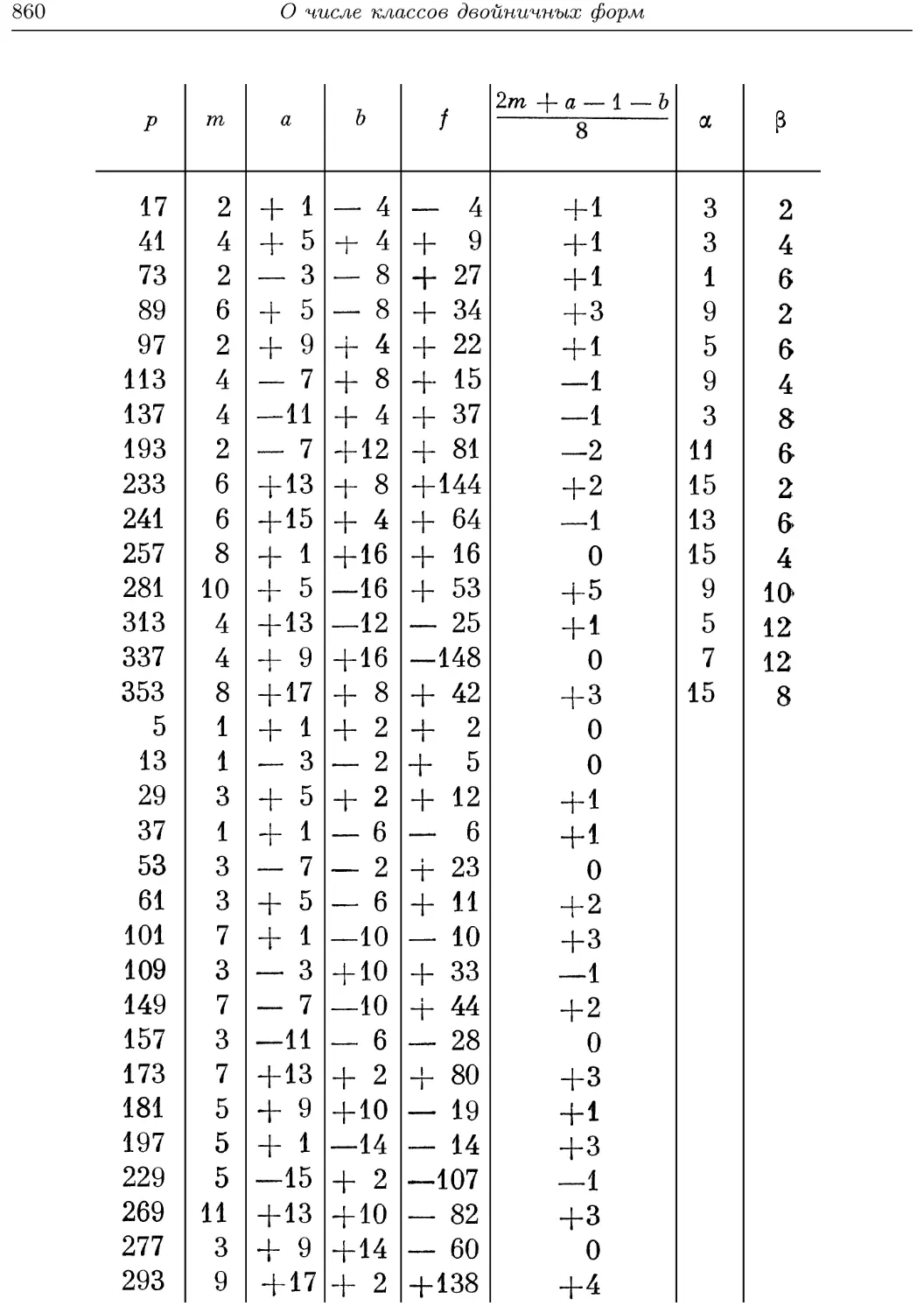
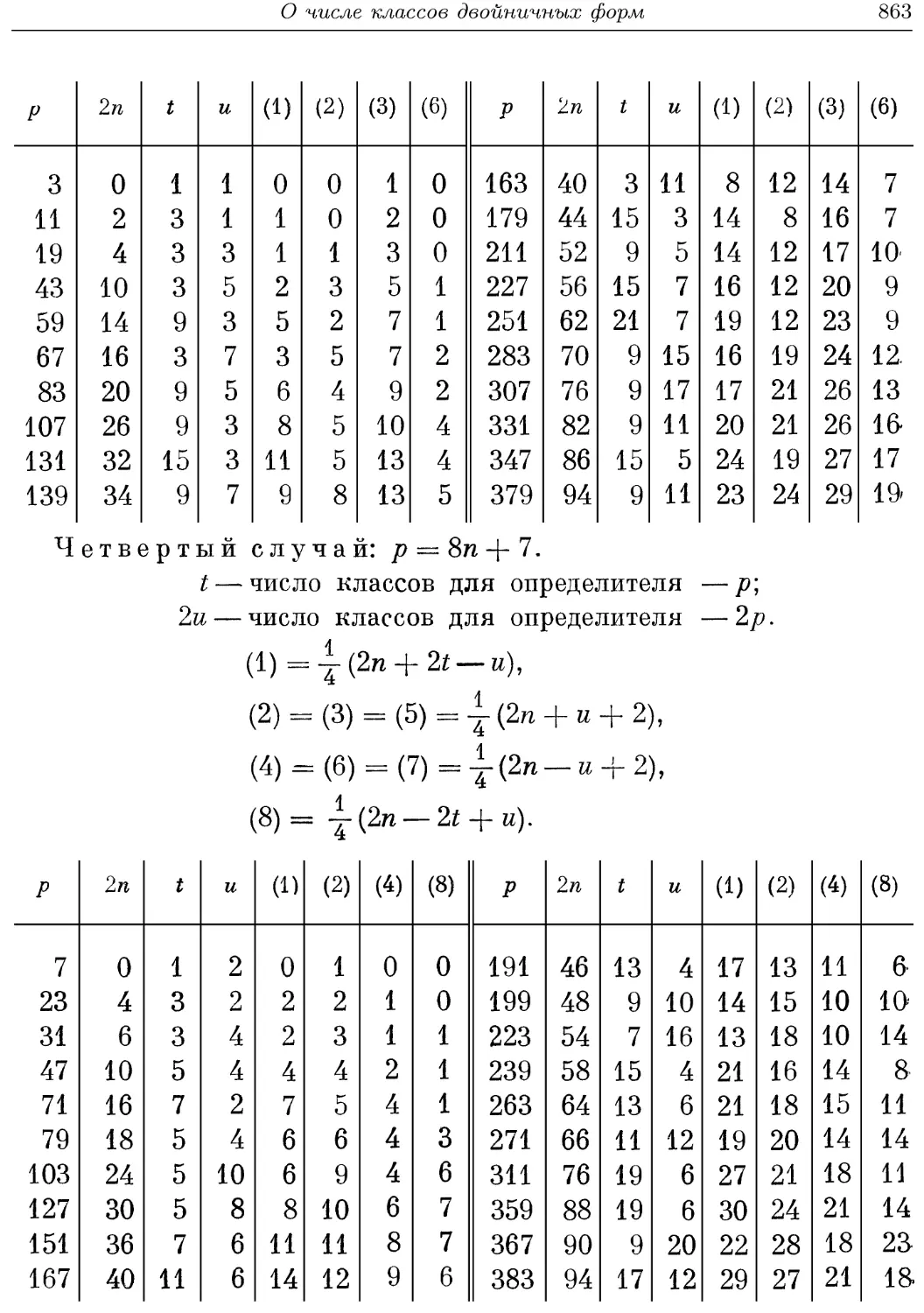
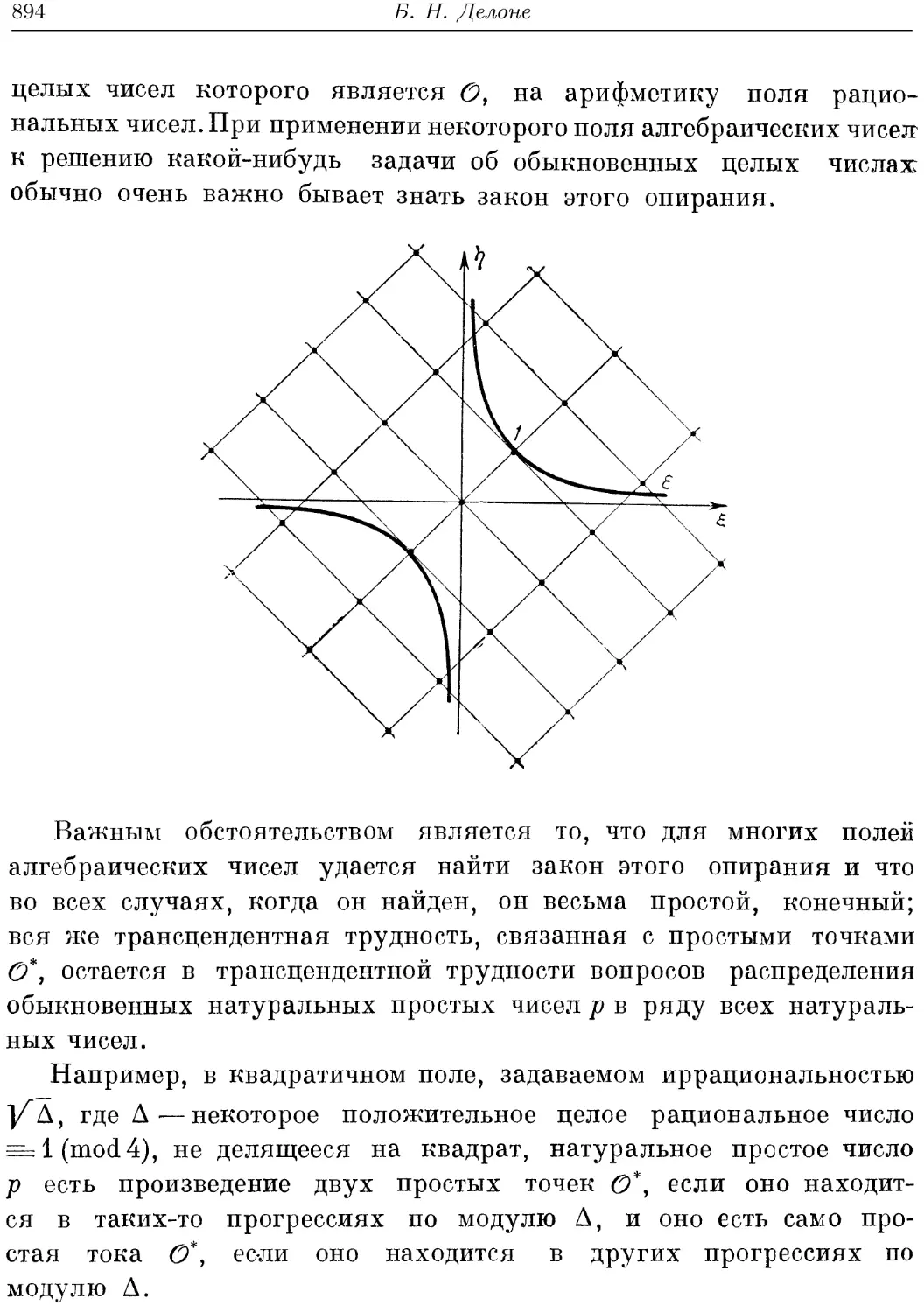
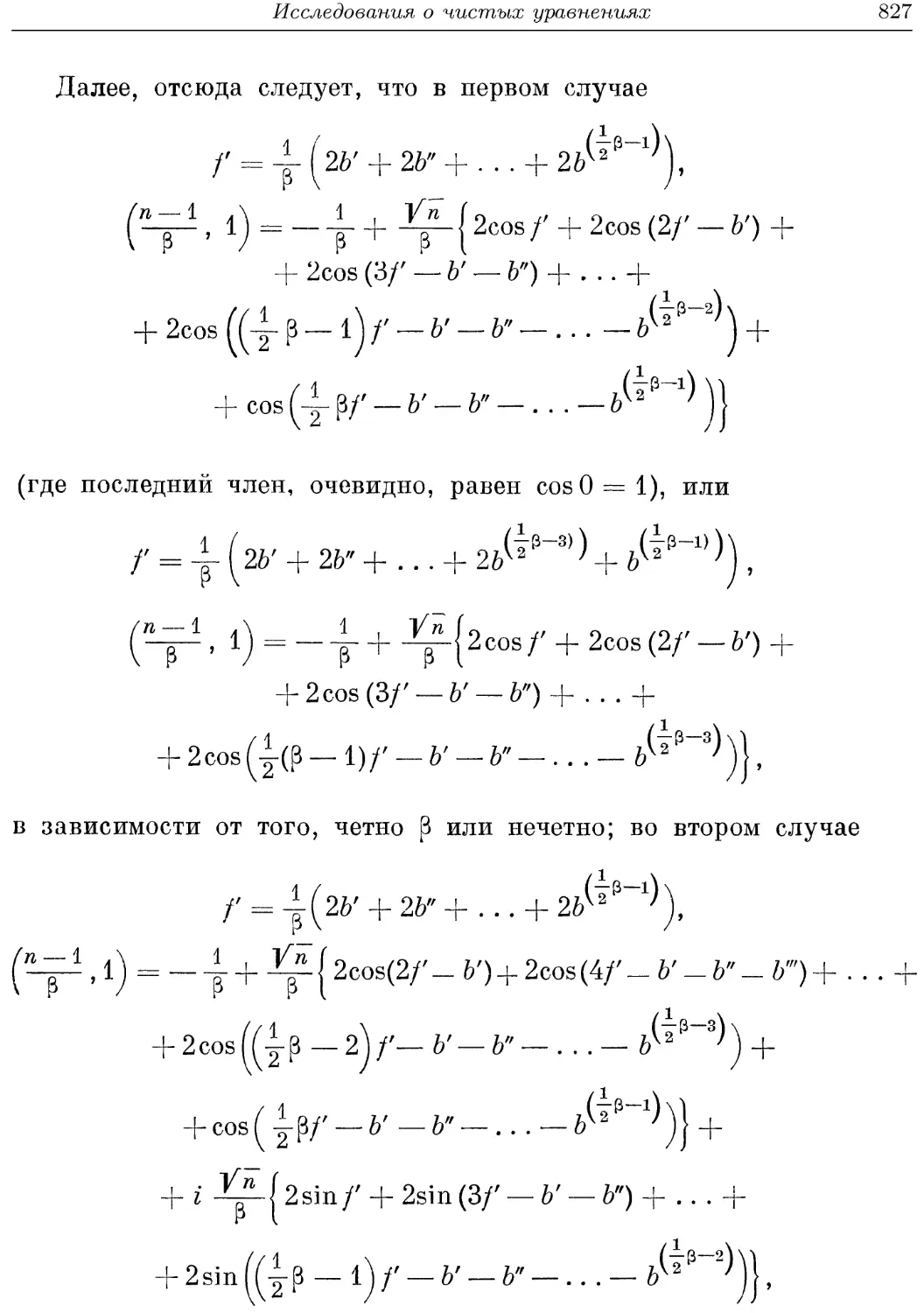Текст
АКАДЕМИЯ НАУК СОЮЗА ССР
КЛАССИКИ НАУКИ
КАРЛ ФРИДРИХ ГАУСС
ТРУДЫ
ПО ТЕОРИИ ЧИСЕЛ
ОБЩАЯ РЕДАКЦИЯ
АКАДЕМИКА И. М. ВИНОГРАДОВА
КО ММЕНТАРИИ
ЧЛЕНА-КОРР. АН СССР Б.Н.ДЕАОНЕ
ПЁРЁВОД
КАНД. ФИЗ.-МАТЕМ. НАУК
В.Б.ДЕМЬЯНОВА
а=в(то& т)
ИЗДАТЕЛЬСТВО АКАДЕМИИ НАУК СССР
МОСКВА- 1959
СЕРИЯ «КЛАССИКИ НАУКИ»
основана академиком С.И.Вавиловым
Редакционная коллегия: академик Я. Г. Петровский
(председатель), академик Я. Я. Андреев, академик В. А. Казанский,
академик Д. Я. Щербаков, академик Я. Ф. Юдин, члеЕ1-корреспондент
АН СССР В. II. Делоне у член-корреспондент АН СССР X. С. Коштоянц,
член-корреспондент АН СССР А. М. Самарин, профессор Д. М. Лебедев,
профессор Я. А. Фигуровскийг кандидат философских наук
Я. В. Кузнецов (зам. председателя)
АРИФМЕТИЧЕСКИЕ
ИССЛЕДОВАНИЯ
ПРЕДИСЛОВИЕ АВТОРА
Содержащиеся в этом сочинении исследования относятся к той
части математики, которая имеет дело с целыми числами, в то время
как дробные числа остаются вне рассмотрения в большинстве случа-
случаев, а мнимые — всегда. Так называемый неопределенный или дио-
фантов анализ, представляющий собой учение о том, как из беско-
бесконечного числа решений, удовлетворяющих неопределенному урав-
уравнению, выбирать те, которые являются целочисленными или хотя
бы рациональными (а в большинстве случаев еще и положительны-
положительными), не исчерпывает этой дисциплины, а представляет собой лишь
очень специальную ее часть, которая относится ко всей дисциплине
приблизительно так же, как учение о преобразовании и решении
уравнений (алгебра) относится к анализу в целом. Именно, как
все исследования, которые касаются общих свойств числовых ве-
величин и связей между ними,принадлежат к области анализа, так целые
числа (а также и дробные, поскольку они определяются через це-
целые) составляют предмет изучения арифметики. Но так как то, что
обычно принято называть арифметикой, почти не выходит за преде-
пределы искусства считать и вычислять (т. е. представлять числа в опре-
определенном виде, например, в десятичной системе, и производить над
ними арифметические операции) с добавлением еще некоторых вопро-
вопросов, которые или вовсе не относятся к арифметике, как, например,
учение о логарифмах, или имеют силу не только для целых чисел,
но и для любых числовых величин, то представляется целесообраз-
целесообразным различать две части арифметики и только что упомянутое при-
причислять к элементарной арифметике, а все общие исследования о
внутренних связях между целыми числами относить к высшей ариф-
арифметике, о которой одной здесь и будет идти речь.
10 Предисловие автора
К высшей арифметике относится то, что Э в к л и д с присущими
древним изяществом и строгостью изложил в «Началах», в книге
VII и следующих; однако это представляет собой лишь первые шаги
этой науки. Знаменитое сочинение Диофанта, целиком посвя-
посвященное проблемам неопределенного анализа, содержит много иссле-
исследований, которые вследствие их трудности и красоты методов застав-
заставляют быть высокого мнения об уме и проницательности их автора,
особенно, если учесть незначительность вспомогательных средств,
находившихся в его распоряжении. Так как, однако, эти задачи
больше требуют находчивости и сообразительности, чем глубоких
методов, и, кроме того, являются слишком специальными и редко
приводят к более общим выводам, то эта книга рассматривается как
эпоха в развитии математики скорее потому, что она содержит в себе
первые следы искусства, характерного для алгебры, а не потому,
что она обогатила новыми открытиями высшую арифметику. Глав-
Главным образом более поздним исследователям, правда, немногочислен-
немногочисленным, но завоевавшим непреходящую славу,— таким, как Ферма,
Эйлер, Лагранж, Лежандр, мы обязаны тем, что они
нашли доступ к сокровищнице этой божественной науки и показали,
какими богатствами она наполнена. Я, однако, не буду здесь пере-
перечислять, какие открытия принадлежат каждому из этих математи-
математиков в отдельности, так как это можно узнать из предисловия к до-
дополнениям, которыми Лагранж снабдил «Алгебру» Эйлера,
и из недавно вышедшего сочинения Лежандра, о кото-
котором скоро будет упоминаться; кроме того, об этом говорится
в соответствующих местах настоящих «Арифметических иссле-
исследований».
Целью этого труда, издать который я обещал еще пять лет назад,
было довести до общего сведения те исследования по высшей ариф-
арифметике, которыми я занимался частью ранее, частью позже указан-
указанного срока. Однако, чтобы никто не удивлялся, что я здесь повторяю
предмет почти с самого начала и заново произвожу многие исследо-
исследования, которыми уже занимались другие, я считаю необходимым
указать на то, что когда я в начале 1795 г. впервые принялся за ис-
исследования такого рода, я ничего не знал о том, что было сделано
за последнее время в этой области, и все средства, при помощи ко-
Предисловие автора 11
торых я получал свои результаты, я изобретал сам. Именно, зани-
занимаясь в то время другой работой, я случайно натолкнулся на одну
изумительную арифметическую истину (если не ошибаюсь, она
изложена в виде теоремы в п. 108), и 1ак как она не только
показалась мне прекрасной сама по себе, но и навела на мысль,
что она связана и с другими выдающимися фактами, я со
всей энергией взялся за то, чтобы выяснить принципы, на которых
она основывается, и получить строгое ее доказательство. После того
как это желание, наконец, осуществилось, прелесть этих исследова-
исследований настолько увлекла меня, что я уже не мог их оставить; так и
получилось, что в то время как одни все время пролагали дорогу
другим в том, что изложено в первых четырех разделах этого труда,
я сам имел о подобных работах других математиков лишь прибли-
приблизительное представление. Когда же мне, наконец, представилась воз-
возможность ознакомиться с работами этих выдающихся умов, то я по-
понял, что большая часть моих рассуждений была посвящена уже
давно известным вещам, но с тем большей охотой решился следовать
по стопам этих ученых, которые двигали арифметику вперед; так
возникли различные исследования, часть которых составляют раз-
разделы V, VI, VII. Когда я, спустя некоторое время, принял решение
опубликовать результаты моих усилий, то я, идя навстречу жела-
желаниям многих, тем охотнее решил не выбрасывать ничего также и из
указанных более ранних исследований, что, во-первых, в то время
еще не было книги, по которой можно было бы ознакомиться с рас-
рассеянными по академическим изданиям работами других математиков
по этому вопросу; затем, потому, что многие из этих исследований
были совершенно новыми и проводились новыми методами, и, нако-
наконец, потому, что все они так тесно переплетались как между собой,
так и с более поздними исследованиями, что новое неудобно было бы
изложить достаточно ясно без того, чтобы сначала не напомнить
некоторые другие вещи.
Тем временем появилось сочинение уже и до того имевшего боль-
большие заслуги в высшей арифметике Лежандра («Essai dune the-
orie des nombres», Paris, a. VI), в котором он не только тщательно
обработал и привел в порядок все, что было сделано в этой науке до
сих пор, но и привнес очень много своего собственного. Так как эта
12 Предисловие автора
книга попала ко мне в руки слишком поздно, когда большая часть
моего сочинения была уже готова, я ее нигде не упоминал в тех слу-
случаях, когда аналогия рассматриваемых вопросов могла бы дать
к этому повод; лишь в отношении нескольких ее мест я счел необхо-
необходимым сделать некоторые замечания в дополнениях, которые,
как я надеюсь, любознательный читатель не оставит без вни-
внимания.
Во время печатания этого сочинения, которое несколько раз пре-
прерывалось и из-за многочисленных задержек растянулось на четыре
года, я не только продолжил далее те исследования, которые начал
еще ранее, но опубликование которых решил отложить до другого
случая, чтобы не делать книгу слишком объемистой, но и принялся
за многие новые исследования. Кроме того, несколько исследова-
исследований, которые я по той же причине только вскользь упоминал, так
как более подробное рассмотрение представлялось менее необходи-
необходимым (например, те, о которых говорится в пп. 37, 82 и следующих,
и в других местах), в дальнейшем были продолжены и дали повод
к более общим исследованиям, которые представляются достойными
опубликования (ср. также сказанное в дополнениях относительно
п. 306). Наконец, так как книга вследствие значительного размера
раздела V оказалась гораздо объемистее, чем я ожидал,— многое,
что первоначально для нее предназначалось, и в частности весь
восьмой раздел (который в этом сочинении уже упоминается в не-
нескольких местах, и который содержит общее изложение теории алгеб-
алгебраических сравнений любой степени), пришлось выбросить, Все
эти вещи, которые легко могут заполнить том, равносильный насто-
настоящему, я опубликую, как только для этого представится
случай.
То, что во многих трудных исследованиях я пользовался синте-
синтетическими доказательствами и опускал анализ, при помощи которо-
которого они были найдены, объясняется главным образом требованиями
краткости, которым я, насколько это возможно, должен был стре-
стремиться удовлетворить.
Теория деления круга или теория правильных многоугольников,
которая рассматривается в разделе VII, сама по себе не принад-
принадлежит арифметике; однако ее принципы следует черпать только в
Предисловие автора 13
высшей арифметике; это будет для математиков, быть может, столь
же неожиданным, сколь, надо надеяться, приятными бывают для
них обычно истины, черпаемые из этого источника.
На это я хотел обратить внимание читателя. О самом предмете
судить не мне. Я ничего не желаю столь горячо, как того, чтобы эти
исследования понравились тем, кто принимает близко к сердцу
успехи науки, как те, которые восполняют имевшиеся до сих пор
пробелы, так и те, что открывают путь к новому.
Раздел I
О СРАВНИМОСТИ ЧИСЕЛ ВООБЩЕ
Сравнимые числа, модули, вычеты и невычеты
1
Если число а входит делителем в разность чисел Ь, с, то Ъ и с на-
называются сравнимыми по а, в противном же случае — несравнимы-
несравнимыми. Число а мы назовем модулем. Каждое из чисел Ь, с в пер-
первом случае называется вычетом, а во втором — невычетом друго-
другого из них.
Эти обозначения применяются в отношении всех целых, как
положительных, так и отрицательных* чисел; на дробные числа они
не распространяются. Так, например, —9 и -f-16 сравнимы по
модулю 5; число —7 является вычетом по модулю 11, но
невычетом по модулю 3 числа -f-15. Так как нуль делится на
любое число, то каждое число следует считать сравнимым с самим
собой по любому модулю.
2
Все вычеты заданного числа а по модулю т содержатся в фор-
формуле а -\- km, где к обозначает произвольное целое число. Из теорем,
которые мы установим позднее, более легкие могут быть без труда
выведены отсюда; однако всякий сможет с такой же легкостью
убедиться в их верности и с первого взгляда.
* Модуль, очевидно, всегда нужно брать по абсолютной величине.
16 Раздел I (пп. 3-6)
В дальнейшем сравнимость чисел мы будем обозначать знаком =,
а модуль, там где это будет нужно, мы будем добавлять заклю-
заключенным в скобки: —16 = 9 (mod5), —7 = 15 (mod 11)*.
Теорема. Если даны т последовательных целых чисел
а, а + 1, а + 2, . . . , а + лг — {
и еще некоторое число А, то из чисел а, а + 1, а + 2, . . ., а + т—1
будет сравнимо с А по модулю т одно и только одно число.
Именно, если (а — А) / т есть целое число, то а=Л; если же
оно дробное, то пусть ближайшее больше^ его целое число (если
дробь отрицательна, то ближайшее к ней целое число, меньшее ее
по абсолютной величине) равно к] тогда A -f- km будет лежать
между а ж а-\- т ж потому будет искомым числом. Но очевидно,
что все отношения
а — Л а + 1 — Л а -\- 2 — Л
лежат между к—1 и А+1; поэтому среди них не более чем одно
может быть целым числом.
Наименьшие вычеты
Таким образом, каждое число обладает вычетом как в ряду
чисел 0, 1, 2, .. . , т — 1, так и в ряду 0, —1, —2, .. . , — (т — 1),
причем мы будем их называть наименьшими вычетами. Очевидно,
что если 0 не является вычетом, то наименьших вычетов всегда
имеется два, один положительный и один отрицательный. Если их
* Это обозначение я выбрал вследствие большой аналогии, которая имеется
между равенствами и сравнениями. По этой же причине Лежандр в своем
сочинении, ниже часто упоминаемом, сохраняет для сравнений просто знак
равенства; однако, во избежание возможных двусмысленностей, я не решился
следовать его примеру.
Элементарные теоремы о сравнениях 17
абсолютные величины не равны, то одна из них меньше чем тп/2,
в противном же случае обе они равны т/2. Отсюда следует, что
каждое число обладает вычетом, который по абсолютной величине
но превосходит половины модуля и называется абсолютно наи-
наименьшим вычетом.
Например, число —13 по модулю 5 обладает наименьшим поло-
положительным вычетом 2 (который одновременно является и абсолютно
наименьшим вычетом) и наименьшим отрицательным вычетом —3.
Число +5 по модулю 7 является своим собственным наименьшим
положительным вычетом, а —2 является его наименьшим отрицатель-
отрицательным и одновременно абсолютно наименьшим вычетом.
Элементарные теоремы о сравнениях
5
После того как мы установили эти обозначения, перечислим те
свойства сравнимых чисел, которые непосредственно очевидны.
Числа, сравнимые по составному модулю, сравнимы также и по
каждому его делителю.
Если несколько чисел сравнимы с одним и тем же числом по одно-
одному и тому же модулю, то они сравнимы (по этому же модулю) между
собой.
В следующих теоремах также предполагается, что модуль остаг
ется одним и тем же.
Сравнимые числа имеют одинаковые, а несравнимые — различные
наименьшие вычеты.
б
Если имеется любое количество чисел Л, В, С,... и столько же
других чисел а, Ъ, с, ..., которые сравнимы с первыми по какому-
нибудь модулю, т. е.
А = а, В = Ъ,
то
Если А^а, # = 6, то А — .5 = а— Ь.
18 Раздел I (пп. 7-11)
7
Если А^а, то и кА^ка.
Если к — положительное число, то это есть просто специальный
случай теоремы предыдущего пункта, который получается, если
положить А = В = С = . .. и а = b = с = . . .. Если к отрицательно,
то—к положительно, поэтому —&Л =— ка, откуда кА = ка.
Если А^а, В^Ь, то также АВ^аЬ.
Действительно, АВ= АЬеееоЬ,
8
Если имеется любое количество чисел А, В, С, ... и столько же
других чисел а, Ъ, с, . . . , которые сравнимы с первыми, т. е. А^ееп,
В^Ь, . . . , то и произведения чисел каждого ряда сравнимы между
собой, т. е. ABC . . . = abc ....
Согласно предыдущему пункту, АВ = аЬ, и по той же причине
ABC = abc; этим же способом можно присоединить и сколько
угодно других сомножителей.
Если все числа А, В, С,... взяты равными, как и соответ-
соответствующие числа а, Ъ, с, .. ., то получается следующая теорема.
Если А = а и к — целое положительное число, то Ак^ак.
Пусть X — алгебраическая функция переменной величины х вида
Аха + Вхь + Схс + . .. ,
где А, В, С, . . . обозначают какие-нибудь целые числа, а а, Ь, с, . . . —
целые неотрицательные числа. Тогда, если переменной х придавать
значения, сравнимые по некоторому модулю, то и получающиеся при
этом значения функции X будут сравнимы между собой.
Пусть /, g — сравнимые между собой значения х. Тогда, согласно
предыдущему пункту, fa = ga и А/а = Aga\ точно так же Bfb~Bgb
и т. д. Поэтому Afa + Bf + С/с + . . . = Aga + Bgb + Cgc + . .. , что
и требовалось доказать.
Легко понять, как эта теорема может быть распространена на
функции многих переменных.
Элементарные теоремы о сравнениях 19
10
Таким образом, если в качестве значений х брать все следующие
одно за другим целые числа, а значения функции X заменять
их наименьшими вычетами, то последние образуют ряд, в ко-
котором после интервала из т членов (где т обозначает модуль)
все время повторяются те же самые члены, т. е. этот ряд будет обра-
образован бесконечно много раз повторяющимся периодом из т членов.
Если, например, X = хъ — 8х + 6 и т = 5, то для х = 0, 1, 2, 3,...
значения X имеют следующие наименьшие положительные вы-
вычеты: 1, 4, 3, 4, 3, 1, 4, ..., где первые пять: 1,4, 3, 4, 3 повторяются
до бесконечности; и если ряд продолжается в обратную сторону,
т. е. если х придаются отрицательные значения, то повторяется тот
же самый период с обратным порядком следования членов. Отсюда
ясно, что во всем ряду нет никаких других членов, кроме тех, ко-
которые образуют этот период.
11
В силу сказанного в рассмотренном примере X не может быть
= 0 или =2 (mod 5), а тем более не может быть = 0 или = 2. Отсюда
следует, что уравнения Xs — 8х -f- 6 = 0 и х3 — 8х + 4 = 0 не раз-
разрешимы в целых числах, а вследствие этого, как известно, и в ра-
рациональных числах. Вообще очевидно, что если функция X от не-
неизвестного х имеет вид
хп + Ах71'1 + Вхп~2 + . . . + Лт,
где А, В, С,... — целые числа, и п — целое положительное числог
то уравнение X — 0 (к такому виду, как известно, могут быть при-
приведены все алгебраические уравнения) не имеет рациональных кор-
корней, если сравнение Х=0 не может удовлетворяться хотя бы по
какому-нибудь одному модулю. Этот критерий, который непосред-
непосредственно очевиден, будет более подробно рассматриваться в разделе
VIII. Однако уже сейчас на этом примере можно составить себе
некоторое представление о пользе этого исследования.
20 Раздел I (пп. 12-13)
Некоторые приложения
12
На теоремах, изложенных в этой главе, основывается большая
часть того, что обычно принято изучать в арифметике, например,
признаки делимости заданного числа на 9, 11 и другие числа. По
модулю 9 все числа, являющиеся степенями 10, сравнимы с едини-
единицей. Поэтому, если заданное число имеет вид а + 10fe + 100с + ...,
то оно будет давать тот же остаток по модулю 9, что и а + Ь + с +•••
Отсюда следует, что если сложить цифры числа, записанного в
десятичной системе, то эта сумма и данное число дают одинаковые
наименьшие вычеты, и потому первая может делиться на 9, когда
второе делится на 9, и обратно. Так же обстоит дело и для делите-
делителя 3. Далее, так как 100=1 по модулю 11, то всегда 102 =1, а
102fe+1=10=—1, и потому число вида а + 10fe + 100c +... имеет по
модулю 11 тот же наименьший вычет, что ж а — b -\- с — ..., откуда
сразу получается известное правило. Из этих же принципов легко
могут быть выведены все подобные признаки.
Точно так же в вышеизложенном следует искать основу тех пра-
правил, которые обычно рекомендуются для проверки правильности
арифметических операций. Именно, если одно число получается из
других посредством сложения, вычитания, умножения или возведе-
возведения в степень, то вместо заданных чисел подставляются их наимень-
наименьшие вычеты по некоторому удобному модулю (обычно, 9 или 11, так
как вычеты по этим модулям в нашей десятичной системе, как мы
уже показали, находятся особенно легко). Получающееся в резуль-
результате операций число должно быть сравнимо с тем, которое получа-
получается после замены чисел их вычетами. Если же этого не случится,
то мы заключаем, что в вычисления вкралась ошибка.
Так как, однако, эти и им подобные вопросы достаточно хорошо
известны, то было бы излишним дольше на них задерживаться.
Раздел II
О СРАВНЕНИЯХ ПЕРВОЙ СТЕПЕНИ
Предварительные теоремы
о простых числах, сомножителях и т. д.
13
Теорема. Произведение двух положительных чисел, каждое из
которых меньше заданного простого числа, не может делиться на
это простое число.
Пусть р — простое число, а а—'Положительное число, меньшее
р\ тогда утверждается, что не существует положительного числа
Ь<Ср, обладающего тем свойством, что аЪ = 0 (mod p).
Доказательство. Предположим, что существуют числа 6, с, d, . ..,
которые все меньше р и для которых ab^O, ас = 0, ай = 0,...
(mod/?). Из всех этих чисел пусть Ь — наименьшее, так что
среди чисел, меньших 6, ни одно уже не обладает указанным
свойством. Тогда, очевидно, 6>1. Действительно, если бы было
6 = 1, то мы имели бы аЬ = а < р (по условию), т. е. аЬ не дели-
делилось бы на р. Следовательно, р, будучи простым числом, не
делится на 6, а лежит между некоторыми двумя следующими одно
за другим кратными Ь, например, между mb и (яг+1N. Если
р — mb = b'1 то Ъ' будет положительным числом, меньшим чем 6.
Так как, по нашему предположению, аб^О (rnodp), то (согласно
п. 7) также и mab = 0, и потому, вычитая это из ар = 0, мы получаем
а (р — т6) = а6'^0, т. е. Ъг должно было бы содержаться среди
22 Раздел II (пп. Ц-11)
чисел Ь, с, d, . . . , хотя оно меньше, чем наименьшее среди этих
чисел число Ь. Это приводит к противоречию.
14
Если ни а, ни Ъ не делятся на простое число р, то и произве-
произведение ab не делится на р.
Пусть наименьшие положительные вычеты чисел а, Ъ по модулю
р суть а, р, из которых ни один (по условию) не равен 0. Если
бы было ab = O (modp), то, так как а& = а[3, также было быоф = О,
что противоречит предыдущей теореме.
Доказательство этой теоремы было дано еще Евклидом («На-
(«Начала», VII, 32). Однако мы не захотели его опустить, во-первых,
потому, что в настоящее время часто или вообще пропускают это до-
доказательство, или основывают его на неубедительных соображениях,
а, во-вторых, потому что суть примененного здесь метода, который
в дальнейшем послужит нам для отыскания значительно более глубо-
глубоких фактов, легче может быть понята на более простом примере.
15
Если ни одно из чисел а, 6, с, d,... не делится на простое числор,
то и произведение abed... не делится на р.
Согласно предыдущему пункту, на р не делится ab, а потому —
также и abc, а потому также и abed и т. д.
16
Теорема. Каждое составное число может быть разложено на про-
простые сомножители только одним единственным образом.
Доказательство. То, что каждое составное число может быть раз-
разложено на простые сомножители, известно из основ; однако то, что
этого нельзя сделать несколькими различными способами, совершен-
совершенно необоснованно по большей части предполагается само собой ра-
разумеющимся. Если мы предположим, что составное число А, равное
аа6Рст..., где а, &, с,... обозначают различные простые числа, раз-
Предварительные теоремы 23
ложимо на простые сомножители еще и другим способом, то прежде
всего ясно, что в этой второй системе сомножителей не может встре-
встречаться других простых чисел, кроме а, Ь, с,..., так как составленное
из этих последних число А не может делиться ни на какое другое
простое число. С другой стороны, в этой второй системе сомножите-
сомножителей ни одно из простых чисел а, &, с,... не может отсутствовать, так
как иначе (согласно предыдущему пункту) число А не делилось бы
на него. Поэтому оба разложения на множители могут отличаться
только тем, что в одно из них какое-нибудь простое число входит
большее число раз, чем в другое. Пусть р такое простое число, ко-
торое в одном разложении встречается т раз, а в другом разложении
п раз, и пусть т > п. Если теперь из обеих систем выбросить по п
сомножителей, равных р, то в одной из них еще будет оставаться
т — п сомножителей /?, а в другой их уже не будет совсем, так что
для числа А/рп мы получим два разложения на множители, из кото-
которых одно совсем не содержит сомножителя р, а другое содержит его
т — п раз. Это, однако, противоречит тому, что мы только что до-
доказали.
17
Таким образом, если составное число А есть произведение чисел
В, С, Z), ..., то ясно, что среди простых сомножителей чисел В, С,
D,... не может быть никаких других, кроме тех, которые встреча-
встречаются среди сомножителей числа А, и что каждый из этих простых
сомножителей должен входить вВ, С, Д... в общем столько же раз,
сколько ж ъ А. Отсюда получается критерий, при помощи которого
можно узнать, делит ли число В другое число А, или нет. Первое
имеет место тогда, когда В не содержит других сомножителей,
кроме входящих в А, а их содержит не большее число раз,
чем А.
Если какое-либо из этих условий не выполняется, то В не явля-
является делителем А.
При помощи комбинаторики отсюда легко выводится, что если
А == ,
где а, Ь, с, ..., как и раньше, обозначают различные простые числа,
24 Раздел II (пп. 18-20)
то количество различных делителей А, включая 1 и i, равно
18
Если поэтому А = аа № cY. . . , К = А* /х яг^ ... и все простыв
числа а, 6, с,. . ., #, Z, т,. . . различны между собой, то А ж К
не имеют общих делителей, кроме 1, т. е. они взаимно просты.
Наибольший общий делитель нескольких заданных чисел
А, В, С,... находят следующим образом: все эти числа раз-
разлагают на простые сомножители, и из них выбирают те, ко-
которые являются общими для всех чисел А, В, С,... (если таких
нет, то нет и общих делителей). Затем смотрят, сколько раз
каждый из этих простых сомножителей содержится по отдельности
в каждом из чисел А, В, С, . . ., т. е. в какой степени каждый
входит в числа А, В, С, .... Наконец, для каждого простого
сомножителя берут наименьшую из всех степеней, которые он имеет
в А, Вщ С, . . ., и образуют произведение всех этих степеней; оно
и будет искомым наибольшим общим делителем.
Если же мы хотим найти наименьшее общее кратное чисел
.4, В, С,..., то следует поступать так. Нужно взять все простые
числа, делящие хотя бы одно из чисел А, В, С, . . . , затем выбрать
для каждого из них наибольшую степень из всех, с которыми оно
входит в числа А, В, С,. . . и образовать произведение всех таким
способом выбранных степеней; оно и будет искомым наименьшим
общим кратным.
Пример. Пусть А = 504 = 23.32-7, В - 2880 = 26.32-5, С = 864 =
= 25-33. Чтобы найти наибольший общий делитель, мы должны
взять простые сомножители 2, 3 в степенях 3, 2, так что этот наи-
наибольший общий делитель равен 23-32 = 72. Наименьшее же общее
кратное есть 26.33.5.7 = 60 480.
Доказательства, ввиду их легкости, мы опускаем. Решение этих
вопросов в том случае, когда разложение чисел А, В, С, ... на мно-
множители не дано, известно из основ.
Предварительные теоремы 25
19
Если числа а, Ъ, с, ... взаимно просты с некоторым числом к, то
и их произведение abc... взаимно просто с к.
Действительно, так как ни одно из чисел а, Ь, с, ... не имеет
с к общего простого сомножителя, а в произведение abc... могут
входить только те простые сомножители, которые являются делите-
делителями хотя бы одного из чисел а, Ъ, с,..., то и произведение abc не име-
имеет с к общих простых сомножителей. Поэтому, согласно предыду-
предыдущему пункту, к и abc... взаимно просты.
Если числа а, Ъ, с, ... попарно взаимно просты и каждое из них
делит число к, то и их произведение есть делитель к.
Это тоже легко получается из пп. 17 и 18. Действительно, если р
есть любой простой делитель произведения abc... и содержится в
нем гс раз, то одно из чисел а, Ь, с,...должно содержать этот делитель
гс раз. Поэтому и к, делящееся на каждое из этих чисел, гс раз со-
содержит делителем р. Аналогично дело обстоит со всеми делителями
произведения abc
Поэтому, если два числа т, п сравнимы между собой по взаимно
простым модулям а, Ь, с, ..., то они сравнимы и по их произведению.
Действительно, так как число т — п делится на каждое из чи-
чисел а, Ь, с, ..., то оно делится и на их произведение.
Наконец, если а взаимно просто с Ъ и ак делится на Ь, то к долж-
должно делиться на Ь.
Действительно, так как число ак делится на а и на Ьч оно
7 ак к
должно делиться на их произведение ао, т. е. —г = -г- есть целое число.
20
Если число А = а* № сг . . . , где а, Ь, с, ... —различные просты
числа, есть степень некоторого другого числа, скажем, А — кп, то
все показатели а, р, т> • • • делятся на п.
Действительно, число к не содержит других простых сомножи-
сомножителей, кроме а, Ъ, с,.. . , а их содержит все. Если сомножитель а
в число к входит а/ раз, то в кп = А он содержится пси' раз. По-*
этому ш'=аиа//2 есть целое число. Точно так же доказывается,
что числа р/ п, . .. —целые.
26 Раздел II (пп. 21-25)
21
Если а, Ь, с, ... попарно взаимно просты, а произведение abc . . .
есть некоторая степень, например, abc. .. — kn, то каждое из чисел
а, Ь, с,... тоже является п-й степенью.
Пусть а = Iх т^ рп, где I, т, р, .. . обозначают различные простые
числа, ни одно из которых, согласно предположению, не является
делителем чисел Ь, с,... Тогда произведение abc. . . содержит X
раз сомножитель Z, [Л раз — сомножитель т и т. д. Таким образом
(согласно предыдущему пункту), X, [л, тс, ... делятся на п и потому
У а = l^rrfif1 .. .
есть целое число. То же самое имеет место и в отношении чисел
б, с, ...
Эти теоремы о простых числах мы должны были предпослать
в первую очередь. Теперь мы обращаемся к тем теоремам, которые
имеют уже более близкое отношение к поставленной нами цели.
22
Если числа а, Ъ делятся на число к и сравнимы между собой по
взаимно простому с к модулю т, то и числа а / к и b / к сравнимы
между собой по этому же модулю.
Действительно, а — b делится на к и, согласно условию, также
и на т\ поэтому (в силу п. 19) а — Ъ/к делится на т, т. е.
Если dice при тех же самых остальных предположениях тик
имеют наибольший общий делитель е, то ~ = -jr-(mod—].
Действительно, к/е и т/е взаимно просты. А так как (а — Ь)
делится как на к, так и на т, и потому (а — Ь) /е делится яэ.к/е
и на /п/е, а следовательно, и на кт/е2, то (а — Ъ) /к делится на
. а Ъ ( , т\
т/е, т. е. T = y(mod-j.
Предварительные теоремы 27
23
Если а взаимно просто с т, и е, f — несравнимые по модулю т
числа, то ае и af тоже несравнимы по модулю т.
Это есть просто обратная теорема к теореме предыдущего пункта.
Отсюда вытекает, что если а умножить на все целые числа от О
до т + 1 и произведения заменить их наименьшими вычетами по
модулю т, то эти последние будут все отличны один от другого.
И так как число этих вычетов, которые все меньше т, равно т, а чисел
от 0 до т — 1 столько же, то, следовательно, ни одно из этих чисел
не может отсутствовать среди этих вычетов.
24
Выражение ах + Ь, в котором а, Ъ обозначают данные числа,
а х — неизвестное или переменное число, может быть сделано
сравнимым по взаимно простому с а модулю т с любым заданным
числом.
Пусть число, которое должно быть сравнимо с указанным выра-
выражением, есть с, а наименьший положительный вычет с — 6 по мо-
модулю т есть е. Тогда, согласно предыдущему пункту, имеется хотя
бы одно значение х<Ст с тем свойством, что наименьший вычет
произведения ах по модулю т равен е. Если это значение есть v,
то av=e=c — b, и потому av + Ъ=с (mod m).
25
Выражение, которое, аналогично уравнению, связывает между со-
собой две сравнимые одна с другой величины, мы будем называть сравне-
сравнением. Сравнение, содержащее неизвестное, называется решенным,
если для этого неизвестного найдено удовлетворяющее сравнению
значение (корень). Отсюда ясно далее, что понимается под разре-
разрешимым или неразрешимым сравнением.
Наконец, легко видеть, что здесь могут представиться те же раз-
различия, что и для уравнений. Дальше встречаются примеры транс-
трансцендентных сравнений; алгебраические же сравнения разделяются
в зависимости от наивысшей содержащейся в них степени неизве-
28 Раздел II (пп. 26-27)
стного на сравнения первой, второй и более высоких степеней. Точно
так же могут встречаться системы сравнений с несколькими неизве-
неизвестными, вопрос об исключении которых нам придется рассмотреть.
Решение сравнений первой степени
26
Сравнение первой степени ах + Ь^с, согласно п. 24, всегда
разрешимо, если модуль взаимно прост с а. Если v — подходящее
значение х, т. е. корень сравнения, то, очевидно, что корнями
являются и все числа, сравнимые с у по модулю этого сравнения
(п. 9). Обратно, легко видеть, что все корни v должны быть сравни-
сравнимы между собой] действительно, если t — другой корень, то
av + b^at + b, и потому av^at, откуда v^t (п. 22). Отсюда
следует, что сравнение x=v (modяг) представляет собой полное
решение сравнения ах + 6 = с.
Так как решения сравнения, которые сравнимы с х, находятся
в нашем распоряжении и в этом отношении сравнимые числа
следует рассматривать как эквивалентные, то мы все такие решения
сравнения будем считать за одно решение. Поэтому если наше
сравнение ах-\-Ь = с не допускает других решений, то мы будем
говорить, что оно разрешимо единственным образом, или имеет
только один корень. Так, например, сравнение 6х + 5 = 13 (mod 11)
не обладает другими корнями, кроме тех, которые = 5 (mod 11).
По иному обстоит дело для сравнений более высоких степеней или
для сравнений первой степени, в которых неизвестное умножается
на число, не взаимно простое с модулем.
27
Остается еще добавить кое-что о нахождении решения сравнения
такого рода.
Сначала заметим, что сравнение ах-\- t = u, модуль которого
предполагается взаимно простым с а, связано со сравнением
а#^ + 1. Действительно, если последнему удовлетворяет # = т%
то первое удовлетворяется посредством х = ЧЬ(гг — t) r. Но, если
Решение сравнений первой степени 29
мы обозначим модуль через Ь, то сравнение а# = + 1 эквивалентно
неопределенному уравнению ах =Ьу + 1ч а как такое уравнение
надо решать, в настоящее время достаточно хорошо известно. Мы
удовольствуемся поэтому тем, что изложим здесь алгоритм
вычислений.
Если величины А, В, С, D, Е,... так зависят от величин
а, р, т, 8, s,. . ., что
А = а, В = $А + 1, С = чВ + A, D = W + В, Е = sD + C,. . . ,
то мы будем для краткости обозначать их следующим образом:
А = [ос], В = [а, р], С = [а, р, т], 2) = [а, р, т, 8], ... *.
Пусть теперь дано неопределенное уравнение ах — by ^hl,
в котором а, Ъ положительны. Мы предположим, что а не меньше,
чем Ъ\ это позволительно. Тогда по образцу известного алгоритма
для отыскания наибольшего общего делителя двух чисел мы
посредством обыкновенного деления образуем равенства
а = <xb + с, Ъ = рс + d, с = ^d + е, . ..,
в которых а, р, т, . .., с, d, е,. .. суть целые положительные числа
и 6, с, d, е, . . . все время убывают, до тех пор, пока не придем
к равенству вида
т = [лтг + 1,
* Это взаимоотношение величин может быть рассмотрено с намного более
общей точки зрения, что мы при случае, возможно, и сделаем. Здесь же мы лишь
добавим две теоремы, которые найдут применение в настоящих исследованиях,
именно:
A) [а, р, т, ...Д, ji]-[P, Т. -Д]-
-[«, Р, Т. -ДЫР, Т. -Д>Н = ±1-
где нужно брать верхний или нижний знак в зависимости от того, четно количест-
количество чисел а, р, ^, ..., X, [Л или нечетно.
B) Последовательность чисел а, C, f, ... можно обратить, т.е.
[а, р, 7, ...Д, [А] - [|Л,Х, ..., т, р, а].
Доказательства не трудны, поэтому мы их опускаем.
30 Раздел II (пп. 28-30)
что, как известно, всегда случится. Тогда
а = [пч [л, . . . , y, р, а], Ъ = [п, (х, . . . , ?, 3].
Поэтому, если взять
я = [(х, • • -,т, PL У = [И-, .. .,т, Р, а],
то будет иметь место ах — Ьг/ + 1, когда количество чисел
а, р, т» • • • > Iх» и четно, и ах = Ъу — 1, когда оно нечетно.
28
Общее решение таких неопределенных уравнений сначала изучал
Эйлер, «Comment. Petrop.», Т. VII, р. 46 *. Метод, которым он
пользовался, состоит в подстановке вместо х, у других неизвестных^
и в настоящее время хорошо известен. Л а г р а н ж подходил к во-
вопросу несколько по-иному. Именно, из теории непрерывных дробей
известно, что если дробь alb разложить в непрерывную дробь
1
и, отбросив в ней последний член 1М, снова превратить ее в обыкно-
обыкновенную дробь х/у, то будет иметь место ах—Ьу+1, если а взаимно
просто с Ъ. Впрочем, оба метода приводят к одному и тому же алго-
алгоритму. Исследования Лагранжа находятся в «Hist, de VAc. de-
Berlin», Аппеё 1767, p. 175, и кроме того, в дополнениях к фран-
французскому переводу «Алгебры» Эйлера.
29
Сравнение ах + t^u, модуль которого не взаимно прост с а
легко может быть сведено к предыдущему случаю. Пусть т — мо-
модуль, и о — наибольший общий делитель чисел а, т. Прежде всего
* Ср. дополнения в конце «Исследований».
Решение сравнений первой степени 31
ясно, что каждое значение х, удовлетворяющее сравнению по модулю
т, удовлетворяет и тому же сравнению по модулю 8 (п. 5). Но так как
8 есть делитель а, всегда имеет место ах^О (mod 8). Поэтому заданное
сравнение разрешимо только тогда, когда ? = w(mod8)} т. е. когда
t — и делится на 8.
Таким образом, если мы положим а = Ье, т = 8/, t — и = Ьк,
то е будет взаимно просто с /, и сравнению Ьех + Ьк = 0 (mod 8/)
будет эквивалентно сравнение ех + к = 0 (mod/), т. е. каждое
значение х, которое удовлетворяет последнему, будет удовлетворять
также и первому, и обратно. Действительно, ех + к может, очевидно,
делиться на / только тогда, когда оех -\- ок делится на 8/, и обратно.
Но сравнение ex -j- & = 0(mod/) мы уже выше научились решать,
и мы получаем, что если v есть одно из значений х, то х = v (mod/)
представляет полное решение заданного сравнения.
30
В случае составного модуля иногда лучше применять следующий
метод.
Пусть модуль = тп, и заданное сравнение есть ах = Ь. Решим
сначала это сравнение по модулю т, и предположим, что оно
удовлетворяется, если х = v (mod m/ 8), где 8 обозначает наиболь-
наибольший общий делитель чисел т и а. Тогда ясно, что каждое значе-
значение х. удовлетворяющее сравнению ах = Ъ по модулю тп должно
удовлетворять и сравнению по модулю т, и потому должно пред-
представляться в виде v + — х', где хг обозначает неизвестное число,
хотя обратное неверно, т. е. не все числа, представимые в виде
v + -у х\ удовлетворяют сравнению по модулю тп. Но если надо
найти такое х, что v -f- -у х' является корнем сравнения ах ==
7 / 1 \ am , ,
^о (modтп), то его можно получить, решая сравнение -у х + av =
=еЬ (modmri), которое эквивалентно сравнению— х' == ^(modrc).
Из этого следует, что решение любого сравнения первой степени
по модулю тп сводится к решению двух сравнений по модулям т
и п. Легко видеть, что если п снова есть произведение двух
32 Раздел II (пп. 31-32)
сомножителей, то решение сравнения по модулю п зависит от решения
двух сравнений, модули которых являются его сомножителями.
Вообще решение сравнения по любому составному модулю зависит
от решений других сравнений, модули которых являются его сомно-
сомножителями. Последние же, когда это целесообразно, могут предпо-
предполагаться простыми числами.
Пример. Если дано сравнение 19х =1 (mod 140), то надо решить его
сначала по модулю 2, откуда получается x = l(mod2). Если
положить х = 1 + 2х', то получается сравнение 38х' = — 18 (mod 140),
которое эквивалентно сравнению 19х' ^ — 9 (mod 70). Если последнее
снова решить по модулю 2, то получится x'==l(mod2), и потому,
если положить х' = 1 + 2х", 38х" == — 28 (mod 70) или 19х" ~
==— 14(mod 35). Последнее, решенное по модулю 5, дает х" = 4 (mod 5),
и если положить х" = 4 + Ьх'", то 95#w = — 90 (mod 35) или
19х'"е= —18 (mod 7). Наконец, из последнего сравнения следует
я'" ==2 (mod 7), и если положить х" = 2 + 1хт, то получится
^ = 59 + 140xw. Поэтому полным решением заданного сравнения
является х = 59 (mod 140).
31
Подобно тому, как корень уравнения ах = Ъ выражается в виде
Ъ/а, мы будем также и корень сравнения ах = Ь обозначать через
b/а и для ясности приписывать модуль. Так, например,
19
т= (mod 12) обозначает всякое число, которое =11 (mod 12) [что по
11
аналогии может быть также обозначено через ^ (mod 12)]. Вообще,
из предыдущего вытекает, что— (mode) не имеет вещественного
значения (или, если так говорить больше нравится, является
мнимым выражением), если а и с имеют общий делитель, который
в то же время не делит Ъ. За исключением этого случая выраже-
выражение— (mode) всегда имеет вещественные значения, и притом беско-
бесконечно много; однако все они сравнимы между собой по модулю с,
если а взаимно просто с с, или по модулю с/8, если Ь есть наи-
наибольший общий делитель чисел с и а.
Сравнения по нескольким модулям 33
С этими выражениями можно оперировать почти так же, как с
обычными дробями. Некоторые свойства, которые легко могут быть
выведены из предыдущего, мы здесь укажем.
1. Если по модулю с имеет место а = а, 6 = {3, то выражения
-T-(modc) и ^-(modc) эквивалентны.
2. v^(modcS) эквивалентно -г-(mod с).
3. rr(modc) эквивалентно -г- (mode), если к взаимно просто с с.
Мы могли бы привести еще много подобных теорем; так как,
однако, они не связаны ни с какими трудностями и не очень
нужны для дальнейшего, мы переходим к несколько иным вещам.
Нахождение числа, которое сравнимо
с заданными вычетами по заданным модулям
32
При помощи изложенного выше легко может быть решена сле-
следующая задача, которая часто будет встречаться в дальнейшем:
найти все числа, которые имеют заданные вычеты по заданным
в любом количестве модулям. Пусть сначала даны два модуля А
и В, по которым искомое число z должно быть сравнимо соответ-
соответственно саиб. Тогда все значения z содержатся в выражении
Ах-\-а, где х — неизвестное число, с тем, однако, свойством, что
Ах -\- а = Ъ (mod 5). Если § есть наибольший общий делитель чисел
А и В, то полное решение этого сравнения будет иметь вид
х == v (mod yj, или, что то же самое, х = v + у , где к обозначает
произвольное целое число. Поэтому формула Av-\-a -| г—- охватывает
все значения z, т. е. z == Av -f- & (mod — j представляет собой пол-
полное решение вопроса.
Если к А и В добавлен еще третий модуль С, по которому
искомое число z должно быть сравнимо с с, то нужно дальше
рассуждать таким же образом, ибо первые два условия уже объеди-
объединены в одно. Если s есть наибольший общий делитель чисел АВ[Ь
34 Раздел II (пп. 33-34)
и С, и я = Ытос1— J есть решение сравнения — х + Av + а ==
=с (mod С), то полное решение задачи дается сравнением z =. —тг--7 +
+ Av -f- a (mod—-—) # Подобным же образом следует поступать и в
случае, когда задано большее число модулей. Заметим, что АВ /Ь,
АВС/Ьг суть наименьшие общие кратные соответственно чисел
А, В и А, В, С. Отсюда легко усмотреть, что сколько бы ни было
задано модулей А, В, С,. . . , полное решение будет иметь
вид z ==е г (modM), где М есть наименьшее общее кратное этих
чисел.
Далее, если какое-нибудь из вспомогательных сравнений неразре-
неразрешимо, то из этого следует^ что и решение всей задачи невозможно.
Это, однако, не может случиться, если все числа А, В, С, ...
между собой взаимно просты.
Пример. Пусть числа А, В, С; а, Ъ, с суть соответственно, 504г
35, 16; 17, —4, 33. Здесь два условия, а именно,
z = 17 (mod 504) и = — 4 (mod 35)
эквивалентны одному: z = 521 (mod2520). Последнее же, объединен^
ное с условием z = 33 (mod 16), дает z = 3041 (mod5040).
33
Если все числа А, В, С, ... взаимна просты, то их произведе-
произведение является, как известно, их наименьшим общим кратным. В этом
случае все сравнения z =е a (mod A), z == Ъ (mod 5),... эквивалентны
одному сравнению z = r(modi?), в котором В. обозначает произве-
произведение чисел А, В, С, ... Отсюда следует, что, и наоборот, одно
условие z = r (modi?) может быть разложено на несколько. Именно,
если R каким-нибудь образом разложено на взаимно простые
сомножители А, В, С,. . ., то условиями z = r (mod A), z = r (mod B)r
z = r (mod C),... исходное условие полностью исчерпывается. Это заме-
замечание открывает нам путь к тому, чтобы не только сразу узнавать
о невозможности решения задачи в случае, когда это вытекает из
заданных условий, но чтобы также проводить вычисления короче
и удобнее.
Сравнения по нескольким модулям 35
34
Пусть, как и раньше, заданные условия суть z = a (modA),
z==&(modJ9), z =EEc(modC), . . . . Разложим все модули на взаимно
простые сомножители, А — на А'А"А'"..., В — на В'В"В'"... и т.д.,
причем так, что числа А', А!\ ... , В', В",. .. либо простые, либо
являются степенями простых чисел. Таким образом, если одно из
чисел А, 5, С, ... само является или простым числом, или степенью
такового, то его раскладывать на множители не нужно. Тогда из
предыдущего получается, что заданные условия можно заменить
следующими:
z = a (mod Ar), zeebcl (mod A"). z~a (mod A'"), . . .,
z = b (mod Я')» z = b (mod 5"), z = b (modBw), . . .
и т. д.
Если бы числа А, В, С,... не были все попарно взаимно просты,
например, А не было бы взаимно просто с В, то, очевидно, про-
простые делители чисел А и В не могли бы быть все различны между
собой, и потому среди сомножителей А', А", А'", . . . имелся бы
такой, для которого среди сомножителей В', В", В"\ .. . нашелся
бы или равный ему, или кратный ему. или делящий его. Если
А' = В', то условия z==a(modA') и z = b (modВ') должны быть
идентичными, т. е. a ==b (mod А' или В'), так что одно из этих
условий можно отбросить. Если а не =: b (mod Л'), то решение задачи
невозможно. Если же В' кратно А', то условие z == a (mod-4')
должно содержаться в условии z == 6 (modi?'), т. е. вытекающее из
последнего условие z~b (mod А') должно быть идентично первому.
Отсюда следует, что условие z = a (mod-4'), если оно не противо-
противоречит другим (в противном случае решения нет), может быть
отброшено. Если выбросить таким способом все лишние условия,
то очевидно, что те из модулей А', А", А'", . .. , В\ В\ В'\ .. . ,
которые после этого останутся, будут взаимно просты. Мы можем
тогда быть уверенными в возможности решения задачи и можем
применять указанные выше правила.
36 Раздел II (пп. 35-37)
35
Пример. Если, как и выше, должно быть z = 17 (mod 504),
==— 4 (mod 35) и = 33i(modl6), то эти условия могут быть разло-
разложены на следующие:
z =e17 (mod 8), =17 (mod 9), ==17 (mod 7);
z=e — 4 (mod 5), = — 4 (mod 7);
z== 33 (mod 16).
Из них можно отбросить условия ? = 17 (mod 8) и z== 17 (mod 7),
так как первое содержится в условии ze= 33 (mod 16), а второе
идентично с z =— 4 (mod 7). Поэтому остаются следующие условия:
17 (mod 9),
— 4 (mod 5),
— 4 (mod 7),
33 (mod 16),
из которых следует z == 3041 (mod 5040).
Отметим еще, что в большинстве случаев удобнее снова объеди-
объединить те из оставшихся условий, которые получились из одного
и того же первоначального условия. Например, если некоторые из
условий z ==a(mod-4'), z = а (mod Л"), .. . отброшены, то составлен-
составленное из остальных условие будет состоять в том, что у = а по
модулю, который равен произведению оставшихся модулей из числа
Л\ А", А'", . . . Так, в нашем примере из условий z =—4 (mod 5),
z ==— 4 (mod 7) снова получается то условие, из которого они
возникли, именно, z е= — 4(mod35). Далее, отсюда следует, что
в отношении краткости вычислений не совсем безразлично, какое
из совпадающих условий отбрасывать; однако в наши намерения
не входит вдаваться здесь подробнее в практические приемы,
которые лучше усваиваются во время работы, чем по готовым
рецептам.
36
Если все модули А., В, С, /),... взаимно просты, то часто
бывает лучше использовать следующий метод. Нужно определить
число а, которое сравнимо с единицей по Л и с нулем но произ-
Сравнения со многими неизвестными 37
ведению остальных модулей; пусть а — любое значение (в боль-
большинстве случаев удобнее всего брать среди них наименьшее) умно-
умноженного на BCD . . . выражения 1/BCD . . . (mod А) (см. п. 32). Точно
так же, пусть р == 1 (mod В) и == 0 (mud ACD . . .), 7 == 1 (mod С)
и =0 (mod ABD. . .) и т. д. Тогда, если ищется число z, которое
по модулям А, В, С, D, . .. сравнимо соответственно с а, Ь, с, d, . . .,
то можно положить
z = аа + $Ь + Тс + 8d + .. • (mod ABCD. . .).
В самом деле, очевидно, что аа = a (mod Л), в то время как осталь-
остальные члены рй, Тс> • • • все = 0 (mod Л); поэтому 2 = a (mod Л).
Аналогично и доказательство для других модулей. Такое решение
следует предпочесть указанным ранее, если нужно решить несколько
задач, в которых модули А. 5, С, ... сохраняют одни и те же
значения; действительно, тогда остаются неизменными и значения
чисел а, р, «у, . . . С подобным положением мы сталкиваемся в одном
вопросе, связанном с исчислением времени; спрашивается, на какой
год в юлианском периоде приходится заданное Рёмеровское число,
золотое число и солнечный круг. Здесь А = 15, В = 19, С = 28.
Так как значение выражения 1/19-28 (mod 15) или 1 / 532 (mod 15)
равно 13, то а = 6916. Аналогично находим, что р = 4200 и ^ =4845.
Поэтому искомое число есть наименьший вычет числа 6916а +
+ 42006 + 4845 с, где а — Рёмеровское число, Ь—золотое число и
с — солнечный круг.
Линейные сравнения со многими неизвестными
37
Предыдущее относилось к сравнениям первой степени с одним
неизвестным. Но мы должны еще рассмотреть и сравнения, в которые
входит несколько неизвестных. Однако, если бы мы захотели с пол-
полной строгостью разобрать все частности вопроса, то нам пришлось
бы вдаваться в этом разделе в слишком большое число подробно-
подробностей, и кроме того, наша задача состоит сейчас не в том, чтобы дать
исчерпывающее изложение, а в том, чтобы лишь отметить вопросы,
38 Раздел II (п. 37)
наиболее достойные внимания; поэтому мы ограничим здесь наше
исследование немногими замечаниями, а подробное рассмотрение
этого предмета отложим до другого случая.
1. Аналогично тому, как для уравнений, мы можем убедиться,
что и здесь мы должны иметь столько сравнений, сколько неизвест-
неизвестных надо определить.
2. Пусть, таким образом, дано столько же сравнений
(.4) ах + by + cz + . . . = / (mod m),
{A') a'x + b'y + c'z+... = /',
(А") а"х + Ъ"у + c"z + . . . = /",
сколько имеется неизвестных х, у, z, ...
Определим теперь числа ?, ?', ?", ... из уравнений
ьг + ьг + кг +... = о,
и притом так, что все эти числа целые и не имеют общего делителя,
что, как известно из теории линейных уравнений, всегда возможно.
Подобным же образом определяем числа f\, v\', ff, ..., С, С, С",...
из уравнений
ay + a'vf + a"yf + ...= О,
crl + c'rl'-tc"rl"+-- =0,
aV + а"С"+... =0,
3. Если сравнения А, А' А'\... умножить соответственно сна-*
чала на ?, ?', %",..., потом на tj, rf < v]'',... и т. д. и затем произве-
произведения сложить, получатся, очевидно, следующие сравнения:
(Й7] + b'yf + b"yf+...)y = fyi + /V + ЛГ+-.
(сС + cV + сГ+...) 2 = /С + fV + /"?"+...,
Сравнения со многими неизвестными 39
которые мы для краткости представим следующим образом:
4. Теперь нужно различать несколько случаев.
Во-первых, если все коэффициенты 2 (#?)> 2(^7])>--- ПРИ неиз"
вестных взаимно просты с модулем сравнения т, то эти сравнения
можно решить по указанным выше правилам, и полное решение
вопроса будет представляться сравнениями вида
Если, например, заданы сравнения
х + Зу + z = l (mod 8),
ix + y + 5z = 7,
2х f 2y + z =3,
то мы находим i = 9, ?' = 1, i" = —14; отсюда — 15х= — 26 и пото-
потому х = 6 (mod 8). Таким же образом находим 15?/ = — 4, 15z = l,
откуда ?/ = 4, z = 7 (mod 8).
5. Во-вторых, ее ли не все коэффициенты 2 (а^)> 2 (^7])>--- взаим-
взаимно просты с модулем, то пусть а, р, т»..« суть наибольшие общие
делители m и, соответственно, 2 (а^Ь 2 (^)> 2(с^)»--- Тогда зада-
задача, очевидно, неразрешима, если они не являются одновременно так-
также и делителями соответственно чисел 2(Я0» З^7])' 2(/^)'--- Если
же эти условия выполняются, то полное решение сравнений в C)
дается сравнениями вида x=plmod — J, y=ql mod-H, z=rfmod-j, ...,
или, другими словами, существует а различных (т. е. несравни-
несравнимых по модулю т, таких, как р, р + —,..., р -\- ) значе-
значений ху р различных значений у, и т. д., которые удовлетворяют
указанным сравнениям; очевидно, что все решения заданных
* Это утверждение, как можно заметить, нуждается в доказательстве, ко-
которое мы здесь опустили. В самом деле, из наших рассуждений следует только
то, что заданные сравнения не удовлетворяются при других значениях неизвест-
неизвестных х, у, z...; а то, что указанные нами значения этим сравнениям удовлетворя-
удовлетворяют, ниоткуда не следует. Именно, эти сравнения могли бы, вообще говоря,
не иметь никаких решений. Подобный же паралогизм часто встречается и в тео-
теории линейных уравнений.
40 Раздел II (п.
сравнений (если они вообще существуют) содержатся здесь. Однако
обратить это утверждение нельзя; действительно, в большинстве
случаев не все комбинации всевозможных значений х со всевоз-
всевозможными значениями у, всевозможными значениями z и т. д. да-
дают решение задачи, а лишь некоторые из них, которые удовлетво-
удовлетворяют одному или нескольким условиям сравнимости. Так как,
однако, полное решение этого вопроса не является необходимым
для дальнейшего, мы не будем здесь более подробно его исследо-
исследовать, и удовлетворимся тем, что продемонстрируем положение ве-
ведущей на примере.
Пусть заданные сравнения суть
3x + 5y + z~4, 2x + 3y + 2z = 7, 5x + y + 3z = 6 (mod 12).
Здесь числа ?, ?', ?"; т], т]', т]"; С, С, С" равны соответственно 1,
— 2, 1; 1,1, —1; —13, 22, —1, откуда вытекает 4# =— 4,
7у= 5, 28z = 96. Отсюда получаются четыре значения для х, имен-
именно, х = 2, 5, 8, 11, одно значение для у, именно г/= 11, четыре
значения для z, именно z = 0, 3, 6, 9 (mod 12). Чтобы теперь уз-
узнать, какие комбинации значений х и значений z мы имеем пра-
право брать, подставим в заданные сравнения вместо #, у, z соот-
соответственно 2-\-3t, 11, Згг? после чего они перейдут в следующие
сравнения:
57 + 9t + Зи = 0, 30 + б? Н- 6и = 0, 15 + 1Ы + 9и = 0 (mod 12),
а они, как легко видеть, эквивалентны следующим:
19 + 3^4-^ = 0, 10 + 2* + 2и = 0, 5 + 5*-г-Зи = 0 (mod 4).
В силу первого из них должно быть гг = t-\-1 (mod 4); если мы
подставим это значение в два других сравнения, то увидим, что оба
они тоже удовлетворяются. Отсюда следует, что значения х = 2, 5,
8, 11 (которые получаются, если положить t = 0, 1, 2, 3) необходи-
необходимо должны комбинироваться соответственно со значениями z = 3, 6,
9, 0, так что всего мы имеем четыре решения, именно
х = 2, 5, 8, 11 (mod.12);
г/= 11, 11, 11, 11;
2ЕЕЕЗ, 6, 9,0.
Различные теоремы 41
К этим исследованиям, благодаря которым мы уже достигли цели
этого раздела, мы добавим еще несколько основанных на подобных
же принципах теорем, которые мы часто будем использовать впос-
впоследствии.
Различные теоремы
38
Задача. Требуется узнать, сколько существует положительных
чисел, которые меньше данного положительного числа А и одновре-
одновременно взаимно просты с ним.
Если количество положительных чисел, которые меньше задан-
заданного числа и одновременно взаимно просты с ним, обозначать бук-
буквой ф, ставящейся перед числом, то нам нужно найти Ц>(А).
I. Если число А простое, то все числа от 1 до А — 1, очевидно,
взаимно просты с А' следовательно, в этом случае
II. Если А есть степень простого числа, именно, А = рт, то
взаимно простыми с А будут все числа, за исключением делящих-
делящихся на р. Поэтому из рт — 1 чисел отбрасываются следующие: р,
2р, Зр,..., (рт— х—1)р\ таким образом, остается рт— 1 — (рт~ 1 — 1)
или рт —!(р — 1) чисел, так что tp (рт) = рт ~г(р — 1).
III. Остальные случаи легко могут быть сведены к двум первым
при помощи следующей теоремы.
Если А разлагается па взаимно простые сомножители М, N,
Р,..., то
= cp(M).cp(N).cp(P)...
Доказывается это следующим образом. Пусть т, т!, т",... суть
числа, которые взаимно просты с М и меньше чем М; количество
их, таким образом, равно <р(М). Точно также пусть п, п', п",...,
соответственно р, р', р",...—числа, которые взаимно просты с iV,
соответственно с Р, и меньше, чем N, соответственно, чем Р, ко-
количество которых равно <p(N)> соответственно <р(Р), и т. д. Тогда,
42 Раздел II (п. 39)
как известно, все числа, взаимно простые с произведением А, вза-
взаимно просты также и с отдельными сомножителями М, N, Р,...,
и обратно (п. 19). Далее, все числа, которые сравнимы по моду-
модулю М с одним из чисел т, т!, т",..., взаимно просты с М и об-
обратно; то же самое имеет место относительно N, Р,.... Поэтому
задача сводится к следующей: определить, сколько среди чисел,
меньших А, имеется таких, которые сравнимы с одним из чисел
т, т!', т",... по модулю М, с одним из чисел п, п\ п",... по мо-
модулю N и т. д. Но из п. 32 следует, что все числа, которые име-
имеют по отдельным модулям М, N, Р,... одни и те же вычеты, срав-
сравнимы по их произведению А, и что поэтому среди чисел, меньших
А, имеется одно единственное, которое сравнимо i. заданными вы-
вычетами по отдельным модулям М, N, Р,... . Следовательно, иско-
искомое число будет равно количеству всех комбинаций отдельных
значений т, т\ т",.-- с отдельными значениями п, п', п",..., от-
отдельными значениями р, р', /?",... и т. д. Но как известно из
комбинаторики, это количество равно
cp(M).cp(N).cp(P)...
IV. Легко видеть, как это применяется к рассматриваемому
случаю. Если А разложено на простые сомножители, т. е. задано
в виде aa6pcY,..., где a, b, с,... обозначают различные простые
числа, то
ср(А) =ср(а«).ср(№)-ср(&)...= аЛ-1(а — 1).ДО ~1(b~ l)c*-i(c—1)...,
или короче
ф(А) = А • —=— • ...
т v ' а Ь с
Пример. Если ,4 = 60 = 22-3-5, то <р(^1) = 1.|-|.60 = 16. Чис-
Числа, взаимно простые с 60, суть 1, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 49, 53, 59.
Первое решение этой проблемы содержится в работе Эйлера
«Theoremata arithmetica nova methodo demonstrata» в «Сотт. nov. Ac.
Petrop»., VIII, p. 74. Позднее доказательство повторяется в другой
работе: «Speculationes circa quasdam insignes proprietates numerorum»,
Ada Petrop., VIII, p. 17.
Различные теоремы 43
39
Если же значение функции ср определить так, что у (А) выра-
выражает количество чисел, которые взаимно просты с А и не превос-
превосходят А, то очевидно, что <рA) будет уже равно не 0, а 1, а во
всех остальных случаях никаких изменений от этого не произой-
произойдет. Принимая это определение, мы получаем следующую теорему.
Если а, а', а",...— всевозможные делители числа А (не исключая 1
и самого А), то
Пример. Если А =30, то <рA) + 9B) + <рC) + 9 E) + 9F) +
+ 9 (Ю) + 9 A5) + 9 C0) = 1 + 1+2 + 4 + 2 + 4 + 8 + 8 = 30.
Доказательства. Если умножить на А/а все числа, которые вза-
взаимно просты с а и не превосходят а, на А/а'—все числа, вза-
взаимно простые с а', и т. д., то мы получим <р(а) + 9(а) + 9(а") +•••
чисел, которые все не превосходят А. Но
1) все эти числа между собой различны. В самом деле, то, что
все числа, которые получаются для одного и того же делителя
числа А, не равны между собой, очевидно. А если бы для различ-
различных делителей М, N и соответственно взаимно простых с ними чи-
чисел [х, v получались бы равные числа, т. е. если бы было
А А.
— {л = — v, то имело бы место jxiV = vM. Если предположить (что
допустимо), что М > N, то М, являющееся взаимно простым с (л
и делителем числа jxiV, должно было бы также быть и делителем
N, т. е. большее число было бы делителем меньшего, что невоз-
невозможно;
2) среди этих чисел содержатся все числа 1, 2У 3,..., А. Имен-
Именно, если t — любое число, не превосходящее Л, и 8 — наибольший
общий делитель чисел А и t, то А/Ь будет делителем А, с кото-
которым t/Ь взаимно просто. Поэтому число t очевидно содержится
среди тех чисел, которые получаются для делителя А/Ь\
3) отсюда следует, что количество всех этих чисел равно Ащ
Поэтому
44 Раздел II (пп.
40
Если [х есть наибольший общий делитель чисел А, В, С D,...^
то можно найти числа a,b,c,d,...c тем свойством, что
аА + ЬВ + сС +...= [х.
Доказательство. Если рассматривать сначала только два числа
А, В, наибольший общий делитель которых равен X, то сравнение-
Ах:=\ (modi?) разрешимо (п. 30). Если его корень =ос, то, пола-
полагая —-^5— = Р» получим &А + $В = X, что и требовалось.
Если присоединяется еще третье число С, и X' есть наибольший
общий делитель X и С, то можно найти такие два числа i и f,
что к\4- ^С = Х\ Тогда к&А + к$В + ^С = X'. Но очевидно, что ХЛ
есть общий делитель чисел А, В, С,..., и притом наибольший, так
как если бы существовал еще больший общий делитель 0, то вы-
ражение кг + Арг--)-^ r = j было бы целым числом, т. е. боль-
большее число 0 было бы делителем меньшего числа. Поэтому мы по-
получаем требуемое, если положим Ы = а, к$ = Ъ, у = с, X7 = jx.
Подобным же образом можно рассуждать, сколько бы новых
чисел мы ни присоединяли.
Если числа А, В, С, D, ... не имеют общих делителей, то оче^
видно можно добиться того, что
а А + ЪВ -f- сС -)-...— 1.
41
Если р — простое число, и имеется р предметов, среди которых
может быть любое количество одинаковых (лишь бы не все они были
одинаковы), то число всех перестановок этих предметов делится на р.
Пример. Пять предметов А, А, А, В, В могут быть размещены
десятью различными способами.
Доказательство этой теоремы легко может быть выведено из изве-
известной теории перестановок. Действительно, если среди этих пред-
предметов имеется а равных А, Ъ равных В, с равных С и т. д. (где числа*
Различные теоремы 45
а, Ь, с, ... могут быть равны и единице), так что
то число перестановок равно
1 -2-3...
1.2-3. . . а • 1.2-3. . .Ъ- 1-2-3. ..с...'
Само собой разумеется, что числитель этой дроби делится на зна-
знаменатель, так как число перестановок должно быть целым числом.
Но числитель делится на /?, а знаменатель, который образован из
сомножителей, меньших р, на р не делится (п. 15). Поэтому число
перестановок делится на р (п. 19).
Однако я надеюсь, что многим не покажется безынтересным и
следующее доказательство.
Если в двух перестановках порядок предметов, из которых они
образованы, отличается только тем, что тот предмет, который в од-
одной из них занимает первое место, в другой находится на другом
месте, но все предметы в обеих перестановках следуют один за дру-
другим в одном и том же порядке (считается, что за последним предме-
предметом следует первый), то мы будем называть эти перестановки подоб-
подобными *. Так, в нашем примере перестановки АВААВ и АВАВА
будут подобными, так как предметы, занимающие в первой первое,
второе и т. д. места, во второй в том же порядке занимают третье,
четвертое и т. д. места.
Так как каждая перестановка состоит из р предметов, то для
каждой, очевидно, можно найти р — 1 подобных перестановок, если
тот предмет, который был первым, передвигать на второе, третье
и т. д. места. Если среди них нет равных, то ясно, что число всех
перестановок будет делиться на р, так как оно в р раз больше, чем
число всех не подобных между собой перестановок.
Предположим теперь, что две перестановки
PQ... TV... YZ, V... YZPQ... Т,
* Если представлять себе эти перестановки записанными по кругу, так что
последний предмет оказывается соседним с первым, то между подобными пере-
перестановками вообще не будет разницы, так как никакое место нельзя будет на-
назвать ни первым, ни последним.
46 Раздел II (п. 42)
одна из которых получается из другой описанной передвижкой чле-
членов, равны, т. е. что Р = V и т. д. Если член Р, являющийся в пер-
первой перестановке первым, во второй является (п + 1)-м, то во вто-
втором ряду (п + 1)-й член будет, таким образом, равен первому,,
(п + 2)-й член — второму, и т. д., так что Bп + 1)-й член снова ра-
равен первому, и по той же причине и (Зп + 1)-й и т. д., вообще*
(кп+т)-й равен m-му. (При этом, если кп + т > р, то надо либо мыс-
мыслить ряд V...YZPQ...T все время снова повторяющимся сна-
сначала, либо вычитать из кп + т ближайшую меньшую кратность
числа /?). Поэтому, если определить число к так, чтобы имело место
кп=1 (mod р), что возможно, ибо р — простое число, то мы полу-
получим, что всегда m-й член равен (т + 1)-му, т. е. каждый член равен
следующему, откуда следует, что все члены равны между собой,
что противоречит предположению.
42
Если коэффициенты А, В, С, ..., TV; a, b, cr ...r n двух функций:
вида
(Р) хт + Ахт~1 + Вхт -2 + Схт -3+...+ N,
все являются рациональными, но не все — целыми числами, и произ-
произведение (Р) и (Q) представлено в виде
то коэффициенты 31, 95,..., 3 ™е могут все быть целыми.
Доказательство. Выразим все коэффициенты А, В,..., а, 6,... в
виде несократимых дробей и возьмем любое простое число /?, ко-
которое входит в один или несколько из знаменателей этих дробей.
Если предположить (на что мы имеем право), что р входит в зна-
знаменатель какого-нибудь дробного коэффициента у (Р), то ясно,
что если (Q) разделить на р, у (Q)/p также будет хотя бы
один дробный коэффициент, знаменатель которого содержит р
(именно, первый коэффициент 1//?). Далее, легко видеть, что среди
коэффициентов (Р) имеется дробь, знаменатель которой содержит
р в степени, большей, чем все предыдущие члены, и не меньшей,
Различные теоремы 47
чем все последующие члены. Пусть этот член есть Gxg, а степень,
в которой р входит в знаменатель дооби G, равна рК Подобный
же член существует в (Q)/p\ пусть это Гхт, и степень, в которой
р входит в знаменатель дроби Г, есть т. Очевидно, что t + т по
меньшей мере равно 2. Тогда член x^ + Y произведения (Р) и (Q)
будет иметь дробный коэффициент, знаменатель которого содержит
(t + т—1)-ю степень числа р. Это доказывается следующим образом.
Пусть 'G^ + x, "G^ + 2,." суть те члены, которые в (Р) пред-
предшествуют члену Gx$, a G'x? —x, G"x?"~2,...— те, которые следуют
после него. Точно так же, пусть TxY + 1> TxY + 2,... суть те члены,
которые в {Q)/p предшествуют члену Г#т, а Г'а^ — 1, Г"#7— 2,...—те,
которые следуют после него. Тогда коэффициент члена xg + ^ в
произведении (Р) и (Q)/p7 очевидно, равен
+ TG'+TG"+...
Слагаемое GT есть дробь, которая после приведения к несо-
несократимому виду содержит в знаменателе р в (t + т)-й степени; ос-
остальные же слагаемые, если они являются дробями, содержат в
знаменателе меньшие степени р, так как все они являются произ-
произведениями двух сомножителей, из которых либо знаменатель одно-
одного содержит р в степени, меньшей, чем т-я, а знаменатель дру-
другого — в степени, не большей, чем t-я, либо знаменатель
одного содержит р в степени, меньшей, чем t-я, а знаменатель
другого — в степени, не большей, чем т-я. Поэтому G Г име-
имеет вид е///?*+ т, в то время как сумма остальных слагаемых
имеет вид е'/}'р1 + х — ь, где 8 есть положительное число, и е, /, /'
не содержат р сомножителем. Вся сумма равна, таким образом,
(е/'-\-е'/ръ)//'р1 + г. Так как числитель этого выражения не делится
на р, то после сокращения дроби знаменатель вса равно будет де-
делиться на pl + T. Поэтому коэффициент члена я^ + f в произведении
(Р) и «?) равен
ef'+e'fp*
frpt + *-i*
т. е. является дробью, знаменатель которой содержит (t -\~ т — 1)-ю
степень числа р. Таким образом, теорема доказана.
48 Раздел II (пп. 43~44)
43
Сравнение т-й степени
Ахт + Вхт~1 + Схт-* +...+ Mx + N = О,
модулем которого является не входящее в А простое число р9 не
может быть разрешимо более чем т различными способами, т. е.
имеет не более уем т не сравнимых по модулю р корней (см. пп.
25, 26).
Если бы это было не так, то предположим, что имеются срав-
сравнения различных степеней т, п,..., которые имеют более чем т,
п,... корней, и пусть т — наименьшая такая степень, так что все
подобные сравнения более низкой степени согласуются с нашей
теоремой. Так как для первой степени мы эту теорему уже дока:
зали выше (п. 26), то ясно, что т или равно 2, или больше, чем 2.
Итак, пусть сравнение
Ахш + Вхт -1 +...+ Мх + N = О
обладает по меньшей мере т-\-1 корнями именно #=<х, ж = р,
х^=у,. •» и предположим, что позволительно, что все числа а, р,
Т,... положительны и меньше, чем /?, и что наименьшее из них
есть а. Подставим в данное сравнение г/ + а вместо х\ пусть оно
перейдет тогда в
А'уш + В'у™ -1 + Сут ~ z+...+ М'у + N' = 0.
Это сравнение, очевидно, будет удовлетворяться, если полагать
?/ = 0, или ?/ = Р—а, или у = т — а и т. д., причем все эти корни
различны между собой и число их равно т-\-1. Но из того, что
у = 0 является корнем, следует, что N1 делится на р. Поэтому
сравнение
т-1 + В'ут-2+...+ М')=в0 (mod/?)
также удовлетворяется, если у придавать т значений р — а, у — а,...,
которые все больше 0 и меньше р, а потому при этих значениях и
A'ym-1 + B'ym-*-l...+ Mf==:Q (п. 22),
т. е. сравнение (т — 1)-й степени
А'у™-1 + В'у™~* + . . . + М' = О,
Различные теоремы 49
имеет т корней, что находится в противоречии с нашей теоремой
(очевидно, что А' = А, и потому А', как и требуется, не делится
на /?), хотя мы предположили, что все сравнения степени, меньшей,
чем т-я, находятся с теоремой в согласии. Тем самым теорема пол-
полностью доказана.
44
Хотя мы предполагали, что модуль р не должен входить в коэф-
коэффициент старшего члена, теорема верна Не только в этом случае.
Именно, если первый коэффициент, а быть может также и несколько
следующих, делятся на р, то эти члены можно спокойно отбросить,
и тем самым прийти к сравнению более низкой степени, у которого
первый коэффициент уже не делится на р; лишь в случае, когда все
коэффициенты делятся на р, сравнение превращается в тождествен-
тождественное, и значение неизвестного совершенно неопределенно.
Эта теорема была впервые высказана и доказана Лагранжем
{«Mem. de ГAc. de Berlin», Аппёе 1768, р. 192). Она встречается так-
также в одной работе Лежандра, «Recherches d'Analyse indHermi-
пёе», Hist de VAc. de Paris, 1785, p. 466. Эйлер доказал в «Сотт.
nov., Ac Petrop.», XVIII, p. 93, что сравнение хп — 1=0 не может
иметь более чем п различных корней. Хотя это есть только частный
случай, однако метод, которым он пользуется, легко может быть
применен ко всем сравнениям. Еще более частный случай он рассмат-
рассматривал даже раньше, в «Сотт. nov. Ac. Petrop.», V, р. 6, но использо-
использованный там метод в общем случае неприменим. Ниже, в разделе
VIII, мы докажем эту теорему еще одним способом; однако, сколь
бы различными на первый взгляд эти методы ни казались, все же
знатоки, которые пожелают их сравнить, легко убедятся, что все
они основаны на одном и том же принципе.
Так как здесь мы должны рассматривать эту теорему лишь как
вспомогательную, и неуместно давать здесь ее исчерпывающее изло-
изложение, мы не будем тратить силы на то, чтобы рассматривать спе-
специально еще и составные модули.
Раздел III
О СТЕПЕННЫХ ВЫЧЕТАХ
Вычеты членов геометрической прогрессии,
начинающейся с единицы, образуют периодический ряд
45
Теорема. В каждой геометрической прогрессии 1, а, а2, а3,...,
кроме первого члена 1, имеется еще и другой член а*, сравнимый с
единицей по взаимно простому с а модулю ру с показателем t <^ р.
Доказательство» Так как модуль р взаимно прост с а, а пото-
потому и с любой степенью а, то среди членов прогрессии нет
= 0 (mod/?), и потому каждый из них сравним с однимиз чисел 1, 2,
3,..., (р—1). Так как количество этих чисел равно р—1, то оче-
очевидно, что если взять более чем р — 1 членов прогрессии, их наи-
наименьшие вычеты не могут быть все различны. Поэтому среди чле-
членов 1, а, а2, а3,..., av~l найдутся по крайней мере два сравнимых
между собой. Пусть ат = ап и т^>щ деля на ап мы, получим
ат~п = 1 (п. 22), где т — п<^р и >0.
Пример. В прогрессии 2, 4, 8,... первым членом, сравнимым с
единицей по модулю 13, оказывается 212 = 4096. В той же прогрес-
прогрессии по модулю 23 имеем: 2П = 2048 = 1. Точно так же шестая
степень числа 5, т. е. 15625, сравнима с единицей по модулю 7,
а пятая, 3125,— по модулю 11. Таким образом, в некоторых слу-
случаях уже сравнима с единицей степень с показателем, меньшим,
чем р — 1, в других же случаях бывает нужно доходить до (р—1)-й
степени.
Вычеты членов геометрической прогрессии 51
46
Если прогрессию продолжить за тот член, который сравним о
единицей, то дальше будут повторяться те же самые вычеты, ко-
которые были в начале. Именно, если а1 = 1, то а1 + * = а, а1 +2 = а2,
и т. д., до члена а2*, наименьший вычет которого опять есть 1,
а затем период вычетов начинается снова. Мы получаем таким об-
образом период, содержащий t вычетов, который после того как он
оканчивается, снова повторяется сначала. При этом во всей про-
прогрессии не может встречаться других вычетов, кроме тех, которые
содержатся в этом периоде. Вообще, ат* = 1 и amt + n^an%
что в наших обозначениях мы представим так;
Если r = p (mocU), то ar = ap (modр).
47
Из этой теоремы получается простой способ отыскания вычетов
степеней со сколь угодно большими показателями, если известно,
какая степень сравнима с единицей. Если, например, нущно \най-
ти остаток от деления степени З1000 на 13, то, так как 33 =
= l(mod 13), мы сначала получаем, что t =3. Так как 1000=1 (mod3),
то 31000 = 3 (mod 13).
Если а1 есть наименьшая степень, сравнимая с единицей (не
считая случая а0 = 1, который мы здесь не принимаем во внима-
внимание), то все t членов, которые образуют период вычетов, различ-
различны, что без труда можно усмотреть из доказательства в п. 45. По-
Поэтому теорему из п. 46 можно обратить, именно: Если ат = ап (mod pO
то m = n(mod?). Действительнб, если бы т, п пО моду-
модулю t были не сравнимы, то их наименьшие вычеты были бы раз-
различны. Но если a** = am, a* = an, то a** = av, т. е. не все степени,
меньшие а*, не сравнимы между собой, что приводит к противо-
противоречию.
Если, в частности, ak^l (mod/?), то & = 0 (mod?), т. ё. к де-
делится на t.
52 Раздел III (пп. 49-50)
До сих пор речь шла о любых модулях, лишь бы они были
взаимно просты с а. Теперь мы специально рассмотрим модули,
являющиеся простыми числами, а потом на основе этого построим
более общее исследование.
Сначала рассматриваются модули,
которые являются простыми числами
49
Теорема. Если р — простое число, которое не входите а, и а 1
есть наименьшая степень а, которая сравнима с единицей по моду-
модулю р, то показатель t или равен р — 1, или является делителем
этого числа.
(Ср. примеры из и. 45.)
Доказательство. Так как мы уже показали, что t или = р — 1,
или <Г р—1» нам остается только убедиться, что в последнем слу-
случае t всегда будет делителем р — 1.
I. Возьмем наименьшие положительные вычеты всех членов
1,а, а2,..., а' — 1 и обозначим через а, а', а",..., так что <х=1, <х'=а,
а"Е=а2,... Очевидно, что все они различны, так как если бы два
члена-ат, ап имели один и тот же вычет, то (считая, что т^> п)
должно было бы быть ат —п=1 и т — n<^t, что невозможно, по-
потому что по условию никакая степень, меньшая, чем а*, не срав-
сравнима с единицей. Далее, все числа ос, а', а",... содержатся в ряду
чисел 1, 2, 3,.. , р—1, но не исчерпывают его целиком, так как
t<Cp—1. Совокупность всех чисел а, а', а"....мы обозначим через
(А). Таким образом, (-4) содержит t членов.
П. Выберем теперь из ряда 1, 2,3,.... р — 1 какое-нибудь число
Р, не входящее в комплекс (-4), перемножим C со всеми числами а,
а', а",.., и обозначим через C, C', р",... наименьшие вычеты этих про-
произведений, число которых тоже равно t. Эти вычеты должны быть
все отличны как один от другого, так и от всех чисел а, а', а",.--
Именно, если бы первое утверждение было неверно, то мы имели
бы, например, $ат = $апу и потому, после деления на р, ат = ап,
что противоречит доказанному выше; если же второе утвержде-
утверждение было бы ложным, то мы имели бы, скажем, pam==an, откуда
Теорема Ферма 53
(считая, что т<.п) p = an~ ш7 т. е. р было бы сравнимо с одним
из чисел а, а', а",..., что противоречит предположению. Если же
т^>пу то после умножения на а1~т мы получим j3a*=Ea* + n —m,
или, учитывая, что a' = l, p = a' + n —m , что невозможно по той же
самой причине. Если совокупность всех чисел р, р\ р",..., количество
которых равно t, обозначим через (В), то в обеих совокупностях (А)
и (В) будет уже 2t чисел из ряда 1, 2, 3,.,., р— 1. Поэтому, если
(А) и (В) охватывают все эти числа, то t = ^— и теорема дока-
доказана.
III. Если же некоторые числа еще не содержатся в (А) и (В),
то пусть одно из них есть у. Перемножим его со всеми числами
а, а', а",..., обозначим наименьшие вычеты произведений через f>
f', т"»---» а совокупность всех этих вычетов — через (С). Тогда (С)
тоже будет содержать t чисел из ряда 1, 2, 3,..., р — 1, и все они
будут отличны как один от другого, так и от чисел, содержащих-
содержащихся в (-4) и (В). Первые два утверждения доказываются так же,
как в п. II, а третье следующим образом. Если бы было Yam^P^n,
то имело бы место или т = Р#п~~т» или Т —Р*2*1""71» в зависи-
зависимости от того, т<С,п или т^>п\ в обоих случаях ^ было бы та-
таким образом, вопреки предположению, сравнимо с одним из чисел,
содержащихся в комплексе (В). Поэтому мы имеем теперь 3? чи-
чисел из ряда 1, 2, 3,...,/?— 1, и если других больше нет, то t =
= ^—— и теорема доказана.
о
IV. Если другие числа все еще имеются, то нужно таким же спо-
способом построить четвертую совокупность чисел (D). Так как коли-
количество чисел 1, 2, 3, ..., р— 1 конечно, оно рано или поздно
будет исчерпано и окажется кратностью t. Таким образом, t есть
делитель р — 1.
Теорема Ферма
50
Таким образом, (р — l)/t есть целое число, и возводя обе части
сравнения а! = 1 в р~ -ю степень, мы получим а^"*^!, т. е.
54 Раздел III (пп. 51-52)
разность av~l~-l всегда делится на р, если р — простое число, не
входящее в а,
Эта теорема, которая заслуживает величайшего внимания как
вслед твие ее изящества, так и ввиду ее выдающейся пользы, обычно
называется по имени нашедшего ее математика теоремой Ферма
(см. «Fermatii Opera Mathematical, Tolosae, 1679, p. 163). Фермане дал
доказательства, но утверждал, что обладает им. Эйлер впервые
опубликовал доказательство в сочинении «Teorematum quorundam ad
numeros primos spectantium demonstration, Comm.Acad. Petrop., T. VIII*.
Оно базируется на разложении степени (а + 1)р, из вида коэффи-
коэффициентов которого очень легко вывести, что (а + 1)^ — аР — 1 всег-
всегда делится на р, а потому (a~\-l)v — (а + 1) будет делиться на р,
если делится аР — а. Но так как 1р — 1 всегда делится на р, то
это имеет место и для 2^ — 2, а потому и для Зр — 3 и т. д., во-
вообще, для аР — а. Поэтому, если р не входит в а, то и ар~г — 1
будет делиться на р. Сказанного достаточно, чтобы сделать ясным
сущность метода. Подобное же доказательство дал Ламберт в
«Ada Erudit.,» 1789, p. 109. Так как, однако, разложение степе-
степени бинома в значительной степени казалось чуждым теории чисел,
Эйлер нашел другое доказательство, которое содержится в «Com-
«Comment, nov. Petrop.)), Т. VII, p. 70 и полностью совпадает с данным
нами в предыдущем пункте. В дальнейшем нам встретятся еще и
другие доказательства. В этом же месте мы приведем пока еще
одно, которое базируется на принципах, подобных первому дока-
доказательству Эйлера. Следующая теорема, для которой теорема Фер-
Ферма является просто частным случаем, найдет ниже применение и
при других исследованиях.
* В более раннем сочинении он еще не достиг цели («Сотт. Acad. Petrop.»,
Т. VI, р. 106). В известном споре между Мопертюи и Кенигом, кото-
который возник по поводу принципа наименьшего действия, но скоро перекинулся
на другие предметы, К е н и г утверждал о существовании письма Л ейбница,
в котором содержится доказательство, полностью совпадающее с доказательст-
доказательством Эйлера («Appel аи public», p. 106). Однако, даже если бы мы и не сомне-
сомневались в этом свидетельстве, все же нужно отметить, что Лейбниц заведомо
нигде не опубликовал своего открытия (ср. «Hist, de VAc. de Berlin», Аппёе
1760, p. 530).
О числе решений сравнения х1 = (mod p) 55
51
Если р— простое число, то р-я степень многочлена а + 6 + с+..-
сравнима по модулю р с выражением а? + bv + cv +...
Доказательство. Как известно, р-я. степень многочлена a -f- Ъ -\-
-\ с... образуется из чисел вида xaa6^cY..., где а + р + т+--- = /?, и
число х указывает, сколькими способами можно переставлять р
предметов, из которых а, р, т»--- соответственно равны а, 6, с,...
Но выше, в п. 41, мы показали, что это число всегда делится на
р, если только не все предметы равны, т. е. если среди чисел а,
p. Y»--- не все? кроме одного, равного р, равны 0. Отсюда следует,
что у (а + 6 + с+...)р все члены, за исключением ар, 6р, ср,..., де-
делятся на р. Поскольку речь идет о сравнении по модулю р, их
можно совсем отбросить, и тогда получится
(а + 6 + c+...)p = ap + 6p-}-cp-f....
Если теперь все величины a, b, с,... равны 1, а число их рав-
равно ft, то будет kv'^k, как и в предыдущем пункте.
О количестве чисел, которым соответствуют периоды,
у которых количество членов равно
заданному делителю числа р—1
52
Так как никакие числа, кроме делителей р— 1, не могут быть
наименьшими показателями степеней, в которые надо возводить ка-
какие-нибудь числа, чтобы сделать их сравнимыми с единицей, то воз-
возникает вопрос, все ли делители р — 1 здесь пригодны, и, далее,
если все не делящиеся на р числа разбить на классы по показате-
показателям их наименьших сравнимых с единицей степеней, то сколько
чисел будет приходиться на отдельные показатели. При этом можно
сразу заметить, что достаточно рассматривать лишь все положитель-
положительные числа от 1 до р — 1. Действительно, очевидно, что сравнимые
между собой числа нужно возводить в одну и ту же степень, чтобы
сделать их сравнимыми с единицей, и потому каждое число соответ-
56 Раздел III (пп. 53-54)
ствует тому же самому показателю, что и его наименьший положи-
положительный вычет. Мы должны, таким образом, направить наше
внимание на то, чтобы установить, как числа 1, 2, 3, ..., р—1 разбива-
разбиваются с этой точки зрения по отдельным сомножителям числа р—1. Если
d — делитель р — 1 (к которым надо причислять также 1 и р — 1),
то ради краткости через ф(с?) мы будем обозначать количество поло-
положительных меньших чем р чисел, для которых d-я степень есть наи-
наинизшая из всех, сравнимых с единицей.
53
Для того чтобы это исследование было легче понять, мы рас-
рассмотрим сначала один пример. Для р = 19 числа 1, 2, 3,..., 18
распределяются по делителям числа 18 следующим образом:
1
2
3
6
9
18
1.
18
7,
8,
4,
2,
11
12
5,
3,
6,
10
9, 16
, 13,
, 17.
14, 15
Таким образом, в этом случае фA) = 1, ф B) = 1, ф C) = 2, ф F) =
= 2, ф(9) = 6, фA8) = 6. Нетрудно подметить, что каждому по-
показателю принадлежит столько же чисел, сколько имеется чисел,
которые не больше его и с ним взаимно просты, или, что, по край-
крайней мере в этом случае, в обозначениях п. 39 имеет место ф (d) =
= cp(d). To, что это замечание верно всегда, мы можем доказать
следующим образом.
I. Если имеется какое-нибудь число а, которое принадлежит по-
показателю с? (т. е. у которого d-я степень сравнима, а все более низ-
низкие степени не сравнимы с единицей), то все его степени а2, а3,
а4, . .., ad или их наименьшие вычеты тоже обладают первым свой-
свойством (именно, тем, что их d-e степени сравнимы с единицей), а
так как это можно выразить еще и так, что наименьшие вычеты
О числе решений сравнения xt = (mod p) 57
чисел а, а2, а3,. .., <zd (которые все различны между собой) явля-
являются корнями сравнения #d = l, а это сравнение не может иметь
более чем d различных корней, то ясно, что кроме наименьших вы-
вычетов чисел a, a2, a3,.,», ad между 1 и р—1 включительно нет
других чисел, d-я степень которых сравнима с единицей. Отсюда
следует, что все принадлежащие показателю d числа содержатся
среди наименьших вычетов чисел а, а2, а3, .. ., ad. Каковы их зна-
значения и как велико их количество, можно определить так: если
к— число, взаимно простое с d, то все степени числа ак, показа-
показатели которых меньше, чем d, не сравнимы с единицей. Действитель-
но, пусть г- = т (mod d) (см. п. 31), тогда ahm = a\ поэтому если бы
е-я степень числа ак с e<id была сравнима с единицей, то было бы
также акте1= lv откуда, вопреки предположению, ае=1. Отсюда
вытекает, что наименьший вычет числа ак принадлежит показателю d.
Если же к имеет с d какой-нибудь общий делитель 8, то наимень-
наименьший вычет числа ак не принадлежит показателю d, так как у не-
него уже d/Ь-я степень сравнима с единицей (именно, kd/Ь будет де-
делиться на d, т. е. == 0 (mode?), и потому akdjb^i). Отсюда следует,
что показателю d принадлежит столько чисел, сколько среди чи-
чисел 1, 2, 3, . . ., d имеется взаимно простых ее?. Однако надо иметь
в виду, что этот вывод основывается на предположении, что одно
число а, принадлежащее показателю d, уже имеется. Поэтому не
исключена возможность, что какому-нибудь показателю вообще не
принадлежит никакого числа, т. е. мы пока получили только то,
что ф(с?) или =0, или =cp(d).
54
П. Если теперь d, d\ с?",... суть все делители числа р — 1, то
так как все числа 1, 2, 3,...,/? — 1 распределены между этими
делителями, имеет место равенство
Но в п. 40 мы доказали, что
58 Раздел III (п. 55)
а из предыдущего пункта следует, что ф(с?) может быть или рав-
равно (p(d), или меньше, но не больше, чем 9(^0» и так же обстоит
дело для ф (df) и 9 (df) и т. д. Если какой-нибудь член (или несколько
членов) ряда ф(с?)> ф(й'), ф(с?"),... был бы меньше, чем соот-
соответствующий член ряда <p\d), <p(d'), <p(d"), . . ., то сумма одного ря-
ряда не могла бы равняться сумме другого ряда. Отсюда мы, нако-
наконец, получаем, что ф(с?) всегда равно cp(d) и тем самым не зависит
от величины р—1.
55
Наибольшее значение имеет, однако, один специальный случай
предыдущей теоремы, а именно то, что всегда существуют числа,
наименьшая степень которых, сравнимая с единицей, есть (р — 1)-«я,
причем между 1 и р—1 их столько, сколько существует чисел,
не превосходящих р—1 и взаимно простых с р — 1. Так как до-
доказательство этой теоремы не столь просто, как это могло бы по-
показаться на первый взгляд, мы вследствие важности этой теоре-
теоремы, дадим еще одно ее доказательство, несколько отличающееся
от предыдущего, тем более, что различие методов обычно очень по-
помогает уяснению более трудных вопросов. Разложим р — 1 на его про-
простые сомножители; пусть р— 1 = aa№cY, . . ., где а, Ь, с,... обозна-
обозначают различные простые числа. Тогда мы можем провести доказа-
доказательство теоремы следующим образом.
I. Всегда можно найти число А, которое принадлежит показа-
показателю аа, и точно так же числа В, С,..., которые принадлежат
соответственно показателям b&, cY,. ..
II. Произведение всех чисел А, В, С, . .. (или наименьший вы-
вычет этого произведения) принадлежит показателю р — 1.
Это мы докажем следующим образом.
I. Если g— какое-нибудь из чисел 1, 2, 3,,,., р—1, не
удовлетворяющее сравнению ж(р—!)/<*== 1 (mod/?), которому не мо-
могут удовлетворять все эти числа, так как его степень меньше, чем
р — 1, то я утверждаю, что если через h обозначить (р — 1)/аа-ю
степень числа g, то h или его наименьший вычет принадлежит по-
показателю аа.
О числе решений сравнения х1 = (mod p) 59
Действительно, аа-я степень числа й, очевидно, есть (р — 1)-я
степень числа g, т. е. сравнима с единицей, в то время как аа~г-я
степень h есть (р—1)/а-я степень g, т. е. с единицей не сравнима;
аа~2-я, аа~3-я и другие степени h подавно не могут быть сравнимы
с единицей. Но показатель наименьшей сравнимой с единицей сте-
степени /г, т. е. показатель, которому принадлежит /г, должен (соглас-
(согласно п. 48) входить в число аа. Так как аа не долится ни на какие
числа, кроме самого себя и более низких степеней ау отсюда необ-
необходимо вытекает, что аа должно быть показателем, которому при-
принадлежит h. Аналогичным образом показывается, что существуют
числа> которые принадлежат показателям 6Р, с^, . .,
II. Если мы предположим, что произведение всех чисел Л, 2?,
С,... принадлежит не показателю р — 1, а меньшему показателю t,
то t будет входить в р—1 (п. 48), т. е. (р — l)/t будет целым чис-
числом, превосходящим единицу. Но легко видеть, что это частное
или равно одному из простых чисел а, 6, с, . . ., или по крайней
мере делится на одно из них (п. 17), пусть, например, на а, так
как для остальных доказательство остается тем же. Тогда t будет
входить в (р — 1)/а, и потому произведение ABC..., возведенное
в (р—1)/а-ю степень, будет тоже сравнимо с единицей (п. 46). Но
ясно, что отдельные числа В, С,... (кроме А), возведенные в
(р—1)/а-ю степень, будут сравнимые единицей, потому что показа-
показатели &Р, cY, . . ., которым эти отдельные числа принадлежат, входят
б (р — 1)/а. Поэтому
Отсюда следует, что показатель, которому принадлежит А1 дол-
должен быть делителем (р — 1)/а (п. 48), т. е. (р — 1)/аа+1 должно
р | Ь^ст
быть целым числом. Но -—^г" = ~~~ не может быть целым
{л. 15); поэтому мы должны сделать вывод, что наше предположе-
предположение не может быть верным, т. е. что произведение ABC. . . действи-
действительно принадлежит показателю р—1.
Последнее доказательство выглядит несколько длиннее первого,
однако, первое является менее прямым, чем второе.
60 Раздел III (пп. 56-58)
56
Эта теорема представляет яркий пример того, какая большая
осторожность часто бывает необходима в теории чисел для того, что-
чтобы не предположить доказанным то, что в действительности еще не
доказано. Ламберт в уже указанной выше работе упоминает об
этой теореме, но и не думает ничего говорить о необходимости ее
доказательства. Никто не пытался дать доказательства, кроме Э й л е-
р a: «Demonstrationes circa residua ex divisione potestatum per numeros.
primos resultantia», Comment, nov. Acad. Petrop., T. XVIII, 177 3r
p. 85 и ел. (см. в особенности параграф 37, где он подробнее распро-
распространяется о необходимости доказательства). Однако доказательство,
которое дает остроумный автор, страдает двумя недостатками. Один
состоит в том, что в параграфе 31 и далее автор молчаливо предпо-
предполагает, что сравнение хп = 1 (переводя употребляемые там способы
выражения на наши обозначения) действительно имеет п различных
корней, хотя до этого было доказано только, что оно может иметь
не больше чем п корней; второй недостаток тот, что формула и»
параграфа 34 выведена только по индукции.
Первообразные корни, основные числа, индексы
57
Числа, принадлежащие показателю р — 1, мы будем называть,
следуя Эйлеру, первообразными корнями. Таким образом, если а —
первообразный корень, то наименьшие вычеты всех степеней а, а2,
а3,..., av~'i будут различны между собой, откуда легко получается*
что среди них должны находиться все числа 1, 2, 3,..., р — 1, кото-
которых столько же, сколько и указанных наименьших вычетов, т. е.
что каждое не делящееся на р число сравнимо с некоторой степенью
числа а. Это замечательное свойство очень важно и может значи-
значительно облегчить арифметические операции, касающиеся сравне-
сравнений, приблизительно таким же образом, как введение логарифмов
облегчает операции обычной арифметики. Мы можем при желании
взять какой-нибудь первообразный корень в качестве основания или
основного числа и выражать через него все не делящиеся на р чис-
Алгоритм индексов 61
ла, причем, если ae=b (mod p), то мы будем называть е индексом
числа Ь, Если, например, для модуля 19 в качестве основания взят
первообразный корень 2, то числам
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, И, 12,
13, 14, 15, 16, 17, 18
буду* соответствовать индексы
0, 1, 13, 2, 16, 14, 6, 3, 8, 17, 12, 15,
5, 7, И, 4, 10, 9.
Впрочем, ясно, что если основание остается одним и тем же, то каж-
каждое число обладает многими индексами, но все они сравнимы между
собой по модулю р — 1. Поэтому, когда речь будет идти об индексах,
то те из них, которые сравнимы по модулю р — 1, будут рассматри-
рассматриваться как эквивалентные, подобно тому, как и сами числа, если
они сравнимы по модулю /?, считаются эквивалентными.
Алгоритм индексов
58
Теоремы, относящиеся к индексам, совершенно эквивалентны тем,
которые относятся к логарифмам.
Индекс произведения любого числа сомножителей сравним по мо-
модулю р — 1с суммой индексов отдельных сомножителей.
Индекс степени какого-нибудь числа сравним по модулю р — \ с
произведением индекса этого числа и показателя степени.
Доказательства, вследствие их легкости, мы опускаем.
Отсюда видно, что если желательно построить таблицу, из кото-
которой можно было бы находить индексы всех чисел для различных
модулей, то в ней можно опустить как все числа, которые больше
модуля, так и все составные числа. Пример такой таблицы дан в
конце этого труда (таблица 1)*. В ней в первом вертикальном ряду
* Таблица помещена на стр. 576.— Прим. ред.
62 Раздел III (пп. 59-60)
стоят простые числа и их степени от 3 до 97, рядом с каждым из них
стоят взятые за основания числа; затем идут индексы последовательных
простых чисел. Точно так же, в первой строке таблицы располо-
расположены простые числа, так что можно легко и надежно найти, какой
индекс соответствует заданному простому числу по заданному
модулю.
Если, например, р = 67 и за основание взято число 12, то ин-
индекс числа 60
= 2 ind 2 + ind 3 + ind 5 == 58 + 9 + 39 = 40 (mod 66).
59
Индекс каждого значения выражения г-(mod/?) (п. 31) сравним па
модулю р — 1с разностью индексов числителя а и знаменателя bi
если только числа а и b не делятся на р.
Именно, если с — какое-нибудь значение этого выражения, то
be == a (mod/?), и потому
ind b + indc= ind a (mod/? — 1),
откуда
ind с == ind a — ind b.
Таким образом, если имеется таблица, из которой можно нахо-
находить индекс, соответствующий любому числу по любому простому
модулю, и другая таблица, из которой можно получить число, при-
принадлежащее заданному индексу, то можно очень легко решать все
сравнения первой степени, так как все они сводятся к таким, у
которых модуль есть простое число (п. 30). Если, например, дано
7
сравнение 29х + 7 = 0 (mod 47), то ж ^-^g-(mod 47), и потому
ind х = ind (— 7) — ind B9) = ind 40 — ind 29 = 15 — 43 = 18 (mod 46).
Но индекс 18 принадлежит числу 3. Поэтому яеееЗ (mod 47).
Впрочем, вторую таблицу мы не приложили. Вместо нее нам
может служить другая таблица, как мы покажем в разделе VI.
О корнях сравнения хп = А 63
О корнях сравнения да" — Л
60
Аналогично тому, как в п. 31 мы обозначали корни сравнений
первой степени, мы в дальнейшем будем употреблять специальное
обозначение и для корней чистых сравнений более высокой степени»
Именно, подобно тому, как у~А обозначает не что иное как корень урав-
уравнения хп =АУ так и любой корень сравнения хп==А (modp) будет обозна-
обозначаться так же,но с добавлением модуля: \/A(modp).Мы будем говорить,
п
что это выражение у A (mod;?) обладает столькими значениями, сколько
оно имеет значений, не сравнимых по модулю р, так как все срав-
сравнимые по р значения следует рассматривать как эквивалентные
(п. 26). Кроме того, ясно, что если А и В сравнимы по модулю р,
то выражения "\/A(modp) и у В (mod p) будут между собой экви-
эквивалентны.
п
Если положить yA==x{modp), то п ind х == ind A (mod р — 1).
Из этого сравнения по правилам предыдущего раздела получаются
значения ind x, а из них,— соответствующие значения х. Легко ви-
видеть, что х обладает столькими же значениями, сколько корней име-
п —
ет сравнение п ind x ~ ind A (mod р — 1). Таким образом, у А имеет
только одно значение, если п взаимно просто с р — 1; если же
числа пир—1 имеют наибольший общий делитель 8, то ind x
имеет 8 значений, не сравнимых по модулю р—1, а потому и у А
имеет столько же значений, не сравнимых по модулю /?, если
только ind А делится на 8. Если же это условие не выполнено, то
у А не будет иметь вещественных значений.
Пример. Пусть нужно найти значения выражения ]/TT(modl9).
Для этого нужно решить сравнение 15 ind x == ind 11 = 6 (mod 18),
откуда находятся три значения ind#==4, 10, 16 (mod 18). Им со-
соответствуют значения я ==6, 9, 4 (mod 19).
64 Раздел III (пп. 61-6
61
Как ни прост этот метод, когда под рукой есть нужные табли-
таблицы, все же не следует забывать, что он является косвенным.
Поэтому имеет смысл потратить усилия на то, чтобы иссле-
исследовать, насколько сильны прямые методы, причем мы приве-
приведем здесь то, что может быть выведено из предыдущего, осталь-
остальное же, что требует более глубоких рассмотрений, оставим до раз-
раздела VIII.
Начнем с простейшего случая, когда .4 = 1, т. е, когда ищут-
ищутся корни сравнения хп == 1 (modp). Таким образом, если за Основа-
Основание взять произвольный первообразный корень, то здесь должно
быть п ind х == 0 (mod р—1). Если п взаимно просто с р— 1, то это
сравнение будет иметь один единственный корень, именно, ind#==
п
= 0(modjD — 1), и потому в этом случае у 1 (mod/?) имеет единст-
единственное значение, именно, ==1. Если же числа пир — 1 имеют
(наибольший) общий делитель 8, то полным решением сравнения
гс ind ж = 0 (mod р—1) будет ind х == 0 [mod —г—) (п. 29), т, е. ind ж
должен будет быть сравнимым по модулю р — 1 с каким-нибудь
из чисел
или, другими словами, обладать 8 значениями, не сравнимыми по
модулю р — 1; поэтому в этом случае х также имеет 8 различ-
различных (несравнимых по модулю р) значений. Отсюда явствует, что
ь
выражение у 1 тоже имеет 8 различных значений, индексы кото-
которых в точности совпадают с указанными перед этим числами.
Поэтому выражение ]/Т (mod/?) совершенно эквивалентно выражению
п
yi (mod р), т. е. сравнение хъ = 1 (mod p) имеет те же корни, что и
хп == 1 (mod p). Однако первое имеет более низкую степень, чем
второе, если только 8 ил не равны между собой.
О корнях сравнения хп = А 65
Пример. )/~1 (mod 19) имеет три значения, потому что 3 есть наи-
наибольший общий делитель чисел 15 и 18, и эти значения одновре-
з _
менно являются значениями j/~l (mod 19). Последние же суть 1,
7, И.
62
Итак, благодаря этой редукции мы получаем то преимущество,
что нам не надо решать никаких других сравнений вида жпе=1,
кроме тех, у которых п является делителем р— 1. Ниже мы пока-
покажем, что сравнения этого вида всегда могут быть еще упрощены,
однако пока изложенного материала для этого недостаточно. Сей-
Сейчас мы можем закончить только один случай, именно, тот, когда
п = 2. В самом деле, очевидно, что -\-1 и —1 дают все значения
выражения }/"l, так как больше двух значений оно иметь не может, а
+ 1 и — 1 всегда несравнимы между собой, кроме случая, когда
модуль равен 2; в этом случае непосредственно ясно, что ]/1
может иметь только одно значение. Из этого следует, что -|-1 и
2т
—1 будут также значениями выражения У\ , в случае, когда т
взаимно просто с (р—1)/2. Это всегда имеет место, если модуль
таков, что (р —1)/2 является простым числом (если при этом в точ-
точности р — i = 2m, то все числа 1, 2, 3,..., р — 1 являются кор-
корнями), например, если р = 3, 5, 7, 11, 23, 47, 59, 83, 107,...
В качестве сле/^ствия здесь можно было бы добавить, что индекс
числа —1 всегда == р~ (mod р — 1), какой бы первообразный ко-
корень мъ1 ни взяли. Действительно, 2 ind (— 1) = 0 (mod p — 1); по-
поэтому ind (— 1) или == 0, или == р 2 (mod р — 1). Но 0 всегда являет-
является индексом числа +1> а +1 и —1 всегда должны иметь раз-
различные индексы (кроме случая р = 2, который мы здесь исключаем).
63
п
В п. 60 мы показали, что выражение у A (mod p) имеет или
8 различных значений, где 8 есть наибольший общий делитель
66 Раздел III (пп. 6^-65)
чисел п и р — 1, или ни одного значения. Подобно тому, как выше
мы доказали, что У А и У А эквиваленты, если А~19 так сейчас
п
мы докажем более общий факт, что выражение У А всегда может
быть сведено к выражению вида У В, с которым оно эквивалентно.
Именно, обозначим какое-нибудь значение нашего выражения че-
через х, так что хп^=А. Если теперь ? —какое-нибудь значение вы-
ражения — (mod р — 1), которое, как явствует из п. 31, обладает
вещественными значениями, то xnt = А1. Но xnt =хъ вследствие то-
того, что tn==b (mod p — 1). Отсюда хъ = А\ и потому любое значе-
п Ъ
ние У А будет также значением У А1. Таким образом, если выра-
жение У А имеет вещественные значения, то оно совершенно экви-
эквивалентно выражению У~А1, ибо последнее не имеет других значений
п
и имеет все значения первого, хотя может случиться, что если У А
5
не имеет вещественных значений, У~А1 все же ими обладает.
21 _
Пример. Если отыскиваются значения выражения У2 (mod 31), то
наибольший общий делитель чисел 21 и 30 равен 3, и одно из зна-
3
чений выражения ^т (mod 30) тоже равно 3. Поэтому, если выраже-
21 _
ние У2 обладает вещественными значениями, то оно будет эквива-
з з
лентно выражению ]/23 или ]/8, и действительно, оказывается, что
значения второго выражения, именно 2, 10, 19, удовлетворяют
также и первому.
64
Для того чтобы избежать опасности, что мы будем применять
эту операцию понапрасну, мы должны получить правило, при по-
помощи которого можно сразу узнавать, допускает У А вещественные
О корнях сравнения хп = А 67
значения или нет. Если имеется таблица индексов, то вопрос ясен;
действительно, из п. 60 вытекает, что вещественные значения су-
существуют или нет в зависимости от того, делится или нет на 8 ин-
индекс числа А относительно какого-нибудь взятого за основание
первообразного корня. Однако это можно узнать и без помощи та-
такой таблицы. Именно, если индекс числа А равен к, то рсли он
делится на 6, к(р—1)/8 будет делиться на р — 1, и обратно. Да-
Далее, индекс числа ^(p-D/5 равен к(р—1)/8. Поэтому, если у~А (mod p)
имеет вещественные значения, то .4(p-D/5 будет сравнимо с
единицей, в противном же случае — нет. Так, в примере предыду-
предыдущего пункта 210 = 1024=1 (mod31), откуда следует, что J/lT(mod31)
имеет вещественные значения. Таким же образом мы убеж-
убеждаемся отсюда, что У— 1 (mod p) всегда имеет два вещественных
значения, если р имеет вид 4/72 + 1, и ни одного значения, если
р имеет вид Am + 3, потому что (— 1JТП =1 и (— lJw+i = — 1. Эта
изящная теорема, которая обычно высказывается в следующей фор-
форме: если р — простое число вида Ат-\-\, то всегда можно найти
квадрат целого числа а2 с тем свойством, что а2 -f- 1 будет делить-
делиться на р; если же р — простое число вида Am — 1, то такого квадра-
квадрата не существует,—была таким же способом доказана Эйлером,
в «Сотт. nov. Acad. Petrop.», Т. XVIII, 1773, p. 112. Другое до-
доказательство он дал еще намного раньше, в «Сотт, nov». Т. V,
р. 5, вышедшем в 1760 г. В более раннем сочинении, в «Сотт.
nov.», Т. IV, р. 25, он еще не пришел к доказательству. Позднее
также и Лагранж дал в «Nouveaux Mem. de Г Ac. de Berlin», A.
1775, р. 342. новое доказательство теоремы. Еще одно доказатель-
доказательство мы дадим в следующем разделе, который будет специально по-
посвящен этому предмету.
65
п
После того, как мы научились все выражения У A (mod p) сво-
сводить к таким, у которых п есть делитель числа р—1, и одновре-
одновременно получили критерий для того, чтобы узнавать, обладают они
68 Раздел III (пп. 66-67)
вещественными значениями или нет, мы рассмотрим теперь такие
п
выражения уА (mod р),у которых п есть делитель р—1, несколь-
несколько подробнее. Сначала мы покажем, в какой связи находятся меж-
между собой отдельные значения выражения, а затем укажем некоторые
специальные приемы, при помощи которых очень часто можно
лайти одно значение выражения.
Во-первых, если i=l и г — какое-нибудь одно из значений вы-
п
ражения yl (mod;?), т. е. гп == 1 (mod;?), то и все степени г будут
значениями этого выражения; а среди них различных между собой
будет столько, сколько единиц содержит показатель, которому при-
принадлежит г (п. 48). Поэтому, §сли г есть значение, принадлежащее
показателю п, то степени г, г2, г3, ..., гп (где вместо последней мож-
можно также взять единицу) будут охватывать все значения выраже-
п
ния у1 (mod;?). Вопрос же о том, какие существуют вспомогатель-
вспомогательные сред тва для отыскания таких значений, которые принадле-
принадлежат показателю п, мы более подробно рассмотрим в разделе VIII.
Во-вторых, если А несравнимо с единицей, и одно значение
п
выражения у А (то&р), которое мы обозначим через z, известно,
то остальные значения можно искать следующим образом Если
(как мы показали выше)
A r r2 rn—l
П
суть все значения выражения у 1, то
7 7Г 7Г2 71—1
п
будут всеми значениями выражения у А. Действительно, то, что
все эти значения удовлетворяют сравнению хп~А, вытекает из то-
того, что если лзять какое-нибудь из них, скажем = zrk, то его п-я
степень, именно znrnke вследствие того, что гп = 1 и zn = А, будет
сравнима с i, а то, что все эти значения различны, легко следу-
следует из п. 23. Других же значений, кроме этих, число которых рав-
О корнях сравнения хп = А
/—
но /2, выражение у А иметь не может. Так, например, если одно из
значений выражения У~А равно z, то другое будет равно —z. Ha-
п —
конец, мы должны сделать вывод, что все значения выражения у А
найти нельзя, если одновременно не известны все значения выра-
п
жения У1 .
66
Вторая задача, которую мы себе поставили, заключалась в томг
чтобы показать, в каком случае может быть непосредственно най-
п
дено одно значение выражения у A (mod p) (где п предполагается
делителем р — 1). Это тот случай, когда какое-нибудь значение срав-
сравнимо с какой-нибудь степенью А, и так как этот случай встречает-
встречается нередко, будет не лишним немного на нем задержаться. Пусть
одно из таких значений, если они вообще существуют, есть z, так что
z == Ак и А == zn (modp). Отсюда следует А = Акп. Поэтому, если
имеется число к с тем свойством, что А == Акп, то Ак будет иско-
искомым значением. А это условие эквивалентно тому, что 1 = кп (mod t),
где t обозначает показатель, которому принадлежит А (пп. 46, 48).
Для того, чтобы это сравнение было возможно, необходимо, чтобы
п было взаимно просто с t. В этом случае &=— (mod ?); если же
t и п имеют общий делитель, то ни одно значение z не может быть
сравнимо со степенью числа А.
67
Так как, однако, для такого решения нужно знать само t, мы
посмотрим, как можно поступать, когда это число не известно. Прежде
всего, очевидно, что t должно входить в (р — 1)/п, если только
п
у A (mod p) имеет вещественные значения, что мы здесь все время
предполагаем. Действительно, если какое-нибудь значение этого
выражения равно г/, то как г/Р—1^1. так и уп = A (mod/?). Если
70 Раздел III (п. 68)
возвести обе части последнего сравнения в (р—1)/п-ю степень, то
получится А^~1)/п == 1, и потому (р—1)/п должно делиться на t
(п. 48). Если теперь (р — 1)/п взаимно просто с п, то сравнение из пре-
предыдущего пункта, а именно, &7г = 1, разрешимо также и по модулю
(р — 1)/гс, и удовлетворяющее сравнению по этому модулю значение
к будет, очевидно, удовлетворять тому же сравнению и по модулю t,
который входит в (р — 1)/п (п. 5). В этом случае цель достигнута.
Если же (р—1)/п не взаимно просто с п, то выбросим из (р—1)/п
все простые сомножители, которые одновременно входят в п. Тогда
мы получим взаимно простое с п число (р—l)/nq, где q обозначает
произведение всех тех простых сомножителей, которые мы выброси-
выбросили. Если теперь условие, к которому мы пришли в предыдущем пунк-
пункте, а именно, что t взаимно просто с п, выполняется, то t будет так-
также взаимно просто eg и потому будет входить и в (р — l)/nq. Поэто-
Поэтому, если решить сравнение кп = 1 (mod p~~ ] (что возможно, так
как п взаимно просто с (р — l)/nq), то значение к будет удовлетво-
удовлетворять также и сравнению по модулю t, что и требовалось. В целом
этот прием состоит в том, чтобы найти число, которым можно за-
заменить неизвестное нам числом. Однако нужно иметь ввиду, что в слу-
случае, когда (р — 1)/7г не взаимно просто с 72, мы предполагали, что выпол-
выполнено условие из предыдущего пункта. Если же это условие не выполне-
выполнено, то все выводы теряют силу; и если при невнимательном следо-
следовании указанным правилам мы найдем значение z, п-я степень ко-
которого несравнима с числом А, то это будет указывать на то, что
условие не выполнено и потому этот метод вообще нельзя применять.
68
Однако и в этом случае потраченные усилия часто бывают по-
полезны, и имеет смысл исследовать, как это неверное значение от-
относится к правильному. Предположим, что к, z определены соглас-
согласно правилам, но что zn не сравнимо с А по модулю р. Если толь-
только мы можем определить значения выражения УА/z71 (modp), то
п
умножая каждое из них на 2, мы получим значения у А. Действи-
О корнях сравнения хп = А 71
тсльно, если v — какое-нибудь значение ~\/~ A/zn, то (vz)n==A. Но
п п
выражение у А/гп проще, чем У А, постольку поскольку
— (mod p) по большей части принадлежит меньшему показателю,
чем А. Именно, если d есть наибольший общий делитель t и q, от
^ (mod р) будет принадлежать показателю d, что доказывается еле-
Z
дующим образом. Если вместо z подставить его значение, мы полу-
получим — ^—^^ (mod р). Но кп—1 делится на (р—l)/nq (согласно
предыдущему пункту), а (р — 1)/п — на t (там же), откуда (р — l)/nd
делится на t/d. Далее, t/d взаимно просто с q/d (по условию), и по-
потому также (р — l)/nd делится на tq/d2, или (р — i)/nq — на t/d, и,
таким образом, кп—1 делится на t/d и (кп — l)d — на t. Из этого
следует, что А(кп~~Vd = 1 (mod /?), откуда легко вывести, что A/zn.
возведенное в с?-ю степень, сравнимо с единицей. А то, что A/zn не
может принадлежать показателю, меньшему, чем d, хотя и может
быть легко доказано, но мы на этом останавливаться не будем,
так как для нашей дели это не требуется. Таким образом, мы за-
заведомо установили, что A/zn (mod p) всегда принадлежит меньшему
показателю, чем Л, за исключением того единственного случая, ког-
когда t входит в q, и потому d = t.
Однако, какая польза в том, что A/zn принадлежит меньшему
показателю, чем А? Чисел, которые могут выступать в роли А,
больше, чем чисел, которые могут выступать в роли A/zn, и если
мы должны получить выражения вида У А по одному и тому же
модулю, то теперь мы имеем то преимущество, что многие из них
можно вывести из одного и того же источника.
Так, например, мы всегда будем в состоянии определить хотя
бы одно значение выражения У~А (mod 29), если только известны
значения ]/¦—1 (mod 29) (которые суть +12). Действительно, из
предыдущего пункта явствует, что значение подобного выражения
всегда можно найти непосредственно, если t нечетно, и что d = 2,
72 Раздел III (пп. 69-70)
если t четно; но показателю 2 не принадлежат никакие числаг
кроме —1.
з
Примеры. Найдем значения ]/31 (mod 37). Здесь р—1 = 36, п = Зг
р~ = 12, и потому q = 3. Поэтому должно бьиъ ЗА=:1 (mod 4)?
и это имеет место, если положить к = 3. Отсюда z = 313 = 6 (mod 37),
и, действительно, мы находим, что б3 = 31 (mod 37). Если значения
з _ з
выражения ]/Ч (mod 37) известны, то и остальные значения j/
з _
могут быть определены. Но значения Vl суть 1, 10, 26, и, умно-
умножая их на 6, мы и получим остальные значения =23 и 8.
Если же отыскивается значение выражения }^3 (mod 37), то здесь
р~~ = 18, и потому q = 2. Поэтому должно быть 2k= I (mod9),
откуда к = 5 (mod9). Следовательно, z== Зб = 21 (mod37). Но
не сравнимо с 3, а сравнимо с 34. Однако о/ = —1 (mod 37) и
Y—1 = + 6 (mod 37). Отсюда получаются верные значения +6*21=
= +15.
Вот примерно то, что мы можем здесь сообщить относительно
отыскания таких выражений. Известно, что прямые методы часто
оказываются довольно длинными, однако этот недостаток присущ
не всем прямым методам теории чи ел, и потому мы не могли
удержаться от того, чтобы не показать, как много они могут
здесь дать. Следует также заметить и то, что в нашу задачу не
входит подробнее развивать специальные приемы, которые нередко
может найти опытный вычислитель.
Связь между индексами в различных системах
69
Мы возвращаемся теперь к корням, которые назвали первооб-
первообразными. Мы покажем, что если за основание взят любой перво-
первообразный корень, то все числа, индексы которых взаимно просты
с р — 1, также являются первообразными корнями, и что, кроме
Индексы в различных системах 73
них, других первообразных корней нет, так что тем самым одно-
одновременно становится известным количество всех первообразных
корней (см. п. 53). Какой первообразный корень мы берем за
основание, вообще говоря, зависит от нашого желания, откуда
видно, что здесь, как и в логарифмическом исчислении, возможны
различные системы *; мы рассмотрим, каким образом они между
собой связаны. Пусть а и Ъ — два первообразных корня, и т—ка-
т—какое-нибудь другое число, и пусть, если за основание взято а,
то у числа Ъ индекс = Р, а у числа т индекс = [х (mod р—1);
если же за основание взято Ь, то пусть у а индекс =а, аут
индекс = v(mod/?— 1). Тогда 0^8 = 1 (mod/?—1). Действительно,
по предположению, а^ = &, и потому аа|3 = 6а = а (mod /?), откуда
a$ = l(modp—1). Аналогичным рассуждением находим, 4tov = oc[a
и [x = Cv (то&р—1). Поэтому, если имеется таблица индексов,
составленная для основания а, она легко может быть превращена
в другую, основание которой есть Ъ. Действительно, если для
основания а индекс числа Ь сравним с C, то для основания Ъ индекс
числа а сравним с -г-(mod/? — 1), и если на это число умножить
все индексы таблицы, то мы получим все индексы для основания Ь.
70
Хотя заданное число может получать различные индексы, если
за основание брать все новые и новые первообразные корни, у этих
индексов все же будет то общее, что все они имеют с р—1 один
и тот же наибольший общий делитель. Действительно, если индекс
заданного числа для основания а есть т, а для основания Ъ есть п7
и мы предположим, что наибольшие общие делители [х, v этих
индексов с р—1 не равны между собой, то один из них будет
больше другого, например, (х > v, и потому [х не будет входить
в v. Но если обозначить через а индекс числа а, когда за осно-
основание взято 6, то, согласно предыдущему пункту, n = am(modp—1),
* Разница состоит только в том, что в случае логарифмов количество воз-
возможных систем бесконечно велико, в нашем же случае оно лишь равно числу
первообразных корней. В самом деле, сравнимые между собой основания, оче-
очевидно, порождают одинаковые системы.
74 Раздел III (пп. 71-72)
и потому [х также будет входить в п, что противоречит нашему
предположению.
То, что этот наибольший общий делитель индекса заданного
числа и числа р — 1 не зависит от основания, вытекает также и
из того, что он равен (р—1)Д, где t обозначает показатель, кото-
которому принадлежит число, об индексе которого идет речь. Действи-
Действительно, если индекс для некоторого произвольного основания
равен А, то t есть наименьшее число (не считая нуля) такого рода,
что произведение к и t будет кратностью р — 1 (ср. пп. 48 и 58),
т. е. есть наименьшее, за исключением нуля, значение выраже-
выражения -г(тоАр — 1); а то, что оно равно наибольшему общему дели-
/с
телю чисел к и р — 1, без труда вытекает из п. 28.
71
Далее, легко доказать, что основание всегда можно выбрать
так, что принадлежащее показателю t число получит любое задан-
заданное значение индекса, лишь бы его наибольший общий делитель
с р — 1 был равен (р—l)/t. Если этот наибольший общий дели-
делитель мы для краткости обозначим через с?, если, далее, заданный
индекс =dm, а индекс заданного числа, когда за основание взят
какой-то первообразный корень a, =dn, то т и п будут взаимно
просты с р~~ и с t. Если тогда е есть значение выражения
т— (modp—1), которое взаимно просто с р—1, то az будет перво-
первообразным корнем, и если его взять за основание, то заданное
число получит требуемый индекс dm (действительно, aEdm = adn =
с заданным числом). А то, что выражение -.— (mod/? — 1) обладает
значением, взаимно простым с р—1, может быть доказано сле-
следующим образом. Согласно пп. 31, 32 это выражение эквивалентно
следующему: — fmod^~ ) или — (mod?), — а все значения этого
последнего взаимно просты с t] действительно, если бы какое-ни-
какое-нибудь значение е имело с t общий делитель, то этот делитель
должен был бы входить и в те, а потому также и в число п,
которое сравнимо с те по модулю t. Но это противоречит предпо-
Основные числа 75
ложению, что т взаимно просто с t. Таким образом, если все
простые делители числа р—1 входят также и в t, то все значе-
значения выражения — (mod t) будут взаимно просты с р — 1 и число их
будет равно d. Если же р — 1 содержит еще и другие простые
делители /, g, h, . .., которые в t не входят, то пусть — (mocU) = e—
какое-нибудь значение выражения — (mocU). Тогда, так как чис-
числа t, /, g, /г, . . . попарно взаимно просты, можно найти такое
число s, которое по модулю t сравнимо с числом е, а по моду-
модулям /, g, /г, . . . — с любыми взаимно простыми с этими модулями
числами (п. 32). Такое число не будет тогда делиться ни на один
простой сомножитель числа р — 1, т. е. будет взаимно просто
с р—1, что и требовалось. Наконец, из комбинаторных сообра-
соображений без труда получается, что число таких значений равно
jp — lf—lg—ih — l ~ r
• —— • • —т— .... Однако, чтобы этот экскурс не слиш-
слишком затянулся, мы доказательство опустим, ибо для нашей дели
оно не является столь уж необходимым.
Основные числа, служащие специальным целям
72
Хотя, вообще говоря, совершенно безразлично, какой перво-
первообразный корень берется за основание, все же иногда одни основ-
основные числа могут иметь преимущества перед другими. В таблице 1
мы всегда брали за основание число 10, если только оно было
первообразным корнем; в остальных случаях мы всегда определя-
определяли основание так, чтобы индекс числа 10 был наименьшим из
возможных, т. е. чтобы он был равен (р—1)/?, где t обозначает
показатель, которому принадлежит 10. Какое преимущество мы
благодаря этому имеем, мы покажем в разделе VI, где эта табли-
таблица будет снова использована для другой цели. Так как, однако,
и здесь еще может остаться некоторый произвол, то мы, для опре-
определенности, из всех удовлетворяющих указанному выше условию
первообразных корней всегда выбирали за основание наименьший.
76 Раздел III (п. 73)
Так, например, для р = 73, когда t = 8 и d = 9, az имеет -g-y = б
значений, а именно, значения 5, 14, 20, 28, 39, 40. Мы взяли за
основание наименьшее из них — число 5.
Метод отыскания первообразных корней
73
Методы отыскания первообразных корней большей частью сво-
сводятся к пробам. Если то, что мы изложили в п. 55, сопоставить с
тем, что будет сказано ниже относительно решения сравнениях71 ={у
то это и будет почти все, что можно получить прямыми методами.
Эйлер в «Opusc. Analyt.», Т. /, р. 152, признает, что ему представ-
представляется исключительно трудным находить такие числа, и что их истин-
истинная сущность должна быть причислена к наиболее глубоким секре-
секретам чисел. Однако посредством проб они довольно легко определя-
определяются следующим образом. (Имеющий навык будет знать, что про-
продолжительность выкладок может быть сокращена многочисленными
специальными приемами; однако научиться этому можно гораздо
быстрее на практике, чем следуя теоретическим предписаниям.)
1. Берем любое взаимно простое с р (так все время будет обозна-
обозначаться модуль) число а (в большинстве случаев ради сокращения
вычислений хорошо брать его по возможности маленьким, например,
брать число 2) и определяем его период (п. 46), для чего находим
наименьшие вычеты его степеней, до тех пор, пока не дойдем до не-
некоторой степени а\ наименьший вычет которой равен 1 *. Если
t = р — 1, то а есть первообразный корень.
2. Если же ?<р — 1, то берем другое число Ь, которое не содер-
содержится в периоде числа а, и ищем подобным же образом его период.
Если показатель, которому принадлежит Ь, обозначить через и, то
легко убедиться, что и не может быть ни равным t, ни делителем t;
действительно, в обоих случаях было бы Ь*=1, что невозможно,
так как период числа а охватывает все числа, t-я степень которых
* Разумеется, нам не обязательно знать сами эти степени, так как наимень-
наименьший вычет каждой из них легко может быть получен из наименьшего вычета
предыдущей степени.
Отыскание первообразных корней 77
сравнима с единицей (п. 53). Если и= р — 1, то Ъ будет первообраз-
первообразным корнем; если же и хотя и не равно р — 1, но является кратно-
кратностью ?, то мы имеем уже, следовательно, число, принадлежащее
большему показателю, и потому оказываемся ближе к нашей цели,
состоящей в отыскании числа, принадлежащего наибольшему по-
показателю. А если и и не равно р — 1 и не кратно t, то мы
все же можем найти число, которое принадлежит показателю, боль-
большему, чем t и и, а именно, показателю, равному наименьшему обще-
общему кратному чисел t и и. Если этот показатель равен г/, то разложим
у на два взаимно простых сомножителя т и п, причем так, что один
из них входит в ?, а другой входит в и *. Если тогда at/m=A, &u/n=
=5(mod /?), то произведение АВ будет числом, принадлежащим по-
показателю у. Действительно, легко убедиться, что А принадлежит
показателю т, а В — показателю щ поэтому произведение АВ при-
принадлежит показателю тп, ибо тип взаимно просты, что можно до-
доказать совершенно тем же способом, которым в п. 55 доказывается
предложение И.
3. Если теперь у = р — 1, то АВ будет первообразным корнем.
Если же это не так, то нужно, аналогично тому, как раньше, взять
другое число, не содержащееся в периоде числа АВ. Оно или будет
первообразным корнем, или будет принадлежать показателю, кото-
который больше, чем у, или по крайней мере при помощи него можно
будет найти (как и перед этим) число, принадлежащее показателю,
большему, чем у. Так как числа, которые получаются при повтор-
повторном произведении этой операции, принадлежат ко все большим и
большим показателям, ясно, что в конце концов будет найдено чис-
число, принадлежащее наибольшему показателю, т. е. первообразный
корень.
* То, как именно это можно сделать, легко получается из п. 18. Разложим
у на такие сомножители, которые являются либо различными простыми числами,
либо степенями различных простых чисел. Каждый из этих сомножителей вхо-
входит в одно из чисел 1и и (а может быть и в оба). Напишем каждый из сомножителей
либо рядом с числом t, либо рядом с числом и в зависимости от того, в какое из
них он входит. Если же он входит в оба эти числа, то безразлично, рядом с ко-
которым из них его писать. Если произведение сомножителей, которые написаны
рядом с t, равно т, а второе произведение равно п, то легко видеть, что т вхо-
входит в t, а п — в и, и что тп = у.
78 Раздел III (пп. 74~76)
74
При разборе примера эти предписания станут более ясными.
Пусть число, для которого нужно найти первообразный корень, есть»
р = 73. Испробуем сначала число 2, период которого оказывается,
следующим:
1, 2, 4, 8, 16, 32, 64, 55, 37, 1, . . .
О, 1, 2, 3, 4, 5, 6, 7, 8, 9,. . .
Так как уже степень с показателем 9 сравнима с единицей, число-
2 не является первообразным корнем. Рассмотрим поэтому какое-
нибудь другое число, не содержащееся в периоде числа 2, напри-
например, 3, период которого есть
1, 3, 9, 27? 8, 24, 72, 70, 64, 46, 65, 49, 1, ...
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...
Поэтому 3 также не является первообразным корнем. Наименьшее
общее кратное чисел 9 и 12, являющихся показателями, которым
принадлежат 2 и 3, есть 36, и будучи разложенным в соответствии с
предписанием предыдущего пункта, оно дает сомножители 9 и 4.
Умножим теперь 2 на третью степень числа 3. Произведение, равное
54, будет принадлежать показателю 36. Если, наконец, вычислить
период числа 54 и снова испытать какое-нибудь не содержащееся
в нем число, например, 5, то оно окажется первообразным корнем.
Различные теоремы
о периодах и первообразных корнях
75
Прежде чем оставить этот предмет, мы хотим добавить еще
некоторые теоремы, которые представляются достойными внимания
вследствие своей простоты.
Произведение всех членов периода любого числа =-fl, если,
количество их, т. е. показатель, которому это число принадлежит^
нечетно, и = — 1, если этот показатель четен.
Теоремы о периодах и первообразных корнях 79
Пример. Для модуля 13 период числа 5 состоит из членов 1,
5, 12, 8, для произведения которых имеет место 480 = — 1 (mod 13).
Период числа 3 по этому же самому модулю состоит из чле-
членов 1, 3, 9, и их произведение 27 = 1 (mod 13).
Доказательство. Если показатель, которому принадлежит число,
равен t, а индекс самого числа есть (р— 1)Д, чего, согласно п. 71,
всегда можно добиться посредством выбора соответствующего осно-
основания, то индекс произведения всех членов периода
= A + 2 + 3 + ... + * — 1) EzJ = (*-l)te-l) ^
t z
т. е. =0(mod/? — 1), если t нечетно, и =(р —1)/2, если t четно.
Поэтому в первом случае это произведение ^е 1 (mod/?), а во вто-
втором = — l(modp) (п. 62).
76
Если в предыдущей теореме число является первообразным
корнем, то его период охватывает все числа 1, 2, 3,..., р— 1,
произведение которых тем самым всегда = — 1 (действительно.
р — 1 всегда четно, за исключением одного случая р = 2, когда
—1 и +1 эквивалентны).
Эта изящная теорема, которая обычно высказывается так: про-
произведение всех чисел, меньших заданного простого числа, увеличенное
на единицу, делится на это простое число, была впервые опубли-
опубликована Варингом и приписана им Вильсону («Meditationes-
algebraicae», ed. 3, p. 380). Однако ни тот, ни другой не могли
ее доказать, и Варинг считал, что доказательство является тем
более трудным, что нельзя себе представить, чтобы было такое
обозначение, которое задавало бы простое число. По нашему мне-
мнению, однако, подобные истины следует черпать не из обозначений,
а из понятий.
Позже доказательство дал Лагранж («Nouv. Mem. de ГАса-
demie de Berlin», 1771). Оно основывается на рассмотрении коэф-
коэффициентов, которые получаются при раскрытии скобок в произ-
произведении
(Х + 1) (х + 2) (х + 3). . . (х + р - 1).
80 Раздел III (пп. 77-8
Именно, если записать это произведение в виде
xv~x + Axv~2 4- Bxv~3 + . .. + Mx + N,
то коэффициенты А, В, . . ., М будут делиться на р, в то время
как N = 1-2-3 . . .(р — 1). Но при х = 1 произведение делится на р;
с другой стороны, оно = 1 + N (mod/?), и потому 1+ N обязатель-
обязательно должно делиться на р.
Наконец, Эйлер в «Opusc. Analyt.», Т. 1, р. 329 дал дока-
доказательство, которое совпадает с приведенным нами. Так как такие
люди не считали эту теорему недостойной своих размышлений,
мы надеемся не вызвать порицания за то, что приведем еще одно
ее доказательство.
77
Если произведение двух чисел а и Ъ сравнимо по модулю р с
.единицей, то, следуя Эйлеру, мы будем называть эти числа а и Ъ
ассоциированными. Тогда, согласно предыдущему разделу, каждое
положительное число, меньшее р, имеет среди положительных и
меньших р чисел одно и только одно ассоциированное. Но легко
доказать, что среди чисел 1,2,3,... только 1 л р—1 ассоцииро-
ассоциированы сами с собой. Действительно, ассоциированные сами с собой
числа являются корнями сравнения х2 = 1, которое имеет вторую
степень и потому не может иметь более двух корней, т. е. не имеет
других корней, кроме 1 и р — 1. Поэтому, если эти два числа
отбросить, то остальные числа 2,3,...,/? — 2 будут попарно ассо-
ассоциированы и потому их произведение =1. Таким образом, про-
произведение всех чисел, именно 1-2-3. . . (р — 1) = р — 1 или = — 1.
Например, по модулю 13 среди чисел 2, 3, 4, . . ., 11 ассоцииро-
ассоциированными одно с другим будут следующие: 2 и 7, 3 и 9, 4 и 10,
5 и 8, 6 и 11; действительно, 2-7 = 1, 3-9 = 1 и т. д. Поэтому
2-3-4. ..11 = 1, откуда 1-2-3 ... 12 = — 1.
78
В более общем виде теорему Вильсона можно высказать так.
Произведение всех чисел, которые меньше некоторого заданного
Теоремы о периодах и первообразных корнях 81
числа А и одновременно взаимно просты с ним, сравнимо по моду-
модулю А с единицей, взятой с положительным или с отрицательным
знаком. С отрицательным знаком единица получается, когда А
имеет вид рт или 2рт, где р обозначает отличное от 2 простое
число, и, кроме того, при А = 4Г во всех же остальных случаях
получается положительная единица. Теорема, высказанная Виль-
Вильсоном, содержится в первом случае. Например, для А = 15 про-
произведение чисел 1, 2, 4, 7, 8, 11, 13, 14 сравнимо с 1 по модулю 15.
Доказательство мы ради краткости не приводим; заметим только,
что оно может быть проведено подобным же образом, как в пре-
предыдущем пункте, с той только разницей, что сравнение х2^!
может иметь и более двух корней, которые требуют некоторых
специальных рассмотрений. Можно было бы также вывести дока-
доказательство из рассмотрения индексов, подобно п. 75, если принять
во внимание то, что сейчас будет сказано о составных модулях.
79
Теперь мы возвращаемся к перечислению остальных теорем
(п. 75).
Сумма всех членов периода любого числа =0. Так, в примере
из п. 75 будем иметь 1 + 5 + 12 + 8 = 26 = 0 (mod 13).
Доказательство. Если число, о периоде которого идет речь,
равно а, и показатель, которому оно принадлежит, равен t, то
сумма всех членов периода
==1 + а + аа + а8 + ...+ аи = ^ (mod p).
Но а1 — 1=0; следовательно, эта сумма =0 (п. 22), если только
а — 1 не делится на р, т. е. а несравнимо с 1. Этот случай мы
должны, таким образом, исключить, если мы хотим называть
периодом также и один единственный член.
80
Произведение всех первообразных корней =1, если исключить
случай р = 3, когда имеется только один первообразный корень 2.
82 Раздел III (п. 81)
Доказательство. Если любой первообразный корень взят за
основание, то индексами всех других первообразных корней будут
числа, которые взаимно просты с р — 1 и одновременно меньше
р—1. Но сумма этих чисел, т. е. индекс произведения всех пер-
первообразных корней = 0(modjD— 1), и потому само произведение
= 1 (mod/?); действительно, легко видеть, что если к есть число,
взаимно простое с р — 1, то и р — 1—к будет взаимно проста
с р — 1, и каждые два таких взаимно простых с р — 1 чис-
числа образуют сумму, которая делится на р — 1 (к никогда не
может быть равно р — 1 — А, кроме случая р — 1=2 или р = 3,
который мы исключили; в самом деле, во всех остальных случаях
(р — 1)/2, очевидно, не взаимно просто с р — 1).
81
Сумма всех первообразных корней или = 0 (когда р — 1 делится
на какой-нибудь квадрат), или = + 1 (mod/?) {когда р — 1 есть про-
произведение различных простых чисел] при этом следует брать поло-
положительный или отрицательный знак в зависимости от того, четно
или нечетно число этих простых чисел).
Пример. 1) Для р — 13 мы имеем первообразные корни 2, 6, 7у
11, сумма которых 26 = 0(mod/?); 2) для р = 11 первообразные
корни суть 2, 6, 7, 8? и сумма их 23 = -f- 1 (mod 11); 3) для р = 31
первообразные корни суть 3, 11, 12, 13, 17, 21, 22, 24, и сумма
их 123= —1 (mod 31).
Доказательство. Мы доказали выше (п. 55, II), что если
р — 1 = aab^cY. . . (где а, Ъ, с, . . . — различные простые числа) и А,
В, С, . . . суть какие-нибудь числа, принадлежащие соответственно
показателям аа, №, cY, . . ., то произведение ABC. .. представляет
собой первообразный корень. Но легко также доказать, что каждый
первообразный корень может быть представлен в виде такого про-
произведения, и притом одним единственным способом *.
* Именно, определим числа а, Ь, с, ... так, что a:E3l(mod<2a) и
ее 0 (mod^cY . . .), Ь=1 (mod6p) H=0(modaacY . . .), и. т. д. (ср. п. 32).
Тогда a + Ь + с + • • • = 1 (mod/?-— 1) (п, 19). Если теперь какой-нибудь пер-
первообразный корень г нужно представить в виде произведения ЛВС..., то
Теоремы о периодах и первообразных корнях 83
Отсюда следует, что вместо первообразных корней можно брать
эти произведения. Но так как в этих произведениях всевозможные
значения А должны комбинироваться со всевозможными значения-
значениями В и т. д., то сумма всех этих произведений равна произведе-
произведению суммы всевозможных значений А на сумму всевозможных
значений В, на сумму всевозможных значений С и т. д., что пока-
показывается в комбинаторике. Если обозначить всевозможные значе-
значения А, В, . . . соответственно через А, А\ А", . . ., В, В', В", . . ., .. .,
то сумма всех первообразных корней будет
= (А + А' + А" + . . .) (В + В' + В" + . . .) . . .
Я утверждаю теперь, что если показатель <х = 1, то сумма
А + А' + А" + . . . = — 1 (modp), а если а > 1, то эта сумма =0,
и так же обстоит дело для [В, -у, •••• Если это будет доказано, то
отсюда будет сразу вытекать справедливость нашей теоремы. Дей-
Действительно, если р— 1 делится на некоторый квадрат, то какой-
нибудь из показателей ос, р, -у, • • . будет превосходить единицу,
и потому какой-нибудь из сомножителей, с произведением которых
сравнима сумма первообразных корней, =0, а значит =0 и само
произведение. Если же р — 1 не делится ни на какой квадрат
то все показатели а, р, "f> • • • будут равны 1; поэтому сумма всех
первообразных корней будет сравнима с произведением такого
количества сомножителей (каждый из которых =—1), сколько
имеется чисел а, Ь, с, . . ., т. е. = + 1- в зависимости от того, четно
или нечетно число этих чисел. Указанные же выше утверждения
доказываются следующим образом.
1. Если ос = 1 и А — число, принадлежащее показателю а, то ос-
остальными числами, принадлежащими этому показателю, будут
А\ А\.. ., Аа~\ Но
1 + А + А2 + А3 + . . . + Аа~г
является суммой полного периода и потому =0 (п. 79); поэтому
А + А2 + А3 + . . . + Аа~' = — 1.
положим А = г , В ^ г , С ^в г , . . .; тогда А будет принадлежать показа
телю аа, В — показателю w и т. д., и произведение всех чисел Л, В, С, . .
будет ^r(modp). Легко видеть также, что числа А, В, С, . . . не могут иметь
никаких других значений, кроме указанных.
84 Раздел III (пп. 82-85)
2. Если же ос > 1 и А — число, принадлежащее показателю аа,
то другие принадлежащие этому показателю числа мы получим,
если из чисел А2, А3, А^, . . ., Аа ~~1 отбросим числа Аа, А2а, Asa, . . .
(ср. п. 53). Поэтому их сумма
= 1 + А + А2 + ... + АаО'-г — A + Аа + А2а + . . . + Аа*-а),
т. е. сравнима с разностью двух периодов и потому =0.
О модулях, которые являются степенями простых чисел
82
Все, что мы изложили до сих пор, основывается на предполо-
предположении, что модуль является простым числом. Остается еще рас-
рассмотреть случай, когда за модуль берется составное число. Так
как, однако, появляющиеся здесь теоремы не столь изящны, как
в первом случае, и для их обнаружения не требуется особенно
тонких приемов, а можно их вывести простым применением ранее
изложенных принципов, то было бы и утомительным и излишним
разбирать здесь все подробности. Поэтому мы лишь кратко изло-
изложим, что этот случай имеет общего с предыдущим и в чем от него
отличается.
83
Теоремы пп. 45—48 были уже доказаны для общего случая; тео-
теорему же из п. 49 нужно изменить следующим образом.
Если через f обозначить количество чисел, которые меньше т и
одновременно взаимно просты cm, т. е. если f = cp(m) (п. 38), то для
заданного взаимно простого с т числа а показатель t наинизшей его
степени, которая сравнима с единицей по модулю т, или равен /,
или является делителем этого числа.
Доказательство теоремы из п. 49 проходит и в этом случае, если
только взять т вместо р, f вместо р — 1, а вместо чисел 1, 2, 3,...
..., р—1— те числа, которые взаимно просты с т и одновременно мень-
О модулях вида рп 85
ше т. Поэтому мы предоставляем это читателю. Впрочем, и другие
доказательства, о которых мы там (пп. 50, 51 ) говорили, без боль-
больших изменений переносятся на этот случай. Однако, в отношении
следующих теорем (п. 52 и далее) имеется большое различие между
модулями, которые являются степенями простых чисел, и теми,
которые делятся на несколько простых чисел. Мы рассмотрим по-
поэтому модули первого типа отдельно.
84
Если модуль т = рп, где р—простое число, то / = рп~1(р — 1)
(п. 38). Если теперь применить к этому случаю исследования
в пп. 53, 54, то, внеся изменения, указанные в предыдущем
пункте, мы убедимся, что все доказанное там верно и в этом случае,
если только доказать сначала, что сравнение вида х1 — 1 ЕЕ 0 (mod//1)
не может иметь больше чем t корней. Для простого модуля мы
вывели этот факт из общей теоремы п. 43, которая, однако, в общем
виде верна только для простых модулей, и потому в рассматривае-
рассматриваемом сейчас случае не может быть применена. Однако мы докажем
особым методом, что для данного частного случая теорема верна.
В дальнейшем (раздел VIII) мы научимся доказывать это проще.
85
Мы хотим доказать следующую теорему.
Если е есть наибольший общий делитель чисел t и рп~1(р — 1)
то сравнение х1 = 1 (modpn) имеете различных корней.
Пусть е = kpv, где к не содержит сомножителем р и потому
входит в р — 1. Тогда сравнение ж* = 1 по модулю р будет иметь &
различных корней, и если обозначить их через А, В, С, .. ., то
каждый корень такого же сравнения по модулю рп должен быть
сравним по модулю р с одним из чисел А, В, С,. .. Теперь мы
докажем, что сравнение хх = 1 (mod pn) имеет pv корней, сравшшых
с А, столько же корней, сравнимых с В, и т. д. по модулю р.
Отсюда будет следовать, что количество всех корней равно &pv,
т. е. равно е, что и утверждается Указанное доказательство мы
Раздел III (пп. 86-87)
проведем следующим образом. Во-первых, мы покажем, что если а
есть корень, сравнимый с А по модулю р, то корнями будут также
и а + Рп~\ а + 2рп~\ а + 3pn~v, . .., ос + (pv — 1)pn-v; во-вторых.
что среди чисел, сравнимых с А по модулю р, нет других корней,
кроме тех, которые имеют вид си-\-крп~^ (где h обозначает произ-
произвольное целое число), откуда следует, что имеется /?v, но не больше,
таких корней. То же самое имеет место и для корней, сравнимых
с числами Z?, С,...; в-третьих, мы покажем, что всегда можно
найти один корень, который сравним с i do модулю р.
86
Теорема. Если t, как и в предыдущем пункте, есть число, кото-
которое делится на pv, но не делится на р^1, то
(ос -f hpv-y — ос' = 0 (mod р* И) или == aJ^hpH (mod pH-v+i).
Вторая часть теоремы не верна, если р = 2 и одновременно
Доказательсто этой теоремы можно было бы вывести из разло-
разложения степени бинома, если показать, что все члены после второ-
второго делятся на jd{x+v+1. Так как, однако, рассмотрение знаменателей
коэффициентов приводит к некоторым затруднениям, мы вместо
этого применим следующий метод.
Если мы сначала предположим, что ц>1 и v = l, то так как
хг _ yt = (х - у) (Xt-i + xt-2y + xt-sy2 + ..._]. yt-i)t
имеет место
(ос + hp»y — ct} = hp» [(ос + tip»)*-1 + (ос + hp^y-2a -f .. . + ос'-1].
Но
ос + hpv* e^ ос (mod p2).
Поэтому каждый член (ос + hpv-y—i, (ос + hp11-)*—2,. . . е^о*—1 (mod/?2),
и значит сумма их всех = to?—1 (mod p2), т. е. имеет вид tai}—1 + vp2*
где v есть некоторое число. Следовательно, (а-\-hp^y — ос' будет
иметь вид
, т. е. =a'-iftp»4(modp'*+2) и = 0 (mod рИ-i).
О модулях вида рп 87
Тем самым для этого случая теорема доказана.
Если теперь по-прежнему остается [х > 1, но для других значе-
значений v теорема не верна, то обязательно должна существовать гра-
граница, до которой теорема все время верна, а за ней уже стано-
становится неверной. Пусть наименьшее значение v, для которого она
больше не верна, равно ср. Тогда легко видеть, что если t делится
на р9~1, но не делится на рф5 то теорема еще верна, но перестает
быть верной, если t заменить на tp. Поэтому
(ос + tip»I = ос' + с^-ЧрН (mod р*+<р) или = а* _|_ tf-ikpH + up^+v^
где и означает целое число. Но так как для v = 1 теорема уже
доказана, мы имеем
(ос' + ^
= оо'р + OL^~lhpu'+4 + оо'Р-^рИ-Ф+i (mod
и потому также
(а + hpv-yv = а'Р + onf^^hpHp (mod рИ-Ф+i),
т. е. теорема верна и при замене t на tp, т. е. верна для v = 9,
что находится в противоречии с нашим предположением. Отсюда
следует, что теорема верна для всех значений v.
87
Остается еще случай, когда [л = 1< При помощи метода, совер-
совершенно аналогичного тому, который применялся в предыдущем
пункте, можно, не прибегая к помощи биномиальной теоремы,
доказать, что
(а + hp)*-1 = а'-1 + а'-2 (t-l)hp (mod p2),
а (ос + Ар)' = и*-1 + ос'-з (t — 2) hp,
ос2 (ос + tip)*-* = oc'-i + af~ (t — 3) hp,
Раздел III (пп. 88-89)
так что многочлен (ибо число слагаемых равно t) будет
= fat-i + (t~~2iU a'-2 hp (mod р2).
Но так как t делится на р, то и (t—1)?/2 будет делиться на р
во всех случаях, за исключением случая р = 2, который мы исклю-
исключили из рассмотрения еще в предыдущем пункте. В остальных же
случаях будет иметь место -—-^— ы1—21гр = 0 (mod/?2), и потому
указанный многочлен будет, как и в предыдущем пункте
= foe'-1 (mod/?2). В остальном доказательство здесь проводится точно
так же, как и там.
Поэтому мы можем сделать вывод, что, за исключением случая
р = 2, всегда имеет место
(ос + hp»)f = ос' (mod j^+v),
и (ос -|~ А/^)* несравнимо с ос' для каждого модуля, являющегося
более высокой степенью р, чем /^+v, где предполагается, что h не
делится на р, и /?v есть наивысшая входящая в t степень р.
Отсюда тотчас же вытекают утверждения 1 и 2, которые мы на-
наметили для доказательства в п. 85. Именно,
во-первых, если а*==1, то и (а + hpn—vy == 1 (modpn)r
во-вторых, предположим, что какое-нибудь число ос', сравнимое
по модулю р с А, & поэтому и с ос, но несравнимое с последним
по модулю pn~~v, удовлетворяет сравнению xt == 1 (modpn), и по-
положим а' = а + 1рх, где Z не делится на р и Х<тг — v; тогда
а-\-1рхУ = и* по модулю /?Л+\ но не по модулю рп, который яв-
является более высокой степенью р. Поэтому в действительности ос'
не может быть корнем сравнения #f=l.
88
В-третьих, мы должны были найти какой-нибудь один корень
сравнения ж* == 1 (mod/?71), который сравним с А, Мы здесь пока-
покажем только, как это можно сделать, если уже известен корень
такого же сравнения по модулю рп~1. Очевидно, что этого дос-
достаточно, потому что мы сможем тогда перейти от модуля р9 для
О модулях вида рп
которого корнем является А, к модулю р2 и точно так же ко всем
последующим степеням.
Итак, пусть ос— корень сравнения xf = I (mod/?71™1), и надо
найти корень этого сравнения по модулю рп. Положим его рав-
равным ос + hpn~v-1; эту форму он должен иметь согласно предыду-
предыдущему пункту (случай, когда v = п — 1 мы затем рассмотрим от-
отдельно; больше же, чем п — 1, v быть не может). Таким образом,
должно быть
(а + hp71-^-1I
Но
(ОС + hpn-v-l)t = а* _|_. а*
Поэтому, если определить /г так, что 1 = а' + ocf~1htpn~v~1 (modpn)
или (ибо, по предположению, 1 ^ ocf (mod/?71") и t делится на pv)
так, что — + af—х/г— делится на ю, то мы и получим то,
что нам нужно. А то, что это всегда возможно, вытекает из предыдущего
раздела, так как мы предположили, что t не должно делиться на более
высокую степень р чем pvf и потому vft—H/p* взаимно просто с р.
Если же v = п — 1, т. е. если ? делится на рп~1 или на еще
большую степень р, то каждое значение А, которое удовлетворяет
равнению #f = l по модулю р, будет удовлетворять ему и по мо-
модулю рп. Действительно, если t = рп~1т9 то ?=t(mod р—1); по-
поэтому, так как Л*== 1 (mod/?), то и Ат = 1 (mod/?). Следовательно,
если положить Лт = 1 + /г/?, то
4« = A + hp)Pn=l (mod/Я) (п. 87).
89
Все, что в пп. 57 и следующих мы вывели при помощи теоре-
теоремы, что сравнение xf == 1 не может иметь более чем 2 различных
корней, сохраняет силу также и для модуля, являющегося сте-
степенью простого числа; и если мы назовем первообразными корня-
корнями те числа, которые принадлежат показателю р71'—1 (р—1), или
те, в периодах которых содержатся все числа, не делящиеся на
р, то и в этом случае первообразные корни будут существовать.
90 Раздел III (пп. 90-91)
Далее, все, что мы говорили выше относительно индексов и их
применений, а также относительно решения сравнения х1 == 1, может
применяться также и в этом случае. Так как никаких трудностей
здесь нет, было бы излишне все это полностью повторять. Кро-
Кроме того, мы уже показали, как можно получать корни сравнения
х1 == 1 по модулю рп из корней этого сравнения по модулю р. Мы
должны добавить кое-что относительно случая, когда модулем яв-
является некоторая степень числа 2 — случая, который выше мы из
рассмотрения исключали.
Модули, являющиеся степенями числа 2
90
Если за модуль взята некоторая степень 2п числа 2, большая,
чем вторая, то степень каждого нечетного числа с показателем 2п~2
сравнима с единицей.
Например, З8 = 6561 =1 (mod 32).
Действительно, каждое нечетное число имеет вид или 1 + 4/г,
или — 1 + 4/г, откуда теорема следует непосредственно (теорема
из п. 86).
Так как, таким образом, показатель, которому принадлежит
любое нечетное число по модулю 2П, является делителем числа
2П~~2, то каждое число должно принадлежать одному из следую-
следующих показателей: 1, 2, 4, 8,. . . , 2П~2. Какому именно из них
оно принадлежит, легко можно определить следующим образом. Если
данное число равно 4/г + 1, и показатель наибольшей степени чи-
числа 2, входящей в /г, равен т (где т может быть и равным 0,
именно, когда h нечетно), то в случае h > т + 2 показатель, ко-
которому принадлежит данное число, равен 2n~~m~2. Если же п рав-
равно или меньше, чем т + 2, то заданное число = +1 и потому
принадлежит показателю 1 или показателю 2. Действительно, как
без труда вытекает из п. 86, каждое число вида +1 + 2т+2А: (что
эквивалентно виду 4/г + 1), возведенное в степень с показателем
2n—m—2t сравнимое единицей по модулю 2П; если же возвести это
число в степень с показателем, являющимся более низкой степенью
О модулях вида 2п 91
числа 2, то оно с единицей сравнимо не будет. Поэтому каждое чис-
число вида 8к -{- 3 Иди 8к -f- 5 принадлежит показателю 2П~А
91
Из сказанного вытекает, что в этом случае не существует пер-
первообразных корней в том смысле, в котором мы употребляли это
выражение выше, т. е. не существует чисел, периоды которых ох-
охватывают все числа, меньшие модуля и взаимно простые с ним.
Однако легко видеть, что некоторая аналогия имеется и здесь.
Именно, оказывается, что степень числа вида 8к -\- 3 с нечетным
показателем всегда имеет вид 8к -\- 3, а степень с четным показа-
показателем— вид 8&4-1; таким образом, никакая степень не может
быть вида 8к + 5 или 8А: + 7. Так как, таким образом, период
числа вида 8к + 3 состоит из 2п~2 различных членов, каждый из
которых имеет вид 8к -\- 1 или вид 8к + 3, и среди чисел,
меньших модуля, чисел такого вида не может быть больше,
чем 2п~~2, то ясно, что каждое число вида 8к + 1 или 8к + 3 срав-
сравнимо по модулю 2п с некоторой степенью любого числа вида 8к +
+ 3. Аналогичным образом можно показать, что период числа ви-
вида 8к -{- 5 содержит все числа вида 8к -\- 1 или 8к + 5. Поэтому,
если за основание взято число вида 8к -\- 5, то все числа вида
8к -\- 1 и 8А+5, взятые положительными, и все числа вида 8&+3
и 8к -\- 1 i взятые отрицательными, будут иметь вещественные ин-
индексы, причем индексы, сравнимые по модулю 2П~2, следует рас-
рассматривать как эквивалентные. В этом смысле надо понимать
нашу таблицу 1*, в которой мы для модулей 16, 32 и 64 (для мо-
модуля 8 таблицы, конечно, не нужно) всегда брали за основание
число 5. Например, для модуля 64 числу 19, которое имеет вид
8я-}-3 и потому должно браться отрицательным, соответствует ин-
индекс 7, что означает, что 57 = — 19 (mod64). Взятым отрицатель-
отрицательными числам вида 8п + 1 и 8п + 5 и взятым положительными чис-
числам вида 872 + 3 и 8п + 7 можно было бы определенным образом
сопоставить мнимые индексы. Если бы их ввести, то действия с
индексами можно было бы свести к очень простому алгоритму.
* Таблица помещена на стр. 576.— Прим. ред.
92 Раздел III (пп. 92-93)
Но так как мы были бы заведены слишком далеко, если бы захо-
захотели изложить это с полней строгостью, мы оставим это до дру-
другого случая, когда мы будем излагать теорию мнимых величин,
которая, по нашему мнению, до сих пор еще никем не была при-
приведена к ясным понятиям. Имеющие навык легко найдут этот ал-
алгоритм сами; впрочем, для того, чтобы употреблять эту таблицу, нужен
лишь небольшой опыт, подобно тому как те, кому не известны но-
новейшие исследования о мнимых логарифмах, могут пользоваться
логарифмами, если они только поняли изложенные выше принципы-
Модули, составленные из нескольких простых чисел
92
В отношении модулей, составленных из нескольких простых чи-
чисел, почти все, касающееся вычетов степеней, может быть выведе-
выведено из общей теории сравнений. Так как, однако, впоследствии мы
более подробно будем показывать, как любые сравнения по моду-
модулям, составленным из нескольких простых чисел, могут быть
сведены к сравнениям, модули которых суть простые числа или
степени простых чисел, здесь нам нет нужды долго задерживать-
задерживаться на этом предмете. Заметим только, что красивое свойство, су-
существующее для модулей, которые суть простые числа или степени
простых чисел, именно, что всегда существуют числа, периоды ко-
которых содержат все числа, взаимно простые с модулем, здесь ужа
не имеет места, за исключением того случая, когда модуль есть уд-
удвоенное простое число или удвоенная степень простого числа.
Именно, если модуль т имеет вид АаВьСс..., где А, В, С,... обо-
обозначают различные простые числа, далее, Аа~1(А — 1) обозначает-
обозначается через ос, ВЬ~1{В — 1) — через р, и т. д., и наконец, z есть чис-
число, взаимно простое с т, то za =в I (mod Аа), z&~ l(modBb) я т. д.
Если теперь [х есть наименьшее общее кратное чисел ос, [3, т,..., то
сравнение 2^=1 будет выполняться по всем модулям Аа, Вь,. . .,
а потому и по модулю т, являющемуся их произведением. Но за
исключением случая, когда т есть удвоенное простое число или
удвоенная степень простого числа, наименьшее общее кратное*
О составных модулях 93
чисел а, (В, ^,... меньше их произведения (так как числа а, [В, f, . . .
не могут быть взаимно просты, ибо обязательно содержат общий
делитель 2). Поэтому ни у какого числа период не содержит столь-
столько членов, сколько имеется чисел, взаимно простых с модулем и
меньших модуля, так как это количество равно произведению чи-
чисел ос, р, т, . . . Так, например, для т = 1001 шестидесятая сте-
степень каждого числа, взаимно простого с т, сравнима с единицей,
потому что 60 есть наименьшее общее кратное чисел 6, 10, 12.
Случай же, когда модуль есть удвоенное простое число или удво-
удвоенная степень простого числа, совершенно аналогичен тому, когда
модуль есть простое число или его степень.
93
Работы, в которых другие математики касались изложенного
здесь предмета, мы уже упоминали мимоходом. Тех, которые хотели
бы ознакомиться с этим предметом несколько более подробно, чем
мы, из желания быть краткими, сообщили здесь, мы отсылаем в
первую очередь к следующим сочинениям Эйлера, которые осо-
особенно достойны быть рекомендованы вследствие ясности изложения,
всегда отличающей этого великого человека от других математиков:
«Theoremata circa residua ex divisione potestatum relicta». Comm.
nov. Petrop., T. VII, p. 49;
Demonstrationes circa residua ex divisione potesiatum per numeros
primos resultantia». Ibid., T. XVIII, p. 85.
Можно указать также на работы 5 и 8 в его «Opusculis Analyti-
cis», T. I.
Раздел IV
О СРАВНЕНИЯХ ВТОРОЙ СТЕПЕНИ
Квадратичные вычеты и невычеты
94
Теорема. Если какое-нибудь число т взять в качестве модуля,
то из чисел О, 1, 2, 3,..., т — 1 могут быть сравнимы с некото-
некоторыми квадратами не более чем -~т-\- 1 чисел, если т четно, и не бо-
1 , 1
лее чем -~т -г-к- чисел, если т нечетно.
Доказательство. Так как квадраты сравнимых чисел тоже, оче-
очевидно, сравнимы, то каждое число, сравнимое с некоторым квад-
квадратом, сравнимо и с квадратом числа, меньшего чем т. Поэтому
нам нужно рассмотреть только наименьшие вычеты квадратов 0, 1,
4, 9,..., (т — IJ. Но легко видеть, что (т — 1J=1, (т — 2J=22,
(т — 3J = 32, и т.д. Поэтому если т четно, то будут совпадать
/1 ,\2 /1 -\2 /1 \2
наименьшие вычеты квадратов 1-к-т—1 и к-т+1 , ro"m—^
\Z J \Z J \А J
A \ 2
-к-т-\-2\ и т. д.; если же т нечетно, то будут сравнимы
/1 1\2 /1 1 \2 /1 3\2 /1 , 3\2
квадраты (ут — у) и (у^ + у) » (ут~у) п VYm + y) и т> д*
Отсюда вытекает, что при четном т не может быть сравнимо с
квадратом ни одно из чисел, кроме тех, которые сравнимы с од-
одним из квадратов- 0, 1, 4, 9, . . ., \-^т) » а при нечетном т каж-
Квадратичные вычеты и невычеты 95
дое число, сравнимое с некоторым квадратом, обязательно сравни-
сравнимо с одним из чисел О, 1, 4, 9, . . ., [рг ш —т) • Поэтому в пер-
первом случае имеется не больше чем -к-m-^i, а во втором не боль-
1 . 1
ше чем -к-т -\--k- различных наименьших вычетов.
Пример. По модулю 13 квадраты чисел 0, 1, 2, 3, . . . , 6 име-
имеют следующие наименьшие вычеты: 0, 1, 4, 9, 3, 12, 10; затем они
снова повторяются в обратном порядке. Поэтому не может быть
сравнимо с квадратом ни одно число, которое не сравнимо с од-
одним из этих вычетов, т. е. которое сравнимо с одним из чисел 2,
5, 6, 7, 8, И.
По модулю 15 получаются следующие вычеты: 0, 1, 4, 9, 1,
10, 6, 4; затем они же повторяются в обратном порядке. Таким
образом, здесь число вычетов, которые могут быть сравнимы с некото-
1 , 1 *
рыми квадратами, даже меньше, чем -к- т -\--к-, ибо такими выче-
вычетами являются только 0, 1, 4, 6, 9, 10. Числа же 2, 3, 5, 7, 8,
11, 12, 13, 14 и все сравнимые с ними не могут быть сравнимы
по модулю 15 ни с каким квадратом.
95
Из сказанного следует, что для каждого модуля все числа
могут быть разбиты на два класса, один из которых содер-
содержит все числа, которые сравнимы с некоторыми квадратами, а дру-
другой— те числа, для которых это не имеет места. Мы будем на-
называть первые квадратичными вычетами взятого в качестве модуля
числа*, а вторые — его квадратичными невычетами, а когда это
* Собственно говоря, мы используем здесь это выражение в другом смысле,
нежели мы это делали до сих пор. Именно, мы должны были бы говорить, что
г есть вычет квадрата а2 по модулю т, если r= a2(mod m). Однако ради крат-
краткости мы в этом разделе всегда будем называть г квадратичным вычетом самого
числа т, не опасаясь, что это может привести к недоразумениям, так как выра-
выражение «вычет» в смысле «сравнимое число» мы, начиная отсюда, будем употреб-
употреблять лишь тогда, когда речь идет о наименьшем вычете, а в этом случае никакой
двусмысленности возникнуть не может.
96 Раздел IV (пп. 96-98)
не сможет привести к недоразумению, будем также использовать
просто выражения «вычеты и невычеты». Очевидно, что если все
числа 0, 1, 2,.. ., т — 1 распределены по обоим классам, то срав-
сравнимые числа содержатся в том же классе.
В этих исследованиях мы также начнем с простых модулей;
это все время будет молчаливо предполагаться, даже когда об этом
и не будет специально упоминаться. При этом простое число 2 ис-
исключается, т. е. будут рассматриваться только нечетные простые
числа.
Если модуль есть простое число,
то среди чисел, меньших его, количество вычетов
равно количеству невычетов
96
Если за модуль взято простое число р, то среди чисел 1, 2,
3,. ¦ ., р — 1 половина будет квадратичными вычетами, а осталь-
остальные — невычетами, т. е. имеется -ту {р — 1) вычетов и столько же
невычетов.
Именно, легко доказать, что все квадраты 1, 4, 9,..., -у~(р—1J
несравнимы между собой. Действительно, если бы имело место г2 =
= г'2 (mod p) и числа гиг' были бы не больше, чем (р — 1)/2, и не
равны между собой, то, предполагая г > г', что законно, мы име-
имели бы, что число (г — г') (г + г') положительно и делится на р. Но
каждый из сомножителей г — г' и г -\- г' меньше р, и потому на-
наше предположение не может иметь места (п. 13). Поэтому среди
чисел 1, 2, 3,..., р—1 имеется (р—1)/2 квадратичных вычетов;
но больше среди этих чисел вычетов быть не может, так как, при-
присоединяя еще вычет 0, мы уже получим (р-\-1)/2 вычетов, а ко-
количество всех вычетов не может превосходить этого числа. Таким
образом, остальные числа являются невычетами, и тем самым их
количество равно (р—1)/2.
Так как нуль всегда является вычетом, то в этих исследовани-
исследованиях мы исключим его из рассмотрения вместе с числами, делящи-
делящимися на модуль; этот случай сам по себе ясен и лишь удлиняет
теоремы. На этом же основании мы исключили также и модуль 2.
Вычеты и невычеты по простому модулю
97
97
Так как многое из того, что мы будем разбирать в этом разделе,
может быть выведено также и на основании принципов предыдущего
раздела, и так как не является бесполезным получать одну и ту же
истину различными путями, мы сейчас поясним эту связь. Легко
видеть, что все числа, сравнимые с некоторыми квадратами, имеют
четные индексы, а несравнимые с квадратами — нечетные. Но так
как р — 1 есть четное число, то количество четных и нечетных ин-
индексов одинаково, именно, и тех, и других по (р — 1)/2, и столько
же будет вычетов и невычетов.
Примеры
Для моду-
модулей
3
5
7
И
13
17
1
1
1
1
1
1
Вычетами
, 4
, 2, 4
, 3, 4, 5,
, 3, 4, 9,
, 2, 4, 8,
являются
9
10, 12
9, 13, 15, 16
остальные же числа, меньшие этих модулей, суть невычеты.
Ответ на вопрос, является ли составное число
вычетом или невычетом заданного простого числа,
зависит от свойств сомножителей
98
Теорема. Произведение двух квадратичных вычетов простого чис-
числа р является вычетом; произведение вычета на невычет является
невычетом; наконец, произведение двух невычетов является вычетом.
Доказательство. I. Пусть А, В— вычеты, получающиеся из ква-
квадратов а2, Ь2: т. е. Л = а2, В = й2; тогда произведение АВ будет
сравнимо с квадратом числа ab, т. е. будет вычетом.
98 Раздел IV (пп. 99-100)
II. Если А есть вычет, например, = а2, а В — невычет, то АВ
будет невычетом. Действительно, если мы предположим, что АВ^
==й;2 и —==&(modjD), то будет иметь место а?В = а?Ь2, и потому
В = Ь2, т. е., вопреки нашему предположению, В будет вычетом.
Другое доказательство. Если все вычеты, содержащиеся среди
чисел 1, 2. 3,..., р — 1 (количество этих вычетов равно (р—1)/2),
умножить на Л, то все произведения будут квадратичными выче-
вычетами и все будут несравнимы между собой. Если теперь умножить
на А невычет В, то произведение не будет сравнимо ни с одним
из ранее полученных произведений. Поэтому, если бы оно
было вычетом, то мы име й бы (р + 1)/2 несравнимых между
собой вычетов, среди которых нет нуля. Но это противоречит
п. 96.
III. Если А и В—невычеты, то, умножая на А все вычеты,
содержащиеся среди чисел 1, 2, 3,..., р — 1, мы, согласно II,
получим (р — 1)/2 несравнимых между собой невычетов. Но ни
одно из этих произведений не может быть сравнимо с произведе-
произведением АВ. Поэтому, если бы оно было невычетом, мы имели бы
(р + 1)/2 несравнимых между собой невычетов, что противоречит
п. 96.
Еще легче можно вывести эти теоремы из принципов предыдущего
раздела. Действительно, так как индексы вычетов всегда четны,
а индексы невычетов нечетны, то индекс произведения двух вычетов
или двух невычетов будет четным, и потому само произведение есть
вычет. Наоборот, индекс произведения вычета на невычет будет
нечетным, и потому само произведение есть невычет.
Оба метода могут быть применены также для доказательства
следующих теорем.
Значение выражения -^-(mod p) является вычетом, если числа а и Ъ
являются одновременно или вычетами, или невычетами; наоборот,
оно будет невычетом, если одно из чисел а и Ъ есть вычет, а другое —
невычет.
Эти теоремы могут быть получены также обращением предыду-
предыдущих теорем.
Вычеты и невычеты по составному модулю 99
99
Вообще, произведение любого количества сомножителей есть вы-
вычет как в том случае, когда все сомножители — вычеты, так и в том,
когда число невычетов среди них четно; если же число невычетов,
находящихся среди сомножителей, нечетно, то произведение есть
невычет. Поэтому легко можно узнать, является ли заданное число
вычетом или невычетом, если мы знаем это относительно его отдель-
отдельных сомножителей. Поэтому в таблицу 2* мы вносили только про-
простые числа. Устройство этой таблицы следующее. Слева расположе-
расположены столбцом модули **, в верхней строке стоят последовательные
простые числа; если какое-нибудь из них является вычетом по неко-
некоторому модулю, то на пересечении соответствующих строки и столб-
столбца ставится маленькая черточка; если же простое число является
невычетом модуля, то соответствующее место оставляется пустым.
О модулях, являющихся составными числами
100
Прежде чем переходить к более трудным теоремам, нам нужно
еще кое-что добавить относительно не простых модулей.
Если за модуль взята любая степень рп простого числа р
(мы предполагаем, что р не равно 2), то среди чисел, которые не
делятся на р и меньше модуля, половина является вычетами, а
остальные невычетами, т. е. количество как тех, так и других
равно (р—1) jDn-V2.
Действительно, если число г есть вычет, то оно будет сравни-
сравнимо с квадратом некоторого числа, не превосходящего половины
модуля (ср. п. 94). Но легко видеть, что существует (р — l)jDn~V2
чисел, которые не делятся на р и меньше половины модуля, и по-
потому нужно только показать, что квадраты всех этих чисел не-
несравнимы один с другим, т. е. дают различные квадратичные вы-
вычеты. Но если бы квадраты двух чисел а и &, которые оба не де-
делятся на р и меньше половины модуля, были бы сравнимы между
* Таблица помещена на стр. 577.— Прим. ред,
** Мы скоро покажем, как можно избавиться от составных модулей.
100 Раздел IV (пп. 101-102)
собой, то а%2 = (а — Ъ) (а -\- Ъ) должно было бы делиться на рп (мы
предполагаем при этом а > Ь, что законно). Это возможно, одна-
однако, только тогда, когда либо одно из чисел а — Ь, а -\- Ъ делится
на рп, что не имеет места, потому что оба они меньше рп, либо
одно из этих чисел делится на рт, а другое на рп~т, т. е. оба де-
делятся на р. Однако и этого не может быть. В самом деле, оче-
очевидно, что тогда сумма и разность этих чисел, именно 2а и 26,
тоже делились бы на р, а потому на р делились бы также а и Ь,
что противоречит предположению. Отсюда, наконец, вытекает, что
среди чисел, которые не делятся на р и меньше модуля, имеется
(р— i)pn~1/2 вычетов, и что остальные числа, которых столько же,
являются невычетами. Эту теорему можно было бы вывести также
и по аналогии с п. 97 из рассмотрения индексов.
101
Каждое не делящееся на р число, которое является вычетом для
р, есть также вычет для рп, а то число, которое есть невычет для
р, будет также невычетом для рп.
Последняя часть этой теоремы очевидна. Поэтому, если бы пер-
первая часть была неверна, то среди чисел, которые меньше рп и од-
одновременно не делятся на р, вычетов для р было бы больше, чем
для рп, т. е. больше чем рп~1(р—1)/2. Но без труда видно, что
среди указанных чисел количество вычетов числа р в точности
равно рп~1(р — 1)/2.
Точно так же легко найти квадрат, который сравним по моду-
модулю рп с заданным вычетом, если известен квадрат, сравнимый с
этим вычетом по модулю р.
Именно, если имеется некоторый квадрат а2, который сравним
с заданным вычетом А по модулю р^, то квадрат, сравнимый с А
по модулю pv (где предполагается, что v > [л, но v<T2[x), находится
следующим образом. Мы полагаем основание искомого квад-
квадрата равным +а + ж/Л ибо именно такую форму оно, как лег-
легко видеть, и должно иметь. Тогда должно быть а2 + 2ахр^ -f- х2р2и- =
== A (mod />v) или, так как 2а > v, А — а2 еее + 2ахр^ (mod pv). Если
Вычеты и невычеты по составному модулю 101
А — а2 = рЫ, то х есть значение выражения +d/2a(modpv~^), ко-
которое эквивалентно выражению +(А — а2)/2ар^ (modjov).
Таким образом, если задан квадрат, который сравним с А по
модулю р, то можно найти квадрат, который сравним с А по мо-
модулю р2; от него можно затем перейти к модулю /?4, затем к мо-
модулю р8 и т. д.
Пример. Если задан вычет 6, который сравним по модулю 5 с
квадратом 1? то мы находим квадрат 92, с которым он сравним
по модулю 25, далее, квадрат 162, с которым он сравним по мо-
модулю 125, и т. д.
102
Что же касается чисел, делящихся на /?, то ясно, что их квад-
квадраты будут делиться на р2, и потому все числа, делящиеся на /?,
но не делящиеся на р2, являются невычетами числа рп. Вообще же,
если дано число ркА, где А не делится на р, то нужно различать
следующие случаи:
1. Если к^п, то ркА = 0 (modpn), т. е. данное число есть вычет.
2. Если к <С п и нечетно, то ркА есть невычет.
Действительно, если бы было ркА = р2*+1А = s2 (mod pn), то
s2 делилось бы на р2>с+1, а это возможно только тогда, когда s
делится на р*+г. Но тогда s2 делилось бы также на /?2*Н~2, а пото-
потому (так как 2х -}- 2, очевидно, не больше ?г)"на это число делилось бы
и р2УС+г А, т. е. А делилось бы на р, что противоречит предположению.
3. Пусть к меньше чем п, и четно. Тогда ркА будет вычетом
или невычетом по модулю рп в зависимости от того, является ли
А вычетом или невычетом по модулю /?. Действительно, если А
есть вычет по модулю р, то он будет вычетом и по модулю pn~h. Но
если А = a2 (mod pn~k), то Арк = а2рк (ш.оАрп) и а2рк есть квадрат. Если
же А невычет для /?, то ркА не может быть вычетом для рп. В самом
деле, если бы имело место ркА = а? (modpn), то а2 обязательно дол-
должно было бы делиться на рк. Частное было бы квадратом, срав-
сравнимым с А по модулю рп~~к, а потому также и по модулю р, т. е.
А было бы квадратичным вычетом для р. Но это противоречит пред-
предположению.
102 Раздел IV (пп. 103-104)
103
Так как раньше мы исключили случай р = 2, сейчас мы должны
кое-что сказать специально о нем. Если число 2 — модуль, то каж-
каждое число является вычетом; невычетов нет. Если модуль равен 4,
то все нечетные числа вида 4А: -f-1 будут вычетами, а вида kk +3
— невычетами. Если, наконец, модуль равен 8 или более высо-
высокой степени числа 2, то все нечетные числа вида 8А: -f-1 будут вы-
вычетами, а все остальные, т. е. числа вида 8к-\~3} 8к + 5, 8к-\-7
— невычетами. Последняя часть этой теоремы следует из того,
что квадрат всякого нечетного числа, будь оно вида Ак + 1 или
kk — 1, имеет вид 8А; + 1. Первую же часть мы докажем следую-
следующим образом.
1. Если сумма или разность двух чисел делится на 2П—1, то ква-
квадраты этих чисел сравнимы по модулю 2П. Действительно, если од-
одно из них равно а, то второе будет иметь вид 2п~^г + а, и для
квадрата его имеем, что он = a2 (mod 2п).
2. Каждое нечетное число, являющееся квадратичным вычетом
по модулю 2П, сравнимо с квадратом некоторого числа, которое
нечетно и меньше чем 2П~2. Именно, пусть а2 — квадрат, с кото-
которым сравнимо данное число, и а = + а (mod2n—*), где а не пре-
превосходит половины модуля (п. 4); тогда а2 = а2. Тем самым и за-
заданное число е= а2. Очевидно, что как а, так и а нечетны, и а < 2П~2.
3. Квадраты всех нечетных чисел, меньших 2П~2, несравнимы
по модулю 2П. В самом деле, пусть г и s—два таких числа. Ес-
Если бы их квадраты были сравнимы по модулю 2П, то (г — s) (r+s)
делилось бы на 2П (где предполагается г > 5). Но легко видеть, что
числа г — s в. г + s яе могут одновременно делиться на 4, и пото-
потому, если одно из них делится на 2, то второе должно делиться
на 2п—х, чтобы произведение делилось на 2П. Это, однако, невоз-
невозможно, так как каждое из этих чисел меньше, чем 2п~2.
4. Наконец, если эти квадраты привести к их наименьшим по-
положительным вычетам, то мы получим 2П~~3 различных квадратич-
квадратичных вычетов, которые меньше модуля* и все имеют вид 8&+L Но
* Потому что количество нечетных чисел, меньших, чем 2П"~2, равно 2П"~3.
Вычеты и невычеты по составному модулю 103
так как среди чисел, меньших модуля, имеется в точности 2П~3 чи-
чисел вида 8& + 1, то все они должны содержаться среди указанных
вычетов. Это и нужно было доказать.
Чтобы найти квадрат, сравнимый с заданным числом вида 8к-\-1
по модулю 2П, можно использовать метод, аналогичный методу из
п. 101 (ср. также п. 88). Наконец, для четных чисел будет верным
все то, что мы изложили в п. 102.
104
Относительно количества различных (т. е. несравнимых по мо~
дулю) значений, которые имеет выражение V =УА(mod/?71), когда
А есть вычет по модулю рп, из предыдущего легко можно вывести
следующее. (Число р мы, как и раньше, предполагаем простым и
для краткости сразу исключаем случай п = 1.)
I. Если А не делится на р, то V имеет одно значение для
р = 2, п — 1, именно V == 1; два значения, если р нечетно, а также,
если /? = 2, п = 2; именно, если одно из них мы обозначим через
= v, то другое будет = — v\ четыре значения для р = 2, п^>2;
именно, если одно из них ==v, то остальные суть == — v> 2n~1-\-Vi
2n~1 — v.
II. Если же А делится на р, но не делится на рп, то пусть
наибольшая степень р, входящая в А, есть рш (очевидно, что ее
показатель должен быть четным), и пусть А = арш. Тогда ясно,
что все значения V делятся на /Л и все получающиеся после деле-
деления величины суть значения выражения V = У a (mod /?п~~2{х).Из
них мы получим все различные значения F, если умножим на
pv- все лежащие между 0 и рп~^ значения выражения V. Поэтому
значения V представляются в виде
vp11, vp* + pn-v<, vp* + 2pri^-^, . . ., vpv- + {p* — 1) pn~v-,
где неизвестное v принимает все различные значения выражения
У, так что число значений V равно /^, 2р^ или 4р^ в зави-
зависимости от того, равно ли число значений V (см. случай I) 1, 2
или 4.
104 Раздел IV (пп. 105-106)
III. Если А делится на рп, то легко видеть, что если мы по-
положим п = 2т или = 2т — 1, смотря по тому, четно п или не-
нечетно, то значениями V будут все числа, делящиеся на рт, и
только они. Поэтому 0, рт, 2рт,.. . , (рп-т — 1) рт дают все раз-
различные между собой значения, и число их равно рп~т.
105
Остается случай, когда модуль составлен из нескольких различ-
различных простых чисел. Если т = аЪс . .. , где а, 6, с, ... обозначают
или различные простые числа, или степени различных простых
чисел, то прежде всего ясно, что если п есть вычет по модулю тг
то оно будет вычетом и по всем модулям а, Ь, с, . . . , и потому пг
очевидно, будет невычетом для т, если оно является невычетом
хотя бы одного из чисел а, 6, с,.... Но и наоборот, если п является
вычетом всех чисел а, Ь, с, . . ., то оно будет и вычетом их произ-
произведения. Действительно, если мы положим п == -42, 52 С2,... соот-
соответственно по модулям а, Ь, с, . .., то для числа N, полученного
согласно п. 32, которое сравнимо с А, В, С,... соответственно
по модулям а, Ь, с,. . . , будет иметь место n^N2* no всем этим
модулям, а потому также и по их произведению т. Так как легко
видеть, что при комбинировании таким способом каждого значе-
значения числа А или выражения Yli (mod а) с каждым значением числа В,
с каждым значением числа С и т. д. получается значение числа N,
т. е. выражения У~п (mod иг), и, далее, из различных комбинаций
получаются различные N, а из всевозможных комбинаций — все-
всевозможные N, то количество всех различных значений N равно
произведению количеств значений чисел -4, В, С, . .. , определять
которые мы научились в предыдущем пункте.
Далее, ясно, что если известно значение выражения Yli (mod m)
или N, то оно будет одновременно значением всех А, В, С, . .. ,
а так как, согласно предыдущему пункту, из него могут быть
выведены все значения этих величин, то, следовательно, из одного
значения N можно получить все остальные.
Пример. Пусть модуль равен 315, и спрашивается, является ли
число 46 вычетом или невычетом. Простые делители числа 315
Критерий для вычетов и невычетов по простому модулю 105
суть 3, 5, 7, и число 46 является вычетом по каждому из них,
а потому и по модулю 315. Так* как, далее, 46 = 1 и ==64
по модулю 9, = 1 и == 16 по модулю 5, =4 и = 25 по модулю 7,
то основаниями квадратов, которые сравнимы с 46 по модулю 315,
являются следующие числа: 19, 26, 44, 89, 226, 271, 289, 296.
Общий критерий того, является ли заданное число
вычетом или невычетом по заданному простому модулю
106
Из предыдущего следует, что если только мы можем узнать,
будет ли заданное простое число вычетом или невычетом по задан-
заданному простому модулю, то все остальные случаи могут быть сведены
к этому. Поэтому мы должны направить наши усилия на то, чтобы
получить точные критерии для решения первого вопроса. Однако,
прежде чем приступить к этому исследованию, мы хотим указать
на один критерий, получающийся на основании предыдущего раз-
раздела, который хотя и не находит себе почти никогда применения
на практике, но все же достоин упоминания вследствие своей про-
простоты и общности.
Каждое число А, которое не делится на простое число 2т + Ь
является вычетом или невычетом по этому простому числу, в за-
зависимости от того, имеет ли место Ат = + 1 или = — 1 (mod 2т +1).
Именно, если для модуля 2т -f- 1 индекс числа А в некоторой
системе равен а, то а будет четным, если А есть вычет числа 2т + 1,
и нечетным, если А — невычет. Индекс же числа Ат равен та,
т. е. он = 0 или = т (mod 2m), смотря по тому, четно а, или не-
нечетно. Отсюда вытекает, что в первом случае Ат = -f 1, а во втором
случае Ат = — 1 (mod2m + 1). (ср. пп. 57 и 62).
Пример. 3 есть вычет числа 13, потому что З6 == 1 (mod 13);
наоборот, 2 — невычет по модулю 13, ибо 26 == — 1 (mod 13).
Однако, если исследуемые числа более или менее большие, этот
критерий становится полностью непригодным вследствие громозд-
громоздкости вычислений.
106 Раздел IV (пп. 107-110)
Исследования относительно простых чисел, по которым
заданные числа являются вычетами или невычетами
107
Итак, для заданного модуля совсем легко указать все те числа,
которые являются для него вычетами или невычетами. Действи-
Действительно, если заданный модуль = тг то нужно только найти ква-
квадраты чисел, не превосходящих половины т, или даже только
числа, сравнимые по модулю т с этими квадратами (практически
существуют еще более удобные методы), и тогда все числа, срав-
сравнимые с каким-нибудь из полученных чисел по модулю т, будут
вычетами, а все числа, не сравнимые ни с одним из них, —не-
—невычетами. Однако обратная задача: если задано некоторое число,
определить все те числа, по которым оно является вычетом или
невычетом,— значительно сложнее. Этой задачей, от решения которой
зависит и решение проблемы, поставленной в предыдущем разделе,
мы будем теперь заниматься и начнем при этом с простейших
случаев.
Вычет—1
108
Теорема. Число — 1 является квадратичным вычетом по всем про-
простым числам вида An -\- 1 и невычетом по всем простым числам
вида An + 3.
Пример. —1 является вычетом чисел 5, 13,17, 29, 37, 41, 53,61,
73, 89, 97,... и сравнимо соответственно с квадратами чисел 2,
5, 4, 12, 6, 9, 23, 11, 27, 34, 22, . . . ; и напротив, —1 является
невычетом чисел 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83, ...
Мы уже упоминали об этой теореме в п. 64. Доказательство
же легко получается из п. 106. Действительно, для про того числа
вида Ап-\-1 имеет место (—1Jпе=1, а для простого числа вида
An + 3 будет (—1Jп~1^ — 1. Это доказательство совпадает с до-
доказательством, приведенным в вышеупомянутом месте. Однако вслед-
вследствие красоты и полезности теоремы не будет лишним доказать
ее еще другим способом.
Вычет -1 107
109
Совокупность всех вычетов простого числа р, меньших р, за исклю-
исключением вычета 0, мы обозначим буквой С. Так как число этих выче-
вычетов всегда равно (р — 1)/2, оно, очевидно, будет четным, если р
имеет вид 4п + 1, и нечетным* если р имеет вид 4п + 3. Аналогично
п. 77, где речь шла о любых числах, мы будем называть ассоциирован-
ассоциированными те вычеты, произведение которых =1 (mod/?); действительно;
если г есть вычет, то и 1/г, очевидно, будет вычетом по модулю /?.
Так как один и тот же вычет не может иметь в С других ассоцииро-
ассоциированных вычетов, ясно, что все вычеты из С могут быть разбиты на
классы, каждый из которых содержит два ассоциированных вычета.
Далее, ясно, что если нет вычетов, ассоциированных с самими со-
собой, т. е. если каждый класс содержит два неравных вычета, то
число всех вычетов должно быть равно удвоенному числу всех клас-
классов. Если же имеются вычеты, ассоциированные сами с собой, т. е.
если имеются классы, содержащие только один вычет, или, если
такое выражение больше нравится, содержащие этот один вычет
дважды, то, полагая число таких классов равным а, а число осталь-
остальных классов равным Ь, мы получим, что число всех вычетов в С рав-
равно а + 2Ь. Поэтому, если р имеет вид in + 1, то а четно; если же р
имеет вид in + 3, то а нечетно. Но среди чисел, меньших /?, ника-
никакие, кроме 1 и р — 1, не могут быть ассоциированы сами с собой
(ср. п. 77), а 1, очевидно, всегда есть вычет. Поэтому р — 1 (или,
что то же самое, — 1) в первом случае должно быть вычетом, а во
втором невычетом, ибо иначе в первом случае имело бы место а = 1,
а во втором а = 2, что невозможно.
110
Этим доказательством мы также обязаны Эйлеру, который
дал и первое доказательство этой теоремы вообще (ср. «Opusc. Ana-
lyt.», Т. I, p. 135), Легко заметить, что оно базируется на принци-
принципах, подобных тем, на которых основано наше второе доказательство
теоремы Вильсона в п. 77. Если же опираться на эту теорему,
то доказательство можно провести еще проще. Среди чисел 1, 2,
108 Раздел IV (пп. 111-113)
3, ..., р — 1 имеется (р —1)/2 квадратичных вычетов по модулю р и
столько же невычетов. Поэтому количество невычетов четно, если
р имеет вид 4^+1, и нечетно, если р имеет вид 4тг+3. Таким обра-
зом, произведение всех чисел 1, 2, 3,..., р — 1 в первом случае явля-
является вычетом, а во втором — невычетом (п. 99). Но это произведение
всегда =—1 (mod р); следовательно, —1 в первом случае есть вы-
вычет, а во втором — невычет.
111
Из сказанного следует, что если г есть вычет простого числа вида
4п + 1, то и —г будет вычетом этого простого числа, и наоборот,
все невычеты такого числа, взятые с отрицательным знаком, оста-
остаются невычетами *. Обратное имеет место в случае простых чисел
вида 4п + 3, вычеты которых при перемене знака превращаются
в невычеты, и наоборот. (Ср. п. 98.)
Наконец, из всего сказанного легко получается следующее общеа
правило: — 1 является вычетом всех чисел, которые не делятся ни
на 4, ни на какое-либо простое число вида in + 3, и невычетом всех
остальных чисел (ср. пп. 103 и 105).
Вычеты -\-2 и —2
112
Теперь мы переходим к вычетам +2 и —2.
Если мы соберем в таблице 2 все простые числа, для которых +2
является вычетом, то получим следующие: 7, 17, 23, 31, 41, 47, 71,
73, 79, 89, 97. Легко заметить, что среди них нет чисел вида 8п + 3
и 8п + 5. Поэтому мы должны постараться строго обосновать это
индуктивное заключение.
Прежде всего, заметим, что каждое составное число вида 8п + 3
или 8п + 5 обязательно содержит простой сомножитель одного из
этих видов; действительно, только из простых чисел вида 8п + 1 и
* Таким образом, если мы говорим о некотором числе как о вычете или не-
невычете числа вида 4/г + 1, то мы можем просто отбрасывать знак рассматрива-
рассматриваемого числа или же снабжать его двойным знаком -4-.
Вычеты +2 и -2 109
8п + 7, очевидно, не могут быть составлены другие числа, кроме
имеющих вид 8п + 1 и 8 я + 7. Поэтому, если наше индуктивное
заключение правильно, то вообще не должно быть чисел вида 8п +3
или 8 тг+ 5, для которых +2 было бы вычетом. Как легко прове-
проверить, среди чисел до 100 действительно нет чисел указанного вида,
для которых +2 было бы вычетом. Если же мы предположим, что
по другую сторону этой границы такие числа есть, то пусть наимень-
наименьшее из них равно ?; таким образом, t имеет вид или 8п + 3, или 8п +5,
и +2 является для него вычетом, в то время как для всех меньших
чисел такого вида — невычетом. Если положить 2 = a2 (mod t), то
всегда можно считать, что а нечетно и меньше t (действительно, а
обладает по меньшей мере двумя положительными значениями, мень-
меньшими t, сумма которых равна t, и из которых поэтому одно четно,
а другое нечетно (ср. пп. 104 и 105)). Если же это условие выполне-
выполнено, и а2 = 2 + tu, или tu = а2 — 2, то а2 будет иметь вид 8/г + 1,
и tu, таким образом,— вид 8п — 1, и потому и будет или вида 8п +3,
или вида 8 п + 5, в зависимости от того, имеет ли t второй или
первый из этих видов. Из равенства а2 = 2 + tu следует, что 2 =
=а2 (mod и), т. е. 2 является также вычетом числа и. Но легко видеть,
что и < t, и потому t, вопреки нашему предположению, не является
наименьшим среди чисел, для которых наше индуктивное заключе-
заключение неверно. Отсюда, очевидно, следует, что то, что мы установили
индуктивным путем, действительно всегда справедливо.
Если мы скомбинируем это с теоремами, найденными в п. 111,
то получим следующие теоремы.
I. Для всех простых чисел вида 8п + 3 число +2 есть невычет,
а —2 — вычет.
II. Для всех простых чисел вида 8п + 5 как +2, так и —2 явля-
являются невычетами.
ИЗ
Аналогичным образом из таблицы 2 мы находим * следующие
простые числа, для которых —2 является квадратичным вычетом:
3, 11, 17, 19, 41, 43, 59, 67, 73, 83, 89, 97. Так как среди них нет
* Рассматривая — 2 как произведение чисел +2 и —1 (ср. п. 111).
110 Раздел IV (пп. 1Ц-115)
чисел вида 8п + 5 и 8п + 7, исследуем, справедливо ли это индук-
индуктивное заключение вообще. Подобно тому, как в предыдущем
можно показать, что каждое составное число вида 8п + 5 или
8п + 7 содержит простой сомножитель вида 8п + 5 или 8п + 7,
так что, если наше индуктивное заключение вообще справедливо,
то —2 не может быть вычетом никаких чисел вида 8тг+5 или 8п + 7.
Если же предположить, что такие числа существуют, то пусть наи-
наименьшее из них равно t, и —2 = а2 — tu. При этом, если, как и выше,
предположить, что а нечетно и меньше, чем t, то и будет иметь вид 8п +
+ 5 или 8п + 7, в зависимости от того, имеет ли t вид 8п + 7 или
8п + 5. Но из того, что а2 + 2 = ?и и а < t, легко вывести, что и
тоже меньше t. Наконец, —2 будет также и вычетом числа и, т. е.
t, в противоречие с предположением, не является наименьшим чис-
числом, для которого наше индуктивное заключение неверно. Итак,
—2 обязательно является невычетом всех чисел вида 8п + 5 и
8п + 7.
Если связать это с теоремой п. 111, то получаются следующие
теоремы.
I. Для всех простых чисел вида 8п + 5 как —2, так и +2 явля-
являются невычетами, что мы уже доказали в предыдущем пункте.
П. Для всех простых чисел вида 8п + 7 число —2 является невы-
невычетом, а +2 — вычетом.
Впрочем, в каждом из двух доказательств мы могли брать для а
также и четное значение; тогда мы должны были бы различать слу-
случаи, когда а имеет вид An + 2 или in. Рассуждения протекают
точно так же, как и выше, и не вызывают никаких трудностей.
114
Остается еще один случай, а именно тот, когда простое число
имеет вид 8п + 1. Но для него прежние методы оказываются не-
непригодными, а нужен специальный искусственный прием.
Если для модуля, являющегося простым числом вида 8п + 1, не-
некоторый первообразный корень равен а, то (п. 62) аАп == — 1 (mod 8n-\-l),
а это сравнение может быть также представлено в виде (а2п + IJ =
== 2а2п (mod 8гс + 1), или в виде (а2п — IJ == — 2а2п. Отсюда следует,
Вычеты +2 и -2 111
что как 2а2п, так и —2а2п являются вычетами по модулю 8га+ 1.
Но так как а2п есть не делящийся на модуль квадрат, то, очевидног
+ 2 и —2 суть вычеты (п. 98)*.
115
Не будет бесполезным добавить и другое доказательство этой тео-
теоремы, которое относится к предыдущему так же, как второе доказа-
доказательство (п. 109) теоремы из п. 108— к первому (п. 108). Разбираю-
Разбирающиеся в этих вопросах тогда легче поймут, что и в том, и в другом
случае оба доказательства не настолько отличаются одно от друго-
другого, как это может показаться на первый взгляд.
I. Для любого простого модуля вида 4#г + 1 среди чисел 1, 2,
3,..., 4т, которые меньше модуля, имеется т чисел, сравнимых
с биквадратами, а остальные Зт — с биквадратами несравнимы.
Хотя это легко можно вывести из соображений предыдущего
раздела, но и без этого доказательство не сложно. Именно, мы уже
доказали, что для такого модуля —1 всегда есть квадратичный
вычет. Если, таким образом, /2 = —1, то для любого не делящегося
на модуль числа z биквадраты четырех чисел +z, —z, -\-fz, —fz
(которые, как легко видеть, не сравнимы один с другим) будут срав-
сравнимы между собой. Далее, ясно, что биквадрат какого-нибудь числа,
не сравнимого ни с одним из этих четырех чисел, не может быть
сравним с их биквадратом (действительно, в противном случае срав-
сравнение четвертой степени #4 ^ z4, в противоречие с п. 43, имело бы
более четырех корней). Отсюда легко следует, что числа 1, 2, 3,...
..., 4иг порождают только т несравнимых биквадратов, с которыми сре-
среди этих чисел имеется т сравнимых, в то время как остальные не
могут быть сравнимыми с биквадратами.
П. По простому модулю вида 8п + 1 число —1 сравнимо с неко-
некоторым биквадратом (—1 является биквадратичным вычетом этого
простого числа).
* Короче доказательство проводится так: имеет место (а3п — апJ =
= 2 + (а*п + 1) (а2" - 2) и (а3" + ап)* = - 2 + (а4п + 1) (а2п + 2). Поэтому
/2 = ± (а3п -an)Hf-2E± (азп + ап) (mod 8л + 1)
112 Раздел IV (пп. 116-117)
Именно, число всех биквадратичных вычетов, меньших, чем8тг + 1
(за исключением нуля), равно 2тг, т. е. четно. Далее, легко пока-
показать, что если г есть биквадратичный вычет числа 8п +1, то таковым
будет и значение выражения! (mod 8п + 1). Поэтому все биквадра-
тичные вычеты могут быть разбиты на классы, подобно тому, как
мы это сделали в п. 109 для квадратичных вычетов. Остальная часть
доказательства может быть теперь проведена совершенно тем же
способом, как и там.
III. Пусть теперь g4 = — 1, и h есть значение выражения
— (mod8rc + l). Тогда (так как gh = 1)
о
(g±hf = g* + h2± 2gh = g2 + h2±2.
Ho gA == — 1, откуда — h? == g^h2 == g2, т. e. g2 + h2 == 0 и (g + hJ ^
^ + 2, и потому как +2, так и —2 являются квадратичными
вычетами по модулю 8п -\- 1.
116
Наконец, из предыдущего легко выводится следующее общее
правило:
+ 2 является вычетом каждого числа, которое не делится на
4 и на любое простое число вида 8п + 3 или 8п + 5, и невычетом
всех остальных (например, всех чисел вида 8п -\- 3 или 8п + 5,
будь они простыми или составными).
— 2 является вычетом каждого числа, которое не делится на
4 и на любое простое число вида 8п + 5 или 8п -\-7, и невычетом
всех остальных.
Эти изящные теоремы были уже известны проницательному
Ферма, «Op. Mathem))., p. 168. Однако он нигде не сообщил дока-
доказательства, о котором утверждал, что оно у него имеется. Позже
доказательство все время безуспешно искал Эйлер; впервые строгое
доказательство дал Лагранж («Nouv. Mem. de I'Acad. de Berlin»,
1775, p, 3?9, 351). Оно, по-видимому, не было известно Эйлеру,
когда он опубликовал свою работу, помещенную в «Opusc. Analyt.»,
Т. /, р. 259.
Вычеты +3 и —3 113
Вычеты +3 и —3
117
Теперь мы переходим к вычетам +3 и —3, причем начинаем
со второго.
Из таблицы 2 мы находим следующие простые числа, для кото-
которых —3 является вычетом: 3, 7, 13, 19, 31, 37, 43, 61, 67, 73, 79, 97.
Среди них нет ни одного числа вида 6/2 + 5. А то, что и за пределами
границы таблицы нет простых чисел такого вида, для которых —3
является вычетом, мы докажем следующим образом. Прежде всего,
ясно, что каждое составное число вида 6/2 + 5 обязательно содержит
простой сомножитель такого же вида. Поэтому до той границы, до
которой нет простых чисел вида 6/2 + 5, имеющих —3 вычетом,
нет также и составных чисел того же вида с тем же свойством. Если
предположить, что за пределами нашей таблицы такие числа суще-
существуют, то пусть наименьшее из них равно t и —3 = а2 — tu. Тогда,
если считать, что а взято четным и меньшим чем t, будет иметь ме-
место u<t и —3 будет вычетом для и. Но если а имеет вид 6/2 it 2,
то tu будет иметь вид 6/2+1, и потому и — вид 6/г + 5. Это,
однако, невозможно, так как по нашему предположению t есть наи-
наименьшее число, для которого наше индуктивное предположе-
предположение неверно. Если же а имеет вид 6/2, то tu будет иметь вид
Збд + 3 и потому tu/3 — вид 12п + 1, а и/3, — вид 6п + 5. Но
ясно, что —3 является вычетом дляи/3 и -^< t. Это, однако, невоз-
невозможно. Поэтому ясно, что —3 не может быть вычетом никакого
числа вида 6/2 + 5.
Так как каждое число вида 6/2 + 5 представляется обязательно
или в виде 12/2 + 5, или в виде 12/г + 11, а потому в первом случае
может быть также записано в виде 4/2 + 1, а во втором — в виде
in + 3, мы имеем следующие теоремы.
I. Для каждого простого числа вида 12/2 + 5 как —3, так и +3
являются невычетами.
П. Для каждого простого числа вида 12/2 + 11 число —3 является
невычетом, а число +3 — вычетом.
114 Раздел IV (пп. 118-121)
118
В качестве чисел, имеющих +3 вычетом, в таблице 2 находятся
следующие: 3, И, 13, 23, 37, 47, 59, 61, 71, 73, 83, 97; среди них
нет ни одного числа вида \2п + 5 или 12лг + 7. То, что вообще
нет чисел вида 12п + 5, 12лг -(- 7, для которых +3 является выче-
вычетом, может быть доказано точно таким же образом, как в пп. 112Г
113, 117, и потому мы не будем на этом останавливаться. В соедине-
соединении с п. 111 мы получаем следующие теоремы.
I. Для каждого простого числа вида 12п +5 как +3, так и —3
являются невычетами (что мы нашли уже в предыдущем пункте).
П. Для каждого простого числа вида 12п + 7 число +3 является
невычетом, а число —3 — вычетом.
119
Таким путем, однако, ничего нельзя узнать относительно чисел
вида 12п + 1, которые поэтому требуют для своего рассмотрения
специальных приемов. Правда, индуктивным способом легко уста-
установить, что +3 и —3 являются вычетами всех простых чисел такого
вида. Кроме того, очевидно, нужно только доказать, что —3 явля-
является вычетом всех таких чисел, потому что тогда и +3 обязательно
будет вычетом (п. 111). Мы, однако, докажем более общий факт,
а именно, что —3 есть вычет каждого простого числа вида Зп -\- 1.
Пусть р — такое простое число, и а — число, принадлежащее по
модулю р показателю 3 (то, что такое число существует, вытекает
из п. 54, так как 3 есть делитель числа р — 1).Тогда а3=1 (mod p),
т. е. а3 — 1 или (а2 -\- а -\- 1)(а — 1) делится на р. Однако, очевид-
очевидно, что не может быть а = 1 (mod p), так как 1 принадлежит пока-
показателю 1, и потому не а — 1, а обязательно а2 + а + 1 делится на
р, а, следовательно, делится и 4а2 + 4а + 4, т. е. Bа + IJ =
= —3 (mod р), и значит —3 есть вычет по модулю р.
Между прочим ясно, что это доказательство (которое не опира-
опирается на изложенное выше) охватывает также и простые числа вида
1272 + 7, которые мы уже рассмотрели в предыдущем пункте.
Можно еще заметить, что это исследование может быть проведено
также методами, аналогичными тем, что применялись в пп. 109,
115, но ради краткости мы не будем в это вдаваться.
Вычеты +5 и —5 115
120
Из предыдущего легко получаются следующие теоремы (ср. пп.
102, 103, 105).
I.—3 является вычетом всех чисел, которые не делятся ни на 8Г
ни на 9 и ни на какое простое число вида 6п -\- 5, и невычетом всех
остальных чисел.
II. +3 является вычетом всех чисел, которые не делятся ни на Аг
ни на 9, ни на какое простое число вида 12п + 5 или \2п -f- 7, и не-
невычетом всех остальных чисел.
Специально можно отметить следующий частный случай..
— 3 является вычетом всех простых чисел вида Зп + 1, или, что
то же самое, всех простых чисел, которые являются вычетами числа
3, и является невычетом всех простых чисел вида 6п + 5, или, за
исключением числа 2, всех простых чисел вида Ъп -\- 2, т. е. всех, ко-
которые являются невычетами числа 3. Легко убедиться, что все осталь-
остальные случаи вытекают отсюда.
Теоремы, касающиеся вычетов +3 и —3, были уже известны
Ферм a, «Opera Wallisii», Т. II, р. 857, хотя доказательства впер-
впервые дал Эйлер, «Сотт Nov. Petr.,» Т. VIII, р. 105 и ел. Поэтому
особенно удивительно, что доказательства теорем относительно вы-
вычетов + 2 и — 2, которые основываются на подобных же прин-
принципах, не поддались его усилиям (ср. также сочинение Л а г р а н-
ж a, «Nouv. Mem. de ГAc. de Berlin», p. 352).
Вычеты +5 и —5
121
Индуктивным путем мы находим, что + 5 не является вычетом
никакого нечетного числа вида Ъп + 2 или Ъп + 3, т. е. никакого
нечетного числа, которое есть невычет числа 5. То, что это правило
не имеет исключений, доказывается так. Пусть наименьшее числоТ
составляющее исключение из этого правила, если такие вообще су-
существуют, равно t, так что оно есть невычет числа 5, в то время как
5 является его вычетом. Пусть, далее, а2 = 5 + tu, где а четно ж
меньше, чем t. Тогда и будет нечетным и меньшим, чем t, a +5 бу-
будет вычетом по модулю и. Если теперь а не делится на 5, то это будет
116 Раздел IV (пп. 122-123)
иметь место и для щ но очевидно, что tu есть вычет числа 5, а так как
t является невычетом по модулю 5, то и тоже будет невычетом. Таким
образом, существует нечетный невычет числа 5, для которого + 5
является вычетом, и которое меньше, чем t. Но это находится в про-
противоречии с нашим предположением. Если же а делится на 5, то пола-
полагая а = 5 Ъ и и = 5v, мы получим tv== — 1=4 (mod 5), т. е. tv бу-
будет вычетом числа 5. Далее доказательство проводится точно так же,
как и в первом случае.
122
Итак, для всех простых чисел, которые одновременно являются
мевычетами числа 5 и имеют вид 4тг + 1, т. е. для всех простых чи-
чисел вида 20тг -j~ 13 или 20тг + 17 числа + 5 и —5 являются невыче-
невычетами; для всех же простых чисел вида 20п + 3 или 20п + 7 число +5
есть невычет, а — 5 — вычет.
Совершенно аналогичным способом можно показать, что —5
является невычетом всех простых чисел вида 20п + 11, 20п +13,
20п + 17, 20п + 19, а отсюда, как легко видеть, следует, что +5
есть вычет всех простых чисел вида 20п + 11 или 20п + 19 и невы-
невычет всех простых чисел вида 20п + 13 или 20п + 17. И так как каж-
каждое простое число, кроме 2 и 5 (для которых-^ 5 есть вычет), пред-
представляется в одном из видов 20п + 1, 3, 7, 9, 11, 13, 17,19, то мы, оче-
очевидно, уже можем решить наш вопрос относительно всех простых
чисел, кроме тех, которые имеют вид 20п + 1 или 20п + 9.
123
Индуктивным путем легко находится, что + 5 и — 5 являются
вычетами всех простых чисел вида 20п + 1 или 20п + 9. Если бы это
было верно вообще, мы имели бы изящную теорему, именно, что + 5
есть вычет всех простых чисел, которые являются вычетами числа
5 (так как эти последние представляются в одном из видов Ъп + 1
или Ъп + 4, т. е. в одном из видов 20гс + 1, 9, 11, 19, а для третьего
и четвертого из этих видов этот факт уже доказан), и невычетом всех
нечетных простых чисел, которые являются невычетами числа 5,
Вычеты +5 и —5 117
что мы уже доказали выше. Ясно, что этой теоремы доста-
достаточно, чтобы уметь решать, является ли +5 (а тем самым и — 5^
если рассматривать его как произведение +5 и —1) вычетом или
невычетом любого заданного числа. Наконец, можно было бы отме-
отметить аналогичность этой теоремы той, которую лш вывели в п. 120
относительно вычета— 3.
Однако доказать это индуктивное заключение не очень легко.
Если задано некоторое простое число вида 20п + 1 или, более общо,
вида 5гс + 1, то с вопросом можно покончить подобным же образом,
как в пп. 114, 119. Именно, если а — какое-нибудь число, принад-
принадлежащее по модулю Ъп -f- 1 показателю 5 (то, что такое существует,
вытекает из предыдущего раздела), то аъ = 1, или (а — 1)(а4 + а3 +
г а2 + а + 1) — 0 (mod Ъп + 1). Но так как не может быть а = 1,
т. е. а — 1 = 0, то обязательно а4 + а3 + а2 + а + 1 = 0. Поэто-
Поэтому также 4(а4 + а* + а2 + а + 1) = Bа2 + а + 2J - 5а2 е= 0, т. е.
5а2 есть вычет числа Ъп + 1, а значит и 5 — вычет этого числа, по-
потому что а2 есть вычет, не делящийся на Ъп + 1 (действительно, «
не делится на Ъп + 1 вследствие того, что а5= 1).
Случай же, когда дано простое число вида Ъп + 4, требует более
глубоких вспомогательных средств. Но так как теоремы, при помо-
помощи которых решается этот вопрос, в дальнейшем будут изложены
в более общем виде, мы коснемся их здесь лишь коротко.
I. Если р — простое число, и Ъ — его заданный квадратичный
невычет, то значение выражения
4
А_
(в котором при раскрытии скобок, как легко видеть, иррациональ-
иррациональность пропадает) делится на р при любом х, в том числе иприя =j0.
Именно, при первом взгляде на коэффициенты, которые получа-
получаются при разложении А, видно, что все члены от второго до пред-
предпоследнего включительно делятся на р, и потому
р-1
А = 2(р + l){xv + хЪ 2 ) (mod p).
Но так как Ъ есть невычет по модулю р, то 5(р~ 1)/2ееее —\ (mod p)-
(п. 106); в то же время хр всегда = .х (согласно предыдущему разделу);
поэтому А =0.
118 Раздел IV (п. 124)
II. Сравнение А = 0 (mod р) имеет относительно х степень р, и
все числа 0, 1, 2, ...,/? — 1 являются его корнями. Если теперь е
есть делитель числа р + 1, то выражение
Уь
(которое мы обозначим через В) после раскрытия скобок будет сво-
свободно от иррациональности, относительно х будет иметь степень
е — 1, и, как известно из первых элементов анализа, А будет (как
многочлен) делиться на В, Теперь я утверждаю, что имеется е —1
значений х, которые будучи подставлены в В, делают В делящимся
на р. Именно, если положить А = ВС, то С будет иметь относительно
х степень р —е + 1, и потому сравнение С = 0 (mod p) обладает не
более чем р — е + 1 корнями. Отсюда легко следует, что все
остальные е — 1 чисел из ряда 0, 1, 2,3, ..., р — 1 являются кор-
корнями сравнения В = 0.
III. Предположим теперь, что р имеет вид 5п + 4, е = 5, Ъ —
невычет по модулю /?, и число а определено так, что выражение
(а + Yhf -(а- УЪ)Ъ
Уь
делится на р. Но это выражение равно
10а4 + 20а26 + 2Ь2 = 2 [(Ь + 5а2J — 20а4],
и потому также (Ъ -\- 5а2J — 20а4 делится на р, т. е. 20а4 есть вычет
по модулю р. Так как, однако, 4а4 есть вычет, не делящийся на р
(действительно, легко видеть, что а не делится на /?), то также и
5 будет вычетом по модулю /?, что и требовалось доказать.
Отсюда следует, что указанная в начале этого пункта теорема
вообще верна.
Заметим еще, что доказательством для обоих случаев мы обязаны
Лагранжу, «Mem. de Г Ac. de Berlin», 1775, p. 352 и ел.
О вычетах ±7 119
О вычетах -4-7
124
Подобным же образом доказывается, что —7 есть невычет каж-
каждого числа, которое является невычетом числа 7.
По индукции же можно заключить, что —7 есть вычет каждого
числа, которое является вычетом числа 7.
Однако до сих пор это никем не было строго доказано. Впрочем,
для тех вычетов числа 7, которые имеют вид 4гс — 1, доказательство
просто. Действительно, уже достаточно хорошо известным из пре-
предыдущего путем можно показать, что +7 всегда невычет, а потому
— 7 — вычет таких простых чисел. Но это дает слишком мало, так
как остальные случаи этому методу не поддаются. Лишь еще один
случай можно исследовать способом, подобным использованному
в пп. 119 и 123. Именно, если р есть простое число вида In -f- 1,
и а — число, принадлежащее по модулю р показателю 7, то легко
видеть, что выражение
4 l^Zi]' = Bа3 + а2 — а — 2J + 7 (а2 + аJ
всегда делится на р, и потому — 7(а2 + яJ есть вычет по модулю р.
Но (а2 + яJ, будучи квадратом, является вычетом числа р и при-
притом не делится на р\ действительно, так как а по предположению
принадлежит показателю 7, оно не может быть ни = О, ни = 1 (mod p),
т. е. на р не делятся ни а, ни а + 1, а потому и квадрат (а + 1Jя2.
Таким образом, также и 7 является, очевидно, вычетом числа р,
что и нужно было доказать. Впрочем, и это доказательство впервые
было найдено Лагранжем в сочинении, упомянутом в конце
п. 123. Ниже, в разделе VII, мы докажем, что вообще выражение
А(хр— 1)/(х — 1) всегда может быть приведено к виду X2ztpY2
(верхний знак нужно брать, когда р — простое число вида 4гс •+ 1,
а нижний — когда оно простое число вида in + 3), где X и Y суть
целые рациональные функции отх. Лагранж для значений р,
превышающих 7, этого разложения не провел (ср. указанное в п.
123 сочинение, стр. 352).
120 Раздел IV (пп. 125-127)
Подготовка к общему исследованию
125
Так как применявшиеся до сих пор методы оказываются недоста-
недостаточными для проведения общего доказательства, пора изложить
другой метод, у которого этого недостатка нет. Мы начнем с теоремы,
которая долго не поддавалась нашим усилиям доказать ее, хотя
справедливость ее с первого взгляда кажется настолько очевидной,
что некоторые даже не признавали необходимости ее доказатель-
доказательства. Эта теорема состоит в следующем. Любое число, за исключе-
исключением положительных квадратов, является невычетом некоторого про-
простого числа. Так как, однако, мы будем пользоваться этой теоремой
только как вспомогательным средством для доказательства других
предложений, мы разберем только те случаи, которые будут нужны
для этой цели. Справедливость остальных случаев позднее получит-
получится сама собой. Сейчас мы докажем, что каждое простое число вида
4п + 1, взятое как положительным, так и отрицательным *, явля-
является невычетом какого-нибудь простого числа, и притом (если задан-
заданное число > 5) такого, которое меньше, чем оно само.
Если сначала задано простое число р вида 4тг+1, которое
нужно брать отрицательным (мы будем считать, что р^>П; —13
является невычетом числа 3, а —17 — невычетом числа 5), то пусть
2а — первое четное число, большее, чем Ур\ тогда легко видеть,
что Аа2<^2р или 4а2 — р<Ср. Но 4а2 — р имеет вид An -{- 3, а + р
есть квадратичный вычет числа 4а2 — р (так как р = 4а2 (mod 4а2— р))»
Поэтому, если 4а2 — р есть простое число, то —р будет его не-
невычетом; если же оно не простое, то хотя бы один из его про-
простых сомножителей обязательно имоет вид 4тг -(- 3, и так как -\- р
есть вычет также и этого сомножителя, —р будет его невычетом.
Относительно простых чисел, которые должны браться положи-
положительными, мы будем различать два случая. Пусть сначала р — про-
простое число вида 8гс + 5. Если а е.ть любое положительное число,
которое < Yv/2, то 8п + 5—2а2 будет положительным числом
вида 8п + 5 или 8п -f- 3 (в зависимости от того, четно а или не-
* Разумеется, число +1 должно быть исключено.
Подготовка к общему исследованию 121
четно) и потому обязательно будет делиться на какое-нибудь про-
простое число вида 8п-\-3 или 8п + 5, ибо произведение любого коли-
количества чисел вида 8п + 1 и 8п + 7 не может иметь ни вида 8п + Зг
ни вида 8п + 5. Если указанное простое число равно q, то 8п -f-
-f- 5 = 2а2 (mod #). Но 2 является невычетом ч^сла </ (п. 112),
а потому невычетами будут также 2а2 и 8п -\- 5 *.
126
Однако то, что каждое простое число вида 8п-\-1, взятое поло-
положительным, является невычетом какого-нибудь простого числа,
меньшего, чем оно само, уже не может быть доказано такими про-
простыми средствами. Но так как эта истина имеет для нас величайшее
значение, мы не можем обойтись без строгого ее доказательства,
хотя оно довольно сложно. Мы начнем со следующей леммы.
Лемма. Если имеется два ряда чисел
(I) А, В, С,...
(II) А\ В\ С',...
(одинаково ли количество членов в обоих рядах или нет — несу-
несущественно) с тем свойством, что если р обозначает простое число
или степень простого числа и входит делителем хотя бы в один
из членов второго ряда, то в первом ряду делятся на р по крайней
мере столько же членов, сколько и во втором, то я утверждаю, что
произведение всех чисел (I) делится на произведение всех чисел (II).
Пример. Если (I) состоит из чисел 12, 18, 45, а (II)—из чисел
3, 4, 5, 6, 9, то на числа 2, 4, 3, 9, 5 в (I) делятся соответственно
2, 1, 3, 2, 1 членов, а в (II) — соответственно 2, 1, 3, 1, 1 членов.
Произведение же всех членов из (I), равное 9720, делится на произ-
произведение всех членов из (II), именно, на 3240.
Доказательство. Если произведение всех членов (I) равно Q>
а произведение всех членов (II) равно Q', то очевидно, что каждое
* П. 98. Именно, очевидно, что а2 является вычетом по модулю q, не деля-
делящимся на q, так как в противном случае на с целилось бы и простое число рг
что невозможно.
122 Раздел IV (пп. 127-128)
простое число, которое является делителем Q\ будет также дели-
делителем Q. Покажем теперь, что каждый простой сомножитель числа
Q' входит в Q по меньшей мере в той же степени, что и в Q'.
Если р — такой делитель, и в ряде (I) а членов делятся на /?,
? членов — на /?2, с членов — на р* и т. д., а буквы а', V, с\ . . .
имеют аналогичное значение для ряда (II), то легко видеть, что р
имеет в Q степень а + Ъ + с -f- . • • , ав^' — степень а' -f- Ъ' + с' + . . .
Но по предположению Q' не больше, чем а, V не больше, чем 6,
и т. д., и потому, очевидно, а' + Ъ' + с' + . . . не больше чем а + & +
-f с . . . Так как, таким образом, ни одно простое число не может
входить в Q' в степени, большей, чем в Q, то Q делится на Q' (п. 17)
127
Лемма. В прогрессии 1, 2, 3, 4,..., п па какое-нибудь число h
может делиться не больше членов, чем в состоящем из стольких же
членов ряде а, а + 1, а + 2, . . . , а-}-п — 1.
Именно, без труда видно, что если п есть кратность числа /г,
то в каждой из прогрессий на h делятся n/h членов. Если же это
не так, то пусть п = eh-\- f9 где /<C^i тогда в первом ряде на h
будут делиться е членов, а во втором или столько же, или е -\- 1
членов.
В качестве дополнения отсюда следует теорема, известная из
теории фигурных чисел, но, если мы не ошибаемся, прямо еще
никем не доказанная, именно, что
1 • 2• 3. .. п
всегда есть целое число.
Наконец, в более общем виде эту лемму можно было бы выска-
высказать так.
В прогрессии а, а-f-l, а -р 2, . . . , а -|- тг — 1 существует по мень-
меньшей мере столько же чисел, сравнимых с заданным числом г по
модулю /г, сколько среди чисел 1, 2, 3, . . . , п имеется делящихся
на h.
Подготовка к общему исследованию 123
128
Теорема. Если а — какое-нибудь число вида 8п + 1, р — какое-
нибудь взаимно простое с а число, по которому -j-a является выче-
вычетом, и, наконец, т — произвольное число, то я утверждаю, что в
прогрессии
11 1
а, у (а — 1), 2 (а— 4), у (а — 9),. . ., 2 (а — т2) или -^ (а — т2),
в зависимости от того, четно т или нечетно, существует по мень-
меньшей мере столько же членов, делящихся на р, сколько и в прогрессии.
1,2,3,. ..,2т+1.
Первую прогрессию мы обозначим через (I), вторую — через (II).
Доказательство. I. Если р = 2, то в (I) на р будут делиться
Бее члены, за исключением первого, т. е. т членов; столько же
членов будет делиться на р и в (II).
П. Если р — нечетное число, или удвоенное, или учетверенное
нечетное число, и а == г2 (mod р), то в прогрессии —т, —(т—1).
— (т — 2), . . . , + т (в которой столько же членов, сколько в (II),
и которую мы обозначим через (Ш)) будет содержаться по меньшей
мере столько же членов, сравнимых с г по модулю р, сколько
в ряде (И) имеется членов, делящихся на р (согласно предыдущему
пункту). Среди первых, однако, не может найтись никаких двух,
которые отличались бы только знаком, но не абсолютной величиной*.
В то же время для каждого из них имеется соответствующий член
в ряде (I), который делится на р. Именно, если -^гЪ — какой-нибудь
член ряда (Ш), сравнимый с г по модулю р, то а — Ъ2 будет де-
делиться на р. Если теперь Ъ четно, то член 2 (а — Ь2) ряда (I) делит-
делится на р. Если же Ъ нечетно, то на р делится член (а — Ъ2)/2\ дей-
действительно (а — Ь2)/р, очевидно, будет четным целым числом, так
как а — Ъ2 делится на 8, а р — самое большее на 4 (в самом деле
л, по предположению, имеет вид 8п + 1, а г2, будучи квадратом
нечетного числа, имеет тот же самый вид, и следовательно, их раз-
* Именно, если бы имело место r~—f~+f(modp),To яа.р делилось бы число
2/, а значит (так как /2 = a(mod /?),и число 2а. Это возможно, однако, только
тогда, когда р = 2, так как по предположению а взаимно просто с р. Случай же
р = 2 мы уже рассмотрели отдельно.
124 Раздел IV (пп. 129-130)
ность имеет вид 8п). Отсюда мы заключаем, наконец, что в ряде (I)
делятся на р по крайней мере столько членов, сколько в ряде (III)
имеется чисел, сравнимых с г по модулю р, т, е. столько же или
больше, чем количество членов в (II), делящихся на р.
III. Пусть р имеет вид 8п и а = г2 (mod 2p). (Действительно
легко видеть, что так как а, по предположению, есть вычет числа
р, оно будет вычетом и числа 2р). Тогда в ряде (III) будет по
меньшей мере столько же членов, сравнимых с г по модулю р>
сколько членов в (II) делится на р, и первые по абсолютной вели-
величине все будут различны. Но каждому из них в ряде (I) будет
соответствовать член, делящийся на р. Действительно, если -\- Ъ
или —6 = г (mod/?), то Ъ2 = г2 (mod 2р) *, и потому член (а — б2)/2
делится на р. Тем самым в (I) существует по меньшей мере столько
же членов, делящихся на р, сколько в (II).
129
Теорема. Если а — простое число вида 8/2+1, то среди чисел,
меньших 2j/~а -\- 1, обязательно существует простое, по которому а
является невычетом.
Доказательство. Пусть, если это возможно, а есть вычет всех
простых чисел, которые меньше 2j/a"+l. Тогда легко видеть, что
а будет также вычетом и всех составных чисел, которые меньше-
2уа + 1 (в силу правил, по которым можно узнать, является ли
данное число вычетом или невычетом составного числа; п. 105). Если
наибольшее целое число, из тех, которые <^Va, равно т,то в
11 1
A) a,y(a —1), 2 (a —4), у (a —9), ... , 2(a — m2) или y(a —m2)
на любое число, меньшее 2 У а + 1, будет делиться по крайней мере
столько же членов, сколько и в ряде
(II) 1,2,3,4,... , 2т+1
(согласно предыдущему пункту).
* Именно, число Ь2 — г2 = (Ъ + г)(Ъ — г) состоит из двух сомножителей,
один из которых (по предположению) делится на р, а второй делится на 2 (так
как и&иг нечетны); тем самым Ъ2 — г2 делится на 2 р.
Формулировка фундаментальной теоремы 125
Но отсюда следует, что произведение всех членов ряда(I) делится
на произведение всех членов ряда (II) (п. 126). Первое же равно
или а (а — 1)(а — 4). . . (а — т2), или половине этого произведения
{в зависимости от того, четно т или нечетно). Поэтому произведе-
произведение а (а — 1)(а — 4)... (а — т2) очевидно делится на произведение
всех членов (II), а так как все эти члены взаимно просты с а, то
на их произведение будет делиться и первое произведение, если
отбросить от него сомножитель а. Но произведение всех членов (II)
зюжет быть представлено следующим образом:
(т + 1) [(т + IJ — 1] [(т + IJ — 4) . . . [(т + IJ — т2].
Поэтому
1 а — 1 а -— 4 а — т2
т + 1 (т + 1J—1 (т + 1J —4 (и? + IJ — т2
будет целым числом, хотя это есть произведение дробей, которые
меньше 1; действительно, так как У а обязательно должно быть
иррациональным, то т -|- 1 > У а и потому {т-{- 1J> а. Отсюда
следует, наконец, что наше предположение неверно.
Но так как а, очевидно, > 9, то 2~)/~а + 1 << а, и потому среди
лростых чисел, меньших а, существует такое, по которому а является
невычетом.
Индуктивным путем находится общая (фундаментальная)
теорема и делаются выводы из нее
130
После того как мы строго доказали, что каждое простое число
вида 4/2 + 1, взятое как положительным, так и отрицательным,
является невычетом некоторого простого числа, которое меньше
его самого, мы тотчас же переходим к более подробному и общему
сравнению простых чисел с точки зрения того, является ли одио
из них вычетом или невычетом другого.
Выше мы со всей строгостью доказали, что —3 и +5 являются
126 Раздел IV (пп. 131-132)
вычетами или невычетами всех простых чисел, которые суть соот-
соответственно вычеты или невычеты чисел 3 или 5.
Из рассмотрения нижеследующих чисел мы находим, что —7Г
-И, +13, +17, -19, -23, +29, -31, +37, +41, -43, -47,+53,
—59 и т. д. являются вычетами или невычетами всех простых чисел,
которые, взятые положительными, являются для указанных чисел
соответственно вычетами или невычетами. Это рассмотрение легко-
можно продолжить при помощи таблицы 2.
При некотором внимании каждый заметит, что из этих простых
чисел те, которые имеют вид 4/2 + 1, взяты с положительным зна-
знаком, а имеющие вид 4/2 + 3 — с отрицательным.
131
Мы скоро докажем, что найденное нами здесь индуктивным путем
верно вообще. Однако прежде чем браться за это дело, нужно ука-
указать все, что следует из этой теоремы, если предположить ее спра-
справедливой. Саму теорему мы выскажем следующим образом.
Если р — простое число вида 4/2 + 1, то -\-р, а еслир — простое
число вида 4/2 — 3, то —р будет вычетом или невычетом каждого
простого числа, которое, взятое положительным, является вычетом
или невычетом числа р.
Так как почти все, что можно высказать о квадратичных выче-
вычетах, основывается на этой теореме, то название «фундаментальная
теорема», которое мы в дальнейшем будем употреблять, не будет
для нее неподходящим.
Чтобы наши выводы представить в возможно более краткой фор-
форме, мы будем обозначать через а, а'', а'',... простые числа вида 4/2 + 1,
через Ъ, Ь', Ъ"',... — простые числа вида 4/2 + 3, далее, через А, А',
А'\... — любые числа вида 4/2 + 1 и через В, В', В"',... — любые
числа вида 4/2 + 3. Наконец, поставленная между двумя величина-
величинами буква R будет указывать, что первая является вычетом второй,
а буква N будет иметь противоположное значение. Например,
+5i?ll,+27V5 означает соответственно, что +5 есть вычет числа
11, а+2 и —2 суть невычеты числа 5. Если соединить теперь фун-
фундаментальную теорему с теоремами из п. 111, то легко получаются
следующие теоремы.
Формулировка фундаментальной теоремы
127
1)
2)
3)
4)
5)
6)
7)
8)
Если
±aRa'
± aNa'
+ aRb \
— aNb j
+ aNb \
— aRb j
±bRa
+ bNa
+ bRb' \
— bNb' j
+ bNb' \
— bRb' \
To
±a'Ra
+ a'Na
±bRa
±bNa
f +aRb
\ —aNb
i +aNb
\ —aRb
\ + b'Nb
\ —b'Rb
f + b'Rb
\ —b'Nb
132
Выше содержатся все случаи, которые могут встретиться при
сравнении двух простых чисел; следующее касается любых чисел,
однако доказательства здесь не так очевидны.
9)
10)
11)
12)
13)
14)
Если
+ aRA
±bRA
+ aRR
— aRR
+ bRR
— bRR
\
\
{
{
To
+ ARa
+ ARb
— ANb
±RRa
±BNa
— RRb
+ RNb
+ RRb
— RNb
128 Раздел IV (п.
Так как доказательства всех этих теорем основываются на одних
ж тех же принципах, нет нужды все их подробно проводить; дока-
доказательство теоремы 9, которое мы приведем, может служить приме-
примером. Вообще же можно заметить, что каждое число вида 4/г + 1 или
совсем не имеет сомножителей вида 4/2 + 3, или содержит два таких
сомножителя, или четыре и т. д., т. е. что количество таких сомно-
сомножителей (среди которых могут быть и равные) всегда четно, а каждое
число вида in + 3, напротив, всегда содержит нечетное число (т. е.
или один или три, или пять и т. д.) сомножителей вида 4тг -f- 3.
Число сомножителей вида 4/2 + 1 остается неопределенным.
Теорема 9 доказывается следующим образом. Пусть А есть про-
произведение простых сомножителей а', а", а", ..., 6, b\ b"', ..., где чис-
число сомножителей 6, Ь', Ъ", ... четно (их может и не быть совсем, что
сводится к тому же самому). Если теперь а является вычетом числа
А, то оно будет также вычетом всех сомножителей а', а", а", ...,
Ь, Ъ', Ъ", ..., а потому, согласно теоремам 1 и 3 предыдущего пункта,
эти отдельные сомножители, а, следовательно, и их произведение А
являются вычетами числа а. Также и —А будет вычетом. Если же
—а есть вычет числа А, а потому и отдельных сомножителей а',
а", ..., Ъ, bf, ..., то отдельные сомножители а', а", ... будут вычета-
вычетами числа а, а сомножители b, b\ ... — невычетами. Так как, одна-
однако, количество последних четно, произведение всех сомножителей,
т. е. А, будет вычетом числа а, а потому вычетом будет я —А.
133
Мы еще обобщим наше исследование. Рассмотрим два любых вза-
взаимно простых между собой нечетных числа Р и Q, взятых с каки-
какими-нибудь знаками. Не обращая внимания на знак числа Р, мы
разложим его на простые сомножители, и обозначим через р коли-
количество тех из этих сомножителей, по которым Q является невыче-
невычетом. Если некоторое простое число, по которому Q есть невычет,
встречается среди этих р сомножителей несколько раз, то и учиты-
учитывать его следует столько же раз. Аналогично, пусть q есть количе-
количество простых сомножителей числа Q, по которым Р является не-
невычетом. Тогда числа р и q находятся в некоторой связи одно с дру-
другим, которая зависит от природы чисел Р, Q. Именно, если одно
Формулировка фундаментальной теоремы 129
из чисел /?, q четно или нечетно, то по виду чисел Р, Q, можно су-
судить, будет ли второе четным или нечетным. Эта связь представле-
представлена в следующей таблице.
Числа /?, q одновременно будут четными или нечетными, если
числа Р, Q имеют вид:
1) + А9 +А';
2) +А, -Л';
3) +А, + В;
4) +А, —В;
О j Л. у /i ,
6) + Я, -В'.
Наоборот, одно из чисел р, q четно, а другое нечетно, когда чис-
числа Р, Q имеет вид:
7) —А, +В;
8) -А, -В\
9) +В, +В'\
Ю) —В, —В'.
Пример. Пусть числа Р и Q суть —55 и -f-1197, что относится
к четвертому случаю. Здесь 1197 является невычетом одного един-
единственного простого сомножителя числа 55, именно, числа 5, а —55
есть невычет трех простых сомножителей числа 1197, именно, чи-
чисел 3, 3, 19.
Если Р и Q обозначают простые числа, то эти теоремы переходят
в те, которые мы привели в п. 131. Именно, в этом случае р и q мо-
могут быть не больше 1; если поэтому предположить, что р четно, оно
обязательно будет = 0, т. е. Q будет вычетом числа Р; если же р
нечетно, то Q есть невычет числа Р, и обратно. Таким образом, если
здесь вместо А, В написать а, Ь, то из 8) следует, что если—а есть
вычет или невычет числа Ь, —Ъ будет невычетом или вычетом числа
а, что совпадает с 3) и 4) из п. 131.
Вообще ясно, что Q может быть вычетом числа Р только тогда,
когда р = 0; поэтому, если р нечетно, то Q заведомо есть невычет
по модулю Р.
130 Раздел IV (п. 134)
Отсюда также могут быть без труда выведены теоремы предыду-
предыдущего пункта.
Кстати, скоро станет ясно, что это общее рассмотрение является
не просто бесплодным умозрением, так как полное доказательство
фундаментальной теоремы едва ли может быть без него проведено.
134
Мы приступаем теперь к выводу этих теорем.
I. Мы будем, как и перед этим, считать, что Р, на знак которого
мы не обращаем внимания, разложено на простые сомножители,
и разложим далее каким-нибудь образом также и Q, но уже учиты-
учитывая его знак. Затем будем комбинировать каждый отдельный сомно-
сомножитель первого разложения с каждым отдельным сомножителем вто-
второго разложения. Тогда, если s обозначает количество всех комби-
комбинаций, в которых сомножитель числа Q является невычетом сомно-
сомножителя числа Р, то р и s будут или одновременно четными, или одно-
одновременно нечетными. Действительно, если/, /', /", ...суть простые
сомножители числа Р, и если среди сомножителей, на которые раз-
разложено Q, имеется т невычетов по модулю /, т' невычетов по мо-
модулю /', т" невычетов по модулю /" и т. д., то легко видеть, что,
s = т + т' -\- т" + ...,
а р выражает, сколько среди чисел т, т', т", ... имеется нечетных.
Отсюда сразу вытекает, что s будет четным, когда рчетно, и нечет-
нечетным, когда р нечетно.
П. Сказанное справедливо всегда, каким бы образом Q ни была
разложено на сомножители. Теперь мы переходим к специальных
случаям, и сначала рассмотрим случаи, когда одно из чисел, Р,
положительно, а другое, Q, имеет или вид -Ь-4, или вид —В. Раз-
Разложим Р и Q на простые сомножители, снабдив отдельные сомножи-
сомножители числа Р положительными знаками, а отдельные сомножители
числа Q — положительными или отрицательными знаками в зави-
зависимости от того, имеют ли они вид а или Ь; тогда Q, очевидно, будет,
как и требовалось, иметь или вид+-4, или вид — В, Скомбинируем
Формулировка фундаментальной теоремы 131
отдельные сомножители числа Р с отдельными сомножителями чис-
числа Q и обозначим, как и раньше, через s число комбинаций, в ко-
которых сомножитель Q является невычетом сомножителя /\ и анало-
аналогично через t — число комбинаций, в которых сомножитель Р явля-
является невычетом сомножителя Q. Тогда из фундаментальной теоремы
следует, что первые комбинации совпадают со вторыми и потому s = t-
Наконец, из только что доказанного следует, что p^s (mod 2), ^? =
= t (mod 2), и потому p=q (mod 2).
Тем самым мы получаем теоремы 1), 3), 4) и 6) из п. 133.
Остальные теоремы могут быть прямо выведены подобным же ме-
методом, но требуют одного нового соображения. Однако их легче
получить из предыдущего следующим образом.
III. Обозначим снова через Р и Q какие-нибудь взаимно простые
нечетные числа, через р и q — количества простых сомножителей
чисел Р, Q, по которым соответственно Q или/* являются невычета-
невычетами. Наконец, пусть р' — количество простых сомножителей числа
Р, по которым является невычетом — Q (если само Q отрицательно,
то — Q, очевидно, будет обозначать положительное число). Разобьем
теперь все простые сомножители числа Р на четыре класса, именно
1) на сомножители вида а, по которым Q является вычетом;
2) на сомножители вида Ь, по которым Q является вычетом;
число их пусть равно %;
3) на сомножители вида а, по которым Q является невычетом;
их число пусть равно ф;
4) на сомножители вида Ь, по которым Q является невычетом;
их число обозначим через со.
Тогда легко видеть, что р = ф + со, р' = х + ф-
Если теперь Р имеет вид +Л, то х +w» a потому также и
X — со будет четным числом; тем самым р' =¦ р ~\- х — со ^р (mod 2).
Если же Р имеет вид +^, то подобным же образом мы находим,
что числа р и р' по модулю 2 несравнимы.
IV. Применим сказанное к отдельным случаям. Если сначала
как jP, так и Q имеют вид +-4, то по теореме 1) р = g(mod 2).
Но, с другой стороны, р' = р (mod 2), и потому //= <7(mod2), что
совпадает с теоремой 2). Аналогично, если Р имеет вид —А,
а О — вид + i, то, согласно только что доказанной теореме 2),
132 Раздел IV (пп. 135-136)
/? == g (mod2). Так как р'==р, отсюда следует также //==#. Тем
самым доказана также и теорема 5).
Тем же способом теорема 7) выводится из 3), теорема 8) — или
из 4), или из 1), теорема 9) — из 6), и из нее же и теорема 10).
Строгое доказательство фундаментальной теоремы
135
Хотя в предыдущем пункте теоремы из п. 133 и не были доказа-
доказаны, но было показано, что их справедливость следует из справедли-
справедливости фундаментальной теоремы, которую мы пока лишь предполо-
предположили. Но из самого способа вывода ясно, что эти теоремы верны для
чисел Р, Q, если только фундаментальная теорема имеет место для
всех комбинаций простых сомножителей этих чисел, даже в том
случае, если бы вообще она была и не верна.
Мы будем говорить, что фундаментальная теорема верна до не-
некоторого числа М, если она верна для любых двух простых чисел,
ни-одно из которых не превосходит М,
Аналогичным образом нужно понимать выражения такого рода,
что теоремы пп. 131, 132, 133 верны до некоторой границы. Легко
видеть, что если доказана справедливость фундаментальной теоремы
до некоторой границы, то и указанные теоремы в пределах этой
границы имеют силу.
136
Непосредственной проверкой легко можно показать, что для ма-
маленьких чисел фундаментальная теорема верна; таким путем опреде-
определяется граница, до которой эта теорема заведомо верна. Мы предпо-
предположим, что эта проверка произведена, причем совершенно безраз-
безразлично, до какого места она сделана. Достаточно, например, устано-
установить справедливость теоремы только до числа 5; а это сразу видно,
так как +5iV3^-t3iV5.
Если бы теперь фундаментальная теорема оказалась вообще, говоря,
деверной, то существовала бы такая граница Т, что до нее теорема вер-
Доказательство фундаментальной теоремы 133
на, а для следующего числа Г+1 она уже не верна. То же самое можно
сказать по-иному, а именно, что существуют два простых числа,
большее из которых есть Т +1, которые находятся в противоречии
с утверждением теоремы, но что для любых двух простых чисел, если оба
они меньше Т + 1, теорема верна; отсюда следует, что до
границы Т верны и теоремы из пп. 131, 132, 133. Однако сейчас мы
покажем, что это предположение не может быть верным. В соответ-
соответствии с различными возможностями для вида числа Т + 1 и того
простого числа, которое меньше Т + 1 и взятое с Т + 1 противоре-
противоречит утверждению теоремы, мы будем различать следующие случаи
(при этом указанное простое число обозначим через р).
Если и Т + 1 и р имеют вид An + 1, то фундаментальная теоре-
теорема могла бы быть не верна, если бы имело место одно из двух:
или одновременно +/?/?(Т + 1) и ± (Т + l)Np,
или одновременно +pN(T + 1) и + (Т + l)Rp.
Если и Т + 1, и р имеют вид An + 3, то фундаментальная тео-
теорема была бы не верна, если бы имело место
или одновременно + pR(T + 1) и —(Т + l)Np
(или, что сводится к тому же, — pN(T + 1) и -\-(Т + 1) Rp)y
или одновременно +рЩТ + 1) и —(Г + l)Rp
(или —рЩТ + 1) и +(Т + l)Np).
Если Т + 1 имеет вид An + 1, а р — вид in + 3, то фундамен-
фундаментальная теорема не верна, если
или одновременно ^~pR{T + 1) и +(Т + l)Np (или —(Т + 1)Др),
или одновременно ± рЩТ + 1) и —(Г + l)Np (или +(^+1)^).
Если Т + 1 имеет вид An + 3, а /? — вид 4п + 1, то фундамен-
фундаментальная теорема не верна, если
или одновременно +рЩТ + 1) (или— рЩТ + 1)) и ±(Т + l)Np,
или одновременно + pN(T + 1) (или—/?/?(Г + 1)) и±Bгл +1)Др.
Если может быть доказано, что ни один из этих восьми случаев не
может иметь места, то мы тем самым, очевидно, получим, что спра-
справедливость фундаментальной теоремы не ограничена никакими пре-
пределами. К этому доказательству мы сейчас и приступаем. Но так
как одни из этих случаев зависят от других, мы не будем придер-
придерживаться той же их последовательности, в которой они здесь пере-
перечислены.
134 Раздел IV (пп. 137-139)
137
Первый случай. ЕслиТ -\- \ имеет вид Ап-{-1 (= а), и р— такого
же вида, и, кроме того, + /?.Да, то не может быть -^raNp. Выше
этот случай фигурировал первым.
Пусть + р = e2(moda), где е четно и меньше, чем а (чего всегда
можно добиться). Тогда нужно различать два случая.
I. Если е не делится на р, то положим е2 = р -f- a/; тогда / будет
положительным числом вида An + 3 (т. е. вида В), которое меньше а
и не делится на р. Далее, е2 = р (mod/), т. е. pRf, и потому, по
теореме 11 из п. 132 (которую мы имеем право применить, так как
р it / меньше, чем а, и значит, для них эти теоремы верны), -\- fRp-
Но и a/Rp, откуда-\-aRр.
П. Если е делится на р, то положим е — gp и е2 — р + ap/г, или
pg2 = 1 -|~ аи. Тогда /г имеет вид 4тг + 3 (В) и взаимно просто с р
и g2. Далее. pg2Rh и потому также /?/?/г, откуда (по теореме 11
из п. 132) zb^Rp- Но и —ahRp, ибо —ah == 1 (mod/?). Следова-
Следовательно, -\-aRp.
138
Второй случай. ?c^w Г + 1 имеет вид Ап-^1(=а), Р
4тг 4- 3, и + pR (Т -\- 1), mo we может быть -f- (Г + 1) ZVp
— (Т -\- 1) Rp. Выше этот случай фигурировал пятым.
Пусть, как и выше, е2 = р + /а, где е четно и меньше, чем а.
I. Если е не делится на р, то и / не будет делиться на р. Кроме
того, / будет положительным числом, имеющим вид An + 1 (или А),
и меньшим, чем а. Далее, + pRf и потому (теорема 10 из п. 132)
-} /Rp. Но и + faRp] следовательно, + aRp или —aNp.
II. Если е делится на р, то пусть е = pg и / = ph. Поэтому
g2p = l+ha. Кроме того, h положительно, имеет вид An + 3 (В) и
взаимно просто с р и g2. Далее, -f g2pRh, и поэтому + pRh. Сле-
Следовательно (теорема 13 из п. 132), —hRp. Но — haRp,
откуда aRp и — aNp.
139
Третий случай. Если Т + 1 имеет вид Ап + l(= a), p — число
такого же вида, и +/?iVa, то не может быть zbaRp. (Выше это
был второй случай.)
Доказательство фундаментальной теоремы 135
Возьмем какое-нибудь простое число, меньшее, чем а, по кото-
которому + а является невычетом; то, что такое существует, мы уже
раньше доказали (пп. 125, 129). При этом, однако, нужно отдельно
рассматривать два случая, в зависимости от того, имеет ли это
простое число вид An -\-1 или An -f- 3; действительно, не было дока-
доказано, что существуют такие простые числа обоих этих видов.
I. Пусть указанное простое число имеет вид 4n -f-1 и равно а''.
Тогда Ч-a'iVa (п. 131), и потому ^ra'pRa. Пусть, таким образом,
е2 == a'/?(modа), где е четно и меньше чем а. Тогда снова нужно
различать четыре случая.
1. Если е не делится ни на р, ни на а', то положим е2 = а'р -\- af,
причем знак выбирается так, чтобы / было положительным. Тогда /
будет <^а, взаимно просто с а' и р и, если взять верхний знак,
будет иметь вид An + 3, а если нижний — вид An + 1. Для краткости
число простых сомножителей числа у, по которым х является не-
невычетом, мы обозначим через [х, у]. Тогда a'pRf, и потому [а'р, /] = О-
Следовательно, [/, а'р] будет четным числом (теоремы 1) и 3) из
п 133), т. е. будет или равно 0, или равно 2. Поэтому / будет или вычетом
обоих чисел а', р, или невычетом каждого из этих чисел. Первое,
однако, невозможно, так как + а/ есть вычет числа а', и +aNa'
(по предположению), откуда + /Лта'. Значит, / должно быть не-
невычетом каждого из чисел а', р. Но вследствие ^rafRp будет ^raNp,
что и требовалось доказать.
2. Если е делится на р, но не делится на а', то пусть е = pg и
g2p ~ a'+ ah, причем знак берется такой, чтобы h было положи-
положительным. Тогда h будет <<а, взаимно просто с a', g и р и в случае
верхнего знака будет иметь вид An -f 3, а в случае нижнего — вид
An-f-1. Из равенства g2p = ar -Az_ah, после умножения его на риа',
без труда выводятся следующие соотношения:
(a) pa'Rh; ф) ±_ahpRa'\ G) aa'hRp.
Из (а) следует [pa', h] = 0, и потому (теоремы 1) и 3) из п. 133)
[/г, раг\ четно, т. е. h является или вычетом, или невычетом обоих
чисел р, а' одновременно. В первом случае из (Р) следует -\-apNa\
и так как по предположению +aiVa', будет ^rpRa'. Отсюда по
фундаментальной теореме, которая верна для чисел р, а', меньших
136 Раздел IV (пп. ЦО-ЦЗ)
Т + 1, получается, что + а'.Д/?. Из этого и из того, что hNp, сле-
следует, согласно (т), -^raNp, что и требовалось доказать. Во втором
случае из ф) следует + apRa' и потому +pNa\ ^za'Npn, наконец,
отсюда и из того, что /г/?/?, получается, согласно (*у), ^raNp,
3. Если е делится на а', но не делится на /?, то доказательство
протекает почти точно также, как и в предшествующем случае,
и не вызывает никаких новых трудностей.
4. Если е делится и на а\ и на р, а потому и на произведение
а'р (действительно, мы можем считать, что числа а' и р различны
между собой, так как иначе то, что мы хотим доказать, а именно,
что aNp, уже содержалось бы в предположении aNa'), то пусть
e = ga'p и g2a'p = 1 + ah. Тогда h будет меньше а, взаимно просто
с а' и р и для верхнего знака имеет вид 4га + 3, а для нижнего —
вид 4га+1. Но легко видеть, что из последнего равенства вытекают
следующие соотношения:
(a) a'pRh; ф) + ahRa'\ (?) + а/г/?/?.
Из соотношения (а), которое совпадает с (а) во втором случае,
вытекает, как и там. что одновременно имеет место или hRp и hRa\
или hNp и hNa'. Однако в первом случае, вследствие соотноше-
соотношения ф), в противоречии с предположением было бы aRa'\ следова-
следовательно, hNp, и потому, в силу (*у), также aNp.
II. Если указанное простое число имеет вид 4га + 3, то доказа-
доказательство настолько похоже на предыдущее, что проводить его из-
излишне. Для тех, кто хочет сделать это самостоятельно (что мы
очень рекомендуем), заметим только, что после того как они при-
придут к равенству е2 = bp^raf (где Ъ обозначает указанное простое
число), ради достижения большей ясности следует рассматривать
оба знака отдельно.
140
Четвертый случай. Если Т +1 имеет вид 4п+!(=#), р —
вид 4га -j-3, и zkpNa, то не может быть aRp или —aNp. (Выше
этот случай был шестым.)
Это доказательство мы также ради краткости опускаем, так как
оно совершенно аналогично доказательству третьего случая.
Доказательство фундаментальной теоремы 137
141
Пятый случай. Если Т + 1 имеет вид An + 3 (= b), р имеет такой
же вид, и + pRb или—/>Лй, то не может быть -f- bRp или — bNp^
(Выше — третий случай.)
Пусть р ==е2 (modi), где е четно и меньше, чем Ъ.
I. Если е не делится на р, положим е2 = р + bf. Тогда / будет
положительным числом, меньшим Ь, взаимно простым с р и имеющим
вид An -f- 3. Далее, будет иметь место pRf, и потому, согласно
теореме 13 из п. 132, —/Rp. Отсюда и из того, что -\-bfRp, следует
— bRp, и потому -\-bNp.
II. Если е делится на р, то пусть е = pg и g2p = 1 -f- Ыг. Тогда h
будет иметь вид An + 1 и будет взаимно просто с р, далее,
р = g2/?2 (mod/г), и потому />7?/г. Отсюда получается + hRp (теорема 10
из п. 132), а из этого и из —bhRp следует —bRp или -\-bNp.
142
Шестой случай. Если Т -f- 1 имеет вид in + 3 (= 6), />— вид
An -\- I и pRb, то не может быть zt_bNp. (Выше — седьмой случай.)
Доказательство, которое совершенно аналогично предыдущему,
мы опускаем.
143
Седьмой случай. Если Т -f- 1 имеет вид An -\- 3 (= b), p имеет
такой же вид, и + pNb или — pRb, то не может быть + bNp<
или — bRp. (Выше — четвертый случай.)
Пусть —/? ==е2 (mod6), где е четно и меньше, чем Ъ.
I. Если е не делится на р, то пусть —р = е2 — bf. Тогда /будет
положительным числом вида An + 1, взаимно простым с р и меньшим,
чем Ъ (действительно, очевидно, что е не больше Ъ— 1, и р < ?— 1,
поэтому bf = е2 + Р < б2 — 6, т. е. / < Ъ — 1). Далее, — P-Rf, и потому
(теорема 10 из п. 132) -\-fRp, а из этого и из того, что -\-bfRp,
следует -f bRp или —bNp.
II. Если е делится на /?, то пусть е = pg и g2p = — l-\-bh.
Тогда h будет положительным числом вида An + 3> взаимно простым
138 Раздел IV (пп. Щ-Ц5)
с р и меньшим, чем Ъ. Далее, —pRh, и потому (теорема 14 из
п. 132) + hRp. Из этого и из того, что bhRp, следует
или — bNp.
144
Восьмой случай. Если Т -\- 1 имеет вид An + 3 (= Ъ), /?
4rc-t-l, и + pNb или —pRb, то не может быть ^rbRp. (Выше —
последний случай.)
Доказательство проводится так же, как в предыдущем случае.
Аналогичный метод для доказательства
теоремы из п. 114
145
В предшествующих доказательствах мы все время предполагали
значение числа е четным (пп. 137—144); заметим, что мы могли бы
использовать и нечетные значения, но при этом нам пришлось бы
отдельно рассматривать еще большее количество случаев. Те, ко-
которые находят в этом удовольствие, потрудятся не даром, если они
потратят свои усилия на исследование этих случаев. Кроме того,
тогда должны были бы предполагаться известными теоремы, касаю-
касающиеся вычетов +2 и —2. А так как наше доказательство было про-
проведено без использования этих теорем, мы получаем тем самым но-
новый способ для их доказательства. Этого не следует недооценивать,
так как методы, которые мы использовали выше для доказательства
теоремы о том, что +2 являются вычетами каждого простого числа
вида 8п + 1, оказываются несколько менее прямыми. Мы будем
предполагать, что остальные случаи (в которых речь идет о прос-
простых числах вида 8п + 3, 8п + 5, 8п + 7) уже доказаны при-
применявшимися выше методами, а эта теорема найдена только
индуктивным путем; следующими далее рассуждениями мы дока-
докажем, что это индуктивное заключение действительно справедливо.
Если бы +2 не было бы вычетом всех простых чисел вида 8п + 1,
то пусть наименьшее простое число такого вида, для которого +2
Доказательство теоремы из п. 114 139
или —2 является невычетом, было бы равно а, так что для всех про-
простых чисел, меньших а, теорема справедлива. Возьмем тогда какое-
нибудь простое число, меньшее, чем а/2, по которому а есть невычет
{то, что такое число существует, легко получается из п. 129). Если
оно равно р, то, согласно фундаментальной теореме, будет pNa.
Поэтому zL^pRa. Пусть е2 == 2/?(mod а), где е нечетно и меньше,
чем а. Тогда надо рассмотреть отдельно два случая.
I. Если е не делится на/?, то пустье2 = 2р + Щ- Тогда q будет
положительным числом вида 8п + 7 или 8п + 3 (в зависимости
от того, имеет ли р вид 4п + 1 или in +3), меньшим, чем а, и не
делящимся на р. Теперь разобьем все простые сомножители числа
q на четыре класса; пусть при этом будет е сомножителей вида
Ъп + 1, / сомножителей вида 8п + 3, g сомножителей вида 8п + 5
и h сомножителей вида 8п + 7; пусть произведение всех сомножи-
сомножителей первого класса равно Е, произведения всех сомножителей
второго, третьего и четвертого классов равны соответственно F,
G, Н *. После того как это сделано, рассмотрим сначала случай,
когда р имеет вид in + 1 и потому q — вид 8п + 7. Тогда легко
видеть, что 2АЕ, 2RH, и потому /?i?-E, pRH, откуда, наконец,
ERp, HRp. Далее, 2, а потому и /?, будут невычетами каждого со-
сомножителя вида 8п + 3 или 8п + 5; поэтому каждый такой сомно-
сомножитель будет невычетом числа р, откуда легко следует, что FG
будет вычетом числа р, если / + g четно, и невычетом, если / + g
нечетно. Но / + g не может быть нечетным; действительно, разбо-
разбором всевозможных случаев легко убедиться, что если / + g нечетно,
то EFGH, или q, будет иметь или вид 8п + 3, или вид 8?г + 5, ка-
каковы бы ни были е, /, g, h в отдельности, что противоречит предпо-
предположению. Следовательно, FGRp, EFGHRp, или qRp, и отсюда,
в силу aqRp, вытекает, наконец, aRp, что находится в противоречии
с предположением. Если же р имеет вид 4тг + 3, то подобным же
образом можно показать, что pRE и потому ERp, — pRF, откуда
FRp, q -\- h четно, и потому, наконец, вопреки предположению,
qRp, aRp.
* Когда совсем нет сомножителей, принадлежащих некоторому классу,
вместо их произведения нужно писать 1.
140 Раздел IV (п. Ц6)
II. Если е делится на р, то доказательство может быть проведена
подобным же образом, и для опытного читателя (а этот пункт на-
написан специально для таких) не представит затруднений. Ради
краткости мы его опускаем.
Решение общей проблемы
146
При помощи фундаментальной теоремы и теорем, относящихся
к вычетам —1 и zh2, всегда можно определить, является ли какое-
нибудь заданное число вычетом или невычетом заданного простого
числа. Не будет бесполезным еще раз повторить здесь и другие
факты, изложенные выше, чтобы иметь вместе все необходимое для
решения следующего вопроса.
Задача. Пусть даны любые два числа Р, Q; определить, является
ли Q вычетом или невычетом по модулю Р.
Решение. I. Пусть Р = aab^cY. . . , где а, Ь, с, . . . обозначают раз-
различные положительные (ибо Р можно считать положительным)
простые числа. Для краткости мы будем здесь называть просто
отношением числа х к числу у ту связь между ними, которая
проявляется в том, что х является вычетом или невычетом по
модулю у. Отношение Q к Р зависит, таким образом, от отношений Q
к аа, Q к 6Р и т. д. (п. 105).
II. Чтобы уметь узнавать отношение Q к аа (для других парг
Q, Ь^ и т. д., дело обстоит так же), нужно разобрать два случая.
1. Если Q делится на а, то положим Q =Qrae, где Q' уже не
делится на а. Если тогда е = а или е > а, то QRaa\ если е < ос
и нечетно, то QNaa; наконец, если е < ос и четно, то отношение
Q к аа будет таким же, что и отношение Q' к аа~е. Следовательно,
этот случай сводится к случаю, когда
2. Q не делится на а. Здесь мы снова будем различать два
случая.
(Л), а = 2. Тогда при а = 1 всегда QRa*', если а = 2, то нужно,
чтобы Q имело вид 4п + 1; наконец, если а — 3 или а > 3, то Q
должно иметь вид 8п -J-1. Если это условие выполнено, то QRa*.
Решение общей проблемы 141
(В), а — какое-нибудь другое простое число. Тогда отношение Q
к а* такое же, как и Q к а (ср. п. 101).
III. Отношение любого числа Q к (нечетному) простому числу а
определяется следующим образом. Если Q>a, то вместо Q подстав-
подставляется его наименьший положительный вычет * по модулю а. Отно-
Отношение этого вычета к а такое же, как и числа Q к а.
Далее, число Q, или то, которым оно заменено, разлагается на
простые сомножители р, р'', //',..., к которым добавляется еще мно-
множитель — 1, если Q отрицательно. Тогда, как известно, отношение
Q к а зависит от отношений отдельных сомножителей к а. Именно,
если среди этих сомножителей имеется Ъп невычетов числа а, то
QRa, a если невычетов 2т + 1, то QNa. При этом легко видеть, что
если среди сомножителей р, р'', //',... имеется два, или четыре, или
шесть, или, вообще, 2к совпадающих, то их можно просто отбра-
отбрасывать.
IV, Если среди сомножителей р, р', р", ... встречаются—1 и 27
то отношение их к а определяется из пп. 108, 112, 113, 114. А отноше-
отношения остальных сомножителей к а зависят от отношений а к этим сом-
сомножителям (фундаментальная теорема и теоремы из п. 131). Если
р — один из них, то можно убедиться (рассматривая числа а и р
так же, как перед этим числа Q и а, которые соответственно больше
их), что отношение акр или может быть определено в соответствии
с пп. 108—114 (именно, если наименьший вычет числа а по модулю р
не имеет нечетных простых сомножителей), или еще зависит от отноше-
отношений р к некоторым простым числам, которые меньше р. То же самое
имеет место и для остальных сомножителей р'', //',... Легко видеть,
что, продолжаяэтотпроцесс,мы в конце концов придем к числам, отно-
отношения между которыми можно определить при помощи теорем из пп.
108—114. На примере это будет яснее.
Пример. Отыскивается отношение числа+453к1236. Имеем: 1236=
- 4-3-103; 453 Л4, согласно II, 2 (А);+453 /?3, согласно II, 1. Ос-
Остается, таким образом, получить только отношение +453 к 103. Оно
будет таким же, что и отношение +41 (=453 (mod 103)) к 103.
* «Вычет» в смысле п. 4. — Часто бывает лучше брать абсолютно наимень-
наименьший вычет.
142 Раздел IV (пп. Ц7-Ц8)
Последнее в свою очередь такое же (по фундаментальной теореме), как
отношение +103 к 41 или —20 к 41. Но —207? 41; действительно,
-20 = —1-2-2-5; — 1 Д41 (п. 108) и +5Л41, ибо (фундаменталь-
(фундаментальная теорема) 41 = 1, и потому является вычетом числа 5. Отсюда еле
дует +453/?103, откуда, наконец, +453Ш236. Действительно,
453=2972 (mod 1236).
О линейных формах, содержащих все простые числа,
по которым заданное число является вычетом
или невычетом
147
Если дано любое число А, то можно указать определенные
формулы,в которых содержатся все взаимно простые с А числа, по ко-
которым А является вычетом, т. е. все числа, которые могут быть
делителями чисел вида х2 — А (где х'2 обозначает произвольный
квадрат)*. Для краткости мы рассмотрим только нечетные делители,
взаимно простые с А, так как остальные случаи легко могут быть
сведены к этому.
Пусть сначала А — или простое число вида 4п + 1, взятое поло-
положительным, или простое число вида 4тг — 1, взятое со знаком —.
Тогда, в силу фундаментальной теоремы, все те простые числа, кото-
которые, будучи взяты положительными, являются вычетами числа А,
будут делителями х2 — А, а все простые числа (за исключением чи-
числа 2, которое всегда есть делитель), являющиеся невычетом для А,
не будут делить х2 — А. Обозначим все вычеты числа А, меньшие, чем
А (за исключением нуля), через г, г', г", ..., а все невычеты — через
п, п', п"... . Тогда каждое простое число, содержащееся в одной из
форм Ак + г, Ак + г', Ак + г", ..., будет делителем х2 — А,
а каждое простое число, содержащееся в одной из форм Ак + п,
Ак + п', Ак + п\ ..., не делит х2 — А\ здесь к обозначает произ-
произвольное целое число. Первые формы мы будем называть формами
делителей, а вторые — формами неделителей выражения х2 — А.
* Такие числа мы будем называть просто делителями выражения х2 — А\
тем самым становится само собой понятным, что такое «неделители».
О линейных формах 143
Число тех и других одинаково и равно (.Л — 1)/2. Если, далее, В —
нечетное составное число, и ARB, то все простые сомножители числа
J5, а потому и само В, будут содержаться в одной из первых форм. Сле-
Следовательно, каждое нечетное число, содержащееся в одной из форм
неделителей, не будет делить х2 — А, Однако обратное утвержде-
утверждение неверно; действительно, если В есть нечетный составной недели-
неделитель выражения х2 — А, то среди простых сомножителей числа В
будет несколько неделителей, но если количество их четно, то само
В будет находиться в какой-нибудь форме делителей (ср. п. 99).
Пример. Для А = —11 указанным способом находим, что формы
делителей выражения х2 + 11 суть 11A + I,3,4,5,9,a формы неде-
неделителей: Нк + 2, 6, 7, 8, 10. Поэтому —11 будет невычетом всех
нечетных чисел, содержащихся в одной из последних форм, и вычетом
всех простых чисел, принадлежащих к какой-нибудь из первых форм.
Такие же формы существуют и для делителей и неделителей выра-
выражения х2 — А, где А — любое число. Легко видеть, однако, что нуж-
нужно рассматривать только такие значения А, которые не делятся ни
на какой квадрат; действительно, если А = а2А', то все делите-
делители* х2—А будут, очевидно, и делителями х2 — А', и то же самое
имеет место для неделителей. Мы будем различать три случая: 1) слу-
случай, когда А имеет вид + Dтг +1) или — Dтг — 1), 2) случай, ко-
когда А имеет вид — Dтг + 1) или + Dтг — 1), 3) случай, когда А
четно, т. е. имеет вид ЧЬ Dтг + 2).
148
Первый случай: А имеет вид +Dтг + 1) или —Dтг — 1). Разло-
Разложим А на простые сомножители, и те из них, которые имеют вид
4тг + 1, снабдим положительным знаком, а имеющие вид 4тг — 1 —
отрицательным знаком (от чего произведение не изменится, т. е.
по-прежнему будет равно .Л). Пусть эти сомножители суть а, Ь, с,
с?,... Разобьем далее все числа, которые меньше А и взаимно просты
с А у на два класса, причем в первом классе соберем все числа, кото-
которые являются невычетами или ни для одного, или для двух, или для
* Имеются в виду делители, взаимно простые с А.
144 Раздел IV (п. Ц9)
четырех, вообще, для четного количества чисел среди а, Ь, с, d..., a во
втором — числа, являющиеся невычетами или для одного, или для
трех, вообще, для нечетного количества чисел среди а, 6, с, d,...
Первые обозначим через г, /•', г", ... , а вторые— через п, п\ п ,...
Тогда формы Ак + г, Ак + г', Ак + г", ... будут формами делите-
делителей выражения х2 — А, а формы Ак + 72, ^4А: + п1, ^4& + тг", ... —
формами неделителей ж2 — А (т. е. каждое простое число, кроме 2,
будет делителем или неделителем выражения х2 — А, в зависимости
от того, содержится ли оно водной из первых, или в одной из вторых
форм). Действительно, если р — простое число, взятое положитель-
положительным, которое по одному из чисел а, Ъ, с, ... является вычетом или невы
четом, то и само это число будет соответственно вычетом или невыче-
невычетом числа р (в силу фундаментальной теоремы). Поэтому, если среди
а, Ъ, с, ... имеется т чисел, по которым р есть невычет, то среди них
будет и т невычетов числа/?, и потому, если р содержится в одной из
первых форм, т будет четным, и ARp, а если в одной из вторых форм,
то т нечетно, и AN р.
Пример. Пусть А= +105 = (—3).(+5)-(—7). Тогда числа г, г',
г",... будут следующие: 1, 4, 16, 46, 64, 79 (которые не являются
невычетами ни одного из чисел 3, 5, 7); 2, 8, 23, 32, 53, 92 (которые
являются невычетами чисел 3, 5); 26, 41, 59, 89, 101, 104 (которые
являются невычетами чисел 3, 7); 13, 52, 73, 82, 97, 103 (которые яв-
являются невычетами чисел 5, 7). Числа же п, п', п", ... будут следую-
следующие: И, 29, 44, 71, 74, 86; 22, 37, 43, 58, 67, 88; 19, 31, 34, 61, 76, 94;
17, 38, 47, 62, 68, 83. Первые шесть являются невычетами числа 3,
шесть следующих суть невычеты числа 5; затем следуют невычеты
числа 7, и наконец, те, числа, которые одновременно являются невы-
невычетами всех трех.
Из комбинаторных соображений и из пп. 32 и 96 легко выводится,
что количество чисел г, г', г", ... равно
-3) :
1 1-2 ' 1.2-3-4 ' '
а количество чисел п, п', п", . . . равно
Л /(/ — !)(/ — 2) Z(/ — 1 > (/ _ 2) (Z — 3) (/ — 4)
Ч/+ Т^З + 1-2.3.4.5
О линейных формах 145
где I обозначает количество чисел а, Ь, с, . . . ,
t = 2"\a— i){b— l)(c— 1). ..,
и оба ряда продолжаются до тех пор, пока не оборвутся. (Действи-
(Действительно, имеется t чисел, являющихся невычетами всех чисел а, Ь,
с, ..., t-h(l—1)/ 1 -2 чисел, являющихся невычетами двух из них,
и т. д.; однако необходимость краткости не позволяет нам проводить
это доказательство подробнее.) Сумма же каждого из этих рядов *
равна 2Z~~1. Для первого ряда это можно получить, объединяя в вы-
выражении
12)
второй член с третьим, четвертый с пятым, и т. д., а для второго —
объединяя в этом же выражении первый член со вторым, третий
с четвертым и т. д. Таким образом, количества форм делителей
и форм неделителей выражения х2— А одинаковы, именно равны
149
Второй и третий случаи мы можем рассмотреть одновременно. Имен-
Именно, здесь всегда можно положить Л равным или (—1)(?, или (-f-2) (?,
или (—2) Q, где Q есть число вида -f- Dтг -f- 1) или —Dтг—1),
которое мы рассмотрели в предыдущем пункте. Пусть вообще
A=olQ, так что а или равно —1, или равно +2. Тогда А есть
вычет всех чисел, по которым оба числа а и Q одновременно
являются вычетами или невычетами, и невычетом всех чисел, по
которым только одно из чисел а и Q является невычетом. Отсюда
легко вывести формы делителей и неделителей выражения х2— А.
Если <х = — 1, то все числа, которые меньше, чем 4Л и взаимно
просты с этим числом, мы разобьем на два класса, относя к первому
классу те числа, которые содержатся в какой-нибудь форме дели-
делителей выражения х2 — Q и одновременно имеют вид 4п + 1, а также
те, которые содержатся в какой-нибудь форме неделителей выра-
* После отбрасывания сомножителя t.
146 Раздел IV (пп. 150-151)
жения х2—Q и одновременно имеют вид An + 3; все остальные
числа отнесем ко второму классу. Если числа первого класса суть
г, г', г"',... , а числа второго класса— п, п\ п", . . . , то А будет
вычетом всех простых чисел, содержащихся в одной из форм ААк + г,
ААк + /"', 4^4& -|- г", . . . , и невычетом всех простых чисел, содержа-
содержащихся в формах ААк -f- n, 4^4A; -f- тг', . . . Если а = + 2, то мы будем
разбивать на два класса все числа, которые меньше, чем 8Q и взаимно
просты с AQ, причем к первому классу будем относить все числа,
которые содержатся в одной из форм делителей выражения х2 — Q
и одновременно, в случае верхнего знака, имеют вид 8п-\-I или
8п + 7, а в случае нижнего знака — вид 8п + 3 или 8п + 5, и все
числа, которые содержатся в одной из форм неделителей выражения
х2—(? и одновременно, в случае верхнего знака, имеют вид 8п -\- 3
или 8n-f 5, а в случае нижнего знака — вид 8/г + 1 или 8п + 7;
все остальные числа отнесем ко второму классу. Если тогда числа
первого класса обозначить через г, г', г", . . . , а числа второго клас-
класса—через п, п\ п", . . ., то +2^ будет вычетом всех простых чисел,
содержащихся в одной из форм 8Qk + г, 8Qk + r', 8Qk + /•", . . . ,
и невычетом всех простых чисел, содержащихся в одной из форм
8Qk + n, 8Qk -j- n', 8(?& + n", .. . Легко также доказать, что и здесь
имеется одинаковое количество форм делителей и форм неделителей
выражения х2 — А.
Пример. Этим способом можно найти, что + 10, есть вычет всех
простых чисел, содержащихся в одной из форм 40& + 1, 3, 9, 13,
27, 31, 37, 39, и невычетом всех простых чисел, содержащихся
в одной из форм 40& + 7, 11, 17, 19, 21, 23, 29, 33.
150
Эти формы обладают многими замечательными свойствами, из
которых мы здесь укажем одно. Если В есть составное взаимно про-
простое с А число, среди простых сомножителей которого имеется 2т
таких, которые содержатся в формах неделителей выражения
х2 — А, то В содержится в одной из форм делителей этого выраже-
выражения; если же число простых сомножителей числа 5, которые содер-
содержатся в формах не делите лей выражения х2 — А, нечетно, то и В бу-
О работах других авторов по этому вопросу 147
дет содержаться в одной из форм неделителей. Несложное доказа"
тельство мы опускаем. Из этого следует, что не только каждое про-
простое число, но и каждое составное нечетное взаимно простое с А чис
ло, которое содержится в одной из форм неделителей, само является
неделителем; действительно, один из простых сомножителей такого
числа обязательно должен быть неделителем.
О работах других авторов,
относящихся к этим исследованиям
151
Фундаментальная теорема, которая, без сомнения, должна быть
причислена к наиболее изящным открытиям в этой области, в той
простой форме, в которой мы ее дали выше, ранее никем не была вы-
высказана. Этому следует удивляться тем более, что некоторые дру-
другие теоремы, которые из нее вытекают и из которых ее в свою очередь
легко было бы вывести, были уже известны Эйлеру. Он зналу
что существуют формы, в которых содержатся все простые делители
чисел вида х2 — А, и формы, в которых содержатся все их простые
неделители, причем все первые формы отличны от всех вторых, и
указал способ находить такие формы; однако все его попытки полу-
получить доказательство были тщетны и лишь приводили к тому, что*
истины, найденные индуктивным путем, становились более вероят-
вероятными. Правда, в одном своем сочинении, «Novae demonstrationes circa
divisores numerorum formae x2-\- my2» (которое поступило в Петербург-
Петербургскую Академию 20 ноября 1775 г. и было издано уже после смерти
этого выдающегося математика в первом томе «Nova Ada» этой Ака-
Академии), как видно из стр. 47 и следующих, он, по-видимому, считал,
что доказательство ему удалось; но здесь вкралась ошибка, так как
на стр. 65 он молчаливо предполагает, ^о формы делителей и недели-
неделителей существуют*, из чего уже нетрудно было вывести, какой они
* Именно, что существуют числа г, г', /',..., п, п', /г", ..., которые все
различны, меньше, чем 4Л, и обладают тем свойством, что все простые делители
выражения х2 — А содержатся в одной из форм ААк + г, 4Ак + г', ..., а все
простые неделители — в одной из форм кАк + п, 4Ак + п',..., (где к — обоа-
начает произвольное число).
148 Раздел IV (п. 152)
должны иметь вид. Однако метод, который он использует для обосно-
обоснования указанного предположения, едва ли пригоден. В другом сочи-
сочинении: «De criteriis aequationis fx2 + gy2 = hz2 untrumque resolutio-
nem admittat necne», Opusc, Analyt.T. I. (где /, g, h являются задан-
заданными, a x, у, z — неизвестными числами) он индуктивным путем на-
находит, что если для h = s уравнение разрешимо, то оно разрешимо и
для всякого значения, сравнимого с s по модулю 4/g, если только оно
является простым числом; на основании этой теоремы предположе-
предположение, о котором идет речь, легко может быть доказано. Однако дока-
доказательство этой теоремы также не поддалось всем его усилиям *, что
и не удивительно, так как, по нашему мнению, следовало исходить
из фундаментальной теоремы. Справедливость этой теоремы будет
сама собой вытекать из того, что мы изложим в следующем разделе.
После Эйлера этим вопросом в своем замечательном труде
«Recherehes d'analyse indeterminee», Hist, de ГAcad. des Sc, 1785,
p. 465, занимался Л е ж а н д р. Он получил (стр. 465) теорему,
которая по сути дела идентична фундаментальной теореме; именно,
если р и q — два положительных простых числа, то если одно из них
имеет вид 4лг -j- 1, то абсолютные наименьшие вычеты степеней
p(q—i)/2 и д<р—1)/2 соответственно по модулям q и/? или оба равны
+1, или оба равны —1; если же/? и #оба имеют вид 4тг+3, то один из
этих абсолютно наименьших вычетов равен +1, а другой равен —1;
согласно п. 106, отсюда следует, что отношения (в смысле п. 146)
р к q и q к р одинаковы, когда хотя бы одно из чисел р и q имеет вид
An + 1, и противоположны, когда и р, и q имеют вид 4тг + 3. Эта
теорема содержится среди теорем из п. 131; она следует также из
теорем 1, 3, 9 п. 133; в свою очередь, фундаментальная теорема может
* Как он свидетельствует и сам в цитированном сочинении, стр. 216:
«Hujus elegantissimi theorematis demonstratio adhuc desiteratur, postquam
a pluribus jamcludum frustra est investigata ... Quocirca plurimum is praestitisse
oensendus est, cui successerit demonstrationem hujus theorematis invenire».
С какой настойчивостью этот бессмертный математик стремился получить
доказательства этой теоремы и других предложений, являющихся лишь част-
частными случаями фундаментальной теоремы, видно из многих других мест
«Opusc. Analyt». (ср. «Additamentum ad. diss.», VIII, Т. I и diss. XIII, Т. II,
а также многие сочинения в «Comment. Ac. Petrop.», которые мы уже упоминали).
О сравнениях второй степени общего вида 149
быть выведена из нее. Л е ж а н д р попытался также дать дока-
доказательство, о котором, так как оно весьма остроумно, мы будем под-
подробнее говорить в следующем разделе. Так как, однако, он принимал
без доказательства многие утверждения (о чем он сам говорит на
стр. 520: «Nous avons suppose seulement...»), часть из которых до сих
пор вообще никем не была доказана, а часть, по крайней мере на наш
взгляд, и не может быть доказана без помощи фундаментальной тео-
теоремы, то избранный им путь, по-видимому, не в состоянии привести
к цели, и потому наше доказательство должно считать первым*.
Впрочем, в дальнейшем мы изложим еще два других доказательства
этой в высшей степени важной теоремы, которые совершенно отлич-
отличны и от приведенного выше доказательства и между собой.
О сравнениях второй степени общего вида
152
До сих пор мы рассматривали «чистое» сравнение х2^ A (mod m)
и показали, как можно решить вопрос о том, разрешимо ли оно.
Отыскание самих корней было, в силу п. 105, сведено к случаю,
когда т является или простым числом, или степенью простого числау
а вторая из этих возможностей, согласно п. 101, также сводится к то-
тому случаю, когда т есть простое число. В отношении же этого послед-
последнего случая почти все, что может быть получено прямыми методамит
охватывается изложенным в пп. 61 и следующих, в соединении с тем,
что мы рассмотрим в пятом и шестом разделах. Вообще же, эти пря-
прямые методы, если и оказываются применимыми, все же в большинстве
случаев бывают намного длиннее косвенных, которые мы изложим
в разделе VI, и потому достойны внимания не столько с точки зрения
практической пользы, сколько вследствие своей красоты.
Произвольные сравнения второй степени легко могут быть сведены
к чистым сравнениям. Если дано сравнение
ах2 + Ъх -\~ с=0,
Ср. дополнения в конце «Исследований».
150 Раздел IV (п. 152)
которое должно быть решено по модулю т, то ему эквивалентно
сравнение
Аа2х2 + iabx + 4ас == 0 (mod 4а7?г),
т. е. каждое число, удовлетворяющее одному из этих сравнений,
удовлетворяет и другому. Второе же сравнение может быть пред-
представлено в виде
Bах + bf ее^Ь2 — Aac (mod 4am),
откуда все значения 2ах + b, которые меньше, чем4 am, могут быть
найдены, если только они вообще существуют. Если эти значения
обозначить через г, г', г", ..., то все решения заданного сравнения
получаются из решений сравнений
2ах ==г — Ь, 2ах == /•' — Ь, . . . (mod 4am),
которые мы научились находить во втором разделе. Впрочем, следует
заметить, что в большинстве случаев решение может быть упрощено
применением различных специальных приемов; например, вместо
заданного сравнения бывает возможно подыскать равносильное
ему сравнение
а'х2 + 2Ь'х-+-с'еееОу
в котором а' входит в т; однако ради краткости мы не будем излагать
здесь это подробно, тем более, что с этими вопросами мы еще встре-
встретимся в последнем разделе.
РАЗДЕЛ V
О ФОРМАХ И НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЯХ
ВТОРОЙ СТЕПЕНИ
Предмет исследования; определение форм и обозначения
153
В этом разделе мы будем главным образом заниматься функциями
двух переменных х, у следующего вида:
ах2 + 2Ьху + су2,
где а, Ь, с являются заданными целыми числами, и будем называть
эти функции формами второй степени или просто формами. Это
исследование достигает своей вершины в решении знаменитой проб-
проблемы об отыскании всех решений любого неопределенного уравнения
второй степени с двумя неизвестными, когда эти неизвестные должны
принимать либо целые, либо лишь рациональные значения. Правда,
эта проблема решена еще Лагранжем, и многое, касающееся
природы форм, было как этим великим математиком, так и Эйле-
Эйлером, частью впервые найдено, частью же доказано после того, как
это было найдено Ферма. Однако при основательном исследова-
исследовании форм нам открылось так много нового, что нам показалось целе-
целесообразным заново изложить весь этот предмет, тем более, что откры-
открытое указанными математиками разбросано во многих местах, и,
как нам кажется, было известно лишь немногим; затем, способ
152 Раздел V (пп. 154-155)
изложения этого предмета в большинстве случаев является нашим соб-
собственным, и, наконец, открытое нами вряд ли было бы понятно без но-
нового изложения, сделанного ранее. Однако, несомненно, что в этом
вопросе еще остается неоткрытым много замечательного, к чему могут
приложить свои силы другие. Впрочем, относящееся к истории отыска-
отыскания наиболее выдающихся свойств мы всегда будем указывать
в соответствующих местах.
Форму ах2 + 2Ъху + су2, когда дело не будет касаться самих
неизвестных х, у, мы будем обозначать через (а, Ь, с). Таким обра-
образом, это выражение будет обозначать произвольную сумму трех сла-
слагаемых, именно, произведения заданного числа а на квадрат любого
неизвестного, удвоенного произведения числа Ъ на это неизвестное
и некоторое другое неизвестное и, наконец, произведения числа с
на квадрат этого второго неизвестного. Например, A, 0, 2) будет
представлять сумму квадрата и удвоенного квадрата. Далее, хотя
формы (а, Ъ, с) и (с, Ъ, а) обозначают одно и то же, если обращать
внимание только на сами слагаемые, они тем не менее, будут разли-
различаться, если мы будем принимать во внимание также порядок рас-
расположения слагаемых; то, что от этого мы получаем пользу, будет
достаточно ясно из дальнейшего.
Представление чисел; определитель
154
Мы будем говорить, что некоторое число представляется некоторой
формой, если неизвестным формы могут быть приданы такие цело-
целочисленные значения, при которых значение формы равно заданному
числу. При этом имеет место следующая теорема.
Теорема. Если число М может быть представлено формой (а, Ь, с
так, что значения неизвестных, дающие это представление, взаимно
просты, то Ъ2 — ас является квадратичным вычетом числа М.
Доказательство. Если значения неизвестных суть т, п, так что
am2 + 2Ътп + сп2 = М,
Представление чисел; определитель 153
и два числа [х, v подобраны так, что \ип + ш = 1 (п. 40), то, как
легко показать, раскрывая скобки,
(am2 + 2bmn + en2) (av2 — 26[xv + qx2) =
= [[x (mb + nc) — v (ma + nb)]2 — (b2 — ac) (m[x + nvJ,
или
M (av2— 26(xv + ф2) - [(x (m6 + nc) — v (ma + n&)]2— F2 — ac).
Поэтому
62 — ac == [[x(m& + nc) — v(ma + nfe)]2 (modM),
т. e. b2 — ас есть квадратичный вычет числа М.
Число Ъ2 — ас, от свойств которого, как мы покажем в даль-
дальнейшем, в основном зависят свойства формы (a, b, с), мы будем
называть определителем этой формы.
Значения выражения ]fb2 — ас (mod Ж),
которым принадлежит представление числа Ж формой (а, б, о)
155
Как мы показали,
[л (mb + пс) — v (та + пЪ)
является значением выражения
Yb2 — ac (mod M).
Однако, как известно, числа [л, v, для которых [хггг + vn = 1,
могут выбираться бесчисленным множеством способов, так что будут:
получаться все новые и новые значения указанного выражения.
Посмотрим, в какой связи они находятся между собой. Пусть не
только (xm + vn = l, но и [л/m + Vn = 1; положим
[х (mb + пс) — v (та + nb) = v, fx' (mb + пс) — v' (та + nb) = ?/.
154 Раздел V (п. 156)
Если из равенства (лттг + vra = 1, умноженного на fx', вычесть
равенство fx'm + v'w = 1, умноженное на [л, то получится fx'— [х =
= rc(fx'v— [xv'); точно так же, умножая первое равенство на v',
а второе на v и вычитая, получаем v' — v = т ([xv'— [^'v). Отсюда
тотчас же следует
v — v' = ([x'v— jxv') (am2 + 26гатг + era2) = (fx'v — ;xv') M,
или v == г;' (modM). Итак, каким бы образом [х и v ни выбирались
формула [х (mfc + тгс) — v (та + тгб) не может давать различных (т. е.
несравнимых) значений выражения ]K&2— ас (modM). Поэтому, если
v есть какое-нибудь значение указанной формулы, то мы будем
говорить, что представление числа М формой ах2 + 2Ъху + су2,
при котором х = т, у = п, принадлежит значению v выражения
уЪ2—ас (modM). Впрочем, легко показать, что если v есть какое-
нибудь значение указанной формулы, и v == v' (modM), то вместо
чисел [л, v; дающих г?, можно подобрать другие числа, (х' и v'.
которые дают г/. Действительно, если положить
, . п (г/ — г?) , т (г/ — г?)
то будет иметь место
[х'т -}- Vn = [xm -(- v^ = 1,
а значение формулы для [л/ и V будет превосходить ее значение
для [х и v на величину (fx'v — fxv') M, которая равна ([xm + vn) (v' — v) =
— v' — г?, т. е. первое значение будет равно г?'.
156
Есл з имеется два представления одного и того же числа одной
и той же формой (а, Ь, с), при которых неизвестные имеют взаимно
простые значения, то они могут принадлежать как одному и тому
же значению выражения ~\fb2 — ас (modM), так и различным зна-
значениям. Если
М = ат2 + 2Ьтп + сп2 = am'2 + 2Ът'п' + en'2,
и
\шь + w — 1, \**'т' + vW = 1,
Значения выраснсения л/b2 — ас (mod M) 155
то ясно, что если
[х (тЪ + пс) — v (та + пЪ) == fx' (т'6 + п'с) — v' (т'а + п'Ъ) (mod M),
то это сравнение будет оставаться справедливым, какие бы другие
возможные значения мы ни брали вместо [л, v, fx', v'; в этом случае
мы будем говорить, что оба представления принадлежат одному
и тому же значению выражения УЪ2— ас (mod M). Если же ука-
указанное сравнение для каких-нибудь значений [х, v, [//, v' не выпол-
выполняется, то оно вообще не будет выполняться ни для каких значений,
и представления в этом случае будут принадлежать различным
значениям. А если
[л (mb -\-пс) — v (та + пЬ) = — [\l' (т'Ъ + п'с) — V(m'a + п'Ъ)],
то будем говорить, что представления принадлежат противоположным
значениям выражения У Ь2 — ас. Все эти термины мы будем исполь-
использовать также и тогда, когда речь будет идти о нескольких пред-
представлениях одного и того же числа различными формами, имеющими,
однако, одинаковые определители.
Пример. Пусть дана форма C, 7, —8), определитель которой
равен 73, Мы имеем следующие представления числа 57 этой
формой:
3-132 +14-13.15—8-252; 3-52 + 14-5.9—8-92.
Для первого из них можно положить [л = 2, v = — 1, откуда
получается значение выражения ^73 (mod 57), которому принадле-
принадлежит это представление:
2 A3.7—25-8) + A3-3 + 25-7) = — 4.
Подобным же образом находим, полагая [х = 2, v = — 1, что второе
представление принадлежит значению + 4. Следовательно, эти два
представления принадлежат противоположным значениям.
Прежде чем идти дальше, заметим, что формы с определителями,
равными нулю, при дальнейших исследованиях будут исключены из
рассмотрения, так как они сильно удлиннили бы теоремы, и потому
их лучше рассмотреть отдельно.
156 Раздел V (пп. 157-158)
Форма, содержащая другую форму или содержащаяся
в другой форме; преобразование, собственное и несобственное
157
Если некоторая форма F, неизвестные которой суть х, г/, может
быть переведена в другую форму F' от неизвестных х', у' посредством
подстановки вида
х = ах' + $у\ у = *\х' + fy\
где ос, р, y> 8 суть целые числа, то мы будем говорить, что первая
форма содержит вторую, или что вторая содержится в первой. Если
форма F есть
ах2 + 2Ьху + сг/2,
а форма F' есть
а V2 + 2Ъ'х'у' + с'г/'2,
то мы имеем следующие три равенства:
а' = аа2
6' = аар -|- Ь (а8 + Рт) +
с' = ар2
Если второе равенство умножить само на себя, первое равенство
умножить на третье и из первого произведения вычесть второе,
то после отбрасывания взаимно уничтожающихся членов получается
Ь'* — а'с' = (Ь2 — ас) (а8 — рТJ.
Отсюда следует, что определитель формы F' делится на опре-
определитель формы F, и что частное является квадратом; таким
образом, эти определители имеют, одинаковый знак. Поэтому, если
форма F' в свою очередь может быть подобной подстановкой пере-
переведена в форму F, т. е. как F' содержится в F, так и F содержится в F'у
то определители обеих форм равны между собой *, а (а8— р^J = 1,
* Из предыдущего анализа вытекает, что эта теорема верна также и для
форм, определители которых равны нулю. Однако равенство (а8 — (З^J = 1
в этом случае уже не обязательно.
Эквивалентность форм 157
В этом случае мы будем называть формы эквивалентными. Итак,
необходимым условием эквивалентности форм является равенство их
определителей, хотя из одного этого условия эквивалентность еще не
вытекает. Подстановку х = сих' + [Зг/', у — *\xf + by' мы будем называть
собственным преобразованием, если аб — ^ является положительным
числом, и несобственным, если число ос8 — р^ отрицательно; относи"
тельно формы F' мы будем говорить^ что она содержится в форме F
собственно или несобственно в зависимости от того, переводится
ли F в F' собственным или несобственным преобразованием. Если
формы F и F' эквивалентны, то (ос8 — р^J = 1, и потому, если пре-
преобразование собственное, то оо8 — р^ = 1, а если несобственное — то
ос8 — р^ = — 1. Если несколько преобразований одновременно являются
собственными или одновременно несобственными, то мы будем
называть их однотипными, а собственное и несобственное преобра-
преобразования — неоднотипными.
Эквивалентность, собственная и несобственная
158
Если определители форм F, F' равны между собой и F' содер*
жится в F, то и F будет содержаться в F\ причем собственно
или несобственно в зависимости от того, собственно или несоб-
несобственно F' содержится в F.
Пусть F переходит в F' при подстановке
Тогда F' будет переходить в F при подстановке
х1 = Ьх — рг/, у' = — чх + аг/;
действительно, при этой подстановке из F' будет получаться то же,
что получается из F, если положить
ж = а(8ж —рг/) + Р(—Т3 + а2/)» у =T(Sx—рг/)+ 8(— Т* + <*г/),
158 Раздел V (п. 159)
ИЛИ
х == (<х8 — Рт) Д5. 2/ = И — Рт) 2/-
Но при этом из jP получается, очевидно, (а&— ^JF, т. е. снова F
(согласно предыдущему пункту). Очевидно, однако, что последнее
преобразование будет собственным или несобственным в зависимости
от того, является ли собственным или несобственным первое пре-
преобразование.
Если как F' в F, так и F в F' содержатся собственно, мы будем
называть эти формы собственно эквивалентными, а если они содер-
содержатся одна в другой несобственно, то — несобственно эквивалент-
эквивалентными. В целесообразности такого подразделения мы вскоре
убедимся.
Пример. Форма 2х2 — 8ху + З?/2 при подстановке х = 2х' + у\
у = Зх' + 2у' переходит в форму — 13#'2— 12х'у' — 2?/'2, а она в свою
очередь переходит в первую форму, если положить х' = 2х—у
у' = — Зх + у. Следовательно, формы B, —4, 3) и (—13, —6, —2)
собственно эквивалентны.
Проблемы, к рассмотрению которых мы теперь переходим,
заключаются в следующем.
I. Если даны какие-нибудь две формы с одинаковыми опреде-
определителями, то требуется узнать, эквивалентны ли они или нет; если
эквивалентны, то собственно, несобственно или одновременно и соб-
собственно и несобственно, так как это тоже возможно. Если же они
имеют различные определители, то нужно уметь определить, содержит
ли одна из них другую, и если содержит, то собственно, несоб-
несобственно или одновременно и тем и другим способом. Наконец,
нужно найти все, как собственные, так и несобственные, преобра-
преобразования одной формы в другую.
П. Если дана некоторая форма, то нужно определить, представ-
представляется ли ею заданное число и найти все представления. Так как
при этом формы с отрицательными определителями требуют при
рассмотрении этого вопроса методов, отличных от тех, которые
требуются для форм с положительными определителями, то мы
сначала укажем все, что является общим для обоих случаев, а
только после этого станем рассматривать формы каждого типа в
отдельности.
Противоположные формы 159
Противоположные формы
159
Если форма F содержит форму F', которая в свою очередь содержит
форму F\ то форма F содержит и форму F".
Пусть неизвестные, от которых соответственно зависят формы
F, F\ F" суть х, у; х\ у'\ х", г/", и F переходит в F' при под-
подстановке
a F/ переходит в F" при подстановке
х' = аУ + ру, у' = ТУ + Ь'у\
Тогда F будет, очевидно, переводиться в F" подстановкой
х = а (а V + РУ) + Р (т'*" + Ь'У"), У = Т К*" + РУ) + 8 (Т'*'' + * V
или
х = (аа' + рт') х" + (ар' + ^') у", у = (Та' + 8Т') х" + (тр' + 88') /.
Следовательно, F будет также содержать форму F".
Так как разность (аа' + Рт') (тР' + ьь') ~ К8' + Р8') (Та' + 8Т')
равна (а8 — р^) (а'8' — р'^') и потому положительна, если числа
cub — Py и си'Ь' — PY либо оба положительны, либо оба отрицательны,
и отрицательна, если одно из этих чисел положительно, а другое
отрицательно, то форма F содержит форму F" собственно или несоб-
несобственно в зависимости от того, содержат ли форма F форму F'
и форма F' форму F" одинаковым или неодинаковым образом.
Отсюда следует, что если имеется любое количество форм F,
F', F", F"\.. ., каждая из которых содержит следующую, то первая
форма содержит последнюю, причем собственно, если число форм,
содержащих следующую за ней несобственно, четно, и несобственно
если это число нечетно.
Если форма F эквивалентна форме F', a F' в свою очередь экви-
эквивалентна форме F", то форма F эквивалентна форме F'\ причем —
собственно, если эквивалентности формы F форме Fr и формы F'
форме F" одного типа, и — несобственно, если эти эквивалентности
различных типов.
160 Раздел V (пп. 160-161)
Действительно, так как формы F, F' эквивалентны соответственно
формам F\ F", то не только первые из них соответственно содержат
вторые (откуда следует, что F содержит также и F"), но и вторые
содержат первые. Поэтому F и F" эквивалентны. Из предыдущего
же следует, что F содержит форму F" собственно или несобственно
в зависимости от того, эквивалентны ли форма F форме F' и форма F'
форме F" одинаковым или неодинаковым образом; так же и форма F"
содержит форму F. Поэтому формы F и F" будут эквивалентны,
в первом случае собственно, а во втором несобственно.
Формы (а, — Ь, с), (с, Ьу а), (с, — Ь, а) эквивалентны форме (а, Ъ, с),
причем первые две — несобственно, а третья — собственно.
Действительно, ах2-\-2Ьху-\-су2 переходит в ах'2 — 2Ъх'у' -f су'2,
если положить х = х' + 0• г/', у = 0-х' — г/', причем это преобразова-
преобразование несобственное, так как 1-(—1) — 0-0 = — 1. В форму же
сх'2 + 2Ьх'у' + ау'2 первая форма переходит посредством несобствен-
несобственного преобразования х = 0-я' + у\ У = х' + 0-г/', а в форму
сх'2 — 2Ьх'у' + щ'г при собственном преобразовании х = 0-х'—у',
У=х' + 0-у'.
Из этого ясно также и то, что каждая форма, эквивалентная
форме (а, Ь, с), собственно эквивалентна либо этой форме, либо
форме (а, — Ъ, с), а также, что если некоторая форма содержит
форму (а, Ь, с) или содержится в ней, то она собственно содержит
форму (а, Ъ, с) или форму (а, — Ь, с), или же собственно содержится
в одной из них. Формы (а,Ь,с) и (а, —Ь, с) мы будем называть
противоположными.
Соседние формы
160
Если формы (а} Ъ, с) и (а', V, с') имеют одинаковые определители,
и, кроме того, с = а' и Ъ == — Ъ' (mod с) или Ъ + V == 0 (modс), то мы
будем называть эти формы соседними, причем в тех случаях, когда
будет нужна большая точность, мы будем называть первую форму
соседней для второй слева, а вторую —> соседней для первой справа.
Так, например, форма G, 3, 2) является соседней справа для
Общие делители коэффициентов форм 161
формы C, 4, 7), а форма C, 1,3) — соседняя своей противоположной
форме C, —1, 3) с обеих сторон.
Соседние формы всегда собственно эквивалентны. Действительно,
форма ах2-\- 2Ъху + су2 переходит в соседнюю форму сх'2-^- 2Ь'х'у'-\- с'у'г
h -\-Ъг , (
при подстановке х = —у , у = х -\ ! у которая является
собственной, ибо 0»—— 1(—l) = l), что легко доказывается
выкладкой с использованием равенства б2 — ас = Ь'2 — а'с'\ число же
(b-\-b')/c по предположению является целым. Впрочем, эти поясне-
пояснения и следствия не имеют силы, если с = а' = 0. Но этот случай
может представиться только для форм, определители которых
являются квадратами.
Формы (а, 6, с) и (а', V с') собственно эквивалентны, если а = а',
b е=Ь' (modа). Действительно, форма (а, 6, с) (согласно предыдущему
пункту) собственно эквивалентна форме (с, —6, а), а последняя
является соседней слева для формы (аг, 6', с').
Общие делители коэффициентов форм
161
Если форма (а, 6, с) содержит форму (а', Ь\ с'), то каждый
общий делитель чисел а, 6, с является также и общим делителем
чисел а', Ь', с', а каждый общий делитель чисел а, 26, с — общим
делителем чисел а', 26', с'.
Именно, если форма ах2 + 2Ьху + су2 переводится в форму
а'х'2 + 2Ъ'х'у' -\- с'у'2 подстановкой х—<хх'-\-$у\ у = чх'~}-Ъу\ то
выполняются следующие равенства:
aoi2 ~\- 26ат + су2 = а',
ар2 + 2бр8 + с82 = с',
из которых теорема следует тотчас же, если для доказательства
ее второй части вместо второго равенства использовать равенство
+ 26 (a8 + Рт) + 2сТ8 = 26'.
162 Раздел V (п. 162)
Из этого вытекает, что наибольший общий делитель чисел аг
6 B6), с входит в наибольший общий делитель чисел а', Ъ' B6'), с'. Если
же, кроме того, и форма (а', 6', с') содержит форму (а, 6, с), т. е.
если эти формы эквивалентны, то наибольшие общие делители чи-
чисел a, 6B6), с и а\ Ъ' B6'), с' будут равны, так как каждый из
них должен входить в другой. Поэтому, если в этом случае числа
а, 6B6), с не имеют общих делителей, т. е. их наибольший общий
делитель равен 1, то и числа а', V B6'), с' не будут обладать об-
общими делителями.
Связь между всевозможными однотипными преобразованиями
одной заданной формы в другую
162
Задача. Пусть форма
F = АХ* + 2BXY + СУ2
содержит форму
/ = ах*+ 2Ъху + су\
и дано некоторое преобразование первой формы во вторую; найти
все остальные однотипные с ним преобразования.
Решение. Пусть задано следующее преобразование: X = ах + (Зг/,
Y — ух + Ьу\ предположим сначала, что имеется и некоторое дру-
другое преобразование X = ои'х + $'у, У = 4х + &'у, однотипное с пер-
первым, и посмотрим, что из этого будет следовать. Если принять,
что определители форм F, f суть D, d, и <х8 — Рт= е-> а'&' —
— PY = е\ то (в силу п. 157) d = De2 = De'2, и так как величи-
величины е и е', по условию задачи, должны быть одного знака, е = е'.
Но мы имеем следующие шесть равенств:
[1] Act? + 25aY + Cf5 = a,
[2] Ла/2 + 25а Y + ^т'2 = а,
[3] .4оф + 5 (а8 + Рт) + С?8 = 6,
[4] . 4а/р/-+, В (а'У + Р'т') + СТ'8.' - 6,
Связь между преобразованиями одной формы в другую 163
[5] #2 + 2#р8 + а2 = с,
{6] A$'2 + 2B$W + СЪ'2 = с.
Если для краткости обозначить числа
А (ар' + Вое') + В (а8' + рт' + тр' + 8а') + С (Т8' + 8Т') ,
через а', 26', с', то из предшествующих равенств выводятся сле-
следующие *:
[7J а'2 — D (аТ' — Та'J = а2,
[8]] 2а'Ь' — Л (аТ' — т<*') («8' + Рт' — Т?' — 8а') = 2аЬ,
46'2— J? [(а8' + рт' — тр' — 8а'J + 2ее'] - 2й2 + 2ас ,
откуда, прибавляя 2Dee' = 2d = 2b2 — 2ас, мы получаем
[9] W2 — D (<*8' + Рт' — ТР' — 8а/J = 4^2»
а'с' _ Д (а8' — Тр') (рт' — 8а') - Ь\
а из этих равенств, вычитая из них D (а8 — р^) (а'8г — р'^') =
= б2 — ас, мы приходим к равенствам
[10] а'с' — D (а?' — Т^О (Р8Г — 8р') = ас ,
[11] 2Ь'с' —
[121
Предположим теперь, что наибольший общий делитель чисел
a, 2bt с равен 7?г, а числа 31, 95, € определены так, что
3ta + 956 + ?с = лг
* Они получаются следующим образом:^ [7] получается из [1]-[2] (т. е.
если мы перемножим равенства [1] и [2], или, точнее, умножим левую часть
первого на левую часть второго и правую часть первого на правую часть второго
и приравняем произведения), [8] получается из [1]-[4]+ [2j-[3], следующее
(непронумерованное) равенство из [1]-[6] + [2]-[5] + [3]*[4] -f [3]-[4];
непронумерованное равенство, идущее после [9] — из [3] -[4], равенство [11] —
из [3]-[6] + [4] -[5], равенство [12] — из [5]-[6]. Обозначений, подобных ис-
лользованным здесь, мы будем все время придерживаться и в дальнейшем.
Выкладки же мы должны предоставить читателю.
164 Раздел V (п. 162)
(п. 40); умножим тогда равенства [7], [8], [9], [10], [И], [12] соот-
соответственно на Э12, 23C5, 952, 231S, 235S, (?2 и сложим произведения.
Если еще для краткости положить
[13] 31а' + 2956' + <?с' = Т ,
[14] 31 (аТ' — Та') + 95 (а8' + рТ' — Тр' — 8а') + S ф8' — Щ = С/ ,
где Т и U, очевидно, являются целыми числами, то мы получим
равенство
Мы приходим, таким образом, к следующему изящному заклю-
заключению: из любых двух однотипных преобразований формы F в f по-
получается решение в целых числах неопределенного уравнения t2—
— Du2 = m2, именно, t = T, u = U. Так как при наших рассужде-
рассуждениях мы не предполагали, что преобразования различны, то и
одно преобразование, примененное дважды* дает решение этого
уравнения. При этом, однако, вследствие того, что а' = а, р' = р,
также и а' = а, Ъ' = 6, с' = с, и, следовательно, получается реше-
решение Т = т, U = 0, очевидное и непосредственно.
Теперь мы предположим известными первое преобразование и ре-
решение неопределенного уравнения и посмотрим, что можно из этого
вывести относительно второго преобразования, т. е. каким образом а',
Р', т', ^' зависят от а5 р, ^, 8, 71, /7. Для этой цели умножим
сначала равенство [1] на 8а' — р*у', равенство [2] — на а8' — ^Р'>
равенство [3] — на ос^' — Та'» равенство [4] — на ?а' — а^' и сло-
сложим произведения. При этом получается равенство
[15] (е + е') а' = (а8' — рТ' — ?р' + 8а') а .
Аналогично из
получается равенство
[16] 2 (е + в') 6' = 2 (ей' — Рт' — ТР' + 8а')ь -
Наконец, из
(8р' - рв') ([3] - [4]) + (о8' - тР') [5] + (8а' - рТ') 16]
вытекает равенство
[17] (e + e')c' = (aS'-pY'_Tp' + 8a')c
Связь между преобразованиями одной формы в другую 165
Если значения [15], [16], [17] подставить в [13], то мы получим
(е + ё) Т = (а8' — р?' — тр' + 8а') Ща + 2%>Ъ + <Бс),
или
[18] 2еГ = (а8' — рт' — тр' + 8а') лг ,
откуда Т может быть выведено много легче, чем из [13]. Если
это равенство связать с [15], [16], [17], то получается та' = Таг
2mbr = 2ТЬ, тс' = Тс. При подстановке этих значений а', 2V, с' в
равенства [7] — [12] и замене Т2 на m2 + DU2 указанные равен-
равенства после соответствующих преобразований переходят в следующие:
' — 8a') @8' — p)
= 2bcU2,
Отсюда при помощи равенства [14] и равенства Э(а +
+ ©с = т легко выводятся (если умножить соответственно на 21,
95, К сначала первое, второе и четвертое равенства, затем второе,
третье и пятое и, наконец, четвертое, пятое и шестое и получен-
полученные произведения сложить) соотношения
(a8' + ВТ' — тр' — За') Urn2 = 2mbU2 ,
из которых при делении на mil * получается
[19] aU = (oif' — та') m ,
[20] 2617 = (а8' + рТг — тр' — 8ar)
[21] с*7 = ф8' — 8р') т;
* Этого нельзя было бы делать, если бы U было равно 0; но в этом случае
справедливость равенств [19], [20], [211 тотчас же получалась бы из первого,
третьего и шестого равенств.
166 Раздел V (п. 162)
из любого из этих равенств U может быть получено намного
легче, чем из [14]. Одновременно отсюда следует, что как бы ни
были определены 91, 35, § (что можно сделать бесконечным числом
способов), значения Т и U будут сохраняться одними и теми же.
Если теперь умножить равенство [18] на ос, [19] — на 2р,
[20] — на —ос, то при сложении получается
2аеГ + 2 (ра — осб) U = 2 (а8 — Ру) а'/га = 2еа'тга .
Аналогичным образом из р * [18] + р • [20] — 2а • [21] получается
2$еТ + 2 (рь — осе) U = 2 (<х8 — Рт) p'wi = 2е$'т .
Далее, из ? • [18] + 28 . [19] — ? . [20] имеем
2чеТ + 2 (8а — fb) U = 2 (а8 — рт) т'тга = 2ет'7?г.
Наконец, из 8 . [18] + 8 . [20] — 2^ . [21] получается
2ЬеТ + 2 (8& — Тс) f/ = 2 (а8 — pY) Srm = 2e8'm .
Если в эти формулы подставить вместо а, 6, с их значения
из [1], [3], [5], то формулы переходят в следующие:
р'т = рГ — (р5 + ЗС) г/ ,
Из вышеизложенного исследования вытекает, что не существу-
существует преобразования формы F в /, однотипного с заданным, кото-
которое не содержалось бы в формулах
(I)
Y = -1
m
где ? и и обозначают произвольные целые числа, удовлетворяю-
удовлетворяющие уравнению t2 — Du2 = m2. Однако из этого еще нельзя заклю-
заключить, что любые значения t и и, удовлетворяющие указанному
* Отсюда легко видеть, что
(Ьч' — fb')mt 2BeU = (аЬ' — Ва' + tf' — $4') m> CeU = (Ра' — а?')/и.
Связь между преобразованиями одной формы в другую 167
уравнению, при подстановке в формулы (I) дают требуемые пре-
преобразования. Но при помощи равенств [1], [3], [5] и равенства
t2 — Du* — т2 легко устанавливается следующее.
1. Форма F может быть преобразована в форму / подстанов-
подстановкой, получающейся из любых значений t и и. Выкладки, которые
скорее громоздки, чем трудны, мы для краткости опустим.
2. Каждое преобразование, полученное по формулам (I), одно-
однотипно с заданным. Действительно,
~ [at - («В + ТС) и] ¦ -i- [Ы + $А + ЬВ) и] -
3. Если формы F и / имеют разные определители, то может слу-
случиться, что при некоторых значениях t и и формулы (I) будут давать
подстановки, которые содержат дроби и потому должны быть отбро-
отброшены. Все же остальные будут годиться и ими будут исчерпываться
все искомые преобразования.
4. Если же формы Fnf имеют одинаковые определители и потому
эквивалентны, то формулы (I) не дают никаких преобразований, со-
содержащих дроби, и потому представляют полное решение задачи для
этого случая. Доказывается это следующим образом.
Из теорем предыдущего пункта следует, что в этом случае т одно-
одновременно является общим делителем чисел А, 2В, С. Так как
t2 — Du2 = т2, то t2 — В2и2 = т2 — АСи2; таким образом t2 —
— В2и2 и тем более At2 — АВ2и2 делится на т2, откуда вытекает
(ибо 2В делится на т), что it2 делится на т2 и, следовательно, 2t
делится на т. Поэтому числа 2(t + Ви)/т и 2(t — Ви)/т являются
целыми, и притом (так как их разность АВи/т четна) либо одновре-
одновременно четными, либо одновременно нечетными. Если бы они оба
были нечетными, то и их произведение должно было бы быть нечет-
нечетным; но произведение, будучи равным учетверенному числу
(t2—В2и2)/т2, которое, как мы показали выше, целое, обязательно
четно. Следовательно, этот случай невозможен; поэтому 2(t -\-Bu)/m
и 2(t — Ви)/т всегда четны, а значит (t + Ви)/т и (t — Ви)/т —
168 Раздел V (пп. 163-164)
всегда числа целые. Из этого уже без труда выводится, что все четыре
коэффициента в (I) всегда являются целыми числами.
Из сказанного вытекает, что если известны все решения уравне-
уравнения t2—Du2=m2, то из этого могут быть выведены все преобразова-
преобразования формы (А, В, С) в форму (а, Ь, с), однотипные с заданным преоб-
преобразованием. Как находить решения указанного уравнения, мы пока-
покажем позднее. Сейчас заметим только, что количество решений конеч-
конечно, если D отрицательно или если D положительной притом является
квадратом, и бесконечно, если D — положительное число, не являю-
являющееся квадратом. Если имеет место этот последний случай и одновре-
одновременно D не равно d (см. выше случай 3), то нужно было бы еще ис-
исследовать, каким образом сразу отличать те значения t, и, которые
дают подстановки, не содержащие дробей, от значений, приводящих
к дробным подстановкам. Однако ниже мы изложим для этого слу-
случая другой метод, который будет свободен от этого неудобства
(п. 214).
Пример. Форма х2 + 2г/2 при собственной подстановке х =
= 2х' + 1у\ у = x/Jr 5y' переходит в форму F, 24, 99); найдем
все собственные преобразования первой формы во вторую. Здесь
D = —2, т = 3, и потому уравнение, которое надлежит решить,
есть t2 + 2w2 = 9. Оно удовлетворяется шестью различными спосо-
способами, именно, при t = 3, —3, 1, —1, 1, —1 и соответственно и = О,
О, 2, 2, —2, —2. Первое и третье решения дают подстановки с дроб-
дробными числами и потому должны быть отброшены; из остальных
получаются четыре подстановки
I 2х'+1у', ( х' + Ъу',
\-2х'-7у', |_ж'_5у',
-2х'-9у', У-) х' + Зу',
{ 2х'+9у', у-Х>-Ъу>,
первая из которых совпадает с заданной.
Двусторонние формы
163
Выше мы мимоходом уже упоминали о том, что некоторая фор-
форма F может содержать другую форму F' одновременно и собственно
Форма, содерэюащаяся в другой и собственно и несобственно 169
и несобственно. Очевидно, что это будет иметь место, если между
формами F и F' можно поместить еще одну форму G, обладающую
теми свойствами, что F содержит G, G содержит F' и G несобствен-
несобственно эквивалентна самой себе. Действительно, если мы предположим,
что F содержит форму G собственно (несобственно), то так как G не-
несобственно содержит G, F будет содержать G также и несобственно
(собственно), т. е. будет содержать как собственно, так и несобственна
(п. 159). Таким же способом мы из предположения, что G содержит
F', выводим, что F содержит F' и собственно и несобственно. То, что
формы, несобственно эквивалентные самим себе, существуют, выте-
вытекает из рассмотрения совсем простых примеров, именно, форм со
средними членами, равными нулю. Такая форма сама себе противо-
противоположна (п. 159) и потому несобственно эквивалентна. Более общо,
этим свойством обладает каждая форма (а, Ь} с), у которой 2Ъ делится
на а. Именно, форма (с, Ь, а) будет для этой формы соседней слева
(п. 160) и потому будет ей собственно эквивалентна; форма же (с, Ь, а),
согласно п. 159, несобственно эквивалентна форме (а, Ь, с); таким
образом, (а, Ь, с) несобственно эквивалентна самой себе. Такие формы
(а, Ь, с), у которых 2Ъ делится на а, мы будем называть
двусторонними. Таким образом, имеет место следующая теорема.
Форма F будет содержать форму F' и собственно и несобственноТ
если имеется двусторонняя форма, содержащаяся в F и содержа-
содержащая F'.
Однако эту теорему можно и обратить.
Теорема, касающаяся случая,
когда одна форма содержится в другой
одновременно собственно и несобственно
164
Теорема. Если форма
F = Ах2 + 2Вху + Су2
содержит другую форму
F' = А'х'*
170 Раздел V (п. 164)
как собственно, так и несобственно, то всегда можно найти дву-
двустороннюю форму, которая содержится в форме F и содержит
форму F'.
Предположим, что форма F переводится в форму F' как под-
подстановкой
х = ах' + р/ , у = тж' + Ьу\
так и неоднотипной с ней подстановкой
Если тогда числа aS — р^, а'^'—PY обозначить соответственно
через е, е\ то Б'2 — 4'С" = е*(В2 — АС) = ё2(В2 — АС), откуда
^2 __ ^/2^ и^ так как? по предположению, е и е' имеют противопо-
противоположные знаки, е = — е' или е + е' = 0. Если теперь в F' положить
х' = Ъ'я? — ру и г/' = — т'ж" + aV» To» очевидно, получится та же
самая форма, которая получается из F, если положить
или
1) х = a (8 V - р V) + Р (- Т'ж" + а'2/") = И' - РТ') *" + (?«' - «Р'J/",
2/ = Т (8'«* — РУ) +S (— т'*' + «У) = (Т*' — 8Т') х" + («а'— Тр') у",
ИЛИ
2) х - а' (8 V - ру) + Р' (- т'^ + «У) = вV ,
У = т' (8'^ - Р'Г) + 8' (- Т'^ + «У) = *У •
Поэтому, если числа a8f — В?', Pa' — ap', ^' — ^т'> ^ос' — ^Р' обозна-
обозначить соответственно через а, Ь, с, d, то форма i7 обеими подстановками
х = ах" + by", у = сх" + dy"\ х = eV, у = е'у"
будет переводиться в одну и ту же форму, откуда получаются
следующие три равенства:
[ 1 ] Ааг + 2Вас + Сс2 = Ае'2,
[2] Лаб + Б (ad + fee) + Ccd = Be'2,
[3] ^62 + 2Bbd + Cd2 = Ce'2.
Из значений же чисел a, fe, c, d находим
[4] ad — be = ее' ^—е2 = — ё2.
Форма, содерснсащаяся в другой и собственно и несобственно 171
Поэтому из d • [1] — с . [2] получается
(Аа + Be) {ad — be) = {Ad — Be) e'2 ,
и потому
^ (a + d) = 0 .
Далее, из (a + d) • [2] — b • [1] — с • [3] вытекает
[Ab + B(a + d) + Cc] {ad —be) = [—Ab + В (a + d) — Cc] e'\
и потому
B{a+d) = 0.
Наконец, из а • [3] — 6 • [2] имеем
+ Cd) {ad — 6c) = (— Bb + Ca) e'2,
и потому
С (a + d) = 0.
Так как все три величины А, В, С не могут быть одновре-
одновременно равными нулю, мы получаем а + d = 0 или а = — d.
Из а • [2] — 6 • [1] следует
(J5a + Cc) (ad — be) = {Ba — Ab) e'2,
откуда
[5] Ab — 2Ba — Cc = 0.
Из равенств е + e! — 0, a + с? = О, или
a§ _ pT + a'8' — p'T' = 0, a8' — pT' — ??' + 8a' = 0,
следует (a + a') (8 + 8') = ф + p') (T + т'), или .
Пусть это отношение, выраженное в наименьших числах, имеет
вид т : п, так что т ж п взаимно просты*; возьмем такие числа
* Если бы все величины a+a', f + Т » Р + f'» ^ + 8' были равны нулю,
то соотношение было бы неопределенным, и потому такой метод был бы не-
неприменим. Но при некоторой внимательности можно заметить, что это при
172 Раздел V (п. 164)
[л, v, что [1т-\-уп = 1. Далее, пусть г есть наибольший общий де-
делитель чисел а, Ь, с, квадрат которого будет, следовательно, вхо-
входить также в а2 + be или be — ad, или е2, так что г является также
и делителем е. Если теперь форму, в которую переходит форма F
при подстановке
х = mt -\ и, г/ = nt — ^—- и,
обозначить через G = Mt2 + 2iVta + Ргг2, то G будет двусторонней
и будет содержать форму F'.
Доказательство, I. Чтобы сделать ясным, что форма G — дву-
двусторонняя, мы покажем, что
М (fy,2 — 2a(xv — cv2) = 2Nr ,
откуда, так как г входит в а, Ь, с, будет следовать, что число
F[л2 — 2a;xv — cv2)/ г целое, и потому 2N есть кратность числа М. Но
[6] М = Л/?г2 + 2#тшг + Стг2, iV> = [Amv — В {т\к — т) — Сщ\ е .
Далее, раскрывая скобки, легко установить, что
2e + 2a = e-e/ + a-d = (a-a/)(^ + ^)-(P-p/)(T + T/M
2b = (a + a') (p -p') - (a - a') (p + p').
Отсюда следует, так как т (у 4- ^') = ft (a + a') m (8 -f- 8') =
= n (P + P')» 4T0 m Be + 2a) = — 2nb или
[7] me + ma + nb = 0 .
Аналогично,
2e — 2a = e — e' — a + d = (a + О (8 — 8') — (p + p') (T — ?'),
2c = (T-T/)(8 + 8')-(T + Y')(8-8#),
и отсюда следует nBe — 2a) = —2mc, или
[8] ne — na -f- me = 0 .
наших предположениях невозможно. Действительно, тогда имело 0ы место
аВ — [}*f = а'В' — Р'^'» т- е- е — е'у и потому, в силу е== — е', было бы
е = е' = 0. Отсюда следовало бы, что и J5'2 — Л'С = 0, т. е. определитель
формы /" равен 0, однако такие формы мы раз и навсегда исключили из
рассмотрения.
Форма, содерэюащаяся в другой и собственно и несобственно 173
Если теперь к m2F(x2— 2u\lv— cv2) прибавить выражение
A — т\ь — пу) [ту (е — а) + (т\к + 1) Ь] + (т<? + ^я + nb) (тру + v) +
-f- (ne — па -f- тс) ту2,
которое вследствие
1 — т\к — пу — О, те + ^<^ + nb = 0, гсе — па + тс = О,
очевидно, равно нулю, то после раскрытия скобок и отбрасывания
взаимно уничтожающихся членов мы получим 2mve + b. Поэтому
[9] т* (fy2 — 2a(xv — cv2) = 2mve + b .
Прибавляя аналогичным образом к m/2 (fyx2 — 2a[xv — cv2) выражение
A — т[л — rav) [(^v — /w[x) б — A + mjx + ^v) a] — (m^ + ma + nb)
+ (ne — na + me) rcv2 ,
находим
[10] mn (fyx2 — 2a\Lv — cv2) = (пу — m\k) e — a.
Наконец, если к п2 (й[х2 — 2a[xv — cv2) прибавить выражение
(т\ь -\- пч — 1) [n[L (e + a) + (yn + 1) c] — (me -\-ma-\- nb) щ2 —
— (ne — na-\- me) (n\Lv -f [^),
то получится
[11] n2 (fe[x2 — 2a(xv - cv2) = — 2n[xe — с .
Теперь из [9], [10], [11] получается
(^4m2 + 2Bmn + Сп2) F[х2 — 2ajxv — cv2) =
= 2е [Ату + В (пу — т\х) — Сщ.] + АЪ — 2Ва — Сс
или, в силу [6],
М (Ьа2 — 2а\ку — cv2) = 2Л> .
II. Чтобы доказать, что форма G содержит форму F', мы по-
покажем, что, во-первых, G переходит в F\ если положить
174 Раздел V (п. 165)
и, во-вторых, что г (ла— ту) / е и г {п$ — тЬ) / е суть целые числа -
1. Так как F переходит в G, если положить
х = mt -\ и. у = nt — и ,
то G преобразуется подстановкой ($) в ту же самую форму, в ко-
которую преобразуется F, если положить
vT) ж' + (jxp + v8) у'] + v
z/ = n [([xa + vy) ж' + (f^P + v8) y'\ — [л [(no. — mT) ж' + (л? — m8) z/'] -
-f 7П[х) xf -f- 8 (nv + /W[x) z/r = y^:' + 8z/ .
Но этой подстановкой F переводится в F'\ поэтому и G подста-
подстановкой (S) будет переводиться в F'.
2. Из значений е, Ъ, d находим, что а'е + уб — осе? = 0, или,
вследствие того, что d = — а, тга/е + тгоса + /2у6 = 0. Отсюда в силу
[7], пси'е + naa = т^е + тггуа, или
[12] (па — my)a = (m^ — па') в .
Далее, <xnb = —&т(е-\-а), ^mb = — /w(a'e + aa), и потому
[13] (па — my) b = (&' — а) те .
Наконец, у'е — ^а -f- ас = 0; если умножить это равенство на п
и подставить вместо па его значение из [8], то получается
[14] (псх,— ту) с = (т — ч')пе •
Аналогичным образом выводится р'е + S6—$d = 0, или гср'е +
+ nS6 + npa = 0, и потому, в силу [7], п$'е + п$а = mbe + m8a
или
[15] (лр — m8) a = (m8 — лр;) е .
Далее, $nb = — ?>т(е + а), 8/ий = —m(fJ'e +pa), и потому
[16] (лр — тЪ)Ъ = (рл — Р) те.
Форма, содержащаяся в другой и собственно и несобственно 175
Наконец, Ъ'е—Sa + ?te = O; если умножить это равенство на п
и подставить вместо па его значение из [8], то получается
[17] (п$ — га8)с = (8 — Ь')пе.
Так как наибольший общий делитель чисел а, 6, с равен г, то
можно теперь найти такие целые числа 3t, 95, (S, что
3ta + 956 + Eс = г.
Если эти числа найдены, то из [12], [13], [14]; [15], [16], [17].
следует
па') + 95 (ос' — а) га -f- ? (т — ?') и = -у (па — га?),
31 (т8 _ пф) + 95 ф; — Р) га + 6 (8 — 8') л = '- (лр — га8),
и потому числа г (пи—тщ) I е и г (п$ — тпЪ) / е—целые.
165
Пример. Форма 3#2+14:п/ — 4г/2 преобразуется в форму
12#'2—l&x'y' + 3%/2 как собственно, если положить
так и несобственно, если положить
х = — 74я' + 8%', у = 15ж' —
Числа a + аЛ Р + ?'» Т + Т'» S Ч-8' равны здесь соответственно
— 70, 100, 14, —20. При этом — 70 : 14 = 100 : —20 = 5 : — 1.
Мы полагаем поэтому га = 5, п = — 1, [а = 0, v = — 1. В качестве
чисел a, b, с находим —237, —1170, 48, наибольший общий
делитель которых г равен 3. Наконец, е = 3. Поэтому преобразо-
преобразование х = Ы — и, y = — t переводит форму C, 7, —4) в двусто-
двустороннюю форму t2— l&tu -j- Зн2.
Если формы F, F' эквивалентны, то форма (?, содержась в F,
будет содержаться также и в F'. Но так как G в свою очередь
содержит F\ G будет эквивалентна F\ а, следовательно, эквйва-
176 Раздел V (пп. 166-167)
лентна также и форме F. Таким образом, в этом случае теорема
может быть высказана в следующем виде.
Если формы F и F' эквивалентны как собственно, так и несоб-
несобственно, то можно найти двустороннюю форму, эквивалентную
обеим этим формам.
Между прочим, в этом случае е — + 1, а потому и г, которое;
входит в е, равно 1.
В отношении преобразований форм мы удовольствуемся изло*
женным и перейдем теперь к рассмотрению вопроса о представлен
ниях чисел.
Общее исследование о представлениях чисел формами
и о связи этих представлений с преобразованиями
166
Если форма F содержит форму F\ то каждое число, которое
может быть представлено формой F', может быть также пред-
представлено и формой F.
Пусть неизвестные форм F, F' суть соответственно х, у; х\ у',
и предположим, что число М представляется формой F' при х' = т,
у' = п, а форма F переводится в F' подстановкой
Тогда очевидно, что если мы положим
х = хт + $п, у = ^т + &п ,
форма F представит М.
Если М представляется формой F' различными способами, на-
например, также и при х' = т', у1 = п\ то отсюда будут получаться
и различные представления М формой F. Действительно, если бы
было ост + ргс = am' + $п' и ^т + Ьп = ^тг + Ьп', то имело бы
место или а8 — Рт == О» что противоречит нашему предположению о
том, что определитель формы F не равен нулю, или т = т\ п = пг
Отсюда следует, что М может быть представлено формой F по
Представления чисел и преобразования форм 177
меньшей мере столькими же различными способами, что и фор-
формой F'.
Поэтому, если как F содержит форму F', так и F' содержит
форму F, т. е. если F и F' эквивалентны, и число М представля-
представляется одной из них, то оно представляется и другой, причем столь-
столькими же различными способами, что и первой.
Наконец, заметим, что в этом случае наибольший общий дели-
делитель чисел т, п равен наибольшему общему делителю чисел
am + fin, ^т-\-Ы. Е ли первый равен А, и числа [л, v подобраны
так, что [xm -f- vn = А, то
F(х — ?v) (am + fin) — (В[х — av) {4m + Ьп) = (a8 — fi*() (fx/ra + ш) = + А.
Поэтому наибольший общий делитель чисел am + (Згс, ^ + &п вхо-
входит также и в А, а А в свою очередь входит в него, так как вхо-
входит в ост -f- fin и Ym + ^- Следовательно, оба наибольших общих
делителя равны. В частности, если m, n взаимно просты, то
am -f- рп, чт + ^ будут взаимно просты.
167
Теорема. Если формы
F = ах2 + 2Ьху + су2,
F' - aV2 + 26'жУ -t c'z/'2
эквивалентны, определители их равны D, вторая форма переводит-
переводится в первую подстановкой
х =ax + fiy, у' = чх + Ьу
и если, далее, число М представляется формой F при х = т,
у = п и потому формой F'— при
х' = am + fin — т', у' = ^т + &п = п\
причем так, что т взаимно просто с п, и потому и т' взаимно
просто с п', то оба представления будут принадлежать или одно-
одному и тому же, или противоположным значениям выражения
Y& (modM) в зависимости от того> является ли преобразование
формы F1 в F собственным или несобственным.
178 Раздел V (пп. 168-169)
Доказательство. Если мы определим числа [л, v так, что \liu +
-f- vn = 1, и положим
ЬУ — 7V = .,/ — Pi* + <*v = /
(эти величины, в силу того, что aS — PT^zfcl» являются целыми
числами), то (согласно сказанному в конце предыдущего пункта)
будет выполняться равенство
Если, далее,
[л (Ьт + сп) — v (am + Ъп) = F, р' {Ъ'т! + cV) — v' (a'm' -f Ъ'п1) - F;,
то V, V будут значениями выражения |^Z)(modM), которым при-
принадлежат соответственно первое и второе представления. Подставляя
в V вместо [//, v', m', п' их выражения, а в V
вместо а выражение a'a2 + 26'а^ + с'^2,
вместо Ь выражение а'&$ + &' (а^ + Рт) + С'Т^»
вместо с выражение аф2 + 2Ь'р8 + с'82,
находим после соответствующих преобразований, что
F = F'(a8 —рт).
Поэтому или V = V\ или Рг = —F', в зависимости от того,
а8 — р^ = -|- 1 или — — 1, т. е. представления будут принадлежать
или одному и тому же, или противоположным значениям выраже-
выражения YD (mod M), в зависимости от того, будет ли преобразование
формы F1 в F собственным или не обственнътм.
Поэтому если имеется несколько представлений числа М фор-
формой (а, Ь. с) при взаимно простых значениях неизвестных х, у,
которые принадлежат различным значениям выражения Y& (mod M^,
то соответствующие представления формой (a', b', с') будут при-
принадлежать тем же самым (противоположным) значениям, а если
для одной из форм нет представления числа М, принадлежащего
какому-нибудь определенному значению, то для эквивалентной
формы нет представления, принадлежащего этому же (противопо-
(противоположному) значению.
Представления чисел и преобразования форм 179
168
Теорема. Если число М представляется формой ах2 + 2Ьху -\- су2,
когда неизвестным х, у придаются взаимно простые значения т, п,
и если значение выражения }Л0 (modM), которому принадлежит
это представление, равно N, то формы (а, Ь, с) и (М, N,(N2—D) / М)
собственно эквивалентны.
Доказательство. Из п. 155 вытекает, что можно найти целые
числа [х, v с тем свойством, что
m\L + m> = 1, [л (bm + en) — v (am + bn) = N.
Если это сделано, то подстановкой х = тх' — vz/', у = пх + [хг/\
которая, очевидно, является собственной, форма (а, Ь, с) перево-
переводится в форму, определитель которой равен D(m\L + ^vJ, т. е.
равен D, другими словами, в эквивалентную форму. Если записать
эту форму в виде (ДГ, N\ (N'2 — D)/Mf), то
М' = am2 + 2bmn + с^г2 = М, Nr = — mva + {m\L — nv) & + щс = iY.
Поэтому форма, в которую переводится (а, Ъ, с) указанным пре-
преобразованием, представляется в виде (М, N, (N2 — D)/M).
Из равенств
m\L + nv = 1, [л (mb + ис) — v (та -f- rc&) = iY
следует, между прочим, что
nN -\- та + пЪ nN -\-та + ^& rnb -\- пс — mN
^ — am2 + 2Ьтп + сп* = М ' V = " М ?
и потому стоящие справа выражения являются целыми числами.
Заметим еще, что эта теорема неверна, если М = 0, так как
тогда член (iV2 — D) / М будет неопределенным*.
169
Если имеется несколько представлений числа М формой (а,Ь,с),
принадлежащих одному и тому же значению N выражения
* Если мы захотим применять нашу терминологию также и в* этом случае,
то выражение «/V есть значение выражения У D(mod M), или /V2=D(mod M)»t
должно означать, что число ./V2—D есть кратность числа М и потому N2— D = 0.
180 Раздел V (пп. 170-171)
\rD(moAM) (причем значения х, у мы все время предполагаем
взаимно простыми), то из этого могут быть выведены несколько
собственных преобразований формы F = (а, 6, с) в форму
G = (М, N, (N2 — D) IM). Именно, если представление получается
при значениях х = т', у = п', то F будет переводиться в G под-
подстановкой
, , , m'N — т'Ь — п'с , , , , п'N + т'а 4- п'Ь ,
х = тх Н ^ у , г/ = 72 .х + ^—L 2/ •
Обратно, из каждого собственного преобразования формы F в G
получается представление числа М формой F, принадлежащее зна-
значению N. Именно, если F переходит в G при подстановке
х = тх' — vj/', у = тгх' + (лг/', то М будет представляться формой F,
если положить ж = т, у — п, и так как здесь m[x + wv = l, значе-
значение выражения |/"Z>(modM), которому принадлежит представление,
будет равно [л (fern + сп) — v(am-\-bri), т. е. N. Из нескольких раз-
различных собственных преобразований будет получаться столько же
различных принадлежащих N представлений *. Отсюда легко сле-
следует, что если имеются все собственные преобразования формы
F в G, то из них можно получить все принадлежащие значению N
представления числа М формой F. Таким образом, задача об
отыскании представлений заданного числа заданной формой (при
которых неизвестные имеют взаимно простые значения) сводится
к задаче об отыскании всех собственных преобразований этой формы
в заданную эквивалентную ей форму.
Если использовать здесь то, что было изложено в п. 162, то
легко получается, что если одно из принадлежащих значению N
представлений числа М формой F есть х = а, у = ?, то общая
формула, охватывающая все принадлежащие значению N представ-
представления того же числа формой F, такова:
* Если мы предположим, что из двух преобразований получается одно
и то же представление, то эти преобразования должны иметь вид
1) х — тх' — vy', у = пх' -\- }±у'\ 2) х = тх' — v'l/', у = пх' + \л'у''.
Но из двух равенств
т[± + nv — т\ь' + wv', [х (mb + nc) — v {та + пЪ) = \х' (тЬ + пс) —<v' (та + пЪ)
легко видеть, что либо М = 0, либо jx = ja', v = v'. Случай М = 0 мы, однако,
исключили.
Формы с отрицательным определителем 181
at— (аЪ + ус) и ^t — (аа
X = J , у =
ГУ) 'О уу.
где т есть наибольпгий общий делитель чисел а, 2Ъ, с, a t, и обозна-
обозначают произвольные числа, удовлетворяющие уравнению t2— Du2 =
170
Если форма (а, Ъ, с) эквивалентна какой-нибудь двусторонней
форме, а значит как собственно, так и несобственно эквивалентна
форме G = (М, TV, (TV2 — L)/M), или собственно эквивалентна как
форме (Af, N, (N2 - D)IM), так и форме (М, -N, (N2 — D)/M\ то
получаются представления формой F числа М, которые принадле-
принадлежат как значению N, так и значению — N. И обратно, если имеется
несколько представлений числа М этой формой F, которые принад-
принадлежат противоположным значениям N и —N выражения ]/"D (mod M),
то форма F эквивалентна форме G как собственно, так и несобствен-
несобственно, и может быть найдена двусторонняя форма, которой F эквива-
эквивалентна.
Этими общими замечаниями о представлениях в этом месте можно
ограничиться. О представлениях, в которых неизвестные имеют не
взаимно простые значения, мы будем говорить ниже. В отношении
остальных свойств формы с отрицательными определителями надо
исследовать совсем другими способами, чем формы с положитель-
положительными определителями. Поэтому мы будем теперь рассматривать
формы с отрицательными и положительными определителями от-
отдельно и начнем с первых как более легких.
О формах с отрицательным определителем
171
Задача. Пусть дана какая-нибудь форма (а, 6, а'), определи-
определитель которой отрицателен и равен —D, где D обозначает положи-
положительное число; найти собственно эквивалентную ей форму
(А, В, С), у которой А не больше чем ]/4jD/3 и С, и не меньше
чем 25.
182 Раздел V (п. 172)
Решение. Мы предположим, что для заданной формы не выпол-
выполняются одновременно все три условия, так как иначе не нужно
было бы искать другую форму. Пусть V — абсолютно наименьший
вычет числа ¦—Ъ по модулю а'*, и а" = ;— (это число целое,
так как Ъ'2 = Ъ2, Ь'2 + D = b2 + D = aa! ==0(moda')). Если теперь
a" < a1', то пусть снова b" — абсолютно наименьший вычет числа
•—V по модулю а", и а" = ъ—. Если и здесь еще а" < а", то
пусть снова Ьт — абсолютно наименьший вычет числа — Ь" по
модулю а", и а"" = ^г— • Эту операцию продолжаем до тех пор,
а
пока в ряду а', а", ат, а"\ ... не достигнем члена а(т+1), который
не меньше, чем предшествующий ему а(т); это в конце концов
должно случиться, потому что иначе получился бы бесконечный
ряд все время убывающих целых чисел. Тогда форма (а , 6 , а х
будет удовлетворять всем условиям.
Доказательство, I. В ряду форм (а, Ь, а') (а', Ь'', а"), (а", Ь", а!"),...
каждая является соседней для предыдущей, поэтому последняя
собственно эквивалентна первой (пп. 159, 160).
II. Так как Ъ^ есть абсолютно наименьший вычет числа —^(m—1)
по модулю а(т), то 6(т) не может быть больше чем а(т)/2 (п. 4).
Ш.2Так как а(т) а(т+1) - D + Ъ(тJ и а(ш+1) не меньше чем а{т\
то а 2 будет не больше, чем D -\- Ъ ' , и так как Ъ^т' не больше
чем а(т)/2, то а(тJ будет не больше чем Z) + -^-a(mJ. и потому
3a(rnJ/ 4 будет не больше чем D и, наконец. a(m) — не больше чем
1/4073".
Пример. Пусть задана форма C04, 217, 155), определитель кото-
которой равен —31. Здесь мы находим такой ряд форм:
C04, 217, 155), A55, —62, 25), B5, 12, 7),
G, 2, 5), E, -2, 7).
* Заметим, что если у формы (а, 6, а') равен 0 первый член а или последний
член а', то определитель этой формы будет положительным квадратом; следова-
следовательно, в настоящем случае указанное обстоятельство не может иметь места.
По аналогичной причине крайние члены а, а' формы с отрицательным определи-
определителем не могут иметь противоположных знаков.
Формы с отрицательным определителем 183
Последняя является искомой. Точно так же для формы A21, 49, 20),
определитель которой равен —19, находим эквивалентные формы
B0, —9, 5), E, —1, 4), D, 1, 5); тем самым D, 1, 5) есть иско-
искомая форма.
Такие формы (А, Вч С), определители которых отрицательны
и у которых А не больше чем |/4?)/3 и С, и не меньше чем 2В,
мы будем называть приведенными формами. Итак, для каждой
формы с отрицательным определителем может быть найдена собст-
собственно эквивалентная ей приведенная форма.
172
Задача. Найти условия, при которых две различные приведенные
формы (а, 6, с) и (а', Ь\ с') с одним и тем же определителем —D
могут быть собственно эквивалентны.
Решение. Если мы предположим (что допустимо), что а' не больше
чем а, и что форма ах2 + %Ьху + су2 переходит в форму а'х'2 +
+ 2Ь'х'у' + с'у'2 при собственной подстановке х = ах' + $у'у
у = ^х' + §?/', то мы имеем равенства:
J1] аа2 + 26аТ-[- с?2 = а',
12] аар + Ъ (а8 + ВТ) + сТ8 = V,
{3] а6-рт = 1.
Из [1] следует что аа' = (аса + b^J + D^2, поэтому произведение
аа' положительно, а так как ас = D + б2, а'с' = D + Ъ'2, то ас и aV
тоже положительны. Поэтому все числа а, а', с, с' имеют одина-
одинаковые знаки. Так как теперь как а, так и а' не больше чем |/Z)/3S
то аа' не больше чем 4D/3, и тем самым .D^2 (которое равно
аа' — (аа + Ь^J) подавно не может быть больше чем 4Z)/3. Следо-
Следовательно, y или равно нулю, или равно +1.
I. Если у = 0? то из [3] следует, что или а = 1, 8 = 1, или
а = — 1, 8 = — 1. В обоих случаях из [1] получается а' = а, а из
[2] вытекает, что 6' — 6=::+:Р<2- Но Ъ не больше чем а /2, и 6' не
больше чем а'/2, и потому также не больше чем а/2. Поэтому
равенство Ъ'—6 = + р<2 может выполняться только тогда, когда:
184 Раздел V (п. 173)
или 6 = 6 , тогда отсюда следовало бы с = ;— = = с,
т. е., вопреки предположению, формы (а, 6, с) и (а\ Ъ', с') совпа-
совпадали бы;
или Ь = —Ь' = ^г-к-а] в этом случае с' = с, и форма (а',Ь',с')
переходит в (а,—6, с), т. е. в форму, противоположную форме
(а, 6, с). Одновременно получается, что эти формы двусторонние,
так как 26 = + а.
II. Если Y^zhl? то из [1] получается сих2 + с — а/ = +26а.
Так как, однако, с не меньше чем а, и потому не меньше чем а!,
то ах2 + с — а' или 26а, очевидно, не меньше чем аа2. Поэтому, так
как 26 не больше чем а, а будет не меньше чем а2; а отсюда не-
необходимо следует, что а = 0 или а = + 1.
1. Если а = 0, то из [1] будет вытекать а' = с, и так как а не
больше чем с и не меньше чем а', то обязательно будет а' = а = с.
Далее, из [3] следует, что [3^ = — 1, и потому из [2] получается
Ъ + Ъ' = ЧЬ Sc = + 6а. Отсюда, подобно тому, как в I, вытекает, что
или Ь = Ъ'\ в этом случае формы (а, 6, с), (а', Ъ', с'), вопреки
предположению, совпадали бы;
или Ь = — Ъ'\ в этом случае формы (а, 6, с), (а', Ь', с') проти-
противоположны.
2. Если а = +1, то из 1 следует, что +26 = а + с — а', и
так как ни а, ни с не меньше чем а', то 26 будет не меньше чем а и
не меньше чем с. Но 26 также не больше чем а и не больше чем с; по-
поэтому обязательно +26 = а = с, а вследствие равенства +26=а +
+ с — а' равно также и а'. Таким образом, из [2] получается
или, вследствие того, что аЬ — Py = 1»
V — Ъ = а (^ + Т8) + 26(ЭТ = а (ар + Т8 + рт);
поэтому, как и раньше, обязательно
или 6 = 6', откуда, вопреки предположению, получалось бы>
что формы (а, 6, с), (а', 6', с' ) совпадают;
или 6 = —6', когда эти формы противоположны. Вследствие того.
Формы с отрицательным определителем 185
что а = +26, формы в этом случае одновременно будут двусторон-
двусторонними.
Из всего этого следует, что формы (а, Ь, с) и (а', Ь', с') только
тогда могут быть собственно эквивалентными, когда они противо-
противоположны и одновременно или являются двусторонними, или имеет
место а = с = а' = с'. То, что в этих случаях формы (а, Ь, с) и
(а', Ь', с') собственно эквивалентны, также легко усматривается из
предыдущего. Действительно, если формы противоположны, они
должны быть эквивалентны несобственно, а если они, кроме того,
двусторонние, то также и собственно. Если же а = с, то форма
^P-f(a—6J^ а ___ ^ ^ будет соседней для формы (а, Ь, с),
и потому эквивалентна ей. Но вследствие того, что D + Ъ2 = ас = а2,
имеет место D + (а~6J == 2а — 26, и форма Bа — 26, а — 6, а) —
двусторонняя. Поэтому форма (а, 6, с) будет также и собственно экви-
эквивалентна своей противоположной.
Так же легко можно теперь узнавать, когда две не противополож-
противоположные приведенные формы (а, Ъ, с) и (а', V, с') могут быть несобственно
эквивалентными. Именно, они будут несобственно эквивалентны,
если формы (а, 6, с) и (а', —Ъ', с'), которые не совпадают, собственно
эквивалентны, и обратно. Отсюда вытекает, что условие, при кото-
котором первые формы несобственно эквивалентны, заключается в том,
что они совпадают, и, кроме того, или они двусторонние, или а — с.
Приведенные же формы, которые не совпадают и не противоположны,
не могут быть эквивалентны ни собственно, ни несобственно.
173
Задача. Пусть даны две формы F и F' с одинаковым отрицатель-
отрицательным определителем; требуется узнать, эквивалентны ли они.
Решение. Найдем обе приведенные формы /, /', которые собствен-
собственно эквивалентны соответственно формам F, F'. Если тогда формы
/, /' эквивалентны собственно, или несобственно, или обоими спосо-
способами, то так же эквивалентны будут и F, F'. Если же /, /' не эквива-
эквивалентны никаким способом, то не будут никаким способом эквивалент-
эквивалентны и F, F'.
186 Раздел V (пп. 174-175)
Согласно предыдущему пункту, может представиться четыре
случая.
1. Если /, /' не совпадают и не противоположны, то F, F' не
эквивалентны никаким способом.
2. Если /, /', во-первых, или совпадают, или противоположны,
и, во-вторых, или являются двусторонними, или имеют какие-ни-
какие-нибудь равные крайние члены, то F, F' будут эквивалентны как соб-
собственно, так и несобственно.
3. Если /, /' совпадают, но не являются двусторонними и не
имеют равных крайних членов, то F, F' будут только собственно
эквивалентны.
4. Если /, /' противоположны, но не являются двусторонними
и не имеют равных крайних членов, то F, F' будут только несоб-
несобственно эквивалентны.
Пример. Для форм D1, 35, 30), G, 18, 47), определители кото-
которых равны —5, приведенные формы A, 0, 5), B, 1, 3) оказываются
не эквивалентными. Поэтому первые формы не эквивалентны ника-
никаким способом. Формам же B3, 38, 63), A5, 20, 27) эквивалентна
одна и та же приведенная форма B, 1, 3), и, так как она одно-
одновременно является двусторонней, то формы B3, 38, 63), A5, 20, 27)
будут эквивалентны как собственно, так и не обственно. Формам
C7, 53, 78) и E3, 73, 102) эквивалентны приведенные формы (9, 2, 9),
(9^ —2, 9), и так как они противоположны и их крайние члены
равны, то заданные формы будут эквивалентны как собственно, так
и несобственно.
174
Число всех приведенных форм, которые имеют данный опреде-
определитель — D, всегда конечно и не очень велико в сравнении с чис-
числом D. Сами же эти формы могут быть найдены двумя способами.
Мы будем обозначать произвольные приведенные формы с опреде-
определителем — D через (а, Ь, с); таким образом, должны быть опреде-
определены все значения а, Ъ, с.
Первый метод. За а берутся все числа, как положительные,
так и отрицательные, которые не больше чем |/Z)/3 и по кото-
которым — D есть квадратичный вычет, и для отдельных а число Ъ
Формы с отрицательным определителем 187
последовательно полагается равным всем, как положительным, так
и отрицательным значениям выражения У—D (mod а), которые не
больше, чем а /2; с для отдельных определенных значений а, Ъ
полагается равным (D — Ь2) / а. Если при этом получатся какие-
нибудь формы, у которых с < а, то их нужно выбросить; осталь-
остальные же, очевидно, будут приведенными.
Второй метод. За Ъ берутся все числа, как положительные, так
и отрицательные, которые не больше чем -у I/ ~^D или j/"Z)/3,
для отдельных Ъ выражение b2 -\- D раскладывается всеми возмож-
возможными способами (учитывая и различие знаков) на такле два со-
сомножителя, которые оба не меньше чем 26, и один из сомножи-
сомножителей, причем, если они не равны, то меньший полагается равным а,
а другой равным с. Так как а не больше чем УkD/3, то все по-
получающиеся при этом формы, очевидно, будут приведенными. На-
Наконец, ясно, что не может быть никакой приведенной формы, кото-
которая не была бы найдена каждым из двух методов.
Пример. Пусть D = 85. Здесь граница значений а равна числу
1^340/3, которое лежит между 10 и 11. Числа же между 1 и 10
(включительно), по которым —85 есть вычет, суть 1, 2, 5, 10.
Отсюда получается двенадцать форм:
A, 0, 85), B, 1, 43), B, -1, 43), E, 0, 17), A0, 5, 11),
A0, -5, И), (-1, 0, -85), (-2, 1, -43), (-2, -1, -43),
(—5, 0, —17), (-10,5,-11), (-10,-5,-11).
При другом методе в качестве границы для значений Ъ полу-
получает я число У 85/ 3, которое лежит между 5 и 6. Для 6 = 0 по-
получаются формы A,0,85), (—1, 0, —85), E,0,17), (—5,0,-17);
для 6 = 4-1 — формы B, ±1, 43), (— 2, +1, — 43). Для b = ±2
не получается ничего, так как 89 не может быть разложено на два
сомножителя, которые оба не меньше чем 4. То же имеет место
для +3, +4. Наконец, из Ъ = +5 получаются следующие формы:
A0, ±5, 11), (-10, +5, —И).
175
Если среди всех приведенных форм с данным определителем из
каждых двух форм, которые не совпадают, но собственно эквива-
188 Раздел V (п. 176)
лентны, выбросить ту или иную, то оставшиеся формы обладают тем
замечательным свойством, что любая форма с тем же определителем
собственно эквивалентна какой-нибудь из них, причем только одной
(так как иначе среди них были бы собственно эквивалентные). Отсю-
Отсюда вытекает, что все формы с тем же самым определителем могут
быть разбиты на столько классов, сколько осталось форм, именно,
если причислять к одному классу формы, собственно эквивалентные
одной и той же приведенной форме. Так, например, для D = 85
остаются формы
A,0,85), B,1,43), E,0,17), A0,5,11),
(—1,0,-85), (-2,1,-43), (-5,0,-17), (-10,5,-11),
так что все формы с определителем — 85 могут быть разбиты на
восемь классов, в зависимости от того, эквивалентны ли они первой,
второй и т. д. форме. Очевидно, что формы, помещенные в один класс,
собственно эквивалентны, а формы из различных классов, напротив,
не могут быть собственно эквивалентными. Впрочем, этот вопрос о
классификации форм мы значительно подробнее будем рассматри-
рассматривать ниже. Здесь мы добавим только единственное замечание. Выше
мы уже показали, что если определитель формы (а, Ь, с) отрицателен
и равен —D, то а и с имеют одинаковые знаки (именно, потому что
ас = b2Jr D и, значит, положительно). Из этих же соображений легко
убедиться, что если формы (а, Ъ, с), (а', Ъг, с') эквивалентны, то все
величины а, с, а', с' будут иметь одинаковые знаки. Действительно,
если первая переходит во вторую при подстановке х = &х' + §у',
у = ух ' + оу', то аа2 + 2Ьау + су2 = а', и отсюда аа' = (аа +
+ byJ + Dy2, и потому, очевидно, неотрицательно. Так как, одна-
однако, ни а, ни а' не могут быть равны нулю, то аа' будет положительно
и, следовательно, знаки у а, а' будут одинаковы.
Поэтому ясно, что формы, крайние члены которых положитель-
положительны, совершенно обосабливаются от тех, крайние члены которых отри-
отрицательны, и можно рассматривать только те из приведенных форм,
которые имеют положительные крайние члены, так как остальные
имеются в таком же количестве и получаются из первых, если край-
крайним членам придаются противоположные знаки; и точно так же об-
обстоит дело для форм, которые выбрасываются или оставляются сре-
среди приве енных.
Формы с отрицательным определителем
189
176
Здесь для некоторых отрицательных определителей дана таблица
форм, по которым все остальные формы с тем же определителем мо-
могут быть разделены на классы. В соответствии с замечаниями в пре-
предыдущем пункте мы помещаем, однако, только половину форм,
именно, те, крайние члены которых положительны.
D
Формы
1
2
3
4
9
10
11
12
A, 0, 1)
A, 0, 2)
A, 0, 3), B, 1, 2)
A, 0, 4), B, 0, 2)
A, 0, 5), B, 1, 3)
A, 0, 6), B, 0, 3)
A, 0, 7) B, 1, 4)
A, 0, 8), B, 0, 4), C, 1, 3)
A, 0, 9), B, 1, 5), C, 0, 3)
A, 0, 10), B, 0, 5)
A, 0, 11), B, 1, 6), C, 1. 4), C, -1.4)
A, 0, 12), B, 0, 6), C, 0, 4), D, 2, 4)
Продолжать здесь эту таблицу дальше было бы излишне, так как
ниже мы покажем значительно более целесообразное ее устройство.
Итак, очевидно, что каждая форма с определителем —1 собствен-
собственно эквивалентна форме ж2 + у2, если ее крайние члены положитель-
положительны, и форме —ж2 — у2, если они отрицательны. Далее, каждая фор-
форма с определителем — 2, крайние члены которой положительны,
будет собственно эквивалентна форме ж2 4- 2у2, так же как каждая
форма с определителем —11, крайние члены которой положитель-
положительны, собственно эквивалентна одной из форм ж2 4- lit/2, 2ж2 + 2ху 4
4- 6гД Зж2 4- 2ху + 4у2, Зж2 — 2ху 4- 4у2.
190 Раздел V (пп. 177-178)
111
Задача. Имеется ряд форм, каждая из которых является сосед-
соседней справа для предыдущей] требуется найти какое-нибудь собст-
собственное преобразование первой формы в любую форму ряда.
Решение. Пусть заданные формы суть
(а, 6, af) = F, (a', Ъ\ a") = F\ (а", Ъ", а") = F\ (а*, Ъ\ а") = F",...
Величины (b + b')/af, (bf + b")/a", (b" + V") /а"',... обозначим соот-
соответственно через /г', /г", К'\ . . . , а неизвестные форм F, Fr F", . . .
пусть соответственно х, у; х', у'\ х", у"\. . . Далее, предположим,,
что F должна переходить
в F' , если положить х = са'х' + PV, 2/ = Т'^' + ^V»
в F" , » » ж = аУ + (Эу\ г/ = TV + 8'у,
в Fw, » » ж = aw^ + p'Y". У = i"x" + 8V»
и т. д.
Тогда, так как
F переходит в F', если положить ж =—?/', г/ = х' -\-h'y'
F' » » F" » » ж' - — г/", г/' = ^ + /г'у,
F" » » Fm » » ^)г/ - — у\ у" = х" + К"у\
и т. д. (п. 160),
легко выводится следующий алгоритм (п. 159):
a'
a"
a'"
a""
или
a'
a"
a'"
a""
= P">
= F>
= 0»
= P;.
= p",
P'
p/;
pw
r
p'
p7
pw
— —1?
= /г/грг -
= /г'"Р" -
= /г"Т
= — 1,
- /г"Р',
= К" Р"
= /zw/ pw
-а',
-а",
и т.
-Г
и т.
Т' =
Т# =
т- =
Д-,
тг:
*С '-
д.
= 1,
= 8',
= 8*,
= 8W,
= 1,
= 8',
= 8",
= 8W,
8'
8"
8W
8r
8"
8W
= A',
— /г'
= A'8' —1,
= ^8* —8',
= /г"" 8'" — 8",
Формы с отрицательным определителем 191
То, что все эти преобразования собственные, без труда может быть
выведено как из их образования, так и из п. 159.
Этот очень простой и удобный при вычислениях алгоритм ана-
аналогичен алгоритму, изложенному в п. 27, и может быть сведен
к нему*. Впрочем, это решение не ограничивается формами с от-
отрицательными определителями, а распространяется на все случаи,
если только ни одно из чисел а', а", ат, ... не равно нулю.
178
Задача. Даны две собственно эквивалентные формы F, f с одним
и тем же отрицательным определителем; найти какое-нибудь собст-
собственное преобразование одной формы в другую.
Решение. Предположим, что форма F есть (А1 В, А'), и что
методом п. 171 найден ряд форм (А', В\ А"), (А", В", А"г), . ..
...,(^4(m), B{m\ J.(m+1)), последняя из которых приведенная; точно так
же, предположим, что форма / есть (а, Ъ, а'), и что тем же методом
найден ряд форм (а', Ъ\ а"), (а", Ъ\ а"), . . . , (а(п\ Ь(п\ а(п+1)), по-
последняя из которых приведенная. Тогда могут представиться два
случая.
I. Формы (А(т\ В{т\ А(т+1)), (а(п\ Ь(п\ а(п+1)) или совпадают,
или противоположны и одновременно двусторонние. Тогда формы
(А{т-{\ 5(т~1}, А(т)) и (а(п), -Ь(п-г\ а(п-1}) будут соседними (здесь
дуп—i) обозначает предпоследний член ряда А, А\ А", .. . , А^т\ и
1~ , а(п~1}, 6(п~х) имеют подобное же значение). Действительно,
)^ а
(п\
) Д
еее — В(т) (mod A(m)), б^1^—6(n)(mod a(n) или
* Именно, в обозначениях п. 27,
В(п) = + [_ /г", К\ — Ь!\ . . , , ],
где двойные знаки должны иметь значения , [-, -| , -\- -f-, если п имеет
соответственно вид 4& -f- 0, 1, 2, 3, и
где двойные знаки имеют значения -| , -f- -\-г , 1-, когда п соответ-
соответственно имеет вид 4Лг + 0, 1, 2, 3. Ради краткости, мы, однако, не будем вда-
вдаваться в это подробнее; впрочем, убедиться в этом каждый легко может и сам.
192 Раздел V (п. 179)
поэтому ?(т-1} — b{n~~l)^b{n) — B{m\ и потому =0, если формы
(А(т\ В(т\ А(т+1)), (а{п\ Ъ{п\ а(п+1)) совпадают, и = 2Ь{п) и тем самым
= 0, если они противоположны и одновременно двусторонние.
Поэтому в ряду форм
(А, В, А'), (А', В', А"), ..., {А(т-'\ В^, А™),
(а<»>, _ b(n~l\ а<п~% (а^, - Ь{п~2\ а^^), ..., (а', -Ь,а), (а, Ь, а')
каждая форма — соседняя для предыдущей, и тем самым, согласно
предыдущему пункту, может быть найдено собственное преобразо-
преобразование первой формы F в последнюю форму /.
II. Формы (А{т\В{т\ ,4(m+1)), (a(n\ b(n\ а(п+1)) не совпадают, но
противоположны и одновременно А(т) = А^т+1) = а(п) = а(п+1). Тогда
ряд форм
(А, В, А'), (А\ В', А"),.. . , (А(т\ В(т\ А(т+%
(а(»), -b^\ а^~\ (а^г\ -6(п-2), а(п~2)),. . . , (а', -Ъ, а), (а, 6, а')
будет обладать тем же свойством. Действительно, ^т+^ — а(п>
H^)_jH) = _(j(n) + jH)) делится на а(п). Тем самым, со-
согласно предыдущему пункту, может быть найдено собственное пре-
преобразование первой формы F в последнюю форму /.
Пример. Так, для форм B3, 38, 63), A5, 20, 27) имеем ряд
B3,38,63), F3,25,10), A0, 5,3), C,1,2), B,-7,27), B7,-20,15),
A5, 20, 27). Поэтому
h! = 1, h" = 3, К" - 2, /г"" - — 3, К"" = — 1, /г""" - 0.
Отсюда в качестве преобразования формы 23х2 + 76ху + 63г/2 в форму
15^2+40^гг + 27гг2 получается следующее: х=—13?—18и, г/ = 8г+11гг.
Из этого решения без труда вытекает решение следующей
задачи: пусть формы F, / несобственно эквивалентны; найти несоб-
несобственное преобразование формы F в /. Действительно, если / = at2 +
+ 2btu -f- а'гг2, то противоположная форма а/?2 — 2bpq -f- а'#2 собст-
собственно эквивалентна форме .F. Если найдено собственное преобразо-
преобразование формы F в форму ар2 — 2bpq -f- а'^2, именно, х = cap -\- $q,
у = ур -^ $qt то .Fj очевидно, будет переходить в /, если положить
х = out — (Згг, у = ^t — 8гг, и это преобразование будет несобственным.
Формы с отрицательным определителем 193
Если формы F, / эквивалентны как собственно, так и несобст-
несобственно, то можно, таким образом, всегда найти как собственное,
так и несобственное преобразование.
179
Задача. Пусть формы F, / эквивалентны, найти все преобра-
преобразования F в /.
Решение. Если формы F, / эквивалентны только одним способом,
т. е. только собственно или только несобственно, то найдем в со-
соответствии с предыдущим пунктом одно преобразование формы F
в /; тогда ясно, что других преобразований, кроме тех, которые
с ним однотипны, быть не может. Если же формы F, / эквива-
эквивалентны как собственно, так и несобственно, то найдем два преоб-
преобразования, одно собственное и одно несобственное. Если теперь
F = (А, В, С), далее, В2 — АС = — Z), и наибольший общий дели-
делитель чисел А, 2В, С равен т, то из п. 162 следует, что в первое
случае все преобразования формы F в / могут быть выведены из
одного преобразования, а во втором случае все собственные преоб-
преобразования— из одного собственного, и все несобственные — из одного
несоб твенного, если только имеются все решения уравнения
t2 -f- Du2 = т2. Итак, если они найдены, то задача решена.
Номы имеем D = АС — В2, 4J9 — kAC — 4i?2, и потому число
4D , АС /2Я\2
—г = 4—т— — целое.
4Х)
1. Если теперь — > 4, то D > т2, поэтому в t2 + Du2 = m2
обязательно должно быть и = 0, и тем амым t не может иметь
других значений, кроме + т или — т. Если поэтому F, / экви-
эквивалентны только одним способом и какое-нибудь преобразование
есть
х = ах' + $у', у = тгж' + 8г/,
то, кроме этого преобразования, которое получается из t — т
(п. 162), и следующего:
х = —ах' — 4Зг/\ у = — тж' — %г,
194 Раздел V (п. 179)
других преобразований быть не может. Если же F, / эквивалентны
как собственно, так и несобственно, и имеется какое-нибудь соб-
собственное преобразование
и несобственное преобразование
то собственных преобразований, кроме первого (получающегося
из t = т) и следующего (получающегося из ? — —т)\
X = —CLX' — $у\ у = — *[Х' — Ьу',
не будет, и аналогичным образом не будет несобственных преоб-
преобразований» кроме
х = «V-f ?У, у = f'x'+ Ъ'у' ях = — а'х'— ру, у = - Т'а;'- 8'у'.
2. Если —г = 4 или Z) = т2, то уравнение t2 -\- Du2 = m? до-
пускает четыре решения, именно: t, и = т, 0; —т, 0; 0,1; 0, —1
Если поэтому F, / эквивалентны только одним способом, и одно
из преобразований есть
х = clx' + ру', у = тя' + 8г/',
то всего имеется четыре преобразования:
х = + ах' + Ру', г/ = drT^'ity'»
Если же F, / эквивалентны двумя способами или, кроме ука-
указанного данного преобразования, имеется еще одно, неоднотипное
с ним, то оно принесет тоже четыре преобразования, неоднотипных
с первым, так что имеется восемь преобразований. Впрочем, легка
доказать, что в этом случае F, / всегда действительно эквивален-
эквивалентны двумя способами. Действительно, так как D = т2 = АС — В2Г
то т входит также и в В. Определитель формы (А / т, В/ т, С / т)
равен —1, поэтому форма эквивалентна или форме A, 0, 1), или
форме (—1, 0, —1). Но легко видеть; что тем же преобразованием.
Формы с отрицательным определителем 195
которым форма (А/т, В / т, С/т) переводится в (+1,0, +1),.
также и (А, В, С) переводится в форму (+?га, 0,+т), которая
является двусторонней. Поэтому форма (А7 В, С), так как она экви-
эквивалентна двусторонней форме, будет эквивалентна как собственно,
так и несобственно каждой форме, которой она эквивалентна вообще.
4Z)
3. Если —7г = 3 или AD = Зт2. то т четно, и всевозможными
решениями уравнения t2 + Du2 = т2 являются следующие шесть:
111 1
t,u = m,0; —m,0; ym,i; — -^т, 1; -j-m, — 1; ^т, — 1.
Если поэтому имеется два неоднотипных преобразования формы F в /:
х = ссх' + РзЛ ?/ = Т*' + ?>
х = о'ж' + р'г/', у = yV + 8У,
то имеется двенадцать преобразований, именно, шесть, однотипных
с первым:
и шесть однотипных со вторым, которые получаются из предыдущих,
если вместо а, р, ^> 8 подставить соответственно а', C', ^', S'.
То, что в этом случае F, / всегда эквивалентны обоими спо-
способами, доказывается следующим образом. Определитель формы
B-4/т, 2В/т, 2С / т) равен 2~ =—3, и потому (п. 176) эта
2
форма эквивалентна или форме (+1, 0, +3), или форме (+2, +1, +2).
Из этого легко видно, что форма (А, В, С) эквивалентна или форме
(+~2 т> 0' — ~2~ тг или Ф°Рме (iw» -0"^»+^) , которые обе дву-
* Можно показать, что {А, В, С) обязательно эквивалентна второй из этих
форм; однако это не является здесь необходимым.
196 Раздел V (пп. 180-181)
к 1? 4D Л / 2В\ , АС Л
5. Если предположить, что ^т = 1, то (-^-) = 4 —5- — 1 ==
сторонние, и потому каждая форма, эквивалентная форме (-4, В, С)
вообще, эквивалентна ей обоими способами»
, ^ 4D о / 2В \2 . АС о
4. Если предположить, что —5-= 2, т0 —— =4—s-— 2, и по-
1 т? \ т ) т2
тому =2 (mod4). Так как, однако, никакой квадрат не может быть
= 2 (mod 4), этот случай не может иметь места.
предположить,
= — I(mod4). Так как, однако, это невозможно, то и этот случай
не может иметь места.
Так как, далее, D не равно нулю и неотрицательно, других
случаев, кроме перечисленных, быть не может.
180
Задачу. Требуется найти все представления заданного числа М
формой F = ах2 + 2Ьху + су2 с отрицательным определителем —D7
у которых х, у имеют взаимно простые значения.
Решение. Из п. 154 явствует, что М может быть представлено
желаемым способом только в том случае, если — D есть квадратичный
вычет числа М. Поэтому сначала отыскиваются все различные, т. е.
несравнимые значения выражения У — Z)(modM); пусть эти значе-
значения суть N% —N, N', —Л', -V", —N",... Для того чтобы вычисле-
вычисления были по возможности проще, все Лт, iV',... могут быть опреде-
определены так, чтобы они были не больше чем М / 2. Так как каждое
представление должно теперь принадлежать какому-нибудь одному
из этих значений, можно рассматривать эти значения по отдель-
отдельности.1
Если формы F и (М, N, (D + N2) / М) не являются собственно
эквивалентными, то не может быть представления числа М, кото-
которое принадлежит значению N (п. 168). Если же они, напротив,
собственно эквивалентны, то найдем собственное преобразование
формы F в форму
Пусть это преобразование есть
Формы с отрицательным определителем 197
х = ах' + рг/', у = цх' + bV''i
тогда я = а, г/ = т есть представление числа М формой F, при-
принадлежащее N. Пусть наибольший общий делитель чисел 4, 2В, С
равен т\ будем различать три случая (ср. предыдущий пункт).
1. Если —а~ > 4, то не может быть других принадлежащих N
представлений, кроме следующих двух: х =^= а, у — у, х = -— а,
?/ = — Т (пп- 169> 179)-
Z. Если —у- = 4, то имеется четыре представлеция:
, , аВ + чС , аА + тВ
3. Если —Г = 3, то имеется шесть представлений:
. / 1 аБ + тС\ . / 1 . аА
.. ¦ _J [ /у ' I \ 9/ _4— I у _1
Подобным же образом отыскиваются представления, принадле-
принадлежащие значениям —N, Л', —N',...
181
Получение представлений числа М формой F, у которых х, у
имеют не взаимно простые значения, легко может быть сведено к уже
рассмотренному случаю. Такое представление можно получить если
положить х = [ке, у = [л/, где [х есть наибольший общий делитель
(ле и [х/, т. е. е и / взаимно просты. Подстановка же х = е, у = /
будет представлением чи ла М/[х2 формой F, в котором ж, г/ имеют
взаимно простые значения. Если поэтому М не делится ни па какой
квадрат (кроме 1), например, если оно есть простое число, то таких
представлений числа М нет. Если же М содержит квадратные
делители, то пусть они суть (л2, v2, тс2,... Сначала отыскиваются все пред-
представления формой (А, В, С) числа М/(х2, у которых х, у имеют
взаимно простые значения; эти значения, умноженные на [л, дадут
198 Раздел V (п. 182)
все представления М; у которых наибольший общий делитель х, у
равен (л. Подобным же образом все представления числа М/у2,
у которых значения ж, у взаимно просты, дают все представления М,
у которых наибольший общий делитель х, у равен v, и т. д.
Поэтому ясно, что при помощи предыдущих правил могут быть
найдены все представления заданного числа заданной формой
с отрицательным определителем.
Специальные приложения к разложению чисел на два квадрата,
на простой и удвоенный и на простой и утроенный квадраты
182
Мы переходим к некоторым специальным случаям, отчасти вслед-
вследствие их исключительного изящества, отчасти же потому, что ими
подробно занимался Эй л ер, благодаря чему они приобрели до не-
некоторой степени классический характер.
I. Ни одно число, по которому — 1 не является квадратичным
вычетом, не может быть представлено формой х2 -f- у2 так, что х
взаимно просто с у (или быть разложено на два взаимно простых
квадрата); для всех остальных чисел, взятых положительными, это,
напротив, возможно. Пусть М — такое число и пусть Лт, —N, N\
— N', iV", — N", ... — всевозможные значения выражения
V^T. Тогда, согласно п. 176, форма (М, N, (N2 + 1)/М)
собственно эквивалентна форме A, 0, 1). Если х = txx' -f- JSz/',
у = ^xf -f by' — какое-нибудь собственное преобразование второй
формы в первую, то принадлежащими N представлениями числа
М формой х2 + у2 являются следующие четыре: х = +а. у — + ^;
Так как форма A, 0, 1) двусторонняя, то, очевидно, и форма
(М, —iV, (N2-\-l)lM) будет ей собственно эквивалентна, и первая
будет собственно преобразовываться во вторую, если положить
х = сих' — $у\ у = — чх' + fy'- Отсюда получаются четыре пред-
представления М, принадлежащих — iV, именно: х = + а, у = + ^;
У^Ч-я- Тем самым ясно, что имеется восемь представлен
* Именно, этот случай содержится, очевидно, в п. 180, 2.
Представления чисел некоторыми специальными формами 199
еий числа М, из которых половина принадлежит N, а половина
принадлежит — N] однако все они дают только одно единственное
разложение числа М на два квадрата: М — а2 + Т2>—если при-
принимать во внимание только сами квадраты, а не порядок их рас-
расположения и не знаки корней из них.
Если поэтому других значений выражения У—1 (mod М), кро-
кроме TV и —N, нет, что, например, имеет место, если число М простое,
то М может быть только одним единственным способом разложено
на два взаимно простых квадрата. А так как —1 есть квадратичный
вычет каждого простого числа вида in + 1 (п. 108), и простое число,
очевидно, не может быть разложено на два не взаимно простых квад-
квадрата, то мы получаем следующую теорему.
Каждое простое число вида in -\- 1 может быть разложено на
два квадрата, причем одним единственным образом.
Так, например, 1-0 + 1, 5 - 1 + 4, 13 - 4 + 9, 17 - 1 + 16,
29-4 + 25, 37 - 1 + 36, 41 - 16 + 25, 53 - 4 + 49, 61 =
-25 + 36, 73 - 9 + 64, 89 - 25 + 64, 97 - 16 + 81, ...
Эта в высшей степени изящная теорема была известна уже Фер-
м а, хотя впервые доказана была Эйлером: «Сотт. nov, Petr.»9
Т. V, 1754, 1755, S. 3 и ел. В четвертом томе, стр. 3 и далее, находит-
находится сочинение, посвященное этому же предмету, хотя тогда он еще и
не закончил полностью эту работу (ср. особенно п. 27).
Поэтому, если какое-нибудь число вида in + 1 или может быть
разложено на два квадрата несколькими способами, или не может
быть разложено вообще, оно, очевидно, не является простым.
Наоборот, если выражение У —1 (mod М), кроме N и —N,
имеет еще и другие значения, то будут и другие, принадлежащие
этим значениям, представления числа М. В этом случае М может
быть, таким образом, разложено на два квадрата несколькими спо-
способами, например, 65 — 1+64 — 16+49, 221 — 25 + 196 —
- 100 + 121.
Остальные представления, в которых х, у имеют не взаимно
простые значения, легко могут быть найдены нашим общим методом.
Заметим только, что если некоторое число, которое содержит сомно-
сомножители вида in + 3, не может быть освобождено от них делением на
некоторый квадрат (что имеет место, если один или несколько из
200 Раздел V (п. 182)
этих сомножителей входят в нечетной степени), то оно никаким спо-
способом не может быть разложено на два квадрата*.
II. Формой х2 + 2у2 не может быть представлено так, что х взаим-
взаимно просто с у, ни одно число, по которому —2 является невычетом,
в то время как для всех остальных чисел это возможно. Если
— 2 есть вычет числа М, и N — какое-нибудь значение выражения
K^dnod M), то (см. п. 176) формы A,0,2) и (M,N, (TV2 + '1I М)
будут собственно эквивалентны. Если первая собственно переходит
во вторую при подстановке х — ах' + $у', у — ух' -|- оу', то
х = а, у = y будет принадлежащим N представлением числа М.
Кроме него и представления х = —а, у — —у, никакие другие
значения N не принадлежат (п. 180).
Аналогично тому, как выше, убеждаемся, что представления
х = +а, у = Ц-у принадлежат значению —N. Все эти четыре пред-
представления дают, однако, только одно разложение числа М на квад-
квадрат и удвоенный квадрат, и если кроме N и —N других значений
выражения У — 2 (mod M) больше нет, то нет также и других пред-
представлений числа М. Отсюда при помощи теоремы п. 116 легко выводит-
выводится следующая теорема.
Каждое простое число вида 8п + 1 или 8п + 3 может быть раз-
разложено на квадрат и удвоенный квадрат и притом только одним
способом.
Так, например, 1 = 1 + 0, 3 = 1 + 2, И = 9 + 2, 17 = 9 + 8,
* Если М = 2llSaab®c~/, . . ., где а, Ъ, с, . . . обозначают различные про-
простые-числа вида 4/г + 1, и ? —произведение всех простых сомножителей чис-
числа М вида 4/г 4- 3 (в такой форме можно представить каждое положительное
число, если положить jjl = 0, когда М нечетно, и ? = 1, когда М не содер-
содержит сомножителей вида 4/г + 3), то М не может быть разложено на два квад-
квадрата, если S не является квадратом. Если же S есть квадрат, то имеется
1
¦Wa 4- 1) (р -f 1) («у + 1) . . . разложений числа М, когда хотя бы одно из чи-
1 1
сел а, р, 7» • • • нечетно, и у (а + 1) (р + 1) (^ -f 1) . . . + у разложений,
когда а, В, -у» • • • все четны (речь идет здесь о самих квадратах). Тот, кто
сколько-нибудь владеет комбинаторикой, без труда получит доказательство
этой теоремы (на котором, как и на других частностях, мы не останавлива-
останавливаемся) из нашей общей теории.
Представления чисел некоторыми специальными формами 201
19-1 + 18, 41 = 9 + 32, 43 - 25 + 18, 59 - 9 + 50, 67 =
- 49 + 18, 73 - 1 + 72, 83 - 81 + 2, 89 - 81 + 8, 97 = 25 +
+ 72 и т. д.
Также и эту теорему, как и многие ей подобные, Ферма знал,
хотя доказательство впервые дал Л а г р а н ж, «Suite des recherches
d' Arithmetique», Nouv. Mem de VAc. de Berlin, 1775, p. 323 и ел.
Многое относящееся к этому предмету исследовал еще Эйлер,
«Specimen de usu observationum in mathesi pura», Comm. nov. Petrop.,
T. VI, р. 185 и ел.; однако полное доказательство теоремы все время
не поддавалось его усилиям (ср. также сочинение в Т. VIII A760,
1761 гг.): «Supplementum quorundam theorematum arithmeticorum»
в конце).
III. Подобным же путем доказывается, что каждое число, по
которому —3 есть квадратичный вычет, может быть представлена
или формой х2 + Зу2, или формой 2х2 + 2ху + 2у2, и притом так,
что значение х взаимно просто со значением у. Так как теперь —3
является вычетом всех простых чисел вида Зп + 1 (п. 119), а формой
2х2 + 2ху + 2у2, очевидно, могут быть представлены только четные
числа, мы, как и выше, получаем следующую теорему.
Каждое простое число вида Зп + 1 может быть разложено на
квадрат и утроенный квадрат, причем только одним единственным
способом.
Так, например, 1 = 1 + 0, 7 = 4 + 3, 13 = 1 + 12, 19 = 16 + 3,
31 = 4 + 27, 37 - 25 + 12, 43 = 16 + 27, 61 = 49 + 12, 67 -
-64 + 3, 73 - 25 + 48 и т. д.
Доказательство этой теоремы впервые дал Эйлер в упомяну-
упомянутом выше сочинении «Comm. nov. Petrop.», Т. VIII, р. 105 и ел.
Подобным путем мы могли бы идти и дальше и, например, пока-
показать, что каждое простое число вида 20п + 1 или 20п + 3, или
20/2 + 7, или 20п + 9 (именно, по которым —5 является вычетом)
может быть представлено одной из форм х2 + Ъу2, 2х2 + 2ху + Зу2,
и притом простые числа вида 20п + 1 и 20п + 9 — первой, а про-
простые числа вида 20п + 3, 20п + 7 — второй формой; далее, что уд-
удвоенные простые числа вида 20п + 1, 20п + 9 могут быть представ-
представлены формой 2#2 + 2ху + Зу2, а удовоенные простые числа вида
20п + 3, 20/2 + 7 — формой х% + Ъу%. Однако каждая из этих
202 Раздел V (п. 183)
теорем и бесчисленное множество других специальных теорем легко
могут быть выведены из предыдущего и из того, что будет изложено
ниже. Мы переходим поэтому к формам с положительным определи-
определителем, и так как их природа совершенно различна в зависимости от
того, является ли определитель квадратом или нет, то мы здесь сна-
сначала исключим формы с квадратным определителем, а рассмотрим
их позднее отдельно.
О формах с положительным неквадратным определителем
183
Задача. Пусть задана любая форма (а, 6, а'), положительный
неквадратный определитель которой равен D\ найти собственно
эквивалентную ей форму (А, В, С), у которой В положительно
и меньше чем jAD, w, кроме того, А, если оно положительно, или — А,
если А отрицательно, лежит между }ЛО -\~ В и }ЛО — В.
Решение. Мы предположим, что для заданной формы еще не
выполняются оба условия, так как иначе нам было бы не нужно
искать другую форму. Далее, заметим, что у формы с неквад-
неквадратным определителем первый или последний член не может быть равен
нулю (п. 171, замечание). Пусть V = — &(moda') и расположено
между границами }f D и J^D^f-a' (где берется верхний знак,
если а' положительно, и нижний, если оно отрицательно). То, что это
возможно, легко доказывается способом, подобным изложенному
в п. 3. Положим тогда ;— = а", что является целым числом,
так как Ь'2 — D = b2 — D = аа' ==0 (modа'). Если теперь а"<Са'у
то пусть снова Ъ"' ==—b'(moda") и расположено между }ЛО и
a" (в зависимости от того, положительно а" или отрицатель-
отрицательно), и, далее, —^— = а", Если здесь снова а" < а", то пусть Ът ==
= — &"(modaw) и расположено между }ЛО и )ЛО + а'", и
—IL— = а"". Эта операция продолжается до тех пор, пока в ря-
ряду чисел а', а", а"\ а"", ... не получится член а(т+1\ который не
меньше, чем предыдущий член а^т\ что рано или поздно должно
случиться, так как иначе мы получили бы бесконечный ряд все
Формы с полоснсителъным неквадратным определителем 203
время убывающих целых чисел. Если положить тогда а^ = А%
Ь(™) = В, a(m+ti = С, то форма (А, В, С) будет удовлетворять всем
условиям.
Доказательство. I. Так как в ряде форм (а, Ъ, а'), (а , Ъ', а"),
(а", Ъ", а"), . .. каждая является соседней для предыдущей, по-
последняя, (А, В, С), будет собственно эквивалентна первой.
II. Так как В лежит между УD и УD + А (где всегда нужно
брать верхний знак, если А положительно, и нижний — если А
отрицательно), то очевидно, что если \fD — В = р, В — (\f D^y-A)=q,
зти величины р, q будут положительны. Теперь легко устанавли-
устанавливается, что q2 -f 2pq + 2р УЪ =D + A2 — B2, тем самым D + А2 —
— В2 будет положительным числом, которое мы положим равным г.
Так как D = В* — АС, то г = А2 ~ АС, и потому число А2 — АС
положительно. Так как, однако, по предположению, А не больше
чем С, то это, очевидно, может иметь место только в том случае,
-если АС отрицательно и потому знаки чисел А ж С противополо-
противоположны. Отсюда следует В2 = D + АС < D и потому В < Y"D.
III. Так как, далее, —АС = D — В2, то будет АС < D и пото-
потому (так как А не больше чем С) A<VD. Тем самым YD + A по-
положительно, а значит положительно и В, которое лежит между
границами YD и f/D^A.
IV. Тем самым }ЛО + В + А подавно положительно, и так как
у D — В + А — — q отрицательно, то + А лежит между ]/D и
VD — B.
Пример. Если задана форма F7, 97, 140), определитель которой
равен 29, то находим ряд форм: F7, 97, 140), A40, —97, 67),
F7, —37, 20), B0, —3, —1), (—1, 5, 4). Последняя является
искомой.
Tatiue формы (А, В, С) с положительным определителем D,
у которых А, взятое положительным, лежит между ]/D -\- В и
YD — В, а В положительно и меньше чем |/D, мы будем назы-
называть приведенными формами. Приведенные формы с положитель-
положительным неквадратным определителем, таким образом, несколько отли-
отличаются от приведенных форм с отрицательным определителем;
однако вследствие большой аналогии между теми и другими мы не
хотим вводить для них различных названий.
204 Раздел V (п. 184)
184
Если бы об эквивалентности двух приведенных форм с поло-
положительным определитем можно было судить также легко, как для
форм с отрицательным определителем (п. 172), то без труда можно*
было бы узнавать эквивалентность и двух любых форм с одним и
тем же положительным определителем. Однако здесь положение
вещей в значительной мере иное, и возможно, что очень многие
приведенные формы эквивалентны между собой. Поэтому, прежде
чем приступать к этой задаче, мы должны сначала глубже вник-
вникнуть в природу приведенных форм (с положительным неквадрат-
неквадратным определителем, что мы здесь все время будем предполагать)
1. Если форма (а, Ь, с) приведенная, то а и с имеют противо-
противоположные знаки. Действительно, если определитель формы положить
равным D, то ас = Ь2— D и потому ас отрицательно, так как
2. Число с, так же, как и а, будучи взято положительным,
лежит между У D + Ъ и У D — Ъ. Действительно, — с =
V
поэтому абсолютная величинам лежит между (D—-Ъ2) / {V D -\- Ь)
и (D — b2)/(VD — b), т. е. между УЪ—Ъ и j/"D + b.
3. Отсюда вытекает, что и форма (с, Ь, а) приведенная.
4. Как а, так и с меньше, чем 2>У D. Именно, каждое из этих
чисел меньше, чем УD + Ь,и потому подавно меньше, чем 2УD.
5. Число Ъ лежит между У D и УD ^f а (где верхний знак
берется при положительном а, а нижний — при отрицательном а).
Действительно, так как + а лежит между УD -\- Ъ и УD — Ь, то
^г-_а—(УВ—6), т. е. b — (|/Z) + а) положительно; b — УО, на-
наоборот, отрицательно; поэтому b лежит между УВ жУD^ya.
Точно таким же образом доказывается, что Ъ лежит между УD
и У ВЦ-с (в зависимости от того, положительно с или отрица-
отрицательно).
6. Для каждой приведенной формы (а, Ь, с) с каждой стороны
имеется одна и только одна соседняя приведенная форма. Если
а'=с, &'== — ^(moda'), и Ъ' расположено между У D и |/D~-\^a'*:,
* Всюду, где фигурируют двойные знаки, нужно брать верхний, когда а'
положительно, и нижний, когда а' отрицательно.
Формы с полоэюительным неквадратным определителем 205
далее, с= —г,— , то форма (а\ Ъ', с')— соседняя справа для
к
формы (а, 6, с), и одновременно ясно, что если бы была приведе-
приведена форма, соседняя справа для формы (а, 6, с), она не могла бы
быть отлична от (а', 6', с'). А то, что она действительно приведен-
приведенная, мы докажем следующим образом.
А. Если положить
то числа р, q, г, согласно B) и в силу определения приведенной
формы, положительны. Если, далее, положить
V - (VD + а') = q', VD-V = r\
то числа q\ г положительны, так как Ь' лежит между ]^D м
]/~D~pa. Наконец, если b -f- Ь' = + та\ то т—целое число.
Теперь очевидно, что р + q' = b + Ъ', и потому Ь-\-Ь\ т. е. +/иа',
а, значит, и т положительны. Отсюда следует, что т — 1 заведомо
не отрицательно. Далее,
r + q'±ma'=:2b'±a', т. е. 26' - г + q' ± (т — 1) а\
к потому 26' и Ь' обязательно положительны; и так как V -\- г' =
= /Д то б' <
В. Далее,
г ± та' - УЪ + Ь\ т. е /• + (т — 1) а' = \r~D + 6' =р аг,
и потому V D-\-Ь'Ц-а' положительно. Из этого и из того, что
+ а' — (У-D — Ъ') = q' и потому положительно, следует, что +я'
лежит между УВ + Ь' и }/"Z) — 6;. Поэтому форма (аг, 6Г, с') при-
приведенная.
Таким же образом доказывается, что если 'с = а, 'Ь = — 6 (mod 'с)
и 'Ь лежит между УВ яУВ + 'с, далее, 'а = —~—, то форма
{'а, '6, 'с) приведенная. Но очевидно, что эта форма является
соседней слева для формы (а, 6, с), и никакая другая приведенная
форма, кроме ('а, '6, гс), этим свойством обладать не может.
206 Раздел V (пп. 185-186)
Пример. Для приведенной формы E, 11, —14), определитель
которой равен 191, соседней справа является приведенная форма
(—14, 3, 13), а соседней слева — форма (—22, 9, 5).
7. Если приведенная форма (a',b',cr) является соседней справа
для приведенной формы (а, Ь, с), то для приведенной формы
(с, &, а) форма (с', Ъ\ а') будет соседней слева; и если для при-
приведенной формы (а, Ь, с) форма ('а, 'Ь, гс) является соседней сле-
слева, то приведенная форма ('с, '&, 'а) будет для приведенной формы
(с, 6, а) соседней справа. Далее, формы (—'а, '&, —'с), (—а, Ь, — с),
(—а', Ь, —с') также будут приведенными, причем вторая для
первой и третья для второй являются соседними справа, или
первая для второй и вторая для третьей — соседними слева, и
подобным же образом обстоит дело с тремя формами (—с', &', —а'),
(—с, &, —а), (—'с, 'fc, —'а). Это настолько ясно, что не требует
пояснения.
185
Количество всех приведенных форм с данным определителем D
всегда конечно] сами же они могут быть найдены двумя способами.
Мы будем обозначать произвольные приведенные формы с опреде-
определителем D через (а, 6, с), так что должны быть определены все
значения а, Ь, с*
Первый метод. Будем брать за а все числа (как положитель-
положительные, так и отрицательные), которые меньше чем 2 }/D и по кото-
которым D является квадратичным вычетом, и для каждого отдель-
отдельного а будем полагать число b равным всевозможным положитель-
положительным значениям выражения }^Z)(moda), которые лежат между УD
и \rD'^a1 а с для отдельных значений а, Ъ будем полагать рав-
равным (b2 — D) / а. Если при этом получатся какие-нибудь формы,
у которых +а лежит вне интервала У~В-\-Ъ и J^D — Ъ, то их
нужно выбросить.
Второй метод. За Ъ берутся все положительные числа, которые
меньше чем }ЛО, для отдельных Ъ выражение b2 — D разлагается
всеми возможными способами на два сомножителя, которые, будучи
взятыми по абсолютной величине, лежат между ]/i) + Ъ и |/Z>—Ъ<
и один из них полагается равным а, а другой равным с. Очевид-
Формы с полоэюительным неквадратным определителем 207
но, что каждое отдельное разложение на, сомножители дает две
формы, потом} что каждый из сомножителей должен быть положен
равным как а, так и с.
Пример. Если D = 79, то значения а будут следующими два-
двадцатью двумя: +1, 2, 3, 5, 6, 7, 9, 10, 13 14, 15. Отсюда нахо-
находим девятнадцать форм;
A, 8, -15), B, 7, -15), C, 8, -5), C, 7, -10), E, 8, -3),
E, 7, -6), F, 7, -5), F, 5, -9), G, 4, -9), G, 3, -10),
(9, 5, —6), (9, 4, —7), A0, 7, —3), A0, 3, —7), A3, 1, -6),
A4, 3, -5), A5, 8, -1), A5, 7, -2), A5, 2, -5),
и столько же других, которые получаются из этих, если меняются
знаки крайних членов, именно, формы (—1, 8, 15), (—2, 7, 15),...,
так что всего форм имеется тридцать восемь. Из них, однако, шесть
должны быть выброшены, именно, (+13, 1, +6), (+14, 3, +5)>
(+15, 2, '+5); остальные тридцать две охватывают все при-
приведенные формы. Вторым методом эти же формы получаются в
следующем порядке*:
(+7, 3, +10), (+10, 3, +7), (+7, 4, +9), (+9, 4, +7),
(+6, 5, +9), (+9, 5, +6), (+2, 7, +15), (+3, 7, +10),
(+5, 7, +6), (+6, 7, +5), (+10, 7, +3), (+15, 7, +2),
(+1, 8, +15), (+3, 8, +5), (+5, 8, +3), (+15, 8, +1).
186
Пусть F приведенная форма с определителем D, и для нее
форма F' является соседней справа, для F' форма F" является
соседней справа, для F" форма F'" является соседней справа
и т. д. Тогда, очевидно, все формы F', F", F'", ... являются
вполне определенными и собственно эквивалентными как между
собой, так и форме F. Так как, однако, число всех при-
* При Ъ = 1 число — 78 не может быть разложено на два сомножителя,
абсолютные величины которых лежат между |/^79 + 1 и ]/~79 — 1; вследствие
этого указанное значение, а по аналогичной причине и значения 2 и 6, нужно
отбросить.
208 Раздел V (п. 187)
веденных форм с заданным определителем конечно, то ясно, что
в бесконечном ряду F, F', F", ... не все формы могут быть раз-
различными между собой. Если предположить, что F(m) и F^m^n) сов-
совпадают, то F{-m~1) и 7?(т+п""г) будут приведенными, соседними сле-
слева для одной и той же приведенной формы и потому будут сов-
совпадать, поэтому F(m~~2) и р(т+п~2) и т. д., наконец, F и F(n) тоже
будут совпадать. Следовательно, в ряду F, Ff F'\ . . ., если только
он продолжен достаточно далеко, обязательно повторится первая
форма F, и если мы предположим, что F(n) — первая форма, сов-
совпадающая с F, или что F', F", . . ., F^71^ все отличны от F, то
легко видеть, что все формы F, F\ F", . . ., F(Ji~~1) различны между
собой. Совокупность этих форм мы будем называть периодом фор-
формы F. Если поэтому ряд будет продолжаться дальше последней
формы периода, то все время будут снова повторяться формы F,
F', F", ...}и весь бесконечный ряд будет образован из этого
бесконечно много раз повторяющегося периода формы F'.
Ряд F, F\ F", . . . может быть продолжен и в обратную сто-
сторону если перед формой F поставить приведенную форму 'F,
которая является для нее соседней слева, перед 'F — форму "F,
которая является для нее соседней слева, и т. д. При этом по
лучается бесконечный в обе стороны ряд форм
"rF "F 'F F F' F" F
и легко видеть, что 'F совпадает с F{n~l\ "F совпадает с р
и т. д., и потому ряд и влево составляется из бесконечное число
раз повторяющегося периода формы F.
Если формам F, F\ F", . . ., 'F, "F. . . . придать соответственно
индексы 0, 1, 2, ..., —1, —2, ..., и вообще форме F^m' — индекс
т, а форме (m)F — индекс — т, то очевидно, что две формы ряда
будут совпадающими или различными в зависимости от того,
сравнимы по модулю п их индексы или нет.
Пример. В качестве периода формы C, 8, —5), определитель
которой равен 79, получается рядC, 8, —5), (—5, 7, 6), F, 5, —9),
(—9, 4, 7), G, 3, —10), (—10, 7, 3). После последней
формы снова получается C, 8 —5). Таким образом, здесь лг = 6.
Формы с полоэюительным неквадратным определителем 209
187
Сейчас мы дадим несколько общих замечаний об этих периодах.
1. Если формы F, F\ F",.../F, "F, mFt... представлены
следующим образом:
(а, Ъ, —а'), (-а', Ь\ а"), (а", Ъ\ — а'"), ..., (-'а, % 'с),
("а, "Ъ, -'а), (-'"а, '"Ъ, "а), . . .,
то #се величины а, а', а", а'", . . ., 'а, "а, '"а, . . . будут иметь одина-
одинаковые знаки (п. 184,1), а Ъ, V, Ь", . . ., 'Ь, "Ъ, ... все будут поло-
положительны.
2. Отсюда вытекает, что число п (количество форм, из которых
состоит период формы F) всегда четно. Действительно, первый
член какой-нибудь формы F(w) из этого периода будет, очевидно,
обладать тем же знаком, что и первый член а формы F, если т
четно, и противоположным, если т нечетно. Поэтому, так как
F(n) и F совпадают, п обязательно будет четным.
3. Алгоритм, при помощи которого отыскиваются числа Ь\ Ъ", Ъ"\ ...
.. ., а", а!"', . . ., согласно п. 184,6, состоит в следующем:
Ь'' = — b(modа') между границами yD и ]/?)+ а'\ а" :=———;
а
b" = — V (mod a") » » УЪ и УЪ + а"\ а1" = D ~ Ь;
У" == — 6" (mod а") » » К^ и /2) + aw! ^ = ^г^ ,
аричем во втором столбце нужно брать верхний или нижний
знак в зависимости от того, положительны а, а', а", ... или
отрицательны. Вместо формул в третьем столбце можно взять и
следующие, которые удобнее, когда число D большое:
и т. д.
210 Раздел V (п. 187)
4. Каждая форма F{, которая содержится в периоде формы F,
будет по сути дела иметь тот же период, что и F. Именно, этот
период будет таков: F(m\ F(m+1), . . ., F(n~l), F, F', . . ., F^-l)- в
нем встречаются те же формы и в том же порядке, что и в пе-
периоде формы F, и он отличается от последнего только в отноше-
отношении своего начала и конца.
5. Отсюда следует, что все приведенные формы с одинаковым опре-
определителем D могут быть разбиты на периоды. Берется по желанию
любая такая формами отыскивается ее период F, Ff, F", ..., F^n-l\
который можно обозначить через Р. Если он еще не охватывает всех
приведенных форме определителем D, то пусть какая-нибудь не со-
содержащаяся в нем форма есть G, а ее период есть Q. Тогда ясно, что
Р и Q не могут иметь общих форм, так как иначе иС должна была бы
содержаться в Р, и периоды вообще совпадали бы. Если Р и Q еще не
исчерпывают всех приведенных форм, то не входящая туда форма
Н даст третий период R, который не имеет общих форм ни с Р, ни
с Q. Таким способом можно поступать, пока не исчерпаются все
приведенные формы. Так, например, все приведенные формы с опре-
определителем 79 разбиваются на шесть периодов:
I. A, 8, - 15), (-15, 7, 2), B, 7, -15), (-15, 8, 1).
II. (-1, 8, 15), A5, 7, -2), (-2, 7, 15), A5, 8, -1).
III. C, 8, -5), (-5, 7, 6), F, 5, -9), (-9, 4, 7), G, 3, -10),
(-10, 7, 3).
IV. (-3, 8, 5), E,7,-6), (-6,5,9), (9,4,-7), (-7,3, 10),
A0, 7, -3).
V. E, 8, -3), (-3, 7, 10), A0, 3, -7), (-7, 4, 9), (9, 5, -6),
(-6, 7, 5).
VI. (-5, 8, 3), C, 7,-10), (-10, 3,7), G, 4,-9), (-9, 5, 6),
F, 7, -5).
6. Мы будем называть ассоциированными формами такие фор-
формы, которые состоят из одних и тех же, но стоящих в противо-
противоположном порядке, членов, например, (а, Ъ, —а'), (—ar, b, а).
Тогда из п. 184,7 легко видно, что если приведенная форма F
имеет период F, F', F", . . ., F^"'^, далее, с формой F ассоцииро-
ассоциирована форма / и с формами F^"^, F(n~2), ..., F", F' — соответ-
соответственно формы /', /", . . ., /(n), f(n—i)^ T0 периодом формы / будет
Формы с положительным неквадратным определителем 211
Л Л А • • •» /(n~2\ /t71), и потому он будет состоять из стольких
же форм, что и период формы F. Периоды ассоциированных форм
мы будем называть ассоциированными периодами. Так, в на-
нашем примере ассоциированы периоды III и VI и точно так же
IV и V.
7. Возможно, однако, и то, что форма / сама содержится в
периоде ассоциированной с ней формы F как в нашем примере
обстоит дело для периодов I и II, и что тем самым период формы
F совпадает с периодом формы / или, что период формы F ассо-
ассоциирован с самим собой. Если это имеет место, то в таком
периоде встречаются две двусторонние формы. Именно, если мы
предположим, что период формы F состоит из 2п форм, или что
F и F совпадают, и если, далее, индекс формы / в периоде
формы F равен 2т + 1 *, т. е. FBm+1) и F ассоциированы, то оче-
очевидно, что ассоциированы также F' и FBm\ F" и р{2т~~1) и т. д.,
и потому также F(m) и F(m+U. Если F(m) = (a(m>, Ы™) , _а<т+1))
<™+1>(т+1) (+1) (+2) tf) (+) (+)
по определению ассоциированных форм, Ыт^ = &(m+i) и тем
самым 2&(m+1> = 0 (moda(m+1)), т. е. форма i^(m+D—двусторон-
i^(m+D—двусторонняя. Точно так же ассоциированы i^Bm+1) и F^n\ поэтому — также
FBm+2) и рBп-1)^ дадее? рBт+з) д рBп-2) и т< д>? и? наКОНбЦ,
р(т+п) и ^(m+n+i). последняя из этих форм является, одна-
однако, двусторонней, что легко доказывается подобным же рас-
рассуждением. Но так как т -f 1 и т -{- п-\- I по модулю 2п не
сравнимы, формы F{m+1) и р{т+п~[~1) не совпадают (п. 186, где п
обозначает то же самое, что здесь 2п). Так, в нашем примере в I
находятся двусторонние формы A, 8, —15), B, 7, —15), в II —
формы (—1, 8, 15), (—2, 7, 15).
8. Обратно, каждый период, в котором имеется двусторонняя
форма, ассоциирован с самим собой. Действительно, легко видеть,
что если F^ есть приведенная двусторонняя форма, то ассоцииро-
ассоциированная с ней форма (которая тоже является приведенной) будет
одновременно для нее соседней слева, т. е. формы jp(m~1) и ()
* Индекс здесь обязательно будет нечетным, так как первые члены форм F,
/, очевидно, имеют противоположные знаки (ср. выше, п. 187, 2).
212 Раздел V (п.
ассоциированы. Тогда, однако, весь период ассоциирован с самим
собой. Отсюда вытекает, что не может быть, чтобы в каком-нибудь
периоде содержалась только одна единственная двусторонняя форма.
9. Однако в одном и том же периоде их не может быть и
больше двух. Именно, если мы предположим, что в состоящем из
2п форм периоде формы F имеется три двусторонних формы
F^\ F^\ F^\ которые принадлежат соответственно индексам X,
[х, v, так что числа X, [л, v — неравные, лежащие в границах от О
до 2п—1 (включительно), то будут ассоциированными формы
F&-V и F{X\ и точно так же F{X~2) и ^(х+1) и т. д., и7 наконец,
F и ^7BХ~~1)# На том же основании ассоциированы F и F^~L\ так
же, как F и F^~x\ Поэтому р^^\ F^~^\ р^~г) совпадают и
индексы 2Х — 1, 2[л—1, 2v—1 сравнимы по модулю 2гс, а значит,
и X^[x = v (modrc). Это, однако, невозможно, так как между гра-
границами 0 и 2п — 1, очевидно, не могут лежать три различных
сравнимых по модулю п числа.
188
Так как все формы из одного и того же периода собственно
эквивалентны, возникает вопрос, могут ли быть также собственно
эквивалентными и формы из различных периодов. Однако прежде
чем показать, что это невозможно, мы должны изложить кое-что
относительно преобразований приведенных форм.
Так как в дальнейшем мы очень часто должны будем иметь
дело с преобразованием форм, то чтобы, насколько это возможно,
избежать длиннот, мы, начиная с этого места, все время будем
пользоваться следующим сокращенным способом записи. Если
форма LX2 + 2MXY + NY2 подстановкой X = ах + jfy, Y = fx + Ц
преобразуется в форму lx2 -f 2mxy + ш/2, мы будем говорить просто,
что (L, ikf, N) переходит при подстановке а, р, ^, 8 в (Z, т, п).
При этом не нужно будет специально обозначать неизвестные
форм, о которых идет речь. Однако, очевидно, что в каждой
форме следует различать первую неизвестную от второй.
Пусть задана приведенная форма (а, Ь, — а') с определителем
D. Образуем аналогично тому, как в п. 186, уходящий в обе
Формы с полоэюительным неквадратным определителем 213
стороны в бесконечность ряд приведенных форм . . ., "/, '/, /,
/', f, .. ., причем пусть
/' = (—а', Ъ\ а"), /" = (а", Ь\ -а'"), ...,
7 = (_ 'а, Ъ, а), 7 = ("а, '6, -'а), . . .
Если положить
Ъ + Ъ'_ , Ь' + Ь" ЬЧ^
а' ~~ ' а" ~~ '
— а' ' а" ' — ат
_ "Ъ + 'Ъ _ тЪ + "Ъ_.и
~~ it * . —— ft a ., —— f fc« • • • .
—а а
it * . ft a .,
а —а а
то, очевидно, что если мы (как в п. 177) образуем числа а', а",
а'", . . ., р7, Р", Р"\ . . . и т. д. по алгоритму
и т. д.,
то / будет переходить в
/' при подстановке a', P', f'» 8',
/" » » а", р% Т", 8",
Г » » а", р'", f\ 8W,
и т. д.,
и все эти преобразования будут собственными.
Так как 7 переходит в / при собственной подстановке 0, —1,
1, h (п. 158), / будет переходить в 7 при собственной подстановке
/г, 1, —1, 0. По аналогичной причине 7 будет переходить в "j
при собственной подстановке '/г, 1, —1, 0, "f в '"/ при собственной
подстановке "/г, 1, —1, 0 и т. д. Отсюда, в соответствии с п. 159,
тем же способом, как в п. 177, можно вывести, что если числа
'а, "а, '"а, . . . , 'р, *р, '"р, ... и т. д. образуются по следующему
алгоритму:
'а = /г, 'р = 1, 4 = -!, '6=0,
-а = 'А 'а — 1, "Р = 'а, "Т - 'А '?, "8 = 'т,
214 Раздел V (п.
'"'a = "'h '"a — "a, ""P = '"a, " = wh '"? — "\, ""8 = "'T',
и т. д.,
то / переходит в
7 при подстановке 'a, 'p, 'y, '8,
7 » » "а, "р, "Т, "8,
7 » » '"a, '"р '"?, "8,
и т. д.,
и что все эти преобразования собственные.
Если положить <х = 1, р = 0, т = 0>8 = 1, т0 эти числа будут
иметь для формы / то же значение, что и числа а', р', *у'> 8' для
/'; а", р", ч", 8" для /", и т. д.; 'а, 'р, '^, '8 для 7» и т- Д- Именно,
при подстановке а, р, у, 8 форма / переходит в /. Но тогда бес-
бесконечные ряды а', а", а'", . . . , 'а, "а, "'а, . . . посредством вставки
члена а приводятся в такую тесную связь, что они могут рас-
рассматриваться как один связанный бесконечный в обе стороны ряд,
который все время строится по одному и тому же закону:
. . . , '"ос, "а, 'а, а, а', а", а'", . . . Закон построения следующий:
"'a + 'a ="h "а, "ел + а = 7г 'а, 'а + а' = /га,
а + ос" = /г'а', а' + а'" = /г"а",
или, вообще (если считать, что отрицательный индекс, добавлен-
добавленный справа, обозначает то же, что положительный индекс, добав-
добавленный слева),
а(™>.
Аналогично является непрерывно связанным ряд . . . , "р, 'C, р, р\
Р", . . . , законом построения которого является
и этот ряд будет совпадать с предыдущим, если все члены сдви-
сдвинуты на одно место: "р = 'а, 'р = а, р = а' и т. д. Закон построе-
построения непрерывного ряда . . . , "if, 'т> Т> т'> Т"> • • • следующий:
Формы с полоэюительным неквадратным определителем 215
и законом построения ряда . . . , "§, '8 8, 8', 8", . . . будет
g(m-l)
и, кроме того, вообще,
Пример. Если заданная форма есть / = C, 8, —5), то она будет
преобразовываться
в форму '" = (—10, 7, 3) подстановкой —805, —152, +143, +27,
» """/ = C,8, —5) » —152, +45, +27, —8,
» = (-5, 7, 6) » +45, +17, -8, -3,
» = F, 5, -9) » +17, -И, -3, +2,
» 7 = (-9, 4 7) » -И, -6, +2, -| 1,
» 7 = G, 3,-10) » -6, +5 +1,-1,
» 7 = (-10, 7,3) » +5, +1, -1, 0,
» /=C,8,-5) » +1, 0, 0, +1,
» /'=(—5,7, 6) » 0, —1, +1, -3,
» Г = F, 5, -9) » -1, -2, -3, -7,
» /" = (_9, 4, 7) » -2, +3, -7, +10,
» Г = G, 3, -10) » +3, +5, +10, +17,
» Г = (-Ю, 7, 3) » +5, -8, +17, —27,
» /""" = C, 8, —5) » —8, —45, —27, —152,
» f"» = (_5, 7, 6) » —45, +143, —152, f 483,
и т. д.
189
Относительно этого алгоритма нужно заметить следующее,
1. Все числа а, а', а'7, . . . , 'а, "а, . . . имеют одинаковые знаки;
все числа &, Ь\ Ь", ...,'&, , . . . положительны. В ряду . . . "h, '/г,
/г, /г', /г", . . . знаки чередуются: именно, если все числа а, а', ...
положительны, то №т) или <т)/г будут положительны при четном т
и отрицательны при нечетном т\ если же а, а', ... отрицательны,
то Ы™) или <т>/г будут отрицательны при четном т и положи-
положительны при нечетном т.
216 Раздел V (п. 190)
2. Если а положительно и потому h' отрицательно, h" положи-
положительно и т. д., то а" =— 1 отрицательно, к'" = h"а" отрицательно
и по абсолютной величине больше чем а" (или равно а", если
Ы' = 1); а"" = h'Jr0Lf" — а" положительно и по абсолютной величине
больше чем а'" (потому что h!"v!" положительно, а" отрицательно);
а"'" = /г"" а"" — а'" положительно и по абсолютной величине
больше чем а"" (потому что /г"" а"" положительно) и т. д. Отсюда
легко видеть, что ряд а', а", а'", . . . возрастает до бесконечности
и что все время два положительных знака чередуются с двумя
отрицательными, так что а(т> имеет знак + , + , —, —, если со-
соответственно т = 0, 1, 2, 3(mod4). Если а отрицательно, то подоб-
подобной же последовательностью рассуждений находим, что а? отрица-
отрицательно, а'" положительно и по абсолютной величине или больше
чем а", или равно а"; а"" положительно и больше чем а'"; а'""
отрицательно и по абсолютной величине больше чем а"" и т. д.,
так что ряд а', а", а'", . . . все время возрастает, и знак члена
a(m) eCTb _j_^ —? —^ _1_ если соответственно т = 0, 1, 2, 3 (mod4).
3. Таким же способом находим, что все четыре бесконечных
ряда а', а", а"', . . . , ?, ?', ?", . . . , а', а, 'а, "а, . . ., ?, '?, Y
а потому и следующие, идентичные с ними ряды j3, j3', j3", . . .
.../8,8, 8', 8", . . . , р/р, "р, . . . , '8, "S, . . . непрерывно возрастают,
и в зависимости от того, имеет ли место т = 0, 1, 2, 3 (mod4),
знаки таковы:
У «(т) +, ±, —, =F, У Р(т) ±, —, =F, +,
У Т(т) ±, +, =Ь —, У 8(т) +, =Ь —, ±,
У (w)a +, ±, —, =F, У (т)Р =F> +> ±, —,
У (т)Т +? —, ±, +, У (m)S +,+,—, ±,
где следует брать верхний знак, если а положительно, и нижний,
если а отрицательно. В частности, можно было бы отметить сле-
следующее свойство. Если т обозначает какой-нибудь положительный
индекс, то а<т) и ^т^ будут иметь одинаковые знаки, если а по-
положительно, и противоположные, если а отрицательно, и анало-
аналогично обстоит дело для р<т> и 8(т>; наоборот, <т>ос и <m>Y или <т>р
и <т)8 будут иметь одинаковые знаки, если а отрицательно, и про-
противоположные, если а положительно.
Формы с полоэюительным неквадратным определителем 217
4. В обозначениях п. 27 величины <x<m>, . . . коротко могут быть
выражены следующим образом. Если положить
' = A', ±h" = к", -fhw = А'", . . .,
. . . , ±h = A, +'h *= rk, ±"h = "к, . . .,
так что все числа к', к", . . , Л, 'Л, .. .положительны, то
= 4. [?", А'", А"", . . . , Л(™-1>], р<™> = + [к", А'", к"", . . . ,
= _)_ [А'? А//? #'", . . . , ^m-D]; 8(w) = + \к\ к\ к"\ . . . , й
= _j_ [й;? 'А^А> ^ #>j (m-i) ^.]? (т)р
(т)Т = ± ['*, ЯК тк, . . . , <т> А], (т>6 = + ['A, "A, WA, .. . , (^-2) А],
причем знаки должны определяться по указанным выше правилам.
По этим формулам, доказательство которых мы, вследствие их лег-
легкости, опускаем, вычисления всегда могут быть проведены крат-
кратчайшим образом.
190
Лемма. Если т, [х9 т', п, v, n' обозначают какие-нибудь целыечисла,
однако такие, что из трех последних ни одно не равно нулю, то я
утверждаю, что если [x/v лежит между границами т/п и т'\п'
(которые сами исключаются), и тп' — птг = ^1, то знаменатель v
будет больше, чем п и п'.
Доказательство. Очевидно, что \тп' лежит между vmn' и vnm',
и потому отличается от обеих границ меньше, чем одна граница
отличается от другой, т. е. vmn' — vnm' > \хпп' — vmn' и > [кпп' —
— vnm', или v > п' ({ьп — vm) и >тг([лп' — vm'). Отсюда следует,,
что так как [кп — vm, очевидно, не равно 0 (ибо в противном слу-
случае, вопреки предположению, было бй — = — J и также \кп' — vm'
не равно 0 (по аналогичной причине), каждое из этих выражений
равно 1, v > п' и v > п.
Поэтому ясно, что v не может быть равно 1, т. е. что если
тп' — пт' = + 1, то между дробями т/п, т'/п' не может лежать
целое число. Поэтому между ними не может лежать и нуль, т. е.
указанные дроби не могут иметь противоположных знаков.
218 Раздел V (п. 191)
191
Теорема. Если приведенная форма (а, 6, — аг) с определителем D
переводится подстановкой а, р, т, 8 в приведенную форму (А, В, — А')
с тем же определителем, то, во-первых, (+V&— Ъ)/а лежит
между а/^ и р/8 (ec^w ни ^, ww S we равны нулю, т. е. если обе
границы конечны), причем верхний знак нужно брать тогда, когда
ни одна из обеих границ не имеет знака, противоположного знаку
числа а (или, яснее, когда обе границы имеют тот же знак, что и а,
или одна из них имеет знак, одинаковый с а, а другая равна нулю);
нижний же — тогда, когда ни одна из границ не имеет того же
знака, что а; во-вторых, (+VD + Ь)Iа' лежит между f/а и 8/C
{если ни а, ни C не равны нулю), где имеет место верхний знак,
если ни одна из границ не имеет знака, противоположного знаку а'
(или а), и нижний — если ни одна из них не имеет того же знака,
что и а' *.
Доказательство. Мы имеем равенства
[1]
[2]
Из них следует
[3j
аса2
ар
а
Т
+ 26 оо? —
+ 26 (З^-—
±1/ DA-
а
а'ч2
aW
аА
= А
= —А'.
~ъ
[4]
аА'
D--w-b
[5] ^ = К , а2
±yrD + ^+b
jf] Т= а' •
* Очевидно, что других случаев быть не может, так как, согласно предыду-
предыдущему пункту, вследствие равенства aS— р^ =+1 обе границы не могут иметь
противоположных знаков и не могут одновременно быть равны нулю.
Формы с положительным неквадратным определителем 219
Если равно нулю какое-либо из чисел т? 8, а, р, то отбрасы-
отбрасывается соответственно равенство [3], [4], [5], [6]. Однако здесь
остается неясным, какими знаками должны быть снабжены вели-
величины корней. Это мы установим следующим образом.
Тотчас же ясно, что в [3] и [4] обязательно должны быть взяты
верхние знаки, если ни а/^, ни р/8 не имеют знаков, противо-
противоположных знаку а, потому что если бы мы взяли нижний знак, то
величины аа/т и ар/8 были бы отрицательными. Так как, однако,
А ж А1 имеют одинаковые знаки, J^D попадает между J^D -f aA /
и J^D—аА' /82, и потому в этом случае (\f D — b) / а лежит между
а / ^ и C/8. Тем самым первая часть нашей теоремы для первого
случая доказана.
Тем же способом убеждаемся, что в [5] и [6] обязательно дол-
должны быть взяты нижние знаки, если ни ^/а, ни 8/C не имеют того
же знака, что а' или а, потому что если бы взять верхний знак, то
величины а'т/а и а'8/{3 обязательно стали бы положительными.
Отсюда тотчас же следует, что в этом случае (— j/Z) -j- b)/ar лежит
между т/а и <VP« Поэтому доказана также и вторая часть теоремы
для последнего случая. Если бы теперь можно было так же лег-
легко показать, что в [3] и [4] нужно брать нижние знаки, если ни
одна из величин а/т, C/8 не имеет того же знака, что и а, и в
[5] и [6]—верхние, если ни т/а, ни 8/C не имеют знака, противо-
противоположного знаку а, то отсюда подобным же образом следовало бы,
что в первом случае (—|ЛО — Ь)/а лежит между а/т и C/8, а во
втором случае (|/ D -j- b)/a' лежит между т/а и 8/C, т. е. первая
часть теоремы была бы доказана также и для последнего слу-
случая, а вторая часть ее также и для первого случая. Однако, хотя
это сделать и нетрудно, все же это не удается напрямик, и по-
потому мы используем следующий метод.
Если ни одно из чисел а, р, т> ^ не равно нулю, то а/т и C/8
будут иметь те же знаки, что т/а и VP- Если поэтому ни одна из
этих двух величин не имеет того же знака, что а' или а, и пото-
МУ (—У & + Щ/а' попадает между т/а и 8/C, то ни одна из величин
.а/т, р/8 не будет иметь того же знака, что и а, и потому -^= =
— у D + Ъ
220 Раздел V (п. 192)
__ —l (вследствие aaf = D —Ь2) попадет между а/т и C/8.
Поэтому для того случая, когда ни а, ни C не равны нулю, пер-
первая часть теоремы доказана также и для второго случая (действи-
(действительно, то условие, что ни т> Нй 8 не равны нулю, было добавлен
но уже в теореме). Аналогичным образом, если ни одно из чисел
а, В, y, 8 не равно нулю, и ни а/т, ни C/8 не имеют знака, про-
противоположного знаку а или а7, и потому (Y~D — b)/a лежит между
а/т и C/8, то также и т/'а и 8/C не будут иметь знака, противопо-
а Yd+ъ
ложного знаку а , и потому = ; попадет между т/я-
и 8/C. Таким образом, если ни т> ни 8 не равны нулю, вторая
часть теоремы доказана также и для второго случая.
Поэтому остается еще только доказать, что первая часть теоре-
теоремы справедлива для второго случая и тогда, когда одно из чисел
a, C равно нулю, и что вторая часть теоремы верна для первого*
случая также и тогда, когда или т = 0, или 8 = 0. Однако все эти
случаи невозможны.
Действительно, предположим для первой части теоремы, что ни
Т, ни 8 не равны нулю, что a/т, р/8 не имеют того же знака,
что а.
1. Пусть a = 0. Тогда из равенства а8 — [Зу = -J- 1 следует, чта
Р = +1, т = + 1- Поэтому, вследствие равенства [1], А — —а' и
тем самым А и а', а потому также а и 4' имеют противополож-
противоположные знаки, откуда следует, что ~\f D — аА'/Ъ2 > Y~D^> b. Из этого
вытекает, что в [4] обязательно должен быть взят нижний знакг
потому что иначе C/85 очевидно, получило бы тот же знак, что и а.
Поэтому будет -|- ^> }> 1 (потому что по определении*
приведенной формы а < ]/?> + Ь). Это, однако, невозможно, так
как р = + 1 и 8 не равно нулю.
2. Пусть р = 0. Тогда из равенства aS — р^ = + 1 получается, что
a — + 1, 8 = + 1. Поэтому из [2] следует, что — А' = — а'\ тем
самым a', a и Л будут иметь одинаковые знаки, откуда следует,
что Y~D + аЛ/a2 >]/"/)> 6. Отсюда вытекает, что в равенстве [3]
должен быть взят нижний знак, потому что при ве хнем знаке-
Формы с полоэюительным неквадратным определителем 221
а/^ получило бы тот же знак, что и а. Поэтому— > ^^-—— >1,
а это невозможно по той же причине, что и в первом случае
(при ос = 0).
Предположим, для второй части теоремы, что ни ос ни C не
равны нулю, что т/а, 8/C не имеют знака, противоположного
знаку а!.
1. Пусть 7 = 0. Тогда вследствие равенства ос8 — (Зт == +1 бу-
будет а = Н=1, § = +1, и потому из [1] вытекает, что А = а; по-
поэтому ^4' и а' будут иметь одинаковые знаки, откуда следует, что
)/~D + я'А'/$2 > j/"Z)>&. Поэтому в [6] должен быть взят верхний
анак, потому что при нижнем 8/C получило бы знак, противопо-
противоположный знаку а'. Таким образом, 8/C >(|/i) + й)/а' > 1. Это, одна-
однако, невозможно, так как 8 — + 1 и C не равно нулю.
2. Если, наконец, 8 = 0, то вследствие равенства cub — fty = -j- 1
будет р = +1, т = + 1 и потому, согласно [2], —А'= а. Отсюда
следует ]ЛО — а'А/а2^> \/"D > &, в силу чего в [5] надо брать
верхний знак. Поэтому — >-*¦—г—->1» а это невозможно.
ос л
Тем самым наша теорема доказана во всей ее полноте.
Так как разность между ос/^ и [3/8 равна 1/^8, то разность
между (zbVD — b)/a и ос/^ или р/8 будет меньше чем 1/^8; но меж-
ДУ (zb V~D — Ъ)/а и а/Т или между первой величиной и C/8 не
может лежать дроби, знаменатель которой был бы не больше чем
Y или 8 (предыдущая лемма). Точно также разность между вели-
величиной (+ }/~D + Ь)/а и дробью т/а или дробью 8/р будет меньше
чем 1/оф, и между первой величиной и одной из этих дробей не
может лежать дроби, знаменатель которой был бы не больше чем
аир.
192
Из применения предшествующей теоремы к алгоритму п. 188
следует, что величина (УD — Ь)/а, которую мы обозначим через L,
лежит между ос'/т' и р'/§', между асГ/8" и |3"/5", между ос7т" и V"№
и т. д. (действительно, из п. 189, 3 легко получить, что ни одна
из этих границ не имеет знака, противоположного знаку а, и
222 Раздел V (п. 193)
потому величина корня }/~Z) должна браться с положительным зна-
знаком), или между ос'/т' и а7т"» между ос"/Т" и &'"ft'" и т. д. Поэтому
все дроби ос'/т'» а'7т'"? а'т'""» • • • будут лежать по одну сторону
от L, а все дроби а"/т ят""> <x"tw"\ ...—по другую сторону.
Так как, однако, т'<Т'"» то ос'/т' лежит вне интервала между а'"/?'""
и L, и по аналогичной причине ос"/т" — вне интервала между L и
ост""> &'7т'" —вне интервала между L и а'""/т'"" и т- Д- Отсюда
ясно, что эти величины лежат в следующей последовательности:
Но разность между а'/т' и L меньше разности между ос'/т' и а7т"у
т. е. меньше чем l/^V» и по подобной же причине разность меж-
между ос'Ут" и ^ меньше чем 1/YY"» и т- Д- Поэтому дроби а'/т'» ^Vt"?
а!"/ч"', • • • все больше приближаются к границе L, и так как т\
Y", y'"» • • • возрастают до бесконечности, разность между дробями
и границей может быть сделана меньше любой заданной величины.
Согласно п. 189, ни одна из величин ^/сс, /(у/'а, "^/"си, ... не имеет
того же знака, что а; отсюда следует посредством совершенно ана-
аналогичного предыдущему ряда заключений, что эти величины и ве-
величина (—]/~D + Ъ)/а\ которую мы обозначим через Z/, расположены
в следующей последовательности:
'a
Но разность между f/a и Z/ меньше, чем l/'oca, разность между
'т/'а и L' меньше чем 1/"ос'а и т. д. Поэтому дроби ^/сс, 'ч/'&, • • •
все больше приближаются к границе Z/, и разность может быть
сделана меньше любой заданной величины»
Т/7(Т о
В примере п. 188 L = ц =^0,2960648 и приближающие
дроби суть 0/1, 1/3, 2/7, 3/10, 5/17, 8/27, 45/152, 143/483, ... Но
143/483 = 0,2960662. Точно так же L' = ~Vl^ + s = — 0,1776388,
и приближающие дроби суть 0/1, —1/5, —1/6, —2/11, —3/17,
—8/45, —27/152, —143/805, ... Но 143/805-0,1776397.
Формы с положительным неквадратным определителем 223
193
Теорема. Если приведенные формы /, F собственно эквивалентны,
то одна содержится в периоде другой.
Пусть / — (а, Ъ, —a'), F = (А, В, —А'), определители этих
форм равны D, и первая переходит во вторую при собственной
подстановке 21, 95, (?, ©. Тогда я утверждаю, что если найти пе-
период формы / и бесконечные в обе стороны ряды приведенных
форм и преобразований формы / в них, как это делалось в п. 188,
то или + 21 равно какому-нибудь члену ряда ..., "ос, 'ос, ос, ос', ос", . . .
и если положить его равным а<т), то + 23 = C(m)T + S = 7(т),
-]-© = 8(т), или — 21 равно одному из членов ос(т) и — 23, — @, — © соот-
соответственно равны t8(m), ^m), 8(m) (где т может обозначать также и
отрицательный индекс). В обоих случаях F, очевидно, идентична /(т).
Доказательство. I. Мы имеем четыре равенства:
[1] a3t2
[2] а2123 + Ь B1© + 232) — a'G© = В,
[3] а232 + 2ШЭ — а'®2 = — А\
[4] 2BD —93E = 1.
Рассмотрим, однако, сначала случай, когда одно из чисел 21, 23, ?,
© равно нулю.
1. Если 21 = 0, то из [4] следует, что 25S = —1, и потому
35 = +l.i S = + l. Поэтому из [1] получается —а' = А, из [2]
получается — Ъ + а'© = Z?, или 5 ^ — 6 (mod а' или 4), откуда следует,
что форма (А, В, — А') является соседней справа для формы (а, 6, — а').
Но так как первая форма приведенная, она обязательно совпадает
с/'. Поэтому В=Ь', и потому, в силу [2], Ь+Ь' = —#'(?©==+#'©; отсюда,
так как—-^Ц— = h\ следует, что ©=+/г\ Отсюда же мы за-
заключаем, что +2t, :=F23, +?, +© соответственно равны 0, — 1,
+ 1, /г', т. е. равны а', C', т', 8'.
2. Если 23=0, то из [4] следует, что 21= +1; ©=+1; из
[3] —что а'= 4', из [2]— что Ь + а%==В, или 6 = 5 (mod а'). Так
как, однако, как /, так и F—приведенные формы, то как Ь, так иВ
будут лежать между "УD и Л/'В'^-а' (в зависимости от того,
224 Раздел V (п. 193)
положительно а' или отрицательно; п. 184, 5). Поэтому обяза-
обязательно Ъ = В и Е == 0. Следовательно, формы / и F совпадают,
и + 21, + 25» + S, + © соответственно равны 1,0, 0, 1, т. е.
равны ос, р, ч% 8.
3. Если © = 0, то из [4] следует, что 21 = + 1» © = + 1, пз
[1] —что а = А, из [2] —что + а25 + Ъ = Б, или & = ? (mod а). Так
как, однако, как Ь, так и 5 лежат между J/~D и ]/"/) +а, то обя-
обязательно будет В = Ъ и 25 = 0. Поэтому этот случай не отличается
от предыдущего.
4. Если © = 0, то из [4] следует, что 25 = +1> 6 = + 1, из
[3] —что а = — А\ из [2] —что +а% — Ъ = В, или B=^ — b (modа).
Поэтому F является соседней слева для формы /, и, значит, сов-
совпадает с формой '/. Поэтому, вследствие ——— = h и В — 'Ь, бу-
будет + 21 = h. Отсюда следует, что +21, +23, + К, +© соответ-
соответственно равны /г, 1, —1, 0, т. е. 'ос, 'C, '^, '8.
Итак, остается только тот случай, когда ни одно из чисел 2t,
95, S, © we доено нулю. Здесь, вследствие леммы п. 190, величины
2t/S, 95/©, S/2t, ©/25 будут иметь одинаковые знаки, и потому мо-
могут представиться два случая, так как эти знаки могут или сов-
совпадать со знаком а, а'', или быть ему противоположными.
II. Если 21/S, 25/© имеют тот же знак, что и а, то величина
— 6)/а (которую мы обозначим через L) будет лежать между
этими дробями (п. 191). Теперь мы покажем, что 2I/S равно одной
из дробей ос"/т"' ат'"» dtn!*{'"* ..-, и 25/© равно следующей, или,
St a(m) s? a(m+l)
что если — = —^- , то -^- = —^q^y- . В предыдущем пункте
мы показали, что величины ос'/т'» а7т"» ат'"» ••• (которые мы
коротко обозначим через A), B), C), . ..) располагаются в следую-
следующей последовательности (I): A), C), E), ..., L,... , F), D), B);
первая из этих величин равна нулю (так как ос' = 0), остальные
имеют те же самые знаки, что L или а. Так как, однако, по пред-
предположению, 21/6, 25/© (вместо которых мы будем писать 9К> 91)
имеют одинаковые знаки, то эти величины, очевидно, будут ле-
лежать справа от A) (или, если угодно, с той же стороны, что и L),
и притом, так как L лежит между ними, одни справа от L, а
Формы с положительным неквадратным определителем 225
другая слева от L. Но легко можно показать, что 3R не может
лежать справа от B), так как иначе 9Z лежало бы между A) и
L, откуда следовало бы, во-первых, что B) лежит между 9К и 91,
и потому знаменатель дроби B) больше, чем знаменатель дроби 91
(п. 190), и во-вторых, что 91 лежит между A) и B), и потому зна-
знаменатель дроби 9} больше, чем знаменатель дроби B), что невоз-
невозможно .
Мы предположим, что Ж не равно ни одной из дробей B), C),
D), ... и посмотрим, что из этого следует. Очевидно, что если
дробь 9R лежит левее, чем L, она обязательно должна лежать или
между A) и C), или между C) и E), или между E) и G) и т. д
(так как L иррационально и потому, очевидно, отлично от 3R, а
дроби С1), C), E), ... могут быть приближены к t на любую за-
заданную величину). Если же SR лежит справа от L, то оно должно
обязательно лежать или между B) и D), или между D) и F), или
между F) и (8) и т. д. Поэтому, если мы предположим, что Ш
лежит между (т) и (т + 2), то величины Ж, (т), (т + 1), (т + 2),
L, очевидно, будут лежать в следующей последовательности:
(И)* (т), 3R, (т + 2), L,(m + 1).
Тогда обязательно 9} = (т + 1). Действительно, 91 лежит справа
от L; если бы оно лежало также и справа от (т -\- 1), то (т-\-\)
лежало бы между Ж и 3J, т. е. было бы ^(m+1) > S, a 9R лежало
бы между (т) и (т + 1)> т. е. было бы S > ^(т+1) (п. 190), что невоз-
невозможно. А если бы 91 лежало слева от (т + 1), т. е. между (т-\-2)
и (т + 1), то было бы © > ^(т+2)} и так как (т + 2) лежит между
3R и 9?, было бы f(m+2) > ©, что невозможно. Поэтому 91 = (ттг-f-l),
«IB a(m-l-i) o(m)
или — = = — .
Так как 21©—25S = 1, то 25 взаимно просто с ©, и по подоб-
подобной же причине р<т) взаимно просто с &т\ Отсюда легко видеть,
* Безразлично, совпадает ли порядок расположения в (II) с порядком
расположения в (I) или является ему противоположным, т. е. лежит ли в (I)
величина (т) слева или справа от L.
226 Раздел V (п. 193)
что равенство — = ^ может выполняться только в том слу-
'—' О
чае, если или 25 = р<т>, © = 8<™>, или 25 = — р<т>, © = — 8<т>.
Но так как форма / при собственной подстановке oo<m), p(m>, ^(™\
S(m) переходит в форму /(m>, которая есть (+а(т>, й<т>, + <
то мы имеем равенства
[5]
[6]
[7]
[8] (х(т)^(т) — p(m)^(w) __ ^
Поэтому (из равенств [7] и [3]) получается + а(т+^ = —А'. Если,
далее, умножить равенство [2] на oo(m)8(m) — р(т)^(т)? равенство [6]
на 2155—23S и вычесть, то, раскрывая скобки, легко установить
равенство
[9] В — 6<™> = (?оо(™) —
и так как либо р<т> = S3, 8<т) = ©, либо р<т> = — 85, S^m) = — ©, то
отсюда следует, что Б — Ыт) = + Fа<т> — 3l7(m)) (^252 + 2625© —
— а'©2) = + {Ы^ — Щ^) А'.
Поэтому В = Ыт) (mod Л'). Так как, однако, как В, так и Ь{т)
лежат между J/~D и Y~D^A, то обязательно В = Ыт\ и потому
_5ЦТ(т) =о, или i = -?L-r, т. е. gR=()
Таким образом, из предположения, что Ж не равно ни одной
из величин B), C), D), .. . , мы вывели, что в действительности
оно равно одной из них. Если же мы теперь с самого начала
предположим, что Ж = (т), то, очевидно, будет или 31 = <х<т) и
© = т(™), или — 31 = а(™>, — (? = 7(m) B обоих случаях из [1] и [5]
следует, что .4=+а(т), и из [9] — что В — &(т) = + (858(т) —
— Щ(т)) А, или В = Ыт) (mod-Л). Отсюда, аналогично тому, как и
выше, получается В = Ыт\ и потому 23S(m) = Э3(т); но так как 25
взаимно просто с ©, и р(т> взаимно просто с 8<m), то, следовательно,
или 23 = В(^), © = 8<™>, или 93 = — р(^»), ©=— 8(т>, и тем самым
Формы с положительным неквадратным определителем 227
из [7] следует, что —А' = -f- а^^. Поэтому формы F и /(ш> сов-
совпадают. Но при помощи равенства 31© — 25(? = oc(m)S(m) — C(m)^(m>
без труда доказывается, что + 23 = р(т), + © = S(m), если -f- 31 =
= ос(т). -f- К = ^(т), и, наоборот нужно положить — 23 = р(ш)
_©=8(т>, если — % = <х,(т\ — d = 7GГ))- Это и нужно было дока-
доказать.
III. Если знак величин 3I/S, 35/25 противоположен знаку а, то
доказательство настолько похоже на предыдущее, что достаточно
указать только на основные пункты. Число (— \/"D -f- h)/ar лежит
между S/91 и ©/25. Дробь ©/25 равна какой-нибудь из дробей
и если считать ее равной (w)S/(rn)p, то
(I) доказывается следующим образом. Если предположить, что
не равно ни одной из этих дробей, то она должна лежать между
какими-нибудь двумя из них: (m)S/(m)p и (^+2)8/(^+2)р. А отсюда тем
же способом, что и выше, можно вывести, что обязательно
(m)
r
и потому или % = (w)a, g = (w)^, или — 31 = (m>a, — 6 — (™>т. Так
как, однако, / при собственной подстановке (т)<х, (т)р, (т)^, (т>8 пе-
реходит в форму
то получаются три равенства, из которых в связи с равенствами
[Ц [2], [3], [4] и равенством (m)a(m)8 = (то)р(т)^ = 1 подобным же
образом, как выше, вытекает, что первый член А формы F равен
первому члену формы <т)/, и средний член [первой сравним со
средним членом второй по модулю А. Отсюда, так как обе формы
228 Раздел V (пп. 194-195)
приведенные и потому средние члены обеих лежат между Y & и
Y-D + A, следует, что эти средние члены равны, а отсюда выво-
дится, что —щ—= -=- . Поэтому здесь справедливость утвержде-
утверждения (I) выведена из предположения, что оно не верно.
гьсли же предположить, чго -г—— = —, то совершенно анало-
аналогичным образом и при помощи тех же равенств доказывается и
(II), т. е что --—р- = -^- . А отсюда вследствие равенств 21© —
— 5?S = I, (™)а<т>8 — (rn)^(m)^ = \ вытекает, что
или
ИЛИ
— 21 = Wa, — 85 = ^m\8, — 6 = (m)y, — © = N8,
н что формы F и (m)/ совпадают, а это и требовалось доказать.
194
Так как формы, которые выше (п. 187,6) мы назвали ассоцииро-
ассоциированными формами, всегда несобственно эквивалентны (п. 159), то
ясно, что если приведенные формы F, f несобственно эквивалентны,
и G есть форма, ассоциированная с F, то формы G, f собственно
эквивалентны, и потому форма G содержится в периоде формы /.
Если поэтому формы F и / эквивалентны как собственно, так и
несобственно, то как F, так и G будут, очевидно, содержаться в
периоде формы /. Поэтому этот период будет ассоциирован с са-
самим собой и будет содержать две двусторонние формы (п. 187, 7).
Тем самым мы получаем красивое подтверждение теоремы из
п. 165, на основании которого мы уже могли бы быть уверенными,
что существует хотя бы одна двусторонняя форма, которая экви-
эквивалентна формам F, /.
Формы с полоэюительным неквадратным определителем 229
195
Задача. Пусть даны какие-нибудь две формы Ф и ф с одинаковым
определителем] требуется узнать, эквивалентны они или нет.
Решение. Найдем две приведенные формы F и /, которые соответ-
соответственно эквивалентны заданным формам Ф и ф (п. 183). В зависимо-
зависимости от того, эквивалентны ли эти формы только собственно, или
только несобственно, или и собственно и несобственно, или ни так,
ни иначе, также и заданные формы будут эквивалентны или только
собственно, или только несобственно, или и так и иначе, или ни так,
ни иначе. Найдем период одной из этих приведенных форм, напри-
например, период формы /. Если в этот период входит форма F, но одно-
одновременно не входит форма, ассоциированная с F, то, очевидно, имеет
место первый случай. Если же входит эта ассоциированная форма,
а сама F не входит, то второй, если обе формы входят — то третий,
а если не входит ни одна из них, то четвертый случай.
Пример. Пусть заданы формы A29, 92, 65), D2, 59, 81) с опреде-
определителем 79. В качестве эквивалентных им приведенных форм нахо-
находим A0, 7, —3), E, 8 —3). Период первой формы следующий:
A0, 7, -3), (-3, 8, 5), E, 7, -6), (-6, 5, 9), (9, 4, -7), (-7, 3, 10).
Так как в нем нет формы E, 8, —3), но есть ассоциированная
с ней форма (—3, 8, 5), то заданные формы эквивалентны только
несобственно.
Если все приведенные формы с одинаковым определителем раз-
разбиты на периоды Р, Q, R,... тем способом, который был указан выше
(п. 187, 5), и из каждого периода выбрана по желанию любая форма,
например, из Р выбрана F, из Q выбрана G, из Л выбрана Н и т. д.,
то среди этих форм F, G, Н,... не может быть никаких двух, которые
собственно эквивалентны. А каждая другая форма с тем же опреде-
определителем будет эквивалентна какой-нибудь из них, причем только
одной. Из этого вытекает, что все формы с этим определителем мо-
могут быть разбиты на столько классов, сколько имеется периодов,
именно, если отнести к первому классу те, которые собственно экви-
эквивалентны форме F, ко второму — те, которые собственно эквивалент-
эквивалентны форме Сит. д. Таким образом, все формы, содержащиеся в одном
и том же классе, будут собственно эквивалентны; формы же из раз-
230 Раздел V (пп. 196-197)
личных классов не могут быть собственно эквивалентными. Однако
здесь мы не будем задерживаться на этом вопросе, который должен
быть подробнее рассмотрен ниже.
196
Задача. Пусть даны две собственно эквивалентные формы Ф и <р;
требуется найти собственное преобразование одной из них в другую.
Решение. Методом п. 183 можно найти два ряда форм
Ф, Ф', Ф", ..., Ф(п) и <р <р', ф", ..., ф(*>
с тем свойством, что каждая следующая форма собственно эквива-
эквивалентна предыдущей, а последние формы Ф(п) и <p(v> — приведен-
приведенные; и так как мы предположили, что Ф и <р собственно эквива-
эквивалентны, то обязательно Ф(п) встретится в периоде формы <рМ. Пусть
<p(v) = / и период ее до формы Ф следующий:
/, /', /",..., i{™\ ф(п),
так что в этом периоде индекс формы Ф(п) равен т\ обозначим еще
те формы, которые противоположны формам, ассоциированным
с Ф, Ф', Ф", . . ., Ф(п) соответственно через
Тогда в ряду <р, <р', т", . ., /, /', /", . .., fm^\ Y{n~l\ W{n~2\ . .., Y, Ф
каждая форма будет соседней слева для предыдущей, и потому,
согласно п. 177, может быть найдено собственное преобразование
первой формы, ф, в последнюю, Ф. Для всех остальных форм,
кроме /(т~г) и Y('n~1\ это непосредственно очевидно. Для этой же
пары форм доказательство следующее. Пусть y(m~1) = (gy fi, i),
/< = ф<*> = (?', к*щ г'),ф^-1> = (8-, h\ П. Форма (g\ h\ V) будет
соседней справа как для формы (g, /г, г), так и для (g"t h", i"),
поэтому i=g' = i" и —h = h'= — /z"(mocU или g, или i").
* Таким образом, lF получается из Ф перестановкой первого и последнего
членов и изменением знака у среднего члена; аналогично обстоит дело и для
других форм.
Формы с полоснсителъным неквадратным определителем 231
Отсюда вытекает, что форма (Г, —h", g"), т. е. форма ^р(п~1) —
соседняя справа для формы (g< h, i), т. е. формы рт'~\
Если формы Ф, ф несобственно эквивалентны, то форма ср будет
собственно эквивалентна той форме, которая противоположна Ф.
Поэтому можно найти собственное преобразование формы ср в ту
форму, которая противоположна Ф. Если предположить, что это
достигается подстановкой ос, C, т» 8, то легко видеть, что ср не-
несобственно преобразуется в самую форму Ф подстановкой ос, — р»
Т, -8.
Отсюда также очевидно, что если формы Ф и ср эквивалентны
как собственно, так и несобственно, то могут быть найдены два
преобразования, одно собственное и одно несобственное.
Пример. Найдем несобственное преобразование формы A29, 92, 65)
в форму D2, 59, 81), которая, как мы установили в предыду-
предыдущем пункте, несобственно эквивалентна первой. Сначала надо най-
найти собственное преобразование формы A29, 92, 65) в форму
D2,—59, 81). Для этого строим следующий ряд форм: A29, 92, 65),
F5, -27, 10), A0, 7, -3), (-3, 8, 5), (б', 22, 81), (81, 59, 42),
D2, —59, 81). Отсюда находим собственное преобразование —47,
56, 73, —87, при котором A29, 92, 65) переходит в D2, —59, 81).
Поэтому первая форма будет переходить в форму D2, 59, 81)
при несобственном преобразовании —47, —56, 73, 87.
197
Если имеется одно преобразование какой-нибудь формы ср =
(а, Ъ, с) в эквивалентную форму Ф, то из него можно вывести все
однотипные преобразования формы ср в Ф, если только можно ука-
указать все решения неопределенного уравнения t2 — Du2 = т2, в кото-
котором D обозначает определитель форм Ф, <р> и т — наибольший
общий делитель чисел а, 26, с (п. 162). За эту проблему, которая
в случае отрицательного значения D уже была решена выше, мы
сейчас возьмемся также и для положительного значения D. Так как,
однако, каждое значение t, удовлетворяющее уравнению, будет
удовлетворять ему и после изменения своего знака, и то же самое
верно для значений и, то нам нужно будет определить лишь все
232 Раздел V (пп. 198-199)
положительные значения t. и, и каждое решение с положительными
значениями будет заменять четыре решения. Эту задачу мы решим
так, что сначала найдем наименьшие значения t, и (кроме само
собой разумеющихся t = m, u=0), а затем научимся выводить
из них все остальные.
198
Задача. Найти наименьшие значения t, и, удовлетворяющие неоп-
неопределенному уравнению t2— Du2 — т2, если дана форма (М, N,P),
определитель которой равен D, и у которой наибольший общий
делитель чисел М, 2N, Р равен т.
Решение. Возьмем любую приведенную форму / = (а, 6, —а')
с определителем D, у которой наибольший общий делитель чисел
а, 26, а' равен т. То, что такая форма существует, ясно уже из
того, что можно найти эквивалентную форме (М, N, Р) приведен-
приведенную форму, которая, согласно п. 161, обладает этим свойством;
однако для нашей цели можно использовать каждую приведенную
форму, для которой это условие выполняется. Найдем период фор-
формы /, который пусть состоит из п форм. При сохранении всех обо-
обозначений, которыми мы пользовались в п. 188, имеет место /(п) =
= (а<п), Ып\ —а^1)), потому что п четно, и / будет переходить
в эту форму при собственной подстановке ос<п>, р<п>, ^п\ S(n). Но так
как / и /п) совпадают, то / будет переходить в /п) и при собствен-
собственной подстановке 1,0, 0, 1. Из этих двух однотипных преобразова-
преобразований формы / в /п)» согласно п. 162, может быть выведено решение
уравнения t2 — Du2 = т2 в целых числах, именно, t = (oc(n> + ^n*) m / 2
(равенство 18 в п. 162), и = ^^т/а (равенство 19 в п. 162)*
Если эти значения, взятые положительными (ибо первоначально они
еще не обязаны быть таковыми), обозначить через Т, U, то Т, U
будут наименьшими значениями t, и, кроме t = m, и = 0 (от этих по-
последних TjiU обязательно отличны, так как ^п\ очевидно, не может
быть равно нулю).
* То, что в п. 162 обозначалось через а, р, j, Ъ; а' C\ j', Ь'\ Ау Вг С;
а, Ъ, с; е, здесь соответственно равно 1, 0, 0, 1; о^п), ^п\ у^п\ Ь^-, а, Ъ,
— а'; а, Ъ, — а'\ 1.
Формы с положительным неквадратным определителем 233
Действительно, если мы предположим, что существуют еще мень-
меньшие значения t, и, например, t и и, которые положительны, и и
не равно н>лю, то, согласно п. 162, форма / при собственной иод-
1 1 11
становке — (t — bn), — а'п. — an, — (t + bn) будет переходить в идеи-
ТТЬ ТТЬ ТТЬ ТТЬ
тичную ей форму. Теперь, из п. 193, II следует, что или —(t — bn),
или (t—bn) должно быть равно одному из чисел ос", а'", ос"", ...,
например, а^> (именно, так как t2 — Dn2-\- m2 = 62tt2+ aa'n2jr m2, то
t2 > 62u2, и потому t — bn положительно; поэтому дробь (t — bn) / an,
которая соответствует дроби 21/E в п. 193, будет иметь тот же
/V 1,1
самый знак, что и а или а ), и что в первом случае — а ц. — an,
— (t + йи), а во втором — эти же величины с противоположными
знаками соответственно равны р(м#), ^\ 8(м#). Так как, однако, tt < U,
т. е. и < и > 0, то ^М будет < ^(п) и > 0; поэтому, так как
ряд y» т'» Т'» • • • непрерывно возрастает, [х обязательно будет ле-
лежать между 0 и п. Но соответствующая форма /(м#) будет совпадать,
с формой /. Это, однако, невозможно, так как все формы /, /'
/", ... до fn~1' предполагаются различными. Отсюда следует, что
Т, U являются наименьшими значениями*, и (заисключением т, 0).
Пример. Если D = 79, т = 1, то можно использовать форму
C. 8, —5), для которой и = 6, и ос<п> = — 8, т(п) = —27, g(n) =
= —152 (п. 188). Отсюда следует Т = 80, G = 9, что дает наи-
наименьшие удовлетворяющие уравнению ?2—79гг2 = 1 значения г, гг.
199
Дая практического использования могут быть получены еще бо-
более удобные формулы. Именно, 2Ь^п) =—а{а№ — S(n)), что легко
следует из п. 162, если умножить равенство [19] на 26, равенство
[20] — на а и заменить использованные там обозначения тепереш-
теперешними. Отсюда а(п) + 8(п) =28(п) — — т(«>, и потому
а
234 Раздел V (п. 200)
Подобным же образом получаются следующие значения:
Как первые, так и вторые формулы будут очень удобными, так
как f(n) = S^"*, a(n) = р(п~), и потому, если пользоваться вто-
вторыми формулами, то нужно вычи лить только ряд р', р", р'", . , ., р(п),
а если первыми — то только ряд 8', 8", 8'",... Кроме того, из
п. 1895 3 легко следует, так как п обязательно четно, что ос(п) и
— р(п) имеют одинаковые знаки, и точно так же S(n) и —-у^, так что
в первых формулах надо брать абсолютную разность, а во вто-
вторых— абсолютную сумму, и потому знаки вообще не нужно при-
принимать во внимание. При возвращении к обозначениям, употреб-
употреблявшимся в п. 189,4, из первых формул получается
Т = m [к', к\ к'",.. ., к{п)] — ^ [*', к\ к'",. . ., к{п-\
а из вторых
Т = ш [к", к'",.... к^»] + "? [к", к'", ..., ft<">],
a L ' J
где для значения Т может быть написано также m к", к'", . .., &(п>— .
Пример. Для D = 61, m = 2 можно использовать форму B, 7,—6),
для которой находим, что п = 6, а к'', к", к"\ к"", к'"", к"""
соответственно равны 2, 2, 7, 2, 2, 7. Отсюда следует
Г = 2[2, 2, 7, 2, 2, 7] —7 [2, 2, 7, 2, 2] = 2888 — 1365 = 1523
по первой формуле; то же значение получается и по второй фор-
формуле:
Г = 2 [2, 7, 2, 2] +у [2, 7, 2, 2, 7]
[/ = [2, 2, 7, 2, 2] = i-12. 7> 2> 2> 7] = 195.
з
и
Формы с полоэюительным неквадратным определителем 235
Впрочем, имеются еще различные приемы, при помощи которых
вычисления могут быть сокращены; однако требования краткости
не позволяют нам говорить о них подробнее.
200
Чтобы из наименьших значений t, и получить все, представим
уравнение Т2 — DU2 = т2 так:
' т г ) \т т
откуда следует, что если е обозначает любое число, то
[1]
L J
\m m j
Теперь ради краткости мы обозначим вообще значения величин
^ + yD]=(
2 Vd \m m J 2 Yd \m
через №\ и^е\ т. е. значения их для е = 0 — через t°, u° (которые
будут равны т, 0), для е = 1—через V, и' (которые будут равны
Г, U), для е = 2 — через t", и", для е = 3 — через ?'", и" и т. д.,
и докажем, что если брать для е все неотрицательные целые чис-
числа, т. е. 0 и все положительные числа от 1 до оо, то эти выра-
выражения дадут все положительные значения t, и, а именно: (I) что
все значения этих выражений действительно являются значениями
?, и\ (II) что все эти значения являются целыми числами; (III) что
не существует положительных значений t, и, которые не содержа-
содержали ь бы в этих формулах.
I. Если вместо №\ и^ подставить их значения, то при помощи
равенства [1] без труда устанавливается, что
(t{e) + и(е) YD) (t{e) - и(е) YD) = m2, т. е. t(eJ - Du(eJ = m2.
II. Таким же образом легко устанавливается, что
I j(e-i) = ?1^(е) и(е+1) 1
1 т ' '
236 Раздел V (п. 200)
Отсюда вытекает, что оба ряда t°7 t', t", ?'",...; м°, и\ и", и'",...
являются рекуррентными, именно,
f^tLt' — t0, Г = —Г —*',...; в" = —в',...
mm m
Так как теперь, по предположению существует некоторая форма
(М, N, Р) с определителем D, у которой М, 2N, Р делятся на т,
мы имеем
и потому 4J12, очевидно, делится на т2. Поэтому 2Т / т является
целым и притом положительным числом. Так как, однако, t° = га,
t' = Т, 1г° = 0, и' = U, и потому эти числа целые, то будут целыми
также и все числа t", t'", . . ., и", и'", . .. Далее, очевидно, так как
Т2 > яг2, что все ?°, t', t", t"\. . . положительны и непрерывно возра-
возрастают до бесконечности, и точно так же — все гг°, и', и", и'",....
III. Если мы предположим, что существуют еще и другие поло-
положительные значения t, и, которые не содержатся в рядах t°, t',
t", ..., гг°, и', и", . .., например, 2, U, то так как ряд гг°, и', . . .
возрастает от 0 до бесконечности, очевидно, что U обязательно бу-
будет лежать между двумя соседними членами и^ и и^п+т\ так что
U > гг(п) и U < и(п+1\ Чтобы доказать невозможность этого предпо-
предположения, сделаем следующие замечания.
1. Уравнение t2 — Du2 — т2 также будет удовлетворяться, если
положить
t = 1 (?*<*> _ DUwW), и =
Это легко может быть установлено простой подстановкой; а то,
что эти значения, которые мы для краткости обозначим через т,
и, всегда являются целыми числами, мы докажем следующим об-
образом. Если (М, iV, P) — форма с определителем D, и т — наиболь-
наибольший общий делитель чисел М, 2N, Р, то на т будут делиться
как Z+N\X, так и № + Nu^ и потому также U(^n) + Л^гг(п)) —
— гг<п) (S? + Nti) или U^(n)—2гг(п). Поэтому о будет целым числом,
а тем самым также и т, ибо т2 == Du2 + ^2.
Формы с полоэюительным неквадратным определителем 237
2. Очевидно, что о не может быть равно нулю, так как из
этого следовало бы, что
пли
U2 (DuW + т2) = u^(DW2 + т2),
или U2 = и(п)\ вопреки предположению, что U > и(п\ Так как, за
исключением значения 0, наименьшее значение и равно U, то и,
очевидно, не меньше чем U.
3. Из значений t^n\ ^(n+1\ u^n\ u(n+lS> легко может быть уста-
установлено, что
mil =
Поэтому Ш(п)—Zu^ заведомо не меньше, чем w<n+1)^n) — ^n
4. Теперь из равенства X2 — DU2 = т2 получаем
и аналогично
откуда легко следует, что- > , . А отсюда и из следствия 3 получаем
tn + И(Л) ^J > (w(«+Dj(n) — i(^+DW(n)) Un) _[_ и(п)
или, если раскрыть скобки и вместо X2, t^*, ^(n+D2 подставить их
значения DW + m2, i)w(nK + m2, Du(n+^2 + т2,
j. (Ц2 _ K(n)
_L_
откуда, так как каждая величина, очевидно, положительна, по-
посредством перестановки следует, что
7,(ПJ G1J
238 Раздел V (п. 201)
Это, однако, невозможно, так как первый член первой величины
меньше первого члена второй, и точно так же второй член первой
величины меньше второго члена второй величины. Поэтому наше
предположение не может выполняться, и ряды t°, tr, t", . . ., н°,
и\ гг", . . . представляют все положительные значения t, и.
Пример. Для D = 61, т = 2 в качестве наименьших положитель-
положительных значений t, и мы нашли следующие: 1523, 195. Поэтому все
положительные значения будут представляться следующими фор-
формулами:
t =
При этом мы находим
г° = 2, t'= 1523, Г - 1523 t' — t° = 2319527,
Г - 1523 f — t'l = 3532618098, . . .;
wo = о, и' = 195, и" = 1523 wr — и0 = 296985,
ww - 1523 в" —и' - 452307960,....
201
Относительно рассмотренной в предыдущем пункте проблемы
мы добавим еще следующие замечания.
1. После того как мы показали, как во всех случаях можно ре-
решить уравнение t2 — Du2-=m2, где т — наибольший общий дели-
делитель трех чисел М, 2/V, Р с тем свойством, что N2 — МР = D,
стоит потрудиться над тем, чтобы определить все числа, которые
могут быть таким делителем, т. е. все значения т для заданного
значения D. Положим D = n2D\ где Dr полностью свободно от
квадратных сомножителей, что достигается, если за п2 взять наи-
наибольший квадрат, входящий в D\ если же D само уже не делит-
делится ни на какой квадратный сомножитель, то нужно положить
/г = 1. Тогда мы утверждаем следующее.
Во-первых. Если D' имеет вид 4А + 1, то каждый делитель чис-
числа 2п является значением т, и обратно. Действительно, если g —
Формы с положительным неквадратным определителем 239
делитель числа 2п, то мы получаем форму (g5 п, п2 A—Dr)/g),
определитель которой равен D и у которой наибольший общий де-
делитель чисел g, 2п, n2(D'— l)/g, очевидно, равен g ^так как
7ia(D' —1) 4гс2 D' — 1 \ „
—-—g = —g- • —г— , очевидно, является целым числом) . Если
О О /
же, наоборот, предположить, что g есть значение т, именно,
наибольший общий делитель чисел М, 2iV, Р и N2— МР = D, то
очевидно, что 4Z) или An2D' будет делиться на g2. Отсюда, однако,
следует, что 2п обязательно делится на g. Действительно, если бы
g не входило в 2га. то g и 2га имели бы наибольший общий дели-
делитель, который меньше чем g, и если он равен 8 и 2п = Ьпг, g =
= bg\ то п'2D' делилось бы на g'2, га' было бы взаимно просто
с ^' и потому также га'2 — с g'2, а значит, /)' также делилось бы
на gr 2, вопреки предположению, по которому Z)r свободно от вся-
всякого квадратного сомножителя.
Во-вторых. Если D' имеет вид 4& -}- 2 или 4А; + 3, то каждый
делитель числа п является значением т, и обратно, каждое зна-
значение т входит в п. Действительно, если g есть делитель п, то мы
получаем форму (g, 0, —n2D' / g)t определитель которой равен D
и у которой наибольший общий делитель чисел g, 0, n2D'/g, оче-
очевидно, равен g. Если же мы предположим, что g есть значение ту
именно, наибольший общий делитель чисел М, 2N, Р и N2— МР = D,
то так же, как и выше, g входит в 2п, или 2п / g является целым
числом. Если бы это отношение было нечетным, то имело бы место
^-еее 1 (mod 4), и потому An2D'/ g2 было бы или = 2, или = 3 (mod 4).
о 4/z2D/ 4D 4А^2 4МР 4/V2 , , /ч , ,,„ ; 9
Но —2-=-^=— _ = __ (mod4), и потому 4A2/g2 или
6 6 6 6 6
^2 или =3 (mod4). Это, однако, невозможно, так как каждый
квадрат должен быть сравним по модулю 4 или с нулем, или с
единицей. Следовательно, отношение 2п /g обязательно четно и тем
самым число п / g целое, т. е. g есть делитель п.
Таким образом, отсюда вытекает, что 1 всегда является значе-
значением т, или что уравнение t2 — Du2 = 1 для каждого положитель-
положительного неквадратного значения, D разрешимо; далее, что 2 только
тогда является значением т, когда D имеет или вид 4А, или вид
4А+ 1.
240 Раздел V (п. 201)
2. Если т > 2, но при этом является допустимым числом, то
решение уравнения t2 — Du2 = т2 может быть сведено к решению
подобного уравнения, в котором т равно 1 или 2. Если, как и
перед этим, положить D = n2D\ то если т входит в п, т2 будет
входить в D. Если предположить тогда, что наименьшие значения
р, q в уравнении р1 -q2 = I суть р = Р, q = Q, то наименьшие
значения t, ив уравнении t2 — Du2 = m2 будут t = mP9 u = Q.
Если же m не входит в п, то оно обязательно будет входить в 2п
и, очевидно, будет четным; a AD/ m2 есть целое число. И если
тогда в качестве наименьших значений р, q в уравнении р2 —
^q2 = A найдены значения р = P. q = Q, то наименьшими зна-
значениями t, и в уравнении t2 — Du2 = т2 будут t=-~-P, u — Q.
В обоих случаях, однако, не только из наименьших значений р, b
могут быть выведены наименьшие значения t, и. но, очевидно, что
тем же методом из всех значений первых могут быть получены все
значения вторых.
3. Если, как в предыдущем пункте, t°, u°, f, и' : t", и"\. . .
обозначают все положительные значения t, и в уравнении t2 —
— Du2 — m2, и оказывается, что некоторые значения из этих рядов
сравнимы но некоторому данному модулю г с первыми значениями
этих же рядов, например, t^p)~t0 (или = иг), и№ = и° (или = 0)
(mod г) и одновременно следующие значения сравнимы со вторыми
значениями, именно, ?(р+1)==?', гг(р+1) == и' (mod г), то также
Это легко следует из того, что каждый из двух рядов t°, t\ t", . . .;
ляется рекуррентным; действительно
t" = — t' — t° t(p+2) = — i(p+1) — t{9)
m ' m '
м°, u',un,... является рекуррентным; действительно, так как
то также
t" =
и точно так же для остальных значений. Отсюда следует, что
вообще
Формы с полоэюительным неквадратным определителем 241
где h обозначает любое число, и еще более общо, что если
(x = v(modp), то также *(fx) = *(v), uw ==u(v) (mod г).
4. Упомянутым в предыдущем замечании условиям всегда можно
удовлетворить, именно, для любого заданного модуля г всегда мо-
может быть найден индекс р, для которого
Чтобы это доказать, заметим следующее.
Во-первых, третьему условию можно удовлетворить всегда. Дей-
Действительно, из данных в замечании 1 критериев без труда уста-
устанавливается, что уравнение р2 — r2Dq2 = т2 также разрешимо, и
если предположить, что наименьшими значениями р, q (кроме т, 0)
являются Ру Q, то среди значений t, и, очевидно, найдутся также
и t = Р, и = rQ. Поэтому Р, rQ будут содержаться в рядах
t°, t', . . .; и0, и', . . ., и если Р = г(Л), rQ = и(Х), то будет и(Х) == 0 == и0
(mod г). Кроме того, легко видеть, что между и0 и и<Л) не будет ни
одного члена, который сравним с и0 по модулю г.
Во-вторых, ясно, что если, кроме того, здесь выполнены и три
остальные условия, именно, если также и(Л+1) = и', ?(Х) = г°, ?(Х+1) = г',
то нужно только положить р = X. Если же то или иное из этих
условий не имеет места, то я утверждаю, что наверняка можно
положить р = 2Х. Действительно, из равенства [1] и общих формул
для г , w } предыдущего пункта следует, что
,BЛ) 1 /.(ХJ , niAX^2\ * /™2 i
i = — (I -+- ии ) = — [т -+-
и потому
" — t °
причем эта величина является целым числом, так как по предпо-
предположению г входит в и^ и точно также т2 — в 4J9, а потому и
подавно т — в 2D. Далее, иBХ) = — t^u^\ и так как
242 Раздел V (пп. 202-203)
и потому делится на т2, то и 2t{X) делится на т и тем самых иBХ)
делится на г или
В-третьих, находим
и так как по аналогичной причине число 2Du^/mr целое, то
Наконец, находим
и = и н
1
и так как 2?(Х+1) делится на т, и w(X) делится на г, то
Впрочем, польза двух последних замечаний обнаружится в даль*
нейшем.
202
Специальный случай проблемы, именно, решение уравнения
t2 —Da2 = 1, рассматривался уже математиками предшествующего
столетия. Остроумный Ферма задал эту проблему английским
аналитикам, и В а л л и с называет Брункера, как нашедшего
решение, которое он приводит в своей «Algebra Kapitel», p. 98 и
«Opera»у Т. //, р. 418и ел.; О з а н а м называет таковым Ферма,
и, наконец, Эйлер (который рассматривал этот вопрос в «Сотт.
Petn, VI, р 175; «Сотт. nov», XI, р. 28; «Algebra» *, Pars II, p. 226\
«Opusc. Analyt», I, p. 310) — англичанина П е л л я, вследствие
чего эта проблема некоторыми авторами называется проблемой
* В этом сочинении для изложенного в п. 27 алгоритма применяются такие
же обозначения, о чем мы в своем месте забыли упомянуть.
Формы с полоснсителъным неквадратным определителем 243
П е л л я. Все эти решения по существу совпадают с тем, которое
получится, если в п. 198 использовать такую приведенную формуу
у которой а = 1. Однако то, что предписываемые операции рано или
поздно обязательно придут к концу, т. е. что проблема действительно
всегда разрешима, никто не доказал строго* до Лагранжа
«Melanges de la Soc. de Turin», T. IV, p. 19, и более коротко в «Hibt.
de VAc. de Berlin», 1767, p. 237. Это исследование находится также
в уже указанных дополнениях к «Алгебре» Эйлера. Впрочем, наш
метод (который основывается на совершенно других принципах и не
ограничивается случаем т = 1) дает намного больше путей для
получения решения, так как в п. 198 мы ведь можем исходить и из
любой другой приведенной формы (а, Ъ, —а').
203
Задача. Пусть формы Ф, 9 эквивалентны] требуется предста-
представить все преобразования одной из них в другую.
Решение. Если эти формы эквивалентны только одним способом
(т. е. или только собственно или только несобственно), то найдем в соот-
соответствии с п. 196 одно преобразование формы 9 в Ф, которое пусть
будет а, р, y> ^» очевидно, что не может быть других преобразо-
преобразований, кроме однотипных с ним. Если же ср, Ф, эквивалентны как
собственно, так и несобственно, то найдем два неоднотипных пре-
преобразования, т.е. одно собственное и одно несобственное, например,
ос, р, т> 8 и а', р', *у'» &'; любое другое преобразование будет
однотипным или с первым, или со вторым. Если поэтому форма 9
равна (а, Ь, с), ее определитель равен D, наибольший общий дели-
делитель чисел а, 2Ь, с (как и все время до сих пор) равен т, и t,
и — всевозможные числа, удовлетворяющие уравнению t2 — Du2 = m2,
* То, что в указанном сочинении (стр. 427, 428) говорит об этом В ал-
лис, не убедительно. Ошибка состоит в том, что он предполагает, что если
задана величина р, то можно найти целые числа z, а с тем свойством, что z/a
меньше чем р, однако разность меньше, чем некоторое определенное число. Это
верно в том случае, если это число постоянно, но здесь как раз оно зависит от
а и z, и потому переменно.
244 Раздел V (пп. 204-205)
то в первом случае все преобразования формы <р в Ф будут содер-
содержаться в формулах (I), а во втором случае — в формулах (I) и (II):
(I)
— [ск/t — (ct'b + if'c) и], — [P'i — (P'fc + Src) и],
(И)
i- [T't + (a'o + т'Ь) в], -1 [8'i + ф'а + 8'6) ц].
Пример. Мы хотим иметь все преобразования формы A29, 92, 65)
в форму D2, 59, 81). То, что они эквивалентны только несобственно,
мы нашли в п. 195, а в следующем пункте мы получили несоб-
несобственное преобразование первой формы во вторую: —47, —56, 73, 87.
Поэтому все преобразования формы A29, 92, 65) в форму
48, 59, 81) представляются формулами
— D71 + 421 а), — E61 + 503 и), 731 + 653 и, 871 + 780 и,
где t, и обозначают всевозможные числа, удовлетворяющие урав-
уравнению t2 — 79 м2 = 1. Эти числа представляются формулами
± и = ^щ [(80 + 9 J/79N + (80 - 9 j/79)e],
где для е нужно брать все целые неотрицательные числа.
204
Очевидно, что формулы, представляющие все преобразования,
будут тем проще, чем проще исходное преобразование, из которого
эти формулы выведены. То, из какого преобразования исходить, за-
зависит от нашего желания; поэтому общие формулы часто могут
быть сделаны проще, если из первоначально найденных формул мы
сначала получим более простое преобразование, придав t, и опреде-
определенные значения, а затем составим для этого преобразования как
исходного новые формулы. Так, например, если в найденных в пре-
Формы с полоэюительным неквадратным определителем 245
дыдущем пункте формулах положить * = 80, и = —9, то получится
более простое преобразование, чем то, из которого мы исходили,
именно, получится 29, 47, —37, —60, откуда получаются общие
формулы 29*—263и, 47* — 424и, —37* + 337и, —60* + 543гг. Та-
Таким образом, если по предыдущим правилам установлены общие
формулы, то можно посмотреть, нельзя ли,придавая *, и определен-
определенные значения_^*\+и';+^+гг'';..., получить болеепростоепреобразо-
вание, чем то, из которого формулы были выведены, и если можно,
то из этого преобразования могут быть выведены более простые
формулы.
Впрочем, при суждении о простоте остается некоторый произвол,
который мы при желании могли бы ввести в твердые рамки и вместе
с тем указать в ряДе *', и'\ *", и"\ ... границу, за пределами которой
преобразования постоянно будут менее простыми, так что дальше
заходить уже не нужно, а следует произвести исследование только
до этой границы. Так как, однако, при пользовании предписанными
правилами простейшее преобразование в большинстве случаев
получается или тотчас же, или при применении для *, и значений
zh?\ db^', то мы ради краткости это исследование опустим.
205
Задача. Найти все представления заданного числи М заданной
формой axi+2bxy -j- су2 с положительным неквадратныМ определи-
определителем D.
Решейие. Заметим сначала, что получение представлений с не-
невзаимно простыми значениями х, у здесь, как и выше (п. 181) для
форм с отрицательным определителем, может быть сведено ^ тому
случаю, :когда ищутся представления со взаимно простыми значе-
значениями неизвестных, и было бы излишне это здесь повторять. ДлЙ
возможности же представления посредством взаимно Простых зна-
значений х, у необходимо, чтобы D было квадратичным вычетом по мо-
модулю М, и если всевозможные значения выражения у D (mod M)
суть TV, —N, Nr\ —N', N", —N"> ... (относительно которых мы мо-
можем предполагать, что ни одно из них не больше чем А//2), то каждое
представление числа М заданной формой будет принадлежать одному
246 Раздел V (п. 205)
из этих значений. Поэтому прежде всего должны быть определены
эти значения, а затем найдены принадлежащие отдельным значениям
представления. Представления, которые принадлежат значению 7V,
могут быть только тогда, когда формы (а, Ь, с) и (М, 7V, —~—) соб-
собственно эквивалентны; если это имеет место, то найдем какое-нибудь
собственное преобразование первой формы во вторую, например,
а, Р, у, 8. Тогда в качестве принадлежащего значению N представле-
представления числа М формой (а, Ь, с) получаем следующее: х = а, у = у, и
все принадлежащие этому значению представления могут быть пред-
представлены формулой
я = ^И-И + Тс)и], у= 1[т*+(аа + Тй)и],
где т обозначает наибольший общий делитель чисел а, 2Ь, с, a ?, и —
произвольные числа, удовлетворяющие уравнению t2 — Da2 = m2.
Впрочем, эта общая формула, очевидно, может быть сделана тем
проще, чем проще преобразование а, C, у» °> из которого она выводи-
выводилась; поэтому будет нелишним предварительно найти в соответствии
с предыдущим пунктом простейшее преобразование формы (а,Ь,с) в
(M,N,(N2—D)/M), и выводить формулу из него.
Точно таким же образом могут быть указаны представления,
принадлежащие остальным значениям —N, N',—TV', ... в виде
общих формул (если такие представления вообще существуют).
Пример. Найдем все представления числа 585 формой 42#2 +
-f- 62xy + 212/2. Что касается представлений с не взаимно простыми
значениями х, у, то тотчас же ясно, что таковых не может быть, кроме
таких, у которых наибольший общий делитель х, у равен 3, так как
585 делится только на квадрат, равный 9. Если поэтому найдены все
представления числа ^ = 65 формой 42я'2 + €>2х'у' + 21у/2,
у
у которых х' взаимно просто с у', то все представления числа 585
формой А2х2 + 62ху + 21у2} у которых х не взаимно просто с у,бу-
у,будут получены, если положить х = Зх\ у = Зу'. Значения выражения
r79 (mod 65) суть +12, +27. В качестве представления числа 65,
которое принадлежит значению —12, находим х'= 2, у'= —1;
поэтому все принадлежащие этому значению представления числа 65
Формы с положительным неквадратным определителем 247
будут охватываться формулой х' = 2*— 41а, у'=—*+53а, и тем
оамым все получающиеся отсюда представления числа 585— фор-
формулой х = 6* — 123а, у = —3* + 159гг. Подобным же образом на-
находим в качестве формулы, которая выражает все принадлежащие
значению +12 представления числа 65, следующую: х' = 22* —
— 199а; у'= —23* — 211а, и в качестве формулы, которая охва-
охватывает все получающиеся отсюда представления числа 585, следую-
следующую: х = Ш — 597а, у = —69* + 633а. Значениям же +27 и —27
не принадлежит ни одно представление числа 65. Чтобы найти пред-
представления числа 585 со взаимно простыми значениями х, у, нужно
сначала получить значения выражения у 79 (mod 585), которые суть
±77, ±103, ±157, +248. Находим, что значениям ±77, ±103,
±248 не принадлежит ни одно представление; значению же —157
принадлежит представление х = 3, у = 1, из которого в качестве
общей формулы, которая дает все принадлежащие этому значению
представления, выводим следующую: х = 3* — 114а, у = * + 157а.
Подобным же образом находим в качестве принадлежащего значению
+ 157 представления х = 83, у = —87, и в качестве формулы, в ко-
которой содержатся все подобные представления, следующую: х =
= 83* — 746а, у = —Sit + 789а. Мы получаем, таким образом,
четыре общие формулы, в которых содержатся все представления
числа 585 формой 42#2 + §2ху + 21?/2, именно
х = 6* — 123а, у = — 3* + 159а;
х = 66* — 597а, у = — 69* + 633а;
x = 3t — 114а, у = t+ 157ц;
х = 83* — 746а, у = — 87* + 789а,
причем *, а обозначают произвольные целые числа, которые удовле-
удовлетворяют уравнению t2 — 79а2 = 1.
На специальных применениях этих исследований о формах с по-
положительным неквадратным определителем мы, ради краткости, не
останавливаемся, так как каждое из них без труда может быть полу-
получено так же, как и в пп. 176,182,и немедленно переходим к единствен*
но еще остающимся формам с положительным квадратным определи*
телем.
248 Раздел V (пп. 206-207)
О формах с квадратным определителем
206
Задача. Пусть задана форма (а, Ь, с) с квадратным определите-
определителем h2, где h обозначает положительное значение корня] требуется
найти собственно эквивалентную ей форму (А, В, С), у которой А
лежит между границами 0 и 2h — 1 (включительно), B — h и С —0.
Решение I. Так как h2 = Ъ2 — ас, то (h — b): a = с: [— (k + Ь)],
пусть этому отношению равно отношение р : 5 где р взаимно проста
с 8; определим а, *у так, что а8— р-у = 1, что возможно. Пусть
подстановкой а, р, ^, 8 форма (a, b, с) переводится в форму (а', Ь\ с'),
которая тем самым собственно эквивалентна первой. При этом мы
имеем
Ъ' =аа$ + Ь (<х8 + Рт) + И^ =
b (a8 + pT) — (h + Ъ) р? =
с' = ар2 + 2бр8 + сЬ2 =
= (А— 6) р& + 2бр8 — (А + Ъ) рб - 0.
Если поэтому, кроме того, а' уже лежит между границами 0
и 2/г — 1, то форма (а!, Ь', с') будет удовлетворять всем условиям.
II. Если же а' лежит вне границ 0 и 2А—1, то пусть А — наи-
наименьший положительный вычет числа а' по модулю 2h, который, оче-
очевидно, будет лежать между этими границами; положим А — а' = 2hk.
Тогда форма (а', Ъ', с'), т. е. (а', А, 0) будет при собственной под-
подстановке 1, 0, Л, 1 переходить в форму (A, h, 0), которая собственно
эквивалентна формам (а', Ъ\ с') и (а, 6, с) и удовлетворяет всем
условиям. Заметим, что форма (а, Ь, с) переходит в форму (^4, /г, 0)
при подстановке a + Р&, Р, Т + 8&, 8.
Пример. Пусть дана форма B7, 15, 8), определитель которой
равен 9. Здесь h = 3; далее, отношениям — 12 : 27 = 8 : (— 18)
в наименьших числах равно отношение 4: (— 9). Если, таким обра-
образом, положить р = 4, Ь = — 9, а = — 1, у = 2, то форма (a\b\cf)
будет следующая: (—1, 3, 0); она переходит при подстановке 1,
0, 1, 1 в форму E, 3, 0). Последняя является, таким образом,
Формы с квадратным определителем 249
искомой формой, и заданная форма переходит в нее при собствен-
собственной подстановке 3. 4, —7, —9.
Такие формы (А, В, С), у которых С = О, В = h и А лежит между
границами 0 и 2h—1, мы будем называть приведенными формами)
их, таким образом, следует отличать от приведенных форм с отри-
отрицательным определителем и положительным неквадратным опреде-
определителем.
207
Теорема. Две не совпадающие приведенные формы (а, /г, 0) и
(а', h, 0) не могут быть собственно эквивалентны.
Доказательство. Действительно, предположим, что они собственно
эквивалентны и первая переходит во вторую при собственной под-
подстановке а, р, т> 8; тогда имеем четыре равенства
[1] а<х2 + 2/mgy = а',
[2] аар + h (а8 + р?) = Л>
[3] up2 + 2&р8 = 0,
[4] а8-рт = 1.
Если умножить второе равенство на р, третье — на аи вычесть, то
получится — h (а8 — р-у) р = р/г, или, в силу [4]. — р/г = р/г, так что
обязательно р = 0. Поэтому из [4] следует, что aS = 1 и а = + 1.
Тем самым из [1] вытекает, что a+ 2% = а'. Но это равенство мо-
может выполняться только в том случае, если y = 0 (так как, по
предположению, а и а' оба лежат между границами 0 и 2й), т. е.
если а —а', или если формы (а, /г, 0) и (а\ h, 0) совпадают, что
противоречит предположению.
Поэтому следующие задачи, которые для неквадратного опреде-
определителя представляют едва ли не наибольшие трудности, могут быть
решены без труда.
I. Если даны две формы F, F' с одинаковым квадратным опре-
определителем, то нужно узнать, являются ли они собственно эквива-
эквивалентными. Найдем две приведенные формы, собственно эквивалент-
эквивалентные соответственно формам F, F'\ если они совпадают, то заданные
формы собственно эквивалентны; в противном же случае—нет.
250 Раздел V (пп. 208-209)
И. При тех же предположениях нужно определить, являются ли
формы несобственно эквивалентными. Пусть формой, противополож-
противоположной одной из заданных форм, например F, является форма G; если
она собственно эквивалентна форме F\ то F и F' будут несоб-
несобственно эквивалентными, и обратно.
208
Задача. Пусть даны две собственно эквивалентные формы F, F'
с определителем /г2; найти собственное преобразование одной из них
в другую.
Решение. Пусть форме F собственно эквивалентна приведенная
форма Ф, которая в силу предположения будет тем самым собствен-
собственно эквивалентна также и форме F'. Найдем, согласно п. 206, соб-
собственное преобразование формы F в Ф, которое обозначим через а,
Р, у, 8, и точно так же — собственное преобразование формы F'
в Ф, которое обозначим через а', р', у', ^'. Тогда Ф будет пере-
переходить в F' при собственной подстановке 5', —Р', —у', а'» и
потому F будет переходить в F' при собственной подстановке
а8' —рт', ра'_ар'5 Т8'_$т', 8ос'_ тр\
Стоит потратить усилия на то, чтобы получить для этого преоб-
преобразования формы F в F' другую формулу, для которой не нужно
предварительно знать приведенной формы Ф. Предположим, что
F = (а, й, с), F' = (а', Ь\ с'), Ф = (A, h, 0).
Так как отношению (h — Ъ): а или с:[—(h-\-b)] равно отношение
п «, h — Ъ а
в наименьших числах р : о, то легко видеть, что —-—=-г- есть це-
лое число, которое мы положим равным /; точно так же -г = ^—-
является целым числом, которое мы положим равным g. Но мы
имеем А = аи2 + 2йа^ + с^2 и потому $А = аа2р + 26офт "Ь С?Т2> или
(если заменить ар на b(h — b) и с — на (Зу)
Bрт — а8) а
Формы с квадратным определителем 251
или (вследствие того, что Ь = — h — bg)
$А = 2а (а8 — рт) h + (а8 — ^Jg = 2а/г + g.
Точно так же
ЬА = aa2S + 26a^S -f 6T2S =
= a2S2T + b BocS — pT) T — рт2/г =
= (a8 - pTJ/ + 2T (a8 - pT) h = 2Т/г + /.
Поэтому
Если совершенно таким же образом положить
ТО
Если эти значения а, ^> а', ^' подставить в выведенную выше
формулу для преобразования формы F в F\ то она перейдет в сле-
следующую:
W — b'g ?>'g-?>g' bf — b'f Ff — bg'
2k1 2h 2h ' 2h
в которой А уже не содержится.
Если даны две несобственно эквивалентные формы F, F' и
ищется собственное преобразование одной в другую, то пусть G
противоположна форме F и собственное преобразование формы G
в F' следующее: а, C, -у, 8. Тогда a, J3, —-у, —8, очевидно, будет
несобственным преобразованием формы F в F'.
Наконец, ясно, что если заданные формы эквивалентны как соб-
собственно, так и несобственно, то тем же способом могут быть найдены
два преобразования, одно собственное и одно несобственное.
209
Итак, остается только показать, как из одного преобразования
могут быть выведены все остальные, однотипные с ним. Но это за-
зависит от решения неопределенного уравнения t2 — к2и2 = т2, где т
252 Раздел V (пп. 210-211)
обозначает наибольший общий дейитель чисел а, 2Ь с, и (а, Ъ, с) —
одну из двух эквивалентных форм. А это уравнение всегда разре-
разрешимо только двумя способами, именно, или посредством t = m, и = О,
или посредством t = —т, и = 0. Действительно, если мы предпо-
предположим, что существует еще и другое решение t = Т, и = 17, для
которого и не равно нулю, то будет —г = —g- + 4, и так как яг2
заведомо входит в 4/г2, как 4Г2/тп2, так и Ah2U2/m2 будут квад-
квадратами целых чисел. Но легко видеть, что число 4 только тогда
может быть разностью двух целых квадратов, когда меньший квад-
квадрат равен нулю, т. е. U = 0, что противоречит предположению.
Поэтому если форма F переходит в форму F' при подстановке аг
Р, «у, 8, то, кроме преобразования —а, — р, —т> —8, других пре-
преобразований, однотипных с ней, не будет. Поэтому если формы
эквивалентны только собственно или только несобственно, то имеете**
лишь два преобразования; если же они эквивалентны как собственног
так и несобственно, то их имеется четыре, именно, два собствен-
собственных и два несобственных.
210
Теорема. Если две приведенные формы (а, /г, 0), (а', /г, 0) несоб-
несобственно эквивалентны, то аа'^т2 (mod 2 яг/г), где т обозначает
наибольший общий делитель чисел а, 2/г или а', 2/г, и обратно,
если а, 2/г и а', 2/г имеет один и тот же наибольший общий дели-
делитель т, и аа' = т2 (mod 2/гг/г), то формы (а, /г, 0), (а', /г, 0) несоб-
несобственно эквивалентны.
Доказательство. I Пусть форма (а, /г, 0) переводится в форму
(а', /г, 0) не обственной подстановкой а, р, ^> 8, так что имеют
место четыре равенства:
[1] аа2 + 2/гат = а',
[2] аар + А(ос8 + рТ) = А,
[3] ар2
[4] а8-
Формы с квадратным определителем 253
Из них следует, если мы умножим [4] на h и вычтем из [2]
{что кратко мы выразим в виде [2] — h [4]), что
[5] (аа + 2%) р = 2/г.
Аналогично из ^ [2] — т2 [3] — (я + ятР + %&) KL после того как
мы отбросим взаимно уничтожающиеся члены, следует, что
[6] — аа8 = а -\- 2А^8, или — (aa + 2/г-у) 8 = а;
наконец, из а [1] получаем aa (aa -f- 2%) = aa', или
(aa + 2%J — aa' = 2/г? (aa +
или
{7] (aa + 2%J = aa' [mod 2/г (aa + 2hf)].
Но теперь из [5] и [6] следует, что aa -f- 2h\ входит в 2/г и а, и
потому также и в т, которое является наибольшим общим дели-
делителем а и 2/г; но очевидно, что т также будет входить в aa + 2%,
поэтому обязательно aa + 2% равно или + т, или —т, а потому
из [7] тотчас же следует, что т2 = аа' (mod 2mh).
II. Если а, 2/г; а', 2/г имеют один и тот же наибольший общий
делитель ту и кроме того, aa'= m2 (mod 2mh), то числа a/m, 2h/my
a' I m, (aa! — m2)/2mh) будут целыми. Но легко убедиться, что
форма (а, /г, 0) переходит в форму (а', /г, 0) при подстановке —а' / т,
— 2h/m, (aa! — m2)/2mh, a / т, и что это преобразование несоб-
несобственное. Поэтому эти формы несобственно эквивалентны.
Следовательно, мы можем также сразу судить о том, эквивалент-
эквивалентна ли несобственно самой себе заданная приведенная форма. Именно,
если обозначить наибольший общий делитель чисел а, 2/г через т,
то должно быть а2=т2 (mod 2mh).
211
Мы получим все приведенные формы с данным определителем
Л%, если в неопределенной форме (Ау h, 0) представим вместо А все
числа от 0 до 2/г — 1 включительно; количество их тем самым равно
2/г. Очевидно, что все формы с определителем /г2 могут быть разбиты
па столько же классов, и они будут обладать теми же свойствами,
254 Раздел V (п. 212)
которые мы получили выше (пп. 175, 195) для классов форм с отрица-
отрицательным и с положительным неквадратным определителем. Так, на-
например, все формы с определителем 25 распадаются на десять клас-
классов, которые могут различаться по содержащимся в каждом из них
приведенным формам. Эти приведенные формы суть @, 5, 0), A, 5, 0),
B,5,0), E,5,0), (8, 5, 0), (9, 5, 0), которые одновременно несобствен-
несобственно эквивалентны самим себе; C, 5, 0), которая несобственно эквива-
эквивалентна форме G, 5, 0), и D, 5, 0), которая несобственно эквивалентна
форме F, 5, 0).
212
Задача. Найти все представления заданного числа М заданной
формой ах2 + 2Ьху + су2 с определителем А2.
Решение этой задачи могло бы быть получено из соображений
п. 168 точно тем же способом, который мы указали выше (пп. 180г
181, 205) для форм с отрицательным и положительным неквадрат-
неквадратным определителем; так как это не может вызвать затруднений,,
было бы излишне повторять здесь то же самое. Однако будет не
лишним вывести решение из других соображений, характерных
именно для этого случая.
Если, как и в пп. 206, 208, положить
(А — Ъ): а = с : [— (А + Ъ)] = р : 8,
h — Ъ а , с —h — Ъ
то легко установить, что заданная форма является произведением
Ьх— Ру и fx — gy. Отсюда вытекает, что каждое представление
числа М заданной формой дает разложение числа М на два мно-
множителя. Если поэтому d, d', d",... — всевозможные делители числа М
(куда причисляются также 1 и М, и каждый отдельный сомножи-
сомножитель учитывается два раза, именно, как положительным, так и
отрицательным), то все представления числа М будут, очевидно,
получены, если последовательно положить
М
Ьх — ру = d, fx — gy = -j- ">
Формы с квадратным определителем 255
М
Ъх — $у= d\ fx — gy = -jr ;
и т. д., найти отсюда значения х и у и выбросить те представле-
представления, в которых х или у получают дробные значения. Очевидно,
кстати, что из двух первых равенств следует, что
_ ftM — gd2 _ ЪМ — fd2
х~ (?>f-bg)d> У -(°>f
а то, что эти значения всегда определенны, вытекает из того, что
Р/ — ty = 2/г, и потому знаменатель заведомо не равен нулю. Между
прочим, из этого же принципа, именно, из того, что каждая форма
с квадратным определителем может быть разложена на два сомно-
сомножителя, могут быть решены и остальные проблемы; однако мы
предпочитали и здесь использовать метод, аналогичный тому, ко-
который мы указали выше для форм с неквадратным определителем.
Пример. Найдем все представления числа 12 формой Зх2-\- ^ху—Ту2.
Она распадается на сомножители х — у и Зх + 7у. Всевозможные
делители числа 12 суть + 1, 2, 3, 4, 6, 12. Если положить х — у = 1,
19 9
Зх + Ту = 12, то получается х = т^, у= г^; эти значения, так как
они дробны, должны быть выброшены. Точно так же получаются
непригодные значения и из делителей —1, +3, +4, +6, + 12.
Из делителя же + 2 получаются значения х = 2, у = 0, и из дели-
делителя — 2 — значения х = —2, у = 0. Других представлений, кроме
этих двух, не существует.
Этот метод неприменим, когда М = 0. Действительно, в этом
случае все значения х, у должны удовлетворять или уравнению
Ьх — р2/ = 0. или уравнению fx — gy = O. Но все решения первого
уравнения содержатся в формуле х = fte, у = 8z- где z обозначает
произвольное целое число (поскольку, как предполагается, C, 8 взаим-
взаимно просты) и точно так же, если наибольший общий делитель чи-
чисел /, g положить равным т, то все решения второго уравнения
будут представляться формулой х = —, у = —. Поэтому в этом
случае обе эти общие формулы охватывают все представления числа Л/.
Теперь все, что относится к вопросу об эквивалентности, к
отысканию всех преобразований форм и к получению всех представ-
представлений заданного числа заданной формой, мы изложили настолько
256 Раздел V (п. 213)
полно, что больше желать уже нечего. Поэтому остается только
еще показать, как узнать, если заданы две формы, которые не могут
быть эквивалентными вследствие того, что не равны их определи-
определители, содержится ли одна из них в другой, и если это имеет место,
то как найти все преобразования первой во вторую.
Формы, которые содержатся в других
и притом им не эквивалентны
213
Выше, в пп. 157, 158, мы, показали, что если форма / с опреде-
определителем D содержит форму F с определителем Е и переходит в нее
при подстановке ос, C, -у, 8, то Е = (ос8 — р-уJ D\ далее, что если
ос8— Py = -j— 1? то форма / не только содержит форму F, но и экви-
эквивалентна ей, и что вследствие этого если / только содержит фор-
форму F, но не эквивалентна ей, то отношение E/D является целым
числом, превосходящим единицу. Поэтому здесь нужно решить за-
задачу о том, как узнать, содержит ли заданная форма / с определи-
определителем D заданную форму F с [определителем De2, причем предпо-
предполагается, что е положительное целое число, большее чем 1. Мы
решим эту задачу таким образом, что покажем, как может быть
найдено конечное число форм, содержащихся в / и обладающих
тем свойством, что если форма F содержится в /, то она обяза-
обязательно должна быть эквивалентна одной из этих форм.
I. Предположим, что все (положительные) делители числа е
(включая 1 ие) суть т, т', т", . . ., и что е = тп = т'п' = т"п" , ...
Для краткости мы будем обозначать форму, в которую / переходит
при собственной подстановке т, 0, 0, п, через (т\ 0); форму, в ко-
которую / переходит при собственной подстановке т, 1,0, п, через (т\ 1)
и т. д., вообще, форму, в которую / переходит при собственной
подстановке т, к, 0, п, через (т\ к). Аналогично, пусть / при соб-
собственной подстановке т\ 0, 0, п1 переходит в (т'\ 0): при подста-
подстановке т'у 1, 0, п' — в (т'\ 1), и т. д., при подстановке т!\ 0, 0,
п", —в (т"\ 0) и т. д., и т. д. Все эти формы собственно содер-
содержатся в /, и определитель каждой из них равен De1. Совокупность
Неэквивалентные формы, содержащиеся одна в другой 257
всех форм (т; 0), (т\ 1), (т; 2),... , (т\ т — 1); (т'\ 0), (т'; 1),...
. . ., (т'; т' — 1); (т"; 0), ..., число которых равно т + т' + т" + . . .,
и которые, как легко видеть, все между собой различны, мы обо-
обозначим череа О.
Если, например, / есть форма B, 5, 7) и е = 5, то О будет
охватывать следующие шесть форм: A; 0), E; 0), E; 1), E; 2), E; 3),
E; 4),— которые в развернутом виде имеют вид B, 25,175), E0, 25, 7),
E0, 35, 19), E0, 45, 35), E0, 55, 55), E0, 65, 79).
П. Я утверждаю теперь, что если форма F с определителем De2
собственно содержится в /, то она обязательно собственно эквива-
эквивалентна какой-нибудь форме из О. Действительно, если / переходит
в F при собственной подстановке ос, р, -у, 8, то ос8— р-у = е. Пусть,
далее, наибольший общий (взятый положительным) делитель чисел -у, 8
(которые не могут быть оба равны 0) равен п и — = т, причем
это число, очевидно, целое. Предположим g, h такими, что ^g +
-\- Ыг = п, и, наконец, пусть к — наименьший положительньй вычет
числа xg -(- р/г по модулю т. Тогда форма (т\ к), которая, очевидно,
содержится среди форм О, будет собственно эквивалентна форме F,
причем первая переходит во вторую при собственной подстановке
7 | ag + gfe — к , k Ь qg+frh — k j_ _b__
Действительно, прежде всего ясно, что все эти четыре числа це-
целые; точно так же легко устанавливается, что подстановка соб-
собственная; наконец, очевидно, что форма, в которую переходит при
этой подстановке (т\ к), будет та же самая, в которую переходит
/ * при подстановке
т
или, так как тп = е = aS — Рт» и потому р-у + тп = °^> °^ — тп =
при подстановке
4 L (pT + р8А), т, 8,
* Которая при подстановке т, к, 0, п переходит в {т\ к) (ср. п. 159).
258 Раздел V (п. 2Ц)
или, наконец, в силу ^g + Ыг = п, при подстановке а, р, у, S, т. е.у
согласно предположению, в i*1. Поэтому формы (т; к) я F собст-
собственно эквивалентны.
Таким образом всегда можно узнать, содержит ли собственно
заданная форма / с определителем D форму F с определителем Z)e2.
Если же спрашивается, содержит ли / форму F несобственно, то
нужно только исследовать, содержится ли собственно в / форма
противоположная F (п. 159).
214
Задача. Пусть даны две формы, f с определителем D и F с опре-
определителем De2, первая из которых собственно содержит вторую',
требуется представить все собственные преобразования фор-
формы / в F.
Решение. Если ?2 обозначает ту же совокупность форм, что
в предыдущем пункте, то нужно выбрать из этой совокупности все
формы, которым F собственно эквивалентна; пусть это формы
Ф, Ф', Ф", . .. Каждая из этих форм дает излагаемым ниже спо-
способом собственные преобразования формы / в F, причем отдельные
формы дают различные преобразования, а все вместе — всевозмож-
всевозможные преобразования (т. е. не существует собственного преобразова-
преобразования формы / в F, которое не получалось бы из одной из форм
Ф, Ф', .. .). Так как метод для в ех форм Ф, Ф', . . . одинаков,
мы будем говорить только об одной из них.
Предположим, что Ф = (М; К) и е = MN, так что / переходит
в Ф при собственной подстановке М, К, О, N. Далее, произвольное
собственное преобразование формы Ф в F мы обозначим через
а, Ь, с, Ь. Тогда / будет, очевидно, переходить в Ф при собственной
подстановке Ма-\-Кс, МЬ-\-КЬ, Nc: Nb, и этим способом из каж-
каждого собственного преобразования формы Ф в F получается соб-
собственное преобразование формы / в F Таким же образом можно
поступать и с остальными формами Ф', Ф", . . . , отдельные собствен-
собственные преобразования которых в F дают собственные преобразования
формы / в F.
Чтобы сделать ясным, что это решение во всех отношениях явля-
является исчерпывающим, нужно показать следующее.
Неэквивалентные формы, содержащиеся одна в другой 259
L Что при этом получаются все возможные собственные преобра-
преобразования формы f в F. Пусть а, р, ^, Ь— какое-нибудь собственное
преобразование формы / в F, и, как и в предложении II предыду-
предыдущего пункта, п — наибольший общий делитель чисел т» 8; числа же
m, g, h, k пусть определены таким же образом, как и там. Тогда
(т; Щ будет находиться среди форм Ф, Ф', .. . , и
будет собственным преобразованием этой формы в Р; а из него мы
по указанному выше правилу получаем преобразование ос, р, *y» &•
Все это было доказано в предыдущем пункте.
II. Что все получающиеся таким образом преобразования раз-
различны, т. е. что ни одно не получается дважды. При этом мы
убеждаемся без труда, что несколько различных преобразований
одной и той же формы Ф, или Ф', и т. д. в F не может дать одно
и то же преобразование формы / в F\ а то, что и различные формы,
например, Ф и Ф', не дают одного и того же преобразования,
доказывается так. Предположим, что собственное преобразование
а> Р» Т> ^ формы / в F получается как из собственного преобразо-
преобразования а, 6, с, Ъ формы Ф в f, так и из собственного преобразова-
преобразования а', 6', с', Ь' формы Ф' в F. Далее, пусть Ф = (М; К), Ф'=(М'; К')\
е = MN = M'N''. Тогда имеют место равенства:
[1] а = Ма + Кс = М'й' + К'с\
[2] р = Mb + iO> - MV + «TV,
[3] т - iVc = N'c',
[4] 8 = /V?) = N'b',
[5] аЬ — Ьс = а/*/ — Ы = 1.
Из а [4] — Ь [3] при помощи равенства [5] получаем, что N = N'X
X(ab' — be'), поэтому N' входит в N; аналогично, из а'[4] — Ь'[3]
следует, что N (а'Ь — Ь'с) — N', и потому N входив в N'; следова-
следовательно, так как и N и N' предполагаются положительными, обя-
обязательно N — N' и М — М', и значит, в силу [3] и [4], с = с',
Ь = Ьг. Далее, из а [2] — Ь [1] следует, что
К = М* (<&' — Ьа') + К' (ab' - Ьс') - М (аЬ' - Ьа') + К'\
260 Раздел V (п. 215)
тем самым К = Kf (mod M), а это возможно только в том случае,
если К = К\ потому что как К, так и К' лежат между грани-
границами 0 и М — 1. Поэтому формы, вопреки предположению, не яв-
являются различными.
Ясно, что если D отрицательно или является положительным
квадратом, то этим методом действительно могут быть найдены все
собственные преобразования формы / в F\ если же число D положи-
положительно, но не является квадратом, то могут быть даны некоторые
общие формулы, в которых содержатся все собственные преобра-
преобразования (число которых бесконечно велико).
Наконец, если форма F содержится в форме / несобственно, то все
Несобственные преобразования первой во вторую легко могут быть
получены указанным методом. Именно, если а, р, у, 8 пробегает
все собственные преобразования формы /в форму, противоположную
форме F, то все возможные несобственные преобразования формы /
в F представляются в виде а, —р, у, —8.
Пример. Требуется найти все преобразования формы B, 5, 7)
в форму B75, 0, —1), которая содержится в первой как собственно,
так и несобственно. Совокупность форм & для этого случая мы указали
уже в предыдущем пункте; исследование дает, что как E; 1), так и
E; 4) собственно эквивалентны форме B75, 0, —1). В соответствии
с изложенной выше теорией находим, что всевозможные собственные
преобразования формы E; 1), т. е. формы E0,35,19), в форму
B75, 0, —1) содержатся в общей формуле
Ш — 275м, — t + 16u, —15* f 275м, * — 15м,
где *, и обозначают всевозможные целые числа, удовлетворяющие
уравнению *2 — 275м2 = 1. Поэтому все получающиеся отсюда соб-
собственные преобразования формы B, 5, 7) в форму B75, 0, —1) будут
содержаться в общей формуле
65* — 1100и, — 4* + 65и, —15* + 275н, * —15м.
Аналогичным образом всевозможные собственные преобразования
формы E;4), т. е. формы E0, 65, 79), в форму B75, 0, —1) содержатся
в общей формуле
14* + 275м, t + Hu, —15* —275м, —*—15м,
Формы с определителем 0 261
и потому все собственные преобразования формы B, 5, 7) в форму
B75, 0,-1), которые отсюда получаются,— в формуле
10*+ 275 и, t + Wu, — 151 — 275 и, —t — 15u.
Обе эти формулы охватывают, таким образом, все искомые собствен-
собственные преобразования*. Подобным же образом находим, что всевоз-
всевозможные несобственные преобразования формы B, 5, 7) в форму
B75, 0, —1) содержатся в следующих двух формулах:
65* — 1100 м, At — 65 и, — 15 ? + 275 и, — ?+15гг;
10*+ 275 и, —t — lOu, — 15^ — 275 гг, ^ + 15 гг.
Формы с определителем 0
215
До сих пор формы с определителем 0 мы из всех рассмотренний
исключали; поэтому, чтобы сделать нашу теорию исчерпывающей во
всех отношениях, мы должны еще добавить кое-что и о них.
Доказано вообще, что если какая-нибудь форма с определителем D
содержит форму с определителем ?)', то D' является кратностью D\
поэтому ясно, что форма, определитель которой равен 0, не может
содержать никаких других форм, кроме тех, у которых определитель
тоже равен 0. Таким образом остается решить только две задачи^
именно: 1) Пусть даны две формы /, F, вторая из которых имеет
определитель 0; требуется узнать, содержит ли первая форма вторую,
или нет, и в первом случае представить все преобразования первой
формы во вторую; 2) найти все представления заданного числа задан-
ной формой с определителем 0.
Первая задача требует различных методов, когда определитель
первой формы / тоже равен 0, и когда он не равен 0. Все это мы те-
теперь и изложим.
I. Прежде всего заметим, что каждая форма ах2 + 2Ъху + су2,
определитель которой Ъ2 — ас = 0, может быть представлена в виде
* Короче все собственные преобразования представляются формулой
10*-}-55w, t + 2u, — 15 г — 55w, — t — Зм,
где tb и пробегают все числа, удовлетворяющие уравнению t2 — 11 и2 = \.
262 Раздел V (п. 215)
m{gx -f- hyJ> где g и h обозначают взаимно простые числа, а т — це-
целое число. Имендо, если т — наибольший общий делитель чисел
а, с, причем взятый с тем же знаком, который имеют сами эти числа
(легко видеть, что эти числа не могут иметь противоположных зна-
знаков), то а/т, с/т будут целыми взаимно простыми неотрицательными
числами, а их произведение равно Ь2/т2, т. е. является квадратом,
а потому и сами они тоже квадраты (п. 21).
Если — — g2, — = /г2, то g и /г также взаимно просты, далее,
g2h2 = —Т и gh = + — . Отсюда вытекает, что
т (gx + hyJ = ax2 -f- 2bxy + су2.
Пусть теперь даны две формы /, F с определителем 0, причем
пусть
f = m(gx + hy)\ F = M(GX + HYf,
так что g взаимно просто с /г, и G — с Н. Тогда я утверждаю, что
если форма / содержит форму F, то т или равно М, или по мень-
меньшей мере рходит в М, причем отношение тогда является квадратом,
и обратно, если М/т есть целочисленный квадрат, то F содер-
содержится в /. Именно, если предположить, что / переходит в F при
подстановке
то
^ (GX + HYf = [К + ТА) X + (pg + 8А) У]2,
откуда легко следует, что М/т есть квадрат. Если положить его
то
е (GX + HY) = ± [(ag + ТА) X + (Pg + 8fe) У],
равным е21 то
т. е.
ag + Тй, +еЯ = pg + 8й.
Если поэтому @, § определены так, что @С + §Я = 4:1, то
+ е = @ (ag + тА) + -5 (Pg + 8А) — целому числу.
Формы с определителем 0 263
Если же, наоборот, предположить, что М /т является целым
квадратом и равно е2, то форма / будет содержать форму F.
Именно, можно будет так определить целые числа ос, р, ^, 8, что
ag + ТА = + eG, $g + bh = zt eH.
Действительно, если целые числа g, fj выбраны так, что $g -j- $h = 1»
то указанные равенства будут выполняться, если положить
а = + eG§ + hz, т =
Р = ±бЯй + hz\ 8 =
где z и z' могут иметь любые целочисленные значения. Поэтому F
будет содержаться в /. Одновременно можно без труда убедиться,
что эти формулы представляют все значения, которые могут при-
принимать а, р, y» 8, т. е. все преобразования формы / в F, если,
только предположить, что z и z' пробегают все целые числа.
II. Если даны две формы, / = ах2 -f- 2bxy -f- су2, определитель
которой не равен 0, и F = М(GX + HYJ, определитель которой
равен 0, то я утверждаю, во-первых, что если / содержит форму F,
то число М может быть представлено формой /; во-вторых, что
«ели М может быть представлено формой /, то F содержится в /;
е-третъих, что если в этом случае произвольное представление
числа М формой / есть х = ?, у = и, то GI, Щ, Go, Но будет про-
пробегать все преобразования формы / в F. Все это мы докажем сле-
следующим образом.
1. Если предположим, что / переходит в F при подстановке
а, р, 7> 8, и определим числа @, § так, что @G + ?)# = 1» то если
положить х = а® + р§, г/ =±= y®+^§» значение формы / будет, оче-
очевидно, равно М, и потому М пред тавляется формой /.
2. Если предположить, что а?2 + 26|d + со2 =М,то при подста-
подстановке G?, Я|, Gu, ZTu форма /, очевидно, переходит в F.
3. То, что в этом случае подстановки G?, H%, Go, Но дают все
преобразования формы / в F, если предположить, что 8, о пробе-
пробегают все значения х, у, при которых / — М, показывается так.
Если а. р, y> 8 — какое-нибудь преобразование формы / в /?, и,
как и раньше, ®G-{- §>Н = 1, то среди значений х, у будут нахо-
находиться также и следующие:
х = а® + р§ г/ = Т@ + 8?,
264 Раздел V (п. 216)
а из них мы получаем подстановку
или
Т + Ь № — т#), 8 + © (ТЯ - 8G).
Так как, однако,
a (aX + рУJ + 26 (аХ + рУ) (?Х + 8У) + с (ТХ + ЗУJ
то
и потому (так как определитель формы /, умноженный на (оо8 — РтJ»
равен определителю формы F, т. е. равен 0, и потому а8 — $4 = 0)
Поэтому наша подстановка переходит в а, р, т, 8, откуда выте-
вытекает, что указанная формула дает все преобразования формы
/вР.
III. Нам остается еще только показать, как можно найти все
представления заданного числа заданной формой с определителем 0.
Если заданная форма есть m(gx + Лг/J, то тотчас же ясно, что
число должно делиться на т, и отношение должно быть квадратом.
Если поэтому положить заданное число равным те2, то очевидно,
что для тех значений х, г/, для которых т (gx + /и/J = те2, gx -j- hy
должно быть равно или + е, или — е. Поэтому мы получим все
представления, если найдем все решения линейных уравнений
gx -f- hy = е и gx -f- hy = — e в целых числах. То, что они разре-
разрешимы, известно (если, как и предполагается, g и h взаимно просты).
Именно, если g, fj определены так, что $g + §h = 1, то первое урав-
уравнение будет удовлетворяться, если положить х = $е + fjz, г/ — fje— gz,,
а второе,— если положить ж = — $е + Az, г/ = — ^е — gz, где z обоз-
обозначает какое-нибудь целое число. Одновременно эти формулы будут
давать все целочисленные значения х, у, если считать, что z про-
пробегает все целые числа.
Решение неопределенных уравнений второй степени 265
Общее решение в целых числах всех неопределенных уравнений
второй степени с двумя неизвестными
216
В качестве заключения этих исследований, мы добавим еще
одну задачу.
Задача. Найти все решения в целых числах общего неопределен-
неопределенного уравнения второй степени с двумя неизвестными:
ах2 + 2Ъху + су2 + 2dx + 2ey + f = 0*
(где а, Ь, с, . . .— любые заданные целые числа).
Решение. Мы введем вместо неизвестных х, у другие:
р = (Ь2 — ас) х + be — cd, q = (Ъ2 -— ас) у -\-bd — ае,
которые, очевидно, всегда будут целыми числами, если х и у целые.
Тогда мы получим уравнение
ар2 + 2bpq + cq2 + f (b2 — асJ + (Ь2 — ас) (ае2 — 2bde + cd2) = О,
или, если для краткости положить
/ (б2 — асJ + (Ь2 — ас) (ае2 — 2bde + cd2) = —M,
то
ар2 + 2bpq + cq2 - М.
Но раньше мы показали, как могут быть найдены все решения
этого уравнения, т. е. все представления числа М формой (а, Ь, с).
Если же из отдельных пар значений р, q определить соответствую-
соответствующие вначения хг у при помощи равенств
г — P + cd — Ъе _ q + ae — bd
b* — ac ' У b* — ac '
то легко видеть, что все эти значения удовлетворяют заданному
уравнению, и не существует целочисленных значений х, у, которые
не получались бы таким способом. Если мы, поэтому, из всех так
* Если бы было дано некоторое уравнение, у которого был бы нечетным
второй, четвертый или пятый коэффициент, то после умножения на 2 оно приве-
привелось бы к виду, предполагаемому здесь.
266 Раздел V (п. 217)
получающихся значений х, у выбросим дробные значения, то
останутся все искомые решения.
Относительно этого решения нужно сделать следующие заме-
чания.
1. Если либо число М не может быть представлено формой
(а, Ъ, с), либо ни из какого его представления не получается целых
значений ж, г/, то уравнение не может быть разрешимо в целых
числах.
2. Если определитель формы (а, Ь, с), т. е. число Ъ2— ас,
отрицателен, или же положителен, является квадратом и одно-
одновременно М не равно 0, то количество представлений числа М
формой (а, Ъ% с) будет конечным, и тем самым будет конечным и
количество решений (если они вообще существуют) заданного
уравнения.
3. Если Ъ2—ас— положительное число, не являющееся квадратом,
или же квадрат, но одновременно М=0, то если число М вообще может
быть представлено формой (а, й, с) хотя бы одним способом, оно
будет представляться бесконечным количеством способов', так как,
однако, невозможно найти все эти представления и исследоватьу
дают ли они целые значения ж, у или дробные, то необходимо
указать метод, при помощи которого в случае, когда ни одно
представление не дает целых значений х, у, можно в этом удосто-
удостовериться (действительно, мы покажем, сколько в этом случае надо
исследовать представлений, в чем ведь никогда нельзя было бы
быть уверенным без такого правила); если же одни представления
дают целые, а другие — дробные значения х, у, то нужно будет
показать, как вообще сразу можно отличать первые от вторых,
4. Если Ъ2— ас — 0, то значения х, у вообще не могут быть
определены по указанным выше формулам; поэтому в этом случае
нужно сообщить специальный способ.
217
Для случая, когда б2 — ас — положительное число, не являющееся
квадратом, мы выше показали, что всевозможные представления
числа М формой ар2 -]- 2bpq -f- сф (если они вообще существуют)
Решение неопределенных уравнений второй степени 267
могут быть определены по одной или нескольким формулам вида
i <f = ¦!-(<&* +©в),
где 21, 25, S, 2)—заданные целые числа, т—наибольший общий
делитель чисел а, 2Ь, с, и наконец, t, и обозначают всевозможные
целые числа, удовлетворяющие уравнению t2— (b2— ас)и2 — т2.
Так как значения t, и можно предполагать как положительными,
так и отрицательными, то вместо каждой отдельной из этих фор-
формул мы можем получить четыре других:
~
так что количество всех формул теперь вчетверо больше, чем до
этого, a t и и выражают уже не все числа, удовлетворяющие урав-
уравнению t2— (b2 — ac)u2 = m2, а лишь положительные числа такого
рода. Каждую из этих формул надо рассмотреть отдельно и иссле-
исследовать, какие значения t, и дают целые значения х, у.
Из^ выражений
д т
[1]
получаются следующие значения х, у:
Ш + 53м -f- mcd — mbe (it + !5)м + ^«^ — mbd
У =
X = m (b2 — ас) ' У = m (&2 — ac) '
Но выше мы показали, что все (положительные) значения t обра-
образуют рекуррентный ряд ?°, t\ t", , . . , и точно так же соответствую-
соответствующие значения и образуют рекуррентный ряд и0, и\ и", . . .; что,
далее, может быть указано число р с тем свойством, что по неко-
некоторому заданному модулю
268 Раздел V (п. 218)
Возьмем за этот модуль число т(Ь2 — ас), и обозначим для крат-
краткости значения ж, г/, которые получаются, если положить t = t°,
и=и° — и которые мы снабдим индексом 0 — через х°, у0; точно
так же те, которые получаются, если положить t = t\ u = uf — и
которые мы снабдим индексом 1 — через х', г/', и т. д. Тогда без
труда видно, что если числа x^h\ yW целые и р определено пра-
правильно, той я<л+р), г/(Л+р), ж<М-2р)? г/(Л+2р) и вообще x(h+ke\ г/<Л+М бу-
будут целыми числами, и что, наоборот, если ж(Л> или г/<Л> дробно7,
то и #(И-ВД или y(h+kp) является дробным числом. Отсюда легко
выводится, что если найдены значения х, г/, снабженные индексами
0. 1, 2, ... , р — 1, и для каждого из этих индексов или х, или у
не является целым числом, то вообще нет индекса, для которого
как х, так и у принимали бы целые значения, так что в этом слу-
случае из формулы [1] не могут быть получены целые значения х, у.
Если же среди этих индексов имеются какие-нибудь, скажем
[л, [л/, [//', ... , которым соответствуют целые значения ж, г/, то всеми
целыми значениями х, г/, которые могут быть получены из формулы [1],
будут те, индексы которых имеют вид [х -(- #р, или jx' + #р» или
[л" -f Ар, ... , где к пробегает все целые положительные числа, не
исключая и нуля.
Остальные формулы, в которых содержатся значения р, q, раз-
разбираются точно таким же способом. В том случае, когда ни из
одной из всех этих формул не получаются целые значения ж, г/,
заданное уравнение само вообще не может быть решено в целых
числах; если же оно в действительности разрешимо, то все цело-
целочисленные решения могут быть представлены по изложенным выше
правилам.
218
Если Ь2 — ас является квадратом и М = 0, то все значения р, q
содержатся в двух формулах вида р = 9tz, q = Sgz; p = STz, q = Э5'2,
где z обозначает произвольное целое число, а 31, 95, 91', 95' суть
заданные целые числа, первое из которых не имеет общих дели-
делителей со вторым, а третье — с четвертым (п. 212). Поэтому все
Решение неопределенных уравнений второй степени 269
целочисленные значения х, у, получающиеся из первой формулы,
содержатся в формуле
m%z A- cd — be 33z + ae — bd
X = — ! ? 11 — !
а все остальные, получающиеся из второй формулы,— в формуле
q1 %'z-\-cd — be *>&'z-\-ae — bd
Так как, однако, каждая из этих формул может давать также и
дробные значения (поскольку не обязательно Ь2 — ас = 1), мы
должны в каждой из этих формул отделить те значения z, для
которых как х, так и у будут целыми числами, от остальных;
впрочем, достаточно рассмотреть только первую формулу, так как
для второй применим в точности тот же метод.
Так как 21, 95 взаимно просты, можно найти два такие числа
а, Ь, что а21 + Ь95 = 1. Если это сделано, то мы имеем
(ах + Ьу) (Ъ2 — ac) = z + a(cd— be) + Ь(ae — bd),
откуда тотчас же вытекает, что все значения z, которые могут
дать целые значения х, у, обязательно должны быть сравнимы
с числом a (be — cd)-{~b(bd — ae) по модулю б2 — ас, т. е. содер-
содержаться в формуле (б2 — ac)zf-{-a(be — cd)-{-b(bd — ae), где zf обо-
обозначает произвольное целое число. Поэтому вместо формулы [1] мы
легко получаем формулу
х = 9tz' + :
которая, очевидно, дает целые значения х, у или для всех значе-
значений z\ или для никаких, причем первый случай будет иметь место,
если 91 Fс?—ае) и 95 (be — cd) по модулю Ь2 — ас сравнимы, а вто-
второй,— если не сравнимы. Точно таким же образом исследуется фор-
формула {2], и целочисленные решения (если они этой формулой
даются) отделяются от остальных.
270 Раздел V (пп. 219-221)
219
Если Ь2 — ас = 0, то форма ах2 + 2bxy -f су2 может быть пред-
представлена в виде т(ах + ^уJ1 где т, а, р являются целыми числами
(п. 215). Если положить <хх -f $у = г, то заданное уравнение пере-
переходит в
mz2 + 2dx + 2ey + f = 0,
и отсюда в соединении с ах -\~ fiy — z следует, что
x— 2ae~2$d ' ^ ~~ 2^ —2ae
Теперь ясно, что если не имеет места ае = [М (каковой слу-
случай мы тотчас же рассмотрим отдельно), то получающиеся из этих
формул при любом значении z значения х, у удовлетворяют задан-
заданному уравнению; поэтому остается только еще показать, как опре-
определяются те значения z, из которых получаются целые значе-
значения х, у.
Так как ах + $у = z, то для z можно брать только целочис-
целочисленные значения; кроме того, ясно, что если для некоторого зна-
значения z как х так и у будут целыми числами, то и все значения
z, которые сравнимы с ним по модулю 2ае — 2$d7 тоже будут да-
давать целые значения. Если поэтому подставить вместо z все целые
числа от 0 до 2ае — 2$d — 1 (в случае, когда ае — $d положительно)
или до 2(М — 2ае — 1 (если ае — [3d отрицательно) включительно,
и ни для какого из этих значений х и у не будут целыми числа-
числами, то вообще никакое значение z не будет давать целочисленных
значений ж, у, и заданное уравнение будет вообще неразрешимо в
целых числах. Если же некоторые из значений z, например, С, С,
С", . .. (которые можно также найти решением сравнений второй
степени по правилам раздела IV), дают для х, у целочисленные
значения, то все решения получаются, если положить z = Bае —
— 2[М) v + С, z = Bае — 2pd) г? + С, . . . , где v пробегает все целые
числа.
Решение неопределенных уравнений второй степени 271
220
Для исключенного случал, когда ае = [3d, мы должы применить
специальный способ. Если мы предположим, что а, р взаимно про-
просты, что, как известно из п. 215, I, позволительно, то — = тг бу-
будет целым числом (п. 19), которое мы положим равным h. Тогда
заданное уравнение принимает вид
(тосх -f т$у + /гJ — /г2 + т/ = О
и потому, очевидно, может быть разрешено рационально только в
том случае, если /г2 — т/ является квадратом. Если /г2 — mf = k2y
то ясно, что заданному уравнению эквивалентны оба следующие
уравнения:
тосх -f т$у -f h + к = 0 и #га# + ^Р2/ + п — к = 0,
т. е что каждое решение заданного уравнения удовлетворяет так-
также тому или другому из этих уравнений, и обратно. Первое ура-
уравнение, очевидно, может быть решено в целых числах только
тогда, когда h -f- к делится на т; аналогично, второе уравнение
только тогда обладает решением в целых числах, когда h — к
делится на т. Но эти условия также и достаточны для разреши-
разрешимости каждого из этих уравнений (так как, по предполо-
предположению, ос и р взаимно просты), и все их решения могут быть най-
найдены по известным правилам.
221
Рассмотренный в п. 217 случай (самый трудный из всех) мы
поясним примером. Пусть задано уравнение
х2 + 8ху + у2 + 2х - 4г/ +1 = 0.
Сначала посредством введения новых неизвестных
р = 15 х — 9, q = 15г/ + 6
мы подучаем из него уравнение
р* + 8РЯ + Я2 = ~ 540.
272 Раздел V (п. 222)
Далее, находим, что все целочисленные решения этого уравнения
содержатся в следующих четырех формулах:
p = — 6*, q = 2At
p = — 6tt q = 24t + 90,
где t, и обозначают всевозможные целые положительные числа,
которые удовлетворяют уравнению t2—15 и1 = 1 и содержатся в
формулах
в = ^1= [D
где 7г обозначает всевозможные целые положительные числа (вклю-
(включая и нуль). Поэтому все значения ж, у содержатся в формулах
= i(8f —ЗОв —2),
Применяя предписанные нами правила, найдем, что для того, чтобы
получились целочисленные значения, в первой и второй формулах
нужно брать те значения t, и, которые получаются при четных пока-
показателях 7г, а в третьей и четвертой — при нечетных п. В качестве
простейших решений мы получаем х = 1, —1, —1, соответственно
у = —2, 0, 12.
Впрочем, нужно заметить, что решение рассмотренной в преды-
предыдущем пункте проблемы в большинстве случаев может быть сокра-
сокращено посредством многочисленных искусственных приемов, в особен-
особенности в отношении непригодных, т. е. содержащих дроби, решений.
Однако, чтобы изложение не было слишком пространным, мы пред-
предпочитаем здесь это опустить.
Исторические замечания 273
Исторические замечания
222
Так как многое из того, что мы до сих пор излагали, рассма-
рассматривалось также и другими математиками, мы не можем обойти
их заслуги молчанием. Относительно эквивалентности форм об-
общее исследование произвел Л а г р а н ж, «Nouv. Mem. de V Ас.
de Berlin», 1773, p. 263\ 1775, p. 323 и ел., где он, в частности,
показал, что для каждого данного определителя имеется конечное
число форм с тем свойством, что каждая форма с этим определи-
определителем эквивалентна одной из них и что тем самым все формы с дан-
данным определителем могут быть разбиты на классы. Позднее
Л е ж а н д р открыл, в большинстве случаев индуктивным
путем, многие изящные свойства этой классификации, которые
мы ниже подкрепим доказательствами. Впрочем, до сих пор никто
не входил в исследование собственной и несобственной эквивалент-
эквивалентности, польза которого особенно обнаруживается в более тонких
исследованиях.
Знаменитая проблема доложенная в п. 216, была впервые решена
Лагранжем, «Hist, de I'Ac. de Berlin», 1767, p. 165; 1768, p. 181
и ел. Решение (менее совершенное) находится также в уже упоминав-
упоминавшихся ранее дополнениях к «Алгебре» Эйлера. Еще раньше на
этот вопрос обратил внимание Эйлер, «Сотт. Petr.», Т. VI, р. 175:
«Сотт. Nov.», Т. IX, р. 3; там же, Т. XVIII, р. 185 и ел.; однако он
все время ограничивался в своем исследовании тем, что из одного
решения, которое он предполагал уже известным, выводил другие,
и, кроме того, его методы могли дать все решения только в немногих
случаях (ср. Lagrange, «Hist, de Г Ac. de Berlin», 1767,
p. 237). Так как последнее из этих трех сочинений имеет дату более
раннюю, чем сочинение Лагранжа, которое разбирает задачу
во всей общности и не оставляет уже ничего желать в этом отноше-
отношении, то Э й л е р в свое время (восьмидесятый том «Комментариев»
относится к 1773 г. и опубликован в 1774 г.) еще не мог знать этого
решения. Впрочем, наше решение (так же, как и все остальное, что
мы до сих пор изложили в этом разделе) базируется на совершен-
совершенно иных принципах.
274 Раздел V (п. 223)
То, что необходимо здесь сообщить о других — Диофанте,
Ферма и т. д.,— касается только частных случаев; так как то, что
особенно достойно упоминания, мы уже указывали выше, мы не
будем тратить силы на то, чтобы перечислять все подробности.
То, что мы до сих пор изложили о формах второй степени, следует
рассматривать только как начало этой теории; при более усердном
продолжении этого исследования нам открылось весьма широкое
поле для изысканий, из которых то, что оказывается наиболее за-
замечательным, мы изложим ниже. Действительно, этот предмет на-
настолько плодотворен, что ради краткости мы должны обойти молча-
молчанием многое другое, что нами сейчас уже найдено; но намного больше
остается еще, без сомнения, не открытым и ждет новых усилий.
Кстати, мы хотим в начале этих исследований заметить, что формы
с определителем 0 из рассмотрения исключаются, если только явно
не оговорено противное.
ДАЛЬНЕЙШИЕ ИССЛЕДОВАНИЯ О ФОРМАХ
Разбиение форм с заданным определителем
на классы
223
Выше (пп. 175,195, 211) мы уже показали, что если задано какое-
нибудь целое (положительное или отрицательное) число D, то можно
указать конечное число форм F', F'', F", ... с определителем D, обла-
обладающих тем свойством, что каждая форма с определителем D соб-
собственно эквивалентна одной и только одной из них. Тем самым все
формы с определителем D (число которых бесконечно велико) мо-
могут быть разбиты на классы, именно, первый класс состоит из всех
форм, которые собственно эквивалентны форме F', второй — из форм,
которые собственно эквивалентны форме F' и т, д.
Из определенного класса форм с данным определителем может
быть выбрана какая-нибудь форма, которая может рассматриваться
как представитель всего класса. Вообще говоря, совершенно безраз-
безразлично, какую форму выбирать из каждого класса, однако предпо-
Разбиение форм на классы 275
чтение всегда будет оказываться той форме, которая проще осталь-
остальных. Простота какой-нибудь формы (а, Ь, с) выражается, очевидно,
в величине чисел а, Ь, с, и форма (а', Ъ', с') с полным правом может
быть названа менее простой, чем (а, Ъ, с), если а'>а, b'>b, c'>c.
Этим, однако, положение вещей еще не полностью определено, и,
например, остается еще зависящим от нашего желания, какую из
форм A7, 0 — 45), E,0, —153) считать более простой. По большей
части, однако, бывает целесообразным соблюдать следующее правило.
I. Если определитель D отрицателен, то в качестве представите-
представителей нужно брать приведенные формы из каждого класса; если же
в одном и том же классе находятся две приведенные формы (которые
тогда противоположны, п. 172), то нужно брать ту из них, у которой
средний член положителен.
II. Если определитель D есть положительное число, не являющее-
являющееся квадратом, то нужно найти период какой-нибудь приведенной
формы, содержащейся в заданном классе; в этом периоде будет или
две двусторонние формы, или ни одной (п. 187).
1. В первом случае пусть (А, В, С), (Аг, В'', С) двусторонние
формы; далее, пусть наименьшие вычеты чисел В, В' по модулям
А, А' соответственно равны М, М' (которые могут быть взяты поло-
D — М2 ..
жительными, если они не равны нулю), и, наконец, —^— ^ **»
—^р— = №' Тогда в качестве представителя берется та из форм
(А, М, —N), (А'', М', —N'), которая проще. При этом предпочтение
отдается той форме, у которой средний член равен нулю; если же
средние члены или у обеих форм равны нулю, или ни у одной не
равны нулю, то предпочитается та форма, которая имеет меньший
первый член, а если первые члены по величине равны, но их знаки
противоположны, то предпочтение отдается положительному знаку
перед отрицательным.
2. Если же во всем периоде нет ни одной двусторонней формы, то
среди всех форм периода выбирается та, которая имеет наименьший
(не принимая во внимание знак) первый член, причем если в этом
периоде имеется две формы, у которых один и тот же первый член,
но у первой с положительным знаком, а у второй с отрицательным,
то первой отдается предпочтение перед второй. Если эта форма есть
276 Раздел V (п. 224)
(А, В, С) и из нее так же как и в предыдущем случае получена другая
форма (А, М, —N) (именно, за М берется абсолютно наименьший
лт D—M\
вычет В по модулю А, и полагается /V = ^—^—;, то эта последняя
и берется в качестве представителя.
Если же случится, что один и тот же наименьший первый член
встречается у нескольких форм периода, то все эти формы должны
быть рассмотрены таким же образом, и из получающихся форм нуж-
нужно взять в качестве представителя ту, у которой средний член наи-
наименьший.
Так, например, для D =3 05 среди других имеется следующий пе-
период: A7, 4, -17), (-17, 13, 8), (8, И, -23), (-23, 12, 7), G, 16,-7),
(—7, 12, 23), B3, И, —8), (—8, 13, 17), из которого сначала выби-
выбирается форма G, 16, —7); из нее выводится затем представитель
G, 2, -43).
III. Если определитель является положительным квадратом и
равен/с2,то отыскивается содержащаяся в заданном классе приведен-
приведенная форма (А, к, 0), и если А<^к, то она и берется в качестве предста-
представителя; если же А>к, то вместо нее берется форма (А — 2к, /с, 0),
первый член которой отрицателен, но меньше чем к.
Пример. Все формы с определителем —235 распадаются на шест-
шестнадцать классов, представителями которых являются A, 0, 235),
B, 1, 118), D, 1, 59), D, -1, 59), E, 0, 47), A0, 5, 26), A3, 5, 20),
A3, —5, 20), и еще восемь других форм, которые отличаются от
предыдущих только знаками крайних членов, именно, (—1, 0, —235),
(-2, 1 , -118), ...
Все формы с определителем 79 распадаются на шесть классов,
представителями которых являются формы A, 0, —79), C, 1, —26),
C, -1, -26), (-1, 0, 79), (-3, 1, 26), (-3, -1, 26).
224
Таким образом, при этой классификации формы, которые соб-
собственно эквивалентны, полностью обосабливаются от остальных.
Два формы с одним и тем же определителем эквивалентны, если они
Принадлежат одному классу; каждое число, которое представляется
одной из них, может быть представлено также и другой, и если какое-
Разбиение форм на классы 277
нибудь число М может быть представлено первой формой так, что
неизвестные имеют взаимно простые значения, то это число может
быть представлено таким же образом и другой формой, причем так,
что оба представления принадлежат одному и тому же значению выра-
выражения J/jD (mod M). Если же две формы принадлежат к различным
классам, то они не являются собственно эквивалентными; из предста-
представимости какого-нибудь заданного числа одной из форм нельзя
заключить о представимости этого же числа и другой формой; наобо-
наоборот, если число М может быть представлено одной из форм так, что
значения неизвестных взаимно просты, то тотчас же ясно, что
подобного представления этого числа другой формой, которое при-
принадлежало бы тому же значению выражения)//) (mod M), быть не
может (ср. пп. 167, 168).
Напротив, вполне возможно, что две формы F, F' из различ-
различных классов К, К' несобственно эквивалентны; в этом случае
каждая форма из одного класса будет несобственно эквивалентна
каждой форме из другого класса, каждая форма из К имеет про-
противоположную себе форму в А"', и классы К, К' сами будут назы-
называться противоположными. Так, в первом примере предыдущего
пункта третий класс форм с определителем —235 противоположен
четвертому, а седьмой — восьмому; во втором примере второй класс
противоположен третьему, а пятый — шестому. Если поэтому даны
какие-нибудь две формы из противоположных классов, то каждое
число Л/, которое может быть представлено одной из них, будет
представляться также и другой,, причем если для первой формы
представление достигается взаимно простыми значениями, то для
второй возможно представление таким же образом, причем оба эти
представления будут принадлежать противоположным значениям
выражения УВ (mod M). Впрочем, указанные выше правила для
выбора представителей таковы, что противоположные классы всег-
всегда имеют противоположных представителей.
Наконец, имеются также классы, которые противоположны са-
самим себе. Именно, если какая-нибудь форма одновременно с про-
противоположной ей формой содержатся в одном и том же классе,
то легко видеть, что все формы этого класса эквивзалентны между
собой как собственно, так и несобствешю, ж для каждой формы
278 Раздел V (пп. 225-226)
встречается и ей противоположная. Таким будет каждый класс,
в котором содержится двусторонняя форма, и наоборот, в каждом
противоположном самому себе классе обязательно будет встречаться
двусторонняя форма (пп. 163, 165), вследствие чего сам класс будет
называться двусторонним. Так, среди классов форм с определителем
—235 имеется восемь двусторонних, представителями которых являют-
ся A, 0, 235), B, 1, 118), E, 0, 47), A0, 5,26), (-1, 0,-235),
( — 2, 1, —118), (—5, 0, —47), (—10, 5, —26); среди классов
<|юрм с определителем 79 двусторонних два, представителями кото-
которых являются A. 0, —79), (—1, 0, 79). Впрочем, если предста-
представители определены по нашим правилам, то двусторонние клас-
классы могут быть найдены без труда. Именно, для положительного
неквадратного определителя двусторонний класс будет, очевидно,
иметь представителем двустороннюю форму (п. 194); для отрица-
отрицательного определителя представители двусторонних классов будут
или классами двусторонними, или такими, что их крайние члены
равны (п. 172); наконец, для положительного квадратного опре-
определителя мы, согласно п. 210, легко убеждаемся, является ли
представитель несобственно эквивалентным самому себе и потому
является ли представляемый им класс двусторонним.
225
Выше (п. 175) мы уже показали, что у формы (а, Ъ, с) с отри-
отрицательным определителем крайние члены имеют одинаковые знаки
как между собой, так и со знаками крайних членов каждой
эквивалентной ей формы. Если а, с положительны, то мы будем
называть форму (а, Ъ, с) положительной формой, и точно также
будем называть весь класс, в котором содержится (а, Ъ, с) и который
состоит только из положительных форм, положительным классом.
Наоборот, (а, Ъ, с) будет отрицательной формой и будет содержаться
в отрицательном классе, если а, с отрицательны. Положительной
формой не могут представляться отрицательные числа, а отрица-
отрицательной формой — положительные числа. Если (а, Ь, с) является
представителем положительного класса, то форма (—а, Ъ,—с)
Разбиение классов на порядки 279
будет представителем отрицательного, откуда следует, что число
положительных классов равно числу отрицательных и что если
определены первые, то тем самым даны и вторые. Поэтому при
исследовании форм с отрицательным определителем нужно, по боль-
большей части, рассматривать только положительные классы, так
как их свойства легко переносятся на отрицательные классы.
Впрочем, такое различие характерно только для форм с отрица-
отрицательным определителем; формами с положительным определителем
могут представляться и положительные и отрицательные числа, и
даже нередко в этом случае две формы вида (а, Ъ, с), (—а, Ъ,— с)
принадлежат одному и тому же классу.
Разбиение классов на порядки
226
Некоторую форму (а, Ь, с) мы будем называть примитивной
формой, если числа а, Ь, с не имеют общих делителей; в противном
случае она будет называться произведенной формой, причем если
наибольший общий делитель чисел а, Ъ, с равен т, то форма
(а, Ъ, с) произведена из примитивной формы (а/т, Ъ/т, с/т). Из
этого определения тотчас же вытекает, что все формы, определи-
определители которых не делятся ни на какой квадрат, кроме 1, обяза-
обязательно являются примитивными формами Далее, из п. 161 следует,
что если в какой-нибудь данный класс форм с определителем D
входит примитивная форма, то все формы этого класса будут при-
примитивными; в этом случае сам класс будет называться примитив-
примитивным. Далее, ясно, что если какая-нибудь форма F с определите-
определителем D произведена из примитивной формы / с определителем
D/m2f и классы, в которых содержатся соответственно формы F,
/, суть К, к, то все формы класса К могут быть произведены из
примитивного класса к; в этом случае мы будем называть поэтому
сам класс К произведенным из примитивного класса к.
Если форма (а, Ъ, с) примитивная, но а, с не являются одно-
одновременно четными (т. е. если или они оба, или по крайней мере
одно из них нечетно), то легко видеть, что не только а, 6, с, но
280 Раздел V (п. 226)
и а, 26, с не могут иметь общих делителей, и в этом случае фор-
форма (а, 6, с) будет называться собственно примитивной или просто
собственной формой. Если же форма (а, 6, с) примитив-
примитивная и числа а, с оба четные, то очевидно, что числа
а, 26, с, будут иметь общий делитель 2 (который одновременно
будет наибольшим), и тогда (а, 6, с) будет называться несобственно
примитивной, или просто несобственной формой *. В этом случае
6 обязательно нечетно (так как иначе форма (а, 6, с) не была бы
примитивной формой); поэтому 62 = l(mod4) и тем самым, так как ас
делится на 4, определитель б2—ас=1 (mod 4). Несобственные
формы имеются поэтому только для определителя вида 4гс+1,
если он положителен, или вида—Dп + 3), если он отрицателен.
Из п. 161, однако, очевидно, что если в каком-нибудь данном
классе находится собственно примитивная форма, то все формы
этого класса собственно примитивны, и, наоборот, что класс, ко-
который содержит одну несобственно примитивную форму, сплошь
состоит из несобственно примитивных форм. Поэтому сам класс
в первом случае будет называться собственно примитивным классом
или просто собственным классом, а во втором случае несобствен-
несобственно примитивным или просто несобственным классом. Так, напри-
например, среди положительных классов форм с определителем — 235
имеется шесть собственных классов, именно, тех, представителями
которых являются A, 0, 235), D, 1, 59), D, —1, 59), E, 0, 47),
A3, 5, 20). A3, —5, 20) и столько же имеется их среди отрица-
отрицательных классов Несобственных же классов будет и тут и там по
два. Классы форм с определителем 79 (это число имеет вид An -f- 3)
все являются собственными.
Если форма (а, 6, с) является произведенной, причем из при-
примитивной формы (а/т, b/т, с/т), то последняя может быть или
собственно, или несобственно примитивной. В первом случае т
* Мы остановились на выражениях «собственная» и «несобственная», по-
потому что не нашли ничего более удобного; мы указываем на это для того,
чтобы кто-либо не стал искать связи между этим обозначением и тем, кото-
которое употребляется начиная с. п. 157, ибо такой связи нет. Впрочем, накаких
недоразумений на этой почве возникнуть, разумеется, не может.
Разбиение классов на порядки 281
является также наибольшим общим делителем чисел а, 2Ъ, с; во
втором случае наибольший общий делитель этих чисел будет равен
2т. Этим самым делается понятным различие между формой, про-
произведенной из собственно примитивной формы, и формой, произве-
произведенной из несобственно примитивной формы, и точно так же (ибо,
согласно п. 161, все формы одного и того же класса тоже нахо-
находятся в этой связи) между классом, произведенным из собственна
примитивного класса, и классом, произведенным из несобственна
примитивного класса.
Посредством этого различия мы получили первую основу, на
которой может быть построено разбиение всех классов форм с задан-
заданным определителем на различные порядки. Два класса, представи-
представителями которых являются формы (а, Ъ, с), (а', Ъ', с'), мы будем
причислять к одному и тому же порядку, если как числа а, Ъ, с
имеют тот же самый наибольший общий делитель, что а', Ъ', с',
так и числа а, 2Ъ, с имеют тот же наибольший общий делитель,
что а', 26\ с'. Если же одно или другое, или оба эти условия не
имеют места, то мы будем причислять классы к различным по-
порядкам. Отсюда тотчас же вытекает, что все собственно примитив-
примитивные формы образуют один порядок, а все несобственно примитив-
примитивные формы — другой порядок. Если т2 является квадратом,
входящим в определитель D, то классы, произведенные из собст-
собственно примитивных классов с определителем D/m2, будут образо-
образовывать отдельный порядок, произведенные из несобственно прими-
примитивных классов с определителем D/m2 — другой порядок и т. д-
Если случайно D не делится ни на какой квадрат (кроме 1), то
порядков из произведенных классов не будет, и потому будет или
один порядок (если D = 2 или 3 по модулю 4), именно, порядок
собственно примитивных классов, или два порядка (если D = 1 (mod 4)),
именно, порядок собственно примитивных и порядок несобственно
примитивных классов. При помощи комбинаторных соображений
без труда обосновывается следующее общее правило. Если
D=D'22il аш Ъ2$ c2Y ..., где D' не содержит квадратных сомножителей,,
и a, fe, с,... — различные нечетные простые числа (в таком виде
может быть представлено каждое число, если положить (х = О,
когда D не делится на 4, и положить равными 0 все а, р, y» • • •
282 Раздел V (пп. 227-228)
или, что то же самое, отбросить сомножителиа2а, Ь2& , c2Y ,..., когда
D не делится ни на какой нечетный квадрат), то имеется или
((х + 1) (а + 1) (Р + 1)(Т + 1) • • • порядков, именно, когда D' = 2
или 3 (mod 4), или ((х + 2) (а + 1) (Р + 1) (т + !)• • • порядков, именно,
когда D' = l (mod 4).
Доказательство этого правила, мы, однако, опустим, так как
оно не является ни трудным, ни очень уж здесь необходимым.
Пример 1. Для D = 45 = 5*32 имеется шесть классов, предста-
представителями которых являются формы A, 0, —45), (—1, 0, 45),
<2, 1, —22), (—2, 1, 22), C, 0, —15), F, 3, —6). Они распадаются
на четыре порядка: именно, первый порядок охватывает оба соб-
собственных класса, представители которых суть A, 0, —45) и
(—1, 0, 45); второй порядок будет содержать оба несобственных
¦класса с представителями B, 1, —22) и (—2, 1, 22); третий поря-
порядок содержит только один класс, произведенный из собственного
класса с определителем 5, именно, тот, представителем которого
является C, 0, —15), и, наконец, четвертый порядок состоит из
одного произведенного из несобственного класса с определителем
5 класса, представитель которого есть F- 3, —6).
Пример 2. Положительные классы с определителем — 99 =
= —11*32 распадаются на четыре порядка. Первый порядок
охватывает следующие собственно примитивные классы*: A,0,99),
D, 1, 25), D, -1, 25), E, 1, 20), E, -1, 20), (9, 0, И); второй
порядок содержит несобственные классы B, 1, 50), A0, 1, 10);
третий порядок содержит классы C, 0, 33), (9, 3, 12), (9, —3, 12),
произведенные из собственных классов с определителем —11; чет-
четвертый— один единственный класс F, 3, 18), произведенный из
несобственного класса с определителем —11. Отрицательные классы
этого определителя могут быть разбиты на порядки точно таким
же образом.
Заметим, что противоположные классы всегда принадлежат
одному и тому же порядку, факт, причина которого видна без
труда.
* Ради краткости мы вместо самих классов указываем их представителей.
Деление порядков на роды 283
227
Из этих различных порядков наибольшего внимания заслужива-
заслуживает порядок собственно примитивных классов. Действительно,
отдельные произведенные классы получаются из некоторых прими-
примитивных классов (с меньшим определителем), из рассмотрения
которых часто сами собой получаются факты, касающиеся первых.
Но ниже мы покажем, что каждый несобственно примитивный класс
люжет быть в некотором смысле ассоциирован или с одним собст-
собственно примитивным классом (с тем же определителем), или с тремя.
Далее, при отрицательном определителе отрицательные классы мо-
могут быть оставлены в стороне, так как каждому из них всегда со-
соответствует некоторый положительный класс. Чтобы теперь глубже
проникнуть в природу собственно примитивных классов, мы преж-
прежде всего введем между ними одно существенное различие, по кото-
которому весь порядок собственных классов может быть разделен на не-
несколько родов. Так как до сих пор мы еще не касались этого очень
важного предмета, мы должны изложить все с самого начала
Деление порядков на роды
228
Теорема. Посредством любой собственно примитивной формы F
может быть представлено бесконечно много чисел, которые не де-
делятся на заданное простое число р.
Доказательство. Если форма есть F = ах1 + 2Ьху -+- сг/2, то р,
очевидно, не может одновременно входить во все три числа а, 26,
€. Если теперь а не делится на р, то ясно, что если для х взять
какое-нибудь число, не делящееся на /?, а для у — делящееся на
р, то значение формы F на р не делится; если же с не делится
на р, то мы добьемся того же, если придадим х значение, деля-
делящееся на jd, at/ — не делящееся на р; если, наконец, а и с делят-
делятся на р, и потому 2Ь не делится на р, то форма F будет прини-
принимать не делящиеся на р значения, если и х и у придавать значе-
значения, не делящиеся на р.
284 Раздел V (п. 229)
Очевидно, теорема будет сохранять силу и для несобственно
примитивных форм, если только р не равно 2.
Так как одновременно могут выполняться многие такие усло-
условия, именно, что одно и то же число должно делиться на некото-
некоторые заданные простые числа и не делиться на другие (ср. п. 32),
то легко видеть, что числа х, у могут быть бесконечным числом
способов определены так, что- примитивная форма ах* + 2Ьху + су2
принимает значение, которое не делится на любое количество за-
заданных простых чисел, из которых исключается одно единствен-
единственное число 2, если форма несобственно примитивна. Отсюда вытека-
вытекает, что в более общем виде теорема может быть высказана следую-
следующим образом.
Посредством любой примитивной формы может быть представ-
представлено бесконечно много чисел, которые взаимно просты с заданным
(нечетным, если форма несобственно примитивна) числом.
229
Теорема. Если F — примитивная форма с определителем D, и
р — входящее в D простое число, то не делящиеся на р числа, ко-
которые могут быть представлены формой F, обладают тем
общим свойством, что либо все они являются квадратичными выче-
вычетами, либо все квадратичными невычетами по модулю р.
Доказательство. Если F — (а, Ь, с) и, далее, т, т' — какие-ни-
какие-нибудь два числа, не делящиеся на р, которые могут быть представ-
представлены формой F, именно,
т = ag* + 2bgh + ch*9 m' = ag'2 + 2bg'h' + ch'2,
то
mm' = [aggf + b {ghf + hg') + chh']* - D {gh' - hg'f-
тем самым произведение mm' сравнимо с квадратом по модулю D,
а потому также и по модулю р, т. е. mm' есть квадратичный
вычет по модулю р. Отсюда следует, что или каждое из чисел т,
т! является квадратичным вычетом, или каждое является квадра-
квадратичным невычетом по модулю р.
Деление порядков на роды 285
Подобным же образом доказывается, что если определитель D
делится на 4, то представляющиеся формой F нечетные числа или
все = 1, или все = 3 (mod 4). Действительно, в этом случае произ-
произведение двух таких чисел всегда будет квадратичным вычетом по
модулю,4, и потому = 1 (mod 4); поэтому либо каждое из них =1,
либо оба = 3.
Если, наконец, D делится на 8, то произведение двух любых
нечетных чисел, которые могут быть представлены формой F,
является квадратичным вычетом по, модулю 8 и потому оно
== 1 (mod 8). Поэтому в этом случае представляющиеся формой F
нечетные числа или все = 1, или все = 3, или все = 5, или все
==7 (mod 8).
Так, например, так как число 10, которое является невычетом
по модулю 7, может быть представлено формой A0, 3, 17), то
все не делящиеся на 7 числа, которые могут быть представлены
этой формой, являются невычетами по модулю 7. Так как —3
представляется формой (—3, 1, 49) и =1 (mod 4), то все пред-
представляющиеся этой формой нечетные числа будут обладать тем же
свойством.
Впрочем, мы могли бы, если бы это было необходимо для на-
наших целей, легко доказать, что представляемые формой F числа
не находятся в постоянном отношении такого рода ни с одним
простым числом, не входящим в Z), т. е. что как вычеты, так и
невычеты каждого не входящего в D простого числа могут быть
представлены формой F. Наоборот, в отношении чисел 4 и 8 неч-
нечто аналогичное имеет место и в других случаях, и мимо этого мы
пройти не можем.
I. Если определитель D примитивной формы F сравним с
3 (mod 4), то нечетные числа, представляющиеся формой F, будут
или все = 1, или все===3 (mod 4). Именно, если т, т1 — два пред-
представляемых формой F числа, то произведение mm1 может быть
тем же способом, как выше, представлено в виде p2 — Dq2. Если
поэтому каждое из чисел т, т' нечетно, то обязательно одно из
чисел р, q должно быть четным, а другое нечетным, а потому из
двух квадратов р2, q2 один == 0, а другой == 1 (mod 4). Отсюда
легко следует, что р2— Da1 == 1 mod 4 , и потому числа т, т' или
286 Раздел V (п. 230)
оба^=1, или оба = 3 (mod 4). Так, например, формой A0, 3, 17)
не могут быть представлены никакие нечетные числа, кроме имею-
имеющих вид 4п + !•
II. Если определитель D примитивной формы F сравним с
2 (mod 8), то нечетные числа, представляющиеся формой F, будут
или все либо = 1, либо = 7, или все либо = 3, либо ===5 (mod 8).
Действительно, пусть т, т' — два представляющихся формой F
нечетных числа, произведение которых тем самым может быть
представлено в виде p2 — Dq2. Тогда, так как оба числа т, т'
нечетны, то р обязательно должно быть нечетно (так как D четно),
и потому р2 = 1 (mod 8); a q2 или = 0, или==1, или =4, и по-
потому Dq2 или = 0, или з=2. Поэтому mm' = р2 — Dq2 будет или
= 1, или = 7 (mod 8). Таким образом, если т или=з1, или == 7,
то и т' будет или = 1, или = 7, а если т или==3, или =е5, то
и т' будет или===3, или = 5. Так, например, все нечетные числа^
представляющиеся формой C, 1, 5), или == 3, или =е 5 (mod 8),
а ни одно число вида 8п + 1 или 8п-\- 7 этой формой представлено
быть не может.
III. Если определитель D примитивной формы F сравним с
6 (mod 8), то этой формой могут быть представлены нечетные
числа или только такого рода, которые === 1 и == 3 (mod 8), или
только такого рода, которые = 5 и == 7 (mod 8). Доказательство,
которое совершенно аналогично предыдущему (в II), каждый
может провести без труда. Так, например, формой E, 1, 7) могут
быть представлены только такие нечетные числа, которые или = 5,
или == 7 (mod 8).
230
Поэтому все числа, которые могут быть представлены задан-
заданной примитивной формой F, с определителем Z), будут находиться
во вполне определенной связи с отдельными простыми делителями
D (на которые сами они делиться не могут); нечетные же числа,
которые могут быть представлены формой F, в некоторых случаях
будут иметь определенное отношение также и к числам 4 и 8,
именно, к числу 4, если D или===0, или == 3 (mod 4), и к числу 8,.
Деление порядков на роды 287
если D или==О, или = 2, или ==6 (mod 8)*. Отношение такого
рода к этим отдельным числам мы будем называть характером или
специальным характером формы F и выражать его следующим
образом: если формой F могут быть представлены только квадра-
квадратичные вычеты простого числа р, то мы будем придавать ей ха-
характер Rp, в противном случае — характер Np\ аналогично мы
будем писать 1, 4, если формой F не могут быть представлены
другие нечетные числа, кроме тех, которые == 1 (mod 4), из чего
тотчас же вытекает, какие характеры будут выражаться обозначе-
обозначениями 3, 4; 1,8 ;3, 8; 5, 8; 7, 8. Наконец, формам, которыми могут
представляться только такие нечетные числа, которые по модулю
8 илие=1, или ==7, мы будем придавать характер 1 и 7, 8, из
чего само собой получается значение характеров 3 и 5, 8; 1 и 3, 8;
5 и 7, 8.
Отдельные характеры заданной примитивной формы (а, Ъ, с)
с определителем D всегда могут быть определены по крайней мере
по одному из чисел а, с (которые оба, очевидно, представляются этой
формой). Действительно, если р — простой делитель D, то одна
из чисел а, с, очевидно, не будет делиться на р\ в самом деле, если
бы оба они делились на ру то р входило бы также и в b2(=D+ ас),
а значит и в Ь, т. е. форма (а, Ъу с) не была бы примитивной. Анало-
Аналогичным образом, в тех случаях, когда форма (а, Ъ> с) имеет опре-
определенное отношение к числу 4 или 8, то по крайней мере одно из
чисел а, с, очевидно, будет нечетным, а по нему и можно будет
узнать это отношение. Так, например, для формы G, 0, 23) по отно-
отношению к числу 23 из числа 7 получается характер 7V23; по от-
отношению к числу 7 из числа 23 для этой же формы получается ха-
характер Rl\ наконец, характер этой формы по отношению к числу 4,
именно, 3,4, может быть получен как из числа 7, так и из числа 23.
Все числа, которые могут быть представлены какой-нибудь фор-
формой F, содержащейся в классе К> представимы также и всякой дру-
другой формой этого класса, и потому, очевидно, отдельные харак-
характеры формы F будут принадлежать и всем остальным формам этого
класса, вследствии чего их можно рассматривать как характеры
* Для определителей, делящихся на 8, отношение их к числу 4 можно не
рассматривать, так как оно уже определяется отношением к числу 8.
288 Раздел V (п. 231)
всего класса. Поэтому отдельные характеры любого заданного при-
примитивного класса можно узнать по его представителю. Противопо-
Противоположные классы всегда будут иметь все характеры одинаковые.
231
Совокупность всех специальных характеров заданной формы или
класса образует полный характер этой формы или класса. Так,
например, полный характер формы A0, 3, 17) или всего представ-
представляемого ею класса есть 1, 4; N7; iV23. Подобным же образом пол-
полный характер формы G, —1, 17) есть 7, 8; i?3; N5; действительно,
специальный характер 3, 4 в этом случае отбрасывается, так как
уже содержится в характере 7, 8. На этом мы основываем деление
всего порядка собственно примитивных (если определитель отрица-
отрицателен, то положительных) классов с данным определителем на не-
несколько различных родов, именно, все классы, которые имеют один
и тот же полный характер, мы причисляем к одному роду, а классы,
полные характеры которых различны,— к различным родам. От-
Отдельным же классам мы придаем тот полный характер, который
имеют содержащиеся в них отдельные формы. Так, например, для
определителя — 161 получается шестнадцать собственно прими-
примитивных положительных классов, которые следующим образом раз-
разбиваются на четыре рода:
1,
1,
з,
з,
характер
4; R1; 7?23
4; N1; 7V23
4; R1; N22,
4; N7; R23
A, 0, 161)
E, 2, 33),
G, 0, 23),
C, 1, 54),
зормы, представляющие классы
, B, 1,
E, -2,
(И, 2,
C, -1
81),
33),
15),
, 54)
(9,
(Ю,
(И,
,F,
1,
3,
1
18),
17),
-2, 15
, 27),
(9,
(Ю,
-1,
-з,
», A4, 7,
F,
—1,
18)
17)
15)
27).
Относительно числа различных полных характеров, которые воз-
возможны a priori, можно заметить следующее.
I. Если определитель делится на 8, то по отношению к числу
8 возможны четыре различных специальных характера; число 4
Деление порядков на роды 289
не дает никаких специальных характеров (замечание к предыду-
предыдущему пункту). Кроме того, по отношению к каждому из отдельных
нечетных простых делителей числа D имеется по два характера.
Если поэтому число таких делителей равно т, то всего будет
2т+2 различных полных характеров (где нужно положить т = О,
если D есть степень числа 2).
II. Если определитель D не делится на 8, но делится на 4, и,
кроме того, на т нечетных простых чисел, то всего имеется 2т+1
различных полных характеров.
III. Если определитель D четен, но не делится на 4, то он
или ==2, или == 6 (mod 8). В первом случае имеется два специаль-
специальных характера по отношению к числу 8, именно, 1 и 7, 8; 3 и
5, 8; во втором случае -—столько же. Если поэтому положить коли-
количество нечетных простых делителей числа D равным т, то всего
будет 2m+1 различных полных характеров.
IV. Если D нечетно, то оно или = 1, или ^ 3 (mod 4). Во вто-
втором случае по отношению к числу 4 имеется два различных ха-
характера, в то время как в первом случае подобное соотношение
в полный характер не входит. Если поэтому т обозначает то же,
что и раньше, то в первом случае имеется 2т, а во втором—2W+1
различных полных характеров.
Впрочем, нужно заметить, что отсюда никак не следует, что
в действительности имеется столько же родов, сколько возможно
различных характеров. В нашем примере только половине из них
действительно соответствуют классы или роды, в то время как не
существует положительных классов, имеющих характеры 1, 4; i?7;
iV23 или 1, 4; Nl\ i?23 или 3, 4; i?7; i?23 или 3, 4; iV7; iV23.
Об этом очень важном вопросе ниже будет сказано подробнее.
Форму A,0,—D), которая, без сомнения, является простей-
простейшей среди всех форм с определителем Z), мы будем отныне на-
называть главной формой, весь класс, в который входит эта форма,—
главным классом, и, наконец, весь род, в котором содержится
главный класс,—главным родом. Поэтому нужно делать различие
между главной формой, формой из главного класса и формой из
главного рода; точно так же — между главным классом и классом
из главного рода. Мы будем придерживаться этих наименований
290
Раздел V (пп. 232-233)
всегда, даже и тогда, когда для какого-нибудь определителя
случайно не будет других классов, кроме главного класса или
других родов, кроме главного рода, как это, например, по боль-
большей части бывает, если D есть положительное простое число вида
232
Хотя то, что было изложено о характерах форм, первоначально
служило только той цели, чтобы обосновать на этом подразделение
положительного собственно примитивного порядка, ничто не ме-
мешает нам распространить это также и на отрицательные или несоб-
несобственно примитивные формы и классы, и подразделить по такому же
принципу на роды как положительный несобственно примитивный
порядок, так и отрицательный собственно примитивный порядок
и отрицательный несобственно примитивный порядок. Так, напри-
например, после того как собственно примитивный порядок форм с опре-
определителем 145 разложен на следующие два рода:
Л5; Л29
7V5; 7V29
A, 0, -145), E, 0, -29)
C, 1, -48), C, -1, -48),
то и несобственно примитивный порядок подобным же образом раз-
разбивается на два рода:
Л5; Л29
7V5; N29
D, 1, -36), D, -1, -36)
B, 1, -72), A0, 5, -12),
или, подобно тому как положительные классы форм с определителем
—129 распадаются на четыре рода:
1, 4, №; Й43
1, 4; iV3; iV43
3, 4; ЯЗ; W43
3, 4; iV3; i?43
A, 0, 129), A0, 1, 13), A0, -1, 13)
B, 1, 65), E, 1,26), E, -1, 26)
C, 0, 43), G, 2, 19), G, -2, 19)
F, 3, 23), (И, 5, 14), (И, -5, 14),
Деление порядков на роды 291
так и отрицательные классы делятся на четыре рода:
3, 4; N3; iV43
3, 4; ЯЗ; Я43
1, 4; N3; Я43
1, 4; i?3; N43
(_1, о, -129), (-10, 1, -13), (-10, -1, -13)
(_2, 1, -65), (-5, 1, -26), (-5, -1, -26)
(_3> 0, -43), (-7, 2, -19), (-7, -2, -19)
(_6, 3, -23), (-11, 5, -14), (-11, -5, -14).
Так как, однако, система отрицательных классов всегда подобна
системе положительных классов, то в большинстве случаев было бы
излишне рассматривать первую отдельно. А то, как несобственно
примитивный порядок может быть сведен к собственно примитив-
примитивному, мы покажем позднее.
Наконец, что касается произведенных порядков, то для их под-
подразделения новых правил не требуется. Действительно, так как
каждый произведенный порядок получается из некоторого при-
примитивного порядка (меньшего определителя) и отдельные классы
первого возникают из отдельных классов второго, то очевидно, что
подразделение произведенного порядка может быть выведено из
подразделения примитивного порядка.
233
Если (примитивная) форма F = (а, Ь, с) обладает тем свойством,
что могут быть найдены два числа g, /г, для которых g2 = a
gh==b, h2 == с по некоторому заданному модулю т, то мы будем
называть эту форму квадратичным вычетом числа т, a gx -\- hy
— значением выражения У ах2 -f- 2bxy -\- су2 (mod m) или, короче, (gr h)
—значением выражения У (а, Ь, с), или УF (mod m). Более общо, если
имеется взаимно простой с модулем т множитель М с тем свой-
свойством, что
h? = cM (mod m),
то мы будем говорить, что М(а, b, с) или MF есть квадратичный
вычет числа т, и (g,h) — значение выражения ]/гМ(а,Ь,с), или
YMF {то&т). Так, например, форма C,1,54) является квадра-
квадратичным вычетом числа 23, и G, 10) есть значение выражения
292 Раздел V (п. 233)
J/"C, I, 54) (mod 23): аналогично, B, — 4) есть значение выражения
у 5 A0, 3,17) (mod 23). Польза этих определений будет показана
позднее; здесь мы хотим только вывести следующие теоремы.
I. Если М (а, Ь, с) — квадратичный вычет числа т, то он будет
входить в определитель формы (а,Ь,с). Действительно, если (gy h)
есть значение выражения У~М (а, Ь, с) (mod m) или
g2 = аМ, gh == ЬМ, h2 == сМ (mod m),
то Ь2М2— асМ2 = 0, т. е. F2 — ас) М2 делится на т. Так как,
однако, М предполагается взаимно простым с т, то и Ь2 — ас
будет делиться на т.
II. Если М(а,Ъ,с) — квадратичный вычет числа т, и т или
простое число, или степень простого числа, скажем, равно /?^, то
специальный характер формы (а,Ъ,с) по отношению к числу р
будет Rp или Np, в зависимости от того, является ли М вычетом
или невычетом по модулю р. Это сразу следует из того, что как
аМ, так и сМ есть квадратичный вычет по модулю т или р, и
по меньшей мере одно из чисел а, с не делится на р (п. 230).
Аналогичным образом, если т = 4 (в то время как все осталь-
остальное остается без изменений), то специальным характером формы
(а,Ь,с) будет 1, 4 или 3, 4, в зависимости от того, М = 1 или = 3;
далее, если т = 8 или более высокой степени числа 2, то специаль-
специальным характером формы (а,Ь,с) будет 1, 8; 3, 8; 5, 8; 7, 8, если со-
соответственно М = 1; 3; 5; 7 (mod 8).
III. Обратно, если т — простое число или степень простого
числа, скажем, р^Л причем р входит в определитель Ъ2 — ас и,
далее, М является вычетом или невычетом по модулю р в зависи-
зависимости от того, каков характер формы (a,btc) по отношению к р}
Rp или Np, то М(а,Ь,с) будет квадратичным вычетом числа т.
Действительно, если а не делится на р, то аМ будет вычетом по
модулю р, а потому и по модулю т\ если g — значение выраже-
выражения ]/~аМ (modm), h—значение выражения 6g/a(modm), то будет
g1 = аМ, ah = bg, и потому
agh == bg2 = аЪМ и gh = ЬМ;
Деление порядков на роды 293
наконец>
ah2 = bgh = Ъ2М = Ъ2М — (Ь2 — ас)М = асМ,
и тем самым h2 = сМ, т. е. (g, h) есть значение выражения
YМ (а,Ъ,с). Если же а делится на ту то с, очевидно, не делится;
отсюда легко видно, что мы придем к тому же результату, если
возьмем для h значение выражения J^cM fmodm), а для g — значе-
значение выражения Ыг/ с (mod m).
Аналогичным образом доказывается, что если т = 4 и входит
в Ъ2— ас, и если, далее, М==\ или = 3, в зависимости от того,
является ли специальным характером формы (а, Ъ, с) 1,4 или 3,4,
то М (а, Ь, с) будет квадратичным вычетом числа т. Точно так
же, если т = 8 или является более высокой степенью числа 2,
на которую делится Ъ2 — ас, и если, далее, предполагается
М==1; 3; 5; 7 (mod 8) в зависимости от того, чего требует спе-
специальный характер формы (а, Ъ, с) по отношению к числу 8, то
М(а,Ъ,с) есть квадратичный вычет числа т.
IV. Если определитель формы (а, Ъ, с) равен D и М (а, Ь, с) есть
квадратичный вычет числа D, то по числу М могут быть сразу
определены все специальные характеры формы (а, Ь, с) как по
отношению к отдельным нечетным простым делителям D, так и по
отношению к числу 4 или числу 8 (если они входят в D). Так,
например, так как 3 B0, 10, 27) есть квадратичный вычет числа
440, именно, значением КЗB0, 10, 27) (mod 440) является A50,9),
и 3iV5, 3i?ll, то характеры формы B0, 10, 27) следующие: 3, 8;
No] i?ll. Только специальные характеры по отношению к числам
4 и 8, если последние не входят в определитель, не находятся ни
в какой обязательной связи с числом М.
V. Обратно, если взаимно простое с D число М содержит в себе
все специальные характеры формы (а, Ь, с) (за исключением харак-
характеров по отношению к числам 4 и 8, если они не входят в D),
то М(а,Ь,с) будет квадратичным вычетом числа D. Действительно,
из III получается, что если число D представлено в виде
+ ^4а5 CY . .. , где А, В, С, ... —различные простые числа, то
М(а,Ь,с) является квадратичным вычетом отдельных чисел А01, В^,
Су , ... Если поэтому Bt, W) — значение выражения УМ (а,Ь,с)
294 Раздел V (п. 233)
по модулю А*, B5, 93') — значение этого же выражения по модулю
В^, ((?, <?') — по модулю CY и т. д., и числа g, h определены так,
что g == 21, S3, 6, . . . , h = 31', 23', 6', . .. соответственно по модулям
А*, В^, Су, . . . (п. 32), то легко видеть, что g2 = aM, gh — ЪМ,
h2 == сМ по всем модулям А*у В^, Ст, . . . , а потому и по модулю D,
который является их произведением.
VI. На основании этого числа, подобные М, называются ха-
характеристическими числами формы (а, Ъ, с), и, согласно V, несколько
таких чисел может быть найдено без труда, если известны все
специальные характеры этой формы; простейшие из них в боль-
большинстве случаев легче всего находить посредством проб. Очевидно,
что если М — характеристическое число заданной примитивной
формы с определителем D, то все числа, которые сравнимы с М
по модулю D, также будут характеристическими числами этой же
формы; далее, формы, содержащиеся в одном и том же классе,
а также в различных классах одного и того же рода, имеют одни
и те же характеристические числа, откуда следует, что каждое
характеристическое число заданной формы может быть придано
также целому классу или целому роду; наконец, 1 всегда есть
характеристическое число главной формы, главного класса и глав-
главного рода, т. е. каждая форма из главного рода является квадра-
квадратичным вычетом своего определителя.
VII. Если (g,h) есть значение выражения }/М (а, Ь, с) (modm),
и g' = g, Ы = й (mod/га), то и {g',ti) будет значением этого же
выражения. Подобные значения могут рассматриваться как экви-
эквивалентные^ если же (g, /г), (g',ti) — такие значения выражения
УМ (а, Ь, с) (mod m), что не имеет места одновременно gf = g,
К = ft(modm), то эти значения нужно считать различными. Оче-
Очевидно, что если (g,h)(—значение такого выражения, то таковым
будет и (—g,—/г), и легко показать, что эти значения всегда
различны, кроме случая т = 2. Точно так же легко показать, что
выражение УМ(а,Ь,с)(тод.т) не может иметь больше различных
значений, чем два (противоположных), если т равно или
нечетному простому числу, или степени нечетного простого числа,
или числу 4; если же т = 8 или является более высокой степенью
числа 2, то всего значений будет четыре. Отсюда при помощи VI
Композиция форм 295
легко получается, что если определитель D формы (а, 6, с) равен
+ 2^АЛВ^ . ., где А, В, . . . обозначают различные нечетные простые
числа, количество которых пусть равно п, и если М — характе-
характеристическое число этой формы, то всего имеется или 2П, или 2n+1,
или 2ni~2 различных значений выражения УМ (а, 6, с) (mod Z)), в за-
зависимости от того, [л < 2 или = 2, или > 2. Так, например, полу-
получается шестнадцать значений выражения 1/7A2, 6,—17) (mod 240),
именно, (+18, +11), (+18, +29), (+18, +91), (+18, +109),
(±78, +19), (±78, +59), (+78, +61), (+78, +101). Подробного
доказательства мы ради краткости не даем, так как для дальнейшего
оно не является особенно необходимым.
VIII. Наконец, заметим, что если D — определитель двух экви-
эквивалентных форм (a,b,c), (a',b',c'), M — их характеристическое
число, и первая переходит во вторую при подстановке а, C, ^, 8,
то при этом из каждого значения выражения j/М (а, 6, с), напри-
например, из (g, /г), получается значение выражения ~]/~М (а', Ь'', с'), именно,
(а? + Т^> $8 + Щ- Доказательство каждый может провести без
труда.
О композиции форм
234
После того как мы предпослали все это о разбиении форм на
классы, роды и порядки и изложили общие свойства, которые
непосредственно получаются из этих подразделений, мы переходим
теперь к другому, очень важному и до сих пор еще никем не
затрагивавшемуся вопросу, именно, к композиции форм. В начале
этого исследования мы, чтобы не прерывать в дальнейшем сплошно-
сплошного ряда доказательств, сразу же дадим следующую лемму.
Лемма. Если имеется четыре ряда целых чисел:
которые состоят из одинакового количества [именно, из п + 1) чле-
членов и обладают тем свойством, что
cdf — dc', cd" — dc\ ..., c'd" — d'c\ ...,
296 Раздел V (п. 234)
соответственно равны
k(ab'-ba'), к{аЪ" — Ъа"),. . . ук{а'Ъ"— Ъ'а"),
или что вообще
где к есть заданное целое число, и X, [х — какие-нибудь различные между
собой целые числа между 0 и п включительно, большее из которых
пусть [х*, м, кроме того, все a(XN(fX) — b{X)a{[L) не имеют общего дели-
делителя, то могут быть найдены четыре таких целых числа <х, р, ^, 8,
что
оса + $Ь = с, аа' + $Ъ' = с!, aa" + §Ъ" = с", . . .,
Та + ЬЬ = d, Та' + 86' = dr, ^а" + W = d",...,
или вообще
aa(v) + 8fe(v) = c(v\ Ta(v) + S6(v) = rf(v).
Если это сделано, то
Так как по предположению числа аЪ' — Ъа', аЪ" — Ъа", . . .
..., а'Ъ" — Ъ'а!', . . . (количество которых равно п(п + 1)/2) не имеют
общих делителей, то может быть найдено столько же других целых
чисел, таких, что если первые перемножить с соответствующими
вторыми, то сумма произведений 6удет равна 1 (п. 40). Эти множи-
множители будут обозначаться через @, 1), @, 2), . . , , A, 2), . . . , вообще
множитель числа а^Ъ^ — Ъ^а^—через (X, (л), так что
(Знаком V мы обозначаем сумму всех значений последующего
выражения, которые получаются, если X, [л придавать все раз-
* При этом а рассматривается как а@* и Ъ — как &@). Отметим, что такое
же равенство, очевидно, выполняется, если X = \х или X > jx.
Композиция форм 297
личные значения между Оип, для которых [/,;> X.) Если положить
затем
= а, ^ (*, V) («(X)^(!i) - c(X)«(rt) = P.
= Tl 2 (X, ц) (Л((*> - Л<¦*>) = 8,
то эти числа а, C, y» 8 будут обладать требуемыми свойствами.
Доказательство. I. Если v обозначает какое-нибудь целое число
между 0 и п, то
) = 2 (\ V) (c(XN(|1)c(v) -
= 1 ^ (X, ц)
Аналогичным подсчетом находим
II. Так как тем самым
то
и аналогично
и из этих формул значения а? [В, у? S могут быть найдены намно-
намного легче, если только числа X, [х взяты такими, что а^Ы^ —
— ?(Х)а(ц) не равно нулю, что заведомо возможно, так как по усло-
условию у всех чисел а^ЬМ—Ь^а^ нет общих делителей, и потому
все они одновременно не могут быть равны 0. Из этих равенств
298 Раздел V (п. 235)
получается, если первое перемножить с четвертым, а второе с треть-
третьим и вычесть, что
и потому обязательно
а8 — р^ = А-
235
Если форма
ЛХ2 + 2BXY + CY2 = F
переходит в произведение двух форм
ах2 + 2Ьху + су2 = /, а'х'2 + Zb'x'y' + с1 у'2 = f
при подстановке вида
X = рхх' + р'ху' + р"ух'+ р"уу\
Y - qxx' + q'xyf + q"yx' + q"yyl
(что мы для краткости всегда в дальнейшем будем выражать так:
если F переходит в //' при подстановке р, р', р'\ р'"\ q, q', q", qrrr)*f
то мы будем говорить просто, что форма F преобразуема в //'
если, кроме того, это преобразование таково, что шесть чисел
pq'-qp', pq"-qp", pq" - qf, P'q"-q'P", pY'-q'p'", p"q'"-q"p'"
не имеют общих делителей, то мы будем называть форму F состав-
составленной (скомпонированной) из форм /, /'.
Мы начнем наше исследование с самого общего предположения,
именно, что F переходит в //' при подстановке р, р', р", р"\ q,
q\ q", q"', и посмотрим, что отсюда следует. Очевидно, что этому
предположению будут полностью эквивалентны следующие девять
* Таким образом, при этом обозначении принимается во внимание поря-
порядок расположения коэффициентов р, рг,... и форм /, /'. Но легко видеть, что
если изменить порядок расположения форм /, /' на обратный, то коэффициенты
р', q' поменяются местами с р", q"', а все остальные коэффициенты останутся
на месте.
Композиция форм 299
равенств (т. е. если эти равенства имеют место, то при названной
подстановке F будет переходить в //', и обратно):
[1] Ар* + 2Bpq + Cq2 = аа',
[2] Ар'2 + 2Bp'q' + Cq'2 = ас',
[3] Ар"* + 2Bp"q" + Cq"* = са',
[ 4 ] Ар' + 2Bp'"q'" + Cq'=cc',
[5] Арр' + В (pq' + qp') + Cqq' = ah',
[6] Арр" + В (pq" + qp") + Cqq" = ba',
{7] Ap'p'" + В (p'q'" + q'p'") + С?У" = be',
[8] V/" + В (p"q" + q'p') + С q"q'" = cb',
[9] A (pp" + p'p") + В (pq'" + qp'" + p'q" + q'p") + С (qq'" + q'q") = 2bb',
Пусть определители форм F, /, /' соответственно равны D, d,
d\ наибольшие общие делители чисел А, 2В, С; а, 2Ь, с; а', 2Ъ',
с — соответственно М, т, т! (которые мы будем предполагать взя-
взятыми положительными); далее, определим шесть таких целых чи-
чисел 21, 95, ?, ЭГ, 23', ?', что
наконец, обозначим числа
ря' — чр\ ря" — чр\ рят — qpw> p'q* — я'р\ p'qw — q'p'", р"<Г — ?V
соответственно через Р, Q, i?, S, T, U, а их наибольший общий
делитель, взятый положительным, — через к. Если положить тогда
[Ю] Аррт + В (pqm + qpr") + Cqq'" = W + A,
то, согласно равенству [9], будет
[И] Ару + В {p'q" + q'p") + Cq'q" = bb' - A.
300 Раздел V (п. 235)
Из этих одиннадцати равенств (с [1] по [И]) мы выводим следую-
следующие новые равенства *:
[12]
[13]
[14]
[15]
[16]
[17]
[18]
1191
[20]
[21]
122]
[23]
DP2 — d a2,
DP(R — S) = 2d'ab,
DPU = d'ac — (A2 — dd'),
D(R — Sf = Ы'Ъ2 + 2 (Д2 — dd'),
D(R — S)U = 2d'bc,
DU2 = d'c*,
DQ* = da'2,
DQ (R + S) = 2da'b',
DQT = da'c' — (Д2 — dd'),
D{R + SJ = ЫЪ -f 2 (Д2 — dd'),
D(R + S)T = 2db'c',
DT2 = dc'2.
Из них снова получаются следующие два:
0 = (А2 — dd'J — 2d'ac (A2 — dd'),
именно, первое из [12]-[15] — [13]-[13], а второе из [14] -[14] —
— [12]-[17], а отсюда легко увидеть, что обязательно А2 — dd1 = 0
независимо от того» равно нулю а или нет **. Мы предположим
поэтому, что в правых частях равенств [14], [15], [20], [21] выра-
выражение А2 — dd' равно нулю.
Если положить теперь
* Эти равенства получаются так: [12] из [5]2 — [1]-[2]; [13] из [5]-[9] —
-[1].[7]-[2].[6]; [14] из [10].[И]-[6].[7]; [15] из [5].[8] + [5].[8] + [10]» -
-[11]2-[1].[4]-[2].[3]-[6].[7]-[6].[7]; [16] из [8].[9] - [3].[7] - [4].[6];
[17] из [8]2 — [3]-[4]. Вывод остальных шести равенств получается таким же
образом, если только поменять местами равенства [2], [5], [7] соответственно
с [3], [6], [8], а остальные равенства [1], [4], [9], [10], [11] оставить на месте,
именно, [18J получается из [б]2 —[1]-[3] и т. д.
** Этот вывод равенства А2 = dd' достаточен для нашей цели; мы могли
бы указать более изящный, но слишком длинный способ для вывода равенства
0 = (А2 — dd'J непосредственно из равенств [1] — [И].
Композиция форм 301
%Р + 35 (R — S) + &U = тп',
»'(? + S5'(i? + S) + ST - iw'n
{причем нужно заметить, что п, п' могут быть и дробными, хотя
тп', т'п обязательно целые), то из равенств с [12] по [17] легко
получается, что
Dm2n'2 = d' Cta + 2356 + ScJ = d'm2,
и аналогично из равенств с [18] по [23] —
Dm'2n2 = d CtV + 2®'Ь' + S'c'J = dm'2.
Поэтому d = Dn2, d'=Dn'2, откуда мы получаем в качестве перво-
первого следствия: определители форм F, /, /' обязательно относятся
один к другому кап квадраты,—и в качестве второго следствия:
D всегда входит в числа dm'2, d'm2. Отсюда вытекает, что D, d, df
имеют одинаковые знаки, и что в произведение //' не преобразуема
никакая форма, определитель которой больше, чем наибольший
общий делитель чисел dm'2, d'm2,
Если умножить равенства [12], 113], [14], а также равенства [13],
115], [16] и [14], [16], [17] соответственно на 91, 35, S, сложить
каждый раз три произведения, суммы разделить на Dmn\ и на-
написать Dn'2 вместо df, то мы получим
р = an', R — S = 2bri. U = cn'.
Аналогичным образом получается, если равенства [18], [19], [20],
далее [19], [21], [22] и [20], [22], [23] умножить соответственно на
Ш', 35', <?', то
Q = а'п, R + S= 2Ь'п, Т = с'п.
Отсюда получается в качестве третьего следствия: числа а, 26, с
пропорциональны числам Р, R — S, U, и если отношение первых ко
вторым положить равным 1:п', то п' есть квадратный корень из
d' ID) точно так же числа а', 2Ь', с' имеют одинаковые отношения к
Qf R -\- S, Т, и если положить их равными 1 : п, то п есть квад-
квадратный корень из d/ D.
Величины 72, п' могут быть как положительными, так и отри-
отрицательными квадратными корнями из d/D, d' /D, на чем мы
302 Раздел V (п. 235)
будем основывать одно различие, которое на первый взгляд кажется
бесцельным, но польза которого в дальнейшем станет ясной. Именно,
мы будем говорить, что при преобразовании формы F в //' форма /
берется прямо, если п положительно, и обратно, если п отрица-
отрицательно, и аналогично /' берется прямо или обратно в зависимости
от того, положительно п' или отрицательно. Если же добавляется
еще условие, что к = 1, то форма F называется составленной или
из обеих форм /, /' прямо, или из обеих обратно, или из / прямо,
а из /' обратно, или из / обратно, а из /' прямо, в зависимости
от того, положительны ли оба числа п, п', или оба отрицательны,
или первое положительно, а второе отрицательно, или первое от-
отрицательно, а второе положительно. Впрочем, каждый может легко
убедиться, что эти отношения не зависят от порядка, в котором
следуют формы /, /' (ср. первое замечание * к этому пункту).
Далее заметим, что наибольший общий делитель чисел Р, Q,
7?, S, Т, U, именно, к, входит в числа тп', т'п (как это выте-
вытекает из выведенных выше для этих чисел значений), и потому
квадрат числа к входит в т2п'2, т'2п2, и Dk2— в d'm2, dm'2. Но и
обратно, каждый общий делитель чисел тп', т'п будет входить в к.
Действительно, пусть е — такой делитель, который, очевидно, бу-
будет входить также в числа an', 2Ъп', сп', а'п, 2Ъ'п, с'п, т. е. также
в числа Р, 7?— S, U, Q, 7? + <?, T и, следовательно, также в 27?
и 2S. Если бы теперь чцсло 2R / е было нечетным, то должно бы-
было бы быть нечетным и число 2S / е (так как сумма и разность
являются четными числами), и тем самым было бы нечетным и их
произведение. Но это произведение равно -\ (Ь'2п2 — Ь2п'2) =
= —г (d'n2 + а'с'п2 — dn'2 — асп'2) = —^ {а'с'п2 — асп'2), и поэтому чет-
четно, так как е входит в а'п, cfn, an', сп'. Поэтому 27? /е обязательно
четно, и потому 7?, а также и S делятся на е. Так как тем самым
е входит во все шесть чисел Р, Q, R, S, T, U, то оно будет вхо-
входить также и в их наибольший общий делитель к. Отсюда следует,
что к есть наибольший общий делитель чисел тп', т'п, откуда
легко видеть, что Dk2 есть наибольший общий делитель чисел dm'2,
* Стр. 298.— Прим. ред.
Композиция форм 303
d'm2. Это четвертое следствие. Очевидно, таким образом, что если
форма F составлена из / и /', то D будет наибольшим общим де-
делителем чисел dm'2 и d'm2, и обратно, и это свойство может быть
взято также за определение составленной формы. Форма, состав-
составленная из форм /, /', имеет поэтому наибольший определитель среди
всех форм, которые преобразуемы в произведение //'.
Прежде чем мы сможем продолжать дальше, мы должны сна-
сначала точнее определить значение Д, которое, как мы показали,
равно }/~dd' = Y~D2n2n'2, но знак которого до сих пор еще не был
определен. Для этой цели мы из основных равенств с [1] по [11]
выведем равенство DPQ = Ааа' (которое получается из [5] [6] —
— [1] • [11]), и тем самым Daa'nn' — каа', откуда, если ни одно из
чисел а, а' не равно нулю, следует А = Dnn'. Но точно таким же
образом из основных равенств могут быть выведены восемь дру-
других равенств, у которых слева будет Dnn', а справа А, умножен-
умноженное на 2а6', ас', 2Ьа', Abb', 2Ьс', са', 2сЬ', ее' *, откуда, поскольку
ни все а, 26, с, ни все а', 26', с', не могут быть равны 0, легко полу-
получается, что во всех случаях А = Dnn', и потому А имеет тот же
знак, что и Dy d, d', или противоположный в зависимости от того,
имеют ли п, п' одинаковые или противоположные знаки.
Далее, заметим, что числа аа', 2аЪ', ас', 26а', 466', 26с', са', 2cb', ее',
266' -f- 2А, 266' — 2А все делятся на mm'. Для девяти первых это
ясно само собой, а для двух остальных может быть доказано по-
подобно тому, как выше показывалось, что R и S делятся на е.
Именно, очевидно, что 466' -f- 4Д и 466' — 4А делятся на mm' (так
как 4А =]fl6dd' и Ad делится на т2, Ad' — на т'2, и тем самым
I6dd' делится на т2т'2 и 4А — на mm'), и разность частных есть
четное число; но легко показать, что произведение частных тоже
четно, откуда следует, что каждое из этих частных четно, и как
266' + 2А, так и 266' — 2А делятся на mm'.
Из одиннадцати основных равенств теперь легко выводятся сле-
следующие шесть равенств:
АР2 = aa'q'2 — 2ab'qq' f ac'q2,
* Вывод, который читатель легко может найти сам, мы здесь ради краткости
должны опустить.
304 Раздел V (п. 235)
AQ2 = aa'q"* — 2ba'qq" + ca'q\
AR2 = aafq"'2 — 2 {bb' + A) qqm + cc'q2,
AS2 = ac'q — 2 (W — A) q'q" + ca'q'2,
AT2 = ac'q"'2 — Ihc'q'q" + cc'q'2,
AU2 = ca'q"'2 — 2cb'q"q"' + cc'q.
Поэтому все величины АР2, AQ2, . . . делятся на mm', откуда, так
как к2 есть наибольший общий делитель чисел Р2, Q2, R2, . . . ,
легко следует, что и А к2 делится на mm'. Если же вместо а, 2&, с,
а', 2Ь\ с' подставить их значения Р /п\ . . . или (pqr — qpf) /' п\ ... ,
то эти равенства перейдут в шесть других, у которых справа бу-
будут стоять произведения величины (q'q" — qq")/nnr и чисел Р2, Q2,
i?2, . .. Очень простую выкладку мы предоставляем читателю.
Отсюда (так как не могут быть одновременно равны 0 все величины
Р2, Q2, . ..) получается Ann' = q'q" — qq",
Аналогичным образом из основвых равенств выводятся шесть
других равенств, которые отличаются от предыдущих только тем,
что вместо А всюду стоит С, а вместо q, q\ q", q"f соответственно
p, p\ p'\ p'", и которые мы ради краткости не выписываем. Из них
таким же образом следует, что Ск2 делится на mm', и Спп' =
= рУ-ррт-
Наконец, из того же источника вытекают следующие шесть ра-
равенств:
ВР2 = — aa'p'q' -f ab' (pq' + qpf) — ac'pq,
BQ* = — aa'p"qf' + ba* {pqrf + qf) — ca'pq,
BR2 = — aafp"'qm + (bb' + A) (pqm + q'p"r)—cc'pq,
BS2 =—ac'p"q" + {bb' — A) {p'q" + q'f) — ca'p'q';
ВТ2 = — ac'f'q'" + be' {p'q'" + q'pm) — cc'p'q\
BU2 = — ca'f'q'" + cb' {p"q" + q"p") — cc'fq",
из которых так же, как и раньше, следует, что 2Вк2 делится на
mm', и 2Впп' = pqrn + qf — p'q" — q'p\
Так как теперь Ак2, 2Вк29 Ск2 делятся на mm', то легко видеть,
что и Мк2 должно делиться на mm'. Но из основных равенств по-
получается, что М входит в аа', 2ab'9 ас', 2ba', Abb', 2bc', са', 2сЪ', ее'
и потому также в am', 2bm!, cm! (которые являются наибольшими
общими делителями соответственно трех первых, трех средних
Композиция форм 305
и трех последних из этих девяти чисел), и, наконец, и в произ-
произведение mm', которое есть наибольший общий делитель этих послед-
последних трех величин. Поэтому в том случае, когда F составлена из
форм /, /', т. е. к = 1, обязательно должно, очевидно, быть М = mm!
Это — пятое следствие.
Если наибольший общий делитель чисел А, Ву С равен Ш, то он
или равен М (в случае, когда форма F собственно примитивна или
произведена из собственно примитивной формы), или равен М/2
(в случае, когда форма F несобственно примитивна или произведена
из несобственно примитивной формы). Если, аналогично, обозна-
обозначить наибольшие общие делители чисел а, Ь, с; а', Ь', с' соответст-
соответственно через ш, ш', то тили^ттг, или = т?г/2, ит'или=т',или = 7п72.
Но теперь, очевидно, т2 входит в d, m'2— в d!, и потому m2m'2 вхо-
входит в dd' или А2 и mm' — в А. Поэтому из шести последних ра-
равенств для ВР2, .. . следует, что mm' входит в Вк2, и потому (так
как оно входит и в Ак2 шСк2) также и в 9№. Следовательно, если F
составлена из /, /', то mm' входит в 3R. Если поэтому в этом слу-
случае каждая из форм /, /' собственно примитивна или произведена
из собственно примитивной формы, или если mm' = mm' = М, то бу-
будет SR = М, т. е. F тоже будет формой этого же типа. Если же
при тех же предположениях или каждая из форм /, /', или по
крайней мере одна из них, например, /, несобственно примитивна
или произведена из несобственно примитивной формы, то из ос-
основных равенств следует, что аа', 2ab', ас', ba', 2bbr, be'', са'', 2cbf,
ее' и тем самым также am', Ът', cm', а, значит, и mm' = -7- mm' —
= -у М делятся на S9?. Следовательно, в этом случае обязательно
9R = -2"Af, т. е. и форма F или несобственно примитивна, или про-
произведена из несобственно примитивной формы. Это представляет со-
собой шестое следствие.
Наконец, заметим, что если не рассматривать п,п' как неизвест-
неизвестные, ни одно из которых не равно 0 (как это мы делали раньше),
а предполагать выполнение девяти равенств
ап' = Р, 2bn'=R — S, cn' = U9
a'n = Q, 2b'n = R-r-S, c'n = T,
306 Раздел V (п. 236)
Ann' = q'q" — qq\ 2Bnnr = pq" + qp" — p'q"— q'p", Cnn' = p'p" — ppm
(которые, так как нам часто придется на них ссылаться, мы обоз-
обозначим через О), то подстановкой легко может быть установлено,
что обязательно выполняются и основные равенства с [11 по [9],
или что форма (^4, 5, С) при подстановке р, р', р'\ р"'; g, q', q",
q" переходит в произведение форм (а, Ъ, с), (а', Ь\ с'), и что,
кроме того,
Вычисления, приводить которые здесь было бы слишком длинно
мы предоставляем усердию читателя.
23G
Задача. Пусть даны две формы, определители которых или равны,
ли по крайней мере относятся один к другому как квадраты двух
чисел; найти составленную из них форму.
Решение. Пусть (а, 6, с) = /, (а;, Ь', с') — f — компонируемые
формы, d, d! — их определители, наибольшие общие делители чисел
а, 26, с; а1\ 2Ь\ с' равны соответственно т, т\ и наибольший об
щий делитель чисел dm'2, d'm2, взятый с тем же знаком, что и
с?, d\ равен D. Тогда dm'2 (D, d'm2 / D будут взаимно простыми
положительными числами, а их произведение будет квадратом;
поэтому и сами они квадраты (п. 21). Следовательно, Y~d/D и
Y^d'/D — рациональные числа, которые мы положим равными п, п\
причем мы будем брать для п положительный или отрицательный
знак в зависимости от того, должна ли форма / входить в компо-
композицию прямо или обратно, и точно так же знак п' мы будем опре-
определять в зависимости от того, как должна входить в композицию
форма /'. Поэтому тп', т'п будут целыми взаимно простыми чис-
числами, в то время как гс, п' могут быть и дробными. После того,
как это сделано, заметим, что числа an', сп'', а'п, с'п, Ъп' + Ъ'п,
Ъп' — Ъ'п целые; в отношении первых четырех это ясно само собой
(так как an' = —тп' и т. д.), в отношении же двух остальных
это доказывается таким же образом, как выше в предыдущем.
Композиция форм
307
пункте показывалось, что R и S делятся на е. Возьмем теперь
четыре произвольных целых числа а, ?}',?Г, О!", с одним только
условием, чтобы в следующих равенствах (I) четыре стоящие слева
величины не были все равны 0 одновременно, и положим
й'ап' + ОГа'п + ?Г (Ьп' + b'n) = [лд,
— йап' + й'"с'п — Q" (Ьп' — Ъ'п) = fi.gr',
й'"сд' — &а'п + Q' (Ьп' — b'n) = y.q\
— ?J"cn' — U'c'n —
(I)
так что q, q , g", qrr будут целыми числами, которые не имеют
общих делителей, что достигается, если за [л взять наибольший
общий делитель четырех чисел, которые в этих равенствах стоят
слева. Тогда, согласно п. 40, могут быть найдены четыре таких
целых числа ф, ф', ф", ф", что
(И)
Если это сделано, то определим четыре числа р, р', р", р'" сле-
следующими равенствами:
ty'an' + %"а'п + У (bn' + b'n) = р,
- tyan' + ф'с'п — ф" (Ьп' — b'n) = р',
$'"сп' — tya'n + ф' (Ьп' — b'n) = р",
_ <§"сп' _ у'с'п _ щьп' + b'n) = рт.
Наконец, положим
q'q* — qqr" = Ann', pq'" + qp"' — p'q" ~ q'f = IBan',
p'p" — ppm = Cnn'.
Тогда числа А, В, С будут целыми, и форма (А, В, С) = F будет
составлена из форм /, /'.
Доказательство. I. Из равенств (I) без труда получаются сле-
следующие четыре равенства:
О = q'cn' - q"c'n — q"r (bnf —Ъ'п),
О = qcn' + q'rra'n — q" (bn' + b'n),
0 = q'"an' + qc'n — q' (bn' + b'n),
0 = q"an' — q'a'n — q (bn' — b'n).
(Ill)
308 Раздел V (п. 237)
II. Если мы теперь предположим, что целые числа 21, 95, 6, 2Г,
35', ?', 31, 31' определены так, что
Ша + 2356 + ?с - т,
то будет
Отсюда при помощи равенств (III) легко устанавливается, что
если положить
+ qs'SR) = q,
— д'"(ГЗг + / C531' — $'Э}) = q',
' + ^'3? — 9' (дз'31' — Э5Ш) = q",
' + д'езг + g (ЗЗЗГ + Э5'3?) - qw,
то имеют место равенства
(IV)
q'an' + ol'a'n + qw (bn' + Ь'п) = g,
— <\an' + qwc'fi — q" (bn' — b'n) = q\
fen' — c\afn + a' {bn1 — b'n) = q",
— <\"cn' — q'c'n — q (bn' + b'n) - q".
Если [x^l, то эти равенства не являются необходимыми, а
вместо них могут быть использованы равенства (I), которым они
вполне аналогичны. Если теперь из равенств (II), (IV) найдены
значения Ann', 2Bnn\ Спп' (т. е. числа q'q" — qq'",...), и то, что
взаимно уничтожается, отброшено, то оказывается, что останутся
слагаемые, являющиеся или произведениями целых чисел на пп\
или произведениями целых чисел на dn'2r или произведениями це-
целых чисел на d'n2, и что кроме того, все слагаемые 2Впп' будут
содержать сомножитель 2. Отсюда мы выводим (так как dn'2 = d'n2
dn'2 d'n2 i/~TTF \
и тем самым —- = —г = у da являются целыми числами), что
числа А, В, С целые.
Композиция форм 309
III. Если подставить значения р, р', р", рш из равенств (II), то
при помощи равенств (III) и равенства
Щ + У'д' + Уд" + ГУ = 1
легко установить, что
РЯ' - ЯР' = ™'. pq" - qpf" - p'q" + q'p" = 26л', jfqm - q''p'" - en',
pq» — qf = a!n, pqm — qpm + p'q" — q'p" = 2b'nf p'qm — q'p'" = c'n,
и эти равенства совпадают с первыми шестью из равенств О в пре-
предыдущем пункте; остальные же три имеют место уже по предпо-
предположению. Поэтому (ср. заключение предыдущего пункта) форма F
переходит при подстановке р, р\ р", p"r\ q, qr, q", q" в //', и оп-
определитель ее равен D, т. е. наибольшему общему делителю чисел
dm'2, d'm2] поэтому, в силу четвертого следствия предыдущего
пункта, форма F составлена из / и /'. Наконец, легко видеть, что
F составлена из /, /' так, как предписывалось, так как знаки чи-
чисел п, п' правильно определены уже сначала.
237
Теорема. Если форма F преобразуема в произведение двух форм
f,f и форма f содержит форму /", то F преобразуема также
в произведение форм /, /".
Доказательство. Сохраним для форм F, /, /' все обозначения
п. 235, и пусть форма /" равна (а", Ъ", с"), и форма /' переходит
в f при подстановке а, р, ч> &•
Тогда без труда видно, что F переходит в //" при подстановке
оф + тр'. Рр + о/, <ч>" + т/'= Р/>" + ?";
щ + те'. Ря + W, <*я" + т?'", К + V".
что и требовалось доказать.
Если для краткости обозначить коэффициенты ар + хр', |3/? + 6р',...
соответственно через ф, ф', ф", tyrrr; ?J, D/, D/, Uw, и число aS — $4—
через е, то из равенств Q, п. 235 легко устанавливаются равенства
310 Раздел V (пп. 238-239)
— ОГф" = сп1'е,
п + fc'n = а"п,
ф'?Г — ?>'$'" = с"дг,
ШУ — &Um = Ann'e,
— W" = Спп'е.
Если теперь обозначить определитель формы f через d", то е будет
квадратным корнем из d" / d'', причем положительным или отрица-
отрицательным в зависимости от того, содержит ли форма /' форму /"
собственно или несобственно.
Поэтому п'е есть квадратный корень из d" / D, откуда вытекает,
что девять предыдущих равенств полностью аналогичны равенствам
Q, п. 235, и что при преобразовании формы F в //" форма / берется
так же, как при преобразовании формы F в //', а форма /" берется
или так же, как /', или противоположным образом, в зависимости
от того, содержит ли /' форму /" собственно или несобственно.
238
Теорема. Если форма F содержится в форме F' и преобразуема
в произведение форм /, /', то и форма F' преобразуема в это же
произведение.
Доказательство. Если мы сохраним.для форм F, /, /' те же обо-
обозначения, что и выше, и предположим, что форма F' переходит
в F при подстановке а, C, ^, 6, то легко видеть, что F' при под-
подстановке
превращается в то же самое, во что превращается F при подста-
подстановке р, р', р", р'"\ g, q\ q", qm, т. е. что F' переходит при этой
подстановке в //'.
Кроме того, посредством вычислений, аналогичных вычислениям
предыдзчцего пункта, легко устанавливается, что F' преобразуема
в //' таким же образом^ что и F, если F' содержит форму F
собственно, и что} напротив, если F содержится в F' несобственно,
Композиция форм 311
то преобразования формы F в //' и формы F' в //' противопо-
противоположны по отношению каждой из форм /, /', т. е. что та из этих
форм, которая в одно из преобразований входит прямо, в другом
берется обратно.
Комбинируя настоящую теорему с теоремой предыдущего пункта,
мы получаем следующую более общую теорему.
Если форма F преобразуема в произведение //', и формы /, /'
-содержат соответственно формы g, g', а форма F содержится в
форме G} то G преобразуема в произведение gg'.
Действительно, по теореме этого пункта G преобразуема в //',
поэтому, по теореме предыдущего пункта, и в /g', и, по той же
теореме,— и в gg'. Далее ясно, что е ли все три формы /, /', G
¦содержат формы g, g', F собственно, то G преобразуема в gg'
таким же образом относительно g, g', каким относительно /, /'
преобразуема F в //'; что аналогично обстоит дело, если первые
три формы содержат последние три несобственно; наконец, так же
легко можно определить, как преобразуема G в gg', если из трех
форм /, /', G одна содержит соответствующую из трех форм g, g', F
не так, как содержат соответствующие формы две другие.
Е ли формы F, /, /' эквивалентны формам G, g, g', то послед-
последние будут иметь те же определители, что и первые, и то, что числа
т, т' обозначают для форм /, /', они будут обозначать и для форм
g, g' (п. 161). Отсюда при помощи четвертого следствия п. 235 без
труда выводится, что в этом случае G составлена из g. g', если F
составлена из /, /', и что форма g входит в первую композицию
таким же образом, как /—во вторую, если F эквивалентна форме
G таким же образом, как / — форме g, и наоборот; и что подобно
этому g' берется в первой композинии или таким же, пли противо-
противоположным образом по сравнению с тем, как берется /' во второй
композиции, в зависимо ти от того, является ли эквивалентность
форм /', gf однотипной с эквивалентностью форм F, G, или нет,
239
Теорема. Если форма F составлена из форм /, /', то всякая
другая форма, которая преобразуема таким же образом, что и F,
€ произведение ff, будет собственно содержать форму F.
312 Раздел V (п. 2Щ
Доказательство. Если сохранить для F\ /, /' все обозначения
п. 235, то равенства Ql будут иметь место и здесь. Если предполо-
предположить, что форма F' = (А', В\ С"), определитель которой пусть
равен D\ переходит в произведение //' при подстановке р, р' р", рт\
q, q', q", q'\ и числа pq'— qp', pq" — qp", pf— qp"\ p'q"— q'p", V'f—
— q'p'", p"qw — q"p'" обозначить соответственно через
P', Q' R', S\ T\ U\
то получится девять равенств, совершенно аналогичных равенствам
?1, именно:
Р' = ап'9 R' — S' = 2йп\ V = сп\
Q' = а'п, R' + S' = 2Ь'п, Т = с'п,
q'q"— qqw= А'пп', pq'"+ qprrf—pV — q>"=2S'nn\ py—№"= Сип'9
которые мы обозначим через ?1'. Величины п, и' являются здесь
квадратными корнями из d/D, dr / D, причем взятыми с теми же
знаками, что и п, п'\ если поэтому положительный квадратный
корень из DID' (который является целым числом) положить рав-
равным А;, то п = йтг, п' = кп\ Вследствие этого и первых шести
равенств из О и О' очевидно, что
Р' = кР, Q' = kQ, R = kR,
S' = kS, Г = kT, U' = Ш.
Поэтому, согласно лемме п. 234, можно определить четыре целых
числа а, р, у, 6 с тем свойством, что
и т. д.
Если подставить эти значения р, q, р', q', . . . в три последних ра-
равенства из ?2\ то при помощи равенств п = кп, п' = Атг' и послед-
последних трех равенств из О легко устанавливаются равенства
A'oL* + 2B'oL4 + C'f = A,
А'к$ + В' (<х8 + Рт) + С'Т5 = ^>
Л'Ра + 2Д'р8 + С'52 = С.
Композиция форм 313
Поэтому форма F' при подстановке а, р, у, 8 (которая является
собственной, так как аЬ — ^ = А положительно) переходит в J7,
т. е. содержит форму F собственно. Это и требовалось доказать.
Если поэтому форма F' также составлена из форм /, /' (таким
же образом, как и F), то формы F9 F' будут иметь одинаковый
определитель и потому будут собственно эквивалентны. Более общо:
если форма G составлена из форм g, g' таким же образом, как F
соответственно из /, /' и формы g9 g' собственно эквивалентны
формам /, /', то и формы F, G будут собственно эквивалентны.
Tan как тот случай, когда обе компонируемые формы входят в
композицию прямо, является простейшим, а остальные могут быть
легко сведены к нему, мы будем в дальнейшем рассматривать только
его9 так что если какая-нибудь форма будет названа составленной
из двух других, то под этим всегда будет подразумеваться, что она
составлена из каждой из них прямо То же самое ограничение бу-
будет иметь место, когда одна форма будет называться преобра-
преобразуемой в произведение двух других.
240
Теорема. Если из форм /, /' составлена форма F9 из F, /" —
форма %9 из U Г — форма F'9 и из F', /'— форма $'', то формы
Qf, g' собственно эквивалентны.
Доказательство. I. Пусть
/ = ах2 -f- 2bxy + су2 у
/' = п'х'* + 2Ь'х'у' + с'у'\
/" = а^2 _|_ 2Ь"ху + сГу"\
р = АХ2 + 2BXY + CY2,
F' = А'Х'2 -Ь 2B'X'Y' -f CT/2,
далее, пусть определители этих семи форм равны соответственно
d, d'9 d'\ D, D', ©, ©'; все они имеют одинаковые знаки и от-
относятся один к другому как квадраты. Далее, пусть т — наиболь-
наибольший общий делитель чисел а, 2Ь, с, и аналогичное значение имеют
314 Раздел V (п.
т', т", М для форм /', /", F. Тогда, в соответствии с четвертым
следствием п. 235, D есть наибольший о^щий делитель чисел dm'2,
d'm2 и потому Dm— наибольший общий делитель чисел dm'2m,
d'm2m!'2\ М = тт'\ ©— наибольший общий делитель чисел Dm,
р"М2 или чисел Dm, d"m2mf2. Отсюда следует, что© есть наиболь-
наибольший общий делитель трех чисел dm'2m , d'm2m, dffm2m'2. Но по
аналогичной причине и ©' есть наибольший общий делитель этих
же трех чисел, поэтому, так как © и ©' имеют одинаковые знаки,
то © = ©', т. е. формы 5, 3*', имеют одинаковый определитель.
II. Пусть теперь F переходит в //' при подстановке
X = рхх' + р'ху' + p"yxf + fyy',
Y = qxx' + q'xy' + q"yxf + q'"yy\
и ^ — в Fj" при подстановке
Ж = рХх" + р'Ху" + p"Yx" + P'"Yy",
U =
и положительные квадратные корни из d/Z), d' / D, /)/©, d"/©
обозначим через п, п\ $1, п". Тогда, согласно п. 235, мы имеем
восемнадцать равенств, из которых половина принадлежит пре-
преобразованию формы F в //', и половина — преобразованию формы
3* в Ff\ Первое равенство е ть pqr — qp' = an' и по его образцу
легко могут быть образованы и остальные которые мы здесь ради
краткости должны опустить. Впрочем, величины п, п\ 3i, n" будут
хотя и рациональными, но не обязательно целыми числами.
III. Если значения X, Y подставить в значения 3?, Q, то полу-
получается следующая подстановка:
ЗЕ = A) хх'х" + B) хх'у" + C) хух" + D) ху'у" +
+ E) ух'х" + F) ух'у" + G) г/г/V + (8) уу'у",
& = (9) хх'х" + A0) хх'у" + (И) ху'х" + A2) ху'у" +
+ A3) ух'х" + A4) ух'у" + A5) уу'х" + A6) уу'у",
при которой g, очевидно, переходит в произведение //'/"• Коэф-
Коэффициент A) равен рф + <7Р"; значения пятнадцати остальных мы не
приводим, так как каждый может определить их без труда. Число
Композиция форм 315
A) A0) —B) (9) мы обозначим через A, 2), число A) A1) —C) (9)—
через A,3), и, вообще, (g) (8 + h) — (h) (8 + g) — через (g, h), где
предполагается, что g, h различные целые числа между 1 и 8,
большее из которых есть h*. Таким образом, всего получается двад-
двадцать восемь знаков. Если обозначить теперь положительные квадрат-
квадратные корни из d/2>, d'/S через п, п' (которые будут равны гМ,
п1), то мы найдем следующие двадцать восемь равенств:
A,2;= аа'п", C, 5) = а'Ъ'п — а"Ьп',
A,3)= аа"п', C,6)= bb'n" + b'b"n — bb"n' — ?>mt'n",
(l,4)=ab'n"+ab"n', C,7)=aVtt,
A,5) = a'a"n, C,8)= bc'n" + b"c'n,
A, 6)= a'bn" + a'b"n, D,5)=b'b"n—bb'n"—bb''n'+?)nn'n",
A,7)= a"bn' + a"b'n, D, 6) = b'c"n — 6c"»',
A, 8) =bb'n"-rbb"tt'+b'b"n+ ©nn'tt", D, 7) = b"c'n — bc'n",
B, 3) = ab"tt' — ab'n", D, 8) = c'Sn,
B,4)=acV, E,6)=caV,
B, 5) = a'b"n — o'6»"f E,7)= ca"tl',
B,6)= a'c'% E,8)= 6'cn" + У en',
B, 7)=ii"n4Wtt-66V— Stm'tt", F, 7) = b"cn' — b'ctl",
B, 8)= kV + fcV», F, 8) = cc"tt',
C,4)=acV, G,8)=cc'n",
которые мы обозначим через Ф, и девять других:
A0) A1) — (9) A2) = an'nt,
A) A2) - B) A1) - C) A0) + D) (9) = 2an'n5,
— (9) A6) + A0) A5) + A1) A4) — A2) A3) =
A) A6) - B) A5) - C) A4) + D) A3) +
+ E) A2) — F) (И) — G) A0) + (8) (9) = 4inV®,
- A) (8) + B) G) + C) F) - D) E) = 25й'п"е,
A4) A5) — A3) A6) = c»V»,
* Теперешний смысл знака (g, h) не следует путать с тем, в котором он
употреблялся в п. 234; действительно, числа, обозначенные этим знаком, здесь
соответствуют тем, на которые в п. 234 умножались числа, обозначенные таким
же знаком.
316 Раздел V (п. 240)
которые мы обозначим через Т *.
IV. Давать вывод всех этих 37 равенств было бы слишком долго;
достаточно установить лишь некоторые, по образцу которых осталь-
остальные могут быть доказаны без труда.
1. Мы имеем
A, 2) = A) A0)-B) (9) =
= fljq' - qp') p* + (pq'" - qp'" - p'q" + q'p") pq +
+ (p"qm - q"p"') Я2 = »" D»8 + 2Bpq + Cq*) = tt'oo',
а это и есть первое равенство.
2. Имеет место
A, 3) = A) (И) -C) (9) = (pq"- qp") (pg'-gp') = а"Шап' = ааГп',
а это и есть второе равенство.
3. Имеем
= (pq'- Ctf') Pf + №т- qpm) pqtn - (p V - q V) <7P" +
+ (pV— q//p'")gg'" =
= П* [Apfr+ B[pq'"+ ЯР'") + Cqqm] + b'fA (pq" - qp") =
= n" [bbr + Ydd') + Ъ"Ш ф'п + bn') = **
= n"bb' + ъ'ЪЪ" + nb'b" + ©tin V.
Это восьмое равенство в Ф. Установить остальные равенства мы
предоставляем читателю.
V. Из равенств Ф следующим образом получается, что двадцать
восемь чисел A,2), A,3),... не имеют общего делителя. Сначала
заметим, что двадцать семь произведений по три сомножителя, в
которых или первый равен п, второй равен какому-нибудь из чисел
* Можно было бы заметить, что мы можем получить 18 других равенств,
аналогичных равенствам Ч7, у которых справа вместо сомножителей а, 26, с
стоят соответственно а\ 2Ь\ с'; а"\ 2Ь", с"; но эти равенства для нашей цели
не нужны, и потому мы их опускаем.
** Это следует из равенства [10] п. 235 и далее. Величина корня Vdd'
?)гш'912 = 2)un\
Композиция форм 317
п\ 2Ъ' с', третий равен какому-нибудь из чисел а", 2Ъ", с", или же
первый равен п', второй — какому-нибудь из чисел а, 2&, с, третий —
какому-нибудь из чисел а", 2Ь", с", или, наконец, первый равен п"',
второй — какому-нибудь из чисел а, 25, с, третий — какому-нибудь
из чисел а', 2Ь', с',— что эти отдельные двадцать семь произведений
вследствие равенств Ф равны либо каким-нибудь из двадцати восьми
чисел A, 2), A, 3),..., либо суммам или разностям нескольких из
них (например, па'а"= A,5), 2ш'Ъ"= A, 6) + B, 5), 4п6'й"= A,8) +
+B, 7)+ C, 6) + D, 5), и подобным же образом для остальных);
поэтому, если бы эти числа имели общий делитель, он должен был
бы обязательно входить и во все указанные произведения. Но от-
отсюда при помощи п. 40 методом, часто применявшимся ранее, легко
получается, что этот же делитель должен входить также и в числа
пт'т", п'тт", п"тт\ а потому их квадраты, которые равны
dm'2m/©, d'm^m / ©, d"m2m'2/&, делятся на его квадрат. Это,
однако, невозможно, так как согласно I, наибольший общий де-
делитель трех числителей равен ©, и потому сами квадраты не могут
иметь никаких общих делителей.
VI. Все это относится к преобразованию формы §г в //'/" и вы-
выводится из преобразований формы F в //' и формы §г в Ff. Но
совершенно аналогичным образом из преобразований формы F' в
//" и формы %' в F'f выводится следующее преобразование формы
W в //'/":
ЗЕ' = A)' хх V + B)' хх'уГ - г C)' xy'af -\ ,
ф' = (9)' хх'х" + A0)' хх'у" + A1)' ху'х" Н
(где все коэффициенты обозначают то же, что и при преобразова-
преобразовании формы % в //'/"» и для отличия к каждому из них добавлен
штрих), из которого точно так же, как и перед этим, получаются
двадцать восемь аналохичных равенствам Ф равенств, которые мы
обозначим через Ф\ и девять других, аналогичных 1Г, равенств,
которые мы обозначим через ХГ'. Именно, если обозначить A)' A0)'—
-B)'(9)' через A,2)', A)'(Ц)'_C)'(9)'-через A,3)' и т д, то
равенства Ф' будут иметь вид
(l,2)' = aaV, A,3)'= aa'n', ...,
318 Раздел V (пп. 241-242)
и равенства Y' —
(Ю)'(И)' — (9)'A2)' = ап'п'Ж,
(Дальнейшее изложение мы представляем ради краткости читателю;
впрочем, опытные читатели найдут, что это вычисление не нужно
еще раз проводить заново, а можно легко перенести сюда по ана-
аналогии первый анализ.) После этого из Ф и Ф' тотчас же следует
A,2) = A, 2)', A, 3) = A, 3)', A, 4) = A, 4)', B, 3) - B, 3)', .. .
А отсюда и из того, что A, 2), A, 3), B, 3), ... (согласно V) не все
имеют общий делитель, получается при помощи леммы п. 234, что
можно так определить четыре целых числа ос, р, ^, 8, что
+ 8(9)' = (9), т B)'+ 8 A0)'= A0),
и а8 — Py = 1-
VII. Отсюда посредством подстановки из первых трех равенств
Т значений а#, аЪ, а? и из первых трех равенств Y' значений
аЭГ, а25', а(?' легко устачавливается, что
а BГа2
а («ар + 33 (а8 + Рт) +
а Ctp2 + 223PS + Е82) = аб',
откуда, в случае если а не равно 0, очевидно, что форма $ ПРИ
собственной подстановке а, р, ^7 8 переходит в $'. Если же вместо
трех первых равенств изТи *?' использовать три следующих, то
мы найдем три равенства, полностью аналогичных вышеуказанным,
в которых лишь вместо сомножителя а всюду стоит Ь, откуда
вытекает, что справедливо то же заключение, если только Ъ не
равно 0. Наконец, если использовать аоследние три равенства из
Т и Т', то мы таким же образом найдем, что наше заключение
верно, если только с не равно 0. Но так как все три числа а, Ь, с
заведомо не равны нулю одновременно, то форма g обязательно
должна переходить при собственной подстановке а, р, у, S в ^',
и потому она будет этой форме собственно эквивалентна. Это
и требовалось доказать.
Композиция форм 319
241
Такую форму, как % или g', которая получается, если одну из
трех заданных форм скомпонировать с той, которая возникает при
композиции двух других, мы будем называть составленной из этих
трех форм, и из предыдущего пункта вытекает, что безразлично,
в каком порядке компонируются три формы. Аналогично, если дано
любое количество форм /, /', /", /", . . . (определители которых
должны относиться один к другому как квадраты), и форма /
компонируется с /', получающаяся отсюда форма — с/", возни-
возникающая после этого форма — с /'" и т. д., то форма, которая полу-
получается в заключение этой операции, называется составленной из
всех форм /, /', /", /'",. . . Легко доказывается, что также и здесь
безразлично, в каком порядке формы составляются, т. е. в каком
бы порядке эти формы ни составлялись, формы, получающиеся
в результате этого составления всегда будут собственно эквива-
эквивалентны. Далее, ясно, что если формам /, /', /", . . . собственно экви-
эквивалентны формы g, g', g", .. . , то и форма, составленная из послед-
последних, будет собственно эквивалентна форме, составленной из первых.
242
Предыдущие теоремы касаются композиции форм в наиболее
общем виде; теперь мы переходим к специальным применениям,
которыми мы не хотели прерывать последовательность теорем. Сна-
Сначала мы снова вернемся к задаче п. 236, которую мы ограничим
следующими условиями. Во-первых, компонируемые формы должны
иметь одинаковые определители, т. е. d = d'\ во-вторых, т, т!
должны быть взаимно просты; в-третьих, искомая форма должна
быть составлена из обеих форм /, /' прямо. Тогда т2 и т'2
также будут взаимно просты и потому наибольший общий
делитель чисел dm'2, d'm2, т. е. D, равен, d = d' и п = п' = 1. Четыре
величины U, ?Г, Q", Q"\ которые могут быть выбраны по желанию,
мы положим соответственно равными—1, 0, 0, 0, что всегда позво-
позволительно, кроме единственного случая, который мы здесь опускаем,
когда а, а1, Ъ -\-Ъ' одновременно равны 0 очевидно, однако, что
этот случай может встретиться лишь для форм с положительными
320 Раздел V (п. 242)
квадратными определителями. Тогда ясно, что (х есть наиболь-
наибольший общий делитель чисел а, а', Ъ -f b', что числа ф', ф", ф'" должны
быть взяты так, чтобы было
ф'а + ф"а' + ф'" (b + b') = [х.
a ф совершенно произвольно. Отсюда, если мы в указанном месте
подставим вместо р, q, p', #',... их значения, получаются равенства
А = ^, В = -±- [Ща' + фаЬ' + фа'Ъ + ф"Fй' + Z))],
а С может быть определено из равенства АС = В2 — D, поскольку
а и а' не равны нулю одновременно.
В этом решении значение А не зависит, таким образом, от зна-
значений $Р, ф', $Р", ф'" (которые могут быть определены бесконечным
числом различных способов); но В получит другое значение, если
придать другие значения этим числам, и есть смысл исследовать,
каким образом связаны между собой все значения В. Для этой
цели мы заметим следующее.
I. Как бы ни были определены числа ф. ф\ ф", ф'", получаю-
получающиеся при этом значения В все сравнимы между собой по мо-
модулю А. Именно, если предположить, что при
ф = р, ф' = р\ ф* = р", ф"= р" будет В = 58,
а при
ф = р + Ь, ф' = j3'+ 6', ф^= *>" + б", ф"= pw + б'" будет 5 = 58 + ©,
то
а5' + а'с" + F + Ъ') о" = 0, аа'б + ab'b' + а'ЪЬ" + (ЪЪГ + D) Ьт = (х©.
Если умножить левую часть второго равенства на ар' + а'р" +
+ (& + ft')pw, правую на [х и вычесть из первого произведения
величину
(аЬу + a'bp" + (b'2 + Z)) pw) (аб' + а'Ь" + (Ь + V) Ьт),
которая вследствие первого равенства, очевидно, равна 0, то после
раскрытия скобок и приведения подобных членов мы получим
Композиция форм 321
откуда следует, что [Л2? делится на аа'', или ?) делится на ааг
т. е. на -4, и
И. Если для значений р, р', р", р"' чисел $, $', $" tym будет
Z? = sg, то можно найти другие значения этих чисел, для которых
В принимает любое заданное сравнимое с 95 по модулю А значе-
значение, скажем, 95 + кА. Сначала заметим, что четыре числа [л, с, с',
Ъ — Ъ' не могут иметь общих делителей; действительно, если бы
они имели общий делитель, то он входил бы в шесть чисел а, а',
6 + 6', с, с', Ъ — b', a потому также как в а, 26, с, так и в а', 2Ь',
с', а, следовательно, в т, т', которые, однако, по предположению
взаимно просты. Поэтому могут быть указаны четыре целых числа
A, h\ h", К11 с тем свойством, что
Aji + h'c + h!'cr + hm (Ь — Ь') = 1.
Если сделать это и положить
kh=t>, к \Ь!' (Ь + Ъ') — К"а'\ = рЬ',
k [hr (b + b') + h'"a] = {хЬ\ — к (Ка1 + h"a) = (л?>'",
то числа с, с\ с", 6'", очевидно, будут целыми; далее, легко уста-
устанавливается, что
ab' + a'b" + (b + b')br" = 0,
аа'Ь + ab'b' + a'bb" + {W + D) Ьт =
= °^h. [[xh + chr + c'h"+ (b — V) hm] = (хЫ.
Из первого равенства вытекает, что и р' + 6, р' + ?>', р" + 6Г/, р'"+ 6W
могут быть взяты в качестве ф, ф', фг/, $Г, а из второго, что эти
значения дают В = 95 + АА
Отсюда видно, что В всегда может быть определено так, что
оно будет лежать между 0 и А — 1 включительно, если А положи-
положительно, и между 0 и —А — 1, если А отрицательно.
322 Раздел V (п. 243)
243
Из равенств
$Р'а + У а' + Т (Ъ + ь') = Р, в = - Щаа'+фаЪ'+У'а'Ъ + У" (ЬЬ'+
следует
В=Ъ + ^ [Щ' + ф' F' - 6) - Г'с] = V + 21 [фа + Г (& - й') - Г С],
и потому
^ = 6'(mod— V
Если а/[х, аг/(^ взаимно просты, то между 0 и А — 1 (или между
О и — А — 1 когда А отрицательно) будет лежать только одно един-
единственное число, которое = Ь (modа /ц) и =6' (modа' /[л); если его
положить равным В и —-— = С, то форма (А7 В, С) будет, оче-
видно, составлена из форм (а, Ъ, с), (а', Ъ\ с'). Таким образом, в
этом случае для отыскания скомпонированной формы не нужно
больше беспокоиться о числах ф, ф', ty", ty" *.
Например, если отыскивается форма, составленная из форм
A0, 3, 11), A5, 2, 7), то а, а', 6 + 6' равны соответственно 10,15, 5; (х =5;
отсюда -4=6; Z? = 3(mod2) и E^2(mod3), тем самым В = 5, и
искомая форма есть F, 5, 21). Впрочем, условие, что а/;л, a' /\l
взаимно просты, вполне эквивалентно условию, что оба числа а, а'
не должны иметь большего общего делителя, чем три числа а, а',
Ъ -\~ Ъ\ или, что сводится к тому же, что наибольший общий дели-
делитель чисел а, а' должен входить также и в число Ъ + Ь\ Можно,
в частности, указать следующие специальные случаи.
1. Если даны две формы (а, 6, с), (а' Ь\ с') с одним и тем же
определителем D и тем свойством, что наибольший общий делитель
чисел а, 26, с взаимно прост с наибольшим общим делителем чисел
а\ 2Ь' с' и, далее, а взаимно просто с а', то мы найдем состав-
* Что всегда достигается при помощи сравнений
аВ аЪ' а'В а'Ъ (Ъ + Ъ')В ЬЬ' + D
Композиция форм 323
ленную из них форму (А, В, С), если положим А = аа', B = b (moda)
и =&' (mod а'), С =—-г—. Этот случай всегда имеет место, когда
одна из компонируемых форм является главной формой, т. е. когда
а = 1, 6 = 0, с = —D. Тогда А=а', В можно положить равным
Ь\ откуда следует, что С = с'. Таким образом, форма, составленная
из главной формы и какой-нибудь второй формы с тем же опреде-
определителем, есть сама эта вторая форма.
2. Если компонируются две противоположные собственно при-
примитивные формы, например, (а, Ь, с) и (а, —Ь, с), то (а = а. Из этого
легко видно, что главная форма A,0, —D) будет составленной из них.
3. Если дано сколько угодно собственно примитивных форм
(а, Ь, с), (а', Ъ', с'), {а", Ъ",с"),... с одними тем же определителем D,
первые члены которых а, а', а"',... являются попарно взаимно про-
простыми числами, то мы найдем составленную из них форму (А, В, С),
если положим А равным произведению всех чисел а, а', а",..., В —
сравнимым с отдельными Ь, Ъ', Ь"',... соответственно по модулям
J52 ?
а, а', а",..., и С =—^—. Действительно, легко видеть, что фор-
формой, составленной из двух форм (а, Ь, с), (а\ Ъ', с'), будет
(аа', В, (В2 — D)/aa'), формой, составленной из нее и из (а", Ъ", с")
будет (аа'а\ В, (В2 — D)/aa'a") и т. д.
4. Обратно, если дана собственно примитивная форма (А, В, С)
с определителем D, и член А разложен на любое число попарно
взаимно простых сомножителей а,а',а", ..., далее, числа b, b\ 6",...
или равны В, или по крайней мере сравнимы с В соответственно по
модулям а, а', а",..., и положено ас = Ь2 —D, а'с' = Ъ'2 —D,
а"с" = Ъ — D, то форма (А, В, С) будет составлена из форм
(а, Ь, с), (а', Ь\ с'), (а", Ь", с"),..., или будет разложима на эти формы.
Без труда доказывается, что такая же теорема имеет место и тогда,
когда форма (А, В, С) является несобственно примитивной или про-
произведенной. Этим способом, следовательно, каждая форма может
быть разложена на другие формы с тем же определителем, первые
члены которых все являются или простыми числами, или степенями
простых чисел. Такое разложение часто может быть с пользой при-
применено, когда из нескольких заданных форм нужно скомпонировать
одну. Например, если отыскивается форма, составленная из форм
324 Раздел V (п. 243)
C,1, 134), A0, 3, 41), A5, 2, 27), то разлагаем вторую форму на сле-
следующие: B, 1, 201), E,—2, 81), — третью — на C,-1,134), E, 2, 81);
тогда форма, составленная из пяти форм C, 1, 134), B, 1, 201),
E, —2, 81), C, —1, 134), E, 2, 81), в каком бы порядке они ни бра-
дись, будет, очевидно, составлена также из трех заданных форм.
Но при композиции первой и четвертой форм получается главная
форма A,0, 401); она же возникает при композиции третьей и пя-
пятой форм; поэтому при композиции всех пяти форм получается
форма B, 1, 201).
5. Вследствие большой пользы этого метода стоит потрудиться
над тем, чтобы развить его еще несколько далее. Из предыдущего
замечания вытекает, что проблема композиции любого числа за-
заданных собственно примитивных форм с одинаковым определителем
может быть сведена к композиции форм, первые члены которых
являются степенями простых чисел (ибо простое число может рас-
рассматриваться как первая степень самого себя). Поэтому мы хотим
специально рассмотреть случай, когда компонируются две собст-
собственно примитивные формы (а, 6, с), (а', Ь', с'), у которых а и а'
являются степенями одного и того же простого числа. Если, та-
таким образом, а = /гх, а1 = /гх, где h обозначает простое число, и
если мы предположим (что допустимо), что х не меньше чем X, то
hx будет наибольшим общим делителем чисел а, а', и если он,
кроме того, входит в Ь -\- Ъг, то мы имеем случай, рассмотренный
в начале этого пункта в. (А, В, С) будет составлена из заданных
форм, если положить А = /гх~х, В = Ъ (mod /гх~х) и = 6' (modi) (это
последнее условие можно, конечно, отбросить), и С = —-т—. Если
же hx не входит в Ъ + Ь\ то наибольший общий делитель этих
чисел обязательно сам будет степенью /г; есяи он равен /гу, то v<X
(если случайно hx и Ъ -\- Ъ' взаимно просты, нужно положить v =0).
Если поэтому ф', $", ф'" определены так, что
ф'/г* + ф'7гх + ф'" (Ь + V) = h\
а ф взято произвольно, то форма (^4, ВЛ С) будет составлена из
заданных форм, если положить
А = &*+*-2v? B=*b+ №— ЩКХ — ф'(Ъ' — Ъ) — Г'с], С = B2~D .
Композиция форм 325
Но легко видеть, что в этом случае и ф' можно брать произволь-
произвольно, так что если положить ф = ф' = 0, то получается
B = b — qTch*-\
или вообще
В = к А + Ъ — фс}р-\
где к обозначает любое число (предыдущий пункт). В эту очень
простую формулу входит только ф'", которое есть значение выра-
т V
жения -т—тт (mod hx) *. Например, если отыскивается форма, состав-
составленная из форм A6, 3, 19) и (8, 1, 37), то h = 2, х = 4, X = 3, v = 2.
Поэтому .4 = 8, ф"— значение выражения -^-(mod8); одним из них
является 1, поэтому В = 8к—73, и тем самым, если положить
А; = 9, то В=- — 1 и С = 37. Следовательно, (8, — 1, 37) является
искомой формой.
Если, таким образом, дано любое число форм, первые члены ко-
которых все являются степенями простых чисел, то нужно посмот-
посмотреть, будут ли первые члены некоторых из них степенями одного
и того же простого числа, и их скомпонировать между собой по
только что указанному правилу. Тогда получатся формы, первые
члены которых все еще являются степенями простых чисел, но уже
сплошь различных; поэтому форма, составленная из них, может быть
определена в соответствии с третьим замечанием. Если, например,
даны формы C, 1, 17), D, 0, 35), E, 0, 28), A6, 2, 9), (9, 7, 21),
A6, 6, 11), то из первой и пятой получается форма B7, 7, 7), из
второй и четвертой — форма A6, —6, 11), из нее и из шестой —
форма A, 0, 140), которая может быть отброшена. Поэтому остаются
только формы E, 0, 28) и B7, 7, 7), из которых получается фор-
форма A35,—20, 4), вместо которой может быть взята также собственно
* Или выражения 7,7, (mod hK~v)f откуда следует, что
/zv
326 Раздел V (пп.
эквивалентная ей форма D, 0, 35). Таким образом, она получается
в результате композиции шести заданных форм.
Впрочем, из этого же источника может быть почерпнуто еще много
других полезных для применения специальных приемов; но чтобы
не быть слишком пространными, мы опускаем более подробный раз-
разбор этого предмета и обращаемся к другим, более трудным вопросам.
244
Если число а может быть представлено какой-нибудь формой /,
а число а' — формой /', и форма F преобразуема в //', то без тру-
труда видно, что произведение аа' представимо формой F. Отсюда
тотчас же следует, что если определители этих форм отрицатель-
отрицательны, форма F положительна, если формы /, /' либо обе положи-
положительны, либо обе отрицательны, и наоборот, форма F отрицатель-
отрицательна, если одна из форм /, /' положительна, а другая отрицательна.
Мы хотим специально остановиться на случае, который мы рас-
рассматривали в предыдущем пункте, именно, когда F составлена из
/, /', и /, /', F имеют один и тот же определитель D. Если мы,
кроме того, предположим, что представления чисел а, а' формами
/, /' осуществляются при взаимно простых значениях неизвестных,
и что первое представление принадлежит значению Ъ выражения
\rD{moAa), а второе — значению Ъ' выражения ]/^D (mod а'), и
положим Ь2— D = ас, Ъ'2— D = a'c\ то, согласно п. 168, формы
(а, 6, с), (а', Ъ', с') будут собственно эквивалентны формам /, /',
вследствие чего F составлена также и из двух первых. Но из этих
же форм составлена форма (At В, С), если мы, обозначив наибольший
общий делитель чисел а, а', Ъ + V через [х, положим А = ^\ , В = Ъ и
= Ъ' соответственно по модулям а/jx, а'/^, и АС = В2 — D. Следо-
Следовательно, эта форма будет собственно эквивалентна форме F. Но
число аа1 представляется формой Ах2 + 2Вху ~\~ Су2, если положить
х = [л, у = 0; эти значения имеют общлй делитель [л; поэтому аа'
может быть представлено и формой F так, что значения неизвест-
неизвестных имеют наибольший общий делитель [х (п. 166). Поэтому если
и = 1, то число аа' може! быть представлено формой F при взаим-
Композиция порядков 327
но простых значениях неизвестных, и это представление будет при-
принадлежать значению выражения Y^D (mod аа'), равному В, которое
по модулям а, а! сравнимо соответственно с числами Ь, b'. Усло-
Условие [х = 1 заведомо выполняется, если а, а' взаимно просты; вооб-
вообще же оно выполняется всегда, когда наибольший общий делитель
а, а! взаимно прост с Ъ -\-Ь'.
Композиция порядков
245
Теорема. Если форма f принадлежит тому же порядку, что и
g, и точно так же f из того же порядка, что и g', то форма F9
составленная из /, /', будет иметь тот же определитель и при-
принадлежать тому же порядку, что и составленная из g, g' форма G.
Доказательство. Пусть формы /, /', F соответственно равны
(а, Ъ, с), (а', Ъ', с'), (А, В, С), а их определители d, d', D. Далее,
пусть наибольший общий делитель чисел а, 26, с равен т, а наи=>
больший общий делитель чисел а, Ь, с равен пт, и аналогичные
значения имеют т', т' по отношению к форме /' и М> УК по от-
отношению к форме F. Тогда порядок формы / определяется числа-
числами d, m, m, вследствие чего те же числа будут принадлежать и
форме g; по той же причине числа d', m\ пт' будут для формы g'
тем же, что и для формы /'. Но в соответствии с п. 235 числа D,
М9 ffi определяются числами d, d', т, т\ пт, пт'; именно, D есть
наибольший общий делитель dm'2 и d'm2, далее, М = mm' и SR ==
= птт' (если одновременно т = т и т' = т') или = 2тт' (если т =
= 2т или т! = 2т'). Так как эти свойства чисел D, M, 3R полу-
получаются из того, что F составлено из /, /', то очевидно, что D, М,
SOc должны иметь те же значения и для G, и потому G будет из
того же порядка, что и F. Это и требовалось доказать.
На основании этого мы будем называть порядок, в котором содер-
содержится F, составленным из порядков, в которых содержатся /, /'.
Так, например, из двух собственно примитивных порядков всегда
составляется порядок такого же типа, а из собственно примитив-
примитивного и несобственно примитивного — несобственно примитивный.
328 Раздел V (п. 246)
Аналогичным образом следует понимать и такие выражения, когда
порядок называется составленным из нескольких других порядков.
Композиция родов
246
Задача. Пусть даны две любые примитивные формы /, /', при ком-
композиции которых получается форма F; тогда, зная роды, которым
принадлежат /, /', нужно определить род, к которому отно-
относится F.
Решение. I. Рассмотрим сначала случай, когда по крайней мере
одна из форм /, /', например, первая, собственно примитивна, и обоз-
обозначим определители форм /, /', F соответственно через d, d', D.
Тогда D есть наибольший общий делитель чисел dm'2, d', где т'
равно 1 или 2 в зависимости от того, собственно или несобственно
примитивна форма /'. В первом случае F будет принадлежать соб-
собственно примитивному порядку, во втором — несобственно примитив-
примитивному порядку. Род же формы F определяется ее специальными ха-
характерами как по отношению к отдельным нечетным простым де-
делителям числа D, так, в некоторых случаях, и по отношению к чи-
числам 4 и 8. Мы должны поэтому определить их отдельно.
1. Если р какой-нибудь нечетный простой делитель D, то он
обязательно входит также в d, d', и потому среди характеров форм
/, /' обязательно будут фигурировать также и их отношения к р.
Если теперь число а представляется формой /, а число а' — формой
/', то произведение аа' будет представимо формой F. Поэтому, если
как формой /, так и формой/'представляются квадратичные вычеты
по модулю р (не делящиеся на р), то и формой F могут представляться
квадратичные вычеты по модулю р, т. е. если каждая из форм /, /'
имеет характер Ир, то и форма F будет иметь этот же характер. По
той же причине F будет иметь характер Ир, если каждая из форм
/, /' имеет характер Np; наоборот, F имеет характер Np, если одна
из форм /, /' имеет характер Яр, а другая — характер Np.
2. Если в полный характер формы F входит отношение к чис-
числу 4, то такое отношение должно фигурировать и в характерах
Композиция родов 329
форм /, /'. Действительно, это имеет место только тогда, когда
Z) = 0 или = 3(mod4). Если D делится на 4, то также и dm'2 и
d' делятся на 4, откуда тотчас же вытекает, что форма /' не мо-
может быть несобственно примитивной и потому т' = 1. Поэтому как
d, так и d' делятся на 4, и в характерах обеих форм фигурирует
отношение к числу 4. Если Z) == 3 (mod 4), то D входит в d, d'\
отношения являются квадратами, и потому d, d' также обязатель-
обязательно или =0, или =3(mod4), и среди характеров форм /, /' нахо-
находятся их отношения к числу 4. Отсюда тем же способом, как и в
A), следует, что характер формы F есть 1, 4, если обе формы /,
/' имеют или характер 1, 4, или характер 3, 4, и, наоборот, ха-
характер формы F есть 3, 4, если одна из форм /, /' имеет харак-
характер 1, 4, а другая — характер 3, 4.
3. Если D делится на 8, то делится на 8 также и d'\ поэтому
форма /' заведомо собственно примитивна, т' = 1 и d тоже делит-
делится на 8. Поэтому среди характеров формы F какой-нибудь из характе-
характеров 1,8; 3, 8; 5, 8; 7, 8 может встретиться только тогда, когда как в
характере формы /, так и в характере формы /' фигурирует по-
подобное отношение к числу 8. Но тем же способом, как и раньше,
легко устанавливается, что характер формы F есть 1, 8, если / и
/' имеют по отношению к числу 8 одинаковый характер; что ха-
характер формы F есть 3, 8, если одна из форм /, /' имеет характер
1,8, а другая — характер 3, 8, или если одна имеет характер 5,8,
а другая — характер 7,8; что форма F обладает характером 5,8,
если формы /, /' имеют характеры 1,8 и 5,8 или характеры 3,8 и
7, 8; наконец, F имеет характер 7, 8, если /, /' имеют характеры
1,8 и 7, 8 или 3,8 и 5,8.
4. Если D е= 2 (mod 8), то d' или=0, или =2 (mod 8); поэтому
т' = 1, и потому также и d или =0, или =2 (mod 8). Однако
оба числа d и d' не могут делиться на 8, так как D является их
наибольшим общим делителем. Поэтому форме F может быть при-
придан тот или иной из двух характеров 1 и 7, 8; 3 и 5, 8 только тог-
тогда, когда или обе формы /, /' обладают одним из этих характеров,
или одна из них имеет один из этих характеров, а другая один
из следующих характеров: 1? 8; 3, 8; 5, 8; 7, 8. Отсюда легко полу-
получается, что ха актер формы F может быть определен по следующей
330
Раздел V (п. 247)
таблице, где находящийся слева характер относится к одной из
форм /, /', а находящийся вверху — к другой:
1
3
и
и
7,
5,
8
8
1 и
или
или
1 и
3 и
7,
1,
7,
7,
5,
8
8
8
8
8
3 и
или
или
3 и
1 и
5,
з,
5,
5,
7,
8
8
8
8
8
5. Подобным же образом доказывается, что форме F не может
быть придан тот или иной из двух характеров 1 и 3, 8; 5 и 7, 8,
если только одним из них не обладает по крайней мере одна из
форм /, /', в то время как другая имеет или тоже один из этих
характеров, или один из следующих: 1,8; 3,8; 5,8; 7, 8, причем ха-
характер формы F может быть найден при помощи следующей таб-
таблицы, в которой характеры форм /, /' находятся слева и вверху:
1
5
и
и
со"
7,
8
8
1 и
или
или
1,
5 и
з,
1,
со"
со"
7,
8
8
8
8
8
5 и
или
или
5 и
1 и
7,
5,
7,
7,
со"
8
8
8
8
8
II. Если обе формы /, /' несобственно примитивны, то D есть
наибольший общий делитель чисел 4й, 4сГ, или D/i — наибольший
общий делитель чисел d, d!. Отсюда легко следует, что и d, и
d't и -?- D = 1 (mod 4). Если положить F = (А, В, С), то наибольший
общий делитель чисел А> В, С равен 2, и наибольший общий
Композиция родов 331
делитель чисел А, 2В, С равен 4. Поэтому F есть форма, произ-
произведенная из несобственно примитивной формы {А/2, В/2, С/2); опре-
определитель последней равен Z>/4, и ее род будет определять род фор-
формы F. Но характер первой формы, так как она несобственно при-
примитивна, не содержит отношений к 4 или 8, а лишь отношения к
отдельным нечетным простым делителям числа Z)/4. Но так как,
очевидно, все эти делители входят в d, d\ и половина каждого
произведения двух сомножителей, один из которых представляется
формой /, а другой формой /', может быть представлена формой
\~2 ' ~2~' Т/ ' т0 легко видать, что характер этой формы по отно-
отношению к каждому входящему в Z>/4 нечетному простому числу есть
Rp, как тогда, когда 2Rp и формы /, /' имеют по отношению к р
один и тот же характер, так и тогда, когда 2Np и характеры форм
/, /' по отношению к р противоположны, и что, напротив, харак-
тер формы —, у, -ту) есть Np, как тогда, когда /, / имеют
/2 ' 2 ' 2,
одинаковые характеры по отношению к р, и 2Np, так и тогда,
когда /, /' имеют противоположные характеры, и 2Др.
247
Из решения предыдущей проблемы вытекает, что если g — при-
примитивная форма из того же порядка и того же рода, что и /, и
точно так же g' — примитивная форма из того же порядка и того
же рода, что и /', то форма, составленная из g и g', принадлежит
тому же роду, что и форма, составленная из /, /'. Отсюда непо-
непосредственно получается понятие рода, составленного из двух (или
нескольких) других родов. Далее, из этого же следует, что если
/, /' имеют одинаковый определитель, и /—форма из главного ро-
рода, a F составлена из /, /', то F будет из того же рода, что и /';
поэтому главный род при композиции с другими родами всегда
может быть отброшен. Если же при сохранении остальных условий
/ не из главного рода, а /' — примитивная форма, то F заведомо
будет не из того рода, что /'. Если, наконец, /, /' — собственно
примитивные формы одного и того же рода, то F будет из глав-
главного рода; если же /, /; обе несобственно примитивные формы с
332 Раздел V (пп. 248-249)
одинаковым определителем, но из различных родов, то F не может
принадлежать главному роду. Поэтому если какая-нибудь соб-
собственно примитивная форма компонируется сама с собой, то полу-
получающаяся при этом форма, которая тоже собственно примитивна
и имеет этот же определитель, обязательно будет принадлежать
главному роду.
248
Задача. Пусть даны две любые формы /, /', из которых составле-
составлена форма F; нужно по родам форм /, /' определить, к какому роду
принадлежит форма F.
Решение. Пусть / = (а, Ь, с), /' = (а', Ъ\ с'), F = {А, В, С), да-
далее, m — наибольший общий делитель чисел а, 6, с, и т'— наиболь-
наибольший общий делитель чисел а', Ь', с', так что формы /, /' произ-
произведены из примитивных форм (а/т, Ь/т, с/т), (а''/т'', Ь'/т', с'/т'),
которые мы соответственно обозначим через f, f. Если теперь но
крайней мере одна из форм f, f собственно примитивна, то наиболь-
наибольший общий делитель чисел А, В, С будет равен mm', и потому F
будет произведена из примитивной формы (А/тт', В/mm', C/mm') =
= $, откуда следует, что род формы F зависит от рода формы %.
Но легко убедиться, что $ переходит в ff при той же подстанов-
подстановке, при которой F переходит в //' и что тем самым форма % со-
составлена из форм ff, и ее род может быть определен в соответ-
соответствии с задачей п. 246. Если же обе формы f, f несобственно
примитивны, то наибольший общий делитель чисел А, В, С равен
2mm', и форма % также и в этом случае составлена из форм f, f,
и, очевидно, произведена из собственно примитивной формы
(^/2тт', В/2тт', С/2тт'). Род этой формы может быть поэтому
определен по п. 246, а так как F произведена из этой формы, то
тем самым тотчас же становится известным и род формы F,
Из этого решения вытекает, что изложенная в предыдущем пунк-
пункте теорема для примитивных форм, именно, что если формы /', g'
из одних и тех же родов, что и формы /, g, то форма, составлен-
составленная из /' g', принадлежит тому же роду, что и форма, составлен-
ная из /, g, сохраняет силу для любых форм.
Композиция классов 333
Композиция классов
249
Теорема. Если формы /, /' из тех же порядков, родов и клас-
классов, что и соответственно формы g, g', то и форма, составленная
из /, /', будет из того же класса, что и форма, составленная из
g u g'-
Из этой теоремы, справедливость которой немедленно следует
из п. 239, делается непосредственно ясным понятие класса, со-
составленного из двух или из нескольких заданных классов.
Если некоторый класс К компонируется с главным классом,
то получается снова класс К, т. е. главный класс при композиции
с другими классами того же определителя может отбрасываться.
При композиции двух противоположных классов всегда получается
главный класс того же определителя (ср. п. 243). Так как каж-
каждый двусторонний класс противоположен самому себе, то при ком-
композиции каждого собственно примитивного двустороннего класса с
самим собой получается главный класс того же определителя.
Верно и обращение последней теоремы, именно: если при ком-
композиции собственно примитивного класса К с самим собой полу-
получается главный класс Н того же определителя, то К обязательно
двусторонний класс. Действительно, если К' есть класс, противопо-
противоположный классу К, то из трех классов К, К, К' при композиции по-
получается тот же класс, что и из Н и К'; но из первых получается К
(так как К и К' дают главный класс Н, а он и К снова дают К),
а из вторых — К'. Тем самым К совпадает с К' и потому является
двусторонним классом.
Далее, может быть выведена следующая теорема: если классы
К, L соответственно противоположны классам К', U, то и класс,
составленный из К и L, будет противоположен классу, составлен-
составленному из К' и L'. Пусть формы /, g, /', g' принадлежат соответственно
классам К, L, К', L'; пусть форма F составлена из / и g, а форма
F' — из /' и g\ Так как формы /' и /, так же, как и формы g' и g,
несобственно эквивалентны, a F составлена из каждой из двух форм
/, g прямо, то F будет составлена и из форм /', gr, но из каждой
обратно. Поэтому каждая форма, которая несобственно экввва-
334 Раздел V (п. 250)
лентна форме F, прямо составлена из /' и g', и потому собственно
эквивалентна форме F' (пп. 238, 239), вследствие чего F, F' несоб-
несобственно эквивалентны, и классы, которым они принадлежат, противо-
противоположны.
Отсюда следует, что если компонируется двусторонний класс К
с двусторонним классом L, то всегда получается двусторонний
класс. Действительно, это есть класс, который составлен из классов,
противоположных классам К, L, и потому он противоположен сам
себе, ибо эти классы противоположны сами себе.
Наконец, заметим, что если даны два любых класса К, L с оди-
одинаковым определителем, из которых первый собственно примити-
примитивен, то всегда можно найти класс М с тем же определителем, кото-
который, будучи скомпонирован с К, дает L. Очевидно, мы добьемся
этого, если возьмем за М класс, который составлен из L и класса,
противоположного классу К; одновременно очень легко усмотреть,
что этот класс является единственным, обладающим таким свойст-
свойством, или что различные классы одного и того же определителя, бу-
будучи скомпонированы с одним и тем же собственно примитивным
классом, дают различные классы.
Композицию классов удобно обозначать знаком сложения +>
и, точно так же, тождественность классов — знаком равенства.
Тогда только что высказанная теорема может быть выражена сле-
следующим образом. Если К' есть класс, противоположный классу К,
то К + К'.' есть главный класс того же определителя, и тем самым
К + К' + L = L; если поэтому положить К' + L = М, то К +
+ М = L, что и требовалось. Если же, кроме М, имелся бы еще и
другой класс М', который обладал бы тем же свойством, т. е. если
бы было К + М' = L, то имело бы место К + К' + М' = L -f-
+ К' = М, откуда следует, что М' = М. Если составляются не-
несколько одинаковых классов, то это можно (по образцу умножения)
обозначать, ставя впереди число, указывающее их количество, так
что, например, 2К означает то же, что К + К, ЗК — то же, что
К + К + К, и т. д. Те же обозначения можно было бы перенести
и на формы, так что (а, Ь, с) + {а1 ,Ъ',с') означало бы форму, состав-
составленную из форм (a, by с), (а', Ъ\ с'); но чтобы избежать всякой дву-
двусмысленности, мы предпочитаем отказаться от этого сокращения,
Композиция классов 335
тем более, что знаку У М(а, Ъ, с) мы уже придали специальное зна-
значение. Мы будем говорить, что класс 2К получается удвоением
класса К, класс ЗК — утроением класса К, и т. д.
250
Если D есть число, делящееся на т2 (где т мы предполагаем
положительным), то существует порядок форм с определителем D,
произведенный из собственно примитивного порядка с определителем
D/m2 (или два таких порядка, если D отрицательно, именно, один
положительный и один отрицательный). Очевидно, что этому порядку
будет принадлежать (положительная) форма (т,0, — D/m), которая
по праву может рассматриваться как простейшая в нем (так же, как
(—т, 0, D/m), в случае отрицательного D, будет простейшей формой
в отрицательном порядке). Если, кроме того, D/m2 = 1 (mod 4),
то существует также порядок форм с определителем D, который
произведен из несобственно примитивного порядка с определителем
Dim2, и которому будет принадлежать форма Bт, т, (т2 — D)/2m),
являющаяся в нем простейшей. (Если D отрицательно, то снова
имеется два порядка, и в отрицательном порядке в качестве про-
простейшей следует рассматривать форму (—2т,—т, (D —т2)/2т)).
Так, например, если мы хотим причислять сюда и случай, когда т = 1,
то в четырех порядках форм с определителем 45 простейшими будут
следующие формы: A, 0, —45), B, 1, —22), C,0,-15), F,3,-6).
В этом смысле надо понимать следующую задачу.
Задача. Пусть дана какая-нибудь форма f из порядка О; нуж-
нужно найти собственно примитивную (положительную) форму, при
композиции которой с простейшей формой из О получается
форма F.
Решение. Пусть форма F = (та, тЪ, тс) произведена из при-
примитивной формы / = (а, Ь, с), определитель которой равен с?, и
предположим сначала, что / собственно примитивна. Заметим преж-
прежде всего, что если а не взаимно просто с 2dm, то заведомо су-
существуют другие, собственно эквивалентные форме (а, 6, с) формы,
которые этим свойством обладают. Действительно, согласно п. 228,
существуют числа, взаимно простые с 2dm и представляемые этой
336 Раздел V (пп. 251-252)
формой; пусть таким числом является а' = аос2 + 26осу + су2; пред-
предположим (это допустимо), что ос, у взаимно просты. Если тогда C,
8 выбраны так, что а8 — р*у = 1, то форма / при подстановке ос, р.
у, 8 переходит в форму (а', 6', с'), которая собственно эквивалент-
эквивалентна ей и обладает требуемым свойством. Но так как формы F и
(а'т, b'm, с'т) также собственно эквивалентны, то легко видеть,
что достаточно рассматривать тот случай, когда а взаимно просто
с 2dm. Тогда (а, bm, cm2) будет собственно примитивной формой
(так как если бы у a, 2bm, cm2 был общий делитель, то он со-
содержался бы также и в 2dm = 2b2m— 2аст) с тем же определи-
определителем, что и у формы F, и легко установить, что форма F при
подстановке 1, 0,—Ь, —ш; 0, т, а, Ът переходит в произведе-
произведение формы (т, О, —dm), —которая, если F не есть отрицатель-
отрицательная форма, является простейшей формой порядка О, — и формы
(a, bm, cm2), откуда, на основании критерия в четвертом замечании
п. 235, вытекает, что F составлена из (т, О, —dm) и (a, bm, cm2).
Если же F — отрицательная форма, то она переходит в произведе-
произведение простейшей формы (— т, О, dm) из того же порядка и поло-
положительной формы (—а, Ьт, —cm2) при подстановке 1, 0, b, —cm;
О, —т, —а, Ьт, и потому составлена из них.
Если же f—несобственно примитивная форма, то можно счи-
считать, что а/2 и 2dm взаимно просты; действительно, если это свой-
свойство для формы / не имеет места, то можно найти собственно экви-
эквивалентную ей форму, которая эти]м свойством обладает. Но отсюда
следует, что (а/2, bm, 2cm2) будет собственно примитивной формой
с тем же определителем, что и у формы F, и так же легко уста-
устанавливается, что F переходит в произведение форм
±2т, ±т, +у (т— dm)), (±y a, bm, ± 2cm2)
(
при подстановке
1, 0, y(l=FЬ), —cm; 0, +2т, ±\а, (Ь± 1) т,
где нужно брать нижние знаки, если F отрицательная форма, и
верхние — в остальных случаях, и что тем самым F составлена из
этих двух форм, первая из которых является простейшей в поряд-
порядке О, а вторая — собственно примитивной (положительной) формой.
Число классов в родах из одного порядка 337
251
Задача. Пусть даны две формы F, f с одинаковым определителем
D, которые принадлежат одному и тому же порядку 0\ нужно
найти собственно примитивную форму с определителем D, которая,
будучи скомпонирована с /, порождает форму F.
Решение. Пусть ср — простейшая форма из порядка О\ далее,
пусть g, f — собственно примитивные формы с определителем D,
которые, будучи скомпонированы с ср, дают соответственно формы
F, /; наконец, пусть /' — собственно примитивная форма, которая
будучи скомпонирована с f, порождает форму $. Тогда форма F
будет составлена из трех форм ср, f, /', или из двух форм /, /'.
Поэтому каждый класс из заданного порядка может рассматри-
рассматриваться как составленный из некоторого заданного класса этого же
порядка и какого-нибудь собственно примитивного класса с тем же
определителем.
Для заданного определителя
в отдельных родах из одного и того же порядка
содержится по одинаковому числу классов
252
Теорема. Для заданного определителя в отдельных родах из
одного и того же порядка содержится по одинаковому числу
классов.
Доказательство. Пусть роды G и Н принадлежат одному и тому
же порядку и пусть G состоит из п классов К, К', К", . . ., К^п~х>;
далее, пусть L—какой-нибудь класс из рода Н. Найдем в соот-
соответствии с предыдущим пунктом собственно примитивный класс
М с тем же определителем, при композиции которого с К полу-
получается класс L, и обозначим классы, получающиеся при компози-
композиции класса М с классами К', К", . . ., А^-*1) соответственно через
Z/, Z/',,. .,Z/n—1>. Тогда из последнего замечания в п. 249 следует,
что все классы L, Z/, L", . .^I/71-*1) различны, и, согласно п. 248,
все они принадлежат одному и тому же роду, т. е. роду Н. На-
Наконец, легко видеть, что Н не может содержать других классов,
кроме этих, так как каждый класс из рода Н может рассматри-
338 Раздел V (пп. 253-254)
ваться как составленный из М и некоторого другого класса того
же определителя, который обязательно будет из рода G. Поэтому
Н, так же, как и G, содержит п различных классов.
Сравниваются количества классов,
содержащихся в отдельных родах из различных порядков
253
Предыдущая теорема предполагает, что порядок один и тот же,
и не может быть применена к различным порядкам. Так, например,
для определителя —171 имеется двадцать положительных классов,
которые разбиваются на четыре порядка. В собственно примитив-
примитивном порядке содержится два рода, каждый из которых охватывает
по шесть классов; в несобственно примитивном порядке оба рода
обладают четырьмя классами, каждый род — по два; в порядке,
произведенном из собственно примитивного порядка с определите-
определителем —19, имеется только один род, который содержит три класса;
наконец, порядок, произведенный из несобственно примитивного
порядка с определителем —19, имеет только один род, состоящий из
одного класса. Так же обстоит дело для отрицательных классов.
Поэтому нужно постараться найти общий принцип, от которого
зависит связь между числом классов в различных порядках. Предпо-
Предположим, что Kt L — два класса из одного и того же (положитель-
(положительного) порядка О с определителем/), и М — собственно примитивный
класс с тем же определителем, при композиции которого с К полу-
получается класс L; такой класс Л/, согласно п. 251, всегда можно ука-
указать. В некоторых случаях М может быть единственным собственно
примитивным классом, который, будучи скомпонирован с К> по-
порождает L; в других случаях может существовать несколько раз-
различных собственно примитивных классов, которые обладают этим
свойством. Мы предположим для общности, что имеется г таких
собственно примитивных классов Л/, М\ М'\ ..., М{г~1I которые при
компонировании их по отдельности с К, дают один и тот же класс
L, и обозначим их совокупность через W. Далее, пусть U — дру-*
гой (отличный от L) класс из порядка О, и Nr — собственно прими-»
тивный класс с определителем Z>, который, будучи скомпонирован
Число классов в родах из различных порядков 339
с L, порождает L'; совокупность классов N' + М, N' + М\
N' + М",..., iV' + M{J~i) (которые все собственно примитивны и от-
отличны один от другого) обозначим через W. Тогда очевидно, что К,
будучи скомпонировано с любым классом из W', дает Z/, откуда сле-
следует, что W и W не имеют общих классов; кроме того, без труда
доказывается, что не существует собственно примитивных, не со-
содержащихся в совокупности W классов, которые, будучи скомпо-
нированы с К, давали бы Z/. Таким же образом убеждаемся, что
если L" — другой, отличный от классов L, U класс из порядка О,
то имеется г собственно примитивных классов, отличных как один
от другого, так и от классов из W, W, которые при композиции их
по отдельности с К дают L"', и так же обстоит дело со всеми классами
из порядка О. Так как, однако, каждый собственно примитивный
(положительный) класс с определителем D, будучи скомпонирован
с К, дает класс из порядка О, то отсюда легко получается, что
если количество всех классов в порядке О равно п, то количество
всех собственно примитивных (положительных) классов с тем же
определителем равно т. Мы получаем поэтому общее правило:
если К, L обозначают какие-нибудь два класса из порядка О, и г —
число различных собственно примитивных классов с тем же опре-
определителем, которые при композиции их по отдельности с К порож-
порождают L, то число всех классов в собственно примитивном (положи-
(положительном) порядке в г раз больше, чем число всех классов в по-
порядке О.
Так как классы К, L ж порядка О могут предполагаться совер-
совершенно произвольными, то можно брать и идентичные классы, при-
причем будет целесообразно воспользоваться тем классом, в котором
содержится простейшая форма из этого порядка. Поэтому, если
взять этот класс вместо К и L, то вопрос сводится к тому, чтобы ука-
указать все собственно примитивные классы, которые при композиции
с К снова порождают К. Путь к этому пролагается теоремой следую-
следующего пункта.
254
Теорема. Если F = (А, В, С) — простейшая форма из порядка
О с определителем D, и f = (а, Ь, с) — собственно примитивная
340 Раздел V (п. 255)
форма с тем же определителем, то число А2 представляется этой
формой /, если F получается при композиции форм /, F, и, обратно,
если F составлена из себя самой а /, то А2 представляется формой /.
Доказательство. I. Если F переходит в произведение /F при
подстановке р, р', р", рт\ q, q'f q", q\ то, согласно п. 235, мы
имеем
A (aq — 2bqq" + cq2) = А3, и потому А2 = aq — 2bqq" + cq2.
II. Предполагая, что А2 может быть представлено формой /,
обозначим значения неизвестных, при которых это достигается,
через #", —q, т. е. будем считать, что А2 = aq — 2bqq" + cq2,
и положим
q"a — q(b + B) = Ap, — qC = Ap\ q" (b — В) — qc = Ар"\
— q"C - Ap'", q"a — q (b — B) = Aq', q" (b + B) — qc = Aqm.
Тогда легко показать, что F переходит в произведение /F при
подстановке р, р', р", р"\ q, q\ q"', q'" и потому составлена из /
и F, если только все числа р, р',. .. целые. Но, по определению
простейшей формы, В или равно 0, или равно -4/2, поэтому число
2В/А целое; оттуда же следует, что и С/А целое число. Поэтому
целыми числами будут q' — р, pf, q" — р'\ р"', и потому остается
только показать, что р и р" целые. Но
если поэтому 5 = 0, то
и тем самым числа р и р" целые. Если же В = -к-, то
откуда так же легко получается, что и в этом случае р и р" це-
целые числа. Из этого следует, что F составлена из / и F.
Число классов в родах из различных порядков 341
255
Проблема теперь свелась к тому, что нужно определить все
собственно примитивные классы с определителем D, формами из
которых представляется число А2. Очевидно, что А2 представляет-
представляется каждой формой, первый член которой равен или А2, или квад-
квадрату какого-нибудь делителя А\ наоборот, если А2 представляется
формой / при значениях неизвестных осе, [Зе, наибольший общий
делитель которых равен е, то форма / при подстановке а, р, ^> 8
будет переходить в форму, первый член которой есть А2/е2, и ко-
которая будет собственно эквивалентна форме /, если ос8 — р^ = 1.
Из этого вытекает, что в каждом классе, формами которого может
быть представлено А2, находятся формы, у которых первый член
есть или А2, или квадрат делителя числа А. Итак, дело сводится
к тому, чтобы определить все собственно примитивные классы с
определителем />, в которых имеются такие формы, и это достига-
достигается следующим образом. Пусть а, а', а", .. . все положительные
делители А; найдем все значения выражения }/TJ(mod а2), которые
лежат между 0 и а2 — 1 включительно, и которые пусть равны Ь>
b\ b", . . ., и положим
b2~D = a*c, b'2 — D = a*c't Ъ — D =
далее, обозначим совокупность форм (а2, Ь, с), (а2, й', с'),... через F.
Тснда легко видеть, что в каждом классе с определителем D, в ко-
котором встречается форма, первый член которой равен а2, должна
содержаться также какая-нибудь форма из F. Аналогичным образом
получим все формы с определителем D, первый член которых есть
а'2, а средний член расположен между 0 и а'2 — 1 включительно, и
обозначим совокупность их через V. Точно так же пусть V" — со-
совокупность аналогичных форм, первый член которых есть а и т. д.
Из форм V, F', V",... удалим те формы, которые не являются соб-
собственно примитивными, остальные разобьем на классы и в каждом
отдельном классе оставим только по одной из них, если случайно
окажется несколько принадлежащих одному и тому же классу. Та-
Таким способом мы получим все искомые классы, и число их будет
относиться к единице как число всех собственно примитивных (по-
(положительных) классов относится к числу классов в порядке О.
342 Раздел V (п. 256)
Пример. Пусть D = —531 ж О — произведенный из несобственно
примитивного порядка с определителем — 59 положительный по-
порядок, простейшей формой в котором является F, 3, 90), т. е. .Л =6.
Здесь а, а', а"', а" равны соответственно 1, 2, 3, 6. Совокупность
V содержит форму A, 0, 531), совокупность V — формы D, 1, 133),
D,3, 135), совокупность V" — формы (9, 0, 59), (9, 3, 60), (9, 6,63),
наконец, совокупность V'" содержит формы C6, 3, 15), C6, 9, 17),
C6, 15, 21), C6, 21, 27), C6, 27, 35), C6, 33, 45). Однако
из этих двенадцати форм шесть нужно отбросить, а именно, из со-
совокупности V" — вторую и третью, а из V"'— первую, третью, чет-
четвертую и шестую, так как все эти формы являются произведенными;
относительно же оставшихся форм можно убедиться, что все они
принадлежат различным классам. Действительно, число собственно
примитивных (положительных) классов с определителем — 531 равно
18, а число несобственно примитивных (положительных) классов с оп-
определителем — 59 (т. е. число произведенных из них классов с опре-
определителем — 531) равно 3; таким образом, первое число относится
ко второму как 6 к 1*
256
Это решение сделается еще более ясным после следующих об-
общих замечаний.
I. Если порядок О произведен из собственно примитивного по-
порядка, то А2 входит в D\ если же порядок О несобственно примитив-
примитивный или произведен из несобственно примитивного порядка, то А
четно, D делится на .Л74, и частное = 1 (mod 4). Поэтому квадрат
каждого делителя числа А будет входить или в D, или по крайней
мере в 4Z), причем в последнем случае частное всегда будет
= 1 (mod 4).
П. Если а2 входит в D, то всевозможными значениями выражения
УВ(тод.а2), которые лежат между 0 и а2 — 1, будут следующие:
0, а, 2а, . . . , а2 — а, и потому число форм V есть а. Но среди них
будет лишь столько собственно примитивных, сколько имеется в
ряду
D D 1 D 4
а*
Число классов в родах из различных порядков 343
чисел, которые не имеют общих делителей с а. Если а = 1, то V
будет состоять только из одной формы A, 0, —D), которая всегда
собственно примитивна. Если а = 2 или есть степень числа 2, то
половина указанных а чисел будут четными, а остальные нечет-
нечетными; поэтому в V будет содержаться а / 2 собственно примитивных
форм. Если р есть какое-нибудь другое простое число или степень
простого числа, то нужно различать три случая, именно: все эти а
чисел будут взаимно просты с а, и потому все формы из V будут
собственно примитивны, если D / а2 не делится на р и одновременно
не является квадратичным вычетом по модулю р\ если же р входит
в В/а2, то в F имеется (р — 1)а/р собственно примитивных форм;
наконец, если D / а2 есть не делящийся на р квадратичный вычет
по модулю /?, то в V имеется (р — 2) а / р собственно примитивных
форм. Все это может быть доказано без труда. Если же положить
вообще а = 2vpnqxrp ... , где р, q< г,... обозначают различные не-
нечетные простые числа, то количество собственно примитивных форм
в V равно NPQR . . ., где нужно положить
N = 1 (если v = 0) или N = 2 (если v > 0),
Р = рп (если D / а2 является квадратичным невычетом по модулю /?),
или
Р = (р — 1) рп—г (если D / а2 делится на /?), или
Р = (р — 2) /?тс~1 (если DI а2 есть не делящийся на р квадратич-
квадратичный вычет по модулю р),
а числа Q, i?, ... определяются соответственно из q, г, ... так же,
как Р из р.
III. Если а2 не входит в D, то kDla2 — число целое и == 1 (mod4);
значения выражения ]^Z> (mod а2) суть: а/2, За/2, 5а/2, ...
..., а2 — у а; поэтому количество форм в V равно а, и из них будет
столько собственно примитивных, сколько среди чисел
D 1 D 9 D 25 ?>/ 1\2
имеется взаимно простых с а. Если -^ == 1 (mod8), то все эти числа
четны, и потому в V нет собственно примитивных форм; если же
— === 5 (mod 8), то все эти числа нечетные, и потому в V все формы
344 Раздел V (п. 256)
будут собственно примитивными, если а равно 2 или есть степень
числа 2, вообще же в этом случае в V будет столько собственно
примитивных форм, сколько среди этих чисел имеется не делящихся
ни на один простой делитель числа а. Если а = 2vpnqxrp.. ., то это
количество равно NPQR ..., где нужно положить 2V = 2V, а осталь-
остальные Р, Q, Л,... выводятся из р, q, г, . . . таким же образом, как
в предыдущем случае.
IV. Итак, этим способом можно определить количество собственно
примитивных форм в F, F', F",...; для суммы всех этих количеств
без труда находится следующее общее правило. Если А = 2v2la95p@X . .г
где 21, 25, (?,... обозначают различные нечетные простые числа, то
общее количество всех собственно примитивных форм в F, F', F", . . .
АпаЬс...
равно погашу ' где НУЖНО положить
Я = 1 (если —? == 1 (mod 8) j, или
П = 2 (если -т-2есть целое число], или
Я = 3 (если ^2-^5 (mod 8)J, далее,
а = 31 (если 2t входит в -ja)» или
ч 4 J
a = 914- 1 (если 21 не входит в -^ , причем нужно брать верхний
или нижний знак в зависимости от того, является
ли 42)I А2 квадратичным невычетом или вычетом по
модулю 2t j;
и Ь, с, ... выводятся из 95, S,. . . так же, как а из 2t. Ради крат-
краткости мы не будем излагать здесь доказательство более подробно.
V. Что же касается числа классов, которые дают собственна
примитивные формы из F, V, F",..., то здесь нужно различать
следующие три случая.
Во-первых, если число D отрицательно, то отдельные собственна
примитивные формы в F, F', ... образуют каждая особый класс,
т. е. число искомых классов выражается формулой, указанной в
предыдущем замечании, за исключением двух случаев, именно, когда
42)/ А2 или =—4, или =—3, т. е. когда D или =—А2, или
= —"Z"^2* Для того, чтобы доказать эту теорему, нужно, очевидно,
Число классов в родах из различных порядков 345
только показать, что не может случиться того, что две различные
формы из V, V, V", . .. собственно эквивалентны. Если предполо-
предположить, что (/г2, г, k), (/i'2, г"', к')— две различные собственно при-
примитивные формы из V, V, V", ..., которые принадлежат одному и
тому же классу, и что первая переходит во вторую при собственной
подстановке а, р, т» 8, так что имеют место равенства
<х8 — рт = 1, /г2а2 + 2гаТ + kf = h'\ /г2аC + i (а8 + Рт) + кЧь = г",
то отсюда легко следует: во-первых, что ^ заведомо не равно О
(действительно, в противном случае было бы а = +1, /г2 =/г'2»
V == г (mod /г2), и потому заданные формы были бы идентичны, что
противоречит предположению); во-вторых, что ^ делится на наиболь-
наибольший общий делитель чисел /г, Ь! (действительно, если положить
этот делитель равным г, то он, очевидно, входит также в 2г, 2г',
но взаимно прост с А; кроме того, г2 входит в h2k — h'2k' = i2 — z'2,
откуда легко следует, что г входит также в i — i'\ но az'—рй/2 =
= az + yA, и потому y^» а» значит, и ^ делятся на г); в-третьих,
что (а/г2 + ifzJ — />^2 = ^2^/2. Поэтому, если положить а/г2 + ^^* = гр,
Y = rg, то р, g будут целыми числами, причем второе не равно О,
, 27 /2
и р2 — Dq2 = —— . Но h2h'2/г2 является наименьшим числом, деля-
делящимся одновременно на /г2 и /г/2, и потому также входит в А2, а
тем самым и в 4D; следовательно, 40т*2/ /г2/г/2 есть целое (отрица-
(отрицательное) число, и если положить его равным —е, то будет р2 —
— Dq2 = или 4=(т^7) + е#2. В этом равенстве член Brp Ihh'J,
будучи квадратом, меньшим 4, обязательно или равен 0, или равен 1.
В первом случае eq2 = 4, и Z) = —(—j , откуда следует, что отно-
отношение 4Z) / А2 есть взятый с отрицательным знаком квадрат и потому
заведомо не сравнимо с 1 (mod 4), так что О не может быть ни
несобственно примитивным, ни произведенным из несобственно при-
примитивного порядка порядком. Поэтому D/А2 есть целое число,
откуда легко следует, что е делится на 4, q2==l1 D = —(—j и
A21D — тоже целое число. Следовательно, обязательно D = — А2
или -р" = — 1, что приводит к первому исключенному случаю. Но
346 Раздел V (п. 256)
втором случае eq2 = 3, так что е = 3 и AD = — 3 (—¦) . Поэтому
-^-j есть целое число, которое может быть равно только о, так
как, будучи умноженным на целочисленный квадрат (ттт) , оно
дает число 3. Следовательно, AD = —ЗА2 или D — —-г А2, что
представляет собой второй исключенный случай. Во всех же осталь-
остальных случаях все собственно примитивные формы из V, V, V",...
будут, таким образом, принадлежать различным классам. Для исклю-
исключенных случаев достаточно сообщить результаты нетрудного, но ради
краткости опускаемого здесь исследования. Именно, в первом случае
среди собственно примитивных форм из V, V, F",... в одном и том
же классе каждый раз оказывается по две, а во втором случае по
три формы, так что число всех искомых классов в первом случае
равно половине, а во втором — третьей части выражения, приве-
приведенного в предыдущем замечании.
Во-вторых, если D положительный квадрат, то отдельные соб-
собственно примитивные формы из V, V, F",... все без исключения
будут образовывать особые классы. Действительно, если предполо-
предположить, что (/г2, г, к), (/г/2, г', к') — две такие различные собственно
эквивалентные формы, и что первая переходит во вторую при соб-
собственной подстановке ос, р, т» 8, то очевидно» что все сделанные в
предыдущем случае заключения, в которые не входило предполо-
предположение, что D отрицательно, остаются в силе и здесь. Поэтому если
р, q, r обозначают здесь то же, что и там, то и здесь ADr2/h2h'2
будет целым числом, но уже не отрицательным, а положительным
и, кроме того,— квадратным, и если положить его равным g2, то
Шг') —g2q2 = ^* Это, однако, невозможно, так как разность двух
квадратов не может быть равна 4. Поэтому предположение не может
быть правильным.
Для третьего случая, однако, когда D является положительным
неквадратным числом, мы до сих пор еще не обладаем общим пра-
правилом для того, чтобы сравнивать число собственно примитивных
форм bF, F',F",... с числом различных получающихся отсюда клас-
классов. Мы можем только утверждать, что второе или равно первому,
или является его делителем; мы обнаружили даже своеобразную
Число классов в родах из различных порядков 347
связь между отношением этих чисел и наименьшими удовлетворяю-*
щими уравнению t2 — Du2 = А2 значениями t, и, излагать которую
здесь было бы слишком долго; но можно ли всегда узнать это от-
отношение только по числам D, А (как в предыдущих случаях), мы
сказать определенно не можем. Здесь мы дадим несколько примеров,
количество которых каждый может легко умножить. Для D — 13,
^4 — 2 число собственно примитивных форм в F,... равно 3, и все они
эквивалентны, т. е. образуют только один класс; для D = 37, А = 2
в F,... также имеется три собственно примитивных формы, которые
принадлежат трем различным классам; для D = 588, А = 7 в
в F,... имеется восемь собственно примитивных форм, которые обра-
образуют четыре класса; для D = 867, А = 17 в F,... встречается во-
восемнадцать собственно примитивных форм, и для D — 1445, А = 17
столько же, но для первого определителя они распадаются на два,
а для второго — на шесть классов.
VI. Из применения этой общей теории к тому случаю, когда О
•есть несобственно примитивный порядок, следует, что число содер-
содержащихся в этом порядке классов относится к числу всех классов
в собственно примитивном порядке как 1 к числу различных соб-
собственно примитивных классов, которые образуют следующие три
формы: A, 0, — D), D, 1, A—Z>)/4), D, 3, (9 — D)/4). Если D =
= 1 (mod 8), то отсюда получается только один класс, так как в этом
случае вторая и третья формы несобственно примитивны; если же
D = 5 (mod 8), то все эти три формы будут собственно примитивны, и
потому при отрицательном D дадут столько же различных классов,
за исключением единственного случая D = —3, когда они образуют
только один класс; наконец, случай, когда D положительно (вида
8лг + 5), относится к тем, для которых общего правила еще не из-
известно. Однако мы можем утверждать, что в этом случае указанные
три формы принадлежат или к трем различным классам, или к од-
одному, но никогда не к двум. Действительно, легко убедиться, что
если формы A,0, — D), D, 1, A — D)/ 4), D, 3, (9 — Z>)/4) принад-
принадлежат соответственно классам К, К\ К\ то К + К' = К', К' +
+ К1 = К", и потому, если предположить идентичными К и К'', то
будут идентичными также К1 и К"\ точно так же, если предполо-
предположить идентичными К и К\ то ж К' ж К" тоже будут идентичными;
348 Раздел V (п. 257)
наконец, так как К' + К" = К, то из предположения об идентич-
идентичности К' и К" следует также идентичность К и К". Отсюда полу-
получается, что или все три класса К, К\ К" различны, или все три сов-
совпадают. Например, среди чисел до 1000 всего будет 125 чисел вида
8п + 5, из которых для 31 определителя имеет место первый слу-
случай, т. е. число классов в собственно примитивном порядке втрое
больше, чем в несобственно примитивном, именно, для 37, 101, 141,
189, 197, 269, 325,333, 349, 373, 381, 389, 405, 485, 557, 573, 677,
701, 709, 757, 781, 813, 829, 877, 885, 901, 909, 925, 933, 973, 997; для
остальных 94 определителей имеет место второй случай, т. е. для
них число классов в обоих порядках одинаково.
VII. Едва ли нужно говорить, что при помощи этого исследо-
исследования могут сравниваться между собой не только число классов
в различных порядках одного и того же определителя, но что оно
применимо также к любым различным определителям, которые от-
относятся один к другому как квадраты. Именно, если О обозначает
какой-нибудь порядок определителя dm2, а О' — порядок опреде-
определителя dm'2, то О можно сравнить с собственно примитивным по-
порядком с определителем dm2, а его — с порядком, произведенным из
собственно примитивного порядка с определителем d, или, что в от-
отношении числа классов сводится к тому же,— с самим этим послед-
последним порядком, и с ним же можно точно так же сравнить порядок О\
О числе двусторонних классов
257
Среди всех классов в заданном порядке с заданным определителем
в особенности требуют подробного исследования двусторонние
классы, и определение числа таких классов проложит нам путь ко
многому другому. Достаточно, однако, определить указанное число
только для собственно примитивного порядка, так как остальные слу-
случаи легко могут быть сведены к этому.Эту задачу мы выполним так:
сначала покажем, как находить все собственно примитивные двусто-
двусторонние формы {А,В, С) с заданным определителем D, у которых или
В— 0, или В = -^ А, а затем, как, зная их число, найти число всех
собственно примитивных двусторонних форм с определителем D.
Число двусторонних классов 349
I. Очевидно, мы найдем все собственно примитивные формы
(А, О, С) с определителем D, если возьмем за А отдельные дели-
делители (как положительные, так и отрицательные) числа D, для кото-
которых С = —-j взаимно просто с А. Поэтому если D = 1, таких
форм имеется две: A,0,-1), (—1,0,1); столько же их будет,
€сли D = — 1, именно A, 0, 1), (— 1,0, — 1); если D простое число
или степень простого числа (будь то с положительным или отри-
отрицательным знаком), то их имеется четыре: A, 0, —D) (—1, 0, D),
(D, 0, — 1), (—D, 0, 1). Вообще же, если D делится на п различных
простых чисел (к которым здесь должно быть причислено и 2), то
всего имеется 2n+1 таких форм. Именно, если положить D = +PQR ...,
где Р, Q, i?,... обозначают различные простые числа или степени
таковых, количество которых равно п, то значениями А будут числа
1, Р, Q, 7?,... и произведения любого количества этих чисел; коли-
количество этих значений равно 2П; однако, его нужно удвоить, так как
отдельным значениям нужно придавать как положительные, так и
отрицательные знаки.
II. Подобным же образом оказывается, что все собственно при-
примитивные формы B5, 5, С) с определителем D получаются, если
за 5 брать все делители (как положительные, так и отрицательные)
числа D, для которых С = -—E ——-> будет целым числом, взаимно
простым с 25. Так как при этом С обязательно нечетно и потому
С2 = 1 (mod 8), то из D = В2 — 2ВС = (В — СJ — С2 следует, что D
или =3(mod4), если В нечетно, или ==0(mod8), если В четно;
поэтому, если D сравнимо по модулю 8 с одним из чисел 1, 2,
4.5, 6, 7, то форм такого вида нет. Если Z) = 3(mod4), то С целое
и нечетное, какой бы делитель числа D ни брать за В\ а для
того чтобы С не имело общих делителей с 25, нужно брать
такие 5, чтобы D/B было взаимно просто с В. Поэтому для
D = — 1 мы получаем две формы B, 1, 1), (—2, —1, —1), а
вообще легко убедиться, что если количество всех входящих в D
простых чисел равно п, то всего имеется 2n+1 форм. Если D де-
делится на 8, то С будет целым числом, если за В брать какой-ни-
какой-нибудь четный делитель числа D/ 2; а другое условие, именно, что
С = ~2 В — 2В Д°лжно быть взаимно просто с 25, удовлетворяется,
350 Раздел V (п. 258)
во-первых, тем что в качестве В берутся все четные, ноне делящиеся
на 4 делители числа D, для которых D / В не имеет с В общих
делителей и количество которых (принимая во внимание возмож-
возможность различных знаков) равно 2 1, где п обозначает количество
различных нечетных простых делителей числа D; во-вторых, тем,
что в качестве В берутся все делящиеся на 4 делители числа D /2,
для которых DI 2В взаимно просто с 5 и количество которых тоже
равно 2n+1, так что всего в этом случае мы получаем 2П+2 таких
форм. Именно, если, положить D = +2[LPQR.. ., где [х обозначает
некоторый показатель степени, больший чем 2, а Р, Q, R, . . . — раз-
различные нечетные простые числа (или степени таких чисел), коли-
количество которых равно п, то и в качестве В/2 и в качестве D j 2B можно
брать значения 1, Р, Q, i?, .. . и произведения лгсбого количества
этих чисел как с положительным, так и с отрицательным знаком.
Из всего этого мы выводим, что если считать D делящимся на п
различных нечетных простых чисел (где нужно положить п = 0>
если D = +1 или — dz 2, или равно степени числа 2), то коли-
количество всех собственно примитивных форм (А, В, С), у которых В
или равно 0, или равно А / 2, равно 2n+1, если D == 1 или == 5 (mod 8),
равно 2П+2, если D = 2, 3, 4, 6 или 7 (mod 8), наконец, равно 2П+3,
если .D = 0 (mod 8). Если сравнить это число с тем, которое мы ука-
указали в п. 231 для количества всех возможных характеров прими-
примитивных форм с определителем D, то можно заметить, что первое
во всех случаях в точности вдвое больше второго. Впрочем, ясно,
что если D отрицательно, то среди указанных форм всегда имеются
столько же положительных, сколько и отрицательных.
258
Очевидно, что все полученные в предыдущем пункте формы
принадлежат двусторонним классам, и, обратно, в каждом двусто-
двустороннем собственно примитивном классе с определителем D должна
содержаться по меньшей мере одна из таких форм; действительно,
в таком классе заведомо встречаются двусторонние формы, и каждой
собственно примитивной двусторонней форме (а, Ь, с) с определи-
определителем D эквивалентна какая-нибудь из форм предыдущего пункта,
Число двусторонних классов 351
именно,
или (а, 0, — — ), или ( а,
а, 0, — — J,
в зависимости от того, сравнимо ли Ъ с 0 или у a (mod а). Задача
поэтому сводится к тому, чтобы определить, сколько различных
классов образуют эти формы.
Если среди форм предыдущего пунш а фигурирует форма (а, 0, с),
то среди них будет и форма (с, 0, а), которая будет всегда
отлична от первой, кроме единственного случая, когда а = с = + 1,
и потому D = — 1; этот случай мы пока не будем принимать ва
внимание. Но так как эти формы, очевидно, принадлежат одному
и тому же классу, то из них нужно оставить только одну, причем
мы отбросим ту, у которой первый член больше третьего; случай,
когда а = —с = + 1 или D = 1, мы тоже оставим в стороне. Таким
образом, мы можем разбить все формы {А, О, С) на две части,
причем из каждых двух все время будем оставлять одну, и во всех
оставшихся будет А < |/+ Р.
Аналогично, если среди форм предыдущего пункта фигурирует
форма B6, 6, с), то среди них будет находиться также и форма
Dс-2Ь,2с-Ь,с) = (-^, -у, с
которая собственно эквивалентна первой и отлична от нее, за исклю-
исключением случая, когда с = b = + 1 ил D = — 1, рассмотрение кото-
которого мы отложим. Из этих двух форм нужно оставить только ту,
у которой первый член меньше, чем первый член другой (быть
равными по величине, но иметь различные знаки они в этом случае
не могут); отсюда вытекает, что также и все формы B5, 5, С)
могут быть сведены к половине их, если из каждых двух все время
сохранять только одну, и что у оставшихся форм В < —, т. е.
В < l^ibD- Таким образом, из всех форм предыдущего пункта
остается только половина форм, совокупность которых мы обозначим
через W, и остается только показать, сколько из них может полу-
получиться различных классов. Между прочим, ясно, что в случае,
352 Раздел V (п. 258)
когда D отрицательно, в W содержится столько же положитель-
положительных форм, сколько и отрицательных.
I. Если D отрицательно, то отдельные формы в W будут при-
принадлежать различным классам. Действительно, все формы (А, О, С)
приведенные, и точно так же среди форм B5, 5, С) все приведен-
приведенные, за исключением тех, у которых С < 25. Но у такой формы
2С < 25 + С, и потому [так как 5 < — т. е. В < 2С — В, и потому
25<2С, т. е, В < с) 2С — 2В <С и С —В <\-С, и тем самым
У
форма (С, С — В, С), которая, очевидно, эквивалентна первой,
является приведенной. Таким образом, мы имеем столько же при-
приведенных форм, сколько имеется форм в W, и так как легко видеть,
что среди них нет ни идентичных, ни противоположных (кроме
случая С — 5 = 0, когда 5 = С = + 1 и потому D = — 1, который
мы уже отложили), то все формы будут принадлежать различным
классам. Отсюда следует, что число всех двусторонних собственно
примитивных классов с определителем D равно числу форм в W,
или половине числа форм предыдущего пункта; в исключенном
же случае D = — 1 дело обстоит так же вследствие того, что имеется
два класса, одному из которых принадлежа! формы A, 0,1), B,1, 1),
а другому—формы (— 1У 0, —1), (—2, —1,—1).Таким образом, вообще,
для отрицательного определителя число всех двусторонних собст-
собственно примитивных классов равно числу всех возможных характе-
характеров примитивных форм этого определителя; число же положитель-
положительных двусторонних собственно примитивных классов равно половине
указанного числа.
П. Если D — положительный квадрат h2, то без труда доказы-
доказывается, что отдельные формы из W принадлежат различным классам;
однако, в этом случае мы можем получить решение проблемы еще
быстрее следующим образом. Так как, согласно п. 210, в каждом
двустороннем собственно примитивном классе с определителем /г2
(и ни в каких других) содержится одна приведенная форма (а, /г, 0),
у которой а является значением выражения У1 (mod 2/г) и лежит
между 0 и 2/г — 1 включительно, то ясно, что собственно прими-
примитивных двусторонних классов с определителем /г2 существует столько
же, сколько значений имеет это выражение. Но из п. 105 легко
Число двусторонних классов 353
получается, что число этих значений равно 2П, или 2n+1, или 2П+2, в
зависимости от того, является ли h нечетным, или четным, но не
делящимся на 4, или делящимся на 4, т. е. в зависимости от того,
Z)==l, или ==4, или == 0 (mod 8), причем п обозначает число нечет-
нечетных простых делителей h или D. Отсюда следует, что число дву-
двусторонних собственно примитивных классов всегда равно половине
числа всех указанных в предыдущем пункте форм, т. е. равно
числу форм в W, т. е. равно числу всех возможных характеров
III. Если D—положительное число, не являющееся квадратом, то
произведем из отдельных форм (А, 5, С), которые содержатся в W, новые
формы (А, В', С"), полагая В'== В (mod А), причем В1 заключено между
границами УD и ]/ D + А (где берется верхний или нижний знак в
зависимости от того, положительно А или отрицательно), и С =
_ —II—; совокупность этих новых форм обозначим через W.
Очевидно, что эти формы будут собственно примитивными двусто-
двусторонними формами с определителем D, различными между собой;
кроме тою, все эти формы приведенные. Действительно, если А < У D,
то, очевидно, В' < |//) и положительно; кроме того, Bf > |//)zf: А, и
потому А > У D — В', и тем самым А, взятое положительным, заведомо
лежит между УD + В1 и У D — В''. Если же A >YD, то не может быть
5=0 (так как эти формы мы отбросили), а обязательно В=—А\ поэтому
В по величине равно -^- Л, но имеет положительный знак деистви-
тельно, так как А < 2 УD, то +y^ лежит в границах, указан-
1
ных для В', и сравнимо с В по модулю А, а потому В' = zty
и тем самым 5' < ^D , т. е. 2В' < J/"D + В' или Л < VDJ- В';
поэтому 4i Л будет обязательно лежать между границами УD -\- В'
и У D — В1. Наконец, W содержит все приведенные собственно
примитивные двусторонние формы с определителем D; действительно,
если (а, Ъ, с) есть такая форма, то или Ь==0 или ^^ya^moda).
В первом случае, очевидно, не может быть Ь < а, а потому также
и а > У D, вследствие чего форма fa, 0, ) заведомо содержится
в W, а соответствующая форма (а, 6, с) — в W. Во втором случае
354 Раздел V (п. 259)
заведомо а < 2 ]/1) и потому (а, -^а,-^а — —J содержится в W,
а соответствующая форма (а, Ь, с) — в W. Из этого мы заключаем,
что число форм в W равно числу всех приведенных собственно
примитивных двусторонних форм с определителем D; так как, однако,
в каждом отдельном двустороннем классе содержатся две приведен-
приведенные двусторонние формы (пп. 187, 194), то число всех двусторонних
собственно примитивных классов с определителем D равно половине
числа форм в W, т. е. половине всех возможных характеров.
259
Число двусторонних несобственно примитивных классов с задан-
заданным определителем D всегда равно числу собственно примитивных
двусторонних классов с тем же определителем. Пусть К главный
класс и К\ К",... — остальные двусторонние собственно прими-
примитивные классы того же определителя, далее, L— какой-нибудь дву-
двусторонний несобственно примитивный класс с этим же определи-
определителем, например, тот, в котором содержится форма B,1, у—Yj'
Таким образом, при композиции класса L с К получается сам класс L;
при композиции же класса L с К', К'1, . . . пусть получаются классы
Z/,L", .-•> которые, очевидно, все принадлежат тому же определителю,
несобственно примитивны и двусторонни. Поэтому наша теорема будет
доказана, если показать, что все классы L, Z/, L", .. . различны, и что,
кроме них, других нес обственно примитивных двусторонних классов с
определителем D нет. Для этой цели мы рассмотримЪледующие случаи.
I. Если число несобственно примитивных классов равно числу
собственно примитивных, то каждый из первых получается при
композиции класса L с определенным собственно примитивным клас-
классом, вследствие чего все L, IJ, L", .. . обязательно различны. Но
если 2 обозначает какой-нибудь несобственно примитивный дву-
двусторонний класс с определителем D, то существует собственно при-
примитивный класс $ с тем свойством, что Ж -f- L = ?; если классу §,
противоположен класс Ж', то будет также и Ж' + L = ? (так как
классы L, ? противоположны самим себе), вследствие чего S и S'
обязательно совпадают, и потому класс 5? является двусторонним.
Число двусторонних классов 355
Поэтому Ж находится среди классов К, К\ К",. .., и?—среди классов
U L\ L'\ ....
II. Если число несобственно примитивных классов втрое
меньше, чем число собственно примитивных классов, то пусть Н —
4, 1, —т—), Н'—класс, в ко-
котором содержится форма D, 3, —т—]. Тогда Н, Н' собственно при-
примитивны и отличны как один от другого, так и от главного класса К\
далее, Н -\- Н' = К, 2Н = Н', 2Н' = Н, и если 2— какой-нибудь
несобственно примитивный класс с определителем D, получающийся
при композиции класса L с собственно примитивным классом Ж,
то будет также 2 = L+ S + ЯиЙ =L+8t+JjP; кроме трех собственно
примитивных и различных между собой классов Ж, Ж + #, Ж + Н\
других классов, которые при композиции с L давали бы fi, не
будет. А так как, если класс 2 двусторонний, и Ж' противоположен
классу Ж, также и L-{-K'=2, то класс Ж' обязательно будет
совпадать с одним из указанных трех классов. Если Ж' = Ж, то
класс Ж двусторонний; если Ж' = Ж + Н, т0 будет К = Ж + Ж' =
— 2Ж + Н = 2 (Ж + Н'), и потому двусторонним будет Ж + Н', и
аналогично, если Ж' = Ж + Н', то будет двусторонним Ж + Н, откуда
следует, что 2 обязательно содержится среди классов L, Z/, L", . ..
Но легко видеть, что среди трех классов Ж, Ж + Н, Ж + Н' больше
чем одного двустороннего быть не может; действительно, если бы
Ж и Ж + Н оба были двусторонними, т. е. совпадали бы соответ-
соответственно с противоположными им классами Ж', Ж' + Н'\ т0 было бы
Ж + Н = Ж + Н'\ то же заключение получается из предположения,
что двусторонни Ж и Ж + Я'; наконец, если бы Ж + Н, Ж + Н' были
двусторонними, т. е. совпадали бы с противоположными им клас-
классами Ж' + #', Ж'+ Я, то было бы Ж + Н + Ж' + Н= Ж'+ #' + Ж + Н\
т. е. 2Н = 2Н' или Н = Н'. Поэтому имеется только один дву-
двусторонний собственно примитивный класс, который при композиции
с L дает 2, и, следовательно, все L, Z/, L", .. . различны.
Число двусторонних классов в произведенном порядке, очевидно,
равно числу двусторонних классов в примитивном порядке, из
которого он произведен, и всегда может быть определено в силу
предыдущего.
356 Раздел V (пп. 260-261)
260
Задача. Собственно примитивный класс К с определителем D
получается удвоением собственно примитивного класса к с тем же
определителем; найти все такие классы, при удвоении которых
получается класс К.
Решение. Пусть Н главный класс определителя D, и Н\ Н",
Н"\ . . . — остальные двусторонние собственно примитивные классы
с тем же определителем; обозначим классы, которые получаются
при их композиции с А, именно, А+ //"', к-\-Н", к -\- Н"', . . . соот-
соответственно через к\ к", к"\ . .. Тогда все к, к' к"', .. . будут соб-
собственно примитивными классами с определителем D, различными
между собой; точно так же легко видеть, что при удвоении этих
отдельных классов получается класс К. Если же $ обозначает
какой-нибудь собственно примитивный класс с определителем D,
который при удвоении дает класс К, то $ обязательно будет содер-
содержаться среди классов к, к/ к", . . . Действительно, если положить
$ = к + §, так что <г> — собственно примитивный класс с опреде-
определителем D (п. 249), то 2к + 2§ = 2$ = К = 2к, откуда легко полу-
получается, что 2?> совпадает с главным классом, § — двусторонний
класс, т. е. содержится среди классов Н, Н', Н", . . . , и $ содер-
содержится среди классов к, к\ к",. . . Следовательно, эти классы будут
представлять полное решение задачи.
Впрочем, ясно, что в случае, когда D отрицательно, среди клас-
классов /с, к', /с",... половина положительных и половина отрицательных.
Так как тем самым каждый собственно примитивный класс с опре-
определителем jD, который может быть получен удвоением подобного же
класса, вообще получается при удвоении стольких подобных клас-
классов, сколько имеется двусторонних собственно примитивных клас-
классов с определителем D, то ясно, что еёли число всех собственно при-
примитивных классов с определителем D равно г, а число всех двусто-
двусторонних собственно примитивных классов с тем же определителем
равно 72, то число всех собственно примитивных классов с этим опре-
определителем, которые могут быть получены удвоением подобных клас-
классов, будет равно г/п. Та же формула получается, если в случае отри-
дательного определителя буквы г, п обозначают количества положи-
Исследование о том, всем ли характерам соответствуют роды 357
тельных классов, именно, первая — количество всех собственно
примитивных классов, а вторая — количество двусторонних соб-
собственно примитивных классов. Так, например, для определителя
D = — 161 число всех положительных собственно примитивных клас-
классов равно 16, а число таких же двусторонних классов равно 4, и
потому число всех классов, которые получаются удвоением подоб-
подобных классов, должно быть равно 4. И действительно, мы находим,
что все классы, содержащиеся в главном роде, обладают этим свой-
свойством; именно, главный класс A,0, 161) получается при удвоении
четырех двусторонних классов; B, 1, 81) — при удвоении классов
(9, 1, 18), (9, -1, 18), A1, 2, 15), (И, -2, 15); (9, 1, 18) —при
удвоении классов C, 1, 54); F, 1, 27), E, —2, 33), A0, 3, 17); на-
наконец, (9, —1, 18) — при удвоении классов C, —1, 54), F, —1, 27),
E, 2, 33), A0, -3, 17).
Половине всех возможных для данного определителя характеров
заведомо не могут соответствовать собственно примитивные
(при отрицательном определителе положительные) роды
261
Теорема. Половине всех возможных характеров не могут соот-
соответствовать при положительном определителе, не являющемся квадра-
квадратом, собственно примитивные, а при отрицательном определителе
собственно примитивные положительные роды.
Доказательство. Пусть т — число всех собственно примитив-
примитивных (положительных) родов определителя D; к — число клас-
классов, содержащихся в отдельных родах, так что km есть число всех
собственно примитивных (положительных) классов, и 72 — число
всех различных возможных для этого определителя характеров.
Тогда, согласно п. 258, число всех двусторонних (положительных)
собственно примитивных классов равно п/2, и потому, в соответствии
с предыдущим пунктом, число всех собственно примитивных классов,
которые могут получаться при удвоении подобных же классов,
равно 2кт/п. Но, согласно п. 247, все эти классы принадлежат
главному роду, в котором содержится к классов. Если поэтому все
358 Раздел V (п. 262)
классы главного рода могут быть получены удвоением некоторых
классов (в дальнейшем будет доказано, что в действительности это
так и есть), то —^ = к или т = -^п\ но очевидно, что не может
быть ^^ > кf и потому не может быть т >-7уП. Так как,следовательно,
число всех собственно примитивных (положительных) родов за-
заведомо не больше, чем половина всех возможных характеров, то
по меньшей мере половине из них такие роды соответствовать не
могут.
Впрочем, нужно отметить, что отсюда еще не следует, что по-
половине всех возможных характеров действительно соответствуют
собственно примитивные (положительные) роды; справедливость этой
в высшей степени важной теоремы будет получена ниже из очень
скрытых свойств чисел.
Так как для отрицательного определителя всегда существует
столько же отрицательных родов, сколько и положительных, то
очевидно, что из всех возможных характеров собственно примитив-
примитивным отрицательным родам может принадлежать не более половины,
о чем, так же, как и о несобственно примитивных родах, мы будем
говорить ниже. Наконец, заметим, что теорема не распространяется
на положительные квадратные определители, и что, напротив, для
них отдельным возможным характерам действительно соответ-
соответствуют роды.
Второе доказательство фундаментальной теоремы
и остальных теорем, касающихся вычетов —1, +2, —2
262
Таким образом, в случае, когда для данного определителя Z), не яв-
являющегося квадратом, возможны только два характера, собственно
примитивный род будет соответствовать только одному из них (кото-
(который обязательно является главным характером), в то время какдругой
не соответствует никакой собственно примитивной положительной
форме этого определителя. Это имеет место для определителей —1,
2, —2, —4, для взятых положительными простых чисел вида 4и + 1,
Второе доказательство фундаментальной теоремы 359
для взятых отрицательными простых чисел вида 4тг + 3, наконец,
для всех взятых положительными нечетных степеней простых чиг
сел вида An + 1 и для степеней простых чисел вида in + 3, причем
взятых положительными или отрицательными в зависимости от того,
являются ли показатели четными или нечетными. На основании
этого мы можем получить новый метод для того, чтобы доказать не
только фундаментальную теорему, но и все остальные теоремы пре-
предыдущего раздела, касающиеся вычетов —1, +2, —2,— метод, ко-
который совершенно отличен от использованного в предыдущем разделе
и по изяществу ему не уступает. При этом, однако, мы отбросим опре-
определитель —4 и определители, являющиеся степенями простых чи-
чисел, так как рассмотрение их не дает ничего нового.
Итак, для определителя —1 не существует положительных форм,
характером которых является 3, 4; для определителя +2 вообще
нет форм с характером 3 и 5,8; для определителя—2 нет положи-
положительных форм характера 5 и 7, 8; для определителя+/?, если р —
простое число вида 4тг + 1, или для определителя —р, если р —
простое число вида An + 3, не имеется собственно примитивных
(в последнем случае положительных) форм характера Np. На ос-
основании этого мы докажем теоремы предыдущего раздела следую-
следующим образом.
I.—1 является невычетом каждого (положительного) числа вида
An + 3. Действительно, если бы —1 было вычетом некоторого та-
такого числа А, то если положить —1 = В2 — АС, форма (А, В, С)
была бы положительной формой с определителем —1, характером
которой было бы 3, 4.
II.—1 является вычетом каждого простого числа р вида An + 1.
Действительно, характером формы (—1, 0, р), равно как и всех
собственно примитивных форм с определителем /?, является Яр;
поэтому —1 есть вычет по модулю р.
III. Как + 2, так и — 2 являются вычетами каждого простого
числа р вида 8п + 1. Действительно, формы (8, 1, ~р \ (—8, 1,^7" )
или формы (8, 3, —¦§"")> (—8, 3, ^-?—) собственно примитив-
примитивны (в зависимости от того, четно п или нечетно), и потому их
360 Раздел V (п.
характер есть Rp. Следовательно, -\-8Rp и —8Rp, а потому так-
также и 2i?p, — 2Rp.
IV. + 2 является невычетом каждого числа вида 8п + 3 или 8п +5.
Действительно^ если бы + 2 было вычетом некоторого такого чи-
числа А, то существовала бы форма (А, В, С) с определителем + 2 с ха-
характером 3 и 5, 8.
V. Точно также — 2 является невычетом каждого числа вида 8п +
+ 5 или 8я + 7, так как иначе существовала бы форма с опреде-
определителем — 2, характером которой было бы 5 и 7, 8.
VI. — 2 является вычетом каждого простого числа р вида 8п +-
+ 3. Эту теорему можно доказать двумя способами. Во-первых,
Так как, согласно IV, 2Np и, согласно I, — liVjo, то обязательно
— 2Rp. Второе доказательство основывается на рассмотрении опре-
определителя + 2р, для которого возможно четыре характера, имен-
именно Rp, 1 и 3, 8; Rp, 5 и 7, 8; Np, 1 и 3, 8; Np, 5 и 7, 8, и из них
по меньшей мере двум не соответствуют никакие роды. Но форме
A, 0, 2р) соответствует первый характер, а форме (—1, 0, 2р) —
четвертый, поэтому должны быть отброшены второй и третий ха-
характеры. Так как характер формы (р, 0, — 2) по отношению к чи-
числу 8 есть 1 и 3, 8, то ее характер по отношению к числу р не мо-
может быть иным, как Rp, и потому — 2Rp.
VII. -(- 2 является вычетом каждого простого числа р вида 8п +
+ 7, что также можно доказать двумя способами. Во-первых, так
как, согласно I и V, —INp, —2Np, то будет -\-2Rp. Во-вторых,
так как или (8, 1, ~tP), или (8, 3, о р) является собственно
\ о / V о /
примитивной формой с определителем —р (в зависимости от того,
четно п или нечетно), то ее характер есть Rp, и потому 8Rp и 2Rp.
VIII. Любое простое число р вида 4тг + 1 является невычетом
каждого нечетного числа q, которое есть невычет по модулю р. Дей-
Действительно, если бы р было вычетом по модулю q, то, очевидно, име-
имелась бы собственно примитивная форма с определителем р, харак-
характером которой было бы Np.
IX. Точно так же, если какое-нибудь нечетное число q является
невычетом простого числа р вида An + 3, то — р есть невычет по
модулю q; действительно, иначе имелась бы положительная собст-
О характерах, которым не соответствуют роды 361
венно примитивная форма с определителем —/?, имеющая харак-
характер Np.
X. Каждое простое число р вида 4тг + 1 является вычетом каж-
каждого другого простого числа q, которое есть вычет первого. Если q
также имеет вид in + 1, то это непосредственно следует из VIII;
если же q имеет вид in + 3, то (вследствие II) также и —q будет
вычетом по модулю /?, и потому pRq (согласно IX).
XI. Если какое-нибудь простое число q есть вычет другого про-
простого числа р вида 4тг + 3, то—р является вычетом числа q.
Именно, если q имеет вид in + 1, то из VIII следует pRq и потому,
согласно II, —pRq\ случай же, когда q имеет вид in + 3, не под-
поддается этому методу, но может быть легко изучен посредством рас-
рассмотрения определителя +pq. Именно, так как двум из четырех
возможных для этого определителя характерам Rp, Rq\ Rp, Nq\
Np, Rq\ Np, Nq не могут соответствовать роды, а характерами форм
A, 0, — pq), (—1, 0, pq) соответственно являются первый и четвер-
четвертый, то второму и третьему характерам не может соответствовать
никакая собственно примитивная форма с определителем pq. Так
как теперь, по условию, характер формы (#,0, —р) по отношению
к числу р есть Rp, то характер этой формы по отношению к числу q
должен быть Rq, и потому — pRq.
Если в теоремах VIII и IX предположить, что q обозначает
простое число, то они в соединении с теоремами X и XI дадут фун-
фундаментальную теорему предыдущего раздела.
Точнее определяется та половина характеров,
которой не могут соответствовать роды
263
После того, как мы заново доказали фундаментальную теоремуf
мы покажем, как та половина характеров, которой не могут еоответ-»
ствовать никакие собственно примитивные (положительные) формы,
может быть определена для данного не являющегося квадратом опреде-
определителя, причем мы решим эту задачу тем более просто, что фунда-
фундамент для решения уже заложен в исследовании пп. 147—150. Пусть
362 Раздел V (п. 264)
е2 есть наибольший квадрат, входящий в заданный определитель
D, и D = D'e2, так что D' не содержит квадратных множителей;
далее, пусть а, Ь, с,... — все нечетные простые делители D', и по-
потому D', с точностью до знака, есть или произведение этих чисел,
или удвоенное произведение. Обозначим далее через Q совокупность
специальных характеров Na, Nb, Nc,..., причем — только их, если
D' = 1 (mod4); с добавлением еще характера 3, 4, если В' = 3 и
е или нечетно, или четно, но не делится на 4; с добавлением харак-
характеров 3, 8 и 7, 8, если ?)' = Зие делится на 4; с добавлением или ха-
характера 3 и 5, 8, или двух характеров 3, 8 и 5, 8, если D'= 2 (mod 8)
и е или нечетно, или четно; наконец, с добавлением или характера
5 и 7, 8, или двух характеров 5, 8 и 7, 8, если D' = 6 (mod 8), и е
или нечетно, или четно. Если это сделано указанным образом, то
все полные характеры, в которых содержится нечетное число спе-
специальных характеров из ?S, не могут соответствовать никаким соб-
собственно примитивным (положительным) родам с определителем D.
Во всех остальных случаях специальные характеры, которые выра-
выражают отношение к не входящим в D' простым делителям числа D, не
имеют влияния на возможность или невозможность существования
соответствующего рода. Из комбинаторных же соображений легко
убедиться, что таким способом исключается действительно поло-
половина всех возможных полных характеров.
Доказательство справедливости этого правила проводится сле-
следующим образом. Из принципов предыдущего раздела или из за-
заново доказанных в предыдущем пункте теорем без труда выводится,
что если р есть какое-нибудь не входящее в D (нечетное положитель-
положительное) простое число, которому отвечает какой-нибудь из отброшенных
характеров, то D' содержит нечетное число сомножителей, являю-
являющихся невычетами по модулю /?, а потому D', а, значит, и D, есть
невычет по модулю р. Далее, легко видеть, что произведение лю-
любого количества нечетных, взаимно простых с D чисел, которым не
отвечает ни один из отброшенных характеров, также не может
быть связано с таким характером; из этого, наоборот, ясно, что каж-
каждое нечетное положительное взаимно простое с D число, которое
принадлежит какому-нибудь из отброшенных характеров, заведомо
содержит какой-нибудь простой сомножитель с таким же свой-
О характерах, которым не соответствуют роды 363
ством, и потому D является его невычетом. Если бы поэтому сущест-
существовала собственно примитивная (положительная) форма с определи-
определителем D, которая соответствует одному из отброшенных характе-
характеров, то D было бы невычетом каждого представимого такой формой
положительного нечетного взаимно простого с D числа, что, оче-
очевидно, не согласуется с теоремой п. 154.
В качестве примеров можно сравнить классификации, указан-
указанные в пп. 231, 232, число которых при желании можно увеличить.
264
Итак, всевозможные для какого-нибудь данного не являющегося
квадратом определителя характеры разбиваются на два типаР, Q, с
тем свойством, что ни одному из характеров Q не может соответство-
соответствовать собственно примитивная (положительная) форма, в то время как
ничто, насколько мы до сих пор знаем, не препятствует тому, что
остальным характерам Р такие формы принадлежат. Относительно
-этого типа характеров можно, в частности, высказать следующую
теорему, которая легко вытекает из их определения: если характер
яз Р компонируется с характером из Q (по способу п. 246, т. е.
точно так же, как если бы второму типу тоже соответствовал род),
но получается характер из Q; наоборот, если компонируются два
характера из Р или два характера из Q, то получающийся характер
принадлежит к Р. При помощи этой теоремы можно также и для
отрицательных или несобственно примитивных родов исключить по-
половину возможных характеров следующим образом.
I. Для отрицательного определителя D отрицательные роды бу-
будут в этом отношении как раз противоположны положительным,
именно, ни один из характеров Р не будет принадлежать собственно
примитивному отрицательному роду, а все такие роды будут иметь
характеры из Q. Действительно, если D' = 1 (mod 4), то —D'
является положительным числом вида 4тг + 3, и потому среди чи-
чисел а, Ь, с,... имеется нечетное количество чисел вида 4тг + 3, по
каждому из которых —1 есть невычет, откуда вытекает, что в пол-
полный характер формы (—1, О, D) в этом случае входит нечетное число
специальных характеров из ?2, т. е. что он принадлежит О. Если
364 Раздел V (п. 265)
D' = 3 (mod 4), то среди чисел а, Ъ, с,... или совсем нет чисел вида
4тг + 3, или их имеется два, или четыре и т. д.; но так как в этом
случае среди специальных характеров формы (—1, О, D) встречается
или 3, 4, илиЗ, 8, или 7, 8, то ясно, что и здесь полный характер
этой формы принадлежит к Q. Тот же вывод так же легко получается
и в остальных случаях, так что отрицательная форма (—1,0? D) всегда
имеет характер из Q. Но так как эта форма при композиции с ка-
какой-нибудь другой отрицательной собственно примитивной формой
с тем же определителем дает положительную форму такого же типа,
то легко видеть, что никакая отрицательная собственно примитивная
форма не может иметь характера из Р.
И. Для несобственно примитивных (положительных) родов по-
подобным же образом доказывается, что дело обстоит или так же, как
для собственно примитивных, или противоположным образом, в за-
зависимости от того, D = 1 или = 5 (mod 8). Действительно, в первом
случае также и В' = 1 (mod 8), откуда легко следует, что среди
чисел а, Ь, с,... или совсем нет чисел вида 8тг + Зи8гс + 5, или та-
таковых имеется два, или четыре и т. д. (действительно, произведение
любого количества нечетных чисел, среди которых чисел вида
8п + 3 и 8п + 5 вместе имеется нечетное количество, всегда будет
или =3, или =5 (mod 8), а произведение всех чисел а, Ь, с,... дол-
должно быть равно D' или —Dr). Отсюда вытекает, что полный харак-
тер формы B, 1, —2~)или не содержит специальных характеров,
из^, или содержит их два, четыре и т. д., и потому принадлежит к Р.
Так как теперь каждая несобственно примитивная (положительная)
форма с определителем D может рассматриваться как составленная из
1—D
B,1, ~2~) и собственно примитивной (положительной) формы того же
определителя, то ясно, что в этом случае никакая несобственно при-
примитивная (положительная) форма не может иметь характера из Q.
Во втором случае, когда D = 5 (mod 8), все обстоит наоборот;
именно, определитель D', который тоже = 5 (mod 8), заведома
содержит нечетное число сомножителей вида 8п + 3 и 8п + 5Г
откуда следует, что характер формы B, 1,—тр), а потому и характер
каждой несобственно примитивной (положительной) формы с опре-
Разлоэюение простых чисел на два квадрата 365
делителем D принадлежит к Q, т. е. никакому из характеров
Р не может соответствовать несобственно примитивный положи-
положительный род.
III. Наконец, для отрицательного определителя отрицатель-
отрицательные несобственно примитивные роды снова противоположны несоб-
несобственно примитивным положительным родам; именно, первые не
могут иметь характеров из Р или из Q, в зависимости от того, D = 1
или = 5 (mod 8), или в зависимости от того, имеет ли —D вид
8п + 7 или 8п + 3. Это без труда выводится из того, что при компо*
зиции формы (—1, О, D), характер которой принадлежит Q, с отри-
отрицательными несобственно примитивными формами того же опре-
определителя получаются положительные несобственно примитивные
формы, и потому, если для последних исключены характеры Q,
для первых обязательно должны быть исключены характеры Р,
и наоборот.
Специальный метод для разложения
простых чисел на два квадрата
265
Из исследований пп. 257, 258 относительно числа двусторонних
классов, на которых базировалось все предыдущее, можно вывести
еще много замечательных следствий, которые мы ради краткости
опускаем; однако мы не можем пройти мимо следующего замечания,
ввиду его изящества. Мы показали, что для положительного опре-
определителя р, являющегося простым числом вида 4и + 1, имеется
только один единственный двусторонний собственно примитивный
класс; поэтому все двусторонние собственно примитивные формы
с таким определителем собственно эквивалентны между собой.
Следовательно, если Ъ есть наибольшее положительное целое число,
которое меньше чем \/"р и р — Ь2 = а', то формы A, Ь, —а').
{—1, Ь, а') будут собственно эквивалентны, и потому, так как обе
они, очевидно, являются приведенными, одна из них будет содер-
содержаться в периоде другой. Если первую форму снабдить в ее периоде
индексом 0, то индекс второй обязательно будет нечетным (так как
первые члены этих двух форм имеют цротивоположные знаки);
366 Раздел V (п. 266)
поэтому можно положить его равным 2т + 1. Далее, легко видеть,,
что если формы с индексами 1, 2, 3,.,. суть соответственно
(-а', Ъ\ а"), (а", Ъ», -а!"), (- а'\ V", а""),. . . ,
то индексам 2/гг, 2/гг — 1, 2т— 2, 2/гг — 3,... будут соответствовать
формы
(а', 6,-1), (-а", 6', а'), (а"\ Ь",-а"), (-а"", ?"', а'"),...
Отсюда следует, что если форма индекса т равна (А, В, С),
то она же равна и (—С, В, —А), и потому С = —А и р = A2 -f-
+ В2. Поэтому каждое простое число вида 4лг + 1 может быть
разложено на два квадрата (данное разложение выше, в п. 182,
мы вывели совсем из других принципов), и такое разложение мы по-
получаем совсем простым и единообразным методом, именно, построе-
построением периода приведенной формы, определитель которой равен
этому простому числу, а первый член равен 1, до формы, крайние члены
которой равны по величине и противоположны по знаку. Так, на-
например, для р = 233 мы получаем следующий ряд форм: A, 15, —8),
(-8, 9, 19), A9, 10, -7), (-7, И, 16), A6, 5, -13), (-13, 8, 13),
и 233 = 64 + 169. Между прочим, ясно, что А обязательно нечетно
(так как (А, В, —А) должна ведь быть собственно примитивной
формой), и потому В будет четно. Так как для положительного опре-
определителя р, являющегося простым числом вида 4?г + 1, также и
в несобственно примитивном порядке содержится только один един-
единственный двусторонний класс, то очевидно, что если g есть наиболь-
наибольшее нечетное число, которое меньше чем У~~р, и р — g2 = 4/г, то
приведенные несобственно примитивные формы B, g, —2h)r
(—2, g, 2h) собственно эквивалентны, и потому одна из них содержится
в периоде другой. Отсюда с помощью рассуждения, которое совер-
совершенно аналогично предыдущему, получается, что в периоде формы
B, g, —2h) находится форма, у которой крайние члены равны по
величине, но противоположны по знаку, так что разложение числа
р на два квадрата может быть выведено также и отсюда. Но оче-
очевидно, что крайние члены этой формы будут четными, а средний
нечетным, и так как известно, что простое число может быть раз-
разложено на два квадрата только одним способом, то найденная этим
Тройничные квадратичные формы 367
последним методом форма будет или (В, +-А, —В), или (—23,4: А, В).
Так, в нашем примере для р — 233 получается следующее:
B, 15,-4), (-4,13, 16), A6,3,-14), (-14, И, 8), (8, 13, -8), и
233 = 64 + 169, как и выше.
Отступление, содержащее исследование
о тройничных формах
266
До сих пор мы ограничивали наше исследование такими функ-
функциями второй степени, которые содержат две переменные, и потому
не было необходимости снабжать их специальным названием. Но
очевидно, что мы можем рассматривать этот предмет как очень спе-
специальный раздел общего исследования об алгебраических рациональ-
рациональных целых однородных функциях любого числа переменных и лю-
любой степени, и подразделять такие функции по степени на формы
второй, третьей, четвертой и т. д. степеней, и по числу перемен-
переменных на двойничные, тройничные, четверичные и т. д. формы. По-
Поэтому то, что до сих пор называлось просто формами, являются
двойничными формами второй степени, а функции вида
Ах2 + 2Вху + Су2 + 2Dxz + 2Eyz + Fz2
(где А, В, С, D, E, F обозначают заданные целые числа) — назы-
называются тройничными формами второй степени и т. д. Сначала на-
настоящий раздел посвящался только двойничным формам второй
степени; но так как остается еще много относящихся сюда фактов,
причем из наиболее красивых, непосредственный источник которых
следует искать в теории тройничных форм второй степени, мы хотим
включить здесь краткое отступление об этой теории, в котором из
первых ее элементов мы приведем то, что необходимо для пополнения
теории двойничных форм, и надеемся, что для математиков это будет
приятнее, чем если бы мы указанные факты или опустили, или вы-
вывели бы менее естественными методами. Более же подробное иссле-
исследование об этом очень важном вопросе мы должны отложить до
другого случая, во-первых, потому, что богатство его уже сейчас
368 Раздел V (п. 267)
очень расширило бы границы этого труда, а, во-вторых, потому, что
имеется надежда на то, что в будущем оно пополнится еще другими
важными фактами. Формы второй степени от четырех, пяти и т. д.
переменных мы, по крайней мере в этом месте, совершенно исклю-
исключаем из рассмотрения *, и довольствуемся тем, что обращаем на эту
весьма обширную область внимание математиков, ибо они найдут
здесь обширный материал для упражнения своих сил и обогащения
высшей арифметики выдающимися открытиями.
267
Для большей отчетливости будет очень полезно, если для трех
входящих в тройничную форму переменных, как и в случае двой-
двойничных форм, мы установим определенный порядок расположения,
так что первая, вторая и третья переменные будут различаться ме-
между собой. При размещении отдельных частей формы мы будем всегда
соблюдать такой порядок, чтобы часть, содержащая квадрат пер-
первой переменной, занимала первое место, а далее следовали бы одна
за другой части, содержащие квадрат второй переменной, квадрат
третьей переменной, удвоенное произведение второй и третьей,
удвоенное произведение первой и третьей, удвоенное произведение
первой и второй переменной. Наконец, постоянные целые числа, на
которые умножаются эти квадраты и удвоенные произведения, мы
будем в том же порядке называть первым, вторым, третьим, чет-
четвертым, пятым, шестым коэффициентами.
Так, например,
ах2 + а'х'2 + а!'х + 2Ъх'х" + 2Ъ'хх" + 2Ъ"хх'
будет правильно расположенной тройничной формой, первая перемен-
переменная которой есть х, вторая х', третья х", первый коэффициент ко-
которой есть а, и т. д., четвертый Ъ и т. д. Так как, однако, в смы-
смысле краткости было бы удобно, если бы нам не нужно было бы
всегда обозначать переменные тройничной формы специальными
буквами, то мы будем записывать такую форму, если мы не
* По этой же причине в дальнейшем под двойничными или тройничными фор-
формами все время будут пониматься формы второй степени.
Тройничные квадратичные формы 369
обращаем внимания на переменные, следующим образом:
(а, а', а"\
[Ь, Ъ\ Ъ") .
Если положить
б2 — а'а" = А, Ь'* — аа" = А', Ъ"* — ал' = А",
ab — Ъ'Ъ" = В, а'Ъ' — ЪЪ" = В', а"Ъ" — W = В",
то получается другая форма
1А,А>,А»,
\В, В\ В") ^ь »
которую мы будем называть дополнительной к форме
a, а\ а"
b, Ь\ P)
Отсюда, если для краткости положить
ab2 + а'Ь'2 + а"Ъ"* — аа'а" — 2ЪЬ'Ъ" = D,
мы снова находим
'B' — BB" = b'D, A"B" — BB' - b"D,
откуда вытекает, что дополнительной для формы F является форма
(aD, a'D, a"D\
[bD, b'D, b"DJ .
Число D, от свойств которого в первую очередь зависят свойства
тройничной формы /, мы будем называть определителем этой формы.
Таким образом, определитель формы F будет равен D2, т. е. равен
квадрату определителя формы /, для которой она является допол-
дополнительной.
Так, например, для тройничной формы
29, 13, 9
7, —1, 14
370 Раздел V (п.
дополнительной будет форма
—68, —260, —181
217, —111, —133
и определитель обеих равен 1.
Тройничные формы с определителем 0 мы из последующего
исследования совершенно исключим, так как они, как будет по-
показано в оставленной до другого случая более полной теории трой-
тройничных форм, только по виду являются тройничными формами,
в действительности же эквивалентны двойничным формам.
268
Если какая-нибудь тройничная форма / с определителем D,
переменными которой являются х, хг, х" (именно, первая равна х,
и т. д.), переходит в тройничную форму g с определителем Е, пе-
переменными которой являются у у у'', у" у при подстановке вида
х — ay + р?/' + yj/",
где все девять коэффициентов а, р,... предполагаются целыми чи-
числами, то мы, ради краткости, будем, отбрасывая переменные, го-
говорить просто, что / переходит в g при подстановке (S)
ос, р, т
«'. Р'. Т'
ос", Р", Т">
и что / содержит форму g или g содержится в /. Из этого предполо-
предположения непосредственно получается, следовательно, шесть равенств
для шести коэффициентов формы g, приводить которые здесь нет
нужды; однако из них несложными выкладками получаются сле-
следующие выводы.
I. Если положить для краткости
рт'а" + уа'Р" — Тр'а" — аТу — р<х Y = к>
Тройничные квадратичные формы 371
то после соответствующих сокращений получается равенство Е =
= k2D, откуда вытекает, что Е делится на D и отношение является
квадратом. Поэтому ясно, что число к является для преобразований
тройничных форм подобным числу ос8 — р^ из п- 157 Для преобразо-
преобразований двойничных форм, именно, квадратным корнем из отношения
определителей, из чего можно было бы предположить, что различие
знаков у к и здесь обусловливает существенное различие между
преобразованиями и собственной и несобственной содержимостью
одной формы в другой. Однако, если рассмотреть вопрос ближе, то
видно, что / переходит в g также и при подстановке
— ос, — р, — т
-а', -{*', -Т'
-а", -(В", -Т",
но если в значение к подставить —авместоа, —(В вместо (В, и т. д.
то получится —/с, и потому эта подстановка будет неоднотипна с под-
подстановкой (S), а, значит, каждая тройничная форма, которая со-
содержит другую форму каким-нибудь образом, содержит ее и другим
образом. Поэтому такое различие здесь делаться не будет, так как
для тройничных форм оно не нужно.
II. Если обозначить через F, G формы, дополнительные к /,
g, то коэффициенты у F будут определяться коэффициентами формы
/, а коэффициенты у G — значениями коэффициентов формы g,
которые известны из равенств, определяемых подстановкой S.
Если выразить коэффициенты формы / буквами, то сравнением
значений коэффициентов форм F, G без труда устанавливается, что
F содержит форму G и переходит в нее при подстановке (Sf)
РТ'-Р'Т, Та'-Т'а. <*Р'- а'Р-
Выкладку, которая не требует преодоления никаких трудностей,
мы здесь не выписываем.
III. При подстановке (S")
PY-PY, р'т-рт*. рт'-Р'т,
Т'а" — TV, -foe —Т«". т«' — т'«.
аф" — а"Р', а"р — а^", аЗ' — а',8
372 Раздел V (пп. 269-271)
форма g переходит, очевидно, в ту форму, в которую переходит
форма / при подстановке
Л, О, О
О, к, О
О, 0, к,
т. е. она переходит в ту форму, которая получается, если отдель-
отдельные коэффициенты формы / умножить на к2. Эту форму мы обозна-
обозначим через /'.
IV. Точно таким же образом показывается, что G при подста-
подстановке (Sm)
а, а', а"
р> Р', р*
т, т'. т"
переходит в форму, которая получается из F, если отдельные ко-
коэффициенты у F умножить на к2. Эту форму мы обозначим через F''.
Мы будем говорить, что подстановка S"' получается из подста-
подстановки S транспонированием', тогда S, очевидно, тоже будет полу-
получаться транспонированием из подстановки S'", и из подстановок
S', S" одна будет получаться транспонированием другой. Под-
Подстановку S' целесообразно назвать дополнительной к подстановке S,
и потому S" будет также дополнительной к подстановке S'".
269
Если не только форма / содержит форму g, но и вторая форма
содержит первую, то формы /, g называются эквивалентными.
В этом случае не только D входит в Е, но и Е входит в D, откуда
легко следует, что D ~ Е. Но и наоборот, если форма / содержит
форму g с тем же определителем, то обе эти формы эквивалентны.
Действительно (если использовать те же обозначения, что и в пре-
предыдущем пункте, и исключить случай D = 0), к = +1, и потому
форма /', в которую переходит g при подстановке *S"', идентична /,
т. е. / содержится в g. Далее, ясно, что в этом случае также и допол-
дополнительные к /, g формы F, G эквивалентны между собой, и вторая
Тройничные квадратичные формы 373
переходит в первую при подстановке S'". Наконец, если, наоборот,
предполагать формы F, G эквивалентными, причем считать, что пер-
первая переходит во вторую при подстановке Т, то и формы /, g будут
эквивалентны, и / будет переходить в g при подстановке, дополни-
дополнительной к 7\ a g в / при подстановке, которая получается из Т
транспонированием. Действительно, при этих двух подстановках
соответственно форма, дополнительная к F, переходит в форму, до-
дополнительную к G, и вторая в первую; но обе эти формы получаются
из /, g умножением отдельных коэффициентов на D, откуда без труда
следует, что при указанных выше подстановках соответственно /
переходит в g, и g в /.
270
Если тройничная форма / содержит тройничную форму /', а по-
последняя, в свою очередь, содержит форму /", то и / будет содер-
содержать форму /". Действительно, легко видеть, что если переходят
/ в /' при подстановке
ос,
ос'
Р
ос", Р", Т"
/' в /" при подстановке
8, 8, С
8', 8', С
S", s", С",
то / будет преобразовываться в /" при подстановке
/х8 + р8' + Т8", as + ре' + Те", *С + рС + ТС",
а'8 + Р'8' -+- т^, а'е + рV + т V, а'С + р'С + Т^
Таким образом, если / эквивалентна форме /', и /' эквивалент-
эквивалентна форме /", то форма / также будет эквивалентна форме /". Ясно,
как эти теоремы распространяются на большее число форм.
271
Отсюда уже вытекает, что все тройничные формы, так же, как и
двойничные, могут быть разбиты на классы, если причислять экви-
эквивалентные формы к одному и тому же классу, а не эквивалент-
374 Раздел V (п. 271)
ные — к различным. Формы с различными определителями будут
поэтому заведомо принадлежать к различным классам, и потому
будет бесконечно много классов тройничных форм; принадле-
принадлежащие же одному и тому же определителю тройничные формы об-
образуют или большее, или меньшее число классов; но как основное
свойство этих форм следует рассматривать то, что все формы с од-
одним и тем же заданным определителем всегда образуют конечное
число классов. Подробному изложению этой очень важной теоремы
мы должны предпослать установление следующего важного разли-
различия, которое имеет место для тройничных форм.
Некоторые тройничные формы устроены так, что ими могут пред-
представляться как положительные, так и отрицательные числа, на-
например, форма х2 + у2— z2\ вследствие этого они называются не-
неопределенными формами. Напротив, другими формами не могут
представляться отрицательные числа, а только положительные (кро-
(кроме нуля, который получается, если все переменные положить рав-
равными 0), например, формой х2 -f у2 + z2\ вследствие этого такие
формы называются положительными; наконец, некоторыми форма-
формами не могут представляться положительные числа, -например, фор-
формой — х2 — у2 -— z2, вследствие чего они называются отрицатель-
отрицательными формами. Положительные и отрицательные формы имеют
общее название: определенные формы. Сейчас мы уже дадим неко-
некоторые критерии, при помощи которых можно судить об этих свой-
свойствах форм.
ЕСЛИ ТРОЙНИЧНУЮ (boDMV
f = ах2 + а'х'2 + а"х + Zbx'x" + 2Ъ'хх" + 2Ъ"ххг
с определителем D умножить на а и так же, как в п. 267, обо-
обозначить коэффициенты дополнительной к / формы через А, А', А",
В, В', В", то получается форма
(ах -f Ь"х' + Ъ'х"J — А"х'2 + 2Вх'х" — А'х = g;
если теперь еще раз умножить на А*, то получим форму
А' (ах 4- 6V + Ъ'х"J — (А'х" — Bx'f + aDx'2 = h.
Тройничные квадратичные формы 375
Из этого тотчас же вытекает, что если как А', так и aD являются
отрицательными числами, то все значения h отрицательны, вслед-
вследствие чего формой /, очевидно, могут представляться только такие
числа, знаки которых противоположны знаку а А', т. е. совпадают
со знаком а или противоположны знаку D. Таким образом, в этом
случае / является определенной формой, причем положительной
или отрицательной в зависимости от того, положительно а или от-
отрицательно, или в зависимости от того, отрицательно D или поло-
положительно.
Если же или оба числа aD, А' положительны, или одно положи-
положительно, а другое отрицательно (ни одно не равно 0), то легко ви-
видеть, что h при соответствующем определении величин х, х\ х"
может принимать как положительные, так и отрицательные значе-
значения. Следовательно, в этом случчае / может принимать значения,
которые имеют или тот же знак, что и аА', или противоположный,
и потому / будет неопределенной формой.
В случае, когда 4'= 0, но а не равно 0, должно быть
g = {ах + Ъ"х' + Ъ'х"У — х' {А"х' — 2Ъх").
Если придать а/произвольное значение (которое, однако, неравно 0
А" х1
и выбрать х" так, чтобы ^в —х" имел0 тот же знак, что
и Вхг (легко видеть, что это возможно, так как В не может быть
равно нулю; действительно, в противном случае было бы В2 —
— А'А" = aD = 0, и потому D = 0, а этот случай мы исключили),
то х\А"х' — 2Вх") будет положительной величиной, откуда легко
вытекает, что х можно определить так, чтобы g получило отрицатель-
отрицательное значение. Очевидно, что при желании эти значения можно по-
подобрать и так, чтобы все они были целыми числами. Наконец, ясно,
что если х\ х" приданы любые значения, то х можно взять столь
большим, что g будет положительно. Поэтому / является в этом
случае неопределенной формой.
Наконец, если а = 0, то
/ = а'х'2 + 2Ъх'х" +- аУ2 + 2х (Ь"х' + Ъ'х"),
Поэтому если взять х', х" произвольными, но такими, что Ъ"х +
-\-Ъ'х" не равно 0 (что, очевидно, возможно, если только Ьг и й"не
376 Раздел V (п. 272)
равны одновременно 0; но тогда было бы D = 0), то легко видеть,
что х можно определить так, чтобы / принимала как положительные,
так и отрицательные значения. Следовательно, и в этом случае /
есть неопределенная форма.
Тем же способом, каким мы здесь по числам aD, А' определяли
природу формы /, можно делать это и при помощи чисел aD и А",
так что / является определенной формой, если как aD, так ж А"
отрицательны, и неопределенной во всех остальных случаях.
И точно так же этой цели может служить рассмотрение чисел a'D
и А, или чисел a'D и А", или чисел a"D и А, или, наконец, чисел
a"D и А'.
Из всего этого следует, что у определенной формы шесть чисел
А, А', A", aD, a'D, a"D отрицательны, причем у положительной формы
а, а', а" положительны, D отрицательно, а у отрицательной формы
а, а', а" отрицательны и D положительно. Отсюда вытекает, что
все тройничные формы с заданным положительным определителем
распадаются на отрицательные и неопределенные формы, все трой-
тройничные формы с заданным отрицательным определителем распа-
распадаются на положительные и неопределенные, и, наконец, что поло-
положительных форм с положительным определителем или отрицательных
с отрицательным определителем вообще не существует. Кроме
того, легко видеть, что для определенной формы дополнительной
всегда является определенная и притом отрицательная форма, а для
неопределенной — неопределенная.
Так как все числа, представляемые данной тройничной формой,
очевидно, представляются также и всеми эквивалентными ей фор-
формами, то содержащиеся в одном и том же классе тройничные формы
будут или все неопределенными, или все положительными, или все
отрицательными. Поэтому эти наименования можно перенести с форм
на целые классы.
272
Высказанную в предыдущем пункте теорему о том, что все трой-
тройничные формы с заданным определителем распадаются на конечное
число классов, мы докажем методом, подобным тому, который мы
Тройничные квадратичные формы 377
использовали для двойничных форм, именно, мы покажем, во-пер-
во-первых, каким образом каждая тройничная форма может быть сведена
к более простой форме, и, во-вторых, что количество простейших
форм (к которым мы приходим при этой редукции) для каждого
данного определителя конечно. Если мы вообще предположим, что
дана тройничная форма / = ( ?' ?,' °!„ ] с (отличным от нуля) опре-
\О, О , и J
делителем D, которая при подстановке
а, Р? Т
(S) а', р' Т'
а" р", Т"
/т, т\ т" \
переходит в эквивалентную форму g = \ , „ , то наша за-
у /t, п , п j
дача состоит в том, чтобы определить а, р, "р . . ., так, чтобы фор-
форма g была проще чем /. Если дополнительными для форм /, g яв-
(А, А', А"\ /М, М', М"\
ляются соответственно формы d d/ В" \ "> \N Nf N" I '
рые мы обозначим через F, G, то, согласно п. 269 ; F переходит
в G при подстановке, дополнительной к S, a G в F при подстанов-
подстановке, получающейся из S транспонированием. Число
кото-
которое должно быть равно или +15 или —1, мы обозначим че-
через к. После этого заметим следующее.
I. Если т = 0, ^ = 0, а" = О, Р" = 0, f' = 1, то
m = аа2 + 2Ь^аа' + ^'а/2, т' = ар2 + 2Ь^Р' + а'р/2, т" = аг/;
/г = Ьр' + Ьф, п' - Ьа' + й'а, п" = аар + 6" (ар; + ра') + а'аф'.
Кроме того, ар' — р<х' должно быть равно или + 1? или — 1. Из это-
этого вытекает, что двойничная форма (а, Ъ", а'), определитель кото-
которой есть А", при подстановке а, р, а', р; преобразуется в двойнич-
двойничную форму (т, п", т') с определителем М", и потому, вследствие
ар' — ра' = + 1, ей эквивалентна, откуда следует М" = А", что лег-
легко может быть установлено и непосредственно. Если поэтому (а, Ъ", а')
378 Раздел V (п. 272)
сама еще не является простейшей формой в своем классе, то a, р,
а', р' могут быть определены так, что (т, п", т!) будет более про-
простой формой, причем из теории эквивалентности двойничных форм
легко следует, что это может быть сделано так, что т не больше
чем У—АА"/3, если А" отрицательно, или не больше чем |/ А"', ес-
если А" положительно, или т = 0, если А" = О, так что во всех слу-
случаях (абсолютная) величина т заведомо может считаться или рав-
равной 0, или по крайней мере не превосходящей ]/~+4-4"/3. Итак,
при этом форма / сводится к другой форме, которая, если это во-
вообще возможно, имеет меньший первый коэффициент, а дополни-
дополнительная к ней форма имеет такой же третий коэффициент, что и
дополнительная к / форма F. В этом состоит первая редукция.
II. Если, напротив, а = 1, р = 0, *( = 0, а' = 0, а" = 0, то к —
— Р'т" — P'V = zh 1; поэтому подстановкой, дополнительной к S,
является
+ 1, О, О
о, г, -р"
о, -т\ Р',
и посредством нее F переводится в G. Мы имеем поэтому
т == а, п'= Ь\" + 6Y» п" = ЬТ + ЬТ,
+ а"$"\ т" = а'ч'2
п = а'р у + & (Р Y
Af' - ,4Y2 —
N = — А'$У' + В ф Y + Т'Р'') — -4"Р Y>
ikf" = ^^ _ 2Вр'Р" -f ^p'2.
Отсюда вытекает, что двойничная форма (А", В, А'), определитель
которой есть Da, при подстановке р;, —т', —Р", ^ переходит в
форму (М", N, М') с определителем Dm, и потому (вследствие то-
того, что PY' — Тф" = it 1> или того, что Da = Dm) эквивалентна ей.
Если поэтому (А", В, А') еще не является простейшей формой сво-
своего класса, то коэффициенты р', т'» Р"» Т" могут быть определены
так, что форма (М", N, М') будет более простой, причем это всег-
всегда может быть достигнуто так, что М", рассматриваемое без зна-
знака, не больше чем ^+41^/3. Следовательно, таким способом фор-
Тройничные квадратичные формы 379
ма / сводится к другой форме с таким же первым коэффициентом,
а форма, дополнительная к этой второй форме, имеет третий коэф-
коэффициент, который, если это вообще возможно, меньше, чем третий
коэффициент дополнительной к / формы F. В этом состоит вторая
редукция.
III. Если поэтому / есть тройничная форма, к которой не при-
применима ни первая, ни вторая редукция, т. е. которая ни одной
из этих двух редукций не может быть сведена к более простой фор-
форме, то по абсолютной величине обязательно будет как а2 ^ 1г^"> так
и A^^~aD. Из этого следует, что а* <^-тг А, и потому а4^
о У
^T^aD или a3^.^D и a^yj/77; отсюда снова А^-
А" ^у УD2. Поэтому если а или А" еще превосходят эти грани-
границы, то к форме / обязательно будет применима одна из предыду-
предыдущих редукций. Впрочем, это утверждение нельзя обратить, так
как часто бывает, что тройничная форма, у которой ее первый ко-
коэффициент и третий коэффициент дополнительной формы уже ле-
лежат в указанных границах, все же может быть сделана еще про-
проще при помощи первой или второй редукции.
IV. Если теперь к любой заданной тройничной форме с опреде-
определителем D попеременно применять первую и вторую редукции,
т. е. если к ней самой применить первую, к получающейся при этом
форме вторую или первую, к так полученной форме снова первую
или вторую редукцию и т. д., то ясно, что в конце концов мы придем
к форме, к которой уже не применима ни одна из этих редукций.
Действительно, так как абсолютные величины как первых коэф-
коэффициентов получающихся при этом форм, так и третьих коэффици-
коэффициентов дополнительных к ним форм попеременно то остаются неиз-
неизменными, то убывают, этот процесс обязательно будет где-нибудь
иметь конец, ибо иначе получились бы два бесконечных ряда по-
постоянно убывающих чисел. Из этого мы уже получаем следующую
красивую теорему. Каждая тройничная форма с определителем D
может быть сведена к другой эквивалентной ей форме, у которой
380 Раздел V (п. 273)
i 3 /
первый коэффициент не больше чем -yD, а третий коэффициент
дополнительной к ней формы не больше чем - уD2 (по абсолютной
величине), если сама заданная форма еще не обладает этими свой-
свойствами. Впрочем, если бы вместо первого коэффициента формы /
и третьего коэффициента дополнительной к ней формы мы точно
таким же образом взяли бы или первый коэффициент самой формы
и второй коэффициент дополнительной, или второй коэффициент
самой формы и первый или третий коэффициент дополнительной,
или третий коэффициент самой формы и первый или второй коэффи-
коэффициент дополнительной, мы тем же самым путем достигли бы своей
цели; однако целесообразно все время придерживаться одного ме-
метода, чтобы иметь возможность легче производить относящиеся сюда
операции по определенному алгоритму. Заметим, наконец, что
для обоих коэффициентов, для которых мы показали, как можно
заключить их в определенные границы, могут быть установлены
еще меньшие границы, если отделить определенные формы от не-
неопределенных; однако для нашей теперешней цели это не нужно.
273
Теперь мы дадим несколько примеров, на которых указанные
перед этим правила сделаются яснее.
Пример 1. Если
, 19, 21, 50
/ =
15, 28, 1
то
1—825, —166, —398
— 398 \
— 370 )
257, 573, — 370,'
и D = —1. Так как A9, 1, 21) является приведенной двойничной
формой, которой никакая другая форма с меньшим первым членом,
чем 19, не эквивалентна, то первая редукция здесь не применима;
напротив, мы находим, что двойничвдя форма (—398, 257, —166),
Тройничные квадратичные формы 381
согласно теории эквивалентности двойничных форм, преобразуема
в более простую эквивалентную ей форму (—2, 1, —10), причем
первая переходит во вторую при подстановке 2, 7, 3, 11.
Поэтому если положить $' = 2, т' = — 7, [3" = — 3, т" — 11, то
к форме / применяется подстановка
1, 0, 0
0, 2, -7,
0, —3, 11
при которой она переходит в форму
/ 19, 354, 4769\
? = \— 1299, 301, —82J •
Третий коэффициент дополнительной к ней формы равен — 2, и в
этом отношении /' проще, чем /.
К форме /' можно применить первую редукцию. Именно, так
как двойничная форма A9, —82, 354) переходит в форму A, 0, 2)
при подстановке 13, 4, 3, 1, то к форме /' нужно применить под-
подстановку
13, 4, 0
3, 1, 0,
0, 0, 1
при которой она переходит в
/1, 2, 4769 \
' =\-95, 16, о)'
К форме /", дополнительной к которой является форма
-513, —4513, — 2 \
- 95, 32, 1520J •
можно снова применить вторую редукцию. Именно, форма
(—2, —95, —4513) при подстановке 47, 1,-1, 0 переходит в
(—1, 1, —2); поэтому к форме /" нужно применить подстановку
1, 0, 0
0, 47, -1,
0, 1,-1
382
Раздел V (п. 274)
при которой она переходит в
1,
1, 0, 16у
Первый коэффициент этой формы дальше уже первой подстановкой
уменьшен быть не может, так же, как и третий коэффициент до-
дополнительной к ней формы, — второй подстановкой.
Пример 2. Если дана форма
, /Ю, 26, 2
f=[ 7, 0,
дополнительной к которой является форма
— 3, -20, — 244\
70, — 28, 8)
и определитель которой равен 2, то, применяя в соответствии с
правилами попеременно вторую и первую редукции, мы находим
подстановки,
1.
JO JO J
о,
1
о,
1.
JO JO J
1,
1,
o,
0,
4,'
2
o!
0,
j_
i
o,
i,
o,
0
0
—1
0
о
1
0
0
—1
0
0
1
при которых
переходит
1
у
г
Г
/
/ 10,
1-1,
1 '
U
( 2
\ 9
\
/
\ —2
2,
0,
Г)
—1
, 2,
, 1,
В
-4 у!
1 —
-2/
2 2 \
z, z
1 0 /
= /'
1"
-г
J'lf
Форма /"" не может быть дальше упрощена ни первой, ни вто-
второй редукцией.
274
Если имеется тройничная форма, у которой первый коэффициент,
так же, как и третий коэффициент дополнительной к ней формы,
Тройничные квадратичные формы 383
уменьшены при помощи только что указанных методов насколько
это возможно, то дальнейшую редукцию дает следующий метод.
Если мы сохраним те же обозначения, что и в п. 272, и поло-
положим а = 1, а' = 0, р' = 1, ос" = 0, Р" = 0, т" = 1, т. е. сделаем под-
подстановку
1» Р» 7
О, 1, т'
О, 0, 1,
то будет
m = a, т'= а'+ 2?"р + аЗ2,
т" - а"
Л = Ъ + a'i + Ъ'$ + Ъ" (Т + рт') + а[ВТ, л' = 6' + аТ + Ъ*ч\
п" = Ъ" + ар;
кроме того,
М" = 4", N = В — Ay, N' = Bf — N$ — A'\.
Итак, при такой подстановке коэффициенты а, А", которые пони-
понижались предыдущими редукциями, не изменяются; поэтому наша
задача состоит в том, чтобы посредством оответствующего выбора
Р, Т» Т' добиться уменьшения других коэффициентов. Для этой це-
цели заметим сначала, что если А" — 0, то можно считать, что и а =
= 0; действительно, если бы а не было равно 0, то была бы еще
раз применима первая редукция, так как каждая двойничная фор-
форма с определителем 0 эквивалентна форме вида @, 0, /г), т. е.
форме, первый член которой равен 0 (ср. п. 215). По совершенно
аналогичной причине можно предполагать, что если а = 0, то и
А" = 0, так что или ни одно из чисел а, А" не равно 0, или они
равны 0 оба.
В первом случае ясно, что р, ^» т' могут быть определены так,
что по абсолютной величине п", JV, N' будут соответственно не боль-
11 1
ше чем rfl, г А"* о~ ^" * ^ак' в первом примере предыдущего пунк-
пункта последняя форма
/1, 257, 2n
U, 0, 16/ '
384 Раздел V (п. 275)
дополнительной к которой является форма
513, - 2, -1\
\ 1, -16, 32 )>
при подстановке
1, -16, 16
О, 1, -1
0, 0, 1
переходит в форму
1, 1, 1\
О, 0, 0)=' >
дополнительной к которой будет форма
-1, -1, -1\
О, 0, 0) •
Во втором случае, когда а = А" = 0 и потому также Ъ" = О,
будет
т = 0, т' = а\ т" =-а" -\- 2b^f -\- 2b'y + а'^'2',
п = b -\- а'ч' + 6'В, лг = 6Г, тг" = 0.
Поэтому
и легко видеть, что р и f' могут быть определены так, что п будет
равно абсолютно наименьшему вычету числа Ъ по модулю, являю-
являющемуся наибольшим общим делителем а'', й', т. е. что по абсолют-
абсолютной величине будет не больше половины этого делителя, и потому
п = 0, если а', Ъ' взаимно просты. Если [В, <у' определены таким об-
образом, то значение т может быть выбрано так, что т" по абсолют-
абсолютной величине будет не больше чем Ъ'\ это было бы невозможно сде-
сделать только в том случае, если Ь' = 0; но тогда было бы D = 0,
однако этот случай мы исключили. Так, для последней формы
во втором примере предыдущего пункта п = — 2 — 3 + 2^', откуда,
если положить [В = — 2, ^' == 0, следует п = 0, далее, т" = 2 — 2*у,
и, если положить <у = 1, то т" = 0. Мы получаем поэтому
подстановку
Тройничные квадратичные формы
385
1, -2, 1
О, 1, О
о, о, 1,
при которой указанная форма переходит в
О, 2, 0\
О, -1, 0)=/ •
275
Если имеются ряд эквивалентных тройничных форм /, /', /",
/'", ... и преобразования каждой из этих форм в следующую, то,
в соответствии с п. 270, из преобразований / в /' и /' в f выво-
выводится преобразование формы / в /"; из него и из преобразования
формы /" в /'" следует преобразование формы / в /'" и т. д., и оче-
очевидно, что таким способом можно найти преобразование формы /
в любую форму ряда. А так как из преобразования формы / в ка-
какую-нибудь эквивалентную ей форму g может быть получено и пре-
преобразование формы g в / (?"' из S, пп. 268, 269), то можно таким
путем найти преобразование любой формы ряда /', /", ... в первую
форму /. Так, для форм первого примера предыдущего пункта мы
находим подстановки
13,
6,
-9, -
4,
2,
-з,
0
— 7
11
13,
6,
-9,
188,
87,
— 130,
— 4
— 2
3
13,
6,
-9,
-20,
-9,
14,
16
7
-И,
которыми форма / переводится соответственно в /", /'", /"", а из
последней подстановки находим следующую:
1, 4, 4
3, 1, 5
3, -2, 3,
при которой /"" переходит в /. Подобным же образом во втором
примере предыдущего пункта получаются подстановки
1, -1, 1
-3, 4, -3
10, —14, 11
2, -3, -1
3, 1, 0
2, 4, 1,
386 Раздел V (пп. 276-277)
при которых соответственно форма
/10, 26, 2\
U 0,4)/
переходит в
и вторая — в первую.
0, 2, 0
0, —1, 0
276
Теорема. Число классов, на которые распадаются все тройнич-
тройничные формы с данным определителем, всегда конечно.
(а, а', а!'\
Доказательство. I. Число всех форм \ h h, 7J с данным опре-
делителем D, у которых а = 0, Ъ" = 0, Ь не больше, чем половина
наибольшего общего делителя чисел а', Ъ\ и а!' не больше чем Ь\
очевидно, конечно. Действительно, так как должно быть а'&'2 = Z),
для значения V не имеется других возможностей, кроме +1, —1
и корней из входящих в D квадратов (если, кроме 1, еще имеют-
имеются таковые) с положительными или отрицательными знаками, а ко-
количество этих значений конечно. Для отдельных же значений V
значения а' определенны, а значения 6, а", очевидно, ограничены
конечным числом возможностей.
/а, а', а"\
И. Точно так же количество всех форм К ^ у,\ с определите-
4 з
лем D, у которых а не равно 0 и не больше чем yf+D, Ъ —
4 з
— аа' = А" не равно нулю и не больше чем у}//J, Ъ" не больше
чем а/2, аЪ — Ъ'Ъ" = В и а'Ъ' — ЪЪ" = В' не больше чем -^ А", ко-
конечно. Действительно, количество всех комбинаций значений а, Ъ",
А", В, В' конечно; если же эти значения заданы, то остальные ко-
коэффициенты формы а', 6, V, а!' и коэффициенты
Ь/2 _ mn = А^ а,,ь„ _ ъъ> = Вп
Тройничные квадратичные формы 387
дополнительной формы определяются из следующих равенств;
а =
а
А" п ~ А"
АВ — В'В"__ Ва' + В'Ъ" h, _ А'В' — ВВ" ВЪ" + В'а
&'2 — /4' Ь2 — А ЪЪ'А-В"
а' Ь"
А так как указанные формы получаются, если из всех комбинаций
значений а, Ъ"', А", В, В' выбрать те, для которых значения а', а",
Ъ, Ь' получаются целыми, то количество этих форм, очевидно, ко-
конечно.
III. Итак, все формы из I и II вместе образуют конечное число
классов, которое может быть и меньше, чем число форм, если ка-
какие-нибудь из них эквивалентны между собой. А так как, в силу
предыдущих исследований, каждая тройничная форма с определи-
определителем D обязательно эквивалентна одной из этих форм, т. е. при-
принадлежит какому-нибудь из классов, образуемых этими формами,
то эти классы охватывают все формы с определителем D, т. е. все
тройничные формы с определителем D распадаются на конечное
число классов.
277
Правила, по которым могут быть найдены все формы в I и II
предыдущего пункта, получаются сами собой из изложенного, вслед-
вследствие чего можно ограничиться приведением нескольких примеров.
Для D = 1 получаются следующие шесть (вследствие двойных
знаков; форм I:
О, 1, 0\ /0, 1. +
О, + 1. ОГ \0, ±1,
у форм II а и А" не могут иметь других значений, кроме + 1 и—I,
а для получающихся из них четырех комбинаций Ъ", В ж В' дол-
должны быть положены равными 0; таким образом, получаются че-
четыре формы:
/1, -1, 1\ /-1, 1, 1\ /1, 1, -1\ /-1, -1, -1\
\о, о, or \ о, о, or \o, о, oj' 1 о, о, or
388
Раздел V (п. 277)
Точно так Же для D = — 1 получается шесть форм I и четыре
формы II, именно:
0,-1, 0\ /0, -1, ±1
0, ±1, 0/' \0, ±1, О
\ /-1 1, -1\
/' \ 0, О, О,/'
¦1,-1, -1\ /-1 1, -1\
0, 0, 0;
/-1,-1, 1\ /1, 1, 1^
[ 0, 0, 0/' 1,0, 0, 0;
Для D = 2 получается шесть форм I:
/0, 2, 0\ /0, 2, ±1>
lo, ±1, OJ' \0, ±1, 0;
и восемь форм II:
1, -1, 2^
1, 1,
О, О,
-1, -1.
о, о, о
-1, 1,
Д 0, 0/' \ 0, 0. О/
/1, -2, 1\ /-1, 2, 1\
1о, о, о), \ о, о, oj
Впрочем, число получающихся из этих форм в этих трех слу-
случаях классов много меньше, чем число форм. Именно, легко уста-
устанавливается следующее.
I. Форма
1, 2, -1\ /-1, -2,
О, О, О), \ О, О,
переходит
/0, 1,
\0, -1,
в
0)
соответственно
1,
о,
о,
а форма
о,
1,
о,
0
0
—1
/о,
U
при
0
0
1
1,
±1,
/0,
(о,
1\
о/'
1
1
>
/
1
подстановках
, о,
, 1,
, 1,
1
1
0
/1,
1
с
),
0
0
1
0
0
о,
-1
0
\
)
1,
±1,
о,
1,
-1,
—1\
oj
1
1
—1
1,
1,
о,
/1,
\°.
о,
1,
—1,
1
0
—1
¦1
1,
-1
0
Тройничные квадратичные формы 389
переходит в
/1, -1, 1\ /-1, 1, 1\
\о, о, о)* [ о, о, о)
простой перестановкой переменных. Поэтому десять указанных
тройничных форм с определителем 1 сводятся к двум:
О, 1, 0\ /-1, -1, -IV
О, 1, О/' [ О, О, О)9
вместо первой при желании можно взять и следующую:
1, О, О
1, О, О
Так как первая форма неопределенная, а вторая определенная, то
ясно, что каждая неопределенная тройничная форма с определи-
определителем 1 эквивалентна форме х2 + 2yz, а каждая определенная —
форме — х2 — у2 — z2.
И. Совершенно аналогично находим, что каждая неопределен-
неопределенная тройничная форма с определителем — 1 эквивалентна форме
— х2 + 2yz, а каждая определенная —форме х2 + у2 + z2.
III. Для определителя 2 из восьми форм II сразу могут быть
отброшены вторая, шестая и седьмая, так как они получаются из
первой простой перестановкой переменных,, и по такой же причи-
причине — пятая, которая получается из третьей подобным же образом,
и восьмая, получающаяся из четвертой. Остальные три образуют
вместе с шестью формами I три класса; именно,
О, 2, О
О, 1, О
переходит в
О, 2, О
,0, -1, 0
390
Раздел V (п. 278)
при подстановке
а форма
переходит в формы
0, 2, 1
.0, 1, 0
1, О, О
О, 1, О
О, 0, -1,
1, 1, -2
О, О, О
О, 2, 1
О, -1, О
О, 2,
О, 1,
О, 2, -1\ /1, -1, 2
О, —1.
О
О, О, О
соответственно при подстановках
1, о, 1
1, 2, О
1, 1, О
1, 0,-1
1, 2,
1, 1,
1, О, О
1, 2, -1
1, 1, -1
1, О, О
1, 2, 1
1, 1, 1
1, О, О
О, 1, 2
О, 1, 1.
Поэтому каждая тройничная форма с определителем 2 приво-
приводится к какой-нибудь из следующих трех форм:
О, 2, 0\ /1, 1, -2\ /-1, -1, -2n
О, 1, 0/' \0, О, О)9 { О, 0, 0 у
вместо первой из которых при желании можно взять также
форму
'2, О, О
1, О, О
Но очевидно, что каждая определенная тройничная форма обяза-
обязательно будет эквивалентна третьей форме,— х2 — у2 — 2z2, так как
первые две формы неопределенные, а каждая неопределенная форма
будет эквивалентна первой или второй, а именно, первой, 2х2 +
-f- 22/2, если ее первый, второй и третий коэффициенты одновременно
четны (так как легко видеть, что такая форма при любом преобразо-
преобразовании переходит в подобную же форму и потому не может быть эк-
эквивалентна второй форме), и второй, х2 + у2 — 2z2, если ее первый,
Тройничные квадратичные формы 391
второй и третий коэффициенты не являются одновременно чет-
четными, т. е. или один из них, или два, или все три нечетны (действи-
(действительно, по аналогичной причине в такую форму форма 2х2 + 2yz
не может перейти ни при какой подстановке).
Таким образом, то, что получилось в примерах пп. 273, 274, а
именно, что определенная форма
/19, 21, 50
\ 15, 28, 1
с определителем — 1 приводится к форме х2 + у2 + z2, а неопре-
неопределенная форма
10, 26, 2
7, 0, 4
с определителем 2 — к форме 2х2 — 2yz или (что сводится к тому же)
к форме 2х2 -j- 2yz, можно было бы на основании приведенного
исследования предсказать заранее.
278
Тройничной формой с переменными х, ж', х" представляются
с одной стороны, числа, когда х, х', х" придаются определенные зна-
значения, а с другой стороны — двойничные формы, посредством под-
подстановок вида
х = mt -\- пи, х' — m't -f- п'и, х" = m"t -j- n"u,
где т, п, т\... обозначают определенные числа, a t, и — перемен-
переменные представляемой формы. Для полноты теории тройничных
форм было бы поэтому нужно решить следующие задачи.
I. Найти все представления заданного числа заданной трой-
тройничной формой.
II. Найти все представления заданной двойничной формы за-
заданной тройничной формой.
III. Определить, эквивалентны ли две заданные тройничные
формы с одинаковым определителем, или нет, и в первом случае найти
все преобразования первой формы во вторую.
392 Раздел V (пп. 279-,
IV. Определить, содержит ли заданная тройничная форма
другую заданную тройничную форму с большим определителем,
или нет, и в первом случае определить все преобразования первой
формы во вторую.
На этих задачах, которые значительно труднее, чем аналогич-
аналогичные задачи для двойничных форм, мы подробно остановимся в дру-
другом месте; здесь мы ограничим наше исследование тем, что пока-
покажем, как первая задача может быть сведена ко второй, а вторая —
к третьей; третью же мы научимся решать для нескольких простей-
простейших и для теории двойничных форм особенно важных случаев; чет-
четвертой задачи мы не будем рассматривать совсем.
279
Лемма. Если даны три любых целых числа а, а\ а" (которые,
однако, не все одновременно равны нулю), то можно найти шесть
других чисел В, В', В", С, С, С" с тем свойством, что
В'С" — В"С = а, В"С — ВС" = а', ВС — В'С = а".
Доказательство. Пусть а — наибольший общий делитель чисел
а, а', а"\ возьмем такие целые числа А, А\А", что
Аа + А'а' + А"а" = а.
Далее, возьмем три любых целых числа @, ?', &" с тем только
условием, что три числа <1'А" — <1пА\ &"А — GL4", &А'— &А, ко-
которые мы соответственно обозначим через Ъ, Ъ\ Ь", а их наиболь-
наибольший общий делитель через р, не все одновременно равны нулю
Если положить тогда
а'Ъ" — а!'Ъ' = а$С, а"Ъ — ab" = а^С", аЪ1 — а'Ъ = а$С"\
то числа С, С, С", очевидно, будут целыми. Наконец, если мы
выберем целые числа 25, 25', 25" так, что
положим
Тройничные квадратичные формы 393
и затем положим
В = а23 — hA, В' = а23' — hA', В" = аЗЗ" — КА\
то эти значения J3, J3', Б", С, С", С" будут удовлетворять предпи-
предписанным условиям.
Именно, мы находим
аВ + а'В' + а" В" = О,
ЪА + Ь'А' + Ъ"А" = 0, и потому ЪВ + Ь'В' + Ъ"В" = ар.
Теперь из значений С", С" мы получаем
оф (Б'С" — J5"C") = аб'В' — а'6Я' — а"ЪВ" + а^Б" =
= а (ЪВ + й'?' + 6"Б") — 6 (aJ5 + а'5' + а"Вп) = а^а,
и потому Б'С" — В"С' = а, и подобным же образом находим, что
?"С _ ВС" = а', ВС — В'С = а".
В остальном анализ, при помощи которого это решение было
найдено, а также метод для отыскания по одному решению всех
других здесь должны быть опущены.
280
Предположим, что двойничная форма
at2 + 2btu + си2 = ср,
определитель которой пусть равен D, представляется тройничной
формой / от переменных х, х\ х'\ если положить
х — mt + пи, xr = m't + п'и, х" = m"t + п"и>
и что дополнительной к форме / является форма F от перемен-
переменных X, Х\ X". Тогда легко установить выкладкой (если обозна-
обозначить коэффициенты форм /, F специальными буквами), а также
сразу выводится из п. 268, II, что число D представляется формой F,
если положить
X = т'п" — т"п', X' = т"п — тп\ X" = тп' — т'п\
это представление числа D естественно назвать дополнительным
к представлению формы <р формой /. Если значения X, X', X"
394 Раздел V (п. 280)
не имеют общих делителей, мы будем называть это представление
числа D собственным, в противном же случае — несобственным, и
будем применять те же наименования и в отношении представле-
представления формы <р формой /, к которому первое представление являет-
является дополнительным. Отыскание всех собственных представлений
числа D формой F основывается на следующем.
I. Не существует представления числа D формой F, которое
не могло бы быть выведено из некоторого представления какой-
нибудь формы с определителем D формой /, т. е. не было бы до-
дополнительным к такому представлению.
Именно, пусть представление числа D формой F следующее;
X = L, X' = Z/, X" = L"; возьмем на основании леммы предыду-
предыдущего пункта, такие т, тг, т", п, п\ п", что
т'п!' — т"п' = L, т"п — тп!' = Z/, тп' — т'п = L",
и пусть / при подстановке
х = mt -f пи, х' = m't + п'и, х" — m"t -\- п"и
переходит в двойничную форму <р = at2 + 2Ыи + си2. Тогда легко
видеть, что D есть определитель формы <р, и заданное представле-
представление числа D формой F является дополнительным к представле-
представлению формы ф формой /.
Пример. Пусть / = х2 + х'2 + х, и потому F = — X2 — X'2 —
— X, D = — 209, и представление D формой i7 следующее: Х=1,
X' = 8, X" = 12. Отсюда для т, т', т", п, п', п" мы находим
следующие значения: —20, 1, 1, —12, 0, 1, и <р = 40212 + 482Ш +
+ 145м2.
II. Если <р, 1—собственно эквивалентные двойничные формы,
то каждое представление числа D формой F, являющееся допол-
дополнительным к некоторому представлению формы <р формой /, будет
также дополнительным и к некоторому представлению формы ^
формой /.
Если переменные формы X суть р, q, при собственной подстанов-
подстановке t = ар + рд, и — чр + 8? форма <р переходит в ^, и некоторым
представлением формы <р формой / является
{R) х = mt + пи, х' = m't + п'и, х" = тЧ + п"и,
Тройничные квадратичные формы 395
то без труда видно, что если положить
am + чп== gi а77г' + Tn' = S'> ат" + Тп" — 8"
$т + Ьп = /г, ртгг' + Ъп' = /г', Вт" + 8?г" = /г",
то форма х будет представляться формой / при
(Rf) x = gp + hq, х' = g'p + h'q, x" = g"p + ft"?,
и если произвести выкладки, то мы найдем (в силу а8 — р*у = 1),
что
g'hff — g"hf = т'п" — тГп\ g"h — gh" = т"п — тп",
gh' — gh = win' — т'п,
т. е. это представление числа D формой F эквивалентно представ-
представлениям (R), (R').
Так, мы находим, что в предыдущем примере форме <р эквива-
эквивалентна форма х = 13р2— iOpq + 18g2, причем первая переходит во
вторую при собственной подстановке t = —Зр + q, и = Ър — 2q.
Отсюда мы находим следующее представление формы % формой /:
х = Aq, х' = — Зр + q, х" = 2р — q, из которого получается то же
самое представление числа — 209, из которого мы и исходили.
III. Наконец, если две двойничные формы <р> X с определителем
D, зависящие соответственно от переменных t, и; р, q, представ-
представляются формой /, и для какого-нибудь представления одной из
них дополнительным собственным представлением числа D формой F
является то же представление, что и для некоторого представле-
представления другой, то эти формы обязательно собственно эквивалентны.
Предположим, что форма 9 представляется формой /, если поло-
положить
х = mt -f- пи, х' = m't -\- п'и, х" = m"t -f- n"u,
а форма х — если положить
х = gp + hq, x' = g'p + h'q, x" = g"p + h"q,
и что
т'п" — т'п' = g'h" — g"h' = L,
т"п — тп" = g"h — gh" = Z/,
inn' — т'п = gh' — g'h = L".
396 Раздел V (п. 281)
Подберем целые числа Z, V, V так, что Ы + L'V + L'T = 1, и по-
положим
пТ— п'Т = М, n"l — nln = M', пГ — п'1 = М\
l>m»^.l»m< =, ]у, V'm — lm" = N', lm' — Vm = N*.
Наконец, положим
gM + g'M' + g"M" = a, hM + h'M' + WMT - p,
giV + g'iV' + ^7V" = T, /iTV + /г'Л7/ + A'JV = 8.
Отсюда легко получить, что
am + 4n=g-l(gL + g'L + g"L") = g7
pm + Ы = h — I (hL + h'L' + A^L') = К
и точно так же
am' + чтг' = g\ $mr + Ьп' = h\ am" + ^nrf = g", $m" + &n* = h*.
Из этого вытекает, что выражения mt + пи, m't + п'и, rrft + д"ггг
при подстановке
(S) t = ap + $q, в = тр + 8gr
переходят соответственно в gp-\-hq, g'p + h'q, g"p + h"q< откуда
явствует, что при подстановке (S) форма 9 переходит в ту же фор-
форму, в которую переходит /, если положить
x = gP + hq, x' = g'p + A'gr, xn = gnp + h"q,
т. е. в форму ^, которой она поэтому эквивалентна. Наконец,
после соответствующих выкладок легко находится, что
aS _ рт = (Ц + L'V + LTJ = 1,
вследствие чего подстановка (S) является собственной, и формы <рг
X собственно эквивалентны.
Из этих замечаний вытекают следующие правила для отыска-
отыскания всех собственных представлений числа D формой F. Нужно
найти все классы двойничных форм с определителем D и из каждого
класса выбрать произвольную форму; далее, нужно найти все соб-
собственные представления этих отдельных форм формой / (причем те
формы, которые формой / не представляются, отбрасываются) ш
Тройничные квадратичные формы 397
из этих представлений вывести представления числа D формой F.
Из I и II следует, что при этом будут получены все возможные соб-
собственные представления, и потому задача будет решена полностью;
из III следует, что преобразования форм из различных классов
заведомо приводят к различным представлениям.
281
Отыскание несобственных представлений заданного числа D фор-
формой F легко может быть сведено к предыдущему случаю. Именно,
ясно, что если D не делится ни на какой квадрат (кроме 1), то
таких представлений вообще нет, а в том случае, ко1да D делится
на квадраты X2, [л2, v2,. . ., все несобственные представления
числа D формой F будут найдены, если найти все собственные
представления этой формой чисел Z)/X2, .D/[x2, D/v2, . . . и умножить
значения переменных соответственно на X, [л, v,. . .
Итак, отыскание всех представлений заданного числа задан-
заданной тройничной формой, являющейся дополнительной к некоторой
тройничной форме, свелось ко второй задаче; а к этому случаю,
который на первый взгляд кажется очень частным, могут быть
следующим образом сведены остальные случаи. Пусть D — число,
которое ружно представить формой! I, определитель кото-
\/2, /2 , lfl j
рой равен Д, и дополнительной к которой является форма
(G, G', G") , _ о „
\=f. Последней форме снова эквивалентна форма
/Д#, Ag\ Ag"\
[ у # = F и ясно, что представления формой F числа
\Дй, ДА, ДА"/
AD (находить которые можно на основании предыдущего) полно-
полностью идентичны представлениям заданной формой числа D. Заме-
Заметим, что если все коэффициенты формы / имеют общий делитель
[х, то все коэффициенты формы F, очевидно, делятся на [л2, вслед-
вследствие чего и AD должно делиться на [Л2 (иначе представлений не
будет), и представления числа D заданной формой будут идентич-
идентичны представлениям числа AD/^2 той формой, которая получается
398 Раздел V (п. 282)
из F, если отдельные коэффициенты формы F умножить на [х2, и
которая является дополнительной для формы, получающейся из
формы /, если ее отдельные коэффициенты поделить на [л.
Отметим, наконец, что это решение первой задачи неприменимо,
если D — 0, так как в этом случае двойничные формы 6 определи-
определителем D разбиваются на бесконечное число классов; ниже мы
разберем этот случай при помощи других принципов.
282
Отыскание представлений заданной двойничной формы, опре-
определитель которой не равен нулю *, заданной тройничной формой
основывается на следующих замечаниях.
I. Из каждого собственного представления двойничной формы
(/>> Я* г) = 9 с определителем D тройничной формой / с определи-
определителем Д могут быть найдены целые числа J5, В' с тем свойством,,
что
= — Ад, ?'2 еее Дг (mod
или, другими словами, может быть получено значение выражения
|/"д (/?, — qf r) (modZ)). Пусть мы имеем следующее собственное
представление формы ср формой /:
х = at + |fc, x' = <*!t + р'и, х" = a"t + Р"гг
(где х, xr, x"\ t, и обозначают соответственно переменные форм /;
<р); подберем целые числа *(, т' Т" так> чтобы число
было равно или-f 1, или—1; пусть при подстановке
* Случай!) = 0, который рассматривается при помощи совершенно других
методов, здесь, ради краткости, опускается.
Тройничные квадратичные формы 399
х /а, а', а"\
форма / переходит в форму = g, дополнительной к
\6 &' 6"/
которой является форма f = G-. Хогдаясно, что а=р,
\#, 5', .В" /
b" = q, a' = r, A" = D, и определителем формы g является Л. По-
Поэтому
В2 = Ар + A'D, ВВ' = —Ад + B"D, 5'2 = Дг + ^^>.
Так; например, форма 19?2 + б^и + 41и2 будет представляться
формой ж2 + х'2 + ^'2 при х = 3^ + 5и, ж' = Зг — 4м? ж" = ?, откуда
следует, что если положить т = — 1, ^' = 1, т" = О' то ^ = —^1,
В' = 27, т. е. (—171, 27} является значением выражения
1/—1A9,-3, 41) (mod770).
Отсюда уже следует, что если Л (/?,—д, г) не является квадра-
квадратичным вычетом по модулю D, то форма ср не может быть собст-
собственно представлена никакой тройничной формой с определителем
Д; поэтому в случае, когда Д, D взаимно просты. Д должно быть
характеристическим числом формы ср.
II. Так как числа y> t'> T" могут быть выбраны бесчисленным
множеством способов, то могут получаться различные значения
для В, В', и мы хотим узнать, в какой связи они находятся ме-
между собой. Предположим, что и числа 8, 8', 8" таковы, что
(аф" _ а»р') 8 + (а"Р — оф") 8' + (оф' —
равно или -(- 1, или— 1, и что форма / при подстановке
ос, р, 8
а', р', 8'
а"/ р*, 8"
. /а, а', а"\
переходит в форму ^ = д, дополнительной к которой
\Ь, Б', Б"/
Bt, 2t', 2t/r\
cJ rj, rv> I == ®- Тогда формы g, g эквивалентны,
аз, 93, 937
400 Раздел V (п. 283)
а поэтому эквивалентны также и формы G, @, и применяя указан-
указанные в пп. 269, 270 принципы, мы находим *, что если положить
(PY - PY)8 + (Р"Т - РТ") 8' + (РТ' - Р'Т) §" = С,
(TV _ TV) 8 + (Т"а - Та") 8' + (Та' - т'а) 8"= ч,
то форма @ будет переходить в G при подстановке
А, 0, 0
0, к, О
С -п, I.
Следовательно,
Ш8, 5'
и потому, в силу того, что !& = + 1, имеет место или В =^$Ь,
В' ^25', или В:= — 25, В' ^^ — 25'(modZ)). В первом случае мы
назовем значения (В, В'), B5, 25') эквивалентными, а во втором —
противоположными; о представлении же формы <р мы будем гово-
говорить, что оно принадлежит некоторому значению выражения
УА(р,—q, r) (mod/)), которое может быть получено из этого пред-
представления методом, изложенным в I. Поэтому все значения, кото-
которым принадлежит одно и то же представление, будут или эквива-
эквивалентны, или противоположны.
III. Наоборот, если, как и раньше в I, представление х — at +
+ fto, .. . формы <р формой / принадлежит значению (В, В'), кото-
которое может быть выведено отсюда при помощи преобразования
а, р, т
ос', Р',т'
а", Р", Т",
то это же представление будет принадлежать также и каждому дру-
другому значению B5, S3'), которое либо эквивалентно, либо противо-
противоположно первому, т. е. вместо т» т'» Т" можно брать другие целые
* Именно, если из преобразования формы/в g вывести преобразование g
в /, из этого последнего и из преобразования формы/в 9 вывести преобразование
формы g в д, и, наконец, отсюда посредством транспонирования получить пре-
преобразование © в С
Тройничные квадратичные формы 401
числа 8, 8', 8", для которых выполняется следующее равенство:
(О) (ос'В" — а"Р') 8 + (а"Р — оф") 8' + (а?' — аф) 8" = ± 1
и которые обладают тем свойством, что четвертый и пятый коэф-
коэффициенты формы, которая является дополнительной к той, в кото-
которую переходит форма / при подстановке (S)
а, р, 8
ос', р', 8'
^, Р", 8",
соответственно равны 25, 25'. Именно, если положить
± В = 25 + т]?>, + 5' = 35' + ZD
(где и здесь и дальше нужно брать верхние или нижние знаки в
зависимости от того, эквивалентны значения (В, В'), (95, S3') или
противоположны), так что С, т] будут целыми числами, и если g
при подстановке
1, 0, С
0, 1, 7J
0, 0,±1
переходит в форму д, то легко видеть, что ее определитель равен
А, а четвертый и пятый коэффициенты дополнительной формы рав-
равны соответственно 95, 95'. Если же положить
- 8, *% + P'tj + t' = 8', ос"С + р"
то без труда получится, что / при подстановке (S) переходит в д,
и что уравнение (О) удовлетворяется.
283
Из этих принципов выводится следующий метод для отыска-
отыскания всех собственных представлений двойничной формы
cp = pt*-\- 2qtu + га2
с определителем D тройничной формой f с определителем Л.
402 Раздел V (п. 283)
I. Найдем все различные (т. е. не эквивалентные) значения вы-
выражения У~А(р, — g, r)(modD). Для случая, когда <р является при-
примитивной формой, и Д взаимно просто с D, эта задача была ре-
решена выше (п. 233), а остальные случаи очень легко могут быть
сведены к этому, что мы, однако, подробнее выяснять ради крат-
краткости не будем. Заметим только, что если Л взаимно просто с D,
то выражение А (р,—q, r) не может быть квадратичным вычетом
по модулю D, если <р не является приведенной формой. Действи-
Действительно, если мы предположим, что
Ар = В2 — DA', — Aq = BB' — DB", Аг = В'2 — DA,
то
{DB" — АдJ = (DA' + Ар) (DA + Аг),
и отсюда, после раскрытия скобок и замены D на q2 — pr, полу-
получается
_ д (Ар + 2B"q + А'г) + А2 = 0,
откуда легко следует, что если бы числа р, q, r имели общий
делитель, то он входил бы также и в А2; но тогда А не могло
бы быть взаимно просто с D. Поэтому р, q, r не могут иметь
общих делителей, т. е. форма 9 является примитивной формой.
II. Если мы обозначим количество этих значений через т и
предположим, что среди них имеется п значений, которые противо-
противоположны самим себе (причем мы полагаем п = 0, если таких значе-
значений нет), то ясно, что остальные т—п значений попарно проти-
противоположны (так как мы ведь предполагаем, что берутся все зна-
значения без исключения); если из каждых двух противоположных
значений одно (любое) отбрасывается, то всего остается (т + п)/2
значений. Так, например, из следующих восьми значений выра-
выражения V—1A9, — 3,41) (mod 770): C9, 237), A71, —27), B69,-83),
B91,-127), (—39,-237), (— 171, 27), ( — 269, 83), (— 291, 127)
— последние четыре надо отбросить, так как они противопо-
противоположны четырем первым. Впрочем, очевидно, что если (В, В')
есть значение, противоположное самому сабе, то 25, 2В\ а пото-
потому также и 2Ар, 2А#, 2Аг делятся на Z); поэтому если А и D
взаимно просты, то 2pt 2q, 2r будут также делиться на D, а так
ко-
Тройничные квадратичные формы 403
как, согласно I, p, q, г не могут иметь общих делителей, то на
D должно будет делиться число 2, что возможно только тогда,
когда либо .D = + l, либо .D = +2. Поэтому для всех значений
D, которые больше чем 2, всегда п = 0, если Л взаимно
просто с D.
III. Теперь ясно, что каждое собственное представление формы
9 формой / обязательно должно принадлежать к некоторому из
оставшихся значений, причем только к одному. Поэтому нужно
брать последовательно эти значения и для каждого из них нахо-
находить принадлежащие им представления. Чтобы найти представле-
представления, принадлежащие заданному значению (В, J?'), нужно сначала
/а, а', а"\
определить тройничную форму g = ( 1, определитель
торой равен А и у которой а = р, Ъ" = q, а' = г, аЪ — Ъ'Ъ" — В,
а'Ъ' — ЪЪ" — В'\ значения а", о, Ъ' находятся отсюда при похмощи
равенств из п. 276, II, из которых легко видно, что в случае,
когда Л, D взаимно просты, числа 6, 6', а" будут целыми (имен-
(именно, потому, что эти три числа дают целые числа при умножении
как на D, так и на Л). Если теперь либо один из коэффициен-
коэффициентов b, b\ а" дробный, либо формы /, g не эквивалентны, то не
может быть принадлежащих значению (В, В1) представлений
формы 9 формой /; если же числа 6, Ъ\ а" целые и формы /, g
эквивалентны, то каждое преобразование первой во вторую, на-
например, преобразование
а, Р, Т
а', Р', Т'
а", Р*, Т"
дает одно такое представление, именно,
х = at + ри, х' = a't + $'и, х" = aft + р*и,
и, очевидно, не может быть такого представления, которое не мо-
могло бы быть выведено из некоторого преобразования. Таким обра-
образом, та часть второй задачи, которая ставит себе целью разыска-
разыскание собственных представлений, уже сведена к третьей задаче.
IV. Далее, из различных преобразований формы / в форму g
всегда получаются различные представления, за исключением
единственного случая, когда значение (В, В') противоположно
404 Раздел V (п. 284)
самому себе и когда по два преобразования дают одно и то же
представление. Именно, если мы предположим, что / переходит в
g при подстановке
а, р, 8
а', ?', 8'
а", р", 8"
(которая дает то же представление, что и предыдущее преобразо-
преобразование) и обозначим через к, I, С, ч] те же числа, что и во втором
разделе предыдущего пункта, то
В = ШВ + т)!Д В' = ЫВ' + СШ;
если поэтому оба числа к, I положить либо равными + 1, либо
равными—1, то (так как мы исключили случай D = 0) будет иметь
место ? = 0, т] = 0, откуда ле/ко следует, что 8 = *у, 8' = y\ S" = ^".
Поэтому о^ба наши преобразования могут быть различны только в
том случае, когда одно из чисел f, к равно + 1> а другое равно
— 1; тогда В = — В, В'= — В' (mod/)), т. е. значение (В, В')
противоположно самому себе.
V. Из того, что выше (п. 271) мы указали относительно критериев
определенных и неопределенных форм, легко видеть, что если А
положительно, D отрицательно, и ср является отрицательной фор-
формой, то g будет определенной отрицательной формой; если же А
положительно, и либо и D положительно, либо D отрицательно
и форма ф положительна, то g будет неопределенной формой. Так
как теперь / и g заведомо не могут быть эквивалентны, если они не
однотипны в отношении этого свойства, то ясно, что двойничные
формы с положительным определителем, так же, как и положитель-
положительные формы, не могут быть собственно представлены тройничной
отрицательной формой, и отрицательные двойничные формы — не-
неопределенной тройничной формой с положительным определите-
определителем, а что, напротив, тройничной формой первого или второго типа
могут собственно представляться только двойничные формы соот-
соответственно второго или первого типа. Аналогичным образом следует,
что определенной (т. е. положительной) тройничной формой с отри-
отрицательным определителем могут представляться только положи-
Тройничные квадратичные формы 405
тельные двойничные формы, а неопределенной тройничной формой —
только отрицательные двойничные формы с положительным опре-
определителем.
284
Так как несобственными представлениями двойничной формы ф
с определителем D тройничной формой /, дополнительной к которой
является форма F, будут те, из которых получаются несобственные
представления числа D формой F, то очевидно, что ф может быть
представлена формой / только несобственно, если D содержит
квадратные сомножители. Если мы предположим, что все входящие
в D квадраты (кроме 1) суть е2, е'2, е, ... (их количество конечно,
так как мы предполагаем, что D не равно 0), то каждое несобственное
представление формы ф формой /будет, очевидно, приводить к пред-
представлению числа D формой F, у которого значения переменных
имеют в качестве наибольшего общего делителя одно из чисел е,
е', е",...; в этой связи мы ради краткости будем говорить, что каждое
несобственное представление формы ф принадлежит квадратному де-
делителю е2, или е'2, или е и т. д. Но все представления формы ф,
принадлежащие одному и тому же заданному квадратному делителю
е2 (корень из которого, е, мы предполагаем положительным), нахо-
находятся по следующим правилам, из синтетического доказательства
которых, избранного нами здесь ради краткости, легко восстано-
восстановить анализ, при помощи которого они были найдены.
Сначала нужно найти все двойничные формы с определителем
D/e2, которые переходят в форму <р при собственной подстановке
вида Т = xt -j- Хгг, U = [lu, где Т, U обозначают переменные такой
формы, t, и — переменные формы <р; х, ;х — положительные целые
числа (произведение которых тем самым равно е) и X — положи-
положительное число, которое меньше, чем [х (включая и нуль). Эти формы
вместе с соответствующими преобразованиями находятся следую-
следующим образом.
Будем придавать х последовательно значения, равные отдель-
отдельным положительным делителям числа е (включая 1 и е), и пола-
полагать [х = —; для отдельных определенных значений х, [х будем
406 Раздел V (п. 284)
придавать X все целые значения от 0 до [х—1, благодаря чему
мы заведомо получим все преобразования. Тогда мы найдем форму,
которая при подстановке Т =y.t-{-'ku, U = \ш переходит в 9, если
разыщем форму, в которую переходит 9 при подстановке t = — T —
С/", и = —U; таким образом мы получим формы, соответст-
е р.
вующие отдельным преобразованиям; однако из всех этих форм
нужно оставить только те, у которых все три коэффициента будут
целыми числами *.
Во-вторых, предполагая, что Ф — какая-нибудь из этих форм,
которая переходит в 9 при подстановке Т = y.t -\- \u% U = [ли, най-
найдем все собственные представления формы Ф формой / (если та-
таковые имеются) и выразим их в общем виде формулами
(Щ Х = Ш + 93*7, х9 = %'Т + 2377, х" = %"Т + $847;
наконец, из каждого отдельного представления (Щ выведем пред-
представление
(р) х = <xt + ри, х' = а'* + р'ю, х" = <хЧ + $"и
посредством равенств
Совершенно таким же образом, как и форму Ф, рассмотрим и ос-
остальные формы, найденные по первому правилу (если их несколь-
несколько), так что из отдельных собственных представлений получатся
все другие представления; тогда, как я утверждаю, таким путем
будут найдены все принадлежащие делителю е2 представления фор-
формы 9> и притом каждое получится только один раз.
Доказательство. I. То. чю тройничная форма / при каждой
подстановке (р) действительно переходит в 9) настолько ясно, что
* Если бы мы могли здесь более подробно рассмотреть этот вопрос, нам уда-
удалось бы существенно сократить решение. Непосредственно ясно, что в качестве
х нет нужды брать никаких других делителей числа е, кроме тех, квадраты кото-
которых входят в первый коэффициент формы 9- Впрочем, при другом удобном слу-
случае мы еще вернемся к этой проблеме, из решения которой также могут быть
получены более простые решения проблем пп. 213, 214.
Тройничные квадратичные формы 407
не требует дальнейшего пояснения; а то, что каждое представление
(р) является несобственным и принадлежит делителю е2, вытекает
из того, что числа ос'Р"— ос"Р', ос"Р— осЗ", оф'— ос'Р будут равны со-
соответственно еBГ23" — Г23'), е(Г23 — 2Г25"), ^ C125' — 2Г'23)? вследст-
вследствие чего их наибольшим общим делителем, очевидно, является е
(так как представление (Щ собственное).
II. Мы покажем, что из каждого заданного представления (р)
формы 9 может быть найдено собственное представление формы с
определителем D/e2, которое содержится среди представлений, най-
найденных по первому правилу, т. е. что из заданных значений ос, ос',
ос", р, р', р" могут быть выведены целочисленные значения х, X, [л,
которые удовлетворяют предписанным условиям, и значения 31, 2Г,
21", 23, 23', 23", которые удовлетворяют равенствам (В.), и притом
только одним единственным образом. Действительно, прежде всего
из первых трех равенств в (R) вытекает, что за х должен быть
взят наибольший общий делитель чисел ос, ос', ос" с положительным
знаком (именно так как 2Г23"—2П8\ ЭГ'85 — 2№", 3195' — 31Г95 не
имеют общих делителей, то и 2t, 2Г, 21" не могут иметь общих де-
делителей); тем самым определяются и 2t, 2t', 2t", а также и [х = —
(легко видеть, что это число обязательно целое). Если мы предпо-
предположим, что три целых числа а, а', а" выбраны так, что <*2t + <*'2Г +
+ аГ = 1, и ради краткости вместо аЯ5 + аг93' + а5" будем пи-
писать к, то из последних трех равенств (R) следует, что ар + <*'?' +
4- а"Р" = X + [л&, откуда тотчас же вытекает, что для X имеется
только одно значение между 0 и ;х — 1. Но так как после того,
как это сделано, 35, 35', 35" тоже получают определенные значения,
нам остается только еще доказать, что они всегда будут целыми.
Но
- — [а" B("р — Эф") — а' Bф' — 2l'P)]
и потому 35, очевидно, является целым числом, и точно так же
408 Раздел V (п. 285)
устанавливается, что и 35', 35" получают целочисленные значения.
Из этих рассуждений следует, что не может быть несобственного
представления формы 9 формой /, принадлежащего делителю е2,
которое указанным методом могло бы либо не получиться вовсе,
либо получиться несколько раз.
Если теперь таким же образом исследовать остальные квадрат-
квадратные делители числа D и найти представления, принадлежащие каж-
каждому из них, то мы получим все несобственные представления
формы ф формой /.
Далее, из этого решения легко получается, что указанная в конце
предыдущего пункта теорема относительно собственных представ-
представлений имеет силу и для несобственных представлений, а именно,
что вообще никакая положительная двойничная форма с отрица-
отрицательным определителем не может быть представлена отрицательной
тройничной формой и т. д. Действительно, если ф есть такая двой-
двойничная форма, которая, в силу указанной теоремы не может быть
представлена формой / собственно, то очевидно, что и все формы
с определителями D/e2, Z)/e'2,...,которые содержат форму ф, не мо-
могут быть собственно представлены формой /, так как все эти формы
имеют определители того же знака, что и определитель формы ф,
и если эти определители отрицательны, то либо все формы будут
положительны, либо все отрицательны в зависимости от того, при-
принадлежит ли ф к первым или ко вторым.
285
Относительно вопросов, которые образуют третью из постав-
поставленных нами проблем (к которой в предыдущем сведены обе первые
проблемы), а именно, если заданы две тройничные формы с одним и
тем же определителем, узнать, эквивалентны они или нет, и в первом
случае найти все преобразования одной из них в другую, мы мо-
можем в этом месте сказать только немногое, так как полное решение,
которое мы указали для аналогичной проблемы в случае двойнич-
двойничных форм, здесь наталкивается на еще большие трудности. По-
Поэтому мы ограничим наше исследование некоторыми специальными
случаями, ради которых мы главным образом и предприняли
отступление от нашего основного предмета.
Тройничные квадратичные формы 409
I. Выше было показано, что для определителя +1 все тройничные
формы распадаются на два класса, один из которых содержит все
неопределенные формы, а другой — все определенные (отрицатель-
(отрицательные) формы. Из этого тотчас же следует, что любые две тройничные
формы с определителем 1 эквивалентны, если либо обе они определен-
определенные, либо обе неопределенные; если же одна из них определенная,
а другая неопределенная, то эквивалентность не может иметь места
(вторая часть теоремы, очевидно, справедлива вообще для форм
с любым определителем). Точно так же некоторые две формы с опре-
определителем —1 заведомо будут эквивалентны, если либо обе они опре-
определенные, либо обе неопределенные. Две определенные формы
с определителем 2 всегда будут эквивалентны; две неопределенные
формы не будут эквивалентны, если у одной из них первые три коэф-
коэффициента все четны, а у другой — не все четны; в остальных случаях
(когда три первые коэффициента все одновременно четны либо у обеих
форм, либо ни у одной из них) они, напротив, будут эквивалентны.
Таким же образом мы могли бы установить еще намного больше
специальных теорем, если бы выше (п. 277) исследовали больше
примеров.
II. Во всех этих случаях, если /, /' обозначают тройничные эк-
эквивалентные формы, можно найти также одно преобразование одной
из них в другую. Действительно, для всех случаев в каждом классе
тройничных форм выше было указано достаточно маленькое число
форм, к которым вполне определенным методом может быть сведена
любая форма этого класса; там же было показано, как можно все
эти формы привести к одной. Если F — это форма в том классе, ко-
которому принадлежат /, /', то при помощи указанных выше правил
могут быть найдены преобразования форм /, /' в F и точно так же
преобразования формы F в /, /'. Отсюда, согласно п. 270, могут
быть выведены преобразования формы / в /' и формы /' в /.
III. Поэтому остается только показать, как из одного преобразо-
преобразования одной тройничной формы / в другую форму /' можно вывести
все возможные преобразования. Эта задача сводится к более простой,
а именно, найти все преобразования тройничной формы f в себя.
Именно, если / при нескольких подстановках (^), (^'), (т"), ... пере-
переходит сама в себя, а при подстановке (t) — в /', то если комбиниро-
410 Раздел V (п. 285)
вать, как было указано в п. 270, преобразование (t) с (т), (?'), (т"),...,
будут, очевидно, все время получаться подстановки, при которых /
переходит в /'; кроме того, выкладкой легко устанавливается, что
каждое преобразование формы / в /' может быть получено таким
путем из комбинации заданного преобразования (t) формы / в /'
с некоторым (и притом только одним) преобразованием формы /
в себя, и что тем самым из комбинаций заданного преобразования
формы / в /' со всеми преобразованиями формы / в себя получаются
все преобразования формы / в /', и притом каждое только один раз.
Отыскание всех преобразований формы / в себя мы ограничим
здесь случаем, когда / является определенной формой, у которой
четвертый, пятый и шестой коэффициенты все равны 0 *. Пусть по-
поэтому / — ( п' г) а )'и пусть произвольная подстановка, при которой
/ переходит в себя, обозначена через
*", Р", Т",
так что должны удовлетворяться равенства
аос2 + а'ос'2 + а"ос = a,
+ aVp' + aV'P''-O,
+ a'aY + flVf - О,
+ a'pY + a"PY - 0.
Теперь нужно различать три случая.
I. Если числа а, а', а" (которые имеют одинаковые знаки) все
различны между собой, то мы предположим, что а < а', а' < а!'
(если бы расположение по величине было другим, то можно было бы
получить те же выводы совершенно аналогичным образом). Тогда
* Остальные случаи, когда / является определенной формой, сводятся
к этому; если же форма / неопределенная, то нужно применять совсем другой
метод, и количество преобразований оказывается бесконечно большим.
Тройничные квадратичные формы
411
первое из равенств (?2), очевидно, дает, что а' = а" — 0, и потому
а = + 1; поэтому из четвертого и пятого равенств следует р = О,
7 = 0; аналогично, из второго равенства получается Р" = 0, и по-
потому Р = + 1, а затем из шестого равенства ^' = 0 и из третьего
7// = + 1, так что мы получаем (за счет независимых друг от дру-
друга двойных знаков) восемь различных преобразований.
II. Если us чисел а, а', а" два -равны одно другому, например,
аг = а", а третье отлично от них, то мы предположим следующее.
Во-первых, что а < а\ Тогда таким же образом, как и в пре-
предыдущем случае, получается, что а'= 0, а" = 0, ос = -+- 1, ft = 0,
^ = 0; а из второго, третьего и шестого равенств легко видеть,
что либо Р' = ±1, Т' = О> Р" = 0, т" = ±1. либо Р'=0, T'^i1»
Р" = ±1, т" до-
довели же, во-вторых, а > а\ то мы получаем те же результаты
следующим образом. Из второго и третьего равенств следует обя-
обязательно, что р = 0, т = 0, и либо Р' = ± 1, т' = °» Р" = 0 Т" = ± 1.
либо р' = 0, ч' — il, Р" = ±1, т" ~ 0- При обоих предположениях
из четвертого и пятого равенств следует, что ос' = 0,J а" = 0,
а из первого, — что а = + 1. Поэтому в каждом случае имеется
шестнадцать различных преобразований. Оба других случая, в ко-
которых либо а = а", либо а = а''. разбираются совершенно аналогич-
аналогичным образом, если только заменить буквы а, а', а" в первом слу-
случае соответственно буквами р, р', р", а во втором — буквами т, ^\ т"-
III. ^с^гг есе т^гг числа а, а', а" равны между собой, то из пер-
первых двух равенств вытекает, что среди трех чисел а, а', а", так же,
как и среди чисел р, р', Р" и т, ^\ Т"> по Два числа равны 0, а
третье равно +1. Но из трех последних равенств легко усмот-
усмотреть, что из трех чисел а, р, т может быть равно +1 только одно,
и также обстоит дело для чисел а', Р', ч' и а''» Р"» Т^- Поэтому
всего имеется только шесть комбинаций:
a
ecu
a'
P
T"
a'
ecu
T
a"
p
a"
ecu
T
= 4- 1
= ±i
= ±i
все остальные коэффициенты — 0,
412
Раздел V (п. 286)
так что за счет двойных знаков всего мы получаем 48 преобразо"
ваний. Эта же схема охватывает также и предыдущие случаи; но
из шести колонок нужно брать только первую, если все числа а,
а', а" различны; первую и вторую колонки, если а' = а", первую
и третью, если а = а\ и первую и шестую, если а = а".
Отсюда получается, что если тройничная форма / = ах2 -{-
+ аV2 + о!гх переходит в другую эквивалентную ей форму /' при
подстановке
то все преобразования формы / в /' содержатся в следующей
схеме:
ж"
ж"
х'
х'
X
х"
х'
х"
X
х"
X
х'
х"
х'
X
¦±(&'у-
щ'
СУ)
¦су),
с учетом того, что нужно использовать все шесть колонок, если
а = а' = а", первую и вторую колонки, если а', а" равны между со-
собой, а а отлично от них, первую и третью, если а —а', первую и
шестую, если а = а", наконец, только первую колонку, если все
числа а, а', а" различны между собой. В первом случае коли-
количество преобразований равно 48, во втором, третьем и четвертом
случае равно 16 и в пятом — равно 8.
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К ТЕОРИИ ДВОЙНИЧНЫХ ФОРМ
Об отыскании формы, при удвоении которой
получается заданная двойничная форма главного рода
От этого краткого изложения первых элементов теории трой-
тройничных форм мы переходим к некоторым специальным приложе-
приложениям, из которых на первом месте стоит следующая проблема.
Отыскание формы результату ее удвоения 413
286
Задача. Пусть дана принадлежащая главному роду двойничная
форма F = (А, В, С) с определителем D; нужно найти двой-
двойничную форму /, при удвоении которой получается форма F.
Решение. I. Найдем собственное представление противоположной
форме F формы F' = AT2 —» 2BTU -f- CU2 тройничной формой х2— 2г/
пусть это представление таково:
То, что это возможно сделать, легко следует из предшествующей
теории тройничных форм. Действительно, так как,по предположению,
форма F принадлежит главному роду, то существует значение вы-
выражения У {А, В, С) (modi)), вследствие чего может быть найдена
тройничная форма 9 с определителем 1, в которую форма (А, — Z?, С)
входит как часть, причем легко убедиться, что все коэффициенты
этой формы являются целыми числами. Так же легко видеть, что
<р является неопределенной формой (так как, по предположению,
F заведомо не является отрицательной формой); поэтому она обя-
обязательно эквивалентна форме х2 — 2yz. Следовательно, можно найти
собственное преобразование второй формы в первую, которое даст
собственное представление формы F формой х2 — 2yz.
Итак, мы имеем
А=а2 — 2*'а", — Я = оф—а'Р" —а"Р', С = $2 — 2C'C";
если, далее, обозначить числа аC'— ос'C, а'C"— а"Р', а"Р — оф" соот-
соответственно через а, Ъ, с, то они не будут иметь общих делителей,
и, кроме того, D = Ь2 — 2ас.
II. Из этого при помощи последнего замечания из п. 235 легко
выводится, что форма F при подстановке 2C', C, р, C"; 2ос', а, а, а"
переходит в произведение формы Bа, — Ъ, с) на себя самое, и точно
также при подстановке р', C, C, 2C"; а', а, а, 2а" — в произведение
на самое себя формы (а, — Ь, 2с). Наибольший общий делитель
чисел 2а, 2&, 2с равен 2; поэтому если с нечетно, то числа 2а, 2&,
с не будут иметь общих делителей, т. е. форма Bа, —Ь, с) будет
собственно примитивной; точно так же, если нечетно а1 то будет
414 Раздел V (п. 287)
собственно примитивной форма (а, — 6, 2с). В первом случае фор-
форма F получается при удвоении формы Bа, —6, с), а во втором —
при удвоении формы (а, —6, 2с) (ср. четвертое следствие п. 235);.
но всегда заведомо будет иметь место один из этих случаев. Дейст-
Действительно, если бы оба числа а, с были четны, то Ъ обязательна
было бы нечетным; но легко убедиться, что р"а + Р& + Р'с = 0>
а"а + аЪ + а'с = 0, из чего следовало бы, что являются четными
числа р&, а&, а потому также и а, р. Вследствие этого А ж С бы-
были бы четными, что противоречит предположению о том, что фор-
форма F принадлежит главному роду, и, следовательно, собственна
примитивному порядку.
Возможно также, что будут нечетными оба числа а и с; в этом
случае мы имеем тем самым две формы, при удвсении которых
получается форма F.
Пример. Пусть дана форма F = E, 2, 31) с определителем —151.
В качестве значения выражения ]/E,2,31) находим здесь E5, 22),
д / 5, 31, 4\
откуда получается тройничная форма 9=1^ п оЬ по прави-
\И, и, — z/
лам, указанным в п. 272, получаем эквивалентную ей форму
1, 1, —1\
I , которая переходит в форму 9 при подстановке
2, 2, 1
1, -6, -2
О, 3, 1.
Отсюда при помощи указанных в п. 277 преобразований следует,
/ 1, 0, 0\
что форма I I переходит в форму 9 при подстановке
\ -ч ^> ^v
3,-7,-2
2, -1, О
1, -9, -3.
Поэтому а =11, Ъ = —17, с = 20; следовательно, так как а нечет-
нечетно, форма F получается при удвоении формы A1, 17, 40) и пере-
переходит в произведение этой формы на самое себя при подстановке
-1, -7, -7, -18; 2, 3, 3, 2.
О характерах, которым соответствуют роды 415
Всем характерам, за исключением тех,
невозможность которых была доказана в пп. 263, 264,
действительно соответствуют роды
287
Относительно решенной в предыдущем пункте задачи мы доба-
добавим еще следующие замечания.
I. Если форма F при подстановке р, р\ р"'. р"\ q, q' q", q" пе-
переходит в произведение двух форм (h, i, k), (h\ г', k') (каждая из
которых, как мы всегда предполагаем, берется собственно), то имеют
место легко выводимые из третьего следствия п. 235 равенства:
p»hn' — p'h'n — р (in' — i'n) = О,
(р* — р') (in + i'n) — р (knf — k'ri) + р" (hnr — h'n) = О,
p'kn' — p"k'n — pm (inr — i'n) = 0,
и три других равенства, которые получаются из этих заменой чисел
Pi Р' •> Р" •> р" на Я, q\ qr\q '] числа п, п' являются положительными
квадратными корнями из частных, которые получаются, если
определители форм (fc, ?, /с), (hf, Г, к') разделить на определитель
формы F. Если же эти две формы совпадают, т. е. п = n', h = h',
i = V, к = к', то указанные равенства переходят в следующие:
(p»—p')hn = 0, (p" — p')in = 0, (f-p')kn^O,
откуда получается, что обязательно р' = р", и, совершенно анало-
аналогичным образом, qr = q". Таким образом, если формы (h, i, k)y
(hf', Г, к') зависят от одних и тех же переменных, ?, и, а перемен-
переменные формы F обозначены через Г, С/, то Сбудет переходить
в (Ы2+ 2itu + ки2J при подстановке
Т = pt* + 2p'tu + pwu2, U = qt2 + 2q'tu + qwu2.
П. Если форма F получается удвоением формы /, то она будет
получаться и при удвоении всякой другой формы, содержащейся
в одном классе с /, т. е. класс формы F будет получаться удвоением
класса формы / (ср. п. 238). Так, в примере предыдущего пункта
форма E, 2, 31) получается также и удвоением формы A1, —5, 16),,
416 Раздел V (п. 288)
которая собственно эквивалентна форме A1, 17, 40). Из одного
класса, при удвоении которого получаетсщ класс формы F, все
остальные такие классы (если их имеется несколько) находятся на
основании изложенного в п. 260; в нашем примере других поло-
положительных классов такого сорта нет, так как существует только
один двусторонний собственно примитивный положительный класс
с определителем —151 (именно, главный класс); так как при
композиции единственного двустороннего отрицательного клас-
класса (—1, 0, —151) с классом A1, —5, 16) получается класс
(—11, —5, —16), то он и будет единственным отрицательным
классом, при удвоении которого получается класс E, 2, 31).
III. Так как благодаря решению задачи предыдущего пункта
установлено, что каждый собственно примитивный (положительный)
принадлежащий главному роду класс двойничных форм может быть
получен удвоением некоторого собственно примитивного класса
с тем же определителем, то теорема п. 261, утверждающая, что по
крайней мере половине всех возможных для данного неквадратного
определителя D характеров не могут соответствовать собственно
примитивные положительные роды, может быть теперь усилена
утверждением, что в действительности такие роды соответствуют
в точности половине всех этих характеров, другой же их половине
такие роды тем самым соответствовать не могут (ср. доказательство
указанной теоремы). Если в п. 264 все возможные характеры были
разбиты на две равных совокупности Р, Q, причем для характе-
характеров из совокупности Q было доказано, что им не могут соответство-
соответствовать собственно примитивные положительные формы, в то время
как для характеров из Р оставалось неясным, действительно ли
каждому из них соответствуют такие роды, то теперь эта неясность
полностью устранена, и мы можем быть уверены, что во всей сово-
совокупности Р нет ни одного характера, которому не соответствовал
бы некоторый род. Но отсюда легко выводится также и то, что для
отрицательного определителя в отрицательном собственно прими-
примитивном порядке, в котором, как мы показали в п.264,1, невозможны
все характеры из Р, а возможны лишь характеры из Q, в дейст-
действительности возможны все характеры из Q. Именно, если обозначить
через К какой-нибудь характер из Q, через /— любую форму из
Разлоэюения чисел и двойничных форм на три квадрата 417
отрицательного собственно примитивного порядка форм с опреде-
определителем D и через К' — ее характер, то последний будет содер-
содержаться в Q, откуда легко следует, что характер, составленный из
К, К' (по правилу п. 246), принадлежит совокупности Р, и потому
существуют положительные собственно примитивные формы
с определителем D, которые ему соответствуют; при композиции
любой из таких форм с формой / получается, очевидно, отрицатель-
отрицательная собственно примитивная форма с определителем D, характером
которой является К. Совершенно аналогичным образом показы-
показывается, что в несобственно примитивном порядке все те характеры,
которые, согласно правилам п. 264, II, III, только и могут быть воз-
возможны, оказываются действительно возможными, независимо от
того, содержатся ли они в Р или в Q. Эти теоремы, если мы
не слишком заблуждаемся, следует причислить к прекраснейшим тео-
теоремам теории двойничных форм, тем более, что хотя они имеют сов-
совсем простую природу, но скрыты так глубоко, что строгое доказа-
доказательство их невозможно без помощи такого большого числа дру-
других исследований.
Теория разложения чисел и двойничных форм
на три квадрата
Теперь мы переходим к другому приложению предыдущего от-
отступления, а именно, к разложению чисел и двойничных форм на
три квадрата, причем предпошлем этому следующую задачу *.
288
Задача. Пусть М обозначает положительное число; найти
условия, при которых существуют отрицательные примитивные
двойничные формы с определителем —М, которые являются квад-
квадратичными вычетами числа М, т. е. для которых 1 является харак-
характеристическим числом.
Решение. Обозначим через Q, совокупность всех специальных
характеров, которые указывают отношения числа 1 как к отдельным
* Ср. дополнения в конце «Исследований».
418 Раздел V (п.
(нечетным) простым делителям числа М, так и к числам 8 или 4,
если они входят в М; очевидно, что этими характерами будут Rp,
Rp', Rp",..., где р, р', /?",-•* обозначают упомянутые простые де-
делители, и 1, 4 или 1, 8, если в М входит соответственно число 4 или
число 8. Далее, будем использовать буквы Р, Q, в том же значении,
что и в предыдущем пункте, или в п. 264. Теперь мы будем различать
следующие случаи.
I. Если М делится на 4, то ?2 является полным характером и из
п. 233, V вытекает, что 1 может быть характеристическим числом
только тех форм, характером которых является Q. Но очевидно,
что О является характером главной формы A, О, М) и принадлежит
тем самым совокупности Р, а, значит, не может соответствовать
никакой отрицательной собственно примитивной форме; поскольку
несобственно примитивных форм для такого определителя нет, в этом
случае вообще не существует отрицательных примитивных форм,
которые являются вычетами числа М.
II. Если М=3 (mod 4), то рассуждения остаются теми же,
за единственным исключением, что в этом случае существует не-
несобственно примитивный отрицательный порядок, в котором ха-
характеры из Р либо возможны, либо нет, в зависимости от того,
имеет ли место М=3 или =7 (mod 8) (ср. п. 264, III). В первом
случае в этом порядке существует, следовательно, род, характером
которого является Q, вследствие чего 1 будет характеристическим
числом всех форм из этого рода; во втором случае вообще не сущест-
существует отрицательных форм, обладающих этим свойством.
Ш. Если M=l(mod 4), то ?1 еще не является полным харак-
характером, так как к нему нужно добавить еще отношение к числу 4; оче-
очевидно, однако, что ?1 обязательно должно входить в характер
формы, для которой 1 является характеристическим числом, и,
наоборот, каждое число, характером которого является либо О;
1, 4, либо Q; 3, 4, должно иметь характеристическое число 1.
Но О; 1, 4 является, очевидно, характером главного рода, при-
принадлежащим к Р, и потому в отрицательном собственно прими-
примитивном порядке невозможным; по той же причине характер Q;
3, 4 принадлежит к Q (п. 263), вследствие чего ему в отрицательном
собственно примитивном порядке соответствует род, все формы
Разложения чисел и двойничных форм на три квадрата 419
которого имеют характеристическое число 1. Несобственно прими-
примитивного порядка в этом случае, так же, как и в следующем, не
существует.
IV. Если М = 2 (mod 4), то для того, чтобы из ?2 получился
полный характер, к Q, нужно добавить еще отношение к числу 8,
а именно, либо 1 и 3, 8 либо 5 и 7,8, если М = 2 (mod 8), и либо
1 и 7,8, либо 3 и 5, 8, если Л/= 6 (mod 8). В первом случае ха-
характер О>; 1 и 3,8, очевидно, принадлежит к Р, а потому харак-
характер О; 5 и 7, 8 — к Q, вследствие чего ему соответствует отрица-
отрицательный собственно примитивный род; и по аналогичной причине
во втором случае будет существовать один род из отрицательного
собственно примитивного порядка, формы которого обладают требу-
требуемым свойством, именно, род с характером Ql\ 3 и 5, 8.
Из этого следует, что отрицательные примитивные формы с оп-
определителем — М, имеющие характеристическое число 1, существу-
существуют, когда М сравнимо по модулю 8 с одним из чисел 1, 2, 3, 5, 6,
причем всегда в одном единственном роде, который будет несобст-
несобственным в случае М = 3,ичто таких форм вообще нет, если М ==
^еО, 4 или 7 (mod 8). Ясно также, что если (—а, — Ъ, —с) является
отрицательной примитивной формой с характеристическим чис-
числом + 1, то (а, Ь, с) будет положительной примитивной формой с
характеристическим числом —1. Отсюда видно, что в пяти первых
случаях (когда М=1, 2, 3, 5, 6) существует один положительный
примитивный род, формы которого имеют характеристическое чис-
число — 1, причем для М^З — несобственный, а в остальных трех
случаях (когда М = 0, 4, 7)' таких положительных форм вообще не
может быть.
289
Относительно собственных представлений двойничных форм трой-
тройничной формой х2 -(- у2 + z2 = / из развитой в п. 282 общей теории
получается следующее.
I. Двойничная форма <р может быть собственно представлена
формой / только если она (форма <р) является положительной при-
примитивной формой, и число — 1 (т. е. определитель формы /) явля-
является ее характеристическим числом. Поэтому для положительных
420 Раздел V (п. 290)
определителей, а также и для отрицательных определителей — Л/,
в случае когда М делится на 4 или имеет вид 8п + 7, не сущест-
существует двойничных форм, собственно представимых формой /.
П. Если же 9 — (Р* Я> г) является положительной примитивной
формой с определителем — М, и — 1 является характеристическим
числом формы <р> а потому и противоположной ей формы (/?, — q, r),
то существуют представления формы <р формой /, принадлежащие
любому заданному значению выражения У — (/?, — q, r). Именно,
все коэффициенты тройничной формы g с определителем — 1 (п. 283)
обязательно будут целыми числами, a g будет определенной фор-
формой и потому заведомо будет эквивалентна форме / (п. 285, I).
III. Число всех принадлежащих одному и тому же значению
выражения у—(р, —q-, т) представлений во всех случаях, кроме
случаев М = 1 и М = 2, равно, согласно п. 283, III, числу пре-
преобразований формы / в g, и потому, согласно п. 285, равно 48'
оттуда же вытекает, что если имеется одно принадлежащее задан-
заданному значению представление, то остальные 47 получатся, если
значения х, у, z всевозможными способами переставлять и брать
со всевозможными комбинациями знаков; поэтому все 48 представ-
представлений дают только одно разложение формы <р на три квадрата,
если иметь в виду только сами квадраты, а не порядок их распо-
расположения и не знаки корней из них.
IV. Если количество всех входящих в М различных нечетных
простых чисел положить равным [х, то из п. 233 выводится,
что число всех различных значений выражения |/—(/?, —q, r) (mod M)
равно 2*, из которых, однако, согласно п. 283, нужно рас-
рассматривать только половину (если М > 2). Поэтому число всех
собственных представлений формы <р формой/ равно 48-2!Л~1 =3-2^+3,
а число различных разложений на три квадрата равно 2fA~1.
Пример. Пусть ср= №2 + 6tu + Alu2, и потому М = 770. Здесь
нужно рассматривать следующие четыре значения выражения
/—A9, —3, 4) (mod 770) (п. 283): C9,237), A71, —27), B69, —83),
B91, —127). Чтобы найти представления, принадлежащие значе-
A9,41,2\
о, Ь, о/
Разлоэюения чисел и двойничных форм на три квадрата 421
в которую, как мы находим по правилам из пп. 272,275, форма /
1,-6, О
переходит при подстановке •
— 3, —2, —1 >, откуда получается
-3, —1, -1
следующее представление формы 9 формой /:
x — t — Qu% у = —3t— 2w, 2 — —3t— и;
остальные 47 представлений, принадлежащих этому же значению,
которые получаются перестановками х, у, z и переменами знаков,
мы ради краткости не выписываем. Все эти 48 представлений дают
одно и то же разложение формы ср на три квадрата:
t2 — 12*и + Зби2, 9*2 + 12tu + 4w2, 9t2 + Ыи + и2.
Совершенно аналогичным образом значение A71, —27) дает
разложение на квадраты Ct + 5wJ, C? — 4wJ, t2\ значение B69, —83)
дает разложение (t -f- 6uJ -f- C? + иJ + C? — 2иJ\ наконец, значе-
значение B91, — 127) — разложение (t + ЗиJ + C* + АиJ + C* — 4иJ;
каждое из этих разложений эквивалентно 48 представлениям.
Кроме этих 192 представлений или четырех разложений, никаких
других нет, так как 770 не делится ни на какой квадрат, и по-
потому несобственных представлений существовать не может.
290
Формы с определителями —1 и —2, которые в некоторых от-
отношениях представляют собой исключения, мы коротко рассмот-
рассмотрим отдельно. Сначала мы предпошлем общее замечание о том,
что если <р, ср' какие-нибудь эквивалентные двойничные формы, и
(О) — заданное преобразование первой во вторую, то при комби-
комбинировании каждого представления формы 9 некоторой тройничной
формой / с подстановкой (в) получается представление формой /
формы <р'> далее, при этом из собственных представлений формы 9
получаются собственные представления форм ср', причем из различ-
различных различные, а из всех — всевозможные такие представления
формы 9- Это очень легко можно доказать выкладкой. Поэтому
422 Раздел V (п. 291)
одна из форм <р, 9' м^жет быть представлена формой / столькими
же способами, что и другая.
I. Пусть сначала ср = t2 + и2 и <р' — какая-нибудь другая поло-
положительная двойничная форма с определителем —1, которой фор-
форма 9 эквивалентна, и пусть <р переходит в <р' при подстановке
t = cut' + Ри', гг = 7^' + ^и\ Форма <р представляется тройничной фор-
формой / = х2 + у2 + 22, если положить х — t, у = и, 2 = 0; при пе-
перестановках значений ж, у, 2 отсюда получается шесть представ-
представлений, а из каждого из них — снова четыре, если изменять знаки
у t, и, так что всего имеется 24 представления, которым соответ-
соответствует одно единственное разложение на три квадрата, и, кроме
них, как легко видеть, никаких других быть не может. Отсюда
следует, что и форма <р' может быть разложена на три квадрата
только одним единственным способом, а именно, на (cut' -f- Pw'J,
(ft' + Su'J и 0, каковому разложению эквивалентны 24 представ-
представления.
II. Пусть 9 = ^2+2w2 и 9' — какая-нибудь другая положитель-
положительная двойничная форма с определителем — 2, и пусть ср переходит
в нее при подстановке t = cut' + $и\ и = ft' +6гг'. Тогда, анало-
аналогично тому, как в предыдущем случае, мы заключаем, что 9, a
потому и 9'» может быть разложена на три квадрата только одним
единственным способом, а именно, форма (р — на t2 -f- и2 -f- и2 и
форма 9' — на (<**' + Pw'J + (Т*' + ^иТ + (Т*' + ^и'J\ легко видеть,
что каждое такое разложение эквивалентно 24 представлениям.
Отсюда следует, что двойничные формы с определителями — 1
и — 2 относительно числа представлений тройничной формой х2 -f-
+ у2 + z2 подчиняются закону, общему и для других двойничных
форм; действительно, так как в обоих случаях [л = 0, то формула
предыдущего пункта также дает 24 представления. Причина этого
заключается в том, что две особенности этих форм компенсируют
одна другую.
Ради краткости мы освободим себя от труда применять к форме
х<2> + У2 + z2 изложенную в п. 284 общую теорию несобственных
представлений.
Разлоэюения чисел и двойничных форм на три квадрата 423
291
Задача об отыскании всех собственных представлений задан-
заданного положительного числа М формой х1 + У2 + z<2>, согласно и. 281,
сводится сначала к отысканию собственных представлений числа
— М формой — х2— у1 — z2 — /; а это в соответствии с предписани-
предписаниями п. 280 делается следующим образом.
I. Находятся все классы двойничных форм с определителем
— Л/, формы которых могут быть собственно представлены формой
X2 4- У2 + Z? = F (которая является дополнительной к форме /).
Если М = 0, 4, 7 (mod 8), то, согласно п. 288, таких классов нет
и потому М не может быть разложено на три квадрата, которые
не имеют общих делителей*. Если же Л/^1, 2, 5, или 6, то су-
существует один положительный собственно примитивный, или, если
М = 3, то несобственно примитивный род, который охватывяет все
такие классы; число этих классов мы обозначим через к.
II. Выберем теперь из этих классов любые к форм, из каждого
класса по одной, которые мы обозначим через 9, ?', ?%•••> найдем
всевозможные собственные представления этих форм формой F,
число которых равно, таким образом 3 • 2^+3к = К, где (л обознача-
обозначает количество (нечетных) простых сомножителей числа М, и выве-
выведем, наконец, из каждого такого представления
X = mt + nu, Y = m't + n'u4 Z ^-m"t + n"u
следующее представление формой х2 + у2 + z2 числа М\
х = т'п" — гп"п\ у = тп"п — mnn, z = тп' — т'п.
В совокупности этих К представлений, которую мы обозначим
через ?1, обязательно содержатся все представления числа М.
III. Поэтому нам нужно еще только исследовать, содержатся ли в
О одинаковые представления; а так как из п. 280, III мы уже зна-
знаем, что те представления из Q, которые получаются из различных
* Это вытекает также и из того, что сумма трех нечетных квадратов обяза-
обязательно EE=3(mod 8), сумма двух нечетных и одного четного либо = 2, либо=6,
сумма одного нечетного и двух четных либоЕЕг1, либо^О, наконец, сумма трех
четных либо = 0, либо = 4; в последнем случае, однако, представление, очевид-
очевидно, является несобственным-
424 Раздел V (п. 292)
форм, например, из форм <р и <р', обязательно различны, то оста-
остается лишь исследовать, могут ли различные представления одной
и той же формы, например, формы ср, формой F привести к одина-
одинаковым представлениям формой х2-\- у2 + z2 числа М. Но тотчас же
ясно, что если среди представлений формы <р имеется представление
(г) X = mt + nu, Y = m't+n'u, Z = m"t + п"и,
то среди них есть и представление
(г') х= —mt — nu, Y = —m't — nfu, Z = — m"t — n"u,
и что из обоих представлений получается одно и то же представ-
представление числа М, которое мы обозначим через (/?); исследуем поэтому,
может ли это представление (R) получиться еще из других пред-
представлений формы <р. Из п. 280, III легко следует, если положить
X = ф, что если все собственные преобразования формы <р в себя
представляются в виде
t — <xt + f3w, и = ^t + <$w,
то все те представления формы <р, из которых следует представ-
представление (R), выражаются формулами
х = (сит )
у = (Лт'+ *(п') t + (pmA + Ы') и,
z = (am"+ Trc") t + ($т"+ЪпГ) и.
Но из изложенной в п. 179 теории преобразований двойничных
форм с отрицательным определителем получается, что во всех слу-
случаях, кроме случаев М = 1 и М = 3, имеется только два собст-
собственных преобразования формы 9 в самое себя, именно, а, р, y> ^
(соответственно) = 1, 0, 0, 1, и = — 1, 0, 0, — 1 (именно, так как 9
является примитивной формой, то, что в п. 179 обозначалось через
т, равно или 1 или 2, и потому всегда, кроме исключенных случаев,
здесь заведомо имеет место случай 1 п. 179), Поэтому представле-
представление (В.) может получиться только из представлений (г), (г'), и, зна-
значит, каждое собственное представление числа М встречается в ?1 два
и только два раза, а количество всех различных собственных пред-
представлений числа М равно ту К = 3 •
Разлоэюения чисел и двойничных форм на три квадрата 425
Что касается исключенных случаев, то число собственных
преобразований формы <р в себя, согласно п. 179, равно 4 для
М = 1 и равно 6 для М — 3,,и, действительно, легко установить,
что количества собственных представлений чисел 1, 3 равны соот-
соответственно К/4, К/6; именно, каждое из указанных двух чисел
может быть разложенно на три квадрата только одним единствен-
единственным образом: число 1—на 1+0 + 0, число 3 — на 1 + 1 + 1;
разложение числа 1 дает шесть, а разложение числа 3 — восемь
различных представлений; число же К равно 24 для М = 1 (когда
^ — 0, к = 1) и равно 48 для М = 3 (когда [х = 1, к = 1).
Кстати заметим, что если h равно числу классов в главном»
роде, которому, согласно п. 252, равно число классов в любом дру-
другом собственно примитивном роде, то к = h для М=1, 2, 5 или
6 (mod 8), и k = ^h для ik/ = 3(mod 8), за исключением единствен-
единственного случая М = 3, когда k = h = l. Поэтому для чисел вида
8п + 3 количество представлений всегда равно 2^+2/г, так как для
числа 3 две особенности компенсируют одна другую.
292
Разложения чисел на три квадрата мы различаем (так же, как
и в случае двойничных форм) от представлений формой х2 + у2 +
+ z2 в том отношении, что в первом случае мы обращаем внимание
только на величину квадратов, а во втором, кроме того, на порядок
их расположения и знаки квадратных корней из них, и потому
представления х = а, у = b, z = с и х = а', у = &', z = с' мы счи-
считаем различными, если не выполняются одновременно равенства
а = а', Ъ = Ъ', с = с'', в то время как разложения на а2 + Ь2 +
+ с2 и а'2 + Ь12 + с'2 считаются одинаковыми, если вторые квад-
квадраты с точностью до порядка расположения равны первым.
I. Из этого вытекает, что разложение числа М на квадраты
а2 + Ъ2 + с2 и а'2 + Ъ'2 + с'2 эквивалентно 48 представлениям,
если ни один из этих квадратов не равен 0 и все они различны между
собой, и эквивалентно только 24 представлениям, если либо один
из квадратов равен 0, а два других различны, либо ни один из квад-
квадратов не равен 0, но два из них одинаковы. Если же в разложении
426 Раздел V (п. 292)
заданного числа на три квадрата два из них равны 0, или один ра-
равен 0, а два других равны, или, наконец, все три равны между собой,
то это разложение будет эквивалентно соответственно шести, двена-
двенадцати или восьми представлениям; однако, если ограничиваться
только собственными представлениями, то так может быть только
в исключительных случаях, когда М = 1 или 2 или 3. Эти случаи
мы из рассмотрения исключим и предположим, что количество
всех разложений числа М на три квадрата (без общих делителей)
равно Е, и среди них имеется е разложений, в которых равен 0 один
квадрат, и е' разложений, в которых два квадрата равны между
собой; первые могут также рассматриваться как разложения на два
квадрата, а вторые — на квадрат и удвоенный квадрат. Тогда ко-
количество всех собственных представлений числа М формой х2 + у2 +
+ z2 равно
24 (е + ef) + i8(E — e~ ё) = 48? — 24 (е + ё).
Но из теории двойничных форм легко следует, что е равно либо
О, либо 2^~1, в зависимости от того, является ли число — 1 ква-
квадратичным невычетом или вычетом по модулю М, и точно так же
ё равно либо 0, либо 2М>~1, в зависимости от того, является невы-
невычетом или вычетом по модулю М число —2, где [х равно количе-
количеству (нечетных) простых сомножителей числа М (см. п. 182; в
большие] подробности мы здесь вдаваться не будем). Из этого
легко выводится, что Е = 2^~2ку если как число —1, так и число
— 2 являются невычетами по модулю М, Е = 2^~2 (к -)- 2), если
оба эти числа являются вычетами, Е = 2^~2(к + 1), если одно
число является вычетом, а другое невычетом по модулю М.
В исключительных случаях М = 1 и М = 2 эти формулы дава-
ли бы значение Е~-, в то время как на самом деле Е = 1; для
М = 3 получается, однако, правильное значение 2?=1, так как
в этом случае две указанные в п. 291 особенности компенсируют
одна другую.
Если поэтому М является простым числом, то [л = 1, и потому
-г 1 1
Е = ^-{к-\ 2), в случае когда M=l (mod 8), Е = -= (к + 1), когда
М = 3 или =5. Эти частные теоремы были получены индуктивным
Разложения чисел и двойничных форм на три квадрата 427
путем Лежандром и опубликованы им в замечательном, ранее
уже упоминавшемся, сочинении, «Hist, de VAc. de Paris», 1785,
p. 530 и след., правда, в несколько иной форме* причина чего в
основном заключается в том, что он не различал собственную экви-
эквивалентность от несобственной и потому объединял между собой
противоположные классы.
И. Чтобы найти все разложения числа М на три квадрата
(без общих делителей) нет нужды находить все собственные пред-
представления всех форм ср, ср', ср",... Действительно, прежде всего
легко установить, что все 48 представлений формы ср, которые
принадлежат одному и тому же значению выражения У— (р, — q, r)
(если положить 9 = (р, q, г)), дают одно и то же разложение числа
Мч и потому достаточно иметь только одно из них, или, что сво-
сводится к тому же, достаточно найти лишь все различные разложе-
разложения* формы ф на три квадрата, и точно так же обстоит дело
для остальных форм срг, 9",... Далее, если ср не содержится в
двустороннем классе, можно пренебречь формой, которая выбрана
из противоположного класса, т. е. из каждых двух противополож-
противоположных классов достаточно рассматривать только один. Действитель-
Действительно, так как совершенно безразлично, какая форма выбирается из
каждого класса, то мы предположим, что из класса, противо-
противоположного тому, которому принадлежит форма ср, выбрана форма
9', противоположная форме 9- Тогда легко видеть, что если
собственные разложения формы ср в общем виде выражаются фор-
формулой
(gt + /шJ + (g't + h'uf + (g"t+h"u)\
то все различные формы ср' будут представляться в виде
(gt - /шJ + (g't - h'uf + (g"t - h"u)\
а также и то, что из последних получаются те же представления чис-
числа М, что и из первых. Наконец, в случае, когда 9 является формой
из двустороннего класса, но не формой главного класса и не фор-
формой, эквивалентной форме B, О, М/2) или форме B, 1, (М + 1)/2)
* Всегда нужно при этом подразумевать «собственные», если угодно пере-
перенести это выражение с представлений на разложения.
428 Раздел V (п. 293)
(в зависимости от того, четно М или нечетно), то половину значе-
значений выражения У— (/?, — q, r) можно отбросить; ради краткости,
однако, мы не будем говорить подробнее об этом преимуществе.
Впрочем, если мы хотим получить все собственные представления
числа М формой х2 + у2 + z2, мы можем использовать это преиму-
преимущество, так как оно легко получается из разложений.
Для примера найдем все разложения на три квадрата числа 770»
Здесь [х = 3, е = е' = 0 я потому Е = 2к. В соответствии с клас-
классификацией положительных двойничных форм с определителем
—770, которую мы здесь, ради краткости, приводить не будем, так
как она легко может быть получена на основании любого из правил
п. 231, мы находим, что число положительных классов равно 48Г
и все они собственно примитивны и распадаются на 8 родов, так
что к = 4, и потому Е — 8. Род, характеристическим числом кото-
которого является —1, должен, очевидно, иметь по отношению к числам
5, 7, 11 специальные характеры i?5; iV7; Nil, из чего, на
основании п. 263, легко следует, что его характер по отношению
к числу 8 следующий: 1 и 3, 8. Но в роде, имеющем характер 1 и
3, 8; i?5; iV7; 7V11, имеется четыре класса, в качестве пред-
представителей которых мы выберем формы F, 2, 129), F, —2, 129),.
A9, 3, 41), A9, —3, 41); второй и четвертый классы мы, однако, от-
отбросим, так как они противоположны соответственно первому и
третьему классам. Четыре разложения формы A9, 3, 41) мы уже на-
нашли в п. 289; из них получаются разложения числа 770 на 9 +
+ 361 + 400, 16 + 25 + 729, 81 + 400 + 289, 576 + 169 + 25.
Подобным же образом находятся четыре разложения формы б?2 -]-
+ 4ta + 129гг2 на
t — 8мJ + B* + иJ + {t + 8wJ, (t — 10иJ + Bt + ЪиJ + (t + 2wJ,
Bt — ЪиJ + (t + 10uJ + {t + 2uJ, Bt + luf + (t— 8uJ + (t + 4wJ,
которые получаются соответственно из следующих значений выра-
выражения К-F,-2, 129): D8, 369), F2, -149), (92, —159), B02, 61).
Из этого вытекают разложения числа 770 на 225 + 256 + 289,
1 + 144 + 625, 64 + 81 + 625, 16 + 225 + 529. Других разло-
разложений, кроме этих восьми, нет.
Доказательство одной теоремы Ферма 429
То, что относится к разложениям чисел на три квадрата, которые
имеют общий делитель, настолько легко получается из общей тео-
теории п. 281, что нам нет нужды на этом останавливаться.
Дсказательство теоремы Ферма о том,
что каждое целое число может быть разложено
на три треугольных числа или на четыре квадрата
293
Предыдущие исследования приводят также к доказательству
знаменитой теоремы о том, что каждое положительное целое число
может быть разложено на три треугольных числа, теоремы, которая
впервые была найдена Ферма, но для которой до сих пор отсутст-
отсутствовало строгое доказательство. Очевидно, что каждое разложение
числа М на треугольные числа
±x(x + l) + ±y(y+l)+±z(z + i)
дает возможность разложения числа 8М + 3 на три нечетных
квадрата
Bx+iy + By+l)* + Bz + l)\
и обратно. Но, согласно изложенной выше теории, каждое целое
положительное число ЪМ -\- 3 разложимо на три квадрата, которые
обязательно нечетны (ср. замечание к п. 291), и количество разло-
разложений зависит от количества простых сомножителей числа ЪМ -\-
+ 3 и от числа классов, на которые распадаются двойничные формы
€ определителем — (8М + 3). Столько же имеется и разложений
числа М на три треугольных числа. При этом мы считаем, что
х(х + 1)/2 рассматривается как треугольное число для любого
значения х; если же нуль желательно исключить, то теорему нужно
формулировать так: каждое целое положительное число либо само
является треугольным числом, либо разложимо на два или три тре-
треугольных числа. Подобное же изменение нужно будет внести и
в следующую теорему, если будет желательно исключить нуль из
числа рассматриваемых квадратов.
430 Раздел V (п. 294)
По такому же принципу доказывается и другая теорема
Ферма, а именно, что каждое целое положительное число может
быть разложено на четыре квадрата. Если вычесть из числа вида
in + 2 любой квадрат (который меньше, чем это число), из числа
вида 4лг + 1 — четный квадрат, или из числа вида 4лг + 3 — не-
нечетный квадрат, то во всех этих случаях остаток будет разложим
на три квадрата, а потому исходное число — на четыре. Наконец,*
число вида in может быть представлено как i^N, где N имеет один
из трех предыдущих видов; а если N разложимо на четыре квадрата,,
то тем самым будет разложимо и i^N. От числа вида 872 + 3 можно*
вычесть также квадрат числа, делящегося на 4, от числа вида
8/2 + 7 — квадрат четного числа, не делящегося на 4, и от числа
вида 8п + 4 — нечетный квадрат, причем остаток каждый раз*
будет разложим на три квадрата.
Впрочем, эта теорема была уже доказана Лагранжем,
«Nouv. Mem. de I Ac, de Berlin», 1770, p. 123, причем это же до-
доказательство (которое совершенно отлично от нашего) более под-
подробно изложил Эйлер в «Actis Ac. Petz.», vol. II, p. 48. Другие-
теоремы Ферма, которые как бы образуют продолжение преды-
предыдущих, а именно, что каждое целое число разложимо на пять пяти-
пятиугольных чисел, шесть шестиугольных,, семь семиугольных и т. д.г
до сих пор не доказаны и требуют других методов.
Решение уравнения ax2+by2
294
Теорема. Если а, Ъ, с обозначают взаимно простые числа, ни
одно из которых не равно 0 и не делится ни на какой квадрат, то
уравнение
(Q) ах2 + by2 + cz2 — 0
не имеет решений в целых числах (кроме решения х = у = z=0r
которое мы не принимаем во внимание), за исключением случаяТ
когда числа —be, —ас,—аЪ являются квадратичными вычетами со-
соответственно по модулям а, Ь, с, и последние числа имеют различные
Решение уравнения ах2 + by2 + cz2 = 0 431
знаки; если же эти четыре условия выполняются,, то уравнение (Q)
в целых числах разрешимо.
Доказательство. Если уравнение (Q) вообще разрешимо в целых
числах, то оно может быть удовлетворено также и такими значе-
значениями х, у, z, которые не имеют общих делителей; действительно,
любые удовлетворяющие уравнению (Q) значения будут по-преж-
по-прежнему ему удовлетворять, если их разделить на их наибольший об-
общий делитель. Если мы теперь предположим, что ар2 + bq2 + сг2 = О,
и числа р, q, r свободны от общих делителей, то они будут также
взаимно просты и попарно; в самом деле, если бы числа q, r имели
общий делитель [а, который был бы взаимно прост с р, то число ^2
входило бы в ар2, а значит, ива, что противоречит предположению;
точно так же взаимно просты одно с другим числа p,r\ р, q. Поэтому
число —ар2 представляется двойничной формой by2 + cz2, когда у,
z принимают взаимно простые значения q, r, вследствие чего опре-
определитель —be этой формы является квадратичным вычетом по мо-
модулю ар2, а значит, и по модулю а (п. 154). Точно так же имеет ме-
место —acRb, —abRc. А тот факт, что уравнение (Q) не может иметь
решений, если знаки чисел а, Ъ, с одинаковы, настолько ясен, что
не требует пояснений.
Доказательство обратного утверждения, составляющего вторую
часть нашей теоремы, мы проведем так, что сначала покажем, как
можно найти эквивалентную форме ( л' п' л ) = / тройничную форму,
у которой второй, третийг четвертый коэффициенты делятся соот-
соответственно на а, Ъ, с, а из этого получим затем решение уравне-
уравнения (О).
I. Найдем такие три числа А, В, С, которые не имеют общих
делителей и обладают тем свойством, что А взаимно просто с чис-
числами Ъ и с, В взаимно просто с а и с, С взаимно просто с а и Ь,
и число аА2 + ЪВ2 + сС2 делится на abc. Это достигается следую-
следующим образом. Пусть 9t,35, S являются соответственно значениями вы-
выражений У-—be (mod а), У^—ас (mod b), |/— ab (mod с), которые
обязательно взаимно просты соответственно с числами а, Ь, с.
Возьмем три целых числа а, Ь, с, которые взаимно просты соответ-
соответственно с а, Ъ, с, а в остальном совершенно произвольны
432 Раздел V (п. 294)
(например, все три равны 1) и определим А, В, С так, что
А = Ъс (mod??) и =с(? (mod с),
В = га (mod с) и =a9t(moda),
С = aft (mod a) и = b35(mod6).
Тогда
а А2 + ЪВ2 + сС2 = а2 (Щ2 + сб2) = а2 (Щ2 — 3t26) = 0 (mod а),
т. е. число аА2 -\- ЪВ2 + сС2 делится на а, и точно так же делится
на Ъ и на с, а значит, и на произведение ate. Кроме того, полу-
получается, что А обязательно взаимно просто с Ъ и с, В взаимно
просто с а и с, С взаимно просто с а и Ъ. Если эти же значения
А, В, С имеют (наибольший) общий делитель [х, то он, очевидно,
будет взаимно прост с a, b, с, а потому и с abc; поэтому если
указанные значения разделить на [л, то мы получим новые значе-
значения, которые не имеют общих делителей и при которых выраже-
выражение аА2 -}• ЪВ2 + сС2 все еще делится на abc, так что они удов-
удовлетворяют всем условиям.
И. Если числа А, В, С определены таким образом то не будут
иметь общих делителей и числа Аа, ВЪ, Сс. Действительно, если бы
они имели общий делитель [х, то он обязательно должен был бы
быть взаимно прост с а (так как а взаимно просто и с ВЬ, и с
Сс), и точно так же взаимно прост с Ъ и с с; поэтому [л должно
было бы входить в Л, В, С, что противоречит предположению.
Поэтому можно найти такие целые числа а, р, т, что аАа -J- $Bb -J-
•\-^Сс = 1\ далее, найдем шесть таких чисел a', J3', т', а", р*, Y\ что
ру — PY = Аа, т'а" — aY = въ, *У ~ Р'а" = <^-
Если теперь / переходит при подстановке
а, а', а'',
р, р\ р".
т. т'. т"
в форму [m> ^ *шп ] = g (которая будет эквивалентна форме /), то
я утверждаю, что числа т!, т", п делятся иа abc. Именно, если
положить
C"Т __ ^ = ^'? Т"а _ а^т = J5', а"Р — Р"а - С",
Решение уравнения ах + by + cz = 0 433
то будет иметь место
а' = В"Сс — С'ВЪ, р' - С'Аа — Л"Сс, Т' = А"ВЪ — ?"Ла,
а" = С'ВЪ — В'Сс, $* = А'Сс — С'Аа, ч" = В'Аа —А'ВЪ.
Если эти значения подставить в равенства
т' = ал'2 + &р + с?'2,
т" = аа + Ь$ + су,
п = atiа" + бР'Р" + ст'т".
то по модулю а получается
т' = ЪсА(В2Ь + С2с) = 0,
тГ=ЪсА'*(В*Ь + С2с) = 0,
2c) =0,
т. е. числа m', w", тг делятся на а; аналогичным же образом нахо-
находят, что эти числа делятся также на Ь, с, а потому и на abc.
III. Если мы положим для краткости определитель форм /, g,
т. е. число —abc, равным d, и
md = М, т' = M'd, m" = M"d, n = Nd, n' =N\ п" = Л",
то /, очевидно, будет переходить при подстановке (S)
aid, ос', а"
К р\ р*
(Md, M'd, M"dx
в тройничную форму ( , v, \ = g с определителем а3, ко-
торая, таким образом, содержится в /. Я утверждаю теперь, что
fd, 0, 0\ „ ^ - y ,
форма ( J = g" обязательно эквивалентна этой форме g .
/М, М7, Мг/\
Действительно, очевидно, что ( ' _/ j = gw является трой-
тройничной формой с определителем 1; далее, так как, по предположе-
предположению, числа а, Ьу с не все имеют одинаковые знаки, то / является
неопределенной формой, откуда легко видеть, что должны быть
неопределенными также и формы g' и gm\ поэтому g" эквивалентна
434 Раздел V (п. 295)
форме ( '
' ' Л (п. 277), и можно найти преобразование {S')
первой формы во вторую; но очевидно, что этим преобразованием
(S') форма gf будет переводиться в g". Следовательно, также и g"
содержится в /, и комбинация подстановок (S), (S') дает преобра-
преобразование формы / в g". Если этим преобразованием является
8, 8', 8"
S, 8', 8"
С С, С",
то ясно, что мы получаем два решения уравнения (?2), а именно,
х = 8', ?/ = е', 2 = С и ж = 8", г/ = s", z = С"; одновременно
получается, что ни одна из этих двух систем значений не может
быть нулевой, так как обязательно
8s'C" + SVC + S"sC — 8s"C — 8'sC"— 8VC = d.
Пример. Пусть задано уравнение 7а:2 — \5у2 -J- 23z2 = 0; оно раз-
разрешимо, так как 345Я7, — 161Д15, 105Л23. Для 31, 25, S полу-
получаются значения 3, 7, 6, и если положить а = Ь = с = 1, то мы
находим А = 98, J? = — 39, С = — 8. Отсюда выводится подста-
| 3, 5, 22|
новка { 1» 2, 281 которой форма / переводится в
\ 8, 25, -7)
[ 1520, 14490, —7245х „
(-2415, -1246, 4735J = ?- ПОЭТ°МУ
(S) =
7 245, 5, 22
-2 415, 2, —28
19 320, 25, —7
/3670800, 6, — Зх
\ -1, -1246, 4735Л
j
IT A w /1' 0) 0\
Далее мы находим, что форма g переходит в . j при под-
становке
3, 5, 1)
-2440, —4066, -813
- 433, - 722, -144
Решение уравнения ах2 + by2 + cz2 = 0 435
и если скомбинировать ее с (S), то получается подстановка
9, И, 121
1> 9> 91 при которой / переходит в g". Мы получаем:
-9, 4, 3)
поэтому два решения заданного уравнения: ж = 11, ?/ = 97 z = 4
и х = 12, г/= —9, z = 3. Последнее решение сделается проще,
если поделить значения на общий делитель 3, после чего полу-
получится х = А, у = — 3, z = 1.
295
Последняя часть теоремы предыдущего пункта может быть также
получена и следующим образом. Найдем целое число h с тем свой-
свойством, что ah = S (mod с) (буквы % 35, 6 мы употребляем в том
же значении, что и в предыдущем пункте), и положим а/г2 -f- Ь = ci.
Тогда легко видеть, что i — целое число, и — ab является опреде-
определителем двойничной формы {ас, ah, i) — ср. Эта форма заведомо не
положительна (действительно, так как, по предположению, а, Ь, с
не все имеют одинаковые знаки, числа аЪ и ас не могут одновре-
одновременно быть положительными); далее, она имеет характери-
характеристическое число — 1, что мы докажем следующим образом.
Если определить целые числа е, е' так, что е = 0 (mod а) и = 35 (mod b)t
се' =9t(modа) и /z35(mod6), то (е, е') будет значением выражения
У—(ас, а/г, i) (mod — ab). Действительно, по модулю а имеет места
е2 = 0 = — ас, ее' = 0 = — а/г,
cV2 = 9B= — 6с = — с2г, и потому в'2 = — г;
а по модулю 6:
е2^^Э52^ — ас, cee' = h$&2 = — ach, и потому ее' = — а/г,
с2е/2 = /г2352 = — ach2 = — сЧ, и потому е'2 = — г.
Но эти же три сравнения, которые выполняются по каждому из^
модулей а, Ь, справедливы и по модулю ab. Из этого на основа*
нии теории тройничных форм легко видеть, что ср представима
/_1 0, 0\ „ .
формой ( ' п]. Пусть, таким образом,
act2 + 2ahtu + ш2 = — (а« + риJ + 2 (Tf + 8к) (ei +
436 Раздел V (п. 296)
тогда, если умножить это равенство на с, получается
a (с* + huf + bu2 = —c (at + $uf + 2c G* + 8и) (e* + to).
Отсюда вытекает, что если придать t, и такие значения, что либо
*[t + Ъи = О, либо st + Ы = 0, то мы тем самым получим решение
уравнения (Q,), которое, следовательно, будет удовлетворяться как
значениями
х = Ьс — ifA, у = т, ^ = aS — рт,
так и значениями
х = Сс — ей, г/ = s, z = осС — ре.
Кроме того, ясно, что как первые, так и вторые значения не могут
быть одновременно все равны 0; действительно, если бы было
8с — ^h = 0 и ^ = 0, то имело бы место также 8 = 0 и <р = — (a^-j-p^J,
откуда а?? = 0, что противоречит предположению, и так же обстоит
дело в отношении других значений. В нашем примере в качестве <р
мы находим форму A61,—63, 24), в качестве значения выражения
У—ср (mod 105) — значение G, — 51), и в качестве представления
Л „ /—1, 0, 0\
формы ср формой ( . п п] — представление
<р = — A3* — АиJ + 2 A1* — Аи) A5* — 5и).
откуда получаются решения х = 7, г/ = 11, z = — 8; ж = 20,
у = 15, z = —5, или, если последнее решение разделить на 5 и
отбросить знак у z, х = 4, у = 3, z = l.
Из этих двух методов решения уравнения (Q) последний имеет
то преимущество, что он в большинстве случаев имеет дбло с мень-
меньшими числами; однако первый, который может быть также соединен
с различными искусственными приемами, на которых мы здесь не
останавливались, представляется более изящным, особенно по той
причине, что числа а, Ь, с рассматриваются здесь как равноправные,
и при перестановке их выкладки совершенно не меняются. Во втором
случае дело обстоит по-иному, так как здесь вычисления по большей
части удобнее всего производить, если принимать за а наименьшее,
а за с наибольшее из трех заданных чисел, как мы и делали в нашем
примере.
О попытке Леснсандра доказать фундаментальную теорему 437
О методе, которым Л е ж а н д р изложил
фундаментальную теорему *
296
Изящная теорема, изложенная в предыдущих пунктах, впервые
была найдена и подкреплена красивым доказательством (совер-
(совершенно отличным от обоих наших доказательств) Л е ж а н д р о м,
«Hist, de Ac. de Paris», 1785, p. 507. Однако одновременно этот за-
замечательный математик попытался в указанном месте вывести до-
доказательство теоремы, которая совпадает с фундаментальной тео-
теоремой предыдущего раздела, из того, что, как мы уже поясняли выше
(п. 151), на наш взгляд, не совсем пригодно для этой цели. Поэтому
будет уместным кратко изложить здесь это (само по себе в высшей
степени изящное) доказательство и указать на причину такого на-
нашего мнения. Сначала предпосылается следующее замечание.
Если числа а, Ь, с <?ce = l(mod 4), то уравнение
(О) ах2 + by2 + cz2 = О
не разрешимо. Действительно, легко видеть, что значение выраже-
выражения ах2 + by2 + cz2 в этом случае обязательно будет либо=1,
либо = 2, либо=3 (mod 4), если считать, что не все величины х,
у, z одновременно четны. Если бы поэтому уравнение (Q) было раз-
разрешимо, то это могло бы достигаться только при четных значениях
х, у, z, что является абсурдом, так как любые значения, удовлетво-
удовлетворяющие уравнению (?)), будуг по-прежнему ему удовлетворять, если
их разделить на их наибольший общий делитель, после чего хотя бы
одно из них обязательно сделается нечетным. Теперь различные
случаи доказываемой теоремы сводятся к следующим основным
моментам.
I. Если /?, q обозначают (положительные различные) простые
числа вида in + 3, то не может одновременно иметь место pRq и
qRp. Действительно, если бы это было возможно, если поло-
положить 1 = а, —р — Ъ, —q = с, выполнялись бы все условия, не-
необходимые для разрешимости уравнения ах2 + by2 + cz2 = 0 (п. 294);
однако оно, согласно предпосланному замечанию, решений не
* Ср. дополнения в конце «Исследований».
438 Раздел V (п. 297)
имеет; следовательно, предположение не может быть верным. От-
Отсюда тотчас же вытекает теорема 7 из п. 131.
II. Если р является простым числом вида in + 1, a q — про-
простым числом вида in + 3, то не может одновременно иметь места
qRp, pNq. Действительно, в противном случае было бы —pRq,
и уравнение х2 + ру2 — qz2 = О имело бы решение, что согласно
предпосланному замечанию, невозможно. Отсюда получаются слу-
случаи 4 и 5 из п. 131.
III. Если р, q являются простыми числами вида in + 1, то не
может одновременно иметь места pRqwqNp. Возьмем некоторое про-
простое число г вида in + 3, которое является вычетом по модулю q
и по которому р есть невычет. Тогда, согласно доказанным выше
(II) случаям имеет место qRr, qNp. Если бы поэтому было pRq,
qNp, то имело бы место qrRp, prRq, pqNr, и потому — pqRr. Сле-
Следовательно, вопреки предпосланному замечанию, уравнение
рх2 + qy2 — rz2 = 0 было бы разрешимо; поэтому сделанное пред-
положение не может выполняться. Отсюда получаются случаи 1 и 2
яз п. 131.
Короче этот случай излагается следующим образом. Если г
обозначает простое число вида in -j- 3, по которому р является не-
невычетом, то также rNp, и потому (если предположить, что pRq,
qNp) qrRp; далее, —pRq, —pRr, и тем самым также —pRqr; по-
поэтому уравнение х2 -\~ ру2 — qrz2 — 0 было бы разрешимо, что про-
противоречит предпосланному замечанию. Следовательно, и т. д.
IV. Если р является простым числом вида 4/2 -f- 1, a q — про-
простым числом вида in -\- 3, то не может быть одновременно pRq
и qNp. Возьмем вспомогательное простое число г вида in + 1, ко-
которое является невычетом по каждому из чисел р, q. Тогда (согласно
II) имеет место qNr, и (согласно 111) pNг; отсюда pqRr. Если поэтому
было бы pRq, qNp, то мы имели бы также prNq, —prRq, qrRp;
тем самым уравнение рх2 — qy1 -\~ rz2 — 0 было бы разрешимо, что
невозможно. Отсюда получаются случаи 3 и 6 из п. 131.
V. Если р, q обозначают простые числа вида in + 3, то не может
одновременно быть pNq и qNp. Действительно, если мы предполо-
предположим, что это возможно, и возьмем вспомогательное простое число г
вида 4/г + 1? которое является невычетом по каждому из чисел
О попытке Леэюандра доказать фундаментальную теорему 439
р, д, то будет иметь место qrRp, prRq; далее, согласно II, pNr, qNr,
и потому pqRr и —pqRr. Следовательно, уравнение —рх2 — qy2 +
+ rz2 = 0 было бы разрешимо, что находится в противоречии с пред-
предпосланным замечанием. Отсюда следует случай 8 из п. 131.
297
Рассматривая предыдущее доказательство подробнее, легко убе-
убедиться, что случаи I и II разобраны так, что против них возразить
нечего. Однако доказательства остальных случаев опираются на
некоторые леммы, и если они еще не доказаны, то и весь метод,
очевидно, теряет свое значение. Хотя эти предположения таковы,
что при поверхностном рассмотрении могло бы показаться, что они
и не требуют доказательства вследствие своей совершенной оче-
очевидности, все же они не могут быть приняты на веру, если желать
полной математической строгости. Что касается предположения
в IV и V о том, что существует простое число г вида in -\- 1, кото-
которое является невычетом по двум другим заданным простым числам />,
д, то из четвертого раздела легко следует, что все числа, которые
меньше чем ipq и взаимно просты с этим числом (количество их равно
2(р — 1) (q — 1)), равномерно распределяются по четырем классам,
один из которых содержит невычеты по каждому из чисел р, g, a
три остальных содержат вычеты по модулю р и невычеты по модулю
д, невычеты по модулю р и вычеты по модулю д, и, наконец,
вычеты по обоим модуям р, q, и что в отдельных классах половина
чисел имеет вид 4тг + 1, а половина — вид 4тг + 3. Поэтому среди
всех этих чисел имеется (р — l)(q — 1)/4 невычетов вида 4тг + 1
по каждому из модулей />, д; эти невычеты мы обозначим через g,
g', g" ,..., а остальные 1(р — 1)(д — 1)/4 чисел — через /г, /г',
/г",... Очевидно, что все числа вида ipqt + g, ipqt + g'', ipqt -f-
+ g",... тоже будут иметь вид in + 1 и будут невычетами по моду-
модулям р, q; совокупность этих чисел обозначим через (G). Теперь ясно,
что для обоснования предположения нужно только доказать, что
в совокупности (G) заведомо содержатся простые числа; само по
себе это очень вероятно, так как формы из (G) вместе с формами
ipqt + /г, ipqt + /г',..., совокупность которых мы обозначим через
440 Раздел V (п. 298)
(Н), содержат все числа, взаимно простые с ipq, а потому и все про-
простые числа (кроме чисел 2, р, q), и не видно причин, по которым ряд
простых чисел не распределялся бы по этим формам равномерно,
так что восьмая их часть принадлежит к (G), а остальные к (Н).
Однако ясно, что такой вывод лишен математической строгости.
Л е ж а н д р сам замечает, что доказательство теоремы о том,
что в каждой форме вида kt + I, где к, I обозначают заданные вза-
взаимно простые числа, a t — произвольное число, обязательно со-
содержатся простые числа, оказывается довольно трудным, и вскользь
указывает метод, который, быть может, способен привести к этому
доказательству. Однако, как нам кажется, для того, чтобы получить
на этом пути строгое доказательство, нужны многие подготовитель-
подготовительные исследования.
Относительно другого предположения (III, второй метод), а
именно, что имеется простое число г вида in + 3, по которому дру-
другое заданное простое число р вида in -\- 1 является невычетом,
Л е ж а н д р вообще не добавляет никакого замечания. Выше
(п. 129) мы доказали, что заведомо существуют простые числа, по
которым р является невычетом, но аш метод оказывается недоста-
недостаточным, чтобы доказать существование таких простых чисел, ко-
которые одновременно имеют вид in -\- 3 (что не требовалось в нашем
первом доказательстве, но требуется здесь). Впрочем, справедли-
справедливость этого предположения мы легко можем доказать следующим
образом. Согласно п. 287, существует положительный род двойнич-
двойничных форм с определителем —/>, имеющий характер 3, 4; Np\ пусть
(а, Ъ, с) — такая форма, и а нечетно (что мы имеем право предпо-
предполагать). Тогда а имеет вид in + 3 и либо само будет простым числом,
либо будет делиться по крайней мере на одно простое число г вида
in + 3. Но —pRa, и потому также —pRr, а, значит, pNr. Однако,
нужно заметить, что теоремы пп. 263, 287 опираются на фундамен-
фундаментальную теорему, и потому, если бы мы захотели доказывать на
основании их часть фундаментальной теоремы, получился бы по-
порочный круг. Наконец, предположение первого метода из III еще
более произвольно, так что нет нужды добавляаь о нем что-либо еще.
Быть может, стоит добавить еще одно замечание относительно
случая V, который хотя и не доказан изложенным только что ме-
О попытке Леснсандра доказать фундаментальную теорему 441
тодом, но легко может быть закончен следующим образом» Если
бы там одновременно имело место pNq, qNp, то было бы —pRq,
— qRp, откуда легко видеть, что —1 является характеристическим
числом формы (/?, О, q), которая тем самым (согласно теории трой-
тройничных форм) может быть представлена формой х2 + у2 + z2. Если
pt2 + qu2 = (at + $uf + (a't + $'uf + (aft + $"uJ,
или
то вследствие первого и второго равенств все числа а, а', ос",
р, р', р" будут нечетны. Но тогда, очевидно, не может выполняться
третье равенство. Подобным же образом может быть рассмотрен
и случай П.
298
Задача. Пусть а, Ъ, с обозначают любые числа; найти усло-
условия для разрешимости уравнения
(со) ах2 ~\- by2 + cz2 = 0.
Решение. Пусть a2, J32, ^2 обозначают наибольшие квадраты,
входящие соответственно в числа be, ас, ab, и пусть оса = ^А,
$Ъ = щВ, ^с=^а^С. Тогда А, В, С являются целыми взаимно
простыми числами; уравнение же (со) будет разрешимо или нет, в
зависимости от того, имеет или нет решение уравнение
(?2) АХ2 + BY2 + CZ2 = 0,
что можно узнать на основании п.294.
Доказательство. Если положить be = 2ta2, ас = 3$р2, ab — (&ч2>
то 31, 95, @ будут целыми числами, свободными от квадратных
сомножителей, и будет иметь место 91 = ВС, 95 = АС, 2 = АВ.
Следовательно, Ш? = {АВСJ, и потому число ABC = А% = В% =Cd
обязательно будет целым. Если т является наибольшим общим
делителем чисел 31, ^431 и 3t = gin, -ЛЭ1 = hm, то g взаимно просто
с h, а также ист (ибо 31 ие имеет квадратных сомножителей)
442 Раздел V (п. 299)
Теперь h?m = gA2$t + g35@, и потому g входит в h2m, что, очевидно»
невозможно, если g не равно +1. Поэтому 91 = +/и, А = -[-h\
тем самым А является целым числом, и точно так же целыми
будут и числа В и С. Так как 91 = ВС не имеет квадратных де-
делителей, то В и С обязательно должны быть взаимно просты.
Наконец, ясно, что если уравнение (О) удовлетворяется при зна-
значениях X = Р, Y = Q, Z = R, уравнению (со) будут удовлетво-
удовлетворять значения х = аР, у =$Q, z = *(R> и наоборот, если второе
уравнение удовлетворяется при значениях х = р, у = q, z = г, то
значения X = $ЧР> ^ == аТ#> % = otf>r будут решениями первого,
так что либо оба эти уравнения разрешимы, либо не разрешимо
ни то, ни другое.
Представление нуля любыми тройничными формами
299
Задача. Пусть дана тройничная форма
f = ах2 + а'х12 + qY2 + 2Ъх'х" + 2Ъ'хх" + 2Ъ"хх'\
определить, может ли быть представлен этой формой нуль {при
значениях неизвестных, которые не все равны 0).
Решение. I. Если а = 0, то значения неизвестных х\ х" могут
быть взяты произвольно, а из уравнения
а'х + гЪх'х" + а"х = — 2х (Ь'х" + Ъ"х)
вытекает тогда, что х получает определенное рациональное значе-
значение; если при этом для х получается дробное значение, то нужно
только умножить значения ж, х', х" на знаменатель этой дроби, по-
после чего получатся целые числа. Невозможными для х', х" являются
те и только те значения, для которых Ьх" + Ъ"х' = 0, причем не
имеет место одновременно а'х'2 + 2Ъх'х" + а"х"г = 0, когда х мож-
можно взять произвольным. Однвременно ясно, что таким путем можно
получить все возможные решения. Случай, когда V — Ъ" = 0, мож-
можно не рассматривать; действительно, тогда х совсем не входит в /,
т. е. / является двойничной формой, и о представимости нуля формой
/ нужно судить на основании теории таких форм.
О представлении нуля тройничными формами 443
П. Если же а не равно 0, то уравнение / = О эквивалентно урав-
уравнению
{ах 4- Ъ"х' + Ъ'х"У — А"х'2 + 2Вх'х" — А'х = О,
если положить
Если теперь здесь А" = 0, но В не равно 0, то очевидно, что если
взять произвольными значения ах + Ь"х' + Ь'х" и х", то х и ж' оп-
определятся рациональным образом, и в случае, когда они не будут
целыми числами, можно будет найти подходящий множитель, кото-
который приведет к целым значениям. Лишь для одного единственного
значения х", именно, для х" = 0, значение ах + Ъ"х + Ь'х" не про-
произвольно, а тоже должно быть равным 0; но тогда можно брать про-
произвольно значения х\ и для х будет получаться рациональное зна-
значение. Если же одновременно А" = 0 и В = 0, то ясно, что если А'
равно некоторому квадрату А:2, то уравнение / = 0 сводится к следую-
следующим двум линейным уравнениям (из которых должно удовлетво-
удовлетворяться либо одно, либо другое):
ах + Ъ"х' + (Ъ' + к) х" = 0, ах + Ъ"х! + {U — к) х" = 0;
если же (при том же предположении) А' не является квадратом,
то очевидно, что решение заданного уравнения равносильно решению
уравнений х" = 0 и ах + Ъ"х' — 0 (которые должны удовлетворять-
удовлетворяться одновременно).
Едва ли нужно указывать, что метод из I может применяться так-
также и тогда, когда равно нулю а' или а", а метод из II,— ког-
когда ^ = 0.
III. Если жени а, ни А" не равно 0, то уравнение /= 0 эквива-
эквивалентно следующему:
А" {ах -t Ъ"х! + Ъ'х"У - {А'х! — Bx"f + Dax"* = 0,
где через D обозначен определитель формы /, т. е. через Da —
число В2—А'А". Если D — 0} то в отношении решения дело об-
обстоит аналогично тому, как в конце предыдущего случая; именно,
444 Раздел V (п. 300)
если А" является квадратом, причем равно к2, то заданное урав-
уравнение сводится к следующим:
ках + {kb" — А") х' + (W + В) х" = О,
ках + (кЪ" + А")х' + (kb" — В)х" = 0;
если же А" не является квадратом, то нужно положить
ах + Ъ"х' + Ъ'х" = 0, А"х' — Вх" = 0.
Если, напротив, D не равно нулю, то мы приходим к уравнению
A"t2 — u2 + Dav2 = 0.
о разрешимости которого мы можем судить на основании предыдуще-
предыдущего пункта. Если теперь последнее уравнение не может быть решена
иначе, как посредством значений t = 0, и = 0, v — 0, то и заданное
уравнение, очевидно, не будет обладать другими решениями, кроме
х = 0, х' = 0, х" = 0; если же уравнение A"t2 — и2 + /)аг;2 = О
разрешимо еще каким-нибудь образом, то из любых значений t, и, v
на основании уравнений
ах + Ъ"х! + Ъ'х" = t, А"х! — Вх" = и, х" = v
получаются, вообще говоря, рациональные значения х, х\ х",
из которых, если они содержат дроби, при помощи подходящего мно-
множителя можно получить целые значения.
Но если найдено какое-нибудь одно решение уравнения / = 0
в целых числах, то задача может быть сведена к случаю I, и так же,
как и там, могут быть найдены все решения. Это достигается следую-
следующим образом.
Пусть уравнению / = 0 удовлетворяют значения (которые мы
предполагаем свободными от общих делителей) а, аг, а" неизвест-
неизвестных х, х' х"\ выберем, далее (в соответствии с пп. 40 и 279), такие
целые числа р, р\ C", ^, т', т"> что
а фу — PY) + а' Ф"Т — Ю + *" Фт' — Р'Т) = 1 >
(и пусть / при подстановке
S) х=ау + $у' + ЧУ", х' =о'у+ ру Н чУ, а" - а"у 4 ру 4 ТУ
переходит в форму
g - q/2 4 с'2//2 4 су2 4 2dyY 4 2dyy 4 Wyy'.
О решении неопределенных уравнений в рациональных числах 445
Тогда, очевидно, с = 0 и g будет эквивалентна форме /, откуда
легко следует, что из всех решений уравнения g = 0 получаются
(при помощи подстановки (S)) все целочисленные решения уравне-
уравнения / = 0. Но из I следует, что все решения уравнения g = 0 содер-
содержатся в формулах
у = _ z {с>р2 + 2dpq + cTq\ у' = 2z {d"p2 + d'pq), у" = 2z (d"pq + d'q*),
где p, q обозначают произвольные целые числа, a z — произвольное
число, для которого можно брать и дробные значения, если только
У-> У, У" остаются при этом целыми числами. Если подставлять
эти значения г/, у\ у" в (S), то мы получим всевозможные цело-
целочисленные решения уравнения / = 0.
Так, например, если дана форма
/ = х2 + я'2 + я — Ах'х" + 2хх" + 8хх'
и дано одно решение х — 1, ж' = — 2, ж" = 1 уравнения / = 0, то,
полагая р, р', {3", ^, т'» Т" равными соответственно 0, 1, 0, 0, 0, 1, мы
получаем, что
Все целочисленные решения уравнения g = 0 содержатся в фор-
формулах
y = — z(p2 — Apq + q*), у1 = 12zpq, у" = I2zq\
и потому все решения уравнения / = 0 — в формула v
х" - — z (p2 — Apq —llq2).
Общее решение в рациональных величинах
уравнений второй степени с двумя неизвестными
300
Из решения задачи предыдущего пункта сразу получается также
решение неопределенного уравнения
ах2 + 2Ъху + су2 + 2dx + 2еу + f =_ 0,
446 Раздел V (п. 301)
когда требуется найти рациональные значения; решение этого же
уравнения в целых числах уже было изложено выше (п. 216 и ел.).
Действительно, все рациональные значения неизвестных х, у могут
быть представлены в виде t/v, u/v, где ?, и, v — целые числа, откуда
вытекает, что решение этого уравнения в рациональных числах
равносильно решению уравнения
at2 + 2btu + си2 + 2dtv + 2euv + fv2 = О
в целых числах; а это уравнение совпадает с рассмотренным в преды-
предыдущем пункте. Должны быть исключены лишь те решения, где v = 0;
однако их не может быть, если число Ъ2 — ас не является квадра-
квадратом. Так, например, все решения в рациональных числах уравнения
х2 + 8ху + уг + 2х — Ау + 1 — 0
(решенного в п. 221 в целых числах) содержатся в формулах
/>2 + 4pg + 2g«
_
— 4pq —
где р, q обозначают произвольные целые числа. Впрочем, мы здесь
лишь кратко коснулись обеих этих находящихся в теснейшей вза-
взаимной связи задач и опустили многие относящиеся сюда замечания,,
чтобы не быть слишком пространными, с одной стороны, а с другой,—
потому что мы владеем другим, основанным на более общих принци-
принципах, решением задачи предыдущего пункта, изложение которого мы
должны оставить до другого случая, так как оно требует более по-
подробного исследования тройничных форм.
О среднем количестве родов
301
Мы возвращаемся к двойничным формам, многие особые свойства
которых мы еще должны привести. Сначала мы добавим некоторые
замечания относительно числа родов и классов в собственно прими-
примитивном (для отрицательного определителя положительном) порядке^
которым мы ограничимся ради краткости.
О среднем количестве родов 447
Число родов, на которые распадаются все (собственно примитив-
примитивные положительные) формы с заданным положительным или отрица-
отрицательным определителем + D всегда равно 1, 2, 4 или более высокой
степени числа 2, показатель которой зависит от сомножителей числа
Д и на основании предыдущих исследований может быть определен
a priori. Но так как в ряду натуральных чисел простые числа пере-
перемешаны с составными, имеющими то большее, то меньшее количество
делителей, то оказывается, что для нескольких следующих один за
другим определителей + D, ± (D + 1)> =Ь (D + 2), ... число родов
то возрастает, то убывает, и в этой запутанной последовательности
не видно никакой закономерности. Тем не менее, если сложить ко-
количества родов, которые соответствуют многим, следующим один
за другим определителям
и сумму поделить на количество этих определителей, то получится
среднее число родов, которое может рассматриваться как соответст-
соответствующее среднему значению zh(Z) + x/2m) определителей и которое
образует очень правильный ряд. Мы будем, однако, предполагать,
что не только т достаточно велико, но что и D еще на много больше,
чтобы отношение крайних определителей не слишком отличалось от
единицы. Закономерность указанного ряда нужно понимать следую-
следующим образом. Если число D' во много раз больше, чем D, то и среднее
число родов, соответствующее определителю +?>', будет значитель-
значительно больше, чем для определителя D; если же D и D' мало отличаются
друг от друга, то и среднее число родов по отношению к D и D' будет
почти одинаково. При этом среднее число родов по отношению к
положительному определителю + D всегда приблизительно равно
среднему числу родов по отношению к отрицательному определите-
определителю —D, причем тем точнее, чем больше D, в то время как для малень-
маленького значения D первое немного больше, чем второе. Эти замечания
сделаются яснее благодаря следующим примерам, которые мы по-
почерпнули из таблицы разбиения двойничных форм на классы, охва-
охватывающей более 4000 определителей. Среди ста определителей от
801 до 900 имеется 7, которым соответствует лишь один единствен-
единственный род, и 32, 52, 8, 1 определителей, для которых число родов рав-
448 Раздел V (п. 302)
но соответственно 2, 4, 8, 16; поэтому всего имеется 359 родов, так
что среднее количество равно 3,59. Сто отрицательных определите-
определителей от —801 до —900 дают 360 родов. Следующие примеры все бе-
берутся из отрицательных определителей. В шестнадцатой сотне (от
—1501 до —1600) среднее количество родов выражается числом 3,89;
в двадцать пятой сотне оно равно 4,03, в пятьдесят первой равно
4,24; из шестисот определителей от —9401 до —10 000 получается
число 4,59. Из этих примеров видно, что среднее количество родов
возрастает значительно медленнее, чем сами определители. Но,
спрашивается, каков тогда закон этого ряда? При помощи довольно
трудного теоретического исследования, излагать которое здесь бы-
было бы слишком долго, было найдено, что среднее число родов для оп-
определителя + D или — D наиболее точно может быть выражено фор-
формулой
где a, p являются постоянными величинами, причем
а «~~ 0,4052847346
ТС2 '
(где тг обозначает половину длины окружности с радиусом 1),
р = 2ag + За2/г — ~ a log 2 ^ 0,8830460462,
где число g равно сумме ряда
^0,5772156649
(ср. Эйлер, «Inst. Calc. Diff.,» p. 444), а число h — сумме ряда
которая приблизительно равна 0,9375482543. Из этой формулы вы-
вытекает, что среднее число родов возрастает в арифметической про-
прогрессии, когда определители растут в геометрической прогрессии.
В качестве значений этой формулы для D = 850,5; 1550,5; 2450,5;
5050,5; 9700,5 мы находим соответственно значения 3,617; 3,86; 4,046,
О среднем количестве классов 449
4,339; 4,604, которые только совсем немного отличаются от приведен-
приведенных выше средних количеств. Чем больше средний определитель и
чем из большего числа определителей вычисляется среднее количе-
количество, тем меньше оно отличается от значения, даваемого формулой.
При помощи этой формулы можно также приближенно найти сумму
чисел, выражающих соответствующие следующим один за другим оп-
определителям +D ,+(/) + 1),..., +(?* + тп) количества родов, если
вычислить средние количества, соответствующие отдельным опре-
определителям и сложить эти числа; при этом крайние определители D и
D + т могут сколь угодно отличаться один от другого. Эта сумма
равна
% [log D + log (D + 1) + log (D + 2) + . . . + log (D + m)) +
или с достаточной точностью равна
ос [(D + т) log (D + m) — (D — 1) log (D — 1)] + ф — a) (m -f 1).
Таким способом для определителей от —1 до —100 сумма количеств
родов получается 234,4, в то время как в действительности она рав-
равна 233; аналогично, для определителей от —1 до —2000 формула
дает значение 7116,6, в то время как в действительности должно быть
7112; для определителей от —1 до —3000 таблица дает число 11166,
а формула — число 11167,9; от —9001 до —10 000, когда эта сумма
равна 4595, формула дает значение 4594,9 — совпадение, которого
почти нельзя было ожидать.
О среднем количестве классов
302
Относительно числа классов (собственно примитивных положи-
положительных, что все время подразумевается) положительные определи-
определители ведут себя совершенно не так, как отрицательные; поэтому мы
будем рассматривать те и другие отдельно. И те и другие обладают
одним и тем же свойством: для заданного определителя в отдельных
родах содержится одинаковое число классов, и потому число всех
450 Раздел V (п. 303)
классов равно произведению числа родов на число классов, содержа-
содержащихся в отдельном роде.
Что касается, сначала, отрицательных определителей, то число
классов, соответствующих многим следующим один за другим оп-
определителям —D, — (D -f- 1), — (D +2),... образует столь же за-
запутанный ряд, что и число родов. Среднее же число классов (пояс-
(пояснять это понятие нет нужды) растет очень закономерно, что видно
из следующих примеров. Сто определителей от —501 до —600 дают
1729 классов, так что среднее количество равно 17,29. Точно так же
в пятнадцатой сотне в качестве среднего числа классов получается
число 28,26; из 24-й и 25-й сотен получается число 36,28, из 61-й,
62-й и 63-й сотен — число 58,50, из 91-й — 95-й сотен — число 71,56,
наконец, из 96-й — 100-й сотен — число 73,54. Эти примеры показы-
показывают, что среднее число классов растет хотя и медленнее, чем опре-
определители, но все же намного быстрее, чем среднее число родов; при
некоторой внимательности мы замечаем, что первое число растет
приблизительно так же, как квадратный корень из определителей.
И, действительно, теоретическим исследованием мы нашли, что
среднее число классов по отношению к определителю — D очень
точно выражается формулой
где
Т= ^ ^0,7467183115,
е равно сумме ряда
.111 1
и
6 = А ^0,2026423673,
Средние значения, вычисляемые по этой формуле, лишь очень не-
немного отклоняются от тех, которые выше мы привели из таблицы
разбиений на классы. При помощи этой формулы можно также
приближенно определить сумму средних количеств всех (собственно
примитивных положительных) классов, которые соответствуют сле-
следующим один за другим определителям —Z>, —(D + 1), —(D +2), ...
О среднем количестве классов 451
..., — (D + т — I), сколь бы ни отличались один от другого край-
крайние определители, для чего нужно сложить соответствующие этим
определителям, согласно формуле, средние количества. Мы полу-
получаем, что эта сумма равна
Т [V~D + V& + 1 + . . . + jfD + m — l] — 8/w,
или приблизительно равна
Так, например, для ста определителей от —1 до —100 эта сумма
по формуле получается равной 481,1, в то время как в действительно-
действительности она равна 477; тысяча определителей от —1 до —1000 дае1, со-
согласно таблице, 15533 класса, формула же дает 15 551,4; вторая ты-
тысяча содержит, согласно таблице, 28 595 классов, формула же дает
значение 28 585,7; точно так же, третья тысяча в действительности
содержит 37 092 класса, в то время как формула дает 37 074,3; де-
десятая тысяча, согласно таблице, имеет 72 549 классов, в то время как
формула дает значение 72 572.
303
Таблица отрицательных определителей, на основании которой
устанавливается различие соответствующих им разбиений на клас-
классы, дает повод и еще ко многим другим специальным замечаниям*
Для определителей вида — (8п + 3) число классов (как тех, которые
содержатся во всех родах, так и тех, которые содержатся в отдель-
отдельных собственно примитивных родах) всегда делится на 3, за исюпо
чением лишь определителя—3, причина чего ясна из п. 256, VI. Для тех
определителей, формы которых составляют только один единственный
род, число классов всегда нечетно; действительно, так как для такого
определителя имеется только один двусторонний класс, именно, глав*-
ный класс, то число всех остальных классов, которые всегда попарно
противоположны, обязательно четно, а потому число всех классов не-
нечетно; впрочем, это последнее свойство имеет место и для положитель-
положительных определителей. Далее, ряды определите лей, которым соответствует
452
Раздел V (п. 304)
заданное разбиение на классы (т. е. заданное количество как родов,
так и классов), всегда оказываются обрывающимися; это неожидан-
неожиданное замечание мы поясним несколькими примерами. (Первая, рим-
римская, цифра показывает число собственно примитивных положитель-
положительных родов, вторая цифра — число классов, содержащихся в каждом
отдельном роде; затем следует ряд определителей, которым соответ-
соответствует такая классификация и отрицательные знаки у которых мы
ради краткости отбрасываем.)
I. 1
II. 3
I. 5
I. 7
II. 1
II. 2
IV. 1
VIII. 1
XVI. 1
1, 2, 3, 4, 7
И, 19, 23, 27, 31, 43, 67, 163
47, 79, 103, 127
71, 151, 223, 343, 463, 487
5, 6, 8, 9, 10, 12, 13, 15, 16, 18, 22, 25, 28, 37, 58
14, 17, 20, 32, 34, 36, 39, 46, 49, 52, 55, 63, 64, 73, 82, 97, 100,
142,148,193
21, 24, 30, 33, 40, 42, 45, 48, 57, 60, 70, 72, 78, 85, 88, 93, 102,
112, 130, 133, 177, 190, 232, 253
105, 120, 165, 168, 210, 240, 273, 280, 312, 330, 345, 357, 385,
408, 462, 520, 760
840, 1320, 1365, 1848.
Аналогично, имеется 20 определителей (наибольший из которых
равен — 1423), которым соответствует классификация 1.9; 4 опреде-
определителя (наибольший равен — 1303), которым соответствует класси-
классификация 1.11, и т. д. Классификациям II.3, II.4, II.5, IV.2 отвеча-
отвечают не больше, чем соответственно 48, 31, 44, 69 определителей, наи-
наибольшие из которых равны — 652, —862, —1318, —1012. Так как
таблица, из которой взяты эти примеры, продолжается далеко за
встречающиеся здесь определители, то представляется бесспорным,
что указанные ряды действительно обрываются, и по аналогии мы
имеем право распространить это заключение и на любые другие клас-
классификации. Так как, например, во всей десятой тысяче определите-
определителей нет ни одного, которому соответствовало бы число классов, мень-
меньшее чем 24, то в высшей степени вероятно, что классификации 1.23;
О среднем количестве классов 453
1.21;..., 11.11; 11.10;...; IV.5; IV.4; IV.3; VIII.2. уже закончились до
—9000, или по крайней мере, что они имеют по другую сторону чи-
числа —10 000 очень мало определителей. Однако, строгие доказатель-
доказательства этих замечаний оказываются очень трудными. Не менее замеча-
замечательно то, что все определители, формы которых распадаются на 32
или более родов, имеют в отдельных родах по меньшей мере по два
класса, и потому классификации XXXII. 1, LX1V.1 и т. д. совершенно
не встречаются (наименьшему из этих определителей, равному
— 9240, соответствует классификация X X X 11.2) и представляется весь-
весьма вероятным, что с ростом числа родов пропадает все больше и боль-
больше классификаций. В этой связи указанные выше 65 определителей,
которым соответствуют классификации 1.1, II. 1, IV.1, VIII.1, XVI.1,
оказываются весьма замечательными, и легко видеть, что все они и
только они обладают двумя исключительными свойствами, а именно,
все принадлежащие им классы форм являются двусторонними, и
любые две формы, содержащиеся в одном и том же роде, обязательно
эквивалентны как собственно, так и несобственно. Между прочим,
эти же 65 чисел (с несколько иной точки зрения, о которой ниже бу-
будет упомянуто и которая связана с одним легко доказываемым кри-
критерием) были указаны уже Эйлером, «Nouv. Mern.de Г Ac. de
Berlin», 1776, p. 338.
304
Число собственно примитивных классов, которые образуют
двойничные формы с положительным квадратным определителем
/с2, может быть вообще определено a priori, и равно количеству чи-
чисел, которые взаимно просты с числом 2k и меньше чем 2/с; отсюда
при помощи несложных рассуждений, которые мы должны здесь
опустить, легко найти, что среднее число принадлежащих таким оп-
определителям классов для определителя к2 очень точно выражается
числом 8к/г.2.
Однако положительные неквадратные определители ведут себя
в этом отношении совершенно своеобразно. Именно, в то время как
классификации с маленьким числом классов, например, 1.1, или 1.3,
или II.1 и т. д., в случае отрицательных или квадратных определите-
454 Раздел V (п. 305)
лей встречаются только для небольших, т. уходящих далеко значе-
значений этих определителей, среди положительных неквадратных оп-
определителей, по крайней мере пока они не очень велики, напротив,
большая часть обладает такими классификациями, когда в каждом
роде имеется только один класс, так что классификации 1.3; 1.5;
II.2; II.3; IV.2 и т. д. весьма редки. Так, например, среди 90 не-
неквадратных определителей, не превосходящих числа 100, имеется 11,
48, 27 определителей, которые имеют соответственно классификацию
1.1; II.1; IV.1; только для одного единственного C7) имеет место
классификация 1.3, два C4 и 82) имеют классификацию II.2 и только
один G9) — классификацию II.3. Если, однако, определители воз-
возрастают, то большие количества классов встречаются заметно чаще;
так, например, среди 96 неквадратных определителей от 101 до 200
два A01 и 197) обладают классификацией 1.3; четыре (именно, 145,
146, 178, 194) — классификацией II.2; три A41, 148, 189) — клас-
классификацией II.3. Из 197 неквадратных определителей от 801 до
1000 три имеют классификацию 1.3, четыре — классификацию И.2,
четырнадцать — классификацию II.3, два — классификацию II .5,
два — классификацию II.6, пятнадцать — классификацию IV.2,
шесть — классификацию IV.3, два — классификацию IV.4, четыре —
класификацию VIII.2; остальные 145 определителей имеют только
один класс в каждом роде.
Было бы красивой и достойной внимания математиков задачей —
определить, по какому закону все реже и реже встречаются опреде-
определители, обладающие в каждом роде только одним классом; до сих пор
мы не можем ни теоретически определить, ни индуктивно с достаточ-
достаточной уверенностью предположить, обрываются ли совершенно в кон-
конце концов такие определители (что, однако, представляется мало
вероятным), или они становятся по крайней мере бесконечно редки-
редкими, или же их частота все ближе подходит к постоянному пределу.
Среднее число классов растет лишь немного быстрее, чем среднее
число родов, и намного медленнее, чем квадратные корни из опреде-
определителей; между 800 и 1000 среднее число классов оказывается равным
5,01. Можно было бы добавить к этим замечаниям еще и другое,
которое в некотором смысле восстанавливает аналогию между по-
положительными и отрицательными определителями. Именно, мы наш-
Алгоритм для собственно примитивных классов 455
ли, что по многим причинам, о которых здесь не будет говориться
подробнее, для положительного определителя D не столько само чис-
число классов, сколько его произведение на логарифм величины t + и j/Z)
(где t, и обозначают наименьшие, не считая 1 и 0, числа, удовлетво-
удовлетворяющие уравнению t2 — Du 2 = 1) аналогично числу классов для
отрицательного определителя, и что среднее значение указанного
произведения также выражается формулой видат|//5 — Щ однако
мы еще не смогли теоретически определить значения постоянных ве-
величин т, п. Если мы имеем право сделать некоторые выводы на ос-
основании сравнения нескольких сотен определителей, то оказывается,
что значение числа т не очень отличается от 21/3. Впрочем, мы остав-
оставляем за собой право в другом удобном случае подробнее остановиться
на принципах предыдущих исследований относительно средних зна-
значений величин, которые возрастают не по аналитическому закону, а
лишь непрерывно асимптотически приближаются к такому закону.
Теперь мы переходим к другому исследованию, в котором сравни-
сравниваются между собой различные собственно примитивные классы
с одним и тем же определителем, чем мы и завершим этот длинный
раздел.
Особый алгоритм для собственно примитивных классов;
регулярные и иррегулярные определители и т. д.
305
Теорема. Если К обозначает главный класс форм с заданным
определителем D, через С обозначен другой класс из главного рода
форм с тем же определителем, и наконец, 2С, ЗС, 4С, . . . обозна-
обозначают классы, которые получаются удвоением, утроением, учетвере-
нием и т. д. класса С (как в п. 249J, то в ряду С, 2С, ЗС,. . .,
если продолжить его достаточно далеко, в конце концов получится
класс, совпадающий с К, и если предположить, что тС является
первым классом, совпадающим с К, и что число всех содержащихся
в главном роде классов равно п, то либо т = п, либо т является
делителем числа п.
Доказательство. I. Так как все классы К, С, 2С, ЗС, . .. обя-
обязательно принадлежат главному роду (п. 247), то первые п + 1
456 Раздел V (п. 306)
классов К. С, 2С, . . ., пС этого ряда, очевидно, не могут быть
все различны. Поэтому либо К совпадает с каким-нибудь из клас-
классов С, 2С, ЗС, . . ., пС, либо по крайней мере два из этих классов
будут совпадать между собой. Пусть rC = sC и г > s; тогда также
(г — 1) С = (s — 1) С, (г — 2) С = (s — 2) С, . . , (г + 1 — s) С = С,
и потому (г — s) С =¦ К.
II. Отсюда легко видеть также, что т или =п, или < п, и
остается поэтому только показать, что в последнем случае т явля-
является делителем числа п. Так как классы
К, С, 2С,..., (т— 1)С,
совокупность которых мы обозначим через (§, в этом случае еще
не исчерпывают весь главный род, то пусть С — какой-нибудь
класс этого рода, не содержащийся в (§, обозначим через (§' сово-
совокупность классов, которые получаются при композиции класса С с
отдельными классами из (§, именно, совокупность
С', С' + С, С + 2С, ..., С" + (т —1)С.
Теперь легко видеть, что все классы в (§' отличны как один от
другого, так и от всех классов из E, и все они принадлежат
главному роду. Если поэтому (§ и E' полностью исчерпывают этот
род, то мы имеем п = 2т, если же не исчерпывают, то 2т < п.
В последнем случае пусть С" — какой-нибудь не содержащийся
ни в (§, ни в (§' класс главного рода; обозначим через ё" совокуп-
совокупность классов, которые получаются при композиции класса С" с
отдельными классами из (§, т. е. совокупность
С", С" + С, С" + 2С, . . ., С" + (тп — 1) С.
Тогда легко получается, что все эти классы отличны один от
другого и от всех классов из & и (?', и что все они принадлежат
главному роду. Если поэтому (?, (§', ё" исчерпывают этот род, то
п = Зт, а если нет, то гс > Зт, и в этом случае новый класс, со-
содержащийся в главном роде, но не содержащийся в совокупностях
6, ё' или ё", если рассмотреть его подобным же образом, приво-
приводит к выводу, что либо п = Am, либо п > 4т и т. д. А так как п
Алгоритм для собственно примитивных классов 457
и т являются конечными числами, то главный род обязательно
рано или поздно будет исчерпан, и п будет кратностью числа т,
т. е. т — делителем числа п.
Пример. Если D = — 356, С = E, 2, 72)*, то мы находим
1С = B0, 8, 21), ЗС = D, 0, 89), 4С = B0, — 8, 21), ЪС = E, — 2, 72),
6С = A, 0, 356). Таким образом, здесь т = 6, а число п для этого оп-
определителя равно 12. Если взять за С' класс (8, 2, 45), то осталь-
остальными пятью классами из (§' будут (9, — 2, 40), (9, 2, 40), (8, — 2, 45),
A7, 1, 21), A7, -1, 21).
308
Видео, что доказательство предыдущей теоремы совершенно
аналогично доказательствам в пп. 45, 49, и действительно, теория
умножения классов во всех отношениях имеет тесную связь с
предметом, рассматривавшимися в третьем разделе. Однако границы
настоящего труда не позволяют изложить здесь указанную теорию
с надлежащей полнотой; мы добавим поэтому лишь несколько за-
замечаний, опуская также и доказательства, которые потребовали бы
более сложного аппарата, и оставим более подробное исследование
до другого случая
I. Если ряд К, С, 2С, ЗС, . . . продолжать за (т— 1)С, то снова
будут получаться те же самые классы:
тС = К, (m + i)C = C, (т+ 2)С = 2С, . . .,
и вообще (если ради краткости рассматривать класс К как ОС)
классы gC, g'C будут одинаковы или различны в зависимости
от того, сравнимы или нет по модулю т числа g и g'. Класс пС
поэтому всегда совпадает с главным классом К.
II. Совокупность классов К, С, 2С,. . ., (т — 1) С, которая выше
обозначалась через (§, мы будем называть периодом класса С, при-
причем это выражение не следует смешивать с рассматривавшимися
в пп. 186 и ел. периодами приведенных форм с положительным
* Классы здесь все время представляются содержащимися в них (простей-
(простейшими) формами.
458 Раздел V (п. 306)
неквадратным определителем. Очевидно, что при композиции любого
числа классов из одного и того же периода снова получается
класс, содержащийся в этом же периоде:
gC + g'C + g"C+... = (g + g' + g" + . . •) С.
III. Так как С + (т — 1) С = К, то классы С и (т—1)С, и
точно так же классы 2С и (т — 2) С; ЗС и (т—3)С и т. д. будут
противоположны один другому. Если поэтому т четно, то класс
2~ тС будет противоположен сам себе и потому будет двусторонним;
наоборот, если в (?, кроме К, имеется еще и другой двусторонний
класс, например, gC, то gC — (т — g) С, и потому g = т — g = -^ т.
Отсюда следует, что если т четно, то в ? не может содержаться
других двусторонних классов, кроме К и -^тС, а если т нечетно,
то — кроме единственного класса К.
IV. Если предположить, что период некоторого содержащегося
в ? класса hC состоит из классов
К, kC, 2kC, 3AC,..., (m'-l)hC,
то m'h будет, очевидно, наименьшим кратным числа h, делящимся
на т. Если поэтому т и h взаимно просты, то т' = т, и оба пе-
периода будут содержать одни и те же классы, только расположен-
расположенные различным образом; вообще же, если[л обозначает наиболь-
наибольший общий делитель чисел т и h, то т' = —. Отсюда вытекает,
что число классов, содержащихся в периоде некоторого класса
из S, или равно т, или равно некоторому делителю числа т,
причем в ? имеют период из т членов столько классов, сколько
чисел среди 0,1, 2,...,иг—1 взаимно просто ст, т.е. ср (т) классов,если
использовать обозначение п. 39; вообще же в ? имеют период из
т/\к членов столько классов, сколько чисел среди 0, 1, 2, ...
..., т—1 имеют cm наибольший общий делитель (л, т. е., как легко
видеть, <р (тп/(л) классов. Поэтому если т = п, т. е. в ? содержит я
весь главный род, то в этом роде имеется всего ср(п) классов, пе-
периоды которых также содержат весь род, и 9 И классов, периоды
Алгоритм для собственно примитивных классов
459
которых состоят из е членов, где е обозначает некоторый делитель
числа п. Этот вывод справедлив всегда, когда в главном роде
имеется некоторый класс, период которого состоит из п членов.
V. При этом же предположении система классов главного рода
не может быть расположена более целесообразно, чем если взять ка-
какой-нибудь класс, обладающий периодом из п членов, в некотором
смысле за основание, и расположить классы главного рода в том по-
порядке, в котором они следуют в периоде этого класса. Если тогда
снабдить главный класс индексом 0, класс, который взят за основа-
основание,— индексом 1, и т. д., то простым сложением индексов можно
найти, какой класс получается при композиции каких-либо клас-
классов главного рода. Здесь приводится пример для определителя
—356, где за основание мы взяли класс (9, 2, 40).
0
1
2
3
A,
(9,
E,
(8, -
о,
2
2
356)
, 40)
, 72)
2, 45)
4
5
6
7
B0
A7
( 4
A7,
, 8, 21)
, 1, 21)
, 0, 89)
-1, 21)
8
9
10
И
B0,
(8,
E,-
(9,-
— I
2,
-2
-2
], 21)
45)
, 72)
, 40)
VI. Хотя как аналогия с разделом III, так и исследование более
чем 200 отрицательных определителей и еще намного большего чис-
числа неквадратных положительных определителей делают правдопо-
правдоподобным, что указанное предположение выполняется для всех опре-
определителей, тем не менее этот вывод был бы неверным и опровергался
бы при дальнейшем продолжении таблицы разбиения на классы. Ра-
Ради краткости мы будем называть те определители, для которых весь
главный род может содержаться в одном единственном периоде, ре-
регулярными, а остальные, для которых это невозможно, иррегуляр-
иррегулярными определителями. Этот предмет, который оказывается принад-
принадлежащим к наиболее скрытым секретам высшей арифметики и дающим
простор для труднейших исследований, мы можем здесь проиллю-
проиллюстрировать лишь немногими замечаниями, которым мы предпошлем
следующее общее замечание.
VII. Если в главном роде содержатся классы С, С, периоды ко-
которых состоят из m, m' членов, и если М является наименьшим чис-
числом, делящимся на т и т', то в этом роде имеются и классы, периоды
460 Раздел V (п. 306)
г
которых содержат М членов. Если М разложить на два взаимно про-
простых сомножителя гиг', один из которых (г) входит делителем в т,
а другой (г') — в т' (п. 73), то класс - С + —, С = С" будет обла-
обладать требуемым свойством. Действительно, если мы предположим,
что период класса С" состоит из g членов, то
K = grC = gmC-
поэтому grm'lr' должно делиться на тг, т. е. gr — на г', и потому
g — на г'. Совершенно аналогичным образом мы находим, что g
делится на г, так что g делится и на тг' — М. Но так как, очевидно,
МС" = К, то и М будет делиться на g, и потому обязательно М =
— g. Отсюда легко видеть, что наибольшее число классов (для заданно-
заданного определителя), содержащихся в одном периоде, делится на число
классов в любом другом периоде (класса из этого же главного рода).
Одновременно отсюда же можно вывести метод для отыскания та-
такого класса, период которого наибольший (и потому в случае регу-
регулярного определителя охватывает весь главный род),— метод, ко-
который совершенно аналогичен методу из пп. 73, 74, хотя на практике
вычисления и могут быть связаны со многими искусственными прие-
приемами. Частное от деления числа п на число классов в наибольшем пе-
периоде, которое для регулярных определителей равно 1, для иррегу-
иррегулярных определителей всегда будет целым числом, большим чем 1,
и будет очень удобным средством для характеристики различных сте-
степеней иррегулярности; поэтому это частное будет называться пока-
показателем иррегулярности.
VIII. До сих пор мы не имеем никакого общего правила для того,
чтобы сразу отличать регулярные определители от иррегулярных,
тем более, что среди последних имеются как простые, так и состав-
составные числа; поэтому мы удовлетворимся здесь лишь несколькими спе-
специальными замечаниями. Если в главном роде содержится более
двух двусторонних классов, то определитель заведомо иррегулярен,
и показатель иррегулярности будет четным; если же в каждом роде
имеется только один или два двусторонних класса, то определитель
или регулярен, или по крайней мере показатель иррегулярности не-
нечетен. Все отрицательные определители вида — B16& + 27), за иск-
Алгоритм для собственно примитивных классов 461
лючением только одного определителя —27, иррегулярны, и пока-
показатели иррегулярности делятся на 3; это же имеет место для отрица-
отрицательных определителей вида — A000/с + 75) и — A000/с + 675)
за исключением лишь определителя — 75, и для бесчисленного мно-
множества других. Если показатель иррегулярности равен простому
числу р или по крайней мере делится на р, то п делится на /?2, откуда
следует, что если п не имеет квадратных делителей, то определитель
заведомо регулярен. Лишь для положительных квадратных опре-
определителей е2 всегда можно сразу узнать, регулярны они или иррегу-
иррегулярны; именно, первое имеет место, когда е равно либо 1, либо 2,
либо нечетному простому числу, либо степени нечетного простого чис-
числа; второе — во всех остальных случаях. Среди отрицательных оп-
определителей иррегулярные встречаются все чаще по мере возраста-
возрастания определителей; так, например, во всей первой тысяче определи-
определителей иррегулярных имеется тринадцать, а именно (отбрасывая
отрицательные знаки), 576, 580, 820, 884, 900, показатель иррегуляр-
иррегулярности которых равен 2, и 243, 307, 339, 459, 675, 755, 891, 974, пока-
показатель иррегулярности которых равен 3 *; во второй тысяче имеется
13 определителей с показателем иррегулярности 2 и 15 определителей
с показателем иррегулярности 3; в десятой тысяче имеется 31 опреде-
определитель с показателем иррегулярности 2 и 32 определителя с показа-
показателем иррегулярности 3. Имеются ли до —10 000 определители с
показателями иррегулярности, большими чем 3, я еще не могу уз-
узнать; по другую же сторону этой границы могут получиться любые
заданные показатели. То, что отношение частоты иррегулярных от-
отрицательных определителей к частоте регулярных по мере роста оп-
определителей все более и более приближается к постоянному значению,
в высшей степени правдоподобно, и определение этого отношения бы-
было бы задачей, достойной внимания математиков. Среди положитель-
положительных неквадратных определителей иррегулярные встречаются намного
реже; таких определителей, у которых показатель иррегулярности
четный, заведомо имеется бесконечно много (например, определи-
определитель 3026, для которого этот показатель равен 2); также представ-
представляется несомненным, что имеются и определители, у которых пока-
* Ср. дополнения в конце «Исследований».
462 Раздел V (п. 307)
затель иррегулярности нечетен, хотя мы должны признаться, что нам
еще ни один такой определитель не известен.
IX. Относительно наиболее удобного расположения системы клас-
классов, которые содержатся в главном роде в случае иррегулярного опре-
определителя, мы здесь, ради краткости, говорить не будем; заметим толь-
только, что так как одного основания в этом случае недостаточно, то необ-
необходимо брать два или даже еще большее число классов, при умноже-
умножении и композиции которых получаются уже все остальные. При этом
получаются двойные и кратные индексы, польза которых состоит при-
примерно в том же, в чем состоит и польза простых индексов при регуляр-
регулярных определителях. Однако подробнее мы рассмотрим этот вопрос при
другом подходящем случае.
X. Наконец, заметим, что так как все рассмотренные в этом и
предыдущем пунктах свойства в основном зависят от числа п, кото-
которое представляет собой нечто подобное числу р — 1 из раздела III,
то это число п заслуживает самого пристального внимания, и потому
было бы весьма желательно открыть общую связь между ним и оп-
определителем, которому оно принадлежит. В этом очень важном воп-
вопросе мы тем более не должны отчаиваться, что по крайней мере для
отрицательных определителей уже известно представление в виде
аналитической формулы для среднего значения произведения числа
п на число родов, которое может быть определено непосредственно
(п. 302) *.
307
Исследования предыдущего пункта охватывают только классы
главного рода; этих исследований, таким образом, достаточно для
положительных определителей, у которых вообще имеется только
один род, и, если не рассматривать отрицательных родов, для отри-
отрицательных определителей, имеющих только один положительный
род. Поэтому нам остается только добавить кое-что еще относитель-
относительно остальных {собственно примитивных) родов.
I. Если в роде G', который отличен отглавногородаС(с тем же оп-
определителем), имеется хотя бы один двусторонний класс, то их в
Ср. дополнения в конце ^Исследований)).
Алгоритм для собственно примитивных классов 463
этом роде столько же, сколько и в G. Пусть в роде G содержатся дву-
двусторонние классы L, M, 7V,... (среди которых находится также и
главный класс К), а в роде G' — двусторонние классы Z/, М',
TV',..., и пусть совокупность первых обозначена через А, а совокуп-
совокупность последних — через А'. Так как все классы L + L', М + Z/,
iV + Z/, ..., очевидно, двусторонние, различны между собой
и принадлежат роду С, т. е. должны содержаться в совокупности
А', то число классов в Л' заведомо не может быть меньше чем в А]
а так как, точно так же, классы V + Z/, М' + Z/, 7V ' + U — дву-
двусторонние, различны между собой и принадлежат роду G, т. е. со-
содержатся в Ау то число классов в А не может быть меньше чем в А'.
Поэтому количества классов в А и А' обязательно равны между
собой.
II. Так как число всех двусторонних классов равно числу родов
(пп. 261, 287, III), то если в G имеется только один двусторонний
класс, то и в каждом роде может содержаться только один двусторон-
двусторонний класс; если же в G существует два двусторонних класса, то в по-
половине всех родов их имеется по два, а в другой половине их вообще
нет; и если в G содержится несколько, скажем, а двусторонних клас-
классов *, то а-я часть родов содержит по а двусторонних классов каж-
каждый, а остальные роды вообще не содержат таких классов.
III. Пусть в случае, когда G содержит два двусторонних клас-
класса, через G, G', G", ... обозначены те роды, которые имеют по два
двусторонних класса, а через Н, Н', Н",... — те роды, которые
не содержат двусторонних классов; обозначим совокупность первых
через @, а совокупность последних через <г>. Так как при компози-
композиции двух двусторонних классов всегда получается снова двусто-
двусторонний класс (п. 249), то> очевидно, что при композиции дьух ро-
родов из @ всегда снова получается род из®. Отсюда следует, далее,
что при композиции рода из @ с родом из § получается род из §.
Действительно, если, например, род Gr + Н принадлежал бы не
к §, а к @, то к @ должен был бы принадлежать и род G' + И -\-G'',
что невозможно, так как G' + G' = G и потому G' + И + G' = Н.
* Это может иметь место только для иррегулярных определителей, причем
а обязательно должно быть степенью числа 2.
464 Раздел V (п. 307)
Наконец, мы легко заключаем, что роды G -\- H, G' -\- H: G" -(- Н, . . .
вместе с родами Н -\- Н, Н' -\- Н, Н" + Н, . . . все различны между
собой, и потому охватывают всю совокупность родов из & и §; но
по только что доказанному все роды G + Н, G' -\-H. G"-\-H,... при-
принадлежат к §, и потому исчерпывают эту совокупность, а, значит,
все о тальные роды Н -\- Н, Иг + И, Н" + Я, . . . принадлежат к ©,
т. е. при композиции двух родов из § всегда получается род из @.
IV. Е ли ? есть класс из рода V, отличного от главного рода G,
то все классы 22?, 42?, 62?, . . ., очевидно, будут принадлежать к G,
а классы 32?, 52?, IE,...— kF. Поэтому, если период класса 2Е
состоит из т членов, то в ряде Е, 2Е, 32?, ... с классом А' будет,
очевидно, совпадать класс 2тпЕ и никакой более ранний, т. е. пе-
период класса Е будет состоять из 2т членов. Поэтому число членов
в периоде каждого класса, не принадлежащего главному роду,
либо равно 2?2, либо является делителем числа 2п, где п обозна-
обозначает число классов в отдельном роде.
V. Пусть С — заданный класс главного рода G, Е — клас • ро-
рода V, при удвоении которого получается С (такой всегда сущест
вует. согласной. 286), и пусть, далее, if, K\ К"..., — все двусторон-
двусторонние собственно примитивные классы (с тем же определителем).
Тогда всевозможными классами, при удвоении которых получается
С, являются классы Е (= Е + К), Е -\- К', Е + К", . . ., совокуп-
совокупность которых мы обозначим через О; число этих классов равно
числу двусторонних классов, т. е. равно числу родов. Ясно, что
среди классов из Q, роду V принадлежит столько, сколько имеется
двусторонних классов в G; поэтому, если обозначить их число че-
через а, то в каждом роде будет, очевидно, содержаться или а клас-
классов из ?2, или ни одного. Из этого легко видеть, что если а = 1,
то в каждом роде содержится один класс из ?1; далее, что если
а = 2, то половина всех родов содержит по два класса из О, а
другая половина не содержит таких классов, причем либо первая
половина совпадает целиком с @, а вторая половина — целиком
с § либо вторая совпадает с @, а первая — с § (@ и § имеют то
же значение, что и выше, в III). Если а еще больше, то классы
из ?1 будет содержать а-я часть всех родов (причем каждый из них —
по а классов).
Алгоритм для собственно примитивных классов 465
VI. Если мы теперь предположим, что С является классом,
период которого состоит из п членов, то легко видеть, что в слу-
случае, когда а = 2 и потому п четно, ни один класс из ?1 не может
принадлежать к G (действительно, в противном случае такой класс
содержался бы в периоде класса С; если поэтому обозначить его
через гС, так что 2гС = С7 то имело бы место 2r = I (modn), что
невозможно); а так как G принадлежит к @, то все классы из Q
обязательно должны распределяться среди родов из <г>. Отсюда сле-
следует, так как всего в G (для регулярного определителя) имеется
<р(п) классов, имеющих периоды из п членов, что в случае, когда
а = 2, в каждом роде из § находится 2ср(п) классов, периоды ко-
которых имеют 2п членов и потому охватывают как их собственный
род, так и главный род; если же а = 1, то в каждом роде, отлич-
отличном от главного, имеется <р(п) таких классов.
VII. На этих замечаниях мы основываем следующий метод наи-
наиболее целесообразного определения системы всех собственно прими-
примитивных классов для каждого данного регулярного (ибо иррегулярные
мы полностью оставляем в стороне) определителя. Выберем по же-
желанию произвольный класс Е, период которого состоит из 2п чле-
членов и потому содержит как его собственный род, который мы обо-
обозначим через F, так и главный род; классы обоих этих родов мы
расположим так, как они следуют в этом периоде. Таким образом,
цель уже будет достигнута, если других родов, кроме этих двух,
нет, или оказывается ненужным их определять (например, в слу-
случае такого отрицательного определителя, для которого имеется
только два положительных рода). Если же нужно определить че-
четыре или больше родов, то остальные получаются следующим обра-
образом. Если V — какой-нибудь род из других, и V + V = F", то
в V и V" имеются два двусторонних класса (либо в каждом из
них по одному, либо в одном два, а в другом ни одного); если
выбрать любой класс А из этих двух, то легко видеть, что если
компонировать А с отдельными классами из С и F, то мы полу-
получим 2п различных принадлежащих к V и V" и потому полностью
исчерпывающих эти роды классов; тем самым описываются и эти
роды. Если, кроме этих четырех родов, имеются еще и другие, то
пусть Vm — один из них, и пусть, далее, F"", V'"\ Vmm — те
466
Раздел V (п. 307)
роды, которые получаются при композиции рода Vm с F, V и F'\
Эти четыре рода F'", V"", V'"", Vmm содержат четыре двусторон-
двусторонних класса, и ясно, что если один из них, А\ выбрать и скомпо-
нировать с отдельными классами из G, F, F\ V", то получатся
все классы из F'",..., F""". Если имеется еще больше классов,
то мы продолжаем таким же образом, пока не исчерпаем их все.
Очевидно, что если число всех подлежащих определению родов
равно 2*\ то всего нужно будет иметь 2fx~~1 двусторонних классов
и каждый класс из этих родов будет получаться либо умножением
класса Е, либо композицией некоторого класса, получающегося
таким умножением, с одним или несколькими двухсторонними клас-
классами. Для пояснения этих правил мы дадим здесь два примера;
относительно пользы таких конструкций и искусственных приемов,
благодаря которым работа может быть облегчена, мы здесь ничего
добавлять не будем.
I. Определитель —161
Четыре положительных рода; в каждом из них по четыре класса
1,
A,
(9,
B,
(9,-
4;
0,
1,
1,
1,
G
i?7;
161)
18)
81)
18)
i?23
= К
=--2Е
= 4?
= 6Е
3,
C
F,-
F,
C,-
4;
, 1,
-1,
1,
-1,
V
N1,
54)
27)
27)
54)
-R23
= Е
= ЗЕ
= ЪЕ
= 1Е
з,
G,
(H,-
A4,
(И,
4;
0,
2,
7,
2,
V
R7
23)
15)
15)
15)
; iV23
= А
= А+2Е
= А4-АЕ
= А + 6Е
A0
E,
E,-
A0,-
1, 4
, з,
2,
-2,
-з,
V"
; iV7; iV23
17)= A + E
33) = A + 3E
33) = A + 5?
17) = Л + 7.Б
Алгоритм для собственно примитивных классов
467
II. Определитель —546
Восемь положительных родов; в каждом из них по три класса
1 и 3,
A,
B2,-
B2,
8;
0,
-2
2,
G
R3; R7; R13
546) = К
, Zb) — IE
25) = AE
3 и 7,
E,
B1
E,-
8;
2,
, 0
-2,
V
N3;
110)
, 26)
110)
N7; N13
= E
=3E
= 5E
1 и
A1
A1
3, 8;
B, 0,
,-2,
, 2,
V
N3, R7; N13
273) = ^
50) = A+
50) =Л +
2E
AE
5 и 7
A0,
A3,
A0,-
,8;
2
0,'
-2,
V"
R3-
55) =
42) =
55) =
JV7,
A-\
A -f
^ 4-
ШЗ
-E
¦3E
¦ЪЕ
1 и 3,8
C, 0,
A7, 7,
A7,-7,
У"
; N3
182)
35)
35)
; N7
= А'
= А'
= А'
; i?13
+ 2Е
+ 4Е
5 и 7
A5,-
G,
A5,
, 8
з,
0,
3,
V""
¦ R3;
37) =
78) =
37) =
R1
А'
А'
А'
; ЛГ13
+ Е
+ ЗЕ
+ 5Е
1 и
F,
A9,
A9,-
3,
о,
9,
9,
8; Re
91) =
33) =
33) =
A
A
A
N7;
+ A'
+ A'
+A'
N13
+ 2E
+ AE
5 и
B3,
A4,
B3,-
7, 8
11,
0,
-11,
тттт
; N3;
29) =
39) =
29) =
R7; R\3
A
A
A
+ A'
+ A'
+A'
+ E
+3E
+5E
Раздел VI
РАЗЛИЧНЫЕ ПРИМЕНЕНИЯ
ПРЕДЫДУЩИХ ИССЛЕДОВАНИЙ
308
Во многих местах до этого мы уже касались того, насколько выс-
высшая арифметика богата истинами, находящими применение также
и в других частях математики; мы считаем, однако, небесполезным
специально рассмотреть некоторые приложения, которые заслужива-
заслуживают более подробного изложения, не столько для того, чтобы исчер-
исчерпать этот предмет, которым легко могли бы быть заполнены многие
тома, сколько для того, чтобы на нескольких примерах пролить на
него более яркий свет. В настоящем разделе мы сначала будем говорить
о разложении дробей на более простые, затем о превращении обык-
обыкновенных дробей в десятичные; после этого мы изложим один новый
метод исключения, который служит для решения неопределенных
уравнений второй степени; наконец, мы укажем простые новые мето-
методы для того, чтобы отличать простые числа от составных и получать
сомножители последних. В следующем же разделе мы дадим обосно-
обоснование общей теории одного специального и очень часто используе-
используемого в общем анализе класса функций, поскольку она находится в
теснейшей связи с высшей арифметикой, и, в частности, попытаемся
обогатить новыми фактами теорию деления круга, из которой до сих
лор были известны лишь первые элементы.
Разлоэюение дробей на более простые 469
Разложение дробей на более простые
309
Задача. Дробь т/п, знаменатель которой есть произведение
двух взаимно простых чисел а, Ъ, разложить на две другие, знаме-
знаменателями которых являются а и Ъ.
Решение. Если искомые дроби суть х/а, у/b, то должно быть
Ьх-\-ау = т; поэтому х является корнем сравнения Ъх = т (mod а),
который мы можем найти на основании раздела II; у же будет
равен (т — Ъх) I а.
Известно, впрочем, что сравнение Ъх = т обладает бесконечно
многими, но сравнимыми по модулю а корнями, но что имеется
только один положительный корень, который меньше, чем а; мо-
может, однако, случиться, что у будет отрицательным. Вряд ли нужно
указывать на то, что у может быть также определен при помощи
сравнения ау == иг (mod 6), а х — из равенства х = т ау . Если,
со
например, дана дробь б8/77> то значением выражения jj (mod 7)
является число 4, и потому б8/77 распадается на -=- + тт.
310
Если дана дробь т/п, знаменатель п которой является произ-
произведением любого количества попарно взаимно простых чисел а, Ь,
с, d, , то, согласно предыдущему пункту, ее можно сначала раз-
разложить на две дроби со знаменателями а и bed...; последнюю снова
разложить на две и т. д., до тех пор, пока наконец заданная дробь
не будет приведена к виду
Числители а, р, т» S,... можно, очевидно, предполагать поло-
положительными и меньшими, чем их знаменатели, за исключением по-
последнего, который, после того, как остальные определены, больше
уже не является произвольным и может оказаться отрицательным,
а также большим знаменателя (поскольку мы не предполагаем, что
470 Раздел VI (пп. 311-312)
т < /г). Тогда по большей части будет целесообразным привести
его к виду — + &, где е — положительное число, меньшее чем е>
а к— целое число. Наконец, ясно, что числа а, Ъ, с,... можно
считать либо простыми, либо степенями простых чисел.
Пример. Дробь 391/924, знаменатель которой равен 4-3-7-11, рас-
* 1 . 40 40 2 38 38
кладывается, таким образом, на — + —;; 231 на "з"~77; —17
17 4 Л 7
на -= JJ, так что если написать jj — 1 вместо — тт, то по-
391 1,2.1,4 -
лучится _ = т + т + у + -г-1.
311
Дробь т/п может быть только одним способом приведена к та-
такому виду — + -j- + .... + к, что а, р, . .. положительны и соот-
соответственно меньше чем а, Ь, ...; действительно, если мы предполо-
предположим, что
и что а', Р', ... тоже положительные числа, меньшие соответственно
чем а, Ъ,..., то обязательно должно быть а = а', р = р', f = т'> . •
...,й = &\ Именно, если умножить равенство на п = abc..., то, оче-
очевидно, будет иметь место m == cubed ... == a'ftcd.,. (mod a), и потому,
так как bed... взаимно просто с а, обязательно a=~a', и тем са-
самым a = а', и точно так же Р = Р' и т. д., откуда само по себе
следует и к = к\ Так как теперь совершенно безразлично, для
какого знаменателя сначала находится числитель, то ясно, что все
числители могут быть найдены так же, как а в предыдущем пунк-
пункте, именно, р — из сравнения $acd... ==т (mod6), ^H3^abd.,. =
= т(то&с) и т. д. Сумма всех так найденных дробей либо равна
заданной дроби т/п, либо разность между ними является целым
числом к, так что мы получаем таким путем одновременно и про-
проверку правильности вычислений. Так, в примере предыдущего пунк-
391 391 391 391
та значения выражений^(mod4), ^jg(aiod3), ^(modT),--^ (modll)
Превращение обыкновенных дробей в десятичные 471
тотчас дают соответствующие знаменателям 4, 3, 7, 11 числители
1, 2, 1, 4, и мы находим, что сумма этих дробей превосходит за-
заданную дробь на единицу.
Превращение обыкновенных дробей в десятичные
312
Определение. Если обыкновенная дробь превращается в деся-
десятичную, то мы будем называть ряд десятичных чисел * (за исклю-
исключением целого числа, если оно имеется), независимо от того, коне-
конечен он или уходит в бесконечность, мантиссой дроби, употребляя
в новом значении выражение, применяемое обычно только в лога-
логарифмах. Так, например, мантисса дроби г/8 равна 125, мантисса
дроби 35/i6 равна 1875, мантисса дроби 2/з7 равна 054054... и т. д.
до бесконечности.
Из этого определения тотчас же вытекает, что дроби l/п, т/п
с одним и тем же знаменателем имеют одинаковые или различные
мантиссы в зависимости от того, сравнимы или нет числители /, т
по модулю п. Конечная мантисса не изменяется, если справа к ней
добавлять любое число нулей. Мантиссу дроби Ют/ п мы получим,
если отбросим первую цифру у мантиссы дроби т/п, и, вообще,
мантиссу дроби 1(Ут/п мы найдем, отбросив v первых цифр у ман-
мантиссы дроби т/п. Мантисса дроби 1/п сразу начинается со зна-
значащей (т. е. отличной от нуля) цифры, если п не больше чем 10;
если же п > 10 и не является степенью числа 10, а число пифр,
из которых состоит /г, равно к, то к — 1 первых цифр мантиссы бу-
будут нулями, и только следующая, к-я цифра будет значащей. От-
Отсюда легко видеть, что если l/п, т/п имеют различные мантиссы
(т. е. если Z, т несравнимы по модулю/г), то эти мантиссы заведомо
не могут совпадать в первых к цифрах, а обязательно отличаются
по крайней мере в к-й цифре.
* Ради краткости мы ограничимся в дальнейшем исследовании обычной де-
десятичной системой, так как она легко может быть преобразована в любую си-
систему.
472 Раздел VI (пп. 313-315)
313
Задача. Пусть заданы знаменатель дроби т/п и первые к цифр
ее мантиссы] нужно найти числитель т, который мы предпо-
предполагаем меньшим чем п.
Решение. Рассмотрим эти к цифр как целое число, умножим его
на п и разделим произведение на 10^ (т. е. отделим последние к
цифр). Если частное есть целое число (т. е. если отделенные цифры
являются нулями), то это частное и является искомым числителем,
и заданная мантисса полна; если же нет, то искомый числитель
является следующим целым числом, т. е. увеличенным на единицу
частным с отброшенными следующими десятичными знаками. Обо-
Обоснование этого правила настолько очевидно из наших замечаний
в конце предыдущего пункта, что не требует дальнейших поясне-
пояснений.
Пример. Если известно, что двумя первыми цифрами мантиссы
дроби со знаменателем 23 являются 69, то мы получаем произве-
произведение 23-69 = 1587; если отбросить от него две последние цифры и
прибавить 1, мы получим, что искомый числитель равен 16.
314
Мы начнем с рассмотрения таких дробей, у которых знамена-
знаменатели являются простыми числами или степенями простых чисел>
и затем покажем, как остальные дроби могут быть сведены к этим.
Прежде всего мы тотчас же заметим, что мантисса дроби a/pv-
(относительно числителя а которой мы все время предполагаем,
что он не делится на простое число р) конечна и состоит из (х цифр,
если р = 2 или р = 5; в первом случае эта мантисса, рассматри-
рассматриваемая как целое число, равна 5^а, а во втором равна 2м" а. Это
настолько ясно, что не требует пояснений.
Если же р — другое простое число, то 10га никогда не будет
делиться на р*, сколь большое г мы бы ни брали, откуда немед-
немедленно следует, что мантисса дроби F = ~ обязательно продолжает-
продолжается до бесконечности. Если мы предположим, что 10е есть наиниз-
наинизшая степень числа 10, которая сравнима с единицей по модулю
Превращение обыкновенных дробей в десятичные 473
ри- (ср. раздел III, где мы показали, что е либо равно числу
(р—1) р^~х, либо является его делителем), то легко убедиться,
что также и 10еа будет первым числом в ряду чисел 10а, 100а,
1000а, ..., которое сравнимо с а по этому же модулю. Но так как,
согласно п. 312, мантиссы дробей 10а/р*, ЮОа//?^, ..., 10еа/р*
получаются, если отбрасывать у мантиссы дроби F соответственно
одну, две, ..., е первых цифр, то ясно, что в этой мантиссе после
первых е цифр, и не раньше, снова повторяются прежние цифры.
Эти первые е цифр, из бесконечного повторения которых образована
мантисса, мы будем называть периодом этой мантиссы или дроби F,
и очевидно, что величина периода, т. е. число цифр, из которых
он состоит, и которое равно е, совершенно не зависит от числите-
числителя а и определяется только знаменателем. Так. например, период
дроби Vn равен 09, период дроби 3/7 равен 428571.
315
Поэтому, если мы знаем период некоторой дроби, мы можем
продолжить мантиссу до любого количества цифр. Далее получает-
получается, что если Ъ = 10xa(mod/?fX), то период дроби Ъ / р^ мы получим,
если первые X цифр дроби F (где мы предполагаем X < е, что до-
допустимо) напишем после остальных е — X цифр, и что тем самым
мы одновременно с периодом дроби F имеем также периоды всех
дробей, числители которых сравнимы по модулю р* с числами 10а,
100а, 1000а,... Например, так как 6 = 3-102(mod7), то из пери-
периода дроби 3/7 тотчас же находится период дроби 6/1ч равный 857 142.
Если поэтому для модуля р^ число 10 является первообразным
корнем (пп. 57, 89), то в случае, когда за основание взято число 10,
из периода дроби 1 / р^ тотчас же можно получить период всякой
другой дроби т I pv- (у которой числитель т не делится на р), от-
отделив у первого из упомянутых периодов слева и приписав затем
к нему справа столько цифр, сколько единиц содержит индекс
числа т, если з& основание взято число 10. Отсюда явствует, поче-
почему в этом случае в таблице 1 всегда берется за основание число 10
(п. 72).
Если же 10 не является первообразным корнем, то из периода
дроби I/jd^ могут быть получены периоды только тех дробей,
474 Раздел VI (п. 316)
числители которых сравнимы по модулю р^ с некоторыми степенями
числа 10. Пусть 10е — наинизшая степень числа 10, которая срав-
сравнима с единицей по модулю р^, далее, (р — l)/?^ = ef, и за осно-
основание взят такой первообразный корень г, что индекс числа 10 ра-
равен / (п. 71). Таким образом, в этой системе числители дробей,
периоды которых могут быть выведены из периода дроби 1 / р^-,
имеют индексы /, 2/, 3/,..., ef — /; аналогично, из периода дроби
г I pv- могут быть найдены периоды дробей, числители которых Юг,
ЮОг, ЮООг, ... соответствуют индексам / + 1, 2/ + 1, 3/ + 1,...;
из периода дроби с числителем г2 (индекс которого равен 2) полу-
получаются периоды дробей с числителями, индексами которых являются
/+2, 2/+ 2, 3/ + 2,..., и вообще, из периода дроби с числите-
числителем г1 могут быть выведены периоды дробей с числителями, индек-
индексами которых являются / + г, 2/ + г, 3/ + г, ... Из этого мы легко
заключаем, что если только мы имеем периоды дробей с числите-
числителями 1, г, г2, г3, ..., г^-, то все остальные могут быть выведены
отсюда простыми перестановками по следующему правилу.
Пусть в системе, в которой за основание взято число г, ин-
индекс числителя т заданной дроби т / р^ равен i (это число мы
предполагаем меньшим чем (р—1) р^~х); положим (деля на /)
г=а/ + Р, где а, р являются целыми положительными числами
(или также равны 0) и р < /. Тогда период дроби т / р^ получится
из периода дроби с числителем г$ (который, следовательно, равен 1,
если р = 0), если первые а цифр в нем поставить после остальных
(тем самым, период останется неизменным, если а = 0). Это доста-
достаточно поясняет, почему при построении таблицы 1 мы следовали
правилу, изложенному в п. 72.
316
По этим принципам мы для всех знаменателей вида /?^, меньших
1000, составили таблицу необходимых периодов, которую мы цели-
целиком или даже в еще продолженном виде опубликуем в свое время.
Здесь в качестве примера достаточно продолженной лишь до 100
таблицы* и пояснения к ней почти не нужны. Для тех знаменателей,
для которых 10 является первообразным корнем, она дает периоды
* Таблица 3; помещена на стр. 578—579.—Прим. ред.
Превращение обыкновенных дробей в десятичные 475
дробей с числителем 1 (именно, для 7, 17, 19, 23, 29, 47, 59, 61, 97),
для остальных знаменателей — периоды, соответствующие / числи-
числителям 1, г, г2,..., rf—1, которые указываются приписанными числами
@), A), B),...; в качестве основания г всегда берется тот же первооб-
первообразный корень, что и в таблице 1. Поэтому период каждой дроби,
знаменатель которой содержится в этой таблице, может быть найден
по правилу из предыдущего пункта, после того как при помощи таб-
таблицы 1 найден индекс числителя. Впрочем, для таких маленьких
знаменателей задача столь же легко может быть решена и без табли-
таблицы 1, если мы простым делением вычислим столько первых цифр ис-
искомой мантиссы, сколько, согласно п. 313, их необходимо иметь, что-
чтобы ее можно было отличить от любой другой мантиссы для этого же
знаменателя (для таблицы 3 не более чем две цифры), и тщательно пе-
пересмотрим все соответствующие этому знаменателю периоды, пока
не найдем наших начальных цифр, которые точно указывают начало
периода; нужно, однако, указать на то, что эти цифры могут также
оказаться разделенными, так что первая (или несколько первых)
будет образовывать конец некоторого периода, а остальные (или ос-
остальная) — его начало.
Пример. Найдем период дроби 12/19. Здесь для модуля 19 мы
имеем (см. таблицу 1) ind 12 = 2 ind 2+3 ind 3 = 39=3 (mod 18)
(п. 57). Поэтому, так как для этого случая имеется только один
период, соответствующий числителю 1, нужно переставить в конец
три его первые цифры, откуда и получается искомый период:
631578947368421052. Так же легко можно было бы найти начало пе-
периода по двум первым цифрам 63.
Если мы хотим найти период дроби 45/53, то, для модуля 53,
ind 45 = 2 ind 3 + ind 5 = 49; количество периодов здесь равно
4 = /, и 49 = 12/ + 1; поэтому в периоде, обозначенном через A),
нужно первые 12 цифр поставить после остальных, и искомый период
есть 8490566037735. В этом случае первые цифры 8 и 4 в таблице от-
отделены одна от другой.
Заметим еще, что при помощи таблицы 3 можно также найти чис-
число, которое для заданного модуля (фигурирующего в таблице под на-
названием знаменателя) соответствует заданному индексу, что мы уже
в п. 59 обещали показать. Действительно, согласно предыдущему
476 Раздел VI (пп. 317-318)
можно, очевидно, найти период дроби, числитель которой (если
он даже и неизвестен) соответствует заданному индексу; достаточна
взять из таблицы столько первых цифр этого периода, сколько цифр
имеет знаменатель; из них, в соответствии с п. 313, мы найдем числи-
числитель, т. е. искомое число, соответствующее заданному индексу.
317
Согласно изложенному, может быть без вычислений найдено лю-
любое число цифр мантиссы всякой дроби, знаменатель которой явля-
является простым числом или степенью простого числа, не превосходящей
границ таблицы; однако на основании исследований в начале этого
раздела применение таблицы распространяется еще гораздо дальше
и охватывает все дроби, знаменатели которых являются произведе-
произведениями простых чисел или степеней простых чисел, если эти степени
не превосходят ее границ. Действительно, так как такая дробь может
быть разложена на дроби, знаменателями которых являются эти со-
сомножители, а эти дроби могут быть превращены в десятичные до лю-
любого знака, то остается только объединить последние в сумму. Впро-
Впрочем, вряд ли нужно даже указывать на то, что последняя цифра этой
суммы может оказаться меньше правильной цифры; но очевидно, что
разница не может превосходить стольких единиц, сколько скла-
складывается отдельных дробей, так что все будет хорошо, если их вы-
вычислить на несколько знаков дальше того места, до которого должна
быть точным выражение для заданной дроби. Для примера мы рас-
6 099 380 351^
смотрим дробь t = 1 271 808 720 ' знаменатель которой есть про-
произведение чисел 16, 9, 5, 49, 13, 47, 59. Согласно изложенным выше
л . И , 4 , 4 , 22 , 5 , 7 , 52
принципам мы находим: F = 1 +i6+"^ + y + 49 + i3 + 47"i~59>
и эти частичные дроби следующим образом превращаются в десятич-
десятичные:
?U 0,6875,
* Эта дробь является одной из тех, которые наиболее близко подходят
к значению квадратного корня из 23, причем ошибка меньше семи единиц в дваг
дцатом десятичном знаке.
Превращение обыкновенных дробей в десятичные 477
|=0,8,
¦|- = 0,4444444444444444444444...,
§ = 0,44897959183673469387 75...,
^ = 0,3846153846153846153846...,
^ = 0,14893617021276595744 68...,
Л = 0,8813559322 0338983050 84 ...,
F « 4.7958315233 127195416617
Разность между этой суммой и верным значением заведомо мень-
меньше, чем пять единиц в последнем, двадцать втором, десятичном раз-
разряде, так что тем самым двадцать первых цифр не может измениться.
Если провести вычисления для еще более далеких десятичных раз-
разрядов, то вместо последних двух цифр 17 получится 1893936...
Впрочем, каждый может заметить, даже если бы мы на это спе-
специально не указывали, что этот метод для превращения обыкновен-
обыкновенных дробей в десятичные особенно предпочтителен в том случае, ког-
когда нужно найти много десятичных знаков; действительно, если дос-
достаточно немногих знаков, то в большинстве случаев столь же удобно
применять простое деление или вычисление с логарифмами.
318
Так как тем самым превращение в десятичные дроби таких дро-
дробей, знаменатели которых составлены из нескольких простых чисел,
уже сведено к тому случаю, когда знаменатель является простым чис-
числом или степенью простого числа, мы хотим добавить только еще
кое-что относительно мантисс первых. Если знаменатель не содер-
содержит сомножителей 2 и 5, то мантисса и здесь будет состоять из перио-
периодов, так как и в этом случае в ряду 10, 100, 1000,... мы в конце кон-
концов дойдем до члена, который сравним с единицей по этому знамена-
знаменателю, и одновременно показатель этого члена, который легко может
быть определен на основании п. 92, будет указывать величину перио-
478 Раздел VI (пп. 319-320)
да, не зависящую от числителя, если он взаимно прост со знаменате*
лем. Если же знаменатель имеет вид 2a5p7V, где N есть число взаимно"
простое с 10, и a, P обозначают числа, хотя бы одно из которых на
равно 0, то мантисса дроби только после первых а или р цифр (в за-^
висимости от того, а дли Р больше) будет состоять из чистых перио-
периодов, которые в отношении своей длины будут совпадать с периода
ми дробей, знаменателем которых является N. Это легко выводится
из того, что первая дробь разложима на две другие со знаменателями
2а5^ и N, первая из которых обрывается после а или р цифр. Впро-
Впрочем, относительно этого предмета мы могли бы добавить много дру-
других замечаний, особенно в отношении искусственных приемов, ко-
которые можно применять, чтобы по возможности быстро конструиро-
конструировать таблицу, подобную таблице 3, однако, ради краткости, мы отка-
откажемся здесь от этого, тем более, что многое относящееся сюда уже-
было указано как Робертсоном в ужецитированномсочинении, так
и Бернулли («Nouv. Mem. de Г Ac. de Berlin», 1771, p. 273)»
Решение сравнения х2=А методом исключения
319
Вопрос о возможности сравнения х2==А (mod m), которое равно-
равносильно неопределенному уравнению х2 = А + Щ)> мы изложили в
разделе IV (п. 146) так, что больше уже ничего не остается желать;
относительно же самого нахождения неизвестных мы уже замечали
выше (п. 152), что косвенные методы значительно предпочтительнее
прямых. Если т есть простое число (к каковому случаю легко мо-
могут быть сведены остальные), то мы могли бы использовать для этой
цели таблицу индексов 1 (согласно замечанию в п. 316, в соедине-
соединении с таблицей 3), как мы подробнее показали в п. 60. Однако этот
метод был бы ограничен пределами таблицы. По этой причине, как мы
надеемся, следующий общий и удобный метод будет небезынтересным
для любителей арифметики.
Прежде всего заметим, что достаточно иметь только те значения
xt которые положительны и не больше чем т/2, ибо каждое другое-
значение сравнимо по модулю т либо с одним из самих этих значе-
Решение сравнения хп = А методом исключения 479
ний, либо с одним из них, взятым с отрицательным знаком; но для
такого значения х значение у обязательно будет содержаться между
А 1 А
границами — — и -^т ——- Метод, который непосредственно
напрашивается, должен был бы состоять в том, что для отдельных,
лежащих в этих границах значений у, совокупность которых мы обоз^
начим через ?}, вычисляется значение А + ту, которое мы обозна-
обозначим через V, и оставляются только те значения, для которых V яв-
является квадратом. Если т — маленькое число (например, меньшее
чем 40), то этот способ настолько короток, что вряд ли требует упро-
упрощений; если же т велико, то при желании работа может быть сокраще-
сокращена посредством следующего метода исключения.
320
Пусть Е — любое целое число, которое взаимно просто с т и
меньше чем 2; далее, пусть все его различные (т. е. несравни-
несравнимые по модулю Е) квадратичные невычеты суть а, &, с, ...; наконец,
пусть корни сравнений
А + ту == а, А + ту = Ь, А-\- ту == с, ... (mod E)
равны соответственно а, р, у» • • •> и все они положительны и мень-
меньше чем Е, что мы имеем право предполагать. Если теперь придать
у значение, которое сравнимо с одним из чисел а, р, Y» • • • по мо-
модулю Е, то получающееся при этом значение V = А + #4/ будет
сравнимо с одним из чисел а, 6, с, ... и потому будет невычетом
по модулю Е\ поэтому оно не может быть квадратом. Отсюда вы-
вытекает, что из О тотчас же могут быть исключены как непригод-
непригодные все числа, которые содержатся в формах Et + a, Et -\- р,
Et + Т> • • -, и будет достаточно произвести испытание остальных
чисел, совокупность которых мы обозначим через Q'. При этой
операции числу Е можно дать название исключателя.
Если же взять в качестве исключателя другое подходящее
число Е\ то мы совершенно аналогичным образом найдем столько
чисел а', р', -у'» • • •> сколько имеется различных квадратичных не-
невычетов, с которыми у не может быть сравнимо по модулю Е'.
Поэтому из О'снова можно будет выбросить все числа, содержа-
480 Раздел VI (пп. 321-322)
щиеся в формах E't-\-<x\ E't-\-$\ Ert-\-^\.t. Таким же образом
исключение можно продолжать и дальше, применяя все новые и
новые исключатели, до тех пор, пока количество чисел в ?1 не
уменьшится настолько, что окажется не более трудно непосред-
непосредственно испытать оставшиеся числа, чем применять новые исклю-
исключения.
Пример. Если дано уравнение х2 = 22 + 97г/, то границы зна-
1 22
чений у равны —22/97 и 24 -г — ~= , так что ?1 охватывает числа
1, 2, 3, . . ,; 24 (ибо непригодность числа 0 непосредственно ясна).
Для Е = 3 получается единственный невычет а = 2; отсюда а=1;
поэтому из ?1 исключаются все числа вида 3?+1; количество остав-
оставшихся чисел О' равно 16. Точно так же для Е = 4 получается
а = 2, Ъ = 3, откуда а = 0, Р = 1; поэтому отбрасываются все числа
вида 4? и 4^+1, и: остаются следующие восемь: 2, 3, 6, 11, 14,
15, 18, 23. Точно так же для Е = Ъ мы находим, что исключаются
числа вида Ы и 5? + 3; таким образом, остаются числа 2, 6, 11, 14.
Исключатель 6 устранил бы числа вида Ы -\- 1 и Ы -\- 4; однако
эти числа (которые совпадают с числами вида 3? + 1) Уже отброшены.
Исключатель 7 устраняет числа вида It + 2, It + 3, It -\- 5 и остав-
оставляет следующие: 6, 11, 14. Если подставить их вместо г/, то полу-
получается V = 604, 1089, 1380; из этих значений только второе яв-
является квадратом. Для него х = + 33.
321
Так как производимая при помощи исключателя Е операция
исключает из значений F, соответствующих значениям у из ?1, все
те значения, которые являются квадратичными невычетами по мо-
модулю Е, а вычеты по этому числу оставляет неприкосновенными,
то легко видеть, что применение Е и 2Е ничем не отличается,
если Е нечетно, так как в этом случае Е и 2Е имеют одни и те
же вычеты и невычеты. Отсюда вытекает, что если в качестве
исключателей использовать последовательно числа 3, 5, 7,..., то
четные числа, не делящиеся на 4, именно, 6, 10, 14, ... должны
пропускаться как ненужные. Далее, очевидно, что дважды произ-
Решение сравнения хп = А методом исключения 481
веденная операция при помощи исключателей Е, Е' устраняет все
те значения F, которые являются невычетами либо обоих чисел
Е, Е', либо по крайней мере одного из них, в то время как зна-
значения, являющиеся вычетами обоих этих чисел, сохраняются. Но
так как в случае, когда Е и Е' не имеют общих делителей, все
устраненные числа являются невычетами, а все оставшиеся — вы-
вычетами по модулю ЕЕ', то ясно, что в этом случае применение
исключателя ЕЕ' приводит в точности к тому же, что и примене-
применение Е и Е\ и потому применять ЕЕ' после Е и Е' уже не нужно.
Таким образом, мы можем отбросить все те исключатели, которые
могут быть разложены на два взаимно простых сомножителя, и
ограничиться теми, которые являются либо (не входящими в т)
простыми числами, либо степенями простых чисел. Наконец, ясно,
что после применения исключателя р11, являющегося степенью про-
простого числа р, исключатели р и р", где v < [х, уже становятся из-
излишними; действительно, так как р11 оставляет среди значений V
только вычеты по себе самому, то тем более не могут остаться не-
невычеты по модулю р или по модулю более низкой чем р^- степени
7?v. Если же исключатель р или pv уже был применен до р*1, то
последний, очевидно, может устранить только те значения V, ко-
которые одновременно являются вычетами по модулю р (или pv) и
невычетами по модулю р^\ поэтому достаточно брать в качестве
а, Ь, с, ... только такие невычеты числа р^-.
322
Отыскание чисел а, р, у» • • •> которые соответствуют некоторому
заданному исключателю Е, может быть значительно сокращено бла-
благодаря следующим замечаниям. Пусть 9(, 95, (?,... суть корни срав-
сравнений ту == а, ту == Ь, ту == с? .. . (mod Е), ж к — корень сравнения
ту == — А; тогда, очевидно, а = 3( + &, р===35 + А, т = @ + А, ...
Если бы теперь нам действительно нужно было находить 21, 95, ©,...
посредством решения указанных сравнений, то этот путь определе-
определения а, р, т» • • • был бы во всяком случае не короче того, который
мы указали выше; однако решать указанные сравнения вовсе не
обязательно. Именно, если, сначала, Е является простым числом,
482 Раздел VI (п. 323)
и т есть квадратичный вычет по модулю Е, то из п. 98 вытекает,
что 9t, 93, ?,..., являющиеся значениями выражений а/т, Ь/т,
с/т,... (modi?), будут различными невычетами по модулю Е, и
потому в точности совпадают с а, р, у? • • •? если не принимать во
внимание порядок их расположения, который здесь не важен; если
же при сохранении остальных предположений т есть невычет по
модулю Е, то числа, 91, 93, К,... будут совпадать со всеми квадра-
квадратичными вычетами (кроме 0). Если Е есть квадрат (нечетного)
простого числа скажем, Е = р2, и если р уже было использовано
в качестве исключателя, то, согласно предыдущему пункту, в ка-
качестве а, 6, с, ... достаточно брать только те невычеты по модулю
р2, которые являются вычетами по модулю р, т. е. числа р, 2р,
Зр, ..., р2 — р (именно; все числа, меньшие чем р2, кроме 0, кото-
которые делятся на р)\ но из этого легко видеть, что в качестве 9t,
95 у ?, .. . должны получиться эти же самые чи ла, лишь располо-
расположенные в другом порядке. Аналогично, если после применения
исключателей р и р2 мы положим Е = р3, то будет достаточно
брать в качестве а, 6, с, ... произведения отдельных невычетов по
модулю р на р2, и 91, 93, ?, .. . окажутся либо этими же самыми
числами, либо произведениями числа р на отдельные вычеты по
модулю р (за исключением 0), в зависимости от того, является ли
т вычетом или невычетом по модулю р. Вообще, если взять в ка-
качестве Е любую степень простого числа, скажем, р*, после того
как все более низкие степени уже были использованы, то в каче-
качестве 91, 93, S,. . . получатся произведения числа ри-~1 либо на все
числа, которые меньше р @ все время исключается), в случае,
когда [х четно, либо на все меньшие чем р невычеты по модулю р,
в случае, когда [л нечетно и mRp, либо на все вычеты, если mNp.
Если Е = 4 и потому а = 2, 6 = 3, то в качестве 9f, 93 мы полу-
получаем либо 2 и 3, либо 2 и 1, в зависимости от того, имеет ли
место т = 1 или =3 (mod 4). Если после применения исключате-
исключателя 4 мы положим Е = 8, то получим а = 5, откуда 31 — 5, 7, 1, 3,
когда соответственно т?г = 1, 3, 5, 7 (mod 8). Вообще же, если Е
есть любая более высокая степень числа 2, скажем, Е = 2^, то
после того как более низкие степени числа 2 уже использованы,
нужно положить а = 2tx~1, b =3-2u'~2, если [х четно, откуда полу-
Решение неопределенного уравнения тх2 + пу2 = А 483
чается 21 = 2tx~~1, 93 = 3• 2^~2 или =2^~2, в зависимости от того,
будет ли т = 1 или = 3; если же [х нечетно, то нужно положить
a = 5-2^~~3, откуда 31 получится равным произведению числа 2^~~3
на одно из чисел 5, 7, 1 или 3, смотря по тому, будет ли т==1,
=3, =5 или =7 (mod8).
Впрочем, искусные математики легко придумают аппарат, при
помощи которого непригодные значения у будут отбрасываться
механически, после того как числа а, р, -у» • • • будут найдены для
достаточного количества исключателей; однако для сокращения
работы мы не будем здесь останавливаться на этом, так же, как
и на других специальных приемах.
Решение неопределенного уравнения тх2-\-пу2=А
методом исключения
323
В разделе V мы указали общий метод для отыскания всех
представлений заданного числа А двойничной формой тх2 + пу2,
или, другими словами, решения неопределенного уравнения
тх2-\-пу2 — А, который не оставляет желать в отношении кратко-
краткости ничего лучшего, если мы уже знаем все значения выражения
1/— тп по самому модулю А и по модулю, получающемуся из А
делением на его квадратные сомножители; однако для того случая,
когда тп положительно, мы изложим сейчас метод, который на-
намного удобнее только что упомянутого метода, если для последнего
еще надо заранее вычислять указанные значения. При этом мы
предположим, что числа т, п и А положительны и попарно взаимно
просты, так как остальные случаи легко могут быть сведены к этому.
Кроме того, достаточно, очевидно, искать только положительные
значения х, г/, так как остальные получаются из них всевозмож-
всевозможными изменениями знаков.
Ясно, что х должен обладать тем свойством, что выражение
(^4 — тх2) I п, которое мы будем коротко обозначать через F,
положительно, является целым и представляет собой квадрат. Пер-
Первое условие требует, чтобы х был не больше чем ]/ А / т\ второе
484 Раздел VI (п. 324)
условие выполняется само собой, если п = 1, в противном же
случае оно требует, чтобы значение выражения - (mod n) было
квадратичным вычетом по модулю п\ и если мы обозначим все
различные значения выражения!/- (modra) через +г, +7*',...,
то значения х должны будут содержаться в одной из форм nt + г
nt— г, nt-\-r',... Поэтому проще всего было бы подставлять
вместо х все не превосходящие границы f/A/m числа такого вида,
совокупность которых мы обозначим через О, и оставлять только
те, для которых V является квадратом. В следующем пункте мы
покажем, как этот способ можно при желании сократить.
324
Метод исключений, при помощи которого мы этого добьемся,
состоит, так же, как и в предыдущем исследовании, в том, что
берутся некоторые числа, которые мы и здесь будем называть
исключателями, затем исследуется, для каких значений х значения
V будут квадратичными невычетами по этим исключателям, и тако-
таковые значения х из ?1 выбрасываются. Из рассуждений, которые
совершенно аналогичны изложенным в п. 321, вытекает, что нужно
использовать только те исключатели, которые являются простыми
числами или степенями простых чисел, и для исключателя второго
типа из значений V нужно отбрасывать только те невычеты этого
исключателя, которые являются вычетами всех более низких сте-
степеней того же простого числа, если для них исключение уже
проведено.
Итак, пусть исключатель Е равен р11 (включая и тот случай, когда
[х = 1), где р есть не входящее в т простое число; предположим,
что pv есть наивысшая степень этого простого числа, на которую
делится п *. Пусть, далее, а, 6, с, .., суть квадратичные невычеты
по модулю Е (причем все, если (л = 1, и лишь те, которые являются
вычетами по более низким степеням, если [х > 1). Если вычислить
корни сравнений
mz == А — па, mzE=A — nb, mz== А — пс,... (mod Ер* =
* Ради краткости мы объединяем оба случая, когда п делится и не делится
на р; в последнем случае надо положить v = 0.
Решение неопределенного уравнения тх2 + пу2 = А 485
которые мы обозначим через а, р, т» • • •» то легко полу-
получится, что если для некоторого значения х имеет место
х2 = a (mod Epv), то соответствующее значение V будет == a (modi?),
т. е. будет невычетом по модулю Е, и аналогично обстоит дело
для р, if» • • • Обратно, столь же очевидно, что если некоторое
значение х приводит к сравнению V = a (mod Е), то для этого зна-
значения будет х2 ~ a (mod Epv)t и потому все значения ж, для которых
х2 несравнимо по модулю Epv ни с одним из чисел а, р, т» • • •»
приводят к таким значениям F, которые несравнимы ни с одним
из чисел а, 6, с, ... по модулю Е. Выберем теперь из чисел
а, р, т> • • • все квадратичные вычеты по модулю Ер*, которые
обозначим через g, g\ g", .. ., и найдем значения выражений
~\/~g, УЩ, Vg"> • • • (modi?pv), которые обозначим через +/г, + /г',
+ /г", ... Тогда ясно, что все числа вида Ep^t + h, Epvt-\-h',
Ер*tЛ^Ь!',. . . заведомо могут быть выброшены из ?1, и что ни
одному из значений х, еще оставшемуся в О после этого исключе-
исключения, не может отвечать значение V, содержащееся в формах ?и + а,
Ей + Ь, Ей + с,. .. Впрочем, такие значения F, очевидно, уже и
сами по себе не могут получиться ни из каких значений х, если
среди чисел а, р, т» • • • нет квадратичных вычетов по модулю Ер*,
и потому в этом случае применение числа Е в качестве исключа-
теля ничего не дает.
Мы можем применять сколько угодно исключателеи, и тем самым
все более и более сужать круг чисел, остающихся в ?2.
Теперь убедимся, что простые числа, которые входят в т, или
степени таких простых чисел нельзя использовать в качестве
исключателеи. Если В есть значение выражения — (mod тп), то по-
получается, что какое бы значение для х ни брать, V будет всегда
сравнимо с В по модулю т, и что тем самым для разрешимости
заданного уравнения необходимо, чтобы В было квадратичным
вычетом по модулю т. Поэтому, если обозначить через р какой-
нибудь нечетный простой делитель числа т9 который по предполо-
предположению не входит в п и А, а, значит, и в В, то V для любого
значения х будет вычетом по модулю р, а потому и по любой
степени числа р\ следовательно, число р и его степени не могут
486 Раздел VI (п. 325)
служить в качестве исключателей. Если т делится на 8, то по
совершенно аналогичной причине для разрешимости заданного
уравнения необходимо, чтобы имело место Б= 1 (mod8), вследствие
чего для любого значения х будет F=l(mod8). так что степени
числа 2 не годятся в качестве исключателей. Если же т делится
на 4, но не делится на 8, то по аналогичной причине должно быть
Б = 1 (mod 4), и значение выражения -(mod8) будет равно 1 или5;
обозначим его через С. Без труда можно увидеть, что для четного
значения х будет F = C, а для нечетного будет V = C + 4 (mod 8),
откуда вытекает, что нужно отбросить четные значения, когда
С = 5, и нечетные, когда С = 1. Если, наконец, т делится на 2,
но не делится на 4, то пусть, как и раньше, С будет значением
выражения —(mod 8), которое равно 1,3, 5 или 7, и D — значение
^1
выражения^1 (mod4), равное 1 или 3. Так как теперь значение F,
очевидно, всегда =С — 2-D#2(mod8), и потому для четного х оно
= С, а для нечетного =С — 2D, то отсюда без труда выводится,
что нужно отбросить все нечетные значения х, если С = 1, все четные,
если С = 3 и D = 1 или С = 7 и D = 3, и что для всех остальных
значений F=^l (mod 8), т. е. F является вычетом по каждой степени
числа 2; в остальных же случаях, именно, когда С = 5, или С = 3и
D = 3, или С = 7 и D = 1, будет иметь F = 3, =5 или = 7 (mod8),
независимо от того, четно х или нечетно, откуда следует, что в этих
случаях заданное уравнение вообще не имеет решений.
Так как точно так же, как мы научились здесь находить посред-
посредством исключений значения х, можно, с необходимыми изменениями
находить и значения г/, то метод исключения для решения постав-
поставленного вопроса всегда можно применять двояким образом (за
исключением случая т = тг = 1, когда оба способа совпадают),
и в большинстве случаев предпочтительнее тот путь, при котором ?1
содержит меньшее количество членов, что легко можно узнать
заранее. Наконец, вряд ли даже нужно указывать на то, что если
после нескольких исключений из О оказываются выброшенными все
числа,— то это можно рассматривать как верный признак неразре-
неразрешимости заданного уравнения.
Решение неопределенного уравнения тх2 + пу2 = А 487
325
Пример. Пусть дано уравнение 3#2+455г/2=10 857 362, которое мы
хотим решить двумя способами: сначала ища значения х, а затем —
значения у. Граница первых значений в этом случае равна числу
1^10 857 362/3, которое расположено между 1902 и 1903; значе-
значение выражения -о-(mod 455) равно 354, и значения выражения
К354 (mod 455) суть +82, +152, +173, +212. Поэтому О состоит
из следующих 33 чисел: 82, 152, 173, 212, 243, 282, 303, 373, 537,
607, 628, 667, 698, 737, 758, 828, 992, 1062 1083, 1122, 1153,
1192, 1213, 1283, 1447, 1517, 1538, 1577, 1608, 1647, 1668, 1738,
1902. Число 3 в данном случае в качестве исключателя брать нельзя,
так как оно входит в т. Для исключателя 4 мы имеем а = 2, Ъ = 3,
откуда ос = О,р = 3; g = 0, ив качестве значений выражения У g (mod 4)
получаются числа 0 и 2; отсюда следует, что все числа вида At и
At + 2, т. е. все четные числа, из О выбрасываются; совокупность
оставшихся (шестнадцати) чисел обозначим через Of. Для числа
Е = 5, которое входит в п, мы получаем в качестве корней сравне-
сравнений mz == А — 2п и mz = А — Зп (mod 25) значения 9 и 24, которые
оба являются вычетами по модулю 25, причем значения выражений
У9 и ]/24(mod25) суть +3, +7; после отбрасывания из ?У всех
чисел вида 25? + 3, 25^ + 7 остается совокупность из следующих
десяти чисел: 173, 373, 537, 667, 737, 1083, 1213, 1283, 1517, 1577
обозначим ее через О". Для Е = 7 мы в качестве корней сравнений
mz == А — Зп, mz = A—5п, mz==A — 672(mod49) имеем значения
32, 39, 18, которые все являются вычетами по модулю 49, а в каче-
качестве значений выражений У32, У39, У18 (mod 49) числа +9, +23,
+19; если выбросить из Q" числа вида 49^+ 9, 49^ + 23, 49^ + 19,
то останется следующая совокупность L1'" из пяти чисел: 537, 737,
1083, 1213, 1517. Для Е = 8 мы получаем а = 5, и потому а = 55
т. е. а есть невычет по модулю 8; поэтому число 8 в качестве
исключателя применять нельзя. Число 9 не годится по той же
причине, что и 3. Для i? = ll числа а, Ь,.. . будут соответственно
равны 2, 6, 1, 8, 10, далее, v = 0, и потому а, р, .. . = 8, 10, 5,0,1;
из этих чисел вычетами по модулю 11 будут только три, именно,
0, 1, 5; из этого следует, что из ?1"' нужно выбросить числа вида
Раздел VI (п.
lit, 11*+ 1, 11*+ 5, так что останутся лишь числа 537, 1083,
1213. Если эти числа испробовать, то для V соответственно полу-
получатся значения 21961, 16129, 14161, из которых квадратами
являются только второе и третье. Поэтому заданное уравнение
обладает двумя решениями в положительных х, у, именно, х = 1083,
у = 127 и ж = 1213, у = 119.
Второе. Если мы хотим найти посредством исключений другое
из двух неизвестных того же уравнения, то целесообразно, поменяв
местами х и у, представить это уравнение в форме 455я2 + Зг/2 =
= 10 857 362, чтобы можно было сохранить все обозначения пп. 323,
324. Граница значений х оказывается здесь между 154 и 155;
значение выражения - (mod п) равно 1, значения |/T(mod3) суть +1
и —1. Поэтому ?2 содержит все числа вида 3* + 1 и 3*—1, т. е.
все числа, не делящиеся на 3, до 154 включительно; количество их
равно 103. Если, однако, применить указанные выше принципы,
то мы найдем, что для исключателей 3; 4; 9; 11; 17; 19; 23 из ?1
выбрасываются соответственно числа следующего вида: 9*+ 4; 4*,
4*4:2, т. е. все четные числа; 27*+ 1, 27*+ 10; lit, 11* + 1,
11* + 3; 17*4:3. 17* + 4, 17*4:5, 17* + 7; 19* + 2, 19* + 3, 19*+8,
19*+ 9; 23*, 23* + 1, 23* + 5, 23*+ 7, 23* + 9, 23* + 10. После
этого остаются лишь числа 119, 127, для которых V оказывается
квадратом и которые приводят к тем же решениям, что мы полу-
получили выше.
326
Указанный только что метод уже и сам по себе настолько удо-
удобен, что почти не оставляет желать ничего лучшего; однако
он может быть еще значительно сокращен при помощи ряда специ-
специальных приемов, которых мы здесь лишь коротко коснемся. При
этом мы ограничимся тем случаем, когда исключатель есть нечетное
простое число, не входящее в А, или степень такого простого
числа, так как остальные случаи либо сводятся к этому, либо
могут быть рассмотрены аналогичным образом. Если мы предполо-
предположим сначала, что исключатель Е = р есть не входящее в т, п
„А па пЬ
простое число, и что значения выражении —, , *
Решение неопределенного уравнения тх2 + пу2 = А 489
,. . . (mod/?) суть соответственно к, 3f, 95, 6, .. . , то числа а,
Р, т, ... мы найдем при помощи сравнений а = й; + 9f, р = й; + 95,
Y = й; + (S,.. . (mod /?). Однако числа 2f, 95, @, . .. можно найти и не
решая сравнений, посредством специального приема, который
совершенно аналогичен приему, использованному в п. 322, причем
эти числа будут совпадать либо со всеми невычетами, либо со
всеми вычетами (кроме 0) по модулю /?, в зависимости от того,
вычетом или невычетом по модулю р будет значение выражения
(mod/?), или, что то же самое, число —тп. Так, во втором
примере предыдущего пункта для Е = П имеем к=1\ —тп —
= — 1365 = 12, т. е. —тп невычет по модулю 17; поэтому числа
3t, 95,... равны 1, 2, 4, 8, 9, 13, 15, 16, а числа а, р, ... равны
соответственно 8, 9, 11, 15, 16, 3, 5, 6; из них вычетами являются
8, 9, 11, 15,16, поэтому+/*,+/*',... будут здесь равны+5,4^3,+7,+4.
Те, которым часто нужно решать подобный вопрос, значительно
облегчат себе дело, если будут вычислять значения h, h', ... ,
соответствующие отдельным значениям к A, 2, 3, ...,/?—1), при
каждом из двух предположений (именно, что —тп является или
вычетом, или невычетом по модулю р) сразу для нескольких зна-
значений р. Заметим еще, что количество чисел h, —/г, /г',... всегда
равно (р—1)/2, если оба числа к и—тп являются одновременно
либо вычетами, либо невычетами по модулю /г, далее, это количе-
количество равно (р—3)/2, если первое число есть вычет, а второе
невычет, и равно (р+1)/2, если первое число невычет, а второе
вычет; однако доказательство этой теоремы мы должны опустить,
чтобы не быть слишком пространными.
Что же касается второго случая, именно, когда Е есть либо
входящее в п простое число, либо степень (нечетного) простого
числа, безразлично, входящего в п или нет, то он может быть
разобран еще проще. Положим, сохраняя все обозначения п. 324,
п = n'pv, где п' не делится на р. Числа a, b, с, ... будут произве-
произведениями числа р**- либо на все числа, меньшие чем р (кроме 0),
либо на все меньшие чем р невычеты по модулю р, в зависимости
от того, четно [х или нечетно; будем записывать эти числа в виде
up11. Если к есть значение выражения - (mod /^+v), то к не делит-
490 Раздел VI (п. 327)
ся на р, потому что по предположению на р не делится А\ далее,
ясно, что все числа а, р, f, ... будут сравнимы с А по модулю р,
и потому ри- не произведет в О никакого исключения, если kNp\
если же кЛр, а потому и &7?/^+\ то пусть г будет (не делящимся
на р) значением выражения У к (mod p^+v), ив — значением выраже-
выражения ^— (mod р); тогда а = г2 + 2erapv (mod p^+v), откуда легко
видеть, что а есть вычет по модулю /^+у, и значения выражения
J^a(modp{J'+v) суть + (г-f-ea/?v). Поэтому все значения h, Ы', /г" , ...
будут представляться в виде г + weplx+v~1. Наконец, мы легко заклю-
заключаем отсюда, что числа /г, /г' Ы', . .. получаются прибавлением
числа г к произведениям числа рИ-v-i либо на все числа, меньшие
чем р (кроме 0), в случае, когда [л четно, либо на все невычеты
по модулю р, не превосходящие той же границы, в случае, когда
(л нечетно и eRp (или, что то же самое, когда — imrn'Rp), либо
на все вычеты (кроме 0), когда [л нечетно и —2mrn'Np.
Впрочем, после того как для отдельных исключателей, которые
мы захотим применить, числа h, Ы', /г", ... будут найдены, само исклю-
исключение можно будет производить также и чисто автоматически, в чем
легко может убедиться всякий, имеющий в этих вещах некоторый
опыт и потративший некоторые усилия.
Наконец, мы должны заметить, что каждое уравнение
ах2 + 2Ьху + су2 = М, у которого Ь2 — ас равно отрицательному
числу —Z), легко может быть сведено к виду, рассмотренному ранее.
Именно, если обозначить наибольший общий делитель чисел а, Ъ
через т и положить
а = та', Ь = mb',
- = а'с — тЪ'2 = п, а'х + Ъ'у = х\
то указанное уравнение, очевидно, будет эквивалентно уравнению
тх'2 + пу2 = а'М} которое можно решить при помощи указанных
выше правил. При этом из решений последнего уравнения нужно
оставить только те, у которых х' — Ъ'у делится на а', т. е из кото-
которых получаются целые значения для х.
Другой метод решения сравнения х2 = А 491
Другой метод решения сравнения х2=Л
в случае, когда А отрицательно
327
В то время как изложенный в разделе V прямой метод решения
уравнения ах2 + 2Ъху + су2 = М предполагает известными значения
выражения УЪ2— ас (mod М), только что изложенный косвенный
метод в случае, когда Ъ2 — ас отрицательно, дает, наоборот^ очень
простой метод для отыскания этих значений, который, особенно
для очень большого значения М, намного предпочтительней метода,
содержащегося в п. 322 и ел. Мы будем предполагать, что число
М простое, или по крайней мере, что если оно составное, то его
сомножители еще неизвестны; действительно, если бы мы знали,
что простое число р входит в М, и что М = р^М'', где М' уже
не содержит сомножителя /?,то нам было бы намного удобнее найти
значения выражения )/ Ъ2 — ас отдельно для модулей р11 и М'
(причем для первого из значений для модуля р, п. 101), и, уже
комбинируя их, получить значения по модулю М (п. 105).
Итак, отыскиваются все значения выражения У—D (mod М),
где ВжМ предполагаются положительными числами, причем М содер-
содержится в форме делителей выражения х2-{-D (пп. 147 и ел.), так
как иначе заранее было бы известно, что никакие числа не могут
быть значениями данного выражения. Обозначим искомые значения,
которые всегда разбиваются на пары противоположных одно дру-
другому, через +г, +г\ it7*"* • • • » и положим D-{-г2 = Mh,
D -\- г'2 = Mti, D -f r = МЫ'. .. ; далее, обозначим классы, к кото-
которым принадлежат формы (М, г, /г), (М,—г, /г), (М, г', h'): (M,—г', К),
(М, г", /г"), (М, — г", /г"),... соответственно через @, —@, ?',
— (?', @", — (?",..., а их совокупность через @. Правда, эти классы,
вообще говоря, следует рассматривать как неизвестные, однако
ясно, во-первых, что все они положительны и собственно примитивны,
и, во-вторых, что все они принадлежат одному и тому же роду,
характер которого легко может быть определен по свойствам числа
М, т. е. по его отношениям к отдельным простым делителям числа D
(и, кроме того, иногда также и к числам 4 и 8; п. 230). Так как
по предположению М содержится в форме делителей выражения
492 Раздел VI (п. 327)
х2 -f- D, мы можем заранее быть уверены, что этому характеру
обязательно соответствует положительный собственно примитивный
род форм с определителем — D, даже если выражение |/ —i) (mod M)
и вовсе не имеет значений; так как теперь этот род нам известен,
можно найти все содержащиеся в нем классы; обозначим их чррез
С, С', С", ... , а их совокупность через G. Тогда ясно, что каждый
класс (?, — (?,... должен совпадать с некоторым классом из G;
при этом может случиться, что несколько классов из © совпадают
между собой, а потому совпадают с одним и тем же классом из G,
а если G содержит только один класс, то с ним будут совпадать
все классы из @. Поэтому если из классов С, С, С", ... выбрать,
по одной из каждого, (простейшие) формы/, /', /"...., то каждый
класс из © будет содержать одну из этих форм. Если теперь
ах2 -f- 2bxy -J- су2 есть форма, содержащаяся в классе S, то суще-
существует два принадлежащих значению г представления числа М
этой формой, причем если одно из них есть х = т} у = п, то другое
будет х = — яг, у = — п; лишь случай D — 1 составляет исключение,
так как здесь имеется четыре представления (ср. п. 180).
Из этого мы заключаем, что если найти (изложенным выше
косвенным методом) все представления числа М отдельными фор-
формами /, /\ /", ... и определить затем все значения выражения
У—Z)(modM), которым отдельные представления принадлежат
(п. 154), то мы получим тем самым все значения этого выражения,
причем каждое по два раза или, в случае D = 1, по четыре раза;
тем самым, задача решена. Если среди /, /', /", ... окажутся формы,
которыми число М представлено быть не может, то это будет
означать, что эти формы не принадлежат к @ и потому должны
быть отброшены; если же М не может быть представлено ни одной
из указанных форм, то—D с необходимостью будет квадратичным
невычетом по модулю М.
Относительно этих операций мы сделаем еще следующие заме-
замечания.
I. Под представлениями числа М формами /, /',..., которые мы
здесь используем, понимаются лишь такие представления, у кото-
которых значения неизвестных взаимно просты; если же получаются еще
и другие представления, у которых указанные значения имеют об-
Другой метод решения сравнения х = А 493
щий делитель (что возможно только тогда, когда (л2 входит в М и
заведомо имеет место, если —DR -у, то при исследовании это-
этого вопроса их нужно просто отбрасывать, хотя в других вопросах
они и могут играть роль.
II. При прочих равных условиях работа будет, очевидно, тем
легче, чем меньше количество классов форм, и потому она будет
всего короче, когда D равно одному из указанных в п. 303 шести-
десятипяти чисел, для которых в отдельных родах имеется только
по одному классу.
III. Так как каждые два представления вида х = т, у = п;
х= — т, у = —п принадлежат всегда одному и тому же значению,
то, очевидно, достаточно рассматривать только такие представления,
у которых у положительно. Различные представления такого
типа всегда соответствуют уже различным значениям выражения
У—D (mod M), так что число всех различных значений равно числу
всех, получающихся представлений такого рода (случай/) = 1, ког-
когда первое число равно половине второго, снова составляет исклю-
исключение).
IV. Поскольку как только мы узнаем одно из противоположных
значений +г, —г, нам тем самым становится известно и другое,
мы можем еще несколько сократить наши операции. Если значение
г было найдено из представления числа М формой из класса С, т. е.
если S= С, то противоположное значение —г получается, очевид-
очевидно, из представления той формой, которая содержится в классе, про-
противоположном классу С, и потому отличном от него, если только С
не является двусторонним классом. Отсюда следует, что если не все
классы из G двусторонние, то из остальных нужно рассматривать
только половину, именно, по одному классу из каждых двух проти-
противоположных, отбрасывая другой, так как из него, как мы уже знаем,
без всяких вычислений получаются значения, противоположные тем,
которые дает оставленный класс. Если же класс С двусторонний,
то из него одновременно получаются оба значения г и —г; именно,
если в С выбрана двусторонняя форма ах2 + 2Ъху + су2, и значение
г получается из представления х = т, у = п, то значение —г по-
получится из представления х — — т —^р, у = п.
494 Раздел VI (п. 328)
V. В том случае, когда D = 1, имеется вообще только один
класс, в качестве представителя которого можно считать выбран-
выбранной форму х2 + у2- Если теперь значение г получается из пред-
представления х = т, у = га, то из представлений х = — т, у = — га;
х — — т, у = п; х = т, у = — га будет получаться это же значе-
значение, а из представлений х = т, у = — га; х = — т, у — га; х = га,
у = т; х = — га, у = — w — противоположное значение — г. По-
Поэтому из этих восьми представлений, которые дают только одно раз-
разложение, достаточно знать лишь одно представление, если только к
значению, получающемуся из него, добавить еще противоположное
значение.
VI. Согласной. 155, значение выражения У—D (тойМ), кото-
которому принадлежит представление М = am2-\-2bmn + era2, равно либо
(л (mb -\-пс) — v {та + пЪ), либо некоторому сравнимому с (л (тЪ -\- пс)—
— v (та + пЬ), по модулю М числу, где (л, v таковы, что (xw + vaz = 1,
Если поэтому обозначить какое-нибудь из таких чисел через v, то
будет иметь место
mv = [xw (mb + пс) — v (M — mnb — п2с) == (fxm + vn) (wb + гас) ^
^ тс + гас (mod M).
Отсюда вытекает, что v является значением выражения
пъЪ -4- пс , -. л /г\ г> г>
(modЖ), и подобным же образом мы находим, что v есть
значение выражения — та п (mod M). Эти формулы очень часто
оказываются предпочтительнее тех, из которых они выведены.
328
Примеры. I. Найдем все значения выражения
У—1365 (mod 5 428 681 =М).
Число Мздесь=1, 1, 1,6, H(mod4, 3, 5, 7,13), и потому содер-
содержится в форме делителей выражений х2 + 1, х2 + 3, х2 — 5
и в форме не делите лей выражений х2 -f 7, ж2 —13, т. е.
содержится в форме делителей выражения х2 + 1365; характер
рода, в котором находятся классы из ©, есть 1, 4; 7?3;
R 5; iV7, iV13. В этом роде содержится только один класс, из
Другой метод решения сравнения х2 = А
495
которого мы выбираем форму 6х2 + бху + 229г/2. Чтобы получить
все представления этой формой числа М, мы положим 2х + у = х'\
тогда получается уравнение Зх'2 -f~ 455г/2 = 2М. Оно имеет четыре
решения с положительными г/, именно, у = 127, х' = +1083; г/ = 119,
#' = + 1213. Отсюда получаются четыре решения с положительными
у уравнения 6я2 -f бяг/ + 229г/2 = М, именно,
478
127
-605
127
547
119
-666
119
Первое решение дает для v значение выражения
30 517
478
или
3249
-^т=- (mod M), откуда мы находим v = 2 350 978; второе дает про-
противоположное значение — 2 350 978, третье — значение 2 600 262,
и четвертое решение — противоположное значение —2 600 262.
II. Если нужно найти значения выражения
то в качестве характера рода, в котором содержатся классы из @, мы
получаем! и 7, 8; 7?11; 7?13; таким образом, этот род является глав-
главным родом, содержащим три класса, представителями которых
служат формы A,0,286), A4, 6, 23), A4,—6, 23); третью из них можно
отбросить, так как она противоположна второй. Для формы #2-f286z/2
мы находим два представления числа М с положительными z/, имевно,
у — ЮЗ, х = +1113, из которых получаются следующие значения
искомого выражения: 1493 445, —1493 445. Формой же A4,6,23)
число М не представляется, откуда следует, что других значений,
кроме двух уже вайденных, не существует.
III. Если задано выражение У—70 (mod 997 331), то классы @
должны содержаться в роде, характером которого является 3 и 5, 8;
R 5; iV7; этот род содержит только один класс, представителем
которого является форма E, 0, 14). Если мы, однако, произведем
вычисления, то убедимся, что число 997 331 формой E, 0, 14)
не представляется, вследствие чего —70 является квадратичным
невычетом этого числа.
496 Раздел VI (пп. 329-330)
Два метода отличать составные числа от простых
и находить сомножители составных чисел
329
То, что задача о том, как отличать составные числа от простых
и разлагать первые на их простые сомножители принадлежит к важ-
важнейшим задачам всей арифметики и привлекала внимание как мате-
математиков древности, так и математиков нашего времени, настолько
хорошо известно, что было бы излишним тратить здесь на это много
слов. Однако, нужно отметить, что все известные до сих пор методы
либо ограничиваются очень специальными случаями, либо настоль-
настолько длинны и трудоемки, что даже для чисел, не выходящих за преде-
пределы таблиц, составленных заслуженными математиками, т. е. чисел,
для которых особо искусные методы не нужны, они утомительны да-
даже для опытных вычислителей, а для еще больших чисел почти со-
совершенно неприменимы. И хотя вышеупомянутые таблицы, которые
доступны всем и которые, как мы надеемся, скоро будут еще расшире-
расширены, обычно оказываются достаточными, тем не менее опытные вычис-
вычислители нередко сталкиваются с таким положением, когда умение
разложить большое число на простые сомножители приносит им
пользу, вполне компенсирующую большую затрату времени; кроме
того, и интересы самой науки как таковой обязывают приложить
все усилия к решению этой столь изящной и знаменитой проблемы.
Именно поэтому мы не сомневаемся, что оба нижеследующих метода,
в действенности и краткости которых мы убедились на долгом
опыте, не должны оказаться бесполезными для любителей арифмети-
арифметики. Впрочем, по самой природе этого вопроса любой метод становит-
становится все более трудоемким по мере того, как числа, к которым он при-
применяется, становятся все большими и большими; однако в случае
обоих приводимых ниже методов трудности нарастают очень мед-
медленно, и числа, состоящие из семи, восьми и даже большего числа
цифр, особенно при применении второго метода, всегда исследуются
с такой быстротой, которую по справедливости следует считать дос-
достаточной для столь больших чисел, работа с которыми при помощи
известных ранее методов представляла бы невыносимый труд даже
для неутомимых вычислителей.
Два метода отличать составные числа от простых 497
Прежде чем применять нижеследующие методы, всегда бывает
целесообразно исследовать предварительно делимость заданного
числа на маленькие простые числа, например, на 2, 3, 5, 7,... до
19 или еще дальше, не только потому, что такие числа, в случае,
если они являются делителями, гораздо проще обнаружить непо-
непосредственным делением, нежели применять к ним тонкие искусствен-
искусственные методы, но и потому, что если ни одно из делений не выполняет-
выполняется без остатка, получающиеся остатки с большой выгодой могут быть
использованы при применении второго метода. Если, например, нуж-
нужно разложить на множители число 314 159 265, то деление на 3 ока-
оказывается выполнимым дважды, а также оказывается выполнимым
деление на 5 и 7, так что мы получаем 314 159 265 = 9-5-7-997 331,
и нам достаточно подвергнуть более подробному исследованию толь-
только число 997 331, которое на 11, 13, 17, 19 не делится. Аналогично,
если задано число 43 439 448, то устраняется сомножитель 8, и более
тонкие методы применяются уже по отношению к числу 5 428 681.
330
В основе первого метода лежит теорема, что каждое положитель-
положительное или отрицательное число, которое является квадратичным вы-
вычетом по некоторому другому числу М, будет квадратичным выче-
вычетом также и по всякому делителю числа М. Известно, что еслиМ не
делится ни на какое простое число, меньшее чем VМ, то М обя-
обязательно является простым числом; кроме того, если все простые чис-
числа, входящие в М и не превосходящие этой границы, суть р, q,...,
то число М делится либо только на эти простые числа (и их степени),
либо, быть может, еще только на одно простое число, которое больше
чем УМ и которое можно найти, поделив М на р, q Поэтому,
если обозначить через Q совокупность всех простых чисел, меньших
чем Ум (за исключением тех, в неделимости на которые числа М
мы уже убедились), то, очевидно, будет достаточно найти все содер-
содержащиеся в Q простые делители числа М. Если мы знаем только, что
некоторое (неквадратное) число г является квадратичным вычетом
по модулю М, то мы уже можем быть уверены, что ни одно простое
498 Раздел VI (п. 331)
число, по которому г является невычетом, не может быть делителем
числа М\ поэтому из Q, можно выбросить все такие простые числа
(в большинстве случаев они составляют примерно половину общего
количества). Если, кроме того, относительно другого неквадратного
числа т' также известно, что оно является вычетом по модулю М,
то из простых чисел, еще оставшихся в О после первого исключения,
мы снова сможем выкинуть те, по которым г' является невычетом и
которые снова составляют примерно половину общего количества
еще оставшихся чисел, если только вычеты г ж г' независимы один
от другого, т. е. если одно из этих чисел не обязательно является
вычетом по всем числам, по которым является вычетом второе, что
имело бы место в том случае, если бы произведение тт' было квадра-
квадратом. Если по модулю М известны еще и другие вычеты г", г"',...,
которые все независимы от остальных, то для каждого из них в от-
отдельности мы можем производить аналогичные исключения, вслед-
вследствие чего количество чисел в О будет очень быстро убывать, так
что скоро окажутся вычеркнутыми либо все числа из О, что будет
свидетельствовать о том, что М заведомо есть простое число, либо
их останется так мало (при этом, очевидно, останутся все простые
делители числа М, если М имеет таковые), что делимость на них
можно будет уже исследовать без труда. Для числа, не превосходя-
превосходящего миллиона, по большей части оказывается достаточным произ-
произвести шесть или семь исключений, для чисел, состоящих из восьми
или девяти цифр, — десять или одиннадцать исключений. Мы долж-
должны, таким образом, коснуться лишь двух пунктов, во-первых, как
находить достаточное количество вычетов по модулю М, и, во-вто-
во-вторых, как наиболее целесообразным способом производить само иск-
исключение. Однако мы начнем со второго вопроса, так как ответ на не-
него покажет нам, какие именно вычеты наиболее удобны для нашей
цели.
331
В четвертом разделе мы подробно показали, как можно отличать
те простые числа, по которым некоторое заданное число г (которое
мы можем предполагать не делящимся ни на какой квадрат) явля-
Два метода отличать составные числа от простых 499
ется вычетом, от тех, по которым оно есть невычет, или, как отли-
отличать делители выражения х2 — г от неделителей; именно, первые
содержатся в некоторых формах вида rz -\~ a, rz + b,..., или вида
Arz + a, Arz + b,..., a вторые — в других аналогичных формах. Ес-
Если г достаточно маленькое число, то исключения очень удобно про-
производить при помощи этих формул; например, нужно исключить все
числа вида Az + 3, если г = — 1, все числа вида 8z + 3, 8z •+ 5,
если г = 2, и т. д. Но так как находить такие вычеты заданного чис-
числа не всегда в наших силах, даже если применение формул для боль-
большого значения г и достаточно удобно, то мы получили бы огромное
преимущество и поразительным образом облегчили свой труд при
исключении, если бы для достаточно большого количества положи-
положительных и отрицательных не делящихся на квадраты чисел г заранее
составили бы таблицу , по которой можно было бы отличать простые
числа, по которым отдельные г являются вычетами, от тех, по которым
они являются невычетами. Такая таблица может быть устроена та-
таким же образом, как ее образец, приведенный в конце этого сочинения
и выше уже описанный; однако для того, чтобы она приносила
достаточно большую пользу для нашей настоящей цели, фигурирую-
фигурирующие в ней простые числа (модули) должны быть продолжены на-
намного дальше, именно, по меньшей мере до 1000 или 10 000; кроме то-
того, удобство таблицы значительно увеличилось бы, если бы вверху
приводились бы также составные и отрицательные числа, хотя, как
вытекает из четвертого раздела, это и не является абсолютно необ-
необходимым. Удобнее же всего применять такую таблицу, если отдель-
отдельные вертикальные колонки, из которых она состоит, вырезать и на-
наклеить на полоски жести или (подобно Н е п е р у) на деревянные до-
дощечки, так что те колонки, которые нужны в каждом отдельном слу-
случае, т. е. которые соответствуют числам г, г', г",..., являющимся
вычетами заданного числа, разлагаемого на сомножители, можно рас-
рассматривать отдельно. Если приложить их правильным образом к пер-
первой колонке таблицы (содержащей модули), т. е. так, что места
отдельных дощечек, соответствующих одному и тому же простому чис-
числу из первой колонки, лежат на прямом направлении с этим про-
простым числом, или, другими словами, оказываются на одной с ним
горизонтальной линии, то те простые числа, которые еще остаются в
500
Раздел VI (п. 332)
&> после исключений при помощи вычетов г, г', г",..., можно будет,
очевидно, узнать с одного взгляда; именно, они будут совпадать с
теми числами из первой колонки, которым во всех приложенных до-
дощечках соответствуют черточки, а все те, против которых хотя бы в
одной дощечке находится пустое место, нужно будет отбросить. Это
станет достаточно ясно на примере. Если мы откуда-нибудь знаем,
что числа — 6, + 13,—14, +17, +37, — 53 являются вычетами
по модулю 997 331, то нужно приложить к первой колонке (которую в
этом случае нужно продолжить до 997, т. е. до наибольшего простого
числа, меньшего чем ]/997 331) полоски, вверху которых стоят чис-
числа —6, +13, ... Мы приведем здесь часть получающейся при этом
схемы:
3
5
7
11
13
17
19
23
—6
+13
—
—
—
—14
—
—
—
—
—
+17
—
—
—
+37
—
—
-53
—
—
—
и т. д.
115
127
131
и т. д.
Подобно тому как мы с одного взгляда узнаем, что из простых чи-
чисел, содержащихся в этой части схемы, после исключений при по-
помощи вычетов —6,+13, ... в Q остается только число 127, точно так
же вся схема, продолженная до числа 997, показывает, что в О вооб-
вообще уже не остается никаких других чисел; попробовав же произвести
Два метода отличать составные числа от простых 501
деление, мы убеждаемся, что 997 331 действительно делится на 127.
Таким образом, разложение указанного числа на простые сомножи-
сомножители есть 127 -7853.
Из изложенного с достаточной ясностью вытекает, что наиболее
удобны не очень большие вычеты или, по крайней мере, вычеты, раз-
разлагающиеся на не очень большие простые числа, так как непосред-
непосредственное применение вспомогательной таблицы ограничивается чис-
числами, находящимися вверху ее, а вообще таблица применима для
чисел, которые могут быть разложены на сомножители, содержащие-
содержащиеся в ней.
332
Для нахождения вычетов заданного числа М мы укажем три раз-
различных метода, изложению которых мы предпошлем два замечания,
при помощи которых из менее удобных вычетов можно будет полу-
получать более простые. Во-первых, если число ак2, делящееся да квад-
квадрат /с2 (который мы предполагаем взаимно простым с М), является
вычетом по модулю М, то и число а будет вычетом; поэтому вычеты,
делящиеся на большие квадраты, могут быть сведены к маленьким
вычетам, и мы будем предполагать, что все вычеты, находимые при
помощи излагаемых далее методов, тотчас же освобождаются от их
квадратных сомножителей. Во-вторых, если два или несколько чи-
чисел являются вычетами, то вычетом будет и их произведение. Если
связать это замечание с предыдущим, то очень часто оказывается
возможным из нескольких вычетов, которые не все являются доста-
достаточно простыми, находить некоторый новый очень простой вычет,
если только первые имеют много общих сомножителей. По этой при-
причине очень большую пользу приносят также и такие вычеты, которые
составлены из большого количества не слишком больших сомножи-
сомножителей, причем целесообразно сразу же раскладывать эти вычеты на
их сомножители. Значение этих замечаний лучше уяснится на при-
примерах и при частом их применении, нежели из теоретических сообра-
соображений.
I. Простейший, а для тех, кто частым упражнением уже приоб-
приобрел некоторый опыт, и удобнейший метод состоит в том, что число
502 Раздел VI (п. 332)
М, или, более общо, некоторая его кратность, раскладывается на
два слагаемых: кМ = а + Ъ (которые либо оба положительны, либо
одно из них положительно, а другое отрицательно); произведение
этих слагаемых, взятое с обратным знаком, будет тогда вычетом по
модулю М, так как — аЪ = а2 = Ъ2 (mod M), и потому — abRM.
Числа а, Ъ нужно брать такими, чтобы их произведение делилось
на большой квадрат, а получающееся при этом частное либо было
маленьким, либо по крайней мере раскладывалось на не слишком
большие сомножители, чего всегда без труда можно добиться.
Особенно рекомендуется брать в качестве а либо квадрат, либо удвоен-
удвоенный, утроенный и т. д. квадрат, который отличается от М либо на
маленькое число, либо на число, разлагающееся на удобные сомно-
сомножители. Например, мы находим: 997 331 = 9992 — 2-5-67 =
= 9942 + 5-1М32 = 2-7062 + 3-17-32 = 3-5752 + 11-31-42 =
-3-5772 - 7-13-42 = 3-5782 -7-19-37 - 11-2992 + 2-3-5-29-42=
= 11-3012 + 5-122, и т. д. Отсюда мы получаем следующие выче-
вычеты: 2-5-67, (-5)-11, (-2)-3-17, (—3I1-31, 3-7-13, 3-7-19-37,
(— 2) -3-5 -11 -29; последнее разложение приводит к вычету (—5)-11,
которыймы уже имеем. Вместо вычетов — 3*11-31, (— 2)• 3-5• 11 • 29
можно взять вычеты 3-5-31, 2-3-29, которые получаются из
первых комбинированием их с вычетом (—5) -11.
II. Второй и третий методы основаны на том, что если две двойни-
двойничные формы (А, В, С), (А'} В', С) с одними тем же определителем Л/,
или — М, или вообще, + кМ, принадлежат одному и тому же роду,
то числа АА', АС, А'С являются вычетами по модулю кМ\ это без
труда устанавливается из того, что каждое характеристическое
число т одной из форм будет характеристическим числом и другой
формы, и потому числа т А, тС, тА',тС все будут вычетами по мо-
модулю кМ. Поэтому если (а, Ь,а') есть приведенная форма с положи-
положительным определителем М, или, более общо, кМ, и если (а[Ъ[а"),
A,0,A ),... суть формы из ее периода, которые поэтому ей эквива-
эквивалентны и тем более содержатся с ней в одном роде, то все числа аа',
аа", аа',... будут вычетами по модулю М. Вычисление большого
количества форм такого периода может быть очень легко проведено
при помощи алгоритма из п. 187; простейшие вычеты большей ча-
частью получаются, если положить а = 1; вычеты, содержащие слиш-
Два метода отличать составные числа от простых
503
ком большие сомножители, следует отбрасывать. Ниже приводят-
приводятся начала периодов форм A, 998, —1327) и A, 1412, —918), опреде-
определители которых равны 997 331 и 1 994 662.
A, 998, —1327)
(—1327, 329, 670)
F70, 341, —1315)
(—1315, 974, 37)
C7, 987, —626)
(—626, 891, 325)
C25, 734, —1411)
(—1411, 677, 382)
C82, 851, —715)
и т. д.
A, 1412, —918)
(—918, 1342, 211)
B11, 1401, —151)
(—151, 1317, 1723)
A723, 406, —1062)
(—1062, 656, 1473)
Г1473, 817, —901)
(—901, 985, 1137)
и т. д.
Поэтому все числа —1327, 670,... будут вычетами по модулю
997 331. Если из них отбросить те, которые содержат слишком боль-
большие сомножители, то останутся следующие: 2*5-67, 37, (—17).83,
(— 5I1 -13, (—2)-3-17,( —2)-59,(—17)-53. Вычет2-5-67, также, как
и вычет (—5)-11, который получается из комбинации третьего вычета
с пятым, мы уже нашли выше.
III. Если С — некоторый класс, отличный от главного, форм с
отрицательным определителем — М или, более общо,— кМ, и
2С, ЗС,... — период этого класса (п. 307), то классы 2С, 4С,... принад-
принадлежат главному роду, а классы ЗС, 5С\... — тому же роду, что и С.
Если поэтому (а, Ь, с) есть (простейшая) форма из С, и (а',Ь", с') —
какая-нибудь форма из некоторого класса указанного периода, на-
например, из пС, то либо а', либо аа', в зависимости от того, четно п
или нечетно, будет вычетом по модулю М (причем в первом случае
вычетом, очевидно, будет также и с', а во втором — ас', са' и ее').
Нахождение периода, т. е. форм, простейших в своих классах, про-
производится с поразительной легкостью, когда а очень мало, особенно
в случае а = 3, чего всегда можно добиться, если сделать предвари-
предварительно кМ = 2(mod 3). Ниже приводится начало периода класса,
в котором содержится форма C,1, 332444).
504 Раздел VI (пп. 333-334)
С = C, 1, 332 444)
2С = (9, —2, 110 815)
ЗС = B7, 7, 36 940)
4С = (81, 34, 12 327)
ЪС = B43, 34, 4109)
6С = G29,-209, 1428)
7С = D76, 209, 2187)
8С = A027, 342, 1085)
9С = (932,—437, 1275)
ЮС -D25, 12, 2347)
Отсюда получаются следующие вычеты (после устранения не-
неудобных): 3-476,1027, 1085, 425, или (если отбросить квадратные
сомножители) :3*7-17,13*79,5-7-31,17,и если их подходящим образом
связать с восемью вычетами, найденными в II, мы получим следующие
двенадцать вычетов: (—2)-3, 13,(—2)-7, 17, 37, —53, (—5)-11, 79,
—83,(—2)-59,(—2)-5-31, 2-5-67. Первые шесть суть те, которыми мы
пользовались в п. 331. Можно было бы еще присоединить вычеты
19 и —29, если бы мы хотели использовать также и те, которые бы-
были найдены в I; остальные полученные там вычеты уже зависят от
найденных здесь.
333
Второй метод разложения заданного числа М на сомножители
исходит из рассмотрения значений выражения вида }/~—D (mod M)
и основывается на следующих замечаниях.
I. Если М есть простое число или степень (нечетного, не вхо-
входящего в D) простого числа, то — D будет вычетом или невычетом
по модулю М в зависимости от того, содержится ли М в форме де-
делителей или в форме неделителей выражения х2 +В,ив первом слу-
случае выражение у —D (mod M) обладает только двумя значениями,
которые противоположны одно другому.
II. Если же М есть составное число, и, например, равно рр'р"...,
где р,р\ р'\... обозначают (нечетные, не входящие в D, различные)
простые числа или степени таких простых чисел, то — D только тог-
тогда будет вычетом по модулю М, когда — D есть вычет по всем отдель-
отдельным числам р, р\ р",..., т. е. когда все эти числа содержатся в формах
делителей выражения х2 + D. Если же значения выражения ]/ —D
по модулям р, р'> р",... обозначить соответственно через it г, ihr\
Два метода отличать составные числа от простых 505
drr",..., то все значения этого же выражения пр модулю М получат-
получатся, если мы найдем числа, которые по модулю р сравнимы с г или с
—г, по р' сравнимы с г' или—г' и т. д., так что количество последних
значений будет тем самым равно 2*\ где ^ обозначает количество
чисел р,р',р",... Если теперь эти значения суть R,— R, R',— R',
i?",..., то само собой R = R по всем числам р,р',р",...; однако, ни по
одному из этих чисел не может иметь места R = — R, так что наи-
наибольший общий делитель чисел М и R — R равен М, а наибольший
общий делитель чисел М и i?-fi? равен 1; всякие же два значения,
которые не являются ни совпадающими,ни противоположными, как,
например, R и R', будут обязательно сравнимы по одному или не-
нескольким (но не по всем) из чисел р,р',р"',..., по остальным же будет
иметь место R ^ — R''; поэтому произведение первых есть наиболь-
наибольший общий делитель чисел М и R —R', а произведение послед-
последних — наибольший общий делитель чисел М и R + R'. Отсюда лег-
легко видеть, что если вычислены все наибольшие общие делители чис-
числа М с разностями между отдельными значениями выражения
у—D (modM) и каким-нибудь данным значением, то эта совокупность
будет содержать числа 1, р, р', р",..., а также их произведения по
два, по три и т. д. Таким образом, мы оказываемся в состоянии по
значениям указанного выражения определить числа р, р'', р",...
Впрочем, так как метод п. 327 сводит эти отдельные значения к
значениям выражении вида - (mod M), где знаменатель п взаимно
прост с М, то сами значения нам и не нужно находить. Действитель-
Действительно, наибольший общий делитель числа М и разности между R и R',
которые совпадают с т/п и т'In', является, очевидно, также и наи-
наибольшим общим делителем числа М и пп' (R — R'), а, значит, так-
также чисел М и гпп — пт', так как последнее число сравнимо с
пп' (R — R') по модулю М.
334
Предыдущие замечания могут быть использованы в настоящем
вопросе двояким образом; используя первый способ, мы не только
сможем узнать, является ли заданное число М простым или состав-
составным, но и сможем в последнем случае найти сомножители; второй спо-
способ заслуживает предпочтения в том отношении, что он в больший-
506 Раздел VI (п. 334)
стве случаев требует более простых вычислений, однако, если не
применять его многократно, он не всегда дает самые сомножители
составных чисел, хотя при помощи него также можно отличать со-
составные числа от простых.
I. Найдем отрицательное число —D, которое является квад-
квадратичным вычетом по модулю М; для этой цели можно использо-
использовать методы, указанные в п. 332,1 и П. Хотя, вообще говоря, и без-
безразлично, какой вычет мы выберем, причем, в отличие от предыду-
предыдущего метода, здесь вовсе нет нужды, чтобы D было маленьким числом,
тем не менее вычисления будут тем короче, чем меньше число клас-
классов двойничных форм, содержащихся в отдельных собственно прими-
примитивных родах с определителем —D, так что особенно благоприятны
те вычеты, если только они годятся, которые содержатся среди 65
чисел п. 303. Так, для М = 997 331 среди всех найденных выше от-
отрицательных вычетов наиболее удобным является вычет —102. Да-
Далее найдем все различные значения выражения J/ —D (mod M)\
если их окажется только два (противоположных), то М заведомо яв-
является простым числом или степенью простого числа; если же их бу-
будет больше, а именно, 2*\ то Мбудет состоять из [^ различных про-
простых чисел или степеней простых чисел, и эти сомножители могут
быть найдены методом предыдущего пункта. Являются ли эти со-
сомножители простыми числами или степенями простых чисел, можно не
только легко определить непосредственно, но и сам метод, при помощи
которого отыскиваются значения выражения |/—D , непосредственно
указывает те простые числа, которые входят в М в некоторых степе-
степенях, больших 1. Именно, если М делится на квадрат простого числа
1г, то при указанных вычислениях мы заведомо придем хотя бы к од-
одному такому представлению М = am2 + 2Ътп + сп2 числа М , для
которого наибольший общий делитель чисел т, п равен тг (вследст-
(вследствие того, что в этом случае —D будет также вычетом и по модулю
М/тг2). Если же не получится ни одного представления, у которого
т и п имеют общий делитель, то это будет верным признаком, что М
не делится ни на какой квадрат, и потому все числа р,р', р",... явля-
являются простыми.
Пример. Указанным выше методом мы находим четыре значения
выражения У—408 (mod 997 331), которые совпадают со зна-
Два метода отличать составные числа от простых 507
.1664 . 2824 , ,
чениями zhjjo"' —"~з~~' в качестве наибольших общих делителей
числа 997 331 и чисел 3-1164 - 113-2824 = 314 120 и 3-1164 +
4-113*2824= 324 104 мы находим соответственно 7853 и 127, поэтому
997 331 = 127-7853, как и выше.
II. Возьмем какое-нибудь отрицательное число —D с тем свой-
свойством, что М содержится в форме делителей выражения х2 -f- D*
Само по себе безразлично, какое именно число такого рода взять;
однако ради удобства нужно в первую очередь обратить внимание на
то, чтобы количество классов в родах с определителем —D было
по возможности маленьким. Кстати, получение такого числа не стал-
сталкивается ни с какими трудностями, если мы ищем его посредством
проб; действительно, в большинстве случаев при достаточном ко-
количестве испробованныхчисел число М оказывается примерно столько
же раз в форме делителей, что и в форме неделителей. Поэтому це-
целесообразнее всего начинать пробы с 65 чисел п. 303 (и притом с наи-
наибольших из них) и только если окажется, что ни одно из них не го-
годится (что, однако, вообще говоря случается один раз из 16 384),
переходить к другим числам, для которых в отдельных родах содер-
содержится по два класса. Затем мы получаем значения выражения
У—D (mod M) и выводим из них, точно таким же образом, как и выше,
сомножители числа М. Если же таких значений не получится, т. е.
—D окажется квадратичным невычетом по модулю М, то, значит, М
заведомо не может быть ни простым числом, ни степенью простого
числа. Если в последнем случае мы хотим найти сами сомножители,
то нужно либо повторить ту же операцию, взяв в качестве D другое
значение, либо прибегнуть к другим методам.
Если мы, например, произведем исследование числа 997 331, то
найдем, что оно содержится в форме неделителей выражений
х2 + 1848, х2 + 1365, х2 + 1320, но в форме делителей выраже-
выражения х2+840; в качестве значений выражения У—840 (mod 997 331)
. 1272 , 3288
мы получаем выражения ±-jgcr> "~Т25'т откуда получаются те
же сомножители, что и выше. Желающие иметь другие примеры
могут обратиться к п. 328, где первый пример показывает,
что 5428681 =307-17683, второй,—что 4272 943 является про-
508 Раздел VI (п. 335)
стым числом, и третий,— что число 997 331 заведомо составлено из
нескольких простых чисел.
Впрочем, границы настоящего сочинения позволили изложить
лишь основные моменты обоих методов нахождения сомножителей;
более подробное исследование с привлечением большего количества
вспомогательных таблиц и других вспомогательных средств мы от-
откладываем до другого случая.
Раздел vii
ОБ УРАВНЕНИЯХ, ОТ КОТОРЫХ ЗАВИСИТ
ДЕЛЕНИЕ КРУГА
335
Среди наиболее блестящих достижений, которыми обогатилась
математика благодаря работам ученых последнего времени, особен-
особенно выдающееся место, без сомнения, занимает теория функций, свя-
связанных с кругом. На этот замечательный тип величин, к которому
приходишь при самых различных исследованиях и без помощи ко-
которого не может обойтись ни одна часть всей математики, крупней-
крупнейшие из новых математиков столь усердно направляли свое приле-
прилежание и остроумие, и создали столь обширную теорию, что почти
невозможно было ожидать, чтобы еще какая-нибудь часть этой тео-
теории, тем более часть, находящаяся у самых истоков и вполне эле-
элементарная, допускала бы еще более важное развитие. Я имею в виду
теорию тригонометрических функций, соответствующих дугам, ко-
которые соизмеримы с длиной окружности, или теорию правильных
многоугольников; настоящий раздел покажет, насколько незначи-
незначительная часть ее была разработана до сих пор. Читатель может уди-
удивиться, что это исследование помещено именно в настоящем труде,
который, на первый взгляд, посвящен совершенно чуждому этим
вопросам предмету; однако само сочинение достаточно убедитель-
убедительно покажет, в какой тесной связи с высшей арифметикой эти вопро-
вопросы находятся.
Впрочем, принципы теории, к изложению которой мы теперь пе-
переходим, распространяются намного дальше того, чем они развиты
510 Раздел VII (пп. 336-337)
здесь. Действительно, они могут быть применены не только к круго-
круговым функциям, но и ко многим другим трансцендентным функци-
Г dx
ям, например, к тем, которые зависят от интеграла \ , , и,
J V 1 — х
кроме того, к различным типам сравнений; но так как об указанных
трансцендентных функциях мы готовим специальное обширное со-
сочинение, а о сравнениях подробно будет идти речь в продолжении
арифметических исследований, нам показалось целесообразным рас-
рассматривать здесь только круговые функции. И даже эти функции,
которые мы могли бы рассматривать во всей общности, мы при помо-
помощи излагаемых в следующем пункте приемов сведем к простейшему
случаю,— с одной стороны, ради краткости, а с другой — потому,
что благодаря этому станут более понятными совершенно новые прин-
принципы этой теории.
Исследование сводится к простейшему случаю,
когда число частей, на которые должен быть разбит круг,
является простым
336
Если обозначить окружность или четыре прямых угла через Р
и предположить, что т и п — целые числа, причем п есть произведе-
произведение попарно взаимно простых сомножителей а, Ъ, с,..., то, согласно*
п. 310, угол А = —- может быть представлен в виде
А = 1— -\- -^ Л- ^L -\-.. .) Р у и соответствующие ему тригонометри-
\ а ос }
ческие функции могут быть известными методами получены из функ-
функций, соответствующих частям аР/а, $Р/Ъ,... Но так как в качестве
а, Ь, с,... можно взять простые числа или степени простых чисел, то
достаточно, очевидно, рассматривать только деление круга на части,
чжсло которых является простым или равно степени простого числа,
а многоугольник с п сторонами тотчас же можно получить из много-
многоугольников с а, Ъ, с ,... сторонами. Мы, однако, ограничимся здесь
в нашем исследовании тем случаем, когда круг нужно делить на ча-
части, число которых является (нечетным) простым, и делаем мы это в
Тригонометрические функций дуг и корни уравнения хп — 1 = 0 511
первую очередь по следующей причине. Как известно, круговые
тР
функции, соответствующие углу —г , могут быть получены по-
посредством решения уравнения р-й степени из функций, соответствую-
тР
щих углу —- , а из первых посредством решения уравнения такой
же степени могут быть получены функции, соответствующие углу
тР
—д- и т. д., так что если мы уже имеем многоугольник с р сторонами,
то для определения многоугольника с рх сторонами нужно решить
^ — 1 уравнений р-й степени. И хотя дальнейшая теория могла бы
быть применена также и к этому случаю, но и на этом пути мы при-
пришли бы к такому же числу уравненийр-ж степени, которая, когда р
простое число, никак не может быть понижена. Например, ниже бу-
будет показано, что многоугольник с 17 сторонами может быть постро-
построен геометрически; однако для определения многоугольника с 289
сторонами никак нельзя избежать уравнения 17-й степени.
Уравнения для тригонометрических функций дуг,
составляющих одну или несколько частей полной окружности;
сведение тригонометрических функций к корням уравнения.
а>п—1=0
337
Хорошо известно, что тригонометрические функции всех углов
кР
вида — , где к пробегает числа 0, 1, 2, . . ., п — 1, выражается
через корни уравнений тг-й степени, причем синус выражается через
корни уравнения
1. х —-^пх -t-jg j-2 х —
1 п(п — 4) (л — 5) , . 1 Л
v LS Lгп-б+. .+ пх = 0,
64 1-2-3 Х —2n-i
косинус — через корни уравнения
ТТ -гп * «/У.П-2 _1_ * П(П — 3) п_4
и. х — -^пх -hjg y^2 x ~
1 п(п — 4)(п — 5) п . . . 1 1 п
i — '-Хп~6+. . .+ -ПХ —г- =0,
64 1-2-3 ~-2n-i 2п~1
512 Раздел VII (п. 338)
и наконец, тангенс — через корни уравнения
тгт « п (п — 1) -» о i nin—1) (л — 2) (/г — 3)
III. яп v, о ; жп~2Н - ; v0 Q , м -
1 • Z 1 • Z • о * 4
Эти уравнения, которые, вообще говоря, имеют место для каждого
нечетного значения п (уравнение II также и для четного), могут
быть сведены, если положить п = 2т-{- 1, к т-и степени; именно,
уравнения I и III нужно разделить на х и положить у = х2. Урав-
Уравнение II, очевидно, имеет корень # = l(=cosO), а остальные его
корни разбиваются на попарно равные (cos — = cos — ,
2Р (п — 2) Р \ Л
cos — = cos ,•••)» поэтому левая часть делится на х — 1,
и частное является квадратом; если из него извлечь квадратный
корень, то уравнение II приведется к уравнению
А. Жт-1 _ _*_ (т _ 1) х2 _ 1
т-2 _ 1_ (т _ 2)
1 (то„3)(т-4) _#
Ж ^2 Г2 Ж
1 16 1.2 " ^32 1-2
корнями которого являются косинусы углов Р/тг, 2-Р/тг, ЗР/п,...
. . . , тР I п. Дальнейших редукций для этих уравнений, по крайней
мере в случае, когда п есть простое числа, до сих пор не было
известно.
Между тем ни одно уравнение не является столь простым для
рассмотрения и удобным для нашей цели, как уравнение хп — 1 =0,
корни которого, как известно, теснейшим образом связаны с корнями
указанных уравнений. Именно, если обозначить для краткости
мнимую величину }/"—1 через г, то корни уравнения хп — 1=0
представятся в виде
кР . . . кР
cos \- i sm — = г,
где в качестве А нужно брать все числа 0, 1, 2, 3, . . . , п— 1. Но
Тригонометрические функций дуг и корни уравнения хп — 1 = 0 513
1 кР . . кР т
так как — = cos г sin — , то корни уравнения 1 представятся
в виде (г )/2i или гA — г2)/2г, корни уравнения II —в виде
1 / . 1 \ 1 + г2 ттт
у ( г -\ J = —±— , наконец, корни уравнения III — в виде
гA—г2)/A-{~г2). По этой причине мы будем основывать наше
исследование на рассмотрении уравнения хп—1 = 0, причем будем
предполагать, что п является нечетным простым числом. А для
того чтобы дальше не пришлось прерывать последовательность
рассуждений, мы предпошлем здесь следующее вспомогательное
предложение.
338
Задача. Пусть задано уравнение
(W) zm + Az™-1 + ... — 0;
нужно найти уравнение (W')f корни которого являются \-ми
степенями корней уравнения (W), где X обозначает заданный поло-
положительный целый показатель степени.
Решение. Если обозначить корни уравнения (W) через а, Ь, с,...,
то корнями уравнения (W') должны быть аЛ, 6х, с\... Согласно
известной теореме Ньютона, по коэффициентам уравнения (W)
можно найти суммы любых степеней корней а, Ь, с,.... Итак, най-
найдем суммы
ах+ bx + cl+ ...; а2Х + 62Х + с2Х + ..., ...до атХ+ 6тХ + стХ + ...
В свою очередь по этим суммам можно будет затем опре-
определить при помощи той же теоремы коэффициенты уравнения (W).
Одновременно из этого вытекает, что если коэффициенты у
(W) рациональны, то и все коэффициенты у (W) тоже будут
рациональными. Другим путем можно даже доказать, что если
первые являются целыми числами, то и вторые будут целыми
числами; однако мы не будем здесь останавливаться на этой тео-
теореме, которая не столь уж нужна для нашей цели.
514 Раздел VII (пп. 339-340)
Теория корней уравнения хп—1=0
(в предположении, что п есть простое число).
Если отбросить корень 1, то совокупность (?1) остальных корней
содержится в уравнении Х = хп~{ +хп~2-\-... + ас+ 1=0
339
Уравнение хп—1=0 (где все время подразумевается, что п
есть простое число) имеет только один вещественный корень х = 1;
остальные п — 1 корней, которые охватываются уравнением
Xй-1 + хп~2 + ... + х + 1 = 0,
все являются мнимыми; совокупность их мы обозначим через й,
а функцию
через X. Таким образом, если г есть какой-нибудь корень из О,
то 1 = гп = г2п, и т. д., и вообще геп = 1 для каждого положи-
положительного или отрицательного значения е\ отсюда очевидно, что
если X, [х суть сравнимые по модулю п целые числа, то гх = г^.
Если же X, [х, напротив, не сравнимы по модулю п, то гх и r[J-
будут но равны; действительно, в этом случае можно найти такое
целое число v, что (X — (л) v == 1 (mod n), откуда следует, что
г(к—и)ч = г и потому гх~^ заведомо не равно 1. Далее, ясно, что
каждая степень корня г также является корнем уравнения
хп— 1=0; поэтому, так как все величины 1 (= г°), г, г2,..., гп~х раз-
различны, они будут представлять собой все корни уравнения хп — 1—0,
и потому совокупность гу г2, г3,..., гп~1 будет совпадать с Q. От-
Отсюда мы л°гко заключаем, что, вообще, О совпадает с любой со-
совокупностью ге, г2е, гзе,..., И71N , где е обозначает некоторое целое
не делящееся на п положительное или отрицательное число.
Поэтому
X = (х — ге) (х — r2e) (x — rSG) ...(x — И71-1N),
откуда следует:
»«е i Г2е I гзе \ I Ли—1)е — \ и \ \ ге _\_ Г2е _
Теория корней уравнения хп — 1 = 0 515
Два таких корня, как г и -у (= г™-1) или, вообще, ге и л~е,
мы будем называть обратными; очевидно, что произведение двух
1
простых сомножителей х— г и ж - вещественно, именно, равно
х2— 2#coso) + l, так что угол со равен либо углу Р/п, либо не-
некоторой его кратности.
340
Так как тем самым, если один из корней из О обозначен через
г9 то все корни уравнения хп-—1=0 представляются в виде сте-
степеней гху то, следовательно, произведение нескольких корней этого
уравнения также может быть представлено в виде гх, где X либо
равно 0, либо положительно и меньше, чем п. Поэтому, если обо-
обозначить через cp(t,u,v,...) алгебраическую целую рациональную
функцию от неизвестных t, м, г?,..., которую можно представить
в виде суммы слагаемых вида htau^v^..., то ясно, что если вместо
ty и, v,... подставить некоторые корни уравнения хп—1 = 0, ска-
скажем, положить t = а, и = b> v = с,..., то функцию ср (а, й, с,...) можно
будет представить в виде
А + А г + А г2 + Атг* + ... + Л(п~1)гп~1,
где коэффициенты А, А ,... (из которых некоторые могут отсутст-
отсутствовать, т. е. быть равны 0) будут определенными величинами, и,
кроме того, все эти коэффициенты будут целыми числами, если все
постоянные коэффициенты у cp(t, и, v,...), т.е. все числа h будут
целыми. Если же затем вместо t, м, #,... подставить соответственно
а2, Ь2, с2,..., то каждое слагаемое вида ht*u&v'r...t которое перед
этим давало га, теперь даст г2а, откуда легко видеть, что
9 (а2, Ъ\ с2,...) = А + А'г2 + А г* + А"г" + ... + ^"V71.
Точно так же и вообще для любого целого значения X
9(аЛ, &\ с\...) =А 4 Агх + А"г2Х + ... + Л(п-1}г(т1~1)х;
эта теорема имеет очень большое значение и составляет основу
дальнейших исследований.
516 Раздел VII (п. 341)
Отсюда следует, далее, что
9A, 1,1,...) =<р(ап, Ьп, с71,...) =А + А + А + ... + ^(п~~1},
/ 1 \ I / О 7 О О Ч / О 7 О О \i
9 (а, Ь, с,...) + 9 (а > ь » с >•••) ~ь ? (а » ь » с >•••) + •••
так что эта сумма всегда является целым числом, делящимся на
п, если все постоянные коэффициенты у cp(t,u, #,...) целые.
Функция X не может быть разложена на сомножители
более низких степеней, все коэффициенты у которых рациональны
341
Теорема. Если функция X делится на функцию
Р = хх -\- Ах7" + Вхх~* -4- ...-)- Кх -f- L
более низкой степени, то коэффициенты A, B,...,L не могут быть
все одновременно целыми числами.
Доказательство. Пусть X — PQ и $ есть совокупность корней
уравнения Р = 0, a Q,-—совокупность корней уравнения (9 = 0,
так что О состоит из $ и Q. Далее, пусть 31 есть совокупность
корней, обратных корням из $, и © — совокупность корней, обрат-
обратных корням из Q, и пусть корни, которые содержатся в 9^,
являются корнями уравнения R = 0 (которое, как легко видеть,
есть хл -j—J- х^ -)-... + -у-х -|—=г- — (J ] , а корни, которые содер-
жатся в @, являются корнями уравнения б1 — 0. Очевидно, что
корни из 91 и © вместе также будут составлять всю совокупность
ii и что i?^ = X. Теперь мы будем различать четыре случая.
I. ф совпадает с 31 и потому Р = /?. В этом случае, очевидно,
корни из $ будут попарно обратны, и потому Р будет произ-
произведением X / 2 удвоенных сомножителей вида х2 — 2х cos to -f- 1;
так как каждый такой сомножитель равен (х — cos соJ + sin2 со, то
легко видеть, что Р при любом вещественном значении х обяза-
Неразлоэюимостъ многочлена X = хп + хп +... + Ж + 1 517
дельно принимает вещественное положительное значение. Пусть
уравнения, корнями которых являются квадраты, кубы, биквад-
биквадраты, и т. д., наконец, (п—1)-е степени корней из ф, суть Р'= О,
Р" = 0, jP" =-0,..., /><*-!) = 0, и пусть значения функций Р, Р\
Р",..., Jp(n~1\ которые они принимают при # = 1, равны соответ-
соответственно р, р', /?",.••> р(п~1); тогда, согласно сказанному перед этим,
р будет величиной положительной, и по совершенно аналогичной
иричине р\ //',... также будут положительными. Но так как р есть
значение функции A — t) A—и) A—г;)..., которое она принимает,
если в качестве ?, м, г;,... подставить корни из $, // — значение
этой же функции, которое она принимает, если вместо t, и, г;,,..
подставить квадраты этих корней, и т. д.; так как, кроме того,
значение функции при t — 1, и = 1, г; = 1, очевидно, равно 0, то
сумма р + // + /?" + ••• + р(п~~1) является целым не делящимся на
Аг числом. Кроме того, легко видеть, что Р-Р' Р"... = Xх, и потому
р.р' .р"... = Агх.
Если бы теперь все коэффициенты у J° были рациональны, то,
согласно п. 338, были бы рациональны также и все коэффициенты
у Р\ Р",...\ согласно же п. 42, все эти коэффициенты обязательно
были бы целыми числами. Поэтому и р, р\р",... были бы целыми
числами, а так как их произведение равно тгх, а их количество
п — 1 > X, то обязательно некоторые из них (по меньшей мере
п—1—X) были бы равны 1, а остальные были бы равны либо п,
либо некоторой степени числа п. Но если бы g из них были бы
равны 1, то, очевидно, имело бы место р + pr -\- ..E=g(mod тг),
и потому эта сумма заведомо не делилась бы на п. Поэтому сде-
сделанное предположение неверно.
II. Если ^5 и 31 хотя и не совпадают, но все же имеют не-
несколько общих корней, то пусть X их совокупность, и Т = 0 — урав-
уравнение, корнями которого они являются. Тогда Т будет наиболь-
наибольшим общим делителем функций Р, R (что известно из теории
уравнений). Но очевидно, что в % корни будут попарно обратными,
и потому, согласно только что доказанному, не может быть, чтобы
все коэффициенты у Т были рациональными. Однако они все были
бы рациональными (что вытекает из природы операций, посредст-
посредством которых находится наибольший общий делитель), если бы
518 Раздел VII (пп. 342-343)
были рациональными все коэффициенты у Р, а, следовательно, и
все коэффициенты у R. Поэтому наше предположение приводит
к противоречию.
III. Если U и S либо совпадают, либо по крайней мере имеют
общие корни, то по совершенно аналогичной причине не может
быть, чтобы все коэффициенты у Q были рациональны; однако они
оказались бы рациональными, если бы были рациональны все
коэффициенты у Р. Поэтому последнее невозможно.
IV. Наконец, если бы ни $ с SR, ни Q, с ©не имели общих
корней, то все корни из *g содержались бы в @, и все корни из
О,— в SR, так что было бы Р = S и Q — R. Поэтому X — PQ было
бы произведением Р и /?, т. е. произведением
+ ... + Kx + L на хх + -^- Xх + ... + -^-ж + 4- ,
откуда, полагая х = 1, мы получили бы
Но если бы все коэффициенты у Р были рациональными, а по-
потому, согласно п. 42,- также и целыми, то L, которое должно было
бы входить в последний коэффициент функции X, т. е. в 1, обя-
обязательно было бы равно +1, вследствие чего п было бы точным
квадратом. Поскольку это противоречит предположению, наше
допущение не верно.
Таким образом, из этой теоремы вытекает, что если бы X можно
было разложить на сомножители, то по крайней мере часть их
коэффициентов была бы иррациональна, т. е. определялась бы
уравнениями более высоких степеней.
Указывается цель дальнейших исследований
342
Цель дальнейших исследований, указать которую представляется
небесполезным, состоит в том, чтобы последовательно разлагать X
па все большее и большее число сомножителей, причем так, чтобы
их коэффициенты определялись при помощи уравнений по возмож-
Разбиение корней уравнения X = 0 на периоды 519
ности более низких степеней, пока мы не дойдем таким путем до
простых сомножителей, т. е. до самих корней из ?2. Именно, мы
покажем, что если число п — 1 каким-либо способом разложено на
целочисленные сомножители а, В, ^.... (которые можно считать
простыми числами), то X можно разложить на а сомножителей
степени (п—1)/<х, коэффициенты которых определяются уравне-
уравнением степени а; далее, что эти отдельные сомножители в свою
очередь могут быть разложены на р сомножителей степени
(п—1)/оф при помощи уравнения степени р и т. д., так что если
v обозначает число сомножителей a, р, ^,..., то нахождение кор-
корней из ?1 сводится к решению v уравнений степеней а, р, ^ и т. д.
Так, например, для п=17, где п — 1=2-2-2-2, придется решить
четыре квадратных, а для п = 73 — три квадратных и два куби-
кубических уравнения.
Так как в дальнейшем очень часто придется рассматривать
такие степени корня г, показатели которых в свою очередь являются
степенями, а писать такие выражения довольно громоздко, мы
в дальнейшем для облегчения изложения будем использовать сле-
следующее сокращенное обозначение: вместо г, г2, г3,... мы будем
писать [1], [2], [3],... и вообще, вместо гх, где X обозначает любое
целое число, будем писать [X]. Таким образом, подобные выраже-
выражения становятся вполне определенными только после того, как
в качестве г, т. е. [1]. взят определенный корень из ?Х Вообще же
[X], [[л] будут равны или не равны в зависимости от того, сравнимы
или не сравнимы X, (л по модулю щ далее, имеет место [0] = 1;
[Х]-]D] = [Х + (х]; [Xr=[Xv]; сумма [0] + [X] + [2Х] + ... + [(п — 1) X)
равна либо 0, либо п, в зависимости от того, не делится X на п
или делится.
Все корни из ?2
разбиваются на некоторые классы (периоды)
343
Если число g является для модуля п числом такого рода,
которые мы в разделе III называли первообразными корнями, то
п — 1 чисел 1, g, g2,..., gn~2 будут сравнимы по модулю п, быть
520 Раздел VII (п. 344)
может, только в другом порядке, с числами 1, 2, 3?..., п—1,
т. е. каждое число одного ряда имеет сравнимое с ним число во
втором ряду. Отсюда непосредственно следует, что совокупность
корней [1], [g], [g2],..., [gn~2] совпадает с Q,, и точно так же вообще
с ?1 будет совпадать любая совокупность
где X обозначает любое цел^е число, не делящееся на п. Далее,
легко видеть, в силу того, что gn~1 = 1 (mod n), что корни [Xg^],
[Xgv] будут совпадающими или различными в зависимости от того,
сравнимы [х, v по модулю п или не сравнимы.
Если теперь G есть другой первообразный корень, то корни
[1]> l8].---Agn~2] будут, с точностью до порядка расположения,
совпадать также с [1], [G],...,\Gn—2]. Но, кроме того, легко дока-
доказывается, что если е есть делитель числа п — 1, и п—1 = е/,
ge = h, Ge = H, то также и / чисел 1, /г, /г2,..., hf—1 будут (с точ-
точностью до порядка расположения) сравнимы с числами 1,//",
Я2,..., Hf~1. Действительно, если мы предположим, что С = #" (mod п),
и [L есть произвольное положительное число, которое меньше чем
/, a v — наименьший вычет числа [лоо по модулю /, то будет иметь
место ve = [хсое (mod п — 1), откуда gve = ?*<**== №е (mod n) или №^/iv,
т. е. для каждого числа второго ряда 1, Н, Я2,... в первом ряду
имеется сравнимое с ним, и наоборот. Из этого вытекает, что со-
совокупность / корней [1], [/г], [/г2],..., [h*—1] совпадает с совокуп-
совокупностью корней [1]. [Н], [Я2],..., [Я*], и, более общо, что [X], [Х/г],
[Х/г2],..., [Х/г'-1] совпадает с [X], [ХЯ], [ХЯ2],..., ]X#/-i]. Сумму 1
корней вида [X] + [Х/г] + [Х/г2] + ••• + [М^], которую нужно рас-
рассматривать как не зависящую от g, так как она не меняется, если
вместо g взять другой первообразный корень, мы будем обозначать
через (/, X), а совокупность этих корней будем называть периодом
(/, X), причем порядок расположения корней не принимается во
внимание *. При представлении такого периода будет целесообразно
заменять отдельные корни, из которых он состоит, их простей-
* Может случиться, что мы, когда из-за этого не смогут возникнуть недора-
недоразумения, будем в дальнейшем называть саму сумму численным значением перио-
периода или просто периодом.
Теоремы о периодах корней уравнения X = 0 521
шими выражениями, а именно, вместо чисел X, Х/г, Х/г2,... подстав-
подставлять их наименьшие вычеты по модулю п, по величине которых
можно при желании также и упорядочивать слагаемые периода.
Пример. Для п = 19, когда в качестве первообразного корня
взято число 2, период F, 1) состоит из корней [1], [8], [64], [512],
[4096], [32 768] или из корней [1], [7], [8], [И], [12], [18]. Точно
так же период F, 2) состоит из корней [2], [3], [5], [14], [16]. [17].
Период F, 3) совпадает с предыдущим. Период F, 4) содержит
корни [4], [6], [9], [10], [13], [15].
Различные теоремы о периодах корней из О
344
Относительно этих периодов сразу же можно сделать следую-
следующие замечания.
I. Так как Х/г^ == X, Х/г^1 == Х/г,... (modn), то очевидно, что (/, Х/г),
(/, Х/г2),... будут состоять из тех же корней, что и (/, X); таким
образом, если [X'] обозначает любой корень из периода (/, X) то
этот период будет полностью совпадать с периодом (/, X'). Если
поэтому два периода, содержащие одинаковое число корней (такие
периоды мы будем называть однотипными) имеют хотя бы один
общий корень, то они, очевидно, будут совпадать. Следовательно,
не может быть, чтобы в одном из двух однотипных периодов со-
содержались какие-нибудь два корня, в то время как в другом
находится только один из них; далее, ясно, что если два корня
[X], [X'] принадлежат одному и тому же периоду из / членов, то
значение выражения — (mod n) сравнимо с некоторой степенью
числа /г, т. е. что можно положить X' == Xgve (mod n).
II. Если f = n—1, е = 1, то период (/,1), очевидно, совпадает
с О; во всех остальных случаях О состоит из периодов (/, 1), (/, g),
(/, g2),..., (/, ge~~x). Поэтому эти периоды полностью различны, и
ясно, что всякий другой однотипный период (/, X) совпадает с одним
из указанных, если только [X] принадлежит к Q, т. е. если X не
делится на п. Период (/, 0) или (/, kri) состоит из / единиц. Точно
так же легко видеть, что если X является не делящимся на п
522 Раздел VII (п. 345)
числом, то совокупность е периодов (/, X), (/, Xg), (/, Х^2),..., (/, Х^)
совпадает с О. Так, например, для п == 19, / = 6 совокупность ?}
состоит из трех периодов F, 1), F, 2), F, 4), и к любому из них
может быть сведен любой другой, кроме F, 0).
III. Если п—1 есть произведение трех положительных чисел
а, Ь, с, то очевидно, что каждый период из be членов состоит из Ъ
периодов по с членов в каждом, а именно, (be, X) состоит из (с, X),
(c,Xga), (c,Xg2a),..., (с, Xgab~a), вследствие чего последние называются
содержащимися в первых. Так, например, для п = 19 период F, 1)
состоит из трех периодов B, 1), B, 8), B, 7), первый из которых
содержит корни г, г18, второй—корни г8, г11, и третий — корни
345
Теорема. Пусть (/, X), (/, ц) суть два однотипных, совпадающих
или различных периода, и пусть (/, X) состоит из корней [X], [X'],
[X"],... Тогда произведение (/, X) и (/, (х) является суммой f однотип-
однотипных периодов, именно, равно
{f, X + (х) + (/, X' + (х) + (/, X" + v,) + m.. = W.
Доказательство. Пусть, как и раньше, п—1 = ef, g — первооб-
первообразный корень по модулю п и h = ge, так что, согласно предыду-
предыдущему, (/, X) = (/, Х/г) = (/, 'kh2) = ... Тогда искомое произведение
равно
W-(f^) + №Щ №*(№*
т. е. равно
[* + {*] + [М + [л]
+ [Х/г2 + [л/г2] + [Х/г8 + [л/г2] + ... +
последнее выражение всего содержит /2 корней. Если теперь сло-
сложить здесь отдельные вертикальные ряды, то мы, очевидно, по-
получим
(/, X + [*) f (/. Х/г + A) + - + (/, Wt>-i + ft),
и легко видеть, что это выражение совпадает с W, так как числа
Теоремы о периодах корней уравнения X = 0 523
X, X', X",..., по предположению, сравнимы (в каком порядке — безраз-
безразлично) по модулю п с числами X, Х/г, Хй2,..., Х/^-1 и потому также
числа
Х + [Х, Х' + (л, Г+ [*,...
должны быть сравнимы с числами
X + (л, Х/г + (л, Х/г2 + (л,..., Х/г/-1 + [х-
if этой теореме мы добавим несколько дополнений.
I. Если к обозначает некоторое целое число, то произведение
(/, к\) на (/, к[ь) равно
(/, к (X + ;л)) + (/, к (X' + р)) + (/, Л (X" + ц)) + ...
II. Так как отдельные части, из которых состоит И^, совпадают
либо с суммой (/,0), которая равна /, либо с одной из сумм (/, 1),
(/»#)» (Ag2)»"-^/,^-1), то ^ можно привести к виду
W = af + b (/, 1) + V (/, g) + fe" (/, g2) + ... + 6(e-1} (/< ^e-j),
где коэффициенты a, fc, fc',... являются положительными целыми
числами (некоторые из которых могут быть равны 0). Далее, ясно,
что произведение (/, к\) на (/, к\ь) равно
я/ + Ъ (/, А) + V (/, Ag) + ... + №-!> (/, %e-i).
Например, для п = 19 произведение суммы F, 1) на себя же,
т. е. квадрат этой суммы равен F,2) +F, 8) +F, 9) +F, 12) +F, 13) +
+ F, 19) = 6 + 2 F, 1) + F, 2) + 2 F, 4).
III. Так как произведение отдельных частей W и однотипного
с рассмотренным выше периодом (/, v) может быть представлено
л аналогичном виде, то ясно, что и произведение трех периодов
(/,Х), (/,[х), (/, v) представляется в виде с/ + d(/, 1) + ...
...+б#е-~1>(/, g6), и что коэффициенты с, d,... будут целыми положи-
положительными числами (или равны 0), и, кроме того, для любого целого
значения к имеет место
= cf + d(f, к) + d' (/, Ag) + ....
Точно так же эта теорема может быть распространена на лю-
любое число однотипных периодов, причем безразлично, являются ли
524 Раздел VII (п.
эти периоды все различными или же они частично или полностью
совпадают между собой.
IV. Из этого мы заключаем, что если в целой рациональной
алгебраической функции F = <р (?, и, г;,...) подставить вместо пере-
переменных t,u,v,... соответственно однотипные периоды (/, X), (/, (х),
(/,v),..., то значение этой функции представится в виде
A + B(fA) + B' (/, g) + В" (/, g2) + ... + B(e-D (/, ge-l),
причем коэффициенты Л, i?, 2?',.-- все будут целыми числами, если
являются целыми все постоянные коэффициенты у F\ если же
вместо t, гг, г;.... подставить соответственно (/, &Х),(/, к\л), (/, Av),...,
то значение F примет вид А -\- В (f, к) -\- В' (/, kg) +....
346
Теорема. Предполагая, что X есть we делящееся на п число и
обозначая ради краткости (/, X) через р, мы доказываем, что каж-
каждый другой однотипный с (/, X) период (/, (л), где [л также предпо-
предполагается не делящимся на п, приводится к виду
где коэффициенты ос, р,... являются определенными рациональными
величинами.
Доказательство. Обозначим для краткости периоды (/, \g), (/, Xg2),
(/, Xg3),..., (/, Xge~x), число которых равно е—1 и с одним из ко-
которых обязательно совпадает период (/, (л), через р',р"} /?"',..• .
Тогда мы тотчас же получаем равенство
(I) 0 = 1+р + р' + р* + рГ' + ...
Если же мы по правилам предыдущего пункта вычислим зна-
значения степеней числа р до (е—1)-й, то получим еще е — 2 ра-
равенств вида
(II) 0 = р* + А + ар + а'р1 + а"р" + а"'р" + ...,
(III) 0 = р* + В + Ър + Ъ'р' + Ъ"р" + Ъ'"р"' + ...,
(IV) 0 = р* + С + ср + с'р' + с"р" + сГ'рГ* + ...,
где все коэффициенты -4, а, а',..., #, Ь, 6',... являются целыми
числами и не зависят (что и само по себе очевидно, а также не-
Теоремы о периодах корней уравнения X = 0 525
посредственно следует из предыдущего пункта) от X; таким обра-
образом, указанные равенства остаются справедливыми, если вместо X
подставить любое другое значение; это замечание распространяется,
очевидно, также и на равенство (I), если только считать X не
делящимся на п.
Положим (/, (х) = р', ибо легко видеть, что если (/, [х),... совпа-
совпадает с некоторым другим периодом из р", р'"',..., то все равно
остаются применимыми следующие рассуждения. Так как число
уравнений (I), (II), (Ш),... равно е—1, то величины р\ //",...,
число которых равно е—2, могут быть при помощи известных
методов отсюда исключены, после чего получится свободное от них
уравнение вида
(Z) 0 - 31 + S5jo + ?р2 -Ь ... + Жре-1 +Ыр',
причем можно попутно добиться того, что все коэффициенты 91,
35,..., 9Z будут целыми числами, хотя бы одно из которых не равно
нулю. Если теперь, например, 9} не равно 0, то отсюда тотчас же
следует, что р' определяется именно тем способом, как утверж-
утверждается в теореме. Таким образом, нам остается только доказать,
что 9Z не может быть равно 0.
Если мы предположим, что 9} = 0, то будет удовлетворяться
уравнение (Z): $Лре~1+ ... + 95/?+ 91=0, — а так как его степень за-
заведомо не может превосходить (е — 1), то ему могут удовлетворять
не более чем е—1 различных значений р. Но так как уравнения,
из которых выведено уравнение (Z), не зависят от X, то ясно,
что и (Z) не зависит от X, т. е. сохраняется, какое бы вместо
X ни подставить целое не делящееся на п число. Поэтому урав-
уравнение (Z) будет удовлетворяться, какую бы сумму (/, 1), (/, g),
(/, g2),..., (/. ge~x) ни подставить вместо р, откуда сразу следует,
что эти суммы не могут быть все различны, а что по крайней
мере две из них должны быть равны. Пусть одна из этих равных
сумм содержит корни [С], [С']? [С"],..., а другая — корни [yj], [y]'],
[y]"]?... предположим (это допустимо), что все числа С, С, С",...,
т], у]г, 7]",.-- положительны и меньше чем п\ очевидно, что они
также будут все различны и не равны 0, Если функцию
526 Раздел VII (п. 347)
старший член которой имеет степень не более высокую чем хп~ху
обозначить через Y, то, очевидно, при х = [1] будет иметь место
У = 0; поэтому Y содержит сомножитель х — [1], причем этот со-
сомножитель будет у Y общим с той функцией, которую мы ранее
обозначали через X. Но легко показать, что это невозможно. Дей-
Действительно, если бы Y и X имели какой-нибудь общий сомножи-
сомножитель, то наибольший общий делитель функций X, Y (то что он
имеет степень меньшую чем п, немедленно следует из того, что У
делится на х) имел бы сплошь рациональные коэффициенты, что
сразу вытекает из природы операций, при помощи которых нахо-
находится наибольший общий делитель двух функций, все коэффици-
коэффициенты которых рациональны. Однако в п. 341 мы показали, что X
не может содержать сомножителей степени ниже п — 1, все коэф-
коэффициенты которых рациональны. Следовательно, предположение,
что 31 = 0, не может быть правильным.
Пример. Для п =» 19, / = 6 будет р2= 6 + 2р + р'+ 2р"', отсюда
и из O = l-fjD + pfJr р" мы находим, что р'= 4 — р2, р"= — 5 —
— Р + Р2', следовательно,
F, 2)= 4 - F,1J, F, 4) = - 5 - F, 1) + F, IJ,
F, 4)= 4 - F, 2J, F, 1) = - 5 - F, 2) + F, 2J,
F, 1)= 4 - F, 4J, F, 2) = - 5 - F, 4) + F, 4J.
347
Теорема. Если F = cp(t, и, г;,...) есть симметрическая* целая ра-
рациональная алгебраическая функция от f переменных t, и, г;,..., и
если е нее вместо этих переменных подставить f корней, содержа-
содержащихся в периоде (/, X), то значение F, в соответствии с п. 340,
* Симметрическими функциями, как известно, называются такие функции,
которые содержат все переменные одинаковым образом, или, точнее, которые
не меняются, как бы мы не переставляли между собой переменные; такими
функциями являются, например, сумма всех переменных, произведение
всех переменных, сумма всевозможных попарных произведений переменных
и т. д.
Теоремы о периодах корней уравнения X = 0 527
можно представить в виде
А + А'[1] + А"[2] + ... = W.
Тогда корни, которые в этом выражении принадлежат одному и
тому же периоду из f членов, будут иметь равные коэффициенты.
Доказательство. Пусть [р], [q]—два корня, принадлежащие
одному и тому же периоду и пусть р, q положительны и меньше
чем п\ тогда нужно доказать, что [р] и [q] имеют в выражении
для W одинаковые коэффициенты. Пусть q = pgve (modn); далее,
пусть содержащиеся в (/, X) корни суть [X], [X7], [X"],..., где числа
X, X', X",... предполагаются положительными и меньшими чем п\
наконец, пусть наименьшие положительные вычеты чисел Х^Уе,
X'gve, X"gve,.-- по модулю п суть соответственно [л, (л/, (л",..-, эти
числа, очевидно, совпадают с числами X, X', X",..., только взятыми
в другом порядке. Тогда из п. 340 вытекает, что выражение
принимает вид
А + Af [gvej + A" [2g"*] +..., или А + А' [9'] + А" [8^] +...= (W),
где 6', 0",... обозначают наименьшие вычеты чисел gve, 2gve,... no
модулю п, откуда видно, что [q] имеет в [W] такой же коэффици-
коэффициент, что и [р] в [W]. Но легко видеть, что при раскрытии выра-
выражения (/) получается тот же результат, что и при раскрытии
выражения ср([[л], [[л'], [[л"],...), так как (x = Xgve, (л/еееХ7^,...; а по-
последнее выражение в свою очередь дает такой же результат, как
и <р(М» 1^']» [^Iv-)' так как Iх» V^'i l**")-- отличаются от X, X', X",.--
только порядком расположения, а для симметрической функции
это не имеет значения. Отсюда мы заключаем, что W полностью
совпадает с W, так что корень [q] имеет в W тот же коэффици-
коэффициент, что и [р].
Поэтому W, очевидно, может быть представлено в виде
A + a(f,l) + а'(/, g) + аж(/, g2) + ...+ а^) (/, g^),
где коэффициенты Л, а,..., а<е—D являются определенными величи-
величинами, которые, кроме того, будут целыми числами, если являются
целыми все рациональные коэффициенты у F. Так, например, если
528 Раздел VII (пп. 348-349)
72 = 19, / = 6, X = 1, и 9 обозначает сумму всевозможных попар-
попарных произведений переменных, то значение ср можно представить
в виде 3 + F, 1) + F,4).
Далее, легко видеть, что если мы затем подставим вместо t9
и, v,... корни из другого периода (/, АХ), то значение F будет равно
А + а (/, к) + а' (/, kg) + а"(/, %2) + ...
348
Так как у каждого уравнения
х*— ах*-1+ $xf~2— fxf-3+ ... = О
коэффициенты а, C, ^,... являются симметричными функциями кор-
корней, а именно, а — суммой всех корней, В — суммой всевозмож-
всевозможных произведений корней по два, ?— суммой всевозможных их
произведений по три и т. д., то в уравнении, корнями которого
являются корни, содержащиеся в периоде (/, X), первый коэффи-
коэффициент равен (/, X), в то время как каждый из остальных может
быть представлен в виде
где все числа А, а, а',... целые; и, кроме того, ясно, что уравне-
уравнение, корнями которого являются корни, содержащиеся в некотором
другом периоде (/, АХ), получается из указанного уравнения, если
заменить в нем коэффициент (/, 1) на (/, к), (/, g)— на (/, kg), и
вообще (/,/?) — на (/, кр). Таким образом, можно указать е урав-
уравнений z = 0, z'=0, z"=0,..., корнями которых являются корни,
содержащиеся соответственно в (/, 1), (/, g), (/, g2),..., если только
известно е сумм (/,1), (/, g) (/, g2),..., или даже если найдена
только одна из этих сумм, так как, согласно п. 346, по одной из
них можно при помощи рациональных операций определить и все
остальные. При этом мы одновременно получаем разложение функции
X на е сомножителей степени /; действительно, произведение функ-
функций z, z'', z"',..., очевидно, равно X.
Пример. Для 72 — 19 сумма всех корней из периода F, 1) равна
F,1) = а; сумма произведений этих корней по два будет равна
Теоремы о периодах корней уравнения X = 0 529
3 + F,1) -f F, 4) = Р; аналогично находим, что сумма произведений
корней по три равна 2 + 2 F,1) + F, 2) = у, сумма произведений
корней по четыре равна 3 + F, 1) + F, 4) = 8, сумма произ-
произведений корней по пять равна F, 1) = е, и произведение всех кор-
корней равно 1. Тем самым уравнение
z = х6— ажБ+ рж4— чх3+ 8ж2— sx +1 = 0
охватывает все корни, содержащиеся в F, 1). Если теперь в коэф-
коэффициентах ос, р, 7^--вместо F, 1), F, 2), F,3) подставить соответ-
соответственно F,2), F,4), F,1), то получится уравнение z'=0, которое
охватывает корни, содержащиеся в F, 2), а если проделать такую же
перестановку еще раз, то получится уравнение z"= 0, которое будет
охватывать корни, содержащиеся в F, 4), и произведение zz'z" будет
равно X.
349
В большинстве случаев, особенно, когда /—большое число,
удобнее находить коэффициенты а, р, ^,... при помощи теоремы
Ньютона из сумм степеней корней. Именно, непосредственно
ясно, что сумма квадратов корней, содержащихся в (/, X), равна
(/, 2Х), сумма кубов равна (/, ЗХ) и т. д. Поэтому, если ради крат-
краткости вместо (/, X) (/, 2Х), (/, ЗХ),... писать соответственно q, q\
<f,..., то
a = g, 2p = ag — q\ 3T = $q — ag'+ g^,...,
причем произведения из двух периодов, согласно п. 345, тотчас
же должны быть преобразованы в суммы периодов. Так, в нашем
примере, если вместо F,1), F,2), F,4) написать соответственно
р, р', р", то величины q, q', q", q"', q"", qH'" будут соответственно
равны p, p' p', p"', p', p"\ поэтому
= C + p + p»)p — pp>+ p>= 6 + 6p + 3p',
= B + 2p + p')p-C + p + p") p'+ pp'- pT= 12 + Ap
и т. д.
530 Раздел VII (пп. 350-351)
Заметим, что таким способом нам нужно вычислять только по-
половину коэффициентов; действительно, не трудно доказать, что
коэффициенты, равноудаленные от концов, равны, именно, послед-
последний коэффициент равен 1; предпоследний равен а, третий от конца
равен р и т. д., т. е. последние коэффициенты получаются из пер-
первых заменой (/, 1), (/, g),... на (/,— 1), (/,— #),... или на (/, п — 1),
(/, п — #),... Первый случай имеет место, когда / четно, а второй,
когда / нечетно; последний же коэффициент всегда равен 1. До-
Доказательство этого факта основывается на теореме п. 79; однако,
ради краткости, мы не будем здесь на нем останавливаться.
350
Теорема. Пусть п—1 есть произведение трех целых положи-
положительных чисел а, р, у; пусть, далее, период (р^, ^)» который имеет
Рт членов, состоит из р меньших периодов, имеющих по т членов,
именно из (*]fi X), (т> X'), (f, X"),...; предположим еще, что если в неко-
некоторой функции от р переменных, обладающей свойством, указанным
в п. 347, именно, в функции F = <p(t, и, v,...), вместо переменных
t, и, у,... подставить соответственно суммы (f, X), G, X'), (т, Х"),...,
то значение функции приводится по правилам из п. 345, IV к виду
А + а(Т, 1) + а' (Т, g) + ... + а«> (т, g«P-«) + ...+ а«» (Т, g*0-i)= W.
Тогда я утверждаю, что если F есть симметрическая функция, то
те периоды в W, которые содержатся в одном и том же периоде
из р? членов, т. в., вообще, периоды вида (т, g*) и (т, gav+^), г^е v
обозначает некоторое целое число, будут иметь одинаковые коэф-
коэффициенты.
Доказательство. Так как периоды (р?» Xga) и (р^, X) совпадают,
то меньшие периоды G, ^ga)] (т» ^/grOtO (т» ^'/^а)'--- из которых, оче-
очевидно, состоит первый период, будут обязательно совпадать с теми,
из которых состоит другой период, лишь расположенными в другом
порядке. Если, таким образом, предположить, что после того как
первые подставлены вместо t, и, г;,..., функция F переходит в W,
то W будет совпадать с W. Но, согласно п. 347,
W'= A +a(T, ga)+a'(
= А + а (Т, g«) + а'
Теоремы о периодах корней уравнения X = 0 531
При этом, так как это выражение должно совпадать с W, то пер-
первый, второй, третий и т. д. коэффициент у W (считая от а)
обязательно совпадает с (a -f 1)-м, (а -f 2)-м, (а + 3)-м и т. д.,
откуда легко заключить, что, вообще, коэффициенты периодов
(Т. в*)> (Т» ga+fx); (Т. g2a+{x),-.., (T> gva+fx), которые стоят на ([х + 1)-мг
(оо + (л-+ 1)-м, Bа + р + 1)-м,..., (va + [х + 1)-м месте, должны сов-
совпадать между собой. Это и требовалось доказать.
Из этого вытекает, что W можно привести к виду
А + а (рт, 1) + а' (рт, g) + ... + a(«-D CT, g«-i),
где все коэффициенты Л, а,... будут целыми числами, если явля-
являются целыми все постоянные коэффициенты у F. Далее, легко ви-
видеть, что если после этого подставить в функцию F, вместо пере-
переменных, р периодов (состоящих из ^ членов), которые содержатся
в другом периоде из ^ членов, например, в (j^, X&), и которые
тогда суть, очевидно, (у, Х&), (»у, Х'А), (*у, Х^А),..., то получающееся
при этом значение будет иметь вид
А + а (рт, Л) + a' (pT, gu) + ...+ а*** (Рт, ga"x *)•
Далее ясно, что теорема остается верной и в том (лучае, когда
оо=1, т. е. ^ = п — 1; именно, здесь все коэффициенты
у W равны и потому W приводится к виду Л+афт, 1).
351
Итак, если мы сохраним все обозначения предыдущего пункта,
то ясно, что отдельные коэффициенты уравнения, корнями ко-
которого являются р сумм (^, X), (»у, X'), (т, X"),...,могут быть пред-
представлены в виде
А + а (рТ, 1) + а' (рТ, g) + ... + a<a-D (pT. §a"i),
и что все числа Л, а,... будут целыми, а уравнение, корнями ко-
которого служат р периодов из у членов, содержащиеся в некотором
другом периоде (Рт, АХ), получается из первого уравнения, если
всюду в его коэффициентах вместо каждого периода (Рт, [л) подста-
подставить (Рт, А[х). Если, таким образом, a = 1, то все р периодов из т
532 Раздел VII (п. 352)
членов определяются уравнением ^-й степени, отдельные коэффи-
коэффициенты которого приводятся к виду А + а ф*(, 1) и поэтому явля-
являются известными величинами, так как (^» 1) — (п— 1Д) — — !•
Ь'сли же ос^>1, то коэффициенты уравнения, корнями которого
являются все периоды из ^ членов, содержащиеся в некотором
заданном периоде из *у членов, будут известны, как только будут
известны численные значения всех а периодов из ^ членов. Впро-
Впрочем, часто, особенно когда р не очень мало, вычисление коэффи-
коэффициентов этих уравнений удобнее производить, находя сначала
суммы степеней корней, и уже из них так же, как в п. 349, полу-
получать при помощи теоремы Ньютона значения коэффициентов.
Пример I. Найдем для ^г = 19 уравнение, корнями которого яв-
являются суммы F,1), F,2), F,4). Если мы обозначим эти корни
соответственно через р, //, р", а искомое уравнение через
ОС jfi.30 j JljOO С/ — U)
TO
A=p + p'+ p", В = pp'+ pp"+ p'p", С = pp'p".
Поэтому
A = A8, 1) = -1;
далее мы имеем
PP'=p + 2p'+ 3p", pp"= 2p + 3//+ p", p'pr= 3p + p'+ 2p",
и потому
B = 6(p+p'+ p") = 6 A8, 1) = - 6;
наконец,
С = (р + 2р'+ Зр") р"= 3 F, 0) -\ И (р + р'+ р") = 18 - И = 7.
Поэтому искомым уравнением является
х3+х2— 6а; — 7 = 0.
Если мы применим здесь другой метод, то получим
р + р'+р"= — 1,
р*= 6 + 2р + р'+ 2р", р'*= 6 + 2р'+ р"+ 2р, р"*= 6 + 2р"+р+ 2р',
поэтому
Р*+ Р'2+ Р= 18 + 5 (р + р'+ f) = 13,
Решение уравнения X = 0 533
и точно так же
рЧ Р'3+ p"s = 36 + 34 (р + р'+ р") = 2.
Отсюда при помощи теоремы Ньютона мы получим то же
уравнение, что и перед этим.
II. Найдем для п = 19 уравнение, корнями которого являются
суммы B,1), B,7), B,8). Если обозначить их соответственно через
q, q', q", то мы найдем
<7 + Ч'+ Я"= F, 1), qq'+ qq"+q'q"= F, 1) + F, 4), qq'q*= 2 + F, 2);
поэтому, если сохранить обозначения предыдущего пункта, то ис-
искомое уравнение запишется в виде
х3— рх2+ (р + р") х — 2 — р' = 0.
Уравнение, корнями которого являются содержащиеся в F,2)
суммы B, 2), B,3), B, 5), получается из предыдущего, если вместо
р, р\р" подставить соответственно р', р", р, а если эту же подста-
подстановку произвести еще раз, то получится уравнение, корнями ко-
которого являются содержащиеся в F,4) суммы B,4), B,6). B, 9)*
На предыдущих исследованиях
основывается решение уравнения Ж = 0
352
Предыдущие теоремы вместе с указанными следствиями из них
содержат основные пункты всей теории, и метод нахождения кор-
корней О может быть изложен теперь в немногих словах.
Прежде всего нужно выбрать число g, которое является по модулю
п первообразным корнем, и найти наименьшие вычеты степе-
степеней g до gn~2 по модулю п. Разложим п — 1 на множители, при-
причем, если желательно свести проблему к уравнениям по возможно-
возможности более низкой степени, то на простые; пусть эти сомножители
(в совершено произвольном порядке) суть а, р, т,-»> С; положим
__ = рт...С = а, -^р- =Т.. .С = &,...
Разобьем все корни из ?2 на а периодов из а членов, каждый
из них снова разобьем на {3 периодов из Ъ членов, каждый из них
534 Раздел VII (п. 352)
снова на *у периодов и т. д. Найдем в соответствии с предыдущим
пунктом уравнение (А) степени а, корнями которого являются
указанные а сумм по а членов; тем самым значения указанных
сумм станут известными после решения этого уравнения.
Однако здесь возникает одна трудность, так как представля-
представляется неясным, какой из корней уравнения (^4) приравнивать каж-
каждой сумме, т. е. какой корень следует обозначить через (а,!),
какой через (a, g),~. Это затруднение можно обойти следующим
образом. Через (а, 1) можно обозначить любой корень уравнения
(^4); действительно, так как каждый корень этого уравнения яв-
является суммой а корней из ?1, причем совершенно безразлично,
какой именно корень из Q, обозначен через [1], то можно, очевидно,
предположить, что через [1] обозначен какой-то из тех корней, из
которых состоит заданный корень уравнения (^4), вследствие чего
этот корень будет равен (а, 1). Однако этим корень [1] будет оп-
определен еще не вполне, так как остается еще совершенно неопре-
неопределенным, какой именно корень из тех, что образуют (а, 1), мы
берем в качестве [1]. Но если сама сумма (а, 1) определена, то из
нее уже могут быть получены все остальные суммы из а членов
(п. 346). Отсюда тотчас же вытекает, что при решении указанного
уравнения нам достаточно найти только какой-нибудь один корень.
Для этой же цели можно применить и следующий, менее пря-
прямой, метод. Возьмем в качестве [1] некоторый определенный корень,
ГЛ1 кР . . . кР 7 g.
т.е. положим [1] —cos 1- г sin —, где целое число к выбрано про-
произвольно, однако так, что оно не делится на п\ тогда и [2], [3],...
тоже будут определенными корнями, а потому и суммы (а, 1),
(а, g),... будут определенными величинами. Если вычислить их по
таблице синусов с весьма незначительной точностью, именно с та-
такой, чтобы только иметь возможность судить, какая из них больше,
а какая меньше, то уже не останется никакой неопределенности
в вопросе о том, как обозначать отдельные корни уравнения (^4).
После того как найдены все а сумм из а членов, найдем, в
соответствии с предыдущим пунктом, уравнение (В) степени р,
корнями которого являются р сумм из Ъ членов, которые встреча-
встречаются в (а, 1); все коэффициенты этого уравнения будут известны
Решение уравнения X = 0 535
Так как еще остается произвольным, который из а — рб корней,
содержащихся в (а, 1), обозначить через [1], то любой корень
уравнения (В) можно обозначить через (Ь, 1), ибо, очевидно, можно
предположить, что в качестве [1] был выбран некоторый из Ъ кор-
корней этого уравнения. Итак, найдем посредством решения уравне-
уравнения (В) какой-нибудь один его корень, обозначим его через (&, 1)
и получим отсюда, в соответствии с п. 346, все остальные суммы
из Ъ членов. Одновременно мы имеем при этом критерий правиль-
правильности вычислений, так как всегда те суммы из Ъ членов, которые
принадлежат одному и тому же периоду из а членов, должны да-
давать известные суммы.
Во многих случаях так же просто было бы найти а — 1 осталь-
остальных уравнений [3-й степени, корнями каждого из которых
являются р сумм из Ъ членов, которые содержатся в других
периодах (a, g), (a, g2),... из а членов, и посредством решения
отыскать все корни как этих уравнений, так и уравнения (В)] од-
однако тогда, так же, как и выше, пришлось бы прибегнуть к по-
помощи таблицы синусов, чтобы определить, каким именно периодам
из Ъ членов должны быть приравнены отдельные полученные та-
таким способом корни. Впрочем, для этой цели можно применить и
много других приемов, изложить которые полностью здесь мы не
можем; лишь для случая C = 2 мы продемонстрируем один прием,
который особенно важен и легче может быть пояснен на примере,
чем при помощи теоретических рассмотрений.
После того как таким путем найдены значения всех <хВ сумм
из Ъ членов, из них совершенно таким же способом при помощи
уравнений 'у-й степени могут быть получены все а$ч сумм из с
членов. Именно, можно либо получить, согласно п. 350, только
одно уравнение ^-й степени, корнями которого являются ^ содер-
содержащихся в F, 1) сумм из с членов, затем найти один его корень,
положить его равным (с, 1) и, наконец, получить отсюда, в соот-
соответствии с п. 346, все остальные подобные суммы, либо же нужно
получить все ар уравнений ^-й степени, корнями каждого из ко-
которых являются ^ сумм из с членов, каждая из которых содер-
содержится в отдельном периоде из Ъ членов, затем решением этих
уравнений найти значения всех корней, и, наконец, определить
536 Раздел VII (п. 353)
порядок их расположения так же, как и выше, при помощи таб-
таблицы синусов или же посредством приема, иллюстрируемого при-
приведенными ниже примерами для у = 2.
Продолжая таким же образом, мы, очевидно, в конце концов
получим все {п—1)/С сумм из С членов; если же получить, в соот-
соответствии с п. 348, уравнение степени С, корнями которого явля-
являются С содержащихся в (С, 1) корней из ?1, то все коэффициенты
этого уравнения будут известными величинами; если при решении
его мы найдем какой-нибудь один корень, то его можно будет по-
положить равным [1], и все остальные корни из ?1 будут его степе-
степенями. Если угодно, можно, решив указанное уравнение, получить
также и все его корни, а затем, решая —= 1 других уравне-
уравнений С-степени, корнями каждого из которых являются С корнейг
содержащихся в отдельных периодах из С членов, найти и все
остальные корни из Q,.
Отметим, что после того как решено первое уравнение (А),
т. е. получены значения всех а сумм из а членов, тем самым не-
немедленно получается разложение функции X на а сомножителей
степени а в соответствии с п. 348, и, далее, после решения урав-
уравнения (J3), т. е. после нахождения значений всех оф сумм из Ь
членов, каждый из указанных сомножителей в свою очередь рас-
распадается на р сомножителей, т. е. X распадается на ар сомножи-
сомножителей степени Ь, и т. д.
353
Первый пример для п = 19. Так как здесь п — 1 = 3-3-2, то
получение корней Q, сводится к решению двух кубических и од-
одного квадратного уравнений. Этот пример понять будет особенно
легко благодаря тому, что необходимые операции в большинстве
случаев уже встречались ранее. Если в качестве первообразного
корня взять число 2, то его степени будут иметь следующие наи-
наименьшие вычеты (показатели степеней написаны в первом ряду, а
наименьшие вычеты во втором ряду под ними):
0 12 3 4 5 6 7 8 9 10 И 12 13 14 15 16 17
1 2 4 8 16 13 7 14 9 18 17 15 И 3 6 12 5 10.
Решение уравнения X = О
537
Отсюда мы, в соответствии с пп. 344, 345, легко находим сле-
следующее разбиение всех корней из О, на три периода, состоящих
каждый из шести членов, причем эти периоды в свою очередь рас-
распадаются каждый на три периода, состоящих из двух членов:
(B,1)...[1], [18]
F,1) B, 8)...[81, [11]
[B, 7) ...[7], [12]
B,2) ...[2], [17]
О = A8,1){ F,2) B,16)...[3|, [16]
(B,14) ...[5], [14]
B,4) ...[4], [15]
B,13)...[6], [13]
B,19)...19], [10].
Уравнение (^4), корнями которого являются суммы F,1), F,2),
F, 4), есть
один из его корней приближенно равен —1,2218761623. Если
взять его в качестве F,1), то
F, 2} =А— F,1J^2,5070186441,
F, 4) - — 5 — F,1) + F,1Jж — 2,2851424818.
После этого X распадется на три сомножителя шестой степени,
которые можно найти в соответствии с п. 348.
В качестве уравнения (В), корнями которого являются суммы
B,1), B,7), B,8), получается следующее уравнение:
хз_ F? 1} Х2 + [F> 1} + F> 4)] х _ 2 - F, 2) = 0,
или, приближенно,
Xs + 1,2218761623х2 — 3,5070186441ж — 4,5070186441 = 0;
находим, что один корень ях —1,3545631433; обозначим его
через B,1). Но при помощи метода п. 346 мы находим следующие-
уравнения, где ради краткости вместо B,1) написано q:
B,2) = 22_2; B,3) = 98 — 39;
B, 5) = <76- 5?3 + 5?;
538 Раздел VII (п. 353)
B, 6) - q* — 6q* + 9?а — 2; B, 1) = q1 - lq* + Uq* - 7q;
B, 8) = q* — 8q* + 20g4 — I6q* + 2;
B, 9) = q9 — 9?7 + 27g5 — 30?3 + 9?.
Удобнее, чем по правилам п. 346, эти уравнения в данном слу-
случае могут быть получены посредством следующих рассуждений.
Положим
кР кР
[1] ^cos-jg + г sin -^q ;
тогда
r4Ql 18/cP . . . 18/сР кР . . кР
[18] = cos -jg-+ ism~ig~ = cosl9~~ iSinl9 ' и П0ЭТ0МУ
о кР . П1 \кР . . . UP
= I cos -тп \ точно так же и вообще [к] = cos -jk- + l sm -jq- • и по-
потому B, X) = [к] + [18Х] - [X] + [- X] = 2 cos ^
Поэтому, если -|- = cos со, то B,2) = 2 cos 2со, B, 3) = 2 cos Зсо, и
т. д., откуда по известным формулам для косинусов кратных углов
выводятся те же формулы, что и выше. Из последних формул мы
получаем следующие численные значения:
B,2)^ — 0,1651586909
B,3) ж 1,5782810188
B, 4) ж —1,9727226068
B, 5) ж 1,0938963162
B,6)ж 0,4909709743
B, 7) ж —1,7589475024
B, 8)ж 1,8916344834
B,9)^ — 0,8033908493
Значения B,7), B,8) могут быть также выведены из уравнения
{В), для которого эти значения являются двумя остальными кор-
корнями, причем вопрос о том, который из них есть B, 7), а который
B, 8), может быть решен либо приближенным вычислением по ука-
указанным перед этим формулам, либо при помощи таблицы синусов,
которая уже при самом поверхностном ее использовании пока-
зывает, что B,1) = 2 cos со, если положить со = г^Р, вследствие чего
1У
^ = 2cos^ и B, 8) = 2cos ^ = 2cos^ .
Точно так же можно найти суммы B, 2), B, 3), B, 5) из уравнения
Решение уравнения X = 0 539
хг _ (б, 2) ж2 + [F,1) + F, 2)] х — 2 — F, 4) = О,
корнями которого они являются, и сомнение в том, какие корни
надо положить равными каким из указанных сумм, разрешается
точно таким же образом, как и перед этим; и подобно этому при
помощи уравнения
хз _ (б, 4) х1 + [F, 2) + F, 4)] х — 2 — F,1) = О
могут быть найдены суммы B,4), B,6) B,9).
Наконец, [1] и [18] являются корнями уравнения
х2 — B, 1)ж + 1 =0,
1 / 1 1
причем один из них равен -у^' ^ ~Ь *у ^— Т^' ^ ~ Т
-Т<2'2)' а другоЙ равен уB,1)-
откуда получается, что их численные значения приближенно равны
— 0,6772815716+ 0,7357239107г.
Шестнадцать остальных значений могут быть найдены либо посред-
посредством возведения в степень одного из этих двух корней, либо по-
посредством решения восьми других подобных уравнений; применяя
первый метод, нужно либо по таблице синусов, либо при помощи
поясняемого на следующем примере способа выя нять, для какого
из двух корней мнимая часть имеет положительный знак, а для
какого отрицательный. Таким способом находятся следующие зна-
значения, причем верхний знак соответствует первому, а нижний —
второму корню:
[1] и [18] ж — 0,6772815716 +0,7357239107*',
[2] и [17] ж —0,0825793455 =F0,9965844930i\
[3] и [16] ж 0,7891405094 ±0,6142127127i\
[4] и [15] ж —0,9863613034 ±0Д645945903г\
[5] и [14] ж 0,5469481581 + 0,83716647831,
[6] и [13] ж 0,2454854871 ±0,9694002659*,
[7] и [12] « — 0,8794737512 + 0,4759473930г,
[8] и [И] ж 0,9458172417 + 0,3246994692*',
[9] и [10] да —0,4016954247 ±0,9157733267*.
540
Раздел VII (п. 354)
Второй пример для и = 17. Здесь мы имеем п —1 = 2-2-2-2,
так что вычисление корней из Q, сводится к решению четырех
квадратных уравнений. В качестве первообразного корня мы возь-
возьмем здесь число 3, степени которого имеют по модулю 17 следую-
следующие вычеты:
0 12 3 4 5 6 7 8 9 10 11 12 13 14 15
1 3 9 10 13 5 15 И 16 14 8 7 4 12 2 6.
Отсюда получаются следующие разбиения совокупности ?1 на два
периода по восемь членов, четыре периода по четыре члена, восемь
периодов по два члена:
(8, 1)
(8,3)
D
D'
D 3)
B'
B,
B' 9) *
1B'
\B, 13)
D 9) /B'
D' У) 1B, 15)
B' 3) •
B, 5) .
B, 10)
[4], [13]
[8], [9]
12], [15]
[3], [14]
151. ]12]
[7], [10]
[6], [И].
Уравнение (А), корнями которого являются суммы (8, 1), (8,3),
согласно правилам п. 351, оказывается следующим: ж2 + х — 4 = 0;
его корни равны — у + у/17 « 1,5615528128 и _±_iyT7«
« — 2,5615528128; первый из них мы положим равным (8, 1). тогда
второй обязательно равен (8, 3).
Далее, в качестве уравнения, корнями которого являются
суммы D, 1) и D, 9), получается следующее уравнение (В):
х1— (8, 1)х— 1 =0; корни его суть |(8,1)± 1/4+(8, lJ^.
ж у (8,1)+у /12+ 3(8,1) + 4(8, 3); тот корень, у которого перед
радикалом стоит положительный знак и который ж 2,0494811777,
мы примем за D, 1), после чего другой корень, у которого вели-
величина радикала взята отрицательной, и численное значение которого
Решение уравнения X = 0 541
« —0,4879283649, автоматически должен быть положен равным
D,9). Остальные суммы из четырех членов, именно, D,3) и D,10),
могут быть определены двояким способом. А именно, во-первых,
— по методу п. 346, который дает следующие формулы, где для
краткости вместо D, 1) пишется р:
D, 3) = - 1 + Зр - 1 р3 ж 0,3441507314,
D, 10) = |- + 2р — р2 — 4- р3 ж — 2,9057035442.
Этот же метод приводит также к формуле D, 9) = — 1 — 6р +
+ Р2 Н~ Т^3? из которой мы находим то же самое значение, которое
мы только что привели. Во-вторых, суммы D, 3), D, 10) можно
также определить посредством решения уравнения, корнями кото-
которого они являются. Это уравнение есть х2— (8, 3) х— 1 = 0,
поэтому его корни суть 1(8, 3) ±|-|А + (8, ЗJ, т. е. 1(8,3) +
+ \ VX12^4(8, 1)+3(8,3)и1(8,3)-1|Л2 + 4(8, 1) + 3(8, 3). А
неопределенность, какой именно из этих корней есть D, 3), а какой
есть D, 10), устраняется при помощи следующего приема, о кото-
котором мы и упоминали в п. 352. Преобразуем произведение D, 1) —
— D, 9) на D,3) — D,10), в результате чего получим 2 (8, 1) —
— 2(8, 3)*; значение этого выражения, очевидно, положительно,
а именно, равно +2|/17, и, кроме того, первый сомножитель про-
произведения тоже положителен,а именно, равен +|/2 + 3(8, 1)+4(8,3);
поэтому и второй сомножитель D, 3) — D, 10) должен обязательно
быть положительным, и потому D, 3) следует положить равным
первому корню, у которого квадратный радикал берется со зна-
знаком + , а D, 10) — второму корню. При этом, конечно, получаются
те же самые численные значения, что и выше.
* Истинная природа этого выражения такова, что это произведение в раз-
развернутом виде не содержит сумм по четыре члена, а выражается только через
суммы из восьми членов; причина этого, на которой мы здесь ради краткости не
останавливаемся, должна быть ясна для понимающего читателя.
542 Раздел VII (п. 354)
После того как все суммы из четырех членов найдены, мы пе-
переходим к определению сумм из двух членов. В качестве уравне-
уравнения (С), корнями которого являются содержащиеся в D, 1) суммы
B, 1) и B, 13), мы получаем ж2— D, 1)х + D, 3) = 0; его корни суть
|D,1)±1у-4D,3)+D,1J, или 1D,1)±1]А + D, 9)-2D, 3).
Тот корень, у которого величина радикала принимается положи-
положительной, и который приближенно равен 1,8649444588, мы полагаем
равным B, 1), так что другой корень, приближенно равный
0,1845367189, есть B, 13). Если остальные суммы из двух членов
мы захотим получить по методу п. 346, то для B, 2), B, 3), B, 4),
B, 5), B,6), B,7), B,8) можно применить те же формулы, которые
мы указали в предыдущем примере для точно так же обозначенных
величин, именно, B, 2) [или B, 15)] = B, IJ — 2, и т. д. Если же
мы предпочтем получать эти суммы попарно решением квадратных
уравнений,то для B, 9) и B,15) мы найдем уравнение х2— D, 9)х +
+ D, 10) = 0, корни которого суть ~ D. 9) ± /4+D, 1)— 2 D, 10);
а то, как здесь разобраться в вопросе с двойным знаком, реша-
решается точно так же, как выше. Именно, при преобразовании произ-
произведения B, 1) — B, 13) на B, 9) — B,15) получается — D, 1) + D, 9),
и так как это выражение, очевидно, отрицательно, а сомножитель
B,1) — B,13) положителен, то B,9) — B,15) обязательно должно
быть отрицательно, и потому в указанном перед этим выражении
верхний знак должен быть взят для B,15), а нижний — для B, 9).
Отсюда мы находим, что B, 9) = — 1,9659461994, B, 15) =
= 1,4780178344. Точно так же мы заключаем (так как произведе-
произведение B,1) —B,13) на B, 3) —B, 5) равно D, 9) —D, 10), т. е. равно
положительной величине), что сомножитель B,3) — B,5) положи-
положителен.После этого таким же вычислением, как и раньше, мы находим:
B, 3)=--1D, 3)+1 /4+ D,10) —2D,9)» 0,8914767116,
B, 5)= 1 D, 3)—1/4+ D,10) —2D,9)» — 0,5473259801.
Решение уравнения X = 0 543
Наконец, посредством совершенно аналогичных операций находим
B,10)= i D,10)— у /4+D,3)— 2D,1) « — 1,7004342715,
B,11)= 1 D,10)+ 1/4+D,3)— 2D,1)« - 1,2052692728.
Теперь мы должны только дойти до самих корней из ?1. В ка-
качестве уравнения (Z)), корнями которого являются [1] и [16], мы
получаем х2— B,1) х -f- 1 = 0, поэтому корни равны
yJ-4, т.е. 1()||
zhyi l/2 — B,15). Верхний знак мы выбираем для [1], нижний —
для [16]. Четырнадцать остальных корней мы получаем либо воз-
возведением в степени корня [1], либо решением семи квадратных
уравнений, каждое из которых дает по два корня, причем неопре-
неопределенность относительно знаков квадратных корней устраняется
при помощи того же приема, что и ранее. Так, например, [4] и
[13] являются корнями уравнения х2—B,13) #+1—0, и потому
равны у B,13) ± у i /2 —B, 9). Но произведение [1] — [16]
на [4] — [13] равно B, 5) — B, 3), т. е. является вещественной
отрицательной величиной; а так как [1] — [16] = г]/2— B,15),
т. е. есть произведение мнимой величины i на положительную
вещественную величину, то, в силу z2 = — 1, [4]—[13] также
должно быть произведением i на некоторую положительную
вещественную величину. Отсюда мы заключаем, что для [4]
нужно взять верхний, а для [13] нижний знак. Аналогичным
образом для корней [8] и [9] мы находим значения -у B,9]+
zb-x-iVZ — BД), причем так как произведение [1] — [16] на
[8] — [9] равно B, 9) — B, 10), т. е. отрицательно, то для [8] нужна
взять верхний, а для [9] нижний знак. Если таким же образом
вычислить остальные корни, то получатся следующие численные
значения, где верхний знак нужно брать для первого корня, а
нижний для второго:
544 Раздел VII (пп. 355-356)
[1], [16J« 0,9324722294+ 0,3612416662 i,
[2], [15] ж 0,7390089172 + 0,6736956436 i,
[3], [14] « 0,4457383558 ±0,89516329141,
[41, [13]« 0,0922683595 ±0,99573417631,
[5], [12] ж - 0,2736629901 + 0,9618256432 i,
[6], [11] ж — 0,6026346364 + 0,7980172273 i,
[71, [10] ж - 0,8502171357 + 0,5264321629 i,
[8], [9] ж — 0,9829730997 + 0,1837495178 i.
Изложенного до сих пор вполне достаточно для решения уравне-
уравнения хп — 1 = 0 и потому также и для нахождения тригонометриче-
тригонометрических функций, соответствующих дугам, сравнимым с полной окруж-
окружностью; однако вследствие важности этого вопроса мы не можем за-
закончить это исследование без того, чтобы не добавить кое-что из этой
сокровищницы, относящееся как к самому этому вопросу, так и к
связанным с ним задачам. При этом мы выберем отсюда то, что может
быть изложено без введения нового громоздкого аппарата, и будем
рассматривать это только как начатки этой обширной теории, которую
в дальнейшем необходимо подробно разработать.
Дальнейшие исследования о периодах корней.
Суммы, у которых количество членов четно,
являются вещественными величинами
355
Так как п всегда предполагается нечетным, то 2 находится
среди сомножителей числа п—1, и совокупность О состоит из
(п—1)/2 периодов по два члена. Период вида B, X) будет состоять
из [X] и [Xg(n~D/2], где g, как и выше, обозначает некоторый перво-
первообразный корень по модулю п. Но g(n—D/2 = —l(modn), и потому
)/a = _X (Ср. п. 62), откуда [Xg(n-D/2] = [— X]. Следовательно,
кР кР кР
если положить [X] = cos + i sin и потому [— X] = cos
кР кР
— i sin — , то B, X) = 2 cos — . Из этого мы пока сделаем только
О разбиении корней уравнения X = 0 на два периода 545
тот вывод, что значение каждой суммы из двух членов есть веще-
вещественная величина. Так как каждый период, число членов которого
четно и равно 2а,может быть разложен на а периодов по два члена,
то значение каждой суммы четного числа членов всегда вещественно.
Таким образом, если в п. 352 мы в ряду сомножителей ос, р, Т> • • •
на последнем месте поместим число 2, то все операции, использу-
используемые вплоть до получения двучленных сумм, будут приводить к
вещественным числам и мнимые величины смогут появиться только
при переходе от двучленных сумм к самим корням.
Об уравнении, определяющем разбиение корней
из О на два периода
356
Большого внимания заслуживают вспомогательные уравнения,
посредством которых для каждого значения п определяются суммы,
образующие совокупность О; эти уравнения оказываются замечатель-
замечательным образом связанными с самыми глубоко скрытыми свойствами
числа п. Однако в этом месте мы ограничим наше исследование
только следующими двумя случаями. Сначала мы рассмотрим квад-
квадратное уравнение, корнями которого являются суммы из (п—1)/2
членов, а затем, в случае, когда п—1 делится на 3, — кубическое
уравнение, корни которого суть суммы из —-(п—1) членов.
о
Если мы ради краткости вместо —(/г—1) будем писать т, и
обозначим через g некоторый первообразный корень по модулю п,
то совокупность О будет состоять из двух периодов (т, 1) и (т, g),
причем первый будет содержать корни [1], [g2], [g4], .. ., [gn~3], a
второй — корни [g], [g3], [g5], . . ., [gn~2]. Если обозначить наимень-
наименьшие положительные вычеты чисел g2, g4, . . ., gn~3 (безразлично в
каком порядке) через R, R'f R"f.. ., а наименьшие положительные
вычеты чисел g, g3, . . ., gn~2 (тоже в произвольном порядке) через
N, N', N", . . ., то корни, из которых состоит (иг, 1), будут совпа-
совпадать с [1], [Д], [R'], [В*],..., а корни из (т, g) - с [iV], [Лг/],
[iV], .... Но ясно, что все числа 1, i?, R', R", . .. являются квад-
546 Раздел VII (п. 356)
ратичными вычетами по модулю п, и так как все они меньше
чем п и притом различны, так что количество их равно -х-(п—1)г
т. е. равно количеству всех положительных вычетов по модулю п,
меньших чем п, то эти числа полностью совпадают с указанной
совокупностью вычетов. Отсюда сразу вытекает, что числ;* N, N'\
N", ..., которые различны как между собой, так и отличны от
всех чисел 1, i?, R\ /?",... и вместе с последними исчерпывают
всю совокупность 1, 2, 3,..., п—-1, обязаны совпадать со всеми
положительными квадратичными невычетами по модулю п, меньшими
чем га. Если мы теперь предположим, что уравнение, корнями кото-
которого являются суммы (иг, 1), (иг, g), есть
то
А = (т, 1) + (m, g) = — 1, В = (т, l).(m, g).
Произведение (т, 1) на (m, g), согласно п. 345, равно
К ^ + 1) + (т, N' + 1) + (m,N" + l) + ...= W,
и может быть представлено в виде а (иг, 0) -f р (иг, 1) + Y (m> §")-
Для определения коэффициентов ос, р, -у мы заметим, во-первых,
что а + Р + Т^^2 (в силу того, что количество сумм в W равно т)г
во-вторых, что р = y (это следует из п. 350, ибо произведение
(иг, 1)-(иг, g) является симметрической функцией сумм (иг, 1), (иг, g)r
из которых состоит большая сумма (п — 1, 1)); в-третьих, так как
все числа N + 1, N' + 1, Л7"" + 1, . . . заключены в границах между
2 и п + 1 (исключая самые границы), то ясно, что либо ни одна
из сумм из W не сводится к (иг, 0) (и потому а = 0), что будет
в том случае, когда среди чисел N9 N', N\... число п—1 не
содержится, либо к (и?, 0) сводится только одна сумма, а именно,,
(иг, /г), что будет в том случае, когда п—1 находится среди чисел
iV, N\ N", ..., и тогда а = 1. Из этого мы заключаем, что в пер-
первом случае а = 0, р = ^ = -^ иг, а во втором случае а = 1, р = -у =
= — (т — 1); одновременно отсюда следует, так как числа р и у
обязательно целые, что имеет место первый случай (или, что то же
О разбиении корней уравнения X = 0 на два периода 547
ч^амое, что п — 1 или — 1 не содержится среди невычетов по мо-
модулю п)у если т четно, т. е, п имеет вид 4&+1; второй же слу-
случай имеет место (это равносильно тому, что п — 1 или — 1 содер-
содержится среди невычетов по модулю п)9 если т нечетно, т. е. п
имеет вид 4& + 3*. Следовательно, так как (т, 0) = т и (т, 1) -f
+ (т, g) = — 1, искомое произведение в первом случае равно
1 1
— у772' а во ВТОРОМ случае равно -^(тгг+1), а потому искомым
уравнением в первом случае является х2 + х -г{п — 1)=0 (корни
— у±у"Кп)> а во втором будет х2 + х + — (п + 1) = 0 (корни
-Т±у* Vn).
Таким образом, какой бы корень из ?1 ни был взят в качестве
[1], разность между суммами У! [ffi] и 2[^> ГДе в качестве Ш нужно
подставить ..все положительные вычеты, а в качестве 31 — все поло-
положительные невычеты по модулю п, меньшие чем п, равна + ]/?г
для п = 1 и равна ± i ]/77 для п = 3 (mod 4). Отсюда легко
видеть также, что если к обозначает целое число, не делящееся
на п, то
cos — 2j cos —^^ = ±Уп и
для n^l(mod4), а для n^3(mod4) первая разность равна 0, a
вторая равна ±- Yn \ эти теоремы исключительно изящны. Заметим
также, что всегда нужно брать верхний знак, если к равно 1, или,
более общо, равно некоторому квадратичному вычету по модулю п,
и нижний знак, если к есть квадратичный невычет по модулю п.
Теоремы эти не только без ущерба, но скорее с выигрышем в изя-
* Таким образом, мы получили новое доказательство теоремы о том, что
—1 является вычетом по всем простым числам вида 4А: + 1 и невычетом по всем
простым числам вида 4А: + 3, которая выше (пп. 108,109, 262) уже была доказана
многими различными способами. Если бы мы захотели здесь предполагать эту
теорему известной, то было бы не нужно обращать внимание на различие двух
случаев в этом условии, так как Р, "f сами по себе уже были бы целыми числами.
548 Раздел VII (п. 357)
ществе могут быть распространены и на составные значения п\
однако этого вопроса, требующего более глубоких исследований,
мы здесь не будем касаться, а отложим это до другого случая.
Доказательство теоремы, упомянутой в разделе IV
357
Если уравнение, корнями которого являются т содержащихся
в периоде (т, 1) корней, есть
z = хт — ахт-^ + Ьхт~°- — . . . = О,
то а — (т, 1), и остальные коэффициенты 6, ... имеют вид Э( +
35 (т, 1) + @(m, g), где 91, 99, ? суть целые числа (п. 348); если
при этом обозначить через z' функцию, в которую переходит z,
если вместо (т, 1) всюду подставить \т, g), и вместо (т, g) подста-
подставить (m, g2) или, что то же самое, (т, 1), то корнями уравнения
zf — 0 будут корни, содержащиеся в (т, g), и будет иметь место
77 t у
X 1
Поэтому z может быть представлено в виде R + S (т, 1) + T{mf gO
где R, S, Т являются целыми функциями от х, все коэффициенты
которых в свою очередь являются целыми числами. После этого
мы будем иметь
z' =R + S(m,g) + T(m, 1).
Отсюда следует, если ради краткости обозначить через р ш q соот-
соответственно (ттг, 1) и (m, g), что
и аналогично
2z' = 2R — S — T+(T— S)(p — q).
Поэтому, если мы положим
2Л — S — T = Y, T — S = Z,
То АХ = У2 — (р — qJZ2, и потому, в силу (р — qJ
Доказательство теоремы из раздела IV
549
причем нужно брать верхний знак, если п имеет вид 4&+1, и
нижний, если п имеет вид 4&+3. Это и есть теорема, доказатель-
доказательство которой мы выше (п. 124) обещали привести. Легко видеть,
что два старших члена функции Y всегда суть 2хт -f- xm~x, а стар-
старший член функции Z всегда есть хт—г; остальные коэффициенты,
которые все, очевидно, являются целыми числами, зависят от раз-
личных свойств числа п и не могут быть охвачены общими анали-
аналитическими формулами.
Пример. Для п = 17 в качестве уравнения, корнями которого
являются восемь корней, содержащихся в (8, 1), мы, согласно пра-
правилам п. 348, находим уравнение
Xs — рх1 + D + р + 2q) xQ — D/? + 3g) хъ + F + Ър + 5q) x* —
откуда получается, что
R = xs + 4я6 + 6х4 + Ах2 + 1,
S = — х7 + х6 — 4хб + Зж4 — 4х3 + ж2 — ж,
Т = 2х« — Зхб + 5я4 — Зх3 + 2ж2,
и потому
Y = 2х8 + х7 + 5х6 + 7хб + 4ж4 + 7ж3 + 5я2 + ж
Z = ж7 + ж6 + .хб + 2х4 + х3 + ж2 + 2.
Ниже приводится еще несколько других примеров.
2,
n
3
5
11
13
19
23
2ж + 1
2ж2 + ж +
2ж3 + ж2 -
2хь + х* -
2жв ФхЧ
+ 2
2ж9 + ж8 -
— 5ж4-
2ж" + х10
— ix6 + 4
'Ju"" "^
2
-X —
-2х3
- 4х4
-4х7
-Зх3
У
•2
+
—
+
+
/ -
lot?
2х2 — х — 2
а;3 + 4ж2 + ж+
3^6 + Ъхъ —
4^ _ х _ 2
- 8ж8 — 7ж7 —
1 + 8ж3 -f- 5ж2—
1
X
ж2-
ж4-
ж5-
ж8-
ж10
—2
+
Z
f X
+¦ ж
—- хв + #б + #4 —
-Х3+^
/у.6 0/у.б /у»4 I /у.2 |
X
550 Раздел VII (п. 358)
Об уравнении для разбиения корней из ?1
на три периода
358
Мы переходим к рассмотрению кубических уравнений, при по-
помощи которых в случае, когда п имеет вид ЗА-f-l, определяются
три суммы из ~тг(п — 1) членов, образующие совокупность ?1.
Пусть g— некоторый первообразный корень по модулю п и
~^{п — 1) = т (т есть целое четное число). Тогда тремя суммами,
из которых состоит О, будут (m, I), (m, g), (m, g2), которые мы
обозначим через р, р', р"', и ясно, что первая содержит корни [1],
[g3h [g8],..., \gn~% вторая —корни [g], [g4[, . . . , [gn~3], третья —
корни [g2], [g5], . . . , [gn~2]. Если предположить, что искомое урав-
уравнение есть
то
А = р + р' + р", В = рр' + р'р" + рр", С = рр'р",
откуда тотчас же получается А = —1. Пусть наименьшие положи-
положительные вычеты чисел g3, g6,. . , gn~4 по модулю п суть (в произ-
произвольном порядке) 9t, Э5; S, . . ., и $ — их совокупность с присо-
присоединением к ней числа 1; точно так же пусть Э(\ 35', S', . . .—наи-
.—наименьшие положительные вычеты чисел g, g4, g7, . . . , gn~s, и f —
их совокупность; наконец, пусть 31", ЗУ', S",... — наименьшие
положительные вычеты чисел g2, g5, g8,.. . , gn~2, и $" — их
совокупность; тогда все числа из 5?, $', Ж" будут различны и
вместе охватывают числа 1, 2, 3,..., п — 1. Прежде всего нужно
заметить, что число п — 1 обязательно находится в Ж, так как
легко видеть, что оно является вычетом числа gsm/2# Отсюда легко
видеть также, что пара чисел типа h и п — h должна содержаться
в одной и той же из трех совокупностей Ж, 5?', 5?", так как если
первое является вычетом числа g\ то другое будет вычетом числа
Зт зт,
л -}- — л — ¦— от
g 2 или числа g 2, если X > —. Обозначим через (Ш) коли-
О разбиении корней уравнения X = 0 на три периода 551
чество таких чисел из ряда 1, 2, 3, .. . , п — 1, что и они сами и
числа, получающиеся из них прибавлением единицы, содержатся в
$, через (ЯЯ') — количество чисел этого же ряда, которые сами содер-
содержатся в Я, но непосредственно следующие за ними числа содержатся
в Я'; аналогичный смысл имеют и обозначения (ЯЯ"), (Я'Я), (Я'Я'),
(Я"Я), (Я"*'), (Я"Я"). Теперь мы утверждаем, во-первых, что
= (Я'Я). Действительно, если мы предположим, что /г, /г',
h", . . . суть всевозможные числа из ряда 1, 2, 3, . . . , п — 1, кото-
которые сами содержатся в Я, в то время как следующие за ними
числа h -f 1, Ы + 1, h" + 1, . .. содержатся в Я', и число которых,
следовательно, равно (ЯЯ')? то ясно, что все числа п — h — 1,
п — К — 1, п — /г" — 1, . .. содержатся в Я', следующие за ними
числа п — /г, п — h',...— в Я; а так как подобных чисел всего
имеется (Я'Я), то не может быть (Я'Я) < (ЯЯ'), и точно так же до-
доказывается, что не может быть и (ЯЯ') < (Я'Я); поэтому оба числа
обязательно должны быть равны. Совершенно таким же образом
доказывается, что (ЯЯ") = (Я"Я), (Я'Я") = (Я"Я'). Во-вторых, так как
каждое число из Я, за исключением только одного наибольшего
числа п — 1, имеет следующее за ним, которое содержится либо
в Я, либо в Я', либо в Я", то сумма (ЯЯ) + (ЯЯ') + (ЯЯ") равна
уменьшенному на единицу количеству всех чисел, т. е. равна т— 1,
и по аналогичной причине
(Я'Я) + (Я'Я') + (Я'Я") - (Я"Я) + (Я"Я') + (Я"Я") = т.
После этих приготовлений мы представим, в соответствии с
п. 345, произведение рр' в виде (т, 31' + 1) + (т, 35' + 1) +
+ (т, (?' + 1) + . . .; это выражение, как легко видеть, равно
(St'§t)p + (Я'Я')/?' + (Й'Я")//' и так как, согласно п.345, I, произведе-
произведение к р'р" получается из рр', если вместо (т, 1), (m, g), (m, g2)
подставить соответственно (m, g), (m, g2), (m, g3), т. е. вместо
p, p'9 p" подставить p't p", p, то р' р" - (Я'Я)/ + (Я'Я')//' +(Я/$Г)/?,
и совершенно аналогично, р"р = (Я'Я)//' + (Я'Я')р + (Я'Я")//. Отсюда
тотчас же следует, что, во-первых,
В =т(р + р' + р") = — т>
и во-вторых, так как подобно тому, как было представлено рр\
552 Раздел VII (п. 358)
можно и рр" записать в виде (Я"Л)/? + (Л"Л')// + (Л"Л")/Л а это вы-
выражение должно быть равно тому, которое было указано для рр"
выше, то обязательно (Л"Я) = (Я'Л') и (ЗНГ) = (Я'Я). Если теперь
положить
(«/Яяг) = (Я'гЯ')=а, (Л"Я") = (*'*) = (*»') = Ь, (Л'Л') = (*"*) - (ЯЯ") = с,
то из сказанного следует, что т — 1 = (ЯЛ) + (ЛЯ') + (ЯЯ") =
== (ЛЛ) + Ъ + с, и а + Ъ -f с = т, т. е. (ЛЛ) = а — 1, так что наши
девять неизвестных величин сводятся к трем, именно, к а, 6, с, a
в силу равенства а -{- b -{- с = т даже к двум. Наконец, квадрат
числа р, очевидно, представляется в виде (т, 1 + 1) + (т> 31 + 1) +
+ (т, 33 + 1) + (т, ? + 1) + . . . ; среди слагаемых этого выражения
имеется (иг, п), которое равно (т, 0), т. е. равно т, в то время
как остальные слагаемые, как легко видеть, сводятся к (Ш)р +
+ (ЛЛ')// + (»")/>"; поэтоту мы имеем р2 = т + (а — 1) р + Ьр' + ср".
Таким образом, мы, согласно предыдущим исследованиям, име-
имеем следующие четыре равенства:
р*^т + (а -1)р + Ьр' + ср",
РР' = Ьр -\- ср' + ар",
РР" = ср + ар' + Ър\
р'р" = ар + Ьр' + ср",
где три неизвестных величины а, 6, с связаны соотношением
(I) a-\- b + с = т,
и, кроме того, заведомо являются целыми числами. Отсюда сле-
следует, что
С = рр'р" = ар* + Ърр' + срр» =
= ат+ (а? + Ь2 + с2 — а) р-\- (ab + ас + bc)p'+ (ab + be + аф".
Но так как рр'р" является симметрической функцией сумм р, р\ р",
то коэффициенты, на которые эти суммы умножаются в предыду-
предыдущем выражении, обязательно должны быть равны, вследствие чего
мы получаем новое уравнение
(II) а2 + Ь2 + с2 — а = ab -f be + ас,
О разбиении корней уравнения X = 0 на три периода 553
откуда следует, что С = am + (ab + be -f- ca) (/? + // + //'), или
(в силу того, что р + р' -}- р" = — 1 и на основании (I))
(III) С = а2 — be.
Хотя теперь С зависит от трех неизвестных, между которыми
мы имеем только два соотношения, тем не менее этого оказыва-
оказывается достаточным для окончательного определения С, если только
использовать еще то условие, что а, Ьщ с являются целыми числами.
Чтобы показать это, представим уравнение (И) в виде
I2a+l2b-t 12с+ 4 =
= 36а2 +3662 + 36с2 — ЗбаЬ — Збас — 366с—24а + 126 + 12с + 4.
Левая часть, согласно (I), равна 12 т + 4 = 4п, а правая — преобра-
преобразуется в
Fа — ЪЪ — Ъс — 2J + 27 (Ь — сJ,
или, если вместо 2а — Ъ — с написать &, в (Зк — 2J -f 27 (b — сJ.
Из этого вытекает, что число An (т. е. вообще четвертая кратность
каждого простого числа вида Зт + 1) может быть представлено
формой х2 + 27г/2, результат, который, впрочем, легко может быть
выведен из теории двойничных форм; все же представляется заме-
замечательным, что такое разложение связано со значениями а, 6, с.
Но число 4п только одним способом может быть разложено на
сумму квадрата и двадцать седьмой кратности квадрата, что мы?
докажем следующим образом*. Пусть
4п = *2 + 27гг2 = t'2 + 27гг'2;
тогда, во-первых,
(«' — 27ии'J + 27 {tur + t'uY = 16n25
во-вторых,
(tf + lluu'f + 27 (tuf — t'uf = 16n2,
в-третьих,
(tuf + t'u) {tuf — t'u) = An (u'2 — u2);
из третьего равенства следует, так как п простое число, что оно*
входит в одно из чисел tuf -\- t'u, tu' — t'u) но из первого и вто-
* Более прямым методом эту теорему можно было бы доказать на основании,
принципов пятого раздела.
554 Раздел VII (п. 359)
рого равенств вытекает, что оба эти числа меньше чем щ поэтому
то из них, которое делится на и, обязательно равно 0, следова-
следовательно и'2— и2 = 0, откуда и'2 = и2 и t'2~t2, т. е. оба разложе-
разложения не являются различными. Поэтому, если предполагать извест-
известным разложение числа An на квадрат и двадцать седьмую крат-
кратность квадрата (это разложение можно получить либо данным в
пятом разделе прямым методом, либо изложенным в пп. 323, 324
косвенным методом), именно, предположить, что An = М2 + 27ЛГ2,
то определятся квадраты (Зк— 2J, (Ь— сJ, и вместо уравнения
(II) мы получаем теперь два уравнения. Но легко видеть, что не
только квадрат (Зк— 2J, но и само число Зк— 2 полностью опре-
определено; действительно, так как оно обязательно равно либо + М
либо — М, то неопределенность знака устраняется условием, что к
должно быть целым числом. Именно, нужно положить Зк— 2 = + М,
или — М в зависимости от того, имеет ли М вид 3z +1 или
3z -f 2 *. Так как теперь к = 2а — Ъ — с = За — т, то а = -~- (т -j- A),
Ь -f с = т — а = -х- Bт — А), и потому
C= a2 — be = a2 — -f (b + cJ + -f (& — cJ =
4 /i 4 4 'I 4
-"¦ / |7\O -^/O 7\Oi •JL Л т о Х79. Xy . X
JV2,
и таким же способом находятся все коэффициенты. Эта формула
станет еще проще, если вместо N2 подставить его значение из
уравнения (Зк — 2J + 277V2 = An = 12т+А\ после соответствующих
вычислений получается
1 1
С — — (m -f- к -\- Зкт) =. —(т -\- кп).
* Очевидно, что М не может иметь вид 3z, так как тогда Ы делилось бы
на 3. На ту неопределенность, имеет ли место Ъ — с — N или = — N, нам
дальше не нужно будет обращать внимания, и она не может быть устранена
по самой природе вещей, так как все зависит от выбора первообразного
корня g, так что для одних первообразных корней разность Ъ — с положи-
положительна, а для других отрицательна.
Сведение уравнения X = 0 к чистым уравнениям 555
Это же значение может быть представлено и в виде (Зк — 2) N2 -f- A3—
— 2к2 + к — km + т, который хотя и менее удобен для примене-
применения, но зато сразу показывает, что С, как это и должно быть,
является целым числом.
Пример. Для п = 19 будет in — 49 -f- 27, поэтому Зк— 2 = -\- 7,
^ = 3, С = -^-F -f- 57) = 7, и искомое уравнение, как и раньше,
«сть х3 + х2 — 6х—7 = 0. Подобным же образом для п = 7, 13, 31,
37, 43, 61, 67 значение к соответственно равно 1, — 1, 2,-—3, —2,
1, — 1, и потому С = 1, — 1, 8, —И, —8, 9, —5.
Хотя вопрос, решенный в этом пункте, является довольно запу-
запутанным, мы не захотели обойти его, отчасти ввиду изящества
решения, а также и потому, что это дало возможность использовать
различные искусственные приемы, которые с большой пользой мо-
могут быть применены и в других исследованиях*.
Сведение уравнений, из которых находятся корни ?2,
к чистым уравнениям
359
Предыдущие исследования относились к отысканию вспомога-
вспомогательных уравнений; теперь мы изложим весьма выдающееся свойство,
касающееся их решения. Как известно, все усилия крупнейших ма-
математиков найти общее решение уравнений, степень которых выше
четвертой, или (выражаясь точнее) найти редукцию произвольных
уравнений к чистым уравнениям, до сих пор были тщетны, и едва
ли можно сомневаться в том, что эта проблема не просто прево-
превосходит силы современного анализа, но и вообще неразрешима.
(Сравните с тем, что по этому поводу замечается в п. 9 сочинепия
* Следствие. Если г есть корень уравнения х3 — 1=0, то (р -\- s/?' -f-
п Г М N /27
-\- s2p"K = — (М -\- Ny — 27). Если положить —т= ~ cos Ф» —7=^" = s^n Ф» т0
и \ кп у кп
1 2 1 г—
р = — Y + ~з cos ~3 У^ п > М = + I(mod3), IeeM A-2-3-•-mK (mod n). Если
положить За? + 1 = г/, то будет иметь место равенство у3 — Зпу — Мл = 0.
556 Раздел VII (п. 360)
«Новое доказательство одной арифметической теоремъп.) Тем не
менее очевидно, что существует бесчисленное множество смешанных
уравнений любой степени, которые допускают такое сведение к
чистым уравнениям, и мы надеемся, что математикам будет инте-
интересно, если мы покажем, что наши вспомогательные уравнения
всегда относятся к такому типу. Однако, вследствие большого
объема этого исследования, мы укажем здесь только основные мо-
моменты, необходимые для доказательства возможности редукции, а
более подробное изложение отложим до другого времени. Сначала
должны быть предпосланы некоторые общие замечания о корнях
уравнения хе—1 ==0, охватывающие также и тот случай, когда е
является составным числом.
I. Эти корни (как известно из элементарных книг) представля-
кР кР
ются в виде cos {- i sin — , где в качестве к нужно взять е чисел
0, 1, 2, 3, . . . , е—1 или каких-либо других, сравнимых с этими по
модулю е. Один корень, получающийся при к = 0 или вообще при
делящемся на е значении к, равен 1; всем остальным значениям к
соответствуют корни, отличные от 1.
(кР кР\^ ХкР "КкР
cos 1- i sin — ) = cos f- i sin , то ясно, что
e ' e I e ' e '
если R есть корень, соответствующий взаимно простому с е значе-
значению к, то в прогрессии R, i?2, i?3, . .. только е-й член впервые
будет равен 1, а все предыдущие будут от 1 отличны. Из этого
тотчас же следует, что все е величин 1, R, i?2, i?3, . . ., Re~1 раз-
различны, а так как все они, очевидно, удовлетворяют уравнению
хе — 1=0* то они представляют собой все корни этого уравнения.
III. Наконец, при том же предположении для каждого целого
не делящегося на е значения X будет иметь место равенство
действительно, сумма, стоящая в левой части, очевидно, равна
A—i?Xe)/(l — i?x), а числитель этой дроби равен 0, в то время как
знаменатель отличен от 0. Если же X делится на е, то указанная
сумма, очевидно, равна е.
Сведение уравнения X = 0 к чистым уравнениям 557
360
Пусть, как и всюду до этого, п есть простое число, g— перво-
первообразный корень по модулю тг, и п — 1 — произведение трех целых
положительных чисел ос, C, у- Ради краткости мы сразу же пове-
поведем исследование так, чтобы оно распространялось и на случай,
когда одно из чисел а или ^ равно 1; если ? = 1, то в качестве
сумм (^, 1), (у, g), . . . надо взять корни [1], [g], . . . Таким обра-
образом, из всех предполагающихся известными а сумм по t8^ членов,
(?Т> *)> (РТ> #)' (?Т> §2)> • • • > (РТ> ёга~)' нужно получить суммы
по т членов—задача, которую выше мы свели к решению уравне-
уравнения степени C, но, как мы теперь покажем, которую можно решить
я при помощи чистого уравнения такой же степени. Ради кратко-
краткости мы обозначим суммы
(Т. 1), (Т,Г)> (Т, ?2а),-.., (Т>Гр-а)>
содержащиеся в (Ру, 1), соответственно через а, 6, с, . . . , т; суммы
(Т. g)> (Т. Г + ')> (Т, ^2а + *), • < •, (Т. Гр ~ а + *).
содержащиеся в {$ч> g), — соответственно через а', Ь\ с',..., т'\
суммы
— соответственно через а", Ь", . . . , т/г", и т. д., до тех сумм, которые
содержатся в ($ч>8*~*)-
I. Пусть теперь R обозначает любой корень уравнения х$ — 1 =0
и пусть выражение для C-й степени функции
t = a -f Rb + R2c + . . . + i?P ~ * т/г,
найденное по правилам п. 345, имеет вид
TV + Аа + 56 + Сс + . . . + Mm + ,4 V + B'V + С с' + . . . + М'т/?' +
+ А"а" + ?" + С"сГ 4 • • • + М'иг" +
где все коэффициенты N, A, S, J', . . . являются целыми рацио-
рациональными функциями от R. Если предположить далее, что [3-е
степени двух других функций
и = i?^a + #6 + i?2c
558 Раздел VII (п.
uf = b + Rc + + + +
суть соответственно U и U', то так как и' получается из t заменой
сумм а, Ь, с, . . . , т соответственно на Ь, с, d, . . . , а, мы, на ос-
основании п.350, легко получим, что
U' = N + Ab +Bc + Cd-\ ... -\-Ma-\-
+ A'V + В'с' + C'd' + . . . + М'а! +
+ А"Ъ" + В"сГ + C'd" + • • • + М"а" +
Далее, так как и = Ru', то, очевидно, U = RW\ поэтому, вслед-
вследствие того, что i?P = 1, соответствующие коэффициенты у U и U'
одинаковы; наконец, легко видеть, что так как t и и отличаются
только тем, что у t сумма а умножена на 1, а у и — на R&, та
все соответствующие коэффициенты (т. е. коэффициенты при одина-
одинаковых суммах) у Т и U равны, а потому равны также и коэффи-
коэффициенты у Т и U'. Отсюда следует, наконец, что А = В = С = . . . = М>
А'= В'= С'= ...=М', А"= В"= С"= ... = М", . . . , так что Т при-
приводится к виду
N + А (рт, 1) f A'(fr, g) + A*(fr, g2) + . .. ,
где каждый из коэффициентов N, А, А\ . . . имеет вид
причем /?, /?', /?", . . . являются заданными целыми числами.
IL Если в качестве R взять некоторый определенный корень
уравнения х$ —1 = 0 (которое мы предполагаем уже решенным)^
причем такой, что никакая его степень, меньшая чем C-я, не равна 1>
то Т также будет определенной величиной, из которой t может
быть получено решением чистого уравнения t$ — Т = 0. Но так
как это уравнение имеет 8 корней, которые равны t, Rt, R4, . . .
. . . , i?P — * t9 то представляется неясным, какой именно корень нужно
взять. Однако это совершенно безразлично, что можно пояснить
следующим образом. Нужно вспомнить, что после того как все
суммы из Py членов определены, корень [1] определен лишь в том
смысле, что так должен быть обозначен один из ^ корней, содер-
содержащихся в (Pf, 1), и потому совершенно безразлично, какую из ^
Сведение уравнения X = 0 к чистым уравнениям 559
сумм, образующих сумму (р^, 1), обозначить через а. Если теперь,
после того как некоторая определенная сумма обозначена через а,
предположить, что t = ?9 то легко видеть, что если затем обозна-
обозначить через а ту сумму, которая раньше была обозначена через Ь,
то суммы, которые раньше обозначались через с, d, . . . , а, 6,
теперь будут Ь, с, . . . , т, а, и потому значение t теперь будет
равно ^ = %R&~1. Точно так же, если через а обозначить ту сумму,,
которая первоначально обозначалась через с, то значение t станет
равным %R$~2y и вообще t можно рассматривать как равное любой
из величин %, %RP — {t SLRp — 2, . . . , т. е. любому корню уравнения
х& — Т = О, в зависимости от того, какая из содержащихся в (р^, 1)
сумм обозначена через (-у, 1).
III. После того как величина t таким путем определена, нужно
найти р—1 других равенств, которые получаются из ?, если R
заменять последовательно на i?2, i?3, Л4, . . . , R&, именно,
V = а + R2b + R*c + . . . + RW - 2 m,
Г - а
Последнее равенство мы, впрочем, уже знаем, так как оно, оче-
очевидно, есть a+b-\-c-\-...-\-m = ((З-у» 1); остальные же могут быть-
получены следующим образом. Если мы точно так же, как в I было
представлено ^, представим, в соответствии с правилами и. 345,
произведение t^~2t\ то методом, совершенно аналогичным преды-
предыдущему, можно будет доказать, что результат можно будет пред-
представить в виде
где 3J, 21, 31',... являются целыми рациональными функциями*
от R, и потому Т' будет известной величиной, из которой получа-
T't2
ется ? = -™- • Если, далее, предположить, что для произведения
?3 — з ?" получается функция 7"', то точно так же это выражение
можно представить в аналогичной форме и получить затем значе-
T"ts
ние t" в виде t" = -^—; точно так же tm находится из равенства
T'"t*
t = ——, где Т" есть известная величина, и т. д.
560 Раздел VII (п. 361)
Этот метод был бы неприменим, если бы t могло равняться 0,
откуда следовало бы тогда, что и Т = Т' = Т" = . . . = 0; но можно
показать, что это невозможно, хотя доказательство мы здесь опу-
опускаем, так как оно слишком длинно. Имеются также специальные
rpt rp if
приемы, при помощи которых дроби ^-, т , . .. преобразуются в
целые рациональные функции от /?, а также в случае а = 1 су-
существуют более короткие методы для нахождения значений t',
t", . .. ; все это мы должны, однако, обойтк здесь молчанием.
IV. Наконец, после того как t, t;, I", . . . найдены, мы, согласно
замечанию III предыдущего пункта, имеем t + t' + t" + • • • = Р&,
откуда определяется значение а, из которого, согласно п. 346,
могут быть получены значения всех остальных сумм из ^ членов.
Значения Ь, с, d,. . . могут быть определены также из следующих
равенств, справедливость которых должна быть ясна для каждого
внимательного читателя:
$Ь= №-Н + №-*1' + Дз-з^ + ... ,
рс - i?23 ~ 21 + RW ~41' + R2& ~6 f + . ..,
Из большого числа замечаний, которые можно сделать в от-
отношении этого исследования, мы приведем здесь только одно. Что
касается решения чистого уравнения х$—Т = 0, то ясно, что Т
в большинстве случаев имеет мнимое значение Р + iQ9 так что это
уравнение, как известно, связано, с одной стороны, с делением не-
некоторого угла (тангенс которого равен Q/P), на р частей, а с дру-
другой— с извлечением корня степени р из некоторого отношения
(отношения единицы к У~Р2 -f Q2). При этом весьма замечательно
(о чем подробнее мы, однако, говорить не будем), что значение
з
}/~Р2 -)- Q2 всегда может быть выражено рационально через уже
известные величины, так что, кроме извлечения квадратного корня,
для решения уравнения нужно только деление некоторого угла,
например, при [3 = 3 — трисекция угла.
Так как, наконец, ничто не мешает положить ос = 1, т=1, и
потому р = п—1, то ясно, что решение уравнения хп—1 =0 тот-
Применение к тригонометрическим функциям 561
час же может быть сведено к решению чистого уравнения
хп~ * — Т — 0 степени п—1, где Т определяется через корни урав-
уравнения хп~1 — 1 = 0. Отсюда при помощи сделанного выше заме-
замечания следует, что деление полного круга на п равных частей
требует: 1) деления полного круга на п — 1 частей; 2) деления
некоторой другой дуги, которая может быть построена после вы-
выполнения первого деления, на п—1 частей; 3) извлечения одного
единственного квадратного корня, причем можно показать, что этим
корнем всегда является у п .
Применение предыдущих исследований
к тригонометрическим функциям.
Метод различать углы, которым соответствуют
отдельные корни из О
361
Теперь мы еще рассмотрим подробнее связь между корнями ?1
v Р 2Р ЗР (n — i)P
и тригонометрическими функциями углов — , — , — , ..., —.
ть ть ть ть
Метод нахождения корней из О, который мы изложили, таков,
что мы еще не можем различать (если не использовать в процессе
вычислений указанным выше образом таблиц синусов, что, однако,
было бы менее прямым способом), какой корень соответствует
Р
каждому из указанных углов, т. е. какой корень равен cos (-
. . Р „ 2Р . . 2Р о
+ i sm — , какой равен cos 1- г sin — , и т. д. dTa неопределен-
неопределенность, однако, легко устраняется, если принять во внимание, что
Р 2Р ЗР (ть 1) Р
косинусы углов — , — , — , ..., —2 все вРемя убывают (если
принимать во внимание и знак), а синусы всех этих углов поло-
(я—1)Р (ть — 2)Р (ть-З)Р (п+\)Р
жите льны; углы i—^— , i , v—^- , . .., *-^__— имеют
соответственно такие же косинусы, что и углы первого ряда, а
синусы углов второго ряда отрицательны, но по абсолютной вели-
величине равны синусам углов первого ряда. Поэтому среди корней О
те два, которые имеют наибольшие вещественные (равные между
собой) части, соответствуют углам — , ^— , причем первому
562 Раздел VII (п. 362)
углу соответствует тот корень, у которого мнимая величина i умно-
умножается на положительную величину, а второму — тот, у которого
она умножается на отрицательную величину. Из остальных п—3
корней те, которые имеют наибольшие вещественные части, соот-
2Р (п — 2)Р г?
ветствуют углам —, и т. д. Ьсли корень, который со-
р
ответствует углу — , уже известен, то остальные можно еще раз-
различать и на основании того, что если указанный корень обозна-
2Р ЗР 4Р
чить через [X], то углам —, —, —,... будут, очевидно, соответ-
соответствовать корни [2Х], [ЗХ], [4Х],... Так, в примере п. 353 тотчас
1 г» »
же видно, что углу — jP не может соответствовать никакой другой
18
корень, кроме [11], а углу -^Р— никакой другой корень, кроме
[8]; углам же tq^» тд^> 19^' Тд^'*'* отвечают соответственно
корни [3], [16], [14], [5],.... В примере п. 354 углу ^Р соответ-
2
ствует, очевидно, корень [1], углу j=P — корень [3] и т. д. Таким
Р 2Р
образом, косинусы и синусы углов — , —, , .. полностью опреде-
определяются.
Тангенсы, котангенсы, секансы и косекансы
определяются по синусам и косинусам
без помощи деления
362
Что же касается остальных тригонометрических функций этих
углов, то их можно было бы определить через синус и косинус
известным методом, именно, секанс и тангенс — определить, деля
соотвественно единицу и синус на косинус, а косеканс и котан-
котангенс— деля соответственно единицу и косинус на синус. Однако в
большинстве случаев удобнее определять эти функции при помощи
следующих формул, в которых не фигурирует деление, а имеется
только сложение.
Определение по синусам и косинусам остальных функций 563
р 2р (п 1) р
Пусть со — один из углов — , — ,. .. , - -— , и cos со
г sin со = R, так что R есть некоторый корень из ?2; тогда
, i\ 1+R2 . i (т> 1 \ Л — R*
. i (т> 1 \
sm w = 2Г СЛ — ^J =
Отсюда следует, что
2R . 1A_Д2) 2Ri
secco- qp^r, tgco= ; + /?2 , cosecco=7?—j,
Покажем теперь, что числители этих четырех дробей можно
так преобразовать, что они станут делящимися на знаменатели,
I. В силу R = Rn + i^ffn + i имеет мест0 2R = R+R2n + \ a
это выражение, очевидно, делится на 1+ R2, так как число п
нечетно. Отсюда получается
sec со = R — R3 + Л5 — R1 + .. . + R2n - \
и потому (так как из sin со = —sinBn—1)со, sin Зсо =
= — sin Bп — 3) со, . . . , очевидно, следует sin со — sin Зсо -f
+ sin5co— . .. + sinBn— 1)со = 0)
sec со = cos со — cos Зсо + cos 5co — .. + cos Bn — 1) со,
или, наконец (в силу cos со = cos Bп—1) со, cos Зсо = cos Bп—3) со, .. .),
sec со = 2 [cos со — cos Зсо + cos 5со — •. . + cos (п — 2) со] + cos mo,
где нужно брать верхние или нижние знаки, в зависимости от того,
имеет ли п вид 4А: + 1 или hk + 3. Очевидно, эта формула может
быть также представлена в виде
sec со = + [ 1 — 2 cos 2co -f 2 cos 4co — . . . + 2 cos (n — 1) со].
II. Если подобным же образом подставить 1 — R2n +2 вместо
1 — i?2, то получится, что
tg со = i A — R2 + i?4 — R* + . . . — i?2n),
или (так как 1— i?2* = 0, R2 — R2n - 2 = 2i sin 2co, i?4 — В2» -4 =
= 2i'sin4co,...)
tg со = 2 [sin 2co — sin 4co + sin 6co — ... + sin (n — 1) со}.
564 Раздел VII (п. 362)
III. Так как имеет место 1 + R2 + R* + ... + /?2™-з = 0, то
п = п — 1 — R2 — R* — . .. — R2n ~2 =
= A - 1) + A - Л2) ++ A - R*) + .. . + A - R^~%
и отдельные скобки этого выражения делятся на 1 — R2. Поэтому
г^ = 1 + A + щ + A + /г2 + i?4) + ... + A + /г2 + д* + ...
откуда, умножая на 2, вычитая затем
О = (п — 1) A + R2 + /?4 + .. . + R2n ~2)
и снова умножая на /?, мы получаем
— (n —
откуда тотчас же следует, что
cosecco = — [(n —l)sin(o +(n —3)sin3co + . .. —(n — l)smBn—1) со] =
2
= ~[(п — l)sin(o + (п — 3)sin3co + . .. + 2sinG2 — 2)со],
причем эта формула может быть представлена также и в виде
cosecco = [2sin2co + 4sin4co + 6sin6co + . . + (п — l)sin(n—1)со].
IV. Если указанное выше значение п/A—R2) умножить на
1 + R2 и затем вычесть
О = (п — 1) A + Л2 + i?4 + ... + R2n ~2),
то получится
'^ГЖ = (п - 2) Д* + (п-4) В* + (п - 6) Д« + ... - (п- 2) iP» - \
откуда тотчас же следует, что
ctg со = — [(п — 2) sin 2со + (п — 4) sin 4со + (п — 6) sin бсо + ...
... —{гс — 2) sin (п — 2) со] = -^ [(п — 2) sin 2co +
-f- (п — 4)sin4co + ... + 3sin(rc — 3)со + sin(n — 1) со],
причем эту формулу можно представить также и в виде
2
ctg<t) = [sinсо + 3sin3co 4- • • • + (п — 2) sin(n — 2) со].
Пониснсение степеней уравнений для тригонометрических функций 565
Метод постепенного понижения степеней уравнений
для тригонометрических функций
363
Точно так же, как при предположении, что п — 1 = ef, функ-
функция X может быть разложена на е сомножителей степени /, если
известны значения Bcejc e сумм из / членов (п. 348), так и для
уравнения Z = 0 степени п—1, корнями которого являются си-
синусы или какие-либо другие тригонометрические функции углов
Р 2Р (п — \)Р х гу е>
—, — , . . ., — , функция Z может быть тогда разложена на е
сомножителей степени /. Основные моменты этого способа состоят
в следующем.
Пусть О состоит из следующих е периодов по / членов: (/, 1) = Р,
Р', Р", . . ., и период Р состоит из корней [1], [а], [Ь], [с],..., пе-
период Р' — из корней [а']} [//], [с'],..., период Р" — из корней [а*],
[&"], [с"], ... Пусть, далее, корню [1] соответствует угол (о, и по-
потому корням [а], [Ь], ... — углы асо, йсо, . .., корням [а'], [&'], ,..—
углы а'со, Ь'а>? . . ., корням [а"], [Ь"], ... — углы а"со, 6"со, ... и т. д.
Тогда легко видеть, что все эти углы совпадают с углами — ,
2Р ЗР (п — \)Р
— , — , . .., — , точнее, что совпадают тригонометрические
функции первых и вторых*. Поэтому, если обозначить тригоно-
тригонометрическую функцию, о которой идет речь, буквой <р, ставящейся
перед значением угла, и положить произведение сомножителей
х — 9(со)» х — ?(асо)> х
равным У, произведение сомножителей х — <р (а'со), х — <р (&'а)), . ..
равным У, произведение сомножителей х — <р(а"со), х — <р(&"со),...
равным У" и т. д., то, очевидно, будет иметь место YY'Y". .. = Z.
Нам еще нужно только показать, что все коэффициенты функций
F, У, У", . .. могут быть представлены в виде
А + В(/, 1) + C{f, g) + D(f,g*) + ..
* В этом смысле два угла совпадают, если разность между ними равна или
полной окружности, или некоторой ее кратности; такие углы можно было бы
назвать сравнимыми по полной окружности, если понимать сравнимость в не-
несколько расширенном смысле.
566 Раздел VII (п. 364)
вследствие чего их, очевидно, можно будет считать известными,
если известны значения всех сумм из / членов. Этого мы доби-
добиваемся следующим образом.
Подобно тому как
совсо = 1[1] + -|[1Г"\ sinco = -y г[П+4" i[i]n~\
так же и остальные тригонометрические функции угла
со могут быть приведены к виду 31 + 95 [1]+ © [I]2 + ?)[1]3 + . . ., и
непосредственно ясно, что если к обозначает некоторое целое чис-
число, то функции угла ксо будут тогда равны 31 + 95 [к] -\- Ё [к]2 -f-
+ Sl&J3 + ... Но так как отдельные коэффициенты у У являются
целыми рациональными симметрическими функциями от ср (со), <р(асо),
ср (Ьа>),. -., то ясно, что если вместо этих величин подставить их
значения, то отдельные коэффициенты станут целыми рациональ-
рациональными симметрическими функциями от [1], [а], [6],..., вследствие
чего они, согласно п. 347, приводятся к виду А-\-В(/, 1)+
-f- С (/, g) + .. . И по совершенно той же причине возможно при-
привести к подобному виду и все коэффициенты функций У, У",...
364
Относительно проблемы предыдущего пункта мы добавим еще
несколько замечаний.
I. Так как отдельные коэффициенты у У являются такими же
функциями от содержащихся в периоде Рг (который можно обо-
обозначить через (/, а')) корней, что и отдельные коэффициенты у У
как функции корней из Р, то из п. 347 вытекает, что У полу-
получается из У, если в выражении для У вместо (/, 1), (/, g), (/, g2), ...
всюду подставить соответственно (/, а'), (/, a'g),(f, a'g2), ... И точно
так же У" получается из У, если в выражении для У всюду вместо
(/, 1), (/, g), (/, g2),... подставить соответственно (/, а"), (/, a"g),
(/, a"g2), .. . Поэтому если функция У найдена, то остальные функ-
функции У, У", ... получаются немедленно из нее.
II. Если мы положим
У = tf — acxf-i
то коэффициенты a, p, ... будут соответственно равны сумме корней
Пониснсение степеней уравнений для тригонометрических функций 567
уравнения У = О, т. е. сумме величин <р((о), (р(асо), ср(Ьы), ..., сумме
произведений этих величин по две и т. д. Однако в большинстве
случаев намного удобнее искать эти коэффициенты при помощи
метода, подобного указанному в п. 349, а именно, сначала найти
сумму корней (р((оO <р(асо), (р(Ьсо),.., сумму их квадратов, сумму
кубов и т. д., а затем получить коэффициенты при помощи тео-
теоремы Ньютона. Если 9 обозначает тангенс, секанс, котангенс
или косеканс,то существуют еще и другие вспомогательные средства,
о которых, однако, мы здесь не будом говорить.
III. Особого рассмотрения заслуживает тот случай, когда / яв-
является четным числом, и потому каждый период Р, Р\ Р", . ..
составлен из — / периодов по два члена. Если Р состоит из перио-
периодов B, 1). B. а), B, 6), B, с),..., то числа 1, а, 6, с,... и п — 1,
п — а, п — Ь, п — с,... вместе составляют всю совокупность 1, а,
6, с, ... или по крайней мере (что здесь сводится к тому же) срав-
сравнимы с последними числами по модулю п. Но <р((п — 1) со) = + 9 (со)
9 ((га — а) со) = +?(асо)» и т- Д-» гДе нужно брать верхние знаки,
если 9 обозначает косинус или секанс и нижние знаки, если 9
обозначает синус, тангенс, котангенс или косеканс. Отсюда сле-
следует, что в обоих первых случаях сомножители, из которых состоит
У, разбиваются на пары равных между собой, и потому У является
квадратом, а именно, У = г/2, где у равно произведению сомножи-
сомножителей
х — 9(С0)> х — 9(асо)> х — <р(Ь(о),...
Точно так же в этих случаях и остальные функции У, Y" ...
являются квадратами, причем, если мы предположим, что Рг со-
состоит из B, а'), B, Ь'), B, с'),..., Р* — из B, а"), B, Ь"), B, с"),...
и т. д., и что произведение сомножителей х — (р(й'со), х — ср(Ь'(о),
х — (р(с'(о), * .. равно у', произведение сомножителей х — (р(<х"ы),
х — 9(в//@)>--- равно у" и т. д., то У = у'2, Y" = y и т. д. Да-
Далее, функция Z также является квадратом (ср. п. 337), а именно,
квадратом произведения уу'у", . . . Легко видеть также, что у\ у",.. .
точно так же получаются из у, как У, У", .. . получаются, со-
согласно сказанному в I, из У; что отдельные коэффициенты у у
568 Раздел VII (п.
могут быть представлены в виде
так как суммы отдельных степеней корней уравнения у = О, оче-
очевидно, равны половинам сумм степеней корней уравнения Y = О
и потому приводятся к такому виду.
В четырех последних случаях Y является произведением сомно-
сомножителей
я2-(9(со)J, я2_(9(асо)J, яа-(ф(Ьсо)J,...
и потому имеет вид
Xf — Хя/~2 + [Lxf ~4 — . . .
и ясно, что коэффициенты X, [л, . . . могут быть получены из сумм
квадратов, биквадратов и т. д. корней ф(со), 9 (aco), 9(bw),...;
так же обстоит дело и с функциями У, У", . . .
Пример I. Пусть п = 17, / = 8, и 9 обозначает косинус. Тогда
и нужно разложить ]/Z на два сомножителя у, у' четвертой сте-
степени. Период i> = (8,l) состоит из B,1), B, 9), B,13), B,15), по-
поэтому у будет произведением сомножителей
х — 9(со)> х — ?(9w), х — 9 A3со), х —
11
Если вместо ср(ко)) подставить -у [к] -\- -^ [п — А], мы найдем
9 (со) + <р (9со) + ф A3со) + ф A5©) = 1(8,1);
(9(со)J + (9(9со)J + (9A3со)J + (9A5со))* = 2 + 1(8,1);
3 1
точно так же сумма кубов равна -^ (8, 1)+-^ (8, 3), сумма биквад-
3 5
ратов равна у + т^ (8Д). Определяя отсюда по теореме Ньютона
коэффициенты функции у, мы получим
11 )]а;2-1[(8, 1)+3(8,3)]х +
+ 1[(8, 1) + (8, 3)];
Пониэюение степеней уравнений для тригонометрических функций 569
у' получается из г/, если поменять местами (8, 1) и (8, 3). Если под-
подставить теперь вместо (8, 1) и (8, 3) значения —у+ yK17 и
— -= — У И, то мы получим
Подобным же образом можно разложить УХ на четыре сомно-
сомножителя второй степени, первый из которых (х — ср(оу))(х—срA3(о)),
второй (х— ср(9(о))(х — срA5(о)), третий есть (х — срC(о))(х — срE(о)),
и четвертый (х— срA0(о)) (х — ср A1со)), и все коэффициенты
этих сомножителей могут быть выражены через четыре суммы
D,1), D,9), D,3), D,10). Очевидно, что произведение первого
и второго сомножителей будет равно г/, а произведение третьего
и четвертого равно у'.
Пример II. Если ср обозначает синус, а все остальное остается
без изменения, так что
Z _ .16 17 хи л_Щх12_ 221 1о , 935 561 357 4 ^51_ 2
^""^ 4 Х "*" 16 ж 32 ^ 56^ 512Ж "^2048Ж 4096 Х "^
17
1 65 536
нужно разложить на два сомножителя ?/, ?/' восьмой степени, то
у будет произведением четырех двойных сомножителей
я2-(9((о)J, sa —(<р(9со))а, ^2-(9A3(о)J, ^2 - (9A5(о)J.
1 1
Но так как ср(ко)) = —— i [к] + — i [n — к], то
(9 (Щ)* = - i- [2А] + 1 [п] - -i [2п - 2А] = | -1 [2А] -| [2п-2А].
Отсюда для суммы квадратов корней ср (со), <р(9со), 9A3со),
срA5(о) мы находим значение 2 — хС^» ^)> ^ля суммы их биквадра-
3 3
тов — значение -j — Та(8> 1), Для суммы их шестых степеней — зна-
СП Л
чение -j ^7(8, 1)—^т(8, 3), и для их суммы восьмых степеней —
значение g -^ (8,1)- 1(8, 3).
570 Раздел VII (п. 365)
Отсюда следует:
а у' получается из у перестановкой (8,1) и (8,3), так что, подстав-
подставляя значения этих сумм, мы получаем
— ({7— 7 1/ТЛг2-!-— — 1
\32 64' ^У "^256 64
4- — 4- — l/"T7
^256 + 64' i/e
Точно так же можно разложить Z на четыре сомножителя, коэф-
коэффициенты которых могут быть выражены через суммы из четырех
членов, причем произведение двух будет равно у, а произведе-
произведение двух других равно у''.
Деления круга, которые можно выполнить
при помощи квадратных уравнений
или посредством геометрических построений
365
Таким образом, предыдущими исследованиями мы свели деле-
деление круга на п равных частей, где п есть простое число, к реше-
решению уравнений число которых равно количеству сомножителей,
на которые может быть разложено число п — 1, а степени урав-
уравнений определяются величиной сомножителей. Поэтому, если п — 1
есть степень числа 2, что имеет место для значений п ~ 3, 5, 17,
257, 65537, .. ., то деление круга сводится к решению только квад-
квадратных уравнений, и тригонометрические функции углов Р / п,
2Р / п,. . . могут быть выражены через более или менее сложные
(в зависимости от величины п) квадратные уравнения. Следова-
О делениях круга посредством геометрических построений 571
тельно, в этом случае деление круга на п равных частей или по-
построение правильного га-угольника может быть выполнено при
помощи геометрических построений. Например, для п = 17 из
пп. 354, 361 для косинуса угла j^P легко выводится следующее
выражение:
-i |/ 17 + 3 УТТ — |/ 34 — 2 УТТ — 2 ]/ 34 + 2 J/T? •
Косинусы кратностей этого угла имеют аналогичный вид, синусы
же содержат на один радикал больше. Весьма замечательно, что
в то время как возможность геометрического деления круга на три
и пять частей была известна уже ко временам Эвклида, к этим
сведениям на протяжении 2000 лет не было добавлено ничего но-
нового, и что все математики считали, что кроме указанных деле-
делений, и тех, которые непосредственно получаются из них, именно,
делений на 15, 3-2а, 5-2^, 15-2^ и 2^ частей, никакие другие де-
деления при помощи геометрических построений не выполнимы. Легко
доказать, впрочем, что если п = 2m -f- 1 есть простое число, то и
показатель m не может содержать никаких простых сомножителей,
кроме числа 2, и потому равен либо 1, либо 2, либо более высо-
высокой степени числа 2; действительно, если бы m делилось на неко-
некоторое нечетное число С (большее чем 1), и именно, имело бы место
m = Ст], то 2W + 1 делилось бы на 271 + 1 и потому было бы со-
составным числом. Таким образом, все значения п, для которых по-
получаются только квадратные уравнения, представляются в виде
22 +1; таким образом, получаются пять чисел 3, 5, 17, 257, 65537,
если полагать v = 0, 1, 2, 3, 4 или m — 1, 2, 4, 8, 16. Однако
геометрическое деление круга можно провести ни в коем случае
не для всех чисел такого вида, а лишь для тех из них, которые
являются простыми. Правда, Ферма утверждал из индуктивных
соображений, что все числа такого вида обязательно являются
простыми; однако Эйлер впервые заметил, что уже для v = 5
или m = 32 это правило оказывается неверным, так как число
232 + 1 = 4294967297 содержит сомножитель 641.
572 Раздел VII (п. 366)
Если же п—1 содержит, кроме числа 2, другие простые со-
сомножители, то мы всегда приходим к уравнениям более высокой
степени, именно, к одному или нескольким кубическим, если чис-
число 3 содержится один или несколько раз среди сомножителей числа
п — 1, к уравнениям пятой степени, если п— 1 делится на 5 и т. д.,
и мы можем со всей строгостью доказать, что эти уравнения более
высоких степеней никак не могут быть исключены или сведены
к уравнениям более низкой степени; хотя границы настоящего
сочинения не позволяют привести здесь это доказательство, мы
считаем своим долгом указать на это, чтсбы никто не надеялся
бы свести еще и другие деления кроме делений, дающихся нашей
теорией, например, деления на 7V 11, 13, 19,... частей к геомет-
геометрическим построениям, и не тратил бы бесполезно свое время.
366
Если нужно разделить круг на аа частей, где а обозначает
простое число, то это, очевидно, всегда можно сделать геометри-
геометрически, если а = 2, но ни для каких других значений а это уже
невозможно, если только а>1; действительно, нам тогда пришлось
бы решать, кроме тех уравнений, которые нужны для деления на
а частей, также и а—1 других уравнений степени а; эти уравнения
также не могут быть исключены или понижены. Степени необхо-
необходимых уравнений, таким образом, всегда (т. е. также и для слу-
случая а = 1) будут равны простым сомножителям числа (а — 1) аа~г.
Если, наконец, нужно разделить круг на N = aab&cf. . . частей,
где а, Ь, с,... обозначают различные простые числа, то достаточно
уметь производить деление на аа, 6р, cY, ... частей (п. 336)
поэтому, чтобы узнать степени требуемых для этой цели
уравнений, нужно рассмотреть простые сомножители чисел
(а — 1)аа~!, (й —1)ДО-1, (с —1)cy-i, ...,
или, что сводится к тому же, произведения этих чисел. Заметим, что
это произведение выражает количество чисел, которые взаимно про-
просты с N и меньше чем N (п. 38). Таким образом, геометрически деление
можно произвести только тогда, когда это число есть степень числа 2;
О делениях круга посредством геометрических построений 573
если же оно, кроме 2, содержит еще и другие простые сомножите-
сомножители, например, р,р',..., то от уравнений р-й, р'-ж и т. д. степеней ни-
никаким образом нельзя будет избавиться. Отсюда мы заключаем вооб-
вообще, что для того, чтобы круг можно было геометрически разделить
на TV частей, нужно, чтобы N было равно либо 2, либо более высо-
высокой степени числа 2, или чтобы TV было либо простым числом вида
2т -f 1, либо произведением нескольких таких простых чисел, или
чтобы TV было произведением одного или нескольких таких простых
чисел либо на 2, либо на более высокую степень числа 2; короче го-
говоря, необходимо, чтобы TV не содержало никаких нечетных простых
сомножителей, кроме имеющих вид 2т+ 1, и никакого сомножите-
сомножителя указанного вида не содержало в степени выше первой. Среди чи-
чисел до 300 такими значениями TV являются следующие 38: 2, 3, 4, 5, 6,
8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85,
96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272 *.
* Если бы все числа вида 22т + 1 были простыми, то достаточно точным вы-
выражением для количества рассматриваемых чисел (N), меньших заданного числа
Л/Г ^ r l/logMV2
М, было бы ^^j
ДОПОЛНЕНИЯ
К п. 28. Решение неопределенного уравнения ах =Ьу + 1 было
впервые дано не Эйлером (как сказано в тексте), а уже одним
математиком семнадцатого столетия, Баше де Мезириаком,
замечательным издателем и комментатором Диофанта, и эту
честь признал за ним Лагранж («Add. а ГAlgebre d'Euler», p. 525,
где одновременно указывается сущность метода). Баше изложил
свое открытие во втором издании своей книги «Problemes plaisans
et delectables qui se font par les nombres»; в первом издании, с которым
я только и мог ознакомиться, его еще нет. хотя оно уже и было
сделано.
К п. 151, 296, 297. Лежандр заново изложил свое доказа-
доказательство в замечательном сочинении «Essai d'une theorie des nomb-
nombres», однако по существу ничего в нем не изменил, поэтому все
возражения против его метода, приведенные в п. 297, остаются
в силе. Хотя теорема (на которой основывается одно предположе-
предположение) о том, что в каждой арифметической прогрессии Z, / + А,
I + 2к, .. . имеются простые числа, если только I и к не имеют
общих делителей, в этом сочинении рассматривается подробнее,
но в смысле математической строгости сделанного еще не
достаточно. Однако, если бы эта теорема и была полностью дока-
доказана, остается еще одно предположение (что имеются простые числа
вида An + 3, по которым заданное положительное простое число
вида An -{- 1 является квадратичным невычетом), и я не знаю, можно
ли его строго доказатьt не предполагая уже известной саму фун-
фундаментальную теорему. Впрочем, надо заметить, что Лежандр
делает это предположение не молчаливо, а и сам обращает на него
внимание.
Дополнения 575
К пп. 288—293. Относительно того вопроса, который здесь рас-
рассматривается как специальное приложение теории тройничных
форм, и который должен быть разобран так, чтобы в отношении
строгости и общности не оставалось желать ничего лучшего, Ле-
жандр в третьем разделе своего сочинения проводит намного
более подробное исследование*. При этом он использует принципы,
совершенно отличные от наших; одвако на этом пути он столк-
столкнулся со многими трудностями, в результате чего не смог обосно-
обосновать основные теоремы строгими доказательствами. На эти труд-
трудности он сам честно указал; однако, если мы не ошибаемся, они
могут быть устранены легче, чем та, что в этом исследовании пред-
предполагается справедливой упомянутая выше теорема («В каждой
геометрической прогрессии и т. д.»).
К п. 306, VIII. В третьей тысяче отрицательных определите-
определителей имеется 37 иррегулярных, из которых 18 имеют показатель
иррегулярности 2, остальные 19 — показатель иррегулярности 3.
К п. 306, X. Недавно нам посчастливилось полностью решить
поставленную здесь задачу; это исследование, которое поразитель-
поразительным образом проливает сьет на многие вопросы как высшей ариф-
арифметики, так и анализа, мы при первой возможности опубликуем
как продолжение настоящего сочинения. Результат состоит в том,
что коэффициент т из п. 304 равен ^«2,3458847616, где f обо-
обозначает ту же величину, что и в п. 302, а тг, как и там, обозна-
обозначает половину длины окружности радиуса 1.
* Хотя мы на это и не указываем, читатель не должен смешивать наши
тройничные формы с тем, что Л е ж а н д р называет «formо trinaire d'un nom-
bre». Именно, под этим выражением он понимает разложение числа на три квад-
квадрата.
Таблиць
3
5
7
9
11
13
16
17
19
23
25
27
29
31
32
37
41
43
47
49
53
59
61
64
67
71
73
79
81
83
89
97
1
2
2
3
2
2
6
5
10
10
10
2
2
10
17
5
5
6
28
10
10
26
10
10
5
12
62
5
29
И
50
30
10
2
1
1
2
1
1
5
*
10
17
8
1
1
И
12
*
И
26
39
30
2
25
25
47
*
29
58
8
50
25
3
72
86
3
3
1
*
8
8
3
И
5
20
7
*
27
13
3
34
15
17
18
13
9
32
42
3
9
18
6
71
*
52
87
2
5
5
5
4
9
1
7
2
15
*
5
18
20
1
1
22
5
17
41
31
34
14
1
39
14
1
34
35
81
18
И
7
4
7
7
2
9
12
21
5
16
20
4
2
28
39
7
38
*
38
44
23
10
7
33
33
19
22
24
7
53
11
И
1
13
6
3
16
13
23
29
5
6
3
6
27
16
46
45
45
5
61
43
55
70
1
72
4
82
13
3
12
13
12
19
8
2
23
7
13
31
40
3
9
28
23
20
15
23
27
59
74
38
67
65
83
17
8
17
13
15
7
1
4
5
33
16
42
31
42
14
49
12
8
7
21
9
15
4
82
19
Таблиц!
19
5
18
12
15
22
7
25
9
29
29
35
41
22
22
7
26
38
62
10
12
59
53
27
23
И
11
24
21
6
21
36
20
39
32
39
27
39
14
20
5
46
52
5
16
31
79
29
27
3
15
7
25
43
24
6
4
25
И
22
4
35
1
7
36
29
47
* 1
31
0
27
28
32
5
7
45
7
13
8
43
13
И
76
14
32
57
26
(пт
37
32
35
24
38
22
41
33
9
44
30
64
23
24
60
77
41
г. 58,91)
41
18
25
27
33
2
18
14
19
55
4
21
29
38
67
71
43
37
36
30
13
41
13
63
44
51
47
10
49
59
44
47
23
8
53
40
12
64
17
31
55
13
69
34
60
53
28
51
5
3
59
53
7
45
13
10
14
59
17
1
54
29
5
17
53
20
45
65
61
3
5
37
58
75
4
34
19
32
67
И
50
54
20
53
32
51
71
44
33
33
17
26
25
73
4
48
43
68
20
79
52
47
46
42
83
27
91
89
18
Таблицы
II
1 1
1 1
68+
III
II
II
1 1
S8+
II 1 1 1 1 1
III
61+
1 1 1 1
II
M
1 1
II
1 1 1 1
11
\L+
il
i i i i i
i I
i i i i
I i I I
T9+
ii
ill
69+
i i i ) i I I и I i I
I I I i
i I I i i i
и
i i I i i i I i f i i
и
i i iIi
ll
I
Ю
a
H
i j i i i
i \
n
i I i i i i i i
ill
i i
mi
62+
m
M
i i
SS+
i 1 I I I I и
I I I I
6И-
и
M
i i i i i I
AI+
I и i I
и
еИ-
I i I i
ill
И+
i I
ill
ii
I i 11
i
ii
I i i i
i I i i i
S+
i I i i i I i 1
Z+
I i I i I I
i i I I I
I—
II
III II 1 1 Г
> CO Ob I>-
¦ О0 0ОЭ
Таблицы
Таблица 3 (п. 316)
3
7
9
11
13
17
19
23
27
29
31
37
41
43
47
49
53
59
61
67
71
73
79
@).. 142857.
@)..1; A)..2; B)..4; C)..8; D)..7; E)..5.
@)..09; A)..18; B)..36; C)..72; D)..45.
@)..076923; A)..461538.
@)..0588235294 117647.
@)..0526315789 47368421.
@)..0434782608 6956521739 13.
@)..037; A)..074; B)..148; C)..296; D)..592; E)..185.
@)..0344827586 2068965517 24137931.
@)..032280645 16129; A)..5483870967 74193.
@)..027; A)..135; B)..675; C)..378; D)..891; E)..459; F)..297;
G)..486; (8)..432; (9)..162; A0)..810; A1)..О54.
@)..02439;A)..14634;B)..87804;C)..26829;D)..60975;E)..65853;
F)..95121; G)..70731.
@)..0232558139 5348837209 3; A)..65116279О6 9767441860 4.
@)..0212765957 4468085106 3829787234 0425531914 893617.
@)..0204081632 6530612244 8979591836 7346938775 51.
@)..0188679245 283; A)..4905660377 358; B)..75471698И 320;
C)..6226415094 339.
@)..016949152542372881355932203389 8305084745 7627118644
06779661.
@)..0163934426 2295081967 2131147540 9836065573 7704918032
7868852459.
@)..0149253731 3432835820 8955223880 597;
A)..1791О44776 1194029850 7462686567 164.
@)..0140845070 4225352112 6760563380 28169;
<1)..8732394366 1971830985 9154929577 46478.
@)..01369863; A)..06849315; B)..34246575; C)..71232876;
D)..56164383; E)..80821917; F)..О41О9589; G)..20547945;
(8)..02739726.
@)..0126582278 481; A)..3670886075 949; B)..6455696202531;
C)..7215189873 417; D)..9240506329113;E)..7974683544 303.
Таблицы 579
Таблица 3 (п. 316) (окончание)
81 @)..012345679; A)..135802469; B)..493827160; C)..432098765;
D)..753086419; E)..283950617.
83 @)..0120481927 7108433734 9397590361 4457831325 3,
A)..6024096385 5421686746 9879518072 2891566265 0.
89 @)..0112359550 5617977528 0898876404 4943820224 7191;
A)..3370786516 8539325842 6966292134 8314606741 5730.
97 @)..010309278350515463917525773195 87628865979 381443298
9690721649 4845360824 7422680412 3711340206 185567.
ОГЛАВЛЕНИЕ
Предисловие автора
Раздел I. О сравнимости чисел вообще
Сравнимые числа, модули, вычеты и невычеты (пп. 1—3). Наименьшие
вычеты (п. 4). Элементарные теоремы о сравнениях (п. 5—11). Не-
Некоторые приложения (п. 12).
Раздел II. О сравнениях первой степени
Предварительные теоремы о простых числах, сомножителях и т. д.
(пп. 13—25). Решение сравнений первой степени (пп. 26—31). На-
Нахождение числа, которое сравнимо с заданными вычетами по задан-
заданным модулям (пп. 32—36). Линейные сравнения со многими неиз-
неизвестными (п. 37). Различные теоремы (пп. 38—44).
Раздел III. О степенных вычетах
Вычеты членов геометрической прогрессии, начинающейся с единицы,
образуют периодический ряд (пп. 45—48). Сначала рассмат-
рассматриваются модули, которые являются про-
простыми числами (пп. 49—81). Теорема Ферма (пп. 50, 51).
О количестве чисел, которым соответствуют периоды, у которых ко-
количество членов равно заданному делителю числа р— 1 (пп. 52—56).
Первообразные корни, основные числа, индексы (п. 57). Алгоритм
индексов (пп. 58, 59). О корнях сравнения хп = А (пп. 60—68).
Связь между индексами в различных системах (пп. 69—71). Основ-
Основные числа, служащие специальным целям (п. 72). Метод определе-
определения первообразных корней (пп. 73, 74). Различные теоремы о пери-
периодах и первообразных корнях (пп. 75—81). О модулях, которые яв-
являются степенями простых чисел (пп. 82—89). Модули, являющиеся
степенями числа 2 (пп. 90, 91). Модули, составленные из нескольких
простых чисел (пп. 92, 93).
Оглавление
Раздел IV. О сравнениях второй степени
Квадратичные вычеты и невычеты (пп. 94, 95). Если модуль есть простое
число, то среди чисел, меньших его, количество вычетов равно коли-
количеству невычетов (пп. 96, 97). Ответ на вопрос, является ли составное
число вычетом или невычетом заданного простого числа, зависит от
свойств сомножителей (пп. 98, 99). О модулях, являющихся состав-
составными числами (пп. 100—105). Общий критерий того, является ли
заданное число вычетом или невычетом по заданному простому мо-
модулю (п. 106). Исследование относительно про-
простых чисел, по которым заданные числа яв-
являются вычетами или невычетами (пп. 107—
150). Вычет—1 (пп. 108—111). Вычеты-f 2 и—2 (пп. 112—116). Вы-
Вычеты +3 и —3 (пп. 117—120). Вычеты +5 и —5 (пп. 121—123). О вы-
вычетах ±7 (п. 124). Подготовка к общему исследованию (пп. 125—
129). Индуктивным путем находится общая (фундаментальная)
теорема и делаются выводы из нее (пп. 130—134). Строгое доказатель-
доказательство фундаментальной теоремы (пп. 135—144). Аналогичный метод
для доказательства теоремы из п. 114 (п. 145). Решение общей пробле-
проблемы (п. 146). О линейных формах, содержащих все простые числаt
по которым заданное число является вычетом или невычетом (пп.
147—150). О работах других авторов, относящихся к этим исследо-
исследованиям (п. 151). О сравнениях второй степени общего вида (п. 152).
Раздел V. О формах и неопределенных уравнениях второй
степени
Предмет исследования; определение форм и обозначения (п. 153). Пред-
Представление чисел; определитель (п. 154). Значения выражения
'Yb2 — ас (mod Л/), которым принадлежит представление числа М
формой (а, &, с) (пп. 155, 156). Форма, содержащая другую форму
или содержащаяся в другой форме; преобразование, собственное
и несобственное (п. 157). Эквивалентность, собственная и несобствен-
ная(п.158). Противоположные формы (п. 159). Соседние формы (п. 160).
Общие делители коэффициентов форм (п. 161). Связь между всевозмож-
всевозможными однотипными преобразованиями одной заданной формы в другую
(п. 162). Двусторонние формы (п. 163). Теорема, касающаяся случая,
когда одна форма содержится в другой одновременно собственно и
несобственно (пп. 164, 165). Общее исследование о представлениях
чисел формами и о связи этих представлений с преобразованиями(пп.
166—170). О формах с отрицательным опреде-
определителем (пп. 171—182). Специальные приложения к разложе-
разложению чисел на два квадрата, на простой и удвоенный и на простой и
утроенный квадраты (п. 182). О формах с положитель-
582 Оглавление
ным неквадратным определителем (пп. 183—
205). О формах с квадратным определителем
{пп. 206—212). Формы, которые содержатся в других, и притом им
не эквивалентны (пп. 213, 214). Формы с определителем
0 (п. 215). Общее решение в целых числах всех неопределенных
уравнений второй степени с двумя неизвестными (пп. 216—221).
Исторические замечания (п. 222). Дальнейшие исследования о формах
(пп. 223—265). Разбиение форм с заданным определителем на классы
(пп. 223—225). Разбиение классов на порядки (пп. 226, 227). Деление
порядков на роды (пп. 228—233). О композиции форм
(пп. 234—244). Композиция порядков (п. 245). Композиция родов
(пп. 246—248), Композиция классов (пп. 249—251). Для заданного
определителя в отдельных родах из одного и того же порядка со-
содержится по одинаковому числу классов (п. 252). Сравниваются ко-
количества классов, содержащихся в отдельных родах из различных
порядков (пп. 253—256). О числе двусторонних классов (пп. 257—
260). Половине всех возможных для данного определителя характе-
характеров заведомо не могут соответствовать собственно примитивные (при
отрицательном определителе положительные роды) (п. 261). Вто-
Второе доказательство фундаментальной те-
теоремы и остальных теорем, касающихся вы-
вычетов —1, +2, —2 (п. 262). Точнее определяется та половина ха-
характеров, которой не могут соответствовать роды (пп. 263, 264). Спе-
Специальной метод для разложения простых чисел на два квадрата
(п. 265). Отступление, содержащее исследование о тройничных фор-
формах (пп. 266—285). Некоторые приложения к теории двойничных
форм (пп. 286—307). О нахождении формы, при удвоении которой
получается заданная двойничная форма главного рода (п. 286). Всем
характерам, за исключением тех, невозможность которых была до-
доказана в пп. 263, 264, действительно соответствуют роды (п. 287).
Теория разложения чисел и двойничных форм на три квадрата
(пп. 288—292). Доказательство теоремы Ферма о том, что каждое
целое число может быть разложено на три треугольных числа или на
четыре квадрата (п. 293). Решение уравнения ах2 + by2 + cz2 = 0
(пп. 294, 295). О методе, которым Л е ж а н д р изложил фундамен-
фундаментальную теорему (пп. 296—298). Представление нуля любыми трой-
тройничными формами (п. 299). Общее решение в рациональных величи-
величинах уравнений второй степени с двумя неизвестными (п. 300). О сред-
среднем количестве родов (п. 301). О среднем количестве классов (пп.
302—304). Особый алгоритм для собственно примитивных
классов; регулярные и иррегулярные определители и т. д. (пп.
305—307).
Оглавление
Раздел VI. Различные применения предыдущих исследований 468
Разложение дробей на более простые (пп.309—311). Превращение обык-
обыкновенных дробей в десятичные (пп. 312—318). Решение сравнения
хъ = А методом исключения (пп 319—322). Решение неопределен-
неопределенного уравнения тх2 + пу2 = Л методом исключения (пп. 323—
326). Другой метод решения сравнения х2^А в случае, когда А
отрицательно (пп. 327, 328). Два метода отличать составные числа от
простых и находить сомножители составных чисел (пп. 329—334).
Раздел VII. Об уравнениях, от которых зависит деление круга 509
Исследование сводится к простейшему случаю, когда число частей, на
которые должен быть разбит круг, является простым (п. 336). Уравне-
Уравнения для тригонометрических функций дуг, составляющих одну или не-
несколько частей полной окружности; сведение тригонометрических
функций к корням уравнения хп — 1 =0 (пп. 337, 338). Теория кор-
корней уравнения хп — 1=0 (в предположении, что п есть простое
число). Если отбросить корень 1, то совокупность (Q.) остальных
корней содержится в уравнении X = xn~~i-\- xn~~2 +...+X + 1=0
(пп. 339, 340). Функция X не может быть разложена на сомножители
более низких степеней, все коэффициенты у которых рациональны
(п. 341). Указывается цель дальнейших исследований (п. 342). Все
корни из Q. разбиваются на некоторые классы (периоды) (п. 343). Раз-
Различные теоремы о периодах корней из Q, (пп. 344—351). На преды-
предыдущих исследованиях основывается решение уравнения X = 0
(пп. 352—354). Дальнейшие исследования о пе-
периодах корней. Суммы, у которых количество членов четно,
являются вещественными величинами (п. 355). Об уравнении, опреде-
определяющем разбиение корней из D. на два периода (п. 356). Доказатель-
Доказательство теоремы, упомянутой в разделе IV (п. 357). Об уравнении для
разбиения корней из Q, на три периода (п. 358). Сведение уравне-
уравнений, из которых находятся корни Q,, к чистым уравнениям (пп. 359,
360). Применение предыдущих исследований к тригонометрическим
функциям Метод различать углы, которым соответствуют отдельные
корни из (?1) (п. 361). Тангенсы, котангенсы, секансы и косекансы
определяются по синусам и косинусам без помощи деления (п. 362).
Метод постепенного понижения степеней уравнений для тригоно-
тригонометрических функций (пп. 363, 364). Деления круга, которые можно
выполнить при помощи квадратных уравнений или посредством гео-
геометрических построений (пп. 365, 366).
Дополнения 574
Таблицы 576
ДРУГИЕ
СОЧИНЕНИЯ
НОВОЕ ДОКАЗАТЕЛЬСТВО
ОДНОЙ АРИФМЕТИЧЕСКОЙ ТЕОРЕМЫ
(Commentationes soc. reg\ sc. Gottingensis,
Vol. XVI, Gottingae, 1808)
1
В вопросах высшей арифметики очень часто имеет место свое-
своеобразное явление, существенно увеличивающее ее прелесть, которое
в анализе встречается значительно реже. В то время как при ана-
аналитических исследованиях к новым истинам большей частью можно
придти лишь тогда, когда мы полностью овладели принципами, на
которых они покоятся, и которые, в известной мере, открывают к ним
путь, в арифметике весьма часто, благодаря какому-нибудь неожи-
неожиданному случаю, бросаются в глаза на индуктивном пути изящней-
изящнейшие истины, доказательства которых, однако, скрыты так глубоко,
что не поддаются никаким попыткам и оказываются недоступными
для остроумнейших изысканий. Далее, между арифметическими
истинами на первый взгляд совершенно различной природы суще-
существует столь тесная и столь поразительная связь, что нередко во вре-
время поисков чего-нибудь совсем иного удается на пути, совершенно
отличном от ожидаемого, получить какое-нибудь давно желанное
доказательство, долгие размышления над которым прежде остава-
оставались тщетными. Большей частью, однако, эти истины такого рода,
что к ним можно придти многими весьма различными путями, и не
всегда кратчайшим оказывается тот, который представился первым.
Поэтому, конечно, весьма ценно, когда в конце концов для одной из
таких истин, которая долго и безрезультатно обдумывалась и затем
588 Новое доказательство одной арифметической теоремы
хотя и была доказана, но длинным окольным путем, удается найти
наиболее простое и естественное доказательство.
Среди вопросов, о которых мы говорили в предыдущем пункте,
выдающееся место занимает теорема, содержащая почти всю теорию
квадратичных вычетов, которую мы в «Арифметических исследова-
исследованиях» (раздел IV) назвали фундаментальной теоремой. Первым, кто
нашел эту чрезвычайно изящную теорему, следует, несомненно, счи-
считать Лежандра, хотя еще задолго до этого великие математи-
математики Эйлер и Лагранж открыли индуктивным путем мно-
многие ее специальные случаи. Я не буду останавливаться здесь на пере-
перечислении попыток этих ученых доказать теорему; тот, кого это ин-
интересует, может обратиться к упомянутому выше сочинению. Позво-
Позволю себе лишь, для подтверждения сказанного в предыдущем пункте,
добавить здесь то, что относится к моим собственным попыткам. К
самой теореме я вполне самостоятельно пришел в 1795 г., когда я еще
совершенно не был знаком со всем тем, что было до этого уже сделано
в высшей арифметике, и был лишен каких-либо литературных вспомо-
вспомогательных средств; эта теорема мучила меня целый год и не под-
поддавалась напряженнейшим усилиям; наконец, я получил доказатель-
доказательство, приведенное в четвертом разделе указанного сочинения. По-
После этого я нашел еще три других доказательства, основанных на
совершенно отличных принципах, одно из которых я сообщил в пя-
пятом разделе, а два остальных, которые по изяществу не уступают пер-
первому, опубликую при другом удобном случае. Однако все эти дока-
доказательства, хотя и не оставляющие желать ничего лучшего в отно-
отношении строгости, выведены из слишком разнородных принципов,
за исключением, быть может, первого, которое, однако, проводится
посредством утомительной цепи умозаключений и страдает чрез-
чрезмерными длиннотами в вычислениях. Поэтому я, не колеблясь, ут-
утверждаю, что естественное доказательство до сих пор отсутствовало;
знатоки смогут судить, заслуживает ли такого наименования доказа-
доказательство, которое нам недавно посчастливилось открыть, и которое
излагается на следующих ниже страницах.
Новое доказательство одной арифметической теоремы 589
Теорема. Пусть р — положительное простое число, к— не деля-
делящееся на р целое число,
А—совокупность чисел 1, 2, 3,..., (р —1)/2,
В— совокупность чисел (р + 1) /2, (р + 3)/2, (р + 5) /2, .. ., р— 1.
Возьмем, далее, наименьшие положительные вычеты произведений к
на отдельные числа из А по модулю р, которые, очевидно, будут
все различны и будут частью принадлежать к А, а частью к В.
Если теперь предположить, что всего к В принадлежит [х из этих
вычетов, то к будет квадратичным вычетом или невычетом по мо-
модулю р в зависимости от того, будет ли число [х четным или не-
нечетным.
Доказательство. Если а, а', а", .. . суть вычеты, принадлежа-
принадлежащие к А, а Ъ, Ъ\ Ъ", . . . — остальные лычеты, принадлежащие к Б,
то очевидно, что дополнения последних, р — Ь, р—Ъ\ р — Ъ", . . .,
будут все отличны от чисел а, а', а",. . . , но вместе с ними будут
исчерпывать всю совокупность А. Поэтому мы имеем
1.2.3....±(р-1) = аа'а"...(р
Последнее же произведение, очевидно, будет
= (—ifaa'a" . .. bb'b" . . . s
= (—lfk-2k-3k ...l(
Следовательно,
1 = {_ifkG>-1)/2,
т. е. к^р~~1^2е= + 1, в зависимости от того, будет ли [х четным или
нечетным, откуда тотчас же и получается наша теорема.
Дальнейшие рассуждения могут быть существенно сокращены
посредством введения подходящих обозначений. Пусть символ (к, р)
590 Новое доказательство одной арифметической теоремы
обозначает количество тех произведений из ряда
*, 2Л, ЗА:,..., ^(p-l)k,
наименьшие положительные вычеты которых по модулю р превос-
превосходят половину этого числа. Если далее, х есть некоторая не-
нецелочисленная величина, то через [х] мы будем обозначать ближай-
ближайшее к х, меньшее чем х целое число, так что х — \х] всегда есть
положительная величина, лежащая между границами 0 и 1. Тогда
без труда получаются следующие соотношения:
I. [х] + [_я] = _1.
II. [х]-\-h= [x-\-h\, если h есть целое число.
III. [х] -\-[h — x] = h — l.
IV. Если х — [х] есть дробь, меньшая чем г/2, то [2х] — 2 [х] = 0;,
если же, напротив, х — [?]>-7г> т0 Г^ж]— 2[ж] = 1.
V. Если поэтому наименьший положительный вычет целого*
числа h по модулю р меньше чем р/2, то [2h/p] — 2[/г/р]=0;
если же этот вычет больше чем jd/2, to [2h/p] — 2[h/р] = I.
VI. Из этого тотчас же следует, что
(к, р) = [2к/р] + [4к/р] + [6к/р] + ¦ ¦ ¦ + {(p-i)к/р] —
— 2[к/Р] — 2[2к/р]—2[Зк/р] 2[у(/> —1)А/р].
VII. Из VI и I легко выводится, что
(к,р) + (-к,р)=±-(р-1).
Отсюда получается, что число — к относится к числу р (в смысле
того, является ли — к вычетом или невычетом по модулю р)
или так же, как + к, или противоположным образом, в зависи-
зависимости от того, имеет ли р вид An + 1 или вид An + 3. В первом
случае число —1 будет, очевидно, вычетом, а во втором — невыче-
невычетом по модулю р.
VIII. Приведенную в VI формулу мы преобразуем следующим
образом. Согласно III, имеет место
[(р — 3)к/р]=к—1—[Зк/р],
Новое доказательство одной арифметической теоремы 591
Если мы произведем замену такими выражениями последних
(pipi)/4 членов ряда из VI, то получим,
во-первых, что если р имеет вид 4п + 1, то
— 2 {[к/р] +[Ък/р]+ [5к/р]^
- {[к/р] + [2к/р] + [Зк/ р] + • • • + [1 (р-1) к/р\\,
и, во-вторых, что если р имеет вид An -+- 3, то
IX. Для специального случая А = + 2 из приведенных выше
формул получается, что B, р) = -т-(.Р + 1)> гДе нужно брать верх-
верхний или нижний знак в зависимости от того, имеет ли р вид
4гс + 1 или An + 3. Следовательно, когда р имеет вид 8п + 1 или
8гс + 7, число B, /?) будет четным, и потому 2 будет вычетом по
модулю р; если же р имеет вид 8п + 3 или 8м + 5, то B, /?), на-
напротив, будет нечетным, и потому 2 будет невычетом по модулю р.
Теорема. Пусть х — положительная нецелочисленная величина,
такая, что среди ее кратностей х, 2х, Зх, ... до пх нет ни од-
одного целого числа; положим [пх] = h, откуда легко получить, что
и среди кратностей 1 /х, 2/х, 3/х, . . до h/x обратной к х вели-
величины тоже нет целых чисел. Тогда я утверждаю, что
[х] + [2х] + [Зх] + • • - + [пх] +
+[1/х] + [2/х] + [3/х] + . •. + [h/x] = nh.
Доказательство. В ряде [х] + [2х] + [Зх] -)-•••+ [пх], который
мы обозначим через ?2, первые члены до [1 / х]~то члена включи-
592 Новое доказательство одной арифметической теоремы
тельно все, очевидно, равны 0, следующие члены до [2 /х]-то все
равны 1, следующие, до [3/^]-го, все равны 2, и т. д. Поэтому
+ 1г.{п — [11/х]} = hn — [l / х] — [2 /х] — [3 /х] [h/x].
Это и требовалось доказать.
Теорема. Если k, р обозначают любые положительные не равные
между собой простые числа, то
+ [р/ к] + [2р/к] + 1Ър/к]+-.-+[± (к- 1)р/к] =
Доказательство. Предположим, для определенности, что к < р,
тогда -j(p — 1) к/р будет меньше, чем к/2, но больше чем (к — 1)/2
у (/? — 1)к/р\ = —-(к — 1). Отсюда вытекает, что настоя-
настоящая теорема тотчас же получается из предыдущей, если положить
~ = х, ^{р— 1) = и, и потому \{к— 1) =h.
Подобным же образом можно показать, что если к есть четное
число, взаимно простое с р, то
Однако мы не будем останавливаться на этой теореме, которая
для нашей цели не требуется.
Новое доказательство одной арифметической теоремы 593
Теперь из соединения последней теоремы с теоремой VIII п. 4
сразу получается фундаментальная теорема. Именно, если обозна-
обозначить через А, р какие-нибудь неравные положительные простые
числа и положить
(к, р) + [к/р] + [2к/р] + [Зк/р] + • • • + [j(p — 1) к/р\ = L,
(Р, к) + lp/к] + [2р/к] + [Зр/к] +... + [i (*-1)/>/*] = М,
то из VIII п. 4 вытекает, что L и М всегда будут четными чис-
числами. Согласно же теореме п. 6,
Поэтому, если -г (к — 1) (р — 1) четно, что будет тогда, когда либо
оба числа к, р, либо по крайней мере одно из них имеет вид
4п-\-1, то (А, р) и (р, к) будут обязательно либо оба четны, либо
оба нечетны. Если же -г (к—1) (р — 1) нечетно, что будет тогда,
когда оба числа к, р имеют вид An -\- 3, то обязательно одно из
чисел (к, р), (/?, к) должно быть четным, а другое нечетным. Сле-
Следовательно, в первом случае отношение числа к к р (в том смыс-
смысле, является ли первое вычетом или невычетом второго) будет со-
совпадать с отношением р к к, а во втором случае будет ему про-
противоположно. Это и требовалось доказать.
СУММИРОВАНИЕ НЕКОТОРЫХ РЯДОВ
ОСОБОГО ВИДА
(Commentationes soc. reg. sc. Gotting.
recentiores, Vol. /, Gottingae, 1811)
Среди наиболее замечательных истин, к открытию которых про-
проложила путь теория деления круга, далеко не последнее место зани-
занимает изложенное в п. 356 «Арифметических исследований» суммиро-
суммирование, причем не только вследствие его особенного изящества и ис-
исключительной плодотворности, более подробное обоснование которой
мы отложим до другого исследования, но также и по той причине,
что строгое и совершенное доказательство этого суммирования
требует преодоления совсем необычных трудностей. Эти трудности
тем более неожиданны, что относятся они не столько к самой теоре-
теореме, сколько к некоторому ее уточнению, причем если на него не об-
обращать внимания, то доказательство тотчас же становится очевидным
и легко получается на основании изложенной в указанной работе
теории. Теорема там была дана в следующем виде. Пусть п — простое
число; обозначим всевозможные квадратичные вычеты по модулю п>
лежащие между границами 0 и п — 1 включительно, через а, а все-
всевозможные невычеты, лежащие между теми же границами, через Ъ\
наконец, через со обозначим дугу 3607/г, и через к — какое-нибудь
не делящееся на п заданное целое число.
I. Тогда для значения п вида Am + 1 имеет место
2 cos ак(о = — у + у V~n,
Суммирование некоторых рядов особого вида 595
2 cos bk со = — у + j/n,
потому
2 cos а& со — 2 cos ^ w ~ it V^ i
2 sin a& со = 0,
2 sin bkco = 0.
П. Для значения п вида 4m + 3 имеет место
2 cosa&co — — у,
2 cos bkco = — у,
2 sin a& со = + у
2 sin feA со = =p у
2 sin ak со— 2j sin й& со = + Уп*
Формулы суммирования были доказаны в упомянутом месте со
всей строгостью, и здесь уже не остается больше никаких других
трудностей, кроме определения знака у квадратного корня. При этом
без труда можно показать, что знак, зависи-т от числа к лишь по-
постольку, поскольку для всех значений А, которые являются квадра-
квадратичными вычетами по модолю тг, он должен быть одним и тем же, а
для всех значений к, которые являются квадратичными невычетами
по модулю п, должен быть противоположным первому. Поэтому
все дело сводится к случаю А=1, и ясно, что если мы узнаем знак
для этого значения, то он сразу станет известным и для всех остальных
значений к. Но при определении этого знака, которое на первый
взгляд кажется относящимся к числу совсем простых задач, мы на-
наталкиваемся на совершенно неожиданные трудности, и метод, при
помощи которого мы до сих прр обходили все припятствия, здесь
совершенно отказывается служить.
596 Суммирование некоторых рядов особого вида
Быть может целесообразно, прежде чем идти дальше, проделать
для нескольких примеров наше суммирование непосредственным
вычислением; однако будет хорошо, если предварительно мы сделаем
некоторые общие замечания.
I. Если в случае, когда п есть простое число вида km + 1, обоз-
обозначить через а' всевозможные квадратичные вычеты по модулю п,
лежащие в границах от 1 до (п — 1)/2 включительно, а через Ъ'
обозначить всевозможные лежащие между теми же границами невы-
невычеты, то, как известно, всевозможные числа п — а1 будут содержать-
содержаться среди чисел а, а всевозможные числа п — Ь1 — среди чисел Ъ\
так как при этом числа а\Ъ' ,п — а', п — Ь1 будут, очевидно, состав-
составлять всю совокупность чисел 1, 2, 3, ..., п — 1, то всевозможные
а1 вместе со всевозможными п — а' будут охватывать всевозможные
числа а, и точно так же всевозможные Ъ' вместе со всевозможными
п — Ь' будут представлять все числа Ъ.
Поэтому
V cos akco = Vcos a'kco -f V(cos (n — a') kco,
У\ cos bko) = ^ cos b'kco -f 2 cos (n — &') Axo,
V sin akco = Vsin a'kco + V sin (n — a') ^@>
y. sin bkco = V sin b'Aw + ^ s^n (n ~~ Щ ^co-
Но так как cos (n — a') kco = cos a'Aco, cos (rc — b') Aco = cos b'kay,
sin(n — a')k(o = —sin a'Aco, sin(^ — Ь')кю = —sin&'&co, то сразу
Очевидно, что имеет место
2 sin akco = 2 sin a'ku> — 2 sin а'Ы = О,
V sin bko> = V sin b'ko) — S\ sin b'kco = 0.
Сумма же косинусов принимает вид
2 cos ako) = 22 cos a'kw,
2 cos bk(o = 2 2 cos б'Лсо,
Суммирование некоторых рядов особого вида 597
так что должно иметь место
1 + 4 2 cos a'k(o =
1 + 4 ^ cos b'fao = H3 Vn,
cos a'Aco — 2 ^ cos fc'Aco = ± )/7г.
П. В случае, когда п имеет вид 4m -\~ 3, дополнение до п каж-
каждого вычета а является невычетом, а дополнение каждого невыче-
невычета b — вычетом; поэтому всевозможные числа п — а совпадают со
всевозможными числами Ъ, а всевозможные числа п — b — со все-
всевозможными числами а. Из этого следует, что
S\ cos akco = V cos (n — b) kco — V cos bkco.
Тем самым, так как всевозможные а и b вместе составляют всю,
совокупность чисел 1, 2, 3,..., п — 1, и потому V cos аксо-\- V cos bkco==
= cos kco -f cos 2 kco -j- c°s 3 Aco +... + cos (n — 1) ku> = — 1, становятся
непосредственно очевидными формулы суммирования
2j cos akco = — ^-» 2j cos 6Aco = — -^ •
Точно так же
V sin aAco = V sin (n — b) kco = — J\ sin bkto,
откуда становится ясным, каким образом одна из двух формул
суммирования
2 ^ sin акю = + ~)fn^
2y\smbkco = + \f n
зависит от другой.
Теперь мы проделаем непосредственные вычисления для нескольких
примеров.
598
Суммирование некоторых рядов особого вида
I. Для п=^Ъ имеется одно значение для а\ именно, а' = 1, и
одно значение для 6', именно, Ъ' = 2. Но
cos со да + 0,3090169944, cos 2 со да — 0,8090169944;
поэтому 1 -+- 4 cos со = -f- V^j 1+4 cos 2 со = — У 5.
IL Для ra = 13 имеется три значения для а', именно, 1, 3, 4, и
столько же значений для Ь', именно, 2, 5, 6; производя вычисле-
вычисления, находим
cos со да+ 0,8854560257
cos Зсода+0,1205366803
cos 4сода—0,3546048870
cos 2co ж + 0,5680647467
cos 5co да — 0,7485107482
cos бсо да —0,9709418174
Суммада+0,6513878190 Сумма»—1,1513878189
Поэтому 1 + 4 ^ cos а'со = + У13, 1 + 4 2 cosй'со = — J/T3~.
III. Д^я п = П мы имеем четыре значения для а', именно, 1,
2, 4, 8, и столько же значений для6', именно, 3, 5, 6, 7. Вычис-
Вычисляем теперь косинусы.
cos Зсо ж + 0,4457383558
cos oco ж — 0,2736629901
cos со
cos 2со
cos 4со
cos 8co
+ 0,9324722294
+ 0,7390089172
+ 0,0922683595
— 0,9829730997
cos бсо « — 0,6026346364
cos 7со^— 0,8502171357
Сумма да + 0,7807764064 Сумма да — 1,2807764065
Поэтому 1 + 4 2 cos а'со = + |^Г7, 1 + 4 ^cos&'co = — ]/"Т7.
IV. Д^я п = 3 имеется одно значение для а, именно а = 1, и ему
соответствует
sin со = + 0,8660254038.
Поэтому 2 sin со = +КЗ.
V. Для п = 7 имеется три значения для ау именно, 1, 2, 4;
поэтому мы имеем такие значения синусов:
sin со да + 0,7818314825
sin 2co да + 0,9749279122
sin 4co да — 0,4338837391
и потому 2
Сумма
а@ = +
+ 1,3228756556,
Суммирование некоторых рядов особого вида 599
VI. Для п = 11 значениями а являются 1, 3, 4, 5, 9, и им соот-
соответствуют синусы
+ 0,5406408175
sin Зсо « + 0,9898214419
sin4w« +0,7557495744
sin 5co^ +0,2817325568
sin 9со^ —0,9096319954
Сумма»+ 1,6583123952
и потому 2 2 smaco = + ]/Ц.
VII. Для гг = 19 значениями а являются числа 1, 4, 5, 6, 7, 9,
11, 16, 17, и им соответствуют синусы
sin со « + 0,3246994692
sin 4co ж + 0,9694002659
sin 5(o « + 0,9965844930
sin6co« +0,9157733267
sin7co» + 0,7357239107
sin 9co да+ 0,1645945903
sin llco» — 0,4759473930
sin 16co» — 0,8371664783
sin 17со^ —0,6142127127
Сумма-^ + 2,1794494718,
и потому 2 V sin aw —+}/9.
4
Во всех этих примерах знак корня получается положительным,
и этот же факт легко установить и для больших значений п = 23,
тг = 29 и т. д., вследствие чего уже становится весьма вероятным, что
это верно и вообще. Но доказательство этого обстоятельства не мо-
может быть получено на основании принципов, изложенных в указан-
указанном выше месте; обстоятельство это с полным правом следует при-
признать лежащим гораздо глубже. Цель настоящего сочинения будет
состоять в том, чтобы дать строгое докавательство этой в высшей сте-
степени изящной теоремы, которое мы безуспешно искали разными спо-
способами на протяжении многих лет и в конце концов счастливо
600 Суммирование некоторых рядов особого вида
осуществили благодаря своеобразным и довольно тонким рассмотре-
рассмотрениям; одновременно мы обобщим теорему, что не только не повредит
ее изяществу, но, скорее, сделает ее еще изящнее. В заключение мы
рассмотрим замечательную тесную связь, имеющуюся между этим
суммированием и другой в высшей степени важной арифметической
теоремой. Мы надеемся, что эти исследования не только будут инте-
интересны для математиков сами по себе, но что и методы, при помощи
которых нам удалось все это получить и которые могут оказаться
полезными и при рассмотрении других вопросов, окажутся достойны-
достойными их внимания.
5
Наше доказательство основывается на рассмотрении своеобраз-
своеобразного типа рядов, члены которых зависят от выражений вида
A — х) A — х2) A — х*)...A — а?*)
Ради краткости мы обозначим такую дробь через (иг, fx) и сначала
сделаем некоторые общие замечания относительно функций такого
вида.
I. Если т является целым положительным числом, меньшим
чем [х, то функция (иг, (х), очевидно, равна нулю, так как числитель
содержит сомножитель A •—х°). Для т = [х сомножители в числи-
числителе будут совпадать с расположенными в обратном порядке со-
сомножителями знаменателя, так что (fx, [х) = 1; наконец, в случае,
когда т есть целое положительное число, большее чем [х, мы имеем
формулы
2, v.) = <* 7i-^(Г-^
^+3)A^+2)A^+1) , ,о оч
и вообще
(т, (л) = (m, m — (л).
Суммирование некоторых рядов особого вида 601
II. Далее, легко устанавливается, что вообще имеет место
(иг, (х + 1) = (т — 1, (х + 1) + жт-»*-1(/№—1, [л).
Но так кай, точно так же, имеет место
(иг—1, |г + 1) = (иг —2, [x + l) + ^-^-2(m_2, (х),
(лг —2, |х + 1) = (лг —3, р. + 1) -Ь жт-^-в (То — з, |х),
(тю — 3, [л + 1) = (т — 4, [х + 1) + хт~^-^ (т — 4, ?л),
и т. д.
и этот ряд может быть продолжен до
(|х + 2, |х + 1) = ([х+1, n + ij + sfn+l, [х) = ([х> [xj+aj^ + l, [*),
если иг является целым положительным числом, большим чем
[х + 1, то
(иг, [л + 1) = ([х, [л) + ж ([х + 1, [л) + х2 ([х + 2, (л) +
+ ?3((л + 3,[л)+...+ ^-^-1(т— 1, |х).
Отсюда вытекает, что если для какого-нибудь определенного
значения числа [л каждая функция (т, [л), где т обозначает целое
положительное число, является целой функцией, то должна быть
целой и каждая функция (иг, [л-fl). Но так как указанное пред-
предположение для [л = 1 выполняется, оно будет справедливо и для
[л = 2, а потому и для [х = 3 и т. д., т. е. вообще для любого
положительного целочисленного значения т функция (иг, [л) будет
целой функцией, т. е. произведение
A — хт) A — хт~^) A — ?т-2)...A — ят-И~1)
будет делиться на
A — х) A — я2) A — х3)...A — ж*).
Теперь мы рассмотрим два ряда, которые оба могут привести
нас к цели. Первый ряд следующий:
, 1-хт A - г)A - а? ) (l-a?)(l-a?)(l-a?)
1— я? "t~ A — яг) A — яга) A — х) A — я?8) A — я3) "Г*"'
602 Суммирование некоторых рядов особого вида
ИЛИ
1 - (т, 1) + К 2) - (иг, 3) + (т, 4) - ...;
мы обозначим его, ради краткости, через / (х, т). Прежде всего,
непосредственно ясно, что если т является целым положительным
числом, то этот ряд после (т+1)-го члена (который равен -f-1)
обрывается, и что поэтому сумма в этом случае^должна быть конеч-
конечной целой функцией от х. Далее, из п. 5, II вытекает, что вооб-
вообще для любого значения т имеет место
1 = 1,
— (лг, 1) = — (т — 1, i)—xm-1,
+ (m, 2) = + (m — 1, 2) + я™~2 (т - 1, 1),
— (m, 3) = — (т — 1,3) — хт~3(т. — 1,2)
и т. д.,
и потому
/(х, т) = i — xm-1 — A— ж™-2)(ти—1,1) + A— хт-*)(т— 1, 2)—
_(l_ST*-4)(m_l>3)+...)
Но очевидно, что
A_Хт-2)(т_1? 1) = A_жт-1 )(m^_2, 1),
A_жт-з)(т_1? 2) = A —ж"*-1)(иг —2, 2),
A_хт-4)(т_1? 3) = A—tf*-l)(jW—2, 3)
и т. д.;
поэтому мы получаем уравнение
[1] /(ж, т) = A — xm~i)f(x, т — 2).
Так как для т = 0 получается /(ж, т) = 1, то согласно только
что найденным формулам мы имеем
f(x, 2) = 1-х,
f(x,A) = (l-x)(l~xs),
f (х, 6) = A - х) A — х3) A — х%
/(ж, 8) = (I — х) (I — xs)(l — Xs) A — х7)
и т. д.,
Суммирование некоторых рядов особого вида 603
т. е. вообще для каждого четного значения числа т
[2] /(ж, т) =A — х)A — ж?)A — х5)...A — xm-i).
Наоборот, так как для т = 1 имеет место / (я, т) =0, то и
/(я,3) = 0,
/(ж, 5) = 0,
/С*,7)=0
и т. д.,
т. е. вообще для каждого нечетного значения числа т
f(x, т) = 0.
Впрочем, последние формулы могут быть выведены и из того,
что в ряде
1 — (иг, 1) + (иг, 2) - (т, 3) +...+ (иг, т — 1) — (иг, иг)
последний член уничтожает первый, предпоследний член уничто-
уничтожает второй и т. д.
8
Хотя для нашей цели достаточно ограничиться случаем, когда
т является нечетным положительным целым числом, но вследствие
важности вопроса будет не лишним добавить кое-что относительно
случаев, когда т или дробно или отрицательно. Тогда наш ряд.
очевидно, уже не будет обрываться, а будет продолжаться до беско-
бесконечности, и, кроме того, легко видеть, что он расходится, если
придавать х значения, меньшие чем 1, так что суммирование воз-
возможно только для значений х, которые больше чем 1.
На основании формулы [1] из п. 6 мы имеем
X
1 — L 1 —_
X X*
604 Суммирование некоторых рядов особого вида
1
1 — - 1 — 1 1 — -
X Xs ХЪ
и т. д.,
так что значение функции / (х, т) и для отрицательного целочис-
целочисленного значения т пред ставимо в конечном виде. Для остальных
же значений т мы следующим образом преобразуем функцию
/ (х, т) в бесконечное произведение.
Если т принимает бесконечно большое отрицательное значение,
то функция / (х, т) переходит в
jO X vU X jO X %Ю X VO X 00 X
Следовательно, этот ряд равен бесконечному произведению
1 1 1 _1
х а?3 хъ х1
Так как, далее, вообще
то будет иметь место
причем эти сомножители будут, очевидно, все больше и больше
приближаться к единице.
Специального рассмотрения заслуживает случай т— — 1, когда
/(Я,_1) = 1 +Я-1-1-2Г-3 _|_Ж-6 -|- ж—Х0 _|_
Этот ряд равен, следовательно, бесконечному произведению
i — x~x 1—a: 1 —a?""'
т. е., если вместо х подставить х~г, мы будем иметь
14- -4- -8 4- 6 4- — 1 ~~х2 1~~х* i~x* i—x8
\ i * \ л /у» л /у«3 Л /у»5 А . ^v*7
Суммирование некоторых рядов особого вида 605
Это равенство двух довольно замысловатых выражений, к кото-
которому мы еще вернемся в другом месте, конечно, в высшей степени
замечательно.
Во-вторых, мы рассмотрим следующий ряд:
-4-Х /| „ i X м „\,/j „2\ Г;
ИЛИ
который мы обозначим через F(x,m). В этом исследовании мы
ограничимся случаем, когда т является целым положительным числом,
так что и этот ряд будет все время обрываться на(т+1)-м члене,
который равен х2 (т, т). Так как
(т?г, т) = 1, (w, m — 1) =? (m, 1), (т, т — 2) = (m, 2),*..,
то этот ряд может быть представлен также и в виде
11 1 1
F(x,m) = x2 -\-х2 (т,1)-{-х2 (т,2)-\-х2 (т, 3)+...
Отсюда следует, что
U + ^2~ГП ^}Р{х, т) == 1 + я^и», 1) +ж(т, 2) + ^2"(т, 3) +...
i 3
Но так как (п. 5, II)
(m, 3) + я™-2 (m, 2) = (т + 1, 3)
и т. д.,
то получается, что
606 Суммирование некоторых рядов особого вида
Но F(x, 0) = 1; поэтому
i i
F (x, 3) = A + x*) A + x) A + x*)
и т. д.,
или вообще
*¦ * F (ж, т) — A -\- х2) A-{- х) A -\- х2)... A -f-a;2™).
10
После того как мы предпослали эти предварительные исследо-
исследования, мы ближе займемся нашей задачей. Так как для значения
/А \ 2
п, равного простому числу, все квадраты 1, 4, 9,..., (^-(п — 1) j не
сравнимы между собой по модулю п, то их наименьшие вычеты
по модулю п будут, очевидно, совпадать с совокупностью всевоз-
всевозможных чисел а, и потому
/А \ 2
V cos ако) = cos кю -f- cos 4й:со -f- cos 9Zxo + •• • + cos f ^ (n — 1) J Aco,
У] sin akoy — sin Лео + sin 4&co -f sin 9й:со + ... + sin (j {n — 1)) kco.
/I \2
PI точно так же, так как эти квадраты 1, 4, 9,...,(:г(п—1) в
обратном порядке сравнимы с квадратами (тг(п + 1)) ? V2~(n~b'
A \2 /1 ^2
j (п -\- 1)) koy -\- cos (j (га + 3) j ксо +•••+ cos(n—1JА:со,
Поэтому, если положить
Т =1 + cos&co + cos4A:co + cos9&« +...+ cos(n—1
U = sinAico + sin4&(o + sin9A:co +...+ sin(n—1J&со
Суммирование некоторых рядов особого вида 607
то будет иметь место
2 = Г,
Отсюда вытекает, что указанные в п. 1 суммирования зависят
от суммирования рядов Т и U\ поэтому, несмотря на то, что нам
нужны первые суммирования, мы сосредоточим наше исследование
на последних, причем рассмотрим их в такой общности, чтобы
охватить не только простые значения числа п, но также и любые
составные значения. Число к мы будем, однако, предполагать вза-
взаимно простым с пу так как к этому случаю легко может быть
сведен и случай, когда к и п имеют общий делитель.
11
Если мы обозначим мнимую величину У— 1 через i и положим
cos кы -\- i sin Aco = г,
то мы получим гп = 1, т. е. г будет корнем уравнения хп —1=0.
Легко видеть, что все числа к, 2ку Зк,...,(п—1)к не делятся на
п и не сравнимы одно с другим по модулю п\ поэтому все сте-
степени
а г Г2 гз гп— 1
числа г различны, а каждая из них тоже удовлетворяет уравнению
хп — 1=0. Следовательно, эти степени будут представлять все корни
уравнения хп —1=0.
Если бы к имело с п общий делит^дь, то эти выводы были бы
неверны. Действительно, если бы v было таким общим делителем,
то число кп[*ч делилось бы на п, а потому была бы равна единице
более низкая степень, чем гп, а именно, rn/v. Таким образом, в
этом случае степени числа г будут представлять самое большее
тг/v корней уравнения хп — 1 =0, причем они действительно будут
представлять в точности столько различных корней, если v являет-
является наибольшим общим делителем чисел к в. п. В нашем случае, когда
кип предполагаются взаимно простыми, число г удобно называть
608 Суммирование некоторых рядов особого вида
собственным корнем уравнения хп — 1 —0; напротив, в том случае,
когда кип имеют (наибольший) общий делитель v, число г будет
называться несобственным корнем этого у равнения; очевидно, однако,
что тогда г будет собственным корнем уравнения хп^—1 =0. Про-
Простейшим несобственным корнем является единица; а в том случае,
когда число п простое, других несобственных корней вообще нет.
12
Если мы положим теперь
то, очевидно, будет выполняться равенство W = Т + iU, и Т будет
вещественной частью числа W, в то время как U будет получаться
из мнимой части числа W отбрасыванием сомножителя i. Таким
образом, вся задача свелась к отысканию суммы W; для этой
цели можно использовать либо ряд, рассмотренный в п. 6, либо
ряд, суммировать который мы научились в п. 9, однако первый
менее удобен в случае, если число п четно. Все же мы надеемся,
что читателю будет приятно, если случай, когда п нечетно, мы
исследуем двумя методами.
Итак, мы предположим сначала, что число п нечетно, что г
обозначает какой-нибудь собственный корень уравнения хп —1=0,
и что в функцию f(x, т) подставлены значения х = г и т = п — 1.
Тогда, очевидно, будут выполняться равенства
1 — хт 1 —г
— f—1»
1-х ~ 1 —г
¦==— Г»
1 _ a;2 ! _ Г2
1—яз 1 —г
И Т. Д.
ДО
Суммирование некоторых рядов особого вида 609
(Не лишне указать, что эти уравнения справедливы лишь по-
постольку, поскольку г предполагается собственным корнем; действи-
действительно, если бы г было несобственным корнем, то в некоторых из
этих дробей одновременно исчезал бы числитель и знаменатель, и
потому дроби становились бы неопределенными.)
Отсюда мы выводим следующее уравнение:
/(г, п— 1) = 1 +Г-1 + г-»+г-в + ...+ г~^(П~1)п=:
= A — г) A — Г3) A — Г5).. .A — Гп~2).
Такое же уравнение будет иметь место, если вместо г подставить
гх, где X обозначает любое число, взаимно простое с п\ действи-
действительно, тогда гх также является собственным корнем уравнения
хп — 1 =0. Поэтому если вместо г мы напишем гп~2 или, что то
же самое, г~2, то получим
1 + г2 + г6 + г12 +...+ Ип-1>п^
= A — Г") A — Г) A — Г-1*)...A — Г-2<п-2>).
Если обе части этого уравнения умножить на
то в силу соотношений
24-4" (^—1>а f("-3J (n-i)n+i(n-l)8 j
e+l(n-i)« i-(n_5K (n-2)(n—l) + j-(n-l)« j
Г4 — Г4 , Г 4 =Г4
12_|JL(n_iJ L(n_7J (n_3)(n-2)+f(n~lJ j
и т.д.
получится следующее уравнение
= (г — Г) (Г3 — Г"8) (Г5 — 7—5)...(Г"-2— Г-"+2),
610 Суммирование некоторых рядов особого вида
или, если по иному расположить члены в левой части,
= (Г — Г ) (Г3 — Г~3)(Г5 — Г~5).. .(>п~2 — Г~п+2),
13
Сомножители в правой части уравнения [5] могут быть предста-
представлены и так: 3
г ;.-i — (г71 г"~п+1),
ДО
после чего указанное уравнение принимает вид
W = (— if^"^ (г2 — г'2) (г4 — г~*)(г* — r-«)...{rn-i—
Если это уравнение перемножить с уравнением [5] в его первона-
первоначальной форме, то получается
W2 = (— 1)<п-1)/2(г _ г-1) (г2 — г'2) (г3 — Г3)...(г-1 — r-n+i),
где (—1)(л—1)/2 или равно + 1, или равно —1, в зависимости от
того, имеет ли п вид 4[л -f-1 или вид 4[л + 3. Отсюда следует, что
W2=± Гп(п-1)/2A _ Г) A _ г-4) A _ Г-в)вв>A _ г-2(п-1))#
Но легко видеть, что числа г, г, r~6,...,r~2nJ представляют
все корни уравнения хп —1=0, за исключением корня # = 1,
так что для каждого значения х должно быть справедливым тож-
тождественное соотношение
{х — г) (х — г) (х — Г6)... (х — г~2п+2) =
= х71 +#п-2 +хп-3+ ... + х+1.
Поэтому, если положить ж = 1, мы получим
A — Г2) A — Г4) A — Г6). ..A — г~2™+2) = п,
Суммирование некоторых рядов особого вида 611
и так как, очевидно, гп<п—х>/2 = 1, то наше уравнение переходит в
следующее:
[6] W* = ± п.
Таким образом, в случае, когда п имеет вид 4[л + 1, будет иметь
место
W = ± Уп, и потому Т = ± Уп, U = 0;
напротив, в том случае, когда п имеет вид 4[л + 3, будет иметь
место
W = + гУп, и потому Т = 0, U = ± У™.
14
Метод предыдущего пункта позволяет определить только абсо-
абсолютные значения величин Т, Ui и остается неизвестным, нужно ли
полагать в первом случае Т, а во втором случаев равными -\~Уп
или —У п. Однако, по крайней мере для случая А= 1, это можно
следующим образом определить из уравнения [5]. Так как для
к = 1 имеет место
г — г'1 = 2i sin со,
г3 — г~3 — 2г sin Зсо,
Г5 — r-5 _ 2i sin 5o)
и т. д.,
то указанное уравнение преобразуется в
W = B^)(n-1)/2sinco.sin3co-sin5co...sm(^ — 2) со.
Но в случае, когда п имеет вид 4[х+ 1, в ряду нечетных чисел
1, 3, 5, 7,...,|(/г-3), |(/г + 1),..., /г-2
содержится (тг—1)/4 чисел, которые меньше чем га/2, и им, оче-
очевидно, соответствуют положительные синусы; напротив, остальные
(п —1)/4 чисел будут больше чем п/2, и им будут соответствовать
отрицательные синусы. Поэтому произведение всех синусов равно
произведению положительной величины на множитель (—l)(n—i)/4f
612 Суммирование некоторых рядов особого вида
и значит W равно произведению вещественной положительной вели-
величины на множитель i71—1, равный единице (так как г4 = 1 и га — 1
делится на 4), т. е. W является вещественной величиной, так что
обязательно должно быть
W = + Уп, Т = +Уп.
А в том случае, когда га имеет вид 4jx + 3, в ряду нечетных
чисел
1,3,5, 7,..., ^(га —1), | (га + 3),..., га —2
первые (га + 1)/4 чисел будут меньше чем га/2, а остальные (га — 3)/4
чисел — больше чем га/2. Поэтому среди синусов дуг со, Зсо, 5со,...
...,(га — 2)со будет (га — 3)/4 отрицательных, и значит W будет
произведением сомножителя jO*—1)/2^ вещественной положительной
величины и сомножителя (—1)(гг—з)/4- третий сомножитель равен г'(п—з)/2?
и вместе с первым он дает in~2 = г, так как гп~3 = 1. Поэтому обя-
обязательно должно быть
W = + *Уй и С/ = + У п.
15
Теперь мы покажем, как те же самые выводы могут быть получе-
получены при помощи ряда, рассмотренного в п. 9. Если в уравнении [4]
мы вместо #1/2 напишем — у~{, то получим
до (т + 1).гочлена =
^ (l_j/-2)A_j/-4)A_2/-6)
= A - у-1) A + г/) A - у-3) A + J,-4). ..(I ± у-т).
Если теперь взять за у собственный корень уравнения уп —1=0,
например, г, и одновременно пологьить т = п — 1, то будут выпол-
выполняться соотношения
i-y
Суммирование некоторых рядов особого вида 613
1 — Г4
— г6
1-г
/1 w—2 /1 Г2П—2
причем нужно отметить, что ни один из знаменателей 1 — г~2,
1 —г"~4,... не равен 0. Поэтому уравнение [7] принимает следующий
вид:
l + r + j* + r9+... + r^-D2 =
= A _r-l) (I + Г) A — Г-») ... A + Г-п+!).
Если в правой части этого уравнения перемножить первый со-
сомножитель с последним, второй с предпоследним и т. д., то мы
получим
A _ Г~1) A + Г-п+!) = Г — Г-1 ,
A _[_ г—4) A г—п+4 ) _ гп-4 Г—п+4
И Т. Д.
Из этих отдельных произведений получается, как легко видеть,
произведение
(г — г-1) (г3 — г-3) (г5 — г-6).. . (гп~* — г-*+4) (г"-2 —
и потому это последнее выражение равно
Это уравнение тождественно с уравнением [5] п. 12, полученным
при помощи первого ряда; остальные выводы могут быть получены
из этого уравнения так же, как в пп. 13 и 14.
614 Суммирование некоторых рядов особого вида
16
Теперь мы переходим к случаю, когда п является четным числом.
Если сначала п имеет вид 4[л + 2, т. е. не делится на 4, то ясно,
что числа-т-га2, (t^ + I) —1> (t^ + ^J —4, . . ., т. е. вообще чи-
A Л2
2-tt + M —^2 ПРИ делении на га/2 дают нечетные част-
частные и потому сравнимы с числом га/2 по модулю га. Отсюда следу-
следует, что если г является собственным корнем уравнения хп —1=0,
и потому гп/2=—1, то выполняются равенства
И Т. Д.
Следовательно, в ряду
член Ип/2)* будет взаимно уничтожаться с первым членом, следую-
следующий за г(п/2>* член — со вторым членом, и т. д., и потому
W = 0, Т = 0, U = 0.
1
Остается еще только случай, когда га имеет вид 4[л, т. е. делит-
A \2
тт-л + м —X2 делятся на л, и потому
Следовательно, в ряду
Суммирование некоторых рядов особого вида 615
член Ип/2)а равен первому члену, следующий за г^2^ член — второ-
второму члену и т. д., так что
(ь-
Если мы теперь предположим, что в уравнении [7] п. 15 поло-
положено т= jr-n — 1, аза у взят собственный корень уравнения
уп —1 = 0, например, корень г, то уравнение, подобно тому, как в
п. 15, принимает вид
1 + T 4- Г4 + . . . + Г^ I a=
откуда
[8] W = 2 A — г-* )A + г-2) A — г-*) A + г-*)... A — г *п+1).
Так как, далее, г"*'2 = — 1, и потому выполняются равенства
И Т. Д.,
а произведение сомножителей — г2 , — г2" ', — г2' , ... до
—п—1 —па п ^
— г2 равно (—IL г16 4 , то последнее уравнение может быть
записано также и в виде
1 11
W = 2( 1Л4 г^ ^ ' ~~"^* / >• ""~*"^ / X
х A — г-»)A — /•-*)... A — j
616 Суммирование некоторых рядов особого вида
Так как
1 — г-2 = — г-2 A — г~п+2),
1 — г-з = — г~3 A — г
и т. д.,
то
A _ г-1) A _ г~2) A _ г-8) . . . A _ г" 2
«(_ 1)
- h1+1" A Г i
--п-3
X A— Г а ) ...A—7-~п+1),
и потому
-1„-2
X A —г *п 3)...A —r-"+i).
Если перемножить это выражение для W с ранее найденным
и к обеим частям добавить множитель 1 — г * } т0 получится
A__-\п _ -\п
Но
\-г *п = 2,
(-1)«-8= _1,
-I» in
Г 4 _ ri
Из этого следует, наконец, что
[9] W* =
Но легко видеть, что г™/4 равно или + г> или — i, в зависимо-
зависимости от того, имеет ли к вид 4^ + 1 или 4[л + 3. А так как
Суммирование некоторых рядов особого вида 617
то в случае, когда к имеет вид 4[л + 1, будет иметь место
W = ± A + 0 Vn, и потому Т == U = + Ки,
а в случае, когда к имеет вид 4[л + 3, получается
W = ± A — i) }/п, и потому Г = — U = +j/"^
18
Метод предыдущего пункта позволяет определить абсолютные
значения функций Г, ?/ и дает условия, при которых они имеют
или одинаковые, или противоположные знаки, но не дает еще воз-
возможности определить сами знаки. Для случая, когда принято к = 1,
мы завершим это следующим образом.
Если положить р = cos^-^ + z'sin 75- со, так что г = р2, то, в силу
равенства рп = —1, уравнение [8], очевидно, можно будет пред-
представить следующим образом:
W = 2 A + р—2) A + р-4) A + р"-0 ) A + р-8) . . . A + р-п+4) A + Р2),
или, если расположить сомножители в другом порядке,
W = 2 A + р2) A + р-4) A + р6) A + р-8)... A + р-^Н) A +
Но
1 + р~4 - 2р cos со,
1+ p6 = 2p3cos|co?
1 + р~8 «= 2р-4 cos 2co
и т. д.
До
1 + р~п+4 = 2р"*"гП+2 cos fen — i) о)
cos ^iw — i) со.
618
Суммирование некоторых рядов особого вида
Поэтому мы получаем
W = 2n/2
cos ^c
со-cos о3 • • • cos(-n —-)w-
Входящие в это произведение косинусы, очевидно, все положитель-
положительны, сомножитель же рп/4 равен cos 45° + г sin 45° = A + О VV2- От'
сюда следует, что W является произведением числа A + 0 на ве-
вещественную положительную величину, вследствие чего обязательно
должно быть
W =
и =
19
Имеет смысл ег^е /?аз сопоставить здесь между собой все произ-
произведенные до сих пор суммирования. Именно, вообще имеет место
т =
±Vn
0
0
0
0
В зависимости
имеет ли п
4[л -j-
4[л -(- ^
4 [л +1
от того,
вид
L
г
3
и в случае, когда предполагается, что А=1, корни должны браться
с положительными знаками. Поэтому то, что для простых значений
числа п мы нашли в п. 3 индуктивным путем, теперь доказано со
всей строгостью, и остается еще только показать, как могут быть
во всех случаях определены знаки для любых значений числа к. Одна-
Однако, прежде чем мы сможем взяться за эту задачу во всей ее общ-
общности, мы должны сначала подробнее рассмотреть те случаи, когда
п является простым числом или степенью простого числа.
Суммирование некоторых рядов особого вида 619
20
Если сначала п — нечетное простое число, то после изложенного
а п. 10 очевидно, что W = 1 + 2 2 r<l = 1 + 22 ^аЛ» где ^ = cos со +
+ i sin со, и а, как и там. пробегает все квадратичные вычеты по
модулю п от 1 до п—1. Если теперь точно так же обозначить через
b всевозможные квадратичные невычеты по модулю /г, лежащие в
тех же границах, то легко видеть, что всевозможные числа ак бу-
будут сравнимы по модулю п (с точностью до порядка расположения)
либо со всевозможными числами а, либо со всевозможными числа-
числами Ь, в зависимости от того, является ли к вычетом или невычетом.
Поэтому в первом случае
W = 1 + 2^Ra = 1 + R + Я4 + Я9 + . . . + i?<n-lJ,
и потому W = + |Лг, если тг имеет вид 4[л + 1» и И^ = + iVn,
если /г имеет вид 4;л + 3.
Во втором случае, когда к есть невычет по модулю п, полу-
получается
w = 1 + 2
Так как всевозможные числа а, 6, очевидно, исчерпывают всю со-
совокупность чисел 1, 2, 3,..., п — 1, и потому
2т?а + 2 л& = л + R2 + R3 + • • •+Я71-1 = — l,
то отсюда вытекает, что
W = — 1 — 2]>]Яа = — A + -# + Я4 + Я9 + ...
и потому W = —Уп , если га имеет вид A[i -\- 1, и W = — С]/п , если
п имеет вид 4;л + 3.
Таким образом,
во-первых, если п имеет вид 4[л + 1 и А является квадратичным
вычетом по модулю /г, то
620 Суммирование некоторых рядов особого вида
во-вторых, если га имеет вид 4[л + 1, и А является квадратич-
квадратичным невычетом по модулю га, то
T = — Yn, U = 0,
в-третьих, если га имеет вид 4(х + 3, ж к является квадратич-
квадратичным вычетом по модулю га, то
в-четвертых, если га имеет вид 4(х -|- 3, и А; является квадратич-
квадратичным невычетом по модулю га, то
Г^О, 17 = — Уп.
21
Пусть, во-вторых, га является или квадратом, или более высокой
степенью нечетного простого числа р, и пусть га = p2y-q, где # или
равно 1, или равно р. Здесь мы хотим прежде всего заметить, что
если X — какое-нибудь целое число, не делящееся на рк, то
Из этого легко видно, что
W = 1 + ^р2к + +
Действительно, остальные члены ряда
могут быть разбиты на (рх—1)д частичных рядов, каждый из ко-
которых содержит рх членов и на основании указанного выше пре-
преобразования имеет нулевую сумму.
Суммирование некоторых рядов особого вида 621
Отсюда мы заключаем, что в случае, когда # = 1, т. е. п явля-
является степенью простого числа с четным показателем, выполняется
равенство
W = р* = + У~п, и потому Т = + Уп, U = 0.
В случае же, когда q — р, т. е. когда п является степенью
простого числа с нечетным показателем, мы положим rv х = р;
тогда р будет собственным корнем уравнения xv—1=0, а имен-
именно, р= cos — 360° + i sin- 360°, и
W = 1 + р + р4 + Р9 + . •. + р
= РхA + Р + Р4 + Р9 + . • • +
Но сумма ряда 1 + р + р4 + р9+---+ p(p~iJ определяется так
же, как в предыдущем пункте, и мы немедленно получаем, что
W = + J^n = Г, если р имеет вид 4[х + 1,
W = + i Vn — iU, если р имеет вид 4;л + 3,
причем следует брать положительный или отрицательный знак в за-
зависимости от того, является ли число к вычетом или невычетом по
модулю р.
22
Из того, что было изложено в пп. 20 и 21, легко выводится так-
также следующая теорема, которая позднее будет нам очень полезна•
Если положить
W = 1 + rh + г4Л + r*h + . . . + r^n-D2,
где h обозначает какое-нибудь не делящееся на р целое число, то
в случае, когда п или равно р, или равно степени числа р с не-
нечетным показателем, имеет место
W' = W, если h есть квадратичный вычет по модулю р,
W = —W, если h есть квадратичный невычет пй модулю р.
622 Суммирование некоторых рядов особого вида
Действительно, W\ очевидно, получается из W, если подставить
kh вместо к\ но в первом случае к и kh однотипны, а во втором —
неоднотипны, если рассматривать их в отношении свойства быть
вычетами или невычетами по модулю р.
Напротив, в том случае, когда п является степенью числа р
с четным показателем, очевидно, выполняется равенство W =
= + j/"w, и потому всегда W = W.
23
В пп. 20, 21 и 22 мы рассмотрели нечетные простые числа и их
степени; поэтому остается еще только случай, когда п является
степенью числа 2.
Для п = 2, очевидно, W = 1 + г = 0.
Для п = 4 получается W = 1 -f- г + г4 + гд = 2 -f- 2г, поэтому
W = 2 -{- 2i, если А имеет вид 4[л -f- 1, и W = 2 — 2г, если А: имеет
вид 4[л + 3.
Для тг = 8 мы имеем W = 1 -f г + т-4 + г* + г16 + г25 + r3Q + т-49 =
= 2 + 4т- + 2т-4 = 4т-. Поэтому
И^ = A -f- 01^8", если А имеет вид 8[а + 1,
TF = (— 1 + 0 V'S"» если А имеет вид 8[х + 3,
И^ = (— 1 — г) |/8", если А имеет вид 8[л + 5,
И^ = A — i) |/8", если А имеет вид 8[л -f 7.
Если я является более высокой степенью числа 2, то мы поло-
положим1 n — 22*q, где q или равно 1, или равно 2, ах больше чем 1»
Здесь прежде всего надо заметить, что если X есть какое-нибудь
не делящееся на 2у-~1 целое число, то
Отсюда легко видеть, что
Суммирование некоторых рядов особого вида 623
Если мы положим г22х~~2 — р, то р будет корнем уравнения
хы _ 1 = о, а именно, р = cos ^ 360° + г sin ~ 360°. Тогда
W = l+p + p4 + p9 + ...+ ^Ч~1У =
= 2—1 A + р + р4 + р9 + • • . + р^-1J).
Но сумма ряда 1 Чг Р +Р4 + Р9 + - •• + рD9~1J определяется на
основании того, что говорилось относительно случаев п = 4, 72 = 8;
поэтому в случае, когда <7=1, т. е. когда п есть степень числа 4,
получается, что
W = A + 02к = A + ОТ^"» если * имеет вид 4[х + 1,
И7 == A — г) 2х = A —г)У~п, если к имеет вид 4[л + 3,
т. е. получаются формулы, которые в точности аналогичны форму-
формулам для случая п = 4; если же q = 2, т. е. тг является степенью
числа 2 с нечетным показателем, большим чем 3, то
^ если к имеет ВИД 8^ + 4>
Р7=-(— 1+гJх|/2" = (— 1 + г)^л, если А; имеет вид 8[л+3,
И^ = (_ 1 —гJ^|/2"= (— 1 — г)}/п", если к имеет вид 8[х + 5,
Т7 = A — гJк|/2" = A — i) Упу если А; имеет вид 8[л + 7;
эти формулы также совершенно аналогичны тем, которые были ука-
указаны для п = 8.
24
Также и здесь есть смысл потрудиться над тем, чтобы опреде-
определить, как связаны между собой сумма ряда
W = 1 + rh + г*л + г^ + . . . + гл<п-1>*,
где /г обозначает какое-нибудь нечетное число, и сумма W. Так
как W получается из W, если к заменить на А/г, то значение Wr
будет так же зависеть от вида числа Л/г, как VT зависит от вида
624 Суммирование некоторых рядов особого вида
W
числа к. Если положить — = Z, то, очевидно, будет справедливо
следующее.
I. В случае, когда п = 4 или когда п есть более высокая сте-
степень числа 2 с четным показателем, имеет место
Z = 1, если h имеет вид 4[л + 1,
I = — i, если h имеет вид 4[л + 3, а к— вид 4[л+1,
1= + i, если h имеет вид 4[х -f- 3, и к имеет такой же вид.
II. В случае, когда п = 8 или когда п есть более высокая сте-
степень числа 2 с нечетным показателем, имеет место
I = 1, если h имеет вид 8[л + 1,
I =± — 1, если /г имеет вид 8[х -f- 5,
Z ===== —1— г, если либо h имеет вид 8[х + 3, а к — вид 4[х + 1>
либо /г имеет вид 8[х -f- 7, а А; — вид 4[л -f- 3,
I = — г, если либо /г имеет вид 8[х + 3, а к — вид 4[л -f- 3,
либо h имеет вид 8[л -\- 7, а А;—вид 4[л+1.
Изложенным до сих пор полностью завершается определение сум-
суммы W в тех случаях, когда п является простым числом или сте-
степенью простого числа; поэтому остается только исследовать те слу-
случаи, когда п составлено из нескольких простых чисел. К этому нам
пролагает путь следующая теорема.
25
Теорема. Если п есть произведение двух целых положительных
взаимно простых чисел а и Ь, и если
Р = 1 -f ra* + г4а2 + г9а3 + . • . + r(b-V*a\
то я утверждаю, что W = PQ.
Доказательство. Если число а пробегает все значения 0, 1, 2,
3, . . ., а — 1, число р — все значения 0, 1, 2, 3,..., Ъ — 1, число
v — все значения 0, 1, 2, 3,..., п — 1, то, очевидно,
w = S
Суммирование некоторых рядов особого вида 625
Поэтому PQ = 2га2Р2+ь2ос2, если для аир брать всевозможные зна-
значения во всевозможных сочетаниях; далее, в силу того, что 2aba$ =
= 2офп, выполняется равенство PQ = ^г^+ь^\ Но без труда вид-
видно, что отдельные значения выражения ар -f ben различны между
собой, и каждое из них равно какому-нибудь значению v. Поэтому
PQ = 2^2 = W.
Заметим, между прочим, что га% является собственным корнем урав-
уравнение хь —1 = 0, а гь% — собственным корнем уравнения ха — 1 =
= 0.
26
Если, далее, п является произведением трех попарно взаимно про-
простых чисел а, Ь, с, то очевидно, что если положить be = b', числа
а и Ъ' также будут взаимно простыми; поэтому W является произ-
произведением двух сомножителей
Но так как га% есть собственный корень уравнения хЪс — 1 = 0, то
первый сомножитель сам есть произведение сомножителей
1 + рс2 + Р4с2 + р9с2 + • • • + р%
где р = га%. Отсюда вытекает, что W является произведением трех
сомножителей
I _|_ гЬ2с2 _j, г4Ь2с2 _|_ г9Ь2с2 _]_ # в ^ _|_ г(а—1JЬ«с»
1 _|_ га2с2 _|_ Г4а2с3 _[_ Г9а2с2 _|_ t # # _|_ Г(Ъ—1Jа«с2 ^
где гЬ2с2, га2с2, га2&| обозначают соответственно собственные корни
уравнений ха — 1 = 0, хъ — 1=0, хс — 1=0.
626 Суммирование некоторых рядов особого вида
27
Из этого мы без труда заключаем, что, вообще, если п есть про-
произведение любого числа попарно взаимно простых сомножителей а,
Ь, с, . . ., то W есть произведение такого же числа сомножителей,,
причем этими последними являются выражения
п2 4П2 9п2 (а—1Jп2
п2 ^п2 9П2 (Ь—1Jп2
п2 4п2 9п2 (с—1Jп2
где гп*1а%, гп2/Ь2, гп2/с2 являются соответственно собственными
корнями уравнений ха — 1=0, хъ — 1 = 0, хс — 1 = 0,...
28
На основании этих принципов переход к полному определению
суммы W для любого значения числа п уже ясен. Именно, нужно
разложить п на сомножители а, Ь, с,. . ., являющиеся или различ-
различными простыми числами, или степенями различных простых чисел *
и положить гп*1а* = А, гп21Ъ2 = В, гп^ = С, . . . Тогда А, В, С, ...
будут собственными корнями уравнений ха —1 = 0, хъ —1 = 0,
хс —1=0,..., a W будет произведением сомножителей
1 + А + А* + А9+ . . . + A^~v\
1 + в + S4 + S9 + . . . + ?(ь-1>2,
и т. д.
Но каждый из этих сомножителей может быть определен на ос-
основании изложенного в пп. 20, 21 и 23, так что тем самым будет
известно и значение произведения. Будет не бесполезным собрать
здесь вместе правила для определения указанных сомножителей, что-
Суммирование некоторых рядов особого вида 627
бы иметь их одновременно перед собой. Так как корень А равен
~ • , то сумма 1 + А + А* + А9 + . . . -]- А^—V2, которую мы
обозначим через L, будет так же определяться числом кп/а, как
в нашем общем исследовании сумма W определялась числом к. Нам
нужно различать теперь двенадцать случаев.
I. Если а равно или простому числу/? вида 4[х+ 1, или его сте-
степени с нечетным показателем, и одновременно кп/а является квад-
квадратичным вычетом по модулю р, то L = -\~У~а.
II. Если при тех же остальных предположениях кп/а является
квадратичным невычетом по модулю р, то L = —У~а.
III. Если а равно или простому числу р вида 4[х + 3, или его
степени с нечетным показателем, и одновременно кп/а является
квадратичным вычетом по модулю р, то L = + i}/~a.
IV. Если при- тех же, что и в III, остальных предположениях
кп/а является квадратичным невычетом по модулю р, то L ¦=
V. Если а является квадратом или более высокой степенью с
четным показателем (нечетного) простого числа, то L = -\-уа.
VI. Если а = 2, то L = 0.
VII. Если а = 4 или а является более высокой степенью числа
2 с четным показателем, и одновременно кп/а имеет вид 4;х+1, то
VIII. Если при тех же, что и в VII, остальных: предположениях
кп/а имеет вид 4[х + 3, то L = A — г) ]/а\
IX. Если а = 8 или а является более высокой степенью числа
2 с нечетным показателем, и одновременно кп/а имеет вид 8[х + 1,
то L = A + 0/я.
X. Если при тех же, что и в IX, остальных предположениях
кп/а имеет вид 8[х + 3, то L = (—1 + i)~]/~a .
XI. Если при тех же остальных предположениях кп/а имеет вид
8[х + 5, то L = (— 1 — г)j/o".
XII. Если при тех же остальных предположениях число кп/а име-
имеет вид 8[а+7, то L = (l — i)Ya.
628 Суммирование некоторых рядов особого вида
29
Пусть, например, п = 2520 = 8-9-5«7 и Л: = 13. Тогда
для а = 8, согласно случаю XII, L = A — i)l/8~;
для сомножителя 9, согласно случаю V, соответствующая сум-
сумма равна 1/9";
для сомножителя 5, согласно случаю II, соответствующая сум-
сумма равна —1/5";
для сомножителя 7, согласно случаю III, соответствующая сум-
сумма равна -j- i *|/У. Поэтому мы получаем:
W = A — г) (— г) 1/2520 = (— 1 — г) 1/2520.
Если п имеет это же значение, а А=1, то
сомножителю 8 соответствует сумма (— 1 + i)Y&,
сомножителю 9 соответствует сумма 1/9",
сомножителю 5 соответствует сумма 1/5",
сомножителю 7 соответствует сумма — г "|/У.
Поэтому для произведения получается W = A -f- г) "J/2520 .
30
Другой метод для определения суммы W в общем случае основы-
основывается на том, что мы изложили в пп. 22 и 24. Если мы положим
вообще cos со + i sin со = р и
так что г = рк, А = afe, S = C/i:, С = y^» • • •» то выражение
1 + р + р4 + р9 + • • • + p(n-i)S
будет произведением сомножителей
1+а + а4 + а9 + ...+ a<°-i)s,
1 + р + Р4 + Р9 + ¦ • • + Г»2,
1 + т + т4 + т9 + • • • + т(с-1>2.
Суммирование некоторых рядов особого вида 629
а потому W будет произведением сомножителей
w = 1 + р + р4 + р9 + • . • + Р(п-1J,
85 =
14 а + а4 + а9 + . . . + а(а~1J
1 + В + В* + Я9 + . . . + в(Ь~1)Я
1 + Р + Р4 + Р9 + • , • + Р(Ь~1J
1 + с + С4 + С'9 + . . . + С(с~1J
Но первый сомножитель w определен выше, в исследованиях
п. 19, а остальные сомножители получаются из формул пп. 22 и
24, которые мы здесь приведем еще раз, чтобы иметь их все вме-
вместе*. Здесь нужно различать следующие двенадцать случаев.
I. Если а равно или (нечетному) простому числу р, или его сте-
степени с нечетным показателем, и к является квадратичным вычетом
по модулю р, то соответствующий сомножитель й равен + 1-
II. Если при тех же остальных предположениях А; является квад-
квадратичным невычетом по модулю р, то 9t = — 1.
III. Если а является квадратом нечетного простого числа или
более высокой его степенью с четным показателем, то 91= +1.
IV. Если а = 4 или а является более высокой степенью числа
2 с четным показателем и одновременно к имеет вид 4[х + 1, то
81= +1.
V. Если при тех же, что и в IV, остальных предположениях
число к имеет вид 4[х + 3, а число п/а—вид 4[х + 1, то 91 = — i.
VI. Если при тех же остальных предположениях, что и в IV,
число к имеет вид 4[х+3, и число п/ а — также вид 4[х -f* 3, то
31 = + г.
VII. Если а = 8 или а является более высокой степенью числа 2
с нечетным показателем, и к имеет вид 8[х+ 1, то 91 = + 1.
VIII. Если при тех же, что и в VII, остальных предположениях
к имеет вид 8[х + 5, то 91 = — 1.
* Очевидно, что то, что ранее обозначалось через к, h, теперь есть п/а и А
для второго сомножителя, п/Ъ и к для третьего сомножителя и т. д.
630 Суммирование некоторых рядов особого вида
IX. Если при тех же, что и в VII, остальных предположениях
число к имеет вид 8[х + 3, а число п/а— вид 4[Л + 1, то 21 = -(- i.
X. Если при тех же, что и в VII, остальных предположениях
число к имеет вид 8[л + 3, а число п/а— вид 4;л + 3, то 2t =—i.
XI. Если при тех же, что и в VII, остальных предположениях
число к имеет вид 8[л + 7, а число п/а— вид 4[х + 1, то 2t =— г.
XII. Если при тех же, что и в VII, остальных предположениях
число к имеет вид 8[л-f 7, а число п/а — вид 4[х + 3, то 21 = -f г-
Случай, когда а = 2, мы пропустили; хотя здесь для -И получи-
получилось бы выражение 0/0, т. е. неопределенность, однако, всегда
W = 0.
Остальные сомножители 35, ?, ... так же зависят от Ь, с, ...
(если последние фигурируют в определении первых), как 21 зави-
зависит от а.
31
При помощи этого второго метода первый пример из п. 29 ре-
решается следующим образом.
Сомножитель w будет равен A -f г) У 2520 .
Для а = 8, согласно случаю VIII, соответствующий сомножитель
9t равен — 1.
Сомножителю 9 числа п соответствует, согласно случаю III,
сомножитель + 1.
Сомножителю 5 соответствует сомножитель — 1 (согласно слу-
случаю II).
Сомножителю 7 соответствует сомножитель — 1 (согласно слу-
случаю II).
Отсюда для произведения получаем W = (— 1 — г) J/2520,
как и в п. 29.
32
Так как значение W может быть определено при помощи двух
методов, один из которых основывается на квадратичных характерах
чисел пк/а, пк/Ъ, пк/с,... соответственно по модулям а, Ъ с, • • •
Суммирование некоторых рядов особого вида 631
а другой зависит от квадратичных характеров числа к по модулям
а, Ь, с, . . . , то между всеми этими квадратичными характерами
должна существовать некоторая взаимообусловливающая связь, в том
смысле, что каждый из этих характеров должен определяться через
остальные. Пусть а, Ь, с, ... — нечетные простые числа и к = 1,
далее, сомножители а, Ь, с, .. . мы разобьем на два класса, один
из которых содержит те сомножители, которые имеют вид 4[л + 1
и которые мы будем обозначать через /?, //, //', ..., а второй со-
состоит из тех сомножителей, которые имеют вид 4[х + 3, и которые
мы будем обозначать через q, q\ q", . .. Количество последних мы
обозначим через т. После этого заметим, что п будет иметь вид
4[х+1, если т четно (сюда же следует отнести и случай, когда
сомножителей второго класса вообще нет, и потому т = 0), и что,
напротив, п будет иметь вид 4[л + 3, если т нечетно. Теперь при
помощи первого метода W определяется следующим образом.
Пусть числа Р, Р\ Р", . . . , (?, Q'', (?", . . . так определяются соот-
соответственно отношениями чисел п/р, п/р\ п/р",..., n/q< njq\ n/q",..
к числам р, р\ р\ . . ., q,q\ q", . . . , что
Р = + 1, если п/р является квадратичным вычетом по модулю /?,
Р — — 1, если п/р является квадратичным невычетом по модулю р,
и точно так же для остальных чисел. Тогда W является произве-
произведением сомножителей Р У~р, Р' Ур\ Р" V"p", ... ., iQ ]/ q, iQf Vq',
iQ" V^i • • • i и потому
W = PPfP"... QQ'Q" ...im Vn.
При помощи второго метода или даже непосредственно на основа-
основании правил п. 19 получается, что
W = -)-|/"п, если п имеет вид 4[х-f- 1, или, что то же самое,
если т четно,
W = + 1У~п, если п имеет вид 4[х + 3, или, что то же самое,
если т нечетно.
Оба эти случая можно одновременно охватить следующей формулой:
imZ~m
632 Суммирование некоторых рядов особого вида
Итак, из сказанного следует, что
РР'Р" ... QQ'Q". .. = im2~m.
Но im~m = l, если т имеет вид 4[х или 4[л+1, и i
если m имеет вид 4;х + 2 или 4;х + 3; таким образом, мы получаем
очень изящную теорему.
Теорема. Если а, Ь, с, . . . обозначают различные положительные
нечетные простые числа, произведение которых равно п и среди ко-
которых имеется т чисел вида 4[х + 3, а остальные имеют вид 4[х -{- 1,
то количество тех из всех этих чисел а, Ь, с, . . ., по которым яв-
являются невычетами соответственно числа п / а, п/ Ь, п / с, ... , четно,
если т имеет вид 4;х или 4[х + 1, и нечетно, если т имеет вид
4[х -f- 2 или 4[х -f- 3.
Так. например, если положить а = 3, Ь = Ь, с = 7, d = 11,
то имеется три числа вида 4;х + 3, именно, числа 3, 7 и 11. Но
5.7-НДЗ; 3-7-1LR5; 3-5-11Л7; 3-5-7ЛГ11, т. е. только n/d
является невычетом по модулю d.
33
Знаменитая фундаментальная теорема о квадратичных вычетах
представляет собой ни что иное, как специальный случай только
что изложенной теоремы. Именно, если мы ограничим количества
чисел а, Ь, с,... двумя, то если вид 4;л -(- 3 имеет или только одно и&
них, или ни одного, очевидно будет иметь место либо одновременна
aRb/ bRa, либо одновременно aNb, bNa; если же оба числа имеют
вид 4[х + 3, то одно из них будет невычетом по другому, а второе
будет вычетом по первому. Таким образом, мы имеем здесь четвер-
четвертое доказательство этой в высшей степени важной теоремы; первое
и второе доказательства мы опубликовали в «Арифметических ис-
исследованиях», третье, недавно, в отдельном сочинении («Новое дока-
доказательство одной арифметической теоремы»); еще два доказатель-
доказательства, которые опять-таки основываются на совершенно иных прин-
принципах, мы изложим позднее. Весьма удивительно, что эта прекрасная
теорема, которая сначала так упорно сопротивлялась всем попыткам
ее доказать, позднее оказалась доступной столь многим совершенна
различным подходам.
Суммирование некоторых рядов особого вида 633
34
Также и остальные теоремы, образующие как бы дополнение
к фундаментальной теореме, а именно, те, на основании которых
можно узнавать, по каким простым числам являются вычетами, или
невычетами числа —1, + 2 и —2, могут быть выведены из этих
же принципов. Мы начнем с вычета + 2.
Если положить п = 8а, где а является простым числом, и 4 = 1,
то на основании п. 28 W будет произведением двух сомно-
сомножителей, один из которых равен +|/а" или + г\Га в случае, если
число 8 или, что то же самое, число 2 является квадратичным
вычетом по модулю а, и, напротив, равен —~\Га или —гуав слу-
случае, если число 2 является невычетом по модулю а. Второй же
сомножитель равен
A -f- i) V^S» если а имеет вид 8[х + 1;
(— 1 + 0 Vo» если а имеет вид 8[х -{- 3;
(— 1 — i) V~8, если а имеет вид 8[х + 5;
A — i) Y~8, если а имеет вид 8[х + 7.
Но согласно п. 18, всегда IF = A + г)уТг"; если разделить эта
значение на четыре значения второго сомножителя, то мы получим,
что первый сомножитель должен быть равен
+ )/~а, если а имеет вид 8[х + 1;
— i У а, если а имеет вид 8[х + 3;
— ]/а, если а имеет вид 8[х -f- 5;
-\-iY~uy если а имеет вид 8[х + 7.
Отсюда непосредственно следует, что в первом и четвертом слу-
случаях число 2 должно быть квадратичным вычетом по модулю а,
а во втором и третьем случаях—квадратичным невычетом.
35
Простые числа, по которым является вычетом или невычетом
число —1, легко можно узнавать при помощи следующей теоремы,
которая и сама по себе достойна внимания.
634 Суммирование некоторых рядов особого вида
Теорема. Произведение двух сомножителей
W = 1 + г~г + г~4 -\ + г~{п~1]\
W = l+r-\-r± + h r(n~1J
или равно п, если п нечетно, или равно О, если п четно, но не де-
делится на 4, или равно 2п, если п делится на 4.
Доказательство. Так как, очевидно, имеет место
W = г + г4 + г9 Н \-гп2 =
и т. д.,
то произведение WW может быть представлено также следующим
образом:
1+г + г* + г»+...+ г(П~1>г +
+ Г'1 (Г + Г4 + г9 + Г16 Н \- ГП) +
+ г-« (Г4 + Г9 + ГИ _|_ Г25 ^ j. r(«+lJ) +
+ г"8 (г9 + г16 + г25 + г™ Н h /-(n+2J) +
и если суммировать по вертикальным рядам, это выражение дает
п +
+ г9 A + г6 + г12 + г18 -1 + г6"") +
+ ,.(n-1J(l + г2" + г4" + гвп~в + Ь /-2(п-1J).
Если теперь п нечетно, то отдельные части этой суммы, кроме
первой, равной п, равны 0; действительно, вторая часть будет,
Суммирование некоторых рядов особого вида 635
гA — Г2П) r4A_r4n}
очевидно, равна —, ___ 2—, третья равна — 4 и т. д. Ьсли
же п четно, то нужно исключить еще и часть
П8/4
которая равна пг .
Таким образом, в первом случае WW = п, а во втором случае
WW =п-\- пгп2/*\ но rnV4 = + 1, если п делится на 4, и тогда
следовательно, WW = 2 п\ напротив, если п четно, но не делится
на 4, то гп/* = —1 и потому в этом случае WW'=0.
36
Из п. 22 мы знаем, что если п является нечетным простым чис-
лом, то либо — =-|-1, либо ттг = — 1» в зависимости от того,
является ли число — 1 вычетом или невычетом по модулю п. По-
Поэтому в первом случае должно быть W2 = -\-п, а во втором
W2 — — п. Поэтому на основании п. 13 мы заключаем, что первый
случай может иметь место только тогда, когда п имеет вид 4[х + 1»
а второй — только тогда, когда п имеет вид 4[х + 3*.
Наконец, комбинируя условия, найденные для вычетов + 2 и
— 1, мы сразу получаем, что число —2 является вычетом по каж-
каждому простому числу вида 8(х + 1 или 8[х + 3 и невычетом по каж-
каждому простому числу вида 8[х + 5 или 8[х + 7.
НОВЫЕ ДОКАЗАТЕЛЬСТВА И ОБОБЩЕНИЯ
ФУНДАМЕНТАЛЬНОЙ ТЕОРЕМЫ В УЧЕНИИ
О КВАДРАТИЧНЫХ ВЫЧЕТАХ
(Commentationes soc. red. sc. Gotting.
recentiores, Vol. IV, Gotting, 1818)
Хотя фундаментальную теорему о квадратичных вычетах, кото-
которая принадлежит к прекраснейшим истинам высшей арифметики,
легко было обнаружить индуктивным путем, доказать ее оказалось
значительно труднее. При исследованиях такого рода чаще оказыва-
оказывается, что доказательства простейших фактов, которые в большинстве-
случаев кажутся исследователю очевидными с первого взгляда т
оказываются скрытыми очень глубоко и извлекаются на свет лишь
после многих тщетных попыток, причем совсем не таким путем, на
котором их раньше искали. Далее, не редко случается, что после*
того как был найден один путь, тотчас же открывается и несколько
путей, ведущих к той же цели, одни из которых короче и прямее,
другие же приводят к цели как будто со стороны и основываются на
совершенно отличных принципах, между которыми и предметом ис-
исследования почти нельзя было предположить никакой связи. Такая
замечательная связь между скрытыми закономерностями не только-
придает этим исследованиям некоторую своеобразную привлекатель-
привлекательность, но и заслуживает тщательного выяснения, так как нередко
благодаря ей открываются новые возможности для развития науки.
Таким образом, хотя рассматриваемая здесь арифметическая тео-
теорема могла бы показаться совершенно исчерпанной благодаря пре-
Новые доказательства фундаментальной теоремы 637
дыдущим усилиям, которые уже доставили четыре * во всех отно-
отношениях отличных одно от другого ее доказательства, я тем не менее
€нова возвращаюсь к этому же предмету и предлагаю еще два дока-
доказательства, которые проливают на этот вопрос новый свет. Первое
из них, правда, родственно третьему доказательству в том отношении,
что исходит из той же леммы; в дальнейшем, однако, оно идет другим
путем, так что его по праву можно считать новым доказательством,
которое если не короче третьего, то и не длиннее. Шестое же дока-
доказательство основывается на совершенно отличном от остальных очень
тонком принципе и дает новый пример замечательной связи между
арифметическими фактами, которые на первый взгляд лежат очень
далеко один от другого. К этим двум доказательствам мы добавляем
еще новый очень простой алгоритм, для того чтобы узнавать, являет-
является ли заданное целое число квадратичным вычетом или невычетом по
заданному простому числу.
Была еще и другая причина, которая заставила меня только
теперь опубликовать новые доказательства, о которых я говорил
еще девять лет назад. Именно, когда я в 1805 г. начал исследовать
теорию кубических и биквадратичных вычетов,— предмет намного
более трудный,— меня постигла почти такая же судьба, как когда-
то в теории квадратичных вычетов. Именно, теоремы, которые пол-
полностью исчерпывали рассматриваемые вопросы, и в которых прояв-
проявляется замечательная аналогия с теоремами, касающимися квад-
квадратичных вычетов, сразу находились индуктивно, как только их
искали на правильном пути, но все попытки достигнуть во всех от-
отношениях совершенных доказательств, долгое время оставались
тщетными. Это как раз и явилось стимулом к тому, что я к уже из-
известным доказательствам относительно квадратичных вычетов старал-
старался добавить все новые и новые, в надежде, что какой-нибудь из мно-
многих различных методов может прибавить что-либо к выяснению род-
родственного вопроса. Эта надежда оказалась отнюдь не напрасной,
и неутомимая работа увенчалась наконец успехом. Вскоре я буду в
* Два доказательства изложены в четвертом и пятом разделах {{Арифмети-
{{Арифметических исследований», третье — в отдельном сочинении {{Новое доказательство
одной арифметической теоремы», четвертое содержится в сочинении {{Суммиро-
{{Суммирование некоторых рядов особого вида».
638 Новые доказательства фундаментальной теоремы
состоянии опубликовать результаты моих исследований; однако>
прежде чем приступить к этому трудному делу, я решил еще раз
вернуться к теории квадратичных вычетов, изложить все, что отно-
относительно нее еще осталось сказать, и в известном смысле распро-
распроститься с этой частью высшей арифметики.
Пятое доказательство фундаментальной теоремы
теории квадратичных вычетов
1
Во введении мы уже говорили, что пятое и третье доказательства
исходят из одной и той же леммы, которую мы здесь для удобства
повторим в обозначениях, целесообразных для настоящего иссле-
исследования.
Лемма. Пусть т — положительное нечетное простое число, М —
целое число, не делящееся на т\ возьмем наименьшие положительные
вычеты по модулю т чисел
М, 2М, ЪМ, Ш у (т — 1) М\
часть этих вычетов будет меньше, а часть больше чем т/2; пусть
количество последних равно п. Тогда М будет квадратичным вычетом
или невычетом по модулю те зависимости от того, четно число п или
нечетно.
Доказательство. Если а, Ь, с, d,... — те из наших вычетов, кото-
которые меньше чем т/2, и a',b',c',d',... —остальные вычеты, которые
больше чем т/2, то дополнения последних до т, т. е. числа т — а',
т — Ъ', т — с', т — dr,... будут, очевидно, все меньше чем т/2 и
будут отличны как одно от другого, так и от вычетов а, Ь, с, d,...,
так что вместе с этими вычетами они, быть может только в другом
порядке, будут образовывать совокупность всех чисел 1, 2, 3, 4,..,
..., (т — 1)/2. Поэтому, если положить
1.2-3.4, .. -(т — 1) = Р,
Новые доказательства фундаментальной теоремы 639
то будет выполняться равенство
Р = abcd. . .(m — a')(m — b')(m — c')(m — d'). . .,
и потому
(_ if р = abed ,..{аг — т) (&' — т) (с' — m){dr — m)...
Далее, по модулю т будет иметь место
РМ{т~т = abed ... a'b'c'd'... = abed...{a1— m){b'—m){c'—m){d' — m)...,
и потому
)/2 _ р (_ jjn^
Следовательно, М(т~~1)/2 = + 1, где нужно брать верхний или
нижний знак в зависимости от того, четно п или нечетно, а отсюда
справедливость нашей леммы сразу вытекает на основании теоремы,
доказанной в «Арифметических исследованиях», п. 106.
2
Теорема. Пусть т, М — положительные нечетные взаимно про-
простые числа, п — количество тех вычетов среди наименьших положи-
положительных вычетов по модулю т чисел
М, 2М, Ж, . . . , i- (т — 1) М,
которые больше чем т/ 2, и точно так же N — количество тех вы-
вычетов среди наименьших положительных вычетов по модулю М чисел
т, 2т, Зт, .. ., -~- (М — 1) т,
которые больше чем М /2\ тогда три числа п, N, (т—1)(М—1)/4
или все четны, или одно из них четно, а два другие нечетны.
Доказательство. Обозначим
через / совокупность чисел 1,2, 3,.. . , (т — 1) / 2,
через /' совокупность чисел т— 1, т — 2, т — 3, ... , (т + 1)/2,
через F совокупность чисел 1, 2, 3, ... , (М—1)/2,
через F' совокупность чисел М— I, М— 2, М — 3,. . . , (М + 1) / 2.
640 Новые доказательства фундаментальной теоремы
Таким образом, число п будет показывать, сколько чисел среди
Mf имеют свои наименьшие положительные вычеты по модулю т
в совокупности /', и точно так же число N будет показывать, сколько
чисел среди mF имеют свои наименьшие положительные вычеты
по модулю М в совокупности F'. Наконец, обозначим
через <р совокупность чисел 1,2,3,..., (тМ — 1) / 2,
через <р' совокупность чисел тМ—1, тМ — 2, тМ — 3,..., (тМ -fl)/2.
Так как каждое целое не делящееся на т число должно быть
сравнимо по модулю т либо с каким-нибудь вычетом из /, либо
с каким-нибудь вычетом из /', и точно так же каждое целое не
делящееся на М число сравнимо по модулю М либо с каким-нибудь
вычетом из F, либо с каким-нибудь вычетом из F', то все числа
совокупности <р, среди которых, очевидно, нет чисел, делящихся
одновременно на т и М, можно следующим образом разбить на
восемь классов.
I. В первом классе находятся числа, которые по модулю т
сравнимы с каким-нибудь числом из /, а по модулю М — с каким-
нибудь числом из F. Количество этих чисел мы обозначим через ос.
II. Второй класс содержит числа, которые по модулям m, M
сравнимы соответственно с числами из /, F'. Количество этих чисел
мы положим равным р.
III. Третий класс содержит числа, которые по модулям m, M
сравнимы соответственно с числами из /', F. Их количество мы
положим равным "р
VI. Четвертый класс содержит числа, которые по модулям т,
М сравнимы соответственно с числами из /'. F''. Их количество
пусть равно 8.
V. Пятый класс содержит числа, которые делятся на т, а но
модулю М сравнимы с вычетами из F.
VI. Шестой класс содержит числа, которые делятся на т, а по
модулю М сравнимы с вычетами из F'.
VII. Седьмой класс содержит числа, которые делятся на М, а
по модулю т сравнимы с вычетами из /.
VIII. Восьмой класс содержит числа, которые делятся на М, а
по модулю т сравнимы с вычетами из /'.
Очевидно, что классы V и VI вместе охватывают всевозможные
Пятое доказательство фундаментальной теоремы 641
числа mF\ но количество чисел, содержащихся в VI, равно 7V, по-
поэтому количество чисел, содержащихся в V, равно у (М — 1) —N.
Точно так же классы VII и V1I1 вместе содержат всевозможные чи-
числа Mf; в классеVIII находится п чисел, а в классе VII находится
~2 (т — 1) — п чисел.
Совершенно аналогичным образом все числа совокупности <?'
распадаются на восемь классов IX — XVI; если при разбиении этих
чисел мы будем придерживаться прежнего порядка, то числа, содер-
содержащиеся в классах
IX, X, XI, XII, XIII, XIV, XV, XVI,
будут, очевидно, дополнениями до тМ чисел, содержащихся соот-
соответственно в классах
IV, III, II, I, VI, V, VIII, VII,
так что в классе IX будет находиться 8 чисел, в классе X будет
находиться т чисел и т. д. Но ясно, что если объединить все числа
первого класса со всеми числами девятого класса, то получатся все
числа, меньшие чем тМ, которые по модулю т сравнимы с некото-
некоторым числом из /, а по модулю М — с некоторым числом из F, и лег-
легко видеть, что количество их равно количеству всех комбинаций от-
отдельных чисел из / с отдельными числами из F. Поэтому мы имеем,
что
и по аналогичной причине
Если собрать вместе все числа из классов II, IV, VI, то мы по-
получим, очевидно, все числа, меньшие чем тМ/2, которые сравнимы
по модулю М с некоторым вычетом из F'. Но эти же числа могут
быть представлены и в виде
t F\
642 Новые доказательства фундаментальной теоремы
так что количество их равно (т—1)(М — 1)/4, т. е. мы имеем, что
Точно так же, собирая вместе все числа классов III, IV,
можно заключить, что
т + 8 + тг = 4-(т—1)(Л/—1).
Из этих четырех уравнений мы получаем следующие:
2а = -j. (т — 1) (М — 1) + п + N,
24 = ~(m
2& = ~(т — 1)(М—1) — п — Лт,
каждое из которых доказывает справедливость теоремы.
Если мы теперь предположим, что т и М — простые числа,
то из соединения настоящей теоремы с леммой из п. 1 тотчас же
получается фундаментальная теорема. Действительно, ясно,
I) что если каждое из чисел т, М или только одно из них
имеет вид 4&+1, то число -г-(т—1)(М—1) четно, и потому
числа п, N или одновременно четны, или одновременно нечетны,
т. е. либо каждое из чисел т и М является квадратичным выче-
вычетом по другому из йих, либо каждое является квадратичным не-
невычетом по другому;
II) если же оба числа т9 М имеют вид 4& + 3, то (т— 1) (М—1) /4
является нечетным числом, а потому одно из чисел n, N четно,
а другое нечетно, и тем самым одно из чисел m, M есть квадра-
квадратичный вычет по другому, а второе есть квадратичный невычет
по первому.
Шестое доказательство фундаментальной теоремы 643
Шестое доказательство фундаментальной теоремы
теории квадратичных вычетов
1
Теорема. Если р обозначает (положительное нечетное) простое
число, п—целое положительное число, не делящееся на р, их —
переменную величину, то функция
х2п + xsn + ... + xnv~n
делится на функцию
Доказательство. Если взять такое целое положительное число gy
что gn = 1 (mod/?), и положить gn = I -\- hp, то
1 4- xn+x2n-\-xSn + • • • +*ПР~П _ A — xnv) A — *)
_ xgn _ ж
A— xn)(l— xv)
V 1-х$п x(i-xnv) 1-
и потому стоящая слева функция, очевидно, будет целой, что и
требовалось доказать.
Таким образом, каждая целая функция от х1 которая делится
на A — xnv) / A — хп), делится также и на A — xv) / A — х).
2
Обозначим через а положительный первообразный корень по
модулю р, т. е. положительное целое число с тем свойством, что*
наименьшие положительные вычеты, по модулю р степеней 1, а, а2г
а3, ... , ар~~2 с точностью до порядка расположения совпадают
с числами 1, 2, 3, 4, . . . , р— 1. Если обозначить далее через / (х)
функцию
644 Новые доказательства фундаментальной теоремы
то функция f(x) — 1 — х — х2 — Xs — • • • — хр—1 будет, очевидно,
делиться на 1 — х^, а значит и подавно на -j—— = 1 + х + #2 +
+ Xs + • • • + %v~lu, на эту последнюю функцию будет, таким обра-
образом, делиться и f(x). Но так как х неизвестная величина,
отсюда следует, что и функция f(xn) делится на A—»жтар)/A — хп),
а потому (согласно пункту 1) также и на A—х?) / A ¦—х),
по крайней мере, если п является целым, не делящимся на р
числом. Если же п есть целое число, делящееся на р, то отдельные
части функции f(xn), уменьшенные на 1, будут делиться на 1 — xv\
тем самым в этом случае и / (хп) — р будет делиться на 1 — xv9
а, значит, и на A — xv) / A — х).
Теорема. Если положить
х — х« +х«2 — х«* + х«4— • • • — x«v~2--= ?,
то 1*Ц^р будет делиться на A—х?)/(I—х), если брать верхний
знак, когда р имеет вид 4Л: + 1, и нижний, когда р имеет вид 4А + 3.
Доказательство. Легко видеть, что из следующих р — 1 функций:
-f Х% — X2 + Яа+! — Ха2+! + • • • + ЖаМ+1,
первая равна 0, а каждая из остальных делится на 1—#р. Поэтому
на 1—xv делится также и их сумма, которая равна
Тем самым это выражение О делится также и на A—хр)/A—х).
Но среди показателей 2, а + 1, а2 + 1, а3 + 1, . . ., a^~2 + 1 только
Шестое доказательство фундаментальной теоремы 645
один, а именно, oc^-D/2 + 1, делится на р, так что, согласно преды-
предыдущему пункту, на A—xv) I A—х) делятся все отдельные части
/ (ж2)> / (^а+1), / (яа2+1), / (я*3"), . . . выражения О, за исключением
лишь члена /(ж*^^2^1). Поэтому указанные части можно отбро-
отбросить, так что делящейся на A—xv)/(l—х) остается функция
где берется верхний или нижний знак в зависимости от того, имеет
ли р вид hk + 1 или Ак + 3. А так как, кроме того, /(ха(р~1)/2+1) — р
делится на A—xv) / A—х), то и ^^Рр будет делиться на
A—xv) I A—х). Это и требовалось доказать.
Для того, чтобы двойной знак не приводил ни к какой неопре-
неопределенности, мы обозначим через s число, равное +1 или —1 в
зависимости от того, имеет ли р вид 4&+1 или вид 4А + 3. Тогда
A—я)(?2 — е/?) / A—xv) будет целой функцией от х, которую мы
обозначим через Z.
Пусть q — положительное нечетное число и потому (q — 1)/2 —
целое число. Тогда (??){q~1)/2 — (sp){q~1)/2 будет делиться нц ?2 — вр
и тем самым также и на A — xv) / A—х). Если мы положим
е<з-1>/2 = 8 и g«-i — 8p(«-i>/2 = ^-^У,
то Y будет целой функцией от х, а 8 = + 1, если одно из чисел
р, q или оба они имеют вид 4&+1, и, напротив, 8 = —1, если
оба числа /?, q имеют вид Ак + 3.
Если мы предположим теперь, что q также является простым
числом (отличным от /?), то, согласно доказанной в «Арифметиче-
«Арифметических исследованиях», п. 51, теореме, функция
646 Новые доказательства фундаментальной теоремы
будет, очевидно, делиться на q, т. е. будет иметь вид qX, где X
является функцией от х с целыми коэффициентами (что справед-
справедливо также и относительно остальных фигурирующих здесь функ-
функций Z, 7, W). Если для модуля р и первообразного корня а мы
обозначим через [л индекс числа q, т. е. если q = oc^(mod/?), то
числа q, q&, q&2, goc3, . . ., qcnv~2 будут сравнимы по модулю р соот-
соответственно с числами скУ-, а^+г, а^2, ..., оср~2, 1, ос, ос2,..., ос^1, и потому
X,
— х«\
Р—2
делятся на 1—х*. Если сложить эти функции, взятые попеременно
то положительными, то отрицательными, то станет ясным, что
функция
делится на 1—яр, причем нужно брать верхний или нижний знак
в зависимости от того, четно [х или нечетно, т. е. в зависимости
от того, является ли q квадратичным вычетом или невычетом по
модулю р. Положим поэтому
xq _ Х^ + xq*2 — х^% + xv«v~2 — TS = A — х*) W,
где мы предполагаем, что ^ = + 1 или = — 1 в зависимости от того,
является ли q квадратичным вычетом или невычетом по модулю р;
тогда W будет целой функцией.
Шестое доказательство фундаментальной теоремы 647
6
После этих приготовлений мы, комбинируя предыдущие уравне-
уравнения, выводим уравнение
qlX = sp (8/>(e-D As - Т) + iT^- (Z (8^-D/2 _ Т) + Г? -Wl(i— x).
Предположим, что при делении функции IX на
xv—1 _|_ xv~~2 + ^р~~3 + • • • + ж + 1
получаются частное U и остаток Г, т. е. что
^ хр
так что функции U, Т имеют целые коэффициенты, причем Т заве-
заведомо имеет степень, меньшую чем делитель. Тогда
qT — sp (8/><e-i>/2 — т) =
_ Lzi^ [Z (8/>(e-D/2 _ T) + Yl2 — Wl A — x) — qU],
а это равенство, очевидно, может выполняться лишь в том случае,
когда одновременно обращаются в нуль как левая, так и правая
части. Таким образом, на q делится как вр (8/?(«—D/?~ y), так и
§p(q—l)/2 ^ а так как §2 _ ^ то и чисдо p(q—l)/2 ^§ ДвЛИТСЯ На q.
Если мы теперь обозначим через р единицу, взятую с положи-
положительным или отрицательным знаком в зависимости от того, является
ли р квадратичным вычетом или невычетом по модулю д, то на q
будет делиться число /?(e—1)/2 — р? а потому также и р — ^'» но это
возможно лишь в том случае, если р = уЪ. Из этого тотчас же
следует фундаментальная теорема. Именно,
I) если либо каждое из чисел р, q, либо по крайней мере одно
из них имеет вид 4А+ 1, и потому 8 = + 1, то будет иметь место
Р = 7» и потому либо одновременно q является квадратичным вы-
вычетом по модулю р и р — квадратичным вычетом по модулю q, либо
одновременно q есть квадратичный невычет по модулю р, и р —
квадратичный невычет по модулю q\
II) если оба числа р, q имеют вид Ак + 3, и потому 8 = —1,
то будет иметь место р = — т> и потому либо одновременно q
648 Новые доказательства фундаментальной теоремы
является квадратичным вычетом по модулю /?, и р — квадратичным
невычетом по модулю qy либо одновременно q есть невычет по
модулю ру а р — вычет по модулю q. Это и требовалось доказать.
Новый алгоритм для определения того, является ли
заданное положительное целое число квадратичным вычетом
или невычетом по заданному положительному простому модулю
Прежде чем изложить новое решение этой задачи, мы хотим
кратко повторить здесь решение, данное в «Арифметических иссле-
исследованиях», так как оно довольно просто может быть проведено при
помощи фундаментальной теоремы и следующих известных теорем.
I. Отношение числа а к числу Ъ (в том смысле, является ли первое
квадратичным вычетом или невычетом по второму) является таким
же, как и отношение числа с к числу Ь, если а ^ с (mod b).
П. Если а является произведением сомножителей а, |3, т> &,...,
и & — простое число, то отношение числа а к числу Ъ так зависит от
отношений этих сомножителей к числу Ь, что а является квадратич-
квадратичным вычетом или невычетом по модулю Ъ в зависимости от того, чет-
четно или нечетно количество сомножителей, которые являются невы-
невычетами по модулю Ь. Таким образом, если какой-нибудь из сомножи-
сомножителей является квадратом, то его при исследовании можно вообще
не принимать во внимание; если же какой-нибудь из сомножителей
является степенью некоторого целого числа с нечетным показателем,
то вместо степени можно взять само это целое число.
III. Число 2 является квадратичным вычетом по каждому про-
простому числу вида 8т + 1 или 8т + 7, и, напротив, невычетом по
каждому простому числу вида 8т + 3 или 8т + 5.
Если поэтому дано число а и отыскивается его отношение к простому
числу bf то прежде всего вместо числа а, если оно больше чем &, бе-
берется его наименьший положительный вычет по модулю &, и если
этот вычет разложен на простые сомножители, то, согласно теореме
II, задача сводится к нахождению отношений к числу Ъ для этих
отдельных сомножителей. Отношение сомножителя 2 (если он входит
Алгоритм для вычисления вычетов и невычетов по простому модулю 649
один раз, или три раза, или пять раз и т. д.) известно на основании
теоремы III; отношение же остальных сомножителей в силу фунда-
фундаментальной теоремы зависит от отношения Ъ к отдельным сомножите-
сомножителям. Таким образом, вместо одного отношения заданного числа к
простому числу Ъ получается теперь несколько отношений числа Ъ
к другим нечетным простым числам, которые меньше чем Ь, а эти
задачи таким же способом сводятся к еще меньшим модулям, причем
эти последовательные редукции, очевидно, рано или поздно будут
иметь конец.
Чтобы пояснить это решение примером, найдем отношение числа
103 к числу 379. Так как число 103 уже меньше чем 379 и само являет-
является простым числом, то сразу же применяется фундаментальная тео-
теорема, которая показывает, что искомое отношение противоположно
отношению числа 379 к числу 103. Последнее в свою очередь равно
отношению числа 70 к числу 103, которое зависит от отношений к
числу 103 чисел 2, 5, 7. Первое из этих отношений известно на осно-
основании теоремы III. Второе, согласно фундаментальной теореме, за-
зависит от отношения числа 103 к числу 5, которое, по теореме I, сов-
совпадает с отношением числа 3 к числу 5; последнее, на основании
фундаментальной теоремы, в свою очередь зависит от отношения чис-
числа 5 к числу 3, которое, по теореме I, совпадает с отношением числа
2 к числу 3, известным по теореме III. Точно так же отношение числа
7 к числу 103, на основании фундаментальной теоремы зависит от
отношения числа 103 к числу 7, которое, в силу теоремы I, совпадает
с отношением числа 5 к числу 7; последнее, согласно фундаменталь-
фундаментальной теореме, в свою очередь зависит от отношения числа 7 к числу 5,
которое, по теореме I, совпадает с отношением числа 2 к числу 5,
известному на основании теоремы III. Если теперь представить этот
анализ синтетически, то ответ на вопрос будет зависеть от четырна-
четырнадцати отдельных моментов, которые мы здесь приведем полностью, что-
чтобы сделать еще более очевидной краткость нового решения.
1. Число 2 является квадратичным вычетом по числу 103 (теоре-
(теорема III).
650 Новые доказательства фундаментальной теоремы
2. Число 2 является квадратичным невычетом по числу 3 (теоре-
(теорема III).
3. Число 5 является квадратичным невычетом по числу 3 (по тео-
теореме I и 2).
4. Число 3 является квадратичным невычетом по числу 5 (фун-
(фундаментальная теорема и 3).
5. Число 103 является квадратичным невычетом по числу 5 (тео-
(теорема I и 4).
6. Число 5 является квадратичным невычетом по числу 103 (фун-
(фундаментальная теорема и 5).
7. Число 2 является квадратичным невычетом по числу 5 (теоре-
(теорема III).
8. Число 7 является квадратичным невычетом по числу 5 (теоре-
(теорема I и 7).
9. Число 5 является квадратичным невычетом по числу 7 (фун-
(фундаментальная теорема и 8).
10. Число 103 является квадратичным невычетом по числу 7
(теорема I и 9).
11. Число 7 является квадратичным вычетом по числу 103 (фун-
(фундаментальная теорема и 10).
12. Число 70 является квадратичным невычетом по числу 103
(теорема II, 1, 6, 11).
13. Число 379 является квадратичным невычетом по числу 103
(теорема I и 12).
14. Число 103 является квадратичным вычетом по числу 379.
В дальнейшем мы ради краткости будем использовать обозначе-
обозначение, введенное в сочинении «Новое доказательство одной арифметиче-
арифметической теоремы». Именно, мы будем обозначать через [х] самое величи-
величину х, если я является целым числом, и, напротив, ближайшее к
х целое число, меньшее чем х, если х является дробной величи-
величиной, так что х — \х\ всегда будет не отрицательной величиной,
меньшей чем 1.
3
Задача. Пусть а, Ъ обозначают положительные взаимно простые
Г1 1
целые числа, и | -^« | = а- ; нужно найти сумму
Алгоритм для вычисления вычетов и невычетов по простому модулю 651
a] ' la] ' la] la] ' ' [_aJ
Решение. Мы обозначим для краткости подобную сумму через
<р (а, Ь), так что будет иметь место также и
если положить \-трЬ\ = Ь'. В третьем доказательстве фундаменталь-
фундаментальной теоремы было показано, что в случае, когда числа а и Ъ нечетны,
выполняется равенство
) = а'Ь',
и тем же методом легко доказать справедливость этой теоремы и
в том случае, когда только одно из чисел а, Ъ нечетно, о чем уже упо-
упоминалось в указанном месте. По аналогии с тем способом, которым
отыскивается наибольший общий делитель двух целых чисел, разделим
число а на Ь; пусть частное равно р, и остаток равен с; затем раз-
разделим Ъ на с и т. д., так что получим равенства
а = р& + с,
При этом в ряду все время уменьшающихся чисел Ъ, с, d, e, /,...,
тяы в конце концов придем к единице, ибо числа а и Ъ по предпо-
предположению взаимно просты, так что последним равенством будет
Ц — 1^1 -\- 1.
Но так как, очевидно, имеет место
[tHp+tl-Ит].
и т. д.,
652
Новые доказательства фундаментальной теоремы
ТО
и потому
9 (а, Ъ) = а'Ъ' - \ р (ft'2 + b')-9 (ft, с).
т-т « Г1 1 / Г1 J
По аналогичной причине, если положить Нт-с = с , Иг^
L ^ J L ^
— g| = е', . .., то будут выполняться равенства
9 (с d) = c'd' — j 8 (d'2 + d') — 9 (d' *)>
9 (d, e) - d'e'
e'2 + e')-cp(e, /),
Отсюда мы получаем (так как, очевидно, <p(Z, 1) = 0) формулу
<р (а, 6) = а'Ь' — Ъ'с' + c'd' — d'e' + . .. + AT —
Из того, что было изложено в третьем доказательстве, легко
вывести, что отношение числа Ъ к а, в случае, когда число а про-
простое, немедленно можно узнать по значению суммы ф(а, 2ft); Именно,
в зависимости от того, четна эта сумма или нечетна, число ft будет
квадратичным вычетом или невычетом по модулю а. Но для этой
же цели может быть использована и сама сумма ср (a, ft), с тем,
однако, ограничением, что случай, когда Ъ нечетно, следует отличать
от случая, когда ft четно. Именно,
I) если ft нечетно, то b является квадратичным вычетом
или невычетом по модулю а в зависимости от того, четно или
нечетно ср (a, ft);
Алгоритм для вычисления вычетов и невычетов по простому модулю 653
II) если Ъ четно, то сохраняет силу это же правило, когда,
кроме того, а имеет вид 8п -\~ 1 или 8п + 7; если же при четном
значении числа Ъ модуль а имеет вид 8п + 3 или 8/2 —(— 5, то пра-
правило будет противоположным, т. е. Ъ будет квадратичным вычетом
по модулю а, когда ср (а, Ь) нечетно, и, напротив, невычетом, когда
ср(а, Ъ) четно.
Все это легко получается из п. 4 третьего доказательства.
Пример. Если отыскивается отношение числа 103 к простому
числу 379, то для получения суммы ср C79, 103) мы имеем
a =
b =
с =
d =
e =
379
103
70
33
4
a' =
b' =
c' =
d' =
e' =
189
51
35
16
2
T
8
e
= 3
Л
= 2
= 8,
поэтому
9C79, 103) =
= 9639 —1785 + 560 — 32 — 3978 + 630 — 272 + 24 = 4786,
так что 103 является квадратичным вычетом по числу 379. Если
же мы захотим использовать для этой цели сумму ср C79, 206), то
мы будем иметь
189
379
206
173
33
103
86
16
4
1
1
5
4,
откуда получается, что
9 C79, 206) = 19 467 — 8858 + 1376 — 64 — 5356 +
+ 3741 — 680 + 40 = 9666;
тем самым 103 является квадратичным вычетом по модулю 379.
654 Новые доказательства фундаментальной теоремы
6
Так как для определения отношения числа Ъ к а нет необходи-
необходимости вычислять отдельные части суммы <р (а, 6), а достаточно
только знать, сколько среди них имеется нечетных, то наше пра-
правило может быть представлено и так.
Пусть, как и выше, а = $Ь + с, Ь = ^с + d, с = bd + еч . . . , до
тех пор, пока в ряду чисел а, 6, с, d, е, . . . не получится единица.
Положим к-а =а', у6 = &', ус =с',..., и пусть |х обозна-
обозначает количество тех нечетных чисел в ряду а', Ь\ с', . . . , за ко-
которыми непосредственно следует также нечетное число; далее, пусть v
обозначает количество таких нечетных чисел в ряду р, ^» 8, . . . ,
которым в ряду Ь'', с', d', .. . соответствуют числа вида 4п + 1 или
вида 4п + 2. Тогда b будет квадратичным вычетом или невычетом
по модулю а в зависимости от того, четно число [х + v или нечетно,,
за исключением единственного случая, когда одновременно b четно
и а имеет вид 8п + 3 или 8п-\-5; в этом случае следует применять
противоположное правило.
В нашем примере ряд a', b\ c\ d\ . . . дает две пары следующих
одно за другим нечетных чисел, так что \к = 2; в ряду же р, ч%
8, s, хотя и имеются два нечетных числа, но им в ряду Ъ\ с', df\
е' соответствуют числа вида Ы + 3, так что v = 0. Поэтому число
(л + v будет четным, и; значит, 103 является квадратичным вычетом
по модулю 379.
ТЕОРИЯ БИКВАДРАТИЧНЫХ ВЫЧЕТОВ
Сочинение первое
(Commentationes soc. reg. sc. Gdtting
recentiores., Vol. VI, Gottingae, 1828)
1
Теория квадратичных вычетов может быть сведена к небольшо-
небольшому числу основных теорем, относящихся к прекраснейшим жемчужи-
жемчужинам высшей арифметики, которые, как мы знаем, сначала легко по-
получались индуктивным путем, а затем были доказаны различными
способами, так что в этом отношении не остается уже желать ничего
лучшего.
Намного труднее, однако, теория кубических и биквадратичных
вычетов. После того как мы начали исследовать эти вопросы в 1805 г.,
у нас, помимо очевидных элементарных предложений, получились
также некоторые специальные теоремы, которые весьма замечатель-
замечательны как простотой формулировок, так и трудностью доказательства;
однако мы скоро пришли к убеждению, что применявшиеся до сих
пор арифметические принципы ни в коем случае не достаточны для
обоснования общей теории, а что эта теория с необходимостью тре-
требует в некотором смысле бесконечно расширить область высшей ариф-
арифметики; а как это следует понимать, будет показано в процессе на-
настоящих исследований. Как только мы вступаем в эту новую область,
тотчас же обнаруживается подход к индуктивному нахождению весь-
весьма простых и исчерпывающих всю теорию теорем; однако доказатель-
доказательства их скрыты столь глубодо, что их удалось извлечь на свет толь-
только после многих бесплодных попыток.
656 Теория биквадратичных вычетов. I
Приступая теперь к опубликованию этих исследований, мы на-
начинаем с теории биквадратичных вычетов, причем в этом первом со-
сочинении изложим те результаты, которые еще могут быть получены
без расширения области арифметики, но которые в известном смыс-
смысле пролагают к нему путь, и одновременно приводят к новым фак-
фактам в теории деления круга.
Понятие биквадратичного вычета мы ввели в п. 115 «Арифме-
«Арифметических исследованию): именно, целое положительное или отрица-
отрицательное число а называется биквадратичным вычетом целого числа р,
если а сравнимо по модулю р с некоторым биквадратом, и биква-
биквадратичным невычетом, если такое сравнение невозможно. Во всех
дальнейших исследованиях, когда не будет оговорено противное,
будет предполагаться, что модуль р является (нечетным положи-
положительным) простым числом, и а не делится на р, ибо все остальные
случаи легко могут быть сведены к этому.
Очевидно, что каждый биквадратичный вычет числа р будет
также и его квадратичным вычетом, а потому каждый квадратич-
квадратичный невычет — также и биквадратичным невычетом. Эту теорему
можно и обратить, если р является простым числом вида An -f- 3.
Действительно, если в этом случае а является квадратичным вы-
вычетом числа р, то положим а = b2 (mod/?), где Ъ будет или квад-
квадратичным вычетом, или квадратичным невычетом. В первом случае
положим & = с2, так что а = с*, т. е. а будет биквадратичным вы-
вычетом числа р; во втором случае число —Ъ будет квадратичным
вычетом числа р (так как — 1 является невычетом каждого про-
простого числа вида 4п + 3), и если положить —& = с2, то, как и
раньше, будет а^с*, т. е. а будет биквадратичным вычетом чи-
•сла р. Одновременно легко видеть, что других решений сравнения
.х4 = a (mod/?), кроме х = с и х — —с, в этом случае нет.
Теория биквадратичных вычетов. I 657
Так как эти очевидные теоремы исчерпывают всю теорию биква-
дратичних вычетов для простых модулей вида 4га + 3t мы полностью
исключаем такие модули из нашего исследования, т. е. ограничим
его простыми модулями вида 4п + 1.
Если р является, таким образом, простым числом вида 4п + 1,
то теорему предыдущего пункта обратить нельзя; действительно,
могут существовать квадратичные вычеты, которые не являются
одновременно биквадратичными вычетами, причем это имеет место
в том случае, когда квадратичный вычет сравним с квадратом ква-
квадратичного невычета. Действительно, если положить a = fe2, где b
является квадратичным невычетом числа р, то если бы сравнение
х* = а удовлетворялось некоторым значением ж = с, имело бы место
с4 = 62, т. е. произведение (с2 — й)(с2 + 6) делилось бы на р, вслед-
вследствие чего р входило бы делителем или в сомножитель с2—Ъ, или
в сомножитель с2 + Ь, т. е. или + 6, или —Ъ было бы квадратич-
квадратичным вычетом числа р, а потому они оба были бы квадратичными
вычетами (так как —1 является квадратичным вычетом), что про-
противоречит нашему предположению.
Таким образом, все не делящиеся на р целые числа могут быть
разбиты на три класса, первый из которых содержит биквадратич-
ные вычеты, второй — те биквадратичные невычеты, которые одно-
одновременно являются квадратичными вычетами, и третий — квадра-
квадратичные невычеты. Очевидно, что достаточно произвести такое
разбиение на классы только для чисел 1, 2, 3,..., р — 1, из ко-
которых половина будет принадлежать третьему классу, а другая
половина распределится по первому и второму классам.
Лучше, однако, определить четыре класса, природа которых
состоит в следующем.
Пусть А — совокупность всех лежащих между 1 и р — 1 (вклю-
(включительно) биквадратичных вычетов, и е — произвольный квадратичный
658 Теория биквадратичных вычетов. I
невычет числа р. Пусть, далее, В—: совокупность всех наимень-
наименьших положительных вычетов по модулю /?,. получающихся из
произведений еАч а С и D — соответственно совокупности наимень-
наименьших положительных вычетов по модулю /?, получающихся из про-
произведений е2А, е3А. Тогда легко видеть, что отдельные числа из В
различны между собой, так же как и отдельные числа из С и
отдельные числа из D, и что среди всех этих чисел не может
встретиться нуль. Далее, ясно, что все числа, содержащиеся в А
и С, являются квадратичными вычетами числа р, а все числа,
содержащиеся в В и D — квадратичными невычетами, так что со-
совокупности А я С заведомо не могут иметь общих чисел с сово-
совокупностями В и D. Но также не могут иметь общих чисел ни А с С,
ни В с В.
I. Действительно, если мы предположим, что какое-нибудь число
из А, например, число а, встречается также и в С; далее, что оно
получается из сравнимого с ним произведения е2а', где а' — неко-
некоторое число из совокупности А\ наконец, что а = а4, а' = а'4, и
целое число в таково, что 9а'= 1, то е2а'4 = а4, и потому, умно-
умножив это сравнение на в4, мы получим
т. е. е2 будет биквадратичным вычетом, и следовательно, е — квад-
квадратичным вычетом, что противоречит предположению.
II. Точно так же, если мы предположим, что у совокупно-
совокупностей В9 D есть какое-нибудь общее число, которое получается из
некоторых произведений еа, е3а\ где а и а' являются числами из
совокупности А, то из сравнения еа=е3а' будет следовать а = е2а',
т. е. найдется число, которое, будучи сравнимо с произведением
е2а\ принадлежит совокупности С, и одновременно принадлежит
совокупности А, что, как мы только что доказали, невозможно.
Далее, легко доказать, что все лежащие между 1 и р — 1 вклю-
включительно квадратичные вычеты числа р обязательно должны встре-
встречаться или в А, или в С, а все лежащие в этих же границах
квадратичные невычеты числа р — или в Б, или в D. Действительног
I) каждый квадратичный вычет, являющийся одновременна
биквадратичным вычетом числа р, по предположению находится в А;
Теория биквадратичных вычетов. I 659
II) квадратичный вычет h (меньший чем р), который одновре-
одновременно является биквадратичным невычетом, положим =g2, где g
будет квадратичным невычетом. Если мы подберем такое целое
число у, что e^^E=gi то ^ будет квадратичным вычетом числа р,
который мы положим =&2. Тогда
Но так как наименьший вычет числа А:4 входит в А, то число /г,
которое получается из произведения этого числа на е2, обязательно
должно содержаться в С;
III) если h обозначает лежащий между границами 1 и р — 1
квадратичный невычет числа р, и между теми же границами взято
такое целое число g, что eg = h, то g будет квадратичным вычетом
и потому будет содержаться или в А, или в С. В первом случае /г,
очевидно, находится среди чисел совокупности В, а во втором —
среди чисел совокупности D.
Из всего этого следует, что все числа 1, 2, 3,...,/?—1 так
разбиваются на четыре совокупности А, В, С, D, что каждое из
этих чисел встречается в одной и только одной из этих совокупно-
совокупностей, и каждая совокупность содержит (р—1)/4 чисел. При этой
классификации классы А ж С определяются однозначно, в то время
как классы В и D могут изменяться, поскольку они зависят от
выбора числа е, которое само всегда причисляется к классу В;
если же вместо е взять какое-нибудь другое число из класса D,
то классы В и D поменяются местами.
6
Так как — 1 является квадратичным вычетом числа р, то можно
положить —1 =/2 (mod/?), так что четырьмя корнями сравнения
#4 = 1 будут 1, /, —1, —/. Если поэтому а является биквадра-
биквадратичным вычетом числа /?, например, а = а4, то четырьмя корнями
сравнения х* = а будут а, /а, —а, —/а, и легко видеть, что они
между собой несравнимы. Отсюда вытекает, что если собрать наи-
наименьшие положительные вычеты биквадратов 1,16, 81, 256, ..., (р—IL,
то среди них каждый будет повторяться по четыре раза, так что
660 Теория биквадратичных вычетов. I
имеете^ (р —1)/4 раздичных биквадратичных вычетов, которые
образуют совокуднрсть А. Есди собрать наименьшие вычеты биква-
биквадратов только до (^-у-) , то каждый будет встречаться только
до два раза.
Произведение двух биквадратичных вычетов, очевидно, тоже
будет биквадратичным вычетом, т. е. при перемножении двух чисел
из класса А всегда получается произведение, наименьший положи-
положительный вычет которого принадлежит этому же классу. Точно так
же будут содержаться в А и наименьшие положительные вычеты
произведения числа из В на число из D, или числа из С на число
яз С.
Классу В принадлежат вычеты произведений А -В и C-D, клас-
классу С — вычеты произведений А -С, В -В и D-D, наконец, классу
D — вычеты произведений A-D и В-С.
Доказательства настолько ясны, что достаточно провести одно
дз них. Пусть, например, с и d — числа из С и Z), и пустьс = е2а,
d^^a', где а, а' обозначают числа из А. Тогда е^аа' будет биква-
дратичным вычетом, т. е. наименьший вычет этого числа принадле-
принадлежит классу А; а так как для произведения cd имеет место cd^e^aa',
его наименьший вычет будет, следовательно, содержаться в В.
Одновременно легко можно узнавать, какому классу принадле-
принадлежит произведение любого числа сомножителей. Именно, если придать
классам А, В, С, D соответственно характер 0, 1, 2, 3, то характер
произведения будет равен или сумме характеров отдельных сомно-
сомножителей, или наименьшему вычету этой суммы по модулю 4.
Не стоит тратить труда на то, чтобы доказать эти элементарные
теоремы без помощи теории степенных вычетов, так как при ее
домощи все может быть доказано намцого легче.
Пусть g — первообразный корень по модулю /?, т. е. число с тем
сврйством, что в ряду степеней g, g2, g3f... ни одна ранее степени
Теория биквадратичных вычетов. I 661
gv^i не сравнима с единицей по модулю р. Тогда наименьшие по-
положительные вычеты чисел 1, g, g2, g3,..., gv~~2 с точностью д«*
порядка расположения будут совпадать с числами 1, 2, 3,...,/?— 1
и будут разбиваться на четыре класса следующим образом. Будут
принадлежать
к классу
A
В
С
D
наименьшие вычеты чисел
I „4 „8 р.12
о
9 «13
1 о »• * * >
*
> 5 > 6
> • * •»
11
8
crlS
6 >•
Отсюда немедленно получаются все предыдущие теоремы.
Точно так же, как здесь, мы разбивали на четыре класса*
обозначенные нами через А, В, С, D, числа 1, 2, 3,...,/?—lf
можно и любое не делящееся на р целое число причислять к одному
из этих классов, в зависимости от того, каков его наименьший
вычет по модулю р.
Если мы обозначим через / наименьший вычет степени gr(p~1)/4
по модулю р, но так как /2 = g^~D/2= — 1 {«Арифметические иссле-
дования», п. 62), буквам / будет иметь здесь то же самое значение,
что и в п. 6. Степень gMp—i)/*f где X обозначает целое положитель-
положительное число, будет, таким образом, сравнима по модулю р с одним
из чисел 1, /, —1, —/, в зависимости от того, имеет ли X соот-
соответственно вид 4m, Am + 1, 4m + 2, Am + 3, или, в зависимости
от того, принадлежит ли наименьший вычет числа gx соответственно
классу А, В, С, D. Отсюда мы получаем очень простой критерий
для того, чтобы узнавать, к какому классу следует причислить
заданное не делящееся на р число /г; именно h будет принадле-
принадлежать к А, Ву С или D в зависимости от того, сравнима ли степень
(D/ п() модуЛЮ р с ЧИсл0М 1, /, — 1 ИЛИ — /.
662
Теория биквадратичных вычетов. I
В качестве следствия отсюда вытекает, что —1 всегда принад-
принадлежит классу А, если р имеет вид 872+1, гг, напротив, принадле-
принадлежит классу Су если р имеет вид 8п + 3. Независящее от теории
степенных вычетов доказательство этой теоремы легко можно про-
провести при помощи рассуждений из п. 115, III «Арифметических
исследований».
10
Так как все первообразные корни по модулю р получаются из
вычетов степеней gx, когда X принимает все значения, взаимно про-
простые с р — 1, то легко видеть, что первообразные корни будут
распределяться по совокупностям В и D равномерно, если основа-
основание g все время содержится в В. Если вместо числа g взять другой
первообразный корень из совокупности В, то классификация оста-
останется прежней; если же взять за основание первообразный корень
из совокупности D, то классы В и D поменяются местами.
Если разбиение на классы произведено в соответствии с указан-
указанным в предыдущем пункте критерием, то различие между класса-
ми В и D будет зависеть от того, какой из корней сравнения
х2 = — 1 (mod p) мы выбрали в качестве характеристического числа /.
11
Для того, чтобы легче иметь возможность пояснять примерами
те более тонкие исследования, к которым мы теперь переходим, мы
приведем здесь разбиение чисел на классы для всех модулей до 100.
Для каждого отдельного модуля мы выбрали наименьший перво-
первообразный корень.
p-
8-
A
В
С
D
= 5
=2,/ =
1
2
4
3
2 «
A
В
С
D
P =
и —
1,
2,
4,
7,
13
2, j
со"
5,
10,
8,
f = &
9
6
12
11
f
g
A
В
С
D
1,
3,
2,
6,
17
3,
4(
5,
oo"
7,
/ = 13
13, 16
12, 14
9, 15
10, 11
Теория биквадратичных вычетов. I
663
С
D
1, 7, 16, 20, 23, 24, 25
2, 3, 11, 14, 17, 19, 21
4, 5, 6, 9, 13, 22, 28
8, 10, 12, 15, 18, 26, 27
В
С
D
В
С
D
? = 2, / = 31
1, 7, 9, 10, 12, 16, 26, 33, 34
2, 14, 15, 18, 20, 24, 29, 31, 32
3, 4, 11, 21, 25, 27, 28, 30, 36
5, 6, 8, 13, 17, 19, 22, 23, 35
/? = 41
g = 6, / = 32
1, 4, 10, 16, 18, 23, 25, 31, 37, 40
6, 14, 15, 17, 19, 22, 24, 26, 27, 35
2, 5, 8, 9, 20, 21, 32, 33, 36, 39
3, 7, 11, 12, 13, 28, 29, 30, 34, 38
В
С
D
8 = 2, / = 30
1, 10, 13, 15, 16, 24, 28, 36, 42, 44, 46, 47, 49
2, 3, 19, 20, 26, 30, 31, 32, 35, 39, 41, 45, 48
4, 6, 7, 9, 11, 17, 25, 29, 37, 38, 40, 43, 52
5, 8, 12, 14, 18, 21, 22, 23, 27, 33, 34, 50, 51
g = 2, /=11
А 1, 9, 12, 13, 15, 16, 20, 22, 25, 34, 42, 47, 56, 57, 58
В 2, 7, 18, 23, 24, 26, 30, 32, 33, 40, 44, 50, 51, 53, 55
С 3, 4, 5, 14, 19, 27, 36, 39, 41, 45, 46, 48, 49, 52, 60
D 6, 8, 10, 11, 17, 21, 28, 29, 31, 35, 37, 38, 43, 54, 59
664 Теория биквадратичных вычетов. I
8 = 5, / = 27
1, 2, 4, 8, 9, 16, 18, 32, 36, 37, 41, 55, 57, 64, 65, 69, 71, 72
5, 7, 10, 14, 17, 20, 28, 33, 34, 39, 40, 45, 53, 56, 59, 63, 66, 68
3, 6, 12, 19, 23, 24, 25, 27, 35, 38, 46, 48, 49, 50, 54, 61, 67, 70
И, 13, 15, 21, 22, 26, 29, 30, 31, 42, 43, 44, 47, 51, 52, 58, 60, 62
= 34
1, 2, 4, 8, И, 16, 22, 25, 32, 39, 44, 45, 50, 57, 64, 67,
73, 78, 81, 85, 87, 88
3, 6, 7, 12, 14, 23, 24, 28, 33, 41, 43, 46, 48, 56, 61, 65,
66, 75, 77, 82, 83, 86
5, 9, 10, 17, 18, 20, 21, 34, 36, 40, 42, 47, 49, 53, 55, 68,
69, 71, 72, 79, 80, 84
13, 15, 19, 26, 27, 29, 30, 31, 35, 37, 38, 51, 52, 54, 58, 59,
60, 62, 63, 70, 74, 76
g = 5, / = 22
1, 4, 6, 9, 16, 22, 24, 33, 35, 36, 43, 47, 50, 54, 61, 62, 64,
73, 75, 81, 88, 91, 93, 96
5, 13, 14, 17, 19, 20, 21, 23, 29, 30, 41, 45, 52, 56, 67, 68, 74,
76, 77, 78, 80, 83, 84, 92
2, 3, 8, И, 12, 18, 25, 27, 31, 32, 44, 48, 49, 53, 65, 66, 70,
72, 79, 85, 86, 89, 94, 95
7, 10, 15, 26, 28, 34, 37, 38, 39, 40, 42, 46, 51, 55, 57, 58, 59,
60, 63, 69, 71, 82, 87, 90
Теория биквадратичных вычетов. I 665
12
Так как число 2 является квадратичным вычетом всех простых
чисел вида 8п + 1 и квадратичным невычетом всех простых чисел
вида 8п + 5, то для простых модулей первого вида число 2 будет
содержаться в классе А или С, а для простых модулей второго ви-
вида — в классе В или D. Так как разница между классами В и D не-
несущественна, ибо она зависит только от выбора числа /, мы оставим
пока модули вида 8п + 5 в стороне. Если же подвергнуть модули ви-
вида 8п + 1 индуктивному исследованию, то мы найдем, что 2 принад-
принадлежит классу А для р = 73, 89, ИЗ, 233, 257, 281, 337, 353,..., и,
напротив, принадлежит классу С для р = 17, 41, 97, 137, 193, 241,
313, 401, 409, 433, 449, 457,...
Далее, так как для простого модуля вида 8п + 1 число — 1
является биквадратичным вычетом, то очевидно, что — 2 всегда
будет принадлежать тому же классу, что и + 2.
13
Если сравнивать между собой примеры п. 12, то, но крайней
мере на первый взгляд, кажется, что нельзя указать простой кри-
критерий для того, чтобы различать между собой модули первого вида
и модули второго вида. Тем не менее имеется два таких критерия,
замечательных по изяществу и простоте, к одному из которых при-
приводят следующие рассмотрения.
Модуль р, как простое число вида 8/z + 1» может быть представ-
представлен, и притом единственным образом, в виде а2 + 2Ь2 («Арифмети-
(«Арифметические исследования», п. 182, II); при этом мы предполагаем, что зна-
значения а, Ъ берутся положительными. Очевидно, что а будет нечетным,
а Ъ четным; мы положим Ъ = 2Лс, где с уже нечетно.
I. Заметим теперь, что если р = a2 (mod с), то р является квад-
квадратичным вычетом числа с, а потому и отдельных простых сомножи-
сомножителей, на которые с распадается; в силу же фундаментальной теоремы
эти отдельные простые сомножители, в свою очередь, будут квадра-
квадратичными вычетами числа р, а потому будет квадратичным вычетом
числа р и их произведение с, а, следовательно, как б2, так и — Ь2
будут биквадратичными вычетами.
666 Теория биквадратичных вычетов. I
И. Поэтому число — 2Ь2 должно принадлежать тому же классу,
что и число 2; так как а2 = — 262, то очевидно, что 2 будет содер-
содержаться в классе А или в классе С в зависимости от того, является ли
а квадратичным вычетом или квадратичным невычетом по модулю р.
III. Предположим теперь, что а разложено на свои простые
сомножители, причем те из них, которые имеют вид 8т + 1 или
8т + 7, мы обозначим через а, а', а", . . . , а те, которые имеют вид
8т + 3 или 8т + 5,—через C, р', Р", .. . ; количество последних
пусть равно {л. Так как /? = 262 (mod а), то р будет квадратичным
вычетом тех простых сомножителей числа а,квадратичным вычетом ко-
которых является число 2, т. е. сомножителей а, а', а",. . . , и, напротив,
квадратичным невычетом тех сомножителей, квадратичным невычетом
которых является число 2, т. е. сомножителей р, р', р", . . . Поэтому,
в силу фундаментальной теоремы, отдельные сомножители а, а',
а", ... в свою очередь будут квадратичными вычетами числа р, а
отдельные сомножители р, р', Р",...— его квадратичными невычетами.
Итак, мы заключаем отсюда, что произведение а является квад-
квадратичным вычетом или невычетом числа р в зависимости от того,
четно [л или нечетно.
IV. Но легко убедиться, что произведение всех а, а', а", . .. бу-
будет всегда иметь вид 8т + 1 или 8т + 7, и что так же обстоит де-
дело для произведения всех р, р', Р", . . ., если количество их четно, так
что в этом случае и произведение а обязательно должно иметь вид
8т + 1 или 8т + 7, и что, напротив, произведение всех р, р',Р", . .. ,
когда количество их нечетно, будет иметь вид 8т + 3 или 8т + 5,
а потому в этом случае также обстоит дело и для произведения а.
Из всего этого получается, таким образом, следующая изящная
теорема.
Если число а имеет вид 8т -\- 1 или 8т -f- 7, то число 2 содер-
содержатся в совокупности А] если же а имеет вид 8т -}- 3 или 8т + 5,
то число 2 находится в совокупности С.
Это подтверждается на примерах, приведенных в п. 11. Именно,
модули первого типа разлагаются следующим образом:
73 = 1 + 2-36, 89 - 81 +2-4, 113 - 81 + 2-16, 233 = 225 + 2-4.
257=225+2-16, 281-81+2-100, 337 = 49 + 2-144, 353-225 + 2-64,
Теория биквадратичных вычетов. I
667
а модули второго типа — следующим образом:
17 = 9 + 2-4, 41 = 9 + 2-16, 97 = 25 + 2-36,
137 = 9 + 2-64, 193 = 121 + 2-36, 241 = 169 + 2-36,
313 = 25 + 2-144, 401=9 + 2-196, 409 = 121+2-144,
433 = 361+2-36, 449=441 + 2-4, 457 = 169 + 2.144.
14
Так как разложение числа р на простой и удвоенный квадраты
имеет такую замечательную связь с вопросом о принадлежности чис-
числа 2 к тому или иному классу, то стоит потрудиться над тем, чтобы
исследовать, не обещает ли подобного результата также и разло-
разложение на сумму двух квадратов, которое, как известно, тоже возмож-
возможно для числа р. Мы приведем поэтому здесь разложения чисел р,
для которых 2 принадлежит классам А и С.
9
25
49
169
1
25
81
289
A
+ 64
+ 64
+ 64
+ 64
+ 256
+ 256
+ 256
+ 64
1
25
81
121
49
225
169
1
9
289
49
441
С
+ 16
+ 16
+ 16
+ 16
+ 144
+ 16
+ 144
+ 400
+ 400
+ 144
+ 400
+ 16
Прежде всего заметим, что из двух квадратов, на которые раз-
разлагается р, один, который мы обозначим через а2, должен быть
668 Теория биквадратичных вычетов. I
нечетным, а другой, который мы будем обозначать через Ь2, — чет-
четным. Так как а2 имеет вид 8п + 1, то очевидно, что значения Ь,
делящиеся на 2, но не делящиеся на 4, будут соответствовать значе-
значениям р вида 8п -f- 5, которые из нашего рассмотрения пока что-
исключены, так как для них число 2 содержится в классе В или D.
А для значений числа р, имеющих вид 872+1, число Ъ должно делить-
ся на 4, и если верить нашему индуктивному заключению, к которо-
которому приводит данная нами схема, то число 2 будет принадлежать
классу А для всех модулей, для которых Ъ имеет вид 8/г, и классу С для
всех модулей, для которых Ъ имеет вид 8/г + 4. Однако эта теорема
требует гораздо более глубокого исследования, чем те, которые мы про-
производили в предыдущей главе, и доказательству ее должны быть
предпосланы многие подготовительные рассмотрения, касающиеся
порядка, в котором следуют одно за другим числа совокупностей
А, В, С, D.
15
Обозначим количество чисел из совокупности А, за которыми
непосредственно следует число из совокупности А, В, С, D, соответ-
соответственно через @0), @1), @2), @3). Точно так же количество чисел иа
совокупности В, за которыми непосредственно следует число иа
совокупности А, В, С, D, обозначим соответственно через A0), A1),
A2), A3); аналогично, пусть й совокупности С имеется B0), B1),
B2), B3) чисел, а в сойокупности D имеется C0), C1), C2), C3)
чисел, непосредственно за которыми следует число соответственно
из совокупности А, В ,С ,D. Мы ставим себе задачу определить a priori
эти шестнадцать количеств. Для того чтобы читателю было удоб-
удобнее проверять на примерах общие выводы, мы считаем целесообраз-
целесообразным привести здесь численные значения членов схемы
@0), @1), @2), @3)
(S) (Ю), (И), A2), A3)
B0), B1), B2), B3)
C0), C1), C2), C3)
для отдельных модулей, для которых выше, в п. 11, мы указали: рас-
распределение чисел по Классам.
Теория биквадратичных вычетов. I
669
О, 1, О, О
О, О, О, 1
о, о, о, о
О, О, 1, О
/7 = 37
2, 1, 2, 4
2, 2, 4, 1
2, 2, 2, 2
2, 4, 1, 2
/> = 73
5, 6, 4, 2
6, 2, 5, 5
4, 5, 4, 5
2, 5, 5, 6
0, 1, 2, О
1, 1, О, 1
0, 1. О, 1
1, О, 1, 1
/> = 41
О, 4, 3, 2
4, 2, 2, 2
3, 2, 3, 2
2, 2, 2, 4
/) = 89
3, 8, 6, 4
8, 4, 5, 5
6, 5, 6, 5
4, 5, 5, 8
0, 2, 1, О
2, О, 1, 1
1, 1, 1, 1
О, 1, 1, 2
/> = 53
2, 3, 6, 2
4, 4, 2, 3
2, 4, 2, 4
4, 2, 3, 4
/> = 97
2, 6, 7, 8
6, 8, 5, 5
7, 5, 7, 5
8, 5, 5, 6
2, 3, О, 2
1, 1, 2, 3
2, 1, 2, 1
1, 2, 3, 1
JD = 61
4, 3, 2, 6
3, 3, 6, 3
4, 3, 4, 3
3, 6, 3, 3
Так как модули вида 8п + 1 и вида 8п + 5 ведут себя по раз-
разному, мы должны рассматривать их отдельно; мы начнем с первых.
16
Число @0) показывает, сколькими различными способами мо-
может быть удовлетворено уравнение ос + 1 = ос', где а, а' обозначают
произвольные числа из совокупности А. Так как для модуля
вида 8п + 1, каковым мы его здесь предполагаем, числа а' и р — а'
принадлежат однор и той же совокупности, то мы будем говорить
короче, что @0) выражает количество различных способов, кото-
которыми можно удовлетворить уравнению 1 + а + а' = р. Очевидно,
что вместо этого уравнения может фигурировать также сравнение
Точно так же
@1) указывает количество решений сравнения 1 + a + Р = 0 (mod p)
@2) » » » » i + a + Y=o
@3) » » » » l+a+8sO
(И) » » » » 1 + р + р'== О
и т. д.,
670 Теория биквадратичных вычетов. I
где через р и р' обозначены произвольные числа из совокупности Бг
через y — числа из совокупности С, через 8— числа из сово-
совокупности D. Отсюда тотчас же получаются следующие шесть
равенств:
@1)= A0), @2) = B0), @3)=C0), A2)=B1), A3)=C1), B3)=C2).
Из каждого решения сравнения 1 + а + р = 0 получается реше-
решение сравнения 1 + 8 + 8' == 0, если взять за 8 то число между гра-
границами 1 и р—1, для которого р8 = 1 (оно, очевидно, будет из
совокупности D), а за 8' — наименьший положительный вычет про-
произведения а8 (который тоже будет из совокупности D)\ точно так
же мы, очевидно, от заданного решения сравнения 1 + 8 + 8' == 0
возвращаемся к решению сравнения 1 + a + р == 0, если выберем р
так, что р8==1, и одновременно положим a===pS'. Отсюда мы за-
заключаем, что оба сравнения имеют одинаковое число решений,
т. е. что @1) = C3).
Аналогичным образом из сравнения 1 + a + ^ == 0 мы получаем
сравнение у' + у" + 1 ^ 0, если выберем у' из совокупно ти С так,
что yt'^1» а за Т" возьмем число из этой же совокупности, срав-
сравнимое с произведением осу'. Из этого мы легко заключаем, что оба
эти сравнения имеют одинаковое число решений, т. е. что
@2) = B2).
Точно так же из сравнения 1 + a + 8 = 0 мы выводим сравнение
Р + р' + 1 = 0, выбирая р, р' так, что р8 == 1 и pa == р', и потому
@3) = A1).
Наконец, из сравнения 1 + р + т ^ 0 мы аналогичным образом
выводим как сравнение 8 + 1 + р' ^ 0, так и сравнение т' + 8' +
+ 1 = 0, и заключаем отсюда, что A2) = A3) = B3).
Мы имеем, следовательно, одиннадцать уравнений, связывающих
наши шестнадцать неизвестных величин, так что они могут быть
сведены к пяти, и схема (S) представляется следующим образом:
к
i,
к,
1.
i,
1,
т,
т.
к,
т,
к,
т.
1
т
т
i.
Теория биквадратичных вычетов. I 671
Но легко можно присоединить еще три новых уравнения. Имен-
Именно, так как за каждым числом из совокупности -4, за исключе-
исключением последнего числа р—1, должно следовать число из какой-
нибудь из совокупностей А, В, С или jD, to мы имеем
@0) + @1) + @2) + @3) = 2п — 1,
и точно так же
B0) + B1) + B2) + B3) = 2щ
C0) + C1) + C2) + C3) = 2п.
Во введенных обозначениях первые три равенства дают
к + m = п.
Четвертое уравнение будет совпадать со вторым. При помощи этих
уравнений можно исключить три неизвестных, благодаря чему
шестнадцать неизвестных уже сводятся к двум.
17
Для того, чтобы достигнуть полного решения, мы хотим сейчас
найти число решений сравнения
где а, р, ^ обозначают произвольные числа из совокупностей Аг
В, С. Очевидно, что значение а = р—1 невозможно, так как не
может быть C-|-Т = 0; если же вместо а подставлять по порядку
остальные значения, то /г, г, к, I будут принадлежащими соответ-
соответственно к А, В, С, D значениями выражения 1+а- Но для каж-
каждого данного принадлежащего совокупности А значения выражения
672 Теория биквадратичных вычетов. I
1 + а, например, для 1 + а ~ а°, сравнение aQ + Р + Т s 0 обла-
обладает столькими же решениями, что и сравнение 1 -f Р' + т' ^ О
(именно, если положить р5==а°р', *у ^ а°т')> т- ?• A2) ~ m решения-
решениями. Точно так же для каждого данного значения выражения <х+ 1,
принадлежащего совокупности 5, например, для 1 + а = р°, срав-
сравнение р° -)- р -)- y ^ 0 имеет столько же решений, что и сравнение
1 + а' + Р' = 0 (именно, если положить р == р°ос', ^ == Р°Р')> т- е-
@1) = i решений. Аналогично, для каждого данного принадлежа-
принадлежащего совокупности С значения выражения 1 + а, например, для
1 ~\- а = y°, сравнение т° + р + т ^= 0 разрешимо столькими же раз-
различными способами, что и сравнение 1 + Ь -f- a' ^ 0 (именно, если
положить р==т°($> ^Е=Т°а')> т. е. число решений будет равно
@3) = I. Наконец, для каждого данного значения выражения 1 + а,
принадлежащего совокупности D, например, для 1 + a = 8°, срав-
сравнение S° -f- p -f- ^ ^ 0 обладает столькими же решениями, что и
сравнение 1 -f- 4' + 8' == 0 (именно, если положить р ^ 8°^',
Y = Ь°^)у т. е. B3) = т решениями. Таким образом, если мы собе-
соберем все эти решения, то получим, что сравнение 1-[-а + р + Т==0
имеет
hm + z2 + kl + lm
различных решений.
Но совершенно аналогичным образом выводится, что если за р
брать по порядку отдельные числа из совокупности В, то сумма
1 + Р будет принимать A0) = i, (И) = I, A2) = т, A3) = т значе-
значений, принадлежащих соответственно совокупностям Ау В, С, D, и
что для каждого данного значения выражения 1 + р сравнение
1+Р + а + т==0 будет иметь @2) = А, C1) = т, B0) = А, A3) = т
решений, в зависимости от того, в какой из совокупностей А, В,
С, D находится 1 + Р; таким образом, число всех решений будет
равно
ik + lm + km + т2.
К этому же значению мы придем, если будем основывать под-
подсчет на рассмотрении значений суммы 1 + т-
Теория биквадратичных вычетов. I 673
18
Из этих двух выражений для одного и того же числа мы по-
получаем уравнение
О = km -f- i2 + Ы — ih — km — т2,
откуда, исключая h при помощи уравнения h = 2т — к — 1, находим
О = (к — mf + г2 + kl — ik — к2 — т.
Но два последних уравнения из п. 16 дают к = -тг (I -\-i), и если
1
подставить это значение, то г2 + М — ik — к2 перейдет в -г{1—IJ,
а потому предыдущее уравнение, после умножения его на 4, перей-
перейдет в следующее:
О = 4 (к — mf + (I — if — 4w.
Так как Ат=2(к + т)—2(к — т) = 2п — 2(к — т), отсюда
следует, что
2п = 4 (к — mf + 2 (к — т) + (I — if,
или
8/г + 1 = [4 {к — т) + I]2 + 4 (I — if.
Если поэтому положить
4 (к — т) + 1 = а, 2l~ 2i = b,
то мы получаем
р = а2 + Ь2.
Но, как известно, р может быть разложено на два квадрата только
одним единственным способом, причем из этих квадратов нечетный
должен быть взят за а2, а четный — за Ъ2, так что а2 и Ъ2 явля-
являются вполне определенными числами. Но и само а будет вполне
определенным числом; действительно, основание квадрата должно
быть взято положительным или отрицательным в зависимости от того,
имеет ли положительное основание вид AM -f-1 или 4М + 3.
Об определении знака числа Ъ мы будем сейчас говорить.
Если скомбинировать теперь эти новые уравнения с последними
тремя уравнениями из п. 16, то пять чисел /г, г, к, I, m будут
674
Теория биквадратичных вычетов. I
однозначно определяться через а, 6, п следующим образом:
8й = 4/2 — За— 5,
8i = in + a — 26 — I,
8m =4/2 — а + 1.
Если вместо /2 желательно ввести модуль р, то схема (S), после
умножения отдельных ее членов на 16, чтобы избавить их от дро-
дробей, будет выглядеть следующим образом:
p —
p —
p +
p +
6a
2a
2a
2a
— 11
— 46 —
— 3
+ 46 —
3
3
p
P
P
+ 2<z
+ 2a
— 2a
— 2a
—
+
+
+
46
46
1
1
— 3
— 3
P +
P —
P +
P —
2a
2a
2a
2a
—
+
—
i
~r
3
1
3
1
P +
P —
P —
P +
2a
2a
2a
2a
+ 46
+ 1
+ 1
— 46
— 3
—3.
19
Остается только еще показать, как может быть определен знак
числа Ъ. Выше, в п. 10, мы уже отмечали, что различие между
совокупностями В и D само по себе несущественно, а зависит от
выбора числа /, за которое нужно брать один из корней сравне-
сравнения х2 = — 1, и что эти совокупности меняются местами, если
вместо одного корня взять другой. Но так как вид приведенной
выше схемы показывает, что подобная перестановка совокупностей
равносильна изменению знака у 6, то можно предвидеть, что
должна существовать связь между знаком числа 6 и числом /.
Чтобы выяснить ее, заметим прежде всего, что если обозначить
через [к целое неотрицательное число и заставить z пробегать все
числа 1, 2, 3, . .. , р—1, то по модулю р будет либо 2zfZ = 0,
если [л не делится на р —-1, либо 2j 2^ = — 1, если [л делится на р—1»
Вторая часть теоремы вытекает из того, что для каждого деляще-
делящегося на р—1 значения [л имеет место z^eeeI; первую же часть мы
докажем следующим образом. Если g обозначает первообразный
корень, то совокупность всех значений z будет совпадать с сово-
совокупностью наименьших вычетов всевозможных чисел gv>9 когда у
Теория биквадратичных вычетов. I 675
принимает все значения О, 1, 2, 3, .. . , р— 2, и потому
2z* = 2«w'. Но
и потому
(в*—!) 22fx = g^*3-0—1 = 0.
А так как для не делящегося на р — 1 значения (х число g^ не
сравнимо с 1, т. е. g*— 1 не делится на р, то отсюда следует,
что ^j
Если теперь разложить степень (z4 + 1)(р~)/4 по формуле бино-
бинома, то, в силу предпосланной леммы будет выполняться сравнение
2 (z4 + 1)(р-1)/4 = _ 2 (mod p).
Но наименьшие вычеты всевозможных z4 представляют все числа
совокупности А, причем каждое из них встречается по четыре
раза; поэтому среди наименьших вычетов чисел z4 + 1 мы имеем
4@0) принадлежащих совокупности А,
4@1) » » В,
4@2) » » С,
4@3) » » Z),
и четыре будут равны 0 (именно, для z4 == /? — 1). Отсюда, прини-
принимая во внимание критерии совокупностей Ау В, С, Z), мы выводим
сравнение
2 (z4 + 1)(р~1)/4 = 4 @0) + 4/ @1) — 4 @2) — 4/ @3),
откуда
— 2 = 4 @0) + 4/ @1) — 4 @2) — 4/ @3),
или, подставляя вместо @0), @1), ... их значения, найденные
в предыдущем пункте, имеем
— 2еее— 2а — 2 — 26/.
676
Теория биквадратичных вычетов. I
Отсюда заключаем, что всегда а + й/ = 0, или, умножая на /, что
и это сравнение служит для определения знака числа 6, когда /
уже выбрано, или, если знак числа Ъ уже предписан, то для
определения числа /.
20
После того как для модулей вида 8/2 + 1 мы полностью решили
нашу задачу, мы переходим к случаю, когда р имеет вид 8п + 5;
теперь мы можем быть в изложении более краткими, так как все
выводы лишь слегка отличаются от предыдущих.
Так как для модуля вида 872 + 5 число — 1 принадлежит
классу С, то дополнения чисел из совокупностей А, В, С, D до
Р будут содержаться соответственно в совокупностях С, D, А, В
Отсюда легко получить, что
знак:
@0)
@1)
@2)
@3)
A0)
(И)
A2)
A3)
B0)
B1)
B2)
B3)
C0)
C1)
C2)
C3)
обозначает количество решений сравнения:
1+а + т =0
1 + а + 8 =0
1 + а + а' еее 0
1+а + р =0
1 + Р + Т =0
l-fp + 8 =0
1 + р + а =0
1 + р + р'=0
1 + Т + Т' = 0
1+т + 8 =0
1+т + а =о
1 + Т + Р =0
1+8 + Т =0
1 + 8 + 8' = 0
1 + 8 + а =0
1 + 8 + р =0,
Теория биквадратичных вычетов. I 677
откуда тотчас же получаются шесть уравнений
@0) = B2), @1) = C2), @3) = A2), A0) =B3), (И) = C3), B1)=C0).
Если сравнение 1+а + т = 0 умножить на число ?' из сово-
совокупности С, которое выбрано так, что тт' —1» и за ?" взять наи-
наименьший вычет произведения осу', который, очевидно, тоже принад-
принадлежит совокупности С, то получается сравнение f' + Т" + 1 = 0»
из чего мы заключаем, что @0) = B0).
Совершенно аналогичным образом мы получаем уравнения
@1) = A3), @3) = C1), A0) = A1) = B1).
При помощи этих одиннадцати уравнений мы можем наши
шестнадцать неизвестных свести к пяти и схему (S) представить
в виде
h,
т,
h,
т.
г,
т,
т,
1.
к,
1,
К
г.
1
i
т
т.
Далее мы получаем уравнения
B0) + B1) + B2) + B3) = 2Л|
C0) + C1) + C2) + C3) = 2и + 1,
или, если использовать введенные выше обозначения,— следующие
три уравнения:
( h + i + k + l = 2n + l9
(I) \2m + i + l =271 + 1,
( h-\- m = п,
при помощи которых число наших неизвестных уя?е может быть
сведено к двум.
Остальные уравнения мы выводим из рассмотрения числа реше-
решений сравнения 1+а+р + т = 0 (причем и здесь мы обозначаем
678 Теория биквадратичных вычетов. I
через ос, C, ^ произвольные числа соответственно из совокупностей
А, В, С). Именно, принимая сначала во внимание, что 1 + а дает
/г, i, к, I чисел соответственно из совокупностей А, В, С, Z), и что
для каждЬго данного значения а в этих четырех случаях получает-
получается соответственно т, Z, г, т решений, мы находим, что количество
всех решений равно
hm + И -)- ik -\- 1т.
Во-вторых, так как 1 + Р представляет m, m, Z, i чисел, при-
принадлежащих соответственно совокупностям А9 В, С, Df и для
каждого данного значения числа р в этих четырех случаях сущест-
существует соответственно hf m, h, m решений, то число всех решений
равно
hm -\- т2 + hi -\- im^
откуда мы получаем уравнение
О = т2 + hi + im — il — ik — lm9
которое при помощи вытекающего из (I) равенства к = 2т — h
переходит в уравнение
О = т2 + hi -\- hi — И — im — Im.
Но из уравнений (I) мы получаем также I -\- i = 1 + 2/г; поэтому
2i = i +2h + (i — Z),
2Z = 1 + 2Л — (i — I).
Если подставить эти значения в предыдущее уравнение, то полу-
получается
О = 4т2 — Am — 1 — 8hm + 4/г2 + (i — IJ.
Наконец, если мы теперь подставим вместо Am выражение 2(/г + т) —
— 2 (h — m), или, в силу последнего из уравнений (I), выражение
2п — 2 (h — т), то мы получим
0 = 4(/г — тJ — 2n + 2{h — m)— I +(i — If,
и потому
8n + 5=[A(h — m) + I]2 + 4 (г — If.
Теория биквадратичных вычетов. I
679
Поэтому, если положить
4(А_ т)
= а, 21 — 21= 6,
то будет выполняться равенство
р = а2 + б2.
Но так как и в этом случае р может быть только одним един-
единственным способом разложено на два квадрата, один четный и один
нечетный, то а2 и б2 будут вполне определенными числами; действи-
действительно, очевидно, что а2 должно быть положено равным нечетному,
а б2— четному квадрату. Кроме того, знак числа а определяется
тем, что должно быть a=l(mod4), а знак числа 6— тем, что
имеет место 6 == a/(mod/?), что легко доказывается при помощи
рассуждений, совершенно аналогичных проведенным в предыдущем
пункте.
Если считать это доказанным, то пять чисел /г, г, k, I, m сле-
следующим образом определяются числами а, 6, п:
= in — За+ 3,
= Ап — а + 1,
4iли, -если предпочитать выражения через р, то умноженные на 16
члены схемы (S) оказываются следующими:
р + 2а — 7
р — 2а — 3
р f 2а + АЬ + 1
р — 2а — 3
р _ 2а — 3
/? + 2а — 46 + 1
/? — 2а + 1
+ 2а — 46 + 1
р + 2а — 7
+ 2а + ib + 1
+ 2а — 46+
2а + 46 + 1
— 2а — 3
? — 2а — 3
680 Теория биквадратичных вычетов. I
21
После того как мы решили нашу задачу, мы возвраща-
возвращаемся к основному исследованию, причем ставим себе теперь целью
окончательное определение совокупности, к которой принадлежит
число 2.
I. Если р имеет вид 872+1, то как уже установлено, число 2
содержится или в совокупности А, или в совокупности С. В пер-
первом случае легко видеть, что совокупности А принадлежат также
и числа у(/?— 1), -^(р + 1), в то время как во втором случае
они принадлежат совокупности С. Примем теперь во внимание, что
если а и а + 1 являются соседними числами совокупности Ау то
соседними же будут и числа р — ос — 1, р — а, т. е. что те числа
совокупности А, за которыми следует число из этой же совокуп-
совокупности, могут быть сгруппированы на пары ассоциированных одно
с другим (именно, ассоциированы а и р—1—а); тогда мы убе-
убедимся, что количество @0) таких чисел будет всегда четным, если
нет числа, ассоциированного с самим собой, т. е. если у(/?— 1) не
принадлежит совокупности А, в противном же случае указанное
количество нечетно. Отсюда мы заключаем, что @0) нечетно, если
число 2 принадлежит совокупности ^4, и четно, если 2 принадле-
принадлежит совокупности С. Но мы имеем
а2 + &2 —6а —И,
или, если положить а = 4д + 1, Ъ = г (ср. п. 14),
@0) = q* — q + r2—l.
Но так как q2—q, очевидно, всегда четно, то число @0) будет
нечетным или четным в зависимости от того, четно или нечетно
число г, и потому число 2 будет принадлежать совокупности А или
совокупности С в зависимости от того, имеет ли Ъ вид 8т или
вид 8т + 4. Это и представляет собой теорему, котррую мы в п. 14
нашли индуктивным путем.
Теория биквадратичных вычетов. I 681
II. Но и во втором случае, когда р имеет вид 8п + 5, мы
можем так же завершить исследование. Число 2 принадлежит
здесь или к 5, или к D, и легко видеть, что в первом случае
число -сг(Р — ^) пРинаДлежит к 5, а число y^+l) — к Z), а во
1 1
втором случае у (/?— 1)— к ^? а ~(/? + 1) — к ^- Учтем теперь,
что если р является таким числом из 5, за которым следует число
из Z>, то и число р — р — 1 будет содержаться в 5, а число
р — р— в Z), т. е. что всегда вместе со всяким числом, обладаю-
обладающим указанным свойством, этим свойством обладает и число, ассо-
ассоциированное с первым. Поэтому количество таких чисел, т. е. A3),
будет четным, за исключением случая, когда одно из них ассоци-
ировано само с собой, т. е. когда -тг(Р — 1) принадлежит совокуп-
совокупности 5, а у(/?+ 1) — совокупности D\ в этом случае число A3)
будет нечетным. Отсюда мы заключаем, что A3) четно, если число
2 принадлежит совокупности Z>, и, напротив, нечетно, если 2 при-
принадлежит совокупности В. Но мы имеем
16 A3) == а2 + б2 + 2а + АЬ + 1,
или, если положить а = iq -f 1, Ъ = 4г + 2,
Поэтому число A3) будет нечетным, когда число г четно; на-
напротив, A3) будет четным, когда г нечетно. Из этого мы заклю-
заключаем, что число 2 принадлежит совокупности 5, если Ъ имеет вид
8т + 2, и, напротив, принадлежит совокупности D, если Ъ имеет
вид 8/?г+ 6.
Результат этих исследований может быть высказан следующим
образом.
Число 2 принадлежит совокупности А, В, С или D в зависи-
зависимости от того, имеет ли число Ь/2 вид 4т, Am + 1, Am + 2 или
Am + 3
682 Теория биквадратичных вычетов. I
22
В «Арифметических исследованиях» мы изложили общую теорию
деления круга и решения уравнения xv —1=0, и между прочим
доказали, что если [л является делителем числа р—1, то функ-
функция (xv — 1)/(#— 1) при помощи вспомогательного уравнения поряд-
порядка [х может быть разложена на [л сомножителей порядка (р—1)/[*.
Кроме общей теории этого решения, мы в пп. 356—358 указанного
сочинения отдельно рассматривали специальные случаи, когда
[х = 2 или [л = 3 и показали, как в этих случаях строить вспомога-
вспомогательное уравнение a priori, т. е. без развертывания схемы наимень-
наименьших вычетов степеней некоторого первообразного корня по мо-
модулю р. Теперь, хотя мы на это и не указывали, внимательные
читатели могут заметить тесную связь следующего случая указан-
указанной теории, т. е. случая [л = 4, с изложенными здесь в пп. 15—20
исследованиями, при помощи которых этот случай также может
быть без труда разобран полностью. Однако мы оставим это рас-
рассмотрение до другого случая, а в настоящем сочинении предпочтем
проводить исследование в чисто арифметической форме, без какой-
либо связи с теорией уравнения xv —1 = 0. Мы в заключение рас-
рассмотрим еще несколько новых чисто арифметических теорем, кото-
которые находятся в теснейшей связи с предметом, разбиравшимся до
сих пор.
23
Если степень (ж4 -j- 1)(р~д)/2 разложить по формуле бинома, то
в разложении будет содержаться три члена, у которых показатель
степени при х делится на р — 1, именно
где Р обозначает средний коэффициент
А. 1. L
Л Л /л
1 -2 -3
Теория биквадратичных вычетов. I 683
Таким образом, если подставлять вместо х по порядку числа
1, 2, 3, ...,/?— 1, то по теореме п. 19 мы получаем
2(^ + 1)(р~1)/2^ — 2 — Р.
Но если принять во внимание то, что было изложено в п. 19,
и то, что числа из совокупностей А1 В, С, Dy возведенные в сте-
степень с показателем (р—1)/2, сравнимы по модулю р соответствен-
соответственно с числами +1, —1, +1, —1, то легко видеть, что
2 (я4 + 1)(р~1)/2 == 4 @0) — 4 @1) + 4 @2) — 4 @3),
и потому, согласно данным в конце п. 18 и в конце п. 20 схемам,
2(я4 + 1)(р-1)/2ЕЕЕ — 2а — 2.
Сравнение этих двух значений дает следующую очень изящную
теорему.
Имеет место
P~2a(modp).
Если четыре произведения
1.2-3. . . |0>-1)
обозначить соответственно через q7 г, 5, t, то формулировка этой
теоремы примет вид
2а = — (mod/?).
684 Теория биквадратичных вычетов. I
Так как у каждого сомножителя числа q его дополнение до р
входит в t, то q = t(modp), если число сомножителей четно, т. е.
если р имеет вид 872+1, и q~—t, если число сомножителей не-
нечетно, т. е. р имеет вид 8п -{- 5. Точно так же в первом случае
будет выполняться сравнение г == s, а во втором — сравнение
г = — s. В обоих случаях qr = st, а так как, как известно^
qrst = — 1, то q2r2 = — 1, и потому qr == Hh/(mod/?). Если связать
это сравнение с только что найденной теоремой, то получается
r2 = -j-2a/, и потому, согласно пп. 19, 20,
Весьма замечательно, что разложение числа р может быть
найдено совершенно прямыми методами] именно, основанием нечет-
нечетного квадрата будет абсолютно наименьший вычет числа r/2qr
a j основанием четного квадрата — абсолютно наименьший вычет
числа г2/2 по модулю р. Выражение r/2q, значение которого для
р = 5 равно 1, для больших значений р может быть представлено
также следующим образом:
6 • 10 • 14 . 18. . . (р — 3)
2-3-4.5 ... х (/>-!)
Так как мы, кроме того, знаем, с каким знаком следует брать
получающееся из этой формулы основание нечетного квадрата,
а именно, с тем, при котором оно имеет вид 8т+ 1, то особенно
достойно внимания, что для основания четного квадрата подобного*
общего критерия до сих пор не найдено. Если бы кто-нибудь era
нашел и сообщил нам, мы были бы за это очень благодарны. Пока
же я считаю полезным привести здесь значения чисел at b} fr ко-
которые получаются для значений р, не превосходящих 200, из наи-
наименьших вычетов выражений r/2q, г2/2, qr.
__ fr — qr*
* А также {(а + Ь) q}2 = а =^ '
Теория биквадратичных вычетов. I
685
р
5
13
17
29
37
41
53
61
73
89
97
101
109
113
137
149
157
173
181
193
197
а
+ 1
2
+1
+ 5
+ 1
+ 5
у
+ 5
— 3
+ 5
+ 9
+ 1
— 3
. 7
—И
— 7
—И
+ 13
+ 9
7
+1
ъ
+ 2
— 2
4
+ 2
— 6
+ 4
— 2
— 6
— 8
— 8
+ 4
—10
+ 10
+ 8
+ 4
—10
— 6
+ 2
+ 10
412
—14
/
2
5
13
12
31
9
23
11
27
34
22
91
33
15
37
44
129
80
162
81
183
ТЕОРИЯ БИКВАДРАТИЧНЫХ ВЫЧЕТОВ
Сочинение второе
(Commentationes soc. reg. sc. Gotting.
recentiores, Vol. VII, Gottingae, 1832)
24
В первом сочинении было полностью изложено то, что необхо-
необходимо для биквадратичной классификации числа.+2. Именно, если
мы будем считать все числа, не делящиеся на модуль р (который
предполагается простым числом вида in + 1) разбитыми на четыре
класса А, В, С, D, причем каждое число относится к первому, вто-
второму, третьему или четвертому классу, если его степень с показа-
показателем (р — 1)/4 сравнима соответственно с + 1, + /, —1, —/, где
/ обозначает один из двух корней сравнения /2=е— 1 (mod p), то
ответ на вопрос, к какой совокупности принадлежит число + 2,
зависит от разложения числа р на два квадрата, а именно, если
положить/? = а2 + Ь2, где а2 обозначает нечетный, а Ъ2 — четный
квадрат, и предположить, что знаки чисел а, Ъ выбраны так,
что а =1 (mod4), b = a/ (mod p), то число + 2 будет принадлежать
к совокупности А, В, С или D в зависимости от того, имеет ли
число 6/2 соответственно вид in, 4?г + 1, in + 2, in + 3.
Отсюда немедленно получается также правило для классифика-
классификации числа —2. Именно, так как число —1 принадлежит классу А
для четного значения 5/2, и классу С для нечетного значения Ь/2,
то, согласно теореме п. 7, число —2 будет принадлежать классу А,
Теория биквадратичных вычетов. II
687
J9, С или D в зависимости от того, имеет ли число Ь/2 соответственно
вид 4?г, 4?г + 3, 4п + 2 или 4^г + 1. Эти теоремы могут быть также
выражены следующим образом.
Число
принадлежит сово-
совокупности
А
В
С
D
+2
если Ъ по модулю 1
0
2а
4а
6а
2
5 сравнимо с
0
6а
4а
2а
Легко убедиться, что выраженные подобным образом теоре-
теоремы уже не зависят от условия а = 1 (mod 4), а имеют силу
и при а ^ 3 (mod4), если только второе условие, af~b(modp)
сохраняется.
Точно так же легко видеть, что содержание этих теорем изящ-
изящным образом может быть объединено в одну единственную форму-
формулу, именно,
если а и b берутся положительными, то всегда
25
Теперь мы посмотрим, что дает индуктивное рассмотрение от-
относительно классификации числа 3. Если таблицу п. 11 продолжить
дальше (беря все время наименьший первообразный корень), то
Теория биквадратичных вычетов. II
она будет показывать, что число +3 принадлежит
совокупности:
А для
р
13
109
181
193
229
277
а
— 3
— 3
+ 9
— 7
—15
+ 9
ъ
+ 2
+ 10
+ 10
—12
4- 2
-t-14
Р
17
29
53
89
101
ИЗ
137
197
233
257
269
281
293
В для
а
+ 1
+ 5
7
+ 5
+ 1
— 7
—И
+ 1
-г 13
+ 1
+ 13
+ 5
+17
ъ
— 4
+ 2
+ 2
— 8
+10
— 8
— 4
—14
+ 8
—16
+ 10
+ 16
+ 2
С для
p
37
61
73
97
157
241
a
+
+
—
+
'
1
5
3
9
11
—15
—6
—6
—8
+4
—6
—4
D для
р
5
41
149
173
а
+ 1
+ 5
— 7
+ 13
+ 2
— 4
+ 10
+ 2
По крайней мере на первый взгляд мы не замечаем связи между
значениями чисел а, Ь, которым соответствует одна и та же совокуп-
совокупность. Однако, если мы учтем, что подобное различие в теории квад-
квадратичных вычетов относительно числа —3 устанавливается по более
простым правилам, чем относительно числа +3,то у нас появляется
надежда на такое же счастливое обстоятельство и в теории биквад-
биквадратичных вычетов. И действительно, мы находим, что число —3
лринадлежит
Теория биквадратичных вычетов. II
689
Л для
р
37
61
157
193
а
+ 1
+ 5
+11
— 7
ъ
— 6
— 6
- 6
-12
р
5
17
89
ИЗ
137
149
173
233
257
281
В для
а
+ 1
+ 1
+ 5
— 7
—И
у
+ 13
+ 13
+ 1
+ 5
совокупности
ъ
+ 2
— 4
— 8
— 8
4
+ 10
+ 2
+ 8
—16
+ 16
Р
13
73
97
109
181
229
241
277
С для
а
з
— 3
+ 9
— 3
+ 9
—15
—15
+ 9
t
ъ
+ 2
— 8
+ 4
+ 10
+ 10
+ 2
4
+ 14
Р
29
41
53
101
197
269
293
D для
а
+ 5
+ 5
7
+ 1
+ 1
+ 13
+ 17
+ 2
— 4
+ 2
+ 10
—14
+ 10
4- 2
и здесь индуктивный закон немедленно бросается в глаза.
Именно, число — 3 принадлежит совокупности
A, если Ъ делится на 3, т. е. & = 0(mod3),
B, если а-\-Ъ делится на 3, т. е. Ъ == 2а (mod 3),
C, если а делится на 3, т. е. а == 0 (mod 3),
Z), если а — Ъ делится на 3. т. е. & = a(mod3).
26
Далее, мы находим, что число -f- 5 принадлежит совокупности
А для р = 101, 109, 149, 181, 269,
В для р = 13, 17, 73, 97, 157, 193, 197, 233, 277, 293,
С для р = 29, 41, 61, 89, 229, 241, 281,
D для р = 37, 53, ИЗ, 137, 173, 257.
Если мы рассмотрим значения чисел а, &, которые соответству-
соответствуют отдельным р, то мы подметим здесь закон так же легко, как и
при классификации числа — 3. Именно, число + 5 оказывается
в совокупности
A, если Ъ = 0 (mod 5),
B, если Ъ = а,
C, если а == 0,
А если & = 4а.
690
Теория биквадратичных вычетов. II
Очевидно, что эти правила охватывают все случаи, так как
для Ъ = 2а или Ъ = За (mod 5) имело бы место а2 + Ь2 = 0, что не-
невозможно, ибо, по предположению, простое число р отлично от 5.
27
Точно так же индуктивное рассмотрение, примененное к чис-
числам — 7, —11, +13, +17, —19, —23 и продолженное достаточ-
достаточно далеко, дает следующие правила.
А
В
С
D
А
В
С
D
А
В
С
D
А
В
С
D
Для числа — 7
а еее Оили & = Q(mod 7),
Ъ = 4а или Ъ == 5а,
Ъ = а или & г= 6а,
5 == 2а или 6 = За.
Для числа — 11
Ъ = 0, 5а или 6а (mod 11),
5 == а, За или 4а,
а == 0 или b == 2а или 9а,
Ь == 7а, 8а или 10а.
Для числа + 13
6 = 0, 4а, 9а (mod 13),
Ъ = 6а, 11а, 12а,
аЕЕЕО; Ъ = ?>а, 10а,
Ь = а, 2а, 7а.
Для числа+ 17
а = 0;&==0, а, 16а (mod 17),
Ъ = 2а, 6а, 8а, 14а,
Ъ = 5а, 7а, 10а, 12а,
6 = За, 9а, 11а, 15а.
Теория биквадратичных вычетов. II
691
А
В
С
D
А
В
С
D
Для числа —19
b = 0, 2a, 5а, 14а, 17а (mod 19),
& = 3а, 7а, 11а, 13а, 18а,
а = 0; & = 4а, 9а, 10а, 15а,
6 = а, 6а, 8а, 12а, 16а.
Для числа — 23
>;йе=О, 7а, 10а, 13а, 16а (mod
b = 2a, За, 4а, 11а, 15а, 17а,
Ь = а, 5а, 9а, 14а, 18а, 22а,
6—6а, 8а, 12а, 19а, 20а, 21а.
28
Найденные таким способом при индуктивном рассмотрении спе-
специальные теоремы оказываются верными, сколь далеко мы бы ни
продолжали индукцию, и дают очень красивую форму критериев.
Если же сравнить их между собой, чтобы сделать общие выводы,
то с первого же взгляда приходят на мысль следующие замечания.
Критерии, при помощи которых узнается, к какому классу при-
принадлежит простое число + д (гДе берется верхний или нижний
знак в зависимости от того, имеет ли q вид An + 1 или 4га + 3),
зависят от чисел а, Ь, если сравнивать их между собой в отноше-
отношении модуля q.
I. Именно, если а = 0 (modg), то +g принадлежит определен-
определенной совокупности, причем этой совокупностью является А для
q = 7, 17, 23, и С для q = 3, 11, 13, 19, из чего можно предполо-
предположить, что первый случай имеет место вообще тогда, когда q имеет
вид 8га+ 1, а второй, — когда q имеет вид 8п zb 3. Совокупности
же В и D уже заранее исключаются для делящегося на q значе-
значения а, так как в этом случае jp = &2(modg), т. е. р является квад-
квадратичным вычетом числа д, а потому, в силу фундаментальной
теоремы, + q должно быть квадратичным вычетом числа р.
II. Если же а не делится на д, то критерий зависит от значе-
значения выражения — (modq). Это выражение может иметь, вообще
692 Теория биквадратичных вычетов. II
говоря, одно из q различных значений, а именно, значений 0, 1,
2, 3,..., q — 1; но если q имеет вид An + 1, то исключаются оба
значения выражения У—l(mod<7), которые заведомо не могут
быть значениями выражения — (mod#), потому что все время пред-
предполагается, что р = а2 + Ъ2 является простым числом, отличным
от q. Поэтому число допустимых значений выражения — (modg)
для #^l(mod4) равно q — 2, в то время как для g = 3(mod 4)
оно остается равным q.
Теперь эти значения распадаются на четыре класса, именно,
так, что одни, обозначаемые в общем виде через а, соответствуют
совокупности А, другие, обозначаемые через р, — совокупности В,
третьи, обозначаемые через т»—совокупности С, и четвертые,
обозначаемые через 8,— совокупности D, причем так, что +д при-
принадлежит совокупности А, В, С, Z), если соответственно имеет место
Однако закон этого разбиения оказывается лежащим довольно
глубоко, хотя некоторые общие замечания и могут быть сделаны
сразу же. Число значений в трех классах одинаково, а именно,
равно (q —1)/4 или (q -f l)/4, в то время как в четвертом классе
(причем в том, который соответствует совокупности с критерием
а = 0) оно на единицу меньше, так что число всех различных кри-
критериев относительно отдельных совокупностей одинаково, именно,
равно (q —1)/4 или (д + 1)/4. Далее, заметим, что число 0 всегда
встречается в первом классе (среди чисел, а), а дополнения чисел
а> Р> Т? ^ Д° Яу т- е- числа q — a, q — р, q — -у» Я — ^ содержатся
соответственно в первом, четвертом, третьем, втором классах. На-
„1 1 1 1 , j
конец, мы видим, что значения выражении —, у, —, — (modg/
принадлежат к первому, четвертому, третьему, второму классам,
если критерий а = 0 соответствует совокупности А, и, напротив,
третьему, второму, первому, четвертому классам, если критерий
а = 0 относится к совокупности С. Этим ограничивается то, что
может быть обнаружено индуктивным путем, если мы не хотим
позволить себе предвидеть также и то, что ниже будет выведено
из естественных источников.
Теория биквадратичных вычетов. II
693
29
Прежде чем идти дальше, мы хотим отметить, что знание кри-
критериев для простых чисел (взятых положительными, если они имеют
вид 4тг-{-1, и отрицательными, если они имеют вид An + 3) доста-
достаточно для того, чтобы классифицировать все остальные числа, если
только использовать теорему из п. 7 и критерии для чисел — 1
и -}- 2. Так, например, если мы хотим иметь критерии для числа
+ 3, то оказывается, что указанные в п. 25 критерии, касающиеся
числа — 3, имеют силу также и для + 3, если число 5/2 четно, а
если оно нечетно, то в этих критериях совокупности А, В, С, D
заменяются соответственно на С, D, А, В, так что мы получаем
следующие правила.
совокупности
А
В
С
D
Число -[- 3 принадлежит
если
Ъ == 0 (mod 12) или одновременно а == 0 (mod 3) и
Ъ~2 (mod 4);
&==8а или 10а (mod 12),
&=6а (mod 12) или одновременно a = 0(mod 3) и
&==0(mod-4),
& = 2а или 4а mod 12).
Точно так же критерии для + 6 выводятся из критериев для
2и —3.
совокупности
А
В
С
D
Число + 6 принадлежит
если
5 = 0, 2a, 22a (mod 24) или одновременно а == 0 (mod 3)
и Ъ == 4а (mod 8),
Ъ ^в 4а, 6а, 8а (mod 24) или одновременно а = 0 (mod 3)
и Ъ = 2а (mod 8),
Ь = 10а, 12а, 14а (mod 24) или одновременно
а == 0 (mod 3) и Ъ = 0 (mod 8),
Ъ = 16а, 18а, 20а (mod 24) или одновременно
а^О (mod 3) и Ъ = 6а(mod 8).
694
Теория биквадратичных вычетов. II
совокупности
А
В
С
D
Число же — 6 принадлежит
если
6 ее= 0,10а, 14а (mod 24) или одновременно а===0 (mod 3)
и Ъ = 4а (mod 8).
Ь == 4а, 8а, 18а (mod 24) или одновременно а = 0 (mod 3)
и Ъ = 6а (mod 8),
6==2а, 12а, 22а (mod 24) или одновременно
аЕ=0 (mod 3) и b== 0(mod 8),
Ъ == 6а, 16а, 20а (mod 24) или одновременно
а = 0 (mod 3) и Ъ = 2а (mod 8).
Аналогичным образом критерии для числа + 21 составляются
из критериев для чисел —3 и —7, критерии для числа —105 —
из критериев для чисел —1, —3, -J- 5, —7 и т. д.
30
Итак, индукция приносит нам богатый урожай специальных тео-
теорем, которые родственны теореме о числе 2; однако между ними от-
отсутствует общая связь, отсутствуют строгие доказательства, так как
метод, которым мы в первом сочинении рассматривали число 2,
дальше, уже неприменим. Правда, нет недостатка в различных мето-
методах, при помощи которых можно получить доказательства для част-
частных случаев, в первую очередь тех, которые относятся к распреде-
распределению квадратичных вычетов по совокупностям А и С; однако мы не
будем на них останавливаться, ибо мы должны желать построить
общую теорию, охватывающую все случаи. После того как мы еще
в 1805 г. начали размышлять об этом предмете, мы скоро пришли
к убеждению, что естественный источник общей теории следует
искать в расширении области арифметики, как мы уже ука-
указывали в п. 1.
Именно, в то время как в рассматривавшихся до сих пор вопро-
вопросах высшая арифметика имеет дело только с целыми вещественными
числами, теоремы, относящиеся к биквадратичным вычетам, только
тогда выступают во всей своей простоте и естественной красоте, когда
Теория биквадратичных вычетов. II 695
арифметики распространяется также и на мнимые числа,
так что ее объектом становятся без ограничения все числа вида
а + bi, где, как обычно, i обозначает мнимую величину у—1,
а и Ъ — всевозможные целые вещественные числа от — оо до + оо.
Такие числа мы будем называть целыми комплексными числами,
причем вещественные числа не противопоставляются комплекс-
комплексным, а рассматриваются как их частный случай. Настоящее сочи-
сочинение будет содержать как элементарное учение о комплексных
величинах, так и начала теории биквадратичных вычетов, пол-
полное развитие которой мы поставим себе целью в продолжении этой
работы *.
31
Прежде всего мы предпошлем некоторые наименования, введение
которых будет способствовать большей краткости и ясности.
Область комплексных чисел а + Ы содержит:
I. Вещественные числа, у которых b = 0, и среди них, в зави-
зависимости от того, каково число а,
1) нуль,
2) положительные числа,
3) отрицательные числа.
II. Мнимые числа, у которых Ъ отлично от нуля. Здесь снова
различаются:
1) мнимые числа без вещественной части, т. е. такие, у которых
а = О,
2) мнимые числа с вещественной частью, т. е. такие, у которых
ни а, ни Ъ не равны нулю.
Первые, при желании, можно называть чисто мнимыми числами,
а вторые — смешанными мнимыми числами.
* Мы хотим только заметить еще, что подобное расширение области теории
биквадратичных вычетов особенно целесообразно. Теория кубических вычетов
подобным же образом должна основываться на рассмотрении чисел вида а + bh,
где h есть некоторый мнимый корень уравнения h3 — 1 =0, например, h =
__ ___ тг 4-1/ —- i, и точно так же теория вычетов более высоких степеней тре-
z V 4
бует введения других мнимых величин.
696 Теория биквадратичных вычетов. II
В настоящей теории мы будем употреблять четыре единицы:
+ 1, —1, +г, —i, которые кратко будут называться соответственно
положительной, отрицательной, положительно мнимой и отрица-
отрицательно мнимой единицами.
Три произведения некоторого комплексного числа на одно из
чисел — 1, +г,—i мы будем называть числами, ассоциированными
с этим числом. За исключением нуля (который ассоциирован с са-
самим собой), всегда, таким образом, ассоциированы одно с другим че-
четыре различных числа.
Напротив, число, которое получается из данного комплексного
числа заменой i на — i, мы будем называть сопряженным с этим
числом. Таким образом, мнимые числа разбиваются на пары различ-
различных между собой сопряженных чисел, в то время как вещественные
числа сопряжены сами с собой, если только мы хотим использовать
этот термин и для них.
Произведение комплексного числа на число, сопряженное с ним,
мы назовем нормой каждого из этих чисел. Для вещественного
числа в качестве нормы должен рассматриваться, следовательно, его
квадрат.
Вообще мы имеем по восемь связанных между собой чисел,
именно:
а + Ы
-Ъ -\~ai
а — Ы
Ъ — ai
а — Ы
— Ъ — ai
— а + Ы
Ь -\~ai;
здесь мы видим две четверки ассоциированных чисел и четыре пары
сопряженных чисел, а общая норма их всех равна а2 + Ь2. Однако
среди этих восьми чжсел будет только четыре различных, если либо
а — + Ъ, либо одно из чисел а, Ъ равно 0.
Из приведенных определений тотчас же получается такое след-
следствие.
Числом, сопряженным с произведением двух комплексных чисел,
является произведение чисел, сопряженных с ними.
Теория биквадратичных вычетов. II 697
Так же обстоит дело и для произведения большего числа сомно-
сомножителей и для частного.
Норма произведения двух комплексных чисел равна произведению
норм этих чисел.
Эта теорема также распространяется на произведение любого
числа сомножителей и на отношения.
Норма каждого комплексного числа (за исключением нуля, что
мы, начиная отсюда, будем в большинстве случаев молчаливо пред-
предполагать) является положительным числом.
Далее, ничто не мешает распространить наши определения на
дробные или иррациональные значения чисел а, Ъ\ однако а + Ы
только тогда будет называться целым комплексным числом, когда
каждое из чисел а, Ъ целое, и только тогда рациональным, когда
каждое из чисел а, Ъ рационально.
32
Алгоритм арифметических операций над комплексными числами
хорошо известен; деление посредством введения нормы может быть
сведено к умножению, так как мы имеем
а + Ы , , .ч с — di ас + bd be — ad .
Квадратный корень извлекается по формуле
если b является положительным числом, или по формуле
если b является отрицательным числом. На том, какую пользу
в смысле облегчения операций играет преобразование комплексных
чисел а + Ы к виду г (cos 9 + z'siiKp), нам нет здесь нужды оста-
останавливаться.
698 Теория биквадратичных вычетов. II
33
Целое комплексное число, которое может быть разложено ва
два отличных от единиц сомножителя*, мы будем называть состав-
составным комплексным числом; напротив, число, не допускающее такого
разложения, называется комплексным простым числом. Из этого
тотчас же вытекает, что каждое составное вещественное число яв-
является также и составным комплексным числом. Однако еещест-
веннное простое число может быть составным комплексным числом,
а именно, это будет иметь место для числа 2 и всех веществен-
вещественных положительных простых чисел вида 4п + 1 (за исключением
числа 1), так как они, как известно, могут быть разложены на
два положительных квадрата; например, 2 —A + г)A—г), 5 =
= A +2г)A—2г), 13 = C + 2i) C — 2г), 17 - A + 4г) A — 4г) и т. д.
Напротив, положительные вещественные простые числа вида
4n -j- 3 всегда являются также и комплексными простыми числами.
Действительно, если бы для некоторого такого числа имело место
q = (а + Ы) (а + $i)9 то было бы также q = (а — Ы) (ос —- pi), и по-
потому q2 = (а2 + &2) (а2 + 482); но q может быть только одним единст-
единственным способом разложено на положительные сомножители, боль-
большие чем 1, именно, q2 = q-q, так что должно было бы быть
q = а2 + б2 = а2 + р2. Это, однако, невозможно, так как сумма двух
квадратов не может иметь вид An + 3.
Для отрицательных вещественных чисел» очевидно, сохраняет
силу та же терминология, что и для положительных, и так же
обстоит дело и для чисто мнимых чисел.
Остается поэтому только показать, как отличать составные
числа от простых среди смешанных мнимых чисел, и это достига-
достигается следующей теоремой.
Теорема. Каждое целое смешанное мнимое число а + Ы является
или комплексным простым числом, или составным числом, в зависи-
зависимости от того, является ли его норма простым вещественным
числом или составным числом.
* Или, что то же самое, на такие сомножители, нормы которых больше
единицы.
Теория биквадратичных вычетов. II 699
Доказательство. I. Так как норма составного комплексного числа
всегда является составным числом, то очевидно, что комплексное
число, норма которого является вещественным простым числом,
обязательно должно быть комплексным простым числом. Это первая
часть теоремы.
II. Если же норма а2 + Ъ2 является составным числом, то пусть
р— вещественное положительное простое число, которое входит в
нее делителем. Рассмотрим тогда два случая.
1. Если р имеет вид An + 3, то, как известно, а2 + Ъ2 может
делиться на р только тогда, когда р одновременно входит ива
и в 6, так что а + Ы будет составным числом.
2. Если р не имеет вида An + 3, то оно заведомо может быть
разложено на два квадрата; положим поэтому р = а2 + р2.
Так как
(ах + йр) (ах — йр) - а2 (а2 + р2) — р2 (а2 + Ь2),
и потому левая часть делится на /?, то р заведомо будет входить
в один из сомножителей ах + Щ, ах — бр, а так ка!к, далее,
(ах + ЬЪJ + (Ъх-ярJ - (ах-Щ? + (Ъх + арJ - (а2 + &2) (а2 + Р2),
и потому левая часть делится на р2, то очевидно, что в первом
случае на р должно делиться также число Ъх — ар, а во втором —
число Ъх + #р. Поэтому в первом случае будет целым комплексным
числом число
а+ Ы _ аа+ Ъ$ Ъа— ар .
а+Р*~ Р + Р 1'
а во втором—число
а + Ы ad — &Р , &а + ар .
а— р*" ~~ р р 1'
Так как вследствие этого заданное число делится или на oc + pi,
или на а — pi, и норма отношения, именно, (а2 + Ъ2)/р, по предпо-
предположению, отлична от единицы, то a -f- Ы в обоих случаях является
комплексным составным числом. Это вторая часть теоремы.
700 Теория биквадратичных вычетов. II
34
Таким образом, совокупность комплексных простых чисел исчер-
исчерпывается числами следующих четырех типов.
1. Четырьмя единицами 1, +г, —1, —г, которые, однако, когда
речь будет идти о простых числах, мы в большинстве случаев мол-
молчаливо будем предполагать исключенными.
2. Числом 1 + i и тремя ассоциированными с ним числами
—1 + i, —1 — i, 1 — i.
3. Вещественными положительными простыми числами вида
An + 3 и тройками чисел, ассоциированных с каждым из них.
4. Комплексными числами, нормами которых являются превос-
превосходящие единицу простые числа вида An -{- 1, причем каждой дан-
данной норме такого вида соответствует в точности по восемь комплекс-
комплексных простых чисел, так как такая норма только одним единственным
образом может быть разложена на два квадрата.
35
Точно так же, как вещественные целые числа разделяются на
четные и нечетные, а первые снова на делящиеся на 4 и не делящиеся
на 4, так и для комплексных чисел имеет место столь же важное
различие. Именно, комплексные числа или не делятся на 1 -\- i,
например, числа а + Ы, у которых одно из чисел а, Ъ нечетно, а дру-
другое четно, или делятся на 1 + г, но не делятся на 2, если каждое из
чисел а, Ънечетно, или делятся на 2, если каждое из чисел а, Ъчетно.
Числа первого класса удобно называть нечетными, числа второго
класса — получетными, а числа третьего класса — четными комплекс-
комплексными числами.
Произведение нескольких комплексных сомножителей всегда не-
нечетно, если все сомножители нечетны; оно получетно, если один из
сомножителей получетен, а остальные нечетны; наконец, оно четно,
если среди сомножителей имеются или по крайней мере два получет-
получетных, или по крайней мере один четный.
Норма каждого нечетного комплексного числа имеет вид An + 1;
норма получетного числа имеет вид 8п -f 2; наконец, норма четного
числа является произведением числа вида An + 1 на число А или на
большую степень числа 2.
Теория биквадратичных вычетов. II 701
36
Так как связь между четырьмя ассоциированными комплексны-
комплексными числами аналогична связи между двумя противоположными ве-
вещественными числами (т. е. между двумя числами, равными по аб-
абсолютной величине, но имеющими противоположные знаки), а из
них положительное обычно по праву рассматривается как первичное,
то возникает вопрос, может ли быть подобным же образом выделено
одно число из каждых четырех ассоциированных комплексных чи-
чисел и будет ли это полезным?Чтобы решить этот вопрос, нужно учесть,
что принцип выделения должен быть таким, что произведение двух
чисел, которые среди ассоциированных с ними рассматриваются
как первичные, всегда должно быть первичным числом среди чисел,
ассоциированных с ним. Но мы сейчас же убеждаемся, что такого
принципа вообще не существует, если выделение первичного числа
не ограничивать только целыми числами; полезным же такое выде-
выделение оказывается лишь для нечетных чисел. А для них поставлен-
поставленная цель может быть достигнута следующими двумя способами.
I. Произведение двух чисел а-\-Ы, a'+b'i с тем свойством,
что а и а'имеют вид 4?г + 1, а Ъ и Ь' четны, снова обладает этим
свойством, т. е. его вещественная часть будет =1 (mod 4), а мнимая
часть будет четной. Но легко видеть, что среди четырех ассоцииро-
ассоциированных нечетных чисел всегда будет одно и только одно число
с таким свойством.
II. Если число а + Ы обладает том свойством, что а — 1 и /;
или одновременно делятся на 4 или одновременно делятся на 2,
но не делятся на 4, то произведение его на комплексное число такого
же вида будет обладать этим же свойством, и легко видеть, что из
каждых четырех ассоциированных нечетных чисел числом такого
вида будет одно и только одно.
Из этих двух приблизительно одинаково целесообразных прин-
принципов мы выберем второй; именно, среди четырех ассоциированных
нечетных комплексных чисел мы будем рассматривать как первич-
первичное то число, которое по модулю 2 + 2i сравнимо с положительной
единицей; благодаря этому мы сможем намного короче формулиро-
формулировать многие замечательные теоремы. Так, например, первичными
702 Теория биквадратичных вычетов. II
являются комплексные простые числа — 1+2?, —1—21, + 3+2?,
+3—2i, +1+4г,+ 1—4г\ ..., так же, как и вещественные отрица-
отрицательные простые числа — 3, —7, —11, —19,... Число, сопряженное
с нечетным комплексным первичным числом, тоже будет первич-
первичным.
Для получетных и четных чисел вообще такое различение было
бы слишком произвольным и почти бесполезным. Хотя среди ассо-
ассоциированных простых чисел 1 + г, 1 — г, —1 + г, —1 -— i мы и мо-
можем выбрать одно число в качестве первичного, но для составных
чисел мы такого различения производить не будем.
37
Если среди сомножителей составного комплексного числа име-
имеются такие, которые сами являются составными, и если они снова
разложены на сомножители, то ясно, что в конце концов мы при-
придем к простым сомножителям, т. е. каждое составное число разло-
разложимо на простые сомножители. Если среди них имеются не пер-
первичные сомножители, то мы подставим вместо них произведения
ассоциированных с ними первичных чисел на г\ —1 или —г.
Таким образом, мы получаем, что каждое составное комплексное
число М может быть представлено в виде
М = ГА*В*С*
где А, В, С, ... являются различными между собой простыми ком-
комплексными первичными числами, и ^ = 0, 1, 2 или 3. Для такого*
разложения справедлива теорема, что оно возможно лишь одним
единственным образом, — теорема, которая при поверхностном рас-
рассмотрении могла бы показаться очевидной сама собой, однако, в.
действительности требующая доказательства. К нему пролагает
путь следующая теорема.
Теорема. Произведение М = АаВ®СТ . . ., где А, В, С, . , . обозна-
обозначают различные простые комплексные первичные числа, не может
делиться ни на одно первичное комплексное простое число, не со-
содержащееся среди чисел А, В, С,...
Доказательство. Пусть Р — первичное комплексное простое число*
не содержащееся среди чисел A, S, С, . . . , и пусть р, а, Ь, с, . *
Теория биквадратичных вычетов. II 703
являются соответственно нормами чисел Р, А, В, С, .... Тогда
легко видеть, что норма числа М равна aab^cY... так что это
число должно было бы делиться на р> если бы М делилось на Р.
Так как отдельные нормы являются или вещественными простыми
числами (из ряда 2, 5, 13, 17, .. .), или квадратами вещественных
простых чисел (из ряда 9, 49, 121,...), то немедленно ясно, что
это может быть только тогда, когда р равно одной из норм а, Ь,
с, . . . ; мы предположим поэтому, что р = а. Но так как, по пред-
предположению, Р ж А являются различными между собой первичными
комплексными простыми числами, то легко видеть, что это может
выполняться лишь если Р и А являются сопряженными комплекс-
комплексными числами, и потому р = а является нечетным вещественным
простым числом (а не квадратом простого числа); положим поэтому
А = k -f- И, Р — к— И. Тогда (если распространить понятие и обо-
обозначение для сравнимости на целые комплексные чисела) будет иметь
место A=E2k(modP), откуда легко видеть, что
Таким образом, если предположить, что М делится на Р. то и
2VB*C\ . .
будет делиться на Р, а потому норма этого числа, которая равна
будет делиться на р. Но так как 2 и к заведомо на р не делятся,,
то из этого следует, что р должно совпадать с одним из чисел Ъ,
с, ... Пусть, например, р = Ь. Но тогда мы заключаем отсюда,,
что или В = к + И, или В = к — И, т. е. или В = А, или В ~ Р,
но и то и другое противоречит предположению.
Из этой теоремы другая теорема, а именно, что разложение
на простые сомножители возможно только единственным спосо-
способом, выводится очень легко, причем методом, совершенно анало-
аналогичным тому, который мы использовали в «Арифметических иссле-
исследованиях» (п. 16); поэтому было бы излишним задерживаться
сейчас на этом.
704 Теория биквадратичных вычетов. II
38
Теперь мы переходим к сравнимости чисел по комплексным мо-
модулям. Однако до начала этого исследования целесообразно пока-
показать, как комплексные числа можно наглядно интерпретировать.
Подобно тому, как каждая вещественная величина выражается
куском бесконечной в обе стороны прямой линии, начинающимся
из произвольно выбранной начальной точки и измеренным произ-
произвольно выбранным в качестве единицы отрезком, и потому может
быть представлена другим концом этого куска, причем точки по одну
сторону от начальной представляют положительные величины, а
точки по другую сторону от начальной — отрицательные, так и
каждая комплексная величина может быть представлена некоторой
точкой бесконечной плоскости, на которой определенная прямая
служит для представления вещественных величин; а именно,
комплексная величина х + iy представляется точкой, абсцисса кото-
которой равна х, а ордината (берущаяся положительнай по одну сторону
от линии абсцисс и отрицательной — по другую сторону) равна у.
Таким образом, можно говорить, что каждая комплексная величина
измеряет различие между положением той точки, которой представ-
представляется эта величина, и положением начала координат, если поло-
положительная единица обозначает произвольное, но фиксированное
уклонение по произвольному, но фиксированному направлению,
отрицательная единица — такое же по величине уклонение по про-
противоположному направлению, наконец, мнимые единицы — такие
же по величине уклонения по направлениям, перпендикулярным
первым, и идущим в обе стороны.
Таким образом, на природу величин, которые мы называем
мнимыми, проливается ясный свет. Если начало координат обозна-
обозначить через @), а две комплексные величины т, т! соответствуют
точкам М, М', положение которых по отношению к точке @) они
выражают, то разность т — т' будет выражать не что иное, как
положение точки М относительно точки М' \ с другой стороны, если
произведение mm! выражает положение точки N относительно
точки @), то легко убедиться, что это положение так же опреде-
определяется положением точки М относительно точки @), как поло-
положение точки М' определяется положением той точки, которой
Теория биквадратичных вычетов. II 705
соответствует положительная единица, так что будет не лишено
оснований сказать, что положения точек, соответствующих комплекс-
комплексным величинам mm', m, тг, 1, образуют пропорцию. Однако более
исчерпывающее изложение этого вопроса мы оставим до другого
случая. Трудности, которыми считается окруженной теория мнимых
величин, по большей части имеют своей причиной мало удачные на-
наименования (некоторые снабдили их даже неудачно звучащим назва-
названием невозможных величин). Если бы, исходя из представлений,
даваемых многообразием двух измерений (которые с большой яс-
ясностью проявляются при пространственных соображениях), назы-
называть положительные величины прямыми, отрицательные — обрат-
обратными, а мнимые — к ним перпендикулярными величинами, то мы
имели бы простоту вместо путаницы, ясность вместо туманности.
39
Изложенное в предыдущем пункте относится к непрерывным
комплексным величинам; в арифметике же, которая имеет дело толь-
только с целыми числами, схемой комплексных чисел является система
точек, так расположенных на одинаковых расстояниях одна от дру-
другой на проходящих на одинаковых расстояниях одна от другой пря-
прямых, что они разбивают бесконечную плоскость на бесконечное число
квадратов. Все числа, делящиеся на заданное комплексное число
а + Ы = т, также будут образовывать бесконечно много квадратов,
стороны которых равны \ а2 + Ъ2 , т. е. площади равны а2 + Ь2;
если ни одно из чисел а, Ъ не равно нулю, то последние квадраты
будут расположены по отношению к первым наклонно. Каждому
числу, не делящемуся на модуль т> будет соответствовать точка,
расположенная или внутри одного из таких квадратов, или на гра-
границе двух квадратов; последний случай, однако, может иметь место
только тогда, когда числа а, Ъ имеют общий делитель; далее, ясно,
что числа, сравнимые по модулю т, занимают в своих квадратах
конгруентные положения. Отсюда легко видеть, что если собрать
все числа, лежащие внутри некоторого определенного квадрата, и все
числа, лежащие на каких-нибудь двух не противоположных его
сторонах, и, наконец, добавить к ним число, делящееся на т, то
мы получим полную систему несравнимых по модулю т вычетов,
706 Теория биквадратичных вычетов. II
т. е. каждое целое число будет сравнимо с одним и только одним
из 3tnx чисел. Было бы тйкже нетрудно показать, что количество
этих вычетов равна норме модуля, т. е. равно а2 + Ь2. Однако нам
кажется целесообразным доказать эту очень важную теорему дру-
другим, чисто арифметическим, способом.
40
Теорема. Л о заданному комплексному модулю т = а + bi9 норма
которого равна а2 + Ъ2 = р и для которого а, Ъ являются взаимно
простыми числами, каждое целое комплексное число сравнимо t одним
и только одним вычетом из ряда 0, 1, 2, 3,...,/? — 1.
Доказательство. I. Если а, C являются целыми числами, для
которых имеет место оса + $Ъ = 1, то
i = cub — [За + т (Р + оа).
Если поэтому дано целое комплексное число А + Bi> то
А + Bi = А + (аЬ — Ра) В + т ($В + aBi).
Поэтому, если обозначить через h наименьший положительный
вычет числа А + (cub — $а)В по модулю р и положить
А + (ub — ра) В = h + kp = h + т (ak — bki),r
то будет выполняться равенство
A + Bi = h + m[$B + ak + (асВ — bk) i"J,
или
Тем самым доказана первая часть теоремы.
II. Если с некоторым комплексным числом сравнимы по мо-
модулю т два вещественных числа /г, /г', то они будут сравнимы и
между собой. Поэтому, если мы положим h — h! = m(c -f di), то
будет выполняться равенство
(Л— hT)(a — bi) = p(c + di),
и потому
(h — h')a = ре, (h — Ъ!)Ъ = — pd,
и, далее, вследствие того, что аа + &Р = 1,
& — Ь! —р(с<х — d$)r т. е. h = /г' (mod // .
Теория биквадратичных вычетов. II 707
Поэтому числа /г, /г', если они не равны, не могут оба одно-
одновременно содержаться в совокупности чисел 0, 1, 2, 3; .. ., р — 1.
Тем самым доказана вторая часть теоремы.
41
Теорема. По комплексному модулю т == а + bi, норма которого
равна а2 + Ь2 = р и для которого а, Ъ не взаимно просты, а имеют
наибольший общий делитель X {который мы предполагаем положитель-
положительным), каждое комплексное число сравнимо с вычетом х + iyt облада-
обладающим тем свойством, что х является одним из чисел 0, 1, 2,
3, . . . , -у- — 1,а у — одним из чисел 0,1,2, 3,..., X — 1, причем
только с одним единственным из всех р вычетов, имеющих такой вид.
Доказательство. I. Если выбрать целые числа а, C так, что
оса + C6 = X, то
U =ab — $a + m($ + ои).
Если теперь А + Bi — заданное комплексное число, далее,
если у — наименьший положительный вычет числа В по модулю X,
и х — наименьший положительный вычет числа A -f (<xb — pa) T"y
по модулю /?/Х, и если положить
А + {*Ъ-$а)В-=^ = х+ -f .*,
то будет иметь место
"У
т. е. стоящее слева число делится на т, а потому A + Bi =
= х -i- yi (mod т). Тем самым доказана первая часть теоремы.
II. Если мы предположим, что с одним и тем же комплексным
числом сравнимы по модулю т два числа х -f yi и х' + y'i, то они
будут сравнимы по модулю т и между собой. Поэтому они тем
более будут сравнимы по модулю X, и потому у = у' (modX). Если
теперь предположить, что каждое из чисел у, у' содержится среди
708 Теория биквадратичных вычетов. II
чисел 0, 1, 2, 3, . . ., X — 1, то обязательно должно быть у = у'.
Но тогда будет иметь место также и х^х' (то&т), т. е. х — х'
будет делиться на ту и потому число (х — х')/Х будет целым, деля-
делящимся на Y+j if т. е. будет выполняться сравнение
х — х' А/ j a b Л
-—?— =0 mod -г- + т- Ч •
А у Л Л у
Но так как числа а/Х, 6/Х взаимно просты, отсюда на основании
второй части предыдущей теоремы следует, что (х — х')/\ делится
а Ь . Л„
также на норму числа т~ + "г1» т- е- на число д/Х2, а потому
А А
х — х' делится на pfk* Поэтому, если предположить, что и каждое
из чисед х, х' содержится в совокупности 0, 1, 2, 3, ...,-? —1,
то обязательно будет х = х\ т. е. вычеты х -f yi1 x' -f y'i будут
совпадать. Тем самым доказана вторая часть теоремы.
Между прочим, ясно, что сюда нужно причислять также случай,
когда модуль является вещественным числом, т. е. Ъ = 0, и потому
X = + а, и случай, когда модуль является чисто мнимым числом,
т. е. а — 0, и потому X = +6. В обоих случаях -^ =± X.
42
Таким образом, если все сравнимые между собой по заданному
модулю комплексные числа причислять к одному и тому же классу,
а несравнимые — к различным классам, то всего будет р классов,
охватывающих совокупность всех целых чисел, где р обозначает
норму модуля. Совокупность такого же количества чисел, взятых
из различных классов, будет давать полную систему несравнимых
вычетов, которую мы научились выбирать в пп. 40 и 41. При этом
выбор представителей в отдельных классах там основывался на том,
что в каждом классе выбирался такой вычет х + г/i, для которого
у имеет наименьшее значение, а из нескольких вычетов с одинако-
одинаковым наименьшим значением у — тот вычет, у которого значение х
меньше всего, за исключением, однако, отрицательных значений
как для х, так и для у. Но для других целей будет целесообразно
придерживаться других принципов, причем особенно следует обра-
Теория биквадратичных вычетов. II 709
тить внимание на тот способ, при котором выбираются те вычеты,
которые, будучи поделенными на модуль, дают самые простые част-
ные. Очевидно, что если а + (Зг, а' + C7, а" + р"г, . . . являются
частными, получающимися при делении на модуль сравнимых между
собой чисел, то как разности между различными величинами ос, а',
а", . . . , так и разности между различными величинами [3, J3', [3", , . .
будут целыми числами, и ясно, что всегда существует вычет, для
которого аир лежат между границами 0 и 1, включая первую
границу и исключая вторую; такой вычет мы будем называть про-
просто наименьшим вычетом. При желании вместо указанных границ
можно брать также границы —^ и + -~- (включая первую и ис-
ключая вторую); вычеты, соответствующие этому ограничению, мы
будем называть абсолютно наименьшими вычетами.
В отношении этих наименьших вычетов встают следующие за-
задачи.
43
Наименьший вычет заданного комплексного числа A -\-Bi no модулю
а + Ы9 норма которого равна /?, находят следующим образом.
Если х + yi является искомым наименьшим вычетом, то (х + yi) X
X (а — Ы) будет наименьшим вычетом произведения (А + Bi) (а — Ы)
по модулю (а-\-Ы)(а — ЫI т. е. по модулю р. Поэтому если поло-
ЯхИТЬ _ А | ~L D ТР 71 I ¦/ п 7? 1~i А — /""* т\ I п
где /, g являются наименьщими вычетами чисел а А + ЬВ, аВ — ЪА
по модулю р9 то выполняется равенство
x + yi =
или
Очевидно, что наименьшие вычеты /, g следует брать или в
границах 0 и р — 1, или в границах <—тгр ж -\--к р в зависимо-
зависимости от того, отыскивается ли просто наименьший или абсолютно
наименьший вычет комплексного числа.
710 Теория биквадратичных вычетов. II
44
Нахождение полной системы наименьших вычетов для заданного
модуля может быть выполнено несколькими способами. Первый ме-
метод состоит в том, что сначала определяются границы, между
которыми должны лежать вещественные части, а затем для отдель-
отдельных значений, лежащих между этими границами, находятся границы
мнимых частей. Общий критерий наименьшего вычета х + yi для
модуля а -\- Ы состоит в том, что как ах + by = ?, так и ау — Ъх = tj
лежат между границами 0 и а2 + Ь2, если речь идет просто о наи-
наименьших вычетах, или между границами —у (я2 + ^2) и +у(я2+&2),
если отыскиваются абсолютно наименьшие вычеты, причем вторая гра-
граница исключается. Специальные правила потребовали бы отдельного
рассмотрения случаев, соответствующих различным возможностям
для знаков чисел а, Ь, но мы не будем тратить здесь время на их
изложение, которое не связано ни с какими трудностями. Доста-
Достаточно будет пояснить сущность метода на одном примере.
Для модуля 5 + 2г просто наименьшие вычеты х + yi должны
быть таковы, что как число Ъх + 2г/ = ?, так и число Ъу — 2х — т]
равны одному из чисел 0, 1, 2, 3,. . . , 28. Равенство 29х = Ы — 2tj
показывает, что положительные значения х не могут быть больше чем
5-28/29, а абсолютные величины отрицательных значений не могут
быть больше чем 2-28/29. Поэтому всевозможными допустимыми
значениями для х являются следующие: —1, 0, 1, 2, 3, 4. Для
х = — 1 число 2г/ должно быть равно одному из значений 5, 6,
7,..., 33, а число Ъу— одному из значений —2, —1, 0, 1, 2,
3, ... ,26; поэтому наименьшее значение для у равно + 3, а наибольшее
равно + 5. Если так же рассмотреть остальные значения х, то по-
лyqaeтcя следующая таблица всех наименьших вычетов:
X
— 1
0
+ 1
+ 2
+ з
+ 4
3, 4, 5
0, 1, 2,
1, 2, 3,
1, 2, 3,
2, 3, 4,
2, 3, 4
У
со"
4,
4,
5,
4,
5,
5,
6
5
6
6
Теория биквадратичных вычетов. II
711
Подобным же образом для абсолютно наименьших вычетов зна-
значения ? и т) должны быть среди чисел —14, —13, —12, . . . , + 14;
следовательно, 29х не может лежать вне границ —7-14 и -|-7-14,
и потому х должен быть равен одному из чисел —3, —2, —1, О,
1, 2, 3. Для х = — 3 число 2у = ? — 5х = ? + 15 будет равно од-
одному из чисел 1, 2, 3, . . . , 29, а число by = i]-\-2x -= г\ — 6 — од-
одному из чисел —20,— 19, —18, . . ., +8. Отсюда для у получает-
получается единственное значение + 1. Если таким же образом рассмотреть
остальные значения х, то получается следующая таблица всех
абсолютно наименьших вычетов:
w
— 3
— 2
— 1
0
+ 1
+ 2
+ 3
+ 1
-2,-1,
-3, -2,
-2,-1,
-2,-1,
9 1
—1
У
0,
1
о,
о,
о,
+1
,0,
+1
+1,
-1-1
, -4-2
+1,
+2,
-f-
>
+2
2
i~3
2
45
При применении второго метода целесообразно различать два
случая.
В первом случае, когда а и Ъ не имеют общих делителей, по-
положим сна -\- $Ь = 1, и пусть А является наименьшим положитель-
положительным вычетом числа (За—^аб по модулю р. Тогда тождественные
соотношения
а (р<х — аЬ) = Р/? — Ъ (аа + C6), Ъ {$а — <*Ь)=—<хр + а (аа + рЬ)
показывают, что а& = — &, bk = a(mod/?). Поэтому, если, как и
выше, положить ах-\-Ъу = ?, аг/ — fe = yj, то будет иметь место
т} = Л, ? = —&Yj(mod/?). Таким образом, мы получим все числа ? + т^г,
которые соответствуют просто наименьшим вычетам х + г/г, если
либо будем брать для ? последовательно значения 0, 1, 2, 3, ...
..., р—1, а для т)— наименьшие положительные вычеты произведений
712
Теория биквадратичных вычетов. II
kl no модулю ру либо, наоборот, для т] будем брать первые значе-
значения, а для ?— наименьшие вычеты произведений — кч]. Тогда из
отдельных значений ? -\~ i\i соответствующие значения х -f- yi нахо-
находятся по формуле
x + yi= •7Г=% = ~ * +
¦Ы р ' р
Далее, ясно, что когда % увеличивается на единицу,
растает на к, или уменьшается на р — к,
певает либо изменение
а — кЬ ак -\-Ь .
и потому х +
или воз-
претер-
претер~1
либо изменение
а — кЬ
это замечание служит для облегчения вычислений.
Наконец, если отыскиваются абсолютно наименьшие вычеты, то эти
правила меняются лишь в том отношении,что теперь числу ? придаются
1 . 1
последовательно значения в пределах от — тгр до + ^ р, в то вре-
время как для т] берутся абсолютно наименьшие вычеты произведений
к\. Здесь приводится таблица полученных таким путем наименьших
вычетов для модуля 5 + 2L
Наименьшие вычеты
1 -
2-
3-
4-
5-
6-
7-
8-
9-
+ ч
0
f 17 г
f 5 г
f 22 г
f Юг
f27 г
f 15 г
f 3 г
f 20 г
+- 8г
X +
0
] _|_
4-
+ 1 +
+
— 1 +
+ 1 +
+ 1 +
yi
Зг
г
4 г
2г
5»
Зг
г
4 г
2г
10-
11-
12-
13-
14-
15-
16-
17-
184
19-
Н25г
h 13*
- г
h 18*
h 6*
г23г
НИг
Ь28г
Н 16/
ь и
.+
+ 1-
+ 2-
+ 1-
+ 2-
+ 1-
+ 2-
+ 1-
+ 2-
+ ЗН
yi
h 5 г
-Зг
- г
1-4 г
1-2 г
^5г
-Зг
-6г
-4г
t-2*
5-
20 Н
21 -
22-1
23-
24-
25-
26 Н
27 Н
28-т
|-21i
- 9»
-26»
-14»
- 2»
-19»
- 7г
-24»
-12»
x + yi
+ 2-
+ 3-
+ 2-
+ 3-
4-4-
4-ЗН
4-4-
+ 3ч
Н5г
-Зг
h 6г
Ь4г
h 2г
-5г
ЬЗг
1-6»
г4г
Теория биквадратичных вычетов. II
713
Абсолютно наименьшие вычеты
5 + tf
— 14 — 6 г
— 13+11г
— 12— г
— И—13г
—10 + 4 г
— 9 — 8 г
— 8 +9 г
— 7 — 3 г
— 6+14г
— 5 + 2/
— 2 — 2л
— 3+ г
— 2— г
—— J. —— <J?,
— 2
— 1 —2г
-2+ г
. А 7
JL 6
— 2 + 2г
— 1
5 + 4
— 4 —
-3 +
— 2 —
-1 +
0
+ 1 —
+ 2 +
+ 3 —
+ 4 +
Юг
7г
5г
12г
12г
5г
7г
Юг
— 1
— 1
0
+ 1
+ 1
— 2г
+ г
— г
+ 2г
— 2г
+ г
— г
+ 2г
5 + 1
+ 5 —
+ 6 —
+ 7 +
+ 8 —
+ 9 +
+ 10 —
+ 11 +
+ 12 +
+ 13 —
+ 14 +
i
2г
14г
Зг
9г
8г
4г
13г
г
Иг
6 г
х + У
+ 1
+ 2 —
+ 1 +
+ 2 —
+ 1 +
+ 2
+ 1 +
+ 2 +
+ 3 —
+ 2 +
i
2г
г
г
2г
Зг
г
г
2г
Второй случай, когда а и & не взаимно просты, легко может
быть сведен к предыдущему случаю. Пусть X — наибольший общий
делитель чисел а, &, и а = Ха', Ъ = Х&'. Обозначим, далее, через F
произвольный наименьший вычет для модуля X, рассматриваемый
как комплексное число, т. е. будем считать, что F — произвольное
число х + yit у которого х, у заключены или в границах 0 и X,
1 1
или в границах — ^"Х и -f ^-X (в зависимости от того, идет ли речь
просто о наименьших или об абсолютно наименьших вычетах);
наконец, обозначим через F' произвольный наименьший вычет для*
модуля а' + b'i. Тогда (а' + b'i) F -\- F' будет некоторым наимень-
наименьшим вычетом для модуля а + bi, и мы получим полную систему этих вы-
вычетов, если будем комбинировать всевозможные значения F со все-
всевозможными значениями F'.
46
Два комплексных числа называются взаимно простыми, если, кроме
единиц, они не обладают другими общими делителями; если же
так!ие общие делители существуют, то наибольшими общими назы-
называются те из них, нормы которых наибольшие.
714 Теория биквадратичных вычетов. II
Если даны разложения на простые сомножители двух данных
чисел, то нахождение наибольшего общего делителя может быть
выполнено точно таким же образом, как и для вещественных чисел
(«Арифметические исследования», п. 18). Одновременно из этого вы-
вытекает, что все общие делители двух данных чисел должны входить
также и в найденный таким способом наибольший общий делитель.
А так как само собой ясно, что три ассоциированных с ним числа
тоже являются общими делителями, то всегда должны называться
наибольшими четыре и только четыре общих делителя, и их норма
является кратным каждого другого общего делителя.
Если разложение двух данных чисел на простые сомножители не
дано, то наибольший общий делитель находится при помощи алго-
алгоритма, подобного тому, который используется в случае веществен-
вещественных чисел. Пусть т, т — два заданных числа; последовательным
делением образуем ряд чисел т", т'",..., такой, что т!' является
абсолютно наименьшим вычетом числа т по модулю т , число т'" —
абсолютно наименьшим вычетом числа т по модулю т" и т. д.
Если нормы чисел т, т , т", т",... обозначить соответственно
через р, р, р\р",..., то рр будет нормой отношения т"/т ,
и потому, по определению абсолютно наименьшего вычета, будет
заведомо не больше чем 1/2; так же обстоит дело для р" 1р" и т. д.
Поэтому положительные вещественные целые числа р', р'\ р'\.. .
будут образовывать непрерывно убывающий ряд, так что в конце
концов мы обязательно придем к члену 0, или, что то же самое, в
/ « tit «
ряду т, т , т , т ,... в конце концов получится член, который
входит в предыдущий член без остатка. Пусть этот член есть J
и пусть
т = km' + m",
т' = к'тГ + т!'\
т'" = к"т!" + т"\
т(п)=
Если пройти этот ряд равенств в обратном порядке, то мы полу-
аим, что m(n+1) входит во все предшествующие члены т{п), ..., т",
т\ т. Если же пройти эти равенства в прямом порядке, то станет
Теория биквадратичных вычетов. II 715
ясно, что каждый общий делитель чисел т, т входит также и в каж-
каждое последующее число. Первое показывает, что m^nJrl) является
общим делителем чисел т> т , а второе —что этот делитель наи-
наибольший.
Если последний остаток m^n+1) окажется равным одной из четы-
четырех единиц 1, — 1, г, —г, то это будет указывать на то, что т и
т' взаимно просты.
47
Если равенства предыдущего пункта, за исключением послед-
последнего, скомбинировать между собой так, чтобы т", т!"', т"...,
исключились, то получается равенство вида
где h и К являются целыми числами, и притом, если использовать
обозначение, введенное в «Арифметических исследованиях», п. 27,
выполняются равенства
h = ±[kr, k\ &'",..., *<*-*>] = ^[Й:^-1), №-2),..., k", k'],
h'= + ]h, If, k\ Г #»-i>] = + [№-
таричем берутся верхние :или нижние знаки в зависимости от того,
четно п или нечетно. Эту теорему мы выскажем следующим обра-
образом.
Наибольший общий делитель двух комплексных чисел т, т' мо-
может быть представлен в виде hm + Km',где huh! являются целы-
целыми числами.
Очевидно, что это справедливо не только для того наибольшего
общего делителя, к которому приводит алгоритм предыдущето
пункта, но и для трех с ним ассоциированных, для которых вме-
вместо чисел h, h! нужно брать либо hi, h!i, либо — h, —/г', либо —hi%
—h'i.
Если поэтому числа иг, т' взаимно просты, то разрешимо урав-
уравнение
1 = hm + h'm\
716 Теория биквадратичных вычетов. II
Пусть, например, даны числа 31 -f Ы = т, 11 — 20г = т\ Мы
находим здесь
к = г, т" = + И — 5г,
V = + 1 — г, т* = + 5 — 4г,
Л* = + 2, т"" = + 1 + Зг\
кт = — 1 —2г, mm* = + i,
к"" = + 3 — г,
откуда
[к', к?',кт] = — 6 — Ы,
[Л, Л', **,*"] = +4—Юг,
и потому
т?г '""= г = F + 5г) m + D — Юг) т',
и
1 = E — 6г) т + (— 10 — 4г) т',
Это равенство легко можно проверить вычислением.
48
Изложенным до сих пор подготовлено все, что нужно для тео-
теории сравнений первой степени в арифметике комплексных чисел;
но так как эта теория не существенно отличается от соответству-
соответствующей теории в арифметике вещественных чисел, которая исчерпы-
исчерпывающе изложена в «Арифметических исследованиях», то будет
достаточно отметить здесь только основные моменты.
I, Сравнение mt =1 (mod m') эквивалентно неопределенному урав-
уравнению mt + т'и = 1, и если последнее удовлетворяется при значе-
значениях t = /г, и ;= h'\ то общее решение первого представляется в виде
t ==/г (mod яг'). Условие же разрешимости заключается в том, что
модуль т! не должен иметь с коэффициентом т общих делителей.
II. Решение сравнения ах + Ъ = с (mod М) в случае, когда а и М
взаимно просты, зависит от решения сравнения
Теория биквадратичных вычетов. II 717
и если второе сравнение удовлетворяется при t = h, то общее ре-
решение первого дается формулой
x = {c — b)h (modAf).
III. Сравнение ах + Ъ = c(modM) в случае, когда а и М имеют
общий делитель X, эквивалентно сравнению
а с — Ъ ? , М\
тж = —г— mod у- .
А А \ А /
Если поэтому за X взят наибольший общий делитель чисел а и
М, то решение заданного сравнения сводится к предыдущему слу-
случаю, и ясно, что условием, необходимым и достаточным для раз-
разрешимости сравнения, является то, что X входит также и в раз-
разность с — Ъ.
49
До сих пор мы излагали только элементарные вопросы, которые
однако, нельзя было опустить, не утратив связности изложения.
В более глубоких исследованиях арифметика комплексных чисел
оказывается подобной арифметике вещественных чисел в том отно-
отношении, что теоремы становятся проще и изящнее, если рассматри-
рассматривать только модули, являющиеся простыми числами; распростра-
распространение их на составные модули в большинстве случаев скорее
длинно, чем трудно^ и требует более технической работы, нежели
искусства. По этой причине в дальнейшем речь будет идти глав-
главным образом о простых модулях.
50
Если X обозначает функцию от переменной х вида
Ахп+ Вхп~1+ Схп-*+ ...
где п — вещественное положительное целое число, А, ?, С,...— ве-
вещественные или мнимые целые числа, и если т есть целое ком-
комплексное число, то мы также и здесь будем называть корнем срав-
сравнения X = 0(mod/n) каждое целое число, которое, будучи подстав-
подставлено вместо х, дает делящееся на модуль т значение функции X.
718 Теория биквадратичных вычетов. II
Решения при помощи корней, которые сравнимы по модулю, мы не
будем рассматривать как различные.
Если модуль является простым числом, то такое сравнение сте-
степени п также и здесь не может иметь больше чем п различных реше-
решений. Если ос обозначает любое определенное (комплексное) целое
число, то X посредством деления на х— а может быть представ-
представлена в виде X = (х — ос)Х'+/г, где h будет определенным целым
числом, а X'—функцией (п — 1)-й степени с целочисленными коэф-
коэффициентами. Если теперь а — корень сравнения X = 0 (mod m), то h,
очевидно, будет делиться на т, т. е. для каждого значения пере-
переменной х будет выполняться сравнение X = (х — ос) X' (modm).
Точно так же, если р обозначает некоторое определенное целое
число, то X' приводится к виду (х — $)X№-\-h', где X" является
функцией (п — 2)-й степени с целочисленными коэффициентами.
Если же мы предположим, что число р является корнем сравнения
Х==0, то оно должно также удовлетворять сравнению (р—а)Х'=0,
а, значит, и сравнению Х'==0, если корни ос, р несравнимы между
собой, откуда мы заключаем, что также и К должно делиться на
т, т. е. что должно быть X = (х — <х)(ж — p)X"(modm) при всех
значениях х.
Аналогичным образом, если имеется третий несравнимый с дву-
двумя первыми корень т, мы получаем, что X ={х—а)(ж—р)(ж—т) ^'">
где Хт является функцией (п — 3)-й степени с целочисленными
коэффициентами. Подобным же образом можно продолжать и дальше,
и, кроме того, ясно, что коэффициент старшего члена у каждой
функции будет равен числу Л, которое мы можем предполагать не
делящимся на т, так как иначе сравнение 1 = 0 по существу
имело бы меньшую степень. Если поэтому имеется п несравнимых:
между собой корней, именно, а, р, f,---» v» то ПРИ всех значениях
х выполняется сравнение
Х=вА (х — <х)(х — р)(ж — т) -• (х —
следовательно, подстановка каждого нового не сравнимого ни с
одной из величин а, р, у,..., v значения будет давать для X значе-
значение, не делящееся на тг откуда и следует справедливость нашей
теоремы.
Теория биквадратичных вычетов. II 719
Впрочем, это доказательство по существу совпадает с тем, ко-
которое мы провели в п. 43 «Арифметических исследований», отдель-
отдельные моменты которого имеют силу для комплексных чисел так же,,
как и для вещественных.
51
То, что в третьем разделе «Арифметических исследований» гово-
говорилось относительно степенных вычетов, с незначительными изме-
изменениями сохраняет силу также и в арифметике комплексных чисел;
в большинстве случаев могут быть сохранены даже доказательства
теорем. Однако, для того чтобы ничего не пропускать, мы хотим,
привести основные теоремы, снабженные краткими доказательствами,,
причем все время будет подразумеваться, что модуль является^
простым числом.
Теорема. Если к обозначает целое число, не делящееся на мо-
модуль т, норма которого равна р, то №—1 == 1 (modm).
Доказательство• Пусть а, Ь, с,... образуют полную систему не-
несравнимых между собой вычетов по модулю т, из которой, однако,
выброшен вычет, делящийся на т, так что количество этих чисел,
совокупность которых мы обозначим через С, равно р — 1. Пусть,
далее, С"—совокупность произведений kaf kb, he,... По предполо-
предположению ни одно из этих произведений не делится на т, и потому
каждое из них имеет сравнимый с ним вычет в совокупности Сг
так что можно положить ak==a\ bk = b\ ck = c',... (modm), где
числа а', Ь', с',.-- содержатся в совокупности С. Совокупность чисел
а\ Ь', с',... мы обозначим через С". Пусть, далее, Р, Р\ Р" явля-
являются произведениями отдельных чисел совокупностей С, С", С", т. е-
Р =abc...,
Так как числа совокупности С" последовательно сравнимы с чис-
числами совокупности С", то Р"=Р' или .Р'еее АР-1.?. Но так как лег-
легко видеть, что каждые два числа совокупности С" несравнимы,.
720 Теория биквадратичных вычетов. II
и потому все они различны между собой, то числа совокупности
С" обязательно будут совпадать с числами совокупности С,
только взятыми в измененном порядке, и потому Р"= Р. Следо-
Следовательно, число (к'Р-1—1)Р делится на т, для чего необходимо,
так как т является простым числом, не входящим в отдельные
делители числа Р, чтобы кр~г— 1 делилось на т.
25
Теорема. Если, как и в предыдущем пункте, к обозначает целое
число, не делящееся на модуль т, a t — наименьший показатель (не
считая нуля), для которого kl= I (modm), то t является делите-
делителем всякого другого показателя и, для которого ки = 1 (mod m).
Доказательство. Если предположить, что t не является делите-
делителем числа и, то пусть gt будет кратностью числа t, которая явля-
является первой, большей чем и, так что gt — и есть целое положитель-
положительное число, меньшее чем t. Из №=1, ки==1 следует,что 0==к&—ки=
==ки(к81—и—1), и потому №г—и == 1 т.е. существует степень числа к
с показателем, меньшим чем t, которая сравнима с единицей. Но
это противоречит предположению.
Как следствие отсюда вытекает, что t заведомо делит р—1.
Такие числа tt для которых t = р — 1, мы будем и здесь назы-
называть первообразными корнями по модулю т. Сейчас мы покажем,
что они действительно существуют.
53
Разложим число р — 1 на его простые сомножители:
р — 1 =а« fcPcY...,
где а, 6, с,... обозначают различные между собой положительные
вещественные простые числа. Пусть, далее, А, Ву С,...— целые (ком-
(комплексные) не делящиеся на т числа, которые не удовлетворяют
соответственно сравнениям
x(V—l)/a== 1? X(V—1)/Ь= 1 ж(р—1)/с=== 1?...;
Теория биквадратичных вычетов. II 721
то, что такие числа существуют, очевидно на основании теоремы
п. 50. Наконец, пусть h сравнимо по модулю т с произведением
Тогда я утверждаю, что h является первообразным корнем.
Доказательство. Если обозначить через t показатель наинизшей
сравнимой с единицей степени Ы, то из предположения, что h не
является первообразным корнем, следовало бы, что t является де-
делителем числа р—1, т. е. что число (р—l)/t было целым, боль-
большим чем 1 числом.
Очевидно, что вещественные простые сомножители этого целого
числа содержатся среди чисел а, Ъ, с,... Предположим поэтому
(что допустимо), что (р—l)/t делится на а и положим р—1 =atu.
Вследствие того, что ht:=l, тогда также и htU:=l, т. е.
р—1 р—1 р—1 р—1 р—1 р—1
А а<х а -В ъ® а -С с'{ а ... = 1.
Но очевидно, что (р—1)/а№ является целым числом, и потому
р—1 р—1
В bP ' а = (^-1)^-1)/^=^
так же, как
р—1 Р—1
С cY ' с =1,
и т. д. Поэтому должно быть
р—1 р—1
А а* а /|
Выберем теперь такое положительное целое число X, что
Х№с*...= 1 (mod а),
что возможно, ибо простое число а не входит делителем в число
Ь$сг..., и положим \№сч...= 1-f а[х. Тогда, очевидно> будет выпол-
ня1ься сравнение
—1
а л -ч Р—-1 Р—1
е^1, или, так как X» >— =
722
Теория биквадратичных вычетов. II
V—1
откуда следует, так как А&—^^I, что и A^—V^e^I, а это про-
противоречит предположению. Следовательно, предположение о том,
что t является делителем числа р — 1, не может быть справедли-
справедливым, и потому h обязательно является первообразным корнем.
54
Если h обозначает первообразный корень по модулю т, норма
которого равна р, то члены ряда
1, /г, /г2, /г3,...,/г^-2
будут попарно несравнимы между собой, откуда легко следует, что
каждое целое число, не делящееся на модуль, должно быть срав-
сравнимо с одним из указанных чисел, т. е. что этот ряд представляет
полную систему несравнимых вычетов, за исключением нуля. По-
Показатель той степени, с которой сравнимо заданное число, может
быть назван индексом этого числа, если h рассматривается как ос-
основание. Мы приведем сейчас несколько примеров, причем рядом
с каждым индексом будет указываться абсолютно наименьший вычет.
Первый пример
т = 5 -f- 4г, р = 41, h = 1 + 2г
о
И
1
К
0
1
2
3
4
5
6
7
Вычет
+1
+ 1+2г
+1- i
+3+ г
—2г
+Зг
—2—2г
—2— i
О
CD
I
Я
8
9
10
11
12
13
14
15
Вычет
4
— 3+ i
+ 2- г
— 1— г
+1—Зг
— 2
+ 3
О
нч
CU
«
ш
К
16
17
18
19
20
21
22
23
Вычет
—2+2г
—1+2г
+4/
+1 + Зг
—1
—1—2г
-1+ г
—3— г
О
со
s
24
25
26
27
28
29
30
31
Вычет
+ 2г
— Зг
+2+2г
+2+ г
+4
+3— г
+ i
-2+ i
о
И
Я
S
32
33
34
35
36
37
38
39
Вычет
+ 1+ i
+ 1+Зг
+2
—3
+2—2г
+1—2г
—4г
—1—Зг
Теория биквадратичных вычетов. II
723
Второй пример
т = 7, р = 49, А = 1 + 2г
о
I
0
1
2
3
4
5
6
7
8
9
Вычет
+ i
+1+2г
—3—Зг
+3—2г
—Зг
—1—Зг
—2+2г
+1—2г
—2
—2+Зг
О
CD
S
10
11
12
13
14
15
16
17
18
19
Вычет
—1— г
+1—Зг
— г
+ 2- г
—З+Зг
—2—Зг
2
-3+ г
+2+2J
-2- г
ндекс
S
20
21
22
23
24
25
26
27
28
29
Вычет
+2г
+3+2г
1 _! т
—3— г
—1
—1— 2г
+3-t-3i
-3+2г
-f Зг
+1+Зг
О
1
s
30
31
32
33
34
35
36
37
38
39
Вычет
+2—2г
—1+2г
+ 2
+2—Зг
+1+ г
—1+3»
+ i
-2+ г
+3—Зг
+2+Зг
О
S
ВС
и
Н
40
41
42
43
44
45
46
47
Вычет
+з
+3- г
—2—2г
+2+ г
—2г
—0 ' ' Zd Ъ
+1- i
+3+ г
55
Относительно первообразных корней и алгоритма индексов мы
добавим еще некоторые замечания, однако доказательства, вслед-
вследствие их легкости, опустим.
I. В заданной системе индексы, сравнимые по модулю р — 1,
соответствуют вычетам, сравнимым по модулю т, и обратно.
И. Вычеты, соответствующие индексам, взаимно простым с чис-
числом р—1, тоже являются первообразными корнями, и обратно.
III. Если t является индексом первообразного корня /г', когда
за основание взят первообразный корень /г, и наоборот, t' является
индексом числа /г, когда за основание взято число /г', то U'' =
= l(mod/?—1); и если при тех же предположениях индексы какого-
нибудь другого числа в этих двух системах равны соответственно
и и и\ то tu'=u9 t'u^u' (modp—1).
IV. Если числа 1, 1+i и ассоциированные с ними исключить
(как слишком тривиальные) из числа рассматриваемых модулей, то
останутся те простые числа, которые в п. 34 были указаны под
724 Теория биквадратичных вычетов. II
рубриками 3 и 4. Нормами последних являются вещественные простые
числа вида 4п + 1, нормами же первых — квадраты нечетных веще-
вещественных простых чисел; таким образом, в обоих случаях р — 1
делится на 4.
V. Если обозначить индекс числа—1 через и, то 2^ = 0 (mod/?—1)
и потому либо ц = 0, либо w=— (р—1). Но так как индекс 0
соответствует вычету + 1, то индекс числа —1 обязательно должен
быть равен -к- (р — 1).
VI. Если точно так же обозначить через и индекс числа i, то
будет выполняться сравнение 2и = у (р — 1) (mod р — 1), и потому
1 3
либо и==-т-(р — 1), либо и=-у-(р — 1). Какая из этих двух воз-
возможностей осуществляется в действительности, зависит от выбора
первообразного корня. Именно, если для взятого в качестве осно-
основания первообразного корня h индекс числа г равен -г(р — 1), то
индекс будет равен -т-(р — 1), когда за основание берется число/г^,
где (л обозначает положительное, взаимно простое с р — 1 целое
число вида 4п+3 (например, само число р — 2), и обратно. По-
Поэтому одна половина первообразных корней дает для числа i ин-
1 3
деке -г (р—1), а другая половина — индекс -г(р — 1), и очевидно,
что число — i будет для первых оснований обладать индексом
3 1
-т(р — 1), а для вторых — индексом -т-(р — 1).
VII. Если модулем является положительное вещественное про-
простое число вида An + 3, например, равное q, так что р = д2, то
индексы всех вещественных чисел будут делиться на q + 1. Дей-
Действительно, если t обозначает индекс вещественного числа к, то
в силу соотношения kq—1=l(modg) выполняется сравнение (q—1J=
= 0(modg2—1), и потому число t/(q + 1) является целым. Точно
так же индексы чисто мнимых чисел вида М делятся на (q + l)/2.
Поэтому очевидно, что первообразные корни для таких модулей
следует искать только среди смешанных мнимых чисел.
Теория биквадратичных вычетов. II 725
VIII. Напротив, для модуля т, являющегося смешанным ком-
комплексным простым числом (нормой которого, следовательно, служит
вещественное простое число вида 4п + 1), любые первообразные
корни могут быть выбраны среди вещественных чисел, так как среди
них можно найти даже полную систему несравнимых вычетов (п. 40).
Но очевидно, что каждое вещественное число, которое является пер-
первообразным корнем по комплексному модулю т, будет одновре-
одновременно и первообразным корнем по модулю р в арифметике веществен-
вещественных чисел, и обратно.
56
Хотя теория квадратичных вычетов и невычетов для арифметики
комплексных чисел содержится в теории биквадратичных вычетов,
мы, однако, прежде чем перейти к последней, отдельно приведем
здесь основные теоремы первой теории; но при этом ради краткости
мы будем говорить только об основном случае, когда модуль является
комплексным (нечетным) простым числом.
Пусть т — такой модуль, и р — его норма. Очевидно, что всякое
целое (и, как здесь все время будет предполагаться, не делящееся
на т) число может или не может быть сравнимо по модулю т с неко-
некоторым квадратом в зависимости от того, четным или нечетным будет
его индекс, если за основание взять произвольный первообразный
корень; в первом случае это целое число называется квадратичным
вычетом, а во втором — квадратичным невычетом по модулю т.
Отсюда следует, что среди р — 1 чисел, представляющих полную
систему несравнимых (не делящихся на т) вычетов, половина будет
относиться к квадратичным вычетам, а половина — к квадратич-
квадратичным невычетам. Всякое же другое число, не содержащееся в этой
системе, имеет в этом отношении тот же характер, что и сравнимое
с ним число системы.
Далее, отсюда следует, что произведение двух квадратичных
вычетов, так же, как и произведение двух квадратичных невычетов,
является квадратичным вычетом, а произведение квадратичного
вычета на квадратичный невычет — квадратичным невычетом; и во-
вообще, произведение любого числа сомножителей будет квадратичным
726 Теория биквадратичных вычетов. II
вычетом или невычетом в зависимости от того, четно или нечетно
число невычетов среди этих сомножителей.
Для того чтобы различать квадратичные вычеты от квадратич-
квадратичных невычетов, мы сразу получаем следующий общий критерий.
Число к, не делящееся на модуль, является по нему квадратич-
квадратичным вычетом или невычетом в зависимости от того, имеет ли место
л<р-1Уй =_! или &(р-1)|2 =__! (mod my
Справедливость этой теоремы немедленно следует из того, что при
выборе за основание произвольного первообразного корня индекс
степени k{v~1)/2 будет или =0, или =V2(p — 1), смотря по тому, четен
или нечетен индекс числа к.
57
Итак, для заданного модуля легко разбить полную систему не-
несравнимых вычетов на два класса, именно, на квадратичные вычеты
и невычеты, чем одновременно определяется, к каким классам отно-
относятся и все остальные числа; однако намного труднее вопрос о кри-
критериях, при помощи которых те модули, по которым заданное число
является квадратичным вычетом, можно отличать от модулей, по
которым оно является невычетом.
Что касается вещественных единиц +1 и —1, то они в арифме-
арифметике комплексных чисел сами являются квадратами, а потому и квад-
квадратичными вычетами по каждому модулю. Точно так же из критерия
предыдущего пункта легко видеть, что число i (а также и — i) яв-
является квадратичным вычетом по каждому модулю, норма которого
р имеет вид 8п + 1, и невычетом по каждому модулю, норма кото-
которого имеет вид 8п + 5. Так как, очевидно, безразлично, брать ли
за модуль число тили одно из ассоциированных с ним чисел шг,—т,
— im, to можно считать, что модулем является первичное число
среди ассоциированных (п. 36, II), т. е., что если модуль равен
а + bi, то а нечетно, а Ъ четно. Так как вследствие этого всегда
а2= 1 (mod 8), а Ь2 или^О, или =4 (mod 8), в зависимости от того,
делится Ъ на 4, или не делится, то числа + i и — i будут, очевидно,
в первом случае квадратичными вычетами, а во втором— квадратич-
квадратичными невычетами по модулю а + Ы.
Теория биквадратичных вычетов. II 727
58
Так как вопрос о характере составного числа, т. е. о том, является
ли оно квадратичным вычетом или невычетом, сводится к вопросу
о характерах сомножителей, то очевидно достаточно ограничиться
выводом критериев для отличия тех модулей, по которым заданное
число к является квадратичным вычетом, от тех, по которым оно
является квадратичным невычетом, для тех значений к, которые
являются простыми числами и, кроме того,— первичными среди
ассоциированных с ними. При этом индуктивное рассмотрение тот-
тотчас же дает нам очень изящные теоремы.
Если начать с числа 1 + /, то мы найдем, что оно является квад-
квадратичным вычетом по модулям
— 1+2/, + 3 — 2/, — 5 — 2/, — 1 — 6/, + 5 + 4/,
+ 5-4/, — 7, + 7 + 2/, — 5 + 6/,...,
и, напротив, квадратичным невычетом по модулям
_1_2г,—3, +3+2/, +1+4*, + 1-4/, -5+2/, -1 + 6/, +7-2/,
—5—6г, -3+8/, —3—8/, +5+8/, +5—8/, +9+4/, +9—4/,...
Если мы внимательно рассмотрим этот обзор, при котором из
каждых четырех ассоциированных модулей мы все время брали
первичный, то мы легко заметим, что все модули а + Ы в первом
классе обладают тем свойством, что для них а + Ъ = +1 (mod 8), а
во втором классе—тем свойством, что для них а + 6 = — 3(mod8).
Очевидно, что если вместо первичного модуля т брать ассоцииро-
ассоциированный с ним модуль — т, то этот критерий нужно будет изменить
таким образом, что для модулей первого класса а + 6 ===— 1, a
для модулей второго класса а + Ъ = + 3 (mod 8). Поэтому, если
наше индуктивное заключение верно, и если а + Ы обозначает про-
простое число, для которого а нечетно, а Ъ четно, то вообще 1 + /
будет квадратичным вычетом или невычетом по нему в зависимости
от того, имеет ли место а + Ъ == + 1 или == + 3 (mod 8).
728 Теория биквадратичных вычетов. II
Для числа — 1 — / выполняется то же правило, что и для
Если же число 1 — i рассматривать как произведение чисел —i и
1 + г, то ясно, что число 1 — / имеет тот же характер, что и 1 + /г
если Ъ делится на 4, и противоположный, ебли Ъ не делится на 4,
откуда легко видеть, что 1 — / является квадратичным вычетом по
простому числу а + Ы, если а — Ь = + 1, и квадратичным невыче-
невычетом, если а — Ъ == + 3 (mod 8), все время в предположении, что а
нечетно, а Ъ четно.
Впрочем, эта вторая теорема может быть выведена из первой
также и при помощи одной более общей теоремы, которую мы вы-
выскажем следующим образом.
В теории квадратичных вычетов характер числа а + Р* по от-
отношению к модулю а + Ы тот же, что и характер числа а — р*
по отношению к модулю а — Ы.
Доказательство этой теоремы получается из того, что оба моду-
модуля имеют одну и туже норму р, и из того, что если (а+Р0(р~~1)/2—1
делится на а + Ы, то и (ос — рг)^~№— 1 делится на а — bi, a если
(а + рг)(р-1)/й+ 1 делится на а + Ы, то и (ос — pi)(p-D/2-|- 1 должно
делиться на а — Ы.
59
Теперь мы переходим к другим нечетным простым числам.
Мы находим, что число—1+2г является квадратичным вычетом
по модулям
+3+2г, +1—4г, — 5+2г, —5—2г, —1—6г, +7—2гг
-3+8г, +5+8/, +5—8г,
и квадратичным невычетом по модулям
—1—2г\ —3, +3—2г, +l+4f, —1 + 6г, +5+4г, +5—4f,
—7, +7+2г, —5+6г, —5—6/, —3—8/, +9—4/,...
Если привести модули первого класса к их абсолютно наимень-
наименьшим вычетам по модулю—1 + 2/, то мы получим только вычеты+1
Теория биквадратичных вычетов. II 729
и —1; именно, +3+2/ = —1, +1— Ai=—1, —5+2/=+1, —5—2/=
==—1, и т. д.
С другой стороны, мы находим, что все модули второго класса
по модулю—1 + 2/ или=+/, или =—/.
Но + 1 и — 1 сами являются квадратичными вычетами по мо-
модулю — 1+2/, а + i и — / — квадратичными невычетами по нему.
Поэтому, если верить индуктивному заключению, то получается
следующая теорема.
Число—l-\-2i является квадратичным вычетом или невычетом
по простому числу а + Ы в зависимости от того, будет ли последнее
квадратичным вычетом или невычетом по числу —1+2/, в предпо-
предположении, что а + Ы является первичным среди четырех ассоцииро-
ассоциированных чисел, или, точнее, что а нечетно, а Ъ четно.
Далее, из этой теоремы немедленно вытекают аналогичные тео-
теоремы относительно чисел +1—2/, —1—2/, + 1+2/.
60
Если мы проведем подобное же индуктивное исследование отно-
относительно числа —3 или +3, то найдем, что каждое из них является
квадратичным вычетом по модулям
+3 + 2г\ +3 —2i\ -l+6i, —1 —6г, —7, —5 + 6г,
—5 — 6/, —3 + 8/, —3 — 8/, +9 + 4/, +9 — 4/,...,
и квадратичным невычетом по модулям
—1 + 2/, —1 — 2/, +1+4/,+1 —4/, —5 + 2/, —5 — 2/,
+ 5+4/,+5-4/,+7 + 2/, +7-2/, +5 + 8/, +5-8/,...
Первые сравнимы по модулю 3 с одним из четырех чисел +1,
—1, +/, —/, вторые же — с одним из четырех чисел +1 + /,
+ 1 — г, —1 + /, —1 — /. Первые сами являются квадратичными
вычетами, последние же — квадратичными невычетами по моду-
модулю 3.
730 Теория биквадратичных вычетов. II
Поэтому наша индукция показывает, что простое число а + Ы
(все время в предположении, что а нечетно, а Ъ четно) так же отно-
относится к числу —3 (и к числу +3), как второе относится к первому
(имеется в виду вопрос о том, является ли одно число квадратичным
вычетом или невычетом другого).
Если подобным же индуктивным способом рассмотреть другие
простые числа, то везде мы обнаружим этот в высшей степени изящ-
изящный закон взаимности и придем, таким образом, к следующей фунда-
фундаментальной теореме относительно квадратичных вычетов в ариф-
арифметике комплексных чисел.
Если а + Ы, A + Bi обозначают простые числа с тем свойством,
что а, А нечетны, а Ь, В четны, то или каждое из этих чисел будет
квадратичным вычетом по другому, или каждое — квадратичным
невычетом.
Несмотря на исключительную простоту этой теоремы, доказа-
доказательство ее представляет очень большие трудности, на которых мы,
однако, не будем здесь задерживаться, так как сама теорема является
лишь частным случаем более общей теоремы, которая содержит в
себе всю теорию биквадратичных вычетов. К ней мы поэтому теперь
и переходим.
61
То, что в п. 2 сочинения первого говорилось относительно по-
понятий биквадратичного вычета и невычета, мы перенесем также и на
арифметику комплексных величин, причем, как и раньше, ограни-
ограничимся рассмотрением модулей, являющихся простыми числами;
одновременно, в большинстве случаев без особого упоминания,
будет предполагаться, что за модуль берется первичное среди ассо-
ассоциированных чисел, т.е. число, сравнимое с 1 по модулю 2+2г\ и,
кроме того, что числа, о характерах которых (т. е. о том, являются
ли они биквадратичными вычетами или невычетами) идет речь, не
делятся на модуль.
Для заданного модуля не делящиеся на него числа можно было
бы разбить на три класса, первый из которых содержал бы биквад-
ратичные вычеты, второй — те биквадратичные невычеты, которые
являются квадратичными вычетами, и третий — квадратичные
Теория биквадратичных вычетов. II 731
невычеты. Однако нам будет удобнее разбить третий из этих классов
на два, так что всего получится четыре класса.
Если взять за основание какой-нибудь первообразный корень,
то биквадратичные вычеты будут иметь индексы, делящиеся на 4,
т. е. имеющие вид 4тг; те невычеты, которые являются квадратичны-
квадратичными вычетами, будут иметь индексы вида An + 2; наконец, среди ква-
квадратичных невычетов часть будет иметь индексы вида 4п + 1»а часть-
индексы вида An + 3. Таким образом, действительно получаются че-
четыре класса; однако различие между двумя последними классами
является не абсолютным, а зависит от первообразного корня, вы-
выбранного за основание; действительно, легко видеть, что для одной
половины первообразных корней заданный квадратичный невычет
имеет индекс вида Ап-\-1, а для другой половины — индекс вида
An + 3. Чтобы избежать этой неопределенности, мы будем предпо-
предполагать, что всегда выбирается такой первообразный корень, для
которого индекс (р —1)/4 принадлежит числу + i (ср. п. 55, VI).
Таким образом, получается разбиение на классы, которое без помо-
помощи первообразных корней можно более коротко описать следующим
образом.
Первый класс содержит те числа А, для которых &(p—i)/4=1; эти
числа являются биквадратичными вычетами по модулю.
Второй класс содержит те числа, для которых k(^p~1^u^i.
Третий класс содержит те числа, для которых &(р—i)/4=— 1.
Четвертый класс содержит те числа, для которых &(р—D/%^—i.
Третий класс будет содержать биквадратичные невычеты, явля-
являющиеся квадратичными вычетами; на второй и четвертый классы
подразделяются квадратичные невычеты.
Числам этих классов мы будем сопоставлять соответственно
биквадратичные характеры 0, 1, 2, 3. Если мы определим характер
X числа к по модулю т так, что он должен совпадать с показате-
показателем той степени числа i, с которой сравнимо число k^—W*, то оче-
очевидно, что характеры, сравнимые по модулю 4, следует рассматри-
рассматривать как эквивалентные. Впрочем, пока это понятие вводится
только для модулей, являющихся простыми числами; в продолже-
продолжении этих исследований мы покажем, как его можно обобщить и на
составные модули.
732 Теория биквадратичных вычетов. II
62
Чтобы можно было легче прийти к индуктивному заключению^
относительно характеров модулей, мы даем объемистую таблицу.
при помощи которой можно будет сравнительно легко найти харак-
характер любого заданного числа по отношению к модулю, норма которого
не больше чем 157, если иметь в виду следующие замечания.
Так как характер составного числа равен (или сравним по мо-
модулю 4) сумме характеров отдельных сомножителей, то достаточна
уметь определять для заданного модуля характеры простых чисел ^
Так как, далее, характеры единиц—1, +г, —i, очевидно, сравнимы
по модулю 4 соответственно с числами (р—1)/2, (р—1)/4, 3{р—1)/4у
то будет достаточно указать характеры только первичных чисел
среди ассоциированные Так как, наконец, числа, сравнимые по
модулю т, имеют один и тот же характер, то достаточно занести,
в таблицу характеры тех чисел, которые содержатся в системе аб-
абсолютно наименьших вычетов. Кроме того, при помощи рассужде-
рассуждений, аналогичных рассуждениям п. 58, можно доказать, что если
для модуля а + Ы характер числа А + Bi равен X, а для модуля
а—Ы характером числа А — Bi является X', то всегда Х=—X'(mod4)y
т. е. X -f- X' делится на 4; поэтому в таблице нужно помещать
только те модули, у которых Ъ или равно 0, или положительно *
Если, например, отыскивается характер числа 11 — Ы по отноше-
отношению к модулю —5 — 6г, то вместо этих чисел мы подставляем числа
11-f Ы и —5+6г, затем определяем (п. 43) абсолютно наименьший
вычет числа 11 -f-6г по модулю—5 + 6г, который оказывается рав-
равным —1 — 4i = — 1 • A + 40- Поэтому, так как для модуля — 5 + Ы
характер числа — 1 равен 30, а характер числа 1 + 4?, согласна
таблице, равен 2, то число 32 (или 0) будет характером числа
11 + Ы для модуля-—5 + 6г, а потому, согласно последнему замеча-
замечанию, также и характером числа 11—Ы для модуля—5—Ы. Точ-
Точно так же, если отыскивается характер числа—5--f-6i по отношению к
модулю ll+6i, то абсолютно наименьший вычет первого, равный
1—5i, разлагается на сомножители — г, 1 + i, 3 — 2г, которым соот-
соответствуют характеры 117, 0, 1, так что искомый характер равен
118 или 2; такой же характер имеет и число—5—Qi по отноше-
отношению к модулю 11 — 6г.
Теория биквадратичных вычетов. II
733
Модуль
о
+ 3 + 2i
+ l + 4i
— 5 + 2i
—1 + 6i
+5 + 4i
— 7
+7 + 2i
—5 + 6i
Харак-
Характер
3
3
1
3
0
1
2
0
1
2
0
1
3
0
1
2
3
0
1
2
3
0
1
2
3
Числа
l + i
l+i
— 1 + 2i
l + i
A 9/
l + i
з
1 + i, —1 + 2i
— 1—2i
l + i
— 3
— 1 + 2i, — 1 — 2i
— 3
— 1 + Zi, 6 — Zi
— 1 — 2i, 3 + 2i
l + i, 3 + 2i, 3 — 2i, 1 — 4i
— 3
— 1 — 2i, 1 + 4i
— 1 + 2i
1 + i, —3, 3 + 2i, 3 — 2i
1 —4i
_ l + 2i, —1 — 2i
734
Теория биквадратичных вычетов. II
Модуль
Q 1 Q7'
—0 —р ос
—\~ О —{— о 1
+9 + 4г
—1 + Юг
+3 + 10г
-7 + 8г
й
СЗ
ПЗ Он
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
1
2
3
0
1
2
3
— 1
1
— 3
— 1
— 1
— 5
— 1
1
_!
1
— 3
1
1
— 3
3
1
1
— 3
— 1
1
3
— 1
1
+ 2г
+ г,
-2г,
-2г
-2г,
+ 2г.
+ i, -
+ 2г,
+ г,
, 1 -f
-4г,
+ г,
— 2г,
+ 4г,
+ i,
, з +
+ 2г,
+ i,
+ 2i,
-2г,
+ 2г
Числа
3 —2г, 1 —4г
3 + 2г
1 -+¦ 4г, — 5 + 2г
—1 + 6г
3 —2г
-3, 3 + 2г. 1+4г,1 —4г
3 + 2г
—1 —2г, 3—2г
4г
— 5 + 2г
— 1 +2г, —1 — 2г, 3+2t
_5 -| 2г, 5 — 4г
1—4г
— 1 — 2г, 1 — 4г
2г, 1 + 4г, — 5 — 2г
3 —2г
7
3 —2г, 1 —4г, — 5 — 2i
1 _|_ 4г, —5+2г, — 1—6г
- 3, — 1 + 6г
Теория биквадратичных вычетов. II
735
Модуль
—и
—11 + 4г
+ 7 + Юг
+ 11 + 6г"
1рак-
X g
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
—3
1+г,с
—1 +
3 +
1 +
_1_
—5 +
-3,3
1 +
—1 +
1 +
—1 —
1+1
_1_
—5 —
-5 +
5 —
2г,
2г,
Числа
2г\ 1 + 4г,
— 1 — 2г
—5 + 2г, 5 +4г
1 — 4г, —5 — 2г, 5 — 4г
г, -1 + 2г,
2г,
2г
<
4г,
2г,
2*\
2г,
2г,'
2г,
—1 + 6г
И, 1 + 4г,
1-4г,-
3 + 2г, -
-3, -5
1+2г\-3,
3 + 2г, 3
-1 +6г,
5 + 4г, 7
3 + 2г, 5 + 4г
1 — 4г, —5—2г
1 -\ 6г, —1—6г
-5 + 2г
— 2г
1+4г,1—4г",—7
5 —4г
— 2г.
63
Теперь мы хотим попытаться получить индуктивным путем
общие критерии для модулей, по которым заданное простое число
имеет один и тот же характер. Мы все время предполагаем, что мо-
модули являются первичными среди ассоциированных с ними чисел,
т. е. имеют вид а + bi, где или а =1,6=0 или а=3, Ъ =2 (mod 4).
В отношении числа 1 + г, с которого мы начнем, на индуктивный
закон натолкнуться будет легче, если мы отделим модули первого
типа (для которых а = 1,& = 0) от модулей второго типа (для
которых а = 3, 6 = 2). При помощи таблицы предыдущего пункта мы
находим, что
736
Теория биквадратичных вычетов. II
характер
соответствует модулям первого типа
О
1
2
3
5 + 4г, —7 + 8г, —7 — 8г\ —И + 4г
1 — 4г, —3 + 8г, —3 — 8г, 9 -f- 4г, —И
5 —4г, —7, —11 — 4z
— 3, 1+4г, 5 + 8г, 5 — 8г, 9 — 4г
Если внимательно рассмотреть эти шестнадцать примеров, то мы
найдем, что каждый раз характер = -г {а— Ь—I)(mod4).
Точно так же
характер
0
1
2
3
3
—5
_1
— 1
-2г,
+ 2г,
+ 2i,
-2i,
соответствует
— 1 — 6г, 7 -
—1 _|_ бг, 7 -
—5 —2г, 3-
3-Ь2г", —5
модулям второго типа
f 2г, ¦
-2i,
-Юг
-Ы,
— 5+6г, —l-t-Юг,
—1
7-
7-
— Юг, 3 + К
-ЬЮг
-Юг, 11 —6г
11+бг
Во всех этих двадцати примерах мы при некоторой внимательно-
сти замечаем, что характер = -г{а — Ъ — 5)(mod4).
Оба эти правила легко можно объединить в одно, имеющее силу
для модулей обоих типов, если учесть, что число Ь2/4 для модулей
первого типа = 0, а для модулей второго типа = 1 (mod 4). Поэтому
характер числа 1 + * по отношению к каждому простому и пер-
первичному среди ассоциированных с ним чисел модулю будет
zzri. (а _ ь — 1 — b2) (mod 4).
Попутно мы хотим здесь заметить, что так как (b -f- 1J всегда
имеет вид 8п -f- 1, т. е. число BЬ + 62)/4 всегда четно, то указан-
указанный характер всегда будет четным или нечетным в зависимости
от того, четно или нечетно число (а + Ъ —1)/4, что согласуется с
указанным в п. 58 правилом для квадратичного характера
Теория биквадратичных вычетов. II
737
1 1
Так как числам (а — Ъ — 1), ^(а — 6 + 3) являются целыми, и
одно из них четно, а другое нечетно, то их произведение четно, и
потому выполняется сравнение щ (а — Ъ — 1) (а — Ъ + 3) = 0 (mod 4).
Поэтому вместо данного выше выражения для биквадратичного ха-
характера может быть взято также и следующее:
~(а — Ъ—
Ъ2)
b—
= ~(— а2+ 2аЪ —
эта форма предпочтительнее потому, что при ней не нужно огра-
ограничиваться лишь первичными модулями, а нужно предполагать
только, что а нечетно, а Ъ четно; действительно, при этом предпо-
предположении одно из чисел а-\-Ы или а — Ы, очевидно, будет первич-
первичным среди ассоциированных, а значение указанной формулы для
обоих этих чисел будет одинаковым.
64
Исходя из последнего найденного в предыдущем пункте пра-
правила, мы видим, что
для
числа
1-1-
характер ее
-~(a2-+2ab — 62 — 1)
-|- (— а2 + 2а6 + б2 + 1)
-тг- (а2 4- 2а6 + 362 — 1^
Это тотчас же следует из того, что для числа i характер
1 11
~ (а2 + Ъ2 — 1), а для числа — 1 характер =^ (а2 + Ъ2 — 1)= -Ь2,
так как а2—1 всегда имеет вид 8п. Очевидно, что хотя эти четыре
правила и получены пока на основании индуктивных заключений,
но связаны между собой они так, что если будет получено доказа-
доказательство одного из них, то тем самым будут доказаны и осталь-
738
Теория биквадратичных вычетов. II
ные. Едва ли нужно напоминать, что и в этих правилах предпо-
предполагается только, что число а нечетно, а число Ъ четно.
Если желательно использовать формулы, применимые только к
первичным модулям, то можно использовать следующую схему.
Для
числа
— 1 — i
характера
(— а — г> -Ь 1 —б2)
(a-b-1 + b*)
{—a — b+1+b2)
Наиболее простые формулы получаются, если, как мы это дела-
делали в начале нашего индуктивного рассмотрения, различать модули
первого и второго типа. Именно, характер
числа
1-М
1 — i
для модулей первого
типа сравним с
1
±(а-Ь-1)
для модулей второго
типа сравним с
4
65
Для числа — 1 -f 2г, к которому мы теперь переходим, мы то-
тоже хотим делать различие между теми модулями а + Ы, для кото-
которых а = 1, ?> = 0, и теми, для которых а = 3, 6 = 2. Таблица п. 62
показывает, что в отношении этого числа
Теория биквадратичных вычетов. II
739
характер
0
1
2
3
— 3
+ 1
+ 1
— 3
соответствует
+ 8/,
+ 4/,
-4/,
, +5-
+ 5
+ 5
+ 5
h4/,
— 8/
— 4/
+ 8/
+ 9
модулям
, +9 +
, -7, -
7
-4/, -
первого типа
4/,
-3
8/,
-7
— И +
— 8/
— И
+ 8/, -
4/
11—4/
Если привести эти отдельные модули к абсолютно наименьшим
вычетам по модулю — 1 -J- 2г, то мы заметим, что все те модули,
которым соответствует характер 0, сравнимы с 1; те, которым со-
соответствует характер 1, сравнимы с г; те, характером которых яв-
является 2, сравнимы с —1; наконец, те, характером которых яв-
является 3, сравнимы с —i. Но характерами чисел 1, i, —1, —i
для модуля — 1 + 2г как раз и являются соответственно числа О,
1, 2, 3; таким образом, во всех этих семнадцати примерах харак-
характер числа —1+ 2i по отношению к модулю а + Ы первого типа совпа-
совпадает с характером числа а + Ы по отношению к модулю — 1 + 2г\
Точно так же при помощи таблицы мы находим, что
характер
соответствует модулям второго типа
О
1
2
3
+ 3 + 2/, — 5 — 2/, — 1 + '.
_|_ 3 — 2/, —1 + 6/, — 5 — i
— 5 + 2г, — 1 + 6г, +7 — 2^'
— 1—2г, +7+2г, —5+6г, +3+10/, +3—10/, +11—6*
Н, — 1 — Юг, +11 + 6f
, +7 + 10/, +7—10/
Если привести эти модули к их абсолютно наименьшим выче-
вычетам по модулю — 1 + 2г, то мы увидим, что все модули, которым
соответствуют характеры 0, 1, 2, 3, сравнимы соответственно е
числами —1, —г, +1, + г; но если, наоборот, взять за модуль-
число — 1 + 2г, то сами эти числа будут соответственно иметь ха-
характеры 2, 3, 0, 1. Таким образом, во всех этих девятнадцати
примерах характер числа — 1 + 2г по отношению к модулю второ-
второго типа отличается от характера самого этого модуля по отно-
отношению к числу — 1 + 2г на две единицы.
740
Теория биквадратичных вычетов. II
Далее, легко видеть, что совершенно так же обстоит дело и
для числа — 1 — 21.
66
Для числа — 3 мы не будем делать различия между модулями
первого и второго типа, ибо результат показывает, что такое раз-
различие здесь ни к чему. Итак,
харак-
характер
0
i
2
3
\ ! f\ j
—1—2г, 1
—11 —
3 + 2г,
-1 + 2»,
-7 +
—1 —(
-4г, -
4i, 7-
3— 2г,
1+4г
8г, -1
соответствует модулям
Зг, -7, -5 -
-5+2г, 5+4г
-Юг
-3+8г, -
, —5 —2г,
1 + 4г, 7 +
{- 6г, —5 — 6г,
, 7+2г, 5—8г,
—11,11 +
6г, И—6г
—1 + Юг, —7—8г,
- 3 —8г, 9 +4г, 3 + Юг,
5 —4г, 7 —2г
Юг
, 5 + 8г, -
3 — Юг
-1 - Юг,
Приведя эти модули к их наименьшим вычетам по модулю 3,
мы увидим, что те, которым соответствует характер 0, либо =1,
либо = — 1, те, характером которых является число 1, либо
= 1—г, либо ^—1 + ^, т^, характером которых является число
2, либо =г, либо ^ — г, наконец, те, которые имеют характер 3,
либо = 1 + г, либо ^ — 1 — г. Отсюда мы индуктивным путем за-
заключаем, что характер числа — 3 по отношению к простому и пер-
первичному среди ассоциированных чисел модулю совпадает с харак-
характером самого этого модуля, если за модуль уже брать число 3,
или, что то же самое, число — 3.
67
Проведя такое же индуктивное рассмотрение по отношению к
другим простым числам, мы найдем, что для чисел 3 + 2г, —l+fo',
7 + 2г, —5 + 6г,... справедливы теоремы, подобные той, к которой
мы пришли в п. 65 для числа — 1 + 2г, и, напротив, для чисел
1 + 4г, 5 + 4г, —3 + 8г, 5 + 8г, 9 + 4г,... дело обстоит так же, как
для числа — 3. Таким образом, индукция приводит к следующей,
Теория биквадратичных вычетов. II 741
очень изящной теореме, которую мы по аналогии с теорией квад-
квадратичных вычетов в арифметике вещественных чисел можем на-
назвать фундаментальной теоремой теории биквадратичных вычетов.
Если а -\- Ы, a'-\-b'i обозначают два различных и среди ассоции-
ассоциированных с ними чисел первичных, т. е. сравнимых по модулю
2 -\- 2i с единицей, простых числа, то биквадратичный характер
числа а + bi no отношению к модулю а'+ ЪЧ совпадает с характе-
характером числа a'-\-b'i no отношению к модулю а+ Ы, если или каждое,
или по крайней мере одно из чисел а-\-Ы, a'-\-b'i принадле-
принадлежит к первому типу, т. е. сравнимо по модулю 4 с единицей; на-
напротив, оба эти характера отличаются один от другого на две
единицы, если ни одно из чисел а -\- Ы, а' + b'i не принадлежит
к первому типу, т. е. оба сравнимы по модулю 4 с числом 3 + 2L
Несмотря на большую простоту формулировки этой теоремы,
доказательство ее принадлежит к наиболее глубоко скрытым тай-
тайнам высшей арифметики, так что, по крайней мере в настоящее
время, оно может быть проведено только при помощи тончайших
исследований, которые далеко вышли бы за рамки этого сочинения.
Поэтому опубликование этого доказательства, так же, как и изло-
изложение связи этой теоремы с теми теоремами, с индуктивного уста-
установления которых мы начали это сочинение, мы отложим до треть-
третьего сочинения. Однако в заключение мы хотим все же привести
уже здесь все, что необходимо для доказательства теорем, выска-
высказанных в пп. 63 и 64.
68
Мы начнем с тех простых чисел а + Ы, для которых 6 = 0
(т. е. с простых чисел третьего типа по терминологии п. 34) и для
которых тем самым а должно быть (чтобы число было первичным
среди ассоциированных) вещественным отрицательным простым
числом вида — Dга + 3), вместо которого мы будем писать —q. К
такому виду принадлежат числа —3, —7, —11, —19...
Если обозначить через X характер числа 1 + i9 когда за модуль
берется одно из указанных чисел, то должно выполняться сравне-
сравнение
1У* (mod q).
742 Теория биквадратичных вычетов. II
Но известно, что число 2 является квадратичным вычетом или
невычетом по модулю q в зависимости от того, имеет ли q вид
Ъп -\-1 или 8га + 3, откуда следует, что вообще
2<в-1)/2 = (_ l)«Z+D/4 = i(
и потому, если возвести это соотношение в степень с показателем
28 = г8 (modg).
Поэтому предыдущее соотношение принимает вид
4 (modg),
и отсюда следует, что
| !-4(<7 + 1) (mod4),
или, так как ^(q+lJ^0 (mod4), что
Это и представляет собой теорему п. 63 для случая Ъ — 0.
69
Намного, однако, труднее исследовать такие модули а + 6г, для
которых Ь не равно нулю (числа четвертого типа по терминологии
п.34), и здесь предварительно должны быть предпосланы различ-
различные исследования. Норму а2 + fe2, которая является вещественным
простым числом вида 4га + 1, мы будем обозначать через р.
Обозначим через S совокупность всех наименьших вычетов по
модулю а~\-Ы = т, за исключением нуля, так что количество со-
содержащихся в S чисел равно р—1. Обозначим далее через х-\-yi
произвольное число этой системыи положим ах-\-Ьу = 1,ау — Ьх=у\.
Числа 2 и т] являются поэтому целыми, заключенными между гра-
границами 0 и р (причем сами эти границы исключаются); в самом деле,
в рассматриваемом случае, когда а и b взаимно просты, формулы
п. 45, именно, т] = &?, ? = — Лт) (mod/?) показывают, что ни одно
Теория биквадратичных вычетов. II
743
из чисел ?, т] не может быть равно 0 без того, чтобы одновременно
не исчезало бы и второе, т. е. чтобы не получалась бы комбина-
комбинация х = 0, у = О, которую мы уже исключили. Таким образом,
критерий того, что число х + yi содержится в S, состоит в том, что
четыре числа ?, т], р — ?, р — т] должны быть положительными.
Далее, заметим, что ни для какого такого числа не может иметь
место 5=7], так как из этого следовало бы, что р (х + у) = #(?+Ч) +
+ Ъ (? — т]) = 2а?, а это невозможно, так как ни один из сомножите-
сомножителей 2, а, ? не делится на р. Подобным же образом равенство
р(х — у + а + Ь) = 2а? + (а + Ь) (р — 5 — tj) показывает, что ? + т]
не может быть равно р. Поэтому мы получаем отсюда, поскольку
числа ? — т], /? — ? — т] должны быть как положительными, так и
отрицательными, разбиение системы S на четыре совокупности
С, С, C"f С", причем мы полагаем содержащимися
в сово-
совокупности
С
С
С
числа, для которых
? — т] положительно, р — ? — т] положительно
? — т] положительно, р — ? — т] отрицательно
? — т] отрицательно, р — ? — т] отрицательно
? — т] отрицательно, р — ? — т] положительно
Таким образом, числа совокупности С характеризуются перво-
первоначально шестью условиями; именно, должны быть положительны-
положительными шесть чисел ?, т], р — ?, р — т], ? — т], р — ?—tj; но очевидно, что
второе, пятое и шестое условия уже содержат в себе все остальные.
Аналогично обстоит дело для совокупностей С", С", С"\ так что
на самом деле полные критерии зависят от трех условий, а именно,
для сово-
совокупности
с
с
С"
должны быть положительны числа
р — ^ 5 —ч. Ъ + 'Ц — Р
/7 — 7], 7] —?, ? + 7] — р
5» ч —6, Р — ? — ч
744 Теория биквадратичных вычетов. II
Далее, каждый, даже если бы мы и не указывали на это, дол-
должен был заметить, что при геометрическом изображении комплекс-
комплексных чисел (ср. п. 39) числа системы S содержатся внутри квад-
квадрата, стороны которого пересекаются в точках, которыми изобра-
изображаются числа 0, а + Ы, A + г) {а -|- bi), i {а + Ы), и что разбиение
системы S соответствует разбиению квадрата его диагоналями. Од-
Однако нам хотелось бы использовать здесь чисто арифметические
средства, почему мы и предоставляем ради краткости наглядные
иллюстрации опытному читателю.
70
Если четыре комплексных числа
г = х + yi, r'=x' + y'i, г" = х" + y"i, rm= x"r+ y"i
так связаны между собой, что выполняются равенства
г'— т -\- ir, r"= т + г>'= A + i)m — ?\ г'" = т + ir"'= im — г>,
и если предположить, что первое число, г, принадлежит совокуп-
совокупности С, то остальные числа, г'', г", г"\ будут принадлежать соот-
соответственно совокупностям С", С", С".
Действительно, если положить
\ = ах + by, г/ = ay — bx,
V=ax'+by', 71'=ау'—Ьх'9
?"= ax"+ by", rC= ay"— bx",
bw=axm + by'"f t{m = ay'"—bx'\
то мы получим
6_щ = Г + г/-р = г/'-Г=р-1'"- i",
р - s _ г, = g'_ n'= r+ f?- р = г{"- Ч",
откуда при помощи критериев для отдельных совокупностей спра-
справедливость утверждения теоремы получается сама собой. И так как
снова г = т + ir, то легко видеть, что если предположить число г
принадлежащим совокупности С", то числа г\ г'\ г1'1 будут при-
принадлежать соответственно совокупностям С", С", С; если предполо-
Теория биквадратичных вычетов. II 745
жить г принадлежащим совокупности С", то остальные числа будут
принадлежать совокупностям С"', С, С"; наконец, если г принадле-
принадлежит совокупности С"', то числа г', г", г'" принадлежат совокупно-
совокупностям С, С', С".
Одновременно из этого вытекает, что в отдельных совокупно-
совокупностях С, С, С", С" содержится по одинаковому количеству чисел,
а именно, по (р —1)/4 чисел.
71
Теорема. Если, понимая под к целое не делящееся на т число,
умножить отдельные числа совокупности С на к, и после того как
наименьшие вычеты этих произведений по модулю т распределены
по совокупностям С, С, С", С", обозначить количества тех, кото-
которые окажутся в этих отдельных совокупностях, соответственно
через с, с', с", с'", то характер числа к по отношению к модулю т
будет сравним по модулю 4 с числом с'+ 2с" + Зс"\
Доказательство. Пусть к С принадлежит с наименьших вычетов
а> Р» Т> ^>«"> к ?" принадлежит с' вычетов т + ia!, т + г(В', т-\-щ'>
т + г'8',...;кС" принадлежит с" вычетов A + i) т — а", A + i) m —(В",
(l-\-i)m — y"» (I + 0 m — ^'V--; наконец, к С" принадлежит с'" вы-
вычетов im — га'", гяг — г(В'", гт — гу", гт — г'8"',... Рассмотрим тогда
четыре следующих произведения:
1) произведение всех (р — 1)/4чисел, образующих совокупность С;
2) произведение произведений, которые получаются при умно-
умножении этих отдельных чисел на к)
3) произведение наименьших вычетов этих произведений, т. е.
произведений чисел а, р, -у, &,..., ш-\-М, т + ф',...,;
4) произведение всех чисел а, р, -у, &,..., а', Р', т'> ^V--> а"> Р">
7", S",..., количество которых равно с + с'-{- с"-\- с'".
Если эти четыре произведения обозначить по порядку через JP,
Р', Р", Р'", то мы, очевидно, будем иметь
и потому
746 Теория биквадратичных вычетов. II
Но легко видеть, что все числа а', р', ^\ 8',..., &", Р", Т", S'V--,
а/", p'", y"'» 8'",... принадлежат совокупности С и отличны как одно
от другого, так и oi чисел а, C, *у, 8,..., причем эти последние
также различны между собой. Поэтому все эти числа вместе взя-
взятые совпадают, с точностью до порядка следования, со всеми чис-
числами, образующими совокупность С, откуда следует, что Р = Р"\
и потому
Наконец, отсюда получается, так как отдельные сомножители
произведения Р не делятся на т, что
так что число с' + 2с" + Зс'" является характером числа & по отно-
отношению к модулю т.
72
Для того чтобы иметь возможность применить общую теорему
предыдущего пункта к числу 1 + г, мы должны совокупность С
снова разбить на две меньшие совокупности G и С, причем к со-
совокупности G мы будем причислять те числа x + yi, для которых
пх-\- by = ? меньше чем /?/2, а к совокупности С— те, для которых
i больше чем р/2\ количества чисел, содержащихся в совокупно-
совокупностях G и С, мы обозначим через g и g', так что g-f-g'=-(^—1).
Таким образом, полным критерием принадлежности числа сово-
совокупности G является то, что положительны три числа т], ? — т],
р — 2?; действительно, третье условие для совокупности С, соглас-
согласно которому должно быть положительно число р — 5 — 7], уже
включается в этот критерий, так как р — 6 — т] = (? — ?]) + (/?—2?).
Точно так же полный критерий для принадлежности числа сово-
совокупности G' состоит в положительности трех чисел % р — Е — ?],
21-р.
Отсюда легко видеть, что произведение каждого числа совокуп-
совокупности G на число 1 + i принадлежит совокупности С"'. Действи-
Теория биквадратичных вычетов. II 747
тельно, если положить
(х + yi) A + i) = х'+ y'i и ax' + by' = ?', ay'—bx'= т)',
то мы получим
т. е. критерий для принадлежности числа х -f- yz совокупности G
совпадает с критерием для принадлежности числа xr-\-y'i совокуп-
совокупности С".
Совершенно аналогичным образом показывается, что произведе-
произведение любого числа совокупности G' на число 1 + i принадлежит со-
совокупности С".
Поэтому, если числу к из предыдущего пункта придать значе-
значение 1 + г, то получится с = О, с' = 0, с"= g', с'"— g, и потому ха-
характер числа 1 + i будет равен 3g + 2g',= T (p — 1) -f g. А так как
1 1
характеры чисел г, —1 равны соответственно т (р—1),^(/?—1), то
характерами чисел —1 + г, —1 — г, 1—г будут соответственно чис-
3 1
лал(/?—!¦) + ?> ^> 4^—"^ "I" ^' ^ем самым вопрос сводится к
определению числа g.
73
Рассуждения пп. 69 — 72 на самом деле не зависели от пред-
предположения, что m является первичным числом; начиная же с этого
места, мы будем во всяком случае предполагать, что а нечетно,
аи четно, и что, кроме того,числа а, Ь, а — Ъ положительны. Преж-
Прежде всего мы должны установить границы значений х для чисел
совокупности G.
Если положить
ау — Ьх = т), (а + Ь) х — (а — Ъ)у = С, р — 2ах — 2Ьу = 9,
то критерий принадлежности числа х -\-yi к совокупности G будет
состоять в трех условиях, а именно, в том, что числа т;, С, 9 должны
748 Теория биквадратичных вычетов. II
быть положительны. Так как рх = (а — 6) ч\ + аС, р (а — 2х) =
= аб + 26т], то должны быть положительны числа х и 2а — ж, т. е.
ж должно быть равно одному из чисел 1, 2, 3,..., ^ (а — 1). Так
как, далее, (а — 6N — 26С +/? (а — 6 — 2ж), то ясно, что если х
меньше чем ^(а — 6), то второе условие (согласно которому долж-
должно быть положительно С) уже содержит в себе третье (по которо-
которому должно быть положительно 6), и что, напротив, если х больше-
чем ;> (а — 6), то второе условие уже содержится в третьем. Поэто-
Поэтому для следующих значений числа х: 1, 2, 3, ... , к (а — 6 — 1)
нужно позаботиться только о том, чтобы были положительны yj и С,.
т. е. чтобы у было больше чем bx/а и меньше чем (а + 6) х/(а—6).
Следовательно, для каждого такого значения х всего имеется
ЬхЛ
V(a + b)xl \Ъх
L a-b J L^
чисел х + г/г, если квадратные скобки имеют тот же смысл, в ко-
котором мы их уже употребляли в других случаях (ср. «Новое дока-
доказательство одной арифметической теоремы», п. 4; «Новые доказа-
доказательства и обобщения фундаментальной теоремы теории квадра-
квадратичных вычетов», «Новый алгоритм и т. д.», п. 3). Напротив, для
11 1
следующих значений числа х: -(а — Ь-\-1)-(а — 6 + 3),..., ^(а — 1)/
достаточно, чтобы у\ и 0 принимали положительные значения, т. е.
чтобы у было больше, чем bx/а и меньше чем (р — 2ах) /26, или, что
1 7 . а2 — 2ах г,
то же самое, чем xb-{ ^—• Следовательно, для каждого тако-
такого значения всего имеется
чисел х + yi.
Отсюда мы заключаем, что количество чисел в совокупности G
равно
у Пи + Ъ)х1 у Г1 , а*-2ах! у ГЪх!
8 - 1Л [ а-Ъ \ + А \2 ° 2Ь~\ ~ & [Т]'
Теория биквадратичных вычетов. II 749
где в первом члене суммирование производится по всем целым зна-
1 1
чениям числа х от 1 до т> {а— Ъ—1), во втором от ^ (я — Ь+1) до
1 1
-(а — 1) и в третьем — от 1 до ^(а—1).
Если мы используем букву <р в том же смысле, что и в указан-
указанном выше месте (ср. «Новые доказательства и обобщения и т. д.»),
а именно, положим
t'u
Ы
где t, и обозначают какие-нибудь два положительных числа, а V
обозначает число У, то первый из указанных трех членов будет
равен ф (а — 6, а + 6), третий равен —<р (а, 6), а второй равен
2 у_
Но если мы напишем члены в обратном порядке, то получим
= №> a)-9(b, a).
г5J
Поэтому наша формула принимает вид
, a) —9(а, &) —?(Ь, а) + |&2-
Рассмотрим сначала член (р(а — ^ а + ^)» который тотчас же
преобразуется в со (а — Ь, 2Ъ) + 1 + 2 + 3+...+ ^(а — 6 — 1) или в
9(а-6; 26) + |((а —бJ —1).
Далее, так как, в силу общей теоремы, cp(t, ^) + (р(ц» 0 =
= LirB L если только t ж и являются взаимно простыми поло-
положительными целыми числами, то
9(а —6, 2b)=r2b(a — b — l) — cpBb, a — b),
и потому
^ 3b2 — 4b — l) — cpBb, a — b).
750 Теория биквадратичных вычетов. II
Если члены выражения <pBb, a—Ъ) мы расположим следующим
образом:
а-ЬЛ ГЗ(а-ЬЛ 15(а-ЬI Г(Ъ-1){а-Ъ) 1
~2b~J + L 2& J + L"^^~J +-+ L 26 J +
a — bl , Г2(а-\
то второй ряд, очевидно, будет равен
<р(Ь, а — Ъ) = 9(Ъ, а) — 1-2-3-...— ±Ъ = <р(Ъ, a)-JF2 + 26);
первый же ряд после изменения порядка расположения на обрат-
обратный мы представим так:
а так как, если t обозначает целое, а и — дробное число, всегда
будет [t — u] = t — 1—[и], 10 это выражение преобразутся к сле-
следующему:
= ifcBa— 4 —Ь) —9B6, а) + 9F, а).
Поэтому
9B5, а-6) = 29E, а) —<рBЬ, а)+[б(а-3-6),
а, значит,
9 (a —6, а + 6) = (рB6, а) —29F, а) + |(а2 —б2 + 26 —1).
Если подставить это значение в приведенную выше формулу
для g и доложить, кроме того, ср(а, b)-\-cp(b, а) =-г Ъ (а — 1), то
мы получим
g = 2ср B6, а) — 29 F, а) + | (а2 — 2а6 + б2 + 46 — 1».
Теория биквадратичных вычетов. II 751
74
При помощи совершенно аналогичных рассуждений исследуется
случай, когда, хотя а, Ъ и остаются положительными, но а — Ъ от-
отрицательно, т. е. Ъ — а положительно. Равенства р(а — 2х) = 2Ьт\-\-
+ аб, р (Ь — а + 2я) = 2К + (& — а) б показывают, что числа - а — х
z*
и х + 2 (^ — а) должны быть положительны, и потому ж должна
1 1
быть равно одному из чисел — ~ (Ъ — а — 1), —-х (Ь — а — 3),
Z Zi
— ^(b— а — 5),...,+ х(а — 1). Далее, из равенства рх + (Ъ — а) ч\ = aZ
следует, что для отрицательных значений х условие, согласно ко-
которому должно быть положительно т], уже содержится в условии,
согласно которому должно быть положительно С, и что, наоборот,,
если числу х придается положительное значение, то из положитель-
положительности числа С вытекает положительность числа yj-. Поэтому значения
числа у для определенного отрицательного значения числах долж-
должны содержаться между (а + Ъ) х/(а — Ь) и (р — 2ax)/2b, a для за-
заданного положительного значения числа х — между bx/а и
(р — 2ах)/2Ъ. Для х — 0 эти границы, очевидно, равны 0 и р/2Ъг
исключая само значение у = 0. Из этого следует, что
где в первом члене суммирование производится по всем отрица-
отрицательным значениям х от — 1 до — ^{Ъ — а — 1), во втором — по всем
значениям х от —-к-(Ъ — а —1 ) до ^ (а — 1), ив третьем — по всем
A Z
положительным значениям х от -\- 1 до ^ (а — 1). Таким образом, в
результате первого суммирования получается ¦— <р (Ь — а, Ь -f- а),
в результате второго, так же, как и в предыдущем пункте, полу-
чается т^2 + 9 BЬ, о) — 9 (&» а)> и> наконец, в результате третьего сумми-
суммирования получается —ср(а, Ь), т. е.
, a) — cp(b, a) — cp(a, b) +\b\
752 Теория биквадратичных вычетов. II
Точно таким же образом, как в предыдущем пункте, мы полу-
получаем теперь
9F —а, Ъ + а) = ср(Ь — а, 26) — § (F — аJ — 1) -
= | C62 _ 2а6 — а2 — 46 + 1) — 9 B6, 6 — а),
и
9B6, Ъ— а) = срBЬ, а) — 2ср(Ь, а) + | 6 F — 1 — а),
откуда
9F —а, 6 +а)-29 F, а) —9B6, а) + g (б2 — а2 — 26 + 1),
и, наконец,
Таким образом, доказано, что g выражается одной и той же
формулой, независимо от того, положительно число а — 6 или от-
отрицательно, лишь бы были положительны числа а, 6.
75
Чтобы получить дальнейшую редукцию, положим
Так как легко видеть, что всегда [и] + w+ у = [2м], какую
вещественную величину w ни обозначало, то L-\-N = cp(b1 a),
Теория биквадратичных вычетов. II 753
а так как очевидно, что L + М = <рBЬ, а), то
9B6, а) — ср(Ь,а) = М — N.
Далее, ясно, что для суммы первого члена ряда N и предпослед-
него члена ряда М имеет место 2Ь М~ —26—I ~2 ^а— '» и
что такова же будет сумма второго члена ряда N и третьего
с конца члена ряда М и т. д. А так как, кроме того, последний
член ряда М равен -^(а — 1), а последний член ряда N равен
\а ~J \ = --(^qz 1)? где нужно брать верхний или нижний знак в
зависимости от того, имеет ли число а вид 4п -{- I или An -f- 3, то
выполняется равенство
и потому
Следовательно, формула для g, найденная в пп. 73 и 74, пере-
переходит в формулу
если положить а4--1 = 4уг, где п есть целое число. Но так как
отсюда получается, что 1 — 16гс2 — 8ап -f- ^2, то эта формула может
быть представлена также и следующим образом:
g = |(-я2 + 2аЪ + Р + 1) + 4(| (а + 1)л-и*-
Но так как g является характером числа — 1 — i по модулю
a + Ы, то этот характер, следовательно, будет =-g-(—я2 -|- 2ab +
+ ^2 + 1) (mod 4), а это как раз и есть теорема, найденная выше
(п. 64) индуктивным путем; отсюда немедленно получаются и тео-
теоремы относительно характеров чисел 1 + г, 1 — i, — 1 + i. Таким
образом, для случая, когда а и Ъ положительны, эти четыре тео-
теоремы доказаны теперь со всей строгостью.
754 Теория биквадратичных вычетов. II
76
Если Ъ отрицательно, в то время как а остается положительным7
то положим Ь = —Ъ\ где Ъ' уже положительно. Так как уже до-
доказано, что по модулю а + b'i характер числа — 1 — i сравним с
?- (— а2 + 2ab' + Ь'2 + 1) по модулю 4, то характер числа — 1 + г
по модулю а — b'i, согласно приведенной в п. 62 теореме, будет
= -«• (а2 — 2аЪ' — Ь'2 — 1), т. е. характер числа ¦—1 + г по модулю
а + bi будет =-«- (а2 + 2аЪ — Ь2 — 1); а это как раз и есть теорема,
указанная в п. 64, из которой сразу получаются и остальные три
теоремы, касающиеся характеров чисел 1 + г, 1 — г, — 1 — i. Таким
образом, эти теоремы доказаны также и для случая, когда Ъ отри-
отрицательно, т. е. для всех случаев, когда а положительно.
Наконец, если а отрицательно, то положим а — —а\ Ь = —Ь'и
Но так как, в силу уже доказанного, характер числа 1 + г
относительно модуля a'-{-b'i будет = тг(— а'2 + 2а'V—3&/2+1) (mod 4),
и так как безразлично, брать ли за модуль число а' -\- b'i
или противоположное число —а' — b'i, то характер числа 1 + г" по
отношению к модулю а + Ы будет, очевидно, = -^ (— а2 + 2а6 —
— 362 + 1) (mod 4), и подобные же утверждения имеют силу для
характеров чисел 1 — г, — 1 + h — 1 — г-
Таким образом, из этого следует, что доказательство теорем о
характерах чисел 1 + г, 1 — г, — 1 -f г, — 1 — i (пп. 63 и 64) теперь
уже свободно от всяких ограничительных предположений.
НЕКОТОРЫЕ
ИССЛЕДОВАНИЯ
ИЗ РУКОПИСНОГО
НАСЛЕДИЯ
ГАУССА
УЧЕНИЕ О ВЫЧЕТАХ
I
Решение сравнения Х™—1=0
237*
В третьем разделе мы показали, что сравнение #п=1, когда
за модуль берется простое число р, обладает [л корнями, где [л
является наибольшим общим делителем п и р— 1, и что эти корни
в точности совпадают с корнями сравнения я^ = 1. Поэтому доста-
достаточно рассмотреть только тот случай, когда п является делителем
числа р — 1. А то, что решение не только этого сравнения яп = 1,
но и любого другого по любому модулю может быть выведено из
решения по модулям, которые являются простыми числами, было
уже показано раньше, а ниже (в восьмом разделе) будет изучено
еще подробнее.
238
Но мы можем еще больше упростить нашу Задачу; действитель-
действительно, в том же разделе мы установили, что решение сравнения #п = 1
зависит от решений подобных же сравнений ха^1, #ь = 1, . . . , где
числа а, 6,... являются либо простыми, либо степенями простых,
а п есть произведение этих чисел. Именно, если А, В, . . . являются
соответственно некоторыми корнями сравнений жа = 1, жь = 1,...,
* Номера отдельных пунктов оставлены те же, что и в рукописи Гаусса.—
Црим. пер ев.
758 Учение о вычетах
то их произведение АВ. . . равно одному из корней сравнения
xn^i. Поэтому мы ограничим наше исследование решением срав-
сравнения #n = l (mod/?), где р является простым числом, а п равно
простому числу или степени простого числа и одновременно яв-
является делителем числа р — 1.
239
Далее, из третьего раздела известно, что среди корней сравне-
сравнения хп=1 всегда имеются такие, степенями которых могут быть
представлены все остальные корни. Если г обозначает один из
таких корней (мы называли их выше первообразными корнями,
когда было п — р—1, и это же выражение мы хотим и далее
употреблять в расширенном смысле), то все корни заданного срав-
сравнения суть
Таким образом, мы должны направить все наши усилия на то,
чтобы получить такие корни, ибо, если они будут найдены, то
остальные корни получатся сами собой. Для краткости мы будем
обозначать некоторую степень числа г посредством ее показателя,
заключенного в скобки, так что @) будет обозначать единицу,
A) — некоторый первообразный корень сравнения хп = 1, B) — квад-
квадрат числа A), и т. д., так что ряд @), A), B), C), . . ., (п — 1)
будет охватывать все корни. При этом известно, что (к) всегда будет
первообразным корнем, когда к взаимно просто с п, т. е. в нашем
случае (где п является степенью простого числа t, скажем, п = Г*),
когда t не входит делителем в к. Очевидно, что обозначения A),
B), . . . сами по себе неопределенны, однако, если A) получает не-
некоторое определенное значение, то и все остальные выражения уже
будут определены.
240
Так как мы поставили себе целью сначала искать первообраз-
первообразные корни, то мы должны прежде всего отделить их от остальных.
Это достигается выбрасыванием из ряда @), A), B), . . . , (п—1)
Решение сравнения Хт — 1 = 0 759
всех членов, в которых к делится на t; если же п является про-
простым числом, т. е. v = 0, то нужно отбросить только один член (О),
Однако, прежде чем переходить к дальнейшему исследованию, мы
очень советуем читателю рассмотреть несколько примеров, для
того чтобы иметь конкретное представление обо всем, что без этого
могло бы показаться слишком абстрактным. Хотя мы приводим-
здесь только один пример, читателю будет не лишне самому разо-
разобрать и другие примеры.
Если р = 29, п = 7, то семью корнями сравнения х1 = l(mod 29)
являются: 1, 7, 16, 20, 23, 24, 25. Так как п является простым
числом, то все эти корни, за исключением 1, являются первообраз-
первообразными; таким образом, если положить 7 = A), то обозначения
@), A), B), C), D), E), F)
будут соответственно иметь следующие значения:
1, 7, 20, 24, 23, 16, 25.
При этом учитывается, что значения (п) и @), (п -\- 1) и A) и т.д.
и вообще (а) и (Ь) эквивалентны, если а = 6 (mod га).
241
Однако, чтобы достигнуть нашей цели, мы должны действовать
еще несколько иным способом. Именно, мы сохраним только те члены
(к), у которых к не делится на ?, и количество которых равно
* —1 . .
. п = к; а все эти числа (или числа, сравнимые с ними по
модулю п) могут быть представлены следующими одна за другой
степенями какого-нибудь одного числа.
Если это число равно р, то все первообразные корни сравнения
,тп=1 будут обозначаться следующим образом:
A), (р), (р2), (р8). • • •, (рМ-
Этим приемом мы добиваемся того, что все непервообразные
корни совершенно исключаются; основания для этого и получаемые
преимущества ниже будут пояснены отчетливее. В нашем примере
мы можем, таким образом, положить р = 3; тогда первообразные
760 Учение о вычетах
корни сравнения #7 = 1 расположатся так:
A), C), (З2), C»), C*), C*),
или A), C), B), F), D), E),
и они равны 7. 24, 20, 25, 23, 16.
242
Для того чтобы читатель знал, куда нацелены дальнейшие ис-
исследования, мы укажем теорему, которую мы хотим доказать и
пояснить.
Если число X (которое равно f~1(t—1)) имеет простые сомно-
сомножители а, Ъ, с, d,. . . , и Х = аа6ст..., то решение сравнения
%п — 1^0 сводится к решению а -f- P + • • • сравнений более низкой
степени, из которых а сравнений имеет степень а, р сравнений —
степень Ъ, у сравнений — степень с, и т. д.
Так, в нашем примере решение сравнения х1 = 1 зависит от
одного сравнения второй степени и одного сравнения третьей сте-
степени, и вообще легко видеть, что степень этих сравнений никогда
не зависит от модуля р. Однако, чтобы получить доказательство
этой теоремы, мы должны предпослать некоторые теоремы, касаю-
касающиеся связи между сравнениями и их корнями, хотя сами эти
исследования будут продолжены только в восьмом разделе.
243
Теорема. Если сравнение
хт + Ах™ + Вхт~2 + . . . + N - =: 0 (по простому модулю)
обладает тем свойством, что для произведения т сомножителей
х — г, х — г\ х — г", х — /", . . . , которое мы обозначим через хт +
+ ахт~1 + Ъх™—* + . . . -f п, имеет место А = а, В =ее6, С ^ с, . . . ,
по модулю р, то величины г, г\ г", . . . будут корнями заданного
сравнения, причем других корней оно иметь не будет.
Доказательство. I. Всегда
хт -4- Ах171-1 + Вхт~2 Н = хт + ах171-1 + Ьхт~2 Н (mod p).
Решение сравнения Хт — 1 = 0 761
Но правая часть будет равна 0, если положить х = г, х = г', х = г",...;
поэтому для этих значений х левая часть сравнима с 0 по модулю р.
Это — первое утверждение теоремы.
И. Если бы заданному сравнению удовлетворяло еще какое-
нибудь значение р, которое не сравнимо ни с одним из чисел г, г'Т
г", . . . , то выполнялось бы сравнение
Оеееер™ + Ар171-1-}- Др™-2-| = рт + ар171-1 + Ьр™-2 + • • - =
= (Р-г)(Р-г')(Р-О-- •
Но так как ни один из сомножителей р — г, р — г', р — г"', . . . не
сравним с 0, то и произведение их всех не может быть сравнима
с 0. Поэтому других корней, кроме г, г', . . . , нет. Это второе утверж-
утверждение теоремы.
244
Задача. Пусть г, г\ г", . . . —неизвестные величины, число которых
равно т, и пусть сумма их равна а, сумма их квадратов равна $г
сумма кубов равна у, и т- д., и сумма т-х степеней равна [л;
даны, однако, не сами эти числа {количество которых тоже равно т)г
а другие числа, а', р', т'» • • • > которые соответственно сравнимы с
ними по модулю р, являющемуся простым числом, большим чем т.
Нужно найти сравнение т-й степени, корнями которого являются
г, г', г", . . .
Решение. Рассмотрим г, г\ г", . . . как корни некоторого урав-
уравнения
хт + Ах™-1 -f Вхт-2 + Схт~3 Н 0,
и определим его коэффициенты А, В, С, . . . (используя вместо урав-
уравнения сравнение) при помощи известного метода, именно, полагая
— AD ее?- 8' -f А4' + В$' 4
— mN = [лг + АГ + . . .
762 Учение о вычетах
Эти коэффициенты не могут, однако, быть неопределенными, потому
что все числа 1, 2, 3, . . . , п < р. Тогда я утверждаю, что сравнение
хт + Ахт~^ + Вх™-2 -| 1- N = О
является искомым.
Доказательство. Предположим, что уравнение, корнями которого
являются г, г\ г", г'",. . . , следующее:
хт _| ахт-1 + Ьхт~2 Н = 0.
Тогда
— а = а,
— 2й = р + аа,
— Зс = y + ар + ^а,
Но тогда, очевидно,
а = A, b = В, с = С,... (mcdp),
и потому, согласно предыдущему пункту, числа г, г' г",.. ., которые
являются корнями уравнения
хт + ах™-1 + 6ж™-2 Н = 0,
будут одновременно и корнями сравнения
хт + Ах™-1 + Вхт~2 Н = 0.
Мы предоставляем читателю привести примеры.
245
Мы возвращаемся к нашей задаче. Сохраняя обозначения, ис-
использованные в п. 242 и предыдущем пункте, мы хотим показать,
что если X является произведением нескольких сомножителей efg...,
то первообразные корни сравнения хп = 1, количество которых равно
X, могут быть так разбиты на е классов, что суммы корней, при-
причисленных к одному и тому же классу, даются сравнением е-й
¦степени; далее, что если классы считать известными, то каждый из
них может быть в свою очередь так разбит на / порядков, что
Решение сравнения Хт — 1 = 0 763
сумма каждого порядка дается сравнением /-й степени, а эти по-
порядки снова могут быть подразделены, и т. д., до тех пор, пока
мы не придем к отдельным корням.
246
Определение. Совокупность всех содержащихся в форме (рЛе+в)
(п. 241) членов мы будем называть полным периодом или просто
периодом. Пусть е обозначает какой-нибудь делитель числа X,
а—какое-нибудь заданное число, к — всевозможные целые числа от 0
до 1; тогда ради краткости мы будем обозначать такой период
через (е * а). Так, в нашем примере члены
A), B), D) образуют период B*0),
C), F), E) » » B*1),
A), F) » » C*0),
C), D) » » C*1),
B), E) » » C*2).
Если теперь все члены некоторым образом разбиты на периоды,
отдельные периоды снова разбиты на меньшие периоды и т.д., то
мы утверждаем, что этим самым мы добиваемся того, что было
высказано в предыдущем пункте.
Однако, прежде чем приступить к изложению этого, мы покажем,
что хотя при образовании такого периода используются в некотором
смысле произвольные величины г, р, тем не менее не получается
никакой неопределенности, т. е. что как бы эти величины не выби-
выбирались, в одном и том же периоде все время будут получаться
одни и те же члены (именно, если предписано, сколько членов
период должен содержать).
Критерий принадлежности двух членов А, В к одному и тому
же периоду получается из того, что каждый из них имеет вид
(pfce-f-a^ т# е что j[==rpke+<x^ В = rpke+(K (modp). При этом г является
первообразным корнем сравнения хп == 1 (modp), а р — первообраз-
первообразным корнем сравнения xx = l(modn) (ср. выше).
764 Учение о вычетах
Нужно доказать, что если вместо чисел г, р выбраны другие-
числа, например, s, с, то А и В будут содержаться в подобных
формах *•'•+*, s°l'e+*.
Пусть sm = r (mod p)f c^ = p (mod n) и m == o^ (mod тг), что воз-
возможно, так как г, р являются первообразными корнями; т взаимна
просто с га, [л взаимно просто с X (раздел III). После соответствую-
соответствующей подстановки мы получаем А == ^е+^а+^ д == ^ft'e+na+i^ что и
требовалось доказать.
247
Теорема. Произведение двух однотипных периодов независимо от
числа р может быть образовано сложением однотипных периодов
и заданных чисел.
(Однотипными периодами мы называем такие периоды, которые
содержат одинаковое количесаво членов, т. е. для которых числа
е одно и то же.)
Пример. Если п = 7, то произведение периодов A) + F) и B) -f-
+ E) (в силу (а)-F) = (а+ &)) равно C) + F) + (8) + (И), т.е.
состоит из периодов C) + D) и A) + F).
Доказательство. Пусть — = / и заданные периоды суть (е * а)
и (в* (В), а суммы —
(Ра) + (Ра+е) + (ра+2е) + • • • + (ра+^)е) = РУ
(рР) + (рЭ+в) + (рр+2е) + . . . + (рй+(/-1) в) = Q.
Произведение PQ будет состоять из /2 членов. Упорядочим их
следующим образом. Образуем / рядов, каждый из которых состоит
из / членов. Первый ряд охватывает произведение Р на (р*3), вто-
второй—-произведение Р на (рр 'е) и т. д. В первом ряду первое место
занимает произведение, которое получается из члена (ра), второе
место — произведение, которое получается из (ра+е), и т. д. по по-
порядку; во втором же ряду первое место будет принадлежать произ-
произведению, получающемуся из члена (ра+е), второе — произведению*
получающемуся из члена (ра+2е), и т. д., наконец, последнее — произ-
произведению, получающемуся из члена (ра); третий ряд пусть начи-
начинается с произведения, получающегося из члена (ра+2е), и т. д., а.
Решение сравнения Хш — 1 = 0 765
за произведением последнего члена пусть следуют произведения
первого, второго и т. д. членов; иными словами, если следующие
один за другим члены периода Р обозначены через 1,2, 3, ...,?,
а следующие один за другим члены периода Q — через I, II, III,..., Z,
то получаются следующие части произведения PQ:
1.1 + 2-1 + 3-1 + 4-1 + ...+2-1,
2.II + 3.II + 4.II + + 1-И,
3-Ш + 4.Ш+ + UII + 2.III,
Составим теперь из членов, которые занимают в отдельных рядах
одинаковые места, / порядков. Тогда я утверждаю, что
1) если какой-нибудь член сравним с 1, то и все остальные
члены того же порядка тоже сравнимы с 1;
2) каждый порядок, в котором нет членов, сравнимых с 1, об-
образует период.
Если мы это докажем, то мы, очевидно, достигнем нашей цели.
Общий вид такого порядка таков:
(р«-НН-2) в _|_ рИ-2е^ (
действительно, вместо pa+(fc—Dе можно написать также р«+<Л+'—De,
ибо ef = X и рх == l(modn), и так же обстоит дело в отношении пре-
предыдущих членов. Если положить р«+ке + р? ^рх (mod я), что допу-
допустимо, если р«+ке + рР не делится на п, то порядок можно будет
представить также и так:
(Рх), (Рх+е), (рх+2е),-..,(рх+(/-1)е),
а это, очевидно, есть период (е*х); если же ра+А:е + рр делится на
п, то все члены порядка будут сравнимы с 1.
Замечание. Это доказательство одновременно дает очень про-
простой прием для нахождения произведения; циже мы дадим другой
прием, который хотя и не предпочтительнее этого, но вследствие
своей простоты также заслуживает большого внимания.
766 Учение о вычетах
248
Все меньшие периоды, которые образуют один больший период,,
мы будем называть системой периодов. Так, например, это наи-
наименование будет употребляться для периодов
(е/*а), (*/*/ +а), (е/* 2/ + а), . . . , (ef * (е- 1)/ + а),
из которых составлен период (/*ос). Система периодов будет пра-
правильно расположена, если числа, стоящие после звездочки *, как
в данном случае числа ос, / + а, 2/ + а, . . . , образуют арифмети-
арифметическую прогрессию (с разностью /); наконец, системы будут одно-
однотипными, если как меньшие, так и большие периоды однотипны.
Теорема. Если перемножить один с другим периоды двух пра-
правильно расположенных систем, а именно, первый перемножить с пер-
первым, второй со вторым, третий с третьим и т. д., то сумма
всех произведений может быть составлена из периодов, однотипных
с большим периодом, и заданных чисел.
Доказательство. Пусть даны системы
(е/*а), (е/*а + /), (е/*а + 2/), . . . ,
(е/*р), (е/«р+Д (е/*р + 2/),...
Произведения отдельных периодов первой системы и соответст-
соответствующих периодов второй системы состоят, согласно предыдущему
пункту, из целых чисел и однотипных периодов. Но небольшая
внимательность при составлении этих периодов показывает, что если
(в/* а) (е/*р) состоит из целого числа N и периодов (ef*A), (ef*B)y
(ef * С), . . . , то произведение (ef * a -f /) (ef * р -f /) будет состоять из
числа N и периодов (ef * Л + /), (в/ * J5 + /), (е/ * С + /),..., произ-
произведение (е/ * а + 2/) (е/ * р + 2/) — из N и периодов (ef* A + 2/),
(ef* В + 2/), (е/ * С + 2/), . . . , и, вообще, произведение (ef * а + Iх/) X
X (в/ * р + (х/) — из числа N и периодов (ef * A -f (x/), (ef * В -{- [х/)г
(в/* С + (л/),. . . Отсюда непосредственно вытекает, что сумма всех
периодов равна
eN + y*A) + (f*B)+{f*C) + ...,
что и требовалось доказать.
Это доказательство также дает нам в руки способ для нахож-
нахождения этой суммы.
Решение сравнения Хш — 1 = 0 767
249
Легко еще обобщить эту теорему, именно, в том отношении, что
если имеется любое число правильно расположенных однотипных
систем, и из первых, вторых и т. д. периодов образованы произ-
произведения, то сумма всех этих произведений состоит из чисел и боль-
больших периодов. Если все эти системы взять одинаковыми, то сумма
некоторых степеней всех периодов будет состоять из чисел и перио-
периодов, однотипных с большим периодом. Уже отсюда видна цель
нашего исследования. Пусть \ = efgh. . ,\ разложим все первообраз-
первообразные корни на е периодов А, А', А", . . .; каждый из них снова раз-
разложим на / периодов Ву В\ В'\ . . .; каждый из них — на g периодов
С, С С", . . . Но сумма всех периодов дана, именно, она сравнима
с —1. Согласно же тому, что было только что изложено, известны
также и суммы
(А)* + {A'f + (Ay + {А'У + . • •,
(А)* НЛЧ(Л3 + (Л3 + -,
и т. д.
Поэтомур согласно п. 244, мы можем найти сравнение е-я степени,
корнями которого являются А, А', А!\ . . . Если теперь эти корни
предполагаются известными, то мы разлагаем каждый период на
меньшие периоды, именно,
,4-на В, В', В»,...,
А'-ы В{п\ В{п+1\ В{п+2\ . . . ,
А"— на В{2п\ В{2п+1\ В{2п+2\
и т. д.
Тогда, т^ким образом, дано и В -f- В' + В" + • • • == А. Но
(В)* + (В')*+ (?")* + ...,
и т. д.
состоят из единиц и периодов А, А', А", . . . Поэтому В, В\ В\...
будут задаваться сравнением /-и степени, из которого они могут
быть найдены; и аналогичным образом могут быть найдены периоды,
из которых состоят А\ А", . . . Но теперь каждый может увидеть,.
768 Учение о вычетах
что совершенно аналогичным образом каждый период может быть
разложен на меньшие, до тех пор, пока мы не дойдем до самих
корней.
250
При применении этих правил имеется, однако, одна трудность,
которую мы должны устранить. Именно, так как каждое сравнение
имеет несколько корней, то мы должны знать, какой знак следует
придавать каждому из них, чтобы можно было верно различать их
один от другого. Так как значение периодов зависит от чисел г, р,
которые могут выбираться произвольно, то и в этом вопросе обя-
обязательно остается некоторый произвол. Впрочем, число р должно
быть с самого начала выбрано раз и навсегда. Сущность нашего
метода в основном состоит в том, что мы из больших периодов
получаем меньшие. Однако этого нельзя проделать без соответствую-
соответствующего упорядочения периодов — упорядочения, коюрое мы получи-
получили посредством обозначений. Поэтому мы должны постараться
различать все периоды, после того как они найдены, по их
знакам.
Пусть период А обозначен через (е*ос) и разложен на / перио-
периодов В, С, Z), . . . , которые мы должны определить. Очевидно, что
каждый из них будет иметь вид (е/# ке + ос); я утверждаю, однако,
что для одного из них, например, для В, число к может быть
выбрано произвольно, после чего уже может быть найдена последо-
последовательность остальных.
Пусть R — какой-нибудь первообразный корень сравнения хп = 1,
и пусть В состоит из членов R11 + Rv + • • •; пусть, далее, — рке+а ==
= — (modn), и так как значение г произвольно (если только период
А получает знак (е*ос), что, очевидно, само по себе имеет место),
то положим г = RV (mo&p). Тогда первым членом периода В будет
грА:в+а, и В можно обозначить через (е/ * ке -f ос). Если бы вместо
R11 мы рассматривали член i?v, то мы получили бы другое значение г;
но легко видеть, что для некоторого корня р корень г может
иметь Х/е/ различных значений.
Решение сравнения Хт — 1 = 0 769
251
Теперь мы посмотрим, как, определив один период, можно раз-
различать остальные по их знакам. Однако для этой цели нужно
поискать другой метод для нахождения остальных корней; дейст-
действительно, поскольку остальные периоды, как и сам Л, являются
корнями некоторого сравнения, для них нет никакого упорядо-
упорядочения. Если мы предположим, что период А обозначен через (е/*0),
то из предыдущего следует, что
А2 имеет вид М + N (ef *0) + О (ef * I) + P (ef *2) + . . . ,
А3 имеет вид М' + N' (ef * 0) + О' (ef * 1) -f- Pr (ef * 2) -\ ,
Ае1~г имеет вид М* + N* (ef * 0) + О* (ef * 1) + P* (ef * 2) -\ .
К тому же имеет место сравнение
(в/* 0) + (ef * 1) + (ef * 2) + . . . + (ef*ef — 1) = - 1.
Таким образом, мы имеем ef—1 линейных сравнений и столько же
неизвестных величин, которые тем самым могут быть определены
посредством исключения.
Замечание. Может представиться случай, когда неизвестные ве-
величины задаются выражениями вида V / Wp\ как обойти эту труд-
трудность, мы покажем позднее. Здесь мы не хотим на этом останавли-
останавливаться, так как такой случай может встретиться только очень редко.
252
В вопросе о решении чистых сравнений этим можно вообще
удовлетвориться. В дальнейшем о них мимоходом будет говориться
еще многое; многое из теории решения чистых уравнений может
быть применено к другим вопросам, на что мы в соответствующих
местах не будем забывать обращать внимания. Мы добавим еще
один пример, при сравнении которого с указанными правилами для
менее опытного читателя все станет яснее.
Пусть п = 31, р = 311, т. е. пусть отыскиваются корни сравнения
х31 — 1=0 (mod311). Сначала нужно найти первообразный корень
сравнения у30 —1=0 (mod 31); одним из них является у~3.
770 Учение о вычетах
Положим поэтому р = 3 и разложим сначала все первообразные
корни заданного сравнения на пять периодов, именно:
E*0) = A) + B6) + B5) + C0) + E) + F),
E*1) = C) + A6) + A3) + B8) + A5) + A8),
E*2) = (9) + A7) + (8) + B2) + A4) + B3),
E*3) = B7) + B0) + B4) + D) + (И) + G),
E*4) = A9) + B9) + A0) + A2) + B) + B1).
После соответствующих вычислений мы находим, что сумма перио-
периодов =— 1, сумма квадратов =25, сумма кубов =26, сумма би-
биквадратов = 249, сумма пятых степеней =564.
Поэтому периоды являются корнями сравнения
+ + х + 5 = о.
Далее мы находим
E * ОJ == 6 + 2 E * 0)-f * + * + 2 E * 3) + E * 4),
E * ОK = 12 + 15 E * 0) + 4 E * 1) + 3 E * 2) + 6 E * 3) + 6 E * 4),
5 * ОL == 90 + 60 E*0) + 28 E*1) + 26 E*2) + 49 E*3) + 38 E * 4),
и отсюда посредством исключения получается
5 E*1) = 3E* ОL —E* ОK — 33E*0J — 24E*0) + 15,
5 E * 2) = — 2 E * ОL — E * ОK + 22 E * ОJ + 31 E * 0),
5 E * 3) = E * ОL — 2 E * ОK + 11 E * ОJ — 12 E * 0) — 20,
5 E * 4) = — 2 E * ОL + 4 E * ОK.
Но один из корней найденного сравнения =17; поэтому, если по-
положить E*0) = 17, то будет иметь место
E*1)-183, E* 2) = 263, E*3) = 91, E* 4) =67.
Теперь каждый из найденных периодов снова разложим на три
периода, именно:
E * 0) на A5 * 0),A5 * 5), A5 * 10), или на A)+ C0), B6) + E), B5)+F),
E * 1) на A5 * 1),A5 * 6),A5 * И), или на C) + B8),A6) f A5), A3)+A8),
и т. д.
Решение сравнения Хт — 1 = 0 771
Если мы предположим, что
периоды, на которые разложен E * 0), являются корнями сравнения
Xs + Ах2 + Вх + С = 0,
периоды, на которые разложен E * 1), являются корнями сравнения
хз + А'х* + В'х + С' = 0,
периоды, на которые разложены E * 2), являются корнями сравнения
Xs + А"х2 -+ В"х + С" = 0,
и т. д.,
то
А = — E * 0), В = E * 0) + E * 3), С = — 2 — E * 4),
Л'= — E*1), J?' = E*l) + E*4), С" = — 2 — E*0),
и т. д. и т. д. и т. д.
Поэтому
A5*0), A5*5), A5*10) являются корнями сравнения
Х3_17х2+ Ю8Х — 69 ЕЕЕ 0,
A5*1), A5*6), A5*11) » » »
A5*2), A5*7), A5*12) » »
х* + Ш2 — 31х + 126^0,
A5*3), A5*8), A5*13) » »
A5*4), A5*9), A5*14)
Но здесь мы имеем
A5*0K — 3A5*0) = A5*1).
A5*1K —3A5*1) = A5*2),
и т. д.
Поэтому, если положить один из корней первого сравнения,
например, 10, равным A5 * 0), то мы получаем отсюда
A5*0)= 10, A5*5) = —116, A5*10)= 123,
A5*1)= 37, A5*6)= 50, A5*11)= 96,
A5*2) = —151, A5*7)= 139, A5*12) = —36,
A5*3) = —39, A5*8)= 28, A5*13)= 102,
A5*4) = —112, A5*9)= 98, A5*14)= 81.
772 Учение о вычетах
Если, наконец, взять члены, которые образуют эти отдельные
периоды, то
A), C0) будут корнями сравнения х2 — A5 * 0)х -\- 1 = 0,
C), B8) » » » х2 — A5*1)ж + 1 =0,
и т. д.
Корнями первого сравнения являются 126 и 195; они будут тем
самым первообразными корнями сравнения ?31 = 1, и остальные
могут быть получены из них без труда.
УЧЕНИЕ О ВЫЧЕТАХ
II
Общие исследования о сравнениях
330
То, что в предыдущих разделах мы сообщили относительно
сравнений, касается только простейших случаев, и по большей части
находится специальными методами. В этом разделе мы хотим по-
попытаться, насколько это в настоящее время возможно, свести теорию
сравнений к более высоким принципам, приблизительно так же,
как рассматривается теория уравнений, с которой, как мы уже
часто отмечали, имеется значительная аналогия. Так как все ал-
алгебраические сравнения с одним неизвестным могут быть приведены
к виду
где X — алгебраическая, не содержащая дробей, функция от пере-
переменного ж, то нужно главным образом рассматривать такие функции.
331
Если Р, Q — функции переменного х вида
А + Вх + Сх2 + Dxs + . . . ,
Н + Jx + Кх* + Lx* + . . .
(в дальнейшем под простым названием «функция» всегда будут
пониматься такие функции), и коэффициенты при одинаковых
774 Учение о вычетах
степенях неизвестного х у каждой из пик сравнимы по некоторому
модулю, то мы будем называть функции сравнимыми по этому мо-
модулю. Очевидно, что когда для неизвестного берутся равные или
сравнимые значения, то сравнимые функции будут принимать срав-
сравнимые значения. То, что в разделах I и II было доказано для
чисел, в большинстве случаев имеет силу и для функций. Если,
например, Р = Р', Q == Q', R = R', . . . , то, очевидно, также будет
иметь место Р + Q + R+... = Pf+Qf+Rr+ . .. ; P — Q=P'—Q'\
PQ = P'Q'\ PQR.. .=P'Q'Rf . ..
Доказательства очень легки и могут быть проведены аналогично
тому, как в первом разделе.
Если PQ ~ R1 то мы будем обозначать функцию Q просто че-
через R/P, отбрасывая модуль, и будем говорить, что Q является
частным от деления R на Р по этому модулю. Очевидно, однако,
что вместо Q можно брать все функции, сравнимые с этой функ-
функцией, и все они буду рассматриваться в качестве одного единст-
единственного значения. В дальнейшем же мы покажем, в каких случаях
такое частное может иметь несколько (несравнимых) значений.
332
Если модуль является простым числом, и делитель Q содержит
только один член Hxh, коэффициент которого Н не делится на
модуль, т. е. если Н не сравнимо с 0, то частное не может иметь
нескольких значений. Действительно, если бы было QA=P и
QB = Р, то имело бы место Q (А — В) ее: 0. Если теперь
(?==...+ Hxh
где Н не делится на р, и
А — В = Lxl + + ,
где L не делится на р (А — В будет иметь такой вид, так как мы
предполагаем, что А несравнимо с Б), то выполнялось бы сравне-
сравнение Q (А — В) be HLxh+l + . . . =0, что невозможно, так как HL
несравнимо с 0.
Общие исследования о сравнениях 775
Теперь легко можно указать правила для деления функции Р
на Q, когда это возможно. Если
Р = аха + tea+1 + сяа+2 + . . . + кх*,
Q = тх* + лжИ-i + дж«*+2 + . . . + txT,
где а, к, т, t не делятся на модуль, то а должно быть не меньше
чем [х, и х — не меньше чем т. Деление же может производиться
аналогично тому, как в элементарной арифметике, если только все
время вместо частного брать целое число, именно, частное все вре-
время будет иметь вид г/т, а это выражение по модулю имеет смысл.
Если теперь, после того как найдено х + [х — он — т + 1 членов, ос-
остается остаток, который будет иметь вид
где не все коэффициенты А, 5, С, ..., сравнимы с 0, то Р не мо-
может делиться на Q.
Впрочем, ясно, что деление могло бы также начинаться с чле-
членов, которые имеют наивысшие степени, т. е. с членов кх*7 txT;
вычисление облегчается, если Q представить в виде
тих»- A + qx + rx2 + ...),
после чего, если положить mv = 1, выполняется сравнение
Р __ vP ix11
"Q" = 1 + qx + . . . '
дальнейшее же деление можно производить обыкновенными мето-
методами.
333
Теорема. Если х = а является корнем сравнения ? = 0, то ? де-
делится по модулю сравнения на х — а.
Доказательство. Действительно, если бы делимости не было, то
имело бы место с = (х — а) %' + Ь, где Ъ не делится на модуль.
Если положить теперь х = а, то по предположению будет ? =е О,
и потому (я — а)?' + 6 = 0; но при этом также и (я — а) ?' = 0, и
потому обязательно 6^0.
776 Учение о вычетах
334
Задача. Пусть даны две функции; нужно найти их общий
делитель (наивысшей степени) по заданному модулю.
Решение. Пусть даны функции А и 5, и пусть А имеет такую
же или большую степень, чем степень В. Разделим А на В;
если деление возможно, то В является искомым общим делителем.
Если же получается остаток С, то он будет степени меньшей, чем В.
Пусть, таким образом,
А~аВ + С, В = ЪС + D, C==cD + E,. . . ,
где -4, В, С, Z), . . . , а, 6, с, ... является функциями, и степени
функций А, В, С, /),... образуют убывающий ряд. Если в конце
концов какое-нибудь деление не даст остатка, например, если D =dE,
то последний делитель будет искомым общим делителем; если же
все время получаются остатки, то мы придем в конце концов к
остатку, не имеющему степени, т. е. к числу; в этом случае функ-
функции А, В ке имеют общих делителей.
Доказательство. Если делитель Е делит предыдущую функцию
без остатка, то он, как легко видеть, будет делить и все пред-
предшествующие функции; тем самым Е будет общим делителем функ-
функций Л, В. Это—первая часть теоремы. А если бы имелся неко-
некоторый делитель, скажем Е\ большей степени, то в силу соотно-
соотношения С = А —аВ он делил бы также и С, и по аналогичной при
чине делил бы Вит. д., а, значит, делил бы и Е, т. е функция
более высокой степени входила бы делителем в функцию более низ-
низкой степени. Это невозможно, и потому второе утверждение до-
доказано.
Отсюда вытекает также, что если имеется общий делитель не-
некоторой степени, то нельзя прийти к остатку, не имеющему сте-
степени, так как иначе функция без степени делилась бы на функцию
с некоторой степенью, что невозможно.
335
Теорема. Если А и В — две взаимно простые по модулю р функ-
функции, и А имеет степень а, а В — степень р, то можно найти та-
такие две функции Р9 Q, степени которых соответственно < р и < ос,
Общие исследования о сравнениях 777
что будет выполняться сравнение
PA + QB—l (mod/?).
Доказательство. Действительно, в этом случае
А~аВ + С7 В = ЪС +D,. .., K = kL + M,
причем степени функций А, Ву С, Z), . . . , if, L, М непрерывно
убывают, и М совсем не имеет степени. Если теперь образовать
такие ряды
а, а', а", а"',..., а<*>,
\,Ъ,Ъ',Ъ",...,Ы*-»,
ЧТО
а' == 6а + 1, а" = са' + а, ат = da" + а', . . . ,
6' == сб + 1, V = db' + b, V" = cb" + b\ . . . ,
то, как легко видеть, будут выполняться сравнения
A — aB= + C,bA — a'B~ — D, VА — а"В= + Е,...,
и, наконец,
Ы*г-ЪА — аЮВ==±М.
Л
Если теперь м = [х? то если положить Р ^ у1.Ыус~1\ Q е= —\ка^-\
будет иметь место
PA + QB—1.
Но ясно, далее, что
степень функции В + степень функции а = степени функции А,
» » с + » » ь = » » i?,
степень функции L + степень функции /с = степени функции К.
Поэтому
степень функции L + сумма степеней функций а, 6, с,..., /с = степени
функции А.
Но, очевидно, что степень функции а(х), и потому также степень
функции Q равна сумме степеней функций а, Ь, с, . .. , т. е. равна
а — степень функции L. Поэтому
степень функции Р равна g — степень функции X.
Это и требовалось доказать.
778 Учение о вычетах
336
Но из этого следует, что если М является общим делителем
наибольшей степени функций А, 5, то всегда можно положить
АР + BQ = М.
Примеры на предыдущую теорему я для краткости опускаю,
однако для читателей было бы не лишним приобрести на таких
примерах некоторую сноровку в решении подобных задач. Впрочем,
стоит указать, что предыдущая теорема верна и для функций, взя-
взятых абсолютно, если их коэффициенты являются рациональными
числами. Это само собой вытекает из способа доказательства.
Однако мы не будем на этом задерживаться. Подобное же обстоя-
обстоятельство, даже и без специального указания на него, читатель заме-
заметит и в дальнейшем.
Если А не имеет общих делителей никакой степени ни с 5, ни
с С, то А не будет иметь общих делителей также и с произведе-
произведением ВС. Действительно, если РА + QB = 1, то РАС + QBC = С.
Если бы теперь А имело бы с ВС общий делитель М, то он, воп-
вопреки предположению, входил бы также и в С. Поэтому и вооб-
вообще, если функция А взаимно проста с функциями Z?, С, D,. . . , то
она будет взаимно проста и с их произведением.
Если А, В, С, D, . . . все вместе не имеют общих делителей, то
можно сделать, чтобы выполнялось сравнение
РА + QB + RC + SD + .. . = 1.
Если М есть делитель наивысшей степени функций А и 5,
М' — делитель наивысшей степени функций М и С, М"—делитель
наивысшей степени функций М' и D и т. д., то последний член этого
ряда (согласно предположению) будет, очевидно, не иметь степени.
Поэтому можно положить
аА + ЪВ = М, mM-i-cC- M\ m'M' + dD = M",... ,
п если произвести подстановки, мы убедимся в справедливости
теоремы.
Общие исследования о сравнениях 779
337
Теорема. Если функции А7 5, С, ... по модулю р попарно вза
имно просты {т. е. никакие две из них не имеют общих делите-
делителей), и если функция М делится по этому же модулю на все эти
функции в отдельности, то М делится также и на их произведение.
Доказательство. Можно положить PA + QB^i, и потому
М п Мр М
Так как функция С взаимно проста с АВ, то М будет делиться
также на ABC и, по аналогичной причине, — на ABCD, и т. д.
338
Если сравнение ? = 0 имеет корни х = а, х = Ъ, х е== с, . . . , то
q делится на произведение (х — а) (х — Ъ){х — с) ... Действительно,
так как числа а, Ъ, с, .. . предполагаются несравнимыми одно с дру-
другим, то функции х — а, х — b, x — с, ... попарно взаимно просты,
и так как функция g делится на каждую из них, она будет де-
делиться также и на их произведение. Отсюда вытекает, что число
корней не может превосходить степени сравнения. Это и есть обе-
обещанное нами доказательство этой теоремы.
Одновременно, однако, из этого усматривается, что решение срав-
сравнений образует только часть значительно более общего исследо-
исследования, именно, исследования о разложении функций на сомножи-
сомножители. Ясно, что сравнение ? = 0 не имеет вещественных корней,
если с не обладает сомножителями первой степени; однако не исклю-
исключено, что Г; может быть разложено на сомножители второй, третьей
или более высоких степеней, вследствие чего функции ? в извест-
известном смысле могут быть приписаны мнимые корни. В действитель-
действительности, если бы мы пожелали воспользоваться той свободой, кото-
которую позволяют себе теперешние математики, и ввести такие мни-
мнимые величины, мы могли бы несравненно сократить наши дальней-
дальнейшие исследования; тем не менее мы предпочли выводить все из
старых принципов.
780 Учение о вычетах
339
Функции называются простыми по некоторому определенному
модулю, если они по этому модулю не делятся ни на какие функ-
функции более низкой степени.
Так, например, все функции первой степени простые; функции
же второй степени являются либо простыми, либо составлены из
двух функций первой степени; при этом ? будет простой функцией
второй степени, если сравнение ? = 0 не имеет вещественных корней.
Так, например, функция х2 + х + 1 по модулю 5 простая, потому что
х2 + х + 1 = (х — 2J — 3 (mod 5),
и 3 является квадратичным невычетом по модулю 5.
Эти простые функции требуют нашего внимания в первую оче-
очередь. Действительно, хотя для нахождения вещественных корней
из них не могут служить никакие, кроме функций первой степени,
тем не менее более подробное рассмотрение этих простых функций
целесообразно как вследствие их замечательных свойств, так и по-
потому, что из них выводятся и другие прекрасные истины.
340
Теорема. Любая функция либо является простой, либо состав-
составлена из простых функций, причем в последнем случае она может
быть составлена из простых функций только одним единственным
образом.
Доказательство. Именно, если заданная функция А не простая,
то она будет делиться на некоторую функцию В более низкой сте-
степени. Если В— не простая функция, то она делится на некоторую
другую функцию С более низкой степени, и если продолжать таким
же образом, то ясно, что в конце концов мы придем к простой
функции, так как в противном случае этот ряд был бы бесконеч-
бесконечным, что невозможно, ибо степени все время убывают. Если теперь
последняя простая функция есть L, то она входит делителем во
все предшествующие функции. Поэтому A—LA', и А' имеет более
низкую степень чем А. Но так как теперь снова A'==L'An и т. д.,
Общие исследования о сравнениях 781
мы, очевидно, в конце концов придем к простой функции, и потому
А будет сравнимо с произведением простых функций L, Z/, L",. . .
Если теперь предположим, что также А = ММ'М". . . , и не все
функции L, Z/, L", . . . совпадают с функциями М, М', М", . . . ,
то отбросим те, которые являются общими для обоих рядов. Если
остаются функции X, X', X", . . . ; [х, [j/, [а", . . . , то функция [х будет
взаимно проста с X, X', X", . . . ? а потому и с их произведением
ХХ'Х". . . Несмотря на это, должно быть
ХХ'Х" . . . = (л(л,у . . . , т. е. Xk'V'' ' ' = fx'fx" ,
что невозможно.
341
Основная задача этих исследований состоит в том, чтобы опре-
определить число простых функций каждой степени. Именно, так как
для определенного модуля число всех различных (несравнимых)
функций каждой степени ограничено, а из них одни составлены из
простых функций более низких степеней, а другие сами являются
простыми, то и количество этих последних конечно. Строгое изло-
изложение этого предмета довольно трудно; мы начнем с более прос-
простых случаев.
Если положить модуль равным /?, то число всех различных
функций n-й степени вида
хп + Ах71-1 + Вхп~* + Схп~з + . . .
равно рп. Действительно, число коэффициентов ^4, 5, С,. . . , равно п,
а так как каждый из них независимо от остальных может быть
= 0, 1, 2, 3,..., р—1 (mod/?), то из комбинаторных соображений
следует, что всего имеется рп различных комбинаций; они и бу-
будут поэтому определять совокупность всех различных функций этой
степени.
Так, имеется р различных функций первой степени, именно функ-
функций х, х + 1, х + 2, . . . , до х -f р — 1; р2 различных функций вто-
второй степени и т. д.
782 Учение о вычетах
342
Выше мы уже указывали на то, что все функции первой степени
являются простыми; если мы ограничимся, что для нашей цели
достаточно, такими функциями, старший член которых имеет коэф_
фициент 1, то всего будет р функций первой степени.
Все функции второй степени либо составлены из двух функций
первой степени, либо являются простыми. Но из комбинаторики
известно, что р различных предметов можно скомбинировать по два
(включая и комбинации одинаковых предметов) р(р-\-1)/1-2 раз-
различными способами. Поэтому столько же будет функций, состав-
составленных из двух простых функций первой степени, и потому сущест-
существует р2 — "Г ' — -тг- (р2 — р) простых функций второй степени.
Подобным же образом из всех функций третьей степени, число
которых равно р3, исключаются те, которые составлены из трех
простых функции первой степени и число которых равно , ^ з '
и, далее, исключаются те, которые составлены из простой функции
первой степени и простой функции второй степени и число кото-
1 1
рых равно р--2~(р2 — р). Если их отбросить, то останется -^ (р3—р)
функций; таким образом, именно столько имеется простых функций
третьей степени. Очевидно, что можно и дальше продолжать по-
подобным же образом.
343
Однако, чтобы легче выполнять эти операции, и одновременно
проложить путь к нахождению общего закона, мы будем рассмат-
рассматривать вопрос в общем виде. Для краткости мы обозначим через
A) число простых функций первой степени, через B) — число прос-
простых функций второй степени и т. д., через (I2) — число функций,
составленных из двух простых функций первой степени, и т. д.,
вообще, через (la2^3Y. . .) — число всех функций, которые со-
составлены из простых функций, причем из а простых функций пер-
первой степени, р простых функций второй степени, ^ простых функ-
функций третьей степени и т. д.; степень такой функции тем самым
Общие исследования о сравнениях 783
равна а + 2C + 3f + . . . Тогда из предыдущего и из комбинатор-
комбинаторной теории явствует, что
A«2^45. . .) = (la) BP) C?) D5). ..,
(А «ч_ (*) К1) + *1 К*) + 21 К1) + 3] ¦ ¦ ¦ [A) + а - 1]
1 ;~ 1.2-3.4...а
или, вообще,
, _ (а) \(а) + 1] [(а) + 2] [(а) + 3] . . [(а) + а - 1]
{ } ~~ 1.2.3-4.. .а
Наконец, ясно, что если собрать все различные способы составле-
составления числа п посредством сложения из чисел 1,'2, 3, ... (эти спо-
способы можно обозначать через а-1 + Р*2 + f-З + . ..), то сумма всех
этих выражений Aа2рЗ^ . . .) будет равна числу всех функций сте-
степени п, т. е. равна рп. Так, например,
Р ^A),
Р* =
jp» =
/^4 = (I4) + (I2 - 2) + A - 3) + B2) + D),
и т. д.
Мы видим, что в выражение /?п, кроме величин A), B), C), . . .
входит также величина (гс),из чего следует, каким образом все ве-
величины могут быть определены чорез предшествующие. Так, мы
находим
(!) = />. D) = 4^4-Л G) = 4 (Р7-Р),
B) = 4-(/>а-/0. E) = -\-{рь-р), (8) = 4-(^-Л
и т. д.
344—346
Из этого начала ряда мы замечаем, что наивысший член выра-
выражения (п) равен рп I п, и если п есть простое число, то к этому
члену добавляется еще — р/п; если же п — составное число, тб за-
784 Учение о вычетах
кон менее очевиден. Если, однако, рассмотреть положение вещей
внимательнее, то мы увидим, что
Р =A), />« = 5E) + A),
р* = 2 B) + A), р» = 6 F) + 3C)+2B)+A),
A), />7 = 7G) + A),
2B) + 1, рв = 8(8)+ 4D)+2B)+A),
и т. д.
где дальнейший закон уже ясен; именно, если ос, !3, f, 5, • ¦ • явля-
являются всевозможными делителями числа п, то
Мы перейдем теперь к тому, чтобы доказать общность этого
замечания.
Мы показали, что сумма всех таких выражений Aа) B^) CY). . . ,
для которых а + 2C + Зу + . . . = п, исчерпывает все функции п-й
степени и потому равна рп. Отсюда вытекает . Если про-
/ 1 У*)/ 1 \&)Г 1 \C) 4 . Л .
изведение (д-z^j \i^r^) {tzt^J • • • разложить в ряд 1 + Ах +
Вх2+ . . . = Р, то
А = р, В = р\ С = рз, .
_ A)а? 2 B) х2 ^ 3 C) х3
/ Хб?Р DX
(отсюда, если вместо -^- подставить -г-^— и разложить отдельные
л (Хх 1 — рх
дроби в бесконечные ряды, немедленно получается справедливость
теоремы).
347
Эта теорема может быть выражена также и другим образом.
Именно, если п, 1, 8, 8', 8", 8W, . . . — всевозможные делители чис-
числа тг, то эта теорема состоит в том, что
рп=п(п) + A) + 8(8) + 8'(8') + 5"(8") + . . .
Но очевидно, что произведение (п) простых функций, имеющих
Общие исследования о сравнениях 785
степень п, будет иметь степень п(п), и так же обстоит дело и для
остальных произведений.
Поэтому произведение всех простых функций степеней 1, п, 8,
§',... имеет степень рп.
Теперь из этой теоремы легко вывести само значение выраже-
выражения (п); ради краткости мы, однако, опустим вычисление, которое
не трудно. Если, таким образом, п = a<xb^cr. . . , где а, Ь, с,. . . —
различные простые числа, то
П(п) = рП—^рп/а+^рп/аЪ_^рп/аЪс+ ...?
где 2/?п/аЬс обозначает совокупность всех выражений вида рп/аъс..^
когда величины а, 6, с, ... каким-либо образом переставляются меж-
между собой. Так, например, для уг = 36
36 C6) = /?36 — р18 — р12 + р\
Мы хотим добавить еще одно замечание. Если п имеет вид а*
и число а простое, то п(п) = рп — рп1а\ тем самым, так как (п)
обязательно целое число, то при любом р
pni= pnla (mod n),
и потому, если р взаимно просто с а,
_ п
р а = 1 (modtt),
и для а = 1
pa-i =
Замечательно, что эти теоремы могут быть получены столь
различными способами.
348
Задача. Пусть дано уравнение
хт + Ах171-1 + Вхт~2 + Cx™"s + ... + М = О,
корнями которого являются х = а, х = Ь, х = с,... ; нужно
найти уравнение, корнями которого являются х = ах, х = 6Т, х = ст, ...
786 Учение о вычетах
Первое решение. Найдем по известной теореме сумму корней
заданного уравнения, сумму их квадратов, кубов и т, д. до суммы
их тх - х степеней. Отсюда получается тогда и сумма корней
искомого уравнения, так же, как и сумма их квадратов и т. д.,
именно, 2аТ> 2а2Т> • • • » из чего на основании той же теоремы могут
быть определены коэффициенты.
Для практики это решение является более легким; однако для
нашей цели, а также и для доказательства того, что коэффициенты
искомого уравнения являются целыми числами, если коэффициенты
заданного уравнения целые, более целесообразно следующее решение.
Второе решение. Пусть 6 — собственный корень уравнения
хТ = 1; если образовать произведение функций
хш + Ах771-1 + Вхт+2 + . . . ,
хт + Адх™-1 + Вд2хт~2 + . . . ,
хт
х
2~-2 хт~2
то корнями этого произведения будут
а, 6а, 6*а,. ..,
с, Ос, е?с,
и т. д.,
т. е. произведение будет равно
(хТ — ах) (хт — Ьт) (хт — ст).. .,
и потому будет иметь вид
х™ + А' ят(™-1) + Bf x<m~2^ + . ..
Если теперь вместо хт мы напишем х, то получим
хт + А' я™-1 + В' хт~2 + . . . = (х — ах) (х — ЬТ) (х — ст). . .,
и потому уравнение
хт + А' хт~>- + В' хт~2 + ... = О
является искомым. А то, что числа А', В\ ... здесь не только
Общие исследования о сравнениях 787
рациональные, а даже целые, легко вытекает из теории уравнения
хх = 1.
Так как в дальнейшем мы часто будем использовать эту опера-
операцию, мы обозначим через (Р, рт) функцию, которая, будучи прирав-
приравнена нулю, дает уравнение, корнями которого являются т-е степени
корней уравнения Р = 0.
Если Р == Q по какому-нибудь модулю, то и (Р, рт) = ((?, рт) по
этому модулю.
349
Теорема. Если т — простое число, то коэффициент члена хп
в функции (Р, рт) сравним по модулю т с коэффициентом члена хтп
в функции Рт (что представляет собой для этого случая третье
решение предыдущей задачи).
Доказательство. Из шестого раздела следует, что некоторый
коэффициент произведения
(xm f Axm~l + . . .) (хт + Лбж™-1 +...)...
после подстановки вместо 6Т единицы принимает вид
е + A + е + е2 + ... + б") F.
Если теперь рассматривать 6 как первообразный корень уравне-
уравнения xv = 1, то все произведение обратится в Е; если же положить
6 = 1, то все произведение превращается в Рт = Е + tF, и потому
коэффициент члена хпт в функции Рт сравним по модулю т с коэф-
коэффициентом члена хпТ в Е, т. е. с коэффициентом члена хп в функ-
дии (Р, рт).
350
Теорема. Если т — простое число, то
(Р, Р^)еее
Доказательство. Пусть в (Р, рт) коэффициент члена хп равен N'Т
а в Р коэффициент того же члена равен N. Если положить тогда
Р = хт + Лж™-1 + . . . + Nxn +. . .,
788 Учение о вычетах
то будет выполняться сравнение
рт _ хтт + ? х(т-1)т + ... +NTxnx + ... (mod т),
и потому (согласно предыдущему пункту) JV' = NT (mod т); поэтому,
так как NT = N, то и N' = N, что и требовалось доказать.
Отсюда очевидно, что (Р, ра) == (Р, рат) и (Р, рт) = (Р, рт2),
и потому вообще
(Р, p«)EEE(P,p-*
351
Теорема. Существует такое значение числа v < /?m, wzo функция
xv — 1 делится по модулю р на заданную функцию Р степени т,
у которой низший член не содержит х.
Доказательство. Разделим на Р ряд функций 1, х, х2, . . . , х?™-1
если они имеют степени, большие чем т\ так как ни одна из этих
функций не может делиться на Р без остатка, то все остатки могут
быть приведены к виду
Ах™-1 + Вхт~2 + . . . + N,
где все коэффициенты положительны и меньше чем р. Но ясно,
что так как все коэффициенты никогда не могут быть равны 0, то
имеется только рт — 1 функций, одной из которых обязательно
должен быть равен каждый остаток; поэтому, так как, пока мы
дойдем до степени х с показателем рт — 1, получится рт остатков,
хотя бы два остатка обязательно должны быть равны. Пусть такие
остатки получаются при делении ха и ха+* на Р, где а + v < рт.
Тогда #a+v — ха будет делиться на Р. Поэтому на Р будет делиться
и xv — 1, так как (по предположению) ж, а потому и ха является
функцией взаимно простой с Р.
Дополнение. Если xv — 1 делится на Р, то и xkv — 1 будет
делиться на Р, где к обозначает любое целое число.
352
Теорема. Пусть обозначения остаются теми же, что и в преды-
предыдущем пункте. Тогда если Р — простая функция, и xv — наимень-
Общие исследования о сравнениях 789
тая степень, такая, что xv—1 делится на Р, то v либо равно
рт — i^ либо является делителем этого числа, за исключением един-
единственного случая, когда Р = х.
Доказательство. Так как Р есть простая функция степени т,
то существует рт — 1 различных функций степеней, меньших чем
т (именно, из всех функций отбрасывается функция 0), которые
все взаимно просты с Р. Так как теперь, по предположению, xv
есть наименьшая степень, которая при делении на Р дает остаток 1,
то ясно, что если все более низкие степени от 1, х, . . . до xyJ~1
разделить на Р, то получатся v различных остатков, которые мы
в общем виде будем обозначать через А. Если теперь эти v остатков
исчерпывают все возможные остатки, то теорема доказана; если же
имеются еще остатки, не содержащиеся среди полученных, то пусть
один из них есть В. Тогда очевидно, что функция Bxv при делении
на Р дает остаток В, и, вообще, Bxv+k = Bxk (mod P). Но все функ-
функции от В до Bxv~x дают остатки, отличные как один от другого,
так и от остатков А; действительно, если бы имело место
Вхх = Вхх+Ъ (modP), то было бы и 1 == x5(mod.P), где 8 < v, что
противоречит предположению; если же было бы Вхх = ^(mod P)y
то было бы также В = x^v~x (mod P), и потому В совпадало бы
с одним из остатков А, вопреки нашему предположению. Поэтому
мы получаем, очевидно, v новых остатков. Таким же образом
можно продолжать и дальше (точно так же, как и выше, вп....),
и ясно, что число всех возможных рт — 1 остатков будет либо = v,
либо = 2v, либо = 3v, т. е. вообще будет равно некоторой кратности
числа v.
353
Из предыдущей теоремы и дополнения к п. 351 следует, что
каждая простая функция степени п входит по модулю р в функцию
жрп-1 —1# Поэтому все функции первой степени, за единственным
исключением тех, которые сравнимы с х, будут входить в xv~1—1;
это есть теорема Ферма; все простые функции второй степени,
т. е. функции вида х2 + Ах + В будут входить в функцию х^~х — 1,
и т. д. Если теперь п, 6, 6', §", . . . , 1 суть все делители числа п>
790 Учение о вычетах
то очевидно, что и рп— 1 будет делиться на ръ— 1, ръ' —1,
ръ" — 1 ,...,/? — 1; поэтому функция х®71'1 — 1 делится на все про-
простые сомножители степеней п, 8, §', 8", . . . вплоть до простых
функций первой степени (за исключением функции х), а, значит
(так как все эти функции абсолютно просты, а потому и попарно
взаимно просты), также и на произведение всех этих функций. Но
это произведение имеет степень рп—1 (п. 347; одна функция, х,
выбрасывается), и потому получается, что это произведение должно
быть сравнимо с функцией х^п~х — 1 по модулю/?.
354
Теорема. Если функция xv — 1 делится на функцию Р9 то
(Р, Р*»+<) = (Р, рО,
где A, t обозначают любые целые числа.
Доказательство. Если
Р = хт + Ах™-1 + Вхт~2 + . . . ,
и если
х™ + Ах™ + . . .
разложить в бесконечный ряд вида
1111
хх х21 ' 1 х3 ' * ж4 ' »
то, как известно, а будет суммой корней уравнения Р — 0, р — сум-
суммой их квадратов и т. д. Отсюда без труда выводится, что суммы
(v -р 1)-х, (v + 2)-х, . . . степеней сравнимы соответственно
с суммой корней, суммой их квадратов ж т. д. Но из этого сле-
следует, что если только модуль не равен и не меньше степени
функции Р, то
(Р, р*+1)^Р, (Р, р^) = (Р, р2), (Р, p*+*) = (J>, р»),...
Оставшийся же случай мы рассмотрим ниже.
Общие исследования о сравнениях 791
355
Теорема. Если в ряду
члены, следующие за v-м членом, сравнимы по порядку с первыми
членами, то xv — 1 будет делиться на Р, если только Р не содер-
содержит одинаковых сомножителей.
dP
Доказательство. Если положить =— = Q, то функция Q будет
взаимно проста с Р. Если
"Р" = аГ ~^~ ~а? ~^ ~х* ~^ ' ' ' '
то после члена N / xv (по предположению) будет следовать
. в , с ,
Поэтому
откуда вытекает, что функция х"—1 делится на Р.
356
Теорема. Если Р есть простая функция от х степени т, и
X — функция от х, xv, xv , xpS, . . . , х^т~1, в которую все эти вели-
величины входят одинаковым образом, т. е. которая остается неизмен-
неизменной, каким бы образом мы эти величины не переставляли между
собой, то функция X при делении на Р дает остаток, являющийся
числом.
Доказательство. Если остаток есть
Ах™-1 + Вт~2 + . . . + N = g,
то все коэффициенты А, В, С, . . . до iV, за исключением этого
последнего, будут сравними с 0.
Это доказывается следующим образом. Так как X — ? делится
на Р,тои Jp — ?р делится на Р. Но легко видеть, что Xv есть то,
792 Учение о вычетах
что получается из X, если вместо х подставить xv, вместо xv подста-
подставить xv\ и т. д., и вместо хрГП~1 подставить х^т или, что то же
самое, х. Поэтому, очевидно, Xp = X(mod.P); тем самым, так как
Xv = ?р и X = ?(mod,.P), имеет место также SP^?(modP), т. е.
Но lv — ? сравнимо по модулю р с произведением функций ?, ?+1,
? + 2, ... до ? + /> — 1, а эти сомножители будут все взаимно просты
с Р, если только ? не является просто числом. Поэтому и ?р—?
ни в каком другом случае не может делиться на Р.
Такими функциями, которые фигурируют здесь, являются сумма
всех указанных величин, с^мма их квадратов, кубов и т. д., суммы
произведений из них по два, по три и т. д. Что представляют из
себя получающиеся числа, мы определим в следующем пункте.
357
Теорема. Если
р^хт- Ах1'1 + Bxm~2 - Cxm~s + • • •
есть простая функция предыдущего пункта, то остаток будет
сравним с А, если поделить на Р сумму величин х, xv, .. .
• . . , xvm~x, будет сравним с J5, если поделить на Р сумму их
произведений по два, будет сравним с С, если поделить на Р сумму
их произведений по три, и т. д.
Доказательство. Пусть указанные функции суть X, Y, Z, . . . у
а их остатки по порядку суть А', В', С", ... Тогда легко видеть,
что х, xv, хр2, . . . являются корнями уравнения
zm — Xz™-1 + Yzm~2 — Zzm~3+ . . . = 0.
Поэтому, если положить z = x, то будет выполняться равенство
хт — Хх171-1 + Yxm-2— Zxm~3+ . .. = 0.
Но функции X—A', Y — В', Z — С, ... делятся на Р, поэтому
на Р делится и функция
хт — А'хт~^ + Bfxm~2 — C'xm~s + ...
Общие исследования о сравнениях 793
Это, однако, возможно только в том случае, если А' = А, В'=ВГ
С = С, ...
Известно, кстати, что всякая другая функция X от х, xv, xv\ . . .
(в которую все эти величины входят одинаковым образом) всегда
может быть вьгражена через эти функции. Так, например,
х2 + х^+х^2 + . . . = А2 — 2В (modp), и т. д.
Пример. Если р =: 5 и Р = х2 -f- 2х + 3, то при делении на Р
функция х + хь будет сравнима с — 2, #6 = 3, и т. д.
358, 359
Теорема. Если Р — простая функция, их" — наименьшая сте-
степень неизвестного х, которая при делении на Р дает остаток 1,
и если, далее, Р = (Р, рп), то п будет сравнимо по модулю v с не-
некоторой степенью числа р.
Доказательство. Выше мы показали, что если
Р = хт + Ах™-1 + Вхт~2 +
то
zm + Azm~^ + Bzm~2 + ... — (z — х) (z — X*) . .. (z — яр™)
делится на Р. Подобным же образом получается, что
zm + Az171-1 + Bzm~2 + . . . — (z — хп) (z — xnv) . .. (z — x71?771'1)
делится на Р. Но так как эти сомножители попарно взаимно просты,
то, очевидно, каждый из вторых должен быть сравним по Рг
р с одним из первых. Поэтому обязательно z — xn = z — #рх, т. е.
р* = п (mod v). Это и требовалось доказать.
О нахождении простых делителей функции acv— 1
по простому модулю
360
Если v делится на модуль р или на некоторую его степень, и,
скажем, v = pk • X, то
x" — i = {xK—\yk (mod/? .
794 Учение о вычетах
Отсюда вытекает, что нужно рассматривать только тот случай,
когда v не делится на р.
Если /?m = l (modv) и: при этом число т — наименьшее из воз-
возможных, то хТ>т~1—1 будет, очевидно, делиться на xv—1. По-
Поэтому xv — 1 не может иметь других сомножителей, кроме сомно-
сомножителей функции х/рГП~1— 1. А это выражение имеет простые дели-
делители степени т и другие делители, степени которых являются
делителями числа т. Поэтому и х"— 1 должно иметь такие дели-
делители. Сколько делителей каждого рода имеет эта функция, мы про-
продемонстрируем на примере, откуда легко можно будет вывести и
общий закон.
Если v = 63 и р = 13, то т = 6. Поэтому х63— 1 будет иметь
по модулю 13 простые сомножители шестой, третьей, второй и пер-
первой степени. Но ясно, что произведение сомножителей первой сте-
степени есть общий делитель (более высокой степени) функций х63 — 1
и х12—1, т. е. есть х3— 1. Поэтому имеется три сомножителя пер-
первой степени. Произведение всех простых сомножителей второй и
первой степеней будет общим делителем функций хез—1 и х168 — 1,
2| з
т. е. будет равно х21 — 1; поэтому имеется —^—~9 сомножителей
второй степени. Произведение простых сомножителей третьей сте-
степени и первой степени будет общим делителем функций х63 — 1
g 3
и я2196— 1, т. е. равно ж9— 1; поэтому имеется » = 2 де-
делителей третьей степени. Наконец, остальные имеют шестую
63 — 6 — 18 — 3
степень и их число, таким образом, равно ^ ,
т. е. равно 6.
При внимательном рассмотрении этого положения вещей мы
легко получаем следующее общее правило.
Пусть 8— делитель числа т, и пусть 8', 8", 8'", . . .— всевозмож-
всевозможные делители числа 8, меньше чем 8. Пусть, далее, наибольшие
общие делители числа v и чисел ръ—1, рь' — 1, рь" — 1, . . . равны
соответственно [х, [х', [л", . . . , и числа (х/[х', (х/[х", [л/[л"', . . . равны
соответственно X', X", V\ . . . Тогда xv — 1 имеет простых дели-
делителей степени 8 в 8 раз меньше, чем имеется чисел, меньших чем [х,
которые не делятся ни на одно из чисел X', X", Х"\ . . .
Общие исследования о сравнениях 795
361
Теорема. Если функция X от переменного х делится на другую
функцию 5, и при замене х на хк функция X переходит в Х\ то
X' делится на (?, pl/k).
Доказательство. Если X = %v и g, v переходят в ?', г/, если
вместо х написать хк, то, очевидно, ,X' = |V. Но ?' делится на
(?, р1/к), а потому делится также и X'.
362
После установления этих закономерностей мы можем теперь
легко определить простые делители функции xv—1. Предположим,
что все те делители, которые делят также какую-нибудь функцию
xv' — 1, где v' < v, уже найдены, и что нужно только получить
остальные. Все они, однако, могут быть соединены в выражении
(Р, pft), где Р есть один из них, а вместо А: подставляются все числа,
которые меньше чем v и взаимно просты с v.
В шестом разделе мы показали, каким образом собственные корни
уравнения xv = 1 могут быть так разбиты на классы, что после
того как все они будут выражены в виде степеней одного из них,
в отдельных классах получается одно и то же разбиение, какой бы
собственный корень ни был взят за основание. Такие совокупности
корней мы будем называть периодами. Теперь ясно, что функции
ж, ха, х&, жт, . . . , где а, р, т, • • • обозначают все взаимно простые
с v числа, могут быть подобным же образом разбиты на периоды,
а каждый больший период снова разбит на меньшие, пока мы
в конце концов не придем к периодам вида хк, хкр, хкр\ . . . , хк1рт~~~1.
Если это сделано, то, очевидно,
1) так как каждый период составлен из таких наименьших пе-
периодов хк + хкр + . . . , то при делении его на некоторую простую
функцию степени т в остатке получится число;
2) так как всегда все члены периода могут быть представлены
в виде х*'аа'ъ^'сУ'", где х, а, 6, с, ... —определенные числа, а для
а, р, *у, . . . можно подставлять все значения, то ясно, что период
переходит сам в себя, если вместо х подставить хк, где к имеет
вид aab^c^. . . (mod v), откуда легко видеть, что если к обозначает
796 Учение о вычетах
такое число, то все функции Р, (Р, рк), . . . при делении на них
периода приводят к одному и тому же остатку;
3) поэтому период после вычитания этого остатка будет делиться
на произведение всех функций (Р, рк).
363
Таким образом, в основном дело сводится к тому, чтобы опре-
определить эти остатки. Сначала определим остаток, который полу-
получается при делении на произведение всех фигурирующих здесь
простых функций наибольшего периода. Если это произведение
сравнимо с
хх — Ах7—1 + . . . ,
то остаток сравним с А. А вид этого произведения найти легко,
и из шестого раздела получается, что А = О, если v делится на не-
некоторый квадрат, а в противном случае, А либо равно +1, либо
равно —1, в зависимости от того, четно или нечетно число простых
сомножителей числа v.
Разложим теперь этот наибольший период на меньшие периоды
и представим периоды каждого члена через xkp7Zu, так что к есть
для каждого периода определенное, но для различных периодов
различное число, а тг и и в каждом периоде являются переменными
числами, однако те значения, которые они имеют в одном периоде,
сохраняются также и в остальных. Если взять пока в качества
основания какую-нибудь простую функцию Р, и если остатки от
деления периодов 2 ^рТГи, 2 %к'рПи, . . . на Р суть соответственна
А, А', ... , то 2 хрПи — -^ будет делиться на произведение всех
функций (Р, ри), 2 ж*'рТСп — А' будет делиться на произведение
всех функций (Р, рк'и) и т. д. Но легко видеть, что величины
А, А', . . . являются корнями заданного сравнения. Именно, если
периоды корней уравнения xv — 1, которое соответствует предыду-
предыдущим периодам, являются корнями уравнения Q = 0, то А, А\ . . .
будут корнями сравнения Q = 0. Действительно,
А + А' + • • • =с суммой периодовг
А2 + A'2 -f- * • • = с суммой квадратов периодов,
и т. д.
Общие исследования о сравнениях 797
Именно, выкладки совершенно аналогичны тем, которые мы про-
проделывали в шестом разделе, если только взять х вместо р, так как
и здесь xv можно заменять единицей, так же, как там pv.
Если мы нашли корни А, А', . . . , то выберем какой-нибудь из
них в качестве остатка периода 2#pTCu и расположим затем остатки
других периодов подобно тому, как мы делали это в шестом разделе.
Указанный выбор здесь также произволен, так дак функция Р до
«сих пор была совершенно неопределенной. Следующая выкладка
целиком аналогична той, которую мы подробно производили в ше-
шестом разделе; изложение здесь всех частностей завело бы нас слишком
далеко. После того как мы, наконец, придем к 2 хрП> все будет
сделано. Действительно, если положить
р = хт _|_ axm~l _|_ bxm-2 -f- . . . ,
то —а=^хрП\ таким же образом мы получаем вторые коэффи-
коэффициенты остальных функций (Р, рЛ), откуда могут быть определены
другие коэффициенты функции Р. Нередко может случиться, что
мы будем приходить к тождественным сравнениям, из которых
казалось бы ничего нельзя получить. Как можно преодолеть эту
трудность, мы покажем ниже.
364
Все это станет намного яснее на примере. Пусть поставлена
задача разложить на множители функцию х15 — 1 по модулю 17.
Здесь т = 5, и так как произведение всех элементарных функций
сравнимо с
(ж15 — 1) (а; — 1) _ 8 7 , б Т4 i тз т _! \
(х3 — 1)(хь — 1) ~~ "~ ' ' ' '
то имеется лишь два простых сомножителя Р и Рг четвертой сте-
степени. Разложим теперь х, х2, ж4, х7, ж8, ж11, ж13, хи на следующие
два периода:
= х' + хп + ж13 + хи.
798 Учение о вычетах
Если по одной из функций Р, Р' имеет место
то
А + А'=1,
л* = 2> 1?а + 2 &1?а + 2 ^1?а + 2
л' 2= 2х«-"а+2 х* 1'а + 2 я»-"а + 2
и потому
5'1?а = 1-4-4
Поэтому ^4, А' являются корнями сравнения
х2 — х + 4 = 0 (mod 17),
и они равны 6, 12. Тем самым Р будет делителем функции
х* + х± + х* + х — 6,
причем
Р = ж4 — 6х3 — 2х2 — 12ж + 1.
Функция же Р' будет сравнима с (Р, р7), и потому
365
Для нас достаточно здесь показать возможность этих решений.
Многочисленные искусственные приемы, посредством которых этн
вычисления могут быть облегчены, мы ради краткости опускаем.
Напротив, мы не можем оставить без упоминания некоторые очень
важные следствия.
Предыдущим было доказано, что все вспомогательные уравне-
уравнения, для решения уравнения xv = 1, будучи превращены в сравне-
сравнения, имеют некоторые корни, если период
х 4- xv + жр2 + . . . + яР™
еще не разложен. Если мы возьмем случай, когда v есть простое
число, то т будет делителем числа v — 1. Таким образом, здесь
вспомогательные уравнения (если число периодов, которые при
Общие исследования о сравнениях 799
помощи их отыскиваются, будет делителем числа (v — l)/m), имеют
вещественные корни. Если поэтому (v — 1) / т четно, т. е. если т
является делителем числа (v—1)/2, т. е. если pty—V/z = l (mod v),
т. е., наконец, если р является квадратичным вычетом по простому
числу v, то квадратное уравнение, при помощи которого корни
разбиваются на два периода, будет обладать вещественными кор-
корнями по модулю р. Но в шестом разделе мы показали, что если
положить v — 4/г + 1, то этим уравнением всегда будет ж2 + х + п = 0.
Поэтому у нас получается следующая замечательная теорема.
Теорема. Если простое число р является квадратичным вычетом
по простому числу 4п + 1, то сравнение
х2 + х + п = 0 (modр),
а потому также и сравнение
будет иметь вещественные корни, т. е. + v будет квадратичным
вычетом по числу р.
366
Это есть, таким образом, третье полное доказательство фунда-
фундаментальной теоремы четвертого раздела, которое тем более замеча-
замечательно, что принципы, из которых оно выведено, совершенно отличны
от тех, которыми мы пользовались при прежних доказательствах.
Но из этого же источника, однако, противоположным путем, мы
выведем и четвертое доказательство. Именно, если v есть простое
число вида 4/г + 1, и р — любое другое простое число, и если +v
является квадратичным вычетом по простому числу р, то мы дока-
докажем, что р является квадратичным вычетом по числу v.
Пусть рт — наименьшая степень числа р, которая сравнима с 1
по модулю v. Элементарные делители функции (xv —1)/(#— 1) по
модулю р буд>т иметь степень т, и потому число их всех будет
равно (v — 1)/т. Но так как + vi?p, то сравнение
х2 + х =р п = 0 (mod p)
800 Учение о вычетах
разрешимо; пусть его корнями будут А и А'. Разобьем функции
ж, ж2, . ..,жу~1 на два класса, которые обозначим через ? и ?'; тогда
? + ?' = ^4 + Л' + A + х + х* + ... + ж*-1),
К' == 44' + X A + х + х2 + . . . + xv~i),
и потому функция (z— ?) (z— S')— (z— 4) (z — -4') будет делиться
на каждый элементарный делитель функции (х? — 1)/(ж—1).
Поэтому каждый такой элементарный делитель будет вхо-
входить либо в ? — 4 и ?'— А', либо в ? — А' и ?'— -4. Из этого
вытекает (так как А несравнимо с А'), что если подставить xv
вместо х, то ? и ?' не изменятся. Действительно, если бы <¦ перехо-
переходило в ?' и обратно, то ? — ^4 и ? — ^Г делились бы на одну и ту
же простую функцию, что невозможно. Отсюда следует, наконец,
что (v —1)/2 делится на т9 т. е. /?(V~D/2 — 1 делится на v. Поэтому
р является квадратичным вычетом по модулю v.
Все случаи фундаментальной теоремы легко вывести из каждой
из этих двух теорем.
367
Хотя мы ограничились здесь случаем, когда v является прос-
простым числом, но аналогичные теоремы без большого труда мо-
могут быть установлены и тогда, когда число v составное, на чем,
однако, мы теперь, ради краткости, подробнее останавливаться не
можем.
Ясно, что подобные же замечания можно сделать также и от-
относительно большего числа периодов. Так, если (v—1) / т делится
на 3, т. е. если р является кубическим вычетом по простому чис-
числу v, то уравнение, при помощи которого корни уравнения xv =1
разбиваются на три периода и которое мы в шестом разделе научи-
научились определять a priori, будет разрешимо по модулю р, и обратно.
Так, например, сравнение х3 + х2—2х — 1 = 0 разрешимо по лю-
любому простому модулю, который имеет вид 7п + 1, в то время как
это невозможно, если модуль имеет не такой вид.
Нам было бы не трудно обогатить эту главу еще многими дру-
другими замечаниями, если бы рамки, которыми мы должны ограни-
Общие исследования о сравнениях 801
читься, не запрещали этого. Для тех замечаний, которые могли
бы повести еще дальше, эти принципы по крайней мере смогут
указать путь.
368
Мы будем говорить, что некоторое сравнение S = 0 имеет рав-
равные корни, или, более общо, равные делители, если S делится на
степень некоторой функции.
Имеет ли заданное сравнение равные делители, можно узнавать
таким же образом, как и в теории уравнений. Если положить
то, очевидно, будет выполняться сравнение
dx —С V dx + * dx)'
поэтому -г- будет делиться на %т~1. Если вообще
где А, В, С,... обозначают различные простые функции, то
dX _ у f a dA Ь dB
1
dx — " \a ' dx ^ в ' ;dx + с"' ш + * • 7>
откуда вытекает, что если ни одно из чисел а, Ь, с, ... не делится
на модуль, то т— делится на Аа~1 ВЬ~1СС~1..., но не делится на
Аа, Въ, Сс,... Из этого вытекает следующая теорема.
Теорема. Если общий делитель наибольшей степени функций X и-г-
равен ?, то X будет обладать всеми простыми сомножителями, ко-
которые имеет ?•, причем каждым из них в числе, на единицу боль-
большем чем Е; если поэтому X и -j— являются взаимно простыми
функциями, то X не будет иметь равных сомножителей.
802 Учение о вычетах
369
Первый пример. Мы хотим узнать, имеет ли функция
хъ + 3^4 _ 6хз + Зж _ 4 = X
равные делители по модулю 17. Имеем
Отсюда мы находим, что функции X ж -г- взаимно просты, вслед-
вследствие чего X не имеет равных сомножителей.
Второй пример. Если
2х — 3 (mod 13),
то
^ = 5х4 — 2х3 + 4х2 + 5х + 2.
Но наибольший общий делитель функций X ж -г- сравним
+ 1х + 7 или, после умножения на 8, сравним с х2 + 4я + 4; и
так как этот делитель сравним с (ж + 2J, то функция X будет
делиться на (х + 2K, а частное (которое равно х2 + 11) уже не со-
содержит других двойных делителей.
370, 371
Если в соответствии с предыдущими пунктами функция X пред-
представлена в виде АаВьСс. .., где А, Б, С, ... — попарно взаимно
простые функции, и числа а, Ь, с,... не равны 1, то разложение
может продолжаться и дальше. Пусть, таким образом, X — функ-
функция, которая больше уже не содержит равных делителей. Мы ви-
видели выше, что xv — х является произведением всех простых функ-
функций первой степени. Если g — общий делитель наивысшей степени
функций X ж х? — х, то | будет произведением всех делителей
первой степени функции I, и I/S уже не будет обладать такими
делителями. Если же мы найдем, что функции X и xv — х взаим-
взаимно просты, то функция X не будет иметь делителей первой степе-
Общие исследования о сравнениях 803
ни и потому сравнение X = 0 не будет иметь вещественных корней.
Так как, далее, х^2 — х является произведением всех простых функ-
функций второй степени и первой степени, то общий делитель наивыс-
наивысшей степени функций хр2— х и Х/?, равный, скажем, &', будет со-
содержать все делители функции X, которые имеют вторую степень.
Если так продолжать и дальше, то видно отсюда, что X может
быть таким способом разложена на сомножители ?, ?', ?", .. ., кото-
которые содержат соответственно все делители первой, второй, третьей
и т. д. степеней.
372
Если же дано произведение нескольких простых функций в
одинаковых степенях, то отдельные функции должны определяться
пробами. Эта задача имеет большое сходство с той, в которой
отыскиваются сомножители составных чисел. Но здесь уже a priori
определено, может ли быть заданная функция еще разложена на
сомножители. Так как, кроме того, здесь количество всех возмож-
возможных сомножителей конечно, мы можем пользоваться подобными же
вспомогательными средствами, как и выше. Однако мы не будем
задерживаться на этом вопросе, так как опытный вычислитель,
свободно владеющий общими принципами, легко найдет, если это
будет нужно, специальные приемы.
Мы переходим к другому вопросу, а именно, к рассмотрению
сравнений, у которых модуль не является простым числом, что
мы до сих пор все время предполагали. Однако здесь особенно ва-
важен случай, когда модуль является степенью простого числа, при-
причем важен как сам по себе, так и потому, что он необходим для
устранения некоторых сомнений (п. ...)»
373
Задача. Пусть функция X разложена по модулю р на попарно
взаимно простые сомножители ^ ?', ?"...; нужно так разложить
X по модулю р2 на подобные же сомножители 3, 2', 3", ...,
& = Н, ?' = 2', Г = 2"... (mod».
804 Учение о вычетах
Решение. Если Х=?ф (mod р), т. е. Х= ?ф +/>Е, и если мы положим
3 = Б + р<р, Y = ф + /ко,
то будет выполняться равенство
ST = X — pi, + (срф + Sw) /? + /?W
Если, таким образом, должно быть HY =X(mod/?2), то срф + Ы—S
обязательно должно делиться на р. Но так как ф и ? по модулю
р являются взаимно простыми функциями, то ф и (о могут быть
определены так, что это условие выполняется (п. 336), и притом,
кроме того, так, что степени функций ср и со на единицу меньше
соответственно степеней функций ? и ф. Тогда будет иметь место
X = HT(mod/?2). Ясно, что подобным же образом Т снова может
быть так разложена на сомножители З'О, что 3/^%'(то&р), и т. д.,
вследствие чего мы в конце концов получаем
Х = ЕЕ'Е" ...(modp2).
374
После этого легко может быть доказано, что X может быть
разложена на сомножители также и по модулям р3, р*,... Если
вообще
X = PQ (modрт), т. е. X = PQ + p™R,
и если функции Р ж Q по модулю /? взаимно просты, то, полагая
Р' = Р + Л/?™, Qf = Q + Bpm,
мы получим
Р'<?' = X — pmR + D<> + БР) рт + АВр*™.
Отсюда для каждого модуля /?v (где v^>m и < 2яг + 1):
P'Q' = X, если i? =
Из этого видно, что если функция X по модулю р не имеет
равных сомножителей, то она разлагается на сомножители по мо-
модулю рк аналогично тому, как и по модулю р. Если же X имеет
Общие исследования о сравнениях 805
равные сомножители, то дело обстоит намного сложнее, и не мо-
может быть полностью исследовано даже при помощи предыдущих
принципов. Поэтому, так как мы не можем сообщить всего, что
сюда относится, мы рассмотрим только один случай, который пред-
представляется важнейшим, и исследование которого нужно для раз-
разрешения некоторых оставшихся от предыдущего сомнений. Это
тот случай, когда в рассмотрение входят только равные сомножи-
сомножители первой степени. Он может быть также целесообразно исполь-
использован для нахождения корней сравнений. В другом месте мы из-
изложим этот вопрос в общем виде.
375
Пусть, таким образом, ХеееХ' (х— а)т(то&р), и функция X'
взаимно проста с х — а\ отыскиваются все делители функции X
первой степени, которые сравнимы с делителем х-—а по модулю р, a
сама функция X делится на них по модулям р2, р3, ... (Мы пред-
предполагаем, что абсолютно функция X не делится на х — а, так как
иначе х — а делило бы функцию X по любому модулю.) Если
вместо х подставить z + #, мы получим
Z = Z'zm (modр), или Z = Z'zm + pA.
Если теперь Z делится по модулю р2 на некоторый делитель
вида z + а/?, то А обязательно должна иметь вид zZ" -f- pB. Если
это не имеет места, то исследование уже закончено. Если мы, та-
таким образом, положим
Z = Z'zm + pZ"z (mod р2), или Z = Z'zm + pZ"z + р2В,
то ясно, что Z делится на 2 и на всякий другой делитель, срав-
сравнимый с 2 по модулю р.
Чтобы иметь перед собой какой-нибудь определенный случай,
положим т = 4; легко видеть, что всякий другой случай может
быть изложен аналогичным образом. Если теперь Z делится по
модулю р3 на некоторый делитель вида z + а/7, то
<x,p,p3) или <x,Z" = B(mo&&z, p).
806 Учение о вычетах
Теперь могут представиться три случая.
1. Если Z" = 0 (modd z, p), и В несравнимо с 0, то ясно, что ни
одно значение а не удовлетворяет сравнению, и потому Z не об-
обладает по модулю рг делителями вида z + ос/?. Тем самым иссле*
довайие закончено.
2. Если ни Z", ни В не сравнимы с 0 по (moddz, //L то а бу-
будет иметь одно единственное значение, именно:
Поэтому будет только один делитель функции Z по модулю
р3, который сравним с z + ар по модулю /?2, и будет выполняться
сравнение
Если мы теперь предположим, что делителем функции Z (mod p4)
является z -{- сир -\- (З/?2, то
0 =
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ ИССЛЕДОВАНИЙ
О ЧИСТЫХ УРАВНЕНИЯХ
1
Так как метод, которым мы в «Арифметических исследованиях»,
п. 360, учили решать уравнение хп —1=0, образует очень пло-
плодотворную и важную теорию, для которой мы в указанном сочи-
сочинении могли отметить лишь простейшие моменты, то мы надеемся,
что математикам будет приятно, если мы снова вернемся к этому
предмету, подробнее займемся тем, чего раньше лишь отчасти и
кратко касались, опуская доказательства, и более детально иссле-
исследуем то новое, что добавилось с тех пор.
Предположим, что п — простое число, а число п — 1 разлагается
на сомножители осх^ХТ» и обозначим, далее, через g какой-нибудь
первообразный корень для модуля п. Пусть г представляет произ-
произвольный корень уравнения хп—1=0, а Л — произвольный корень
уравнения х& —1 = 0. Тогда если обозначить длину окружности,
радиус которой равен 1, через Р, и мнимую величину jf— 1 через
if то все корни уравнения х& —1=0, т. е. все значения Л будут
представляться формулой
кР , . . кР
cos -Q-* + i sin -д- ,
Р Р
где к пробегает все целые числа 0, 1, 2, 3, .. ., C — 1. Далее, ясно,
что все степени каждого корня Л также являются корнями, и что
если Л ест;ь корень, соответствующий взаимно простому с р значе-
значению к, то все степени Л°, Л, Л2, Л3, . . ., Л^ различны между
Исследования о чистых уравнениях
собой и потому исчерпывают всю совокупность корней; в этом случае
мы будем называть Л собственным корнем уравнения х& — 1 = 0;
напротив, корень Л, соответствующий не взаимно простому с $
значению к, будет называться несобственным; если 8 есть наиболь-
наибольший общий делитель чисел Лир, то, как легко видеть, Л^/5=1;
и, далее, все степени R°, Л, Л2, Л3,..., Л5 между собой раз-
различны и потому R есть собственный корень уравнения^/5 — 1 =0.
То же самое имеет место и для уравнения хп —1=0, но здесь все
корни, за исключением корня 1, обязательно будут собственными
корнями.
После того как предпосланы эти замечания, наше исследование
будет в основном иметь дело с состоящими из [Зу членов функция-
функциями следующего вида:
которые мы ради краткости будем обозначать через [г, R]. Отдель-
Отдельные члены такого выражения являются произведениями степени
числа г на степень числа Л; показатели первых образуют геомет-
геометрический ряд, а показатели вторых — арифметический ряд. Все по-
показатели
1 nr<x р-2а „За р-<*?у—а
х> б » о 9 5 » •• ч б
несравнимы по модулю п> и потому эти степени числа г различ-
различны между собой; однако, если их продолжить дальше, то начнет
повторяться тот же самый ряд, так как ga&4 == 1 (modrc), и
потому г^у = г. Вторые же сомножители
1, Л, Л2, Л3. ...,ДРт-1
образуют у равных периодов, так как R& = 1, Л*3 = Л
и т. д.
Из этого вытекает, что функция [г, Л] может быть представле-
представлена также и в виде
Исследования о чистых уравнениях 809
+ Л (г?а + г^+Л + rg^+« + • • • + г^а/3у~а3+а) +
+ ДЭ-1 (г^/ + г*2ар + г^33+ . . . + г^т),
или, вводя обозначение из п. 343 «Арифметических исследований»,
в виде
[г, Л] = (Т, 1) + R (T, g«) + Л2 (T, g**) + . . . + Д*-1(Т> g^-a).
3
Если мы в качестве корня г возьмем единицу, то получим
[1, R] = 1 + R + R2 + R3 + . .. + R^~i =
= т A + R + Л2 + Л3 + ... + ДР-1),
и значение этого выражения равно р^, если за Л также взят ко-
корень 1, и, напротив, равно 0 для всякого другого значения Л.
Если же г остается неопределенным, и полагается Л —1, то по-
получается
[г, 1] = г + rs* + r^ + г*3а + . . . + г?аРт~а,
или, используя введенное в «Арифметических исследованиях» обо-
обозначение, [г, 1] = (Ру, 1), т. е. [г, 1] будет состоять из одного пе-
периода из Ру корней, одним из которых является само г. Еслиа=1,
то этот период будет охватывать все корни г, г2, г3,. .., г71^1, толь-
только в другом порядке.
Отметим еще следующие соотношения, причина которых ясна
сама собой:
[г, R]=R[rga, R] = R* [re2*f R], или вообще = Rk И**, Л],
где к обозначает любое положительное целое число. Отсюда выте-
вытекает, что функция [гт, Л] либо равна [1, Л], именно, если т де-
делится на пу либо, в остальных случаях, может быть приведена к
виду R^lr^tR], и притом так, что v < а. Действительно, если
т не делится на п, то т будет сравнимо по модулю п с некоторой
810 Исследования о чистых уравнениях
степенью числа g, показатель которой, согласно «Арифметическим
исследованиям», удобно обозначить через indm; поэтому, если по-
положить mdtf2 = Xa + v, что, очевидно, можно сделать так, что
v < а, то
[rm, R] = [т*Хв+\ R] = Д-* И\ Д];
поэтому нужно положить [л = — X, или, если желательно иметь по-
положительный показатель, [х = — X (mod p).
Теорема. Если г', так же, как и г, обозначает произвольный ко-
корень уравнения хп—1=0, и, далее, R', так же, как и R, обозна-
обозначает произвольный корень уравнения х& —1 = 0, то
[г, R] х [/•'. R'\ = [rr\ RR'] + R [rsar\ RR']+ R2 [^2V, RR'] +
+ i?3H8V,JRi?/]+ ... + RVy-i[rZa^-ar', RR).
Доказательство. Если произвести ууножение [г, R] на отдель-
отдельные члены функции [r',R']t то произведение можно будет предста-
представить в следующем виде:
[г, R] г' + RR' [г^а,Л],г^а+ RZR'* И2а, R] г^2а+
Если потом объединить первые члены отдельных получающихся
при этом частей, то получится [rr'9 RR']\ если точно так же со-
собрать вторые члены, то получится R [г$аг', RR'\, и т. д., откуда мы
в конце концов и получаем указанный вид произведения.
Далее, простой перестановкой чисел г, R с г', R' получается,
что это же произведение может быть представлено также и в сле-
следующем виде:
[rr\ RR'\ +R'[rr'g\RR'] + R'2 [rr'g2* ,RR'] +
+ Rs [rr'gSa, RR] + ... + R^-1 [rr'g*^~a , RR].
Из этого следует далее, что если и г", г"', . . . являются произ-
произвольными корнями уравнения хп —1=0, а R'\ R"\ ... — произ-
Исследования о чистых уравнениях 811
вольными корнями уравнения х& —1 = 0, то произведение функ-
функций [г, R], [г', Rf], [г", Д"], [rm, R"'],..., как бы велико ни бы-
было их число, равно сумме
если брать в качестве к!, к", к"\ .. . всевозможные различные ком-
комбинации чисел 0, 1, 2, 3, ...,Py — 1, вследствие чего всего полу-
получится p^-iy^-i членов, если через [х обозначено число перемножае-
перемножаемых функций.
Формула, которой мы в предыдущем пункте представили произ-
произведение любого числа функций, является общей и не предполагает
никакой связи между корнями г, г', г", гг",... или между корня-
корнями R, R', Д", Д",.. . Отсюда без труда выводится, что так как
корни г', г", г", . . . можно рассматривать как степени корня
г, а корни R', R", R'",...— как степени корня Л, то отдельные ча-
части произведения могут быть приведены к виду RM [rm, Rx], где
показатель X все время один и тот же, именно i?x = RRrR"R" .. .
Поэтому, согласно тому, что было указано в п. 3, такое произ-
произведение редуцируется к следующему виду:
А [1, i?x] + В [г, Rx] + В' [г*, Rx] + В"
+ В'" [rs\ Д*] + . .. + ?(a-D [г^-1
где отдельные коэффициенты А, В, В\ В'\ В"\ ... имеют вид
h + h'R + h"R2 + h'"R* + ... + h^
и Л, Ы\ /г", К", . . . обозначают определенные целые числа.
Простейшим случаем является тот, когда г = г' = г" = гт = ...
и i? = R' = R* = R" = .. .; тогда наше произведение переходит в
степень [г, Л]х, которая, таким образом, всегда может быть пред-
представлена в указанном выше виде.
812 Исследования о чистых уравнениях
6
Поэтому, если положить X = р, то степень [г, R]& примет сле-
следующий вид:
А [1,1] + В [г, 1] + В' [г*, 1] + . .. + B<e-» [г*"",1] =
(рт, 1) + В' (рт, g) + 2?" (pT, g2) + • • • + 5(«-
Если поэтому предполагать известными не только корень R
(а, значит, и значения коэффициентов -4, В, В',. . .), но и значения
отдельных сумм фу, 1), (Рт, g),... из р^ членов, то тем самым не-
немедленно будет известно значение 6', так что значение [г, R] мож-
но будет найти по формуле |/V. Это выражение допускает р раз-
различных значений, так что могла бы возникнуть неопределенность
в отношении того, какое из них следует брать; но легко показать,
что это совершенно безразлично, если R является собственным кор-
корнем уравнения х$ — 1 =0. Действительно, в этом случае указан-
з _
ными р значениями корня |/"б' будут, очевидно, следующие зна-
значения:
[г, R], [гЛ R], [г*8", R],..., Kp-«, R],
ибо р-е степени этих функций, согласно п. 3, равны между со-
собой, а сами эти функции пропорциональны р различным корням
уравнения х&—1 = 0. Если же известны только суммы (ру, 1),
фу, g), ...из ру членов, то сам корень г определен лишь в том
смысле, что он должен содержаться в совокупности (ру, 1), и оста-
остается произвольным, какой из корней этой совокупности берется за г.
Но эти корни суть г, г^а, г?2а,. .., и потому из функций [г, JR],
[г?в,Д], [г^2а,Л],... мы тоже можем любую взять в качестве [г,i?].
Эти заключения не имели бы силы, если бы R не было собст-
собственным корнем уравнения х® —1=0. Действительно, если предпо-
предположить, что R является собственным корнем уравнения #&' — 1 =0,
где р' есть делитель числа р, но легко получается, что
[г, R] = [r*#\ R], [тЛ R] = Иар'+а, R],...,
Исследования о чистых уравнениях 813
и потому в совокупности из р функций [г, Л], \r8a, Л],. . .,
будет только р' различных, т. е. из значений выражения
_
' допустимы не более чем р' значений, остальные р— Р'зна-
Р'значений должны быть отброшены. Но легко видеть, что в этом слу-
случае не нужно доходить до р-й степени функции [г, Л], а что уже
[г, Л]р' приводится к нашему виду
рт^ + в (рт, 1) + в1 (вт, g) + вп (рт, g*) +...
Мы получаем поэтому [г, Л] в виде выражения уЬ', и безразлично,
какое значение этого выражения мы берем.
Так же, как [г, Л], можно определить и функции [г, Л2],
[г, Л3],. . ., или вообще [г, Rk\\ действительно, если мы предположим,
что при подстановке в б7 вместо R степеней Л2, Л3, .. ., Rk полу-
получаются функции 6", 6W, ...,8(А\ то, очевидно, будет иметь место
[г, Л2р = 6", [r,Rs]& = 6W, . . . , и вообще [г, /?*р = 6W, вследствие
чего и эти функции могут быть представлены в виде корней:
[г,Л2]= УЬ" и т.д. Однако, если какую-нибудь величину нужно
выразить через одну из функций [г, Л], [г, Л2],. . ., то эти выраже-
выражения в виде корней использовать не целесообразно. Именно, так
как значения отдельных корней не вполне определенны, то остава-
оставалась бы неопределенность в том, какие значения можно комбини-
комбинировать между собой, а это, очевидно, не безразлично; действитель-
действительно, легко видеть, что если для [г, Л] взято определенное значение,
то и все функции [г,Л2], |>,Л3],..., должны получить вполне оп-
определенные значения, которые, однако, не указываются выражения-
выражениями через корни. Поэтому эти выражения нужно отбросить и най-
найти другие, при помощи которых [г, Л2], [г, Л3],. . . рационально
представляются через [г, Л] и известные величины; это легко до-
достигается следующим образом.
Согласно теореме п. 4 и тому, что было изложено в п. 5,
произведение [г, Rk] X [г, R]®~k тоже может быть представлено в
814 Исследования о чистых уравнениях
таком виде:
^А + В (рт, 1) + В' (pTf g) + В" (pTf g») + .. . +»«-D (pT, g«-i)f
где -4, 5, В\ В", ... будут рациональными функциями от R. По
этому, если положить
[г, Я8] х [/-,*]&-» =6"\
[г,Д4]х[г,Др-4 = 6""
и т. д.,
то 6", 6'", 6"", .. . также будут рационально заданными величина-
величинами, и будут выполняться равенства
[г, **]=¦?¦ [г, Д]а,
и т. д.
Таким образом, эти выражения рационально представляют значе-
значения функций [г, i?2], [г, Л3],..., если только [r,R] не равно О,
когда они будут неопределенны; мы можем, однако, строго дока-
доказать, что никогда не может быть [г, R] = 0, по крайней мере если
г обозначает корень, отличный от 1, хотя изложение этого дока-
доказательства мы, чтобы не быть здесь слишком пространными, долж-
должны отложить до другого случая.
8
Рассмотрение предыдущего пункта оказывается полезным, если
поставлена задача спуститься от периодов из $ч членов к перио-
периодам из у членов. Действительно, легко видеть, что если R обозна-
обозначает собственный корень, то мы получаем
Р (Т, 1) = (рт, 1) + [г, R] + [г, Л2] + [г, Л3] + . . . + [г, ЯМ,
Р (Т, ?а) = (РТ, 1) + Д*-11?, R] + №~2 [г, Я2] + ЛЗ-з [г, Л3] + . . .
Исследования о чистых уравнениях 815
...+R*[r,№~i
и т. д.
Если бы здесь для отдельных функций [г, R], [r, R2], ... были
взяты их выражения в виде корней ]/~6', |/б", .. ., то значение
каждого ряда определялось бы лишь с точностью до В^ различ-
различных значений, в то время как, когда мы берем для [г, i?2], . . .
рациональные выражения, то не остается уже никакой неопреде-
неопределенности, кроме тех неопределенностей, которые неизбежны по самой
природе вопроса. Это замечание ускользнуло от внимания Лаг-
ран ж а, считавшего, что указанный нами в п. 360 «Арифметиче-
«Арифметических исследований» метод, где мы умышленно пользовались только
рациональными выражениями и не употребляли выражений в виде
корней, можно было бы упростить, подставив вторые вместо первых
(«Traite de la resolution numerique des equations», edition 2-ieme, p. 311).
Далее, вряд ли даже необходимо указывать на то, что как толь-
только получены значения периодов (у, 1), (у, g*), . . . или только одно-
одного из них, то отсюда уже могут быть рациональным образом полу-
получены значения всех остальных периодов из ^ членов. Поэтому
спуск от периодов с C^ членами к периодам с т членами требует
решения уравнений х&=1, х& = Ь'9 а все остальные операции вы-
выполняются рационально.
9
Все это почти таким же образом рассматривалось в «Арифмети-
«Арифметических исследованиях»: однако кое-что там было сообщено без дока-
доказательств, привести которые здесь является небесполезным. Мы
утверждали там, что нахождение значения корня ]Лб', которое, по
крайней мере тогда, когда 6' является мнимой величиной, на пер-
первый взгляд требует деления на C частей как некоторого отрезка,
так и некоторого угла, на самом деле зависит только от послед-
последнего, а первое всегда может быть сведено к извлечению одного ква-
квадратного корня. Это мы докажем следующим образом.
816 Исследования о чистых уравнениях
Если, как и выше, обозначить мнимую величину ]/ — 1 через i
з
и положить 6' = Р + iQ, а какое-нибудь значение выражения у?
положить равным р + iq, где Р, Q, р, q вещественны, то, как извест-
известно, если положительные величины ?, е и углы F, f определены
так, что
q = esinf,
то
и / равен одному из углов
±F, -1(^ + 360°), 1(^ + 720°),..., i(jp+(p_ 1K60°).
Поэтому / будет определяться делением угла F на (В частей, а
извлечения корня |/Е мы можем избежать следующим образом.
Каждое произведение rkRK имеет одинаковую вещественную часть
с r-kR~~K\ а мнимые части, содержащие множитель i, у этих произ-
произведений равны по величине, но противоположны по знаку. Отсюда
немедленно следует, что
[г, R'1] = р — iq = e (cos / — i sin /),
ж потому
[г, R] х [г~\ R-Ц = е\
Но указанное произведение, согласно теореме п. 4, равно
[1,1] + R [г*"-*, 1] + Л2 И2"-*, 1] + . . . + R^-1 [r*'PY—-1,1} =
• • + л^-1 (pTlg«P^-«_ 1),
а эти величины можно определить, если R и все периоды из [Зу
членов предполагаются известными. Таким образом, определение е
требует только извлечения квадратного корня.
Исследования о чистых уравнениях 817
В специальном случае, когда а = 1, отдельные периоды (Рт>?а—1),
(Рт> §2а—1)» • • •> очевидно, равны г+ г2 + г3 + г4 + • • • Ч-^71, и потому
е2 = рт + (Л + Л2 + й3 + . . . + R^) (г + г2 + г3 + . . . + г*-*) =
= рт + 1 = щ
если считать, что г ж R представляют собой корни, отличные от 1,
и потому всегда е = ]/гс {{{Арифметические исследования», в конце
п. 360).
10
До сих пор мы проводили наше исследование во всей общности,
так что охватывали любые значения чисел а, В, ч\ однако, начиная
отсюда, мы переходим к более специальному случаю а= 1, который
проложит нам путь к плодотворнейшему и изящнейшему исследова-
исследованию.
Пусть поэтому знак [r9 R] представляет функцию
где п — простое число, г — произвольный корень уравнения хп—1=0
(не исключая и корня 1), R — произвольный корень уравнения
х$ — 1 = 0; далее, р обозначает некоторый заданный делитель числа
п — 1, и, наконец, g — некоторый определенный первообразный
корень для модуля п. Далее, мы положим ради краткости
г71-1 =
откуда следует, что s = п для г = 1 и s = 0 для всякого другого
значения г, и точно так же S = п — 1 для R = 1, но ? = 0 для
любого другого значения R.
Тем самым, согласно п. 3, мы имеем
далее, для каждого не делящегося на тг значения 7?г
818 Исследования о чистых уравнениях
или более общо
где ind m обозначает показатель степени числа g, сравнимой по
модулю пет. Если мы применим это преобразование к тому,
о чем говорилось в п. 5, то мы получим, что произведение двух
или большего числа сомножителей вида [rh, R ] приводится к виду
где А ж В являются рациональными функциями от R с целыми
коэффициентами, а X есть сумма всех значений Н. Очень важно
свести такие преобразования к простому алгоритму; для этой
цели мы должны, в частности, подробнее рассмотреть природу
произведения двух функций.
И
Произведение [г, R!1] x [г, i?v], согласно теореме п. 4, равно
Из n— 1 показателей 2, g + 1, g2 -f 1, . . ., gn~2 + 1 здесь встре-
встречается только один делящийся на пу именно, показатель g-(n~1)/2-f- 1;
соответствующий член нашей суммы будет, таким образом, равен
этот член равен 0, если i?^+v не равно 1, и равен (га — 1) R{n~1)[1/2 =
= + (п—1) для i?^+v = l. Остальные части нашего выражения,
сумму которых мы положим равной О, преобразуются следующим
образом:
[r\ R^] = R~ilx+V) ind 2 [г,
r
(g2+l) r
ind (?3+D r
И Т. Д.
Исследования о чистых уравнениях 819
Отсюда вытекает, что
I. Q = [г, Д^+Ч х 2^ind X~(f"+V) ind (X+1\
если вместо х подставлять последовательно значения 1, g, g2, gs, . ..
...,^п"~2, исключая только значение g{-n~1)/2, или, что то же самое,
если вместо х подставлять значения 1, 2, 3, 4, . . ., п — 2, так как
вторые значения сравнимы с первыми (быть может только в другом
порядке) по модулю п.
Если мы предположим, что целое число у является обратным
для х по модулю п, т. е. определено так, что ху = 1 (mod/г), то
будет иметь место ind:r =— ind?/ (mod n—1) и
ind (x + 1) + ind у = ind (жг/ + у) == ind A + г/) (mod n — 1).
Поэтому
[xindz — ([х + v)ind(? + 1) = — fx ind г/ — ([х + v) {ind (у +1)—ind?/} =
^ v ind?/—([л + v) ind (г/ + 1).
А так как числа, обратные к числам 1, 2, 3, . . ., п — 2, совпа-
совпадают с ними, только расположены в другом порядке, то
II. О = [г, Д"+Ч X 2i?vlndy-((H-v)ind {v+1),
если вместо у подставлять последовательно числа 1,2,3, ..., п — 2.
Эта же формула немедленно получается и из I, так как числа (х,
v, очевидно, можно поменять местами.
Если, наконец, предположить, что целое число z является об-
обратным по модулю п для х + 1, т. е. xz + z = 1 (modn), то
ind A — z) = ind x + ind z (mod n — 1),
ind(? + 1) = — ind z (modn — 1),
и потому
f/,ind? — ([x ^- v) ind (ж + 1) == [x [ind A —z) — indz] + ([x + v)indz==
^ [x ind A — z) + v ind z.
Так как когда ж пробегает значения 1, 2, 3, . . .,и — 2, число я
должно пробегать (быть может только в другом порядке) значения
2, 3,4, ..,,га — 1, мы получаем тем самым третье выражение
ш. а = [г9л^] х
820 Исследования о чистых уравнениях
где вместо z последовательно подставляются числа 2, 3, 4, . . ., п — 1,
или, если угодно, выражение
1-z)+v ind z
= [г, R^] X 2
ind z+v ind ^+1—;г
Так как ind(l — z) = -^-(n—l)+md(z—1), то наше произве-
произведение можно представить и так:
X [r,R"]=R{{{] + [,] 2
+ ^ д^+vj х 2дк ind ,+v ind (z-i
где все время числами, подставляемыми вместо zf являются числа
2,3,4,...,п-1.
Заметим, что во всех этих формулах вместо чисел
[л ind ж— ([х + v)ind (х + 1), v ind?/ — (fx + у) ind (у +1),
[х ind A — z) + v ind z, и т. д.
можно, очевидно, подставлять их наименьшие вычеты по модулю р.
Если (л + v = 0 (mod p), то
[г, R*] х [г, Rv] = {п—1) &п~^/2 + (г + г2 + г3 + .. . + /--!) х
х A + /Г + R2* + i?3fx + ... + i?( )
12
Произведение [1,7?^] X [г, Rv], согласно теореме п. 4, равно
[г, i?^+v] + R* [r, R^] + R2* [r, R^v] {-... + R{n~^ [г, R^} =
- [г, i?^v] x A + i?u + i?2fx + R^ + . . . + i?(n~2)fx) =
= [r, i?K+v] X ^ A + ^ + i?2fx + R^ + . . . + i?(p-1)fx).
Поэтому произведение [1,7?^] X [l,i?v] может быть преобразова-
преобразовано в
—^ И, ^+v] х A + R» + R^ + Rs* + ...
Исследования о чистых уравнениях 821
Теперь без труда можно получить и любое произведение
[r™,R*] х [rm\ R*']; действительно, так как [r^R*] = Я~~^ind т [г, Л*
для не делящегося на п значения т, и равно [1, /?**] для
делящегося на п значения т, и так как подобное же преобразова-
преобразование сохраняет силу и для других сомножителей [rm\ R* ], то умно-
умножение сводится или к задаче предыдущего пункта, или к тем
случаям, которые мы рассматривали в настоящем пункте.
13
После того как мы показали, как преобразовывать произведе-
произведение двух сомножителей, преобразование произведения нескольких
сомножителей уже не представляет труда. Если произведение
[г,Н*] X [r,i?v] приведено к виду А[1,Л*+"] + В [г, 7T+V], то ясно,
что если добавить третий сомножитель [г, i?"], произведение будет
равно С [1, R^+n] + D[r, Н"+"+п], где положено
[г, R^] X [г, Пп] = с [1, ^+V+7X] + d [г,
С - Be, D = Bd + A{l
Поэтому [г, i?]x легко может быть приведено к виду
.4[1,ДЛ] + ?[г,Дх].
Ради примера мы найдем степени функции [г, R] для гс^И,
р = 5, причем мы положим g = 2. Здесь числам
1, 2, 3, 4, 5, 6, 7, 8 9, 10
соответствуют индексы
0, 1, 8, 2, 4, 9, 7, 3, 6, 5.
Поэтому для разложения квадрата [г, R]2 по формуле I п. 11 мы
имеем
(Л=1, V=l.
822 Исследования о чистых уравнениях
Значения х 1, 2, 3, 4, 5, б, 7, 8, 9.
ind х О, 1,8,2, 4, 9, 7, 3, 6.
2ind(x + l) 2,16,4,8,18,14,6,12,10.
Наименьший вычет
числа indx — 2 ind (а? + 1) (mod 5) 3, 0, 4, 4, 1, 0,1,17, 1,
откуда мы получаем
п = [Г, 7?2] х {2 -t 47? + 7?3 + 27?4},
и
1) [г, 7?]2 = [1, 7?2] + [г, 7?2] х {2 + 47? + 7?3 + 27?4}.
То же самое выражение получается из формулы III п. 11, именно
Значения z 2, 3, 4, 5, 6, 7, 8, 9, 10.
indz 1,8,2,4,9,7,3,6,5.
ind(rc + l — z) 5,6,3,7,9,4,2,8,1.
Наименьший вычет
числа ind z + ind (n + 1 — z) (mod 5) 1,4,0,1,3,1,0,4,1.
Совершенно аналогичным образом мы находим
2) [г, 7?2] х [г, 7?] = [1, 7?з] + [г, 7?з] х {2 + 7? + 47?2
3) [г, Л3] х [г7 Д] = [1, 7?4] +[г, Л4] X {2 + 47? + 7?з + 27?*}.
Наконец,
4) [г, 7?4] х [г, 7?] = [1,1] + [г, 1] X {1 + 27? + 27?2 + 27?3 + 27?4}.
Если умножить равенство 1) на [г, R] и подставить вместо
[г, R2] х [г, R] его значение из 2) и далее подставить
[1, 7?2] х [г, R] = [г, Л3] х {2 4 27? + 27?2 + 27?3 + 27?4},
то мы получим равенство
[г, R]3 = [1, 7?3] х {2 + 47? + 7?3 + 27?4} +
+ [г, 7?3] х {12 + 227? + 187?2 + 247?3 + 157?4},
и точно так же
[г, 7?]4 = [1, 7?4] х {12 + 227? + 187?2 + 247?3 + 157?4} +
+ [г, 7?4] X {164 + 1707? + 2057?2 + 1807?3 + 1907?4}.
[г, 7?]5 = [1,1] х {164 + 1707? + 2057?2 + 1807?3 + 1907?4} +
Исследования о чистых уравнениях 823
[г,1] х{1836 + 1830/? + 1795i?2+1820i?3+-1810i?4} =
1640 + 1700J? + 2050Д2 А- 1800Д3 + 1900J?4 +
A836 + 1830Л + 1795/?2 + 1820/?3 + 1810Д4) (s—l) =
QiSSs — 98S — FД -r 41i?2 + 16i?3 + 26Д*) s +
66R + 451i?2 + 176Д3 + 286i?4.
14
Вычисления, которые до сих пор проводились таким образом,
что они были пригодны для всех значений г и i?, могут быть зна-
значительно сокращены, если мы с самого начала будем рассматривать
R как собственный корень уравнения х$ —1=0. При этом пред-
предположении произведение [г, R^] x [r, i?v] преобразуется к виду
В [г, i?1^], если только [х -f v не делится на р. Если же [л + v де-
делится на р, то указанное произведение будет равно (п— 1) ^(П~1)ГЛ'2 _|_
-f-[г, 1]2^^Ш х> если вместо inda; подставлять все значения 0, 1,
2, 3, . . ., п — 2, за исключением значения (п— 1)/2. Отсюда легко
видеть (если [х, а потому также и v не делится на [3), что в этом
случае
[г, Л"] X [г, /Г] =- Д^1*'2 {Л _ 1 _ [г, 1]},
и потому [г, Д14] X [г, i?v] равно 0 для г = 1, и равно nR{n~1)[l12 для
всякого другого значения г. Так как, далее, J?(n~1)fz/2 = -)- 1 или
= — 1, в зависимости от того, является ли число (п — 1)[х/р
четным или нечетным, то наше произведение в первом случае будет
равно п, а во втором равно —п.
Далее, из этого следует, что можно положить
[r,B*]x [r,R] = A'"[r,R%
824 Исследования о чистых уравнениях
откуда мы получаем
и т. д.,
и, наконец,
[г, Rf = ± пА'АщАт . . . Аф~2\
где следует брать верхний или нижний знак в зависимости от того,
является ли число (п—1)/В четным или нечетным.
Отсюда, следовательно, вытекает, что после того, как найдено
значение [г, R], остальные функции
могут быть здесь определены намного легче, чем в тех случаях,
когда ос не равно 1, на что мы уже указывали в «Арифметических
исследованиях» (п. 360, III). Эти операции могут быть упрощены
еще более детальным рассмотрением природы функций А', А", . ..
15
В п. 9 мы показали, что значение функции [г, Л] может быть
приведено к виду J^n(cos/ + isin/), и таким же образом могут
быть приведены к подобному же виду и функции [г, R2], [r, R3], и
т. д. до функции [г,^]. Если мы положим
[г, R] = Vn (cos /'+ г sin Л,
[г, Л3] = Уп (cos f + г sin Г),
и т. д.,
то будут выполняться равенства
А' = 1/n [cos B/' - Л + * sin B/' - /')],
Л" = |/n [cos (/' + /" - Г) + i sin (/' + /" - /")],
ЛГ - )/n [cos (/' + Г - Г) + * sin (/' 4 Г — Г)]
и т. д.
Исследования о чистых уравнениях 825
Если представить функции А\ А"', Ат, ... в виде
А' = af (cos Ъ'-\- i sin b'),
А" = a" (cos Ъ" + г sin Ъ"\
Ат = a'"(cosbm + isinbrrr),
и т. д.
причем так, что все числа а', а" а"\ . . . положительны, то мы полу-
получаем, что
а1 - а" = а" = .. . = У~п,
Г = -j(b' + Ъ" + Ъ" + ... + Ь<"-2>)>
если (п — 1)/Р четно, или
/' = у A80° + 6' + 6* + Ьт + • •. + 6<п-2>),
если (п — 1) / р нечетно, и, далее,
[Г| Л2] = ]/^(cosB/ — 6') + i sin B/ — 6')),
[г, дз] = y^(cosC/'_ 6' — 6") + г sin C/ — Ъ' — V%
и т. д.
Наконец, согласно формулам п. 8,
^ /' + cos B/ - 6') + cos C/' - V - Ъ") +
cos((p- 1)/'- b'-b" -6*- . . .- 6(p-2))} +
+ sin ((p — 1)/' — 6'_6" — ft" — .. . — 6C~2))},
v „ (П— 1 \ /Л—1 o\
и точно так же получаются значения функции ( —^— , g 1, (—«— , g j,
/л —1
f—q—, g3),.--, если в этой формуле вместо /' подставлять соот-
ветственно значения / о— , / — 2 • —^— , / — о —^— , .. . ,
где it = cos —q h г sm —q~
826 Исследования о чистых уравнениях
16
Еще одно упрощение получается на основании следующего заме-
замечания. Так как, согласно п. 14, имеет место
± [г, R] X [г, R*-1] = [г, Я2] X [г, i?p~2] = ± [г, i?3] [г, Лр~3] = ... = п,
где (в первом, третьем и т. д. произведениях) нужно брать верх-
верхние или нижние знаки в зависимости от того, четно или нечетно
число (п — 1)/Р, то в первом случае должно быть
cos (/' + /(Р))= cos (/" + /(p-2)) = cos (Г +/C~3)Н ... - 1,
во втором случае
- cos (/' + Z03-1*) = cos (/" + f~2)) = - cos (/'" -f f~s)) = . .. = 1,
и в обоих случаях
sin (/' + f~1]) = sin (/" + /@-2)) = sin (/'" + f~3)) = .. . = 0.
Поэтому можно положить в первом случае
/>-*> = -/', /р-2) = -/", /р-3> = -г,...,
во втором случае
Л&—1) л ОП° 4' Л$—2) л ОГ\° 4" А$—3) л ОГ\0 гт
у — 151) •— / , / ¦= lol) —fit === ^"^ — / » • • •
Но из этого следует, что в первом случае
дф—2) /j/ /jC—3) At/ /j C — 4) дпг
A — Л , Л — А , А — -Л , . . .,
а во втором случае
так что общее число функций А', А", А'",... сводится к половине.
Исследования о чистых уравнениях 827
Далее, отсюда следует, что в первом случае
2cos C/' — Ь' — b") + . ..
cos D- P/' - V - b" - ... -
(где последний член, очевидно, равен cosO = 1), или
' + 2со8B/'-6')
+ 2cos C/' — V — Ъ") + . . . +
2cos (i(p — 1)/' —&' —ь» —... — ь^
в зависимости от того, четно р или нечетно; во втором случае
/' = -iB6' Нг 2Ъ" + . .. + 2Р1*'1
'- 6') + 2cosD/'_ b'-b"-b'")
2cos((ip — 2)/'— b' — b' — . ..—
2sin/' + 2sin C/'
¦2sin[( j$ — l)f —b' — b" —...
828 Исследования о чистых уравнениях
ИЛИ
/' = 4- fa + 2b" + ... + 2b^ *' + 180°) ,
^ , l) = - j + ^~ {2cos {If - V) + 2cos D/' - 6' - 6* - V") +
+ i J^L J2sin/' + 2sinC/' —6' —6") + . . . +
2sin ((lp -2)f-V-V- . .. - 6^~
sin ((y p — l) /' — 6' — b" — . ..
в зависимости от того, четно или нечетно число ?3/2. Для осталь-
остальных периодов из (п — 1)/р членов имеет место то же, что мы за-
заметили выше. Итак, мы заключаем из этого вообще, что для опре-
определения этих периодов требуется деление полного круга на р ча-
частей, от которого рационально зависит построение углов Ь', Ъ", Ът',...,
далее, деление на р частей угла b' -f b" + b"' + ... , и, наконец,
извлечение квадратного корня УН. Если теперь положить одно-
одновременно р = -я- (п — 1), то указанные периоды будут, очевидно,
совпадать с удвоенными косинусами углов 360°/п, 2-360°/п,
3-360°/п,.. .,-у (п — 1K60°/^, и потому деление круга на п частей
зависит от деления всего круга на (п—1)/2 частей, от деления
на (п—1)/2 частей угла, который может быть построен после
выполнения первого деления и от корня У~п • Если же нужно найти
и синусы углов 360°/я, • • ., то требуется еще одна операция.
17
Ради большей ясности мы снова используем пример п. 13, где*
мы нашли
А' = A" = 2 + 4R + Rs + 2R*^ 2R — 2R2 — R*,
= —R + 2R2 — 2RK
Исследования о чистых уравнениях 829
Если взять за R значение cos 72° + i sin 72°, то
А1 = А" - 2 cos 72° — 3 cos 144° + i B sin 12° — sin 144°),
A" = — 3 cos 72° + 2 cos 144° + i (sin 72° + 2 sin 144°).
Поэтому углы b\ b", . . . определяются уравнениями
2 sin 72°— sin 144°
2 cos 72°—3 cos 144°
1) sinb'=
2) cos V =
оч ^ ,, 2 sin 72°—sin 144:
3) tgb
4) sin &" =
5) cos b" -
6) tgi
2 cos 72°—3 cos 144° '
sin 72°+ 2 sin 144°
— 3 cos 72°+ 2 cos 144°
sin 72° -f 2 sin 144°
W8- —3 cos 72°+2 cos 144° "
Каждое из уравнений 1), 2), 3) достаточно для определения уг-
угла V', если известен квадрант, в котором его следует брать; этот
квадрант следует определять по знакам величин 2 sin 72° — sin 144°,
2 cos 72° — 3 cos 144°; то же самое имеет место для угла Ь".
В нашем случае угол Ь' берется между 0° и 90°, а угол Ь" —
между 90° и 180°. Если числитель и знаменатель уравнения 3) умно-
умножить на —3 cos 72° + 2 cos 144°, то оно перейдет в уравнение
tg V = Jj- {— sin 72° + 13 sin 144°} ,
и точно так же, если числитель и знаменатель уравнения 6) умно-
умножить на 2 cos 72° — 3 cos 144°, из него получится следующее урав-
уравнение:
tg b" = ~ {— 13 sin 72° — sin 144°}.
Отсюда получаются такие численные значения:
tg Ь'ж + 0,4316226944; log tgb'« 9,6351042715; V ж 23о20Ч6",04603;
830 Исследования о чистых уравнениях
tg 6*» —0,8355819332;logtgbir« 9,9219890411 n; 6^140°7'6", 52441,
откуда следует, что
5/' ж 186°48'38",61647, f ж 37°21'43",723294.
Поэтому мы получаем:
B,1) ж — g- + ^ {2 cos 37°21'43",723294 + 2 cos 51°22'41",400558},
B, 2)ж — i- + ^ {2 cos 325°2Г43",723294+ 2 cos 267°22'41", 400558},
B, 4) ж — g- + Ц± {2 cos 253°21'43",723294+2 cosl23°22'41",400558},
B, 8) ж — ?- Ь -^ {2 cos 181°21'43",723294 + 2 cos 339°22'41",400558К
B, 5) ж — у + Щ± {2 cos 109°21'43",723294 + 2 cos 195o22'41*,400558),
откуда мы находим, что
B,1)ж + 1,6825070652 ж 2 cos360°
B, 2)ж + 0,8308299 ^2 cos
B,4)= 2 cos
B, 8)= 2 cos
И
720°
И '
1440°
И
2880°
B,5) = 2 cos 1800°
И
18
Другой пример доставляет нам уравнение х17—1=0, которое
мы другим методом разобрали уже в «Арифметических исследова-
исследованиях». Мы полагаем, таким образом, п = 17, ?3 = 8, g = 3. Тогда
числам 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 со-
соответствуют индексы
0, 14, 1, 12, 5, 15, И, 10, 2, 3, 7, 13, 4, 9, 6, 8.
Исследования о чистых уравнениях 831
Отсюда мы находим
А' = А""п = * + 2R + 2R2 + * + ЗЯ4 + 4i?5 + 2i?6 + 2Л7,
А" = А"т = 2 + 3R+ * + R3 + Л4 + 3i?5 + 4Л6 + Л7,
Л" = Л"" - 3 + 37? + 2i?2+ 3i?3 + * + R5 + 2i?6 + R\
или, так как в этом случае i?4 -f I = О,
А / А ПИН Q 0 7? О 7?3
хх — j\ — О ~—— uil ?jJ\ ,
Art А""' \ Л/?2
А!" = .4"" = 3 + 2R + 2Я3.
Поэтому если положить i? = cos 45° + i sin 45°, то
A' = A""" = — 3 — 2г^2, 4" = Л"" = 1 — 4г, ^'" = ^"" = 3
Таким образом, величины 6', 6", V" находятся из уравнений
sin Ъ' = — 1/ —
cos &' =
tg 6' = -
из этих уравнений получим
X {2cos 137°39'57" + 2 cos 52°1'5" + 2 cos 265°38'52"+ 1},
B,3) ж— \+ ^Х
X {2 cos 92°39'57" + 2 cos 322°1'5" + 2 cos 130°38'52" — 1},
X {2 cos 47°39'57" + 2 cos 232°1'5" + 2 cos 355°38'52" + 1},
8 ' 8 Л
X {2 cos 2°39'57" + 2cos 142°1'5" + 2cos 220°38'52' — 1},
832 Исследования о чистых уравнениях
X
X {2cos317°39'57" + 2 cos 52°1'5" + 2 cos 85°38'52" + 1},
«-§- + ^х
X {2 cos 272°39'57" + 2 cos 322°1'5" + 2 cos 310°38'52" — 1},
X {2 cos 227°39'57" + 2 cos 232°1'5" + 2 cos 175°38'52" + 1},
X {2 cos 182°39'57" + 2 cos 142°1'5" + 2 cos 40°38'52" — 1};
2^B,1) « + 0,092268» cos ^360°,
|-B,3) = cos ^ 360°,
I-B,9) = cos ^360°,
~ B,10) = cos Д 360°,
|- B,13) » + 0,93247 » cos ^ 360°,
i- B,15)= cos ^360°,
2
jB,ll) = cos
?-B,11) = cos 1= 360°.
* * *
От этих более общих исследований о функциях [г, R], которые
проливают более яркий свет на вторую, начатую в «Арифметиче-
«Арифметических исследованиях», п. 360, теорию, и развивают ее, мы переходим
к более подробному рассмотрению некоторых специальных случаев
Исследования о чистых уравнениях 833
(именно, когда для р берутся определенные значения); при этом
получаются многие сколь плодотворные, столь и изящные факты,
некоторые из которых, правда, уже излагались, однако другим
методом, в «Арифметических исследованиях», а другие должны рас-
рассматриваться как совершенно новые. Однако развитие замечатель-
замечательной связи между этими исследованиями и высшей арифметикой,
которая при этом получает весьма значительное и неожиданное обо-
обогащение, мы оставим до другого сочинения, которое скоро будет
опубликовано. Во всем дальнейшем исследовании мы будем пред-
предполагать, что за г взят собственный корень уравнения хп—1 =0,
и за R — собственный корень уравнения R& — 1=0.
19
Мы начнем со значения В = 2, когда для R, следовательно, нуж-
нужно взять значение —1. Наша функция [г, R] будет поэтому равна
и мы имеем
[г, R] = - И, R] = + И8, R] = — И3, R] = . ..,
и вообще, если X обозначает любое не делящееся на п целое чи-
число, то
[r\ R] = -f- [r, R], если X есть квадратичный вычет по модулю п\
[rx, R] = — [г, Я], если X есть квадратичный невычет по модулю п.
Далее, если произвольные квадратичные вычеты по модулю п,
содержащиеся среди чисел 1, 2, 3,..., п — 1, обозначать через а,
и произвольные квадратичные невычеты по модулю п, заключенные
в том же интервале, обозначать через Ъг то очевидно, что если не
обращать внимания на порядок расположения, то числа
будут сравнимы по модулю п с числами а, и точно так же числа
а о3 дб рП—2
5> Ь ' 5 > "' * Ь
будут сравнимы с числами 6, так что [г, R] = 2jra —
834 Исследования о чистых уравнениях
ТТ 360° 7,7
Поэтому, если мы положим = со и г = cos ясо + sin ясо, то
будет выполняться равенство
[ry R] =2 cos ak(D—2C0S bkoi~\~ г 2 sin a^— ?*2 sinfe&co.
Но, согласно п. 14, квадрат функции [г, R] равен + п или ра-
равен — п, в зависимости от того, имеет ли п вид 4z + 1 или 4z — 1,
и потому в первом случае [г, 7?] = + Уп, а во втором случае [г, Л] =
= + i У~п\ знаки же перед корнями остаются неопределенными. От-
Отсюда получаются следующие формулы для сумм:
1. Если п имеет вид 4г + 1, то
2 cos ако) — ^
2j sin а!ш — 2 sin Ькы = 0.
II. Если п имеет вид 4z—1, то
2 cos акы —2 cos ^w = ^»
2 sin akoi —2 sin Ькю = + j/n".
Далее, так как совокупность всех чисел а, Ь, очевидно, совпа-
совпадает с числами 1, 2, 3,..., п—1, то
2г° + 2гЬг=г + г2 + гВ+ . ..гп-1 = —1,
и потому
2 cos аАсо + 2 cos Ькоо = — 1,
2 sin а&со + 2 sin bkco = 0.
Поэтому из предыдущих формул для сумм получаются следую-
следующие соотношения.
I. Для первого случая
2 cos аЫ = — ^ ± 2" V^"»
2 cos feAco = — — =j= — j/n",
2 sin aAco = 2 sin feAco = 0.
Исследования о чистых уравнениях 835
II. Для второго случая
2j cos akco =2 cos ^^ = ^>
2 sin akoy = + у
2 sin №о = + у
Эти суммирования при помощи метода, не очень отличающегося
от настоящего, были произведены уже в «Арифметических исследо-
исследованиях» п. 356; хотя ни один из этих методов не смог устранить
неопределенность знаков корней, нам все же недавно удалось в
специальном исследовании восполнить этот пробел; мы доказали,
что при к = 1 во всех указанных формулах нужно брать верхние
знаки.
ДОКАЗАТЕЛЬСТВО НЕКОТОРЫХ ТЕОРЕМ
О ПЕРИОДАХ КЛАССОВ ДВОЙНИЧНЫХ ФОРМ
ВТОРОЙ СТЕПЕНИ
Теорема I. Число {собственно примитивных) классов с одним и
тем же определителем, которые при возведении в Р-ю степень, где
Р является либо простым числом, либо степенью рп простого чи-
числа р, дают главный класс К, либо равно 1, либо равно степени
того же простого числа р.
Доказательство. Пусть (О) — полная группа всех классов, о ко-
которых идет речь, и п — их число. Так как главный класс К обя-
обязательно содержится в (Q), то теорема очевидна, если туда входит
только он один. Если же туда входят и другие классы, то число
классов, содержащихся в периоде каждого из них, будет степенью
адсла р. Пусть А один из этих классов и пусть его период (9t) со-
содержит р* классов, которые все будут входить в (Q). Если теперь
классы этого периода B1) исчерпывают совокупность (Q), то мы име-
имеем ра = п, и теорема доказана; если же нет, то пусть В— любой
не входящий в (91) класс из (О); предположим, что его период про-
продолжен до тех пор, пока не получился класс ЪВ, который одно-
одновременно содержится среди классов периода (9t); это обязательно
должно случиться, так как по крайней мере главный класс явля-
является общим для этого периода и для периода (91). Если предполо-
предположить теперь, что ЪВ является первым классом в периоде класса В,
входящим также и в (91), т. е. что b по возможности наименьшее,
то я утверждаю,
1) что Ь является степенью числа р. Действительно, ясно, что
если положить Ъ = p$hf ЪВ == iA и hk == 1 (mod pn) (что возможно),
Некоторые теоремы о периодах классов квадратичных форм 837
то будет иметь место кЪВ = p^hkB = р$В = ikA, т. е. р&В также
будет находиться среди классов периода B1), откуда следует, что
Ыи6 = /;
2) что если совокупность классов К, В, 25,..., (Ь — 1) В обо-
обозначить через (95), то всевозможные композиции класса из (91) с
классом из (95) дадут /?а+^ различных классов. Действительно, если
предположить, что тА + пВ = m' A + п'В и п — п', то обязательно
т = т'\ если же п > тг', то (п — п') В = (mf — т)А, что невозмож-
невозможно, если п не равно тг';
3) что эти /?а+Р различных классов содержатся в (О), что оче-
очевидно.
Если теперь эти р* & классов исчерпывают совокупность (О), то
теорема доказана; если же нет, то выберем другой, не содержащий-
содержащийся среди них класс из (О), скажем, класс С, и продолжим его пе-
период до тех пор, пока не получим класса, который уже содержит-
содержится среди классов, составленных из (91) и (95). Посредством рас-
рассуждений, подобных предыдущим, показывается, что показатель
этого класса должен быть степенью числа р(=ру) и что компози-
композиция pY первых классов периода класса С с уже найденными /?а+Р
классами дает ра+/Ч-т различных классов, которые все содержатся
в (О). Если эти классы еще не исчерпывают (О), то мы таким же
образом рассмотрим четвертый класс D, и т.д., и ясно, что так как
(О) состоит из конечного числа классов, то эта операция тоже бу-
будет конечной, и п будет равно степени числа р.
Теорема II. Если число всех классов главного рода равно aa6^cY...,
где a, b, с, ... обозначают различные простые числа, то в этом ро-
роде существует аа, Ь&, с^ . . . классов, которые, будучи возведены со-
соответственно в степень а", 6^, cY, . . . дают главный класс.
Доказательство. Если А, А\ А",... — всевозможные классы, ко-
которые при возведении в степень aa дают главный класс К, и B1) —
их совокупность; далее, если В, В', 2?", ..., (Я5); С, С", С",..., (К)
и т. д. имеют аналогичные значения, то я утверждаю, что при ком-
композиции всевозможных классов из (91), со всевозможными классами
из (95), со всевозможными классами из (@) и т. д. получаются
различные классы. Действительно, если А + В + С + . . . =
= А' + В'+ С + . . . , то, полагая А — А' = А", В — В/ = В//
838 Некоторые теоремы о периодах классов квадратичных форм
и т. д., мы имеем
А" + В" + С" + . .. = К\
возводя в степень №с* . . ., мы получаем (№& . . .) А" = К, откуда
легко видеть, что А" = К и А = А', и таким же образом мы полу-
получаем В = В\ С = С и т. д. Пусть совокупность этих классов рав-
равна (S). Ясно, далее, что все эти классы принадлежат главному ро-
роду. Наконец, в главном роде нет ни одного класса, который не со-
содержался бы в (S). Пусть. . .
О СВЯЗИ МЕЖДУ ЧИСЛОМ КЛАССОВ,
НА КОТОРЫЕ РАСПАДАЮТСЯ ДВОЙНИЧНЫЕ ФОРМЫ
ВТОРОЙ СТЕПЕНИ, И ИХ ОПРЕДЕЛИТЕЛЕМ
Прошло уже тридцать три года с тех пор, как я открыл принципы
замечательной связи, которой посвящено настоящее сочинение;
я уже указывал на это в конце «Арифметических исследований».
Однако другие дела долгое время отвлекали меня от этого исследо-
исследования, пока недавно я не вернулся к нему и не смог благодаря но-
новым усилиям его расширить. Так как, однако, эта новая часть выс-
высшей арифметики выходит за рамки одного сочинения, то это первое
сочинение будет посвящено формам с отрицательным определите-
определителем; формы же с положительным определителем, которые требуют
совершенно своеобразного рассмотрения, должны быть оставлены
до другого сочинения.
Основу всего вопроса образует своеобразное исследование о ко-
количестве всех комбинаций целочисленных значений, которые при-
принимают два неопределенных целых числа внутри некоторой предпи-
предписанной области. Очевидно, что эта задача может быть поставлена
также и геометрически, именно: найти количество комплексных чи-
чисел, изображающихся точками внутри некоторой заданной фигуры.
840 О числе классов двойничных форм
Свойства фигуры зависят от свойств ограничивающей ее линии, т. е.
либо от одного уравнения между координатами х, у (если границей
является одна замкнутая кривая), либо от нескольких таких урав-
уравнений (если она состоит из нескольких криволинейных или прямоли-
прямолинейных частей), и от нашего желания будет зависеть, причислять ли
к рассматриваемому количеству те целые комплексные числа, для
которых соответствующие точки лежат на границе, или исключать их.
При аналитическом представлении этой задачи указанные гра-
граничные условия всегда могут быть выражены так, что одна или не-
несколько заданных функций Р, Q, i?,... от переменных х, у должны
принимать положительные или неотрицательные значения (в зави-
зависимости от того, исключается или допускается значение 0).
Так, например, если предписанной фигурой является круг, ра-
радиус которого равен У А, в то время как его центр совпадает с точ-
точкой, соответствующей некоторому целому комплексному числу, то
аналитическим условием этого является то, что выражение А—х2—
— у2 неотрицательно, если допускать (что мы все время и будем
делать) также и точки, лежащие на самой границе. Если фигурой
является треугольник, то должны иметь неотрицательные значения
три линейные функции ах + Ъу-\-с, ах + Ъ'у + с', а"х + Ъ"у -\-с"У
и аналогично обстоит дело и в других случаях.
Точное решение задачи должно, вообще говоря, призводиться
так: сначала, исходя из природы условий, одна из переменных,
например, х, должна быть заключена в границы, внутри которых
она последовательно пробегает все целые значения, а затем нужно
определить, сколько целочисленных значений другой переменной
у соответствует каждому отдельному значению переменной х; все
эти числа затем нужно сложить. В частных случаях по большей
части имеются специальные искусственные приемы для сокращения
работы.
Пусть, например, как и выше, фигурой является круг с радиу-
радиусом У А, и пусть г — наибольшее целое число, меньшее чем УАу
или само число У А, если А является квадратом. Точно так же,
О числе классов двойничных форм
841
пусть г', г", гт,..., Иг) — наибольшие целые числа, меньшие, соот-
соответственно, чем "[/"-4 — 1, У А — 4, У А — 9,..., У А — г2. Тогда ис-
искомое количество равно
2г + 1 + 2 Bг' + 1) + 2 Br" i- 1) + 2 Bг'" + 1) + .. . =
= 1 + 4г + 4г' + 4 г" + 4г" + . . . + 4ИГ>.
Короче, однако, в этом примере использовать следующий метод.
Пусть q — наибольшее целое число, меньшее чем У А/2 (или рав-
равное У А/2, если это число целое), и точно так же пусть г^+г\
r(g+2)? r(q+3)^ ## # — наибольшие целые числа, меньшие соответ-
соответственно чем yA — (q+ IJ, У А — (q + 2J, /Л — (д + ЗJ, .... Тог-
Тогда искомое количество равно
По этой формуле получаются следующие значения:
А
100
200
300
400
500
600
700
800
900
1000
317
633
949
1257
1581
1885
2209
2521
2821
3149
А
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
3149
6293
9425
12581
15705
18853
21993
25137
28269
31417
А
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
31417
62845
94237
125629
157093
188453
219901
251305
282697
314197
Для нашей цели не требуется нахождения точного значения;
нам нужно только получить выражение, которое дает точное коли-
количество с любым приближением, если границы стремятся к бесконеч-
842 О числе классов двойничных форм
ности. Однако, так как здесь еще возможен некоторый произвол,
мы должны прежде всего точнее обрисовать положение вещей.
Итак, мы предположим, что функции Р, Q, R,..., кроме перемен-
переменных х, у, содержат постоянный элемент к, так что отдельные функ-
функции Р, Q, i?,... являются однородными функциями трех величин х,
у, к. Таким образом, фигура, определенная уравнениями Р = О,
Q = О, R = 0,... будет так зависеть от к, что различным значениям
к будут соответствовать подобные и подобно расположенные отно-
относительно начала координат фигуры, и соответствующие линейные
измерения будут пропорциональны значениям к, а площади пропор-
пропорциональны значениям к2. Если обозначить теперь количество точек
внутри фигуры через М?а площадь через V, то при возрастании к долж-
должны, очевидно, также возрастать М и V; но если к будет стремиться
к бесконечности, то М и V будут сколь угодно близко подходить к от-
отношению равенства, или, если желательна элементарная ясность,
сколь бы малая величинах ни была задана, всегда можно будет ука-
указать такую границу, что для каждого значения /с, превосходящего
эту границу, отношение M/V заведомо должно будет лежать между
1 — ^ и 1 + X. Обычным образом это может быть выражено так:
для бесконечно большого значения к выполняется равенство
М = V.
В нашем примере требуемое условие выполняется, если положить
к = У~А \ при этом фигура будет кругом с площадью тс А, где тг обоз-
обозначает половину длины окружности с радиусом 1. Приведенные выше
числа позволяют ясно убедиться в сходимости.
При желании мы могли бы провести доказательство этой теоре-
теоремы с полной строгостью, однако мы предпочитаем его в этом
месте опустить и перейти к более трудным вещам.
В этом сочинении граница определяется одним единствен-
единственным уравнением вида ах2 + 2Ьху + су2 = А, где а, Ь, с — целые чи-
числа, и Ъ2 — ас — отрицательное число, которое мы положим равным
—D. Очевидно, что кривая, определяющая фигуру, будет эллипсом,
и легко получается, что квадраты полуосей являются корнями
О числе классов двойничных форм 843
уравнения (ас — Ъ2) q2—А ( а+ c)q + А2 — О, т. е. равны
А
2 (ас — Ь2)
42 Л2
Произведение этих корней будет равно ]_ &2 ~ j?2» и П0Т0МУ пло"
тсА
щадь эллипса равна
Таким образом, отсюда следует, что число всех комбинаций це-
целочисленных значений переменных х, г/, для которых выражение
ах2 + 2Ъху-\-су2 не превосходит значения А, с ростом А все более
и более приближается к величине кА/}/~О, и для бесконечно боль-
большого А должно быть положено равным этому значению. Далее, яс-
ясно, что в этом отношении безразлично, причислять ли к остальным
комбинацию х = 0, у = 0 или исключать ее. Таким образом, иско-
искомое количество (в последнем смысле) является ничем иным, как
суммой количеств представлений отдельных чисел 1, 2, 3,..., А
двойничной формой второй степени ах2 + 2Ьху + СУ2, и так как из
этих чисел одни вообще не могут быть представлены этой формой,
а другие представляются большим или меньшим числом способов,
то величину k/Y~D следует рассматривать как среднее значение ко-
количества представлений неопределенного положительного числа ка-
какой-нибудь формой, определитель которой равен — D.
Прежде чем переходить к общему изложению дальнейшего, нам
представляется целесообразным разобрать некоторые специальные
случаи, чтобы легче можно было проникнуть в суть аргументации.
Поэтому мы сначала снова возьмем форму х2 -\- у2, для которой
количество представлений неопределенного числа имеет среднее
значение тт. А количество действительных представлений заданного
числа может быть без труда определено при помощи обоснован-
обоснованных в «Арифметических исследованиях» общих принципов. Если мы
обозначим через / (А) количество представлений числа А, то оно
равно 4, если .4 = 1, или равно 2, или же равно некоторой степени
844 О числе классов двойничных форм
числа 2; /(^4) равно 8, если А является простым числом вида An + 1
или произведением такого простого числа на степень числа 2;
/ (А) = О, если А является простым числом вида An + 3 или делится
на такое простое число, но не делится на его квадрат; наконец,,
вообще, если А представлено в виде 2^&га&рст.. . ,, где а, Ь, с,
обозначают различные простые числа вида 4n+l, a S — произве-
произведение простых чисел вида An + 3, если простые числа такого вида
имеются среди сомножителей числа А, то
либо /(А) = 4 (а + 1) (р + 1) (т + 1). • • ,
либо / (А) = О,
в зависимости от того, является ли число S квадратом или нет.
Таким образом, ясно, что /(А) полностью определяется теми прос-
простыми числами среди 3, 5, 7, 11, 13,..., которые встречаются среди
сомножителей А, так что вообще нужно положить
f{A) =4C). E). G). (И). A3)...,
где C), E), G),. . . определяются так. Если р обозначает простое
число, то
во-первых, (р) = 1, если р не входит в А]
во-вторых, (р) = а + 1, если р имеет вид An -f- 1 и ра есть наи-
наивысшая степень, входящая в А;
в-третьих, (р) = 0, если р имеет вид An + 3 и показатель наи-
наивысшей входящей в А степени числа р нечетен; наконец,
в-четвертых, (р) = 1 если р имеет вид An + 3, и показатель
наивысшей входящей в А степени числа р четен.
Очевидно, что первый случай содержится во втором и четвертом.
Таким образом, члены ряда /A), /B), /C), /D), .. . расположены
в высшей степени неправильно, хотя по мере увеличения числа все
точнее получается среднее значение, равное тт. Сумму /(l) + /B)-f*
+ / C) + • .. + f(A) мы обозначим через F (А),
7
Если мы теперь положим вообще f(m)-\-fCm) = /' (т), то легко
видеть, что
/'(^)= 4.E).G).(И).A3)...,
О числе классов двойничных форм 845
т. е. /' (А) не зависит от отношения, в котором А стоит к числу 3,
так что неправильность ряда /' A), /' B), /' C), /' D), /' E), . .. будет
не только позднее начинаться, но и будет намного меньше. Если
мы, далее, положим
/' A) + /' B) + /' C) + /' D) + . . . + /' (т) = F' (т),
ТО
F' (ЗА) = F (ЗА) + / C) + / F) +/(9) +... + / (ЗА) = F (ЗА) + F (А).
Отсюда легко видеть, что если А возрастает до бесконечности, то
нужно положить
т. е. что среднее значение членов ряда /'A), /'B), /'C), /'D),..
4
равно -^- тт.
о
Если положить вообще — /' (т) -|- /' Eт) = /"(т), то подобным же
образом
f (А) = 4G). (И). A3)...,
т. е. из нового ряда /"A), /"B),... устраняются неправильности,
зависящие от отношения А к числу 5. И если положить
/" A) + /" B) + /" C) + . . . + /" (т) = F" (т),
ТО
F" Em) = —F' (т) + F' Em),
откуда следует, что если т возрастает до бесконечности, то нужно
положить
F" (Ьт) — ~тг- 4т,
4 4
или что среднее значение членов ряда равно -^ • -=- к.
Если мы будем продолжать таким же образом и дальше, образуя
новые ряды, и исключая последовательно сомножители G), A1),
A3), A7), . . . , то эти ряды будут все более и более походить на
постоянные, а средние значения будут последовательно приобретать
846 О числе классов двойничных форм
новые сомножители 8/7, 12/ш 12/13, 16/17, 20/i9, • • • , знаменателями
которых являются простые числа в их натуральном порядке, а чи-
числители на единицу больше или меньше знаменателей в зависимости
от того, имеют ли эти простые числа вид 4п — 1 или 4п + 1. Так
как при продолжении этого процесса до бесконечности постоянное
значение 4 должно все ближе подходить к среднему значению, мы
получаем
, 4 4 8 12 12 г
~3" * ~5~ ' "Т ' ТГ ' ТТ * • • до бесконечности,
или
3 5 7 И 13
3 + 1 о — 1 7 + 1 11 + 1 13 —I"*
Если отдельные дроби разложить в бесконечные ряды
О А Л Л
6 _4 L_L_i L_L
3 + 1 3 r9 27 "т" • • • '
А+ —4- —4-
5 -1 ~ х ' 5 ' 25 ' 125
7 + 1 7 '49 343 ' ' ' ' '
и т. д.,
то произведение легко преобразуется в
i_i_.—-- + — L + _±__
3^5 7^9 11 ^ 13 ' " '
и сумма этого ряда, как известно вообще, равна тг/4. В действи-
действительности Эйлером обратным путем давно было получено отсюда
/г 4 4 8
равенство между тг/4 и бесконечным произведением -=- • -=- •-=-...
(Introd. in analysin inf., T. /, Cap. XV, § 285).
Во вторую очередь мы рассмотрим форму х2 -f- 2y2, для которой
количество представлений неопределенного числа будет иметь среднее
значение, равное к/У 2. Если мы обозначим через /(А) количество
представлений этой формой заданного числа А, то оно равно 2 для
О числе классов двойничных форм 847
А = 1 или А = 2, или когда Л является степенью числа 2; далее,
/ (А) = 4, если Л является одним из простых чисел, для которых —2
является квадратичным вычетом, т. е. простых чисел вида 8А + 1 у
8k + 3, именно, для А = 3, 11, 17, 19, 41, 43, . .. ; наконец, /(^4) = О,
если А является простым числом, для которого —2 есть квадра-
квадратичный невычет, т. е. простым числом из ряда 5, 7, 13, 23, 29, 31, ...
или простым числом вида 8k + 5 или 8Л; + 7. Вообще, если число А
представлено в виде 2u'Saab cY.. . , где а, 6, с, ... обозначают различные
простые числа вида 8&-f 1, 8& + 3, a S обозначает произведение
остальных чисел (вида 8k + 5, 8k + 7), причем если такие числа
содержатся среди сомножителей числа А, то нужно положить
либо
либо /(^4) = О,
в зависимости от того, является ли S квадратом или нет. Затем,
совершенно аналогично тому, как в п. 7, мы переходим от ряда
/A), /B), /C), /D), /E),..., т. е. ряда 2, 2, 4,2, 0, 2,...,
последовательно к рядам, все больше и больше приближающимся
к постоянным, средними значениями которых являются по порядку
числа тг/}/, 2W3}/, 2-6-к/3-5'У2, 2 • 6 • 8- тс/3 -5- 7 У2,. . .\
причем так, что мы приходим к равенству
2=-?=
2
3" '
6
5
8
т
10
и
14
13
16
17
18
19
где знаменатели образуют натуральный ряд простых чисел, а числи-
числитель на единицу меньше знаменателя, если он имеет вид 8к -\- \
или 8А; + 3, и напротив, на единицу больше знаменателя, если
последний имеет вид 8k + 5 или 8k + 7.
II
1
Прошло уже тридцать шесть лет с тех пор, как я открыл прин-
принципы рассматриваемой в этом сочинении замечательной связи, на
что я уже указывал в конце «Арифметических исследований». Однако
848 О числе классов двойничных форм
другие дела долгое время отвлекали меня от этого исследования,
пока я недавно снова не вернулся к нему и не смог благодаря новым
усилиям его расширить. Так как, однако, объем этой новой части
высшей арифметики выходит за рамки одного сочинения, то это пер-
первое сочинение будет посвящено формам с отрицательным определи-
определителем; формы же с положительным определителем, которые требуют
совершенно своеобразного рассмотрения, должны быть оставлены
до другого сочинения.
Для нашей цели мы используем одну теорему, которая сама по
себе хотя и является арифметической, но природу которой удобнее
и отчетливее можно уяснить, если проводить рассмотрения в геомет-
геометрической форме.
Если на бесконечной плоскости задана фигура, ограниченная не-
некоторой линией, то площадь этой фигуры может быть приближенно
определена, если разбить плоскость на квадраты, и подсчитать коли-
количество как тех из них, которые целиком лежат внутри фигуры, так
и тех, которые пересекаются границей фигуры, причем площадь,
очевидно, будет меньше или больше в зависимости от того, отбрасы-
отбрасываются ли последние квадраты, или считаются вместе с первыми.
Если же квадраты, лежащие на границе, на основании какого-либо
принципа желательно частью исключать, а частью учитывать, то
ошибка будет либо положительной, либо отрицательной, но обяза-
обязательно меньшей, чем сумма всех квадратов, лежащих на границе.
Чем меньшие квадраты брать, тем точнее будет при этом опреде-
определяться площадь, и такое приближение можно продолжать до беско-
бесконечности, т. е. можно брать квадраты настолько малыми, что ошибка
будет меньше любой заданной величины. Хотя это кажется очевид-
очевидным само по себе, мы тем не менее не преминем дать строгое доказа-
доказательство.
Каждые два квадрата могут иметь либо только одну общую вер-
вершину, либо две, либо вообще ни одной; в первом и втором случаях
они будут называться соседними, а в третьем случае — разделен-
разделенными. Очевидно, что квадратов, которые все являются соседними
О числе классов двойничных форм 849
один с другим, может быть не более четырех, и потому среди любых
пяти различных квадратов всегда должно быть по крайней мере
два разделенных между собой. Но так как расстояние между двумя
1 очками, лежащими в разделенных квадратах, не меньше стороны
квадрата, которую мы обозначим через а. то очевидно, что если точка,
выйдя из какого-нибудь места одного квадрата, пересекает по поряд-
порядку второй, третий, четвертый квадрат и, наконец, достигает пятого
квадрата, то длина пути заведомо будет не меньше чем а. И так как,
если линия далее пересекает другие квадраты, то по аналогичной
причине ее части, заключенные между пятым и девятым квадратами,
далее, между девятым и тринадцатым квадратами и т. д.— не могут
быть меньше чем а, то мы легко заключаем, что замкнутая линия,
которая всего затрагивает п различных квадратов, заведомо не мо-
может быть меньше чем (п — 4) а/4. Таким образом, наоборот, замкну-
замкнутая линия, длина которой равна Z, заведомо не может затрагивать
4/
более чем 4+ — различных квадратов. Так как их площадь, рав-
равная 4а2 + 4aZ, может быть сделана меньше любой заданной величи-
величины, если а бесконечно уменьшается, то это же подавно имеет место и
для ошибки квадратуры, о которой мы говорили выше.
Принцип, по которому учитываются или исключаются квадраты,
лежащие на границе фигуры, может быть установлен многими раз-
различными способами; наиболее простым представляется обращать
внимание только на положение центра каждого квадрата, так что
квадраты, центры которых лежат внутри фигуры, учитываются,
а квадраты, центры которых находятся вне фигуры, исключаются,
причем те квадраты, центры которых лежат на самой границе, учиты-
учитываются или исключаются в зависимости от нашего желания. Вместо
центров можно было бы брать также любые другие точки, лежащие
в отдельных квадратах аналогичным образом.
Таким образом, дело сводится к тому, что мы представляем себе
на плоскости точки, расположенные на одинаковых расстояниях
одна от другой и так лежащие на равноудаленных между собой
прямых, что получаются квадраты. Тогда, на основании теоремы
850 О числе классов двойничных форм
предыдущего пункта, мы можем утверждать, что число точек, содер-
содержащихся внутри фигуры, умноженное на квадрат расстояния между
двумя соседними точками, будет столь мало, сколь мы хотим,
отличаться от площади фигуры, если только указанное расстояние
взято достаточно малым, или выражаясь обычным образом, что это
произведение представляет собой площадь, если расстояние беско-
бесконечно мало.
4
Кривая, которая представляется уравнением
ар2 + 2bpq + Cq2 = l
в прямоугольных координатах р, д, является коническим сечением,
и притом эллипсом, если величины а, с, и ас — Ъ2 положительны;
ограниченная этим эллипсом площадь оказывается равной тг /У ас —Ь2.
Значение величины ар2 -f- 2bpq -f- cq2 вне эллипса всюду больше
чем 1, а внутри эллипса меньше чем 1, но нигде не отрицательно.
Представим себе на плоскости, на которой лежит эллипс, систему
точек, расположенных так, что они образуют квадраты, стороны
которых равны X и параллельны координатным осям, причем без-
безразлично, совпадает ли начало координат, т. е. центр эллипса,
с одной из этих точек или нет. Если количество точек внутри эллипса,
считая и те, которые лежат на границе, равно яг, то, согласно теореме
предыдущего пункта, число к/Уас— Ъ2 является границей для
величины тХ2, к которой она приближается настолько, насколько
нам угодно, если X бесконечно уменьшается.
Если предположить, что начало координат совпадает с какой-
нибудь точкой системы, то если положить р = Хж, q = Хг/, числа
х и у для отдельных точек системы будут, очевидно, целыми,
и, наоборот, каждая комбинация целочисленных значений х, у будет
соответствовать некоторой точке системы. Поэтому число т является
ни чем иным, как количеством всех комбинаций целочисленных
значений величин х, г/, для которых F будет не больше чем М,
если мы для краткости обозначим функцию или форму второй
степени ах2 + 2Ъху + су2 через F, а величину 1/Х2 — через М. Опреде-
О числе классов двойничных форм 851
литель этой формы равен Ъ2 — ас, и вместо этого мы будем писать — D.
Поэтому наша теорема теперь будет высказываться следующим
образом.
Теорема I. Количество т всех комбинаций целочисленных значений
неизвестных х, у, для которых значение формы с отрицательным
определителем —Вне превосходит границы М, будет равно кМ/VD,
причем лишь приближенно, но с бесконечно увеличивающейся точностью
приближения, если М бесконечно возрастает. Вряд ли нужно ука-
указывать на то, что бесконечно увеличивающуюся точность приближения
надо понимать здесь (как и в дальнейшем) не в том смысле, что
сама разность между кМ/ УБ и m бесконечно уменьшается, а в том,
что отношение этих величин все ближе подходит к единице, т. е.
что разность ¦=¦ — 1 бесконечно убывает.
Чтобы произвести точный подсчет, можно для отдельных целых
значений ху лежащих между границами — у ^уу и + 1/ -^г- , рас-
рассматривать по два соответствующих уравнению F = М значения у
откуда немедленно получится количество целых чисел, лежащих
между ними. Так как это количество одинаково для противо-
противоположных значений х, мы тем самым освобождаемся почти от
половины работы. Можно делать и так: подсчитывать значения х,
которые соответствуют отдельным значениям у между границами
— 1/ %=г- и + l/ ^jr-. При целесообразном соединении обоих методов
работа может быть облегчена еще более, на чем, однако, мы здесь
подробнее останавливаться не будем; будет достаточно, если мы
добавим кое-что о простейшем случае.
Если формой является F = х2 + г/2, т. е. кривая есть окружность,
и если г, г', г", г",. . ., № обозначают наибольшие целые числа, кбторые
соответственно меньше чем
УЖ, ум — 1, ум — 4, ум — 9,..., ум — г2,
852
О числе классов двойничных форм
или равняются им самим, если среди этих величин содержатся
целые числа, то искомое количество т равно
2г + 1 + 2 Bг' + 1) + 2 Bг" + 1) + 2 Aгт + 1) + . . . + 2(гС> + 1) =
= 1 + 4г + 4г' + 4г" + 4/" + . . . + 4И1*).
Однако то же самое мы получим проще, если обозначим через q
наибольшее целое число, меньшее чем'УМ/2 (или эту самую величину,
если она является целым числом), при помощи формулы
т = Aq2 + 1 + 4г
Таким образом, получаются следующие количества:
м
100
200
300
400
500
600
700
800
900
1000
т
317
633
949
1257
1581
1885
2209
2521
2821
3149
м
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
т
3149
6293
9425
12581
15705
18853
21993
25137
28269
31417
М
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
т
31417
62845
94237
125629
157093
188453
219901
251305
282697
314197
Теперь мы следующим образом обобщим теорему п. 4.
Теорема II. Если собраны не все комбинации целочисленных значений
величин х, у, для которых F не превосходит значения М, а лишь часть из
нихч именно, те, для которых х сравнимо по некоторому заданному
модулю g с некоторым заданным числом G, а у сравнимо по некоторому
заданному модулю h с некоторым заданным числом Н, то количе-
количество т' этих комбинаций приближенно будет выражаться значением
О числе классов двойничных форм 853
кМ I gh^D, причем приближение будет беспредельно становиться
все более точным, если М возрастает до бесконечности.
Действительно, если положить х = gx' + G, у = hy' -f- #, то т'
будет, очевидно, количеством всех комбинаций целочисленных зна-
значений величин х\ у', для которых
+ f J+М*'+т)(^+-?1)+chiyf+-?
не превосходит значения М. Поэтому, если мы представим себе на
плоскости систему точек, которые расположены почти так же, как
в п. 4, но, кроме того, еше и так, что с некоторой точкой системы
совпадает не начало координат, а точка с координатами р = — ,
нк , . 8
q = -г- f то т будет выражать количество точек внутри эллипса,
уравнение которого есть
считая также и точки, лежащие на самой границе. И площадь этого
эллипса, которая равна ™ = —^г=> будет границей, к кото-
gh у ас — Ь2 ghyD
т
рой приближается произведение т'Х2 = —, когда X бесконечно убы-
убывает или М бесконечно возрастает.
Ясно, что эта теорема охватывает также и тот случай, когда
только одна из двух неизвестных х, у должна изменяться скачками,
в то время как значения другой не ограничены никакими усло-
условиями. В самом деле, это, очевидно, равносильно тому, чтобы
положить h или g равным 1.
До сих пор рассмотрения не зависели от свойств коэффициентов
формы ах2 + 2Ьху + су2; однако, начиная с этого места, мы будем
предполагать, что эти коэффициенты являются целыми числами.
Таким образом, каждая комбинация целочисленных значений вели-
величин ж, у будет давать целое значение самой формы, т. е. будет
соответствовать представлению этой формой некоторого целого числа.
854 О числе классов двойничных форм
Отсюда вытекает, что совокупность всех комбинаций целочисленных
значений величин х, у, при которых форма F = ах2 + 2Ьху + су2
принимает значения, не превосходящие границы М, есть ни что
иное как совокупность всех представлений целых чисел, которые
не превосходят границы М, или целых чисел до этой границы вклю-
включительно, если сама она является целым числом. Поэтому, если мы
ради краткости обозначим количество различных представлений
формой F определенного целого числа тг через F (п), или, чтобы избежать
двусмысленности, через Fny то обозначенное выше через т число
будет равно F0 + Fl + F2 + F3 + . . . + FM, и первая теорема
примет следующий вид.
Теорема III. Сумма F0 + Fl + F2 + . . . + FM приближенно
равна кМ /~f/~D, и точность приближения увеличивается беспредельно,
если М возрастает до бесконечности.
8
К третьей теореме, касающейся представлений всех чисел, мы
хотим добавить еще одну, которая относится только к нечетным
числам. Очевидно, что формой F не могут представляться нечетные
числа, если а и с одновременно четны; поэтому исследование огра-
ограничивается следующими тремя случаями.
I. Если а нечетно, а с четно, то нечетное число будет пред-
представляться при нечетном значении х, в то время как значение у
остается произвольным. Поэтому теорема II, если положить в ней
g = 2, G = 1, /г = 1, показывает, что количество всех комбинаций
таких значений ж, г/, для которых форма принимает нечетные зна-
значения, не превосходящие границы М, при бесконечно растущем М
с любой степенью точности представляется формулой кМ/2\fD.
II. Если а четно, а с нечетно, то для представления нечетного
числа нужно, чтобы у было нечетно, вследствие чего мы, полагая
g = 1, h=^2, H = 1, приходим к тем же выводам.
III. Если нечетны как а, так и с, то для того, чтобы получилось
нечетное значение формы, нужно чтобы либо нечетное значение х
комбинировалось с четным значением г/, либо четное значение х
О числе классов двойничных форм 855
комбинировалось с нечетным значением у. Количество всех комбина-
комбинаций как первого, так и второго типа, при которых значение формы
не превосходит границы М, с любой степенью точности выражается
формулой 7иМ / 4]/"Z); поэтому количество всех комбинаций, которые
дают нечетные, не превосходящие границы Мч значения формы,
также и здесь с любой степенью точности выражается формулой
7UM/2JAD.
Но так как совокупность всех таких комбинаций есть ни что иное
как совокупность всех представлений всех чисел 1, 3, 5, 7,. . ., М,
если М — нечетное целое число, или всех чисел 1, 3, 5, 7, .. ., Л/ — 1,
если М — четное целое число, то мы получаем следующую теорему.
Теорема IV. Сумма
Fl + F3 + F5 + F1 + . .. + F (М — 1)
или Fl + F3 + F5 + F1 + . . . + FM,
-в зависимости от того, четно М или нечетно, с любой степенью
точности выражается формулой itM-/ 2УВ, если F есть форма,
у которой один или оба коэффициента а, с нечетны.
Пусть С — совокупность представителей всех классов собственно
примитивных форм для определителя —D. Обозначим через (п)
количество всех представлений числа п формами из совокупности С.
Пусть р — нечетное простое число. Тогда
1. (рп)= (п), если р есть делитель числа D.
2. (рп) = (п) + (А) \ п /делит х2 + D
где п= hpv-, \х — любое число и h не делится на р.
В случае 1 имеет место (h) = (ph) = (p2h) = (p3h) — ...;
» » 2 » » (ph) = 2 (ft), (p2h) - 3 (h), (psh) = 4(й)
» » 3 » »
856
О числе классов двойничных форм
Пусть из каждого собственно примитивного класса для опреде-
определителя — D, количество которых равно X, выбрана некоторая форма
и совокупность этих форм обозначена через L.
Обозначим через f(A) количество всех представлений числа А
формами из L.
Пусть, далее, f(A; р) = f(A /ра)? где р* — наивысшая степень
простого числа р, которая входит в А; далее, f(A; p, q) = /(A/p*q&),
если q — другое простое число, наивысшая степень которого, входящая
в А, есть q&; f(A; р, q, г) = f(A /p^qPrt), если г — третье простое
число, наивысшей степенью которого, входящей в Ау является rY>
и т. д.
[IV]
Обозначим через (п) количество значений х из совокупности
О, 1, 2, 3, 4,..., рп-1,
для которых х2 — D = х2 — ар^ делится на рп.
1) (х нечетно, например, = 7,
2) [х четно, например, = 6
{2)=р
(8) = О
И Т. Д.
aNp
?"'.
E) = />2
F) = p*
G) = 0
и т. д.
aRp
D) = p*
E) = P2
F) = ps
G) = 2/
и т. д.
О числе классов двойничных форм
Положим
р
(*>-f
и т.
теперь
-(!)'
= B)'
= C)'
= D)'
д-
f(p)
т
f(p3)
fip1)
Тогда
= i +
= (ir
= i +
и
B)'
+ C)'
B)' +
т. д.
D)'
Следовательно, полагая
Р-1(а i f(P)
мы имеем
Р + *Г = 1 | С1)' i B)' | C)' ¦ D)' ,
Р Р Р2 РВ />4
Таким образом, Т = 1.
= !+<!)
[V]
Среднее число классов для отрицательного определителя — D очень
близко к
Истинное же значение выражается следующей формулой, где
ради краткости пишется m для среднего числа и М — для истинного;
р, q представляют собой все нечетные простые числа, не входящие
в Z>, причем р — делители, a q — неделители выражения х2 + D;
г обозначает входящие в D простые числа.
858 О числе классов двойничных форм
т л /г Р3 + Р
1. М = т х произведение выражении 3__Л
тт л>г tc>TD „
11. М = —-^— X произведение выражении
rS Г
? —1 г2—1
;
III. NB. М = —-— х произведение выражений _^ • —^— ;
IV. М = I/ — х произведение выражений ?__. - ^~ • ~ ;
V. M =
NB. Формула III непосредственно выводится из сравнения обоих
способов для подсчета представляемых чисел до некоторой границы.
[VI]
Теорема. Число классов, на которые распадаются все собственно
примитивные двойничные формы, для отрицательного определителя
—D равно
п .r-j^r » Р — 1 9 + 1 г2— 1
-т- х у D х произведение выражении • —-— • —^— >
где
р обозначает все (нечетные) простые числа, по которым — D
является невычетом,
q обозначает вде (нечетные) простые числа, по которым —D
является вычетом,
г обозначает все (нечетные) простые числа, входящие в D;
-y-YD X произведедие выражений
„ Г2— 1
О числе классов двойничных форм 859
где в знаменателе положительный знак имеют те дроби, знаменатели
которых содержатся в форме неделителей выражения #2 + D, а отри-
отрицательный знак — те дроби, знаменатели которых содержатся в форме
делителей; те дроби, знаменатели которых не взаимно просты с D,
вообще отбрасываются;
_ у ^У1=? 3 ^ 5 ^ ") __ ctg6 ± ctg36 ± ctg56±> - ¦ ±ctg дб
если положить б=^г, iV = j,^Z)H3a^ брать все взаимно простые
с D числа с определенными выше знаками.
Для положительных определителей число классов
\og{T+UVD)
где Т, U обозначают наименьшие значения величин t, и, удовле-
удовлетворяющие уравнению t2 — Du* = 1;
13 5
log sin ~y 6 ± log sin -y 6 ± log sia -у б ± • • •
~ iog(r+ и Yd) '
[VII]
Для отрицательного определителя — p, который является простым
числом вида 4га+1, число классов равно (а — Р), где а обозначает
число квадратичных вычетов в первом квадранте
1-2-3... 4- (Р-1),
Р — число невычетов.
[VIII]
b = 2m + a — I(mod8),
где m есть половина числа классов для определителя —р.
860
О числе классов двойничных форм
р
17
41
73
89
97
ИЗ
137
193
233
241
257
281
313
337
353
5
13
29
37
53
61
101
109
149
157
173
181
197
229
269
277
293
т
2
4
2
6
2
4
4
2
6
6
8
10
4
4
8
1
1
3
1
3
3
7
3
7
3
7
5
5
5
11
3
9
п
+ 1
+ 5
— 3
+ 5
+ 9
— 7
—И
7
+ 13
+15
+ 1
+ 5
+ 13
+ 9
+ 17
+ 1
— 3
+ 5
+ 1
— 7
+ 5
+ 1
— 3
— 7
—11
+13
+ 9
+ 1
—15
+ 13
+ 9
+ 17
h
0
— 4
+ 4
— 8
я
+ 4
+ 8
+ 4
+ 12
+ 8
+ 4
+16
—16
—12
+16
+ 8
+ 2
— 2
+ 2
— 6
— 2
— 6
—10
+ 10
—10
— 6
+ 2
+ 10
—14
+ 2
+ 10
+14
+ 2
4
1
— 4
+ 9
+ 27
+ 34
+ 22
+ 15
+ 37
+ 81
+144
+ 64
+ 16
+ 53
— 25
—148
+ 42
+ 2
+ 5
+ 12
— 6
+ 23
+ 11
— 10
+ 33
+ 44
— 28
+ 80
— 19
— 14
—107
— 82
— 60
+138
2т + а — 1 — Ъ
8
+ 1
+ 1
+ 1
+з
+1
—1
/[
—2
+2
—1
0
+5
+ 1
0
+з
0
0
+1
+1
0
+2
+3
—1
+2
0
+з
+1
+з
—1
+з
0
+4
ОС
3
3
1
9
5
9
3
11
15
13
15
9
5
7
15
о
Р
2
4
6
2
6
4
8
6-
2
6
4
10
12
12
8
О числе классов двойничных форм
861
р
317
349
373
389
397
т
5
7
5
11
3
а
—11
+ 5
— 7
+ 17
—19
ъ
+14
+18
+ 18
—10
— 6
/
+ 114
—136
+ 104
—115
+ 63
2т + а — 1 — Ъ
8
—2
0
—2
+6
[IX]
Распределение квадратичных вычетов по октантам
р — простое число; (г) — число квадратичных вычетов по модулю р,
^которые лежат между (г—!)-§- и г-^ •
Первый случай: р = 8п -(- 1.
2t— число классов для определителя —р\
2и — число классов для определителя — 2р.
B) = D) = E) = G) =
р
17
41
73
89
97
ИЗ
137
193
2га
4
10
18
22
24
28
34
48
t
2
4
2
6
2
4
4
2
и
2
2
8
4
10
4
6
10
A)
2
4
7
8
9
9
11
15
B)
1
3
3
6
4
7
8
10
C)
0
0
5
2
7
5
7
13
я
233
241
257
281
313
337
353
401
58
60
64
70
78
84
88
100
t
6
6
8
10
4
4
8
10
и
4
10
8
4
18
12
12
6
A)
17
19
20
21
25
25
27
29
B)
15
14
16
19
16
19
21
26
C)
11
13
12
11
21
21
19
19
862
О числе классов двойничных форм
Второй случай: р = 8п-\-5.
2t — число классов для определителя — р\
2м — число классов для определителя —2р.
A) = C) = F) = (8) =i-Bn-* + и),
p
5
13
29
37
53
61
101
109
149
157
173
2га
0
2
6
8
12
14
24
26
36
38
42
t
1
1
3
1
3
3
7
3
7
3
7
(
и
1
3
1
5
3
5
3
5
3
13
5
4) =
A)
0
1
1
3
3
4
5
7
8
12
10
E) =
B)
1
1
4
2
5
5
11
8
14
9
15
~7~~ (
D)
0
0
1
1
2
2
4
5
7
6
8
2n —
p
181
197
229
269
277
293
317
349
373
389
397
In
44
58
56
66
68
72
78
86
92
96
98
+ 2)
t
5
5
5
11
3
9
5
7
5
11
3
и
9
5
13
5
11
9
7
13
13
7
21
A)
12
12
16
15
19
18
20
23
25
23
29
B)
13
15
15
24
17
23
22
24
24
31
22
D)
3
10
10
13
14
14
17
17
19
20
19
Третий случай: р = 8п-\-3.
t — число классов для определителя — рг
2и — число классов для определителя —2р.
C) = i Bга + t + и + 2),
F)=4-Bп-*-в + 2),
О числе классов двойничных форм
р
3
11
19
43
59
67
83
107
131
139
2га
0
2
4
10
14
16
20
26
32
34
t
1
3
3
3
9
3
9
9
15
9
и
1
1
3
5
3
7
5
3
3
7
A)
0
1
1
2
5
3
6
8
11
9
B)
0
0
1
3
2
5
4
5
5
8
C)
1
2
3
5
7
7
9
10
13
13
F)
0
0
0
1
1
2
2
4
4
5
р
163
179
211
227
251
283
307
331
347
379
2га
40
44
52
56
62
70
76
82
86
94
t
3
15
9
15
21
9
9
9
15
9
и
11
3
5
7
7
15
17
11
5
11
A)
8
14
14
16
19
16
17
20
24
23
B)
12
8
12
12
12
19
21
21
19
24
C)
14
16
17
20
23
24
26
26
27
29
F)
7
7
10
9
9
12.
13
1&
17
19
Четвертый случай: р = 8п-\-1.
t — число классов для определителя —р;
2и— число классов для определителя —2р.
(8)= lBn-
р
7
23
31
47
71
79
103
127
151
167
2ге
0
4
6
10
16
18
24
30
36
40
t
1
3
3
5
7
5
5
5
7
11
и
2
2
4
4
2
4
10
8
6
6
A)
0
2
2
4
7
6
6
8
11
14
B)
1
2
3
4
5
6
9
10
11
12
D)
0
1
1
2
4
4
4
6
8
9
(8)
0
0
1
1
1
3
6
7
7
6
р
191
199
223
239
263
271
311
359
367
383
2га
46
48
54
58
64
66
76
88
90
94
t
13
9
7
15
13
11
19
19
9
17
и
4
10
16
4
6
12
6
6
20
12
A)
17
14
13
21
21
19
27
30
22
29
B)
13
15
18
16
18
20
21
24
28
27
D)
11
10
10
14
15
14
18
21
18
21
(8)
6
10
14
8
11
14
11
14
23
18
864
О числе классов двойничных форм
[X]
Распределение квадратичных вычетов по двенадцатым частям.
р— простое число; (г) — число квадратичных вычетов по модулю
г — 1 г
р} которые лежат между —т^— р я-jj р.
Первый случай: р = 2Ап + 1.
2t
Аи
число классов для определителя —р.
число классов для определителя —Зр.
B) = D) = F) = G) = (9) = (И) = ± Fл - Зг
C) = E) = (8) = A0) = | (вп + 3* - Аи).
р
73
97
193
241
п
3
4
8
10
t
2
2
2
6
и
3
3
6
3
A)
5
6
И
14
B)
3
4
9
8
C)
2
3
5
И
Второй случай: р = 2Ап + 13.
2t — число классов для определителя — р\
Аи — число классов для определителя —Зр.
A) = C) = A0) = A2) = 1 Bп + 1 + t),
B) = F) = G) = (И) = 1 Bп + 1 - t),
= (8) = 1Bп+1+*-2и).
О числе классов двойничных форм
865
р
13
37
61
109
157
181
229
п
0
1
2
4
6
7
9
t
1
1
3
3
3
5
5
и
1
2
2
3
4
3
3
A)
1
2
4
6
8
10
12
B)
0
1
1
3
5
5
7
D)
1
3
3
6
9
8
10
E)
0
0
2
3
4
7
9
Третий случай: р = 2Ы + 5.
2t — число классов для определителя — р;
2и — число классов для определителя —Зр.
A) = B) = (б) = G) = A1) = A2) = п,
р
5
29
53
101
149
173
197
269
п
0
1
2
4
6
7
8
11
i
1
3
3
7
7
7
5
11
1
3
5
5
7
9
11
7
A)
0
1
2
4
6
7
8
11
C)
1
3
4
8
10
11
11
17
D)
0
1
3
3
6
8
11
9
E)
0
0
0
2
3
3
3
8
866
О числе классов двойничных форм
Четвертый случай: /? =
2t — число классов для определителя — р:
Ъх — число классов для определителя —Зр.
A) = B) = F) = G) = (И) = A2) = 1 Fга -t- 3 + и);
р
17
41
89
113
137
233
257
п
0
1
3
4
5
9
10
t
2
4
6
4
4
6
8
и
3
3
3
9
9
15
9
A)
1
2
4
6
7
12
12
C)
1
3
6
4
5
8
12
D)
0
0
1
4
5
9
8
E)
0
1
3
2
3
5
8
БОЛЕЕ ПОДРОБНОЕ РАССМОТРЕНИЕ
НЕКОТОРЫХ ВОПРОСОВ,
ОТНОСЯЩИХСЯ К ДЕЛЕНИЮ КРУГА
367
То, что мы изложили в последней части седьмого раздела, на-
начиная с п. 355, представляет собой убедительный пример как боль-
большой плодотворности учения о делении круга, так и замечательной
связи этой дисциплины с различными арифметическими исследова-
исследованиями. Однако, будучи слишком ограничены и объемом работы и
временем, мы смогли там лишь слегка коснуться этого круга во-
вопросов, который вознаграждает наши усилия тем более богатыми ре-
результатами, чем дальше мы в нем продвигаемся. Поэтому мы на-
намерены снова вернуться здесь к некоторым начатым там исследо-
исследованиям и разобрать их более подробно, причем читатель несомненно
не очень удивится, увидев, что решение многих проблем, издавна
рассматривавшихся всеми по-разному, базируется на этом фунда-
фундаменте,
368
Плодотворнейшие возможности открывает исследование, начатое
в п. 356, где мы, после того как совокупность корней уравнения
хп — 1 =0 (за исключением единицы) была разбита на два класса,
показали, как находить сумму корней в каждом из классов, при-
О некоторых вопросах теории деления круга
чем эти суммы оказались равными ^~+ "^У11 и —Т — ~тУп для
случая, когда п имеет вид 4т+ 1, и равными ^+т г —п и
— Y — Т^"—п для слУчая> когда п имеет вид 4т + 3. Однако мы
там не только ограничились случаем, когда п является простым
числом, но, что еще более существенно, оставили также неопре-
неопределенными знаки корней, не подкрепив их определение, лишь крат-
кратко набросанное, строгим доказательством. Поэтому мы прежде все-
всего должны восполнить этот пробел.
369
Итак, пусть теперь п — любое целое положительное число, R —
такой корень уравнения хп—1 = 0, что никакая его степень, бо-
более низкая, чем п-я, не равна единице (ср. п. 359, II), и пусть,
как и в седьмом разделе, через [X] обозначена степень i?A, так что
[0]=1, [1], [2], [3],..., [п—1] представляют все корни уравне-
уравнения хп —1 = 0. Далее, обозначим сумму
[0] + [1] + [4] + [9] + • • • +[(п - IJ] через 2 [»],
и более общо
[0] + [X] + [4Х] + [9Х] + • • • + [X (п— IJ] - через 2 [«*],
так что 31 пробегает квадраты чисел 0,1,2,3,. . . , п—1. Таким об-
образом, очевидно, что так же, как вообще [X] — [jx], если X, [л явля-
являются некоторыми (положительными или отрицательными) целыми
числами, сравнимыми по модулю п, так и 2 [31^1 = 2 t^L если
Х = {л. После этих приготовлений мы имеем следующую задачу.
370
Задача. Определить произведение сумм 2 1ЭД и 2f—ЭД*
Решение. Так как гс2 = 0, (п + 1J = 1, (n + 2J=e4,... (modn),
то легко получается, что
О некоторых вопросах теории деления круга
2 № = [И + [4] + [9] + [16]+ • • • + [п2] =
= [4] + [9] + [16] + [25] +... + Цп + IJ] =
= [9] + [16] + [25] + [36]+ • • • +[(п + 2J] =
или вообще
= [А2] + [(* + IJ] + [(* + 2J] + [(А + 3J]+... +[(П + ft -1)«].
Отсюда
[-#4x2 [Я] =
= [0] + [2ft + 1] + [4ft + 4] + [6ft + 9] + ... + [(л — IJ + 2(n — l)ft].
Поэтому 2 [— И] X 2 [ЭД преобразуются в
[0] + [l] + [4] + [9]+.-.+ [(n-lJ] +
+ [0] + [3] + [8] + [15] + • • • + [n2 — 1] +
+ [0] + [5] + [12] + [21] + • • • + [n2 + In — 3] +
+ [0] + [7] + [16] + [27] + • • • + [n2 + 4n -5] +
+ [6] + [2n — 1]'+ [An]'+ [6ii + 3]'+ •'• • + [3n2 — 6n + 3].
Если сложить отдельные вертикальные ряды, мы получим
и если гс нечетно, то в этом выражении исчезнут все части, кроме
первой, так как будут равны нулю все числители 1 — [2п], 1 — [4п],
1 — [6м],..., и напротив, не равны нулю все знаменатели 1 — [2],
1 —[4], 1 —[6], 1 — [8], ..., 1 — [2п — 2]. Если же п — чету
ное число, то будет равен нулю и один из знаменателей,
именно, 1 — [п], которому соответствует член U- п2 л ~г i > но
сумма частей, из которых этот член получился, будет равна п \-г п2 .
Здесь снова нужно различать два случая. Если п делится на 4,
1 Г1 1
то ^-712 = 0 (mod п), и потому -т- п2 = 1; если же п четно, но не
870 О некоторых вопросах теории деления круга
делится на 4, то -гПг == -к- n(mod ri), и потому обязательно 1-т- п2 ==
= — 1. Из этого, наконец, следует:
1) для нечетного значения п искомое произведение равно п\
2) для значения я, делящегося на 4, оно равно 2п\
3) для четного, но не делящегося на 4 значения п оно равно 0t
371
Стоит потрудиться над тем, чтобы подробнее рассмотреть при-
природу суммы 2№
L Так как вместо квадратов 0, 1, 4, 9, 16, ... можно подстав-
подставлять их наименьшие вычеты по модулю п, то ясно, что если М
пробегает квадратичные вычеты по модулю п среди чисел от 0 до
п — 1, и т обозначает количество корней сравнения х2;=М (mod я),
то 2 ВД = ^т[М]. Как определяется число т, мы показали в пп.
104 и 105.
II. Если п есть (нечетное) простое число, то т == 1 для М = 0,
и т = 2 для каждого другого значения М. Если же п является
степенью нечетного простого числа, например, равно pv, то т = 2
для каждого значения М, не делящегося на р,
372
Если п — (нечетное) простое число, то совокупность вычетов М
состоит из нуля, для которого т= 1, и из (п—1)/2 других чисел,
для которых т = 2. Если [л пробегает эти вычеты (за исключением
вычета 0)г то наш ряд равен 1 + 2^г^. Если, далее, v пробегает все
остальные числа, меньшие чем п, количество которых тоже равно
(п —1)/2 и которые охватывают все квадратичные невычеты по мо-
модулю п, меньшие чем п, то очевидно, что
1 + S^ + 2>*v = 1 + г + г2 + г3 + - - . + г*-* = уЕт^ 0.
Поэтому, если положить сумму нашего ряда, т. е. 1 + ^^j^, рав-
равной А, то 1 + 22^v = — А, и 2г1Х — SrV = А-
О некоторых вопросах теории деления круга 871
Согласно п. 356, мы имеем тем самым А = +У"п или ЧЬУ^—п,
в зависимости от того, га = 1 или =3 (mod 4). Однако знак этим
еще не определяется.
Если в наш ряд, который мы обозначим через II, подставить
вместо г другой подобный же корень уравнения хп — X «г 0, ска-
скажем, г' = гх, то получающийся ряд будет обозначаться через Н\
373
Если п является квадратом или более высокой степенью про-
простого числа, скажем, = рп, то одни из вычетов М будут являться
числами, не делящимися на р, другие будут делиться на р2, но
не будут делиться на более высокую степень числа р, третьи бу-
будут делиться на /?4, но не будут делиться на р6 и т. д., до тех
вычетов, которые делятся на рп~*у но не делятся на р7*—1 или де-
делятся на рп~г, но не делятся на /?те, в зависимости от того, четно к
или нечетно; наконец, имеется еще вычет 0, который является един-
единственным, делящимся на рп (ср. п. 102). Если теперь [л пробегает
квадратичные вычеты числа р} меньшие чем р (за исключением ну-
ля), количество которых равно ^(^—1)» т0 указанные различные
типы вычетов будут представляться следующим образом. Первые,
которые не делятся на /?, будут представляться в виде [х + kp, где
в качестве А нужно брать все целые числа от 0 до pn'r-i — 1, так
что количество всех вычетов такого вида равно у (р—1)ртс~1;для
каждого из них т = 2. Сумма всех членов в II, соответствующих
этим вычетам, равна
Второй класс вычетов представляется в виде [jljd2 + kp3, где в
качестве к нужно брать все целые числа от 0 до рп~3 — 1, так что
количество всех вычетов такого вида равно -k-(j> — 1) рп~3\ для каж-
каждого из них будет т = 2р. Сумма получающихся отсюда членов в
872 О некоторых вопросах теории деления круга
рдде II будет равна
ГР —1
если к > 3. Аналогичным образом третий, четвертый й т. д. клас-
классы представляются соответственно в виде [хр4 + кръ, [хр6 -f кр1, . . .,
где за А нужно брать все целые числа от 0 до (соответственно)
рп~5 — 1, рп~~7 — 1, . . .; для них т — 2р2у т = 2ps, ... . И в ряде
II обращаются в нуль суммы членов, получающихся из третьего,
четвертого и т. д. классов^ если соответственно тс > 5, тс > 7,...
Отсюда для случая, когда тг четно, следует, что в II остаются
только те члены, которые соответствуют вычету 0 и равны 1. Но
для них т = рп/2, так что сумма всех членов в II равна р*/2.
ПРИЛОЖЕНИЯ
ОТ РЕДАКЦИИ
Почти все работы великого математика Гаусса были опубли-
опубликованы им на латинском языке, В настоящем издании впер-
впервые публикуются в русском переводе все работы Гаусса по
теории чисел. Перевод выполнен кандидатом физико-матема-
физико-математических наук В. Б. Демьяновым в основном с прекрасного
немецкого перевода Мазера (Н. Maser; изд. Springer, 1889),
но некоторые места перевода были, кроме того, сверены чле-
членом-корреспондентом АН СССР Б. Н. Делоне с подлинным
латинским текстом. В «Приложениях» даны статья академи-
академика И. М. Виноградова «Карл Фридрих Гаусс» и статья-
комментарий члена-корреспондента АН СССР Б. Н. Делоне
«Работы Гаусса по теории чисел», облегчающая чтение
текста работ Гаусса.
Академик И.М.Виноградов
КАРЛ ФРИДРИХ ГАУСС*
Великому немецкому математику Карлу Фридриху Гауссу при-
принадлежат глубокие и основополагающие исследования почти во всех
основных областях математики: в теории чисел, в геометрии, в тео-
теории вероятностей, в анализе, в алгебре, а также важные исследова-
исследования в астрономии, в геодезии, в механике и в теории магнетизма.
Математический гений Гаусса развивался на исследованиях
по теории целых чисел, завершившихся опубликованием в 1801 г.
его знаменитой книги «Disquisitiones arithmeticae». В дальнейшем
Гаусс возвращался к этим исследованиям и дал в области теории
чисел еще две важные работы.
В «Disquisitiones arithmeticae» Гаусс изложил все существенное,
что было известно в теории чисел до него, но часто исходя из более
общих и более принципиальных соображений. Кроме того, «Dis-
«Disquisitiones arithmeticae» в четвертом, пятом и седьмом своих разделах
заключают три крупнейших открытия самого Гаусса: доказательство
квадратичного закона взаимности, композицию классов и родов
квадратичных форм и теорию деления круга.
Квадратичный закон взаимности является центральной теоремой
теории квадратичных вычетов, доказательство которой долго и
* Речь акад. И. М. Виноградова на торжественном заседании, организован-
организованном Всесоюзным обществом культурной связи с заграницей и Отделением физи^
ко-математических наук АН СССР 23 февраля 1955 г., по случаю столетия со
дня смерти К. Ф. Гаусса.
876 И. М. Виноградов
безуспешно пытались получить крупнейшие математики того времени.
Исследования Гаусса по квадратичному и, позже, по биквадратич-
ному закону взаимности послужили исходным пунктом длинного
ряда работ, приведших в конечном итоге к отысканию общего закона
.взаимности, представляющего собой одну из важных теорем теории
алгебраических чисел.
Исследования Гаусса по композиции классов и родов квадратич-
квадратичных форм явились важным первым этапом в труднейшем вопросе
о построении арифметики полей алгебраических чисел. Исследова-
Исследования Гаусса по целым комплексным числам, опубликованные позже
(в 1832 г.), дали пример поля алгебраических чисел, отличного от
рационального, в котором действуют законы обычной арифметики.
Продолжение обоих этих исследований привело во второй половине
XIX столетия к построению общей теории алгебраических чисел,
которая является в настоящее время одним из основных методов,
теории чисел.
Теория деления круга, занимающая последний, седьмой раздел
«Disquisitiones arithmeticae», содержит подробное рассмотрение дву-
двучленного уравнения хп = 1, в котором, применяя методы теории
чисел, Гаусс сводит решение этого уравнения на цепь уравнений
низших степеней. Это исследование представляет собой частный,
но вполне завершенный случай теории, построенной впоследствии
Галуа, которая является одной из основных теорий алгебры. Теория
деления круга дала замечательный чисто геометрический результат.
К тем правильным многоугольникам, которые умели строить при
помощи циркуля и линейки древние математики, Гаусс прибавил еще
правильный семнадцатиугольник. Более того, он нашел вообще все
те правильные многоугольники, которые можно построить при по-
помощи циркуля и линейки. Теорема о правильном семнадцатиуголь-
нике была опубликована Гауссом без доказательства, когда он был
еще 19-летним студентом, и создала ему первую известность.
В связи с теорией деления круга Гаусс рассмотрел в 1811 г. осо-
особые тригонометрические суммы, называемые теперь суммами Гаусса.
Дальнейшее обобщение этого исследования привело впоследствии
к рассмотрению более общих тригонометрических сумм, которые
являются сейчас одним из самых сильных средств аналитической
Карл Фридрих Гаусс 877
теории чисел и способствовали доказательству важных теорем, ка-
касающихся обыкновенных целых чисел.
О работах Гаусса, не относящихся к области теории чисел, я
скажу уже более кратко. Подобно тому, как это было у Архимеда,
Ньютона, Эйлера и, впоследствии, у Чебышева, большинство из
этих работ было вызвано задачами, которые ставили естествознание
и практическая деятельность. Так, работы по геодезической съемке,
которые были поручены Гауссу, привели его к исследованиям по
внутренней геометрии поверхностей. Они были опубликованы в
1828 г. в знаменитом мемуаре «Disquisitiones generates circa super-
superficies curvas». В этом мемуаре содержится также доказательство важ-
важной теоремы Гаусса о неизменяемости кривизны при изгибании по-
поверхностей. Непосредственным обобщением идеи Гаусса о внутрен-
внутренней геометрии поверхностей явилась впоследствии геометрия Ри-
мана, послужившая в свою очередь основным аппаратом для общей
теории относительности.
Обширные приближенные вычисления, которые приходилось
практически производить лично Гауссу при решении задач, относя-
относящихся к астрономии и к геодезии, привели его к более глубокой
разработке способа наименьших квадратов и к выяснению централь-
центрального значения нормальной кривой распределения в вопросах, свя-
связанных с теорией вероятностей.
Работы Гаусса по теории магнетизма привели его к важным тео-
теоремам теории потенциала.
Размышляя над основными принципиальными вопросами меха-
механики, Гаусс пришел к известному своему принципу наименьшего
действия.
Еще в самый первый период своей научной деятельности, в связи
с необходимостью обнаружить на небе потерянную малую планету
Цереру, Гаусс придумал замечательный метод определения орбиты
по трем наблюдениям. Успех этого метода, давшего возможность
снова найти Цереру, был первым обстоятельством, которое сделало
имя Гаусса всемирно известным.
Сделаю несколько общих замечаний об особенностях стиля твор-
творчества Гаусса. Все общие математические идеи появлялись у Гаусса
в связи с решением совершенно конкретных задач. Но эти задачи
878 И. М. Виноградов
большей частью относились к важным узловым вопросам современной
ему математики. В дальнейшем, в руках его продолжателей, идеи
Гаусса привели к созданию новых областей математики. В частно-
частности, работы Гаусса по теории чисел предопределили развитие теории
чисел более чем на столетие; такую же роль сыграли и работы Гаусса
по внутренней геометрии поверхностей.
После Гаусса осталось обширное рукописное наследие, которое
было опубликовано много позже его смерти. В рукописях Гаусса
математики с изумлением нашли целый ряд теорем, данных без дек
казательства и касающихся самых различных отделов математики:
аналитической теории чисел, теории эллиптических и, в частности,
модулярных функций, неэвклидовой геометрии и т. д. Некоторые
из этих теорем были, задолго до обнародования посмертных рукопи-
рукописей Гаусса, независимо от Гаусса, открыты и опубликованы дру-
другими математиками, а многие не были еще известны и послужили
стимулом для работ последующих ученых.
Русские математики всегда высоко ценили и глубоко изучали
работы Гаусса. Некоторые исследования русских математиков яв-
являлись непосредственным продолжением работ Гаусса, например:
исследования русских математиков о минимумах определенных и не-
неопределенных квадратичных форм, работы по общей теории алге-
алгебраических чисел, а в последнее время — работы по общему закону
взаимности и исследования, переносящие гауссову внутреннюю гео-
геометрию поверхностей на случай не аналитических поверхностей.
Указанная глубокая связь, которая всегда существовала между
немецкими и русскими математиками, должна служить примером
того дружеского сотрудничества, к которому мы стремимся во всех
областях нашей жизни и которое принесет пользу обоим нашим ве-
великим народам.
Б. Н. Делоне
РАБОТЫ ГАУССА ПО ТЕОРИИ ЧИСЕЛ
1. Теория чисел до Гаусса
Важные теоремы о целых числах были доказаны уже в древно-
древности. Так, например, в школе Пифагора (V в. до н. э.) были найдены
в бесконечном числе такие взаимно простые квадраты целых чисел,
сумма которых тоже квадрат х2 + у2 = z2. В «Началах» Эвклида
(III в. до н. э.) мы находим доказательство бесконечности числа про-
простых чисел. В сочинении Диофанта (III в. н. э.) рассмотрены способы
решения различных неопределенных уравнений в рациональных
числах.
Первый, кто в новое время начал глубокие исследования целых
чисел, был Пьер Ферма A601—1665) из Тулузы. Задачи, решенные
Ферма, и особенно теоремы, высказанные им, но доказательства кото-
которых он скрыл по обычаю того времени, произвели большое впечатле-
впечатление на последующих математиков. Ферма имел особую способность
проникать в самые глубокие тайны чисел. Укажем два примера.
В 1651 г. Ферма, в виде вызова всем современным ему математикам,
поставил задачу доказать, что если Д — целое положительное число,
отличное от полного квадрата, то уравнение х2 — Д?/2 = 1 (которое
теперь называется уравнением Пелля) всегда имеет решения в целых
числах х, у (уф 0). Теорема эта в руках Эйлера и Лагранжа, кото-
который первый ее доказал в 1768 г., оказалась ключом ко всему неопре-
неопределенному анализу 2-й степени. Другой пример: на полях своего
экземпляра книги Диофанта Ферма записал утверждение, что, тогда
как сумма двух квадратов целых чисел может быть опять квадратом
целого числа, сумма двух кубов или двух одинаковых высших сте-
Б. Н. Делоне
пеней не может быть такой же степенью целого числа (так называе-
называемая великая теорема Ферма). Теорема эта в общем виде не доказана
и не опровергнута до сих пор, но уже самые попытки ее доказать
привели к созданию глубоких теорий.
Большая часть задач, оставленных Ферма последующим поколе-
поколениям математиков, была решена Эйлером A707—1783) и Лагранжем
A736—1813), которые также поставили и решили многие дальней-
дальнейшие собственные задачи. Эйлер, в частности, построил теорию сте-
степенных вычетов (см. о, них дальше на стр. 897); доказал (в его дока-
доказательстве, правда, есть пробел), что уравнение х3 + у3 = z3 не
имеет решений в целых числах; нашел на числовых примерах (однако
не смог этого доказать), что простые числа р, такие, для которых
заданное целое число а есть «квадратичный вычет» (т. е. те р, для ко-
которых существуют такие квадраты х2, что число а отличается от них
лишь на кратности р), суть те и только те простые числа, которые
содержатся в некоторых определенных арифметических прогрессиях
(так называемый квадратичный закон взаимности в рациональном
поле), а также многое и многое другое. Лагранж глубоким и тонким
методом доказал утверждение Ферма об уравнении Пелля и показал,
что этот метод дает способ для полного решения в целых числах лю-
любого неопределенного уравнения 2-й степени с двумя неизвестными
ах2 + 2Ьху + су2 + %dx + 2еу + / = 0. Кроме того, Лагранж до-
доказал замечательную теорему, верность которой утверждал уже
Ферма, что любое целое положительное число N есть сумма четырех
квадратов целых чисел: N = х2 + у2 + z2 + t2, частный случай
так называемой общей теоремы Варинга, доказанной в общем виде
только в 1909 г. Гильбертом.
Леждндр A752—1833) опубликовал первый большой трактат о
теории чисел, в котором собрал все сделанное до него и добавил много
нового.
Таково было положение теории чисел до Гаусса.
2. «Арифметические исследования» Гаусса
Гаусс A777—1855) с самого раннего возраста обнаруживал не-
необыкновенные способности к математике. Сохранилось предание,
что он, когда ему едва минуло 3 года, присутствовал при расчете
«Арифметические исследования» Гаусса 881
своего отца, бывшего водопроводным мастером, с подсобными рабо-
рабочими и заметил, что расчет сделан неверно, а верно так-то. Расчет
был проверен, и присутствующие с неподдельным удивлением уви-
увидели, что число, указанное трехлетним мальчиком, правильное.
Уже 18 лет Гаусс получил: в математике результаты первостепенной
важности. С 1797 г. Гаусс начал печатать свою знаменитую книгу
«Арифметические исследования» («Disquisitiones arithmeticae»)*. По
тогдашним условиям печатание шло медленно, и в течение этого вре-
времени Гаусс дорабатывал разные части книги, особенно пятый ее
раздел. «Арифметические исследования» вышли в свет в 1801 г.,
когда Гауссу было 24 года. «Арифметические исследования» — пер-
первая книга, в которой теория чисел, или, как говорит Гаусс, высшая
арифметика, излагается как стройная наука, причем во всех вопросах
Гаусс обращает особое внимание на принципиальную сторону дела.
Книга Гаусса оказывала решающее влияние на работы всех матема-
математиков мира по теории чисел в течение целого столетия, а многие
идеи, в ней заложенные, оказали влияние на всю математику в це-
целом. Все результаты работ в теории чисел предыдущих ученых, та-
таких, как Ферма, Эйлер, Лагранж, Лежандр, включены в тот или
иной из семи разделов, на которые разделено это фундаментальное
сочинение, имеющее более 600 страниц, но большей частью эти ре-
результаты изложены, исходя из более общих, глубоких и объединяю-
объединяющих принципов. Кроме того, книга содержит в четвертом, пятом и
седьмом разделах три совершенно различных первоклассных и
фундаментальных для теории чисел и алгебры новых открытия са-
самого Гаусса: 1) доказательство закона взаимности, 2) теорию компо-
композиции квадратичных форм и теорию их родов и 3) теорию деления
круга. Два других крупнейших открытия Гаусса в теории чисел:
4) гауссовы суммы и 5) арифметика целых комплексных чисел, были
сделаны уже позже, после выхода в свет «Арифметических исследо-
исследований», и опубликованы соответственно в 1811 и в 1828—1832 гг.
Относительно общего стиля «Арифметических исследований»
Гаусса надо сказать следующее. Гаусс был несравненным вычисли-
* С. F. G auss. Werke, Bd. I; см. также: С. F. G auss. Untersuchungen
uber hohere Arithmetik. Deutsch. hrsg. von H. Maser, 1889.
882 Б. Н. Делоне
тел ем и, подобно тому, как это делали многие другие выдающиеся
арифметики, обычно получал свои новые результаты, исходя из об-
обширных численных вычислений, которые позволяли ему подмечать
новые, глубоко скрытые арифметические истины, доказательства
которых он получал затем нередко лишь в результате упорной,
продолжительной, иногда многолетней работы. Книга Гаусса про-
проникнута стремлением решить каждый вопрос так, чтобы получить
удобнейший вычислительный алгоритм. Многие места книги пояс-
поясняются численными примерами и небольшими численными таблич-
табличками, которые делают непосредственно ясным то, о чем идет речь и,
так сказать, вводят в самую практику рассматриваемых арифмети-
арифметических вопросов.
Когда углубляешься в изучение книги Гаусса, то прямо недоу-
недоумеваешь, как мог двадцатилетний молодой человек создать такой
грандиозный комплекс сложнейших и глубочайших методов и тео-
теорем, так хорошо слаженный и построенный и, кроме того, содержа-
содержащий, как было указано выше, три первоклассных открытия, каждое
из которых уже одно обессмертило бы имя любого математика. Не-
Несомненно, что умственный подвиг молодого Гаусса, приведший к
написанию «Арифметических исследований», имеет мало себе равных
в мировой науке.
Попробуем теперь по порядку рассмотреть открытия Гаусса в*
теории чисел и выяснить то значение, которое каждое из них имело*
для дальнейшего развития математики. Но прежде, чем это делать,,
нам придется довольно много сказать о теории чисел вообще и о тео-
теории алгебраических чисел в частности.
3. О теэрии чисел вообще
и о современных нам ее методах
Обыкновенные целые числа...,— 3, —2, —1, 0, 1, 2, 3,... являются
основой всей математики. В отношении сложения они образуют
весьма простую совокупность (бесконечную циклическую абелеву
группу), а именно: ...,— 1—1, —1, 0, 1, 1+1, 1+1+1, ..., единствен-
единственным исходным кирпичом которой является число 1. В отношении
же к умножению тот же ряд целых чисел имеет уже вовсе не простую
О теории чисел и ее современных методах 883
структуру. А именно тех простейших кирпичей, из которых строятся
умножением все целые числа, бесконечно много — это простые чис-
числа, 2, 3, 5, 7,11, 13,17, 19, 23, 29, 31, 37,... Натуральные числа, боль-
большие 1, получаются из них умножением так: 2, 3, 2-2, 5,2-3, 7,2-2-2,
3-3, 2-5, 11,2-2-3, 13, 2-7, 3-5, 2-2-2-2,17, ... Для того же, чтобы
умножением получить все целые рациональные числа, надо еще
привлечь обе единицы; 1 и — 1 и число 0.
Уже даже самый простой вопрос, как идут в ряду натуральных
чисел 1,2,3,4,5,6,... простые числа, до настоящего времени представ-
представляет непреодолимые трудности. Со времен Эвклида доказано, что их
бесконечно много. Но только Чебышеву в 1849 г. удалось показать,
что число ttGV) простых чисел, меньших данного предела N, при-
приблизительно равно ^-г-, а затем Адамару и Валле-Пуссену — что
ln/V
отношение k(N): —— стремится к пределу 1. Лишь совсем недавно,
в 1937 г., И. М. Виноградову в знаменитой работе удалось доказать,
что любое достаточно большое натуральное число N есть сумма четы-
четырех простых чисел. Но, например, до сих пор не удается выяснить,
встречаются ли сколь угодно далеко так называемые «близнецы»,
т. е. простые числа, отличающиеся друг от друга на число 2, как пара
101 и 103 или пара 8004119 и 8004121.
Вся трудность теории чисел состоит в том, что свойства целых
чисел относительно умножения (мультипликативные свойства) с их
свойствами относительно сложения (с их аддитивными свойствами)
связаны очень сложно.
Перейдем теперь к рассмотрению современных нам методов тео-
теории чисел.
На современном нам этапе теории чисел для решения вопросов
теории обыкновенных целых рациональных чисел используются»
кроме элементарного, в основном четыре метода:
1) теория алгебраических чисел (и других алгебр);
2) теория алгебраических функций;
3) аналитическая теория чисел;
4) геометрия чисел.
Отметим тех главнейших математиков, кроме Гаусса, которые
до настоящего времени создавали эти методы.
884 Б. Н. Делоне
К использованию метода алгебраических чисел относятся ра-
работы Валлиса об уравнении Пелля, работы Лагранжа о неопреде-
неопределенных уравнениях 2-й степени, доказательство Эйлера теоремы
Ферма для кубов, работы Эйзенштейна и Куммера о законе взаим-
взаимности, работы Дирихле о теории единиц, работы Куммера об идеаль-
идеальных числах, работы Дедекинда, Золотарева, Кронекера по теории
простых делителей, работы Гильберта, Такаги, Артина, Хассе по
теории поля классов, работы Фробениуса и Чеботарева, обобщаю-
обобщающие теорему Дирихле о прогрессии, работы Шафаревича об общем
законе взаимности и работы Тэта о группах когомологий.
К обобщению этого метода на теорию квадратичных форм с мно-
многими переменными относятся работы Венкова, Хассе, Хекке, Зи-
геля, Витта, Эйхлера.
Основные сводки по этому методу принадлежат Гильберту A896) —
по общей теории алгебраических чисел, Хассе A924) — по спе-
специальному вопросу теории алгебраических чисел, теории поля клас-
классов, и Эйхлеру A952) — по применению алгебр к арифметике ква-
квадратичных форм со многими переменными.
Использование теории алгебраических функций, родственной
теории алгебраических чисел, но имеющей свои специфические ме-
методы, начал Пуанкаре, затем в этом направлении работали Морделл,
А. Вейль, Хассе и др.
Аналитическая теория чисел ведет свое начало от Эйлера. Ди-
Дирихле и Чебышев продолжали развитие этих идей в вещественной
области. Новую струю влил Риман, который вышел в комплексную
плоскость и начал использовать аналитичность функции и аналити-
аналитическое продолжение. Методы аналитической теории чисел употреб-
употребляли в теории алгебраических чисел Дирихле, Дедекинд, Кроне-
кер, Фробениус, Чеботарев, Хекке, Зигель, Хейльбронн и др. Важ-
Важный прием для аддитивных задач придумал Вороной. Блестящее раз-
развитие та же идея, хотя, по-видимому, и независимо от Вороного,
получила в работах Рамануджана и Харди и Литтльвуда.
Важной главой аналитической теории чисел является оценка
тригонометрических сумм, первый далеко идущий результат в кото-
которой был получен в 1914 г. Г. Вейлем. Наиболее глубокие новые идеи
в этой области были развиты Виноградовым, который, между
О теории алгебраических чисел 885
прочим, получил оценки тригонометрических сумм по простым
числам.
Основателями геометрии чисел были Минковский, Вороной и
Клейн. Ее методами работали у нас автор этих строк и Венков, а
также их используют многие современные математики.
Работы Гаусса по теории чисел дают первые образчики почти во
всех этих направлениях, но наибольшее значение они имеют для
развития метода алгебраических чисел и метода тригонометрических
сумм.
4. О теории алгебраических чисел
1. Основные понятия. Уже самые первые крупные арифметики,
которые пытались решать более глубокие вопросы теории целых
чисел, начали убеждаться в том, что часто для их решения надо так
или иначе привлекать некоторые вспомогательные, так называемые
алгебраические, иррациональности, т.е. корни некоторых уравнений
с рациональными коэффициентами. Этот метод играл роль уже в ра-
работах Валлиса A616—1703) об уравнении Пелля, в работах Лагран-
жа о неопределенных уравнениях 2-й степени, в которых j/A раз-
разлагался в непрерывную дробь. В доказательстве невозможности урав-
уравнения х3 + у3 + 23 — 0 в целых числах х, у, z Эйлер привлекает
иррациональность \ — 3 и т. д.
Что же такое поле алгебраических чисел данной степени? Рас-
Рассмотрим какое-нибудь алгебраическое уравнение п-и степени с ра-
рациональными коэффициентами ах, я,,..., ап:
х™ + a^-i + а2хп~ 2+ . . . + ап^х + ап - 0, A)
неприводимое в поле рациональных чисел, т. о. такое, что его левая
часть не раскладывается на два множителя низших степеней опять
с рациональными коэффициентами, и пусть а — один из его действи-
действительных или комплексных корней. В таком случае число а назы-
называется алгебраическим числом п-й степени. Совокупность К всех
тех чисел, которые получаются из числа а, если соединять его само
с собой любым конечным числом действий сложения, вычитания,
умножения и деления, называется полем алгебраических чисел п-я
степени, являющимся расширением рационального поля присоеди-
Б. Н. Делоне
нением к нему числа а. Можно показать, что присоединение к полю
рациональных чисел нескольких алгебраических иррациональностей
равносильно присоединению одной такой иррациональности высшей
степени.
Легко далее показать, что в силу тождества ап + а^—1 + • • • +
-f ап = О всякое число со поля К, являющегося результатом при-
присоединения числа а, можно привести к виду со = и^71 + и2(хп~2 +
+ ---+ип, где ии и2, . . ., ип — рациональные числа, и обратно. Ес-
Если aW, a<2>, . . ., a<n) все корни уравнения A), то числа:
cod) = щФ^-1 + щф)п~^-\ Нп,
1 + и2аB)"-2 -\ [-ип,
которые называются сопряженными между собой, суть все корни
некоторого уравнения
ж" + M"-i + ^п~2 + Ь бп-1^ + Ьп = 0, B)
также с рациональными коэффициентами Ьъ Ь2,. . ., ЬП} но которое
может уже быть и приводимым (степенью неприводимого).
Нетрудно показать, что все те числа поля i?, для которых в
уравнении B) blf b2}. . ., bn — целые рациональные, называемые це-
целыми алгебраическими, образуют в поле К так называемое коль-
кольцо, т. е. такую подсовокупность О чисел поля К, что сумма, раз-
разность и произведение ее чисел суть опять ее же числа. Наконец,
можно показать, что в этом кольце О всех целых чисел поля К
можно выбрать систему п таких его чисел соь со2,. . ., соп — базис
кольца О всех целых чисел поля К,— что любое целое число со
поля К имеет вид
СО = С1(О1 + С2СО2 -| 1- СПСОП,
где си с2,. . ., сп — целые рациональные, и обратно.
Арифметика кольца О всех целых чисел того или иного поля
К алгебраических чисел и играет часто роль при решении разных
вопросов теории целых рациональных чисел.
Все, что сейчас сказано, можно изложить и иначе — геометри-
геометрически .
О теории алгебраических чисел
887
2. Геометрическое изложение. Начнем с обыкновенных целых
рациональных чисел. Возьмем координатную ось и будем называть
суммой, разностью и произведением двух точек этой оси точку, коор-
координата которой есть сумма, разность или произведение координат
этих точек. В таком случае легко видеть, что ряд целых рациональ-
рациональных точек ..., —2, —1, 0, 1, 2, ... представляет собой дискретную,
-3
-1
г з
•—4 H
1
4, t
1
1
1
у 1 1
> —(
• ,
1 0
I
—
неу плотня ему ю совокупность точек оси — такую, что такие сумма,
разность и произведение ее точек суть ее же точки, и наоборот, если
«совокупность точек оси обладает этими свойствами (и отличается от
одной точки 0), то она есть ряд целых рациональных точек. Неуплот-
няемость совокупности здесь понимается в том смысле, что нельзя
к ней прибавить дальнейших точек так, чтобы старые ее точки вместе
с этими новыми опять давали совокупность, удовлетворяющую всем
другим потребованным условиям.
Такая совокупность называется неуплотняемым дискретным коль-
кольцом точек (по отношению к введенным покоординатным сложению,
вычитанию и умножению).
То же самое можно делать на плоскости, если на ней зафиксиро-
зафиксирован некоторый заданный координатный репер Е = Оехе2 и введено
покоординатное по отношению к нему сложение, вычитание и умно-
умножение точек, так что если, например, заданы точки C, 11) и E, —7),
то их сумма есть точка (8,4), а произведение — точка A5, —77).
На плоскости имеется одно очевидное, тривиальное дискретное,
неуплотняемое кольцо — это решетка всех точек с целыми рацио-
рациональными координатами. Действительно, покоординатные сумма,
Б. Н. Делоне
разность и произведение точек этой решетки есть, очевидно, опять
точка с целыми рациональными координатами; эта совокупность
дискретна и, как нетрудно показать, неуплотняема. Но на плоско-
плоскости, кроме этого (единственного) приводимого дискретного неуплот-
няемого кольца, есть еще сколь угодно много других различных ко-
колец, которые все уже неприводимы, т. е. не имеют точек на осях коор-
координат, кроме начала.
Л=3
Как можно показать, каждое из них может быть построено так:
надо взять любое положительное целое рациональное число А, не
делящееся на квадрат, и рассмотреть репер Е, построенный на век-
векторах A, 1) и (}/Д, — |/Д)> и решетку точек, на нем построенную
(т. е. с целыми рациональными относительно него координатами).
Если A^l (mod 4), то сама эта решетка, представляющая собой
решетку прямоугольников, а если A=l (mod 4), то та, которая полу-
получается из нее, если добавить по точке в центрах всех ее прямоуголь-
прямоугольников, будет двумерным неприводимым дискретным неуплотняемым
кольцом и никаких других таких колец нет.
Можно показать, что каждое из этих колец представляет собой
не что иное, как совокупность всех целых чисел некоторого веще-
вещественного квадратичного поля алгебраических чисел, если каждому
О теории алгебраических чисел
числу этого поля сопоставлять точку плоскости, координаты которой
суть это число и ему сопряженное, и обратно. Квадрат d площади
основного параллелограмма (заштрихованного) такой решетки ра-
равен в первом случае 4Д, а во втором Д. Он называется дискриминан-
дискриминантом соответственного квадратичного поля. Итак, дискриминанты
вещественных квадратичных полей суть числа 4-2, 4-3, 5, 4*6, 4-7,
4-10, 4-11, 13, 4-14, 4-15, 17, 4-19, 21, 4-22, 4-23, 4-26, 29, 4-30,...,
причем со всяким таким дискриминантом имеется только одно квад-
квадратичное поле.
Аналогичное имеет место для ?г-мерного вещественного или ком-
комплексного пространства, где всякое гс-мерное неприводимое (т. е.
не имеющее точек, отличных от точки 0, хоть одна из координат ко-
которых равна нулю) не^нлотняемое кольцо О по отношению к по-
покоординатным сложению, вычитанию и умножению есть ^мерная
решетка точек, координатами которых являются целые числа неко-
некоторого поля алгебраических чисел п-й степени и им сопряженные,
и обратно. Таких колец О бесконечно много, и дискриминанты (квад-
(квадраты гс-мерных объемов основных параллелепипедов) их суть неубы-
неубывающие целые числа, причем число различных колец О с одним и
тем же дискриминантом конечно (теорема Эрмита).
890 Б. Н. Делоне
Рассмотрим теперь арифметику такого кольца О. В отношении
сложения и вычитания такое кольцо построено совсем просто —
всякая его точка со = с1со1 + с2со2 + • • • + сп^п, где соь со2, . . ., соп
#уть концы векторов его основного репера Е, а сь с2,. . ., сп —
целые рациональные числа. Что же касается умножения, то при
п > 1 уже вопрос о единицах кольца, т. е. о таких его точках е,
от умножения на каждую из которых кольцо О переходит само в
себя, не так прост. При п=1 единицы кольца две: +1 и —1.
При п > 1 оказывается единиц, кроме как для квадратичных мни-
мнимых полей, бесконечно много, но все они суть произведения степе-
степеней конечного числа так называемых основных единиц. Теорема эта
была впервые доказана для действительных квадратичных полей
Лагранжем в 1768 г., а в общем случае Дирихле в 1846 г., при-
причем в свое время это исследование Дирихле считалось одним из
самых трудных в теории чисел.
Далее, в О можно выделить так называемые простые точки,
т. е. такие точки, которые уже нельзя представить в виде произведе-
произведения нескольких точек О, отличных от единиц.
Примеры показывают, что уже при п = 2 существуют кольца
О, в которых любая точка однозначно разлагается на простые точ-
точки (если не учитывать множителей единиц), и существуют другие
кольца О, в которых это разложение, вообще говоря, неоднознач-
неоднозначно. В таких «плохих» кольцах арифметика несовершенна, и они
поэтому непосредственно не могут быть успешно использованы.
Возможно, что уже и Гаусс знал об этом обстоятельстве. Но не
видно было, как от него избавиться, пока Куммер A810—1893) в
1844 г. для частных случаев полей, зависящих от корней уравне-
уравнений деления круга xv~1Jr xv~2 + • • • + ж + 1 = 0, где р — простое
число, не показал, что такое кольцо О можно дополнить некото-
некоторыми так называемыми идеальными элементами так, чтобы в до-
дополненном кольце О* (которое само уже не является кольцом, но
является мультипликативной системой, т. е. такой, что произведе-
произведение любых двух ее элементов есть ее же элемент) разложение бы-
было уже однозначно. Позже, в начале 70-х годов, одновременно и
независимо друг от друга, разными способами показали то же са-
самое для общего поля алгебраических чисел Дедекинд A831—1916)
О теории алгебраических чисел 891
ж Золотарев A847—1878). Еще один способ изложить этот вопрос
нашел позже Кронекер A823—1891). Наконец, в 1896 г. Клейн
A849—1925) для частного случая квадратичных полей нашел очень
наглядный новый подход, который был впоследствии обобщен на
любое поле алгебраических чисел.
3. Теория идеалов Дедекинда. Изложим сначала теорию идеалов
Дедекинда. Пусть Lx и L2 — две п-мерные подрешетки решетки О\
нетрудно доказать, что если составить все попарные произведения
•их точек и затем рассмотреть все суммы и разности полученных
произведений, то получится опять некоторая подрешетка L3 решет-
решетки 0. Решетка L3 называется произведением ЬХЬ2 решеток Lx и L2.
Если 3 такая тг-мерная подрешетка решетки 0, что 03 = 3> то 3
называется идеалом в 0. Очевидно, что если v — точка из 0, от-
отличная от нуля (т. е. от начала), то решетка 3 — VO> есть идеал
в 0, так как 0-v0=v0, ибо 00 = 0 ввиду того, что в 0 есть
точка 1 = A,1, . . ., 1) и уже 10 = 0. Такой идеал v0 называется
главным идеалом, соответствующим точке v. Дедекинд показал,
что если в 0 нет никаких идеалов, отличных от главных, то лю-
любая точка из 0 однозначно, с точностью до множителей единиц,
разлагается в произведение простых его точек, т. е. уже в самом
кольце 0 арифметика совершенна. Если же в 0 есть идеалы 3, °т~
личные от главных, что, как это показывают примеры, бывает
очень часто (даже, по-видимому, большей частью, например, для
мнимых квадратичных полей всегда, кроме как для конечного чис-
числа таких полей), то разложение точек 0 в произведение простых
точек 0 уже неоднозначно. Если, однако, вместо точек 0 рассмот-
рассмотреть идеалы в 0, то оказывается, что среди них имеются простые
идеалы, т. е. такие, которые нельзя представить в виде произведе-
произведения других идеалов, отличных от так называемого единичного иде-
идеала 0@, очевидно, тоже идеал в 0), и можно доказать основную
теорему, что любой идеал в 0 однозначно разлагается в произве-
произведение таких простых идеалов, отличных от единичного идеала 0.
Два идеала Si и $2 в 0 называются эквивалентными, или по-
подобными, если существует такая точка X в пространстве i?n, в ко-
котором лежит 0, от умножения на которую один из идеалов пере-
переходит в другой, другими словами, если эти идеалы 3i и 32 полу-
892 Б. Н. Делоне
чаются друг из друга «растяжениями» по осям координат. Совокуп-
Совокупность идеалов 0, подобных друг другу, образует класс идеалов в
0. Все главные идеалы, очевидно, подобны идеалу 0 — это
главный класс. Можно показать, что число h классов идеалов в 0
конечно.
4. Теория побочных решеток Клейна. Перейдем теперь к тому
Дальнейшему развитию теории Дедекинда, которое предложил Клейн„
Оказывается, что если взять по представителю 82, Зз> • * •, Sh в
каждом из неглавных классов идеалов, то можно их помножить
на такие точки Х2, Х3,. . . , Хп из /?п, что полученные так называ-
называемые побочные решетки 0', О",. . ., O(^i~1) вместе с «главной» ре-
решеткой 0 образуют нормальную фигуру (Normalfigur) 0*, кото-
которая уже не есть решетка и обладает следующими свойствами:
1) объемы (вообще говоря, комплексные) основных параллелепипедов
всех решеток, 0, 0', 0", . ¦ ., О^1~1) одинаковы; 2) любые две из h
решеток 0, 0', 0",. . ., O^h~1) не имеют общих точек, кроме точки
О, общей им всем; 3) произведение любых двух точек нормальной
фигуры 0* есть опять точка этой нормальной фигуры (но сумма
двух точек нормальной фигуры, вообще говоря, уже не есть точ-
точка нормальной фигуры); 4) произведение любых двух решеток
Q(i)@{k) есть Опять одна из этих решеток О{1\ причем таким умно-
умножением решетки О, . .O{h~1) образуют абелеву группу, единицей
которой является О\ 5) единицы 8 главной решетки О суть одно-
одновременно единицы и каждой из побочных решеток в отдельности и,
следовательно, и всей нормальной фигуры 0* в целом, причем ни-
никаких других единиц нормальная фигура не имеет; 6) всякая точ-
точка нормальной фигуры 0*, с точностью до множителей единил,,
однозначно разлагается в произведение простых точек этой нор-
нормальной фигуры.
Связь между теорией идеалов Дедекинда и теорией нормальной
фигуры 0* Клейна та, что если \ — какая-либо точка нормальной
фигуры (отличная от нуля) и 0^ — решетка, «обратная» той ре-
решетке О{1\ в которой эта точка \ лежит, т. е. такая, что 0(Л>0(О =О7
то /0W = 3 есть идеал Дедекинда, лежащий в 0, соответствующий
этой точке \ нормальной фигуры 0*, и обратно. Умножению точек О~
отвечает умножение соответствующих им идеалов, и обратно
О теории алгебраических чисел 893
5. Причины успеха применения алгебраических чисел в теории
обыкновенных целых чисел. Поставим себе вопрос: на каких обсто-
обстоятельствах основан успех применения алгебраических чисел при
решении вопросов об обыкновенных целых числах? Таковых об-
обстоятельств три.
Во-первых, переход в подходящее поле алгебраических чисел
часто дает «линеаризацию» задачи. Вместо рассмотрения нелиней-
нелинейного выражения, составленного из обыкновенных целых чисел, рас-
рассматриваются его линейные, но иррациональные, алгебраические
множители. Пример: уравнение Пелля х2 ¦—Д?/2 = 1 заменяется
таким образом (х — V&у) (х + У~&у) = 1, и далее все сводится к
рассмотрению линейных выражений х—)/Д?/ и х-{-|/Дг/.
Во-вторых, при таком рассмотрении задачи происходит так на-
называемое «распроектирование» задачи, т. е. задачу (которая при
непосредственном к ней подходе является, скажем, одномерной)
рассматривают в пространстве высшего измерения, где она распу-
распутывается. Возьмем тот же пример уравнения Пелля. При переходе к
квадратичному полю мы получаем на плоскости решетку точек, со-
соответствующих целым числам этого поля, и вопрос решения урав-
уравнения х2 — Дг/2 = 1 сводится к разысканию тех точек в этой ре-
решетки, которые лежат на гиперболе ?т] = 1. Отсюда весьма неслож-
несложно получается знаменитый результат Лагранжа об уравнении
Пелля.
В-третьих, заметим следующее. В любом кольце О всегда есть
точка 1 = A,1,. .., 1), а следовательно, и точки 1 + 1 = 2 = B,2,..., 2),
14-1+1 = 3 = C,3, . . ., 3) и т. д., так называемые натуральные
точки кольца О. Всякая точка О* есть делитель некоторой нату-
натуральной точки О (и всех ее кратных, конечно). Всякая простая точка О*
есть, оказывается, делитель некоторой натуральной точки р в О,
где/?—натуральное простое число, причем такая точкар разлагает-
разлагается не больше, чем на п (если п—степень поля) простых множителей О*.
Поэтому для того, чтобы обозреть все простые точки О*, достаточ-
достаточно знать, как разлагается каждое натуральное простое число
2, 3, 5, 7, 11, 13, 17, ... в произведение простых точек E*.
Мы будем в этом случае говорить, что мы знаем, как опира-
опирается арифметика того поля алгебраических чисел, кольцом всех
894
Б. Н. Делоне
целых чисел которого является 6?, на арифметику поля рацио-
рациональных чисел. При применении некоторого поля алгебраических чисел
к решению какой-нибудь задачи об обыкновенных целых числах:
обычно очень важно бывает знать закон этого опирания,
Важным обстоятельством является то, что для многих полей
алгебраических чисел удается найти закон этого опирания и что
во всех случаях, когда он найден, он весьма простой, конечный;
вся же трансцендентная трудность, связанная с простыми точками
О*, остается в трансцендентной трудности вопросов распределения
обыкновенных натуральных простых чисел р в ряду всех натураль-
натуральных чисел.
Например, в квадратичном поле, задаваемом иррациональностью
|/Д, где Д—некоторое положительное целое рациональное число
^=l(mod4), не делящееся на квадрат, натуральное простое число
р есть произведение двух простых точек 6?*, если оно находит-
находится в таких-то прогрессиях по модулю Д, и оно есть само про-
простая тока 6?*, если оно находится в других прогрессиях по
модулю Д.
Разделы I-III «Арифметических исследований» Гаусса 895
В поле деления круга на п равных частей, где гс простое, т. е. в
поле, зависящем от корня неприводимого уравнения хп~г
+ 1 = 0, простое натуральное число ^разлагается на простые
делители так или иначе в зависимости от того, в какой прогрессии
по модулю п лежит число р, и т. д.
Мы описали в самых общих чертах и с современной нам точки
зрения основные обстоятельства, связанные с теорией алгебраиче-
алгебраических чисел. Во время Гаусса все это совершенно не было еще изве-
известно, и делом Гаусса в теории чисел, в большой его части, было как
раз глубоко и последовательно проникать во все эти обстоятельства,
исследуя частные, но уже совсем не тривиальные относящиеся сюда
вопросы, в основном связанные с теорией квадратичных полей, ко-
которые дали важные исходные факты для всех дальнейших исследо-
исследований в этой области.
Гаусс сам, несомненно, еще не видел всей грандиозной развер-
развернутой сейчас картины, но, очевидно, уже предугадывал многие важ-
важные ее стороны.
После этого отступления мы можем перейти к подробному после-
последовательному рассмотрению содержания различных разделов «Ариф-
«Арифметических исследований» Гаусса.
5. Первый, второй и третий разделы
«Арифметических исследований» Гаусса
«Арифметические исследования» разделены на 7 разделов (глав),
поделенных на мелкие пункты (параграфы), имеющие сквозную ну-
нумерацию. Эти пункты мы будем обозначать буквой «п». Всего в «Ариф-
«Арифметических исследованиях» 366 пунктов.
Первые три раздела «Арифметических исследований», озаглавлен-
озаглавленные: 1) «О сравнимости чисел вообще», 2) «О сравнениях первой сте-
степени», 3) «О степенных вычетах», представляют собой как бы введе-
введение в книгу и не содержат новых открытий, но изложение в них
ведется так, что все, до того известное, относящееся к рассматривае-
рассматриваемым в них вопросам, приводится в порядок, если нужно, снаб-
снабжается недостающими доказательствами и т. д.
896 Б. Н. Делоне
Уже в первых строках первого раздела «Арифметических иссле-
исследований» Гаусс вводит новое важное понятие сравнения, которое,
по существу, употреблялось, конечно, и до Гаусса, но не было еще
никем сформулировано. Это понятие и всем известный удобный зна-
значок для него: а = b (mod m), обозначающий, что числа а и Ъ дают оди-
одинаковые остатки при делении на модуль т, вошли с тех пор в тео-
теории чисел во всеобщее употребление, так как подчеркивают далеко
идущую аналогию между сравнениями и уравнениями.
С более современной точки зрения можно сказать, что введением
понятия сравнения положено начало рассмотрению алгебры над ко-
конечным полем.
Во втором разделе в п. 16 доказывается однозначность разложе-
разложения натурального числа на простые множители. По этому поводу
Гаусс говорит: «То, что каждое составное число может быть разло-
разложено на простые сомножители, известно из основ; однако то, что
этого нельзя сделать несколькими различными способами, совер-
совершенно необоснованно по большей части предполагается само собой
разумеющимся», хотя надо сказать, что эта однозначность уже до-
доказана у Эвклида.
Далее рассматривается решение сравнения 1-й степени
ах + t = 0 (mod р)
и системы таких сравнений.
В п. 42 этого раздела несколько неожиданно вставлено доказа-
доказательство известной и по настоящее время так часто используемой
леммы Гаусса. Если многочлен с целыми рациональными коэффи-
коэффициентами и старшим коэффициентом 1 разлагается в произведение
многочленов со старшими коэффициентами, равными 1, и рацио-
рациональными остальными коэффициентами, то эти коэффициенты тоже
целые.
В третьем разделе о степенных вычетах Гаусс, естественно, пе-
переходя от сравнений 1-й степени к сравнениям высших степеней,
исследует сначала степенные вычеты, т. е. остатки, которые дают
степени разных чисел при делении их на данный модуль. Особенно
важен случай простого модуля р. Для каждого числа а, не деля-
делящегося на р, существует наинизшая степень ad, дающая остаток 1.
Разделы I-III «Арифметических исследований» Гаусса 897
Число d — всегда делитель числа р — 1 и называется показателем,
«к которому принадлежит» число а по модулю р.
В пп. 52—57 Гаусс дает способ определить число ф (d) не сравни-
сравнимых по модулю р чисел, принадлежащих к данному делителю d
числа р — 1. А именно он показывает, что ф (d) ^Сф(й), где ер —
число натуральных чисел, меньших d и взаимно простых с d. Но если
d, d', d",...— все различные делители р — 1, то
известно, что
откуда следует, что ф (d) = ф (d), ф (df) = ф {d') и т. д. и, в частности,
что ф (р — 1) = ф (р — l)=hO.
Таким образом, оказывается доказанным существование перво-
первообразных корней g простого числа р, т. е. существование таких чи-
чисел g, которые принадлежат к показателю р — 1 по модулю р. Это
доказательство Гаусса является одним из самых блестящих арифме-
арифметических рассуждений. Существованием первообразного корня g
по простому модулю р постоянно пользовался Эйлер, однако, по-ви-
по-видимому, он лишь ошибочно считал, что дал доказательство этого
существования. Степени 1, g, g2,...,gp~2 имеют то свойство, что любое
число, не делящееся на р, сравнимо с одной и только одной из этих
степеней по модулю р.
В 1918 г. И. М. Виноградов показал, что всегда существует пер-
первообразный корень простого числа р, меньший, чем 22 Ур lnp, где
к — число различных простых делителей р — 1.
6. Четвертый раздел «Арифметических исследований».
Первое доказательство закона взаимности
Четвертый раздел «Арифметических исследований» озаглавлен
«О сравнениях второй степени». Он содержит знаменитое первое до-
доказательство предложения, называемого в настоящее время квадра-
квадратичным законом взаимности над полем рациональных чисел. Закон
этот эмпирически, или, как говорил Гаусс, «индуктивно», впервые
был найден Эйлером (см. его статью 1744—1746 гг. «Theoremata
898 Б. Н. Делоне
circa divisores numerorum in hoc forma pa2 + qb2 contentorum». В фор-
форме, почти в точности совпадающей с той, которую придает этой тео-
теореме Гаусс, теорема эта была сформулирована Эйлером позже, в
1772 г. (опубликована в «Opuscula Analytical в 1783 г.). Лежандр в
«Histoir ede V Academie Royale des Sciences, Annee 1785» (опублико-
(опубликовано в 1788 г., стр. 465), очевидно, не зная об этих работах Эйлера,
снова нашел эту теорему. Однако доказательство этой теоремы не
поддавалось всем усилиям Эйлера и Лежандра. Лежандр сам счи-
считал, что он ее доказал, но, как справедливо указывает Гаусс, «до-
«доказательство» Лежандра содержит предположение о существовании
некоторых простых чисел, удовлетворяющих некоторым условиям,
доказательства которого Лежандру дать не удалось.
В начале четвертого раздела Гаусс рассматривает вопрос о тех
числах а, которые суть так называемые квадратичные вычеты по
заданному модулю т, т. е. о тех числах а, для которых сравнение
х2=а (mod m) имеет решение. Этот вопрос легко сводится к рассмот-
рассмотрению такого же вопроса для того случая, когда модуль — простое
число р, и затем легко решается. В п. 107 раздела 4 Гаусс говорит:
«Однако обратная задача: если задано некоторое число, найти все
те числа (модули — Б. Д.), по которым оно является (квадратич-
(квадратичным — Б. Д.) вычетом или невычетом — значительно сложнее».
Эту задачу в силу выше сказанного также достаточно решить для про-
простых модулей р. Уже Эйлер решил вопрос для а = — 1 и 3, а Ла-
гранж — для а = 2, 5 и 7. Знаменитая теорема Эйлера о том, что
число — 1 есть квадратичный вычет простых чисел р вида 4гс + 1
и невычет простых чисел р вида 4гс + 3, была той теоремой, попытка
доказательства которой, как об этом свидетельствует сам Гаусс,
безвозвратно увлекла его на путь занятия высшей арифметикой.
Гаусс решает вопрос о том, для каких модулей данное число а есть
квадратичный вычет, сначала для чисел а — — 1,+2,+3,+5,+7,
а затем переходит к доказательству теоремы (закона взаимности),
которая решает этот же вопрос для любого числа а, причем опять
достаточно рассмотреть случай, когда заданное число а простое.
Гаусс выражает эту теорему так:
«Если р — простое число вида 4гс + 1> то + р, а если р — про-
простое число вида 4гс + 3, то — р будет (квадратичным — Б. Д.) вы-
Разделы I-III «Арифметических исследований» Гаусса 899
четом или невычетом каждого простого числа, которое, взятое поло-
положительным, является вычетом или невычетом числа ръ.
Гаусс делает вслед за этим следующее замечание: «Так как почти
все, что можно высказать о квадратичных вычетах, основывается на
этой теореме, то название «фундаментальная теорема», которое
мы в дальнейшем будем употреблять, не будет для нее неподхо-
неподходящим».
Доказательство Гаусса основано на полной индукции. Кроне-
кер справедливо называет это доказательство пробой сил Гауссова
гения. Наибольшую трудность представил для Гаусса тот пункт
этого замечательного доказательства, в котором доказывается, что для
любого простого числа а вида 8п + 1 всегда имеются простые числаt
меньшие 2l/a-f-l, для которых а — квадратичный невычет. Эта
лемма как раз и позволяет Гауссу провести полную индукцию. По
словам самого Гаусса, доказательство этой леммы мучило его целый
год и противостояло всем его усилиям («per integram annem me tor-
sit operamque enixissmam effugit»), пока наконец, ему не удалось
решить вопроса при помощи совершенно элементарного, но глубокого-
соображения, изложенного в п. 129 менее чем на одной странице.
Лишь более 100 лет после появления «Арифметических исследова-
исследований» Гаусса И. М. Виноградову удалось выяснить природу таких
лемм и дать целый комплекс теорем, к ним относящихся.
Фундаментальная теорема дает, как это показывает Гаусс в
п. 147, полное решение поставленной задачи: найти те простые чис -
,ла р, для которых заданное число А есть квадратичный вычет.
Действительно, пусть, например, А — некоторое заданное целое
положительное число = 1 (mod 4). Разложим А на простые множи-
множители и припишем тем из них, которые вида in + 1, знак + , а тем,
которые вида in — 1, знак — , и пусть они, взятые с такими зна-
знаками, суть а, Ъ, с, d,...; тогда произведение abed... равно А . Обозна-
Обозначим через г, г' , г",... те целые числа, которые меньше А и взаимно
простые с4и каждое из которых — квадратичный невычет четного
числа чисел a,b,c,d,... Тогда,как это легко вывести из фундаменталь-
фундаментальной теоремы, прогрессии Ак + г, Ак + г', Ак + г",... содержат
все те и только те простые числа р, по которым число А есть квадра-
квадратичный вычет.
900 Б. Н. Делоне
Для случаев других видов А результаты совершенно аналогичны.
В последнем п. 152 четвертого раздела Гаусс, используя закон
взаимности, дает полное решение общего сравнения второй степени:
ах2 + Ьх + с = 0 (mod m).
Отметим, что Лежандр еще до Гаусса ввел символ (—J (символ
Лежандра), определив его так: ( — J = + 1, если а — квадратич-
ныи вычет р, и (—) = —1, если а — квадратичный невычет. При
помощи этого символа фундаментальная теорема записывается так:
V—1 Q—1
2 2
где р ж q — два нечетных простых числа. Формула эта обычно на-
называется законом взаимности двух простых чисел.
7. Целые комплексные числа Гаусса
и биквадратичный закон взаимности
В пятом разделе Гаусс дал второе доказательство квадратичного
закона взаимности, а впоследствии — еще 6 других его доказа-
доказательств, основанных на различающихся между собой соображениях.
Затем Гаусс в течение многих лет работал над отысканием кубиче-
кубического и биквадратичного законов взаимности, т. е. над решением
вопроса о том, каковы те простые числа р, для которых заданное
число А есть вычет 3-й или 4-й степени, т. е. сравнение х3= A (mod p)
или #4= A (mod p) имеет решение. О кубическом законе взаимности
Гаусс ничего не опубликовал и только в 1828 г. напечатал первую
свою работу о биквадратичных вычетах, содержащую частные ре-
результаты, а в 1832 г.— свою знаменитую вторую работу о биквадра-
биквадратичных вычетах. В этой работе он говорит, что хотя «индукция при-
приносит нам богатый урожай специальных теорем (о биквадратичных
вычетах — Б. Д.)...; однако между ними отсутствует общая связь...».
В п. 1 первой статьи Гаусс говорит: «Намного труднее (чем теория
квадратичных вычетов — Б. Д.), однако, теория кубических и
Целые комплексные числа и биквадратичный закон взаимности 901
биквадратичных вычетов. После того как мы начали исследовать
эти вопросы в 1805 г., . . мы скоро пришли к убеждению, что применяв-
применявшиеся до сих пор арифметические принципы ни в коем случае не
достаточны для обоснования общей теории, а что эта теория с необ-
необходимостью требует в некотором смысле бесконечно расширить об-
область высшей арифметики; а как это следует понимать, будет пока-
показано в процессе настоящих исследований». Это же утверждение Гаусс
повторяет в п. 30 второй статьи, начиная с которого он и присту-
приступает к этому «расширению поля арифметики».
Гаусс вводит кольцо О так называемых целых комплексных чи-
чисел а-\-Ы, где а и Ъ — все возможные целые рациональные числа.
Другими словами, Гаусс предлагает рассматривать целые числа
квадратичного поля, происходящего от присоединения к полю ра-
рациональных чисел числа i = j/Т, т. е. корня неприводимого квадрат-
квадратного уравнения х2 + 1 = 0. Произведение такого числа на ему со-
сопряженное (а + hi) (а — Ы) = а2 + Ъ2 называется нормой числа
а + Ы. Гаусс показывает, что единицами кольца О являются чис-
числа 1, i,— 1,— i (и только они). Далее он показывает, что простыми
числами этого кольца являются: 1) числа а + bi, нормы которых —
рациональные простые числа вида 4я + 1, и 2) сами рациональные
простые числа р вида 4я + 3. Наконец, Гаусс доказывает, что любое
число а + Ы рассматриваемого кольца О, с точностью до множите-
множителей 1,1,— 1, — i, однозначно раскладывается в произведение таких
простых чисел. Таким образом, в смысле вышеизложенной теории
алгебраических чисел оказывается, что в этом кольце число клас-
классов h = 1.
После всего этого Гауссу уже удается, опираясь на численные
примеры, сформулировать основную теорему о вычетах 4-й степени
(т. е. биквадратичный закон взаимности) для чисел рассматриваемого
кольца О, причем опять достаточно это сделать только для простых
чисел этого кольца. Сам Гаусс в своем мемуаре, однако, доказатель-
доказательства этой теоремы не дает, и не известно, обладал ли он этим дока-
доказательством. Доказательство этой теоремы непосредственно в духе
идей Гаусса было дано Бушем в начале XX в. Вообще же биквадра-
биквадратичный и кубический законы взаимности были доказаны в первой
половине XIX в. Эйзенштейном (из теории комплексного умножения
902 Б. Н. Делоне
специальных эллиптических функций) и Якоби (из соображений,
связанных с теорией деления круга).
Важность этого второго мемуара Гаусса о биквадратичных выче-
вычетах заключается, конечно, не в нахождении биквадратичного закона
взаимности, а в том «расширении поля арифметики», о котором го-
говорит Гаусс. Вся трудность была в том, чтобы понять, что простой
вид теория биквадратичных вычетов приобретает только в поле }/~Т,
и показать, что в этом поле такая же простая арифметика, как в поле
рациональных чисел. Этим был сделан существенный шаг в построе-
построении метода алгебраических чисел, хотя обе главные его трудности —
общая теорема о единицах и теория идеальных делителей — в этом
простейшем случае не были еще затронуты.
8. О законах взаимности вообще и о задаче,
которую они решают
Что представляют собой законы взаимности с точки зрения той
схемы применения метода алгебраических чисел, которую мы рас-
рассмотрели в параграфе 4? Начнем с самого простого: квадратичного
закона взаимности над полем рациональных чисел.
Можно показать, что в квадратичном поле с дискриминантом d,
т. е. в поле, получаемом от присоединения к полю рациональных
чисел корня а неприводимого квадратного уравнения х2 + ах +
+ Ъ = 0 с рациональными коэффициентами а и 6, если А — целое
рациональное число, не делящееся на квадрат, и такое, что оно отли-
отличается от числа ^ Ъ целым или дробным квадратным множителем и
d = А, если А = 1 (mod 4), и d = 4А, если А =2 или 3 (mod 4),
простое число р следующим образом раскладывается на простые
делители:
1) р разлагается на два разных простых идеальных делителя,
если (})=+!;
2) р — само простой идеальный делитель, если (~~)= — 1;
3) р есть квадрат простого идеального делителя, если р — мно-
множитель d, причем можно легко найти и сами соответственные про-
простые идеальные делители.
О законах взаимности вообще 903
Таким образом, содержится или не содержится простое число р
в тех прогрессиях, которые были из квадратичного закона взаимно-
взаимности выведены на стр. 899, решает вопрос об «опирании» арифме-
арифметики квадратичного поля на арифметику поля рациональных чисел.
Наоборот, можно показать, что, зная законы разложения натураль-
натуральных простых чисел в квадратичных полях, можно из них вывести
закон взаимности.
Только в свете этого обстоятельства, показывающего, что квадра-
квадратичный закон взаимности есть то главное звено, которое делает воз-
возможным полноценное употребление квадратичного поля для решения
соответственных вопросов теории обыкновенных целых чисел, ясно,
почему Гаусс придавал ему такое большое значение, и предложил
до восьми различных его доказательств.
После Гаусса многие математики упорно занимались отыска-
отысканием законов взаимности для вычетов высших степеней. Мы уже ука-
указывали, что кубический и биквадратичный законы взаимности до-
доказали Якоби и Эйзенштейн. Закон взаимности для вычетов р-х
степеней между рациональным простым числом q и простым делите-
делителем поля i?(]/T) нашел тоже Эйзенштейн. Много лет работы посвятил
разысканию доказательства общего закона взаимности для вычетов
р-х степеней в поле i?(]/T) создатель теории идеальных делителей
Куммер, причем в этих исследованиях Куммер наткнулся на важ-
важность некоторой логарифмической производной, появление которой
в теории чисел казалось совершенно необъяснимым. Долгое время
закон взаимности Куммера считался крайним, чего удается достиг-
достигнуть на этом пути. Но многие математики и дальше упорно занима-
занимались разысканием еще более общих законов взаимности. Наиболь-
Наибольший успех был достигнут в этом вопросе знаменитым немецким ма-
математиком Гильбертом A862—1943) и его школой. Гильберт показал
при помощи теории поля классов (о которой будет речь в следующем
параграфе), что правая часть равенства, записывающего закон
взаимности, может быть представлена как произведение конечного
числа некоторых символов, которые он назвал «норменными симво-
символами» и простейшие свойства которых он установил. Однако дать
прямую конструкцию этих символов, т. е. их явное функциональное
904 Б. Н. Делоне
выражение через числа, стоящие в левой части равенства, и харак-
характеристики поля ему не удалось. Это было сделано в самые последние
годы советским математиком И. Р. Шафаревичем, который, основы-
основываясь на новых идеях, дал, наконец, полное решение вопроса, а
именно нашел и доказал общий закон взаимности. Между прочим,
в методе Шафаревича логарифмическая производная Куммера по-
получила естественное объяснение. Таким образом, знаменитый во-
вопрос, у начала которого стоят гениальные работы Гаусса, наконец,
решен окончательно.
Каков же смысл, в свете схемы § 4, всех этих законов взаимности?
Все они суть частные случаи закона взаимности Шафаревича, следо-
следовательно, достаточно разобрать, каков его смысл. Закон взаимности
Шафаревича решает следующий вопрос: если задано любое поле
к алгебраических чисел т-й степени, содержащее корень п-& степени
из 1,и оно расширяется до поля К присоединением к нему ]/со, где
(о — число поля к, узнать, как опирается арифметика поля К на
арифметику поля к. Квадратичный закон взаимности, как мы сей-
сейчас видели, решает этот вопрос для того частного случая, когда
к — поле рациональных чисел и п = 2; кубический и биквадратич-
ный законы взаимности Эйзенштейна и Якоби — для частного слу-
случая, когда к — поле деления круга на 3 или 4 равные части и п =
= 3 или 4; закон взаимности Куммера — для частного случая,
когда п = р и к — поле деления круга на р частей.
9. О теореме Кронекера и о теории поля классов
Легко показать, что всякое квадратичное поле есть подполе не-
некоторого поля деления круга. Еще в 1854 г. Кронекер наметил до-
доказательство одной из самых замечательных теорем всей алгебры —
корень любого уравнения с рациональными коэффициентами, группа
Галуа которого абелева (коммутативная), выражается рационально
через некоторый корень из 1. Это, несомненно, самая красивая тео-
теорема теории Галуа, доказанная после Галуа. Таким образом, весьма
просто описываются все абелевы (т. е. с абелевыми группами Галуа)
расширения рационального поля — все они суть подполя полей
деления круга, и обратно. Ввиду того, что вопрос о том, как они-
О теореме Кронекера и о теории поля классов 905
рается арифметика поля деления круга на арифметику рациональ-
рационального поля, решается совсем просто, а тогда уже просто решить этот
вопрос для любого подполя поля деления круга, теорема Кронекера
решает вопрос об опирании на арифметику рационального поля для
любых абелевых расширений поля рациональных чисел. Рациональ-
Рациональные простые числа р так или иначе разлагаются в произведение
простых делителей данного абелева поля в зависимости от того,
заключаются ли они или не заключаются в таких-то прогрессиях.
Теорема о разложении натуральных простых чисел р в квадратичном
поле, указанная выше, есть просто частный случай этой общей тео-
теоремы, так как квадратичное поле абелево.
Так как всякое абелево расширение поля рациональных чисел
р-й степени над полем корня />-й степени из 1 получается присоеди-
Vr—
нением одного J/co, где со — число этого поля, а арифметика таких рас-
расширений регулируется законом взаимности Куммера, обратно из
этого закона взаимности можно получить теорию абелевых распш-
рений рационального поля, включая теорему Кронекера, как это
было сделано в 1915 г. автором этих строк. Понадобился даже, только
более простой, закон взаимности Эйзенштейна, а для циклических
полей степени рк — закон взаимности Вестерна.
Полное доказательство теоремы Кронекера дал только Вебер
в 1886 г.* Позже, начиная с 1892 г., сначала на наиболее простом
случае относительно квадратичных полей, Гильберт начал разви-
развивать общую теорию поля классов, т.е. теорию классификации и тео-
теорию опирания арифметик относительно абелевых расширений К
любого заданного поля к (а не только рационального) алгебраиче-
алгебраических чисел. После углубленных работ самого Гильберта, Фуртвен-
глера и японского математика Такаги такая теория была построена.
Важную теорему, опираясь на один метод, употребленный для дру-
другой цели Н. Г. Чеботаревым, дал в этой теории Артин. Более отра-
отработанное изложение дал Хассе,а затем, из иных принципов,— фран-
французский математик Шевалле.
Теорема Кронекера и связанная с ней теория есть частный слу-
случай общей теории поля классов, а именно: это теория полей классов
* Acta Math., 8.
906 Б. Н. Делоне
для того случая, когда к — поле рациональных чисел. Подобно
тому, как эта частная теория поля классов может быть получена из
закона взаимности Эйзенштейна или Вестерна (как это было указано
выше), общая теория поля классов может быть получена из общего
закона взаимности Шафаревича. Это было показано учеником
И. Р. Шафаревича — А. И. Лапиным.
10. Первая часть пятого раздела
«Арифметических исследований»
Пятый раздел «Арифметических исследований» Гаусса (пп. 153—
307), озаглавленный «О формах и неопределенных уравнениях вто-
второй степени», посвящен теории квадратичных форм. Этот раздел
самый обширный из семи разделов и необыкновенно богат содержа-
содержанием. Он, естественно, разделяется на 4 части. Первая его часть
(пп. 153—222) содержит классификацию и теорию представления
чисел двойничными квадратичными формами, а также решение в це-
целых числах общего неопределенного уравнения 2-й степени с двумя
неизвестными. Вторая его часть (пп. 223—265), озаглавленная
«Дальнейшие исследования о формах», содержит теорию компози-
композиции классов двойничных квадратичных форм и теорию их родов.
Третья часть (пп. 266—285), озаглавленная «Отступление, содержа-
содержащее исследование о тройничных формах», посвящена теории трой-
тройничных квадратичных форм. Четвертая часть (пп. 286—307), оза-
озаглавленная «Некоторые приложения к теории двойничных форм»,
содержит доказательство теоремы о родах, теорию разложения чи-
чисел в сумму трех квадратов или трех треугольных чисел, решение
неопределенного уравнения ахъ + by2 + cz2 = 0, решение общего
неопределенного уравнения 2-й степени с двумя неизвестными в ра-
рациональных числах и соображения о среднем числе классов в роде.
Все, что изложено в первой части пятого раздела, в принципе
было уже сделано до Гаусса, в основном Лагранжем, однако изло-
изложение Гаусса формально (но не по существу) сильно отличается от
изложения Лагранжа.
1. Сведение основных задач теории целочисленных двойничных
квадратичных форм к задаче об эквивалентности двух таких форм.
Первая часть раздела V «Арифметических исследований» Гаусса 907
Выражение вида
ах2 4- 2Ъху + су2,
т е. двойничную квадратичную форму, Гаусс называет формой 2-сте-
пени, или просто формой, и обозначает (а, 6, с). Коэффициенты
а, Ь, с предполагаются целыми рациональными. Если существуют
такие целые рациональные х = т, у = п, что am2 + 2Ьтп + сп2 = М,
то число М называется представимым формой (а, Ъ, с). Число
D = Ъ2 — ас = — , называется определителем формы. Пусть
т, п — примитивное представление числа М, т. е. т и п взаимно
простые, и пусть [л и v — такие целые рациональные числа, что
\хт + vra = 1; тогда Ъ2 — ас = [[л (тЪ + пс) — v (та + пЪ)]2 (mod M), что
следует из тождества
{am2 + 26mn + сп2) (ay2 — 2Ьр> + с[л2) —
пс) — v (та -\- пЪ)]2 — (Ъ2 — ас) (т[л
Определитель D = Ъ2 — ас формы есть, следовательно, квадра-
квадратичный вычет каждого представляемого ею числа М. Каждое при-
примитивное представление числа М, как легко показать, независимо
от выбора чисел [л и v, «принадлежит» к некоторому определен-
определенному «значению» v выражения
— ас (modM).
После этих вводных замечаний излагается теория линейных и
линейных унимодулярных преобразований двойничной квадратич-
квадратичной формы F
х = *х' + $у', у = чх' + &у'
в форму F'.
Выводится формула
V2 — а'с' = (Ь2 — ас) (а8 — ртJ,
т. е. то правило, что определитель преобразованной формы равен
определителю преобразуемой формы, помноженному на квадрат оп-
определителя преобразования.
908 Б. Н. Делоне
Формы F и F' называются собственно эквивалентными (proprie
п ft
aequivalentes), если !: = + 1, и несобственно эквивалентными
(improprie aequivalentes), если !: = — 1.
Лагранж не различал собственной от несобственной эквивалент-
эквивалентности. Он считал две формы эквивалентными, если одна переходит
в другую при помощи линейной подстановки с определителем
п ft
!: , равным +1 или —1, все равно.
Таким образом, класс эквивалентных форм Лагранжа составляет
два класса Гаусса, т. е. классификация Гаусса более дробная. Если
рассматривать то геометрическое толкование, которое мы разбираем
ниже, то собственно эквивалентным формам соответствуют одина-
одинаково ориентированные основные реперы решетки, соответствующей
классу форм, а несобственно эквивалентным — равно ориентиро-
ориентированные, т. е. при помощи различения этих понятий можно учитывать
относительную ориентацию реперов. Но различение Гауссом соб-
собственной и несобственной эквивалентностей имело, по-видимому, в
основном другую, более глубокую причину. Дело в том, что компо-
композиция квадратичных форм, которую Гаусс вводит во второй части
пятого раздела и которая имела такое капитальное значение для
развития как теории чисел, так и алгебры, как это будет нами пока-
показано, дает стройную теорию, только если рассматривать эквивалент-
эквивалентность в этом более узком смысле, по Гауссу, так как только в этом
случае можно говорить не о композиции форм, а о композиции
классов.
После введения всех указанных выше понятий Гаусс ставит две
основные задачи:
I. Если даны две формы F и F' с одним и тем же определителем
D, узнать, эквивалентны ли они и притом собственно или несобствен-
несобственно, а если с разными определителями, то не содержит ли одна форма
другую, и найти все собственные и несобственные преобразования
одной формы в другую.
II. Если дана форма F, узнать, представляется ли ею число М,
и найти все такие представления, если они есть.
При этом Гаусс доказывает теорему: если число М представляется
формой ах2 + 2Ъху + су2 при х = т, у = п, где тип взаимно
Первая часть раздела V «Арифметических исследований» Гаусса 909
простые, и если «значение» выражения ]/*.D (mod M), к которому при-
принадлежит это представление, равно N, то формы F = (а, 6, с) и
G = (M,N, —jyj—) — собственно эквивалентны, и F переходит в G
при помощи подстановки:
х = икс' + vj/', у = пх' + ?хг/', A)
где [а и v находятся из уравнений:
иг[х + wv = 1, [х (Ът -\- сп) — v {am -f- bn) = iV.
Наоборот, если F и G эквивалентны и G получается из F подста-
подстановкой A), то х = т, у = п есть представление числа М формой F,
принадлежащее «значению» ]/~~D (mod M), равному N.
Таким образом, решение задачи II сводится к решению задачи 1.
2. Теория приведения Гаусса для случая определенной двойничной
квадратичной формы. Рассмотрим более подробно решение первого
основного вопроса, к которому в конечном счете сводятся все задачи,
решаемые в первой части пятого раздела. Подобно тому, как это
делал уже и Лагранж, этот первый вопрос Гаусс решает при помощи
алгоритма последовательного преобразования заданных форм к
эквивалентным им, так называемым приведенным формам. Вопрос
этот, естественно, решается совсем разно для случаев, когда ZX0
и когда D>0.
Однако Гаусс формально в обоих случаях прибегает к одному п
тому же средству: к вычислению последовательных соседних справа
форм, — что очень красиво. Формой соседней справа (contigua a
parte prima) к форме (а, Ь, а') Гаусс называет форму (а', Ъ', а"), ко-
0 1
—1
где Ь —
торая получается из формы (а, Ь, а') подстановкой
некоторое целое число.
Для случая Z)<0, а>0, т. е. когда форма положительная опреде-
определенная, Гаусс показывает, что если выбирать 8 каждый раз так,
чтобы Ъ' = — Ъ -\- а'Ь заключалось между — -уиу, т.е. чтобы было
2|&'|<Са', и строить такую форму (а', Ъ', а"), соседнюю с заданной
(а,Ь,а') справа, а затем, далее,такую же форму (а",Ь", а"), соседнюю
с (а', &', а") справа, и т. д., то после конечного числа шагов
получится форма (А, В, С), эквивалентная данной, для которой
910 Б. Н. Делоне
выполняются так называемые неравенства приведения:
2|5|<^<С. A)
Такая форма (А, В, С) называется приведенной. Гаусс далее по-
показывает, что, кроме двух специальных случаев, две формы эквива-
эквивалентны тогда и только тогда, когда эквивалентные им приведенные
формы тождественны.
Все это становится гораздо более прозрачным, если это рассмат-
рассматривать геометрически. Возможно, что уже при писании «Арифмети-
«Арифметических исследований» и сам Гаусс рассматривал многое в теории
квадратичных форм геометрически, как это думает, например, Бах-
манн, хотя геометрию квадратичных форм, которую мы сейчас рас-
рассмотрим, Гаусс и обнародовал гораздо позже, лишь в 1831 г.
Всякая положительная (т. е. если D = Ъ2 — аа'<0, а>0) двой-
двойничная квадратичная форма (а, 6, а') с действительными коэффи-
коэффициентами есть (если говорить современным языком), как легко по-
показать, скалярный квадрат линейного векторного выражения, т. е.
ах2 + 2Ъху -f- а'у2 = (<?i# + е2уJ =
= I ei !2^2 + 2 | ег j | e21 cos 9 xy + | e2 \2y2,
где (б!|, \e2\ — длины векторов ег и е2, а <р — угол между ними.
Построим решетку Г на репере Оеге2, т. е. совокупность всех точек
плоскости, координаты которых относительно репера Оехеъ целые
рациональные.
Переход к форме (а', Ъ', с'), эквивалентной форме (а, 6, с), со-
состоит в переходе от репера Оеге2 к другому основному реперу
Ое[е2 той же решетки Г, а именно, если (а', Ь', с') = (а, 6, с)/а з\ ,
\г ь)
то ег = ае1 ~\- ^е2 и е'2 = ^е1 + 8е2, и обратно, причем, если форма
собственно (proprie) эквивалентна, т. е.
т 5
= + 1, то этот новый
репер Оёхё2 имеет ту же ориентацию, как заданный Оеге2, если же
несобственно (improprie эквивалентна, т.е. !? = — 1), то — обрат-
обратную. Таким образом, классу собственно эквивалентных форм соот-
соответствует совокупность всех основных реперов рассматриваемой ре-
решетки Г одной и той же ориентации. Как говорят, решетке соот-
Первая часть раздела V «Арифметических исследований» Гаусса
911
ветствует класс форм, и обратно. То же самое имеет место и в да-
далее рассматриваемой геометризации неопределенных форм, а также
в том и другом случае, если коэффициенты а, Ь, с не считать це-
целыми, а любыми действительными числами. Форме (а', Ъ', а"), со-
соседней справа с формой (а, 6, а'), т. е. форме
а@.х' + г/Т 4 26 @-х' + г/') (-х' + 8г/') + а' (- х' + 5г/'J =
= а'х 2 -t- 2 (— Ъ 4- а'8) я'г/' + (а + 265 + а;62) г/'2 -
= [вх (О -х' + у') + в2 (- х' -ь 8г/')]2 =
= (—e^' + te
получаемой из нее преобразованием (, L соответствует репер, пер*
вый вектор е[ которого равен вектору —е2, обратному второму
вектору е2 исходной формы (а, Ь, а;), и второй вектор е2, которьп!
равен е1 + Ье2. Если, кроме того, Ь подобрано так, как указано
выше, т. е. чтобы было 2\ЪГ \^а\ или, иначе, 2 11 е± \ \ е2\ cos(pf
912 Б. Я. Делоне
^ |6i|2 или 11^21 cos ф' I "Ч-Ц""' то проекция второго вектора е'2 на
первый е\ по абсолютной величине меньше или равна половине
длины \е\| первого вектора, т. е. конец второго вектора принад-
принадлежит полоске, ограниченной перпендикулярами, восставленными
в серединах первого вектора е\ и ему обратного вектора — е\.
Если, следовательно, переходить от заданной формы (а, 6, а'
к соседней с ней справа форме (а', Ъ'', а"), от нее снова к соседней
с ней справа форме (а", Ъ", а"') и т. д., то в этом ряду форм, на-
начиная с формы (а\ Ь', а"), будет каждый раз выполняться первое
условие приведения 2[J5|<^-4. Но через конечное число шагов вы-
выполнится и второе условие приведения А^С, так как, если бы
все время было а'>а"^>а"г и т. д., то получилось бы, что в дан-
данной решетке есть внутри круга радиуса "Уа', описанного вокруг цен-
центра О, бесконечно много точек, все более и более близких к точ-
точке О, а этого быть не может.
Из этого геометрического рассуждения мы видим, таким обра-
образом, что, после конечного числа шагов алгоритма Гаусса соседних
справа форм, мы от любой положительной формы (а, 6, а') придем,
в конце концов, к собственно эквивалентной ей приведенной форме.
Все полученные таким способом последующие реперы будут той
же ориентации, как и исходный репер, т. е. формы, им соответ-
соответствующие, будут собственно эквивалентны исходной форме.
То, что приведенная форма только одна, если у нее в обоих
случаях имеют место неравенства, а не равенства, также легко
показать геометрически.
3. Теория приведения Гаусса для случая нес пред елейной двой-
двойничной квадратичной формы. Случай D > О, т. е. когда (а, 6, а7) —
неопределенная двойничная квадратичная форма с вещественными
коэффициентами, приводит к совсем другой теории. В этом случае
форма разлагается на линейные множители с вещественными
коэффициентами 1Ъ |2| 7]ъ 7j2, где ^ ^ =f= 0:
(а, Ь, а') = р (^х + 12у)~Ых + ЪУ),
причем даже бесконечным числом разных способов, так
как вещественный множитель р можно выбирать произвольно.
Первая часть раздела V «Арифметических исследований» Гаусса 913
Зафиксируем как-нибудь множитель р и рассмотрим репер
векторы которого относительно некоторой выбранной декартовой
координатной системы имеют координаты (?ь т^) и E2, т^)-
Рассмотрим решетку, построенную на этом репере, и будем пред-
предполагать, что она не имеет, кроме начала, точек на координатных
осях, что равносильно тому, что форма не разлагается на множи-
множители, пропорциональные рациональным. Неопределенную форму
(А, В, С) Гаусс называет приведенной, если она удовлетворяет
условиям:
УЪ — В<\А\<УТ) + В, В>0. B)
Если обратиться к рассмотренной сейчас геометрии таких форм
и геометрически истолковать эти неравенства, то получается, что
они обозначают следующее. Если называть па-
параллелограмм, вершина которого — в рассмат-
рассматриваемой точке М (не лежащей на осях 01 и
Ог\), центр которого — в начале и стороны па-
параллельны координатным осям О\ и Ог\, коор-
координатным параллелограммом точки М', то усло-
условия B) обозначают то, что: 1) координатные
параллелограммы концов первого и второго
векторов репера, соответствующего форме
(А, В, С), скрещиваются, как на верхнем рисун-
рисунке, а не охватывают один другой, как на
нижнем рисунке, и 2) вдоль первой оси, т. е.
оси 0?, координатный параллелограмм второго
вектора длиннее, чем первого.
Легко показать (это можно сделать и геометрически), что если
от заданной неопределенной формы (а, Ь, а') переходить к соседней
с ней справа, такой, что в V = —Ъ-\-а'Ъ число S берется между
УТ)—| а'| и YT) , то через конечное число шагов придем к при-
приведенной в этом смысле форме — собственно эквивалентной форме
(а, Ь, а').
Если же продолжать этот же алгоритм дальше, то будут полу-
получаться последовательные дальнейшие приведенные формы, соседние
одна с другой, все более и более «длинные» вдоль оси О\.
—
1
1
—
914 Б. Н. Делоне
Аналогично тому, как это сделал уже Лагранж, Гаусс показы-
показывает, что если коэффициенты формы—целые числа, то, хотя раз-
различных таких приведенных вдоль оси О\ реперов бесконечно много,
различных соответствующих им форм конечное число и они по-
повторяются периодически. Геометрически это происходит от того, что
решетка Г, построенная на репере, соответствующем целочисленной
определенной квадратичной форме, имеет гиперболические повороты
в себя, т. е. имеет такие множители р, что если помножить все
координаты ? ее точек на р и разделить на р все координаты т] ее
точек, то решетка Г совместится с собой.
Приведенные реперы, расположенные в одинаковых местах раз-
различных периодов, получаются один из другого таким автоморфиз-
автоморфизмом решетки Г, и потому им соответствуют одинаковые квадра-
квадратичные формы.
Для того чтобы решить задачу 1,надо, таким образом, вычислить
полный период приведенных форм, эквивалентных первой из за-
заданных форм, и найти хотя бы одну приведенную форму, эквива-
эквивалентную второй заданной форме, и тогда, если она встречается в пе-
периоде первой формы, то заданные формы эквивалентны, если нет,
то — неэквивалентны.
В последних пп. 216—221 первой части пятого раздела Гаусс
прилагает теорию двойничных форм, построенную им в предыду-
предыдущих пп. 153—215 этого раздела, к решению в целых числах общего
неопределенного уравнения 2-й степени с целыми коэффициентами;
ах2 + 2Ьху + су2 + 2dx + 2ey + f = 0.
Заключительный п. 222 первой части пятого раздела посвящен
исторической справке о предшествующих «Арифметическим исследо-
исследованиям» Гаусса работах Эйлера, Лагранжа и Лежандра, относящихся
к тому же вопросу.
11. Вторая часть пятого раздела «Арифметических исследований».
Композиция классов и композиция родов квадратичных форм
Вторая часть пятого раздела, озаглавленная «Дальнейшие иссле-
исследования о формах» (пп. 223—265), содержит теорию композиции
Вторая часть раздела V «Арифметических исследований» Гаусса 915
классов целочисленных квадратичных двойничных форм данного
определителя, всецело принадлежащую уже лично Гауссу.
То, что не все целочисленные двойничные квадратичные формы
данного определителя эквиваленты и что они разбиваются на конеч-
конечное число классов эквивалентных форм, было известно уже Лагран-
жу, но то, что эти классы можно компонировать друг с другом и что
они образуют в смысле этой композиции конечную коммутативную
(абелеву) группу, есть замечательное открытие Гаусса, оказавшееся
как бы далекой и весьма нетривиальной разведкой в область теории
алгебраических чисел, которая была совершена Гауссом задолго
до того, как сама эта теория была окончательно построена. Трудно
гадать, каков был путь, приведший Гаусса к открытию композиции
классов, но, во всяком случае, предвидение ее важности не обмануло
Гаусса.
1. Основные определения — определение понятия «род». Сово-
Совокупность всех целочисленных двойничных квадратичных форм, соб-
собственно эквивалентных данной такой форме, образует класс (собствен-
(собственный) форм данного определителя. Как это непосредственно следует
из теории приведения, в каждом классе форм данного определителя
есть формы, все коэффициенты которых по абсолютной величине меньше
данной функции от определителя; поэтому в случае форм с целыми
коэффициентами число классов таких форм данного определителя
конечно. В случае отрицательного определителя D — Ъ2 — ас < О,
т. е. когда форма определенная, достаточно рассматривать лишь
положительные классы, т. е. классы форм, у которых D < 0 и а > О,
так как отрицательные классы получаются из них просто изменением
знаков всех коэффициентов всех форм на обратные.
Форму (а, Ь, с), у которой а, Ь, с не имеют общего делителя, Гаусс
называет примитивной, а если при этом а и с не оба четные, т. е. и чи-
числа а, 2&, с, не имеют общего делителя, то он называет форму собствен-
собственно примитивной. Тогда и все ей эквивалентные формы тоже прими-
примитивные или собственно примитивные. Соответственно этому рассмат-
рассматриваются и классы примитивные и собственно примитивные. Два
класса одного и того же определителя Гаусс относит к одному и тому
же порядку (ordo), если (а, Ь, с) и (а\ Ь', с') — формы этих классов,
и как числа а, Ь, с и а', Ъ', с' имеют один и тот же наибольший общий
916 Б. Н. Делоне
делитель, так и числа а, 26, с и а', 26', с' имеют один и тот же наи-
наибольший общий делитель.
Наиболее важное значение имеет собственно примитивный поря-
порядок, так как непримитивные формы просто связаны с примитивными.
Совокупность классов собственно примитивного порядка данного
определителя D Гаусс далее еще разделяет на роды (genera), относя
в один и тот же род все те классы, формы которых имеют один и тот же
характер. Под характером примитивной формы, или примитивного
класса форм, так как у всех форм одного и того же класса, как легко
показать, одинаковые характеры, Гаусс понимает следующее.
Пусть т — какой-нибудь простой делитель Z>, а в некоторых
случаях надо еще рассмотреть числа т = 4 и т — 8, и пусть число
всех этих различных модулей т равно X. Можно показать, что
если mi — один из этих X модулей, то для всех чисел п, представ-
представляемых данной собственно примитивной формой определителя D и
взаимно простых с 2D для данного тг, квадратичный характер
[—) (символ Лежандра) имеет одно и то же значение. Выпишем
эти квадратичные характеры, которые все равны +1 или —1, для
всех X указанных модулей тъ т2, .. ., т\, взятых в каком-либо
раз навсегда выбранном порядке; тогда для данной формы полу-
получается некоторая определенная последовательность X чисел +1.
Эту последовательность Гаусс называет характером (Totalcharacter)
рассматриваемой собственно примитивной формы определителя D
или характером класса, ею представляемого. Так как число всех
вообще возможных различных последовательностей, составленных
из X членов, равных +1 или —1, равно 2х, то число различных
характеров форм данного определителя, а следовательно, и число
родов никак не больше, чем 2х. Однако неясно, всякая ли такая
последовательность есть характер некоторого класса — a priori,
может быть, что число родов и меньше?
Для того, чтобы дать ответ на глубокий вопрос о том, каково
истинное число родов, Гаусс вводит особое исчисление, в котором
элементами являются не числа, а классы форм.
2. Композиция классов Гаусса и ее изложение по Дирихле. Форма
F = ЛХ2 + 2BXY + CY*
Вторая часть раздела V «Арифметических исследований» Гаусса
917
называется по Гауссу компонированной из форм
/ = ах2 + 2Ъху + су2 и /' = а'х'2 + 2Ъ'х'у' + с'у'2,
если она переходит в их произведение при помощи целочисленной
билинейной подстановки вида:
X = рхх' + р'ху' + р'ух' + ртуу'\
Y = qxx' + q'xyr + q"yxf + qmyy\
где числа
р р'
ч ч'
р р"
я <?"
•>
р р">
q q'"
Р' Р"
q' q"
»
Р' Р'"
q' q">
Р" Р'"
q" q">
не имеют общего им всем множителя, отличного от 1. При этом
оказывается, что класс, к которому принадлежит форма F, вполне
определяется тем, к каким классам принадлежат компонируемые
формы / и /'.
Убедиться в возможности компонирования собственно прими-
примитивных форм одного и того же определителя проще не из изло-
изложения, данного самим Гауссом, а при помощи того упрощения
этого изложения, которое предложил Дирихле. Наметим
основные пункты этого упрощенного изложения теории Гаусса.
Пусть / = ах2 + 2Ъху -\- су2 — собственно примитивная форма, т. е.
числа а, 26, с не имеют общего им всем делителя, отличного от 1.
Заметим прежде всего, что среди чисел, представляемых такой
формой /, всегда существуют числа, взаимно простые с любым
наперед заданным числом К. Действительно, если хотя бы один из
крайних коэффициентов формы /, например а, не делится на про-
простое число р, то для того, чтобы / не делилась на р, достаточно
взять такие х и у, чтобы х не делилось на р, а у делилось на р.
Если же оба крайние коэффициента / делятся на р, то средний 26
уже не делится на р, так как форма собственно примитивная,
и достаточно взять такие х и у, чтобы оба они не делились на р.
Поэтому, если ри р2, . . ., Pk —вс^ различные простые делители
числа Ку то для того, чтобы / = ах2 + 2Ьху + су2 была взаимно
простой с К1 достаточно так взять х, чтобы оно делилось на одни
из этих простых чисел и не делилось на другие, и то же самое
918 Б. Н. Делоне
сделать с у. При этом можно еще, очевидно, всегда выбрать х ж у
так, чтобы они были взаимно простыми.
Выберем теперь по форме из компонируемых классов, и пусть
представитель второго из этих классов есть форма (а', Ъ'', с'). Возьмем
такие взаимно простые числа х = а, у = ^, чтобы при подстановке
их в представителя первого класса получалось число а, взаимно
простое с числом а'', что, как мы сейчас видели, всегда можно
сделать. Тогда, если взять такие р и 8, чтобы было aS — р^ = 1г
/а р\
то подстановка ( IT) переводит представителя первого класса в экви-
эквивалентную форму (a, b, с), первый коэффициент которой а взаимно
прост с первым коэффициентом а' представителя второго класса.
Перейдем теперь еще от этих представителей (а, Ъ, с) ж (а', Ъ\ с')
рассматриваемых классов с взаимно простыми а ж а' далее к другим,
им эквивалентным «параллельным» формам при помощи подстано-
подстановок @ *) и l!|. Эти формы будут иметь прежние первые коэф-
коэффициенты а ж а', средние же их коэффициенты будут а[л + Ъ ж
a'v + &'. Подберем теперь так [л и v, чтобы удовлетворялось сле-
следующее неопределенное уравнение 1-й степени:
что всегда можно сделать, так как числа а ж а' взаимно простые.
Обозначив a\L + Ъ через В, мы получим формы (а, 5, с) и (а', Ву с').
Но определители этих форм равны, поэтому В2 — ас = В2—а'с',
откуда, так как а ж а' взаимно простые, с = а'С, с' = аС. Выбран-
Выбранные нами, теперь уже окончательно, представители рассматривае-
рассматриваемых нами классов имеют такой вид:
/ = (а, В, а'С) и /'= (а', В, аС).
Определители обеих этих форм равны В2 — аа'С = d.
Разложим обе эти формы на линейные множители следующим
образом:
f=(Vax +
Вторая часть раздела V «Арифметических исследований» Гаусса 919
Перемножая первые множители, мы получим следующее тож-
тождество:
= Vaa' (хх' -Суу')+ ^Ц^ (аху' + а'х'у + 2Вуу'), (*)
у аа
а перемножая вторые множители,— аналогичное тождество, в кото-
котором только вместо Y^d стоит—|/"d. Перемножая оба эти тождества,
мы получаем, что форма
F - (аа\ В, С)
того же определителя В2 — аа'С = d переходит в произведение форм/
и /' при помощи билинейной подстановки
X = хх'
Коэффициенты ее
'; F = а^г/' + а'х'у + 2Бг/г/'.
A)
суть
определители
Р Р Р Р
я я' ч" я
1 0 0 — С
О а а' 25
—1
0
0
а
и
1
0
0
а'
взаимно простые.
Если были бы выбраны не эти специальные представители / и /'
рассматриваемых классов (называемые Дирихле «einige» — «соглас-
«согласные»), а какие-либо произвольные, например, получаемые из них
подстановками:
B)
х = ах + [Зг/, х' = ocV + р'г/',
г/ = Тх + Ьу и г/' = ^'х' = Ь'у\
то результатом их композиции можно считать ту же форму F,
но билинейная подстановка, при помощи которой она переходит
920 Б. Н. Делоне
в произведение заданных форм, будет уже более сложная, а именно
та, которая получается из билинейной подстановки A) при помо-
помощи замены в ней х, у, х', у' по формулам B).
3. Связь с умножением решеток Клейна. С той геометрической
точки зрения, которую мы рассмотрели выше, теория Гаусса ком-
композиции классов принимает следующий вид.
Предположим для определенности, что определитель d положи-
положительный; если бы d было отрицательно, дальнейшее изложение
было бы совершенно аналогичное. Решетка L, соответствующая
форме /, построена (если d > 0) на векторах (]/а\ У~а) и
—l_l— 9 ^— ? а решетка L , соответствующая форме / , по-
\ у а уа J
строена на векторах (у а , у а ) и I JL , —^— . Тождество (*)
\ \ а' У а' /
показывает, что произведение точки решетки L с координатами х9
у, относительно указанного ее основного репера, на точку решет-
решетки U с координатами х', у', относительно ее указанного основного
репера, т. е. произведение любой точки решетки L на любую точку
решетки Z/, дает некоторую точку решетки L, соответствующей
форме F, с координатами (ххг — Суу', аху' + а'х'у -\-2Byy'). Легко
показать, что, соответственно выбирая точки решеток L и Z/ и
складывая и вычитая их произведения, можно получить любую
точку решетки L, т. е. что решетка L есть произведение в рас-
рассматриваемом нами на стр. 891 смысле решеток L и Z/. Для этого,
очевидно, достаточно показать, что концы М1 и М2 векторов основ-
основного репера решетки L могут быть получены следующим способом»
Точка Мх с первой координатой У~аа\ очевидно, получается в ре-
результате умножения точек A,0) и A,0) решеток L и L'. Для того
? 1\/Г - " B + Vd
же чтобы получить точку М2 с первой координатой —у-1-— , пере-
Yaa'
множим сначала точки A,0) и @,1) решеток L и U и затем их
точки @,1) и A,0), тогда мы получим точки с первыми координа-
В + Vd у— в + ^лГ-, . .
тами —-=— у а и —^=— у а (вторые координаты будут из
у а' Vа
них получаться заменой f/^d на —V^d). Складывая эти точки
zt раз первую и еще z2 раз вторую, мы получим точку с первой
Вторая часть раздела V «Арифметических исследований» Гаусса 921
координатой:
Vd-./— B + Vd-i/—, B + Yd , , , ч
а' у а у аа'
у а' у а у аа'
а так как а ж а' взаимно простые, то можно так выбрать zx и z2,
чтобы было azt -f a'z2 = 1, и тогда мы получим точку М2.
Итак, с геометрической точки зрения рассмотренная нами на
стр. 917 композиция классов Гаусса есть не что иное, как умно-
умножение решеток, соответствующих этим классам, в том смысле, как
умножение решеток было рассмотрено на стр. 891.
В своих лекциях «Избранные главы теории чисел» 1 Клейн
говорит, что можно себя спросить, почему Гаусс вместо того, чтобы
говорить об умножении решеток, говорит о композиции соответ-
соответствующих им квадратичных форм. Клейн думает, что не невоз-
невозможно, что уже при писании «Арифметических исследований» Гаусс
знал о связи квадратичных форм с решетками, но не изложил
вопроса так из каких-то своих личных соображений. А между тем,
это изложение при помощи решеток дает больше, чем изложение
при помощи форм, уже потому, «что отдельный линейный множи-
множитель, задающий решетку, учитывает абсолютную величину + ази-
азимут, а форма учитывает только абсолютную величину». «Компози-
«Композиция форм,— говорит Клейн,— есть, так сказать, лишь следствие,
а не эквивалент теории умножения решеток». Идея рассмотрения
решеток могла легче привести к связи с модулярными функциями.
Кроме того, идея рассмотрения при композиции не самих форм,
а линейных множителей форм, могла скорее привести к решению
самого глубокого, связанного со всеми этими исследованиями ариф-
арифметического вопроса, к построению теории делимости в полях алге-
алгебраических чисел.
4. Связь с теорией квадратичных полей. Какой же смысл имеет
теория композиции двойничных квадратичных форм данного опре-
определителя, созданная Гауссом, с точки зрения теории алгебраиче-
алгебраических чисел? С той геометрической точки зрения, на которую мы ста-
стали в § 8 в изложении теории алгебраических чисел, дело обстоит так.
1 F. К 1 е i n. Ausgewahlte Kapiteln der Zahlentheorie, Teil II. Gottingen,
1907, стр. 133 (литограф.).
922 Б. Н. Делоне
Пусть А — целое положительное число, не делящееся на квадрат;
тогда (см. § 8) кольцо 0 всех целых точек квадратичного поля
Н(УЪ), если А = 2 или 3(mod4), имеет базис A,1) (]/"А, — j/"A),
а если А =1 (mod 4), имеет базис A,1) Г 2 -, ~~2 ), Квад-
ратичные формы, построенные на этих реперах, суть (х -f- У^Ау) х
X (x — у Ay) = z2—Ay2 и \x + —
H—^—г/2. Формы эти целочисленные, но вторая из них не имеет
двойки в коэффициенте при ху. Но надо заметить, что теорию
композиции форм Гаусса можно изложить и для целочисленных
двойничных квадратичных форм вида ах2 + Ъху + су2, т. е. таких,
у которых при ху стоит коэффициент 6, а не 26, как у Гаусса.
Определителем d формы тогда называется число б2 — 4ас. Вся тео-
теория будет ровно такая же, как изложенная выше, только тожде-
тождество (*) надо будет заменить следующим:
уах Н L. у) [у ах
Vd
у =
' - Суу') + ^±_^ (a ay' + aVy + Buy').
В случае, когда А ~2 или 3(mod4), rf будет равен 4А, а в слу-
случае А == 1 (mod4), d = 1 — 4-1 • —j— = А. Главный класс такого
определителя d будет представляться как раз формой х2 — А?/2 или
соответственно формой х2 + ху -\—^—у2. Этим формам соответ-
соответствует главная решетка 0. А остальным h — 1 классам примитив-
примитивных форм определителя d соответствуют побочные решетки 0',
0",. . ., О^1~1\ если для каждого из них соответственно выбрать
множитель р. Выбор этих множителей, как показал Клейн, связан
с рассмотрением базиса абелевой группы классов квадратичных
форм определителя d. Композиции классов соответствует умноже-
умножение решеток 0, 0', О", . . ., O{h~1) друг на друга.
Всякая точка всякой из так выбранных (в смысле выбора мно-
множителей р) решеток 0, 0', 0", . . ., Q{h~1) разлагается однозначно
в произведение простых точек этих решеток с точностью до
Вторая часть раздела V «Арифметических исследований» Гаусса 923
множителей единиц 8, которые все суть точки главной решетки б,
лежащие на гиперболах ?vj = +1. От умножения на любую из них
каждая из решеток б, б', ,. ., O{h~1) переходит в себя, и каждая
из форм соответствующего этой решетке класса целочисленно ли-
линейно унимодулярно преобразуется в себя.
С точки же зрения теории идеалов Дедекинда дело обстоит так.
Если помножить решетку О{к) на какую-либо точку \ решетки
(О4)'1, то получается подрешетка 8 главной решетки б, которая
есть идеал к-то класса решетки б, и обратно. Квадратичная форма,
соответствующая решетке 8, отличается от квадратичной формы
определителя d, соответствующей решетке б , целым рациональ-
рациональным множителем, который есть норма идеала 8 в решетке б, т. е.
число, показывающее, во сколько раз площадь основного паралле-
параллелограмма решетки 8 больше, чем площадь основного параллело-
параллелограмма решетки О, Это число, очевидно, равно норме по отноше-
отношению к осям ОЪ] точки j, т. е. произведению ?т] ее координат.
Стоило Гауссу сделать в теории композиции форм еще один
шаг дальше, а именно, разумно подобрав множитель р (т. е. пра-
правильно повернув решетки О'', О", . . ., О по отношению к решет-
решетке б), начать умножать один на другой отдельные линейные мно-
множители квадратичных форм, лежащих в рассматриваемых классах
(т. е. отдельные точки решеток б, б',..., О ), как он обнаружил
бы однозначность разложения и построил бы, задолго до Куммера,
Дедекинда и Золотарева, арифметику полей алгебраических чисел.
Трудно сказать, что остановило Гаусса на этом пути. Быть может,
одной из главных трудностей, которую, как кажется, так и не уда-
удалось преодолеть Гауссу, была для него теорема о базисе абелевой груп-
группы, без которой трудно сообразить, как выбирать множители р для
форм, представляющих отдельные классы.
Классы форм данного определителя в смысле композиции, рас-
рассмотренной Гауссом, образуют абелеву группу. Главный класс яв-
является единицей этой группы. Два обратных класса, т. е. те, ко-
которые содержат формы (а, Ь, с) и (а, —Ь, с), являются обратными
элементами и т. д. Группа классов Гаусса была первой нетривиальной
абелевой группой, которая обратила на себя внимание матема-
математиков. Ха актеры классов, рассматриваемые Гауссом в его теории
924 Б. Н. Делоне
родов,— первый нетривиальный пример характеров группы, при-
причем даже не очень простой, так как характеры Гаусса — не числа,
а последовательности чисел, правда, очень простых, только +1. О той
роли, которую сыграла теория композиции классов Гаусса в исто-
истории абелевых групп, мы скажем дальше (стр. 954), где будем рас-
рассматривать соображения Гаусса о регулярных и иррегулярных опре-
определителях, рассмотренных им в самом конце пятого раздела, в п. 306.
5. Композиция родов и вывод неравенства g^2x—г. Вернемся
теперь снова к вопросу о числе родов целочисленных собственно при-
примитивных двойничных квадратичных форм данного определителя
D, т. е. к той глубокой задаче, для решения которой Гаусс создал
свою композицию классов.
В п. 246 Гаусс рассматривает композицию родов, а именно он от-
отмечает, что при композиции классов характеры этих классов пере-
перемножаются, а следовательно, род, к которому принадлежит класс,
являющийся результатом композиции двух каких-либо классов>
вполне определяется тем, в каких родах лежат эти классы, т.е., как
теперь бы сказали, характеры классов дают обычным своим умно-
умножением гомоморфное представление группы классов.
В п. 252 Гаусс, опираясь на этот результат, естественно при-
приходит к тому, что в каждом роде одно и то же число классов*
Обозначая поэтому, как ранее, число классов через /г, число
родов — чере?. f, а число классов в роде — через g, Гаусс получает
h = g1^. Гаусс называет двусторонними (ambiges) классами те клас-
классы , квадраты которых (в смысле композиции классов) дают глав-
главный класс.
В п. 257 и следующих Гаусс доказывает, что число двусторон-
1 а
них классов равно уХ> где х = % есть число всех возможных
различных последовательностей, состоящих из X чисел, равных + 1.
Далее, опять, как бы мы сейчас сказали, просто из групповых
соображений, Гаусс показывает, что если обозначить число дву-
двусторонних классов через а, а число тех классов, которые суть
квадраты некоторых классов, через 8, то h = а8. Но все классы,
которые суть квадраты некоторых классов, принадлежат к главно-
главному роду, так как характер каждого из таких классов есть квадрат
Третья часть раздела V «Арифметических исследований» Гаусса 925
характера того класса, квадратом которого он является, т. е.
состоит только из +1, а это характер главного рода. Поэтому
?<^g\ Учитывая это неравенство и то, что h = g*( и h = ос8, Гаусс
в п. 261 получает, что т^а> т- е- число родов не более, чем
2Х'~1. Другими словами, по крайней мере половина из всех воз-
возможных последовательностей из X чисел +1 не представляет собой
характера никакого собственного примитивного класса определи-
определителя D.
В п. 262 Гаусс из этого неравенства для числа родов получает
новое, второе, доказательство квадратичного закона взаимности,
которое некоторые математики считают наиболее глубоким из всех,
данных Гауссом.
Итак, число родов ^^2А~11 но сколько именно родов — остается
и на этом месте «Арифметических исследований» все же невыяснен-
невыясненным. Для выяснения этого важного вопроса Гаусс употребляет
новое средство — теорию тройничных целочисленных квадратичных
форм.
12. Третья часть пятого раздела «Арифметических исследований».
Отступление о тройничных формах
Эта часть пятого раздела «Арифметических исследований» оза-
озаглавлена: «Отступление, содержащее исследование о тройничных
формах» (пп. 266—285).
В этом «Отступлении» Гаусс рассматривает теорию форм
/ = ах2 + а'х'2 + аУ2 + 2Ъх'хп + 2Ъ'х"х + 2Ъ"хх',
которые он обозначает (&?'?")» гДе а, а', а", Ь, Ъ', Ъ"— целые ра-
рациональные числа.
Число
А = аЪ2 + а'Ь'2 + а"Ь — аа'оГ — 2Ъ'ЪЪп
Гаусс называет определителем такой формы и предполагает его
неравным нулю.
В этой части пятого раздела Гаусс кладет начало обширной обла-
области исследований, посвященных арифметической теории квадратич-
квадратичных форм от многих переменных, в которой впоследствии дали важ-
926 Б. Н. Делоне
ные результаты Зеебер, Эйзенштейн, Дирихле, Арнольд Мейер,
Зеллинг, Коркин и Золотарев, Смит, Минковский, Вороной, Вен-
Венков, Хассе, Зигель и др. Сам Гаусс построил только самые элементы
этой теории, необходимые ему для решения вопроса о числе родов
двойничных квадратичных форм.
1. Рассмотрение Гауссом параллельно с данной тройничной
формой ей союзной формы, геометрический смысл этого и значение
для кристаллографии. Рядом с заданной тройничной формой / Гаусс
рассматривает всегда так называемую союзную с ней форму (forma
adjuncta)
F = Ах2 -}- Afx/2 + A"x + IBx'x" + 2Brx"x + 2B"xx\
где
A = b2 — a'a", A'= b'2 —aa\ A" = Ь — аа';
В = аЪ — Ъ'Ъ", В1 = а'Ъ' — ЬЬ\ В" = а"Ъ" — ЪЪ'.
Сделаем в этом месте геометрическое замечание. Если форма /
положительная, т. е. все числа, ею представляемые, положительны,
то, как нетрудно показать, / = (хех-\- х'е2-\~ эс"е3J, т. е. равна ска-
скалярному квадрату линейного векторного выражения, причем если
А^ 0, то векторы е±, е2, е3 не компланарны. Трехмерная «решетка»
Г всех точек, имеющих целые рациональные координаты относительно
репера Ое±е2е3 (совершенно подобно тому, как в случае двойнич-
двойничной квадратичной формы двумерная решетка, построенная на репере
Ое±е2, ей соответствующем), связана с формой / так, что эквивалент-
эквивалентным с / формам, т. е. формам, получаемым из / линейными подста-
подстановками
X = (XX + Грх' + ЧХ"
х' = а'х + р V + т V
х" = <х."х + $"х' + ч"
с целыми рациональными коэффициентами и определителем +1,
соответствуют другие основные реперы этой же решетки Г, т. е.
решетке соответствует в этом смысле класс эквивалентных форм,
а отдельным формам класса — отдельные основные реперы решетки.
Репером, союзным (—взаимным = полярным = обратным) к
данному реперу Ое^е^ называется репер #е*е*е*, такой, что
Третья часть раздела V «Арифметических исследований» Гаусса 927
скалярное произведение (хе1 + х'е2 + х"е3) (:r*e* + x'*el + х"*е*з) равно
просто хх* -(- х'х'* + %"х"*', т. е. такой репер, что
*
1
[eiea])'
где [ ] обозначают векторное, а ( ) — скалярное произведение.
Решетка Г*, построенная на союзном репере, называется союз-
союзной с решеткой Г. Важнейшее для кристаллографии свойство
союзной решетки состоит в том, что всякий вектор союзной решет-
решетки Г* перпендикулярен к некоторой плоской сетке (т. е. двумер-
двумерной подрешетке) заданной решетки Г и по длине равен площади
ее основного параллелограмма, и обратно. Это обстоятельство
позволяет свести изучение плоских сеток решетки Г параллельно-
переносной повторяемости кристалла (которые играют существенную
роль как в вопросах о плоских гранях кристалла, параллельных
наиболее густым таким сеткам, так и в вопросах рентгеновского,
электронного и нейтронного анализа структуры кристаллов) к изу-
изучению векторов взаимной решетки Г*.
Рассмотрение Гауссом союзной формы было очень важным шагом,
так как эта форма или, скорее, связанная с ней геометрическая кон-
концепция союзной (^взаимной) решетки впоследствии стала играть
(и играет сейчас) большую роль в практической кристаллографии.
Надо, однако, сказать, что рассмотрение трехмерного репера, взаим-
взаимного с данным, к которому все сводится, было сделано гораздо раньше
Гаусса Лагранжем в его статье «О треугольных пирамидах» * в 1773 г.,
в которой Лагранж изучал разные геометрические свойства тетраэд-
тетраэдров, исходя из задания тетраэдра, имеющего одну вершину в на-
начале координат, девятью координатами трех других его вершин.
Эта статья Лагранжа, по-видимому, осталась мало замеченной,
и француз кристаллограф Браве, первый введший взаимную решетку
в кристаллографию, ссылается на Гаусса.
Рассмотрение Гауссом далее теории представления тройничной
формой / двойничной квадратичной формы <р (п. 280) связано как
* Solutions analytiques de quelques problemes sur les pyramides triangulai-
res, 1773 (Oeuvres, t. III).
928 Б. Н. Делоне
раз с этой взаимностью, в силу которой всякому такому представ-
представлению соответствует представление определителя D этой формы <р,
союзной с / формой F.
2. Как Гаусс решает вопрос о положительности тройничной
квадратичной формы. Отметим, между прочим, как Гаусс в п. 271
решает вопрос о том, является ли заданная тройничная квадратич-
квадратичная форма / положительной определенной или нет. Помножив /
на а, Гаусс получает форму
g = (ах + Ъ"х' + Ъ'х"У — А" х'2 + 2Вх'х" — Ах,
а помножив форму g еще на А', он получает форму
k = А' (ах + Ъ"х' + Ъ'х"У — (А'х" — Bx'f + aAx'2
и говорит: если 4' и аД отрицательны, то h представляет только
отрицательные числа, почему / тогда представляет только числа,
знак которых обратен знаку аА\ т. е. числа того же знака, как а.
Таким образом, в этом случае форма / определенная и притом по-
положительная, если а > 0, и отрицательная, если а < 0. Если же
числа аД и i' положительные или одно из них положительно,
а другое отрицательно (но оба не равны нулю), то легко видеть,
что соответственным подбором х, х'', х" форма h может быть сделана
как положительной, так и отрицательной, т. е. форма / неопре-
неопределенная. Далее отдельно еще исследуются случаи А1 = 0, a=f=0 и
а = 0 ж доказывается, что в этих случаях форма / неопределенная.
Из всего этого Гаусс выводит следствие, что у положительной формы
числа А, А\ A", aA, a'A, а"А отрицательны, числа а, а', а" по-
положительны и число А отрицательно.
Любопытно, что Гаусс не задается целью найти систему незави-
независимых необходимых и достаточных условий положительности формы /.
Сейчас мы знаем, что эти условия следующие:
а Ъ" V
b" a' b
b' b a"
а Ъ"
a>0r
или в обозначениях Гаусса: А <0, А"<0, а >0. Гаусс даже не
отмечает, что девять выведенных им условий не только необходимы,
Третья часть раздела V «Арифметических исследований» Гаусса 929
но и достаточны. То же самое замечание надо сделать относительно
рассмотренных на стр. 910 и 913 условий приведения двойнич-
двойничной положительной и неопределенной квадратичной формы. Как
в тех, так и в других условиях у Гаусса к выписанным нами прибавле-
прибавлено еще по одному лишнему условию, которое есть следствие остальных.
3. Доказательство Гауссом конечности числа классов целочисленных
тройничных квадратичных форм при помощи теории приведения
таких форм. В пп. 272—275 Гаусс дает способ приведения тройничной
квадратичной формы, причем способ такой, который одновременно
годится как для случая,когда форма / определенная, так и для слу-
случая, когда она неопределенная. В силу уже этого обстоятельства
условия приведения Гаусса для положительной тройничной квад-
квадратичной формы не приводят к одной приведенной форме (как это
имеет место у Зеебера). Они лишь таковы, что абсолютные величины
всех коэффициентов приведенной формы, как в случае, когда форма
определенная, так и в случае, когда она неопределенная, могут быть
ограничены в зависимости от определения А формы /. Поэтому,
если коэффициенты а, а' а", 6, Ъ', Ъ" формы / целые рациональные,
число различных таких приведенных форм определителя А конечно.
Отсюда в п. 276 получается теорема о том, что, подобно тому, как
для двойничных целочисленных квадратичных форм, число классов
целочисленных тройничных квадратичных форм данного определи-
определителя А конечно. Итак, эту основную теорему условия приведения
Гаусса дают. Но условия Гаусса приведения тройничных квадра-
квадратичных форм в том смысле несовершенны, что если даны две эквивалент-
эквивалентные между собой такие формы / и /', то может быть, что ни одна фор-
форма, приведенная в смысле Гаусса, эквивалентная второй из них, не
будет совпадать ни с одной из форм, приведенных в смысле Гаусса,
эквивалентных первой. Таким образом, эта теория приведения Га-
Гаусса тройничных квадратичпых форм не дает возможности решить
вопрос об эквивалентности двух таких форм / и /'.
4. Сведение Гауссом представления чисел тройничной квадратичной
формы к задаче эквивалентности двух таких форм. В п. 280 Гаусс
начинает рассматривать теорию представления тройничной квадра-
квадратичной формой / определителя А двойничной формы
930 Б. Н. Делоне
определителя i), если положить в форме /
х — mt + пи, х' = m't + п'и, х" = m"t -f га"и.
Легко убедиться, что в этом случае форма F, союзная с /, пред-
представляет число D, если положить в ней
X = т'п" — т"п\ X' = т"п — тп", X" = тп' — т'п.
Наоборот, оказывается, что всякое представление X, X', X"
числа D союзной формой F таким образом получается из некоторого
представления некоторой двойничной формы ф определителя D фор-
формой /. Геометрический смысл этого обстоятельства мы выяснили выше
на стр. 928.
Отсюда следует, что решение задачи: найти все собственные пред-
представления числа D формой F сводится к тому, чтобы выписать пред-
представителей всех классов целочисленных двойничных квадратичных
форм определителя D и найти все собственные представления этих
представителей формой /, если они есть. Все эти представления и да-
дадут все представления числа D формой F,
В п. 283 предлагается следующий способ находить все соб-
собственные представления двойничной формы
ср = pt2 -\- 2qtu + гм2
определителя D тройничной формой / определителя А.
Пусть В и В' — такие целые рациональные числа, что В2 = аг
ВВ' =Ь, В'ъ == с (modi)); тогда линейную форму Вх + В'у Гаусс
называет значением jfax2 + 2bxy + су2 (modi)). Гаусс показывает,
что всякое собственное представление формы ср формой / принад-
принадлежит к некоторому «значению» (В, В'), и выводит следующее
правило для нахождения всех собственных представлений формы <р
формой /.
Найти все различные «значения» |^А(/?/2 + 2qtu + ru2)(modD).
Если два таких «значения» обратны по знаку, надо брать только
одно из них. Чтобы найти все собственные представления фор-
формы ср формой /, принадлежащие к данному «значению» E, B')t
одно найти тройничную форму g = la °:, ^„ ) определителя А, в ко-
Третья часть раздела V «Арифметических исследований» Гаусса 931
торой а = р, Ъ" = g, а' = г, аЪ — Ъ'Ъ" = В, а'Ъ' — ЪЪ" = В\ откуда уже
найдутся a", b, b', но, вообще говоря, в виде дробных чисел. Если
либо один из коэффициентов а", Ь, Ъ' выйдет нецелым, либо формы /
и g не будут эквивалентны, то представлений формы <р формой /г
соответствующих «значению» E, Б'), нет, Если же а", Ь, V выйдут
целые и формы / и g эквивалентны, то каждое преобразование
а' р' Т'
а* р- г
формы / в форму g дает такое представление:
х = at + ?и, х' =r <x!t + р'и, ^ = 7ft + $"и,
и обратно.
В силу вышеописанной связи между представлениями числа D
формой F и представлениями двойничной формы ср формой / задача
о представлении чисел тройничной целочисленной квадратичной
формой сводится к задаче установления эквивалентности двух трой-
тройничных целочисленных квадратичных форм / и g, и в случае, если они
эквивалентны, к нахождению всех подстановок, при помощи которых
одна из них переходит в другую, совершенно аналогично тому, как
это было в вопросе о представлении чисел двойничной целочислен-
целочисленной квадратичной формой.
5. Недостаток теории приведения Гаусса тройничных квадратич-
квадратичных форм. К сожалению, теория приведения Гаусса тройничных
квадратичных форм, как это было указано выше, не дает возможности
решить вопрос об эквивалентности двух целочисленных тройничных
квадратичных форм / и g, а потому и задача представления чисел
такой формой также не получает у Гаусса полного решения. Сам
Гаусс говорит об этом в п. 285 следующее: «Относительно вопросов,,
которые образуют третью из поставленных нами проблем (к которой
в предыдущем сведены обе первые проблемы), а именно, если за-
заданы две тройничные формы с одним и тем же определителем, узнатьг
эквивалентны они или нет, и в первом случае найти все преобразо-
преобразования одной из них в другую, мы можем в этом месте сказать только
немногое, так как полное решение, которое мы указали для анало-
932 Б. Н. Делоне
гичной проблемы в случае двойничных форм, здесь наталкивается
на еще большие трудности. Поэтому мы ограничим наше исследо-
исследование некоторыми специальными случаями, ради которых мы главным
образом предприняли это отступление (т. е. изложение теории трой-
тройничных форм — Б. Д.) от нашего основного предмета (т. е. от иссле-
исследования теории двойничных квадратичных форм — Б. Д.)».
Еще раньше в п. 277, посвященном теории приведения тройнич-
тройничных квадратичных форм, Гаусс прямым вычислением показал, что
всякая целочисленная неопределенная тройничная квадратичная
форма определителя А = + 1 может быть преобразована в форму
х2— 2yz. Собственно, этот частный результат о том, что существует
только один класс целочисленных тройничных неопределенных квад-
квадратичных форм с определителем А = +1 только и нужен Гауссу
дальше из всей теории приведения тройничных форм.
6. Работа Зеебера 1831 г. о положительных тройничных квадра-
квадратичных формах, аннотация Гаусса к ней и работа Дирихле 1841 г.
Возможно, как мы это уже выше говорили, что геометрическое тол-
толкование теории квадратичных форм было уже близко Гауссу в то вре-
время, когда он писал «Арифметические исследования», хотя в них он
нигде ни слова об этом не упоминает. Опубликовано это геометриче-
геометрическое толкование было Гауссом гораздо позже, в 1831 г., в его анно-
аннотации (Anzeige) к работе Зеебера о приведении положительных трой-
тройничных квадратичных форм *.
В первой статье Зеебер рассматривает разбиение пространства
на одинаковые параллелепипедальные молекулы, причем рассмотре-
рассмотрение квадрата расстояния между вершинами таких параллелепипедов,
образующими некоторую решетку Г, приводит его к геометрическому
смыслу положительной тройничной квадратичной формы. В обшир-
обширной A32 стр.) второй работе Зеебер решает задачу приведения поло-
положительных тройничных квадратичных форм так, что в каждом клас-
классе оказывается, как у Гаусса в случае положительных двойничных
форм, лишь одна приведенная в его смысле форма. Зеебер говорит,
* Seeber. Versuch einer Erklarung des inneren Baues der festen Korper,
1824; Untersuchungen uber die Eigenschaften der positiven ternaren quadrati-
schen Formen, 1831.
Третья часть раздела V «Арифметических исследований» Гаусса 933
что его привела к этому решению предыдущая кристаллографическая
работа. Таким образом, «Теория положительных тройничных квадра-
квадратичных форм,— говорит Зеебер,— становится полезным или даже
необходимым орудием кристаллографии». Интересно отметить, как
в этом месте при создании теории переплетаются между собой вопро-
вопросы теории чисел и кристаллографии.
В «Anzeige» к работе Зеебера Гаусс дает доказательство неравен-
неравенства аа'а"<С 2А, которому удовлетворяет приведенная по Зееберу
форма. Это неравенство Зеебер нашел лишь эмпирически, на приме-
примерах, но не дал его общего доказательства, а доказал лишь, что
аа'а"<ЗЛ. Доказательство, которое предлагает Гаусс, получается
из одного арифметического тождества. Впоследствии Коркиным и Золо-
Золотаревым, Минковским и др. это неравенство было обобщено на слу-
случай положительных квадратичных форм от п переменных. Оно обо-
обозначает, что в каждой решетке есть основной репер, мало отличаю-
отличающийся от ортогонального». Остальная часть «Anzeige» Гаусса посвя-
посвящена изложению геометризации двойничных и тройничных квадра-
квадратичных форм (положительных), рассмотренной нами выше на стр. 926.
В самом конце Гаусс замечает, что положительная тройничная
квадратичная форма будет приведенной по Зееберу тогда, когда
параллелепипед, построенный на соответствующем ей репере, такой,
что каждое из его ребер не длиннее диагоналей тех граней, которым
они принадлежат, и не длиннее внутренних его диагоналей. Указан-
Указанное же выше неравенство Зеебера, замечает Гаусс, означает просто
то, что объем такого параллелепипеда, помноженный на У29 не
меньше, чем объем прямоугольного параллелепипеда с такими же
ребрами.
Простое и весьма изящное геометрическое доказательство суще-
существования в каждой трехмерной решетке основного параллелепипеда,
удовлетворяющего условиям приведения Зеебера, дал в 1850 г.
Дирихле в работе «fiber die Reduction der positiven quadratischen For-
men mil drei unbestimmten ganzen Zahlen» (Crelle, 40, 1850). Эта ра-
работа Дирихле, опубликованная еще задолго до смерти Гаусса, была, по
нашему мнению, первой в истории математики серьезной работой по
геометрии чисел. В этой работе Дирихле впервые вводит тот шести-
шестиугольник, который сейчас принято называть областью Дирихле точка
934 Б. Н. Делоне
решетки. Для других целей этот шестиугольник позже рассматривал
Эрмит в работе об обобщении непрерывных дробей, предложенном
Чебышевым. Общую теорию таких областей для решеток любого числа
измерений дал в своей знаменитой работе «Recherches sur les paral-
leloedres primitifs» A908—1909) Г. Ф. Вороной.
7. Способ задавать трехмерную решетку. Скажем еще несколько
слов о том, как задают решетку. Кристаллографы обычно задавали
решетку длинами ребер и величинами углов какого-нибудь ее основ-
основного репера. Это во всех смыслах неоднородное задание — даже
размерность выбранных параметров неодинакова.
Гаусс задавал основной репер решетки квадратами длин его ре-
ребер а, а', а" и скалярными произведениями его ребер друг на друга
Ь9 Ъ', Ъ", и записывал это так: (?/////)• Задание Гаусса однородно в
смысле размерности выбранных параметров.
Первый, кто после Гаусса сделал дальнейший шаг в вопросе о за-»
дании решетки, был Зеллинг (Selling)* В работе 1873 г. « Uber die bi-
na'ren und terndren quadratischen Formen» ("Crelle, 74, 1873) Зеллинг
предложил кроме векторов еи е2, е3 репера всегда рассматривать
еще четвертый вектор е4= —е1 — е2 — е3. Задание Зеллингав некото-
некотором смысле более однородно, чем задание Гаусса. Численно такой
четырехвекторник Зеллинг задает шестью параметрами — попар-
попарными скалярными произведениями его векторов друг на друга (е2е3),
(e3ei)» (eie2)» (eie4)> (e2e4)» (e3e±)i обозначая их g, h, k, Z, m, n —¦ и запи-
записывает это так: f f' ' ]. Своей записью Зеллинг
\19 т., п)
снова уничтожает достигнутую им симметрию.
Еще более совершенна запись решетки,
предложенная в работе «Neue Begrundung der
geometrischen Kristallographie» (Zeistchr. fur
7 ^ Kristallographie, 1932) автором настоящей
статьи, при помощи символа, представляющего
пространственный тетраэдр, на ребрах которого написаны парамет-
параметры Зеллинга. Только в этой записи непосредственно по приведен-
приведенному (по Зеллингу) символу обнаруживаются все симметрии решетки
(группа ее «поворотов» в себя, тип ее параллелепипеда Браве и т. д.).
Третья часть раздела V «Арифметических исследований» Гаусса 935
8. 7 голоэдрий решеток и 32 кристаллографических класса, 14 ре-
решеток Враее и 73 арифметических класса кристаллов. Кристалло-
Кристаллографы много занимались вопросом о тех группах «вращений» (вра-
(вращений вокруг точки решетки и таких же вращений плюс отражение
в плоскости, проходящей через эту точку), при которых трехмерная
решетка Г совмещается с собой. Таких групп 7 — это так называемые
голоэдрии. Если рассмотреть и все их подгруппы, то получается
32 группы, называемые кристаллографическими классами. Каждая
из этих подгрупп причисляется к наименьшей из тех голоэдрий, ко-
которых она есть подгруппа. Так получается разбиение 32 классов
на 7 сингоний. Кристаллограф Браве в своей знаменитой работе
1851 г. «Sur les points distrihues regulierement sur le plan et dans Ves-
pace» вывел, кроме того, все возможные существенно различные
решетки, имеющие ту или иную голоэдрию: три — для кубической
толоэдрии, одну — для ромбоидальной, две — для квадратной (=
тетрагональной) голоэдрии, четыре — для ортогональной ( = ромби-
ромбической) голоэдрии, две — для моноклинной, одну — для триклин-
ной и одну — для гексагональной голоэдрии — всего 14 типов
решеток Браве. Параллелепипедом Браве данной решетки Г назы-
называется наименьший из параллелепипедов решетки Г (т. е. парал-
параллелепипедов, вершинами которых являются точки решетки Г),
вообще говоря, уже не основной, который (как тело) имеет туже груп-
группу «поворотов» в себя, какую имеет сама решетка Г, или наимень-
наименьший из прямоугольных таких параллелепипедов, если такие в
решетке есть. Гексагональная решетка не имеет параллелепипеда Бра-
Браве, так как никакой параллелепипед не может иметь шестерной оси
«симметрии.
Совокупность всех преобразований данной положительной трой-
тройничной квадратичной формы в себя это не что иное, как голоэдрия
решетки, т. е. группа всех ортогональных преобразований решетки
в себя, оставляющих одну ее точку на месте, записанных цело-
целочисленными унимодулярными (вообще говоря, неортогональными)
матрицами по отношению к некоторому основному реперу решетки.
Если преобразовать все матрицы такой группы матриц одной и той же
произвольной унимодулярной матрицей, то мы получим так называе-
называемую эквивалентную запись голоэдрии решетки, т. е, запись ее голо-
936 Б. Н. Делоне
эдрии по отношению к некоторому другому основному реперу решет-
решетки. Если считать различными такие группы целочисленных матриц,
записывающих голоэдрию решетки, которые не эквивалентны в этом
смысле, то различных таких групп оказывается 14, каждая соответ-
соответствует своей решетке Браве. Если же взять и все их подгруппы, раз-
различные в этом же смысле, то получится всего 73 кристаллографиче-
кристаллографических класса. Эту точку зрения проводит сейчас школа известного
швейцарского кристаллографа Ниггли.
В этом смысле 7 голоэдрий можно называть геометрическими
голоэдриями, а 14 решеток Браве — арифметическими голоэдрия-
голоэдриями; 32 кристаллографических класса — геометрическими клас-
классами, а введенные сейчас 73 кристаллографических класса—
арифметическими классами.
9. Теория приведения положительных квадратичных форм с тремя
и с п переменными. Что касается дальнейшей истории теории при-
приведения целочисленных тройничных квадратичных форм, то о
случае определенных форм мы уже говорили, для них весь вопрос был
в высшей степени удовлетворительным образом решен Зеебером. До-
Дополнение к нему оставалось сделать лить в отношении вопроса
о подстановках, преобразующих данную форму в себя; теорию таких
подстановок разработали Эйзенштейн и Борисов. Затем Зеллинг в упо-
упомянутой работе 1873 г., исходя из своего четырехвекторника, дал
новую, отличающуюся от зееберовой, теорию приведения трой-
тройничных положительных форм. Автор настоящей статьи в упомянутой
выше работе 1932 г. связал эту теорию приведения положительной
тройничной квадратичной формы с теорией области Вороного решет-
решетки, и довел ее до завершающей таблицы 24 сортов решеток, закон-
законченно решающей весь этот вопрос, так что результат стал удобен для
использования в кристаллографии*.
Обобщение теории приведения Зеллинга на положительные
квадратичные формы с четырьмя переменными дал Шарв (Charve).
Первый, кто показал, что можно и для положительной квадратичной
формы с п переменными выделить при помощи (может быть, и беско-
* Этот метод автора приняли сейчас в международном справочнике па
структурному анализу кристаллов A952). Им перевычислены почти все извест-
известные до сих пор структуры; см. справочник Donneuy Crystal data, 1956.
Третья часть раздела V «Арифметических исследований» Гаусса 937
нечного числа) линейных неравенств область изменения их коэффи-
коэффициентов (основную область приведения) такую, что: 1) никакие две
формы из этой области неэквивалентны и 2) любая положительная
квадратичная форма с п переменными имеет себе эквивалентную в этой
области,— был Эрмит (Hermite); то же, что можно выделить такую
область при помощи конечного числа линейных неравенств, показал
в замечательной работе «Discontinuitdtshereich fur arithmetische Aqu-
valez» (Ges. Abh., Bd. II) Минковский. Исходя из идей Вороного,
Б. А. Венков показал в работе «О приведении положительных квад-
квадратичных форм» *, что если п > 2, то существует континуум различ-
различных разбиений области положительных квадратичных форм с п пе-
переменными на фундаментальные области приведения, каждая из ко-
которых задается конечным числом неравенств, причем разбиение Мин-
ковского является лишь одним из таких разбиений. Для получения
разбиений Венкова надо рассмотреть произвольную положительную
форму и все ей эквивалентные ?,?'»?",... Разбиение Венкова полу-
получается, если рассмотреть пирамиды, на которые разбивается в прост-
пространстве коэффициентов конус положительных форм, каждая из кото-
которых является областью Вороного соответственной формы ср(г) в смысле
мероопределения Вороного. Если п>2 и исходную форму ср непре-
непрерывно изменять, разбиение это тоже непрерывно изменяется. В про-
противоположность этому, как заметил еще раньше автор этих строк, для
п = 2 существует только одно такое разбиение, так как при измене-
изменении ф все стенки разбиения Венкова сохраняются.
10. Теория приведения неопределенных тройничных квадратичных
форм и квадратичных форм с п переменными сигнатуры п — 2. Что
касается теории приведения неопределенных квадратичных форм,
то она гораздо труднее. Для произвольного п и произвольной сигна-
сигнатуры она не завершена еще и теперь. Для неопределенных тройничных
форм теория эта сейчас совершенно закончена. Наиболее далеко
идущий результат принадлежит здесь также Б. А. Венкову. Пояс-
Поясним, в чем дело. В случае определенной двойничной или тройничной
квадратичной формы существует одна и только одна эквивалентная
ей приведенная (в случае двойничной приведенная по Гауссу, а в
случае тройничной приведенная по Зееберу) форма и только в том
* «Известия АН СССР», № 4, 1940.
938 Б. Н. Делоне
случае, если решетка имеет симметрии, то — несколько (конечное
число) таких приведенных форм, но они все могут быть легко найдены.
В силу этого в случае положительной двойничной или тройничной
квадратичной формы всегда можно узнать, эквивалентна ли она дру-
другой заданной такой форме, т. е. являются ли реперы, соответствую-
соответствующие этим формам, разными реперами одной и той же решетки или
нет; все равно, целые или любые действительные числа — коэффи-
коэффициенты этих форм.
Совсем иные обстоятельства характеризуют неопределенные формы.
Если задана неопределенная двойничная квадратичная форма
(а, Ь, с), то указанным на стр. 913 алгоритмом можно посредством
конечного числа шагов прийти от нее к эквивалентной ей приве-
приведенной (в смысле стр. 913) форме и далее находить тем же алго-
алгоритмом последовательные следующие формы цепочки приведенных
форм, эквивалентных заданной форме. Если коэффициенты а, Ъ, с
не пропорциональны целым числам, то все формы этой цепочки
будут различные, если же а, 6, с целые (или пропорциональны
целым числам), то различных форм в этой (бесконечной в обе сто-
стороны) цепочке будет лишь конечное число — они будут периоди-
периодически повторяться. Дело в том, что если а,Ъ, с пропорциональны
целым числам, то решетка Г, построенная на репере, соответствующем
форме 9 = (а, Ь, с), будет при ее гиперболическом «вращении» отно-
относительно асимптот <9?, От], получаемых, если положить ср = 0
т. е. при изменении числа р в ее разложении (а, Ь, с) = р fax + ?2J/) X
X — {г\хх + 7]2у) , периодически совмещаться с собой. Каждая такая
решетка Г имеет свой вполне определенный конечный наименьший
гиперболический угол совмещения с собой, так называемый ее
угол Пелля П. Если дана неопределенная тройничная квадра-
квадратичная форма / == ах2 + а'х'2 + а"х + 2Ъх'х" + 2Ъ'х"х + 2Ь"хх', коэф-
коэффициенты которой пропорциональны целым числам, то, если поло-
положить /(х, х\ х") = 0, получится некоторый конус К второго порядка,
и если рассматривать целочисленные линейные унимодулярные пре-
бразования Л пространства (х, х'', х"), при которых этот конус
совмещается с собой (преобразования Лорентца, соответствующие
этой форме), и называть эквивалентными точки, переходящие одна
Четвертая часть раздела V «Арифметических исследований» Гаусса 939
в другую при таких преобразованиях Л, то можно внутри К тоже
выделить фундаментальную область V такую, что: 1) каждая точка
внутри К эквивалентна точке из V, 2) две различные точки
внутри V неэквивалентны. Эта область V играет для целочислен-
целочисленной неопределенной тройничной формы / ровно ту же роль, какую
играет угол Пелля П для неопределенной двойничной целочислен-
целочисленной формы (а, Ь, с).
Если для данной формы / найдена эта область, то можно ре-
решить задачу эквивалентности.
В работе Б. А. Венкова «Об арифметической группе автомор-
автоморфизмов неопределенной квадратичной формы» * устанавливается
существование фундаментальной области V (удовлетворяющей усло-
условиям 1 и 2) для неопределенных целочисленных форм с п пере-
переменными сигнатуры п — 2, состоящей из конечного числа выпуклых
пирамид с конечным числом граней.
13. Четвертая часть пятого раздела «Арифметических
исследований», содержащая приложение теории тройничных
квадратичных форм и исследования о числе классов
Эта часть, озаглавленная «Некоторые приложения к теории
двойничных форм», изложена в пп. 286—307.
1. Доказательство теоремы о родах: -у = 2х. В п. 286 Гаусс,
используя построенную им теорию тройничных форм, доказывает глу-
глубокую теорему: всякий класс главного рода получается удвоением (воз-
(возведением в квадрат) некоторого класса. Делает он это так. Пусть
F = (A, В, С) — некоторая двойничная квадратичная форма главного
рода определителя D. Рассмотрим ей обратную форму F' = (А9 — В, С)
и будем представлять эту последнюю тройничной формой / = х2 —2yz.
В силу вышеизложенной теории представления двойничных форм
тройничной формой это возможно. Действительно, Д — 1, поэтому
надо искать «значение» У (А, В, С) (modD), а в силу того, что фор-
форма F — главного рода (только тут учитывается то, что F — главного
рода), можно показать, что такие «значения» имеются. Далее,
* «Известия АН СССР», № 2, 1937.
940 Б. Н. Делоне
в силу специальных свойств формы /, тройничная форма g опре-
определителя А = 1, такая, что ее коэффициенты а, а', а", b, b', Ъ" удов-
удовлетворяют нужным условиям, тоже существует, причем для формы /
и коэффициенты а", Ь, V формы g выходят целые, а полученная
форма g определителя А = 1 оказывается неопределенной. Но так
как выше было доказано, что имеется только один класс неопре-
неопределенных тройничных квадратичных форм определителя А = 1 и
что все они эквивалентны форме /, то форма g эквивалентна /.
Можно, следовательно, найти хотя бы одно преобразование
ос р т
а' р' Т'
а" р* Т"
формы / в форму g. Каждое из таких преобразований дает пред-
представление
х = <xt + ри, хг = n't + р'и, of = aft + $"и
формы F' формой /. Именно, мы будем иметь
А = а2 — 2аV, — В - оф — ос'р" — а*р', С = р2 — 2р'Р".
Если обозначить числа оф' — а'р, а'р" — а'ф', а'ф — а^' через:
а, 6, с, то они будут взаимно простые, и мы будем иметь
D = b2 — 2ac.
Но учитывая, как получается двойничная форма, которая есть
композит двух двойничных квадратичных форм, можно непосред1-
ственным вычислением проверить, что форма
F = (A,B,C) = AX2 + 2BXY + СУ2
при помощи подстановки
X = 2$'хх' + ру' + $ух' + р"г/г/'; У -= Ъх!хх' + ажг/' + аух' + а^г/г/'
переходит в произведение
Bах2 — 2Ьху + су2) {2ах'2 — 2Ьх'у' -f су'2),
Четвертая часть раздела V «Арифметических исследований» Гаусса 941
т. е. в квадрат (в смысле композиции форм Гаусса) формы
Bа,—Ъ, с),
а при помощи подстановки р', р, [З2, [3"; а', а, а, 2а" — в квадрат
формы
(а, -6, 2с).
Одна из этих двух форм, как легко видеть, собственно прими-
примитивная. Таким образом, всякая форма (А, В, С) главного рода
есть квадрат некоторой собственно примитивной формы того же
определителя.
Вернувшись к соображениям п. 261, мы видим, что раз всякий
класс главного рода есть квадрат некоторого класса, то 8 = g.
Теперь уже, сравнивая равенства h = gy и h = 8а, мы видим, что
число родов равно числу а тех классов, квадраты которых суть
главный класс. А это число, как показал Гаусс, равно -к-Х==2х~1.
Число родов, значит, равно 2х-1.
Гаусс говорит, что если он не ошибается, этот результат пред-
представляет собой, может быть, самое красивое, что удается доказать
о целочисленных двойничных квадратичных формах. С этим нельзя
не согласиться, так как таким образом о таинственном числе клас-
классов h квадратичных форм с данным определителем (или, что все
равно, числе классов идеальных делителей в данном квадратичном
поле) получен глубокий и простой результат: если определитель D
делится на разные простые числа и их число равно X (иногда надо
еще рассматривать модули 4 и 8), то число родов в точности равно
2Л~1, а, следовательно, число классов h есть кратное этого числа:
h = g2x~1. Каково же число g классов в каждом роде — это неиз-
неизвестно и до сих пор. Наиболее далекий в настоящее время полу-
полученный результат в этом вопросе состоит в том, что если D = Ь2—
— ас < 0, то, какое бы ни зафиксировать положительное число е,
для всех достаточно больших (по абсолютной величине) D имеют
место неравенства
(результат Хейльбронна и Зигеля).
942 Б. Н. Делоне
2. Теория родов Гаусса с точки зрения теории алгебраических
чисел. После описания того, каким образом Гаусс доказал основ-
основную теорему о родах, стоит остановиться на том, что такое тео-
теория родов с точки зрения современной теории алгебрадческих
чисел.
Дело в том, что определение понятия рода у Гаусса (см.
стр. 916) очень формальное. К одному роду Гаусс относит те классы
данного определителя, характер (Totalcbaracter) которых одина-
одинаков. Можно подойти к понятию рода гораздо более по существу,
если опираться на теорию алгебраических чисел.
Заметим прежде всего, что простые числа, которые представ-
представляют хотя бы одной из форм данного определителя, это те и только
те простые числа, по которым число 4D есть квадратичный вычет,
а тогда, как это следует из закона взаимности, это те и только те
простые числа, которые содержатся хотя бы в одной из конечного
числа некоторых определенных прогрессий: ADt -J- 1Ъ ADt -f- h, . . >
. . . ,Ш + 1к (см. стр. 902).
Известно, что аналогичное утверждение не имеет места для от-
отдельного класса форм. Например, для формы х2 ~\- ху + 6у2 опре-
определителя 23 нельзя указать таких прогрессий: Nt + l±, Nt -{- l2, ...
.. . , Nt + lk .. .
Возникает следующая задача: каким образом можно так раз-
разбить все h классов Къ . . . , Kh квадратичных форм данного опре-
определителя на группы (Къ . . . , Кп) (КГ1+1, .. ., Krz) ...(... Kh),
такие, что для того, чтобы простое число р представлялось хотя
бы одним из классов заданной группы, было бы необходимо и до-
достаточно, чтобы оно содержалось хотя бы в одной из некоторых
заданных прогрессий.
Разбиение, при котором все классы попадают в одну группу,,
этому условию удовлетворяет, а разбиение, при котором каждый
класс образует отдельную группу, вообще говоря, не удовлетворяет.
Интересно найти, конечно, разбиение на такие самые маленькие
группы, которые этому условию удовлетворяют. Таким разбиением
является разбиение на роды.
Для того чтобы доказать это обстоятельство, обратимся к тео-
теории алгебраических чисел.
Четвертая часть раздела V «Арифметических исследований» Гаусса 943
Пусть А — произвольное нормальное поле алгебраических чи-
чисел, и оно получается от расширения поля R рациональных чисел
присоединением к нему целого алгебраического числа а, и р — ка-
какой-нибудь простой идеальный делитель поля К, не входящий в
дискриминант числа a, a p — то натуральное простое число, кото-
которое делится на р. Легко показать, что с} ществует одна и только
одна подстановка s группы Галуа @ поля А, для которой выпол-
выполняется сравнение
а/5 =zap (modp).
В таком случае говорят, что простой делитель р принадлежит
«в смысле Фробениуса» к автоморфизму s поля А^. Другие про-
простые делители числа р принадлежат, в этом смысле, к подстанов-
подстановкам, сопряженным с s, и поэтому говорят, что простое натураль-
натуральное число р принадлежит «в смысле Фробениуса» к классу сопря-
сопряженных подстановок группы @. Очевидно, что всякое натуральное
простое число /?, не входящее в дискриминант числа а, принадле-
принадлежит, в этом смысле, к одному и только одному классу сопряженных
подстановок группы @. Поэтому все натуральные простые числа р,
кроме конечного их числа, разбиваются относительно поля А^ на
классы Фробениуса, число которых равно числу классов сопряжен-
сопряженных элементов группы @.
Н. Г. Чеботарев доказал важную теорему о том, что к любому
классу сопряженных элементов группы @ принадлежит, в указан-
указанном смысле, бесконечно много простых чисел р.
Можно показать, что если А, тоже нормальное над Л, подполе
поля А, то всякий класс Фробениуса поля А есть совокупность
кнескольких целых классов Фробениуса поля А.
Если поле К есть поле деления круга на т частей, то каждый
класс сопряженных подстановок его группы @ состоит только из
одной подстановки (так как @ абелева). Простые числа /?, принад-
принадлежащие к данной подстановке поля деления круга, суть, как
легко показать, не что иное, как все простые числа некоторой
арифметической прогрессии mt-\-l, где I — то или иное из <р (т)
чисел, меньших т и взаимно простых с т, в зависимости от того,
какую из ср (т) подстановок мы рассматриваем.
944 Б. Н. Делоне
Всякое абелево над R поле алгебраических чисел есть некото-
некоторое подполе некоторого поля деления круга (теорема Кронекера —
Веб ера), и поэтому, учитывая вышесказанное, получается, что класс
Фробениуса для абелева поля есть совокупность всех простых чи-
чисел, представляемых некоторыми прогрессиями mt -f- 1Ъ mt -f-12, ...
..., mt -f- U-
При помощи теории поля классов можно доказать следующую
теорему.
Пусть R Q/~d) — квадратичное поле определителя d. И пусть
К—наибольшее абелево над RQ/H) неразветвленное его расши-
расширение, т. е. наибольшее поле алгебраических чисел, которое полу-
получается от присоединения к полю R(yd) корня абелева, относи-
относительно него, уравнения с коэффициентами из этого поля, отно-
относительный дискриминант которого по отношению к полю RQ/H)
равен 1. Как это доказывается в теории поля классов, группа
Галуа G (абелева) этого поля К по отношению к полю RQ/H) изо-
изоморфна группе классов идеалов поля RQ/H) и имеет, следова-
следовательно, порядок h. Степень поля К над рациональным полем равна
2/г; поле К относительно рационального поля тоже нормальное
поле, но его группа Галуа @ относительно рационального поля R
уже, вообще говоря, не абелева.
Легко видеть, что если подстановка s группы @ входит в ее
подгруппу G, то класс сопряженных с s в группе (? подстановок со-
состоит из двух подстановок s и s. При помощи теории поля клас-
классов можно показать, что те простые числа р, которые представля-
представляются данным примитивным классом квадратичных форм определителя
d (без двоек при Ъ), суть те и только те простые числа, которые в
поле К принадлежат «в смысле Фробениуса» к классу $, s'1 сопря-
сопряженных подстановок группы @, образуемых той подстановкой $
группы G, которой соответствует рассматриваемый класс квадратич-
квадратичных форм.
Из этой теоремы получается два следствия.
I. Все простые числа р, представляемые формами, принадлежа-
принадлежащими к разным, но не обратным друг другу классам примитивных
форм данного определителя d, различны, а представляемые формами
Четвертая часть раздела V «Арифметических исследований» Гаусса 945
обратных классов — одинаковы. Последнее — очевидно, так как форме
(а, Ь, с) обратна форма (а, —Ъ, с), а эти формы, очевидно, пред-
представляют одинаковые числа при х = т, у = п и х = т, у = — п.
II. Всякая примитивная форма представляет бесконечно много
простых чисел, —это следует из теоремы Чеботарева для рассмат-
рассматриваемого поля К, но может быть, правда, доказано и минуя тео-
теорему Чеботарева.
Перейдем теперь к разбиению классов Къ . . . , К^ на группы
(Ки . . . , КГ1), (КГ1+и . . . , КГ2), ... (. . . Kh), о которых мы го-
говорили выше.
Рассмотрим наибольшее абелево над R подполе К поля А", рас-
рассматривавшегося нами сейчас. Само поле К (степени 2/г) тоже мо-
может быть абелевым над R, но может им и не быть. Во всяком
случае, квадратичное его надполе RQfd) абелево над R; поэтому
та подгруппа Н группы @ поля К, которой принадлежит К, есть
подгруппа группы G. При помощи теории поля классов можно по-
показать, что ее подстановкам соответствуют классы главного рода, а
подстановкам смежных с Н в G систем — классы других родов.
Таким образом, теория родов связана с вопросом о наибольшем
абелевом относительно R подполе, которое содержится в так
называемом абсолютном поле классов К рассматриваемого квадра-
квадратичного поля Я(УA).
Если поле К само абелево, то Н = 1 и главный род, а следова-
следовательно, и все роды, имеют по одному классу. Другой крайний слу-
случай, когда наибольшее абелево подполе К есть поле R(j/"d); тогда
Н = G и все классы образуют один род. Но могут быть и проме-
промежуточные случаи.
Классы Фробениуса поля К суть некоторые комплексы клас-
классов Фробениуса поля К, но какие?
Разложим группу @ поля К на смежные системы по ее под-
подгруппе Н:
© = H + s2H + s3H+... + srH-
тогда эти смежные системы своей композицией образуют группу
@ поля К, Так как группа @ абелева, то классы ее сопряженных
946 Б. Н. Делоне
элементов совпадают с отдельными ее элементами. Так как Н czG,
то у каждой из этих смежных систем либо все ее элементы лежат
в G, либо все не лежат в С, в зависимости от того, лежит ли в G
соответственный коэффициент разложения Si. Поэтому те из этих
систем, которые лежат в G, суть просто все смежные системы G по
Н. Классы Фробениуса поля К, соответствующие классам s, s'1
сопряженных в @ элементов, где s— подстановка G, как можно
показать, объединяются в некоторые классы Фробениуса поля К,
если объединять те из них, у которых s принадлежит одной и той
же смежной системе G по Н. Отсюда, учитывая сказанное вышег
и получается, ^то совокупность простых чисел р, представляемых
хотя бы одной из форм одного и того же рода, есть не что иное,
как некоторый класс Фробениуса поля К. Но так как поле К абе-
лево, то эта совокупность простых чисел р есть не что иноег как
совокупность всех простых чисел р, представляемых некоторыми
определенными прогрессиями.
Итак, разбиепие классов на роды есть одно из разбиений на груп-
группы, о которых мы говорили выше. Можно из этих же соображений по-
показать, что не может быть более дробного такого разбиения.
Совершенно иной подход к теории родов квадратичных форм
следующий,
Две целочисленные квадратичные формы / и g с п переменными
и матрицами А ж В называются принадлежащими к одному и тому же
роду, если для любого целого q существует такая матрица с ра-
рациональными элементами Г, что Т*АТ = В и знаменатели всех эле-
элементов Т взаимно просты с q.
Этот подход к теории родов ценен тем, что он сразу охватывает
квадратичные формы с любым числом п переменных. К сожалению,
мы не имеем возможности останавливаться на этой теории родов.
Можно показать, что две формы принадлежат к одному и тому же
роду, если они целочисленно р-адически эквивалентны при любом р
и, кроме того, вещественно эквивалентны.
3. Дальнейшие приложения теории тройничных квадратичных
форм. Вернемся к дальнейшему описанию содержания четвертой
части пятого раздела «Арифметических исследований». После изло-
изложения в первых двух пунктах (пп. 286 и 287) этой части доказатель-
Четвертая часть раздела V «Арифметических исследований» Гаусса 947
ства теоремы о родах Гаусс в дальнейших его пунктах (пп. 288—
300) разбирает ряд классических задач, которые решаются при помо-
помощи построенной им теории. Задачи эти следующие: теория разложе-
разложения чисел или двойничных квадратичных форм на три квадрата
(пп. 288—292); доказательство теоремы, высказанной Ферма, о том,
что любое натуральное число может быть разложено на три треуголь-
треугольных числа или на четыре квадрата (как известно, эта последняя зна-
знаменитая теорема была впервые доказана Лагранжем) (п. 293). Что же
касается теоремы, высказанной также Ферма, о том, что всякое на-
натуральное число есть сумма пяти пятиугольных, шести шестиуголь-
шестиугольных чисел и т. д., то она была лишь гораздо позже доказана Коши.
Далее Гаусс дает решение неопределенного уравнения ax2jr by2 +
-J-cz2=0 в целых числах (пп. 294—295), излагает соображения о мето-
методе, которым Лежандр пытался доказать закон взаимности (пп. 296—
298); решает вопрос о представлении нуля любой тройничной квадра-
квадратичной формой (п. 299); наконец, дает общее решение неопределен-
неопределенного уравнения 2-й степени с двумя неизвестными в рациональных
числах (п. 300). В последних заключительных пунктах (пп. 301 —
307) Гаусс снова возвращается к двойничным квадратичным формам
и рассматривает в п. 301 вопрос о среднем числе их родов, впп. 302—
304 — вопрос о среднем числе классов и, наконец, в пп. 305—307—
понятие о регулярных и иррегулярных определителях. Во всех этих
пунктах Гаусс старается более глубоко, чем он это сделал до того,
проникнуть в свойства группы классов квадратичных форм данного
определителя, но исследования этих пунктов носят определенно неза-
незаконченный и фрагментарный характер.
Поясним, в чем они состоят.
4. Исследования Гаусса о среднем числе классов. Ввиду того,
что число родов зависит от числа различных простых делителей опре-
определителя Z), для ряда идущих подряд определителей ~f- D,
+ (Z>-f-l), + (-D + 2), . . . число родов скачкообразно, то увеличи-
увеличивается, то опять уменьшается; однако, как замечает Гаусс, если
сложить число родов для идущих подряд определителей + Z),
+ (/) -f 1)> . . . -Ь (D -]- т— 1) и разделить их на их число га, то
получится «среднее» число родов, которое можно оценить. Для
этого надо считать, что т берется очень большим (например, фик-
948 Б. Н. Делоне
сированным), а затем D берется еще гораздо большим, чем т.
Гаусс говорит, что это среднее число родов может быть хорошо
представлено формулой oclogD + p, где а и р — некоторые найден-
найденные им постоянные.
Аналогично Гаусс ставит вопрос о среднем числе классов дан-
данного определителя D, причем он получает, что «среднее» число
классов может быть хорошо представлено формулой
—8,
2ти ,.1,1,1.1. . 2 Тз
где T=7S' б = 1+ 8- + 27 + 64 + 125+-'-' а ^ = —. В свя-
зи с этим Гаусс получает следующую приближенную формулу
для числа ^j h (— Д) всех собственно примитивных классов всех
А=1
отрицательных определителей, которые по абсолюгной величине
меньше или равны т:
уТ(К mf — 8т,
где y и 5 — числа, указанные выше.
Гаусс говорит, что он получил эту формулу «при помощи теоре-
теоретических исследований» и что она очень близко сходится с тем,
что он получил при помощи непосредственных численных проб.
Сейчас можно только гадать, как Гаусс мог найти эту формулуг
учитывающую и второй член — 8т, в то время.
Формула эта была впервые доказана в работе 1918 г. И. М. Ви-
Виноградовым со следующим остаточным членом:
A=l
3
иг7 (log иг)»).
5. Дальнейшие исследования Гаусса о числе классов целочисленных
двойничных квадратичных форм. Среди посмертно (в 1876 г.) издан-
изданных работ Гаусса (Nachlass) имеются две статьи, озаглавленные
«О связи между числом классов, на которые распадаются двой-
двойничные формы второй степени, и их определителем» (De nexu inter
Четвертая часть раздела V «Арифметических исследований» Гаусса 949
multitudinem claseium in quas formae binariae secundi gradus di-
stribuuntur earumque determinantem) и доложенные Гёттингенскому
королевскому обществу: первая — в 1834, а вторая — в 1837 г., но
не напечатанные при жизни Гаусса.
Эти статьи заключают в себе дальнейшие исследования Гаусса
о числе классов h целочисленных двойничных квадратичных форм дан-
данного определителя D. Обе эти статьи являются лишь незаконченными
фрагментами. Однако из них видно, что Гаусс уже до Дирихле
подошел к выводу тех же формул для числа классов, которые дал
затем Дирихле в знаменитой своей работе 1840 г.: «Recherches sur di~
verses applications de Vanalyse infinite simale a la theorie des nombres»*.
Вывод этих замечательных формул основан на двух различных спо-
способах найти некоторую «плотность». Первый способ дает эту плот-
плотность как произведение числа классов h на некоторую величину *,
которая легко вычисляется и выражается через дискриминант D и ос-
основное решение уравнения Пелля х2 — By1 = 1. Второй способ дает
* vi (D\ i
эту плотность в виде бесконечного ряда 2J \~^) 7г~ » не зависящего
(явно) от числа классов. Сравнение этих двух выражений этой плотно-
плотности дает число классов h.
Из статей Гаусса ясно видно, что принципы для получения пер-
первого выражения искомой плотности у Гаусса и у Дирихле совпадают.
Что же касается второго выражения искомой плотности, то его
Гаусс получил, по-видимому, уже очень давно (в декабре 1800 г.), но
как он к нему пришел, из оставшихся после него фрагментов не впол-
вполне ясно. Путь, который, по-видимому, привел Гаусса к этому вто-
второму выражению, выясняет Дедекинд в своих комментариях к этим
работам Гаусса **.
Поясним с той точки зрения, на которую мы стали на
стр. 887, 892, о какой плотности идет речь и в чем состоит вывод
первой формулы для нее. Пусть, например, задано вещественное
квадратичное поле к и дискриминант его равен Z), а число его
классов h. Предположим для простоты (хотя и общий случай рас-
рассматривается совершенно аналогично), что не только решетка О
* D irich I et. Werke, Bd. I.
** С. F. G a u s s. Werke, Bd. II, стр. 292—303.
950 Б. Н. Делоне
вещественная, но и все ее побочные решетки Клейна 0', 0", . . .
...,0(k—*) тоже вещественные (дело в том, что даже при вещественности
поля к некоторые из тех множителей Х2, Х3, . . . , ХЛ, на которые
мы помножали (стр. 892) представителей g2, g3> • • • > 3to идеалов
неглавных классов, для того чтобы получилось правильное распо-
расположение решеток Клейна 0', 0", . . . , 0(/1-1), иногда могут полу-
получаться комплексными). Предположим также еще, что норма основной
единицы е0 положительная.
Рассмотрим угол Пелля кольца 0, т. е. угол, образованный
произвольным лучом, исходящим из начала и лежащим в первом
квадранте ОЪ\, и тем лучом, в который он переходит при помощи
того наименьшего «гиперболического» (относительно асимптот 01,
Ог[) поворота плоскости, при котором решетка О переходит в себя.
Этот поворот получается от умножения всех точек плоскости на
основную единицу е0.
Не только решетка 0, но и каждая отдельная из решеток 0',
О", . . . , O^h~1\ периодична в том смысле, что она при этом гипер-
гиперболическом повороте совмещается с собой. В силу этого совокуп-
совокупность всех точек системы 0*, лежащих в таком углу Пелля, есть
совокупность всех точек О* с положительной нормой, попарно не
ассоциированных одна с другой, т. е. не отличающихся между со-
собой лишь множителями единицы. Точки 0*, лежащие во 2-м и 4-м
квадрантах, имеют отрицательные нормы, а точки 0*, лежащие в
3-м квадранте, ассоциированы с точками, лежащими в 1-м, при
помощи единицы: —1.
Обозначим через П(?) ту часть угла Пелля, которая отрезается
от него гиперболой Ъ\ = t (где t > 0), и обозначим площадь ПA)
через Пх; в таком случае площадь области П(?) равна Шь так
как область П(?) получается из области ПA) гомотетией с коэф-
коэффициентом Уь относительно начала координат.
Число Т точек 0*, лежащих в области П(?), представляет со-
собой число всех различных идеалов поля к с положительными нор-
нормами, не превышающими t.
Ввиду того, что площади основных параллелограммов всех ре-
решеток 0, О\ О", . . . , O^h~1) одинаковы и равны }/Т), что решетки
эти попарно не имеют общих точек, кроме начала, и что число
Четвертая часть раздела V «Арифметических исследований» Гаусса 951
точек решетки с данной площадью основного параллелограмма,
принадлежащих данной области, приблизительно равно площади
этой области, деленной на площадь этого параллелограмма, или,
точно говоря (при увеличении коэффициента гомотетии }/^t ), асимп-
асимптотически равно этому отношению,— число Т точек 0*, лежащих в
П (t)f асимптотически равно h—= . Отсюда следует, что предел
Т
lim—- — /гх,
t
где х = —4=. Этот предел называется плотностью идеалов поля &.
Это, попросту говоря, плотность точек системы 0*, если за еди-
единицу площади принимать площадь Пх.
Вывод второй формулы для этой «плотности» проводится так.
Пусть F (т) есть число различных идеалов поля к с положи-
положительной нормой т, т. е. число точек 0*, лежащих на гиперболе
|т] = т в угле Пелля. Искомый предел
lim-f = lim F(l) + FB) + ... + F(t) _
Но если расположить идеалы к с положительными нормами по
увеличению нормы и они суть $ь $2, . . . , $т', . . . , а их нормы
<^. . . <^гсг<С . . . , то мы имеем очевидные неравенства
FB) + .. . +F(nT — l) < Г <FA) + FB) + .. . + F{nT\
или, если разделить на пт>, то неравенства
и поэтому, так как lim ( 1 ] = 1, то, какое бы малое по-
грр -^ I Игр/ I
ложительное 5 ни взять, мы будем, для всех достаточно больших
Т\ иметь /гх— 8 < < их -|- 8, или деля на J", —^т— < <
tlrp, 1 ^Т'
. foe + В о
< —тр— . Возведя все части этого последнего неравенства в 5-ю
952 Б. Н. Делоне
степень, где s>l, умножая на (s — 1) и суммируя по всем Т',
большим некоторого достаточно большого Уо, мы получим неравен-
неравенства
Гр f Л rpf TLrpt rpf JL
sr\ 1
Но известно: 1) что ряд 2j~t пРи s> ^ сходится и 2} что
s->l t t
Поэтому, приближая в предыдущих неравенствах s к 1, мы
получим равенство
Левая часть этого равенства является второй формулой для
искомой «плотности»; она явно не зависит от ft, в ней суммирова-
суммирование производится по всем идеалам поля к с положительной нормой.
Дальнейшее преобразование левой части этого равенства произ-
производится, во-первых, опираясь (два раза) на знаменитое «тождество
Эйлера» ^ ~ = П =7 » где п пР°бегает все натуральные, а р—
л 1 — р
все простые числа, и которое имеет следующее обобщение на все
идеалы g и все простые идеалы р некоторого поля к:
здесь п —¦ значок нормы. Ряд V. называется дзета-функцией
Дедекинда данного поля к и обозначается C(s).
Во-вторых, в этом преобразовании левой части равенства (*)
учитывается закон разложения натуральных простых чисел р на
простые идеалы квадратичного поля к. Используя этот закон,
можно получить, что
Четвертая часть раздела V «Арифметических исследований» Гаусса 953
где (—) — символ Лежандра. Отсюда величина lim ((s — 1) С (s)),
называемая вычетом дзета-функции, получается равной
или, если учесть, что
то
lim(($ — l) С ($))== lim'
Воспользовавшись снова тождеством Эйлера, но уже в обратном
направлении, мы получаем
или, окончательно, формулу
/с-Х — / . (
\J п '
которую уже знал Гаусс.
При помощи дальнейшего упрощения этой формулы получаются
следующие формулы Дирихле для числа классов h квадратичного
поля, которые содержат уже лишь конечные суммы.
В случае kQ/m), m<C0
а в случае к(\/~т), ту О
bin bin
2' II(.--.--
954 Б. Н. Делоне
где П распространены на все квадратичные вычеты а и квадратич-
квадратичные невычеты Ъ (modi)).
В течение 90 лет после опубликования этих формул Дирихле мате-
математикам не удавалось избавиться от средств анализа при выводе
этих конечных формул, выражающих искомое натуральное число h.
Первый, кто сдвинул этот вопрос, был Б. А. Венков. В своей ра-
работе «Uber die Klassenzahl positiver bindrer quadratischen Formen»
(Math. Zschr., 1931, 33) он вывел формулы Дирихле при т<0 для слу-
случая d^ I (mod 8) из совсем другого принципа, а именно, применяя
арифметику кватернионов, вовсе не прибегая к средствам анализа,
и тем самым более глубоко вник в чисто арифметические свойства
этого числа.
6. Регулярные и иррегулярные определители Гаусса и история
теории абелевых групп. В п. 305 Гаусс называет определитель D ре-
регулярным, если в главном роде есть такой класс, что всякий класс
главного рода есть степень этого класса, т.е. если группа классов
главного рода циклическая. Если определитель D нерегулярный, то
эта группа — некоторая нециклическая абелева группа.
В п. 306 Гаусс говорит: «Относительно наиболее удобного распо-
расположения системы классов, которые содержатся в главном роде в слу-
случае иррегулярного определителя, мы здесь, ради краткости, говорить
не будем; заметим только, что так как одного основания (базиса, про-
производящего элемента — Б. Д.) в этом случае недостаточно, то необхо-
необходимо брать два или даже еще большее число классов, при умножении
и композиции которых получаются уже все остальные. При этом
получаются двойные и кратные индексы, польза которых состоит
примерно в том же, в чем состоит и польза простых индексов при ре-
регулярных определителях. Однако подробнее мы рассмотрим этот во-
вопрос при другом подходящем случае». Насколько, однако, известно, не
сохранилось записей Гаусса также и в его «Рукописном наследии»г
в которых была бы дана теорема о базисе абелевой группы.
В предисловии к своей известной работе «О группах перестано-
перестановочных элементов» A879) Фробениус и Штикельбергер говорят: «Ос-
«Основания теории конечных групп перестановочных элементов (конеч-
(конечных абелевых групп — Б. Д.) были положены, с одной стороны,
Эйлером и Гауссом, а с другой,— Лагранжем и Абелем, первыми в их
Четвертая часть раздела V «Арифметических исследований» Гаусса 955
арифметических исследованиях по теории степенных вычетов, а вто-
вторыми — в их алгебраических работах, относящихся к решению урав-
уравнений. После этих, положивших начало, исследований Гаусс и Ше-
ринг продолжили эту теорию. Гаусс (Werke, II, 266; Nachlass, 1876)
дает разложение группы на примарные группы, порядки которых
взаимно простые (в прямое произведение таких групп — Б. Д.), а
Шеринг (Gott. Nachr., 1869, S с h е г i n g. Werke, Bd. I) дает ее
разложение в элементарные группы, порядок каждой из которых де-
делится на порядок следующей». Таким образом, теорему о базисе абе-
левой группы на примере гауссовой композиции классов впервые
нашел Шеринг в 1869 г. В 1870 г. Кронекер перенес ее на абелевы
группы вообще.
В этом месте стоит отметить, что в упоминавшейся не раз выше
теории поля классов арифметический подход Эйлера и Гаусса и ал-
алгебраический подход Лагранжа и Абеля для случая абелевых групп
оказываются как бы соединены и являются там двойственными опи-
описаниями одних и тех же фактов.
7. Значение собственной эквивалентности в теории композиции
классов Гаусса. Поясним в заключение этого параграфа, какое преиму-
преимущество имеет для теории композиции классов различение, делаемое Га-
Гауссом между собственной и несобственной эквивалентностью форм,
Если классом считать, по Гауссу, совокупность собственно эквива-
эквивалентных между собой форм, то получается группа классов, рассмот-
рассмотренная в теории композиции, изложенной выше. Если же, как это
делал Лагранж, относить в один класс как собственно, так и не-
несобственно эквивалентные между собой формы, то теория компози-
композиции запутывается. Действительно, формы (а, Ь, с) и (а, —Ь, с) несоб-
несобственно эквивалентны одна другой, вторая получается из первой под-
подстановкой [q _л. В смысле билинейной композиции произведение
этих форм дает, как легко убедиться, главную форму A,0, Z>), т. е.
классы, соответствующие этим формам, обратные. Каждый класс
Лагранжа есть, следовательно, сумма двух взаимнообратных классов
Гаусса. Пусть имеются два класса Лагранжа а + а, Ъ + Ъ'1, где
а и Ъ —классы Гаусса. Рассмотрим произведения afr, сГхЪ, аЪ \
аГ1^1. Из них аЪ и аГ1^1 принадлежат взаимнообратным клас-
классам, а а^Ь и ab1 — двум другим взаимнообратным классам. Поэтому
956 Б. Н. Делоне
произведения форм двух классов Лагранжа дают не формы одного
определенного класса Лагранжа, а формы одного или другого из
некоторых двух классов Лагранжа. Поэтому композиция форм не
ведет к группе композиции классов (в смысле Лагранжа), а к некоей
мультигруппе.
14. Шестой раздел «Арифметических исследований».
Различные приложения теории чисел
Раздел этот озаглавлен: «Различные применения предыдущих
исследований» (пп. 308—334).
Гаусс начинает его словами: «Во многих местах до этого мы уже
касались того, насколько высшая арифметика богата истинами, на-
находящими применение также и в других частях математики; мы счи-
считаем, однако, небесполезным — специально рассмотреть некоторые
приложения, которые заслуживают 6oiee подробного изложения,
не столько для того чтобы исчерпать этот предмет, которым легко
могли бы быть заполнены многие тома, сколько для того, чтобы на не-
нескольких примерах пролить на него более яркий свет».
Гаусс подробно рассматривает решение следующих задач.
В пп. 309—311 рассматривается разложение дроби в сумму более
простых дробей, основанное на теореме: если знаменатель п дроби ~
равен произведению взаимно простых чисел а, Ь7 с, d, ..., то можно
представить дробь в виде
В пп. 312—318 подробно рассматривается теория обращения обык-
обыкновенных дробей в десятичные.
В пп. 319—322 решается сравнение х2 = A (mod m). Гаусс гово-
говорит, что, конечно, можно решать это сравнение при помощи таблиц
индексов, но что делать, если вычисления выходят за пределы этой
таблицы; поэтому Гаусс дает другой удобный способ, который он
подробно разбирает.
В пп. 323—326 предлагается близкий к предыдущему способ для
решения неопределенного уравнения тпх2 + пу2 = А.
Раздел VII «Арифметических исследований» Гаусса 957
В пп. 327—328 дается другой способ решения сравнения
х2 "еее: A (mod m)
для случая, когда А < 0.
В пп. 329—334 рассматриваются два различных способа узна-
узнавать, простое ли заданное число.Один основан на теории квадратичных
вычетов, а другой — на одном соображении, связанном с теорией
квадратичных форм.
15. Седьмой раздел «Арифметических исследований».
Теория деления круга Гаусса
Этот последний раздел, озаглавленный «Об уравнениях, от которых
зависит деление круга», посвящен одной алгебраической теории, в
которой играют существенную роль некоторые соображения теории
чисел, а именно теории уравнения хп = 1.
Уравнение это называется уравнением деления круга потому,
что корни его суть точки комплексной плоскости, лежащие на ок-
окружности радиуса 1 с центром в начале и делящие эту окружность
на п равных частей.
1. Возникновение этой теории у Гаусса и основной его результат.
В рассматриваемом седьмом разделе Гаусс строит во всех деталях для
этого частного уравнения теорию, совпадающую с теорией Галуа
A811—1832). Галуа построил свою общую теорию алгебраических
уравнений около 1830 г., т. е. через 30 лет после выхода в свет книги
Гаусса, причем эта теория была опубликована лишь через 15 лет после
смерти Галуа, в 1846 г., Лиувиллем, а сделалась общим достоянием
алгебраистов только в конце 50-х годов прошлого столетия, после
появления в свет курса высшей алгебры Серре. Теория Галуа имеет
как бы две стороны — алгебраическую и арифметическую. Если
подготовкой алгебраической стороны теории Галуа были работы по
теории алгебраических уравнений Лагранжа, то подготовкой ее
арифметической стороны была теория деления круга Гаусса. Сам
Галуа в своем основном мемуаре ссылается на теорию деления кру-
круга Гаусса, которая, очевидно, послужила для него как бы прообразом
при построении его общей теории.
Исследование уравнения хп= 1 дало, кроме того, Гауссу возмож-
958 Б. Н. Делоне
ность решить знаменитый вопрос о том, каково должно быть число
сторон правильного многоугольника для того, чтобы его можно
было построить циркулем и линейкой. Оказалось, что кроме пра-
правильных многоугольников, у которых число сторон равно 2k9 3*2kf
5-2Л или 15 -2Л, возможность построения которых была известна
уже древним, можно построить циркулем и линейкой многие дру-
другие, например, правильный семнадцатиугольник.
Это поразительное открытие Гаусс сделал еще до того, как он
начал писать «Арифметические исследования». В июне 1796 г. в
«Литературной газете», издававшейся тогда в Иене, была помещена
следующая заметка:
«Новые открытия
Всякому начинающему геометру известно, что можно геометрически (т. е.
циркулем и линейкой — Б. Д.) строить разные правильные многоугольники,
а именно треугольник, пятиугольник, пятнадцатиугольник и те, которые полу-
получаются из каждого из этих путем последовательного удвоения числа его сторон.
Это было уже известно во времена Эвклида, и, как кажется, с тех пор было рас-
распространено убеждение, что область элементарной геометрии дальше не распро-
распространяется: по крайней мере, я не знаю удачной попытки распространить ее
в эту сторону. Тем более кажется мне заслуживающим внимания открытие, что
кроме этих правильных многоугольников может быть геометрически построено
еще множество других, например семнадцатиугольник. Это открытие является
собственно лишь следствием одной еще не совсем законченной большой теории^
Как только она получит эту законченность, она будет предложена публике.
К. Ф. Гаусс из Брауншвейга,
Студент-математик в Геттингене».
В рассматриваемом седьмом разделе Гаусс доказывает, что если
число п сторон правильного многоугольника имеет вид n = pipr..pi-2hf
где pi,Pj, . . ., pi—различные простые числа вида р = 2m-j- 1, то он
может быть построен циркулем и линейкой. (Для того чтобы число
2т-\- 1 было простым, показатель т не должен иметь нечетных про-
простых делителей, так как если бы т = qml9 где q нечетное, то число
это можно было бы написать так: 2т+ 1 = Bт^+ lq, но число
это делится на 2т*-|- 1 и, следовательно, непростое. Показатель т
здесь, следовательно, может быть сам только степенью двойки,,
т = 2*\ т. е. простые числа Pi,p$,. . . , имеют следующий вид;
Раздел VII «Арифметических исследований» Гаусса 959
В предпоследнем п. 365 Гаусс говорит, что он имеет верный
способ доказать и обратное, а именно, что ни при каких других р,
кроме указанных, правильный многоугольник построить циркулем
и линейкой уже нельзя. Он говорит далее, что «хотя границы на-
настоящего сочинения не позволяют привести здесь это доказатель-
доказательство, мы считаем все же своим долгом указать на это, чтобы никто
не надеялся бы свести еще и другие деления, кроме делений, да-
дающихся нашей теорией, например, деления на 7, 11, 13, 19, .. . ча-
частей, к геометрическим построениям (т. е. к построениям циркулем
и линейкой — Б. Д.) и не тратил бы бесполезно свое время».
Доказательство этой обратной теоремы сразу следует из общей
теории Галуа, но оно может быть проведено и непосредственно.
Перейдем теперь к изложению содержания самого седьмого раз-
раздела. В п. 336 Гаусс сводит задачу к случаю, когда п — простое
число. В последующем изложении поэтому число п уже везде пред-
предполагается простым. В п. 341 дается доказательство того, что мно-
хп ^
гочлен j— = xn~1Jr хп~2-\- ... -\- х -\- 1 = X, где п простое, не
приводим в поле рациональных чисел. Доказательство это сложновато,
сейчас найдены совершенно простые доказательства этого факта.
Совокупность корней уравнения X = 0 Гаусс обозначает через О.
В п. 342 Гаусс кратко резюмирует, какую основную теорему
он будет далее доказывать. Он говорит: «Цель дальнейших исследо-
исследований, указать которую представляется небесполезным, состоит в
том, чтобы последовательно разлагать X на все большее и большее
число сомножителей, причем так, чтобы их коэффициенты опреде-
определялись при помощи уравнений по возможности более низких степе-
степеней, пока мы не дойдем таким путем до простых сомножителей,
т. е. до самих корней из О. Именно, мы покажем, что если число
п — 1 каким-либо способом разложено на целочисленные сомножи-
сомножители а, р, т, • • • (которые можно считать простыми числами), то X
можно разложить на а сомножителей степени (п—1)/а, коэффици-
коэффициенты которых определяются уравнением степени а; далее, что эти
отдельные сомножители в свою очередь могут быть разложены на р
сомножителей степени (п—1)/оср при помощи уравнения степени р
и т. д., так что если v обозначает число сомножителей а, р, f, • • • ,
960
Б. Н. Делоне
то нахождение корней из О сводится к (последовательному — Б. Д.
решению v уравнений степеней а, р, f и т. д. Так, например, для
д = 17, где п —1=2-2-2-2, придется решить четыре квадратных,
а для п = 73(где п—1=2-2-2-3-3 — Б. Д.) — три квадратных и
два кубических уравнения».
2. Леммы о периодах и доказательство основной теоремы. Для^
доказательства этой основной теоремы Гаусс переходит к рассмот-
рассмотрению так называемых периодов.
Пункт 343 озаглавлен: «Все корни из О разбиваются на неко-
некоторые классы (периоды)».
Дело в следующем. Пусть г — какой-нибудь из корней ?1, тогда
все корни О суть г, г2, г3,... , гп~11 что доказать нетрудно. Если
теперь g — какой-либо первообразный корень простого числа п, то
числа 1, g, g2, .. ., gn—2 представляют собой по модулю п числа 1,.
2, 3, . . ., п— 1, но, может быть, взятые в другом порядке. Поэтому
г, г&, г?2, . . . , г?п~2—тоже все корни О. Каждый из этих корней
есть g-я. степень предыдущего, а так как gn~ 1=l(modn), то (r?n~~2J —
= г?п~~1= г, и поэтому первый из них есть в свою очередь g-я сте-
степень последнего.
Расположим мысленно эти корни последовательно, например,
против часовой стрелки, в точках, делящих некоторую окруж-
окружность на п—1 равных частей (эта окружность не есть окружность
комплексной плоскости) так, чтобы образовался правильный
(п—1)- угольник Р; тогда g-я степень каждого из этих корней
Раздел VII «Арифметических исследований» Гаусса 961
будет равна последующему за ним.Пусть теперь п—l = ef. Посмотрим,
какими свойствами обладают суммы по / этих корней такие, что соот-
соответствующие им / вершин многоугольника Р образуют правильный
/-угольник. Эти суммы Гаусс называет периодами длины /.
Если строить такую сумму, исходя от корня гх, то она будет
равна
\w+ яшш + r*hf~\ (I)
где h = ge, и каждое следующее ее слагаемое будет /г-й степенью
предыдущего и первое /г-й степенью последнего. Гаусс обозначает
эту сумму (/, X). Очевидно, что всё равно, с какой из его вершин
начинать такой /-угольник, т. е. что (/, \hk) = (/, X). Если в фор-
формуле (I) положить X —0 [или вообще X = 0(modn)], то получится
сумма (/, 0) -= /; эту сумму Гаусс тоже называет периодом. Но это
особый период, не входящий в число тех, которые мы выше пояс-
пояснили многоугольниками. Относительно периодов Гаусс доказывает
ряд лемм.
Лемма. Произведение двух разных или одинаковых периодов
одной и той же длины выражается линейно с целыми рациональ-
рациональными коэффициентами через периоды той же длины.
Например, если п = 19, т. е. п—1 =18, то
F,1J= F, 2) + F, 8) + F, 9) + F,12) + F,13) + F,19) =
Эта лемма очевидна, так как при умножении (/, X) на (/, |х)
надо составить сумму всех возможных произведений / корней г
входящих в (/, X) и / корней, входящих в (/, fx) но эту сумму
можно разбить на суммы тех / произведений, в которых расстоя-
расстояния по окружности против часовой стрелки корня из (/, jx) от ум-
умноженного на (/, [х) корня из (/, X) одинаковы. Каждая из этих
частных сумм произведений будет, очевидно, периодом той же дли-
длины /, или числом /, если показатели при г при этом получатся вес
делящиеся на п.
Следствие. Любая целая рациональная функция периодов
одной и той же длины с рациональными коэффициентами равна
линейной комбинации периодов этой длины с рациональными коэф-
коэффициентами.
962 Б. Н. Делоне
Это следствие получается повторным применением предыдущей
леммы.
Лемма. Если X не делится на п, то любой период (/, [х), где (л
тоже не делится на п, имеет следующее выражение через период
(/, X), который мы обозначим тут через /?, если п—1 = ef:
а + $р + Т/>2+ • • • + Vе-
При доказательстве этой леммы Гауссу приходится использо-
использовать доказанную им в п. 341 неприводимость многочлена X.
Лемма. Всякий симметрический многочлен с рациональными
коэффициентами от / корней периода длины / выражается линейно
с рациональными коэффициентами через периоды длины /.
Эта лемма доказывается при помощи предыдущих лемм.
Лемма. Пусть п — 1 = оф^ и пусть период ф^? ^) состоит из [3
более коротких периодов (*у, X), (-у, X'), . . .; тогда всякий симметри-
симметрический многочлен с рациональными коэффициентами от этих более
коротких периодов («у, X), (-у, X'), . . . выражается линейно с рацио-
рациональными коэффициентами через периоды длины р-у-
Эта лемма выводится из предыдущей леммы.
Применив эту лемму к частному случаю, когда рассматриваются
элементарные симметрические функции от периодов («у, X), (f, X'),...,
Гаусс получает, что то уравнение степени р, корнями которого
являются эти периоды, имеет коэффициенты, выражающиеся линей-
линейно с рациональными коэффициентами через периоды длины р^, откуда
сейчас же и получается указанная выше основная его теорема.
Рассмотрим пример. Пусть п = 19, тогда п — 1 = 18 = 3-3-2 и
получается следующее разложение на периоды:
A8,1)=
F,
F,
F,
1)
2)
4)
1
1
1
B,1).
B,8).
B, 7).
B,2)
B,16)
B,14)
B, 4).
B,1).
B,9).
. . г, г18
. . г8, г11
. . . Г , Г
. . . Г5, Г14
. . г4, г15
. . г6, г13
. г9, г10
F,1),
Х3+Х
B,1),
Xs—(е
9 /Г)
F,2)
2—бж
B,8)
,,1)ж2
, F, 4) — корни
-7 = 0;
B, 7) — корни
+ [F,1)+ F,4)]*-
— 2 — F, 2) = 0;
- корни
Л)х
+ 1=0.
Раздел VII «Арифметических исследований» Гаусса
963
Если п = 2т+ 1, т. е. п— 1 — 2т, то каждый из более длинных
периодов раскладывается в сумму двух более коротких периодов и
все уравнения цепи получаются квадратные, т. е. задача решения
уравнения хп—1=0 сводится к решению цепи квадратных урав-
уравнений.
Например, если п = 17, то п—1 = 16 = 2-2«2-2 и получается
такое разложение на периоды:
A6,1) =
(8,
(8,
1)
3)-
D,
D,
D,
D,
1)
9)
3)
1С
B,1)
B,13)
B,9)
B,15)
B,3)
г, г" (8,1), (8,3)-корни
г4, г
г8, г
13
х*
4=0;
D,1), D,9) —корни
..г2, г16 я2— (8,1) х— 1 = 0;
.. г3, г14 B,1), B,13) — корни
3. Связь теории деления круга Гаусса с теорией Галуа. Стоит
отметить в этом месте, какую связь имеет эта основная теорема
теории деления круга Гаусса с основной теоремой общей теории
Галуа, доказанной Галуа через 30 лет после появления «Арифме-
«Арифметических исследований» Гаусса.
Напомним, что Галуа начинает свою теорию с того, что если
дано алгебраическое уравнение с коэффициентами, лежащими в не-
некотором поле /с, то можно свести его решение к решению некото-
некоторого другого, так называемого соответствующего ему нормального,
уравнения с коэффициентами из того же поля к, т. е. такого:
1) которое неприводимо в поле к, и 2) все корни которого выра-
выражаются рационально через один из его корней и элементы поля к.
Это замечание было сделано до Галуа еще Абелем.
Для нормального уравнения Галуа следующим образом вводит
его группу. Если К — то поле, которое получается от расширения
поля к присоединением к нему корня г заданного нормального
уравнения т-ж степени с коэффициентами из поля к и если <р2(г)>
фз(г\ • • •, 9™(г) — другие его корни, то если во всех элементах
поля К заменить г через срг(г), то произойдет автоморфизм поля К,
964 Б. Н. Делоне
т. е. при такой замене элементы поля К перейдут в такие новые
его элементы, что любое рациональное с коэффициентами из к со-
соотношение между его элементами останется верным, если их заме-
заменить на те элементы, в которые они перешли. Эти т автомор-
автоморфизмов поля К образуют группу — так называемую группу Галуа
G над полем к рассматриваемого уравнения.
Основной результат теории Галуа состоит в следующем. Галуа
вводит понятие нормального делителя группы. Если Н — подгруппа
G, то она называется нормальным делителем G, если для любого
элемента g из G имеет место g^Hg = Н, т. е. если Н совпадает со
всеми своими сопряженными.
Пусть F (х) — многочлен, стоящий в левой части рассматрива-
рассматриваемого нормального уравнения, и пусть группа Галуа его имеет
нормальный делитель индекса а (т. е. такой, число элементов ко-
которого в а раз меньше числа всех элементов группы); пусть этот
нормальный делитель в свою очередь имеет нормальный делитель
индекса 3 и т. д.; в таком случае, как это показывает Галуа (и это
его основная теорема), многочлен F (х) разлагается на а множителей
„ т Y y
степеней —, коэффициенты которых выражаются рационально через
корень уравнения степени а с коэффициентами из поля к; далее,
каждый из этих множителей разлагается на р других множителей
степеней -g, коэффициенты которых выражаются рационально че-
через корень уравнения степени р, коэффициенты которого выража-
выражаются рационально через корень предыдущего уравнения степени а
и элементы поля А и т. д. Но ведь это и есть теорема Гаусса, но
для более общего случая.
Уравнение X = О Гаусса степени т — п— 1, где п — простое чи-
число: 1) неприводимо в поле рациональных чисел и 2) все его корни
выражаются рационально через один, т. е. оно нормально над по-
полем к рациональных чисел. Корни его суть г, r^, (r^)s,. .. , т. е.
группа автоморфизмов — циклическая. Если порядок циклической
группы равен т — ару . . . , то оно имеет подгруппу индекса а, ко-
которая тоже циклическая; эта подгруппа имеет в свою очередь подгруп-
подгруппу индекса р, которая тоже циклическая, и т. д. Но любая под-
подгруппа циклической группы есть ее нормальный делитель. Таким
Раздел VII «Арифметических исследований» Гаусса 965
образом, мы видим, что основная теорема теории Галуа есть непо-
непосредственное обобщение теоремы Гаусса, о чем упоминает и сам
Галуа.
Что же собственно понял Галуа? Галуа понял, что успех теории
деления круга Гаусса основан совсем не на том, что уравнение
X = 0 имеет весьма специальный вид, а на том, что оно нормаль-
нормальное, и не на том, что его группа весьма специальная (циклическая),
а на том, что все ее последовательные делители суть нормальные
делители. Как только Галуа понял эти истинные причины успеха
Гаусса — он построил свою общую теорию. Для этого, кроме того,
ему должна была быть близка идея Лагранжа о том, что истин-
истинной «философией» теории алгебраических уравнений является тео-
теория подстановок.
4. Вещественность всех корней всех промежуточных уравнений, кроме
последнего, если оно квадратное. В п. 355 Гаусс делает еще следу-
следующее замечание. Так как п нечетное, число п—1 четное. Множи-
Множитель 2 числа п — 1 можно, при разложении на периоды, всегда
ставить на последнее- место. Тогда разложение это кончится дву-
/о >ч и х к 360° . . . Л 360°
членными периодами (z, X). Ьсли положить rK= cos И sin—— >
то г~А= cos i sin . Но (z, X) = rK + г , где п = ge =
= g 2 =—1 (mod гс), т. е. B, X) =гх+ г~л.Поэтому B, X)=2cos ——.
Двучленные периоды, таким образом, — веществепные числа,
а следовательно, в выбранном разложении и все предыдущие им, бо-
более длинные, из них составленные периоды — тоже вещественные
числа. При таком разложении на периоды, т. е. когда последние
периоды, отличные от самих корней, двучленные, все вспомога-
вспомогательные уравнения, кроме последнего квадратного уравнения, да-
дающего сами корни, имеют все корни вещественные.
„ к 360° B, X) /о 1\
проме того, получается, что cos = ^—, где (z, X) можно
получить при помощи решения цепи уравнений с вещественными
корнями.
Чтобы найти то X, при котором & = 1, достаточно, очевидно,
найти наибольший положительный двучленный период B, X). Посту-
Поступая таким образом в случае п = 17, т. е. решая вспомогательные
966 Б. Н. Делоне
уравнения: х2+ х — 4 = 0; х2—(8,1)ж—1= 0; х2— D,1)х + D,3) = 0,
Гаусс находит, что
4" }/ !7 + 3 |/ТУ — }/~34~— 2 J/T7 — 2 ]/ 34 + 2 J/f? ¦
Эта формула содержит только квадратные корни, которые мо-
могут быть, как известно, построены циркулем и линейкой. Она дает
поэтому возможность дать построение циркулем и линейкой по ра-
радиусу окружности, который тут принят за 1, отрезка, равного
360° 360°
cos —г=- , т. е. угла -^г , а следовательно, дает возможность пост-
построить циркулем и линейкой правильный семнадцатиугольник.
5. Разрешимость всех промежуточных уравнений в радикалах
Наконец, в п. 359 Гаусс показывает, что во всех случаях все
вспомогательные уравнения решаются в радикалах. Он говорит:
«Предыдущие исследования относились к отысканию вспомога-
вспомогательных уравнений; теперь мы изложим весьма выдающееся свойство,
касающееся их решения. Как известно, все усилия крупнейших ма-
математиков найти общее решение уравнений, степень которых выше
четвертой, или (выражаясь точнее) найти редукцию произвольных
уравнений к чистым (двучленным — Б. Д.) уравнениям до сих пор
были тщетны, и едва ли можно сомневаться в том, что эта проб-
проблема не просто превосходит силы современного анализа, но и вообще
неразрешима . . . Тем не менее очевидно, что существует бесчислен-
бесчисленное множество смешанных (т. е. не двучленных — Б. Д.) уравне-
уравнений любой степени, которые допускают такое сведение к чистым
уравнениям, и мы надеемся, что математикам будет интересно, если
мы покажем, что наши вспомогательные уравнения всегда относятся
к такому типу». И далее Гаусс, используя резольвенты Лагран-
жа, доказывает, что все его вспомогательные уравнения решаются
в радикалах.
Этим, по существу дела, и кончается знаменитое сочинение Га-
Гаусса «Арифметические исследования».
Гауссовы суммы 967
16. Гауссовы суммы
1. Содержание работы Гаусса 1811 г. В 1811 г. Гаусс опубликовал
статью «Суммирование некоторых рядов особого вида» (Summatio
quarundam serierum singularium). Гаусс начинает п. 1 работы сле-
следующей фразой: «Среди наиболее замечательных истин, к открытию
которых проложила путь теория деления круга, далеко не послед-
последнее место занимает изложенное в п. 356 «Арифметических исследова-
исследований» суммирование, причем не только вследствие его особенного изя-
изящества и исключительной плодотворности, более подробное обосно-
обоснование которой мы отложим до другого исследования, но также и по
той причине, что строгое и совершенное доказательство этого сумми-
суммирования требует преодоления совсем необычных трудностей».
Дело идет о вычислении значении периодов длины т = —<г~ , где
п простое, т. е. когда совокупность всех корней О уравнения X = О
разбивается на два периода (/тг, 1) и (т, g). В силу основной теоремы
теории деления круга Гаусса не представляет труда составить то
квадратное уравнение с рациональными коэффициентами, корнями
которого являются эти периоды, но как узнать, какой из этих корней
2тс/
есть (т, 1), а какой (т, g), предполагая, что г — е п ? Дело сводится
к определению знака + в формуле для этих корней. И Гаусс говорит,
что решение многих трудных вопросов теории чисел не отняло у него
столько дней, сколько взяло лет работы решение вопроса об этом
знаке. Выяснению этого вопроса посвящены пп. 5—32 работы; в
п. 33 Гаусс показывает, что рассмотрение указанных периодов длины
2 дает также доказательство квадратичного закона взаимности.
Итак, периоды (т, 1) и (/гг, g) суть, в силу основной теоремы тео-
теории деления круга, корни некоторого квадратного уравнения
с рациональными коэффициентами.
Эти коэффициенты Гаусс в п. 356 «Арифметических исследований»
находит так. А = (m, I) -f (m, g), т. е. равно сумме всех корней
уравнения X — хп~х-\- хп~2+ . . . + % + 1 = 0, т. е. равно — 1. Что
же касается В, то оно равно (/тг, 1)• (/гг, g).
Б. Н. Делоне
Это произведение в силу леммы, приведенной нами на стр. 961,
может быть представлено в виде
(т, N +1) + (т, N' + 1) + (т, N"+ 1) + ... = W,
где слева т слагаемых, каждое из которых равно (т, 1), (m, g)9
или (т, 0). Таким образом, В = а (т, 0) + р (т, 1) + у (т, g), где
а, р, *y — целые положительные числа, причем а -f- р + у — т. Из
доказательства леммы (стр. 961) сразу видно, что р — у и что либо
ни одно слагаемое W не равно (т, 0), либо такое слагаемое только
одно, т. е. что а = 1 или 0. Таким образом, либо а = 0, р — у =
1 1
= Ym* либ° а = 1, Р = Т — ~т (т — ^-)» a так как а» Р> Т целые, то
первое имеет место, если т = —-—четное,т.е. п = 4Z+1, а второе, ес-
если т нечетное, т. е. п = 4Z + 3. А так как (т, 0)= т = w и (т, 1) +
4- (т, g) = —1, то в первом случае (т, l).(m,g) = (п — 1),
1
а во втором -к- щ поэтому искомое квадратное уравнение есть
х2+ х — ~(п — 1) = 0 или х2+ х + ~ (п + 1) = 0.
Периоды (т, 1) и (т, g) имеют следующий вид:
(т, 1) = г + rS2-f
(m, g) = г^+ г^4
2кг
где г = е п , т. е. они могут быть записаны и так:
2кг„ 2кг 7
где а пробегает все квадратичные вычеты, а Ъ — все квадратичные
невычеты по модулю п.
«Определение знака», таким образом, сводится к разысканию
—а
значения суммы: /л еп . Оно проводится Гауссом в пп. 5 — 32
Гауссовы суммы 969
работы при помощи преобразования рассматриваемой суммы в произ-
произведение (г—г) (г3—г~3). . . (гр~2—г~р+2), что в свою очередь до-
достигается при помощи исследования двух особых рядов:
, /)=- - : -, каждый из которых
A— x)(l— x2). . .A— xJ) ' F
приводит Гаусса к желаемой цели.
Доказательство это принадлежит к числу трудных, поэтому мы его
здесь воспроизводить не будем.
2. Дальнейшие исследования о гауссовых суммах в XIX столетии.
В XIX в. рядом крупных математиков были предложены другие, от-
отличающиеся от гауссова, решения вопроса о знаке в гауссовой сумме,
основанные на разных принципах. В. А. Лебег A840) прибег для этой
цели к эллиптическим функциям; проще решил вопрос Коши A840)
и из тех же соображений в 1856 г. Кронекер. Дирихле A837) опре-
определил значение гауссовой суммы при помощи определенного интег-
интеграла. Кронекер A880) вернулся к способу, ранее предложенному
Коши и основанному на основной теореме Коши о комплексном
интегрировании.
Свойства гауссовых сумм были использованы при пребразовании
оо
ряда 2(—)— в конечную сумму для вывода формул Дирихле
числа классов h квадратичного поля.
Во всяком случае, можно сказать, что в течение ровно целого
столетия после появления мемуара Гаусса 1811 г. совершенствова-
совершенствовались решения вопроса, поставленного Гауссом, но никакого прин-
принципиального расширения задачи о гауссовых суммах получено
не было. В статье Бахмана (P. Bachmann. Uber Gauss zahlen-
theoretische Arbeiten), появившейся в 1911 г., гауссовым суммам
посвящены только две страницы, причем Бахман, видимо, недо-
недоумевает, к чему относится замечание Гаусса о необыкновенной
важности метода его сумм. Работы XIX в., посвященные теории
гауссовых сумм, были замкнуты в узкие рамки.
970 Б. Н. Делоне
3. Второй этап развития теории тригонометрических сумм
в аналитической теории чисел. В 1914 г. были сделаны две совсем
разные работы, с которых началось неожиданно мощное дальнейшее
развитие метода тригонометрических сумм в теории чисел.
Две работы, о которых мы говорим, это работа Германа Вейля
(Н. Weyl) 1914 г., в которой была оценена абсолютная величина суммы:
х=1
где ап9 an—1 , ..., аг — заданные действительные числа, причем хотя
бы одно из них иррациональное, и работа И. М. Виноградова о рас-
пределении квадратичных вычетов. Хотя оценка Г. Вейля лишь не-
немного лучше тривиальной <^ р (которая получается, если все слагаемые
заменить 1), однако и она уж ведет к замечательным приложениям.
Использовав ее, Харди и Литтльвуд создали первый мощный
аналитический метод для решения аддитивных задач теории чисел.
Осуществление этого метода Харди и Литтльвудом состоит в исполь-
использовании целой цепи глубоких соображений, из которых главные:
1) применение интегрирования по контуру, 2) применение ряда Фарея,
с которым связано разбиение контура интегрирования на большие
и малые дуги (впервые примененное к подобным вопросам Вороным
в его работе 1903 г.) и 3) использование неравенства Г. Вейля, кото-
которое позволяет оценивать интеграл по малым дугам.
Этим методом Харди и Литтльвуду удалось, в частности, дать
более совершенное, чем у Гильберта, доказательство теоремы Ва-
ринга: N = х\ + х\ +...+ #", — дающее асимптотическую формулу
для числа представлений суммой к п-х степеней целых чисел любо-
любого достаточно большого целого числа, из которой получилась хоро-
хорошая оценка для числа к слагаемых, при которых уравнение Варинга
имеет решение для любого такого N.
Метод Харди и Лйттльвуда дал решение также ряда других важ-
важных задач.
Другая из двух упомянутых в начале этого пункта работ была
работа И. М. Виноградова, которую он представил в 1914 г. на
Математический факультет Петербургского университета для того,
чтобы быть «оставленным при Университете для подготовки к про-
Гауссовы суммы 971
фессорскому званию» (напечатана она была позже, в 1918 г.,
в значительно расширенном виде). В этой работе, используя спе-
специальным образом гауссову сумму, Виноградов показывает, что аб-
абсолютная величина суммы символов Лежандра по р, подряд идущим
натуральным числам, каково бы ни было р, не больше, чем jfpln p, от-
откуда, в частности, получается, что среди натуральных чисел, меньших
Ур In p, всегда есть хотя бы один квадратичный невычет модуля р.
Мы позволим себе привести это замечательное доказательство.
Но раньше сделаем несколько общеизвестных замечаний о гаус-
27тг
совых суммах. Во-первых, гауссова сумма 2je v , где г — все выче-
г
ты по модулю р и а не делится на р, легко сводится к сумме
—ах2
е*> ¦
х=о
Действительно, слагаемое этой последней суммы при х = О рав-
равно 1, вычеты же (mod/?) квадратов I2, 22, ...,(/?— IJ суть все
квадратичные вычеты г (mod/?), но каждый взятый два раза, так
как х^—х^~ (#!+ х2)(х1—х2), если жх+ х2 делится на р, то х^ и я2
сравнимы (mod/?), если же нет, то несравнимы. Вычеты (mod/?)
двух равно отстоящих от концов этого ряда квадратов поэтому
одинаковы. Мы имеем, таким образом, 2j ev — 1 Jr%Ziev -
х=0 г
Во-вторых, если п — все невычеты (mod/?), то
irci 2iri
—(хт sr\ —an
поэтому
ахг v^ —
е р =2ер
Х=0 Г
/Г\ \ л {П\ л
а так как(—J = + 1, (—) — — 1, то
972 Б. Я. Делоне
ах __
Заметим еще, что модуль суммы /jev равен \f р. Это следу-
ет из того уравнения х2— Ах + 5 = 0, корнями которого являются
периоды (т, 1) и (т, g). Но сейчас это обычно выводят непосред-
непосредственно так. Помножая сумму на ей комплексно сопряженную
Р~~1 2тгг . V—1 2ттг . , еч
\~1 ах sry —а(х2—уг)
2j e р , получаем /J е р • Сделав здесь подстановку x=yJr
х=о х,у=0
+ t, так как х2 — г/2 = у2 + 2гг/ + г2 — ?/2 = 2^г/ + t2, получаем
^ =— af2 ^п —2atV тт ^S1 — 2aty о
2j е v ' 2je р • ^° -^ е v у если 2а^ не делится на р, равно
t=o у=о у=о
нулю. Число 2at делится на р только при t = 0. Следователь-
2тгг Р-1
но, мы получаем е р • ^j I = 1р = р. Таким образом, модуль ис-
следуемой суммы равен Ур , а следовательно, сама эта сумма рав-
равна 8 1^/?, где |е| = 1.
Переходим теперь к доказательству теоремы Виноградова, Так
/т \ fma2\ ( а \ /та\
как — )= — =(-.)—) то
\р) V р J \pJ\pJ'
m=i тп=1
откуда мы получаем
m=l
Просуммируем это равенство по а от 1 до р1у где р± — любое нату-
натуральное число:
п \ \ Р~1 /
m=i a=i
Гауссовы суммы
973
Перейдем к модулям (звездочками указаны ссылки на примечания):
a==l
2тсг , % 2ттг
-(P.+l)m _r
*<
тп=1
р)
sin-1
sin a?
тт Л .тот тс n 7u sin a?
Но здесь 0 <— < T , а на интервале 0 < я < — , >
т. е. sin х > — х. Другими словами,
sin у 2
пт 2 пт 2т
sin — > = —.
р те р Р
Следовательно,
р-1
m=l
Р—1
2
m=l
7С
У
Этот метод был распространен И. М. Виноградовым на вопрос
о распределении вычетов высших степеней и применен к ограниче-
ограничению наименьшего первообразного корня g простого числа р.
Р* am
* Если У1 в р рассмотреть как геометрическую прогрессию.
** Здесь мы употребляем формулу Эйлера.
*** Здесь мы используем свойство, что равноотстоящие от концов суммы
слагаемые равны.
974 Б. Н. Делоне
Виноградов показал, что
где к — число различных простых делителей.
Период, начавшийся в 1914 г. описанными выше работами Г. Вей-
ля и И. М. Виноградова и по 1934 г., можно назвать вторым этапом
развития теории тригонометрических сумм в теории чисел. По мне-
мнению И. М. Виноградова, характерными чертами этого этапа были две:
1) отказ от нахождения точных значений сумм и переход к их оцен-
оценкам, но зато 2) освобождение от требования, чтобы высказывания,
при их помощи получаемые, относились только к полной системе вы-
вычетов. Однако сохранялось условие, чтобы суммирование произво-
производилось по отрезку чисел натурального ряда, взятых подряд.
Уже в 1916 г. начали рассматривать куски полных рациональных
тригонометрических сумм, причем трудности, возникающие при этом,
не больше тех, какие имеются в теории иррациональных сумм (т. е.
таких, как суммы Г. Вейля, где а, иррациональные), так как много-
многочлен с иррациональными коэффициентами все равно не периодичен
по модулю р. Иногда даже и в случае рациональной суммы выгодно
брать рациональные приближения коэффициентов, но зато с малыми
знаменателями, как это делается в случае иррациональной суммы.
В этот второй период были решены методом тригонометрических сумм
многие важные задачи. Мы уже упоминали о знаменитых работах
Харди и Литтльвуда. Были получены важные теоремы о распреде-
распределении дробных долей многочлена, о представлении чисел в форме
целого многочлена от многих переменных:
(где ф — многочлен степени не выше п — 1), о некоторых системах
диофантовых уравнений и т. д.
В 1928 г. Р. О. Кузьминым была получена следующая весьма
общая оценка тригонометрической суммы. Если f(x) на отрезке
A
где 0 < 9 < ^
ь 2
/'(#) монотонна, то ^e2ni^x> <"q" .
Гауссовы суммы 975
Здесь х пробегает все целые числа между а и Ъ включительно.
Геометрически это означает, что если имеется ломаная, состоящая
из векторов длины 1, и такая, что каждый следующий вектор по-
повернут относительно предыдущего на все больший и больший угол,
заключающийся между 6 и 1 — 9, то конец этой ломаной лежит не-
недалеко от ее начала.
Отметим, что в настоящее время знак гауссовой суммы, пожа-
пожалуй, наиболее просто можно определить, используя эту лемму Кузь-
Кузьмина. А именно, полную гауссову сумму 2е р нетрудно свести
к. вычислению двух следующих сумм:
w = 2 в1^*1 и2= 2 в1р~*2-
l<x<Vp Vp<x<V—l
1 /—
Относительно W легко показать, что Re{(l—i)W}^-jYp, где
Re { } обозначает вещественную часть { }. Что же касается до Z,
то, применяя лемму Кузьмина, можно показать, что
\z\<VJ-
Соединяя оба эти обстоятельства, получаем определение знака
в гауссовой сумме.
4. Третий этап развития теории тригонометрических сумм в тео-
теории чисел. Характерной чертой третьего этапа, начавшегося рабо-
работой И. М. Виноградова 1934 г., является освобождение от того усло-
условия, чтобы суммирование проводилось по всем натуральным числам
некоторого отрезка подряд. Так, чтобы было, например, возможно сум-
суммировать по простым числам или по числам, имеющим не более, чем
столько-то простых множителей и т. д., И. М. Виноградов показал,
что получаются хорошие оценки двойных сумм
по различным областям, где х и у пробегают достаточно густые незави-
независимые одна от другой последовательности целых чисел, и функция
976 Б. Н. Делоне
f(x, у) не разлагается в сумму двух функций, каждая от одной пере-
переменной. Этот способ оказался очень сильным; при помощи него
И. М. Виноградов получил свою более тонкую оценку суммы Г. Вей-
ля и оценки сумм, при помощи которых он доказал теорему Гольд-
Гольдбаха.
Конечно, мощный современный метод тригонометрических сумм,
давший в последнее десятилетие столько глубоких теорем теории
чисел, далеко ушел за рамки того, что дал Гаусс, но все же у исто-
истоков его стоит рассматриваемая работа Гаусса 1811 г. «Суммирование
некоторых рядов особого вида».
5. Причины успешного применения тригонометрических сумм
в теории чисел. Подобно тому, как это мы сделали в заключении па-
параграфа об алгебраических числах, разумно и здесь поставить такой
вопрос. Во-первых, говорит И. М. Виноградов, целые числа идут
в ряду вещественных чисел периодически, и потому, очевидно,
можно удобно описывать их свойства при помощи периодической
функции e2niz. Но можно сделать и другое замечание. Тригонометри-
Тригонометрические суммы являются тем орудием, которое позволяет какую-ни-
какую-нибудь искомую в теории чисел величину выразить формулой. Напри-
Например, число решений сравнения
а±х^ + а2х™ + . . . + акх™ = О (mod /?),
где аг — заданные целые числа, как нетрудно убедиться, равно
-J-2 ••• 2 2 е^а>х"+';+а^.
А когда искомое число записано формулой, то можно уже забыть
задачу теории чисел и находить величину, определяемую формулой,
или оценивать эту величину — это уже совсем другая задача, и ча-
часто, ввиду удобных свойств функции e2mz, ее можно решить.
Здесь мы видим аналогию тому положению, которое имеется
в теории дифференциальных уравнений. Решая какую-нибудь задачу
геометрии, механики или физики, составляют соответствующее ей
дифференциальное уравнение; а затем занимаются второй, уже сов-
совсем другой задачей: как решить это уравнение; эта вторая задача ос-
основана на теоремах о дифференциальных уравнениях как таковых.
СОДЕРЖАНИЕ
АРИФМЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ (DISQUISITIOWES ARTTHMETICAE)
Раздел 1.0 сравнимости чисел вообще 15
Раздел II. О сравнениях первой степени 21
Раздел III. О степенных вычетах 50
Раздел IV. О сравнениях второй степени 94
Раздел V. О формах и неопределенных уравнениях второй степени 151
Раздел VI. Различные применения предыдущих исследований . . . 468
Раздел VII. Об уравнениях, от которых зависит деление круга . . . 509
Дополнения 574
Таблицы 576
Оглавление 580
ДРУГИЕ СОЧИНЕНИЯ
Новое доказательство одной арифметической теоремы 587
Суммирование некоторых рядов особого вида 594
Новые доказательства и обобщения фундаментальной теоремы в учении
о квадратичных вычетах 636
Теория биквадратичных вычетов. Сочинение первое 655
Теория биквадратичных вычетов. Сочинение второе 686
НЕКОТОРЫЕ ИССЛЕДОВАНИЯ ИЗ РУКОПИСНОГО
НАСЛЕДИЯ ГАУССА
Учение о вычетах 757
I. Решение сравнения Хт —1= 0 757
II. Общие исследования о сравнениях 773
Дальнейшее развитие исследований о чистых уравнениях 807
Доказательство некоторых теорем о периодах классов двойничных форм
второй степени 836
978 Содерснсание
О связи между числом классов, на которые распадаются двойничные фор-
формы второй степени, и их определителем 839
Более подробное рассмотрение некоторых вопросов, относящихся к делению
круга 867
ПРИЛОЖЕНИЯ
От редакции 874
И. М. Виноградов. Карл Фридрих Гаусс 875
Б. Н. Делоне. Работы Гаусса по теории чисел 879
1. Теория чисел до Гаусса (879).— 2. «Арифметические исследова-
исследования» Гаусса (880).— 3. О теории чисел вообще и о современных нам ее мето-
методах (882).— 4. О теории алгебраических чисел (885).— 5. Первый, второй
и третий разделы «Арифметических исследований» Гаусса (895).— 6. Чет-
Четвертый раздел «Арифметических исследований». Первое доказательство
закона взаимности (897).— 7. Целые комплексные числа Гаусса и биквад-
ратичный закон взаимности (900).— 8. О законах взаимности вообще и о
задаче, которую они решают (902).— 9. О теореме Кронекера и о теории
поля классов (904).— 10. Первая часть пятого раздела «Арифметических
исследований» (906).— 11. Вторая часть пятого раздела «Арифметических
исследований». Композиция классов и композиция родов квадратичных
форм (914).— 12. Третья часть пятого раздела «Арифметических исследова-
исследований». Отступление о тройничных формах (925).— 13. Четвертая часть пятого
раздела «Арифметических исследований», содержащая приложение теории
тройничных квадратичных форм и исследования о числе классов (939).—
14. Шестой раздел «Арифметических исследований». Различные приложения
теории чисел (956).— 15. Седьмой раздел «Арифметических исследова-
исследований». Теория деления круга Гаусса (957).— 16. Гауссовы суммы (967).
Карл Фридрих Гаусс
Труды по теории чисел
Утверждено к печати
Редакционной коллегией серии «Классики науки»
Академии наук СССР
*
Редактор издательства А. 3. Рывкин
Технический редактор И. А. Макогонова
РИСО № 2-103В. Сдано в набор 20/VI 1959 г.
Подписано к печати 31/X 1959 г. Формат 70Х92уи
Печ. л. 61,25. Усл. печ. л. 71,66. Уч.-изд. л. 49,8
Изд. № 3675. Тип. зак. № 2078. Тираш 2500 экз.
Цена 36 р. 86 к.
Издательство Академии наук СССР
Москва Б-62, Подсосенский пер., 21
2-я типография Издательства АН СССР
Москва Г-99, Шубинский пер., 10