Теория поля. Современный вводный курс - Рамон П.

Автор: Рамон П.

Теги: физика теория поля

Год: 1984

Похожие

Теория суперструн Т.1. Введение

Введение в теорию суперструн

Солитоны и инстантоны в квантовой теории поля

Топология калибровочных полей и конденсированных сред

Текст

П.Рамон
ТЕОРИЯ ПОЛЯ. СОВРЕМЕННЫЙ ВВОДНЫЙ КУРС
М.: Мир, 1984,336 с.
В книге П.Рамона (США) последовательно излагается квантовая теория поля
(в рамках теории возмущений) на основе понятия функционального интеграла.
Все важнейшие выкладки представлены полностью, что дает возможность
читателю не только ознакомиться с основными идеями новейшей квантовой
теории поля, но и овладеть техникой сложных вычислений. После каждой главы
даются упражнения и задачи. Книга может служить основой для дальнейшего
изучения предмета по более специализированным обзорам, монографиям и
оригинальным статьям, так что она заполняет существенный пробел в учебной
литературе по современной квантовой теории поля.
Для студентов старших курсов, аспирантов и начинающих научных
работников в области физики элементарных частиц.
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА 5
ПРЕДИСЛОВИЕ 9
Глава 1. Функционал действия 11
§ 1. Элементарные сведения 11
§ 2. Группа Лоренца (беглый обзор) 15
§ 3. Группа Пуанкаре 21
§ 4. Локальные поля и преобразования группы Пуанкаре 24
§ 5. Общие свойства действия 36
§ 6. Действие для скалярных полей 43
§ 7. Действие для спинорных полей 47
§ 8. Действие со скалярными и спинорными полями и суперсимметрия 53
Глава 2. Функционал действия в квантовой механике: 61
фейнмановский интеграл по траекториям
§ 1. Канонические преобразования в классической и квантовой механике 62
§ 2. Фейнмановский интеграл по траекториям 67
§ 3. Интеграл по траекториям и гармонический осциллятор, наводящийся 74
под действием силы
Глава 3. Фейнмановский интеграл по траекториям в теории поля 80
§ 1. Производящий функционал 80
§ 2. Фейнмановский пропагатор 83
§ 3. Эффективное действие 88
§ 4. Вычисление интеграла по траекториям методом перевала 94
§ 5. Первые квантовые поправки. Вычисление детерминантов с помощью 102
(^-функции
§ 6. Изменение масштаба детерминантов Константа связи, зависящая от 107
масштаба
Глава 4. Вычисление фейнмановского интеграла по траекториям 111
методом теории возмущений: теория ф4
§ 1. Фейнмановские правила для теории ср4 111

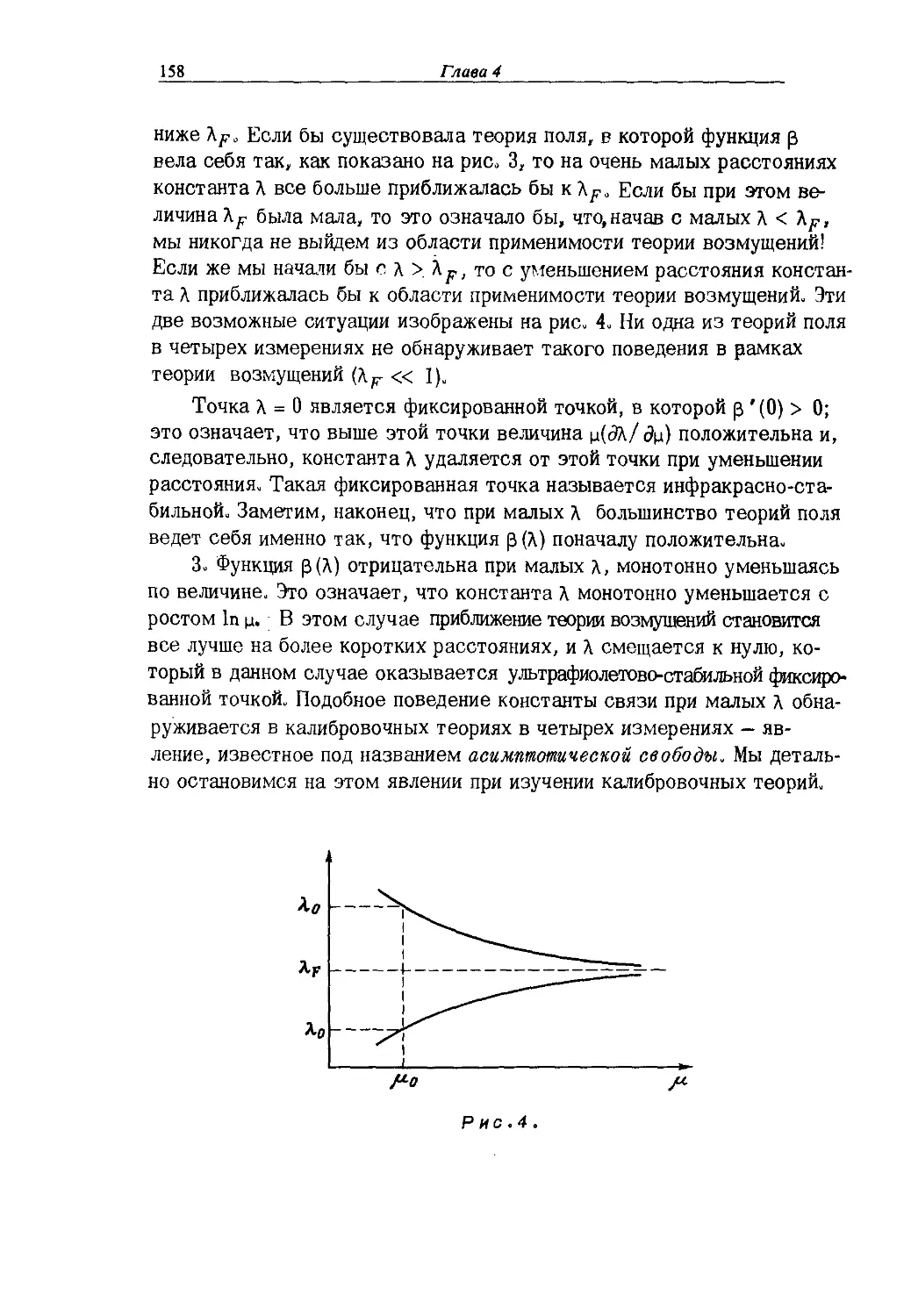
§ 2. Расходимости фейнмановских диаграмм 120
§ 3. Размерная регуляризация фейнмановских интегралов 127
§ 4. Вычисление фейнмановских интегралов 132
§ 5. Перенормировка 141
§ 6. Рецепты перенормировки 152
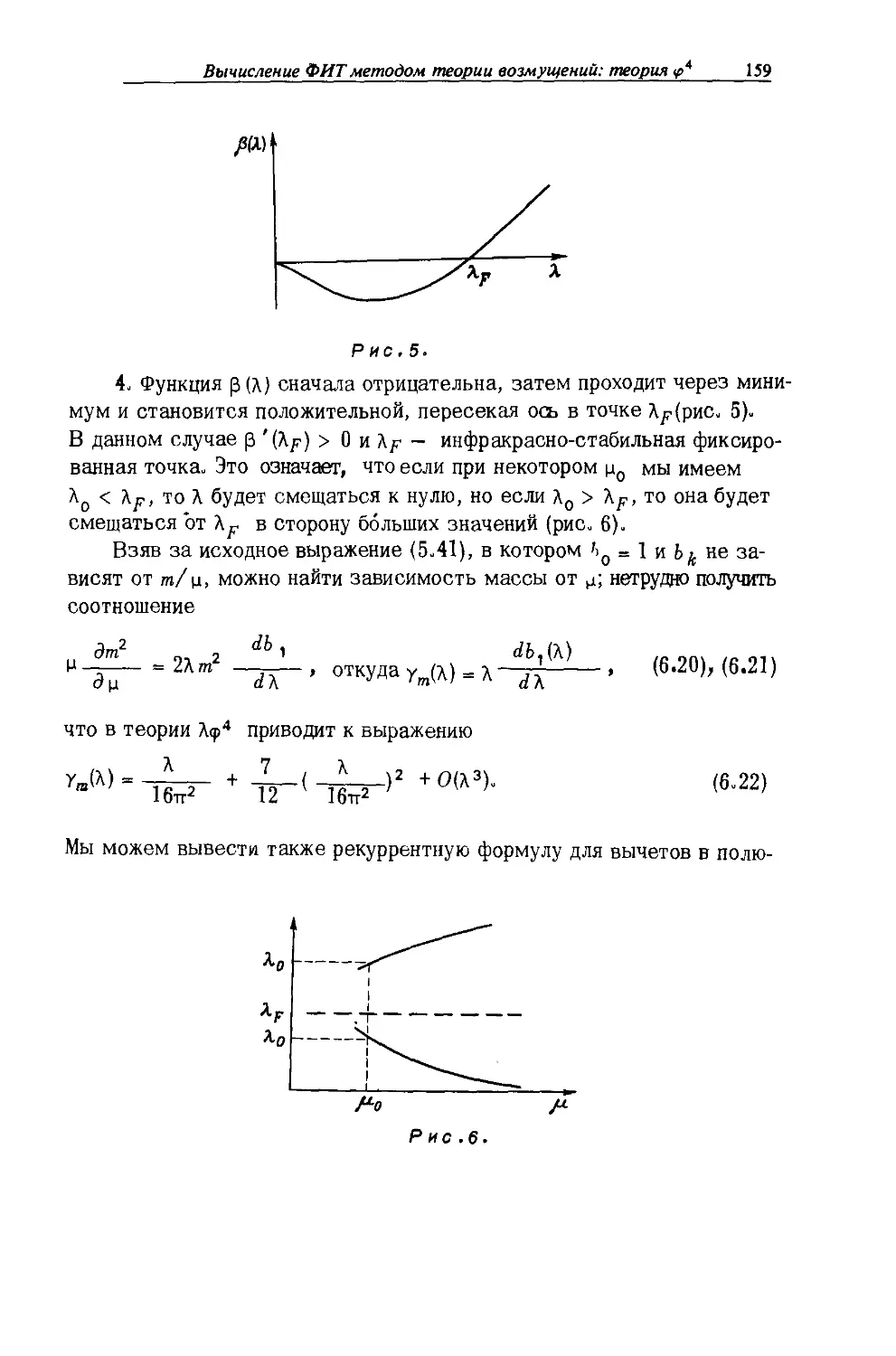
§ 7. Зависимость коэффициентов ренормгруппы от рецепта 164
перенормировки
§ 8. Продолжение в пространство Минковского, аналитичность 166
§ 9. Сечения и унитарность 172
Глава 5. Интеграл по траекториям при наличии фсрмиопов 181
§ 1. Интегрирование по грассмановым числам 181
§ 2. Интеграл по траекториям для свободных ферми-полей 185
§ 3. Фейнмановские правила для спинорных полей 191
§ 4. Вычисление и масштабное преобразование фермионных 196
детерминантов
Глава 6. Калибровочные симметрии, конструкция Янга — Миллса 203
§ 1. Глобальные и локальные симметрии 203
§ 2. Построение локально симметричных лагранжианов 214
§ 3. Чисто янг-миллсовская теория 220
Глава 7. Интеграл по траекториям в калибровочных теориях 232
§ 1. Гамильтонов формализм в калибровочных теориях, абелев случай 232
§ 2. Гамильтонов формализм для калибровочных теорий, неабелев случай 241
§ 3. Непосредственное определение янг-миллсовского ФИТ, процедура 249
Фаддеев а — Попова
Глава 8. Вычисления по теории возмущений в калибровочных 253
теориях
§ 1 Фейнмановские правила для калибровочных теорий в евклидовом 253
пространстве
§ 2. КЭД, однопетлевая структура 261
§ 3. КЭД, тождества У орда 274
§ 4. КЭД, применения 280
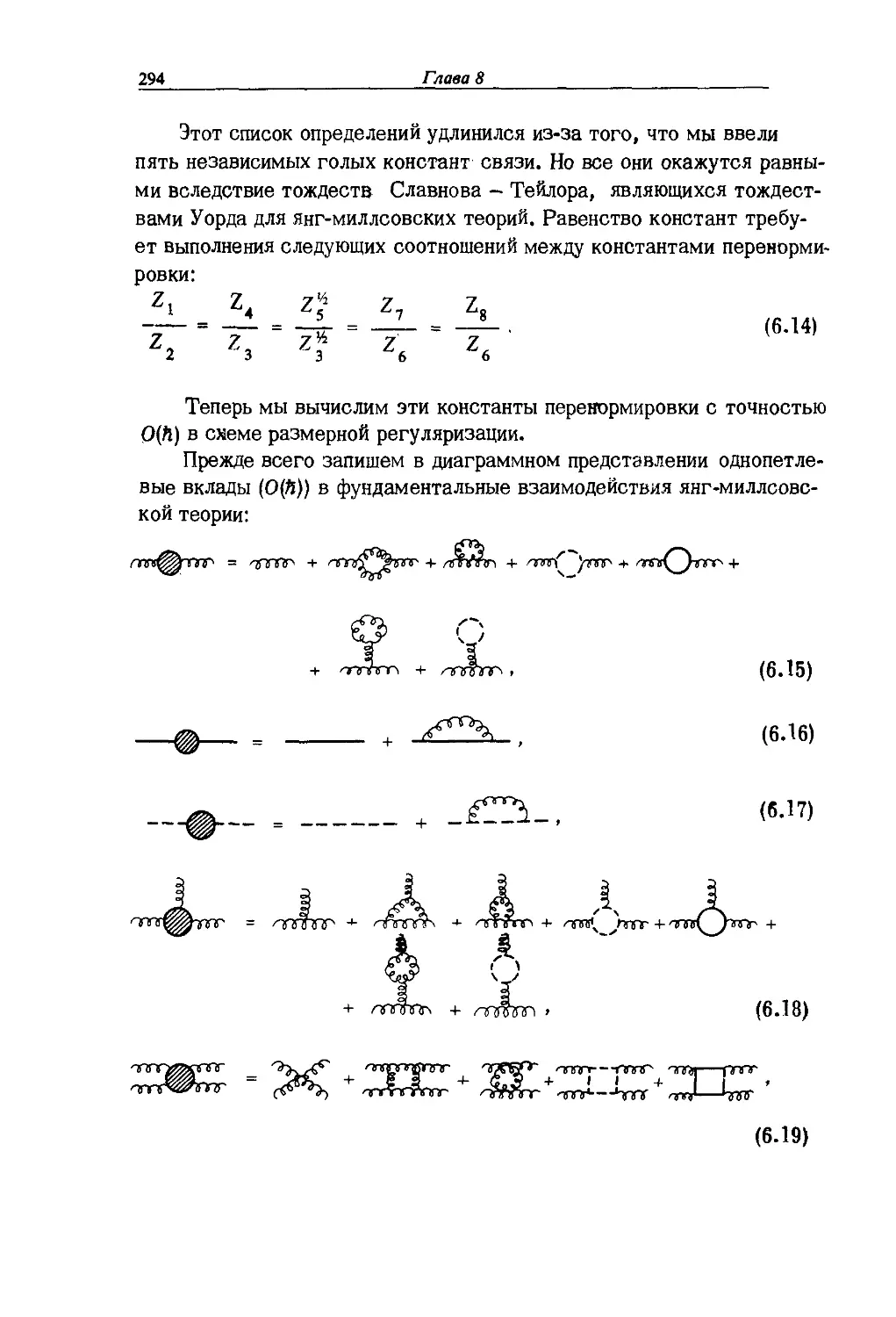
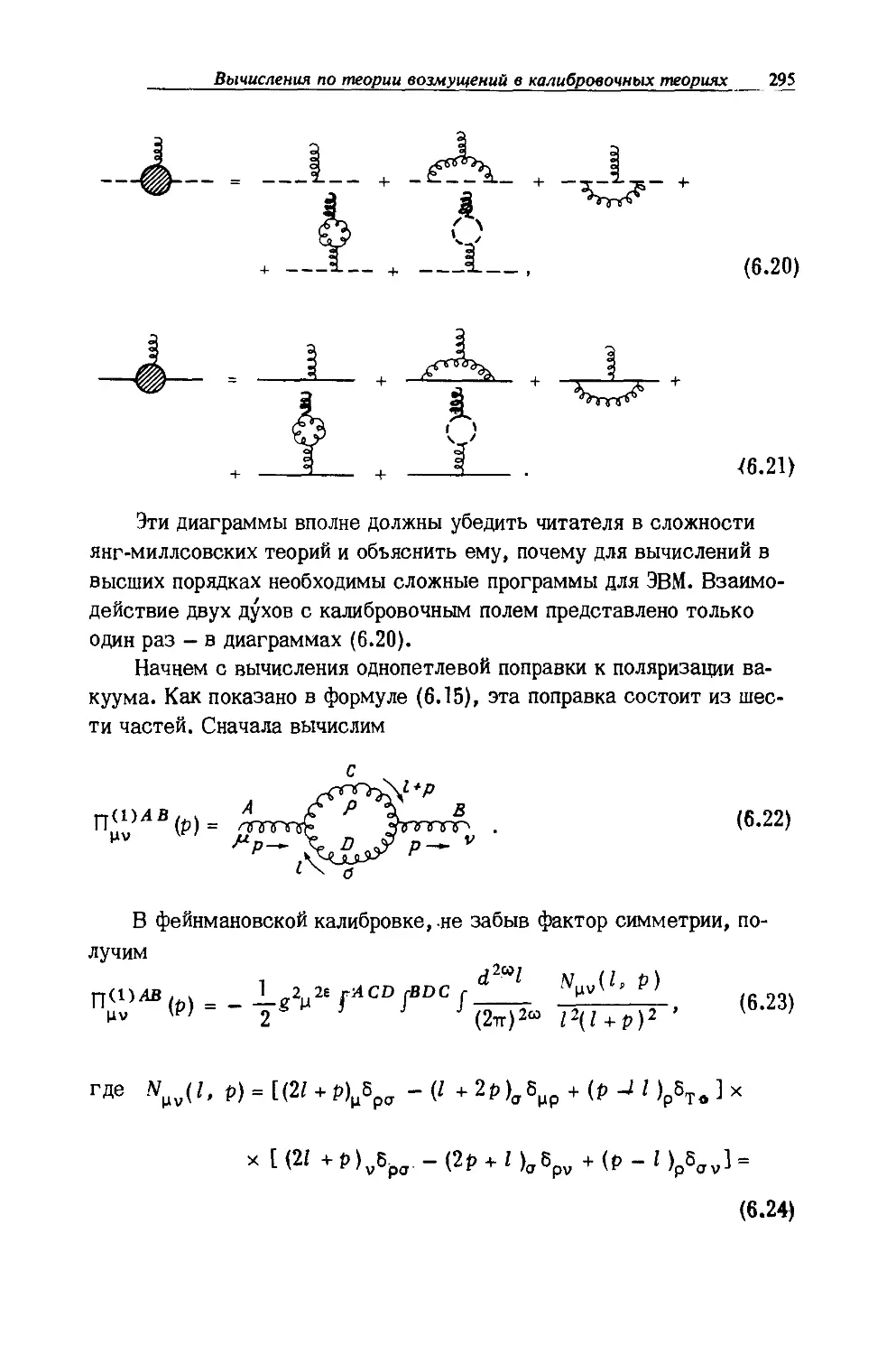
§ 5. Янг-миллсовская теория, предварительные замечания 287
§ 6. Янг-миллсовская теория, однопетлевая структура 292
§ 7. Янг-миллсовская теория, тождества Славнова - Тейлора 305
§ 8. Янг-миллсовская теория, асимптотическая свобода 311
Приложения 317
A. Гауссово интегрирование 317
Б. Интегрирование при произвольном числе измерений 320
B. Фейнмановские правила в ковариантной калибровке в евклидовом 323
пространстве Bсо измерений)
БИБЛИОГРАФИЯ 324

Предисловие переводчика
Книга П.Рамона "Теория поля. Современный вводный курс" была
опубликована в 1981 г. под № 51 в известной серии "Рубежи физики".
Многие издания этой серии получили широкую известность и были пере-
переведены на русский язык. Достаточно упомянуть книги Фейнмана
"Квантовая электродинамика" ("Мир", 1964) и "Взаимодействие фото-
фотонов с адронами" ("Мир", 1975) и др., книгу Адлера и Дашена "Алгебры
токов и их применение в физике частиц" ("Мир", 1970), книгу Коккедэ
"Теория кварков" ("Мир", 1971). В этой же серии вышли и переведен-
переведенные с русского монографии советских ученых И.М.Халатникова "Вве-
"Введение в теорию сверхпроводимости", А.Б.Мигдала "Метод квазичастиц
в теории ядра", а также (под № 50) близко примыкающая по теме к дан-
данной книге монография А.А.Славнова"и Л.Д.Фаддеева "Введение в кван-
квантовую теорию калибровочных полей".
Бессменный издатель серии "Рубежи физики" известный амери-
американский физик Дэвид Пайнс так определил в 1961 г. задачи серии:
"В наши дни настоятельно необходимо решение задачи понятного изло-
изложения последних достижений в наиболее волнующих и активных облас-
областях физики.. . Ведущие ученые часто читают циклы лекций и специ-
специальные курсы лекций для аспирантов, посвященные интересующей их
узкой области физики. Цель таких лекций - суммировать современное
состояние быстро развивающейся области, и чаще всего они оказыва-
оказываются единственным в данный момент более или менее полным и после-
последовательным изложением предмета. Часто появляются и конспекты
этих лекций (подготовленные самим лектором, студентами старших
курсов или аспирантами), распространяемые ограниченным тиражом.
Одна из главных задач серии "Рубежи физики" - сделать такие кон-
конспекты доступными более широкому кругу физиков. Необходимо под-
подчеркнуть, что конспекты лекций, конечно, не очень хорошо обработа-
обработаны и не отличаются особой строгостью как стиля, так и содержания...
Смысл всей серии в том, чтобы предложить новью, быстрые, более свобод-
свободные по форме и, как можно надеяться, более эффективные способы
обучения одних физиков другими..."
Все сказанное Пайнсом в полной мере относится и к предлагае-
предлагаемой книге П.Рвмона. Во-первых, это учебник, пригодный для перво-

Предисловие переводчика
начального ознакомления с современными идеями и методами теории
поля. Читателями книги могут быть студенты старших курсов физи-
физических факультетов университетов и других вузов с аналогичной про-
программой и аспиранты, приступающие к самостоятельной работе в об-
области физики высоких энергий и квантовой теории поля. Во-вторых,
она представляет собой конспекты лекций, и весь стиль изложения в
ней, в котором отсутствует стремление к изяществу, несет на себе
отпечаток данного обстоятельства. В-третьих, предмет этой книги
еще не нашел достаточного отражения в существующих монографиях
и учебниках на уровне, доступном новичку.
Необходимость подобного рода пособия по современной теории
поля продиктована временем. Развитие квантовой теории поля за пос-
последние 15 лет было чрезвычайно бурным и плодотворным. Если гово-
говорить о приложениях, то достаточно упомянуть единую теорию электро-
электрослабого взаимодействия (в справедливости которой сейчас вряд ли
кто-нибудь сомневается) и квантовую хромодинамику (КХД) - главно-
главного претендента на роль истинной теории сильного взаимодействия.
Эти две теории, в основе которых лежит современная квантовая тео-
теория неабелевых калибровочных полей, стали фундаментом конкретных
расчетов наблюдаемых явлений в физике частиц. Таким образом, зна-
знание основ современной квантовой теории поля - необходимый эле-
элемент образования любого специалиста-физика, как теоретика, так и
экспериментатора.
Это требует значительной ломки традиционного подхода к препо-
преподаванию квантовой теории поля, существующего уже три десятилетия.
Если до недавнего времени стандартные курсы лекций сводились к из-
изложению канонического квантования свободных полей, а в качестве
единственного примера теории с взаимодействием подробно рассмат-
рассматривалась квантовая электродинамика (КЭД), для которой развивалась
диаграммная техника и обсуждались правила вычислений наблюдаемых
величин, перенормировка и т.п., то сейчас КЭД воспринимается уже
как некоторый весьма частный случай общего класса калибровочных
теорий. Кроме того, развитие квантовой теории поля за последние го-
годы сопровождалось разработкой новых методов и подходов и усовер-
усовершенствованием техники вычислений. Так, наиболее экономным при вы-
выводе фейнмановских правил для разложения в ряд по теории возмуще-
возмущений в калибровочных теориях оказался метод континуального интегра-
интеграла (интеграла по траекториям). Был развит метод размерной регу-
регуляризации расходящихся интегралов в теории, последовательно со-
сохраняющий на всех этапах вычислений калибровочную инвариантность.
В связи с развитием суперсимметричных теорий и теории супергра-

Предисловие переводчика
витации существенными стали формальные правила обращения с грао
смановыми переменными.
Цель книги П.Рамона в том, чтобы познакомить читателя имен-
именно с современными методами квантоипй теории поля. Главный итог
книги — обоснование фейнмановских правил для янг-миллсовских
теорий (в частности, для КХД) и примеры вычислений по теории воз-
возмущений в КЭД и КХД, прежде всего связанных с выявлением асим-
асимптотического поведения инвариантного заряда. При этом все изло-
изложение базируется на методе интеграла по траекториям. Попутно
излагаются такие вопросы, как группа Лоренца и группа Пуанкаре,
преобразования суперсимметрии, построение лагранжианов, инвари-
инвариантных относительно определенных групп симметрии, и построение
соответствующих сохраняющихся величин, классические решения
уравнений янг-миллсовского поля, вычисление первых квантовых по-
поправок к классическим решениям, техника размерной регуляризации
и ряд других вопросов.
Отличительной чертой книги является стремление научить чита-
читателя технике конкретных вычислений. В то же время автор отказал-
отказался от попыток излагать строгие доказательства (например, перенор-
перенормируемости янг-миллсовских теорий). Книга очень прагматична, и
в этом, на* наш взгляд, ее большое достоинство. Специалисты, несом-
н енно, заметят то влияние, которое оказали на структуру книги и
стиль изложения известные лекции С.Коулмена (см. библиографию
в конце книги).
Ограниченный объем не позволил автору охватить многие важные
вопросы современной теории. Об этом сам П.Рамон пишет в своем
предисловии. Кроме того, в книге полностью отсутствуют физические
приложения. Но это отвечает справедливому убеждению автора, что
конкретные вычисления в теории электрослабого взаимодействия и в
КХД должны сегодня составлять содержание отдельного учебника.точ-
но так же, как и все методы, связанные с выходом за рамки теории
возмущений.
Мы думаем, что книга ПРамона будет ценным пособием для всех
приступающих к изучению современной квантовой теории поля и ее
приложений. Она прекрасно дополняет известный учебник Н. Н.Бого-
Н.Боголюбова и Д.В.Ширкова "Квантовые поля", также рассчитанный на на-
начальное обучение. Читатели, желающие глубже изучить проблему кван-
квантования калибровочных теорий, могут обратиться к уже упомянутой
монографии А.А.Славнова и Л.Д.Фаддеева.
При переводе мы воздержались от развернутых комментариев,
ограничившись лишь мелкими замечаниями. В противном случае это

Предисловие переводчика
нарушило бы замысел и стиль всей книги. Для тех читателей, которые
захотят углубить свои знания по отдельным вопросам, лишь бегло упо-
упомянутым в книге, представлен список дополнительной литературы.
Мы добавили в него несколько ссылок, в основном на монографии
советских авторов. При переводе были исправлены замеченные опечат-
опечатки в формулах. Я благодарен И.Б.Хрипловичу за указание на некото
рые из них.
А.Верков

Предисловие
Доказательство перенормируемости янг-миллсовских теорий, дан-
данное »т Хофтом, повлекло за собой бурное развитие методов и прило-
приложений квантовой теории поля. Однако за прошедшие годы Зыло напи-
написано мало учебников, так что аспирант, специализирующийся в области
теории поля, вынужден обращаться к оригинальной литературе или к
обзорам. Сейчас много прекрасных обзорных статей, но они, к сожа-
сожалению, часто пишутся не для начинающих, а для специалистов. Пред-
Предлагаемые конспекты лекций, читанных в Калифорнийском технологи-
технологическом инститите в 1978 - 1980 гг. в виде курса теории поля для ас-
аспирантов первого года обучения, преследуют цель заполнить этот про-
пробел путем простого изложения вычислений, в которых применяется
современный аппарат, используемый специалистом по теории поля.
С педагогической точки зрения теперь уже немыслимо рассказать
за один год пертурбативную теорию поля — времена одногодичного
учебного курса, основанного на КЭД, ушли навсегда. Поэтому предла-
предлагаемые конспекты лекций освещают лишь избранный круг вопросов;
Современное изложение предмета должно состоять по крайней мере
из трех частей: из первого курса, в котором внимание сосредоточено
на структуре и методах пертурбативных теорий поля, знакомящего
аспиранта с теорией перенормировок и вычислением фейнмановских
диаграмм в калибровочных теориях; из второго курса, имеющего дело
с приложениями калибровочных теорий и в основном сконцентрирован-
сконцентрированного на вычислениях по теории возмущений в квантовой хромодинами-
ке (КХД), динамике ароматов (модель Глешоу - Вайнберга - Салама)
и, возможно, в теориях великого объединения; и из третьего курса по
непертурбативной технике. Наши конспекты относятся к первой части.
Сначала в них излагается на элементарной уровне классическая тео-
теория поля, причем детально рассматриваются группа Лоренца, дираков-
ские и майорановские массы: и суперсимметрия, а затем описываются
методы регуляризации, теория перенормировок и другие формальные
стороны предмета. Все изложения ведется в форме вычислений; дока-
доказательство перенормируемости не дается, а указывается лишь, поче-
почему это свойство представляется правдоподобным. Очень подробно
рассмотрена перенормировка теории Аф4, а о перенормировке калибро-

10 Предисловие
вочных теорий речь идет лишь вскользь. Переход от классической
теории поля к квантовой описан с помощью фейнмановского интегра-
интеграла по траекториям, что приемлемо с точки зрения и пертурбативных,
и непертурбативных исследований. Кроме того, для простых теорий
описана техника вычисления функциональных детерминантов, осно-
основанная на ? -функциях.
Весь материал излагается достаточно подробно, с тем чтобы
читатель мог проследить каждый шаг. Однако при этом вообще опу-
опущен ряд очень существенных теоретических вопросов, таких, как
инфракрасная структура ненарушенных калибровочных теорий и вы-
вычисления в калибровочных теориях с нарушенной симметрией. Мы все
же надеемся, что наши конспекты смогут служить введением в пер-
турбативные вычисления в-калибровочных теориях. В конце каждого
параграфа помещены задачи, причем степень" их трудности отмечена
звездочками. Чтобы указать пути дальнейшего изучения предмета,
приведен список литературы.
Я хотел бы выразить свою признательность проф. С.Фраучи и
ДжДарви за внимательное прочтение рукописи и конструктивную кри-
критику. Особо приношу благодарность Ю.Корригэну и Дж.Харви за то,
что они познакомили меня с техникой'? -функций, а также аспирантам
группы Физика-230 за их терпение и многочисленные предложения.
Наконец, я глубоко признателен Роме Гейне и Хелене Так, современ-
современным копиистам, без героических усилий которых эти конспекты ни-
никогда не увидели бы света.
Пасадена, лето 1980 г. П.Рамон

Глава 1
Функционал действия
§1. Элементарные сведения
Щсть нечто прекрасное и способное внушить благоговейные чув-
чувства в том, что все основные законы классической физики можно вы-
вывести из одной-единственной математической конструкции, именуе-
именуемой действием. Из нее вытекают классические уравнения движения,
а анализ условий инвариантности действия позволяет найти величины,
сохраняющиеся при классическом движении. Вдобавок, как показали
Дирак и Фейнман, роль понятия действия полностью раскрывается в
квантовой физике. Благодаря этому обеспечивается ясный и элегант-
элегантный язык для описания перехода от классической к квантовой физике
с использованием фейнмановского интеграла по траекториям (ФИТ).
Таким образом, наша задача ясна: сначала мы научимся строить
приемлемые функционалы действия (ФД), а затем выведем квантовые
свойства системы, описываемой заданным ФД, вычисляя связанный с
ним ФИТ. Прежде всего исследуем ФД для элементарной системы —
точечной частицы, вектор положения которой в момент времени t
есть ж(. ({) (i = 1, 2, 3) и которая движется в независящем от времени
потенциале V(x-). Соответствующий ФД дается выражением
S ([*• ]; tl, t2) a I dt ( 4- "I ^L _^f V(xt )). A.1)
t s * dt dt
Он является функцией начального и конечного моментов времени t,
и i 2 и функционалом от траектории *; (t) при 11 <' t <t2. (По повторяю-
повторяющимся латинским индексам проводится суммирование.) Все это означа-
означает, что заданной траектории xt (t) мы сопоставляем некое число, име-
именуемое функционалом (в данном случае S). Функциональный аргумент
мы будем заключать в квадратные скобки [...].< Например, длина тра-
траектории есть функционал от траектории.
Посмотрим, как меняется S при малой деформации траектории
*i(O + e*,(O. A.2)

12 Глава I
Имеем
S[xt *:6*,]
Пренебрегая
d{xt к6*,)
dt
V(xt fSx,- ) =
h
= / dt(-
h
членами i
J(*, 4-
dt
-- V(xt ) +
1
2.
0(t
¦5x
Sx
d(xt v.
dt
S*i )
>xJi можно написать
•i ) dxt
dt
+ 2 d
dt
i dt V.
dxt
dt
dxi
' dt
d(Xi +:5xi
dt
-У(х1 + 5х{)
о i &
I -_ 5;
¦).
1. A.3)
4 f
A.4)
A.5)
(Здесь д .= 8Idx^ Таким образом,
+ m} dt J- (Sx. d*i ). A.6)
Последнее слагаемое есть "поверхностный" член. Его можно устра-
устранить, если ограничиться вариациями траекторий, обращающимися в
нуль в концевых точках: 5xt (t i) = 5xi (t 2) = 0. Если принять это усло-
условие, то из требования постоянства действия S при любых 8х{ вытекают
классические уравнения движения системы. Символически запишем
это как равенство нулю функциональной производной, определяемой
соотношением
ЕС
S[*. +*Xi } = SI* ] f:/ *бх{ -^- + ... . A.7)
Б*,-
Итак,
_SS_ =_(mi!!L ,diV)-Q. (U)
6x( dt2
Следовательно, мы установили взаимное соответствие между урав-
уравнениями движения и условием экстремальности действия S. Заметим,
однако, что условие экстремальности действия S приводит к целому

Функционал действия
классу возможных траекторий. По какой из них на самом деле проис-
происходит движение, зависит от граничных условий, задаваемых как на-
начальные значения величин ж,- и dxi/dt.
Следующий и самый важный момент, который нужно отметить,
это наличие взаимного соответствия между симметриями действия
S и существованием величин, сохраняющихся в процессе движения
системы. Приведем пример. Пусть V(xi ) - функция длины вектора ж,- ,
т.е. величины г =-(xixi) \ Тогда действие S, очевидно, инвариант-
инвариантно по отношению к вращениям трехмерного вектора xi , поскольку
оно зависит только от длины этого вектора, а она при вращениях не
меняется. При бесконечно малом произвольном вращении имеем
5х; = tijXj, б,-,- = -е.-,-, причем t-i) не зависит от времени. ^1.9)
Далее, так как действие S инвариантно, выполняется равенство
6S = 0. Но ранее мы видели, что 5S состоит из двух слагаемых: функ-
функциональной производной, равной нулю для классической траектории, и
поверхностного члена. Однако для данной конкретной вариации мы не
можем наложить на bxt (t) граничные условия, и поэтому инвариант-
инвариантность действия S совместно с уравнениями движения приводит к ра-
равенству
tj at t.
Поскольку это верно при любых е . ., величины
m(Xi
{ dx:
L X ± ) A.11)
Xi —L -Xj -±- )
удовлетворяют равенству
lij{tx)=lij(t2) A.12)
л потому сохраняются в процессе движения* Как известно, это
компоненты углового момента. Инфинитезимальную форму зако-
закона сохранения можно получить, положив t2 -> t v 'Итак, мы
доказали в одном простом случае знаменитую теорему Эмми Нетер,-
связывающую инвариантность (здесь по отношению к вращениям) с
законом сохранения (углового момента). Суммируем уроки, извлечен-
извлеченные нами из этого элементарного примера: 1) классические уравне-
уравнения движения получаются из условия экстремальности действия S;
2) граничные условия должны задаваться извне; 3) симметрии дейст-
действия S находятся во взаимном соответствии с сохраняющимися вели-
величинами и поэтому отражают основные симметрии физической систе-

14 Глава 1
мы.Пример относился к классической механике. Его можно обобщить
и на классическую теорию поля, например максвелловскую электроди-
электродинамику или общую теорию относительности Эйнштейна.
Действие есть всего лишь некая математическая конструкция, и
число возможных конструкций такого рода неограниченно. Но дейст-
действие должно описывать физический мир, который, как мы полагаем,
устроен совершенно определенным образом. Следовательно, среди
многих возможных должен существовать один очень специальный ФД,
правильно описывающий то, что происходит на самом деле. Возникает
вопрос: как отличить это единственное действие от других действий?
Ответ нам подсказывает теорема Нетер, указывающая на связь меж-
между симметриями системы и симметриями функционала. Нам хорошо
известны некоторые симметрии,вроде тех, которые вытекают из специальной,
теории относительности, и из всех возможных действий мы должны
выбрать только те, которые отражают эти симметрии. Другие симмет-
симметрии, вроде сохранения электрического заряда, еще более ограничи-
ограничивают вид искомого ФД. Есть основания полагать, что природа предпо-
предпочитает определенные типы действия, которые обладают всякими инва^
риантностями, меняющимися от точки к точке. Подобные инвариантно-
инвариантности приводят к калибровочным теориям, о которых будет идти речь
далее в этой книге. Пока что научимся строить ФД для систем, ¦удовле-
¦удовлетворяющих законам специальной теории относительности. Формальным
признаком таких систем является инвариантность относительно
преобразований, порождаемых неоднородной группой Лоренца или,
что то же, группой Пуанкаре, к изучению которых мы и перейдем.
Задачи
Замечания: 1) задачи приведены в порядке возрастающей сложности;
2) решайте задачи, пользуясь функционалом действия,
даже если вам знакомы более элементарные способы ре-
решения.
А. 1). Докажите, что при движении, описываемом действием
S =fdtJL тх2, х = dx/dt,
2
сохраняется импульс.
2) Предполагая, что V(x() = v[ I - cos (г/а)}, найдите выражение
для скорости изменения импульса.
Б* Выведите выражение для скорости изменения углового момен-
момента точечной частицы, движущейся в произвольном потенциале.
*В. Найдите инвариантности ФД в случае точечной частицы, дви-

Функционал действия 15
жущейся в потенциале V=— a/r. Указание: ньютоновские орбиты
не прецессируют, что приводит к нетривиальной сохраняющейся ве-
величине, вектору Рунге - Ленца.
*Г. Считая ФД инвариантным относительно однородных трансля-
трансляций во времени, выведите выражение для связанной с этим сохраня-
сохраняющейся величины. Возьмите в качестве примера точечную частицу,
движущуюся в независящем от времени потенциале. Что произойдет
если потенциал будет зависеть от времени?
§ 2. Группа Лоренца (бегпый обзор)
В специальной теории относительности постулируется, что ско-
скорость света одинакова во всех инерциальных системах отсчета. Это
означает, что если xi - координаты светового сигнала в момент
времени t в одной системе и тот же самый световой луч регистриру-
регистрируется в точке жГ в момент времени t' в другой системе, то должно
выполняться равенство
''«^-«.¦«i = cV2- хГхГ. B.1)
Множество линейных преобразований, связывающих {х\ ,t') с (ж,- , t)
и сохраняющих неизменным приведенное выше выражение, образует
группу, называемую группой Лоренца (см. задачи). Выберем систему
единиц, в которой выполняется равенство с = 1, и введем обозначения
xv, ц = 0, 1, 2, 3, где х° = t, (ж», х\ х») = ¦(*' ) = х,
т.е. х»=.(х°,х{ )=•(*, х), i=l,2,3.
В этих компактных обозначениях величину s 2 можно записать в виде
*2= х°х°
= х°х° _
B.2)
где метрический тензор g^v= gv[i равен нулю во всех случаях, кроме
случая ц = v, причем g00 =¦- gu = -g22 = - ^зз =•*• ^сли нет особых
оговорок, то по повторяющимся индексам проводится суммирование.
Теперь уравнение B.1) принимает вид
xv ~/\$ x° + fiif х? , B.4)
Рассмотрим множество линейных преобразований
„V _ Л и „О
•у
сохраняющих*2. ГЬ этой причине величины Л v должны удовлетворять
условию
«цу*-ц*'" = gMV Л^ Л" хРх° = gpa xPx°. B.5)

16 Глава 1
Поскольку соотношение B.5) должно выполняться при любых х^.мы
имеем
«Ра=-«|дуЛ?Л?. B.6)
Во многих отношениях удобнее матричные обозначения: будем paw
сматривать х» как вектор-столбец и обозначать его через х, a g -
как матрицу, обозначаемую через g. Тогда
»2=-*V- *' = *<*, B.7), B.8)
где L - матрица, эквивалентная коэффициентам A{J, а индексом Г
обозначена транспонированная матрица. Чтобы матрицы L были матри-
матрицами преобразований Лоренца (ПЛ), они должны удовлетворять соотно-
соотношению
g = LV- B-9)
Исследуем уравнение B.9). Во-первых, вычислим детерминанты обеих
его частей:
det g= det L^det g det L, B.10)
откуда мы заключаем, что
det L= ±1. B.11)
Случай det L = 1 (-1) соответствует собственным (несобственным)
ПЛ. Например, ПЛ, задаваемое численно матрицей L = g, является не-
несобственным; физически такое преобразование отвечает заменам
х° -» х°, хх -*-х1 , т.е. пространственному отражению. Во-вторых^выпи-
шем компоненту уравнения B.6) с индексами 00:
откуда следует, что | Л °|« 1. B.13)
Если Лjj г 1, то ПЛ называют ортохронными, аЛ00^ - 1 отвечает не-
ортохронным ПЛ. Таким образом, все ПЛ можно разделить на четыре
категории (см. задачу):
1) собственные ортохронные, иначе называемые ограниченны*.
ми (L\) с det L =+ 1, Ло° >1;
2) собственные неортохронные (L*.) с det L =-к1; Л§^ — 1;
3) несобственные ортохронные (L± ) с det L = — 1; Л' > 1;
4) несобственные неортохронные (L[_) с det L = - 1; ЛЦ^'— 1.
Приведем несколько примеров.

Функционал действия 17
1).Вращения: х'° = х°, х'1 = оч xj, где ач - ортогональная
матрица.
Матрицу L можно записать в блочной форме
l-tf-i-y. <2.,4,
так что det L = det a, Возможны случаи det a = +1, отвечающие
собственным и несобственным вращениям, при этом L относится к
2, Бусты: преобразования
1 =-
описывают буст в направлении оси L Тогда в блочной форме 2х 2
имеем
ch ti -sh г| ,
b0V B.16)
(, ch
1_Bb
о ; 1
det L = ch2 л - sh2 л = 1, До =¦ ch л > 1. BЛ7), B 18)
Такое преобразование принадлежит к типу L\ Отметим» что перейдя
к новой переменной v (скорости движущейся системы отсчета), свя-
связанной с г| соотношениями
ch л = A - v2)- *, shT1 = v(l - va)-«> , BЛ9)
мы получим более знакомую форму этого преобразования,
3 Обращение времени, определяемое как преобразование
х - - х , х 1 =-х1 , Такое преобразование имеет det L = ¦— 1 и
Ag = - 1 и принадлежит поэтому к категории L-L,
4, Полное отражение, определяемое как преобразование x'v- = —х^
В этом случае det L = f 1, Л? = -1 и преобразование принадлежит
к категории Ц+ Полное отражение можно представить как произведе-
произведение пространственного и временного отражений.
Любое преобразование Лоренца можно представить в виде произ-
произведения преобразований указанных четырех типов (см. задачи). Сле-
Следовательно, мы можем ограничиться изучением вращений и бустов.
Поскольку возможны три вращения и три буста, по одному на каждое
пространственное направление, преобразование Лоренца характеризу-

Г8 Глава 1
ется шестью параметрами. Займемся построением шести соответст-
соответствующих генераторов. Рассмотрим бесконечно малое ПЛ
A"v= B"v + «"v, B.20)
где 5 ^v - символ Кронекера, равный нулю при ц 4 v и единице в ос-
остальных случаях. Подстановка выражения B.20) в уравнение B.6)
дает с точностью до О(е)
Используем метрический тензор для опускания индексов, например:
*и = g»v *v = (*° - х). B.22)
Тогда уравнение B.21) принимает вид
O = evtl + eMV, B.23)
т.е. е - антисимметричный тензор с 4 * 3/2 = 6 (как и ожидалось)
независимыми компонентами. Введем эрмитовы генераторы
L^ s i (V<9V - =чЛ). где ди н -L- =.(J- , 7 ). B.24), B.25)
Тогда можно написать
жйв.е1дрЖр# B.26)
Легко видеть, что генераторы LMV образуют алгебру Ли:
¦¦^uv» ^рсг 1 = г gVp Lya - l'gup^va ~ igva^np + 1йца ^vp> B.27)
которую можно отождествить с алгеброй Ли группы SO C,1). Наибо-
Наиболее общее представление генераторов SO C.1), удовлетворяющих пе-
перестановочным соотношениям B.27), имеет вид
где S^v - эрмитовы операторы, которые образуют ту же алгебру Ли,
что и LMV, и коммутируют с ними. Эрмитовы генераторы Мц , где
i, j = 1, 2, 3, сами образуют алгебру
[H..,Mkl] = -i5jk Мц + i?>ik Mji+ iSjiMik - i8uMjk, B.29)
отвечающую группе вращений SU B). Можно получить более знакомое
выражение, если ввести новые операторы
Ji s—e,7* M{k, B.30)
где е,. .? - символ Леви-Чивиты, полностью антисимметричный по всем

Функционал действия 19
своим индексам, и е 123 = + 1- (По повторяющимся латинским индек-
индексам проводится суммирование.) Тогда
Введем генераторы бустов
&i = Moi . B.32)
Из алгебры Ли следует, что
[ К,- , К;-] = - HljkJk,[Ji ,Kj}= itijk Kk. B.33), B.34)
Генераторы X и/t- эрмитовы, но при этом К. некомпактны. Пере-
Перестановочные Соотношения можно расцепить, введя новые линейные
комбинации
Ni s -у- (/» * iKi )• <2-35>
Хотя они и неэрмитовы, т.е. N{ t N,- , у них имеется то преимущест-
преимущество, что для них выполняются простые перестановочные соотношения
[tfi(tf/] = 0, B.36)
[tii,Nf]~-UifkNkl B.37)
[Nf.N^-itijbNl B.38)
Это означает, что и /V,- , и N,- образуют алгебру Ли группы SU B). По-
Поэтому можно воспользоваться хорошо известной теорией представле-
представлений этой группы. Из общеизвестных результатов этой теории для (спи-
(спиновой) группы SU{2) следует, в частности, что в данном случае суще-
существуют два оператора Казимира (операторы, которые коммутируют со
всеми генераторами)
"i "i с собственными значениями п(п + 1),
t t
Nt N{ с собственными значениями т(т+- 1),
где т, п = 0, 1/2, 1> 3/2, ... . Полученные представления индицируют-
индицируются парой чисел (п, nil, a состояния внутри представления различаются
дополнительно по собственным значениям операторов /V3 и /V]. Заме-
Заметим, что две группы SUB) не являются независимыми, так как их мож-
можно менять местами, производя операцию четности Р, в результате ко-
которой имеем
и операцию эрмитового сопряжения, меняющую знак мнимой единицы

20 Глава 1 .
и поэтому превращающую /V,- в щ • в общем случае представления
группы Лоренца не являются собственными состояниями ни четности,
ни (эрмитового) сопряжения. Поскольку Ji = /V; ±N)\ можно отож-
отождествить спин представления с т + п . Рассмотрим для примера сле-
следующие представления:
а) @, 0):спин равен нулю, скалярное представление с определен-
определенной четностью (может быть скаляром и псевдоскаляром);
б) A/2, 0): спин равен 1/2, левый спинор (определение левого
и правого условное)-,
в) @, 1/2): спин равен 1/2, правый спинор.
Эти спиноры имеют по две компоненты ("спин вверх" и "спин вниз"),
и их называют вейлевскими. Когда требуется учитывать четность, сле-
следует рассматривать линейную комбинацию @, 1/2) фA/2, 0), образу-
образующую дираковский спинор.
Любопытно, что, задав эти спинорные представления, мы можем,
умножая их друг на друга, построить любое другое представление. Это
эквивалентно построению состояний с высшими спинами путем образо-
образования (кронекеровского) произведения многих состояний со спином 1/2
в группе вращений. Приведем два примера.
а) Произведение A/2, 0) ® @, 1/2) = A/2, 1/2) дает представ-
представление со спином 1 с четырьмя компонентами. В тензорном обозначении
оно записывалось бы как 4-вектор.
б) A/2, 0) ® A/2, 0) = @, 0) ф A, 0). Здесь скалярное представле-
представление дается антисимметричным произведением. ЬЬвое представление
A, 0) описывается антисимметричным самодуальным тензором второ-
второго ранга, т.е. тензором Вми, удовлетворяющим условиям
V ="- ?vM> V = -^- ?uvpCT fipa> B.39), B.40)
где е MVPa - символ Леви-Чивиты в четырех измерениях, полностью
антисимметричный по своим индексам, причем е ° ' 2 3 =¦+ 1. Представ-
Представление @, 1) отвечает антисамодуальному тензору
V = —y~ ^vpa V- <2-41)
Например, максвелловский тензор напряженности поля Fuv преобразу-
преобразуется по отношению к группе Лоренца как @, 1)® A» 0).
Подчеркнем, наконец, один важный момент. Предположим, что мы
рассматриваем ПЛ в так называемом_^евклидовом пространстве", где
переменная t заменена величиной \/- 1 t. Тогда перестановочные со-
сотношения сохранятся, с той только разницей, что §ц„ заменится кро-

Функционал действия
некеровским дельтач;имволом - 6MV , и в результате мы придем к ал-
алгебре Ли группы S0D), т.е. группы вращений в четырех измерениях.
Теперь уже расщепление на две коммутирующие группы SUB) дости-
достигается с помощью эрмитовых комбинаций /,- ±Х{- . Эти две группы
SUB) полностью независимы, поскольку они не могут быть переведе-
переведены друг в друга сопряжением. Четность может все еще связывать эти
две группы, но в евклидовом пространстве, где все направления экви-
эквивалентны, это уже значительно'менее интересно.
Задачи
A. Покажите, что преобразования Лоренца удовлетворяют груп-
групповым аксиомам, т.е. что если L1 и L2 - два ПЛ, то и произведение
L XL 2 - тоже ПЛ; существует тождественное преобразование, и если
L — ПЛ, то и обратное преобразование L~l — тоже ПЛ.
Б. Покажите, 4TodetL и знак величины А°о являются лоренц-
инвариантными и могут быть поэтому использованы для классифика-
классификации преобразований Лоренца.
B. Покажите, что если L - ограниченное ПЛ (det L = + 1,
Л°о > 1), то все преобразования Лоренца могут быть записаны в виде
L х пространственное отражение для lJ_
L к обращение времени для L*_ ,
L х пространственное отражение к обращение времени для l| .
Г. 'Покажите что ограниченное преобразование Лоренца можно
однозначно представить в виде произведения буста и вращения.
*Д. Задача о перетасовке индексов: покажите, что компоненты
самодуального антисимметричного тензора второго ранга преобразу-
преобразуются друг через друга, т.е. неприводимо по отношению к группе Ло-
Лоренца.
§ 3. Группа Пуанкаре
Другой фундаментальный принцип - это инвариантность поведе-
поведения изолированной физической системы по отношению к однородным
трансляциям в пространстве и времени. (Чтобы генерировать грави-
гравитационные взаимодействия, этот принцип следует обобщить на произ-
произвольные трансляции.) Такое преобразование записывается в виде
*n-»s'M=.xnf-enf C.1)
где а м _ произвольный постоянный 4-вектор. Следовательно, общей
группой инвариантности является десятипараметрическая группа, на-

22 Глава 1
зываемая группой Пуанкаре, для которой"
жИ-»х'и = Лиу «vf a». C.2)
Трансляции C.1) не коммутируют с ПЛ. Действительно, рассмотрим
два последовательных преобразования группы Пуанкаре (ГП) с пара-
параметрами (Aj, а,) и (Л2, о 2):
«м-Л^^ + а11! -Л^рЛР^х^Л^-роР, + а»а. C.3)
Мы видим, что параметры трансляции подвергаются вращению. Здесь
нет ничего удивительного, поскольку так и должно быть в случае 4-
векторов. Подобное связывание группы трансляций с группой Лоренца
называется полупрямым произведением. Тем не менее, как явствует
из самого названия, преобразования ГП образуют группу (см. зада-
задачу А). Чтобы получить алгебру генераторов, заметим, что изменение
координат мировой точки х при бесконечно малой трансляции можно
записать в виде
-1еРРрх» =е^, C.4), C.5)
где е м - параметры, а
Pp=-idp C.6)
— эрмитовы генераторы этого преобразования. Очевидно, что они ком-
коммутируют друг с другом:
[P»,PV] = O, C.7)
но не коммутируют (ибо они 4-векторы) с генераторами группы Ло-
Лоренца:
<3-8>
Перестановочными соотношениями C.7) и C.8), а также перестановоч-
перестановочными соотношениями для М^ определяется алгебра Ли группы Пуан-
Пуанкаре. "Длина" Р^Р^ вектора Рр, очевидно, инвариантна по отноше-
отношению к преобразованиям Лоренца, а потому в силу формулы C.7) явля-
является оператором Казимира. Ке столь очевидно, как построить другой
оператор Казимира, но, как мы только что заметили, таким операто-
оператором может служить длина любого 4-вектора, коммутирующего с гене-
генераторами Р . Как раз таким вектором является Фвектор Паули - Любанско»
го W»:
2
С учетом формул C.7) и C.8) и антисимметрии символа Леви-Чивиты

Функционал действия 23
получаем
[W*, РР]-0, (ЗЛО)
а поскольку W преобразуется как 4-вектор, мы имеем
i. C.11)
Поэтому длина W* W^ данного вектора является инвариантом Казими-
ря. Самые общие выражения для десяти генераторов группы Пуанка"-
ре таковы:
так что
Гм = - ~- «uvp0 Spodv, C.12)
Теория представлений ГП была разработана I'1 Фигнером. Ее представ-
представления распадаются на три класса.
1. Собственное значение оператора РрРР = т2 есть действитель-
действительное положительное число. Тогда собственное значение оператора
W WP равно - m?s(s +• 1), где s - спин, принимающий дискретные зна-
значения s =0, 1/ 2, 1, ... . Такие представления индицируются массой
ти спином s. Состояния внутри представления различаются третьей
компонентой спина s3 = -s , - s + 1, ... , s - 1, s , а также непре-
непрерывными собственными значениями Р,- . Физически это состояние со-
соответствует частице массой т, со спином s, трехмерным импульсом pi
и проекцией спина s3, Массивные частицы со спином s имеют 2s + 1
степеней свободы.
2. Собственное значение оператора РрРр равно нулю, что отве-
отвечает частице с нулевой массой покоя. При этом собственное значение
оператора WpW р тоже равно нулю, а так как PPW = 0, операторы
!Р и Рц пропорциональны друг другу. Соответствующий коэффици-
коэффициент пропорциональности называется спиральностью и равен ±s, где
s =0, 1/2, 1, 3/2, ... - спин представления. Таким образом, безмас-
безмассовые частицы со спином s ф 0 имеют две степени свободы. Они до-
дополнительно различаются тремя значениями их импульса вдоль осей
х, у, z. Примером частиц, попадающих в эту категорию, могут слу-
служить фотон со спином 1 и двумя состояниями со спиральностью ± 1,
нейтрино со спиральностью ± 1/2 и гравитон с двумя состояниями по-
поляризации ± 2.
3. РрРр = 0, но при этом спин непрерывен. Длина вектора W рав-
равна квадрату положительного числа, взятому со знаком минус. Этот тип
представления описывает частицу с нулевой масоой покоя и с бесконеч-

24 : Глава 1
ным числом состояний поляризации, индицируемых непрерывной пере-
переменной. Такие представления, по-видимому, не реализуются в приро-
природе.
За подробностями мы отсылаем читателя к статье В. Баргмана
и Ю.Вигнера [ I]1); Существуют также "тахионные" представления
с PQPP < 0, которые мы не рассматриваем.
Имеются и другие представления ГП, но они неунитарны. Кван-
Квантовая механика допускает отождествление с состояниями частиц толь-
только унитарных представлений. Вигнеровские представления бесконеч-
бесконечномерны, что соответствует частицам с неограниченным импульсом.
Полезно сравнить этот случай с тем, что мы получили для группы Ло-
Лоренца, где речь шла о конечномерных, но неунитарных представлени-
представлениях. Введя в рассмотрение поля, мы сможем использовать эти пред-
представления.
Задачи
A. Покажите, что преобразования C.2) образуют группу.
B. Покажите, что если РрРр = т2 > 0, то собственное значение
оператора W W Р действительно равно - m2s (s + 1)Г"
*В. Найдите представление генераторов ГП на пространственно-
подобной поверхности х0 = 0 в случае, когда т2 = 0 и s =0.
Указание. Положив х0 = 0, следует выразить сопряженную вели-
величину Ро через оставшиеся переменные. Для этого используйте опе-
оператор Казимира. Затем выразите все генераторы ГП через xi , Pj и
т2. См. по этому поводу статью [ 2].
*Г. Решите предыдущую задачу в случае пространственноподобной
по9ерхности х° = х3.
** Д.Решите задачу Г в случае, когда s ^ 0 и т2 > 0.
§ 4. Локальные поля и преобразования
группы Пуанкаре
Рассмотрим произвольную функцию пространственно-временной
точки Р. В одной инерциальной системе отсчета, в которой точке Р
соответствуют координаты x^t это будет функция /"(*ц); в другой сис-
системе отсчета, где точке Рсоответствуют координаты x'vt это будет
функция f'(x'v), поскольку функциональная зависимость, вообще го-
говоря, зависит от выбора системы отсчета. Запишем изменение функ-
^Литература помещена в конце глав. Кроме того, в конце книги имеет-
имеется аннотированная библиография. — Прим. перев.

Функционал действия 25
ции при бесконечно малом преобразовании координат в виде
ц
С точностью до О Exv) можно заменить d^f ' величиной дц/". Тогда
6f = 50f +S^duf, D.2)
где через BQf обозначено изменение функции в данной точке х:
50f-f'(x)-f(x). D.3)
Второй член в формуле D.2) называется переносным членом. Равен-
Равенство D.2) можно формально записать как операторное:
D.4)
При трансляциях в пространстве-времени локальное поле не ме-
меняется, т.е.
Bf = О = Sof + t^d^f, D.5)
или 5o/' = -eM<V = -;*%/¦> D.6)
где Рц - оператор, опеределенный формулой C.6). При лоренцевых
же преобразованиях ситуация более сложная, и для ее выяснения мы
рассмотрим несколько примеров.
а) Скалярное поле
Построим (или представим себе) некоторую функцию <р(х) коорди-
координат xv, принимающую одно и то же значение при измерении в различ-
различных инерциальных системах отсчета, связанных преобразованием Ло-
Лоренца, т.е.
ф'(*') = Ф(*). D.7)
Этим условием определяется некое скалярное поле ( по отношению к
к ПЛ). В случае бесконечно малого преобразования, используя форму-
формулы D.7) и D.2), находим, что
0 = 5ф = 50q> + 8х^ дijf> D.8)
где Sx» дается формулой B.26). Полагая
D.9)
и сравнивая с D.8), мы видим, что представление генераторов группы

26 Глава I
Лоренца Д/цу в случае скалярного поля есть просто i{xudv - ц
Это означает, что введенный ранее оператор S^, действуя на скаляр-
скалярное поле, дает нуль. Как возникает нетривиальное SMV, можно увидеть,
рассмотрев конструкцию д^ (х). Заметим, что это выражение - ска-
скаляр по отношению к трансляциям, так же как и ф, поскольку оператор
производной не меняется при трансляциях (конечно, только при одно-
однородных трансляциях). Имеем
5г?цФ = [6,<Эц]фк<^бф. D.10)
Так как ф - лоренцовский скаляр, величина 5ф равна нулю. Но из фор-
формулы D.4) мы видим, что
[МцМво.^ЬСб*"^,^]. D.11)
Оператор 5 0 не меняет величины х» и поэтому коммутирует с Эц, но
к 5xv это не относится. Вычисление последнего коммутатора дает
[6„<?ц]=е/<Э0. D.12)
Собирая все полученные результаты, находим, что
где (Spff)/=»
Как нетрудно убедиться, найденные операторы удовлетворяют тем же
перестановочным соотношениям, что и генераторы L „ Сравнивая
соотношение DЛЗ) с канонической формой
50 (что угодно) =— — 6 Рст Мра (что угодно), D15)
мы получаем представление лоренцовоких генераторов для поля м
Поле, преобразующееся какд^х), называется векторным полем. За-
Заметим, что роль "спиновой части" М заключается в перестановке
индексов.
Тензорное поле со многими лоренцовскими индексами будет пре-
преобразовываться тоже по закону D.13). Действие оператора SpCT на
такое поле будет представляться суммой выражений типа D.14), по
одному на каждый индекс. Например, действие оператора S на тен-
тензор второго ранга Вцу дается формулой
Теперь уже легко построить из скалярных полей инварианты по отно-
отношению к группе Пуанкаре. Это любые скалярные функции q>(x), такие,

как <рп, cos q>(x) и т.д., 5Aс?Иф(ж)( (д^){д^) и т.д. (см. задачу). Но
величина *м?цф, будучи лоренц-инвариантной, не является пуанкаре-
инвариантной.
б) Спинорные поля
Спинорные представления A/2, 0) и @, 1/2) группы Лоренца реа-
реализуются двухкомпонентными комплексными спинорами. Обозначим
эти спиноры через ^ (*) и уд(*)- Двузначные спинорные индексы яр
но не выписаны. [ В литературе спинорные индексы L-типа отмечают
точкой сверху, а индексы /?-типа пишут без точки.] Запишем преобра-
преобразование спиноров в виде
Tf(*)-»t,'(*VA.T,W для A/2, 0)
L Li L и
У (ж) -» У '(*') = Л У (*) Для @, 1/2).
L, R R Л
гДе АЛ, L - матрицы 2х 2 с комплексными элементами. В случае
когда преобразование является вращением, явный вид матрицы Л^ д
известен из спинорных представлений группы SUB):
AL(/J) = е 1 ~2~ Ю (вращение). D.17)
Здесь со1' - параметры вращения, а а • - эрмитовы 2х 2-матрицы
Паули:
Эти матрицы удовлетворяют соотношению
а1 ст/ =5'/ + 1вс'как. D.19)
Сопоставив таким образом генераторы вращений /,- с 1/2ст1 t Мы мо-
можем записать в такой же 2х 2-форме и генераторы бустов. Нам уже
известно, что генераторы Ki не должны быть унитарными, так как
расщепление на две SC/B)-rpynnbi неунитарно. Представление генера-
генераторов в виде
К = - -i- a D.20)
удовлетворяет всем требуемым перестановочным соотношениям. По-
Поэтому
А -5Г— СТ • (СО — i V) /J IIV
Лг = e 2 D.21)

28 Глава 1
где v — параметры буста, связанные с генераторами К . Поскольку
представления A/2, 0) и @, 1/2) связаны между собой преобразова-
преобразованием четности, можно, зная Л^, построить Лд, изменив знак парамет-
параметров буста:
— а -((в + iv)
Лл=е 2 . D.22)
Эти выражения для Л^ и Лд дают возможность вывести ряд важных
свойств. Во-первых, мы видим, что Л^ и Лд связаны между собой со-
соотношением
Л7Х = Л^. D.23)
Во-вторых, в силу магического свойства матриц Паули
ст 2ст ' ст 2 = - (ст ' )*, D.24)
где звездочкой обозначена, как обычно, комплексно сопряженная ма-
матрица, можно написать соотношение
0 . — о * • [ at — i v) *
ct2Alct2 = е 2 '= Лд. D.25)
В-третьих, из эрмитово-сопряженного равенства D.24) с учетом эрми-
товости матриц Паули следует, что
Л[=а!Л1'Л D.26)
откуда a 2A[ct2Al = 1, илиЛ?ст2Л?, = ст2. D.27)
Такое же равенство справедливо и для Лй. Все эти соотношения пона-
понадобятся при построении лоренц-инвариантных выражений, содержащих
спинорные поля. В качестве первого применения, используя комплек-
комплексно сопряженное равенство D.25), находим, что при лоренцовских
преобразованиях выполняются соотношения
<J24>*L -» <72Л* у* = а2Л* а2а2ц>1 = Лдст2^*. D.28)
Формула D.28) показывает, что, если задан спинор у , преобразую-
преобразующийся как A /2, 0), можно построить связанный с ним спинор ст 2у* , преоб»
разующийся как @, 1/ 2). Точно так же, если спинор у преобразует-
преобразуется как @, 1/2), то спинор <72у* преобразуется как A/2, 0).
Ранее отмечалось, что можно построить скалярное представление,
взяв антисимметричное произведение двух представлений A/2, 0). Те-
Теперь это можно явно показать. Пусть ц/ и х, - два спинора, преобра-
преобразующиеся по представлению A/2, 0). Как следует из формулы D.27),

Функционал действия 29
при лоренцовских преобразованиях
Это и есть искомый скаляр. С точки зрения теории групп скалярное
произведение возникает как антисимметричное произведение; поэтому,
взяв xL =yL , мы должны получить, что скалярный инвариант не су-
существует. В явной форме находим, что *
D.30)
и это выражение обращается в нуль, если у^ и у?2 - обычные чис-
числа. Но если взять в качестве ц^ и yi грассмановы числа, антиком»
мутирующие друг с другом, то такой скалярный инвариант будет иметь
ненулевое значение. И действительно, как мы увидим ниже, спинорные
поля будут рассматриваться как классические грассмановы (антиком-
мутирующие) числа.
Можно также взять х, =°\*. Тогда инвариант принимает вид
Ни один из этих инвариантов не является действительным. Заменяя
L на R и наоборот, мы получим комплексно сопряженные инварианты.
Из двух спиноров можно построить и представление, отвечающее
4-вектору. Простейший путь - начать со спинора yL~(\/2, 0), так
как из него можно сконструировать спинор @, 1/2), а затем перемно-
перемножить эти два спинора. Известно, что величина 4\ У?, инвариантна по
отношению к вращениям, которые представляются унитарными опера-
операторами, действующими на спиноры. Но она не инвариантна по отноше-
отношению к бустам, поскольку
^L^X'X^l^z/"*^9^ +0^2)' D.32)
Однако дополнительно возникшая величина преобразуется по правилу
t , t J- e-v . J-C v . .
VL° 4>L* VIе 2 ole2 у =• ц/ a'y +
L L l
+ — v; ц/ \ <у1 t 'a} ! 4\ + 0{v) м ^ а1 у + vl у* ^ + O(v2),
2t *-* *-" Li Li Li U
D.33)

30 Глава I
где фигурными скобками i I обозначен антикоммутатор. Следователь-
Следовательно,; под действием бустов две указанные величины преобразуются
друг в друга:
t .
а по отношению к вращением величина yLo l у. ведет себя как трех-
трехмерный вектор. Сравним соотношения D.34) с законом преобразова-
преобразования 4-вектора
кт/ц _ ?ц f/v D 35^
где е ff! = ¦ - v1' - параметры буста. Отсюда вытекает, что величина
i ш ст^ш =i (и, ф и, а1 и; \ D.36^
является 4-вектором. Здесь мы обозначили через а ° единичную 2x2-
матрицу. Начав с фл и изменив знак пространственных компонент,
можно получить другой 4-вектор
Эти два вектора действительны, поскольку ц^ии у/? - грассмановы
переменные: (v?vr)* = y[ 4^ = -^ ^L> их сумма (разность)
имеет положительную (отрицательную) четность.
Каждый из этих 4-векторов, скомбинированный с другим, может
дать лоренцовский инвариант. Как мы видели ранее, простейшим
4-вектором является оператор производной д^, который вдобавок еще
и трансляционно-инвариантен. Так как оператор д может действовать
на любое из полей, получаем следующие билинейные по спинорным по-
полям инварианты:
4 *\°*В\ D.38)
Подразумевается, что оператор производной действует направо и толь-
только на ближайшую соседнюю величину. Указанные лоренцовские инва-
инвариантны уже не являются действительными; однако можно образовать
действительные комбинации, например
~Т *1аЧ^- -j- 3^1*%L E ±-^Lo^d^L D.39)
и аналогичное выражение, в котором L заменено на R, a a w - на а^.
Если четность существенна, то следует объединить представле-
представления A/2, 0) и @, 1/2). Поскольку невозможно приравнять спинор ц^

Функционал действия 31
спинору <т2у*? , не придя к противоречию или к условию
у ? = 0, необходимо построить четырехкомпонентный спинор, называе-
называемый дираковским спинором:
D.40)
для которого операция пространственной инверсии хорошо определе-
определена:
Р: *. *=¦{ и," =/ " М vp оТ, D.41)
где введена 4к 4-матрица у0. С помощью проекционных операторов
-у- A ±ys), D-42)
где (в блочной форме)
г. -( » -1 )•
можно спроектировать дираковский спинор на левый или правый спи-
спиноры.
Все построенные ранее инварианты можно выразить через дира-
ковские спиноры. Например,
D.44)
ф ¦ 0
где ф = iy ¦ у0 — дираковски-сопряженный спинор. Так как величина
D.44) является лоренцовским инвариантом, спинор ^J преобразуе" ся
контраградиентно по отношению к Y. Аналогично
(ч/ а^ц ^ + ^ 5^M^)= -у VY^1*' D'45)
где введены 4 х 4-матрицы
D-46)
Поскольку величина D.45) - лоренцовский инвариант, индекс ц у у -
матриц является истинным 4-векторным индексом, Ясно, что это дира-
ковские матрицы в вейлевском представлении. Они удовлетворяют со-
соотношению
{ yH yVi _ 9_)av /л 4?\

32 Глава 1
Матрица у5 связана с другими у-матрицами формулой
У5 = iyVyV • D.48)
Учитывая эквивалентность спиноров yL и а 2у? по отношению к
преобразованиям Лоренца, можно построить соответствующий дираков-
ский спинор
Заметим, что
(Yc)c = У. D.50)
Спинор Ч называется (зарядово) сопряженным. Поскольку а2у*
преобразуется так же, как уц, можно построить и специальный тип
четырехкомпонентного спинора, называемый майорановским спинором,
D.51)
Он (зарядово) самосопряжен; Майорановский спинор - это вейлевский
спинор, записанный в четырехкомпонентной форме. Мы остановимся
на физической интерпретации этого спинора, когда построим из спи-
норных полей функционалы действия. Сейчас же заметим лишь, что
майорановский или вейлевский спинор описывает объекты с вдвое мень-
меньшим, чем у дираковских спиноров, числом степеней свободы.
Как мы отмечали в конце § 2, в евклидовом пространстве нельзя
связать друг с другом две S С/B)-группы, образующие (евклидову) груп-
группу Лоренца. Теперь мы можем показать, почему это так. Каждая из
групп 51/B) реализуется унитарными операторами, и поэтому мы име-
имеем новые выражения
?
1 ~ \ ' D.52)
„ — а •(«>— v)
Лй - Л| = е 2
откуда видно, что между Л^ и Л^ нет никаких связей. Следователь-
Следовательно, в евклидовом пространстве не существуют майорановские спино-
спиноры, так как невозможно связать yf и ш?. Однако мы свободны в
выборе if^ или Ч^ по отдельности и даже можем образовать дираков-
ский спинор Т?, понимая при этом, что введенная ранее операция за-
зарядового сопряжения перестает существовать.

Функционал действия 33
в) Векторное поле
Векторное поле преобразуется по представлению A/2, 1/2). Мы
уже видели, как действует оператор S pff на произвольное векторное
поле А^(х). К этому можно добавить, что существует другое пред-
представление векторного поля в виде эрмитовой 2 х 2-матрицы
*A~\ ЛоЛ / D.53)
Преобразования Лоренца определяются как такие преобразования, при
которых сохраняется условие А=А ' и инвариантна величина det A.
Можно рассмотреть ряд инвариантов, таких,как
дйА„(х)д*Аи(х), д^Ау,(х)9Ыч{х),9хi {x)tti т.д. Поскольку для
ного представления четность определена, можно определить как век-
векторные, так и аксиально-векторные поля.
г) Поле со спином 3/2
Можно по-разному определять поле со спином 3/2 в зависимости
от того, какую роль должна играть четность. Один из возможных спо-
способов заключается в том, чтобы образовать произведения трех пред-
представлений A/2, 0):
A/2, 0)® A/2, 0)9A/2,0) = C/2,0) вA/2,0)вA/2,0). D.54)
Полностью симметричное произведение отвечает спину C/2 [ два пред-
представления A/2, 0) имеют смешанную симметрию]* Таким образом, по-
поле со спином 3/2 представляется полем, полностью симметричным
относительно перестановок трех его спинорных индексов L-типа. Трансформа-
Трансформационные свойства такого поля получаются путем соответствующего обоб-
обобщения действия оператора Sp0. на индекс L-типа (см. задачу). В этом
случае собственные состояния оператора четности даются комбина-
комбинацией представлений C/2, 0)~@, 3/2). Однако подобное представление
довольно громоздко из-за большого числа индексов у символа поля.
Более удобное представление поля со спином 3/2 дает произве-
произведение вектора и спинора:
A/2, 1/2)® A/2,0)= A, 1,/2)9@, 1/2). D.55)
Соответствующая полевая величина имеет 4-векторный и спинорный
индексы. Собственным состоянием оператора четности будет в этом
случае четырехкомпонентное поле Рариты - Швингера
D.56)

34 Глава 1
(спинорные индексы опущены). Записанное в таком виде поле описы-
описывает все состояния, содержащиеся в произведении D.55), вместе с
их партнерами по четности. Следовательно, необходимо лоренц-инва-
риантным образом отбросить лишние компоненты A/2, 0) ®@, 1/2).
Поэтому мы налагаем на поле дополнительные условия
= 0 <4-57)
или, с использованием матриц Дирака,
0 D.58)
Можно построить те же типы ковариантов и инвариантов, что и в спи-
норном случае, с той только разницей, что теперь имеется еще один
векторный индекс. Инвариантами, например, будут
^II °2 ^' vlRa2^R> 4>»R 4>t> — • D-59)
Используя набор векторов
D.60)
в комбинации с оператором д^, образуем инварианты вида
d»4>lL°PVvLivapv и т.д. D.61)
Действительным скалярным инвариантом является комбинация
D.62)
Наличие знака минус, или, что то же, матрицы у5, диктуется свойства-
свойствами тензора е по отношению к преобразованию четности. Наконец, за-
заметим, что, как и в случае поля со спином 1/2, на поля Рариты -
Швингера можно наложить майорановские условия.
д) Поле со спином 2
И в этом случае существует много способов описать поле со спи-
спином 2: B, 0), @, 2), A, 1). Выберем последний способ. Такое представ-
представление возникает в произведении
D.63)
где индексами S и А обозначены симметричная и антисимметричная
части. Следовательно, поле со спином 2 может быть описано симме-

Функционал действия 35
тричным тензором второго ранга Ацу. Следу этого тензора соответ-
соответствует скалярная компонента, которую можно отбросить, наложив ус-
условие бесследовости
(*) = 0. D.64)
Инвариантны легко строятся путем "насыщения" векторных индексов
и использования оператора cL. Вот примеры:
А^ V ... . D.65)
Такое тензорное поле возникает в общей теории относительности, где
оно используется для описания гравитона.
Завершая параграф, заметим, что можно построить и много дру-
других полей, обладающих определенными свойствами по отношению к
лоренцовским преобразованиям. Мы выбрали для более детального об-
обсуждения только те из них, которые используются для описания физи-
физических явлений. Это как раз те поля, которым мы можем сопоставить
фундаментальные частицы. Так, дираковским спинорам мы ставим в
соответствие заряженные фермионы, подобные электрону, мюону, тау-
лептону, кваркам; вейлевским спинорам - нейтрино ve, vw, vT. Вектор-
Векторным полям мы сопоставляем фотон, глюоны, посредством которых
осуществляются сильные взаимодействия, и W- бозоны, посредством
которых осуществляются слабые взаимодействия. Наконец, тензор-
тензорному полю соответствует гравитон, посредством которого осущест-
осуществляется гравитационное взаимодействие.
Задачи
A. Найдите в явной форме результат действия оператора S а на
Б. Выразите результат действия оператора S ро на дираковский
спинор через дираковские матрицы, т.е. представите в виде, не зави-
зависящем от представления.
B. Постройте явное выражение для поля, билинейного по спинорам
X. и у ии преобразующегося по представлению A, 0). Можно ли пос-
построить такое поле только из поля ш ?
Г. Используя матрицы Л^ и Л#, найдите форму, которую прини-
принимают преобразования Лоренца, действующие на матрицу D.53).
Д. Исходя из полей у. (х) и Л^(х), постройте по крайней мере два
инварианта, в которые входят оба эти поля.
Е. Найдите представление матриц Дирака, в котором компоненты
майорановского спинора действительны. Такое представление называ-
называется майорановским представлением.

36 Глава 1
§ 5. Общие свойства действия
В предыдущих параграфах мы познакомились с тем, как построить
Пуанкаре-инвариантные выражения из полей, имеющих вполне опреде-
определенные трансформационные свойства по отношению к группе Пуанкаре.
Теперь мы можем объединять эти инварианты в выражения для функ-
функционалов действия, которые могли бы служить основой для более или
менее приемлемых физических теорий. Требование инвариантности по
отношению к группе Пуанкаре гарантирует, что эти теории будут под-
подчиняться аксиомам специальной теории относительности. Но, освоив-
освоившись с таким построением, мы увидим, что получается слишком мно-
много вариантов теорий и что одного требования пуанкаре-инвариантности
недостаточно для того, чтобы выделить истинное действие, описываю-
описывающее мир. Попытаемся сузить круг наших поисков и перечислим некото-
некоторые искусственно налагаемые требования, которые, как выяснилось,
достаточны ¦ для того, чтобы отобрать приемлемые теории.
1. Мы используем функционалы действия вида
S = [ <*«*?, E.1)
где Tj и т2 - пределы интегрирования, а
d*x = dt dx^x'dx^ E.2)
есть мера интегрирования в четырехмерном пространстве Минковско-
го. Иногда по математическим соображениям мы будем менять число
измерений пространства-времени или даже рассматривать меру в ев-
евклидовом пространстве, где d4- х заменяется евклидовой мерой
d*x = dxodx4x4x3, E.3)
причем х°= ix°, х1 _.ж« .Подынтегральное выражение ? называется
лагранжевой плотностью или, короче, лагранжианом. Лагранжиан
является функцией только полей и их производных, чем обеспечивается
трансляционная инвариантность. Кроме того, он зависит от полей, взя-
взятых только в одной пространственно-временной точке жц, следствием
чего оказывается локальный характер теории поля. Ясно, что такой
выбор - простейший из возможных: нетрудно вообразить и нелокальные
теории поля, но они, конечно, будут более сложными. Однако наша ве-
вера в локальную теории поля такова, что мы считаем такую теорию при-
пригодной даже для описания нелокальных явлений!
2. Мы требуем, чтобы функционал S был действительным. Это тре-
требование, как установлено, совершенно необходимо для получения удов-

Функционал действия 37
летвррительных квантовых теорий поля, в которых сохранялась бы пол-
полная вероятность., Комплексный потенциал в классической физике озна-
означает поглощение, т.е. превращение материи в ничто; ясно, что это нам
не подходит.
3. Мы требуем, чтобы из действия S следовали классические урав-
уравнения движения, содержащие производные не выше второго порядке. В
классических системах, описываемых дифференциальными уравнения-
уравнениями более высокого порядка, обычно имеются непричинные решения. Хо-
Хорошо известный пример - уравнение Лоренца - Дирака в электроди-
электродинамике. Это дифференциальное уравнение третьего порядка, включаю-
включающее эффекты реакции излучения и обнаруживающее такие непричинные
явления, как ускорение частиц до их взаимодействия с излучением.
Чтобы удовлетворить указанному требованию, мы рассматриваем такие
лагранжианы ?, которые содержат не более двух операторов д . Вслед-
Вследствие этого классические уравнения движения (возведенные в квадрат
в случае спинорных полей) будут содержать действующий на поле опе-
оператор д^дР. Когда уравнения движения превращаются в условие на соб-
собственные значения этого оператора, мы говорим, что имеем дело со
свободной теорией поля, так как можно отождествить дцд^ с операто-
оператором Казимира группы Пуанкаре, а уравнения движения ограничивают
наш выбор представлением, отвечающим (свободной) частице.
4. Принимается, что действие S инвариантно по отношению к
группе Пуанкаре, как уже говорилось выше.
5. Могут быть дополнительные требования инвариантности-дейст-
инвариантности-действия S . И действительно, феноменологический успех калибровочных
теорий указывает на то, что функционал действия должен быть инва-
инвариантным относительно необычных новых преобразований, включаю-
включающих новые степени свободы, подобные электрическому заряду, слабо-
слабому заряду, цветовому заряду и другим зарядам, которые еще пред-
предстоит открыть. Калибровочные теории строятся на действиях, инва-
инвариантных относительно локальных (т.е. зависящих от х) преобразова-
преобразований, совершаемых среди этих внутренних степеней свободы. Позже
мы подробнее рассмотрим этот вопрос.
В классической теории действие имеет вполне определенную раз-
размерность ML2T~* углового момента, или, что эквивалентно, постоян-
постоянной %. В естественной системе единиц, в которых h = 1, действие S
становится "безразмерным". Следовательно, лагранжева плотность
в четырех измерениях имеет естественную размерность L~4 %).
15 Далее в книге автор часто указывает только показатель л в выраже-
выражении Ln для размерности каких-то величин. — Прим. перев.

38 Глава 1
Рассмотрим действие
S(Ti> Т2> [Ф])Е Г d*x ?(ф,д^Ф), E.4)
где Ф(х) - любое локальное поле или любая совокупность локальных
полей ( они могут быть скалярами, спинорами, ...; все индексы мы
опускаем); т, ит2 - границы области интегрирования. Изменение дей-
действия S при произвольном изменении Ф на величину 6Ф таково:
5S = ; Гх 5? -/ Их (-|А- вф,¦?-- 5(ЭиФ)). E.5),E.6)
Так как при этой вариации х не меняется, мы имеем
5EЦФ) = <?УEФ). E.7)
Выражение E.6) можно преобразовать к виду
55 =•/ *x(JL ~дЛ- ) 5Ф + / rf*« ^(^-. 8Ф).
5Ф 5(ЭФ) ^(^Ф)
E.8)
Последнее слагаемое здесь - поверхностный член, который можно пе-
реиисать в виде интеграла по поверхности
E-9)
где сг - граничная поверхность, a da - элемент этой поверхности.
Потребуем теперь, чтобы вариация 5Ф была равна нулю на поверхнос-
поверхности ст . Из требования стационарности действия S при произвольном из-
изменении 5Ф, равном нулю на границах, мы получаем уравнения Эйлера
Лагранжа
дФ
_0
которые представляют собой классические уравнения поля для систе-
системы, описываемой действием 5. Можно рассматривать выражение
E.10) как функциональную производную действия S по Ф. Еще раз под-
подчеркнем, что она хорошо определена только для таких вариаций, кото-
которые обращаются в нуль на границах области интегрирования. Как од-
одно из важных следствий отбрасывания поверхностного члена отметим,

Функционал действия 39
что можно получить те же самые уравнения движения, задавшись но-
новой лагранжевой плотностью
?'=.?н-:<у\и E.11)
с произвольными Ли. Подобное изменение лагранжиана ? приводит к
изменению действия S, полностью зависящему от выбора граничных
условий для полей, входящих в ?' (такой свободы нет в присутствии
гравитационного поля). Преобразование, связывающее ? и ?', в клас-
классической механике называется каноническим преобразованием. Заме-
Заметим также, что добавление к лагранжиану ? постоянной величины не
меняет характера классической системы, но оказывает влияние на
связь системы с гравитационным полем, поскольку такая добавка по-
порождает бесконечную энергию.
Посмотрим теперь, как меняется действие в результате пока еще
неконкретизированных (но не произвольных) изменений координат 8х^
и полей 5Ф. Изменению координат отвечает изменение меры интегри-
интегрирования, даваемое формулой Якоби
6(d«*) = d*x ди5х». E.12)
Отсюда следует, что
Т2
5S = / rf4* 0,,б*?? н- 5?). E.13)
С учетом формулы D.4) получим
(*?f 6o?= E.13)
ц? + — 50Ф +J? 5О5ЦФ. E.15)
Так как 50 - изменение только самой функции, имеем
20<Э(,Ф = [5„, др]ф f ^й60Ф = др50Ф. E.16), E.17)
Простые выкладки приводят к выражению
E.18)
Привлекая классические уравнения движения, можно записать измене-

40 Глава I
ние действия в виде
8S- ТЛг*[&,.в»мкв*май? + *.(^— 50Ф)Ь E.19)
= ¦ f d*x ди(?5х» + —2±— 50Ф). E.20)
Можно также, выразив 50 через 5, написать
Г Г.
Щ. E.2.)
Выразим вариации координат и полей через глобальные (т.е. не зави-
зависящие от х) параметры преобразования:
5*Р = °*г 5wa , E.22)
б»а
5Ф = 5» . E.23)
Здесь индекс а нумерует параметры преобразования. Следовательно,
6S =• f d4x 6
E.24)
Если действие инвариантно по отношению к преобразованиям E.22) и
E.23), то отсюда вытекает, что плотность тока
сохраняется, т.е.
«3^/^ =0. E.26)
Это уравнение сохранения есть следствие того, что выражение E.24)
справедливо при всех 5соа. Таким образом, мы доказали для класси-
классической теории поля теорему Нетер, связывающую уравнение сохране-
сохранения с инвариантностью действия.

Функционал действия 41
Но если действие не сохраняется, то и это уравнение сохранение
более не справедливо. Например, при бхР « 0 оно имеет особенно прос-
простой вид
E-27)
Предположим, что мы нашли совокупность преобразований E.22) и
E.23), оставляющих действие инвариантным. Проинтегрируем обе
части равенства E.26) в бесконечных пределах по пространственным
направлениям и в конечном интервале по времени. Тогда
Г2 +эо Т2
0= [ dx° f d3x duj» = f dx° -I- f d3*
+ f dx°fPx Э, /'. E.28)
Если пространственные границы выбраны подходящим образом, то пос-
последний член обращается в нуль. В результате
0= f d3* /о° (T,,*)- U d*x /°(Г2,*). E.29)
— 00
— 00
Следовательно, заряды, определенные формулой
#о(Г)а / d3x /° (Т, х), E.30)
— 00
не зависят от времени, поскольку приведенные выше рассуждения вер-
верны независимо от выбранных пределов интегрирования по времени.
Итак,
dQn
— = 0. E.31)"
dt
Из условия 5S = 0 нам удалось вывести существование сохраняющих-
сохраняющихся зарядов.
Когда параметры преобразований безразмерны, как в случаях пре-
преобразований Лоренца и внутренних преобразований (но не трансляций),
получающиеся токи всегда имеют размерность L~D+ J в D измерениях
так что заряды оказываются безразмерными.

42 Глава 1
Заметим далее, что сохраняющийся ток определен неоднозначно,
так как к нему всегда можно добавить четырехмерную дивергенцию
антисимметричного тензора dp t?4 Это особенно ясно видно, если
учесть формулу E.11). Кроме того, поскольку /м сохраняется только
после использования уравнений движения, мы свободны добавлять к
нему любую величину, обращающуюся в нуль в силу уравнений движе-
движения. Это существенно, в частности, тогда, когда а - лоренцовский ин-
индекс, как в случае трансляций, для которых
5*м = 6ц;_5*^_ ц (о } E#32)
5соа р
и в случае преобразований Лоренца, для которых
5жЦ=6цУх . _Ё^ -> J_ (gM*y _gtJ*p). E.33)
v 5coa 2 P
В последнем случае параметр а заменяется антисимметричной парой
индексов [ pv ].
В заключение отметим, что преобразование, оставляющее инва-
инвариантным действие S, может изменять лагранжиан ? на полную ди-
дивергенцию, и это означает, что операция симметрии сопровождается
каноническим преобразованием. В квантовой теории, где уже нельзя
полагаться на уравнения движения, утверждение о сохранении тока
теряет свое значение, но заменяется соотношениями между функция-
функциями Грина, так называемыми тождествами У орда.
Задачи
А. Покажите, что конформные преобразования
где с - бесконечно малый 4-вектор, в совокупности с дилатациями
5хМ = axV-, где a - бесконечно малая величина, и преобразованиями
группы Пуанкаре образуют 15-параметрическую группу (она называет-
называется конформной группой). Найдите генераторы этой группы и их пере-
перестановочные соотношения.
Б. Дилатации и группа Пуанкаре образуют вместе так называемую
группу Вейля. При дилатациях поле Ф размерности d преобразуется, по
правилу 5Ф = + сй>. Предполагая, что действие S инвариантно по отно-
отношению к группе Вейля и содержит Ф, найдите сохраняющийся ток, соот-
соответствующий дилатациям.

Функционал действия 43
§ 6. Действие цпл скалярных полей
Лагранжева плотность, содержащая только одно скалярное поле
Ф(х), записывается в наиболее общем виде как
? = _L_ эиф) д? Ф) - У{ф), F.1)
где коэффициент 1/2 чисто условен, а V - скалярная функция. Первое
слагаемое носит название кинетического члена, а второе — потенциаль-
потенциального. Кинетический член обладает более широкой, нежели потенциаль-
потенциальный, группой инвариантности: он инвариантен по отношению к сдвигу
поля ф -»ф + а, где а - глобальная постоянная. Поэтому в четырех из-
измерениях ф(ж) имеет естественную размерность L~x (или размерность
массы). В классической теории форма функции V(<p(x)) ничем не огра-
ограничена. Простейшим примером может служить лагранжиан
?о= J_ ЭAф эИф- -L- rtV, F.2)
где т имеет размерность массы. Такое действие описывает свободную
частицу массой т (как мы позднее выведем, исходя из интеграла по
траекториям.) Заметим, что лагранжиан ?0 инвариантен также по от-
отношению к дискретному преобразованию симметрии
Ф(х) - -ф). F.3)
Более сложный пример - лагранжиан
? ,.? _ ± ф\ F.4)
о 4!
описывающий теорию с самодействием. Отметим, что ,А - безраз-
безразмерный параметр (в четырех измерениях). Знаком минус обеспечива-
обеспечивается положительность функции V. Такое действие приводит к приемле-
приемлемой квантовой теории поля. Д)угой пример - синус-гордоновский лаг-
лагранжиан
?,.'1 ^Ф^ф +JL (cos ^ -1), F.5)
1 Л
где Л — безразмерная константа. При уДу/т« 1 этот лагранжиан
сводится к предыдущему с отличием лишь в знаке члена Сф4. К сожалению,
неизвестно, приводит ли такой лагранжиан к приемлемой квантбвой
теории поля в четырех измерениях; но он дает хорошую квантовую тео-
теорию в двух измерениях!
Какова бы ни была форма функции V, легко получить уравнения

44 Глава 1
движения
F.6)
где штрихом обозначена производная по полю <р. Следуя сказанному
в предыдущем параграфе, можно построить сохраняющуюся величину.
1. При бесконечно малой трансляции, для которой8х^ = et* H6q>- О,
уравнения E.25) и E.26) принимают вид
V — *цч?. + э^ ***• Э^ iw = °- FЛ)> (О)
Мы видим, что в этом случае / - симметричный тензор; он называ-
называется тензором энергии-импульса. Соответствующий сохраняющийся за-
заряд таков:
РЦ = М3* /ио = М3*(-?Мо? + <ЭоФ<Эцф). F.9)
Поскольку Ро есть энергия системы, плотность энергии дается выра-
выражением
/00= -?+ dQyd0<f=— д0<?д0 Ф+:-2~7 9 7Ф+ F(q>)
F.10), F.11)
и, как нетрудно видеть, положительно определена, если V> 0. Та по-
полевая конфигурация, которая приводит к наименьшему значению /00,
отвечает основному состоянию. Поскольку члены с производными да-
дают положительный вклад, такая конфигурация всегда возникает для
статического поля <р0 (Эо ф0 =Bi ф0 = 0), и в этом случае плотность
энергии есть значение потенциала Р(ф0) для этого конкретного поля.
2. При лоренцовских преобразованиях сохраняющийся нетеровский
ток представляет собой трехиндексную величину .
i»vp = (- «мЛ^ + 3t& д*№\> хр ~ gp х\>) * hvxp - /up*v.
F.12), F.13)
Соответствующие сохраняющиеся заряды - это генераторы лоренцов-
лоренцовских преобразований
Mvp = f d3x /ovp = f d3x (jovxp -jopxv). ^щ
Сохранение этих зарядов есть следствие инвариантности действия по
отношению к преобразованиям группы Пуанкаре.
В качестве примера применения теоремы Нетер к таким преобра-
преобразованиям, по отношению к которым действие S не обязательно инвари-

Функционал действия 45
антно, рассмотрим бесконечно малую дилатацию
6*и = ос*и, 5<р= -о<р., F.15)
Нетеровский ток имеет вид
F.16), F.17)
Пользуясь формулой F.8), получаем, что
d J 2- FЛ8)
Если ? = 1/2 (З^фЭ^ф - (Х/4!)ф4, то легко доказать, что диверген-
дивергенция тока /И равна нулю (в четырех измерениях; см. задачу). Однако,
если бы мы добавили к ? "массовый член" - 1/2т2ф2, его вклад ока-
оказался бы равным
duj? = m292# 0. F.19)
Причина того, что в этом случае ток /g перестал сохраняться, заклю-
заключается в появлении в лагранжиане ? размерного параметра.
Напомним, что вид тензора /мунеоднозначен. В качестве приме-
примера рассмотрим новое определение
e - gMV дрд?) 92, F.20)
где а — безразмерное число. При этом все еще выполняется условие
-0. F.21)
Зафиксируем а, потребовав, чтобы в теории, инвариантной- относитель-
относительно дилатаций, тензор 9pv имел нулевой след. Если взять для примера
лагранжиан F.4) с т2 = 0, то
ejf = A +¦ баХ-дрфдрдРф-фдрдРф), F.22)
откуда мы получаем, что а =¦- 1/6. Более того, разность величин
0 и /mV есть поверхностный член, не меняющий сохраняющихся за-
зарядов. Можно теперь определить новый ток дилатаций в виде
?р F.23)
С учетом формулы F.21) найдем
д» /5Ц = в"; , F.24)

46Глава 1
откуда следует, что инвариантность относительно дилатаций эквива-
эквивалентна бесследовости тензора 0pv. Новый ток дилатаций связан со
старым соотношением
/^ =*р/мр- 4 Х?№9
о
= -/g -ь — <9p[*M5P-*PaH]92, F.25)
которое получается, если использовать формулу F.17). Мы видим, что
эти два тока отличаются друг от друга на полную дивергенцию, и по-
поэтому заряд дилатаций не меняется. Тензор 9 носит название "но-
"нового улучшенного тензора энергии-импульса" [3, 4]. Разности тен-
тензоров 9pv и /^ и векторов /ц0 и / Jo _ это поверхностные члены.
Указанные новые формы тензора энергии-импульса и тока дила-
дилатаций можно получить каноническим образом, если добавить к лагран-
лагранжиану скалярного поля поверхностный член вида д^Л^1, где
F.26)
6
так что его добавление соответствует некоторому каноническому пре-
преобразованию.
В полевых теориях для полей с высшими спинами инвариантность
относительно дилатаций всегда связана с бесследовостью тензора
энергии-импульса. Как будет видно далее, даже если .инвариантность
относительно дилатаций присутствует в исходном лагранжиане, она
нарушается квантовыми эффектами.
Теория поля с несколькими скалярными полями во многом анало-
аналогична изложенной выше, но в ней возникают новые интересные сим-
симметрии. Рассмотрим для примера N действительных скалярных полей
9„ , где ael, ... /V, и лагранжиан
? =¦ -i- Z ди Фа д» 9а - F.27)
2
а =1
Помимо обычных инвариантностей, этот лагранжиан очевидно инвари-
инвариантен по отношению к глобальному (т.е. не зависящему от х) вращению
N действительных скалярных полей, переводящему одно поле в другое,
5<Ра =*аЪ П> Еа6 = ~ * Ьа ¦ F.28)

Функционал действия 47
В результате появляется 1/2 N{N —1) сохраняющихся нетеровских то-
токов
'
-
об
Это пример внутренней симметрии, возникающей из-за наличия многих
полей одного типа. Если дополнить теорию потенциалом, зависящим
только от инвариантной по отношению к вращениям "длины" фа фа » то
внутренняя инвариантность относительно вращений сохранится.
Задачи
А. Покажите, что в четырех измерениях дивергенция каноническо-
канонического тока дилатаций равна нулю, если ? =1/2 <?мф<?Иф- (Л/4!)ф4_
Б. Выведите в D измерениях выражение для дивергенции тока ди-
дилатаций, если ? =1/2 д„фдН - Р(ф).
*В. Канонический тензор энергии-импульса в общем случае ооя-
зан быть симметричным. Покажите, что всегда можно найти член BP»V,
антисимметричный при заменах р -¦ ц или р -> v, такой, что тензор Белин-
фанте
у PV _ jliV ^ q DPMV
В Р
симметричен и сохраняющийся нетеровский ток для лоренцовских пре-
преобразований записывается в виде
U В >В '
Указание: для скалярного поля SP^V =0, так что эта величина 1меет
отношение к S ^v.
*Г. Найдите бф'для конформного преобразования. Покажите, что
действие S = / d4x 1/2 Э^фдНф инвариантно относительно конформ-
конформного преобразования. Постройте сохраняющийся нетеровский ток.
Д. Выведите выражение для сохраняющихся токов, соответствую-
соответствующих преобразованиям F.28), если лагранжиан ? задан в виде F.27).
§ 7. Действие цпя спинорных полей
В данном параграфе мы прежде всего займемся построением вы-
выражений для действий, включающих спинорные грассмановы поля
ц> и у . Если воспользоваться результатами § 4, то простейшие
формы спинорного кинетического члена будут такими:
Г) 1 t ц t* Й _ О# 1П 1\

48 Глава 1,
?й=?л*. G.2)
или, если четность существенна,
?Дирак = Y*Y»W = ?R+?L. G.3), G.4)
В частном случае уЛ = — <*2 ч>% легко показать, что лагранжиан ?# экви-
эквивалентен S.L с точностью до полной дивергенции (см. задачу А). Сле-
Следовательно, если fM - четырехкомпонентный майорановский спинор,
лагранжиан записывается в виде
? Майорана --J- ^У^^М G.5)
и совпадает с i.^, в чем можно убедиться, используя грассмановы
свойства спинора у; . В литературе часто можно встретить кинетичес-
кинетический член G.3), записанный так, что оператор производной действует
только направо и при этом отсутствует множитель 1/2. Хотя на пер-
первый взгляд такая форма лагранжиана отличается от формы G.3), все
различие сводится к полной дивергенции. Подобное отличие не имеет
значения до тех пор, пока система не взаимодействует с гравитацион-
гравитационным полем.
Из приведенных выражений явствует, что в D измерениях спинор-
ное поле имеет (по построению) размерность Z,-'7^0); B четырех
измерениях размерность спинорных полей равна - 3/2.
Указанные возможные кинетические члены инвариантны относи-
относительно конформных преобразований (см. задачу Ж), так же как это бы-
было для кинетического члена скалярного поля, но вдобавок эти члены
обладают своими фазовыми инвариантностями. Рассмотрим, напри-
например, лагранжиан ?L (то же самое относится и к ?#). Поскольку ч^ ~
комплексный спинор, можно подвергнуть его фазовому преобразованию
yL+eiay^, G.6)
оставляющему S.L инвариантным, если а не зависит от х. У дираков-
ского лагранжиана G.3) две такие инвариантности. Пользуясь четы-
рехкомпонентной формой записи, их можно разделить на общее фазо-
фазовое преобразование
У + е'РУ G.7)
и киральное преобразование
Ч^ -»'в*'Р У$ Ч1 /7 Q\
1 ^ с т . у i.о/

Функционал действия 49
Наконец, как и в скалярном случае, действие с ? = ?^(или?д) инва-
инвариантно относительно постоянного сдвига полей, поскольку
?L(YL +:ol)-?l + — 3^*1**44 -VLo^o-l). G.9)
На основании теоремы Нетер можно построить сохраняющиеся токи,
отвечающие преобразованиям G.7) и G.8):
/и=.» чу у = w taM ip -i-j^^^ GЛ0)
L L R R
/[ = ;Т/у'Г=('Л> -j>Ta% G.11)
" L /? Л
Соответствующие сохраняющиеся заряды таковы:
^ t G.12)
L L R R
L L R R
Для майорановского поля существует только киральное преобразова-
преобразование, поскольку поле у „ сопряжено полю у, , и потому фазовые преоб-
преобразования полей ^ И1ря противоположны.
Из спинорных полей можно построить другие некинетические квад-
квадратичные инварианты (§ 4). Используя только поле у , получим
L
!j
JfL
G.14), G.15)
где m - параметр с размерностью массы (в любом числе измерений).
Выражения G.15) и G.16) - это так называемые массовые члены. Так
как для описания майорановского спинора ^ можно использовать по-
поле yL, выражение G.14) может служить массовым членом для майора-
майорановского спинора. Записанное в четырехкомпонентных обозначениях,
выражение G.14) называется майорановской массой. Итак, наличие толь-
только одного поля уь еще не гарантирует безмассовости, как столь часто
неправильно утверждают. (Например, это относится к модели Вайнбер-
га — Салама слабых и электромагнитных взаимодействий, в которой
нейтрино описывается двухкомпонентным левым спинором без правого
партнера. В этом случае безмассовость нейтрино есть результат отсут-
отсутствия определенных хиггсовых бозонов, и сохранение фермионного чис-
числа оставляет нейтрино безмассовым даже после учета радиационных
поправок.) Замечание представляется особенно уместным в связи с тем,
что нейтрино принято описывать левым полем. Отметим, что выражение

50 Глава 1 _
?"• нарушает непрерывную симметрию относительно фазовых преобра-
преобразований G.6), и от нее остается только воспоминание в виде дискрет-
дискретной симметрии относительно замены f^ -> - У/,. В майорановских обо-
обозначениях
?» =._i?L тмтм, ??5 - - ~ ТМУ5ГМ. G.16), G.17)
L 2 ?
2
Если присутствуют оба поля у/, и у#, то можно построить еще два
квадратичных инварианта, что приводит к выражениям
Они оба инвариантны по отношению к общему фазовому преобразова-
преобразованию G.7), но неинвариантны по отношению к киральному преобразова-
преобразованию G.8), при котором
vp-.e'Pysi^ 9,4^0,9^5 G#20)
и, следовательно,
fm .• — ш „2' Р Уч 41 11 91\
<Д_" -»1ште3т. [1.1.1)
Применяя формулу E.27), находим, что
д /^ = - 2тТу5Т, G.22)
тогда как дивергенция тока j», определяемого формулой G.10), оста-
остается равной нулю. Из этого не следует делать вывод, что нельзя пост-
построить квадратичных по дираковским полям членов, не содержащих про-
производных и сохраняющих киральную инвариантность. Нижеследующий
пример демонстрирует это. Рассмотрим выражение
гг (лЛ ^VItv\<V 1яЛ ' тг4 «А ^ /*Л Ч-' /лЛ 11 Г)СХ\
U yXf Т \Х) Т \Х) + Ь TlyXj Т \%) Ус Т \%) \ ' • **1*}
равное сумме &? и ?^ , но с коэффициентами, зависящими на этот
раз от х. Чтобы сохранить киральную инвариантность, величины а и тт
должны при киральных преобразованиях трансформироваться следую-
следующим образом:
G.24)
При бесконечно малых р поля а и тг поворачиваются,переходя одно в

Функционал действия
другое:
6сг =-+ 2Cтт, 6тг = -2|3а. G.25)
Такое преобразование оставляет инвариантной величину а 2 + тт2. Сле-
Следовательно, лагранжиан
Sf = -L Фуи^ Г к»А'Ф(<7 + »у5тт)Г G.26)
кирально-инвариантен. Если а и тт - канонические поля, то А - безраз-
безразмерная постоянная (называемая обычно юкавской константой взаимо-
взаимодействия). Можно вдохнуть жизнь в сами поля а- и тт, добавив к ? их
кинетические члены, а также самодействие этих полей, сохраняющее
условие G.25). Это приводит к лагранжиану
? =.J_ сруи" Г + ih Ф(а + tys -гт) f + — дцод^а-*— <Эмтгдмтт-
-f>2+Tr2). G.27)
Такой лагранжиан обладает следующими симметриями (все они гло-
глобальные) :
а) общая дираковская фазовая симметрия
f -, eta f; а . тг -> а , тт;
б) киральная симметрия
6У=-?&у5У, 5сг = 2 C тт, 6тт = -2|3сг,
оставляющая инвариантным выражение a2 f тг2;
в) дискретная симметрия относительно преобразования четно-
четности 4>->уоу,сг ¦» сг, тг-»-тт; отсюда следует, что а (х) - ска-
скалярное поле, а тг(я) — псевдоскалярное.
Лагранжиан подооного типа был впервые построен Гелл-Манном
и Леви. Теории такого рода называются а -моделями и подходят для
описания физических тт-мезонных взаимодействий. (В рассмотренном
примере изоспин пиона не принимался во внимание.)
Мы видим, что требование сохранения во взаимодействии симмет-
симметрии кинетического члена приводит к введению дополнительных полей.
Это общее свойство: расширение симметрии -> добавочные поля.
Заметим, что в четырех измерениях инвариантные члены, содер-
содержащие более двух спинорных полей, имеют размерность по меньшей
мере - 6, так что для восстановления размерности ? требуются раз-
размерные константы. Но в двух измерениях члены типа fpTJ или
имеют ту же размерность, что и ?.

52 Глава 1 .
Поскольку двухкомпонентные спинорные поля всегда комплексны,
уравнения движения получаются независимым варьированием по полям
у и цл j . Здесь нужно быть крайне осторожным, так как мы рассма-
рассматриваем у.- и уТ» как грассмановы поля и не можем протащить 5 ч1 че-
через у> не изменив знака. Например
- ^r^^^Vl = G.28)
ILL,
= ¦ 5ц/ ст^ду - (д^ ац) 6у f:noB. члены, G.29)
\j" *¦* Li
что приводит к сопряженным уравнениям
а»д^ = 0 или йц^^стМ= °* G-3°)
В случае дираковского спинора, чтобы получить уравнения движения,
нужно произвести независимые вариации по Т и 9.
В заключение заметим, что можно построить, и более сложные инва-
инварианты, содержащие спинорные поля, напримерd^d^f. Хотя в чле-
членах такого типа нет ничего плохого с точки чрения требований инвариантно"
сти, их включение не приводит к удовлетворительным теориям по той
причине, что они нарушают связь между спином и статистикой. Мы
вернемся к этому вопросу позднее при рассмотрении калибровочных
теорий.
Задачи
A. Покажите, что лагранжиан S.R, в котором у = сг2у* , равен
лагранжиану ?^ с точностью до полной дивергенции.
Б. Найдите тензор энергии-импульса Белинфанте для лагранжиа-
й
на ^ Дирак*
B. Покажите, что для ?= ? цирак ток дилатаций можно записать в ви-
виде /^ = *p/gP> где ]У$- тензор энергии-импульса в форме Белинфанте. Тем
самым вы покажете, что тензор Белинфанте совпадает с новым улуч-
улучшенным тензором энергии-импульса для дираковского поля.
Г. Пусть задан лагранжиан
Используйте киральное преобразование для того, чтобы исключить
псевдоскалярный член. Какова будет масса получившегося дираковско-
дираковского поля?

Функционал действия 53
*Д. Пусть задан квадратичный лагранжиан, содержащий поля ш
Д'
и включающий дираковскую и майорановскую массы. Диагонализуйте
поля таким образом, чтобы получить несмешанные массы. Каковы бу-
будут массы полей? Каков физический смысл различных степеней сво-
свободы?
*Е. Рассмотрите лагранжиан а-модели- а) Пользуясь теоремой
Нетер, выведите выражение для сохраняющегося кирального тока,
б) Предположим, мы добавили к ? член, линейный по а; найдите дивер-
дивергенцию кирального тока. Это последнее уравнение отображает гипоте-
гипотезу ЧСАТ (частично сохраняющегося аксиального тока) пионной физи-
физики.
*Ж. Как преобразуется при конформных преобразованиях поле у ?
Покажите, что лагранжиан ?^ конформно-инвариантен.
§ 8. Действие со скалярными и спинорными полями
и суперсимметрия
Между простейшим кинетическим членом ?/, для спинорных полей
и его аналогом для скалярного поля S имеются определенные разли-
различия. В то время как !?L содержит одну производную, скалярный кине-
кинетический член содержит две производные; поле у является грассмано-
вым полем, a S - обычное поле; наконец, ?/, обладает фазовой инва-
инвариантностью G.6), а кинетический член для одного скалярного поля ею
не обладает. В то же время имеется и сходство, поскольку оба кине-
кинетических члена конформно-инвариантны. В данном параграфе мы рас»-
смотрим вопрос о возможности существования симметрии между поля-
полями, связывающей фермионный и скалярный кинетические члены. Та-
Такая симметрия называется суперсимметрией - благодаря ей возмож-Vl
ны нетривиальные взаимодействия между скалярными и спинорными
полями. Чтобы легче было выявить новую симметрию, запишем кинети-
кинетический член скалярного поля в виде, как можно более похожем на ?^.
Для этого введем кинетический член для двух скалярных полей, кото-
которые мы обозначим через S и Р, и сравним его с кинетическим членом
для майорановского спинорного поля, которое мы обозначим через х-
Тогда каждый кинетический член будет обладать своей фазовой инва-
инвариантностью. В самом деле, лагранжиан

54 Глава 1
помимо того, что он конформно-инвариантен, обладает двумя незави-
независимыми глобальными фазовыми инвариантностями
, S + .P-. e'P(Sf»fl. (8.2)
Любая дальнейшая инвариантность будет включать преобразования, пе-
переводящие бесспиновые поля S иРв спинорное поле х- Общие свойства
преобразования этого типа таковы: а) параметр преобразования, обоз-
обозначим его через а, должен быть грассмановым спинорным полем, т.е.
глобальным бесконечно малым майорановским спинорным параметром;
б) в простейшем случае преобразование полей S и Р не должно включать
оператора производной, а преобразование поля х должно включать одну
производную, так как фермионный кинетический член имеет на одну
производную меньше, чем скалярный кинетический член. Таким образом,
мы приходим к преобразованию
6 (S или Р) = 5Мх, (8.3)
где М - некоторая 4х 4-матрица. Так как сюда не входят никакие 4-век-
торные индексы, матрица М должна содержать только матрицы / иу5.
Следовательно, можно зафиксировать преобразование в виде
5S =ааХ, 6P=t6ay5X, (8.4), (8.5)
где а и Ь - неизвестные действительные коэффициенты. Здесь мы вос-
воспользовались фазовой инвариантностью (8.2), чтобы определить вариа-
вариацию S через матрицу /, а вариацию Р— через матрицу гу5. Правая часть
этих вариаций построена так, чтобы они были действительными. (В май-
орановском представлении для матриц Дирака все четыре компоненты
майорановских спиноров действительны, а все матричные элементы
у-матриц чисто мнимы, так что iy5 имеет действительные матричные
элементы). Далее (предполагая, что дц не изменяется; см. задачу Е)
находим
2 М 2 м s рХ-
(8.6)
Чему может равняться вариация поля х? Заметим, во-первых, что с
точностью до полной дивергенции
4 Y ^x " T XY UX~T
Используем теперь векторную часть свойств "майорановского перево-
переворота": при замене § ->ц комбинации fn, fy5r) и |уцУ5г) четны, а ?уцл и

Функционал действии 55
нечетны. Это справедливо для любых двух майорановских спино-
спиноров § и г| (см. задачу). Учитывая это в преобразовании (8.7), получа-
получаем с точностью до поверхностных членов
б[ JL х
б? WQZ = Fxyp^-o^Sa *-1ЬдиРау5)д*Х+ Пов. член = (8.9)
Соберем все полученные результаты:
— ^S)(yu ^ад^ SS f ibd^FbY5) х 4- Пов. член, (8.10)
причем при переходе _от (8.9) к (8.10) выполнено интегрирование по
частям. Итак, если бх удовлетворяет уравнению ( о = Э^)
дд5Хум+ aaSa + iba PaYs = 0, (8.11)
то лагранжиан ?^z изменяется лишь на полную дивергенцию. Реше-
Решение этого уравнения легко находится:
(8.12)
Здесь мы использовали равенство YpYadiPda = <9иЭ1р. Таким образом,
мы достигли поставленной цели: найдена совокупность преобразований
между бесспиновым полем и полем со спином 1/2, оставляющих инва-
инвариантной сумму их кинетических членов (с точностью до каноническо-
канонического преобразования). Для большей убедительности нужно проверить,
является ли эти преооразования замкнутыми и образуют ли они группу.
Вначале посмотрим, как действуют на поля два суперсимметрич-
суперсимметричных преооразования. Имеем
[6lf62]S =aa2slX -A~2) =
= a52[aypai<?PS - ibYpY5adPP]- A — 2)= 2a* a 2/p a ^P S .
(8.13)
В последнем равенстве мы воспользовались свойствами майорановско-
го переворота для аксиально-векторной части. Следовательно, действие
двух суперсимметричных преобразований на поле S сводится к трансля-
трансляции поля S на величину 2 i a2 a 2ypa j. Посмотрим, что происходит с
полем Р.*
[8V 52]P=i6a2y561x-(l*-*2) = 2b2a2ypa^Pp, (8.14)

_56 Глава 1
опять с учетом тождества для майорановского переворота аксиального
вектора. Поскольку преобразования полей S, Ри х должны быть одина-
одинаковы, необходимо положить
Ь = ±о. (8.15)
Убедимся, наконец, в том, что два суперсимметричных преобразования
поля х представляют собой трансляцию. Имеем
[51,62]Х = «УР« 2<ЭРб ,5 - ib уру5<х ^PS ,Р - A ~ 2) =
РA-*2). (8.16)
Хотелось бы переписать правую часть этого равенства в форме, похо-
похожей на остальные, т.е. содержащей комбинацию а 2ур a j, анеа2'
Для этого применим прием, предложенный Фирцем. Возьмем любые два
дираковских спинора (не обязательно майорановских) Т и Л; 4< 4-мат-
рииу AY можно представить в виде линейной комбинации 16 дираков-
дираковских ковариантов/, у 5) у5 уц, ум, crpv= 1/4[уц, yv]. Коэффициенты
вычисляются путём взятия соответствующих следов. В результате
имеем
ЛТ = - 2_ ТЛ - J_ у^УзЛ + J_ у . ~~
4 4 4
1 -
Числовые коэффициенты всех членов образуют первую строку знамени-
знаменитой матрицы Фирца. Они содержат всю необходимую информацию для
построения матрицы в целом. В применении к нашему случаю нахо»
ДИМ
2 112 2 1 2 P РСТ
если одновременно исполь зовать свойства майорановского переворо-
переворота. С учетом формул (8.15) и (8.18) получаем
<. (8.19)
Воспользовавшись антикоммутатором для у-матриц, переришем это
выражение в виде
[6lt S2]x=2a2a2y^ai^X -°2«2УМа1УмУР'?рХ- (8-20)
Первый член и есть нужный нам результат, но, к сожалению, у нас воз-
возник дополнительный член, пропорциональный ypcL х* Этот дополнитель-

Функционал действия 57
ный член исчезает только в том случае, когда справедливы классичес-
классические уравнения движения. Чтобы устранить этот член, мы можем расши-
расширить определение вариации 6х и посмотреть, к чему это приведет. За-
Заметим, что если добавить к выражению (8.12) для 6х дополнительную
вариацию вида
бдопХ= (Ffiy5G)a, (8.21)
где F и G - функции координаты м, но не канонические поля, так как
их размерность равна L~2, то выражения (8.13) и (8.14)-не изменятся
благодаря свойствам майорановского переворота. Например,
[5i, 62]flOnS = aa26lflon х- A — 2) =
= oa2(F * iysC)a, - A *¦* 2) = 0. (8.22)
Однако эта добавочная вариация дает вклад в преобразование х» а
именно:
^i. Sj-lnonx-^f fiy^jOaj-a— 2). (8.23)
Дополнительный член в формуле (8.20) можно переписать подходящим обра-
образом с помощью фирцевского преобразования
1м 2У5 ~{\*г* 2). (8.24)
Сравнеше с выражением (8.23) показывает теперь, что выбрав
S.F-a^yP^x, 61G = -ia2S1y5yP^pX, (8.25), (8.26)
мы сократим дополнительный член и получим желаемый результат. Ос-
Оставляем в качестве упражнения (см. задачу) доказательство того что
в применении к функциям F и С выполняется операторное соотношение
[6,,52] = 2a2 a2y^a,au. (8.27)
К сожалению, новое выражение для бх не оставляет инвариантным
исходное действие из-за наличия члена бдопх. Но заметим, что
2
-—6(F2 + C2). (8.28)
Следовательно, действие
о 2 ^

58 Глава 1
инвариантно относительно преобразований суперсимметрии
6S=aaX; 6P=iaSysx; 5F = а 2 ЗуР^х; 6С = - i a 2 ay5
SX = aypadpS - ia ypy5oc<?PP + (F + гу5С)ос.
(8.30)
Все эти преобразования удовлетворяют теперь операторному уравне-
уравнению (8.27). Такое действие впервые было написано Вессом и Зумино
[5].
Благодаря введению вспомогательных полей F и G у нас теперь
независимо от уравнений движения имеется одинаковое число бесспи-
бесспиновых (S, Р, F и G) и спинорных (четыре действительные компонен-
компоненты поля х ) полей. Читатель может сам убедиться, что "на массовой по
верхности" (т.е. на классической траектории), где поля F и G не явля-
являются необходимыми, баланс между бесспиновыми и спинорными степе-
степенями свободы все равно сохраняется* Этот баланс между числом бозон-
ных (целый спин) и фермионных (полуцелый спин) степеней свободы
есть общая закономерность суперсимметричных теорий.
Из выражения (8.27) следует, что результатом двух суперсиммет-
суперсимметричных преобразований является трансляция. Вдобавок к этому, пос-
поскольку суперсимметричные параметры - спиноры, генераторы супер-
суперсимметрии преобразуются как спиноры. Поэтому нужно расширить
группу Пуанкаре, включив в нее генераторы суперсимметрии (см. за-
задачу). У полей F iaG нет кинетических членов в действии; они служат
лишь вспомогательными полями и в свободной теории полностью от-
отделены от других полей.
Красота преобразований суперсимметрии (8.30) заключается в
возможности их обобщения на теории с взаимодействием. Например,
можно ввести суперсимметричную юкавскую связь, сохраняющую гло-
глобальную киральную инвариантность,
aBa -2GSP) (8.31)
или
' (8.32)
Можно выписать и массовые члены
Л (хх L SF -
= _,- Л (хх - -L SF - _L_ PC). (8.33)
т 2 а а
Последнее выражение позволяет обнаружить одну важную и фа-
фатальную) особенность суперсимметричных теорий. Рассмотрим урав-

Функционал действия 59
нения движения для лагранжиана Весса - Зумино с массой. Эти урав-
уравнения имеют вид
0Х-» — х. DS = — F, nP = Jl_G, (8.34) - (8.36)
2 2а ¦ 2а
(8.37), (8.38)
а2 2а а2 2а
Без особого труда можно, решив последние два уравнения относитель-
относительно F и G, выразить их через S и Ри подставить полученные выраже-
выражения в уравнения (8.35) и (8.36) для S и Р. Тогда они примут вид
oS=—2l S, иР = - — P. (8.39)
4 4
Следовательно все три поля х, S и Р имеют одинаковую массу. Тако-
Таково общее свойство суперсимметрии: все поля, входящие в супермуль-
типлет,, имеют одну и ту же массу. Это объясняется тем, что массо-
массовый оператор Рц Рц коммутирует со всеми генераторами суперсим-
суперсимметрии. Отсюда немедленно вытекает, что в природе не может быть
точной суперсимметрии, поскольку у частиц с разными спинами нет
вырождения по массе.
Проделанные простые вычисления показывают, какова роль вспомогатель-
вспомогательных полей в том случае, когда могут быть решены уравнения движения. Проил-
Проиллюстрируем теперь роль вспомогательных попей, не обращаясь к уравнениям
движения, с помощью следующей примитивной модели. Пусть р(х) - некое
скалярное поле, а А(х) — некое вспомогательное поле. Возьмем лагранжиан
в виде
?=— д фд^Ф +• — А2 + Лф2. (8.40)
2 Ц 2
Пополнив это выражение до полного квадрата, получим
2 2 2*
Определив новое, теперь уже невзаимодействующее вспомогательное попе
А' -А -|-ф2, мы придем к лагранжиану взаимодействияО/2)^(9^ — A/2)ф4.
Мы рассмотрели простейший пример суперсимметричной теории в
4 измерениях. В настоящее время суперсимметрия - это чисто "теоре-
"теоретическая симметрия", не имеющея никакой экспериментальной поддер-
поддержки. Но мы думаем, что было небесполезно обратить внимание чита-
читателя на существование нетривиальных симметрии между полями с раз-
разными спинами.

60 Глава 1
Задачи
A. Докажите свойства майорановского переворота.
Б. Пользуясь тождествами для у-матриц, убедитесь в справедли-
справедливости разложения Фирца (8.17).
B. Проверьте киральную инвариантность действия S^z и найдите,
как действуют киральные преобразования на поля.
Г. Покажите, что интеграл /"[ (i/2) ху5 X + (V°) SG — A/a)PF)]x
х d4x инвариантен относительно преобразований суперсимметрии.
*Д. Введите майорановские спинорные генераторы суперсимметрии
Q, записав конечное преобразование супереимметрии в виде е'а(?. Вы-
Выведите выражения для антикоммутатора двух генераторов Q и для ком-
коммутатора Q с генераторами группы Пуанкаре. Получившаяся алгебра, включаю-
включающая как коммутаторы, так и антикоммутаторы, образует градуирован-
градуированную алгебру Ли (супералгебру). Покажите, что,как следствие этого,
генератор Q коммутирует с массой.
*Е. Найдите изменение координаты х^ при преобразованиях супер-
суперсимметрии и убедитесь, что д^ - инвариант относительно этих преоб-
преобразований.
**Ж. На основании теоремы Нетер выведите выражение для сохра-
сохраняющегося суперсимметричного тока. Здесь нужна осторожность, так
как при суперсимметричном изменении к ?.wz добавляется полная ди-
дивергенция.
ЛИТЕРАТУРА
1. Bargmynn V., Wigner E;P., Proc. Nat. Acad. Sci. (USA), vol. 34, №5,
211A946).
2. Dirac P.A.M., Rev. Mod. Phys., 21, 392 A949).
3. Gursey F., Ann. of Phys., 24, 211 A963).
4. Coleman S., Jackiw R., Ann. of Phys., 67, 552 A971).
5. Wess ]., Zumino В., Nucl. Phys., B78, 1 A974).

Глава 2
Функционал действия
в квантовой механике:
фейнмановский интеграл по траекториям
В предыдущей главе мы занимались построением функционалов
действия, которые порождают (классические) теории, согласующиеся
с постулатами специальной теории относительности. Эта глава посвя-
посвящена использованию ФД в квантовой теории. Для простоты и ясности
мы сначала остановимся на роли действия в квантовой механике, а в
следующей главе перейдем к квантовой теории поля.
Первыми осознали роль действия в квантовой механике Дирак и
Фейнман. Дирак искал такую формулировку квантовой механики, в ко-
которой время и пространственные переменные рассматривались бы сход-
сходным образом. Напомню, что в обычной формулировке квантовой механи-
механики задается квантовая система, находящаяся в начальный момент вре-
времени в определенном состоянии, одном из собственных состояний пол-
полного набора операторов, коммутирующих с гамильтонианом и друг с дру-
другом. Затем, пользуясь гамильтонианом, находят, в каком состоянии ока-
окажется система в более поздний момент времени t. После этого вычис-
вычисляют амплитуду перехода из состояния 50 в момент времени tQ в сос-
состояние S в момент времени t и т.д. Как нетрудно видеть, время в таком
описании играет центральную роль, и в случае релятивистской системы
это вызывает беспокойство, поскольку теряется явная лоренцовская
инвариантность теории, хотя окончательный результат и оказывается ре-
релятивистски-инвариантным. Поэтому Дирак и искал такую формулиров-
формулировку, в которой время не было бы особо выделено. В своих поисках Дирак
обратился вновь к классической механике, в которой известны два (эк-
(эквивалентных) подхода: гамильтонов, в котором с самого начала выде-
выделяется время, и лагранжев, в котором этого нет. Конкретно Дирак выяс-
выясняя, каков смысл ФД в классической механике, с намерением обобщить
это понятие в квантовой механике. В классической механике действие
является генератором канонического преобразования, переводящего
систему от одного момента времени к другому. Поэтому будет непло-
неплохо освежить наши знания о канонических преобразованиях.

62 Глава 2
§ 1. Канонические преобразования в классической
и квантовой механике
Рассмотрим частицу, движующуюся в одном измерении. Состояние
движения этой частицы в момент времени t задается ее координатой
q и импульсом р, являющимися независимыми функциями времени t.
Изменение этих функций со временем определяется системой двух диф-
дифференциальных уравнений первого порядка (уравнений Гамильтона)
dff dp дН
1 —
at dp dt д q
МЛ
где гамильтониан Н зависит от qt р и t и представляет собой энер-
энергию системы. Уравнения Гамильтона можно изящно записать, если ввес-
ввести скобки Пуассона
, <.2
Я'Р dq dp dp dq
где А и В — две произвольные функции переменных q, p и t. Тогда
уравнения Гамильтона принимают вид
Ар>н\. A,3)
\q,H\t р>
dt dt
Отсюда следует, что если F — любая функция переменных q% p и t,
то ее производная по времени равна
dF
dt
* FtH)itL. A.4)
Последний член учитывает любую явную зависимость функции F от
времени. Уравнения Гамильтона можно вывести из вариационного прин-
принципа
б/'2 dt{p*3-- H(p. <?))=0, A.5)
11 dt
причем независимые вариации 6 р и 6 q принимаются равными ну-
нулю в концевых точках.
Определим каноническое преобразование
Р ¦* Р, 9 -<? A'б)
как такое преобразование, при котором не меняется форма уравнений
Гамильтона, т.е. в новой системе переменных (Q, Р) существует та-

Функционал действия в квантовой механике 63
кой новый гамильтониан К (Q, Р), что
j?_ i, ()
dt dP it dQ
Ясно, что эти уравнения также можно вывести из вариационного прин*
ципа
6/^ dt{P^~ -K(<?,P))=0e A.8)
Отсюда вытекает условие, что подынтегральные выражения в форму-
формулах A.5) и A.8) могут отличаться не более чем на полную производи
ную по времени:
Piiz__tf(9,p) = pi2_-K(<?, P)+¦*?-'¦ A.9)
dt it di
Функция G называется производящей функцией канонического преобра^
зованияс Она может зависет от г и от .любой "смешанной" пары пере-
переменных (q, Q), (q, Р), (p,Q) или (р, Р). Пусть С зависит от пары
независимыж переменных (<?, ^)« Тогда
dG _ dG + dG ig 4. dG dQ {\.Щ
dt dt dq dt dQ dt
Рассмотрим теперь выражение A.9), считая q и Q независимыми пе-
переменными. Мы получаем, что
-*-H +-|?, A.11)
(p;4,P)<? |
и остающиеся переменные (р, Р) выражаются теперь в виде
а новый гамильтониан определяется формулой
K=//+JLG-. A.13)
dt
Можно с равным успехом начать с того, что взять функцию G,
зависящую от переменных (q, P). Тогда аналогичные рассуждения
приводят к уравнениям
Г) , Q.*Gii,P) . AЛ4)
dq d P

64 Глава 2
В частности, выбор G в виде
G= qP t A.15)
приводит к тождественному преобразованию, как можно убедиться
с помощью уравнений A.14). Поэтому бесконечно малое каноничес-
каноническое преобразование с параметром е << 1
Q=q + O(t), P=p + O{e) A.16)
будет порождаться производящей функцией, отличающейся от выра°
жения A.15) членом, пропорциональным е ¦:
G(q, P)= qP*zF(q,P) + O(*2)= O-17)
= qP+BF(q9fi) +OF2), A.18)
так как р обличается от Р на величину О (в). Функция F[q, р), ко-
которая зависит теперь только от исходной системы, называется генера-
генератором канонического преобразования. Подстановка выражения A.18)
в A.14) дает
p,
dq
ИЛИ
8qsQ~q = e =
о г
dp
6P-P-,
6 dq
A.
A.
¦19),
P»
21),
A
Fl
A.
.20)
,22)
= e [q, F\,
Отсюда следует, что бесконечно малое изменение .любой функции f
переменных q и р, вызванное бесконечно малым каноническим преобра-
преобразованием с генератором F {<?, р) и параметром е дается выражением
5f(p,q)=lf(p,q),eF\. A.23)
В частности, сравнивая это выражение с A.4), мы видим, что гамиль-
гамильтониан является генератором бесконечно малых трансляций во време-
времени.
Представим себе теперь очень специальный тип канонического
преобразования, которое отображает переменные q, p на множество
других переменных Q, Р, не зависящих от времени. В этом рлучае зна=
ние уравнений преобразования
q = q(Q,P>t), p=P(Q,P,t)
эквивалентно решению динамической задачи,, поскольку Q и Р явля-
являются константами, которые можно определить из начальных условий.
Было бы неплохо узнать, чем порождается такое преобразование. Так

Функционал действия в квантовой механике 65
как мы требуем равенства
= AL = О, A.24)
dt dt
новый гамильтониан не зависит от Q и Р„ Он может быть трлько кон-
константой, зависящей пли не зависящей от времени. Для простоты прло-
жим Н равным нулю. Тогда, приняв за независимые переменные q и Q,
получим, что выражение A.13) будет иметь вид
H(q>p = is_ft)=_ds_} (L25)
д q д t
где S(qf Q = const, t) — производящая функция. Мы пришли к уравнению
Гамильтона — Якоби, решением которого является функция S(oHa называ-
называется главной функцией Гамильтона). Из формулы A.12) имеем
Р = const = -i^- {q,Q,t)\0= const , A.26)
и обращение этого выражения дает q как функцию переменных Q, Р и
t, а тем самым решена динамическая задача.
Далее, производная по времени функции S
= -H(q,P, t) + p*3- A.27),(U8)
dt dt dq dt dt
есть не что иное, как ,лапранжиан. В результате интегрирования полу-
получаем
S = J* L€t' A.29)
и обнаруживаем, что S есть действие, рассматриваемое как функция
переменных q(t) и q(tQ ) = Q в случае, когда решение задачи уже
подставлено в L и проведено интегрирование по времени. Таким об-
образом, мы приходим к основному результату: действие есть производя*
щая функция канонического преобразования, т.е. преобразования пере-
переменных, описывающих систему, от одного момента времени к другому.
Посмотрим, как интерпретировать этот результат в рамках квантовой
механики.
Перейдем к квантовому описанию системы с одной степенью сво-
свободы в одном измерении. Рассматривая операторы q и р (операторы
будем помечать шляпкой "А"), удовлетворяющие фундаментальным
перестановочным соотношениям

бб Глава 2
[ 9> ?J = [ Р» pJ = Oj [ 9» pJ = t^, ('1.30)
где t - постоянная Планка, состояния системы в данный момент вре-
времени можно взять как состояния | q > |, отвечающие заданному поло-
положению и удовлетворяющие соотношениям
q\q> - q | Q> , < q \ q'> = &{q -q' ), fdq \q>< q\~ \.
(Ul)-A.33)
(Здесь q - обычное число или функция, но не оператор!) В квантовой ме-
механике определяется каноническое преобразование между операторами
(q, р) и (Q, Р) как такое преобразование, которое не изменяет форму
фундаментальных перестановочных соотношений (L30). Тогда система
будет описываться состояниями ] Q > , обладающими теми же свойства-
свойствами, что и состояния \q> (конечно, с заменой q на Q).
Следуя Дираку, cocpeflt точим внимание на "смешанном" матричном
элементе < q \ Q>* Исходя из формулы A.31),,легко получить, что
\Q? = q< q\Q>,
или, эквивалентно.
( 1.34), A-35)
Кроме того, так как р ] q > = -it -^— | q > , A.36)
dq
мы имеем
< ч I p\Q> = »ft— < ?!<?>»<?! p\Q> = -т—< q \Q>
dq dQ
A.37), A.38)
Но операторы Q и 'q не обязаны коммутировать между собой, так что соб
ственное значение произвольного оператора F {q, Q) в смешанном пред-
представлении может и не быть хорошо определенным, пока не наложены допол-
дополнительные учловия на форму оператора F. Например, из .соотношений
A.34) и (L35) явствует, что
< я\ fi(q)f2(Q)\$> = /1(?)/2(<?)< ч\ <?>• A-39)
Поэтому мы будем рассматривать только "хорошо упорядоченные"
функции, для которых
<?| F(q. Q)\ <?> = F(q, Q)<q\Q>. A.40)

Функционал действия в квантовой механике 67
(Хорошее упорядочение означает, что эти функции представимы в ви-
виде произведения функции оператора q на функцию оператора Qo ) Тог-
Тогда, если мы прложим (с дираковской способностью предвидеть!)
< q\Q> * e-(i/h)G(q, Q)} A.41)
где G — функция переменных q и Q, то уравнения A.37) и A.38)
примут вид
3q
A.42), A.43)
Затем, если предположить, что d'G/dq и дG/дQ -"хорошо упоря-
упорядоченные" функции в смысле определения A.40), то последние уравне-
уравнения могут стать уже уравнениями для операторов
A.44)
dq 9Q
Итак, мы видим, что определенная соотношением A.41) функция G
есть квантовый эквивалент производящей функции. Дирак назвал ее
"аналогичной" производящей функции [ 1,2].
Задачи
А. Покажите, что скобки Пуассона инвариантны относительно ка
ионического преобразования.
Б, Рассмотрите бесконечно малое каноническое преобразование
a
где е а — параметры преобразования, a Fa — генераторы. Покажите,
что операция [ 5^5 ] f сама есть каноническое преобразование. Ин-
Индексы здесь отвечают двум различным параметрам е 1о и е 2а. Что
является генератором этого канонического преобразования? Удовлет-
Удовлетворяют ,ли канонические преобразования групповым аксиомам?
В. Рассмотрите систему с координатами qi и импульсами р,- ,
i = 1, 2, 3. Найдите генераторы бесконечно малых вращений и проверьте
результаты задачи Б.
§ 2. Фейнмановский интеграл по траекториям
Далее Дирак попытался применить эту аналогию к гдавной функ-
функции Гамильтона, в которой q = <?' в момент времени t и Q = q в
момент времени Т:

68 Глава 2
Подчеркнем, что тильда "~ " означает всего лишь некоторую неопре-
неопределенную связь между правой и левой частями, так как при выводе фор-
формулы A.44I) Дир'аку пришлось сделать множество предположений без
какого-либо обоснования, В самом деле, как нетрудно видеть, знак равен-
равенства в формуле B.1) был бы неправилен, если считать временной интер-
интервал Т — t конечным. Действительно, разобьем Т -1 на N бесконечно
малых временных интервалов tа = t + а е; /Vs = Т — t. Пусть qa = qt ;
тогда, используя соотношение полноты A.33) для каждого ta, можно"
написать
... < In ~i \чт> - B.2)
Это точная квантовомеханическая формула. Если считать, что соотноше-
соотношение B.1) есть равенство, то интеграл в экспоненте можно разбить на
много областей интегрирования и это приведет к неправильной форму=
ле
< q't \qT> = <q't | ql><q1 \ q2> ... < qN „ x ] qT >, B.3)
отличаюшейся от правильной отсутствием промежуточных интегрировав
ний. В последней формуле qx, q2> ^. — классические значения траек-
траектории, взятые в моменты времени t19 12> ... .
Но если предположить, что в формуле B.1) выполняется равенство
(с точностью до константы) только для бесконечно малого промежутка
времени, т.е.
< It I 4t + 5t >= Ae ' <2'4)
где L (как в теории Гамильтона — Якоби) понимается как функция
переменных q* и qt + 5 t } то мы не вступим в противоречие с кван«-
товомеханической формулой B.2 ). Именно это и сделал Фейнман [3]!
Если подставить B.4) в B.2), то это приведет к фейнмановскому
интегралу по траекториям амплитуды перехода:
1} Номер главы будет указываться только в ссылках на формулы из
предыдущих глав.

Функционал действия в квантовой механике 69
/f dtL(q,q)
<q'AqT> = Hm AN f ( П dqt ) e =
t * N-» o» j = 1
^'фиксировано B.5)
=/ 3)9e-C</A)S(t. T,[?]) ^ B.6)
где второе выражение есть просто хитрый способ скрыть то, что мы
не знаем меру интегрирования. Граничными условиями служат значения
траектории, взятые в начальный и конечный моменты времени.Формула
B.5) означает, что ецли вы хотите вычислить амцлитуду вероятности
того, что частица, находящаяся в момент времени Т в точке q, будет
находиться в момент времени t в точке q', то вам нужно представить
эту амплитуду как сумму по всем возможным траекториям, которые на-
начинаются в момент времени Т в точке q и кончаются в момент време-
времени г в точке q', с весом, равным экспоненте от произведения отноше-
отношения (- i1%) на действие, вычисленное для конкретной траектории. Из
такой формулировки ясно видно различие между классической и кван=
товой механикой. В первом случае частица движется только по одной
траектории, идущей от q до q', а во втором вклад дают все траектории.
Формула B.6) очень ясно указывает на то, какова связь между
классической и квантовой механикой. В классическом пределе % ¦* О
подынтегральное выражение при изменении q будет осциллировать со
все большей частотой и само себя гасить, если только действие S не
является почти постоянным; но это так и есть, когда S стационарно
и q — классическая траектория (а может ,ли быть несколько стационар-
стационарных точек?). Таким образом, мы видим, что при h ¦* 0 классическая
траектория естественным образом выделяется и восстанавливается
формула B.3), но только в классическом пределе.
Благодаря указанной связи, отмеченной впервые Дираком, функ"
ционал действия и становится столь важным понятием. Мы видели, что
действие S, как оно ни прекрасно, играло лишь очень незначительную
щпъ в классической механике, поскольку там требовалось только знать
положение его экстремумов. В квантовой же механике действие исполь-
используется во всех точках. Обращаясь к прощлому, как не задуматься над
тем, задавали ,ли себе физики прошлого столетия вопрос, почему так
мало берется от понятия действия!
Проверим теперь путем явных вычислений, насколько справедли-
справедлива гипотеза Фейнмана B.4). Пусть Н - независящий от времени опе-
оператор Гамильтона нашей одномерной системы. В гейзенберговской кар-

70 Глава 2 __
тине состояние | q > в момент времени t + б t получается из состоя-
состояния в момент времени * оледуюшим образом:
I ?* + б*>~1 ?«•> + - 5« ff |9t > + O(EtJ ). B.7)
ft
Отсюда
< v't+st I ?г> = <?; I qt >-¦—< ?; |Я| ,^5{-:-о (so2).
B.8)
В качестве простого примера положим
ftJP $ B.9)
2
чтобы избежать (на время) трудностей с упорядочением. Тогда
Al Л— + V(q)]< q't | q. > = B.10)
2 л l> l>
J-°* 2tt 2 a?2
B.11)
еоли использовать формулу A.32) и интегральное представление 5-функ-
ции
8(х~х')= /+- ^i- е^(*-*') „ B.12)
Собирая все формулы и выполняя дифференцирование по q , получаем
+ OEt2)], B.13)
где
H{ltq)=*L 12 + V(q). B.14)
2
Положим
9' _ q = Al. 5t = q5t B.15)
dt

Функционал действия в квантовой механике 71
и поднимем Н в показатель экспоненты [ вводя при этом ошибку
O((8t J )]. В результате
¦ _ r+oo di
B.16)
На этой стадии манипуляции становятся формальными и не очень хоро
шо определенными. Мы хотим взять интеграл по I, а подынтегральное
выражение - чисто осциллирующая функция. Есть два способа выйяи из
этого положения: .либо искусственно ввести для сходимости множитель
вида е-81 , либо формально считать i5 t "действительной" величи-
величиной, т.е. продолжить выражение в евклидово пространство, заменив t
на it . Сохраним на время множитель i бt и будем рассматривать его
как действительную константу. Тогда,производя замену переменных
приходим к выражению
HL [ -L- q2 - V(q)]
s ' I 1 h 2
Вычисляя гауссов интеграл, получаем
<?;+«.i?«> - пг-4^- с^[~? "F(9)]- BЛ9)
Напомним, что величина <J определена формулой B.15) и в нее вхо»
дит как q', так и ^« Величина, стояшая в квадратных скобках, дей-
действительно является .лагранжианом. Следовательно, гипотеза Фейнма-
на оказывается правильной, если не считать того, что возникшая кон-
константа по меньшей мере необычна. Таким образом, для конечного ин-
интервала времени
<qf\q* > = lim f«. / ' П I dq. ( 1 ) Уг \ х
' Т 8»-0 /= 1 ; 2тг»беА
Л' 6 ( фиксировано
(t/h>f*Ldt B.20)

72 t Глава 2
Предполагая, что этот предел имеет смысл, мы видим, что вряд ли можно
опустить константу пропорционадьности между амплитудой перехода и
интегралом по траекториям. Этот вывод является строгим для систем,
описываемых гамильтонианом вида B.9).
Предположим теперь, что мы хотим вычислить амплитуду пе-
перехода для системы с классическим гамильтонианом вида
H=±p2v(q), B.21)
2
где v{q) - некоторая функция переменной q. Нужно очень аккуратно
определить соответствуюший оператор Гамильтона, поскольку р и q
не коммутируют. Теперь очередь за предписанием об упорядочении. Опре-
Определим симметричное упорядочение "..." так, что
2тг 2 '2
х е "<*'-?) B.22)
Как нетрудно убедиться, таким условием действительно определяется не-
некое упорядочение. При этом q и q' рассматриваются равноправно.
Далее, полагая А = 1, путем непосредственных вычислений получа-
получаем, что
dl \) +
qt> = f^AL e 2
17 +O(F«J), B.23)
так что интегрирование по / становится более сложным. Производя
замену переменных
Г= sfis7{l v* ~ v* q), B.24)
где q — величина, определенная формулой B.15), находим
1 -iSt—q2 1 , +в. ,,. -1'21г -
B.25)
B.26)

Функционал действия в квантовой механике 73
Выражение в показателе экспоненты можно интерпретировать как ла-
лагранжиан
L=J^v-lq2, B.27)
2
в чем нетрудно убедиться, образовав каноническим способом гамиль»
тониан (см. задачу); но в B.26) имеется и дополнительный член
t>"~^[(g + qr')/2], который в данном олучае вносит вклад в интеграл
по траекториям, имеющий вид
N -1 dqi w +i Г * Lit
<Ч\ I > = / / П '«~* (?+? ) е Г
B.28)
Заметим, что это выражение отличается от наивного выражения, в
котором траектория берется трлько с весом е '^. Таким образом, ма-
магическая мера " ? q " иногда содержит странные сюрпризы, вроде мно-
множителя v~^ в данном случае. Отсюда можно извлечь один урок: пра-
правильное выражение для амплитуды перехода получается только в том
случае, если сначала используется гамильтонов формализм. Более
правильное выражение имеет вид
< q^ qj,> ~ ) ... ) ±>р Up е
где "?р" означает T\(dpi /2тт), а < q> — среднее значение перемен-
переменной q на данном интервале. Итак, выражение для амплитуды перехода в
виде экспоненты от действия следует рассматривать как выведенное из
фундаментальной формы B.29), содержащей гамильтониан.
Задачи
A. Выведите формулу B.11), непосредственно вычиолив матричные
элементы оператора ц в импульсном представлении и затем выпо,лнив
обратное преобразойрлие в ^-представление.
5v Найдите точные выражения для "qnp" и n/qnp2" в соответст-
соответствии с определением, содержащимся в соотношении упорядочения B.22).
B. Пользуясь обычной процедурой,покажите, что лагранжиан
L = Уг v~lq2 приводит к гамильтониану Н ~ Уг р2 v(q).
Г. Покажите, что если Т < tltt2< t, то
iCLdt[pq -H]
$pq(t )q(t2)e = < q\ \ T [ q(tr) q(t 2)]\ qv>,

74 Глава 2
где симврл Т [...] означает хронрлогически упорядоченное произве-
произведение:
при ц> t2,
1) При t2 > tx.
§ 3. Интеграл по траекториям и гармонический осциллятор,
находящийся под действием внешней силы
Очень хорошей иллюстрацией к применению метода интеграла по
траекториям может служить задача о гармоническом осцилляторе, на
который действует внешняя сила. Мы хотим вычислить амплитуду пере-
перехода при наличии действительной вынуждающей силы F
iCtdt[JL q2 --L со2?2 + F(f)q(t )]
2 2
со следующими граничными условиями: q = Q' в момент времени t и
q = Q в момент времени Т. Записанное так подынтегральное выраже-
выражение будет чисто осциллирующим; один из способов восстановить сходи-
сходимость таков: добавить затухающий член
у е ^Tdtq2(t), e > 0,
C.2)
и устремить s к нулю по окончании вычислений. Тогда подынтеграль-
подынтегральное выражение примет вид
— Ч2 (w2_ je)?2
2 2
Предположим теперь, что в случае осциллятора с внешней вынуждающей
силой мы хотим вычислить амплитуду перехода из состояния Q в бес-
бесконечно далеком прошлом в состояние Q' в бесконечно далеком буду-
будущем. Чтобы осуществить это, удобно ввести преобразование Фурье
e
iEt
Z(E) C.3)
и обратное ему преобразование
G(E) = f^~^e~iEt'G(t), C.4)
V 2тг

Функционал действия в квантовой механике 75
где G - любая функция времени t, a G - ее фурье-образ. Выразим
q (t) и F (t), входящие в C.1), через их фурье-образы:
J- [ чг _ („2. ,. , , 2 ] =± J*J/f НЕ^ В',
2 2
q(E'), C.5)
Интегрирование по «, использование интегрального представления B.12)
для S-функпии и затем интегрирование по Е" приводит к выражению в
показателе экспоненты
— /12 dE[{E2 -co2 + «е)?( ?)?(-?) +?(?)?(-?) +
+ '?(-?)?'(?)]. C.7)
Определяя новые переменные в ^-пространстве
Г(Д)=Т(Д)+ f(?i C.8)
Е2 -а2 + г'Е
или в (-пространстве
приходим к выражению для амплитуды перехода
Теперь-то и проявляется магия интеграла по траекториям, поскольку
якобиан преобразования C.8) равен единице. Следовательно,
V=S)9 C.11)
и в последнем множителе в формуле (ЗЛО) мы узнаем амплитуду пере-

76 Глава 2
хода при F = 0, так что в результате
i г +
,,.
C.12)
Зависимость от F выделена в явном виде. Можно еще немного преоб-
преобразовать это выражение, придав ему форму интеграла по времени
expi - — / 1" dtF(t)D(t~t')F(t')dt'\, C.13)
где D(t~t') = ft™ 11 L. -—_. C.14)
z-rr E2~ az + ie
Каков физический смысл выражения C.13)? Допустим, что вынужда-
вынуждающая сила отсутствует в моменты времени «=+«•. Тогда в эти мо-
моменты времени вакуумные состояния не будут зависеть от существо-
существования силы F. Пусть | Q + „, > — вакуумные состояния в бесконечно
далеких будущем и прошлом. Выразим их через состояния | Q ±ов, кото-
которые входят в выражение C.12). Имеем
J ^_D
= fdQ'dQ<Q+
Q'+
= 0 x
где мы учли выражение C.12) и ввели обозначение < ... > для указания
интегрирования по t и t''. Пользуясь теперь выражением C.15) с
F - 0, можно переписать C.16) в виде
_ L < FDF>
<^+J^-м>F=-^+<»>^„к>F = o е 2 • C.17)
Но величина < Q+(J й_„.> р= 0 есть амплитуда того, что система,
находившаяся в бесконечно далеком прошлом в основном состоянии ,
окажется в бесконечно далеком будущем в отсутствие всякой вынуждающей

Функционал действия в квантовой механике 77
силы. Такая амплитуда должна равняться 1 (если она нормируема).
Следовательно, выражение C.13) мы отождествляем с амплитудой
перехода системы из основного состояния в пропцлом в основное сос-
состояние в будущем при наличии внешней вынуждающей силы.
Обозначим величину C.13) символом W[ F] и введем Z[ F]
в соответствии с равенством
rtF]-e~r<FiD»*2>i.-a,e.!Z[F]e C.1SU3.19)
Здесь вновь символ <...> 12 означает интегрирование по немым пере-
переменным "Iм и ", при этом Fj означает F и т.д. Заметим, что
функционал W нормирован так, что W[ 0]— 1.
Нетрудно показать (см. задачу), что
D(t) =_i [Q{t)e-iat + Q(-t )e iat], C.20)
2 ico
где 9 (x) — ступенчатая функция:
fl, *>0,
C.21)
Далее, непосредственно дифференцируя выражение C.14), мы убеждаем-
убеждаемся, что
(.?_ + co2)D(«) = -5@. C.22)
it2
Следовательно, D (t) есть функция Грина оператора (d2/dt2) + в^
а правилом добавления - fe , предписываемым интегралом по траекто-
траекториям, фиксируются граничные условия. Как явствует из выражения
C.20), D{ t) представляет собой смесь запаздывающего и опережа-
опережающего сигналов. Это "предшественник" фейнмановского пропагатора,
описывающего распространение сигнала как обусловленное двумя фак-
факторами: движением состояний с положительной энергией (частиц) в
положительном направлении во времени и состояний с отрицательной
энергией (античастиц) назад во времени.
Отметим еще одно интересное обстоятельство: выражение C.13)
можно продолжить на мнимые значения Е, не встретив1 при повороте
контура никакой сингулярности (рис. 1), Возможность выполнения та-

78 Глава 2
ЫЕ
p и c.1.
кой операции, называемой виковским поьоротом, очень существенна, по-
поскольку эта операция соответствует рассмотрению с самого начала
"евклидова" (t -* it) определения интеграла по траекториям. Такой
способ альтернативен введению i e -затухания, ибо подынтегральные
выражения в евклидовом пространстве уже не осциллируют. Например,
мы могли бы начать с выражения
WE[F)= } $qe J "~ 2 d-r 2 f C.23)
полученного подстановкой л - it в формулу ( 3.1). Тогда ответ в
действительном времени получается аналитическим продолжением вы-
выражения для WE[ F]. Такой процесс приводит к той же полюсной струк-
структуре функции D(t), что и добавление - ie ( см. задачу). Мы подробнее
проследим за этой процедурой при вычислении фейнмановских диаграмм.
Однако отсутствие сингулярностей в евклидовом пространстве, хотя и
привлекательно с математической точки зрения, затемняет физический
смысл теоретико-полевых амплитуд. На практике, конечно, каждый счи-
считает себя вправе продолжать функции и вычисляет так, как ему легче.
Но по формальным причинам разница между описанием в евклидовом
пространстве и пространстве Минковского может быть огромной (смысл
добавки -и в случаефермионов, "калибровка" на световом конусе"
и т.п.).
Задачи
А. Методом, изложенным в приложении А, покажите, что
i= I det С
Каким условиям должна удовлетворять матрица С (если она эрмитова)?

Функционал действия в квантовой механике 79
Дополнительное упражнение для желающих: доказать приведенную выше
формулу в случае, когда С — неэрмитова матрица.
В. Вычислите функции Грина
-iEt .г .-iFt
методом теории вычетов. Выясните, каков физический смысл граничных
условий для этих функций Грина. Можете ,ли вы каким-либо способом
получить указанные функции с помощью интеграла по траекториям? Вы-
Выразите через функции Da и DT функцию D [ формула C.20) ].
*В. Исходя из выражения
покажите, что
WE[F] = WE [0]ехр{ _ % / dz do F(t)De(t - о ) F(a)\,
причем выражение для DE (т) следует найти. Затем путем аналити-
тического продолжения выведите выражение C.20) для функции D.
Г. Покажите, что
D(t)= f e"' *
_i_ [Q(t)e Q(l)e)
2тт Е2 -со2 + te 2ico
(e > 0).
ЛИТЕРАТУРА
L Dirac P,AcM., Physo Zso Sowjetunion, 3, Hf. 1 A933).
2o Dirac P.AoMo — in: Selected Papers on Quantum
Electrodynamics, ed* J. Schwinger, Dover, 1958.
3. FeynmqnR. P. , Rev, Mod.1 Phys., 20, 267 ( 1948) .

Глава 3
Фейнмановский интеграл
по траекториям в теории поля
§ 1. (Производящий функционал
Обобщим теперь интеграл по траекториям на случай теории поля.
Рассуждая по аналогии с квантовой механикой и взяв для удобства
в качестве примера действительное скалярное поле, мы можем описы-
описывать состояния системы в данный момент времени t кет-вектором
| ф(х)>#. Назовем это состояние конфигурацией. Можно вычислить
амплитуду перехода между конфигурацией в момент времени t и но-
новой конфигурацией в более поздний момент времени t, но при этом
мы немедленно сталкиваемся с необходимостью выразить кет-вектор
конфигурации через возможные физические состояния системы. Иден-
Идентификация состояний системы обычно существенным образом зависит
от возможности использовать метод малых возмущений. Сначала рас-
рассматривают теорию в нулевом приближении, и в этом случае состояние
легко определяются. Переход к полной теории осуществляется добавле-
добавлением малого возмущения к идеализированной теории нулевого порядка.
Затем вычислякт влияние этого малого возмущения на идеализирован-
идеализированные состояния в нулевом порядке. Указанные шаги возможны только
в том случае, если удается построить полную теорию, рассматривая
малое возмущение простой системы, и на основе такой теории вычис-
вычислить поправки к идеализированным состояниям нулевого порядка.
Примером может служить квантовая электродинамика (КЭД), в кото-
которой легко обнаруживается малый параметр а ~ A37). Теория нуле-
нулевого порядка отвечает значению а = 0. Такая теория без труда опи-
описывается с помощью идеализированных состояний фотона и электрона
(или мюона, тау, кварка, . . .). Последовательно в каждом порядке по
а вычисляется влияние взаимодействия на указанные состояния и их
взаимодействия. После некоторых ухищрений (а именно, теории пере-
перенормировок) обнаруживается, что эти поправки приводят к физическим
состояниям электрона и фотона и их взаимодействиям. Цель всего
сказанного - подчеркнуть, что успех КЭД основан на том, что нам

Фейнмановский интеграл по траекториям в теории поля 81
удалось выявить идеализированные электронно- и фотоноподобные сос-
состояния в теории нулевого порядка. Такое выявление стало возможным
только благодаря тому, что а - малое число. Примером еще нерешен-
нерешенной теории может служить КХД, квантовая хромодинамика, которая,
как полагают, описывает взаимодействия кварков и глюонов (эквива-
(эквивалент фотонов в КХД). Считается, что кварки не являются физически-
физическими частицами, а таковыми являются связанные состояния кварков -
протоны, тт-мезоны и т.д. Но априори ничто не заставляет считать,
что кварки - не физические состояния. Поэтому, чтобы двигаться даль-
дальше, мы должны решить, каковы константы взаимодействия кварков
друг с другом. Если они малы, то кварки можно рассматривать как
физические состояния (здесь "физические" означает, что состояния
"выживают" в изоляции); если же константы велики, то говорить о
кварках как о частицах не имеет особого смысла, поскольку кварки
будут связываться друг с другом, а не существовать в виде асимпто-
асимптотических состояний.
Таким образом, знание физических состояний теории поля во мно-
многом зависит от решения. Но его-то мы и ищем! Нам нужно найти такую
формулировку теории, основанную на интегралах по траекториям, при
которой не требовалось бы знать ее физические состояния (это будет
выведено). Прием, который позволяет выбраться из этой западни,
очень прост. Всякий согласится, что, какими бы ни были состояния,
должно существовать состояние с наименьшей энергией, которое мы
назовем вакуумным. Оно может иметь очень сложную структуру (на-
(например, сверхпроводимость) и может быть заселено всеми видами
странных объектов, но тем не менее считается, что оно существует.
Предположим теперь, что нас интересует амплитуда перехода системы
из вакуумного состояния при t = -<» в вакуумное состояние при t = +~
в присутствии произвольной вынуждающей силы. Это означает, что в
любой момент времени мы сохраняем за собой право как угодно воз-
возбуждать систему по своему желанию и наблюдать за ее откликом.
Тогда мы можем получить ответ на все вопросы, если только мы дос-
достаточно умны, чтобы применять такие пробы, которые дают распозна-
распознаваемые отклики. Следовательно, план действий будет таким: а) решить
задачу о построении амплитуды < Q | й >, для произвольного источни-
источника / (х)|. б) интерпретировать результаты, т.е. опознать амплитуды
рассеяния; в) исходя из этих амплитуд, рассчитать физические след-
следствия теории.

82 Глава 3
По традиции источник привязывается к локальному полю, так как
это приводит к вынуждающему члену общего вида, с помощью которого
могут быть построены все возможные источники. В случае, когда при-
применима теория возмущений, локальные поля естественным образом ин-
интерпретируются как частицы.
Начнем с простейшей теории поля — самодействующего скалярного
поля, описываемого действием
2 <J
A.1), A.2)
Чтобы построить гамильтонову плотность К, определим канони-
канонический импульс
и выполним затем преобразование Лежандра
Н(тт, ф,Уф) = тгф-?= — (tt2+V<p • V<p+mV)
Если тг> 0 и F > 0, то функция Н положительно определена.
Амплитуда перехода вакуума в вакуум определяется как
A.6)
где N - постоянная (обычно плохо определенная), символ <. . . > оз-
означает теперь интегрирование по пространственно-временным пере-
переменным, а / (х) - произвольный источник. Интегрируя по тт методом,
изложенным в предыдущей главе, получим
В этом случае через Юф (или 3)тт) обозначено произведение всех
dyk, где фА - значение ф при х = лг,.
Подынтегральное выражение в A.7) осциллирует.и даже интегра-
интегралы по траекториям плохо определены. Существуют два способа изба*-
виться от этой трудности: а) ввести множитель ехр(-Ц е< ф2>)се > О,
обеспечивающий сходимость; б) определить W в евклидовом простран-
пространстве, положив х0 = ix0, d*x - -i d*x, д^ аИр = -<?цф вц«р, Где

Фейнмановский интеграл по траекториям в теории поля 83
чертой отмечены переменные в евклидовом пространстве и д =
Тогда выражение A.7) примет вид
_< Л^фй.ф +— т\2
« 2 " М 2
Теперь уже показатель экспоненты под интегралом отрицательно оп-
определен при положительных т2 и V.
В обоих случаях производящий функционал используется для по-
отроения функций Грина, являющихся коэффициентами функциональ-
функционального разложения
W[J] = 2 -^ </г/2 . . • JN^NH\, 2 N)>, N A.9)
ИЛИ
где, как обычно, J{ = j(x() и т.д., символ <•••>!,.,.(W означает
интегрирование по d4*^ ,, .d4»; . Главная задача теперь'в том, чтобы вычис-
вычислить функции G(Ar)(«1 xN) методом теории возмущений или иным спосо-
способом. В р-пространстве эти функции будут отождествлены с амплитудами пе-
перехода. Это нетривиально, поскольку амплитуды перехода должны удовлет-
удовлетворять требованиям унитарности и полноты. Для построения таких функций
G^^Xj ?v) используется функционал WE[J] в евклидовом про-
пространстве; функции G^' связаны с Gw) аналитическим продолжение
ем (виковским поворотом), и это заранее предполагает, что в процес-
процессе поворота контура не пересекаются сингулярности. Такого условия
достаточно для определения структуры особенностей Gw\ но нетриви-
нетривиальной задачей становится доказательство того, что подобная проце-
процедура совместима с унитарностью. Мы надеемся, что все эти несколько
смутные замечания станут яснее после явных вычислений.
§ 2, Фейнмановскнй пропагатор
В данном параграфе мы вычислим W[j] для случая V = 0. Сдела-
Сделаем это в пространстве Минковского с помощью е- процедуры. Положим

84Глава 3
B.1)
Легче всего проделать вычисления в пространстве фурье-образов
(импульсном пространстве) тем же методом, что и в случае вынужден-
вынужденного гармонического осциллятора. Введем четырехмерное преобразо-
преобразование Фурье
7B-2)
7
_« BттL
eH*-*')-Pf B.4)
где х-р = х° • р° - х°- р, a F - любая функция с достаточно хорошим
поведением. Экспонента под интегралом легко выражается через фурье-
образы функций ф и /; в результате в показателе экспоненты возника-
возникает выражение
- "»2 + 'Оф'(-р) -Т(р){р2 -™2 + «О
B.5)
где Ф>) = Ф(Р) + (Р2 -™2 + и -1f(P)- B.6)
Новая переменная ф' отличается от ф на константу в пространстве
функций, так что
3)ф =3)ф'. B.7)
Объединяя все результаты, находим
< 2 2 B.8)
причем мы замечаем, что зависящий от ф' член оказался точно таким
же, как член, зависящий от ф, в выражении B.1) при / = 0. Следова-

Фейнмановский интеграл по траекториям в теории поля 85
теЛЬНО,
1
р - m
Выбрав должным образом N, можно положить WQ[0] = 1. Заметим, что
Wq[I-] можно формально вычислить, пользуясь формулами приложе-
приложения А. Важно то, что нам удалось найти явную зависимость W0[j] o5K/,
Пользуясь обратным преобразованием Фурье, получаем
12 , B.1.0)
где через AF12 обозначено AF(xl - х2):
Bтт)
Это — фейнмановский пропагатор. Теперь можно интерпретировать по-
получающиеся из WQ функции Грина. Мз выражения A-10) находим
B.12)
+ AF(Xl -x3)AF(x2 -x4)+Af(x1 -x4)AF(x2 - x3)]
B.13)
и т.д. причем одновременно с этим все G с нечетным числом перемен-
переменных обращаются в нуль. Последнее легко понять, так как W0[j] зави-
зависит только от / 2. Попутно заметим, что все G являются функциями
только разностей координат, в чем отражается трансляционная инва-»
риантность теории. Другой вывод заключается в том, что все функции
Грина более высоких порядков можно выразить через G@2\ Поэтому
может оказаться более удобным положить
BЛ4)
и определить новые функции Грина с помощью Z[J]:
i!f---,N)J1. . . JN>1...N- BЛ5>
N

86 Глава 3
Теперь мы видим, что по крайней мере в случае WQ величина Gc на мно-
много проще, чем G.
Выясним теперь физический смысл функций Грина, порождаемых
функционалом WQ. Прямым вычислением находим, что
(дид» + т2)Ар(х) = -ъ(*Цх), B.16)
тем самым отождествляя Д с функцией Грина оператора d + т2-
Граничные условия для нее определяются из (- (е) -процедуры, диктуе-
диктуемой интегралом по траекториям. Поэтому можно отождествить Д (х - у)
с пропагатором некоего сигнала из точки х в точку у. Сигнал представ-
представляет собой состояния одиночной частицы или одиночной античастицы,
поскольку эти состояния являются решениями уравнения Клейна - Гор-
Гордона
( n + w2)9 = 0. BЛ7)
О том, какие решения распространяются, говорит нам (-к) -процеду-
-процедура. Можно показать, что решения с положительной энергией уравнения
Клейна - Гордона распространяются вперед во времени, а решения с
отрицательной энергией - назад во времени (см. задачу).
Поскольку эти решения должны быть сопоставлены состояниям
частицы (или античастицы) с энергией Е = р° = \ р2 + т2 (или
—ф2 + т2), мы приходим к очень симметричной физической картине:
информация переносится вперед во времени частицами, а назад во
времени - античастицами. Спросим себя, например, сколькими спосо-
способами можно перенести какое-то квантовое число из точки х в точку у,
если у нас имеется частица, несущая одну единицу этого квантового
числа, и античастица, несущая минус одну единицу. Квантовым числом
может быть электрический заряд, а частицей тт+-мезон. Ответ - дву-
двумя способами: либо за счет распространения тт+-мезона из х в у с
уничтожением заряда +1 в точке х и переносом его в точку у, либо за
счет распространения тг~-мезона, античастицы для тт+-мезона, с пере-
переносом отрицательного заряда из у в х.
Выводы: 1) мы установили, что рассматриваемая функция Грина
есть пропагатор определенных сигналов, и 2) мы знаем, какие сигна-
сигналы она распространяет. Отсюда естественно вытекает, что в нашем
примере состояния должны быть состояниями частид с массой т2, а
функцию G^\x - у) мы интерпретируем как амплитуду перехода час-
частицы из точки х:-.в точку у. Можно ввести диаграммное представление
в х-пространстве, сопоставив с Д^ (х - у) линию, связывающую две

Фёйнмановский интеграл по траекториям в теории поля 87
пространственно-временные точки х и у:
Gl2)(*,y): * у
Для функций Грина высших порядков мы с помощью диаграмм добав-
добавляем вклады, скажем, соответствующие формуле B.13):
i' *v
хг\ lxt х3\ \х, хч
+
Ч *¦/ № х* \хг х3)
Ясно, что G g — существенно несвязный объект. Эту функцию можно
интерпретировать как амплитуду, например, перехода из х х.в
*3, х4. В данном приближении имеется лишь столько способов распро-
распространения сигнала, сколько изображено выше с помощью диаграмм.
Значительно более ясной оказывается интерпретация в простран-
пространстве Фурье- образцов. Мы видели, что структура оператора Ар вынуж-
вынуждает нас интерпретировать р как 4-импульс состояния частицы. Это
совместимо с трансляционной инвариантностью и приводит к сохране-
сохранению р. Действительно, поскольку G зависит только от разностей коор-
координат х, простой фурье-образ
обязательно содержит 6-функцию от (рх + . . . +pN). Поэтому мы по-
полагаем
XN>
B.18)
где функция &Р)(ри . . . ,pN) определена лишь при условии
Pt + • . . + PN = 0.
Например, G™(p, -p)= L— B.19)
р2 _ от2 + |Е

88 Глава 3
представляет собой амплитуду распространения частицы с импульсом
р и массой от2. Это же можно изобразить с помощью диаграммы
(И= ~~J B.20)
Но в общем случае мы будем представлять функцию Грина
j, . . . , pN) кружком с входящими в него N линиями с символа-
символами Pv р2, . . . ,- pN при условии рг +. . . + pN = 0, выражающем
сохранение импульса:
l -,PN)= рТЧ^Р^- B.21)
Такая диаграмма будет интерпретироваться, скажем, как ампли-
амплитуда рассеяния состояний с импульсами рх, „ „ . , р: в состояния с
импульсами р.+ v ... t pN> если при ^тпм считать ляйии / + 1, . . ., N
выходящими. Снова заметим, что именно видом функции G(n2) определяется
характер внешних состояний. На тех ограничениях, которые накладыва-
накладываются на ё унитарностью, мы остановимся позже.
Задачи
A. Исходя из евклидова выражения для WE[J], выведите соответ-
соответствующее выражение для фейнмановского пропагатора и покажите, что
после аналитического продолжения в пространство Минковского он
сводится к обычному.
Б. Покажите, что Др(х) - пропагатор сигналов с положительной
энергией вперед по времени и с отрицательной - назад по времени.
B. Найдите действительную и мнимую части пропагатора AF(x);
выясните их физический смысл. Можете ли вы выразить AF через
§ 3. Эффективное действие
С помощью производящего функционала можно сконструировать
локальные величины, допускающие привычную интерпретацию. Напри-
Например,
SW
JL <зл>

Фейнмановский интеграл по траекториям в теории поля 89
так что
61пИЬ SZn
ФЛ)C.2)
6Дх) 5J(x)
удовлетворяет [ для доказательства нужно воспользоваться формулой
B.16)] классическому уравнению движения
(n+^V^ (*) = /(*). C.3)
В самом деле, на основании уравнения C.3) можно заменить / (х) вы-
выражением, содержащим ф(к°п'(х). Формально это сводится к осуществ-
осуществлению функционального преобразования Лежандра; вводя
KJ oKn C.4)
мы с учетом формулы C.2) находим, что Го не зависит от /. В этом
случае легко найти явное выражение для Г , выразив / через ф@).
Пользуясь формулой BЛ6), получаем (интегрируя по частям по ходу
дела)
roU(S]= " у <[< D + m2)<f™ MfuN о +ш2)Ф(к°Д> -
-<Ci*+»W2,>-y'-№Q >«*>№• C-5)
Интегрирование по частям приводит к окончательному выражению
C.6)
y
представляющему собой то свободное действие, с которого мы начи-
начинали.
Аналогичную процедуру можно осуществить и в общем случае,
когда V Ф 0. Образуем
C7)
и попробуем вычислить эффективное действие
>, C.8)

90 Глава 3
фкл
где теперь /(*) = - , C.9)
в чем нетрудно 'убедиться, продифференцировав C.8) по <р . (Конечно,
кп
Г[фкп] зависит только от фкп, a Z [/] - только от /.) Между прочим,
мы видим, что, поскольку Г - эффективное действие, величина C.9)
входит в правую часть уравнения движения, возникающего из условия
экстремальности Г. В случае V = 0 это явствует из выражения C.3).
Чтобы вывести уравнение движения для <р (*), нам следует запи-
записать W [J ] в какой-либо приемлемой форме. Напишем
1 1 2 • \ 2
2 ** 2
C.11)
А теперь — главный трюк: заметим, что
1 />' ^J Ф "* m/v\«'<~/ Ф^ /О 1О\
с = ф\*/ " j V'* ^/
i 67 (х)
а так как / и ф - независимые переменные, то же самое будет верно
и для любой функции от ф. В частности,
e-i<vW>eKJ<t> = e l°Jei<J9>. C.13)
Это позволяет вынести из-под знака интеграла множитель, зависящий
от V:
» ,<ц
* "[З)? е 2
C.14)
— — )>
J Wi <ЗЛ5>

Фейнмановскип интеграл по траекториям в теории поля !М
_,<F(J_i-)> - —</1AFl2/ >
или eiz[j]=w[jUNe i s?- e 2 .C.16)
.
Это выражение будет отправным при вычислении W[J] методом теории
возмущений. В данный момент выведем из него уравнение для q> .
Из выражения CJ6) имеем
5Лс
6
Отсюда следует, что
/ i-i „2\ и" .' г] U7 Г Г 1 14 1Q\
I Q + т I = • ^ г" lj J| (d.lOl
X Яг
О I
б В
где бх = « S/ Ixe 5/ • C.19)
Величину 6х можно вычислить, применив еще один трюк. Положим
• — \> • • —
х(Л) = е 7хг i C.20)
где Л — некий параметр. Ясно, что
C.21)
Но [V(-i -^-), Jx] * -i V'{- i ¦?- ) 5<% - y), C.22)
где F' - производная функции F по ее аргументу. Интегрируя по у,

92 Глава 3
находим
C.23)
Это уравнение интегрируется теперь по А, так что в результате
dX 6/-,
/r'Hrf)- C.24)
S^x
Следовательно,
( п х+т2)™- =i(J(x)-V'{-i^-))W[J], C.25)
или ( Dje + m2)?Kn(*) = /(*)- FE7]T/'H^)W7[/]' C'26)
Очевидно, что последний член похож на силу. Например, возьмем
V = -— ф4, где Л - безразмерная величина. Тогда
4!
и окончательно
<°«+»Чл<*)-/(*)зТ»кл(*)+ 3! 5/ 2(х) Т
C.29)
Два первых члена в правой части соответствуют классическому урав-
уравнению движения, но к ним добавляются два последних члена, которые
представляют собой поправки, даваемые квантовой теорией (см. зада-
задачу).
В случае V ф 0 явный вид эффективного действия, конечно, неиз-
неизвестен. Его можно представить в виде функционального разложения по

Фейнмановский интеграл по траекториям в теории поля 93
Фкп В виде
Г[фкп] = /d4x[-;Fe((pKn) + —_ Р(?кп)д„9кпд\П + производные вые-
]
фкп] = /dx[F((pKn) + кп„9кп\П рд
ших порядков].
C.3Q)
причем, включив производные функции фкл произвольно высоких поряд-
порядков, мы учли теперь нелокальные эффекты. Произвольные функции
Ре(фкп), F(yKn) и т.д. подлежат определению. Функция Vе - это, оче-
очевидно, эффективный потенциал. Выражая / через ф по формуле
C.29) и интегрируя выражение C.9), находим
Kn) = 1 + поправки. C.32)
Можно также действовать иначе - нелокальным образом разложить
эффективное действие по ф •
К Л
( N)9m(\) . ..чтт>х n. C.33)
Коэффициенты Г ^ \xv . , . , xN) называются собственными вершин-
вершинными частями. В силу трансляционной инвариантности они зависят от
разностей х(. _ *., так что фурье-образы вершинных частей опреде-
определяются формулой
C.34)
где Г (N) определены только при условии, что сумма их аргументов
равна нулю.
Задачи
А. Включив там, где это требуется, постоянную Й, покажите, что
неклассические члены в уравнении для фкп действительно исчезают
при Л -»0.

94
Глава 3
Б. Допустим, что в действии для скалярного поля V = 1/2бт2<р2.
Выведите уравнение, которому подчиняется <р
кл
§ 4. Вычисление интеграла по траекториям
методом перевала
Интегралы вида
/ = fdx e-a(x), D.1)
где а (х) — функция координаты х, можно приближенно вычислить, раз-
разложив а (х) в ряд вблизи точки xQ, в которой функция а (х) стационарна:
х)~а(хо)+--(х-хо)Ч (*„) + ... . D.2)
~(а(хп) -1/2(х - х.
Тогда I ~е ' 0> fdx e l °
D.3)
и интеграл легко вычисляется, если а"(х0) > 0 и можно пренебречь
высшими производными (этот интеграл гауссов). Такое приближение
допустимо в том случае, если подинтегральное выражение максималь-
максимально, когда величина а (х) минимальна, и точки вдали от минимума не
дают существенного вклада, как это показано на рис. 2.
В данном параграфе мы применим подобный метод вычислений к
производящему функционалу в евклидовом пространстве.
Начнем с определения производящего функцион лла в евклидовом
пространстве
-sf[q>> /]
W
D.4)
где
а(х)
а(х)
(Хорошо) (Плохо)
Рис, 2.

Фейнмановскип интеграл по траекториям в теории поля 95
Разложим затем действие в ряд вблизи полевой конфигурации ф0:
SSE
S?[<P, Л = S?t90, /] + < —- (ф - <po)> +
где функциональные производные вычислены в точке ф0. Примем, что
действие S? стационарно в точке ф0, т.е. что ^ подчиняется классичес-
классическим уравнениям движения с источником
' ^ т2фо + F'(<po) - 7 = °' D'7)
6ф
После интегрирования по частям находим, что
с г . п * С A^Zl*) _ m ——— \ ( f m + V(<D \ D 8\
тогда как
1 - х2) D.9)
является оператором. В соответствии с методом перевала производя-
производящий функционал принимает вид 2
1< Е
2. DЛ0)
Гауссов интеграл может быть взят (приложение А), что приводит к фор-
формальному результату
WE[j]~4'Ee~SEl'*0'j]\det([-dildll+m2+V"(<f0)]5l2)rV2 . D.11) .
Очевидно, что не очень-то понятно, как пользоваться таким выраже-
выражением. С учетом тождества
D.12)

96 Глава 3
его можно переписать в несколько более осмысленном виде
так что становится ясным, что мы вычисляем поправки к Z[j], Физи-
Физический смысл такого приближения можно понять, если внимательно
восстановить все множители h. После этого можно убедиться, что
приближение соответствует асимптотическому ряду по h (см. задачу).
Первый член S?[q>0, J] Дает классический вклад в функцию Грина
(вспомните гипотезу Дирака!). Следующий член порядка О(й) представ-
представляет первую квантовую поправку к функции Грина. (Детерминант опера-
оператора следует понимать как произведение его собственных значений.)
Начнем с вычисления классического вклада в W[J]. При этом следует
помнить, что так как функция <ро есть решение уравнения D.7), она
является функционалом от /. Поэтому процедура вычислений очень прос-
проста: а) вычислим функциональную зависимость q> от /; б) подставим
найденное выражение в D.8); в) сравнив получившееся выражение с раз-
разложением BЛ5), извлечем функции Грина 0^A, . . . , N). К сожале-
сожалению, при выполнении шага "а" мы сталкиваемся с серьезными теоре-
теоретическими трудностями. Уравнение, которому удовлетворяет <р , пред-
представляет собой нелинейное дифференциальное уравнение (в случае
V' 4 0)i и оно еще никем не решено в замкнутой форме. Лучшее, что
можно сделать, это попытаться решить его в рамках теории возмуще-
возмущений. Конкретно, возьмем потенциал q>4 и будем раскладывать вблизи
А = 0.
Запишем разложение
»0-?<°> + A,<»+aV« + .... D.U)
так что
= - -1 Jd
2
D.15)
Тг"ф
D.16)

Фепнмановскии интеграл по траекториям в теории поля 97
Если теперь (в очевидных обозначениях) определить евклидову функ-
функцию Грина
(д ~b -m2) G =_б D.1?)
Ц ц ' ху иху ' v '
то тогда ф@)(х) = < ^ха]а> а,
?A)(*) = - \<Gxy%a%bGycJaJbJc> abcy »^*° <4Л8)
о
Таким образом,
+ _L- <GxaGxbC,xcnxdJaJbJcJd> a
D.19)
Соответственно этом,) '".вязные) евклидовы функции Грина определяют-
определяются как
D.20), D.21)
В рассматриваемом классическом приближении связные функции Грина
оказывается равными
(*!, y)G{x2> y)G(x3>y)G(x4> у), D.23)
2fd4x dAyG(x, y) x
x P& y, ~xv x2> xy xA, xy x,), D.24)
где P(x,y, \x.\)= z G^x,. ) G(x, x}) C(g xk)G(y, xe) x
x G(y, *m) Gfc xn)

98 Глава 3 '
и сумма берется по всем нижеследующим тройкам чисел (» / к) = A23),
A24), A25), A26), A34), A35), A36), A45), A46), A56), причем предаю*
латается, что (lmn) принимает дополнительные значения [например,
(lmn) = D56), если (ijk) = A23). Заметим, что индексы (ijk) пробегают
только половину возможных значений. Это связано с тем, что выраже-
выражение для Р симметрично относительно замены х ¦* у.
Указанные функции являются единственными ненулувыми функ-
функциями Грина в данном классическом приближении в порядке X 2.
Как легко видеть, функции Грина в импульсном пространстве, оп-
определяемые формулой
D-26)
1
P 4 + »и
D.28)
e(?6)(Pl,...,p6)=[ П -J_2 ] Z _^2 -— +О(Л2),
« = l P,- + m (i/*) (p,- + py + pkJ + m2
f4.29)
где опять сумма берется по тем же тройкам чисел, что и в D.25).
В приведенных выражениях функции о должны вычисляться только
при условии, что сумма их аргументов равна нулю.
Вычисляя ф0 методом теории возмущений, мы видим, что ср(*)
всегда зависит от / 1+ 2к. Следовательно, порядок Хк вносит вклад
только в функцию G2(* + х). Это артефакт данного приближения, в ко-
•тором пренебрегается вкладами порядка Н. Следуя Фейнману, разра-
разработаем графическое представление полученных функций Грина. Будем
изображать О^) (pt,. . ., pN) кружком с N внешними линиями

Фейнмановский интеграл по траекториям в теории поля 99
pz —_~jfgfP , каждая из которых отмечена символом р, причем
все стрелки входят внутрь. Этот кружок можно представить в виде
диаграмм, если воспользоваться следующими правилами:
1
—•— означает пропагатор —; т— >
рг + т1
означает вершину - Л.
X
При этом подразумевается, что сумма всех р, текущих через вершину,
сохраняется. Сама вершина X не имеет стрелок на линиях, и это указы-
указывает на то, что пропагаторные множители для линий не включены в опре-
определение вершины. Сравнение с формулами D.27) - D.29) приводит к ди-
диаграммам
'рз = Рг\/Р3
р' р* Pi Pi
*ч у3 5ч
б t 6 j 6
3 *Ч /г 5\ /г
\4
1 5 1 6 1 6
6 3 ¦» 2 5. 2
37^4 4
0G?).
7^
7 5 1
6 Z
Таким образом, фейнмановские правила в данном порядке по Л
заключаются в следующем: пользуясь элементами —иXкак основными
строительными блоками, изобразить все возможные сочетания линий
так, чтобы не возникало замкнутых контуров (называемых иначе пет-

100 Глава 3
лями). Подобные диаграммы называются древесными. Не составляет
труда убедиться, что в рассматриваемом приближении функции Грина
представляются древесными диаграммами.
Рассмотрим диаграмму с ? внешними линиями, / внутренними
линиями и Vn вершинами, каждая из которых содержит п линий (в на-
нашем случае п = 4). Каждая внутренняя линия соединяется с двумя лини-
линиями от вершин. Следовательно, число внешних линий в точности равно
числу линий в вершинах минус удвоенное число внутренних линий:
Е = nVn - 11.
В приближении O(h°) мы имеем Е = 2k + 2, п = 4, V^ = k, откуда
/ = VА - 1 (только в порядке 0{Ь°)), так что в фейнмановской диаграм-
диаграмме не может быть никаких замкнутых петель и, следовательно, эти
диаграммы древесные. Правило изображения произвольной (древесной)
диаграммы заключается в том, чтобы нарисовать все топологически
неэквивалентные диаграммы с установленной нумерацией внешних ли-
линий. Например, в ОF), когда одни и те же линии выходят из вершины,
такая диаграмма учитывается только один раз, поскольку перестановка
линий будет давать топологически эквивалентные диаграммы
~ з-^ 4т "-т.д.]. С помощью этих правил нетрудно запи-
/ N J
сать выражение для П(?) ,,.; сначала мы изображаем все возмож-
возможные неэквивалентные древесные упорядочения с пронумерованными
внешними линиями, а затем, пользуясь правилами соответствия, по-
получаем аналитическое выражение. Подобное диаграммное представ-
представление оказалось очень удобным при вычислении функций Грина мето-
методом теории возмущений.
Интересно выразить полученные результаты через классическое
поле<ркл(л:) и посмотреть на вид получающегося эффективного дейст-
действия. Мы определяем классическое поле в евклидовом пространстве
как
Ф tx) = 1 « 1 +O(ft). D.30)
мК Б/(ос) 5/И
Используя формулу DЛ9), можно найти ф (х) как функционал от /
последовательно в каждом порядке по \. Затем мы обращаем это урав-
уравнение по теории возмущений и находим / (х) как функционал от m
кл

Фепнмановский интеграл по траекториям в теории поля 101
В результате
Примечательно, что в этом уравнении нет членов более высокого по-
порядка по X. Сравнивая с выражением D.7), заключаем, что
Интегрирование уравнения C.9) немедленно приводит к следующему
виду эффективного действия в данном порядке:
г?[Фкл] = -/Л-[|фкл(^-«2)фкл-^фк4л(,-)]. <4'33>
Таким образом, Г? есть классическое действие. Следовательно, мож-
можно вывести выражения для собственных вершинных частей. В данном
приближении Г B), очевидно, равняется обратному пропагатору, взято-
взятому со знаком минус, а Г (n)c n > 4 обращаются в нуль. Диаграммы бо-
более высокого порядка не возникают. Это объясняется тем, что Г (лг)
порождают только такие фейнмановские графики, которые не могут
стать несвязными при разрезании одной из их внутренних линий. Подоб-
Подобные диаграммы называются одночастично-неприводимыми. Мы видели,
что все древесные диаграммы одночастично-приводимы, кроме диаграм-
диаграммы низшего порядка.
Зацачи
А. Покажите, что вычисление интеграла по траекториям методом
перевала соответствует асимптотическому разложению по fi.
Б. Решите уравнение
(шф)ф ;
последовательно в каждом порядке по Л вблизи X = 0. Положив
Ф = ф@) + ЛфA) + Л2фB)+ . . . , выведите явные выражения для <рB) и
В. Для теории Лф4 найдите эффективное классическое действие в
порядке Л3 и выведите как в х-, так и в р-пространстве выражения дл
классических евклидовых функций Грина в порядке Л3.

102 Глава 3
§ 5. Первые квантовые поправки. Вычисление
детерминантов с помощью ?-функции
Поправка порядка О(Ь) к эффективному действию находится путем
вычисления детерминанта в выражении D.11). Этот детерминант следу-
следует понимать как произведение собственных значений оператора. Один
из возможных способов вычисления - ограничить пространство, напри-
например, ящиком, что приведет к дискретным собственным значениям. Вы-
Вычисляется произведение этих значений, а затем размер ящика устрем-
устремляют к бесконечности. Ниже для вычисления детерминанта операторов
мы будем пользоваться мощным формальным методом.
Рассмотрим оператор А с положительными и действительными
дискретными собственными значениями а,, . .. . , ап; обозначим через
fn(x) собственные функции этого оператора:
Образуем теперь выражение
I 1ч \ - у ____ . С\ 9\
А » к
называемое ? -функцией, связанной с опрератором А. (В случае когда
А - гамильтониан одномерного гармонического осциллятора, она сов-
совпадает с римановской ? -функцией, если не считать энергии основного
состояния.) Затем сумма распространяется на все собственные значе-
значения и А становится действительной переменной. Заметим, что
*-Zlna e'sXnan =-1п(Пап), E.3)
On *=° п
откуда det4 = По = е А . E.4)
п
п
Преимущество такого представления для det4 заключается в том, что
для многих имеющих физический интерес операторов функция ^несин-
^несингулярна при s=0. Действительно, введем "тепловую функцию"
G(x, у, т) = Ъе-'^Ш„V E.5)

Фейнмановскип интеграл по траекториям в теории поля 103
которая, как можно убедиться прямой подстановкой, удовлетворяет
дифференциальному уравнению (уравнению теплопроводности)
АхС(х, у, т) = -4 G(x, у, т). E.6)
Если теперь воспользоваться ортогональностью собственных функций
и хорошо известным представлением Г-функции, то можно без труда
выразить (^функцию через введенную "тепловую функцию":
Г (S)= _L fdj rs~lfdx G{x, x, т). E.7)
A Г (s ) о
Это и есть нужное нам аналитическое представление функции ? . (s).
Заметим, что
G(x, у, т = О)-б(*-у) E.8)
в силу ортонормированности собственных функций. Таким образом,
один из возможных способов вычисления detA состоит в следующем:
1) найти решение уравнения E.6), подчиненное начальному условию
E.8); 2) подставить найденное решение в E.7), вычислить lA(s) л,
пользуясь формулой E.4), найти det4.
Рассмотренную процедуру можно обобщить на случай нашей за-
задачи. Теперь оператор имеет вид [ - <Э2 + т2 + (A/2)q>j2(x)], где
Ф0(х) — решение классических уравнений с источнико,м /. Легко убе-
убедиться, что решение уравнения
~дх G0(x, у, т) —1 (ЬЛ)
О Т
с граничным условием E.8) имеет (только в четырех измерениях!)
Это еще не решает нашей задачи. В частности, получающаяся вы-
вычислением по формуле E.7) функция ?з гE) не существует. Мы хотим
найти функцию G(x, J,. т), удовлетворяющую условию E.8) и уравнению
от

104 Глава 3
Ясно , что при произвольной функции фо(х) это уравнение очень
трудно решить. Тем не менее посмотрим, что здесь можно сделать.
Написав эффективное действие в виде
к ..., E.12)
нетрудно заметить, что
если заменить <pQ на q> , что не вносит никакой ошибки с точностью
О(Н), и воспользоваться формулами E.4) и D.11).
С другой стороны, можно положить
? ^кп^Фкл(х) + ...]. E.14)
Следовательно, если мы хотим вычислить вклад порядка ОGг) в F(q> )f
то достаточно рассмотреть постоянную полевую конфигурацию. Поло-
Положим, например,
где v - константа, не зависящая от х. Тогда
г?[фкл] = /^ т» E.16)
и действие пропорционально бесконечному объему fd4x, так как евкли-
евклидово пространство R неограниченно. Но если допустить, что мы на-
находимся на поверхности S4 сферы в ряти измерениях, то мы получим
конечный элемент объема ^поверхность сферы). Подобный прием по-
позволяет избежать указанной инфракрасной расходимости. Позднее
можно устремить радиус сферы к бесконечности.
Из предыдущего следует, что вклад порядка О(Й) в потенциал дает-
дается выражением
T»J^ = -i-r A 2 @) E.17)
2 [-д +mz + — v \
2
Уравнение E.11) при постоянном v можно очень легко проинтегри-
проинтегрировать. Имеем

Фейнмановский интеграл по траекториям в теории поля 105
где для того, чтобы показатель степени был безразмерным, величина
т поделена на произвольную величину у 2 с размерностью массы в
квадрате. Затем, пользуясь формулой E.7), полунаем
_(т2+—«*'
1 °° ' -е 2 = E.19)
ГИ о
= -— ( 2 J~s JJi^iL fd% E.20)
1бтг2 Ц2 ' r(s) J
изменив попутно масштаб величины т (строго говоря, интегрирование
по т возможно только при s - 2 > 0, но путем аналитического продол-
продолжения мы определяем ?(s) всюду). Обратим внимание на появление
объемного множителя :Jd4x, который сокращается с соответствующим
множителем в формуле EЛ7) Сравнение формул приводит к результату
п
ds (s-2)(s-\) Mz
E.21)
2^2
64тг:
±
Выяснив функциональный вид f, мы можем утверждать, что эффектив-
эффективный потенциал в теории дается выражением
2 _A_ 2
+ JL {m2+ ^Ф2КПJ[- - + In \ 1 + O(H2).
64it2 2 Kn 2 u E23)
Полученный результат выглядит довольно странно, так как ка-
кажется зависящим от введенного совершенно произвольно неизвестно-
неизвестного масштаба ц2. Означает ли это, что полученный потенциал произ-
произволен? Заметим, что V зависит от параметров т2 и Д. Они по сущест-

106 Глава 3
ву еще не были определены, если не считать того, что они входили
как начальные параметры в классический лагранжиан. Для простоты
возьмем сначала т2 = 0. Тогда легко убедиться, что автоматически
d2v
- 0 при ф = 0. E.24)
Определим квадрат массы как коэффициент перед <р2 в лагранжиа-
лагранжиане ?, вычисленный при <р = 0; оказывается, что если его классическое
значение равно нулю, то это же верно и здесь с точностью O(h). А как
обстоит дело с Л? Определим этот параметр как коэффициент, равный
четвертой производной V, вычисленной в какой-то постоянной точке
Ф = М:
Л = J-!L при Ф = М. E.25)
d4
Отметим, что здесь нельзя, как в предыдущем случае, положить
Ф = 0 из-за расходимости, содержащейся в логарифме (инфракрасная
расходимость). Это типично для теорий, в которых классическое значе-
значение т2 = 0.
Из условия E.25) вытекает, что
In 1!^. = _ _§_ E.?6)
2ц2 3 '
в чем можно убедиться, продифференцировав E.23), положив т2 = 0
и использовав E.25). Следовательно, можно исключить комбинацию
2ц2А, заменив ее величиной М2, и записать результат в виде
25 ] E 27>
] E2?)
в согласии с тем, что получили С. Коулмен и Ю. Вайнберг [ 1]. Это не-
небольшое упражнение показывает, что когда имеешь дело с квантовыми
поправками, нужно внимательно определять входные параметры лаг-
лагранжиана. Выражение E.27) все еще представляется зависящим от од-
одного произвольного масштаба М2, но на самом деле это не так,посколь-
так,поскольку, меняя при заданном условии нормировки масштаб от М 2 до М'2, мы
должны одновременно заменить X на \', где

Фейнмановский интеграл по траекториям в теории поля 107
A'-X + i^l in*L' E.28)
1бтт2 М '
[с учетом E.25)]. Мы видим, что потенциал
F(q> ) = А1ф^+ * ^ [in!^L - Ц-] + О(\3) E.29)
«W 4! Фкп 25бтт2 М'2 6
оказывается форм-инвариантным по отношению к такой репараметриза-
ции:
V{\', M') = V(\, M). E.30)
Это свидетельствует о том, что меняется не физика, а только наш спо-
способ интерпретации констант.
Задачи
А. Допустим, что классический потенциал имеет вид Ркл= 1/6/ф3,
где / - константа с размерностью массы. Методом перевала найдите
первую квантовую поправку к этому потенциалу. Выясните физический
смысл полученного потенциала.
Б* Решите ту же задачу при VKn = 1/6/ф3 + -^- <р4. Найдите физи-
физический смысл. 4
**В. Найдите решение уравнения теплопроводности (д2 —m2)G(x, у, т) =
= <?G/<9t, GCc, у, 0) = 5(лГ- у) в d измерениях. На основании получен-
полученного результата вычислите эффективный потенциал в теории, определя-
определяемой действием
6[ацфдмф+тУ + -Ьр3]
в шести измерениях. В частности, найдите то изменение масштаба \,
которое необходимо, чтобы обеспечить инвариантность результата по
отношению к масштабным преобразованиям. Интерпретируйте знак до-
добавки к \ и нарисуйте график изменения \ с изменением масштаба.
§ 6. Изменение масштаба детерминанте!.
Константа смзи, зависящая от масштаба
Метод вычисления детерминанта операторов с помощью ? -функции
позволяет особенно просто вывести масштабные свойства этих де-
детерминантов. При изменении масштаба мы имеем
A-+A' = eadA, F.1)

108 Глава 3
где d - (естественная) размерность величины А.. Из определения
5 -функции следует, что
lA'c(s) = e-sadlA(s), F.2)
откуда iel(eadA)=ead^AW iet(A), F.3)
Приведем пример применения этой формулы. При дилатации
*n-V'eV Фкп-Фк'л='"Чл (б-4)
классическое действие с т2 = О
не изменяется. Но интеграл по траекториям для этого действия не
является масштабно-инвариантным. Действительно, в приближении
метода перевала мы находим, что изменение эффективного действия
с точностью 0{Н) равно
,-2 + 1ф2л] @). F.6)
Можно вычислить ?-функцию для оператора —~д2 + (Л/2)ф2 t предпо-
предполагая, что G(xy у, т) имеет асимптотическое разложение (полагаем
2
F.7)
16тг т' п = 0
где мы ввели искусственный множитель, обеспечивающий сходимость
с е> 0. Читатель, не довольный такой процедурой, может с самого на-
начала вообразить, что т2 Ф 0. В силу граничного условия E.8) имеем
ао(х,. х) = 1. F.8)
Далее, дифференциальное уравнение E.11), примененное к выражению
F.7), приводит к рекуррентным соотношениям для коэффициентов
а„& у):
&-у11^ао(*>У) = Ъ, F.9)

Фейнмановский интеграл по траекториям в теории поля 109
п = 0, 1,... . F.10)
Можно решить эти ,уравнения:
_ _ л 2 ,-, , v _ ALm4 Eс) - — Р<? (х) +
В результате получаем для ?-функции, вычисленной при s = 0, выра-
выражение
1 il fd«x + l2x
Цтг
Е@)ш _L2[^- Jd* + ±j- fd%Zn(x) + fd**^-rtnCx) F.12)
с учетом определений E.7), F.7) и (б.П). Член с Ъ1 в выражении для
а 2{х, х) выпал при интегрировании. Полагая в равным нулю, приходим
к окончательному результату
5-этф =5эфф_^а__А^ fd*x Ф4(х). F.13)
Е Е 8 • 16-гг2
Таким образом, единственным следствием дилатации (в данном порядке
по Ъ) является изменение константы связи \:
Ь. ,Л.' = A. --fia-bl— 3А1
4! 4! 4! 8-1бтт2
т.е.
Из этой очень важной формулы явствует, что константа связи, в клас-
классической теории безразмернмй параметр, приобретает в результате
квантовых эффектов зависимость от масштаба. В данном конкретном
случае из этой формулы следует, что при больших масштабах констан-
константа связи уменьшается, и это означает, что теория без взаимодействия
в определенном смысле является хорошим приближением для асимпто -
тических состояний. При уменьшении масштаба константа связи начи-
начинает расти и, даже если мы начали с некоторого малого значения Л
при некотором масштабе, дальше Л может настолько вырасти, что это
обесценит те результаты, которые получены методом теории возмуще-
возмущений по X. Отметим, что этот масштабный закон полностью совпадает
с тем, который получен в предыдущем параграфе (напомним, что

ПО Глава 3
а = -luAf'/М). Этот результат точен в порядке О(Ъ). Принято вводить
Р-функцию
которая в данном случае оказывается положительной.
Итак, мы разными путями убедились в том, что в квантовых тео-
теориях поля следует определять константы связи в некотором масштабе,
поскольку, даже если в классическом пределе константы не зависят
от масштаба, они приобретают квантовые масштабные зависимости.
Задачи
**А. При т2 Ф 0 .классическое действие с потенциалом
Т7кл= 1/2 т2^2 + (Л/4!)ф*л уже более не инвариантно относительно
дилатаций. Найдите изменение эффективного действия, возникающее
в результате дилатаций. В частности, найдите как в классическом при-
приближении, так и с учетом квантовых поправок [с точностью Оф.) ] из-
изменение величины т2.
**Б. Исходя из нового асимптотического разложения для функции
G(x, у, т)
отвечающего оператору - д 2 + (Л/2)ф2(эс), выведите рекуррентное соот-
соотношение для коэффициентов Ьп , а также выражения для коэффициентов
Ьп(х, х)прип = 0,1, 2, 3.
ЛИТЕРАТУРА
1. Coleman S.,Weinberg E., Phys. Rev., D7, 1888 A973).

Глава 4
Вычисление фейнмановского интеграла
по траекториям методом теории
возмущений: теория (р4
§ 1. Фейнмановские правила для теории Л?4
Перейдем к обычному вычислению по теории возмущений функций
Грина в евклидовом пространстве. Исходить будем из выражения
(U)
где /V - произвольная (бесконечная) нормировочная постоянная. Связ-
Связные функции Грина определяются как
Мы будем вычислять их, рассматривая потенциал V как малое воз-
возмущение. Для простоты ниже мы будем обходиться без индекса Е и без
черты над х, указывающих на евклидово пространство. Позднее же в тех
случаях, когда будет возможна путаница с пространством Минковского,
эти символы будут восстановлены. Пользуясь приемом, изложенным в
гл. 3, § 3, находим
A.3)
где
" = - ^- < J(x)bF(x-y)J(y)>xy, A.4)
Jp(x -у)

112 Глава 4
После небольших алгебраических преобразований получаем выражение
S _
которое уже допускает разложение в ряд теории возмущений по потен-
потенциалу V. Если положить
A.7)
то
Z[/] = -ln/V + Z°[/.]-5[/]+I_52[/]--l-63[/] + ... . 0.8)
В частности, если V ¦ (Ai/4!-jq>4, то можно провести разложение по сте-
степеням безразмерной (в четырех измерениях) константы связи Л.
'Записывая
S-S^ + SjA2 + ... » A.9)
находим, что Z[/]=-In/V + Z° [/]-А5Д/] _л2 E2[/]_-1_ 52 [/])-
-^<8t/]5[/j6[/JS? []).... A.10)
Разлагая экспоненту в формуле A.7), получаем
2
A.12)
Подставляя выражение A А) для Z0, приходим к выражению
5[/] l<bbbbJhhl
+ 3<А2ХЖ>], (U3)
в котором под знаком < . . . > нроизводится интегрирование по соот-
соответствующим переменным ж, о, Ь, с, d. Аналогично, но несколько
более искусственным образом можно вычислить 52. Заметим, что если

Вычисление ФИТ методом теории возмущений: теория <р* 113
вставить оф I -Z°}exp i Z0} в середину формулы A.12), то
ь*{п~~ -W"/0< tf~ >1 e~z°5i[}] ¦ AЛ4)
Затем, с учетом разложения
R2 r -Z
о ое
Сравнение с разложением A.10) для Z[/ ] показывает, что "несвязная"
часть 1/25* выпадает. Под несвязной частью мы понимаем вклад в вы-
выражение, который может быть записан как произведение двух или более
функционалов от / . Этот термин станет очевидным в диаграммном пред-
представлении. То, что Z порождает только связные куски, верно во всех
порядках (см. задачу). Например, вклад порядка Л3 в разложении A.10)
связный; действительно, напишем
5 __ <¦ Pz° V V V o-"z°> * w -~Z°T, 70\(ez°V -Z°
3 tt ^ e xyyy ze xyz~ ~ ~yT< (e Vxe Уе
-|т-5? [/] + Sj/]5c2[/]+6c3[/]. A.18)

114 Глава 4
В последнем выражении через 5С2 и 5С3 обозначены связные куски.
Чтобы получить это выражение, мы использовали то обстоятельство,
что имеются только два типа "несвязности": либо все три переменные
х, у, -г несвязны, либо одна переменная несвязна с двумя другими, при-
причем последний вариант можно получить тремя способами. Скобки в вы-
выражении A.17) служат для того, чтобы защитить другие члены от дей-
действия операторов производной внутри скобок. С учетом формулы A.18)
член, возникающий в разложении Z, можно переписать в виде
S 5Л+ 45' 8 5? 5C(C 4
+ j-5? = B<. A.19)
Наконец, явное вычисление связной части 5 приводит с точностью
до независящей от / части к выражению
5С2Ш= — </вДвжA-д|у + 1Г&хх&у
2
O.20)
С помощью формулы A.2) находим выражения для связных функций
Грина:
, -х2) - -L_ fd4уД (*, - у )д(у _у)д(у -

Вычисление ФИТ методом теории возмущений: теория <р* 115
A2
-*)Д(* -х)Ь(х -у)Д(у -у)Д(у -х2) +
+ 0(А3), A.21)
G (*,, х2, х3, хА) ш - A [d хй(х^ -яг)Д(я;2 -ж)Д(зс3 -х)Д(«4- х) +
, А2 ..,
-*)Д(*2 -з»)Д(*4 -у) + Д(ж, -
-,2
х Д(у -у)Д(ж -у)[Д(ж, -дг)Д(ж2 -ж)Д(*з -*)Д(*4 ~
-у) + циклическая перестановка ] + 0(А3), A.22)
п -у) + О(А3Ь A.23)
причем сумма в последнем выражении берется по тройкам чисел (ijk) =
= A23), A24), A25), A26), A34), A35), A36), A45), A46), A56), а трои-
ка чисел (Imn) принимает дополнительные к ним значения, т.е. (Imn) =
= D56), если (ijk) = A23) и т.д. В данном порядке-по А вклад в остальные
функции Грина отсутствует. Заметим, что вклады порядка А0 в G|2', по-
порядка А в G*2», порядка А в G(*> и порядка А2 в G <«> уже были получены
ранее в классическом приближении, рассматривавшемся в предыдущей
главе.
Прямым вычислением, пользуясь формулой D.36) гл. 3, можно
найти функции Грина в р-пространстве. Имеем
р) = -J _ Л_ г г *Ач 1
р2 + т2 2 (р2 + ^2J J BitL

116 Глава 4
BтО4
А
3
m2)(Q2 + т2) + Т"
+ m2J J BttL 92 + m2 p2 +
1
X
X
+О(Л3), A.24)
А 1
f
j., p2 + m2 2 J BttL B^L X
4 П 5w4 2T 2 5(gi+g2-Pi -p )BтгL+О(Л3)Ы.25)
В последнем выражении сумма берется только по (j/) = A2), A3) и A4).
Наконец, G161 дается выражением D.29) гл. 3. Полученные выражения
очень громоздки, но существуют так называемые феинмановские правила,
позволяющие довольно просто записывать их. Эти правила таковы.
1. Каждому множителю 1 /(р2 + т2) сопоставляется линия с текущим
по ней импульсом р:

Вычисление ФИТ методом теории возмущений: теория <р* Ш
2. Каждому множителю - А/4! сопосгазляегоя четырехточечная вер-
вершина, причем подразумевается, что полный импульс, втекающий в вер-
вершину, равен нулю:
" Р2 + Р3 + Р4 =
3. Чтобы получить вклад в &N) (р P/v)> нужно, обозначив
внешние хвосты диаграммы, нарисовать все возможные топологически
неэквивалентные перестановки. Число способов, которым может быть
нарисована данная диаграмма, называется ее топологическим весом.
4. После того как обеспечено сохранение импульса в каждой верши-
вершине, берется интеграл по импульсам внутренних петель fd*q/Bтт*).
В результате мы придем к желаемой функции Грина. Пожалуй, бо-
более последовательно было бы сопоставлять каждой вершине множитель
(- Л/4!MBр)BтгL, где Zp представляет собой полный импульс, входя-
входящий в данную вершину. Тог^ца интегрировать нужно по всем внутренним
импульсам. При таком способе возникает общий множитель BтгL5Bр),
где Zp - полный импульс, входящий в функцию Грина. Например, на
диаграммном языке выражение A.24) запишется в виде
A.26)
По сформулированным правилам нетрудно написать аналитические вы-
выражения, соответствующие этим диаграммам.
/ г
1. Нам нужна одна вершина и три пропагатора. Можно четырьмя спо-
способами прицепить первый хвост вершины к точке 1 и тремя - второй
хвост к точке 2. Следовательно, вес равен A /4!L - .3 = 1/2.Сама вершина
вносит вклад - Л. После этого правила приводят к выражению
Bтг)<

П8Глава 4
2. У нас две вершины. Можно четырьмя способами прицепить первый
хвост первой вершины к точке 1, четырьмя способами прицепить первый
хвост второй вершины в точке 2, тремя способами связать второй
хвост первой вершины со второй вершиной и двумя способами связать
третий хвост первой вершины со второй. Следовательно, вес равен
A/4!) • A/4!) 4 . .4 • .3 . .2 = 1/6. Мы не учитывали, что у нас с самого
начала две вершины. Дело в том, что диаграммы остаются теми же самы-
самыми независимо от того, с какой вершины начать. Вклад диаграммы про-
пропорционален (- \)г = \2. Если обозначить импульсы внутренних линий
через q^t q2 и q3, то, согласно фейнмановским правилам, вклад диа-
диаграммы равен
3. В нашем распоряжении две вершины. Можно четырьмя способами
прицепить первый хвост к точке 1, тремя —второй хвост к точке 2, че-
четырьмя - третий хвост уже связанной вершины к другой и тремя же - чет-
четвертый хвост первой вершины ко второй вершине. Следовательно, вес
равен A/4!) .A/4) 4.3..4..3 = Т/4. Вклад диаграммы пропорционален
4. У нас две вершины. Можно четырьмя способами прицепить первую
вершину к точке 1 и четырьмя - вторую вершину к точке 2. В результате
у каждой вершины остается по три свободных хвоста для того, чтобы
связаться друг с другом. Каждая вершина может тремя способами
замкнуться в петлю. Следовательно, вес равен A/4!) . A/4!) 4 х
х 4 . 3 • 3 = 1/4. Вклад диаграммы пропорционален (— ЛJ.

Вычисление ФИТ методом теории возмущений: теория <р* И9
Таким образом, фейнмановские правила сводят все к задаче,
которую решает ребенок, собирающий игрушку из элементов кон-
конструктора. Основные элементы - пропагатор (линия) и вершина. Не-
Немного наловчившись, можно научиться читать сопоставляемые им мно-
множители прямо в лагранжиане. По тем же правилам в соответствии с анали-
аналитическим выражением A.25) получим для четырехточечной функции
следующее диаграммное представление:
A.27)
Предоставляем читателю проверить правильность численных множителей
в формуле A.25). ^
Заметим теперь, что в выражении для G('v>(p,,-.., Pv ) имеетоя
мультипликативный множитель П (р? + т2)~, соответствующий пропага-
(=1
торам внешних хвостов.
Значительно удобнее иметь дело с функциями Грина, порождаемыми
эффективным действием. Связь этих функций Грина с G(n| очень проста:
в то время как функции G(n> связнн, функции [7 <п| одночастично-непри-
водимы. В частности, функция Г t2)(p) р&ена обратному пропагатору,
взятому со знаком минус. Мы уже столкнулись с этим результатом в связи
с древесными диаграммами, но он верен во всех порядках теории возму-
возмущений. Таким образом, г D) содержит только диаграммы
причем внешним хвостам^е соответствуют пропагаторы. Чтобы пока-
показать, что функции Грина г<п) одночастично-неприводимы, можно исхо-
исходить из определяющих уравнений
5ГЫ 6ZU1 ...
-^ =' -57 =ф (U9)
и дифференцировать их.

120 Глава 4
После всего сказанного вернемся к лагранжиану, в котором можно
легко идентифицировать все компоненты фейнмановских правил: четьрех-
точечную вершину, возникающую из члена Аф4, и пропагатор, возникающий
из кинетического и массового членов. Отсюда следует, что после неболь-
небольшой .практики можно просто считывать фейнмановские правила с лагран-
лагранжиана ?. Основная трудность в том, чтобы получить при этом правиль-
правильные знаки и весовые множители перед диаграммами.
Задачи
A. Нарисуйте вклады порядка Л4 в двухточечную функцию GB).
Е. Нарисуйте вклады порядка Л3 в СD).
B. Напишите аналитические выражения для диаграмм задачи А с
учетом весов.
¦ *Г. Выведите фейнмановские правила в случае V = (Л/4!)ф4 +
+ (ц/3!)фз.
**Д. Покажите, что Z[/ ] порождает только связные фейнмановские
диаграммы.
**Е. Найдите вид эффективного действия 5э**[фкп] в порядке Л2
и покажите, что в порождаемых им функциях Грина не возникают одно-
частично-приводимые диаграммы.
§ 2. Расходимости фейнмановских диаграмм
Красота фейнмановских правил несколько блекнет, когда мы осозна-
осознаем, что большинство интегралов по петлям расходится ! Например, вклад
порядка О(Л) в G™ содержит интеграл
Л 1
BтгL д^Тщ^'
Очевидно, что он расходится при q -»°°, так как подынтегральному
выражению не хватает сил побороть меру интегрирования. Подобная рас-
расходимость называется ультрафиолетовой. Она возникает при больших
импульсах или, что эквивалентно, на малых расстояниях [в «-простран-
«-пространстве расходимость возникает от Д@)] и, очевидно, связана с тем, что
приходится вычислять слишком много производных по / в одной точке.
Другой пример - диаграмма под названием "рыба":

Вычисление ФИТ методом теории возмущений: теория <р*
BттL 2 "j"
В этом случае при q -» » интеграл ведет себя как интеграл от d*q/q*,
т. е. как логарифм Inq. Он тоже расходится! Попутно заметим, что
когда т2 = 0 и (pt + р2J = 0, этот интеграл расходится и при малых ?.
Подобная расходимость называется инфракрасной. Обычно такие расходи-
расходимости возникают только в безмассовом случае и при некоторых специаль-
специальных значениях внешних импульсов (в данном случае pt + р - 0, посколь-
поскольку мы находимся в евклидовом пространстве). Положим на некоторое вре-
время w2 4 0 и сосредоточим внимание на ультрафиолетовой расходимости.
То, что столь заботливо сконструированные функции Грина рас-
расходятся, выглядит как полное крушение нашей программы. Но не будем
предаваться отчаянию, а попробуем узнать несколько больше об этих
расходимостях. Мы вскоре обнаружим, что они возникают легко просле-
прослеживаемым образом и исчезают при подходящем переопределении полей
и констант связи! Таково чудо перенормировки, которое, как мы уви-
увидим, возникает только в определенных теориях.
Покажем, как путем топологических рассуждений и подсчета сте-
степеней узнать, имеется ли расходимость. Рассмотрим фейнмановскую
диаграмму с V вершинами, Е внешними линиями и / внутренними линия-
линиями. Сначала будем считать, что имеются только скалярные частицы.
Число независимых внутренних импульсов равно числу петель L в
диаграмме. Для / внутренних импульсов выполняется V -1 соотношений
(единицу нужно вычесть, чтобы учесть облюй закон сохранения импульса),
так что
L = / -V + 1. B.1)
Это соотношение позволяет наивно подсчитать степени импульса для
диаграммы. Такой подсчет даст кажущуюся степень расходимости диа-
диаграммы, обозначаемую через D" . Чтобы вычислить D, заметим, что у
нас имеются L независимых интегрирований по петлям, причем в d
измерениях каждое вносит d степеней импульса, и / внутренних импуль-
импульсов, каждый из которых соответствует пропагатору, вносящему две
обратные степени импульса. Следовательно,
DmdL-21. B.2)
'В отечественной литературе величина D назувается индексом диаграм-
диаграммы,- Прим.пврев.

122 Глава 4
Нам нужно еще одно соотношение между V, Е и /. Пусть VN обозна-
чает число вершин с /V хвостами. В диаграмме с VN такими вершинами
имеется NV^ линий, являющихся либо внешними, либо внутренними.
Каждая внутренняя линия учитывается дважды, поскольку она начина-
начинается и заканчивается в вершине, так что
MN =, Е + 2/. B.3)
Соотношения B.2) и B.3) позволяют выразить D через число внешних
линий и вершин:
D = d-l-(d-2)E + VN(N~2 d-N). B.4)
В четырех измерениях имеем
D = 4 - Е + (N -4)VN (четыре измерения). B.5)
Далее, в рассматриваемой нами сейчас теории /V = 4. Следовательно,
D = 4 —Е (для теории Лф4 в четырех измерениях) B.6)
Полученный здесь важный результат заключается в том, что кажущая-
кажущаяся степень расходимости зависит не от числа вершин, а только от числа
внешних, хвостов! Таким образом, имеются лишь два возможных ва-
варианта с D > 0:
GB) с кажущейся квадратичной расходимостью d = 2,
G*4) с кажущейся логарифмической расходимостью D = 0. =0.
Заметим, что указанные двух- и четырехточечные взаимодействия уже
присутствуют в лагранжиане и это обстоятельство окажется решающим
для перенормировки. Кроме того, D = 0 не обязательно означает логариф-
логарифмическую расходимость: фундаментальная вершина имеет D = 0.
Проведенный анализ не доказывает, что функции б"'61, (Г18», . . . ,
для которых величина D отрицательна,сходятся.Поэтому D и называется
кажущейся степенью расходимости. Рассмотрим "п-частично-приводимую"
диаграмму с Е внешними линиями; это такая диаграмма, которую можно
разделить на части, разрезав не менее п внутренних линий. В общем
случае если D^ и D2 - кажущиеся степени расходимости двух блоков,
показанных ниже, то для всей л-частично-приводимой диаграммы
D-D,+Оа+4(|»-1)-2|1, . B.7)

Вычисление ФИТ методом теории возмущений: теория <р*
123
поскольку два блока связаны т» пропагаторами и п -1 петлями:
N
п-
Заметим, что по определению блоки I и II сами по меньшей мере
частично-приводимы.
В нашем случае, когда п = 1, мы можем иметь D, = D2 = о и при
этом получим D = -2, что соответствует на первый взгляд сходящей-
сходящейся диаграмме. Примером этой ситуации может служить диаграмма
'динозавр" ^^,—^^Г , которая очевидным образом расходится
из-за двух расходящихся интегрирований по петлям. Другой пример
одночастично приводимой диаграммы таков:
О 1
В этом случае Dу = 2, D2 = - 2; кажется, что диаграмма сходится, но
это не так из-за "бородавки" на одном из хвостов. Последний пример
показывает также, что четырехточечная функция может расходиться
сильнее, чем кажется при наивном подсчете: доказательством служит
квадратично-расходящаяся четырехточечная функция _L2_
Отметим, что, рассматривая Г <"', мы избегаем таких одночастично-
приводимых диаграмм. При п = 2 мы имеем D = Df + D2 и вполне может
быть так, что степень Dt (или D2) отрицательна и достаточно велика,
чтобы перекрыть D2 (или D,) и привести к отрицательной степени D.
Примером служит диаграмма "омар"
при п - 3 могут быть диаграммы типа
(в этой сложной диаграмме из каждой вершины выходит не более
одной внешней линии). В теории ЛИ могут существовать не более чем
трехчастично-приводимые диаграммы, так как каждую вершину, связанную
Аналогично

124 Глава 4
с одной внешней линией, можно отделить от диаграммы, разрезав ос-
оставшиеся три хвоста.
Теперь ясно, как вылавливать диаграммы, которые, имея отрица-
отрицательную степень D, все же расходятся. Возьмите любую фейнмановс-
кую диаграмму и классифицируйте ее по степени приводимости; в нашем
случае всякая диаграмма 1-, 2- или 3-частично-приводима. Если она
трехчастично-приводима, то разложите ее на составные части и поищите
возможность разбиения вида Щг—И^^': N±5 t Тогда в этом
типе диаграмм имеется примитивно расходящаяся четырехточечная
функция, а второй блок должен быть сам по себе разложен таким
же образом.
Аналогично, скрытые расходимости в двухчастично-приводимых
диаграммах будут возникать в диаграммах вида Щ Щ^1
Щ j N>z с повторением такого разбиения во втором
блоке. Наконец, одночастично-приводимые диаграммы, которые мож-
можно представить в виде
' n>5 ; =S ШХ1 N>3 , будут иметь СКРЫ-
СКРЫЛА ^^ —N
тые расходимости. Такое же разложение можно провести для вторых
блоков, до тех пор пока не будут выявлены все подобные структуры.
Это исчерпывающее перечисление показывает, что истинно сходя-
сходящиеся диаграммы не содержат скрытых двух- и четырехточечных функ-
функций.
Можно и еще проще объяснить происхождение скрытых ультрафио-
ультрафиолетовых расходимостей в любой диаграмме. Рассмотрим любую петлю,
помещающуюся внутри диаграммы. Интегрирование по импульсу в пет-
петле в четырех измерениях приведет к ультрафиолетовой расходимости,
если эта петля образована не более чем одним или двумя пропагатора-
ми (внутренними линиями). Большее число приведет к ультрафиолетовой
сходимости. Петля, образованная одним пропагатором, содержит толь-
только одну вершину О ; при этом остаются два свободных хвоста,

Вычисление ФИТ методом теории возмущений: теория у4 125
которые в свою очередь могут быть присоединены к остальной части
диаграммы (или один хвост может быть внешним, а другой - присоеди-
присоединенным). В этом случае можно изолировать такую двухточечную функ-
функцию от внутренней части диаграммы.Петля, ограниченная двумя пропа-
гаторами, содержит две вершины и, следовательно, четыре свободных
хвоста Y^ jl , которые можно присоединить к оставшейся части
диаграммы, либо какие-то из этих хвостов, числом до трех, могут яв-
являться внешними линиями. Во всех этих случаях мы должны изолировать
от остальной части диаграммы четырехточечную функцию или двухто-
двухточечную функцию, если два из четырех хвостов соединены вместе (в
этом случае расходимость становится квадратичной). Тогда можно уви-
увидеть, что ультрафиолетовые расходимости внутри диаграммы обуслов-
обусловлены такими петлями и что такие петли возникают в двух- и четырех-
четырехточечных функциях, гнездящихся внутри диаграммы.
Итак, в теории Лср4 в четырех измерениях фейнмановская диаграм-
диаграмма является действительно сходящейся, если ее кажущаяся степень рас-
расходимости D положительна и если диаграмма не может быть расщепле-
расщеплена на трех-, двух- или одночастично- приводимые части описанного вы-
выше типа, которые могут содержать изолированные двух- и четырехто-
четырехточечные блоки. Более изящно выглядит такая формулировка: фейнманов-
фейнмановская диаграмма сходится, если кажущаяся степень расходимости самой
диаграммы и всех ее поддиаграмм положительна. Это так называемая
теорема Вайнберга, которая верна независимо от типа теории поля.
Все сказанное означает, что причиной расходимостей являются
только двух- и четырехточечные функции и ничто более. В них все зло!
Так что если мы можем контролировать их в функциях GB) и G<4), то
у нас есть возможность контролировать расходимости всех других
функций GiN).
Диаграммы, содержащие указанные основные расходимости, назы-
называются примитивно расходящимися. То обстоятельство, что в теории
Лф4 число примитивно расходящихся взаимодействий конечно (двух-
и четырехточечные взаимодействия), а сами эти взаимодействия того
же типа, что и содержащиеся в лагранжиане, является необходимым
условием успешного устранения ультрафиолетовых расходимостей
путем ловких переопределений. Теория, в которой подобное возможно,
называется перенормируемой. Из формулы B.4) можно увидеть, что
этим требованиям удовлетворяют очень немногие теории взаимодей-
взаимодействующих скаляров (см. задачу).

126 Глава 4
При d = 4 степень D растет с ростом числа вершин, для которых
К > 4. Следовательно, теории <р6, q>6, . . ., хотя и совершенно приемле-
приемлемы с классической точки зрения, приводят к бесконечному числу при-
примитивно расходящихся диаграмм (чем больше вершин, тем сильнее
расходимость!). В этом случае ситуация быстро выходит из-под контро-
контроля и надежда навесить ярлыки на все расходимости, а следовательно,
и перенормируемость, исчезает.
Когда d=2 (одно пространственное и одно временное измерения),
положение меняется на обратное. В данном случае
d = 2~2VN <2 измерения) B.8)
и степень D оказывается независящей от числа /V, отмечающего тип
взаимодействия! Величина D зависит только от числа вершин, причем
чем больше вершин, тем более сходящейся оказывается фейнмановская
диаграмма! Кроме того, D не зависит от числа внешних'хвостов! Таким
образом, единственные примитивно расходящиеся диаграммы либо
имеют одну вершину, либо не имеют ни одной. Так как расходимости воз-
возникают из-за интегрирований по петлям, это означает, что расходимости
появляются только в том случае, когда хвост некой вершины связан
с той же самой вершиной, а не в случае взаимодействия двух или более
вершин. Подобные расходимости называются расходимостями "нормаль-
"нормального упорядочения", В двух измерениях ультрафиолетовые расходимос-
расходимости происходят только от "нормального упорядочения", а не от типа
взаимодействия.
Заметим, наконец, что при d > 7 не существует теорий с конечным
числом примитивно расходящихся диаграмм. Последняя из возможных
теорий в высших измерениях это теория Л<р3 в шести измерениях, при-
причем здесь величина Л безразмерна, так как размерность величины q>
теперь уже равна - 2. Число примитивно расходящихся диаграмм неве-
невелико, поскольку V не входит в выражение для D:
D = 6 - 2? '(ф3 в 6 измерениях), B.9)
так что примитивно расходятся одно-, двух- и трехчастичные функции
(как четвертая степень, квадратично и логарифмически). Хотя потен-
потенциал в этой теории неудовлетворителен, так как он неограничен снизу,
сама теория интересна, поскольку она наряду с более сложными калиб-
калибровочными теориями обладает свойством асимптотической свободы.
Итак, в данном параграфе мы обнаружили в фейнмановских диаграм-
диаграммах с петлями ультрафиолетовые расходимости (плохие новости), но

Вычисление ФИТ методом теории возмущений: теория <р* Ш
убедились, что по крайней мере в нашей теории эти расходимости
проистекают только от двух примитивно расходящихся функций Грина
(хорошие новости). Следовательно, если нам удается предотвратить
появление расходимостей в G<2> и G™, то у нас будет надежда предот-
предотвратить катастрофу и получить сходящиеся ответы.
Задачи
А. Найдите все примитивно расходящиеся диаграммы в теории
Ф3 в четырех измерениях. Для каждой такой диаграммы приведите
пример в низшем порядке теории возмущений.
Б. Перечислите все теории взаимодействующих скаляров с конеч-
конечным числом примитивно расходящихся диаграмм в трех измерениях
(d = 3).
В.Повторите задачу Б при П = 5 и покажите, что при d > 7 не су-
существует теорий с конечным чиолом примитивно расходящихся диа-
диаграмм.
Г. Для случаев d = 2, 3, 5, 6 найдите размерности различных кон-
констант связи в теориях с конечным числом примитивно расходящихся
диаграмм.
§ 3. Размерная регуляризация фейнмановских
интегралов
Ниже мы продолжим вычисление фейнмановских диаграмм.
Вычисление ультрафиолетово-сходящихс диаграмм производится не-
непосредственно, в случае же расходящихся диаграмм требуются осо-
особые меры. В этом случае мы сталкиваемся с интегралами вида
I4.{k)-f°dAlF{l,.k), C.1)
— СО
где при больших / функция F ведет себя как / ~2 или I -* . Суть метода
размерной регуляризации в том, что при понижении числа измерений,
по которым ведется интегрирование, расходимости тривиальным об-
образом исчезают. Например, если F -»I ""*, то в двух измерениях интег-
интеграл C.1) на ультрафиолетовом пределе сходится.
С математической точки зрения мы вправе ввести функцию
/(со, k) = fd2a>lF(l, к) C.2)
как функцию (комплексной) переменной и. Вычислим ее в той области,

128 Глава 4
где / не имеет сингулярностей в с*плоскости. Затем придумаем функ-
функцию / '(ш» к), совпадающую с / в области сходимости интеграла C.2)
в со-плоскости и имеющую хорошо , определенные сингулярности вне
области сходимости. Осуществляя аналитическое продолжение, мы
можем утверждать, что функции / и /' совпадают.
Прекрасным примером, демонстрирующим суть, метода аналити-
аналитического продолжения, может служить разница между эйлеровским
и вейерштрассовским определениями Г-функции. При Rez > 0 эйлеров-
ское представление имеет вид
rM-frte-V-1. C.3)
о
Этот интеграл расходится при Rez < 0, поскольку при t -» 0 он ведет
себя как dt/t1 +IRezl, т. е. стремится к бесконечности. Однако, поль-
пользуясь выражением C.3), можно отщепить причиняющую беспокойство
область интегрирования, написав
оо / 1 \п а ос
Г(г)= 2 _J=li_/&tn + I -1 +/«fre-V-1, C.4)
п =0 п! О сх
где а - совершенно произвольная величина. Второй интеграл хорошо
определен даже при Rez < 0 до тех пор, пока ос > 0. Первый интеграл
имеет простые полюса во всех точках, где z - отрицательное целое
число или нуль. Тогда
п =0
(z + п)
+fdte-*t*-\ C.5)
Это выражение справедливо всюду в г-плоскости. Более того, оно не
должно зависеть от произвольного коэффициента ос (читатель может
сам убедиться, что с/Г /da = 0). При а = 1 мы получаем вейерштрас-
совское представление Г-функции. Все же, чтобы изолировать особен-
особенности, нам пришлось ввести в процессе вычислений произвольный
масштаб, хотя конечный результат от него не зависит.
Наша проблема заключается в том, что интегралы типа C.2) по-
похожи на эйлеровский интеграл. Мы же хотим найти эквивалент вейер-
штрассовского представления. Процедура будет следующей: 1) устано-
установим конечную область сходимости интеграла по петле в огплоскости;
для расходящихся интегралов эта область обычно будет лежать слева
от прямой ш= 2; 2) построим новую функцию, которая перекрывается с
интегралом по петле в его области сходимости, но определена в более

Вычисление ФИТ методом теории возмущений: теория <рА 129
широкой области, включающей точку со =2; 3) перейдем к пределу при
м-» 2,
Покажем, как это делается в случае однопетлевых диаграмм, сле-
следуя методу 'т Хофтаи Вельтмана [1]. Возьмем в качестве примера
квадратично-расходящуюся диаграмму "головастик'. Прежде всего
расщепим область интегрирования, написав
Затем введем в пространстве размерности 2 со - 4 полярные координаты
и обозначим через L длину Bсо- 4)-мерного I-вектора. Тогда интеграл
примет вид
J2»> ) C.6)
) .
\LZ + ( z + т2)
Можно провести интегрирование по углам (приложение Б), что приводит
к выражению
/ = *"""' fi*l fdL L2 «- в ! C.7)
Г (со- 2) 0 (L2 + I2 + т2)
Оно определено не очень хорошо, поскольку при ш> 1 у него ультрафио-
ультрафиолетовая расходимость, а,кроме того, интеграл по L расходится на нижнем
пределе (в "инфракрасной" области) при всех со< 2. Следовательно,
в со-плоскости отсутствует перекрывающаяся область, в которой интеграл
/ хорошо определен. Однако инфракрасная расходимость является арте-
артефактом разбиения меры интегрирования. Заметим, что написав
L2»-¦-._! 1_ (L2)"-2, C.8)
со-2 dL2
проинтегрировав по частям по L2 и отбросив поверхностный член, мы
получим
) ()
если еще воспользуемся равенством Г (со - 1) = (со -т 2) Г (со — 2). Теперь
уже представление C.9) обладает инфракрасной расходимостью при
''Вторая диаграмма в выражении A.26). - Прим. пврев

130 Глава 4
ш<; 1 и все той же ультрафиолетовой расходимостью при со> 1, так что
перекрывающаяся область сходимости все еще отсутствует. Повторим
эту процедуру и в результате придем к выражению
Г И
которое уже хорошо определено при 0 < «< 1. Отметим, что для полу-
получения ненулевой области сходимости нам пришлось сдвинуть область
инфракрасной сходимости на две единицы. Если бы интеграл по петле
расходился логарифмически, было бы достаточно одного такого шага.
Получив для I выражение C.10), сходящееся в конечной области
(в данном случае в области 0 < со< 1), мы хотим продолжить его к
физической точке ш= 2. Это делается следующим образом. Подставим
в подынтегральное выражение хитроумную конструкцию
и проинтегрируем по частям в области сходимости. Получим
5 г (со) J с; * д1ц 1JX а2 + 12+пгу
C.12)
После небольших алгебраических преобразований, выразив правую
часть через /, придем к выражению
В нем в явной форме выделен полюс при ш= 1. Интеграл теперь расхо-
расходится на верхнем пределе при ш> 2. Поэтому мы повторяем процесс и
вновь подставляем (З.11) в C.13). Результат можно предсказать:
» I • ,й • Am IT
1
IT . j, f ,. 2 X
Именно к нему мы и стремились. Вся расходимость теперь обязана
простому полюсу при со= 2, так как интеграл теперь сходится.

Вычисление ФИТ методом теории возмущений: теория <р* Ш
Подведем итоги. Вначале мы определили конечный интеграл в
ш-плоскости, который по смыслу должен совпадать с тем, что мы обоз-
обозначили выше fd2a>lF(l, к); в нашем случае это выражение C.10), ко-
которое и является исходным для дальнейшего. Затем, если область схо-
сходимости не включает в себя точку со = 2, мы совершаем аналитическое
продолжение с помощью трюка C.11).
Было бы хорошо показать, что для сходящихся интегралов проце-
процедура, приводящая к (ЗЛО), действительно дает правильный результат.
Возьмем в качестве примера сходящийся интеграл
I(d24
Нетрудно видеть, что описанная процедура приводит к выражению
СО—2 оо j 1
/(со) = JL JdAl fdL2(L2)»-2( . _L_) I , C.15)
Г(со-1Г о dL2 ' {L2 + l2 + rr?)* K
которое прекрасным образом конечно при со» 2. Как нам и хотелось,
Таким образом, процедура действительно самосогласована.
После всей этой нудной работы обратимся к более бесцеремонной
интерпретации интегралов в 2ш измерениях, представленной в приложе-
приложении Б. Если бы мы слепо воспользовались формулами приложения Б,
то получили бы
f d2*l e гA-со) 1
¦FT^j -w T) п^т
Разложим это выражение вблизи »= 2, используя при п = О, 1, 2, ...
и е -» 0 формулу
C.17)
Ыв)т dl^is) ]t C.i8)
as

132 Глава 4
ц/Он-D- +2 -L-, ^'(l)._|L, C.19)
а у - постоянная Эйлера -Маскерони:
фA) = _у = _ 0,5772 .... C.20)
В результате имеем
Можно показать, что этот результат совпадает с тем, который получа-
получается интегрированием выражения C.14).
Далее мы будем пользоваться наивными формулами приложения
Б, не задумываясь об их обосновании, поскольку благодаря >т Хофту и
Вельтману мы знаем, что эти формулы законны.
Задачи
А.Покажите, что наивные вычисления по формулам приложения
Б и более строгая процедура, изложенная в данном параграфе, приво-
приводят для интегралов
к одним и тем же результатам.
Б. Докажите последние четыре формулы приложения В.
§ 4. Вычисление фейнмановских интегралов
Продолжим вычисление фейнмановских диаграмм низшего поряд-
порядка в теории Л<р4, пользуясь методом вычислений, изложенным в § 3,
и формулами приложения Б.
Мы видели, что метод размерной регуляризации основан на вычис-
вычислении фейнмановских интегралов в 2а измерениях, где константа свя-
связи Л уже более не безразмерна. Для удобства введем новую, безразмер-
безразмерную константу связи Лнов в соответствии с соотношением

Вычисление ФИТ методом теории возмущений: теория <р* 133
где р* — произвольная константа с размерностью массы. Иначе говоря,
мы вычисляем функции Грина в теории, определяемой действием
Фейнмановские правила для нее совершенно такие же, как и для теории
в четырех измерениях, кроме трех пунктов: 1) в скалярном произведении
векторов сумма берется по.их 2со компонентам; 2) петлевые интегралы
имеют вид fd2al/BтгJи>; 3) константа - Л в вершине заменяется кон-
константой (- Л)(ц2J ~а.
Вычислим диаграммы низшего порядка в такой теории. Начнем
с диаграммы "головастик" (такая диаграмма возникает от ненормаль-
ненормального упорядочения в члене взаимодействия). Вклад этой диаграммы
дается выражением
2DттJ
D.4)
где мы использовали формулу (Б.16) и вынесли вперед множитель т2,
поскольку размерность вклада этой диаграммы равна квадрату массы.
Разлагая в ряд вблизи со= 2, получаем
Am
4тт ц
D.5)
D.6)
Заметим, что благодаря введению произвольного масштаба \х2 мы можем
в этой формуле проследить за размерностью и что полюс в разложении
функции Г сокращается с первым членом разложения величины
Dтт|д2/те2J -», в результате чего остается конечный вклад при со-» 2.
Такое положение сохранится при вычислении всех расходящихся диаграмм.
Таким образом, мы заключаем, что расходимость в Т проявляется в
виде простого полюса, а конечная часть Т, которая в данном случае

134 Глава 4
не зависит от внешних импульсов, полностью произвольна, поскольку
на нее влияет изменение ц2.
Следующая диаграмма — "рыба"'. рг Р* р. + р = р н
р, Pi
По фейнмановским правилам
= -1-(-АJ(м2L-2".
D.7)
Так как здесь в интеграле по петле имеется более одного пропагатора,
можно для удобства ввести фейнмановскую параметризацию, осно-
основанную на формуле
1 Г (о, +o2 + ...+.oft) 1 1
D.8)
Она позволяет в удобной форме перегруппировать импульсы в петле.
В данном случае используем ее в виде
fdx
Знаменатель можно переписать в виде ' '
1'2 + п? + р2х(\-х), Г=1-р(\-х). D.10)
Так как мы имеем дело со сходящимися интегралами, можно положить
d2 Ч ' = d2wl и обозначить I' через I в интеграле по петле. В резуль-
результате имеем
D.П)

Вычисление ФИТ методом теории возмущений: теория у4 135
Благодаря указанному приему можно теперь воспользоваться форму-
формулой (Б.16) и взять интеграл, получив при этом
. ** / 2u-2co/, Г B - со) 1
2 о Dтт)« Ы2+Р2х(\-х)]2-"'
D.12)
Прежде чем производить разложение, вспомним, что размерность
диаграммы равна (ц2J ~°°; это мы и получили. После разложения
имеем
0B - „)| - D.13)
2\2 -со
)
х2
Л
т2 + p2z(l - х)
xln( —— ) + 0B-«)]. D.14)
4т^
Еще раз отметим, что конечная часть произвольным образом зависит
от р2 , хотя в данном случае она зависит и от внешних импульсов.
Подчеркнем, что такой произвол в конечной части связан с методом
вычислений, а именно с тем, что расходящееся выражение разделяется
на расходящуюся и конечную части (ведь оо + 5 = «> + 6!)-
Остается проинтегрировать по фейнмановскому параметру х. Так
как величина х{\ — х) всегда положительна [0 < х{\ - х) < 1/4] в об-
области интегрирования, аргумент логарифма всегда положителен, что
позволяет легко вычислить интеграл. Воспользуемся формулой
[dx\n[l + — х(\ - х)] ^ - 2 + y/T7Zln( ^Ll^lJ— ),a > 0.
0 а у/\ + а _ 1
D.15)
В результате получим
— со

136Глава 4
* 1
При вычислении четырехгочечной функции возникнут три подобных
вклада с р = р^ + р2> р = р1 + рз и р = р, + рд) отвечающих вкла-
вкладам S-, t- и u-каналов (предупреждение: все импульсы считаются
входящими). Рассмотренная диаграмма вычислена в евклидовой об-
области; продолжение в пространство Минковского повлечет за собой
изменение знака величины р2 и потребует внимательной интерпретации
результата.
Но в том виде, как это пока что записано, конечная часть не содержит
никакой интересной аналитической структуры до тех пор, пока
р2 > 0. Мы вернемся к этому вопросу, когда дойдем до интерпретации
результата в пространстве Минковского.
Тем же методом вычислим диаграмму "двойной ковш":
4 jBttJco 1г + тгЩ
D.17)
JАУ 11
1024**
m2
2
+ 2ln W2 D,B) + y(l))+¦ J—[(фB)
D.18)
Отметим появление двойного полюса и произвольность вычета в
простом полюсе и конечной части.

Вычисление ФИТ методом теории возмущений: теория <р4 137
Наконец, детально вычислим диаграмму "заходящее солнце"
Полезно сделать это подробно, так как
диаграмма содержит две петли. Обозначим вклад этой диаграммы
через 2(р). По фейнмановским правилам
В диаграммах, содержащих несколько петель, ультрафиолетовые
расходимости проникают в интегралы по параметру. Желательно иметь
в этих интегралах возможно меньше расходимостей. Это означает, что,
прежде чем вводить фейнмановские параметры, нужно с помощью спе-
специальной техники преобразовать выражение D.19), несмотря на то что
интеграл в худшем случае расходится логарифмически. Воспользуемся
следующим приемом. Преобразуем подынтегральное выражение в фор-
формуле D.19) с учетом равенства
и выполним интегрирование по частям; находим
причем мы отбросили поверхностные члены, имея в виду аналитическое

138 Глава 4 ___
продолжение, о котором говорилось в связи с однопетлевыми диаграм-
диаграммами (см. работы [1, 2]).
После явного дифференцирования получаем
_?_ (ц, /_^_ ^
Bш-3) б B1ТJШ BтгJШ х
D.23
' D'24)
B^2» {q2 + т2){1, + п2)[(9 _; + рJ + т2]2 »
D.25)
причем по ходу вычислений мы не задумываясь произвели несколько
линейных замен переменных в импульсах в петлях. Теперь видно, что
Кц(р) расходится логарифмически, а К (р) - линейно. Вычислим сна-
сначала К(р).
Введем фейнмановские параметры сначала для одной петли, начав
с сильнее расходящейся. Получим
<TW? 1
BттJсо BттJ" ~Tqi~
i
/ Г; 2 9 , ,. ¦ /л пр\
О L' + ffr + (р + аJх(\ — х)У* П«*о)
Пользуясь формулой (Б.16), интегрируем по I, что дает

Вычисление ФИТ методом теории возмущений: теория <р4 139
ГB -ее) !, г Л 1
Dтг)с0 о Bтг) (q + m J
1
Х [m2 + (p + ?Jx(i-^F-«' D'27)
Вновь используя формулу D.8), перепишем выражение в виде
p2y(l - у) + тЦ\ - у +. _У j jo - Д. DB8)
*A -ж)
Наконец, интегрирование по q дает
»./ > ГD-2со) 1
х[р2уA -у)+ 11^A -У + -1 г)]2". D.29)
жA - ж)
Для удобства введем величину
2 — со= е
(которая положительна из-за аналитического продолжения) и разложим
D.29) вблизи е т 0. Интеграл по параметру имеет полюс при е = 0,
возникающий от точки у - 0, Напишем
ГBе) 1
/&Ы1)Г
1 ' о о
х [pzyV - у) + т2A - у + У \-\~2t (а Ч1 v
Пользуясь соотношением

140 Глава 4
и интегрируя по частям, находим
_¦ J о* L«(l — х)
1 ~ ' е о о
х j 1 + 26 A - у) -?_ In [р2уA - у) + ^A - у + _2L
rfy ^.^1
х [р2уA - у) + «2A - у + ,У,. )]-26, D.33)
!СA — ж)
Теперь уже можно взять интеграл по параметру, разлагая вблизи
е =0.
Вычисление К производится аналогично и приводит к выражению
«- -2 rliL I dx[x{^x)r 1-
J
)]-«•;¦ D.34)
В данном случае интеграл по параметру сходится, так что сингулярност]
по р2 сводится только к простому полюсу.
Разложение вблизи е = 0 дает
К{р) ' /ГЛ1) 2. — П + е - 2е lnm2 + O(s 2)i, D.35)
DттL ~26 е
2 ^-28 14~ + О(?)]. D.36)
Члены О(е 2) и О(е) в интеграле по параметру для К(р) и р К (р)
очень сложны и дают вклад в конечную часть 2 (р).
Собирая все результаты вместе, находим
¦ р2 + конечная часть]. D.37)

Вычисление ФИТ методом теории возмущений: теория <р* Ш
Заметим, что теперь уже произвол возник и на уровне простого
полюса (так же как и в конечной части).
Конечную часть функции 2(р) вычислить очень трудно. Это невоз-
невозможно сделать в замкнутой форме, и приходится вводить "дилога-
рифм" (или функцию Спенса), определяемый как
Li2U) = - / -^— ln(l - xt), D.38)
о t
Опыт показывает, что,когда присутствуют массы, вычисление конеч-
конечных частей двухпетлевых диаграмм требует очень длинных выкладок.
Задачи
A. Покажите, что при а > О
1 4
о а
*Б„ Положите теперь z « 4/р. Найдите структуру сингулярностей
функции /(г) в комплексной г-плоскости и установите вид /(г) при
действительных г.
B. Найдите вид конечной части функции 1(р) при т2 = 0.
Г. Выведите выражение для р К {формула D.34)].
**Д .Найдите К(р) в порядке е ^и вкразите получившиеся интегра-
интегралы через дилогарифмы.
§ 5. Перенормировка
В предыдущих параграфах мы показали, как вычислять фейнма-
новские интегралы. Мы установили, что в теории Аф4 некоторые диа-
диаграммы имеют ультрафиолетовые расходимости, причем расходимости
появляются только в двух- и четырехточечных функциях Грина (при-
(примитивно расходящиеся диаграммы). Когда к этим диаграммам была
применена размерная регуляризация, бесконечности свелись к полю-
полюсам по переменной е =» 2 - л/2 > 0 в комплексной плоскости числа
измерений, где п — число измерений пространства-времени; вдобавок,
конечная часть этих диаграмм оказалась произвольной, зависящей в
нашей схеме от загадочного параметра массы ц.
Теперь мы покажем, как можно устранить эти полюса последова-
последовательно в каждом порядке по А. Метод очень прост: изменим фейнманов-

142 Глава 4
ские правила в каждом порядке так, чтобы получить конечный резуль-
результат при ? -» 0. В качестве первого примера рассмотрим диаграмму
"головастик":
л
I J - т —— [ + 4^B) — In m + О(е)], E.1)
2 е
lotr 4тгц^
Содержащуюся здесь бесконечность можно устранить, добавив к лагранжи-
лагранжиану ? дополнительный член
E.3)
который мы рассматриваем как дополнительный член взаимодействия.
Здесь F, - ннроизвольная безразмерная функция, аналитическая при
е -¦ 0; наличие этой функции отражает произвольность самой процеду-
процедуры. Дополнительный член приводит к новому фейнмановскому прави-
правилу, изображаемому следующим образом:
J__ + /г,). E.4)
It ?
Поэтому если мы вычисляем обратный пропагатор в порядке 0{К), то
№ (Р) -Р2+тЧ1- -1- ЛМ2) - 1п т2 - F,)] + О(\г) E.5)
(следует помнить, что поправка к обратному пропагатору при обращении
приобретает знак минус). Эта весьма наивная процедура делает теорию
конечной в порядке Л. Дополнительный член E.3) называется контрчле-
контрчленом. Чрезвычайно важно то,, нто его зависимость от поля (и производ-
производных поля) такая же, как и у члена, уже имеющегося в лагранжиане ?,
(в данном случае массового члена).
Переходим к порядку X2. Одночастично-неприводимая (ОЧН) четы-

Вычисление ФИТ методом теории возмущений: теория у4
143
рехточечная функция дается диаграммами
z ч г 4 г 4 г—х—* г
1 3
<Р1
где
5 ж
»
.Р2
А(,
t,
(Pi
' рз« Р*'
^ 1 А,
з s> '
4;
и - мандельстамовские
+ Р,J' ' " (Pi +Р3J'
3 л ]
2 ч €
;. Ц| Т \J\C lli "Г L/(A />
Vl + 4mV« -I
переменные:
«-(P1+p4J.
E.6)
В том виде, как она написана, функция rw расходится при е -» 0. Что-
Чтобы исправить положение, добавим еще один член к ?:
л 1
Л _^_[J_ + Gl(e,a2)V. E.9)
1
где G, - произвольная безразмерная функция переменной е , аналити-
аналитическая при е -» 0. Этот новый контрчлен приводит к дополнительному
фейнмановскому правилу, изображаемому в виде
х-
.26:
E.10)
Он добавляется при вычислении новой функции ГD>, приводя при
е -» 0 к конечному результату:
T~
2 - In m2 -
E.11)

144 Глава 4
Аналогично можно вычислить вклад в ГB' порядка О(К2), но здесь уже
нужно использовать дополнительные фейнмановские правила E.4) и
E.10). В диаграммном представлении для обратного пропагатора по-
получим
= + —5lJ—
+ -О- +
где дополнительные фейнмановские правила привели в данном порядке
к двум новым диаграммам. Они легко вычисляются (см. задачу). Ока-
Оказывается, что
О " —г- *2i —3— + М1) + F. -1пт2] + . . - I, E.13)
где мы показали только полюса по е ; кроме того,
С) ж —j Л 1 —j— + [уB) "*¦ G) — In от J + • • «1, E.14)
Сравнивая с диаграммой " двойной ковш" из предыдущего параграфа
—**— 4 ?2 ?
E.15)
замечаем, что двойной полюс в последнем выражении в точности сок-
сокращается с контрчленной диаграммой E.13), хотя простой полюс оста-
остается. Это явствует из диаграмм, поскольку сумма
по определению конечна. Складывая все диаграммы, находим
3G,-!) + ...!+О(Л2), E.16)
где опять не выписана конечная часть. И вновь мы сталкиваемся с
расходящимся выражением при ? -» 0. Но, о чудо! Члены с In m2, при-
присутствующие при простых полюсах отдельных диаграмм, исчезли, так
же как и эйлеровская постоянная, содержащаяся в каждой функции

Вычисление ФИТ методом теории возмущений: теория у* 145
но отсутствующая в разности
1) () J
E.17)
Чтобы сократить полюса в E.16), мы вводим новый массовый контр-
контрчлен, так что феинмановское правило для массового контрчлена прини-
принимает вид
, +3G, -1))
A2F
1], E.18)
где F — функция переменных ? и т , произвольная, но конечная при
е -» 0. Этот член порождается добавочным контрчленов в лагранжиане
2 А2 1 Л ^2
^ E.19)
Он отвечает только за один тип бесконечностей в Г '2>. Другой тип
бесконечностей сокращается путем добавления к нашему все разрастаю-
разрастающемуся лагранжиану еще одного члена
E.20)
где Uг - произвольная функция, аналитическая при с -» 0. Таким обра-
образом, проделав"все это, мы получаем возможность устранить ультра-
ультрафиолетовые расходимости в порядке Л2. Ясно, что такую игру можно
продолжать, пока не надоест: вычисляем диаграммы порядка Л3, поль-
пользуясь исходным лагранжианом ? и контрчленами E.19) и E.20); за-
затем вводим новые контрчлены, которые выбраны с точностью О(к2)
так, чтобы сократить новые расходимости, и т.д. До сих пор примеча-
примечательным в этом процессе было то, что все необходимые для устране-
устранения расходимостей контрчлены порождали новые взаимодействия того
же типа, как и те, которые уже содержатся в исходном лагранжиане;
нам не пришлось [с точностью О(Л2)] вводить контрчлены, соответ-
соответствующие членам отсутствующего в ? типа. Если бы удалось показать,
что столь примечательное соответствие сохраняется во всех порядках

146 Глава 4
по Л, то мы сказали бы, что теория перенормируема,_Мы не будем
здесь пытаться доказать это для теории Лф4, а лишь укажем на то
место, где вся процедура может оказаться несостоятельной.
Рассмотрим типичную двухпетлевую диаграмму
в которой удалены все внешние хвосты. Из-за различных петлевых
интегрирований эта диаграмма расходится. В соответствии с нашими
новыми правилами для контрчленов к указанной диаграмме следует
добавить три контрчленные диаграммы
Здесь каждая линия —¦#— представляет контрчленную вершину низ-
низшего порядка, необходимую для сокращения бесконечности, возникаю-
возникающей в однопетлевой диаграмме. Поэтому такие контрчленные диаграммы
будут содержать член 1/е, проистекающий от вклада диаграммы
—•— , умноженный на 1пр2, где р - некоторый импульс, возни-
возникающий при интегрировании по петле, Следовательно, все это будет
выглядеть так, будто указанные члены порождают в лагранжиане
контрчлены вида 1пр2/е, которые не соответствуют никакому члену
в ?, так как вычет 1пр2 чрезвычайно нелокален в координатном про-
пространстве. Подобные члены - это ложка дегтя в бочке меда. В этом
заключается знаменитая проблема перекрывающихся расходимостей.
Внимательное изучение приведенных диаграмм показывает, что сумма
всех диаграмм не содержит никаких полюсов с логарифмическим вы-
вычетом: они сокращаются с соответствующими полюсами, содержащими-
содержащимися в двухпетлевой диаграмме. Мы на самом деле видели пример этого
чуда, когда члены с 1пот2 сократились с вычетом простого полюса в
формуле E.16). (Подробнее см. в работе [ 1],) Критическим пунктом
при доказательстве перенормируемости является возможность .дока-
.доказать, что эти перекрывающиеся расходимости действительно сокраща-
сокращаются.
Предположим, что все это так и есть и что для обеспечения конечнос-
конечности теории в произвольном порядке по Л нужны только такие контрчле-
контрчлены, которые соответствуют исходному лагранжиану ?. Это означает.

Вычисление ФИТ методом теории возмущений: теория <р4 147
что тот лагранжиан, который приводит к конечным ответам, имеет вид
?ПвР " ? + ?контр. E-21)
где ? — наш исходный лагранжиан,
? -_^_ д^д^ + -*_ mV + -JrM2V. E.22)
а ?контр — лагранжиан контрчленов,
?^<9м9«9м<р+ _^_т25<р2 + _Л_ц2?СФ\ E.23)
Он имеет (по предположению, которое проверено в порядке 0(Л2)) в точ-
точности тот же вид, что и ?, но со специально подобранными А, В к С,
так что функции Грина, порождаемые ;лагранжианом?пеР, конечны
при е -¦ 0. Определив новые поля и параметры, можно переписать ?пеР
в виде
20 9о2 +-^-9о> E-24)
гдеср0 ^ (\ + А)*<*в гиф, E.25)
E.26)
А0 - Ац" .^р =Ам2?A + OZ^ E.27)
так называемые г ол«в поле, масса и константа связи. Заметим, что
?пеР выглядит совершенно так же, как ?, если не считать обозначе-
обозначений параметров и поля. В то же время LneP приводит к конечной теорт, а
? - нет. Это показывает, что, хитроумно запрягав все бесконечнооти в <р0(,
щ и Ло, мы можем сделать теорию конечной. После этого бесконечности
поглощаются перенормировкой, Все голые величины расходятся при t ¦* О,
тогда как (перенормированные) величины тпри е ¦* 0 принимают конечные
(но произвольные) значения. Последние следует отождествить с физи-

148 Глава 4
ческими параметрами теории. В подходе, основанном на интеграле
по траекториям, производится интегрирование по полям; отсюда можно
убрать изменение масштаба полей в множитель Z , если одновременно
соответствующим образом изменить масштаб источника, определив
голый источник
/о - 2-*/ E.28)
или голое классическое поле
Взяв за исходный новый лагранжиан E,21), мы получим функции
Грина предыдущего параграфа, в которых т и К заменены величинами
mQ и Ао. Но выразив голые параметры через физические параметры
т и Л и подходящим образом перенормировав / , мы получим конечные
функции Грина. В случае ОЧН-функций Грина это равенство имеет вид
i р„; *о. "о» ?) = V/2 г{"'<р, Рп;Л, щ ц, Е),
E.30)
где г о > _ функции, конечные при е -> 0. В этом равенстве можно либо
рассматривать голые параметры как функции перенормированных, либо
считать голые параметры независимыми переменными; в последнем
случае одетые параметры являются функциями голых. 3 аметим теперь,
что левая часть равенства E.30) не зависит от ц, тогда как правая
явно, а также и неявно (через Лит) зависит от ц. Поэтому, дифференци-
дифференцируя обе части равенства E.30) по ц, мы получим дифференциальное
уравнение, отражающее всю магию перенормировки1):
i д Ж
E.31)
Красота этого уравнения в том, что оно содержит только перенормиро-
перенормированные функции Грина Г ^, которые конечны при е -* 0. Различные
производные возникают вследствие неявной зависимости Г ^ от ц
1)Эго уравнение, отражающее групповой характер конечных перенормиро-
перенормировок функций Грина, отвечающих различным рецептам перенормировки, называ-
называется уравнением ренормапизационной группы (ренормгруппы). — Прим. перев.

Вычисление ФИТ методом теории возмущений: теория <р4 149
через Лита Определим коэффициенты
р (Л , _^— , е) ^ ц дХ , E.32)
m , 1 din Z .. оо.
)Ф, E.33)
, )!^ц
ц 2 дм'
1 din
m
,, m .1 din m /с о .,
ут(Л , , ?) = ___ ц _ , E.34)
ц I д\х
Они аналитичны при е -* О, безразмерны и зависят только от А и т/ц.
С другой стороны, Г (п| по построению имеет размерность, рав-
равную 4 — п + е (га -2), которую можно понимать как суммарную степень
однородности функции Г (п) по ее размерному параметру, т.е.
!ц A +s д . +т1 [4- ге + ?(тг -2)]J х
ац (?s dm
ш А. Р» е) = 0 , E.35)
где мы ввели масштаб s для импульсов» Это уравнение в сочетании с
E.31) можно, .исключив \хд/д\х, превратить в уравнение, описывающее
масштабные свойства Г ("'. Переходя к пределу при е -¦ 0, получаем
m . 6 ±. x i\ m \ П
ц (9Л m ц (Эт
-nYd(\, _) + 4-тг!Г(п>(«Р, т, А, и)-0. E.36)
ц
В выписанном уравнении суммировано поведение Г (" • при изменении мас-
масштаба входящих в Г '"' импульсово (Впервые уравнение подобного типа
для КЭД было получено Гелл-Манном и Лоу [ 3] .)Если бы мы могли его
решить, то узнали бы» как функции Грина при значениях импульсов sp
связаны с теми же функциями при некоторых исходных значениях р.
Трудность решения уравнения Eо36) связана с тем, что коэффициенты
Р» Yd и Ym зависят от двух переменных Л и m/ц. Эти коэффициенты
можно вычислить явно в каждом порядке теории возмущений, но в дан-
данный момент они совершенно произвольны, поскольку мы еще не устано-
установили, чему равны конечные части контрчленов. Это будет сделано в

150 Глава 4
следующем параграфе, где будут исследованы различные "рецепты пере-
перенормировки" . Сейчас отметим лишь, что указанные коэффициенты за-
зависят от способа выбора конечных частей контрчленов»
Голые параметры можно представить в виде рядов Лорана по пере-
перенормированным параметрам:
2 » ), E.37)
/с=1 Ек
m,Q = т2(Ь0(\ , ,е)+ 2 ц )> E.38)
М 4=1 6
m .
Z- =с0(А,^-,е)+2 С' '6П -' E.39)
где а 0, Ь 0, и с 0 аналитичны при е -¦ 0. Сравнивая с уже вычисленными
с точностью О(К2) контрчленами, находим
г, /1 / \ -i /1 х 1 г1 \ Л/13\ ^"л4П^
а0(А, тга/ц, е) = ЛЦ + Л G^) + U \\ Ь VJo4U/
-i-(XF, +AF2)+Aff2+O(A), E.41)
2»(/)ОC) E.42)
О(Л3), E.43)
1 +3G, -1)] + Л2/24 + О(А3), E.44)
E.45)
1 О(А3). E.46)
Заметим, что в этих формулах коэффициенты а, Ь и с зависят от
тц'/ц только через неизвестные функции Fy, F , Gy, H2 . Эвристи-
Эвристически э то можно объяснить следующим образом. Контрчлены исполь-

Вычисление ФИТ методом теории возмущений: теория <рА Ш
зуются для исключения тех расходимостей, которые возникают при
очень больших масштабах импульсов (масс). Поэтому любой фиксиро-
фиксированный массовый параметр не должен играть никакой роли* Следо-
Следовательно, до тех пор пока последовательно в каждом порядке теории
возмущений контрчлены не имеют конечной части, вычеты в их полю-
полюсах не должны зависеть от т. Именно это и отражают формулы
E.40) - E.46)- Сказанное лежит в основе независящего от масс ре-
рецепта перенормировки, на котором мы остановимся в следующем
параграфе. В зависимости коэффициентов от произвольных конечных
частей контрчленов отражается зависимость р- и у-функцийот выб-
выбранного априори рецепта. Отсюда вытекает, что не следует пытаться
найти решение уравнения ренормгруппы E.31) до тех пор, пока не выб-
выбран рецепт перенормировки. Техническая трудность при нахождении
решений связана с тем, что коэффициенты зависят одновременно от
А и m/ц. Но, как мы увидим, существует рецепт, при котором коэффи-
коэффициенты становятся не зависящими от масс, что чрезвычайно облег-
облегчает решение уравнения E.31). Иначе приходится решать E.31) в об-
области, где можно пренебречь массами, т.е. там, где импульсы вели-
велики по сравнению с исходными массовыми параметрами.
В заключ ение заметим, что можно вывести и другой тип уравне-
уравнения ренормгруппы, полученный впервые Калланом [ 4] и Симанчиком
[ 5]. В уравнении этого типа изучается изменение функций Г в зависи-
зависимости от физической массы. Коэффициенты |3 и у зависят только от
Л; члены сути \хд[д\х вообще отсутствуют, а вместо них имеется
неоднородный член, которым можно пренебречь в пределе малых
масс или, что то же, больших импульсов.
Задачи
А. Рассчитайте вклад дополнительных контрчленных диаграмм
E.12) и E.13) с учетом конечных частей.
Б. Покажите, что с точностью О(Л2) сам пропагатор конечен.
Указание: пропагатор содержит одночастич но-приводимые диаграммы.
* *В. Покажите, что в теории Л<р3 перекрывающиеся расходимости от
диаграммы (Т\ в действительности компенсируются контр-
контрчленной Диаграммой, регуляризующей однопетлевую диаграмму

152 Глава 4
§ 6. Рецепты перенормировки
В предыдущем параграфе мы детально осуществили процеду-
процедуру перенормировки в теории Л<р4» Исключение расходимостей
привело, помимо произвольного масштаба ц, к дополнительному
произволу, отраженному в функциях F,, F2t G,, Н2 состав-
составляющих конечную часть контрчленов,, Из структуры того лагранжиана,
который приводит к конечным результатам,
?пер=? + ?контр, FЛ)
явствует, что конечная часть ?контр может быть устранена
переопределением (или конечной перенормировкой) исходных начальных
параметров, содержащихся в?, поскольку ? и ?контр имеют одинако-
одинаковую структуру» Отсюда вытекает, что конечную часть контрчленов мож-
можно фиксировать, только определив параметры, входящие в ?» Однако
способ определения т,Аиф содержит много произвола, и он выбира-
выбирается либо из соображений удобства, либо с учетом требований сходи-
сходимости теории возмущений»
В некоторых случаях можно непосредственно связать перенормиро-
перенормированные параметры с физически измеримыми величинами» Именно так
обстоит дело в КЭД, где физический электрический заряд приравнивает-
приравнивается значению вершинной функции в томсоновском пределе»
Конкретное задание масштаба путем приравнивания перенорми-
перенормированных параметров соответствующим функциям Грина в значитель-
значительной степени произвольно (в евклидовом пространстве); есть лишь од-
одно важное ограничение в случае теорий, включающих безмассовые час-
частицы» Такие теории приводят к инфракрасно-расходящимся функциям
Грина при нулевых значениях входных импульсов» Было бы неразумно
выбирать точку вычитания при том значении масштаба, при котором
функция Грина расходится» Подобных точек следует избегать» Позже,
когда амплитуда будет продолжаться в пространство Минковского,
масштаб вычитания проявится при пространственно-подобных значе-
значениях входных импульсов и не будет оказывать влияния на те сингуляр-
сингулярности, которые функции Грина должны иметь и имеют для того, что-
чтобы они были амплитудами перехода» Такие сингулярности возникают
в физической области, где по меньшей мере некоторые из импульсов
всегда времениподобны.
Приведем несколько примеров вычитаний, называемых иначе
рецептами перенормировки»

Вычисление ФИТ методом теории возмущений: теория <fi* 153
А. Это чаще всего применяемый рецепт фиксации параметров.
Мы определяем входные параметры равенствами
А р \ 2 = 0, F.2)
Г*?,, Р2, р3, Р4)~-»2'ЪА при р. -0. F.3)
В отсутствие инфракрасных расходимостей, возникающих при т2 = 0,
такой рецепт хорошо определен» Чтобы подчеркнуть способ, которым
определены входные параметры, мы приписали им соответствующий
индекс» Отметим, что F*2) содержит два условия, так как это равен-
равенство фиксирует не только массу, но и нормировку поля. Приведенными
условиями фиксируется конечная часть контрчленов» В частности,
мы находим, что
Е?~ ч>B) - Ь т2А ; G? - уA) - In т2А ; НЛ2 = 0 и т»д» F-4)
В идеале было бы более предпочтительным отождествить константу
связи с ГD) в физической точке, где частицы находятся в простран-
пространстве Минковского на своих массовых поверхностях {р2 = т2)-
Б» Можно по желанию изменить точку вычитания, лишь бы это
не оказывало влияния на продолжение в пространство Минковского
или на инфракрасные сингулярности» Добавим, что коль скоро вычи-
тательная процедура осуществляется над евклидовыми функциями
Грина, она приводит к пространственно-подобному вычитанию в про-
пространстве Минковского» Таким образом, наш второй ре"епт [6] анало-
аналогичен рецепту А, но проводится при произвольном значении р:
«Л/2, F.5)
ГD|(Р,, р2, р3, Р4) = -и2?*в при p. P/ =W2Fi7 -1/4), F.6)
причем последняя точка выбрана так, что s = t = и = М2. Конечно,
можно выбрать любые значения величин s, t, и и любое значение
Р2, при котором нормируется Г12>. Неизвестные функции в этом
рецепте фиксированы и равны
1пй|; #2Б«0, F.7)

154 Глава 4
- lnm| - / <Ып [ 1 + М1 х(\ - х)] И ТоДо F.8)
о
В данном случае масштаб ц полностью устраняется и заменяется
масштабом М 2, который в равной степени произволен» Ясно, что
теперь при выборе М существенным становится численное значение
о
Недостатком такого рецепта перенормировки является то, что
уравнение ренормгруппы из предыдущего параграфа трудно решить где-
либо, кроме глубокоевклидовой области, в которой, по-видимому,
можно пренебречь всеми массами» Все же приравнивание констан-
константы связи значению амплитуды при некотором масштабе имеег определен-
определенную привлекательность с физической точки зрения, даже если такое
сравнение имеет место в нефизической точке. Дело в том, что
при этом в вычисления явно включаются массы и можно непосредст-
непосредственно идентифицировать разные физические пороги.
В. Очень красивый рецепт предложен 'т Хофтом [ 7] и Вайнбер-
гом [8], Он весьма просто формулируется и позволяет без труда
найти решение "уравнения ренормгруппы" E.36) из предыдущего
параграфа. Рецепт состоит в том, что просто все конечные части
контрчленов полагают равными нулю последовательно в каждом по-
порядке Л, т.е. принимают
Ff = F*=G* =я|=0ит.д. F.9)
Тогда, сравнивая с выражениями E.40) — E.46) предыдущего парагра-
параграфа, мы замечаем, что все коэффициенты о, Ь, с не зависят от т.
Такой рецепт называется " не зависящей от массы" перенормировкой.
Независимость от массы сохраняется вплоть до произвольно высоко-
высокого порядка; эвристически это нетрудно объяснить следующим образом.
Когда у контрчленов нет конечной части, они имеют лишь ту "голую
скелетную" структуру, которая нужна для компенсации бесконечностей
на очень малых расстояниях, но там, при бесконечных импульсах,
всеми массами, по-видимому, можно пренебречь, считая при этом, что
амплитуды хорошо себя ведут при р -»во. Отсюда и вытекает независи-
независимость от масс. И действительно, в рецептах .А и Б зависимость от
массы обусловлена только конечной частью контрчленов. Такое коло-
колоссальное упрощение позволяет непосредственно вычислить коэффици-

Вычисление ФИТ методом теории возмущений: теория у4 155
енты р, у и ут, входящие в E»36)« Например, мы можем теперь на-
написать
()
Ао = М«[А + 2 _Д ]о FЛ0)
Дифференцируя по ц при фиксированном Ао, получаем
• .*ft(i-^Li«»(.tjJiw ,6..,,
где штрихом обозначено дифференцирование по А» В этой формуле Л
и \i<dK/d\i) — функции, аналитические при е = 0„ Отсюда вытекает, что
Ц а ¦- 2бЛ-2а,(Л)-2Ла'(Л), F.12)
или, в пределе при е -» 0 ,
Р(Л)-1ш ц _^_.-2A-aJ—)а,(Л). F.13)
р -¦ О ОЦ ОЛ
Тово р-функция, входящая в "уравнение ренормгруппы", зависит толь-
только от Л и определяется вычетом в простом полюсе по е.. С уч етом
уравнения F» 12) и того обстоятельства, что вычеты в разных полюсах
по е должны обращаться в нуль в выражении FЛ1), находим
A - Л -^-К+ , (Л) = в?(Л)A - A^_)at(X). F.14)
Смысл уравнения FЛ2) ясен: успешная перенормировка означает,
что голая константа связи не зависит от ц, так как изменение величи-
величины ц сопровождается таким изменением X, что соотношение FЛ0) не
меняется,, Вычислим теперь р в теории возмущений,, Пользуясь фор-
формулой Eо43), получаем
5А ЗА2
Пренебрегая членами О(Х3), можно без труда проинтегрировать F* 15),
так что в результате имеем
А =Л0 I , Fо16)

156 Глава 4
где Ао — значение величины А в точке цо„
Из формулы F-15) видно, что А растет с ростом ци Таким обра-
образом, если мы начнем с малого значения Ао(« 1) при заданном масш-
масштабе ц0, то эффективная константа связи с ростом ц будет расти»
Но при этом мы будем иметь дело со все большими Л и рано или поздно
выйдем за область применимости теории возмущений А « 1, или,
точнее, C/16тт2)Л01пц/ц0 « L Поэтому на более коротких расстоя-
расстояниях мы должны добавить члены более высокого порядка в правую
часть равенства F„15)о
Итак, в теории А<р4 теория возмущений становится все более при-
применимой на больших расстояниях, Тое« в той области, где проявляются
дальнодействующие свойства взаимодействия", следовательно, можно
доверять определению асимптотических состояний, основанному на
теории возмущений. Если бы в теории поля обнаружилось, что правая
часть равенства F.15) отрицательна, то это означало бы, что способ,
основанный на теории возмущений, не пригоден для определения асим-
асимптотических состояний но очень хорош для определения поведения
на малых расстояниях.
Дапее мы увицим, что так обстоит депо в квантовой хромодинамике (КХД),
которая описывает взаимодействие между кварками. Кварки позволяют пра-
правильно описать короткодействующее взаимодействие двух протонов, но они
не являются асимптотическими состояниями, а лишь входят как составные
части в асимптотические состояния, подобные протону.
Отметим, что полученное здесь выражение для р (А) совпадает с
тем, которое было получено при вычислении детерминантов методом
?-функций. Этому не следует удивляться, поскольку точность преды-
предыдущего метода была равна О(й), а здесь мы получили лишь результат,
связанный с однопетлевым приближением, точность которого тоже
равна О{%).
Посмотрим теперь, отвлекаясь от теории возмущений, какой мо-
может быть форма зависимости А от ц. Прежде всего заметим, что если
fj (А) дается формулой F.15) даже при больших А, то эта функция
обратится в бесконечность при масштабе
Ц = Цоехр[—_И ], Fо17)
ЛАо
очень большом, если исходное значение Ао мало. Эта точка называется
точкой Ландау, ибо оно обнаружил подобную закономерность в КЭД.
Однако нет никаких оснований считать, что выражение для однопетле-

Вычисление ФИТ методом теории возмущений: теория <р4 157
Рис.3.
вого вклада в р справедливо при больших Ло Мы не знаем, как вычис-
вычислить р при больших А, но рассмотрим несколько возможных вариантов
поведения р, начав с C = 0 при Л = 0, т^е „ с точки без взаимодействия.
1о Функция р (Л) остается положительной при больших а; тогда Л
продолжает расти с ростом масштаба, описывая выпуклую или вогну-
вогнутую кривую в зависимости от знака р ' (А). Если р (А) обращается в
бесконечность при некотором значении А» то и сама константа А ста-
становится в этой точке бесконечной (точка Ландау).
2о Функция р(А) сначала положительна при малых Л, а затем про-
проходит через максимум и становится отрицательной, пересекая ось в
точке KF:
(рис 3)о Точка А^ называется фиксированной точкой, так как если
по каким-то причинам константа была первоначально равна А^, то
она и остается в этой точке. Можно проанализировать поведение кон-
константы Л вблизи \р, разложив р вблизи Af, что приводит к уравнению
ц JL. = (A-AF)p'(M + «. • • FЛ9)
Мы видим, что все зависит от знака производной р '(А^)„ Если
Р '{^р) < 0, как на рис, 3, то величина \\{<fk/d\i) положительна при А,
немного меньших А^, в связи с чем величина А смещается в сторону
больших значений, т.е. к фиксированной точке AF ; когда же А дальше
фиксированной точки lF, величина ц(<9л/<?р), отрицательна, и при этом
опять А смещается к AF. Таким образом, с ростом ц константа А бу-
будет приближаться к А^„ Такая фиксированная точка называется ультра-
ультрафиолетово-стабильной, поскольку А асимптотически приближается к
значению Af при ц -* °о, причем сверху или снизу в зависимости от
положения начальной точки Ао, которая может быть взята выше или

158
Глава 4
ниже Л^„ Если бы существовала теория поля, в которой функция р
вела себя так, как показано на рис» 3, то на очень малых расстояниях
константа Л все больше приближалась бы к Л^, Если бы при этом ве-
величина ~KF была мала, то это означало бы, что, начав с малых Л < \F,
мы никогда не выйдем из области применимости теории возмущений!
Если же мы начата бы с Л >. Af, то с уменьшением расстояния констан-
константа Л приближалась бы к области применимости теории возмущений. Эти
две возможные ситуации изображены на рис- 4- Ни одна из теорий поля
в четырех измерениях не обнаруживает такого поведения в рамках
теории возмущений (\к « I).
Точка Л = 0 является фиксированной точкой, в которой р '@) > 0;
это означает, что выше этой точки величина \х{дк/ д\х) положительна и,
следовательно, константа Л удаляется от этой точки при уменьшении
расстояния. Такая фиксированная точка называется инфракрасно-ста-
инфракрасно-стабильной. Заметим, наконец, что при малых Л большинство теорий поля
ведет себя именно так, что функция р(Л) поначалу положительна.
3. Функция р(Л) отрицательна при малых Л, монотонно уменьшаясь
по величине. Это означает, что константа Л монотонно уменьшается с
ростом In ц. В этом случае приближение теории возмущений становится
все лучше на более коротких расстояниях, и Л смещается к нулю, ко-
который в данном случае оказывается ультрафиолетово-стабильной фиксиро-
фиксированной точкой. Подобное поведение константы связи при малых Л обна-
обнаруживается в калибровочных теориях в четырех измерениях — яв-
явление, известное под названием асимптотической свободы. Мы деталь-
детально остановимся на этом явлении при изучении калибровочных теорий.
Хо
/*
Рис.4,

Вычисление ФИТ методом теории возмущений: теория <р4
159
Р ис. 5.
4. Функция В (Л) сначала отрицательна, затем проходит через мини-
минимум и становится положительной, пересекая ось в точке Л^(рис 5).
В данном случае в '(кр) > 0 и Л/г — инфракрасно-стабильная фиксиро-
фиксированная точка- Это означает, что если при некотором ц0 мы имеем
Ао < Ар, то Л будет смещаться к нулю, но если Ло > Л^, то она будет
смещаться от XF в сторону больших значений (рис- 6).
Взяв за исходное выражение E-41), в котором hQ - 1 и Ък не за-
зависят от т/р, можно найти зависимость массы от ^; нетрудно получить
соотношение
дт2
db,{\)
F.20), F.21)
что в теории Л<р4 приводит к выражению
16-п-2 ' 72~VT6^~' "'" " F2)
Мы можем вывести также рекуррентную формулу для вычетов в полю-
Р ис .6.

160Глава 4
сах более высокого порядка:
dbl +. db .
1 ""
F.23)
Наконец, из определения функции 1^, в котором с 0 = 1 и ск не
зависят от т/ ц, можно вывести уравнение
J =-2Л _ll_, F.24)
аЛ
ац т аЛ
а"с,
откуда yrf(A) = - Л -—— , F.?5)
ал
так что в теории Лф4
F,26)
Коэффициенты ск в свою очередь удовлетворяют соотношению
F.27)
Приведенные рекуррентные соотношения позволяют вычислять вычеты
в полюсах более высокого порядка, исходя из вычетов в простых полю-
полюсах. В этом и состоит ценность изложенной процедуры: если теория
перенормируема, то многие коэффициенты можно вычислить косвенным
путем без помощи фейнмановских диаграмм.
Пользуясь рассмотренным не зависящим от масс рецептом перенор-
перенормировки >тХофта — Вайнберга, легко проинтегрировать уравнение
ренормгруппы, так как коэффициенты утратили зависимость от т. Те-
Теперь уравнение имеет вид
ds д\ "" dm n
хГ|л|(«р; m, A, u) = 0. F.28)
Введем зависящие от масштаба переменные A(s) и m(s ) в соот-
соответствии с равенствами

Вычисление ФИТ методом теории возмущений: теория у4 161
|), A(s - 1) - А, F.29)
ds
m(s)[Ym(l(s))}}, т(з)т
as
Тогда уравнение F.28) легко интегрируется, так как оно превращает-
превращается в дифференциальное уравнение первого порядка по s ; в результате
получаем ,
s as .-,. ,
Г<"»(*Р; т. А, ц) = 5 "Г<п»(р; m(s ),*(*). и)* 1 F.31)
Из этого равенства явствует несколько неожиданное масштабное
преобразование функций Грина при изменении масштаба внешних
импульсов: константа связи и масса преобразуются нетривиальным
образом, а функции Грина наряду с естественной размерностью dn
обнаруживают еще и аномальную размерность yd для каждого внеш-
внешнего хвоста.
Допустим, что с самого начала мы приняли т - 0. Тогда класси-
классическая теория была бы инвариантной по отношению к дилатациям
(и конформным преобразованиям, гл. 1). Но в квантовой теории это
не выполняется, так как при регуляризации вводится некий масштаб
либо через обрезание при больших импульсах, либо через параметр
и размерной регуляризации, а тем самым нарушается инвариантность
относительно дилатаций (см. по этому поводу лекцию Коулмена
[9]).
Кроме того, мы видим, что поведение функций Грина при изме-
измененных значениях импульсов определяется функциями 7(s ) и ~in{s ),
которыми, стало быть, определяется и физика при больших масштабах.
Интересно исследовать поведение функций Грина при больших
s . Предположим, что в теории имеется ультрафиолетово-стабильная
фиксированная точка при значении А •= А^. При больших масштабах
величина А будет смещаться к A t?. Следовательно, ут и yrf будут
сдвигаться к ym(AF) и у</(Л/г), так что решение уравнения F.21)
F.32)
можно проинтегрировать, получив в результате
F.33)

162 Глава 4
если только предположить, что интеграл определяется областью боль-
больших s. Аналогичное предположение относительно интегрирования
у^ приводит к формуле
b)(sp; т, К, ц)„», -
F.34)
Таким образом, если величина 1 - ym(hF) положительна, то при боль-
больших масштабах вообще можно пренебречь массой и, кроме того, дей-
действительно Yj(\p) появляется как аномальная размерность.
Как явствует из формулы F.33), справедливость наивного предпо-
предположения, что массы выпадут из теории при больших масштабах, су-
существенно зависит от значения интеграла от аномальных размерностей,
который мы запишем в виде
F-35)
Такая форма записи показывает, что если C(Л) и ут(\) не имеют
одновременно нулей, то наибольший вклад в интеграл будут давать
фиксированные точки, чем "отчасти" и подтверждается сделанное на-
нами выше предположение.
Если ультрафиолетово-стабильная точка находится при Af л О
(как в калибровочных теориях), то тогда вообще нет проблем, пос-
поскольку поведение теории при больших импульсах определяется тео-
теорией возмущений, т.е. ут@) = 0.
Можно проинтегрировать различные уравнения в теории Лф4, поль-
пользуясь результатами, полученными для ут и у^ в низшем порядке тео-
теории возмущений. Это дает
Ц^1/4 *<*)* F.36)
A 36 16тт2
для зависящей от масштаба массы и
dr, - —
36 ^Т2 Г1"'(р) F.37)
для аномальной размерности. Эти результаты верны только при малых
масштабах масс, так как мы видели, что вычисленная по теории возму-

Вычисление ФИТ методом теории возмущений: теория у4 163
щений р-функция положительна, и поэтому по достижении некоторого
масштаба теория возмущений теряет применимость.
Задачи
А. Задав $(К) - р(дЛ,/<Эр), проанализируйте гипотетические теории
поля, в которых
2. $(kk) - О, Ц - \F + а/к, к - 1, 2, ...,«.
Б. Пусть
т20 ,™2(! + 2 ) = т Zm.
п = 1 Е
Покажите, что
1 ^Ь Zm db,
5ш ^
п + 1 ^ 1 1
Выведите формулу, связывающую Ъп> п + , с 6 ь 2, если
В. Пусть Фо = ФA +
Покажите, что yd(K) » _» ц _ = - X ,
Г. Убедитесь в правильности уравнения ренормгруппы в теории
4, пользуясь результатами теории возмущений для р, у^и yrf.

164 Глава 4
§ 7. Зависимость коэффициентов ренормгруппы от
рецепта перенормировки
В предыдущем параграфе мы вычислили коэффициенты р
и у в низшем нетривиальном порядке по А, пользуясь не завися-
зависящим от массы рецептом перенормировки «тХофта— Вайнберга.
Исследуя их поведение, мы сделали важные физические выводы.
Внимательный читатель вправе задать вопрос, в какой мере эти коэф-
коэффициенты зависят от рецепта перенормировки. В случае общего рецеп-
рецепта типа А или Б они будут, вообще говоря, зависеть от масс через
конечные части контрчленов.
Исходя из формул E.37) - E.39), дифференцированием по ц при
фиксированных голых параметрах находим
П 9 Г Oi u <^А г ' л. °1 1 . / dm m .
0-2е[я + ] + ц__[о'+ _!_]+(_ - )х
? д\х ° е op p
. ] + полюсы высших порядков,
((.1)
откуда выводим, что
^ i «I j. * г \ а. за
^ = 8 (— ^А + G.) + .j.
О 1 2
G.2)
В этих формулах штрихом обозначено дифференцирование по А, а точ-
точкой - по тУц» Сравнивая с выражением F.15), мы видим, что из-за
G, возникла явная зависимость от рецепта. В частности, мы замеча-
замечаем, что зависимость от рецепта возникает в низшем порядке из-за
массы. При выводе уравнения G.2) становится очевидным, что члены
порядка А3 в G.2) зависят непосредственно от G, без мультиплика-
мультипликативных массовых факторов. Аналогично можно показать, что
din m ,1 A ,1m A * .
у = |д = ( + р I +
О(К3),

Вычисление ФИТ методом теории возмущений: теория <р* 165
д , 7к 1 /^ ,2 т .А ,
1г() ~(^ +
4_BJ(*) G.4)
2
Полагаем е -> 0 и получаем окончательно
/„»
G.7)
Эти формулы показывают, что, когда присутствуют массы, зависимость
от рецепта входит уже в низшем порядке. Следовательно, только в
случае, когда можно пренебречь массами, мы можем говорить, что
коэффициенты низшего порядка в уравнении ренормгруппы не зави-
зависят от рецепта перенормировки. Обычно при использовании рецепта
типа А или Б уравнение ренормгруппы решается в условиях, когда
можно пренебречь массами. Если ц — точка перенормировки, то мы
можем считать т/ ц сколь угодно малой величиной, выбрав очень
большое ц.
Предположим, что у нас имеются два рецепта перенормировки.
Они должны быть связаны друг с другом конечной перенормировкой,
поскольку различаются только определением перенормированных
параметров. Следовательно, параметры в одном рецепте будут связа-
связаны с параметрами в другом соотношениями
G.8)
; U = 1 + О(\), G.9)
; J/ = 1 + О(Л3). G.10)

166 Глава 4
В частности, отсюда следует, что
G.11)
где А - некоторая функция переменных X и щ/ р. В глубоко-евклидо-
глубоко-евклидовой области это сводится к уравнению вида
G.12)
которое показывает, что фиксированная точка К = XF превращается в
фиксированную точку \'F ~ A(XF) ? \F. Отметим, что этот результат
получен без применения теории возмущений. Следовательно, как мож-
можно было ожидать, наличие (или отсутствие) фиксированной точки не
зависит от рецепта перенормировки. Можно также показать что и
знак первой производной функции В в фиксированной точке не зависит
от рецепта (см. задачу).
Другие параметры ренормгруппы ут и yd тоже обладают некото-
некоторыми не зависящими от рецепта перенормировки свойствами; в част-
частности, таковы их численные значения в фиксированной точке в глубоко-
глубокоевклидовой области.
Задачи
A. Докажите правильность формул G.2) - G.4).
Б. Докажите правильность в низшем порядке уравнения ренорм-
ренормгруппы для Г12) и ГD>, удерживая конечные части F^, F2, Я2 иС,.
B. Пренебрегая массами покажите, что знак величины rfp / </Л
в фиксированной точке X р не зависит от рецепта перенормировки.
.*Г. Найдите связь между y'd{\') и у'т(Кг) и yd (Л), ут(Л), В(Л),
где штрихованные и нештрихованные величины относятся к двум неза-
независящим от масс схемам перенормировки (функции F, G и Н берутся
сначала независящими от т/ \х, но могут иметь численные значения).
Покажите, что значения параметров ув и ут в точке \р не зависят
от рецепта.
§ 8. Продолжение в пространство Минковского,
аналитичность
Мы получили конечные функции Грина ценой введения произволь-
произвольного масштаба. Но из уравнения ренормгруппы мы знаем, что если
изменить этот масштаб, то с функциями Грина ничего не случится,

Вычисление ФИТ методом теории возмущений: теория <р* 167
поскольку их изменение компенсируется одновременным изменением
перенормированных параметров и прля. Чтобы не отрываться от реаль-
реальности, нам нужно представить функции Грина в пространстве Минковско-
го.
Это достигается путем аналитического продолжения. Рассмотрим
евклидову функцию Грина, зависящую от импульсов р,,..., pN .
Прежде всего изменим все временные компоненты импульсов р, сделав
их мнимыми:
Р * (Р0» Pi ) "> Р - (Ро = iPo^ Pi = Pi)'
Посмотрим,например, что случится с пропагатором. В соответствии
со сказанным выше произойдет замена
1 1
p2 + m2 —p2 + m2 '
так как мы используем метрику в пространстве Минковского g00 =•
* ~Ец » + !• Такая замена не совсем удовлетворительна, поскольку
выражение, полученное в пространстве Минковского, имеет полюс при
р2 = т2, т.е. пои
Процесс продолжения можно рассматривать как переход от мнимой
к действительной оси в плоскости р0, осуществляемый поворотом
по часовой стрелке; возможность такого перехода зависит от того,
можно ли избежать любого полюса...Отсюда следует, что полюса по
Ро следует считать лежащими несколько ниже (выше) положительной
(отрицательной) действительной оси, т.е. продолжение происходит
от 1/(р2 + т2) к -1/(р2 -т2 + i е), где в > 0, а в конце всех вычис-
вычислений нужно перейти к пределу при е -¦ 0+. В более сложных случа-
случаях полюса следует выбирать так, чтобы они не мешали вращению по
часовой стрелке мнимой временной оси к действительной временной
оси. В этом (- ?<г)-предписании мы узнаем знакомый (см. выше)
способ сделать сходящимся интеграл по траекториям. Можно так-
также сравнить фейнмановские правила в пространствах Евклида и
Минковского, скажем, для теории q>4:

168
Глава 4
(Евкл.),
(Минк.),
(8.1)
(8.2)
Интегрирование по петлям: -— (Ьвкл.),
(Минк.).
(8.3)
TW
Рассмотрим фейнмановскую диаграмму с L петлями, V вершинами и
/ внутренними линиями. Разница между вычислением такой диаграм-
диаграммы в пространствах Евклида и Минковского будет заключаться в
множителе -i для каждой вершины и каждого пропагатора и в множи-
множителе г для каждой петли, так как d^k =. id*k. Кроме того, величина
тп2 в евклидовой функции Грина заменяется зеличиной m2 -it в
соответствующем выражении в пространстве Минковского. Таким
образом, мы приходим к соотношению
-it
(8.4)
заменив в евклидовой функции все импульсы продолженными в про-
пространство Минковского, т.е. заменив импульсы р = {р0, р{ ) импуль-
импульсами р = (i pQf р. ). Пользуясь топологическим соотношением
L = 1 -V + 1G 4 0), получаем соотношение
GW (Р> и2) - (' )°е* ii} = Р! ™2 "'О. (8.5)
справедливое для любой фейнмановской диаграммы с V-4 0. Исключе-
Исключением из этого правила является выражение для самого пропагатора

Вычисление ФИТ методом теории возмущений: теория у* 169
(V = 0), в котором i заменяется на -i, что можно увидеть из (8.4),
положив L = V = 0 , / =1.
В качестве примера использования такой процедуры рассмотрим
четырехточечную функцию в пространстве Минковского. Имеем
~ К2
х fdx In(ffl2 ~U -sx^~x) ) + t- и и-каналы]. (8.6)
о m2 -tE +M2x(l - x)
Здесь мы умножили евклидово выражение на i , заменили р2 на.-р2
и и2 на и2 -IE. Вычитание в евклидовой функции Грина было сдела-
сделано при pt р. = М2E-- - 1/4), так что Г^4> = -А в этой симметричной
точке (рецепт Б). Заметим, что точка вычитания входит как параметр
и не подвергается изменению в процессе продолжения. Добавка —г в
в знаменателе не нужна, так как знаменатель нигде не обращается в
нуль. Числитель не может изменить знак при некотором значении
¦s - (Ру + Р2J. Когда это происходит, у логарифма появляется разрез в
комплексной 5-плоскости. Рассмотрим аргумент логарифма
F(s, x)= m2 -it -sx(l x), (8.7)
Величина хA - х) положительно определена и изменяется от 0 до 1/4.
Следовательно, наименьшее значение 5, при котором F обращается в
нуль, равно
50 = 4т2, (8.8)
где предполагается, что произведение х{\ — х) равно своему максималь-
максимальному значению. В этой точке у функции Г D> появляется точка ветвле-
ветвления. По традиции из этой точки проводят разрез в комплексной 5-плос-
5-плоскости, идущий от 4т2 до + оо вдоль положительной действительной оси.
Аналогичным образом вклады t- и u-каналов дают разрезы, начинающи-
начинающиеся при 10 и и 0 -4т 2. В силу соотношения
s + t +w» 4m2 (8.9)
не все эти разрезы независимы. Физический смысл возникших точек
ветвления нетрудно выяснить, если интерпретировать ГD> как ампли-
амплитуду рассеяния для рассеяния двух частиц с импульсами рум.рг в

170 Глава 4'
две частицы с импульсами р% и рЛ :
Предположив, что начальные и конечные частицы находятся "на мас-
массовой поверхности", т.е. что
р2а ,т2, а = 1,2, Я, 4,
легко увидеть, что значение s 0 « 4т2 соответствует тому, что две
частицы имеют минимальные энергии Еа = т. Только при sQ> 4 m2
две частицы имеют достаточно энергии, чтобы нетривиальным обра-
образом рассеяться в две другие. Поэтому s 0 называется физическим
двухчастичным порогом. Ниже этого порога функция Г D) — действи-
действительная функция своих аргументов, но при s > s Q у нее появляется
мнимая часть.
Резюмируем: продолжив функцию Г 14) в пространство Минковско-
го, мы обнаружили возникновение нетривиальной аналитической струк-
структуры; эта структура, конечно, определяется условиями унитарности
и причинности, что и позволяет нам рассматривать функции Грина в
пространстве Минковского как амплитуды перехода.
Другой пример нетривиальной аналитической структуры, возника-
возникающей в результате продолжения в пространство Минковского, связан
с диаграммой "заходящее солнце" . В этом случае лучший способ най-
найти точки ветвления - посмотреть на аргумент логарифма в интеграле
по параметру. В данном случае интересующий нас аргумент имеет вид
А - -у(\ - у)р2 + гп2A - у + у ). (8.10)
хA - х)
Он обращается в нуль, если
Р^тг{1 \ >
.11)
и положение точки ветвления будет определяться наименьшим таким
значением р2. Чтобы найти это наименьшее значение, нам нужно ми-
минимизировать параметрическое выражение,на которое умножается
т2. В случае двухточечной функции точки ветвления будут, вообще
говоря, возникать при минимальных значениях р2, для которых
P2 = m2f{xy, х2> . . . , xN), (8.12)

Вычисление ФИТ методом теории возмущений: теория у>4 171
где х,, . . . , xjy - Фейнмановские параметры, необходимые для
N-петлевой диаграммы. Тогда точка ветвления расположена при
P2-m2f(x0,, . . . , х%), (8.13)
где точки х° определяются уравнениями (8 Л 4)
df
— = 0 при X,- = х? (нужно убедиться в том, что при *;. = *° действи-
<Э*.
телью достигается минимум). По имени Ландау, разработавшего системати-
систематическую процедуру охоты за точками ветвления фейнмановских диаграмм, та-
такие уравнения назьгоаются уравнениями Ландау. Применяя эту процедуру к
нашему случаю, прлучим из (8.14), что минимум возникает при х= 1/2, у =
= 1/3, так что точка ветвления расположена при значении
Р2 = %т2. ¦ (8.15)
Если вспомнить вид диаграммы "заходящее солнце" -Q-, то станет
ясно, что эта точка соответствует минимальной энергии, необходимой для
возбуждения трех частиц, почему она и называется трехчастичным
порогом.
Итак, лропагатор в пространстве Минковского имеет следующую
структуру особенностей: полюс при р2 = т2 [должным образом сдви-
сдвинутый с помощью правила (- »е)] и точка взтвления при Р2 * 9т2
с разрезом, проведенным по традиции вдоль действительной оси р2
и простирающимся до р2 ¦ + «>. Когда включаются более высокие по-
порядки по Л, то должны, по-видимому, встречаться точки ветвления при
больших значениях р2. Такая структура особенностей (конечно) сог-
согласуется с интерпретацией GB1 как пропа^атора.
Задачи
*А, Пользуясь диаграммами и учитывая физические соображения,
найдите положение точек ветвления в Г^'4' с учетом членов О(К4).
*Б. Повторите задачу А для пропагатора.
i*B. Покажите, что функция Г|4) удовлетворяет дисперсионному
соотношению, выраженному действительную часть ft4> через ее
мнимую часть. [Используйте только выражение для fD>, найденное
по теории возмущений с точностью О(Л2).]

172 Глава 4
§ 9. Сечения и унитарность
Теперь мы уже почти у цели. Мы хотим отождествить функции
Грина в пространстве Минковского с амплитудами перехода. Но не
все функции могут быть амплитудами перехода, так как они должны
удовлетворять определенным требованиям, в частности тем, которые
вытекают из унитарности и причинности. Как вы, наверное, уже дога-
догадываетесь, функции Грина из предыдущего параграфа удовлетворяют
этим требованиям.
Чтобы точно сформулировать требования, вспомним формализм
S-матрицы и применим его к теории tap4.
Допустим, что можно определить состояния очень далеко от об-
области взаимодействия, в частности в очень отдаленном прошлом или
будущем. Смысл таких состояний вполне ясен в случае короткодей-
короткодействующих сил, например в случае слабого или сильного взаимодейст-
взаимодействия. Когда же включаются и дальнодействующие силы, дело усложняет-
усложняется и при определении таких состояний нужно быть особенно внима-
внимательным. Пусть состояния описываются кет-вектррами ] ос; ± Т>,
где Т -очень большое время, а а - полный набор наблюдаемых. Эти
состояния удовлетворяют требованиям полноты и ортогональности
2| ос ; ±ТХ±Т; ос| - 1, < а; ± Т| |5; ±Т> = 6аВ. (9.1),(9.2)
а
Если наша система - гармонический осциллятор, то а - число запол-
заполнения и т.д. Очень важно то обстоятельство, что приведенные соотно-
соотношения выполняются только в данный момент времени и поэтому не
учитывают никакой динамики, а только кинематику. Если при больших
Т взаимодействие можно выключить (короткодействующие силы), то
такие состояния легко опознать как диагонализующие невозмущенный
гамильтониан.
В теории Аф4 при т2 ? 0 не составляет труда опознать такие сос-
состояния. Они составлены из одночастичных вигнеровских состояний,
отмеченных значениями тп р, причем энергия определяется как
+ ур2 + т2. Если мы перейдем к обозначениям более релятивистского
вида, т.е. обозначим эти состояния символом \р >, где р - вектор
4-импульса, то требуется, чтобы они удовлетворяли соотношениям
/i!L \p>Q(p
(Ztt)
<р\ р'> = 2BттK /р2 + т2 5{р -р'). (9.4)

Вычисление ФИТ методом теории возмущений: теория <р* 173
Тогда любое многочастичное состояние будет суперпозицией невзаи-'
модействующих одночастичных состояний
(9.5)
В теории tap4 имеется некоторое оправдание нашей уверенности в том,
что эти состояния дают асимптотические состояния: поведение кон-
константы связи при больших масштабах таково, что свободный фейн-
мановский пропагатор точно описывает распространение сигнала,
а мы знаем, что Д^ — действительно пропагатор одночастичных сос-
состояний описанного выше типа. (Здесь мы рассуждаем несколько бес-
бесцеремонно, поскольку, строго говоря, AF — пропагатор состояний
как с положительной, так и с отрицательной энергией,) Попутно за-
заметим, что если на больших расстояниях константа связи растет с
расстоянием, то как асимптотические состояния следует идентифи-
идентифицировать лишь конструкции, которые могут избежать влияния столь
огромных сил. По-видимому, именно так обстоит дело в КХД, где
на кварки действуют такие силы. Поэтому кварки не могут служить
асимптотическими состояниями. Но эти силы действуют только на
объекты с цветом, что позволяет определить асимптотические состоя-
состояния, не имеющие цвета (адроны).
С физической точки зрения интерес представляет вычисление
амплитуды перехода
Тар =<а, + ~| р,-~>. (9.6)
Следуя Гейзенбергу, определим S-матрицу, обладающуя свойством
| р, + оо> = S | Р,- сс>. (9.7)
Такая S-матрица должна содержать всю динамическую информацию
об эволюции физических состояний во времени. Из условия полноты
состояний на + «¦ и на — «
л
следует, что оператор S унитарен. (Вы можете также показать, что
StS = 1). Физический смысл унитарности в том, что система не может
превратиться в ничто (черные дыры ?). Когда состояния рассеиваются,
то большую часть времени ничего не случается - они значительно

174 Глава 4
охотнее пропускают друг друга, чем взаимодействуют. По этой при-
причине положим
S-1 + iR, (9.9)
л
где Я содержит интересующую нас информацию. Отсюда следует, что
Тар -<а,-оо| S+\ P, -~>
-5вр -г .<а,-«,|Д+| р, -«о. (9.11)
Поскольку взаимодействие лоренц- инвариантно, можно написать
(9.12)
где ра (р ) - сумма импульсов в конечном (начальном) состоянии.
Тогда вероятность перехода во всем пространстве-времени дается
выражением
х<ос ,-<*>{ Т+\ р, - «><р,-«| Т\ а,-~>. (9.13)
Легко сообразить, какой смысл имеет квадрат б-функции: величина
BттL8'4'@) есть объем пространства-времени (в чем нетрудно убе-
убедиться, поместив систему в некий ящик). Отсюда вытекает, что вероят-
вероятность перехода в единице объема пространства-времени равна
Qep-BWLS«4»(P4 -pp)|<o| Т|р>|2. (9.14)
Это выражение справедливо для состояний, удовлетворяющих соотно-
соотношению (9.2). В нашем случае состояния с заданным импульсом нор-
нормированы не на 1, а согласно (9.4). Поделив на нормировочный коэф-
коэффициент, находим
где Еа(?а) означает произведение энергий в состояниях ос(р), причем
каждая энергия определяется как
+ma. (9.16)

Вычисление ФИТ методом теории возмущений: теория <р* 175
В экспериментах по рассеянию обычно измеряют сечение рассеяния
двух частиц (мишени и налетающей частицы) с превращением в нес-
несколько частиц. Такое сечение находится по формуле
B-it)
3TV
(9.17)
Здесь vab - относительная скорость частиц а и Ь; в случае частиц
с одинаковой массой она дается выражением
Vab
Собирая все результаты, получаем
da (а + 6- 1 + 2+ . . . + N)-
а +РЬ ~Р, -. .
d3P;
Wjr—. (9.19)
Заметим, что мера интегрирования d3p/2Е релятивистски-инвариантна,
поскольку
d*p/2E-d*pe(po)S(p2 -m2). (9.20)
Рассмотрим интересный частный случай упругого рассеяния, для ко-
которого N ж 2. Определим систему центра масс, в которой
ра +рь = р, = р2 = 0. (9.21)
Тогда из простых соображений кинематики можно написать
а +Ь -1 + 2)- -I Tl2 dQ, (9.22)
64tt2s

176 Глава 4
Рь
РИС. 7.
где dQ « <i9<i(cos6), причем б - угол между начальным и конечным
направлениями импульсов (рис 7), a s — мандельстамовская перемен-
переменная: s -(ра +рь)\
Как и можно было ожидать перенормированные функции Грина
А
мы отождествим с матричными элементами оператора Т. Поэтому
важно перейти от требования унитарности к условиям для Т и убе-
убедиться в том, что они выполняются при таком отождествлении.
Из условия унитарности для S вытекает, что
Л л Л А ЛЛ
р р + V /? i" /? ,' рр + /Q ОQ\
В этом операторном уравнении собраны все ограничения на Rs диктуе-
диктуемые унитарностью. Возьмем, например, матричный элемент этого соот-
соотношения между двухчастичными состояниями | 1, 2 > или | 3, 4 > •:
< 3, 4 | Д| 1, 2> - <3,4| ДТ| 1,2> -t < 3У 4 | RRt\ 1,2 > . (9.24)
Как нетрудно видеть, в случае, когда внешние частицы бесспиновые,
< 3, 4 | fft| 1, 2 > - < 1, 2 | fit | 3,4 > . (9.25)
С учетом равенства < 1,2 | R t | 3, 4 > - (< 3,41 R | 1,2 >)* (9.26)
л л л
получаем 2Im< 3,4 | R \ 1, 2 > - < 3,4 | RRt\ 1,2 > . (9.27)
Правую часть можно переписать иначе» если ввести набор промежуточ-
промежуточных состояний. Так как мы хотим ограничиться взаимодействиями»
включающими четное число состояний (инвариантность при замене
Ф -» - ф), низшим по энергии промежуточным состоянием будет двух-
двухчастичное состояние \ a, b > -\ а >\Ь> * Поэтому с учетом формулы
(9.3) приходим к выражению

Вычисление ФИТ методом теории возмущений: теория у4 177
2Im< 3,4]
Д
х 8{Ь2 -гг?) < 3,41 R\ a, b ><а, Ь\ ЯЦ 1,2 > + ..., (9.28)
где многоточием обозначена сумма по 4-„ 6-, • . . -частичным проме-
промежуточным состояниям. В случае Г-матрицы (9.1 2) выражений (9.28)
принимает вид
Л
|
Л дп Jh
2Im<3,4| T| 1,2 > - f —~-j— Q(ao)Q(boM(a2 -
x5(P -т2)Б(а +6 - 1 - 2)< 3,4| Tt| a, b ><as b\ T\ 1,2 > +
(9.29)
Так как а и 6 находятся на массовой поверхности, это выражение бу-
будет отлично от нуля только в том случае, если начальное состояние
I 1,2 > обладает достаточной энергией, чтобы породить промежуточное
состояния | а, Ъ>, т.е. если s = (р, 4 р2)? > 4т2. Таким образом»
вследствие унитарности и полноты Т-матрицы ее элементы действи-
действительны при ^ < 4т2 и приобретают мнимую часть после того, как
пересекается двухчастичный порог, а для всех других, более высоких
порогов имеются дополнительные вклады в мнимую часть.
Сравним теперь это с четырехточечной функцией, полученной по
теории возмущений,
(9„30)
Мы видели» что интеграл по параметру действительно приобретает
мнимую часть и имеет точку ветвления при s = 4m2, так что все
это согласуется с соотношением унитарности (9.29). Таким образом,
мы получаем возможность отождествить функции Грина с величиной
— i, умноженной на 7*-матрицу. В данном случае
Г14>A, 2, 3, 4)= -г < 3, 4| Т| 1, 2>„ (9.31)
В самом деле, мы уже вычислили мнимую часть функции rD)i; она
имеет порядок Л2 и появляется только при 5 > 4т2о Но можно вычис-

178 Глава 4
лить эту мнимую часть из соотношения унитарности (9.29), подставив
в его правую часть вершину низшего порядка теории возмущений.
Это приводит к выражению
21т(гГD»)= \ / d*ad*bQ(ao)Q(bQM(a
2 -
xS(b* _т2MП + 2-а -Ь) + 0(\4), (9о32)
показать правильность которого мы предоставляем читателю. Оно
содержит только вклад низшего порядка в мнимую часть; 4-, 6- ,_» » .
-частичные пороги будут давать вклад в мнимую часть лишь в более
высоких порядках по \.
Если учесть эту связь между функциями Грина и амплитудами
рассеяния, то возникает новый способ вычисления мнимой части диа-
диаграмм, основанный на соотношении унитарности. Такой способ приго-
пригоден для вычислений по теории возмущений, поскольку правая часть
равенства (9.29) имеет квадратичную структуру; это означает, что
если амплитуда < а, Ь \ Т| 1, 2 > вычислена в порядке \А,то мни-
мнимая часть будет определяться в порядке \к + ' . Сказанное имеет
важное значение благодаря существованию оптической теоремы,
которая связывает мнимую часть амплитуды рассеяния вперед с
полным сечением. Эта теорема легко доказывается подстановкой
| 3, 4 > = | 1,2 > в формулу (9.29) и сравнением правой части полу-
получившегося выражения с проинтегрированным выражением (9.22).
Можно получить и диаграммное представление унитарных огра-
ограничений, если вспомнить смысл фейнмановского пропагатора.
Имеем
ikx
1
в(+*0N(*2-т2),
и здесь в явном виде выражается то обстоятельство, что Д^ — про-
пагатор состояний как с положительной, так и с отрицательной энер-
энергией в зависимости от знака xQ „ Если теперь ввести новый набор
правил, в котором полный пропагатор Д^ заменен произведением
B(kQ M{k2 -m2), то мы получим графический способ вычисления

Вычисление ФИТ методом теории возмущений: теория <р* 179
мнимых частей и, следовательно, полных сечений. Конечно, новое
правило применимо только в пространстве Минковского. Вместо ста-
старого правила
р2 -п? + it
введем новое правило для пропагатора с разрезом
-» Bту)е(р0)б(*>02 -и2).
Заметим, что разрезанный пропагатор несимметричен, как показы-
показывает штриховка. Дело в том, что, поскольку мы должны вычислять
ТТ^ в правой части (9.29), части диаграммы, лежащие слева от раз-
разреза, должны соответствовать сопряженной диаграмме справа от него,
хотя они могут быть и неодинаковыми. Мы отсылаем заинтересованно-
заинтересованного читателя за деталями к работе 'т Хофта и Вельтмана " Диаграм-
матика" [10].
Итак, равенство (9.32) в диаграммном представлении запишется
в следующем виде: im К X = к I x • Окончательный
результат заключается в том, что можно вывести общие форму-
формулы, в которых мнимая часть диаграмм представляется в виде
суммы всех возможных разрезов этих диаграмм. (Это не так
плохо, как кажется, поскольку многие из разрезанных диаграмм дают
нуль в силу закона сохранения энергии, ибо разрезание фейнмановс-
кого пропагатора ограничивает поток энергии одним направлением).
На этом мы завершаем изучение теории \<f* в рамках теории
возмущений,
Задачи
А. Исходя из выражения (9.19), покажите, что da/dQ =
= AД)|Т|2б41т2.
Б. Покажите, что для упругого рассеяния бесспин вых частиц
< 3,41 S j 1,2 > -< 1,2| 5j3,4>.
в. Исходя из соотношения унитарности вычислите Im(i Г'4') и
сравните с результатом, полученным ранее по теории возмущений.

180 Глава 4
Г. Покажите, что в общем случае при е > О
„, 1 ,
X + I ? X
где РA/ х) — главное значение величины 1/х в смысле Коши, опре-
определяемое как
Р{ )=¦-?' / dyeixy [вЫ - 6(- у)].
-*'Д. Вычислите мнимую часть диаграммы "заходящее солнце" ,
пользуясь соотношением унитарности im [i ~Q-~\ =
**> Е, Пусть задан лагранжиан ?.Е = д <р д ф + т2ф2 +
а) выведите феймановские правила; б) найдите изменение т, h
и А в результате изменения масштаба с точностью O(h); в) решите
уравнения, полученные в пункте б, и дайте физическую интерпрета-
интерпретацию результата. Можно пользоваться любым рецептом перенормировки,
но мы рекомендуем рецепт, не зависящий от масс.
ЛИТЕРАТУРА
1. Ч Hooft G.; Veltman М„, Nucl. Phys., E44, 189 A972).
2. Curtright, Ghandour, Ann. of Phys., 106, 209 A977).
3. Gell-Mann M., Low F., Phys. Rev., 95, 1300 A954).
4. Callan C, Phys. Rev., D5, 3202 A972).
5. Symanzik K,, Comm. Math. Phys.» 23, 49 A971).
6. Georgi H,, Politzer 1LD., Phys. Rev., D14, 1829 A976).
7. V Hooft G«, Nucl. Phys., B61, 455 A973).
8. Weinberg S., Phys. Rev., D8, 3497 A973).
9. Coleman S., in: Proc. of the 1971 Int. School of Subnuclear Physics,
Erice, Italy, ed. A. Zichichi, Acad. Press, 1973.
10. 't Hooft G., Veltman M°, In: Patricle Interactions at Very High Energy,
part B, eds. D. Speiser et al., Plenum Press, N.Y., 1974 •

Глава 5
Интеграл по траекториям
при наличии фермионов
§ 1. Интегрирование по грассмановым числам
В гл. 1 мы привели несколько примеров функционалов действия, содер-
содержащих ферми»поля, т.е. поля, преобразующиеся по представлениям группы
Лоренца с полуцелым спином» Там же было отмечено, что ферми-по-
ля должны рассматриваться как антикоммутирующие классические по-
поля и что такое классическое условие не означает квантования. Если
рассуждать по аналогии с квантованием, скажем, скалярного поля, то
мы придем к рассмотрению интеграла "по траекториям" от антикомму-
тирующих полей. В лучшем случае это может быть формальным поня-
понятием , лишенным прямого физического смысла, но, как обычно бывает
в подобных случаях, окончательный результат будет представлять ин-
интерес,хотя метод его получения таков, что можно лишь пожать пле-
плечами.
Сначала рассмотрим случай одной грассмановой (антикоммутирую-
щей) "переменной" в. Она удовлетворяет условию
!е,е!=о, или е2 = о d.i)
(символ!,! означает антикоммутатор). Определим дифференциальный
оператор d/dQ равенством
И =1. A.2)
dB
В силу соотношения A.1) разложение любой функции/(б) переменной
в будет иметь простой вид
/(в)= а * рв. A.3)
Дня удобства будем считать C величиной грассманова типа, а а - действи-
действительным коммутирующим числом. (Далее грассмановы переменные
будем обозначать греческими буквами.) Отсюда следует, что
Цг р, 4т о' A-4)- A-5)
dQ dQ2
если принять {d/dQ) a = S d/dQ, pi = 0. Из уравнения A.5) следует,

182 Глава 5
ЧТО
i^-,4-| = o' (l-6)
dQ dQ
т.е. что для дифференцирования нет обратной операции. Это очень
неудобно, так как все привыкли думать об интегрировании и дифферен-
дифференцировании как об обратных операциях. Но тем самым мы предупрежде-
предупреждены о том, что интегрирование следует вводить формальным путем.
Определим его как операцию, обозначаемую символом fdQ..., со свой-
свойствами
/"rf© =-0, fdQ 6=1, A.7)
т.е. эта операция действует в точности как дифференцирование. При
таком определении операция интегрирования удовлетворяет критерию
инвариантности относительно трансляции переменной интегрирования
на постоянную величину.
Мир одной грассмановой переменной довольно уныл, а потому рас-
рассмотрим N грассмановых переменных 6г- , i =1, ..., N, удовлетворяю-
удовлетворяющих условиям
[в,-, Bj\ = 0, i, /= 1, ..., /V. A.8)
Введем соответствующие операторы производных в соответствии с
равенствами
!^- .М'=Л-/. h^'^?-l=0. A.9), A.10)
Любую нормальную (т.е. не грассманову) функцию переменных в,- мож-
можно записать в виде
/(в,- ) =а ±:$i%i + CijQi&j +¦ ... -ксв^... BN, A.11)
где последний коэффициент является грассмановым или нормальным
в зависимости от /V. Интегрирование определяется так же, как и в
случае одной переменной:
fdQi =0, ffl&tQi =1 (по i нет суммирования). A-12)
Когда мера интегрирования и подынтегральное выражение содержат более
одной переменной, условимся проводить интегрирование в соответст-
соответствии с процедурой вложения. Так, например,
в2в2)в1=-1. (ЫЗ)
В качестве примера рассмотрим интеграл
A.14)

Интеграл по траекториям при наличии фермионов 183
где М - антисимметричная N х /V-матрица с нормальными элемента-
элементами т( ¦, а экспонента определяется своим разложением в рад. При
/V = 2 имеем
i2(M) = fide1de2[ 1 - 2т12е,е2 ]= A.15)
2ш12 =¦ 2х/"±ПГ. A.16)
При нечетном N можно показать, что интеграл / обращается в нуль; это
согласуется с тем, что интеграл / пропорционален квадратному корню из де»
терминанта, так как детерминант нечетномерной антисимметричной матрицы
равен нулю. Чтобы угадать вид общей формулы, рассмотрим случай /V = 4.
Нетрудно видеть, что соответствующие члены в разложении экспоненты имеют
вид
е "e 1 г
() + .„ 4e1eae34
+ :т14 т2з 1 + ••• > A-17)
откуда /4(М) = 4[m12m34 -77ii3m24 ^тит23]= 4,y/dfet M,
A.18), A.19)
так что общая формула может быть записана в виде
1N(M) = B)N/2sffcTW. A.20)
Это первая интересная формула. Ее следует сравнить с эквивалент-
эквивалентной формулой для бозонных (нормальных) полей, в которую квадрат-
квадратный корень из детерминанта входит в знаменатель.
Далее рассмотрим интеграл
Х'в' , A.21)
где X; - грассмановы числа,
ix,-,X/i=0. 1x^9/} =0. A.22)
Чтобы упростить задачу, вычислим A.21) сразу при /V = 2. Тогда
е-егл/е + хге = i _ 2т12е1д2 -xiX2Q1e2i A.23)
так что 12{М; х) = 2(ш,а + у

184 1 'лава 5
Этот результат можно было бы получить и более простым путем, фор-
формально дополнив до полного квадрата показатель экспоненты и сдви-
сдвинув переменную интегрирования так, как будто мы имеем дело с обыч-
обычным интегрированием, т.е. положив
е' = е+-1лг»х A.25)
и записав
= I ,dttj ... «Од, e " '" " 4 A '" * = A.26)
= e 4 Лу(.И). A.27)
В частном случае /V = 2 мы приходим к формуле A.24). Цель этого
небольшого упражнения двоякая: во-первых, вывести формулу A.27) ,:,
во-вторых, показать, что благодаря определению A.7) при грассмано-
вом интегрировании разрешен сдвиг переменных.
Приведенные выше формулы можно обобщить на случай интегри-
интегрирования по комплексным грассмановым переменным. Для примера
п оложим
п (9f 'в>; * (Ql ~ iQl)> A#28)
так что dQ1d%2= dx]*dr\, вт MQ = - 2in* т12ц. A.29), A.30)
Если ввести 1x1- матрицу 2m12, то на основании формулы A.16) по-
получим
fdt) (/n*ei'Tl*Wn = det M, М=2тп. A.31)
Эту формулу можно обобщить на случай/V комплексных грассмановых
чисел. Аналогично доказывается, что
•¦?*л + *?л* =det ,Ие-^*(л/)~Ч; A.32)
где 5 и ^ * - комплексные грассмановы числа. Формулы A.27) и
A.32) чрезвычайно важны для вычисления интегралов по траекториям
при наличии фермионов, связанных с внешними грассмановыми ис-
источниками.

Интеграл по траекториям при наличии фермионов 185
Задачи
A. Дайте общее доказательство формулы A.20).
Б. Докажите формулу A.27) при /V = 4 явным вычислениям.
B. Докажите соотношение A.31), если М' есть матрица 2* 2.
Г. Докажите формулу A.32).
Д. Покажите, что / da <ф еаЛ/Р = det M, где а и C — незави-
независимые грассмановы переменные.
§ 2. Интеграл по траекториям для свободных
ферми-полей
Существуют три способа описания свободных частиц со спином
1/2 в пространстве Минковского.
А. Вейлевский лагранжиан
?ц> =-у\ а • ду, B.1)
описывает с помощью двухкомпонентного комплексного спинора ц>^
левую безмассовую частицу одновременно с ее правой античастицей
(например, безмассовое левое нейтрино и правое антинейтрино), при-
причем эти частицы связаны между собой дискретным СР-преобразова-
нием
ГР: Vl- °2V*L ¦ B.2)
Б. Майорановский лагранжиан
?> A n im , г +
*-И - VL а • dvL "-у- (Ч^ a2yL+VL°2V*L) B.3)
описывает массивный вейлевский спинор. Он интерпретируется как
самосопряженная частица со спином 1/2 и двумя степенями свободы,
отвечающими спину, направленному вверх или вниз. Массивный вей-
вейлевский спинор можно выразить через четырехкомпонентное майора-
новскэе поле
так что майорановский лагранжиан принимает вид
? ^^ f ^ B-5)

186 Глава 5
В. Дираковский лагранжиан
^ К
описывает частицу с двумя степенями свободы и отдельную от нее
античастицу (например, электрон и позитрон). Этот лагранжиан имеет
вдвое больше степеней свободы, нежели вейлевский и майорановский,
и помимо СР сохраняет и Р. Для удобства этот лагранжиан выражают
через четырехкомпонентный дираковский спинор
ч
?)
в виде ?D = TD(y.d.-H im) TD. B.8)
Если ввести связь с внешними источниками, то для каждого из
этих лагранжианов можно построить производящий функционал. Вейлев»
ские поля у - могут быть связаны с источниками в выражениях вида
Эти два вида связи эквивалентны при замене х р = СТ2 Х*г • Следователь-
Следовательно, можно рассматривать только один тип связи с источником.
В вейлевском случае рассмотрим функционал
L
B.10)
Как и во всех свободных теориях, он без труда вычисляется. Введем
фурье-образы
^ i ит.д, B.11)
как в гл. 3. Показатель экспоненты принимает вид
S 4^(p )ст T
w fp[^_ (
Перепишем его в виде BЛ2)
B.13)

Интеграл по траекториям при наличии фермионов 187
где q>\ (р) — решение уравнений движения
B.14)
При такой форме записи мы видим, что можно сразу провести интегри-
рование по у , заменив переменную интегрирования на ц>,, что при*
ведет к изменению произвольной нормировки:
BЛ5,
а2а.ра2 = ст ¦ р.. B.16), B.17)
где мы использовали соотношения [ гл. 1, формула D-37) ]
о.ра-р = р2, а2а.ра2 = ст ¦ р..
Если мы, как и в бозонном случае, положим
V=-eiz, 2.18)
где Z - производящий функционал связных функций Грина, то
ZlxL, x\]= ~^d*x X\(x) (iu • д)~* iL(x). B.19)
Отсюда мы извлекает двухточечную связную функцию Грина
)-» 6 »(*. -ж2) B.20)
или в импульсном пространстве
сЬ>(р)=._ _i_ =_,- СТ'Р ; B.21\
а.р р2
это, конечно, не что иное, как пропагатор. В такой форме данное вы-
выражение не имеет смысла, если не задано правило обхода полюса при
Р2 = 0. Мы можем задать его по аналогии с бозонным случаем, но нуж-
нужно иметь в виду, что в фермионном случае применение (- is ^правила
не обосновано соображениями сходимости, так как мы имеем дело с
формальным грассмановым интегрированием. Поэтому для подтвержде-
подтверждения того же самого предписания обходя полюса, что И[В бозонном слу-
случае, видимо, нужно перенести проблему в евклидово пространство.
Другие два случая рассматриваются аналогично» В майорановском
случае исходим из
1^4^*^1 B.22)

№ Глава 5
и, дополняя до полного квадрата, получаем
r.TV-., B.23)
где р-уирц, B.24;
что приводит к пропагатору
Р ? т р2 -т2
если учесть равенство рр= р2. И в этом выражении нужно в явной фор-
ме добавить правило обхода полюса. Дираковский случай исследуется
сходным образом, исходя из функционала
где теперь ? и ? - четырехкомпонентные дираковские грассмановы
источники. Аналогичные выкладки приводят к выражению
WD = N'e~ (d4tiD (P + -») Ed ^ B.27)
из которого мы извлекаем пропагатор
G«(P)=_^ =-i P~m , B.28)
D Р + т р2_ш2
куда следует добавить (- i e ^предписание.
Как и в бозонном случае, можно построить производящий функ»
ционал непосредственно в евклидовом пространстве, а затем продол-
продолжить функции Грина в пространство Минковского.
Группа Лоренца в евклидовом пространстве становится компакт-
компактной, что означает (гл. 1), что она состоит из двух совершенно неэкви-
неэквивалентных 5^/B)"КОМпонент. Однако оператор производной все так же
преобразуется по представлению A/2, 1/2,), и если мы теперь захо-
захотим составить лоренцовский скаляр, линейный по производной, то нам
потребуется два разных поля ^ ~A/2, 0) и у „ ~@, 1/2) для постров"
ния векторных величин, преобразующихся как A/2, 1/2). Можно пос-
построить два таких действительных вектора с компонентами
>Ь + '^i» -^l"^r + 4>\c^l), B.29)

Интеграл по траекториям при наличии фермионов 189
помня при этом, что, так как ш и у„- грассмановы числа,
Li Л
Если ввести четырехкомпонентный евклидов дираковский спинор
B.32)
то можно переписать рассматриваемые векторы в виде
I B-33)
где у — евклидовы у-матрицы
О i\ - /0 -о
B-34)
удовлетворяющие соотношению
19ц, yJ'=-25,v; B.35)
У5 = (о _,j. B.36)
Возможные массовые члены имеют вид (в евклидовом пространстве
существует только один тип массы)
fiv ^i**' <2-37)
так что евклидов лагранжиан дается выражением
? ^^ ^ B.38)
причем мы позаботились о том, чтобы лагранжиан был действитель»
ным,
?* =? . B.39)
Соответствующий производящий функционал таков:
•№/$> 5ТЯ] = /V Г.Ю^о^е" .^4ж'[?? + ••EW + •¦4.??]=» B.40)
} BЛ1)

190 Глава 5
откуда получаем выражение для пропагатора
С?(Р)=_±_ .,- Р— } B#fi)
Р + т Р2 + т2
где учтено, что рр = - р2, Отметим, что,как и ожидалось, в знаме-
знаменателе пропагатора стоит величина р2 + г^.Мы с удовлетворением
видим, что у него такая же структура, как и у дираковского пропагатора
в пространстве Минковского.
В случае вейлевских полей, по-видимому, не должно быть подоб-
подобного соответствия: в евклидовом пространстве невозможно построить
уравнение первого порядка для поля, преобразующегося по представ-
представлению A/2, 0), исходя из инвариантного лагранжиана, содержащего
только это поле (как мы только что видели, это легко можно сделать,
если рассматривать два вейлевских поля). Если ФИТ может быть хоро-
хорошо определен только в евклидовом пространстве, как утверждают спе-
циалисты по аксиоматике, то тогда, вероятно, мы столкнемся с впол-
вполне реальной проблемой там, где приходится иметь дело с вейлевскими
полями, например в теории слабых взаимодействий или в ее объедине*
нии с КХД. Подчеркнем, что в рамках теории возмущений с теорией
поля, содержащей вейлевские поля в пространстве Минковского, вроде
бы не происходит ничего плохого. Но может оказаться, что при более
полном исследовании обнаружатся сюрпризы, которые потребуют удво-
удвоения числа вейлевских фермионов, что при некотором (большом) мао
штабе восстановит векторно-подобную структуру слабых взаимодей-
взаимодействий.
С другой стороны, поскольку ферми-поля входят в перенормируе-
мый лагранжиан квадратично, их интегрирование приводит только к
детерминантам. Поэтому можно думать, что нам требуется лишь какой-
нибудь евклидов функционал, который приводил бы к правильному ( в
смысле его продолжения в пространстве Минковского) детерминанту.
Такой подход требует удвоения числа независимых грассмановых по-
полей (см. лекции Коулмена "Применения инстантонов" [ 1 ] и задачу Д).
Задачи
А, Вычислите производящий функционал для майорановского и ди-
дираковского полей в пространстве Минковского.
Б, Покажите, что в евклидовом пространстве оператор д преоб-
преобразуется по представлению A/2, 1/2).

Интеграл по траекториям при наличии фермионов 1?1
В. Пусть в евклидовом пространстве задано ф^—A/2, 0). По-
Постройте квадратичную форму, преобразующуюся по представлению
A. 0).
Г. Покажите, что спинорный лагранжиан в евклидовом простран-
пространстве обладает следующим любопытным свойством: массовый член в
лагранжиане инвариантен относительно так называемого кирального
преобразования уЕ -» e'aVs fE, а. кинетический член - нет!
л
Д. Формально определим i. = х0,+ 1т)ц>, где х и у - независимые
четырехкомаонентные грассмановы поля. Покажите, как нужно инте»
грировать, чтобы получить обычный дираковский детерминант. Проана-
Проанализируйте в этом случае киральную инвариантность.
§ 3. Фейнмановские правила для спинорных полей
В предыдущем параграфе говорилось о фейнмановских правилах
для свободных ферми-полей. Здесь мы выведем правила для взаимо-
взаимодействующих спиноров. Спиноры могут взаимодействовать по-разному,
лишь бы выполнялось условие сохранения спина, которое требует, что-
чтобы все вершины взаимодействия содержали четное число пар спинорных
полей. В гл. 1 мы уже приводили примеры теорий со взаимодействую-
взаимодействующими фермионами.
Число возможных фермионных взаимодействий резко сокращается,
если мы накладываем условие перенормируемости, которое требует,
чтобы число примитивно расходящихся диаграмм было конечным. По-
Поэтому вычислим кажущуюся степень расходимости D произвольной
фейнмановской диаграммы с фермионами.
Рассмотрим диаграмму с L петлями, 1Ь бозонными внутренними
линиями, If фермионными внутренними линиями, V вершинами, каждая
из которых имеет /Vb бозонных и Nf фермионных хвостов, Еь внешни-
внешними бозонными линиями и Ег внешними фермионными линиями. Как мы
только что отметили, числа Nj и Ее должны быть четными. Число пе- '
тель дается соотношениями
L =/ -V + \ = Ib +If -V + 1. C.1)
Кажущаяся степень расходимости в d измерениях равна
Dd = dL-If-2Ib, C.2)
так как каждая внутренняя спинорная линия вносит только одну обрат-
обратную степень импульса. Далее, полное число фермионных линий равно
N,V = Ef+.2If C.3)

192 Глава 5
и аналогично полное число бозонных линий -
NbV=Eb+21b. C.4)
Эти соотношения позволяют записать Dd в виде
Dd= d- (d-\)E{ - — (d- 2)Eb -V[d- _L (d~l)Nf-
- — (d-2)Nb]. C.5)
При N r - Er =0 данное выражение сводится к полученному ранее
выражению для случая одних бозонов. В других измерениях выражение
C.5) имеет вид
D2 = 2 - ~ Ef - VB - — Nf) B измерения), C.6)
откуда следует, что /Vy< 4 B измерения), C.7)
так как в противном случае расходимость будет расти с ростом числа
вершин. Следовательно, даже в двух измерениях существует ограни-
ограничение на тип разрешенных фермионных взаимодействий: в нем не дол»
жны содержаться степени выше (уL. Можно сказать иначе: в противо-
противоположность бозонным полям, которые в двух измерениях безразмер-
безразмерны, спинорные поля имеют размерность (- 1/2), так что взаимодей-
взаимодействие наибольшей степени, не требующее введения размерной констан-
константы связи, — это у4.
В четырех измерениях имеем
D4= 4-JL Ef -Еь -V[4- — Nf -Nb]. C.8)
2 2
Если мы не хотим, чтобы число примитивно расходящихся диаграмм
росло с ростом числа вершин, то нужно потребовать, чтобы выпол-
выполнялось условие
4 - A Nf - Nb > 0, C.9)
¦2 ;
где Nf - четное число. Решение этого неравенства Nb = 0, Nf = 2 по-
похоже на включение массового члена, а не на вершину взаимодействия;
решение Nf= 0, Nb = 2, 3, 4 приводит к рассмотренным ранее взаимо-
взаимодействиям 92t ф3 и ф4. Единственное новое решение, включающее как
фермионы, так и бозоны, таково:
Nf = 2, Nb = 1, C.10)

Интеграл по траекториям при наличии фермионов 193
что дает
D4 = 4- -I Ef-Eb. C.11)
Это новое решение, описывающее единственное разрешенное перенорми«
руемостью фермионное взаимодействие, невероятно ограничивает все
возможности: перенормируемые фермионные взаимодействия должны
содержать не более двух фермионных полей и одного бозонного поля.
Следовательно, в четырех измерениях фермионы входят в лагранжиан
Х- только квадратично! Данное обстоятельство можно выразить иначе:
в четырех измерениях фермионы имеют размерность (- 3/2), а бозо-
бозоны - (- 1). Стало быть, единственная нетривиальная связь размерно-
размерности 4 - это связь двух фермионов и одного бозона
Сделанный нами примечательный вывод чрезвычайно упрощает
анализ теорий, включающих взаимодействие спиноров. Если заданы
два поля со спином 1/2, то можно образовать комбинации либо со спи-
спином 0, либо со спином 1. Связи с полем спина 0 - это юкавские связи,
и они возникают во многих обличиях. В пространстве Минковского для
дираковского поля имеем связи
где 9 — скалярное, a q>* — псевдоскалярное поле. Для вейлевского по-
поля имеем
•VlWPi. ^tcr2v*q,2, C.13)
L h
где q>j и <р2 не обладают определенной четностью. В евклидовом про-
пространстве возможные связи имеют вид
i t\> ф, ^ -¦ у.Т <р' (евклидово пространство) C.14)
Связи со спином 1 для дираковской частицы в пространстве Минковс-
Минковского имеют вид
C.15)
где A w - векторное поле, ач4м - аксиально-векторное поле. Для вей-
левских полей имеем связи
iyU^^, i^^RB'^ C.16)

194 Глава 5
где Вц и В'ц не обладают определенной четностью. Векторные связи
в евклидовом пространстве таковы:
Взаимодействие спинорных и векторных полей будет подробно рассма*
триваться в следующих главах. Фейнмановские правила для вершин
юкавского взаимодействия сводятся просто к самим безразмерным
юкавским константам связи:
i
' — if: ifYVy, C.18)
— f'Ys- /'^V C.19)
Здесь штриховыми линиями обозначено бозонное поле, а сплошными -
спинорное, причем спинорные индексы опущены.
Грассманова природа спинорного поля находит отражение в одном
кардинальном изменении фейнмановских правил: если в диаграмме име-
имеется замкнутая фермионная линия (петля), эту диаграмму нужно брать
со знаком минус, что иллюстрируется следующим примером.
Рассмотрим выражение (скажем, в евклидовом пространстве)
,,+ \А{х)]
J1 = 1, C.20)
A]
где А (х) - скалярное поле, а детерминанты следует понимать как
функциональные. Мы можем выразить их через интегралы по траекто-
траекториям, причем детерминант в знаменателе, дается интегралом по бозон-
ным полям, а в числителе - по грассмановым полям, В результате
имеем
C.21)
В такой форме это выглядит как теория грассманова поля у, взаимо-
взаимодействующего с комплексным скалярным полем через внешнее поле

Интеграл по траекториям при наличии фермионов 195
А(х). Фейнмановские правила таковы:
• : -bj для ерассмановой линии,
¦ ¦ — для линии бозонного поля,
Л.
где поле А изображается волнистой линией, В такой теории пропагатор
поля А будет иметь поправки, связанные с диаграммами "поляриеации
вакуума" ~~^^\v~^^ +¦ ллл/ ^ч^л^ , вклады которых,
согласно приведенным фейнмановским правилам, совершенно одинаков
вы* Но эти диаграммы не должны изменять пропагатор А, поскольку
мы, начав с W = 1, знаем, что теория должна быть тривиальной! Сле-
довательно, при сложении эти две диаграммы должны взаимно уничто"
жаться: грассманова петля должна приобрести знак, обратный знаку
бозонной петли.
Итак, где бы не встречались грассмановы (спинорные) поля, сог-
согласно фейнмановским правилам, нужно умножать диаграмму с п раз-
разными фермионными петлями на (- 1)". Можно объяснить это правило
тем, что разрезанная фермионная петля в соответствии с обобщенной
ферми-статистикой должна быть антисимметричной относительно пере-
перестановки ее хвостов, так как в силу условия унитарности такая петля
связана с физической амплитудой.
В заключение заметим, что юкавская связь допускает перенорми"
руемые самодействия среди скалярных полей (см, задачу),.
Задачи
А. Найдите размерности, при которых существуют перенормирув"
мые теории, содержащие фермионы.
Б, Задан лагранжиан
1) выведите фейнмановские правила; 2) найдите на однопетлевом
уровне зависимость юкавскойконстанты связи от масштаба; 3) иссле-
исследуйте перенормируемость лагранжиана; в частности, проанализируйте

196 Глава 5
все однопетлевые диаграммы и исследуйте структуру требуемых контр-
контрчленов., Является ли лагранжиан в такой форме перенормируемым?
Если нет, исправьте его.
§ 4. Вычисление и масштабное преобразование
фермиониых детерминантов
Начнем с производящего функционала в евклидовом пространст-
пространстве для теории, описывающей взаимодействие скалярного поля с четы^
рехкомпонентным спинорным полем
D.1)
где 5 ~fd*[ ц
2 4!
- /ф+ + ^ (д + im +*/>q>)T1-iEtT1-iT-t?]. D.2)
Спинорные поля входят в это выражение квадратично и поэтому
могут быть функционально проинтегрированы. В результате приходим
к выражению (S g[ip} /] дается формулой D,5) из гл. 3)
где после дополнения до полного квадрата мы использовали формулу
A.31). Можно переписать его в виде
$ ? Г>> -S?t9, /1. Л .,
J .Х1ф е detE.f гт + if if),
D.4)
Это очень хорошая формула, позволяющая вычислять WE по теории
возмущений, В данном параграфе мы сосредоточимся на вычислении
WE методом перевала Для начала разложим S# вблизи классической
полевой конфигурации q>0, f 0, Y . Функциональное разложение имеет
вид
52S

Интеграл по траекториям при наличии фермионов 197
+
D=5)
гдел = ?-?0, Р =Ф-Фо-
Как и в гл. 3, § 4,мы проводим разложение вблизи тех полевых
конфигураций, которые оставляют действие стационарным, т.е. удов-
летворяют классическим уравнениям движения:
D 6)
D.7)
_SS_| _{_д2 + т2+2^_ 2) . t
5ф ° "з7" <90™0 + l' o^o ~ •* = * '*'
Отбрасывая эти линейные члены, мы получаем приближенное вы-
выражение для SE, которое квадратично по отклонениям полей от их
ционарных значений^ В явной форме
С С • ^ t /5 • ' • /• \ ^ ^ /12 2 Ъ. 2 ч
Эр ~ ор п. + <л (о + im + itФп)т\> + — <р{— of + m + — Ф )р>
? fc о 2 2 °
+ f / < rtt pT0 > + г /¦ < Т1" pri > . D.9)
Так как мы хотим функционально проинтегрировать по п,, л^ и р, то
дополняем это выражение до полных квадратов, получая
SE = Se\o + <г)'1[(д.+ im' + if<fo)r\'> + — <p[-d2+n2t
где n' = ^ +
Кроме того, в данном приближении
Юу = 2)л = 2)я', 3)ф=-2)р, D.12), D.13)
поскольку якобиан преобразования равен 1. Это позволяет выполнить
функциональное интегрирование выражения D.10), пользуясь формула"

198 Глава 5
ми приложения Л и § 1 этой главы. В результате имеем
_, — Sp „. Л ,
+ *Г т1 (d+:im +:if<p)~ f )] , D.14)
где обратный оператор во втором детерминанте действует как на^0,
так и через iyQi
Так же как и в приближении метода перевала для скалярной тео^
рии поля, действие SE\ Оз рассматриваемое как функционал от источник
ков /, ? и ^' ^ порождает все древесные диаграммы, тогда как детер-
детерминанты дают однопетлевые вклады, имеющие первый порядок пой.
Выполним функциональное преобразование Лежандра между источ^
никами J ,{ и { ' и новыми классическими источниками
D.15)
5!{х)
8ZE
и введем эффективное действие
DЛ7)
порождающее одаочастачно-неприводимые функции Грина, В классическом
приближении это не что иное, как классическое действие с классичес"
кими источниками D.15) и D.16), играющими роль полей:
п тип > 19 Т К"' ' К" '
Первые квантовомеханические поправки к DЛ8) даются детерми^
нантами D.14). Пользуясь методом ^-функций, (гл. 3), установим неко-
торые их свойства. Эти детерминанты более сложны из^за наличия спи"
норных индексов и обратного оператора во втором детерминанте в фор-
формуле D.14).
Будем рассматривать частный случай постоянных полевых конфи-
конфигураций и пренебрежем всеми массами. Тогда

Интеграл по траекториям при наличии фермионов 199
1 л 1
(? if)
— , D.
так что аргумент детерминанта скалярного поля принимает вид
D^0)
Кроме того, при постоянном <р0 фермионный детерминант равен (см.
задачу)
det (l+ i/9o) = [det (- д2 + f> f .фа )]\ D.21)
о
На основании формулы D.20) производящий функционал можно пере"
писать в виде
0 2
^ . .... % 1 Ы
D.22)
О
что, правда, допустимо только при постоянных q>0 иТ0. Чтобы еще боль-
больше упростить дело, предположим, что f0 - киральное поле, т.е. что
ytv у =0 (или ш =0): 4^ У * 0. D.23)
„Гц о тл
Тогда аргумент второго детерминанта можно переписать в виде
(-д? + А)(-д2 + В), D.24)
где А и В - константы, содержащие <р0 и УJ Y„ и удовлетворяющие
равенствам
А + В = (/2+ -Л-)<р2, D.25)
лв = J_ x/v - г^'^ФоЧ'о» D«26)
2 °
Таким образом, задача сводится к вычислению детерминантов вида
det(- d2 +C), где С - константа. Из изложенного в гл. 3 мы зна-
знаем, что
-5 'г @)
det(-d2+ C)=e f-^ + CJ , /4ф27)

200 Глава 5
где
/,v м4 / С 2-s г (в -2)
C]() = T6^V -—j-/^4*, D.28)
или
'[-«•¦el."»"—И^С!(-Т+ЬТ'- <4'29)
Вооружившись этими формулами, нетрудно найти однопетлевой вклад
в эффективный потенциал (см. задачу). Приведем лишь результат при
256тт2 ° Т
+ In ^ уо ). D.30)
Здесь первый член такой же, как и в чисто скалярном случае; его дают
бозонные петли. Второй член - это вклад фермионных петель в потен-
потенциал; как и полагается, он взят со знаком минус.
Масштабные свойства этих детерминантов выясняются столь же
просто. Напомним (гл. 3), что при изменении масштаба
где I - функция, даваемая выражением D.28), так что
det" [е-20 (-д2 +¦ С)] = е~2па f1
det (_^2 + Q
8 • 16 тг2
D.32)
если принять, что константа С при масштабных преобразованиях меня"
ется с такой же размерностью, как и -Ж Более строго вопрос рас
сматривается в гл. 3, § 6. Таким образом, однопетлевая масштабная
поправка равна
Ге - Ге + ^ ^d"x t 2(— )(/• М2 + (- 2)(- -L)D2 + В2)].
2 2
D.33)

Интеграл по траекториям при наличии фермионов 201
D.34)
Написав
42 + В2 = (Л + ВJ -2АВ =
мы видим, что при изменении масштаба функция р? приобретает
ны того же типа, что и в классиче'ском лагранжиане, а это прив'одит к
изменению безразмерных констант связи:
4! 4! 4! 128 тг2 (^~ ' Ь ( * '
f*f'-f--%h-f2- D-36)
6й ТГ
Таков пример зависимости от масштаба в теории с несколькими кон-
константами связи. Новое здесь в том, что изменения масштаба образуют
связанную систему. Такое явление легко объяснить, пользуясь диаграм-
диаграммами: фермионная петля, очевидно, вносит вклад в константу <р4, а с
точностью О{%) фермионная константа связи определяется только при*
сутствием исходной фермионной вершины:
\
П
где штриховые линии отвечают скалярным, а сплошные - спинорным
полям.
Заметим, что при изменении масштаба должны также возникать
добавки к фермионному и скалярному кинетическим членам, но в на'
шем приближении постоянных полей эти добавки не появились [ фор"
мулы D.35) и D.36)]. Например, фермионный детерминант det § + (/<р)
нельзя записать в виде D.21), если q> зависит от х. В общем случае
в закон масштабного преобразования этого детерминанта будет вхо-
входить кинетический член; это соответствует тому, что сами поля приоб-
приобретают на однопетлевом уровне аномальные размерности, проистекаю-
проистекающие от диаграммы Q . В чистой теории q>4 скалярное
поле приобретает аномальную размерность только на двухпетлевом
уровне, так что при изменении масштаба детерминантов данный эффект
не проявляется. Итак, формулы D.35) и D.36) должны быть поправлены
с учетом перенормировки волновой функции.

202 Глава 5
Задачи
А . Покажите, что если пренебречь членами O(fi), то
Г?[<Ркл*^кл ^ 1 есть классическое действие.
Б. Покажите, что в четырех измерениях det (д + im) = [det(-<?? +
В. Найдите однопетлевой вклад в потенциал, включая вклад ферми=
онов.
*Г. Пользуясь диаграммами, выведите на однопетлевом уровне
формулы для зависимости Л и / от масштаба (с учетом перенормиров"
ки волновой функции) и сравните с формулами D.35) и D.36).
ЛИТЕРАТУРА
1. Coleman S., in: Proc. of the 1977 Int. School of Subnuclear Physics,
Erice, Italy, ed. A. Zichichi, Acad. Press, 1979.

Глава 6
Калибровочные симметрии,
конструкция Янга-Миллса
§ 1. Глобальные и локальные симметрии
В гл. 1 мы привели примеры .лагранжианов, содержащих поля со спи-
спином 0 и К, но не стали рассматривать какие-либо теории, содержаще
взаимодействие с полями более высоких спинов. Дело в том, что поля со
спином 1, *4 и 2 можно очень красиво ввести, просто потребовав, чтобы
все симметрии, какие только имеются в системе со спинами % и 0, vior-
ли произвольным образом меняться от точки к точке в пространстве-вре-
пространстве-времени. Поля со спином 1 соответствуют обобщению внутренних (т.е. не-
доренцовских) симметрии; поля со спином 2 возникают тогда, когда прос-
пространственно-временные симметрии (гдобальная инвариантность относи-
относительно группы Пуанкаре) становятся локальными в пространстве-време-
пространстве-времени; поля со спинами '/, и 2 появляются при обобщении глобальных су-
суперсимметричных теорий и превращении их в .локально суперсимметрич-
суперсимметричные.
Мы не будем рассматривать .локальное обобщение пространственно-
временных симметрии, а, следуя Янгу и Миллсу [ 1 ] , сосредоточим вни-
внимание на построении теорий, локально инвариантных относительно'
внутренних симметрии. Самый старый пример теории с скальной
симметрией - электродинамика Максвелла Общий характер поня-
понятия "калибровки" (т.е. локализации) впервые осознала Э.Нетер [ 2].
Процедура калибровки в ее современной форме была разработана в
20-х годах Вейлем.
Рассмотрим простейший возможный .лагранжиан, содержащий спи-
норное поле,
?Q =— ^i о . дц^ = ц^ aw дц ч>^ + Поверхностный член, A*1)
который, как нам известно, инвариантен относительно фазового прв-
образования

204 Глава 6
где а — константа. Основная идея "калибровки" этой фазовой симмет-
симметрии заключается в том, чтобы сделать .лагранжиан ? инвариантным
относительно фазовых преобразований того же вида, что и A.2), но
с константой а , произвольным образом зависящей от я, т.е. инва-
инвариантным относительно преобразований
yL(x) >e'«<*>4,L(*). A.3)
Инвариантность лагранжиана ? относительно .локального фазового
преобразования A.3) нарушается из-за наличия в нем оператора произ-
производной д , так как в результате преобразования A.3) мы имеем
так что
Чтобы получить нужное обобщение лагранжиана ?. , введем новый опе-
оператор S (который будет обобщением оператора д ), обладающий тем
свойством, что при локальном фазовом преобразовании
или, на операторном языке,
?u_efa<«) фце-'я<ж>. A.7)
Этот новый оператор производной называется ковариантной производной.
Теперь оказывается тривиальным следствием, что новый лагранжиан
1^1 о»Ъ^ь A.8)
инвариантен относительно преобразования A.3). Все это превосходно,
но нужно построить саму ковариантную производную. Мы допускаем,что
она имеет вид
где А (х) - некая функция координаты х. В таком случае требование
ковариантности
%~+К = д»+ *^(*>= е^Сж)[дц + Мм(*)]в-'а(ж5 A.10)

Калибровочные симметрии, конструкция Янга — Миллса 205
становится трансформационным свойством функции А^:
А»(*)~+ <(*)= A]l(x)-aila(x). A.11)
Теперь уже новый лагранжиан
?= ц>1 о»(ди+ iA»(x))vL = ?„ + »>/ °»Ч>ьА»(х) A.К)
инвариантен относительно одновременных .локальных преобразований
yL(x) _—e'°<*> yL, Лм(«) —+ Лм(*)- 5ца(Ж). A.13)
Глобальная симметрия .лагранжиана ?Q обобщается на .локальную сим-
метрию, т.е. калибруется, ценой введения нового векторного поля
А (х), взаимодействующего с сохраняющимся током. Как нетрудно ви-
видеть, новое гщле 'А (х) имеет ту же размзрность, что и д ••; поэтому
его можно отождествить с каноническим полем в четырех измерениях
(при другом числе измерений поле А нужно умножить на размерную
константу связи, прежде чем его можно будет таким образом интерпре-
интерпретировать). Кроме того, так как оператор г'о^ эрмитов, поле А (х) дей-
действительно.
Заметив, что комбинация
р^ = дЛ~дЛ о.н)
инвариантна относительно калибровочного преобразования (U3), не-
нетрудно теперь записать кинетический член для поля А (х) так, чтобы
сохранить эту инвариантность. Размерность комбинации A.Т4) равна
-2, и поэтому мы можем построить из нее новый лагранжиан
?- 1 F' F»v, A.15)
где g - безразмерная константа, которую можно устранить, положив
А^ = gAy , так что если переписать все через А' то эта константа
войдет в произведение А" на ток кЛа\ в формуле A.12). Множи-
Множитель 1 /4 соответствует принятому определению константы g. Ко-
Конечно, как можно было бы уже догадаться, выражение A.15) - это
максвелловский лагранжиан. У нас получилась замкнутая теория взаи-
взаимодействующих полей со спином 1 и 1/2, описываемая лагранжианом
(ой + ^(х))^. A.16)

206 Глава б
Хотя эта теория и очень хороша, она неперенормируема ( в чем мы убе -
димся ниже) из-за одного неожиданного осложнения, совершенно пра-
правильно называемого аномалией (Адлера - Белла - Джекива) и имеюще-
имеющего отношение к левоспиральной природе поля ц> . Если мы калибро-
вочно-инвариантным образом свяжем А с четырехкомпонентным ди-
раковским полем, то никаких проблем не возникнет и мы придем к лаг-
лагранжиану
^ ^ A.17)
который описывает КЭД, если отождествить А (х) с фотоном, Y с элек-
электроном и g с электрическим зарядом. Лагранжиан ? инвариантен
относительно локальной симметрии
А^{Х) ,Ац(х) - дц сс(х),
а в отсутствие массового члена для поля ч/ еще и относительно глобаль-
глобального кирального преобразования
П*) -» *%у(*)- AЛ8>
В квантовой теории поля эта киральная симметрия не точна (вновь аномалия)
даже в отсутствие массы у электрона, но это не создает никаких проблем,
так как с ней не связано никакое калибровочное поле.
Калибровочная инвариантность не допускает наличия какого-либо мас-
массового члена для А .
Прежде чем обощать это построение на более сложные симмет-
симметрии, кратко остановимся на разных типах глобальных симметрии.
Лагранжиан для N действительных скалярных полей q> , . . . , q>
? = _!_2 д д% ш±д^д»Ф A.19)
4 1 = 1 i
инвариантен относительно глобальных вращений в N измерениях O(N),
под действием которых iV-мерный вектор- столбец Ф меняется по правилу
Ф-Ф' = ЙФ, .0-20)
где R — матрица вращений (собственных и несобственных). Так как
произведение ФТФ (длина вектора Ф) О(Л0-инвариантно", для матри-
матрицы R выполняется соотношение

Калибровочные симметрии, конструкция Янга — Миллса 207
Матрицы собственных вращений можно записать в виде
R = exp(— co''2.;.), П.22>
где ш'; = —со'; - действительные параметры группы вращений, число
которых равно N(N — 1)/2, a Z.. — генераторы этой группы, число
которых тоже равно N(N — 1)/2. Рассматривая бесконечно малое из-
изменение вектора Ф
5ф= — со''1,.7Ф A.23)
-и требуя, чтобы выполнялись групповые свойства, можно доказать,,
что генераторы 1{. образуют алгебру Ли
[A.24)
Выше мы получили алгебру Ли для группы SO(N), пользуясь N х iV-мат-
рицами 2.., действующими на N-мерный вектор Ф. Из формул A.21) и
A.22) легко видеть, что эти матрицы действительны и антисимметрич-
антисимметричны. Но можно построить много разных матриц, удовлетворяющих соот-
соотношениям A.24). Это объясняется тем, что можно многими разными
способами представить группу SO{N). Мы выбрали способ, при котором
используется /V-мерное представление, но с таким же успехом можно
было выбрать присоединенное представление, число измерений которо-
которого равно числу параметров группы. В случае группы SO(N) присоеди-
присоединенным представлением может служить антисимметричный тензор вто-
второго ранга А.. = -Лг-. При этом элементы Л-. удобно рассматривать
как элементы некой антисимметричной матрицы А. Тогда при вращени-
вращениях
A^A' = RART; AT = -А, A.25)
где R — N х /V-матрица A.22). Затем легко построить инвариантный лаг-
лагранжиан, в котором А - скалярные поля:
A.26)
Симметричное "квадрупольное " представление S(y = +S;I- можно рас-
рассмотреть аналогичным образом, если только известно, что след тензо-

208 Глава б
pa S инвариантен относительно преобразований группы SO(N). Начав
с представления N группы SO(N), можно построить более сложные пред-
представления, описываемые тензорами более высокого ранга. В общем
случае тензор произвольно высокого ранга есть комбинация тензоров,
преобразующихся неприводимо (друг через друга) при преобразовани-
преобразованиях группы. Рассмотрим, например, тензор третьего ранга Т , и возь-
возьмем для определенности i, j, k = 1, . . . , 10. Этот тензор следующим
образом разлагается на неприводимые представления группы SOA0):
1) полностью антисимметричная часть T\ih\, имеющая
10-9. 8/1 • 2- 3 = 120 компонент;
2) полностью симметричная часть Т . имеющая
10• 11 • 12/1 • 2 • 3 = 220 компонент, которая содержит, после свертки
по двум индексам, вектор Ти- с 10 компонентами; следовательно,
Т...д разлагается на неприводимое представление с 2Т0 компонентами
и представление с 10 компонентами;
3) тензоры со смешанной симметрией относительно перестановки
индексов: антисимметричный относительно перестановки двух индексов
с 320 компонентами (= 45 ¦ 10 - 10 -120), и симметричный только по
двум индексам с 320 + 10 компонентами.
Итак, мы получили разложение приводимого тензора третьего ран-
ранга в группе SOA0) с 1000 компонентами на неприводимые части:
1000 = 120 + 220 + 10 + 10 + 320 + 320.
Подобное построение неприводимых представлений осуществляется
просто (хотя и утомительно); единственная тонкость возникает в том
случае, когда N-четное число, и тогда можно использовать тензор Ле-
ви-Чивиты е.. ^ ^ k с N индексами, чтобы расщепить пополам полностью
антисимметричный тензор ранга N/2. Кроме того, когда N/2 - четное
число, антисимметризованный тензор ранга N/2 расщепляется на два
действительных и неэквивалентных представления. Когда же N/2 - не-
нечетное число в результате получаются два сопряженных друг другу
представления. Например, в группе SOA0) полностью антисимметрич-
антисимметричный тензор 5 ранга имеет 252 компоненты, которые расщепляются на
126-мерное представление и сопряженное ему, причем операцию соп-
сопряжения выполняет е -символ.
Путем образования тензорных произведений векторов мы не полу-
получим всех представлений, поскольку у группы SO(N) имеются дополни-
дополнительно спинорные представления (например, группа SOC) имеет пред-

Калибровочные симметрии, конструкция Янга — Миллса 209
ставление с полуцелым спином). Если N - Ъх + 1, п = 1,2, . . . , то груп-
группа SO(N) имеет только одно действительное фундаментальное спинор-
ное представление размерности 2п\ например, группа SOC) имеет
действительное двумерное представлениз, S 0E) - действительное
четырехмерное спинорное представление и т.д., и из этих представле-
представлений могут быть построены все остальные. Если N = 2п, п = 2, $ 6 ..., то
группа S O(N) имеет два действительных и неаквивалентных фундамен-
фундаментальных спинорных представления размерностью 2" ~ 1 'каждое. Нако-
Наконец, при /V = 2п, п = 3, 5, . . . , группа SO(N) имеет два фундаменталь-
фундаментальных комплексных сопряженных друг другу спинорных представления.
Например, группа S 0F) имеет сопряженные представления 4 и 4 и
т.д. Все представления могут быть построены из описанных спинор-
спинорных представлений, так что они в этом смысле более фундаментальны,
чем векторное представление.
Рассмотрим теперь кинетический член для .V двухкомпонентных
спинорных полей
где а пробегает значения от 1 до JV и производится суммирование по
а . Мы видели, что в случае а = 1 выражение A.27) инвариантно отно-
относительно фазового преобразования. При а > 1 лангранжиан ?F инва-
инвариантен относительно гораздо более широкой симметрии. Рассмотрим
(опустив индекс а) преобразование
4>L+UyL, A-28)
где V - матрица N х N; тогда
Ясно, что если матрица V не зависит от х и унитарна, т.е.
I/I/f =U1U= 1, A30)
то лагранжиан ?f инвариантен по отношению к преобразованию A.28).
Из унитарности матрицы V следует, что ее можно выразить через
эрмитову N х N-матрицу Н в виде
U = еш; Н = нК A.31)

210 Глава 6
Эта эрмитова матрица Н зависит от N2 действительных параметров.
Заметим, что взяв матрицу Н пропорциональной единичной матрице,
мы вернемся к рассмотренной ранее фазовой инвариантности. Следо-
Следовательно, дополнительные новые преобразования порождаются бессле-
бесследовой частью матрицы Н, выражающейся через N2 - 1 действительных
параметров в виде
И= i ю Т , j4 = Г1, (U2)
где &У4 - действительные параметры, а ТЛ - эрмитовы <V х .V = матри-
матрицы с нулевым следом. Эти матрицы порождают унитарную группу SU(N)
в N измерениях и удовлетворяют соответствующим перестановочным
соотношениям алгебры Ли
[Тл, TB] = ifABCTc, A.33)
где fABC- действительные полностью антисимметричные коэффициен-
коэффициенты, называемые структурными константами алгебры [ это соотношение
поможе на A.24), но содержит другие коэффициенты /]. Приведем неко-
некоторые знаменитые примеры: /V = 2: ТА = Угол, ил - спиновые матрицы
Паули, А = 1, 2, 3; N = 3: ТА = КАЛ, Ал - матрицы Гелл-Манна, А = 1,
, . . . , 8. Матрицы Гелл-Манна удовлетворяют условию нормировки
A.34)
и имеют следующий вид:
/о 1 (Л
л1= 1 о о ,
\ о о о/
/О 0 04
U t 0/
Таким образом, в группе SU(N) имеются следующие фундаментальные

Калибровочные симметрии, конструкция Янга — Миллса 211
представления:
у ~N означает, что 5ц> = iаАТАц/, A.36)
ф'~ jy 03начает» что 5<+»' = -шАТА ц>', A.37)
где последнее свойство преобразования получено из требования, что-
чтобы произведение у' ц> было инвариантом. Тензорная структура в груп-
группе S U(.V) проще, чем в группе SO(N): сопоставим нижний (верхний) ин-
индекс а величине, преобразующей по представлению N(N) группы
SU(N): у ~ v, ya~.ty. Рассматривая эти представления как строитель-
строительные блоки, можно путем образования тензорных произведений получить
все представления группы SU(N). Одним из интересных представлений
является присоединенное представление М? , где М - бесследог ,я эр-
эрмитова матрица, содержащая N2 - 1 - элементов; как указывают ин-
индексы, она построена как произведение представлений N и N:
/VxN = (N2-l)+l. Удобно записать это представление как матрицу
М, преобразующуюся по правилу
или 5M = twA[TA, M]. A.38), A.39)
Можно также рассматривать присоединенное представление как {Ы2— 1)-
мерный действительный вектор, и ц этом случае матрицы представле-
представления ТА будут (N2 -1)(/V2 - 1)-мерными.
Другие типы представлений можчо построить в виде тензоров с
произвольным числом верхних и нижних индексов. Чтобы образовать
синглеты, можно свертывать верхние индексы с нижними, но не пару
верхних или нижних индексов. Так, например, представление Т , мож-
можно разложить на неприводимые компоненты просто по симметрии отно-
относительно индексов ab: на симметричные и антисимметричные. Так, в
группе SUE)
ТаЬ = Т(аЬ) + Т[аЬ]-
5 х 5 = 15 + 10.
Здесь круглые скобки означают полную симметрию, а квадратные -
полную антисимметрию по индексам.
Рассмотрев кинетические члены фермионных и скалярных полей,
мы убедились, что можно построить лагранжианы, инвариантные от-
относительно унитарных и ортогональных преобразований. С помощью

212 Глава 6
кинетического члена оказывается возможным получить и инвариант-
инвариантность относительно симплектической группы. Заметим, что кинетичес-
кинетический член грассманова майорановского поля, взятый в форме
тождественно равен нулю, если имеется только одно майорановское
поле. Рассмотрим, однако, случай четного-числа майорановских полей
уш ,»¦=!,..., 2л/, связанных с помощью антисимметричной число-
числовой матрицы Е(. . = -?•., элементы которой таковы:
+1, i >ь
°> • =Ь A.41)
1, i </.
В этом случае можно образовать инвариантные выражения вида A.40)
и получить ненулевой результат, обеспечив антисимметризацию по бе-
бегущим индексам i . Таким способом мы получаем отличный от нуля
кинетический член
? = ^м.-?оУ5гЧгм, • О-42)
Он инвариантен относительно преобразований, оставляющих неизмен-
неизменным антисимметричное квадратичное выражение. Подобные преобразо-
преобразования составляют симплектическую группу SpBN), а * . преобразует-
преобразуется как основное действительное 2\?-мерное представление. Как указы-
указывает наличие антисимметричного тензора Е{., синглет группы SpBN)
содержится в антисимметричном произведении двух 2|\?-представлений.
[ Вследствие этого невозможно построить кинетический член для ска-
скалярного поля, преобразующийся по представлению 2.V группы SpB/V).]
Действительно, неприводимые представления симплектических групп
входят в симметризованные тензорные произведения, а приводимые —
в антисимметризованные (для групп вращений все наоборот). В част-
частности, присоединенное представление задается симметризованным
произведением BМ х 2М).сим и поэтому содержит NBN + 1) элементов.
Интересный случай соответствует значению N = 1. Мы видим, что тог-
тогда лагранжиан A.42) инвариантен по отношению к группе SUB),, посколь-
поскольку матрицу Е можно отождествить с символом Леви-Чивиты е^. . Это не
случайно: алгебры Ли групп SpB), SUB) и SVC) одинаковы. Заметим, что в

Калибровочные симметрии, конструкция Янга — Миллса 213
действительности размерность группы SpBN) такая же, как и группы
SOBN + \). Сравнивая представления, находим, что можно отождест-
отождествить группы S 0E) и Sp{4), поскольку размерность представления 4
группы SpD) такая же, как и спинора группы S0E). Но 5ОG).уже не
совпадает с SpF), так как в группе S0G) нет шестимерного представ-
представления. (Более того, даже когда алгебры Ли находятся в соответствии,
их глобальные свойства могут различаться.)
Итак, путем построения различных типов кинетических членов нам
удалось получить лагранжианы, инвариантные относительно групп
0(N), U(N) и SpB). В наш список не вошли другие группы Ли, назы-
называемые исключительными, так как их нельзя определить на основе
только квадратичных инвариантов, подобных кинетическому и массово-
массовому членам; для описания этих групп нужны инварианты более высокого
порядка. Подобные инварианты могут входить в ту часть лагранжиана,
которая связана с взаимодействием. Таким образом, исключительные
симметрии — это симметрии взаимодействия. Мы не приводим здесь
примеров лагранжианов, инвариантных по отношению к исключительным
группам, а просто перечислим сами эти группы; G с 14 генераторами,
рангом 2 и только действительными представлениями, порождаемыми
фундаментальным семимерным представлением; F4 с 52 генераторами,
рангом 4 и только действительными представлениями, порождаемыми
фундаментальным 26-мерным представлением; ?6 с 78 генераторами,
рангом 6, имеющая действительные и комплексные представления, по-
порождаемые фундаментальными представлениями 27 или 27; ?.с 133 ге-
генераторами, рангом 7 и только действительными представлениями, по»)
рождаемыми представлением 66; наконец ?g с 248 генераторами и тем
уникальным свойством, что присоединенное 248-мерное представление
этой группы является также и ее фундаментальным представлением.
Задачи
А. Пусть задана алгебра Ли [ТА, Тв] = ifABCTc, As Р9 С = 1,
. . . , К, где fABC— полностью антисимметричные действительные
коэффициенты. Их можно рассматривать как К матриц {fA)BC размер-
размерности К х К. Пользуясь тождеством Якоби, покажите, что эти К х К-
матрицы образуют ту же алгебру Ли, что и матрицы ТА, если только
взят надлежащий множитель (-г ).

214 Глава g
Б* Разложите комплексный тензор третьего ранга ТаЬс, а, Ь, с =
= 1, ... 5, на S [/E)-неприводимые компоненты.
В. Пусть заданы V - 1 разных полей TJ, Т%, . . . , Т% ~1. Пока-
Покажите, что всегда можно построить из их произведения поле, преобра-
преобразующееся как представление N группы S U(N) (т.е. как представление
с одним верхним индексом).
Г. В группе S [/C) выразите произведение двух матриц Гелл-Манна
через такие же матрицы.
Д. Докажите, что алгебры Ли групп SU{2) и SOC), SUD) и SOF)
изоморфны.
Е. Пусть задан лагранжиан ? = ^ <9ЦФТ<Э МФ, где Ф - вектор-столбец
из N действительных скалярных полей: Найдите нетеровские токи и за-*
ряды. Какие условия следует наложить на поля, чтобы нетеровские за-
заряды образовали алгебру Ли группы S O(.V)?
Ж. Покажите в явной форме, что при V = 2 лагранжиан, даваемый
выражением A.42), S [/B)-инвариантен.
§ 2. Построение локально симметричных лагранжиане!
В предыдущем параграфе мы показали, как включить в лагранжиан
локальную фазовую инвариантность. Теперь покажем, как сделать это
в случае более сложных симметрии по отношению к неабелевым груп-
группам Ли, о которых мы только что говорили.
Для иллюстрации мы будем рассматривать лагранжиан комплексных
двухкомпонентных спинорных полей. Но читатель должен помнить, что
вследствие аномалий Адлера — Белла - Джекива "калибровка" унитар-
унитарных симметрии в случае левых полей приводит к неперенормируемой
теории. Поскольку на данной стадии нас интересуют только классичес-
классические выводы, мы временно игнорируем эту тонкость. При желании чита-
читатель, чтобы чувствовать себя спокойнее, может проделать то же по-
построение с Л' дираковскими четырехкомпонентными спинорами.
Как мы только что видели, лагранжиан
где по а берется сумма от 1 до N, инвариантен по отношению к гло-
глобальным преобразованиям группы U(N)
1, B.2)

Калибровочные симметрии, конструкция Янга — Милпса 215
где и = е'ае'"ЛтА, B.3)
а через ТА обозначены (V2 - 1) бесследовых эрмитовых матриц, явля-
являющихся генераторами группы SU(N). Теперь мы хотим обобщить выра-
выражение B.1) так, чтобы включить инвариантность по отношению к ло-
локальным преобразованиям вида B.2),т.е. преобразованиям
4>L{x(-U{xfo/L(x), B.4)
где теперь
Заметим, что решение вопроса о том, какую часть глобальной симмет-
симметрии желательно калибровать, в значительной степени зависит от нас
самих:. Например, мы могли бы калибровать только какую-нибудь под-
подгруппу группы SU(N). Здесь же мы калибруем всю группу! Когда V
зависит от х, член с производной d^L уже не преобразуемся должным
образом; действительно,
д№ <*> - №(хУуь (х) = [ dilU(x)]4,L (х) + U(x)d^L (x) 4 B.6)
t Ud^lx). B.7)
Таким образом, нам нужно обобщение производной, которое не на-
нарушало бы инвариантности лагранжиана ?. Поэтому мы вводим кова-
риантую производную ф требуя, чтобы выполнилось соотношение
\vL{x) + U(x)%vL№, B.8)
или, в операторной форме,
^(х). B.9)
Подчеркнем, что в данном случае оператор 3) представляет собой
N х iV-матрицу, так что, если мы хотим показать все индексы, соот-
соотношение B.8) следует написать в виде
Таким образом, если нам удастся найти подобный оператор 2)ц, то но-
новый лагранжиан

216 Глава 6
будет локально инвариантным по отношению к группе U(N). Поскольку
операт
в виде
оператор 3)^ должен быть обобщением оператора д , будем искать его
где мы опустили индексы группы V(N); А (*) - эрмитова /Vx/V-матрица
с векторными элементами, так как id - эрмитов вектор:
B.13)
где через Тв обозначены (Л/2- 1) эрмитовых генераторов группы
S U(N). Из закона преобразования B.9) следует, что
iV(x)A]l(x)uUx), B.14)
или Л^(х) = -Ш(х)[д^ (х)] + иШ^(х)иЧх). B.15)
Легко показать, что поля В (х) и 4в(х) преобразуется раздельно. Дей-
Действительно, взяв след выражения B.1,1!), находим
Р,» = - -^Sp(Щх)[д^(х)]) + ВЦ(Х). B.16)
С учетом равенства (см. задачу)
Sp{V{x)[d иЧх)]) = -iNd a(x) B.17)
имеем
B>) = -^oW + eu(x), B.18)
т.е. полученное ранее преобразование. Умножив теперь B.15) на Тс
и взяв след, получим закон изменения N2 - 1 полей А^ г если восполь-
воспользуемся свойствами следов Т-матриц
SPTA = 0, Sp(TATB) = УёАВ, B.19)
записанными в обычной нормировке. Пожалуй, проще рассмотреть
бесконечно малые "калибровочные преобразования" B.15). Полагая
+ . . . , B.20)

Калибровочные симметрии, конструкция Янга — Миллса 217
получаем
5Лц(х) = Aj(x) - Ац(х) = -T%wB(x) + icoB(x)[TB Ац(х)] + 0(со2).
B.21)
Умножив на Тс и взяв след, с учетом формул B.19) и B.13) находим
6Л^(х) = -dMcoc(x) + 2kob(x)Sp([Tb, А^(х)]тс) + О(со2). B.22)
Так как для операторов ТА выполняются перестановочные соотношения
алгебры Ли группы SV(N)
[ТА TB] = ifABCTc, B.23)
мы в результате получаем
Примечательным в этом калибровочном преобразовании B.24) являет-
является то, что, будучи записано в таком виде, оно не зависит от представ-
представления исходных фермионных полей.
Вариацию B.21) можно очень изящно переписать, перейдя к кова-
ковариантной производной. При преобразованиях SU(N)
. B.25)
Следовательно, ковариантная производная величины со дается выраже-
выражением (см. задачу)
Дцш=5цю+|[ЛЦ. со]. B.26)
Сравнивая с B.21), получаем
о/у*) = _Suco, B.27)
откуда следует, что, даже если само поле А (х) не преобразуется ко-
вариантно по отношению к SU(N) из-за члена Ud ifi, бесконечно малое
изменение поля А (х) преобразуется ковариантно, так как его можно
выразить через ковариантную производную.
Итак, мы расширили наш лагранжиан, чтобы обеспечить его локаль-
локальную и(Д/)-симметрию. Мы добились этого ценой введения N2 векторных
полей, необходимых для построения ковариантной производной. Чтобы
поля могли существовать самостоятельно, мы должны включить их ки-
кинетические члены, не нарушив при этом исходной локальной симметрии.

218 Глава 6
Для поля В~ (х), отвечающего общим фазовым преобразованиям, можно
просто повторить действия предыдущего параграфа. Поэтому мы сосре-
сосредоточим внимание на тех N2 — -1 полях, которые появились в связи с ло-
локальной SU(N) -инвариантностью. Прием, используемый при построении
кинетического члена, инвариантного по отношению к преобразованию
B.15), заключается в том, чтобы при образовании различных выраже-
выражений применять ковариантную производную 2) .
Рассмотрим эрмитов опреатор
*> -¦ l\. 5U B-28)
Он, конечно, преобразуется ковариантно, поскольку так преобразует-
преобразуется оператор ф , т.е.
?^(х)^и(х)Г^(х)иЧх)- B.29)
Подставляя выражение B.12) для 3) в фундаментальном представлении
и опуская поле В , находим
Так как Р^(х) - эрмитова бесследовая N х W-матрица, ее можно раз-
разложить по матрицам Тв:
где Ft vi — н 4а (y\ Л A°(y\ — { DKaUА ^/чЛ л*^/*л /о qov
причем мы использовали формулу B.13) с отброшенным Р и формулу
B.23). Конечно, величины F — это янг-миллсовское обобщение на-
пряженностей поля в электромагнетизме. Не все они независимы, так
как подчиняются тождествам Бьянки
®nF ст +® Fcm + ^aFn =0» B.33)
в которых операторы Ъ , действующие на F следует понимать в
смысле соотношения B.26), так как величины 'F преобразуются по
присоединенному представлению группы SU(N). Указанные тождества
являются прямым следствием тожества Якоби для ковариантной произ-
производной
t® , [ф , фа]] + [ф , [3K, 3) ]] + [Фа, [3) ,2) ]] = 0. B.34)

Калибровочные симметрии, конструкция Янга — Миллса 219
Они представляют собой просто кинематические ограничения, которым
тривиальным образом удовлетворяют напряженности поля.
Теперь уже легко построить инвариантный кинетический член. Он
имеет вид
при условии нормировки B.19) для т-матриц; это выражение есть обоб-
обобщение максвелловского лагранжиана и, как нетрудно видеть, имеет долж-
должную размерность (константа связи g безразмерна).
Заметим, что лагранжиан ?ям не зависит от конкретного представ-
представления фермионов и поэтому сам по 'себе описывает весьма нетривиаль-
нетривиальную теорию. Кроме того, выбирая структурные функции fABC, отвеч tio-
щие другим группам Ли, мы можем получить соответствующие янг-мил-
лсовские теории для этих групп Ли.
Вдумчивый читатель может задать вопрос, почему мы не рассмотре-
рассмотрели другой инвариант
^pa B.36)
в качестве возможного кинетического члена. Ведь он лоренц-инвариан-
тен, калибровочно-инвариантен и имеет правильную размерность. Дело
в том, что его можно представить в виде полной дивергенции. Действи-
Действительно, напишем
o +iApAa])~ B.37)
где член с ЛААА исключен в силу свойств цикличности следа. Далее
t^P°SP(A^AvdpAo)= -bpe"VPaSP<VHab №)
так что, поскольку еЩфСГ(? <?цЛу = О,
Таким образом, получаем
pWP, B.41)

220 Глава 6
где WP = eP*nvSpUadu/lv + -~АаЛ^]. B.42)
Это означает, что, взяв / в качестве кинетического члена в лаг-
лагранжиане, мы не смогли бы получить какое-либо уравнение дви-
движения для A t так как этот член влиял бы на действие только в кон-
концевых точках. Однако этот член можно добавить к ?ям, что приведет
к каноническому, преобразованию поля А .
Задачи
А. Пусть задано вейлевское поле, преобразующееся по представ-
представлению 6 группы 5[/C). Постройте с помощью матриц Гелл-Манна S?/C)-
ковариантную производную, действующую на это поле.
Б, Покажите, что Sp[U^ (х)д^Ц(х)] = iNd а(х).
В. Покажите, что если функция со преобразуется по присоединен-
присоединенному представлению группы SV{N), то ее ковариантная производная да-
дается выражением 3)^со = да + i [А , со], где А - матрица калибровоч-
калибровочных полей, и преобразуется так же, как а..
Г. Исходя из свойств калибровочного преобразования поля А ,
покажите, что напряженность поля F^v = d^Av - dvA^ + i [Лр, Av] дей-
действительно преобразуется по присоединенному представлению группы
SU(N)..
Д. Взяв лагранжиан ? = Угд фтдиф, где ф{х) - вектор-столбец из
N Действительных скалярных полей, обобщите его так, чтобы он стал
локально инвариантным по отношению к группе SO{N), повторив описан-
описанную в тексте процедуру. Сколько нужно ввести векторных полей? Пока-
Покажите, что бесконечно малое изменение этих полей при преобразованиях
группы SO(N) также можно выразить через ковариантную производную,
действующую на калибровочные параметры.
§ 3. Чисто янг-миппсовская теория
В данном параграфе мы исследуем классические свойства янг-мил-
лсовского действия, имеющего вид
fdx pF^Fn. C-1)
где Fw= дЛ ~ дЛ + i[\> АЛ V*) = tfW' C-2), C.3)

Калибровочные симметрии, конструкция Янга — Миллса 221
Матрицы Тв представляют собой генераторы одной из алгебр Ли
[Тв, Тс] = ifBCDTD, C.4)
причем индексы В, С, D принимают значения от 1 до К, где К - раз-
размерность алгебры Ли, определяемой полностью антисимметричными
структурными константами fBCD. В силу равенства C.4) матрицы Тв
имеют нулевой след; они нормированы так, чтобы выполнялось соотно-
соотношение
SP(TBTC) = 1/2SBC. C.5)
Возможные алгебры Ли были классифицированы в диссертации Карта-
на; к ним относятся: классические алгебры SU(N) размерности N2 — 1,
N > 2; SO(N) размерности N(N - 1)/2, N > 2; SpBN) размерности
NBN + 1), N > 1, и исключительные алгебры Ли G2A4), F4E2), ?6G8),
Е7A33) и (?gB48), размерности которых указаны в скобках.
Можно также записать янг-миллсовское действие в виде, не зави-
зависящем от матриц Тв,
где теперь F«y= д^Ав - д,Ав - f BCDA^ADV . C.7)
Отсюда следует, что
+ g/ ВСОЛСЛ»^ЛУВ - llf BCDf BEEAffiA»EAvF. C.8)
Как нетрудно видеть, первые два члена - того же типа,что и в мак-
свелловском лагранжиане (не считая суммирования). Однако два следу-
следующие члена указывают на то, что векторные поля обладают весьма не-
нетривиальными кубическим и квартичным взаимодействиями друг с дру-
другом.
Вывод уравнений движения легче всего провести в матричной фор-
форме. Начнем с вариации действия
5S =- -L/rf4*SP(F SFn, C.9)

222 Глава 6
где 5 Fuv = d»bAv + iSA»Av + iA»5A" - (д -vV). (ЗЛО)
С учетом антисимметрии поля F имеем
65 = - — fd4x Sp[F {№AV + iSA»Av + M»*6.4W)]. C.11)
Затем мы интегрируем первый член по частям, отбрасывая поверхност
ный член, поскольку вариации обращаются в нуль на границах. Учиты-
Учитывая свойства цикличности следа, приходим к выражению
55 = А_ fdAx Sp [ (d^F^ + i [ A», FMV ]) 5-4v], C.12)
откуда и получаются в матричной форме уравнения движения
= 0. C.13)
Так как F у преобразуется по присоединенному представлению, это
уравнение можно непосредственно записать через ковариантную произ-
производную в виде
откуда видно, что само уравнение ковариантно. Вдобавок поля удовлет-
удовлетворяют кинематическим ограничениям (Бьянки) (как и поля F в
электромагнетизме)
Vuv = °' <ЗЛ5>
представляет собой тензор, дуальный тензору F . Подчеркнем, что
уравнение CJ5) не является уравнением движения, так как оно три-
тривиально решается путем выражения F через потенциалы.
Из уравнения движения C.13) явствует, что можно ввести некий
сохраняющийся ток ;у; действительно, величина
v^v = t-U^,Fuv] C.17)
удовлетворяет уравнению <?v/v = О, (ЗЛ8)
что приводит к сохраняющимся зарядам (записанным в матричной фор-

Калибровочные симметрии, конструкция Янга — Миллса 223
Me QAT*)
Q = fd3xjo = _ /d3xdfc|4) = -^dVF.o., C.19)-C.21)
где последний интеграл берется по бесконечно удаленной пространст-
пространственной поверхности. Хотя у тока jv ужасные трансформационные свой-
свойства по отношению к калибровочным преобразованиям, заряды Q, как
это видно из C.21), преобразуются очень просто по отношению к весь-
весьма широкому классу калибровочных преобразований. Из формулы C.21)
получаем
QVQ' = _?dV"t/F.oi/t, C.22)
где U - операторы, заданные на граничной поверхности на бесконеч-
бесконечности. Следовательно, потребовав, чтобы операторы U были постоян-
постоянны в пространстве на пространственной бесконечности, мы можем вы-
вынести их из-под знака интеграла по поверхности и получить ковариант-
ное преобразование сохраняющихся зарядов. Добавим, что выписанный
нами ток совпадает с нетеровским током, полученным каноническими
методами.
Можно ввести взаимодействие в янг-миллсовскую систему, доба-
добавив к SnM член вида
J- fd*xSp(A»J ), C.23)
S
где ] (х) - внешний источник, записанный здесь в матричной форме
/Ц(*) = /*(*)ТВ. C.24)
Тогда уравнение движения примет вид
3)%v = /v. C.25)
На основании этого уравнения мы можем для сохранения ковариант-
ковариантности уравнения движения требовать, чтобы источник Jv преобразо-
преобразовывался ковариантно:
J»^UJ»uK C.26)
Более того, как нетрудно показать, источник / и обязан ковариантно

224 Глава 6
сохраняться в силу уравнения движения (см. задачу)
C.27)
Заметим, что нетеровским током является не / , а
Теперь, если вернуться к рассмотрению дополнительного члена
C.23), мы увидим, что он не инвариантен по отношению к калибровоч-
калибровочному преобразованию. Предполагая, что источник /ц преобразуется
ковариантно, находим
^) = - /d4xSP(/^co) = /d4xSPM^), C.29)
и это означает, что можно восстановить инвариантность, если внешний
источник / ц сохраняется. В максвелловской теории в этом месте не
возникает проблем, поскольку при изменении калибровки источник /ц
не преобразуется. В янг-миллсовской же теории утверждение д ] ц = О
не ковариантно. Иначе говоря, подобная связь с источниками разруша-
разрушает калибровочную инвариантность. Это не должно вызывать удивления.
В конце концов, если обратить наше предыдущее построение, то станет
ясно, что способ калибровочно-инвариантного описания взаимодейст-
взаимодействия А заключается в добавлении кинетического члена для полей, из
которых состоит источник /ц. Внешний нединамический источник для
этого не годится.
Конечно, нельзя запретить исследовать решения классических
уравнений C.25) совместно с условием C.27), но мы лишь заметим,
что связывание янг-миллсовских полей с нединамическими внешними
источниками представляется сомнительным занятием.
Вернемся к уравнениям движения C.14) без источника. В простран-
пространстве Минковского существует много решений этого уравнения. Как и
в электродинамике, имеются решения этого уравнения в виде плоских
волн (см, задачу). У них бесконечная энергия (но конечная плотность
энергии). Однако в противоположность максвелловской теории из-за
нелинейного характера теории Янга-Миллса такие решения нельзя нала-
налагать друг на друга с тем, чтобы получить решения с конечной энерги-
энергией, несмотря на то что плоские волны движутся в одном направлении.
Существует много других очень интересных решений этого уравне
ния с конечной энергией, но они содержат некоторые сингулярности и

Калибровочные симметрии, конструкция Янга — Миплса 225
потому требуют существования сингулярных источников (см. задачу).
Янг-миллсовское уравнение движения в евклидовом пространстве
чрезвычайно содержательно „ Евклидово пространство можно рассмат-
рассматривать как пространство Минковского с мнимым временем, а в кванто-
квантовой механике процессы эволюции в мнимом времени формально соответ-
соответствуют процессам тунеллирования, происходящим мгновенно в действитель-
действительном временно Поэтому Хофт назвал несингулярные решения янг-мил-
лсовского уравнения без источника в евклидовом пространстве ан стан-
тонами. С другой стороны, мы уже видели ранее, что ФИТ может быть
лучше определен в евклидовом пространстве» Поэтому изучение реше-
решений в евклидовом пространстве вдвойне интересно.
Следуя Белавину, Полякову, Шварцу и Тюпкину [ 3], остановимся
на решениях в евклидовом пространстве, имеющих конечное действие.
В евклидовом пространстве
SP[<Fm, -VKFMV-^v)b0, C.30)
поскольку это сумма квадратов. Следовательно,
SP<Vmv + ^iv^iv) > 2Sp(FuwFM4), C.31)
откуда в силу соотношения
^OJ C-32)
приходим к неравенству
Av. C.33)
которое после интегрирования устанавливает нижнюю границу значе-
значения янг-миллсовского евклидова действия. Ясно, что знак равенства
достигается, когда
рцУ = К*' <3-34>
что соответствует самодуальным решениям. Антисамодуальные реше-
решения также соответствуют нижней границе. Нетрудно показать, что са-
модуальным и антисамодуальным решениям соответствует равный ну-
нулю евклидов тензор энергии-импульса, (см. задачу). Интеграл от пра-
правой части неравенства C.33) можно переписать в виде интеграла от
дивергенции [формула B.41)]
fd*x SP(F^v) = 4/d4* <yrp) C.35)

226 Глава 6
где
2i
-g-^vV»1' Cl36)
так что
-L2 /Л Sp FuvFMV > -
где последний член проинтегрирован по граничной поверхности на евкли-
евклидовой бесконечности. Следовательно, минимальное значение действия
будет зависеть от свойств калибровочных полей на бесконечности.
Чтобы действие SnM было конечным, поля FB должны достаточно
быстро убывать на евклидовой бесконечности:
О*>, Г0' C'38)
I x I"*00
а это в общем случае означает, что А^ стремится к конфигурации
V~'4L/t при *2"°°' C.39)
получающейся из А = 0 в результате калибровочного преобразования;
значит, F v = 0.
Напомним теперь, что действие S^M ограничено снизу величиной,
полностью зависящей от поведения потенциалов на евклидовой беско-
бесконечности. Действительно, подставляя C.39) в C.36), мы видим, что
на поверхности 5
W* - ^^Р^идУидриЧдаи^, C.40)
причем мы учли антисимметрию по р и а и условие UU*= 1. Следова-
Следовательно,
Ъ^^ C.41)
что полностью зависит от группового элемента U(x)\ Мы пришли к при-
примечательному результату: минимальное значение евклидового дейст-
действия зависит только от. свойств оператора V(x), а не от деталей полевой
конфигурации при конечных х.
Рассмотрим конкретный случай группы S[/B). Тогда групповые
элементы U(x) зависят от трех параметров, которые мы обозначим

Калибровочные симметрии, конструкция Янга — Миллса 227
через 9t, <p2, <р3> и которые сами зависят от х. Поверхность же интегри-
интегрирования S — это сфера очень большого (бесконечного) радиуса. Следо-
Следовательно, мы можем воспринимать U как отображение между тремя
групповыми параметрами и тремя координатами, задающими нашу сфе-
сферу, т.е. отображение трехмерной сферы в трехмерную сферу. Подобные'
отображения характеризуются своим гомотопическим классом. Грубо
говоря, гомотопический класс соответствует тому, сколько раз одна
сфера накрывает другую. Например, гомотопический класс, равный 1,
означает, что сфера S ~ на евклидовой бесконечности только один раз
накрывает сферу S 3 группового множества, помеченного углами <р,- .
В общем случае гомотопический класс п означает, что п точек сферы
S™ отображены в одну точку сферы S3 и т.д.
Если положить
C.42)
а = 1 дх <9э
v га
то получим
V C.43)
или, с учетом антисимметрии символа в,
5, * f db^pe^y
E g2 C.44)
При такой форме записи ясно виден якобиан преобразования между
переменными, задающими поверхность S, и углами <рц . Но, как мы
только что говорили, такое отображение характеризуется своим го-
гомотопическим классом п, если сфера 53°° и-кратно отображается на
групповое множество SUB). Параметризуя V, скажем, углами Эйлера,
можно путем простых выкладок получить, что
-^4-n, C.45)
где п — целое число
f
Sp{F F ), C.46)
n -—fx Sp{F F
называемое понтрягинским индексом

228 Глава 6
Таким образом, евклидовы решения с конечным действием поме-
помечены своими гомотопическими классами, которые определяют нижнюю
границу (евклидова) действия. Эта нижняя граница достигается в том
случае, когда полевые конфигурации либо дуальны, либо антисамодуаль-
ны, т.е. когда
f = ±F . C.47)
Рассмотрим в качестве примера первое из найденных инстантон-
ных решений; в этом случае евклидов SU{2) -потенциал дается выраже-
выражением
C-48)
где V = —. (х0 - ix • а), C.49)
V х
причем сг -матрицы действуют в пространстве SU{2), a
*2 = *о +х • х.
Это решение удовлетворяет требованию C.39) для конечного действия
(Л2 - константа). Можно показать, что данное решение самодуально, а
из вида оператора U следует, что понтрягинский индекс равен +1.
Заметим, наконец, что в янг-миллсовских теориях те функции, ко-
которые преобразуются под действием калибровочных преобразований,
вообще говоря, нельзя считать постоянными, поскольку им всегда мож-
можно путем калибровочного преобразования придать зависимость от х.
Ближе всего к понятию постоянной функции понятие ковариантной по .
стоянной, которая определяется как функция <р, удовлетворяющая усло-
условию
ФцФ-(Эм+|Лм)9-0, C.51)
где опущены все групповые индексы. Решая это уравнение относитель-
относительно ф, мы обнаружим очень интересный объект - упорядоченный интег-
интеграл по траекториям. В самом деле, заметим, что
<р(х + dx) = q>(x) + <&мдцФ + . . . , C.52)
где dxu - произвольно малое смещение. Используя условие C.51), полу-
получаем
Ф(х + dx) = ф(х) - idx^A^x) + . . . - e-u*UA»f(x) + O((dxJ). C.53)

Калибровочные симметрии, конструкция Янга — Миллса 229
Так как при калибровочных преобразованиях
Ф(*) - V(xb(x), C.54)
из формулы C.53) следует, что
Это и есть то фундаментальное соотношение, которое нам нужно. Теперь
можно проинтегрировать уравнение C.51), итерируя по смещениям:
ф(у) можно получить из <р(х), взяв малые смещения вдоль кривой, начи-
начинающейся в точке'* и кончающейся в точке у, так что
— Ф dx • А
(Ре * Ш, C-56)
где введено обозначение для "упорядоченной по траекториям экспонен-
экспоненPe-ifdx .а_ п (. _ idxc . A{x^))t C.57)
причем dxk - смещение от точки xk на кривой С (рис. 8). Из форму-
формулы C.55) следует соотношение
у у
-if dx- A -i4 dx- A
х х +
Ре -+U(y)Pe {/'(х). C.F;8)
В частности, упорядоченная по траекториям экспонента вдоль замкну-
замкнутой траектории преобразуется как локальная ковариантная величина:
Pe-ij,dx-A _ и{х)Ре-1Фйх-АиЦх), C.59)
так что ее след калибровочно-инвариантен. Оя представляет собой функ-
функционал от траектории. Заметим, что из условия C.51) вытекает равенст-
Рисв.

230 Глава 6
во нулю напряженностей поля. Однако ничто не мешает рассматривать
упорядоченный по траекториям функционал для любого поля А .
Мы не касались многих .других аспектов классической янг-миллсов-
ской теории, например решений в виде монополей, обобщения инстантон-
ных решений, меронных решений с бесконечным евклидовым действием
(но конечным действием в пространстве Минковского и сингулярными
источниками) и т.п. Увы, нам нужно двигаться вперед и подумать о том,
как определить квантовую янг-миллсовскую теорию.
Задачи
А. Покажите, что полевая конфигурация
гае F^ —произвольные функции, является решением'янг-миллсовских
уравнений движения [4]. Сравните эти решения с решениями в виде
плоских волн в максвелловской теории.
*Б* Проанализируйте анзатц By - Янга для 5{7B)-инвариантной
янг-миллсовской теории
где С — есть 5{/B)-индекс, С = 1, 2, 3, а г - длина вектора положения
х. (Напомним, что в группе SUB) коэффициенты f^BC _ еАвс ^ те>
это тензор Леви-Чивиты.) Выведите уравнения, которым должны удов-
удовлетворять коэффициенты / и g. Покажите, что этим уравнениям удов-
удовлетворяют значения / = 1, g = const. Найдите для такого решения по-
потенциал и полевые конфигурации, вычислите плотность энергии и энер-
энергию.
В. Покажите, что в случае 5{/B)-калибровочной теории из анзатца
'т Хофта - Корригэна - Фэрли - Вильчека для потенциалов, выражен-
выраженных через одно скалярное поле <р,
АС0=-±дСЬ Af = -L[6?30q.-efdyq.]
вытекает, что <р удовлетворяет уравнению движения теории \Ф4, где \
— произвольная константа.

Калибровочные симметрии, конструкция Янга — Милпса 2П
Г. Покажите что нетеровскиЙ тензор энергии-импульса для евкли-
евклидовой янг-миллсовской теории может быть записан в виде
Q _ (г + F \{F F \
Д. Определите, как изменяется W При калибровочном преобразова-
преобразовании, и покажите, что производная д W калибровочно-инвариантна.
Е. Вычислите след упорядоченной по траекториям экспоненты
вдоль замкнутой петли для инстантонного решения, о котором говорит-
говорится в тексте. Выберите простую траекторию, которая вам покажется
удобной.
ЛИТЕРАТУРА
1. Yang СМ., Mills R., PhysoRev., 96. 191 A954).
2. Mother E., Nachr. KgL Ges. Wise., Gottingen, 235 A918).
3. Belavin A., Polyakov A., Schwarz A., Tyupkin Yu., Phys. Lett.,
59B. 85 A975).
4. Coleman S., Phys. Lett., 70B. 59 A977).

Глава 7
Интеграл по траекториям
в калибровочных теориях
Определение ФИТ для калибровочных теорий связано с трудностя-
трудностями особого рода- Как мы только что видели, в таких теориях действие
инвариантно по отношению к преобразованиям, зависящим от простраст-
венно-временных координат: S[A^\ = S[A' ] „ Поэтому бездумное ин-
интегрирование по всем полевым конфигурациям привело бы к чудовищно-
чудовищному увеличению числа лишних бесконечных интегрирований и сделало
бы интеграл по траекториям еще более бесконечным, чем обычно*
В приложении А мы рассмотрим случай, когда подынтегральное выра-
выражение зависит не от всех переменных, по которым ведется интегриро-
интегрирование- Мы увидим, что в этом случае интеграл можно определить пу-
путем ловкого изменения меры; новая мера, сохраняя ковариантный вид,
содержит ограничивающие множители, благодаря которым интегриро-
интегрирование производится только по существенным переменным,- На приме-
применении подобного метода к ФИТ для калибровочных теорий основана
процедура Фаддеева - Попова.
Но можно также потребовать, чтобы ФИТ имел реальный смысл
только на уровне гамильтонова формализма в духе квантовомехани-
ческого соответствия гл„ 2„ Оказывается, что оба метода дают один
и тот же результат» Тем не менее полезно рассмотреть и тот и другой
методы»
§ 1. Гамильтонов формализм в калибровочных
теориях, абелев случай
Для начала рассмотрим случай абелева поля (максвелловская
теория). Лагранжиан имеет вид (F^v = <ЭцЛу _<ЭуЛц)
l-F^F^- JL
.[2FoiFoi +Fi/P/]. A.1), A.2)
Определим канонические импульсы

Интеграл по траекториям в калибровочных теориях 233
1Г„= ^ ^ A.3)
и постулируем следующие значение фундаментальных скобок Пуас-
Пуассона (СП) при совпадающих временах:
а все остальные СП при совпадающих временах обращаются в нуль-
Плотность гамильтониана дается выражением
К(х, О«1гЧЛм-?. A-5)
Для любой функции / канонических переменных А и тт уравнения
движения имеют вид
/ = 1/, Я}сп, A.6)
где Н — энергия, определяемая как
H = fd3xK(x, О- A-7)
Намеченная нами каноническая процедура легко проводится во многих
случаях, например в скалярной теории поля* Но если мы применим ее
к калибровочным теориям, то сразу же столкнемся с трудностями*
Действительно, подставив A.2) в A.3), найдем, что в абелевой теории
откуда в силу антисимметрии F следует, что
т^О. A-9)
Это. противоречит фундаментальным СП при ц = v = 0» Поэтому, если
мы хотим сохранить фундаментальные СП, нам следует подходить к
равенству A.9) как-то по-особому. Все же продолжим еще немного вы-
вычисления и найдем наивный гамильтониан, который мы обозначим че-
через HQ. Из формул A.5) и A.7) путем интегрирования по частям
получим
Но = fd з *[ _J_ Fij f/ - 4~ ^ ^ +A odi *'']' <U0>
и мы видим, что скорости исчезли из этого выражения; в этом и зак-
заключается весь смысл гамильтонова формализма. Но равенство

234 Глава 7
тг ° = 0 означает, что замена переменных, связанная с переходом
от скоростей к импульсам д0 Ац -*ттц, сингулярна (вы не можете ото-
отобразить четыре вещи в три, не заплатив за это)» Следовательно, оп-
определение гамильтониана К неоднозначно: к нему можно добавить
любую произвольную функцию, пропорциональную тг0 » Запишем новый
гамильтониан в виде
H = H0+jd3xFrrQ, (Ы1)
где F -произвольная функция» Чтобы выяснить смысл функции F,
воспользуемся уравнениями движения (L6) при f - AQ. Тогда
Л> =U0, H\cn = F, A.12), (ЫЗ)
причем мы использовали фундаментальные СП A.4). Если бы функция
F зависела от канонических переменных, то в выражении A.12) были
бы дополнительные слагаемые, но они все равно умножались бы на
тг0 и в конце концов обращались бы в нуль. Поэтому без потери общ-
общности можно считать, что F не зависит от канонических переменных.
Отсюда вытекает, что если в заданный момент времени tQ мы имеем
некоторое определенное значение функции AQ, то в момент времени
10 + 5* ее значение будет определяться совершенно произвольной
функцией. Что же это означает ? Дополнительный член / d3xF-nQ
вызывает изменение переменной Ао, но оставляет неизменными
Ai, что эквивалентно калибровочному преобразованию
ЛЦ-ЛЦ + (ЭЦХ, A.14)
в котором Цх, 10) = 0, но Цх, to),4 О» Таким образом, дополнитель-
дополнительный член в формуле A.11) приводит к специальному типу калибровоч-
калибровочного преобразования»
Но это еще не все» Посмотрим теперь, пользуясь формулами
(L4) и (L10), как изменяется тт° :
*о = К , Я }сп = - di *•'(*, t). A.15)
Но, согласно канонической процедуре, тт0 = 0 во все моменты времени»
Отсюда мы получаем другое ограничение
*,*•' =0, A.16)
в которое входят только канонические импульсы! Прервем на мгновение
наши выкладки. Сначала, исходя из канонической процедуры, мы получили,

Интеграл по траекториям в калибровочных теориях 235
что тт° = О U Дирак называет такой", тип ограничений первичной связью,,
Затем, пользуясь уравнениями движения, мы нашли другое ограничение
на величины тг. Этот тип ограничений Дирак называет вторичной связью
[ 1]„ Таким образом, у нас стало еще больше соотношений между вели-
величинами тт. Создается впечатление, что мы отображаем четыре скорости
на два независимых импульса тт., Чтобы отразить этот дополнительный
произвол, мы должны добавить еще один (дополнительный) член к
гамильтониану Н, имеющий вид
HROn=fd3xG(x, 0<?,V(*> О- A.17)
Пользуясь уравнением (L6) и соотношениями (L4), можно увидеть, к
какого типа изменениям приводит этот дополнительный член:
ЬАо =U0> НД0П!Сп=°. И =U/' йдоп*=^с° ПЛЬ A.19)
Следовательно, он осуществляет постоянное во времени калибровочное
преобразование; функция G не должна зависеть от t. Таким образом,
изменение канонического формализма привело к гамильтониану, кото-
который, определяя эволюцию системы во времени, производит при этом
калибровочные преобразования. Включив AQ в G, можно переписать
наш новый и окончательный гамил ьтониан в виде
йнов = /<Р*[ 4~F» РИ ' ~Г ТГ' ** + Gdi ^ ]• П'Щ
Заметим, что член с тг ° выпал из выражения A.20), поскольку йнов
уже более не зависит от AQ , Теперь мы в состоянии описать
получившуюся в результате физическую систему. Пусть / - любая
функция переменных А{ и тт,- . Производная этой функции по времени
определяется выражением
и содержит произвольный вклад, связанный с членом dt тг1 ¦> Это неприем-
неприемлемо, так как изменение физической величины во времени не произвольно.
Поэтому мы потребуем, чтобы выполнялось равенство
которое означает, что функция /физ не должна зависеть от переменной,

236 Глава 7
сопряженной с <?f тт' « Другими словами,-физическая величина долж-
должна быть определена только на некоторой поверхности в плоскости
(Ai , TTj- ). Такую поверхность всегда можно описать уравнением
«Ц , и, ) = О, (L23)
подразумевая при этом, что замена переменных g -* г, где z - пе-
переменная, сопряженная к di тг1 , несингулярна, т.е.
det|_!?_| =det|i& «Э'тг }сп|,^ 0, A.24)
где использовано определение СП. Отметим, что г определяется фор-
формулой
6C,- тг' )(у) 5 ., ,.- ...
= {d*x I ={ ,5, тт'Ь A-25)
5z(yY
Физический смысл соотношения A.25) ясен: производная д{ тт' порож-
порождает калибровочные преобразования, а функция g должна быть способ-
способна зафиксировать калибровку.
Предполагая, что условие A.24) выполняется, можно произвести ка-
калибровочное преобразование
(Л-. щ ) - (?•> щ ).
в котором мы положили
g(Ait тт?) = Лз- A-26)
Далее, так как Аг и тг^ - сопряженные переменные,
detig, д^ тс, !СП = deti $
представляет собой просто якобиан преобразования &ъ. -> т?э. Если
он несингулярен, то можно разрешить уравнение д' Trf = 0 с целью
выразить тг3 через оставшиеся переменные. Заметим, что при таком
преобразовании гамильтониан не меняется. Приведем примеры.

Интеграл по траекториям в калибровочных теориях 237
\.Кулоновская калибровка определяется условием
. A.28)
Образуем детерминант
detld' Л. , djtri 1СП = det[<9i<9iy5(x -у)], A.29)
который следует понимать, как произведение собственных значений
оператора Лапласа di д'; • Хорошо известно, что у этого оператора
нет нулевых собственных значений, кроме постоянного решения, ко-
которое мы исключаем подходящим выбором граничных условий. Следо-
Следовательно, кулоновская калибровка удовлетворяет нашему критерию
хорошей калибровки. Это означает, что можно, пользуясь уравнением
д1 тг(. = 0, выразить сопряженную к A.28) переменную через оставшие-
оставшиеся канонические переменные. Опуская тильду над буквами, напишем
it; -irf +-П-Г, Ai-A^+A?, A.30) ,A.31)
где по построению дивергенция поперечных мод равна нулю:
а*ттГ =а* л?" -о. A.32)
Тогда кулоновская калибровка записывается как
А\ =0, A.33)
а связь A.16) принимает теперь вид
d'lrf =<Э1'<Э. ф = 0, A.34)
если выразить тт^ через ф. Именно обратимость оператора Лапласа
позволяет нам положить <р = 0. Таким образом, в этой калибровке у
нас остаются канонические переменные тт^и aJ с равной нулю дивер-
дивергенцией. Гамильтониан, выраженный через эти переменные, имеет
вид
Н- ^jdMBiBi +ттМ). (L35)
где В., l ....*.л1. О«36)

238 Глава 7
2„ Аксиальная калибровка Арновижа - Фиклера определяется
как
?=Л3 = 0. A.37)
В этом случае условие для детерминанта имеет вид
det [ д 5(х -у)],4 0, A.38)
дх3
и оно выполняется, поскольку оператор д,/дх3 обратим» Следователь-
Следовательно, можно найти тг3 пользуясь уравнением AЛ6). В результате
имеем
¦п3(х, у, z, t) = -f dz'C1Tr, +а2тг2)(х, у, г1, t), A.39)
— оо
где мы (произвольно) наложили граничное условие на тг3 . Теперь
система описывается каноническими переменными Л,, Л2, тг1 , тт2
и (нелокальным) гамильтонианом
*
+тт22+тт|(тг, ,тт2)], A.40)
_L_
в котором тг3 определяется формулой (L39), а
В, = -азЛ2, В2 = д3А,, В3 = (д,А2-д2А,). A.41)
Теперь уже легко записать ФИТо Пусть AL и та - независимые
переменные» Тогда ФИТ имеет вид
гДе тт3(тг1) ~ Функция тг3 , выраженная через поперечные переменные
путем обращения соотношения A.16). Теперь
det| |3« тГг , ?,!cn |. A.44)
'^ A.45)

Интеграл по траекториям в калибровочных теориях 239
Это позволяет переписать A.43) в виде
Мы добавили (без всяких последствий из-за наличия 5[Л^]) член
тг3^ в показателе экспоненты, так что теперь гамильтониан
HI Л> ?»
= -_— (тг^ 1^+ тг3тг3 + Dj B(- J (-1.40
содержит все компоненты Bt , Выполним обратное каноническое
преобразование от переменных с тильдой к переменным без тильды.
Единственно, что при этом произойдет (помимо отбрасывания тильды),
это превращение А3 в калибровочную функцию g. После этого ФИТ
примет вид
i Г rf4*[ ТГ; А; -К + Апд1 ТГ; ]
A.48)
Проинтегрируем, наконец, по тг^ . Заметим, что, интегрируя по частям
член 40<Э'тт; , можно переписать показатель экспоненты в виде
тт» (d0At -dt Ao) - -^— *,• тт? - -^— Bi Вг . A.49)
Дополняя до полного квадрата, получаем
где S [ А] -максвелловское действие, выраженное через потенциалы. По-
Полагаем теперь
< -щ -д0А( +diA0 A.51)
и производим замену переменных. Если g не зависит от тт, то такая
замена переменных не влияет на g и на скобки Пуассона. Следователь-
Следовательно, эти величины можно вынести из-под знака интеграла по тт, сохра-
сохранив при этом интерпретацию СП как бесконечно малого изменения
функции g в результате калибровочных преобразований. Интегрирова-

240 Глава 7
ние по тт' дает бесконечную постоянную, которую мы игнорируем.
Окончательный результат имеет вид
/ 6[*]det| J_|*H A.52)
осо
где S[A] - максвелловское действие, g - калибровочная функция, а
Sg/Sco- ее изменение при бесконечно малых калибровочных преобра-
преобразованиях. Применив эту формулу к случаю кулоновской калибровки,
получим
^д1А.]а*\д2\е*. A.53)
и при этом видно, что детерминант не содержит какой-либо зависимости
от А; следовательно, его можно включить в нормировку. Заметим,
что входящая линейно в S переменная Ао приводит после интегрирова-
интегрирования к функциональной 6-функции. Это показывает, что Ао не является
динамической переменной, хотя часто можно встретить утверждение,
что условие Ло = 0 представляет собой калибровочное условие (это
не так!). Но если мы все-таки требуем выполнения условия Ао = О,
то мы теряем ограничение diui = 0 (теорема Гаусса), которое затем
должно быть восстановлено.
В заключение заметим, что можно определить ковариантную
калибровку
9х А^ = 0, A.54)
которая действительно представляет собой калибровочное условие,
так как содержит динамическую переменную A t.
Задачи
А. Рассматривая <р, , q>2 и х как канонические поля, выполните
каноническую процедуру применительно к действию
S = j ^ 2 21
и определите соответствующий интеграл по траекториям.
Б. Проанализируйте применимость равенства А{ Л,- = т2 в
качестве калибровочного условия и запишите соответствующий
интеграл по траекториям для электродинамики в такой калибровке.

Интеграл по траекториям в калибровочных теориях 241
В. Бовторите предыдущую задачу для калибровочного условия
(д. Л3)<ЭМз = 0.
Г. Рассмотрите условие 0 = * дг . ^(zt 0» где интеграл берется
по некоторой кривой С. Можно ли использовать его в качестве кали-
калибровочного условия?
§ 2. Гамильтонов формализм для калибровочных
теорий, неабелев случай
Исходя из янг-миллсовского лагранжиана, можно повторить все
рассуждения предыдущего параграфа и прийти к очень похожим резуль-
результатам. Но мы начнем все же с формализма первого порядка, в котором
fnv и ^ц считаются независимыми переменными, а действие S[F, A]
берется таким, чтобы FMV можно было выразить через Лц исходя из
уравнения движения. Итак, возьмем действие в виде
B.1)
Ясно, что вариация такого действия по F приводит к уравнению
C.2) из гл. 6, но F не имеет динамического смысла, так как не име-
имеет производной по времени; это всего лишь вспомогательное поле.
Однако при такой форме действия его легче переписать в виде, не со-
содержащем квадратичных по временным производным членов. Введем
"электрическое" и "магнитное" поля
Et =Foi, В,- = ^-4jkFiky. B.2),B.3)
или, альтернативно,
jj B.4)
Используя уравнение движения
Fif -dtAf -djAi +i[A{ , Aj], B.5)
можно переписать S в виде
S = - _ly fd*x Sp[B. В. + ?. ?. _2?,- (д0А{ -dt Ao +
+ i [^0, At ])] = B.6)

242Глава 7
- 2A0 (*. ?. + i [Д, , Et ])], B.7)
использовав циклическое свойство следа и выполнив интегрирование
по частям. Переписанное таким образом действие S легко преобразу-
преобразуется к гамильтоновой форме. Взяв след, получаем
B.8)
где ?| - канонический импульс, сопряженный с А{ (точка означает
дифференцирование по времени), 4^ играет роль лагранжева множите-
множителя, а
(S.?.)B«d.?f +/ВССЛС?О. B.9)
Динамическими переменными являются ?? и Лв , для которых мы пос-
постулируем следующие фундаментальные скобки Пуассона при совпадающих
временах:
U?(x, 0. ?/С<У> 01сп =бВС5[75(х^у), B.10)
причем все остальные СП при совпадающих временах равны нулю. Не
все из этих переменных независимы, так как они должны удовлетво-
удовлетворять уравнению связи
($.?.)*.<?. ?f +fBCDACED =0, B.11)
получаемому варьированием по А В , Уравнения движения имеют
вид
где
^3[fi BJBi]. B.13)
Таким образом, как и в предыдущем параграфе, изменение во времени
содержит дополнительный член, обязанный лагранжеву множителю.

Интеграл по траекториям в калибровочных теориях 243
Чтобы выяснить смысл этого члена, вычислим скобку Пауссона
ЪАВ (х> ,) - U? (*, t), jd*yAC{y, 0B),- Et )с(у, 01СП . BЛ4)
которую следует интерпретировать как изменение переменной А(в при
бесконечно малом преобразовании, вызываемом дополнительным чле-
членом. Пользуясь соотношением B.10), находим, что
5А.В (», 0 « - а. Ав0{х, р) - fBCDAC {x> t)AD{X} t)> B.i5)
что представляет собой калибровочное преобразование. Следовательно,
как и в абелевом случае, дополнительный член в гамильтониане Н
осуществляет калибровочное преобразование с калибровочным парат
метром А^ .
Нетрудно видеть, что производная по времени от связей B.11) са-
сама пропорциональна этим связям (см. задачу). Следовательно, ника-
никаких других связей быть не может.
Как и ранее, мы принимаем, что функции Ав и Ев являются
физическими, если их изменение при бесконечно малой трансляции
во времени не произвольно, т.е. если
{/,C). ?,• )fiicn -° при (В,-Е. )в - 0. B.16)
Далее, СП всегда можно рассматривать как интегральный оператор
1¦=! , (В,-?,-)*(*, 01. B.17)
О
'
если выполняется условие интегрируемости
5 5 5
О s*C(y> 0 8zC(yt О 5zS(x, О
Пользуясь тождеством Якоби и СП между двумя величинами 3). ?•
(при равных временах), нетрудно показать, что это условие действи-
действительно выполняется (см. задачу). Таким образом, наше физическое
подпространство может быть определено двумя условиями
$;?;)й = 0. 1 .(В,- ?,¦ )в1-0. B.19)
Эти условия соответствуют переходу от функционального простран-
пространства, покрываемого функциями Ав и ?f (i = 1, 2, 3), к функциональ-

244 Глава 7
ному пространству, покрываемому функциями И^ , а? и Жв, Т[?
в подходящим образом выбранном базисе.
Можно также описать это подпространство иначе, заменив неудоб-
неудобное условие с СП другим набором условий
gB(A^(Xf t), ??(*, *))«0. B.20)
которые мы называем калибровочными условиями. Такое измененное
определение не должно включать какие бы то ни было сингулярные
замены переменных, связанные с переходом от функций ъс к функци-
ям qc, т.е. (функционально)
=det|Uc, C),-?,. )в!| *0. B.21)
Это условие необходимо для того, чтобы функция gB описывала жела-
желаемый выбор калибровки. В противном случае она не будет фиксировать
калибровку. Предполагая, что условие B.21) выполнено, поступим
несколько умнее и ограничимся таким выбором калибровок, которые
удовлетворяют (вновь при совпадающих временах) условию
{gB, gc!cn = 0. B.22)
Тогда мы можем рассматривать gB как каноническую переменную.
Рассмотрим каноническое преобразование
(Ав , ЕВ) + (АВ, Ёв), B.23)
где индексы / используются просто как метки и не обязательно пре-
преобразуются как векторные индексы при вращении, а
Ц-ев(Л. , ?. ). B.24)
Теперь условие B.21) принимает вид
<2-25>
так как переменные с тильдой сопряжены друг другу. Если мы теперь
положим gB =^?\ = 0, то уже невозможно придать смысл СП B.10),
включающей Евг. Это означает, что Щ нужно выразить через оста-
остающиеся переменные. Но именно это и позволяет сделать условие

Интеграл по траекториям в калибровочных теориях 245
B.25): с его помощью можно разрешить уравнение связи B.11), выра-
выразив Ев3 через остальные переменные. Таким образом, янг-миллсов-
ская система определяется теперь в независимых переменных
Л® = (%в, А\) и EBL = (Ёв, Ев2) плотностью гамильтониана
Н = i- [е1Ё{ + [EA3(EL, A^V+ЩЩ], B.26)
где ЕАг{Е±, А^) - функщя, являющаяся решением уравнения связи
B.21), а Щ даются формулами B.5) и B.3). Не стоит и говорить,
что теперь гамильтониан Н стал очень сложным, так как помимо того,
что он нелокален, он еще содержит кубичные и квадратичные члены
взаимодействия.
Приведем теперь примеры часто встречающихся калибровочных
условий.
1. Кулоновская калибровка, определяемая, как и в абелевом слу-
случае, условием
#А? = 0. B.27)
Как нетрудно видеть, для того чтобы равенство B.27) было хорошим
калибровочным условием, оператор
B.28)
не должен иметь нетривиальных нулевых собственных значении.
Учитывая B.27), перепишем B.28) в виде
{ ^E'. B.29)
Недавно Грибов [ 2] указал на то, что существуют нетривиальные
решения уравнения
OfiC/c = 0 B.30)
и потому кулоновская калибровка не является хорошо определенной
для янг-миллсовских теорий в том смысле, что она не позволяет одно-
однозначно извлечь независимые канонические переменные. Но и в этом
безумии есть свой порядок: совсем не просто прийти к потенциалам
Ав , удовлетворяющим кулоновскому условию, для которых оператор
B.28) имеет нулевые собственные значения. В качестве примера,

246 Глава 7
иллюстрирующего эту проблему, рассмотрим потенциал (в матричных
обозначениях)
A. m-iUrd. U; д1 А. =0. B.31)
Если бы условие B.27) было достаточным для фиксации калибровки,
то мы должны были бы иметь возможность доказать, что единственным
решением уравнения B.31) является Л; = 0. Ограничимся случаем
группы SUB) и напишем
U = cos + i о < nsin__— , B.32)
где п • п = 1 и ш зависит только от х. Тогда путем прямых вычисле-
вычислений можно убедиться, что [а -индекс группы SUB)]
д{ А<\ = A + cosco)( <3;со) <Э' па + A - coscc) iabcnbdidi nc +
+ sinctf<9. ^abcnbdinc +smudidina +п°сЭЦ ы, B.33)
Такое уравнение явно безнадежно, но мы его упростим: следуя
Грибову, ограничимся сферически-симметричными решениями, для
которых
л° -сЭаг = _fl_. B.34)
г
Тогда находим, что со зависит только от г и как следствие кулоновского
условия со(г) удовлетворяет уравнению
+ _— - sin 2co = 0, B.35)
где t = In г. Из требования несингулярности U следует, что
ф = -«) = 0, 2тт, 4тт, . . . B.36)
Полученное уравнение представляет собой уравнение затухающих коле-
колебаний маятника в постоянном гравитационном поле. Граничное условие
B.36) требует, чтобы колебания начинались при u(t - -«>) из положе-
положения неустойчивого равновесия. Затем, в зависимости от начальной ско-
скорости грузика, возможны три варианта: 1) либо он все время будет ос-
оставаться в положении и - 0; 2) либо он начнет падать по ч асовой стрел-

Интеграл по траекториям в калибровочных теориях 247
ке и при t - + о» достигнет положения устойчивого равновесия со= - тг;
3) либо он начнет падать против часовой стрелки и все кончится так же,
как в предыдущем случае.
Вдобавок к этому маятник может много раз прокрутиться и только
затем попасть в одну из трех категорий. Первое решение соответствует
значению А ,• =0, что можно было сказать заранее, но два других типа
решений соответствуют нетривиальным Ai . Существование таких Л,-
и приводит к неоднозначности Грибова. Если положить
А. ж-ie-il^^- д,¦eil*^T1- , B.37)
где / = 0, ± 1, ± 2, . . . , то значение / = 0 отвечает случаю 1, а значе-
значения / = ± 1 - двум другим случаям. При t -* + °° имеем следующие гра-
граничные условия:
при / = 0,
± i "' * при / = ± 1. B.38)
Далее, если вычислить понтрягинский индекс для различных грибов-
ских решений, то окажется, что
п- —
1
( О, / = 0,
/1
B,39)
Таким образом, нетривиальные решения Грибова имеют топологичес-
топологический заряд +1/2 (у инстантонов +1). Такие решения явно не соот-
соответствуют обычным конфигурациям потенциала!
Поэтому можно, вероятно, допустить, что оператор B,28) имеет
нулевые собственные значения только для Ai с нетривиальной топо-
топологической структурой, т-е» с п Л 0 (доказательство такого предполо-
предположения мне не известно). Таким образом, если ограничиться возмуще-
возмущениями вблизи нулевых потенциалов, имеющих п = 0, то проблему мож-
можно игнорировать. Однако решение ее все еще является открытым во-
вопросом в тех случ аях, когда рассматриваются непертурбативные
янг-миллсовские явления. По этому поводу можно сказать лишь то,
что кулоновская калибровка требуемым образом ограничивает фазовое

248 Глава 7
пространство, но только с точностью до копий, соответствующих
; _ +1, ± 2 Мы вернемся к данному вопросу после того, как
рассмотрим аксиальную калибровку.
2. Аксиальная калибровка Арновитпа - Фиклера характеризуется
условиями
n'Af =0, я1" я,- = 1. B.40)
где п -постоянный вектор. В этом случае оператор
5ссс
B„41), B.42)
приводится к тому же виду, что и в абелевом случае, и, по-видимому,
обратим, так что кажется, что в этой калибровке не должно возникать
проблемы Грибова (подробнее об этом ниже). Таким образом, можно
обратить уравнение связи BЛ 1) и, решив его относительно ЕА2 , полу-
получить в результате Ц- = 5? 3)
Е\(Х, У) г, О = - / dz'(\EL)A{x, У, г1, t), B.43)
— 00
причем единственная ненадежная вещь здесь - граничное условие
при z = -<х> (самое слабое место этой калибровки). После этого не-
непосредственно находится гамильтониан, представляющий собой столь
устрашающее выражение, что приводить его здеи> не стоит.
Вернемся теперь к проблеме Грибова. На первый взгляд, аксиаль-
аксиальная калибровка не сопряжена с неоднозначностями, обнаруженными
в кулоновской калибровке. Однако они могут скрываться в граничном
условии для ?3, необходимом для обращения nl dt : Поэтому возмож-
возможны два варианта: 1) либо проблема не специфична ддя теории Янга -
Миллса и дело лишь в том, что кулоновская калибровка — неудачный
выбор; 2) либо проблема коренится в самой теории,и тогда она долж-
должна проявиться и в аксиальной калибровке, а единственное место, где
это может случиться, - пространственная бесконечность. Никто не
знает ответа, но Сингер показал, что если определить интеграл по
траекториям на сфере S 4 в евклидовом пространстве, то грибовская
проблема присуща самой теории и корни ее в том, что невозможно
обойтись одним и тем же калибровочным условием во всем простран-
пространстве-времени. Так как нас главным образом интересуют вычисления
янг-миллсовского интеграла по траекториям по теории возмущений, тс
мы просто, будем игнорировать в дальнейшем грибовскую проблему.

Интеграл по траекториям в калибровочных теориях 249
ФИТ для янг-миллсовской теории можно теперь построить в точ-
точности так же, как и в абелевом случае, лишь с небольшим усложнением,
связанным с индексами. Мы просто приведем результат:
Л
B.44)
где gA - калибровочная функция, a S Ям [ А] - янг-миллсовское дей-
действие, записанное только через Тютенциалы.
Задачи
А. Вычислите скобки Пауссона
I (9),- Et )Л(х, t\R] и \ (Ю. ?. )А(х, О, {% ?,• )В{У, О!
и покажите, что если удовлетворяются уравнения связи, то измене-
изменение фь ЕА) во времени равно нулюо
Б., Пользуясь некоторыми результатами задачи А, покажите, что
выполнены условия интегрируемости для функции г, определяемые
как
SzA(x, О
x, t)\.
В. Выразите гамильтониан янг-миллсовской системы в кулонов-
ской и аксиальной калибровках через соответствующие независимые
канонические переменные,
Г. Выведите уравнение движения затухающего маятника в пос-
постоянном гравитационном поле и сравните с уравнением Грибова,
Вычислите топологический заряд Bо39) для нетривиальных решений
этого уравнения»
Д. Покажите, что ,в кулоновской калибровке возможность избавить-
избавиться от продольных составляющих ?(. , используя связь (Ю8- ?,- ) = О,
зависит от обратимости оператора д12)f- „
§ 3. Непосредственное определение янг-миллсовского
ФИТ, процедура Фаддеева - Попова
В двух предыдущих параграфах мы показали, как можно вывести
янг-миллсовский ФИТ, пользуясь классическим гамильтоновым форма-
формализмом,, Окончательный результат оказался сложным выражением,

250 Глава 7
что объясняется наличием в гамильтоновом формализме ограничений,
обусловленных калибровочной инвариантностью исходного действия.
Существует другой, более прямой способ получить это выражение -
процедура, предложенная Фаддеевым и Поповым [ 3],
Янг-миллсовское действие по построению калибровочно-инвариант-
но, т,е«
snMU^] = snMUt/L (ЗЛ)
где
Л1 = VA»tf -iUd^tf, U(x) = е'«(Ф Т. C,2)
Это означает, что наивное выражение (в евклидовом пространстве)
/3LV

че очень хорошо определено, если символом Юл обозначено сум-
суммирование по всем А даже по тем, которые связаны калибровоч-
калибровочным преобразованием, В приложении А мы покажем, как обойти эту
трудность: нужно определить новую меру, которая не давала бы
лишних вкладов, т,е, меру, в которой сумма берется только один
раз по всему калибровочному семейству. Грубо говоря, мы должны
отделаться от лишних интегрирований (задача, известная математи-
математикам как определение меры Хаара)о
Рассмотрим величину
A UM] = /St/5[gB(^)], C,3)
где Аии - функция, определенная в формуле C,2), Символ 'S)U означа-
означает сумму по всем элементам группы, a gB - функции, обращающиеся
в нуль для некоторых А^.Величина Д~^ инвариантна (мы пренебрега-
пренебрегаем нетривиальными гомотопическими классами и проблемой Грибова),
Действительно, так как
^j^17)].» C,4)
изменим переменные интегрирования и перейдем от UkU", где

Интеграл по траекториям в калибровочных теориях 2Я
В результате получим
поскольку V" - переменная интегрирования* Таким образом, путем
хитроумного вставления 1 в наивную сумму по траекториям получаем
^ ^gS№. C,7)
Выполнив в подынтегральном выражении калибровочное преобразование
от Л^ к Л^, получим
если воспользуемся формулами (ЗЛ) и (Зоб), а также учтем, что
2L^ и ЭЛ^ одинаковы^ Но теперь ничто уже в подынтегральном
выражении не зависит от U, и можно убрать 3I/ вместе с мультипли-
мультипликативной бесконечностью, от которой мы и хотели избавиться в пер-
первую очередь,, Следовательно, мы определяем правильный ФИТ для
теории Янга -Миллса как
Остается вычислить А [Л]. Прием заключается в том, чтобы рас-
рассмотреть gA(Au) как функцию группового элемента U(x<), Тогда
можно произвести замену переменных U(x) ¦* gA* Символически записы-
записывая
3)U = 3)g det | i?_ | , (ЗЛО)
5
получаем Д [А] = /3) g det | IE- | 5 [gl _ (ЗЛ1)
или
AgU] = det|ig_||g=o' <ЗЛ2>
Подобные манипуляции можно производить, если замена переменных
U -» g хорошо определена и несингулярна: одному групповому элементу
U(x) отвечает только одна функция g и наоборот. Как мы видели, в ку-
лоновской калибровке это условие не выполняется (проблема Грибова).

252 Главе 7
Более того, U(x) определяется тем же числом параметров, что и g,
но U(x) может иметь нетривиальные граничные условия и принадлежать
к ненулевому гомотопическому классу» Мы игнорируем в последующем
подобные проблемы до тех пор, пока будем иметь дело с вычислениями
по теории возмущений в квантовой теории поля вдали от значения
Если параметризовать U(x) функциями <яА(х), то Д можно записать
в виде
(ЗЛЗ)
8 со* (у)
Собирая все выражения, приходим к окончательному выражению
для ФИТ в калибровочной теории (опустив индексы)
C.14)
6 со
которое совпадает с выражением, полученным с помощью гамильтонова
формализма» Это выражение калибровоч но-инвариантно (смо прило-
приложение А и задачу)»
Задачи
А. Покажите, что величина Д [А] = det| 5йЛ;/5со в| калибровоч-
но-инвариантнао
Бо Покажите, что окончательное выражение
5со
не зависит от выбора калибровки g (указания см„ в приложении А),
**В. При наличии неоднозначности Грибова величина Д~1 не су-
существует. Попробуйте обобщить процедуру Фаддеева - Попова, т.е.
определите заново величину Д~10
ЛИТЕРАТУРА
1. Dime РАМ, Can» Journ. Math., 2, 1 29 A950).
2. Gribov V.N., NucL Phys., В139, 1 A978).
3. Faddeev L:D., Popov V.N., Phys. Lett., >25B, 29 A967).

Глава 8
Вычисления по теории возмущений
в калибровочных теориях
§ 1.Фейнмановские правила для калибровочных теорий в
евклидовом пространстве
Будем исходить из выведенного в предыдущей главе выраже-
выражения для интеграла по траекториям для калибровочных теорий, к кото-
которому мы с целью получить функции Грина добавим члены с источника-
источниками. Таким образом, рассмотрим в евклидовом пространстве функционал
A.1)
Чтобы вывести фейнмановские правила, нужно переписать дополни-
дополнительные множители в мере. Прежде всего заметим, что выражение
A.1) не зависит от калибровочных функций g4. Поэтому можно выбрать
новую калибровочную функцию
g'A=gA-cA, A.2)
где с - некоторая функция переменной х, не зависящая от А^ ,
Кроме того, можно провести в выражении A Л) функциональное интегри-
интегрирование по с А с любым весом; это просто приведет к изменению норми-
нормировки функционала W[J], Калибровочная функция обычно линейна по
Ау, так что если мы хотим, чтобы калибровочная функция входила
квадратично в показатель экспоненты, то рассмотрим
$<S)cAe~2*tiSd*XcAcAbUA-cA\=e~12Jd*xtA&A> <L3>
где а - произвольный коэффициент. Тогда исходное выражение примет
вид
(ЪАА A.t\5gA i ~SEM ~ ^nr< gA6A > +< J,,aaA > A.4)
Далее нам нужно переписать детерминант в виде функционально-
функционального интеграла. Поскольку детерминант входит в числитель, он соот-
соответствует интегралу по траекториям, взятому по грассмановым пере-

254 Глава 8
менным:
A.5)
Эти грассмановы поля - знаменитые поля-духи Фейнмана и Фаддеева -
Попова, преобразующиеся как члены присоединенного представления
группы. Теперь можно записать ФИТ в виде
/Ют^/Юл^-*!** г A.6)
где
ф = s ЯМ + _J_ < gAgA > -i < tfA(x
Это выражение позволяет сформулировать фейнмановские правила, ко-
которые, очевидно, зависят от выбора калибровки. Заметим, что
5Aj(x)
(х)
и это приводит к локальному взаимодействию г| -полей» Такое же выра-
выражение справедливо и в абелевом случае, с той только разницей, что
в нем отсутствуют групповые индексы* Ниже мы будем рассматривать
оба случая, абелев и неабелев. Прежде всего рассмотрим ковариант-
ную калибровку
^ = Vm = °- A.9)
Нетрудно видеть, что
в неабелевом случае и
S[ ' = д^5(х-у) A.11)
в абелевом. Сравнивая с выражением A.7), мы заключаем, что в абе-
левом случае в такой калибровке духи не взаимодействуют с калибро-
калибровочными полями» Поэтому от них можно избавиться путем интегриро-

Вычисления по теории возмущений в калибровочных теориях 255
вания в интеграле по траекториям: в ковариантной калибровке A»9)
для КЭД духи не являются необходимыми»
В неабвлевом же случае выражение AЛ0) указывает на наличие
нетривиального члена взаимодействия» После интегрирования по час-
частям, если учесть условие A»9), часть действия, содержащая поля-духи,
принимает вид
\p,*\r,4 A.12)
При такой форме записи грполя можно интерпретировать как скалярно-
подобные поля, взаимодействующие через свой ток с калибровочными
полями» Но не следует забывать, что эти поля представляют собой
грассмановы числа и потому фейнмановские правила для них радикаль-
радикально отличаются от правил для скалярных полей: всякую замкнутую петлю,
составленную из тополей, нужно брать со знаком минус (гл. 5). Связь
тока с дивергенцией калибровочного поля антиэрмитова, тогда как ос-
остальная часть лагранжиана д/хов эрмитова» Но можно пренебречь
антиэрмитовой частью, так как детерминант должен вычисляться при
условии д • А = 0„ Как мы увидим ниже, вытекающее отсюда изменение
фейнмановских правил для духов оказывает влияние только на распро-
распространение продольной части калибровочного поля, которую всегда мож-
можно устранить путем перенормировки калибровочного параметра а. Фейнма-
Фейнмановские правила, учитывающие наличие полей-духов, таковы:
nponaimop духа
р - р2 '
вершина взаимодействия духа с калибровочным полем
1
ABCt
где спиральная линия отвечает калибровочному полю Ас „ Кроме то-
того, мы для ясности восстановили множитель g. Импульсы р, q, r
входят в вершину и, конечно, удовлетворяют уравнению закона сох-

256 Глава 8
ранения
A.15)
Квадратичная ч асть эффективного действия для калибровочных полей
имеет вид
где мы произвели изменения в определениях А -* qA, a -> g2a; далее,
причем каждый член был проинтегрирован по частям, Пропагатор ра-
равен обратной величине оператора в квадратных скобках, (Заметим,
что в отсутствие калибровочного члена выражение в квадратных скоб-
скобках есть оператор проектирования и для него нет обратной величины;
поэтому и требуется добавлять калибровочный член, что сделал еще
Ферми для КЭД.) Мы можем без потери общности записать пропагатор
в импульсном пространстве в виде ДрMцу + Y(p)pilpv. Тогда, потре-
потребовав, чтобы выполнялось условие
0 )\ (Ы8)
мы получаем для фейнмановского пропагатора, изображаемого гра-
графически спиралью, выражение
^ A.19)
До сих пор мы считали параметр а произвольным. С точки зрения
вычислений проще всего калибровка Фейнмана, в которой a = 1:
А в 1 , „
плплпгт —» 5ЛЙ5 (Калибровка Фейнмана). A.20)
f р — v р2 »v

Вычисления по теории возмущений в калибровочных теориях 257
Если положить а = 0, то числитель пропагатора A.19) превращается
в проекционный оператор, необходимый для запрета распространения
лишней моды. Такая калибровка называется калибровкой Ландау.
Она не очень удобна для вычисления фейнмановских диаграмм, но
полезна при проверке унитарности амплитуд в пространстве Минковс-
кого.
Далее, эффективное действие содержит член, кубичный по калибро-
калибровочным полям,
-gfd*xfABCA*AvB д^ . A.21)
Чтобы получить соответствующее фейнмановское правило, мы должны
переписать этот член в импульсном пространстве в>виде
-1- A* (р)АВ (q)ACp (r)VABpC (p, q» ф A.22)
Множителем - V, полностью симметричным относительно перестанов-
перестановки полей А, и определяется фейнмановское правило. В частности, нам
уже известна структура индексов V, которая просто есть /^sc. Сле-
Следовательно, можно написать
p(p> q, r), A.23)
где функция УЦур(р, q, r) должна быть антисимметричной относитель-
относительно перестановки пар (м, р), (v, q), (р, г), так как множители f^-BC
сами полностью антисимметричны. Из выражения A.21) следует, что
в Рцур должно входить произведение i гц5ур „ Этого достаточно, чтобы
из соображений симметрии выписать все остальные члены. Результат
таков:
A p-— --r P
где, конечно (р + q + г)ц = О.
Аналогично эффективное действие содержит квартичныи член
J_ g2fABEfCDEAAABACADt A.25)

258 Глава 8 ^___
который следует переписать в виде
-1_^(р)лЯ (q)Acp (r)A^{s)V^CaD[p> q> r> s)> (]26)
где множитель V полностью симметричен относительно перестановки
троек {А, \х, р), (В, v, q), (С, р, г) и (D, a, s). Из выражения A „25)
явствует, что этот член не содержит никаких импульсов и, следова-
следовательно, его структура такова:
1 2fABEfCDEr к
— S f f 5цр5уа •
Исходя из этого выражения, мы должны построить выражение, симмет-
симметричное относительно замен {А, \л) -»(В, v) и [С, р) -»(D, ст)о Так как
множители / антисимметричны, нам нужно по отдельности антисиммет-
ризовать выражение по отношению к заменам ц -> v и р -» ст, т„ео поло-
положить
5iap5vcr -> -j—Eup5vc -5Ур5Ца)>
чтооы учесть оба требования. Затем следует обеспечить еще две сим-
симметрии - относительна замен (А, ц) -»(D, р) иD, м -»(D, Ь). Для этого до-
бавим соответствующие чланы и поделим результат на 3. Это даст нам
последнее фейнмановское правило
_g2ifABEfCDE(s
х Up°va
per -
5ap5via -5vp5ua;
Два последних фейнмановских правила не зависят от калибровки и
отсутствуют в абелевом случае. Все выписанные фейнмановские пра-
правила в ковариантной калибровке собраны в приложении В„

Вычисления по теории возмущений в калибровочных теориях 259
Рассмотрим теперь калибровку Арновитта - Фиклера, которую мы
запишем в евклидовом пространстве в необычной форме
Vf-'0' W=l- A.28)
Легко видеть, что в этой калибровке выражение
5(х-у)= A.29)
ud[i5(x-y) (ЬЗО)
не зависит от А^ „ Следовательно» как в абелевой, так и в неабелевой
теории духи не связаны с калибровочными полями, а потому можно
без них обойтисЬо Именно в калибровке такого типа структуры аЬ •левой
и неабелевой теорий наиболее близки друг другу. Нам остается только
позаботиться о пропагаторе калибровочного поля- Квадратичный по
А член имеет теперь вид
jd*x[ 1_ EцЛ* - dvA^)(duABv -д„Ав ) - _*_ пиАВпрАв} ,
или, после интегрирования по частям,
_1_ fd*xA* [ - W,v - d[idv - -L- %nv] AB . A.31)
Фейнмановский пропагатор равен обратной величине выражения в квадрат-
квадратных скобках. В импульсном пространстве (см. задачу) получаем
A.32)
Как нетрудно видеть, преимущества такой калибровки сомнительны:
духов нет, но очень сложна структура пропагатора^
Заметим, что в выведенных нами фейнмановских правилах
имеется некоторый произвол: знак пропагатора ду*ха и вершины взаимо-
взаимодействия духа с калибровочным полем не существен, так как мы всег-
всегда будем иметь дело с четным числом линий духово

260 Глава 8
В заключение вьшишем дополнительные фейнмановские правила
для связи калибровочных полей с фермионами. Хотя калибровочные
поля можно связать независимо с левыми и правыми фермионными
полями, мы остановимся на чисто векторной связи, в которой левые
и правые фермионы связаны одинаково» В этом случае в дополнение
к калибровочному лагранжиану нужно написать
?/ = Фг • 3>V + inW, A.33)
где ц/(х) - дираковское спинорное поле массы щ а Ф — соответствую-
соответствующая ковариантная производнаяо Мы опустили все индексы. Дополнитель-
Дополнительные фейнмановские правила таковы:
фермионная линия
A,34)
т
где р = р у и а, Ъ - индексы фермионного представления;
вершина взаимодействия фермиона с калибровочным полем
где (ТА)$ — матричные элементы генераторов группы в соответст-
соответствующем фермионном представлении* До тех пор пока мы имеем дело
с дираковскими фермионами, нет существенной разницы между рас-
рассмотрением их в,пространстве Минковского или Евклида, если не счи-
считать замены ц> на цД * Ниже мы сохраним более уместную систему обоз-
обозначений, отвечающую пространству Минковского, хотя и пишем фейнманов-
фейнмановские правила в евклидовом пространстве,,
Задачи
А. Выведите выражение для пропагатора калибровочного поля в
калибровке п^Лц = 0, пипи = 1, гац фиксировано»
Б. Выведите фейнмановские правила для комплексного скаляр-
скалярного поля, взаимодействующего с янг-миллсовским полем. Для опре-
определенности рассмотрите локальную инвариантность относительно
группы SU(N) и предположите, что поле преобразуется по iV-мерному
представлению.

Вычисления по теории возмущений в калибровочных теориях 261
**В. Рассмотрите для S {/(ЛО-калибровочных теорий калибровочное
условие д А + а{А , А \ (записанное здесь в матричной форме), где
а — произвольный коэффициент. Выведите фейнмановские правила*
Проанализируйте влияние калибровочных условий на вершины. Заметим,
что это странное калибровочное условие возможно только в том слу-
случае, когда оператор {А А \ имеет те же групповые свойства, что и
д- А.
§ 2. КЭД , однопетпевая структура
Переходим к исследованию в рамках теории возмущений простей-
шай из калибровочных теорий, которая описывает взаимодействие фото-
фотона с заряженными частицами. Определяющий эту теорию классический
лангранжиан имеет вид
B.1)
Здесь Т — четырехкомпонентное дираковское поле, а е - электрический
заряд» В природе существует много заряженных полей: лептоны е~, \л~,
т ~с зарядом - е, "верхние" кварки и, с (и, возможно, t) с зарядом
2/Зе, "нижние" кварки d, s, b с зарядом - 1,/Зе, промежуточный век-
векторный переносчик слабых взаимодействий И^и, возможно, многие
другие поля, еще не открытые. Мы ограничимся полем со спином 1/2,
Так как мы собираемся проводить вычисления в пространстве 2ш
измерений, заменим размерную константу связи е безразмерной:
е-к?ц2"ш, B.2)
где ц - традиционный массовый параметр в схеме размерной регуляри-
регуляризации. (Напомним, что в 2соизмерениях поля со спином 1/2 имеют
размерность - со+ 1 /2, а поля со спином 1 имеют размерность
- со+ L) Таким образом, фейнмановские правила в евклидовом про-
пространстве (в фейнмановской калибровке а = 1) имеют вид
B.3)
р+т

262 Глава 8
где мы опустили все спинорные индексы и, кроме того, каждой фер-
мионной петле приписывается знак минус.
Руководствуясь этими правилами, приходим к однопетлевым диа-
диаграммам
г т ~~~rjr~\^*r^ i__—t Bi4)
которые дают поправки к фундаментальным параметрам теории и по-
полям, и диаграммам
B.5)
которые на первый взгляд порождают новые взаимодействия. Разбе-
Разберемся сначала с диаграммами B.5).
Хорошо известно, что дираковский кинетический член инвариан-
инвариантен относительно операции зарядового сопряжения
Y -» Т € = CY т • B.6)
При таком дискретном преобразовании дираковские коварианты Фчл
^у5Уи ^УвУц^ четны, тогда как векторный 4V,y и тензорный
Ч'&шД коварианты нечетны. Отсюда следует, что лагранжиан B.1)
инвариантен относительно комбинации дискретных преобразований
Ч'-Ч'С.л^-^. B.7)
Поэтому ?КЭД не может порождать взаимодействий, для которых не-
нечетно число фотонных линий (напомним, что в аналогичном случае
теории Лф4, которая симметрична относительно замены ф -» - q>, не мо-
могут существовать функции Грина с нечетным числом линий). Данное
положение , называемое теоремой Фарри, избавляет нас от диаграмм
B.5).

Вычисления по теории возмущений в калибровочных теориях 263
Мы намеренно пренебрегли диаграммой
B.8)
описывающей рассеяние света на свете. При простом подсчете степе-
степеней эта диаграмма логарифмически расходится (в четырех измерени-
измерениях), поскольку каждый фермионный пропагатор ведет себя как (р)-„1
Но так как диаграмма содержит четыре фотонные линии и возникает в
калибровочно-инвариантной теории, она должна быть пропорциональна
(F vL и иметь размерность восемь (при со= 2). Таким образом, мо-
может показаться, что мы нашли диаграмму, которая расходится и не
соответствует фундаментальным взаимодействиям, входящим в ла-
лагранжиан. Следует ли из этого, что КЭД неперенормируема? На пер-
первый взгляд, кажется невозможным устранить эту расходимость, перео-
переопределив входные параметры. Но вопреки простому подсчету степеней,
ящичная диаграмма B.8) - ультрафиолетово-сходящаяся, и тем самым
вопрос снимается. Отсюда вытекает первый урок: в калибровочных
теориях нельзя доверять простому подсчету степеней, поскольку рас-
расходящиеся диаграммы могут оказаться на самом деле конечными или
по крайней мере не так сильно расходящимися.
После такого мудрого предостережения займемся вычислением
однопетлевых диаграмм B.4), Начнем с поправки к фермионной линии
(опуская спинорные индексы)
B-9)
р-1
»J J-*!!L y . I".' > у _^_ B.10)
Используя свойства у-матриц в евклидовом пространстве
i»Vyvi=-25nv, BЛ1)
перепишем фермионный пропагатор в виде
=i
q + m q2 + m
B.12)

264 Глава 8
Вводя интегрирование по фейнмановским параметрам, получим
- rrf-T-*K BЛЗ)
Перейдем к новой переменной интегрирования
l'=l-px; B.14)
имеем
- X)] 2 '
B.15)
Член с /' в числителе обращается при интегрировании в нуль, а два
другие члена дают [в силу формулы (Б.16)]
х [р2х{\ -x) +m2x]«-2# B.16)
Прежде чем проводить разложение вблизи со= 2, нужно использовать
алгебру у-матриц, которая теперь зависит от размерности. Действи-
Действительно, из B.11) находим
ГцУц = -^«, уцУрГц = [2-2B-со)]ур. B.17), B.18)
Положив е = 2 — со, можно теперь написать
х [р{\ -х) + 2т-е(рA - х) + ^].
После разложения вблизи е = 0 находим
J9A +y)+m(l + 2у)
-x)+2m]ln( P2*A-*) + m2* )] + 0(е)<
42

Вычисления по теории возмущений в калибровочных теориях 265
где у - постоянная Эйлера - Маскерони. Сохраним этот результат на
будущее-
Рассмотрим теперь поправку к фотонной линии, называемую также
диаграммой поляризации вакуума:
B.21)
B.22)
где знак минус взят из-за фермионной петли, а след берется по спинор-
ным индексам, т.е. от произведения у-матриц. Это выражение перепи-
переписывается в виде
t-m)Yv(t--m)]. B.23)
Вводя феинмановский параметр и новый импульс в петле
1' = I + Р* > B,24)
получаем
пм„(р) = -(*ц2-»J;<**
гЛ11— Sp [у (Г + 0A - х) - niSyJ'-^x -m)]
BттJсо L/'2 +т2+р2хA -х)]2 •
B.25)
Как обычно, члены, нечетные по /', выпадают при интегрировании по
петле» Если в 2 со измерениях рассматривать у-матрицы как 2е0 х 2 ю-
мерные, то будем иметь следующие формулы для следов:
, B.26)
S,p6vcr + бцсгбру - 6,v6pa). B.27)

266 Глава 8
Поэтому след, входящий в числитель выражения B.25), мы переписы-
переписываем в виде
['р'а -РрРахA ~ *)]SP(y|aypyvytT) + m2S?(YiiYv), B,28)
где мы воспользовались тем, что след нечетного числа матриц равен
нулю. Пользуясь формулами B.26) и B.27), приходим к выражению
для следа B.28)
2"! 2Г Г _2хA - х){р^ ~Swp2) - 6^[ Г2 + m2 + р*х{\ - х)]},
B.29)
причем мы добавили и вычли величину 5^р2хA - *)¦ Собирая все
результаты, получаем
1 -х)]2
2хA - x)(p^pv -5^-p2)
41 - X)] ~ ~[12 + т2 + р2х(\ _х)]2
B.30)
Интегрирование по импульсу в петле с использованием формул (БЛ 6)
и (Б. 18) приводит к тому, что первые два члена взаимно унич тожают-
ся, и мы получаем
B.31)
После разложения вблизи е = 0 приходим к выражению
1
И ~ - 4-у -fdxx(l -х)х
DE О
причем мы использовали значение интеграла
/ dxx(l - х) = -1- . B.33)
о 6

Вычисления по теории возмущений в калибровочных теориях 267
Последняя однопет левая диаграмма представляет собой поправку
к вершине
РХ
р + 1 \ q + l /n пл\
- А л '
х Т(Т B.35)
Она сложнее двух предыдущих диаграмм. Введем два фейнмановских
параметра и перепишем B-35) в виде
9 ' о о ^ттг~
хуа(р + 7 -m)yp(l + q -т) уа [I2 + тг(х + у)+ 21. (рх +
+ qy) + Р2х + q2y I" B.36)
После перехода к новой переменной интегрирования
Г = / +px + qy B.37)
выражение B.36) принимает вид
Гр{р, q) = -2t(e» » fdxf dy /____ х
у„ [I -qy + РA - х) -mi Yoil -Рх + 9A - у) - яг]уст
х
[/2 + тЦх + у) + р 2хA т х) + q2y{\ -у)-2р. qxy]3'
B.38)
Только квадратичная по / часть числителя приводит к расходящему-
оя интегрированию по петле. Если написать
(р, q), B.39)

268 Глава 8 .
где ГA1> содержит только часть числителя, квадратичную по I, то,
пользуясь формулой (БЛ 8), получим для расходящейся части
/_..2-Ю\3 1 1 ~Х
I г- /П \ Г 1.. Г Jy ^
+ y)+pzx(l -x) + 9^A -
а пользуясь формулой (БЛ 6), найдем
Dп)« о о
^, '2.40)
/.,,2 -со\3 1 1 -ж
*' 7 ГC<4/Ях/ dyx
Итг) 0 0
Уст Ы1 - *) - ЧУ -т]у [q(\ - у) - рх -пАуа
х 1
[т2(х + у)'+ р2х(\ -х) + q2y{\ - у) - 1р . qxy]3 ~ш '
B.41)
В последнем выражении мы можем безбоязненно положить со= 2, так
как
ГрB)
интеграл
(Р, ч) =
X
сходится1;
— i (en 2 ~с
А
В
•)
«]
результате
е2 1
Г ЙУ
Ifi 2 J UX
16 тН о
Л
получим
1-*
/ dy >
0
р
. B.42)
тЦх + у) + р2х(\ - х) + q2y(\ -y)-2p- qxy
К этому выражению мы вернемся позже. Полезное тождество
УстУссУрГрУст = 2УрУрУо - 2B ~ ")Уа'УрУр B-43)
совместно с формулой B.18) позволяет переписать B.40) в виде
2 1 1 -ж
<?)=-*• ем еур.-?_ Г(е)A -eJfdxf dyx
8тг о о
х / п?(х + у) + р2х(\ - *) + q2y(\ - у) - 2р * qxy -?_
4тгМз

Вычисления по теории возмущений в калибровочных теориях 269
е2 1 11-*
- j _L_ -у_ 1-2/ <&/ *
16 ТГ2 Е О О
xln [ "j(x + >') + P:>c<1 -ж) + 92уA -У) ~ Ь • «*У
Мы еще вернемся к этим выражениям, так как они содержат
много интересной физики- Чтобы должным образом их проанализиро-
проанализировать, нам придется совершить продолжение в пространство Минковс-
кого и вычислить полученные выражения на фермионной массовой
поверхности» Мы обнаружим, что они инфракрасно расходятся (все,
кроме ТТ^.у), и рассмотрим вопрос о том, как обойти эту трудность.
Но пока что сосредоточимся на структуре теории поля. Вычисление
однопет левых диаграмм позволяет выяснить необходимую для пере-
перенормировки КЭД структуру контрчленов.
Можно показать, что число примитивно расходящихся диаграмм в
КЭД конечно (гл. 5). Как мы уже отмечали, для перенормируемости
необходимо, чтобы вклад диаграммы рассеяния света на свете был
конечным в ультрафиолетовой области. Предположим, что это дейст-
действительно так (см. задачу).
Исходный лагранжиан в фейнмановской калибровке имел вид
4- tmTY + i ец2-со ЯРЛЧ'. B.46)
Попробуем записать лагранжиан контрчленов в виде
ellllJ. B.47)
Тогда перенормированный лагранжиан
?пер _ Р .
B.48)
можно выразить через голые величины
B.50)

270 Глава 8
е _ 2 —со 1 + *М 21
mo = m(l+ Km)/A +^21 = mZm/Z2, B.52)
_, —1 /1 js \//1 t^ \ 7 /7 /О HQ\
f» g = \ 1 + A ) (\i + Л -j = L / Lt 2 \Л«иО/
в виде
. 1 -а - B.54)
+ ~2^ (д • Л0J = Z2T5Y + imZmf^ + eZ^AY +
где мы ввели дайсоновские множители Z. Такая форма записи пока-
показывает, что калибровочная инвариантность лагранжиана ?Kn сохра-
сохранится и в ?пеР, если положить Z, = Z2, с тем чтобы сохранить струк-
структуру ковариантной производной, которая, очевидно, имеет в ?пеР вид
ч+<>4^ v B-56)
Однако отсюда еще не следует, что Z, = z2 (хотя так и окажется!),
потому что мы нарушили калибровочную инвариантность нашего лагран-
лагранжиана, включив член, фиксирующий калибровку, так что множители
Z стали зависеть от калибровки.
Контрчлены можно найти путем однопет левых вычислений. Во-пер-
Во-первых, вычисление поправки к фермионной линии
е2 1
(р + 4т) + Конечные члены B.57)
1 бтг2
приводит к контрчленам
16тт2
L +F(«m/u)) B.58)
1
— +FJe №/»)). B.59)
e

Вычисления по теории возмущений в калибровочных теориях 271
где F2 и Fm — произвольные конечные части, аналитичные при
е -» 0 и зависящие только от т/\х. Во-вторых, поправка к фотонной
линии
е2 1
Ruv iP> = (РцР\> -5mv? ^fr~2 + Конечная часть), B.60)
приводит к новому пропагатору
+ — Пп„ : + . . . = B.61)
A -
Р2
е2 1 w ^v e2 1
+
Е
B.62)
так что
где F3 _ произвольная безразмерная функция. Продольная часть про-
пагатора дает
° = Г2^(— +F«>« B.64)
что, конечно, равносильно перенормировке величины а. Заметим, что
в калибровке Ландау, где а = 0, поправка к пропагатору калибровочного
поля содержит тот же самый оператор проектирования, что и в голом
пропагаторе, и потому а не изменяется из-за поправок, но это верно
только в калибровке Ландау»
Наконец, поправка к вершине
е2 1
rpiP, Q) = »ецЕУр(—— —I + Конечная часть) B.65)
приводит к выражению

272 Глава 8
где F, - конечная часть контрчлена. Итак, суммируя все результаты,
имеем
?(_L- + *,)+<>(««). B.67)
2(
m(_L +о ---. <>
12тт2 ?
Мы видим, что предполагаемое соотношение Z y=Z2 в данном поряд-
порядке теории возмущений вьшолняется с точностью до конечной части
контрчленов. Поэтому на основании формулы B.51) мы можем записать
голый заряд в виде
2
е0 = ем? [ 1 + JL— _J + Конечные части + О(е3I B.72)
24тт2 е
Таким образом, если игнорировать конечную часть контрчленов, приняв
независящий от масс рецепт перенормировки, то мы можем найти из
этого соотношения, как изменяется калибровочная константа связи в
зависимости от масштаба [гл« 3, формула F.13)}:
de e3
М ^ B<73)
Знак здесь такой же, как и в скалярной теории* Решение этого уравне-
уравнения имеет вид
1 1 ¦¦ 1п(ц/ц0), B.74)
где ц0 - произвольный масштаб» В иной форме, которая, пожалуй,
более содержательна, она записывается так:

Вычисления по теории возмущений в калибровочных теориях 273
еЦ\х) = , B.75)
2К)
6тт2
причем имеется сингулярность при
(знаменитая сингулярность Ландау), Но задолго до того, как мы дос-
достигнем столь больших масштабов, уравнение 'B,74), выведенное в рам-
рамках теории возмущений, придется исправить с учетом эффектов выс-
высших порядков, которыми нельзя пренебрегать при больших масштабах
масс из-за знака в правой части. Когда имеется много заряженных
фермионов, каждый из них вносит вклад в B.74) в соответствии со своим
зарядом (см, задачу).
То, что электрический заряд становится все слабее и слабее на
больших расстояниях (т.е, при малых масштабах), означает, что вполне
оправданна интерпретация свободного лагранжиана (е = 0) на осноэе
представления о физических фотонах и.например, электронах. Правда,
дальнодействующий характер электромагнитного поля делает такую
интерпретацию не совсем надежной „ но факт остается фактом, что
электроны и фотоны можно наблюдать в лаборатории в свободном сос-
состоянии,
Задачи
А. покажите, что логарифмически расходящаяся, на первый взгляд.
ящичная диаграмма рассеяния света на свете
самом деле сходится,
Б. Покажите прямым вычислением, что диаграммы
на
обращаются в нуль»
В. Найдите зависимость е от р в низшем порядке, если имеется
Зяц кварков с зарядом 2/3, 3nd кварков с зарядом - 1/3 и пг лепто-
нов с зарядом - 1 „ Предположите, что е2(ц0)/4тг= 1/137 при ц0 =

274 Глава 8
= 1 МэВ, и найдите положение сингулярности Ландау в случае, когда
включены известные заряженные фермионьь Сколько сортов фермионов
нужно для того, чтобы особая точка Ландау соответствовала планковской
массе?
*Г, Рассмотрите электродинамику (заряженного) скалярного
поляо Выведите фейнмановские правила и вычислите поляризацию
вакуума от скалярной петли* Сравните результат с тем, который
уже получен для фермионной петли,
,*Д. Вычислите контрчлены Zv Z2, Z3, Zm, Za в произвольной
ковариантной калибровке, тиеа считайте при вычислениях величину
а произвольной. Покажите, что хотя контрчлены z зависят от кали-
калибровки (от а )> E - функция от нее не зависит.
§ 3. КЭД. тождества Уорда
Вследствие локальной калибровочной инвариантности КЭД
не все функции Грина, порождаемые функционалом
e-zUu> X. xl = #/2L 2)jpg)ye-s*M> -< V^ + ixy+^X^
C.1)
независимы. В этом выражении
Jd«x[-1_ (FuvJ+ -^_ (d- AJ
C,2)
и ^y X» X - источники, причем последние два - грассмановьь Произ-
Производящий функционал (Зо1) не инвариантен относительно калибровочных
преобразований
SA = _1_ л Л(х), 6* = -i Л(г)Т(х), б? = i Л(хтх), C.3)
где А{х) - произвольная функция. Это объясняется наличием в 3(
члена, фиксирующего калибровку, и источников. Мы выведем в этом
параграфе систему функциональных уравнений связи для Z, из которых
получим соотношения между функциями Грина, называемые тождествами
Уорда.
Метод, который мы намереваемся использовать, легко обобщается
на более сложный случай янг-миллсовских теорий; он основан на работе
Бекки, Руэ и Сторы (БРС) [ 1 ]» Первый шаг заключается в том, чтобы,
пренебрегая на время источниками, восстановить определенный тип ин-

Вычисления по теории возмущений в калибровочных теориях 275
вариантности даже при наличии члена, фиксирующего калибровку- Это
достигается восстановлением лагранжиана духов, что в данном абелевом
случае равносильно всего лишь переопределению (бесконечной) постоянной
нормировки N. Новое эффективное действие дается выражением
Х fd*x[ -L (F^J
где ti и rj* - комплексные грассмановы поля. Теперь действие ^^
инвариантно относительно специального калибровочного преобразова-
преобразования
:'\ - -L- д^*ц + ?П*). C,5)
+ ^*), C,6)
(д • Л%, 5П* =-¦ _L_ (a • А% * , C.7)
се
где ^ и ?.* — комплексные грассмановы переменные, не зависящие от
х. В результате таких преобразований мы получаем выражение
± fd^[±_(d. A)d2(l*r) + 5п*) ~
сс
_ J_ {д . А) д%*п - ±_{д. А) дЧч% C.8)
а а
если проинтегрировать по частям вариацию последнего члена в форму-
формуле (Зо4)о Выше мы использовали следующее правило для двух грассма-
новых чисел а и %'¦
так что произведение о^ действительно, если действительны «и
Будем исходить теперь из нового производящего функционала
е~7- У», х. X.
^ Л"
^ (ЗЛ0>

276 Глава 8
где а и а * - комплексные грассмановы источники для полей-духов.
Сместим в этом выражении поля с помощью преобразования БРС
C.5) - C.7): поскольку действие S дфф инвариантно относительно это-
этого преобразования, а якобиан преобразования БРС равен единице (смо
задачу), при этом изменятся только члены с источниками,. Сравнивая
два спосооа записи производящего функционала (ЗЛО), легко нахо-
находим, что
_5 'Л(Ь +</ • А + • • ->~< I ' 5А + iX54> + i5VX + 5i**v +5пст*> (ЗЛ1)
х е
где вариации даются выражениями C,5) - C,7), Заметим, что если ог-
ограничиться преобразованиями БРС, для которых ? - действительная
величина, т,е„
?* = ?, . (ЗЛ2)
то можно без труда разложить экспоненту, так как ?2 = 0о В резуль-
результате
- х(г) + г)*)Ч + Пг) + Ц*)х + — (д- А)а - _L_ (д- А)о*>1
ае ае (ЗЛЗ)
Это и есть нужное нам соотношение, хотя оно и получено в несколько
громоздкой форме,, Но если мы введем производящий функционал для
одночастично неприводимых диаграмм
, 4W Пкл- Л*кл^= Z^J\х> Х> X, о, а*] -<] • Лкл +
>. C.14)
где А^кп и т.д. - классические источники, то
/м = - -^— и т.д. (ЗЛ5)
Таким образом, если выразить все через Г, то можно сразу же перепи-
переписать (ЗЛ 3) в виде

Вычисления по теории возмущений в калибровочных теориях 277
5Лцкл 5Ткп
' (Я А \ 5Г ^ п (ЗЛ6>
. —- (<Э- Лкл) ___ > = о.
ав 5т1кл
Ъо самая простая для анализа форма тождеств Уорда в КЭД. Приме-
Применим теперь эту формулу к простейшим случаям- Зависимость Г от
Пкп и Пкл очень проста, так как эти поля не взаимодействуют:
Г=«7^4УП#кл(*)Л~1(*-У)ЛклЫ +Г'ицкп,Ч'КП1Фкп], C.17)
где Г ' не зависит от riKr) и г)\п, а Д' - обратный свободный безмас-
безмассовый пропагатор:
Д-1(х -у) = - <Э25(х -у). CJ8)
Выражение для Г ' более сложно и начинается с членов
(х, у, «^(z) + . . . , C.19)
где Д-J _ полный обратный фотонный пропагатор, S ~1 - полный об-
обратный фермионный пропагатор, а Гр - трехточечная функция. Конечно,
Г ' содержит много других членов, которые соответствуют индуцирован-
индуцированным взаимодействиям, отсутствующим в исходном лагранжиане.
Начнем с того, что применим соотношение (Зо 16) к (Зо17) и C„19),
удерживая только члены, содержащие А^ и ц + ц*. Результат (в импульс-
импульсном пространстве) оказывается таким:
АцД-\,(А)+1_АцА2 = 0. (Зо20)
Если написать
C-21)

278 Глава 8
то тождество Уорда C.20) приводится к виду
А + Bk* + J k2 = 0. C.22)
а
Например, в фейнмановской калибровке а = 1 это тождество означает,
что
Л~Л = " 5uv*2 + <Snv*2 ~WF(k2), C.23)
где F(k2) имеет порядок по крайней мере*2. Мы уже проверили этот
результат во втором порядке по_е.
Далее, члены, содержащие У, Y, ц (или любое г)*), приводят к дру-
другому тождеству
— Гц(х, у, г) - iS-'(X~z)(x - y) + iS-<(x -z)8(x ~y) = 0. C.24)
То же самое уравнение можно записать в импульсном пространстве:
(Р -«)/Ц(Ь Р -Ч, Q) = 5-ЧР) ~ S-'(<?). C.25)
Это первоначальная форма тождеств Уордао Нетрудно проверить это
соотношение в теории возмущений:
Гц-•>,, + ..., C.26)
S-4p)-i($ + n) + .... C.27)
Более того, так как 5 -1 (р) мультипликативно перенормируется мно-
множителем Z2, а Г у — Множителем Z,, из данного тождества Уорда
следует, что
Z, =Z2, C.28)
как мы и говорили ранее. Было бы глупо применять такую процедуру
вычитаний, которая нарушала бы равенство C.25). Поэтому конечные
части Z1 и Z2 всегда выбираются равными - прямыми вычисления-
вычислениями мы убедились в том, что полюсные части равны. Заметим попутно,
что если написать
ГЦ(Р, Р -Q, Q) = С, Гц + С2а^(р -q)v, C.29)
то член магнитного момента С2 выпадает из C.25) в силу антисиммет-
антисимметрии.

Вычисления по теории возмущений в калибровочных теориях 219
Уже не раз отмечалось, что теории с безмассовыми частицами
страдают инфракрасными расходимостями, и КЭД из-за безмассовости
фотона не является исключением. Один из способов избежать этих рас-
ходимостей - ввести малую массу фотона. Заметим,.что в случае
КЭД это не нарушает тождеств Уорда, так как можно сохранить инвари-
инвариантность БРС даже при наличии фотонного массового члена, если
считать, что дух приобрел ту же массу. Дело в том, что массовый
член меняется как
6—14 = -Хд • А((,*ц + 5л*) + Поверхностный член, C.31)
В фейнмановской калибровке а = 1 эта вариация оказывается равной
+ ц*5ц) = - А6(т!*т]). C.32)
Это означает, что БРС-инвариантность может быть сохранена ценой
появления массивной духовной частицы, которая ни с чем не взаимо-
взаимодействует! Такое дополнительное преимущество, по-видимому, не обоб-
обобщается на случай неабелевых теорий, о чем будет сказано ниже.
Задачи
А. Покажите, что якобиан преобразования БРС равен единице.
Б. Пусть задан функционал
Покажите, что
6q> кп
где Г[ф ] = Z[J] - </ф> *'
**В. Выведите тождества Уорда для скалярной электродинамики
(комплексное скалярное поле, взаимодействующее с фотоном) в фейн-
мановской калибровке.
*Г. Выведите тождества Уорда для КЭД в аксиальной калибровке.
**Д. Выведите тождества Уорда для КЭД в калибровке

280 Глава 8
§ 4. КЗД, применения
Прежде чем переходить к практическому применению результатов,
полученных нами для КЭД, мы должны продолжить функции Грина в
пространство Минковского и выбрать рецепт перенормировки.
Фотонный пропагатор в евклидовом пространстве дается выраже-
выражением (чтобы избежать путаницы, мы восстановили черту над евклидо-
евклидовыми импульсами)
6 У р~4 2тт2^ 6-6 2tV
-2-Fe] + 0te4). D.1)
6
Конечные части контрчленов Z3 и Za фиксируются требованием, чтобы
пропагатор Д^у при р2 -» 0 выглядел так же, как исходный пропагатор:
Б...,
так что F3=Fa =-у-In ^-2. D.3)
1ТТЦ
Аналогично в порядке О(е 2) имеем
„ 1 , е2 , 1 + У г 1 /1 . , Б2хA - х) + т2х 1 г
S-X(P =«Р[1 +-Ч( -~+/^A -ХIп" V ; +T"f
8тт2 2 о
+ гт[ 1 + -—г A + 2у + 2 fdx In — 2F )],
Чт'1 о w|i
D.4)
и может показаться, что подходящая процедура вычитания будет заклю-
заключаться в продолжении в пространство Минковского, т.е. в замене
р -» -р vlp2 -» -р2, и требовании
S~HP) = i (me - р) при Р2 = т2 D.5)

Вычисления по теории возмущений в калибровочных теориях 281
которое фиксирует конечные части
F2 = -у + 2 - In ш2/4тгм2, D.6)
Fm= у _ 1 + у In (т2/4ттМ2). D.7)
Однако такой выбор вычитательной процедуры неоднозначен. Дело в
том, что наш рецепт предполагает, что разложение S(p) вблизи р = т
хорошо определено. Но простые рассуждения показывают, что это не
так. Из требования D.5) следует, что
2(?>) = О при р = т, D.8)
так что проведем разложение исходного выражения для 2(р) зблизи
р = т. Это легче вещего сделать, разложив фермионный пропагатор в
B.10) по степеням р~ + т:
я—J ="У"[1 " у-(^ + щ) + •••]• D.9)
Мы сразу же видим, что возникшие в этом разложении члены плохо оп-
определены. Например, член, линейный по р + т, приводит к интегралу
{е„1-»J г dJ^L _L, D.10)
(ец ' J BттJ" /4
который расходится не только на верхнем пределе интегрирования при
со = 2, но и на нижнем пределе. Подобного типа расходимость называет-
называется инфракрасной расходимостью, и ее надо рассматривать отдельно от
ультрафиолетовых расходимостей, с которыми мы имели дело ранее.
Один из способов решить эту проблему заключается в том, чтобы
приписать фотону фиктивную массу Л и удерживать ее в процессе вы-
вычислений. Тогда инфракрасной расходимости нет и все снова хорошо.
Подобная процедура в КЭД дает еще и то преимущество, что она не вли-
влияет на калибровочную инвариантность вычислений. Отметим, что ин-
инфракрасные расходимости возникают на "массовой поверхности" внеш-
внешних частиц: величина D.10) равна д^/др на евклидовой массовой по-
верхности р + т = 0.
То обстоятельство, что инфракрасные расходимости в КЭД могут
быть устранены добавлением массы фотону и возникают на массовой
поверхности внешних частиц, указывает на то, что эти расходимости

282 Глава 8
связаны с наличием дальнодействующих сил, делающих неоднозначным
определение асимптотических состояний.
Другой способ устранения инфракрасных расходимостей заключа-
заключается в использовании размерной регуляризации. В этом случае прово-
проводится интегрирование по параметрам в 2ю-мерном пространстве и за-
затем разложение вблизи со = 2. Инфракрасные (так же как и ультра-
ультрафиолетовые) расходимости будут возникать как полюса в плоскости
размерности. Подробнее об этом ниже.
Остается зафиксировать вершинный контрчлен. Прежде чем сде-
сделать это, нам следует переписать вычисленное выше Г (р, q) в более
подходящей форме. Мы собираемся использовать рецепт, при котором
фермионы находятся на своих "массовых поверхностях". Это застав-
заставляет нас считать, что Г (p~s q) помещается между спинорами, для ко-
которых справедливы (евклидовы) уравнения движения. Поэтому мы пере-
перепишем Г в виде
rp(F, 9)=Tp(^ q) + (P + m)Ap+Bp(q+m), D.11)
где Г и есть то, что мы ищем, так как члены с Л и В в силу урав-
уравнении движения не будут давать вклада. В процессе сведения к тако-
такому виду оказываются полезными тождества Гордона
УрУ **-%- 2г'стрт,?т = mYp + Гр(<? + т)> D.12)
Д _ _ л
PYp =Pp + 2hpTpr = -mYp + (р+т)Гр, D.13)
где V = 1 [V vj. D.14)
Они легко выводятся, если представить произведение двух у-матриц
в виде полусуммы коммутатора и антикоммутатора. Вооруженные таким
образом, мы подготовлены к небольшой порции неприятной "дираколо*
гии".
Используя тождества (справедливые только для Г )
D.16)
D.17)

Вычисления по теории возмущений в калибровочных теориях 283
и выражение B.42), можно свести числитель подынтегрального выра^
женя в ГB) к виду
(* + уJ - 2A -х-у)] - 2*2A - *)A - у)ур +
рдт[ х-у(у + *)] - 8imjpTpT[y - х{х + у)]. D.18)
Этот результат позволяет разбить вклад от ГB) на две части, одна
из которых пропорциональна ур, а другая - арт . Займемся пока что
частью, содержащей у Она имеет вид
ГР(Р> 9) - Г A)fo q) - «>цеУрТ^-2 / dx)~ \ х
г к к 16ttz о о
(х + уJ - 2A - х - у) - 2РA - *)A - у)
х —; — — ^-^ . D.19)
ml(x + y) + p2x(li -x) + q2y{\ - у) - 2р . qxy
Когда мы вычисляем это выражение на массовой поверхности
5*. ?*.-«*. *2 = 0' <4-20>
последний интеграл сводится к
и мы с огорчением убеждаемся, что он расходится. Это наша старая
приятельница — инфракрасная расходимость. Как уже отмечалось выше,
можно избавиться от нее, придав фотону фиктивную массу Л, что сво-
сводится к замене т2(зс + у) величиной т2(х + у) +К(\ — х —у) в знаменате-
знаменателе. Тогда интеграл D.21) заменяется интегралом
V" '
/AcV dy ("У)'*1-*-* , . D.22)
0 о (х + уJт2 + Ц\ — х — у)
который прекрасно сходится. Этой инфракрасной расходимости нет в
членах, пропорциональных а у, ни в ГB), ни в ГA). Все же она стоит
на-пути использования рецепта перенормировки на массовой поверхнос-
поверхности, записанного здесь в пространстве Минковского,
Гр(р, q) = -ецеур при p2 = g2 = m2, (P-qJ = °> <4-23)

284 Глава 8
так как если мы не справимся с расходимостью в D.21), то это будет
означать, что Ft (инфракрасно) расходится. Заметим, что эту проце-
процедуру можно осуществить и в евклидовом пространстве с той разницей,
что к2 я 0 будет означать, что р = q. Из выражения D.22) находим
1 1-х т2(х + уJ+ ЛA -х -у)
F. = 1 + у + f dx Г dy [ 2 In '. 5 ~
1 op 4тг^
ЛA -х-у)
Вычислить эти интегралы представляем читателю.
Как уже отмечали, другой способ регуляризации инфракрасных рас-
ходимостей заключается в том, чтобы взять интегралы по параметру,
прежде чем переходить к пределу при со -» 2. Начнем, например, с выра-
выражения B.40) для Г' . Числитель вычисляется аналогично предыдуще-
предыдущему, за исключением того, что в D.18) появятся поправочные члены,
стремящиеся к нулю как (со — 2). Пренебрегая ими, найдем, что для
всех частиц на массовой поверхности
- х - у)]
+ у)]
D.25)
причем мы использовали симметрию подынтегрального выражения от-
относительно замены х -»у, чтобы переписать член с а у. Поскольку нас
интересует только бесконечная часть при е -» 0, рассмотрим вниматель-
внимательнее интеграл
оЦ-%(Х + У)^-) = ^1=тA-^-4Ь-^- прие.О.
D.261
Таким образом, мы в явной форме показали, что инфракрасная расходи-
расходимость в Г возникает теперь в виде полюса в плоскости размерности
точно так же, как и ультрафиолетовая расходимость. Однако в отличие

Вычисления по теории возмущений в калибровочных теориях 285
от последней инфракрасная расходимость возникает только в случае,
когда частицы находятся на своих массовых поверхностях и по край-
крайней мере одна из них безмассовая. Далее окажется, что этот полюс,
остающийся после регуляризации, в случае величин, представляющих
физический интерес, взаимно уничтожится с вкладом других диаграмм,
проинтегрированных по 2со-мерному фазовому пространству. Однако
изложенный нами прием представляет собой изящный расчетный метод
и не влияет на калибровочные свойства теории.
Раз уж мы занимаемся вершинной функцией, вычислим вклад члена
с a ~k в ГB). Так как он и ультрафиолетово, и инфракрасно сходится,
то незачем изощряться: положим со= 2. Тогда этот вклад равен
D'27)
D-28)
Физический смысл этого индуцированного взаимодействия между фо-
фотоном и фермионом очевиден, поскольку он вносит в эффективное
действие член вида
— 4t^Ki^-P)MP -«)*(«), D.29)
т 8ttz k
или, в координатном пространстве,
^ H^Fp^m)d\ D.30.)
Он приводит к поправке к собственному магнитному моменту g фер-
миона (в единицах магнетона Бора)
a =
4тг
Мы видим теперь, каким образом теория поля приводит к поправке к
дираковскому магнитному моменту фермиона. Отметим, что эта по-
поправка конечна. Дело в том, что индуцированный член взаимодействн-
вия D.30) отсутствует в исходном лагранжиане (его размерность
равна 5) и, так как теория перенормируема, все контрчлены входят
только в выражения для фундаментальных вершин, а не в индуциро-

286 Глава 8
ванные новые взаимодействия. Заметим, что мы не доказывали пере-
перенормируемости КЭД, но недоверчивый читатель может обратиться к
одному из многих превосходных учебников на эту тему.
Оставшаяся часть функционала Гр дает также поправку к электро-
электромагнитным силам между двумя заряженными фермионами, соответст*
вующую вкладу
^ ^ D.32)
Пользуясь нашим рецептом, нетрудно найти F(k2) с точностью О(е2).
Результат в евклидовом пространстве имеет вид (см. задачу)
F(A2) = 1+J-Ji JL [\aHL- — ] + О(а2),к2«т2. D.33)
3 т2 2тт Л 8
Подчеркнем, что эта поправка зависит от способа, которым мы выбра-
выбрали а, т.е. от вычитания D.23).
Такая конкретная вычитательная процедура была выбрана
потому, что она позволяет провести прямое сравнение с экспери-
экспериментом и найти таким путем численное значение заряда е. Напри-
Например, можно сравнить значение е, определяемое условием D.23),
с нерелятивистским пределом сечения рассеяния электрона куло-
новским полем. Это не совсем строго, так как обмениваемый фо-
фотон никогда в действительности не находится на своей массовой
поверхности, но вследствие малости массы электрона разница неве-
невелика.
Поправка D.33) к вершине снимает вырождение между состоя-
состояниями 2S % и 2Р% в (релятивистском) атоме водорода. Вычисления
показывают, что эта поправка понижает уровень 2Р% относительно
уровня 2S% на величину 1010 МГц, тогда как экспериментальное зна-
значение лэмбовского сдвига равно 1057,77 МГц. Но, как и во всех пра-
правильных теориях, положение спасают дополнительные поправки. Преж*
де всего, аномальный магнитный момент также снимает вырождение
и вносит дополнительные 68 МГц. Теперь у нас слишком много, но
модификация фотонного пропагатора, обязанная поляризации вакуума,
вычитает целых 27 МГц, и мы получаем 1052 МГц, что вполне приемле-
приемлемо при точности О(а). На самом деле расчеты с учетом поправок О(а 2)
приводят к идеальному согласию между теорией и экспериментом!

Вычисления по теории возмущений в калибровочных теориях 287
Мы не рассматривали всех приложений КЭД, но, наверное, уже яс-
ясно, что, несмотря на все промежуточные шаги, которые потребовались
для ее регуляризации, это необычно успешная теория.
Задачи
А. Вычислите часть функции Г пропорциональную ур, придав фо-
фотону малую массу, и найдите выражение для Fy в случае, когда для
вершины используется рецепт перенормировки на массовой поверхно»?
сти.
Б. Пользуясь результатами предыдущей задачи, вычислите вер-
вершинную поправку к лэмбовскому сдвигу в первом порядке теории воз-
возмущений, а затем вычислите вклад поляризации вакуума.
В. Вычислите вклад аномального магнитного момента в лэмбов-
ский сдвиг.
§ 5, Янг-миппсоаская теория, предварительные замечания
Наконец-то мы переходим к давно обещанным вычислениям по теории
возмущений в янг-миллоовских теориях. В частности, мы изучим теорию
янг-миллсовских полей во взаимодействии с дираковскими спинорами в
евклидовом пространстве.
Эффективный лагранжиан в ковариантной калибровке д • Ав = О запи-
записывается в виде
эфф
2а
E.1)
где Fuv = ЗА* " ^v^S - gv.l-afBCDACA» E.2)
A
Мы опустили групповые индексы у фермионов и сохранили обозначения,
соответствующие пространству Минковского (используя TjJ вместо ут),
хотя мы и рассматриваем евклидово пространство; как уже отмечалось
выше, это не меняет функций Грина до тех пор, пока мы имеем дело с
дираковскими спинорами. Спинорное поле У преобразуется по d - мерно-

288 Глава 8
му неприводимому представлению группы G,a(dfxdf )-мерные эрмито-
эрмитовы матрицы Т, (число их равно N) образуют алгебру Ли группы G:
[ 7}в, Tf] ш ifв CDTf, В, С, D = 1, . . . , N, E.3)
где fBCD — структурные константытруппы G, а N - ее размерность.
Принято считать, что если в качестве G рассматривается восьми-
восьмимерная унитарная группа 5С/C), а каждый дираковский фермион преоб-
преобразуется по ее трехмерному представлению, то такая теория описывает
взаимодействие между составными частями ядерной материи - кварка-
кварками. Фермионам сопоставляются кварки, а восемь обладающих самодей-
самодействием векторных частиц, называемых глюонами, порождают межквар-
ковые силы. Степени свободы каждого кварка, связанные с группой
Sf/C), называются цветами ("красным", "белым" и "голубым"). В при-
природе существует пять (а может быть, шесть) таких разновидностей
кварков, называемых ароматами; они обозначаются символами и (up),
d (down), s (strange), с (charm), b (bottom) и t (top) (предполагается, что
кварк t существует, но он еще не открыт). Такая теория межкварковых
взаимодействий называется квантовой хромодинамикой (КХД).
Ниже мы будем рассматривать все в общем виде. Фейнмановские
правила для теории, описываемой лагранжианом E.1), были выведены
в § 1; они суммированы в приложении В. Отметим неоднозначность,
содержащуюся в фейнмановских правилах для духовой части лагранжиа-
лагранжиана. Он содержит член вида
-—gil2-u>fABCn*Ar]Bd- Ac, E.4)
2
пропорциональный калибровочной функции д • Ас = 0. Этот член возни-
возникает из детерминанта Фаддеева — Попова, представляющего собой де-
детерминант изменения калибровочного условия, вычисленный при задан-
заданном калибровочном условии, т.е." когда д • Ас= 0. Следовательно, член
E.4) можно отбросить из эффективного лагранжиана, и это не повлия-
повлияет на физические следствия, так как отбрасываемый член включает взаи-
взаимодействие фиктивной продольной части калибровочного поля. Формаль-
Формальное преимущество такого отбрасывания заключается в том, что остаю-
остающаяся часть лагранжиана, связанная с духами, становится действитеиь-
ной, поскольку член E.4) чисто мнимый. Однако вычисления в явной
форме (Т. Куго, частное сообщение) показывают, что элементы S -мат-

Вычисления по теории возмущений в калибровочных теориях 289
рицы при отбрасывании E.4) меняются во всех случаях, кроме случая
калибровки Ландау. Хотя мы этого и не будем использовать, отметим,
что пренебрежение указанным членом приводит к новому фейнмановско-
му правилу для вершины дух - дух - калибровочное поле:
^ fABC(p -q) Измененное
_А 2 _s 2 Р правило
Р — —7
E.5)
Внимательный читатель, вероятно, уже обратил внимание на то,
что безразмерная константа связи g входит во многие члены лагран-
лагранжиана E.1). Из-за калибровочной инвариантности лагранжиана в клас-
классической теории в нем содержалась только одна константа связи. Од-
Однако наш эффективный лагранжиан содержит члены, нарушающие ка-
калибровочную инвариантность, и создается впечатление, что мы не
имеем права считать все эти разные константы связи равными друг
другу, если только нет причины, по которой квантовые поправки
не нарушали бы эквивалентности. Ниже мы увидим, что такая при-
причина есть и она заключена в преобразовании БРС, которое мы уже
анализировали для абелевого .случая в § 3.
В качестве первого применения вычислим вклад низшего поряд-
порядка в неабелеву комптоновскую амплитуду, что послужит нам провер-
проверкой знаков в фейнмановских правилах. Имеем следующие диаграммы:
Вклад первых двух диаграмм таков:
p
+
V
л 1С
q + m
(Р
+ 9J +
г
тг
ч
ЧУ
тв
с л,
ТЛ
"'
— г
'-? +
/\»
Р -
'а(р'
А
-я)'-
?'
т
hi
E
п2
E
.7)
УРЬ
.8)

290 Глава 8
а третья диаграмма (в фейнмановскоЙ калибровке) дает вклад
С — t5aM'-?-2fe)p+Spa(A-9)U
Сумма этих трех диаграмм должна удовлетворять требованию ка-
калибровочной инвариантности, которое означает, что в силу нашего ка-
калибровочного условия д • Ав = 0 продольная часть калибровочных
частиц не должна давать вклада. Поэтому мы свертываем выражение
с q и смотрим, что получится. Вклад в свертку от первых двух диаг-
диаграмм равен
-ig2u.*-2°{Tfrfq
л. л
р + q -т
V-
{p' -
A
q —m
qJ + m-
Л
E.
E
E
E.
10)
.11)
.12)
.13)
Пользуясь соотношениями
лл 2
qq = -q ,
q{p-m) = -2q. p *. $ + m)q ,
(p ' — m) q = —2p ' • q — q (p'+ m)
и условиями для фермионов на евклидовой массовой поверхности, сог
ласно которым члены р + т слева нр' + т справа в амплитуде дают
нулевой вклад, так как выражение E.10) входит в обкладках из вол-
волновых функций внешних фермионов, а также соотношением
р2 = р'2 = -т2, E.14)
перепишем E.10) в виде
¦ 2 4-2СО/-ГЛ д -2д ¦ р -д2 в1а -2р*. д + ч2 (_
i * 2q • р + q2 ' > ~2р ' q + q2
E.15)
= *5Т» ~ M[7]t , Т^ ]уа = -g2M4~2c0/ABCT^ya . E.16)
В абелев ом случае этих двух диаграмм доетаточно и вклад продоль-
продольных калибровочных частиц действительно равен нулю (так как / лвс=0)
даже при произюльных значениях q2nk2.B янг-миллсовской теории имеется

Вычисления по теории возмущений в калибровочных теориях 291
еще одна диаграмма, с которой нам надо справиться. Ее вклад в про-
продольную часть равен
{q+k)
1 , -
= _g 2M 4 -icof Л ВС ТС 1 [. ya{ql+Zk. q)-kkg]. E.18)
' (q + kJ
В последнем выражении мы использовали уравнение Дирака для ферми-
онов, чтобы исключить член k + q и переписать qk, как —kk . Оконча-
Окончательный результат получается, если сложить E.16) и E.18):
1 -*Л), E.19)
%рае;
(q + k)
и это выражение в противоположность аналогичному результату для
КЭД не равно нулю! Но оно пропорционально проекционному оператору
для второй калибровочной частицы. Следовательно, продольная комп-
комптоновская амплитуда, свернутая с вектором поляризации второго калиб-
калибровочного поля, равна нулю, если считать, что калибровочное поле удов-
удовлетворяет уравнению движения (в противоположность этому, в КЭД не
накладывается никаких ограничений на вторую фотонную линию). Раз-
Различие обусловлено тем, что в янг-миллсовских теориях линии калибро-
калибровочных полей несут заряд (в КЭД этого нет) и потому их источники
должны иметь заряд (см. задачу) и взаимодействовать с другими ли-
линиями калибровочных полей, если только калиброьочное поле не нахо-
находится на массовой поверхности.
Задачи
*А. Вычислите комптоновскую амплитуду в древесном приближе-
приближении в аксиальной калибровке п А = 0 в евклидовом пространстве.
Сверните одну из векторных линий амплитуды с п . Поясните резуль-
результат.
*Б. Придумайте такое новое фейнмановское правило для источни-
источника вне массовой поверхности, чтобы после добавления соответствую-
соответствующей диаграммы продольная комптоновская амплитуда E.19) обрати»
лась в нуль.
*В. Повторите задачу Б в аксиальной калибровке.

292 Глава 8
§ в. Янг-миппсовская теория, однопетпевая структура
В данном параграфе мы подробно исследуем однопетлевую струк-
структуру янг- миллсовских теорий. Так как теория очень сложна, нам не-
необходимо ввести какой-то руководящий принцип, прежде чем что-то
вычислять: предположим, что теория перенормируема (благодаря
'т Хофту мы знаем, что это верно). Это означает, что мы можем уст-
устранить все ультрафиолетовые расходимости, добавив к лагранжиану
EЛ) контрчленный лагранжиан, который выглядит так же, как и ис-
исходный, но содержит неизвестные коэффициенты перед каждым членом,
которые расходятся при е -> 0, где в = 2 - d/2. Запишем этот лагранжи-
лагранжиан в виде
* К I А АВ г) А^2 -К m,ef АВС Ав Ас -> ЛА .
2а
mW. F.1)
Перенормированный лагранжиан
?пеР=?^ + ? F.2)
эфф контр v '
дает функции Грина, которые в пределе при е ¦* 0 ультрафиолетово-
конечны. В этом суть теории перенормировок. Теперь можно записать
перенормированный лагранжиан, выразив его через голые поля и пара-
параметры, в виде
,D лЕ 1 , ,
V»0+7

Вычисления по теории возмущений в калибровочных теориях 293
Голые поля, константы, связи и массы связаны со своими пере-
перенормированными (конечными) двойниками соотношениями
Z*v, F.4)
F-6)
m( 1 + Кт)/(\ + К2) = mZjZ2, F.7)
F.8)
1 +К.
-^- s gtfZjZ* F.10)
A + К,)й
3 Z6
Z3Z6
F.11)
F.13)

294
Глава 8
Этот список определений удлинился из-за того, что мы ввели
пять независимых голых констант связи. Но все они окажутся равны-
равными вследствие тождеств Славнова - Тейлора, являющихся тождест-
тождествами Уорда для янг-миллсовских теорий. Равенство констант требу-
требует выполнения следующих соотношений между константами перенорми-
перенормировки:
-.Г" = ~ = -A = -4- = -Л • FЛ4)
Теперь мы вычислим эти константы перенормировки с точностью
O(h) в схеме размерной регуляризации.
Прежде всего запишем в диаграммном представлении однопетле-
вые вклады (О(Л)) в фундаментальные взаимодействия янг-миллсовс-
кой теории:
+ /TTV\
—ш— =
F.15)
FЛ6)
F.17)
Д,
• \
+ rrrWRPi
F.18)
F.19)

Вычисления по теории возмущений в калибровочных теориях 295
' \
__!__.
F.20)
Эти диаграммы вполне должны убедить читателя в сложности
янг-миллсовских теорий и объяснить ему, почему для вычислений в
высших порядках необходимы сложные программы для ЭВМ. Взаимо-
Взаимодействие двух духов с калибровочным полем представлено только
один раз - в диаграммах F.20).
Начнем с вычисления однопетлевой поправки к поляризации ва-
вакуума. Как показано в формуле F.15), эта поправка состоит из шес-
шести частей. Сначала вычислим
F.22)
В фейнмановской калибровке, не забыв фактор симметрии, по-
получим
F.23)
BтгJс0 12A+рJ '
P) =
x [ B1
)p5
p5Tft
-BP + l )a6pv + (p - I )p5av] =
)a6pv
F.24)

296 Глава 8
=(8со- 6)yv + Dсо- 3)(/MPw + lvpj + Bсо-
F.25)
и учтено, что 5 = 2со. Это выражение содержит в четырех измерени-
измерениях как инфракрасную, так и ультрафиолетовую расходимость. Заме-
Заметим, что традиционное лекарство от инфракрасной расходимости, свя-
связанное с добавлением калибровочной частице малой массы, приводит
в данном случае к куче неприятностей, так как при этом не сохраня-
сохраняется калибровочная инвариантность. Поэтому ниже мы будем старать-
стараться находиться подальше от точки р2 = 0, в которой и возникает инфра-
инфракрасная расходимость. Когда же это окажется невозможным, мы обра-
обратимся к методу размерной регуляризации (§ 4),
Вводя фейнмановский параметр и производя замену перемен-
переменной интегрирования в петле, получаем
F.26)
После небольших алгебраических преобразований находим
uv, F.27)
где мы пренебрегли линейными по / членами, так как при интегрирова-
интегрировании они все равно дадут нуль. Интегрирование по переменной в петле
приводит к выражению
Vl ACDfBCD \й„х Fсо-3Mц,ГA-со)
о
" 6 - (8«- 6)*A-
F.28)
Оставим пока этот результат в том виде, как он получился, и вычислим
вклад духовой петли.

Вычисления по теории возмущений в калибровочных теориях 297
Этот вклад определяется диаграммой
С
А / В
Пц1МВ(Р)= тглплп Ьппппг . F.29)
Ъ
Вспомнив про знак минус для духовой петли, с помощью правил
приложения В найдем
»;^ ^р- ,,зо,
Это выражение также инфракрасно расходится. После введения фейн-
мановского параметра оно принимает вид
1 F.31)
2 м
Drr)
F.32)
Если бы мы использовали измененное правило E.5) для вершины духа,
то пришлось бы изменить только член с р pv (см. задачу).
Третья диаграмма имеет вид
F.34)
Но эта диаграмма, так же как и две другие диаграммы-головастики в
формуле F.15), обращается в нуль при размерной регуляризации. Она
имеет структуру диаграммы-головастика, и, так как в вершине не воз-
возникает зависимости от импульса, эта диаграмма может давать только
поправку к массе калибровочной частицы. Но в силу калибровочной ин-

298 Глава 8
вариантности у калибровочных частиц отсутствует массовый член.
Если же мы примем любую процедуру регуляризации, нарушающую ка-и
либровочную инвариантность, то диаграмма будет приводить к ненуле-
ненулевому массовому члену. Это было бы артефактом, а потому не могло
бы повлиять ни на какой физический результат. Например, если доба-
добавить калибровочным частицам малую массу, чтобы регуляризовать
инфракрасную расходимость, то диаграмма F.33) будет вносить вкад
в эту фиктивную массу. Это еще один пример мощи метода размерной
регуляризации, который контролирует бесконечности, не нарушая ка-
калибровочной инвариантности .
Теперь извлечем из ГТA) и ГТB) полюсные части. После неболь-
небольших алгебраических преобразований находим, что
ACDfBCD
fACDf
+ }dx In ( р2*^ ~ Х) ) [ 2ppv (U 5ж A - «)) -
- P\v E - 1Ь A - *))] + О(е)\. F.34)
Отметим появление lap 2, указывающее на наличие инфракрасной рас-
расходимости на массовой поверхности при р2 = 0 (только в пространст-
пространстве Минковского, так как в евклидовом пространстве из условия р 2 = О
следует, что и^ = 0). Кроме того,
+ \pvx0 -x)l +O(e)l, F.35)
Сумма ПA) и ПB) Дает полный чисто янг-миллсовский вклад в поли-

Вычисления по теории возмущений в калибровочных теориях 299
ризацию вакуума
2
Ю 1 62 10
+
Г6.36)
и мы вновь получаем магическую структуру проекционного оператора.
Конечная часть имеет аналогичную структуру и содержит множитель
In р2/4тгц2, который, как уже отмечено, инфракрасно расходится.
Элементы матриц ТЛ, образующих алгебру Ли группы G в присоеди-
присоединенном представлении, можно отождествить со структурными кон-
константами
(Т4)вс = ^.ifABC. F.37)
Далее, для любого представления R группы G с матрицами представ-
представления Т„ можно положить
к
Sw(TrTr) = Cr*AB> F.38)
где след берется по индексам представления. Число С называется
индексом Дынкина представления R; оно равно квадратичному опера-
оператору Казимира, умноженному на размерность представления и делен-
деленному на размерность группы. Точное значение индекса Дынкина за-
зависит от нормировки Х-матриц, которая раз и навсегда фиксируется
заданием структурных констант теории. Шкала структурных констант
в свою очередь фиксируется определением констант g, так как они
всегда входят в комбинации gfABC. Очень удобно переписать все на-
наши выражения через индексы Дынкина. Тогда получим
<* <) АВ |^с<6^ - W • т" 7 + ' •' • F'39)
Заметим, что в структуре проекционного оператора нет ничего
священного: ее можно изменить, если только мы примем измененное
правило E.5) для духов.

300 Глава 8
Вклад фермионов в поляризацию вакуума
n^vB (р) . ^r^A^J-rrsirr F.40)
не нужно вычислять заново, так как структура его та же, что и в
КЭД, не считая некоторых теоретико-групповых множителей. Дейст-
Действительно,
f?™up)= F.41)
причем мы использовали формулы F.38) и B.32). Сравнив F.42) с
F.39), можно видеть, что вычеты в полюсах имеют противоположные
знаки (подробнее об этом ниже). Сумма выражений F.42) и F.39)
Дает полную однопет левую поправку к поляризации вакуума.
Следующая поправка к фермионнои линии (если игнорировать
головастики) дается диаграммой
F.43)
и является матрицей как в спинорном пространстве, так и в простран-
пространстве представления фермионов. Нетрудно видеть, что
~Z{p) = TATflK5a(P), F.44)
где 2 определяется формулой B.19). Кроме того, матрица размер-
размерности d, xdf перед выражением F.44) диагональна и равна
ТА ТА = J- Cf, F.45)
f
где мы не указали индексы представления. Отсюда получаем
-i Ct —2-тг (р + 4т) — + • • • , F-46)
df ' 16тг2 е

Вычисления по теории возмущений в калибровочных теориях 301
Однопетлевая поправка к фермионной вершине состоит, если пре-
пренебречь диаграммами-головастиками, из двух диаграмм. Первая из
них РЦА
г>.«)= I <6-47>
имеет ту же структуру, что и в абелевом случае, В самом деле,
Г1р & q> = TfTfTfT^{pt q). F.48)
Матрицу d, x df можно записать как
Тв TAfTBf = [ 7*, Tf]TBf + TfTfTf = F.49)
= if ВАС jC TB + JV_ Cf jAm F.50)
df
Теперь с учетом антисимметрии по С и В перепишем это в виде
TBTATBj_fBACfDCBTD^JtTf= F.51)
1112 ' d, '
= у Wi + f-0'7?' F>52)
пользуясь формулами F.37), F.38) и F.45). Вспоминая результаты
§ 2, получаем
Г>, Я) - ~^Т?Гр ( I Сприс + Cfj- ) ?2 ± + • • • • F.53)
Мы замечаем, что вычет второго члена в точности такой же, как и в
F.46), поскольку в нем не отражается неабелевый характер теории и,
стало быть, должно выполняться старое тождество Уорда КЭД. Если
должны выполняться тождества Славнова — Тейлора, то отношения
Zt/Z2 и Zg/Z6 должны быть равны. Но последнее отношение не
содержит вклада фермионов на однопетлевом уровне, как это видно
из F.17) и F.20); следовательно, перенормировка фермионной волно-

302 Глава 8
вой функции должна в точности сокращаться членом в Z1. Именно
так и происходит.
Второй вклад в вершину определенно неабелев по своей структу-
F-54
По установленным правилам
F.55)
Теоретико-групповые множители легко преобразуются, так как с
учетом формул F.37) и F.38)
fABCTBTC t fABCfBCDTD I
' ¦ fTf = т"' ' Tf =t
F.56),F.57)
Вводя фейнмановские параметры и соответствующим образом сдви-
сдвигая переменную интегрирования в петле, получаем
о о
Np(l'. р. Ч)
* ТТ7! ТГл [ 2 2 ', ^Тз ' F.58)
L« L + m у — х - у) + q х + ру - (qx - ру)\
где Np = 2/p'yvt'yv + "р = 4ГГ'A - е) + Afp, F.59)^6.60)
причем N содержит только члены, линейные по /' к выпадающие при
интегрировании, а также члены, не содержащие I'. Последние приве-

Вычисления по теории возмущений в калибровочных теориях 303
дут к сходящемуся интегралу по петле. Таким образом, находим
^7 -
*(\ - х - у) + qlx + ру - (qx - руJ
от
5
2A - х - у) + q2x + ргу - (qx -
Эта формула очень сложна, но из нее легко извлекается полюсная
часть
Г? (Р, я) - -.«.Vplf ф^ 1 + , . . , F.62)
так что полный полюсной вклад в фермионную вершинную функцию
равен
С, ?> 1 + . . . , (б.б3)
Теперь, после того как мы вычислили полюсную структуру попра-
поправок низшего порядка к фермионному и калибровочному полям и к фер-
мионной вершине, мы можем из формул F.39), F.42), F.46) и F.63)
извлечь соответствующие перенормировочные константы. Они оказы-
оказываются равными
l-C/)f +^з) + -«- . F.86)
где Fv F2, F3 - произвольные конечные части контрчленов. Все эти
выражения зависят от калибровки. (Например, в аксиальной калибров-
калибровке эффективный лапранжиан не содержит духов и имеет ту же структу-

304 Глава 8
ру, что и в КЭД, откуда следует, что выполняется тождество Zx = Z2,
которое явно неверно В феинмановскои калибровке.) Заметим, что
если тождества Славнова - Тейлора F.14) должны выполнятвся, то
фермионный вкдад в четверное векторное самодействие должен расхо-
расходиться, поскольку мы явно фидим, что отношение Z^ Zl/Z2 содержит
вклад фермионов. Эта ситуация противоположна тому, что происходит
с ящичной диаграммой в КЭД, которая конечна. Как же может быть,
чтобы одни и те же диаграммы были конечны в одном случае (КЭД) и
расходились в другом (КХД)? Дело очевидно, в том, что диаграммы
не одинаковы: в КЭД расходимость ящичной диаграммы исчезает пос-
после симметризации по внешним фотонным линиям, отмеченным только
их векторными индексами; в янг-миллсовском же случае симметризацию
по внешним линиям можно осуществить двумя путями, либо симмет-
ризуя как по векторным, так и по групповым индексам, что, как и в
КЭД, не приводит к расходимости, либо антисимметризуя по отдель-
отдельности по векторным и групповым индексам. Именно этот новый вклад
расходится (см. задачу). Такие же рассуждения можно провести и для
вклада фермионов в тройную вершину F.18).
Задачи
А. Вычислите вклад духов в поляризацию вакуума, используя
измененное фейнмановское правило E.5). Покажите в явной форме,
что это влияет только на содержащую р pv (продольную) часть
Пцу. Найдите Za и сравните с тем значением, которое получается
по ооычным правилам приложения В.
Б. Вычислите интегралы по параметру в Пцу в 2со измерениях,
исходя из выражений F.28) и F.32). Затем произведите разложение
вблизи «= 2; выясните смысл лишних полюсов по е.
*В. Вычислите в феинмановскои калибровке в однопетлевом
приближении константу перенормировки духового поля Z а также
константу перенормировки вершины дух - калибровочное поле Z7 и
убедитесь, что Z?/Z6 действительно равно Zl/Z2.
**Г В феинмановскои калибровке вычислите наибряее расходя-
расходящиеся части диаграмм
ТТППГТ рЛГ «V
лпгпг—Цлплг '
и проверьте тождества Славнова - Тейлора для фермионной части .

Вычисления по теории возмущений в калибровочных теориях 305
§7. Янг-миппсовская теория, тождества Славнова — Тейлора
Мы видели, что эффективное действие, являющееся исходным
пунктом квантовой теории янг-миллсовского поля, уже не является
более калибровочно-инвариантным - из-за наличия члена, фиксирую*,
щего калибровку, и духов (в ковариантной калибровке). Члены, нару-
нарушающие калибровочную инвариантность, имеют вид
где г\в и ц в -доля духов, a G л - калибровочные условия. Оказы-
Оказывается, что удобнее использовать вместо комплексных действитель-
действительные грассмановы поля со'4 и рл ; они связаны со старыми полями со-
соотношениями
ца=*(ол + грл), G.2)
T,M--l_(«'1i-ip'1). G.3)
V 2
Тогда с помощью шл и рл калибровочно-неинвариантные члены пере-
переписываются в виде
^^^VCPC. G.4)
Рассмотрим теперь их поведение при калибровочном преобразовании
6ЛВ=фВслс, G.5)
где дс — калибровочный параметр. Имеем
G.A)
мы за
мечаем, что первый и второй члены могут взаимно уничтожиться, ее-
если считать, что калибровочное условие линейно по А Тогда мы за-

за306 Глава 8
ли только мы выберем как надо калибровочный параметр. Действитель-
Действительно, взяв
Лс = ?рС, всИ-- — &Ч, G.7),
G.8)
убеждаемся, что два первых члена в вариации G.6) взаимно уничтожа-
уничтожаются. Более того, поскольку рс - действительное грассманово поле,
параметр ? сам должен быть действительным грассмановым числом с
тем, чтобы Лс было обычным числом, т.е.
?2=0. G.9)
Таким образом, если можно добиться, чтобы выполнялось условие
*(\р)В = 0, G.10)
то отсюда будет вытекать инвариантность полного эффективного дей-
действия, так как преобразование поля А имеет вид (зависящего от поля)
калибровочного преобразования. В явном виде
Члены, включающие одну производную, имеют вид
так что, если положить
у нас останется
4%p)B = lfBCEfEFGAGpFPc + ±-UBEGtffEFCPFP€ GЛ4)
Если учесть, что
G.15)
то можно переписать выражение G.14) в виде
R/T) \В г/tFtCvGB.G F С ' гtpCEtrf,E\GB tG F С in лс\

Вычисления по теории возмущений в калибровочных теориях 307
Теперь, пользуясь антисимметрией при перестановке F и С и соотноше-
соотношениями алгебры Ли для матриц Т, мы можем убедиться, что при условии
G.13) это выражение обращается в нуль. Итак, эффективный лагран-
лагранжиан E.1) инвариантен относительно комбинации преобразований
G.17)
= _1_ ; fABCpBPc,
причем мы явно указали зависимость от константы связи, положили
GA = д • АА и включили фермионы. Эффективное действие инвариантно
относительно этих преобразований БРС только при условии, что все
константы связи одинаковы. Так как преобразования БРС ие меня-
меняются при изменении размерности пространства-времени, они оста-
останутся невредимыми при размерной регуляризации, а это означает,
что как ^Эфф, так и ?конт_ останутся инвариантными при таких пре-
преобразованиях. Отсюда вытекает первое следствие: все голые констан-
константы связи должны быть одинаковы, т.е. мы вправе теперь положить в
F.3)
g°-go = *o =*0 =го , G.18)
откуда вытекает, что выполняются соотношения (б.14) и, таким обра-
образом, помимо Za и Zm, имеются только четыре независимые констан-
константы перенормировки, например Z u z2, Zv Z6, причем три из них мы
уже вычислили.
Как и в абелевом случае, можно на основании БРС-инвариантно -
сти вывести тождества для янг-миллсовских функций Грина. Чтобы
предотвратить появление сложных нелинейных членов, удобно ввести
такие источники, которые связаны с изменениями полей при преобра-
преобразовании БРС, т.е. добавить к обычному набору источников Jв, &в, (,в,
X. X» связь которых с фундаментальными полями имеет вид
-<JB*l +со8ств+р85в+«х^ + «4;х>) G.19)
другие источники РА,иА, Л, X, связь которых с нелинейными изме-
изменениями полей в результате преобразования БРС имеет вид
g ц м 2

308 Глава 8
Мы будем исходить из производящего функционала
Z[/B а*.?*,Х,х; ^.ив, А,Н G.21)
определяемого соотношением
e~z =/2)Л 2>р фу Фи Фр<?~эфф, G.22)
ГДе S3*(fc.ecTb Де^ствие 5Эфф из § 5 с добавленными источниками
G.19) и G.20). Выполним преобразование БРС переменных интегриро-
интегрирования в G.22). Такое изменение переменных не должно повлиять на Z.
Поэтому всякое изменение подынтегрального выражения по сравнению
с G.22), связанное с таким изменением переменных, должно быть
равно нулю, что и приводит к янг-миллсовскому варианту тождеств
Уорда.
Во-первых, можно показать, что мера интегрирования не меняет-
меняется при преобразовании БРС (см. задачу). Во-вторых, мы только что
показали, что действие S . ^ инвариантно относительно преобразо-
преобразований БРС, следовательно, меняться могут только члены с источни-
источниками. Линейные по полям члены приведут к дополнительным членам в
показателе экспоненты
Члены выражения G.20) не дают дополнительного вклада, так как
преобразование БРС нильпотентно: два преобразования БРС дают нуль.
Дейётвительно,
') = 0, G.24)
0 G.25)
и выполнено равенство G.10). Это нетрудно доказать (см. задачу). Та-
Таким образом, единственный результат нашего преобразования заклю-
заключается в добавлении в показателе экспоненты под интегралом членов
G.23). Они все линейны по грассмановой переменной 5, так что эта
дополнительная экспонента легко разлагается - член, линейный по 5,
должен равняться нулю, так как это единственное изменение подынтег-
подынтегрального выражения. Это приводит к тождествам

Вычисления по теории возмущений в калибровочных теориях 309
-L /bcdpcpV
2
G.26)
Выписанное функциональное уравнение чрезвычайно нелинейно, и рабо-
работать о: ним ужасно трудно. Теперь ясно, зачем были нужны дополни-
дополнительные источники - мы можем заменить вс.е эти нелинейные члены
функциональными производными, так как по построению
К - -sjb ' «W
1 r
(Юр) =—g, G.Щ
ц
}_fABCBCm б f G29)
2 5мл
9ATfAV =-i-, G.30)
причем все эти равенства выполняются в применении к ехр I s
Поэтому можно теперь записать эти тождества в виде линейного
функционального дифференциального уравнения
. о 8 я 1 5 „в 5' 5 т б . _z
G.31)
Более целесообразно выписать эти тождества для эффективного
квантового действия Г, порождающего в теории собственные вершин-
вершинные части. Для этого выполним функциональное преобразование Ле-
жандра
/*^«кп, G.32)
°в -»*f G.33)
гА -Рк„. G-34>

310 Глава 8
X -Ч'кп. G.35)
X -*кп, G.36)
2 -Г, G.37)
где теперь А^ кп> а^п, рвп> ф и у^ _ новые источники, играющие
роль полей в классическом приближении. В явном виде
Г = Z - < J » • Лквл + ^кл + 1*КПХ + * ЧВП + §ВРКВЛ > • G.38)
Мы не изменили нелинейные источники, так что действие Г является
также функционалом от чА, иА, X и Л. Тогда
•'*¦
так что в результате тождества Славнова - Тейлора принимают вид
, л
бг 1 , лв 5Г 6Г 5Г
JSL>-0. G.40)
5Ткп 6Л 5Л 6ТКП
На эту формулу тоже страшно смотреть, но это {почти) лучшее, что
можно придумать в столь сложной теории (см. задачу). Нелинейные
члены с источниками просты только в классическом приближении,
где можно положить
Бт* g
В абелевом случае мы включили в вариацию Т нелинейный член
(г\ - г|*) У, который в формуле C.16) заменили классическими источ-
источниками (цкп „. ц кп)Укп! так можно было сделать только потому, что
в данном случае духовое поле не взаимодействует с фермионным по-
полем. Теперь же дело обстоит иначе, что и приводит к значительно
более сложной форме тождеств Уорда. Однако в аксиальной калибров-

Вычисления по теории возмущений в калибровочных теориях 311
ке, в которой отсутствуют ду"хи, янг-миллсовские тождества выглядят
так же, как и в КЭД, и дают тот же результат Z1 = z2.
Хотя полученные тождества и кажутся громоздкими, они очень
существенны для доказательства перенормируемости теории. Они
уменьшают число независимых ультрафиолетовых расходимостей,
позволяя устранить их путем переопределения входных параметров.
Но, как и ранее, мы не будем останавливаться на технических под-
подробностях. В заключение заметим, что если у калибровочной части-
частицы и у ду'хов имеется фиктивная масса, то преобразования БРС, по-
видимому, невозможно обобщить, так как это можно было сделать
в КЭД. Поэтому инфракрасные расходимости в янг-миллсовском слу-
случае, вероятно, нужно также устранять методом размерной регуляри-
регуляризации (§4).
Задачи
A. Выведите тождества Уорда в янг-миллсовской теории в акси-
аксиальной калибровке с учетом фермионов.
Б. Покажите, что янг-миллсовская функциональная мера лево-
инвариантна по отношению к преобразованию БРС.
B. Покажите, что преобразования БРС нильпотентны.
Г. Покажите,-что <?ц(8Г/6т?) = -FГ/5<я^п).
¦Д..Выясните, как тождество Уорда КЭД, связывающее продоль-
продольную часть вершины с обратным фермионным пропагатором, меняется
в янг-миллсовском случае в ковариантной калибровке д • Ав = 0.
§ 8. Янг-Миллсовская теория, асимптотическая свобода
С помощью преобразования БРС мы показали, что янг-миллсов-
янг-миллсовская теория содержит только одну константу связи g. Теперь можно,
пользуясь любой из формул F.9) - F.13), связать голую константу
g0 с перенормированной константой g. Поскольку мы вычислили Zlt
%2 и Z3 в фейнмановскей калибровке, начнем с соотношения F.9)
С учетом формул F.64) - F.66) можно записать это уравнение в виде

312 Глава 8
(разложив по g при фиксированном е
(8.2)
Если принять независящий от масс рецепт перенормировки, сог-
согласно которому все конечные части контрчленов полагаются равными
нулю, то мы немедленно находим, что
или u{dg/dn) =p(g), (8.4)
Таким образом, до тех пор пока
11 4
константа связи уменьшается с ростом ц! Такая ситуация называет-
называется асимптотической свободой (она независимо обнаружена авторами
работ [2, 3}). Это открытие имеет колоссальное значение. Из него сле-
следует, что если на данном расстоянии ц константа связи мала и при-
применима теория возмущений, то при уменьшении расстояния эта конс-
константа будет и дальше уменьшаться, благодаря чему при таких масш
табах можно с еще большей уверенностью пользоваться теорией возму-
возмущений. При увеличении же расстояния константа связи растет и вы-
выходит из той области, где можно доверять теории возмущений (рис.9).
В пертурб^тивной области можно проинтегрировать уравнение
(8.4), что дает
i-]-' (8.7)
В этой формуле тоже можно произвести разложение, если

Вычисления по теории возмущений в калибровочных теориях. 313
? \ Непертурбативная
область
Пертур^ативная
\^ область
Р и с. 9.
Поэтому величину g 2(ц) можно рассматривать как некую эффектив-
эффективную константу связи, равную в низшем порядке g2(n0) и содержащую
поправку O(g%0)):
11
8it:
c
прис
_4_
3
i — + . . . . (8.9)
Такое поведение можно, конечно, воспроизвести диаграммами, даю-
дающими поправку к фундаментальной вершине, но полные поправки к
вершине более сложны. Поправки, возникающие при интегрировании
уравнений ренормгруппы, обычно содержат только главные логариф-
логарифмы. Так, в следующем порядке формула (8.7) даст только член с
1п2(и/и0).
При ц < и0, т.е. на больших расстояниях, вычислениям по тео-
теории возмущений доверять нельзя. Ъо означает, что состояния, с ко-
которыми мы имели дело, проводя вычисления по теории возмущений,
имеют смысл только на малых расстояниях, где теория асимптотичес-
асимптотически свободна, но в области больших расстояний становятся сильносвя-
сильносвязанными и не могут иокинуть область взаимодействия и стать асимп-
асимптотическими состояниями, если только по какой-то неведомой причи-
причине связь не ослабляется снова на еще больших расстояниях (поскольк
куда этой области еще не проводилось никаких вычислений, мы вольны
в своих предположениях). В таком случае у пертурбативных состоя-
состояний единственная возможность выжить и образовать асимптотические
состояния - образовав сложные составные состояния, нейтральные
по отношению к дальнодейетвующим калибровочным силам. Такие ней-
нейтральные, или синглетные, комбинации будут все же испытывать муль-
типольные взаимодействия, но последние короткодействующие и не ме-

314 Глава 8
няют характера составных состояний. Так мы приходим к гипотезе
конфайнмента (инфракрасного пленения), согласно которой в асимпто-
асимптотически свободной теории асимптотическими состояниями могут яв-
являться только,синглеты по отношению к калибровочным силам (в про-
противном случае они не могут избежать влияния сильной связи).
Разберем эту гипотезу в рамках квантовой хромодинамики (КХД),
которая, как считается, правильно объясняет физику сильных взаимо-
взаимодействий. Калибровочная группа в этом случае - SKC), а пертурбатив-
ные состояния - дираковские фермионы, преобразующиеся по фунда-
фундаментальному представлению 3 группы SL/C) и отождествляемые с
кварками, и восемь векторных частиц, называемых глюонами. С по-
мощбю теории групп нетрудно найти, что
С, = 1/2 для каждого дираковского фермиона<~3.
Следовательно,
(8.10)
если учесть п^ ароматов кварков (экспериментально п^ = 5, но теоре-
теоретически число п. должно быть, вероятно, равно 6). Вывод: КХД асимп-
асимптотически свободна. Поэтому в соответствии со сказанным выше асимп
готическими состояниями в теории должны быть не кварки и глюоны, а
составные частицы, состоящие из кварков, антикварков и глюонов, ко-
которые и должны отождествляться с сильновзаимодействующими части-
частицами, известными в лаборатории, такими, как протоны, нейтроны, тт-
мезоны и т.д. Мы узнаем эти частицы, просто образуя синглеты по
отношению к цветным силам! Имеются составные частицы с целым
спином, состоящие из кварк-антикварковых пар (qq) и имеющие спиь
0 или 1 в низших состояниях, в которых спины выстроены параллельно
или антипараллельно. На теоретико-групповом языке это соответству-
соответствует разложению
3x3 = 1+8.
Фермионные асимптотические состояния можно образовать как
C ® 3 ® 3)л = 1 + 8 + 8' + 10.
что соответствует барионам (qqq) и антибарионам {qqq) с наименьши-
наименьшими спинами 3/2 и V2 в зависимости от того, как выстроены

Вычисления Но теории возмущений в калибровочных теориях 315
спины кварков. Связанные системы qq, qqq и qqq очень хорошо
согласуются с наблюдаемыми состояниями. Хуже обстоит дело с
состояниями, составленными из глюонов. Так как
(8 0 8)s = 1 + . . . ,
должно быть асимптотическое состояние, составленное из двух глю-
глюонов. Такие состояния не найдены, возможно, из-за значения их мас-
массы и распадных параметров. Недостает также синглетных состояний
типа (qq-глюон), где (qq) образует состояние 8. Приемлема ли КХД
в качестве теории сильных взаимодействий, это в конечном счете за-
зависит от того, позволяет ли она рассчитать в рамках калибровочной
теории процессы сильной связи. Однако природа дала нам в руки зонд
для малых масштабов, а именно фотоны вне массовой поверхности,
образованные либо во времениподобной моде в процессе у+е "-анниги-
"-аннигиляции, либо в пространственно-подобной моде при излучении налетаю-
налетающим электроном. Эксперимент подтвердил, что по отношению к про-
странственно-подооному зонду протон выглядит так, бу^то он сос-
составлен из трех кварков (партонная модель), что подтверждается
знаменитыми свойствами скейлинга, обнаруженными в опытах по
электророждению. Хотя сравнение теории с экспериментом обычно
осложняется из-за трудностей, связанных с инфракрасной расходимо*
стью, все же пространственно-подобные зонды непосредственно свя-
связаны с глубоко-евклидовой областью, где, как мы видели, структура
теории поля проще всего. Недостатком же данной теории является
отсутствие ясности в области сильной связи, затрудняющие принятие
обычной физической идентификации калибровочной константы связи,
в противовес КЭД, где заряд е почти непосредственно измерим. Та-
Таким аналогом идеальной идентификации в КХД блла бы нормировка
по отношению, например, к константе tt\W- взаимодействия, но, к со-
сожалению, мы просто не знаем, как увязать ее с кварк-кварковой кон-
константой связи. Поэтому были разработаны окольные (и очень хитроум-
хитроумные) способы сравнения с экспериментом, но мы здесь на этом не
останавливаемся, так как они сами могут составить книгу!
В заключение заметим, что существует размерный параметр, ко-
который должен характеризовать рассматриваемую теорию, так как ес-
если, скажем, из сравнения с опытом, известна величина g2 при некото-
некотором масштабе цг, то можно определить, при каком масштабе теория

316 Глава 8
возмущений теряет применимость. По традиции вводят масштабный
параметр Л в соответствии с равенством
§1? (8.11)
Сравнение с формулой (8.7) приводит к выражению
1пЛ = 1пц — : • (8.12)
2/ w J1 с - — С )
В этом порядке, зная ц0 и g2(\i0), мы можем найти масштаб Л, но эта
формула не определяет Л однозначно, так как она получена интегри-
интегрированием уравнения (8.5), а потому лишь приближенная.
ЛИТЕРАТУРА
1. ВессЫ С, Rouet A., Stora R., Phys. Lett., 52Br«44 A974).
2. Politzer H.D., Phys. Rev. Lett., 26, 1346 A973).
3. Gross D., Wilczek F., Phys. Rev. Lett., 26, 1343 A973).

Приложения
Функциональные гауссовы интегралы будут пониматься как проиэ*
ведение большого числа обычных гауссовых интегралов. Простейший
из них
G(a) = +(° dx e~ax\ (АЛ)
— во
если воспользоваться приемом Пуассона, заключающимся в том, что"
бы возвести в квадрат этот интеграл и перейти в подынтегральном вы"
ражении к полярным координатам, оказывается равным
С(в) = /^. (А*2)
Мйжно обобщить это на случай N степеней свободы. Пусть
•)- во -X; а 1 • X •
G(A)= / dxtdxa ... dxNe ч , (АЛ)
— во
где А - действительная симметричная N< Л'-матрица с матричными
элементами а ... Напишем
xiaijxj =ХТАХ, где АТ = А « (А.4)
Матрицу А можно диагонализовать путем поворота:
A = RTDR, RTR = RRT=\, (AJ5)
где D - диагональная матрица со значениями dlt d2, .M <//y Тогда
{А?)
(A.7)
где Y = RJL Якобиан равен единице (докажите это). В переменных у

318 Приложения
интеграл G(A) распадается на N множителей:
GN(A)=G(dl)G(d2)...G(dN)=
*- (АЛ)
если допустить, что все собственные значения матрицы А положитель"
ны. Аналогично можно доказать, что если Z; - комплексные перемен^
ные (число их равно /V), то
Г П dzi dz*e~lUz =Bn)*(det C)~\ (A.11)
где С - эрмитова/УхЛ^матрица с положительными собственными зна-
значениями. Формально можно теперь определить гауссов интеграл по
траекториям, перейдя к пределу при /V -» ~.
Эти формулы справедливы в случае., когда детерминант отличен от
от нуля. Если же он равен нулю, то, значит, некоторые di равны нулю,
что приводит к бесконечности при интегрировании по бесконечному ИН"
тервалу. Но нельзя ли получить осмысленный ответ даже в том случае,
когда детерминант обращается в нуль? Было бы идеально, если бы уда"
лось отделаться от этих гадких бесконечных интегралов. Можно ли
найти такую процедуру? Предположим, что у симметричной N* /У^матри"
цы А имеется п нулевых собственных значений. В переменных у опре-
определим ограниченный гауссов интеграл
Согр(Л)
где мы интегрируем только по тем переменным, которые соответст-
соответствуют ненулевым собственным значениям матрицы А. Такая форма ин-
интеграла GQr (А) неудобна, так как он зависит от правильной системы
координат у. Чтобы избавиться от этого, введем новые переменные
YN -п + 1>-"> YN и перепишем (А.12) в виде
"• dYN-n
Затем перейдем от переменных у к переменным х, пользуясь форму-
формулой Якоби
dxt... dxNdet \&- | , (AJ4)

Приложения 319
и в результате придем к окончательному выражению
СвГр(Л)-/.( П rf*,)det |l|L_ I П Ь(Уа)е-*Тл\ (А.15)
> <?* а = N -п + 1
Этот интеграл вполне определен. Здесь уа - некоторые произволь"
ные функции переменных х, а дополнительные множители det |Эу/йк| Пб(у)
в мере эффективно ограничивают интегрирование по Л^мерному
пространству интегрированием по (N - п)-мерному пространству. Как
явствует из самого построения, GQr (А) не зависит от конкретного вида
функций уа (х), a ~i> N - п» Само собой разумеется, что необходимо
правильно выбрать функции уа (х), чтобы они действительно ограничь
вали область интегрирования, так как иначе якобиан det | ду/Эх\ бу»
дет сингулярным. (Такой метод изменения меры применен для интегра-
интегралов по траекториям в калибровочных теориях. Это привело к знамени"
тым духам Фаддеева - Попова в ковариантной калибровке.)
В заключение докажем еще одно соотношение. Рассмотрим теперь
N T . т
П dXie~x Ax + <*'*
1
(А.16)
Перепишем показатель экспоненты, дополнив его до полного квадра^
та:
хтАх-а-*х ш.(Х-1- А-1ы)Т А(х_ J_ Л со)- — «ТЛ-'М,
l 2 4
(А. 17)
при условии, что обратная матрица А'1 существует. Полагая
*' = *- 1 Л со, (А.18)
так что dx' = dxt , находим
F[A, „1—-T " "''" f, П dx: e~*'T**'= (A.19)
» =1 1
1 ТА~*
= //2е"ТМ " (det A)'*. (A.20)
И вновь результат для интеграла по траекториям формально получает"
ся переходом к пределу N -» ~.

320 Приложения
Б. Интегрирование при произвольном чиспе измерений
Рассмотрим интеграл
IN = fdNl F(l), (БЛ)
где F(l) - произвольная функция только длины 1^ (ц = 1,...., /V), а
N - целое число. Введем полярные координаты в N измерениях
где L* = ZMV (Б.2)
Тогда
-LN-idL rf<p sine^e, sin2 e2<fe2-csin^-2 ед,_
где считается, что переменные принимают значения в интервалах
0<L<OOj0<9<'2ttj 0< в,- <тт, i = 1, ...,N-2 * (Б.4)
Нетрудно показать, что
N -1 v ж
/ k f LN-'dL F(L). (Б.5)
*= 1 О ' о
Пользуясь хорошо известной формулой
У' (sin О2*'1 (cos О2' dt = ±- Г(*>Г<У> , Re*, Rey> 0,
о 2 Г (х +¦ у)
(Б.6)
причем у = 1/2, получаем
тг тт/2 ^' ^ I"(-Г")
о' ' S1" = г ( к + г )
Г(-*±1_)
Подставляя этот результат в (Б.5), приходим к формуле
(Бл)

Приложения
_/V/2
в которой х = L2^
В общем случае F(*) имеет вид
F(*)=-(*+ а2)-^ , л =-2, 3, .„, (Б.9)
что приводит к формуле
°с {N -2\/ ¦<.
I'"" \X+aY B{aa)-A*N/i J * ^-2)/2(Ur)-^(B.10)
Сравнивая с выражением для бета^функции
±
ПА)
справедливым при Re(/V/2) >I0 и Re[ А - (N/2)]> Oj получаем оконча-
окончательный результат
(^2+а2)^ Г(Л) (о 2)Л _yv/2 ° <БЛ2)
Мы вывели это выражение в случае целого N при Re[4 - (/V/2)] >10,
Re (/V/ 2) >Ю, Примем теперь, что при аналитическом продолжении вы-
выражение (БЛ2) верно и в случае нецелых /V.
Далее, полагая I = I ' -кр и вводя обозначение 6 2= о2+ р2, мы
жем записать (Б.12) в виде
f?l
)A
(lU2p-l+b2)A Г (А) (Ь2 _р2у4_ДГ/2 •
(БЛЗ)
Теперь, последовательно дифференцируя выражение (БЛЗ) по р , не
трудно получить формулы м
(-Рм)
A^2Р-1+а2)А Г {A) (a2_p2)A-N/2'
(БЛ4)

322 Приложения
f
2 _ р2)Л-Л/а
1 N 2 2
2 • •- - ?~ Suvr 2~ ° ~P
(Б.15)
Эти формулы выведены для евклидова пространства, и в каждом слу"
чае принимается, что правая часть является правильным продолжение
ем левой части на нецелые значения N.
Сводка формул размерной регуляризации
d2c*l 1 Г (А - со) 1
S
BтгJш A^М2+21-Р)А
(БЛ6)
BттJш (/2f M2 + 21-р)я
>
— со
(Б.17)
г Г (/4 -со) 1 Г (Л — 1 — со) , R1
LpuPv з— + т 5uv —^ -,—' 1» (ь.Щ
{М2-р2)Л-и> 2 (л/2 _ р2)Л - 1- — со
d2wl l\xlvlp _i Г (^4-со) -
' /9„\2со ,ц ,1/2.0 ;.„\Л =" Т; чл-, _ . ¦. LPuPvPp —¦ -1"
BttJC0 (/2 +M2+ 2Z-P)-4 Dir)«r(i4)
{A -co) — [6Ц„ ppPtT + SVCT РцРр + 5pa PtlPv +
z—p'i) *

Г(Л-2-М)
В. Фейнмановекие правила в ковариантной калибровке
в евклидовом пространстве B «о измерений)
фермионная линия.

Библиография
Цель этой аннотированной библиографии в том, чтобы несколько
сгладить вводный характер основного текста книги, предложив чита-
читателю список литературы, в которой материал изложен значительно под»
робнее и глубже. Автор приносит извинения за возможные пропуски.
Существует много превосходных учебников по квантовой теории
поля. Приводим здесь лишь некоторые из них в алфавитном порядке
авторов.
Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Релятивист-
екая квантовая теория, ч. 1. - М.: Наука, 1968.
Боголюбов Н. Н., Жирков Д.В. Введение в тебрию квантованных
полей. - М.: Наука, 1976.
Bjorken J.D., Drell S.D. Relativistic Quantum Mechanics; Relativi-
stic Quantum Fields. - N.Y.: McGraw-Hill, 1965. (/Имеется перевод:
Бъеркен Дж. Д., Дрелл С.Д. Релятивистская квантовая теория, т. 1,
II . - М.: Наука, 1978.)
Лифшиц E.U., Питаевекий Л.П. Релятивистская квантовая тео-
теория, ч. II. - М.: Наука, 1971.
Mandl F. Introduction to Quantum Field Theory. - N.Y.tWiley-Inter-
science, 1959.
Nash C. Relativistic Quantum Fields. — N.Y.: Academic Press,
1978.
Славное А.А., Фаддеев Л.Д. Введение в квантовую теорию кали-
калибровочных полей. - М.: Наука, 1978.
Taylor J.C. Gauge Theory of Weak Interactions. — Cambridge: Cam-
Cambridge University Press, 1976. (Имеется перевод: Тейлор Дж. Калибро-
Калибровочные теории слабых взаимодействий. - М.: Мир, 1978.)
Schweber S. An Introduction to Relativistic Quantum Field Theory. —
N.Y.: Harper and Row, 1961. (Имеется перевод: Швебер С. Введение в
релятивистскую квантовую теорию поля. -т М.: ИЛ, 1961.)
Jauch J.M., Rohrlick F. The theory of Photons and Electrons. —
Cambridge: Addison-Wesley, 1955.

Библиография' 325
Рекомендуем также замечательные лекции Коулмена, прочитан-
прочитанные им на Международной школе субъядерной физики "Этторе Майо"
рана":
"Дилатации" (о нарушении конформной инвариантности квантовы"
Ми эффектами)(Со/етпога S. Dilatations. In: Properties of Fundamental
Interactions (Proc. of the 9. Course of "Ettore Majorana" Intern. School)/
Ed. A. Zichichi. - N.Y.:. Acad. Press, 1973.)
"Перенормировка. Обзор для неспециалистов". (Coleman S. Renor-
malization: a Review for Non-Specialists. In: "Properties of Fundamental
Interactions" (Proc. of the 9. Course of "Ettore Majorana" Intern. School)/
Ed. A. Zichichi. - N.Y., Acad. Press, 1973.)
"Тайная симметрия" (о механизме Хиггса и калибровочных тео-
теориях). (Coleman S. Secret Symmetry. In: Laws of Hadronic Matter (Proc.
of the 11. Course of "Ettore Majorana" Intern. School) /Ed. A. Zechichi.
— N.Y".; Acad. Press, 1975.) (имеется перевод в сб.: Квантовая теория
калибровочных полей. - М.: Мир, 1977.
''Применения инстантонов". (Coleman S. The Uses of Instantons.
In: The Whys of Subnuclear Physics (Proc. of the 1977 Int. School of
Subnuclear Physics, Erice, Italy)/Ed. A. Zichichi. — N.Y., Plenum,
1979.)
Более подготовленные читатели получат удовольствие от чтения
обзоров:
Abers E.S., Lee B.W. Gauge Theories. - Physics Reports, 9C, 1,
1973. (Имеется перевод в сб.: Квантовая теория калибровочных полей. -
М.: Мир, 1977.)
Balian R., Zinn-Justin J. In: Methods in Field Theory (Proc. of the
1975 Les Houches Summer School). - Amsterdam: North-Holland, 1976.
Ниже мы приводим дополнительные ссылки по каждой главе основ»
ного текста.
ГЛАВА 1
§ 1. Подробное исследование связи между инвариантностями ла-
лагранжиана и законами сохранения можно найти в статье:
Hill E.L., Rev. Mod. Phys., 23, 253 A951).
§ 2, 3. Стандартные ссылки по поводу группы Лоренца: ГелъфандИ.М.,
Минлос Р.А., Шапиро З.Я. Представления группы вращений и группы Ло-
Лоренца и их применения. - М.: Физматгиз, 1968.
Гелъфанд ИМ., Граев ММ., Виленкин НЯ. Обобщенные функции,
Т. 5. - М.: Физматгиз, 1962.
Много оригинальных работ по теории представлений групп Лорен-
Лоренца и Пуанкаре перепечатано в книге:

326 Библиография
Dyson F.J. Symmetry Groups in Nuclear and Particle Physics. —
N.Y., Benjamin, 1966.
Еще одно прекрасное изложение теории представлений содержится в
конспектах лекций Ф.Гюрши по теории поля A970 г.) (неопубликовано).
§ 4 - 7. Трансформационные свойства полей обсуждаются в
работе:
Kibble T.W., Journ. Math. Phys., 2, 212 A961).
§ 8. Суперсимметрия впервые появилась в работах, связанных с
моделями струны:
Ramond P., Phys. Rev., D3, 2415 A971).
Neveu A., Schwarz /., Nucl. Phys., B31, 86 A971).
Она же возникла как обобщение группы Пуанкаре в работах:
Гольфанд Ю.Ф., Лихтман ЕЛ. - Письма в ЖЭТФ, 1971, т. 13,
с. 452.
Волков Д.В., А пулов В.П. - Письма в ЖЭТФ, 1972, т. 16, с. 621.
Wess /., Zumino В., Nucl. Phys., В70, 39 A974).
Подробный обзор суперсимметрии:
Fayet P., Ferrara S., Phys. Reports, 32C, 249 A977).
ГЛАВА 2
§ 1. Подробнее о канонических преобразованиях см. книги:
Goldstein H. Classical Mechanics. - Reading, Mass., 1950. (Имеет-
(Имеется перевод: Голдстейн Г. Классическая механика. - М.: Наука, 1975.)
Muhunda N., Sudarshan E.C.G. Classical Dynamics: A Modern Per-
Perspective. - N.Y.: Wiley-Interscience, 1974.
§ 2, 3. Первые работы, посвященные интегралам по траекториям,
можно найти в сборнике репринтов:
Selected Papers on Quantum Electrodynamics/Ed. J. Schwinger. —
N.Y.: Dover, 1958.
Применения интеграла по траекториям детально освещены в книге:
Feynman R. Р., Hi ЬЬ s A. R. Quantum Mechanics and Path Integrals,—
N.Y.: McGraw-Hill, 1965. (Имеется перевод: Фейнман Р.П., Хибс А.Р.
Квантовая механика и интегралы по траекториям. - М.: Мир, 1968.)
ГЛАВА 3
§ 1 - 4. Наше изложение близко цитированной работе Аберса и Ли;
см. также:
Lurie D. Particles and Fields. -N.Y.: Interscience, 1968.
§ 5, 6. По поводу вычисления детерминантов с помощью 5 "функ-
"функций см. работы:
Ray D.B., Singer I.M., Adv. Math., 7, 145A971).
Dowker J.S., Qntchley R., Phys. Rev., D13, 3224 A976).

Библиография 327
Corrigan E., Goddard P., Osborn #., Templeton S., Nucl. Phys.,
В 159, 469 Q979).
ГЛАВА 4
§ 3. Общепринятые ссылки по поводу размерной регуляризации
(помимо тех, которые приведены в тексте):
Bollini C.G., Giambiagi /./., Nuovo Cimento, 12B , 20 A972).
Ashmore J.F., Nuovo Cimento Lett., 4, 289 A972).
Обзор на эту тему:
Leibbrandt G., Rev. Mod. Phys., 47, 849 A975).
§ 5. Понятное объяснение перенормировки можно найти в цитиро"
ванных лекциях Коулмена. См. также:
Collins J.C., Phys. Rev., D10, 1213 A974).
По поводу доказательства перенормируемости см.:
Zimmermann V. In: Lectures on Elementary Particles and Quantum
Field Theory/Eds. S.Deser, M.Grisaru, H.Pendleton. — Cambridge, Mas-
Massachusetts: MIT Press, 1970
и цитированную работу Аберса и Ли. Ренормгруппа обсуждается в ра-
работах :
Stuckeberg E.C.G., Petermann A., Helv. Physica Acta, 25, 499
A953).
Gell-Mann M., Low F., Phys. Rev., 95, 1300 A954).
Callan C.C. In: Methods in Field Theory, Amsterdam: North-Ho Hand,
1975.
Отличительные черты разных уравнений ренормгруппы обсуждаются в
работе:
Weinberg S., Phys. Rev., D8, 3497 A973).
§ 8,9
Eden R.J., LandshoffP.V., Olive D.I., Polkinghorne J.C. The Ana-
Analytic S-Matrix. — Cambridge: Cambridge Univ. Press, 1966 И цитирован"
ная книга Лифшица и Питаевского,
ГЛАВА 5
Основная ссылка к материалу этой главы:
Березин Ф.А. Метод вторичного квантования. - М.: Наука, 1965.
Кроме этого, см., конечно, лекции Коулмена "Применения инстанто-
нов", цитированные выше.
ГЛАВА 6
§ 1, 2. В дополнение к цитированным работам Янга и Миллса и Киб«
бла см.:
Utiyama R., Phye. Rev., 101, 1597 A956).

328 Библиография
Gell-Mann M., Glashow S.L., Ann. Phys. (N.Y.), 15, 437 A961).
§ 3. По поводу инстантонов см. лекции Коулмена "Применения
инстантонов" и цитированную книгу Тейлора. Упорядоченные по траек-
траекториям экспоненты впервые были введены в работе:
Mandelstam S., Ann. Phys. (N.Y.), 19, 1 A962).
ГЛАВА 7
§ 1. Прекрасное изложение теории гамильтоновых систем со свя-
связями содержится в лекциях Дирака:
Dirac P.A.M. Lectures on Quantum Mechanics. — N.Y.: Yeshiva-
University, 1964.
Dirac P.A.M. Lectures on Quantum Field Theory. — N.Y.: Yeshiva
University, 1965. (Имеется перевод в книге: Дирак П.A.M. Принципы
квантовой механики. - М.: Наука, 1979.)
§ 2. См. книгу Славнова и Фаддеева, а также лекции Фаддеева в
книге "Методы теории поля" (Methods in Field Theory), цитированной
выше.
ГЛАВА 8
§ 1. Необходимость введения полей-духов в ковариантных калибров^
ках впервые была отмечена в работах:
Feynman R.P., Acta Physica Polonica, 24, 697 A963).
De Witt B.S., Phys. Rev., 162, 1195 A967).
§ 2, 4. Квантовая электродинамика широко обсуждается во многих
учебниках. В дополнение к уже цитированным укажем книги:
Ахиезер А.И., Берестецкий В.Б. Квантовая электродинамика.
Изд. 3"е. - М.: Наука, 1969.
Feynman R.P., Quantum Electrodynamics. — N.Y.: Benjamin, 1961.
(Имеется перевод: Фейнман Р.П. Квантовая электродинамика. - М.:
Наука, 1964.)
Kallen G. Quantum Electrodynamics. — Berlin: Springer-Verlag,1972.
По поводу размерной регуляризации в КЭД см., например, работу:
Collins J.C., McFarlane A.J., Phys. Rev., D10, 1201 A973).
§ 3
Ward J.C., Phys. Rev., 78, 182 A950).
- Takahashi Y., Nuovo Cimento, S, 370 A957).
§ 4. Использованию размерной регуляризации для выявления инфра-
инфракрасных расходимостей посвящены работы:
Gastmans R., Mendermans R., Nucl. Phys., B63, 277 A973).
Marciano W.J., Phys. Rev., D12, 3861 A975).
§ 5. Доказательство перенормируемости янг-миллсовских теорий

Библиография 329
содержится в работе:
'tllooft G., Nucl. Phys., B33, 173 A971).
См. также цитированную работу Аберса и Ли.
§ 7
Славное А.А., ТМФ, 1972, т. 10, с. 153.
Taylor J.C., Nucl. Phys., В33, 436 A971).
§ 8. Впервые явление асимптотической свобода было отмечено
'т~Хофтом в 1972 г. на конференции по лагранжевой теории поля в Марселе;
за большими деталями и дополнительными ссылками мы отсылаем читате-
читателя к обзору:
Politzer H.D. "Asymptotic Freedom: An Approach to Strong Interac-
Interactions", Phys. Reports, 14C, 129 A974).
Применения КХД изложены в лекциях Филда "Применения квантовой
хромодинамики",. прочитанных в 1978 г. (Field R.D. "Applications of
Quantum Chromodynamics", Lectures given at the La Jolla Institute Sum-
Summer Workshop, 1978).
Литература, добавленная при переводе
1. Боголюбов Н.Н., Жирков Д.В. Квантовые поля. - М.: Наука, 1980.
2. Волошин М.Б., Тер-Мартиросян К.А. Теория калибровочных взаимо-
взаимодействий элементарных частиц. - М.: Энергоатомиздат, 1984.
3. Ициксоп К., Зюбер Ж-Б. Квантовая теория поля. Т. 1, 2. - М.: Мир,
1933.
4. Попов В Л. Континуальные интегралы в квантовой теории поля и
статистической физике, — М.: Атомиздат, 1976.
5. Новожилов Ю.В. Введение в теорию элементарных частиц. - М.:
Наука, 1972.

Оглавление
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА 5
ПРЕДИСЛОВИЕ 9
Глава 1 .Функционал действия 11
§ 1. Элементарные сведения 11
§ 2. Группа Лоренца (беглый обзор) 15
§ 3. Группа Пуанкаре 21
§ 4. Локальные поля и преобразования группы Пуанкаре 24
§ 5. Общие свойств а действия 36
§ 6. Действие для скалярных полей 43
§ 7. Действие для спинорных полей .47
§ 8. Действие со скалярными и спинорными /талями и
суперсимметрия 53
Глава 2 . Функционал действия в квантовой механике: фейнмановский
интеграл по тракториям 61
§ 1. Канонические преобразования в классической и квантовой
механике 62
§ 2. Фейнмановский интеграл по траекториям 67
§ 3. Интеграл по траекториями гармонический осциллятор,
находящийся под действием силы 74
Глава 3. Фейнмановский интеграл по траекториям в теории поля 80
§ 1. Производящий функционал . . , . 80
§ 2. Фейнмановский пропагатор 83
§ 3. Эффективное действие 88
§ 4. Вычисление интеграла по траекториям методом
перевала 94
§ 5. Первые квантовые поправки. Вычисление детерминантов
с помощью ?-функции 102
§ 6. Изменение масштаба детерминантов. Константа связи,
зависящая от масштаба , 107
Глава 4. Вычисление феЛнмановского интеграпа по траекториям методом
теории возмущений: теория ф4 # ^ 11
§ 1. Фейнмановские правила для теории Л<р4 111
§ 2. Расходимости фейнмановских диаграмм „ 120

Оглавление 331
§ 3. Размерная регуляризация фейнмановских интегралов .... 127
§ 4. Вычисление фейнмановских интегралов 132
§ 5. Перенормировка 141
§ 6. рецепты перенормировки 152
§ 7. Зависимость коэффициентов ренормгруппы от рецепта . .
перенормировки 164
§ 8. Продолжение в пространство Минковского,
аналитичность 166
§ 9. Сечения и унитарность 172
Глава 5. Интеграп по траекториям при наличии фермионов 181
§ ^Интегрирование по грассмановым числам 181
§ 2. Интеграл по траекториям для свободных ферми-полей ... 185
§ 3. Фейнмановские правила для спинорных полей 191
§ 4. Вычисление и масштабное преобразование фермионных
детерминантов 196
Глава 6 .Калибровочные симметрии, конструкция Инга — Миппса 203
§ 1. Глобальные и локальные симметрии 203
§ 2. Построение локально симметричных лагранжианов 214
§ 3. Чисто янг-миллоовская теория 220
Глава 7= Интеграп по траекториям в калибровочных теориях 232
§ 1. Гамильтонов формализм в калибровочных теориях,
абелев случай „ 232
§ 2. Гамильтонов формализм для калибровочных теорий,
неабелев случай , .. .241
§ 3. Непосредственное определение янг-миллсовского ФИТ.
процедура Фаддеева - Попова 249
Глава 8. Вычисления по теории возмущений в калибровочных
теориях » 253
§ 1. Фейнмановские правила для калибровочных теорий
в евклидовом пространстве 253
§ 2. КЭД, однопетлевая структура 261
§ 3. КЭД, тождества Уорда 274
§ 4. КЭД, применения 280
§ 5. Янг-миллсовская теория, предварительные
замечания 287
§ 6. Янг-миллсовская теория, однопетлевая
структура 292
§ 7. Янг-миллсовская теория, тождества Славнова - Тейлора . . 305
§ 8. Янг-миппсовская теория, асимптотическая
свобода 311

332 Оглавление
Приложения 317
A. Гауссово интегрирование 317
Б. Интегрирование при произвольном числе измерений ..... 320
B. Фейнмвновские правила в ковариантной калибровке
в евклидовом пространстве Bа> измерений) . 323
БИБЛИОГРАФИЯ 324