МАТЕМАТИКА
В ТЕХНИЧЕСКОМ УНИВЕРСИТЕТЕ
Ах + By + Cz + D = О
А.Н. Канатников А.П. Крищенко
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Издательство МГТУ имени Н.Э.Баумана
Математика в техническом университете Выпуск III
Комплекс учебников из 21 выпуска
Под редакцией В. С. Зарубина и А. П. Крищенко
I.	Введение в анализ
II.	Дифференциальное исчисление функций одного переменного
III.	Аналитическая геометрия
IV.	Линейная алгебра
V.	Дифференциальное исчисление функций многих переменных
VI.	Интегральное исчисление функций одного переменного
VII.	Кратные и криволинейные интегралы. Элементы теории поля
VIII.	Дифференциальные уравнения
IX.	Ряды
X.	Теория функций комплексного переменного
XI.	Интегральные преобразования и операционное исчисление
XII.	Дифференциальные уравнения математической физики
XIII.	Приближенные методы математической физики XIV. Методы оптимизации
XV. Вариационное исчисление и оптимальное управление XVI. Теория вероятностей
XVII.	Математическая статистика
XVIII.	Случайные процессы
XIX.	Дискретная математика
XX.	Исследование операций
XXI.	Математическое моделирование в технике
А.Н. Канатников, А.П. Крищенко
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3-е издание
Под редакцией д-ра техн, наук, профессора В.С. Зарубина и д-ра физ.-мат. наук, профессора А.П. Крищенко
Допущено
Министерством образования Российской Федерации в качестве учебника для студентов высших технических учебных заведений
Москва Издательство МГТУ им. Н. Э. Баумана 2002
УДК 517.1(075.8)
ВБК 22.151.5
К19
Рецензенты: проф. В.И. Елкин, проф. Е.В. Шикин
К19 Канатников А.Н., Крищенко А.П. Аналитическая геометрия: Учеб, для вузов. 3-е изд. / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. -388 с. (Сер. Математика в техническом университете; Вып. III).
ISBN 5-7038-1671-8 (Вып. III)
ISBN 5-7038-1270-4
Книга является третьим выпуском серии „Математика в техническом университете" и знакомит читателя с основными понятиями векторной алгебры и ее приложений, теории матриц и определителей, систем линейных алгебраических уравнений, кривых и поверхностей второго порядка. Материал изложен в объеме, необходимом на начальном этапе подготовки студента технического университета.
Содержание учебника соответствует курсу лекций, который авторы читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен преподавателям и аспирантам.
Ил. 111. Библиогр. 25 назв.
Выпуск книги финансировал
Московский государственный технический университет им. Н.Э. Баумана
УДК 517.1(075.8)
ББК 22.151.5
ISBN 5-7038-1671-8 (Вып. III)
ISBN 5-7038-1270-4
© А.Н. Канатников, А.П. Крищенко, 2000
© Московский государственный технический университет им. Н.Э. Баумана, 2000
© Издательство МГТУ им. Н.Э. Баумана, 2000
ПРЕДИСЛОВИЕ
Эта книга — третий выпуск комплекса учебников „Математика в техническом университете64. Ее содержание выходит за рамки аналитической геометрии и отражает тот курс, который стал уже традиционным во многих вузах технической ориентации. В этом курсе можно выделить три раздела: векторную алгебру, аналитическую геометрию и теорию матриц и систем линейных алгебраических уравнений (СЛАУ).
Векторная алгебра, составляющая первую часть книги (главы 1, 2), тесно переплетается с элементарной геометрией и представляет собой, по существу, современный язык той части геометрии, которая связана с понятиями параллельных прямых и подобия. Мы предполагаем, что читатель хорошо знаком с такими терминами, как точка, прямая, плоскость и знает их свойства (в частности, признаки параллельности прямых, признаки равенства и подобия треугольников, признаки параллелограмма и т.д.).
Аналитическая геометрия, основным методом которой является метод координат, составляет вторую часть книги. Понятие системы координат, так же как и многие факты аналитической геометрии, известно любому начинающему студенту со школьной скамьи. Изучение этого раздела геометрии в техническом вузе отличается большей строгостью и систематичностью. В книге изложение аналитической геометрии, в частности введение декартовой системы координат, опирается на векторную алгебру. Ей посвящены главы 3 — 5. Основное внимание уделено теории прямых и плоскостей, а также кривых и поверхностей второго порядка (главы 11 и 12).
6
Предисловие
Третья часть книги посвящена основам матричной алгебры (главы 6 — 8) и системам линейных алгебраических уравнений (главы 9 и 10).
При отборе и изложении материала авторы стремились предусмотреть возможные различия в объеме его изучения. Сложные и второстепенные вопросы, обычно не входящие в программу, даны в виде дополнений в конце соответствующей главы.
Книга, как и другие выпуски комплекса учебников, имеет развитый аппарат для поиска нужной информации, позволяющий использовать книгу как справочник. Ключевые понятия, которые должны быть известны читателю, в тексте книги выделены курсивом. Любой определяемый термин в тексте выделен полужирным курсивом, а номер страницы указан в предметном указателе, который находится в конце книги. Термины в предметном указателе даны в алфавитном порядке по существительному в именительном падеже. Ссылки предметного указателя разделяются на основные (даны в прямом начертании) и неосновные (даны курсивом), которые указывают на дополнительные сведения о термине. Ссылки на термины, введенные в других выпусках комплекса, содержат номера этих выпусков. Например, 1-215 означает страницу 215 первого выпуска, а II — второй выпуск (соответствующее место в этом выпуске можно найти по его предметному указателю).
В тексте также имеются ссылки, облегчающие поиск нужных определений и других сведений. Такие ссылки могут относиться как к данной книге, так и к другим выпускам комплекса учебников. Например, (см. 1.2) отсылает читателя ко второму параграфу первой главы этой книги, тогда как [1-7.5] означает ссылку на пятый параграф седьмой главы в первом выпуске. Определения, теоремы, замечания, формулы и т.п. имеют двойную нумерацию. Например, теорема 2.1 — это первая теорема в главе 2, (2.1) — первая формула в главе 2, рис. 1.5 — пятый рисунок в главе 1.
Большинство используемых обозначений помещены в перечне основных обозначений. В н^м наряду с их краткой расшифровкой даны ссылки на раздень1 этого или других выпусков серии, в которых вводится обо#начение- Приведены также написание и русское произношений букв латинского и греческого алфавитов.
Перед чтением этой книги преДлагаем в целях самоконтроля выполнить несколько несложны/ заданий. В тексте каждого задания прямым полужирным шрифтом выделены ключевые термины, значение которых должно быть известно читателю, а в конце указан выпуск комплекОа? в котором можно справиться об этих терминах при помощи пРеДметного указателя выпуска.
Задания для самопроверки
1.	Является ли множеств0 действительных чисел упорядоченным и образуют ли натуральные числа его подмножество? Что такое абсолютное значение (модуль) числа? [I]
2.	Имеют ли операции сложения и умножения действительных чисел свойства коммутативности, ассоциативности и В чем СОСТОИТ ИХ СВОЙСТВО дистрибутивности? [I]
3.	В чем выражается свойство антикоммутативности некоторой бинарной операции? [I]
4.	Что понимают под критерием некоторого утверждения? [I]
5.	Из каких этапов состоЯт доказательство по методу математической индукции? [I]
6.	Что такое функция, алгоритм и рекуррентное соотношение? Приведите пРимеРы функций, заданных с помощью рекуррентных соотношений- [I]
7.	Укажите область определения (существования) и область значений и постр°йте графики однозначных ветвей многозначной функции у2 = х. [I]
8
ПРЕДИСЛОВИЕ
8.	Проверьте, является ли функция = а) четной;
б) нечетной. [I]
9.	Сформулируйте определение взаимно однозначного отображения двух множеств. [I]
10.	Какие свойства имеют функции, непрерывные на отрезке? [I]
11.	Что такое вертикальные и наклонные асимптоты графика функции и как их находят? [II]
12.	На каких интервалах функция у = х + 1/х является возрастающей (убывающей)? [II]
13.	Сформулируйте достаточное условие выпуклости вверх графика функции у = f(x). [II]
14.	Как вычисляется производная сложной функции У = /(<7(я:))? [И]
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
◄ и ► — начало и окончание доказательства
#	— окончание примера, замечания
а € А, А Э а — элемент а принадлежит множеству А (множество А содержит элемент а) 1-1.1
А С В, В D А — подмножество А включено в множество В (В включает 4) 1-1.2
А С В, В Э А — подмножество А включено в множество В или совпадает с ним 1-1.2
N — множество натуральных чисел 1-1.3
R	— множество действительных чисел 1-1.3
АВ	— отрезок, соединяющий точки А и В 1.1
\АВ\ — длина отрезка АВ 1.1
AJ&,AB — геометрический вектор с началом в точке А и концом в точке В 1.1
— длина геометрического вектора 1.1
а,|а|	— вектор и его длина 1.1, 1.2
О — нулевой вектор 1.1
а + Ь — сумма векторов а и Ь 1.3
Ха	— произведение вектора а на число А 6 R 1.3
пр/а	— ортогональная проекция вектора а на направление
вектора I 1.4
а, Ь — угол между векторами а и Ь 1.4
Li±L2 — вектор а ортогонален вектору Ь, прямая L] перпендикулярна прямой L} 4.1
а||Ь, L\ || L2 — вектор а коллинеарен вектору Ь, прямая L\ параллельна прямой 4.3
10
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
п
£2	— к=1	сумма п слагаемых си,	• • • • •	ч	1-2.6
m ^акО.к —	линейная комбинация	векторов	ai,	
к=1	коэффициентами aj, ..	•? &к ? ♦• *,		1.5
а~{х;у} (a = {x}y,z}) — задание вектора а из V2 (Уз) с помощью его координат в фиксированном базисе в V2 (У3) 1.5
Vi (У2 и Уз) — пространство коллинеарных векторов (компланарных векторов и всех свободных векторов) 1.6
i (i,j и — ортонормированный базис в Ц (правый ор-тонормированный базис в V2 и Уз) 1.6
аЬ	— скалярное произведение векторов а и Ь 2.2
ахЬ	— векторное произведение векторов а и Ь 2.3
аЬс — смешанное произведение векторов а, Ь и с 2.4
Оху, Oij (Oxyz, Oijk) — правая прямоугольная система координат на плоскости (в пространстве) 3.1
М(х; у) — точка М плоскости с координатами х (абсцисса) и у (ордината) 3.1
7Vf(x;t/;z) — точка М пространства с координатами х (абсцисса), у (ордината) и z (аппликата) 3.1
р и — полярные координаты (полярные радиус и угол) точки на плоскости 3.6
|х|	— абсолютное значение числа х 1-1.3
А => В — из высказывания А следует В (В — необходимое условие для Д, а А — достаточное условие для В) 1-1.5
А <=> В — высказывания А и В равносильны 1-1.5
£?, I	— единичная матрица 6.1
©	— нулевая матрица 6.1
Ат — матрица, транспонированная к А 6.3
det/l — определитель матрицы А 7.1
11
А~г — матрица, обратная к матрице А 8.1
RgA — ранг матрицы А 8.4
Ах = Ь — система линейных алгебраических уравнений (СЛАУ) 9.2
(А|6) — расширенная матрица СЛАУ Ах — b 9.3 у = /(ж) — переменное у — функция переменного х 1-2.1 /(a), f(®)|	— значение функции /(ж) в точке а 1-2.1
ж = /-1(у) — функция, обратная к функции у — /(ж) 1-2.3, 1-11.1 п
П о,т — произведение п сомножителей ai, ат1 ап m=1	1-2.6
к — 1,п — число к принимает последовательно целые значения от 1 до п включительно 1-2.6
12
Основные обозначения
Буквы латинского алфавита
Начертание	Произношение	Начертание	Произношение
A a A a	a	N n N п	эн
В b В Ь	бэ	0 о О о	о
С с С с	ЦЭ	Р Р Р Р	ПЭ
D d D d	ДЭ	Q q Q я	КУ
Ее Ее	e	R г R г	эр
F f F f	эф	S s S s	эс
G g G g	же	Т t Т t	тэ
H h H h	аш	U u U и	У
I i I i	и	V v V и	вэ
J j J i	йот	W w W w	дубль-вэ
К k К к	ка	X х X X	икс
LIL/	эль	у У Y у	игрек
Mm Mm	эм	Z z Z z	зэт
Представлен наиболее употребительный (но не единственный) вариант произношения (в частности, вместо „йот44 иногда говорят ,,жи“).
Буквы греческого алфавита
Начер-	Произно-	Начер-	Произно-	Начер-	Произно-
тание	шение	тание	шение	тание	шение
А ос	альфа	I 1	йота	р р	ро
В (3	бета	К х	каппа	Е a	сигма
Г т	гамма	А А	ламбда	Т т	тау
А 6	дельта	М м	ми	Т v	ипсилон
Е £	эпсилон	N р	ни	Ф	фи
z С	дзета	н е	КСИ	X X	хи
Н Т)	эта	О о	омикрон	ф 'ф	пси
0 #0	тэта	П 7Г	пи		омега
Наряду с указанным произношением также говорят „лямбда44, „мю44 и „ню44.
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
1.1. Векторные и скалярные величины
В прикладных науках оперируют величинами различного характера. В качестве примера обратимся к величинам, встречающимся в физике и механике. Такие величины, как массу и объем, характеризуют количественным значением, которое по отношению к некоторому эталону (единице измерения) задают действительным числом. Поэтому их называют скалярны-ми. Напротив, скорость, ускорение, сила характеризуются не только количественным значением, но и направлением. Их называют векторными величинами.
Скалярные и векторные величины не исчерпывают всех возможных вариантов. Например, свойства кристаллических тел передавать теплоту и деформироваться под действием нагрузки не удается описать при помощи скалярных и векторных величин. Для таких свойств в физике и механике используют более сложные тензорные величины.
Перейдем к строгим определениям и понятиям.
Определение 1.1. Геометрическим вектором (также направленным отрезком) называют любой отрезок, на котором выбрано одно из двух возможных направлений (рис. 1.1).
Любой отрезок однозначно определяется своими концами, поэтому одно из двух возможных направлений для данного отрезка можно задать, указав порядок концов, т.е. от какого конца отрезка надо начать движение в заданном направлении, для того чтобы, двигаясь по отрезку, попасть в его другой
14	1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
конец. Это позволяет определить геометрический вектор просто как упорядоченную пару точек: первую точку в паре называют началом геометрического вектора, а вторую — его концом. Начало геометрического
В вектора называют также точкой его приложения.
Обозначение геометрических векто-ров отражает указанную интерпрета-А	цию: если точка А является началом
геометрического вектора, а точка В — Рис. 1.1 его концом, то геометрический вектор обозначают АВ или Второе обозначение явно подчеркивает, от какого конца отрезка к какому происходит движение в заданном направлении. В первом варианте направление определяется порядком букв, обозначающих концевые точки, а черта сверху предназначена для выделения геометрических векторов среди других геометрических объектов.
Важной характеристикой геометрического вектора является его модуль, или длина, |А?1|, равный длине |АВ| отрезка, соединяющего его начало А и конец В. Длина геометрического вектора может выражаться любым неотрицательным числом. Геометрический вектор называют ненулевым, если его длина положительна. Длина, равная нулю, соответствует ситуации, когда начало и конец геометрического вектора совпадают. В этом случае геометрический вектор называют нулевым или нулъ-вектором и обозначают О. Если длина геометрического вектора равна единице, его называют ортом или единичным.
Для нуль-вектора понятие направления теряет смысл, так как начало и конец у него совпадают. Однако такому геометрическому вектору удобно приписать произвольное направление, которое устанавливают в зависимости от конкретной ситуации.
1.2. Типы векторов и их взаимное расположение	15
1.2. Типы векторов и их взаимное расположение
Определение 1.2. Два геометрических вектора называют коллинеарными, если они лежат на одной прямой1 или на параллельных прямых.
Про пару коллинеарных геометрических векторов иногда говорят, что один из них коллинеарен другому.
Все пары коллинеарных геометрических векторов можно разделить на две группы:
- однонаправленные (или с онаправ ленные) коллинеарные геометрические векторы, имеющие совпадающие направления;
- противоположно направленные коллинеарные геометрические векторы, имеющие противоположные направления.
Если коллинеарные геометрические векторы АЙ и сЗ не лежат на одной прямой, то точки А, В, С и D образуют четырехугольник, который является трапецией (рис. 1.2). В случае однонаправленных геометрических векторов отрезки АС и BD, соединяющие соответственно два начала векторов и два их конца, определяют боковые стороны трапеции (рис. 1.2, а). Если же эти геометрические векторы противоположно направленные (рис. 1.2,6), то отрезки АС и BD являются диагоналями трапеции.
По определению считаем, что нуль-вектор коллинеарен любому другому. Определение 1.2 распространяется очевидным образом на любое число геометрических векторов.
Определение 1.3. Три геометрических вектора называют компланарными, если эти векторы лежат на прямых, параллельных некоторой плоскости.
1 Говоря, что геометрический вектор лежит на прямой, мы подразумеваем очевидную ситуацию, когда начало и конец вектора лежат на этой прямой.
16
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Это определение теряет смысл, если его сформулировать для двух геометрических векторов, потому что любые два геометрических вектора лежат на прямых, параллельных некоторой плоскости. Однако можно говорить о четырех компланарных геометрических векторах или об их большем числе.
Определение 1.4. Два геометрических вектора называют равными, если:
-	они коллинеарны и однонаправлены;
-	их длины совпадают.
В соответствии с определением 1.4 равные геометрические векторы могут иметь различные точки приложения, но задают одно и то же направление и имеют одинаковые длины, В этом случае, т.е. когда заданы направление и длина, но не фиксируется точка приложения, говорят, что задан свободный вектор. Термин подчеркивает, что точка приложения геометрического вектора может меняться произвольно. В дальнейшем для удобства свободные векторы мы будем называть просто векторами. Векторы обозначают одной строчной буквой с дополнительной чертой или стрелкой вверху: а или Распространенным является также обозначение вектора полужирным шрифтом а, которое в дальнейшем мы и будем использовать.
Разный характер действия векторов в прикладных задачах приводит к необходимости рассматривать другие типы век
1.2. Типы векторов и их взаимное расположение
17
торов. Например, вектор угловой скорости и вектор силы, действующей на абсолютно твердое тело, можно перемещать только вдоль прямых, на которых они находятся. Такие векторы называют скользящими векторами. Наконец, геометрические векторы, точка приложения которых не может изменяться, называют еще связанными векторами. К ним относятся скорости в потоке жидкости или газа.
Пример 1.1. В зависимости от учета тех или иных конкретных условий одну и ту же векторную величину иногда удобно рассматривать как свободный, скользящий или связанный вектор. Например, вектор ускорения земного притяжения является связанным вектором, поскольку его модуль и направление зависят от расположения точки приложения относительно центра Земли. Поэтому при расчете траектории полета, например с Земли на Луну, его считают связанным вектором. Однако в задаче о движении снаряда при стрельбе на небольшую по сравнению с радиусом Земли дальность изменения вектора ускорения земного притяжения вдоль траектории снаряда незначительны и его принимают постоянным по модулю и направленным вертикально вниз, т.е. считают свободным вектором. Учет кривизны поверхности Земли приведет к необходимости считать этот вектор уже скользящим, т.е. постоянным при перемещениях лишь вдоль радиуса к центру Земли.
Замечание 1.1. Многие понятия, связанные с геометрическими векторами, переносятся и на свободные векторы. Так, говорят о начале {точке приложения) вектора, конце вектора, модуле {длине) вектора. Различают векторы ненулевые (включая единичные, или орты) и нулевые {нуль-векторы), векторы коллинеарные и векторы компланарные. Коллинеарные векторы могут быть однонаправленными {сонаправленными) и противоположно направленными.
18 1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
1.3. Линейные операции и их свойства
Над векторами можно выполнять различные операции. Свойства этих операций определяют правила преобразования выражений, содержащих векторные величины» Эти правила и составляют предмет векторной алгебры.
Обсуждение векторных операций начнем с двух из них — сложения векторов и умножения вектора на число. Эти операции часто объединяют общим термином линейные операции.
Определение 1.5. Суммой а + Ь двух векторов а и Ь называют вектор с, построенный по следующему правилу параллелограмма. Выбрав для векторов а и Ь общее начало, строим на этих векторах параллелограмм. Тогда диагональ параллелограмма, выходящая из общего начала векторов, определяет их сумму (рис. 1.3).
Замечание 1.2. Наряду с правилом параллелограмма существует равносильное ему правило треугольника. Совместим начало вектора Ь с концом вектора а. Тогда суммой этих векторов будет вектор с, начало которого совпадает с началом а, а конец — с концом Ь (рис. 1.4). Отметим, что если векторы а и Ь коллинеарны, то их сумму по правилу параллелограмма определить нельзя, а правило треугольника в этом случае применимо.
Рис. 1.3
Рис. 1.4
1.3. Линейные операции и их свойства
19
Замечание 1.3. В определении 1.5 существует произвол в выборе точки приложения векторов. Чтобы определение было корректным, надо убедиться, что результаты, получаемые с различными точками приложения, равны между собой. Убедитесь в этом самостоятельно! #
Операция сложения векторов по своим свойствам напоминает операцию сложения чисел.
1°. Сложение векторов коммутативно: a + b — b + a.
◄ Если складываемые векторы неколлинеарны, то свойство непосредственно вытекает из правила параллелограмма, так как в этом правиле порядок векторов не играет роли. Если же векторы коллинеарны, то их сложение сводится к сложению или вычитанию их длин в зависимости от того, являются ли складываемые векторы однонаправленными или противоположно направленными, ►
2°. Сложение векторов ассоциативно: (а + Ь) + с = а +
+ (Ь + с).
◄ Доказать это свойство проще всего при помощи правила
треугольника. Выберем в качестве начала вектора а точку
А (рис. 1.5), и пусть а = АЛ~1, Совместим начало вектора b с точкой В, и пусть b = В (5, На
конец, начало вектора с совместим с концом С вектора Ь, и пусть тогда с = сй.
Непосредственно из постро
ения получаем
лЙ = лЗ + ВЙ = лЙ + (ВЙ + СЙ)=а + (Ь + с), = Л? + ct> = (АЙ + 1Й) + ci> = (а + Ь) + с,
20
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
т.е. геометрический вектор AD изображает и левую часть доказываемого равенства, и правую. ►
3°. Существует такой вектор 0, что для любого вектора а выполняется равенство а + 0 = а,
◄ Действительно, непосредственной проверкой можно убедиться, что указанному условию удовлетворяет нулевой вектор. Проверку удобно проводить при помощи правила треугольника. ►
4°. Для любого вектора а существует такой вектор 6, что а + Ь = 0.
◄ Действительно, таким является вектор (—а), противоположный к вектору а, т.е. вектор, коллинеарный а, той же длины, что и а, но противоположно направленный. Если в качестве точки приложения этого вектора выбрать конец вектора а, то конец противоположного вектора совпадет с началом вектора а. Согласно правилу треугольника, суммой векторов а и (—а) будет вектор с совпадающими началом и концом, т.е. нулевой вектор. ►
5°. Для любых векторов а и b существует такой вектор ж, что а + х = Ь. При этом вектор х определен однозначно.
I
◄ Указанному условию удовлетворяет вектор (—а) +6, так как с учетом свойств 2°-4°
а + х = а + ((-а) + Ь) = (а + (-а)) + 6 = 0 + 6 = 6.
Если вектор х удовлетворяет равенству а + х = 6, то, прибавив слева к обеим частям последнего равенства вектор (—а), получим с учетом свойств 1°, 2°, что х = (—а) + 6. Действительно,
(—а) + (а + х) — ((—а) + а) + ж = 0 + ж = ж = (—а) + 6.
Значит, вектор х определен однозначно. ►
1.3. Линейные операции и их свойства
21
Свойство 5° позволяет ввести операцию вычитания векторов.
Определение 1.6. Разностью Ь~а двух векторов а и Ь называют такой вектор х, что а + х = Ь.
С алгебраической точки зрения переход от а + х = Ь к х = Ь — а (в соответствии с определением 1.6) означает, что при переносе вектора в другую часть равенства перед ним надо менять знак.
Корректность определения разности векторов, т.е. существование и единственность вектора х устанавливает свойство 5°. Практически для вычисления разности векторов можно воспользоваться правилом тре-угольника. Совместим начала век-торов а и Ь, тогда вектор с началом	/ Ц
в конце вектора а и концом, совпа-	Jr	|
дающим с концом Ь, равен разности b — а этих векторов (рис. 1.6).
Операцию вычитания векторов	рис 1>6
также относят к линейным, так как она определяется операцией сложения и является обратной сложению.
Определение 1.7. Произведением вектора а на число А называют вектор Ла, коллинеарный вектору а, с длиной |А| |а|, однонаправленный с а при А > 0 и противоположно направленный при А < 0.
Замечание 1.4. Если А = 0, то, согласно этому определению, вектор 0а должен иметь длину 0 |а| = 0, т.е. должен быть нулевым вектором. Поэтому, хотя остальные характеристики в определении и не определены (коллинеарность, направленность), произведение вектора на число 0 определено однозначно: 0а есть нулевой вектор.
Пример 1.2. Произведение вектора а на число —1 есть вектор, противоположный к а, т.е. (-1)а= (—а). #
22 1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Операция умножения вектора на число обладает свойством ассоциативности, а совместно с операцией сложения она удовлетворяет двум свойствам дистрибутивности.
6°. Умножение вектора на число ассоциативно: (A/z)a = = A(/za).
◄ Действительно, обе части равенства представляют собой векторы, коллинеарные исходному вектору а. Поэтому равенство будет верным, если совпадут длины векторов и их направления. Равенство длин векторов очевидно. Если числа А и р имеют один и тот же знак, то векторы в обеих частях будут однона-правлены с вектором а. Если же А и/i имеют противоположные знаки, то оба вектора в равенстве являются противоположно направленными по отношению к а. Итак, в любом случае в равенстве стоят векторы одного направления и одинаковой длины, т.е. равные векторы, ►
7°. Умножение вектора на число дистрибутивно относительно векторов: А(а + Ь) = Ха + АЬ.
◄ При А = 0 свойство очевидно, так как в этом случае слева будет нулевой вектор (произведение вектора на число 0), а
1.4. Ортогональная проекция
23
справа — сумма двух нулевых векторов. Если А О, свойство вытекает из правила параллелограмма и свойств подобных параллелограммов. На рис. 1.7 представлены случаи для А > О и А < 0. ►
8°. Умножение вектора на число дистрибутивно относительно чисел: (A + /z)a => Xa + fia.
◄ В указанном равенстве — три коллинеарных вектора. Поэтому доказательство сводится к подсчету длин векторов, которым присвоены знаки, учитывающие направление. Если А и fi имеют положительные знаки, то все три вектора в равенстве имеют одно направление, совпадающее с направлением вектора а. При сложении этих векторов справа складываются их длины, а доказываемое равенство равносильно следующему: (А + fi) |а| = А |а| + /z|a|. Случай, когда А и fi отрицательны, аналогичен.
Пусть А и fi имеют противоположные знаки. Для определенности будем считать, что А > 0, /1 < 0. Противоположный случай сводится к этому заменой обозначений и учетом коммутативности сложения чисел и векторов. Если А > 0, fi < 0, то при сложении векторов Ха и fia вычитаются их длины, так как складываются векторы противоположного направления. Получаемый при этом вектор будет однонаправленным с а при |А| > \fi\ и противоположно направленным при |А| < |д|. Его длина, согласно определению произведения вектора на число, равна |А + /х||а|. Учитывая направление этого вектора, заключаем, что он равен (А + д)а, т.е. доказываемое равенство верно и при противоположных знаках коэффициентов А и fi. ►
1.4. Ортогональная проекция
Пусть на плоскости заданы прямая L и точка А. Опустим из точки А на прямую L перпендикуляр (рис. 1.8, а). Тогда его основание (точку О) называют ортогональной проекцией точки А на прямую L. Если прямая L и точка А заданы
24
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
в пространстве, то в этом случае ортогональной проекцией точки А на прямую L называют точку О пересечения прямой L с перпендикулярной ей плоскостью, проходящей через точку А (рис. 1.8, б). Если точка А лежит на прямой L, то она совпадает со своей ортогональной проекцией на L.
А
О
L
а
Рис. 1.8
Для вектора А^ (на плоскости или в пространстве) можно построить ортогональные проекции на прямую L его начала и конца (рис. 1.9). Тогда вектор ОаОв, соединяющий эти проекции О а и Ов и лежащий на прямой L, называют ортогональной проекцией вектора AJ& на прямую L.
Прямую, на которой задано одно из двух возможных направлений, называют осью. Выбранное направление на оси изображают с помощью стрелки на соответствующем конце оси. Ортогональную проекцию ОаОв вектора А$ на ось I мож
но полностью описать длиной вектора ОаОв, приписав ей знак, указывающий направление вектора. Если направление ОаОв совпадает с заданным направлением оси, то берут знак плюс, а если направление вектора противоположно направлению оси, то берут знак минус. Длину вектора ОаОв со знаком, определи-
1.4. Ортогональная проекция
25
ющим направление этого вектора, называют ортогональной проекцией вектора А1$ на ось I и обозначают пр^а.
Обратим внимание на то, что ортогональной проекцией вектора на ось является число, в то время как ортогональная проекция вектора на прямую — это вектор. Чтобы вектору соответствовало число как его проекция, на прямой нужно выбрать одно из двух возможных направлений.
Каждый ненулевой вектор I однозначно определяет ось: его можно рассматривать расположенным на некоторой прямой и задающим на ней направление. Поэтому ортогональную проекцию вектора на такую ось называют ортогональной проекцией вектора на направление вектора I.
Угол между направлениями двух ненулевых векторов называют углом между этими векторами. Угол может изменяться в пределах от 0 до тг. Крайние значения 0 и тг отвечают коллинеарным векторам, соответственно однонаправленным и противоположно направленным. Если хотя бы один из двух векторов является нулевым, то угол между такими векторами не определен. Удобно, однако, считать, что в этом случае угол имеет произвольное значение. Так, нулевой вектор коллинеарен любому другому, что формально соответствует углу 0 (или тг). Конкретное значение, приписываемое углу между нулевым вектором и каким-либо другим, выбирают исходя из конкретной ситуации.
Теорема 1.1. Ортогональная проекция вектора а на направление ненулевого вектора I равна длине |а|, умноженной на косинус угла <р между векторами а и I, т.е.
npza = |a|cos(a,Z),
где (a,Z) — угол между векторами а и I.
◄ Пусть вектор I лежит на прямой L, а его началом является точка А. Совместим начало вектора а с точкой А, и пусть его концом будет точка В (рис. 1.10). Построим ортогональную
26
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
проекцию С точки В на прямую L. Тогда вектор АС является ортогональной проекцией вектора а = AJ^ на прямую L.
а	б
Рис. 1.10
Если угол <р между векторами а и I острый (как это показано на рис. 1.10, а), то конец вектора I и точка С лежат по одну сторону от точки А. В этом случае проекция а на направление вектора I равна длине |АС| = |AB|cos<£> катета АС треугольника АВС.
Если угол <р тупой (см. рис. 1.10,6), то конец вектора I и точка С лежат по разные стороны от точки А. Это значит, что векторы А(5 и I имеют противоположные направления, а проекция вектора а равна — |АС|. В треугольнике АВС угол Vs прилежащий к катету АС, равен тг — </?, поэтому |АС| = = |AB|cos(tt — <р) — — |AB|cos9?.
Если же <р — ~ или а = 0, то точка С совпадает с точкой А и вектор А& является нулевым вектором. Однако cos^ = 0, следовательно, и в этом случае утверждение теоремы справедливо. ►
Теорема 1.2. Ортогональная проекция суммы векторов на направление ненулевого вектора равна сумме их ортогональных проекций на направление этого вектора, а при умножении вектора на число его ортогональная проекция на направление ненулевого вектора умножается на то же число:
прДа + Ь) = npza-|-npzb, npz(Aa) = Апр^а.
1.5. Линейная зависимость и независимость векторов
27
4 Доказательство следует из рис. 1.11. В случае а имеем пР/а = |ЛВ|, пР/Ь=-|ВС|, пР/(а + Ь) = |АС| = |АВ|-|ВС|. В случае б пР/а = \АВ\ и, если А > 0, прДАа) = |4Е| = А|4В|. Остальные варианты (точка С не принадлежит отрезку АВ в случае а, А 0 в случае б) рассматриваются аналогично. ►
Рис. 1.11
1.5. Линейная зависимость и независимость векторов
Введенные нами линейные операции над векторами дают возможность составлять различные выражения для векторных величин и преобразовывать их при помощи установленных для этих операций свойств.
Исходя из заданного набора векторов си, ..., ап, можно составить выражение вида
п
~ 0*1 <Х1 + • • • “F OfnGn)	(1«1)
г=1
где oi, ..., ап — произвольные действительные числа. Это выражение называют линейной комбинацией векторов ai, ..., ап. Числа i= 1,п, представляют собой коэффициенты линейной комбинации. Набор векторов называют еще системой векторов.
28
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
В связи с введенным понятием линейной комбинации векторов возникает задача описания множества векторов, которые могут быть записаны в виде линейной комбинации данной системы векторов ai, ап. Кроме того, закономерны вопросы об условиях, при которых существует представление вектора в виде линейной комбинации, и единственности такого представления.
Если каждый вектор может быть представлен в виде линейной комбинации данной системы векторов и притом единственным способом, то мы можем интерпретировать вектор как набор коэффициентов соответствующей линейной комбинации. Тогда взаимосвязи между геометрическими объектами — векторами — будут представлены некоторыми числовыми соотношениями, а мы получим возможность изучать свойства векторов и других геометрических объектов алгебраическими методами.
Определение 1.8. Векторы сц, ..., ап называют линейно зависимыми, если существует такой набор коэффициентов «1, ..., ап, что
aiai + ... + апап = О	(1.2)
и при этом хотя бы один из этих коэффициентов ненулевой. Если указанного набора коэффициентов не существует, то векторы называют линейно независимыми.
Если cq = ... = ап = 0, то, очевидно, сцсц + ... + апап = = 0. Имея это в виду, можем сказать так: векторы сц, ..., ап линейно независимы, если из равенства (1.2) вытекает, что все коэффициенты ai, ..., ап равны нулю.
Следующая теорема поясняет, почему новое понятие названо термином „зависимость^ (или „независимость“), и дает простой критерий линейной зависимости.
Теорема 1.3. Для того чтобы векторы были линейно зависимы, необходимо и достаточно, чтобы один из них являлся линейной комбинацией остальных.
1.5. Линейная зависимость и независимость векторов 29
◄ Необходимость. Предположим, что векторы aj, an линейно зависимы. Согласно определению 1.8 линейной зависимости, в равенстве (1.2) слева есть хотя бы один ненулевой коэффициент, например cq. Оставив первое слагаемое в левой части равенства, перенесем остальные в правую часть, меняя, как обычно, у них знаки. Разделив полученное равенство2 на «1, получим
а2	«п
<11 —	<12
»1	€*1
т.е. представление вектора в виде линейной комбинации остальных векторов <12, ап.
Достаточность. Пусть, например, первый вектор ai можно представить в виде линейной комбинации остальных векторов:
<11 = /?2а2 + •. * + Рпап-
Перенеся все слагаемые из правой части в левую, получим
«1 - 02Я2 ~	- /?п«п = О,
т.е. линейную комбинацию векторов ai,..., ап с коэффициентами «1 _ 1, а2 = ~/?2> • • •>	= —/Зп, равную нулевому вектору. В
этой линейной комбинации не все коэффициенты равны нулю. Согласно определению 1.8, векторы ai, ..., ап линейно зависимы. ►
Определение и критерий линейной зависимости сформулированы так, что подразумевают наличие двух или более векторов. Однако можно также говорить о линейной зависимости одного вектора. Чтобы реализовать такую возможность,
2У нас нет такой операции „деление вектора на число Поэтому формально вместо „разделим равенство на число ai u мы должны были бы говорить „умножим равенство на число 1/ai Однако подобная педантичность усложняет изложение, в то время как формально не определенное понятие деления достаточно очевидно.
30
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
нужно вместо „векторы линейно зависимы** говорить „система векторов линейно зависима4*. Нетрудно убедиться, что выражение „система из одного вектора линейно зависима** означает, что этот единственный вектор является нулевым (в линейной комбинации имеется только один коэффициент, и он не должен равняться нулю).
Понятие линейной зависимости имеет простую геометрическую интерпретацию. Эту интерпретацию проясняют следующие три утверждения.
Теорема 1.4. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
<4 Если векторы а и Ь линейно зависимы, то один из них, например а, выражается через другой, т.е. а — ХЬ для некоторого действительного числа Л. Согласно определению 1.7 произведения вектора на число, векторы а и Ь являются коллинеарными.
Пусть теперь векторы а и Ь коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их линейная комбинация равна нулевому вектору. Пусть один из этих векторов не равен 0, например вектор 6. Обозначим через А отношение длин векторов: А = |а|/|Ь|. Коллинеарные векторы могут быть однонаправленными или противоположно направленными. В последнем случае у А изменим знак. Тогда, проверяя определение 1.7, убеждаемся, что а = ХЬ. Согласно теореме 1.3, векторы а и Ь линейно зависимы. ►
Замечание 1.5. В случае двух векторов, учитывая критерий линейной зависимости, доказанную теорему можно переформулировать так: два вектора коллинеарны тогда и только тогда, когда один из них представляется как произведение другого на число. Это является удобным критерием коллинеарности двух векторов.
Теорема 1.5. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
1.5. Линейная зависимость и независимость векторов 31
◄ Если три вектора а, Ь, с линейно зависимы, то, согласно теореме 1.3, один из них, например а, является линейной комбинацией остальных: a = /ЗЬ + ус. Совместим начала векторов Ь и с в точке А. Тогда векторы /ЗЬ, ус будут иметь общее начало в точке А и по правилу параллелограмма их сумма, т.е. вектор а, будет представлять собой вектор с началом А и концом, являющимся вершиной параллелограмма, построенного на векторах-слагаемых. Таким образом, все векторы лежат в одной плоскости, т.е. компланарны.
Пусть векторы а, Ь, с компланарны. Если один из этих векторов является нулевым, то очевидно, что он будет линейной комбинацией остальных. Достаточно все коэффициенты
линейной комбинации взять равными нулю. Поэтому можно считать, что все три вектора не являются нулевыми. Совме
стим начала этих векторов в общей точке О. Пусть их концами будут соответственно точки А, В, С (рис. 1.12). Через точку С проведем прямые, параллельные прямым, проходящим через пары точек О, А и О, В. Обозначив точки пересечения через Л' и В', получим параллелограмм ОА'СВ', следовательно, 0(5 = ОА' + ОВ'. Вектор ОА' и ненулевой вектор а = о! коллинеарны, а потому первый из них может быть получен умноже-
нием второго на действительное число а: О А* — аоХ. Аналогично OB' = [3015, (3 Е R. В результате получаем, что О$ = aoX + fio1^ т.е. вектор с является линейной комбинацией векторов а и Ь. Согласно теореме 1.3, векторы а, Ь, с являются линейно зависимыми. ►
Теорема 1.6. Любые четыре вектора линейно зависимы.
◄ Доказательство проводим по той же схеме, что и в теореме 1.5. Рассмотрим произвольные четыре вектора а, Ь, с и d.
32	1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Если один из четырех векторов является нулевым, либо среди них есть два коллинеарных вектора, либо три из четырех векторов компланарны, то эти четыре вектора линейно зависимы. Например, если векторы а и b коллинеарны, то мы можем составить их линейную комбинацию аа + (ЗЬ = О с ненулевыми коэффициентами, а затем в эту комбинацию добавить оставшиеся два вектора, взяв в качестве коэффициентов нули. Получим равную 0 линейную комбинацию четырех векторов, в которой есть ненулевые коэффициенты.
Таким образом, мы можем считать, что среди выбранных
четырех векторов нет нулевых, никакие два не коллинеарны и никакие три не являются компланарными. Выберем в качестве их общего начала точку О. Тогда концами векторов а, 6, с, d будут некоторые точки Л, В, С, D (рис. 1.13). Через точку D проведем три плоскости, параллельные плоскостям ОВС, ОСА, О АВ, и пусть А', В', С' — точки пересечения этих плоскостей с прямыми О А, ОВ, ОС соответственно. Мы получаем параллелепипед О А'С" В'С В" D А", и векторы а, Ь, с лежат на ребрах параллелепипеда, выходящих из вершины О. Так как четырехугольник ОС"DC' является параллелограммом, то ot> = — ОС^' + ОС. В свою очередь, отрезок ОС" является диагональю параллелограмма ОА'С'В', так что ОС^' = = ОА' + OB'. Значит,
Рис. 1.13
ot) = OA' + ОВ' + ОС.
Остается заметить, что
пары векторов о! / О и ОА', Оё и OB', ОС 0 и ОС коллинеарны, и, следовательно, можно подобрать коэффициенты а, (3, у так, что О А' = acdl,
1.6. Базис
33
OB' = /301-} и ОС' = уО(5. Окончательно получаем
of = aOl + /30$ + jOf.
Следовательно, вектор О В выражается через остальные три вектора, а все четыре вектора, согласно теореме 1.3, линейно зависимы. ►
1.6. Базис
Аналогично трем моделям геометрии (геометрии на прямой, на плоскости и в пространстве) мы рассмотрим три множества свободных векторов, или, как говорят, три пространства векторов: пространство Vx всех коллинеарных между собой векторов, т.е. параллельных некоторой прямой, пространство V? всех компланарных между собой векторов, т.е. параллельных некоторой плоскости, и пространство V3 всех свободных векторов.
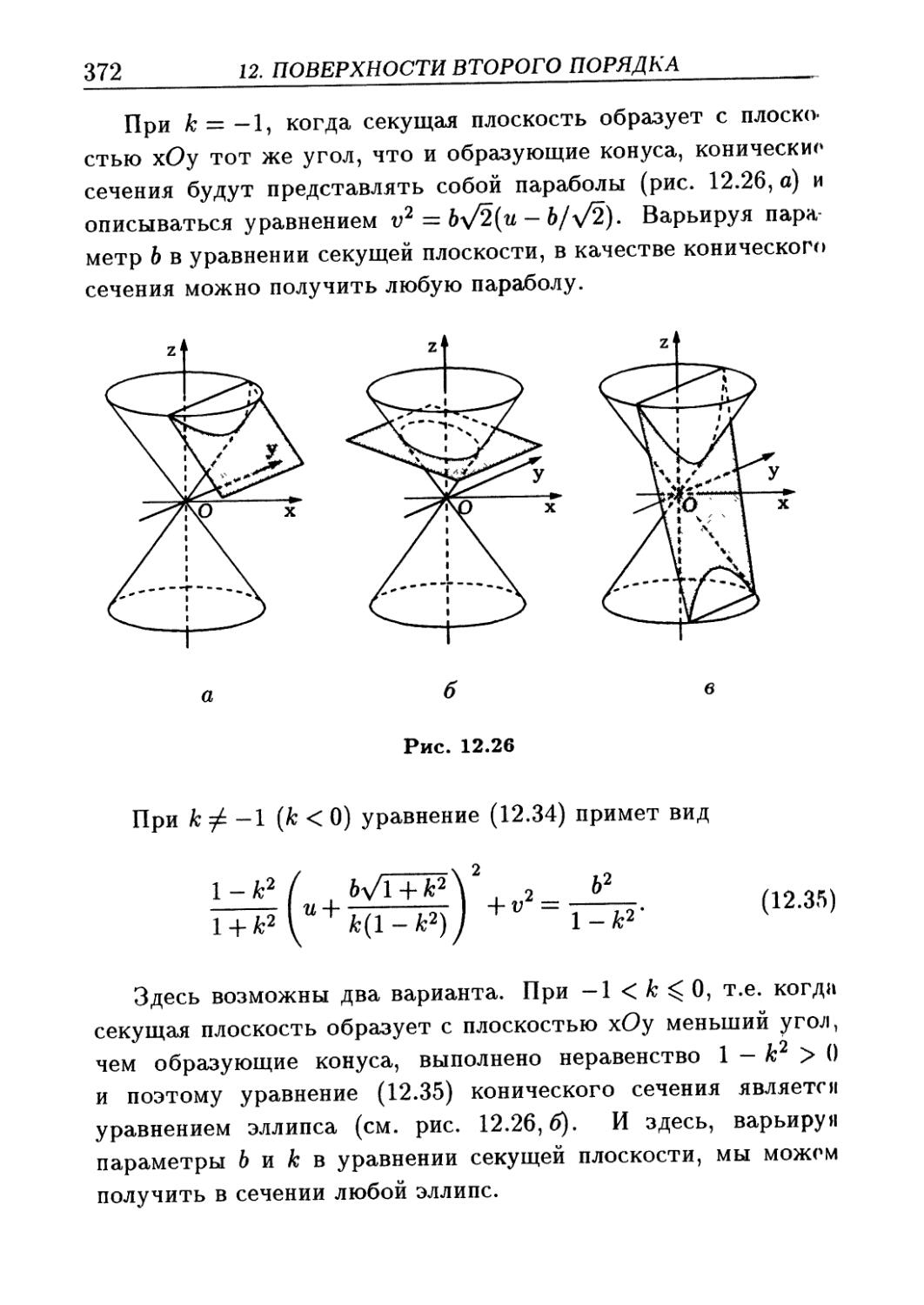
Рассмотрим пространство Ур Любой ненулевой вектор пространства Vi называют базисом в Ур Любые два вектора этого пространства, будучи коллинеарными, линейно зависимы, т.е. один из них может быть получен из другого умножением на число. Выберем и зафиксируем в Ц базис, т.е. вектор е =4 0. Тогда любой вектор х 6 Ц представляется в виде х = Ае. Это равенство называют разложением вектора х в базисе е, а число А — координатой вектора х в этом базисе. Отметим, что коэффициент А при этом определен однозначно. Действительно, этот коэффициент равен А = ±|ж|/|е|, причем выбирают знак плюс, если векторы х и е однонаправлены, и знак минус в противоположном случае.
Рассмотрим пространство 4%. Любую упорядоченную пару неколлинеарных векторов в пространстве называют базисом в У2. Выберем в этом пространстве базис, т.е. два неколлинеарных вектора ei, e2. Согласно теореме 1.5, эти два
2 Аналитическая геометрия
34 1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
вектора и любой третий вектор ж, будучи компланарными, линейно зависимы. Поэтому один из них является линейной комбинацией двух других. При этом можно утверждать, что вектор х выражается через ei и €2. Действительно, запишем линейную комбинацию этих векторов
ах + Д1€1 + /?2е2 = 0,	(1.3)
в которой один из коэффициентов не равен нулю. Сразу делаем вывод, что а ф 0, так как в противном случае в равенстве (1.3) слева можно опустить первое слагаемое, и мы получим, что векторы ei, в2 линейно зависимы. Но этого быть не может, так как они неколлинеарны (см. теорему 1.4). Так как а О, мы можем разделить равенство (1.3) на а. В результате, перенося последние два слагаемых в правую часть, получаем представление вида
X — А1С1 + Л2^2,	(1*4)
которое называют разложением вектора х в базисе ei, в2, а коэффициенты Ai, А2 этого представления — координатами вектора х в базисе ei, в2-
Отметим, что в представлении (1.4) коэффициенты Ai и А2 определены однозначно. Это можно обосновать, анализируя доказательство теоремы 1.5 (используемый в доказательстве параллелограмм однозначно определен диагональю и прямыми, на которых лежат смежные стороны). Однако то же можно установить, используя лишь факт линейной независимости векторов в! и в2-
В самом деле, если есть два представления
х = А1С1 + А2в2 =//161+ //2е2,
то, перенеся в последнем равенстве все слагаемые влево и используя свойство 8° (см. с. 23) дистрибутивности умножения вектора на число относительно чисел, получим
(Al — /Zl)ei + (А2 — Р2)е2 — 0.
1.6. Базис
35
Коэффициенты в этом равенстве слева равны нулю, так как векторы ei, е2 линейно независимы (они неколлинеарны, см. теорему 1.4). Таким образом, Ai = Д1,	= и ДВа взятых
нами представления вектора х совпадают.
Рассмотрим пространство Уз. Любую упорядоченную тройку некомпланарных векторов называют базисом в У3. Выберем в Уз базис, т.е. любые три некомпланарных вектора ei, е2, е3. Эти три вектора с добавленным к ним произвольным четвертым вектором х линейно зависимы (см. теорему 1.6). Можно доказать так же, как мы это делали в случае пространства V2, что вектор х является линейной комбинацией векторов
е2, е3:
х = AiCi + А2е2 + А3е3.	(1*5)
При этом коэффициенты в представлении (1.5) определены однозначно, так как векторы ei, е2, е3 линейно независимы. Представление вектора х в виде (1.5) называют разложением вектора в базисе е1у е2, е3, а коэффициенты Ai, А2 и А3 разложения — координатами вектора х в базисе ej, е2, е3.
Векторы в базисах пространств V2 и Уз, согласно определению базисов, являются упорядоченными. Порядок векторов в базисе устанавливает порядок среди координат любого вектора, и поэтому координаты всегда считают тоже упорядоченными. Если базис, например, в пространстве V3 фиксирован, то каждому вектору из Уз соответствует единственная упорядоченная тройка чисел, составленная из его координат. Кроме того, каждой упорядоченной тройке чисел соответствует единственная линейная комбинация векторов базиса, т.е. вектор из Уз, координаты которого совпадают с этой тройкой чисел. Поэтому, если базис фиксирован, то векторы можно рассматривать как упорядоченные наборы их координат в этом базисе.
Эту возможность часто используют, отождествляя векторы с упорядоченными наборами их координат. Например, если вектор х из Уз в базисе ej, е2, е3 имеет разложение х = 2ei + Зе2 — 4е3, то этому вектору соответствует упорядо-2*
36
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
ченная тройка его координат, которую часто записывают так: {2; 3; —4}. Более того, отождествляют вектор с упорядоченной тройкой координат и пишут х = {2; 3; —4}, вкладывая в это равенство указанный выше смысл.
Итак, если базис в пространстве Vi, V2 или У3 фиксирован, то любой вектор из этого пространства однозначно определен своими координатами, записанными в порядке следования векторов базиса. Поэтому можно сказать, что координаты вектора являются представлением, или „изображением “, этого вектора в данном базисе.
1.7. Вычисления в координатах
Выясним, что происходит с координатами векторов при выполнении линейных операций.
Теорема 1.7. При сложении двух векторов их координаты в одном и том же базисе складываются. При умножении вектора на число координаты этого вектора умножаются на это число.
4 Для простоты остановимся, например, на пространстве У3. Фиксируем в V3 базис ei, в2, е3. Возьмем два произвольных вектора х и у и запишем их разложения в выбранном базисе:
х = Ж1в1 + х2е2 + ж3е3, у = у\ех + у2е2 + у3е3.
Используя свойства линейных операций, вычисляем сумму этих векторов:
X + у = (iriei + Ж2е2 + ж3е3) + (yiei + Угв2 + у3е3) =
= (®1 + У1)в1 + (®2 + J/2)e2 + (х3 + у3)е3.
Мы получили разложение суммы векторов в фиксированном базисе. Отсюда заключаем, что координаты Xi и исходных слагаемых, соответствующие одному вектору е, в базисе (г = = 1,2,3), складываются.
1.7. Вычисления в координатах
37
Аналогично с учетом свойств линейных операций имеем
Аж = Х(ж1е1 4- х2е2 + х3е3) = (Аж^в! + (Аж2)е2 + (Аж3)е3.
В итоге получаем разложение вектора Аж в фиксированном базисе. Из этого разложения видим, что каждая из координат исходного вектора ж умножена на число А. ►
Разложение вектора в базисе имеет простой геометрический смысл. Рассмотрим, например, пространство V3. Разложение вектора d в базисе, скажем а, Ь, с, показано на рис. 1.13. Координатами вектора d будут отношения
4 = ±
|ОАГ
db = ±
|ОВГ
dc = ±
|ОС"|
\ос\'
где знаки выбирают в зависимости от того, является соответствующая пара коллинеарных векторов (например, оА и ОА' для da) однонаправленной или нет.
Теорема 1.8. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их одноименные координаты в одном и том же базисе были пропорциональны. ◄ Докажем теорему в случае пространства V3. Фиксируем в V3 базис ei, е2, е3. Рассмотрим разложения в выбранном базисе векторов ж и у:
х = Х1вг + х2е2 + х3е3, у = ухех + у2е2 + у3е3.	(1.6)
Если одноименные координаты этих векторов пропорциональны, т.е. существует такое А € R, что выполнены равенства
Ж1 = Ау1, х2 = Ау2, ®з = Ауз,	(1.7)
то
ж = ххех + ж2е2 + х3е3 - Хухег + Ау2е2 + Ау3е3 =
= A(j/iег 4- у2е2 4- j/3e3) = Ху
и из теорем 1.3, 1.4 следует, что векторы ж и у коллинеарны.
Достаточность условия доказана. Для доказательства его
38 1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
необходимости предположим, что векторы х и у коллинеарны. Но тогда по теореме 1.4 они линейно зависимы и в силу теоремы 1.3 один из них, например ж, является линейной комбинацией „остальных**, т.е. х = Ху. Подставляя в это равенство разложения (1.6), получаем
Ж1в1 + х2е2 + х3е3 = A(t/iei + у2е2 + у3е3),
или
(xi - Ayi)ei + («2 - Ау2)е2 + (х3 - Ху3)е3 = 0.
А поскольку вектор 0 в любом базисе имеет нулевые координаты, то из последнего равенства следуют соотношения (1.7). ►
Следствие 1.1. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы отношения их одноименных координат в одном и том же базисе были равны.
◄ Выражая А из соотношений (1.7) и приравнивая полученные дроби, находим, что
=	=	(1.8)
У1 У2 Уз
Отметим, что в условии (1.8) в знаменателях дробей могут стоять нули, но при этом подразумевается, что и в числителё? соответствующей дроби стоит нуль. Для пространства условие (1.8) сводится к равенству только первых двух дробей. ► А
Пример 1.3. Пусть векторы в1,в2 образуют базис в У2-Векторы а = 2ei — Зв2, Ь — —ei + Зе2 линейно независимы, так как 2/(-1)	-3/3. Поэтому они тоже образуют базис в
том же Ц- Найдем разложение в этом базисе векторов ei и С = 3в1 — 6в2-
Чтобы найти разложение вектора ej, вычислим сумму векторов а и Ь:
a-pb = ер
Следовательно, искомым разложением является ei = а + Ь.
1.7. Вычисления в координатах	39
Чтобы найти разложение вектора с, поступим следующим образом. Пусть с =: Aja + АгЬ. Подставив в это равенство разложения векторов с, a, Ь в базисе ei, в2, приведем подобные слагаемые в правой части равенства. Получим, что
3в1 — 6в2 = А1 (2в1 — Зв2) + А2( —€1 + Зв2) =
= (2А1 — Аг)^! + (-ЗА! + ЗА2)в2.
Поскольку каждый вектор в любом базисе имеет единственное разложение, то Ai, А2 должны удовлетворять системе уравнений
Г 2Ai — А2 = 3,
X ЗА1 — ЗА2 = 6.
Решая эту систему, находим, что Ai = 1, А2 = — 1. Это значит, что с — a - b.
Определение 1.9. Базис называют ортогональным, если он состоит из векторов, лежащих на взаимно перпендикулярных прямых. Базис называют ортонормиров анным, если он ортогональный и состоит из единичных векторов.
Параллелепипед, изображенный на рис. 1.13, в ортонормированием базисе в V3 является прямоугольным, а точки Л', В', С — ортогональными проекциями точки D на соответствующие прямые. Координаты вектора d = оЬ в ортонормированием базисе равны ортогональным проекциям этого вектора на направления векторов, образующих этот базис.
Ортонормированный базис в пространстве V3 принято обозначать, с учетом порядка, буквами г, j, к, в — соответственно г, j и в Vi — г.
В случае ортонормированного базиса в пространстве V3 /югко найти расстояние от точки О до произвольной точки V. По теореме Пифагора |ОХ|2 =	+ |OXfc|2
(рис. 1.14), где точки Хг, Xj, Xk — ортогональные проекции точки X на соответствующие оси. Но длины отрезков ОХ{,
40
1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
OXj, OXk — это абсолютные значения координат вектора х = 0$ в базисе г, j, к. В результате получаем формулу для вычисления длины вектора х с координатами ®2; »з} в ортонормированном базисе i, j, к пространства V3:
1®1 =	+ +	® 6 Уз-	(1-9)
Аналогично вычисляют длину вектора из пространства V2 по его координатам ®i, Х2 в ортонормированном базисе:
1®1 = \/x\ + x2i ® е Иг, (1-Ю) и длину вектора из Vj с координатой Xi в ортонормированном базисе:
1®1 =	1Ж1|, ®€.У1- (1-11)
Пусть ненулевой вектор х Е V3 образует с направлениями векторов ортонормированного базиса г, j, к углы а, /3 и 7 соответственно. Величины cos а, cos/?, cos 7 называют направляю-
щими косинусами вектора х (рис. 1.15).
Направляющие косинусы вектора можно использовать при вычислении его координат. Если ненулевой вектор х € V3 имеет в ортонормированном базисе г, j, к координаты {^i; ж2; я3} и направляющие косинусы cos a, cos/?, cos 7, то
х\ = |®|cosa, х2 = |ж| cos/?, x3 = |®|cos7.	(1-12)
Используя формулу (1.9) для вычисления длины вектора, получаем
|ж|2 = |®|2cos2a + |ж|2 cos2 /? + |®|2 cos2 7,
Вопросы и задачи
41
откуда после сокращения на |ж|	0 вытекает следующая фор-
мула связи для направляющих косинусов:
cos2 a + cos2 /3 + cos2 7 = 1.	(1-13)
В начале главы мы говорили о том, что векторные величины имеют скалярную характеристику (длину) и направление. Направляющие косинусы не зависят от длины вектора: при
умножении вектора на положительное число направляющие косинусы не изменяются. Именно они и характеризуют направление вектора. Если известны длина вектора и его направляющие косинусы, то вектор определен однозначно.
Направляющие косинусы могут быть заданы углами а, /3, 7 из отрезка [0,тг], удовлетворяющими соотношению (1.13). В качестве примера можно взять вектор {cosa; cos/3; cos7}. Согласно формулам (1.9) и (1.13) этот вектор имеет единичную длину, а значения coso, cos/3, COS7 представляют собой напра
вляющие косинусы этого вектора.
В случае ортонормированного базиса в пространстве У2
направление вектора удобно указывать одним углом </?, кото-
рый отсчитывается от первого вектора базиса против хода часовой стрелки (в случае положительного значения). Угол </?, длина вектора х и его координаты {^i; Х2} связаны соотношениями:
а?! = |o?|cosv?, ж2 = |ж| sin	Рис. 1.16
Вопросы и задачи
1.1. Что можно сказать о сумме векторов?
дЁ + в<5 + с% трех
1.2. Доказать, что если медианы треугольника АВС пересе-
каются в точке А/, то:
а)Д^=(4^+Д^)/3; б)М^ + М^ +
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
2.1. Определители второго и третьего порядков
В этой главе приведены начальные сведения об определителях второго и третьего порядков. Это вызвано тем, что некоторые формулы векторной алгебры, записанные через определители, имеют достаточно компактный вид и удобны как при изложении теории, так и при решении задач. Более полная теория определителей изложена далее (см. 7).
Четырем числам «ц,	«2? &2 можно поставить в соот-
ветствие выражение ai&2 “ а2&1, которое называют определителем второго порядка и обозначают в виде следующей таблицы из двух строк и двух столбцов, отделяемой слева и справа вертикальными линиями:
ai&2 й2&1 =
ai bi
Ct2 £>2
(2-1)
Числа ai и &2 из-за их расположения в определителе (2.1) называют диагональными элементами определителя второго порядка и говорят, что они расположены на его главной диагонали. Аналогично числа «2 и Ъ\ расположены на второй (или побочной) диагонали определителя. Можно сказать, что определитель второго порядка равен произведению его элементов главной диагонали минус произведение элементов побочной диагонали, например:
3 7
5 -2
= 3(—2) — (5 -7) = —41.
2.1. Определители второго и третьего порядков
45
Подобным же образом из девяти чисел составляют определитель третьего порядка. По определению полагают
а1 Q
а2 ^2 с2 а3 ^3 сз
= Я1&2С3 + &1С2«3 + й2^3с1 “
~ а3Ь2С1 - а2Ь1Сз - ai&3c2. (2.2)
Элементы <ц, b2 и с3 располагаются на главной диагонали определителя (2.2), а а3, Ь2 и ci — на побочной.
В формулу (2.2) вычисления определителя третьего порядка входят шесть тройных произведений, сомножители которых расположены в разных строках и разных столбцах. Произведения имеют разные знаки, и запомнить формулу сложно. Для ее запоминания используют правило Саррюса, или правило треугольника. Оно состоит в следующем: со знаком плюс берут слагаемые, являющиеся произведением элементов главной диагонали и произведением элементов, лежащих на параллелях к этой диагонали. Члены, имеющие знак минус, формируются таким же образом относительно побочной диагонали. Схематически это правило выглядит так:
ai bi ci а2 Ь2 с2 аз Ь3 сз
Линиями соединены элементы определителя, произведения которых дают слагаемые с соответствующим знаком.
Пример 2.1. Используя правило треугольника, вычислим определитель третьего порядка:
1 -3 О
4 2 1
5 0 6
= 1-2-6+0-4-0+5(—3)1 —5-2-0 —6-4(—3) —1-1-0=69. #
46
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Вычисление определителя третьего порядка можно свести к вычислению трех определителей второго порядка. Для получения соответствующей формулы воспользуемся тем, что в правой части равенства (2.2) каждое слагаемое содержит один из элементов ai, или ci первой строки определителя. Собирая в (2.2) подобные члены по этому признаку и вынося общие множители за скобки, получаем
ai
«2 «з
bl Cl i>2 C2 Ъз Сз
— ai(i>2C3 - 63C2) -
— bi (агсз — «3С2) + ci («2&з — «3^2) > (2-3)
где из второй скобки дополнительно вынесен знак минус.
Выражения в скобках представляют собой определители второго порядка
&2C3 — ЬзС2 =
62 с2
Ьз сз
«2С3 — азс2 =
с2
«3 с3
tt2 ^2
Ьз
«263 —«з^^
что позволяет записать равенство (2.3) в следующем виде:
ai «2 «з
bl
Ьз
С1
С2 сз
= аг
^2
Ьз
С2 к «2 — 01 СЗ	«3
С2 сз
+ С1
«2
«3
&2
Ьз
(2.4)
Равенство (2.4) называют разложением определителя третьего порядка по первой строке.
Можно аналогичным образом получить разложение определителя по любой строке (столбцу), если тройные произведения в правой части (2.2) группировать по элементам этой строки (столбца).
Обратим внимание на структуру формулы (2.4). Элемент ai умножается на определитель второго порядка, который можно
2.1. Определители второго и третьего порядков
47
получить из вычисляемого определителя третьего порядка вычеркиванием в нем 1-й строки и 1-го столбца, на пересечении которых расположен элемент Аналогично, элемент bi (cj умножается на определитель второго порядка, который можно получить из вычисляемого определителя вычеркиванием в нем 1-й строки и 2-го (3-го) столбца, на пересечении которых расположен этот элемент. Отметим, что знаки слагаемых в правой части (2.4) чередуются начиная со знака плюс.
Пример 2.2. Вычислим определитель третьего порядка
а b с 2-13 -4 5	1
а,6,с€ R,
используя его разложение по 1-й строке:
а b
2 -1
—4 5
= -16а + 146 + 6с. #
Определители второго и третьего порядков находят применение при решении систем линейных уравнений. Рассмотрим, например, систему двух линейных уравнений
(aix + bly = ci, (а2а: + 62у = с2
(2-5)
относительно неизвестных ж, у и найдем ее решение методом исключения неизвестных. Для этого первое уравнение умножим на —а2, второе — на и после почленного сложения этих выражений и приведения подобных членов получим соотношение
(ai62 - a26i)t/ = aic2 - a2Ci.
48
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Исключив аналогичным приемом из уравнений системы (2.5) неизвестное т/, найдем
(aib2 - «2^1)^ = С1&2 ~ ^2&1 •
Если определитель
ai 61
<12	^2
4 =
который называют определителем системы второго порядка (2.5), не равен нулю, то единственное решение этой системы имеет вид
где определители
получаются из определителя 4 заменой столбца коэффициентов при соответствующем неизвестном на столбец правых частей системы (2.5).
Решение системы (2.5) в виде (2.6) называют формулами Крамера (Г. Крамер (1704-1752) — швейцарский математик).. Они выражают при 4^0 единственное решение системы (2.5) через ее коэффициенты.
Аналогичным образом может быть записано решение системы трех линейных уравнений
a1x + biy + c1z = di,
< а2х + b2y + c2z = d2, „ а3х + b3y + c3z = d3
(2-7)
относительно неизвестных x, у, z. Формулы Крамера в этом случае имеют вид
(2-8)
2.2. Скалярное произведение
49
где
	ai	bi	Cl		di	bi	Cl
д =	«2	bi	С2	—	d2	bi	c2
	«3	Ьз	сз		ds	Ьз	Сз
	с&1 d\ Ci		ai ^1 d\
Ду —	tt2 ^2 c2	, Д? =	CM CM CM e
	«3	^3 Сз		«з &з d$
и позволяют найти единственное решение системы при условии, что определитель А системы третьего порядка не равен нулю.
Пример 2.3. Система трех линейных уравнений
' 2х - Зу — 4г = 6, < Зх + 5у + 2г — 1, к 5х + 2у — Зг = 8
имеет единственное решение, так как ее определитель
не равен нулю. Вычисляя еще три определителя
по формулам Крамера (2.8) находим, что единственным решением рассматриваемой системы является х = 1, у = О, г = — 1.
2.2. Скалярное произведение
Есть несколько операций умножения векторов. В резуль-гате первой из них мы получаем действительное число, т.е. гкалярную величину.
50
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Определение 2.1. Скалярным произведением двух векторов а и Ь называют число, равное |а| |Ь| cos92 — произведению длин |а| и |Ь| этих векторов на косинус угла <р между ними.
Скалярное произведение векторов а и b далее будем обозначать аб, хотя в литературе встречается и обозначение (а,Ь).
Используя теорему 1.1, можно выразить скалярное произведение двух векторов через ортогональную проекцию на направление. Если вектор а ненулевой, то скалярное произведение аЬ векторов а и b получается перемножением длины вектора а и ортогональной проекции вектора b на направление вектора а: аЬ — |а|пра6. Аналогично при Ь 0 имеем равенство аЬ = |Ь| прьа.
Если угол между двумя ненулевыми векторами прямой (т.е. равен 90°), то такие векторы называют ортогональными.
Если хотя бы один из двух векторов является нулевым, то их скалярное произведение будет равно нулю независимо от того, какое значение выбрано в качестве угла между векторами. Нулевой вектор считают ортогональным любому другому вектору.
Теорема 2.1. Для того чтобы два вектора были ортого? нальны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
◄ Согласно определению 2.1, скалярное произведение ненулевых векторов а и Ь равно |а| |Ь| cos</?. Поэтому его знак определяется углом <р между векторами а и Ь:
-	угол <р острый: аЬ > 0;
-	угол <р тупой: аЬ < 0;
-	угол <р прямой: аЬ = 0.
Мы видим, что два ненулевых вектора ортогональны тогда и только тогда, когда угол между ними прямой. Если один из векторов является нулевым, то скалярное произведение также равно нулю. При этом угол между векторами не определен,
2.2. Скалярное произведение
51
но, как уже было отмечено, считают, что нулевой вектор ортогонален любому другому. ►
Скалярное произведение имеет следующие свойства.
1°. Скалярное произведение коммутативно: ab=ba.
◄	Свойство непосредственно вытекает из определения 2.1, так как, согласно этому определению, скалярное произведение не зависит от порядка сомножителей. ►
2°. Совместно с умножением на число операция скалярного умножения ассоциативна: (Xa)b= X(ab).
◄	Если 6 = 0 — нулевой вектор, то обе части доказываемого равенства равны нулю. Если же 6	0, то, используя выраже-
ние скалярного произведения через ортогональную проекцию вектора на направление вектора 6 и утверждение теоремы 1.2, получаем
(Аа)6 = 6(Аа) = |6| пр&(Аа) = А |6|прьа = А(а6).	►
3°. Скалярное умножение и сложение векторов связаны свойством дистрибутивности: (а + b)c = ас + Ьс,
◄ Доказательство аналогично предыдущему. При с = 0 обе части доказываемого равенства равны нулю. Если же сф 0, то удобно выразить скалярное произведение через ортогональные проекции векторов на направление вектора с. Используя теорему 1.2, находим
(а + 6)с = |с| прс(а + Ь) = |с| (прса + прсЬ) =
= |с| прса + |с| прс6 = ас + Ьс. ►
Величину аа называют скалярным квадратом вектора а и обозначают а2.
4°. Свойство скалярного квадрата: а2 0, причем а2 = О тогда и только тогда, когда а = 0.
52
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
◄ Действительно,
а2 = аа = |а| |a|cosO = |а|2.
Поскольку квадрат длины вектора — неотрицательное число, то неравенство а2 О выполнено всегда. Равенство а2 = О эквивалентно соотношению |а| = 0, т.е. тому, что а — нулевой вектор. ►
Замечание 2.1. Свойства 2°-3° часто объединяют в свойство линейности скалярного произведения относительно первого сомножителя. Благодаря коммутативности скалярного произведения (свойству 1°) скалярное произведение линейно и по второму сомножителю. Действительно,
а(АЬ) = (АЬ)а = А(Ьа) = А(аЬ), а(Ь + с) = (Ь + с)а = Ьа + са = аЬ + ас. #
Свойства скалярного произведения часто используют при решении задач.
Пример 2.4. Найдем длину вектора а = Зс — 2d при условии, что |с| = 5, \d\ = 4, а угол (р между векторами с и d равен 60°.
Поскольку |а| = г/а2, то, вычисляя скалярный квадрат век-^ тора а, находим, что
а2 = (Зс — 2d) (Зс — 2d) =
= 9с2 — 12cd + 4d2 = 9 |с|2 — 12 |с| |d| cosy> + 4 |d|2 —
= 9-25-12-5-4-0,5 + 4-16 = 225-120+ 64 =169.
Следовательно, |а| = Va? — 13.
Пример 2.5. В треугольнике АВС угол при вершине А равен 120°, а длина стороны АС в три раза больше расстояния между вершинами А и В. Найдем острый угол <р между стороной ВС и медианой AM треугольника.
2.2. Скалярное произведение
53
Угол <р между стороной ВС и медианой AM (рис. 2.1) равен углу между векторами В(5 и АЙ. Согласно определению 2.1 скалярного произведения, косинус угла выра
жается через скалярное произведение этих векторов и их длины с помощью формулы
cos =
Пусть \АВ\ = s. Тогда |АС\ = 3s, и поскольку В(3 = А^ — А^,
то
АЙ =	+ ВЙ = А& + 0,5В<3 = 0,5 (А& + А^)
и поэтому
АЙ • В& = 0,5(411 + А?) (А& - А^) =
= 0,5(|А?|2 - | Д^|2) = 0,5(9s2 - s2) = 4s2.
Вычислив длины векторов АЙ и В(3:
| Ал1| = а/ал!-А^ = 0,5\/(А^ + А^)(А^+А^) =
= 0,5 V (^2 + 241L А? + А^2 =
= 0,5 9s2 + 6s2 cos 120° + s2 = 0,5s\/7,
= y(A& - 2 A^ • A^ + A/h = \/9s2 - 6s2 cos 120°+ s2 = s>/13,
54
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
найдем, что 4s2	8
0,5sa/7s^13	V7a/13
и поскольку <р € (0, тг/2), то <р = arccos(8/x/9l). #
Пусть векторы а и Ь из V3 заданы своими координатами в ортонормированном базисе г, j, k: а = {ха\уа; za}, b — = {хь', Уь] zb}. Это означает, что имеются разложения
а — xai + уа j + zak, b = xbi + ybj + zbk.
Используя их и свойства 1°-4° скалярного произведения, вычислим
ab — (xai + yaj + zak) (xbi + ybj + zbk) = = xaxbii + xaybij + xazbik + + УахЪЗг + УаУЬЭЗ + yaZbjk + + zaxbki + zaybkj + zazbkk =
= жаж6г2 + УаУЬЭ2 + zazbk2 = xaxb + УаУЬ + zazb.
Окончательный ответ получен с учетом того, что ортонор-мированность базиса г, j, к означает выполнение равенств ij = ik = jk = 0, i2 = j2 — к2 = 1. Таким образом,
ab = xaxb + yayb + zazb,	(2.9)
т.е. скалярное произведение векторов в ортонормированном базисе равно сумме попарных произведений одноименных координат.
Из теоремы 2.1 и формулы (2.9) получаем следующий критерий ортогональности векторов а и Ъ:
хахЬ 4“ УаУЬ 4* zazb — 0.	(2.10)
Вспомним, что, согласно определению 2.1 скалярного произведения,
аЬ = Ы|6| cosy?,
2.2. Скалярное произведение
55
где </? = (а,Ь) — угол между векторами а и Ь. Зная, как выражается скалярное произведение и длины векторов через их координаты в ортонормированном базисе, можно вычислить и косинус угла между ненулевыми векторами. Действительно, исходя из формулы
ab cosv=njbi’ получаем
Я'аЗ'Ь 4“ УаУЪ 4*	/о i й
COS Ср = ——.	(2.11)
VXa + + ^VXb + УЬ + Zb
В случай, когда а,Ь € Vj и известны координаты этих векторов в ортонормированном базисе г, j:
а = xai + yaj, b = xbi + ybj,
справедливы формулы, аналогичные (2.9)—(2.11): для вычисления скалярного произведения
аЬ = хахь + уауь,	(2.12)
для критерия ортогональности
ХаХЬ + УаУЬ = О
и для косинуса угла между ненулевыми векторами а, b
XgXb + УаУЪ
VXa + y«Vxb+yb
Пример 2.6. Найдем значения параметра t, при которых векторы а = {t; 1 —1-,7} и b = {t 4* 1; 2; — 2}, заданные своими координатами в ортонормированном базисе, ортогональны.
Используя критерий (2.10) ортогональности векторов, получаем уравнение
£(£4* 1) 4*2(1 — £) — 14 = 0
относительно параметра t. Решая это квадратное уравнение, находим, что лишь при t — -3 и t = 4 данные векторы ортогональны.
cos (а, Ь) =
56
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
2.3.	Векторное произведение
Векторное произведение вводится для двух векторов из V3. Оно опирается на следующее понятие.
Определение 2.2. Упорядоченную тройку некомпланарных векторов а,Ь,с называют правой, если направление вектора а совмещается с направлением вектора Ь при помощи кратчайшего поворота вектора а в плоскости этих векторов, который со стороны вектора с совершается против хода часовой стрелки. В противном случае (поворот по ходу часовой стрелки) эту тройку называют левой.
Так как три некомпланарных вектора образуют базис в Уз, то также говорят о правых и левых базисах. Каждый базис является либо правым, либо левым, т.е. все базисы в V3 разделяются на два класса: класс правых базисов и класс левых базисов. Класс, к которому относится фиксированный базис, называют его ориентацией.
Определение 2.3. Векторным произведением векторов а и Ъ называют такой вектор с, который удовлетворяет следующим трем условиям.
1.	Вектор с ортогонален векторам а и Ь,
2.	Длина вектора с равна |с| = |а| |Ь|sin 9?, где — уго^л между векторами а и Ь.
3.	Упорядоченная тройка векторов а,6,с является правой (рис. 2.2).
Векторное произведение векторов а и Ь далее будем обо-*	значать ахб, хотя в литературе
встречается и обозначение [а, 6]. Если векторы а и Ь коллине-арны, то условие 3 в определении 2.3 теряет смысл, так как трой-Рис. 2.2	ка векторов будет компланарна
2,3. Векторное произведение
57
Однако при этом, согласно условию 2 определения, длина векторного произведения должна равняться нулю. Это однозначно определяет векторное произведение как вектор, равный нуль-вектору. Поэтому дополним определение 2.3, полагая, что векторное произведение двух коллинеарных векторов есть нуль-вектор. В это дополнение входит и случай, когда хотя бы один из двух векторов является нулевым, так как в этом случае эти два вектора коллинеарны.
Векторное произведение используют, например, в механике. Так, момент силы F, при-	—►
2	,,	OMxF
ложеннои к точке М, относи-	j l
тельно некоторой точки О равен OaIxF (рис. 2.3). Однако роль векторного произведения выхо-
дит далеко за рамки его механи-	рис 3
ческой интерпретации.
Свойства векторного произведения можно разделить на две категории: геометрические и алгебраические. Рассмотрим первую категорию — геометрические свойства.
1°. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нуль-вектору.
◄ Необходимость следует из приведенного выше обсуждения определения 2.3 векторного произведения в случае коллинеарных сомножителей. Докажем достаточность. Если ахЬ = О, то |ах6| =0, т.е. |а| |Ь|sin </? = 0, где <р — угол между векторами а и Ь. Но тогда выполнено, по крайней мере, одно из трех равенств: |а| = 0, |6| = 0 или sin(р = 0. Однако каждое из этих равенств влечет коллинеарность векторов а и Ь. ►
2°. Если векторы а и b неколлинеарны, то модуль |ахЬ| их векторного произведения равен площади параллелограмма, построенного на этих векторах как на смежных сторонах (рис. 2.4).
58
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
◄ Свойство объясняется тем, что модуль векторного произве-
а
Рис. 2.4
дения и площадь параллелограмма по двум смежным сторонам и углу между ними вычисляют по одной и той же формуле как произведение длин векторов (сторон параллелограмма) на синус угла между ними. ►
3°. Если ненулевые векторы а и Ь ортогональны, то для геометрического построения вектора ахЬ достаточно совместить их начала и в плоскости, перпендикулярной вектору Ь, повернуть вектор а на 90° вокруг вектора b по ходу часовой стрелки (если смотреть с конца вектора Ь), а затем умножить повернутый вектор на число |Ь|.
◄ Действительно, так как векторы а и Ь ортогональны, их
векторное произведение есть вектор, ортогональный и а, и Ь,
Рис. 2.5
который по модулю равен |а| |Ь|. Векторы а и ахЬ лежат в плоскости, перпендикулярной вектору Ь. Поэтому мы можем получить вектор ахЬ поворотом вектора а вокруг вектора b на прямой угол с последующей корректировкой длины прц, помощи умножения на число |Ь|. Так Kaiy тройка векторов а, Ь, ахЬ, по опредет лению векторного произведения, является правой, поворот должен выполняться по ходу часовой стрелки (рис. 2.5). ►
Для геометрического построения векторного произведения в общем случае нам потребуется следующее понятие. Проекцией пр^а вектора а — А& на плоскость я назовем вектор, соединяющий ортогональные проекции на плоскость тг начала А и конца В вектора а (рис. 2.6). Напомним, что ортогональной проекцией точки на плоскость называю!1 основание перпендикуляра, опущенного из этой точки на плоскость.
2.3. Векторное произведение
59
Проекция вектора на плоскость сохраняет свойства проекции вектора на прямую: проекция суммы векторов равна сумме их проекций, при умножении вектора на число его проекция на плоскость умножается на это число.
Рис. 2.6
4°. Пусть я* — плоскость, перпендикулярная вектору Ь.
Тогда а х Ь = (пр^ а) X Ь.
◄ На рис. 2.7 векторы а, Ь и а1 = пр^а изображены с общим началом в некоторой точке плоскости тг.
Прежде всего отметим, что эти векторы компланарны, так как направление вектора Ь и перпендикуляр из конца а на плоскость тг параллельны. Поэтому векторы axb и (пр7Га)х6 колли-
неарны, так как они перпендику-	рис. 2.7
лярны плоскости, параллельной
векторам а, b и пр^а. Более того, векторы axb и (пр7Га)х6 однонаправлены. Поэтому они равны, если равны их длины. Проверим равенство длин:
|ах6| = |a||6|sin<p, |(npwa)x6| = |npwa| |6|.
Но Inp^a) = |a|sin<jP, значит, длины совпадают. ►
5°. Чтобы геометрически построить векторное произведение векторов а и 6, надо, совместив их начала, спроектировать вектор а на плоскость л, перпендикулярную вектору Ь. Полученную проекцию в плоскости, перпендикулярной вектору 6, повернуть вокруг вектора Ь на угол 90° по ходу часовой стрелки (если смотреть с конца вектора Ь) и результат поворота умножить на число |Ь|.
60
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
4 Сформулированное свойство непосредственно вытекает из свойств 3° и 4°. ►
Алгебраические свойства векторного произведения используют при преобразовании выражений, в которые входят векторные величины. Важнейшими алгебраическими свойствами являются следующие три:
-	свойство антикоммутативности ахЬ= — Ьха;
-	свойство ассоциативности совместно с умножением на число (Аа)хЬ= А(ахб);
-	свойство дистрибутивности относительно сложения (а + + Ь)хс = ахс + 6хс.
◄ Доказывая свойство антикоммутативности, заметим, что если векторы а и Ъ коллинеарны, то в обеих частях равенства ахЬ = — Ьха в соответствии со свойством 1° стоит нулевой вектор. Если же векторы а и Ь неколлинеарны, то существует плоскость, которой они параллельны. В силу первого условия определения 2.3 векторного произведения векторы ахЪ и Ьха перпендикулярны этой плоскости и, следовательно, коллинеарны. Ясно, что и длины векторов ахЬ и Ьха равны, поскольку совпадают с площадью одного и того же параллелограмма (свойство 2°). Остается доказать, что векторы axb и Ьха имеют противоположное направление. Это следует из того, что если тройка векторов а,Ь,ахЬ правая, то тройка Ь,а,ах6 — левая. Поэтому, заменив в последней тройке третий вектор на противоположный, получим правую тройку векторов Ь,а,—ахЬ, причем вектор —ахЬ коллинеарен вектору Ьха и имеет ту же длину. Согласно определению 2.3, это означает, что вектор —ах6 равен векторному произведению векторов Ь и а, т.е. axb= -Ьха.
Свойство ассоциативности доказывается аналогично. В случае коллинеарных векторов а и 6, а также при А = 0 векторы (Аа)хЬ и А(ахЬ) равны нуль-вектору, поскольку каждый из них является или векторным произведением коллинеарных
2.3. Векторное произведение
61
векторов, или произведением вектора на число, равное нулю. Следовательно, в рассматриваемых случаях равенство (Аа)хЬ= А(ахЬ) выполнено.
Предположим теперь, что векторы а и b неколлинеарны, а А 0. Покажем сначала, что в левой и правой частях доказываемого равенства стоят коллинеарные векторы, равные по длине. Действительно, если считать, что векторы а, b и Ха имеют общее начало, то пары а, Ь и Аа, b неколлинеарных векторов порождают одну и ту же плоскость, которой перпендикулярны их векторные произведения ахЬ и (Аа)хЬ. Поэтому векторы А(ахЬ) и (Аа)хЬ коллинеарны. Вычисляя их длины, убеждаемся, что эти длины равны, так как
|А(ахЬ)| = |А| |ах6| = |А| |а| |Ь|sin<р,
где — угол между векторами а и 6, а
|(Аа)хЬ| = |Аа| |Ь|sint/> = |А| |а| |fe|sin^ = |А| |а| |Ь|sin9?,
где ф — угол между векторами Ха и Ь и использовано равенство sin = sin 9?, выполненное при всех А / 0.
Два коллинеарных вектора, равные по длине, либо совпадают, либо являются противоположными друг другу. Нам достаточно исключить последнюю возможность, доказав, что векторы (Аа)хЬ и А(ахЬ) являются однонаправленными.
Если А > 0, то векторы а и Аа однонаправлены. Следовательно, векторы (Аа)хб и ахЬ тоже являются однонаправленными. А поскольку векторы ахЬ, А(ахЬ) тоже однонаправлены, то однонаправлены и векторы (Аа)хЬ и А(ахЬ).
Если А < 0, то векторы а и Аа являются противоположно направленными. Следовательно, векторы (Аа)хЬ и ахЬ тоже являются противоположно направленными. Умножение вектора ахЬ на отрицательное число А меняет его направление на противоположное. Поэтому векторы (Аа)хЬ и А(ахЬ) имеют одинаковое направление.
62
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Остановимся на доказательстве свойства дистрибутивности1. Если с — О, то равенство является очевидным, так как и слева, и справа будут стоять нулевые векторы. Поэтому этот случай далее не рассматриваем и полагаем, что с ф 0. Мы также можем считать, что |с| — 1, так как равенство в общем случае
(а + Ь)хс = ахс + Ьхс
при помощи свойства ассоциативности легко преобразовать к форме
|с| (а + Ь)хс/ = |с|ахс/+ Ic^xc',
с'=Л
т.е. к частному случаю тройки векторов а, Ь, с', для которой |C'| = L
Итак, пусть |с| = 1. Вспомним геометрическое свойство 5° (см. с. 59), дающее геометрическую интерпретацию произведения двух векторов. При нашем дополнительном условии |с| = 1 преобразование произвольного вектора х в векторное произведение ххс происходит за два шага: проектирование х на плоскость тг, перпендикулярную вектору с, и поворот проекции в этой плоскости на прямой угол. Согласно свойству 4° векторного произведения (см. с. 59), получаем	*
(а + Ь)хс = (пря.(а + Ь))хс= (прзга + пр7ГЬ)хс, ахс + 6хс = (пр^а)хс + (пр7ГЬ)хс,
и нам остается показать, что
(прк а + пРя. 6) хс = (пр^а) хс + (npw 6) хс.
1 Следующее далее доказательство опирается на геометрическое представление векторного произведения и в этом смысле достаточно наглядно, так как в нем в основном используются понятия элементарной геометрии. Далее будет приведено и другое доказательство, более короткое, но и более формальное (см. 2.4).
2.3. Векторное произведение
63
Обозначим а' = пр^а, Ь' = пркЬ. Согласно свойству 5°, векторное умножение этих векторов на вектор с заключается в их повороте на прямой угол в плоскости тг. Согласно правилу па-	с
раллелограмма, сумма повернутых векторов получается из сум-	др
мы исходных a' + bf поворотом па прямой угол, или, другими словами, умножением на вектор	рис 2 g
с (рис. 2.8). ►
Замечание 2.2. Доказанные свойства ассоциативности и дистрибутивности векторного произведения объединяют, аналогично случаю скалярного произведения, в свойство линейности векторного произведения относительно первого сомножителя. В силу свойства антикоммутативности векторного произведения векторное произведение линейно и относительно второго сомножителя:
ах(АЬ) = -(АЬ)ха = —А(6ха) = А(ахЬ),
ах(Ь + с) = — (Ь + с)ха = — (Ьха + сха) = ахЬ + ахс.
Пример 2.7. Найдем площадь S треугольника, построенного на векторах а = Зе — 2d nb = cid при условии, что |с| = 1, |<Z| =4, а угол <р между векторами с и d равен 30°.
Для решения задачи воспользуемся формулой
S = 0,5 |а х Ь|.
Используя алгебраические свойства векторного произведения, находим, что
axb = (Зс - 2d)x(c + d) = Зсхс + 3cxd -2dxc- 2dxd — = 3cxd + 2cxd = 5cxd.
Поэтому
S = 0,5|axb| = 0,5|5cxd| — 2,5|c| |d|sin</? = 5. #
64 2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Алгебраические свойства позволяют вычислить векторное произведение через координаты векторов и векторные произведения векторов, образующих базис. Наиболее просто соответствующие формулы выглядят в ортонормированном базисе.
Рассмотрим правый ортонормированный базис г, j, к. Векторные произведения всевозможных пар векторов базиса (всего 9 пар) выглядят следующим образом:
ixj = fc, j X к = i, kxi — j,
jxi = -к, kxj — -i, ixk = —j.
(2.13)
Рис. 2.9
Векторные произведения базисных векторов на себя не приведены, так как все они равны нуль-вектору.
Таблицу произведений (2.13) удобно трактовать как правило циклической перестановки: произведение двух базисных векторов равно третьему, причем знак плюс выбирается, если тройка векторов (первый сомножитель, второй сомножитель, произведение) получается из исходного базиса г, к циклической перестановкой. На рис. 2.9 этот порядок соответствует движению против хода часовой стрелки. При движении на рис. 2.9 от первого сомножителя ко второму по ходу часовой стрелки в правых частях соответствующих равенств (2.13) появляется знак минус.
Рассмотрим два вектора а и Ь, заданных своими координатами в правом ортонормированном базисе г, j, к: а — = {ха; уа\ га}, Ъ = уь; ^}. Тогда имеют место разложения этих векторов
a = xai + yaj + zak, b = xbi + ybj + zbk.
2.3. Векторное произведение
65
Исходя из этих представлений и алгебраических свойств векторного умножения, получаем
axb = (xai + yaj + zak)x(xbi + ybj + zble) =
— X aXbZXZ “I- XaybZX J "f" XaZbtX k ~|“
+ yaXbi X i + yaybj X j + yaZb j Xfc +
+ zaXbkxi + Zaybkxj + zazblexk =
= (Уа?Ь - ybZa)i + 0a^6 - ZbXa)j + (xayb - Zfet/a)& =
Уа
УЬ
Za • Xa г —
Zb хь
Za a j %a
3 +
Zb Xb
Уа
УЬ
k.
Чтобы упростить полученную формулу, заметим, что она похожа на формулу разложения определителя третьего порядка по 1-й строке, только вместо числовых коэффициентов стоят векторы. Поэтому можно записать эту формулу как определитель, который вычисляется по обычным правилам. Две строки этого определителя будут состоять из чисел, а одна — из векторов. При вычислении определителя, умножение векторов на числа и сложение векторов выполняются по обычным правилам, введенным для этих линейных операций в гл. 1. Итак, формулу вычисления векторного произведения в правом ортонормированном базисе г, j, к можно записать в виде
axb =
3 к
Уа Za .
УЬ zb
(2-14)
Пример 2.8. Найдем все векторы, ортогональные векторам тц = {3; 1; -2} и п2 = {1; -1; 1}.
Отметим, что векторы nj и п2 неколлинеарны, так как их координаты непропорциональны, например:
Совместим начала этих векторов в некоторой точке. Тогда существует единственная плоскость, содержащая эти векто-
3 Аналитическая геометрия
66
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
ры. Искомое множество векторов, ортогональных данным, совпадает с множеством векторов, перпендикулярных указанной плоскости, а это множество совпадает с множеством векторов, коллинеарных векторному произведению
П\ ХП1 =
i 3
3 1
1 -1
к
-2
1
— — i — 5j — 4fc.
Ответ: А(—i — 5j — 4&), где A € К.
t
2.4. Смешанное произведение
Определение 2.4. Смешанным произведением трех векторов а1 Ь, с называют число, равное (ахЬ)с — скалярному произведению векторного произведения первых двух векторов и третьего вектора.
Смешанное произведение отличается от скалярного и векторного произведений в первую очередь тем, что имеет три сомножителя, а не два. Обозначают смешанное произведение трех векторов а, Ь, с так: аЪс.
Смешанное произведение имеет простой геометрическйй смысл.
Теорема 2.2. Смешанное произведение трех некомпланарных векторов аЪс равно объему параллелепипеда, построенного на этих векторах как на ребрах, выходящих из одной вершины, взятого со знаком плюс, если тройка векторов а, Ь, с — правая, и со знаком минус, если эта тройка — левая.
◄ Вектор ахЬ перпендикулярен грани указанного параллелепипеда, построенной на векторах а и Ь, и в силу свойства 2 векторного произведения (см. с. 57) имеет длину, равную площади S этой грани (рис. 2.10). Обозначив через е единичный вектор, ортогональный векторам а и b и однонаправленный
2.4. Смешанное произведение
67
( векторным произведением ахЬ, получим
axb = Se.
Рис. 2.10
Смешанное произведение abc равно скалярному произведению вектора Se на век-гор с и равно S|c|cos</?, где угол между векторами
axb и с. Отметим, что число |с|cos$p равно проекции вектора г ла направление вектора е, а его модуль, т.е. ||c|cos</?|, равен высоте h параллелепипеда. Знак проекции определяется углом / между сие. Если <р < 90°, то векторы сие находятся по одну сторону от плоскости векторов а, Ь. Значит, тройки векторов а, Ь, е и а, Ь, с имеют одну и ту же ориентацию — правую. В этом случае смешанное произведение положительно и равно объему параллелепипеда со знаком плюс. Если же 7» > 90°, то ориентация указанных троек различная, т.е. тройка а, Ь, с является левой, и смешанное произведение будет равно объему параллелепипеда со знаком минус. ►
Замечание 2.3. Если векторы а, 6, с компланарны, то параллелепипед, построенный на них, вырождается (лежит в плоскости). Поэтому ему следует приписать нулевой объем. Непосредственно из определения заключаем, что для компланарных векторов а, Ь, с векторы axb и с ортогональны, т.е. (ахЬ)с = 0. Значит, теорема верна и в случае, когда векторы компланарны. #
Как видно из определения, смешанное умножение векторов является вторичной операцией и определяется при помощи । калярного и векторного умножений. Однако смешанное умножение играет важную роль в геометрических приложениях, что и подтверждает теорема 2.2. Исходя из этой теоремы, а также ил свойств скалярного и векторного произведений, можно полу-чип» несколько важных свойств для смешанного произведения.
68
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
1°. Для смешанного произведения действует правило циклической перестановки:
(ахЬ)с = (Ьхс)а = (сха)Ь = — (Ьха)с = — (схб)а = — (ахс)Ь.
◄ Действительно, все шесть указанных произведений по абсолютной величине дают объем одного и того же параллелепипеда, а знак произведений определяется ориентацией тройки сомножителей. При циклической перестановке векторов в тройке ориентация не меняется, при перестановке местами двух векторов в тройке ориентация меняется на противоположную. ►
Замечание 2.4. Из доказанного свойства получаем, что
abc = (axb)c = а(Ьхс),
т.е. порядок двух операций, дающих смешанное произведение, не является существенным. Это объясняет, почему в обозначении смешанного произведения знаки образующих операций опускаются.
2°. Три вектора а, Ь, с компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
4 Это вытекает из теоремы 2.2 и замечания 2.3. ►
3°. Для смешанного произведения выполняется свойство ассоциативности относительно умножения векторов на число: (Аа)Ьс— Л(аЬс).
◄ Обозначив Ьхс = е и используя свойство 2° ассоциативности скалярного произведения относительно умножения на число, получим
(Аа)Ьс = (Ха)(Ьхс) = (Аа)е = А(ае) = Х(а(Ьхс)) = А(аЬс). ►
4°. Для смешанного произведения выполняется свойство дистрибутивности (ai + a2)bc = aibc + a^bc.
2.4. Смешанное произведение
69
4 Обозначив Ьхс = е и используя свойство 3° дистрибутивно-। ти скалярного произведения, получим
(«I + а2)Ьс = (ai + а2)(Ьхс) = («1 +<*2)е = сце + а2е =
= ai(bxc) +а2(Ьхс) = aibc + a2bc. ►
Замечание 2.5. Свойства 3° и 4° смешанного произведения сформулированы для первого сомножителя. Однако при помощи циклической перестановки можно доказать аналогичные' утверждения и для второго и для третьего сомножителей, т.е. верны равенства
а(АЬ)с = А(аЬс), аЬ(Ас) = А(аЬс), а(Ь1 + Ь2)с = abic + ab2c, ab(ci + с2) = abc\ + abc2,
и в итоге имеем свойство линейности смешанного произведения по каждому сомножителю.
Замечание 2.6. Отметим, что при доказательстве свойств смешанного произведения мы не использовали свойства векторного произведения. Наоборот, обоснование свойств векторного произведения можно строить на основе свойств смешанного произведения. Покажем это на примере свойства дистрибутивности векторного произведения, доказательство которого мы обещали привести.
Сначала обратим внимание на следующее. Если векторы х\ и х2 таковы, что для любого вектора у выполняется равенство
=	(2.15)
го х\ — х2. Действительно, равенство (2.15) означает, что (.Г| - х2)у = 0. Так как вектор у любой, мы можем положить у - xi — х2. Тогда получим (®i — х2)2 = 0, но это возможно только при Xi — х2 = О, т.е. при х\ = х2.
Согласно доказанному, равенство
(в! + a2)xb = aixb + a2xb
70
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
будет выполняться, если для любого вектора с ((а! + а2)хб)с = (aixb)c+ (а2х6)с,
или
(<zi + a2)bc = а^Ьс + а2Ьс.
Но последнее равенство верно, так как выражает доказанное свойство 4 дистрибутивности для смешанного произведения. #
Пусть векторы а, Ь, с заданы своими координатами в правом ортонормированном базисе: а = {жа; уа; га}, Ь = уь; зъ}, с = {жс; ус; zc}. Чтобы найти их смешанное произведение, воспользуемся формулами для вычисления скалярного и векторного произведений:
abc — а(Ьхс) =
— Ха
УЬ
Ус
Zb • г — zc хс
Zb
Zc
хь хс
Уь
Ус
ХЬ
хс
УЬ
Ус
Ха хь хс
Уа
УЬ
Ус
Za Zb Zc
э +
Согласно полученной формуле, свойство 2 смешанного произведения можно сформулировать так: необходимым и достаточным условием компланарности трех векторов, заданных координатами в ортонормированном базисе, является равенство нулю определителя третьего порядка, строками которого являются координаты этих векторов.
Пример 2.9. Найдем объем треугольной пирамиды, построенной на векторах а = {—2; 1; -2}, Ь = {1;0;—1} и с = = {1; 1; 1} как на смежных ребрах.
Трем векторам с общим началом можно сопоставить как треугольную пирамиду, так и параллелепипед, причем объем
2.5. Приложения произведений векторов	71
пирамиды будет в 6 раз меньше объема параллелепипеда, равного модулю смешанного произведения аЬс данных векторов. II гак, объем пирамиды равен V = |abc|/6 = 1, поскольку
аЬс =
-2 1
1 О
1 1
-2
-1
1
= -6.
2.5. Приложения произведений векторов
Рассмотрим различные приложения произведений векторов на следующих примерах.
Пример 2.10. Работа А постоянной силы F при прямолинейном перемещении материальной точки из положения М\ в положение М2 равна А = |F| |A/iЛ/2|cos(рис. 2.11, а). Поэтому г помощью скалярного произведения эта работа вычисляется по формуле
Рис. 2.11
Рели к материальной точке приложено п постоянных сил i' = 1,п, то при том же ее перемещении сумма А их работ Аг рннна работе равнодействующей силы

72
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
поскольку
г=1	г=1	г=1
Из этого равенства следует, что система сил не совершает работу, если их равнодействующая ортогональна вектору перемещения s. Ясно, что равенство А = Fs = 0 справедливо и в случае, когда равнодействующая равна нулю или отсутствует перемещение, или верно и то и другое.
Пример 2.11. Круговой диск вращается с постоянной угловой скоростью со вокруг перпендикулярной ему оси вращения L, проходящей через его центр О (рис. 2.11,6). Пусть v — скорость точки Р. Тогда
v = их(Э$,
где со — вектор угловой скорости.
Пример 2.12. На движущуюся со скоростью v частицу с электрическим зарядом q магнитное поле с магнитной индукцией В действует с силой Лоренца
f = qvxB.
Если векторы v и В коллинеарны, то vxB = 0 и при постоянном магнитном поле частица будет совершать прямолинейное равномерное движение. Если же векторы v и В неколлинеарны, то f 0, но мощность, развиваемая этой силой, равна нулю:
W — fv — q(vxB)v = qvBv = О, поскольку смешанное произведение компланарных векторов равно нулю. Следовательно, заряженная частица массой т в постоянном магнитном поле сохраняет свою кинетическую энергию mv2/2.
Д.2.1. Двойное векторное произведение
73
Рассмотрим случай, когда векторы v и В ортогональны, г.р. vВ — 0. Поскольку и сила Лоренца f ортогональна В, то частица остается в плоскости, перпендикулярной вектору В, и /пин ается по окружности радиуса /?, который определяется из у< ловия равновесия возникающей при этом центробежной силы и действующей силы Лоренца,
mv2/R — q\vxB\ — ^|v||B|sin90°.
()тсюда
m|t>|
Ж
Дополнение 2.1. Двойное векторное произведение
Трем векторам а, b и с можно поставить в соответствие вектор, равный ах(Ьхс). Этот вектор называют двойным векторным произведением векторов а, Ь и с. Двойное векторное произведение встречается в механике и физике.
Двойное векторное произведение выражается через линейную комбинацию двух из трех своих сомножителей по формуле
ах(Ьхс) — Ь(ас) - с(аЬ).
/(окажем это. Обозначим через х разность левой и правой частей этого равенства
х = ах(Ьхс) — Ъ(ас) + с(аЬ).
Пам достаточно показать, что х — 0.
Предположим, что векторы Ь и с коллинеарны. Если они оба нулевые, то в выражении для вектора х все слагаемые равны пулевому вектору и поэтому равенство х — 0 выполнено. Если же один из коллинеарных векторов Ь, с ненулевой, например
74
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
с’ т° для другого вектора при некотором а € К выполнено раве^СТво 5 — ас> Но тогда
х = ох (асхс) - ас(ас) + са(ас) = 0.
предположим теперь, что векторы Ь и с неколлинеарны. Тогд^ их векторное произведение не равно нулевому вектору и ортогонально ненулевому вектору Ь. Векторы
Ь . Ьхс ,	. .
,= Н’ ’ = fc = ,XJ
образу ют правый ортонормиров анный базис в Рз (это и отражено в обозначениях). В этом базисе справедливы следующие разложения векторов:
Ь = |Ь|г, с = С1г + с2&, а = aii + aij + azk,
И поэтому
Ьхс= -|6|c2j, ах(Ьхс) = -|6|c2(aife - а3г).
Кром^ того, ас = «iCi — азС2, = «1|Ь|.
В резулЛьтате находим, что и в случае неколлинеарных векторов & и с выполнено равенство
х ~ — |b|c2(aife — «зг) - (fliCi - азс2)|b|i + ai|fe|(cji + c2fc) = 0.
Вопросы и задачи
2*^* Вычислить определители:
Вопросы и задачи
75
2.2.	Решить уравнения и неравенства:
а)	1 — X 0 0		39 2 — х 0	7Г 2х 5 + х		= 0;	б)
		X	-1	0			
|») <	)<	1	X	1	/Л GO		г)
		0	-1	X			
1	1	1		
X2	5	3		0;
X3	25	9		
X	ж2	„3 X		
-1	3		4	= 0;
2	-6		6	
	3	х —4		2 х + 2 -1	
д)	2-13	= 0;	е)	1	1	—2	>0.
	ж + Ю 1	1		5	—3 а:	
2.3.	Найти все значения параметра t, при которых система циух линейных уравнений
( tx — Зу = 2, | 2х + (t — 5)у = 5
имеет единственное решение. Найти зависимость этого един-< '( ценного решения от параметра t.
2.4.	Доказать справедливость равенств:
а! + а\ bi а2 + а'2 b2
«1 bi	а\
а2 Ь2	а'2
bi
b2 ’
б)
Aai
Ла2
bi _ д а1 ^*1 .
Ь2 а2 Ь2 ’
	а? &2 с2		ai bi ci		с&1 Ci bi
и)	ft]	Ci	= —	а2 ^2 С2		а2 с2 ^2
	#3 Ьз Сз		а3 Ьз Сз		из сз Ьз
«И 0	0		«1 0 0		bi ci	
«2 Ь2 0	—	0 Ь2 0	=	0 b2 с2	
аз Ьз с3		0	0 Сз		0	0 сз	
2.5.	Найти длину вектора с = а — 2Ь, если известно, что |<i| = 3, |Ь| = 5 и угол между векторами а и b равен 45°.
76
2. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
2.6.	Найти угол между векторами с~ а — 26 и d= За + 2Ь, если известно, что 1а| — 3, |6| = 5 и угол между векторами а и 6 равен 120°.
2.7.	Найти значения параметра £, при которых векторы c~a-tbnd = a + tb имеют одинаковую длину.
2.8.	Найти площадь треугольника, построенного на векторах а = 2г — j + 3fc и 6 = i + j — к,
2.9.	В треугольнике АВС угол при вершине А равен 45°, \АВ\ = 1, |ЛС| = 4. Найти угол между медианой и биссектрисой, которые проведены из вершины А.
2.10.	Точки Bi и В2 принадлежат соответственно прямым Li и Z/2, которые пересекаются в некоторой третьей точке А. Выразить через ABi и АВ2 векторы, направленные по биссектрисам углов между прямыми.
2.11.	Найти угол между векторами а и 6, если они имеют одинаковую длину, а векторы с — а — 2Ъ и d = а + 36 ортогональны.
2.12.	Найти объем параллелепипеда, построенного на векторах а = i — j + 3fc, 6 = 2i + j — к, с = Зг + j + 2fc.
2.13.	При каких значениях t векторы а = ti — t2j + i3fe, 6 = 2г — j — fc, с = -Ai + 2j + 5fc компланарны.
2.14.	При выполнении какого условия равнодействующая двух сил, приложенных к одной точке, будет направлена по биссектрисе угла между ними?
2.15.	Найти работу силы F = i + k при перемещении материальной точки на вектор а = Зг — 2j + fc.
2.16.	Найти угол между ненулевыми векторами а и 6, если они удовлетворяют соотношению |ах6| = а6.
2.17.	Векторы а, 6 и с некомпланарны, а векторы ах(бхс) и 6 коллинеарны. Найти угол между векторами а и 6.
Вопросы и задачи
77
2.18.	Доказать, что для любых трех векторов справедливо равенство
(ахЬ)хс = (ас)Ь - (Ьс)а, причем в его правой части в круглых скобках стоят скалярные произведения соответствующих векторов.
2.19.	Доказать, что любые векторы а, Ь и с удовлетворяют соотношению
ах(Ьхс) +сх(ахЬ) + 6х(сха) = 0.
2.20.	Доказать, что для любых четырех векторов а, Ь, с и d выполнено тождество
(axb)(cxd) = (ас) (fed) — (ad)(6c).
2.21.	Доказать, что если два вектора равной длины лежат па, одной прямой и однонаправлены, то их моменты относительно любой точки равны между собой.
2.22.	Доказать, что если частица массой т с электрическим нарядом q со скоростью v попадает в постоянное магнитное поле с магнитной индукцией В и векторы v и В неколлинеарны и неортогональны, то она будет двигаться по цилиндрической « пирали. Вычислить радиус основания соответствующего прямого кругового цилиндра и расстояние между соседними витками спирали.
2.23.	Для каких векторов a, Ъ и с выполнены соотношения: а) |а — Ь| = |а + Ь|; б) |а — Ь| > |а + Ь|; в) |а - Ь| < |а + 6|; ।) ab = |а| |Ь|; д) |аX6| =*|<х| |6|; е) аЬс = |а| |6| |с|.
2.24.	Найти все векторы х удовлетворяющие данному условию: а) ах — 0; б)ахж = 0; в) ах» = 6; г)ахж = Ьхж.
2.25.	Какому условию удовлетворяют векторы а и 6, если ц/i я любого вектора х € Из выполнено равенство ох® — Ьхх.
2.26.	Доказать, что для векторов а, Ь и с, удовлетворяющих новию а + b + с = 0, выполнены равенства ахЬ = Ьхс = сха.
2.27.	Доказать компланарность векторов а — Ь, Ь — сис — а.
3.	СИСТЕМЫ КООРДИНАТ
В основе аналитической геометрии лежит возможность однозначного описания точек при помощи наборов чисел, называемых координатами. Описание множества с помощью соотношений между координатами входящих в него точек позволяет привлечь для его исследования алгебраические методы, что значительно расширяет возможности анализа. Обратно, зависимости (уравнения, неравенства и их системы) можно интерпретировать как зависимости между координатами точек и ассоциировать с ними множество, составленное из точек, координаты которых удовлетворяют этим зависимостям, и, следовательно, получить наглядное представление чисто алгебраической задачи (например, в случае поиска решений уравнений и их систем). Таким образом, возникает своеобразный мостик, связывающий алгебру и геометрию. Его роль выполняет система координат.
3.1.	Декартова система координат
Существуют различные способы задания точек набором координат. Аналитическая геометрия опирается на простейшую систему координат — прямоугольную, которая известна из школьного курса математики. Мы дадим определение прямоугольной системы координат, используя векторную алгебру. Фактически мы построим систему координат более общего вида, в которой оси координат могут находиться по отношению друг к другу под произвольным углом. Прямоугольная система координат будет частным случаем, когда углы между осями координат будут прямыми.
Назовем декартовой {аффинной) системой координат пару, состоящую из фиксированной точки О и некоторого
3.1. Декартова система координат	79
оазиса. Соответственно трем пространствам Vi, V2, Уз получаем три варианта декартовой системы координат: на прямой, па. плоскости и в пространстве. Декартовыми (аффинными) координатами произвольной точки М являются координаты вектора ОА% в заданном базисе.
С декартовой системой координат связаны следующие понятия:
начало (системы) координат — точка О в составе декартовой системы координат;
-	репер — базис в составе декартовой системы координат, цля векторов которого выбирается общая точка приложения в начале координат;
-	оси координат (координатные оси) — прямые, на которых лежат векторы репера, задающие направление на .них прямых. Оси имеют специальные названия (в порядке нумерации): ось абсцисс, ось ординат и ось аппликат. Координаты точки именуются по осям: абсцисса, ордината и аппликата. На плоскости отсутствует ось аппликат, на прямой также нет оси ординат.
координатные плоскости — плоскости, определяемые парами векторов репера. Понятие используется для декартовой системы координат в пространстве;
-	радиус-вектор точки М — вектор ОМ, соединяющий начало координат О с этой точкой.
Декартову систему координат общего вида часто называют косоугольной системой координат.
Если репер декартовой системы координат является орто-нормированным базисом, то такую систему координат называют декартовой прямоугольной системой координат, ил и просто прямоугольной системой координат, а декартовы координаты точки — ее прямоугольными координатами.
Далее будем использовать в основном прямоугольные сис-|гмы координат, т.е. будем предполагать, что репер предста
80
3. СИСТЕМЫ КООРДИНАТ
вляет собой ортонормированный базис, причем обязательно правый. Отметим, что базис в V2 (т.е. на плоскости) называют правым (левым), если первый его вектор совмещается со вторым с помощью кратчайшего поворота против хода (по ходу) часовой стрелки.
Итак, под системой координат подразумевается прямоугольная система координат с правым базисом, а под координатами точки — ее прямоугольные координаты. Использование других систем координат будет обязательно оговариваться. Для обозначения декартовых систем координат, например в пространстве, будем использовать обозначения типа Oijk, где О — начало системы координат, а г, j, к — ортонормированный репер (базис), или Oxyz [I], где указаны обозначения для координатных осей.
3.2.	Преобразование прямоугольных координат
Все прямоугольные системы координат в изучаемом пространстве, вообще говоря, равноправны, т.е. выбор одной из них ничуть не хуже (и не лучше) выбора другой. Те или иные предпочтения отдают исходя из особенностей конкретной задачи. Использование различных систем координат ставит задачу преобразования координат точки, т.е. задачу вычисления ее координат в одной системе координат по ее координатам в другой системе.
Пусть Oijk — некоторая прямоугольная система координат в пространстве, которую мы условно назовем старой, а O'i'j'k' — вторая прямоугольная система координат, которую будем называть новой (рис. 3.1). Считаем, что известны координаты точки Of(bc, Ьъ] &з) и векторов
г' = {ац; a2i; #31/ — {^125 ^22; #32}, к' = {<*135 »235 »зз}
в старой системе координат. Пусть для точки М известны ее координаты (x;t/;z) в старой и координаты (ж'; г/'; >гг') в
3.2. Преобразование прямоугольных координат
81
новой системах координат. Это значит, что выполняются два равенства
O^x'i' + y'j' + z'k'
и
+ (УМ, причем координаты вектора 00' являются также координатами начала координат (У новой системы координат относительно старой, т.е.
00' = bii + b2j + b3k.
Поэтому
ОЙ = 00' + (УМ = bri + b2j + b3k + x'i' + y'j' + z'k' =
= bii + b2j + b3k +
+ x'(ani + a2ij + a3i&) +
+ y'(&i2i + &22j + »32^) +
+ *'(<*13* + a23] + <*зз&) —
—	+ Oi\2y' + ol\3z' + bi)i +
+ («21^' + a22y' + a23^' + b2)j +
+ («31^' + o^32yf + oc33z' + b3)k, (3.2)
82
3. СИСТЕМЫ КООРДИНАТ
т.е. получено разложение вектора ОМ в репере старой сис-1 темы координат. Оно должно совпадать с (3.1) в силу един-, ственности координат вектора в одном и том же базисе. Приравнивая соответствующие коэффициенты разложений в (3.1) и (3.2), получаем
х = anxf + а12у' + ai3zf + bi,
У =	+ <*22У' + q23^Z + ^2,	(3.3)
z — «31^' + <*32 j/ + <*33^ + ^3-
Соотношения (3.3), выражающие старые координаты через
новые, представляют собой систему трех линейных уравнений
относительно неизвестных ж', у', z'. Чтобы найти новые координаты ж', у', zf по известным старым, необходимо решить
эту систему относительно новых координат. Система (3.3) при любых ж, у, z имеет единственное решение, поскольку
ее определитель отличен от нуля, выполнены равенства
Это следует из того, что j
1 г
«11	«12	«13		«11	«21	«31	
«21	«22	«23		«12	«22	«32	= = 1,
«31	«32	«33		«13 «23	«33	
.1 так как векторы г', j', fc' образуют правый ортонормированный базис и объем построенного на них параллелепипеда равен 1 (или —1 в случае левого базиса).
Набор коэффициентов в системе (3.3) отражает положение репера новой системы координат, а свободные члены i>2, 63 характеризуют изменение начала координат. Если репер системы координат не изменился, а поменялось лишь начало координат, то формулы преобразования выглядят более просто:
х — х1 + 61, у = у' + 62, z = z' + 63.
(3-4)
3.2. Преобразование прямоугольных координат
83
Преобразование (3.4) называют параллельным переносом системы координат в пространстве на вектор 0(У.
Все вышеизложенное относится к прямоугольной системе координат в пространстве. Прямоугольная система координат па плоскости отличается от пространственной лишь тем, что репер состоит из двух векторов, а точки имеют всего две координаты. Преобразование системы координат на плоскости описывается уравнениями
х = anx' + a^y' + bi, у = a2ix' + а22у' + Ъ2,
(3-5)
где	г= 1,2, — координаты векторов г', jf нового
репера относительно старого а (&Г?&2) — координаты точки О' начала новой системы координат в старой системе координат.
Преобразование параллельного переноса системы координат на плоскости выглядит так:
х = х1 + £>i, у = у' + ь2.
Если начала новой и старой систем координат на плоскости совпадают, а изменяется лишь репер системы координат, то формулы преобразования координат имеют вид:
X = ttni' + <*121/, у = a2ix'+ а22у'.
(3-6)
Здесь возможны два случая. В первом из них новый репер может быть получен из старого поворотом последнего на некоторый угол <р вокруг общего начала систем координат, причем полагают, что <р > 0 (</? < 0) при повороте против хода (по ходу) •псовой стрелки. В этом случае преобразование (3.6) называют поворотом системы координат на плоскости на
84
3. СИСТЕМЫ КООРДИНАТ
угол ср. Нетрудно убедиться, что координаты векторов if и j' нового репера относительно старого выражаются через угол поворота <р: i! = {cos</?; sin </?}, jf = {— sin cost/?} (рис. 3.2).
Зная координаты векторов нового репера относительно старого, мы
можем записать уравнения для поворота системы координат на плоскости:
х = x'coscp — и'sin о?, , .	(3-7)
у — Х s\n<p + y cos<p.
Если преобразование состоит в последовательном выполнении поворота и параллельного переноса, то оно имеет вид:
3.8
х = xf cos <р — у1 sin </? + &!, у — x'sin^ + y'cos^ + i^-Система (3.8) легко решается относительно ж', у', и обратное преобразование координат, отражающее переход от новой системы координат к старой, будет иметь вид:
х1 = xcos^ + ysin^ + bp yf = — xsin</? + ycos</? + 62,
где b[ = bicosy? + i>2sin</?, i>2 = —&isin</? + &2cos</?. Как видим, старая система координат получается из новой с помощью поворота на тот же угол </?, но в противоположную сторону (на угол — в положительном направлении), и параллельного переноса (на вектор 0'S).
Во втором случае с помощью поворота старого репера вокруг начала координат на некоторый угол <р можно совместить лишь векторы i и г', но при этом векторы j и jf окажутся противоположными и для их совмещения потребуется выполнение преобразования зеркального отражения плоскости относительно первой оси координат.
3.3. Простейшие задачи аналитической геометрии
85
В первом случае о двух реперах на плоскости говорят, что они имеют одинаковую ориентацию, а во втором — противоположную.
Аналогичную терминологию используют и для пространства. Если начало новой и старой прямоугольных систем координат в пространстве совпадают и изменяется лишь репер системы координат, то формулы преобразования координат имеют вид:
х — оцх' + €*12*/ + €*13У,
у = «212:'+ a22j/' +«232',	(3.9)
z = «312:' + «згу' + «33^'-
Преобразование (3.9) называют поворотом системы координат в пространстве, если реперы новой и старой систем координат имеют одинаковую ориентацию, т.е. являются оба правыми или левыми. Как и в случае плоскости, это связано с тем, что реперы с одинаковой ориентацией можно совмещать с помощью поворотов. Например, можно сначала совместить векторы г и г' с помощью поворота старого репера вокруг век-гора гхг', а затем выполнить второй поворот вокруг вектора г' для совмещения повернутого вектора j с вектором j'. При этом векторы к и kf автоматически совпадут для реперов одной ориентации и будут противоположными для реперов противоположной ориентации. В последнем варианте требуется, как и в случае плоскости, выполнение дополнительного преобразования зеркального отражения (относительно координатной плоскости, определяемой векторами г' и J')-
3.3.	Простейшие задачи аналитической геометрии
Рассмотрим некоторые задачи аналитической геометрии, < вязанные со взаимным расположением точек на плоскости или в пространстве.
86
3. СИСТЕМЫ КООРДИНАТ
Векторы и точки. Задача состоит в том, чтобы выразить координаты вектора через координаты точек его начала и конца.
Рассмотрим в пространстве прямоугольную систему координат и вектор лё с координатами {Z;m;n}, у которого известны координаты точек его начала А(ха;уа- za) и конца В(хь', уь\гь). Обозначим через О начало системы координат. Тогда координаты точек А и В представляют собой координаты их радиус-векторов 0% и О&. Следовательно, О& — 0% = = {яь — ха\уь — уа; гь — za} и из соотношения AJ& = О& — заключаем, что {/; т; п} = {хь - ха; уь — уа\ Zb - za}, т.е.
l-xb-xa, т = уь-уа, n — Zb-za. (3.10)
В случае прямоугольной системы координат на плоскости координаты вектора 4^ = {1',т} на этой плоскости и координаты точек его начала А(ха\уа) и конца В(хь;уь) связаны аналогичными соотношениями
1 = ХЬ-~Ха, ТП = уь-уа-	(3.11)
Из (3.10) и (3.11) вытекают правила:
-	координаты вектора получают вычитанием из координат его конца координат его начала;
-	координаты конца вектора получают сложением координат вектора с координатами его начала;
-	координаты начала вектора получают вычитанием из координат его конца координат вектора.
Деление отрезка в заданном отношении. Задача состоит в том, чтобы на данном отрезке М1М2 найти точку М, делящую отрезок в заданном отношении: |Л/1 М\: |Л1Л12| =р: q.
Для точки М из отрезка М1М2 векторы A/iA^ и ММ2 коллинеарны и однонаправлены (рис. 3.3). Следовательно, один из них может быть получен из другого умножением на поло-
3.3. Простейшие задачи аналитической геометрии
87
жительное число. Пусть, например, ММ2 — ХМ^. Число А равно отношению длин отрезков ММ2 и М\М, т.е. X = q/p. Поэтому
М)
Рис. 3.3
= Mi л) + мм\ = -ллл) = л/1Д р	р
откуда
М1Л) = —(3.12) Р + 9
Пусть концы М\ и М2 отрезка М\М2 заданы своими координатами в произвольной прямоугольной системе координат Oijk в пространстве: Mi(xi; t/i; 2^), М2(ж2; t/2; ^2)- Найдем координаты точки М в этой же системе координат. Для этого запишем равенство (3.12) через радиус-векторы входящих в него точек
ой - ом[ = -?—(ом>2 - ой)
Р + 9
и найдем, что
ой = -^-оЙ + (i - оЙ = p + q \ р + 9/
= -j— ОЙ + ОЙ = -j— {х2; у2; z2} + —{Ж1; yr,zi} -р+9 p + q p + q	P+q
_ fpx2 + qxi py2 + qyi. pz2 + qzi ) I p + q ’ p + q ’ p + q )'
Итак, если обозначить координаты точки М через (х;?/;г), то
рх2 + qxx	_ ру2 + qyi	_ pz2 + qzi
i 1 У	।	>	।
p+q	p+q	p+q
(3.13)
88
3. СИСТЕМЫ КООРДИНАТ
Если точка М — середина отрезка MiM2, то р = q= 1, и поэтому из (3.13) следует, что координаты М равны полусумме соответствующих координат начала и конца отрезка, т.е.
Ж1+®2	У1+У2 Zi +z2	,	.
I = ' (ЗД4)
В случае плоскости нет аппликат и из (3.12) следует, что координаты точки Л/(ж;у), делящей отрезок МуМ2 в отношении |Л/1Л/| : |ЛШ2| = р : q, определяются через координаты точек Ali(®i;j/i) и Мг(®25 !te) концов этого отрезка с помощью равенств рх2 + qxi ру2 + qyi х =-----------------------, у =---------,
р+я р+я
которые для середины отрезка переходят в соотношения
£1 + х2	3/14- У2
2	’ У 2
Пример 3.1. В вершинах 4(4; 4; 4), В(—2; 6; 4), С(-4;4;2) треугольника АВС расположены материальные точки равной массы. Найдем координаты центра масс этой системы точек.
Центр масс указанной системы точек совпадает с точкой М пересечения медиан треугольника АВС, Пусть точка N — середина стороны ВС, Тогда ее координаты (ж; у; z) равнял полусумме соответствующих координат точек В и С, следовательно, х = —3, у = 5, z = 3. Медиану 4N точка М делит в отношении \АМ| : |MN\ = 2:1, поэтому координаты (ж0; уо5 ^о) центра масс рассматриваемого треугольника в соответствии с (3.13) равны
__2-(-3) + 1-4_ 2	_2-5+1-4_14	_2-3+1-4_10
Х°~ 2+1 ~"з’ У°~ 2+1	Z°~ 2+1
Длина отрезка. Задача вычисления длины отрезка (или расстояния между двумя точками) по координатам его концов в прямоугольной системе координат известна из школьного
3.4. Вычисление площадей и объемов
89
курса геометрии. Мы выведем эту формулу при помощи векторной алгебры.
Длина отрезка — это длина вектора, соединяющего его концы, а длину вектора можно определить, вычислив его скалярный квадрат. Пусть концы отрезка Mi и М2 заданы своими координатами в прямоугольной системе координат Oijk:
2/1; лг1), М2(х2;у2-, z2). Тогда
ЛТ1М2 = {х2 - xi; у2 - yi; z2 - 2Х}.
Скалярный квадрат вектора М1М2, заданного своими координатами в ортонормированном базисе г, j, к, находится с помощью формулы (2.9) для вычисления скалярного произведения:
МгМ^2 = (х2 - xi)2 + (у2 - i/i)2 + (z2 ~ -si)2-
Итак, длина отрезка М1М2 вычисляется по формуле
|М1М2| = у/(а>2 - xi)2 + (у2 - yj2 + (z2 - Z1)2.
3.4.	Вычисление площадей и объемов
Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.
Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.
Пример 3.2. Пусть три вершины треугольника заданы своими координатами: А(4;4;4), В(1;2;3), С(3; —1;2).
90
3. СИСТЕМЫ КООРДИНАТ
Для определения площади ДАВС с помощью (3.10) найдем координаты векторов ДЁ и 4&
= {1 - 4; 2 - 4; 3 - 4} = {-3; -2; -1},
А& = {3 - 4; -1 - 4; 2 - 4} = {-1; -5; -2}.
Затем по (2.14) вычислим их векторное произведение:
к
-1 =— г — 5j + 13fc.
-1 -5 -2
Модуль этого векторного произведения равен
|4^х 4^| = V(-l)2 + (-5)2+132 = \/195,
и, следовательно,
S&abc=
|4^х4^|	\/Т95
2	2
Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 2.8), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах А$, А? и
Таким образом, объем этой пирамиды равен Vsabc = |4^4^4^|/6.
Пример 3.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: 4(2; —1;1), В(5;5;4), С(3;2;-1), 5(4;1;3).	I
3.5. Кривые и поверхности
91
Используя (3.10), вычисляем координаты векторов, направленных по ребрам пирамиды:
= {5-2;5- (-1);4- 1} = {3; 6;3}, А$= {3 —2;2-(—1);—1 - 1} = {1;3; -2}, 4^ = {4 — 2; 1 — (—1); 3 — 1} = {2; 2; 2},
и определяем объем с помощью смешанного произведения найденных векторов:

3
1
2
6
3
2
3
-2
2
= -18,
V = ^|4^4^4^| = 3.
6
3.5.	Кривые и поверхности
Множество точек на плоскости или в пространстве можно описать системой уравнений и (или) неравенств, связывающих координаты точек из этого множества. И одна из важнейших задач аналитической геометрии — построение уравнения или сйстемы уравнений и неравенств, описывающих заданное множество.
Определение 3.1. Если уравнению F(x,y,z) = 0 удовлетворяют те и только те тройки чисел х, у, z, для которых точка Л1(я; у; z) принадлежит множеству S в пространстве, то уравнение F(x,y,z) = 0 называют уравнением множества S, а само множество S — геометрическим образом этого уравнения.
Вышесказанное также относится и к описанию множеств на плоскости, но с единственным отличием — уравнению соответствует функция F(x,y) двух переменных х и у, а не грех.
92
3. СИСТЕМЫ КООРДИНАТ
Определение 3.2. Если уравнению F(x,y) =0 удовлетворяют те и только те пары чисел х и у, для которых точка М(х] у) принадлежит множеству Г на плоскости, то уравнение F(z,y) = 0 называют уравнением множества Г, а само множество Г — геометрическим образом этого уравнения.
Рассмотрим простейший вариант, когда множество точек в пространстве описывается одним уравнением вида F(x,yyz) = 0, где F(x,y,z) — функция трех переменных, а переменные ж, у, z представляют собой координаты точки в пространстве относительно фиксированной прямоугольной системы координат. Если не налагать на функцию F(x,y,z) никаких ограничений, то от подобного описания мало проку, так как тогда при помощи уравнения можно описать любое множество точек в пространстве. Действительно, вспомним общее толкование функции как закона, который любому набору, в данном случае из трех, аргументов ставит в соответствие единственное число. Такой закон можно задать различными способами. Например, выберем произвольное множество S в пространстве. Положим F(x,y,z) = 0, если точка с координатами (ж; у; z) принадлежит множеству 5, и F(x,y,z) = 1 в противном случае. Тогда уравнение F(#,y,z) = 0 будет задавать в точности множество S.
В рамках аналитической геометрии рассматривают уравнения F(x,y,z)=0 (F(z,y) — 0 на плоскости), для которых функция F является многочленом.
Определение 3.3. Многочленом от п переменных Ж1, ..., хп называют функцию вида
т
F(X\f.,Xn)—
г1+-‘«+«П=0
где ii, ..., in — целые неотрицательные числа;	—
действительные числа, причем хотя бы один из коэффициентов
Для которых + ... + in = m, не равен нулю. Число т называют степенью многочлена от п переменных.
3,5. Кривые и поверхности
93
Определение допускает нулевое значение степени многочлена. Независимо от числа переменных многочлены нулевой степени имеют вид F = ao,...,o и являются постоянными функциями. Вид многочленов первой степени зависит от количества переменных. Например, F = 2х - 4у + 5z - 1 — многочлен первой степени от трех переменных, a F = х - у + З — многочлен первой степени от двух переменных. При п < к любой многочлен степени m от п переменных можно рассматривать как многочлен той же степени от к переменных, т.е. от большего числа переменных.
Уравнение F(xi,...,xn) = 0, в левой части которого стоит многочлен от п переменных, называют алгебраическим.
Определение 3.4. Алгебраической поверхностью называют геометрический образ в пространстве, соответствующий уравнению F(x,y,z) = 0, где F — многочлен от трех переменных ж, у, z.
Степень многочлена F в уравнении F = О называют порядком уравнения, или его степенью.
Определение 3.5. Алгебраической кривой (или линией) на плоскости называют геометрический образ на плоскости, соответствующий уравнению F(x,y) = 0, где F — многочлен от двух переменных х, у.
При преобразовании системы координат уравнение поверхности (кривой) изменяется. Пусть х, у, z — старые координаты, ж', yf, zf — новые координаты, связанные со старыми уравнениями (3.3), а поверхность в старой системе координат описывается уравнением F(x,y,z) = 0. Тогда, чтобы получить уравнение поверхности в новой системе координат, необходимо в исходное уравнение подставить вместо переменных х, у, z их выражения через новые переменные xf, yf, z'.
В случае алгебраической поверхности (алгебраической кривой) преобразование координат в уравнении приводит к многочлену той же степени, что и степень первоначального урав
94
X СИСТЕМЫ КООРДИНАТ
нения. Действительно, при преобразовании координат степень многочлена не может возрасти, но тогда она не может и уменьшиться, так как при обратном преобразовании она должна была бы возрасти. Следовательно, степень многочлена в уравнении отражает характер самой поверхности (кривой) и не связана с выбором системы координат.
Степень многочлена в уравнении, описывающем данную алгебраическую поверхность (кривую на плоскости), определяется неоднозначно. Например, поверхность, которая задается уравнением F(x,y,^) = 0, где F — многочлен, может быть также описана и уравнением (Р(ж,у,г))2 = 0, порядок которого вдвое больше. Но среди всех уравнений, описывающих данную алгебраическую поверхность (кривую на плоскости), есть уравнение наименьшего порядка.
Определение 3.6. Минимальный порядок уравнения, описывающего алгебраическую поверхность (алгебраическую кривую на плоскости) в прямоугольной системе координат, называют порядком этой поверхности (кривой).
Отметим, что наиболее распространенные кривые на плоскости (прямые и окружности) и поверхности в пространстве (плоскость, сфера, конус), которые изучаются в курсе школьной геометрии, являются алгебраическими порядка 1 или 2.
Кривая в пространстве может рассматриваться как линия пересечения двух поверхностей. Описывая каждую из поверхностей при помощи уравнения в одной и той же системе координат, например Fi(x,y,z) = 0, Р2(х,у,г) = 0, задают и линию пересечения этих поверхностей системой двух уравнений
>1(2Г,У,2) = О,	’
F2(x,y,z) = 0.
Кривые на плоскости или в пространстве можно описывать и другими способами. Так, кривую можно рассматривать как
3.5. Кривые и поверхности
95
траекторию движущейся точки и описывать, задавая коорди-паты точки как функции времени. Мы приходим к системе грех уравнений
< y = V’(«),	(3.15)
Кривая на плоскости может быть описана аналогичной системой двух уравнений. Такие системы называют параметрическими уравнениями кривой, а переменное t — параметром [II]. Его содержательный смысл (время) не является существенным, да и происхождение параметра может быть различным — не только исходя из механической интерпретации кривой как траектории движения.
Если удается исключить параметр из системы (3.15), то получается система двух уравнений, которая характеризует кривую в пространстве как пересечение двух поверхностей. Возможен и обратный переход, при котором в систему двух уравнений вводят дополнительный параметр так, чтобы новая система могла быть представлена в виде (3.15).
Пример 3.4. Кривую в пространстве, заданную системой двух уравнений
Г х2 + у2 - z2 - О,
х — z + 1 — О,
можно задать параметрически. Для этого исключаем из первого уравнения переменную z и получаем ж2 + у2 — (1 + ж)2 = О или у2 = 2ж + 1. Решая последнее уравнение относительно ж, приходим к системе двух уравнений, эквивалентной исходной:
у2 - 1 2
У2 + 1 2
96
3. СИСТЕМЫ КООРДИНАТ
Остается ввести параметр, положив t = у, и записать парам» трические уравнения рассматриваемой кривой:
t2-l х =------
2
y = t, t2 + l Z~ 2
Поверхность в пространстве может быть также задана параметрическими уравнениями, но параметров в этом случае должно быть два.
Пример 3.5, Сфера радиуса R с центром в начале координат описывается параметрическими уравнениями
' х = Rcosdcoscp, < у = jRcos$sin<£>, z = flsintf,
в которых параметр д соответствует географической широте на поверхности Земли, а <р — географической долготе. Пара метры должны изменяться в пределах |$| тг/2, —л < тг.
3.6.	Полярная система координат
Кроме прямоугольной системы координат на плоскости на сто используют полярную систему координат, которая полностью определяется упорядоченной парой несовпадающих
точек О и 01. Первую из них -точку О — называют полюсом полярной системы координат. Из полюса в направлен нии второй точки 01 проводят луч Ор, называемый полярной осью (рис. 3.4).
3.6. Полярная система координат
97
Расстояние между точками О и О\ выбирают в качестве единицы масштаба. Ясно, что полюс полярной системы координат О, ее полярная ось I и установленная единица масштаба однозначно определяют на плоскости положение точки 01. Поэтому выбор этой тройки геометрических объектов часто рассматривают как выбор конкретной полярной системы
координат.
Положение точки М в полярной системе координат фиксируется расстоянием р между точкой М и полюсом О, называемым полярным радиусом, и углом <р между полярной осью и вектором — полярным углом. Полярный радиус и полярный угол составляют полярные координаты точки М па плоскости, которые записывают так: М(р;<р). Полярный угол измеряют в радианах и отсчитывают от полярной оси. Если значение угла положительно, то его отсчитывают против хода часовой стрелки, в противном случае — по ходу часовой стрелки (см. рис. 3.4). Для полюса р = 0, а угол <р не определен. Для остальных точек плоскости р > 0, а полярный угол р определен с точностью до целого кратного 2л*. Поэтому для полярного угла иногда фиксируют промежуток его изменения, например (—тг,тг], [—л*,л*) или [0,2л*).
Координаты точки на плоскости часто записывают как в полярной, так и в прямоугольной системах координат и используют преобразования этих координат друг в друга. Если нет специальных указаний, то при этом подразумевают следующее
взаимное расположение прямоугольной и полярной систем координат (рис. 3.5): полюс полярной системы координат совмещен с началом прямоугольной системы координат; полярная ось совпадает с положительной частью оси абсцисс, а масштаб в полярной системе для вычисле-
I Аналитическая геометрия
98
3. СИСТЕМЫ КООРДИНАТ
ния расстояний берется равным единице длины в прямоугольной системе координат. В этом случае прямоугольные координаты (ж; у) точки М на плоскости выражаются через ее полярные координаты с помощью соотношений (см. рис. 3.5)
х = pcostp, у = psinip.
(3.16)
С учетом ограничения <^€(—7Г,7г] на полярный угол полярные
координаты точки определяются через ее прямоугольные ко
ординаты следующим образом:
Р = \/х2 + у2,
(arctg(y/a:), л-+ arctg(y/a:), —тг + arctg(y/a:), 7г/2,
—тг/2,
х > 0; х < 0, х < 0, х = 0, х = 0,
У> 0;
У	< 0;
У	> 0;
У	< 0.
(3-17)
Пример 3.6. Найдем полярные координаты точек М(3;4) и1У(—1;1).
Для точки М имеем: р = л/З2 + 42 = 5, = arctg(4/3), а для точки N — р= у^(-1)2 + I2 = \/2> <Р = тг + arctg(-l) = Зтг/4.
3.7.	Цилиндрическая и сферическая системы координат
Для введения цилиндрической системы координат в пространстве выберем плоскость Р и зафиксируем на ней некоторую полярную систему координат с полюсом О и полярной осью Ор. Через точку О перпендикулярно плоскости Р проведем ось Oz, выбирая ее направление таким образом, чтобы возрастание полярного угла со стороны положительного направления оси Oz происходило против хода часовой стрелки (рис. 3.6, а). Фиксируем единицу масштаба для расстояния между точками.
3.7. Цилиндрическая и сферическая системы координат
99
Цилиндрическими координатами точки М в пространстве называют упорядоченную тройку чисел р, <р, 2, в которой (р; ср) — полярные координаты ортогональной проекции точки М на плоскость Р, a z — ортогональная проекция игктора 0$ на ось Oz (см. рис. 3.6, а).
Координата р точки М равна ее расстоянию до оси Oz. Название этой системы (цилиндрическая) связано с тем, что точки с одинаковой первой координатой р образуют боковую поверхность неограниченного прямого кругового цилиндра радиуса р.
На рис. 3.6, б показано стандартное взаимное расположение цилиндрической и прямоугольной систем координат в пространстве. Плоскость Р совмещена с координатной плоскостью прямоугольной системы координат, проходящей через оси абсцисс и ординат, и в этой плоскости согласованы полярная и прямоугольная системы координат. Ось Oz цилиндрической системы координат автоматически совпадает с осью аппликат. При таком взаимном расположении цилиндрической и прямоугольной систем координат прямоугольные координаты (х; у; z) точки М выражаются через ее цилиндрические координаты (р; <р; z) с помощью равенств
х = pcoscp, у = psin<p,
(3.18)
Z — Z.
100
3. СИСТЕМЫ КООРДИНАТ
Для нахождения цилиндрических координат по прямоугольным можно воспользоваться (3.17) с учетом того, что третьи координаты любой точки в этих системах совпадают.
Сферическая система координат в пространстве вводится примерно так же, как и цилиндрическая. Отличие имеется лишь в определении первой и третьей координат точки. Сферическими координатами точки М в пространстве называют упорядоченную тройку чисел р, <р, $, в которой р — длина вектора <р — полярный угол ортогональной проекции точки М на плоскость Р, а д — угол, который образует вектор с положительным направлением оси Oz (рис. 3.7, а).
Замечание 3.1. Используют и другой вариант сферической системы координат, в которой в качестве угла д берется угол между вектором ОЙ и плоскостью Р. #
Отметим, что д G [0,яг], а сферическая координата р точки равна ее расстоянию до точки О. Название системы (сферическая) соответствует тому, что точки с одинаковой первой координатой р образуют поверхность сферы радиуса р с центром в точке О.
Рис. 3.7
Для стандартного взаимного расположения сферической и прямоугольной систем координат в пространстве (рис. 3.7, 6) преобразования координат имеют вид:
х = psin$cos<p,
у = psintfsincp,	(3.19)
z = pcostf
Вопросы и задачи
101
р= \/x2 + y2 + z2,
'О = arccos
z y/x2+y2 + z2>
arctg(y/ar), л + arctg(y/a;), -7r + arctg(j//a:), 7Г/2, -7t/2,
x > 0; x < 0, x < 0, x — 0, x — 0,
y> 0;
У < 0;
У > 0;
У < 0.
(3.20)
Замечание 3.2. В цилиндрической и сферической системах координат могут накладываться ограничения на возможные значения угла у?, отмеченные выше для полярной системы координат, с тем чтобы этот угол определялся для каждой точки однозначно. Значение второй координаты <р в этих системах дли точек оси Oz не определено, и положения таких точек полностью определяются значениями двух других координат.
Вопросы и задачи
3.1.	Доказать, что если уравнение х2 + ху + у — 1 = 0 записать в новых координатах ж', yf с помощью преобразования
координат
х = оцх'+ fiiy', у = а2х‘ + 02у',
то при
«1 01
«2 02
/0
порядок уравнения не изменится. Привести пример, показы-пающий, что при нарушении этого условия порядок может уменьшиться.
3.2.	Найти преобразование координат на плоскости: а) при параллельном переносе системы координат на вектор {-3;5}; 6) при повороте на угол — л/3.
102
3. СИСТЕМЫ КООРДИНАТ
3.3.	Выяснить, задают ли формулы: а) х = xf + yf, у = х1 -- у7; б) х = 0,5а/ - л/з у'/2? У ~ V^x*/2 + 0,5у' поворот системы координат на плоскости. Если задают, найти угол поворота.
3.4.	Найти расстояние между точками М\ и М2, если они заданы своими полярными координатами и ^2,^2 соответственно.
3.5.	Окружность радиуса а катится без скольжения по оси абсцисс в ее положительном направлении, вращаясь с угловой скоростью 1 рад/с. В момент времени t = 0 точка М окружности совпадает с началом системы координат. Доказать, что эта точка движется по циклоиде x — a(t — sinf), у = а(1 — cos^). Построить эту кривую.
3.6.	Нарисовать на плоскости кривую, по которой движется точка с координатами я = sin£, г/ = sin2Прокомментировать это движение точки.
3.7.	Доказать, что множество точек на плоскости, произведение расстояний от которых до точек Fi(—а; 0), ^(0; а) есть величина постоянная, равная а2, представляет собой кривую (лемнискату), которая описывается уравнением (ж2 + у2)2 = = 2а2(х2 — у2). Записать уравнение этой кривой в полярной системе координат и построить кривую.
3.8.	Что представляют собой множества точек в пространстве, равноудаленных от точек: а) 4(0; 0; -10), В(0;0;10); б) 4(1; 1;0), В(-1; -1;0); в) 4(1; 2; 3), В(-1; -2; -3) ? Построить соответствующие геометрические образы и найти их уравнения.
3.9.	Найти координаты центра масс системы четырех материальных точек одинаковой массы т, расположенных на плоскости, если даны их координаты (5; 9), (1; -7), (-4; -8), (2; 2).
3.10.	Найти объем четырехугольной пирамиды SABCD, если в ее основании лежит параллелограмм ABCD и известны координаты вершин S(-5;l;9), 4(1; 3; -7), В(-4;-2;8),
Вопросы и задачи
103
( ’( 2; 1;2). Чему равна высота этой пирамиды, опущенная из вершины 5?
3.11.	Луч света, исходящий из точки А(-2;4) в сторону «н и абсцисс, после зеркального отражения от этой оси прошел через точку В(4; 12). Найти координаты точки отражения и гочки пересечения луча с осью ординат.
3.12.	Найти угол, под которым из начала прямоугольной системы координат виден отрезок, соединяющий точки //(4; 10; 8) и С(2;2;2).
3.13.	Доказать, что два ортонормированных базиса в пространстве, имеющих одинаковую ориентацию, можно совместить друг с другом при помощи поворота вокруг некоторой оси. Найти вектор, задающий направление этой оси, и угол поворота.
3.14.	Найти координаты центра масс треугольника с вершинами А(-1; 7; 4), В(13; 5; 2), С(7; —1; -4), если масса треугольника равномерно распределена по его площади.
3.15.	На плоскости расположены три точки А(1+£; 3 — f), /1(3 - 6 + 2Z) и С(—1+£;£). Выяснить, при каких значениях параметра t из точки А не видна точка С.
3.16.	Доказать, что в полярной системе координат расстояние между точками	и М2(р2^2) вычисляется по
формуле
|М1М2| = Jp\ -2/>ip2cos(<£i - у?2)+р2.
4.	ПРЯМАЯ НА ПЛОСКОСТИ
4.1.	Алгебраические кривые первого порядка
Остановимся на изучении алгебраических кривых первого порядка на плоскости, т.е. кривых, которые в некоторой прямоугольной системе координат описываются алгебраическим уравнением первого порядка ах + Ьу + с = 0, где хотя бы один из коэффициентов а или b отличен от нуля1. Это уравнение называют также линейным уравнением.
Теорема 4.1. Любая прямая на плоскости представляет собой алгебраическую кривую первого порядка и любая алгебраическая кривая первого порядка на плоскости есть прямая.
◄ Рассмотрим произвольную прямую L на плоскости. Пусть точка Мо(жо;уо) лежит на L, а ненулевой вектор п = {а; Ь} перпендикулярен этой прямой. При таких исходных условиях произвольная точка М(х;у) принадлежит прямой L тогда и только тогда, когда вектор ортогонален вектору п
(рис. 4.1)
Зная координаты векторов Mq
Рис. 4.1
= {ж — ж0; у — уо} и п, запишем условие ортогональности этих векторов через их скалярное произведение: а(ж — жо) + + Ь(у - у0) = 0 или ах + by + с = 0, где с = —ажо - Ьуо- Так как п / О, то либо а / 0, либо 6/0. Первое утверждение теоремы доказано.
1 Условие, что коэффициенты а и b одновременно не обращаются в нуль,
коротко можно записать так: а2 4- Ъ2 0.
4Л. Алгебраические кривые первого порядка	105
Для доказательства второго рассмотрим произвольное уравнение первого порядка с двумя неизвестными ax + Ьу + с= 0, а2 |-62 0. Это уравнение имеет хотя бы одно решение. Например, если а / 0, то решением уравнения является х = —с/а,у = 0. )то значит, что геометрический образ уравнения является непустым и содержит какие-то точки. Пусть точка Мо(а?о;Уо) принадлежит указанному образу, т.е. выполняется равенство н.г0 + Ьуо + с = 0. Вычтем это равенство из рассматриваемого уравнения. В результате получим новое уравнение, эквивалентное исходному. Это новое уравнение после перегруппировки слагаемых примет вид
а(х - ж0) 4- b(y - t/o) = 0.	(4.1)
Нетрудно увидеть, что полученное уравнение представляет со-Пой условие ортогональности векторов п '= {а; Ъ} и где Л/ — это точка с координатами (z; у). Следовательно, если точка М(х;у) принадлежит геометрическому образу уравнения ах + by + с —0, то вектор п ортогонален вектору МоЛ/, т.е. точка М лежит на прямой, проходящей через точку Mq перпендикулярно вектору п. ►
Определение 4.1. Уравнение вида
аж+ &/ + с= 0, а2 + 62^0,	(4.2)
называют общим уравнением прямой.
Из доказательства теоремы 4.1 следует, что коэффициенты а и b в общем уравнении прямой имеют простой геометрический смысл. Это координаты вектора, перпендикулярного прямой. Такой вектор называют нормальным вектором прямой. Он, как и общее уравнение прямой, определяется с точностью до (ненулевого) числового множителя.
Пусть прямая L задана уравнением (4.2). Если точка (а:© 5 З/о) лежит на прямой L, то ее координаты удовлетворяют
106
4. ПРЯМАЯ НА ПЛОСКОСТИ
уравнению (4.2), т.е. ахо + Ъуп + с = 0. В любой точке Mi(xi; j/i), не лежащей на прямой L, значение левой части уравнения (4:2) равно
axi + byi + с = axi + byi - axQ - Ьуо =
- a(a:i - xQ) + b(yi - t/0) = пМ0М1 / 0.
Знак скалярного произведения nMQM\ определяется углом между вектором MqMi и нормальным вектором прямой п. Если точки Mi и М2 расположены по одну сторону от прямой L (рис. 4.2, а), то, подставив их координаты в левую часть уравнения (4.2), мы получим значения с одним знаком. Если такая подстановка координат точек М\ и М2 приводит к значениям с разными знаками, то эти точки лежат по разные стороны от прямой L (рис. 4.2, б).
а	б
Рис. 4.2
Пример 4.1. Выясним, как по отношению к прямой Зж-4у + 5 —0 расположены точки А(4; 4) и В(б;6).
Подставив координаты точки А в левую часть общего уравнения прямой, получим положительное число 1, а подстановка координат точки В приводит к отрицательному числу —1. Значит, точки А и В расположены по разные стороны от данной прямой. #
4.2. Специальные виды уравнения прямой
107
Уравнение (4.1) очень полезно при решении задач. Оно 1НМ1ЮЛЯСТ по координатам точки на прямой L и координатам нормального вектора прямой L записать уравнение прямой без промежуточных вычислений.
4.2. Специальные виды уравнения прямой
Кроме общего уравнения прямой на плоскости часто исполняют и другие уравнения прямой. Это связано с тем, что, в записи мости от геометрического описания прямой на плоскости, пр уравнение может быть получено в некотором специальном ни де. Кроме того, каждому виду уравнения соответствует свой геометрический смысл его коэффициентов, что также важно. Фиксируем на плоскости прямоугольную систему координат (Лчу.
Уравнение с угловым коэффициентом. Определим
прямую L на плоскости, задав точку Мо(ж0;уо) на этой прямой и угол у?, на который надо повернуть против хода часовой • грелки ось абсцисс Ох до совмещения с прямой (рис. 4.3).
Предположим, что <р^7г/2.
Точка М(х;у) принадлежит прямой L тогда и только тогда, когда вектор Мо^ составляет • ОСЬЮ Ох УГОЛ <р ИЛИ 7Г — у?, при этом отношение координат • roi'o вектора равно tgy>. Это vc/ювие можно записать в виде
У-Уо f -----= tg¥>.
X — Xq
Рис. 4.3
Находя у, приходим к уравнению
у — kx + 6,
(4-3)
। д<- k = tgy?; b = у0 - zotg¥>.
108
4. ПРЯМАЯ НА ПЛОСКОСТИ
Уравнение вида у = кх + b называют уравнением прямой с угловым коэффициентом. Параметр к (угловой коэффициент прямой) равен тангенсу угла наклона прямой. Па* раметр b равен ординате точки пересечения прямой с осью Оу.
Векторное и параметрические уравнения прямой. Определим прямую L на плоскости точкой Мо(яо;Уо) на этой прямой и ненулевым вектором s —	параллельным ей
(рис. 4.4). Такой вектор з называют направляющим вектором прямой L.
Если точка М(х-,у) принадлежит прямой L, то это эквивалентно тому, что вектор A/qAI коллинеарен вектору з, т.е. эти
Воспользовавшись тем,
векторы принадлежат одному и тому же пространству Vi. Так как вектор з не равен нулевому^ он образует базис в этом пространстве Vj. Следовательно, для некоторого числа t выполняется равенство = ts.
что — {х - хо] у - уо}, з =
= {/; т}, запишем это равенство в координатах:
X	Xq —— It,
У “ Уо = rnt,
или
х = Xq + It, У = Уо + mt.
(4-4)
Уравнения (4.4) называют параметрическими уравнениями прямой. Точка Л1(жо;уо), лежащая на прямой, соответствует значению параметра t = 0.
Если равенство MqA% = ts записать через радиус-векторы г0 и г точек Mq и М соответственно, то в результате получим
4.2, Специальные виды уравнения прямой
109
векторное уравнение прямой
r — rQ — ts, или г —r0 + fs.	(4.5)
Каноническое уравнение прямой. Модифицируем вы-мид параметрических уравнений прямой. Коллинеарность век-юров и з, согласно следствию 1.1, эквивалентна равен-। гну отношений их одноименных координат:
х-хр^у-уо	(46)
Z т
Уравнение (4.6) называют каноническим уравнением прямой. Это уравнение можно также получить, исключив из нпраметрических уравнений (4.4) параметр t.
Уравнение прямой, проходящей через две точки. Зададим прямую L на плоскости двумя различными точками A/i(xi,yi) и М2(х2,у2) на ней.
'Тогда вектор М1М2 параллелен L и ее каноническое урав-н<ч1ие (4.6) как уравнение прямой, проходящей через точку
Л/|(^1,У1), с направляющим вектором з = М1М2, имеет вид
х~х' = У~У1 Х2 ” Xi У2- У1
Уравнение (4.7) называют уравнением Прямой, проходящей через две точки.
Уравнение прямой в отрезках. Определим прямую L ее Iочками А(а,0) и В(0,6) пересечения с осями координат, предполагая, что эти две точки не совпадают с началом системы координат, т.е. что а^0и6/0 (рис. 4.5).
Записывая уравнение прямой L в виде (4.7) по двум ее точкам А и В, получаем
х — а у — 0
0-а = 6-0’
110
4. ПРЯМАЯ НА ПЛОСКОСТИ
Рис. 4.5
(4,<Ч)
откуда — х/а + 1 = у/b, или
х у - + i = i. а о
Уравнение прямой (4.8) называют уравнением прямой в отрез-
ках.
Нормальное уравнение прямой. Определим прямую L при помощи перпендикулярного ей единичного вектора п и расстояния
р > 0 до прямой от начала системы координат. Существуют два единичных вектора, перпендикулярных прямой L. Из этих двух выберем тот, который имеет начало в точке О и направлен „в сторону прямой44 L (рис. 4.6).
Выбранный вектор п однозначно определяется своим углом с осью Ох, который отсчитывается против хода часовой
стрелки. Координаты вектора п легко вычисляются через этот угол: п = {cos<^; sin
Условие, что точка М(х\ у) принадлежит прямой L, эквивалентно тому, что ортогональная проекция радиус-вектора точки М на направление нормального вектора прямой равна рассто-
янию р от точки О до прямой: прп— р (см. рис. 4.6). Проекция прп Ол1 совпадает со скалярным произведением векторов 0$ и п, так как длина нормального вектора п равна, единице, и это приводит к равенству Ол/п = р. Записав скалярное произведение Ол1п в координатах, получим уравнение прямой L в виде
х costp + ysin <р — р = 0.
(4-9)
4.3. Взаимное расположение двух прямых
111
Уравнение (4.9) называют нормальным уравнением прямой. Параметрами в этом уравнении являются угол между нормальным вектором прямой и осью Ох и расстояние от напила системы координат до прямой.
Общее уравнение прямой ах + by 4- с = 0 можно преобра-юпать в ее нормальное уравнение делением на нормирующий множитель ±л/я2 + 62, знак которого выбирается противоположным знаку с. По абсолютной величине нормирующий множитель представляет собой длину нормального вектора {а; Ь} примой, а выбор знака означает выбор нужного направления из двух возможных. Если с = 0, то прямая проходит через начало ьоординат (р = 0). В этом случае знак нормирующего множителя можно выбирать любым.
Пример 4.2. Для получения нормального уравнения прямой из ее общего уравнения Зх — 4у+10 = 0 вычисляем нормирующий множитель + Ь2, который для данной прямой отрицателен и равен —д/32 + 42 = —5. Поэтому нормальное уравнение прямой имеет вид
3	4 Л Л
--ж + -у-2 = 0.
5	5
В данном случае имеем р = 2, cosy? =—3/5, sin9? = 4/5, а 7* arccos(—3/5).
4.3.	Взаимное расположение двух прямых
Фиксируем на плоскости прямоугольную систему координат. Две прямые на плоскости могут быть параллельными или пересекаться. Пересекающиеся прямые могут быть перпендикулярными. Какая из этих возможностей реализуется для прямых Zi и Лз? всегда можно выяснить с помощью их общих уравнений
Ц: aix + hy + ci = 0,
Z/2’ CL2X + b2y + C2 = 0.
112
4. ПРЯМАЯ НА ПЛОСКОСТИ
Действительно, для параллельности прямых L\ и L2 необходп мо и достаточно, чтобы были коллинеарными их нормальны! векторы ni = {ад Ь\} и П2 = {ад ^2}, а, коллинеарность вокто ров равносильна пропорциональности их координат. Поэтому
Li||L2 о — = ^.	(4.10)
а2 &2
Так как последнее равенство преобразуется в соотношениг ai&2 — <*2^1 = 0, то полученное условие параллельности двух прямых можно записать при помощи определителя второго порядка:
л,нл2 «	«и>
Прямые Li и L2 перпендикулярны тогда и только гг<» гда, когда ортогональны их нормальные векторы. Условие ортогональности нормальных векторов п\ — {ад 61} и = {адб2} эквивалентно равенству нулю их скалярного проиэ ведения П\П2 ~ 0, т.е., согласно (2.12), условию
^1^2 +^1^2 — 0-	(4.12)
И условие параллельности, и условие перпендикулярности можно записать через угловые коэффициенты прямых. Для этого необходимо выразить угловые коэффициенты прямых через коэффициенты их общих уравнений: ki — —a\/b\, к2 — —02/1)2- Эти выражения позволяют записать условия (4.10) и (4.12) следующим образом:
-	условие параллельности:	к\ ~к2\
-	условие перпендикулярности: к\к} = — 1.
Две пересекающиеся прямые и L2 образуют два смежных2 угла. Один из этих углов совпадает с углом между нормальными векторами. А угол между двумя векторами можно вычислить при помощи скалярного произведения. Отметим, что
2Два смежных угла в сумме дают 180°.
4.4. Расстояние от точки до прямой
ИЗ
косинусы двух смежных углов различаются знаками, так как cos(tt — </?) = — cos<p. При этом положительное значение косинуса, соответствует острому углу. Значение <р (меньшего из углов между прямыми L\ и Л2) вычисляется согласно формуле
_ |П1П2| _	|<31<а2 + 6162!
lnl I 1п2 |	д/а? + &1 х/°2 + Й2
Угол между прямыми можно также выразить через угловые коэффициенты прямых. Этот угол представляет собой разность углов наклона прямых. Если k\ — tg</?i и fc2 = tg</?2 — угловые коэффициенты прямых L\ и £2, то
+ (	\ кх-к2
tgv? = tg(<^i - р2) = : ;тг 1 + к\к2
Приведенная формула учитывает не только значение угла, но и направление поворота вокруг точки пересечения
при котором прямая L2 совмещается с прямой L\. Прямую L2 можно поворачивать как по ходу часовой стрелки, так и в противоположном направлении. Два возможных угла поворота (без учета знака) в сумме равны 180°. Значение острого угла поворота с учетом его направления определяется по формуле
кг - к2
прямых,
4.4.	Расстояние от точки до прямой
Для вычисления расстояния от данной точки М до прямой L можно использовать разные способы. Например, если на прямой L взять произвольную точку Л/о, то можно определить ортогональную проекцию вектора на направление нормального вектора прямой. Эта проекция с точностью до знака и есть нужное расстояние.
Другой способ вычисления расстояния от точки до прямой основан на использовании нормального уравнения прямой.
114
4. ПРЯМАЯ НА ПЛОСКОСТИ
Пусть прямая L задана нормальным уравнением (4.9). Если точка М(х;у) не лежит на прямой L, то ортогональная про екция прпОл! радиус-вектора точки М на направление еди яичного нормального вектора п прямой L равна скалярному произведению векторов ОА% и п, т.е. xcos^ + ysinc^. Эта же проекция равна сумме расстояния р от начала координат до прямой и некоторой величины 8 (рис. 4.7). Величина 8 по аб солютной величине равна расстоянию от точки М до прямой. При этом 8 > 0, если точки М иО находятся по разные стороны от прямой, и 8 < 0, если эти точки расположены по одну сто рону от прямой. Величину 8 называют отклонением точки
М от прямой.
Рис. 4.7
Отклонение 8 для точки М(х\у) от прямой L вычисляется как разность проекции прпОА^ и расстояния р от начала ко
ординат до прямой (см. рис. 4.7), т.е. 6 — xcos<^ + ysin</? — р.
По этой формуле можно получить и расстояние p(M,L) от точки М(х\у) до прямой L, заданной нормальным уравнением:
p(M,L) = \8\ = \xcos<p+ysin<p--p\.
Учитывая приведенную выше процедуру преобразования общего уравнения прямой в ее нор
мальное уравнение, получаем формулу для расстояния от точки М(х\у) до прямой L, заданной своим общим уравнением:
(4.13) V а2 + Ъ2
Пример 4.3. Найдем общие уравнения высоты АН, медианы AM и биссектрисы AD треугольника АВС, выходящих из вершины А. Известны координаты вершин треугольника А(—1; —3), В(7; 3), <7(1; 7).
4.4. Расстояние от точки до прямой
115
Прежде всего уточним условие примера: под указанными уравнениями подразумевают уравнения прямых Ьдн, и / на которых расположены соответственно высота АН, медиана AM и биссектриса AD указанного треугольника (рис. 4.8).
Чтобы найти уравнение прямой Ьдм, воспользуемся тем,
чт<> медиана делит противоположную сторону треугольника по-
полам. Найдя координаты (а^; t/i) середины стороны ВС х± =
(7 + 1)/2 = 4, У1 = (3 + 7)/2 =
Г), записываем уравнение для 1..\М в виде уравнения прямой, проходящей через две точки,
а + 1 _ у + 3 4+1 “ 5 + 3’
После преобразований получаем общее уравнение медианы
Рис. 4.8
8х — 5у — 7 = 0.
Чтобы найти уравнение высоты Ьдн, воспользуемся тем, •i'1'о высота перпендикулярна противоположной стороне треугольника. Следовательно, вектор перпендикулярен высоте АН и его можно выбрать в качестве нормального вектора прямой Ьдн- Уравнение этой прямой получаем из (4.1), подставляя координаты точки А и нормального вектора прямой 1'АН-
(-6)(х + 1) + 4(у + 3) = 0.
После преобразований получаем общее уравнение высоты
Зя-2у —3 = 0.
Чтобы найти уравнение биссектрисы Lad, воспользуемся тем, что биссектриса AD принадлежит множеству тех точек
116
4. ПРЯМАЯ НА ПЛОСКОСТИ
N(x; у), которые равноудалены от прямых Lab и Lac- Уравнение этого множества имеет вид
p(N,LAB) = p(N,LAC),	(4.14)
и оно задает две прямые, проходящие через точку А и делящие углы между прямыми Lab и Lac пополам. Воспользовавшись уравнением прямой, проходящей через две точки, найдем общие уравнения прямых Lab и Lac'-
. ж+1_у+3	. ж+1_у+3
Ав: 7 + 1	3 + 3’ АС: 1 + 1“7 + 3’
После преобразований получаем
Lab- Зя —4у—9 = 0, LAc- 5я-у + 2 = 0.
Уравнение (4.14) с помощью формулы (4.13) для вычисления расстояния от точки до прямой запишем в виде
|3x-4t/ —9| _ |5я —t/ + 2| ^32+(_4)2 = ^52 + (_1)2-
Преобразуем его, раскрыв модули:
5х — v + 2 Зя-4у-9 = ±5-----.
л/26
В итоге получим общие уравнения двух прямых
(3 т 25/л/26)ж + (-4 ± 5/Т26)г/ + (-9 Т 10/726) = 0.
Чтобы выбрать из них уравнение биссектрисы, учтем, что вершины В и С треугольника расположены по разные стороны от искомой прямой и поэтому подстановки их координат в левую часть общего уравнения прямой Lad должны давать значения с разными знаками. Выбираем уравнение, соответствующее верхнему знаку, т.е.
(3 - 25/726)* + (-4 + 5/75б)у + (-9 - 10/7^6) = 0.
Вопросы и задачи
117
Подстановка координат точки В в левую часть этого уравнения дает отрицательное значение, поскольку
(3 - 25/л/26)7 + (-4 + 5/>/26)3 + (-9 - 10/^26) =
= 21 - 12 - 9 + (-175 + 15 - 10)/V26 = -170/v^6, и такой же знак получается для координат точки С, так как (3 - 25/х/26)1 + (-4 + 5/л/2б)7 + (-9 - 10/\/5б) =
= 3 - 28 - 9 + (-25 + 35 - 10)/\/5б = -34 < 0. Следовательно, вершины В и С расположены по одну сторону прямой с выбранным уравнением, а потому уравнением биссектрисы является
(3 + 25/-\/26)ж + (-4 - 5/-\/26)у + (-9 + 10/^26) = 0.
Вопросы и задачи
4.1.	Найти общее уравнение прямой: а) проходящей через начало системы координат; б) параллельной оси абсцисс (ординат).
4.2.	Выяснить расположение точек 4(2;—1), 13(8; 19) и (7(7; 17) относительно прямой х = 1 +t, у = — 2 + 3L
4.3.	Найти точку пересечения прямых х = 2 + £, у = — 4 — 2t и Зя + 5у- 7 = 0.
4.4.	Найти координаты точки, симметричной точке 4(3; 7) относительно прямой: а) х = -2 - t, y — ^ + t\ б) 2х - 5у + 5 = 0.
4.5.	Найти координаты точки пересечения высот треугольника с вершинами в точках 4(3; -4), 13(—5; 10) и С(6;4).
4.6.	Луч света, вышедший из точки 4(1; 4), прошел на одинаковом расстоянии от точек 13(-2; 6) и С(7;3). Найти уравнение его траектории.
118
4. ПРЯМАЯ НА ПЛОСКОСТИ
4.7.	Найти уравнения сторон параллелограмма ABCD, если известны координаты его двух вершин А(—1;-2), В(3;—4) и точки Л/ (0; 1) пересечения диагоналей.
4.8.	Прямая, проходящая через точку Л/(1;4) и не проходящая через начало системы координат, отсекает от первой четверти координатной плоскости треугольник минимальной площади. Найти ее уравнение.
4.9.	Найти уравнение прямой, которая касается окружности радиуса 2 с центром в начале системы координат и проходит через точку Af(3; 1).
4.10.	Найти расстояние между прямыми: а) х = — 2 + £, у = = 3 + 2t и 2х - у + 8 = 0; б) х = 2-3t, у=Ц-£и2ж + у + 3 = 0.
4.11.	Найти координаты вершин квадрата по уравнению одной из его сторон Зх — 4у + 20 = 0 и точке М(—3; 4) пересечения его диагоналей.
4.12.	Найти угол между медианой и высотой треугольника АВС, выходящими из вершины Л (Г, —5), если известны координаты точки М(2; 1) пересечения его медиан и вершины В(5; 0).
4.13.	Найти уравнение множества точек на плоскости, которые удалены от прямой (ж — 2)/3 = (у + 1)4 в два раза дальше, чем от прямой х = 1 — 12£, у = 5 + 5t.
4.14.	Доказать, что медианы (высоты, биссектрисы) треугольника пересекаются в одной точке.
4.15.	Найти площадь треугольника, если известны координаты его двух вершин А(1; 6), В(3; 8) и точки пересечения: а) медиан Af(4; -4); б) высот Я(5;0).
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
5.1.	Алгебраические поверхности первого порядка
Уравнение первого порядка с тремя неизвестными имеет вид Ах + By + Cz + D = 0, причем хотя бы один из коэффициентов Л, В, С должен быть отличен от нуля. Оно задает в пространстве в прямоугольной системе координат Oxyz алгебраическую поверхность первого порядка.
Свойства алгебраической поверхности первого порядка во многом аналогичны свойствам прямой на плоскости — геометрическому образу уравнения первого порядка с двумя неизвестными.
Теорема 5.1. Любая плоскость в пространстве является поверхностью первого порядка и любая поверхность первого порядка в пространстве есть плоскость.
◄ Как утверждение теоремы, так и ее доказательство аналогичны теореме 4.1. Действительно, пусть плоскость 7Г задана своей точкой Мо и ненулевым вектором п, который ей перпендикулярен. Тогда множество всех точек в пространстве разбивается на три подмножества. Первое состоит из точек, принадлежащих плоскости, а два других — из точек, расположенных по одну и по другую стороны плоскости. Какому из этих множеств принадлежит произвольная точка М пространства, зависит от знака скалярного произведения пМ^яЖ. Если точка М принадлежит плоскости (рис. 5.1, а), то угол между векторами п и MoJll прямой, и поэтому, согласно теореме 2.1,
120	5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Рис. 5.1
Если же точка М не принадлежит плоскости, то угол между векторами п и А10л) острый или тупой, и поэтому пМоЛ/ > 0 или пМол/ < 0 соответственно (см. доказательство теоремы 2.1), причем знак этого скалярного произведения один и тот же для всех точек, расположенных по одну сторону от плоскости (рис. 5.1, 6).
Обозначим координаты точек Mq, М и вектора п через (ж0; Уо; ^о), (я; у; и {А; В; С} соответственно. Так как Mq$ = = {х — xq; у — уо; z — zq}> то, записывая скалярное произведение из (5.1) в координатной форме (2.9) как сумму попарных произведений одноименных координат векторов п и MqA%, получаем условие принадлежности точки М рассматриваемой плоскости в виде
А(х - Xq) + В(у - Уо) + C(z - Zq) = 0.	(5.2)
Раскрытие скобок дает уравнение
Ах + By + Cz + D — 0,	(5.3)
где D = — Axq — Byo — Czq и хотя бы один из коэффициентов А, В, или С отличен от нуля, так как вектор п = {А; В; С}
5.1, Алгебраические поверхности первого порядка	121
ненулевой. Это означает, что плоскость является геометрическим образом уравнения (5.3), т.е. алгебраической поверхностью первого порядка.
Проведя изложенное доказательство первого утверждения теоремы в обратном порядке, мы докажем, что геометрическим образом уравнения Ах + By + Cz + D = О, А2 + В2 + С2 О, является плоскость. Выберем три числа (ж = жо, у = уо> удовлетворяющих этому уравнению. Такие числа существуют. Например, при А / 0 можно положить у0 = 0, zq = 0 и тогда хо = —D/А. Выбранным числам соответствует точка Л^о(^о; Уо; ^о)? принадлежащая геометрическому образу заданного уравнения. Из равенства Axq + Ву0 + Czq + D = 0 следует, что D = — Axq — Вуо - С z$. Подставляя это выражение в рассматриваемое уравнение, получаем
Ах + By + Cz - Axq - Syo - Cz$ = О,
что равносильно (5.2). Равенство (5.2) можно рассматривать как критерий ортогональности векторов п = {Л; В; С} и М0Л%, где точка М имеет координаты (х; у, z). Этот критерий выполнен для точек плоскости, проходящей через точку Mq перпендикулярно вектору п = {А;В;С}, и не выполнен для остальных точек пространства. Значит, уравнение (5.2) есть уравнение указанной плоскости. ►
Уравнение Ax + By + Cz + D = 0 называют общим уравнением плоскости. Коэффициенты А, В, С при неизвестных в этом уравнении имеют наглядный геометрический смысл: вектор п = {А; В; С} перпендикулярен плоскости. Его называют нормальным вектором плоскости.
По известным координатам точки, принадлежащей некоторой плоскости, и ненулевого вектора, перпендикулярного ей, с помощью (5.2) уравнение плоскости записывается без каких-либо вычислений.
122
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Пример 5.1. Найдем общее уравнение плоскости, перпендикулярной радиус-вектору точки Л(2; 5; 7) и проходящей через точку Л/о(3; —4; 1).
Поскольку ненулевой вектор оХ = {2; 5; 7} перпендикулярен искомой плоскости, то ее уравнение типа (5.2) имеет вид
2(х - 3) + 5(г/ + 4) + 7(z- 1) = 0.
Раскрывая скобки, получаем искомое общее уравнение плоскости 2х + 5у + 7z + 7 = 0.
5.2.	Специальные виды уравнения плоскости
Векторное и параметрические уравнения плоскости. Пусть Го и г — радиус-векторы точек Mq и М соответственно. Тогда MqA% = г — го, и условие (5.1) принадлежности точки М плоскости, проходящей через точку Mq перпендикулярно ненулевому вектору п (рис. 5.2, а), можно записать с помощью скалярного произведения в виде соотношения
п(г - Го) = О,
(54)
которое называют векторным уравнением плоскости.
Рис. 5.2
Фиксированной плоскости в пространстве соответствует множество параллельных ей векторов, т.е. пространство
5.2. Специальные виды уравнения плоскости
123
Выберем в этом пространстве базис е1?е2, т.е. пару неколли-неарных векторов, параллельных рассматриваемой плоскости, и точку Mq на плоскости. Если точка М принадлежит плоскости, то это эквивалентно тому, что ей параллелен вектор MqAJ (рис. 5.2, б), т.е. он принадлежит указанному пространству V2-• )то означает, что существует разложение вектора MqA^ в базисе ei,e2, т.е. существуют такие числа и t2) Для которых
= t\ei + t2e2-
Записав левую часть этого уравнения через радиус-векторы го и г точек Mq и М соответственно, получаем векторное параметрическое уравнение плоскости
г = го + hei + t2e2,	(5.5)
Чтобы перейти от равенства векторов в (5.5) к равенству их координат, обозначим через (xq; уо5 ^0), (я; У', z) координаты точек Mq, М и через {е^;	е^}, {е2х; е2у\e2z} координа-
ты векторов ei, е2. Приравнивая одноименные координаты векторов г и го +	+ t2e2, получаем параметрические
уравнения плоскости
{х = xq -j- t\e\x + t2e2x,
У — Уо +	(5-6)
z~ Zq + t\e\z + t2e2z-
Плоскость, проходящая через три точки. Предположим, что три точки Mi, М2 и М% не лежат на одной прямой. Тогда существует единственная плоскость тг, которой эти точки принадлежат. Найдем уравнение этой плоскости, сформулировав критерий принадлежности произвольной точки М данной плоскости тг. Затем запишем этот критерий через координаты точек. Указанным критерием является описание плоскости тг как множества тех точек М, для которых векторы М1Л/2, М1М3 и MiA^ компланарны. Критерием
124 5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
компланарности трех векторов является равенство нулю их смешанного произведения (см. 2.4). Смешанное произведение вычисляется с помощью определителя третьего порядка, строками которого являются координаты векторов в ортонор-мированном базисе. Поэтому, если (x^y^Zi) — координаты точек Мг, г =1,2,3, а (ж; y\z) — координаты точки М, то Mil\i = {х-х1- y-yr, z-Zi}, MlM2 = {x2-x1-, y2-yr, Z2-Zi}, M1M3 — {х^-х^; уз-УС z3~zi} и условие равенства нулю смешанного произведения этих векторов имеет вид
х — #1
Х2 - Х\ хз ~ Х\
У ~ У1
У2-У1
Уз-У1
z — Z1
^2-^1
*3-^1
= 0.
(5-7)
Вычислив определитель, получим линейное относительно х, У> z уравнение, являющееся общим уравнением искомой плоскости. Например, если разложить определитель по 1-й строке, то получим
У2-У1
Уз~У1
Z2-Z1
Z3-Z!
(х -Ж1) -
Ж2-Ж1
ЯЗ-Я1
*2-21
23-21
(у-У1) +
X2-Xi
X3-X1
У2-У1
Уз~У1
(z-zi) = 0.
Это равенство после раскрытия скобок преобразуется к общему уравнению плоскости.
Отметим, что коэффициенты при переменных в последнем уравнении совпадают с координатами векторного произведения М1М2ХМ1М3, Это векторное произведение, будучи произведением двух неколлинеарных векторов, параллельных плоскости тг, дает ненулевой вектор, перпендикулярный тг, т.е. ее нормальный вектор. Так что появление координат векторного произведения в качестве коэффициентов общего уравнения плоскости вполне закономерно.
Рассмотрим следующий частный случай плоскости, проходящей через три точки. Точки Mi(a;0;0), Л/2(0;Ь;0), Л7з(0; 0; с),
5.2. Специальные виды уравнения плоскости	125
abc^ 0, не лежат на одной прямой и задают плоскость, которая отсекает на осях координат отрезки ненулевой длины (рис. 5.3). Здесь под „длинами отрезков66 понимают значение ненулевых координат радиус-векторов точек Мг, г — 1,2,3.
Поскольку М1М2 = {—а; 6; 0}, Mi М3 = {—а; 0; с),	=
= (ж—а; у; г), то уравнение (5.7) принимает вид
х — а у
—a b
—а 0
Вычислив определитель, найдем
Ьс(х — а) + асу + abz = 0, разделим полученное уравнение на abc и перенесем свободный член в правую часть,
Это уравнение называют уравнением плоскости в отрезках.
Пример 5.2. Найдем общее уравнение плоскости, которая проходит через точку с координатами (1; 1; 2) и отсекает от осей координат отрезки одинаковой длины.
Уравнение плоскости в отрезках при условии, что она отсекает от осей координат отрезки равной длины, скажем а 0, имеет вид х	у	z
—I---1— — 1.
а	а	а
Этому уравнению должны удовлетворять координаты (1; 1; 2) известной точки на плоскости, т.е. выполняется равенство 4! a — 1. Поэтому а —4 и искомым уравнением является я + + у + г-4 = 0.
126
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Нормальное уравнение плоскости. Рассмотрим некоторую плоскость л в пространстве. Фиксируем для нее единичный нормальный вектор п, направленный из начала координат „в
Рис. 5.4
сторону плоскости64, и обозначим через р расстояние от начала О системы координат до плоскости л (рис. 5.4). Если плоскость проходит через начало системы координат, то р = 0, а в качестве направления для нормального вектора п можно выбрать любое из двух возможных.
Если точка М принадлежит плоскости л, то это эквивалентно тому, что ортогональная проекция вектора 01$ на направление
вектора п равна р, т.е. выполне-
но условие пО1$ = прп 01$ = р, так как длина вектора п равна
единице.
Обозначим координаты точки М через (ж; у; z) и пусть п = = {cosa; cos/?; COS7} (напомним, что для единичного вектора п его направляющие косинусы cos a, cos/?, cos7 одновременно являются и его координатами). Записывая скалярное произведение в равенстве пО1$ = р в координатной форме, получаем нормальное уравнение плоскости
х cos а + у cos/? + г cos 7 — р = 0.
Аналогично случаю прямой на плоскости, общее уравнение плоскости в пространстве можно преобразовать в ее нормальное уравнение делением на нормирующий множитель.
Для уравнения плоскости Ах + By + Cz + D = 0 нормирующим множителем является число ±\/А2 + В2 + С2, знак которого выбирается противоположным знаку D. По абсолютной
5.3. Уравнения прямой в пространстве	127
величине нормирующий множитель представляет собой длину нормального вектора {А; В; С} плоскости, а знак соответствует нужному направлению единичного нормального вектора плоскости. Если плоскость проходит через начало системы координат, т.е. D = 0, то знак нормирующего множителя можно выбрать любым.
5.3.	Уравнения прямой в пространстве
Общие уравнения прямой в пространстве. Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Если плоскости
тг 1: Aix 4- В\у + C\z 4- D\ — О, ?Г2- А2Х 4* В2У 4*^2^ 4* D2 ~ О
непараллельны, то пересекаются по прямой. Точка М(ж; у; z) принадлежит этой прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению каждой из плоскостей, т.е. являются решениями системы уравнений
А\х 4* Biy 4* Ciz 4- Di = О,
_	(5.8)
^2^ 4“ В2У 4* С*2^ 4“ -^2 -- О,
которую называют общими уравнениями прямой.
Векторное уравнение прямой. Описание прямой в пространстве при помощи общих уравнений — не единственный способ. Прямую L в пространстве можно также однозначно задать любой ее точкой Mq и параллельным ей ненулевым вектором s.
Любой ненулевой вектор, параллельный прямой, называют направляющим вектором прямой.
Если точка М принадлежит прямой L, то это эквивалентно тому, что вектор коллинеарен вектору s (рис. 5.5). Так как s 0, то вектор s является базисом в пространстве Vi
128
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
коллинеарных ему векторов. Поэто-L му для некоторого числа t выполни-ется равенство MQd = ts. Так как
_	Л/оЛ/ = OaJ — OMq — г — гп, гДе г и
Рис. 5.5	’
го — радиус-векторы точек М и Mq соответственно, то условие М € L можно записать в виде уравнения
r = r0 + fs,	(5.9)
которое называют векторным уравнением прямой в пространстве.
Параметрические уравнения прямой в пространстве. Предположим, что известны координаты {1',т;п} направляющего вектора s прямой L и точки Mq(xq-, t/о; ^о) € L в прямоугольной системе координат. Обозначим через (ж; у; г) координаты произвольной точки М,
Критерием принадлежности точки М прямой L является условие коллинеарности векторов MqD^ = {х — хо5 у — уо; г — zq} и s (см. рис. 5.5), что равносильно пропорциональности их координат (см. теорему 1.8). Обозначив через t коэффициент пропорциональности, получим равенства х — xq = tl, У~Уо — tm, z — z0 = tn. Но тогда
x = Xq + It, У = Уо + mt, z = Zq + nt,
(5.10)
и (5.10) называют параметрическими уравнениями прямой в пространстве. Шесть коэффициентов в системе уравнений (5.10) имеют наглядный геометрический смысл: они представляют собой координаты одной точки на прямой, соответствующей t = 0, и координаты направляющего вектора прямой, который соединяет точки, соответствующие значениям параметра t = 0 и t = 1.
5.3. Уравнения прямой в пространстве	129
Итак, если задана система трех уравнений вида (5.10), в которой хотя бы один из коэффициентов Z, m, п отличен от нуля, то эта система определяет в пространстве прямую, причем тройка коэффициентов жо, уо> задает на прямой точку, а тройка коэффициентов /, m, п представляет собой координаты направляющего вектора прямой.
Канонические уравнения прямой в пространстве. Как и в случае прямой на плоскости, из параметрических уравнений (5.10) можно исключить параметр t и записать результат в виде
x-xQ у-уъ z-zq
—7— =--------=------•	(5Л1)
I m п
Уравнения (5.11) называют каноническими уравнениями прямой в пространстве.
Канонические уравнения представляют собой, по существу, другую форму записи условия коллинеарности векторов и s, состоящую в пропорциональности их координат (см. следствие 1.1).
В знаменателе канонических уравнений допускается нулевое значение. Чтобы понять смысл нулевых значений параметров Z, т, п, обратим внимание на параметрические уравнения прямой (5.10), в которых нет проблемы нулевых знаменателей. Например, при I = 0 из (5.10) следует, что х = xq. Мы видим, что если в канонических уравнениях один из знаменателей (или два, но не все три) равен нулю, то соответствующий числитель тоже равен нулю.
Уравнения прямой, проходящей через две точки. Каждая прямая в пространстве однозначно задается любыми двумя своими различными точками. Если известны координаты этих точек Mi(xi; t/i; z\) и M2(x2; Уг\z2\ то в качестве направляющего вектора прямой подходит ненулевой вектор MiM2 = {х2 — Xi; у2 — У1; z2 — zi}. Зная его координаты и координаты точки Mi на прямой, можно записать канонические
г> Аналитическая геометрия
130
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
уравнения прямой (5.11). В результате получим
х-хг _ У-У1 _ Z-Zj _ Х2 -Хг У2- У1 z2 - Z!
уравнения прямой, проходящей через две точки. 1
Пример 5.3. Точки Mi(l;2; 3) и М2(3;2;1) определяют проходящую через них прямую
х — 1 у — 2 z — 3 3-1 ~ 2 — 2 = 1 -3’
Нуль в знаменателе второй дроби означает, что для координат всех точек прямой выполнено равенство у = 2. Поэтому прямая расположена в плоскости у — 2 = 0, параллельной координатной плоскости xOz и пересекающей ось ординат в точке с ординатой 2.
Изменение формы уравнений прямой. Переход от канонических уравнений прямой к параметрическим и обратно достаточно очевиден и сводится к введению или исключению параметра t. Одна форма уравнений непосредственно записывается по другой, так как в них используются одни и те же параметры, задающие координаты точки на прямой и координаты направляющего вектора.	,
Пример 5.4. Найдем координаты точки В, симметричной точке А(2; 3; —1) относительно прямой
х - 1 _ у + 2 __ z-1 :	1 - -1 ~ 2 
В вычислениях будем опираться на следующее геометрическое построение точки В: а) через точку А проводим плоскость тг, перпендикулярную прямой L; б) находим точку М пересечения прямой L и плоскости тг; в) отрезок AM удлиняем до отрезка АВ так, чтобы точка М оказалась в середине отрезка АВ (рис. 5.6).
5.3. Уравнения прямой в пространстве
131
Так как плоскость тг перпендикулярна прямой L, то в качестве нормального вектора п плоскости можно выбрать направляющий вектор прямой L: n = {1; — 1; 2}. По известным координатам нормального вектора плоскости тг и принадлежащей ей точки А записыва-
ем уравнение плоскости 7Г в ви-	Рис. 5.6
Де (5.2):
1(х - 2) + (-1)(у- 3) + 2(^+1) = 0.
Чтобы найти координаты точки М пересечения прямой и плоскости по их уравнениям, запишем параметрические уравнения прямой L:
x = l + t, у = —2 —г=1 + 2£.
Подставив эти выражения для координат точки на прямой в уравнение плоскости, получим уравнение для параметра t
(1 +t- 2) - (—2 - t- 3) + 2(1 + 2t + 1) = 0,
решение которого дает значение параметра для точки М. Найдя это значение t = -А/3 и подставив его в параметрические уравнения прямой, получим координаты точки пересечения
х = 1 - 4/3 = —1/3, у = -2 + 4/3 = -2/3, z = 1 - 8/3 = -5/3.
Поскольку эта точка должна делить отрезок АВ пополам, ее координаты, согласно (3.14), равны полусумме соответствующих координат точек А и В. Следовательно, обозначив через (ж'; у'; У) координаты точки В, получим равенства
- 1 /2	3 + yz
2	7 ’	2
-2/3, -2+£ = _5/3.
Отсюда х' = -8/3, у' = —11/3, / = —7/3.#
132
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Достаточно просто выполняется переход от канонических уравнений к общим. Нетрудно увидеть, что на самом деле канонические уравнения представляют собой особую форму записи общих уравнений. Действительно, двойное равенство (5.11) равносильно системе двух линейных уравнений
' х~х* _ У~Уо _ 0
I	т
X~Xq Z - Zq _ /	n
(5.12)
которые представляют собой частный вид общих уравнений прямой в пространстве.
Самым сложным является переход от общих уравнений к каноническим или параметрическим.
Так как плоскости ти и 7Г2, соответствующие отдельным уравнениям из общих уравнений (5.8) прямой, непараллельны, то хотя бы один из определителей второго порядка
Ах Bi а2 В2 ’
А а2
с2
Вх Сх
В2 С2
представляющих собой координаты векторного произведения нормальных векторов этих плоскостей, не равен нулю. Предполагая, что первый из этих определителей является ненулевым:
Ах
А2
Вх
В2
/О,
изложим три способа перехода от общих уравнений к каноническим или параметрическим.
Первый способ состоит в том, что в системе (5.8) для z назначают два различных значения и по формулам Крамера находят два различных решения системы двух уравнений с двумя неизвестными х п у. Эти два решения системы (5.8) дают координаты двух разных точек Мх и М2 на прямой. А две известные точки прямой позволяют найти уравнение прямой,
5.3. Уравнения прямой в пространстве
133
проходящей через две точки, которое фактически совпадает с каноническими уравнениями прямой.
Отметим, что в качестве направляющего вектора s прямой, заданной общими уравнениями (518), можно выбрать П1ХП2 — векторное произведение двух нормальных векторов плоскостей (рис. 5.7).
Действительно, это векторное произведение является вектором, который ортогонален каждому нормальному векто-
ру, а потому он параллелен как	5 7
одной, так и другой плоскости,
т.е. параллелен их линии пересечения. Нахождение одной точки на прямой и ее направляющего вектора можно рассматривать как второй способ перехода от общих уравнений прямой к ее
каноническим уравнениям.
Пример 5.5. Найдем канонические уравнения прямой, совпадающей с линией пересечения плоскостей
^1* ж —г/ + г~2 = 0, 7Г2- ж + у — z = 0.
Чтобы найти координаты некоторой точки на прямой, подставляем в уравнения плоскостей z = 0 и решаем соответствующую систему двух линейных уравнений относительно х и у
х-у = 2, х + у = 0.
Значения х = 1 и у — — 1 единственного решения системы получаются сложением и вычитанием уравнений системы. Итак, точка с координатами (1; -1; 0) расположена на прямой.
В качестве направляющего вектора прямой берем векторное произведение niXn-2 нормальных векторов ni = {1;-1; 1} и
134
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
П2 = {1;1;— 1} плоскостей 7Г1 и тгг- По формуле (2.14) для вычисления векторного произведения в координатах находим
m хп2 =
i j к
1 -1 1
1 1 -1
= 2j + 2fc,
т.е. направляющим вектором прямой будет s = {0; 2; 2}. Найденный вектор s для простоты заменим коллинеарным ему вектором {0; 1; 1}.
Проведенные вычисления позволяют написать канонические уравнения искомой прямой
х-1 у+1 Z
Третий способ перехода от общих уравнений прямой к ее каноническим или параметрическим уравнениям состоит в следующем. Решаем систему (5.8) по правилу Крамера относительно неизвестных х и у, рассматривая неизвестное z как параметр:
Вг C2Z-VD2 В2 — А Вг~ А2 В2

Л1
А2 C2z^D2 ~ А. Вг~
А2 В2
— —(Ciz+Di)--—(C2Z+D2) —
Обозначив z через t и добавив уравнение z = t, получим параметрические уравнения прямой:
' х ~ «1^ + /?!, < y = &2t + 02, J = t-
5.4. Взаимное расположение прямых и плоскостей	135
5.4.	Взаимное расположение прямых и плоскостей
Взаимное расположение плоскостей. Пусть даны две плоскости, заданные в прямоугольной системе координат своими общими уравнениями,
тгр А^х + В\у + C\z 4~	= О, 7Г2^ А2Х 4- В2У 4*	4* D2 — 0.
Один из двух углов между этими плоскостями (обозначим его через (р) равен углу между их нормальными векторами П\ = = {Ai; Bi; Ci} и п2 = {А2; В2; С2} (рис. 5.8), а другой угол равен 7Г — <р.
Рис. 5.8
Поэтому, согласно определению 2.1 скалярного произведения,
(ni?n2)	^1 Аъ + BXB2 4”С1С2
cos ----~ —-----------------------------------
|ni I |n21	А\ + Bl + Cl У42 + Bl + Cl'
Если две данные плоскости перпендикулярны, то это эквивалентно тому, что их нормальные векторы ортогональны. Критерием ортогональности двух векторов является равенство нулю их скалярного произведения (см. теорему 2.1). Поскольку скалярное произведение двух векторов, заданных в координатах, вычисляется как сумма произведений их одноименных
136
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
координат, критерием перпендикулярности плоскостей ttj и 7Г2 является выполнение равенства
Л1А2 + В\ В2 + С1С2 ~ о.
Аналогично две плоскости параллельны, если их нормальные векторы коллинеарны. Критерием же коллинеарности двух векторов является равенство отношений их координат (см. следствие 1.1). Поэтому условие параллельности двух плоскостей записывается в виде двойного равенства
A = = д2 в2 С2
Замечание 5.1. Это двойное равенство имеет смысл и в том случае, когда в знаменателе одной из дробей стоит нуль. Это значит, что и в числителе той же дроби стоит нуль. #
Параллельные плоскости могут совпадать или быть различными. Левые части общих уравнений совпадающих плоскостей отличаются на ненулевой числовой множитель, и это можно записать как равенство отношений соответствующих коэффициентов их уравнений:
а2	В2	С2 D2
Случай же
Д2 В2	С2	D2
соответствует тому, что плоскости параллельны, но не совпадают.
Угол между прямыми. Угол между двумя прямыми можно найти, используя направляющие векторы прямых. Острый угол между прямыми равен углу между их направляющими векторами (рис. 5.9) или является дополнительным к нему,
5.4. Взаимное расположение прямых и плоскостей
137
('ели угол между направляющими векторами тупой. Таким образом, если для прямых Li и L2 известны их направляющие векторы 3| И S2, то острый угол ср между этими прямыми определяется через скалярное произведение:
cos 9? =
|3132| 1*11W
Например, пусть = {/г; тг; пг}, г — 1,2. Используя формулы (1.9) и (2.9) для вычисления длины вектора и скалярного произведения в координатах, получаем
_	IM2 + ^1^2 + nin2|
+mi + niV{2 + т2 + П2
Взаимное расположение прямых. Для двух прямых в пространстве возможны четыре случая:
-	прямые совпадают;
~ прямые параллельны (но не совпадают);
-	прямые пересекаются;
-	прямые скрещиваются, т.е. не имеют общих точек и непараллельны.
Рассмотрим два способа описания прямых: каноническими уравнениями и общими уравнениями. Пусть прямые L\ и 1>2 заданы каноническими уравнениями:
Ж-Ж1 У-У! Z-Zi	X — Х2 У-У2 Z — Z2
М- — =----------=------, Ь2: —J =---------=------• (5.13)
Li mi ni	/2 т2 п2
138 5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Для каждой прямой из ее канонических уравнений сразу определяем точку на ней М\(хг-, уг-, хД G Li, М2(х2; у2; z2) G L2 и координаты направляющих векторов sj =	для Lj,
s2 = (/2,m2,n2) для L2.
Если прямые совпадают или параллельны, то их направляющие векторы Si и з2 коллинеарны, что равносильно равенству отношений координат этих векторов:
(5-14)
G __ т\ _ П1 h т2 п2
Если прямые совпадают, то направляющим векторам коллинеарен и вектор М\М2\
*2 -^1 _ У-2 ~ У1 _ Z2 - Zj
/1	7П1	П1
(5.15)
Это двойное равенство также означает, что точка М2 принадлежит прямой Li. Следовательно, условием совпадения прямых является выполнение равенств (5.14) и (5.15) одновременно.
Если прямые пересекаются или скрещиваются, то их направляющие векторы неколлинеарны, т.е. условие (5.14) нарушается. Пересекающиеся прямые лежат в одной плоскости и, следовательно, векторы s2 и М\М2 являются компланарными. Условие компланарности этих векторов можно записать через смешанное произведение как равенство нулю определителя третьего порядка, составленного из их координат (см. 2.4):
я 2 - У 2 - У1
ll	nil
h	rn2
?2 “ *1
П2
= 0.
(5.16)
Условие (5.16) выполняется в трех случаях из четырех, поскольку при Д / 0 прямые не принадлежат одной плоскости и потому скрещиваются.
5.4. Взаимное расположение прямых и плоскостей
139
Сведем все условия воедино:
L\ и Z/2 совпадают
£1 и Z/2 параллельны,
но Li ф Ь2
Li и Ь2 пересекаются О
L1 и L2 скрещиваются О
выполнены условия
(5.14) и (5.15);
выполнено (5.14), нарушено (5.15);
выполнено (5.16), нарушено (5.14);
нарушено (5.16).
Если две прямые заданы общими уравнениями
f Aix + B\y+Ciz+ Di — О, A2xA‘B2yA‘C2zA‘D2 = 0,
Азж + Взу+Сз>г+/?з —О,
А4Х 4* В4 у 4~ С4 z -J-* D4 — О,
то мы можем рассмотреть систему уравнений:
А\х + В\у 4* C\z 4* Di = О, А2х 4" В2у 4” C2z 4* D2 — О, А%х 4* В$у 4* C^z 4* Ds = О, k А4Х 4* В4У 4* C4Z 4* D4 — 0.
(5.17)
Взаимное расположение прямых характеризуется количеством решений у системы (5.17). Если прямые совпадают, то система имеет бесконечно много решений. Если прямые пересекаются, то эта система имеет единственное решение. В случае параллельных или скрещивающихся прямых решений нет. Последние два случая можно разделить, если найти направляющие векторы прямых. Для этого достаточно вычислить два векторных произведения п\Хп2 и П3ХП4, где пг = {Д; Вг; Сг}, i= 1,2,3,4. Если полученные векторы коллинеарны, то данные прямые параллельны. Иначе они скрещивающиеся.
Пример 5.6. Исследуем взаимное расположение прямых
х — 1 у — 2	^4*1 г (х~ У — ^4*1 = 0,
----=------=------,	L2: <
1	3	-2	x + y + 2z-2 = 0.
140
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Направляющий вектор Si прямой Li находим по каноническим уравнениям этой прямой: Si = {1; 3; —2}. Направляющий вектор S2 прямой £2 вычисляем с помощью векторного произведения нормальных векторов плоскостей, пересечением которых она является:
32 = П1ХП2 =
3
-1
1
к
-1
2
— —i — 3j +2fc.
i
1
1
Поскольку si — —s2, то прямые параллельны или совпадают. Выясним, какая из этих ситуаций реализуется для данных прямых. Для этого подставим координаты точки Mq(1; 2; —1) € € L\ в общие уравнения прямой L2- Для первого из них получаем 1=0. Следовательно, точка Mq не принадлежит прямой £2 и рассматриваемые прямые параллельны.
Расположение прямой и плоскости. Взаимное расположение прямой и плоскости в пространстве допускает три случая. Прямая и плоскость могут пересекаться в одной точке. Они могут быть параллельны. Наконец, прямая может лежать в плоскости. Выяснение конкретной ситуации для прямой и плоскости зависит от способа их описания.
Предположим, что плоскость тг задана общим уравнением тг: Ах + By + Cz + D = 0, а прямая L — каноническими уравнениями
X-Xq _ У-Уо _ Z — Zq
I т п '
Уравнения прямой дают координаты точки Mq(xq; у0; ^о) на прямой и координаты направляющего вектора з = {/; т\ п} этой прямой, а уравнение плоскости — координаты ее нормального вектора п — {Л; В; С},
Если прямая L и плоскость тг пересекаются, то направляющий вектор з прямой не параллелен плоскости тг. Значит, нормальный вектор п плоскости не ортогонален вектору з, т.е. их скалярное произведение не равно нулю. Через коэффициенты уравнений прямой и плоскости это условие записывается
5.4. Взаимное расположение прямых и плоскостей
141
в виде неравенства
Al + Bm + Cn^ 0.
Если прямая и плоскость параллельны или прямая лежит в плоскости, то выполняется условие s ± п, которое в координатах сводится к равенству
А1 + Вт + Сп = 0.
Чтобы разделить случаи „ параллельны “ и „прямая принадлежит плоскости “, нужно проверить, принадлежит ли точка прямой данной плоскости.
Таким образом, все три случая взаимного расположения прямой и плоскости разделяются путем проверки соответствующих условий:
т	( Axq-j-Byo-k Сzq-k D =
L принадлежит *	«	{	+ В™ + С» = 0;
L параллельна тг <=>
Г Ахъ + Bt/o + Czq + D^o, | Al + Bm + Cn = 0;
L пересекается с тг <=> Al + Bm + Cn / 0.
Если прямая L задана своими общими уравнениями:
L:
Ахх + Biy + Ciz + Di = 0,
А2Х + В2У +	+ D2 = 0,
то проанализировать взаимное расположение прямой и плоскости тг можно следующим образом. Из общих уравнений прямой и общего уравнения плоскости составим систему трех линейных уравнений с тремя неизвестными
А}Х + Biy + C\z + D\ — 0,
< А2х + В2у + C2z + D2 = 0,	(5.18)
Ах + By + Cz + D =0.
Если эта система не имеет решений, то прямая параллельна плоскости. Если она имеет единственное решение, то прямая и плоскость пересекаются в единственной точке. Последнее
142
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
равносильно тому, что определитель системы (5.18)
Ai Вг С.
А2 В2 С2 АВС
отличен от нуля. Наконец, если система (5.18) имеет бесконечно много решений, то прямая принадлежит плоскости.
Угол между прямой и плоскостью. Угол <р между прямой
L X-XQ _ у-уо _ Z-Zy I т п и плоскостью
тг: Ах + By + Cz + D — О
находится в пределах от 0° (в случае параллельности) до 90° (в случае перпендикулярности прямой и плоскости). Синус этого п д	угла равен |cos^|, где ф — угол
/* L	между направляющим вектором
ф Яs
прямой s и нормальным векто-ром п плоскости (рис. 5.10). Вы-
тчислив косинус угла между двумя векторами через их координа-
Рис. 5.10	Ты (см. (2.11)), получим
\А1 + Вт + Сп\
1 х/A2 + в2 + С2 VI2 + т2 + п2
Отсюда
\А1 + Вт-рСп\
VA2 + В2 + С2 VI2 + гп2 + п2
(5.19)
Условие перпендикулярности прямой и плоскости эквивалентно тому, что нормальный вектор плоскости и направляющий вектор прямой коллинеарны. Через координаты векторов это условие записывается в виде двойного равенства
А__ В С
I т п’
(5.20)
5.5. Расстояние до плоскости и до прямой	143
5.5. Расстояние до плоскости и до прямой
Расстояние от точки до плоскости. Рассмотрим в пространстве некоторую плоскость тг и произвольную точку Mq. Выберем для плоскости единичный нормальный вектор п с началом в некоторой точке М\ Е тг, и пусть />(Мо,тг) — расстояние от точки Mq до плоскости тг. Тогда (рис. 5.11)
р(Л/0,тг) = |прпЛ/1Л/о| = |пЛ/1Мо|,
(5.21)
так как |n| = 1.
Если плоскость тг задана в прямоугольной системе координат своим общим уравнением
Рис. 5.11
тг'. Ах + By + Cz+ D = О,
то ее нормальным вектором является вектор с координатами {А; В; С) и в качестве единичного нормального вектора можно выбрать
{А; В; С} \Л42 + В2 + С2’
Пусть (ясьУсь^о) и (#i; у\; zi) — координаты точек Mq и М\. Тогда выполнено равенство
Ах\ + Ву\ + Cz\ + D — О, так как точка М\ принадлежит плоскости, и можно найти координаты вектора M\Mq\
MiMo = {xQ-xr, уо-уг, z0-Zi}.
144
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Записывая скалярное произведение пМ^Мо в координатной форме и преобразуя (5.21), получаем
\ И(хо-Ж1) + В(уо-У1)+С'(^о-^1)| Р(М,7Г) = ------------------------------ =
VA2 + B2 + C2
| Axq + Вуо + Czq — (Ля?! + Ву\ + Czi)|
хЛ42 + В2+С2
| Ахд + Вуо + Czq + D | Уа2 + в2+с^
поскольку Axt + Byi + Cz\ = -£>. Итак, чтобы вычислить расстояние от точки до плоскости нужно подставить координаты точки в общее уравнение плоскости, а затем абсолютную величину результата разделить на нормирующий множитель, равный длине соответствующего нормального вектора.
Расстояние от точки до прямой. Расстояние от точки До прямой L, заданной каноническими уравнениями
L x-xq _ у-уо = Z-Zq
I тп п ’ может быть вычислено при помощи векторного произведения. Действительно, канонические уравнения прямой дают нам точку Mq(xq] г/0; ^о) на прямой и направляющий вектор s = {/; т; п} этой прямой. Построим параллелограмм на векторах s и AfoMi. Тогда расстояние от точки Mi до прямой L будет М
равно высоте h параллелограмма (рис. 5.12). Значит, нужное рас-Л	стояние может быть вычислено
\по формуле
L	----
гч |М0Л/1Хз|
Рис. 5.12	= 1	, .--L,
lsl
5,5. Расстояние до плоскости и до прямой
145
где числитель представляет собой площадь этого параллелограмма. Используя формулы вычисления длины вектора и векторного произведения векторов через их координаты, получаем

3/1-Уо т п
Zi-Zq
I n
x/l2+m2+n2
(5.22)
zi-zo У1~Уо
I т
Расстояние между прямыми. Если прямые пересекаются, то очевидно, что расстояние между ними равно нулю. Случай совпадающих прямых также малосодержателен. Поэтому о расстоянии между прямыми имеет смысл говорить, только если они параллельны или скрещиваются. Два указанных случая с точки зрения вычислений заметно расходятся.
Чтобы найти расстояние между параллельными прямыми, достаточно вычислить расстояние от произвольной точки, например, второй прямой до первой прямой, т.е. можно воспользоваться формулой (5.22). Таким образом, если две параллельные прямые заданы каноническими уравнениями
Х-Х! у-Ух Z-Zx	X — Х2 У-У2 Z — Z2
Lx'- —  =--------=--------, L2: —; =----------—------,
/1	тх Пх	«2	™2 п2
то расстояние между ними вычисляется по формуле
Р(Ь1,1/2) =
У2-У1 *2-21
772 j	Пх
Ж2-Ж1	^2-^1
/1 П1
Х2-Хх У2-У1
1х Шх
y/ll + ml + nl
Расстояние между скрещивающимися прямыми можно находить, используя смешанное произведение. Пусть, как и выше, прямые Lx и L2 заданы каноническими уравнениями. Так как
146
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
они скрещиваются, их направляющие векторы si, «2 и вектор соединяющий точки на прямых, некомпланарны. Поэтому на них можно построить параллелепипед (рис. 5.13). Тогда расстояние между прямыми равно высоте h этого параллелепипеда. В свою очередь, высоту параллелепипеда можно вычислить как отношение объема параллелепипеда к площади его основания. Объем параллелепипеда равен модулю смешанного
произведения трех указанных векторов, а площадь параллело-
грамма в основании параллелепипеда равна модулю векторного произведения направляющих векторов прямых. В результате получаем формулу для расстояния p(Z/i,Л2) между прямыми:
|згз2 M1M2I |S1XS2|
р(^ьЬ2) =
Записывая смешанное и векторное произведения в коорди
натах, окончательно получаем

Расстояние между прямой и плоскостью. Если прямая L и плоскость л пересекаются, то расстояние между ними равно нулю. Если же они параллельны, то расстояние от прямой до плоскости есть расстояние от любой точки прямой до плоскости. Пусть плоскость задана общим уравнением л: Аж + + By + Cz + D = 0, а прямая — каноническими уравнениями
L:
X-XQ _ у-уо _ £-Zo
I
т
п
Д.5.1. Пучки и связки
147
Канонические уравнения прямой позволяют сразу найти координаты одной точки на этой прямой: Л1о(жо> Уо! й))- Поэтому расстояние р(£,тг) между прямой L и параллельной ей плоскостью тг равно
р(Ь,7г) = р(М0,п) =
| Аатр -f- Byo -j-Czp + -D| VA2 + B2 + &
Дополнение 5.1. Пучки и связки
Пучок плоскостей. Пучком плоскостей в пространстве называют семейство всех плоскостей, содержащих фиксированную прямую. Пучок однозначно определяется любой парой своих различных плоскостей. Любые две непараллельные плоскости однозначно определяют некоторый пучок плоскостей.
Рассмотрим вопрос о том, как, зная уравнения двух различных плоскостей пучка, найти уравнения остальных плоскостей пучка.
Теорема 5.2. Для того чтобы плоскость принадлежала пучку плоскостей, определяемому парой непараллельных плоскостей
7Г1'. А^х 4“ В\у 4- C\Z 4~ D\ = 0, 1^2'' &2Х 4* В2У 4* C2Z 4* D2 = О, необходимо и достаточно, чтобы ее общее уравнение можно было записать в виде
4* thy 4* Ciz 4* Ci) 4*
4“ /3(Л.2*е + В2У 4~	4“ D2) =: 0, а2 4~	0. (5.23)
◄ Достаточность. Покажем, что при любых значениях параметров а и Д, одновременно не равных нулю, уравнение (5.23) задает плоскость тг, содержащую общую прямую плоскостей 7Г1 и 7Г2- Отметим, что после приведения в (5.23) подобных
148 5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
слагаемых получим уравнение
(aAi + 0A2)x + (aBi + /ЗВ2)у + («Ci + l3C2)z + (a£>i + /W2) = О, являющееся уравнением первого порядка, так как в нем хотя бы один коэффициент при переменных отличен от нуля. В самом деле, поскольку плоскости tfi и 7Г2 непараллельны, их нормальные векторы п\ = {Ai; Bi; С\} и П2 = {А2;	С2}
неколлинеарны, а значит, векторное произведение П1ХП2 не является нулевым вектором. Поэтому хотя бы один из определителей второго порядка
Ai Bi
А2 В2
Al G
А2 С2
в. С,
В2 С2
представляющих собой координаты этого векторного произведения в прямоугольной системе координат, отличен от нуля. Пусть, например, первый из них не равен нулю. Тогда система
Aia + А2/3 = 0,
Bi& + В20 = О
имеет единственное решение и им является а = (3 = 0. Это значит, что если а и (3 одновременно не обращаются в нуль, то либо коэффициент Ai& + A20 при переменной х, либо коэффициент + В2(3 при переменной у в уравнении (5.23) отличен от нуля.
Итак, (5.23) является уравнением плоскости. Остается убедиться, что эта плоскость проходит через прямую пересечения плоскостей 7Г1 и 7Г2. Но если точка Mq(xq; уо; zq) принадлежит одновременно плоскостям тгх и 7Г2, то одновременно выполняются соотношения
Ахо + В1у$ + Ci zq + Di — 0, + В2У0 + С*2^о + D2 — 0.
(5.24)
Следовательно, для координат точки Mq выполняется и соотношение (5.23), т.е. точка Mq лежит в плоскости тг. Тем самым
Д.5.1. Пучки и связки
149
мы показали, что точки пересечения плоскостей 7Г1 и тг2 лежат па плоскости тг.
Необходимость. Пусть плоскость тг3: А$х + В^у + + Сз^ + Z?3 = 0 содержит общую прямую плоскостей 7Г1 и тг2. Докажем, что ее уравнение можно записать в виде (5.23) при некоторых значениях параметров а и /3. Заметим, что нормальные векторы ni, п2, пз трех плоскостей 7Г1, 7Г2, 7Гз, имеющих общую прямую, лежат в одной плоскости 7ГП, перпендикулярной этой общей прямой (рис. 5.14). Векторы п\ и п2 неколлинеарны, так как соответствующие им плоскости непараллельны. Поэтому эти два вектора образуют базис в пространстве V2 векторов, параллельных тгп. Это значит, что вектор Пз является линейной комбинацией векторов П\ и п2, т.е. при некоторых значениях а и /3
пз = ani + /3п2.
Рис. 5.14
На прямой, общей для трех плоскостей, зафиксируем точку ЛЛ)(^о5 Уа', ^о) И рассмотрим произвольную точку M(x;y,z) и вектор Мол) = 013- ом>0.
Координаты точки Mq удовлетворяют равенствам (5.24). С помощью этих равенств можно выразить свободные члены Di и D2 в уравнениях плоскостей через координаты точки Mq и записать векторные уравнения этих плоскостей:
ТГЦ П1	=0, тг2: п2 (ол^-олй) =0. (5.25)
150
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Но
тогда векторное уравнение пз
(ОЙ-ОМо)
= 0 плоско-
сти 7Гз преобразуется к соотношению
(aril + /3п2)
или
ап\ (бл1 - Cwj) +^П2	- ОМ^ = 0.
Преобразуя векторные уравнения плоскостей 7Г1 и тг2 к их общим уравнениям, получаем уравнение вида (5.23), т.е. плоскость 7Гз пучка описывается этим уравнением. ►
Пучок прямых на плоскости. Аналогично пучку плоскостей в пространстве рассматривают пучок прямых на плоскости. Пучком прямых на плоскости называют семейство всех прямых, проходящих через фиксированную точку плоскости. Пучок однозначно определяется любой парой своих прямых. Для пучка прямых на плоскости справедлив следующий аналог теоремы 5.2.
Теорема 5.3. Для того чтобы прямая входила в пучок прямых, определяемый парой непараллельных прямых
Li: aix + biy + ci =0, L2: a2x + b2y + c2 = 0,
необходимо и достаточно, чтобы ее общее уравнение можно было записать в виде
а^агх + bit/ + ci) + /?(«2^ + Ь2у + с2) = 0, а2 + /?2 / 0. (5.26)
Связка плоскостей. Связкой плоскостей называют семейство всех плоскостей в пространстве с одной общей точкой. Связка плоскостей однозначно определяется любой тройкой своих плоскостей, не принадлежащих одному пучку плоскостей.
Действительно, две различные плоскости связки пересекаются по прямой и определяют тем самым пучок плоскостей.
Д.5.1. Пучки и связки
151
1£сли третья плоскость связки не принадлежит этому пучку, то у таких трех плоскостей имеется единственная общая точка, определяющая связку плоскостей.
Три различные плоскости могут не иметь общих точек (рис. 5.15, а), иметь их бесконечно много (рис. 5.15, б) или иметь единственную общую точку. В первых двух случаях нормальные векторы плоскостей компланарны. Если же нормальные векторы трех плоскостей некомпланарны, то о таких плоскостях говорят, что они находятся в общем положении. Три плоскости, находящиеся в общем положении, пересекаются в единственной точке и однозначно определяют связку плоскостей. Это следует из того, что условие некомпланарности нормальных векторов плоскостей тгг: А±х + Biy + CiZ + Di = О, i— 1,2,3, в координатной записи означает, что определитель
Ai Вг Ci
A<i В2 С2
Аз Вз Сз
Рис. 5.15
152
5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
отличен от нуля и это приводит к существованию единственного решения у системы трех линейных уравнений с тремя неизвестными
Aix + Biy + C\Z + D\ — О,
< А%х + В2У + C2Z + D2 — О, А$х + Взу + C3Z + D3 = 0.
Теорема 5.4. Для того чтобы плоскость входила в связку плоскостей, определяемую тройкой плоскостей тгг-: Aix + Biy + + CiZ + Di = 0, i = 1,2,3, общего положения, необходимо и достаточно, чтобы ее общее уравнение можно было записать в виде
а(А\х + В\у + C\Z +	4-	+ В2у + C2Z + D2} +
+ 7(Азж + Взу + C3z + D3) = 0, (5.27)
где а2 + Д2 + 72 7^ 0.
4 Доказательство аналогично доказательству теоремы 5.2. Различие состоит лишь в том, что в случае пучка плоскостей нормальные векторы двух непараллельных плоскостей образуют базис в V2) а нормальные векторы трех плоскостей общего положения образуют базис в V3. ►
Если дана точка A4o(xo,yo,^o), то связку плоскостей, проходящих через эту точку, легко определить, рассмотрев три плоскости, параллельные координатным, т.е. х = жо, у = уо, z = zq. По теореме 5.4 получим уравнение связки:
а(ж - ж0) + Д (у - уо) + 7(^ ~ го) = 0.
Коэффициенты а, (3 и 7, являясь координатами нормального вектора плоскости в базисе из трех нормальных векторов выбранных плоскостей, в данном случае есть его координаты в прямоугольной системе координат.
Вопросы и задачи
153
Вопросы и задачи
5.1.	Найти общее уравнение плоскости: а) проходящей через начало системы координат; б) параллельной координатной плоскости хОу (yOz); в) параллельной оси ординат (аппликат); г) проходящей через ось ординат (аппликат).
5.2.	Найти канонические уравнения прямой: а) проходящей через начало системы координат; б) параллельной оси абсцисс (ординат, аппликат); в) совпадающей с осью абсцисс (ординат, аппликат); г) параллельной координатной плоско-гти хОу (yOz).
5.3.	Найти общее уравнение плоскости, проходящей через начало системы координат и перпендикулярной плоскостям 2х — Зу — z + 5 = 0, 4ж — 3z + 1 = 0.
5.4.	Найти общее уравнение плоскости, проходящей через точки Л/1(—1; 3; 2), М2 (4; 1; 0) и параллельной прямой
ж + 2 _ у — 1 _ z + 5
3 = -4 = ~Г”’
5.5.	Найти общее уравнение плоскости, проходящей через точку Afi(l; —2; 1) и прямую
х - 1 _ t/+ 1 _ г - 1
2 = 3 “ 2
5.6.	Исследовать взаимное расположение пар плоскостей:
а)	Зх — у + 2z — 4 = 0, — 6х + 2у — 4z — 4 = 0;
б)	х + 2у - 2z - 4 = 0, 2х + 4у - 4z - 8 = 0.
5.7.	Найти все значения параметра £, при которых плоскости tx — у — z — 4 = 0, х + 2у — 3z — 5 = 0, (2 — t)x + у — 24г + 1 = 0 находятся в общем положении.
5.8.	Найти общее уравнение плоскости, проходящей через точки М1(0;1;—2), Л/2(1;2;1) и перпендикулярной плоскости х — у + 3z — 12 = 0.
5.9.	Найти канонические уравнения прямой, параллельной плоскостям х — у — z — 5 = 0, x + 2y + 2z = 0 и проходящей через . точку Л/1(1; 0; -2).
154 5. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
5.10.	Найти параметрические уравнения перпендикуляра, опущенного из точки М\ (1; 1; -2) на прямую
я + 2 __ у— 1 __ z + 5
3 = 2 “ 2 ’
5.11.	На плоскости х + у — z — 0 найти точку с наименьшим расстоянием до начала системы координат.
5.12.	Найти уравнение множества точек, равноудаленных от плоскостей:
а)	х — 2г/ + 4г - 3 = 0, Зя - 6г/+ 12,? + 7 = 0;
б)	х - 2у + Az + 5 = 0, Ах + у + 2z - 11 = 0.
5.13.	Выяснить, в какой из двух углов между плоскостями я + Зг/-2^ + 1 — 0, Зя - у + 2г + 2 = 0 попадает точка Л/(1; 1; -1), в острый или тупой.
5.14.	На каком минимальном расстоянии от начала системы координат пройдет точка при прямолинейном ее движении из точки TVf (5; 0; 1) в направлении точки A/i(—5; 1; 3).
5.15.	Найти канонические уравнения прямой, симметричной прямой я — 1 = 1 — у — z относительно плоскости я + Зг/ — -2г+ 1 = 0.
5.16.	Найти координаты основания перпендикуляра, опущенного из точки Л/(3; -1; 2) на плоскость 2я - 2г/+ z - 1 = 0.
5.17.	Для треугольника с вершинами А(2; 3; -2), В(4; -1; 4), С(2;— 3; 2) найти канонические уравнения медианы, высоты и биссектрисы, проходящих черёз вершину А.
5.18.	Найти уравнение геометрического места точек, равноудаленных от точек Л(1; 4; —3), В(3; 0; —5).
5.19.	Найти канонические уравнения проекции прямой
я - 1 _ г/ - 2 _ ,?+ 1 1 = 2
на плоскость 2я — Зг/ + z — 1 = 0. Составить уравнение проектирующей плоскости.
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
6.1.	Виды матриц
Определение 6.1. Матрицей типа (или размера) тхп называют прямоугольную числовую таблицу, состоящую из тп чисел, которые расположены в т строках и п столбцах. Составляющие матрицу числа называют элементами этой матрицы. Как правило, их обозначают строчной буквой с двумя индексами, например агу, где i — номер строки (г = 1, m), j — номер столбца (J = 1, п), в которых расположен этот элемент.
Матрицы обозначают
прописной буквой: А, В и т.д. Элемент матрицы А, стоящий в г-й строке и j-m столбце, мы будем также записывать в виде [A]tj, что удобно при проведении доказательств.
Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, мы будем встречаться с матрицами, элементами которых будут многочлены или матрицы.
Множество всех числовых матриц типа тхп, элементами которых являются действительные числа, будем обозначать
156
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Если матрица имеет тип 1хп, т.е. если у матрицы всего одна строка, А = (ап, ai2, ..., «in)? то матрицу называют матрицей-строкой, Индекс строки можно опустить: А = = (ai, a2, ..., an). Число элементов в матрице-строке называют ее длиной.
Если матрица имеет тип mxl, т.е. у матрицы один столбец:
( «11
«21
\ «7П1 /
то ее называют матрицей-столбцом. Число элементов в матрице-столбце называют ее высотой. Индекс столбца
можно опустить:
А =
«2
При т — п, т.е. когда матрица имеет столько же столбцов, сколько и строк, ее называют квадратной порядка п:
(ац	а12	...	а1п	>
«21	«22	• • •	а2п
\ ani	ап2	...	ann	j
а при т / п — прямоугольной. Множество всех квадратных матриц порядка п, элементами которых являются действительные числа, обозначают Mn(W), У квадратных матриц выделяют последовательности элементов ац? «22) • ••, апп — главную диагональ, и ani, ап_i}2? ..., «in — побочную диагональ. Элементы главной диагонали называют диагональными. Понятия диагонального элемента и главной диагонали распространяют и на прямоугольные матрицы.
6.1. Виды матриц
157
Если в квадратной матрице порядка п все элементы, стоящие вне главной диагонали, равны нулю, т.е. если матрица имеет вид
/«11	о	...	о	>
О	О>22	• • •	О
о	о	...	о
\ 0	0	... G>nn /
то ее называют диагональной и обозначают diag (ац,..., апп). Если в диагональной матрице порядка п на диагонали стоят единицы, то ее называют единичной и обозначают обычно Е или I:
/1 о
Е = О
О ... 0\
1 ... о о ... о
\0 О ... 1/
Матрицу типа mxn, все элементы которой равны нулю, называют нулевой матрицей соответствующего типа и обозначают буквой 0 или цифрой 0.
Часто используют матрицы и других видов, например верхние треугольные матрицы
< Дц а12 ... ain^ 0	а22	•• • «2п
0	0	... а3п
\ 0	0	... апп)
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых,
158
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
наоборот, элементы над главной диагональю равны нулю:
/ ап 0	0	...	О	\
а21	а22	0	•••	О
\ dn\ &п2 ^пЗ • • • ^пп /
Отметим, что диагональные матрицы являются частным случаем как верхних, так и нижних треугольных матриц. Более того, множество диагональных матриц совпадает с пересечением множества верхних треугольных матриц и множества нижних треугольных матриц.
К трехдиагоналъным матрицам относят такие квадратные матрицы, у которых ненулевыми элементами могут быть лишь диагональные элементы и соседние с ними в строке или столбце:
( а11	012	0	0	0	0	0 \
021	022	«23	0	0	0	0
0	«32	«33	аз4	0	0	0
0	0	0	0	• •• ^п—1,п—2	1,п— 1	®п— 1,п
\ 0	0	0	0	0	®п,п—1	®пп /
Прямоугольные матрицы вида
( а11	012	013	..		• • ttln
0	022	023	..		• • a2n
0	0	033 ••		• • a3n
\ 0	0	0	... атт ... атп /
у которых элементы, расположенные под главной диагональю, равны нулю, называют верхними трапециевидными.
Важную роль в дальнейшем изложении играют ступенчатые матрицы (матрицы ступенчатого вида). Так называют
6.2. Линейные операции над матрицами
• 159
матрицу типа mxn, если для любой ее строки выполнено следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами строки все элементы матрицы равны нулю. Следующие матрицы имеют < тупенчатый вид:
/02 3 0\	/3 1 3 3\	/113	3\
100—11), 10021), 1030	1.
\0 0 03/	\0 О 0 0/	\0 0 1 -1/
6.2.	Линейные операции над матрицами
Прежде чем обсуждать какие бы то ни было операции над матрицами, договоримся, какие матрицы мы будем считать равными.
Определение 6.2. Две матрицы называют равными, если они имеют один и тот же тип и если у них совпадают соответствующие элементы.
Определение 6.3. Суммой матриц А = (a,j) и В = - (bij) типа тхп называют матрицу С = (cij) того же типа с элементами сг; = aij + b{j, i = 1,т, j = 1,п.
Для суммы матриц используют обозначение: С = А + В. В подробной записи
/«12	... «ы \
«21	«22	... «2п
\ «ml «m2	• • • «тп /
/ &11	&12	...	bin	>
&21	Ь22	...	Ь2п
\ Ьт1 Ьт2 • • • Ьтп /
^«11+ Ьц	«12 + ^12	... «1п + ^1п
«21+&21	«22 + ^22	... «2п+&2п
\ «ml “Ь ^т1 «m2 Н“* Ьт2 •.. «тп +ь тп
160
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Замечание 6.1. Сумма определена только для матриц одного типа.
Пример 6.1. Найдем сумму двух матриц
/12	3 0\	/013	3\	/13	6 3\
2 1 -1 1+1430	1	= 64-12.
\0 5	2 3/	\2 3 1 -1/	\2 8	3 2/
Определение 6.4. Произведением матрицы А = (atJ) типа тхп на число а € К называют матрицу С — (cij) типа тхп с элементами = aav.
Подробно это произведение выглядит так:
/ «и «12
«21	«22
«1п
«2п
/ ^«11
€Ш21
oai2
Oftt22
««In
««2п
\ «ml «m2
«тп /
у Q«ml СШт2 •••
^«тп /
Замечание 6.2. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами. Эти операции также называют линейными.
Для любых матриц А — (aij), В — и С = (cij) из Mmn(TRL) верны следующие свойства линейных операций.
1°. Сложение матриц коммутативно: А + В = В + А.
◄ Доказательства равенств матриц часто проводят, основываясь на определении 6.2, т.е. доказывают, что матрицы, стоящие в левой и правой частях равенства, имеют на одинаковых местах равные элементы. Так, свойство коммутативности суммы матриц следует из равенств
[4. + B]tJ — aij + bjj — bij + aij — [JB + A] i j,
среди которых первое и третье следуют из определения 6.3 суммы двух матриц, а второе верно в силу коммутативности сложения действительных чисел. ►
6.2. Линейные операции над матрицами 161
2°. Сложение матриц ассоциативно: (А + В) + С = А + (В + I
◄ Как и в случае коммутативности, свойство ассоциативности вытекает из равенств
[(Л + В) + C]ij — [А + В]г-у +	= (aij + bij) + Cij =
= aij + (bij +	+ [B + C]ij = [A + (B +
которые имеют место в силу определения 6.3 суммы двух матриц и ассоциативности сложения действительных чисел. ►
Свойства 1° и 2° позволяют не заботиться о порядке операций сложения матриц и порядке слагаемых в матричных выражениях.
3°. Существует такая матрица О €	что для любой
матрицы А € Mmn(W) выполнено равенство А + О = А.
◄ Матрица О — это нулевая матрица 0 типа тхп. Действительно, [А + 0]^ = [A]ij + [0]ij = aij + 0 — aij = [A]2j. ►
4°. Для любой матрицы А €	существует такая
единственная матрица В €	для которой выполнено
равенство А + В = 0, где 0 — нулевая матрица.
◄ Если А + В = 0, то [А + B]ij =	+ bij = [0]2j — 0 и, сле-
довательно, + bij = 0. Значит, элементами bij матрицы В являются bij = ~aij, и это доказывает как единственность, так и существование матрицы В. ►
Матрицу В, о которой говорится в свойстве 4°, называют противоположной А и обозначают через —А. Эта матрица получается из матрицы А умножением на число —1.
Свойства 3° и 4° позволяют ввести операцию вычитания матриц. Разностью Р — Q матриц Р и Q одного типа называют матрицу Р+(—Q).
6 Аналитическая геометрия
162 6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
5°. Умножение матрицы на число ассоциативно: (А/х)Л = = Л(дА)-
=: (^M)«v ~ Mm«v) =	►
6°. Умножение матрицы на число дистрибутивно относительно суммы действительных чисел: (A + /z)A = ХА + рА.
◄ [(А + /л) А] гj — (А +	— Xaij + fiaij = [AA]2-j + [/zA]2j = [АЛ +
+ pA]tJ. ►
7°. Умножение матрицы на число дистрибутивно относительно суммы матриц: А(А + В) = АЛ + АВ.
4 [А(А + B)]ij = А[А + B]ij =	+ b{j) = Xaij + Xbij = [АА]г^ +
+ [AB]ij = [АА + XB]ij. ►
8°. Умножение матрицы на 1 не меняет ее: 1 • А = А.
< [1 • A]ij = 1 • [A]tj = [A]2j. ►
6.3. Транспонирование матриц
Определение 6.5. Для матрицы А= (a;j) типа тхп ее транспонированной матрицей называют матрицу Ат = = (сг7) типа пхт с элементами Cij — aji.
При транспонировании матрицы ее строки становятся столбцами новой матрицы с сохранением их порядка. Точно так же столбцы исходной матрицы превращаются в строки транспонированной. Поэтому транспонирование можно рассматривать как преобразование симметрии матрицы относительно ее главной диагонали. Подробнее:
т
(а\\	«12	•••	«1п \	/«11	«21	•••	<*т1
«21	«22	•••	«2п	_	«12	«22	•••	«m2
\ «ml	«m2	• • •	«тп /	\ «1п	«2п	• • •	«тп /
6.3. Транспонирование матриц
163
Пример 6.2. Транспонируем следующие три матрицы:
(«1, й2,
Свойства операции транспонирования.
1°. (Дт)т = А.
◄	Отметим, что матрицы (Ат)т и А имеют одинаковые размеры. Кроме того, [(^4Т)Т]»у — [(4Т)]Л- = [A]jj. ►
2°. (А + В)Т = Ат + Вт.
◄	[(Л + В)т] i 3 = [(А +	= [А]л- + [В] ji = [Лт]у + [Вт]у = [Ат +
3°. (АА)Т = ААТ, Аек.
[(^^) ]о —	= МЛЬ»= ]и = [-^ hr ►
Если А1 = А, то матрицу А называют симметрической, а если Лт = —А — кососимметрической. И в том и в другом случае матрица должна быть квадратной. Элементы симметрической матрицы, расположенные на местах, симметричных относительно диагонали, равны между собой. Действительно, [AT]V = [4]ji и из равенства Ат = А следует, что = [А]гу. Элементы же кососимметрической матрицы, расположенные на местах, симметричных относительно главной диагонали, отличаются знаком, а диагональные — равны нулю. Действительно, [AT]sj = и из равенства Ат = —А следует, что [A]Jt = — [А]у. В частности, при i = j выполняются равенства Ил = -Мг = 0.
164
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Пример 6.3. Матрицы
-2
О
—4
1\
—4 I — симметрические, 2/
—2
1\
—4 I — кососимметрические.
О/
6.4. Умножение матриц
Определение 6.6. Пусть даны матрица А = (а,у) типа тхп и матрица В = (bij) типа пхр. Произведением матриц А и В называют матрицу С = (cij) типа тхр с элементами
Cij —	' aikbkj >
fc=i
которую обозначают С = АВ.
Произведение определено лишь в том случае, когда количество столбцов первого сомножителя равно количеству строк второго. В формировании элемента Cij произведения АВ участвуют элементы г-й строки матрицы А и у-го столбца матрицы В. Поэтому правило умножения матриц называют также правилом умножения „строка на столбец":
Пример 6.4. Найдем произведение двух матриц /2\
1 2	3	0 |	/ 1-2 + 2-0 + 3-3 + 4-1 \ = / 15\
-1 1 —2 2/ 3 “ у-1-2+1-0-2-3 + 217 “ V-6/
О
4
= г •
6.4. Умножение матриц
165
Пример 6.5. Произведением прямоугольной матрицы и матрицы-столбца является матрица-столбец:
«п	«12	... ttin
«21	«22	••• «2п
«ml ат2 • • • ^тп
( йцЖ1+«12ж2+-*-+«1пжп а21ж1+«22ж2 + ---+«2пжп
\«7П1	'Т«т2^'2'Т •	а тпхп/
Пример 6.6. Найдем произведение трех квадратных матриц второго порядка, перемножив сначала первые две матрицы, а затем результат их произведения и третью матрицу:
1 2\ /-1	0 \ /0 -4\
3 4J V 2 -ЗД2 -1/
/ — 1+4 0-б\/0 -4\ V-3 + 8 0 — 12/ \2 -1 /
-12 -б\
-24 -8 /
Умножение матрицы-строки X типа 1хп на матрицу-столбец Y типа nx 1 дает матрицу типа 1x1, которую отождествляют с числом:
У1 У
У2
XY — (#1, ^2, ... , хп) .	—
\Уп/
п
= (х1у1+х2у2 + ... + хпуп) = уУхкук.
fc=l
Таким образом, произведение любой матрицы-строки и любой матрицы-столбца, имеющих одинаковое количество элементов, есть число, равное сумме произведений их элементов с одинаковыми индексами. Если матрица-строка и матрица-столбец имеют разное количество элементов, то их перемножить нельзя.
166
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Замечание 6.3. Для числовых матриц типа 1x1 матричные операции суммы, разности, умножения и умножения матриц на действительные числа совпадают с соответствующими арифметическими операциями суммы, разности и умножения над действительными числами. Вот почему их и отождествляют с числами.
Существование произведения АВ двух матриц не означает существования их произведения ВА. Например, матрицы из примера 6.4 нельзя умножить в другом порядке.
Чтобы матрицу А типа тхп можно было умножить на матрицу В и слева, и справа (т.е. чтобы были определены оба произведения ВА и АВ), матрица В должна иметь тип пхт. Квадратные матрицы А и В можно перемножить, если они имеют один порядок, причем в этом случае определены оба произведения (АВ и ВЛ), хотя равенство АВ = В А обычно нарушается.
Пример 6.7. Найдем произведения двух пар матриц А, В и С, D в одном и другом порядке:
1 2\ /1 1\	/1 3\
34j\0 1J"“\3 7/’
0	= (° И
оо; \0 1/ \оо;’
1 1W1 2\	/4 б\
О 1) \34/ ~ \34/’
00\ /0 1\	(00\
Q 1) \0 0 ) ~ \0 0 ) '
Обратим внимание, что CD = С, DC = О, хотя ни одна из этих двух матриц не является нулевой. #
Если определены оба произведения АВ и ВА и выполнено равенство АВ = ВА, то матрицы А и В называют коммутирующими или перестановочными. Коммутирующие матрицы всегда квадратные и одного порядка.
Пример 6.8. Произведение диагональных матриц одного порядка есть диагональная матрица, элементами которой
6.4. Умножение матриц
167
являются произведения соответствующих элементов перемножаемых матриц. Диагональные матрицы одного порядка являются перестановочными. Действительно,
( «1&1 О О
\ О 0	... j
/ах	0 ... О \
О а2 ... О
\ о 0 ... ап)
Операция умножения матриц имеет следующие свойства.
1°. Умножение матриц ассоциативно, т.е. [АВ}С — А(ВС).
◄ Если матрицы 4,В,С имеют типы mxn, nxfc, kxl соответственно, то
к	к / п	\
= У^[АВ]|Г [C*]rj = I	j [C*]rj =
r=l	r=l \s=l	/
к tl	k fl
F=1 5=1	F = 1 5=1
п	к	n
=Ж Е[вЬг[с]п==[a(bc)]0-.	►
5=1	Г = 1	5=1
2°. Умножение матриц дистрибутивно относительно сложения матриц, т.е. (А + В)С = АС + ВС.
168 6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
4 Если матрицы А, В имеют тип тхп, а матрица С — тип nxfc, то
п	п
[(А + В)С%- = Да + B]ir[C]r> = Д [A]ir + [B]ir)[C]rj = r=l	r=l
71	71	71
= Д ([A]ir[C]rJ + [B]ir[C]rJ) = Да],г[С]г,- + Дж [C]ri = r=l	r=l	r=l
= [AC]^ + [BC]^ = [AC + BC]t>. ►
3°. Существует такая матрица E € Afn(R), что для любой матрицы А € Mn(R) выполнены равенства АЕ = ЕА = А.
4 В качестве матрицы Е можно взять единичную порядка п. ►
4°. Для любой матрицы А € Mn(R) и нулевой матрицы 0 € Afn(R) выполнено равенство А0 = 0.
◄ Вычислим элементы произведения А0:
п	п
[A0]ij = У^[А]гг[0]г?- = У~^[А],ГО = 0.
r=l	r=l
Видим, что все элементы матрицы А0 равны нулю. ►
5°. Для любых матриц А и В типов тхп и nxfc выполнено равенство (АВ)Т = ВТАТ, т.е. транспонированное произведение двух матриц равно произведению в обратном порядке транспонированных матриц,
п
◄ [(АВ) ]г-у = [АВ]^ = У"2[ДЬ‘г[В]гг- =
Г=1
= £[ЛТ]Г)[ВТ],Г = fXM»’].-, = № ► Г=1	Г=1
Операция умножения матриц позволяет ввести операцию возведения квадратной матрицы в натуральную степень. Положим А1 = A, An+1 = AAn, n = 1,2,... Отметим, что две степени
6.5. Блочные матрицы
169
Ап и Ат одной и той же матрицы являются матрицами одного порядка и перестановочны: АпАгп = АтАп = Дп+т. Введем также нулевую степень квадратной матрицы, полагая А0 = Е, где Е — единичная матрица того же порядка.
Введенная степень матрицы позволяет для квадратной матрицы вычислять выражения вида
апАп + ап_ 1 Ап 1 + ... ogA^, G i ~ 0, п,
т.е. многочлены от одного матричного аргумента.
Пример 6.9. Вычислим значение квадратного трехчлена р(х) = Зя2 — 4ж + 5 для квадратной матрицы
А =
О 2\
-1 1) *
Поскольку р(х) = Зя2 - 4я + 5ж°, то р(А) = ЗА2 - 4А + 5А°, где А0 = Е — единичная матрица второго порядка. Вычислив
О 2\ / 0 2\ _ Z-2	2\
-1 1 / у —1 1/	-1 у ’
находим
Q/-2	2\	./ О
р(А) = 3( 1 _1)-4( х
0\ 1J
-6 /О ~8\ , /5	-2^
-3 -37 + \4 -4У + \О 5/	\ 1 —2/
6.5.	Блочные матрицы
Если разделить некоторую матрицу А на части вертикальными и горизонтальными прямыми, то получаются прямоугольные ячейки, являющиеся сами по себе матрицами. Эти ячейки называют блоками матрицы. Сама матрица А может
170
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
рассматриваться как таблица, элементами которой являются более мелкие матрицы Мац: А = (Мар). При таком построении матрица А составляется из блоков, и поэтому ее называют блочной. Например, матрицу
	( «11	«12	«13	«14	«15
	«21	«22	«23	«24	«25
Л =	«31	«32	«33	«34	«35
	«41	«42	«43	«44	«45
	\ «51	«52	«53	«54	«55/
разобьем на следующие блоки:
/ Оц «12	«13 «21	«22	«23 «31	«32	«33	«14	«15 \ «24	«25 «34 «35
«41	«42	«43 \ «51	«52 «53	«44	Я45 «54 «55 /
и обозначим их
(«и «21 «31
«12
«22
«32
«13
«23
«33
(«14	«15
«24	«25
«34	«35
Л/21 —
«42	«43
«52	«53
«45
«55
Тогда матрицу А можно записать в виде блочной матрицы, элементами которой будут эти матрицы Ма@:
Мп
М21
Ml 2
М2 2
Для составления блочной матрицы из серии матриц Мар необходимо, чтобы подмножества матриц из серии с одинаковым значением индекса а имели одинаковое количество строк, а подмножества матриц с одинаковым значением индекса /3 —
6.5. Блочные матрицы
171
одинаковое количество столбцов. Эти подмножества образуют соответственно „блочные44 строки и „блочные44 столбцы (соответствующие нескольким строкам или столбцам обычной записи матрицы).
Пример 6.10. Указанным требованиям удовлетворяют следующие четыре матрицы:
fan	«12	«1з\	f Ъц	bi2\
Мп = I	I ,	M12 = I 7 I J ,
\«21	a22	a23 J	\ &21	b22 /
(cn	«12	С1з\	/ du	di2\
C21	c22	c23 I , M22 = I d2i	d22 j .
С31	«32	c33 /	\d31	C?32 /
Поэтому из них можно составить блочную матрицу
(Мц \ M2i
Mi2 \ м22 J
/ оц а12 «13
«21	«22	«23
Си	С12	С13
С21	С22	С23
\ С31	С32	сзз
Ьц bi2\ 621 ь22 dn di2 d2i d22 dsi ^32 /
Основное свойство блочных матриц состоит в том, что операции над блочными матрицами совершаются по тем же правилам, что и операции над обычными матрицами. В самом деле, это в достаточной степени очевидно для суммы матриц и произведения матрицы на число. Однако относительно суммы эго можно утверждать лишь в том случае, когда размеры слагаемых блочных матриц, равно как и размеры отдельных блоков с равными индексами у слагаемых, совпадают.
Подробнее рассмотрим ситуацию с умножением блочных матриц. Пусть блочные матрицы А — (Да^) и В = (Вру) удовлетворяют двум условиям.
1.	Число „блочных44 столбцов матрицы А совпадает с числом „блочных44 строк матрицы В (т.е. индекс /3 для Л и 13 изменяется в одинаковых пределах).
172
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
2.	Для любых индексов а, /?', у число столбцов у матрицы совпадает с числом строк у матрицы
Тогда

Ссг? — Aot/3 В/Зу •
Для доказательства этого равенства достаточно расписать обе его части через элементы матриц.
Указанные два условия довольно сложны, но все упрощается, если блоки матриц — это квадратные матрицы одного порядка. В этом случае условия близки к обычным: число „блочных*4 столбцов множимого должно совпадать с числом „блочных44 строк множителя.
Представление матриц в блочном виде часто оказывается удобным при нахождении суммы и произведения, если матрицы имеют достаточно большие размеры, а их согласованные разбиения на блоки содержат нулевые, единичные, диагональные, треугольные матрицы.
Пример 6.11. Найдем произведения следующих блочных матриц предполагая, что все операции определены:
А Е\(С\(АС\ (е Е\(А В\_(С D\ 0 вДву Vе/ V# 0/\с D)~\A ВГ
А ЗЕ\ (С\ = ( AC + W\
-Е В)\DJ \-C+BD)
При транспонировании блочной матрицы транспонированию подлежат и ее элементы. Например,
Ми Л/12\Т_/М1Т1
Л/21 М22 /	\ М^2 М-22
6.6. Прямая сумма матриц
173
Пример 6.12. Транспонируем блочную матрицу
(«11	«12
«21	«22
«31	«32
\ «41	«42
«13	«14	«15 \
«23	«24	«25	_ / >411
«33	«34	«35	\	^21
«43	«44	«45	/
>412 \
>422 /
/ Дт
I Л11
I Ат X Л12
( «11	«21
«12	«22
«13 «23
«14	«24
\ «15 «25
«31	«41
«32	«42
«33 «43
«34	«44
«35	«45 /
6.6.	Прямая сумма матриц
Определение 6.7. Пусть даны квадратные матрицы А порядка т и В порядка п. Прямой суммой матриц А и В называют квадратную блочную матрицу С = >4 ф В порядка тп + п, равную
С“ в)'
где 0 обозначает нулевой блок (нулевую матрицу типа тхп вверху справа и пхт внизу слева).
Укажем основные свойства прямой суммы матриц.
1°. Ассоциативность: (АфВ) фС = Аф (ВфС)
4 В результате выполнения операций в левой и правой частях равенства получается одна и та же блочно-диагональная матрица
/А 0 0\
I 0 В 0|, \0 0 С)
где нулевые матрицы имеют соответствующий тип. ►
174 6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
2°. Пусть квадратные матрицы Ai и А2 имеют порядок т, а квадратные матрицы Bi и В2 — порядок п, Тогда
(Ai ф Bi) + (Д2 Ф В2) — (Ai + А2) Ф (Bi + В2),
(Л1 ф Bi)(A2 Ф В2) = А1А2 Ф В1В2.
◄ Действительно, эти записи означают следующее:
Ai 0 \	/ А2 0 \/ Ai Т* А2 0	\
0 Bi J у 0 В2)	\ 0	Bi + В2 / 1
/ Ai 0 \ / А2 0 \ А1А2	0 \
V© Bi) V 0 в2)~ v е Я1В2/’
что соответствует операциям над блочными матрицами. ►
6.7.	Линейная зависимость строк и столбцов
Строки и столбцы матриц можно рассматривать как матрицы-строки и, соответственно, матрицы-столбцы. Поэтому над ними, как и над любыми другими матрицами, можно выполнять линейные операции. Ограничение на операцию сложения состоит в том, что строки (столбцы) должны быть одинаковой длины (высоты), но это условие всегда выполнено для строк (столбцов) одной матрицы.
Линейные операции над строками (столбцами) дают возможность составлять строки (столбцы) в виде выражений «1О1 + ... + а5а5, где ai, ..., as — произвольный набор строк (столбцов) одинаковой длины (высоты), а #1, ..., as — действительные числа. Такие выражения называют линейными комбинациями строк (столбцов).
Определение 6.8. Строки (столбцы) ai, ..., as называют линейно независимыми, если равенство
aiai + ... + asas = O,
(6.1)
6.7. Линейная зависимость строк и столбцов
175
где 0 в правой части — нулевая строка (столбец), возможно лишь при ах = ... = as = 0. В противном случае, когда существуют такие действительные числа ах, ..., «5, не равные пулю одновременно, что выполняется равенство (6.1), эти строки (столбцы) называют линейно зависимыми.
Следующее утверждение известно как критерий линейной зависимости.
Теорема 6.1. Строки (столбцы) ах, ..., as линейно зави-симы тогда и только тогда, когда хотя бы одна (один) из них является линейной комбинацией остальных.
◄ Доказательство проведем для строк, а для столбцов оно аналогично.
Необходимость. Если строки ах, ..., as линейно зависимы, то, согласно определению 6.8, существуют такие действительные числа ах, ..., не равные нулю одновременно, что cviai + ... + asas = 0. Выберем ненулевой коэффициент «г-. Для простоты пусть это будет «р Тогда
«101 = (-«2)а2 + • • • + (-Ots)as
и, следовательно,
( ^2 \	.	. ( &s \
<Х1 — [--I 02 + • • • + I-I
\ «1 / \ «1 /
т.е. строка oi представляется в виде линейной комбинации остальных строк.
Достаточность. Пусть, например, oi = А2О2+ •••+ Тогда loi + (—Лг)о2 + ... + (—Л$)о5 = 0. Первый коэффициент линейной комбинации равен единице, т.е. он ненулевой. Согласно определению 6.8, строки ах, ..., as линейно зависимы. ►
Теорема 6.2. Пусть строки (столбцы) аХ) ..., as линейно независимы, а хотя бы одна из строк (столбцов) 6Х, ..., Ь/ является их линейной комбинацией. Тогда все строки (столбцы) ах, ..., as, bi, ..., Ъ[ линейно зависимы.
176
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
◄ Пусть, например, bi есть линейная комбинация ai, ..., a5, т.е.
bi =a1a1 + ... + asas, ог-€ R, i = 1,$.
В эту линейную комбинацию добавим строки (столбцы) Ь2, ..., bi (при I > 1) с нулевыми коэффициентами:
bi — ai<xi + ... + osas + 0&2 + • • • + ОЬ/.
Согласно теореме 6.1, строки (столбцы) ai, ..., as, Ьх, ..., bi линейно зависимы, к
6.8. Элементарные преобразования матриц
Следующие три операции называют элементарными преобразованиями строк матрицы:
1°. Умножение г-й строки матрицы на число 0:
( ап	012	• •	<%1п		ац	«12	• •	^1п
	ад	• • din	।	>	Лаи	Ааг2 .	.. Аагп
\ ат1	ат2	• • О'тп /		\ 0"тЛ	^7712	- • ^тп /
которое будем записывать в виде (г) —> А(г).
2°. Перестановка двух строк в матрице, например г-й и &-й строк:
/	ап	ап	...	ain \
^г2	• • •	<Нп
^kl	0>k2	• • •	^kn
\ ^ml	• • • ^mn /
<*12
^kn
\ aml	• • • ^mn
^k\	&к2
<*г’2	• • • <Нп
которую будем записывать в виде (г) о (&).
6.8. Элементарные преобразования матриц
177
3°. Добавление к коэффициентом А:
i-й строке матрицы ее к-й строки с
«и	«12 •	.. а1п \
б'Ц	ai2 .	• • агп
б'к!	O-k2 •	• • ^кп
	0-7712 •	• • ^тп /
( «11	«12	• •	Oln
Ог'1+Afl^i ai2-F^G>k2 •		• • Пгп~}~ ^&kn
Ukl	«£2	• •	akn
\ ®ml	&т2	• •	&mn /
что будем записывать в виде (i) —> (г) + А(&).
Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.
Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную. Например, обратным преобразованием для перестановки двух строк является перестановка тех же строк.
Каждое элементарное преобразование строк (столбцов) матрицы А можно трактовать как умножение А слева (справа) на матрицу специального вида. Эта матрица получается, если то же преобразование выполнить над единичной матрицей. Рассмотрим подробнее элементарные преобразования строк.
Пусть матрица В получается в результате умножения i-й строки матрицы А типа тхп на число А 0. Тогда В = ЕДА) А, где матрица ЕДА) получается из единичной матрицы Е порядка т умножением ее i-й строки на число А.
Пусть матрица В получается в результате перестановки i-й и к-й строк матрицы А типа тхп. Тогда В = FikA, где матрица F^ получается из единичной матрицы Е порядка т перестановкой ее i-й и к-й строк.
Пусть матрица В получается в результате добавления к i-й строке матрицы А типа mxnee к-й строки с коэффициентом А. Тогда В = Gik{X}A, где матрица Gik получается из единичной матрицы Е порядка т в результате добавления к i-й строке
178
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
к-й строки с коэффициентом А, т.е. на пересечении г-й строки и к-го столбца матрицы Е нулевой элемент заменен на число А.
Точно так же реализуются элементарные преобразования столбцов матрицы Л, но при этом она умножается на матрицы специального вида не слева, а справа.
С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду. Один из важнейших таких алгоритмов составляет основу доказательства следующей теоремы.
Теорема 6.3. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду, 4 Доказательство теоремы состоит в построении конкретного алгоритма приведения матрицы к ступенчатому виду. Этот алгоритм состоит в многократном повторении в определенном порядке трех операций, связанных с некоторым текущим элементом матрицы, который выбирается исходя из расположения в матрице. На первом шаге алгоритма в качестве текущего элемента матрицы выбираем верхний левый, т.е. [А]ц.
1*. Если текущий элемент равен нулю, переходим к операции 2*. Если же он не равен нулю, то строку, в которой расположен текущий элемент (текущую строку), добавляем с соответствующими коэффициентами к строкам, расположенным ниже, так, чтобы все элементы матрицы, стоящие в столбце под текущим элементом, обратились в нуль. Например, если текущий элемент — то в качестве коэффициента для к-й строки, к = г+ 1,..., нам следует взять число — [Л]^/[А]гу Выбираем новый текущий элемент, смещаясь в матрице на один столбец вправо и на одну строку вниз, и переходим к следующему шагу, повторяя операцию 1*. Если такое смещение невозможно, т.е. достигнут последний столбец или строка, преобразования прекращаем.
2*. Если текущий элемент в некоторой строке матрицы равен нулю, то просматриваем элементы матрицы, расположен-
6.8. Элементарные преобразования матриц
179
iiue в столбце под текущим элементом. Если среди них нет ненулевых, переходим к операции 3*. Пусть в к-й строке под текущим элементом находится ненулевой элемент. Меняем местами текущую и к-ю строки и возвращаемся к операции 1*.
3*. Если текущий элемент и все элементы под ним (в том же столбце) равны нулю, меняем текущий элемент, смещаясь в матрице на один столбец вправо. Если такое смещение возможно, т.е. текущий элемент находится не в самом правом столбце матрицы, то повторяем операцию 1*. Если же мы уже достигли правого края матрицы и смена текущего элемента невозможна, то матрица имеет ступенчатый вид, и мы можем прекратить преобразования.
Так как матрица имеет конечные размеры, а за один шаг алгоритма положение текущего элемента смещается вправо хотя бы на один столбец, процесс преобразований закончится, причем не более чем за п шагов (п — количество столбцов в матрице). Значит, наступит момент, когда матрица будет иметь ступенчатый вид. ►
Пример 6.13. Преобразуем матрицу
1 2 1 1\
2 3 2 4
4 5 4 6/
к ступенчатому виду с помощью элементарных преобразований строк.
Используя алгоритм из доказательства теоремы 6.3 и записывая матрицы после окончания выполнения его операций,
получаем
1
2
4
2
3
5
1
2
4
1\
4
6 /
/1	2 1
~ [ 0 —1 О
\0 -3 о /1	2
~| (3)	(3) — 3(2)~]~ 0 -1
\0 О
(2)	(2) - 2(1)
(3)->(3)-4(1)
1\
2 ] ~
2 /
1 Л
О 2 I .
0—4/
180 6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Вопросы и задачи
6.1.	Какого вида будет матрица Ат, если сама матрица А является: а) единичной; б) нулевой; в) верхней треугольной; г) нижней треугольной; д) трехдиагональной; е) диагональной; ж) блочной?
6.2.	Для матриц
(-1 2 4 \	\ I
' 7 п b В= I 2 3 2 ,	1
7	\0 -1 1/	\ 3
вычислить: а) АВ; б) А(В + ВТ); в) (АС)ТА; г) ВАТ; д) СТВ; е) АТАВ; ж) СТВАТ + 2СТАТ; з) ЗАВС-АС.
6.3.	Показать, что для любой матрицы А € Mmn(W) определены произведения Ат А и ААТ.
6.4.	Привести примеры ненулевых квадратных матриц А и В третьего порядка, для которых АВ = 0.
6.5.	Доказать, что если две матрицы перестановочны, то они квадратные и одного порядка.
6.6.	Доказать, что сумма и произведение двух верхних (нижних) треугольных матриц из Afn(R) есть верхняя (нижняя) треугольная матрица из Mn(R). Чему равны диагональные элементы у произведения двух верхних (нижних) треугольных матриц из
6.7.	Являются ли симметрическими следующие матрицы: а) единичная; б) квадратная нулевая; в) нулевая? Какие из этих матриц являются кососимметрическими?
6.8.	Доказать, что если матрица является одновременно и симметрической, и кососимметрической, то она квадратная нулевая.
Вопросы и задачи
181
6.9.	Доказать, что для любой матрицы А € Mn(R) матрица Л + Ат является симметрической, а А — Ат — кососимметрической.
6.10.	Вычислить А1999, Д2000, А2001, если
\Л /0 «Ч Л ( 0 "А ЧЛ-f0 “О а)Л\1 0/’ б)Л\-1	О/’ В) (1	О/’
6.11.	Найти Ап, п = 2,3,..., если
а)л=(о 1)’ б)Л=(о ")’aeR-
6.12.	Построить пример ступенчатых матриц А и В, сумма которых не является ступенчатой матрицей.
6.13.	Представить элементарные преобразования столбцов матриц как умножение преобразуемой матрицы справа на матрицы специального вида.
6.14.	Вычислить значение квадратного трехчлена р(х} = = —4ж2 + 2х + 3 для матриц
/3 —2\	/ 1 -1	°\
а) А=	); б) А= 3	2 -1 .
V 7	\-1	0	2/
6.15.	Найти произведение двух матриц, перейдя к блочным матрицам согласно заданному разбиению на блоки
1 0 0 1	1 0 2 1 1 1	1 °\ 0 1
0 0	2 0 0	0 0
0 0	0 2 0	0 0
0 0	0 0 2	0 0/
/1 2 3 4	1 °\ 0 1
0 0	2 2
0 0	3 2
0 0	1 1
1 0	0 0
\0 1	0 0/
и вычислив произведение блочных матриц (см. пример 6.11).
182
6. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
6.16.	При помощи элементарных преобразований привести к ступенчатому виду следующие матрицы:
/ 1 -3 —2\	/ 3	1	0\
а) А = I 2	1	1 ; б) А= I 1 -2 -1 .
\-3	2	2/	\—2 —3 — 1/
6.17.	Определено ли произведение АВ, если А — матрица-столбец, а В — матрица-строка?
6.18.	Можно ли произвольную квадратную матрицу представить в виде суммы симметрической и кососимметрической матриц? Если такое представление существует, то единственно ли оно?
6.19.	Для каких матриц А и В выполнено равенство: а) (А + + В)2 = А2 + 2АВ + В2] б) А2-В2 = (А + В)(Л~В)?
6.20.	Существуют ли матрицы А и В, удовлетворяющие равенству: а) АВ + ВтАт — Е\ б) АВ - ВтАт = Е?
7. ОПРЕДЕЛИТЕЛИ
7.1.	Определители n-го порядка
Мы уже познакомились с определителями второго и третьего порядков, которые использовали в векторной алгебре и при решении систем двух и трех линейных уравнений. Теперь мы приступаем к изучению определителей произвольного порядка. В теории таких определителей используются понятия перестановки, подстановки и их четности. Соответствующий материал подробно изложен в [1-4.5], а мы напомним только с амые необходимые сведения.
Всякое расположение чисел 1, 2, 3, ..., п в определенном порядке называют перестановкой из п чисел. Из п чисел можно образовать п! различных перестановок. В общем случае перестановку записывают в виде матрицы-строки О' — («1, &2, ап). Перестановку (1, 2, 3, 4, ..., п) называют нормальной.
Два числа и в перестановке а = (а1? ct2, ..., ап) образуют инверсию, если а3 > аг, но при этом стоит в перестановке правее а3 (т.е. i > j). Общее количество инверсий в перестановке а обозначают |а|, и если это число четное, то перестановку называют четной, а если оно нечетное — нечетной.
Пример 7.1. Определим, какова четность перестановки а — (4, 5, 1, 3, 6, 2), т.е. выясним, является она четной или нечетной. Для этого подсчитаем в а количество инверсий. Правее числа 4 стоят три числа, меньшие его: 1, 3 и 2. Следовательно, числу 4 соответствует три инверсии с числами, стоящими справа от него. Справа от числа 5 стоят также три числа, которые меньше 5. Следовательно, числу 5 тоже
184
7. ОПРЕДЕЛИТЕЛИ
соответствует три инверсии с числами, стоящими справа от него. Аналогично находим, что число 1 не образует инверсий с числами, стоящими правее его, числа 3 и 6 образуют по одной такой инверсии. Общее количество инверсий в перестановке а равно |а| = 34-3 + 0+1 + 1 = 8, т.е. четно. Следовательно, перестановка а является четной. #
Транспозицией перестановки называют такое ее преобразование, при котором в ней меняются местами какие-либо два элемента, а другие остаются на своих местах.
Теорема 7.1. Любая транспозиция меняет четность перестановки.
4 Пусть транспозиция состоит в том, что в перестановке а меняются местами ее г-й и j-й элементы, т.е.
Of = (..., Of2‘, ..., Ofj, ...)	>• (..., Ofj, ..., Of2', ...),
где многоточиями обозначены числа, сохраняющие свои места. Если числа и aj являются соседними в перестановке, т.е.
3 = г+1,
а = (..., аг-, оу, ...),
и образуют инверсию, то при транспозиции эта инверсия исчезнет, а если ее не было, то она появится. Для любой другой пары элементов из перестановки их взаимное расположение при транспозиции не меняется. Поэтому общее количество инверсий в перестановке при транспозиции изменяется ровно на единицу. Следовательно, перестановка меняет свою четность.
Если числа и оу стоят в перестановке через т промежуточных чисел, т.е. j = г + т + 1,
Of— (..., Of2’, Of^-j-i, Of{-|-2? •••> ^t+m>	• • •) 5
то их транспозицию можно реализовать с помощью последовательных транспозиций только соседних пар чисел. Действительно, число можно поменять местами последовательно с
7.1. Определители n-го порядка
185
<4’+ь <4+2, •••> затем уже в перестановке
(• • • ? ^4’4-11 £4+2} •••? ^44-тп, ^4,	• • •)
поменять местами с aj, после чего число ау, уже стоящее слева от аг, поменять местами последовательное oti+тп, ..., <4_|_2, <4+1. В результате нужная перестановка
dig, <4’4-1 > <4+2) •••)	• • •)
будет получена за счет выполнения 2m + 1 транспозиций соседних чисел. Поскольку при этом четность перестановки каждый раз изменялась, а всего этих изменений было нечетное число, то в результате четность перестановки изменилась на противоположную. ►
Из двух перестановок («1, а2,	&п) и (/?i, /32, /Зп)
одних и тех же чисел можно составить новый объект
/?1 @2 --- fin
ai а2 ... &п
(7.1)
который называют подстановкой n-й степени.
Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в противоположном случае. Четность подстановки (7.1) совпадает с четностью числа |/3| +1а| — общего количества инверсий в строках подстановки, которое обозначают |<т|.
Транспозицией подстановки называют любую перестановку ее столбцов. Поскольку транспозиция подстановки вызывает транспозиции и в образующих ее перестановках, то, согласно теореме 7.1, очевидно, что транспозиция подстановки не меняет ее четность.
Каждая подстановка вида (7.1) задает взаимно однозначное отображение множества чисел 1, 2, 3, ..., п на себя, при котором /3i отображается в «1, /32 — в а2 и т.д. В соответствии с
186
7. ОПРЕДЕЛИТЕЛИ
интерпретацией подстановок как отображений две подстановки считают равными, если они отличаются только порядком записи своих столбцов. Например, подстановки
/1 3 4 2\	/1 2 3 4\
^2 4 13/ И V2 3 4 1J
равны, так как вторая получается из первой перестановкой столбцов.
Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок п-й степени имеется ровно п\
Определение 7.1. Определителем порядка п, соответствующим квадратной матрице
/ Иц «12	••• Gin \
Л= “2‘ °22 " “2"	(7.2)
\ а>п\ ап2 ... апп /
порядка п (определителем квадратной матрицы порядка п), называют сумму п! слагаемых
det А =	^(—1)' '«Icqа2«2 • • • апап ?	(7*3)
(У
которая берется по всевозможным подстановкам вида
( 1	2 ... п \
а = I
\ «1 а2 • • • &п /
Определитель матрицы А часто называют просто определителем, или детерминантом, и обозначают
«и а12 ... а1п
«21	«22	•••	^2п
®nl ®п2	• • • ^пп
или det А, называя А матрицей этого определителя.
7.1. Определители n-го порядка
187
Определение 7.1 в частных случаях п = 2 и п = 3 дает то же, ’Iто и введенные ранее в 2.1 определения. Например, при п — 2 из элементов матрицы
А = | 011 °12 | \^21	«22/
можно составить только два указанных в определении произведения ацв22 и oi2«2i, которым соответствуют подстановки
/1 2\	/1 2\
ai=b 2) и а2=Ь J’
четная и нечетная соответственно, так как |ai| = 0, а |сг21 = 1-Поэтому, согласно формуле (7.3),
det А = (— 1)°«11«22 + (“1)1«12«21 ~ «1 1 a22 ~~ «12«21 •
Каждое слагаемое в сумме (7.3) представляет собой произведение п элементов матрицы (7.2). При этом все сомножители находятся в разных строках и в разных столбцах матрицы, по одному в каждой строке (каждом столбце). В произведении сомножители упорядочены по номерам строк (другими словами, по первому индексу), и этот порядок определяет знак слагаемого. Однако на самом деле выбранный порядок не является существенным. Если мы изменим порядок сомножителей конкретного слагаемого, то подстановка, образованная номерами строк и столбцов сомножителей, будет иметь тот же знак, что и подстановка, использованная в сумме (7.3). В частности, сумма (7.3) совпадает с суммой
det А =	(-1),т|аЛ 1	   а0пп,
которая берется по всем подстановкам т вида
f 01 02 ••• 0п\
\ 1	2 ... п У
188
7. ОПРЕДЕЛИТЕЛИ
7.2.	Свойства определителей
Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология (порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей, транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов и др.). При изучении определителей используют эту возможность, подразумевая однако, что терминология относится к матрице определителя.
Свойство 7.1. Определитель не меняется при транспонировании.
◄ Фактически требуется доказать, что для любой квадратной матрицы А вида (7.2) выполнено равенство det Ат = det А.
Прежде всего отметим, что если произведение
^1а 1’ ^пап
является слагаемым в определителе det А, то оно является слагаемым и в определителе det Ат. Действительно, если сомножители этого произведения расположены в разных строках и разных столбцах в матрице А, то они обладают этим же свойством и в транспонированной матрице Ат. Знак этого слагаемого в det А определяется подстановкой
/ 1	2 ... п \
ст = I
\ <*1	012 Otn J
Однако в транспонированной матрице сомножители этого слагаемого расположены на симметричных относительно диагонали матрицы местах. Поэтому в det Ат его знак определяется подстановкой
/ ai а2 • • • &п \
11 2 ... п Г
7.2. Свойства определителей
189
Четности подстановок а и г совпадают, так как общее число инверсий в их строках равно числу инверсий в перестановке (fV], «2? •..} ап). Поэтому совпадают и знаки рассматриваемого слагаемого в det А и det Ат. Следовательно, det Дт = det А. ►
Согласно свойству 7.1, строки и столбцы определителя равноправны в том смысле, что любое доказанное утверждение о строках определителя сразу переносится на столбцы и наоборот. Учитывая это, мы, хотя и формулируем нижеследующие утверждения для строк и столбцов, доказательства проводим только в одном варианте.
Свойство 7.2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
◄ Обозначим через Д определитель матрицы А вида (7.2), а через Д1 — определитель, полученный из Д перестановкой г-й и j-й строк:
	«11	«12	... ain		«и	«12	•••	aln
		«t’2	...		ajl	aj2   •	
д =	aji	aj2	.. . Ujn	, Ai =		ai2 ...	
	ani	0"п2	• • • 0>nn		ani		
Если произведение aiQ1... •... ajaj...апсХп является слагаемым в определителе Д, то оно является слагаемым и в определителе Д1? и наоборот. Это следует из того, что если сомножители этого произведения расположены в разных строках и разных столбцах в матрице определителя Д, то они обладают этим же свойством и в матрице определителя Д1, и наоборот. Знак этого слагаемого в Д определяется подстановкой
г
п
3
190
7, ОПРЕДЕЛИТЕЛИ
Однако в Ai знак этого же слагаемого определяется подстановкой
(1	...	j	... i	...	п \
#1	...	ai	...	aj	...	ап J
Поскольку первая строка подстановки г получается из первой строки подстановки а при помощи одной транспозиции, а вторые строки у них совпадают, эти подстановки имеют разную четность. Значит, определители Д и Aj содержат одинаковые по абсолютной величине слагаемые, но с противоположными знаками. ►
Свойство 7.3. Если все элементы j-ro столбца определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все столбцы, кроме j-ro, такие же, как и в данном определителе, а j-й столбец первого определителя состоит из первых слагаемых j-ro столбца данного определителя, а второго — из вторых слагаемых:
«11	...	«ijH“*«ij	•••	«1п
«21	•••	’**
«ni	...	anj-\-anj	...	ann
«11 •	.. а'ъ .	.. а\п		«11 •	• • a"j •	• • «In
«21 •	•• «2, •	•• «2п	+	«21 •	•• «2j •	• • «2п
«п1 •	-<] 	• • «пп		«п1 •	-<•	• • «пп
Аналогично, если все элементы г-й строки определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме г-й, такие же, как и в данном определителе, а г-я строка первого определителя состоит из первых слагаемых г-й строки данного определителя, вторая — из вторых слагаемых:
«И «12	•••	«1п
«11 «12 • • • «1п
«11 «12 • • • «1п

<1 <2
«п1	«п2	• • • «пп
«п1 «п2 • • • «пп
<4 <2-<4
«п1 «п2 •• • «пп
7.2. Свойства определителей
191
◄ Пусть, например, элементы i-й строки определителя пpeд-c гавлены в виде суммы двух слагаемых. Тогда
«11	«12	•••	«In
atl+fflil	ai2+ai2 • • • ain+ain
anl	Cln2	• • •	®nn
= 52(-l)l“laia1a2a2...		+ aiai) • • -anan —	
— У ^(—1)' '«lai • • -aia, • • ф«па„ + <7 an «12 ...	D-a «1п	-1)	। 'aiai • • • a,aj... anan — ац an ••• ain
= ail ai2 anl «,п2 ito и требовалось доказать. ►	a'-n «пп	+	af!	a'-'	af/ ail	ai2	• • •	ain	> «nl	«n2	• • •	«nn
Свойство 7.4. Общий множитель			элементов строки или
столбца может быть вынесен за знак определителя. Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца:
ац	«lj	• • «In			an •	a\j	... «in
Aa,i .		> . X(lin	= A		a2i	aij	• • • «m
ani	.. «nJ	1 • «nn			anl	• • dnj	• • • ®nn
an •	. A«ij .	• • ®ln		an • •		alj	••• «In
«г1	. . A«{j	•	• • «гп	= A	«г 1		aij	••• «гп
ani	• • Xanj	• • «nn		«nl		. dnj	• • • «пп
192 7. ОПРЕДЕЛИТЕЛИ
◄ Пусть, например, элементы г-й строки определителя имеют общий множитель А. Тогда
СЬц ... CLij . . . din
... \d^g ... Aflj^
—	2( 1)'	• • • (^fliaj) • • *апап —
a
dni ... dnj .. . dnn
	«11 •	.. d]j .	• • ®ln
—	v( 1)'	;• • • ^пап — (У	аг1 •	.. dij .	• • djn
	®nl •	• • dnj .	• • ®nn
где первое и последнее равенства выполняются в силу определения 7.1. ►
Доказанное свойство диссонирует со свойствами умножения матрицы на число. Действительно, при умножении матрицы на число все ее элементы умножаются на число. Но умножение определителя на число — это лишь умножение одной строки или столбца матрицы определителя на это число. Поэтому, если А — квадратная матрица порядка п, то det(AA) = Andet А.
Свойство 7.5. Определитель равен нулю, если он имеет:
1)	нулевую строку (столбец);
2)	хотя бы две одинаковые строки (столбца);
3)	хотя бы две строки (столбца), элементы которых пропорциональны;
4)	хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
◄ 1) Так как определитель является суммой произведений элементов из каждой строки, то в каждом таком произведении есть нуль — какой-то элемент из нулевой строки. Следовательно, все слагаемые в сумме (7.3) равны нулю, как и сам определитель.
7.2. Свойства определителей
193
2)	В соответствии со свойством 7.2 определитель меняет знак при перестановке строк. Если некоторый определитель Д имеет одинаковые строки, то при их перестановке он изменяет знак, но в то же время при такой перестановке он не изменяется, так как переставляемые строки одинаковы. Следовательно, Д = — Д, т.е. 2Д = 0, откуда Д = 0.
3)	Пусть, например, элементы 1-го столбца пропорциональны элементам j-ro столбца с коэффициентом пропорциональности А. Тогда в силу свойства 7.4 общий множитель элементов 1-го столбца можно вынести за знак определителя:
Ха j j	«12 •	.. aij .	• • aln		«ij	«12 •	.. aij .	• • aln
Xa2j	«22 •	.. a2j .	.. a2n	= A		«22 •	.. a2j .	• • a2n
Xanj	ttn2 •	• • anj .	• • ®nn		anj	an2 •	> • a>nj .	• • ^nn
Последний определитель равен нулю, так как имеет два одинаковых столбца.
4)	Пусть, например, 1-й столбец определителя Д является линейной комбинацией всех остальных столбцов:
п
53 ^kalk а12 ••• aln
к-2 п
У2 ^к^2к а22 • • • a2n
к=2	,
Xk eR, к = 2, п.
п
53 ^к^пк ®п2 • • • ®пп к=2
Некоторые коэффициенты линейной комбинации, представляющей 1-й столбец, могут быть нулевыми. Это равносильно тому, что соответствующие столбцы не участвуют в линейной комбинации. Используя свойства 7.3, 7.4 определителя, полу-
/ Аналитическая геометрия
194
7. ОПРЕДЕЛИТЕЛИ
чаем
	«12	«12	•	• •	«1п			«1п	«12 •	• • «In
д = а2	«22	«22	•	••	«2п	+ ..	• • + Ап	«2п	«22	•	• •	«2п
	«п2	«п2	• • «пп			«пп	«п2	• • «пп
— А2О + ... + Ап0 — О, где последние определители равны нулю, так как имеют по два одинаковых столбца. ►
Свойство 7.6. Определитель не изменится, если к любой его строке (столбцу) прибавить линейную комбинацию других строк (столбцов):
п
«и+52 ^feaifc ai2 ... din
к=2
п
«21+52 ^fc«2fc «22 ... «2п
к=2
п
«nl + 52 ^к^пк «п2	• • • «пп
к-2
«11	«12
«21	«22
«1п
«2п
«п1	«п2
«пп
Afc € В (к 1-му столбцу прибавлена линейная комбинация остальных столбцов);
«11+52 kian i=2 «21	n а12+52^гаг‘2 • i=2 «22	n •	• «ln4“52 ^i^in i=2 •	•	a2n
®nl	On2	• •	«nn
«11 012 ••• «1п
«21 «22 ••• &2п
«п1 Оп2 ... «пп
k{ € К (к 1-й строке прибавлена линейная комбинация остальных строк).
7.2. Свойства определителей
195
◄ В силу свойства 7.3 определитель можно представить в виде гуммы двух определителей, один из которых равен нулю в силу свойства 7.5. Например, для 1-го столбца это означает, что
п
«11 + 52 ^k^lk а12 ••• а1п
к-2
п
«21 + 52 ^ка2к а22 ••• а2п
к=2
п
«п1 + 52 ^к^пк «п2 • • • «пп к=2
п
52 ^ка1к «12 ••• «1п к=2
п
12 ^fca2k «22 • • • «2п k=2
п
52 ^к^пк «п2 • • • «пп к=2
«И «12	...	«1п
«21	«22	• • •	«2п
«п1	«п2	• • • «пп
«И «12	...	«1п
«21	«22	• • •	«2п
«п1	«п2	• • • «пп
В матрице А вычеркнем г-ю строку и j-й столбец, в которых стоит элемент atJ . Из оставшихся элементов можно составить новую квадратную матрицу (п— 1)-го порядка, сдвинув строки и столбцы после вычеркивания. Такой способ образования этой матрицы означает, что элемент аы матрицы А, расположенный в к-й строке, при к > г оказывается в (к — 1)-й строке новой матрицы. Аналогично, при I > j этот же элемент оказывается в (Z — 1)-м столбце новой матрицы. Определитель построенной матрицы обозначают через Мгз и называют минором (матрицы А и ее определителя Д), соответствующим элементу Число Ai3 = (—	называют алгебраическим дополне-
нием, соответствующим этому же элементу а^.
Миноры и алгебраические дополнения позволяют, в частности, вычислять определитель n-го порядка путем сведения его к вычислению п определителей (п— 1)-го порядка.
196
7. ОПРЕДЕЛИТЕЛИ
Свойство 7.7. Определитель А квадратной матрицы А = = (а^) порядка п можно представить в виде
п	п
А =	= £(-1)г+ЧЛ^,	(7.4)
7 = 1	7=1
ИЛИ п	п
А = ^aij = 22(-1)^аъМ0-.	(7.5)
г=1	г=1
◄ Докажем равенство (7.4). Поскольку, согласно определению 7.1 определителя, в каждое его слагаемое в качестве сомножителя входит один элемент г-й строки, можно разделить все слагаемые в сумме (7.3) на п групп так, чтобы в каждой группе слагаемые имели один и тот же элемент г-й строки. Вынеся в этих группах общий элемент г-й строки за скобку, получим
Д = det А —	^( 1)1	1	• • • ®пап —
а
= аИ (“I)' ( ’ ^l^lai • • • ^г—• • • апап 4“
а(г,1)
4~ ®г’2 2 ("""I)' ( ’	• * * ^пап 4” • • • 4“
a(i,2)
4“ din 2 (“’О' ( * )l®lai • • •	®г4-1>а»+1 •••^'пап
<т(г,п)
п
— djj ^ ^ ( 1)1 ’^l^lai • • • ®г—®г'4-1>«^1 • • • ®пап ?
7=1	<т(г,7)
где a(i,j) (j = l,n) обозначает подстановку, в которой под числом г стоит число j — индексы общего множителя ау, вынесенного за знак суммы.
Остается доказать, что сумма
^2	...а,_1,а,_1а,+1)„,+1 ...апап (7.6)
^(^7)
7.2. Свойства определителей
197
равна алгебраическому дополнению Aij. Для этого достаточно выразить количество инверсий в подстановке а(г, j) через количество инверсий в подстановке г, которая получается из а(г, j) вычеркиванием столбца (i,j)T и уменьшением на единицу элементов, больших г в 1-й строке и больших j во 2-й. Отметим, что этот способ получения подстановки (п — 1)-й степени г из подстановки n-й степени a(z,j) полностью соответствует построению матрицы минора Mij. Подстановка г соответствует гем местам в матрице минора Mij, на которых оказались сомножители произведения aiai...аг-1,а^1аг-|-1,а|+1	Поэтому
Mij =	. (li—#г‘+1 ,at+1 • • • anan •
Для подсчета инверсий в подстановке a(i,j) столбец (i,j)T переставим г — 1 раз с соседним слева столбцом, что переместит его на место 1-го столбца, не изменив относительного порядка остальных столбцов. В полученной подстановке
i
3
1
ai
г — 1 г + 1
аг_1 аг+1
п
... an
четность которой совпадает с четностью ст(г, j), вычеркнем 1-й столбец и получим
1
«1
г — 1 г + 1
аг_1 аг+1
п
®-п
При вычеркивании 1-го столбца количество инверсий в 1-й строке уменьшится на i — 1, а во 2-й — на j — 1. Следовательно, общее число инверсий уменьшится на г + j — 2, и поэтому

(7-7)

198
7. ОПРЕДЕЛИТЕЛИ
где |т'| равно сумме инверсий в 1-й и 2-й строках г'. Теперь уменьшим на единицу те элементы в т', которые больше i в 1-й строке и больше j во 2-й. При этом количество инверсий в строках не изменится, а в результате получим подстановку т. Поэтому сумма (7.6) с учетом равенства (7.7) принимает вид
2(~ ) "^ (— 1)'	• • • ai—	• • • ^пап ~
= (-iy^Mi} = Ai3,
что и завершает доказательство. ►
Представления определителя в виде (7.4) и (7.5) называют его разложениями по i-й строке и j-му столбцу соответственно.
Разложения по строке (7.4) и столбцу (7.5) дают правила, в соответствии с которыми определитель n-го порядка сводится к п определителям (п — 1)-го порядка, раскладывая которые получим n(n — 1) определителей (п —2)-го порядка и т.д. Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей. Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей. Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений. В этом полезно убедиться самостоятельно, вычисляя разложением по 2-му столбцу следующи и определитель.
Пример 7.2. Вычислим определитель четвертого порядка
3	1-1	2
-5	13-4
20	0	1 -11
1-5	3-3
7.2. Свойства определителей
199
Определитель удобнее всего раскладывать по 3-й строке:
= 20(—9 — 20 + 6 + 30+ 12 — 3) + 1(-9 — 4 + 50 - 2 — 60 — 15) + + 11(9-25+ 3+1+ 45+15) = 20-16-40 +И-48 = 808.
Пример 7.3. Вычислим определитель n-го порядка
1
1
1 1
0 1
1 О
1 1
1
1
1
0
Не меняя величины этого определителя, вычитаем 1-ю строку из всех остальных строк (см. свойство 7.6) и, раскладывая полученный определитель по 1-му столбцу (см. свойство 7.7),
находим, что
Свойство 7.8. Определитель верхней (нижней) треугольной матрицы равен произведению элементов ее главной
200
7. ОПРЕДЕЛИТЕЛИ
диагонали, т.е.
«11 «12 ••• «1п 0	«22 • • • «2п
«и 0 ... О
«21 «22 • • • О
О 0	... «ПП
«п1 «п2 • • • «пп
= «11«22 • • -апп
◄ Воспользовавшись свойством 7.7, последовательно раскладываем определители верхнего треугольного вида по 1-му столбцу и получаем
«11	«12	•••	«1п
0	«22	• • • «2п
«22 «23	• • •	«2п
«33
«Зп
о о
0	0	... «пп
пп
= «11 «22
«33 «34
0 а^
«Зп
«4п
«пп
= «11«22 •• • «пп
0	0
Для вычисления определителей нижнего треугольного вида используется их разложение по 1-й строке. ►
Пример 7.4. Поскольку диагональная матрица является верхней треугольной матрицей, ее определитель равен произведению диагональных элементов. В частности, определитель единичной матрицы Е равен единице. #
С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду (см. теорему 6.3). Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 7.8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет
7.2. Свойства определителей
201
знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на — 1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения ее определителя.
Пример 7.5. Вычислим определитель четвертого порядка
12 3 4
2 3 4 1
3 4 12
4 12 3
Этот определитель называют циркулянтом четвертого порядка, поскольку его строки являются так называемыми циклическими перестановками элементов 1-й строки. Его вычисление основано на преобразовании к треугольному виду. На первом этапе получаем нули в 1-м столбце ниже главной диагонали:
12	3	4 ,	2	3	4	1 d=	3	4	1	2 ~ 4	12	3	(2)-4 (2)-2(1) (3) —> (3) — 3(1) (4) -4(4) -4(1)	12	3	4 0 -1	—2	—7 ~ 0 —2	-8	-10 0 —7 -10 -13
На втором этапе получаем нули во 2-м столбце ниже главной диагонали:
12	3	4
0 -1 -2 —7
0	0 -4	4	’
0	0	4	36
(3) -4 (3) -2(2)
(4) -4(4) -7(2)
На третьем этапе получаем нуль в 3-м столбце под диагональю:
(4) —> (4) + (3) ~
12 3 4
О -1 -2 —7
0	0-44
0	0 0 40
= 1(—1)(—4)40= 160. #
202
7. ОПРЕДЕЛИТЕЛИ
Если в процессе преобразований оказывается, что равные нулю элементы расположены по одну сторону от побочной диагонали, то можно последовательно раскладывать определитель по 1-му столбцу (или по 1-й строке) или, изменяя порядок строк (столбцов) на обратный и учитывая свойство 7.2, преобразовывать определитель к треугольному виду.
Пример 7.6. Вычислим определитель n-го порядка:
0 0	0 0	0 ...	&2,п—1		^1п ^2п		
0 ^nl	^п—1,2 ^п2	1 £ £	1,п-1 -1,п 0	^п—1,п к Лпп 0		•	^1п
		l)n+1fcm	^п—1,2	^п—1,3		.	^п—1,п
= (-l)n(n-1)/2^niA:n-i,2 • • • &2,n-i&in-
Свойство 7.9. Сумма произведений элементов какой-либо строки (столбца) определителя Д матрицы А (7.2) на алгебраические дополнения, соответствующие элементам другой строки (столбца) этого же определителя, равна нулю:
п
'aijAkj = 0? к i;
J=1 п
A-ik — 0, к j* г=1
(7.8)
(7.9)
◄ Докажем равенство (7.8), соответствующее утверждению для строк. Для этого рассмотрим вспомогательный определитель
7.2. Свойства определителей
203
Ai, полученный из Д заменой элементов к-й строки (к ф г) числами ci, С2, ..., сп:
	au	«12	•••	
	«21	а22 ...	а2п
Д1 =		«г2	•••	^in
	С1	с2 ...	сп
	®nl	®п2	^пп
Разложим определитель Д1 по к-й строке:
п
Д1 —
J=i
где Akj — алгебраические дополнения, соответствующие элементам к-й строки как в определителе Д1? так и в определителе Д. Положив Cj = ai3, j = 1, п, получим, что в определителе Д1 совпадают г-я и к-я строки. В соответствии со свойством 7.5 этот определитель равен нулю, т.е.
п
a^3 Akj — 0, к ^i. j=i
Аналогично доказывается равенство (7.9). ►
Свойство 7.10. Если А и В являются квадратными матрицами порядков пит соответственно, то det(X®B) = = det Л det В.
◄ Нужно доказать, что блочная матрица
а е\ ев)
имеет определитель, равный det Л det В.
204
7. ОПРЕДЕЛИТЕЛИ
Мы докажем более общий результат, состоящий в том, что определитель блочно-треугольной матрицы
(7.10)
при любой матрице С тоже равен det A det В.
Как уже отмечалось, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением ее определителя. Выполним над первыми п строками матрицы (7.10) такие элементарные преобразования строк, которые приводят матрицу А к верхнему треугольному виду А' с сохранением ее определителя. Затем выполним над последними т строками полученной матрицы такие элементарные преобразования строк, которые приводят матрицу В к верхнему треугольному виду Bf с сохранением ее определителя. Отметим, что эти преобразования не зависят от элементов матрицы С и при их выполнении определитель матрицы (7.10) не будет меняться, а сама матрица примет верхний треугольный вид
типа пхт, получившаяся в
где Ci — некоторая матрица результате преобразования матрицы С.
Согласно свойству 7.8, определитель матрицы D' треугольного вида равен произведению ее диагональных элементов, которое в данном случае получается умножением произведения диагональных элементов матрицы А' треугольного вида, равного det А', на произведение диагональных элементов матрицы В' треугольного вида, равного det В'. Таким образом, det D = det D' = det A' det B' = det A det B. ►
Свойство 7.11. Определитель произведения двух квадратных матриц А, В € Mn(R) равен произведению их определителей, т.е. det(AB) = detAdetB.
7.2. Свойства определителей
205
4 Пусть С = АВ. Рассмотрим две блочные матрицы
„ ( а	_( А с\
М1~\-Е в) и М* \-Е е/ ’
где Е — единичная матрица порядка п.
Из доказательства свойства 7.10 следует, что det Mi = - det М1 = det Ат det Вт = det A det В.
Для вычисления определителя det М2 сделаем в матрице М2 п перестановок строк с изменением знака одной из переставляемых строк так, чтобы определитель при этом не менялся: (?z + 1)-ю строку матрицы М2 умножим на —1 и поменяем местами с 1-й строкой; (п + 2)-ю строку умножим на —1 и поменяем местами со 2-й строкой и т.д. и закончим умножением на — 1 последней строки и перестановкой ее с n-й строкой. В результате матрица М2 примет вид
М3 =
е е\
А с)'
и опять, как и выше, получаем, что det М3 = det Е det С = detC.
Следовательно, det М2 = det М3 = det С = det (АВ).
Осталось доказать, что матрицу Mi элементарными преобразованиями строк можно преобразовать в матрицу М2, не изменив ее определителя. Записав матрицы Mi и М2 через их элементы
	^«11 •	• • ®1п	0 .	.. 0		•	• • ^1п	Си .	• • С17?
	*	* • @"пп	0 .	.. 0			• • &пп	СП1 .	• • Спп
Mi =					1 М2 =				
	-1.	.. 0	6ц .	• • bin		-1.	.. 0	0 .	.. 0
	( 0 .	.. -1	£*п1 •	• •bnn)		( 0 .	.. -1	0 .	.. 0 /
отмечаем, что первые п столбцов у них совпадают.
206
7, ОПРЕДЕЛИТЕЛИ
В матрице Mi к (п + 1)-му столбцу прибавим 1-й, умноженный на 6ц; 2-й, умноженный на &2Ь и т.д. и закончим прибавлением n-го столбца, умноженного на bni- В результате в (n-f-l)-M столбце в строках п+1,...,2п образуются нули, а в остальных строках, например г-й строке, г = 1,...,п, —
&=1
Повторим аналогичные преобразования со столбцами (п + 2)-м, (п + 3)-м, ..., (2п)-м. В результате получим матрицу М2, не изменив при преобразованиях определитель в силу свойства 7.6. Вывод: матрицы Mi и М2 имеют одинаковые определители и, следовательно, det(AB) = det4det!3. ►
7.3. Методы вычисления определителей
При вычислении определителей применяются различные методы, основанные на свойствах определителей. Часто используемый метод состоит в преобразовании определителя к более простому виду, что мы видели в рассмотренных примерах.
Иногда удобно вычислять определители, комбинируя применение различных их свойств. Рассмотрим конкретные примеры.
Пример 7.7. Вычислим определитель (п+1)-го порядка
А =
х Ci
С1 X
С1 с2
С2
С2 X
Сп
Сп
Сп
С1 С2 Сз ... X
7.3. Методы вычисления определителей
207
Прибавим к 1-му столбцу все остальные:
® S с« С1 с2 • • • Сп 2=1
Л _ X 4- Ci х с2 ... сп -	1=1
п
X+X,Ci с2 С3 ... X
2=1
п
(выносим за знак определителя общий множитель х + £2 ci и 1=1
вычитаем из каждой строки, начиная с последней, предыдущую строку)
1 Ci С2 • • • Сп
п	0	х - ci 0	...	0
х + X?С*)	О	С2~ х	х — с2	...	0
2=1
0	0	0	... х - сп
(раскладываем по 1-му столбцу)
х — ci 0
0
0
х-сп
(используем свойство 7.8)
2 = 1	2 = 1
208
7. ОПРЕДЕЛИТЕЛИ
Пример 7.8. Вычислим циркулянт шестого порядка
д =	1	2	3	4	5	6 2	3	4	5	6	1 3	4	5	6	1	2 4	5	6	1	2	3 5	6	1	2	3	4 6	1	2	3	4	5
Выполняя последовательно преобразования (б) —> (6) —(5), (5) —> (5)-(4), (4) -4 (4)—(3), (3) -4- (3)-(2), (2) -4 (2)-(1), получаем
1	2	3	4	5	6
11111-5 1	1	1	1-5	1
1	1	1-5	1	1
1	1-5	1	1	1
1-51111
(вычитаем из первых пяти строк шестую и раскладываем
определитель по 1-му столбцу)
0	7	2	3	4	5
0	6	0	0	0	-6
0	6	0	0-6	0
0	6	0	-6	0	0
0	6	-6	0	0	0
1-51111
7	2	3	4	5
6000-6 600-60 6	0 -6	0	0
6-6000
(выносим общий множитель 6 из четырех строк и прибавляем к 1-му столбцу остальные)
II 1	7 2 3 4 5 1 0 0 0 -1 100-10 10-100 1-1000	О 1 II
21	2	3	4	5
0	0	0	0	-1
0	0	0	-1	0
0	0-100
0-1000
= —64-21. #
7.3. Методы вычисления определителей
209
Основой одного из подходов является получение некоторого соотношения, связывающего значение определителя Дп порядка п с определителями, например, той же структуры, но более низких порядков:
Дп — /(Дп_1, Дп_2? • • •, "Дп—А:), к < 71.	(7.11)
Такого рода соотношения (7.11) называют рекуррентными 11], как и соответствующий метод вычисления определителей.
Этот метод заключается в том, что сначала непосредственно по общему виду определителя вычисляют столько определителей низших порядков, сколько их имеется в правой части рекуррентного соотношения. Далее, по общему виду определителя или с помощью рекуррентного соотношения вычисляют еще некоторое количество определителей низших порядков и подбирают вид их записи. Это делается для того, чтобы можно было уловить закономерность и записать формулу (в виде гипотезы), выражающую определитель Дп непосредственно через его элементы. Наконец, справедливость гипотезы при любом п доказывается с помощью метода математической индукции.
Общую формулу, выражающую определитель Дп непосредственно через его элементы, можно получить и другим путем. Для этого в рекуррентное соотношение, выражающее определитель n-го порядка, подставляют выражение определителя (п — 1)-го порядка из того же рекуррентного соотношения с заменой п на (п — 1) и т.д.
Пример 7.9. Вычислим определитель n-го порядка
к\	х	х	...	х	х
х	к2	х	...	х	х
х	х	кз	...	х	х
х	х	х	...	kn-i	х
ф	Ф
dU	dj	d/	• • •	«V
210
7. ОПРЕДЕЛИТЕЛИ
Представим элемент в правом нижнем углу в виде кп = = х + (кп — ж), а остальные элементы последнего столбца — в виде х = х + 0. Используя свойство 7.3 и учитывая указанные представления для элементов последнего столбца, разобьем определитель на сумму двух:
Дп-	ki	х	х	...	х	х х	к2	х	...	X	X х	х	кз	...	х	х х	х	х	...	кп~х	х Ф	Ф	ПР	ПР	ПР tLf	w	• • •	•</	•</	+	к\	х	х	...	х	0 х	к2	х	...	х	0 х	х	кз	...	х	0 х	х	х	...	kn-i	0 ПР	Ф	ПР	ПР	К* - ПР Af	iU	W	• • •	•</
В первом определителе вычитаем последний столбец из остальных, а второй раскладываем по последнему столбцу
	к\ — х	0	0	X	
	0	к2 - х ...	0	X	
Дп-	0	0	кп-1 х	X	(кп ж)Дп_> 1,
	0	0	0	X	
откуда					
Дп	= x(ki	-х)...{кп_1	— ж) (кп	-2:)Дп_1.	(7.12)	
Полученный результат представляет собой рекуррентное соотношение для вычисления Дп через Дп-1«
Чтобы найти формулу для вычисления Дп непосредственно через его элементы, начнем вычислять определители низших порядков и записывать их значения в такой форме, чтобы можно было уловить общую закономерность и высказать гипотезу о формуле для Дп.
Поскольку Д1 = |&i| = к\ (здесь, очевидно, |fci| есть обозначение определителя первого порядка, а не модуля), то выражение
7.3. Методы вычисления определителей
211
для Ai можно представить в виде
Д1 = х +	- я) = x(ki - х) ( - + —-—
ki — х
/(алее, используя полученное рекуррентное соотношение, вычисляем значение для Д2 и выполняем необходимые преобразования:
Д2 = х(к\ - ж) + (к2 - ж)Д1 —
= х(кх - х)^-^ + х(кх - х)(к2 - х) ( | +
/т	ч/,	1	1	\
= x(ki -х)(к2-х) - + 7----Н---- •
\ х к\-х к2 - х J
Диализируя выражения для Д1 и Д2) можно заметить следую-щуюзакономерность, которой подчиняется последовательность определителей Дп, n € N:
Формула (7.13) пока еще является гипотезой и ее нужно доказывать. Воспользуемся методом математической индукции.
1. При n— 1 формула (7.13) совпадает с полученным ранее выражением для Др
2. Предположим, что уже доказана справедливость формулы (7.13) для Дп-1, т.е.
Дп—। — х[к\ ж)... {kfn—\ ж) х
111 1
—h -----h -j---h •.. + ~j--
x A/j x k2 x	—i
212
7. ОПРЕДЕЛИТЕЛИ
Подставляя выражение (7.14) для Дп-1 в рекуррентное соотношение (7.12), находим
Дуг — #(&1 ж) ... (&п_J ж) ~f“ (&?г »^) Дуг—1 —
—- (&уг ж)ж(А/’1 ж)...(/?п_J 3?) | ~	| Н J	)
\кп—х х к\—х kn_\—xj
= x(k1-x)...(kn-x) (1 + -1- + —1—+ .„+^-1-), \ •£/ Tv J vU 1^2	/
т.е. формула (7.13) верна для определителя Дп.
Пример 7.10. Вычислим часто встречающийся в приложениях определитель Вандермонда п-го порядка (А.Т. Вандермонд (1735-1796) — французский математик):
1	1	1	1
«1	Х2	• •	^71 — 1	
Дп-
Х1		т^-2 •• хп-1	^п—2
„п—1	7г—1	^п—1	п — 1
Х1	х2	•• Жп-1	
Все строки начиная с 1-й, но кроме последней, умножаем на хп и из каждой полученной строки вычитаем стоящую ниже строку. Чтобы эти умножения не изменили определитель, запишем перед ним компенсирующий коэффициент 1/х™~г и получим
	«п *^1	Хп х2	• •	^71	*^71—1	0
1	(жп—Ж1)	^2^хп ^2)	••	^71 —1 (^П~^7г—1)	0
	•^1	(#п ^1)	•^2 (*^п ^2)	••	^п-1(^п *^п— 1)	0
	~п-1 Ж1	л 2	•^n-l	л» 71	1
Последний столбец в последнем определителе умножим на стоящий перед определителем коэффициент, а затем разложим
7,3. Методы вычисления определителей	213
определитель по этому столбцу. В определителе (п— 1)-го порядка
Xn Xi	#n *^2	..	xn xn—i
Х1(хп-хг)	X2(xn-X2)	. .	(.Tn xn—i
(жп #1) X.}	(#n ^2)		„.п—2 ( •• Xn—1 \Xn %n—1
вы носим из каждого столбца общий множитель:
Дп — (*^П	*^1) (*^П	*^2) • • • (*^п	%п— 1 )
1 1 ... 1
Х2 • • •	*^n—l
X
п—2 1
п—2 п—1
Таким образом, приходим к рекуррентному соотношению п— 1
Дп =	(«п	^г) Дп—1 •
г=1
Используя его, последовательно находим (п—1	\
(#п	*^г) ) Дп—1 —
г=1	/
Продолжая редукцию и учитывая, что Aj = 1, окончательно получаем
i<j
еде произведение распространяется на все пары индексов г, j =
1,77, удовлетворяющие неравенству i < j.
214
7. ОПРЕДЕЛИТЕЛИ
Пример 7.11. Вычислим определитель n-го порядка
5
2 О
Д
п
О 0 ... О
3 0 ... О
5 3 ... О
О 0 0 0 ... 5
Разложим Дп по 1-му столбцу:
3 0 0
2 5 3
0 2 5
Дп — 5ДП_1 2
ООО
О О
О
5
Разложим определитель (п — 1)-го порядка во втором слагаемом по 1-й строке. В результате получим рекуррентное соотношение
Дп = 5Дп—1 6Дп—2-
Чтобы вычислить Дп при помощи этого рекуррентного соотношения, сведем соотношение к формуле геометрической прогрессии. Запишем полученное выражение в двух вариантах:
Дп ~ 2Дп—1 — 3(Дп_ 1 — 2Дта—2),
Дп ~ ЗДп—1 = 2(Дп-1 — ЗДп—2)-
Тогда
Дп-1 — 2Дп_2 = 3(Дп-2 — 2Дп_з),
Дп-1 ~ ЗДп_2 = 2(Дп_2 — ЗДп_з).
Подставив два последних равенства в предыдущие, находим
Дта - 2Дп—1 = 3 (Дп—2 2Дп_з),
Дп ~ ЗДп— 1 — 2 (Дп—2 ЗДп_з)
Вопросы и задачи
215
и, продолжая процесс, получаем
ДП-2ДП_1=3”-2(Д2-2Д1),
Д„ - ЗДП_4 = 2П-2(Д2 - ЗД1).
Исключим из двух последних равенств Дта-1:
Дп = (Зп-1 - 2п-1)Д2 - 6(3П-2 - 2та-2)Д1.
Гак как
5 3
2 5
Д! = |5| = 5, Д2 =
= 19,
то Дп =	- 2”-1) - 30(3n~2 - 2n“2) = 3n+1 - 2n+1.
Вопросы и задачи
7.1. Вычислить определители:			
	5 12 7		0 5 2 0
	3 0 0 2	.	Л'!	8 3 5 4
а)	13 4 5	? б)	7 2 4 1
	2 0 0 3		0 4 10
7.2.	Не раскрывая определители, доказать равенства:
1 a
1 Ь
1 с
а)
Ьс
са ab
= (Ь — а) (с — Ь)(с — а);
б)
sin2 а sin2 (3 sin2/?
cos2 а cos2 /3 cos2/?
cos 2а cos 2/? cos 2(3
= 0.
7.3.	Записать циркулянт n-го порядка и вывести формулу для его вычисления в зависимости от числа п, воспользовавшись вычислениями из примера 7.8.
216
7, ОПРЕДЕЛИТЕЛИ
7.4.	Элементы квадратной матрицы являются непрерывными функциями на отрезке [а; 6]. Доказать, что ее определитель является непрерывной функцией на этом отрезке.
7.5.	Найти все кососимметрические матрицы второго порядка с нулевым определителем.
7.6.	Доказать, что определитель кососимметрической матрицы нечетного порядка равен нулю. Верно ли это утверждение для кососимметрических матриц четного порядка? Привести соответствующие примеры.
7.7.	Доказать, что
	1	2	3	...	п -10	3	...	п — 1 —2	0	...	п	—п\
7.8. Доказать,	-1 -2 -3 ... 0 что 1	1	1	...	1 1	2	1	...	1 1	1	3	...	1 =(п-1)! 1	1	1	...	п
7.9. Выясните, имеют ли решения следующие уравнения:
	1	1	1		1	1	1	
а)	е2х	е~2х	ех	= 0; б)	sin ж	cos ж	ех	= 0
	2е2а;	—2е~2х	ех		cos ж	— sin ж	ех	
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
8.1.	Обратная матрица и ее свойства
Определение 8.1. Пусть А — квадратная матрица порядка п. Квадратную матрицу В того же порядка называют обратной к А, если АВ = ВА = Е, где Е — единичная матрица порядка п.
Обратную матрицу обозначают А"1. Она позволяет определить целую отрицательную степень матрицы А. А именно, для п > 0 полагают А“п = (А-1)п.
Теорема 8.1. Если квадратная матрица А имеет обратную матрицу, то обратная матрица единственная.
<	Предположим, что матрица А имеет две обратные матрицы В и В'. Тогда, согласно определению 8.1 обратной матрицы, выполнены, в частности, равенства АВ1 — Е и В А = Е. Используя ассоциативность умножения матриц, получаем
В = ВЕ = В(АВ'} = (ВА)В' = ЕВ1 = В',
т.е. матрицы В и В1 совпадают. ►
Квадратная матрица не всегда имеет обратную. Установить, имеет ли данная матрица обратную, позволяет следующий критерий.
Теорема 8.2. Для того чтобы квадратная матрица А порядка п имела обратную, необходимо и достаточно, чтобы < 1(4, А / 0.
218 8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
◄	Необходимость. Пусть А”1 — матрица, обратная к А. Тогда det(AA”1) = detE = 1, но, согласно свойству 7.11 определителей, det(AA”x) — det A det А-1. Поэтому det A det А-1 = 1 и, следовательно, det А 0.
Достаточность. Пусть det А 0. Рассмотрим алгебраическое дополнение Aij = (—матрицы А, соответствующее элементу а^ (Mij — минор этого же элемента).
Согласно свойству 7.7 определителей, для любого г — 1,п выполнены равенства (7.4)
п
T^aijAij =det А.
J=i
Согласно свойству 7.9 определителей, для любых индексов k^i выполнены равенства (7.8)
п
Afcj — 0.
i=i
Рассмотрим теперь квадратную матрицу В порядка п с элементами
h — det А*
Матрица С = АВ имеет элементы
п п а 1 п
Cik =	= 22aVd^tA = d^tA = <
J=1	j=l	J=1
k — i,
k i,
т.е. C — это единичная матрица.
Аналогично матрица С' = В А имеет элементы
П	п	д	J п
c'kj =	= d^tA	=
г=1	г=1	г=1
j = k,
следовательно, матрица С является единичной.
8.1. Обратная матрица и ее свойства
219
Согласно определению 8.1, матрица В является обратной дли Л: В = А-1. ►
Следствие 8.1. Если квадратная матрица А имеет обратную, то det А”1 = (det А)”1.
◄	Действительно, det A”1 det А = det(A”1 А) = det Е = 1. ►
Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы А”1 необходимо и достаточно, чтобы сама матрица А была невырожденной.
Теорема 8.3. Если квадратные матрицы А и В порядка п имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем (АВ)”1 = В“1А”1.
◄	В соответствии с определением 8.1 обратной матрицы достаточно доказать два равенства:
(АВ)В~1А~г = Е, (В~1А~1)(АВ) = Е.
Используя ассоциативность умножения матриц (см. 6.4), полу-чаем
(АВ)(В~1 A"1) = A(BB~1)A~l = АЕА"1 = АА"1 = Е,
(В~1А~1)(АВ) = В-1 (А-1А)В = В-'ЕВ = 3'^ = Е, что и требовалось доказать. ►
Теорема 8.4. Если матрица А порядка п имеет обратную, то и транспонированная матрица Ат имеет обратную, причем (ат)-1 = (а-1)т.
◄	Нужно убедиться, что АТ(А-1)Т = Е и (А-1)ТАТ = Е. Используя свойство произведения матриц относительно операции транспонирования, имеем
АТ(А-1)Т = (А-1А)Т = ВТ = В,
(А~1)ТАТ = (АА-1)Т = ВТ = В. ►
220
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
8.2.	Вычисление обратной матрицы
Применяют два основных метода вычисления обратной матрицы. Первый вытекает из теоремы 8.2 и состоит в следующем. Пусть дана квадратная матрица А порядка п. Матрицу А*, транспонированную к матрице (AtJ) алгебраических дополнений, называют присоединенной. Как следует из доказательства теоремы 8.2, если А — невырожденная матрица, то обратная к ней имеет вид
Таким образом, чтобы для квадратной матрицы порядка п найти обратную матрицу, надо вычислить один определитель порядка п и составить присоединенную матрицу, т.е. вычислить п2 определителей порядка п — 1. Метод присоединенной матрицы эффективен при п = 2 или п = 3, но при росте п становится слишком трудоемким.
Пример 8.1. Выясним, имеет ли матрица
обратную и если имеет, то найдем ее.
Поскольку det А = —2, матрица А является невырожденной и, согласно теореме 8.2, имеет обратную. Для ее вычисления последовательно находим
Отметим, что для квадратной матрицы А второго порядка присоединенная матрица А* получается перестановкой в А диагональных элементов и изменением знака двух других.
8.2. Вычисление обратной матрицы
221
Проверка ответа выполняется в соответствии с определением 8.1 обратной матрицы:
Второй метод вычисления обратной матрицы состоит в преобразовании исходной матрицы к более простому виду с помощью элементарных преобразований строк. Чтобы найти матрицу А'*’1, обратную к А, фактически надо решить матричное уравнение АХ = Е. Отметим, что если над матрицей А выполняется какое-либо элементарное преобразование строк, го это же преобразование осуществляется и над матрицей АХ, поскольку любое элементарное преобразование строк матрицы эквивалентно умножению ее слева на соответствующую матрицу специального вида (см. 6.8). Таким образом, если в уравнении АХ = Е над матрицами А и Е одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение AiX = Bi. Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк. Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица А превратилась в единичную матрицу. В результате этих з шагов получается уравнение ASX = Bs, где As = Е, т.е. X = В$. Итак, поскольку Л”1 является решением уравнения АХ = Е, которое эквивалентно X = В3, то А"1 = В3.
Чтобы синхронно выполнять преобразования над матрицами в левой и правой частях матричного уравнения АХ = записывают блочную матрицу (А| Е) и выполняют такие элементарные преобразования строк этой матрицы, чтобы вместо Л получить единичную матрицу Е.
222	8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
Пример 8.2. Продемонстрируем изложенный метод нахождения обратной матрицы для матрицы из примера 8.1. Для этого записываем матрицу (Al#) и выполняем элементарные преобразования ее строк в следующем порядке:
1 2
3 4 /1
J \0
Таким образом,
1
—0,5
8.3.	Решение матричных уравнений
Мы рассмотрим два вида матричных уравнений относительно неизвестной матрицы X: АХ — В и ХА = В, где А и В — известные матрицы, причем матрица А квадратная и невырожденная. Некоторую матрицу называют решением матричного уравнения относительно неизвестной матрицы X, если при ее подстановке вместо X матричное уравнение превращается в тождество.
Начнем с уравнения АХ = В и изложим два метода его решения.
Первый метод предполагает вычисление обратной матрицы А”1 (например, при помощи присоединенной матрицы) и дает запись решения матричного уравнения в виде X = А~ХВ. Действительно, подставляя X = А~гВ в уравнение АХ = В, получаем А(А“1В) = В, т.е. В = В, и X = А-1В является решением матричного уравнения АХ = В. Более того, это решение единственно, так как для любого другого решения Xf выполнено тождество АХ' = В, после умножения которого слева на
8.3. Решение матричных уравнении
223
оказывается, что A-1 (AX') = А-1 В, т.е. (А"”1А)Х/ = Х и, следовательно, X' = X,
Второй метод основан на элементарных преобразованиях строк блочной матрицы (А|В) и имеет своей целью преобразование ее к виду (BlBi), в котором вместо матрицы А стоит единичная матрица Е. Тогда матрица Bi и будет решением уравнения. Если матрица В совпадает с единичной, то в этом частном случае получается метод элементарных преобразований вычисления обратной матрицы.
Пример 8.3. Найдем решение матричного уравнения АХ = ~ В, имеющего вид
1
3 4/Л “ V5 * 7 8/
Воспользуемся методом элементарных преобразований. Для этого запишем матрицу (А|В) и выполним те же элементарные преобразования ее строк,| что и в примере 8.2 (так как матрицы А и цели преобразований^совпадают):
1 2 5 б\	/1	2
3 4 7 8/	\0 -2
5 б\
-8 -10/
1 0 -3 -4\ /1 0 -3 -4\
0 -2 -8 -10/ \0 1 4 5/
Итак,
-3
4
-4
5
Проверка ответа выполняется подстановкой найденного решения в исходное уравнение:
1 2\ /-3 -4\ = /5 б\
3 4/ \ 4	5/ ”\7 8/
Матричное уравнение ХА = В также можно решить двумя способами. Если известна матрица А-4, то умножаем справа
224
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
на А 1 матричное уравнение ХА = В и после очевидных преобразований
(ХА)А~1 = ВА~\ Х(АА-1) = ВА-1, ХЕ=ВА~г
получаем ответ в виде произведения двух матриц X = ВА-1.
Пример 8.4. Найдем решение матричного уравнения ХА = = В, имеющего вид
/1 2\_/5 б\
\3 4/	\7 8/
Поскольку обратная матрица А 1 известна (см. пример 8.2), то
-0,5	\ —2 3 ) '
Другой метод решения матричного уравнения ХА = В состоит в транспонировании его левой и правой частей (ХА)Т = = Вт, АТХТ = Вт. После введения новой неизвестной матрицы Y = Хт получаем уравнение вида АТУ = Вт, которое решается методом элементарных преобразований.
Пример 8.5. Чтобы решить матричное уравнение из примера 8.4, транспонируем его
1 3\„т_/5 7 А
2 4/	“ уб 8J ’
После элементарных преобразований строк блочной матрицы получаем
13 5 7
2 4 6 8
1	3 5<
0	1 2
1
0
-2
3
8.4. Ранг матрицы
225
Итак,
/1 _2\ Y(-l 2\ х V 2 3/’А V"23/’
что, конечно же, совпадает с решением этого уравнения, найденным в примере 8.4.
8.4.	Ранг матрицы
Определение 8.2. Минором порядка к матрицы А типа тхп называют определитель, который составлен из элементов этой матрицы, стоящих на пересечении произвольно выбранных к строк и к столбцов с сохранением порядка этих строк и столбцов.
Если выбранные строки имеют номера г\, 4, ..., 4, а столбцы — ji, J2, •••> то соответствующий минор будем обозначать
О миноре "if говорят, что:
-	строки zi, iz, ...,4 й столбцы ji, jz, ..., jk матрицы входят в него;
-	он образован этими строками и столбцами;
-	он располагается на пересечении этих строк и столбцов;
-	он располагается в этих строках и столбцах матрицы.
Строки, входящие в минор, попарно различны, и в обозначении минора естественно упорядочить их по возрастанию номеров. Это же относится и к столбцам. Правило возраста-ния номеров означает, что, например, Мг ’3’4 является минором некоторой матрицы, расположенным на пересечении 1-й, 3-й и 1-й строк с 3-м, 5-м и 6-м столбцами, в то время как минором не является, потому что нарушен порядок столбцов (5-й столбец указан в верхних индексах перед 3-м). Это просто
к Аналитическая геометрия
226	8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
определитель третьего порядка, который получается из минора ’J’! матрицы при перестановке в нем первых двух столбцов. Поэтому, согласно свойству 7.2 определителей, 4 = - -м3’5’6
Итак, мы следуем соглашению, что обозначение	со-
ответствует минору матрицы, если верхние и нижние индексы в нем строго возрастают. В противном случае, если индексы расположены в ином порядке, это обозначение соответствует определителю, который получается из соответствующего минора перестановкой строк и столбцов.
Пример 8.6. У матрицы третьего порядка
(ап ai2 «13 \ «21 «22 «23 I «31	«32	«33 /
девять миноров первого порядка, девять миноров второго порядка и один минор третьего порядка.
Определение 8.3. Рангом матрицы называют число, которое равно максимальному порядку среди ее ненулевых миноров.	h
Для ранга матрицы А используют обозначение Rg А.
Если квадратная матрица порядка п невырождена, то ёе ранг равен ее порядку п: ненулевым является единственный минор максимального порядка п, совпадающий с определителем матрицы. В частности, ранг единичной матрицы Е порядка п равен п.
Если квадратная матрица вырождена, то ее ранг меньше ее порядка: единственный минор максимального порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок. Ранг нулевой матрицы полагают равным нулю.
8.4. Раит матрицы
227
Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его характеризующее.
Свойство 8.1. Если ранг матрицы равен г, то матрица имеет хотя бы один минор порядка г, не равный нулю, а все ее миноры больших порядков равны нулю.
Теорема 8.5. При транспонировании матрицы ее ранг не меняется, т.е. Rg Ат = Rg А.
Ч Если мы покажем, что при транспонировании матрицы А ее ранг г не убывает, т.е. RgAT г, то сможем прийти к следующему заключению. Поскольку (Ат)т = А, то г = Rg А < Rg Ат Rg(AT)T = Rg А = г, и поэтому Rg Ат = г.
Итак, докажем, что RgAT г. Согласно определению 8.3 ранга матрицы, существует ее минор порядка г, отличный от нуля. Пусть это будет минор М = М3^‘При транспонировании строки и столбцы меняются местами. Поэтому минору /V/, образованному строками г2, .ir и столбцами ji, j2, •••> jr матрицы А, соответствует минор N =	матРиЦы Ат,
образованный строками ji, j2, •••> jr и столбцами ц, г2, ..., гг. Ясно, что эти миноры получаются один из другого операцией транспонирования. Согласно свойству 7.1 определителей, они равны. Таким образом, найден минор r-го порядка в матрице Лт, а именно минор ЛГ, который не равен нулю. Следовательно, RgAT г. ►
Теорема 8.6. Ранг матрицы не меняется при элементарных преобразованиях ее строк и столбцов.
◄ Согласно теореме 8.5, ранг матрицы не будет меняться при элементарных преобразованиях ее столбцов, если он не изменяется при элементарных преобразованиях ее строк. Поэтому ?<*
228
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
случай столбцов можно не рассматривать. Так как элементарные преобразования обратимы, нам достаточно доказать, что ранг матрицы при элементарных преобразованиях строк не увеличивается, а для этого нужно показать, что произвольный минор N =	преобразованной матрицы Л' равен нулю,
если его порядок I превышает ранг г исходной матрицы А.
При умножении г-й строки матрицы А на число А О возможны два случая.
1. Элементы г-й строки не входят в минор N. Тогда минор N является минором матрицы А и равен нулю, так как I > г.
2. Элементы г-й строки входят в минор N. Тогда, согласно свойству 7.4 определителей, N = ХМ = 0, где М =	—
минор матрицы А, который равен нулю, так как его порядок I больше г.
При перестановке двух строк в матрице А с номерами г и к возможны три случая.
1.	Элементы обеих строк входят в минор N. Тогда, согласно свойству 7.2 определителей, перестановка соответствующих строк в миноре N изменяет его знак, но превращает в минор М =	матрицы А порядка I > г. Следовательно, N =
= -м = о."
2.	Элементы обеих строк не входят в минор N. Тогда минор N является минором матрицы А и равен нулю, так как I > г.
3.	Одна из строк (г-я) входит в рассматриваемый минор 7V, а другая (&-я) не входит. Не нарушая общности доказательства, можем считать, что г-я строка матрицы есть 1-я строка минора, т.е. г = гр Минор N матрицы А' представляет собой определитель, составленный из строк и столбцов матрицы А. Но этот определитель, вообще говоря, не является минором А из-за нарушения порядка строк. Восстановив естественный порядок строк, мы получаем минор М матрицы А порядка I > г, который совпадает с N или отличается от него знаком. Следовательно, N — М — 0.
При добавлении к г-й строке матрицы А ее к-й строки с коэффициентом А возможны три случая.
8.4. Ранг матрицы
229
1.	Элементы обеих строк входят в минор N. Не нарушая общности доказательства можем считать, что i = ii, а к = i2-Тогда, согласно свойствам 7.3, 7.4 определителей,
ДГ __ *13132-31 _ i^f3132—3l I \ *13132-31 _ л
поскольку минор	равен нулю как минор матрицы
Л порядка I > г, а определитель	равен нулю как
определитель, имеющий две одинаковые строки.
2.	Элементы г-й строки не входят в минор ЛГ. Тогда минор W является минором матрицы А и равен нулю, так как I > г.
3.	Элементы г-й строки входят в рассматриваемый минор, а элементы fc-й строки не входят. Не нарушая общности доказательства, можем считать, что г = ц. Тогда, согласно свойствам 7.3, 7.4 определителей,
N = N^2^1 = MW2'?1 + ХМ&2”?1 = О, 1г2*“г1	К12—Ч	’
/
поскольку	равен нулю как минор матрицы А порядка
I > г, а	равен нулю как определитель, который, возмож-
но, отличается от минора матрицы А порядка I > г следованием строк.
Итак, элементарные преобразования строк матрицы А не увеличивают ее ранг. Но тогда ранг сохраняется. Действительно, если предположить, что при некотором элементарном преобразовании строк матрицы ранг уменьшился, то выполнение соответствующего обратного элементарного преобразования строк привело бы к исходной матрице. Следовательно, ранг должен возрасти, чего быть не может.
Наконец, при последовательном выполнении элементарных преобразований строк матрицы А ее ранг не меняется, поскольку он сохраняется на каждом шаге при выполнении конкретного элементарного преобразования. ►
230
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
8.5. Теорема о базисном миноре
Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.
Определение 8.4. Минор М матрицы А называют базисным, если выполнены два условия:
а)	он не равен нулю;
б)	его порядок равен рангу матрицы А.
Матрица А может иметь несколько базисных миноров. Строки и столбцы матрицы А, в которых расположен выбранный базисный минор, называют базисными.
Следующую теорему, занимающую одно из центральных мест в теории матриц и ее приложениях, называют теоремой о базисном миноре.
Теорема 8.7. Базисные строки (столбцы) матрицы А, соответствующие любому ее базисному минору Л1, линейно независимы. Любые строки (столбцы) матрицы А, не входящие в М, являются линейными комбинациями базисных строк (столбцов).
◄ Доказательство проведем для строк. Пусть ранг матрицы А = (а^) типа тхп равен г. Фиксируем какой-либо ёе базисный минор М и соответствующие ему базисные строки матрицы А.
Докажем, что базисные строки линейно независимы. Предположим, что они линейно зависимы. Тогда по теореме 6.1 одна из них является линейной комбинацией остальных базисных строк. Согласно свойству 7.5 определителей, минор М равен нулю. Это противоречит тому, что минор М базисный.
Теперь докажем, что любая строка матрицы А, не входящая в базисный минор, является линейной комбинацией базисных строк. Предположим, не ограничивая общности доказательства, что базисный минор М расположен в верхнем левом углу
8.5. Теорема о базисном миноре
231
матрицы. Пусть i — номер строки, не являющейся базисной, т.е. г + 1 iт. Покажем, что определитель порядка г + 1
	«п «21	«12	• «22	•	• • O'lr .. tt2r	a^j a2j
д =				
	ОГ1	«г2	.. arr	arj
	аИ	«£2	•	air	aij
полученный добавлением к минору М элементов г-й строки и произвольного J-ro столбца матрицы A, j = 1,п, равен нулю. При jг определитель равен нулю, так как он содержит два одинаковых столбца. Если же j > г, то А = 0, так как в этом случае А является минором матрицы А, порядок которого равен г + 1 и больше ранга матрицы. Итак, А = 0.
Раскладывая определитель А по последнему столбцу, получаем равенство
Ai ,г+1 aij + A2,r-i-ia2j +... + Ar?r+iary + Ar+i>r+iat-j = 0,
в котором через А1Л+1, А2,г+ь •••? Ar>r+i, ^r-bi^-t-i обозначены алгебраические дополнения соответствующих элементов определителя. Отметим, что эти алгебраические дополнения не зависят от номера J, т.е. не зависят от того, элементы какого из столбцов матрицы А взяты в качестве последнего столбца определителя А. Кроме того, Ar+i,r+i = Л/ / 0. Поэтому из последнего равенства следует, что для всех j — 1, п
aij = b^a^j + £>2a2j + • •. + brarj,
где коэффициенты 6^ =-A^r+dMr+V+i, fc=l,r, не зависят от j, а это означает, что г-я строка (г + 1 г т) матрицы А является линейной комбинацией первых г ее строк, т.е. линейной комбинацией ее базисных строк. ►
Следствие 8.2. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы ее строки (столбцы) были линейно независимы.
232
8, ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
◄ Необходимость. Если квадратная матрица А невырождена, то ее ранг равен ее порядку, а ее определитель является базисным минором. Поэтому все строки (столбцы) являются базисными и по теореме 8.7 о базисном миноре они линейно независимы.
Достаточность. Если все строки (столбцы) квадратной матрицы А являются линейно независимыми, то они являются базисными. Действительно, если бы только некоторые из них были базисными, то, согласно теореме 8.7 о базисном миноре, оставшиеся были бы линейными комбинациями базисных и, следовательно, строки (столбцы) матрицы 4, согласно теореме 6.2, были бы линейно зависимыми. Так как все строки и столбцы квадратной матрицы А являются базисными, а им соответствует определитель матрицы, то он является базисным минором и, следовательно, согласно определению 8.4, отличен от нуля, т.е. квадратная матрица А невырождена. ►
Теорема 8.8. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).
◄ Докажем теорему для строк. Зафиксируем произвольный набор из г линейно независимых строк матрицы, где г — это ранг матрицы. Нам достаточно показать, что хотя бы один из базисных миноров расположен в фиксированных строках. Отбросим остальные строки матрицы и докажем, что ранг новой матрицы, содержащей г строк, равен г. Так как новая матрица не имеет миноров порядка больше чем г, то ее ранг не может превосходить г. Если бы он был меньше г, то только часть этих г фиксированных строк были бы базисными в новой матрице, а остальные, согласно теореме 8.7 о базисном миноре, являлись бы их линейными комбинациями. Согласно теореме 6.2, последнее означало бы линейную зависимость фиксированных г строк, что противоречит условию теоремы.
Итак, ранг новой матрицы равен г. Ее базисный минор имеет порядок г и является ненулевым минором порядка г исходной
8.в. Вычисление ранга матрицы
233
матрицы, расположенным в рассмотренных фиксированных г г троках. ►
Теорема 8.9. Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).
4 Доказательство теоремы проведем для строк. Согласно теореме 8.7 о базисном миноре, базисные строки линейно независимы. Следовательно, максимальное количество к линейно независимых строк матрицы не может быть меньше ранга г матрицы. Итак, г.
Остается доказать, что к г. Отбросим те строки матрицы, которые не входят в число рассматриваемых к. Тогда ранг полученной матрицы из к строк равен к. Действительно, если бы он был меньше к, то только часть из этих к строк были бы базисными в новой матрице, а остальные, согласно теореме 8.7 о базисном миноре, являлись бы их линейными комбинациями. Согласно теореме 6.2, это означало бы линейную зависимость рассматриваемых к строк, что не так. Итак, ранг новой матрицы равен к. Ее базисный минор имеет порядок к и является не равным нулю минором порядка к исходной матрицы. Следовательно, к <С г. ►
Следствие 8.3. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.
8.6. Вычисление ранга матрицы
Для вычисления ранга матрицы применяют два метода: метод окаймляющих миноров и метод элементарных преобразований.
Метод окаймляющих миноров. Минор М' матрицы А называют окаймляющим для минора Л/, если он получается из последнего добавлением одной новой строки и одного нового
234
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
столбца матрицы А. Ясно, что порядок окаймляющего минора М' на единицу больше, чем порядок минора М.
Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем. Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот процесс рано или поздно закончится из-за ограниченных размеров матрицы.
Теорема 8.10. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.
◄ Утверждение теоремы следует из доказательства теоремы 8.7 о базисном миноре. Тем не менее приведем доказательство теоремы 8.10 полностью.
Не ограничивая общности доказательства, предположим, что минор М порядка г матрицы А = (а^) отличен от нуля, расположен в верхнем левом углу матрицы А и все его окаймляющие миноры равны нулю. Рассмотрим минор
	а11 «21	«12	• «22	•	.. а^г .. а2г	aij a2j	
д =	«г1	«г2	.. агг	arj	* >
	аг1	аг2 •	.. а{г	aij	
полученный добавлением к минору М элементов г-й строки и j-ro столбца матрицы А. Он равен нулю при любых значениях г = г+1, т и j = 1, п. Если j г, то А = 0, поскольку этот определитель содержит два одинаковых столбца. Если же j > г, то А = 0, так как в этом случае А является окаймляющим для минора М. Итак, А = 0.
8.6. Вычисление ранга матрицы
235
Фиксируем для i любое из значений г + 1, т. Раскладывая определитель Д по последнему столбцу, получаем равенство
^i.r+i^ij + ^2,г-|-1^2; + ... + Ar>r+iarj + Ar+i>r+iat-j = О,
в котором через Ai>r+i, A2,r+i> • ••,	Аг+1,г+1 обозначены
алгебраические дополнения соответствующих элементов определителя. Отметим, что эти алгебраические дополнения не зависят от номера j, т.е. не зависят от того, элементы какого из столбцов матрицы А взяты в качестве последнего столбца определителя Д. Кроме того, Аг+1)Г+1 = Л// 0. Поэтому из последнего равенства следует, что для всех j = 1, п
aij = bitti j + &2a2j + ... + brarj,
где коэффициенты bfc = -Afc)r+i/Ar+1>r+1, fc=l,r, не зависят от j, а это означает, что г-я строка матрицы А является линейной комбинацией первых г ее строк. Вычитая из г-й строки матрицы А линейную комбинацию первых г ее строк с коэффициентами bi, &2> • ••, &г, получаем нулевую строку, не меняя при этом ранга матрицы А.
Проделав это для всех i = г+1, т, получим матрицу с теми же первыми г строками, но нулевыми остальными строками. Ранг полученной матрицы равен рангу исходной матрицы А и, очевидно, равен г, так как в ней есть неравный нулю минор М порядка г, а любой минор г + 1 или большего порядка будет иметь хотя бы одну нулевую строку и, следовательно, будет равен нулю. Это означает, что минор М является базисным в исходной матрице А. ►
Пример 8.7. Найдем ранг матрицы
/2—431 0\
1 -2	1—42
0	1-1	3 1 *
\4 -7	4—45/
236
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
На первом шаге выбираем любой ненулевой элемент матрицы, например левый верхний элемент, т.е. 2. Это ненулевой минор первого порядка.
На втором шаге строим окаймляющий минор второго порядка. Добавляем 2-ю строку и 2-й столбец и вычисляем получающийся окаймляющий минор
= 0.
Это окаймление не подходит. Меняем 2-й столбец на 3-й. Получаем минор второго порядка
= -1/0.
Это окаймление подходит.
Третий шаг: добавляем к этому минору 3-ю строку и можно снова попытаться использовать 2-й столбец. Оказывается, что
2 1 О
-4
-2
3
1 = 44-3-4-2=1/0,
-1
значит, выбранный минор третьего порядка подходит.
Четвертый шаг: добавляем 4-ю строку (других нет) и 4-й столбец и вычисляем определитель четвертого порядка
2-431
1-2 1-4
0 1-13
4-7 4-4
0 0 19
1-2 1-4
0 1-13
0 1 0 12
0 1 9
1 -1 3
1 0 12
= 0.
Выбранный окаймляющий минор не подходит. Меняем 4-й столбец на 5-й:
2-4 3 0
1-2 12
0 1-11
4-7 4 5
0 0 1-4 1-212 0 1-11
0 10-3
0 1 -4
1 -1 1
1 0 -3
= 0.
8.6. Вычисление ранга матрицы
237
Итак, ненулевой минор третьего порядка з имеет Два окаймляющих минора четвертого порядка и оба они равны нулю. Других окаймляющих миноров четвертого порядка нет. Поэтому делаем вывод, что — базисный минор, а ранг матрицы равен трем.
Метод элементарных преобразований. При элементарных преобразованиях строк (столбцов) матрицы ее ранг, согласно теореме 8.6, не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.
Например, согласно теореме 6.3, с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк. Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных преобразований строк позволяет вычислить ранг матрицы.
Пример 8.8. Найдем ранг матрицы методом элементарных преобразований. Для этого достаточно привести матрицу к ступенчатому виду, воспользовавшись, например, алгоритмом из доказательства теоремы 6.3 (см. с. 178). Отметим, что вычисления удобно проводить, если текущий элемент равен единице. Поэтому операцию 2* алгоритма (перестановка строк) будем выполнять не только для замены нулевого текущего элемента (так было заложено в алгоритме), но также и для того, чтобы в качестве текущего элемента получить единицу или другое небольшое целое число. Отметим также, что можно в любое время умножать ту или иную строку матрицы на ненулевое число, в частности сокращать элементы строки
238
8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
на общий множитель, хотя это и не предусматривается алгоритмом. Эта дополнительная операция позволяет упростить
вычисления:
А =
1 О
—2
-1
1
-3
-4
-2
1
-7
3
1
-1
4
1
-4
3
—4
О
2
1
5
-1
-2
1
-3
-2
-4
1
—7
1
3
-1
4
—4
1
3
-4
2
О
/1—1—2	1-4
0	11-13
0 0	0	1 9
\0 1	1 0 12
/1—1—2	1-4
011-13
0 0	0	1 9
\0 0	0	1 9
/1	-1	—2	1	—4	2\
011-131 0	0	0	1	9	-4
\0	0	0	0	0	0/
Полученная матрица ступенчатого вида имеет три ненулевые строки, поэтому ранг этой матрицы и, следовательно, матрицы А равен трем. Базисным минором в последней матрице является
Вопросы и задачи
239
Замечание 8.1. Приведенные два метода существенно отличаются друг от друга. При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из ее базисных миноров.
При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений. Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением ее вида. Но этот метод позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных преобразований. Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже известного ранга матрицы. В примере 8.8, вычислив наудачу минор третьего порядка, стоящий в тех же строках и столбцах, что и в преобразованной матрице ступенчатого вида, получим
	2-2	3		2	0	3	
	1 -1 1	—	1	0	1	= 1/0.
	0	1 -1		0	1	-1	
(‘ледовательно	, он является одним				из базисных миноров мат-	
рицы А.
Вопросы и задачи
8.1. Для заданной матрицы выяснить, существует ли обрат-
ная матрица, и, если существует, найти ее:
(‘делать проверку ответов.
240	8. ОБРАТНАЯ МАТРИЦА И РАНГ МАТРИЦЫ
8.2.	При каких а € R следующие матрицы имеют обратные:
2 \ а ) ’
1 — а
1
а)
б)
4 + а
3
/1	1	1	\
в)	I 2	3	а	1	.
\ 4	9	а2	/
8.3.	Пусть А — невырожденная матрица. Что можно утверждать о виде матрицы А-1 и (или) ее элементах, если матрица А является: а) единичной; б) диагональной; в) симметрической; г) кососимметрической; д) нижней треугольной; е) верхней треугольной?
8.4.	Доказать, что матричное уравнение ХА — В с невырожденной матрицей А имеет единственное решение.
8.5.	Решить матричные уравнения:
8.6.	Найти матрицу X из матричного уравнения:
а)	АТ(Х — В-1)А-1 = (АВ)-2;
б)	ВА(ЗХ + 2ВТ)-1Д-1 = АВ~1А.
8.7.	Найти определитель матрицы А, если известно, что АтА = 4А""1 Ат. Зависит ли он от порядка матрицы А? Приве-т сти пример матрицы второго (n-го) порядка, удовлетворяющей указанному равенству.
8.8.	Какой порядок имеет невырожденная матрица, если она удовлетворяет условию А3 + ЗА = 0?
8.9.	Методами окаймляющих миноров и элементарных преобразований найти ранг матрицы:
/3 1 —2 0\
12 1-1
5 5 0 -2 \4 3 -1 -1/
/2 1 0 1\
1 3-12
1-1-2 0
\ 4 3 -3 3/
/2 1 3\
1 -1 1 1 1 1 \0 1 1/
Вопросы и задачи
241
8.10.	При всех	а € R	найти	ранг матрицы:
(8	2	а\	/а	1	-1\	/а	0	1\
3	0	1	)	;	б)	I 0	—2	2 I	;	в)	I 0	2а	1 ] .
4	1	2а/	\ 1	2	а/	\ 1	1а/
8.11.	Доказать, что если для матриц А и В определено их произведение АВ, то всегда Rg(4£f) max{RgA, RgB}.
8.12.	Привести примеры таких матриц А и В, что:
a) Rg(4B) <max{Rg4, RgB}; б) Rg(4B) — max{Rg4, RgB}.
8.13.	Пусть матрицы А и В имеют один и тот же тип. Всегда ли выполнены следующие неравенства:
a) Rg(4 + B)^Rg4 + RgB; б) Rg(4 - В) < Rg А + RgB?
8.14.	Привести примеры таких матриц А и В, что:
a) Rg(4 + В) < Rg Д + RgB;	б) Rg(A - В) < Rg4 + RgB;
в) Rg(A +В) = Rg4+ RgB;	г) Rg(4 - В) = Rg4 + RgB.
8.15.	Доказать, что ранг матрицы А не изменится, если ее умножить слева (справа) на любую невырожденную матрицу.
8.16.	Пусть А — квадратная матрица, элементы которой являются функциями, непрерывными на отрезке [а; Ь]. Можно ли утверждать, что ранг этой матрицы является функцией, непрерывной на этом отрезке? Привести иллюстрирующие примеры.
8.17.	Найти все матрицы X второго порядка, удовлетворяющие условию: а) X2 = Е\ б) X2 = —В; в) X2 = 0; г) X3 = X; д) ХХТ = Е; е) ХТХ = -Е.
8.18.	Доказать, что если невырожденная матрица А перестановочна с матрицей В, то и матрица Л-1 перестановочна с матрицей В.
8.19.	Доказать, что если некоторая квадратная матрица А удовлетворяет равенству Л3 — А2 + А + Е = 0, то она невырожденная. Выразить матрицу Л-1 через матрицу А с помощью многочлена второй степени.
9. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
9.1.	Основные определения
Система т линейных алгебраических уравнений с п неизвестными (сокращенно СЛАУ) представляет собой систему вида
ацЖ1 + «12X2 + ...+ ainxn = &i,
< «21^1+ ®22^2 4" • • • 4“ «2п^п = Ь2,	(9
k ат1х1 4“ О"гп2х2 4“ ... 4“ ^тп^п —
Уравнения системы (9.1) называют алгебраическими потому, что левая часть каждого из них есть многочлен от п переменных xi, ..., хп, а линейными потому, что эти многочлены имеют первую степень.
Числа a{j € К называют коэффициентами СЛА У. Их нумеруют двумя индексами: номером уравнения i и номером неизвестного j. Действительные числа Ьх, ..., Ът называют свободными членами уравнений.
Запись СЛАУ в виде (9.1) будем называть координатной.
СЛАУ называют однородной, если Ь\ = Ь2 — • • • — Ьт = 0. Иначе ее называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных х\,...,х^, при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют ее частным решением.
Решить СЛАУ — значит решить две задачи:
-	выяснить, имеет ли СЛАУ решения;
-	найти все решения, если они существуют.
9.1. Основные определения
243
(!ЛАУ называют совместной, если она имеет какие-либо решения. В противном случае ее называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор шипений ее неизвестных всегда является решением. Как пока-1ывает следующий пример, для неоднородных СЛАУ возможны различные случаи.
Пример 9.1. Рассмотрим три системы двух уравнений с двумя неизвестными:
\ f 4“ — 3,	f X} -j- ж2 — 3,	\ Г х^ 4“ ^2 — 3,
1 [xi — ж2 = 1; (Xi 4-^2 = 4; В (2a;i 4-2х2 = 6.
С геометрической точки зрения уравнения каждой из этих СЛАУ задают прямые на плоскости XiOx2 (рис. 9.1). Решениям СЛАУ соответствуют точки пересечения указанных прямых. Складывая почленно уравнения в первой системе, получаем xj = 2, ж2 = 1 — единственное ее решение. Геометрически это подтверждается тем, что соответствующие прямые пересекаются в единственной точке (2; 1) (рис. 9.1, а). Из уравнений второй системы следует, что 3 = 4. Следовательно, эта СЛАУ несовместна, и геометрически это соответствует двум параллельным несовпадающим прямым (рис. 9.1, б). Наконец, третья СЛАУ такова, что второе ее уравнение является следствием первого: оно получается из первого умножением на 2.
Рис. 9.1
244
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Геометрически это означает, что уравнения задают одну и ту же прямую (рис. 9.1, в). Следовательно, координаты любой точки этой прямой удовлетворяют каждому из уравнений системы, т.е. третья СЛАУ совместна и имеет бесконечно много решений. #
Если СЛАУ (9.1) имеет решение, и притом единственное, то ее называют определенной, а если решение неединственное — то неопределенной. При m = n, т.е. когда в (9.1) количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
9.2.	Формы записи СЛАУ
Кроме координатной формы (9.1) записи СЛАУ часто используют и другие ее представления.
Рассматривая коэффициенты а,гд СЛАУ при одном неизвестном Xj как элементы столбца, a Xj как коэффициент, на который умножается столбец, из (9.1) получаем новую форму записи СЛАУ:
«п
«21
xi +
/ «12 \ «22
\ «m2 /
«1п
«2п
\ «тп /
или, обозначая столбцы соответственно aj, ..., an, 6,
Xiai + ... + хпап = b.
(9-2)
Таким образом, решение СЛАУ (9.1) можно трактовать как представление столбца Ъ в виде линейной комбинации столбцов ai, ..., ап. Соотношение (9.2) называют векторной записью СЛАУ.
Обратим внимание на то, что слева в каждом уравнении системы (9.1) стоит сумма попарных произведений — так же,
9.3. Критерий совместности СЛАУ
245
как и в произведении двух матриц. Если взять за основу произведение матриц, то СЛАУ (9.1) можно записать так (см. пример 6.5):
< ац ац a2i а22
ain а2п
Х2
\атп1 &т2
(Ь1\
&2
\ /
®тпп
или Ах = Ь, где А — матрица типа тхп; неизвестных; Ь — столбец свободных членов:
/ ац	ai2 ... ain
a2i	а22 ... а2п
х — столбец
/Ь1\
\ Ът /
\	®m2	• • • ®тпп
Поскольку А, х и 6 являются матрицами, то запись СЛАУ (9.1) в виде Ах = Ь называют матричной. Если 6 = 0, то СЛАУ является однородной и в матричной записи имеет вид Ах = 0.
Приведенные рассуждения показывают, что задачи:
а)	решения СЛАУ (9.1);
б)	представления столбца в виде линейной комбинации данных столбцов;
в)	решения матричных уравнений вида Ах = Ь являются просто различной формой записи одной и той же задачи.
9.3.	Критерий совместности СЛАУ
„Триединство" форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
246
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицу
«11	«12	•••	«1п
«21	«22	•• •	«2п
\ «ml	«m2	• • •	«тп	/
называют матрицей (коэффициентов) СЛАУ (9.1), а мат
рицу
(А|Ь) =
«12
«22
«m2
«1п
«2п
«тп
расширенной матрицей СЛАУ (9.1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Критерий совместности СЛАУ дает следующая теорема Кронекера — Капелли (Л. Кронекер (1823-1891) — немецкий математик, А. Капелли (1855-1910) — итальянский математик).
Теорема 9.1. Для совместности СЛАУ Ах = Ь необходимо и достаточно, чтобы ранг ее матрицы А был равен рангу ее расширенной матрицы (А|Ь).
◄ Необход и мост ь. Отметим, что ранг матрицы А СЛАУ Ах = Ь не превосходит ранг расширенной матрицы (А | Ь). Поэтому нам достаточно показать, что ранг матрицы А системы не меньше ранга ее расширенной матрицы (А 16). Если система совместна, то, записывая ее в векторной форме, делаем вывод, что существуют такие значения неизвестных xi, ..., хп, для которых aixi +... + апжп = 6, где аг — столбцы матрицы А, Ь — столбец свободных членов. Это означает, что последний столбец Ь в расширенной матрице системы является линейной комбинацией остальных столбцов. Выберем какой-либо базисный минор матрицы А. Для простоты пусть он содержит
9,3. Критерии совместности СЛАУ
217
i t роки с номерами 1, 2, ..., к и столбцы с теми же номерами, ГТ.
ап а12 ... aifc
Л/Г— а21	а22	••• ^2к
&к1 &к2 • • • акк
Согласно теореме 8.7 о базисном миноре, базисные столбцы линейно независимы, в то время как для каждого j > к существуют такие Xij € К, i = 1, к, что aj = Aijaj +... + А^а^. Поэтому столбец
6 = 01^1 + ... + акхк + ак+ххк+1 + ... + апхп -
= a^xi + ... + акхк + (Ai^+iai + ... + Xkjc+io^xk+i +
+ ... + (Ainai + ... + Хкпак)хп
является линейной комбинацией базисных столбцов матрицы А. )то означает, что М является также базисным минором и и расширенной матрице (во-первых, он ненулевой; во-вторых, если взять какой-либо окаймляющий минор Mf, то либо он будет минором матрицы А, т.е. нулевым, либо он будет содержать столбец Ь и, следовательно, не может быть ненулевым, так как его столбцы линейно зависимы). Поэтому Rg(A|b) — RgA.
Достаточность. Пусть Rg(A|6) = RgА. Выберем в А базисный минор М (как и выше). Тогда он будет базисным и в матрице (А| Ь). Значит, столбец Ь можно представить как линейную комбинацию базисных столбцов cq, ..., ак:
b-x^ai + ... + хкак.
Полагая x£+i хк±2 “ • • • = хп — О? получаем решение	...,
исходной СЛАУ, поскольку
Ь = x^ai + ... + хкак = x^ai + ... + хкак + Oafc+i + ... + Оап.
)то означает, что СЛАУ совместна. ►
248
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
9.4.	Формулы Крамера
Рассмотрим СЛАУ (9.1) с квадратной невырожденной матрицей А в матричной записи Ах = Ь. В такой форме СЛАУ представляет собой частный случай матричного уравнения АХ = В при В = Ь и X = х (см. 8.3). Поэтому она имеет единственное решение х = А~ХЬ, где А”1 — матрица, обратная к А, Чтобы выразить это единственное решение через коэффициенты СЛАУ, запишем А”1 в виде: А”1 = (<*о)? гДе = = Aji/detA, a Aji — алгебраическое дополнение элемента aji матрицы А. Перейдем от матричного равенства х — А~ХЬ к его координатной записи. Тогда для первых элементов в столбцах левой и правой частей последнего равенства имеем
, .	, .	.	, _ Ац61 + A2i&2 + • • • + Ani&n
— аи01 + <*1202 + ... + &inbn —----------TTl-------------*
Числитель представляет собой разложение по 1-му столбцу
определителя
61	«12
&2	а22
Ьп ^т2
G'ln
®2п
&тп

получающегося, если в матрице А заменить 1-й столбец на столбец свободных членов. Аналогично находим, что

(9.3)
где Aj — определитель матрицы, получающейся из матрицы А заменой j-ro столбца на столбец свободных членов. Таким образом, установлено следующее правило Крамера,
Теорема 9.2. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера (9.3).
9.5. Однородные системы
249
Следствие 9.1. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
9.5.	Однородные системы
Следующая теорема описывает важнейшее свойство множе-гтва решений однородной системы т линейных алгебраических уравнений с п неизвестными
^11^14* О12ж2 + ---+ а1п^п = О, < a2ixi+ а22^ + ...+ «2п^п = 0,	(д 4)
®тп1*£1 4“ ^т2^2 4" • • • 4* ^тп^п ~~ О*
Теорема 9.3. Если столбцы а^1),	..., ж($) — решения
однородной СЛАУ Ах = 0, то любая их линейная комбинация также является решением этой системы.
◄ Рассмотрим любую линейную комбинацию данных решений:
s
x = Y^Xkx(k\ AfceR.
k—1
Тогда
s	s	s
Ax = A(j2 Xkx^ = 22 XkAx & =	AfcO = 0,
k=l	fc=l	k=l
т.е. столбец x является решением однородной СЛАУ Ах = 0. ►
Следствие 9.2. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
250
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
◄ Если х — ненулевое решение однородной СЛАУ, то для любого А € R решением однородной СЛАУ является и Ах. ►
Естественно попытаться найти такие решения а^1), системы Ах = 0, чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение 9.1. Любой набор из к = п — г линейно независимых столбцов, являющихся решениями однородной СЛАУ Ах = 0, где п — количество неизвестных в системе, аг — ранг ее матрицы А, называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице А однородной СЛАУ Ах = О фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Теорема 9.4. Пусть дана однородная СЛАУ Ах = О с п неизвестными и RgA = r. Тогда существует набор из к = п — г решений а^1), ..., этой СЛАУ, образующих фундаментальную систему решений.
◄ Не ограничивая общности, можно считать, что базисный минор матрицы А сосредоточен в верхнем левом углу, т.е. расположен в строках 1, 2, ..., г и столбцах 1, 2, ..., г. Тогда остальные строки матрицы А, согласно теореме 8.7 о базисном миноре, являются линейными комбинациями базисных строк. Для системы Ах =. 0 это означает, что если значения xi, ..., хп удовлетворяют уравнениям, соответствующим строкам базисного минора, т.е. первым г уравнениям, то они удовлетворяют и остальным уравнениям. Следовательно, множество решений
9.5. Однородные системы
251
< ис гемы не изменится, если отбросить все уравнения начиная с (г + 1)-го. Сделав это, получим систему
^11*^1 4“ ®12*^2 4“ • • • 4~ ®1п*^п — О?
а21ж1 + а22х2 + • • • + Л2пжп — О?
к 4“ flr2*^2 4“ • • • 4“ аГпхп — 0.
Разделим базисные «1, ..., хг и свободные яг+1, •••? хп неизвестные, перенеся последние в правую часть, а в левой оставив базисные:
{^11X1 4" ®12*^2	4“ ... 4“ &1гхг	=	^1,г4-1^г+1	• • •	^lnxni
0>21х1 4” ^22х2	4“ ... 4“ 0^2rxr	=	—а2,г+1а'г+1	^2пхпч	(д
«rl^l + 0>г2х2	4“ ... 4“ O“rrxr	®r,r+l^r+l	• • •	0>гпхп*
Если мы зададим произвольные значения независимых неизвестных яг+1, ..., жп, то относительно базисных неизвестных получим квадратную СЛАУ с невырожденной матрицей, решение которой существует и единственно. Таким образом, любое решение однородной СЛАУ однозначно определяется значениями независимых неизвестных жг+1, ...? хп- Рассмотрим следующие к = п — г серий значений независимых неизвестных .Г|. 4-1, ..., Хп.
М Хг+1	= 1,	42+\=0,	^r + l	= 0,	
Ж(1) •*>+2	= 0,	4+2=с	XW xr+2	= 0,	(9-6)
J1)	= 0;	42) = 0;	XW	= 1.	
Здесь номер серии указан верхним индексом в скобках, а сами серии значений выписаны в виде столбцов. В каждой серии .rj.^ = 1, если j = i, и x^+j = 0, если j / i.
252
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Далее, г-й серии значений независимых неизвестных одно-(г)	(г)
значно соответствуют значения х\', ..., зависимых не-известных. Значения независимых и зависимых неизвестных в совокупности дают решение системы (9.5). Покажем, что столбцы
/ж«\
•V *|
(О
4
образуют фундаментальную систему решений. Так как эти столбцы по построению являются решениями однородной системы Ах = 0 и их количество равно к, то, в соответствии с определением 9.1 фундаментальной системы решений, остается доказать линейную независимость решений (9.7). Пусть есть некоторая линейная комбинация решений а^1), ..., х^к\ равная нулевому столбцу:
+ ... + OikX^ = 0.
Тогда левая часть этого равенства является столбцом, компоненты которого с номерами г + 1, ..., п равны нулю. Но (г + 1)-я компонента равна «11 + «20 +... + а^О = «1. Аналогично, (г + 2)-я компонента равна «2 и, наконец, к-я компонента равна Поэтому «1 = «2 = • • • = <*к = 0? что означает линейную независимость решений я^1),...,®W. ►
Построенная при доказательстве теоремы 9.4 фундаментальная система решений (9.7) имеет достаточно специальный вид, поскольку, согласно (9.6), в любом из решений (9.7) все значения независимых неизвестных равны нулю, кроме одного, которое равно единице. Такие фундаментальные системы решений называют нормальными.
9.5, Однородные системы
253
Следствие 9.3. С помощью нормальной фундаментальной системы решений (9.7) однородной СЛАУ (9.4) множество всех решений можно описать формулой
х = с^х^ + ... + Ckx^k\	(9.8)
где постоянные с,-, г = 1, k, принимают произвольные значения.
4 Согласно теореме 9.3, столбец (9.8) является решением рассматриваемой однородной СЛАУ Ах = О. Поэтому остается доказать, что любое решение
3 =
51 >
92
\9п/
п ой однородной СЛАУ можно представить в виде (9.8). Рас-< мотрим столбец х = t/r+ia^1) + • • • + 9п^к^• Этот столбец совпадает со столбцом g по элементам с номерами r+ 1, ..., п и ипляется решением СЛАУ (9.5). Поэтому столбцы g и х совпадают, так как решения системы (9.5) однозначно определяются набором значений ее независимых неизвестных xr±i, ..., хп, и у столбцов g и х эти наборы совпадают. Следовательно, у ~ х =	т.е. решение g есть линейная ком-
бинация столбцов х^\ ..., нормальной фундаментальной системы решений, что завершает доказательство. ►
Следствие 9.4. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, ч тобы ее матрица была вырождена.
◄ Если матрица однородной системы невырождена, то, согласно следствию 9.1, однородная СЛАУ имеет только нулевое решение. Если же матрица однородной системы вырождена, то ее определитель, являющийся в квадратной матрице единствен-п ым минором максимального порядка, равен нулю. Значит, ранг г матрицы системы меньше ее порядка и, следовательно,
254 9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
меньше количества п неизвестных. Поэтому к = п — г > 0 и однородная СЛАУ имеет нормальную фундаментальную систему из к > 0 решений (9.7). Каждое из этих решений является ненулевым (значение одного из неизвестных в каждом решении равно единице). ►
Однородная СЛАУ (9.4) может иметь не только нормальные фундаментальные системы решений, но и другие фундаментальные системы решений. Оказывается, что утверждение следствия 9.3 имеет место не только для нормальной фундаментальной системы решений, но и для произвольной фундаментальной системы решений, что и утверждает следующая теорема.
Теорема 9.5. Если а^1), ...,	— произвольная фун-
даментальная система решений однородной СЛАУ Ах = 0, то любое ее решение х можно представить в виде
х = с\х^ + ... + Ckx^k\	(9.9)
где ci, ..., q — некоторые постоянные.
Эту теорему называют теоремой о структуре общего решения однородной СЛАУ. Это вызвано тем, что, согласно теоремам 9.3 и 9.5, при заданной фундаментальной системе решений ЖП), ... , однородной СЛАУ (9.4) выражение
®оо =	+ ... + CkX^k\	(9.10)
где ci, ..., q принимают произвольные значения, описывает все множество решений. Соотношение (9.10) называют общим решением однородной СЛАУ.
4 Пусть некоторое решение однородной СЛАУ Ах = 0 имеет вид
/х(°)\
\Жп0)/
9.5. Однородные системы
255
Не ограничивая общности, опять будем предполагать, что базисный минор матрицы А сосредоточен в верхнем левом углу, г.г. в первых г строках и столбцах. Тогда (см. доказательство теоремы 9.4) рассматриваемая однородная СЛАУ (9.4) имеет !•<* же решения, что и система
а11ж1 + #12ж2 + •.. + a>inxn — О? «21^1 + «22^2 + • • • + «2п^п = 0,
4“ ^г2х2 4“ • • • 4“ О,гпХп —
которую можно записать в виде
4“ СЬ12^2 4“ • • • 4“ (%lrxr — ^1,г4’1'^гТ1	• • •	^lnxnj
<	П21ж1	4- «22^2 4“ • ’ • 4“ «2г^г = ~а2,г+1#г+1	“ •• • —
СЬГ\Х\	аг2%2 4“ ... 4- аггХг flr,r+l*£r+l	• • •	^гпхп*
)та система, рассматриваемая как СЛАУ относительно базисных неизвестных xi, ..., хг, имеет невырожденную матрицу, гак как ее определитель совпадает с базисным минором матрицы А исходной СЛАУ (9.4). Решая систему относительно базисных неизвестных (например, с помощью формул Крамера), получаем соотношения
Х1 — ^1,г4-1*^г4-1 4“ ... 4“ &1пхт х2 = ^2,г4-1^г-|-1 4“ ... 4“ &2пхп>
(9.11)
хг — ^г,г4-1*^г4-1 4“ ... 4“ &гпхп>
где otij € К — некоторые числа. Запишем фундаментальную систему решений ..., в координатной форме:
г = 1, к,
256
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
и составим из столбцов ж, а^1), ..., матрицу
	(г? 4”	... .<-> ...	Ак} \ Л*)
в =	4“>	_(i) • • •	_(*) •Ъ у
	,<«) ^r + l	J1) ^г+1	•••	Л*) з-г-н
	1 х(о)	ЛО	7 /
Последние к столбцов матрицы В образуют фундаментальную систему решений и, согласно определению 9.1, линейно независимы, а так как по теореме 8.9 ранг матрицы равен максимальному числу линейно независимых столбцов, то RgB к. Покажем, что RgB к. Так как столбцы матрицы В являются решениями системы Ах = О, их элементы удовлетворяют соотношениям (9.11), т.е.
(О	(0 ।	.	(О
•^1 —	4“ • • • 4“ ОС1п*£п ,
(г)	(г) .	.	(г)
< «2 = a2,r+l®r+l + • • • + «2пЖп ,
(г)	(г)	.	.	(г)
— ^r,r-|-l ^г+1 4" • • • 4” ®гп$п ,
(9.12)
где г = 0, г. Вычтем из первой строки матрицы В линейную комбинацию последних к = п — r строк с коэффициентами <*1,г+ь • ••> а1п- Тогда, согласно первому равенству из (9.12), получим нулевую строку. Аналогично преобразуем строки 2-ю, ..., r-ю, используя оставшиеся равенства (9.12). В результате этих преобразований мы получим матрицу, у которой первые г строк нулевые. Так как при этом ранг матрицы но меняется, то RgB п — г = к.
Поскольку RgB — к, а последние к столбцов матрицы В, как уже отмечалось, линейно независимы, то, согласно теореме 8.8, они являются базисными и, следовательно, первый столбец ж,
9.6. Неоднородные системы
257
согласно теореме 8.7 о базисном миноре, является их линейной комбинацией. Это означает, что существуют такие постоянные <\ (г = 1, А;), что выполнено равенство (9.9). ►
9.6. Неоднородные системы
Рассмотрим произвольную СЛАУ Ах = Ь. Заменив стол-гм'ц Ь свободных членов нулевым, получим однородную СЛАУ /1ж = 0, соответствующую неоднородной СЛАУ Ах — Ь. Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема 9.6. Пусть столбец ж0 — некоторое решение СЛАУ Ах = Ь. Произвольный столбец х является решением этой СЛАУ тогда и только тогда, когда он имеет представление ж - ж0 + j/, где у — решение соответствующей однородной СЛАУ Аг/-О.
4 Если х — решение СЛАУ Ах = Ь, то
А(х — ж0) = Ах — Аж° = Ь — 6 = 0.
Поэтому столбец у — х — х° является решением соответствующей однородной СЛАУ, и мы получаем представление х — ж° + |/.
Обратно, если у — произвольное решение соответствующей однородной системы, то х = ж0 + г/ — решение системы Аж — Ь, гак как
А(ж° + у) — Ах° + Ау = Ь + 0 = Ь. ►
Следствие 9.5. Пусть ж' и ж" — решения неоднородной « нс гемы Аж = Ь. Тогда их разность у = ж' — ж" является решением соответствующей однородной системы Ау = 0.
Теорема 9.6 сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной
> Аналитическая геометрия
258 9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
СЛАУ, достаточно знать одно ее решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме 9.1 Кроне-кера — Капелли), а во-вторых, найти частное решение этой системы, чтобы свести ее к однородной системе.
Следствием теорем 9.5 и 9.6 является теорема о структуре общего решения СЛАУ.
Теорема 9.7. Пусть ж° — частное решение СЛАУ Ах = Ъ и известна фундаментальная система решений ..., соответствующей однородной системы Ах = 0. Тогда любое решение СЛАУ Ах = Ь можно представить в виде
х = Х° + С\Х^ + С2&№ + ... + CkX^k\	(9.13)
где Ci € R, i — 1, к.
Как и в случае однородной СЛАУ, название теоремы отражает то, что формула
х = х°-\-хоо, гвоо = с1®(1) + ... + Скх(к\ (9.14)
при произвольных постоянных сг е R, г = 1, Аг, описывает все множество решений СЛАУ Ах = Ь, Формулу (9.14) называют общим решением СЛАУ,
Как найти частное решение неоднородной СЛАУ Ах = 6? Пусть для соответствующей однородной системы Ах = 0 выбраны базисные и свободные неизвестные. Базисный минор матрицы А является базисным и для расширенной матрицы (А | Ь), если СЛАУ Ах = Ь совместна. Поэтому строки базисного минора определяют те уравнения СЛАУ Ах = Ь, из которых следуют остальные. Эти остальные можно отбросить. Итак, пусть есть СЛАУ
^11^1+ Л12ж2 + ---+
^21^1+ «22^2+ •••+ ^2n^n — ^2,
, amlxl + ^т2х2 + • • • + ^тпхп —
9.7. Как решать СЛАУ ?
259
и базисный минор матрицы СЛАУ сосредоточен вверху слева:			
М =	«11	«12	• «21	«22	•	..	Я],. ••	«2г	/0.
	Ctrl ®г2	.. агг	
Тогда исходная система эквивалентна следующей:			
{а11ж1 + а12ж2 + ... + (^1пхп — &1, а21ж1 + а22х2 4“ • • • 4“ (^2пхп ~ ^2,
ttri«i 4“ (%г2х2 4“ • • • 4“ ^гпхп — Ьг*
Зададим нулевые значения хг+\ = ,,, = хп = 0 для свободных неизвестных и получим СЛАУ с невырожденной матрицей
ац£1 4-* «12ж2 4-.. • 4-* airxr = bi, < ^21^1 4" &22х2 4“ • • • 4" 0>2rxr — ^2?
к ar^xi 4“ ®r2*^2 4“ • • • 4“ arrxr — br^
имеющей единственное решение. Решая последнюю систему, находим значения х°, ..., х°. Тогда частным решением будет столбец
/®;\
о
\0/
9.7. Как решать СЛАУ ?
В принципе все уже изложено в предыдущих разделах. Однако описанная схема может быть достаточно трудоемкой из за того, что некоторые вычисления будут несколько раз повторяться. Покажем, как этих повторений можно избежать.
260
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть задана СЛАУ Ах = Ь. Запишем ее расширенную матрицу (А|Ь). Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ:
а)	умножение г-й строки матрицы на число А 0 означает умножение г-го уравнения СЛАУ на это же число;
б)	перестановке г-й и k-и строк в матрице отвечает перестановка г-ro и к-го уравнений СЛАУ;
в)	добавление к г-й строке матрицы ее fc-й строки равнозначно замене г-ro уравнения его суммой с к-м уравнением СЛАУ.
Эти преобразования СЛАУ не меняют ее множество решений. Поэтому приведение расширенной матрицы системы с помощью элементарных преобразований ее строк к ступенчатому виду означает сведение СЛАУ к эквивалентной системе, имеющей ступенчатую матрицу.
Итак, сначала приводим расширенную матрицу (А| Ь) заданной СЛАУ с помощью элементарных преобразований строк к ступенчатому виду (А'|Ь')- При этих преобразованиях ранги матриц не меняются, поэтому Rg(A|b) = Rg(A'|b')> а RgA = = RgA'. Ранги матриц А' и (А'|Ь') равны количеству их ненулевых строк. Если эти ранги равны, то по теореме 9.1 Кронекера — Капелли СЛАУ совместна, а в противоположном случае — несовместна.
В случае совместности в матрице А' ступенчатого вида выбираем, следуя 8.6, базисный минор и фиксируем соответствующие ему базисные и свободные неизвестные. В матрице (А'|Ь') ступенчатого вида отбрасываем нулевые строки (им соответствуют тривиальные уравнения) и по получившейся матрице восстанавливаем СЛАУ. В уравнениях этой СЛАУ слагаемые со свободными неизвестными переносим в правые части и получаем систему, матрица которой является верхней треугольной и невырожденной, так как ее определитель совпадает с базисным минором матрицы А'. Последовательно исключая неизвестные, выражаем базисные неизвестные через свободные.
9.7. Как решать СЛАУ ?
261
(Свободные неизвестные обозначаем как произвольные постони пые и записываем общее решение СЛАУ в виде линейной комбинации столбцов, выделяя в правых частях полученных выражений в отдельные столбцы: а) свободные члены; б) коэффициенты при каждой произвольной постоянной. В этой in писи столбец свободных членов есть частное решение СЛАУ, в столбцы при произвольных постоянных образуют нормальную фундаментальную систему решений однородной СЛАУ, соот-h<‘тствующей заданной неоднородной системе.
Если исходная СЛАУ является однородной, то изложенный метод решения чуть упрощается, поскольку в расширенной матрице последний столбец является всегда нулевым и не меняется при элементарных преобразованиях строк. Имея >го в виду, его опускают, т.е. все преобразования проводят с матрицей системы.
Пример 9.2. Решим однородную СЛАУ
Xi- Х2+ Х3- Х4 = О, £1 + я2 + 2:гз+ Зх4 = 0, 2^i + 4х2 + 5ж3 + 10х4 = О, 2x1 —4^2+ хз~ 6х4 = 0.
Чтобы найти общее решение, запишем матрицу системы и преобразуем ее при помощи элементарных преобразований строк к ступенчатому виду:
/1 -1	1	/1 -1	1	/1 -1	1
1 1	2 3 j	0	2	1	4	0	2	1	4
2	4	5 Ю |	0	6	3 12	0	0	0	0
\2 -4	1 -6/	^0 -2	-1 -4)	\0 0	0 0/
Базисный минор в преобразованной матрице стоит вверху с лева и имеет второй порядок. Это значит, что ранг г матрицы системы равен двум, фундаментальная система решений
262
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
состоит из п — г = 4 — 2 = 2 решений, а сама СЛАУ эквивалентна следующей системе, которая соответствует преобразованной матрице:
Г xi - х2 + х3 - х4 = О, (	2х2 + #з + 4X4 = 0.
Базисными неизвестными являются и х2, а свободными — х3 и Х4. Выражаем базисные неизвестные через свободные:
f Х\ —	1,5хз	Х3,
( х2 = — 0,5хз — 2x4.
Вводим обозначения Х3 = ci, Х4 = с2 и записываем общее решение СЛАУ:
Xj — 1,5с^ С2, < х2 = -0,5^-2с2, Х3 = Cj,
^4 = С2.
Используя матричную форму записи, получаем
/ -l,5ci - с2
—0,5ci — 2с2
С1
\ с2
= С1
/-1,5\
-0,5 1 \ 0 /
+ с2
где
нормальная фундаментальная система решений, a Q, с2 — произвольные постоянные.
9.7. Как решать СЛАУ 7
263
Пример 9.3. Решим неоднородную СЛАУ
xi — х2 + хз - х4 = 4, «1 + х2-|-2хз4- Зх4 = 8, 2xi + 4^2 + 5хз + 10х4 — 20, 2xi - 4x2 + хз — 6х4 = 4.
Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:
/1	-1	1 -1	4\	/1	-1	1 -1	4\
1	1	2	3	8 1	0	2	1	4	4
2	4	5 10	20	0	6	3 12	12
\2	—4	1 -6	4/	ко	—2	-1 —4	-4?
0
-1 1
2 1
0 0
0 0
4\
4
0
0/
4
0
0
Теперь видно, что для преобразованной матрицы минор является базисным. Поэтому Rg А = Rg(A|b) = 2 = г, и, согласно теореме 9.1 Кронекера — Капелли, СЛАУ совместна. Кроме того, СЛАУ свелась к эквивалентной системе
Я1-Я2 + Я3- ^4 = 4,
2ж2 + жз + 4ж4 = 4,
которая соответствует преобразованной матрице. Однако можно продолжить преобразования в матрице, упрощая базисные столбцы (1-й и 2-й) с помощью элементарных преобразований строк так, чтобы в каждом из них остался один ненулевой ик'мент, причем нулевые строки можно отбросить:
/' -1 1
0	2	1
0	0	0
\0	0	0
-1
4
0
0
4\
4
0
о/
1 -1 1
0	2 1
-1 4\ /1 0 1,5 1 б\
4 4/ \0 1 0,5 2 2/
264
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
По этой матрице восстанавливаем систему
f хг + 1,5я3+ Xi = 6, ( х2 + 0,5яз + 2я4 = 2.
Перенося свободные неизвестные жз, ж4 в правые части уравнений, получаем
( хг = 6 — 1,5жз — х4, [ х2 = 2 — 0,5жз — 2ж4.
Для свободных неизвестных положим ж3 = ci, ж4 = с2у и тогда
хг = 6 — 1,5ci — С2, х2 = 2 - 0,5ci - 2с2,
ЯЗ = С1,
к «^4 — ^2,
ИЛИ
/ 6 - l,5ci - с2 > 2 - 0,5ci - 2с2
С1
\	«2	/
Полученное общее решение очень наглядно: 1-й столбец — частное решение неоднородной СЛАУ, а два последних — нормальная фундаментальная система решений соответствующей однородной СЛАУ (ср. пример 9.2).
Пример 9.4. Решим неоднородную СЛАУ
Ж1 - х2 + х3 - х4 = 4, ®1+ х2 + 2х3 + Зх4 = 8, 2xi + 4х2 + 5хз + 10x4 = 20, 2X1 —4х24- %з — 6x4= 5,
отличающуюся от системы из примера 9.3 лишь одним коэффициентом.
9.7. Как. решать СЛАУ ?
265
Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:
/1 -1	1 -1	4\		/1 -1	1 -1	4\
1 1	2	3	8		0	2	1	4	4
2	4	5 10	20		0	6	3 12	12
\2 —4	1 -6			^0 —2	-1 —4	-з/
/1 -1 1 -1
0	2	14
0	0	0	0
\0	0	0	0
/1 -1 1
0	2	1
0	0	0
\0	0	0
-1
4
0
0
4
4
1
0
Ггнерь видно, что в преобразованной матрице минор М}’? явля-нтся базисным для матрицы системы, а минор М123 — для расширенной матрицы. Поэтому RgA = 2, Rg(A|b) = 3 и, согласно теореме 9.1 Кронекера — Капелли, СЛАУ несовместна. Впрочем, несовместность очевидна и так, потому что последней матрице соответствует СЛАУ, в которой третье уравнение имеет вид: Oxi + Оз? 2 + Оз?з + Оз; 4 = 1-
Пример 9.5. Найдем все матрицы, перестановочные с матрицей
Обозначим искомые матрицы через X. Условие перестановочности означает выполнение матричного равенства АХ = ХА. Чтобы существовало произведение в левой части этого равен-। тва, матрица X должна иметь две строки, а чтобы существовало произведение в правой части — два столбца. Следовательно, X — квадратная матрица второго порядка, т.е.
Ж1
яз
^2
Х4
266
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
и для ее нахождения требуется решить матричное уравнение
Перемножая матрицы в этом уравнении и приравнивая элементы, стоящие на одинаковых местах в получающихся матрицах, приходим к равносильной системе четырех уравнений
xi+2x3 = Я1+Зх2, х2 + 2х4 = 2^1 + 4х2, 3xi+4x3= х3 + Зх4, Зх2 + 4х4 = 2хз + 4х4,
или
Зх2 - 2х3 = О, 2xi + Зх2 - 2х4 = О, £1+ ^з- х4 — О, Зх2 - 2х3 = 0.
Эта система имеет простой вид, и мы можем отойти от общей схемы решения однородных СЛАУ, продемонстрированной в примере 9.2. Легко увидеть, что если из второго уравнения вычесть удвоенное третье, то получится такое же уравнение, как первое и последнее. Поэтому первые два уравнения в этой системе можно отбросить и тогда
( xi + х3- х4 = 0,	( xi = -хз + х4,
I Зж2 — 2х3 = 0, ИЛИ |х2 = 2хз/3.
Итак, хз, х4 — независимые неизвестные, a xi, х2 — зависимые неизвестные. Для независимых неизвестных положим x3 = ci, х4 = с2 и тогда получим ответ в виде
' ^1 = -С1 +с2, х2 — 2ci/3, ЯЗ = С1,
. ^4 = С2,
или в матричной форме
С2-С1
С1
2ci/3\
с2 /
Д.9.1. СЛАУ с комплексными коэффициентами
267
где С2 € R — произвольные постоянные. Если фиксировать цля ci, С2 конкретные значения, то из множества всех перестановочных с А матриц будет выделена одна. Например, при < । — 0 и С2 = 0 получается нулевая матрица, а при Ci = 0 и q - 1 — единичная.
Дополнение 9.1. СЛАУ с комплексными коэффициентами
Изложенный в главах 6-9 материал относится к „действительному “ случаю, поскольку элементами матриц и определителей, коэффициентами СЛАУ являлась действительные чи-< ла. В качестве решений СЛАУ также рассматривались наборы действительных чисел. Оказывается, что имеется „комплекс-ное“ обобщение указанного материала. Для получения соответствующего комплексного варианта того или иного из приведенных результатов достаточно заменить в формулировках и доказательствах действительные числа на комплексные [1-4.3].
Специально подчеркнем, что для уравнений с комплексными коэффициентами сохраняется вся теория СЛАУ. В том числе остаются справедливыми: условия совместности СЛАУ (см. 9.3) и свойства их решений; правило и формулы Крамера (см. 9.4) для квадратных СЛАУ с невырожденной матрицей; условие существования ненулевого решения у однородной ('ЛАУ; метод решения СЛАУ на основе приведения расширенной матрицы к ступенчатому виду.
Пример 9.6. Решим квадратную СЛАУ второго порядка с комплексными коэффициентами (г — мнимая единица, г2 = —1)
Xi — ix2 = г + 1, х\ + 2x2 = 2г.
Вычисляем определитель det А матрицы СЛАУ:
det А =
1 —г
1 2
= 1-2- 1(-г) = 2 + г'/0.
268
9. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Ai _ 1 г + 1 —г det А “ 2 + i 2i 2
Следовательно, матрица СЛАУ невырождена, и система имеет решение, притом единственное. Чтобы его найти, воспользуемся формулами (9.3) Крамера:
(г+ 1)2 +2г2 _
2 + г ~
_ 2г _ 2г(2-г) _ 2 + 4г
~ 2+7 ~	5	” 5 ’
-	- 1	1 i + 1	2г- (г+1) _ -1 + г _ -1 + Зг
Х2 det А 2 + г 1 2г 2 + г 2 + г 5
Вопросы и задачи
9.1.	Решить СЛАУ и найти нормальную фундаментальную систему решений соответствующей однородной системы:
3xi+4x2 + 2x3- х4 = 3, 2xi +2x2 + Зхз — 2x4 = — 1, xi+2x2- хз+ х4 = 4, 6xi — 8x2 + 4хз — 2x4 = 3;
1X1 +2хз— Х4 = 5, 3x1— х2 + Х3 +2x4 = 1,
Х1 — 2X2 + Хз +2X4 = 3, 5xi — 3x2 + 4хз + Зх4 = 9, 5xi — 5x2 + Зхз + 6x4 = 7.
9.2.	Решить матричное уравнение
9.3.	Найти общее решение СЛАУ Ах = Ь\ — 2Ьг, если известны общие решения систем Ах = bi и Ах = Ь2-
9.4.	Может ли неоднородная СЛАУ Ах = b быть неопределенной, если столбцы ее матрицы линейно независимы (линейно зависимы)?
9.5.	Может ли неоднородная СЛАУ Ах = Ь быть неопределенной, если соответствующая однородная СЛАУ является определенной (неопределенной)?
Вопросы и задачи
269
9.6.	Совместна или несовместна СЛАУ, если столбцы ее расширенной матрицы линейно независимы (линейно зависимы)?
9.7.	Может ли неоднородная СЛАУ Ах = Ь быть совместной (несовместной), если соответствующая однородная СЛАУ является определенной (неопределенной)?
9.8.	Привести примеры совместной и несовместной СЛАУ, V которых строки матрицы системы линейно зависимы. Что можно утверждать о совместности СЛАУ, если строки ее матрицы (расширенной матрицы) линейно независимы?
9.9.	Квадратная СЛАУ Ах = Ь имеет невырожденную матрицу А, а свободные члены являются непрерывными функциями на отрезке [а, 6]. Доказать, что любое решение этой СЛАУ । остоит из функций, непрерывных на этом отрезке.
9.10.	Найти условие, при выполнении которого линейная комбинация решений неоднородной СЛАУ будет: а) решением ггой же СЛАУ; б) решением соответствующей однородной СЛАУ.
9.11.	Сколько решений может иметь неоднородная (однородная) СЛАУ, если столбцы ее матрицы линейно независимы?
9.12.	Доказать, что неоднородная СЛАУ совместна, если < сроки ее матрицы линейно независимы.
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
10.1.	Проблемы, связанные с вычислениями
При разработке любого численного метода решения какой-либо математической задачи возникает несколько общих проблем.
Первая проблема состоит в том, что теоретически корректный метод, приводящий к решению за конечное число операций, может оказаться плохим или вообще неприемлемым, если это конечное число операций окажется слишком большим. Например, при решении СЛАУ с квадратной невырожденной матрицей порядка п по правилу Крамера необходимо вычислить п+1 определитель n-го порядка. При вычислении только одного из этих определителей „в лоб“, согласно определению 7.1, требуется n!n— 1 арифметических операций. Таким образом, всего для решения системы требуется (n + l)(n!n— 1) + п операций. Уже при п = 23 это число имеет порядок 1021. Даже при скорости 109 операций в секунду потребуется не менее 30000 лет!
Вторая проблема связана с тем, что в практических задачах приходится иметь дело с неточными данными. При решении СЛАУ с квадратной матрицей требуется, чтобы определитель А матрицы системы был отличен от нуля. Однако нарушение этого условия, т.е. соотношение А = 0, никогда не выполняется точно, так как коэффициенты СЛАУ содержат, вообще говоря, погрешности, и определитель можно вычислить лишь приближенно. При этом, если определитель А мал по сравнению с коэффициентами системы, то небольшие погрешности могут приводить к существенному изменению решения.
10.1. Проблемы, связанные с вычислениями	271
Пример 10.1. Рассмотрим системы
Гж+ у= 1,	( х+ у = 1,
(ж + 1,01у = 1;	[я + 1,01у = 1,1.
Решение первой них — х = 1, у = 0, решение второй — х = —9, у 10. Как видим, изменение всего лишь одного коэффициента па 10% приводит к совсем другому результату. Понять причину этого феномена проще всего с помощью геометрической интерпретации СЛАУ. Данные системы можно рассматривать пак пары прямых на плоскости. Тогда их решения изображаются точками пересечения этих пар прямых. В нашем случае прямые „почти параллельны“ (рис. 10.1). Поэтому незначительное изменение положения одной из них приводит к большому < мощению точки пересечения. #
Говорят, что СЛАУ плохо обусловлена, если незначительные изменения ее коэффициентов могут привести к суще-। твонному изменению ее решения. Если этого не происходит, (‘ЛАУ называют хорошо обусловленной.
Третья проблема, возникающая в процессе вычислений, такам' связана с погрешностями и вызвана тем, что вычисления при помощи компьютера или калькулятора выполняются лишь
272
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
с конечным числом значащих цифр и потому их результаты содержат ошибки округлений (этого можно избежать только при вычислениях в целых числах, но диапазон целых чисел, используемых в компьютере, очень узкий, и это может привести к переполнению его разрядной сетки). В силу этой особенности, даже если все коэффициенты в СЛАУ заданы точно, решение получается, как правило, приближенным.
10.2.	Прямые и итерационные методы решения СЛАУ
Мы остановимся на решении только таких СЛАУ, у которых матрица является квадратной и невырожденной. В этом случае система имеет решение, и притом единственное. Для его нахождения используются различные методы. Выбор метода решения СЛАУ определяет не только объем вычислений, но и точность получаемого этим методом результата.
Прямые методы решения СЛАУ выполняются за фиксированное число арифметических операций, не зависящее ни от значений коэффициентов, ни от требуемой точности вычислений (но зависящее, разумеется, от порядка системы). Если вычисления проводятся точно (например, в целых числах), то прямой метод всегда дает точное решение. Поэтому такие методы иногда называют точными. Пример точного метода (хотя и неприемлемого на практике для больших систем) — это правило Крамера.
Итерационные методы решения СЛАУ принципиально иные и априори строятся на том, что ответ в любом случае будет приближенным. Каждый итерационный метод сводится к построению последовательности столбцов
...,	..., которая в пределе дает решение СЛАУ. Каж-
дый очередной столбец вычисляется на основе уже найденных и является более точным приближением искомого решения. Вычисление очередного столбца называют итерацией. В опре-
10.3. Метод Гаусса
273
целенный момент процесс прерывают, а последний полученный । голбец принимают за приближенное решение данной СЛАУ.
Как уже отмечалось, прямые методы решения СЛАУ выпол-п и ю гея за фиксированное число шагов, зависящее для каждого конкретного прямого метода лишь от размеров системы. Точность получаемых при этом решений зависит как от свойств методов, так и от того, является СЛАУ хорошо обусловленной или нет. В некоторых случаях прямые методы могут давать неверные результаты.
Итерационные методы решения СЛАУ в сравнении с прямыми методами, как правило, более устойчивы к погрешностям вычислений. Это связано с тем, что при использовании итерационных методов ошибки вычислений, содержащиеся в — результате n-й итерации, могут компенсироваться при вычислении я(п+1) — следующей, (п 4* 1)-й итерации. Плохая обусловленность СЛАУ обычно приводит к тому, что замедляется « ходимость последовательности к решению системы и увеличивается число итераций для обеспечения нужной точности решения.
10.3.	Метод Гаусса
Рассмотрим квадратную СЛАУ
®11^1 + • • • 4“	= ^1 )
< ...................
k finial 4“• • • 4* ^пп^п “
с невырожденной матрицей А.
Если в методе решения этой СЛАУ, изложенном в 9.7, зафиксировать определенный порядок преобразований (а любой численный метод должен базироваться на точном порядке вычислений), то получится численный метод, известный как метод Гаусса исключения неизвестных (или просто метод Гаусса). Метод Гаусса имеет следующий алгоритм, состоящий
274
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
из 2п — 1 шага. Запишем
расширенную матрицу системы
	«11	«12	«13	•	• •	®1п	ьА
	«21	«22	«23	•	• •	®2п	62
(Д|6) =	«31	«32	«33	•	• •	®3п	Ьз
	\ ®nl	^п2	®пЗ	• • О'ПП	Ьп)
На первом шаге делим 1-ю строку расширенной матрицы на ее 1-й элементам и получаем новую строку (1, а} 2 ,
Верхние индексы в коэффициентах а^ и Ь; указывают на то, что соответствующий элемент расширенной матрицы СЛАУ был пересчитан на к-м шаге метода Гаусса. Затем из каждой последующей г-й строки вычитаем 1-ю, умноженную на коэффициент ац. В результате получаем матрицу
/1	«12	«13	•	•	01п	
0	ч«22	«23	•	•• а2п	*4
0	«32	«33	•	а3п	ьз
\0	ап2	апЗ •	• • апп	b'J
На втором шаге делим 2-ю строку на ее диагональный элемент а22 и получаем новую 2-ю строку (0, 1, а23, ..., а2п, Ь2) расширенной матрицы. Затем из каждой последующей г-й строки (г = 3,..., п) вычитаем полученную строку с коэффициентом а|2 из 2-го столбца. В результате получаем матрицу
/1	«12	«13	•	••	«1п	Ь}\
0	1	«23	•'	••	®2п	62
0	0	«33	•• а3п	М
\ 0	0	а2 з ... а2 п Ь2 /
10.3. Метод Гаусса
275
Процесс продолжаем до последней строки расширенной матрицы. На n-м шаге остается разделить последнюю строку ini ее диагональный элемент и мы получим матрицу
/1	й12	а13	•	•• а1п	
0	1	а23	•	•• а2п	
0	0	1 ..	• • а3п	Ь3з
\0	0	0	..	.. 1	
В результате выполненных преобразований приходим к <ЛЛУ, эквивалентной исходной. Матрица этой СЛАУ являет-। и верхней треугольной и имеет диагональные элементы, равные единице. На этом завершается первая часть алгоритма метода Гаусса, которую называют прямым ходом метода Гаусса.
Вторая часть алгоритма состоит в преобразовании верхней треугольной матрицы в единичную, эту часть называют обратным ходом метода Гаусса. Итак, продолжаем преобразования.
На (п+ 1)-м шаге (первый шаг обратного хода) вычитаем последнюю строку из всех предшествующих с коэффициентами ил n-го столбца. Получаем матрицу
/1	а12	а13	•	•• а1,п-1	0	6п+1>
0	1	а23	•	•	а2,п-1	0	б^1
0	0	1 .	•	а3,п-1	0	с1
0	0	0 ..	1	0	е!
\0	0	0 ..	0	1	ч /
На (п + 2)-м шаге вычитаем (п— 1)-ю строку из всех предше-твующих с коэффициентами из (п — 1)-го столбца. Получаем
276
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
матрицу
/1	a12	a13	•••	al,n—2	0	0	b^+2\
0	1	a23	• • •	a2,n—2	0	0	bn2+2
0	0	1 ...	a3,n-2	0	0	b3+2
0	0	0	...	1	0	0	e!
0	0	0	...	0	1	0	bn+1 °n-l
	0	0	...	0	0	1	bn /
Процесс продолжаем до 2-й строки. На последнем (2п— 1)-м шаге вычтем из 1-й строки 2-ю с соответствующим коэффици ентом а\2 и в результате получим расширенную матрицу вида (Е|У), где
ъ'={ь2п-\ь2п-2,	-
столбец, представляющий собой искомое решение.
Последовательные шаги алгоритма могут быть сведены к серии формул (в них = (щ,
• прямой ход
— г-й шаг, г = 1,...,п — 1:
а)	— 2_i j j г + 1,..., тг, аи
гг—1
= ——
1	а’"1 ’
гг
b)	akj = aik~j1 -ak~ilaliv j = i +
bk = bk~1 ~akllbb k = i + l,...,n-,
10.4. Особенности метода Гаусса	‘2 7 /
• обратный ход
- г-й шаг, г = п+ 1,...,2п-Г.
п
xa = bss- ^2 asjxh s-2n-i.
j = s+l
В приведенных формулах представление процесса вычислении как преобразования расширенной матрицы системы терпится. Двойной нижний индекс в буквенных обозначениях ншачает, что в процессе вычислений необходимо использовать цпумерный массив. Верхний индекс отражает лишь шаг про-Н1ч га вычисления. Отметим, что коэффициенты агк - и Ьк, вычи-• 1 немые в процессе прямого хода метода Гаусса, при обратном и<»д<‘ непосредственно используются для определения решения । ж темы, значит, никаких преобразований расширенной матрицы при обратном ходе вообще выполнять нет необходимости.
10.4.	Особенности метода Гаусса
Разумеется, изложенный в 10.3 метод пригоден только в ।им случае, если матрица СЛАУ невырождена (иначе единичная матрица в результате элементарных преобразований г трок не получится). Но даже если это требование выполнено, мы можем на каком-то шаге получить нуль в качестве диагонального элемента, на который необходимо делить. Это может । «учиться даже на первом шаге.
Пример 10.2. К системе с расширенной матрицей
О 1 2 3\ 1 2 3 4 } 2 5 6 1/
мы не можем непосредственно применить изложенный алгоритм и вынуждены предпринять дополнительные действия, например предварительно переставить на первое место 2-ю или 3 io строку. #
278
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
В практике численных методов диагональные элементы матрицы, на которые в методе Гаусса приходится делить, называют ведущими, или главными. При каких условиях ведущие элементы не обращаются в нуль?
Рассмотрим угловые миноры матрицы А системы, сосредоточенные в ее верхнем левом углу: Д1 = Л1/, Д2 =	• ••,
= м1,Zk’---’ д« =	=det А-
Теорема 10.1. СЛАУ Ах = Ь может быть решена методом Гаусса тогда и только тогда, когда все угловые миноры матрицы А системы отличны от нуля.
◄ Отметим, что элементарные преобразования прямого хода метода Гаусса являются также элементарными преобразова ниями определителей Д*. В результате таких преобразований угловые миноры изменяются, но не меняются ранги соответствующих матриц. Это значит, что угловой минор fc-ro порядка равен нулю тогда и только тогда, когда равен нулю угловой минор того же порядка верхней треугольной матрицы, полученной в результате прямого хода. Но это возможно лишь в том случае, если один из ведущих элементов равен нулю. Наоборот, если все миноры Дд, отличны от нуля, то и все ведущие4 элементы метода Гаусса являются ненулевыми. ►
Сформулированный критерий проверить трудно, может быть, не легче, чем решить саму систему. Поэтому он интересен, скорее, с теоретической точки зрения, чем с практической. Однако в одном важном случае выполнение критерия следует из вида матрицы. Говорят, что в матрице А = (atJ) диагональные элементы преобладают, если для каждой строки с номером i выполняется неравенство
1аи| > /^2 lavl>	(^0.1)
т.е. каждый диагональный элемент по абсолютной величине превосходит сумму абсолютных величин всех остальных эле
10.4. Особенности метода Гаусса
279
ментов своей строки. Такие матрицы называют матрицами г диагональным преобладанием.
Отметим, что в матрице с диагональным преобладанием е диагональные элементы отличны от нуля. Действительно, •и ли бы некоторый диагональный элемент ац матрицы равнялся нулю, то из (10.1) следовало бы неравенство
0 — |ац| >	1^4? | 0,
и 'Iи 0 > 0.
Теорема 10.2. Если в матрице А преобладают диагональные элементы, то все угловые миноры этой матрицы отличны •и нуля.
4 Отметим, что преобладание диагональных элементов в ма-। рице означает, что и в каждом угловом миноре диагональные ♦ /и‘менты преобладают. Поэтому достаточно доказать, что определитель матрицы с преобладанием угловых элементов от-'Iи чен от нуля.
Рассмотрим определитель
	«и	«12	.	• • а1п
д =	«21	«22	•	а2п
	G-nl	ап2	• • ®пп
у которого диагональные элементы преобладают. Тогда ац^0 и для его матрицы можно выполнить первый шаг метода Гаус-। и. В результате первого шага получим определитель
	1	а12	«13	•	•• а1п
	0	«22	«23	•	• • а2п
Д1 =	0	«32	«33	•	•• а3п
о агп2 апЗ  ап
280
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
с элементами
1	?	1	7	•	1 —
01, = —, akj = akj--------“kl,	3 - 2, П.
Оц	Оц
Убедимся, что у нового определителя Д1 диагональные эле менты также преобладают. Для этого оценим сумму модулей всех элементов к-й (к > 1) строки, кроме 1-го (он равен нулю) и к-го (он диагональный):

3*1	11	3*1	1 111 3*1
3^	3^k	j^k	j^k
(используем преобладание оц в 1-й строке)
-	' £4 «-..I - i«,ti)=+i«,i - 444=
1«п1	7^	1«и1
3*Ъ
_ V^I„ I lafcl||«lfc| lalll <
(используем преобладание акк в к-й строке)

|Ofcl||Qlfc| lalll
а1к dkk
an
= l<4|.
Итак, после первого шага прямого хода метода Гаусса пре обладание диагональных элементов в матрице сохранилось. Ис пользуя разложение определителя Ai по 1-му столбцу, прихо дим к определителю (п — 1)-го порядка с преобладанием диаго нальных элементов, который является минором определителя Д1, соответствующим единице в верхнем левом углу. Дока зательство завершается методом математической индукции по порядку определителя. Для определителей первого порядка, т.е. чисел, утверждение теоремы очевидно. ►
При транспонировании матрицы ее угловые миноры транс понируются и потому сохраняют свое значение. Поэтому если
10.4. Особенности метода Гаусса
281
ь । истоме с данной матрицей применим метод Гаусса, то он применим и к системам с транспонированной матрицей. Дру-। ими словами, метод Гаусса применим к системам, в матрицах ко горых диагональные элементы являются преобладающими в » юлбцах.
Если метод Гаусса не проходит, т.е. один из угловых минорок обращается в нуль, то в алгоритм приходится включать ншолпительные действия, например перестановку строк. С цнполпительной перестановкой строк метод Гаусса можно применить к любым системам с невырожденной матрицей, и он пудет давать правильное решение в предположении, что все вычисления выполняются точно.
()днако, даже если метод Гаусса проходит без модификаций, in г равно могут возникнуть неприятности. Дело в том, что из-hi ошибок вычислений вместо ведущих элементов, на которые предстоит делить, мы получаем лишь их некоторое приближение. Значит, вместо теоретического нуля мы можем получить число, хотя и малое, но не нуль. Тогда дальнейшие вычисления могут привести к переполнению разрядной сетки компьютера, вызванному делением большого числа на малое (это фактически можно расценивать как деление на нуль). Если же переполнение не произойдет, то дальнейшие вычисления не будут иметь никакого отношения к реальному решению. Конечный резуль-нгг будет определяться не исходными данными, а причудливой игрой ошибок вычислений.
Пример 10.3. Система
4я+	Зу = 3,
Юж + 7,51у + 3z = —0,49, 2х —	у — z — О
имеет решение (0, 1, —1), в чем можно убедиться непосред-। гнгнной проверкой.
Применим метод Гаусса, предполагая, что вычисления выполняются с точностью до четырех значащих цифр. После
282
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
первого шага получаем матрицу
1	0,75
0	0,01
0 -2,5
0
8
-1
0,75
-7,99
-1,5
Следующий шаг рассмотрим подробнее. Делим 2-ю строку на ее диагональный элемент
1	0,75	0	0,75 \
0	1	800 -799
0 -2,5	-1	-1,5 /
и вычитаем ее из 3-й строки с коэффициентом —2,5. В последнем столбце мы должны из —1,5 вычесть произведение (-2,5)(-799) = 1997,(5). Заданная точность требует, чтобы мы отбросили последний пятый знак и в качестве вычитаемого взяли число 1997. Вычтя его из —1,5, получим —1998,(5) и снова должны отбросить лишний знак. В итоге получим:
1 0,75	0	0,75 \
0 1	800	-799
0 0	1999 -1998	/
Деление 3-й строки на ведущий элемент в последнем столбце дает —0,9995. В результате обратного хода метода Гаусса получаем в качестве решения х — 0,3, у = 0,6,	—0,9995, чти
значительно отличается от верного решения. #
Рассмотренный пример показывает, что дополнительная перестановка строк может помочь и в борьбе с ошибками округления. Действительно, если перед выполнением второго шага прямого хода переставить 2-ю и 3-ю строки, то, каи показывают непосредственные расчеты, ошибки в результат» не появляются, и мы получаем верное решение. Отметим, что указанная перестановка строк перед вторым шагом приводит к матрице системы с преобладанием в строках диагональных элементов.
10.4. Особенности метода Гаусса
283
Итак, перестановкой строк матрицы в процессе вычислений ин методу Гаусса можно улучшить характеристики матрицы и ннныгить надежность метода. Точно так же можно перестали и, (‘ голбцы, что равносильно изменению порядка неизвестным 'Таким способом не всегда можно получить матрицу с преобладанием диагональных элементов в строках, но тем не • ii’Him» перестановки улучшают работу метода.
Перестановку строк и столбцов матрицы можно выполнять и» inн родственно в процессе вычислений перед выполнением • ««’родного шага прямого хода. Перестановка столбцов должна Фиь< ироваться, так как потом, когда будет получено решение, тдует расставить значения найденных переменных в нужном нирндке. Перестановку строк запоминать нет необходимости.
()гповная цель перестановки строк и столбцов — получение н |.ц»к»( гве ведущего элемента возможно большего коэффициен-। । матрицы. Поэтому на г-м шаге прямого хода метода Гаусса в • и । троке выбирают наибольший по абсолютной величине эле-ит и соответствующий столбец меняют местами с г-м. В р» iy/ц/гате перестановки новый ведущий элемент становится наибольшим по абсолютной величине в своей строке (хотя, воз-Hhkiio, и не преобладающим). Выбор наибольшего ведущего ♦ н'м«»пта г-й строки делают в столбцах с номерами г, г* + 1,..., п, * ih как первые г — 1 элементов строки к г-му шагу обнуляют-« Описанный алгоритм модифицированного метода Гаусса с юполпительной перестановкой столбцов называют методом I nyrca с выбором главного элемента.
Выбор главного элемента можно также проводить по столб-•• \, переставляя строки так, чтобы на г-м шаге ведущий элемент ни абсолютной величине превосходил элементы своего столбца нгшпая с (г+1)-го. Оба подхода не имеют преимуществ друг “»1Н*Д ДРУгом? каждый может использоваться, когда стандартен и метод Гаусса не работает (т.е. один из угловых миноров । »1нн1 пулю). С точки зрения ошибок округления и выбор по । и/|Гщу, и выбор по строке не являются безупречными, хотя н пи/|ыиинстве случаев дают хороший результат. Оба подхода
284 10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
можно комбинировать, и тогда выбор главного элемента вы полняется и по строкам, и по столбцам, а именно: в качестве главного элемента на г-м шаге выбирается наибольший из элементов k,j = i,n. Всего, следовательно, возможны три стратегии выбора главного элемента.
Пример 10.4. Применим метод Гаусса с выбором главного элемента по строке к системе из примера 10.3. Первый шаг совпадает с первым шагом метода Гаусса. Перед вторым шагом меняем местами 2-й и 3-й столбцы. Получаем
1	0	0,75	0,75 \
0	8	0,01 —7,99 ]
0 -1 -2,5	-1,5 /
На втором шаге делим 2-ю строку на 8 и прибавляем к 3-й (вычитание с коэффициентом —1). Получаем следующую матрицу (с учетом округлений):
1 0	0,75
0 1	0,00125
0 0 -2,499
0,75 \ -0,9987 .
-2,499 /
В конечном счете ошибки вычислений появляются, но с учетом округлений мы получаем точное решение.
10.5.	Метод прогонки
Рассмотрим СЛАУ с трехдиагональной матрицей
	( аи	«12	0	0 .	.. 0	0	0 \
	«21	«22	«23	0 .	.. 0	0	0
А =	0	«32	«33	«34	•	.. 0	0	0
\ 0	0	0	0	... 0	O/fi— 1	/
10.5. Метод прогонки
285
Для СЛАУ с такой матрицей метод Гаусса упрощается. На а а ж дом г-м шаге прямого хода нужно пересчитывать только цш* строки: г-ю и (г + 1)-ю. После прямого хода расширенная "шприца СЛАУ будет иметь вид
/1	«1	о	...	о
О	1	«2	• • •	0	02
О	0	1	...	О	03
\0 О О ... 1 0J
Моменты этой матрицы можно вычислить по формулам
«12	л h
О| =----, 01 =------,
«11 «11
«i,t'+l	a bi 0i—l«t,t—1	no	1
П,	, 0i—	, 1 — 2,3,...,71	1,
a a Oii—iat)2_ i	ац	j at)i—j
ti  	Ai—l^n,n- 1
Ph —	.
®nn — ^n— 1 ^ПуП— 1
Обратный ход метода Гаусса также упрощается:
— Рп}
— (3i OtiXi-^-i i — П 1,72	2,...,1.
Описанный алгоритм для решения СЛАУ с трехдиагональной матрицей называют методом прогонки.
Замечание 10.1. При решении СЛАУ с трехдиагональ-ной матрицей методом Гаусса перестановки строк и столбцов приводят, вообще говоря, к нарушению трехдиагональности матрицы. Исключение составляет ситуация перед (п — 2)-м шагом, когда перестановка двух последних строк оставляет матрицу трехдиагональной. Учитывая это, в методе прогонки перестановки строк и столбцов не используют.
286
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Следующий пример показывает, что ошибки округления при использовании метода прогонки столь же опасны, как и при использовании метода Гаусса.
Пример 10.5. Несколько изменим СЛАУ из примера 10.3, добавив еще одно уравнение и введя четвертую переменную так, чтобы получилась система
' 4х+ Зу	=3,
Юж + 7,51у+ 8z	=—0,49,
- 2,5у — z + t = -1,50, k	z-pt= —1
с трехдиагональной матрицей. Ее точным решением является ж = 0, у = 1, z = — 1, t = 0, в чем можно убедиться непосредственной проверкой.
Применим метод прогонки, предполагая, что вычисления выполняются с точностью до четырех десятичных знаков. После выполнения первых двух шагов метода прогонки, так же как в примере 10.3, получаем матрицу
(1
0
0
0
0,75	0
1	800
0	1999
0	1
0	0,75 \
0 -799	I
1 -1998	I
1 -1 /
Выполнив третий и четвертый шаги, приходим к следующей матрице:
(1	0,75 0
0,1	800
0	0	1
0	0	0
0
0
0,5002 • 10"3
0,75
-799
-0,9995
-0,5003 • IO"3
В результате обратного хода получаем в качестве решения х — 0,3, у = 0,6, z — —0,9995, t — —0,5003 • 10-3, что, как и в примере 10.3, значительно отличается от верного решения.
Д.10.1. Мультипликативные разложения матриц
287
Дополнение 10.1. Мультипликативные разложения матриц
Рассмотрим СЛАУ Ах = Ь. Если представить каким-либо образом матрицу А в виде произведения A — PQR трех (или другого числа) невырожденных матриц Р, Q, j?, то СЛАУ til* Ь можно разложить на три системы:
' Pz = 6, < Qy = z, Rx = у.
Последовательно решая эти системы, мы получим решение in ходной СЛАУ.
Представление невырожденной матрицы в виде произведения нескольких матриц называется мультипликативным разложением матрицы. Решение любой СЛАУ в конечном счете сводится к обращению матрицы (т.е. вычислению обратной к ней). Поэтому наиболее важны такие мультипликативные разложения матрицы, в которых сомножители легко обратить. Назовем наиболее известные виды легко обращаемых матриц.
Для обращения диагональной матрицы достаточно заменить все ее диагональные элементы на обратные к ним числа.
Ортогональная матрица А (удовлетворяющая соотношению АТА = Е) обращается при помощи операции транспониро-инпия: А-1 = Ат.
Верхняя треугольная матрица, у которой все элементы под главной диагональю равны нулю, интересна тем, что решение । ис гемы с такой матрицей методом Гаусса упрощается: фактически требуется выполнить лишь обратный ход.
Нижняя треугольная матрица, у которой все элементы над гиавной диагональю равны нулю, аналогична верхней треу-iильной матрице, и в случае такой матрицы метод Гаусса
288 10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
также упрощается: прямой ход метода Гаусса сразу приводи ! к ответу.
Оказывается, что метод Гаусса можно интерпретировать как один из способов построения мультипликативного разложс ния матрицы А системы в произведение А = LU двух матриц, где L — нижняя треугольная матрица, a U — верхняя тре угольная с диагональными элементами, равными единице. Это разложение матрицы А называют LU-разложением.
Отметим, что произведение верхних треугольных матриц тоже является верхней треугольной матрицей. При этом соот ветствующие диагональные элементы просто перемножаются Обратная к верхней треугольной матрице также является верх ней треугольной. Все это верно и для нижних треугольных матриц.
Наиболее важное наблюдение заключается в том, что лю бое элементарное преобразование строк какой-либо матрицы равносильно умножению этой матрицы слева на невырожден ную матрицу специального вида (см. 6.8). То же верно и для последовательных шагов метода Гаусса. Таким образом, выполнение прямого хода метода Гаусса означает умножение* уравнения Ах = Ь слева на некоторую невырожденную матрицу 5, равную произведению матриц специального вида для элементарных преобразований прямого хода, причем в результате такого умножения система преобразуется к виду Ux = V = Sb, где U — верхняя треугольная матрица с единицами по главной диагонали. Обозначив L = S”1, заключаем, что А = LU.
Выясним, какой вид имеет матрица L. Для восстановления fc-й строки в матрице А надо k-ю строку матрицы U умножить на и к результату последовательно прибавить 1-ю, 2-ю, ..., (к — 1)-ю строки с коэффициентами соответственно a^i, а£2, ...,
Это равносильно умножению матрицы U слева на матрицу-строку
(akl, ак2, •••? ак,к ’	•••’ о)
Д.10.1. Мультипликативные разложения матриц
289
длины п. Следовательно, если из таких строк составить
матрицу
	( ац	0	0 .	..	0 \
	«21	«22	0 .	..	0
L =	«31	«32	«зз •	..	0
	\	ап2	апЗ •	‘ • апп /
го матрица А получается из матрицы U умножением слева на L. Как видим, использование прямого хода метода Гаусса, приводящего к верхней треугольной матрице /7, дает коэффициенты н* , позволяющие записать матрицу L.
Теорема 10.3. Если для квадратной матрицы А существует L/7-разложение А = £(7, то это разложение единственное.
4 Пусть А = L\U\ — Lzlh- Матрицы £2 и ^2 невырождены. Поэтому, умножив равенство L\U\ — L2U2 на обратные матрицы слева и справа, запишем
(Z,2-1L1)(L/1t/2-1) = E.
Мы получили мультипликативное разложение единичной матрицы Е. Установив, что единичная матрица имеет единственное L/7-разложение (с единицами на главной диагонали [/), а именно Е — ЕЕ, мы тем самым докажем, что
L^L^E, UiU^ = E.
Из этих равенств следует, что L\ — L2 и (7i = [/2, т.е. теорема будет доказана.
Итак, покажем, что представление Е = LU единственно. Обозначим
/1П	0	0	...	О	\
/21	I22	о	...	о
\ Ini ^п2 ^пЗ • • • ^пп /
/1 «12 «13 ... «1П\ О 1	«23 •• • «2п
\0 О 0 ...	1 /
I () Аналитическая геометрия
290
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Рассмотрим произведение г-й строки матрицы L на 1-й столбец матрицы U. Оно равно 1ц. Но LU = Е, поэтому произведение г-й строки L на 1-й столбец U равно нулю при г = 2,..., п. Таким образом, 1ц =0 при г = 2, . ,.,п и все элементы 1-го столбца матрицы L, кроме первого, равны нулю. Первый же равен /ц = 1.
Теперь рассмотрим произведение г-й строки L на 2-й столбец U начиная с третьей и учтем, что 1ц = 0 при г = 2,..., п. Получим, что/22 = 1, Ц2 = 0 при г = 3, . ..,п. Продолжая процесс последовательно по столбцам матрицы (7, приходим к заключению, что L является единичной матрицей. Но тогда из равенства LU = Е следует, что и U является единичной матрицей. ►
Л(7-разложение может выполняться по формулам метода Гаусса. Если несколько изменить порядок операций (не меняя причинно-следственных взаимосвязей), то алгоритм можно записать в виде формул. На г-м шаге (г = 1,2,...,п) сначала вычисляются элементы r-го столбца матрицы L:
г-1
Цг ~ сцг 2 hkH'kr j г = г,г-|-1,...,гг, к=1
а затем г-й строки матрицы U:
г-1
иг}~------7^------, 3 = г + 1,г + 2,п.
^ГГ
При реализации алгоритма на компьютере матрицы L и U можно хранить в одном двумерном массиве, так как диагональные элементы матрицы U известны заранее и их хранить не нужно. При этом они записываются как одна матрица, у которой на главной диагонали и под ней стоят элементы L, а над главной диагональю — элементы U.
Д.10.1. Мультипликативные разложения матриц
291
/^/-разложение существует для тех матриц, для которых injполним прямой ход метода Гаусса. Его можно использовать цл я решения различных задач:
для решения нескольких систем с одинаковой матрицей и различными правыми частями;
для обращения матриц;
для вычисления определителей (det А = det L det /7, где <|<«t U ~ 1, adetL равен произведению диагональных элементов).
Есть небольшая асимметрия между нижней треугольной и верхней треугольной матрицами в £{Лразоложении матрицы А, поскольку лишь диагональные элементы матрицы U раины единице. Матрица L может быть представлена в виде произведения L = LD нижней треугольной матрицы L с единицами на главной диагонали и диагональной матрицы />, состоящей из диагональных элементов 1ц матрицы £, т.е. I) ~ diag(/n, ..., /пп). Это представление приводит к новому разложению А = LDU матрицы А в произведение нижней треугольной, диагональной и верхней треугольной матриц, причем диагональные элементы обеих треугольных матриц равны единице. Такое представление матрицы называют LDU-разложением. Из единственности L/7-разложения вытекает единственность и LDU-разложения.
Предположим, что матрица А является симметрической, 'Запишем ее LDU-разложение: А = LDU, В силу свойств произ-ведения матриц и операции транспонирования получаем А ~ UrDLT — £'DUf, т.е. £О{7-разложение транспонированной ма трицы. Но по условию А = Ат. Поэтому, согласно единственности Z/D/7-разложения, заключаем, что для симметрической матрицы А выполняются равенства L = UT и LT — U, эквивалентные друг другу. Значит, для симметрической матрицы ее //^//-разложение имеет вид А = LDL\
Пусть симметрическая матрица А к тому же является положительно определенной, т.е. все ее угловые миноры имеют ноложительноезначение. Исходя из алгоритма L/7-разложения,
292
10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
можно показать, что в этом случае диагональные элемеп ты матрицы L все положительны. Значит матрица D из LD(7-разложения А имеет на диагонали только положительные значения, а потому ее можно представить в виде D = DD -= DZ?T, где D = diag(\//n, V?22, •••, д/^пп)- Учитываем это в 77?(7-разложении симметрической матрицы:
А = LDL1 = (LD)(DTLT) = (LD)(LD)T.
Мы получили еще одно мультипликативное разложение дли симметрической положительно определенной матрицы в виде А = SST, где S — это нижняя треугольная матрица. Это разложение называют S S^-разложением или разложением Холецкого.
Симметрические положительно определенные матрицы ча сто встречаются в прикладных задачах (например, в матема тической физике). Выполнение разложения Холецкого, вытека ющего из Г(7-разложения, может быть проведено по таким же простым формулам, как и само £(7-разложение. Но хранение* информации о разложении Холецкого требует меньше опера тивной памяти, так как нужно хранить только одну нижнюю треугольную матрицу S.
Вопросы и задачи
10.1.	Решить СЛАУ методом Гаусса. Сделать проверку
найденных решений:
f 5х - 5у + 52 = 2,
г 25х + 15г/ + 102 =
а)	Зх - 5у + 52 = 3,
б)	15х + 13г/ + 42 =
5,
3,
2х — у + 22 = — 1;
k 10х + 4у + 62 — -2.
10.2.	Решить СЛАУ с трехдиагональной матрицей методом прогонки:
2x1+ х2	=5,	( 2xi + х2	= 4,
. xi + 3x2 + 2x3	= 9,	J xi+2x2+ х3 = 8,
'	2х2 ~ х3+ х4 = 1,	' |	х2+2х3+ х4 = 12,
х3 + Зх4 = 5;	(	х3 + 2х4 = 11.
Вопросы и задачи
293
10.3.	Составить программу на одном из алгоритмических м ников, реализующую: а) метод Гаусса; б) метод Гаусса с iibifiopoM главного элемента.
Используя составленную программу, решить систему
0,1Х1 — 8,0а:2 + 9,Зхз — 8,2а:4= 1,5, -3,3х1 + 2,4х2-2,8хз + 2,4х4= 2, —2,6x1 + 1,9х2 — 2,2хз + 1,9х4 = -1, — l,3xi+ 9,3х2 - 1,1хз + 9,5х4 = 0
ме тодом Гаусса и методом Гаусса с выбором главного элемента, f раппить результаты.
10.4.	Найти LU- и ££>{7-разложения следующих матриц:
/5 -5 5\ а) I 3 —5 5 1;
\2 -1 2/
/2 -10	4\
б) I 3 -14	2 | .
у 5 -28 21 /
Выполнить проверку полученных ответов.
10.5.	Найти 55т-разложение симметрических матриц:
/4	6 10\
а) 6 10 12 1;
\ 10 12 35/
/25 15 10\ б) 15 13 4 I .
\10	4	6/
Выполнить проверку полученных ответов.
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Кривая второго порядка на плоскости в прямоугольной системе координат описывается уравнением
Ах2 + Вху + Су2 + Dx + Еу + F ~ 0,	(11.1)
в котором коэффициенты Л, В, С одновременно не обращаются в нуль.
В этой главе мы не ставим себе задачу выявить все кривые', которые могут быть представлены уравнением второй степени, т.е. мы не будем проводить их полную классификацию. Это удобно выполнять при помощи методов линейной алгебры [IV]. Здесь же мы опишем известные кривые второго порядка и их свойства, а также покажем, как можно упростить неко торые частные виды уравнения второго порядка при помощи преобразования параллельного переноса системы координат и определить вид кривой и ее характеристики.
11.1. Эллипс
Определение 11.1. Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 есть заданная постоянная величина, называют эллипсом.
Определение эллипса дает следующий способ его геометри ческого построения. Фиксируем на плоскости две точки F] и F2, а неотрицательную постоянную величину обозначим через 2а. Пусть расстояние между точками Д и F2 равно 2с. Пред ставим себе, что нерастяжимая нить длиной 2а закреплена в точках Fi и F2, например, при помощи двух иголок. Ясно, что
11.1. Эллипс
295
но возможно лишь при а с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 11.1).
Рис. 11.1
Итак, описываемое множество не пусто, если а с. При и г эллипс представляет собой отрезок с концами Fi и /j, а при с = 0, т.е. если указанные в определении эллипса фиксированные точки совпадают, он является окружностью рлдиуса а. Отбрасывая эти вырожденные случаи, будем далее и родполать, как правило, что а > с > 0.
Фиксированные точки Fi и F} в определении 11.1 эллип-||| (см. рис. 11.1) называют фокусами эллипса, расстояние между ними, обозначенное через 2с, — фокальным расстоянием, а отрезки F^M и F}M, соединяющие произвольную Iочку М на эллипсе с его фокусами, — фокальными радиусами.
Вид эллипса полностью определяется фокальным расстоянием IF1F2I = 2с и параметром а, а его положение на плоско-। ти - парой точек Fi и F2.
Из определения эллипса следует, что он симметричен отно-। ительно прямой, проходящей через фокусы Fi и F2, а также итпосительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 11.2, а). Эти прямые называют осями эллипса. Точка О их пересечения является центром
296
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
симметрии эллипса, и ее называют центром эллипса, а точ ки пересечения эллипса с осями симметрии (точки А, В, С и I) на рис. 11.2, а) — вершинами эллипса.
Число а называют большой полуосью эллипса, а b -= \/а2 — с2 — его малой полуосью. Нетрудно заметить, что при с > 0 большая полуось а равна расстоянию от центра эллипса до тех его вершин, которые находятся на одной оси с фокусами эллипса (вершины А и В на рис. 11.2, а), а малая полуось b равна расстоянию от центра эллипса до двух других его вершин (вершины С и D на рис. 11.2, а).
Уравнение эллипса. Рассмотрим на плоскости некоторый эллипс с фокусами в точках F\ и F2, большой осью 2а. Пусть 2с — фокальное расстояние, 2с = |/*i-F2I < 2а. Согласно определению 11.1 эллипса, его образуют те точки М, для которых \F1M\ + \F2M\=2a.
Выберем прямоугольную систему координат Оху на плоскости так, чтобы ее начало совпало с центром эллипса, а фокусы находились на оси абсцисс (рис. 11.2, б). Такую систему координат называют канонической для рассматриваемого эллипса, а соответствующие переменные — каноническими.
В выбранной системе координат фокусы имеют координаты Fi(c; 0), F2(—c;0). Используя формулу расстояния между
11.1. Эллипс
297
।НЧМ1МИ, запишем условие |FiM| +	= 2а в координатах:
у/(х-с)2 + у2 + у/(х + с)2 + у2 = 2а.	(11-2)
hn уравнение неудобно, так как в нем присутствуют два итд ратных радикала. Поэтому преобразуем его. Перенесем н уравнении (11.2) второй радикал в правую часть и возведем н квадрат:
(я - с)2 + у2 = 4а2 - 4а\/(х + с)2 + у2 + (х + с)2 + у2.
1Ьи ле раскрытия скобок и приведения подобных слагаемых нмпучаем
\/(х + с)2 + у2 = а+ ех,	(11-3)
।	1 = с/а. Повторим операцию возведения в квадрат, чтобы
\ ора ть и второй радикал:
(ж + с)2 4- у2 = а2 4- 2гах 4- м2х2,
alii, учитывая значение введенного параметрам,
т2
/2	2\ х ।	2	2	2
(a -cz)— + у = а-с. а2
I пк как а2 — с2 = Ь2 > 0, то
дел.2
~? + т7 = 1, <*>Ь>0.	(11.4)
сг о2
Уравнению (11.4) удовлетворяют координаты всех точек, |<’/кащих на эллипсе. Но при выводе этого уравнения использо-ihi /1ись неэквивалентные преобразования исходного уравнения 11 1.2) — два возведения в квадрат, убирающие квадратные pain калы. Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины
298
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
с одинаковым знаком, но мы этого в своих преобразованиях иг проверяли.
Мы можем не проверять эквивалентность преобразований, если учтем следующее. Пара точек Fi и F2, 12*12*21 — 2с, на плос кости определяет семейство эллипсов с фокусами в этих точ ках. Каждая точка плоскости, кроме точек отрезка F1F2, при надлежит какому-нибудь эллипсу указанного семейства. При этом никакие два эллипса не пересекаются, так как сумма фо кальных радиусов однозначно определяет конкретный эллипс. Итак, описанное семейство эллипсов без пересечений покры вает всю плоскость, кроме точек отрезка F1F2. Рассмотрим множество точек, координаты которых удовлетворяют уран нению (11.4) с данным значением параметра а. Может ли это множество распределяться между несколькими эллипсами? Часть точек множества принадлежит эллипсу с большой по луосью а. Пусть в этом множестве есть точка, лежащая пл эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
т»2	?/2	._.
- + ^- = 1, Ь2 = а2-с2,	(11.5)
а2 Ъ2
т.е. уравнения (11.4) и (11.5) имеют общие решения. Однако легко убедиться, что система
{х2 у2 а2 а2, — с2 л.2 — + —у— = 1 а2 а2 - с2
при а/а решений не имеет. Для этого достаточно исключить, например, х из первого уравнения:
2 /	1	а2 \ а2
У	" (а2 - с2)а2
11.1, Эллипс
299
по после преобразований приводит к уравнению
(а2 - с2) (а2 - с2)
по имеющему решений при а^ а, поскольку (а2 — с2) (а2 — с2) — Ь2Ь2 > 0.
Итак, (11.4) есть уравнение эллипса с большой полуосью а > 0 и мп ной полуосью b = \/а2 — с2 > 0. Его называют каноническим уравнением эллипса,
Пид эллипса. Рассмотренный выше геометрический спо-* иг> построения эллипса дает достаточное представление о пиешпем виде эллипса. Но вид эллипса можно исследовать и * помощью его канонического уравнения (11.4). Например, можно, считая у 0, выразить у через х: у = Ьу/1 — х2/а2, и, следовав эту функцию, построить ее график [II]. Есть еще оцип способ построения эллипса. Окружность радиуса а с цен-i |><>м в начале канонической системы координат эллипса (11.4) описывается уравнением х2 + у2 = а2. Если ее сжать с коэффициентом a/b> 1 вдоль оси ординат, то получится кривая, мвторая описывается уравнением х2 + (j/a/Ь)2 = а2, т.е. эллипс.
Замечание 11.1. Если ту же окружность сжать с коэффи-пиептом а/b < 1 вдоль оси ординат, т.е.	у п
фактически растянуть в этом напра-тении, то получится кривая, которая /Л" \ описывается уравнением (11.4), в ко- /	\
юром а < Ь. Это тоже эллипс, но в	I	\
< н< теме координат Оху (рис. 11.3) его	|_________|
фокусы расположены на вертикальной	I	° Iх
in и симметрии. Каноническую систе-	\	/
му координат для этого эллипса можно \	/
получить в результате поворота сис-гемы Оху на 90°, что соответствует шмоне переменных xf = у, у1 = —х.	Рис. 11.3
300 1L КРИВЫЕ ВТОРОГО ПОРЯДКА
Эксцентриситет эллипса. Отношение фокального рас стояния эллипса к его большой оси называют эксцентриситетом эллипса и обозначают через £. Для эллипса, задан ного каноническим уравнением (11.4), г = 2с/2а = с/а. Если же в (11.4) параметры а и Ь связаны неравенством а < Ь, то фокусы расположены на вертикальной оси симметрии эллипса, с = у/Ь2 — а2, е — 2с/2Ь = с/Ь.
При с = 0, когда эллипс превращается в окружность, и е = 0. В остальных случаях 0 < е < 1. Если зафиксировать фокусы эллипса и менять его форму, устремляя эксцентриситс i к единице, то в пределе получим отрезок, соединяющий фокусы, который можно назвать вырожденным эллипсом с а = с и 6 = 0 Если же, наоборот, зафиксировать параметр а и устремить .• к нулю, то в пределе мы получим окружность радиуса а. Эта предельная ситуация соответствует равенству параметров а и b уравнения (11.4).
Уравнение (11.3) эквивалентно уравнению (11.4), поскольку эквивалентны уравнения (11.4) и (11.2). Поэтому уравнением эллипса является и (11.3). Кроме того, соотношение (11.3) интересно тем, что дает простую, не содержащую радикалок, формулу для длины |^2Л/| одного из фокальных радиусов точки М(х\у) эллипса: |F2М\ = а + ех.
Аналогичная формула для второго фокального радиуса мо жет быть получена из соображений симметрии либо повторени ем выкладок, в которых перед возведением в квадрат уравнении (11.2) в правую часть переносится первый радикал, а не второй Итак, для любой точки М(х\у) на эллипсе (см. рис. 11.2)
\F\M\~a-sx,
<	(11.0)
IF2MI = а + ех,
и каждое из этих уравнений является уравнением эллипса.
Пример 11.1. Найдем каноническое уравнение эллипса । большой полуосью 5 и эксцентриситетом 0,8 и построим его.
11.1. Эллипс
301
Зная большую полуось эллипса а = 5 и эксцентриситет е = 0,8, найдем его малую полуось Ь. Поскольку b = у/а2 — с2, а г /- а = 4, то Ь = у/52~^42 = 3. Значит каноническое уравнение имеет вид
х2 у2
52 +^2 = ’•
/|/1н построения эллипса удобно изобразить прямоугольник с центром в начале канонической системы координат, стороны которого параллельны осям симметрии эллипса и равны его । оответствующим осям (рис. 11.4). Этот прямоугольник пересекается с осями эллипса в его вершинах А(—5;0), В(5;0), ( *((); -3), Z?(0; 3), причем сам эллипс вписан в него. На рис. 11.4 указаны также фокусы ^^(±4; 0) эллипса.
Геометрические свойства эллипса. Перепишем первое уравнение в (11.6) в виде |FiM| = (а/е — х)е. Отметим, что величина a/s — х при а > с положительна, так как фокус Fi не принадлежит эллипсу. Эта величина представляет собой расстояние до вертикальной прямой d: х — а/е от точки М(ж;у), лежащей левее этой прямой. Уравнение эллипса можно записать
и виде
Ы а/е — х
302
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Оно означает, что этот эллипс состоит из тех точек М(х]ц) плоскости, для которых отношение длины фокального радиуса F\M к расстоянию до прямой d есть величина постоянная, равная 8 (рис. 11.5).
У прямой d есть „двойник44 — вертикальная прямая d', сим метричная d относительно центра эллипса, которая задает< и уравнением х = —а/8. Относительно d' эллипс описывается так же, как и относительно d. Обе прямые d и d' называют директрисами эллипса. Директрисы эллипса перпендикулярны той оси симметрии эллипса, на которой расположены его фоку сы, и отстоят от центра эллипса на расстояние а/8 — а2/с (см рис. 11.5).
Расстояние р от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса. Этот пара метр равен
а а2 а2 — с2 Ь2 р =----с—-----с =-------= —.
8	С	С С
Эллипс обладает еще одним важным геометрическим свои ством: фокальные радиусы F\M и F}M составляют с каса тельной к эллипсу в точке М равные углы (рис. 11.6). Преж/и
_________________11.1. Эллипс________________ 303
н’М доказывать это, убедимся, что касательная к эллипсу суще ♦ । ну<‘Т в любой его точке. Рассматривая у как функцию от х, 1нчш||о заданную уравнением (11.4) [II], и дифференцируя его:
/а1 + 2yyf/b2 = 0, находим производную
у'(х) = -xb2/(ya2), У^О.
Рис. 11.6
Видим, что для всех точек эллипса, кроме вершин Л и В, производная, а значит, и касательная существуют. Найдем ее сравнение в произвольной точке М(хо; уо) эллипса. Воспользовавшись уравнением касательной
У-Уо = у'(хо)(х-Хо)
ь графику функции у = у(х) в точке Л/, получим
ЖО62
У~УО=--------2\Х~Х0)
Уоа2
I11 и
хх0 ууо _х20 у20
+ а? + Р'
304
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
а2 + Ь2 ~ ’ поскольку координаты точки М удовлетворяют уравнении! (11.4) эллипса. Касательные в вершинах А и В также су пи* ствуют, в чем можно убедиться, рассматривая х как неявку к» функцию у. Полученное уравнение касательных распространи ется и на касательные в точках А и В,
Нормальным вектором касательной к эллипсу является ь тор п с координатами {хо/а2; у$/Ь2}. Утверждение, что кальные радиусы F\M и F%M составляют с касательной । эллипсу в точке М равные углы, эквивалентно утверждении! о параллельности нормального вектора касательной и бис< н. трисы MN угла FiMF} (см. рис. 11.6). Убедимся в том, ти> последнее верно для любой точки М эллипса. Рассмотрим век торы Fi и F^A^. Векторы п\ = |F$\F$ и п2 = l'i AI коллинеарны векторам и Г2л/ и имеют одинаковую длину равную |Fiл!| |F2a1|. Поэтому их сумма ni +П2 предстапли ет собой диагональ построенного на них ромба, являющукм и как известно, биссектрисой внутреннего угла ромба. Таким образом, согласно теореме 1.8, достаточно доказать пропорци овальность координат вектора п\ +п,2 и нормального вектора п касательной, что следует из равенств
|	|	+ | F\^ |	=
= (а + £з:о){яо -c;yo} + (a - sx0'){x0 +c; y0} =
= {(a + earo) (xQ - c) + (a - ex0) (xo + c); 2ay0} = = {2ax0 - 2c£x0-, 2ay0} = 2a|	- ^) x0; yo) =
_o ( b2	1 _o ,2 Г«о. Уо 1
[a2	J I a2 bz J
Доказанное геометрическое свойство имеет наглядный фи зический смысл. Если в фокусе Fi расположить источник свеч а
11.2. Гипербола
305
го луч, выходящий из этого фокуса, после отражения от эллипса пойдет по второму фокальному радиусу, так как после отражения он будет находиться под тем же углом к кривой, что и до отражения. Таким образом, все лучи, выходящие из фокуса Fi, сконцентрируются во втором фокусе F2, и наоборот. Исходя из данной интерпретации доказанное свойство называют оптическим свойством эллипса.
11.2. Гипербола
Определение 11.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.
Замечание 11.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса. Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
Фиксированные точки в определении гиперболы (обозначим их Fi и F2) называют фокусами гиперболы. Расстояние между ними (обозначим его 2с) называют фокальным расстоянием, а отрезки F^M и F?M, соединяющие произвольную точку М на гиперболе с ее фокусами, — фокальными радиусами.
Вид гиперболы полностью определяется фокальным расстоянием IF1F2I = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов Fi и F2.
I I Аналитическая геометрия
306 И. КРИВЫЕ ВТОРОГО ПОРЯДКА
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 11.7). Первую из этих осей симметрии называют действительной осью гиперболы, а вторую — ее мнимой осью. Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы.
Середина отрезка FiF2, соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы.
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F1MF2 (см. рис. 11.7) справедливо неравенство
IlFxMl- |F2M|| |ВД|.
Равенство а = с выполнено только для тех точек М, которые лежат на действительной оси симметрии гиперболы вне интервала FiF2. Отбрасывая этот вырожденный случай, далее будем предполагать, что а < с. Отметим также, что случай а = 0 соответствует геометрическому месту точек, равноудаленных от фиксированных точек Fi и F2. Как известно из курса школьной геометрии, это геометрическое место представляет собой прямую, перпендикулярную отрезку FtF2 и проходящую через его середину. Этот случай мы также не будем рассматривать.
11.2. Гипербола
307
Уравнение гиперболы. Рассмотрим на плоскости неко-|ирую гиперболу с фокусами в точках Fi и Fi и действительной hi i.io 2a. Пусть 2с — фокальное расстояние, 2с = IF1F2I > 2а.
Согласно замечанию 11.2, гипербола состоит из тех точек Af(x;t/), для которых |\FiM| — IF2MI| = 2а. Выберем прямоугольную систему координат Оху так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс (рис. 11.8). Такую систему координат для рассматриваемой гиперболы называют канонической, а соответствующие переменные — каноническими.
Рис. 11.8
В канонической системе координат фокусы гиперболы имеют координаты Fi(c; 0) и Fj(—с; 0). Используя формулу рассто-мния между двумя точками, запишем условие 11FiМ| — |F2MI | = - 2а в координатах
|У(® - с)2 + у2 -	+ с)2 + у2| = 2а,
где (ж; у) — координаты точки М. Чтобы упростить это уравнение, избавимся от знака модуля:
у/(х- с)2 + у2- \/(х + с)2 + у2 = ±2а, перенесем второй радикал в правую часть и возведем в квадрат:
(ж — с)2 + у2 = (ж + с)2 4- у2 ± 4а (ж 4- с)2 4- у2 4- 4а2.
11*
308
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
После упрощения получим
—£Х — а = ±д/(ж + с)2 + У21
или
л/(ж + с)2 + У2 = Iе® + а1,	(И-7)
где £ = с/а. Возведем в квадрат вторично и снова приведем подобные:
(е2 - 1)ж2 — у2 = с2 — а2
или, учитывая равенство £ = с/а и полагая Ь2 = с2 — а2,
а2 Ъ2 ~
(11.8)
Величину Ь > 0 называют мнимой полуосью гиперболы.
Итак, мы установили, что любая точка на гиперболе с фо кусами Fi(c;0) и Fa(—с;0) и действительной полуосью а удо влетворяет уравнению (11.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовле творяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами Fi и F^. У этого семейства гипербол о< и симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих ни действительной оси симметрии вне интервала FjF2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов Fl и F2 меняется от гиперболы к гиперболе. Пусть координаты точки М(ж; у) удовлетворяют уравнению (11.8), а сама точка принадлежит гиперболе семой ства с некоторым значением а действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению
•Е2 У2 1 Т2 2 ~2
— — = 1, о = с — а . а2 Ь2
11.2. Гипербола
309
Следовательно, система двух уравнений с двумя неизвестными
'я2 у2 а2 с2-а2	’
х2 _ у2 _ к а2 с2 — а2
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при а а это невозможно. Действительно, исключив, например, х из первого уравнения:
2 / а2	1 \ _ а2
V \(с2 —а2)а2	с2 — а2) а2
после преобразований получаем уравнение
у2 с2 (а2 —а2)	_ _, 2 _ 2}
(с2 — а2) (с2 — а2)	’
которое при а / а не имеет решений, так как
(с2 - а2) (с2 - а2) = Ь2Ъ2 > 0.
Итак, (11.8) есть уравнение гиперболы с действительной полуосью а > 0 и мнимой полуосью b = \/с2 — а2 > 0. Его называют каноническим уравнением гиперболы.
Вид гиперболы. По своему виду гипербола (11.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при х 0, у 0, каноническое уравнение гиперболы однозначно разрешается относительно у.
у = — у/ х2 — а2.	(11,9)
а
Исследование функции у(х) дает следующие результаты [II].
I ' Аналитическая геометрия
310
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Область определения функции — {х: х а} и в этой области определения она непрерывна как сложная функция, причем в точке х = а она непрерывна справа. Единственным нулем функции является точка х — а.
Найдя производную функции у(х)
заключаем, что при х > а функция монотонно возрастает. Кроме того,
lim ff(x) — +оо, x~+a+oJ v 7	’
а это означает, что в точке х = а пересечения графика функции с осью абсцисс существует вертикальная касательная. Функ ция у(х) имеет вторую производную
у" = -ab(x2 - а2)~3/2
при х > а, и эта производная отрицательна. Поэтому график функции является выпуклым вверх, а точек перегиба нет.
Указанная функция имеет наклонную асимптоту, это выт<* кает из существования двух пределов [II]:
7	1- f(X) Ь 1-	х/*2 - «2 Ь
к = hm —— = - lim --------------------=
х—>4-00 X d	X	d
b= lim (f(x) — kx) = — lim fу/x2 — a2 — x x-++oq v	' a a7—>4-oo \
Ь ..	-a2 n
= — hm -=====-------= 0.
d x~+4-00 X2 — d2 4“ x
Наклонная асимптота описывается уравнением у = (b/d)x.
Проведенное исследование функции (11.9) позволяет постро ить ее график (рис. 11.9), который совпадает с частью гипор болы (11.8), содержащейся в первой четверти.
11.2. IhiKjihxo
311
Гак как гипербола симметрична и i тн и i нмц СВОих осей, пен кривая имеет вид, изображенный ни ри« 11 Is Гипербола им тоит из двух симметричных ветвей, Р,м н,ин*иЧНЫХ по разные стороны от ее мнимой оси симметрии ветви но ограничены с обеих сторон, причем прямые у Нь/а)ж являются одновременно асимптотами и правой и левой ветвей । иперболы.
Рис. 11.9
Рис. 11.10
Оси симметрии гиперболы различаются тем, что действи-г<’л ьная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересе-юн'т (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют верши-нами гиперболы (точки А(а; 0) и В(—а; 0) на рис. 11.10).
Построение гиперболы по ее действительной (2а) и мнимой (20 осям следует начинать с прямоугольника с центром в начале координат и сторонами 2а и 2Ь, параллельными, соответ-। твенно, действительной и мнимой осям симметрии гиперболы (рис. 11.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной oi ыо симметрии. Отметим, что прямоугольник и его положение* на плоскости однозначно определяют форму и положение । иперболы. Отношение Ь/а сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального
312
1L КРИВЫЕ ВТОРОГО ПОРЯДКА
расстояния к действительной оси. Эксцентриситет обозначь ют через е. Для гиперболы, описываемой уравнением (11.8), £~с/а. Отметим, что если эксцентриситет эллипса может принимать значения из полуинтервала [0,1) (значение 0 соот ветствует предельному варианту эллипса — окружности), то эксцентриситет гиперболы всегда попадает в интервал (1,+оо).
Построим прямоугольник с центром в начале системы ко ординат Оху и сторонами 2а, 26, параллельными осям абсцисс и ординат соответственно. Проведем прямые у = (Ь/а)х и у = — (b/a'jx, на которых лежат диагонали прямоугольника. Существует две гиперболы, соответствующие построенному прямоугольнику (рис. 11.12). Первая из них описывается ка ионическим уравнением (11.8), а вторая — уравнением
х2 у2
а2 Ь2
(11.10)
Вторую гиперболу называют сопряженной по отношению к первой, а уравнение (11.10) — каноническим уравнением сопряженной гиперболы. Действительная и мнимая оси
11.2. Гипербола
313
первой гиперболы являются соответственно мнимой и действи-нчп»ной осями сопряженной гиперболы, а асимптоты у них общие.
Рис. 11.12
Пример 11.2. Найдем каноническое уравнение гиперболы по ее действительной полуоси а = 4 и фокальному расстоянию 7с 10. Построим гиперболу и определим координаты ее псршин, фокусов и уравнения асимптот.
'Гак как действительная полуось а гиперболы известна, то, чтобы найти каноническое уравнение гиперболы, достаточно определить мнимую полуось Ь. Поскольку с = 5, 6= vc2 —а2, । о 6 = \/52 — 42 = 3. Итак, искомое уравнение имеет вид
42 З2 ~
Построим прямоугольник, соответствующий заданной гиперболе (рис. 11.13). Продолжим его диагонали до асимптот । пперболы и построим саму гиперболу. Уравнениями асимптот ИН/1ЯЮТСЯ у = ±Зж/4, вершины находятся в точках (±4; 0), а фо-ьусы совпадают с точками (±5; 0).
314
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Геометрические свойства. Геометрические свойства гиперболы во многом повторяют свойства эллипса. Вернемси к формуле (11.7). Она эквивалентна каноническому уравнении» гиперболы и дает выражение для длины фокального радиус а F2M ее точки М(х\ у):
lF2Mj =	+ с)2 + у2 = ±(еж + а),	(11.11)
где знак плюс соответствует правой ветви гиперболы, а знак минус — левой.
Аналогично можно получить формулу для длины другого фокального радиуса, если при выводе канонического уравнении гиперболы перед первым возведением в квадрат в правую часть равенства перенести не второй, а первый квадратный радикал При этом вместо (11.7) получим
ех - а — ±д/(ж - с)2 + у2,
откуда
| = д/(ж - с)2 + у2 — ±(ех - а),
(11.12)
11.2. Гипербола
315
। д<\ как и в (11.11), знак плюс соответствует правой ветви । ипгрболы, а знак минус — левой. Каждое из уравнений (11.11), (11.12) является уравнением гиперболы.
Гипербола не проходит через свои фокусы (при 0 < a < с). Поэтому фокальные радиусы любой ее точки М имеют нену-H«4iyio длину, т.е. |FiM| / 0 и |F2A/| /0. Но тогда в (11.11) и (11.12) правые части тоже отличны от нуля, и эти уравнения । пперболы можно переписать в следующем виде:
£.	(11.13)
|ж + а/е|	\х-а/е\
Рассмотрим прямую d': х = -а/е (рис. 11.14). Выражение |i I а/е\ представляет собой расстояние от точки М(ж; у) до прямой d'. Аналогично выражение ±(ж — a/s) равно расстоянию 11 а/е\ от точки М гиперболы до прямой d: х = а/е. Поэтому hi уравнений (11.13) следует, что гипербола состоит из таких |<>’п'к, для которых отношение расстояния до фокуса F2 (фо-ьу< a Fi) к расстоянию до прямой d' (прямой d) есть величина постоянная, равная ее эксцентриситету е. Эти две прямые d и »/' называют директрисами гиперболы.
Рис. 11.14
316
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Геометрически директрисы определяются как прямые, пер пендикулярные действительной оси симметрии гиперболы и удаленные от ее центра на расстояние, равное отношению дей ствительной полуоси к эксцентриситету.
Расстояние р от директрисы гиперболы до ближайшего к директрисе фокуса, как и у эллипса, называют фокальным параметром гиперболы. Отметим, что
а	а2	с2 — а2	Ь2
р = с---— с----—--------— —.
8	С	С	С
Гипербола также имеет и оптическое свойство, анало гичное оптическому свойству эллипса. Оно состоит в том, что лучи, вышедшие из одного фокуса, после отражения от ближай шей ветви гиперболы распространяются так, будто вышли ил другого фокуса (рис. 11.15).
Оптическое свойство гиперболы доказывается примерно так же, как и эллипса. Это свойство эквивалентно утверждг нию о параллельности направляющего вектора касательной н точке М(xq; j/о) гиперболы и биссектрисы угла F1MF2. У(м* димся в этом. Вычислим вектор, направленный по биссектрис г угла F1MF2, и сравним его с направляющим вектором каси тельной.
11.2. Гипербола
317
Пусть точка М гиперболы не является ее вершиной. Рас-। мо грим функцию у от ж, неявно заданную уравнением (11.8). /|цфференцируя (11.8), получаем 2ж/а2 — 2уу'/Ь2 = 0, откуда наводим производную
y'{x} = xb2/{ya2}.
сравнение касательной в точке М можно записать в виде
у-Уо = у'{хр}{х-хо}.
Подставив выражение для значения производной в точке Л/, получим
a:°62 ,	.
У~Уо =-----2УХ~Х°)'
Уоа2
11 /I и
ХХр уу0 _ х% у2 а2 Ь2 а2 Ь2 ’
ч го приводит к уравнению касательной
ххр yyQ _ а2 Ь2 ’
in и кольку координаты точки М удовлетворяют уравнению (I 1.8) гиперболы. Это уравнение справедливо и для касательных к гиперболе в ее вершинах, которые в этих точках вер-1икальны. Следовательно, в качестве направляющего вектора мигательной к гиперболе можно выбрать вектор з с координатами {уо/b2} хо/а2}.
Рассмотрим векторы и Векторы п\ — |f^|fv^ и = |Fi л!| F2л! коллинеарны векторам FiA1 и F^ и имеют । щи паковую длину, которая равна |FiA1| |СгЛ) |. Поэтому их । умма п\ + П2 представляет собой диагональ построенного на них ромба, являющуюся, как известно, биссектрисой внутрен
318
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
него угла ромба. Вычисляем эту сумму:
=
= (£х0 + а){ж0 - с; Уо} + (^0 - а){ж0 + с; Уо} =
= {(€х0 + а) (х0 - с) +	- а) (ж0 + с); 2гхоуо} =
f а2
= {2ех% - 2ас; 2ехоУо} = 2£{xq - а2; жоуо} = 2е< хоуо
о 2 f УО
-2еуоа
Видим, что этот вектор коллинеарен вектору з.
Гипербола, приведенная к асимптотам. Если у гипер болы совпадают действительная и мнимая полуоси, т.е. а = 6, то угол между асимптотами равен 2arctg(6/a) = 2arctgl = тг/2, т.е. является прямым. Такую гиперболу называют равнобочной, Для нее кроме канонической системы координат, в которой оси координат совпадают с осями симметрии гипер болы, рассматривают также и другую, осями которой являются асимптоты. Выведем уравнение гиперболы в этой системе ко ординат, которую обозначим Оху. Пусть г, j — ее репер, а г', jf — репер канонической системы координат Ох'у' (рис. 11.16).
Каноническая система координат повернута относительно системы Оху на угол тг/4. Поэтому (см. 3.2)
v 2 . V2 . ,=Т,+ Т3'
3 =“V + ’T3'
Значит, координаты х', у' канонической системы координа'1 выражаются через координаты х, у с теми же коэффициентами:
, V2 х/2 х = —г~х + ——у, 2	2 ’’
.	л/2	х/2
у =“Т1 + Т’-
11.2. Гипербола
319
Уравнение равнобочной гиперболы в канонической системе координат имеет вид (ж')2 — (у')2 = °2? гДе a — действительная (она же мнимая) полуось гиперболы. Заменив в этом уравнении кпионические переменные на ж, у, получим
|(* + у)2-^(*-у)2 = а2,
ИЛИ
а2
.	(11.14)
Уравнение (11.14) называют уравнением гиперболы в асимптотах.
Рис. 11.16
Замечание 11.3. Уравнение
а2 ху = -2
задает сопряженную гиперболу для равнобочной гиперболы (11.14).
Пример 11.3. Найдем координаты вершин, фокусов и уравнения асимптот гиперболы ху = — 8 и построим ее.
320	11. КРИВЫЕ ВТОРОЕ^ 
Данное уравнение является	В асимптотах Длн
сопряженной равнобочной гип^рбол^Н^/|пЬ',ому Оси k^PA1*1^’1 • т.е. прямые х = 0, у = 0, являются ^тотами. Для этоп гиперболы -а2/2 = -8, поэтому а2 Се V) ® = 4- И° ТОГЛ}‘ с= v^Tb2^ vW42 = 4V/2, и, учИЪ|Г»1,,бОЗНа^НИЯ вери,им и фокусов, находим: А(-2\/^; 2л/2) T1,U|	~2у2), F1(-4;4)1
^2(4; —4) (рис. 11.17).	’
11.3, Пар^
Рассмотрим на плоскости пряк/j этой прямой. И эллипс, и гипер6\ единым образом как геометрически отношение расстояния до данной т< прямой есть постоянная величина эллипс, а при е > 1 — гипербола, центприситетом как эллипса, так положительныхзначений параметр зывается незадействованным. Эт<
। не лежащую ни Шть определены н’К) для которы х пинию до данной
< 1 получаете и г является экг I Из возможных нюино 1, ока in соответствует
11.3. Парабола
321
। гометрическое место точек, равноудаленных о*г данной точки и от данной прямой.
Определение 11.3. Геометрическое место точек, равно удаленных от фиксированной точки и от фиксированной при мой, называют параболой.
Фиксированную точку называют фокусом параболы, а прямую — директрисой параболы. При этом полагают, что эксцентриситет параболы равен единице.
Из геометрических соображений вытекает, что парабола. । имметрична относительно прямой, перпендикулярной дирек-ipHc’c и проходящей через фокус параболы. Эту прямую называют осью симметрии параболы или просто осью параболы. Парабола пересекается со своей осью симметрии в единственной точке. Эту точку называют вершиной параболы. Она
расположена в середине отрезка, /I i.i с точкой пересечения ее оси с
Уравнение параболы. Для цы вода уравнения параболы вы-гк’рсм на плоскости начало координат в вершине параболы, в качестве оси абсцисс — ось параболы, положительное направление на которой задается положением фокуса (см. рис. 11.18). ) гу систему координат называ-ю| канонической для рассма-|риваемой параболы, а соответ-। гвующие переменные — кано-
соединяющего фокус парабо-ее директрисой (рис. 11.18).
Рис. 11.18
ническими.
Обозначим расстояние от фокуса до директрисы через р. I л о называют фокальным параметром параболы.
Тогда фокус имеет координаты F(p/2;0), а директриса д описывается уравнением х = —pfe. Геометрическое место
322 11. КРИВЫЕ ВТОРОГО ПОРЯДКА
точек М(х;у), равноудаленных от точки F и от прямой (I, задается уравнением
Ус®-!)+у2=|®+!! (наг»)
Возведем уравнение (11.15) в квадрат и приведем подобные Получим уравнение
у2 = 2рх,	(11.16)
которое называют каноническим уравнением параболы.
Отметим, что возведение в квадрат в данном случае — экви валентное преобразование уравнения (11.15), так как обе части уравнения неотрицательны, как и выражение под радикалом.
Вид параболы. Если параболу у2 = ж, вид которой считаем известным, сжать с коэффициентом 1/(2р) вдоль оси абсцисс, то получится парабола общего вида, которая описывается уравнением (11.16).
Пример 11.4. Найдем координаты фокуса и уравнение директрисы параболы, если она проходит через точку, канонические координаты которой (25; 10).
В канонических координатах уравнение параболы имеет вид у2 = 2рж. Поскольку точка (25; 10) находится на параболе, то 100 = 50р и поэтому р = 2. Следовательно, у2 = 4х является каноническим уравнением параболы, х = — 1 — уравнением ее директрисы, а фокус находится в точке (1; 0).
Оптическое свойство параболы. Парабола имеет еле дующее оптическое свойство. Если в фокус параболы поместить источник света, то все световые лучи после отражения от параболы будут параллельны оси параболы (рис. 11.19). Оптическое свойство означает, что в любой точке М параболы нормальный вектор касательной составляет с фокальным радиусом MF и осью абсцисс одинаковые углы.
Проверим это. Выберем произвольную точку М(жо; t/о) па параболе, описываемой уравнением (11.16). Рассматривая в
И. 4. Неполные уравнения кривой второго порн,Ц1\а	.17.1
vримнении (11.16) переменное х как функцию у (х = y2/(‘tp}h •»“ ниiiiPM уравнение касательной в точке М: х — xq = ^,(.Vo)(?/ J/n)• Him кильку x' = у/p, то я'(уо) = Уь/Р- Подставляем выражение -ни производной в уравнение касательной х — xq = уъ(у ~ уо)/р и получаем рх — рх$ = у$у — уд. Координаты точки М удов 'ie творяют уравнению параболы, т.е. уд = 2р^о- Значит, уран пение касательной можно записать в виде рх — уоу + р%о = 0.
По уравнению касательной наводим ее нормальный вектор в пикеМ: п — {р,-уо}- Убедим-।и, что этот вектор коллинеарен вектору + |AfF|t, который направлен вдоль биссектри-। ы угла, образованного прямым и о траженным лучами (г — орт, hi дающий направление оси Ох). Отметим, что, согласно (11.15), расстояние MF равно я0 + р/2. Полному
мФ + |MF|i = {| - х0; —j/о) + (х0 + р/2){1; 0} = {р;-уо},
г.<*. этот вектор совпадает с выбранным нормальным вектором касательной.
11.4. Неполные уравнения кривой второго порядка
Исли в уравнении
A,r2 + Bxy + Cy2+Dx + Ey + F = 0, A2 + B2+C2^q, (11.17)
кривой второго порядка на плоскости либо В = 0 (нет слагаемого с произведением переменных), либо А = С = 0 (нет слагаемых г квадратами переменных), то такое уравнение называют неполным.
324
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Неполное уравнение второго порядка при помощи парил лелъного переноса системы координат и, возможно, дополни тельного поворота системы координат на плоскости на у го i тг/2, —тг/2 или тг можно преобразовать либо в канонически уравнение эллипса, либо в каноническое уравнение гиперболы, либо в каноническое уравнение параболы, либо в уравнение ли перболы в асимптотах. Кроме того, есть особые случаи, когда уравнение не сводится ни к одному из вышеперечисленных (сл\ чаи вырождения кривой второго порядка).
Замечание 11.4. Поворот системы координат на плосю» сти Оху на угол тг/2 (—тг/2, тг) соответствует введению новы* переменных х — у, у——х, (х — —у, у — ж; х = — х, у = ~у) Такие замены переменных удобно называть переобозначение ями переменных.
Рассмотрим преобразование неполного уравнения кринок второго порядка. Если уравнение второго порядка не содержи i слагаемого с произведением переменных (В = 0), то для oi о преобразования используют выделение полного квадрата ш» каждому из переменных, которые входят в уравнение во второй и в первой степени. Напомним, что для квадратного трехчлоии ах2 + Ъх + с, а 0, выделением полного квадрата по х называю ! следующее его тождественное преобразование:
2 г f 2 ь \	/ 2 . Ь Ь2 Ь2\
ах +ож + с=а I х +-ж I +с=а I х +2—хН--z--—т I + с~
\ a J	\ 2а	4а2 4а2 J
= а( ж2+ 2—х + —- ) - —+ с= а(ж - я0)2 + < \ 2а 4а2/ 4а
где ж0 = -Ь/(2а); d = с - Ь2/(4а).
При В = 0 возможны три варианта.
1.	В первом варианте при 4^0иС/0 уравнение (11.17) путем выделения полного квадрата по х (при D 0) и по у (при Е 0) приводится к виду
А(х-хо)2 + С(у-уо)2 = F',	(11.Ш)
11.4. Неполные уравнения кривой второго порядка
325
где
D	Е	„ D2 Е2
х°~ 24’ Уо~ 2С' F~ F+ 44 + 4С"
Если в (11.18) F' / 0, то, введя обозначения a2 = |F'|/|4|, b2 = |F'|/|С| и учитывая знаки коэффициентов в (11.18), приходим к одному из следующих четырех уравнений:
(ж-ж0)2	(у-уо)2
а2	Ь2 ’
(* ~ го)2 _ й/-Уо)2 _
а2	Ь2 ~	’
(ж-ж0)2	(у-уо)2
а2 + Ь2 ’
(s - ж0)2 (у - у0)2	_
а2	Ъ2
Геометрическим образом последнего уравнения является пустое множество, которое иногда называют мнимым эллипсом. Первое (второе, третье) из этих уравнений называют смещенным уравнением гиперболы (сопряженной гиперболы, эллипса), поскольку после параллельного переноса системы координат
х' - X - Жр, у' = у - Уо
в новых переменных эти уравнения примут соответственно вид
W-1 а2 Ь2 ~ ’ (sT_W__ а2 Ъ2 ~ (Н2.(у')2 ,
Отметим, что среди последних трех уравнений канонический нид всегда имеют первые два и третье (при а 6) уравнения.
I I Аналитическая геометрия
326
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Если же в последнем уравнении а и b удовлетворяют неравен ству а < Ь, то это уравнение примет канонический вид после переобозначения переменных х = у', у = —ж'.
Если в уравнении (11.18) Ff = 0, то оно имеет вид
А(х - хо)2 + С [у - уо)2 - 0.
Геометрическим образом этого уравнения при АС > 0 буде i точка с координатами (жо; уо), а при АС <0 — пара пересеки ющихся прямых
Иа| (ж - xq) ±	- 2/о) = о.
2.	Второй вариант соответствует А / 0, С = 0. При Е / 0, т.е. когда в уравнении присутствует слагаемое с у в первой степени, выделяем полный квадрат по переменному х (при Р/0). Перенеся затем остальные слагаемые в правую часть, получим
А(ж-ж0)2 = -Ey + F',
где xq = —£>/(2А); Ff = D2/(4А) — F. В результате приходим к уравнению
Д(ж-ж0)2 = —£7(у — у0),
где yQ = Ff/E. Полагая р = |Е|/(2|А|), найдем смещенное уравнение параболы (х — xq)2 = 2р(у — у0) (при АЕ < 0) или (ж — жо)2 = — 2р(у — уо) (при АЕ > 0). После параллельного переноса системы координат
x' = x-xQ, у' = у-уо
эти уравнения сводятся к (ж')2 = 2ру' и (ж')2 = —2/ру1 соответ ственно. Наконец, полученные уравнения преобразуются в ки ионическое уравнение параболы у2 = 2рх после переобозначении переменных х = у\ у — —xf и х = —у', y — xf соответственно.
Если в этом варианте слагаемое с у в первой степени и уравнении отсутствует (Е = 0), то уравнение имеет вид
Ах2 + Dx + F = 0, А /0,
11.4. Неполные уравнения кривой второго поряди а

। •*. является квадратным относительно х. Это один ил выро еденных случаев, поскольку (11.17) является уравнением отш» «итольно одного переменного. Выделение полного квадрата н н ом случае сводит уравнение к одному из трех видов:
(х - Хо)2 = а2, (ж - ж0)2 = 0, (ж - ж0)2 = -а2,
। до хо = -£>/(24), a = y/\-F + £>2/(4А)| / 0. Первое из этих уравнений описывает на плоскости пару параллельных прямых г Xq ± а, которые во втором случае сливаются в одну прямую । хо. Третье уравнение задает на плоскости пустое множе-। тио (уравнение пары мнимых параллельных прямых).
3.	Третий вариант 4 = 0, С/0 аналогичен второму (сводится к нему переобозначением переменных х = у, у = — х). Поэтому при D ф 0, т.е. когда в уравнении присутствует । лягаемое с ж в первой степени, выделяя полный квадрат по переменному у (при Е 0) и перенося остальные слагаемые в правую часть, находим
С(у — уо)2 =-Dx + F',
где Уо = — Е/ (2С); F' — Е2/ (46*) — F. В результате приходим к уравнению
С’(у-уо)2 = ~D(x -х0),
где Хо = F'/D. Полагая р = |£>|/(2|С'|), мы опять получим смещенное уравнение параболы {у — уо)2 = 2р(х — хо) (при ( ’I) < 0) или (у — уо)2 = —2р(х — хо) (при CD > 0). После параллельного переноса системы координат
х' = х - х0, у' = у - уо
первое из этих уравнений преобразуется в каноническое уравнение параболы (у')2 = 2рх\ а второе сведется к уравнению (yf)2 = —2рх'. Последнее уравнение преобразуется в канониче-। кое уравнение параболы у2 = 2рх после переобозначения переменных х = —ж', у = —у1.
328
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Если в этом варианте слагаемое с х в первой степени и уравнении отсутствует (D = 0), то уравнение имеет вид
Cy2 + Ey + F = 0, С^О,
т.е. является квадратным относительно у. Это тоже один и:» вырожденных случаев, в котором выделение полного квадрата по у дает уравнение одного из трех видов:
(у~Уо)2 = «2, (у —Уо)2 = 0,	(у-Уо)2 =-а2,
где у0 = -Е/(2С); а = y/\-F + Е*/(4С)\ / 0. Так что и в этом случае получаем пару параллельных (различных, совпадающих, мнимых) прямых, параллельных оси Ох.
Рассмотрим случай, когда в уравнении (11.17) отсутствуют квадраты переменных, т.е. оно имеет вид
Вху + Dx + Еу + F = 0, В/0.	(11.19)
Такое уравнение можно привести к виду (ж-яго)(у-уо) + Г/ = 0, где х0 = -Е/В-, у0 — —D/B-, F' = F — хоуо. Полагая |F'| = а2/2, в зависимости от знака Ff приходим к одному из уравнений
а2	а2
(х-хо)(у-уо) = —,	(х-хо)(у-уо) = -—-	(11.20)
Если а 0, мы получаем смещенное уравнение гиперболы в асимптотах. Название отражает то, что после параллельного переноса системы координат xf = х — жо, у' = у — уо уравнение превратится в уравнение гиперболы в асимптотах xfyf = а2/2 или в уравнение сопряженной гиперболы в асимптотах ж'у' = —а2/2.
Если а = 0, оба уравнения (11.20) будут одинаковы, их геометрическим образом будет пара пересекающихся прямых х = xQ и у = у0.
11.4. Неполные уравнения кривой второго порядка
329
Несложный анализ приведенных преобразований неполного уравнения кривой второго порядка показывает, что при АС > О, II 0 геометрическим образом уравнения могут быть лишь »п/i и пс (окружность при А — С), точка или мнимый эллипс. Поэтому случай АС > О, В = 0 называют эллиптическим.
В то же время в случае АС <0, В — 0 геометрическим образом уравнения могут быть лишь гипербола или пара пересекающихся прямых, которую можно рассматривать как вырожденный случай гиперболы. Аналогична ситуация и в случае 4 С = 0, В 7^ 0. Эти случаи называют гиперболическими.
Наконец, если в уравнении из трех коэффициентов при ।лягаемых второго порядка отличен от нуля только один, А или С, то геометрическим образом может быть или парабола, или пара параллельных (совпадающих) прямых. Этот случай называют параболическим.
В задачах на исследование кривых второго порядка, заданных в прямоугольной системе координат неполными уравнениями, обычно требуется определить каноническое уравнение и вычислить в системе координат Оху: для параболы — координаты вершины и фокуса, уравнение директрисы, для эллипса — координаты центра, вершин и фокусов, полуоси и эксцентри-I итет, уравнения директрис, а для гиперболы — еще и уравнения асимптот.
Пример 11.5. Исследуем кривую второго порядка, заданную своим уравнением 9ж2 + 4у2 - 18ж + 1бу- 11 = 0.
В этом неполном уравнении второго порядка коэффициенты при квадратах переменных имеют одинаковый знак. Значит уравнение относится к эллиптическому типу. Выделяя полные квадраты по обоим переменным, получаем
9(а>2 - 2х + 1 - 1) 4- 4 (у2 + 4у + 4 - 4) - 11 = 0,
9(х-1)2 + 4(у + 2)2 = 36,
(х-1)2 (у + 2)2 _
330
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Следовательно, после параллельного переноса системы ко ординат х' = х — 1, у' — у+ 2 получим уравнение
Н2. (у£ = 1
22 f 32
которое задает эллипс с полуоси ми а = 2, 6 = 3. Так как а < 6, то фокусы лежат на вертикаль ной оси симметрии. Поэтому с = у/Ь2 — а2 = у/5, а эксцентриси тет е = с/b = у/5/3. Центр элли пса находится в точке О' с ко ординатами (1;-2) (рис. 11.20) Отметим, что полученное уран
нение эллипса не является капо Рис. 11.20
ническим, для перехода в капо ническую систему координат требуется дополнительный пово рот системы координат О'к'у' на угол 90°.
Приведем остальные характеристики кривой:
Система координат
О'х'у'
Координаты вершин
Координаты фокусов
Уравнения директрис
Л(-2;0) В(2;0)
С(0; -3)
D(0; 3) Fi (0; -75) F2(0; 75) 7 = ±9/75
Оху
Л(1- 2; —2) В(1 + 2; —2) 0(1; -2-3) 0(1; -2 + 3)
Fi(l; -2-Тб) F2(l;- 2 + 75) у + 2 = ±9/Т5
Пример 11.6. Неполное уравнение 4®2 + 16у2 + 8ж — 64j/ -I + 4 = 0 кривой второго порядка тоже относится к эллиптичо скому типу. Выделяя полные квадраты по обоим переменным,
11.4. Неполные уравнения кривой второго норндьп
.1.11
получаем
4(х2 + 2ж 4-1 - 1) + 16(у2 - 4у + 4 - 4) + 4 = О,
4(яг + I)2 4-16(у — 2)2 = 64,
(ж + 1)2 , (У-2)2
42	+	22
Выполнив параллельный перенос системы координат х' = х 4- I, у' — У — 2, запишем каноническое уравнение эллипса
, (уТ=1 42	22
г полуосями a = 4, 6 = 2. Так как a > 6, то фокусы лежат на горизонтальной оси симметрии. Поэтому с = \/а2 — 62 = 2\/3, и эксцентриситет £ = с/a = х/^3/2. Центр эллипса находится в точке О' с координатами (—1; 2) (рис. 11.21).
Приведем остальные характеристики кривой:
Система координат	О'х'у'	Оху
Координаты вершин	А(-4;0)	А(—1 —4; 2)
	В(4; 0)	В(-1+4; 2)
	С(0; -2)	С(—1;2 —2)
	0(0; 2)	О(—1;2 + 2)
Координаты фокусов	Fi (—2д/3; О)	Fi (-1 - 2>/3; 2)
	F2(273;0)	F2(-l + 2>/3;2)
Уравнения директрис	х' =	х + 1 = ±8/^/3
332
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Пример 11.7. В неполном уравнении кривой второго по рядка 4а:2 - 9у2 - 24а: + 18у — 9 = 0 коэффициенты при квадрата х переменных имеют противоположный знак. Поэтому уравнение относится к гиперболическому типу. Выделяя полные квадра ты по обоим переменным, получаем
4(а:2 - 6а: + 9 - 9) - 9(у2 - 2у + 1 - 1) - 9 = О,
4(а: — З)2 — 9(у — I)2 = 36,
(а; — З)2	(у-1)2
З2 22
В канонических координатах х' = х — 3, у' = у — 1 уравнение имеет вид
(И2 (у')2
З2 22
Оно задает гиперболу с центром в точке О'(3; 1), действи тельной полуосью а — 3, мнимой полуосью Ъ = 2. При этом С = Va2 + ь2 = у/13, £ = с/а= 713/3 (рис. 11.22).
Рис. 11.22
11.4. Неполные уравнения кривой второго норндьн

Приведем сводку остальных характеристик по .пои i ин< р Гм >л<»:
Система координат О'х'у'
Оху
Координаты вершин
Координаты фокусов
Уравнения директрис
Уравнения асимптот
Л(-3; 0) В(3; 0)
Fi (-ЛЗ; 0) Р2(ЛЗ;0) х1 = ±9/Лз у' = ±2/Зх'
А(3 —3; 1)
В(3 + 3; 1)
Fi(3-ЛЗ; 1) Г2(3 + ЛЗ;1) х-3 = ±9/ЛЗ
у—1 = ±2(х —3)/3
Пример 11.8. Неполное уравнение кривой второго по-ридка х2 + 2х — 6у + 7 = 0 относится к параболическому типу, поскольку содержит только одно слагаемое с переменным в квадрате. Выделяя полный квадрат по х, получаем
(ж2 + 2ж + 1 - 1) — бу + 7 = 0, (ж + I)2 = б(у - 1).
В координатах xf = ж + 1, у' — у — 1 уравнение имеет вид (ж')2 = 2 • Зу'.
)то параболас вертикальной осью симметрии, для которойр = 3, ар/2 = 1,5. Вершина параболы находится в точке О'(—1; 1) (рис. 11.23).
Рис. 11.23
334
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
Укажем остальные характеристики кривой:
Система координат
Координаты фокуса
Уравнение директрисы
О'х'у'	Оху
F(0; 1,5)	F(—l; 1 + 1,5)
х1 = —1,5 х + 1 = —1,5
Пример 11.9. Неполное уравнение ху — x — 2y + 6 — Q кри вой второго порядка относится к гиперболическому типу, по скольку оно не содержит слагаемых с квадратами переменных, но имеет слагаемое с их произведением. Преобразуем у равно ние:
х(у — 1) - 2(у—1 + 1) + 6 = О,
(у — 1)(а; — 2)+4 = О, (ж — 2)(у — 1) = —8/2.
В канонических координатах х' = х — 2, у' — у — 1 уравнение имеет вид
xV = -(2x/2)72,
т.е. представляет собой уравнение сопряженной гиперболы и асимптотах с полуосями а = b = 2у/2. Далее находим с -— у/а2 + Ь2 = 4, г = с/а = 4/(2\/2) = у/2. Центр гиперболы находится в точке О'(2; 1) (рис. 11.24).
Рис. 11.24
Д. 11.1. Полярные уравнения
335
Даем сводку остальных характеристик по этой кривой:
Система координат	О'х'у'	Оху
Координаты вершин	А(-2; 2)	А(2 —2; 1 + 2)
	В(2; -2)	В(2 + 2; 1-2)
Координаты фокусов	Fi(-2y/2;2y/2)	Fi(2-2y/2-, 1 + 2^2)
	F2(2y/2; -2у/2)	F2(2 + 2V2; 1-2л/2)
Уравнения директрис	у'=х'± 2>/2	у-1 = ±2л/2(г-2)
Уравнения асимптот	у' = о	у-1=0
	х' = 0	г —2 = 0
Дополнение
11.1. Полярные
уравнения
Часто используют уравнения эллипса, гиперболы и парабола в полярной системе координат. На вид этих уравнений и/I и нет взаимное расположение канонической системы координат кривой и полярной системы координат. Мы фиксируем полюс полярной системы координат в фокусе кривой. При этом цля эллипса выбираем левый фокус, а для гиперболы правый, in ли рассматривать их расположение в канонической системе координат. Полярную ось выбираем так, чтобы ее направление । овпадало с положительным направлением оси абсцисс канонической системы координат.
Все три вида кривых описываются общим свойством: для нобой их точки отношение расстояний до фокуса и до директрисы постоянно и равно эксцентриситету кривой. Значение но центриситета определяет тип кривой. Если зафиксировать фокальный параметр, так что положение директрисы в выбранной системе координат будет оставаться неизменным, мы, нпрьируя эксцентриситет, получим единый ряд эллипсов, параболы, правых ветвей гипербол (рис. 11.25, а), кривая определяется своим эксцентриситетом е уравнения
Конкретная при помощи
-±-=£
\МР\ ’
где* р — полярный, он же фокальный, радиус кривой; МР — перпендикуляр, опущенный из директрису d (рис. 11.25, б).
(11.21)
точки М на точки М на
Так	а
\	|Л/Р| =p + pcos</>,
то, поде' к	«ажение в (11.21), получим
/ ______р_____=с
'вив это выр' p + pcosv? ’
или р=—^--------------------------------.	(11.22)
1—£COS</?
Уравнен	^явают полярным уравнением эллипса, napt^	ветви гиперболы.
Если	>( 11.26) принадлежит левой ветви гиперболы, тс^	назй
\олы и право' \чкаЛ/(рис MP\ = -pcos<p-p, и поэто^	Ьлярное уравнение левой ветви гиперболы
получав!)	|/;
I	I	—р€
(11.21)	по< Р=Г+£	•	(11-23)
* виде
Вопросы и задачи
337
Вопросы и задачи
11.1.	Доказать, что у сопряженных гипербол фокальные расстояния совпадают.
11.2.	Доказать, что при повороте канонической системы координат на угол л/2 уравнение сопряженной гиперболы превратится в каноническое уравнение гиперболы.
11.3.	Найти уравнение эллипса, если его оси симметрии ‘параллельны осям координат, которых он касается, а центр находится в точке (—3; 2).
11.4.	Найти уравнение гиперболы с центром в точке (2; 1), гели ее оси симметрии параллельны осям координат, ее асимптота проходит через начало системы координат и эта гипербола касается: а) оси абсцисс; б) оси ординат.
11.5.	Найти уравнение равнобочной гиперболы с центром в точке (2; 1) и проходящей через начало системы координат, если одна из ее асимптот: а) вертикальна; б) горизонтальна; в) параллельна прямой у = х.
11.6.	Найти уравнение параболы с вершиной в точке (1;3), проходящей через точку (3; — 1), ось симметрии которой: а) вертикальна; б) горизонтальна.
338
11. КРИВЫЕ ВТОРОГО ПОРЯДКА
11.7.	Преобразовать уравнение кривой второго порядка и построить его геометрический образ в системе координат Оху, определив: для параболы — координаты вершины и фокуса, уравнение директрисы; для эллипса — координаты центра, вершин и фокусов, полуоси и эксцентриситет, уравнения ди ректрис; для гиперболы — еще и уравнения асимптот:
а)	ху-х-у+1-0;
б)	ху — х — у + 5 = 0;
в)	4ж2 - 9г/2 - 16ж — 36г/ — 56 — 0;
г)	4ж2 - 25г/2 - 16ж - 100г/+16 = 0;
д)	х2 - 16г/2 - 2х - 64г/ - 47 = 0;
е)	х2 - Юж - 4г/ + 57 = 0;
ж)	ху - 9ж - 4г/ + 72 = 0;
з)	2х2 + 2у2 + 4х — 8г/+11 = 0;
и)	2х2 - у2 + 4х - 8г/ + 36 = 0.
11.8.	Составить уравнение параболы, если ее фокусом является точка (2; —4), а директрисой: а) ось ординат; б) ось абсцисс; в) прямая у = 8.
11.9.	Доказать, что в полярных уравнениях кривых второго порядка знаменатели не обращаются в нуль.
11.10.	Найти каноническое уравнение кривой второго порядка по ее полярному уравнению:
.	15	.	15 ч 5
а) р=----------: б) р=------------: в)	.
5-3cos</>	3 —5cos</?	1 — cos</2
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
12.1.	Поверхность вращения и преобразование сжатия
Поверхность вращения. Простейшие поверхности в пространстве — это плоскости. Они являются геометрическими образами уравнений первой степени от трех переменных. Другой достаточно простой тип поверхностей составляют поверхности вращения.
Определение 12.1. Поверхность Q называют поверхностью вращения, если она образована окружностями с центрами на некоторой прямой L (оси вращения), которые расположены в плоско- .	.
гтях, перпендикулярных L (рис. 12.1).	Л..........\
Уравнение поверхности вращения О	/__________ \
имеет наиболее простой вид, когда нача- г-._______
ло О прямоугольной системы координат	\	I
лежит на оси вращения, а ось Oz совпа-	L*... -J
дает с ней. Пересечение поверхности fi	] "	\
< координатной плоскостью Oxz — это	Л-----------Д
некоторое множество S (рис. 12.2), вра- | --------' I
щение которого образует fi.	L
Предположим, что множество S в рИСе 12,i плоскости Oxz описывается уравнением
<p(x,z) = 0. Рассмотрим произвольную точку М(х; у; z). Она удалена от оси Oz на расстояние d = \/х2 + у2. Если точка М лежит на поверхности вращения Q, то точки A/i(xi; 0; z), Лl2 fa] 0; z) с той же аппликатой z, что и М, и абсциссами x\=d,
340
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
х2 = —d принадлежат множеству S, Поэтому о = ¥>(хъг) = <p(d,z) = <p(y/x2 + y2,z), 0 = 9?(ж2, z) = <f>(-d, z) = <fi(--\/x2 + у2, z)
и условие М € Q сводится к
Рис. 12.2
тому, что координаты точки М удовлетворяют равенству
<р(±\/х2 + y2,z) — 0.	(12.1)
Уравнение (12.1) и есть уравнение поверхности Q, которая образова на вращением подмножества S -= {(x;z): <p(x,z) = 0}, расположен ного в координатной плоскости Oxz. Из уравнения множества 5 уравнение (12.1) соответствую щей поверхности вращения полу чается заменой х на ^.у/х2 + у2.
Преобразование сжатия. Под преобразованием сжатия к координатной плоскости Oxz мы понимаем такое пре-образование, при котором точка М(х; у\ z) смещается в точку y/k-,z), к > 0. Параметр к называют коэффициентом сжатия. При к > 1 точки пространства, расположенные на одной прямой, перпендикулярной плоскости Oxz, в результа те такого преобразования сближаются, т.е. преобразование -действительно сжатие. При 0 < к < 1 преобразование фактически является растяжением.
Пусть в пространстве в прямоугольной системе коорди нат Oxyz некоторое множество Q задано своим уравнением F(#,y,2) = 0. При преобразовании сжатия к координатной плоскости Oxz с коэффициентом к это множество превратится в новое множество Q' с уравнением F(x, &у,г) = 0. Это следует из того, что точка (ж; у; z) тогда и только тогда принадлежи!1 множеству Q', когда точка (ж; ky\z) принадлежит множеству Q,
12.2. Эллипсоиды
341
12.2.	Эллипсоиды
Поверхность, которая получается при вращении эллипса вокруг одной из его осей симметрии, называют эллипсоидом вращения (рис. 12.3)
Уравнение эллипсоида вращения выведем, расположив начало прямоугольной системы координат в центре эллипса и совместив ось аппликат От с осью вращения, а координатную плоскость Oxz — с плоскостью эллипса (рис. 12.4). Тогда уравнение эллипса будет иметь вид
ж2 z1 ~
Если в этом уравнении заменить х на ±у/х2 + у2 (см. 12.1), то получится уравнение
X2 +у2 Z2 ---——4-----= 1
а2 V2
соответствующей поверхности вращения. Итак, эллипсоид вращения с осью вращения Ог описывается уравнением
ж2	у2	Z2
----I- — 4------= 1.
а2	а2	Ъ2
(12.2)
Рис. 12.4
Рис. 12.3
342 12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Применив к эллипсоиду вращения преобразование сжатия h координатной плоскости Oxz, получим эллипсоид общего ви да. Если к — коэффициент сжатия, то уравнение эллипсоида будет иметь вид
ж2 к2у2 z2
а2 + а2	Ь2~ ’
или, после переобозначения параметров,
а2 + Ь2 + с2 L
(12.3)
Уравнение (12.3) задает поверхность второго порядка. Его называют каноническим уравнением эллипсоида. Три па раметра а, Ъ и с, входящие в него — это полуоси эллипсоида (рис. 12.5). Если все три полуоси эллипсоида попарно различны, то эллипсоид называют трехосным.
Рис. 12.5
При совпадении каких-либо двух полуосей (как, например, в уравнении (12.2)) эллипсоид является поверхностью вращения (эллипсоидом вращения). Если равны все три полуоси (а = Ь~ = с = г), то эллипсоид превращается в сферу радиуса г, которая описывается уравнением
2.2.2	2
х +у +Z =Г .
12.3. Гиперболоиды
343
12.3.	Гиперболоиды
При вращении гиперболы вокруг одной из ее осей симметрии получается поверхность, называемая гиперболоидом вращения. Выбор оси вращения влияет на тип гиперболоида. Нели осью вращения является действительная ось симметрии гиперболы, то поверхность вращения будет состоять из двух частей (полостей). Это двуполостный гиперболоид вращения (рис. 12.6). При вращении гиперболы вокруг ее мнимой оси симметрии поверхность будет состоять из одной полости (рис. 12.7). Такую поверхность называют однополостным гиперболоидом вращения.
Для вывода уравнений гиперболоидов вращения расположим прямоугольную систему координат так, чтобы ось вращения, являющаяся осью симметрии гиперболы, совпадала с осью аппликат Oz, а сама гипербола располагалась в координатной плоскости Oxz с центром в начале системы координат.
Для случая двуполостного гиперболоида вращения уравнение гиперболы будет иметь вид
Рис. 12.7
Рис. 12.6
344
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Заменив в нем х на ±\Д2 +у2 (см- получим уравнение
а2 а2 Ъ2
(124)
В случае однополостного гиперболоида вращения гипербола будет описываться уравнением
Опять меняем х на радикал ±-\/ж2 + у2, получаем
уравнение однополостного гиперболоида вращения.
Гиперболоиды вращения преобразованием сжатия к коор динатной плоскости Oxz превращаются в двуполостный и однополостный гиперболоиды общего вида. При коэффициенте сжатия к их уравнениями будут соответственно
а2 а2 Ь2
х2 к2у2 z2
После переобозначений параметров эти уравнения преобразу ются в каноническое уравнение двуполостного (рис. 12.8)
и однополостного (рис. 12.9) гиперболоидов
а2 Ь2 с2
(12.7)
12.4. Эллиптические параболоиды
345
Как видно из уравнений (12.6), (12.7), оба гиперболоида являются поверхностями второго порядка.
Рис. 12.9
Рис. 12.8
12.4.	Эллиптические параболоиды
При вращении параболы вокруг ее оси получаем параболоид вращения (рис. 12.10). Чтобы найти его уравнение, выберем прямоугольную систему координат, направив ось Oz во оси вращения и совместив координатную плоскость Oxz с плоскостью параболы. Пусть при этом парабола описывается уравнением х2 = 2pz, р > 0. Тогда для получения уравнения поверхности вращения нужно заменить в этом уравнении х на t\/^2 + у2 (см. 12.1):
2р2 = ж2 + у2.
Преобразование сжатия параболоида вращения к координатной плоскости Oxz с коэффициентом k дает поверхность
346
12, ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
более общего вида — эллиптический параболоид, уравнением которого будет
2pz = х2 + k2y2.
После переобозначения параметров получаем каноническое уравнение эллиптического параболоида
х^ и2
=	(12.8)
Видим, что эллиптический парабо
лоид является поверхностью вто-
рого порядка. При а = b он превращается в параболоид вра
щения.
12.5.	Конусы
При вращении прямой L, пересекающейся с осью враще-
ния, образуется прямой круговой конус (рис. 12.11). Точка
Рис. 12.11
пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса.
Как и ранее, уравнение будем выводить в прямоугольной системе координат, ось Oz которой совпадает с осью вращения, а начало системы координат — с вершиной конуса. Ось Ох расположим так, чтобы прямая L находилась в координатной плоскости Oxz и описывалась уравнение ем z = к\х. В этой системе координат уравнение поверхности вращения получается из уравнения прямой заменой х на
12.6. Цилиндрические поверхности
347
I \/ж2 + у2 (см. 12.1). В результате такой замены получаем z ~ ±^!у/х2 + у2. Возведя уравнение в квадрат, придем к соот ношению z2 = k2(x2 + у2), а разделив его на с2 = Аг2 а2, получим каноническое уравнение прямого кругового конуса
ж2 у2 ~ Z2 а2 + а2 с2
Преобразование сжатия прямого кругового конуса к координатной плоскости Oxz с коэффициентом к дает эллиптический конус. Его уравнение имеет вид
х2 k2y2 _ z2 а2 + а2 с21
или, после переобозначения параметров,
Уравнение (12.9) называют каноническим уравнением эллиптического конуса. Эллиптический конус при а = b совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка.
12.6.	Цилиндрические поверхности
При вращении прямой вокруг оси вращения, параллельной зтой прямой, образуется поверхность, которую называют круговым цилиндром (рис. 12.12). Эта поверхность является частным случаем цилиндрической поверхности, получающейся при движении прямой в пространстве, которая остается параллельной своему исходному положению (рис. 12.13). Если на движущейся прямой фиксировать точку, то она опишет кривую, которую называют направляющей цилиндрической поверхности (см. рис. 12.13). Можно также сказать, что цилиндрическая поверхность представляет собой множество
348
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
точек на прямых, параллельных фиксированной прямой. Эти параллельные прямые называют образующими цилиндрической поверхности.
Рис. 12.12
Рис. 12.13
В качестве направляющей цилиндра можно взять любую кривую, образованную пересечением цилиндрической поверх ности с плоскостью, не параллельной образующим. Выберем прямоугольную систему координат так, чтобы образующие цилиндрической поверхности были параллельны оси Ох. В ка честве направляющей выберем кривую, являющуюся пересече нием цилиндрической поверхности с координатной плоскостью хОу (рис. 12.14).
Рис. 12.14
12.6. Цилиндрические поверхности
349
Направляющая в плоскости хОу описывается некоторым уравнением двух переменных </>(я,у) = 0. Точка M(x*,y\z) ле-/кит на цилиндрической поверхности тогда и только тогда, когда ее абсцисса и ордината (фактически координаты точки N (х; у; 0) на плоскости хОу) подчиняются уравнению направляющей. Поэтому в выбранной системе координат цилиндрическая поверхность описывается уравнением <£>(я,у) = 0 — уравнением своей направляющей, которое трактуется как уравнение грех переменных ж, у и z. Верно и обратное утверждение: если в некоторой прямоугольной системе координат в пространстве поверхность описывается уравнением, не содержащим одного из переменных, то эта поверхность является цилиндрической. Итак, критерием для цилиндрической поверхности является отсутствие в ее уравнении в подходящей системе координат одного из переменных.
Цилиндр второго порядка — это цилиндрическая поверхность, направляющая которой в плоскости, перпендикулярной образующим, представляет собой кривую второго порядка. В выбранной выше прямоугольной системе координат цилиндр второго порядка описывается уравнением второй степени
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0,
где А2 + В2 + С2 /0.
Это уравнение можно упростить подходящим выбором системы координат. Фактически речь идет о приведении к каноническому виду уравнений второго порядка от двух переменных (см. 11.4, а также [IV]). Канонические уравнения кривых второго порядка приводят к трем видам цилиндров второго порядка:
- эллиптическому (рис. 12.15, а) с каноническим уравне-х2 у2 нием Н- — = 1;
а2 о2
350 12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
-	гиперболическому (рис. 12.15, б) с каноническим уран-ж2 у2
нением — — — — 1;
а2 о2
-	параболическому с каноническим уравнением у2 = 2рх (рис. 12.15, в).
Отметим, что если направляющей является пара пересекаю щихся (параллельных, совпадающих) прямых, то соответствующая им цилиндрическая поверхность представляют собой пару пересекающихся (параллельных, совпадающих) плоскостей.
Рис. 12.15
12.7. Метод сечений
351
12.7. Метод сечений
Для выяснения формы поверхности в пространстве по ее уравнению
Ф(ж,у,г)=0	(12.10)
часто используют так называемый метод сечений. Он состоит в анализе пересечений поверхности с плоскостями, параллельными координатным плоскостям, например с плоскостями вида z = с, где параметр с пробегает все действительные значения. Для каждого значения с система уравнений
f*(W) = 0,
Z — с к
задает соответствующее пересечение. Критерием принадлежности точки М(х; у; z) этому пересечению являются следующие условия: a) z = с; б) координаты х и у ее проекции на координатную плоскость хОу, т.е. координаты точки ЛГ(ж;у; 0), удовлетворяют уравнению
Ф(ж,у,с) = 0.	(12.12)
Зная эти пересечения, т.е. кривые (12.12), можно представить форму поверхности. Отметим, что указанный „рентген“ поверхности можно проводить другими плоскостями, но они должны быть параллельными между собой.
Обычно при исследовании формы поверхности методом сечений используют две точки зрения на уравнение (12.12). Первая состоит в том, что его интерпретируют как уравнение проекции на координатную плоскость хОу сечения (12.11). Согласно второй точке зрения предполагают, что в секущей плоскости имеется прямоугольная система координат с началом в точке О' пересечения секущей плоскости с осъюОг и осями, О'х и О'у, которые проектируются на соответствующие оси Ох и Оу системы координат Oxyz. Это позволяет говорить о (12.12) как об уравнении сечения (12.11) в секущей плоскости.
352
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Пример 12.1. В качестве примера рассмотрим уравнение эллиптического параболоида (12.8)
ж2 I/2
-------1- — — 2z а2 + 62 -
и исследуем его форму методом сечений.
Пересечение этой поверхности с плоскостью z = с описывается уравнением
Ж2 у2 _ “7 + 12 =2с-а2 о2
При с < 0 пересечение пусто, при с = 0 оно совпадает с началом системы координат Oxyz, а при с > 0 представляет собой эллипс
ж2	у2 _ 1
(ау/2с)2 + (6vt)2 “
Оси этого эллипса с ростом параметра с увеличиваются, и можно представить форму поверхности (рис. 12.16, а). Кстати, слово „эллиптический" в названии поверхности и указывает на то, что среди ее сечений имеются эллипсы.
Пересечения этой (рис. 12.16, б), так и с ляют собой параболы
же поверхности как с плоскостью х = с плоскостью у = с (рис. 12.16, в) представ-
с2 у2
а2 о2
и
х2 с2
“2 + То = 2^ а2 о2
соответственно. Параболы в каждом из этих семейств сечений имеют равные параметры (они не зависят от значения с). Эти сечения позволяют дать еще одно геометрическое построение эллиптического параболоида. Рассмотрим параболу Pi, находящуюся в плоскости у = 0, и аналогичную параболу Pj
12.7. Метод сечений
Vi I
а
б
в
Рис. 12.16
354
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Рис. 12.17
в плоскости х = 0 (рис. 12.17, а). Пусть вторая парабола перемещается в пространстве так, что:
-	вершина параболы Р2 все время находится на параболе Р|;
-	ось параболы Р2 параллельна оси параболы Pi;
-	плоскость параболы Р2 перпендикулярна плоскости пара болы Рр
Тогда в результате такого перемещения и образуется элли птический параболоид. При этом роли парабол Pi и Р2 можно поменять,, т.е. перемещать параболу Pi, используя параболу Pj как направляющую. #
Уравнение
^~¥ = 2z (12лз>
отличается от уравнения (12.8) эллиптического параболоида лишь знаком одного слагаемого и тоже задает поверхность вто рого порядка. Ее называют гиперболическим параболой-дом, а само уравнение (12.13) — каноническим уравнением гиперболического параболоида.
12.8. Неполные уравнения поперхности второго пормдкн ’.Ihh
Исследуем вид гиперболического параболоида методом «г пений. Его пересечения с плоскостями у = с при любом анлчг пии с являются параболами:
х2 с2 = 2z‘
Пересечения с плоскостями х = с тоже при всех значениях с являются параболами:
с2 у2 ____— 9г о2 Ь2 ~
Обозначим через Pi параболу, находящуюся в сечении у = 0, а через Р2 — аналогичную параболу в сечении х = 0. Перемещая, как и выше, параболу Р} по параболе Pi (рис. 12.17,6), получаем седлообразную поверхность гиперболического параболоида.
Пересечения гиперболического параболоида с плоскостями z — с при с 0 являются гиперболами
X2 'Ll2
а2 Ь2 ' а при с = 0 — парой пересекающихся прямых
а2 Ь2
Выбор названия поверхности объясняется характером сечений: горизонтальные сечения гиперболического параболоида — это гиперболы, а два других семейства рассмотренных сечений — параболы.
12.8.	Неполные уравнения поверхности второго порядка
Поверхность второго порядков пространстве в заданной прямоугольной системе координат описывается уравнением с десятью коэффициентами:
Ах2 + By2 + Cz2 + Dxy + Exz-H Fyz + Gx + HyA-Kz + L = 0,
356
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
причем среди первых шести коэффициентов, от А до F, должен быть хотя бы один ненулевой.
Мы, как и в случае кривых второго порядка, не будем про водить полную классификацию поверхностей второго порядка, отложив ее до изучения курса линейной алгебры [IV].
В этом разделе мы рассмотрим случай неполного уравнения поверхности второго порядка, т.е. когда в уравнении отсут ствуют попарные произведения переменных:
Ax2 + By2 + Cz2 + Gx + Hy + Kz + L = O.	(12.14)
Такое уравнение второго порядка при помощи параллельно го переноса системы координат и, возможно, переобозначения, переменных можно преобразовать в одно из канонических уран нений поверхности второго порядка или в уравнение вырожден ной поверхности второго порядка, хотя в некоторых особых случаях для упрощения уравнения параллельного переноса но достаточно. Такие особые случаи подробно анализируются в [IV].
Для преобразования уравнения (12.14), используют выделе ние полного квадрата по каждому из переменных, входящих в уравнение во второй и первой степени (см. 11.4 или [I]). При этом возможны три варианта.
1.	В первом варианте уравнение (12.14) содержит квадраты всех трех переменных. Выделение полного квадрата по х (при G^O), по у (при Н ф 0) и по z (при К 0) преобразует уравнение (12.14) к виду
А(х - Хо)2 + В(у - t/о)2 + C(z - 20)2 = L',	(12.15)
где
G	Н	К , G2 Н2 К1
хо- 2А, Уо — 2В, го — 2С,	-	+ 4Л + 4В + 4((.
Пусть в полученном уравнении (12.15) L'^0. Тогда, введя обозначения а2 = |Z/|/1А|, b2 = |Z/|/ |В|, с2 = | Z/1 / |С|, придем к
12.8. Неполные уравнения поверхности второго порядка
357
смещенному уравнению поверхности второго порядка, В зависимости от знаков коэффициентов уравнения (12.15) это могут быть уравнения эллипсоида
(х-хо)2 (у —Уо)2	(г-г0)2
+ ’Г (12Л6)
однополостного гиперболоида
(а - До)2 , (у — Уо)2 _ (г~го)2 _ 1
а2	Ь2	с2	~	’
(а ~ ар)2 _ (У~Уо)2 + (*-*о)2 = j	(12.17)
а2	Ь2	с2	1
(х-хо)2	(у-уо)2	(г-х0)2_
а2	Ь2	с2	~	’
двуполостного гиперболоида
(а - ар)2 , (у — Уо)2 _ (г-гр)2 _
а2 + Ь2	с2	~	’
(а ~ ^р)2 _ (У-Уо)2 _ (z ~ *о)2 = j	(12.18)
а2	Ъ2	с2	’
(а - жр)2 _ (у-Уо)2	(z-z0)2	_
а2	Ь2	с2
или мнимого эллипсоида
(х-хо)2	(у-уо)2 (г-г0)2_
а2 + Ь2 + с2 ~	’
называемого так потому, что уравнение напоминает уравнение эллипсоида, но в отличие от последнего описывает пустое множество.
Если L'= 0, то, вводя обозначения а2 = 1/|А|, Ь2 = 1/1В|, с2 = = 1/ |С|, также приходим к смещенному уравнению поверхности второго порядка. В зависимости от знаков коэффициентов
I 1 Аналитическая геометрия
358
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
уравнения (12.15) это могут быть уравнения конуса				
(ж - ж0)2 а2 (ж - Жр)2	, (У~Уо)2 + Ь2 (У — Уо)2 ,	(-г ~ г0)2 С2 (г - г0)2	= 0, = 0.	(12.1!))
а2 (ж - Жр)2 а2 или точки (ж - Жр)2 а2 Замечание 12.1.	Ь2	с2 (У~УЬ)2 (z~zo)2_n Ь2	с2 , (у - уо)2 , {г - гр)2 _ п 1 Ь2	с2 После параллельного переноса			системы
координат
х' = х - «о, у' - У - Уо, z1 = z — z0
в точку O'(x0; уо; ^о) уравнение (12.16) и первые в тройках уран нений (12.17)—(12.19) в новых переменных примут канониче ский вид, в то время как остальные уравнения в (12.17)-(12.19) преобразуются к каноническому виду дополнительным перс* обозначением переменных в соответствующей координатной плоскости. Это переобозначение переменных важно с тсо ретической точки зрения, так как позволяет определить тип поверхности, хотя положение этой поверхности в системе ко ординат O'x'y'z' принципиально иное, нежели в канонической системе координат (на рис. 12.18 приведены три варианта по ложения однополостного гиперболоида). На практике допол нительное изменение системы координат не реализуют и изо бражают поверхность в системе координат O'x'y'z', получаю щейся параллельным переносом. Переобозначение переменных рассматривают как чисто алгебраическую операцию, поз вол и ющую выяснить положение поверхности относительно системы координат.
12.8. Неполные уравнения поверхности второго порнцин
Ihll
Рис. 12.18
2.	Во втором варианте уравнение (12.14) содержит квадраты двух переменных. Здесь выделяются три подварианта:
а)	А /О, В ^0, С = 0;
б)	А ф 0, В = 0, С / 0;
в)	А = 0, В ^0, С ^0.
Эти подварианты сводятся друг к другу переобозначением переменных. Поэтому они дают одни и те же результаты, и нам достаточно рассмотреть лишь один из них, например первый.
Если А / 0, В ф 0, а С = 0, то в случае К = 0 третье переменное z вообще не входит в уравнение (12.14), которое в этом случае является уравнением цилиндра второго порядка. Все возникающие ситуации и тип поверхности полностью характеризуются направляющей цилиндра в плоскости хОу (см. 11.4).
360
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
В случае К 0 выделение полного квадрата по х (при G / 0) и по у (при Н / 0) преобразует уравнение (12.14) к виду
А(х - хо)2 + В (у - у0)2 = -K(z - z0),	(12.20)
где
G	Н L' т, т G2 Н2
Х°~ 24’ Уо~ 2В' Z°~ К' ~~ +4А + 4В'
Введя обозначения а2 = 1/|4|, Ь2 = 1/|В|, р=\К\/2, придем к смещенным уравнениям поверхности второго порядка. В зависимости от знаков коэффициентов в (12.20), это могут быть уравнения или эллиптического параболоида
х-х0)2	(у-у0)2 _
а2 + J2 — 2р(г zq), s~»o)2 . (У-Уо)2 _ _9 , _ . х
а2 + J2 — 2р(-г Zq), или гиперболического параболоида
-®о)2	(у-Уо)2_9/,	.
а2	J2 — 2р(г z0),
х ~ жо)2 _ 0/-Уо)2 = _2_/г _ 2 ч
а2	^2	2р(г zq).
3. В третьем варианте уравнение (12.14) содержит квадрат только одного переменного. Здесь также возникают три симметричных подварианта (квадрат ж, квадрат у, квадрат z). Остановимся на случае А ^0. Если уравнение не содержит или слагаемого с у в первой степени, или такого же слагаемого с z, то реализуется случай цилиндра второго порядка, который сводится к исследованию направляющей цилиндра. Если же в уравнении присутствуют оба указанных слагаемых первой степени, как, например, в уравнении x2 + y + 2z = 0, то приведение уравнения к каноническому виду требует поворота системы координат в пространстве. Анализ таких уравнений приведен В [IV].
12.8. Неполные уравнения поверхности второго порядка 361
Пример 12.2. Упростим уравнение
4х2 4- 9у2 + 36г2 - 8® - 36у + 72г + 40 = О
поверхности второго порядка с помощью параллельного переноса прямоугольной системы координат.
Уравнение содержит каждое из трех переменных в первой и во второй степени. Поэтому по каждому переменному выделяем полный квадрат:
4(®2 - 2х + 1 - 1) +
4- 9(у2 - 4у 4- 4 - 4) 4- 36(г2 4- 2г 4-1 - 1) 4- 40 = 0, 4(х - I)2 + 9(у - 2)2 + 36(г+ I)2 = 36, (х -1)2 (у — 2)2	.	,2
L-55J- + a^rL + (2+1) =1'
Приходим к смещенному уравнению эллипсоида с центром в точке О'(1; 2; -1) и полуосями а = 3, Ь = 2, с= 1. Соответствующее каноническое уравнение получается после параллельного переноса системы координат xf = х — 1, yf = у — 2, z* = z + 1 и
имеет вид
З2 22
(г')2 = 1.
Пример 12.3. Выясним, какая поверхность является гео-метрическим образом уравнения
ж2 - У2 + z2 - 2х + 4у - 2z - 3 = 0.
Как и в примере 12.2, по каждому переменному выделяем полный квадрат:
(х2 - 2х + 1 - 1) - (у2 - 4у + 4 - 4) + (г2 - 2г + 1 - 1) - 3 = 0, (х — I)2 — (у — 2)2 4-(г — I)2 = 1.
362
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Приходим к смещенному уравнению однополостного гиперболо ида вращения с центром в точке О'(1; 2; 1). После параллельно го переноса системы координат в эту точку х' = х — 1, у' = у — 2, z' = z — 1 уравнение принимает вид
(x')2-(y')2 + (y)2 = l.
Это уравнение не является каноническим из-за несоответствия знаков. Осью вращения гиперболоида является ось О'у' новой системы координат (рис. 12.19, а).
Выясним, какую поверхность определяет
Пример 12.4.
уравнение второго порядка
х2 - 4z2 + 8у + 8z - 12 = 0.
В уравнении нет слагаемого х первой степени и слагаемого у второй степени. Полный квадрат выделяем только по переменному z:
X2 - 4(z2 - 2z +1 - 1) + 8у - 12 = 0,
х2-4(2- 1)2 + 8у-8 = 0,
х2 - 4(z - I)2 = -8(у - 1), т»2
__(г_1)2 = _2(у_1).
Д.12.1. Конические и линейчатые поверхности	363
Приходим к смещенному уравнению гиперболического параболоида. Выполнив параллельный перенос системы координат .г' = х, yf = у — 1, z' = г— 1 в точку <?'((); I; I) получим уравнение вида
которое преобразуется в каноническое дополнительным переобозначением переменных (рис. 12.19,6).
Замечание 12.2. Для определения ни да поверхности и построения ее в новой системе коордипач* (после параллельного переноса) можно использовать мл рыд сечений. Конечно, если, как в примере 12.2, уравнение поверхности имое'г канонический вид, то можно воспользоваться приведенным выше выводом канонических уравнений поверхностей второго порядка. Однако в примерах 12.3, 12.4 (см. рис. 12.19, п, 6) ситуация сложнее, и использование метода сечений представляется целесообразным для исключения ошибок.
Дополнение 12.1. Конические и линейчатые поверхности
Поверхность, которая образуется при движении прямой, проходящей через некоторую фиксированную точку А, называют конической. Точка А — это вершина конической поверхности, а всевозможные прямые на поверхности, представляющие собой положения движущейся прямой, — это образующие конической поверхности (рис. 12.20). Примеры конических поверхностей дают прямой круговой и эллиптический конусы.
Траекторию у некоторой фиксированной точки В на движущейся прямой (но не вершины) можно рассматривать как направляющую конической поверхности. При этом коническую поверхность можно определить как множество всевозможных прямых, проходящих через фиксированную точ
364
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ку А (вершину) и пересекающих заданную кривую у (направляющую).
Рис. 12.20
Если начало прямоугольной системы координат Oxyz совпадает с вершиной конической поверхности, то уравнение F(x,y,z) = 0 этой поверхности будет иметь следующее свойство. Если Е(жо?Уо^о) = 0, то и F(Xxq, Ayo, А^о) = 0 для любого действительного числа А. Это следует из того, что через любую точку конической поверхности, не являющуюся вершиной, проходит образующая. Точки М(х$\ уо; zq) и Л/'(Ажо; Аг/о; А^о) лежат на этой прямой. Уравнения с описанным свойством называет однородными. Итак, при указанном выборе системы координат уравнение конической поверхности будет однородным. Верно и обратное утверждение: геометрическим образом однородного уравнения является коническая поверхность. Алгебраическое уравнение будет однородным, если оно содержит слагаемые одной и той же степени. Например, каноническое уравнение (12.9) эллиптического конуса состоит из слагаемых второй степени.
Коническая поверхность относится к более широкому классу линейчатых поверхностей, образуемых движущейся прямой (рис. 12.21). Если движущаяся прямая все время проходит через фиксированную точку (что, вообще говоря, необязательно), то линейчатая поверхность будет конической. Если ппсгк/гая /гпижется поступательно, оставаясь параллельной свое-
Д.12.1. Конические и линейчптые понгрхши ih
Ш
му исходному положению, мы получаем другой вид нвилйча г«»Й поверхности — цилиндрическую поверхность.
Рис. 12.21
Линейчатыми, но не коническими, поверхностями являют г я однополостный гиперболоид и гиперболический параболоид. Чтобы убедиться в этом, рассмотрим однополостный гиперболоид, заданный своим каноническим уравнением
а2 + Ь2 с2 ~ '
Перенесем второе слагаемой левой части уравнения в его правую часть
(12.23)
ж2 _ г2 _ _ у2
а2 с2 ~ Ь2
и преобразуем уравнение к следующему виду:
с/ \а cJ \ о/ \
При любом значении параметра А система
p-i = A(14),
ас \ Ь/
(12.24)
(12.25)
представляет собой общие уравнения прямой. Эта прямая при любом А принадлежит однополостному гиперболоиду, поскольку при А / 0 уравнение (12.24) гиперболоида получается перемножением уравнений системы (12.25) и сокращением на А. При
366 12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
А = 0 (12.24) следует из (12.^5), поскольку обе части уравнения (12.24) содержат множители, равные нулю. Таким образом, однополостному гиперболоиду принадлежит бесконечно много прямых, описываемых общими уравнениями (12.25). Если к этим прямым добавить еще одну прямую
РЧ=°’ о
(12.26)
которую естественно соотнести с бесконечным значением пара-метра А, то через каждую точку однополостного гиперболоида будет проходить одна прямая семейства, лежащая на гиперболоиде. Соответствующее значение А можно найти из системы (12.25). Итак, гиперболоид, который задается уравнением (12.23), представляет собой множество прямых, описываемых уравнениями (12.25). Эти прямые называют прямолинейными образующими однополостного гиперболоида.
Однополостный гиперболоид имеет также второе семейство прямолинейных образующих, которое описывается системой уравнений
Рис. 12.22
аналогичной (12.25), с тем же соглашением о значениях параметра А (рис. 12.22). Наглядным примером однополостного гиперболоида с двумя семействами прямолинейных образующих являются секции Шаболовской телебашни. Автор оригинальной идеи, заложенной в конструкцию телебашни, он же ее конструктор — русский инженер В.Г. Шухов (1853-1939).
Д.12.1. Конические и линейчатые поверхности	3(17
Прямолинейные образующие гиперболического параболой да находятся так же, как и однополостного гиперболоида. Преобразуем каноническое уравнение гиперболического пара
болоида	^4—
к виду
<12-27> \а о/ \а Ь/
'Гак же как и в случае однополостного гиперболоида, это уравнение можно „расщепить" в систему двух линейных уравнений
(12.28)
или по-другому
(12.29)
Каждая из систем (12.28), (12.29) задает семейство прямолинейных образующих гиперболического параболоида (рис. 12.23).
Рис. 12.23
368	12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
В случае однополостного гиперболоида вращения, т.е. при а = Ь, каждое из двух семейств прямолинейных образующих по лучается вращением одной прямой семейства вокруг оси враще* ния поверхности. Это значит, что однополостный гиперболоид вращения можно получить вращением прямой, которая являет ся скрещивающейся по отношению к оси вращения.
Рассмотрим, например, семейство (12.25), полагая, что а = Ь. Каждая прямая семейства пересекает координатную плоскость хОу в точке, лежащей на окружности х2 + у2 = а2 (других точек гиперболоида в плоскости хОу нет). С другой стороны, прямолинейная образующая не может быть парал лельна этой плоскости, так как соответствующим сечением гиперболоида является эллипс). Выбрав произвольную точку М(acos</?; asin</?; 0) на указанной окружности, найдем значение параметра А для прямой семейства (12.25), проходящей через М. Отметим, что прямолинейная образующая, соответствующая А = 0, пересекает эту окружность в точке (0; - а; 0), а соответствующая бесконечному значению А — в точке (0; а; 0). Это непосредственно следует из (12.25). Подставим в первое уравнение системы (12.25) координаты точки М
acosip х (л	asinc/?
------- — Д I — -------- а \ а
и решим уравнение относительно А:
cosy?
1 — sin <р*
(12.30)
Зная параметр А, мы можем найти направляющий вектор 9 прямой (12.25) как векторное произведение нормальных векторов двух плоскостей, определяемых уравнениями системы (не забывая при этом, что а = 6):
i 3 1/а Х/а Х/а —1/а
к
-\/с А/с
А2 - 1. 2А . А2 + 1, ------г-----j------к.
ас ас а1
Д.12.2. Конические сечения 369
Длина полученного вектора раина
_ У(А2 - 1)2а2 + 4А2а2 + (А2 +~0^ (Ц-А2)^2^?
S ~	а2с	а2с
Разделив вектор s на его длину, получим единичный направляющий вектор
д2 _ 1 2Д
s° = А2+"17>*~ А2 + 1Р^ ~qk~ ptiin“pCOS™ ~ qk'
где р = аД/«2 + с2, q = с/\/а2 + с2, а параметр А заменен на р согласно формуле (12.30)- Можно Показать, что вектор з0 получается из вектора с координатами {0; —р; —q}, соответствующего А = 1, поворотом на угол р вокруг оси Oz [IV]. Следовательно, прямая семейства (12.25), соответствующая параметру А, получается поворотом вокруг оси аппликат прямой того же семейства, соответствующей параметру А= 1.
Дополнение 12.2. Конические сечения
Важнейшей особенностью прямого кругового конуса является то, что все кривые второго порядка трех типов: эллипсы, гиперболы, параболы — могут быть получены как конические сечения, т.е. сечения конуса различными плоскостями.
Рассмотрим прямой Круповой конус, который в прямоугольной системе координат Oxyz описывается уравнением
ж2-|_ У2 - 22 = 0	(12.31)
и геометрически получается^ при вращении вокруг оси Oz прямой z = х, принадлежащей координатной плоскости xOz. В силу круговой симметрии поверхности (12.31) можно ограничиться только сечениями при помощи плоскостей, перпендикулярных координатной плоскости xOz. Таким плоскостям соответствуют уравнения А х + Bz + D = 0, А2 + В2 0.
370 12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Если В = 0, то секущая плоскость описывается уравнением х = хо, где хо = — D/А, и параллельна координатной плоско сти yOz. Подставив значение абсциссы х0 в уравнение конуса (12.31), найдем, что сечение в плоскости х = xq описывается уравнением z2 - у2 = х% (см. 12.7) и при xq / 0 представляет со* бой равнобочную гиперболу (рис. 12.24, а), а при х$ = 0 — пару прямых, которые являются образующими конуса (рис. 12.24, б).
Рис. 12.24
Пусть в уравнении секущей плоскости коэффициент В 0. Тогда плоскость можно представить уравнением z = кх + 6, где к = —А/В, Ь= —D/В. В силу симметрии конуса относительно плоскости Оху достаточно ограничиться случаем, когда к < 0. Коническое сечение для рассматриваемой плоскости в пространстве будет описываться системой двух уравнений
X2 + у2 - Z2 = 0, <
z — kx + b.
(12.32)
Чтобы получить уравнение кривой в секущей плоскости, рассмотрим прямоугольную систему координат O'vu, взяв в качестве координатных осей О'п и O'v прямые, являющиеся Пересе
Д.12.2. Kohh'ivi hUt> 1гч«11ия
371
чениями секущей плоскости с координатными плоскостями xOz и хОу (рис. 12.25).
Координаты и и v произвольной точки I» секущей плоскости будут связаны с ее координатами г, у и z в пространстве соотношениями
и
X = Xq + WCO8</> ~ То
V 1 I А'2 у = и, к и 2="5шу=-7г+Р'
(12.33)
еде <р — угол между коническим сечением, перпендикулярным координатной плоскости xOz, и координатной плоскостью хОу (см. рис. 12.25), причем к = tgys, а То - 1>/к.
Рис. 12.26
Подставляя (12.33) в первое уравнение системы (12.32),
получаем уравнение конического сечения в системе координат (Xvu
/	и \ 2	,	/ ки \ 2
( Xq--) + V2 - (--------7=== ) - 0.
'	\/1 + А;2'	' \/1 +
I ’аскрывая скобки и приводя подобные, находим
1 - к2
1 + к2
и2 +
2Ь Ь2 -
= 0.
(12.34)
372
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
При к = — 1, когда секущая плоскость образует с плоско* стью хОу тот же угол, что и образующие конуса, конические сечения будут представлять собой параболы (рис. 12.26, а) и описываться уравнением v2 = by/2(u ~ b/y/2). Варьируя параметр b в уравнении секущей плоскости, в качестве конического сечения можно получить любую параболу.
Рис. 12.26
При к — 1 (к < 0) уравнение (12.34) примет вид
1-к2 ( by/l+k^y2 2_ 62
1 + Р k(l-k2)J + v ~l — k2'
(12.35)
Здесь возможны два варианта. При -1 < к 0, т.е. когда секущая плоскость образует с плоскостью хОу меньший угол, чем образующие конуса, выполнено неравенство 1 — к2 > 0 и поэтому уравнение (12.35) конического сечения являете» уравнением эллипса (см. рис. 12.26,6). И здесь, варьируя параметры b и к в уравнении секущей плоскости, мы можем получить в сечении любой эллипс.
Вопроси и плдлчи
Il I
При к < —1, т.е. когда секущая плоскость обрплун! । и н«м костью хОу больший угол, чем образующие кппуги, имн-н 1 — к2 < 0, так что коническое сечение, описываемое урнвн»’ нием (12.35), является гиперболой (рис. 12.26, а). Вирьмр\и параметры b и &, можно получить в коническом ((‘’hmihb л о • бую гиперболу.
Вопросы и задачи
12.1.	Исследовать форму поверхности второго поряди.» методом сечений:
а) х2 — 2у — z2 = 1; б) х2 - у2 — 4 = 0;
в) 4ж2 + 4у2 + 5г2 + 1 = 0; г) у2 — z2 - х2 — 0;
д) у2 + z2 - х2 = 0; е) у2 - z2 + х2 = 0;
ж) ху = 0; з) 2ж2 + 2t/2 + 4ж — 8у + 11 = 0.
Установить названия этих поверхностей и сделать рисунок в заданной системе координат.
12.2.	Найти уравнения проекций на координатные плоско сти пересечений поверхностей:
а)	х2 + у2 + z — 4 = 0, х2 + у2 — z — 0;
б)	х2 + у2 — z — 9 = 0, х2 + у2 — 1 = 0;
в)	х2 + у2 — z — 0, 4ж - 4у — z + 8 — 0.
12.3.	Найти уравнение конуса с вершиной в точке (1; —3; 2), образующие которого составляют угол 60° с координатной плоскостью: а) хОу; б) xOz; в) yOz.
12.4.	Доказать, что уравнение х2 — Зу2 + z2 = 2х — 2z - 2 задает конус, и найти его вершину.
12.5.	Найти уравнение конуса с вершиной в начале системы координат, если в него вписана сфера х2 + у2 + (z — 4)2 = 1.
12.6.	Найти каноническое уравнение эллипсоида с полуосями 5, 3 и 2.
374
12. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
12.7.	Преобразовать уравнение поверхности второго порядка с помощью параллельного переноса системы координат и построить ее в новой системе координат:
a)	xz — х — z + 1 = 0; б) у2 + z2 — 4у — 4г + 4 = 0;
в)	4ж2 + 9у2 + z2 — 16ж — 36у + 2г + 296 = 0;
г)	4ж2 — у2 + г2 — 24ж + 2у — 4г + 35 = 0;
д)	х2 — у2 — г2 — 4у — 2г — 1 = 0.
12.8.	Установить название поверхности второго порядка при всех значениях параметра t:
а)	х2 — 2х — г +1 = 0; б) х2 — ty2 + (t + 1)г2 — 4у — 4г + 4 = 0;
в)	х2 + 2у2 + Зг2 — 16а; — 8у + 12г +1 = 0;
г)	х2 — у2 + г2 — 4х + 2у — 4г +1 = 0;
д)	tx2 - (t - 1)у2 - (t + 2)г2 -1 = 0.
12.9.	В прямоугольной системе координат задана прямая
х — 1 _ у + 2 _ г+ 1
2 “ t “ 1
Найти все значения параметра t, при которых поверхность, образованная при вращении данной прямой вокруг оси: а) Ох; б) Оу; в) Oz, является конусом, и определить вершину этого конуса.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Учебники и учебные пособия
Александров П.С. Курс аналитической геометрии и линейной алгебры: Учеб, для вузов. М.: Наука, 1979. 512 с.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры: Учеб, пособие для физ.-мат. и инж.-физ. специальностей вузов. 6-е изд., стереотип. М.: Наука, 1984. 319 с.
Беллман Р. Введение в теорию матриц / Пер. с англ, под ред. В.Б. Лидского. М.: Наука, 1969. 368 с.
Гантмахер Ф.Р. Теория матриц. 3-е изд. М.: Наука, 1967. 576 с.
Ефимов Н.В. Краткий курс аналитической геометрии. 12-е изд., стереотип. М.: Наука, 1975. 272 с.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия: Учеб, для университетов. 4-е изд., доп. М.: Наука, 1988. 224 с.
Курош А.Г. Курс высшей алгебры. 8-е изд. М.: Наука, 1965. 432 с.
Ланкастер П. Теория матриц / Пер. с англ. (7.77. Демушкина, М.: Наука, 1978. 280 с.
Погорелов А,В, Аналитическая геометрия: Учеб, для мат. и физ. специальностей вузов. 4-е изд., стереотип. М.: Наука, 1978. 208 с.
Постников М.М. Аналитическая геометрия. 2-е изд., перераб. М: Наука, 1986. 414 с.
Хорн Р., Джонсон Ч. Матричный анализ / Пер. с англ, под ред. Х.Д.Икрамова. М.: Мир, 1989. 655 с.
Справочные издания
Александрова Н.В. Математические термины: Справочник. М.: Высш, шк., 1978. 190 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. 13-е изд., испр. М.: Наука, 1986. 544 с.
Воднев В.Т., Наумович А.Ф., Наумович Н.Ф. Математический словарь высшей школы / Под ред. 70.(7. Богданова. Минск: Вышэйш. шк., 1984. 528 с.
376
Список рекомендуемой литературы
Выгодский М.Я. Справочник по высшей математике. 13-е изд., стереотип. М.: Физматлит, 1995. 872 с.
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров) / Пер. с англ, под ред. И,Г. Арамановича. М.: Наука, 1973. 832 с.
Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров, М.: Сов. энцикл., 1988. 848 с.
Сигорский В.П. Математический аппарат инженера. 2-е изд., стереотип. Киев: Техшка, 1977. 768 с.
Фор Р., Кофман А., Дени-Папен М. Современная математика / Пер. с франц, под ред. А.П. Колмогорова. М.: Мир, 1966. 272 с.
Задачники
Беклемишева Л. А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре: Учеб, пособие / Под ред. Д.В. Беклемишева. М.: Наука, 1987. 496 с.
Данко П.Е., Попов А.Г., Кожевникова Т.Н. Высшая математика в упражнениях и задачах: В 2 т. Т. 1. 4-е изд., испр. и доп. М.: Высш, шк., 1986. 304 с.
Клетеник Д.В. Сборник задач по аналитической геометрии. 14-е изд., исправл. М.: Наука, 1986. 222 с.
Окунев Л.Я. Сборник задач по высшей алгебре. М.: Просвещение, 1964. 184 с.
Сборник задач по математике для втузов: Ч. 1. Линейная алгебра и основы математического анализа: Учеб, пособие для втузов. / Под ред. А.В. Ефимова и Б.П. Демидовича. 2-е изд. М.: Наука, 1986. 428 с.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. 29-е изд., стереотип. М.: Наука, 1968. 366 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса точки 1-78, 79
Алгебра векторная 18
Аппликата точки 79
Базис в Vi 33
-	- V2 33
---правый (левый) 80
-	- Уз 35
---правый (левый) 56
-	ортогональный 39
-	ортонормированный 39
Блок матрицы 169
Вектор 16
-	геометрический 13
—	единичный 14
—	ненулевой 14
—	нулевой 14
-	единичный 17
-	направляющий прямой 108, 127
-	ненулевой 17
-	нормальный плоскости 121
—	прямой 105
-	нулевой 17
-	противоположный 20
-	свободный 16
-	связанный 17
-	скользящий 17
Векторы геометрические коллинеарные 15 однонаправленные (сонаправленные) 15 противоположно направленные 15 компланарные 15 равные 16 коллинеарные 17
-- однонаправленные (сонаправленные) 17
— противоположно направленные 17
-	компланарные 17 - линейно зависимые 28 — независимые 28
-	ортогональные 50
Величина векторная 13 - скалярная 1-215, 13 Вершина гиперболы 311 - конической поверхности 363 - конуса 346 - параболы 321 - эллипса 296
Высота матрицы-столбца 156
Гипербола 1-107, 305
-	равнобочная 318 - сопряженная 312
378
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Гиперболоид вращения 343
—	двуполостный 343
—	однополостный 343
-	двуполостный 344
-	однополостный 344
Детерминант 186
Диагональ матрицы главная 156
—	побочная 156
-	определителя вторая 44
—	главная 44
—	побочная 44
Директриса гиперболы 315
-	параболы 321
-	эллипса 302
Длина вектора 17
—	геометрического 14
-	матрицы-строки 156
Дополнение алгебраическое 195
Запись СЛАУ векторная 244
—	координатная 242
—	матричная 245
Инверсия 1-166, 183
Итерация 272
Квадрат вектора скалярный 51
Комбинация линейная векторов 27
—	строк (столбцов) 174
Конец вектора 17
—	геометрического 14
Конус прямой круговой 346
-	эллиптический 347
Координата вектора 33
Координаты вектора 34, 35
Координаты точки 1-78, 80
—	декартовы (аффинные) 79
—	полярные 7-/5/, 97
—	прямоугольные 79
—	сферические 100
—	цилиндрические 99
Косинус направляющий вектора 40
Коэффициент линейной комбинации 27
-	сжатия 340
-	угловой прямой 108
Коэффициенты СЛАУ 242
Кривая второго порядка 294
-	(линия) алгебраическая на плоскости 93
Критерий ортогональности векторов 54
«Лемниската II, / 02
Линейность произведения векторного 63
—	скалярного 52 — смешанного 69
]Матрица 155 - блочная 170 - блочно-диагональная 173 - блочно-треугольная 204 - вырожденная 219 - диагональная 157 - единичная 157
-	квадратная порядка п 156
-	кососимметрическая 163
-	невырожденная 219
-	неособая 219
-	нулевая 157
379
Матрица обратная 217
-	определителя 186
-	ортогональная 287
-	положительно определенная 291
-	присоединенная 220
-	противоположная 161
-	прямоугольная 156
-	с диагональным преобладанием 279
-	симметрическая 163
-	СЛАУ 246
—	расширенная 246
-	ступенчатая, 158
-	транспонированная 162
-	трапециевидная верхняя 158
-	треугольная верхняя 157
-	- нижняя 157
-	трех диагональная 158
Матрица-столбец 156
Матрица-строка 156
Матрицы коммутирующие 166
-	перестановочные 166
-	равные 159
Метод Гаусса 273
-	- исключения неизвестных 273
—	с выбором главного элемента 283
-	прогонки 285
- решения СЛАУ итерационный 272
--прямой 272
--точный 272
-	сечений 351
Минор 195
-	базисный 230
-	окаймляющий 233
Минор порядка к 225 угловой 278
Многочлен от п переменных 92
Модуль вектора 17 геометрического 14
Направляющая поверхности конической 363 цилиндрической 347
Начало вектора 17 геометрического 14 (системы) координат 79
Неизвестное базисное 250 зависимое 250 независимое 250 свободное 250
Нуль-вектор 14, 17
Образ геометрический 91,92
Образующая поверхности конической 363
-	- цилиндрической 348
-	прямолинейная гиперболоида однополостного 366
Операция линейная 18, 160
Определитель 186
-	Вандермонда 212
-	второго порядка 44
-	матрицы 186
-	порядка п 186
-	системы второго порядка 48
—	третьего порядка 49
-	третьего порядка 45
Ордината точки 1-78, 79
Ориентация базиса 56
-	реперов одинаковая 85
—	противоположная 85
380
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Орт 14,17
Ось 24
-	абсцисс 79
-	аппликат 79
-	гиперболы действительная 306
—	мнимая 306
-	координат 79
-	ординат 79
-	параболы 321
-	полярная 96
-	эллипса 295
Отклонение точки от прямой 114
Отрезок направленный 13
Парабола 1-107, 321
Параболоид вращения 345
-	гиперболический 354
-	эллиптический 346
Параметр фокальный гиперболы 316
—	параболы 321
—	эллипса 302
Пара упорядоченная 1-78
Переменные канонические 296, 307, 321
Перенос параллельный системы координат в пространстве 83
-----на плоскости 83
Переобозначение переменных 324
Перестановка 1-83, 183
-	нечетная 1-166, 183
-	нормальная 183
-	четная 1-166, 183
Плоскость координатная 79
Поверхность алгебраическая 93
-	второго порядка 355
Поверхность вращения 339
-	коническая 363
-	линейчатая 364
-	цилиндрическая 347
Поворот системы координат в пространстве 85
	-на плоскости 83
Подстановка 1-164, 185
-	нечетная 1-166, 185
-	четная 1-166, 185
Подстановки равные 186
Положение общее плоскостей 151
Полуось гиперболы действительная 306
—	мнимая 308
-	эллипса большая 296
—	малая 296
-	эллипсоида 342
Полюс полярной системы координат 96
Порядок поверхности (кривой) алгебраической 94
-	уравнения 93
Правило Крамера 248
-	параллелограмма 18
-	Саррюса 45
-	треугольника 18, 45
Преобразование сжатия 340
-	элементарное обратное 177
—	столбцов матрицы 177
—	строк матрицы 176
Проекция вектора на плоскость 58
-	ортогональная вектора на направление 25
-----ось 25
-----прямую 24
381
Проекция ортогональная точки на плоскость 58
---прямую 23
Произведение вектора на число 21
-	векторное 56
—	двойное 73
-	матриц 164
-	матрицы на число 160
-	скалярное 50
-	смешанное 66
Пространство Ц 33
-	v2 33
-	Уз 33
Пучок плоскостей 147
-	прямых 150
Радиус полярный 1-151, 97
-	фокальный 295, 305
Радиус-вектор 79
Разложение вектора в базисе 33, 34, 35
-	матрицы мультипликативное 287
-	- LDU 291
-	- LU 288
—	SST 292
- определителя по столбцу 198
---строке 198
—	третьего порядка по первой строке 46
-	Холецкого 292
Размер матрицы 155
Разность векторов 21
-	матриц 161
Ранг матрицы 226
Расстояние фокальное 295, 305
Репер 79
Решение СЛАУ 242
общее 258
однородной общее 254
частное 242
уравнения матричного 222
Свой< тво оптическое гиперболы 31(1
параболы 322
лллипса 305
('вилка плоскостей 150
(‘вменив коническое 369
(‘истема векторов 27
двух линейных уравнений 47
координат 80
декартова (аффинная) 78
прямоугольная 79
каноническая 296, 307, 321
косоугольная 79
полярная 96
прямоугольная 1-77, 79
сферическая 100
 цилиндрическая 98
решений фундаментальная 250 нормальная 252
трех линейных уравнений 48
уравнений линейных
алгебраических 242
СЛАУ 242
-	квадратная 244
-	неоднородная 242
-	неопределенная 244
-	несовместная 243
-	обусловленная плохо 271
—	хорошо 271
- однородная 242
382
СЛАУ онрпдплгпиэд 244
совмт гили J43
Степень многочлена от
it переменных 92
уравнения 93
Столбец базисный 230
Строка базисная 230
Строки (столбцы) линейно зависимые 175
---независимые 174
Сумма векторов 18
- матриц 159
— прямая 173
Теорема Кронекера— Капелли 246
- о базисном миноре 230
Тип матрицы 155
Точка приложения вектора 17
---геометрического 14
Транспозиция перестановки 1-166, 184
- подстановки 185
Тройка некомпланарных векторов левая 56
---правая 56
У гол между векторами 25
-	полярный 1-151, 97
Уравнение алгебраическое 93
-	гиперболы в асимптотах 319
---смещенное 328
-	- каноническое 309
—	полярное 336
-	- смещенное 325
—	сопряженной каноническое 312
---смещенное 325
предметный указатель
Уравнение каноническое гиперболоида двуполостного 344 ----однополостного 344-- - конуса прямого кругового 347 ----эллиптического 347 - - параболоида гиперболического 354 ----эллиптического 346 — эллипсоида 342 - кривой второго порядка неполное 323 - линейное 104 - матричное 222 - множества 91, 92 - однородное 364 - параболы каноническое 322 — полярное 336 — смещенное 326, 327 - плоскости векторное 122 ----параметрическое 123 — в отрезках 125 — нормальное 126 -- общее 121 - поверхности второго порядка смещенное 357
-	прямой векторное 109, 128
-	- в отрезках 110 — каноническое 109 -- нормальное 111 — общее 105
-	- проходящей через две точки 109 — с угловым коэффициентом 108 - эллипса каноническое 299 — полярное 336 — смещенное 325
Уравнения плоскости параметрические 123 - прямой канонические 129 -- общие 127	Цилиндр гиперболический 350 “ круговой 347 - параболический 350 - эллиптический 349
-- параметрические 108, 128 -- проходящей через две точки 130	Член уравнения свободный 242
«Э&окус гиперболы 305 - параболы 321 - эллипса 295	Эксцентриситет гиперболы 311 -	параболы 321 -	эллипса 300 Элемент ведущий 278
Формулы Крамера 48, 248	- главный 278
Ход метода Гаусса обратный 275 	прямой 275	- диагональный 44, 156 - матрицы 155 Эллипс 294
Центр гиперболы 306 - эллипса 296	- мнимый 325 Эллипсоид 342 - вращения 341
Циклоида И, 102 Цилиндр второго порядка 349	- мнимый 357 - трехосный 342
ОГЛАВЛЕНИЕ
Предисловие	5
Основные обозначения	9
1.	Линейные операции йад векторами	13
1.1.	Векторные и скалярные величины................... 13
1.2.	Типы векторов и их взаимное расположение....	15
1.3.	Линейные операций и их свойства.................. 18
1.4.	Ортогональная проекция .......................... 23
1.5.	Линейная зависимость и независимость векторов . .	27
1.6.	Базис...........................................  33
1.7.	Вычисления в координатах......................... 36
Вопросы и задачи.................................. 41
2.	Произведения векторов	44
2.1.	Определители второго и третьего порядков....	44
2.2.	Скалярное произведение........................... 49
2.3.	Векторное произведение........................... 56
2.4.	Смешанное произведение .......................... 66
2.5.	Приложения произведений векторов................. 71
Д.2.1.	Двойное векторное произведение................... 73
Вопросы и задачи.................................. 74
3.	Системы координат	78
3.1.	Декартова система координат...................... 78
3.2.	Преобразование прямоугольных координат........... 80
3.3.	Простейшие задачи аналитической геометрии ....	85
3.4.	Вычисление площадей и объемов.................... 89
3.5.	Кривые и поверхности............................. 91
3.6.	Полярная система координат....................... 96
3.7.	Цилиндрическая И сферическая системы координат .	98
Вопросы и задачи................................. 101
_______________________ 385
4.	Прямая на плоскости	НИ
4.1.	Алгебраические кривые первого порядка.......... 104
4.2.	Специальные виды уравнения прямой.............. 107
4.3.	Взаимное расположение двух прямых.............. Ill
4.4.	Расстояние от точки до прямой ................. 113
Вопросы и задачи................................ 117
5.	Прямая и плоскость в пространстве	119
5.1.	Алгебраические поверхности первого порядка ....	119
5.2.	Специальные виды уравнения плоскости........... 122
5.3.	Уравнения прямой в пространстве................ 127
5.4.	Взаимное расположение прямых и плоскостей ....	135
5.5.	Расстояние до плоскости и до прямой............ 143
Д.5.1. Пучки и связки................................. 147
Вопросы и задачи................................ 153
6.	Матрицы и операции над ними	155
6.1.	Виды матриц.................................... 155
6.2.	Линейные операции над матрицами................ 159
6.3.	Транспонирование матриц........................ 162
6.4.	Умножение матриц............................... 164
6.5.	Блочные матрицы................................ 169
6.6.	Прямая сумма матриц............................ 173
6.7.	Линейная зависимость строк и столбцов.......... 174
6.8.	Элементарные преобразования матриц............. 176
Вопросы и задачи................................ 180
7.	Определители	183
7.1.	Определители n-го порядка...................... 183
7.2.	Свойства определителей......................... 188
7.3.	Методы вычисления определителей ............... 206
Вопросы и задачи................................ 215
8.	Обратная матрица и ранг матрицы	217
8.1.	Обратная матрица и ее свойства................. 217
8.2.	Вычисление обратной матрицы.................... 220
8.3.	Решение матричных уравнений.................... 222
386
ОГЛАВЛЕНИЕ
8.4.	Ранг матрицы..................................... 225
8.5.	Теорема о базисном миноре........................ 230
8.6.	Вычисление ранга матрицы......................... 233
Вопросы и задачи.................................. 239
9.	Системы линейных алгебраических уравнений	242
9.1.	Основные определения............................. 242
9.2.	Формы записи СЛАУ ............................... 244
9.3.	Критерий совместности СЛАУ....................... 245
9.4.	Формулы Крамера.................................. 248
9.5.	Однородные системы............................... 249
9.6.	Неоднородные системы ............................ 257
9.7.	Как решать СЛАУ ?................................ 259
Д.9.1. СЛАУ с комплексными коэффициентами............... 267
Вопросы и задачи.................................. 268
10.	Численные методы решения СЛАУ	270
10.1.	Проблемы, связанные с вычислениями.............. 270
10.2.	Прямые и итерационные методы решения СЛАУ . .	272
10.3.	Метод Гаусса.................................... 273
10.4.	Особенности метода Гаусса....................... 277
10.5.	Метод прогонки.................................. 284
Д.10.1. Мультипликативные разложения матриц............. 287
Вопросы и задачи.................................. 292
11.	Кривые второго порядка	294
11.1.	Эллипс.......................................... 294
11.2.	Гипербола....................................... 305
11.3.	Парабола........................................ 320
11.4.	Неполные уравнения кривой второго порядка ....	323
Д. 11.1. Полярные уравнения............................. 335
Вопросы и задачи.................................. 337
12.	Поверхности второго порядка	339
12.1.	Поверхность вращения и	преобразование сжатия . .	339
12.2.	Эллипсоиды...................................... 341
12.3.	Гиперболоиды.................................... 343
12.4.	Эллиптические параболоиды....................... 345
387
12.5.	Конусы.......................................... 346
12.6.	Цилиндрические поверхнос ти..................... 347
12.7.	Метод сечений .................................. 351
12.8.	Неполные уравнения поверхности второго порядка .	355
Д.12.1. Конические и линейчатые поверхности............. 363
Д.12.2. Конические сечения ............................. 369
Вопросы и задачи............................. 373
Список рекомендуемой литературы	375
Предметный указатель	377
Учебное издание
Математика в техническом университете Выпуск III
Канатников Анатолий Николаевич Крищенко Александр Петрович
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Редактор Н.Г, Ковалевская Художник С.С, Водчиц Корректоры Е.В. Авалова, О.В. Калашникова
Оригинал-макет подготовлен в Издательстве МГТУ им. Н.Э. Баумана под руководством А.И. Канатникова
Изд. лиц. №020523 от 25.04.97
Подписано в печать 27.03.2002. Формат 60x88 1/16
Печать офсетная. Бумага офсетная № 1 Усл. печ. л. 24,25. Уч.-изд. л. 23,48 Тираж 5 000 экз. Заказ № 839
Издательство МГТУ им. Н.Э. Баумана 107005, Москва, 2-я Бауманская, 5
Отпечатано с готовых диапозитивов во ФГУП ИПК «Ульяновский Дом печати» 432980, г. Ульяновск, ул. ГЬнчарова, 14
ISBN 5-7038-1671-8