Текст
В.Д. РАЙЗЕР
ТЕОРИЯ
НАДЕЖНОСТИ
В СТРОИТЕЛЬНОМ
ПРОЕКТИРОВАНИИ
V.D. RAIZER г
THEORY OF
RELIABILITY IN
STRUCTURAL DESIGN
В.Д. РАЙЗЕР
ТЕОРИЯ
НАДЕЖНОСТИ В
СТРОИТЕЛЬНОМ
ПРОЕКТИРОВАНИИ
V.D. RAIZER
THEORY OF
RELIABILITY IN
STRUCTURAL DESIGN
Издательство Ассоциации Строительных Вузов
Москва1998
ББК
i.
УДК 624,046.5
Рецензенты : кафедра строительной механики Московского
строительного государственного университета (зав. кафедрой, доктор техни-
ческих наук, профессор Н.Н. Леонтьев)
Теория надежности в строительном проектировании: Монография/
/ВД.Райзер— М.: изд-во АСВ, 1998. — 304 стр. с илл.
ISBN 5-878294)59-6
The book contains a probabilistic
analysis of modern design code making
procedures and of test control for buil-
ding constructions. Methods of failure
probability calculation are expounded.
Methods of bars and bar's systems relia-
bility estimations are described.
Comparisons with foreign stan-
dards are given. A new conception of
building structures codification and
standardization based on general
consumer's requirements is described.
The book is addressed to the atten-
tion of engineering and technical staff of
research, design and building organize-
lions and of real estate experts.
This edition is realized with the financial
help of investing and budding company RIF
(3, Shiiuzpvaia quay, Moscow, Russia, tel
(095) 235-1667,fax (095) 235-1369).
Приведен вероятностный анализ совре-
менных методов нормирования расчетов в
приемочного контроля конструкций. Изло-
жены методы вычисления вероятности отка-
за. Описаны методы расчета на надежность
стержней и стержневых систем.
Содержится сопоставление с зарубежны-
ми нормами. Описаны новая концепция нор-
мирования и стандартизации расчетов
строительных конструкций, основанная на
нормативных потребительских требованиях.
Для научных и инженерно-технических
работников научно-исследовательских, про-
ектных, строительных организаций и специ-
алистов по оценке недвижимости.
Издание осуществлено при финансовой
поддержке инвестиционно-строительной
компании “Риф” (Москва, Шлюзовая наб. 8,
тел. 235-16-67, факс 235-13-69).
33010000000-010
К-без объяв л.
009(03) - 98
ISBN 5 -87829 -059-6
© Райзер В.Д,, 1998
© Издательство АСВ, 1998
ОГЛАВЛЕНИЕ
Предисловие ........................—...................... 8
Глава 1. Вероятностные основы современных норм
проектирования и приемочного контроля .................... 19
L L Вероятностный анализ метода предельных
состояний .................................... 19
1.2. Нормы расчета и надежность конструкции ....... 27
1.3. Статистический контроль несущей способности .. 35
1.4. Байесовский подход в анализе обеспеченности
механических свойств ............................. 41
Глава 2. Вероятностные модели климатических
и технологических нагрузок .............................., 47
2.1. Классификация нагрузок и их сочетания ........ 47
2.2. Снеговые нагрузки ............................ 57
2.3. Ветровые нагрузки ...............,............ 72
2.4. Темпсратуриыеклиматичсские воздействия ....... 87
2.5. Нагрузки иа перекрытия зданий .............. 95
2.6. Нагрузки от веса конструкций ............... 101
Глава 3. Методы вычисления вероятности отказа ......... 107
3Л. Общие замечания .........,.................... 107
3.2. Меч од двух моментов ........................ 109
3.3. Метод “горячих точек” ...................... 115
3.4. Метод статистических испытании ............ 123
3.5. Метод Монте-Карло ........................... 129
3.6. Модификация метода Монте-Карло с моделирова-
нием стратифицированных выборок ................ 134
Глава 4. Надежность внецентренно-сжатых и
сжато-изогнутых стержней .......,........................ 139
4.1. Области неразрушимости ..................... 139
4J2Г Вероятность отказа впецентренно-ежатого
стального стержня ...........,............... 144
4.3. Вероятность отказа сжато -изогнуто го стального
стержня ......................................... 149
4.4. Вероятностный метод определения коэффициента
сочетания нагрузок .............................. 153
3
4.5. Вероятностный мет од расчета внецентренно-сжатых
стоек с разными эксцентриситетами ................ 158
4.6. Анализ надежности внецензренно-сжатого
железобетонного элемента ......................... 167
Глава 5. Некоторые вопросы надежности
стержневых систем ....................................... 177
5.1. Последовательное соединение элементов ....... 177
5.2. Параллельное соединение элементов ........... 181
5.3. Вероятностный метод предельного равновесия .. 186
Глава 6. Надежность железобетонного каркасного здания,
запроектированного ио российским и европейским нормам ... 199
6.1. Предварительные замечания ................... 199
6.2. Проектирование железобетонного каркасного
здания по российским и европейским нормам ........ 201
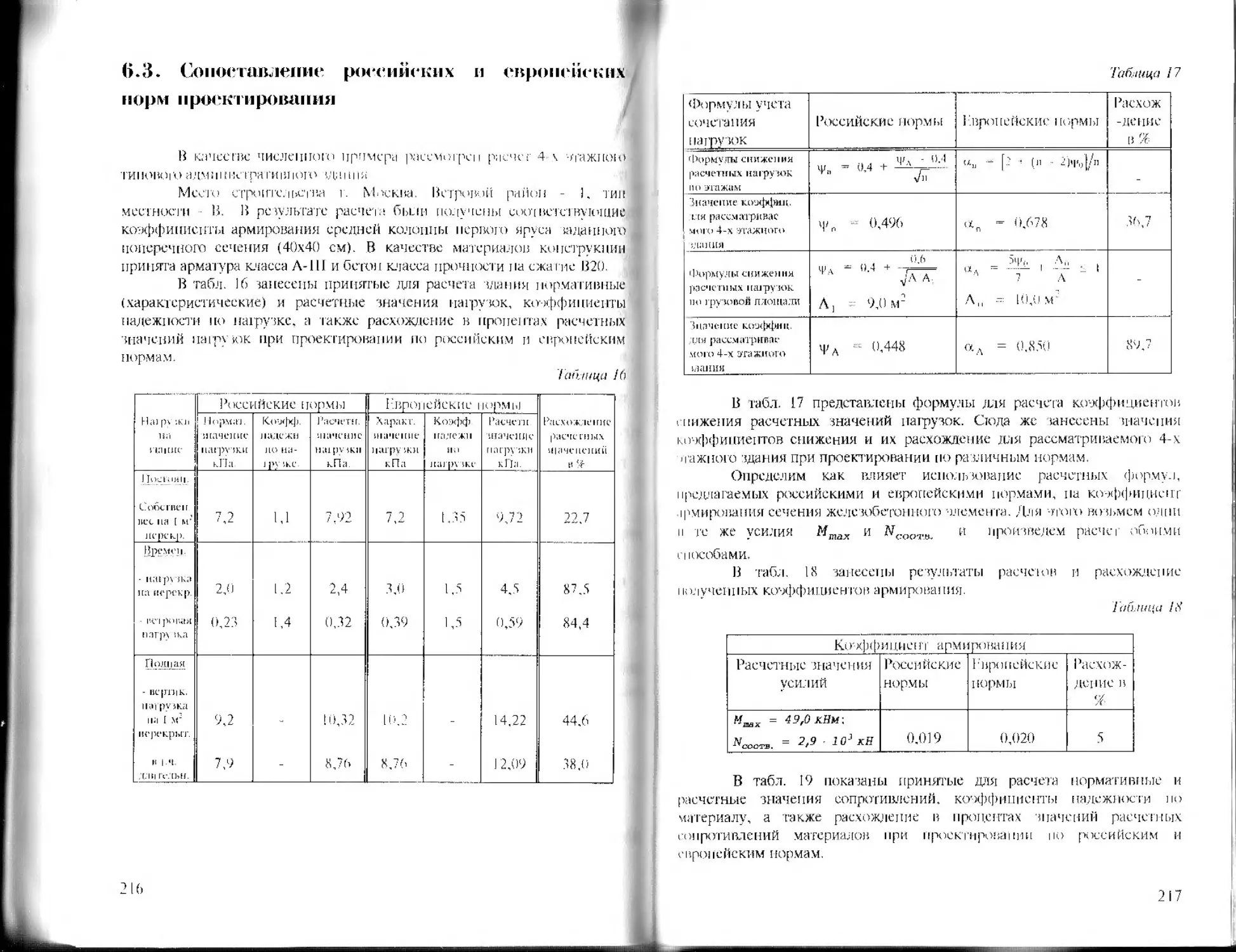
6.3. Сопоставление российских и европейских норм
проектирования ................................... 216
6.4. Вероятностный расчет железобетонного
каркасного здания ................................ 219
Глава 7. Новые расчетные требования проектирования ...... 230
7.1. Общие замечания ............................. 230
7.2. Концепция нормирования и стандартизации
требовании к строительным конструкциям ........... 234
7.3. Характеристики вероятностной модели
работы конструкции ............................... 236
7.4. Выбор и формирование нормативных
надежностных требований .......................... 238
7.5. Нормативные показатели надежности и их
целесообразные значения .......................... 241
Литература ........................................ 247
Приложение I. Рекомендации по выбору вероятностных моделей
климатических и технологических нагрузок .............. 254
1.1. Статистическое обоснование моделей временных
нагрузок и воздействий ....................... 254
1.2. Сглаживание статистических данных ........... 265
Литература ....................................... 274
4
Приложение II. Асимптотическая теория
экстремальных значений ............................... 274
II. 1. Цель теории экстремальных значений ....... 274
II.2. Математическая модель. Точные распределения
экстремальных значений .......................... 276
II.3. Асимптотические распределения
экстремальных значений случайных величин ........ 282
11.3.1. Предельные теоремы для экстремумов ...... 283
II.3.2. Асимптотические распределения экстремумов. 288
П.З.З. Об эквивалентности функций
на "хвостах" распределений ................. 292
II.4. Заключение ................................ 300
Литература ....................................... 301
TABLE OF CONTENTS
Introduction ....................................................................................... 8
Chapter 1. Probabilistic base of modern codes
of design and test control........................................................................ 19
1.1. Probabilistic analysis of the limit state
design method ................................................................. 19
1.2. Codes of design and reliability of structures ..................................... 2'7
1.3. Statistic control of carring opacity ............................................. 35
1.4. Bayes approach in the analysis of mechanical qualities
of laminated steel in sample control .......................................... 44
Chapter 2. Probabilistic models of climatic and
technological loads ................................................................................. 47
2.1. Classification of loads and their combinations ..................................... 47
2.2. Snow loads ....................................................................... 57
2.3. Wind loads ......................................................................... 72
2.4. Temperature and climatic actions ................................................... 87
2.5. Loads due to occupancy in buildings ................................................ 95
2.6. Loads due to weight of structures ................................................. 102
5
Chapter 3. .Methods of analysis of failure probability ............................ 119
? j General observations ................................................................ 119
^2. Two moments method .................................................................. 121
? 3 "Hot points” method ................................................................. 125
3 4. Statistic simulation method...................................................... 136
j у Monte-Carlo method .................................................................. 144
3 d Monte-Carlo method modification with stratified
samples modelling .......................................................... 149
Chapter 4. Reliability of eccentric compressed and
compressed bent bars .............................................................................. 155
4 Areas of survival ..................................................................... 155
4 2. Failure probability of eccentric compressed steel bars ............................. 160
4 3. Failure probability of compressed bent steel bars .................................. 166
4 4. Probabilistic method for determination of
loads combination facto...................................................... 171
4 у Probabilistic method for calculation of eccentric compres-
sed bars with different eccentricities ................................ 176
4 у Reliability analysis for eccentric compressed
reinforced-concrete elements ............................................................. 187
Chapter 5. Some questions about reliability of bar systems .................................... 178
j j. Jn-series connection of elements ....................................................178
5 2. Parallel connection of elements .................................................... 182
у 3 Probabilistic method of limit equilibrium ........................................... 187
Chapter 6. Reliability of reinforced-concrete framework
building design^ according to Russian and European codes .................. 200
6 j. Preliminary notes................................................................. 200
2 . Design of reinforced-concrete frame, building
according to Russian and European codes ............................................... 202
$ 3. Comparison of Russian and European design codes ................................... 216
5 4. Probabilistic design of reinforced-concrete frame
building.................................................................... 220
Chapter 7. New procedures of designing ................................................ 231
7 /. General notes ...................................................................... 231
7 2. Conception of codification and standardization
of structural procedures .............................................. 235
7 3. Characteristics of probabilistic models of structures .............................. 236
у 4. Choice and formation of reliability codes .......................................... 239
7,5. Code factors of reliability and their expedient values ............................. 242
Literature ...................•.................................................................... %48
6
Appendix I. Recommendations for the choice of probabilistic
models of loads ............................................................ 254
1.1. Statistic base for models of temporal loads and actions .... 254
1.2. Smoothing of statistic data .................................. 265
Literature ........................................................ 273
Appendix II. Asymptomatic theory of extreme values ............................ 274
II. I. Purpose of extreme values theory ........................... 274
11.2. Mathematical model. Exact distributions of extreme val.... 276
11.3. Asymptomatic distributions of extreme random values ...... 282
3.I. Limit theorems for extremes ......................... 283
3.2. Some asymptomatic distributions of extremes ....... 288
3.3. Equivalence of functions on "tails" of
distributions ............................................. 292
11.4. Conclusion ................................................. 300
Literature ........................................................ 301
7
INTRODUCTION
ПРЕДИСЛОВИЕ
The conduct of building
structures in course of opera-
tion is described as depending on
the factors of random nature.
Construction materials (steel,
concrete, reinforced armature)
possess properties of statistic
variability. Loads on structures
represent random processes un-
folding during a certain period
of time.
Modern codes of prac-
tice for building structures take
into account probabilistic natu-
re of loads and of earring capa-
city of constructions only on the
level of initial data treatment.
Limit slate design method used
in codes of design is semipro-
babilistic, and structure relia-
bility is ensured by partial coef-
ficients - coefficients of relia-
bility for different loads and
materials, model coefficients,
coefficients of liability, whose
values have no sufficient theore-
tical and experimental basis.
building structures de-
sign reflecting their real con-
duct in course of operation
should be totally based on the
theory of reliability faking into
account probabilistic methods
which give a more unbiassed
evaluation of the structure and
of its fillingness to the expected
exploitation
Theory of reliability
methods give a theoretical foun-
dation in order to properly find
and organize necessary
Поведение строительных кон-
струкций в эксплуатации описыва-
ется факторами случайной природы.
Статистической изменчивостью об-
ладают свойства консгрукциошпах
материалов (прокат, бетон, стальная
арматура). Действующие нагрузки
на сооружения предсгавляют собой
случайные процессы, развертываю-
щиеся во времени.
Современные нормы проекти-
рования строительных конструкций
учитывают вероятностный характер
нагрузок и несущей способности
конструкций только в части обра-
ботки исходных данных. Метод пре-
дельных состояний, заложенный в
нормах проектирования, является
полувероятпостным, и надежность
конструкций при проектировании
обеспечивается на основе исполь-
зования частных коэффициентов за-
пасов - коэффициентов надежности
по нагрузкам, по материалам, коэф-
фициентов условий работы, коэффи-
циентов надежности по назначению,
величшпл которых не имеют доста-
точное теоретическое и эксперимен-
тальное обоснование.
Расчет строительных конст-
рукций, отражающий их реальное
поведение в эксплуатации, должен в
полной мере базироваться па теории
надежности, основанной па веро-
ятностных методах, которые позво-
ляют дать более объективную оцен-
ку конструкции о се пригодности к
нормальной эксплуатации.
Методы теории надежности
дают теоретическую основу для
правильной организации сбора и
обработки статистических данных,
относящихся к воздействиям на
8
statistical data dealing with ac-
tions on building constructions,
characteristics of materials and
structures and other design pa-
rameters The se methods most
correctly reflect the random
nature of basic design values
and the interconnection between
external actions and the
strength of the structures.
If in the process of
designing and building a neces-
sary level of reliability of the
structures is attained on the
whole, this level then is realized
in course of exploitation, that is
the building possesses the capa-
city to fulfil its functions during
the established lime of service,
usually named "reliability". If
the building cannot fulfil its
/unctions, this stale is called
"failure". So, reliability is mea-
sured in probability of nonfailure
work during the established time
of service.
Probabilistic approach is
conditioned by the fad that all
strength, geometric and defor-
mation characteristics of struc-
tures as, well as all actions on
them are random values or ran-
dom processes..
Appropriate levels of
reliability are achieved by means
of various expenses in building a
construction and lead to
different numbers of failure tn
the process of exploitation and
i orrespondingly to different le-
vels of damage. To reduce
expenses in building a const-
ruction one is forced to lower
the reliability, and to reduce
expenses in exploitation this
сооружения, характеристикам мате-
риалов и конструкций из них и
других расчетных параметров. Эти
методы наиболее правильно отра-
жают случайную природу основных
расчетных величин и взаимосвязь
между внешними воздействиями и
прочностью конструкций.
Если в результате проектиро-
вания, изготовления и возведения
формируется уровень надежности
конструкций или объектов в целом,
то во время эксплуатации этот
уровень реализуется, т.е. прояв-
ляется способность объекта выпол-
нять свои функции в течение уста-
новленною срока службы, которую
принято называть "надежностью".
Реализация состояний объекта, при
которых он не сможет выполнять
свои функции, называется "озка-
зом". Мерой надежности является
вероятность безотказной работы за
заданный срок службы.
Вероятностный подход обус-
ловлен гем, что все прочностью,
геометрические и деформационные
характеристики конструкций, а так-
же вес воздействия на них пред-
ставляют собой случайные величины
или случайные процессы.
Соответствующие уровни
надежности достигаются за счет
различных затрат на создание
конструкции и приводят к неоди-
наковому числу отказов в процессе
эксплуатации и соответственно к
различным уровням ущерба. Для
снижения затрат на создание соору-
жения следует уменьшить надеж-
ность, а для снижения затрат на
эксплуатацию необходимо эту
надежность повысить.
9
reliability has to be raised
A reasonable compromise
to these conflicting require-
ments is found in a certain
"expedient level of reliability",
as close as possible io an
"optimal" level, which in prac-
tice is hardly definable. In this
case the purpose of designing
becomes the creation of a
building structure with a neces-
sary expedient level of relia-
bility. that is with a definite risk
of failure. Such a level must be
established by codes of struc-
tural design.
The main area of prac-
tical application of reliability
theory in building structures are
the methods of codes making
procedures of design and of tes-
ting in process of manufactu-
ring.
The development of com-
puter technics allows to change
the approach in probabilistic
design and to abandon traditio-
nal statistic methods of structu-
ral mechanics.
Modern quick computers
give the possibility to automate
complex calculations, which al-
lows Io use, in course of cal-
culating failure probabilities,
numerical methods (method of
statistic simulation and others).
Their most valuable characteris-
tics are simplicity, absence of
any limitations concerning the
nature of initial statistic infor-
mation, as well as the possibi-
lity of using real data (measures
of loads, experimental values of
physical and geometrical para-
meters of the structure etc.)
Разумным удовлетворением
этих противоречивых требований
является некий "целесообразный
уровень надежности", по возмож-
ности близкий к практически дос-
таточно трудноопределимому ее
"оптимальному" уровню. Тогда
целью проектирования является соз-
дание строительной конструкции с
необходимым целесообразным уров-
нем надежности, т.е. с определен-
ным заданным риском отказа. Такой
уровень должен устанавливаться
нормами проектирования.
Основная область практичес-
кого применения теории надежности
строительных конструкций - методы
нормирования правил расчета при
проектировании и контроле при
изготовлег гии конструкций.
Развитие вычислительной тех-
ники позволяет изменить подход к
вероятностным расчетам и отка-
заться от традиционных статис-
тических методов строительной
механики.
Современные быстродействую-
щие ЭВМ дают возможность авто-
матизировать сложные вычисления,
что позволяет использовать для
вычисления вероятности отказа
численные методы (метод статис-
тического моделирования и .др.),
наиболее ценными качествами кото-
рых является трос гота, отсутствие
каких-либо ограничений на харак-
тер исходной статистической инфор-
мации, а также возможность исполь-
зования реальных данных (замеры
нагрузок, экспериментально полу-
ченные значения физических и
геометрических параметров кон-
струкции и т.п.) без предва-
рительного создания теоретических
вероятностных моделей стохасти-
ческих факторов, учитываемых в
10
without making preliminary
theoretical probabilistic models
of stochastic factors taken into
л count in calculation. This
opens I ar g e opportunities to use
probabilistic methods of design.
The statistic nature of the
uifetу factor was first shown by
Mayer in his work published in
1926 /96/ where the author,
instead of design on permissible
vi r esses, suggested to use
methods of probabilities theory
lor the choice of parameter va-
lues. In 1929 /77/ N.F.
Ilotsialov, taking into account
the randomness of basic
parameters, suggested to make
viriicttiral design on the base of
optimal sums of both capita!
expenses and probabilities of
"defective deviations” and losses
bom accidents, that is the notion
of p robab il ist ic opt in li: at ion was
already discussed in this book.
liefore these works ap-
peared. in the engineering prac-
tice it HYi.y usually considered
that the safety factor way a par-
ticular number with exceptional
properties provided by the natu-
re It HYi.y assumed that its exact
observance prescribed by its nu-
merical value ensured the
reliability of structures, and on
the other hand even its smallest
diminution jeopardized the
•aructtire. Nevertheless, for a
aides calculator the safety fac-
tor always remained a genera-
lized reflection of security mea-
sures ensuring at large a satis-
hutory level of reliability.
The works of N.S. Sire-
letsky /67. 68/, as well as of
расчете. Эго открывает широкие
возможности использования вероят-
ностных методов в практике проек-
тирования.
Впервые статистическая при-
рода коэффициента запаса проч-
ности была показана в опублико-
ванной в 1926 г. работе Maiiqia /96/,
в которой автор вместо расчета по
допускаемым напряжениям предло-
жил для выбора значений пара-
метров, вводимых в расчет, исполь-
зовать методы теории вероятностей.
В 1929 г. в ПИ Н.Ф. Хоциалов
предложил, принимая во внимание
изменчивость основных параметров,
вести проектирование конструкций,
исходя из оптимальной суммы как
капитальных затрат, гак и вероят-
ности "дефектных уклонений" и
суммы убытков от аварий, г.е. в
этой работе уже обсуждается идея
вероятностной оптимизации.
До появления этих работ в
инженерной практике обычно счи-
талось, что коэффициент запаса
является особенным числом, наде-
ленным природой какими-то исклю-
чительными свойствами. Предпола-
галось, что точное его соблюдение,
предписанное его численным значе-
нием, обеспечивает надежность
конструкций, в то время как даже
незначительное его преуменьшение
влечет за собой опасность дюг
сооружения. Однако, для соста-
вителя норм расчета коэффициент
запаса всегда оставался обобщен-
ным отражением мер предосто-
рожности, обеспечивающих в целом
удовлетворительный ypoaeiп, надеж-
ности.
Разработке и введению в прак-
V.A. Baldin /2/, A.A. Gvozdev
/17, 18/, V.M. Keldysh and 1.1.
Goldenblat /27/ contributed to
the elaboration and practical
application of the limit state
design method.
Analysis using limit state
design method presently gained
the recognition both in our
country and abroad /94/. The
foundation of elaborated in re-
cent years Eurocodes is the limit
state design method. Code ma-
king procedures based on the li-
mit state design method promo-
ted the creation of reliability
coefficients system in which sta-
tistic data are used in either ca-
se and the design is made in
deterministic form.
General basic questions
concerning the application of
probabilistic methods to the
analysis of reliability of structu-
res were developed in fundamen-
tal researches by К 1'. Bolotin
/10-12/and A.11. Rzanilsin /55/.
Substantial contributions
to the methods of the reliability
of structural design and to the
selling of the basis for the code
making procedures of design
parameters are made in the re-
searches of A.l. Driving /24/,
B.l. Snarskis/57, 61-62/, U.D.
Suhov /69-71/ N.N. Skladnev
/60/, S.A. Timashev /73-74/,
VP. Chirkov /79/ A.P. Kudzis
/31-32/ A.S. Lychev /37/ and
others.
Progressive development
of code procedures methods in
building constructions on the
base of probabilistic approach
тику проектирования конструкции
метода предельных состояний спо-
собствовали труды Н.С. Стрелец-
кого /67, 68/, а также работы В.А.
Балдина /2/, А.А. Гвоздева /17, 18/,
В.М. Келдыша и И.И. Гольденблата
/27/.
Расчет по предельным сос-
тояниям завоевал в настоящее время
широкое признание как у нас в
стране, гак и за рубежом /94/. В
основе разработанных за последние
годы Еврокодов лежит метод
предельных состояний. Процедуры
нормирования, основанные на
методе предельных состоянии,
привели к системе коэффициентов
надежности, когда в той или иной
мерс используются статистические
данные, а расчет ведется в
детерминированной форме.
Общие принципиальные воп-
росы применения вероятностных
методов к анализу надежности
сооружений получили развитие в
фунда м витальны х исследования х
В.В. Болотина /10-12/ и А.Р.
Ржаницына /55/.
Существенный вклад в совер-
шенствование методов расчета
надежности конструкций и обос-
нование процедур нормирования
расчетных параметров внесли
исследования А.Я. Дривинга /24/,
Б.И. Снарскиса /57, 61-62/, Ю.Д.
Сухова /69-71/, Н.Н. Складнева /60/,
С.А. Тимашсва ПЗ-141, В.П. Чиркова
/79/, А.П. Кудзиса /31-32/, А.С.
Льгчева /37/и др.
Совершенствование методики
нормирования расчета строи-
тельных конструкций па основе
вероятностного подхода поставило
вопрос о необходимости глубокого
изучения нагрузок, действующих на
сооружения. Серьезный вклад в
12
made necessary a profound stu-
dy of loads acting on structures.
Serious contributions to the re-
search of loads, of their combi-
nations and of code procedures
related with them are made in
ihe studies by M.F Barnstein
/(/, A. A. Bai /7/, I.A. Belyshev
/8-9/, A.P. Bulychev /24/, L. V.
Kle-pikov /28/, K.S. Lossilskaia
/75/. V.A. Otstavnov, L.S.
Rosenberg /41/, V.N. Pischikov
/47/ and others.
Researches made by V. V.
Bolotin /13/, K.S. Lossilskaia
/35/ A.R. Rzanitsin and U.D.
Suhov /58/, El. Fedorov /75/
V.N. Pischikov /47/ and others
•mbstantially contributed to the
volution of combinated loads
problem in structural design.
Foreign researchers also
obtained important results in the
theory of building structures
reliability. In this respect we can
draw the attention to the studies
made by Ditlevcen /83, 84/
A.M. Freudental /90/ C.A.
< 'ornell /82/ Hasofer and Lind
/91/. R. Rack wit z /100/ and
others. Books by G. Augusti, A.
Bar at fa, F. Casciati /2/, K.
Kapur, L. Lamberson /26/ F.
Borges, M. Castaneta /89/ J.
Murzevski /99/, G. Spaethe /80/
also should be mentioned.
Scientific elabor at ions
determined the level of design
. odijications. Regulations ope-
rating in the Russian codes pro-
cedures system and defining the
rules of structural design on the
base of limit state design met-
hod developed to a large degree
spontaneously, so, because of
исследование нагрузок, учета их
сочетаний и обоснование процедур
их нормирования внесен работами
М.Ф. Барштейна /6/, А.А. Бать ГН,
И.А. Белышепа /8-9/, А.П. Булычева
/24/, Л.В, Кдепикова/28/, К.С.
Лосицкой /75/, В. А. Отставнова,
Л.С. Розенберга /41/, В.Н. Писчи-
кова /47/ и др.
Исследования В.В. Болотина
/13/, К.С. Лосицкой /35/, А.Р.
Ржаницына и Ю.Д. Сухова /58/, В.И.
Федорова /75/, В.Н. Писчикова /47/ и
др. существенно продвинули реше-
ние проблемы учета сочетания
назрузок в расчетах конструкций.
За рубежом получены также
значительные результаты в теории
надежности строительных конструк-
ций. К ним относятся исследования
Дитлевсена /83, 84/, А.М. Фрей-
денталя /90/, Корнелла /82/,
Хасофера и Линда /91/, Р. Раквитца
/100/ и др. Следует также отметить
книги Г. Аугуста, Баратга, Каши-
ати/2/, Капура К., Ламберсона /26/,
Ф. Боржеса, М. Кастанеты /89/, И.
Мужевского /99/, Г. Шпете /80/.
Научные разработки опреде-
лили уровень нормирования рас-
четов. Заложенные в системе
СНиПов принципы нормирования,
регламентирующие правила рас-
чета строительных конструкций на
основе метода предельных состо-
яний, развивались в большей
степени стихийно, поэтому отсут-
ствие общей теоретической базы
приводит к тому, что конструкции
проектируют с уровнем надежности,
который колеблется в широких
13
spontaneously, so, because of
the absence of a general theore-
tical basis, structures are de-
signed with a level of reliability
oscillating within a broad range.
Codes development on the
base of reliability theory should
lead to a necessary inclusion of
indications for the choice of the
required level of reliability ta-
king into account the optimiza-
tion of expenses. Codifications
should also contain indications
about the means to determine
design parameters of structures
with defined level of reliability.
it is essential to formu-
late a probabilistic methodology
of codes design rules with gene-
ra! algorithms for the determi-
nation of designed parameters
of different building construc-
tions.
The book offered to the
attention of the reader consists
of seven chaptersand two appen-
dices.
The first chapter con-
tains probabilistic analysis of
the limit slate design method
and expounds test control rules.
It is shown that with the appl-
ication of the limit stale design
method levels of structural relia-
bility implying the same requi-
red liability can differ by several
dozens of times. It is concluded
that the existing basic reliabilis-
lic requirements consisting in
the comparison of design values
should be replaced by the com-
parison of design probability of
failure with the codified expe-
dient value of this probability.
The methodology of statistic
который колеблется в широки
пределах.
Совершенствование норм на
основе теории надежности должно
привести к необходимости включе-
ния в них указаний по выбору
необходимого уровня надежности с
учетом оптимизации затрат.
В нормативных требованиях
должны быть также указания о
способах определения проектных
параметров конструкций с задан-
ным уровнем надежности
Н еоб ходим о сфор мулир оа а гь
вероятностную методику норми-
рования правил расчета, содер-
жащую общие алгоритмы опреде-
ления расчетных параметров
различных конструкций.
Предлагаемая вниманию чита
tcjdi книга состоит из семи глав I
двух приложений.
В первой главе содержится
вероятностный анализ метода пре-
дельных состояний, а также правил
приемочного контроля. Показано,
что уровень надежности кон-
струкций одинаковой ответствен-
ности при применении метода
предельных состояний может
отличаться в несколько десятков
раз. Сделан вывод о том, что
существующее основное надеж-
ностное требование сопоставления
расчетных значений следует заме-
нить требованием сопоставления
проектной вероятности отказа с
нормируемым целесообразным
значением этой вероятности. Здесь
же рассмотрена методика статис-
тического контроля несущей
способности индустриальных
14
pre valent industrial building
constructions is also examined.
I'he methodology establishes the
link between the value of refe-
rence load during a lest,, the
number of tested structures, the
customer's risk and the required
level of reliability during the
tests. 1‘he same chapter deals
with the Hayes approach of
laminated steel quality control.
The second chapter exa-
mines probabilistic models of
the main climatic and techno-
logical loads on buildings and
constructions. The exposition
takes into account the results of
complex researches in the field
of analysis concerning variable
structure of initial meteorolo-
gical information about climatic
actions, as well as the results of
natural examinations of loads
on ceilings in civil, public and
industrial buildings. Classifica-
tion of loads and their combina-
tions is considered. Probabilis-
tic models of snow and wind
loads, of temperature and clima-
tic actions, of technological
loads on ceilings and of weight
loads are discussed.
The third chapter is con-
secrated to modern methods of
failure probability analysis. It
deals with the method of two
moments, the method of statistic
linearization, the "hot points"
method (defined by B.I. Snars-
kis) which in foreign literature
is knowm as llasofer-Und met-
hod (method of the first ap-
proach). /1л to numerical proce-
dures of failure probability cal-
culation, the statistic simulation
сового применения. Методика
устанавливает связь между зна-
чением величины контрольной наг-
рузки при испытании, числом
испытываемых конструкций, рис-
ком заказчика и требуемым
уровнем надежности при испыта-
ниях. В этой же главе рассмотрен
байесовский подход .для контроля
качества стального проката.
В гора я глава содержит вероят-
ностные модели основных кли-
матических и технологических
нагрузок на здания и сооружения. В
ней нашли отражение результаты
комплексных исследований анализа
структуры изменчивости исходной
метеорологической информации о
климатических воздействиях, а
также результаты натурных обсле-
дований нагрузок на перекрытия в
жилых, административных и
промышленных зданиях. Рассмот-
рена классификация нагрузок и их
сочетания. Обсуждаются вероят-
ностные модели снеговых и вет-
ровых патрузок, температурных
климатических воздействий, техно-
логических нагрузок на перекрытия
зданий и нагрузок от веса
конструкций.
Третья глава посвящена сов-
ременным методам вычисления
вероятности отказа. Излагается
метод двух моментов, метод статис-
тической линеаризации, метод
горячих точек (по определению Б.И.
Снарскиса), который в зарубежной
литературе получил название мето-
да Хасофера-Линда (метода первого
приближения). Для численных
процедур вычисления вероятности
отказа в монографии рекомендуется
метод статистических испытаний,
15
method, Monte-Carlo method,
is recommended, as well as its
modifications with modelling of
stratified samples.
The forth chapter is con-
secrated to the analysis of relia-
bility of one of the most impo-
rtant element of bar systems -
eccentric compressed or com-
pressed bent steel and reinfor-
ced-concrete bars. Practical
applications of probabilistic
methods in structural design are
illustrated, as a rule, by simple
examples (tension, straight ben-
ding). As to the main element of
bar systems - eccentric com-
pressed bars - a research of
carring capacity in probabilistic
version is made and algorithms
of design are. proposed.
The fifth chapter deals
with some questions related to
the reliability of bar systems
and gives the exposition of the
probabilistic method of limit
equilibrium. The use of the
methods of linear programming
(simplex method) and of
statistic simulations allowed to
examine the randomness of limit
carring capacity in multiele-
ment systems.
The sixth chapter con-
tains a comparative analysis of
reinforced-concrete frame buil-
ding reliability designed accor-
ding Russian and European
codes.
New structural design re-
quirements in the conditions of
transition to market economics
imply an alteration in code
making procedures. The seventh
chapter is consecrated to the
метод Монте-Карло, а также его
модификация с моделированием
стратифшщрова иных выбор ок.
Анализу надежности одного
из основных элементов стержневых
систем виеценгрснно-сжатого или
сжато-изогнутого стального и желе-
зобетонного стержня посвящена
четвертая глава. Практическое
применение вероятностных методов
в расчетах конструкций иллюст-
рируется, как правило, простыми
примерами (растяжение, чистый
изгиб). Для основного элемента
стержневых систем, внецентренно-
сжатого стержня, прове-дено
исследование несущей способности
в вероятностной постановке и
предложены алгоритмы расчета.
В пятой главе рассмотрены
некоторые вопросы надежности
стержневых систем и дано изло-
жение вероятностного метода пре-
дельного равновесия. Исполь-
зование методов линейного про-
граммирования и статистических
испытаний позволило исследовать
изменчивость предельной несущей
способности многоэлементных сис-
тем.
В шестой главе содержится
сопоставигельньгй анализ надеж-
ности железобетонного каркасного
здания проектируемого по европей-
ским и российским нормам.
Новые расчетные требования к
проектированию сооружений в усло-
виях перехода к рыночной эконо-
мике требует изменения правил
нормирования расчетов конструк-
ций. Формулированию новых
процедур нормирование посвящена
седа мая глава.
16
chapter is consecrated to the
formulation of new code proce-
dures. A concept of codification
and standardization is here
expounded.
Characteristics of proba-
bilistic model of a structure,
procedures of reliable choice and
codified indexes of reliability are
riven. Facts exposed in this
chapter are results of many
rears of researches and dis-
cussions about l he ways and the
methods to promote new rules of
codification. Conceptual elabo-
rations by B.l. Snarskis and
t!.D. Suhov should be here
mentioned.
The book includes two
appendices. The first of them
contains recommendations about
the choice of probabilistic
models of loads and actions,
the second gives a brief expo-
rt lion of extreme values theory.
The first appendix has a
reference character. It contains
data about statistic foundation
of models with different types of
actions. The solution of many
problems concerning the
vtrenglh and stability requires
knowledge of maximum values
in process of loading.
The second appendix
acquaints the reader with
important results obtained in the
theory of extreme values. The
void of extreme values theory is
pointed out, as well as their
exact distributions and asym-
ptomatic assignments of random
extreme values.
In this , book the author
has restricted his goals to the
Изложены концепция норми-
рования и стандартизация
требований к конструкциям. При-
ведены характеристики вероят-
ностной модели работы конст-
рукции, процедуры выбора
надежностных требований и
нормативные показатели надеж-
ности. Представленным в этой
главе результатам предшествовали
многолетние исследования и
дискуссии о путях и методах
перехода к новым правилам нор-
мирования. Здесь необходимо отме-
тить концептуальные разработки
Б.И. Снарскиса и Ю.Д. Сухова.
В книгу включены два при-
ложения. В первом из них
содержатся рекомендации по выбору
вероятностных моделей нагрузок и
воздействий, а второе содержит
краткое изложение теории экстре-
мальных значений.
Первое приложение носит
справочный характер. Оно содержит
материалы по статистическому
обоснованию моделей различных
видов воздействий. В решении
многих задач прочности и устой-
чивости необходимо иметь инфор-
мацию о максимумах процессов
нагружения.
Второе приложение знакомит
читателя с важными результатами,
полученными в теории экстремаль-
ных значений. Указана цель теории
экстремальных значений, и,х точные
распределения, а также асимпто-
тические распределения экстремаль-
ных значений случайных величин.
При подготовке книги автор
ограничился рассмотрением только
статических задач вероятностного
17
examination of mere statistic
purposes of probabilistic design
of carring structures in indus-
trial and civil buildings.
The book is based on
elaborations made by the
author, his post-graduates and
his assistants in the laboratory
of structural reliability of
TSN11SK (the central research
institute for building struc-
tures).
To all of them the author
expresses his profound gratitude.
расчета несущих конструкций про
мышленных и гражданских зданий.
В основу книги положены раз
работки автора, его аспирантов, ;
также сотрудников лабораторш
прочности и надежности со ору же
ний ЦНИИСКа.
Всем им автор выражает глу-
бокую благодарность.
18
Глава /
ВЕРОЯТНОСТНЫЕ ОСНОВЫ СОВРЕМЕННЫХ
НОРМ ПРОЕКТИРОВАНИЯ И ПРИЕМОЧ
КОГО КОНТРОЛЯ
1.1. Вероятностный анализ метода предельных
состояний
Проектирование конструкций - это процесс принятия решения,
при котором должны учитываться различные неопределенности для
достижения приемлемой вероятности отказа. Приемлемые вероятности
различны для различных предельных состояний, так как последствия их
реализации различны.
Для вероятностных расчетов прежде всего необходимо иметь
детерминированную зависимость между характеристиками конструкции и
ее несущей способности.
Состояние конструкции в условиях эксплуатации может быть
охарактеризовано конечным числом независимых параметров /1/. Часть
этих параметров характеризуют нагрузки, другое - прочность материалов,
третьи - отклонение реальных условий работы конструкции от принятой
расчетной схемы. Уравнение границы области допустимых состояний
конструкции представляется в виде
д(Х1, х2,...,хп) = о
(1)
где
д(х17 х2, ...) - функция работоспособности.
Все расчетные величины можно разделить на две основные
группы. Первая группа включает в себя характеристики, относящиеся к
свойствам самой конструкции , другая включает в себя характеристики
внешних воздействий. Тогда условие нспревышения границы области
допустимых состояний конструкций может определяться как выполнение
предельного неравенства
19
?(х„х2,....хп) =
= «(x1,x2,....xm)-Q (хт.1,хтФ2..х„)>0
или
д = R - Q > О
Здесь и далее (”) обозначается случайная величина.
В приложении к задачам расчета на прочность:
Q - наибольшее значение нагрузочного эффекта - усилия илт
напряжения в конструкции, выраженные через внешнюю нагрузку (т.е
задача опреде-ления напряженного состояния предполагается решенной);
Я - несущая способность, выраженная в тех же единицах и отвечающш
предельному состоянию конструкции по прочности (предел текучести
предел прочности, пластический момент1);
д - характеристика, которую А.Р. Ржаницын назвал резервом прочности.
В общем случае усилия и несущая способность являютш
случайными функциями времени, но в рассматриваемой постановки
С и К считаются случайными величинами, с заданными законамг
распределения. Следует также отметить, что для получения более просты?
результатов условие (2) записано для того случая, когда Q и Я
являются скалярными функциями, хотя во многих случаях необходима
рассматривать соответствующие вектор-функции.
Если принять, что вероятность выполнения неравенства (2) ест!
вероятность неразрушения конструкции то вероятность разрушения -
отказа (превышения 1раницы области допустимых состояний;
определяется выражением
о
Pf = f P?(?)d?
(3)
где
рд (?) ' распределение плотности резерва прочности.
Плотность распределения резерва прочности можно определить,
используя формулу определяющую плотность распределения суммь
случайных величин. При взаимонезавиеимости Q и R
20
р9(д) = J ря(? + o)pq(q)^q
(4)
где
p?(gr) - плотность распределения несущей способности;
Ри(д + (?) - та же функция, но с аргументом (д, Q);
ро(О) - плотность распределения нагрузочного эффекта.
Подставляя (4) в (3), можно записать формулу для определения
вероятности безотказной работы - вероятности неразрушения
со
Рв = 1 - J Рр(О) Ш dQ (5)
или
Ps = Jp^JP^dR
-со
где
PR (О) , Pq (R) - функция распределения несущей способности
и нагрузочного эффекта.
Такой же подход можно использовать и при проектировании
конструкций по жесткое™ (вторая группа предельных состояний). В этом
случае под мерой надежности понимается вероятность того, что
максимальное перемещение w не превысит заданного, т.е. уравнение (5)
примет вид
Ра = J Р М dw , (6)
-00
11ри любых законах распределения Q и R
д - R - Q ; sq = ^в2я + з£ (7)
21
Здесь, как всюду далее, чертой обозначено математическое ожидание, а
Si - стандартное отклонение. Число стандартов s9 укладывающихся в
интервале от д = 0 до д - д , Л.Р. Ржаницын называет характерно-;
тикой безопасности. В зарубежной литературе используются термин
“индекс надежности”. Б.Й. Снарскис использует термин “дальность отка-
за”. Мы будем придерживаться термина, введенного Д.Р. Ржаницыным
д = к- g
s4 fii + Sp
(8)
Вероятность отказа представляет заштрихованную площадь на
рис. 1, где изображена плотность распределения резерва прочности.
Рис. 1. Плотность
распределения
случайной величины
Соотношение между вероятностью отказа Pf и характерис-
тикой безопасности 0 может быть проиллюстрировано, если предполо-
жить, что скалярные функции Q и R подчиняются нормальным
законам распределения /49/.
Вероятность отказа можно выразить в виде
1 °
Pf = Р(д < 0) = ---------т= J ехр
Sg V ^71 -эд
(9)
2
2
Тогда
pf = 2 ~
где
22
I Р (' v2\
Ф (₽) = -7== .( exp - — dx
\ 2ti о \ )
(10)
Ф (р) - интеграл вероятности Гаусса.
Данные таблицы 1 дают представление об изменении вероятности
нказа в зависимости от изменения характеристики безопасности.
Таблица 1
2,25 3,25 3,75 4,25 4,75 5,25
р. 1(Г2 КГ’ К)'4 К)'5 Ю'6 КГ’
На рис. 2 представлен график зависимости вероятности безот-
I. а 1ПОЙ работы Ps от р.
Рис. 2. Зависимость вероятное<
ш неразрушения от |)
Вместо резерва прочности возможно также ввести
(II)
Вероятность отказа при атом определяется формулой
(12)
Выражение (12) оказывается удобным, когда нагрузочный эффект Q и
Ид ущая способность R подчиняются логнормальному распределению.
23
Характеристика безопасности вычисляется при этом по формуле
(13)
где
vR = , vR = -=• - коэффициенты вариации несущей
способности и нагрузочного эффекта.
Полезной будет геометрическая интерпретация характеристик
безопасности, приведенная на рис. 3.
Рис. 3. Граница области
допустимых состояний
R - Q = О
Если усилие и несущая способность подчинены нормальном)
распределению, то изображенные на рис. 3 линии pRQ(R, (?) = const
представляют собой эллипсы.
В координатах q0 = Q/sR, г0 = R/sr эллипсы переходят f
окружности (рис. 4) и соответственным образом изменяется наклог
прямой, ограничивающей область допустимых состояний.
Если ввести нормированные случайные величины
г = (я - r)/sr , q = (с - q)/sq , (14)
то начало координат сместится в центр окружностей (рис. 4).
Учитывая, что
R = rsR + Я, Q = qsq + Q (15)
и подставляя (15) в (2), можно записать:
24
д = R - Q = rsR + R - qs0 - Q
(16)
Phc. 4. Границы облает допус-
тимых состояний r0 - д = О
Граница области допустимых состояний определяется уравнением
rsj? - gsQ + [R - Q) = О
(17)
чем меньше расстояние от прямой, описываемой уравнением (17), до
начала координат (г = д = 0) на рис. 4, тем больше вероятность
отказа Р{ . Из простых геометрических соображений вытекает, что
кратчайшее расстояние между началом координат и граничной линией,
равно характеристике безопасности р . Из этого следует, что р равна
длине вектора ОА, нормального граничной линии (рис. 5).
Направляющие косинусы этой нормали будут равны
cos Qq = - а0 = sQ (s2r +
Il \l/2 (18)
cos ©R = - aR = - sr/(sr + S*)'
Точку А некоторые авторы называют “расчетной” точкой. Тогда
координаты точки А в осях г; д представляют собой расчетные
значения гр и др
др = - ар Р
гР = - (Хк Р
(19)
25
Рис. 5. Характеристика безопасности
В координатах R и Q (рис. 3) координаты расчетной точки
запишутся в виде
Qp — Q c<,q Psq
Rp = R - «•« I’sr
(20)
Формулами (20) it определяются расчетные значения усилия и
несущей способности. Подставляя (18) в (20)
Qp = Q1 + s0 f>vQ/(s^ + s^f2
Согласно методу предельных состояний можно записать
QP ~ "If ^(1 +
Rp ~ ~ - Pjj v\r)
(21)
(22)
где
У/ и У,,. - коэффициенты надежности по нафузке и материалу
соответствен но.
26
В действующих нормах нормативные значения нс совпадают с
математическим ожиданием и сдвинуты ио отношению к среднему
щачению на число стандартов и . Сопоставляя (22) с (21)
7г =
1 + SR p VB/(s^+ S%
1 + Sq$ VQl(si+ S2Q
(23)
Соотношения (23) показывают как коэффициенты надежности
связаны с характеристикой безопасности и между собой.
1.2. Нормы расчета и надежность конструкций
Метод предельных состояний подвел единую идейную базу под
уже существующие надежностные требования, но не сформулировал
правил их установления. В результате многое кардинальные положения
современных норм расчета строительных конструкций не имеют общей
теоретической базы.
Невозможно найти сколько-нибудь разумного объяснения тому,
что надежность сооружений одного и того же назначения, выполненных
из различных материалов, запроектированных по действующим нормам,
оказывается различной. Более того, невозможно сказать, какой уровень
надежности требуют нормы проектирования, должен ли он быть
одинаковым для всех сооружений или различаться, и если должен
различаться, то в каких пределах и в зависимости от чего.
Существующие методы проектирования нс позволяют оценивать
надежность конструкций, и тем более проектировать их с заданным
уровнем надежности. Основным надежностным требованием этого метода
является сравнение расчетных значений нагрузочного эффекта и несущей
способности. Но предельное состояние не может определяться лишь
сопоставлением этих расчетных значений. Оно может наступить при
пзачениях нагрузок, меньших расчетных, если реализовано
соответственно меньшее значение несущей способности.
Поэтому при нормировании надежностных требований нельзя
шраиичиться так называемым полувероятностпым подходом, как обычно
трактуется метод предельных состояний, то есть применять методы
теории вероятностей для рассмотрения каждой исходной случайной
величины в отдельности и не решать задачу надежности конструкций.
27
Полезным представляется анализ действующих норм расчета с
точки зрения надежности проектируемых по ним конструкций /51/.
Введем предположение, что при использовании методики предельных
состояний предполагается, что уровень надежности конструкций, опреде-
ляется только выбором расчетных значений нагру;юк и сопротивлений.
Из всех возможных предельных состояний, определяемых равенством
9q («J0J. ^2> • • • , anQn ) = g R (ЬЯ)
(24)
выбирается одно, соответствующее расчетным значением исходных вели-
чин, а параметры конструкции определяются из условия
9q a2Q2p, > ал(2лр) < gR (ы?р)
(25)
В (24) и (25) Qi и Qlp - случайное значение величины
нагрузки и ее расчетное значение, R и Rp случайное значение
величины сопротивления и его расчетное значение (aiQJ,bi?) -
случайные значения нагрузочного эффекта и несущей способности,
ajQjp, bRp - расчетные значения нагрузочного эффекта и несущей
способности). В какой мере выбор расчетных величин определяет
надежность можно рассмотреть при действии одной нагрузки на.
конструкцию.
В этом случае предельное состояние определяется выражением
aQ = bR
(26)
и расчетное неравенство
aQp — bRP
(27)
работы
Уровень надежности характеризуется вероятностью безотказной
Р3 - p{aQ < Ьк)
(28)
Расчетные значения Qp и Rp определяются их обеспечен-
ностями
28
pq = P(Q < QP) = *(₽0);
Pg = P(R > Rp) = ф(рв),
(29)
= Ф 2(^q) и PR - Ф J(pR) - дальность расчетного значе-
ния нагрузки и сопротивления - аналог характеристики безопасности;
dt - интеграл вероятности.
Если принять в (27) строгое равенство (идеально запроектирован-
ная конструкция) и разделить (26) на (27), то предельное состояние будет
определяться выражением
g = г
q = Q/Qp , г = R/Rp - безразмерные значения нагрузки и
сопротивления, для которых расчетные значения
gR = rp = 1 , а коэффициенты вариации и дальность расчет-
ных значений
vQfvr = = p0,pr =
Тогда
ps = P(q < г) = J Fg(x)pr(x) dx
(30)
Для проведения анализа желательно получить аналитическое
решение. Это можно сделать, приняв «данном случае для описания обеих
случайных величин логарифмически нормальный закон, учитывая то
обстоятельство, что обе эти величины по природе своей неотрицательны.
(Для проводимого здесь качественного анализа вид закона распределения
не имеет большого значения).
Интеграл (30) представляется в виде
рв = 1- «(₽)
(31)
29
где
(si? + s»)
При этом
р = In Г, со = In q .
Параметры s(l) и sp выражаются через числовые
распределения
s2a = ln(l +
Sp = In (l + V2).
характеристики
(32)
При коэффициенте вариации v < 0,4
In (l + ~ v2
тогда
Su, = Vq i Sp ~ V(
и выражение для характеристики безопасности будет
Р = (Prvr + Pg^j/fvr + Vg)
ИЛИ
Pr% + Pq
Р =--------ГУ
(+Z2f
где
X = vr/vg
(33)
(34)
30
Отсюда следует, что характеристика безопасности зависит не
только от обеспеченностей (дальностей) расчетных значений нафузок и
сопротивлений но и от отношения их коэффициентов вариаций (рис. 6).
Рис. 6. Зависимость
характеристики безопас-
ности от отношения
коэффициентов
вариации
Можно заметить, что при детерминированной прочности
(v = % = 0)₽ = ₽д
а при детерминированной нагрузке
(v = х = 0)р = рг
Продифференцировав Р по х и приравняв производную
нулю,
d р _ М1 + ~ (р^х + Р?)х _ п П5,
«X + ~ =
следует, что так как х > ° • то Рг - РдХ = °
Таким образом, максимальная вероятность безотказной работы
достигается при X = Pr/Pg • ПРИ этом Ртах = (Pr + Pg)
При одних и тех же обеспеченностях расчетных значений
прочности и нагрузки надежность может изменяться в больших пределах
в зависимости от отношения коэффициентов вариации нафузки и
прочности, не завися при этом or значений этих коэффициентов.
Если, например, принять vr = 0,08, vg = 0,4 (х = 0,2), то
получим 0 = 2,12 , т.е. вероятность безотказной работы Ps = 0,983, а.
вероятность отказа Pf = 1 - Ps~ 0,017 , а для vr= 0,2, vg = 0,1
(х = 2,0) соответственно 0 = 3,02 и Ps = 0,9987, Ps = 0,9987 , Pf =
0,0013. То есть, вероятность отказа для этих двух случаев отличается в 13
31
раз, а это значит, что и последствия отказов будут отличаться примерно
также.
Из этого следует вывод о том, что даже необходимая унификация
обеспеченности расчетных значений различных нагрузок и
сопротивлений различных материалов, не может обеспечить единый
уровень надежности конструкций. При этом, устанавливая
обеспеченности расчетных значений, мы нс можем предсказать уровень
надежности проектируемой конструкции.
Попутно заметим, что если исходные величины распределены ио
нормальному закону, то формула (34) сохраняется в том же виде с
заменой в ней коэффициентов вариации на стандартные отклонения, т.е.
vr, vq на sr, sg ,а х = sr/sg
Формулы (33) и (34) были введены без учета коэффициента
ответственности в расчетном неравенстве. Если ввести в (27)
коэффициент ответственности, то уnaQp < Rp и aQ = R . Тогда
через безразмерные величины предельное состояние определится
выражением
1 ~
— д
Yn
(36)
Вероятность безотказной работы
S
(37)
где
1 ~
т = — q
Y в
Формула (31) преобразуется к виду
, ~ g + in уд
/ 2 7
X д/Sj- + Sg 7
= <Р)
(38)
Огсюда
32
или
P (Pr ®r+ Pg &q+ ^7л)/\/sr + Sq
(39)
PrX + Pg , 1П у „
(, 2\V2 + I 2 2\^2
(1 + X ) + Vg)
(40)
При ya = 1 (40) совпадает c (34), при этом надежность
колеблется в широких пределах в зависимости от соотношения
изменчивостей исходных величин. При у, * 1 в выражении для
характеристики безопасности появляется дополнительный член
In у n/(v^ + и, следовательно, р зависит не только от отношения
коэффициентов вариации исходных величин х , но и от их абсолютных
значений.
На рис. 7 представлены графики зависимости fl-х (кривая!),
|iq = 1,3; Pr/Pg “ 2, а также графики зависимости ул от % для тех же
шачепий [ig и рг при vg = 0,15 (кривая 2) и v = 0,35 (кривая 3).
Рис. 7.
Зависимость р отх (кривая 1);
Зависимость уп от % (кривая 2 и
3)
В таблице 2 показаны области возможных значений вероятностей
отказа Pf и характеристик безопасности р в случае обеспеченностей
расчетных значений нагрузок и сопротивлений = 1,65, = 2,56 для
разных значений уо.
33
Таблица 2
X vr (V,1 1 <)|Д Уд t У.от0,95 У„ " 0,9
Р Pf Р Pf Р Pf
0.1 0,05 0,50 0,502 1,90 0,0287 1,80 0,0359 1,69 0,0455
0,2 0.10 0,05 0,50 0,25 0,510 0,255 2,12 0,0170 2.02 1,92 0,0217 0,0274 1.9) 1,71 0.0281 0,0436
0.5 0,25 0,05 0.50 0,10 0,559 0,112 2,62 0,0044 2,53 2,16 0,0057 0.0154 2,43 1,68 0,0075 0,0465
1 0.30 0,05 0.30 0,05 0,424 0,071 2,98 0,0014 2.86 2,26 0,0021 0,0119 2,73 1.50 0,0032 0,0668
2 0,30 0,10 0,15 0,05 0,335 0,112 3,02 0,0013 2,87 2.56 0,0021 0,0052 2.71 2,08 0,0034 0,0188
3 0.30 0,15 0,10 0,05 0,316 0,158 2.95 0.0016 2.79 2.63 0.0024 0.0043 2,62 2.28 0,0044 0,0113
Из таблицы следует, что современные методы проектирования
могут приводить к абсурдным результатам, когда вероятность отказа при
ул = 0,9 оказывается меньше чем при yn = 1 .
Таким образом, проектная надежность конструкций зависит не
только от установленных уровней расчетных значений исходных величин,
но и от соотношения их изменчивостей. Анализ надежности
проектируемых конструкций в предположении их идеальной доработки с
точки зрения установления расчетных значений (унификация
обеспеченностей расчетных значений) показывает, что уровень надеж-
ности конструкций одинаковой ответственности может отличаться в
несколько десятков раз. Вполне возможны случаи, когда конструкции
сооружений уникальною класса (наиболее ответственных) оказываются
менее надежными, чем конструкции сооружений третьего класса, наиме-
нее ответственные.
Сложившуюся ситуацию в нормировании правил расчета
строительных конструкций можно охарактеризовать следующим образом
— проектировщик почти ничего нс знает о том, насколько успешно он
выполнил свою главную задачу - проектное обеспечение нормального
функционирования конструкции.
Критическое осмысливание существующих концепций основных
положений расчета и позволяет перейти к принципиально новой
методике проектирования.
В этой методике основное надежностное требование
сопоставления расчетных значений следует заменить требованием
34
сопоставления проектной вероятности отката с нормируемым
целесообразным значением этой вероятности.
1.3. Статистический контроль несущей способ-
ности
Задача обеспечения надежности тесным образом связана с
едачей статистического контроля. Метод расчета по предельным
состояниям предусматривает систематический контроль и уточнение
исходных данных. К последним относятся сопротивления материалов, их
обеспеченность, параметры распределения механических свойств. Все эти
снедения можно получить только на основе обработки представительных
данных по однородности механических характеристик.
Стандарты на материалы устанавливают определенные
требования к характеристикам строительных конструкций. Однако они не
могут полностью соответствовать значениям, принимаемым в нормах
проектирования, так как стандарты на материалы должны учитывать, что
их требования могут быт ь выполнены лишь с определенной вероятност ью
и можно говорить лишь о вероятностной оценке близости данных
требований.
На стадии заводского изготовления конструктивных элементов
необходимо производить контроль соответствия вероятности отказа этой
сталии проектной вероятности отказа. Однако этот контроль также не
может обеспечивать полного соответствия из-за выборочное™ контроля и
его несовершенства.
Основная задача заводского приемочного контроля состоит в
отбраковке партий, засоренность которых дефектной продукцией
превышает уровень, установленный нормативно-технической доку-
ментацией для нормального хода производства. При этом под
нормальным ходом производства понимают такие его состояния, когда
соблюдены основные требования технологии изготовления конструкций.
Суть приемочного статистического контроля состоит в
следующем. От партии изделий, соблюдая принцип случайности,
отбирают выборку в несколько образцов, как правило, много меньше
объема партии. Все изделия выборки подвергаются контролю, в
результате которого определяется степень пригодносги каждого изделия
для дальнейшего использования. Затем рассчитывают те или иные
обобщенные характеристики, которые сравнивают с нормативными. В
результате сравнения выносяг суждения о качестве всей партии и
решение о ее дальнейшем использовании.
35
Так, для оценки надежности индустриальных строительньд
конструкций массового изготовления обычно проводятся статически!
испытания нескольких экземпляров (выборки) из партии изготовленные
конструкций. Испытания заключаются в нагружении их согласн<
расчетной схеме возрастающей нагрузкой до появления отказ
(нарушение любою вида предельного состояния) в каждом испытании
Несущая способность конструкции R определяется величине!
испытательной нагрузки Q* при отказе /49/. Надежность коиструкцш
при испытании характеризуется вероятностью безотказней работы npi
испытаниях ^(ppj Д™ заданного значения расчетной нагрузки Q*p
Условие годности партии можно представить в виде
р4°р)= р(р > qp) -р* - (41)
здесь
Рт - требуемый уровень надежности.
Значение Qp и соответствующее значение Д, обычщ
задаются в технической документации на данный тип конструкции.
В существующих стандартах на испытания несущих конструкций
партия конструкций считается годной, если значение испытательно;
на!рузки Q" в п испытаниях больше контрольной нагрузки
й = ср;
здесь
с - R/Rp > 1 - контрольный коэффициент, определяемы!
как отношение средней прочности материала R к расчетному сопротив
лепию Rp .
Однако существующая методика оценки несущей способности ш
включает в себя связи между значениями контрольных коэффициенте!
с, числом испытываемых конструкций п риском заказчика a i
требуемым уровнем надежности при испытаниях Рл. .
Если несущая способность конструкции имеет нормально!
распределение, то вероятность (41) запишется в виде
(42)
36
iriCCIi
*(у) - Функция Лапласа;
у = - £>pj/sPj; считается известным.
Если задан требуемый уровень надежности Рт для партии,
поступившей на контроль, то квантиль v£ заданного уровня
--- 1 - Рт равен
vp„ - ^р + ф (-Рот) SQp
(43)
Вероятность безотказной работы при испытаниях конструкций па
ипрузку Q'k равна
vL ~ q\
•Р»((?х
- ф-'(рот)
(44)
Если - фиксированное значение квантиля уровня Рот,
ранное величине расчетной нагрузки Q*p , то доя < v° - Qg
. праведливо неравенство
p(<?k * vpot) - ^(<2* > vp™.)
Это неравенство удовлетворится с вероятностью 7.,
। ас
л - нижняя граница Ps (q* , вероятности безотказной
риСхяы при испытании.
Если обозначить р случайную величину, равную числу отказов
при испытаниях на контрольную нагрузку Q'k , то для заданных
чищений л, р, %, = Qp и sQ^ выражение для контрольной
1Ы) рузки получит вид
Qk > VP„ - { ф-1[р(л' Р' >)]
(45)
37
где
Р (л, р, X) < ф
Из (45) при р = 0 (как принято при испытаниях
конструкций) следует результат
О* = vp
- [ *’V2) +
(46)
где
а < (l - X) - риск заказчика.
Значение контрольной нагрузки Qk возрастает с увелич
F и 1 и уменьшается с увеличением числа испытаний п
фиксированном значении v® = Q‘p .
Вероятность приемки партии конструкций для
vL vL = (?р+ <Иро*) %
равна
Из (47) можно найти
(47)
38
X > Vp
JrW
{* Vox) +
+ ф1 a^n p Ф
(-Rjt) ’ SQp
(48)
В случае, если Q*+1 = У < Qk и Q(’+2 < х , то партия
конструкций бракуется и для тех же значений Рт, х, 1 и Qk может
быть переаттестована на меныпую расчетную нагрузку Q^1 ,
определяемую по формуле
Qp = Q\ + {<ИР <n’ *)] + Ф 2(Р-)} scP > <49>
где
р0 - число отказов р0 < р , полученное в результате испыта-
ний п конструкции на интервале | 0, Q*p I .
Дальнейшая проверка несущей способности конструкций на
расчетную нагрузку £>’ возможна при дополнительном испытании
конструкций на контрольную нагрузку Q*k [Q'p < , j) Общее
число испытаний No = п + п0 для тех же значений Рт, X, р
определится из уравнения относительно No
Pp(N0, Р, М = ф
о *1
vp~ ~ Qk
(50)
Для случая р = 0 из решения уравнения (50) следует
(51)
В качестве примера может быть рассмотрена задача определения
плана контроля партии железобетонных балок (класс бетона В25,
арматура класса А-II) для заданного числа испытываемых балок п = 3
39
и допускаемого числа отказов р = 0 на интервале изменения
испытательной нафузки (0 - .
В паспоргс на данный тип балок указан вид отказа - текучесть
продольной растянутой арматуры (расчетное сопротивление Rp -
=27,00 кН/см2). Значение расчетной нагрузки считается равным
Qp = aR = 27 кН/см2 (где: а - геометрическая характеристика).
Соответствующий расчетной нагрузке требуемый уровень вероятности
безотказной работы при испытаниях принят Рт = 0,95 и задано значение
доверительной вероятности X = 0,9 .
При назначении требуемого уровня X (риска заказчика
а = 1 - X ) должны учитываться такие факторы, как новизна разработки
данного типа конструкции, опыт эксплуатации, степень ответственности
сооружения, технология производства.
Распределение предела текучести арматуры принято по
нормальному закону sk = 2,24 кН/см2. Аналогично для расчетной
нафузки sPp = 2,24 кН/см2 значение расчетной нафузки в долях от Qp
равно 12s0p кН/см2. Тогда согласно (46) = 13,7 sQp.
Если при испытании 3-х балок > Qk - I3,7sPp , то с
вероятностью 'к ~ 0,9 справедливо = 0,05 > Q"p = 12sQ и
партия балок принимается.
Пусть Q* = 13,5sQp < Qkf, Q*2 = 14,3sQp . Согласно (48)
x = 14fisQp . Поскольку Q*2 = 14,3sQp < x = 14,6 sQ , to
партия бракуется и может’ бьпъ переаттестована согласно (49) на
расчетную нагрузку Q*p = 1 l,8sQ
Дальнейшая проверка партии на прежнюю нагрузку Qp может
быть проведена, например, для контрольной нагрузки Q'k = 13sv <
= 13,5sOp. В этом случае общий объем испытаний No ~ 8,
п = 5.
Если при дополнительных испытаниях пяти балок число отказов
р - 0 на интервале изменения нагрузки от 0 до 13sQp , то партия
будет’ принята.
Изложенная методика может быть использована при разработке
стандартов на испытания отдельных видов конструкций и материалов и
40
иля уточнения методов приемки конструкций в действующих стандартах
па испытания.
1.4. Байесовский подход в анализе обеспечен-
ности механических свойств металлопроката
Как правило контроль проката ведется по нескольким признакам
(временное сопротивление, предел текучести и т.д.). Условно рассмотрим
случай контроля по одному признаку. В основу положен байесовский
подход для кошроля качества стального проката по среднему значению
для выборок малого объема /49/ .
Для оценки вероятности проникновения некондиционного
металла к потребителю при данных результатах контрольных испытаний
используется тот факт, что каждая отдельная партия проката представляет
собой частную совокупность, принадлежащую генеральной совокупности
металла данного типоразмера и данной марки стали, произведенной за
продолжительный период на данном заводе. Таким образом, генеральная
совокупность состоит из большого числа партий (частных совокупностей).
Контролируемый признак рассматривается как случайная
величина х , характеризуемая некоторой функцией распределения.
Допускается, что при контроле очередной партии металла было
проведено л испытаний, которые показали значения контролируемого
। (ризнака
х1г х2,...,ха
Для дискретных распределений, когда число частных совокуп-
ностей невелико, P(Ai/x1, х2, . . . , согласно формуле Байеса /26/
вероятность того, что полученные результаты принадлежат i-й частной
совокупности, т.е. на. контроль предъявлена i-я партия, можно
представить в виде
P^/Xj, х2,...,х„) =
Р(Д1)Р(Х1, х2,.. . ,хв/А^
к
Хр(л1)р(хз> Х2.....Xn/Aj)
(42)
41
где
Р(Д2) - вероятность i-Й партии до контрольных испытаний;
Р(х2, х2, .... хл/А^) - вероятность получить при контроль-
ных испытаниях i-й партии результаты xlt х2, . .. , хп ;
к - число партий в генеральной совокупности.
Гак как на металлургических заводах выпускается достаточно
большое число партий, а средние значения контролируемого признака от
партии к партии изменяются непрерывно (хотя и округляются при
замерах), т.е., переходя к непрерывным распределениям, выражение (52)
следует записать в виде
р(у/х1, х2,- -’хп) =
= Р(У)Р(Х1> х2,...,х„/у) (
J Р (у)р (xi> х2,..., ха /у) dy
-со
где
р(у) и р(у/х1, х2, • • » xd) - соответствующие плотности
распределений.
Ио результаты испытаний хь х2,...,хл независимы и
поэтому
Р (хъ х2, . . . , хл/Ах) = П₽(хя/Ах) (54)
m-I
Используя (52), можно определить вероятность р(х < С/х2)|
того, что в данной партии стали, показавшей при контрольным
испытаниях результаты х}, х2, .... хп , имеется металл со значением
контролируемого признака меньше наперед заданной величины
к
Р(х < С/х;, х»...,^,) = <с) > (55)
т=1
где
р(х2 < С) - вероятность того, что в i-й партии проката
признак имеет значение меньше С.
42
Плотность распределения признака в генеральной совокупности
обозначается как р?(х) , а через р^(х) - плотность распределения
признака внутри некоторой произвольной i-й частной совокупности.
Для непрерывных распределений выражение (55) принимает вид
р(х < С/хь х2,..., х„) =
со С
= jp(y/xh x2,...,xB)j Pi(x)dxdy
С учетом выражения (53) формула (55) примет вид
р(х < C/xlt х2,..., хл) =
J Р (У)П Р {хп/у) J Р1(х) &<3у
-<ху т-1
Jp(y)flp(xm/y)^
-СО Л] 1
(56)
(57)
Изучение эмпирических данных, полученных по результатам
контрольных испытаний на растяжение показывает, что для генеральной
и частных совокупностей можно использовать нормальный закон
распределения для предела текучести, временного сопротивления разрыву
и относительного удлинения.
Если диапазон рассеяния значений дисперсий частных
совокупностей невелик, то их величина может быть принята постоянной
и равной s2. . Тогда
Рз(х) =
(58)
1
представляет собой плотность распределения вероятности контролируе-
мого признака в частной совокупности, a xi = z математическое
ожидание контролируемой характеристики в частной совокупности
рассматривается как случайная величина
43
2
(59)
Тогда (59) представляет собой плотность распределения
вероятности контролируемого признака в генеральной совокупности.
Здесь хд и s2^xgj - соответственно математическое ожидание и
дисперсия контролируемого признака в генеральной совокупности.
Предполагается, что среднее значение xi контролируемой
характеристики в частной совокупности представляет собой нормально
распределенную случайную величину z с математическим ожиданием
z = хд и дисперсией, определяемой по формуле
si - я2(х?) -
(60)
Тогда
(61)
есть плотность распределения средних значений частных совокупностей.
Используя выражения (53), (55), (57) и (58), можно получить выражение
для плотности распределения частной совокупности
Р(У/ХЪ ^...,х„) = р(у/хт,п) =
1 I” (у -
=
(62)
где
S2(xJ + S2(z)
fi2(Xz) + n2S2(z) '
s2(y)
44
Формула (57) с учетом (58), (59), (61) и (62) приобретает вид
р (х < C/xm, л) =
du dt
(63)
Это основная формула для вычисления обеспеченности С в
контролируемой партии стали, позволяющая определить вероятность
некондиционного металла.
С помощью ЭВМ получены вычисленные значения
Р (х < Cjxm, л) применительно к пределу текучести стали марки
СтЗсп (спокойная).
Р(-х<с/ля, п)
Рис. 8. Зависимость вероятности р{х < С)хтп) от среднего значения
результатов испытании хт ври различных браковочных уровнях С и
числа испытаний п
Значения х, s (x_J, s (Z.J варьировались в широком интервале
<начений, близких к экспериментальным для листовой стали. На рис. 8
45
представлена зависимость р(х < С/хт,л) от среднего значения
результатов испытаний, браковочного уровня С , числа испытаний л ,
параметров sz, sx .
Результаты вычислений позволяют сделать вывод, что при зна-
чении результатов контрольных испытаний, равных или даже несколько
превьппающих браковочный минимум С , вероятность наличия
некондиционного металла в данной партии проката может быть
достаточно велика. Так, при С~ 240 МПа и хл?= 250 МПа эта
вероятность приблизительно равна 0,15 для различных значений л.
Алгоритм оценки свойств проката основан на соотношении (63).
Приняв р(х < С/хт, л) = 0,05 из (60) находится то минимальное хт
среднее значение результатов испытаний, которое обеспечивает
выполнения условия х > С с обеспеченностью 0,95,
46
Глава 2
ВЕРОЯТНОСТНЫЕ МОДЕЛИ КЛИМАТНЧЕС
НИХ И ТЕХНОЛОГИЧЕСКИХ НАГРУЗОК
2.1. Классификация нагрузок и их сочетания
Классификация нагрузок
Окружающая сооружение среда вызывает в нем внутренние
усилия, деформации, перемещения, износ применяемых в конструкциях
материалов и другие кратковременные и длительные эффекты.
I филинами этих эффектов являются воздействия (нагрузки). Воздействия
определяются как природными факторами (снег, ветер, землетрясения и
т.п.), так и в результате человеческой деятельности (движение
транспорта, вес оборудования, собственный вес конструкций,
складируемых материалов и т.п.). Обычно на сооружение действует
несколько нагрузок каждая из которых обладает рядом конкретных
особенностей, которые необходимо изучить.
Следует отметить, что величина и другие характеристики
шндействий, которые используются в расчетах, ассоциируются с
принятой моделью нагрузки, а не с реальным процессом нагружения.
Статистическому и вероятностному моделированию нагрузок и
воздействий должен предшествовать содержательный физический анализ :
- причин их возникновения и изменения в связи с природными и
и хнологическими факторами и явлениями;
- пространственно-временной структуры изменчивости нагрузок
п связи с условиями их проявления и группировкой этих условий по
территории, типам и формам сооружений, режимам использования и т.п.;
- способов наблюдений и измерений с оценкой однородности и
стабильности условий наблюдений и представительности полученных
результатов;
- способов обработки и упорядочения результатов измерений.
На основания такого анализа формируется статистическая
модель нагрузки, включая описание ее генеральной совокупности и
47
области обоснованного использования результатов.
Модель нагрузки содержит ряд параметров и переменных,
которые должны быть оценены до использования модели. При вероягч
ностном описании воздействия все переменные считаются случайными.
По изменчивость может носить не только случайный, но и сисгемати-;
ческий характер, например, период повторяемости. При этом как случай-
ным, так и систематическим характером изменчивости обладают не
только сами воздействия, но и методы их измерения.
Нагрузки обладают большим статистическим разбросом. При
математическом описании нагрузки могут быть представлены в виде
случайных величин, случайных функций времени, а также изменяющихся
не только во времени, но и в пространстве по случайным или детерми-
нированным законам.
Для оценки надежности конструкций при расчете по несущей
способности интерес представляет максимальные значения нагрузок за
определенный период времени (хотя при проверке эксплуатационной
пригодности, долговечности важными становятся не только значения
величины нагрузки, но и продолжительность ее действия).
Если предположить, что нагружение хорошо описывается
стационарным процессом, и учесть, что достаточно удаленные,
максимумы этого процесса могут считаться статистически независимыми,
тогда вполне допустимо считаться с максимумами процесса нагружения.
Если срок службьг сооружения Т разбить на интервалы т достаточно
большие, чтобы считать значения максимумов процесса нагружения в
соседних интервалах статистически независимыми, тогда процесс
нагружения можно рассматривать как процесс испытаний.
При проектировании нромьпггленных и гражданских зданий
массового применения значительная часть расчетов относится к учету
статистического действия атмосферньгх нагрузок. Для них интервал
разбиения можно принять равным 1 году. Тогда под распределением
максимумов можно подразумевать распределение годовых максимумов, а
число испытаний л является сроком службы сооружения.
Дискретное представление нагрузки в виде стационарной
случайной последовательности (рис.9) позволяет записать
Р«шх(О) = {1 - [1 - РДО)]}” . (64)
где
PmaJt(f2) - функция распределения максимальной нагрузки за
срок службы;
48
Pi(Q) - функция распределения постоянной (в том числе
минимальной) в пределах интервала разбиения нагрузки. Вероятность
111пи1лепия нагрузки в промежутке т обозначена р} .
Рис. 9. Модель нагрузки
Конструкции и основания зданий и сооружений обычно
подвергаются действию нескольких нагрузок. Вероятность
одновременного возникновения нескольких нагрузок существенно ниже,
к и вероятность появления любой из них, если значения приняты такими
пне при действии одной нагрузки. Поэтому при проектировании
н< пользуются коэффициенты сочетаний (меньше единицы) учитывающие
уменьшение вероягности одновременного появления нескольких
инрузок.
> чет совместного действия нагрузок
При сочетании нагрузок, представляемых случайньгми
шличинами, а также при совместном рассмотрении максимумов
|1|«>цсссов нагружения (например, годовых максимумов снеговых и
1>гг|ч>вых нагрузок) возможен подход основанный на следующих
П| и-in (сложениях /49, 58/.
Принимается, что нагрузки представляют собой независимые
пчайные величины, что обеспеченность расчетного значения нагрузки
определяется числом ее стаггдартов и что различные расчетные нагрузки
(/пыдают равной обеспеченностью.
Если действует одна нагрузка, то ее расчетное значение
п 11 >сдсляется формулой
<?Р1 = R Р sOi
(65)
49
где
у f. - коэффициент надежности по 1 -ой нафузке;
- математическое ожидание, принимаемое в качестве
нормативного значения QH. ( = О);
sQ. - стандарг 1 -ой нагрузки;
Р - характеристика безопасности (число стандартов).
В формуле 65 знак минус принимается в том случае, когда
опасность возникает не при перегрузке, а недогрузке конструкции.
Расчетное значение усилия выражается через нафузку линейно
= aiQPi = аД± Р aisQt = Р %. = Yfx Nh, , (66)
где
Ns - математическое ожидание, принимаемое равным усилию
аг нормативной нафузки NH
sN. - стандарг усилия от i -ой нагрузки.
Тогда из (66) следует
Для расчетного суммарного усилия, возникающего при действии
нескольких нафузок принимается также обеспеченность, что и для
усилия от каждой расчетной нагрузки. Тогда
Np = N+ р sN , (68)
N. sN - математическое ожидание и стандарт суммарного
усилия.
Если все нагрузки, а следовательно и усилия от них -
некоррелированные случайные величины, то по теореме о дисперсии
суммы случайных величин
fт V2
= Е SnJ . (69)
Vj = J /
50
<i дня суммарного нормативного усилия по теореме о математическом
мжицлнии суммы случайных величин
л>
i = 1
пит । m - число учитываемых в расчете нагрузок.
Подставляя (67), (69), (70) в (68) можно записать
tfp = £ ±
(70)
(71)
2
Если же расчетное значение усилия получено суммированием
у, плий от каждой расчетной нагрузки, то оно оказывается равным
«1 П1 т
np = Z w₽, = L NHi ± Z -7) • <72>
1 = 1 1 = 1 i=l
Определение суммарного усилия по формуле (72) приводят к
перерасходу материала, в сравнении с формулой. (71) (средне-
мшдратическое всегда меньше среднего арифметического при т > 2.
Использование формулы (71) приводит к снижению расчетного усилия до
1<| 15%, в зависимости от числа нагрузок в сочетании и доли каждой из
них.
Вероятностную зависимость двух усилий например, изгибающего
момента М и нормальной силы N в стойке можно представить
приближенно в виде прямых регрессий М на N или N на М .
И. пользуя регрессию М на N , выразим .математическое ожидание
момента Мр , соответствующее расчетному значению нормальной силы
N,.
Мр Мд + (®р
(73)
гмм ‘ коэффициент корреляции суммарных, усилий.
Из (73) с учетом (72) и (67)
.га I m , 2
мр = £ MHi ± rw £ м2 (yf - I) . (74)
1=1 \i = i Hi y '
51
Аналогично, используя регрессию N на М , можно выразити
ожидаемое среднее значение нормальной силы Np , соответствующая
расчетному значению момента Мр .
Для определения коэффициента корреляции запишем выражение1
корреляционного момента
кмя = rMnsMsn (75)|
11ри действии нескольких независимых нагрузок
кмн = ^км^± = S гмЛ sm,sw. (76)I
i = J i~l
Учитывая, что усилия, вызываемые одной нагрузкой связаны
функциональной зависимостью, т.е. rM N = 1 , из (75) и (76) с
использованием (67) и (69) получаем
/I Г т , . э~| Г ™ . л
J 1Х(ч - ZXta - <77>
I Ь-’З jL-ы
Подставляя (77) и (74) и заменяя для общности М и N на X и
У получаем
(78)
Таким образом для каждой комбинации нагрузок необходимо
проверить два варианта расчетных усилий (хр , Yp} и (хр > *₽) •
Усилия Хр и Ур получаются, соответственно, по формулам (71) и (78),
52
и Yp и Xp - по получающимся из них заменой X на У и наоборот.
Применение моделей пуассоновского типа
Для оценки несущей способности важной характеристикой
нпляются пиковые значения величин нагрузок, возникающие в отдельные
м>|хггкие промежутки времени и значительно превышающие обычный
уровень нагружения конструкции. Эти пиковые нагрузки можно
рт сматривать не как непрерывные случайные процессы, а как некоторые
1¥чайные последовательности импульсов, появляющихся через
чучайные промежутки времени т и обладающие случайной
ичпгельностью Л .
Тогда могут быть приняты следующие гипотезы. Изменение
нагрузок во времени представляет собой простой. Пуассоновский поток
. иЬьггий; моменты появления воздействий независимы между собой;
период повторяемости и продолжительность действия нагрузки являются
не 1ависимыми случайными величинами. Принимается также, что усилия
в конструкции линейно выражаются через нагрузки
w(t) = t N^) = t » (79)
1 = 1 2 = 1
i ДС
n - число нагрузок.
Закон распределения максимального усилия N для заданного
н|юмсжутка времени t может бьпъ представлен в виде
Ре (^щах) = У. Рет Рп> (^) i (80)
л> = 1
I НС
рт (t) - вероятность появления нагрузки ш раз за промежуток
I1» • d;
Psm - Функция распределения усилия в одном
испытании.
Принимается, что число испытаний конструкции нагрузкой
имеет распределение Пуассона
53
. (vtf exp (-vt)
Psm(t) = “--.V-----------2 (81
m !
Здесь
v = v - ожидаемая частота появления naipyaoK.
Из принятой схемы независимых испытаний, полагая, что зако!
распределения всех случайных величин Nm одинаков, можно записать
Psa(Nn,/t) = p”(w) . (82)
Если подставить (81) и (82) в (80), то интегральный закон
распределения максимального усилия примет вид
Ps(w™x) = cxp{-vt[l - PS(W)]] (83)
Обозначая 1 - PS(N) - Pf(N) , выражение (83) может быть
представлено в виде:
Ps(^x) = exp[-vtPf(N)] (84)
Если на конструкцию действует несколько независимых
нагрузок, то не учитывая моменты одновременного их появления, можно
для максимального усилия, определяемого по формуле (79) записать
лшх ) • (85)
1=1
Учитывая, что PSi(wmax) определяется формулой (80), функция
распределения максимального усилия представляется в виде
P«(Nmax) exp -X v;tPf(Wj
(86)
Если теперь предположить, что моменты одновременного
появления воздействий также образуют пуассоновский поток событий
тогда в интервале |0, Г| функция распределения максимального усилия
может быть представлена в виде
54
Р«(^ах) = riPsNHPsKj) nPsKj,J --
j=2 i*j i*j*k
’-- flPs(WU.*..i)’
it j* kt...tl
I .'|C
,1) " Функция распределения усилия определяемого
ini формуле (79) в моменты одновременного появления нескольких
нагрузок.
С учетом формул (80) и (8J) выражение (87) преобразуется к виду
РД^тах) =
ехр
-£ - tt
i~l itj
-
-i f -
i*j*k
л n n n
- - £ £ £ • • ♦ £
a* j* k*,..........xl
(88)
i.iecb
Vi j - частота одновременного появления двух нагрузок.
Средняя частота одновременного появления двух воздействий
может быть выражена через ожидаемые значения частот х’2иу2 и
.реднюю продолжительность действия Aj = Д2 и Д2 = Д2 .каждого
и I воздействий
v12 - vlv2 (Aj + ^2)
(89)
Для п воздействий
vi,j.k -.i = vivivk’ • • > vi(^i + Aj + A*+- - -+AJ (90)
1<>гда (88) преобразуется
55
- t z ++* - zz Z- - • (9i)
ir j* fc=...
- • • ZWk- - - VjjAi + A# + Afc + • - • + А1)*3(«£Л. J
'.Л1
В частном случае для двух нагрузок выражение (91) примет вид
Ps(^max) = expI-VjtPf^j) -
(92)
-^Л, + A2)Pf(NI2) - v2tPf(W2)]
Здесь
W2 и N2 - усилия в конструкции от действия недолговременно
появляющихся нагрузок;
Ni2 - усилие в конструкции от двух нагрузок одновременно.
Таким образом, функция распределения максимального усилия
зависит от удельного веса отдельных нагрузок в суммарном усилии, от
законов распределения, частоты появления и длительности действия
каждой нагрузки и от срока службы.
Если закон распределения всех случайных величин Ni , ,
» одинаков, равны ожидаемые частоты и продолжительности
действия пиковых значений нахрузок, а также ai = а = const , то из
(91) следует
Ps(^maX) = exp -t , (93)
1 = 1
где
С* - число сочетаний из Д1 нагрузок по к (к - число
одновременно появляющихся воздействий).
56
2.2. Снеговые нагрузки
Основными физическими факторами, под действием которых
Формируется снеговая нагрузка на сооружения являются выпадающие в
:имнее время осадки, температурный режим местности, господствующее
направление ветра и геометрия покрытия. Перераспределения снега по
покрытию из-за ветрового переноса осуществляется после каждого
снегопада. Процесс таяния также зависит от перечисленных факторов и
от термического сопротивления покрытия, Ежегодные колебания
количества снега составляют причину многолетней изменчивости
снеговой нагрузки.
Интенсивность снеговой нагрузки
Интенсивность снеговой нагрузки на покрытие может быть
представлена в общем виде как случайная функция координат (х, у) ,
времени t , факторов местности q и факторов сооружения С :
q (х,у, t/g,C) =
' _ ' , (94)
= go(W) к&С/Яо) У/?/ С, до)
где
- основной климатологический параметр снеговой
нагрузки, характеризующий накопленную к моменту t реальную сумму
твердых и жидких осадков, выпадающих из атмосферы в данной
местности - запас воды в снеговом покрове (в мм), вес снегового покрова
(кПа) на горизонтальной поверхности земли ;
к(д,С/до) - Функция перехода от веса снегового покрова
земли до к средней интенсивности снеговой нагрузки на площади
покрытия ;
Й (х. У/<7> С, qo) ' Функция перераспределения снеговой
нагрузки по покрытию (функция схемы нагрузки)
К факторам местности д относятся ее географическое
положение, топография, шероховатость, определяющие характер и
интенсивность снегонакопления на земле, ветровой, снеговетровой и
температурно-влажностный режим местности, защищенность
метеостанции и сооружения.
К факторам сооружения С относятся его форма, размеры,
57
ориентация, шероховатость поверхности, внутренний температурный
режим, теплофизические свойства конструкции покрытия, определяющие
во взаимодействии с факторами местности снеговую нагрузку на
покрыгии.
Функции k(g, С/дго) и р (х, yjg, С, до) исключительно
сложны для статистического изучения и вероятностного моделирования,
которые сводятся, главным образом, к отдельных, частным случаям,
определенным формам покрытий, конкретным местным условиям и
заканчиваются разработкой частных рекомендаций по схемам снеговой
нагрузки и коэффициентом перехода.
Поэтому далее рассматривается только случайный процесс
qo(t/g) , реализации которого являются результатом наблюдений
метеостанций.
Применяются два способа измерений g„(t) :
- ежесуточные измерения высоты снегового покрова но
постоянным рейкам, установленным на метеоплощадке или около нее, и
независимые от них (по месту взятия проб) измерения плотности
снегового покрова;
- ежедекадные совместные измерения высоты и плотности
снегового покрова с помощью снегосъемок на характерных участках
местности (нолевых, лесных), с последующим подсчетом запаса воды и
снеговом покрове.
Оценка go(t) как характеристики выпавших и накопленных на
поверхности земли атмосферных осадков зависит от условий
защищенности метеоплощадки и участков снегосьемки от воздействия
ветра. Снегосъемки на лесных участках (под кронами, на лесных
полянах) обеспечивают более надежные оценки до . Возможные
нарушения однородности рядов наблюдений вызываются переносом
участков, на которых выполняются измерения, или изменением условий
их защищенности в период многолетних наблюдений.
Данные измерений метеостанций по снеговому покрову обобщены в
справочнике по климату б. СССР /66/.
В справочнике приведены для отдельных метеостанций
осредненныс по ансамблю зим данные о запасе воды по спегосъемкам на
последний день декады, характеризующие календарный ход
математического ожидания До(^) нестационарного процесса, т.е.
осредненную форму зимнего импульса запаса воды, обусловленного
случайным потоком выпадающих осадков, влиянием таяния снега при
оттепелях и его испарения. Форма этого импульса может быть описана
неслучайной функцией <p(t) , а его максимум, принят как среднее из
зимних максимумов запаса воды q^ по множеству лет наблюдений.
58
однако отсутствуют данные для статистической оценки функции
распределения запаса воды Fgo(g/t) , плотности и
параметров распределения, кроме go(t) .
Полная совокупность многолетних наблюдений go(t) по всем
декадам каждой зимы представляет собой определенную па регулярном
потоке реализацию прямоугольных импульсов (рис. 10).
Рис. 10. Реализация прямоугольных импульсов
Временная структура реализации определяется нс только
пойствами реального процесса, но и регулярным потоком измерений,
выполняемых с фиксированной частотой и неслучайным интервалом At.
Фтичсской переменной, непрерывно длящейся в этом интервале,
приписывается значение, измеренное в начале или конце интервала или
1и-рсдне1пюе по At . или максимальное на Дг , а форма импульса
условно принимается прямоугольной.
Отметим, что если характеристики длительности снеговой
нагрузки не изучаются, процесс может быть представлен реализацией из
мгновенных импульсов с дискретным временем (рис.11).
59
Рис. 11. Распределение
максимумов
Рассматривая реализацию на рис. 10 как условно стационарную и
используя всю совокупность значений интенсивности импульсов как
случайной величины получим одномерную статистическую (верхний
индекс 0) функцию распределения F°o(c[0) и ее параметры
iiW-!4W = i^=,-7=!-U ,95>
где
Д.
N = " - общее число прямоугольных несвязанных
импульсов;
пдя - число выбросов на интервале Т , определяемое по числу
интервалов At , в которых g0(t) > q0 ;
Fgo At - относительная частота появления выбросов.
Выражение (q0) является одномерной функцией
распределения мгновенных значений g0(t) прямоугольных импульсов
(рис. 10) на интервале , и вместе с тем, одномерной функцией
распределения максимумов Fg дс (<?о) , соответствующей реализации
максимумов па рис. 11. Параметры распределения
I м 1 N г <
ЧГд] <96>
Для сглаживания функции распределения во всем интервале
наблюдаемых значений трудно подобрать единую теоретическую
60
функцию, но в области значений, превышающих математическое
ожидание q0 для метеостанций с устойчивым снеговым покровом
приемлемо нормальное распределение.
При расчете сооружений на длительные сроки требуется знание
максимальной снеговой нагрузки за много лет.
11оскольку корреляция между годовыми на1рузками практически
отсутствует, многолетнюю снеговую нагрузку можно получить
теоретически, зная функцию распределения максимальной годовой
нагрузки.
Кривая распределения плотности вероятности максимальной
снеговой нагрузки за один год f(q01) несимметрична, причем f(gOra)
нс может быть меньше нуля.
Изменчивость QOm довольно высока и для её аппроксимации
может быть использован двойной экспоненциальный закон интегрального
распределения (распределение Гумбсля) /23/ (рис. 12)
Р(д<ц) = ехр -ехр
(97)
I’ас пределение плотности вероят ности здесь будет
1 1 rvn I ехп ° 4- ° ^0J 1
•M4o.il ~ ехр - ехр ---------------- + ----------
z \ z z >
(98)
- оо < U < оо, Z > О
параметры и и z связаны с математическим ожиданием q01 и
дисперсией ^((Гот)
следующим образом
Рис. 12. Интегральный
закон распределения qOa
61
q01 = u + 0,5776 z
sZ(<Joi) = 1,645 z2 .
(99)
Коэффициенты □ и z имеют различные значения для разных
местностей. Например, для Москвы получено и - 931 н/м2, z = 365 н/м2.
Для определения максимально допустимой снеговой нагрузки на
сооружение, рассчитанное на п лет, запишем вероятность
непревышсния ею значения
fyoi) = Fn(Zoi] • (100)
Обозначив через V заданную вероятность превышения
величины дОп за п лет, будем иметь
V = 1- F°(q0]); п = 108 ~ ;
(loi)
= V1-V.
Графически этот закон представлен на рис. 12. Применяя
формулу (100) к распределению (97) получим
Ffaon) = exp I — схр
ид- Чо1
z
(102)
где
ив = и + zlnn
Для математического ожидания д01 и ц0о можно
написать
'Jon - Qoi 1лл
(ЮЗ)
дисперсии же при этом не меняются s2(gOn) = s2(g6j .
Анализ случайного процесса накопления снега
При расчете конструкций по второй группе предельных
состоянии при анализе деформаций в сооружениях, необходимо
рассматривать случайный процесс накопления снега. Если разбить
62
папесс накопления снега на сечения, то случайную функцию можно
вменить совокупностью случайных величин.
Далее по каждому из N сечений процесса производится подсчет
числовых характеристик случайной величины q(t) по формулам:
- _ 1 А
" (104)
7 N
Si =
Каргина распределений (гистограммы) в выборочных
характерных сечениях представлена на рис. 13.
Рис. 13. Случайный процесс ио сечениям:
(I декабря, I января, 20 января, 20 февраля, 10 марта, 1 апреля).
63
В начале зимы преобладают несимметричные распределения,
мода и медиана не совпадают1, но по мере приближения процесса к его
середине, когда уже кончается переходный осенний процесс, осенние
подтаивания снега прекращаются, распределения становятся
нормальными. В конце зимы (конец марта, апрель) наблюдается обратная
тенденция.
Такие явления объясняются тем, что в начале зимы и в сс конце
велика вероятность оттепелей, вероятность выпадения незначительных
осадков увеличивается, а больших, соответственно, уменьшается.
Для моделирования случайного процесса накопления снеговой
нарузки может быть использован профильтрованный пуассоновский
процесс.
Эта модель предполагает, что изменения веса снегового покрова в
течение зимы образуют целочисленный счетный поток. Изменение
высоты снежного покрова считается случайным процессом дискретного
типа со счетным числом состояний, а именно простейшим потоком
случайных событий; этот поток считается стационарным и обладает
свойством ординарности.
в любой момент времени
Параметры снеговой нафузки g(t)
t можно для больших выборок представить
Jn(n - 1)
(N - 2) NSj
Е<
(N~i)
' (W - 2\N - 3) [ Ns}
, (105)
д/ - 3N + 3
N + 1 Л
где
д^ - среднее;
A-j - коэффициент асимметрии;
Ej -коэффициент эксцесса случайной величины д~,;
д,ц- значение в j-ом сечении и 1 -ой реализации случайной
функции g(t) .
Далее строится гистограмма частот, по которой, с использованием
одного или нескольких критериев согласия подбирается один из
известных законов распределения непрерывной случайной величины.
Наблюдения за снеговым покровом начинаются с 1-ой или 2-й
декады ноября и заканчиваются, как правило, 3-ей декадой апреля или
1-й декадой мая, таким образом рассматриваются 18 - 19 сечений
64
ирщесса. Неопределенности момента начала и конца зимы в модели
ж меняются случайной ее протяженностью.
На рис. 14 и 15 показаны математическое ожидание и стандарт
। ijx тесса по всем годам и снегосъемным участкам.
Рис. 14.
М атемазм ческое
ожидание нагрузки
Из рисунков видно, что среднее д3 и стандарт Sj возрастают
но максимума в начале марта, затем происходит ускоряющееся таяние
снега.
Рис. 15. Стандарт
нагрузки
Для разработки модели снеговой нагрузки как случайного
|||х>цесса использовались данные в виде декадных величин запаса воды в
снеге с 1947 по 1979 гг. по северу России (Алтай, Ермакове и т.п. , всего
'> снсгосьемных площадок). Данные по каждой площадке включают 32
11|х>цесса, разбитых на 17 сечений в период с ноября по апрель.
Процесс накопления снега можно представить в виде
n(t) г - 1
g(t) = , (106)
ш = 1
65
где
t - текущее время;
хт - т -ос время ожидания изменения нагрузки;
u(tm) - случайная величина, имеющая распределение
приращения нагрузки в момент т - го скачка;
хт функция приращения веса снега в момент
т -го скачка.
Здесь случайными величинами считаются приращения снега.
Случайные величины n(tj + 1} - «(t#) - приращения потока события
за месяц (j = 0,1,2,3) имеют распределение Пуассона (по критерию
Пирсона на уровне значимости 5%) с постоянным значением X :
ф (tju) - л (tj) = n] = ехр|-А(^|2- t^/n! ,(107)
причем при X = 0,78 закон будет справедлив для любого tj (т.с. для
любого месяца, кроме первых полутора). Это означает, что поток
стационарный. Время ожидания событий в нем подчиняется
показательному закону P(t) = 1 - exp(--Xt) . Точнее скачать К
очень слабо -зависит от времени. В первый месяц, когда идет процесс
перехода осени в зиму, X за отдельные декады меньше, чем за
последующие месяцы зимы. 'Гак, X за 1-й месяц равен 0,66 дек’.
Для более точного приближения модели к естественному
процессу снегонакопления было решено представить процесс со
слабовыраженной нестационарностью в первый месяц-полтора в виде
кусочно-стационарного процесса. Т.с. вся продолжительность зимы
разбивается на 2 этапа: первые 1,5 месяца - интервал с интенсивностью
X ~ 0,66 дек1 и остальное время X - 0,78 дек’1 .
Оценку распределений приращений нагрузки можно выполнить
также по частям. Так статистическая обработка скоростей приращений
процесса в виде подекадных разниц показала слабовыраженную
тенденцию к смещению моды относительно среднего, особенно в начале
зимы. Поэтому было решено принять в переходный период (первые
полтора месяца) распределение Лапласа-Шарлье, а дальше - нормальный
закон.
В процессе выработки параметров берутся числовые
характеристики из смежных моментов времени tj и tjtl или,
возможно tj и tjt2 и т.п. ; среднее нормального распределения для
66
мждого момента приращения нагрузки определялись так:
д<ь = — <jik) , <Ю8>
где
М - количество реализаций случайного процесса и имеющейся
выборке;
к - количество ступеней случайною процесса;
дк - нагрузка, накопленная к моменту к -го скачка.
Аналогично считается стандарт - как стандарт разностей нагрузки
п смежные моменты времени.
Такой подход, когда весь процесс (нестационарный) разбивается
ин 2 (а возможно и больше) интервалов стационарности для численной
реализации не представляет принципиальных трудностей.
Алгоритм реализации процесса следующий:
1. Вырабатывается значение нормально распределенной
। лучайной интенсивности X потока п (t) со средним X и стандартом
иА в зависимости от положения процесса на кусочно-стационарных
участках;
2. Вырабатывается время ожидания событий в потоке п (t) по
экспоненциальному закону с помощью обратного преобразования
। (-In у)/Х , где у - случайная величина, равномерно
распределенная на интервале |0, 1|;
3. В момент, совпадающий с состоянием процесса в настоящий
момент и до момента = tk + т назначается постоянное
приращение нагрузки, которое вырабатывается в соответствии с законом
Ни пласа-Шарлье в первые 1,5 месяца и по нормальному закону в
остальной период. Параметры закона вычисляются здесь же по ходу
определения х и следующего момента времени tk+1 ;
4. Для каждых календарных декад, совпадающих с новым
прсменем ожидания, нагрузка назначается как сумма приращения веса
< нега до момента изменения нагрузки ;
5. Так продолжается до тех пор, пока сумма времени ожиданий не
превысит установленную продолжительность зимы. Средняя величина
превышения меньше среднего времени ожидания т .
Таким образом, разбив процесс на интервалы, можно не только
регулировать интенсивности на них, но и задавать различные законы
рис пределения приращений снеговой нагрузки n(t) , одинаковые в
пределах каждого интервала.
67
Представление снеговой нагрузки в виде марковского;
процесса
Предположение о марковости процесса существенно расширяет
класс процессов нагрузки, который можно использовать в анализе:
сооружений. Процесс считается марковским .по интенсивностям к
моментам времени, если последующие воздействия и моменты времени
их появления зависят лишь от предыдущих воздействий и моментов]
времени и не зависят аг всей предшествующей истории нагружения.
Дискрегная марковская цепь представляет собой марковский случайный
процесс, пространство состояний которого счетно или конечно, а
множество индексов Т(1,2,...) , которое пробегает время, совпадает с
множеством целых чисел или частью этого множества.
Анализ марковской цени связан главным образом с вычислением
вероятностей возможных ее реализаций, важнейшей характеристикой
которых является матрица вероятностей перехода за к -шагов
= |Р1?| , где pW - вероятность того, что процесс перейдет из
состояния i в состояние j за к- переходов . Когда одношаговые
переходные вероятности не зависят от временной переменной (т.е. от
значения к , процесс обладает стационарными переходными
вероятностями и тогда Р27 - вероятность перехода из состояния 1 в
состояние j за одно испытание.
Систему дифференциальных уравнений - уравнений
Колмогорова для вероятностей состояний можно записать в виде /49/
^Р0 _ in. dt ~ ~^Р°' ~Г~ - -^-оРо ~ ^1?!', □ L (109)
^РХ _ _ у р IP dt
Начальные условия
при t = О, Ро = 1, Р2 = Р2 = . ..= Рк = 0 . (НО)
Представляя вес снежного покрова как дискретный марковский
процесс (марковскую цепь) 1радацию процесса по значению нагрузки и
68
Hl и мени выбираем так, чтобы не нарушалась однородность процесса и
чтобы приближение модели к нагрузке не было грубым.
Предварительный анализ показал, что для соблюдения условия
инородности процесса по критерию Н. Смирнова, получена следующая
оценка = Х= 0,136, где X - параметр распределения времени
пребывания процесса в состоянии Yk , принятого в виде закона
lie Обуяла
F(x) = 1 - e‘xt (111)
Учитывая, что среднее время пребывания процесса в состоянии
и параметр распределения А связаны соотношением
tep = Y <112>
имеем t » 7 суток. Это значит, что для выполнения условия
однородности процесса необходимо принять градацию процесса по
времени, равную 7 суткам. Обычно замеры высоты снежного покрова
проводятся раз в 5 или 10 дней, поэтому их можно использовать без
в 1менения, а статистику ежедневных замеров перевести в 5-ти, в 7-ми
или 10-дневную.
Таким образом, для процесса снеговой нафузки фадации
времени составляют 5 дней, фадации значений веса снежного покрова,
выбранные из тех же соображений, составляют 200 11а. Эго значит, что за
состояние Yo принимаются значения веса снежного покрова от 0 Па до
ЛИ) Па, за состояние - от 200 Па до 400 Па и т.д., т.е. величина
градации нафузки равна 200 Па. Краевые значения относим к любой из
двух фадаций, например, к предыдущему состоянию, т.е. в точной
щписи: Yo - от 0 Па до 200 Па включительно. - свыше 200 Па до 400
11а включительно и т.д. Максимальное значение веса снежного покрова
д.'1я выбранной статистики составляло 2200 Па (событие,
^фиксированное один раз для района Москвы), следовательно, начиная с
шло значения, статистических данных нет, и эта область входит в зону
редких событий.
Вычисления дали следующие статистические значения
переходных вероятностей за один шаг, т.е. из состояния 1 в одно из
грех возможных: в предыдущее i - 1 , в доследующее 1 + 1 и с
вероятностью Рц процесс продолжает оставаться в том же состояли!
1 (табл.З).
Таблица 3
i 0 1 2 3 4 5 6 7 8
0 0,16 0,11 0,2 0,18 0,14 0,2 0,3 0,32
₽> i 0,7 0,57 0,51 0,54 0,55 0,52 0,5 0,2 0,54
0,2 0.18 0,3 0,15 0,12 0,23 0,1 0,3 0
Графики для переходных вероятностей даны на рис. 16-18.
Из статистического вычисления переходных вероятностей видно
что матрица переходных вероятностей для процесса веса снежного
покрова в течение зимы имеет трехдиагональный вид. Это означает, что
для выбранных градаций времени и значений процесса с очень малой;
вероятностью процесс переходит через соседнее состояние, что позволяя
такие события не рассматривать.
Следующим важным этапом является аппроксимация значени!
переходных вероятностей а область редких событий, т.с. установление
аналитических значений переходных вероятностей для состояли!
процесса свыше Уй = 1800 Па . Аппроксимация проводится следующие
образом: через 3 значения Р±j , близкие к Уе , проводим кривую <
продолжением в область Yk , к > 8 .
70
Рис. 17. Переходящая
вероятность Pi/
Определяем аналитическое описание этой кривой с помощью
। истемы однородных линейных алгебраических уравнений, дающих
ненулевое решение в том и только в том случае, когда ее определитель
равен 0. Установив аналитическую зависимость для переходных
ш |>оятностей в области редких собьггий, определяем значения Pi? по
Iгой кривой для любого состояния Yk , где к = 7 , которые называем
аналитическими в отличие от тех, что получены непосредственно из
патистических данных.
Но означает, что при моделировании процесса снежного покрова до
состояния Yk , где к = 7 , ход процесса - возрастание значения
нагрузки, уменьшение значения или сохранение значения - определяется
ио статистическим переходным вероятностям, а начиная с Yk , где
к ~ 7 , ход процесса определяют аналитические переходные
вероятности.
Рис. 18. Переходящая
вероятность i +1
На рис. 16-18 пунктиром проведены аналитические кривые для
переходных вероятностей, описанные следующими зависимостями для
к » 7:
Pii_1 = 0,1(4,31 - 25,6)1/г a
pi,i = 4,51(251 -161) 6 (113),
pi,i4 = °>7/(31 ~ 2 °)
Из формул (113) видно, что начиная с уровня нагрузки, равного
1600 На, с ростом нагрузки переход процесса в предыдущее состояние
более вероятен (зависимость (а) - возрастающая ветвь параболы), чем
переход процесса в состояние с большим значением веса снежного пок-
рова (зависимость (в) - нисходящая ветвь гиперболы), что, вообще говоря,
понятно.
2.3. Ветровые нагрузки
Ветровая нагрузка на сооружение определяется как сумма средней и
пульсационной составляющих и вычисляется через игггенсивность
ветрового давления (Па) :
W(t) = 0,61 V(t) , (114)
где
V(t) - скорость ветра (м/с), основной климатологический
фактор ветровой нагрузки, зависящий от географического положения
местности и связанного с ним характера атмосферных возмущении
(циклонов, штормов, гроз), от топографических особенностей
распределения ветровых потоков и режима ветров, от шероховатости
местности (характер поверхности, растительности, преград, зданий и
сооружений).
Характеристика условий измерения скорости ветра на станциях
гидрометеорологической службы включает координаты и высоту станции
над уровнем моря, тип окружающей местности, условия защищенности
метеоплощадки; способ измерений - ветроизмсрительный прибор (тип
флюгера, анемометра), высота его установки над уровнем земли (около 10
м), интервал осреднения скорости ветра (2 мин., 10 мин.), число сроков
наблюдений (4, 8, 24 раза в сутки); продолжительность непрерывного
ряда однородных наблюдений.
72
В возможные причины неоднородности рядов наблюдений
< нсдует включить перенос метеоплощадки, изменение условий
иицищенности; замена прибора (в 1950-ые г.г. переход к флюгеру с
гижелой доской, с 1965 г. - постепенный переход гидрометеорологической
службы к анеморумбометру М-63), изменение высоты его установки;
изменение формы записи информации (с 1969г. публикация данных о
максимальной суточной и месячной скорости ветра с учетом порыва);
в 1менение частоты наблюдений (с 1966 г. вместо 4-х введено 8 сроков в
i уз ки, а. в аэропортах возможны 24 срока).
Полная совокупность многолетних наблюдений метеостанции по
всем срокам и направлениям представляет собой определенную на
регулярном потоке измерений недифференцируемую реализацию и если
результат изменения средней за 10 мин (2 мин) скорости ветра
распространяется на весь интервал или реализацию в виде мгновенных
импульсов.
Обработка и сглаживание срочных значений модуля скорости
петра для многих метеостанций показывает, что наилучшее согласие со
статистическими данными имеет несмещенное распределение Вейбулла :
F(V) = 1
(115)
где
F(V) - вероятность того, что в наперед заданный момент
времени скорость ветра не превысит значения V ;
ц , а - коэффициенты, определяемые по каждой метеостанции
и зависящие от ветрового режима данной местности.
Например, для района Москвы оценка параметров ц , а может
(пять получена с использованием выборки суточных максимумов
скоростей ветра методом максимума правдоподобия. Это наиболее общий
метод нахождения оценок.
Функция плотности вероятности зависит не только от значений
хр х2, . . . , хп , которые принимают случайные величины
Ху, х2, . . ., хл , но и ехг значений параметров т]ь п2, .. . , т|0 . Эта
Функция, рассматриваемая как функция параметров при
фиксированных выборочных значениях случайных величин х
называется функцией максимального правдоподобия
l(x7> х2, ..., хв/%) = max (116)
Метод максимального правдоподобия состоит в том, что в
73
качестве оценок параметра rji принимается то значение , цри
котором ь(х2, х2, • , хп/тц) достигает максимума. В случае л
независимых опытов
z(x2, х2, . . . , хо> Hj) = £ Р(хк, nJ . (117)
к=0
Оценки максимального правдоподобия находятся максимизируя
In L (х2> х2, . . . , хл, т) J , используя то обстоятельство, что у = In х
строю возрастающая функция. Опенки определяются из решения
уравнения правдоподобия
” Sin L(xk, т| -) Л n 1
У------L2LLJO = о . (118)
к--о ^Пх
Эти оценки при достаточно общих условиях состоятельны,
асимптотически нормальны и асимптотически эффективны.
Если обозначить С = ц“ , b = а , то
Ла
In L - Пд In Ь + in С + (b - 1) In х_£
i-j
-С£х| ,(119),
i 1
где
л0 - объем статистических данных.
Уравнения (118)запишутся в виде
dlnL
д ь
Пр
ь
°C
= °
1 = 1
п0
+ Е In xi
i-1
(х£ In xi|
(120)
a In L _ п0
~~д~С~ ~ С
= О
Из решения (120) получены а = 1,15, ц = 4,42 .
Квантиль скорости ветра заданной обеспеченности (через перио)
повторяемости) определяется при известных параметрах ц , а в явнои
виде:
74
V* = Г| In — м/е
к At/
(121)
Если получена по статистическим данным сглаженная функция
рнспредсления и определены два ее квантиля Vj*,
пнчветствующие выбранным значениям периода повторяемости
Т*г . 3V2 >то оценки параметров ц, а , вычисляются по формулам:
а
In. Tyjbt
In
in (yr/v^)
In /д tj1,a
(122)
Для повышения точности оценки частоты выбросов и соот-
ветствующих квантилей скорости ветра целесообразно использовать
поричныс выборки из исходной совокупности срочных наблюдений,
образуемые месячными или годовыми максимумами скорости ветра
(табл.4), независимость которых практически обеспечена.
Статистический ряд годовых максимумов скорости ветра
«чительностью 20 лет (1966-1986 гг.), полученной в метеорологической
обсерватории МГУ им. М. В.Ломоносова приведен в таблице 4.
Таблица 4
Годы Скорость м/сек.
1966 16,0
1967 23,0
1968 14,0
1969 13,0
1970 18,0
1971 12,0
1972 20,0
1973 24,0
1974 24,0
1975 21,0
Годы Скорость м/сек.
1976 18,0
1977 21,0
1978 23,0
1979 20,0
1980 18,0
1981 20,0
1982 25,0
1983 21,0
1984 28,0
1985 20,0
Так как исходное одномерное распределение V в области
наибольших значений относится к распределениям экспоненциального
гипа и число срочных наблюдений в течение месяца (года} достаточно
пслико для приближения к асимптотическим результатам, для
75
сглаживания статистического распределения месячных (годовых)
максимумов Уд выбирается двойное экспоненциальное распределение
Гумбеля (распределение экстремальных значений 1 типа):
Fv.(V) - ~^о < V _ -ZfV-U) е (123) < со, z > 0 ,
где
и = (уд 0,55 7} м/с - мода распределения; z )
л Z = 4б Квантиль 1 — с/м . Sy скорости ветра заданной обеспеченности при
известных параметрах и, z вычисляется по формуле:
К
1 . , 1
и + — - In In ---------т—
z[ 1 - д/т;,
(124)
где:
А равно месяцу или году.
Вычисленные по (121) квантили скорости для Ту = 5 ; 20 лет
для большинства метеостанций превышают на 2. . .4 м/с квантили по
(123) для тех же лет наблюдений и значений Ту . Принимая квантиль
V' сглаженного распределения Гумбеля за достоверный можно
установить на основе (121) из условия = Л ('п такой
интервал исходной выборки
4-1
Дя = Tje = тф - Fy(v;)] , (125)
который обеспечивает эквивалентность квантилей по (121), (123) при
выбранном Ту . Переход к интервалу As по (125) является косвенным
способом учета в исходной выборке только независимых наблюдений,
доля которых приближенно равна — . По данным обработки
Аз
76
метеостанций осредненная оценка Ды = 1 сутки.
Параметры u, z устанавливаются из
|чк н ределения по двум известным квантилям
повторяемости
сглаженного
для периодов
1
(126)
Математическое ожидание и среднее квадратическое отклонение
месячных (годовых) максимумов скорости ветра:
т7 °'577 ,
- и + ------ м/с; sv
В небольших совокупностях (менее 10) годовых максимумов
i корости достоверность сглаживания снижается из-за большого разброса
малочисленных данных. В этом случае целесообразно сглаживание
годовых максимумов функций (123) с аналитическими оценками
пнраметров и = ил , z = zm , вычисленными через параметры а , ц
i глаженного исходного распределения (115):
um = ц(1пл?)^'Х м/с ; zm = a0n с/м > (128)
। кт:
А
Д1 = — - число независимых наблюдений в частной исходной
As
hi.Нюрке длительностью А (месяц, год), из которой выбирается один
максимум.
Тогда вместо (124) и (127)
1 ( 1 }
= “ + 2Т|п'" д • (12’>
77
0,577 . п 1
Vo = ит + —— м/с; sVi = - м/с .
zm yjb zm
(130)
Коэффициент вариации
v.
Tt/V6
a In m + 0,517
(131)
Для интенсивности ветрового давления W , соответствующей
исходной совокупности срочных измерений скорости ветра V ,
сохраняется распределение Вейбулла, нос измененными параметрами:
Гп(Ю =
W > 0,
1-е vn- ;
ц > 0, а. > О,
(132)
где
а
Тогда
qm = 0,61 т| Па, т) и а по(117).
f 1\ f 21 э 11
tf = Tvri + — = tJt 1 + — -Г2 1+ — ffi. (133)
x [ x c**' x 0^7
Параметры годовых максимумов ветрового давления по
аналогии с (128):
= pw(ln Па; (in ~ . (134)
Квантиль годовых максимумов
1
-In In
1
i - д/т;
Па
(135)
математическое ожидание и среднее квадратическое огклонение
78
« 0,577 о
- ит» + ~ Па ’
ZmH
(136)
м > >ффициент вариации годовых максимумов
п/у/б______
а„ 1пл1 + 0,577
(137)
Для характерных значений а„ - 0,75 ; Л1 = 365; к. 0,25 .
В переходе к л - летним максимумам Wn ветрового давления
|| качестве исходного используется распределение годовых максимумов
1умбеля, тогда
Wn = »k+ “ = *Л + “ On «)
zmW 71
• - -----=—4---------- ; « Sj,
”b /x- ’ %
1 + (In n) v„
7T
(138)
при v„t = 0,25; n = 50 летимеем = 0,14 .
Учет случайного направленна скорости ветра
Ветровой поток характеризуется не только случайным
и (менением величины скорости, но и случайным изменением
направления. В метеорологии направление ветра, фиксируется по восьми
румбам. В первичных метеорологических источниках и в Справочнике по
климату б. СССР /66/ имеются данные о повторяемости ветров
различных румбов, по которым можно построить розу ветров для
различных районов нашей страны. Так по данным для Москвы была
построена среднегодовая многолетняя роза ветров. Как видно из рис. 19
преобладающими направлениями ветра являются западное и юго-
ш надвое
Для учета в вероятностном расчете сооружений случайного
характера изменения направления Beipa можно использовать следующие
апа способа.
79
Рис. 19. Роза ветров
Первый способ базируется на предположении о том, что все
горизонтальные направления ветра равновероятны. Предположение о
равновероятности направлений максимального ветра допустимо по
причине того, что сооружение ориентируется в пространстве обычно не
по розе ветров, а в соответствии с принятой планировкой с учетом
рельефа местности и т.п.
Применение этого способа можно рассмотреть на примере мачты
имеющей по три оттяжки в каждом оттяжечном узле (рис.20). Узловая
нагрузка перемещается по окружности от оттяжки с номером 1 по часовой
стрелке и фиксируются номера расчетных случаев, которые при этом
будут возникать. В результате этого получилась последовательность из 12
членов, смысл которых есть номер расчетного случая
Уд = (1,3,2,3,1,3,2,3,1,3,2,3) (139)
Таким образом, на окружности можно указать 12 расчетных
случаев.
Число случаев типа 1 равно трем, типа 2 - трем, а типа 3 равно
шести. Номер расчетного случая Уд можно представить в виде
дискретной случайной величины, принимающей значения 1, 2, 3 с
вероятностью = 0,25 , РЯ/Д=2 = 0,25 , Кн,д_з = °,50 •
80
Рис. 20. Случайный характер направленна негра
Для моделирования методом Монте-Карло дискретной случайной
величины окружность 0" разворачивается в отрезок, который
разбивается на 12 равных частей (рис.21) и имеющей границы | 0, 1| .
32313232323
о
L
2221АА212/2Д
12 12 12 12 12 12 12 12 12 12 12
Рис. 21. Развертка
окружности
1
Вырабатывается последовательность равномерно распределенных
на отрезке | 0, 11 случайных чисел . По тому, в какую из 12 частей
линного отрезка попадет очередное выработанное число, и выбирается
помер расчетного случая, по которому необходимо производить
детерминированный расчет.
Например, случайное число = 0,513 попадает в интервал от
6/12 до 7/12, которому соответствует номер расчетного случая Nn = 2.
Число интервалов, соответствующих расчетному случаю типа 1 равно
трем, типа 2 - трем, типа 3 - шести.
Следовательно, как и было отмечено ранее = 0,25 ,
= 0Д5 > Рц,д- з = 0,50 .
Отличие второго способа, от первого состоит в том, что здесь не
используется гипотеза о равновероятности направлений ветра, а
используется роза ветров.
Окружность 0* разворачивается в отрезок с границами | 0, 11 ,
который разбивается на 8 участков (рис.22) по числу румбов.
81
Рис. 22. Учет случайного направления ветра
перемещаться по розе ветров (рис. 19) аг с
по часовой стрелке, то тогда длина первого
Если
направления
соответствующего северному направлению ветра, будет числено равна
повторяемости данного направления, выраженной в относительных
единицах (рис.22).
Аналогично поступают с остальными участками отрезка,
имеющим длину равную повторяемости соответствующего направления
ветра (рис.20).
^-(1,3,3,3,2,1,3,2)
Nd = (l, 3,3, 3,2, 3,3,3)
Hd=(l,2, 3,1,2,1,3, 2)
Рис. 23. Уче т направления ветра
Как и в первом способе если перемещать узловую нагрузку от
отгяжки с номером 1 по часовой стрелке и фиксируя номера расчетных
случаев, которые при этом будут возникать, то тогда в силу того, что
имеет место несовпадение направлений оттяжек в плане с направлениями
ветра (рис.23) (при четырех оттяжках в плане подобных нс совпадений не
возникает), получается четыре варианта последовательности из 8 членов,
смысл которых есть номер расчетною случая
82
Nfi - (1,2,3,1,2,1,3,2) a);
N„ = (33,3,3,2,3,3,3) 6);
N„ = (1,3,3,3,23,3,2) в);
Мд = (32,3,1,2,3,3,3) в).
(140)
Значения вероятностей появления расчетных случаев 1, 2, 3 для
каждого из четырех вариантов последовательностей N„ с учетом
реальной розы ветров представлены в таблице 5.
Таблица 5
11 Лучаи Последовательность из формулы (140)
140 а) 140 б) 140 в) 140 г)
1 = 0,370 = 0,075 = 0,256 = 0,189
2 FN U 0,336 Яд Fw ]= 0,130 Ид ' f J = 0,474 FN ( = 0,194 "л
3 0,294 [= 0,795 = 0,270 [= 0,617
Влияние протяженности строительного объекта на выбор
расчетного значения скоростного давления ветра
Полезно упомянуть еще один аспект рассмотрения ветровой
нагрузки, связанный с учетом протяженности строительного объекта /49/.
Надежность линии электропередачи (ЛЭП) зависит, очевидно, и от ее
протяженности, так как чем больше длина линии, тем больше
т рогггность появления скорости ветра, способной вызвать разрушение
пор, и, следовательно, отказ линии. Тогда при проектировании ЛЭП это
(ктоятельство необходимо учитывать при выборе расчетного значения
мцюети ветра. Если поставлена задача равпонадежности ЛЭП
иещвисимо от их протяженности, то для ЛЭП большей длины должно
пи (начаться большее расчетное значение скорости ветра.
Допустимы следующие предположения:
I. Опоры ЛЭП подвергаются воздействию только ветровой нагрузки;
Динамическое действие ветра не учитывается;
I. Значение максимума скорости ветра V появляющегося па участке
il H I, длиной 1 за время Ту является независимой реализацией одной
и гой же случайной величины;
4 Для ЛЭП, запроектированной на расчетное значение скорости
83
ветра, равную , значения несущей способности опор х .выражены.!
единицах скорости ветра и являются независимыми реализациями одно!
и той же случайной величины с плотностью распределения pV1(x)
Значения несущей способности опор, запроектированных на рас
четное значение скорости ветра, равной V2 являются такж!
независимыми реализациями одной и той же случайной величины <
плотностью распределения р^(х) . Если принять, что V2 = Vjn , т<
по формуле преобразования функций случайных величин
2
Pvjx) = Pv^/n)-
(141)
Плотность распределения несущей способности
принимается по нормальному закону
, \ 1
= ехр
2s2x
.2"
(142)
Математическое ожидание x и дисперсия s2 определяют
расчетным значением скорости всгра Vj, . Тогда функция надежное1
ЛЭП, запроектированной на расчетную скорость и имеющую дли,
1 может быть представлена в виде
«, t/t,
P(t) = J pVj(x)[pVj(x)j dx
о
(143)
Здесь предполагается, что максимумы расчетных скоростей ветра,
статистически независимые, одинаково распределенные в интервалах
случайные величины; t - заданный срок службы.
Подставляя в (143) (142) и (102) можно записать
г Г fu - х + zln 1 (х-х)2 ,,л..
P(ty = j ехр -схр^------------ехр - ' ' dx . (144)
Функция надежности ЛЭП, запроектированной на расчетное
84
ншчсние скорости ветра равной V2 и имеющую дайну ml с учетом
dll) записывается аналогично
'n/t) = fop-op
0
u - x + zki rrf/ti
z
1
ns^/Zr
dx . (145)
Чтобы обеспечить равную надежность ЛЭП равной длины
Функции надежности (144) и (145) должны совпадать при любом t .
Задача состоит в выборе такого значения и , чтобы эти функции
<>ыли в каком то смысле близки друг к другу. Приближенная оценка
получена из условия
dP
dt
t=o
dPm
dt
t-o
(146)
Условие (146) с учетом (144) и (145) приводит к соотношению
Сп2 + Cjn + С2 = О
(147)
I ГЦ-
Со = 0,5 ~ \ С2 = - — ; — - 0,5 -^1 + 1п т .
Z Z Z Z2
Вместо параметров z, х , s2 можно ввести безразмерные
параметры:
£ = - коэффициент вариации несущей способности опор;
х
© - коэффициент вариации максимумов скорости ветра,
х
Используя известное соотношение — =
Z
НК
у 0,577 - постоянная Эйлера;
ффициенты Сй , Сг, С2 переписываются в виде
85
Л
2
Со = 0,5 р©
= -р
(148)
л
-т= - Y ;
л
С2 - р
I I 71
- у - 0,5 р © -----------j= - у
2
+
In Л1 .
параметров
Результаты расчетов при заданных значениях
приведены в таблице 6.
Таблица 6
£ Р © Л1 л
0,125 3 0.2 2 1,055
0,125 3 0,2 10 1,235
0,125 3 0,3 2 1,075
0,125 3 0,3 10 1,258
0,125 3 0,2 2 1,066
0,125 3 0,2 10 1,235
Из таблицы видно, что если длина ЛЭП удваивается, то
значение скорости ветра увеличивается на 2,7%.
Ниже приведены значения Р (t/t^,
где
т = t/t^ 2. - числе лет при £ = 0,125, р = 3,
Р(5) Р(10) PG5) Р(20) Как практически = 0,99955635 Р(5) = 0,99955842 = 0,99911097 Р(10) = 0,99912128 = 0,99867585 Р(15) = 0,99869675 = 0,99824924 Р(20) = 0,99828243 видно вероятности безотказной работы о равны, что подтверждает правильность
предпосылок. Однако остается открытым вопрос, какую ЛЭП
0 = 0,2
86
•in,'юнной (дайна 1 ). Для этого требуются дополнительные технико-
жоиомические обоснования.
2.4. Температурные климатические воздействия
Конструкции зданий и открытых сооружений подвергаются
по «действию во времени температуры воздуха и солнечной радиации,
кич>рые вызывают изменение температуры элементов конструкций, их
леформации и перемещения. В статически неопределимых системах при
•том мо1ут возникнуть температурные усилия.
Основным видом температурных климатических воздействий на
несущие конструктивные системы сооружений являются
неб лагоприятные приращения Т, (t), Т (t) средней по сечению
i.'icmchtob температуры конструкций , ?k,(t) тк (t) в теплое (+),
ныодное (-) полугодия по отношению к начальной температуре
>•.инструкций т°, т\' , при возможном их замыкании в
ii| >< п’ивоположном полугодии:
ЗД “ 4+(t) - тк°. , T_(t) = ?k_(t) - ?k°+
Далее рассматриваются только те приращения, которые
обусловлены изменением во времени среднесуточной температуры
наружного воздуха /9/ та, (t) , ij (t) , т.с.
£<(t) = ^i(t) - ?(t) = ъ (t) - • 049)
Температура наружного воздуха измеряется термометрами
(срочные наблюдения) или термографами (непрерывные записи),
установленными па метеоплощадках в психрометрических будках на
высоте 2 м от поверхности земли. Нарушение однородности рядов
наблюдений связано, главным образом, с переносом метеоплощадки.
Результаты последовательных измерений среднесуточной
температуры воздуха во времени представляют собой реализацию,
определенную на регулярном потоке осреднеппых по каждым
календарным суткам наблюдений.
Наиболее существенной особенностью случайного процесса
среднесуточной температуры является (рис.24) периодическая
пестационарностпь, проявляющаяся в годовом ходе температуры, ее
Функции распределения, плотности и параметров.
87
ti(T-)
Рис. 24.
a) - пример реализации процесса среднесуточных температур;
6) - годовой ход математического ожидания процесса и плот-
ности распределения ординаты процесса;
в) - годовой хол стандарта среднесуточной температуры.
при этом изменчивость среднесуточной температуры воздуха в зимние
месяцы значительно больше чем в летние, и отношение sTj js^
может достигать 3...4.
Результаты первичной статистической обработки данных о
температуре воздуха представлены в справочнике по климату б. СССР
/66/.
Данные справочника о повторяемости среднесуточной
температуры воздуха в отдельные месяцы года дает возможность
приближенно оценить функцию распределения FT ^/t) , плотность
А, (Vе). xi(0 •
Анализ этих данных для многих метеостанций показывает, что
распределение т j (t) близко к нормальному с плотностью
Т| () sTj (t)V2n
[т~тМ
2<0) “
(150)
exp <
88
Данные о междусу'гочной изменчивости позволяют оценить
щит годную VTj(t) процесса среднесуточной температуры и привески
iii wiiibie реализации к условно дифференцируемым (рис.25) .
Рис, 25. Определение
среднего числа выбросок
нестационарного про-
цесса выше уровня t
Функция распределения VTj (t) в отдельные месяцы года близка
► нормальной с нулевым математическим ожиданием, а значения средней
мс жду суточной изменчивости являются оценкой условною
математического ожидания H + (t) положительных или V (t)
-прицательных значений производной в отдельные месяцы года.
'Гак как V^(t) = u ‘ , то оценка среднего квадратичного
> ri клонения производной в отдельные .месяцы года равна:
<%(*) =
^;(t)
—+
(151)
। цс для нормального распределения и* = -=^ = 0,80 .
\12it
Полученные оценки дают возможность вычислить для
нестационарного процесса среднесуточной температуры воздуха
«редкою частоту положительных выбросов TJh(t) > т теплого
полугодия v*(t) и среднюю частоту отрицательных выбросов
।, (t) < т холодного полугодия v’(t) .
Выполненные для нескольких метеостанций вычисления
89
пока зывактг, что основной вклад в число выбросов за теплое (холодное)
полугодие составляю!’ выбросы в трехмесячном летнем (зимнем) сезоне.;
Учитывая, что на интервале этих сезонов изменение
sv (t)
Tj(t) , —незначительно, допустимо рассматривать процесс
среднесуточных температур T7(t) на этих интервалах как
стационарный, пользуясь при вычислении частоты выбросов
осредненными значениями статистических характеристик.
Для стационарных взаимно независимых процессов
vi = 4 Й+’ “ (zx) > (152)
Sx
где
f z (zx) - значение плотности стандартной формь
распределения х для нормированного уровня zx = --------- ;
sx
J и f(u) du
O' = ------7-r— - условное математическое ожидание
Gu (0)
(координата центра тяжести) положительных значений нормированное
V - V
производной и = ---------- :
su
-для нормального распределения производной
u' = = 0,80 ;
72л
__ з/З
-дляравномерного - и = -у - 0,86 ;
Ga - вероятность превышения уровня.
Произведение usv в формуле (152) следует заменить
осредненными за три летних (или зимних) месяца значениями (или
, тогда
1
90
где
т - т.+ — + ~
zt = -------— и V, , тп , sT относятся к летнему сезону.
Sti+
Аналогично вычисляется v“ для зимнего сезона.
Для определения квантиля среднесуточной температуры
шданной обеспеченности следует исходить из условия
1 1 ^r, , I \ fl
= (zTi) или
"ГО z srlt
Для нормального распределения Fz zT = .— e 2
' 11 -J 2k
квантиль нормированной переменной для летнего сезона
JV‘ Тх
2 In —г2 1
sXn
и т‘1+ = т2 + z*it sXu
Аналогично для зимнего сезона
т*. = - z^_ sX:_
(153)
Период повторяемости должен быть выражен в сутках, при этом в
каждом год)' учитывается лишь число суток .за летний ( зимний) сезон, т.е.
Т* = 90 N* , где: N* - период повторяемости, выраженный в годах.
Так, для зимнего сезона в Москве:
тг. = -9,1° С; sTj = 8,6° С ; 7tj = 3,1° С/сутки ;
для периода повторяемости N*^ — 50 лет:
y*(J) = эд • 50 = 4500 суток
о
- U 4^ = V 2V2TT • 8,6
т’(? = - 9,1 - 3,40 • 8,6 = - 38,3° С
91
для периода повторяемости = 5 лет:
y*(J) = 45Q суток; - 2, 64 •
Tj J TI
TjL’’ ” -9.1 - 2,64 8,6 = -31,8° C
На основании рассмотренной модели выбросов можно
определить такой интервал As в исходной реализации
недифференцируемого процесса среднесуточной температуры, при
котором обеспечивается такой же квантиль, как и в (153):
&s = Т* р - Fz(<)] - (154)
где
Fz (z’j - значение функции распределения нормированной
переменной, соответствующее квантилю по (153)
Для условий приведенного выше примера :
ДЛЯ N*[1} = 50 лет Fz(3,40) = 0,99966; As= 1,53 суток,
для N*{1} = 5 лет Fz(2,64) = 0,99585; As= 1,87 суток,
Пользуясь значением Дь, для вычисления обеспеченности
среднесуточной температуры в модели недифференцируемого процесса
<пй = 1 - ~~ (155)
•т.
можно повысить точность оценки квантилей в этой, более простой
модели.
= |(1,53 + 1,87) =
1,7 суток, получим:
Действительно, принимая As
для W**1'* = 50 лет «д1 =
для = 5 лет fo-5' =
0,99962 ; = 3,37 ; = - 38,1° С .
0,9962 ; г/2) = 2,67 ; т*(1) = - 32 Г* С .
И- J- ’
что практически совпадает с вычисленными выше результатами для более
точной модели выбросов.
Для нормирования температурных воздействий, принимаемых в
расчетах конструкций па однократное загружение высокой
интенсивности, целесообразно использовать еще более простую модель
среднесуточной температуры воздуха в виде стационарной
92
|нкледовательности годовых экстремумов (летних или зимних),
интенсивность которых описывается случайной величиной т2л1ах или
’inl£n /8/
Выполненный для нескольких метеостанций анализ многолетних
выборок годовых экстремумов из первичных таблиц наблюдений показал,
что для сглаживания статистических распределений летних и зимних
жстремумов приемлемы как нормальное распределение, так и
распределение Гумбеля, при этом для периодов повторяемости более 50
чет распределение Гумбеля дает более осторожные оценки квантилей т} .
Различие между квантилями для модели годовых экстремумов и
процессных моделей не превышает’ 1,5° С для периодов повторяемости
Y ..50 лет.
В связи с трудностями получения выборок годовых экстремумов
и । первичных метеорологических таблиц, можно оценить параметры
годовых экстремумов, выбрав тот или иной тип их распределения и
используя значения двух квантилей, вычисленных для процессной
м< щели.
Например, периодам N*'1- = 50 лет, N*^1! = 5 лет в
выборках годовых экстремумов соответствуют обеспеченности:
о?) =1 —— = 0,98 ; О)',21 = 1 - - = 0,8 и квантили
д 50 4 5
нормированной нормально распределенной переменной:
= 2 05 ’ z*^ • = 0 84
ЛИЛ DUB >
тогда:
в 'ЗУ - 31,8 _ 0
Tj ппо 2,05 - 0,84
Tljnin = -38,3 - 2,05 5,4 = -27,2" С
Из непосредственной обработки выборки годовых экстремумов
получены значения s, т!„ = 5,6° С ; = - 26,3° С .
г Vj 3*1.1 (J 7 ' _1 xJi_L.il
Таким образом, косвенный способ оценки параметров годовых
жстремумов дает приемлемые результаты.
На основе модели годовых экстремумов среднесуточной
температуры приращения T,(t) , Т_ (t) можно представить как
случайные величины
~ Х1 max ~ г- г = Т1 min ~ т+ f
93
В соответствии с подходом, принятом при разработке СНиП
2.01.07-85 "Нагрузки и воздействия" /64/ начальные температуры
конструкций т° , т? , оцениваются осреднением по времени
соответствующих полугодовых гармоник среднесуточной температуры
воздуха со случайной амплитудой А:
-0 _ 2 Ч2 ~ . 2л t _ 2 -
т, - т ± — Asin ------------ dt = т ± — А
Тк д тк 71
где
Тк - период, равный году ;
т - среднегодовая температура воздуха.
—о —о — , 2 ~ 2
т, ; т± = т ± —- А ; sT = — яА - параметры,
л ° л
Принимаются следующие оценки:
т = + . д _ ^уц ~ *1
2 ' 2 '
где xVIJ ; т, - среднемесячные температуры июля и января ;
SA = 4 Jsf + sf
Тогда
max
л + 2 _
~ Tvn
2л
л - 2 _
—-----Ту
2л
~ 0,8 TVIy + 0,2 Ту ;
т® ~ 0,8 Ту + 0,2xVII ;
4V
и в предположении независимости т2 гаах и rf
min
94
- х 1 max ~ (pr&xl + 0,2xvii)>
1 2
+ -j- S*
%2 ,Bio
(156)
X. “ XI min ~ (P^XVII + 0/2 Tj) J
Sf — (I 1 + — | S^x i
jC_ tf< У J Tjt пип у T. r rmV
7Г/ 7Г lmX
Для условий Москвы:
Tj = -10,2° c, lJmia = -26,3° С;
tVjj = 18,1° С, т1тах = 25,3° С;
н)гда по (156)
Т+ = 29,9° С; sT> = 3,3° С;
Т = - 38,8° С; sT = 6,1° С .
2.5. Нагрузки на перекрытия зданий
Вероятностное моделирование технологических нагрузок имеет
особенности по сравнению с климатическими нагрузками и воздействи-
ями. Вследствие исключительного разнообразия функциональных и
и хнологических условий, реализуемых в зданиях с различными объемно-
।панировочными и конструктивными схемами, возможности статисти-
ческого подхода для непосредственного нормирования нагрузок резко
ограничены, а изменение технологических условий во времени,
поражающееся в перепланировке и замене оборудования, перспективном
ржте нагрузок препятствует прямому переносу статистических данных на
будущие условия.
Наличие внутренних технологически обусловленных связей в
реализациях и выборках технологических нагрузок затрудняет вероят-
ностное истолкование результатов наблюдений и подбор адекватных
Функций распределения интенсивности нагрузок, а также накладывает
95
I
существенные ограничения на формирование однородных статистических
совокупностей ио технологическим признакам. Как правило, статисгичес!
кие оценки относятся к однородным пространственным совокупностям^
например, образованным из зон влияния однотипных конструктивны]
элементов одного или нескольких однотипных производственных участ
ков, и связаны с произвольностью выбора элемента из тако(
совокупности. (Зоной влияния конструктивного элемента считается част||
площади перекрытия, загружение которой произвольно расположенной
сосредоточенной силой вызывает перемещения и внутренние усилия ))
рассматриваемом элементе). Очертание зоны влияния определяется
обычно в предположении балочной схемы перекрытия с шарнирным'
опиранием элементов. Зона влияния является областью определения
поверхности влияния для эффекта того или иного вида - силы давления на
колонну, изгибающего момента в середине пролета ригеля и т.п. На этом
основании вводятся характеристики пространственной изменчивости!
интенсивности технологических нафузок как случайных' переменных,I
хотя эта изменчивость обусловлена, детерминированным»
тех нологическйм решением.
Вероятностное моделирование технологических нагрузок может
быть отчасти оправдано гем, что строительное проектирование зданий
осуществляется часто в условиях технологической неопределенности, при
отсутствии конкретной технологической планировки и каких-либо
данных о ее возможных изменениях в процессе эксплуатации здания.
Вероятностная модель статических нагрузок от технологического}
оборудования может быть основана на следующих исходных данных:
- типовой набор элементов основного технологического,
оборудования для производственного участка определенного назначения
с указанием веса оборудования типа " j “; Qj - площади по его
габариту , относительной частоты его применения vj (на данном!
участке );
- относительная платность размещения оборудования па участке
а0 , оцениваемая долей занятой оборудованием площади (возможные на
остальной части площади ос0 = 1 - нагрузки от людей.}
вспомогательных материалов, отдельных транспортных средств здесь нс
рассматриваются и должны быть учтены дополнительно).
Загружение площади зоны влияния Д() конструктивного!
элемента рассматривается как реализация пуасоновского потока события
где под событием понимается появление элемента оборудования в
некоторой элементарной ячейке со случайной площадью (поскольку в
типовом наборе площади по габариту оборудования различаются).
Математическое ожидание площади ячейки
96
д = Е
3
(157)
HIT
Vj - служит оценкой условной вероятности появления элемента
.^орудования типа j в произвольно выбранной ячейке (при условии,
•но ячейка загружена, а не свободна и в предположении, что значение
v । по площади не изменяется, хотя плотность его распределения
может быть в принципе и неравномерной).
Среднее число ячеек зоны Др , в которых потенциально
пи .можно появление оборудования
пд = . (158)
А Д
Относительная плотность размещения оборудования а0
ниодится как средняя для данного производственного участка оценка
(1Г|юятности появления элемента оборудования в произвольной
(циничной ячейке.
Тогда загружение зоны влияния конструктивного элемента
рассматривается как результат пА = пА независимых испытаний по
простой схеме Бернулли с вероятностью появления и вероятностью
непоявления (1 - ар) элемента оборудования в одном испытании
(единичной ячейке).
Число загруженных ячеек зоны влияния есть дискретная
случайная величина с биноминальным распределением пол .
Параметры
Л(?А ' Лол = а£> ПА > SnQA ~ ~ ар) ПА • (159)
Это означает, что относительная плотность размещения
оборудования в произвольной зоне влияния также является случайной
иг личиной
< параметрами
97
а„ ~ а°> . (160)'
ПА °* «1
Приемлемость простой схемы Бернулли как модели для оценки
пространственной изменчивости была подтверждена анализом
планировочных схем подвесных конвейерных систем автомобильных
заводов и результатами обследования нагрузок от мебели в основных
помещениях административных зданий /51/,
Для определения значений а^л в наиболее нагруженных зонах
влияния, принадлежащих к совокупности зон влияния данного
производственного участка, вычисляется © - квантиль п’0А , появ-
ляклцийся или превышаемый с вероятностью Fln03 г п0Д - 1 - ® ,
Значение п^А определяется как корень уравнения
Дд / Т1 \
1 - » . Е А «?(! - «<,)"" (161)
Л1 = '
подбором подходящего целого числа п^А , начиная перебор от пл с
>1
последовательным уменьшением на единицу. Соответствующий © г
• HqA
квантиль а о» = —— .
пл
Интенсивность нагрузки ст оборудования Q в произвольной
единичной ячейке определяется как результат одного из несовместных
событий появления нагрузки Qj с вероятностью vy , образующих
(v
полную группу vj :
Q = I vj ; Q = £ Vj Qy ;
7 Г /- (I62)
sq = L vj|4+ (e~ Qj) |-
j L J
Значения Qi устанавливаются по паспортным данным
2
оборудования или заданию на проектирование; дисперсией веса
98
отдельного элемента оборудования в большинстве случаев можно
пренебречь.
Параметры Q, Sq характеризуют интенсивность нагрузки в
। онокупности загруженных единичных ячеек производственного участка.
Осредненная нагрузка на площади единичной ячейки
— 2
дд " д ’ дд ' д ’ д& ~ д2 63
Результирующая нагрузка от л0Л элементов технологического
< ^орудования в зоне влияния Др будет равна
Z — KQAQ > — >
si = aonz[si+ (-1 + «р) Q2]
(164)
где параметры z , sf характеризуют технологическую нагрузку в
совокупности всех зон влияния производственного участка ; при
использовании вместо а0 значения О - квантиля a*QA параметры z ,
в2 относятся только к (1 - й))-ой части этой совокупности.
Осредненная по площади зоны влияния технологическая
нагрузка:
ЯА = Z - - _ _ _ А<п (165)
s~ 3<3л ’ *4 < Itr id i + ч Cil 5 1 4
Случайно расположенная технологическая нагрузка оказывает
различное влияние на внутренние усилия и перемещения
конструктивного элемента в зависимости от их вида и положения
сечений, к которым они относятся.
Эго влияние может быть учтено:
- выбором возможного неблагоприятного положения загруженной
площади арАр (или a^Ap ) в области определения поверхности
илияния <pz(x, у) рассматриваемого эффекта z ;
99
- приведением также фактических нагрузок с известной
плотностью распределения случайных координат f{x, у) к
эквивалентным по эффекту равномерно распределенным нагрузкам qs,
z9 = дэ fj Фг(*, y)dxdy = q3 фг Aip = q3Vz , (^6)
А,
где
Vx - объем, ограниченный поверхностью влияния;
V_
< pz = — - среднее значение функции влияния.
Др
Фактический эффект' нагрузки от случайно расположенного
элемента оборудования с равнодействующей Q :
Зфо = ёфг(х, у);
эквивалентная нагрузка из условия (166):
- _ 0Ф2(*,у)
ЧэО - —
Фг Др
При равномерной плотности случайных координат f (х, у) = —
Др
а = = 9л s2 _ (S^+ _ Qi
Чэ° ’ Ар ’ - пгА ’ nf
Фг = — Я ((>2ЛХ' У) dXdY-
А<р
Фактический эффект нагрузки от п0А
технологического оборудования в зоне влияния А
(267)
элементов
гФ = Дм гФв ’
эквивалентная нагрузка из условия (166)
100
1К1)ивалентиая нагрузка из условия (166)
Фг
(168)
параметры эквивалентной нагрузки будут
Чэ = <*Q Ча = Ча ;
ч1) ^7 ~
Ф2
(169)
коэффициент вариации эквивалентной нагрузки
(170)
где
50
v0 - ~ определяется по (162).
Коэффициент вариации vq, учитывает все основные факторы
технологической эквивалентной нагрузки: изменчивость интенсивности
натрузки от элементов оборудования, плотность расположены
оборудования в зоне влияния, вид рассматриваемого -эффекта в связи со
случайным расположением оборудования, площадь зоны влияния (через
2.6. Нагрузки от веса конструкций
Нафузка, определяемая собственным весом несущих
консфукций действует в течение всего срока службы, сооружения.
Нафузка от веса ненесущих элементов (например, перегородок) может
изменяться во время эксплуатации здания в результате реконструкции.
>|'И изменения могут касаться величины нафузки и ее положения в
1 (росфанстве. Нормативное значение веса консфукпии определяется на
101
основе стандартов, рабочих чертежей или паспортных данных заводов
изготовителей, а также по проектным размерам и плотности материалов и
грунтов с учетом их влажности в условиях возведения и эксплуатации.
Условия изготовления диктуют различия в значениях коэффициентов
надежности. Так для бетона изготовленного в заводских условиях
yf = 1,2 , на строительной площадке - у t = 1,3 .
Элементарный вес dG конструкций можно записать в виде
d G = у dV , (171) I
где
у - плотность материала ;
V - элементарный объем.
Возможные флуктуации веса определяются изменчивостью
плотности материалов, геометрических размеров, веса под влиянием
факторов (например, вес защитных покрытий, пренебрежение
отверстиями и швами и т.п.).
Отмеченные факторы влияют на нагрузку от собственного веса.
Они носят как случайный так и систематический характер.
В соответствии с уравнением (171) нагрузка от собственного веса
вычисляется с учетом плотности материала и размеров элементов.
Поэтому целесообразно рассмотреть вероятностные модели для
плотности и для размеров. Эти две модели и определяют вероятностную
модель нагрузки от собственного веса.
Размеры конструктивных элементов могут бьггь представлены, 1
как
а = ааор1 + д а , (172)
где
алот ' номинальное значение согласно чертежам;
Да- отклонение от номинального значения.
Для ансамбля элементов
Да = Д as+ Д аг , (173)
где
Д ад - систематическое отклонение;
Д аг - случайной отклонение.
В общем случае отклонения могут бьггь представлены как
102
да = д а + и + v + w(x, у, z)
(174)
I цс
Да- математическое ожидание по всей партии конструкций;
и - случайная величина (и= 0), характеризующая
межпартионную изменчивость;
v - случайная величина (V = 0), характеризующая
ппутрипартионный разброс;
у, z) - случайная функция (w =0), характеризующая
п 1менчивость размеров в пределах элемента (как правило ее влияние на
шипение величины нагрузки от собственного веса несущественно).
Значения отклонений зависят от принятой системы допусков,
обычно контроль по допускам более важен при определении прочности
в.'ш жесткости, чем при определении собственного веса. Концепция
номинальных значений очевидна и для модели плотности
Y = 7лога +
(175)
где
Ду - отклонение от у вот .
Это отклонение также можно представит в виде суммы
поминальных отклонений Ду 3 и случайных отклонений Ду г:
Ду = Ду8 + дуг
(176)
Иерархическая модель может быть также применена для анализа
1пкггности с учетом ее изменчивости в пределах элемента, между
цементами в одинаковых условиях и с учетом разных технологий
п потовления. Изменчивость плотности зависит от многих факторов. На
первое место выступает структура материала и его физические и
химические характеристики (например, гигроскопичность). Для ряда
материалов (бетон, дерево) имеется статистическое соответствие между
математическим ожиданием плотности и математическим ожиданием
(>противления.
В результате интегрирования уравнения (171) получается
G = J у dV . (177)
v
Для линейных элементов (балки, колонны и т.п.) с площадью
поперечного сечения А нагрузка от собственного веса на единицу
103
длины будет
9(х) = f ydA
А
(178)'
где
у - плотность материала, которая изменяется случайно вдоль
длины элемента.
Можно ввести такое представление
д(х) = д + Дд(х);
А(х) = А + Дй(х); (179)
у(х, у, г) = у + Ду (х, у, z).
Из этого следуют приближенные выражения
Я = Ад; 1
_ _ (180) ।
Ад (х) = д ДА (х) + АШ(х),
где
Ду (х) = ~ J у dA - у ;
Л л
Ду (х) характеризует флуктацию плотности у по площади!
поперечного сечения.
Дисперсия <у(х) определяется соотношением
sJ(x) = sa + s7 J (181) |
для некоррелированных значений плотности и площади поперечного',
сечения
sy = s9 ~~2 f J Р (хп У1; х2> у2) dA} dA2 , (182)
” А1 Аз
где
р - корреляционная функция, р = 1 при
х; = х2 ; У1 = у2.
Аналогично для плит, стеновых элементов и т.п. нагрузка от
104
собственного веса на единицу площади будет равна
9(xf у) = f vdz
(183)
где
Интегрируя по толщине элемента t (zoTOflot)
д{х, у) = д + Дд(х, у);
Ф". у) = t + At(x,y);
у (х, у, z) = у + Ду (х, у, z).
Так же и для линейных элементов
g = t у;
у) = у At (х, у) + t (ж, у),
(184)
(185)
Дисперсия определяется соотношением вида <J8I) =
s& + Sy для некоррелированных значений толщины и плотности.
11ри ЭТОМ Sy « Sy .
Аналогичная модель может применяться для описания измен-
чивости собственного веса в пределах одного элемента, между
элементами изготовленными в одинаковых условиях и между элементами
изготовленными в различных условиях.
Усилия (нагрузочный эффект), возникающие в конструкции от
шпрузки собственного веса можно записать в виде
F = J Ту dV
(186)
ь
где
I - функция влияния нагрузочного эффекта;
Ь - характерный размер элемента;
V - объем.
Приближенное представление будет
105
(187)
(188)
у = у + Ду
ь = ь+ д ь
Тогда с учетом (187), (186) запишется как
F = F + 4F;
F=f/yd^;
ь
AF = \l^dV+\lydV.
b лЬ
Можно упростить вышеприведенное выражение для линейных
элементов
L
Г = J Ig(x) d* . (189)
о
где
д(х) - собственный вес на единицу площади поперечного
сечения.
Из (189) следует
L
F = j Ig dx;
0 LL П90)
Sf = sy П 1 (х1) 1 (х^) р (хь ха) dxidX2
о о
Предполагается, что:
sg = const вдоль длины элемента;
р(хпх2) - корреляционная функция, р = 1 при х2 = х2 .
Для пространственных элементов
F = J I д(х, у) dA;
Л
F = $Ig(x,y)dA; (191)
А
= s9 | J Т(хл> У1) Т(х2’ уг) р(хъ Уь х2, у2) dAjdAi .
А А
106
Глава 3
МЕТОДЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТИ
ОТКАЗА
3.1. Общие замечания
Все показатели надежности, которые могут быть использованы
при формулировании нормативных требований к строительным
конструкциям представляют собой достаточно простые функции вероят-
ности отказа за какойлибо определенный промежуток времени. Поэтому
основной задачей вероятностных расчетов является вычисление вероят-
ности отказа.
Условие отказа математически выражается неравенством
R - Q < О
(192)
В общем случае R и Q - случайные величины. В некоторых
случаях (например, при рассмотрении требований жесткости) К может
Гл.ггь детерминированным ограничением.
Вероятность отказа есть вероятность реализации неравенства
(192)
00
Pf = Prob.{R “ Q < 0} = f ^(x) dx , (193)
о
где
Pf - вероятность отказа;
Р^оь/А) - вероятность реализации события А;
Fjj - функция распределения вероятностей величины R ;
fQ - плотность распределения вероятностей величины Q .
Интеграл (193) может быть представлен в виде
107
Pf = p™b.{g(R’Q) < 0} = fl 4(x2, x2) f0(xb x2) dx2dx2 , (194)
co
где:
g(R, Q) = R - Q - функция рабогоспособностиж;
ю - область отказовых состояний в пространстве (R, Q)
граница которой определяется условием д - О
Величины К и Q могут быть функциями многих случайных
переменных (нагрузок, характеристик прочностных и жесткостных
свойств материалов, геометрических параметров). Поэтому интеграл (194)
может вычисляться в виде
Зоь.{ g(xI,x2>...,^) <0} =
, (195)
= f... Jffl(xj,x2,...,^1)^(xi,x2,...,xa)dxj)...,d^
<оа
где
®а - область отказовых состояний в п -мерном пространстве
[Х], х2, • • . , ха) , граница которого определяется условием д = 0 .
В некоторых случаях интеграл (195) удобно записать в виде
о
pf = ртЬ.{д < о} = , (196)
-а>
где
£„ - плотность распределения вероятностей величины
д = R - Q , определяемая как композиция законов распределения
величин R и Q .
Все рекомендуемые ниже методы есть методы вычисления интег-
рала (193) в различных видах его записи, сформулированные Ю.Д.
Суховым /71/ и содержащиеся в /40/.
108
Я.2. Метод двух моментов
Если несущая способность R и нагрузочный эффект Q распре-
пгиены по нормальному закону, то интеграл (193) выражается через
интеграл вероятностей
pf = I - <Кп)
(197)
щс
„ R ~ Q
р _ — - . ..— - индекс надежности (характеристика
№ + .^)
<>г юпасности);
R и Q - средние значения величин R и Q ;
sK и sQ - стандартные отклонения величин R и Q .
Преимуществом такого подхода является его простота.
Недостаток метода состоит в ограниченности применимости нормального
ш кона. Метод может также быть использован при применении
Hi « нормального закона. При этом нужно учесть, что если R и Q есть
Функции нескольких случайных переменных, то они могут иметь
нормальное распределение только в том случае, когда все исходные
переменные распределены нормально.
Пример 1
В качестве примера рассмотрим сферическую оболочку радиусом р ,
нагруженную внутренним давлением Q (рис. 26).
Требуется определить толщину оболочки h , соответствующую
«/данному уровню надежности Рд = 0,97712, [} — 2.
Напряжение о = — = AQ .
Критерием отказа является достижение напряжением о предела
прочности R . Выражение для индекса надежности запишем в виде
и . ...«-лё
(«?< ЛЧ2)
Нагрузка и предел прочности распределены по нормальному закону с
числовыми параметрами:
109
R = 500 МПа, sR =50 МПа, Q = 5 МПа, sQ = 0,5MHa.
Рис. 26. Оболочка, нагруженная внутренним давлением
Обозначив
а = Q2 - $2я2 ; b = 2RQ ; с = R2 - $2s2R ,
из (197) получим
я _ Ь ± ^Ь2 - 4ас
2a
Для р = 100 см; А = 75 и h = 0,66 см.
Для нелинейных функций работоспособности
в ряде задач находит применение метод статистической линеаризации,
основанной на разложении в ряд Тейлора нелинейной функции в
окрестности приближенного положения центра распределения случайного!
вектора (хь х2, . . . , хп) . Формулы для приближенного вычисления
числовых параметров нелинейной функции независимых случайных
аргументов записываются в ваде
9
дд'
.дх,,
s2
S9
2
S2 +
(дд}2 2 (198)
[dxj-
а'ха
foV s2
+
НО
и Щ 98) определяется ₽ = g/sg .
Пример 2
В качестве примера (предложен Ю.Д. Суховым) рассмотрим
гшецентренно сжатый стержень в виде сварного стального двутавра (рис. 27).
Рис. 27. Поперечное сечение стойки
Геометрические характеристики сечения I - 1920 см4, W = 240 см),
А - 48 см2. Эксцентриситет нормальной силы е - 1,2 см.
Критическая нагрузка
=l,2-l(fH
Определяем вероятность текучести крайнего волокна. Функция
работоспособности
.ч)е
1
г| = -------jj- ; ат - предел текучести.
1 - —
Условие отказа g < 0 , а граница области безотказной работы g - 0 .
Нагрузка принимается распределенной по двойному экспоненциальному
мкону.
Функция распределения нормальной силы
111
Fjf = exp -exp
x - a
Плотность распределения
x - a
fW(x) = J“exP
exp - exp
x - a
Параметры распределения a = 51(f H, 0. = 610* H. Используя известные
соотношения
N - a + 0,5 7 70. и s2 = 1,6450?
определяем N = 5,3510s H, — 7,6910* H.
Предел текучести принимается распределенным по логарифмически
нормальному закону
Числовые характеристики аГ = 31(f Па, sc? = 31 О' Па Обозначив
х2 = N и х2 = <уТ, запишем
х2 - Х1
60 106
1,2 106
+ 208,3
да 7,2 1012
дх2 ~ ^1,2 - 106 - Xj)
= !
дх2
Подставляя в (198), находим g =14,0510', s9 = 3,46 IO7. Тогда, следуя
(197)
0 = 4,06 и ему соответствует Pf = 3,18- Iff5, Pg = 0,9999682.
112
Полученное значение вероятности безотказной работы является
ыч 1.ма приближенными, и как будет показано в следующем параграфе
hi ничается существенно (в большую сторону) от его реального значения.
.1,3. Метод “горячих точек”
Если исходные величины распределены не по нормальному
шн.цу, то теоретически можно предложить такое их преобразование,
'нибы привести их распределение к нормальному. Однако, точное
рппгние здесь возможно только для законов, производных от
нормального (логарифмически нормальный, Рэля и т.п.). В остальных
пучаях преобразование представляет собой приближенную аппрок-
шмпцию исходных законов нормальным. Эта аппроксимация должна
иi.iподняться на границе области отказа в точке (точка подгонки) с
инксимальной совместной плотностью распределения всех исходных
мгличин, так как в окрестной этой точки сосредоточены наиболее
|н'|юятные их сочетания.
Для вычисления вероятности отказа (193) может быть
Hi пользован метод, который был разработан в б. СССР Б.И. Снарскисом
/(. 1, 62/ и названный им "методом горячих точек". Практически тот же
метод в тот же период времени был сформулирован Хасофером и Линдон
/’>!/. За рубежом он получил название "метод первого приближения".
Позднее метод дорабатывался и совершенствовался многими
•пгорами. В предлагаемой методике используется метод горячих точек с
и шальной аппроксимацией распределений исходных величин нормаль-
ным законом. Аппроксимация производится в "горячей точке" - точке
подгонки. Т.к. положение точки подгонки, как правило заранее опрсде-
||ц г невозможно, то метод требует итерационного подхода.
В общем случае нескольких исходных величин при нелинейной
Ччтице области безотказной работы процедура “метода горячих точек"
еостоит в следующем.
Пусть х}, х2, . .. , ха - исходные случайные величины с
и шестными интегральными Ех. и дифференциальными fx функци-
ями распределения. Граница области безотказной работы задана уравне-
нием
д(х1,х2, ...,хп) = 0 ,
utc
113
д - функция работоспособности, выбираемая так, чтобм
вероятность безотказной работы определялась как вероятность того, чтС
д > 0. На первой итерации на границе области д = 0 произвольно
выбирается точка подгонки (хъ х2, . . . , хв) .
Так, например, координаты точки подгонки могут выбираться как
квантили вероятности 0,95 распределении всех исходных величин кроМ|
одной. Эта последняя координата находится из условия д = 0 , т.е. и!
условия принадлежности точки подгонки границе области безотказной
работы. Таким образом, координаты "точки подгонки” опрсделяютс|1
формулой
о-г
Х1 = F^(0,95)|i=i , (199)
а х° определяется из условия д = 0 .
В точке подгонки производится локальная нормализация исход-
ных величин; локальная нормализация заключается в том, что определя-
ются среднее значение х± и стандарт sx такого нормального
распределения величины xi у которого значения интегральной и
дифференциальной функций распределения в точке подгонки равны
значениям соответствующих функций исходного распределений
величины х±
(200)
здесь
Ф и ф
интегральная функция и плотность нормального
стандартного распределения.
Центрирование осуществляется преобразованием
.п
(201)
114
Если граница области отказа д = О нелинейна, то функция
1>п1>отоспособности д линеаризуется также в точке подгонки.
Линеаризованная функция работоспособности запишется в виде
п ~ К" *?)
й(х2,х2, ...,хя) = ....' (202)
i=lcxi
хп=<
Т.к. точка подгонки выбрана на границе области безотказной
(тботы, то д = 0 , тогда
h(xltx2,...,xB) =
А / ч Л А , (203)
= -s Mxi - *1) = - £aixi
1 = 1 1 = 1 1 = 1
। де
a =
1 dxi xi - x“
Условие безотказной работы определяется неравенством h > 0
или
> faixi (2(J4>
i = l 1 = 1
В левой части (204) - детерминированная величина
л л
с = £ а1х1 > а в правой части - случайная величина z = У а^,
i = 1 1 = 1
распределенная по нормальному закону с параметрами:
Л
- среднее значение z - ;
1 = 1
-стандарг sz = • (205)
V 1 = 1
Вероятность выполнения условия безотказной работы будет
115
p„ » J fz(z) dz = ф(р) , (206)
где
(207)
Если нормализованные исходные величины стандартизировать,
т.е. провести преобразование , то в пространстве этих
s_
стандартизированных нормальных величин расстояние от центра
распределения (от начала координат) до линеаризованной границы
области безотказной работы (до “горячей точки”) h - 0 будет равно
р. Точка пересечения перпендикуляра, опущенного из центра
распределения к прямой h = О , с этой прямой есть "горячая точка".
Итерации продолжаются до тех пор, цока выбранная в очередной раз
точка подгонки не окажется "горячей точкой", т.с. расстояние до точки
подгонки в пространстве стандаргизованвых нормальных величин от
центра их распределения
(208)
не окажется равным р .
Эго означает, что линеаризация границы области безотказной
работы была проведена в точке с максимальной по этой границе
плотностью совместного распределения исходных величин и погрешность
от нормализации и линеаризации минимальна, т.е. индекс надежности
Р = р , а вероятность безотказней работы Ps = ф(0) .
Если в результате очередной итерации оказалось, что р * г ,
то точку подтопки для следующей итерации задаем следующим образом;
все ее координаты, кроме одной, принимаем равными соответствующим
координатам "горячей точки" предыдущей итерации, а. последнюю
координату всегда ищем из условия д = 0 . Таким образом,
116
Х? - Xi +
(209)
Преимуществом метода является его универсальность и простота
п норитма. Недостаток метода состоит в том, что функция д , опреде-
ли иная область отказа, должна быть всюду дифференцируемой и
111ПДКОЙ. При кусочной границе области отказа, требуются
шнюлиительные меры, усложняющие алгоритм. Отметим также
in гру длительность в оценке погрешности.
11/т мер 3
Рассмотрим тот же внецентренно сжатый двутавр, как ив
предыдущем параграфе. Параметры логнормального распределения предела
тек унести определяем из выражений:
т = In стт - 0,5t2
t2 = In 1 -
t2 = In 1,01 = 0,01 , t = 0,1
m = In 3 • 10s - 0,05 = 19,51
Для нахождения значений функций КстДх) и £аДх) будем
ы пользовать таблицы нормального закона, применяя преобразование
1паг - 19,51
Мх) = ф[Ф0] , Ч(х) = v (р[и(х)]
Ф и <р - нормальный стандартный закон:
Обозначив х1 = N и х2 = от запишем также выражение для
функции работоспособности
117
х2 -
Х1
60 • 106
1,2 106 -
— + 208,3
Х1
дд
Ох2
7,2 101г
[1,2 if -
- 208,33 ;
дд
дх2
д
1-я итерация
Координаты точки подгонки определяем согласно (199)
X? = F-^0,95);
exp
- exp
х? - 5 JO5"]
6 if J
= 0,95,
отсюда
In (- In 0,95)
X? - 5 105
6 104
x? = 6 - 104 - [in (-In 0,95)] + 5 105 = 678200
Подставляя x° в равенство g = 0
x% = 678200
60 if
1,2 Iff - 0,6782 • if
+ 208,33
= 2190 • 10s
Числовые параметры определяем согласно (201)
Xj = 678200 - ®~40,95)sXi 678200 - 1,645s.
s = <?(1,645)
1 f
-------z exP “
6 io4 4
6,78 IQ5 ~ 5 105
6 104
ехр[-
6,78 105 - 5 105
6 • 104
= 8,123 IO 4 ;
118
sXj = 1,27 105 ; Xj = 4)69 • IO5
Аналогично определяются x2 и sx?:
x2
flnx? - 19,51
» * --±---------
I 0,1
flnx? - 19,51}
<p-----------------
I 0,1 )
10 flnx? - 19,51}
— <p ------------------
xj 4 0,1 )
vn
x2
10
219 105
x2 = 2868 105
Центрирование
о
xf = 678200 - 469390 = 2,08 105
о
xn2 = 2190 105 - 2868 105 = -678 - 105
Согласно (203) определяем ктффициенты
Si
dXjX‘
1 xi
72 • 106
----------- + 208,33 = 472,4
(1,2 - 0,67V
a2 - -1
Следуя (205)
s2 = /472/4 1,27 105)2 + (219 IO5)2 = 638,4 105 .
Дня определения p находим (207)
о
X? = 472A 2J08 1CP + 678 1CP = 1664,4 l(f
119
1664,4
Р " 638А ~ 2fil
Из (208) получим
2
= 3,50 6
Следовательно, проводится следующая
2-я итерация
Координаты точки подгонки согласно (209)
2
- • 2,61 = 7)8 • 10?
„ , 472,4 (1,27 105\
х? = 4,69 10? + ----------L.----- 1
638,4 10?
60 )
—-----— + 20В,33\ = 2741,2 10?
1,2 - 0,78 )
х% = 7,8 105
Нормализация
х2 = 7,8 105
s.
w 17 а 7л5\ ( 7^- 105 - 5 105
FX1\7^ Ю ) = ехр -expj-^--—~~4-------
Ф 1(0,9 906 7) = 2,34 6
1
-------т ехР
6 104
= 0,99067
7,8 105 - 5 105
6 • 104
- ехр
7^ 105 - 5 105'
6 104
= 1,546 10~7 ;
120
<р (2,346)
fXi(7r8 105)
= 1,646 105
X! = 7,8 10s - 2,35 1,65 • IO5 = 3,94 105
X2 = 2741 - IO5 - ф-ЧгхД2741,2 Ю5)1 %
Ф"1 ^Fx^2741,2 105)] = 10(in 2741,2- 105 - 19,51) = -0,84
2741,2 • 105
10
= 274,1 - 105
x2 = 2741,2 IO5 + 0,84 274,1 105 = 2971,2 105
Центрирование
о
x? = 7,8 105 - 3,93 • 105 = 3,86 10s
0
xn2 = 2741,2 -IO5 - 2971,2 105 = -23 0 105
Коэффициенты .
72 1012
a2 = ---------7.------------- + 208,33 = 616,63
1,2 1</ - 0,78 - 105
a2 = -1
Определяем г и p
s2 = ^[616^3 • 1^5 105^ + [274 105f = 1051,67 -IO5 ;
о
xf = 616,63 3,86 l(f + 230 • 105 = 2611,9 lo6
121
2611,9 105
1051,67 IO5
r
+
yk 1,65)
230 V
274,1)
= 2,49 p
Вероятность отказа Pf = 0,0064 .Вероятность безотказной работы
Ps = 0,9936 .
Предложенные итерационные процедуры проиллюстрированы на
рис. 28.
Рис. 28. Зависимость - N
122
3.4. Метод статистических испытаний
Если осуществляется оценка вероятности отказа по частоте
события (Q > R) , то производится достаточно большое число
t гн гистических испытаний по схеме Бернулли, т.е. на каждом испытании
генерируются случайные реализации всех исходных величин.
Выполняется детерминированный расчет значений Q и R и как
Функций этих реализаций и проверяется условие Q > R . Если условие
выполняется исходом испытания считается отказ. Частота v появления
отказа рассматривается как оценка его вероятности Р£ :
Jc
V = — и pf
Л1
(210)
где
Jc - число отказов;
Л1 - общее число испытаний.
Метод крайне прост и универсален, однако он чребует обяза-
кльного анализа близости оценки v к искомой вероятности Pf .кото-
рая зависит от числа испытаний т .
Известные методы такого анализа основываются на предельных
теоремах:
- Бернулли, утверждающей, что при л? -> да, v —> Р£ и что
имеет асимптотически нормальное распределение;
- Хинчина (закон больших чисел), утверждающей, что средние
частоты v при т -» да стремится к се математическому ожиданию;
- Лиццсберга-Леви (центральная предельная теорема), утвержда-
ющей, что среднее значение частоты v имеет асимптотически
нормальное распределение.
Однако теоремы сложения гласят, что биномиальное распре-
деление (а число отказов распределено именно по биномиальному
закону) устойчиво при сложении независимых величин
(самовоспроизводится) и что сумма взаимно независимых случайных
величин имеет нормальное распределение тогда и только тогда, когда все
они нормально распределены. Поэтому возникает вопрос: при каком
общем числе испытаний можно пользоваться предельными теоремами и
принимать асимптотические распределения для построения практических
процедур проверки точности и достоверности полученных оценок.
Ответить на этот вопрос практически невозможно. Кроме того,
известные процедуры используют асимптотическое распределение
123
частоты v и имеют целью построение доверительного интервала для ее
математического ожидания, а не искомой вероятности. Процедуры эти
достаточно сложны и недостаточно убедительны, что часто приводит
вообще к отказу от анализа близости оценки.
В /71/ разработана простая процедура построения доверительного
интервала для вероятности отказа Pf , использующая распределение
этой вероятности. Суть процедуры состоит в следующем.
Число к отказов в т испытаниях при вероятности отказа
Р = -Pf в одном испытании распределяется по биномиальному закону
^Р,т(к) = С^Рк(2 - РГ’к • (211)
Это распределение дискретно, т.к. к - целое число. В реальной
ситуации нам известны к и т и неизвестно р .
Мы можем только предполагать с некоторой вероятностью,
каково было значение р в каждом из проведенных испытаний. Это
предположение характеризуется плотностью распределения вероятностей
величины р , которая выражается из формулы (211), если в ней за
аргумент принять не к , а р и ввест и нормирующий множитель у :
- *Скрк(1 - р)тк . (212)
I
11ормируюший множитель % определяется из условия
j *₽(р) dp = 1
-00
и равен (гл + I) . С учетом этого формулы для плотности распределения
вероятностей (211) представляется в виде
fpA,ro(p) = (™+ l)Ckpk(l - pf к . (213)
и выражает собой бета-распределение (непрерывное распределение)
Гр(р) = +р“’а(1 - р)р 1 . (214)
(а - 1) ,'(р - I) ! *
при
124
(a - 1) = к ;
(0 - 1) = Л1 - к .
Для получения границ доверительного интервала для р
необходимо вьптисление значений функции распределения Fp для бета-
рлопределении, что представляет собой крайне сложную задачу.
Таблицы этой функции имеются лить для небольших значений
тик. Однако, путем элементарных, но громоздких преобразований
можно доказать, что
Рр/к,т(р) = 1 - Fk/p,(mi 1)(т) > (215)
где
FPi'kr т ~ Функция распределения р при заданных Л1 и к (бега
распределение) ;
Fk/P,ni ' Функция распределения к при заданных т и р
iбиномиальное распределение).
Для вычисления функции биномиального распределения при
больших т , малых р (р < 0,!) и конечном т, р можно
пос пользоваться пуассоновским приближением
= <4p*(1 - р)~‘ . е -г <216)
г.е. в нашем случае
к r i к
1 - Ъ>/к,ш(р) = Ш <217)
2 = 0 2=0
где
к = (т + 1) , a fk(i) вычисляется по рекурентной формуле
4(-0 = fk(P) = е-К
(218)
Практически строится функция > из которой
преобразованием к = (лт + 1)к можно получить функции Fp/t(p)
125
для любого Л1 . По этой функции можно определить квантили
вероятности у :
А.
X, = Г^(у) и доверительные коэффициенты ду(к) = — .
к
Произведение т| v2 ееть 1раница доверительного интервала,
к
соответствующая достоверности у , где v, = ------- .
т + 1
При больших т и малых к - v} к, v . В табл. 7 приведены
значения ц095 и ц0/99 в зависимости от числа отказов к .
Покажем применение данного метода на практике. Допустим,
нами проведено 5000 испытаний, из которых в к = 20 произошли
отказы. Частота отказов таким образом составила v =0,004.
Тогда с доверительной вероятностью 0,95 можно утверждать, что
pf Ho,95v =1,453 • 0,004 = 0,005812
и с вероятностью 0,99
Pf =1,655-0,004=0,00622.
Доверительные коэффициенты ц зависят только от числа
зафиксированных отказов к и не зависят от числа испытаний. Это дает
возможность составить полную таблицу практически необходимых
значений коэффициентов. Процедура анализа результатов статисти-
ческого моделирования становится крайне простой и выражается
формулой
ргоь.{рг 5 = у . (219)
Можно задаться желаемым доверительным коэффициентом (т.е.
точностью и достоверностью) и выполнять испытания до тех пор, пока не
получим соответствующее число отказов. Этим решается проблема
определения необходимого числа испытаний.
Как известно, теоретически истинное значение любой
характеристики, определяющей случайную величину, может быть учтено
при бесконечно большом N - числе экспериментов. В инженерных
исследованиях строительных конструкций, где требуются высокие уровни
надежности порядка 0,999 - 0,9999, приходится иметь дело с очень
малыми значениями вероятности отказа и исследовать “хвосты” функций
126
распределения парамеч-ров. Эти “хвосты” определяются с достаточной
го-шостью При N не менее 106 - 109 (в зависимости от типа задачи).
Таблица 7
Значения доверительных коэффициентов т|0 д5 и rj0 99
к Ло,95 00,99 к По,95 Ч\0,99
1 4.74390 6.63900 31 1,34961 1.50353
2 3.14790 4.20300 32 1.34320 1.49414
3 2.58460 3.34850 33 1.33714 1.48532
4 2.28840 2.90137 34 1.33134 1.47688
5 2.10261 2.62200 35 1.32583 1.46884
6 1.97375 2.42850 36 1.32058 1.46117
7 1.87832 2.28579 37 1.31556 1.45382
8 1.80435 2.17537 38 1.31076 1.44683
9 1.74503 2.08717 39 1.30615 1.44012
10 1.69623 2.01450 40 1.30174 1.43370
И 1.65524 1.95368 41 1.29750 1.42756
12 1.62025 1.90175 42 1.29343 1.42161
13 1.58990 1.85688 43 1.28951 1.41593
14 1.56332 1.81768 44 1.28574 1.41044
15 1.53981 1.78290 45 1.28211 1.40513
16 1.51884 1.75191 46 1.27862 1.40005
17 1.49996 1.72412 47 1.27522 1.39513
18 1.48288 1.69900 48 1.27197 1.39038
19 1.46733 1.67613 49 1.26880 1.38582
20 1.45312 1,65525 50 1.26574 1.38135
21 1.44002 1.63600 51 1.26279 1.37706
22 1.42795 1.61823 52 1.25992 1.3729С
23 1.41676 1.60180 53 1.25714 1.36888
24 1.40636 1.58656 54 1.25445 1.36500
25 1.39664 1.57236 55 1.25185 1.36118
26 1.38756 1.55902 56 1.24929 1.35750
27 1.37906 1.54656 57 1.24683 1.35389
28 1.37105 1.53488 58 1.24443 1.35045
29 1.36350 1.52379 59 1.24210 1.34705
30 1.35635 1.51340 60 1.23983
Таким образом, основная сложность задачи, решаемой методом
статистических испытаний, заключается в длительности проводимых
расчетов. Однако, уже сейчас бурное развитие вычислительной техники и
127
увеличение быстродействия ЭВМ ведет к сокращению длительности
расчетов.
Общий алгоритм расчета строительных конструкций методом
статистических испытаний следующий.
Все параметры конструкции R1.....Ro и нагрузки Q}.....QB ,
обладающие изменчивостью, считаем случайными величинами с
известными законами распределения. Законы распределения задаются
численно с помощью генераторов случайных чисел. Предполагается
известным также детерминированный метод расчета конструкции.
Отказом конструкции считается невыполнение принятою основного
расчетного условия.
Определение частоты отказов и построение гистограммы
функции резерва прочности осуществляем по следующему алгоритму.
1. Методом статистическою моделирования, согласно известным
законам распределения, назначаем п реализаций случайных величин -
параметров конструкции и нагрузок Я1е,..., Кдц ; Qie,--<Qji
(i - 1, . .. , n) . Количество испытаний л назначаем, исходя из затрат
машинного времени;
2. Проводим л детерминированных расчетов конструкции
согласно выбранному методу. В результате расчетов л раз определяем
значение функции резерва прочности д .
3. При значении д < 0 фиксируем отказ. Частоту отказов
вычисляем по формуле (210).
4. Далее сравниваем полученную частоту отказов с наперед
заданной вероятностью отказа Pf . Изменяем один из параметров,
например процент армирования (для железобетонных конструкций), и
возвращаемся к шагу 2. Методом итераций повторяем вычисления до
достижения нужной частоты отказов.
5. По достижении заданной частоты отказов для полученных
значений строятся гистограммы относительных частот функции
распределения резерва прочности на интервале равном т стандартам
д . При этом правая и левая границы интервала лежат на расстоянии
т/2 стандартов вправо и влево от математического ожидания д .
Метол статистических испытании с достаточной точностью
позволяет определить оценку вероятности наступления отказа тех строи-
тельных конструкций, которые рассматриваются в данной книге. При
этом расчет может осуществляться эффективным образом на
современных быстродействующих ЭВМ.
Применяемый метод определения верхней границы
доверительного интервала для величины оценки вероятности отказа
является достаточно простым и эффективным.
128
Описанный метол построения доверительного интервала
> июляет производить нормирование не необходимою числа испытаний,
I необходимого числа отказов. Затем по этому числу отказов по табл. 7
можно получить коэффициент т]о 95 или Лорр , на который нужно
умножить полученную вероятность отказа, чтобы получить верхнюю
границу доверительного интервала, которая не будет превышена с
нс|Х)ягностью соответственно 0,95 и 0,99.
1 [реимуществом метода является его простота и универсальность.
I |е достаток метода состоит в т ом, что при оценке малых вероятностей Р{
i приемлемой достоверностью (т.е. требуемых малых значений
доверительного коэффициента, а следовательно, достаточно большого
числа отказов) может потребоваться большое число испытаний. И если на
каждом испытании выполняется сложный детерминированный расчет, то
общая потребность машинного времени становится непомерно большой и
метод оказывается неэффективным.
3,5. Метод Монте-Карло
Более эффективным, т.е. дающим меньший разброс оценки
вероятности отказа по сравнению с предыдущим, является метод
статистического моделирования, получивший название метода Монте-
Карло. Интеграл (193) по определению есть нс что иное, как
математическое ожидание функции Fk , а несмещенной эффективной
оценкой математического ожидания является среднее выборочное
шачение.
Поэтому
Р{ = j dx = Fr(Q) * , (220)
0 m i-l
где
£, - математическое ожидание величины F ,
т - число испытаний.
Т.е. на каждом испытании по плотности вероятностей величины
У моделируется ее реализация Q± и определяется значение функции
распределения величины R при аргументе Q . Затем определяется
среднее из этих значений по всем проведенным испытаниям.
Если величина Q есть функция нескольких переменных
129
Q = 4Q(4i, Чг, - •, q„)
(221)
то на каждом испытании по плотностям вероятностей величин qt
моделируются их реализации gi;?- , вычисляется значение и далее как в
одномерном случае.
Если же и величина R есть функция нескольких переменных:
-R = <Рк(Г1, г2, . . . , г„) , (222)
то ее функция распределения должна быть получена заранее
аналитически либо путем статистической обработки результатов
физического или математического моделирования.
Выражение (220) можно представить в виде
Г-' г _______ 1 у ш
р£ = = «-zp-зМ<22з>
о ‘ 1П 1=1
Тогда должна быть заранее известна функция распределения
величины Q , а величины Rj моделируются по их плотностям
веро5ггностей.
Преимуществам метода является его простота и повышенная
эффективность по сравнению с методом оценки вероятности по частоте,
т.е. меньшая потребность машинного времени.
Недостаток метода состоит в том, что в многомерном случае одна
из функций распределения величин R и Q должна быть заранее
задана. Кроме того, анализ точности и достоверности результата здесь
приходится выполнять с использованием асимптотических распределений
получаемой оценки, а нс искомой вероятности как в предыдущем методе.
Для этого используются более сложные и менее эффективные известные
процедуры.
Пример 4
Для примера решаем ту же задачу, что и методом "горячих точек"
1
mi=i
Моделируем значение нормальной силы N Используем для этого
датчик случайных чисел с равномерным распределением на интервале | 0 , 1 |
и преобразование с помощью функции распределения FN (N) (рис. 29).
130
Датчик дал первое случайное число = 0,084 , т е.
Г„(^) = ее = 0,084
N1 = 6 10^-In (-In 0,084)] + 5 • 105 = 445490H =
= 4,4549 105 .
Находим предел текучести из условия его равенства напряжению в
крайнем волокне от силы
&Т1
60 10s
1,2 106
+ 208,3
1281,7 105Па
Этому значению предела текучести соответствует значение
функции распределения
гат[^(^)| = ф[10(Ь1ат, -19,51)
= Ф(-8/4^ = 1 - Ф(8/Г8) = 0Д00
Операцию проводим 1000раз и находим среднее значение
131
J 1000
Pf = ------- У p. (nJ = 0,0049
1000 тЛ 11
Получив этот результат, мы еще ничего не можем сказать о его
точности и достоверности, т.е. достаточности тысячи испытаны
Необходимой операцией во всех статистических методах является оцени
этой достаточности.
Для этого формируем и рассчитываем 20 выборок по 1000 испытание
в каждой и получаем 20 значений оценки вероятности отказа Pf , которун
рассматриваем как случайную величину, математическое ожидание к оторв
есть Pf . Так как среднее квадратическое отклонения этой случайной
величины нам известно, то для нахождения доверительного интервала Р{
используем критерий Стьюдента.
Доверительный интервал
v = ± tp
Различным
^Pfi2 - МР2.
У М(М- 1)
значениям tp соответствуют различные значения
доверительной вероятности p(t)
В нашем случае М —20 и искомая вероятность Pf оценивается
следующим образом:
Pf = Pf, ± tp
I 20
tPf/ ~ 20 P2
i- 1
20 19
Таблица S
Таблица вероятностей Pf, наступления текучести
в краевых волокнах стержня
85333F.-02 64393Е-02 50887F.-02 46491 Е-02
67381Е-02 63440 Е-02 50115 Е-02 42542Е-02
66616Е-02 57279Е-02 50007Е-02 37344Е-02
66438Е-02 55120Е-02 49169F.-02 33796Е-О2
66137Е-02 539О9Е-О2 48898 Е-02 10305 Е-02
132
Расчеты проводились на ЭВМ и сведены в таблицы В табл. 8
представлены 20 значений оценки Pf по выборкам объема 1000. В табл. 9
представлены значения доверительного интервала для различных значений
^верительной вероятности.
Таблица 9
< (ненка доверительного интервала с использованием критерия Стъюдента
Доверительная вероятность P(t) Доверительный интервал Доверительная вероятность P(t) Доверительный интервал
99000 35525Е-03 93000 33372 Е-ОЗ
98000 35167 Е-ОЗ 92000 33013Е-ОЗ
97000 34808 Е-ОЗ 91000 32655 Е-ОЗ
96000 34449 Е-03 90000 32296Е-03
95000 34090 Е-ОЗ 89000 31937Е-03
94000 33731Е-03 88000 31578 Е-ОЗ
Среднее значение оценки Pf по 20000 испытаний равно 0,0058.
Например для доверительной вероятности p(t) = 0,95 можно ожидать,
•)НЧ>
Pf = 0,00579 ± 0,00034, т.е.
0,00613 >Pf > 0,00545
Вели ширина доверительного интервала слишком велика, следует
увеличить объем выборок или их число. Среднее значение выборки Р, -
С317Е-02.
133
3.6. Модификация метода Монге-Карло с модели
реваншем стратифицированных выборок
Известно несколько модификаций метода Монте-Карло,
которых эффективность метода повышается за счет уменьши
дисперсии оценки. Одним из способов уменьшения дисперсии оцет
является стратификация моделируемой выборки, например, выбор
значении Q± при использовании выражения (220). Для этого интер!
интегрирования разбивается на п классовых интервалов:
д 0±
pf = / ^(x)fe(x) dx = X [ Fs(x)fQ(x) dx =
1
п й —
= £ J fc(x)dx Fk
S Pqj Fr
i=i L
/224)
Л
д J га7
X PQi — I
, Л1
где
p^ - вероятность попадания величины Q в j-ый классовый
интервал;
FR\Q-j) - математическое ожидание функции FS(Q) при
условии нахождения Q в j-om классовом интервале]
О’.д < Q. < Q* ; I
тп7 число реализаций величины Q , попавших в j-ый
классовый интервал;
Qi:j - i-ая реализация случайной величины Q в j-ом
классовом интервале.
Очевидно, что дисперсия оценки в этом случае резко умень-
шается, т.к. она является суммой весьма малых дисперсий случайных
величин, ограниченных на одном классовом интервале. Однако, при
вычислении малых вероятностей классовые интервалы, дающие основной
вклад в опенку' (224), лежат в области маловероятных значений величины
Q . Поэтому значительная часть выборки оказывается ненужной и
необходимое число реализации будет довольно большим.
134
Для исправления этого недостатка предложена модификация
метода Монте-Карло, в которой вместо того, чтобы сначала моделировать
пыборку значений величины Q , а затем производить ес стратификацию,
разу формируется стратифицированная выборка только на нужных
массовых интервалах и с заданными объемами классовых выборок.
Для этого моделируются ограниченные случайные величины
Q'i- I < Qj £ q;
< нлотност'яйи распределения вероятностей
7
*о(Х) = fQj(x)
(225)
Преимуществом метода является его очень высокая
'Ффсктивность, что позволяет резко снизить потребность в машинном
времени.
Недостаток метода состоит в более сложной, чем в обычном
методе Монте-Карло, процедуре формирования выборки. Кроме того,
при решении многомерных задач не всегда просто выделить нужные
классовые интервалы для исходных величин. Анализ точности и
||остоверности выполняется так же, каки в обычном методе Монте-Карло
и создаст те же .затруднения.
Пример 5
Для примера решаем ту же задачу, что и методом “горячих точек".
р< » i р», ЕффлМ
Определяем интервал интегрирования ^лев, , Nпраа^ . Правую
границу определяем из условия
Р^прав.) = 0,9999
(0,9999) =
= 6 - 1 & [- In (- In 0,9999) + 5 JO5] = 10,5 IO5 .
135
Левую границу определяем из условия
^рИ^лев.)] = 0,0001
^Д^тКев.)] = ф{10[1пот(^ев.) - 19,51]) = -3,72 ;
от(^ев.) = 2055
Из уравнения g - О
*лев.
60 106
,---------+ 0,0208
1,2 106 - N„^
= 2055 105
^лев. = 6,5 105 Н
Разбиваем интервал интегрирования на четыре классовых интервала
(j = 1,2,3,4) с левыми границами
N1 = N»eB. = 0,5 105, N2 = 7,5 IO5,
N3 - 8,5 IO5, N4 = 9,5 105.
Определяем значение функции распределения на границах интервалов
10s 5-JO5)
•F’w(Wj) = e e = 0,9212 .
Аналогично
fn(.ni) = 0,9846, FN(N2) = 0,9971,
fn(^3) = 0.9994, Fn(n4) = 0,9999,
где
— NnpaB.
Вероятности попадания значения нагрузки в классовые интересы
равны:
Рн, = Fn{N2) - Fn(N,) = 0,0634
136
Рн2 = 0,0125, pN, = 0,0023, pNi = 0,0005
Для
чПлемом т
(рис. 30).
каждого из классовых интервалов моделируем свою выборку
с помощью датчика равномерно распределенных случайных чисел
Рис. 30. Разбиение на классовые интервалы
Случайное значение нагрузки NJ2 для j -ого классового интервала
определяем как функцию случайного числа 2
Nji = ~ =
= + PW^] = PN_1[PW(WjJ]
Затем определяем значение предела текучести из
уравнения g - О
ат(^>1) —
„ f 60 • 106
N < i----->-------
] \1,2 • 106 -
X J Л
+ 208,3
а значение функции распределения
137
кЦсДл^)] = - 19,51
Производим эту операцию т раз для каждого классового интервала
и по формуле, приведенной в начале примера находим оценку вероятности
отказа Р{ .
Анализ точности при заданной достоверности выполняется такжЛ
как и для обычного метода Монте-Карло (см. предыдущий пример).
138
Глава 4
НАДЕЖНОСТЬ ВНЕЦЕНТРЕННО СЖАТЫХ И
СЖАТО-ИЗОГНУТЫХ СТЕРЖНЕЙ
4.1. Области неразрушимости
Внеценгренно-сжатый или сжато-изогнутый стержень является
одним из несущих элементов, широко применяемых в проектировании
стержневых систем. При оценке надежности стержня при чистом изгибе
или центральном растяжении-сжатии область работоспособности
представляет линейную функцию, что и позволяет достаточно простыми
способами вычислять вероятность отказа. Учет эксцентриситета
продольной силы и сближения концов при деформировании приводит к
нелинейной функции работоспособности. Вероятностному анализу этой
проблемы и посвящен материал данной главы.
Рассмотрим шарнирно-опертый стержень прямоугольного
сечения сжатый продольной силой N с эксцентриситетом е0 (рис. 31,
а), или с начальным искривлением е0 (рис. 31, б) или с поперечной
нагрузкой , момент от которой равен Мо = Ne0 (рис. 31, в).
Для стержня прямоугольного сечения с площадью А = bh
рассмотрим в пространстве N, Мо области неразрушимости
(предельного равновесия) и границы области упругой работы. Уравнение
границы области упругой работы определяется из условия
Мо_ + N
W А
Г 'l
< = - —
< N )
(226)
(227)
где
- <jTW - момент фибровой текучести;
стг - предел текучести;
139
W - момент сопротивления W = —
а) б) в)
Рис. 31. Схемы нагружения внецентрснио-сжатого стержня
Уравнение границы области неразрушимости (предельное равновесие)
определяется из условия
(228)
т.е.
Мопр
(229)
мт 1 ~
здесь
bh2
Мт = W = —— - предельное значение изгибающего
о
момента, принимаемое поперечным сечением при чистом изгибе;
Nr = Аст - предельное значение нормальной силы при
центральном сжатии.
Графики уравнений (227) и (229) представлены на рис. 32.
140
-Кб,
Рис. 32. Область неразрушимости (% = 120}
Для расчета по деформируемой схеме геометрическая
нелинейность учитывается выражением
ео = е0/(1 - N/N3)
где
„ п2Е1
«э = —р— - эйлеровая критическая сила для шарнирно
опертого стержня.
Условие (226) преобразуется к виду (обычно принимаемому при
расчете по деформированной схеме)
м0 + W =
W(1 - N/N3) А
(230)
Моуд = МФТ\1 - — 1 - — • (231)
k NT N3 )
141
где
М^л , N%” - изгибающий момент и продольная сила упругого
деформирования.
График этого уравнения представлен также на рис. 32.
Для построения границы области неразрушимости с учетом
деформированной схемы можно использовать приближенный подход. Для
приближенных методов, основанных на наглядных механических,
принципах, предложена формула Мерчанта дая расчета рам /16, 97/
111
Nap(e0) ’ + N%(e0) ’ '!
где
W"₽(e0) - искомый параметр предельной нагрузки для
деформированной схемы;
= NKP - параметр критической нагрузки для стержня
(рамы) из линейно-упругого материала;
Naw(eo) - параметр предельной нагрузки для жестко-пласти
ческой модели деформирования.
Из графика уравнения (232) в пространстве (N, Мо) на рис. 32
видно, что для отдельного стержня формула Мерчанта неприемлема, хотя
бы по той причине, что при Мо - 0 она не удовлетворяет
необходимому условию N3 - NKP . В /33/ предложена для расчета рам
модифицированная формула Мерчанта, исправляющая этот недостаток.
__________+ j_ _ и*.) (233.
fv(e0) N„,(e«) N, w, ’
здесь
Ny(eoj - предельная сила, при которой возникает краевая
текучесть.
График этого уравнения также показан на рис. 32.
Гели принять приближенно, что в пластической стадии
деформирование стержня описывается той же кривой, что и в упругой
стадии, то наряду с (233) может бьггь предложена формула
142
(234)
Это заведомо верхняя граница проходит ниже (рис. 32) границы,
in щучаемой по формуле (233) и может быть также принята в качестве
ипнроксимации границы области неразрушимости стержня. На рис. 32
представлены случаи когда N3 < NT . На рис. 33 показаны все
подученные границы при №э > NT . Здесь граница области
неразрушимости определяемая условием (234) оказывается несколько
пыше границы, определяемой условием (233). Близость границ
неразрушимости по формулам (233) и (234) позволяет в дальнейшем
использовать уточненную формулу Мерчанта.
Рис, 33. Область иеразрушения (А=70)
143
4.2. Вероятность отказа внецентренно-сжатого
стального стержня
Рассмотрим задачу сравнения показателей надежности (вероят»
ностей отказа) внецептренно-сжатого стального стержня я
предположении различных моделей его деформирования, а именно :
- упругой модели - за отказ принимается появление краевой
текучести;
- упруго-пластической модели - за отказ принимается
образование в сечении пластического шарнира, при этом материал
стержня принимается идеально упругопластическим (т.е. зависимое^
принимается в виде диаграммы Прандтля);
- модели деформирования, основанной на уточненной формуле
Мерчанта (233) - отказ фиксируется при невыполнении условия,
основывающегося на уточненной формуле Мерчанта.
Будем исходить из упрощенного подхода к расчету, при кагором
искривленная ось стержня принимается за синусоиду. При этом стержень
сводится к системе с одной степенью свободы, что не вносит большой
погрешности в результаты расчета при обычных видах загружения и
приемлемо для практики.
При сделанных предположениях представим расчетную формулу
прочности внецептрснно-сжатого стержня, положенную в основу
обычных практических расчетов:
N Мо
max = — + -----7--------рг °пр (235)
/4 I N1 I
W 2 - -V—
I it2 El)
Этой формуле можно придать более простой вид, если ввести
следующие обозначения:
- осевое сжимающее напряжение - а0 = N/A ;
- относительный эксцентриситет приложения сжимающей силы и
расчетном сечении без учета прогиба стержня, отнесенный к ядровому
Я0А
расстоянию сечения - т0 = ;
NW
Гд
- гибкость стержня - X = 1J— .
Окончательно расчетная формула прочности примет вид
144
°0
+ me
л.2 Ea0
^лгЕ -
(236)
। ле
a0 = N/A ;
A = h2 ;
me - относительный эксцентриситет приложения продольной
11лы (для прямоугольного сечения Л1е = бе/h) ;
X - гибкость элемента ;
стт - предел текучести стали.
Формула (236) является основной при вероятностном расчете
ш [сцентренно-сжатого стального стержня по упругой модели деформи-
рования.
При рассмотрении упругопластической модели деформирования
воспользуемся решениями, полученными Ежеком /16, 93/ . Эти решения
основаны на следующих допущениях:
- сечения при деформации стержня остаются плоскими и
перпендикулярными коси стержня;
- сечения не изменяются при деформации стержня;
- влияние деформаций сдвига не учитывается;
- дифференциальные уравнения изгиба составляются в предполо-
жении, что прогибы малы и допустима линеаризация задачи;
- материал стержня имеет так называемую идеальную диаграмму
или диаграмму Прандтля;
- точная кривая изогнутой оси стержня заменена приближенной
кривой в виде синусоиды.
Основное расчетное положение имеет вид
N
А
о
(237)
где
- критическое напряжение, которое определяется из формул,
полученных Ежеком:
- в случае односторонней текучести при
/пе < 3 [ 1 - —
145
°т _ j _ _______(Ук
к2 Е ок _ 3 (стга - о
(238)
- в случае двусторонней текучести при
2 тве ок
(239)
ЛТ
Следует отметить, что уравнения (238, 239) справедливы только
для стержня прямоугольного поперечного сечения.
И наконец, принимается модель деформирования в виде уточ-
ненной формулы Мерчанта (233) - формулы суммирования опасностей.
Пример 6
Для расчета примем следующие исходные данные:
материал стержня - сталь ВстЗпсб-1;
модуль упругости Е = 2060000 кг/смг .
Математическое ожидание величины относительного эксцентри-
ситета приложения нагрузки примем равным те - 1,5 Предел текучести
<тП| эксцентриситет е0 и продольная нагрузка N вводятся в расчет в
качестве случайных величин. Дзя предела текучести принимаем нормальное
распределение. Параметры распределения предела текучести
ат = 305,25 МПа , s„t = 25 МПа.
Расчетный предел текучести о р - 245,0 МПа. Случайный
эксцентриситет также принимаем нормально распределенным с измен-
чивостью ve = 0,1. Дита стержня 1 = 300 СМ .
Принимаем нормальное распределение для случайной продольной
нагрузки N . Принимаем изменчивость нагрузки равной vN = 0,32 . За
величину математического ожидания нагрузки принималось максимальное
воспринимаемое стержнем продольное усилие N , полученное при расчете по
деист вующ им нормам.
Учитывается случайный эксцентриситет приложения сжимающей
нагрузки, обусловленный несовершенством монтажа и изготовления конструк-
146
ций. Закон распределения случайного эксцентриситета принимается нормаль-
ным.
Примем, что математическое ожидание случайного эксцентри-
.чтета соответствует относительному эксцентриситету тв = 1,5 (т.е.
, тержень изначально внецентренно сжат и разброс эксцентриситета наблю-
дается вокруг этого значения). Стандарт отклонения случайного
in ецентриситета поставим в зависимость от ядрового расстояния и примем
равным Вво = 0,1 р , где р = W/A - ядровое расстояние сечения. При
равнении частоты отказа стержней при каждом из 3-х критериев отказа,
частота появления отказов определялась для 10 гибкостей К .
При определении частоты отказов для каждой гибкости производи-
нк ь по 100000 испытаний, что продиктовано затратами машинного времени.
Была решена также и обратная задача. Т.е. для каждой из 10-ти
чпределенных по /65/ предельно допустимых нагрузок, соответствующих
принятым 10-ти гибкостям X , методом последовательных приближений
находилось значение высоты сечения h при условии, что для данного
поперечного сечения частота появления отказов не превысит
v = 0/10135 Количество испытаний было принято равным
п = 10000.
В табл. 10 показано расхождение коэффициентов снижения
(опускаемых напряжений д/ в процентах по отношению к упругоплас-
। ическому стержню для частоты отказов v = 0,00135.
Для упругой модели при гибкостях % - 50-100 получаем
(качения на 10-25% меньше чем для упругопластической модели, что идет
и запас и приводит к перерасходу материала. Расчет по уточненной
Формуле Мерчанта (233) для тех же гибкостей дает значения у на 15-
.'()% больше чем для упруго-пластической модели.
При сравнении рассматриваемых моделей видно, что формула
Мерчанта дает удовлетворительные результаты.
Для сравнения полученных результатов построены (рафики
коэффициентов снижения допускаемых напряжений. Па рис. 34 показана
также кривая, полученная на основе метода статистической
ынеаризации, использованного А.Р. Ржаницыным /55/. За отказ здесь
принимается появление краевой текучести.
Следует’ отметить, что метод статистической линеаризации дает
результаты близкие к результатах полученным по методу статистических
испытаний (кривые 2 и 4).
147
Таблица 1(1
Гибкость X Упругопласти- ческая модель стержня Упругая модель стержня Стержень рассчитанный по формуле Мерчанта Стержень рассчитанный по формуле Мерчанта с учетом К
25 100% 70% 108% 102%
50 100% 75% 115% 101%
75 100% 83% 122% 100%
100 100% 91% 121% 99%
125 100% 94% 130% 98%
150 100% 95% 117% 100%
175 100% 97% 107% 101%
200 100% 97% 106% 101%
225 100% 97% 105% 102%
250 100% 98% 104% 101%
Рис. 34. График зависимости коэффициента ip от гибкости стержня
I - упругопластический стержень; 2 - упругий стержень; 3 - стержень,
рассчитанный по <1х>рмуле Мерчанта с учетом К; 3' - стержень, рассчитанный по формула
Мерчанта; 4 - стержень, рассчитанный методом статистической линеаризации
При сравнении видно, что нсучет неупругого деформирования
для стержней гибкостью А. = 75 - 120 приводит к занижению
несущей способности на 20-30%, хотя при гибкости X > 150
148
Iчп-хождение полученных значений для всех случаев незначительное.
Полученная кривая 3 для гибкости X <150 также не полностью
отпадает с кривой 1. Но здесь следует отмстить, что расчет по формуле
Мерчанта значительно проще чем по обычным формулам расчета
уиругопластическях стержней. В этой связи представляется
целесообразным подобрать некоторый эмпирический коэффициент К ,
м ч-орый при учете его в формуле Мерчанта сглаживал бы расхождение
между кривыми 1 и 3.
Уточненная формула Мерчанта примет вид
к____1 = 1 + l_ _ NY(eo}
Nap(e0) Nn„(e0) N3 ^(е0) N3
(240)
На рис. 34 показана кривая 3 , построенная на основе формулы
i.’4O). Вычисленное методом подбора значение коэффициента К равно
К = 0,87 . Расхождение коэффициента снижения допускаемых напря-
жений ту для стержня, рассчитанного по формуле (240) для всего
рассматриваемого диапазона гибкостей X = 25 - 250 составляет
песто лишь 1-2%.
1.3. Вероятность отказа сжато-изогнутого сталь-
ной) стержня
Существующие методы определения вероятности отказа
нредполагакхг наличие детерминированных решений, на основании
которых выполняется вероятностный расчет.
Точные детерминированные решения получены только для неко-
торых частных случаев и являются достаточно громоздкими. При попытке
поспользоваться этими решениями для выполнения вероятностного рас-
чета возникают непреодолимые математические трудности.
В расчетах сжато-изогнутых стержней с учетом пластических
свойств материала отсутствуют точные детерминированные решения.
Поэтому представляется целесообразным применение приближенных
истодов расчета, дающих достаточную точность для практических целей.
Одним из таких методов расчета, как было показано выше, является
использование модифицированной формулы Мерчанта (240).
Для сравнения используется также решение, полученное С.Д.
ЛсЙтесом для упруго-пластического стержня прямоугольного поперечного
сечения шарнирно опертого но концам /34/.
149
Дифференциальное уравнение оси стержня
где
И2 , _ J
9Е V а0 ,
п = -
2 lap
е = M/N
М - изгибающий момент;
N - продольная сила;
й - высота сечения;
о - предел текучести;
<т0 = N/A - среднее напряжение в сечении (рис. 35).
Численным методом решаем дифференциальное уравнение (241)
и определяем предельную несущую способность стержня Nnp . Тогда
основное расчетное положение можно записать как
N
= тГ < °т (242)
Ось стержня принимается изогнутой по полуволне синусоиды.
Рассматривается только случай односторонней текучести.
150
Вероятностный расчет стержня производился с использованием
метода статистических испытаний. При этом на каждом шаге вычислений
решалось дифференциальное уравнение (241).
Пример 7
Были приняты следующие исходные данные:
материал - сталь ВстЗпсб-1, Е = 2060000 кг/см? , 1 -300см;
параметры предела текучести <з т приняты равными:
= 305,25 МПа, sCj, = 250 МПа .
Математическое ожидание нагрузки принималось соответственно
iCih каждой из рассматриваемых 10-ти гибкостей стержня равным величине
силы N при которой возникает краевая текучесть.
При этом следует отметить, что продольная и поперечная нагрузки
। вязаны между собой зависимостью
26 N
q = ; £, = О ДО 5 ( 243)
Но при расчете методом статистических испытаний значение
вычисляется на каждом шаге и таким образом продольная и поперечная
нагрузки входят в расчет в качестве независимых случайных величин.
Изменчивость N принята равной 0,32 /49/, а изменчивость q
принята равной 0,3.
В результате расчета получаем значение h для частоты отказов
стержня v = 0,00135 . Сравниваем полученное значение h со значением
h для той же частоты отказов, полученном при использовании
модифицированной формулы Мерчанта (240). В этом расчете при подборе
поправочный коэффициент оказался равным единице (К ~ 1) .
Количество испытаний было принято равным 10000, исходя из
wnpam необходимого для расчета машинного времени.
На основе полученных результатов построены трафики снижения
допускаемых напряжений для обоих случаев (рис. 36).
151
Gg - краевое яа/гряткеяне от действия поперечной нагрузки q;
Оу напряжение от действия продольной нагрузки N;
Пр - суммарное напряжение от действия продольной и поперечной
нагрузок.
Рис. 36. График зависимоеги коэффициента от гибкости стержня X
1 - упругопластический стержень; 2 - стержень, рассчитанный по <]к>рмуле
Мерчанта
В табл. 11 отражены результаты сравнительного анализа для
стержня, рассчитанного обоими способами.
Таблица 11
Математичес- кое ожидание продольной наррузки N, Н h см для стержня, рассчитал ною по Лейтесу, v = 0,00135 h см для стержня, рассчитанною по модифи- цированной формуле Мерчанта, v = 0,00135 Расхождение в %
2984480,0 142,5 143,0 0,4
728599,5 71,0 71,0 о,о
460311,1 56,0 56,0 о,о
252743,6 42,0 42,0 о,о
105167,8 27,0 27,0 -1,81
52829,7 19,5 20,0 2,6
15256,0 12,0 11,2 -6,7
6756,2 9,5 9Д5 -3,7
2245,3 7,1 6,95 -2,1
1102,7 5,9 5,8 -1,7
152
Эти результаты позволяют сделать вывод о том, что при
использовании модифицированной формулы Мерчанта мы получаем
гдовлетворительную для практических целей точность вычислений при
пгачительном сокращении времени расчета.
Мы также получаем возможность производить вероятностный
расчет для стержня любого поперечного сечения, натуженного
н[юизвольной продольной и поперечной нагрузкой и имеющего
различные условия закрепления концов. Все это может стать предметом
дальнейшего анализа.
4.4. Вероятностный метод определения коэффи-
циента сочетания нагрузок
В /51 /описывается метод определения коэффициента сочетания,
скованный на вероятностном подходе. При этом рассматриваются
сочетания кратковременных нагрузок. Для решения задачи усилия в
конструкции представляются в виде последовательности независимых
случайных величин, являющихся максимальными годовыми усилиями от
одной или нескольких совместно действующих нагрузок.
Пусть на конструкцию действуют нагрузки 0;(t), Q2(t),
.. . , QD(t) . Их расчетные значения согласгго нормам обозначаются как
y,p(t) , 02₽(с) • - - • » Qn p(t) • Предполагается, что усилия линейно за-
висят от Q^t), Q2(t) ,•••> и условие безотказной работы опре-
деляется выражением
+ a2Q2(t) + ... + aaQn(t) < R , (244)
где
R - несущая способность.
Коэффициенты а,- > 0 зависят от' параметров конструкции и
выбираются таким образом, чтобы выполнялось основное условие метода
предельного состояния
Ч'(атС?1р+ агб2Р +
+ апбпр) Rp
(245)
где
xjz - коэффициент сочетания нагрузок ;
153
Rp - расчетное значение несущей способности.
Для идеально запроектированной конструкции (245) обращается
в равенство, и условие (244) можно с учетом (245) записать в виде
УМ
QiP®
Q2(t)
Q2p(t)
Qn(t)
^p(t)
< yR , (246)
+ ^2
n
где
X = .. aiQjp -
3 n ’
2L ал^ир
k-1
j = 1,2, . .., п характеризуют долю j -ой нагрузки в совмест-
Л
пом расчетном воздействии, при этом л,,- > 0 и £ л * = I .
к = 1
Условием определения коэффициента сочетания может бьггь при-
нято равенство показателя надежности конструкции, запроектированной
при принятых нормами расчетных значениях нафузок, на совместное
действие этих нагрузок, некоторому эталонному значению /35/. Таким
образом, задача сочетания решается на сравнительном уровне. В качестве
показателя надежности может быть выбрана вероятность безотказной
работы
р = J р<?(х)Ря(х)
о
(247)
где
ря(х) - плотность распределения несущей способности ;
Р0(х) - эмпирическая функция распределения максимальных
годовых усилий от нескольких нагрузок, построенная на основе
статистических данных.
Рассматривается стальной стержень, подверженный действию
продольной и поперечной нагрузки. Критерием отказа принимается
достижение краевой текучести. Такой критерий является достаточно
условным. Однако при использовании здесь принципа равнопадежности
оп оказывается достаточным с точки зрения точности получаемых
результатов.
Уравнение для определения у имеет вид
154
ЛчО = Рэт
(248)
(Ж
Р(у) - вероятность безотказной работы, определяется по (247) ;
РЭт - вероятность безотказной работы конструкции,
рассчитанной на одну на!рузку.
В качестве основного расчетного положения было принято
условие
W 7f0
_ + ---о----- < (249)
A W(1 - N!N3) т
те
стет - предел текучести стали ;
N - осевая сжимающая сила;
W - момент сопротивления сечения ;
А - площадь поперечного сечения стержня ;
Мо - момент, определенный в предположении, что прогибы
стержня равны нулю;
N3 - эйлеровская критическая сила .
Из формулы (249) видно, что внутреннее усилие, возникающие в
расчетном сечении стержня, нелинейно зависит от внешней нагрузки.
Поэтому при определении доли каждой из нагрузок в возникающим
усилии рассмотрим следующий способ.
Пусть имеется стержень, нагруженный продольной нагрузкой N
и поперечной нафузкой д таким образом, что в его расчетном сечении
со стороны сжатых волокон возникает краевое напряжение сг0 = а т .
Определим напряжение от действия одной поперечной нагрузки д , оно
будет равно од (рис. 36).
Тогда долю (юперечной нафузки д в суммарном воздействии
можно будет определить как
I
Ч = “ (250)
°™
I
Соответственно доля продольной нагрузки составит
= I - . (251)
155
Зададимся целью получить зависимость величины коэффициента
сочетания нагрузок ц/ от доли в суммарном воздействии поперечной
нагрузки Хд . Нагрузим стержень только поперечной нагрузкой. По /65/
определим расчетное значение максимальной воспринимаемой стержнем
поперечной нагрузки др . Нормативное значение будет равно
д„ = Чр/yt (Yr - коэффициент надежности по нагрузке). Методом
статистических испытаний произведем вероятностный расчет и
определим вероятность отказа стержня, принимая в качестве
математического ожидания нормативное значение нагрузки qH. Данную
вероятность отказа примем эталонной и обозначим уЭш . Очевидно, что
при этом коэффициент сочетания = 1 .
Нагрузим тог же самый стержень продольной и поперечной наг-
рузками и определим но СНиП /65/ предельную несущую способность
стержня, которую при заданном Хд можно выразить через нормативное
значение максимальной воспринимаемой сечением продольной силы
NH . Используя то же значение лд производим вероятностный расчет
стержня при заданной эталонной вероятности отказа v3at .
В результате получаем математическое ожидание продольной
силы N , соответствующее эталонной вероятности отказа v3n) .
Полученное математическое ожидание продольной силы N
соответствует нормативному значению . Коэффициент сочетания
определяем как отношение несущей способности стержня, полученной по
СНиП, к несущей способности, полученной в результате вероятностного
расчета
V = (252)
Аналогично определяем коэффициент сочетания цг для других
значений , в результате чего получаем искомую зависимость.
Пример 8
В качестве примера рассмотрим стальной шарнирно опертый
стержень, имеющий 1 - 300 см , h = 10 СМ . Материал стержня -
сталь ВстЗпсб-1. Модуль упругости Е = 2060000 кг/см2 . В
качестве случайных, величин примем: продольную нагрузку, поперечную наг-
рузку, предел текучести стали.
Все величины примем распределенными по нормальному закону.
156
Предположим, что на стержень действует вертикальная снеговая
нагрузка. Тогда изменчивость продольной нагрузки vN = 0,32 /49/ . В
качестве горизонтальной нагрузки предположим действие ветра., тогда
можно принять, что изменчивость поперечной нагрузки vq = 0,44 /49/.
Цля предела текучести стали были приняты следующие характеристики:
rim - 305,25 МПа, SCjt - 250 МПа , расчетный предел текучести
ыр = 2450 МПа .
Результаты расчетов приведены в табл. 12 и на рис. 37.
Рис. 37. График зависимости коэффициента сочетания
нагрузок '|> от доли вклада в несущую
способность поперечной нагрузки л.д
Таблица 12
Доля поперечной нагрузки Xq Вероятность отказа стержня, запроектирован- ного по СНиП Коэффициент сочетания ншрузок
0,9 0,0121 0,86
0,8 0,01 Ю 0,86
0,7 0,0090 0,85
0.6 0,0058 0,83
0,5 0,0070 0,84
0,4 0,0082 0,85
о,з 0,0095 0,86
0,2 0,0120 0,92
0,1 0,0237 0,95
157
4.5. Вероятностный метод расчета внецентренно-
с жатых стоек с разными эксцентриситетами
Рассмотрим шарнирно опертую стойку с разными экс центри-
ст via ми приложения продольной силы (рис. 38).
При отсутствии поперечной нагрузки формула для момента при
внецентренном сжатии с разными эксцентриситетами имеет вид /56/ :
, . Мв sin кх + Мд sin к(1 - х)
М(х) = ------------------*-----, (253)
sin kl
где
Д.
\Е1
При МА = -NeA, Мв = - NeB .
М(х) - - - - [(е8~ ел °°s *4sin кх +
+ еА sin kl cos kx] (254)
Рис. 38. Расчетная схема стержня
Для синусоиды у = a sin х + b sin х максимальная ордината
равна
158
max у = ya2 + b2
Поэтому максимальное значение М(х) в формуле (254) будет
max М
(*) = —~ 7е1 + е2 - 2 ейев cos kl
sin KJ.
(255)
(>iio достигается в точке, для которой
(ев- еА cos kl) cos Jex - eA sin kl sin Jex = 0
или
< >гс1ода
eR
—— - sinkltgkx + cos kl (256)
eA
Для того, чтобы максимум достигался в промежутке
О < х < 1 необходимо, чтобы согласно (256)
, , е„ 1
cos kl < — < ----------
ел cos kl
В противном случае в качестве наибольшего расчетного момента
следует принимать один из опорных моментов НеА или NeB .
Формулу для максимального момента можно представить в виде
^л>ах = №пр '•
епр = .. — /е2 + е2 - 2елев cos kl
Sin Al
(257)
Предел текучести ат , эксцентриситеты ел , ев , и внешнюю
продольную нагрузку N принимаем в качестве случайных величин.
При определении вероятностных характеристик случайных
параметров исходим из следующего.
159
Для предела текучести от принимаем нормальное распре-
деление.
Случайные эксцентриситеты принимаем равными :
е --- ар ,
где
р = W/A - ядровое расстояние сечения;
W - момент сопротивления;
А - площадь поперечного сечения стержня.
В качестве чакона распределения а естественно принять нор-
мальный закон с центром в начале координат, т.е. при а -- 0 ( а -
математическое ожидание).
Как показано в /55/ наиболее вероятные значения среднего
квадратичного отклонения sa лежат в пределах 0,01 - 0,5.
Предположим, чго сила N есть результат действия на конст-
рукцию снеговой нагрузки, для которой распределение максимуме!!
интенсивности д наиболее точно описывается двойным экспонен-
циальным законом
Р(д) = ехр
(258)
с параметрами
и 836,4 н/м2 , z = 279,3 н/м2 .
Тогда значение силы равно W = Arpq , где Агр - грузо-
вая площадь, с которой собирается снеговая нагрузка.
Моделирование случайной снеговой нагрузки осуществляется L
применением метода Монте-Карло. Путем обращения функции двойною
экспоненциального распределения можно получить так называемую
функцию процентных точек
х (р) = х (У) и — z In (- 1пу)
где
у = Р(х < у)
Можно представить последовательность равномерно
распределенных случайных чисел
160
о < Yi < 1(± - 1,2, ...,т)
Эти числа рассматриваются как вероятности появления величин
х(у±) ’ полученных преобразованием
x(yi) - u - z In (- In yi) = Hi
[ДС
Hi(i -- 1,2, ... , m) - последовательность случайных чисел,
распределенных по двойному экспоненциальному закону.
Пример 8
Рассмотрим пример расчета внецентренно сжатого шарнирно
опертого стального стержня квадратного поперечного сечения.
Исходные данные: Модуль упругости стали ВстЗпеб-1 равен
Е - 2060000 кг/см2 . Данная сталь имеет следующие параметры
распределения: ст= 305,25 МПа , s„ - 25 МПа
В качестве функции резерва прочности принимаем q = R - N ,
где:
R - максимальное воспринимаемое усилие (усилие, при котором
возникает краевая текучесть) ;
N - внешняя нагрузка, которая определяется из формулы
т + , (259)
/1 ГТ
где
ст т - предел текучести стали.
Зададимся вероятностью отказа Р( 0,01 . Примем количество
испытаний, исходя из затрат машинного времени, равным п - 10000 ,а
стандарты величин аА , ав , равными sa* •- Saa --- 0,01 . Эксцентри-
ситеты приложения нагрузки могут принимать как положительные так и
отрицательные значения. Эксцентриситеты еА и ев являются корреля-
ционно независимыми случайными величинами.
Зададимся определенной гибкостью к и соответствующей вели-
чиной h . Также зададимся математическим ожиданием нагрузки, напри-
мер, равным максимальной допустимой силе, найденной из детерминированного
расчета стержня.
161
После генерации стт , ел , ев и N по соответствующим
алгоритмам определим частоту отказов при заданном количестве испытаний
(п - 10000) по формуле
v = k/п , (260)
где
к - количество отказов (отказом является невыполнение условия
g > 0).
Далее сравниваем полученную частоту отказов с заданной
- 0,01 . Изменяя h методом итераций повторяем вычисления до дос-
тижения нужной частоты отказов. Для вероятности отказа Pf - Ofil
обрабатываем полученные значения g и строим гистограмму относительных
частот статистического распределения функции резерва прочности g ,
Анализ полученных гистограмм представляет интерес в связи с определенной
близостью к реальности рассматриваемого случая расчета.
Гистограммы строятся следующим образом.
Методом моментов находим математическое ожидание, и стандарт
статистического распределения по формулам
9=1^ (261)
1=2 п
1^1
i = l
На оси абсцисс откладываем интервал, правая граница которого
лежит на расстоянии 4-х стандартов вправо от математического ожидания,
а левая на расстоянии 6-ти стандартов влево от математического ожидания
Весь интервал разбиваем на 25 частичных интервалов А равных между
собой. Высоты прямоугольников гистограммы равны отношению W^/А •
(плотность относительной частоты), где
Wf = пДп - относительная частота;
п j - количество попаданий в i-ый частичный интервал величины
д;
П - объем выборки.
162
По изложенной методике построены гистограммы при трех значениях
гибкости. Результаты показаны на графиках (рис. 39-41).
Рис. 39. Гистограмма распределения дм гибкое™ X = 15
W/д
Рис. 40. Гистограмма распределения.для гибкости X = 86
Также были произведены расчеты для различных значений стандартов
случайной величины а . При этом вероятность отказа была принята равной
Pf = 0,01 .
Рассматривались два варианта:
а) случайными величинами являются N, ап1 , аЛ и ав ;
б) случайными величинами являются только <хЛ и ав .
Для каждого варианта рассматривались два крайних случая:
- эксцентриситеты являются корреляционно несвязанными случайными
величинами,
163
Рис. 41. Гистограмма распределеиия для гибкости X =: 111
- эксцентриситеты являются полностью корреляционно связанными
случайными величинами.
Очевидно, что истинная корреляция эксцентриситетов находится rt
обозначенных выше пределах.
Но результатам расчетов построены графики (рис. 42- 43)t
отражающие зависимость X - с0 , где о0 == N/A - математическое
ожидание величины напряжения в сечении, при котором Pf ~ 0,01 дли
данного поперечного сечения.
Рис. 42. График зависимости X - а0
— для корреляционно несвязанных случайных эксцентриситетов:
--- для ноллостыо корреляционно связанных случайных эксцентриситетов
164
Помимо этого выполнены расчеты, результаты которых отражают
Проктер зависимости вероятности отказов Pf от стандарта величины S
М различныхгибкостей стержня. Дня чего было принято:
/V, 5т , осА и ав вводятся в расчет в качестве случайных величин:
чистоты отказов вычисляются для значений стандартов величины а ,
умных 0,05; 0,1; 0,15; 0,2; 0,25; 0,3; 0,35; 0,4; 0у45; 0,5.
Рис. 43. График зависимости X - а0
— для корреляционно несвязанных случайных эксцентриситетов:
--- для полностью корреляционно связанных случайных эксцентриситетов
Рис, 44. График зависимос т частоты отказов v
При этом схА и ав принимались независимыми, но имеющими
ранные стандарты з;Ла = s,.^ . Результаты отражены на графиках (рис.
i-J).
165
Анализируя результаты расчетов отмстим:
1. Левая часть гистограмм более пологая чем правая и имеет
"хвост" в области отрицательных значений. Асимметрия увеличивается с
увеличением гибкости. Очевидно, что с уменьшением изменчивости
внешней нагрузки распределение функции резерва прочности будет
приближаться к нормальному, а при возрастании дисперсии внешней
нагрузки удлиняется "хвост” функции резерва прочности в область
отрицательных значений, И поэтому, желательно иметь внешнюю
нагрузку с меныпей дисперсией, чем пытаться сдвинуть кривую
распределения д вправо по оси, имея внешнюю нагрузку с меньшим
математическим ожиданием или увеличивая математическое ожидание
максимального воспринимаемого стержнем усилия, прибегая к
увеличению размеров его поперечного сечения. Но, к сожалению, ни
практике возможности выбора выгодных по вероятностным свойствам
нагрузок елраничецы или вообще отсутствуют.
2. Из графиков (рис. 42, 43) при сравнении видно, что
критические напряжения для гибкости X = 0-40 больше у стержней
с зависимыми эксцентриситетами. Для гибкостей X > 4 0 критические
напряжения становятся больше у стержней с независимыми эксцентри*
ситетами. Причем наиболее существенно различие для стержней
гибкостью 'к = 50 - 130 и достигает в среднем 4-5%. Это
соотношение остается постоянным и при изменении характеристик
величин N и при одной и той же заданной вероятности отказа,
Полученные графики позволяют определить гибкость стержня при
заданной частоте отказов по математическому ожиданию величины
среднего напряжения для зависимых и независимых эксцентриситетов.
Например, при <30 = 200 МПа ; sa = 0,1; Pt - 0,01 :
- для независимых эксцентриситетов X = 78 ;
- для полностью корреляционно связанных X = 70.
Данные результаты разнятся на 10%. Таким образом, нсучет возможности
возникновения разных эксцентриситетов по концам стержня, »
некоторых случаях, приводит к получению завышенного значении
вероятности отказа, те. расчет с учетом различия эксцентриситетов ведет
к экономии материала. Хотя для малых гибкостей наблюдается обратная
картина.
3. При гибкости X - 100 наблюдается резкое снижение
влияния дисперсии эксцентриситетов на частоту отказов. При гибкости
X > 150 это влияние практически отсутствует, чего нельзя сказать о
стержнях гибкостью X < 100 . Следует также отметить, что изменение
величины а в пределах 0-0,1 на частоте отказов v сказывается
несущественно.
166
4.6. Анализ надежности внецентренно-сжатого
железобетонного элемента
Расчетные формулы принимаются по действующим нормам
щюсктирования железобетонных конструкций /63/. При этом отказом
Конструкции считается невыполнение требования по прочности. Исполь-
|уется также метол статистических испытаний.
Исходя из затрат машинною времени, количество реализаций
случайных величин на каждом шаге метода статистических испытаний
назначаем равным п ~ 10000 . По результатам вычислений строятся
1иетограммы функций распределения несущей способности и резерва
прочности. Гистограммы строятся на интервале равном 10-ти стандартам
sg , при этом правая и левая границы интервала лежат на расстоянии 5-
ги стандартов вправо и влево от математического ожидания д .
Используя данный алгоритм были решены следующие задачи:
- определение обеспеченности несущей способности железобетонного
впецснтренпо-сжатого стержня прямоугольного поперечного сечения,
запроектированного по действующим нормам;
определение величины несущей способности с заданной
обеспеченностью;
определение процента армирования для заданной обеспеченности
несущей способности;
определение величины математического ожидания внешней нагрузки
при заданной вероятности отказа;
- определение процента армирования при заданной вероятности отказа.
При выполнении детерминированного расчета использовалась
йвисимость между напряжением в растянутой арматуре и относительной
высотой сжатой зоны бетона /63/. Расчет сечений, нормальных к
продольной оси элемента, когда внешняя сила действует в плоскости оси
симметрии сечения и арматура сосредоточена у перпендикулярных к
указанной плоскости граней элементе может производится в зависимости
от соотношения между величиной относительной высоты сжатой зоны
бетона = x/h0 (рис. 45) и граничным значением относительной
высоты сжатой зоны .
Основное расчетное положение при рассмотрении внецентренно-
сжатого железобетонного элемента прямоугольного сечения (рис. 45)
согласно /63/
167
Рис. 45. Расчетная схема сечения железобетонного элемента
Ne < Rbbx(h0 - 0,5х) + RscA's(h0 - а') , (263)
где
е == еот] + h/2 - а ;
Rb - расчетное сопротивление бетона сжатию;
Rsc - расчетное сопротивление арматуры сжатию ;
Аз - площадь поперечного сечения сжатой или наименее
растянутой арматуры ;
г) - коэффициент, учитывающий продольный изгиб.
Высоту сжа той зоны х определяют из следующих уравнений:
* = х/Ь0 < ; N Rbxb + RSCA'S- RSAS
= x/h0 > ГR- n = Rhxb + RSCA'S- os As
где
Rs - расчетное сопротивление арматуры растяжению;
As - площадь поперечного сечения растянутой арматуры;
os - напряжение в растянутой или наименее сжатой арматуре,
при использовании бетонов классов не выше ВЗО и ненапрягаемой
арматуры классов А-1, A-II, А-ТП.
os = [2(1 - ?)/(7 - ₽й) - l]«s , (265)
где
- фаничная отпоситсд|>пая высота сжатой зоны бетона
168
(Л
s—- fl - -W I
(266)
i ne
ш - характеристика сжатой зоны бетона .
Для выполняемого нами расчета по /63 / :
w = 0,85 - 0,008Rh -
° SR ~ '
oscu - 500 МПа .
Для элементов из бетона классов выше В30 с арматурой классов
выше А-Ш (напрягаемой и ненапрягаемой) напряжение cs следует
"прсдслять по зависимости
CTS = osp + Osc„^y - (267)
Гибкий внецентренпо сжатый элемент под влиянием момента
прогибается, вследствие чего начальный эксцентриситет е0 продольной
гиды N увеличивается. При этом возрастает изгибающий момент и
p.i 1рушение происходит при меньшей продольной силе N в сравнении с
коротким (негибким) элементом.
Нормами рекомендуется расчет таких элементов выполнять по
сформированной схеме. Допускается гибкие внецентренно-сжатыс эле-
менты при гибкости Ig/i >14 рассчитывать е учетом экспентриси-
пта, получаемого умножением начального его значения е0 на
коэффициент т| > 1 .
Значение коэффициента q устанавливается но зависимости
р ^(1 - N/Ncr)
(268)
Выражение для критической продольной силы Wcr при прямо-
угольном сечении с симметричным армированием As = A's (без пред-
варительного напряжения) имеет вид
W,
6,4 ЕЬА ( 0,11
I2 [^7кО,1+"5
(h V
+ - aJ
(269)
169
где
Eb - начальный модуль упругости бетона;
А - площадь поперечного сечения колонны, А - bh;
10 - расчетная длина элемента;
г - радиус ядра сечения (для прямоугольного сечения
г =: 0,289h );
- коэффициент, учитывающий влияние длительного
действия нагрузки на прогиб элемента в предельном состоянии (для
тяжелого бетона ср2 - 1 +
М}л и й, - моменты соответственно от длительной и полной
нагрузок относительно оси, проходящей через центр тяжести наименее
сжатой (растянутой) арматуры;
5 - принимают наибольшим из 5 = e0/h ,
б =: 0,5 - 0,01- Rb;
а. = Es/Eb - отношение модулей упругости арматуры и бето-
на; ц2 - коэффициент армирования, цх = 2AsjA .
Предельную несущую способность железобетонного элемента
определяем по следующему алгоритму.
Предполагаем, что , тогда предельную несущую
способность W* определяем из совместного решения уравнений (263) и
(264). Далее проверяем условие с, < . Если это условие нс
выполняется, значит N* необходимо определять из условия £, >
При анализе надежности внецентренно сжатого элемента средние
значения сопротивления бетона Rb и средние квадратические
отклонения sRb призменной прочности бетона определяются по
формулам
DIJ _
R = ------------------ ; Sj? = Rb vb . (270а)
b 1,07(1 - 2vb) Rb b b
При вычислении средних значений и средних квадратических
отклонений сопротивления арматуры использовали трсбования/63/
ри
Rs = --------*---- ; = Rsvs (270b)
s 1 - l,64ve s s
170
Зададимся целью определить обеспеченность несущей способ-
ности железобетонного внецентренно сжатого стержня прямоугольного
I [оперенного сечения, запроектированного по действующим нормам.
Определим величину предельной несущей способности из
совместного решения уравнений (264-266, 268, 269) и уравнения
Ne - Rbbx(h0 - 0,5х) + - а') (271)
полученного заменой знака неравенства в выражении (264) на знак
равенства.
В формуле (269) примем равным <pj; = 1 (т.е. предпо-
ложим отсутствие длительно действующих нагрузок), случайный эксцен-
триситет приложения продольной силы принимаем равным минималь-
ному допустимому значению ед = 1 см.
Обозначим полученное значение несущей способное™ NCH„n .
Произведем вероятностный расчет данного стержня методом
статистических испытаний и определим величину обеспеченности
несущей способности.
В качестве случайных величин принимаем: прочность бетона
Rb , прочность арматуры RB и эксцентриситет приложения продольной
силы ё0 . За отказ принимаем невыполнение основного расчетного
положения
Й»ер. , (272)
т.е. отказ фиксируется при величине несущей способности меньшей чем
та, что получена при расчете по нормам.
Значение Nsep получаем из совместного решения уравнений
(264-267), (268, 269, 271) При этом значение 8 в формуле (269)
принимаем равным 8 =-. e0]h .
Примем полученную в результате верозпностного расчета частоту
отказов v в качестве оценки вероятности отказа конструкции Pf ,
тогда обеспеченность несущей способности Ps можно определить как
Рэ = 1 - Pf.
Рассмотрим пример определения обеспеченности несущей спо-
собности шарнирно опертого железобетонного стержня, запроекти-
171
р< званного по действующему СНиП /63/. Расчет производим в
соответствии с изложенным выше алгоритмом.
Пример 9
Возьмем стержень квадратного поперечного сечении:
h b =-- 30 см (рис. 45). Длину стержня примем равной 1 480см.
Коэффициент армирования ц2 0,025 . Произведем расчет, по СП нН /63/.
В результате вычислений получим предельную несущую способность , которая
составляет для данного стержня МСНи(1 1 718,25 кН .
Произведем вероятностный расчет и определим частоту отказов в
соответствии с выбранным критерием отказа.
Для случайного сопротивления бетона и арматуры принимаем
нормальный закон со следующими параметрами распределения:
для арматуры класса Л-П1 Rs - 466,5 МПа ;
sRtj --- 45,7 МПа :
для класса бетона по прочности на сжатие В 20:
Rb 19,2MHa;sRb 2,59 МПа /69/.
Случайный эксцентриситет также принимаем распределенным по
нормальному закону Математическое ожидание эксцентриситета принимаем
равным е0 — 0 . В /45/ приводятся статистические данные по наблюда-
емым значениям относительных эксцентриситов: 0,34
Относительный эксцентриситет равен еота ~ ео/р (р ~ ядровое
расстояние сечения).
Тогда стандарт случайного эксцентриситета можно определить как
s =-. se р
l~0 см'м1
Количество испытаний назначаем равным 10000. Вычисленная
чистота отказов составляет v == 0,0042 . Таким образом обеспеченность
несущей способности запроектированного по нормам железобетонного стержня
составит Ps ~ 1 - 0,0042 -- 0,9958 .
На рис. 46 изображена гистограмма относительных частот
функции распределения несущей способ пост и рассматриваемого стержня.
Ниже приводится порядок расчета, позволяющий определять
требуемое для данного стержня значение несущей способности N* при
'заданной обеспеченности Рзад .
172
Рис. 46. Гистограмма апюситсльиыч частот функции
распределения несущей способное ш железобе-
тонного стержня, занроск1ированн01(> но СНиП
Основное расчетное условие вероятности расчета
N* < N (273)
В качестве критерия отказа принимаем невыполнение условия
(273), Методом статистических испытаний определяем частоту откаюв
v. Принимаем частоту отказов v равной вероятности отказа Pf и
определяем обеспеченность несущей способности Р.. --- 1 - Pf .
Сравниваем полученное значение Ps с Рзад . Изменяем значение ЛГ*
и методом итераций продолжаем расчет до выполнения условия
Р Р
^зад .
Полученное значение /V* является искомой величиной несущей
способности при заданной обеспеченности Р,1ДД .
Рассмотрим пример определения величины несущей способности
стержня заданной обеспеченности. Все исходные данные примем такими
же как и в предыдущем примере. В результате расчетов получили, что для
рассматриваемого стержня обеспеченности Рзад 0,9999
соответствует несущая способность - 154 0 кН .
Используя приведенный выше алгоритм, можно решить образную
адачу, когда для заданной несущей способ!юсти определяется се
обеспеченность Р* . Для чтого последовательно задаваясь различными
шачениями Ызад каждый раз определяем со<лжтству|ощую -ггой
несущей способности обеспеченность.
В табл. 13 и па рис. 47 а, б показаны результа ты расчетов для при-
нятого к рассмотрению стержня. На рис. 47 б изображена та же зависи-
мость Р от ц ; , что ц на рис. 47 а, но для значений Р близких к I.
173
Рис. 47. Зависимость обеспечепности несущей способности Р
от величины несущей способности N
Таблица 13
Несущая способность ^зад кН Обеспеченность несущей способ- ности р: Несущая способность ^зад кН Обеспеченность несущей способности P's
1550 0,9999 1850 0,9844
1600 0,9993 1900 0,9774
1650 0,9986 1950 0,9661
1700 0,9959 2000 0,9496
1750 0,9943 2500 0,4365
1800 0,9909 3000 0,0135
174
Из графиков на рис. 47 следует, что при увеличении несущей
способности в 1,4 раза ее обеспеченность снижается с 0,995 до 0,9.
Ниже приводится алгоритм, позволяющий определять коэффи-
циент армирования железобетонного стержня , соответствующий
шданной обеспеченности несущей способности Рэа„ . Значение самой
несущей способности остается постоянным. В качестве критерия отказа
принимаем невыполнение условия (273).
1. Задаемся коэффициентом армирования = 2Asjbh ;
2. Методом статистических испытаний определяем частоту
отказов v ;
3. Принимаем v = Pf ;
4. Определяем обеспеченность несущей способности
Р.. = 1 - Pf ;
5. Сравниваем полученное значение Ps с Рэад ;
6. При расхождении изменяем значение , возвращаемся к п.2
и методом итераций продолжаем расчет до выполнения условия
Р ~ Р
1 s зад *
Полученное значение является искомой величиной коэффи-
циента. армирования, соответствующее заданной обеспеченности Рэад .
Рассмотрим численный пример расчета. Для принятого стержня
ори несущей способности N - 1718,25 кН ее обеспеченность равная
Рэад = 0,95 соответствует коэффициенту армирования р2 = 0,01 7.
Используя приведенный алгоритм, решим обратную задачу: для
заданного коэффициента армирования определим обеспеченность
Рд несущей способности N = 1718,25 кН . Результаты расчета
занесены в табл. 14 и показаны на рис. 48 а, б (графики на рис. 48 а, б
изображены в разных масштабах).
Анализ полученных результатов показывает, что при коэффи-
циенте армирования = 0 обеспеченность несущей способности
становится равной 0,115. Это связано с тем, что свой вклад в несущую
способность продолжает вносить бетон.
Из полученных графиков (рис. 48) видно, что при снижении
с 0,03 до 0,02 обеспеченность несущей способности уменьшается с 0,999
до 0,98. Т.е. снижение коэффициента армирования на 30% приводит к
снижению обеспеченности несущей способности лишь на 2%.
А при уменьшении на 50% обеспеченность несущей
способности становится равной С,675, снижаясь при этом на 32,4%.
175
Рис. 48. График зависимости обеспеченное m Р несущей способности
17 18,25 кН от коэффипиен сов армирования ц
Таблица 14
Коэффициент армирования 14 Обеспеченность несущей СКОСОб- ПОСТИ Р* Коэффициент армирования Р-! Обеспеченность несущей способ-пости р:
0,030 0,9993 0,010 0,7463
0,025 0.9958 0,005 0,4121
0,020 0,9819 0,001 0,1590
0,015 0,9228 0,000001 0,1156
176
Глава 5
11 ^КОТОРЫЕ ВОПРОСЫ
СТЕРЖНЕВЫХ СИСТЕМ
НАДЕЖНОСТИ
5.1. Последовательное соединение элементов
При последовательном соединении элементов >'пис. 49) разруше-
ние происходит по наиболее слабому из них. Выход из строя одного
элемента означает разрушение всей конструкции. В частности, это отно-
сится к статически определимым конструкциям, которые при исключении
любого элемента превращаются в подвижную систему (механизм).
6
6 Рис. 49. Последовательное
соединение элементов
<
о
Очевидно, что надежность такой системы будет меньше
надежности каждою се элемента, поскольку выход из строя одного из
многих элементов более вероятен, чем выход из строя определенного,
наперед заданного элемента. Если интегральный закон распределения
прочности i-ro элемента Pfi(r < q) = Pf±(q) , то вероятность
нсразрушения этого элемента под действием нагрузки g равна
I - Pi(q) •
При последовательно соединенных элементах вероятность нсраз-
рушения системы
177
(274)
Ps(q) = 1 - Pf(g) = П P ~ Ъ(?)]
i 1
где
Pf(g) представляет собой вероятность того, что при нагрузке
g (или меньшей) разрушится хотя бы один элемент и, следовательно,
разрушится вся конструкция.
В формуле (274) предполагается, что прочность каждого элемента
является независимой случайной величиной. При проектировании важное
значение приобретают подходы, связанные е анализом надежности не
только отдельного элемента сооружения. В этом параграфе приводятся
методы оценки надежности системы по известным законам,
распределения вероятности отказа их элементов.
Если все элементы имеют одинаковые распределения своей
прочности, выраженные в единицах внешней нагрузки (при подборе
сечений всех элементов по одному и тому же напряжению), то вместо
(274) можно написать
Ps(g) = [1 - Pn(g)]n (275)
Распределение плотности вероятности разрушения системы равно
₽Дд) - -
dg
4 (276)
1 п п п л
- £пр-м<?)]= Zt^-пр-^).
a(J Ji 1 i 1 1 ~ i =. 1
где
z , dPi(g)
рДд) -- —~ - - плотность вероятности прочности ьго
элемента.
При одинаковых напряжениях во всех элементах системы
плотность распределения прочности примет вид
рДд) = л [I - Р,(д)]П 'рг(д) (277)
178
Пример 10
Пусть прочность каждого элемента подчиняется нормальному закону
распределения, а характеристика безопасности системы [3 = 3 , т.е.
= 0,99865 . Пусть система состоит из 25 одинаковых элементов,
тогда согласно (275)
Pi(q) = 1 - 2^0,99865 = 0,000054
Но таблицам интеграла вероятности определяем характеристику
Ье юпасности элемента
ф(^) = 0,5 - 0,000054 = 0,49946 , 0^ = 3,8 7 .
Г.е. как уже отмечалось, надежность системы будет меньше надежности
к аждого из ее элементов.
При проектировании следует учитывать, что элементы конструк-
ции не всегда совпадают с элементами системы. Например, пояс ферм
может представлять собой один стержень, проходящий через несколько
капелей. Тогда его следует считать за один элемент. Если же раскос
состыкован по длине из двух стержней, то его надо считать за два
цемента.
Схему последовательного соединения элементов можно
проиллюстрировать при анализе надежности изгибаемой балки, которая
япнроксимируется цепью, звенья которой воспринимают изгибающие
моменты (рис. 50) /55/.
Рис. 50. Схема балки
В отличие от растянутой цепи усилия в звеньях здесь будут не
одинаковыми, а пропорциональными изгибающим моментам, возникаю-
щими в балке от внешней нагрузки. Надежность i-го звена будет
Psi = 1 - , (278)
179
где
mi - момент в i-ом звене;
“ вероятность тога, что i-oe звено разрушится при
Л1 < т1 .
Считая прочность на изгиб звеньев некоррелированной между
собой, надежность балки определится выражением
Ps П [1 - р(тД] (279)
1 -1
Здесь п - число звеньев. Уравнение (279) можно записать
1пРя
л
JL - J
[1 - p(mi)]
полагая вероятность Р(т±) малой получим
1п[1 - -РгЫ] s
(280)
(281)
Тогда
Ps
Л
ехр -X pf(raJ
(282)
переходя в пределе к сплошной балке длиной 1
ехр
1
< и [ш(х)] dx
ч о
(283)
где
и[л1(х)] - погонная интенсивность отказов;
% - длина балки, в пределах которой прочности сечений можно
считать полностью коррелированными;
Л1(х) - эпюра моментов при заданной нагрузке.
Если надежность балки достаточно высока, то из (283) следует
180
1
Р3 = 1 - f u[ni(x)] dx
О
(284)
Для нормального распределения прочности сечения
п Л1(х) - т
0,5 - Ф —------------
1 - Р(т) = 0,5
(235)
juih вероятности отказа получим
Pf
1
2К
dx
(286)
Можно отметить, что для статически неопределимой системы
выход из строя хотя бы одного элемента уже является сигналом опасности
для сооружения в целом. Поэтому в ряде случаев проектирования соору-
жений при оценке надежности возможно рассматривать его как систему с
последовательным соединением элементов. Такой подход будет в запас
надежности,
Г>.2. Параллельное соединение элементов
В отличие от последовательного соединения элементов в схеме
параллельного соединения надежность системы оказывается выше надеж-
ности любого отдельного элемента (рис. 52). Достижение предела
прочности в одном элементе выводит последний из строя и повышает
напряжения в других элементах, что может повлечь за собой цепную
реакцию последовательного разрушения всех элементов.
Рассмотрим в качестве примера систему из двух одинаковых
параллельно работающих хрупких элементов (рис. 51). Обозначим
вероятность разрушения одного стержня при усилии в нем равном q
через Pf(g) .
Вероятность нсразрушения системы можно подсчитать по
формуле с использованием понятия условной вероятности.
181
(287)
₽s(q) = i - Ш = [I - -Pf - Pf(^q)] +
+2Pf (0,5q\l - Pf (q)|.
Рис. 51. Параллельное соединение
элементов
Рис. 52. Схема нараллельного
соединения элементов
Первый член в правой части формулы (287) представляет собой
вероятность неразрушсния обоих элементов при усилиях в них равных
q/2 . Второй член представляет собой вероятность разрушения первого
стержня при условии сохранности второго, умноженную на вероятность
неразрушсния второго стержня, при условии, что первый стержень
разрушился. Коэффициент 2 введен вместо третьего члена, равного по
величине второму и получаемою из последнего перестановкой порядки
разрушения элементов.
После раскрытия скобок и приведения подобных членов
формула. (287) получает вид
Ps(q) = 1 - 2P/(0z5q)Pf(q) + P/(0z5q)
(288)
Формулу (288) можно /15/ записать в более общем виде пригод-
ном для системы п параллельных одинаковых идеально хрупких
стержней (рис. 52). На. основе формулы полной вероятности получим
вероятность отказа i - элементов из п.
(289)
С* = п l/i 1(п - 1) I - число случаев, благоприятствующих
этому событию - вероятности отказа j - элементов;
182
p(n-i)(9) = [J - pW(n - - вероятность события,
ч стоящего в том, что (n - i) элементов останутся в работоспособном
о ютоянии;
Р1(п)(<?) - условная вероятность события, заключающегося в
юм, что откажут ровно i элементов, при условии сохранения оставшихся
и работоспособном состоянии.
Для систем состоящих из элементов от одного до трех
примут вид
L п= !. роЦ)(<1) = *. р1(1)(?) == р(?)
2 п==2 Р°^ = Ц Мд) = р(0г5д) -
’ Р2(2)(Я) = ~P2(0,5q) + 2P(0,5q)P(q).
роМ = I. Р1(3](Ч) - P(q/3)-,
3 п = 3 Р43)(?) = -р2^/3) + 2P(q/3)p(q/2);
’ РЛЗ)(Д) = Р'(?Р) - 3P2(q/2)p(q/2) +
+ 6P(q/3)p(q/2)p(q).
Используя метод математической индукции, можно показать, что
имеет место рекуррентная формула
рдю(д) = -хс<'k с}к р1 4--^1р*.я!м <29°)
к о \п - к/
яри i - п из (288) и (290) получаем
РДП)(-?) = рл(л)(д)
п тогда вероятность отказа системы
= -I ('-!)" ‘ СГ‘ р- 4—2-ф (q) (SI>
к о - к/
183
т.е. получена рекуррентная формула, выражающая вероятность отказ»
системы посредством вероятностей последовательного отказа элементов
системы.
С другой стороны, пользуясь тем же методом математической
индукции, МОЖНО получить формулу ДЛЯ Pf , которая
рекуррентно выражается через вероятности отказа частичных систем
заданной системы
= -£(-»" 'с; ‘г- Йц.,(,)
к-О
(292)
Соотношение (289) совместно с развернутой записью еш
сомножителей (291, 292) полностью исчерпывает решение поставленной
задачи.
Представленные формулы оценки надежности конструкций,
состоящих из параллельных соединенных элементов не учитываю!
мгновенною хрупкою разрушения.
При мгновенном хрупком разрушении i-ю элемента в системе
неизбежно возникают динамические (импульсивные) эффекты в
образующейся при этом системе из (п - 1) элементов в последующий
за разрушением этого элемента момент времени будут- превышать усилия,
соответствующие статическому нафужению системы из (л - 1)
элементов.
Можно воспользоваться соотношением предложенным Г.Л.
Гениевым /19/
дв,а 1 = - g?,u . (293)
Здесь динамическое усилие д£п 2 в произвольном элементе
(n - 1) статически неопределимой стержневой системы, образующейся
в результате хрупкою разрушения одного из элементов исходной п рю
статически неопределимой системы, определяется как разность
удвоенного усилия в нем для (л - 2) системы и значения усилия в этом
элементе для п системы при статическом действии заданной нафузки,
соответствующей моменту разрушения.
Для стержневой системы на рис. 52 состоящей из п элементов и
нафуженной силой q усилие в каждом из стержней оказывается равным
184
При статическом выключении из работы одного из стержней усилия в
КС <3
остальных будут q^„ _± = —-— .
' п - 1
Используя (293) можно найти динамическое усилие
л (л - 2)
При одновременном разрушении к стержней из п
о-3 - ст v ЛЛ
41, a-к - 4 /
П (п - к)
(294)
(295)
Формула (292) преобразуется к виду
к = 0
,2%)
и при п ~ 2 из (296) следует
Р*(ч) = 1 - 2P(q/2)p(3/2 q) + P2(q/2) (297)
Из сравнения (288) и (297) очевидно, что надежность при учете
мгновенного разрушения снижается.
Отметим при этом, что системы с параллельным соединением
элементов не могут быть использованы для анализа надежности
статически неопределимых систем, т.к. в них необходимо учитывать
перераспределение усилий в остающихся работоспособными элементах
после выхода из строя некоторых ив них.
185
5.3. Вероятностный
равновесия
метод
предельного
Неупругое деформирование конструкций
Очевидно, что упругий расчет обладает ограниченными
возможностями для опенки действительной несущей способности, а
следовательно и надежности конструкций. Предположение о том, что
конструкция работает упруго вплоть до предельного состояния
равносильно отождествлению этого состояния с появлением предельного
напряжения (предела текучести, например) в какой-либо точке
конструкции т.е. предположению, что конструкция работает по принципу
слабого звена.
Это справедливо в ограниченном числе случаев, например, для
статически определимых конструкций или конструкций, выполненных из
хрупкого материала.
Для статически неопределимых конструкций перераспределение
напряжений, вследствие выключения сечений или элементов приводит в
большинстве случаев к тому, что нафузка может возрастать, превышая
тот уровень, который соответствует появлению текучести, или отказу
одного из элементов мпогоэлсментной системы.
Предельная нагрузка, соответствующая превращению конст-
рукции в механизм, может быть определена методом предельного
равновесия. Преимущества применения этого метода в вероятностной
постановке с позиции простоты расчета очевидны.
Определение промежуточного напряженного состояния стати-
чески неопределимой конструкции со случайными характеристиками
материала и случайными геометрическими характеристиками крайне
сложно из-за большого числа дополнительных неопределенностей и
вычислительных трудностей, возникающих при переходе в область
неупругой работы.
Поэтому представляется достаточно перспективным распро-
странить метод расчета по предельному равновесию на конструкции со
случайной прочностью.
Основные гипотезы метода остаются в силе, но предельная
прочность материала определяется случайными характеристиками. При
расчете по методу предельного равновесия обычно формулируются пре-
дельные условия нагружения, которые затем сравниваются с действую-
щими нагрузками, т.е. предельное неравенство, ограничивающее область
работоспособности, формируется в пространстве нагрузок.
186
Вероятностный расчет по методу предельного равновесия на
действие монотонно возрастающих нагрузок может заключаться в опреде-
лении условной вероятности отказа при заданных нафузках с последую-
щим введением ее в выражение для вычисления вероятности отказа.
Далее рассматриваются сжато-растянутые стержневые системы
типа ферм, структур и т.п., хотя излагаемая методика может быть
успешно использована для вероятностного расчета изгибаемых систем
(рамы) и других видов конструкций.
Поверочный расчет стержневой системы методом
предельного равновесия
Для детерминированного расчета стержневой системы обьвшо
। |ринимаются следующие допущения:
- все нафузки являются сосредоточенными, узловыми и квази-
статическими;
- материал стержней - идеальный упруго-пластический, подчи-
няющийся диафамме Прандтля;
- деформация системы и перемещение ее узлов незначительны,
что позволяет записать уравнения предельного равновесия для
) ^деформированной системы;
- в стержнях системы действуют только продольные силы;
- при достижении напряжениями в стержне предельного значения
считается, что при дальнейшем нагружении они остаются постоянными
(при этом зона пластичности равномерно распределена по всей длине
стержня), увеличение же несущей способности происходит за счет
перераспределения усилий между другими элементами.
Понятие опасных сечений для системы может бьггь заменено
понятием опасных стержней. Для обобщения расчета все стержни опи-
саются опасными, в каждом из них могут быть нарушены условия
прочности (для растянутых стержней) или устойчивости (для сжатых
стержней).
Внутренние усилия характеризуются продольными силами, сос-
тавляющих n-мерный вектор N , компоненты которого
(1 - 1,2.....и) .
Максимальные и минимальные 'продольные усилия в стержне в
предположении упругой работы обозначаются и Ni
соответственно.
Усилия в системе при нулевой нагрузке - остаточные усилия
представляются п-мерным вектором пл с компонентами
пл1 (1 = 1,2, .. . , п). Растяжение считается положительным, сжатие -
отрицательным.
187
Предельные растягивающие и сжимающие усилия обозначаются
wi,np и ^1,пр Решение задачи состоит в определении параметра
внешней нагрузки, при которой произойдет простое пластическое
разрушение. При этом геометрия системы, форма и размеры сечений,
места приложения внешних нагрузок считаются заданными.
Для решения используется статическая теорема, о разрушающей
нафузке, в которой указано, что на всех статически допустимых
распределениях остаточных усилий в системе при исчерпании несущей
способности, действительным является то, при котором мощность цикла
внешних нагрузок максимальна.
Построим математическую модель задачи. Предположим, что
система внешних нагрузок состоит из независимых сил, места
приложения которых, а также направления заданы. Необходимо
определить пределы изменения каждой из этих внешних сил. Для
определенности принимается, что верхний предел д’ > 0 , а нижний
< 0 (р = 1,2, ... , к) .
Найти
Задача поверочного расчета формулируется следующим образом.
max ср при условиях
К-р )
(I = 1,2,..., п);
Ь->д° - Е Ni = 0 [j = V, . • • , (и - к)]; (298)
i 1
q° > 0.
где
q° - параметр предельной нагрузки;
к - степень статической неопределимости фермы;
Nd - продольное усилие в i-ом стержне;
j - элемент матрицы статической совместности;
bj - продольное усилие в j-ом стержне, когда q° = 1 .
Таким образом, приведена математическая модель задачи
поверочного расчета для случая однократного нагружения, соответ-
ствующая теореме о разрушающей нагрузке для случая простого пласти-
ческого разрушения. Статически допустимому распределению усилий в
системе при разрушении соответствует максимальное значение параметра
предельной нагрузки.
188
( Определение предельных продольных сил
Для определения предельных продольных сил, применительно к
стальной стержневой системе можно использовать формулы
, jjp ~ Т2 ^2
где
aTi - предел текучести i-ro элемента;
Ал - площадь поперечного сечения i-ro элемента.
Предельное усилие сжатия определяется по формуле
Ni,Dp = <?TiAi<P.£
(299 а)
(299 б)
(дссь:
cpjt - коэффициент продольного изгиба i-ro элемента, зависящий
<гг случайных величин эксцентриситета е , предела текучести и
являющегося поэтому также случайной величиной.
В случае малого эксцентриситета коэффициент срх
определяется как для центрально сжатого стержня, а в случае
рачительного эксцентриситета - как для внецентренно сжатого стержня.
Формула дня относительного эксцентриситета будет
Л Д
ш = — . (300)
Wc
где
е - эксцентриситет;
Wc - момент сопротивления сечения для наиболее сжатого
волокна.
Затем определяется приведенный относительный эксцентриситет
л?е - Em , (301)
где
£, - коэффициент влияния формы сечения.
После этого проверяется условие
те < 0,1 . (302)
189
Если те < 0,1 , то расчет- производится как для центрально
сжатого стержня, если нет, то расчет производится как для внецентренно-
сжатого с эксцентриситетом е .
Для центрально сжатого стержня
332
л.2у[51 - лу)
при 1 > 4,5 .
где
Ху - условная гибкость элемента, вычисляемая по формуле
X = — - гибкость элемента;
1
lo - приведенная длина элемента;
i - радиус инерции.
Для внецентренно сжатого элемента ф находится по таблице
/65/ в зависимости от Л1е и Ху .
При определении предельного сжимающего усилия принимается
допущение о том, что и в сжатой области материал стержня подчиняется
диаграмме Прандтля, т.е. при достижении действующим сжимающим
усилием предельного, стержень продолжает нести предельную нагрузку.
Таким образом поверочный расчет стержневой системы состоит
из следующих этапов:
- на нервом этапе необходимо обработать исходные данные но
геометрическим размерам, сечениям стержней, направлениям и
соотношениям между внешними воздействиями, степень статической
неопределимости и т.п.
- следующий этап состоит в определении предельных усилий в
стержнях.
190
- третий этап заключается в реализации метода линейною
профаммирования и форме Симплекс-метола.
Вероятностный расчет стержневой системы
Детерминированный расчет конструкции методом предельного
равновесия позволяет определить максимальную предельную нафузку, а
также распределение усилий и перемещений в системе в момент
разрушения. Для вероятностного расчета системы целесообразно
использовать метод статистического моделирования. Расчет состоит из
последовательности этапов:
- генерирование внутренних вероятностных параметров системы;
на этом этапе производится генерирование таких случайных параметров,
как пределы текучести стержней, эксцентриситеты приложения усилий.
- вычисление параметра внешней нафузки при каждой
случайной реализации вероятностных параметров;
- генерирование случайной нафузки па систему; такая нафузка
может представлять собой атмосферное воздействие (снеговая, ветровая и
т.п.) в сочетании с технологическими и собственным весом конструкции.
В конце каждого статистического испытания производится про-
верка выполнения неравенства Q > Qap , здесь Qnp - предельная
нагрузка, получаемая из поверочного расчета; Q - действующая
нафузка.
Если действующая нафузка превышает предельную, то происхо-
дит отказ. Число отказов суммируется, и одновременно на каждом статис-
тическом испытании вычисляется частота отказа делением числа отказов
па число испытаний. Для того, чтобы по полученному значению частоты
оценить вероятность отказа используются процедуры, предложенные в
третьей главе.
Для уменьшения времени вычислений может быть использована
следующая процедура.
Расчет проводится лишь для тех случаев, конца либо действующая
нафузка превышает некоторую заранее заданную величину, либо предел
текучести в одном из стержней был не ниже заданного, либо
жецеггтриситет превышал заданный. Эти заранее заданные величины
। |азываются граничными.
191
Рис. 53. Область допустимых состояний предельной нагрузки
Для определения граничных значений необходима следующая
последователигость операций:
- задание математического ожидания и стандарта пределов теку
чести и эксцентриситетов;
- определение граничных значений пределов текучести и
эксцентриситетов по формулам
^тР = - 3 s.
егр = ё + 3 se
(304)
- проведение детерминированного расчета с использованием
наихудших (граничных) значений величин пределов текучести и
эксцентриситетов;
- определение в результате детерминированного расчета
граничного значения полной нагрузки.
Для наглядности данные ограничения представлены на рис. 53.
Следует отметить, что расчет будет производиться, даже если только в
одном стержне предел текучести или эксцентриситет будет выходить за
пределы граничного значения, хотя это не означает, что обозначенная на
рис. 53 иссушая способность будет меньше своего граничного значения.
Такой подход позволяет значительно сократить число расчетов. Это
192
п'11кхлрируется тем, что из расчетной юны почти полностью
исключается юна Л, вероятность отказа системы в которой равна пулю.
В качестве примера рассмстгрсна стальная плоская ферма из
уголков с перекрестной решеткой пролетом 18м (типовой проект серии
I 460.3-18) - рис. 54. Раскосы выполнены из парных уголков, пояса из
днойных уголков. В местах пересечения раскосы соединяются с помощью
|||цсонок. Шаг ферм принят 6 м. Материалом стержней является сталь
марки ВстЗпсб-1 с расчетным сопротивлением R - 24 5 МПа.
Допускаемая нагрузка включает в себя:
- вес покрытия, нс включая вес фермы,
- снеговую нагрузку.
1Ш снеговая .нагрузка ____________кШ
Рис. 54. Расчетная схема фермы
Район строительства - г. Москва, что соответствует III снеговому
району с 0яорм = 1 кН/м2 , yf = 1,4. Суммарная эквивалентная
нагрузка на покрытие составит Q - Q„ + Qc, где
(?п = 3,2 7 кН)м2 - расчетная постоянная нафузка для отапливаемых
|даний с железобетонными плитами покрытия 3 х 6 м, а
Qp - 1,4 кн/м2 - расчетная снеговая нагрузка.
Суммарная расчетная нагрузка будет Qp = 4fi7 кн/м2 и,
соответственно, погонпая суммарная нагрузка g = 4,67 - 6 =
= 28,02 кН/м.
Данная ферма является шесть раз статически неопределимой (из-
ia симметрии число неизвестных уменьшается до трех). Геомегричсские
параметры представлены в таблице 15.
На рис. 55 изображен механизм разрушения фермы с указанием
усилий в стержнях и выделением стержней, в которых усилия достигли
предельных.
Этот расчет был произведен для случая, когда пределы текучести
равны расчетным 245 МПа и эксцентриситеты равны нулю. Второй расчет
193
производился для случая, когда все пределы текучести и эксцентриситеты
вычислялись по формулам
— ат — 3sOt , в = 3se .
Рис. 55. Предельное равновесие фермы
По расчетному пределу текучести era л и ВстЗпсб-1 было опреде*
ле но математическое ожидание ат -- 305,25 МПа и ~ 25 МПа ,
Таблица /5
Элемент Сечение Площадь сечения см2 Радиус инерции см Момент сопротивлсни я см3
Г — 100x6,5 25,6 3,09 91,04
В — 70x6 16,3 2,15 38,76
1 =11= 70x6 16,3 2,15 38,76
Г 4 63x5 12,26 1,94 26,55
2 J-L 63x5 12,26 1,94 26,55
2’ — 63x5 12,26 1,94 26,55
3 4 63x5 12,26 1,94 26,55
У 63x5 12,26 1,94 26,55
Параметры вероятностной модели снеговой нагрузки определя-
лись по выборке метеорологических данных годовых максимумов веса
квадратного метра снегового покрова за зимний период. Объем выборок
составил 37 лет для Москвы.
Статистическая обработка выборки дала следующие результаты
среднее значение д0 = 649,7 н/м2 ;
стандартное отклонение sqo = 427,1 н/м2;
минимальное значение = 0,0 н}м2 ;
максимальное значение q0 - 2120 н!м2 .
194
Ранее отмечалось, что чаще вес id распределение максимумов
псса снежного покрова удовлетворительно аппроксимируется кривой
распределения Гумбеля, имеющей вид
Г(х) ~ ехр
(305)
где
и и Р* - параметры положения и масштаба соответственно.
и = 454,1 н/м2 , = 340,5 н/м2 .
На рис. 56 построен трафик, характеризующий степень близости
жспериментальной (полученной методом порядковых статистик) и
гиоретической (полученной методом моментов кривой распределения).
Рис. 56. Функция распределения снеговой нагрузки
Имеющееся совпадение может быть оценено как достаточное,
критерий Пирсона у/ - квадрат дал уровень значимости равного
приблизительно 0,27. Известно, что формула (305) для общего случая
может бьггь записана в виде
Гя(х) = ехр -ехр
и - х + р 1п п
(306)
195
где л - число лет.
Графики этой функции распределения для л - 1 году, 2 года, 5
лет, 10 лет, 20 лет и 50 лет приведены на рис. 57.
Для .задачи вероятностного расчета рассматриваемой фермы
приведение вышеуказанных параметров снеговой нагрузки к
сосредоточенным нагрузкам для шага ферм 6м и с учетом расстояния
между соседними панелями верхнего пояса позволяет записать:
среднее значение Q = 11676,6 Н ;
стандарт SQ = 7687,8 Н \
минимальное значение Q„^a = 0,0 Н;
максимальное значение Qmax = 38160 Н .
Рис. 57. Функция распределения снеговой нагрузки за п лет
Распределение предела текучести принималось по нормальному
закону (рис. 58). Было принято, что обеспеченность расчетного значения
равна 0.996, а стандарт - 25 МПа , тогда математическое
ожидание
196
Рис. 58. I Lio иметь распределения предела текучести
предела текучести вычислялось из уравнения
, - \2
(О у "" О )
cfcT
= 0,996
(307)
2 s
2
0 JI
Поскольку закон распределения эксцентриситета, исходя из
природы его возникновения является симметричным, то для пего также
был принят нормальный закон распределения с нулевым математическим
ожиданием и стандартом, равным 0,1 см.
Вероятностный расчет данной фермы представляя собой
2 104 статистических испытаний. На рис. 59 представлен 1рафик
ивисимости частоты отказов от числа лет эксплуатации. На нем
изображена верхняя граница доверительного интервала.
197
Рис. 59. Зависимость вероятности отказа фермы
от срока эксплуатации
198
Глава 6
НАДЕЖНОСТЬ ЖЕЛЕЗОБЕТОННОГО КАР
КАСНОГО ЗДАНИЯ, ЗАПРОЕКТИРОВАННОГО
ПО РОССИЙСКИМ И ЕВРОПЕЙСКИМ
НОРМАМ
0.1. Предварительные замечания
Применяемый в настоящее время при расчете конструкций метод
предельных состояний пе позволяет оценивать надежность конструкций и
тем более проектировать их с заданным уровнем надежности. Основным
расчетностным требованием этого метода является сравнение расчетных
(качений нагрузки и несущей способности, т.е. мы не можем получить
ответ на вопрос о том, какова вероятность безотказной работы
конструкции за заданный промежуток времени.
С девяностых годов в Западной Европе ведется работа по
созданию "Европейских" норм проектирования /85-88/. Основные
положения этих норм базируются на разработанном, с участием
российских ученых. Техническим комитетом (ГК 98) международной
организации по стандартизации (ИСО) стандарта ИСО 2394 "Основные
положения расчета строительных конструкций на надежность" /94/.
Основу этого стандарта составляет метод расчета по предельным
состояниям, названный методом частных коэффициентов надежности.
В европейских нормах нашел отражение накопленный
национальный опыт проектирования. Это выражается в том числе и в
щачениях частных коэффициентах надежности и расчетных значениях
прочности и нагрузок. Представляется целесообразным сопоставить
уровень надежности конструкций, проектируемых по отечественным и
Европейским нормам. Такое сопоставление возможно при применении
вероятностных методов.
В качестве примеров рассматриваются 7-ми и 4-х этажные
железобетонные каркасные здания с подвальными -этажами, имеющие
размер в плане 22,5 х 30 м и сетку колонн 7,5 х 7.5 м (рис. 60).
199
План
Рис. 60- Кинсзруктавиый план типового лажа и продольный
разрез проектируемого каркасного здания
Высота этажей 3,75м. Ригели продольных рам
четырех!jpojicTHbic на опорах жестко соединены со средними колоннами и
шарнирно с наружными стенами. Поперечное сечение колонн 40 х 40 см.
В поперечном направлении жесткость здания обеспечивается
вертикал иными связями.
200
6.2. Проектирование железобетонного каркасного
здания но российским и европейским нормам
За отказ в работе конструкции здания принимаем исчерпание
несущей способности средней колонны первого этажа (колонны 1, рис.
60). Для расчета выбрана средняя, а не крайняя колонна, нагому что
приходящаяся на нее грузовая площадь больше чем па крайнюю колонну.
Средняя колонна более нагружена и сильнее вовлечена в работу
конструкции здания.
Российские нормы
При расчете средней колонны прямоугольною сечения (рис. 61)
согласно СНиП "Бетонные и железобетонные копструкции‘763/ мы
исходим из основного расчетного положения
Ne < Rbbx(h0 - 0,5х) + RscA;(h0 - а’)
(308)
где
е = еог| + h/2 - а ;
Rb - расчетное сопротивление бетона сжатию;
Rsc - расчетное сопротивление арматуры сжатию;
Аз - площадь поперечного сечения сжатой или наименее
растянутой арматуры;
а - .защитный слой бетона;
h0 - рабочая высота сечения h0 - h - а;
Я - коэффициент, учитывающий увеличение изгибающего
момента в результате продольного изгиба.
Высоту сжатой зоны х определяют из следующих уравнений:
при = x/h0 < ^ ; N = Rbx8 + RSCA'S- RgAg'
при £ = x/h0 > ; N = Rbx8 + RSCA'S - vsAs\
где
Rs - расчетное сопротивление арматуры растяжению;
As - площадь поперечного сечения раст янутой арматуры;
<з3 - напряжение в растяну гой или наименее сжатой арматуре .
201
Рис. 61. Расчетная схема внецснтреняо сжатого элемента
= [2(1 - £)/(! - - 1]й3 , (309)
где
- граничная относительная высота сжатой зоны бетона .
fl f
I 1.1J
(310)
Здесь
ю - характеристика сжатой зоны бетона;
со = 0,85 - 0,008Rb , для выполняемого нами расчета по/63/
osR = Rs > ^scu = 500 МПа .
Значение коэффициента ц устанавливается по зависимости
ц = У(1 - N/Ncr) (311)
Выражение для критической продольной силы Ncr при
прямоугольном сечении с симметричным армированием As = A's (без
предварительного напряжения) имеет вид
202
Ncr = [6r4EbA/ +
+ 5) + 0,1] + - a) i
(312)
где
Еь - начальный модуль упругости бетона;
А - площадь поперечного сечения колонны А = bh ;
1й - расчетная длина элемента (расчетную длину колонн
многоэтажных зданий при жестком соединении ригелей с колоннами в
сборных перекрьпиях принимаем равной высоте этажа 10 = 1;
г - радиус ядра сечения (для прямоугольного сечения
г = 0,289h);
Ф; - коэффициент, учитывающий влияние длительного действия
нафузки на. прогиб элемента в предельном состоянии (для тяжелого
бетона q>; = 1 + М11/М1 ;
5 принимают наибольшим из б = l0/h
(5 = 0,5 - 0/)110 - R);
а = ЕБ/ЕЬ - отношение модулей упругости арматуры и
бетона;
р = 2АБ/А - коэффициент армирования .
Европейские нормы
Расчет железобетонной колонны (рис. 62) по европейским
нормам производим согласно/88/.
сжатая
Рис. 62. Расчел пая схема элемент
(к расчету по европейским нормам
проектиро вания)
203
Основным расчетным условием является
при Nd < (xbhfyd)2
[^sfyd(h - 2d,) + hNd(l -
- Nd)/(abhfcd)]/2 - Md > 0 ; °13)
при Nd > v.bhfyd/2
k2[Asfyd(h - 2d,)/2 +
+ CLbh2fcd/8\ - Md > 0, (314)
где
As - площадь поперечного сечения арматуры
Asi - &s2 ~ ^s/-2;
fyd - расчетное сопротивление арматуры;
fcd - расчетное сопротивление бетона сжатию;
Nd - расчетная продольная сила в сечении;
Md - расчетный изгибающий момент в сечении;
а - коэффициент, учитывающий длительность действия
нщрузки (<х = 0,85 );
кг - коэффициент определяется как
= (Wud - Wd)/(Nud - Nhalrd) , (315)
где
Nud - критическая продольная сила:
Nud = abhfcd + Asfyd\
Nbai = 0,5afcdAc; Ac = bh
204
Нагрузки на здание
Постоянные нагрузки
Всю постоянную нагрузку (нагрузку от веса колонн, плит
перекрытия, ригелей и перегородок) заменяем эквивалентной равномерно
распределенной нагрузкой. Эквивалентная равномерно распределенная
нагрузка, собранная с одного этажа
^ЭХВ. ~ •^ЭКВ.Рс ’ (316)
где
рс = 0,024 МН/ы3 - плотность железобетона;
Фэхв - эквивалентная высота перекрытия (h3KB = 0,3 м).
временные нагрузки
- кратковременные:
1) нормативные значения равномерно распределенной временной
нагрузки на плиты перекрытия принимаем по соответствующим нормам
или по имеющимся общим данным для проектирования;
2) нормативную нагрузку от действия ветра при расчете по
российским нормам принимаем по /64/.
Для Москвы (тип местности В) нормативное значение ветрового
давления
Wo - 0,23 кн/м2 .
Нормативное значение средней составляющей ветровой нагрузки
Wm на высоте z над поверхностью земли
Wm = Wokc , (317)
где
к - коэффициент, учитывающий изменение ветрового давления
по высоте;
с - аэродинамический коэффициент.
Нормативное давление ветра для Москвы по европейским
нормах /87/
»0 = , (318)
205
где
(jref - скоростной напор .
<Jret = Vref р/2 , (319)
где
р - плотность воздуха ( р = 1,25 кг/м3 ;
Vref ' скорость ветра .
vref = Calt ref , (32°)
Vref/0 ' базисное значение скорости ветра;
c„lt = 1 + 0,001as , (321)
где
as - высота над уровнем моря (м);
ср0 - аэродинамический коэффициент ( = 1,3);
c0(z) - коэффициент учитывающий изменение скорости ветра в
зависимости от высоты над землей .
c(z) - k2\.n(zlz0] , (322)
( k2 = 0,22 ; z0 = 0,3 м ).
- длительные:
Принимаем по соответствующим нормам или но имеющимся
общим данным для проектирования.
Расчет рамы
Вертикальные нагрузки
Рассматриваемая многоэтажная рама имеет регулярную
расчетную схему с равными пролетами ригелей и равными длинами стоек
(высотами этажей), сечения ригелей и стоек по этажам принимаем
постоянными. Узлы стоек таких рам, расположенные на одной вертикали,
имеют примерно равные углы поворота и, следовательно, равные узловые
моменты с нулевой точкой моментов в середине высоты этажа. Это дает
основание расчленить многоэтажную раму на ряд одноэтажных рам со
стойками (колоннами) высотой, равной половине высоты этажа, с
шарнирами по концам стоек кроме первого этажа (рис. 63 а). Стойки
206
первого этажа принимаются жестко защемленными в фундаменте (рис. 63
б).
При числе пролетов рамы больше трех, раму практически
«меняют трехпролетной рамой и полагают изгибающие моменты в
средних пролетах многопролетной рамы такими же как и в среднем
пролете трехпролетной рамы. Расчет такой рамы можно выполнять с
использованием таблиц /3/ (хотя можно и использовать стандартные
программы расчета рам).
Рис. 63. Расчетная схема рамы среднего и нижнего этажей
и эпюры изгибающих моментов
При этом изгибающие моменты в местах примыкания ригелей к
колонне
М = (ад1 + (3q')i2 , (323)
где
а и |) - табличные коэффициенты. зависящие от схемы
йгружения ригеля постоянной и временной нагрузками и коэффициента
к - отношения погонных жесткостей ригеля и колонны
= > (324)
Горизонтальные ветровые нагрузки
Распределенную горизонтальную ветровую нагрузку заменяем
сосредоточенными силами, приложенными к узлам рамы. Нулевую точку
эпюры моментов стоек всех этажей рамы, кроме первого, считаем
расположенной в середине высоты этажа, а в первом этаже (при
«щемлении стоек в фундаменте) - на расстоянии 2/3 высоты, считая от
места -защемления (рис. 64).
Ярусные поперечные силы рамы
207
Qi = F, + F,+. . -4-F„; t
J 1 2 B (325)
Q2 = F2 + F3*' 9 ~+Fn и T'
Они распределяются между отдельными стойками рамы
пропорционально жесткостям
где
В - жесткость сечения стойки;
л? - число стоек в ярусе.
Рис. 64. К расчет}' рамы на горизонтальную ветровую нагрузку
По найденным поперечным силам определяем изгибающие
моменты в стойках всех этажей, кроме первого
Я*етра = Q1/2 (327)
Для первого этажа изгибающий момент соответственно в верхнем
и нижнем сечениях стойки
2^ ветра
= Q1/3-,
Мве,трл = 2Q1/3
(328)
208
Определение усилий в расчетном сечении
Продольная сила в расчетном сечении колонны возникает в
результате действия постоянной вертикальной нагрузки (нафузки аг
собственного веса) и временной равномерно распределенной нагрузки на
ii.iiiTiii перекрытия. Предполагаем, что изгибающий момент в расчетном
сечении колонны возникает вследствие действия постоянной и
времен!юй равномерно распределенных нагрузок, действующих на
вышележащие перекрытие и горизонтальной ветровой нагрузки.
Российские нормы
I) У силия от вертикальные нагрузок
Продольные нмы от расчетных нагрузок
Груювая площадь - А . Постоянная цагружа па перекрытие
• иного-лажа с учетом коэффициента надежности но назначению здания
0,95 .
G - "псТ;л&
(329)
7 -- - постоянная нормативная нагрузка.
Временная нагрузка на перекрытие одною этажа с учетом
0,95
Q ~ ynvvfA , (330)
г. г.ч. длительная
Q1 " 7 ?; V О f А п (33 I)
I 'If
v - полная временная нормативная нагрузка;
Vj - даительвая времепг -я нормативная нагрузка.
Продольная сила, возникающая в колонне 1 от длительных
нагрузок равна
^maxfl П (G + Cj'Pjj) ; (л.?2)
то же ог полной нагрузки
209
Nn)*x = n{G + ^>n) , (333)
где
n - количество этажей;
\(/я - коэффициент, учитывающий сочетание поэтажных
нагрузок
ш — О А
Фл = 0,4 + , (334)
VD
где
1|/л - коэффициент, учитывающий снижение расчетной
нафузки при увеличении грузовой площади
ц/л = 0,4 + . ; А, = 9 м2 . (335)
Изгибающие моменты в колонне от расчетных нагрузок
Изгибающие моменты стоек определяем по разности абсолютных
значений опорных моментов ригелей в узле ДМ , которая
распределяется между стойками, примыкающими к узлу снизу и сверху, I)
средних этажах поровну М = 0,5/\М , а в первом ярусе М - 0,4АМ .
При этом для определения изгибающих моментов стоек вычисляем
опорные моменты ригелей для первою яруса при значении к ,
увеличенном в 1,2 раза. Анализом усилий можно установить, что при
расчете средней колонны следует принять комбинацию из
Ягаах и WeoorB. при следующей схеме зафужения (рис. 65)
Рис. 65. К расчету рамы на вертикальную нагрузку
Максимальный момент в расчетном сечении колонны 1 от
вертикальных нагрузок определяем по формуле
210
М = (ад' +
(336)
I J|C
д’ и д' - соответственно постоянная и временная равномерно
риспределенная нагрузка на 1 м длины ригеля;
v' - вычисляется с учетом коэффициента фЛ , а также с учетом
коэффициента сочетания 0,95 для длительной и 0,9 для кратковременной
нагрузок, т.к. расчетное сочетание включает две кратковременные
н.прузки (временную равномерно распределенную и ветровую нагрузки).
Находим опорные моменты ригелей в узле рамы от действия полной и
/11ительпой нагрузок
М21 и М23 , М1/21 и М]23 .
Вычисляем разность абсолютных значений опорных моментов в узле
рамы при длительной и полной нагрузках соответственно
= М1/21 - М1/23 ; \М = М21 - М23 . (337)
Момент в колонне подвала от длительной вертикальной нагрузки
MmaXll = 0,4 AM, , (338)
<>i полной вертикальной нафузки
Мтах = 0,4АМ . (339)
Соответствующая максимальному моменту продольная сила
определится при загружении всех пролетов на всех этажах постоянной и
временной нафузками, за исключением временной нафузки в среднем
пролете первого этажа. Таким образом, соответствующая продольная сила
МСООТВ.,1 ~ Мтах , ~ Q1/2 ,
(340)
МСООТВ. = М1пах — Q/2 .
2) Усилия от действия ветра
Расчетный момент от действия ветра находим, умножая
нормативное значение момента на коэффициент’ надежности по ветровой
па грузке yf =1,4 /(А/
211
мветра.р
деветра
Полное расчетное значение момента
Мтах = Мвер™к'р- + 0.9 мветра'р
Мтах>1 = Мвертик-р- -I- 0.9 мветра-р
ЯШ
. (341)
•1
Европейские нормы
Максимальный расчетный изгибающий момент определял
согласно /85/ по формуле
М<30 - 'fc^w,k +
( ) (342)
* Уо maxjM^^ + y\>oM„in^k ; М^п(1'к + Ч'оМдпр,*/’
где:
yG = 1,35 - ко'эффиггиепт надежности по постоянной нагрузке)
Ур коэффициент надежности по временной нагрузке;
Mimp,k ~ момент от нормативной постоянной нагрузки;
Mw,k " момент от нормативной временной нафузки;
^wiad к ' момент от нормативной ветровой нагрузки;
- коэффициент сочетания, равный 0.7 для равномерно
распределенной временной нагрузки и 0,6 для ветровой нагрузки.
Соответствующая максимальному моменту расчетная продолы®
сила равна
— У C^W, k + 1 qNimp, к
(343)
где
^н,к ' Продольная сила от нормат ивной постоянной нагрузки; I
^imp,k ' продольная сила аг нормативной временной нагрузки!
^хшр, к пАрimptl Я<Л д
(344)
где
п - количество этажей;
А - грузовая площадь;
212
Pimp ~ нормативная равномерно распределенная нагрузка на
и нггы перекрытия;
<хп - коэффициент сочетания при количестве перекрытий
л > 2;
ал - коэффициент сочетания, снижающий нормативную
нагрузку при увеличении грузовой площади А ,
ай = [2 + (л - 2)у0]/п , (345)
ПН'
\рй - коэффициент сочетания нагрузок ;
ад = 5 \у0[7 + Ао/А <1,0; Ад = 10,0 м2 (346)
Если временная нагрузка входит в расчет с коэффициентом
сочетания ф0 в виде '•Vo^imp,^. . то коэффициент <хй в расчете не
гнп’ывается.
3) Подбор сечения арматуры
Российские нормы
Расчет выполняем по принятой комбинации JL,„ и
* Шал сиО’Гп,
Рабочая высота сечения Ьо = Л - а .
Эксцентриситет силы е0 = M/N . Случайный эксцентриситет
р(| = h/ЗО или е0 = lCQ1/600 , но не менее 1 см. Для расчета
принимается наибольшее .значение эксцентриситета е0 .
Находим значение моментов в сечении относительно оси,
проходящей через центр тяжести наименее сжатой (растянутой
арматуры).
При длительной нагрузке
Miri = мз '• Ncootd. (h/2 - а) ; (347)
при полной яафузке
Мх = М + Ncoov„. (h/2 - а) (348)
213
Критическую продольную силу вычисляем по формуле (3J2),
Задаемся коэффициентом армирования
= 2Аа/А , (349)
где
А - bh - площадь сечения колонны.
Вычисляем критическую силу Ncr . Определяем значенШ
коэффициента г| по формуле (311), а значение эксцентриситета ПО
формуле
е = еоц + h]2 - а (350)
Вычисляем 1раничную относительную высоту сжатой зоны
по формуле (310).
Далее производим вычисления по следующим формулам
°"
< - ~ + 2 ?. ; (351)
^n^ha - 1 + aa/2)
cts = —-------7--ту-------s = а/Д, •
При afi < 0 принимаем As = A's конструктивно но мини-
мальному проценту армирования. При as > О определяем
N e/h0 - (1 - £>/2)ив
R3(l - §')
(352)
Вычисляем коэффициент армирования ц2 = 2AS/A и сравН
ваем его с принятым при определении Ncr . При их расхожден!
изменяем р2 и делаем перерасчет.
Европейские нормы
В сечении колонны действует момент
Md = Мм + Wd(ea + е2)
(353)
214
где
Md0 - начальный изгибающий момент в расчетном сечении
колонны.
Мм = Мввтра'р + мверти*-р , (354)
где
м»етра.р _ расчетный изгибающий момент в сечении колонны
от действия ветра;
мвеРтик:.р _ расчетный изгибающий момент в сечении колонны
(хг действия вертикальных нагрузок на перекрытие над расчетным
сечением;
еа - эксцентриситет, возникающий вследствие отклонения ос
геометрических размеров и неточности монтажа;
е2 - эксцентриситет, возникающий вследствие продольного
изгиба колонны
еа = 1,12 L/400 = 0,0028 L , (355)
где
L - длина колонны;
е2 = ОДк^Цг) , (356)
где
- коэффициент, зависящий от гибкости,
при к > 35 Jtj = 1;
1]г - кривизна.
1/г = 2k2Eyd/\0,9{h - dj] , (357)
где
коэффициент к2 определяем по формуле (315) ;
eyd =
fud - расчетное сопротивление арматуры, МПа ;
Es - модуль упругости арматуры, МПа.
215
(ъЗ* Сонотшлепие российских и европейских
норм 11роекгировапмя
В качестве численного примера рассмотрен расчет 4 \ чтажиою
типовою админ нс трнги иного здании
Место строительства г. Москва. Ветровой район - I, тип
местности В. В результате расчета были получены соответствующие
коэффициенты армирования средней колонны первого яруса гада иного
поперечною сечения (40x40 см). В качестве материалов конструкции
принята арматура класса А-Ш и бетон класса прочности на сжатие В20.
В табл. 16 занесены принятые для расчета здания нормативные
(характеристические) и расчетные значения нагрузок, коэффициенты
надежности но нагрузке, а также расхождение в процентах расчетных
значений иагруюк при проектировании по российским и европейским
нормам.
Таа-нща /6
Hai ру *.кл liil панне Российские нормы I jjpO] 1СЙСКИС нормы Расхождение расчетных и|ачспенип и '3-
! Норма], жачсиие нагрузки кПа Ko-xjx|). падежи ио иа- 1 ру 'КС- Расчет». IIKI’ICHJJC нахру $кн кПа. Ха рак г. nni'ieniie иагру жи кПа Коэфф надежи ин нагрузке PacHej'H значение нагрузки кПа.
J I ОС I i 1Й1|_.
Собе г не ir лес па [ м? игрек]). 7,2 1,1 7,92 7,2 1.35 9,72 22.7
Времен.
- нагрузка па «срскр. 2,0 1.2 2,4 3,0 1,5 4,5 87,5
• нейро лая пзгру *.ка 0,23 1,4 0,32 0,39 1,5 0,59 84,4
Полная
- liCjH JlK. nai рузка па I м: перекрыт. 9,2 - 10,32 10,2 - 14,22 44,6
К |-Ч. Д.1Ц ГсЛЬЕК 7,9 - 8,76 8,76 - 12,09 38,0
216
Таблица 17
Формулы учета сочетания нагрузок Российские нормы Европейские нормы Расхож -денис в %
ЯХ>рму-ты снижения расчетных нагрузок по этажам ш. - 0.J 4<и - 0.4 + -Ь. tf ]| (/.„ - [? < (л 2)ч-„[/п -
Значение ксгл|)фиц. ия рассматривав моги 4-х этажного ?;(лния - 0,496 ап = 0.678 30,7
114>рму.! [ ы с н и же н н я расчет»! ых । uupy чок ио грузовой плошали С',6 Ч’л “ <М + А - Aj - 9,0 м2 а, = Ж , л 7 Л Л„ ~ 10,0 \Г -
Значение коэффлц. для рассматривав мого 4-х этажного иания ул - 0,448 ал = 0,850 89,7
В табл. 17 представлены формулы для расчета коэффициентов
снижения расчетных значений нагрузок. Сюда же занесены значения
коэффициентов снижения и их расхождение для рассматриваемого 4-х
лажного здания при проектировании по различным нормам.
Определим как влияет использование расчетных формул,
предлагаемых российскими и европейскими нормами, па коэффициент
.|рмирования сечения железобетонного элемента. Для этого возьмем одни
и те же усилия Мтл1Г и и произведем расчет обоими
способами.
В табл. 18 занесены результаты расчетов и расхождение
। юлучеппых коэффициентов армирования.
Таблица 18
Ki) х]) (| > и ц т । с е г । а р м и ро ва н и я
Расчетные значения усилий Российские нормы Рвроисйскис нормы Расхож- дение в %
Ммх = 49г0кНм; NmoTB. = 2,9 103 кН 0,019 0,020 5
В табл. 19 показаны принятые для расчета нормативные и
расчетные значения сопротивлений, коэффициенты надежности по
материалу, а также расхождение в процентах значений расчетных
сопротивлений материалов при проектировании iю российским и
европейским нормам.
217
Таблица 19
Материал Российские нормы Европейские нормы Расхождение расчетных значснсний сопрот. в %
Нормат. сопротив леи не МПа, Коэфф, мадежн. по на териалу Расчета, соп ратин пенис МПа. Нормат. сопротив ление МПа, Коэфф, надежи, по на териалу Расчетн, сопротив ление МПа.
Бетон ВЗО 15 1,3 11,5 15 1,5 10 13
Арматура А-Ш 390 1.07 365 390 1,15 339 13
Для сравнения рассмотрено 7-ми железобетонное каркасное
здание. В результате расчетов был определен коэффициент армирования
Vj при использовании бетонов класса 1320, В25, ВЗО.
Результаты сведены в табл. 20.
Таблица 20
Коэффициент армирования
Класс бетона по прочости Российские нормы Европейские нормы
4-х этажное здание 7-ми этажное здание 4-х этажное здание 7-ми этажное здание
1320 0,019 - 0,048 -
1325 0,011 - 0,041 -
ВЗО 0.005 0,032 0,035 0,088
Анализ результатов детерминированного расчета по российским и
европейским нормам проектирования показывает, что европейские
нормы дают в 2,5-3,5 раза больший коэффициент армирования чем
российские нормы. В данном случае это объясняется в частности тем, что
европейские нормы проектирования предписывают использование
больших коэффициентов надежности но нагрузке, коэффициентов
надежности но материалу, а также использование расчетных формул
учета сочетания нагрузок, которые приводят к увеличению коэффициента
армирования (табл. 16-20).
Анализ результатов детерминированного расчета по российским и
европейским нормам проектирования показывает, что европейские
нормы дают в 2,5-3,5 раза больший коэффициент армирования чем
российские нормы. В данном случае это объясняется в частности тем что
европейские нормы проектирования предписывают использование
больших коэффициентов надежности по нагрузке, коэффициентов
218
надежности но материалу, а также использование расчетных формул
учета сочетания нагрузок, которые приводят к увеличению коэффициента
армирования (табл. 16-20).
Следует также отметить, что при расчете по европейским нормам
в расчет вводятся большие значения нормативной равномерно распреде-
ленной нагрузки на плиты перекрытия и большие значения нормативного
ветрового давления (табл. 16). Проведенный анализ показал, что отечест-
венные нормативные документы допускают при проектировании более
низкий уровень надежности. Объяснению этому может, в частности,
служить и тот факт, что в течение десятилетий в нашей стране к специа-
листам предъявлялись директивные требования экономии металла в
строительстве, что и вызвало необходимость глубокого исследования
нагрузок на сооружения и привело к более смелому назначению
расчетных нагрузок. При этом многолетний опыт безаварийной
эксплуатации зданий массового применения свидетельствует об
оправданности сделанных предположений.
6.4. Вероятностный расчет железобетонного
каркасного здания
Исходные положения
При выполнении вероятностного расиста случайными
принимаем:
- постоянную нагрузку;
- временную нагрузку ыа плиты перекрытий;
- ветровую нафузку;
- дополнительный эксцентриситет, возникающий вследствие
неточности монтажа и отклонения от геометрических размеров сечения;
- сопротивление бетона сжатию;
- сопрот ивление арматуры.
При вероятностном расчете средней колонны будем исходить из
того же расчетного положения (выражение 308), что и при
детерминированном расчете.
Величину коэффициента д , учитывающего возрастание момента
вследствие продольного изгиба колонны, вычисляем по формулам (311,
312).
При этом
219
Л - bh ; г - 0f289h ; ср, 1 * ;
Mti Nl + N,(h/2 a>- M: M + NW2 a):
a • ErJEb i pi2 - 2 А3/А\ e() h \ e0 = MN .
Момент M]fl и продольную силу 7VI принимаем в качестве
постоянных величин. 'Г.к. ветровая нагрузка нс относится к длительным
нагрузкам, то мь1 и NL определяем. собирая постоянные и
временные вертикальные нагрузки. Для временных нагрузок принимаем
пониженное значение, равное 0,7 от полного в соответствии со СНиП
/64/ для л дм н iihc'j рати иных зданий. При этом нормативные значения
нагрузок принимаем pariпями их математическим ожиданиям. ’Ото
позволяет увеличить количество Пкпьпаипй в десятки раз и довести до 1
млн. Такое количество диктуется затратами машинного времени.
Высоту сжатой юны х определяют из следующих уравнений:
яри - x/h0 ._р; N Rhxb i RSCA'S - RaA.. ;
при 2 --- x/’/Lj • N 7?hxb RVCA'S - c>sA!5.
(358)
i-’ie ГТ.. [3-’ •)/(! ;R) 1]RS .
При этом алгоритм всрозгпюстпото расчета следующий. Проверка
иссушен способ! юстп колонны производится в предположении
вын<-л нс и ня условия г x/hf) < ZR .
В нищем случае при и Rsc - R3 выест сжатой
зоны из условия (358) равна х = N/Rbb . Досс вычисляем по
(формуле (310).
Проверяем условие х < и, если оно соблюдено, то при
найденном шипении х проверяем несущую способность элемента по
формуле (308).
i lcc-хбл к ги.енме условия £ = x/h0 < указывает на то, что
х необходим! > определять при условии z ~ x/h0 > по формуле
(358). I [роизвеля преобраювапия, получим
__________________________________
[йьДь - N + °scuA? 1(1 - ГЛ/1,1
k 1 - (В 1,1/
(359)
.220
Изменчивоеть прочп'и*тных характеристик бетона и
арматуры
Принимаем класс бстопа по прочности на сжатие В20, класс
арматуры Л 111. Распределение прочности бетона и арматуры принимаем
но i юрмал ы юму закх» i у / х 1 /. 11 ара м ст ры распределен им с? гу1 ш й i юй
и роч н к ус гм 01 j редел яс м ни с| । к >р м у ла м /6 8/
«О £b,K<>p../'[T0/'U •• %)]; sRb = Rbvb;
^..юрЛ1 sRe - Rav., .
Для бетона клгсса
арматуры класса A- 111:
B2(): Rb 19.2 Ml la ; sRi> = 2.59 МПа ; для
-466.5 Mila ; -46,7 Mila.
(лучинный ЗКГЦ.Г11 rpiirnтег
Случайный •)Кс[[С11трис(це: приложения продольной нагрузки
возникает в результате отклонений гсомстрнческмх размеров и
i ictc >4i [ости moi п ажа kojioi ты. ; (ля случай ноги эксцентриситета
принимаем нормальный закон распределения. Математическое ожидание
жеиеитристета принимаем равным еа 0 . Согласно проведенным
/45/ исследованиям, стандарт случайного кИноситслыюго эксцентриси-
тета приложения продольной нагрузки в [верхнем сечении колонн для
желе зобстопных каркасных зданий составляет- - 0f34.
Огносителыпяй эксцсптр1|с|пс'| равен So™. = ео/Р Р " ядровое
расстояние сечения). 1огда ,.1ндарг случайною чксЕИ'НТристп'ега можно
о предел нт i> как
se = 5' р .
Нагрузки ин здание
Сбор нагрузок в расчетном ссчснип при верояз’ностном расчете
отличается от сбора нагрузок при детермпнированном расчете. В
соответствии с принятой схемой расчета /3/ . действие па1рузок
учитываем следующим образом. Изгибающий момент в расчетном
сечении
W = MseTP' М(, -f м,:
(360)
221
где
WBe.rp. - момент от действия ветровой нафузки;
Мо - момент от нафузок на перекрытие над расчетным
сечением (остальные вышележащие вертикальные нагрузки момент в
расчетном сечении нс создают);
Ме -момент, возникающий в результате наличия случайного
эксцентриситета.
Продольная сила в расчетном сечении
N = No + , (361)
где
No - продольная сила от вертикальных нагрузок на перекрытие
над расчетным сечением;
- продольная сила от остальных вышележащих постоянных и
временных нагрузок.
Ветровая нагрузка, согласно принятой схеме расчета, нормальной
силы в сечении колонны не создает.
При рассмотрении нагрузок принимаем следующее допущение:
постоянные и временные вертикальные нафузки представляют собой
независимые случайные величины. Исходя из принятого допущения,
математическое ожидание и стандарт случайной суммарной нагрузки
определяем по правилам сложения случайных величин.
'Гак как, изгибающий момент в расчетном сечении колонны
возникаем от действия ветровой нагрузки и вертикальной равномерно
распределенной нагрузки, приходящейся на вышележащее перекрытие, то
рассмотрим нагрузку на это перекрытие отдельно. Примем, что
постоянная нагрузка от собственного веса постоянна во всех пролетах
рассматриваемого этажа. Это позволяет избежать генерирования
дополнительно еще двух случайных величин (постоянной и временной
нагрузок на вышележащее перекрытие) и сократить время расчета.
С целью учесть возможную изменчивость временной нагрузки в
самих пролетах, исходим из следующего. Средняя интенсивность
временной [загрузки на перекрытие от веса оборудования и людей также
постоянна, но меняется интенсивность нагрузки в пролете в результате
оттока людей и перемещения оборудования из одного пролета и
сосредоточение их в другом (рис. 66). Предположим, что qx является
равномерно распределенной случайной величиной на интервале
|б; 2дср| , тогда q'2 = дср - q\ .
- постоянная нагрузка;
Vj' - временная нагрузка в крайних пролетах;
^2' - временная нагрузка в средних пролетах -
Рис. 66. Расчетная схема к вероятностному расчету
Нагрузки от собственного веса
Для постоянной нагрузки (вес частей сооружения, в том числе вес
несущих и ограждающих строительных конструкций) принимаем
нормальный закон распределения с математическим ожиданием g =
О,3рс = = 7,2 кн/м2 и стандартом sg = 0,72 кН/м2 ;
изменчивость постоянной нагрузки равна vg = 0,1 .
Временною нагрузки на перекрытия
Временные нагрузки представляют собой временные длительные
и кратковременные нафузки определенные в /64/. Естественно, что
изменчивость временных нагрузок больше изменчивости постоянных
нагрузок. В /51/ приведены данные о нагрузках на перекрытия (мебель,
оборудование, работающий персонал), собранные при обследовании
некоторых административных зданий в г. Москве (общая обследованная
площадь 13000 м2). Эти данные позволяют рассмотреть следующую
модель временной равномерно распределенной нагрузки на плиты
перекрытия. Для участков перекрытия с площадью более 36 м2 в качестве
закона распределения для временной нагрузки принимаем нормальный
закон со следующими параметрами распределения: q = 0,88 кН/м2, s
= 0,21 кН/м2.
Ветровые нагрузки
11ри рассмотрении случайной ветровой нагрузки будем исходить
из следующего. Значения годичных максимумов скорости ветра примем
223
распределенными но двойному >ксцоне|1Ина;1Ы1ому закону /49/,
Интегральная функция распределения
P(V) = exp [- exp (u - Vj/[3„]
(362)
где
и u |3, - параметры распределения.
Используя формулу максимумов независимых случайных
величин можно перейти от максимума за год к максимуму за п лег.
Интегральная функция распределения примет вид
Р(У) - exp [ exp (и - V + {3 In п)/(3]
<363)
где
л - количество лет, за которое вычисляется вероятность отказа.
Следуя /64/ щачепие ветрового давления определится как
Wo = 0,61V2 (364)
Для Москвы параметры двойного экспоненциальной.) распреде-
ления головых максимумов скорости ветра по /49/ следующие:
V ~ 19,95 м/с ; sv = 4,1 м/с ; и = 18,105 м/с ;
[3 =- 3,197 м/с.
Определение усилий в колонне при вероятностном расчете
Изгибающий момент от вертикальных нагрузок вычисляем по
формуле (323) с учетом сделанных предположений
при Qi > g/; М [аДд’ + д^) + [)7(д* - g^)]l2 ; (365)
при д\ < \ М - |а2(д' + gj) -I |)2(д2 - д';)]12 . (366)
Изгибающий момент в расчетном сечении колонны
Й = мвертик- + Мве1’₽а , (367)
где
^вертнк. _ момснт от иергикалъных нагрузок;
224
Йввр™- _ ; ДЙ = М21 - М23 ;
Йввтра _ момснт от действия ветровой нагрузки ;
jjse^pa = Q Ц3 , (368)
где
1 - расчетная длина стойки, равная высоте этажа;
Q - поперечная сила от действия ветровой нафузки.
Продольная сила в расчетном сечении
Я = Ыэт_ + Nm , (369)
где
Йэт. - продольная сила от постоянной и временной нагрузок,
собранная с грузовой площади вышележащих над расчетным сечением
перекрытий кроме перекрытая подвала.
Продольное усилие в расчетном сечении колонны представляет
собой случайную величину, распределенную по нормальному закону с
параметрами распределения, определяемыми по формулам:
(370)
где
^эт,г ’ w тематическое ожидание усилия в колонне от
нагрузки на перекрытие i-ro этажа;
s воот. - стандарт усилия в колонне от нгпрузки на перекрытие i-
tv этажа от постоянной нафузки;
s - стандарт усилия в колонне от нафузки на перекрытие
i-ro этажа от временной нафузки.
Продольная сила ^подв. от нафузки на перекрытие над
расчетным сечением
подв. ~ Л[? + (<?т + , (371)
где
А - грузовая площадь.
225
Построение функции надежности
Методом сгагистичсских испытаний определяем частоту отказов
колонны здания, запроектированного по российским и европейским
нормам (рис. 67).
лс’лодгшх данных
Г " "г
Генерирование случайных
величин
Определение действующих
в расчетном сечении усилий
И и N
вычисление в предполохенни
да
Определение
Мг.ллшо И Мвнутр
нел1 Вычисление X в лред-
лопо женин ч > £.м
нет
да
“и&ы " М|
___
счетчик
отказов
k-kt-1
Вывод на печати исходных
данных и частоты отказов
v=k/n
Рис. 67. Блок-схема вероятностного расчета колонны
За отказ принимаем исчерпание колонной своей несущей
способности, т.е. отказ фиксируется при невыполнении условия (308). В
данном выражении левая часть представляет собой момент от внешней
нафузки - Мваешн. , а правая часть - максимальный воспринимаемый
сечением момент - Мвиутр .
Таким образом, выражение (308) можно записать
Я < м
' “ внутр.
(372)
226
Используя метод статистических испытаний, описанный в главе 3
дли запроектированных зданий строим функцию надежности
। ипшсимости вероятности безотказной работы от срока службы).
Пример вероятностного расчета
Были построены функции надежности для 4-х этажного здания,
1щ|роектированного по российским нормам для следующих классов
Летона: В20, В25, ВЗО, Результаты сведены в табл. 21 и показаны на
рафиках (рис. 68).
Анализ данных результатов показывает, что проектируя элемент
одной и той же несущей способности, по применяя различные классы
бетона, мы получаем различную вероятность безотказной работы.
Таблица 21.
Частота отказов v для количества лет:
Класс бетона но прочности 1 5 15 20 50
В20 17 29 37 44 61
В25 37 58 74 82 113
ВЗО 46 65 85 97 122
Примечание: данные таблицы необходимо умножать па 10 .
—------доверительный интервал (у-0,9 5)
Рис. 68. График зависимое in вероятности безотказной работы от
количества лет для 4-х этажного здания
При неизменной несущей способности конструкции применение
бетона большей прочности влечет за. собой снижение коэффициента
прмирования железобетонного сечения. При этом вклад арматуры в
несущую способность элемента уменьшается. Так как арматура имеет
мспыпую но сравнению с бетоном изменчивость прочности, то уменыпе-
227
пие вклада арматуры в несущую способность приводит к снижению
надежности элемента.
Применяя бетон более низкого класса (соответственно с большим
коэффициентом армирования), мы получаем более надежную
конструкцию.
При использовании бетона В20 (соответственно при - 0,01 9)
вероятность безотказной работы 4-х этажного здания в течении 50 лс|
после возведения составит 0,99994, что соответствует вероятность
безотказной работы здания за 5-ти летний срок эксплуатации при
использовании бетона ВЗО (р.г = 0,005).
Был также рассмотрен пример вероятностного расчета 7-ми этаж-
ного типового административного здания, запроектированного по россий-
скими европейским нормам. ,
Для расчета был принят рекомендуемый европейскими нормами
для данного случая бетон класса С70/85 с нормативным сопротивлением
70 МПа. Результаты расчета показаны на рие. 69.
—------доверительный интервал (у -0г95)
Рис. 69. График зависимости вероятности безотказной работы от
количества лет дня 7-ми этажного здания
Сравнивая 4-х и 7-ми этажные здания, запроектированные не
российским нормам, следует отметить, что надежность более высоко
здания снижается сильнее в зависимости от количества лет. Так
вероятность отказа 4-х этажного здания за 15 лет эксплуатации
увеличивается примерно в 2 раза, а 7-ми этажного здания в 3,5 раза.
Был произведен расчет 7-ми этажного здания при различных
коэффициентах вариации прочности бетона. Оказалось, что вероятность
отказа для здания с коэффициентом вариации прочности бетона vb
0,2 в 2,5 раза больше чем для здания с vb = 0,135. Из этого следует, что
228
нпдежность железобетонной конструкции существенным образом зависит
иг прочностных характеристик материалов. Чего нельзя сказать о
случайном эксцентриситете. В результате проведенного расчета было
огмечено, что при увеличении стандарта случайного относительного
•кецентриситста в 2 раза (с se = 0,34 до se = 0,68) частоты отказов
I х этажного здания при использовании бетона В20 остались прежними
кия всех рассматриваемых временных офезков.
Из графиков на рис. 69 видно, что надежность здания, запроекти-
рованного по европейским нормам выше чем надежность здания,
спроектированного по российским нормам. Здание, запроектированное
ш> европейским нормам за 50 лет эксплуатации имеет такую же
игроятность безотказной работы (примерно, 0,99998), что и здание,
спроектированное по российским нормам, сразу после возведения. Если
с 50 лет эксплуатации для европейских норм мы имеем вероятность
игказа v - 0,00002, то для российских норм v = 0,00024, что в 12 раз
Гюлыпе.
Отметим, что был выбран достаточно условный критерий отказа -
нарушение условия прочности в одном сечении железобетонного вне-
иептренно-сжатого элемента. Но такой подход позволил с
использованием метода статистических испытаний произвести
сопоставление надежности сооружения, проектируемого по разным
нормам.
Разработанный алгоритм вероятностного расчета позволяет
проектировать здания с заданным уровнем надежности. Так, в качестве
примера для 7-ми этажного здания при использовании бетона класса ВЗО
ii'i я заданного уровня безотказной работы равного 0,99999 получен
коэффициент армирования =0,033
229
Глава 7
НОВЫЕ РАСЧЕТНЫЕ
ПРОЕКТИРОВАНИЯ
ТРЕБОВАНИЯ
Г •*
7.1. Обилие замечания
Действующая в настоящее время в России система строительных
норм и правил разрабатывалась в б. СССР и предназначалась для
применения в условиях административно-командной системы управления
экономикой, находящейся полностью в ведении государства. Эти нормы
характерны тем, что в них регламентируются действия по созданию
строительных сооружений. Постоянно дорабатываясь, эти нормы
охватывали все больший и больший круг действий и в идеале должны
были превратиться в свод обязательных правил и указаний по
выполнению всех операций, производимых при проектировании,
производстве, приемке и эксплуатации сооружений. Другими словами
нормы предписывали как нужно делать тот или иной шаг процесса
создания сооружения. При этом считалось, что если все шаги выполнены
в соответствии с предписаниями норм, то будет получен единственно
правильный результат.
Такой подход к нормированию неприемлем в условиях рыночной
экономики, где государство не может указывать владельцу, как ему
распорядиться своей собственностью, т.е. решение о том, как создават!|
сооружение, принимает владелец (или он доверяет это нанимаемым
специалистам). В соответствии с этим нормативные документы должны
предоставлять свободу действий создателям строительных сооружений.
Но тогда возникает особо острая необходимость нормировании
требований к конечному результату. При государственной монополии
такие требования сводились к экономии средств и материалов. В условиях
рыночной эконо-мики нормативные документы должны быть средством,
при помощи которого государство защищает потребителя от произвели
производителя. Основным содержанием этих документов становятсй
нормативные потребительские требования. При свободе выбора средств
конечный результат строительного производства должен обладать
комплексом совершенно определенных потребительских качеств.
Строительное сооружение никогда не является самоцелью. Она
всегда создается для того, чтобы обеспечить условия протекания какого-
230
либо технологического процесса. Здесь термин "технологический процесс"
используется не только в связи с технологией производства, но как
процесс, определяющий назначение сооружения, например, проживание
людей в жилом здании, демонстрация фильмов в кинотеатре, обучение
детей в школе, организация выставок в выставочном зале, обеспечение
осмотра монументов и т.п. Строительное сооружение можно считать
падежным, если оно обеспечивает функционирование технологического
процесса. Т.с. надежность сооружения есть его способность обеспечивать
нормальное функционирование технологического процесса.
Если сооружение оказывается в таком состоянии, при котором
нарушается нормальное протекание технологического процесса или
происходит его полная остановка, то говорят, что произошел "отказ
сооружения". Вероятность реализации отказовых состояний, т.е.
"вероятность отказа", является основной численной мерой надежности
сооружения. С использованием этой численной меры потребительские
требования в нормах проектирования формулируются в виде
нормативных надежностных требований.
В действующих нормах основное расчетное требование для
строительных конструкций формулируется в виде неравенства
RP Qp , (373)
где
Кр и Q,, - расчетные значения несущей способности и
нагрузочного эффекта (т.е. любого механического следствия внешнего
воздействия).
Выполнение этого неравенства считается достаточным условием
для обеспечения надежности, хотя оно не дает возможность получить
численную меру надежности и ее уровень остается неизвестным и
оказывается различным для различных конструкций под различными
нагрузками. Подобным образом формулируются требования и к другим
частям сооружения, уровень надежности которых также остается
неизвестным. Т.е. неравенство (373) нс отражает потребительских
требований к сооружению.
Основное расчетное требование для всех частей сооружения
следует формулировать исходя из потребительского требования в виде
Prob.(R < Q) = Р™ . (374)
где
R и Q - случайные величины несущей способности и
нагрузочного эффекта;
231
РгоЬ. - означает вероятность события (в данном случае отказа);
Рвх - целесообразное значение этой вероятности.
Расчетное требование (374) есть математическая формализация
потребительского требования к строительному сооружению или его части.
Нормативные документы должны содержать комплекс
требований к строительным сооружениям, охватывающий права и
обязанности всех, кто так или иначе вовлекается в технологический
процесс.
Первую группу требований, защищающих интересы владельца,
составляют требования нормального функционирования техно-
логического процесса. Следует иметь в виду, что "нормальное
функционирование" не то же самое, что "безотказное функци-
онирование”. Оно допускает оптимальную вероятность отказа,
соответствующую максимальной прибыльности сооружения.
Требования второй и третьей групп направлены на обеспечение
безопасности сооружошя.
Вторую группу требований составляют требования безопасности
людей, материальных ценностей и окружающей среды в процессе
нормального функционирования технологического процесса, т.е. во всех
предвидимых и учтенных при проектировании ситуациях.
Однако, не все предвидимые ситуации можно и нужно учитывать
при проектировании. Существуют так называемые аварийные ситуации,
при которых возникают воздействия большой интенсивности. Потребова-
лось бы значительное удорожание сооружения для восприятия этих
воздействий. В то же время вероятность возникновения таких ситуаций
крайне мала и затраты на полную нейтрализацию воздействий нецелесо-
образны. Из экономических соображений оказывается выгодных допус-
тить в этих редких ситуациях значительные разрушения, но при этом
нужно стремиться свести до минимума опасности для жизни людей.
Возникает понятие "разумного риска".
Третью группу требований составляют требования разумного
риска в аварийных ситуациях. Эти требования устанавливаются и
удовлетворяются совместно с мероприятиями не входящими в проблему
надежности строительных сооружений и не имеющими прямого
отражения в нормах проектирования. Например, требования огнестой-
кости строительных конструкции устанавливаются в зависимости от
используемых в сооружении систем оповещения и тушения пожара.
Все эти требования, формализуются в отличие от неравенства
(373) в виде равенства (374), поскольку было бы неправильно
устанавливать некоторый предельный уровень надежности и требовать
чтобы во всех случаях надежность сооружения была бы выше этого
уровня. Повышение уровня надежности сооружения требует увеличения
затрат на его возведение. С другой стороны повышение надежности
означает уменьшение вероятности отказов, а следовательно и частот их
232
появления, и ведет к снижению затрат на ремонты-восстановления в
процессе эксплуатации. Существует некоторый разумный или
"целесообразный" уровень надежности сооружений, обеспечивающий
оптимальное соотношение единовременных затрат на возведение
сооружения и распределенных во времени потерь от отказов. Этот
уровень надежности характеризуется целесообразным значением
вероятности отказа
В недалеком прошлом постановка вопроса о целесообразном
уровне безопасности считалась кощунственной, т.к. отождествлялась с
। планированием числа жертв при разрушениях строительных сооружений
В действительности же утверждение о недопустимости жертв сводилось к
фактическому игнорированию проблемы безопасности. Каждое сооруже-
ние имеет некоторую вероятность разрушения. Попытка приблизить эту
вероятность к нулю сопровождается стремлением начальной стоимости
сооружения к бесконечности. Следовательно, проектирование соору-
жения с неизвестной вероятностью отказа означает допущение неопреде-
ленного числа жертв. Анализ уровня безопасности необходим хотя бы для
раскрытия этой неопределенности и возможности оценивать принятое
решение.
В 1992-1994 гг. /40/ разработан проект СНиП России
Надежность зданий и сооружений. Основные положения", который
предписывает вероятностный подход к обеспечению надежности сооруже-
ний и их частей и трактует позрсбительские требования к их надежности.
Ниже излагается основное содержание этого проекта. Отметим,
что здесь вводится ряд новых терминов, которые не согласуются с ГОСГ
27002-89 "Надежность в технике. Основные понятия. Термины и
определения”. Основная причина этого в том, что ГОСТ 27002-89 не
соответствует новой концепции нормирования потребительских требова-
ний. Ключевой термин "надежность” определяется в нем, как свойство
объекта сохранять значения установленных эксплуатационных
показателей в заданных пределах. Соответственно, и все показатели
надежности так или иначе связаны с вероятностью выполнения
требований норм. Т.е. ГОСТ 27002-89 исходит из того, что нормы
устанавливают требования к эксплуатационным показателям, а
надежность есть вероятность выполнения этих требований, тогда как по
предлагаемой новой концепции, напротив, нормы устанавливают
требования к надежности, как к основному потребительскому качеству, а
эксплуатационные показатели (т.е. характеристики сооружения)
устанавливаются как следствие требуемой (целесообразной) надежности.
Отметим также что базовым документом для действующих в настоящее
время норм строительною проектирования является ГОСГ 27751-88
"11адежность строительных конструкций и оснований.
Основные положения по расчету", основанный на методе
предельных состояний в детерминированной форме изложения.
233
Предлагаемые ниже процедуры нормирования могут применяться при
проектировании по действующим нормам для количественной опенки
надежности несущих строительных конструкций, поскольку действующие
документы не содержат указаний по такой оценке. Примеры такого
применения содержатся в предыдущих главах.
7.2. Концепция нормирования и стандартизации
требований к строительным конструкциям
Нормы проектирования, приемочного контроля и освидетель-
ствования строительных конструкций должны формулировать такие
требования, которые обеспечивают защиту прав и охраняемых законом
интересов потребителей продукции строительства. Основными же
потребительскими требованиями к строительным конструкциям являются
их безопасность и способность обеспечивать нормальное функцио-
нирование технологических процессов, объединяющиеся общим поня-
тием надежность.
Требуемый уровень надежности должен устанавливаться из усло-
вия оптимального согласования потребительских качеств конструкция с
их экономичностью, т.е. как целесообразный уровень надежности.
Нормами проектирования устанавливаются в качестве обязательных
принципы выбора этого уровня. Надежность конструкции представляет
собой ее способность выполнять без отказов заданные функции в течение
заданного времени. Численно надежность характеризуется показателями
надежности. Надежность при этом зависит аг внутренних свойств
конструкции и внешних воздействий на нее. Способностью конструкции
сохранять во времени внутренние свойства является ее долговечность .
Численно долговечность характеризуется показателями долговечности,
основными из которых являются морозостойкость, огнестойкость,
выносливость, коррозионная стойкость и повреждаемость (показатель
накопления повреждений).
Нормативные требования к конструкциям формулируются для
двух видов ситуаций:
а) ситуация проектного выбора;
б) ситуация контрольно-браковочного выбора.
В ситуациях типа (а) нормативные требования удовлетворяются
выбором параметров конструкции из непрерывного или дискретного (сор-
таменты, каталоги и т.п.) множества значении.
В ситуациях типа, (б) нормативные требования удовлетворяются
приятием одного из двух возможных решений (пропуск или отбраковка,
реализации).
234
Анализ надежности конструкции производится вероятностными
методами, учитывающими случайный характер внутренних свойств и
внешних воздействий, при этом реальные конструкция и воздействия
обычно заменяются расчетной схемой. Отметим, что отдельные
возможные варианты развития процессов изготовления конструкции, ее
механической работы и связанных с нею последствий, рассматриваемые
как случайные события, называются вероятными реализациями этого
процесса. При количественном вероятностном анализе реализаций
рассматриваются три вида различий между ними (и тем самым три вида
признаков, выделяющих отдельную реализацию среди множества иных):
- внутрисхемные механические случайности, заключающиеся в
том, что учитываемые в расчетной схеме механические показатели
(нагрузки, усилия, характеристики прочности и т.п.) случайным образом
принимают тс или иные значения, т.е. определенным образом
реализуются процессы и поля механических показателей,
непосредственно участвующих в расчетной схеме;
внесхемпые механические случайности, обусловленные
случайными реализациями механических показателей, не имеющих
адекватного отражения в расчетной схеме;
- посторонние немеханические случайности, заключающиеся в
том, что при одной и той же механической картине реализации
конструкции и воздействий возможны различные случайные
обстоятельства, влияющие на последствия отказов (например, наличие
людей, стоимость оборудования и т.п.).
Для анализа надежности конструкции используется
вероятностное описание реализаций, учитывающее лишь характеристики
внутрисхемных механических случайностей. Совокупность всех
реализованных в данный момент времени внутрисхемных механических
случайностей определяет мгновенное состояние анализируемого объекта
(конструкции и воздействия на нее). Внесхсмные механические случай-
ности; учитываются косвенным образом, например, при математической
формализация условий отказа. Посторонние немеханичсские случайнос-
ти используются при установлении целесообразного уровня анализи-
руемой надежности.
Для определения целесообразного уровня надежности устанав-
ливается показатель тяжести последствий отказов, характеризующий пос-
торонние пемеханические случайности.
235
7.3. Характеристики вероятностной модели
работы конструкции
Основой выбора нормативных надежностных требований к
конструкции является математическая модель се функционирования,
предусматривающая деление ее реализаций на два класса:
- класс ущербных (или огказовых) реализаций, в которых
внутрисхемные механические случайности реализуются таким образом,
что они предопределяют существенный экономический либо
неэкономический ущерб, или, по крайнем мере, причинение такого
ущерба становится существенно зависимым от внесхемпых механических
и посторонних немеханических случайностей;
- класс нормальных реализаций, в которых вышеупомянутый
ущерб отсутствует, либо может считаться несущественным.
Отказ конструкции определяется как событие, состоящее в том,
что рассматриваемая реализация оказывается ущербной. При этом
зависимость ущерба от параметров реализации для ситуации с четким
отказом представляет собой ступенчатую функцию, а для ситуации с
нечетким отказом непрерывную монотонную зависимость.
Проявление ущерба во времени учитывается одной из двух
следующих моделей:
1) модель мгновенного образования ущерба, согласно которой
множество мгновенных состояний конструкции подразделяются на
отказовые состояния и нормальные состояния таким образом, что ущерб,
характерный для данного вида отказа, появляется при первом
возникновении отказового состояния, а реализации, состоящие только из
нормальных состояний, не сопровождаются ущербом;
2) модель линейного накопления ущерба, согласно которой
множество мгновенных состояний конструкции подразделяются на
ущербные состояния и нормальные состояния таким образом, что при
возникновении ущербного состояния начинается накопление ущерба,
который считается пропорциональным общей длительности пребывания
конструкции в ущербных состояниях. Реализации, состоящие только из
нормальных состояний, не сопровождаются накоплением ущерба.
Если модель линейного накопления ущерба применяется к
ситуациям с нечетким отказом, то за условный порог отказа принимается
некоторый критический уровень скорости нарастания ущерба.
Отказы, последствия которых определяются моделью
мгновенного образования ущерба, называются отказами-срывами.
Отказы, последствия которых определяются моделью линейного
накопления ущерба, называются отказами-помехами.
Расчетное условие отказа имеет вид:
236
g(r2, r2,. . -, rn) < Д
(375)
где
g - функция работоспособности, играющая роль индикатора
отказа;
Д - порог отказа, ограничивающий область значений функции
д , соответствующих безотказной работе конструкции;
Tj - параметры, характеризующие внутрисхемные механические
случайности реализации (в общем случае эти параметры являются
функциями времени).
Функция работоспособности д есть функция внутрисхемных
механических случайностей, а при выборе значения порога отказа могут
учитываться внесхсмные механические случайности.
Фундаментальным показателем надежности конструкции
является вероятность отказа Pf (Г) , т.е. вероятность того, что за время
предстоящею функционирования конструкции возникает отказ заданного
вида
Pf(?) = Ргоь.{д(г1’Г2,-. .,г„) < Д)
, (376)
где
РгоЬ {-&} ' означает вероятность реализации события.
В некоторых случаях удобно характеризовать надежность
конструкции дальностью отказа (индексом надежности, характеристикой
безопасности) р , однозначно связанной с вероятностью отказа
соотношением
0 = Ф~\1 - Pf)
(377)
где
Ф - интеграл вероятностей
(378)
Параметры, характеризующие внутрисхемные механические слу-
чайности реализации и являющиеся аргументами функции работоспособ-
ности в (375) подразделяются на параметры внутренних свойств
конструкции и параметры внешних воздействий на нее.
237
Последствия отказов харакгсризуюгся показателем тяжести пос-
ледствий отказов, который представляет собой усредненную но вероят-
ности оценку посторонних нсмехапических случайностей. Эта опенка
субъективна и зависит от технике-экономических и социальных условий.
По ответственности решения возможны следующие типы ситуа-
ций:
а) ситуации с экономической ответственностью решения;
б) ситуации с неэкономической ответственностью решения;
в) ситуации со смешанной ответственностью решения.
К типу (а) относятся те случаи, когда последствия учитываемых
отказов поддаются экономической оценке или, по меньшей мере,
возможность такой оценки нс вызывает принципиальных возражений.
К типу (б) относятся те случаи, когда среди последствий учитыва-
емых отказов существенно преобладаю!’ экономически неоценимые,
например, гибель, ранение или иное причинение ущерба здоровью
людей, уничтожение уникальных культурных и исторических ценностей,
тяжкие осложнения в политической и социальной сфере и т.п.
К типу (в) относятся тс случаи, когда последствия учитываемых
отказов включают как экономический ущерб, так и экономически нео-
ценимые последствия, причем оба эти вида последствий существенны для
выбора целесообразною уровня надежности.
Отметим, что для различных видов отказов одной и той же
конструкции может возникнуть необходимость рассмотрения ситуаций с
различными видами последствий.
7.4. Выбор и формирование нормативных надеж-
ностных требований
Нормативные надежностные требования к несущим
строительным конструкциям для стадии проектирования формируются с
помощью расчетною условия отказа (375) и вероятности его выполнения
(376)в виде
Л/Г) -- РгоЬ-ЫП' г2........гл) < Д2} = РГ(Т) . (379)
где
д± - функция работоспособности относительного отказа 1-го
вида, i = 1.....Л1;
лт - число типов отказов;
238
rj - параметры, характеризующие внутрисхемные механические
случайности реализации (в общем случае - функции времени),
j = 1, - •, п ;
п - число учитываемых параметров реализации;
Ai - порог отказа, определяющий область отказовых значений
функции работоспособности;
Т - период времени, на кагором определяется вероятность
отказа;
Pf - вероятность отказа i-ro вида;
Р/х - целесообразное значение вероятности отказа i-ro вида.
При наличии нескольких переменных во времени механических
случайностей рекомендуется в качестве показателя надежности вместо
вероятности отказа _Pf(T) использовать мгновенную вероятность
pitiSt попадания в отказовое или ущербное состояние в наугад
выбранном бесконечно малом интервале времени, определяемую без
учета предыстории процесса жизни конструкции.
Соотношение между' вероятностью отказа за определенный
период времени и мгновенной вероятностью попадания в отказовое или
ущербное состояние определяется формулой
Pinst
рЛт )
J-COV
(380)
где
Tcov - продолжительность равных интервалов времени, на
которые разбивается время предстоящего функционирования
конструкции 'таким образом, что отказы на различных интервалах могли
рассматриваться как независимые события (при учете климатических
воздействий обычно принимается Tcov = 1 год);
Т*о„ - часть интервала Tcov , на которой возможна реализация
отказового или ущербного состояния (например, если одним из
воздействий, вызывающих отказ, является снеювая нагрузка, то T*ov.
есть средняя продолжительность зимы с существенным снежным
покровом);
ТО1 - средняя суммарная длительность опасных перегрузок
суммарного воздействия на интервале.
Если в качестве показателя надежности используется мгновенная
вероятность попадания в отказовое или ущербное состояние, то
нормативное надежностное требование записывается в виде
239
(381)
где
v - случайно выбранный момент времени;
г?(у),..., rk(v) - сечение процессов r^t). • • . rk(t) !!
момент времени v.
Если в качестве показателя надежности используется дальность
отказа (индекс надежности, характеристика безопасности) р , то
нормативное надежностное требование записывается в виде
Pi = РГ
(382)
или
Piast
= ве*‘
г in st
(383)
где
Pi = - ^(7)];
- ф ф - р;х(т)|;
PLst = Ф ф - Р/ль-г]
PSt = * Ф - P&t]
(384)
где
Ф - интеграл вероятностей (378)
Нормативные надежностные требования к несущим
строительным конструкциям для стадии изготовления формируются с
помощью контрольного условия отказа и условной контрольной
вероятности сю выполнения в виде:
Pf, = Prob{(7i (s2.s2,..., sD.gk) < = P*** (385)
или при использовании в качестве показателя надежности дальности
отказа (индекса надежности)
240
₽* = р®х*
(386)
где
д* - контрольная функция работоспособности относительно
отказа i-ro вида;
3^ - контролируемые параметры (случайные величины);
дк - условная контролируемая нагрузка (случайная величина);
- порог отказа, определяющий область отказовых значений
контрольной функции работоспособности;
Р^ - условная контрольная вероятность отката i-ro вида;
Pf*k - целесообразное значение условной контрольной
вероятности отказа i-ro вида;
Рт = ф - условная контрольная дальность отказа i-
го вида;
Р®х* = Ф'2^1 - - целесообразное значение условной
контрольной дальности отказа i-ro вида;
Ф - интеграл вероятностей.
7.5. Нормативные показатели надежности и их
целесообразные значения
Уровень надежности строительных конструкций может
характеризоваться либо вероятностью отказа Pf(T) и однозначно
связанной с ней дальностью отказа р , либо следующими показателями,
производными от вероятности отказа:
- вероятность первого отказа конструкции в текущий момент
времени
Р(0 = - ~ > (387)
где
t - время, за которое вероятность первого отказа не превысит
заданное значение Р .
т = F/(P)
(388)
241
где
fT(t) = 1 - pr(t)
т - среднее время до первого отказа (среднее время жизни)
т = Jtp(t)dt = jp(t)dt , (389)
о о
X (t) - интенсивность отказов, определяемая как условная веро-
ятность того, что конструкция, проработавшая безотказно до момента
времени t , откажет в последующий малый интервал времени dt.
?v(t) =
p(t)
Pf(t)
(390)
H - среднее число отказов восстанавливаемой конструкции в
предположении, что па интервале времени At , большем, чем время
восстановления, повторный отказ конструкции невозможен
к
Н =
к-1
(391)
где
к
hk = £ Pihk,h0 = 1, h2 = Pj;
i 1
т
Pi (М, к = ----- ;
к , 1 - номер интервалов продолжительностью At.
Целесообразный уровень надежности конструкции устанавлива-
ется па основании анализа работы и уровня надежности существующих и
ранее существовавших конструкций, анализа последствий аварий (имев-
ших место и моделируемых), а также на основании анализа
эффективности использования материальных ресурсов для па и лучшего
удовлетворения экономических потребностей и требований безопасности.
В еизуациях с экономической ответственностью анализ
эффективности затрат производится путем минимизации целевой
функции
С - ся(т|) + ^(т], гэ,Ея,Т) , (392)
где
242
С - суммарные затраты на конструкцию, существенно
связанные с ее надежностью;
Св - часть стоимости конструкции, состоящая из тех начальных
затрат, которые существенно влияют на ее надежность (применительно к
рассматриваемым видам отказов);
П° - экономически оценимые средневероятные потери от
отказов конструкции за срок ее службы, приведенные
(дисконтированные) к эквивалентным затратам в момент времени начала
эксплуатации;
Ен - норматив для приведения (дисконтирования) разно-
временных затрат. (Дисконтирование - уменьшение затрат, отдаленных
во времени, при сравнении их с более ранними затратами, учитывающее
возможность накопления прибыли за счет отложенного платежа);
2Э - показатель тяжести экономических последствий отказов;
т] - показатель, используемый для характеристики уровня
надежности конструкций.
При этом в качестве показателя тяжести экономических послед-
ствий отказов Z3 , используется денежная опенки ущерба (например,
слагающаяся из стоимости ремонта поврежденною сооружения, суммы
потерянной прибыли в связи с остановкой производства и т.п.).
Дисконтирование (приведение) средпевероятных потерь
производится по формуле
f 1 V
П° = ДД---------- »
9 U + Е„) 3t
(393)
где
' средневероятные потери, ожидаемые в момент времени от
начала эксплуатации.
В расчетных процедурах возможно дисконтирование норматив-
ною показателя тяжести последствий отказов 2Э , т.е. приведение в
общем случае к некоторому ’ базисному" моменту времени оценки внеш-
них случайностей, реализованных на срок т позднее.
£ = 23te Е°ь
(394)
где
Z° - приведенный показатель тяжести последст вий отказов;
243
Z3t - показатель тяжести последствий отказов, произошедших в
момент времени t от начала эксплуатации, как правило, этот
показатель можно считать постоянным, т.с. Z3t = Z3 .
В случае применения модели линейного накопления ущерба со
скоростью и
Z3 = j udx - u[ dr , (395)
Ту ту
Z" = j ue = uj e , (396)
Ту Ty
где
Ty - множество моментов времени, в которых состояние конст-
рукции ущербно.
При этом в целевой функции (392) должна учитываться случай-
ность момента отказа, а в некоторых обоснованных случаях и его повтор-
ность.
В некоторых случаях удобно использовать натуральный (без
дисконтирования) показатель тяжести последствий отказов, а дисконти-
рование учитывать введением эквивалентною срока службы
Тед = 1/Еп вместо полного Т . Тогда приведенные потери в целевой
функции (392) определяются формулой
= TeqPf(Tcov)Z, (397)
или с учетом (380)
Т Т*
= z3pinst . (398)
В этом случае минимизация целевой функции (392) дает
уравнение для определения оптимального значения нормальной
дальности отказа
lh.„ - J2 hl _ 1„ р„) , (.,99)
где
244
dCH
S =---------------- эффективность затрат, соответствующая
d Piлst
оптимальному уровню надежности. Уравнение (399) решается итерацион-
ным методом.
В случаях нечетких отказов 2Э в (399) определяется не только
как усредненная по вероятности оценка посторонних немеханических
случайностей, но и с учетом усреднения по внутрисхемным, а в
некоторых случаях и внесхемным механическим случайностям.
4 = f tf[8 (?ъ г2у..., г„ )] гг,..., гл) drb dr2,..., dr0 (400)
L
где
ri - параметры, отображающие механические случайности
реализации;
5 - функция механических случайностей;
U - ущерб, однозначно определяемый функцией 8 ;
fr - плотность распределения параметров г ;
L - пространство значений г .
В ситуациях с неэкономической ответственностью решения нсоб-
dCH
ходимо сопоставить скорость нарастания затрат ------ со скоростью
dp
d/7
снижения экономически неоценимых потерь —— , где
Пвэ = Х(п)^нэ > (401)
а Х(ц) - некоторая функция показателя надежности, имеющая смысл
среднего числа нежелательных событий, тяжесть реализации которых
()це- нивается показателем тяжести экономически неоценимых
последствий отказов 2НЭ . Из этого сопоставления устанавливается
предел эффектив-ности затрат на повышение надежности. В некоторых
случаях возможно использование масштабного коэффициента Д
умножением на который показатель переводится в шкалу измерения
жономических потерь. Этот коэффициент представляет собой
монетарную оценку возможностей общества но защите жизни человека
или уникальных ценностей.
245
Устанавливаемое с помощью коэффициента Д единство шкалы
показателя тяжести экономических и неэкономических последствий
вытекает из:
технически неизбежной соразмерности средств в
сопоставляемых случаях (т.е. использования качественно однородных
физических ресурсов для обеспечения надежности как при
экономической ответственности, так и при неэкономической
ответственности, и, следовательно, неизбежности количественной
соразмерности сопоставляемых критериальных 'требований);
- неизбежной ограниченности ресурсов, заставляющей принимать
конечные измеримые уровни запасов даже в случае высокой неэкономи-
ческой ответственности.
В ситуациях со смешанной ответственностью решения
необходимо сопоставить скорость изменения суммарных экономически
□ценимых затрат ~~ 1сн+П“) со скоростью изменения экономически
с7г| ' '
dnH3
неоценимых потерь —— .
CfT|
246
Литература
1. Андреев 0.0. Оценка несущей способности железобетонных сечений
с учетом вероятностной природы прочности бетона и стали //
Строительная механика и расчег сооружений. - 1984. - № 6.- С. 16-19.
2. Аугусти Г., Баратта Л., Кашиати Ф. Вероятностные модели в
строительном проектировании. - М.; Стройиздат, 1988.- 584 с.
3. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий
курс: Учеб, для вузов, - 5-е изд., перераб. и доп. - М.: Стройиздат,
1991. - 767 с.
4. Байков В.Н., Складней 11.11- Применение вероятностного подхода для
оптимального проектирования железобетонных балок // Напря-
женно-деформированное состояние и оптимизация железобетонных
конструкций. Сб. тр. № 151 МИСИ им. В.В. Куйбышева. - М.: 1977. -
с. 3-10."
5. Балдин В.Л., Гольденблат И.И., Кочсцов В.И., Пнльдиш М.Я., Галь
KJ. Расчет строительных конструкций по предельным состояниям. -
М.: 1951. - 272 с.
6. Барштейн М.Ф. Руководство по расчету зданий и сооружений на
действие ветра,- М.: ЦНИИСК. - 1978,- 2)5 с.
7. Бать А.Л., Гвоздев А.Л., Отставной В.А. О классификации нагрузок в
расчете строительных конструкций // Промышленное строительство.
- 1971,-№2,-с. 35-37.
8. Белышев И.А. Нормирование температурных климатических воздей-
ствий для расчета конструкций // Тр. ЦНИИСК им. В.А. Кучеренко.
- 1976. - Вып. 42. - с. 23-36.
9. Белышев И.А., Клепиков Л.В. Статистический анализ данных о
температуре воздуха для расчета конструкций // Тр. II,НИ ИСК им.
В.А. Кучеренко. - 1976. - Вып. 42. - с. 11-34.
К). Болотин В.В. Применение методов теории вероятностей и теории
надежности в расчетах сооружений. - М.: Стройиздат. - 1971. - 255 с.
II. Болотин В.В. Статистические методы и строительной механике,- М.:
Стройиздат.- 1965.- 202 с.
12. Болотин В. В. Методы теории вероятностей и теории надежности в
расчетах сооружений. - М.: Стройиздат. - 1982. - 351 с.
13. Болотин В.В. О сочетании случайных натрузок, действующих на
сооружения // Строительная механика и расчет сооружений. 1962. -
№2 -с. 1-5.
14. Булычев А. II., Сухов Ю.Д. Применение теории надежности для
нормирования расчетных значений нагрузок // Строительная
механика и расчет сооружений. ЦНИИСК. - 1987. - № 2. - с. 3-6.
247
15. Визир ПЛ. Оценка надежности параллельной структуры с учетом
перераспределения нагрузки. Строительная механика и расчет
сооружений. -1981. - № 1.- с. 15-18.
16. Вольмир А.С. Устойчивость деформируемых систем. - М.: Наука. -
1967. - 983 с.
17. Гвоздев А.А. К вопросу о ближайших перспективах расчета конст-
рукций но предельным состояниям // В кн.: Развитие методики
расчета по предельным состояниям. - М.: Стройиздат. - 1971. с. 38-43.
18. Гвоздев А.А. По поводу статьи ’’Основные положения вероятностно-
экономической методики” И Строительная механика и расчет
сооружений. - 1979.- № 3. - с. 71-72.
19. Гениев Г. А. Об оценке динамических эффектов в стержневых
системах из хрупких материалов. Бетон и железобетон. - 1993. - № 3.
- с. 25-27.
20. Гмурман В.Е. Теория вероятностей и математическая статистика. И.:
Мир. - 1977.- 480 с.
21. Гнеденко Б.В. Курс теории вероятностей. - М.: Гостехиздат,- 1954. -
411 с.
22. Гнеденко Б.В., Беляев Ю.К., Соловьев А Л. Математические методы в
теории надежности. - М.: Паука,- 1965. - 524 с.
23. Гумбель Э. Статистика экстремальных значений. - М.: Мир.- 1965. -
449 с.
24. Дривинг А.Я. Рекомендации по применению экономико-
статистических методов при расчетах сооружений с чисто
экономической ответственностью. - ЦПИИСК. - М., 1972. - 61 с.
25. Знаменский Е.М., Сухов Ю.Д. О расчете конструкций с заданным
уровнем надежности // Строительная механика и расчет сооружений.
- 1987. - №2. - с. 7-9.
26. Капур К., Ламберсон Л. Надежность и проектирование систем -М.:
Мир. - 1980. - 604 с.
27. Келдыш В.М., Гольденблат И.И. Некоторые вопросы метода
предельных состояний // Материалы к теории расчета по
предельному состоянию, вып. II. - М.: Стройиздат.- 1949. - с. 6-17.
28. Клепиков Л.В., Отставное В.А. Определение нагрузок при расчете
строительных конструкций // Строительная механика и расчет
сооружений. - 1962. - № 5. - с. 39-45.
29. Ковальский 3., Зубжицки С. О безопасности стержневых систем //
Строительная механика и расчет сооружений. - 1970. - № 2. с 7-9.
30. Краковский М.Б. Определение надежности конструкций методами
статистического моделирования // Строительная механика и расчет
сооружений. - 1982. - № 2. - с. 10-13.
31. Кудзис A ll. Оценка, надежности железобетонных конструкций. -
Вильнюс: Моклас. - 1985. - 155 с.
248
12. Кулзис A. 11. О всрозггносгном расчете железобетонных конструкций
// Бетон и железобетон. - 1988. - № 7. - с. 41-42.
<3. Кузнецов Б. И. Рекомендации по расчету стальных рам как единых
нелинейных систем. -М.: ЦНИИСК им. В.А. Кучеренко. - 1987. - 98
с.
14. Лейтес С.Д. Устойчивость сжатых стальных стержней. -М.:
Стройиздат. - 1952,- 217 с.
15. Лосицкая К.С. Определение коэффициента, сочетания нагрузок //
Исследования но строительной механике и методам расчета,
ЦНИИСК им. В.А. Кучеренко,- М.: 1981. - с. 129-136.
36. Лужин О.В. Вероятностные методы расчета сооружений. - М.: МИСИ
им. Куйбышева, 1983. - с. 122.
17. Лычев А.С. Безопасность конструкций производственных зданий //
Тр. конф. Надежность и реконструкция - 88 - Волгоград. - 1988. - с.
5-7.
18. Митропольский А.К. Техника статистических вычислений. - М.:
Наука. - 1971. - 576 с.
19. Мкргьгчев О.В. Определение частоты отказов внецентренно сжатого
стального стержня. - Дсп. ВНЦИНТПИ, № 11558. - М.: - 1995. - 9 с.
40. Надежность строительных конструкций. Основные положения.
Проект СНиП России. Внесен ЦНИИСК 1994. - 25 с. Исполнители
В.Д. Райзер, Ю.Д. Сухов.
II. Отставное В.А., Розенберг Л.С. О некоторых особенностях сбора и
первичной обработки исходного климатического материала по
снеговым нагрузкам // Расчет строительных конструкций. -ЦНИИСК
им. В.А. Кучеренко. - 1976. - Вып. 42. - с. 91-98.
42. Отчет НИР ЦНИИСК им. В.А. Кучеренко. Разработка основных
положений расчета и проектирования несущих стальных конструкций
на основе вероятностных методов обеспечения их надежности. М.:-
1991. - 9.с. Исполнители В.Д. Райзер, Ю.Д. Сухов, В. В. Астряб.
43. Отчет НИР ЦНИИСК им. В.А. Кучеренко. Разработать вероят-
ностные модели климатических и техногенных воздействий на
конструкции зданий и сооружений, инженерное оборудование и
внешние сети. М.: - 1994. - т. 1. - 223 с. Исполнители В.Д. Райзер,
Л. В. Клепиков.
44. Отчет НИР ЦНИИСК им. В.А. Кучеренко. Разработка единой
системы нормативных документов по проектированию, строи-
тельству, эксплуатации и восстановлению зданий и сооружений,
городов населенных пунктов в опасных зонах. М.: - 1991. - 97 с.
Исполнитель В.Д. Райзер.
45. Парасонис И И. Надежность каркасов одноэтажных производ-
ственных зданий с учетом точности геометрических параметров
монтажа. - Вильнюс: Техника. - 1995. - 392 с.
249
46. Пиковский А.А. Статика стержневых систем со сжатыми элементами.
- М.: Физматгиз. - 1961. - 317 с.
47. Писчиков В.Н. Методика учета изменчивости и вероятности
сочетаний ветровых, снеговых и вертикальных крановых нагрузок.
Международный совет по научным исследованиям и обмену опытом а
области строительства. - Киев. - 1967. - с. 1-22.
48. Райзер В.Д. Развитие теории надежности и совершенствование норм
проектирования // Строительная механика, и расчет сооружений. -
1983. - № 5. - с. 1-4.
49. Райзер В.Д. Методы теории надежности в задачах нормирования
расчетных параметров строительных конструкций. - М.: Стройиздат,
1986.-192 с.
50. Райзер В.Д. Вопросы опенки надежности строительных конструкций
при износе // Исследования по строительной механике. - М.:
ЦНИИСК им. В.А. Кучеренко. - 1985. - с. 61-67.
51. Райзер В.Д. Расчет и нормирование надежности строительных
конструкций. - М.: Стройиздат. - 1995. - 348 с.
52. Райзер В.Д,, Бать А.А., Отставной В.А., Сухов Ю.Д.
Совершенствование нормирования строительных конструкций и
оснований // Строительная механика и расчет сооружений, - 1988. -
№ 3. -с. 59-61.
53. Райзер В.Д., Сухов Ю.Д. Теория надежности и новая концепция
строительных норм. Промышленное и гражданское строительство. -
1996. - № 5.
54. Райзер В.Д., Складней И.П. Количественная оценка надежности,
долговечности и последствий отказов при проектировании
строительных конструкций // Перспективы развития строительных
конструкций. - Л. - 1987. - с. 7.
55. Ржаницын А.Р. Теория расчета строительных конструкций ни
надежность. - М.: Стройиздат. - 1978. - 239 с.
56. Ржаницын А.Р. Устойчивость равновесия упругих систем. - М.:
Госстройиздат. - 1955. - 476 с.
57. Ржаницын А.Р., Снарскис Б.И., Сухов Ю.Д. Основные положения
вероятностно-экономической методики расчета строительных
конструкций // Строительная механика и расчет сооружений. -1979. -
№ 3. - с. 67-71.
58. Ржаницын А.Р., Сухов Ю.Д. Учет совместного действия нагрузок на
сооружения// Строительная механика и расчет сооружений. - 1974. -
№ 4. - с. 40-43.
59. Саульев В.К. Статистическое моделирование: Метод Монте-Карло.
М.: МАИ,- 1974. - 67 с.
60. Складнее Н.Н., Дрейер Ф.Э. О вероятностном расчете и проекти-
ровании железобетонных изгибаемых элементов // Строительная
механика и расчет сооружений. - 1983. - № 3. - с. 1-4.
250
61. Снарскис Б. И. Оптимальные расчетные и контрольные значения
случайных параметров как средство оптимизации надежности //
Проблемы надежности в строительном проектировании. - Сверд-
ловск. - 1972. - с. 202-206.
62. Снарскис Б.И. О связи метода оптимальных расчетных значений с
методикой предельных состояний // Проблемы надежности в
строительном проектировании. - Свердловск . - 1972. - с. 206-211.
63. СНиП 2.03.01-84. Бетонные и железобетонные конструкции /
Госстрой СССР. - М.: ЦИТП Госстроя СССР. - 1985. - 79 с.
64. СНиП 2.01.07-85. Нагрузки и воздействия / Госстрой СССР. -М.:
ЦИТП Госстроя СССР. - 1986. - 36 с.
65. СНиП П-23-81. Стальные конструкции / Госстрой СССР. - М.:
ЦИТП Госстроя СССР. - 1982. - 96 с.
66. Справочник по климату СССР. Л. Гидрометеоиздат. 1964-1968 гг.
67. Стрелецкий Н.С. Основы статистического учета коэффициента
запаса, прочности сооружений. - М.; Стройиздат. - 1947. - 92 с.
68. Стрелецкий Н.С. Метод расчета конструкций зданий и сооружений
по предельным состояниям, применяемый в СССР и основные
направления его применения к строительным конструкциям. - М.:
Стройиздат. - 1961, - 34 с.
69. Сухов Ю.Д. Некоторые особенности теории надежности
строительных конструкций // Строительная механика и расчет
сооружений. 1975. - № 4. - е. 13-16.
70. Сухов Ю.Д Учет начальных искривлений стержней фермы покрытия
при определении ее надежности // В кн. Расчет строительных
конструкций. - Труды Щ1ИИСК им. В.А. Кучеренко, вып. 12. - М.: -
.1976. - с. 127-132. ”
71. Сухов Ю.Д. Рекомендуемые методы определения показателя
надежности / Научно-технический отчет. - Труды ЦНИИСК им. В.А.
Кучеренко. - М.: - 1993. - с. 3-7.
72. Галь К.Э., Корсунцев И.Г. О надежности расчета несущей
способности изгибаемых элементов // Бетон и железобетон. - 1967. -
№ 4. - с. 34-36.
73. Тимашев С.А. Рекомендации по оценке надежности строительных
конструкций. - Свердловск. - Уральский Промстройпроект. 1974.- 103
с.
74. Тимашев С.А. Надежность больших механических систем. - М.:
Паука. - 1982. - 184 с.
75. Федоров Е.И. Вероятностно-оптимизационный расчет конструкций,
находящихся под действием нескольких нагрузок // В кн.:
Исследование нагрузок па сооружения и надежность строительных
конструкций. - М.: 1976. - с. 108-124.
76. Хан Г., Шапиро С. Статистические модели в инженерных задачах. -
М.: Мир. - 1969. - 396 с.
251
76. Хаи Г., Шапиро С. Статистические модели в инженерных задачах. -
М.: Мир. - 1969. - 396 с.
77. Хоциалов Н.Ф. Запасы прочности // Сфоитсльная промышленность.
- 1929. - № 10. - с. 840-844.
78. Черячукин В.В. Применение метода Монте-Карло к некоторым
статистическим задачам устойчивости и надежности // Проблемы
надежности в строительной механике. - Вильнюс. - 1968. - с. 79-85.
79. Чирков В.П. Вероятностные методы расчета мостовых
железобетонных конструкций. - М.: - 1980. - 134 с.
80. Шпете Г. Надежность несущих строительных конструкций,- М.:
Стройиздат. - 1994. - 227 с.
82. Cornel С.A. Stochastic Process models in structural engineering. Dept. Of
Civ. Engineering. Stanford University. Technical Report. №> 34. pp. 14-18.
1969.
83. Ditlcvsen O. Narrow reliability analysis of frame structures. J of Struct.
Mechanics, vol. 1, № 4. 1979, pp. 453-472.
84. Ditlcvsen O. Stochastic model of self-weight load, J. of Struct. Engineering,
ASCE, vol. 113, № 1, 1988, pp 38-49.
85. ENV 1991-1: Eurocodc 1: Basis of design and action on structures - Part 1:
Basis of design, CEN 1994.
86. ENV 1991-2-1: Eurocode 1: Basis of design and actions on structures - Part
2.1; Denstics, self-weight and imposed loads. CEN 1994
87. ENV 1991-2-4: Eurocode 1: Basis of design and actions on structures - Part
2.4: Wind loads. CEN 1995.
88 Env 1992-1: Eurocode 2: Design of concerte structures - Part 1: General
rules and rules for buildings, CEN 1993.
89. Ferry Borges J. Castanheta M. Structural safety. 2nd ed. Laboratorio
Nacional de Engeharia Civil. Lisbon, 1971, p. 217.
90. Freudenthal A M. Safety, reliability and structural design. J. of Stmct.
Div.,Proc. ASCE. 87. ST31961. pp. 814-823.
91. Hasofer, Lind. An exact and invariant first-order reliability format. J. of the
Engineering Meeh., Div., ASCE. vol. 100. № EMJ. February'. 1974. pp.
111-121.
92. Holicky M„ Vrouwenvelder T. Reliability analysis of a reinforced concerte
column designed according to the Eurocodcs. JABSE Colloquim Delft.,
Report, 1996. pp.251-265.
93. Jezek K. Die Festigkcit von Dnickstaben aus Stahl Verlag von J. Springer.
Wien, 1937.
94. JSO/TK 98 ST 2394 General Principles on Reliability for
Structures, 1994,. S. 50.
95 Joint Commitee on Structural Safety Reports. General Principles on Quality
Assurance for Structures. General Principles on Reliability for Structural
Design. Lisbon, pp 168.1981.
252
96. Mayer M.Die Sicherheit der Bauwerte und ihre Bcrechnung nach Granz-
kraften Statt nach zulassigen Spamiungen. Springer Verlag, Berlin, 1926,
pp. 111-126.
97. Merchant W. The failure load of rigid jointed frameworks as influenced by
stability.Structural Engrs, v.32. N 7. 1954, pp. 185-190.
98. Metropolis N., Ulatn S. The Monte-Carlo method. J. Amer. Stat. Assoc.,
vol. 44, N 247, 1949.
99. Murzewski J.Niezawodnosc konstrukeji inzynicrskich Warszawa, 1989, s.
231
100. Rackwitz R.,Fiessler B. An algorithm for the calculation of structural
reliability under combined loading. Bericbtc zur Sicherheitsthorie der
Bauwerke. Lab. f.Konstr. Ingb., pp. 489-494. Munchen, 1977.
253
Приложение I
РЕКОМЕНДАЦИИ ПО ВЫБОРУ ВЕРОЯТ-
НОСТНЫХ МОДЕЛЕЙ КЛИМАТИЧЕСКИХ И
ТЕХНОЛОГИЧЕСКИХ НАГРУЗОК
1Л. Статистическое обоснование моделей времен-
ных нагрузок и воздействий
Основной количественной характеристикой нагрузок и воздейст-
вий является их интенсивность как функция пространственных
координат и времени. Вероятностные свойства иэтенсивности как
случайной переменной оцениваются: для случайных величин - по
статистическим выборкам, для случайных функций - по выборочным
функциям (реализациям).
Основные виды исходных реализаций измеренных значений
нагрузок представлены на рис. 1.1:
а) дифференцируемые - "а", "б";
б) недифференцируемые (ступенчато-импульсного типа):
- со связанными импульсами - "в”;
- с несвязными импульсами - "г” - "и”, в том числе
с мгновенными - "е", "и”.
Каждый импульс начинается от нулевого значения интенсив-
ности. Последовательность затру жений в реализациях "б" - “е”
обусловлена случайным потоком событий, состоящих в появлении
реальных (ненулевых) импульсов нагрузки случайной длительности
d < А , где А - случайный интервал между моментами появления
событий (период повторяемости событий).
Стационарные потоки появления многих нагрузок, например, на
подкрановых и мостовых конструкциях, на перекрытиях зданий,
согласуются с моделью пуассоновского потока и соответствующим ему
экспоненциальным распределением
Fjt) =- 1 ~ e'5t , t > 0, v > 0 , (1.1)
— 1 1
параметры которого А = — , sA = — , где
v v
254
v - интенсивность (плотность) потока или средняя частота
появления событий.
Рис. 1.1.
Для пространственных реализаций интервал А может быть
моментом длины, площади, объема.
Случайное число событий потока WT в интервале т
описывается распределением Пуассона:
И
N i
рЛУ = р
[n,
(1.2)
е
« - т 2 -
параметры = vt = s„ - vt ; в частности, вероятность
А ’
непоявления событий в интервале т равна:
P0(t) = Ррх = (?] = е vt . (1.3)
Нестационарный пуассоновский поток с переменной мгновенной
плотностью v(t) может быть заменен на выбранном интервале т
начиная с некоторого tj , стационарным с эквивалентной средней
плотностью
255
v(tj; tj + т) = J v(t)dt
4
Для реализаций с перерывами между' реальными импульсами, т.е,
с Д - а > 0 , вводятся вероятности непоявления q > 0 и
появления р = 1 - д нагрузки в произвольный момент времени,
причем q оценивается по относительному времени отсутствия нагрузки
в реализации. Если моменты окончания импульсов также считать
г - 1 - у
событиями потока, то соответствующая частота л = - — , a v - р)..
а
Независимо от этого, v = —• и оценка р может быть получена из
Д
а
реализации в виде р .
Временная структура реализаций "ж", "и" определяется не только
свойствами реального процесса, но и регулярным потоком измерений,
выполняемых с фиксированной частотой X (например, для метеороло-
гических переменных - 4, 8, 24 раза в сутки) и неслучайным интервалом
Физической переменной, непрерывно длящейся в интервале At,
приписывается значение, измеренное в его начале или конце, или осред-
ненное по , или максимальное на Дь , а форма импульса условно
принимается прямоугольной. При этом осреднение интенсивности на
интервале Д(. не исключает возможности изучения пульсаций
исходного процесса относительно средних по Дь значений.
Для регулярного потока, включающего измерения с нулевыми
значениями интенсивности, также вводятся вероятности дир, где
q оценивается по относительному числу нулевых импульсов в
реализации. Средняя частота реальных импульсов в регулярном потоке
v = = рХ = ~ .
At
Если характеристики длительности нагрузки не изучаются, про-
цесс может быть представлен реализацией из мгновенных импульсов с
дискретным временем (случайная последовательность), см. рис. 1.1, и.
В импульсе непрямоугольной формы (рис. 1.1., б, в, д) его интен-
сивность характеризуется мгновенными значениями X(t) и максималь-
256
ным значением Хл . В импульсе прямоугольной формы (рис. 1,1,, г, ж)
нее мгновенные значения равны максимальному.
Все виды преобразований исходных реализаций в процессе обра-
ботки, в том числе при аппаратурном определении статистических
характеристик могут быть представлены как:
а) дискретизация реализаций по аргументу с приведением их к
виду "ж" или "и" (рис. 1.1.), т.е. с заменой выборочной функции
дискрет! гой выборкой ;
б) квантование реализаций по интенсивности X , в том числе в
процессе измерений, с переходом от непрерывной случайной переменной
к дискретной;
в) предварительное сглаживание данных с помощью фильтров,
например, скользящего сред! iero ;
г) получение вторичных статистических выборок, например,
выборок месячных, годовых максимумов из многолетней реализации
скорости ветра..
Способы измерений и обработки исходных данных должны быть
четко оговорены в статистической модели переменной.
Основные вероятностные свойства интенсивности нагрузки
X(t) характеризуются се одномерной функцией распределения Ех(х) ,
определяемой как вероятность события X < х и произвольный момент
времени, т.е. Fv(x) ~ < х). Дополнение функции распределения
до 1 ("хвост" распределения) определяет вероятность противоположного
события X > х:
Gx(x) = 1 - Гх(х) = р(х > х)
Значение х* , соответствующее заданной обеспеченности, т.е.
вероятности непревышения р(х < xj - м , называется квантилем
распределения: х* - Fx2(®) .
1 Io известной функции распределения Fx(x) Moiyr быть опре-
делены:
- плотность распределения fx(x) ;
- параметры распределения: математическое ожидание X ,
среднее квадратическое отклонение sx и другие.
Значения функции распределения, плотности распределения и
его параметров, получаемые в результате обработки статистических
данных, называются статистическими оценками и обозначаются в
дальнейшем верхним индексом 0 (нуль).
257
Вследствие ограниченности статистических выборок, нестрогого
выполнения требований однородности наблюдений статистические оцен-
ки содержат неопределенность, характеризуемую их доверительными
интервалами.
Для стационарных процессов с реализациями вида "а" - "д” (рис,
1.1.) одномерная статистическая функция распределения Г°(х) опреде-
ляется как относительная длительность пребывания процесса, ниже
уровня х , рис. [.2.:
£a,:(x(t) > х]
Г°АХ) = ^ - <?х(х) = 1--------------, (1.4)
где
Т - общая продолжительность реализации;
пх - число выбросов X(t) > х на. интервале Т ,
определяемое непосредственным подсчетом;
a^x(t) > Oj - непрерывная длительность i-ro выброса.
Для реализации вида "б” - "д" с конечными интервалами
= flj нулевых значений интенсивности вводятся вероятности
д, р , тогда
^(х) = д + PF°X (х I X > 0\
G^(x) = pG°(x|x > 0),
где
г£(х| х > 0 - условная одномерная функция распределения
по множеству ненулевых значений случайной переменной,
Fx°(x|x > О) =
Е а1рь) х] • °'6)
= 1 - G°x(x\x > 0) = 1---------------------
Основные параметры одномерного распределения определяются
по реализации x(t) как средние по времени:
т т т т •>
Х° = ~ I x(t) dt- s* = И M “ *1 dt • (L7)
‘о 1 о
Отметим, что стационарные случайные процессы, неразложимые
на несовместные процессы разных типов и наблюдаемые в однородных,
стабильных во времени условиях (в конкретной местности и окружающей
среде, при устойчивом технологическом процессе), обладают, как
258
правило, эргодическим свойством но отношению к математическому
ожиданию и корсляционной функции (а значит, и по отношению к
дисперсии), и соответствующие средние по времени с достаточной
точностью характеризуют свойства, пронесся.
Параметры условной функции распределения F°(x|x > 0)
осредняются по части интервала рТ .
Плотность распределения Fx(x) или ^х(х1 х > 0
целесообразно определять после сглаживания функции распределения.
Поток выбросов X(t) > х стационарного процесса с повыше-
нием уровня х приближается к пуассоновскому со следующими
характеристиками:
vx = - средняя частота выбросов X(t) > х ; (1.8)
Т 1
Тх - — - - средний период । ювторясмости выбросов;
лх
z «дад х] т
ссх - o|x(t) > xj =------------------= -----средняя
длительность одного выброса.
При наличии экспериментальных оценок осх и Тх
Gx(x) = ~ =
х _ (1.9)
Fx(x) = 1 - ~ = 1 ~
1-х
Если в реализациях вида "б” - "д" {рис. [.!.), определенных на
1
пуассоновском потоке с частотой импульсов v = =• , выбираются
только максимальные значения интенсивности каждого импульса ,
то они приводятся тем самым к реализации вида ”е”. При этом положение
максимума на интервале а не требует точного определения, так как не
влияет на v и Д .
В отличие от FAx) здесь вводится одномерная функция
Fx (х) распределения случайных максимумов Хд , которая является
оценкой вероятности события < х в произвольно выбранном
импульсе:
259
^(*) = J - <X<*) = i 1 - PXi . (110)
где
т
N = — - vT - число реальных (ненулевых) импульсов на
А
интервале Т ; объем статистической выборки для случайной величины
nXjj - число выбросов ХЛ > х па интервале Т ,
определяемое непосредственным подсчетом;
рх - относительная частота появления выбросов Х-. > х.
При построении статистической функции распределения и
опенке значений гД(х) для крайних членов выборки рекомендуется
вместо N принимать N + 1 (поправка Гумбеля).
Параметры одномерного распределения определяются
осреднением выборочных значений Хд. по N , заменяющим
осреднение по времени :
х° = - Z ; 4 = —— у (хА - х?)
N > х“ N - 1 й/
При больших W выборочные значения ХА группируются по
градациям.
Характеристики потока выбросов ХЛ > х в реализации вида
"е":
пх ... пх
v„ = —А- ~ v —-- -- vp„ ;
у /у -
т ; (Г-Н)
тх = — = —;
пхл
тх - 1
Nx^ = = \-Тх^ = —— - средний интервал повторя-
емости выбросов Хд > X .
11ри наличии статистических оценок А и Тх :
260
G(,(x) - ф -
'• - _ (1.12)
CM = 1 - y- = 1 - 'V-
В стационарных процессах с реализациями вида "ж" (рис. 1.1.),
определенными на регулярном потоке измерений, каждый выброс
X(t) > х , действующий на интервале At отдельного импульса, явля-
ется самостоятельным событием. Поэтому для всех
i(i = 1, 2,..., пх)
> xj = At, £ ai[x(t) > xj = Atnx и вместо (1.4)
вводится более простое равносильное выражение
Fx°(x) = I - б‘(х) =
где
Т
N = — - общее число прямоугольных несвязанных
At
импульсов, включая импульсы с нулевыми значениями, на интервале Т ;
объем статистической выборки для случайной величины Х&
(максимальная интенсивность прямоугольного импульса);
пх - число выбросов на интервале Т , определяемое по числу
интервалов At , в которых X(t) > х ;
рх^ - относительная частота появления выбросов.
Выражение Fx(x) является одномерной функцией распреде-
ления мгновенных значений X(t) прямоугольных импульсов на
интервале Т и, вместе с тем, одномерной функцией распределения
максимумов (х) соответствующей реализации максимумов вида "и"
(рис. J.I.).
Для реализаций вида "ж" с нулевыми значениями импульсов
вводятся вероятности q, р и условные одномерные функции
распределения мгновенных значений.
Параметры распределения X, sx (или sxit )
определяются аналогично.
261
Характеристики потока выбросов X(t) > х (в реализации
вида "ж" или X,it > х (в реализации вида "и") (рис. [.!.):
Vx = Т - -‘•X ”х = т т пх JLl_ AtW I . Vx ’ . nx
Tx 1 Ny ^ ~ = = At Pxit (1.14)
Если известна статистическая оценка Тх , то: . , . At
Тх = vx At; (1.15)
= 1 - kt — J. v At •
Прямой подсчет выбросов по всем интервалам At , в которых
X(t) > х , т.е. в предположении независимости интенсивностей
импульсов смежных интервалов, приводит к завышению частот выбросов,
если At меньше интервала корреляции.
Для повышения точности опенки vx исходные реализации вида
"ж”, “и" преобразуют в реализации максимумов интенсивности ХЛ на
интервалах As . равных или превышающих возможный интервал
корреляции исходного процесса. Так как действительные моменты
появления ХЛ случайны, их последовательность образует реализацию
вида "е" на пуассоновском потоке с А = До .
Для нестационарных процессов (рис. 1.2.) статистическая
функция распределения определяется обработкой ансамбля т
реализаций xi(t) длительностью Тк по равноотстоящим сечениям
процесса, отвечающим фиксированным моментам времени
t (г = 1,2,..., к) , причем каждый момент tr определяет
середину интервала А к = — .
262
Рис. 1.2.
Характерный интервал нестаниопарности Тк устанавливается
из предварительного анализа закономерностей, управляющих изучаемым
процессом.
Так, всем климатологическим переменным свойственна
периодическая нестапионарность с периодом, равным I году, а
некоторым из них - и с периодом, равным 1 суткам.
При t = tr из ансамбля реализаций образуется статистическая
выборка объема л? , для которой:
гДх/tJ = 1 - <£(x/t,) = 1 -
nX/m(tr) - число выбросов X(tr) > х в выборке:
7 ш
X°(tr) = А £ xx(tr);
лт /т,
1 » г - ,2 <116)
s° W = '
Условно мгновенная частота выбросов X(tr) > х , отнесенная
к интервалу А для момента tr
_ , . nx M(tr) Gx(x/tr)
vx(tj = ' V 1 = . (1.17)
' 7 ЩДк Ak
Нестационарный поток выбросов с частотой vx может быть
приведен на интервале г > &к , начиная с момента tr - , к
стационарному со средней частотой:
vx(tr/tr + т) = ”- = - LGx(^/tj) , (1.18)
263
где tj - tr + (j - l)Ak , а на интервале Tk , начиная c t = О
, к стационарному со средней частотой:
7 к . . 7 к
т‘ > = Е ч = ± I g; x/tj , (1.19)
mlk j = 7 1k j 1
где
tj = ^ + (J - •
Для условно стационарной реализации с общей
продолжительностью Т - Ткт средний период повторяемости
выбросов x(tr) > х:
1
= vx(0, Tk) ‘
Многолетние реализации климатологических переменных с
нестационарностью типа годового хода допустимо рассматривать и
обрабатывать как условно стационарные ; в этом случае Х° является
оценкой многолетней средней процесса, a s* включает существенный
вклад дисперсии годовой гармоники Х° (t) относительно X ° .
Для теоретической оценки частоты выбросов дифференцируемых
процессов информация об автокорреляционной функции может быть
заменена данными о производной процесса.
Реализация v(t) производной V(t) получается
дифференцированием по времени исходной реализации x(t) вида "а"
, ч dx(t)
или б (рис. 1.1.): при этом непрерывное диффе-
ренцирование .может быть заменено отношением приращений исходной
переменной и ар|умента на малых интервалах At (рис. 1.3.):
,де) = ДУ2Л) - *<4
At
Такой прием возможен и для приведения недифференцируемых
ступенчато-импульсных реализаций вида "в" к условно дифференцируе-
мым, для которых vA(t) является оценкой мсждуимпульсной изменчи-
вости.
264
Рис. 1.3.
Обработка реализаций v(t), vA(t) выполняется с получением
статистических оценок кДи/t), V°(t), s® , при этом для
стационарных процессов X(t) по определению X(t) = const , поэтому
V = = о плотность распределения fv(v) симметрична
dt
относи-тельно 0, т.е. положительные и отрицательные значения I7(t)
равнове-роятны.
1.2. Сглаживание статистических данных
Сглаживание исходных данных для повышения точности статис-
тических оценок выполняется с помощью теоретических распределений
изучаемой случайной переменной, принимаемых на основании предвари-
тельного анализа действительных условий её возникновения и
реализации, структуры её временной и пространственной изменчивости.
Перечислим основные применяемые способы сглаживания:
а) непосредственное сглаживание статистической функции рас-
пределения Гх(х) во всем интервале сё эмпирических значений с
подбором наилучшего положения теоретической функции распределения
выбранного типа относительно данных наблюдений по критериям: макси-
мального правдоподобия, модифицированного способа наименьших
квадратов Гумбеля, способа наименьших прямоугольников Г.Л.
265
Алексеева, с графоаналитическим представлением данных на
вероятностной бумаге;
б) подбор конкретного вида теоретической функции распре-
деления выбранного тина по статистическим параметрам (моментам)
наблюдаемого распределения с последующим зачислением критериев
согласия теоретического и статистического распределений;
в) неполное сглаживание - по нескольким выбранным значениям
квантилей и соответствующих им относительных частот, сглаживание для
части статистического распределения (в области наибольших или
наименьших значений), формальная подгонка к опытным данным без
предварительного выбора адекватного типа распределения.
Но сглаженной функции распределения может быть ретена
обратная задача определения параметров распределения. Например, для
двухпараметрического распределения X , выражая значения двух
квантилей и х2 через X и sx , находим:
sx = —------~ , X хг - Z]SX , (1.20)
Zj - z2
где
Xj, х2 - квантили- сглаженного распределения X ,
соотистствующие обеспеченностям а>2, о>2 ;
z2, z2 - квантили тех же обеспеченностей в стандартной форме
распределения данного типа для нормированной случайной величины
X - X _
Z =----------,2 = 0, sx = 1 .
sx
Вместо sx, X таким же способом могут быть вычислены и
аналогичные им параметры, принятые в известных формах
аналитического описания распределений.
Если сглаживание выполнено только для части статистической
функции распределения то определяемые из (1.20) параметры следует
использовать только для этой части.
Для решения задач надежности при применении метода "горячих
точек" различные -типы распределений их интенсивности приводятся к
нормальному распределению.
Строгое приведение распределения случайной переменной X к
нормально распределенной случайной переменной У выполняется на
всей области определения X с помощью непрерывного
функционального преобразования - либо в замкнутом виде, либо
численными способами.
Возможно приведение распределения X к нормальному
распределению У лишь па части области определения (в практически
266
важном интервале экстремальных значений переменной) или в отдельных
выбранных точках.
По способу Раквитца в выбранной “горячей точке” для
переменных X и У должны быть выполнены следующие условия:
а) равенство квантилей х(0 = уа ;
б) равенство обеспеченностей Fx(xw) = Fy(yQ) = ® ;
в) равенство плотностей fx(xM) = fy(ya) ,
из которых определяются параметры нормально распределенной пере-
менной:
sy = Л \ ; у = ^ - , (I.2D
W<»)
где
Zyn - го - квантиль нормированной нормально
распределенной переменной;
' значение плотности для стандартной формы
нормального распределения, соответствующее .
Значения sy, Y , вычисленные по (1.21), зависят от выбора
"горячей’'точки и типа Fx(x) , не связаны явно с sx, X и выполняю !
роль формальных параметров, пригодных только для описания
в окрестности "горячей" точки. В применении к реальным
данным (1.21) часто приводит к значениям У < 0 и определение
коэффициента вариаций vy не имеет смысла.
Учитывая, что коэффициент вариации является основным
показателем изменчивости интенсивности нагрузок, используемым и в
теоретических, и в нормативных моделях, целесообразно вместо условия
равенства плотностей ввести равенство коэффициентов вариации
vx ~ vy • Тогда вместо (1.21):
У = -----; sy = vxY
1 + vxzy»
Здесь коэффициент вариации сохраняет свое значение, связанное
с первичными исходными данными, и не зависит от выбора "горячей"
точки. Условие равенства плотностей нарушается, но равенство
обеспеченностей, как более важное условие, сохраняется.
Средняя частота выбросов X(t) > х (пересечений уровня с
положительной производной) дифференцируемых процессов, вычисляе-
((.22)
267
мая во сглаженным или априорным распределениям интенсивности
X(t) и ее производной V(t) , равна:
а) для стационарных взаимно независимых процессов
X(t), y(t)
vi = -u’ ~^fz(zx) , (1.23)
z sx
где
fz(zx) - значение плотности стандартной формы
- х - X
распределения X для нормированного уровня zx - --------- ;
sx
сО
j u4(u)du
u+ = -----—— - условное математическое ожидание
(координата центра тяжести) положительных значений нормированной
V - V
производной и = --------- :
sv
- для нормального распределения производной
2
й+ = =• 0,80,
— 4. 3
- для равномерного - и - — = 0,86 ;
б) для нестационарных процессов X(t), f(t) , приводимых к
стационарным нормированным взаимно независимым процессам
z(t), u(t), рис. 1.4
268
x(t)
Рис. 1.4.
2(t) = ХФ X#) , z(t) = 0, Sz = !
SX\4
“(0 = Y^)~X^) t u(t) = 0, sa(t) = 1;
мгновенное значение частоты выбросов X(t) > х равно:
v^(t) = - Ut) 4(^X/t) , d-24)
где
269
z _ x - x(fc) .
хл Sx(t) ’
0 - v(fc)
ц. = ----- , . - значение нормированной производной для
sv\4
момента t , соответствующее V(t) = 0 ;
Gu(ut) - вероятность превышения уровня ut нормированной
производной;
J u W
jj = -i--------—---- - условное математическое ожидание
<Mut)
(координата центра тяжести) значений нормированной производной,
превышающих уровень ut ;йги - ut = ис - расстояние or уровня
ut до центра тяжести ;
средняя частота выбросов в интервале (tr , tr + т)
1 £г+т
^г, tr + т) = - J v;(t)dt (1.25
Х tF
Средняя частота выбросов X(t) > х (или Х& > х ) нсдиф-
ференцируемых процессов, вычисляемая по сглаженным или априорным
распределениям X, Х& равна:
а) для стационарной последовательности максимумов
интенсивности импульсов, определенной на стационарном
пуассоновском потоке импульсов -
1
= vG^(x) = -G^(x) (1.26)
для стационарного процесса X(t) интенсивности прямоугольных
импульсов на раулярном потоке, рис. [.1, ж, с перерывами или без
перерывов между импульсами -
v; = GAx) ; u.27)
б) мгновенная и средняя на интервале т частота выбросов
нестационарной последовательности максимумов
интенсивности импульсов, определенной на нестационарном
пуассоновском гютоке-
270
^A(t) = v(t)G^(x/t);
- + / \ ltrf+T+/x <L28)
tr + г) - - f v^(t)dt;
T tr
на стационарном пуассоновском потоке -
< (t) = ^(x/t);
- / ч V Ч+т , ч <Г.29)
vXi(tr, tr + т) = - f GXi(x/t)dt;
c tr
для нестационарного процесса X(t) интенсивности прямоугольных
импульсов на регулярном потоке -
* х(с) = ?-<МхА);
t, ♦ у - i f
где
k = ft ’ tj = tr + ’ I)At'
Квантиль интенсивности нагрузки устанавливается как фиксиро-
ванное значение х* , вероятность превышения которого за срок (напри-
мер, нормативный срок службы сооружения) заранее обусловлена:
Рт = 1 - <вг , где тт - .заданное значение обеспеченности
квантиля для интервала Т.
Требуемый ©т - квантиль х’ является корнем уравнения
*хг(х) = ют или
,, . (1.31)
X =
Где ЕХт(х) - функция распределения максимума интенсивности Х3,
на интервале Т .
Так как непосредственное статистическое обоснование ?х (х)
невыполнимо, следует установить связь между FXf (х) и статистически
подтвержденным распределением FXi(x) , построенным на пуассонов-
ском потоке максимумов со случайным интервалом Д или
ры ударном потоке с интервалом Д в.
На основании простой схемы независимых испытаний Бернулли
с двумя возможными исходами "непоявление выброса" - "появление
выброса" с неизменными вероятностями этих исходов в каждом из
271
интервалов Д (или Дя ) дх = FXi(x), fx = 1 - qx = <?хДх)
функция распределения максимумов на интервале Т, Fx (х)
определяется как вероятность непоявления выбросов £ х в
Т
последовательности N = — случайных испытаний пуассоновского
Д
т
потока или N = — испытаний регулярного потока:
As
пуассоновский поток (х) = , (1.32)
регулярный поток FXt(x) = [*\д(х)]"
/ Т \N
или Fx (х) = 1----------1 -> е'3’,г« . (1.33)
7 I NTXJ
При этом условие неизменности дх рх соответствует стацио-
нарным последовательностям и приближенно соблюдается в
нестационар-ных при условии, что характерный интервал
нестационарности многократно повторяется на интервале Т .
Условие эквивалентности (1.31) и (1.32): е”г'г* = ®г опреде-
ляет требуемое значение периода повторяемости выбросов
как стабильного носителя вероятностных требований к интенсивности
временной нагрузки, не зависящего от способа образования статисти-
ческой выборки.
При значениях Т , характерных для строительных конструкций,
требование независимости испытаний по схеме Бернулли практически
выполняется, так как в общей совокупности No испытаний, включая и
зависимые, всегда найдется такое число N независимых испытаний, при
котором реализуется асимптотическая форма е“ т'Тх для Fx^ (х). Если
N < 10 и го г < 0,5 , значение Т* следует уточнить по формуле :
При известном Тх уравнение (1.31) заменяется эквивалентным
по уровню квантиля уравнением
v; = [?;] , (1.зб)
где
272
v^j = —— - допустимая средняя частота выбросов при задан-
Тх
пых Ти0г.
Для недифферепцируемых стационарных процессов уравнение
(1.36) приводится с учетом (1.26) , (1.27) к виду
G’-W = ф;] (]ЭТ)
ИЛИ Fx (х) = m д ,
где
год = 1 - - 1 - - обеспеченность, приведенная к
интервалу Д (т.е. к Д , Дч или Дг ).
Определению Тх по (1.35) соответствует <од = C0jW , что
непосредственно следует из (1.31) и (1.37).
/[ля дифференцируемых стационарных процессов уравнение
(1.36)
приводится с учетом (1.23) к вид)':
о
• <IJ8)
( s "l
откуда z* = fz}\ 2 --—- , где
k svu + Tx)
zx - положительный корень, определяемый по правому "хвосту”
распределения нормируемой переменной ; и требуемый квантиль
интенсивности нагрузки х" - X + zxsx . Аналогично может быть
представлено и решение (1.37).
Приближенное определение требуемого квантиля х* возможно
и для нестационарных процессов при использовании в левой части (1.36)
частоты выбросов, осреднснной по характерному интервалу нестационар-
ное™.
273
Литература
1. Алексеев Г.А. Графоаналитические способы определения и
приведения к длительному периоду наблюдений параметров кривых
распределения: 'Гр. ГГИ. - 1960. - Вып. 73.
2. Вентцель Е..С. Теория вероятностей. -М.: Наука. - 1964.
3. Гумбсль Э. Статистика экстремальных значений. -М.: Мир. - 1965.
4. Феллер В. Введение в теорию вероятностей и ее приложения. -М.:
Мир. - 1984.
5. Хан Г., Шапиро С. Статистические модели в инженерных задачах. -
М.: Мир. - 1969.
274
Приложение II
АСИМТОТИЧЕСКАЯ ТЕОРИЯ ЭКСТРЕМАЛЬ-
НЫХ ЗНАЧЕНИЙ
11.1. Цель теории экстремальных значений
В любой области практики возникают случаи, когда математи-
ческое решение проблемы дается только в терминах наибольшего или
наименьшего из возможных значений.
Так, при выборе максимальных значений снеговых или ветровых
нагрузок на сооружения и решение проблемы выхода из строя системы
при отказе одной из компонент, так называемого "слабого" звена - налицо
жстремальная ситуация. Можно перечислить множество также задач из
техники, экономики, статистики, когда интерес представляет получение
распределения вероятностей или каких-то параметров этого распределе-
ния для экстремального значения в выборке (или крайних значений в
упорядоченной выборке, называемой порядковой статистикой) на основа-
нии информации о распределении в генеральной совокупности или,
напротив, составление суждения о генеральной совокупности из основа-
нии экстремальных значений в выборке. Задачи такого рола настолько
важны для решения многих практических вопросов, что внутри самой
теории порядковых статистик выросло целое ответвление статистики
экстремальных значений.
Экстремальные величины связаны с малыми вероятностями. В
связи с этим необходимо отметить закон Пуассона, относящийся к малым
вероятностям. Этот закон устанавливает число появлений редких
событий, тогда как теория экстремальных значений рассматривает их
размер.
Цель теории экстремальных значений - найти распределения
определенных порядковых статистик и различных их комбинаций в
малых выборках из генеральной совокупности с заданным
распределением, а также получись аналогичные асимптотические
результаты для некоторых типов распределений. Решение первой из этих
мдач необходимо для анализа резко наделяющихся наблюдений,
решение второй - для проверки серии экстремальных значений на
однородность и для предсказания их. Задачи второй группы составляют
275
предмет асимптотической теории экстремальных порядковых статистик.
Самый замечательный результат теории экстремальных значений
теперь является классическим: если экстремальное значение (случайная
величина), нормированное надлежащим образом, имеет предельное
распределение, то оно должно быть распределением одного из трех типов.
Каждому из трех предельных распределений присуще специфическое
поведение для больших абсолютных значений переменной. Основная
часть исходного распределения играет небольшую роль, от нее зависят
только параметры предельных распределений.
Одним из центральных вопросов теории экстремальных порядко-
вых статистик является вопрос о том, оправдано ли применение
классического распределения экстремальных значений, т.е.
распределения, которое получается как предельное для соответствующим
образом нормализованных экстремумов независимых одинаково
распределенных случайных величин. Для некоторых моделей ответ
положителен. Но в некоторых случаях получены предельные
распределения, которые не принадлежат трем классическим типам.
Существует и вторая проблема в теории экстремальных значений
не встречающаяся в большинстве областей прикладной статистики. Даже
если предполагать, что основные случайные величины независимы и
одинаково распределены, то с помощью стандартных статистических
методов (критериев согласия) нельзя решить вопрос о распределении
совокупности. Известны примеры, когда решение в терминах
экстремумов существенно зависит от выбора исходного распределения,
т.е. в основе своей содержит субъективность.
Для случайных явлений, в которых экстремальные значения
играют главную роль (например, наводнения, отказы в системах, и т.д.),
асимптотическая теория экстремальных порядковых статистик дает в
некоторых случаях точные, а в большинстве случаев приближенные
вероятностные модели. Поэтому, если основные условия реальной
ситуации похожи на допущения модели, исходную сложную ситуацию
можно заменить сравнительно простой асимптотической моделью. Если
изучаемую случайную величину можно выразить как минимум или
максимум величин, связанных с произвольно большим разбиением, то
асимптотическая модель может привести к точному стохастическому
описанию случайного явления.
276
11.2. Математическая модель. Точные распреде-
ления экстремальных значений
Располагая статистикой интересующего нас события, мы можем
провести статистический анализ экстремальных значений. Обычно
требуется ответить на следующие вопросы:
1) не выпадает ли за разумно ожидаемые рраницы какое-либо
отдельное наблюдение в выборке из совокупности, распределение
которой предполагается известным;
2) проявляет ли последовательность экстремальных значений
регулярность в своем поведении;
3) какова оценка для распределения экстремумов при конечном
числе наблюдений;
4) что можно сказать об асимптотических свойствах
экстремальных значений и т.п.
Для проведения статистического анализа имеющиеся наблюдения
Х2, Х2,..., Хп расположим в порядке их возрастания и обозначим
Х(1), Х<2),..., Х(а). Таким образом, получаем порядковые статистики
X(i), i = 1, 2....n .
Первая порядковая статистика Х(1) имеет наименьшую
величину, последняя Xf£fJ - наибольшую. Оба эти значения называются
экстремальными. Число л есть объем выборки из исходной генеральной
совокупности. Повторение этой операции N раз образует выборку,
состоящую из N экстремальных значений. Их свойства изучаются
теорией экстремальных значений.
Так как величины Х1г Х2, . . . , Ха случайны, то случайными
являются и величины:
Х(п) = ZD = max(Xj, Х2, . . . , Хп) и
Х(1) = Wo = min (Хъ Х2, . • , Х„) .
Следовательно, вопросы и решения связанные с Za и Wn не
являются детерминированными, о значениях ZB и ?7С можно говорить
только в вероятностном смысле.
Другими словами, вопросы и решения в математической модели,
отражающей интересующую нас практическую проблему, могут и должны
содержать только величины вероятностей того, что ZB и №п попадают в
некоторые области.
В частности, желательно было бы уметь оценивать точно или
приближенно функции распределения
277
HD(x) = P(ZB < x)
и
ZD(x) = p(Wa < x)
(Ill)
(П.2)
Как проводится анализ экстремальных случайных величин? Рас-
смотрим для примера прочность на разрыв R листа металла прямоу-
гольной формы.
Прочность Я - случайная величина и имеет некоторую
функцию распределения L(x) = P(R < х) . Разделим гипотетически
лист на л7 равных частей, разбив каждую сторону на л частей. Пусть
случайная прочность j-й части будет Xj . Поскольку лист металла
потеряет прочность при разрушении хотя бы одной cm части (наименее
прочной), величина Я , очевидно, совпадает с ИГП - минимальной из
всех величин Х^1 < j < л7| .
Это означает, что 1>л(х) = L(x) при всех значениях п . В
частности, L (х) совпадает с пределом функции Ln(x) при п -> оо .
Ввиду того, что нахождение распределения величины и,
следовательно, Wn так же затруднительно, как нахождение функции
Ln(x) , то асимптотическая теория для Ln(x) может позволить
получить L (х) , не находя фактически функции Ln(x) .
Некоторые задачи исследуются именно таким образом. Предель-
ное выражение для Нл(х) или ЬЛ(х) будет одним и гем же (или одним
из небольшою числа возможных) вне зависимости от фактического
распределения величин Ху . В данном примере определяется точный вид
l(x) на основе теории, гарантирующей существование предела
Яв(х) или LB(x) .
В некоторых задачах можно предположить (что вполне
согласуется с физической ее стороной), что Нл(х) нс меняется
существенно, начиная с некоторых значений л , Так как функция
распределения Нд(х) выражает случайные изменения Zn , точный
математический эквивалент приведенного выше предположения состоит в
том, что после некоторой нормировки константами ао и b > О
величина (ZD - aQ}]bn сростом п становится все более независимой
от л . Эго означает, что для фиксированного Z существует предел
278
limP<—----< z
I П
11тНд(ап + bDZ) = H(Z)
n • -><J0
(П.З)
Поэтому, если можно найти н(2) , то величины Xj и их рас-
пределения уже не имеют значения для анализа экстремальных значений.
Вся теория экстремальных значений построена на анализе
простого и точною соотношения
p{ZB < х} = Н0(х) - [F(x)]n (П.4)
означающего, что вероятность тою, что все п независимых элементов
выборки из совокупности с известной функцией распределения F(x)
окажутся меньше некоторого значения х составляет [F(x)]fl .
следовательно, и такова же вероятность, что наибольшее среди п
независимых наблюдений меньше х .
Предположение независимости наблюдений очень важно и в
дальнейшем оно почти всегда сохраняется.
Свойства функции Яд(х) зависят от характера функции f(x)
преимущественно в области больших значений. Влияние остальной части
функции f(x) становится все меньше по мере возрастания. При
увеличении л кривая Нп(х) сдвигается вправо, и важно выяснить,
стремится ли она при этом в какой-либо асимптотической форме.
Аналогично соотношению (И.4) вероятность того, что наименьше
значение превзойдет х , определяется формулой
p{wn > х) = 1 - L0(x) = р - f(x)]r . (П.5)
Выражениям (II.4) и (П.5) соответствуют функции плотности
распределения
Фп(х) = п[г(х)]° lf(x)
(JI.6)
Х(/О(х) = n[l - F(x)p7f(x)
Если исходная функция плотности симметрична, наибольшее и
наименьшее значения распределены взаимно симметрично, т.е.
Фд(-х) " фд(*) , поэтому, зная распределение наибольшего значения,
можно получить распределение наименьшего.
В общем, для несимметричного исходного распределения
функция плотности фДх) наименьшею значения будет симметрична
функции плотности фл(х) наибольшею значения в выборках из
совокупности с взаимно симметричным исходным распределением.
279
Эту взаимосвязь называют принципом симметрии. Практически
это означает, что исследование экстремальных значений можно свести к
исследованию только наибольшего значения.
Если исходное распределение симметрично относительно нуля,
вероятность, что наибольшее значение окажется положительным (или
что наименьшее окажется отрицательным), быстро стремится к единице
при увеличении объема выборки.
Точные распределения экстремальных значений записываются в
виде функций от исходного распределения и объема выборки л .
Первые исследования экстремальных значений (Борткевич,
Мизес, Нейман, Типпет, Трикоми, Финетти) основывались на
нормальном исходном распределении. Полученные при этом
аналитические результаты очень сложны, так как ни одна из
фундаментальных теорем статистической теории экстремумов не связана
простым способом с нормальным распределением. Если за основу взять
экспоненциальное распределение, то основные теоремы теории
экстремальных значений выводятся достаточно легко.
Чтобы охарактеризовать распределение экстремальных значений
недостаточно общепринятых средних: медианы, моды и математического
ожидания. Для этого необходим новый тин средних, введенный Мизесом
и названный Гумбсдсм характеристическим экстремумом. С мим связано
большинство интересных свойств экстремальных значений.
Характеристический экстремум определяется как квантиль
исходного распределения
F(ил) = 1 - - , f(u2) = - , (П.7)
' ’ п ' ' л
где
ий , Uj характеристические наибольшее и наименьшее
значения.
По смыслу определения ожидаемое число наблюдений, больших
п„ (или мепыпих щ), равно 1.
Очевидно, что с увеличением объема выборки ип возрастает, а
и1 убывает. Для симметричных распределений и1 - -ив .
Характеристические экстремумы являются основой критерия
Шовепэ для принятия или отбрасывания экстремальных значений. Он
состоит в следующем. Для данного исходного распределения определим
два теоретических значения un , и} из уравнений
1
n 1 - F
2 ’
2
(11.8)
Тогда ожидаемым числом наблюдений, больших и„ и меныпих
280
u_j является 1/2. Если ожидаемые числа, соответствующие двум
наблюдаемым значениям хв и х2 больше или равны 1/2, то они
принимаются, если нет - то отвергаются. В последнем случае параметры
распределения должны быть пересчитаны без учета отброшенных
значений.
Это приводит к новым значениям ип , Uj , которые теперь
используются для проверки новых крайних членов выборки, второго и
предпоследнего.
Выпишем основные характеристики распределения наибольшего
значения для случая, когда исходное распределение является экспонен-
циальным F(x) = 1 - е~х ; оно асимметрично и ограничено слева,
все моменты у него существую!'. Из (П.4) следует:
Яд(х) = U - е - функция распределения наибольшего
значения ; из (II.7) следует:
ип = In п - характеристическое наибольшее значение ;
медиана хп наибольшего значения приближается к выражению
хп -> In n - In bi 2 ;
математическое ожидание наибольшего значения хп =
= In п + у , где у = 0,577216 постоянная Эйлера ;
с 2 К
дисперсия наибольшего значения sB -> — .
6
Огметим, что моде наибольшего значения (т.е. наиболее
вероятное наибольшее значение ) и характеристическое наибольшее
значение равны.
Все результаты, полученные для экспоненциального исходного
распределения, асимптотически справедливы для распределений экспо-
ненциального типа.
Для распределений экспоненциального типа вероятность
Р (х) = 1 - F (х) . что наблюдение превзойдет х , сходится к нулю
по крайнем мере не медленнее, чем ех . Для них справедливы
равенства
У распределений экспоненциального типа существуют все
моменты исходной случайной переменной и наибольшего значения.
К экспоненциальному типу относятся большинство применяемых
281
па практике распределений: нормальное, логарифмическое нормальное,
логистическое, гамма-распределение и экспоненциальное. Различают три
класса распределений экспоненциального типа, в записи мости от того,
какое из равенств выполняется для критического отношения
(IT.10; 11.11; 11.12)
где
lim 1 (х)| - ’
Таблица IL 1
Понятие Обозначение Первый класс Второй класс Третий класс
Интенсивность р(ил) = ссл возрастаетс ростом постоянна убывает с ростом
Критическое отношение. Q >1 1 <1
Характери стичес кое значение Un возрастает медленнее, чем и1 возрастает как возрастает быстрее, чем ц2
Кривизна вогнутая прямая выпуклая
Мода X» > «д < “л
Плотность *₽я(ил) возрастает постоянна убывает
Гак, функция распределения F(x) ~ 1 - ехр(-х)* , х > 0
принадлежит к первому классу, если к > 1 , ко 2-ому - если к = 1 и к
3-ему - если к < 1 . Свойства трех классов распределений обобщены в
таблице ILL
Интенсивность ц(х) определяется по формуле
Экстремальная функция интенсивности
282
И Ю = ап . Н (Ч1) = «2
11.3. Асимптотические распределения экстремаль-
ных значений
Точные формулы для распределения экстремальных значений,
имеющие простой аналитический вид для экспоненциального распреде-
ления, асимптотически справедливы для распределений экспоненциаль-
ною вида. Большая часть исследований точных распределений экстре-
мальных значений проведена для нормальной исходной совокупности.
Аналитические выражения в этом случае довольно сложные и в общем
виде задача решается непросто.
Согласно равенству (IL4) функцию распределения Ял(х)
наибольшею значения можно записать в виде Яя(х) = exp [л In F(x) ] .
При больших п соответствующая часть F(x) при х -> х
стремится к 1, а экспонента сходится к неопределенности вида ос, 0 ,и
поэтому значение Ял(х) определяется характером приближения F(x)
к L
Чтобы получить асимптотические выражения для экстремальных
значений, необходимо сделать предположения об асимптотических
свойствах исходною распределения. Таким образом, существование
асимптотических выражений связано с некоторыми условиями ; если они
нс соблюдаются, то не существует никакого асимптотического
рас I федел ения экстремальных зна чени й для да 1 п юго исходного
распределения.
Приведем основные результаты асимптотической теории экстре-
мальных значений.
Необходимые и достаточные условия, чтобы исходная функция
распределения принадлежала к одному из трех типов : к распределению
экспоненциальною типа, к распределению типа Коши или к распреде-
лению, имеющему границу были сформулированы В.В. Гнеденко. При
выполнении этих условий распределение наибольших значений сходится
к одному из 3-х асимптотических типов.
Так как линейное преобразование переменной не изменяет вида
распределения, то в дальнейшем нужно говорить не о единственном
предельном (асимптотическом) распределении, а о целом семействе,
которое можно рассматривать как некоторый тип распределения.
Понятие тип-.-. дается следующим определением: функции распределения
Н (х) и Н*(х) относятся к одному типу, если существуют такие
вещественные числа А, В > 0 , для которых выполняется равенство
283
Я‘(х) = = Н(А + Вх).
11.3.1. Предельные теоремы для экстремумов случайных
величин
Введем два обозначения, которые будут использоваться в
изложении асимптотической теории экстремальных значений.
Говорят, что величина a(F) , определенная соотношением
a(F) = inf(x:F(x) > 0} (11.13)
является нижней крайней точкой функции распределения F(x) .
Аналогично, верхняя крайняя точка функции распределения F(x)
определяется соотношением
®(F) = sup (х: F(x) < 1} (11.14)
запись (x:F(x) > 0) читается так: множество значений х , для
которых F(x) > 0 .
Очевидно, что либо a(F) -» го , либо a(F) конечно, а «(F)
либо конечно, либо «(f) = 0 . Например,
для экспоненциального распределения a(F) = 0, «(F) = оо;
для логистического распределения F(x) = 1/1 + е'х имеем
a(F) = -ос , . ®(F) = ос ; если F(x) - функция распределения
случайной величины, принимающей только значения 0 и I, то
a(F) = 0, a(F) = 1
для равномерного распределения на. отрезке /0, 1 / получим
a(F) - О, «(F) 1 .
Для упрощения формулировок теорем введем еще одно понятие.
Пусть Я(х) - невырожденная функция распределения, являющаяся
одним из возможных пределов в соотношении (11.3)
lirn^ Нп(ав + Ьвх) - Н(х)
Говорят, что функция распределения F(x) принадлежит
284
области притяжения Я(х) , сели существу ют последовательности
а„ и Ьв > 0 , для которых справедливо соотношение
Urn Г"(ал + Ьах) - Я(х)
п ->
Запись: F(x) е С (Н) Константы ап , Ьл , называются нормирую-
щими и центрирующими. Заметим, что если F е С (Я) , то
F е С(Я*1 , т.е. F(x) принадлежит также области притяжения
любой другой функции Я*(х) , относящейся к тому же типу.
Приведем обобщенную формулировку' предельных теорем для
экстремумов на основе результатов исследований в этой области,
изложенных в /1-4/. Теоремы доказаны для независимых и одинаково
распределенных случайных величин Xj .
Теорема 1
Функция распределения F(x)
1) Я2/У(х) тогда и
существует такая постоянная X
1 - F(tx)
lim--------- = х :
‘ >. 1 - F(t)
принадлежит области притяжения:
только тогда, когда
> 0 , что для всех х >
а(Г) --
О
(11.15)
и
здесь
если х > О
если X < О
нормирующие константы Ьа метут быть выбраны в виде
bo = infjx: 1 - F(x) < ;
2) Wx) - тогда и только тогда, когда or(F) < «> и ,
функция f*(x) = _ Vх]’ х > ° удовлетворяет
соотношению (II.15)
1 если X > О
expf-(-x) Н если х < О
Константы ап и bn moi у г быть:
285
f
bn = o(F) - infjx: 1 - F(x) < , ал = ®(F) ;
3) Я3/(?(х) тогда и только тогда, когда при некотором конечном
а справедливо соотношение
j [1 - F(y)] dy < ж (11.16)
&
и для всех вещественных х существует предел
1 - Fit + xR(t)]
lim -----Л----- АЛ = е х , ([[.17)
t »« 1 - F(t)
где
w(F)
F(t) = [1 - F(t)] 1 J [1 - F(y)]dy ([[.18)
t
для
<x(F) < t < ©(F), Я3,0(х) = exp(-e ,
-oo < X < a) ,
f 11
a„ = inf(x: 1 - F(x) < -4, bD = R(an) .
I J
Обозначения Hiy(x), Н2у(х), Я5 £?(х) введены Мизесом. Если
F(x) не относится ни к одной из трех категорий из приведенной
теоремы, когда не существует таких констант ап и Ьп > для которых бы
выполнялось соотношение (11.3), следовательно нс существует
предельного распределения дня максимумов; пример такого
распределения будет приведен ниже.
Следует отметить, что константы а0 и Ьп могут быть выбраны
не единственным образом. Доказаны теоремы, позволяющие находить
ао и bD другими способами.
Теорема для минимумов случайных величин формулируется
аналогично с заменой Х?- на (-2Гу) согласно принципу симметрии.
Теорема 2
Функция распределения F(x) принадлежит области притя-
жения:
1) Lj у(х) тогда и только тогда, когда a(F) = -ос- и
существует такая константа у > 0 . что для всех х > 0 выполняется
286
соотношение
i™ =
t-к» r(t)
, . 1 - ехр - (-х) у если х < О
Ч?(х) = 1 J
[1 если X > О
Константы dn можно выбрать следующими:
da = supjx: F(x) < —I ;
2) L2/7(x) тогда и только тогда, когда a(F) - - ос и
функция F*(x) = f[(x(x) - Vх]’ х < в удовлетворяют (11.19)
, х 11 - ехр(-х) 7 если х > О
] *
[0 если х < О
сп = = sup jx: F(x) —I - a(F) ;
3) Lj,o(x) тогда и только тогда, когда при некотором конечном
а выполняется
f F(y) dy < ос a(F) (11.20)
и для всех вещественных х существует предел
Fit + xr(t)l lim -1 —v ;J = ex (11.21)
t ->a(Fi F(t)
где
1 t = । F(y)dy Л?!Я t a(F) afF) •>
LJ/0(x) = 1 - exp [- e x)
-со < X < со ,
са - sup^x: F(x) < dn ~ r(cn) .
I л)
Соотношение (11.3) для минимумов случайных величин имеет вид
lim Ld(co + dnx) L(x) .
Многими авторами исследовано, что к функциям распределения.
287
принадлежащим области притяжения:
I) = ехр(-е х) > относятся исходные распределения
экспоненциального типа (например, экспоненциальное, нормальное,
логнормальное, логистическое, гамма-распределение) ;
2) области притяжения Ял 7(х) = expj(-x) j, х> О
относятся распределения, типа Коши (распределения Коши, Парето);
3) области притяжения Я2?(х) = expJ-(-x) J относятся
распределения, имеющие границу.
Характер приближения точного распределения наибольших
значений к асимптотической форме не одинаков для различных исходных
распределений. Так, для экспоненциального распределения это
приближение происходит быстро, для нормального - медленно.
Из трех асимптотических распределений самое важное
Я3/1(х) = ехр(-е‘х) .
Ему больше всего посвящено аналитических, численных и
практических исследований. В приводимом виде Н30(х) не содержит
никаких параметров (к такому виду можно привести, использовав
линейное преобразование), чего нельзя добиться для асимптотических
распределений Я2 (х) и Я2/У(х) , исключая тривиальные случаи,
когда у = 1 .
Распределение L2z?(x) = 1 - схр(-х) ' , х > 0 для
наименьших значений имеет важные практические приложения
(усталостные испытания материалов, исследование прочности и
надежности конструкций) и носит название "распределение Вейбулла".
Конкретное применение асимптотической теории проводится
следующим образом.
Используя некоторое количество наблюдений, делаем
статистическую оценку исходной обшей функции распределения F (х)
затем определяем нормализующие постоянные ал , Ьа с помощью
которых преобразуются экстремумы.
Затем, используя теоремы 1 или 2 устанавливаем
асимптотическое распределение для преобразованного экстремума. Но
все предельные теоремы определяют тип предельного распределения, т.е.
если Я(х) является предельным законом, то все функции Я (Ах + в)
являются тоже возможными асимптотическими распределениями для
288
исходной функции F(х) . Параметры распределения А, В следует
оценить по наблюдениям за экстремумом Z .
1J.3.2. Асимптотические распределения экстремумов
Применим теорему 1 или теорему 2 для некоторых видов
распределений и установим предельное распределение для максимумов
или минимумов случайных величин, а также вычислим константы
ап , Ьв , которые нормируют Za (или ) таким образом, что с
ростом п величина (z„ - ап}/Ьв становится независимой от п , т.е.
для некоторою фиксированного z выполняется
lim р]—------— < z\ - lim нДад + bnx) = ff(z) .
л-ж I Ьп I п->«>
1) Равномерное распределение на отрезке / 0,1 /
Р(х) =
О, если х < О
х, если 0 < х < 1
1, если х > 1
(П.22)
а) выясним, имеет ли F(x) предельную функцию распределе-
ния дая максимума и каков ее вид.
Имеем «(F) = 0, «(f) = 1 , поэтому для случайной величи-
ны zn = max Х2, ..., Хл) можно применять разделы 2 и 3
теоремы 1.
Проверим вьшолнение соотношения (11.17). Так как функция
l-[t + xR(t)l P(t)
~ ~’1 ' 1" — Д_ л. '
1 - t t
не стремится к е х при t -> 1 , то (11.17) не выполняется.
Остается проверить выполнение условий раздела 2. Для х > О
введем F*(x) = Г{1 - J/х). Для равномерного распределения (11.22)
вводим F*(x) = F(l - I/x) , если х > 1. Проверяем вьшолнение
(И. 15)
1 - F’(tx) t 2
lim -------- = lim — = х , х > О
1 _ F (t) n->« tx
следовательно, справедлив раздел 2 теоремы ley = 1 . Учитывая, что
inf {х: 1 - F (х) <, l]n} = 1 - 1/п ,
289
получаем ап = 1 , bn - 1/п . Тогда
limP|zfl < 1 + x/n| = H2J(x) .где
Н2д(х) = е* , если х < 0 и , ссли х > 0 .
б) Если рассмотреть величину = min {Xj, Х2, .. ., Хл} , то
в этом случае может быть применена теорема 2 (разделы 2, 3).
Проверим выполнение соотношения (11.19), взяв
F*(x) = f(- 1/х) для х < 0. В пашем случае
F*(x) = - 1/х для х < -1. Для всех х > 0 существует I
предел
F*(tx) 1
lim —, следовательно у = 1 и выполняется
t->«0 F (t) х
условие раздела 2 теоремы 2.
Из соотношения (II, 19) имеем dD = 1/п , cD - a(F) = 0 .
Таким образом,
lim < х{ = Ь22(х),где
L2,i(x) = 1 - ех , если х > 0 и L2,i(x) - » если 1
х < 0 .
2) Стандартное нормальное распределение
х
F(x) ~ (2т1)"1!2 | е 2~dy, a(F) = = оо
-СО
К величине zn применимы разделы 1 и 3 теоремы 1, Исследуем
асимптотическое поведение функции 1 -
х > 0 . Интегрируя по частям, получим
<л и2
(2л)х'2[1 - F(x)] = J е 2 du =
X
= (-u)"Je 2 - j е 2 и 2du .
X х
Или
(2я)*2[1 - F(x)] - х-1е~ =
Продолжая этот подход, можно получить столько членов асимто- I
290
при X —> ОС . Пусть
F х
и *du
ие
2
е 2 и 2du, х > 0 .
2
тического разложения, сколько нам нужно. Например, еще один шаг
приводит к неравенствам
7 1 А - —
- - ~ е 2 < 1 ~ F(x) <
X л 2
1 --
< ----е 2 , х > О (П.23)
Следовательно, справедливо соотношение
х2
lim xfl - F(x)]e^ = (2я)’1;2 (11.24)
в силу чего предел в соотношении (11.15) не является конечным. Следова-
тельно, нужно обратиться к разделу 3 з^оремы 1,
Йз правой оценки в (11.23) заключаем, что условие (11.16)
выполняется, например, при а = 1 . Проверим условие (11.17), Для
этого аппроксимируем R (t) из соотношения (1L18), Интегрируя (11.23),
получим
F(y)]dy <
. (11.25)
О
t2
2 , где последнее
t t
неравенство следует из правой части неравенства в (11.23), а также учиты-
вая (11.24) и (11.25), приходим к равенству
t 00.
Тогда
1 - Fit + xfjR(t)ll
!im -.....-
t 1 —
_Z_
e 2t~2 - 3j e 2 y 3dy < [1 -
t t
_t2. y2
< e 21~2 - e 2 y~3dy для t >
t
Учитывая, что
oo У2 -С У2
е 2 у 3 dy < t 3 f е 2 dy < f 4e
291
t
lim ----------
i +«> t + x£(t)
е
ехр |-xR (t) t + ~ xR (t)
Это означает, что можно применить раздел 3 теоремы 1. Предель-
ной функцией распределения для величины
(и0 - ав)/Ьп
является функция Л30(х);
bo = (2 log n)’1/2 ,
<aB = (2 log n)'2/2
log log л + log 4л
2 (2 log л)2'2
3) Распределение Коши.
F(x) = — 3- — arclgx, - co < x < a>,
2 к , поэтому к
ix(F) = -CO, ©(F) = CO
величине za применимы разделы 1 и 3 теоремы 1.
1
dx = оо.
Интегрируем по частям (11.16)
or?
J[1 - F(x)]dx = x[l - F(x)] '+ J
О о 0
Следовательно, условия раздела 3 не выполняются. Обратимся к условиям
раздела 1.
По правилу Лопиталя
1 - F(tx) (-1 + t2)x
lim —------i—- - lim -—--------'-у
1 _ F(t) t->«> + tx)2
-1
это означает, что у = 1. Имеем
lim Ffz„ < bnx\ = exp 1-—k x > 0;
л -> '< ’ ( X I
, ( 71
bn = “
Симметрия F (x) относительно нуля позволяет сразу найти пре-
дельное распределение для Мл. Так как
Р \Ыа < -х} = P{z„ > х}, х > 0 , то
lim < dox} - 1 - ехр 1-4, х < 0, dn = Ьп.
4) Приведем пример распределения, не имеющего предельного
распределения для zB .
Пусть функция распределения F(x) имеет вид
F(x) = 1 - —— , х а е, ®(Г) = <ю
7 10geX V '
Нужно проверить выполнение условий раздела 1) и 3) теоремы 1.
Третий раздел применить нельзя, так как не выполняется условие (11.16).
Проверим условие (11.15)
lim ----= pm 1Oge- . = 1 . Условие (11.15)
1 - F(t) t->co logctx
не выполняется. Следовательно, максимум (zo - anj/bn случайных
величин, имеющих распределение вида
F(x) = 1---------— , х > е не имеет предельного распреде-
logex
ления.
II, 3.3. Об эквивалентности функций на "хвостах"
распределений
В некоторых задачах возникает вопрос о поведении функции
распределения F на ее ’’хвосте", т.е.
а(х) = Р{Х > х) = 1 - Г(х) .
Понятие эквивалентности двух функций распределения на
"хвостах" распределений было введено Резником /5/.
Положим х0 = inf^y: F(y) < 1} для функции
распределения Г(х) .Если Г (у) < 1 для всех у .тогда х0 .
Если рассматриваются две функции распределения Г(х) и G(x) . то
л- F G
писать х0 , х0 .
Определение. Две функции распределения Г(х) и
эквивалентны на "хвостах" распределений, если xj ~ x„ х(, и
292
1 - F(x)
lim --------H
x >x0 1 — G (X)
(11.26)
1
Заметим, что для двух произвольных распределений отношение
[1 - F (х)]Д1 - G (х)] может вообще не иметь предела при х -> х0
слева.
Анализ эквивалентности 2-х функций распределения и эквива-
лентности их на "хвостах" распределений тесно связан с вопросом о
принадлежности этих двух функций распределения одной и той же
области притяжения.
При этом используются следующие положения.
1. Теорема Хинчнна (/6/, с. 308).
Пусть U (х) и 7(х) - две невырожденные функции распреде-
ления. Если для последовательности Гл(х) функций распределения и
констант > 0, Ьп и ап > 0 , fln выполняется
Гл(апх + Ьп) [7(x)v Fn(aBx + рл) -> У(х) (11.27)
тогда имеют место соотношения
--л- -> А * 0; ~ Ь" -> В (11.28)
и выполняется
V(x) = U (Ах + 5) (Ц.29)
Обратно, сели верно (11.28), то каждое из соотношений (11.27)
влечет за собой и другое соотношение (П.29).
2. Распределение экстремального значения, возведенное в
положительную степень, есть снова распределение экстремального
значения и гою же типа.
Поясним положение 1
Под невырожденностью функций распределения понимается, что
ни одно из распределений U (х) и У(х) не сосредоточено в единствен-
ной точке.
Теорема Хинчина содержит в себе следующее. Известно, что нор-
мализующие и центрирующие константы
> 0. Ьп
можно выбрать не единственным образом. Но найдены они должны быть
294
таким образом, чтобы приведенное значение экстремального значения
—------— ( в данной записи - максимума) с ростом п становилось все
более независимым от л , т е. выполнялись соотношения (11.27).
Это означает, что константы ап ♦ и ал , |3П должны быть
между собой эквивалентны.
Из теоремы Гнеденко следует, что предельные распределения для
такою максимума случайных величин должны относиться к одному и
тому же типу, т.е. должны быть связаны между собой линейным
преобразованием переменной через константы А 0. В.
Теорема связывает между7 собой соотношения двух групп
констант ап > 0, Ьп и ал > О, Рп (для величины zn ) и
констант А * 0, В (для двух предельных распределений,
принадлежащих одному типу).
Принято считать последовательности констант ап > 0,
bn , п > 1 асимптотически эквивалентными последовательности кон-
стант ал > 0 , рл , n > 1 , если отношения между ними принимают
вид
~ ь°. о , (П.зо)
ап ап
т.е. в (11.28) А - 2, В = 0 .
11оложепие 2 означает следующее
Но теореме Гнеденко пределы юе распределение для экстремума
случайных величин (максимума ) должно принадлежать одному из трех
типов:
0 , х < 0
Нъ.Дх) = ехр- -х 7 , X > (11.31) 0
Н2у(х) = ехр х < 0
(11.32)
[о . х > о
нз,о(х) = схр| -ех}, X < (11.33)
Тогда для экстремальною значения, возведенною в степень
имеем:
295
= Jx) ; (11.34)
= Jxj ; (11.35)
пзд{хУ ~ аз,о(х ~ (Л.36)
Резник в /5/ исследовал более общий случай эквивалентности
распределений F(x) и G(x) когда
1 - F(x)
hm ------= a, 0 < a < x> (11.37)
x->x<> 1 - G(X)
в котором, как частный случай, при а = 1 наблюдается
эквивалентность на "хвостах" распределений. Им доказана следующая
теорема.
Теорема 3.
Пусть F(x) и G(x) - функции распределения, Ф(х) - распре-
деление экстремального значения. Пусть F(x) принадлежит области
притяжения Ф(х) > т.е. F (х) е Д (ф), следовательно для
нормализующих констант ап> 0, bn , п > 1
Fa(anx + Ья) -» Ф(х).
Тогда Gn(anx + Ьл) -> Ф'(х). Ф'(х) - невырожденная функ-
ция, тогда и только тогда, когда для некоторых А > 0, В:
Ф'(х) = ф(дх + В), х$ = x0F = х0 (11.38)
1 - F(x)
и существует предел--------~ , причем если
1 - G(x)
Ф(х) - Яъ„(х), тогда В = 0 и lim ------------= А7 ;
х->го 1 - G[x)
Ф(х) = Н2гУ(х), тогда В = 0 и lim -— ? = А7
1 - g(x)
Ф(х) = Н30(х), тогда А = 1 я lim —-----------— = ев
1 ~ G(x)
Эта теорема устанавливает необходимые и достаточные условия
эквивалентности двух распределений и характер этой эквивалентности в
зависимости от принадлежности распределений одному из трех предель-
ных типов. Кроме того, согласно теореме 3, для распределения максимума
и в случае F(x) ив случае G (х) можно использовать одни и тс же
нормализующие константы ав > О, Ьв .
Де Хаан и Балкема /7/ исследовали эквивалентность на "хвостах"
распределений как сравнимость функций F (х) из области притяжения
функции Я3/в(х) с функциями G (х) , удовлетворяющими критерию
Мизеса (функциями Мизеса),
r d [1 - G(x)
lim — -----------------г--. л
x->w(f) dx [ g(x)
(11.39)
= 0
где g(x) - плотность распределения вероятностей.
Теорема 4.
Пусть F(x) - функция распределения и пусть при некотором
х2 и всех х таких, что х2 < х < w(F) существуют производные
f(x) = F'(x) и F"(x) , Пусть, кроме того, для F(x) выполняется
условие Мизеса (11.39), т.е.
d Г1 - F(x)
lim — -------, ч
dx f (х)
= 0 .Тогда F(x) принадлежит облас-
ти притяжения Я3/в(х) .
Эта теорема в простой форме дает достаточное условие принад-
лежности функции распределения F(x) области притяжения Я3 0(х).
Используя эту теорему, де Хаан и Балкема доказали /7/, что для
произвольной функции распределения F(x) из области притяжения
Н3/0(х) существует функция распределения F.(x) , удовлетворяющая
условиям теоремы 4 и такая, что выполняется (П.26)
1 — F (х)
lim --------= 1, т.е. Fix) и F.(x) эквивалентны на
х->е(г) 1 - F.(x) v ’
"хвостах" распределений.
296
297
Теорема 5
Функция распределения F (х) находится в области притяжения
H3f0(x) тогда и только тогда, если существует функция Мизеса ГДх) ,
такая, что х0(рФ) = х0(г) = х0 и
11ГП -------= 1
х->х0 1 - ГД Х)
Теорема 4, содержащая критерий Мизеса , позволяет’ найти
функцию распределения Л.(х) из области притяжения HJ/Z?(x) ,
эквивалентную на ‘хвостах" распределений произвольной функции
F (х) из той же области прит яжения.
Для функций распределения принадлежащих области прит яжения
Н2у(х) установлена тесная связь между медленно меняющимися функ-
циями и “хвостами" распределений при условии, что наблюдения незави-
симы и одинаково распределены /9/.
Медленно меняющейся па бесконечности называется функция,
заданная на ( 0, со ), положительная, тогда и только тогда, когда она
удовлетворяет условию
L(tx)
lim — L = 1 при любом х > 0 . (11.40)
t >00 _L(t)
Отметим, что анализ эквивалентности распределений на
"хвостах" может проводиться, вообще говоря, и без привлечения теории
порядковых статистик, в частности теории экстремальных порядковых
статистик, Задача состоит в том, чтобы в каждом конкретном случае
отыскать предел, к которому стремится отношение "хвостов" двух
заданных распределений, т.е. исследовать соотношение (11.26). Этот
предел, вообще творя, может и не существовать.
Теория экстремальных порядковых статистик в применении к
анализу эквивалентности распределений дает необходимые и достаточные
условия эквивалентности и, в частности, эквивалентности на "хвостах"
распределений.
Проанализируем эквивалентность на "хвостах" некоторых видов
распределений.
1)
F(x) - 1 - е-х , О < х < сс,
G (х) - е е х , оо < х < оо
экспоненциалыюе распределение
двойное экспоненциальное
распределение.
298
G(x) - является предельным распределением для максимума
случайных величин, распределенных по закону f(x), т.е.
F(x) е Д . Имеем
По теореме 3
*0 = Х^ = хо = оо .
ев
Вычислим В .
1 - Л*)
lim П
х->ф 1 — G(x)
2 - 1 ~ е *
lim ---------—i
_ е е '
Применим правило Лопиталя, тогда
е *
lim ---------Tr-
*>*> ; _ е е
следовательно, В = 0 .
Функции распределения F(x) и
’хвостах"
lim---------—
*->« е хе-е
lim-----—
е е
G (х) эквивалентны на
= 1 ,
2)
(Их) = 1/1 т е’х - оо < х < оо, логистическое распрсдсле-
< ' 7 1 ’ НИС
G (х) = е~е я , - ос < х < оо, двойное экспоненциальное
распределение.
G(x) - является предельным распределением для максимума
случайных величин, распределенных по закону f(x), т.е.
F(x) е Д(нго). Имеем хог = х^
По теореме 3
1 ~ Fto в
lim ------= ев .
х->«> 1 - G(x)
Вычислим В .
299
г
1 - F (х)
lim -------^—7
х >«> 1 - G(x}
1 - 1/(1 - е-х\
lim -------
x-»=° 1 - I + e x
= lim---------— = 1
x->® 1 + e x
следовательно, F(x) и G(x) эквивалентны на "хвостах" распределений,
В = 0 .
3)
1 1 распределение Коши,
F\x) = ~2 + ~ arct® х ’ “ 00 < х < ’ предельная функция
- , , распределения для
G(x) = expl-— j , х > 0, Г(х),т.е.
F(x) e Д(Н1/У) ,
у = 1 , Xq = Xq = oo , следовательно,
1 ~ F(x) в
hm -------—= e существует и равен A > 0 ,
x -X» 1 - G(x)
Вычислим A .
1 - Fix}
lim ----------
x •>«> 1 - G(x)
lim
, 1 1
1 - - - — arctg x
2 л____________
1 - e-^x
1
- — arctg x
lim
-><» 1 - e
0
0
Применим правило Лопиталя, тогда
11 11
-- - -arctgх ----------
lim 2------я ------- = Ит х П ?
1 - е ,х «->«> „-Дх 1
„2
1
—, следовательно,
л
A = — и функции распределения F(x)
n ’
эквивалентны на "хвостах" распределений.
и
G (х) не будут
4)
300
1,2/2 du,
нормальное
распределение
двойное
G(x) = ee
- oo < x < 00 ,
экспоненциальное
распределение.
F(x) е Д(НЛО) .
По теореме 3
I - F(x)
lim —-—
существует и равен = ев
Вычислим В .
В
1 - F(x)
lim —----W
1 -
lim------
-<ц
х -►«> 1 - G (х) х ->«j 1-е
Применим правило Лопиталя, тогда
•1 ~ ~2 хг
~Т— е X х
г .. е 2
hm —— ----------- = lim — =
х-»=о е е е х х->к е-е
- оо и функции распределения f(x) и G (х)
следовательно.
не эквивалентны
О
О
о
на "хвостах” распределений.
II.4. Заключение
Изложение асимптотической теории экстремальных значений
ограничивалось рамками поставленной задачи - в краткой форме
ознакомить с основными теоремами (предельными законами) для
экстремальных значений и с результатами исследований, касающихся
анализа эквивалентности двух произвольных распределений и в
частности, эквивалентности их на "хвостах" распределений.
Вопросам, касающимся асимптотической теории экстремальных
значений, посвяшено много статей в зарубежных изданиях. Среди работ,
переведенных на русский язык, есть только монографии Гумбеля /3/,
Галамбоша /1/ и Дейвида /4/, в последней этой теме посвящена 9 глава.
Эквивалентности распределений, как удалось установить,
посвящены только 3 статьи на английском языке /7-9/. Применяя
теоремы, доказанные в этих статьях, к распределениям, принадлежащим
области притяжения одного их трех предельных распределений для
301
экстремального значения, можно проанализировать эквивалентность 2-х
распределений.
Для произвольных распределений, не принадлежащих области
притяжения предельных распределений, следует анализировать
Предельное соотношение (II.26), не имея предварительных сведений о
существовании предела и характере экви валентности распределений.
Литература
1. Я. Галамбош. Асимптотическая теория экстремальных порядковых
ста тистик. - М.: Наука - 1984, 303 с.
2. Сархан, Гринберг. Введение в теорию порядковых статистик. -М/.
Статистика - 1970 (перевод под ред. А. Я. Боярского), 41) с.
3. Э. Гумбсль. Статистика экстремальных значений. -М.: Мир - 1965,
444 с.
4. Г. Дейвид. Порядковые статистики. - М.: Наука - 1979, 335 с.
5. S.l. Resnick. Tail equivalence and applications. I. Appl. Probability -
1971, v.8, p. 136-156.
6. В. Феллер. Введение в теорию BqtoaTHOcrefl и ее приложения. Т. 2 -
М.: Мир - 1967, 746 с.
7. А.А. Balkema, L. de Haan. On R. von Mises’ condition for the domain
of attraction of exp (-c'e) • Ann. Math. Statist, v. 43, 1972, p. 1352-1354.
8. L. de Haan. On regular variation and its application to the weak
convergence of sample extremes. Mateinalical Centre Tracts, vol. 32,
1970, Amsterdam.
9. Senela E. Regulary varying functions. Lecture notes in Matematics.
1976, vol. 508, Heidelberge, Springer Verlag.
302
Монография
Райзер Владимир Давыдович
Теория надежности в
строительном проектировании
Технический редактор К. М. Виноградов
Компьютерная верстка АВ. Удовиченко
Лицензия ЛР 0305(14 от 09.03.93
Сдано в iiii6u|>20.! 1.97. Подписано к печати 15.02.98.Формат 60x90/16.Бумага
офсетная. I le’iari. офсетная. Усд. печ. г 19.0. Заказ № 29 . Тираж 1000 ткч.
Ит,1.;г| сльство Ассоциации строительных вузов (АСВ)
129337. Москва, Ярославское шоссе, 26
(095) 183-5742, 183-5683, факс (095) 183-5557
Отпечатано в типографии ЦНИИ «Электроника»
117415, Москва, проспект Вернадского, д. 39
(095) 432-91-69