Министерство образования Российской Федерации
Тульский госудаственный университет
Механико-математический факультет
В.В.Глаголев
МЕТОДЫ
ДИСКРЕТНОЙ МАТЕМАТИКИ
Учебное пособие
Тула 2000
УДК 517.5
Методы дискретной математики. : Учебное пособпе /
В.В.Глаголев. — Тула: ТулГУ, 2000, — 232 с.
ISBN 5-7679-0279-8
В пособпп налагаются основные разделы дискретной математики,
сформировавшиеся к настоящему времени: комбинаторика, теория гра-
фов, булевы функции и их реализации, конечные автоматы, формаль-
ные языки, элементы теории алгоритмов. Большое внимание уделя-
ется прикладной стороне рассматриваемых вопросов: введение новых
понятий мотивируется, на разнообразных примерах показывается как
работают изучаемые методы.
Предназначено для студентов направлений ’’Прикладная матема-
тика и информатика” и ” Математика, прикладная математика”.
Пл. 70. Табл. 20. Бпблпогр.: 10 назв.
* * *
Печатается по решению редакционно-издательского совета Туль-
ского государственного университета.
Рецензент: проф. кафедры матем. кибернетики факультета ВМК Мо-
сковского гос. университета, доктор физ.-мат. наук А.А.Сапоженко.
1602010000 - 76
М ----—----------- Без объявл.
76 П(03) - 2000
©
В. В. Глаголев
ISBN 5-7679-0279-8
@ Тульский государственный
университет, 2000
Предисловие
Слово ’’дискретный” означает в переводе прерывистый, состоящий
из отдельных изолированных частей. Таким образом, это понятие про-
тивоположно понятию ’’непрерывный”. Единство непрерывного н дис-
кретного характерно для математики. Оно проявляется уже в число-
вой системе: множество натуральных чисел - это дискретный объект,
множество действительных чисел - непрерывный. Другой пример; при
решении на ЭВМ какой-либо задачи, связанной с исследованием н рас-
четом непрерывного объекта — движение материального тела, опре-
деление формы поверхности, преобразование непрерывного сигнала н
др. — главным этапом является дискретизация задачи, т.е. выбор пра-
вильной дискретной модели, результаты расчета которой' с заданной'
степенью точности позволяют найти искомые величины в непрерывно!!'
задаче.
Классическая математика - это математика непрерывных величин.
Основное понятие классической математики, понятие предела, связано с
представлением о непрерывной действительной'прямой'— континууме.
Основная модель классической математики — система дифференциаль-
ных уравнений, описывающая движение по непрерывной'траектории в
фазовом пространстве.
Элементы дискретной математики зародились в рамках классиче-
ской, но не занимали в ней заметного места. Главное развитие дискрет-
ная математика получила в последние годы, когда сформировались н
быстро развивались такие дисциплины, как теория графов, комбина-
торный анализ, теория булевых функций, теория автоматов н формаль-
ных языков II др.
Перечисленные разделы н составляют, в основном, содержание дан-
ного учебного пособия. При изложении материала основное внимание
уделено теории: формулировке понятий н утверждений, описанию ма-
тематических моделей н методов решения задач. Кроме того, в каждый
раздел включено несколько чисто прикладных задач, иллюстрирующих
как ’’работает” соответствующая теория.
- 3 -
Глава 1
Теоретико-множественное введение
1.	1. Основные понятия и обозначения
Множество принадлежит к числу исходных неопределяемых поня-
тии, на его основе строятся все без исключения математические кон-
струкции. Обычно множество разъясняют как совокупность объектов
произвольной природы, рассматриваемую как единое целое. Объекты,
составляющие множество, называются его элементами. Слова ’’произ-
вольной природы” означают, что для некоторого элемента н множества
следует отвлечься от всех нх свойств, кроме одного: входит элемент в
состав множества нлн нет. Если элемент а входит в множество А,
то это обозначается так: а Е А (читается: а принадлежит А ), в
противном случае пишут о Е ,\ (а не принадлежит А.)
Для указания конкретного множества существуют различные спо-
собы.
1)	Некоторые множества имеют общепринятые обозначения:
N — множество натуральных чисел;
Q — множество рациональных чисел;
TZ — множество действительных чисел;
С — множество комплексных чисел.
2)	Множество можно задать перечислением: для этого в фигурных скоб-
ках выписываются чеоез запятую все его элементы. Например,
{0,1, 2,3,4, 5,6,7,8,9}-
это множество десятичных цифр.
3)	Чаще всего множество задается описанием свойств его элементов.
Например, отрезок [0, 1] вещественной прямой определяется так
[О, 1] = {х | х Е , 0 < х < 1} ,
а множество
{(ж, у) | х Е , у Е , х2 + у2 < 1}
- 4 -
представляет собой круг на плоскости.
4)	Рекурсивное задание множества.
Этот способ заключается в следующем:
1° . Указываются некоторые исходные объекты, входящие в множество;
2° . Описывается механизм, позволяющий строить новые объекты из
уже имеющихся;
3° . Объявляется, что в множестве нет никаких других объектов кроме
тех, что можно построить из исходных, применяя описанный'в
и. 2° механизм.
Например, подмножество А натурального ряда, состоящее нз все-
возможных степенен двойки, можно задать так
1° . 1 е А ;
2° . х е А => 2т е А ;
3° . А — наименьшее подмножество натурального ряда, удовлетворя-
ющее 1° н 2° .
Обратим внимание на необходимость пункта 3° : если опустить
это требование, то в качестве А можно взять весь натуральный ряд
нлн множество четных чисел нт. д. Условие, что А — наименьшее
подмножество, можно расшифровать таким образом: если В — любое
множество, удовлетворяющее 1° н 2° , то А С В. Можно показать
также, что А является пересечением всех множеств, удовлетворяющих
1° н 2° .
В дальнейшем при рекурсивном задании множеств пункт 3°, как
правило, не указывается, но всякий раз это требование подразумева-
ется.
В качестве другого примера использования рекурсивного задания
множества определим совокупность всех слов в данном алфавите. Пусть
А = {ai,. . ., ат} — произвольное конечное множество, элементы кото-
рого будем называть буквами, а само множество алфавитом. Элементы
определяемого множества А* будем называть словами.
1° . at — слово, aj 6 А* , г = 1, 2,..., т ;
2° . Результат приписывания к слову любой буквы является словом:
х е А* => xaL е А*, ха2 £ Л’,..хат е А*.
-5-
Например, если А = {О, 1}, то А* содержит такие элементы
0,1 (согласно 1° );
00, 01 п 10, 11 (результат приписывания букв 0 п 1 к словам пз преды-
дущей строки, согласно 2° )
000, 001, 010, 011, 100, 101, ПО, 111 (результат приписывания букв 0 и
1 к словам из предыдущей строки, согласно 2° );
и так далее.
В приведенных примерах некоторые множества составляют часть
другого множества. Если все элементы множества А являются в то
же время элементами множества В, то этот факт записывается сле-
дующим образом: АС В ( читается: А содержится в В. ) Знак С_
называют знаком включения.
Различают конечные п бесконечные множества. Для конечного
множества А имеет смысл говорить о числе его элементов, оно обо-
значается |Л|.
1.2.	Операции над множествами.
Булевы тождества
Если некоторые множества взять в качестве исходных, то пз них
можно образовывать новые множества, применяя теоретико-множест-
венные операции:
объединение (сумма):
A U В = {х | х G А или х G В} ;
пересечение (произведение):
А П В = {х | х G А п х G В} ;
разность:
Д \ В = {х | х G А п х В} .
Сумма множеств А п В иначе обозначается А+В, а пересечение
— А  В. Как в случае обычного умножения чисел, точка, как правило,
опускается: А О В = АВ.
- 6 -
Более удобной по сравненпю с разностью является операция допол-
нения. В большинстве случаев можно считать, что все рассматрива-
емые множества являются частями некоторого множества-унпверсума
U. Напрпмер, в математическом анализе прп пзученпп функций од-
ной переменной все фпгурпрующпе в теорпп множества являются под-
множествами вещественной прямой, то есть U = TZ. Прп переходе к
функциям двух, трех п т.д. переменных в качестве универсума будут
выступать множества 7?J,77 3, . . .
Еслп принять предположенпе о налпчпп множества-унпверсума U,
то операция дополненпя определяется следующим образом:
А = U \ А плп А = {ж | х Л} .
После введенпя этой операцпп разность можно не рассматривать,
так как
А \ В = А В .
Выполняя по-разному операцпп над множествамп, можно прпйтп к
одному п тому же результату. Напрпмер, для любых множеств А п
В справедливо равенство
А+В=АВ.
Такого рода соотношенпя называют теоретпко-множественнымп
тождествамп. Тождества устанавливаются с помощью так называемого
принципа равнообьемности: показывается, что множества, стоящие в
левой п правой частях тождества, состоят пз однпх п тех же элементов.
Пропллюстрпруем прпнцпп на рассматриваемом примере:
х G А	+	В	=>	х £ А + В => х	А п х	В	=>
=>	х G А п х G В =>	х G А В .
Наоборот,
х G	А	В	=>	х G А п х G В => х	А п х	В =>
х	А Т В х G А Т В .
Аналогичным образом можно убедиться в справедлпвостп нпжесле-
дующпх соотношений, называемых бу левыми тождествамп (знаком 0
обозначено пустое множество ):
- 7 -
А+ В = В + А	(1)
А+(В + С) = (А + В) + С	(2)
А + А = А	(3)
А + ф =А	(4)
A + U = U	(5)
А-В = В-А	(6)
А  (В  С) = (А  В)  С	(7)
А-А = А	(8)
А - ф = ф	(9)
A-U = А	(Ю)
1 = А	(П)
= и	(12)
й = Ф	(13)
А  (В + С) = А  В + А  С	(14)
А+ (В -С) = (А + В)  (А + С)	(15)
А + В = А-В	(16)
а-в = а + в	(17)
А + А = U	(18)
А-А = ф .	(19)
Булевы тождества можно рассматривать как законы, которым под-
чиняются операции над множествами. Подобно тому, как на основа-
нии арифметических законов можно производить различные алгебраи-
ческие преобразования: раскрытие скобок, вынесение за скобки, приве-
дение подобных членов н т.д., на основании тождеств (1) — (19) можно
производить преобразования теоретико-множественных выражений.
Оказывается, что система тождеств (1) — (19) полна в том смысле,
что любое соотношение между множествами является следствием буле-
вых тождеств. Тождества названы по имени английского математика
- 8 -
XIX в. Дж. Буля, который считается основателем математической
логики. Основная цель этой науки состоит в том, чтобы такие тон-
кие функций человеческого разума, как доказательство утверждений,
проверка гипотез, разработка теорий, связанные с проведением логиче-
ских рассуждений, сделать механическими, так чтобы нх можно было
выполнять автоматически, например, на компьютере. В идеале это мо-
жет выглядеть так: имеется некоторое математическое утверждение,
про которое неизвестно, верно оно нлн нет. Его записывают с помощью
подходящей символики, вводят в компьютер н запускают специальную
программу, которая по окончании работы дает ответ: истинно утвер-
ждение нлн нет. В настоящее время имеется уже достаточно много
программ такого рода, приспособленных для вывода теорем в специ-
альных областях математики. Но первой областью, в которой удалось
автоматизировать логические рассуждения, было так называемое исчи-
сление высказываний, появившееся в работах Дж. Буля. Не вдаваясь
в подробности, достаточно сказать, что основную задачу, решаемую в
исчислении высказывании, можно свести к следующей.'
Даны два множества, построенные из исходных множеств
Ai,A2,...,An при помощи операций объединения, пересечения и до-
полнения. Спрашивается: совпадают ли эти множества?
Пример. Совпадают лн множества
А — (Д1 Aq + Д1 А%)  Аз н В — (Д1 А3 + А^ Дз)  А-± А^ Аз ?
1.3.	Алгоритм для проверки
ТЕОРЕТИКО-МНОЖЕСТВЕННЫХ ТОЖДЕСТВ
Коль скоро зашла речь об алгоритме н компьютерной программе,
необходимо уточнение постановки задачи: именно, нужно более точно
определить, что значит ’’множество, построенное нз исходных мно-
жеств А-1, А?, . . ., Ап при помощи операций объединения, пересечения
н дополнения”.
Этому понятию мы сопоставим некоторый формальный объект, (то
есть узнаваемый только по форме, без выяснения смысла). Как будет
видно в дальнейшем, в большинстве случаев таким формальным объек-
том является слово в некотором алфавите. Заметим также, что именно
такие объекты — последовательности знаков нз определенного набора
— обрабатывает компьютер. Поэтому указанный способ формализации
является, в известной степени, основным.
- 9 -
Определение формулы булевой алгебры
Рассмотрим алфавит, содержащий такие символы
Ai, А'2,   , Ап — обозначения исходных множеств;
+	— обозначения операций объединения, пересечения и дополне-
ния ;
(,) — левая п правая скобки.
Рассмотрим всевозможные слова в этом алфавите п прп помощи ре-
курсивного определения выделим пз них правильно построенные слова
— формулы.
Замечание. Чтобы все формулы имели вид слов (цепочек символов),
дополнение обозначается значком ” А’, поставленным перед множе-
ством:
А =-А ; (фф + фф) = -(-(Л) -Л+Л -'(Ч2)) .
После того, как будет сделано определение, вернемся к старому, более
удобному обозначению.
Определение
1° . А-!, А2, ...,Ап — являются формулами.
2° . Если 5] п 52 — формулы, то формулами будут также
(Ч + Ч) , (л  Ч) п ЧЛ) 
Напомним, что в определении подразумевается еще третий пункт:
последовательность символов введенного алфавита является формулой
в том п только в том случае, если эта последовательность может быть
построена прп помощи 1° п 2°. Чтобы убедиться, что строка символов
является формулой, необходима так называемая процедура граммати-
ческого разбора (по-англпйскп - парсинга). Разбор выглядит примерно
так: если дана строка символов, то проверяется имеет лп эта строка
одну пз следующих форм
(51 + 52) ,	(51  52) плп -1(51) ,
где 5i,52,5 — некоторые строки. Согласно пункту 2°, эти строки
также должны быть формулами, поэтому снова проверяется имеет лп
- 10 -
каждая из них одну из трех указанных форм и так далее. Процедура
проверок заканчивается, когда она доходит до строки At, которая
явяется формулой по определению.
Уточним теперь постановку задачи следующим образом:
Даны две формулы булевой алгебры У\ и У2. Спрашивается:имеет
ли место теоретико-множественное тождество = У2 ?
Опишем в словесной форме алгоритм для решения поставленной
задачи. Этот алгоритм без труда можно перевести в программу для
ЭВМ.
Будем рассматривать произведения (пересечения), составленные пз
исходных множеств и их дополнений Ai, А2, . . ., Ап Ai, А2, . . ., Ап. На
основании тождеств (8), (9) и (19) можно считать, что каждая буква
(с черточкой или без черточки) входит в произведение не более одного
раза, потому что, например,
А-! А2 A-i А3 А2 = А-! А2 А3 , а АДА2А1А3А2 = ф .
Потребуем, чтобы каждая буква входила в произведение ровно один
раз. Такие произведения назовем конституентами (составляющими).
Пользуясь тождеством (6), будем располагать буквы в порядке их но-
меров.
Итак, констптуента — это произведение, в котором:
1) ровно п сомножителей;
2) г-й сомножтель — это либо Ai, либо Л;, г = 1,2, . .. ,п.
Например, в случае п = 3 имеется 8 конституент:
Ai А2 А3 Ai А2 А3 Ai Л2Л3 Ai А2 А3
Ai А2 А3 Ai А2 А3 Ai Л2Л3 Ai А2 А3 .
Будем называть формулы и У2 эквивалентными, если имеет
место тождество = У2. Очевидно, если в какой-либо формуле сде-
лать замену на основании одного пз тождеств (1)—(19), то получится
эквивалентная формула.
Алгоритм для проверки теоретико-множественных тождеств осно-
ван на следующих двух утверждениях.
- 11 -
I. Каждая формула булевой алгебры эквивалентна формуле, имею-
щей вид суммы констптуент.
Будем говорить также, что формула может быть представлена в
виде суммы констптуент.
2. Тождество = А2 имеет место в том и только в том случае,
когда Ту н У2 одинаковым образом представляются в виде суммы
констптуент.
Для доказательства первого утверждения опишем процесс приве-
дения к сумме констптуент. Он распадается на ряд этапов.
I. Пользуясь тождествами (16,17), добиваемся того, чтобы чер-
точки стояли только над буквами. При этом с помощью тождества (11)
убираем двойные черточки.
Для приведенного выше примера эти преобразования выглядят сле-
дующим образом:
А = (А1 Aj+AfA2)  А3 = A-l А?- AiA2  Аз =
= (Aj+А2)(Aj+А2)Аз = (Aj+А2)(Aj+А2)  Аз .
й=(А1А3+А2АДА1А2Аз=(А1Аз+А2АД(А^А^А_Д.
II. Пользуясь тождеством (14), раскрываем скобки н приходим к
выражению вида ” сумма произведений” ;
А — А^А^Аз-ЬА^ А2АзЗ~А2А-1АзЗ~А2А2Аз .
13—А[ Аз А[ -|- А[ Аз А2 -|- А-± А3 А3 -|- А2 А3 Ах4-
-|- А2 Аз А2 -|- А2 Аз А3 .
III. Одинаковые множители в произведений заменяем одним. Про-
изведение, содержащее некоторую букву н ту же букву с черточкой,
удаляем (применяя тождества (8), (9) н (19)):
А — А[ А2 Аз -|- А[ А2 А3 .
13 — А[ А2 Аз -|- А[ А2 А3 -|- А2 А3 .
IV. Если некоторое произведение К состоит менее чем нз п букв,
то с помощью тождеств (10), (18) н (14):
К = к -и = К- (Д + А) = к А + К А~
- 12 -
добавляем недостающие буквы;
В = Al А2 Аз + Л1 А2 Аз + (Hi + ЛД А2 А3 =
— А[ А2 Аз -Е А[ А2 Аз -Е А-± А2 A3 -Е А-± А2 A3.
\f. Если некоторое слагаемое входит в сумму более одного раза, то
на основании тождества (3) оставляем только одно вхождение:
В — А-± А2 Аз -Е А[ А2 Аз -Е А-у А2 Аз .
Окончание примера:
А — Ау А2 Аз -Е Ау А2 Аз .
В — Ау А2 Аз -Е Ау А2 Аз -Е Ау А2 Аз .
Для доказательства второго утверждения заметим, что если Ту
н У2 одинаковым образом представляются в виде суммы констнтуент,
то У2 можно получить из Ту цепочкой эквивалентных преобразо-
вании: от Ту к сумме констнтуент и от суммы констнтуент к У2.
Следовательно, эквивалентно У2.
Допустим теперь, что представления У у и У2 в виде суммы кон-
стнтуент не совпадают. Приведем пример таких множеств Ау . . ., Ап ,
что ?у	Т2.
Пусть U, — множество всевозможных двоичных слов длины п :
U = {a.ia'2    О'п | а; £ {0, 1} , i = 1, 2, . .., п } .
Обозначим через Ai — подмножество слов, у которых г-я буква равна
единице:
Ai = {aia'2 . . . ап | &i = 1} , i = 1, 2, . . ., п .
Дополнение к Ai , очевидно, состоит нз слов, у которых г-я буква
равна нулю:
Ai = {aia'2 . . . ап | &i = 0} , г = 1, 2, . . ., п ,
а пересечение множеств Ai нлн нх дополнений будет состоять нз слов, в
которых соответствующие буквы зафиксированы. Например, Д1Д3Д4
- 13 -
состоит из всевозможных слов, у которых 1-я буква равна нулю, 3-я
— единице и 4-я — нулю. В частности, каждая констптуента состоит
пз одного слова, г-я буква которого равна 1, если г-н сомножитель
конституенты равен Ai, и 0, если г-н сомножитель конституенты
равен Ai.
Отсюда имеем, что если представления ЗА и ЗА в виде суммы
констнтуент не совпадают, то найдется слово входящее в одно нз мно-
жеств н не входящее в другое, то есть тождество JA = JA не имеет
места.
1.4. Декартово произведение
Пусть даны множества А н В. Их декартовым произведением
называется множество, обозначаемое А х В, составленное нз всевоз-
можных упорядоченных пар (а, Ь), таких, что первый элемент пары
берется нз множества А, а второй — нз множества В :
А х В = { (а, 6) | a G A, b G В } .
Эта операция над множествами, в отлнчне от рассмотренных ра-
нее, изменяет природу элементов : в новом множестве элементами явля-
ются пары.
Хорошо известными примерами декартова произведения служат
координатная плоскость Tv2 = R. х R., прямоугольник на плоскости
[а, Ь] х [с, d] = {(ж, у) \a<x<b,c<y<d}.
Произведение трех н большего числа множеств можно определить
формулой (Л х В) х С или как совокупность всевозможных упорядо-
ченных троек (а, Ь, с), таких, что a G A, b G В, с G С.
Отношения
Пусть имеется декартово произведение k множеств А = А± х
A'i х . . . х Ak. Всякое подмножество р С_ А называют ^-местным
отношением.
Если (aj, а?, . . ., а/~) G р , то говорят, что данные элементы нахо-
дятся в отношении р, в противном случае — нет.
Примеры. 1. Отношение < на множестве действительных чисел с
точки зрения введенного определения рассматривается так: р CAR х R.
- 14 -
состоит из всех пар (х, у), в которых первое число меньше второго.
Напрпмер, (0,1) £ р , (3,2) р , (1,1) р. Вместо такой записи
общепринято писать 0 < 1 , 3 yt 2 , 1-^1.
2. Пары (т, п) Е Z х Z, такие, что п = т  d , d Е Z, образуют
отношение <5 делимости на множестве целых чисел. Имеем
(3, 15) Е 6 , (6,42) Е 6 , (6, 15) <5.
Над отношениями можно производить операции, получая нз одних
отношений другие. Возникающее таким образом исчисление отношений
(алгебра отношений) находит применение при разработке реляционных
баз данных.
- 15 -
Глава 2
Элементы комбинаторики
В комбинаторике, или в комбинаторном анализе, изучаются кон-
струкции из элементов конечных множеств. Типичная ситуация та-
кова: имеется исходное множество, из его элементов ио определенным
правилам требуется построить систему подмножеств или систему более
сложных объектов с заданными свойствами. Прежде всего возникает
вопрос, можно ли вообще выполнить такое построение, т.е. вопрос о
существовании системы объектов с требуемыми свойствами. Если этот
вопрос решается положительно, то возникает задача подсчета: сколь-
кими способами можно выполнить построение?
Необходимость в подсчете вариантов почти всегда появляется при
решении сложной задачи на ЭВМ, поскольку нужно заранее спланиро-
вать объем занимаемой памяти и время решения задачи. В качестве
примера можно указать задачу о поиске на ЭВМ наилучшего хода в
шахматной позиции.
Рассмотрим основные приемы, применяемые при подсчете комби-
наторных объектов. Будем называть их принципами или правилами
подсчета.
2.1.	Принципы подсчета
1	.Правило сложения.
Если множества А и В не пересекаются, то |Л + В| = |Л| + |В|.
Несмотря на кажущуюся тривиальность этого правила, оно приме-
няется практически при каждом подсчете. Идея его применения следу-
ющая: если в исходной задаче прямой'подсчет затруднителен, то нужно
рассмотреть ряд случаев и провести более простые подсчеты в каждом
из них.
Пример. Сколько имеется путей из вершины а в вершину b в сети,
показанной на рис. 2.1 ?
- 16 -
Рис. 2.1
Обозначим множество всех путей пз а в h через Ьаь п разобьем
его на два непересекающпхся подмножества:
Lach — путп, проходящие через вершину с ;
Ladb — пути, проходящие через вершину d.
Имеем, | Lab | =	+ \Ьаьь | 
Очевидно, что пнтересующее нас количество путей завпспт только
от размеров решеткп, поэтому обозначим через 1т ц количество путей
в сетп, имеющей т горизонтальных п п вертикальных рядов. Тогда
последнее равенство можно записать так: /4 ,5 = /3 ,5 + /4
Вообще, lmn = n	Пользуясь этпм соотношенпем,
легко подсчитать количество путей на рпс. 2.1: /45 = /35 + /4	=
/35 Т Аз,4 Т Аз,4 Т ^4,3 — ^2,5 Т ЗАз,4 — ^1,5 Т 4/зд Т ЗАз,3 — 5 Т 10^2,3 — 35.
- 17 -
2	.Правило умножения.
Число элементов декартова произведения двух множеств равно
произведению числа элементов одного из сомножителей на число эле-
ментов другого сомножителя:
\Ах В\ = \А\-\В\ .
Пример. Рассмотрим матрицу, состоящую из т строк и п столбцов.
Пусть А = {1, 2, . .., т} —множество номеров строк, В = {1, 2, .. ., и}
— множество номеров столбцов. Место пропзвольного элемента ма-
трицы задается парой (i,j), т.е. элементом декартова пропзведенпя
Ах В. Всего в матрице т  п элементов.
Правило умножения справедливо для любого числа сомножителей в
декартовом пропзведенпп:
Hi х Л2 х ... хАк\ = 1Л1 .|Л2|.....|Л| .
Наиболее часто последнее соотношенпе применяется в случае, когда
A-l = А2 = ... = Ак = А :
|Hfc| = |H|fc.	(2.1)
В этом случае множество А называют алфавитом, его элементы —
буквами, а элементы декартова пропзведенпя Ак , т.е. упорядоченные
наборы пз к букв (ai, a2, . . ., ак) называют словами в алфавите А.
Число к естественно называть длиной слова. Пусть |Л| = т, тогда
правило (2.1) можно сформулировать следующим образом:
число слов длины к в алфавите из т букв равно тк .
Примеры. 1. Сколько имеется различных 6-значных телефонных
номеров?
Здесь алфавит состоит пз 10 цифр, номер — слово длины 6 в этом
алфавите; поэтому количество номеров — 106.
2. В сессию студент сдает 5 экзаменов. Сколько возможных ре-
зультатов сесспп? Ответ:45.
3. Сколько имеется двоичных слов длины п ? Ответ: 2".
- 18 -
3. Принцип взаимно однозначного соответствия. (Правило биек-
ции).
Если можно установить взаимно однозначное соответствие (би-
екцию) между множествами А и В, то |Л| = |В|.
В качестве примера применения этого принципа подсчитаем коли-
чество всевозможных подмножеств множества М, состоящего пз п
элементов. Так как это количество не зависит от природы элементов
множества М, возьмем
М = {1, 2,..., п} .
Произвольному подмножеству А С М поставим в соответствие дво-
ичное слово ача'2    по следующему правилу:
_ ( 1, если i G А ;
°г [ 0, если i £ А .
Это соответствие взаимно однозначное. Отсюда число всех подмно-
жеств п-элементного множества равно числу двоичных слов длины п,
то есть равно 2".
Разобьем подмножества n-элементного множества на классы по
числу элементов в подмножестве. Число всех подмножеств, состоящих
ровно пз к элементов, принято обозначать (этп подмножества
называют также сочетаниями пз п элементов по к.)
Например,
с° = Сп = 1 С'1 = п
Отметим следующие свойства введенных чисел:
п
а) £С* = 2".
к = ()
Это непосредственно следует пз определения чпсел С^.
гг\ z'*/e   s~m — k
Для доказательства поставим в соответствие подмножеству А его
дополнение А = М \ А. Это соответствие взаимно однозначное. Прп
этом, если |Л| = к, то |Л| = п — к. Следовательно, подмножеств,
- 19 -
составленных пз к элементов, столько же сколько подмножеств, со-
ставленных пз п — к элементов.
„1 Г'к _	I z~<fc
Щ — Gn-1 ' Gn-1'
Для доказательства разобьем все Ar-элементные подмножества мно-
жества М = {1,2,...,п} на два класса:
1)	подмножества, не содержащие элемента п. Это будут к-эле-
ментные подмножества множества {1, 2, .. ., п — 1}, поэтому число их
равно С^_1 
2)	подмножества, содержащие элемент п. Если пз каждого такого
подмножества удалить элемент п, то получится (к — 1)-элементное
подмножество А' множества {1, 2, .. ., п — 1}. Соответствие А ь-> А'
взаимно однозначное, поэтому число подмножеств в этом классе равно
С-'п-г Свойство ”в)” вытекает, таким образом, нз правила сложения.
Замечание. Введенные числа по определению имеют смысл при
следующих значениях п н к :
п = 0, 1, 2, .. . к = 0,1, . . .п .
Легко проверить, что соотношения б) н в) останутся в силе для
п = 0,1,2,... н любых к, если придерживаться такого соглашения:
= 0, если к < 0 нлн к > п.
Применяя свойство в), легко вывести по индукции следующую фор-
мулу для вычисления сочетаний':
к _ п! _ п  (п — 1)  ...  (п — к + 1)
“ к\(п — к)\ ~	к\	'
Примеры. 1.Сколько всего партий играется в шахматном турнире с
п участниками ?
Ответ: С„, так как каждая партия однозначно определяется двумя
ее участниками.
2.	В выпуклом n-угольннке общего положения проведены все диа-
гонали. Посчитать число точек пересечения диагоналей.
Слова ’’общего положения” означают, что никакие три диагонали
не пересекаются в одной точке. Обходя многоугольник против часо-
вой стрелки, занумеруем вершины числами 1, 2, . .., п. Тогда имеется
- 20 -
биекция между множеством точек пересечения диагоналей н четвер-
ками (подмножество нз 4 элементов) чисел	указывающих
концы персекающнхся диагоналей. Действительно, если дана точка пе-
ресечения, то выписывая концы персекающнхся диагоналей,’ получим
четверку. Наоборот, если задана четверка, то ей соответствует ровно
одна точка пересечения: если, например, i < j < k < /, то пересе-
каются только диагонали {г, АД н {j, I}. По правилу бнекцнн число
точек пересечения диагоналей равно С'„.
3.	Возвращаясь к первому примеру этой главы (рнс.2.1), подсчи-
таем иначе количество путей нз вершины а в вершину h. Каждому
пути можно поставить в соответствие двоичное слово, обозначая еди-
ницей перемещение по горизонтали н нулем — по вертикали. Чтобы
попасть нз а в Ь, надо сделать 4 перемещения по горизонтали н 3 по
вертикали. Поэтому получающиеся двоичные слова будут иметь длину
7 н состоять нз 4 единиц н 3 нулей. Наоборот, каждому такому слову
соотвествует некоторый путь нз вершины а в вершину h. По правилу
бнекцнн число всевозможных путей равно СД = 35. (Определенное при
рассмотрении этого примера число 1(т, п) = С^+п).
4.	Подсчитать количество решений уравнения
Ж 1 4" Ж 2 4"    4" Ж т = п ,
в котором переменные жд, жд, . . ., хт принимают натуральные значе-
ния.
Эту задачу можно решать проводя индукцию по числу слагаемых
т. Обозначим количество решений через £)(т, п). Имеем
D(l,n) = 1, одно решение жд = п ;
D(2, п) = п — 1, решения: {(1, п — 1), (2, п — 2), . . ., (п — 1, 1)} .
Для вычисления D(3,n) зафиксируем значение хз = г, тогда
жд + х? = п — i н число решений этого уравнения равно п — i — 1.
Отсюда
D(3, n) = J2(n - i - 1) = п - 2 + п - 3 + . . . + 1 =	~	~	.
2 = 1
- 21 -
Таким же путем можно пдтп дальше, но здесь это приведено только
для сравнения: использование сочетании' и остроумного рассуждения,
приписываемого Л.Эйлеру, позволяет сразу решить задачу для произ-
вольных п п т.
С рассматриваемым уравнением можно связать такой наглядный
образ: п точек, расположенные в ряд, разделены перегородками на
т отрезков, первый — из х± точек, второй из ж 2 точек и т. д.:
Перегородки в количестве т — 1 штук расставляются в проме-
жутки между точками, число этих промежутков равно п — 1, поэтому
число способов расстановки перегородок равно , это п есть число
решений уравнения (2.3) в виду очевидной бпекцпп.
5.	Подсчитать количество решений уравнения
ЖД + Ж 2 +    + Хт = П,
в котором переменные Xi, х2,   , хт принимают целые неотрицатель-
ные значения.
Осуществив обратимую замену переменных
?У1 = ж 1 + 1 , гу2 = х2 + 1 , ... ут = хт + 1 ,
получаем для новых переменных следующую задачу:
подсчитать количество решений' уравнения
?У1 + ?У2 +    + Ут = п + т,
в котором переменные у-±, у2, . . ., ут принимают натуральные значе-
ния. Следовательно, искомое число равно _х = С'”+т
Замечание. Пусть {ai,...,am} —множество пз т элементов. Мно-
жество, составленное пз а-±, . . ., ат, в котором элементы могут повто-
ряться называют мультимножеством. Для задания мультимножества
надо указать сколько раз в него входит каждый' из элементов
Л4 = (, fgi > о , i = 1, . . ., т .
\ м    кт )
- 22 -
Величину ki + . . . + km естественно считать мощностью мультимно-
жества.
Из рассмотренного примера следует, что число мультимножеств
мощности п, составленных нз т элементов, равно С„+т _х.
Мультимножества называют также сочетаниями с повторениями.
2.2. Принцип включения-исключения
Поставим задачу: подсчитать количество элементов в объединении
нескольких множеств. Для двух множеств имеем
Hi + А?1 = |А| + Нз1 — Hi  A1 	(2-2)
Рассмотрим далее объединение трех множеств. Обозначим АСА = А
н применим предыдущую формулу:
I +Л2+Аз |= | А+ A31 = | А | +1 Аз| — | А Аз| = А+Ф1 + Нз |— |41Ф+ААз1 
Применяя к |А+А| и |А'А + А'Аз| формулу (2.2), приходим к
такому соотношению
|А+А+Аз| = lAI + IAI + IAI-Н1'А| —НгАз| —Нз'Аз| + НгА'Аз| 
Аналогичное вычисление позволяет перейти от объединения k
множеств к объединению k + 1 множеств (это вычисление сложнее
технически, но не требует новых идей). В результате по индукции
получаем следующую формулу:
i а+а+-. .+Ап । = |л^ । — 52 in  и? 14" 52 iA'A'Ah
2 = 1	l<2<j<n	1<2<J </с<П
...+ (-l)fc+1	£	|A1A2 .. .AJ +...+ (-1)"+1|4H.. .a„|,
1 <2 1 <?2 <   A k
которая в словесной формулировке выглядит так:
чтобы найти количество элементов в объединении множеств,
нужно сложить количества элементов в каждом множестве, затем
вычесть количества элементов во всевозможных попарных пересече-
ниях, прибавить количества элементов во всевозможных пересечениях
по три и т.д. (принцип включения-исключения).
- 23 -
Пример. Рассмотрим слова длины п в алфавите {0,1,2}. Сколько
имеется слов, в которых встречаются все три цифры?
Обозначим Ai множество всех слов длины п, в которых не встре-
чается цифра i , i = 0, 1,2. Тогда |Ло| = |Л1| = |Л2| = 2" . Кроме
того, | Ад  Ai | = | Ад  Л21 = | Ai  Л21 = 1. Наконец, | Ад  А-^  А2 | = 0.
В множество Aq + Ai + А2 входят слова, в которых отсутствует хотя
бы одна цифра. По принципу включений-исключений
| Ао + А-! + А21 = 2" + 2" + 2" - 1 - 1 - 1 + 0 = 3 (2" - 1) .
Следовательно, число слов, в которых присутствуют все три цифры,
равно 3" — 3 (2" — 1).
Пример. Задача о беспорядках.
Перестановкой будем называть бнекцню множества {1, 2, .. ., п}
на себя
тг : {1, 2,..., п} —> {1, 2, . .., п} , г ь-> тг(г').
Для задания перестановки достаточно указать строку
тг( 1) , тг(2) , . . . , 7г(п) ,
которую так же называют перестановкой.
При п = 2 имеется всего две перестановки: 12 н 21, при п = 3
имеются шесть перестановок: 123, 132, 213, 231, 312, 321. Чтобы под-
считать количество перестановок для произвольного п, применим рас-
смотренные выше правила. Разобьем все перестановки на п классов,
фиксируя последний элемент:
Pi = {тг | тг(п) = г}, г = 1, . . ., п .
Между любыми двумя нз этих классов Pi н Pj легко установить
бнекцню, меняя местами в каждой перестановке символы г н j.
Следовательно,
|Л| = |Р2| = ...= |Р„|.	(2.3)
Например, для п = 4 рассматриваемое разбиение имеет вид
- 24 -
V1	Р2	Р.3	Р4
2341	1342	1243	1234
2431	1432	1423	1324
3241	3142	2143	2134
3421	3412	2413	2314
4231	4132	4123	3124
4321	4312	4213	3214
Обозначим число всех перестановок п элементов через рп. Оче-
видна биекция между множеством всех перестановок п — 1 элементов
н множеством Рп : к (п — ^-перестановке надо в конце дописать
элемент п. Следовательно, |РП| = рп-1- Используя (2.3) н правило
сложения, получаем рп = п  рп-1- Повторно используя это соотноше-
ние, находим
рп = прп_-[ = п(п - 1)р„-2 = ... = п(п - 1) ... Зр2 = п! .
Таким образом, число всех перестановок п элементов равно п1..
Перестановку тг назовем беспорядком, если в ней каждый элемент
стоит не на своем месте, то есть тг(г) i ,i = 1,2,...п. Задача о
беспорядках состоит в том, чтобы подсчитать число Dn перестановок-
беспорядков. Например, 1)2 = 1 , Дз = 2.
Обозначим Ai — множество всех перестановок тг, в которых
элемент i стоит на г-м месте,
Ai = { тг |тг(г) = г}, г = 1, 2, . . ., п.
Множество Л1 U Л2 U . . . U Ап будет состоять нз перестановок, в ко-
торых хотя бы один элемент стоит на своем месте, а все остальные
перестановки будут беспорядками, следовательно,
Dn = п! - |Л1 U А2 U ... U Л„| .	(2.4)
Подсчитаем далее число перестановок в каждом нз множеств Ai
н в нх пересечениях. Если тт(г) = г, то сужение отображения тг на
множество {1, 2, .. ., п} \ {г} является бнекцней этого множества на
себя. Следовательно, |Л;| = (п—1)!, г = 1,...,п.
Множество Ai  Aj составлено нз перестановок тг, в которых
тг(г) = г, tt(j') = j. Сужение отображения тг на множество
{1,2,...,п]\{г',Я
- 25 -
является биекцией этого множества на себя.
Следовательно, |А,  АД = (п — 2)!, 1 < i < j < п.
Аналогично находим, что |А^  Д,2 . . . .1,, | = (п — &)!, 1<г'1<г2<
   < ik < п.
Применяя принцип включений-исключений, получаем
п
|A1uA2U...UA„| = £(n-l)!-£(n-2)!+... + (-l)fc+1
г = 1	i<j	ii<i'2<...<ik
В каждой нз этих сумм слагаемые одинаковые, поэтому для вычи-
сления надо знать только нх количество. В первой сумме п слагаемых,
число слагаемых во второй сумме равно количеству всевозможных пар
{г, j}, которые можно составить нз п индексов 1,2, ... ,п, то есть
равно С?. Точно так же в k-ii сумме слагаемых. Отсюда
|Ai U А2 U ... U Ап| = п(п — 1)! — С'п(п — 2)! + ... +
+ (—l)fc+1C^(n —/г)! + ... + (—1)"+1 .
После подстановки в (2.4) н несложных преобразований находим
11 (-1)"\
— n. 11— 1+ — — — + ...-I--j— I .
\	21	3'.	п. J
Стоящее в скобках выражение представляет собой частичную сумму
п!
ряда, сходящегося к е , поэтому Dn . Можно показать, что
е
„	п!
I)., равно целому числу, блнжаншему к — .
е
2.3. Рекуррентные соотношения
Для подсчета дискретных объектов широко применяется техника
рекуррентных соотношений н производящих функций. Поясним ее сущ-
ность на примерах.
Пример 1. Рассмотрим следующую задачу: подсчитать количество
двоичных слов длины п, в которых единицы не могут стоять на со-
седних местах. Будем называть такие слова правильными н обозначим
- 26 -
через Ап число правильных слов длины п. Разобьем множество пра-
вильных слов длины п на два класса: слова, оканчивающиеся на ноль
н слова, оканчивающиеся на единицу. Количество слов в этих классах
обозначим Л^ н А„\ соответственно. Имеем по правилу сложения
Ап = А(п°> +	.	(2.5)
Очевидно, что у слова, оканчивающегося на ноль, первые п— 1 сим-
вол образуют правильное слово длины п — 1, нлн, другими словами,
имеется бнекцня между множеством правильных слов длины п, окан-
чивающихся на ноль, н множеством всех правильных слов длины п — 1.
Следовательно, . 1^'" = An~i.
Если правильное слово длины п оканчивается на единицу, то пре-
дыдущий символ этого слова ( п — 1-й) должен быть нулем, а первые
п — 2 символа должны образовывать правильное слово длины п — 2. Как
н в предыдущем рассуждении, снова имеем бнекцню между множеством
правильных слов длины п, оканчивающихся на единицу н множеством
всех правильных слов длины п — 2. Следовательно, . С? ' = Лп_2-
Подставляя в (2.5), получаем соотношение
Ап = Лп_1 + Лп_2 .
Оно называется рекуррентным, в переводе — возвратным, так как для
подсчета интересующей нас величины для некоторого п нужно воз-
вратиться к предыдущим значениям этой величины. В общем случае
рекуррентное соотношение имеет вид
= С(Л„_1, Лп_2,... Лп_/;) .	(2-6)
Рекуррентное соотношение в известном смысле решает задачу под-
счета, но требует для данного п вычисления всех предыдущих вели-
чин. Например, если нам нужно знать количество правильных слов нз
10 символов, то его можно найти, заполняя следующую таблицу
п	1	2	3	4	5	6	7	8	9	10
Ап	2	3	5	8	13	21	34	55	89	144
(Первые два значения находятся непосредственно, а затем вычисляем
Л.з — А? “Ь А[ , Л4 — Л.з -|- Л2 ,...)
- 27 -
Пример 2.
Пусть ” о ” обозначает некоторую бинарную операцию, рассмо-
трим выражение
ах о а2 о . . . о ап .	(2.7)
Если операция ” о ” неассоцпатпвна, то результат вычисления
выражения (2.7) зависит от расстановки скобок. Сколько имеется раз-
личных способов расстановки скобок в выраженннн (2.7)?
Замечание. Как пример неассоцнатнвнон операции можно привести
векторное произведение. Другой удивительный пример: ”о” —обыч-
ное сложение нлн умножение, но выполняемое на компьютере. В силу
того, что представление каждого числа в памяти компьютера ограни-
чено определенным количеством разрядов, при выполнении каждон опе-
рации возникает погрешность н суммарный'результат этих погрешно-
стей зависит от расстановки скобок. Пусть, например, е максимальное
положительное число такое, что 1 + е = 1. Это так называемый машин-
ный ноль. Тогда (1 + е) +е = 1, в то время как 1 + (е + е) = 1 + 2е 1.
Обозначив число всевозможных способов расстановки скобок через
Dn, имеем
Di =	П2	= 1
D.3 =	2	(ai о а2) о а3 ,	ах о (а2 о а3)
D4 =	5	((ai о а2) о а3)	о а4 ,	(ах о (а2	о	а3))	о	а4	, (ах о а2) о (а3 о а4) ,
ai о ((а2 о а3)	о а4) ,	ах о (а2	о	(а3	о	а4))	.
В случае произвольного п разобьем все способы расстановки ско-
бок на классы, включив в k-ii класс способы, при которых сначала
вычисляется’’произведение” первых к н последних п — к операндов (с
какой-то расстановкой скобок), а потом вычисляется нх произведение
(ai о . . . о ак) о (afc+1 о . . . о a„) .
(2-8)
( к = 1, 2,..., п — 1 .)
Согласно определению, количество способов расстановки скобок
для вычисления ” произведения” первых к операндов равно /)к, по-
следних п—к — Dn-k, следовательно, число расстановок скобок
- 28 -
вида (2.8) равно Dk  Dn~k- Суммируя по всевозможным к (правило
сложения !), находим
п— 1
Dn = Dk  Dn_k п = 2, 3,....	(2.9)
к = 1
Например, О5 = DiD4 + kFD3 + D3kF + D4Dy = 1 -5+1 -2 + 2 1+5 1 = 14
Хотя рекуррентное соотношение в принципе решает задачу под-
счета, в ряде случаев желательно иметь выражение для искомой вели-
чины в явном виде. Такое явное выражение можно получить для реше-
нии одного класса рекуррентных соотношении'— линейных рекуррент-
ных соотношений с постоянными коэффициентами.
Решение линейных рекуррентных соотношений
Пусть функция F в общем определении (2.6) является линейной,
Ап = ал Ап_1 + аз Ап~2 + ... + Ofc An_k , п = к, к + 1,... ,
(2.1U)
<11, <12,..., ак — заданные числа .
Тогда соотношение (2.10) называют линейным рекуррентным со-
отношением к-го порядка: (Более точно надо бы говорить ’’линейное
рекуррентное соотношение с постоянными коэффициентами”.)
Соотношение (2.10) мы будем далее рассматривать как уравнение
(относительно неизвестной функции Л(п) = Ап ) н каждую последо-
вательность
А = (Ло, Л1,..., Ап,...) ,
для которой выполнены соотношения (2.10), будем называть решением
рекуррентного соотношения.
Основные моменты теории линейных рекуррентных соотношений
произвольного порядка можно понять на примере уравнении'второго
порядка — общий случай сложней только в обозначениях. Поэтому,
далее исследуем подробно уравнения второго порядка
Ап = ai Л„_1 + 0'2 Л„_2 , тг = 2,3,... ,	(2.П)
делая необходимые замечания для общего случая.
- 29 -
Описание совокупности решений
Лемма 1. Пусть
А = (Ло, Ai,, Ап,...)
является решением рекуррентного соотношения (2.11), a С —любое
число. Тогда последовательность
СА = (С А0,С А-!,...,С Ап,...)
также является решением рекуррентного соотношения (2.11).
Подставив вторую последовательность в (2.11) п поделив на С,
убеждаемся, что вторая последовательность является решением, по-
скольку решением является первая последовательность. Если С = О,
то последовательность С А состоит пз одних нулей. Такая последова-
тельность, очевидно, будет решением любого линейного рекуррентного
соотношения.
Лемма 2.Пусть
А = (Ло, Ai,..., Ап,...) и В = (Вц, Bi,..., Вп,...) —
два решения рекуррентного соотношения (2.11).
Тогда последовательность
С = Л + В = (Ло + Bq , Ai + Bi ,..., Ап + Вп ,...)
также является решением рекуррентного соотношения (2.11).
Так как Л п В являются решениями, то
Л п — О: I Ап — 1 Т CI2 Ап — 2
Вп — ОД Вп-1 Т 0'2 Вп- 2 , п — 2,3,... .
Сложив эти соотношения, убеждаемся, что С также является реше-
нием.
Пз этих двух простых лемм можно сделать важный вывод. Сово-
купность всевозможных последовательностей
Л = (Ло, Л1,..., Ап,  .)
- 30 -
вместе с операциями покоординатного сложения (как в лемме 2) и умно-
жения на скаляр (как в лемме 1) образует векторное пространство. Из
лемм 1 и 2 вытекает, что совокупность последовательностей, являю-
щихся решениями (2.11), представляет собой подпространство этого
пространства. Объемлющее пространство всевозможных последовате-
льностей бесконечномерно, но подпространство решений линейного ре-
куррентного соотношения пмеет конечную размерность, равную по-
рядку уравненпя.
Лемма 3.Размерность пространства решений рекуррентного соот-
ношения (2.11) равна двум.
Для доказательства заметим, что еслп последовательность (Ап)
удовлетворяет рекуррентному соотношению (2.11), то она полностью
определяется задавшем первых двух членов. Действительно, еслп
Ао = а , Al = Ъ ,	(2.12)
то
A'i = ai Л1 + 0'2 Aq = ск^Ь + 0'2 а
A3 = aq Аз + 02 A-i = aq (ал h + 02 а) + 02 b
Другпмп словамп, чтобы задать последовательность-решенпе, доста-
точно задать первые два члена последовательностп. Определпм базис-
ные решенпя п так
Е(00) = 1 , е[0) = 0 , Е^ = О'!	+ 0'2 4°-2 ,« = 2,3,...
Е1^ = 0 , Е^ = 1 , Е^ = О! Е^ + 02 Е^_ , п = 2, 3,...
Еслп пмеется произвольное решенпе А, первые два члена которого
задаются формулами (2.12), то, очевидно,
А = аЁ(0'1 + b .
Лемма 3 доказана.
Отыскание базисных решений
Итак, чтобынаптп все решенпя уравненпя (2.11) достаточно как-то
отыскать два линейно независимых решенпя — каждое решенпе будет
составляться как лпнепная комбинация базисных.
- 31 -
Путь для отыскания базисных решении подсказывает рассмотрение
рекуррентного соотношения первого порядка
An = XAn.L.	(2.13)
Если Aq = 1, то нз (2.13) получаем
Ап = Хп,	(2.14)
то есть решением рекуррентного соотношения первого порядка явля-
ется геометрическая прогресспя.
Будем п в общем случае пскать решенпе рекуррентного соотно-
шения в впде геометрической прогресспп (2.14). Подстановка (2.14) в
(2.11) дает
Хп = a-L А"”1 + 0'2 А"-2 .
Прп А = 0 пмеем нулевое решенпе, оно не представляет для нас инте-
реса. Счптая А 0, поделпм предыдущее соотношенпе на А"-2 :
А2 = а 1 А + 0'2 .	(2.15)
Итак, геометрическая прогресспя (2.14) является решенпем линейного
рекуррентного соотношенпя (2.11), еслп знаменатель прогресспп А
является корнем квадратного уравненпя (2.15). Это уравненпе называ-
ется характеристическим уравнением для рекуррентного соотношенпя
(2.11).
Для построенпя базисных решений необходимо различать два слу-
чая.
1) Характеристическое уравнение имеет два различных корня Ai
и А2.
В этом случае пмеем два решенпя А" п X". Чтобы убедиться,
что онп независимы, покажем, что пз формулы
Ап = Ci X" + С2 X"	(2.16)
путем подходящего выбора констант можно получпть любое решенпе
(2.11). Этот факт выражают словамп: формула (2.16) — это общее
решение рекуррентного соотношенпя (2.11).
- 32 -
Для доказательства последнего утверждения рассмотрим произ-
вольное решение А*. Выберем константы С* и С* так, чтобы
С* А" + С2 А2 и А* совпадали прп п = 0 и п = 1 :
Ср° + Ср°=А* ,
Ср! + ср2 = А* .	Ь ’
Условия (2.17) имеют форму линейной системы, определитель этой
системы
1 ( = А2 - А1 7^ 0 .
ле2
Следовательно, система имеет единственное решение. Из формул (2.17)
следует, что два решения С* А" + С*2 X" 11 совпадают в первых
двух членах, как мы выдели выше, это означает, что они совпадают при
всех п, то есть
а* = с* х^ + с; х™.
2) Характеристическое уравнение имеет кратные корни Ai = А2.
В этом случае имеется только одно решение в виде геометрической
прогрессии — А", однако пространство решений двумерно н необхо-
димо построить второе решение. Оказывается, что в рассматриваемом
случае решением является последовательность Ап = п А".
Действительно, так как Ai — кратный корень характеристиче-
ского уравнения (2.15), то само уравнение имеет вид
(А — АД" = 0 нлн А" = 2 Ai А — Aj ,
то есть исходное рекуррентное соотношение (2.11) в данном случае
имеет следующий вид
Ап = 2 Ai Ап_1 А! Ап_2 .
Подставляя в него Ап = nA", получаем
п А" = 2 Aj (п - 1) А"-1 - А2 (п - 2) А?“2 .
После деления на А", получим тождество
п = 2 (п — 1) — (п — 2) .
- 33 -
Доказательство того, что решения А" и п А" образуют базис в
пространстве решении проводится так же, как в п.1). Формула
Ап = С'1 А" + С'2 п А" -	(2.18)
общее решенпе, так как для любого решения Л* можно подобрать С\
и С'2 так чтобы это решение и (2.18) совпадали в первых двух членах.
Система для определения констант имеет вид
= Л*
Ср! + С2 А1 = Л^
и ее однозначная разрешимость не вызывает сомнения.
Общий случай
В случае соотношения k-vo порядка (2.10) имеют место утвер-
ждения, аналогичные тем, которые были подробно рассмотрены для
уравнений 2-го порядка.
1)	Совокупность всех решений линейного рекуррентного соотно-
шения k-vo порядка является подпространством в пространстве всех
последовательностей.
2)	Размерность этого подпространства равна к. (Каждое решение
однозначно определяется своими первыми к значениями.)
3)	Для построения базиса подпространства решений составляется
характеристическое уравнение
Afc = a1Afc-1 + a2Afc-2 + ... + afc .	(2.19)
(Оно получается, если в рекуррентное соотношение (2.10) подставить
Л„ = А". ) Многочлен
Я(т) = хк — aq Tfc-1 — а2 хк~2 — ... — Ofc	(2.20)
будем называть характеристическим многочленом рекуррентного со-
отношения (2.10).
4)	Если характеристическое уравнение имеет к различных корней
Ai , А2 , ... , Afc ,
- 34 -
то общее решение линейного рекуррентного соотношенпя (2.10) имеет
вид
с\х^ + с2 х™ +... + С'кхпк.
При заданных начальных значениях решения Ai = (ii, i = 0, 1, . .., к — 1,
константы Ci можно найти, решая систему
C'l Aj + С'д А® + . . . + Ск Х°к = Яд
Ci Ai + С2 Ад + ... + Ck Afc = aj
C'i Aj 1 + C'g A!) 1 + ... + Ck Xk 1 = ak- i 
5)	Если A — корень характеристическое уравнение кратности е,
то рекуррентное соотношение (2.10) имеет следующие решения
А" , пХп , ... , п^А” .
(Очередное решенпе получается пз предыдущего умножением на п. )
Пусть характеристическое уравнение (2.19) имеет корни
Ai кратности ei ,
Ад кратности ед ,
Аг кратности ег ,
61 + ед + . . . + ег = к
(Таким образом,
Я(ж) = (ж - А1)е1(т - Ад)62 .. .(ж - Аг)вг ).
Тогда общее решенпе линейного рекуррентного соотношенпя (2.10)
имеет вид
Ап = £ (cf + С'$!) п + ... + С^_. /С-1) А" .
- 35 -
Продолжение примера 1. Для рекуррентного соотношения
Ап — Ап-1 +	,
которому удовлетворяет число двоичных слов, в которых не встреча-
ется подряд двух единиц, имеет вид
А2 = А + 1 .
..	1 + V 5
Напдя его корни Ai = -----—
1 - V5
----—, получим общее решенпе
Ап = С\ X" + С'2 А" .
Для определения констант, учитывая, что А} = 2, Aq = 3, составляем
систему
C'jAi + С'2А2 = 2
GA? + С'2А2 = 3 .
Решая ее, найдем
с = А' с -
! Aj - А2 J Aj - А2 '
Выше говорилось о преимуществе явной формулы, подтвердим это
на примере Ап. Допустим, что длинную последовательность 0 и 1
(например, бинарный файл) нужно передать по каналу связи. Канал
имеет два состояния: одно для передачи 0 и одно для передачи 1, од-
нако, из-за технических ограничении'состояния, в которых передаются
1, не могут следовать друг за другом. В этих условиях исходная после-
довательность 0 п 1 предварительно кодируется: последовательность
- 36 -
разбивается на блоки длины т и каждый блок заменяется правиль-
ным словом длины п.
Практический интерес представляет такой вопрос. Во сколько раз
увеличивается длина блока в результате его кодирования — в это же
количество раз увеличивается время пересылки последовательности по
рассматриваемому каналу по сравнению с двоичным каналом без огра-
ничений на чередование состояний'.
Для того чтобы правильных слов длины п хватило для кодирова-
ния 2т возможных блоков длины т, число п надо выбирать под
условием Ап > 2т нлн после логарифмирования
log2 Ап > т .	(2.22)
Найдем как ведет себя log2 Ап, при п —> ос. В формуле (2.21) Ах =
1 I л/й	1 — л/й	/ А? \ "
—----- as 1,618, А2 =  -  as —0,618, следовательно, ——> 0
22	у AiJ
.	ТТ	1	г	1оё2Лп
при п —> ос . Используя этот факт легко находим, что lim ---- =
ПЭК) П
log2Ai as 0,694 . Следовательно, log2 Ап as 0,694n н условие (2.22)
принимает вид
0, 694 п > т нлн п > ------т = 1, 44 т .
’	-	“0,694
Таким образом, после кодирования длина последовательности увеличи-
вается примерно в полтора раза.
2.4. Производящие функции
Пусть
А = (Ло, А1г..., Ап,...)	(2.23)
некоторая последовательность. Функция
Д(т) — До 4“ Д1 т -|- Д2 х~ -|- ... -Ь Ап хп -|- ...
называется производящей функцией последовательности (2.23).
- 37 -
Из определения вытекает, что сами числа Ап могут быть найдены
как коэффициенты разложения А(х) ио степеням х :
Ап = coeffj.» А(х) .	(2.24)
Пусть, например, А = (1,1,...,!,...), тогда
Л(т) = 1 + х + ж2 + ... + хп + ... = -- .	(2.25)
1 — х
Точно так же
А = (1, А, А2,..., А",...) ->Л(т) = V Хпхп = -----5—;
1 — А х
п=()
А" = coeffy »-----—.
1 - А х
Ирепмущества от введения производящих функций состоят в сле-
дующем. Во-первых, при переходе к производящей функции много объ-
ектов (целая последовательность) заменяются одним, с одним объектом
легче работать. Во-вторых, каждому алгебраическому плп аналитиче-
скому соотношению для производящих функций соответствует некото-
рое, подчас неожиданное, соотношение для последовательностей (2.23).
Отметим некоторые пз таких соответствий.
1° . Линейной комбинации производящих функций соответствует
линейная комбинация последовательностей:
С(х) = а А(х) + b В(х) <=> С = а А + b В , то есть
Сп = а Ап + b Вп , п = 0, 1, 2,...
2° . Дпфференцпрованпе производящей функции.
Если Л(ж) — Aq -|- Ai х -|- Ац х~ -|- ... -Ь Ап хп -)-...
то А'(х) = Ai + 2 А'2 х2 + 3 Аз х2 + ... + п Ап xn~L + ... .
Например, дифференцируя соотношение (2.25), получим
1 + 2т + Зж" + ... + п хп + ... = —------т-
(1 - ж)2
- 38 -
то есть производящей функцией последовательности (1,2,... , п , . ..)
1
является функция --------т-.
(1 - х)2
Дифференцируя соотношение (2.25) т раз, приходим к формуле
т\ + [(m + 1) . . . 3  2] х + . . . + [(ш + п) . . . (п + 1)] хп + . . . =
11 х)
или после деления на т\
1 + С™+1 х + С'”\2 т2 + ... + хп + ... =	_ *	.	(2.26)
(1 х)
Это производящая функция для сочетаний с повторениями.
3° . Умножению производящей функции на х соответствует сдвиг
последовательности А :
(Ло, А-[ , А'2,... , Ап ,...) —> А(х)
(О , Ао, Л1,... , Л„_1,...) -> хА(х).
Например, производящей функцией последовательности (0, 1, 2, 3, .. .)
х
является функция --------т-.
(1 - ж)2
4° . Интегрирование производящей функции. Если
= v4q -|- у4х т -|- Из . -|- Ап хп 4- ... ,
то
I A(t) dt = Aq х + 4г х2 + “Т ж'3 +    + хП+1 +    
J	2	3	п + 1
о
" ск
В качестве примера использования 4° найдем (Г ~ 
fc = 0K + 1
Имеем (бином Ньютона)
^Cnxk = (x+Qn .	(2.27)
/с=0
- 39 -
Это равенство также пример производящей функции: производящей
функцией последовательности С'°, Ск . . . Ск ,    , С™ ,0,0... является
функция (1 + ж)". Можно также написать
Ск = coefV (ж + 1)" .
(2.28)
Интегрируя левую часть соотношения (2.27), получаем
/х. п	п	х	П	£
£ Ск tkdt = ^ Сп tkdt = Z скп
0 к=()	к=() q	к=()
Для правой части имеем
+ 1)" dt =
(ж + 1)"+1 - 1
п + 1
Таким образом,
Подставляя в полученное равенство ж = 1, находим
2„+i _ х
п + 1
Замечание. Формула бинома Ньютона (2.27) справедлива для про-
извольного вещественного показателя степени п = a G R, если в
качестве биномиальных коэффициентов использовать числа
,к = а (а — 1) . . . (а - fe + 1)
а	k\
£с1ж* = (1 + ж)
к = ()
(2.29)
(2.30)
- 40 -
Эта формула весьма общего характера: нз нее многие рассмотрен-
ные нами производящие функции получаются как частные случаи. Во-
первых, классическая формула бинома Ньютона (2.27) получается нз
(2.30) при а = п, так как нз (2.29) видно, что С^ = 0 при k > п.
Во вторых, полагая а = —(т + 1) н заменяя х на —х ; приходим
к формуле (2.26) для сочетаний с повторениями.
разбираемом ниже, мы используем формулу (2.30)
Наконец, в примере,
Свертка
Пусть А = (Ло , Al ,А2,.. ,,А„,...) н В = (B0,Bi,B2,.. .,Вп,...)
— две последовательности. Их сверткой называется последователь-
ность С = (С'о , С'1 , С2 , . . . , Сп ,   •), — элементы которой вычисля-
ются по правилу
С'о = Ад Bq
С'1 = Aq Во + Ao Bq
С2 = Ао В2 + Ао Во + А2 Во
Сп =	' Ао Вп _
i = 0
Операция свертки является основной в цифровой обработке сигналов:
после свертывания последовательности отсчетов сигнала со специально
подобранной последовательностью происходит фильтрация — усиление
одних частот н подавление других.
Свертка обозначается звездочкой: С = А * В.
5° . Производящая функция свертки равна произведению произво-
дящих функций свертываемых последовательностей.
С = А * В => С(х) = А(х) В(х) .
Действительно, при перемножении А(х) н В(х) n-я степень пере-
менной х складывается нз всевозможных произведений АохгВп_охп~г,
в которых первый сомножитель нз А(х), а второй нз В (ж).
- 41 -
Пример 3.
А(Ж) = (1 + ЖГ = ЕС>!
2 = 0
п
в(Ж) = (1 + Ж)" = Е^^
j=o
m-j-n
С(х) = (1 + хГ+п = Е Скт+п Хк .
к = 0
Следовательно,
k
усгтск~г = ск.	(2.31)
i = 0
(формула Вандермонда).
Производящие функции используются для решения рекуррентных
соотношении. Покажем это на двух примерах.
Число расстановок скобок
Возвратимся к примеру 2 этого параграфа, где мы установили фор-
мулу (2.9) для числа Dn расстановки скобок в неассоцпатпвном про-
изведении. Введем теперь производящую функцию
ОД = Е хп .
п = 1
Заменим коэфпцпенты Dn их выражениями пз рекуррентного
соотношения (2.9). Так как это соотношение имеет место, начиная с
п = 2, то первый член Dj х = х придется отделить от суммы:
ос /п —1	\
D(x) = Ж + Е ( Е Dn~k )ж" 
п = 2 \/с = 1	/
/п — 1	\
Последовательность	Dn~k представляет собой свертку
\fc=i	/
последовательности (Dn) с собой. В силу свойства 5° получаем
D(t) = х + .О2 (ж) .
- 42 -
Таким образом, D(x) можно найти как решение полученного квадрат-
ного уравнения:
П(т) = 7,(1- VI - 4т) .
(Перед корнем выбран знак минус, так как D(0) = 0). Чтобы найти
Dn, надо разложить в ряд правую часть (2.32). Для этого используем
формулу бинома Ньютона (2.30) с а = - :
(2.32)
Vi - 4ж = (1 - 4т)1/2 = ^2 С'Г/2 (-4т)" 
Найдем более удобное выражение для :
1 Г 1
2 \ 2
1
2
1 -3 •...•(2п—3)
Умножим числитель и знаменатель последней дроби на произведе-
ние последовательных четных чисел от 2 до 2п — 2 :
2 - 4-... • (2п -2) = 2"-1(п - 1)! .
Тогда
т ____
1/2 -
П-!	(2п —2)!	=	j
2" n! 2"-1(n — I)1.	1
Отсюда
Значит число расстановок скобок
Dn = соеФ^П(т) = -C'Z-, 
п ~
- 43 -
Линейные рекуррентные соотношения и производящие функции
Пусть последовательность А = (Ло, Ai,..., Ап, . . .) является реше-
нием линейного рекуррентного соотношенпя (2.10). Рассмотрим про-
изводящую функцию этой последовательности
А(х) = Ад + Ао х + ... + Ап хп + ... .
Будем обозначать начальные отрезки этого ряда
a.j (ж) = Aq + А-[ х + ... + Aj_i ж-7-1 , j = 1, 2,..., k, а0(ж) = 0 .
Заменим коэффициенты, начиная с k-ro, по формуле (2.10):
ос / к	\	к	ос
А(хj — (Lfe (жj -|-	I Q'j An_j I X — afc(x) Q'j Xj A.n—j X .
n=k \j=l	/	j=1	n=k
(2.33)
Внутреннюю сумму
5 c^n-j xn J = Ak_jXk J + . . . + Anxn + . . .
n=k
можно представить как A(x) — ak-j(x). Подставив в (2.33) получим
к
Л(ж) = ак(х) + 57 а-j xj (Л(ж) - ak_j(x')') .
j=i
Это уравнение, пз которого можно найти А(х)
4(а =	.	(2.34)
где
/с
Р(ж) = ак(х) — aj xJ ak_j(x) — многочлен, степени не
1=1
превосходящей k — 1 ;
<2(ж) = 1 — 0'1 Ж — ... — Ofc хк.
- 44 -
Сравнивая Q(x) с характеристическим многочленом Н(х) (см.
(2.20)), видим, что
Q(x) = хк Я(1/ж) .
Если
Н{х) = (х — АД®1 (х — As)62 ... (ж — Аг)вг ,
то
Q(x') = (1 — Ai ж)®1 (1 — Л2 ж)62... (1 — Аг ж)®г .
Раскладывая дробь (2.34) на простые, получаем
А(х) = У f, С\е' '
“Д \(1 - Аг Ж)
где C’ij — константы.
Используя степенные ряды (2.26) для этих простых дробен, полу-
чим
н, собирая коэффициент при хп, убеждаемся, что Ап = coeffxnA(x)
представляется как линейная комбинация функций
АГ ,т = 0,...,^-1;г=1,...,г.	(2.35)
Другими словами, функции (2.35) образуют базис в пространстве
решений линейного рекуррентного соотношения (2.10). В конце пара-
графа 2.3 было сформулировано без доказательства, что решения ли-
нейного рекуррентного соотношения (2.10) являются линейными ком-
бинациями функций
пт X™ , т = 0,..., е{ — 1 ; i = 1,..., г .	(2.36)
Ио легко видеть, что функции (2.35) линейно выражаются через функ-
ции (2.36). Например,
Таким образом, аппарат производящих функций позволил полно-
стью обосновать процедуру решения линейных рекуррентных соотно-
шений, сформулированную в конце параграфа 2.3.
- 45 -
Глава 3
Теория графов
3.1. Основные определения
Если необходимо представить в наглядной форме систему взаимо-
связанных объектов, прибегают к такому построению: на плоскости
нлн в пространстве выбирается несколько точек п некоторые пары то-
чек соединяются лпнпямп.
Объект, который получается в результате указанного построенпя,
называется графом. В качестве примеров можно указать блок-схему
алгоритма, граф соедпненпй в электрической схеме, сеть путей сооб-
щения п др.
Одну п ту же систему объектов п связей между нпмп можно по-
разному пзобразпть, применяя указанное выше построенпе: различным
образом располагать точки, в качестве соедпняющпх пх лпнпй брать
те нлн пные кривые п т.д. Более того, можно вообще не рисовать, а
указать систему связей объектов в какой-лпбо пной форме, напрпмер, в
словесной. Это рассужденпе показывает, что необходимо определенпе
графа, как некоторого формального объекта, который можно разными
способамп представлять наглядно.
Определенпе графа
Говорят, что задан конечный неориентированный граф, еслп за-
даны следующие два объекта:
1) конечное множество X = {яд, х?,   , ж„}, элементы этого мно-
жества называются вершинами графа;
2) некоторое множество неупорядоченных пар элементов пз X,
это множество обозначается U, его элементы, то есть пары вершпн,
называются ребрами.
Тот факт, что граф определяется парой множеств X п U, записы-
вают в впде G = (X, U). Прп наглядном представленпп графа вершпны
изображаются точками, ребра — лпнпямп, соедпняющпмп точки.
Пример. G = (X, U), где
X = {яд, Т'2, т.3, ЯД, ЯД, Яд), U = {{яд, X?}, {яд, Т'з}, {яд, Х4}, {яд, Яд}} .
В наглядной форме этот граф представлен на рпс. 3.1,а.
- 46 -
Рис. 3.1
Наряду с введеным определением графа возможны и другие. Так,
напрпмер, иногда возникает необходимость рассматривать графы, в
которых одну и ту же пару вершин соединяет несколько ребер. Такие
графы называются му.льтиграфами. Рассматриваются также графы,
в которых некоторые ребра могут иметь совпадающие концы. Такие
ребра называют петлями. В большинстве приложении теории графов
можно отбрасывать петли и заменять кратные ребра одним ребром.
Поэтому в дальнейшем данное выше определенпе будет основным и сло-
вом ’’граф” будет обозначаться конечный неориентированный граф без
петель н кратных ребер.
Ориентированные графы
Понятие ориентированного графа возникает, если ребрам графа
придать направление, ориентацию, так что один нз концов ребра будет
началом, а другой — концом.
Говорят, что задан ориентированный граф, если указаны два объ-
екта:
1) непустое конечное множество X — вершины графа;
2) множество U, составленное нз упорядоченных пар вершин.
Элементы множества U называют дугами. Дуга ориентирован-
ного графа изображается отрезком со стрелкой (рнс. 3.2).
(Ж1, Х2)
(ж2, Ж1)
Рнс. 3.2
- 47 -
Пример. Пусть X = {жд, жд, ж.з, жд, Ж5}, a U = {(ад, жд), (жд, т.з),
(ж'4, ж.з), (ж.5, Ж4), }. Граф G = (X, U) показан на рис. 3.1,6.
Пусть дан граф G = (X, U). О ребре и = {ж, у} этого графа
говорят, что оно соединяет вершины ж и у. Вершины, соединен-
ные ребром, называют смежными. О ребре и = {ж, у} и вершине
ж говорят, что они инцидентны, то же можно сказать о ребре и н
вершине у.
В дальнейшем будем стандартно обозначать число вершин графа
буквой п, а число ребер — буквой т : |Х| = п, |U| = т. Это
основные числовые характеристики графа.
Число ребер, инцидентных данной вершине ж, называется степе-
нью этой вершины н обозначается <т(ж). Вершина, у которой степень
равна нулю, называется изолированной ; вершины, имеющие степень,
равную единице, называют висячими. Например, вершины жд н Ж5
на рнс. 3.1,а висячие, вершина ж-g —изолированная.
Справедливы следующие два простых утверждения:
-	сумма степеней всех вершин графа равна удвоенному числу ребер;
-	число вершин, имеющих нечетную степень, четно.
Для ориентированных графов вместо степени вершины вводят по-
нятия полустепеней: полустепень захода <т_|_(ж) — это количество
дуг, входящих в вершину ж, т.е. направленных стрелкой'к вершине;
полустепень исхода <Т-(х) —это количество дуг, выходящих нз вер-
шины ж.
Граф, не имеющий ребер (X = ф ), называется пустым. Все вер-
шины пустого графа изолированные. Граф, в котором каждая пара
вершин соединена ребром, называется полным. Полный п -вершинный
граф обозначается Кп, для каждой его вершины ж имеем <т(х) = п— 1
( рнс. 3.3 ).
К$	К4	К5
Рнс. 3.3
- 48 -
Подграфы
Пусть дан граф G = (X, U). Удаляя нз графа некоторые ребра и
вершины, будем получать подграфы исходного графа.
Граф Gy =	называется подграфом графа G = (X, U),
если Ху С X и U-у С U.
Граф Gy = (Ху,Uy) называется остовным подграфом графа G =
(X,U), если Ху = X и Uy CU. Остовный подграф получается, если
в графе G удалить часть ребер, не трогая вершин.
Матрица смежности
Не всегда удобно задавать граф в том виде, как это указано в опре-
делении. Например, при обработке графа на ЭВМ его удобно предста-
влять в матричной форме.
Пусть дан граф (ориентированный граф) G = (X, U) н |Х| = п.
Занумеруем вершины графа числами 1,2,...,п. Рассмотрим п х п-
матрнцу R = (r'ij), элементы которой определяются по следующему
правилу: ryj = 1, если {г, J} £ U, в противном случае ryj = 0.
Матрица R называется матрицей смежности вершин графа G.
Для случая графа эта матрица симметрична н имеет нули на диагонали.
Пример.
Для графа, изображенного
на рнс. 3.4, матрица смежности
такова:
/°
1
R= 1
0
\1
1 1 0 1\
0 10 0
10 11
0 10 1
0 110/
Число единиц в какой-либо строке матрицы смежности равно сте-
пени соответствующей вершины.
Рнс. 3.4
- 49 -
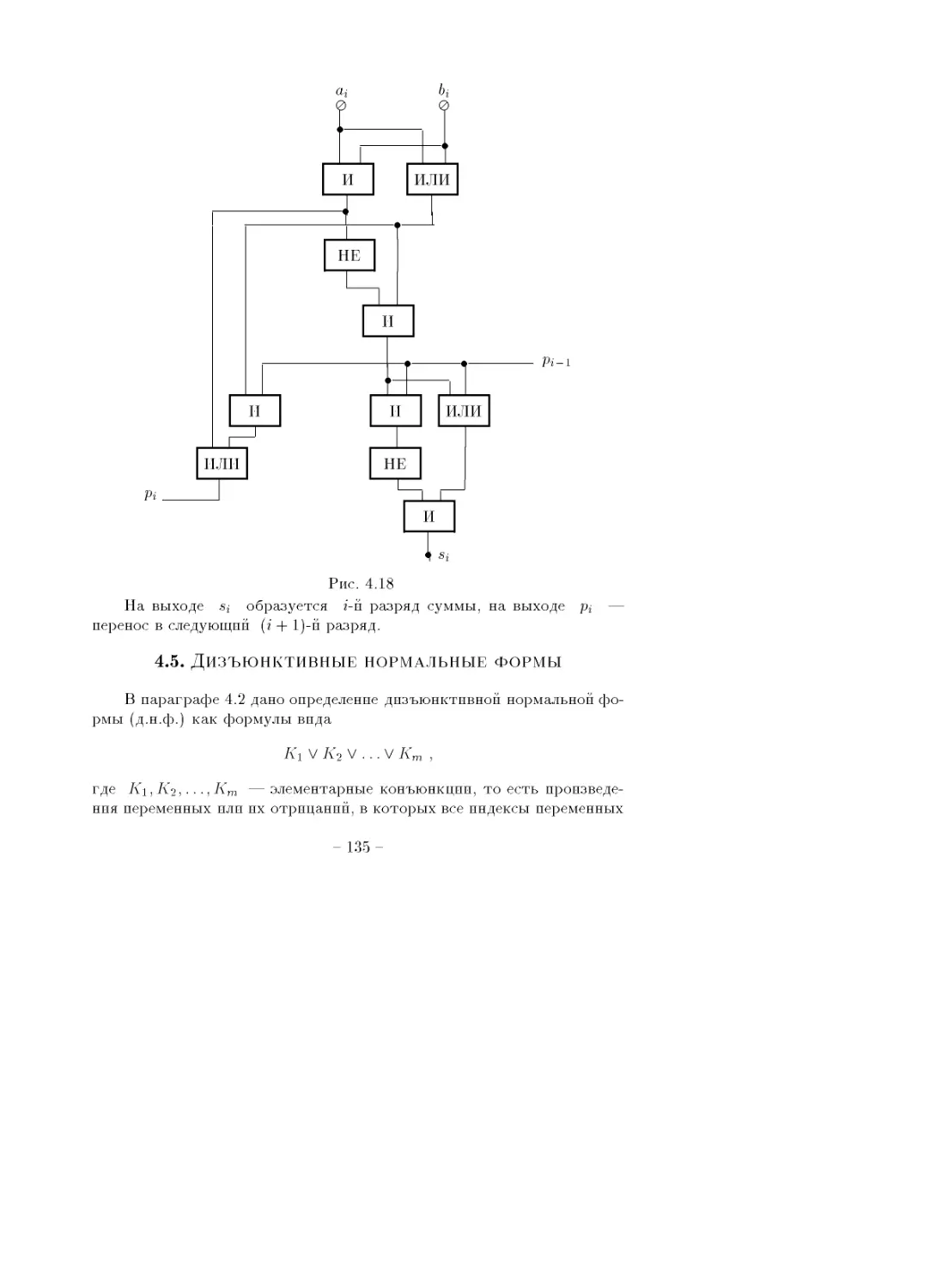
Изоморфизм графов
Ири введении какого-либо математического понятия всегда дого-
вариваются, какие объекты считаются одинаковыми и какие необхо-
димо различать. Изоморфные объекты — это такие объекты, которые
в дальнейшей теории не различаются н рассматриваются как один объ-
ект. Например, два графа, показанные на рнс. 3.5, отличаются только
обозначением вершин н способом размещения на плоскости.
Рнс. 3.5
Если во втором графе переобозначить вершины по схеме
а — 1 , b — 2 , с — 3, <7 — 4 ,
то множества вершин н ребер в первом н во втором графах совпадут н
получится один н тот же граф.
Графы G = (X, U) н Gi = (JVi, tZi) называются изоморфными,
если между множествами нх вершин можно установить взаимно одно-
значное соответствие, такое, что любые две вершины смежны в одном
нз графов в том н только в том случае, когда соответствующие нм
вершины смежны в другом графе.
Пример. Графы, показанные на рнс. 3.6, изоморфны.
Рнс. 3.6
- 50 -
3.2. Связность ГРАФОВ
Пусть G = (X, U) — граф. Конечная последовательность вершин
и ребер графа
Т0М1Т1М2Ж2 . . . T/-1W/T/ ,	(3-1)
в которой каждое м; есть ребро, соединяющее вершины и тд,
называется маршрутом на графе G.
Говорят, что маршрут (3.1) соединяет вершины xq н ж/. Чи-
сло / называют длиной маршрута. Таким образом, длина — это коли-
чество ребер, входящих в маршрут. Маршрут называют замкнутым,
если xq = xi.
Маршрут, в котором все ребра различны, называется цепью.
Замкнутая цепь называется циклом.
Цепь называется простой, если все ее вершины различны. Простой
цикл — это цикл, в котором все вершины, кроме первой'н последней)
различны.
Пример. В графе, показанном на рнс. 3.7,
X1U3X3U3X1U3X3U2X2U4X4U5X3U3X1 — маршрут;
Ж1МзТзМ2Ж2М4Т4М5Т.зМ7Т5 — цепь;
T1M1T2W4T4M6T5 —простая цепь.
Пусть в графе имеется маршрут, соединяющий вершины а н h.
Если часть маршрута вида
- 51 -
содержащую дважды вершину ж , заменить на
. . . х . . . ,
то в результате преобразования снова получится маршрут, соединяю-
щий вершины а и h. Применяя такое преобразование несколько раз,
можно удалить пз маршрута повторяющиеся вершины. Следовательно,
если в графе существует маршрут, соединяющий вершины а и Ь, то
существует и простая цепь, соединяющая те же вершины.
Компоненты связности
Граф называется связным, если любые две его вершины можно со-
единить цепью.
Рассмотрим произвольный граф G = (X,U), пусть жд £ X
— некоторая его вершина. Обозначим через Ад множество вершин
графа, которые можно соединить цепью с вершиной жд. Если данный
граф связный, то Ад = X, в противном случае АДАд 0 0 . Очевидно,
что в графе G нет ребер {ж, у}, соединяющих некоторую вершину
ж £ A'i с некоторой вершиной у нз А'\ Ад : в противном случае цепь,
соединяющую жд с ж, можно было бы продолжить до вершины у.
Обозначим через Ui множество ребер графа G, оба конца которых
принадлежат множеству Ад.
Пусть G'i = (A'i, Ид). Тогда Gi —связный граф. Действительно,
пусть ж £ Ад н у Е Ад. Соединяя цепь от ж к жд с цепью от жд к
у, получим маршрут, соединяющий ж н у. Как было отмечено выше,
этот маршрут можно преобразовать в цепь.
Повторим приведенное выше построение для некоторой вершины
ж2 £ X \ A'i н построим граф G? = (X^U^), обладающий теми же
свойствами, что н G\ , то есть связный н такой, что любое ребро исход-
ного графа либо соединяет вершины нз Х? , либо соединяет вершины
нз Х\Х2.
Если множество A'i U Ад не исчерпывает всех вершин исходного
графа, продолжим построение для вершины ж.з £ X \ (A'i U А'2) н так
далее. В результате для некоторого р будут построены связные графы
Gi = (Xi, Hi) , G2 = (Х2, &2)    Gp = (Хр, Up),
- 52 -
такие, что
X = XL U Х2 U . . . U Хр , X, П Х3 = 0 (г' 0 j) ;
и = Ur и гл и... и ир, иг п и3 =ф Цф j) .
Другими словами, графы Gi,i = 1, . . ,,р связны, не имеют общих
вершин и ребер, а каждая вершина и каждое ребро исходного графа
принадлежит одному пз этих графов.
Графы Gi, G2,   , Gp называются компонентами связности
графа G. Число р — еще одна числовая характеристика графа. Для
связного графа р= 1, если граф несвязный, то р >Д2.
Если данный граф не является связным н распадается на несколько
компонент, то решение какого-либо вопроса относительно этого графа,
как правило, можно свести к изучению отдельных компонент, которые
связны. Поэтому в большинстве случаев имеет смысл предполагать,
что заданный граф связный.
Метрика графа
Пусть дан связный граф G = (X,U). Расстоянием между двумя
вершинами х н у графа G будем называть наименьшую нз длин
цепей, связывающих эти вершины (напомним, что длина цепи — это
количество ребер в ней). Расстояние обозначается с1а(х,у) нлн, если
ясно, о каком графе идет речь, просто d(x, у).
Нетрудно проверить, что введенное расстояние удовлетворяет из-
вестным аксиомам метрики:
1)	d(x, т/) > 0 ; d(x, у) = О <==> х = у ;
2)	d(x, у) = d(y, х) ;
3)	d{x, у) < d(x, z) + d{z, у).
Диаметром графа называется величина
d(G) = тах<7(ж,?/) ,
где максимум берется по всевозможным парам вершин графа.
Определим для каждой вершины х графа G величину
)?(т) = тах<7(ж,?/) ,
- 53 -
т.е. расстояние от х до самой далекой от нее вершины графа. Ми-
нимум этой величины по всем вершинам графа называется радиусом
графа G :
r(G) = min г (ж) = min max <7 (ж, у) .
Вершина xq, в которой достигается этот минимум: г(жо) = r(G) ,
называется центральной.
Пример. Найти диаметр и радиус для графа, показанного на рис. 3.8.
Рис. 3.8
Для решения этой задачи удобно предварительно вычислить так
называемую матрицу расстояний между вершинами графа. В данном
случае это будет матрица размера 9x9, в которой на месте (г, j)
стоит расстояние от вершины г до вершины j' :
/°	1	1	2	2	3	3	3	з	3\
1	0	1	2	1	2	2	2	з	3
1	1	0	1	1	2	2	2	2	2
2	2	1	0	2	3	3	2	1	з
2	1	1	2	0	1	1	1	2	2
3	2	2	3	1	0	2	1	2	з
3	2	2	3	1	2	0	1	2	3
3	2	2	2	1	1	1	0	1	3
\3	3	2	1	2	2	2	1	0	3/
Согласно определению, диаметр равен наибольшему элементу ма-
трицы расстояний. Таким образом, для рассматриваемого графа он
- 54 -
равен трем. Для вычисления радиуса находим в каждой строке ма-
трицы расстоянии наибольшее число ( эти числа выписаны справа от
черточки). Наименьшие нз них дают значения радиуса: г = 2. Вер-
шины 3-я и 5-я являются центральными.
Задача о кратчайшей цепи
При вычислении расстоянии между вершинами графа необходимо
решать следующую задачу:
в связном графе G заданы две вершины а н h ; найти цепь
наименьшей длины (кратчайшую цепь}, связывающую а с Ь.
Имеется простои алгоритм решения этой задачи. Он состоит в
последовательном присвоении вершинам графа целочисленных отметок;
отметка любой вершины оказывается равной длине кратчайшей цепи
между этой вершиной и вершиной а.
Перейдем к описанию алгоритма. Пометим вершину а отмет-
кой ”0”. Все вершины, смежные с вершиной а, пометим отметкой
”1”. Непомеченные вершины, смежные с вершинами, имеющими от-
метку ”1”, пометим двойкой, смежные с ними — тройкой и так далее,
пока не будет помечена вершина h. Допустим, что вершина h полу-
чила отметку k. Возвращаемся от h к а , отыскивая последовательно:
смежную с h вершину к*-!, имеющую отметку k — 1, смежную с
Tfc_i вершину Tfc_2, имеющую отметку А- —2, и т.д. до тех пор, пока
нз некоторой вершины яд с отметкой ”1” не придем в вершину а.
Цепь а — яд — ... —	— b искомая, она имеет длину k.
На рнс. 3.9 показаны отметки, которые получают вершины в про-
цессе работы алгоритма.
Так как вершина h получила отметку ” 7”, то длина кратчайшей
- 55 -
цепи от а до h равна семи. Эта цепь выделена на рисунке.
Замечание. Описанный выше алгоритм иногда называют волновым:
процесс расстановки отметок напоминает распространение возмуще-
ния, которое возникает в вершине а и движется со скоростью одно ре-
бро в единицу времени; вершины, имеющие одинаковые отметки, пред-
ставляют собой фронт волны.
Рассмотрим обобщение задачи о кратчайшей цепи.
Задача о кратчайшей цепи в графе с нагруженными ребрами
Поставим в соответствие каждому ребру и графа G = (X, U) це-
лое неотрицательное число /(м) н будем называть его длиной ребра и.
Объект, который при этом получается, называют графом с нагружен-
ными ребрами, он обозначается G = (X,U,l). Длиной цепи в таком
графе назовем сумму длин входящих в цепь ребер н вновь рассмотрим
задачу об отыскании цепи наименьшей длины между двумя заданными
вершинами а н Ь.
Как н предыдущий, алгоритм решения этой задачи состоит в вы-
числении по определенным правилам числовых отметок вершин. От-
метку вершины х будем обозначать Аж, кроме того, для длины ребра
ы={ж,у} наряду с обозначением 1(и) будем использовать обозначение
1(х, у).
После окончания процесса вычисления отметок они должны удовле-
творять определенным требованиям - условиям оптимальности. Эти
условия сформулированы в следующем утверждении.
Утверждение.Предположим, что в графе с нагруженными ребрами
G = (.V. U,/) каждой вершине х Е X приписана отметка Хх так,
что выполнены следующие условия
1°. Аа = 0 ;
2°. Для каждого ребра и = {ж, у} Ху — Хх < /(ж, у) ;
3°. Для каждой вершины у найдется смежная с ней вершина
х, такая что
Ху - Хх = 1(х, у) .
Тогда
-	длина кратчайшей цепи между вершинами а и h равна Хь ;
- 56 -
-	сама кратчайшая цепь проходит по вершинам
а = Xq —> Xi —> Z'2 —> . . . —> £fc-l —> Xk = b ,	(3.2)
таким что Xx — Xx _t = /(xj_i, xj) , j = 1, 2,..., k .
Для доказательства заметим, что цепь (3.2), о которой говорится
в утверждении, можно построить, используя свойство 3°. Для этого
надо, начав с вершины b = жд, найти смежную с ней вершину Xfc-i,
для которой
Хь Хх^_г — /(х^ — хД) ,
Далее найти смежную с Xfc-i вершину Xfc-2, для которой выпол-
няется 3°, то есть разность отметок вершин Xfc-i н Xfc-2 равна
длине соединяющего нх ребра. Построение продолжаем до попадания
в вершину а.
Длина построенной цепи равна
I(а, х Д -|- /(х 1, xq) -|- . . . -|- I(хс_ 1,6) —
= Хх 1 — Ха + АЖ2 — АЖ1 + ... + А^ — AI.fe_1 = At, — Ха = At .
Покажем, что длина любой другой цепи между вершинами а н b не
меньше, чем А/,. Пусть
а = Уо У1 У2	ys-i ys=b
(3.3)
произвольная из таких цепей.
В силу свойства отметок 2° для ребер цепи (3.3) выполняются
неравенства	АУ1 - Ха < 1{а, ух) - АУ1 < 1(.У1,У2)
Ays_t - Ays_2 < l(ys_2,ys-i)
Аь - А,Л_ < l(ys-i,b) .
Сложив эти неравенства, получим
Хь < 1{а, yi) + l(y-i, У2) + . . . + l(ys-2,ys-i) + l(ys-i,b) ,
- 57 -
то есть длина цепи не меньше, чем А/,.
Утверждение доказано.
Описываемый далее алгоритм Дейкстры обеспечивает присвоение
вершинам графа отметок, удовлетворяющих 1° — 3°.
Алгоритм состоит нз двух этапов:
-	начальная расстановка отметок и
-	циклически повторяющаяся процедура исправления отметок.
На каждом шаге алгоритма все отметки делятся на предваритель-
ные и окончательные. Алгоритм обрабатывает только предваритель-
ные отметки и заканчивает работу, когда все отметки станут оконча-
тельными.
Описание алгоритма Дейкстры.
Начальная расстановка отметок. Полагаем
Ха = 0, Хх = ос (ж а).
Все отметки объявляем предварительными.
Исправление отметок. Средн всех предварительных отметок нахо-
дим наименьшую. Пусть это отметка Хх вершины х. Для каждой
вершины у, смежной с х и имеющей' предварительную отметку, ис-
правляем Ху по следующему правилу
Ху = min{Ay, Хх +1(х,у)} .
После исправления отметок всех смежных с х вершин объявляем от-
метку вершины х окончательной'.
Как видно нз описания, каждый шаг исправления отметок делает
одну нз них окончательной. Таким образом, шаг исправления отме-
ток будет выполняться п раз, где п — число вершин графа. Без
труда проверяется, что окончательные отметки удовлетворяют усло-
виям оптимальности 1° — 3°.
Кратчайшая цепь строится, как это описано выше.
Пример. Для графа, изображенного на рнс. 3.10,
- 58 -
3
14
12
6
Рис. 3.10
18
показаны окончательные отметки и кратчайшая цепь.
3.3. ЦИКЛОМАТИКА ГРАФОВ
Цикломатика - это изучение циклов в графе. Чем больше в графе
циклов, тем запутаннее он выглядит. Цель этого параграфа навести
порядок в множестве циклов.
Задача об эйлеровом цикле
Одной пз первых задач теории графов, возникшей в трудах выда-
ющегося математика XVIII в. Л.Эйлера, была задача о кенигсбергских
мостах. Город Кенигсберг (Калининград) расположен на реке, через
которую имеется семь мостов (рис. 3.11).
b
Рис. 3.11	Рис. 3.12
- 59 -
Популярной головоломкой средн жителей города была такая: как
обойти все мосты, проходя по каждому не более одного раза ? На
языке графов эта задача формулируется так: можно лп в мультиграфе,
показанном на рнс. 3.12, обойти все ребра, проходя по каждому ровно
одни раз ?
Эйлеровым циклом (цепью) в мультиграфе G называется цикл
(цепь), содержащий все ребра мультпграфа. (Напомним, что, согласно
определению, каждое ребро может входить в цепь не более одного раза).
В одно время были распространены головоломки на тему: можно
лп данный рисунок выполнить, не отрывая карандаша от бумаги п не
проводя никакую линию дважды ? Это тоже задача об эйлеровом ци-
кле; она имеет практическое прпложенпе, как задача мпнпмпзацпп хо-
лостого хода пера графопостроителя.
Теорема.Мультиграф обладает эйлеровым циклом в том и только в
том случае, когда он связный и все его вершины имеют четные сте-
пени.
Необходимость. Пусть мультиграф G обладает эйлеровым циклом.
Поскольку в этот цикл входят все ребра мультпграфа, то в нем встреча-
ются п все его вершины. Следовательно, любые две вершины соединены
цепью.
Рассмотрим произвольную вершину х п выделим все ее вхождения
в эйлеров цикл:
. . . W1TW2 . . . W3TW4 . . . U2k-lXU2k   
Очевидно, что «j, 112, ... «2*-1, W2fc — это п есть все ребра мультпграфа
G, инцидентные вершине х. Таким образом, <т(х) = 2k.
Достаточность. Покажем, что если мультиграф связный п степени
всех вершин четны, то он обладает эйлеровым циклом. Доказательство
будем вести индукцией по числу т ребер в мультиграфе.
Имеется всего одни мультиграф с т = 2, удовлетворяющий усло-
виям теоремы (рнс. 3.13), п он, очевидно, обладает эйлеровым циклом.
Рнс. 3.13
Предположим, что теорема верна для всех мультпграфов с числом
ребер, меньшим т, п рассмотрим мультиграф G с т ребрами.
- 60 -
Будем строить обход ребер мультиграфа G в достаточной степени
произвольно, следя лишь за тем, чтобы не проходпть ребро дважды:
начнем с произвольно выбранной вершины а, возьмем какое-нпбудь
ребро, пнцпдентное вершине а, отметпм его как пройденное п перей-
дем в другой конец этого ребра. В дальнейшем действуем однотипно:
попав в некоторую вершину, выбираем наудачу одно пз пнцпдентных
этой вершине непройденных ребер, отмечаем его п переходпм в другой
его конец. На некотором шаге такого построения обнаружится, что
дальше двигаться нельзя: все ребра, пнцпдентные вершине, до кото-
рой дошло построение, отмечены как пройденные. Утверждается, что
такой вершиной может быть только начальная вершина а. Это очевид-
ным образом вытекает пэ того, что степень каждой вершины четная.
Такпм образом, пройденные ребра образуют некоторый цпкл, обо-
значим его /У. Еслп этот цпкл содержит все ребра мультпграфа G,
то он п есть эйлеров. Рассмотрим, как действовать в случае, когда
осталпсь непройденные ребра. Удалив пз G все пройденные ребра,
получпм мультпграф G', в котором по-прежнему все вершины пмеют
четную степень, но он будет несвязным. Пусть G'Y, . . ,Gp — компо-
ненты связности G', пмеющпе более одной вершины. Так как каждая
пз компонент представляет собой связный мультпграф с четными сте-
пенями вершин п с чпслом ребер, меныппм т, то по предположению
пндукцпп она обладает эйлеровым цпклом. Обозначим эйлеровы цпклы
компонент Ц1, . . .ц'. Заметим также, что первоначально построенный
цпкл //' заходпт в каждую пз компонент, т.е. в каждом мультпграфе
G' можно найтп вершину яд, через которую проходпт цпкл //'. Это
вытекает пз того, что после добавления к несвязному мультпграфу G'
ребер цпкла //' получается связный мультпграф G.
Эйлеров цпкл мультпграфа G строптся теперь следующим обра-
зом: в цпкле //' находпм первую вершину яд, входящую в одну пз
компонент G'x,...G'p : яд £ 6д. Включаем в цпкл //' цпкл ц' (то
есть заменяем вершину яд последовательностью ц' = яд... яд. ) В
оставшейся частп цпкла //' снова находпм первую вершину яд, входя-
щую в одну пз компонент п включаем цпкл для этой компоненты. Так
действуем пока не будут включены все эйлеровы цпклы компонент.
Пример. В графе, показанном на рнс. 3.14, степени всех вершин
четные.
- 61 -
a
Рис. 3.14
Допустим, что на первом этапе рассмотренного выше алгоритма
построен цикл, показаннвш на рнс. 3.15.
а
Рнс. 3.15. Цикл // .
Непропденные ребра образуют несвязный граф, показаннвш на рнс.
Строим эйлеровы циклы компонент (рнс. 3.17).
- 62 -
Соединяя их при помощи цикла , получаем эйлеров цпкл поход-
ного графа (рнс. 3.18).
Рнс. 3.18
Дополненпя к теореме
1. Еслп связный мультпграф пмеет ровно две вершпны с нечетной
степенью, то он обладает эйлеровой цепью.
Действительно, временно добавим к мультпграфу новое ребро, со-
единяющее вершпны с нечетной' степенью; в результате степенп всех
вершпн станут четными. Построим в новом графе эйлеров цпкл, а за-
тем удалим добавленное ребро: цпкл разорвется п станет цепью. Эта
- 63 -
цепь начинается и заканчивается в вершинах нечетной степени.
2. В общем случае число вершин мультнграфа, имеющих нечетную
степень, равно 2s (оно всегда четно). Все ребра такого мультнграфа
можно включить в s ценен. Другими словами, мультнграф можно
нарисовать, s—1 раз отрывая карандаш от бумаги. Обоснование этого
факта такое же, как н выше: добавляем новые s ребер, соединяющие
пары вершин с нечетной степенью, строим эйлеров цикл, удаляем новые
ребра.
Цикловые ребра н перешейки
Пусть задан граф G = (X, U). Ребро графа, через которое прохо-
дит хотя бы один цикл, назовем цикловым ребром. Ребро, которое не
входит нн в один цикл, будем называть перешейком.
Пример. В графе, изображенном на рнс.3.19, ребра и± н и? —
перешейки, остальные ребра цикловые.
Рнс. 3.19
Лемма. При удалении из связного графа циклового ребра он остается
связным. При удалении из связного графа перешейка граф распадается
на две компоненты.
Действительно, если удаляемое ребро {a,h} цикловое, то после
его удаления вершины а н h по-прежнему можно соединить цепью —
остатком цикла, в который входило ребро {а, Ь}. Отсюда вытекает,
что н любые две вершины графа после удаления ребра {a, h} оста-
ются связанными цепью. Напротив, если {a, h} — перешеек, то после
его удаления вершины а н h нельзя связать цепью, иначе эта цепь
вместе с ребром {a, h} образует цикл в исходном графе. С другой
стороны, каждая вершина остается связанной либо с вершиной а, либо
с вершиной h.
Следствие. При удалении нз графа циклового ребра число связных
компонент графа не изменяется. При удалении перешейка число связ-
ных компонент графа увеличивается на единицу.
Цнкломатнческое число
Пусть дан граф G = (X, U) , |Х| = п , |[7| = т н пусть G имеет
р компонент связности.
- 64 -
Величина А = т — п + р называется цикломатическим числом
графа.
Теорема. Для любого графа цикломатическое число неотрицательно:
А > 0 .
Доказательство. Будем удалять пз графа по одному ребру и следить
за изменением величины А. Параметры исходного графа обозначим
т, п,р, те же величины после удаления ребра обозначим т', п',р'.
В процессе удаления ребер могут представиться два случая:
а)	удаляемое ребро цикловое. Тогда
т' = т — 1, п' = п, р' = р; X' = т' — п' + р' = А — 1.
б)	удаляемое ребро — перешеек. В этом случае
т' = т — 1, п' = п, р' = р + 1', X' = т' — п' + р' = А.
Итак, при удалении ребра величина А либо не изменяется, либо
уменьшается на единицу. После удаления всех ребер получится пустой
граф, в котором то = 0 , по = п , ро = п , т.е. Ао = 0. Следовательно,
в исходном графе А > 0.
Доказательство теоремы указывает на связь цпкломатпческого чи-
сла с наличием циклов в графе. Действительно, если А > 0, то в графе
есть, по крайней мере, один цпкл. При удалении циклового ребра не-
которые циклы разрываются, и это приводит к уменьшению А. Если
продолжать удаление ребер, то в конце концов разрываются все циклы
п А становится равным нулю. После этого А уже не изменяется, так
как все ребра стали перешейками.
Пример. Пусть требуется связать несколько населенных пунктов се-
тью дорог или телефонной сетью, вообще как-то связать друг с другом.
Предлагаемый проект показан на рис. 3.20,а.
Рис. 3.20
- 65 -
В дальнейшем потребовалось удешевить проект, в результате не-
которые связи были исключены (рис.3.20,б и 3.20,в).
В графе на рис. 3.20,в больше уже никакие связи исключить нельзя,
иначе граф перестанет быть связным и поставленная задача не будет
решена. Такого рода графы называются деревьями.
Деревья
Деревом называется связный граф без циклов. В следующей тео-
реме перечисляются свойства деревьев, каждое нз этих свойств полно-
стью характеризует дерево.
Теорема.Следующие определения дерева эквивалентны:
а) дерево - это связный граф без циклов;
б ) дерево - это связный граф, в котором каждое ребро является
перешейком;
в)	дерево - это связный граф, цикломатическое число которого
равно нулю;
г)	дерево - это граф, в котором для любых двух вершин имеется
ровно одна соединяющая их цепь.
Перечисленные утверждения несложным образом выводятся одно
нз другого по схеме а) => б) => в) => г) => а).
В силу свойства в) имеем т — п + 1 = 0 нлн т = п — 1, т.е. в
любом дереве число ребер на единицу меньше числа вершин.
Рнс. 3.21 некоторым образом объясняет название ’’дерево”. Выде-
лим в дереве некоторую вершину а (корень). Поскольку примыкающие
к ней ребра — перешейки, то после удаления любого нз них от дерева
отделяется компонента. На рисунке они обозначены Т\, . . .Ti~. Каждая
нз этих компонент также является деревом.
- 66 -
Остовное дерево графа
Рассмотрим связный граф н будем удалять нз него по одному ци-
кловые ребра до тех пор, пока их не останется. В результате получится
дерево Т = (X' ,U') такое, что:
1) X' = X, т.е. множество вершин дерева Т совпадает с множе-
ством вершин графа G ;
2) U' С U, т.е.каждое ребро дерева является в то же время ребром
графа G.
Любое дерево Т, удовлетворяющее условиям 1) н 2), называется
остовным деревом графа G.
Так как удаление цикловых ребер можно вести разными способами,
то один н тот же граф имеет, вообще говоря, много остовных деревьев.
Пример.
На рнс.3.22 показан граф G н три его остовных дерева.
Пусть в графе G выделено остовное дерево Т. Ребра графа, не
вошедшие в Т, будем называть хордами дерева Т.
Лемма.Каковы бы ни были остовное дерево Т и хорда h этого
дерева, в графе: G существует единственный цикл, содержащий хорду
h и не содержащий других хорд.
Доказательство. Пусть h = {а, Ь}. В дереве Т имеется единствен-
ная цепь, соединяющая вершины а н Ь. Присоединяя к этой цепи
ребро h, получаем требуемый цикл.
Задача о кратчайшей связывающей сети
Пусть G = (X, U, /) — нагруженный граф. Требуется построить
остовное дерево Т графа G, сумма длин ребер которого минимальна.
- 67 -
Этой задаче можно дать такую интерпретацию: п пунктов на
местности нужно связать сетью дорог, трубопроводов пли линии теле-
фонной связи. Для каждой пары пунктов i и j задана стоимость их
соединения — это и есть ’’длина” l(i, j) ребра {г,}} в данном слу-
чае. Требуется построить связывающую сеть минимальной стоимости,
ее называют кратчайшей связывающей сетью.
Очевидно, что кратчайшая связывающая сеть будет остовным де-
ревом графа G, при этом средн всех остовных деревьев она будет
иметь минимальную сумму длин входящих в нее ребер.
Алгоритм построения кратчайшей связывающей сети состоит нз
п — 1 шагов, на каждом шаге присоединяется одно ребро. Правило для
выбора этого ребра следующее: средн еще не выбранных ребер берется
самое короткое, не образующее цикла с уже выбранными ребрами.
Пример. В матрице С элемент, стоящий в г-н строке н j-м столбце,
указывает в условных единицах затраты, необходимые для того, чтобы
связать пункт г с пунктом j :
/-		5	6	2	1	7	5	4	6 \
	5	—	7	7	5	1	4	6	5
	6	7	—	5	6	6	2	5	4
	2	7	5	—	1	7	6	4	5
с =	1	5	6	1	—	5	6	3	7
	7	1	6	7	5	—	4	5	5
	5	4	2	6	6	4	—	6	2
	4	6	5	4	3	5	6	—	7
	\ 6	5	4	5	7	5	2	7	-/
Задача заключается в том, чтобы с наименьшими затратами свя-
зать все пункты друг с другом.
Применение сформулированного выше алгоритма выглядит так. В
матрице С отыскивается минимальный элемент. Он вычеркивается
нз матрицы, а соответствующее ему ребро зачисляется в сеть, если при
этом не образуется циклов. Эти действия повторяются. Таким обра-
зом, на первых пяти шагах работы алгоритма будут выбраны ребра
{1,5}, {2, 6}, {4, 5}, {3,7}, {7, 9}.
Пз оставшихся ребер минимальную длину имеет ребро {1,4}, но
в сеть оно не включается, так как образует цикл с уже выбранными
- 68 -
ребрами. На последующих этапах алгоритма в сеть будут включены
ребра {5, 8}, {2, 7} и {1,2}.
Для обоснования алгоритма предположим, что дерево Т, которое
он стропт, состопт пз ребер
ui , и2 ,	. . . , w„_i
/(мД < /(м2) < . . . < Z(un-1)
Рассмотрим любое другое дерево Т', п упорядочим его ребра по воз-
растанию длпн. Пусть первые к — 1 ребер дерева Т' такпе же, как
в дереве Т, а k-е ребро отличается от u* , (1 < к < п — 1). При-
соединим к дереву Т' ребро и/., тогда возникнет цпкл, в который
входят ребро Mfc п какпе-то ребра пз дерева Т'. Средн этпх послед-
них обязательно найдется ребро и, длпна которого не меньше, чем
длпна ребра Uk : пначе ребро Uk образовало бы цпкл с ребрамп
меньшей длпны, что исключается правилом выбора очередного ребра
в рассмотренном алгоритме. Удалпм пз дерева Т' ребро и, заме-
нив его ребром и*. В результате получпм дерево, длпна которого не
больше, чем длпна дерева Т'. Аналогичным путем вводпм в дерево
Т' ребра . . ., м„_1, прп этом всякий раз длпна дерева не уве-
личивается. Это означает, что дерево Т, построенное по алгоритму,
действительно, кратчайшее.
Пространство циклов. Система базисных циклов
Пусть дан граф G = (X, U) , |К| = тп. Занумеруем в произвольном
порядке ребра графа: М1,...,мт. Напомним, что остовным подграфом
графа G называется граф G' = (X,U') с тем же множеством вершпн
п множеством ребер, которое является частью U : U' С U. Другпмп
словами, остовный подграф можно получпть, еслп пз графа G удалпть
некоторые ребра. Удобно поэтому, задавать остовный подграф прп
помощп двоичного слова а = ада2   -От, в котором нулп указывают,
какпе ребра удалены, а едпнпцы — какпе оставлены:
( 1, еслп щ Е U.'	.
6 ^«(G)=aia2...am,	= еслпМК, , г = 1,...,т.
(3.4)
Очевидно, что соответствие (3.4) является бпекцпей.
Пример. Слово 11... 1 задает исходный граф G, слово 00... О —
его пустой остовный подграф.
- 69 -
Двоичные слова длины т образуют векторное пространство над
полем пз двух элементов {0, 1 ;+, }, в котором операции определены
так
0 + 0 = 0 0+1=14-0=1 1+1 = 0
0-0 = 0-1 = 10 = 0 1-1=1.
Суммой слов aia'2   а'т и /?1/?2 • •  Дт в этом пространстве является
слово О1 + Д, 0'2 +	. om + Дт . Сумму двух слов можно также опре-
делить как слово, имеющее нули в тех разрядах, где разряды слагаемых
совпадают, и единицы там, где разряды слагаемых различаются.
В силу бнекцнн (3.4) мы можем не различать остовные подграфы н
соответствующие двоичные слова н говорить о пространстве остовных
подграфов графа G — это векторное пространство размерности т
над полем нз двух элементов. Сумму двух остовных подграфов G\ н
G2 будем обозначать G\ + СД. В силу указанной бнекцнн это остов-
ный подграф, задаваемый словом a(Gi) + аДСД), он состоит нз всех
тех ребер, которые входят ровно в один нз подграфов-слагаемых. Что
касается операции умножения на скаляр, то она в рассматриваемом про-
странстве тривиальна: умножение на 1 не меняет подграф, умножение
на 0 дает пустой подграф.
В качестве базиса в пространстве остовных подграфов можно взять
совокупность нз т однореберных подграфов. Им соответствуют дво-
ичные слова с одной единицей'.
В пространстве остовных подграфов выделим подпространство,
содержащее все циклы графа.
Остовный подграф называется квазициклом, если степень каждой
его вершины четна.
Всякий цикл является квазнцнклом. Приставка ’’квазн” означает
’’как бы”, ’’похожий на”. Из теоремы об эйлеровом цикле следует,
что кроме циклов, в число квазнцнклов входят подграфы, состоящие
нз нескольких компонент, каждая нз которых является циклом (необя-
зательно простым). Отметим также, что пустой подграф является ква-
знцнклом.
Лемма. Сумма двух квазициклов является квазициклом.
Доказательство. Пусть С\ н С'2 — квазнцнклы, покажем, что
C'i+C'2 тоже квазнцнкл. Рассмотрим произвольную вершину графа G.
- 70 -
Допустим, что в квазицикле Су к этой вершине примыкает 2ку ребер,
в квазицикле С? — “Ikyt ребер и пусть к ребер пз них общие для Су и
Су>- В сумму Ci С С? войдут ‘2ку — к ребер, входящих только в Су, и
‘2ку> — к ребер, входящих только в Су>, всего — 2(&i ку> — к) ребер.
Следовательно, степень рассматриваемой вершины будет четной, т.е.
Су С С'у — квазнцнкл.
Лемма показывает, что совокупность квазнцнклов так же является
векторным пространством над полем {0, 1}. Оно называется про-
странством циклов графа G. Ясно, что пространство циклов является
подпространством в векторном пространстве остовных подграфов.
В следующей теореме находится размерность н базис этого подпро-
странства.
Основная теорема.В графе G с цикломатическим числом X можно
найти X простых циклов Су,...,С\, со следующими свойствами:
1) любой квазицикл ( в частности, любой цикл ) можно предста-
вить в виде суммы некоторых циклов Су, ..., С\ ;
2) циклы Су, . . . ,СХ независимы, т.е. никакой из них нельзя вы-
разить в виде суммы через остальные.
Система векторов, удовлетворяющая условиям 1) н 2), называется
базисом, количество векторов в базисе называют размерностью соот-
ветствующего пространства. Поэтому совокупность циклов Су, . . ., С\
носит название системы базисных циклов графа G, а основную тео-
рему можно сформулировать так:
размерность пространства циклов графа
равна его цикломатическому числу.
Доказательство будем вести для связного графа G (система ба-
зисных циклов произвольного графа получается объединением систем
базисных циклов компонент). Так как G связный, то X = т — п Т 1.
Выделим в графе G какое-либо остовное дерево Т. В него входит
п — 1 ребро графа, остальные т — (п — 1) = X ребер графа являются
хордами этого дерева. Занумеруем ребра графа так, чтобы первые X
номеров получили хорды, а остальные — ребра дерева. Для каждой
хорды иу выполним следующее построение: присоединим хорду к де-
реву Т н построим цикл Су, состоящий нз хорды иу н цепи в де-
реве, соединяющей концы хорды. Построенные таким образом циклы
Су, . . ., С\ н образуют систему базисных циклов.
- 71 -
Чтобы в этом убедиться, выпишем для каждого из базисных циклов
соответствующее двоичное слово:
«(С'З = 1 0 0 ... О a-i.A+i   -а'1,т
а(С2) = 0 1 0 ... О а2,А+1   -а'2,т
а(С\) = 0 0 0 ... 1 ал,А+1   	
хорды ребра дерева
Никакой цикл Ci нельзя выразить через остальные: соответству-
ющее слово a(C'i) имеет единицу в г-м разряде, а у остальных слов в
этом разряде стоит нуль.
Рассмотрим далее произвольный квазнцнкл С и покажем, как
его представить в виде суммы базисных циклов. Пусть а(С') слово,
соответствующее С. Средн первых А разрядов этого слова найдем
все те, которые равны единице. Пусть Д, г2, . . ., ik — номера этих
разрядов. Рассмотрим квазнцнкл С = СД С С   . Ф С\к. Он имеет
единицы в тех же разрядах средн первых А, что и рассматриваемый
квазнцнкл С. Двоичные слова а(С') и а(С") совпадают в первых А
разрядах, следовательно, слово а(СсС') в первых А разрядах имеет
нули, то есть квазнцнкл С С С составлен только нз ребер дерева.
Учитывая, что любой квазнцнкл либо пустой, либо имеет компоненту,
являющуюся циклом, н тот факт, что в дереве нет циклов, заключаем,
что квазнцнкл С С С пустой нлн С С С = 0. Отсюда С = С, т.е.
С = СД ФС2 ф ...ФСД.
Теорема доказана.
Пример. Построим систему базисных циклов для графа G, показан-
ного на рнс. 3.22.
Выделим остовное дерево Т\ (рнс. 3.23,а).
6)
W1	U?
W.3	U4
Рнс. 3.23
- 72 -
Присоединяя к дереву по очереди хорды ui, и?, u^, 114, получаем 4
базисных цикла, показанные на рнс.3.24.
Рнс. 3.24
Для того же графа можно построить систему базисных циклов,
основываясь на дереве Т? (рнс.3.23,б). Действуя аналогично предыду-
щему, получаем базисные циклы, показанные на рнс.3.25.
Рнс. 3.25
Циклы одной нз систем можно выразить как линейные комбинации
циклов нз другой системы. Для этого надо действовать как указано
в доказательстве основной теоремы. Например, цикл С4 содержит
хорды «2 и U4 дерева Т), поэтому С4 = С'2  С4. В итоге получим
С'1
С'2
С3
С4
С\ ф С'2 Ф
С'2 Ф
ф
ф
ф
ф
с4
с4
с4
с4
Это знакомые по курсу линейной алгебры формулы перехода к но-
вому базису в векторном пространстве (в данном примере 4-мерном).
Матрица перехода
/1 1
о 1
о о
\0 1
1 1
О 1
- 73 -
невырожденная и имеет обратную
/1 1 0 0\
0 110]
0 10 1
\0 1 1 1/
которая является матрицей обратного перехода: от 6\, С?, б'з, 6'4 к
6\,С2,С3,С4 .
3.4. Транспортные сети
Слово ’’сеть” употребляют в тех случаях, когда в графе выделены
некоторые вершины. Выделенные вершины называют полюсами, ино-
гда полюсы делятся на входные и выходные.
Определенпе транспортной сети.
Транспортная сеть — это ориентированный граф G = (X, U), в
котором:
1) каждой дуге и приписано целое неотрицательное число с(и),
называемое пропускной способностью дуги;
2) выделены две вершины s н t. При этом в графе G нет дуг,
заходящих в вершину s, н нет дуг, выходящих нз вершины t. Эти
две вершины называются соответственно источником н стоком.
На рисунке 3.26 приведен пример транспортной сети.
Можно дать различные интерпретации транспортной сети. Пусть,
например, в вершине s имеется неограниченный' запас некоторого
- 74 -
продукта и нужно организовать доставку этого продукта в вершину
t по сети путей сообщения с промежуточными вершпнамп х,у, . . . .
Пропускная способность дуги — это количество груза, которое можно
перевезти в единицу времени по данной дуге. Тогда возникает задача:
организовать перевозки по сети таким образом, чтобы, не превышая
пропускных способностей дуг, перевозить пз s в t максимальное
количество груза в единицу времени.
Определение потока
Основным понятием теорий транспортных сетей является понятие
потока по транспортной сети.
Для каждой вершпны сети х будем обозначать символом Г/+
множество всех дуг, входящих в х, а символом U~ —множество всех
дуг, выходящих пз х. Для вершин s п t пмеем U+ = Г/Д = 0 .
Целочисленная функция ср, определенная на дугах сети, называ-
ется потоком, еслп выполнены следующие три условия:
ср(и) > 0 , (и G U) ;
^2	~ У2 = 0 , (ж £ X, х 0 s, х ;
ср{и) < с(и) , (и £ U) .
(3.5)
(3.6)
(3-7)
На рнс. 3.27 показан одни пз возможных потоков для сети, при-
веденной выше (см. рнс. 3.26). Каждой дуге приписываются (через
запятую) два числа: первое — пропускная способность дуги, второе —
значение потока.	„
Рнс. 3.27
- 75 -
Поток представляет собой план организации перевозок, при этом
<р(и) показывает, какое количество груза проходит по дуге и в единицу
времени. Это количество в силу условии (3.5) и (3.7) неотрицательно н
не превышает пропускной способности дуги. Условия (3.6) называются
уравнениями сохранения: количество груза, приходящего в какую-либо
вершину, равно количеству груза, выходящего нз нее.
Сложим все уравнения сохранения. Если оба конца дуги и отли-
чаются от s н от t, то член <р(и) в получающейся сумме встретится
дважды: со знаком ” —” в уравнении для одного конца дуги и н со зна-
ком ”+” — дяя другого. Отсюда следует, что после сложения останутся
только члены, соответствующие дугам нз U~ н :
52	~ 52	= 0 
иЕ Up	иЕ и +
Таким образом, для любого потока величина груза, выходящего нз
источника s, равна величине груза, прибывающего в сток t. Эту
общую величину обозначают Ф н называют величиной потока. Итак,
по определению
ф = 52	= 52	
u£Up	u£U+
Вообще говоря, потоков по данной транспортной сети может быть
много. Отметим, что всегда имеется нулевой поток:
у?(м) = 0 , и G U,.
Основная задача: для данной транспортной сети найти поток,
имеющий наибольшую величину.
Такой поток называется максимальным.
Для решения поставленной задачи необходимо предварительно изу-
чить специальные подмножества дуг сети, называемые разрезами. К
понятию разреза можно прнйтн, если разбить все множество вершин
(населенных пунктов ) на два района н рассмотреть дороги, ведущие
нз первого района во второй.
- 76 -
Разрезы
Пусть А С X — некоторое подмножество вершин сети, обладаю-
щее тем свойством, что s G А, а I А. Обозначая А = X \ А, имеем
s A, t £ А. Рассмотрим множество всех дуг сети, имеющих начало в
множестве А, а конец — в А.
Это множество дуг обозначается (А, А) н называется разрезом,
определяемым множеством вершин А.
Пример. Пусть в сети, приведенной на рнс.3.26, А = {.s, ж}, тогда
л = {?/,/}. п меем
(Л Д) = {(x,f), (s,y), (х, у)} .
Сумму пропускных способностей всех дуг, входящих в разрез, назо-
вем пропускной способностью разреза. Будем обозначать эту величину
с(А, А).
Замечание. Наряду с разрезом (А, А) далее рассматривается мно-
жество дуг (А, А). В него входят все дуги, имеющие начало в А , а
конец в А.
Лемма. Пусть ср — поток по транспортной сети, Ф — величина
этого потока, а (А, А) — некоторый разрез. Тогда
Ф < с(А, А) ,
т.е. величина любого потока не превосходит пропускной способности
любого разреза.
Доказательство. Рассмотрим уравнения сохранения (3.6) только для
вершин х G А н сложим все эти уравнения. Получится соотношение
вида
и
Коэффициенты еи в этом соотношении могут принимать значения
-1,0,1 н зависят от того как вершины х н у — концы дуги и = (х, у)
располагаются относительно множеств А н А, определяющих разрез.
На рисунке 3.28 показаны рассматриваемые ниже шесть случаев такого
расположения.
- 77 -
Рис. 3.28
1.	х Е А, х s, у Е А. В этом случае величина <р(и) входит в склады-
ваемые уравнения дважды: со знаком ”+” в уравнение сохранения
для вершины у, н со знаком ” —” для вершины х. Следовательно,
=0.
2.	х £ А, х s, у G А. В этом случае величина <р(и) входит только
в уравнение сохранения для вершины х, еи = — 1.
3.	х Е А, у Е А. В этом случае величина <р(и) входит только в
уравнение сохранения для вершины у, еи = 1.
4.	х Е А, у Е А. В этом случае величина <р(и) вообще не встречается
в складываемых уравнениях, еи = 0.
5.	х = s, у £ А. Величина <р(и) входит только в уравнение для
вершины у, еи = 1.
6.	х = s, у £ А. Величина <р(и) не встречается в складываемых
уравнениях, еи = 0.
Для дуг и шестого типа в сумму (3.8) добавим н вычтем <р(и).
Тогда можно утверждать следующее
еи = 1 для дуг, выходящих нз источника (и £ U~), н для дуг нз
множества (А, А) (идущих против разреза);
- 78 -
Еи = —1 для дуг разреза (и G (А, Л)) ;
еи = 0 для остальных дуг.
Таким образом, соотношение (3.8) фактически имеет следующий
вид
52	- 52 н«)+ 52 л(«) = о 
иеи~ ue(a,A) ue(a,a)
Отсюда
ф= 52 н«) - 52 н«) < 52 н«) < 52 с(«) = с(л,л).
иё(А,А)	иё(А,А)	иё(А,А)	иё(А,А)
(3-9)
Лемма доказана.
Теорема. Наибольшая величина потока в транспортной сети равна
наименьшей пропускной способности разреза.
Доказательство. По лемме для любого потока и любого разреза Ф <
с(А,А), следовательно, для любого потока Ф < minс(Л, Л), значит, и
А
для максимального потока справедливо последнее неравенство, т.е.
тахФ < min с(Л, Л) .
Ч>	А
(ЗЛО)
Для завершения доказательства ниже описывается алгоритм по-
строения потока н разреза таких, что величина потока равна пропуск-
ной способности разреза. Пз неравенства (ЗЛО) непосредственно сле-
дует, что такой поток будет максимальным, а разрез — минимальным.
Алгоритм построения максимального потока
Анализ неравенств (3.9) показывает, что величина Ф потока у?
совпадает с пропускной способностью разреза (Л, Л) тогда н только
тогда, когда выполняются два условия:
<р(и) = с(и) для всех дуг и G (А, А) ;
<р(и) = 0 для всех дуг и G (Л, Л) .
(.3.11)
Алгоритм, который приводится ниже, направлен на каждом этапе на
построение такого разреза, для которого выполняются условия (3.11).
- 79 -
При этом либо удается построить такой разрез, тогда задача решена,
либо выясняется, как рассматриваемый поток можно увеличить.
Увеличение потока производится с помощью прибавляющих цепей,
остановимся на них подробнее. Рассмотрим в сети цепь нз источника
в сток, т.е. последовательность вершин
S = Хо, Xl, Х2, . . . , Tfc-1, Xk = t ,
такую, что между Xi н есть дуга сети (г = 0, 1, . .., к — 1). Такой
дугой может оказаться дуга (т;,т;_|_1), в этом случае она называется
прямой, либо дуга	— такая дуга называется обратной.
Пусть в сети задан поток р. Цепь нз s в t называется приба-
вляющей, если для каждой ее прямой дуги и выполняется неравенство
р(и) < c(w), а для каждой обратной дуги и — неравенство р(и) > 0.
Предположим, что для потока ср удалось найти прибавляющую
цепь. Тогда, увеличивая р на единицу на прямых дугах, уменьшая
на единицу на обратных дугах н оставляя неизменным на дугах, не
входящих в цепь, можно получить новый'поток, величина которого на
единицу больше, чем величина р.
Пример. Прибавляющая цепь имеет вид, показанный на рнс.3.29.
3,2
8,3
5,2	6,4
—--------►©
Рнс. 3.29
На каждой дуге указаны два числа: первое — пропускная способ-
ность дуги, второе — поток по дуге. С помощью этой цепи можно
перейти к новому потоку ( рнс. 3.30).
Рнс. 3.30
Переходим к описанию алгоритма построения максимального по-
тока. Алгоритм состоит в последовательном просмотре вершин сети
н присвоении нм отметок. На каждом шаге этого процесса любая нз
вершин находится в одном нз трех состояний':
- 80 -
а)	не помечена;
б)	помечена, но не просмотрена;
в)	помечена п просмотрена.
Оппсанпе алгоритма
0-й шаг. Зададим какой-нпбудь, напрпмер, нулевой поток по сетп.
1-й шаг. Пометим псточнпк s (любой отметкой, напрпмер, звез-
дочкой *. ) После этого вершпна s помечена, но не просмотрена,
остальные вершпны сетп не помечены.
2-й шаг. Берем очередную помеченную, но не просмотренную вер-
шину х. Просматриваем все дугп, прпмыкающпе к этой вершпне. Еслп
вторая вершпна дугп не помечена, то помечаем ее отметкой ” х” в сле-
дующих двух случаях:
а)	дуга выходит пз вершпны х, п поток по ней строго меньше
пропускной способностп;
б)	дуга входит в х, п поток по ней строго больше нуля.
После завершенпя этого шага вершпна х объявляется помеченной
п просмотренной, а вершпны, получпвшпе прп просмотре отметку ” х” ,
объявляются помеченными, но не просмотренными.
Шаг 2 повторяется цпклпческп до тех пор, пока не пропзойдет одно
пз двух событий, рассматриваемых нпже (3-й нлн 4-й шаг ).
3-й шаг. Сток t получпл отметку, напрпмер, отметку ” у”.
Переходим в вершпну у, по отметке вершпны у отыскиваем следу-
ющую вершпну п т.д. до тех пор, пока не дойдем до вершпны s. В
результате будет построена прибавляющая цепь. Увелпчпваем с помо-
щью этой цепп текущий поток, стираем отметкп всех вершпн п начи-
наем выполнение алгоритма с 1-го шага.
4-й шаг. Процесс расстановкп отметок закончился тем, что все
помеченные вершпны просмотрены, но сток t прп этом не помечен.
Пусть А — множество помеченных вершпн. Так как t A, a s G А,
то можно определить разрез (А, А). Для каждой дугп и£(А,А), т.е.
дугп, идущей пз помеченной вершпны в непомеченную <р(и) = с(и),
пначе другой конец этой дугп был бы помечен. По той же прпчпне для
каждой дугп и G (A, A) <р(и) = 0. Следовательно, для построенного
потока п разреза (А, А), образованного помеченными вершпнамп, вы-
полняются условпя (3.11). В таком случае поток максимальный.
- 81 -
Пример. На рис.
ней.
3.31 изображена транспортная сеть п поток по
Процесс расстановки отметок будет пропсходпть в данном случае
так, как это показано в таблице 3.1.
Таблица 3.1
Номер шага	Отметкп вершпн							
	S	а	b	c	d	e	f	t
1	*							
2	*							
3	*	”s”			” a”			
4	*	”s”			” a”	”d”		
5	*	”s”	” e”		” a”	”d”		
6	*	”s”	” e”	”b”	” a”	”d”	’’b”	
7	*	”s”	” e”	”b”	” a”	”d”	”b”	
Поскольку сток получпл отметку, стропм прибавляющую цепь (рнс.
3.32).
- 82 -
5,3
Увеличиваем поток на две единицы на прямых дугах этой цепи и
уменьшаем на две единицы на обратных. В результате приходим к
потоку, изображенному на рис. 3.33.
В процессе расстановки отметок для нового потока удается по-
метить только вершины s и а. Пусть А = {.s, а}, тогда разрез
(А, А) = {(s, с), (a,b), (a, d))— минимальный. Его пропускная способ-
ность
с(А, А) = с(а, d) + с(а, b) + c(.s, с) = 14
совпадает с величиной потока.
- 83 -
Теорема Кенига-Эгервари
Эта теорема вытекает нз основной теоремы Форда-Фалкерсона для
транспортных сетей и показывает, что приложения теории транспорт-
ных сетей могут быть весьма неожиданными.
Мы будем рассматривать так называемые (0,1)-матрицы, то есть
матрицы произвольного размера т х п
А =
/ ап
а21
0.12
022
а-in \
О2п
\ От1
^тп
составленные пз нулей и единиц:	£ {0, 1}, i = 1, . . ., т, j = 1, . . ., п.
Элементы такой матрицы иногда интерпретируют как разрешен-
ные ( ajj = 1 ) и запрещенные (	= 0. )
Множество разрешенных элементов называется независимым, если
эти элементы расположены в различных столбцах н строках:
М = {(«'1J1), («2 ,Ь),   , (ik,jk)} - независимо,
если
1)	aii Ji — ai'2	—    — aik jk — 1;
2)	при .5 7Ч is it,js jt.
Будем называть рядами строки н столбцы матрицы. Покрывающее
множество рядов — это совокупность строк н столбцов матрицы та-
кая, что каждый единичный элемент попадает в какой-либо ряд нз этой
совокупности:
,5' = I U J = {г'1, г2, . . ., is} U {ji, j2, ..., jt}-покрывающее множество,
если
aij = 1 => i £ I нлн j £ J.
Если M —любое независимое множество элементов, а ,5' —любое
множество покрывающих рядов, то всегда
\М\ < \S\,
(3.12)
- 84 -
так как в независимое множество может входить не более одного эле-
мента пз каждого ряда.
Теорема. (Кенпг-Эгерварп). Максимальное число клеток в независи-
мом множестве равно минимальному числу рядов в покрывающем мно-
жестве.
Доказательство. Для данной (0, 1)- матрицы А размера т х п
построим транспортную сеть следующим образом:
Вершины:
Источник s и сток t ;
Вершины-строки щ, . . ., гт по одной для каждой строки матрицы;
Вершины-столбцы щ,...,с„ по одной для каждого столбца матрицы.
Дуги:
Источник s соединен дугой с каждой вершиной-строкой;
Каждая вершина-столбец соединяется дугой со стоком t ;
Вершина-строка щ соединяется дугой с вершиной-столбцом cj в том
н только в том случае, когда = 1.
Пропускные способности:
Пропускная способность каждой дуги равна 1.
Решим для построенной сети задачу о максимальном потоке, при-
меняя алгоритм расстановки отметок. Рассмотрим нашу сеть в тот мо-
мент, когда найден максимальный'поток, то есть процесс расстановки
отметок закончился, но сток t не получил отметки. Это означает, что
построен максимальный поток, обозначим его величину через /.
Из определения сети вытекает, что значение потока на любой дуге
может равняться либо 0, либо 1. Пусть
  >	(3.13)
все дуги в ’’средней” части сети, поток по которым равен 1. Из урав-
нении сохранения вытекает, что
м = {(Ч, Jr), (i2, J2),..., (v, j>)}	(3.14)
независимое множество элементов матрицы. В самом деле, каждая
вершина-строка, по построению, имеет только одну входящую дугу (от
источника), то есть для каждой такой вершины сумма значений потока
- 85 -
по дугам, входящим в вершину, может равняться либо нулю либо еди-
нице, следовательно, и сумма значении потока по дугам, выходящим из
вершины, не больше единицы. Значит, для каждой вершины-строки г\к
нз (3.13) поток равен 1 только на одной нз выходящих нз вершины дуг,
поэтому все индексы Д, г2, . . ., if различны. Аналогично рассуждаем
Для ji, J2, ,;/
Кроме того, имеем, что на дугах
(s,rl2), . . ., (s,rlf) н (дуД), (cj2,t), . . ., (с^Д).
поток равен 1, а на остальных дугах в ’’средней” части сети поток равен
нулю.
Рассмотрим теперь какие вершины имеют отметки. На первом
шаге работы алгоритма при просмотре вершины s, все вершины-
строки, входящие в множество {г^,. . ., г^}, пометку не получат, так
как поток по дугам, идущим нз s в эти вершины равен единице (то
есть равен пропускной способности). Все остальные вершнны-строкн
получат отметку ”.s”, так как поток по дугам, идущим в них от ис-
точника, равен нулю.
При дальнейшей работе алгоритма в результате просмотра поме-
ченных на первом шаге вершин-строк будут помечены вершнны-стол-
бцы, в которые ведут нз них дуги. В силу максимальности потока,
помеченным может оказаться только какой-либо столбец нз множества
{cji, cj2, . . ., Cjf}, так как в противном случае происходит ’’прорыв” в
вершину I н увеличение потока.
На следующем шаге при просмотре вершины-столбца Cjk пометку
может получить только одна вершина-строка rjk — нз всех дуг, входя-
щих в вершину Cjk только по дуге (rjk,Cjk) поток больше нуля (равен
единице).
Пусть I — множество номеров непомеченных строк, a J — мно-
жество номеров помеченных столбцов. Пз рассуждений предыдущего
абзаца следует, что
I С {г'1,г2, . . ,,if} a J С {л, Д2, . . ., jf} ,
н что вершина-строка rjk является помеченной в том н только в
том случае, когда помечена вершина-столбец Cjk. Другими словами,
- 86 -
в паре (rjk,Cjk) либо обе вершпны помеченные, либо обе непомечен-
ные. Отсюда
\I\ + \J\ = f-	(3.15)
Заметим, наконец, что так как процесс расстановки отметок оста-
новился, в ’’средней части” сети нет дуг, у которых начало помечено,
а конец не помечен. Следовательно, каждая дуга либо имеет начало в
множестве I, либо конец в множестве J, то есть ,5' = I U J —
покрывающее множество рядов, н в силу (3.15)	|,5'| = /.
Итак, построено независимое множество элементов н покрывающее
множество рядов с одинаковым числом элементов. Теорема доказана.
Алгоритм построения максимального независимого множества
Опишем алгоритм построения максимального потока для рассмо-
тренной выше сети как действия непосредственно с заданной (0,1)-
матрнцей (не строя сеть фактически.)
Сначала построим какое-нибудь независимое множество элементов.
Можно, например, просматривать столбцы по порядку н в каждом на-
ходить первый попавшийся единичный элемент. Найденный элемент
зачисляется в независимое множество, а строка н столбец, в которых
он находится вычеркивается нз матрицы. Если в каком либо столбце
нет единичных элементов, переходим к следующему.
Пусть на этом шаге построено независимое множество
м = {(С,я),(*2,;2),---,(^,л)} 	(3.16)
Если к = т (в каждой строке выбран какой-то элемент) нлн к = п
(в каждой столбце выбран какой-то элемент), то, очевидно, построено
максимальное независимое множество н алгоритм окончен.
В противном случае начинаем процесс расстановки отметок, позво-
ляющий либо увеличить независимое множество (3.16), либо убедиться,
что оно максимальное.
Пометим как-либо, например, звездочкой ’’пустые” строки, то есть
строки, в которых нет элемента, входящего в независимое множество М
(3.16). Далее, как в общем алгоритме, выполняем циклически шаги
просмотра вершины (то есть строк н столбцов). После каждого шага
ряды матрицы делятся на три группы: непомеченные, помеченные н
- 87 -
не просмотренные, помеченные п просмотренные. Ряды пз последней
группы в последующих шагах не участвуют.
Описание шага просмотра. Берем очередной помеченный, но не
просмотренный ряд.
- Еслп это строка с номером г, то помечаем отметкой ”г” все
непомеченные столбцы, пмеющпе едпнпцу в данной строке.
- Еслп это столбец с номером js, то находпм в незавпспмом множе-
стве М элемент	п помечаем отметкой ”js” строку is.
Имеется два варианта остановки оппсанного процесса.
I. Ирп просмотре столбца в нем не оказалось элемента, входящего в
текущее незавпспмое множество М .Пусть
qi— номер такого столбца;
Р1— его отметка;
rj2— отметка строки pi; (то есть (pi, <72) £ М)
Р2— отметка столбца rj2',
qs— отметка строки р2; ( (р2, </з) € М)
qr— отметка строки pr-i;
рг— отметка столбца qr
п строка рг помечена звездочкой. Тогда элементы
(Р1,Ы, (Р2,?з),   -ЛРг-ЪЧг)
в незавпспмом множестве М можно заменить на элементы
(Р1Л1), (Р2Л/2),   ., (рг,?г) ,
увелпчпв на 1 число независимых клеток.
II. Просмотрены все ряды, то есть помеченных п непросмотренных
рядов больше нет. В этом случае совокупность помеченных столб-
цов п непомеченных строк образует покрывающее множество ря-
дов. Число рядов равно числу элементов в незавпспмом множестве,
откуда следует, что оно максимально.
- 88 -
3.5. Сетевые графики
В этом параграфе сетью будем называть ориентированный граф в
котором выделены две вершины: одна пз них называется началом и не
имеет входящих дуг, другая — концом, она не имеет выходящих дуг.
Последовательность различных дуг, в которой начало каждой дуги
совпадает с концом предыдущей, будем называть путем. Замкнутый
путь называется контуром нлн ориентированным циклом. Если в сети
нет ориентированных циклов, она называется ациклической.
Примерно с 60-х годов получила широкое распространение система
сетевого планирования н управления (СПУ), основным элементом ко-
торой является сетевой график. Представим себе, что планируется со-
здание некоторой сложной системы, строительство предприятия, разра-
ботка н создание сложного технического устройства, проведение боевой
операции н т.д. Весь комплекс действий по созданию системы обычно
разбивается на отдельные единицы — работы, которые в совокупности
после нх выполнения приводят к конечной цели. Отдельные работы
увязаны во времени: в силу логики самого процесса создания системы
выполнение одних работ должно предшествовать другим иначе говоря,
чтобы начать выполнение определенной работы необходимо закончить
некоторые другие.
Сетевой график представляет собой изображение хода выполнения
проекта при помощи ациклической сети. Дуги этой сети изображают
отдельные работы, а вершины — события, состоящие в завершенны од-
ной нлн нескольких работ. Каждой дуге в сетевом графике приписано
целое неотрицательное число — продолжительность соответствующей
работы.
Пример. Сетевой график на рнс.3.34 отражает порядок работ по
решению некоторой прикладной задачи на ЭВМ.
Рнс. 3.34
- 89 -
Перечислим отдельные работы, изображаемые дугами сети. Ка-
ждую дугу будем задавать парой i,j, где i —номер начала дуги j
— номер ее конца:
0,1 — выбор алгоритма решения задачи н разработка укрупненной
блок-схемы программы (эта работа занимает шесть, дней);
1,2	— программирование отдельных модулей;
1,3	— сбор числовых данных для решения задачи;
2,3	— окончательная компоновка программы;
2,4	— разработка контрольного примера;
3,4	— отладка программы;
3,5	— подготовка исходных данных;
4,5	— просчет контрольного примера;
5,6	— решение задачи.
Вершинам сетевого графика соответствуют события, отражающие
те нлн иные этапы работы: 0 — начало работ, 1 — окончание подгото-
вительного этапа, 5 — завершение всех предварительных работ н т.д.
Будем обозначать продолжительность работы i,j буквой tij.
Рассмотрим некоторый путь на сетевом графике ф —	— . . . — ik-i —
ik- Длиной пути назовем сумму продолжительностей входящих в него
работ:	+ ti-2i3 +    + tiк_riк 
Рассмотрим все пути нз начальной вершины в конечную. Тот нз
этих путей, который имеет наибольшую длину, называют критическим.
Длина критического пути tKp — это основная характеристика сете-
вого графика. Смысл ее состоит в том, что если каждая работа i,j
будет начинаться в тот момент, когда произойдет событие i (раньше
она начаться не может), н выполняться точно за время Cj, то вся сово-
купность работ будет выполнена за время, равное длине критического
пути tKp.
Опишем алгоритм для построения критического пути в сетевом
графике. В процессе работы алгоритма для каждой вершины i рас-
считывается величина /р(г) — максимальная длина пути нз начала в
вершину г.
- 90 -
Алгоритм отыскания критического пути
1.	Правильная нумерация сети.
Нумерация вершин сети называется правильной, еслп номер начала
любой дуги сети меньше, чем номер ее конца. Правильная нумерация
ациклической сети всегда возможна н производится следующим обра-
зом. Нумеруем начальную вершину нулем н удаляем ее нз сети вместе
со всеми выходящими нз нее дугами. В получающейся сети непременно
образуются вершины, не имеющие входящих дуг ( это следует нз аци-
кличности), назовем эти вершины вершинами первого ранга н зануме-
руем числами 1,2, ... Далее удалим все вершины первого ранга н вы-
ходящие нз них дуги, появившиеся вершины без входящих дуг назовем
вершинами второго ранга н дадим нм очередные номера. Этот процесс
продолжается до тех пор, пока не будут занумерованы все вершины
сети.
2.	Расстановка отметок.
Пусть сеть правильно занумерована. Для каждой вершины i вы-
числяем отметку /р(г) по следующим правилам:
-	полагаем /р(0) равным нулю;
-	просматриваем вершины в порядке нх номеров н для j'-ii вершины
вычисляем tp(j) по формуле
tpti) = max(fp(j) +tij) ,
где максимум берется по всем вершинам г, имеющим дугу
направленную в вершину /.
По окончании процесса вычисления отметок величина tKp может
быть найдена как отметка концевой вершины.
3.	Построение критического пути. Начиная с вершнны-конца, по-
следовательно находим дуги для которых tp(j) — tp(i) = tij- Эти
дуги н образуют критический путь.
- 91 -
Пример. На рис. 3.35 представлены сетевой график и результаты ра-
боты рассмотренного алгоритма.
В верхней половине кружка, изображающего событие, указан его
номер прп правильной нумерации, в нижней половине дана отметка
tp(i). Критический путь, длина которого равна 170, показан жирными
лпнпямп.
- 92 -
Глава 4
Булевы функции
4.1.	Булевы функции
Булевой называют функцию /(яд, х?,   , хп), аргументы кото-
рой и сама функция могут принимать только два значения. В литера-
туре употребляются также названия ’’логические функции”, ’’функции
алгебры логики”, ’’переключательные функции” н др. Два возможных
значения функции н каждого нз ее аргументов в различных областях
применения булевых функций обозначаются по-разному: И,Л (истина,
ложь ) — в математической логике; да, нет — на блок-схемах алгорит-
мов; .TRUE. .FALSE. — в алгоритмическом языке ФОРТРАН.
Проще всего обозначать эти два значения единицей н нулем, что в
дальнейшем н делается.
Булевы функции впервые появились в работах по математической
логике (Дж. Буль — один нз создателей этой науки), н первые нх при-
менения связаны с решением следующей задачи: выяснить, истинно нлн
ложно сложное высказывание, если известна истинность нлн ложность
составляющих высказываний.
В математике сложные высказывания образуются нз исходных про-
стых при помощи ограниченного запаса средств, нх называют логиче-
скими связками.
Будем обозначать простые высказывания буквами Д, В, С, . . . Из
них можно составить такие новые высказывания:
”	Д н В ”, обозначается Д&В ;
”	Д нлн В ”, обозначается Д V В ;
”не Д ” (то есть, неверно что Д ), обозначается Д ;
’’если Д, то В ”, обозначается Д => В.
Перечисленными связками, по существу, исчерпываются средства
образования сложных высказываний нз простых.
Пример. Пусть буквами А, В, С обозначены такие высказывания:
Д — ” числовой ряд сходится” ;
В — ” все члены ряда положительны” ;
С — ’’общий член ряда стремится к нулю”.
- 93 -
Образуем при помощи связок некоторые составные высказывания
п дадим пх перевод:
А => С — ’’если числовой ряд сходится, то его общий член
стремится к нулю”;
С — ’’общий член ряда не стремится к нулю”;
В&С — ’’члены ряда положительны п общий член ряда стре-
мится к нулю”;
С => А — ’’еслп общий член ряда не стремится к нулю, то ряд
расходится”.
Применяя логические связки многократно, можно образовать до-
вольно сложные высказывания, напрпмер, (А => С')к(В => С')к(А\/ В),
относптельно которых возникает вопрос, истинны они нлн ложны. От-
вет на этот вопрос завпспт от пстпнностп нлн ложности составляющих
высказываний, тем самым с каждым высказыванием связывается бу-
лева функция.
С развитием вычислительной техники выявилась другая роль буле-
вых функций: они выступают как средство (математическая модель)
для оппсанпя работы дискретных устройств переработки информации.
В самой общей форме такое устройство можно представить в виде
ящика с входами и выходами (рис. 4.1).
Рис. 4.1
В процессе работы такого устройства каждый вход и каждый вы-
ход может находиться в одном пз двух различимых состоянии:1 высо-
кий пли низкий' уровень напряжения, намагниченность топ'пли пноп '
полярности, одно пз двух положений переключателя и т.д. Не вдава-
ясь в подробности конкретной реализации устройства, говорят, что на
входы поступает комбинация нулей и единиц и устройство преобразует
ее в некоторую комбинацию нулей и единиц на выходе. Прп помощи
- 94 -
комбинаций нулей и единиц — двоичных слов — кодируются общепри-
нятые знаки представления информации: буквы, цифры, знаки препи-
нания, служебные знаки. Представленная в двоичной форме информа-
ция поступает на вход устройства, оно производит обработку и на вы-
ходе появляется двоичное слово, которое затем можно снова перевести
в естественную форму. Каждый выход дискретного преобразователя
определяется значениями входов, т.е. представляет собой функцию от
входов. Эта функция булева.
Способы задания булевых функций
Число булевых функций от п переменных
Обозначим множество, составленное пз двух элементов, нуля и еди-
ницы, буквой Е, Е = {0, 1}. Областью определения булевой функ-
ции Х2, . . , хп) является совокупность всех n-ок: ац . . ,ап, где
ai G Е , i = 1, ... ,п. В главе 1 эта совокупность была названа де-
картовым произведением и обозначалась Еп. Таким образом, булевой
функцией от п переменных называется функция с областью определе-
ния Еп п областью значений Е :
/ : Е" —> Е, ац . . . ап	, ап) 
Поскольку область определения состоит пз конечного числа эле-
ментов (|Е"| = 2"), то булеву функцию можно задавать при помощи
таблицы, указывая в ней для каждого набора значений аргументов зна-
чение функции (табл. 4.1 ).
Таблица 4.1
Х2  	• % П — 1 п	/(Ж1, т2,..	5 % П — 1 5 % П )
0 0	..00	/(0,0,.	 .,0,0)
0 0	..01	/(0,0,.	..,0,1)
0 0	.. 10	/(0,0,.	..,1,0)
1 1	.. 10	/(1,1,.	.,1,0)
1 1	..11	/(1,1,.	.,1,1)
В качестве примера в таблице 4.2 задана функция /(ад, т2, ж.з)
от трех переменных, которая равна единице, еслп нечетное количество
переменных равно единице, и нулю — в остальных случаях.
- 95 -
Таблица 4.2
Xi Х2 Хз	f
ООО	0
0 0 1	1
0 1 0	1
0 1 1	0
1 0 0	1
1 0 1	0
1 1 0	0
1 1 1	1
Отметим, что наборы значении аргументов в таблице выписывают
в естественном порядке, т.е. так, чтобы г-н по порядку набор предста-
влял собой двоичную запись числа г , г = 0, 1, 2,... 2" — 1.
Рассмотрим в таблице 4.1 столбец значений функции. Он предста-
вляет собой двоичное слово длины 2". Отсюда вытекает, что число
различных булевых функций, зависящих от п переменных, равно 22 .
Это ’’трехэтажное” выражение очень быстро возрастает при увеличе-
нии п.
Возможности задания булевых функций при помощи таблиц огра-
ничены. Например, при п = 10 нужно составлять таблицу нз 210 =
1024 строк. Поэтому используются другие способы задания, средн ко-
торых основным является задание при помощи формул. Этот способ
состоит в том, что некоторые функции выделяются, нх называют эле-
ментарными, а другие функции строят нз элементарных, подставляя
нх друг в друга.
Такой способ задания функций хорошо известен: функции действи-
тельного переменного, изучаемые в математическом анализе, образу-
ются нз ограниченного запаса элементарных функций. Например, функ-
ция sin3 фж2 + I построена нз многочлена ж2 + 1, квадратного корня,
синуса н функции у = ж3.
Рассмотрим в связи с этим простейшие булевы функции.
Булевы функции одного н двух аргументов
В таблице 4.3 перечислены всевозможные булевы функции одного
аргумента.
- 96 -
Таблица 4.3
X	/о	fl	А	А
0 1	0 0	0 1	1 0	1 1
Среди этих функций /о (ж) =0 и /з(ж) = 1 представляют со-
бой константы, функция /1 (ж) = х совпадает с аргументом. Интерес
представляет только функция /2 (ж) . Она называется отрицанием п
обозначается ж . Итак,
Г 1, еслп ж = 0 ;
1 0, еслп ж = 1 .
В таблице 4.4 перечислены все 16 функций от двух аргументов.
Таблица 4.4
Xi Х2	А	fl	А	А	А	А	А	А
0 0	0	0	0	0	0	0	0	0
0 1	0	0	0	0	1	1	1	1
1 0	0	0	1	1	0	0	1	1
11	0	1	0	1	0	1	0	1
Xi Х2	А	А	Ао	Ai	/12	Аз	/14	/15
0 0	1	1	1	1	1	1	1	1
0 1	0	0	0	0	1	1	1	1
1 0	0	0	1	1	0	0	1	1
11	0	1	0	1	0	1	0	1
Некоторые пз этпх функций не представляют интереса, так как
сводятся к функциям одного аргумента:
/о(ж-1, Ж2) = 0 ; /з(ж-1, Ж2) = Ж'1 ; А/жд, ж2) = ж2
Ло(ж1,ж2) = ж? ; /12(ж1,ж2) =ж? ; /15(ж1, ж2) = 1
Из остальных функций семь выделены, онп имеют специальные назва-
ния п обозначенпя. Этп функции вместе с отрпцанпем образуют сово-
купность элементарных булевых функций, пз нпх строятся формулы.
- 97 -
Конъюнкцией называется функция, задаваемая столбцом Д та-
блицы 4.4. Обозначается конъюнкция жд&жд или жд Л жд (читается
” жд н ад ”) Конъюнкция иначе называется логнчекнм умножением.
Из определения видно, что значение функции действительно равно про-
изведению значений аргументов. Поэтому принято н такое обозначение
конъюнкции: жджд . Как наиболее простое оно используется в дальней-
шем. Отметим еще, что конъюнкция вычисляет истинность высказыва-
ния ” А н В ” в следующем смысле: пусть жд — значение истинности
высказывания А, т.е. х\ равно единице, если А истинно, н нулю,
если А ложно. Обозначим ж 2 значение истинности высказывания В.
Тогда истинность высказывания ” А н В ” равна жджд .
Дизъюнкцией называется функция, задаваемая столбцом Д та-
блицы 4.4. Обозначение дизъюнкции— ждХ/жд (читается’’жд нлн жд”).
Другое название дизъюнкции — логнчекое сложение. Эта функция вы-
числяет истинность высказывания ” А нлн В”: данное высказывание
ложно в том н только в том случае, когда А н В оба ложны.
Отметим еще, что
жджд = min{Ti, жд} , жд V жд = тах{ж'1, жд} .
Импликацией называется функция, задаваемая столбцом Дз та-
блицы 4.4. Обозначается импликация— жд —> жд (читается’’если жд,
то ж 2 ” нлн” жд влечет ж 2 ” нлн” нз жд следует ж 2 ”). Эта функция
вычисляет истинность высказывания’’если А, то В ”.
Суммой по модулю £ называется функция, задаваемая столбцом Д
таблицы 4.4. Обозначение Д(ж1,жд) = жд х?- Значение функции
равно сумме аргументов, сумма приводится по модулю 2, т.е. заменя-
ется остатком от деления на 2.
Кроме перечисленных, еще три функции от двух аргументов встре-
чаются в литературе по булевым функциям со специальными названи-
ями н обозначениями:
Д(ж'1,жд) = жд ~ жд —эквивалентность;
Д(ж1, жд) = жд f жд —стрелка Инрса;
ДДжджд) = жд | жд — штрих Шеффера.
- 98 -
4.2.	Представление булевых функций формулами
Формулы в базисе ’’дизъюнкция, конъюнкция, отрицание”
Изучим основные свойства дизъюнкции, конъюнкции и отрицания.
Справедливы следующие тождества;
1.	Xl V Х2 = Х2 V Ж'1
2.	T1 V (х2 V хз) = (x-i V Х2) V т.з
з.	i'i Vi-] = «1
4.	Xi V 0 = Xi
5.	Т1 V 1 = 1
6.	Т'1  Х2 = Х2  Ж'1
7.	Т'1  (т'2  Т.з) = (т'1  Х2)  т.3
8.	тц  тц = тц
9.	Ti • 0 = О
10.	тц  1 = тц
11.	ТГ = тц
12.	0 = 1
13.	Т= 0
14.	Т'1 (т'2 V Т.з) = ТДТ'2 V ТЦТз
15.	Т'1 V Т'2 Т.З = (тц V Т'2)(Т1 V Т.з)
16.	Т'1 V Т'2 = ТДТ'2
17.	тц Т'2 = тТ V т-7
18.	тц V тГ = 1
19.	тц  тТ = 0
Каждое из этих соотношений устанавливается таким образом: со-
ставляются таблицы функций, записанных в левой и правой частях то-
ждества, затем проверяется, совпадают ли эти функции.
Сравнивая тождества 1—19 с теоретико-множественными тожде-
ствами 1 — 19 нз главы 1, легко обнаружить, что одни тождества полу-
чаются нз других в результате следующей замены знаков: объединение
— дизъюнкция, пересечение — конъюнкция, дополнение — отрицание.
Рассмотрим некоторые следствия нз тождеств 1 — 19.
Тождество 2 позволяет рассматривать логические суммы с любым
числом слагаемых
V Х2 V ... V хп ,
- 99 -
результат не зависит от того, как расставить скобки. Для последней
п
суммы иногда применяется сокращенное обозначение \/ •' , . В силу
2 = 1
тождества 1 эта сумма не зависит также от порядка слагаемых. Эту
независимость можно выразить и в такой форме: функция
/(т1 , Х2,    , Хп) = T1 V Х2 V . . . V Хп
равна нулю, только когда Ху = х2 = . . . = хп = 0, в остальных случаях
эта сумма равна единице.
Аналогичным образом имеет смысл записывать без скобок произ-
ведение произвольного числа сомножителей х-у  х2  . . .  хп. Это произ-
ведение не зависит от порядка сомножителей. Функция
f(xy,X2, ...,£„)= Ж1  Х2      хп
равна единице, только когда х-у = х2 = ... = хп = 1, в остальных
случаях произведение равно нулю.
Тождества 16 н 17 по индукции распространяются на любое число
слагаемых н сомножителей':
Ху V Х2 V . . . V Хп = X у  х2  . . .  хп
Ху  Х2  . . .  Хп = хТ V Х2 V . . . V тД 
Будем называть конъюнкцией любое произведение, составленное
нз букв ху, х2,. . ., хп н нх отрицаний тф, Жг, . . ., тД. Пользуясь то-
ждествами 8 , 19 н 9, любую конъюнкцию можно преобразовать либо
к нулю, либо к произведению, составленному нз букв с различными ин-
дексами. Такое произведение называют элементарной конъюнкцией.
Формула, имеющая вид ’’дизъюнкция элементарных конъюнкций”
F = Ку V К2 V . . . V Кт ,
называется дизъюнктивной нормальной формой (д.н.ф.)
В главе 1 была рассмотрена процедура приведения произвольной
формулы, составленной нз знаков U , П ,—, к виду ’’объединение пе-
ресечений”. Поскольку законы (1.1) — (1.19), которым подчиняются
- 100 -
теоретико-множественные операции, формально не отличаются от за-
конов 1 — 19 для логических операций, приходим к следующему утвер-
ждению:
.любую формулу, построенную с помощью знаков дизъюнкция,
конъюнкция и отрицание, можно преобразовать к д.н.ф.
Пример.
F = Х[ Ж 2 V Хз хТ Х2 Хз = Ж1 ЖД Жз (жД V Ж? V Жз) = (ж? V Ж?) Жз (ж'1 V
V жД V ж.з) = Ж1Ж3Ж1 V Ж1Ж3Ж2 V Ж1Ж3Ж3 V Ж2Ж3Ж1 V жджзжд V Ж2Ж3Ж3 =
= О V жДб>2 Ж3 V О V Ж1 б>2 Ж3 V б>2 жД V 0 = ЖД ЖД ЖД V жд жД жД V жДжД .
Булевы тождества можно использовать для упрощения д.н.ф. Рас-
смотрим два простых способа.
Правило поглощения. Если в д.н.ф. присутствуют конъюнкция
К' н конъюнкция К = К'-К” (то есть в конъюнкции К встречаются
те же сомножители, что н в К', н плюс еще какие-то), то более длинную
конъюнкцию К можно удалить нз д.н.ф.
Это правило вытекает нз следующей цепочки формул;
К' V К = К' V К'К” = К'(1 V К”) ^К' -1 ^К' .
Применение правила поглощения к рассмотренному выше примеру
дает следующее упрощение:
F = жд жд жД V жд жД жД V жД жД = жд жД жД V жД жД = жД жД 
Правило склеивания: хК V ж К = К.
Действительно, хК V ж К = (ж V х) К = 1  К = К.
Применение этого правила к рассматриваемому примеру дает та-
кое преобразование:
F = жД жД жД V жд жД жД V жД жД = жД жД V жД жД = жД жД .
Покажем, что каждую булеву функцию можно представить фор-
мулой, используя только знаки дизъюнкции, конъюнкции н отрицания.
Рассмотрим сначала пример, приведенный в табл.4.5.
- 101 -
Таблица 4.5
Xi Х2 Хз	f	Конъюнкция
ООО 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 1 1 0 0 0 0 1	^7^2" Хз FfХ2 ~Хз Х'1 Х2 Хз
Для каждого набора значений переменных адо^оз, на котором
данная функция равна единице, составим произведение переменных или
их отрицаний по следующему правилу:
еслп &i = 1 , то в произведение берется тд ,
еслп &i = 0 , то в произведение берется , г = 1, 2, 3.
Составленные таким образом конъюнкции выписаны в правом сто-
лбце табл.4.5. Рассмотрим одну пз них, например, хХк>%з и выясним,
когда она равна единице:
Ж1 Х2 Хз = 1 <=> ЯД = 1 , Х2 = 1 , Хз = 1 <=> ЯД = 0 , ЯД = 0 , Х3 = 1 .
Таким образом, каждая пз конъюнкций правого столбца табл.4.5 равна
единице только на ’’своем” наборе значений переменных, т.е. на том на-
боре, по которому она составлялась, и равна нулю на остальных семи
наборах. Отсюда следует, что дизъюнкция всех составленных конъ-
юнкций будет равна функции f :
/(яД , Х'2, Хз) = ЯД ЯД Хз V хТ Х2Х3 V ЯД ЯД ЯД 
Формулы, в которых используются только знаки V,&,—, называют
формулами в базисе (V,&,—).
Теорема. Каждая булева функция может быть представлена форму-
лой в базисе (V,&,—).
Доказательство. Рассуждение для общего случая, по существу, то
же, что п в примере. Необходимы лишь некоторые обозначения.
- 102 -
Определим булевскую степень ха следующим образом:
Г х >
1 % >
еслп а = 1 ;
еслп а = 0 .
Рассмотрев четыре возможных случая, проверяем, что
Рассмотрим теперь произвольную булеву функцию f(xi, . . ., хп).
Для каждого набора значений переменных aia2-..an такого, что
/(aia'2 . . . on) = 1, составим конъюнкцию х^1х^2 . . . ж“п. Относи-
тельно этой конъюнкции справедливо утверждение
Ж'/^жД'2 . . . Ж'“п = 1 при ЖД = 0'1 , Х2 =0'2 ... хп = ап ,
ж/1 ж/2 . . . ж“п = 0 при остальных значениях переменных. .
С учетом этого имеем
/(ж1,ж2, . . .,ж„) = У	ж/1 жД2...ж“п .	(4.1)
f(a1a2...an) = l
Под знаком логической суммы в формуле (4.1) записано условие
суммирования: оно означает, что сумма распространяется на все на-
боры 0102 . . ,ап, на которых функция равна единице. Правая часть
формулы (4.1) является д.н.ф., она называется совершенной д.н.ф. бу-
левой функции /.
Примеры. Вернемся к таблице функций двух переменных 4.4 . Пз
только что доказанной теоремы вытекает, что все элементарные функ-
ции можно выразить через три: дизъюнкцию, конъюнкцию н отрица-
ние. Применяя приведенный в доказательстве алгоритм, получаем сле-
дующие формулы :
Ж'1 ф Ж'2 = жДЖ'2 V Ж'1 жД ;
Ж'1 —> Ж'2 = жДжД V жДЖ'2 V Ж'1 Ж'2 ;
Ж'1 ~ Ж'2 = жфжД V Х1 х2 ;
Ж'1 f Ж'2 = Ж'1 Ж'2 ;
Ж'1 |ж'2 = жфжД V жДжд V жджД 
- 103 -
Тот факт, что все булевы функции можно выразить через три,
имеет следующий практический смысл. Предположим, что имеется не-
ограниченный запас элементов, работа которых описывается функци-
ями V,&,— (рнс. 4.2).
Рнс. 4.2
Тогда, соединяя эти элементы подходящим образом, можно собрать
дискретный преобразователь с любым наперед заданным функциониро-
ванием.
Системы булевых функций, с помощью которых можно выразить
любую булеву функцию, называют полными. Изложенное выше в дан-
ном параграфе кратко формулируется так: система функций (V, & , —)
— полная. Поставим задачу: описать другие системы функций, обла-
дающие свойством полноты. Для решения этой задачи необходимо дать
точное определение формулы нлн суперпозиции булевых функций.
Понятие суперпозиции. Постановка задачи о полноте
Пусть имеется элемент, работа которого описывается некоторой
булевой функцией /(ад, тд, ж.з) (рнс.4.3,а). Представляется естествен-
ным проделать с элементом такие операции:
-	изменить обозначения входов ( рнс. 4.3,6);
-	подать один н тот же сигнал на несколько входов ( рнс.4.3,в).
£1— 		f		 f(X[,X2,X^ Хз		f	£'1-|— f (^Х2,Хз,Х	f	У (ж 1,Ж1,Ж2}
Ж.з —	а)	Ж1 —	6)	Х2		в)	
Рнс. 4.3
- 104 -
Определим на множестве булевых функций операцию подстановки
переменных V :
Р (/(^1 J ^2,    ) Хп)) - f 1 , *^«2 ,   - J •*-!») J
где Xit, xt2,. . ., Xin — любые переменные, не обязательно различные.
Пример. Из функции Ж1|ж2 (штрих Шеффера) с помощью опера-
ции Р можно получить отрицание:
/(Ж1, т2) = Ж1|т2 ; Р f{x-y,x7) = f(x, х) =х .
Предположим, что имеется пара функций, скажем, /(ж1,т2,т.з)
и д(у\,Уг1) и соответствующие им элементы. Иропзведем соединение
элементов так, как это показано на рнс. 4.4.
Х'1,У{У\,У'1))
Рнс. 4.4
Функция на выходе схемы рнс. 4.4 получается в результате под-
становки функции д на место третьего аргумента функции /.
Определим на множестве пар булевых функций операцию 5 под-
становки функции в функцию следующим образом: паре булевнх функ-
ций f и д операция 5 ставит в соответствие функцию, получа-
ющуюся в результате подстановки функции д на место последнего
аргумента функции /
5 (/(жд, . . ., Tfc_i, хк'),д(у-1, . . ., я)) = /(жд, . . ., хк_-1,д(у-1, . . ., я)) .
Пусть задана система булевых функций (/i, /2, . . ., /г). Говорят,
что функция / является суперпозицией данных функций, если функ-
цию / можно получить из них, применяя некоторое число раз операции
V и 5.
- 105 -
Пример. Рассмотрим систему функций (Л, УД Уз), где
/1(Т1,Т2) = Т'1 V Т'2 , /2(^'1, Х2) = Х1кх? , /з(х-) = X .
Пусть /(Х!,Х2) = х-1 (Ъ х2. Выше была получена формула х\ Ф х2 =
ЯДХ2 \/ ЯД Х2 ИЛИ
f(x-i,x2) = /1(/2(/з(х-1), х2), /2(Х1, /з(х2))) .
Аналогично формулу для стрелки Пирса можно записать так:
Х-1 t Х2 = /2(/з(Ж1),/з(ж2)) 
Пз приведенных примеров видно, что понятие суперпозиции явля-
ется уточнением понятия формулы: если функцию f можно постро-
ить нз /1, f2,. . ., fr с помощью операций V н 5 , то, следуя этому
построению, можно получить н формулу для /, в которой будут при-
сутствовать только знаки функций /1, /2,   , Л 
Примеры полных систем:
1)	(V,&,—). Полнота этой системы вытекает нз теоремы, дока-
занной в данном параграфе;
2)	(&,—). Полнота вытекает нз формулы х\ \/ х2 = яд&яд н
полноты дизъюнкции, конъюнкции н отрицания;
3)	(V,—). Полнота следует нз формулы х-^х2 = яд Х/яд н пол-
ноты дизъюнкции, конъюнкции н отрицания.
4)	система (яд f яд), состоящая нз одной функции — стрелки
Пирса — является полной. Действительно, яд f яд = яд яд. Отсюда
х = х f х, н
ЯД&ЯД = (яд t Яд) t (ж2 t Х2) .
Таким образом, отрицание н конъюнкцию можно выразить через стре-
лку Пирса. Остается заметить, что отрицание н конъюнкция образуют
полную систему.
Поставим следующую задачу: для данной системы булевых функ-
ций
выяснить, является лн эта система полной.
Исчерпывающее решение этой задачи дается в теореме Э.Поста.
- 106 -
4.3.	Критерий полноты. Теорема Поста
Для формулировки критерия полноты необходимо предварительно
изучить пять классов булевых функции. Каждый пз них обладает тем
свойством, что если производить операцию суперпозиции над функци-
ями, взятыми нз класса, то в результате будут получаться только функ-
ции нз того же класса. В связи с этим упомянутые классы называются
замкнутыми — они замкнуты относительно суперпозиции.
1.	Класс То (класс функций, сохраняющих нуль).
Обозначим через То совокупность всех булевых функций (от лю-
бого числа переменных), которые равны нулю на нулевом наборе зна-
чений переменных:
То = {/ | /(0,0,..., 0) = 0 } .
Пример. Из четырех функций
fl (ti , X?) = T1&T2 , /2(^1, жд) = VT2 , /з(Ж1, жд) = t Т'2 , /4(2) =Х
первые две входят в То, a fy и Д не входят.
Лемма. Суперпозиция функций из класса То является функцией
класса То.
Для доказательства необходимо проверить тот факт что примене-
ние операций Р и S, к функциям, сохраняющим нуль, всякий раз
дает функцию, сохраняющую нуль.
Пусть f(x-i, Х2, . . ., хп) G То, т.е. Д0,0,...,0) = 0. В ре-
зультате подстановки переменных (операция Р ) получается функция
f(xit, Xi2,. . ., xirJ, которая при нулевых значениях своих аргументов
совпадает с /(0, 0, . . ., 0) = 0
Пусть f(xi, . . ., Tfc_i, Tfc) и g(yi, . . ,,уф — две функции, сохраня-
ющие нуль, а функция
h(x-i, . . .,xk_\,y\, ...,У1) = f(x-i, . . ,,xk_i,g(yi, . . ,,yi)) -
результат применения операции 5. Тогда
/г(0,..., 0) = /(0,..., 0,5(0,..., 0)) = /(0,..., 0, 0) = 0 ,
- 107 -
следовательно, h £ Tq.
Лемма доказана.
Пример. Дизъюнкция и конъюнкция входят в То, поэтому любая
суперпозиция этих функции, иными словами, любая функция, которую
можно представить формулой, содержащей только знаки V и &,
будет сохранять нуль. Следовательно, система (V,&) неполная.
2.	Класс Т\ (класс функций, сохраняющих единицу).
Этот класс полностью аналогичен классу То :
Ti = {/|/(1, 1,..., 1) = 1 } .
Пусть, напрпмер, /Джд, жд) = жд V жд, /2(жд,жд) = жд Ф жд. Тогда
/1£Т1,/2^Т1.
Лемма. Суперпозиция функций из класса Ту является функцией
класса Ту.
Доказательство этой леммы повторяет доказательство предыдущей
леммы с заменой нуля на единицу.
3.	Класс S ( класс самодвойственных функций).
Пусть /(жд, . . ., жд) — булева функция, функция
Г (x-i,. ,.,хп) = f(Ti, . . . ,жД)
называется двойственной к функции f.
Будем называть нуль и единицу противоположными значениями
аргумента; аналогичным образом два набора значений аргументов
ад,..., ад н ад, . . ., ад (во втором наборе значение каждого аргумента
заменено на противоположное) будем называть противоположными на-
борами. Тогда определение двойственной функции можно переформу-
лировать так: значение двойственной функции f* на некотором на-
боре значений переменных противоположно значению функции f на
противоположном наборе. Например, если /(О, 1) = 0, то /*(1,0) = 1
нлн /(0,1,1,0) =1 => /*(1, 0, 0,1) = 0 н т.д.
- 108 -
Пример. Таблицу двойственной функции f* можно получить пз та-
блицы функции /, еслп всюду в таблице для f заменить нули и
единицы друг на друга. Произведем такую замену в табл.4.6 для функ-
ции T1&T2-
Таблица 4.6
Xi Х2	/
0 0	0
0 1	0
1 0	0
1 1	1
Таблица 4.7
Xi Х2	Г
1 1 1 0 0 1 0 0	1 1 1 0
В результате получим табл.4.7, нз которой видно, что (тд&тд)* =
V Х2.
Из определения двойственности следует, что f** = /, таким обра-
зом, булевы функции разбиваются на двойственные пары.
Лемма.(принцип двойственности). Если функцию f можно предста-
вить формулой, содержащей знаки функций fy, f2,   , fr, то двой-
ственную функцию f* можно представить такой же формулой, но с
заменой знаков fy,f2,...,fr на знаки f) , /* ,..., /* , соответственно.
Пусть, например,
/(«I, Х2, Х3) = fy(f2(xy),X2, f3(x3, fy(x2,X3, Ж1))) .
Тогда
Г(ж1, ж2, Ж.з) = /1 (Л (Ж1), Ж2, f3(x3, f*y (х2, х3, T1))) .
Чтобы доказать лемму, необходимо проверить ее справедливость
для элементарных шагов суперпозиции V и 5.
Пусть, например, функция /(ti,t2) получается нз функции
g(x-y, х2, т.з, хф) в результате подстановки переменных:
/(т-i, т2) = д(х2, Ху, Ху, х2) .
Тогда
f*(x-y,x2) = /(хфхф) = д(хфхфхфхф) = д* (х2,ху,ху,х2),
- 109 -
т.е. f* получается из д* в результате той же самой подстановки
переменных.
Доказательство справедливости утверждения леммы для шага 5
проведем на примере (общее рассуждение такое же). Пусть
f(xi, ж2, ж3, ж4) = Л(ж1, ж2, /2(ж3, х4)) 
Тогда
/*(ж1, ж2, ж.з, ж4) = f(xT,xf,xf,xf) = fi(xi,xi, f2(xf,xf)) =
= fi(xi, xi, f?(x3, xi)) = fi(xT, Xi, f2(x-3, X4)) = f* (xi,x2, f2 (x3, x4)) .
т.е. f* получается нз f* н f2 так же, как f нз /j н f2.
Пз принципа двойственности можно извлечь ряд практически по-
лезных приемов.
Построение формулы для отрицания функции
Определение двойственной функции можно переписать в эквива-
лентной форме:
/(ж1 , х2,..., хп) — / (т1,х2,..., хп) .
Применяя принцип двойственности, получаем следующее правило:
пусть дана формула для булевой функции f, содержащая знаки
fl, f2, . . ., fr. Чтобы получить формулу для функции f, нужно
в данной формуле заменить знаки всех функций на знаки двой-
ственных функций и над каждой буквой поставить чёрточку.
Примеры.
1.	f(xi , Х2, Ж.з) = Xl Х2 V (х2 V Xl х3).
Так как (V)* = & , (&)* = V , (—)* = — , то
f(xi, х2, хз) = (тТ V xf) xf (xf V Т3) .
2.	f(xi, x2, X3, x4) = Xi x2 X3 x4) f(x-i, x2, X3, x4) = xfVxf VT3 VT4.
3.	f(xi, x2, T3) = x-i xf X3 V xfx2 X3 V xfxf X3
f(x-i, x2, X3) = (x-i V xf V T3) (Tj“ V x2 V T3) (Tj“ V xf V T3) .
- 110 -
Представление булевой функции конъюнктивной нормальной формой
По аналогии с понятием элементарной конъюнкцпп (см. выше) вве-
дем понятие элементарной дпзъюнкцпп — это логическая сумма пере-
менных нлн нх отрицаний'
D = х°) V т“2 V ... V ,
Z 1	I 2	I k >
в которой все индексы переменнвк различны.
Формула, имеющая впд пропзведенпя элементарных дпзъюнкцпй,
К — Di  D2 •	• Dm ,
где Di — элементарная дпзъюнкцпя, i = 1,2,..., m, называется
конъюнктивной нормальной формой (к.н.ф.)
Теорема.Каждую булеву функцию можно представить конъюнктив-
ной нормальной формой.
Доказательство. Пусть требуется представить в к.н.ф. функцию f.
Представим f совершенной д.н.ф. (формула (4.1)):
f(x-L,x2, . . ,,хп) =	т"1^'2 . .	.
/(aia2...a„)=l
Перейдем к отрпцанпям в левой п правой частях этой формулы. Слева
получпм f = f, справа в сплу правила для построенпя отрпцанпя фор-
мулы необходимо поменять знаки V п & друг на друга п поставить
отрпцанпя над всеми буквами. Получаем
/(жд, х2, . . ., х„) = _	&	(ж"1 V х)2 V . . . Vi““) .
/(aia2...a„)=l
Заметим, что ха = ха, кроме того, условие f = 1 равносильно
условию f = 0. Окончательно пмеем следующее представленпе:
/(жд, х2, . . ., х„) =	& (тС1 V х)2 V . . . V т"п) ,
/ (а 1 а 2    л п) = О
которое называется совершенной конъюнктивной нормальной формой
(с.к.н.ф.) функции f.
- Ill -
Пример. Записать формулой функцию f (табл.4.8).
Таблица 4.8
Xi Х2 Хз	/	Дизъюнкция
ООО 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	1 0 1 1 0 1 1 0	Т1 V Х'2 V Хз T]“V Х'2 V Хз T]“V Х2 V Хз
Если данную функцию представлять в впде д.н.ф. по формуле (4.1),
то получится логическая сумма пз пятп слагаемых. Такпм образом,
всего в формуле будет 15 букв. Здесь выгоднее попользовать к.н.ф.
Для построенпя к.н.ф. по каждому набору значений переменых, на ко-
тором функция равна нулю, составляются дизъюнкции (они показаны
в правом столбце таблицы), а затем берется пропзведенпе всех соста-
вленных дизъюнкций:
Пример. Пусть функция от четырех аргументов равна нулю, когда
значения всех аргументов совпадают (все равны 0 нлн все равны 1). В
остальных случаях функция равна единице. Тогда
f = (ад V Х2 V т.з V жд) (тД V Х2 V хз V Х4) .
Перейдем к определению класса ,5'. Функция f называется само-
двойственной, еслп f* = f.
Такова, напрпмер, функция /(ж) = х. В качестве другого примера
рассмотрим функцию /(яд, жд, Жз) = Х\ хз\/х-у хз\/х^ Х3. По определению
двойственной для нее является функция
Раскрывая скобки, убеждаемся, что f* = f.
- 112 -
Самодвойственность удобно проверять по таблице функции. Усло-
вие f = f* пли f(xi,...,xn) = /(тф,   , можно сформулиро-
вать так: самодвойственная функция на каждой паре противополож-
ных наборов значении аргументов принимает противоположные значе-
ния. Заметим еще, что, если при составлении таблицы наборы значений
аргументов располагать в естественном порядке, то противоположные
наборы равно отстоят от концов таблицы.
Обозначим через ,5' совокупность всех самодвойственных функ-
ций:
s = {/1 f = Г }.
Лемма.Суперпозиция самодвойственных функций является самодвой-
ственной функцией.
Лемма вытекает нз принципа двойственности. Пусть
/1 = Л , Л = Л ,   , Л = Л ,
а функция f является суперпозицией функций fi, f2 ,    , fr  Для опре-
деленности возьмем какую-нибудь конкретную формулу, например,
, т2, х3) = Л(х'2, /2(ж.з,Ж1)) 
Тогда по принципу двойственности
Л (si, х2, т.з) = /* (ж2,/2(т3,Т1)) = /1(Т2,/2(Т3,Т1)) ,
т.е. f* совпадает с /.
4.	Класс L (класс линейных функций}.
Предварительно изучим одну полную систему булевых функций.
Лемма. Система функций {Л>Л>Л}, где /1 = 1 , /2(т1, х2) = х-ух2
( конъюнкция), /з(ж1,ж2) = х-i Ф х2 (сложение по модулю два), явля-
ется полной.
Полнота данной системы следует нз того, что х = х Ф 1 (это озна-
чает, что нз функций данной системы можно построить отрицание), а
также нз того факта, что отрицание вместе с конъюнкцией образуют
полную систему .
- 113 -
Пример. Дизъюнкцию можно выразить через конъюнкцию и отрица-
ние, а затем через функции рассматриваемой системы:
Т'1 V Т2 = Х-[ Т2 = (ж'1 Ф 1) (т2 Ф 1) Ф 1 .	(4.2)
Операция сложения по модулю два и конъюнкция по своим алге-
браическим свойствам ничем не отличаются от обычных сложения и
умножения. Вычислением левой и правой частей легко убедиться в спра-
ведливости тождеств (4.3) — (4.7):
Х\ ф Х2 = Х2 Ф Т'1 ;	(4-3)
xi Ф (х2 Ф ж.з) = (si Ф х2) Ф Хз ;	(4-4)
Т1 (ж2 ф Т.з) = Х2 Ф Т'1 т.3 ;	(4-5)
х Ф 0 = х ;	(4-6)
х Ф х = 0 .	(4-7)
Учитывая тождества 6 — 10 для конъюнкции, получаем такое пра-
вило: формулы, содержащие знаки & и ф, можно преобразовы-
вать по обычным алгебраическим законам: переставлять множители и
слагаемые, раскрывать скобки, выносить общий множитель за скобки.
Отметим только, что правило приведения подобных в алгебре с опера-
циями & п ф следующее: еслп в сумме встречаются два одинаковых
слагаемых, то оба они вычеркиваются ( тождества (4.7) и (4.6)).
Пример. Применение алгебраических преобразований к формуле (4.2)
для дизъюнкции дает
Ж1 V Х2 = (ж'1 Ф 1) (х2 Ф 1) Ф 1 = T1 Х2 Ф T1 Ф Ж2 Ф 1 Ф 1 = Т'1 Х2 Ф Т'1 Ф Х2 
Таким образом,
Х\ \/ Х2 = Т'1 Х2 Ф Т'1 Ф Х2 
(4-8)
Рассмотрим произвольную булеву функцию /(яд , т2, . . ., хп).
Представим ее формулой в базисе V,&,—, например, совершенной
д.н.ф. (4.1); после этого заменим в этой формуле каждую операцию V
по формуле (4.8), а каждое отрицание на ф1. В полученном выражении
- 114 -
раскроем скобки и приведем подобные плены. В результате полупится
многонлен от переменных жд, Х2,   , хп :
f(x-[, Х2, . . ., хп) = а0 ф a-i x-i ф а2 х2 Ф . . . Ф ап хп ф бДджд х2 Ф . . . Ф
Ф <Ф — 1 ,n Xn — i Хп Ф </12,3 Ж1Ж 2 Ж'З Ф    Ф </1,2,..., п Ж1Ж2    Хп .
(4-9)
Коэффициенты многочлена равны либо нулю ( если соответствую-
щий член отсутствует), либо единице. В честь русского логика конца
XIX в. И.И.Жегалкина выражение (4.9) называют многочленом Жегал-
кина булевой функции f. Приведенное выше рассуждение доказывает
справедливость следующего утверждения.
Теорема.Каждую булеву функцию можно представить многочленом
Жегалкина.
Пример. Представить многочленом Жегалкина функцию, заданную
табл. 4.9.
Таблица 4.9
Ж1 Х2 Ж3	/
ООО	1
0 0 1	0
0 1 0	1
0 1 1	1
1 0 0	0
1 0 1	0
1 1 0	0
1 1 1	1
Рассматриваемый ниже алгоритм построения многочлена Жегал-
кина применим для любой булевой функции.
1.	Представим / совершенной д.н.ф.:
/(жд, Т'2, т.з) = Ж1 Ж'2 т.3 v T1 Т'2 T.3 V ЖД T.3 V T1 Т'2 т.з 	(4.10)
Заметим, что если А В = 0 , то А \/ В = А бг В. Это выте-
кает из формулы (4.8) или из сравнения таблиц дизъюнкции и суммы
ио модулю 2. Булевы функции А и В, которые одновременно не
- 115 -
обращаются в единицу, т.е. такие, что АВ = 0, называют орто-
гональными. Логическая сумма, слагаемые которой ортогональны, не
изменяется, если знаки V заменить на знаки Ф. Воспользовавшись
этим, выполним следующий шаг.
2.	Заменим в совершенной д.н.ф. функции f (4.10) все знаки V
на знаки Ф :
f(xi, Т'2, Т.з) = тТтЦТз ф Х^Х2 хз Ф хТ Х2 Тз Ф Х\ Х2 Тз 
3.	Заменим каждое отрицание по формуле А = А ф 1, после этого
раскроем скобки н приведем подобные члены:
/ = (т'1 ®1) (х2 ф1) (т3ф1) Ф(Ж1 Ф1) Х2 (т3ф1) Ф(Ж1 ф1) Х2 Т3ФТ1 Т2 Х3 =
= ТД Х2 Т'З ФЖ1 Х2 фТД Т'З ФТ‘2 Х3 фТД фТД фТ.з Ф1 фТД Х2 Т'З фТД Тдф
фТД т.3 фт'2 фт'1 Х2 Т'З фт'2 Т'З фТД ТД Т'З = 1 фТД фТ.з фТД Т.з фТД Т'З .
Окончательно,
/(Т1, Т2, Тз) = 1 ф Т1 ф Тз ф Т1 Тз ф Т2 Тз .
Замечание. Вернемся к общей форме многочлена Жегалкнна (фор-
мула 4.9). Количество членов в ней равно 2" — для каждого под-
множества индексов переменных {ф, г’г, . . ., ik} в многочлене имеется
слагаемое тд1тд2...тдь с коэффициентом	Можно устано-
вить бнекцню между многочленами н двоичными словами
Q,qCLх d2   • ^1,2   • — 1 ,п^1,2,3 •   1,2,,,,,п
длины 2". Следовательно, количество разных многочленов Жегалкнна
от п переменных равно 22 . Это совпадает с количеством всех бу-
левых функций от п переменных. С учетом доказанного только что
утверждения получаем, что имеется ровно по одному многочлену Же-
галкнна для каждой функции.
Функция f называется .линейной, если ее многочлен Жегалкнна
содержит члены только степени не выше первой':
/(т-i, т2, . . ., т„) = а0 ф ai т-i ф а2 т2 ф . . . ф ап хп .
- 116 -
Пусть L — множество всех линейных функции. Константы 0 и 1,
отрицание х , сумма по модулю 2 — примеры линейных функций.
Дизъюнкция xi V Х2 = xi х3 Xi х3 — нелинейная функция. Не-
линейной является также конъюнкция, многочлен Жегалкпна, которой
имеет вид тдтд.
Лемма. Суперпозиция линейных функций является линейной функцией.
Очевидно.
Лемма (о нелинейной функции).Пусть f(xi,X2,...,xn) — нели-
нейная функция и п> 2. Подстановкой констант ( нуля и единицы)
на места п — 2 аргументов функции f можно получить нелинейную
функцию от двух аргументов.
Доказательство. Рассмотрим многочлен Жегалкпна функции f ; по
условию он содержит, по крайней мере один член степени выше первон'.'
Переименовывая переменные мы можем считать, что в этот член входят
буквы x-i н Х2 (возможно н какне-то другие). Произведем такую
группировку членов многочлена Жегалкпна функции f : соберем
вместе члены, в которые входят xi н ж2, н вынесем xi х3 за скобки.
Средн оставшихся соберем члены, содержащие x-i, н вынесем x-i за
скобки; точно так же соберем члены, содержащие ж2, и вынесем х3
за скобки. В результате получим
/ = Т1Т2Л(тз,..., хп) фЖ1В(т3,..., хп) фт2С’(т3,   , хп) С D(x3,.. ,,хп).
Здесь А, В, С, D — некоторые булевы функции от х3, . . ., хп, причем
А ^0. (Это следует нз единственности многочлена Жегалкпна: если
А = 0, то это означало бы, что функция f имеет два многочлена
Жегалкпна — в одном имеется член с произведением xi х3, а в другом
такого члена нет). Итак, для некоторого набора а.з, . . ., ап значений
переменных х3,...,хп имеем Л(а.з, . . ., an) = 1. Тогда
f(xi, т2, а3 . . ., а„) = ад т2 Ф Д ад Ф 7 т2 Ф <5
(Д = В(а3 . . ., а„) , 7 = С’(а3 . . ., а„) , д = D(a3 . . ., а„)) .
Лемма доказана.
- 117 -
5. Класс М (класс монотонных функций).
Рассмотрим множество всех двоичных слов длины п. Зададим на
этом множестве отношение порядка следующим образом: будем гово-
рить, что слово
a =	• • • <тп
предшествует слову
/3 = p-ylh ...рп,
если
Q'l < Р\ у Q'2 С Р2 ,    , ®п < Рп 
(обозначение < понимается обычным образом: 0 <_0, 0 <_1, 1 <_1. )
Тот факт, что слово а предшествует слову Р, будем обозначатв
так: a < Р.
Напомним общее определение отношения порядка на пропзволвном
множестве X. Так назвшают отношение р, для которого ввшолняются
следующие аксиомы:
(рефлекспвноств );
2.x ру , у р х => х = у (антисимметричность);
Z.xpy , у р z => xpz (транзитивность) .
Без труда проверяется, что введенное выше отношение на множе-
стве двоичных слов данной' длины удовлетворяет этим аксиомам.
Пример. Справедливы следующие неравенства;
00 <10 <11; 0010 <0111 <1111.
В то же время пз двух слов 01 и 10 ни одно не предшествует другому.
Такие слова называют несравнимыми.
- 118 -
На рис. 4.5 отношение ” < ” на множестве двоичных слов длины п
представлено графически для п = 3. Слово а предшествует слову /?,
еслп от (3 к а можно пройти по стрелкам.
Булева функция f называется монотонной, еслп для каждой пары
наборов значений переменных, один пз которых предшествует другому,
значение функции на меньшем наборе не превосходит значения функ-
ции на большем:
а < ~(3 =>	< fCP) 
Обозначим через М совокупность всех монотонных булевых функ-
ций.
Лемма. Суперпозиция монотонных функций является монотонной
функцией.
- 119 -
Доказательство леммы проведем на примере конкретной суперпо-
зиции, рассуждение для общего случая фактически то же самое.
Пусть / (х ! , X 2 , У1 , У'2 ) = /1 (ж 1, х 2 , /2 (У1 , У'2 ) ) , ИрНЧвМ фуНКЦНН /1
и /2 нз класса М ; убедимся, что f £ М. Рассмотрим два сравнимых
набора значений аргументов функции f :
0'10'27172 < Д1Д2<5Д2 
Тогда 7172 < <Ы2, и в силу монотонности функции /2 имеет место
неравенство а3 =/2(71,72) < f'2^1, <Д) = Дз
Поэтому O1O2O3 < Д1Д2Д3 и в силу монотонности /1 справедливо
неравенство /1(01, о2, о3) </ДД, Д2, Дз)- В итоге получаем:
/(01,02,71,72) = hia-i, 02, /2(71,72)) = /i(ai, «2, а.з) <
< /1(Д1,Д2,Д.з) = /1(Д1Д2,/2№Д2)) = /(Д1Д2ЛЛ2) 
Таким образом, / £ М.
Лемма (о немонотонной функции).Из немонотонной функции пу-
тем подстановки констант на места некоторых п — 1 аргументов
можно получить отрицание.
Доказательство. Пусть / М. Это означает, что для некоторой
пары наборов о н Д значений переменных нарушено условие моно-
тонности:
о < Д в то время как /(о) > /(Д) .
Наборы о н Д называют соседними, если они отличаются только
одной координатой. Покажем, что для функции / найдется пара
соседних наборов, на которой нарушается условие монотонности. Пару
наборов а н Д такую, что а < Д, всегда можно связать цепочкой
соседних наборов, как это показано ниже на примере
5 = 001000 < 001001 < 011001 <011101 <011111 = Д .
Так как в начале цепочки /(й) = 1, а в конце /(Д) = 0, то для
некоторой пары соседних наборов цепочки происходит смена единицы
на нуль.
- 120 -
Возьмем пару соседних наборов
<ах    О'г — 1 Oa'i+i . . . Q'n , ai . . . а2_ 11ач_|_1 . . . ап,
для которых
У(а'1г  -i^i — 1 5 0 5 АЧ + Ъ-  -jA-'n) - 1 J /(Q'lr  -i^i — 1 5 1 5	+	 -jA-'n) - О?
и рассмотрим функцию одного аргумента
= f(a-y, . . ., а;_1, х, ai+i, . . ., а„).
По построению <р(х) = х. Лемма доказана.
Теорема Э.Поста. Для того чтобы система булевых функций
была полной, необходимо и достаточно, чтобы она содержала
1)	функцию, не сохраняющую нуль;
2)	функцию, не сохраняющую единицу;
3) несамодвойственную функцию;
X) нелинейную функцию;
5) немонотонную функцию.
Необходимость условии теоремы вытекает пз доказанной в лем-
мах замкнутости классов
То , Ту , S , L , М относительно суперпозиции. Нарушение хотя бы од-
ного пз условии теоремы означает, что все функции заданной системы
входят в соответствующий замкнутый класс, поэтому и нх суперпози-
ции будут принадлежать тому же классу. Следовательно, функцию,
не входящую в рассматриваемый класс, нз функций данной системы
построить нельзя. Как видно нз рассмотренных выше примеров, для
каждого нз пяти классов существуют функции, не входящие в класс.
Для доказательства достаточности убедимся, что нз функций за-
данной системы можно построить отрицание н конъюнкцию. Пз пол-
ноты системы, состоящей нз этих двух функций, вытекает в таком слу-
чае н полнота заданной системы. Построение проводится в два этапа:
- 121 -
I. Построение констант и отрпцанпя;
II. Построение конъюнкции.
I. Найдем в данной системе функции fi и fj, такие, что fi То,
a fj (f , п построим функции одного аргумента:
Нж) = fi(x,   , х) и ^(х) = fj(x,   -,х) 
Прп сделанных предположениях относительно fi и fj пмеем
НО) = 1 , Hi) = о.
В зависимости от того, какие значения имеют у?(1) и V’(O) могут
представиться четыре случая а),б),в) и г).
Случай а). у?(1) = 0 , НО) = 0.
Пмеем Нж) = х , Нж) = 0. Подставляя одну пз этих (функ-
ций в другую, получаем ННЖ)) = I. Таким образом, отрицание и
константы построены.
Случай б). y?(I) = I , -0(0) = I.
В этом случае Нж) = I , Нж) = х- Строим НН(Ж)) = 0, и
первый этап закончен.
Случай в). </?(!) = 0 , V’(O) = I.
Пмеем Нж) = ’ф(х) = х. Воспользуемся тем, что в рассматрива-
емой системе имеется функция fk(xi,. . .,хп)	,5'. Для этой функции
найдется пара противоположных наборов ац, . . ., ап и aj", . . ., аД,
на которых функция Д принимает одно и то же значение. Рассмо-
трим функцию А(ж) = fk(xai,. . ., хап). (Наместо г'-го аргумента Д
ставится х, если а; = I, или х, если &i = 0. )
Для функции А (ж) справедлива цепочка равенств:
А(0) = fk (0ai,..., 0“ Д = Д (аД ..., аД) =
= fk(ai,...,an) = Д(1аД...Д“Д = А(1),
откуда следует, что А(ж) = const. С помощью отрпцанпя построим
другую константу.
- 122 -
Случай г). у?(1) = 1 , -0(0) = 0-
Следовательно, <р(х) = 1 , Д(т) = 0- Найдем в данной системе не-
монотонную функцию. По лемме о немонотоной функции пз нее путем
подстановки констант можно получить отрицание.
II. Покажем, что нз функций рассматриваемой системы можно по-
строить конъюнкцию. При этом будем использовать уже построенные
на первом этапе константы н отрицание.
Найдем в заданной нам системе функций нелинейную функцию.
Подставляя в нее константы, построим нелинейную функцию ц от
двух аргументов, это возможно по лемме о нелинейной функции:
//(ж 1, Х2) = Ж'1 Ж2 Ф Л ф Р Х2 Ф 7 .
Рассмотрим функцию тг(ж1, ж2) =//(яд ф Д, ж2 ф а) ф (а Д ф 7). Для по-
строения функции тг нужно только отрицание, поскольку прибавление
двоичной константы либо ничего не изменяет (если константа — ноль),
либо меняет переменную на ее отрицание. Например, при а = 1,Д =
0,7=1 функция тг равна тг(а?1, ж2) = ц(ху, т2ф 1) Ф 1 = /Д, тц, хр). Так
как отрицание уже построено на первом этапе, то функцию тг можно
построить нз функций данной системы.
В общем случае получим
тг(т1, т2) = fpxy ф [3, х2 Ф а) Ф (а Д ф 7) =
= (тц Ф Д) (ж2 Ф а) Ф а (яд Ф Д) Ф Д(т2 Ф а) Ф 7 Ф а Д Ф 7.
Раскрыв скобки, убеждаемся, что тг(а?1, ж2) = тдяд. Таким обра-
зом, конъюнкция построена нз функций системы (Д, /2, . . ., /г).
Теорема доказана.
Для проверки полноты конкретной системы функций удобно запол-
нять таблицу, в которой отмечается единицей нлн нулем вхождение нлн
невхожденне функции в классы Ту , Ту , S, L н М . Такое построение
для системы функции
(Л,/2, Уз) , где /1(т) = X, f2(xy, Х2) = Ху Х2, f3(xy, Х2) = Ху V х2 ,
выполнено в табл. 4.10.
- 123 -
Таблица 4.10
Функция	Класс				
	То	Ту	S	L	м
/1	0	0	1	1	0
А	1	1	0	0	1
/з	1	1	0	0	1
Система функций будет полной, еслп в каждом столбце таблицы
имеетоя нуль. Из табл. 4.10 видно также, что пз системы (/i,/2,/з)
можно удалить функцию /2 или /3, — останется полная система.
Однако, система функций (/2,/з) не является полной.
Пример. В системе функций (Л, /2, /з, А), где А = 0 , А = 1,
Уз(ж1, жд) = яд , /4(^1, яд) = яд V яд все четыре функции монотонны.
Система неполная.
Пример. Функция
А (яд, яд) = яд —> яд имеет следующую таблицу.
Xi	Х2	—> Х2
0	0	1
0	1	1
1	0	0
1	1	1
Из таблицы видно, что А не сохраняет нуль, несамодвойственна и
немонотонна. Кроме того,
/Дяд, яд) = яд Ж'2 = Ж1 (х2 ф 1) ф 1 = 1 ф T1 ф T1 х2 ,	(4.11)
следовательно, A L. Добавляя к А любую функцию, не сохра-
няющую единицу, получим полную систему. Рассмотрим, напрпмер,
систему (А, А) , где f2 = 0. Покажем, следуя доказательству тео-
ремы Иоста, как из функций А и f2 можно построить отрицание и
конъюнкцию.
Имеем /1 То, f2 Ту. Функции д и ф в рассматриваемом
случае такие: <р(х) = fy(x,x) = 1 , ф(х) = 0 . Следовательно, имеет
место случай ”г)”. Находим в системе немонотонную функцию, это
А. Выбираем два соседних набора значений переменных, на которых
нарушается монотонность : /1(0,0) = 1, /1(1,0) = 0. Подставляем
- 124 -
в fi вместо второго аргумента константу нуль, т.е. в данном случае
функцию /2 : fi (ж, /г(ж)) = х. Итак, х = х —> 0.
Для построения конъюнкции находим в системе ДД) нелиней-
ную функцию, это снова Д. Из (4.11) х-ух^ = /Дт^тД). Таким
образом,
Х1 ЖД = (Х1 —> (Х2 —> 0)) —> 0 .
Полученный в этом примере результат можно интерпретировать
так: для любой булевой функции можно написать формулу, в которую
будут входить только стрелки н нули. Иапрнмер,
ф Х2 = ЖфЖД V xfxf = ЖфЖД ' Xfxf =
= (Д1 -э 0>2 -э 0) (ti(t2 0)	0) о.
4.4. Схемы из функциональных элементов
Как отмечалось в параграфе 4.1, в настоящее время основные при-
менения булевых функций связаны с цифровой техникой. Технология
изготовления элементов цифровой техники за последние десятилетня
многократно изменялась в направлении миниатюризации, повышения
быстродействия, снижения потребляемой мощности, удешевления н т.п.
Как следствие, имеется большое разнообразие физических принципов,
на которых построены элементы цифровой техники. Общим для такого
рода устройств является наличие входов н выходов, каждый'нз кото-
рых может находиться в одном нз двух отличающихся друг от друга
физических состояний.
Рассмотрим в качестве примера электрическую схему нз трех дио-
дов н сопротивления, показанную на рнс. 4.6 .
а)	б)
Х1	а------Н
ж 2	о------И
Хз	°------Н
ИЛИ
Рнс. 4.6.
- 125 -
В точках схемы, изображенных кружком, в различные моменты
времени возможно появление напряжения либо высокого уровня, при-
близительно равного 5В, либо низкого уровня, приблизительно равного
нулю. В точке схемы, отмеченной черточкой, поддерживается посто-
янно нулевой уровень напряжения.
Точки, отмеченные ад, тд, т.з будем интерпретировать как входы,
точку у — как выход. При появлении на любом нз входов высокого
уровня напряжения через соответствующий диод н сопротивление R
протекает ток, в результате в точке у будет высокий уровень напря-
жения.
В словесной форме работа схемы на рнс. 4.6,а описывается так:
если на всех входах низкий' уровень напряжения, то на выходе — тоже
низкий, если хотя бы на одном нз входов высокий уровень напряжения,
то на выходе — высокий. Обозначив состояние с высоким уровнем
напряжения единицей', а с низким — нулем, приходим к выводу: зави-
симость выхода от входов можно задать при помощи булевой функции
у = V Х2 V т.з ,
На основании этого схему рнс. 4.6,а условно обозначают так, как это
показано на рнс. 4.6,6 н называют логическим элементом ”ПЛП”.
Отметим, что схема на рнс. 4.6,а не единственная в своем роде:
подобные схемы можно построить нз электронных ламп, электромеха-
нических переключателей, пневмоэлементов н др. Зависимость выхода
от входов может описываться не только как дизъюнкция, но так же при
помощи конъюнкции, отрицания н более сложных булевых функций.
Будем в связи с этим рассматривать логические элементы с раз-
личной зависимостью выхода от входов (рнс. 4.7) .
Рнс. 4.7
Эти элементы можно соединять друг с другом, подавая выходы
некоторых элементов на входы других. Математическая модель возни-
кающего при этом объекта называется схема из функциональных эле-
ментов (СФЭ).
- 126 -
Чтобы определить СФЭ, вначале дадим определение сети. Сеть со-
стоит из полюсов и элементов, каждый элемент имеет, несколько вхо-
дов и одни выход. Полюсы изображаются перечеркнутыми кружками,
а элементы прямоугольниками с отростками
Определение сети
1.	Полюс является сетью. Он будет единственной вершиной этой
сети.
2.	Объединение двух сетей без общих вершин является сетью. Мно-
жество вершин этой сети состоит нз вершин первой'н второй'сетеш
3.	Результат присоединения всех входов некоторого элемента к
каким-либо вершинам сети является сетью. Ее вершинами являются
все вершины старой сети н выход присоединенного элемента.
Пример. На рнс. 4.8 показана последовательность шагов применения
пунктов 1-3 определения сети. Согласно определению, объект, полу-
чаемый на каждом шаге, является сетью.
Рнс. 4.8
- 127 -
Определение схемы пз функциональных элементов
Схемой пз функциональных элементов называется сеть, в которой
1)	каждому элементу с к входами поставлена в соответствие бу-
лева функция f(xi, . . ., жд) от к переменных;
2)	каждому полюсу поставлена в соответствие одна пз переменных
жд, . . ., хп , разным полюсам соответствуют разные переменные;
3)	выделены некоторые вершины, называемые выходами схемы.
ЖД	Х2
Рис. 4.9
Пример. Из сети предыдущего примера может быть получена схема,
показанная на рис. 4.9 .
С каждой вершиной схемы можно связать булеву функцию, о ко-
торой говорят, что она реализуется в соответствующей вершине. Это
делается следующим образом:
1) с полюсами связываем функции, равные ад, . . ., хп ;
2) пусть уже известны функции , . . ., ерь , реализующиеся на вхо-
дах некоторого элемента, которому поставлена в соответствие функция
/(жд, . . ., жд) . Тогда на выходе этого элемента реализуется функция
Лп  -,Ы 
Пример. Иа выходе схемы, показанной на рпс. 4.9 , реализуется функ-
ция
Ж1 ЖД (ж 1 V жд) = (лфГ V Ж2")(Ж1 V жд) = Ж'1 ф жд .
Иа рпс. 4.9 указаны также функции, реализующиеся в вершинах схемы.
- 128 -
Для СФЭ возникают задачи анализа и синтеза.
Задача анализа: дана схема, выяснить, какие функции реализуются
на ее выходах.
Алгоритм решения этой задачи таков: следуя шагам 1 — 3 построе-
ния сети, последовательно вычисляем функции, реализующиеся во вновь
появляющихся вершинах.
Задача синтеза: задан набор функциональных элементов (см. рнс.
4.7). Предполагается, что имеется неограниченный запас элементов
каждого типа. Задана также булева функция f(xi,...,xn) . Требуется
нз заданных элементов построить схему, на одном нз выходов которой'
реализуется функция f .
При решении задачи синтеза прежде всего возникает вопрос: су-
ществует лн такая схема? Этот вопрос решается теоремой Поста: если
система функций (Л ,   , Л) полная, то любую булеву функцию можно
реализовать схемой, построенной нз элементов, показанных на рнс. 4.7.
Действительно, функцию f можно представить в виде суперпозиции
функций (/i,...,/r) , а каждому шагу суперпозиции соответствует
определенное соединение элементов.
Пример. Для функции
/(Ж1, х2, х3) =	x-i, х2), ь(х2, х3), /з(ж.з)), х3)	(4.12)
схема, соответствующая суперпозиции в правой части формулы (4.12),
показана на рнс. 4.10.
Рнс. 4.10
После того как вопрос о существовании схемы решен, возникает за-
дача оптимального синтеза: нз всевозможных схем, реализующих дан-
- 129 -
ную функцию, выбрать наплучщую по тому или иному признаку. На-
прпмер, можно поставить задачу: построить для данной функции схему
с наименьшим числом функциональных элементов.
Рассмотрим далее примеры СФЭ , построенные пз элементов так
называемого классического базиса, т.е. пз функциональных элементов,
реализующих дизъюнкцию, конъюнкцию и отрицание (рис. 4.2) .
Система булевых функций, состоящая пз дизъюнкции, конъюнкции
п отрицания, полная, поэтому пз элементов, показанных на рис. 4.2,
можно построить схему для любой булевой функции. Практически, это
означает, что любой дискретный преобразователь информации можно
построить пз элементов классического базиса.
Пример. Функция /(ад, жд, ж.з) задана таблицей 4.11 . Требуется
построить схему, реализующую f .
Таблица 4.11
Х2 Жз	/
ООО	0
0 0 1	1
0 1 0	0
0 1 1	1
1 0 0	0
1 0 1	1
1 1 0	0
1 1 1	0
Запишем данную функцию формулой в базисе (V,&,—) , исполь-
зуя, напрпмер, совершенную ДНФ (формула (4.1)):
/(т1 , Т'2, т.з) = T1T2T.3 v T1T2T.3 V T1T2T.3 	(4-13)
Для каждой логической операцпп в формуле (4.13) возьмем соот-
ветствующие функциональные элементы и произведем их соединение
так, как этого требует формула (4.13) .В результате получим схему,
показанную на рис. 4.11 .
- 130 -
Рис. 4.11
f
В схеме на рис. 4.11 использовано 10 элементов. Предварптельное
упрощение формулы (4.13)
/(жд, Х2, т.з) = Ж1Ж2Ж.З V Ж1Ж2Ж.З V Ж1Ж'2Ж.З =
= (ti V Т1)Т2Ж.З V Ж1(ж2 V Ж2)ж.З = Жз^'З V Ж1Ж.З = Ж1Т2Ж3.
Схема дешифратора
Дешифратором называется схема, имеющая п входов х±, ... ,хп
п 2" выходов, на которых реализуются всевозможные элементарные
конъюнкцпп, состоящие пз п букв. (См. рпс. 4.13 для п = 2 .)
Рпс. 4.13
- 131 -
При подаче на входы дешифратора какой-либо комбинации нулей
и единиц единичный' сигнал появляется только на одном из выходов,
остальные выходы находятся в состоянии нуль. В ЭВМ дешифратор
применяется для записи или считывания из памяти: на вход подается
двоичный адрес определенной ячейки памяти, это вызывает появление
единичного сигнала ровно на одном из выходов, которып'связан с со-
ответствующей ячейкой, благодаря чему операция записи-считывания
будет производиться именно для этой ячейки.
Схему дешифратора можно построить индуктивно, добавляя для
каждого входа хп блок из 2" элементов ”11”. На рис. 4.14 показана
построенная таким образом схема для п = 3 .
Рис. 4.14
В заключение рассмотрим схему, имеющуюся в каждом компью-
тере.
- 132 -
Схема двоичного сумматора
Двоичный сумматор — это схема, осуществляющая сложение двух
целых чисел, при этом слагаемые н сумма представляются в двоичной
системе счисления. Условно схема сумматора показана на рнс. 4.15.
ап Ьп ... щ b'2 ai 61
___I___L________L 1___I____I 
£
—I------I-------------I----I—
•S„ + l	*п   	-5'2	-5'1
Рнс. 4.15
На 2п входов подаются двоичные разряды слагаемых:
ап . . . Я2Я1 н hn . . . 62^1 
На выходах (число нх равно п + 1 ) образуются двоичные разряды
суммы.
Будем выполнять сложение наиболее простым способом : для по-
лучения какого-то разряда суммы складываются соответствующие раз-
ряды слагаемых н результат переноса нз предыдущего разряда. Тогда
схему сумматора можно построить нз однотипных блоков, как это по-
казано на рнс. 4.17.
ап	Ь3 а3	Ь3 аз	bi
Рнс. 4.16
Зависимость выходов от входов следующая:
.5'1 = ai + 6i ; p-L =	.	(4.14)
Si = at + bi + Pi-1 ; Pi = Oibi V OiPi-iy biPi-1 , i >2 .	(4.15)
- 133 -
Перейдем к построению отдельных блоков. Запишем функцию .5ц
в виде КНФ :
«1 = (Я1 V 61)(«1 V ф) .
(4.16)
Формуле (5.6) соответствует схема, показанная на рпс. 4.17. Прп
подаче на входы а± и ф этой схемы младших разрядов слагаемых на
выходе .5'1 образуется младший разряд суммы, а на выходе pi перенос
во второй разряд.
Рпс. 4.17
Для построения схем при г = 2,...,п заметим, что Si =
(di Э bi) Pg Pi-I , TO есть ВЫХОД Si можно получить, используя две
схемы, показанные на рис. 4.17. Это приводит к схеме, представленной
на рпс. 4.18.
- 134 -
at	hi
Рис. 4.18
На выходе Si образуется г-й разряд суммы, на выходе pi —
перенос в следующий (г + 1)-й разряд.
4.5. Дизъюнктивные нормальные формы
В параграфе 4.2 дано определение дизъюнктивной нормальной фо-
рмы (д.н.ф.) как формулы вида
A'i V 7<2 V ... V Кт ,
где Ki, Кц, . . ., Кт — элементарные конъюнкции, то есть произведе-
ния переменных пли их отрицании, в которых все индексы переменных
- 135 -
различны:
К = жДжД2 . . . ж“г, 1 < г'х < i2 < . . . < ir < п .
Число г, то есть количество букв в конъюнкции, называется ее рангом.
Элементарной конъюнкции К можно сопоставить слово
7172   - 7„
в алфавите {0,1,*} по следующему правилу:
=0, если К содержит ж; ;
= 1, если К содержит тд ;
= *, если К не содержит тд .
Указанное отображение, очевидно, является бнекцнен множества
элементарных конъюнкций'от переменных xi,...,xn на множество
всех слов длины п в алфавите {0,1,*}. Отсюда
число элементарных конъюнкций от п переменных равно 3" .
Замечание. Слову нз одних звездочек соответствует конъюнкция, в
которой нет нн одной буквы. ’’Для ровного счета” будем н такое пустое
произведение называть элементарной'конъюнкцией' н считать, что оно
задает функцию, тождественно равную единице.
Замечание. Нетрудно подсчитать, что число конъюнкций ранга г ,
то есть конъюнкций, составленных ровно нз г букв, равно С'”2Г
(С'” способами можно выбрать буквы, нз которых состоит конъюнкция,
2” способами расставить над ними черточки). Отсюда еще раз находим
общее число элементарных конъюнкций:
п
£С”2” = (1 + 2)" =3” .
г = 0
Если для некоторой булевой функции / имеет место формула
/(т-I, т2, . . ., хп) = 7<1 V К2 V . . . V Кт ,	(4.17)
- 136 -
/1(Ж1, т2, Жз) =
то говорят, что функция f представлена в виде д.н.ф- Д.н.ф в формуле
(4.17) называют д.н.ф. функции f или говорят, что д.н.ф. реализует
функцию f .
Одна нз первых теорем о булевых функциях утверждает, что ка-
ждая функция может быть представлена совершенной д.н.ф. (4.1). Од-
нако, представление функции в виде д.н.ф., вообще говоря, не един-
ственно. Это показывает такой простой подсчет: число булевых функ-
ций от п переменных равно 22 , а число различных д.н.ф. равно 23 ,
то есть в среднем на каждую функцию приходится много реализующих
ее д.н.ф. Например, функция
О, если Xi = Х2 = т.з
1 в остальных случаях
может быть представлена совершенной д.н.ф.
/1(т'1, Т'2, Т.з) = Т1Т2Т.З V ТДТДТ'З V ТДТДТ'З V ТДТДТ'З V ТДТДТ'З V ТДТДТ'З ,
а также следующими д.н.ф. :
/1(т'1, Т'2, Т.з) = Tli'2 v Т1Т2Т.З V ТДТДТ'З V ТДТДТ'З V ТДТДТз
(4.18)
/1(т'1, Т'2, Т.з) = TlT'2 V ТДТ'З V Т1Т.З ,
которые можно получить нз совершенной, применяя булевы тождества.
В связи с этим можно поставить следующую задачу:
для данной булевой функции найти реализующую ее д.н.ф. с
наименьшим количеством букв.
Д.н.ф., реализующая данную булеву функцию f , н имеющая наи-
меньшее число букв по сравнению с другими д.н.ф. функции f , называ-
ется минимальной д.н.ф. функции f . Таким образом, задача состоит в
том, чтобы для заданной булевой функции найти ее минимальную д.н.ф.
Задача отыскания мннмальных нлн близких к ним д.н.ф. в литературе
называется задачей минимизации булевых функций.
n-мерный единичный куб н грани.
Область определения булевой функции /(яд , жд, . . ., хп) , то есть со-
вокупность всевозможных двоичных слов длины п , можно рассматри-
вать как множество вершин единичного n-мерного куба.
- 137 -
Единичный n-мерный куб определяется как декартово произведе-
ние п отрезков: Еп = [0, 1]" :
Еп = {(яд, Х'2,    , Хп) | 0 < Xi < 1,2= 1, 2,..., п}.
Еслп некоторые переменные, например, переменные с номерами
г'1, г'2, . . .,ir зафиксировать на их крайних значениях - 0 или 1, и рас-
смотреть подмножество Q С Еп
Q = {(x-i, Х2, . . ., хп) G Еп | Xit = aq, = 0'2, . . ., Xir = О'г} ,	(4.19)
то, очевидно, Q будет представлять собой декартово произведение
п — г единичных отрезков, то есть куб размерности п — г .
Определение. Пусть oi, 02,..., ог — произвольный набор нулей и
единиц. Множество Q, определяемое формулой (4.19), называется
п — r-мерной гранью куба Еп.
Номера фиксируемых переменных ф, г'2, . . ., ir можно выбрать С„
способами, а зафиксировать значения г переменных — 2” способами.
Поэтому число п — r-мерных граней куба Еп равно С„  “2Г.
Число г будем называть рангом грани и обозначать rang (Q) , та-
ким образом, сумма размерности и ранга грани равна п. Размерности
граней куба (ранги) могут изменяться в пределах от 0 до п. Нульмер-
ные грани (все переменные зафиксированы) - это вершины куба Еп;
одномерные грани называют ребрами; грань размерности п - это сам
куб Еп (никакие переменные не фиксируются).
Замечание. Куб и совокупность его граней образуют топологический
объект, называемый комплексом (кубическим). Это весьма сложный
объект: многие вопросы относительно него остаются нерешенными до
настоящего времени. Например, неизвестно каково минимальное мно-
жество вершин, обладающее тем свойством, что в этом множестве есть
по крайней мере один представитель от каждой Ar-мерной грани (задача
О.Б.Лупанова о ’’протыкании” граней).
Замечание. В дальнейшем кубический комплекс рассматривается как
дискретный, а не как непрерывный объект. Говоря о кубе и его гранях,
мы всякий раз будем иметь в виду множество вершин куба или множе-
ство вершин данной грани. Эти (конечные) множества мы попрежнему
будем называть кубом или гранью.
- 138 -
Геометрическая интерпретация задачи минимизации.
Каждой булевой функцпп /(яд, . . ., хп) будем сопоставлять под-
множество вершпн Nf С Еп, в которых эта функция равна едпнпце:
Nf = {a-ia2 . . . а„ | f(a-L, а2, . . ., ап) = 1}.
Прп этом булевым операциям над функциями будут соответствовать
теоретико-множественные операцпп над подмножествамп Еп . В сле-
дующей таблице перечислены соответствующие друг другу аналитиче-
ские п геометрические объекты.
Соответствие аналитических п геометрических объектов.
Аналитический объект	1 Геометрический объект
Двопчные слова длпны п	Вершпны n-м ерного куба Еп
Булева функция /(жд, . . ., жп)	Подмножество вершпн Nf С Еп
Элементарная конъюнкция К = xf^xf^ . ..xfj	Nk — грань куба Еп Xir = ci'i,	= а'2, . . ., Xir = <ar
Формулы f = <7 V h f = 9 -h f = 9	Соотношения Я/ = Ng U Nh Nf =Ngn Nh Nf = En\Ng
Д.н.ф. Ki V K2 V . . . V Km	Объединение граней NKl иЛф2и ...U#k„
Представление функцпп д.н.ф. f = Аф V K2 V . . . V Km	Покрытие Nf гранями Nf =NKl U#K2U...U#Km
Пз таблицы соответствия аналитических п геометрических объек-
тов мы впдпм, что каждому представленпю булевой функцпп в впде
д.н.ф. отвечает покрытие подмножества вершпн Nf Еп гранями.
Напрпмер, двум д.н.ф. функцпп Д (тд, х2, т.з) пз рассмотренного выше
примера (см. (4.18)) соответствуют покрытия множества Nft ребрамп,
показанные на рпс.4.20.
- 139 -
fl = Ж1Ж2 V Ж1Ж2Ж.з\/	fl = Ж1Ж2 V Ж2Ж3 V Ж1Ж.З
\/Ж1Ж2Жз V Ж1Ж2Ж3 V Ж1Ж2Ж3
Рис. 4.20
Если дано какое либо покрытие множества Nj гранями:
= Q i U ... U Qm ,
то, очевидно, число букв в соответствующей этому покрытию д.н.ф.
будет равно сумме рангов граней
rang (Qi) + . . . + rang (Qm) .
Следовательно, минимальной д.н.ф. отвечает покрытие с наименьшей
суммой рангов. Итак, на геометрическом языке постановка задачи ми-
нимизации звучит следующим образом.
Дано подмножество вершин единичного п—мерного куба.
Найти покрытие этого подмножества содержащимися в
нем гранями с наименьшей суммой рангов.
Переход от аналитической задачи к геометрической в ряде случаев
помогает быстро найти минимальную д.н.ф. Например, для функции
- 140 -
fl из рассмотренного выше примера гранями, содержащимися в мно-
жестве , являются либо одномерные грани (такая грань покрывает
2 вершпны), лпбо нульмерные (такая грань покрывает 1 вершпну). От-
сюда получаем, что любое покрытие множества Nft , (состоящего пз б
вершпн) должно состоять не менее чем пз трех гранен. Следовательно,
вторая пз приведенных в (4.18) д.н.ф. — мпнпмальная.
Сокращенная д.н.ф. Общпп план мпнпмпзацпп.
Геометрическая пнтерпретацпя задачи мпнпмпзацпп дает некоторые
соображенпя по ее решенпю. Выгодно покрывать множество едпнпц
функцпп ’’болыппмп” гранями (т.е гранями большой размерностп) :
больше покрывается вершпн, а ранг - меньше. Дадпм соответствую-
щие определенпя.
Конъюнкция К называется импликантой функцпп f , еслп f
равна 1 на любом наборе а = ац . . . ап значений переменных, на ко-
тором К равна 1:
VS ( К(а) = 1 => Дй) = 1) .
Так как любая д.н.ф. функцпп f представляет собой формулу впда
’’дпзъюнкцпя конъюнкций”, то очевидным образом получаем, что ка-
ждая входящая в д.н.ф. функцпп f конъюнкция является пмплпкантой
этой функцпп. Другпмп словамп, любая д.н.ф. функцпп f составля-
ется пз пмплпкант функцпп f . Прп рассмотренном выше соответствпп
аналитических п геометрпческпх объектов пмплпканте, как это сле-
дует пз определенпя, отвечает грань, целиком содержащаяся в множе-
стве Nf. В частностп, пмплпкантамп являются все члены совершенной
д.н.ф. функцпп (констптуенты). Пусть функция f представлена в впде
д.н.ф. как в формуле (4.17). Допустим, что в некоторой конъюнкцпп,
напрпмер в Ki можно вычеркнуть одну пз букв, такпм образом, что
получающаяся прп этом конъюнкция 7Д также является пмплпкантой
функцпп f . Утверждается, что тогда
/(жд, т2, ...,!'„) = K'l V К2 V . . . V Кт ,
(4.20)
(д.н.ф. (4.20) пмеет на одну букву меньше, чем д.н.ф. (4.17).) В самом
деле, еслп на некотором наборе значенпй переменных а правая часть
- 141 -
формулы (4.20) равна нулю, то и правая часть формулы (4.17) будет
равна нулю (так как К[ = 0 => К} = 0 потому что ’’длиннее”),
следовательно, /(а) = 0) . Если же на некотором наборе значений пере-
менных а правая часть формулы (4.20) равна единице, то н /(а) = 1 ,
так как все конъюнкции в правой части - нмплнканты функции f .
Конъюнкция К называется простой импликантой функции f ,
если
-	К - нмплнканта функции f ;
-	после вычеркивания в К любой буквы она перестает быть
нмплнкантой функции f .
Из проведенного только что рассуждения вытекает, что любую
д.н.ф., в которой хотя бы один нз членов не является простой нмплн-
кантой, можно упростить. Отсюда вытекает следующая теорема.
Теорема. Минимальная д.н.ф. функции f составлена из простых
импликант функции f .
Д.н.ф. функции f , составленная нз всех ее простых нмплнкант,
называется сокращенной. Предыдущую теорему можно переформулиро-
вать так
Теорема. Минимальная д.н.ф. функции f получается из сокращенной
путем удаления некоторых ее членов.
Из этой теоремы вытекает следующий план минимизации.
1. Ио исходному заданию функции построить сокращенную д.н.ф.
2. Различными способами удалять конъюнкции нз сокращенной д.н.ф., та-
ким образом, чтобы д.н.ф., полученная в результате удаления какой-
либо конъюнкции, оставалась д.н.ф. заданной функции.
Пример. Для рассмотренной выше функции /1 (гд, гд, ^.з) сокращен-
ная д.н.ф. имеет вид
/i(xi, ад, хз) = х-1Х? V глад V £1^3 V £1£з V Х'рхз V ждхз. (4-21)
Различными способами удаляя нз нее отдельные члены, приходим к сле-
дующим д.н.ф., нз которых нельзя удалить никакую конъюнкцию:
/l(z'l, Z'2, Х3) = Z'lZ'2 V Z'lZ'2 V Х2Х3 V Х4Х3	(4.22)
- 142 -
ЖД, Жз)	=	ЖДЖД	V	ЖДЖД V	ЖДЖз V	ЖДЖз	(4.23)
/1(ж'1, жд, ж.з)	=	Ж1Ж3	V	Ж1Ж3 V	ждж.з V	ждж.з	(4.24)
/1(ж'1, ЖД, Ж'з)	=	ЖДЖД	V	ЖДЖ3 V	Ж1Ж3	(4.25)
/1(ж'1, Ж'2, Ж'з)	=	Ж1Ж3	V	Ж2Ж3 V	Ж'1Ж'2	(4.26)
Из этих пяти д.н.ф. только две последние минимальные. В то же
время нп одну пз них нельзя упростить рассмотренными средствами
(вычеркивание буквы пз конъюнкции, удаление конъюнкции). Такне не-
упрощаемые д.н.ф. называют тупиковыми.
Определение. Д.н.ф., составленная пз простых пмплпкант функцпп
f , пз которой никакую пмплпканту нельзя удалить так, чтобы остав-
шаяся д.н.ф. также реализовывала бы функцию f , называется тупи-
ковой д.н.ф. этой функцпп.
Таким образом, пункт 2 плана мпнпмпзацпп можно уточнить:
2.	Иостропть тупиковые д.н.ф. п найтп средн нпх мпнпмальную.
Алгоритмы.
Определим следующие операцпп над д.н.ф.
ж  К V ж  К = К - склепванпе;
ж  К V ж  К = К V ж  К V ж  К - неполное склепванпе;
V  7<2 = К1 ~ поглощенпе; .
Здесь К,	— некоторые конъюнкцпп. Наппсанные тождества
являются следствием булевых тождеств для дпзъюнкцпп, конъюнкцпп
п отрпцанпя.
Построение сокращенной д.н.ф.
1.	Иредставпть заданную функцию совершенной д.н.ф.;
2.	Проводить операцпп неполного склепванпя до тех пор, пока это
возможно;
3.	Выполнить все поглощенпя.
В результате получится сокращенная д.н.ф. Для обоснованпя ал-
горитма надо доказать пндукцпей по k , что на этапе 2 получаются
все пмплпканты заданной функцпп ранга п — k .
- 143 -
Наиболее ясное обоснование алгоритма получается если прибегнуть
к геометрической интерпретации: операции склеивания отвечает полу-
чение к -мерной грани пз двух ее к — 1 -мерных ’’половинок”.
Алгоритм Нельсона построения сокращений д.н.ф.
Представить заданную функцию какой либо к.н.ф., раскрыть в ней
все скобки п выполнить все поглощения.
Пример. Имеем для функцпп Д :
Д (ж'1, Т'2, т.з) = (ж'1 V Ж'2 V т.з)  (Д V Д V Ж.з) 
Раскрывая скобки, приходим к сокращенной д.н.ф. (4.21).
Построение тупиковых д.н.ф.
Пусть
АД АД   , Кт
все простые имиликанты функцпп f . Для каждого набора значений
переменных а , такого что /(а) = 1 , отберем те простые имиликанты,
которые на этом наборе обращаются в единицу. Пусть Д Д . . ., ik(a) -
номера отобранных имиликант. Рассматривая номера {1,2,..., т} как
булевы переменные, составим произведение (конъюнкцию)
&(?i V г2 V ... V гДгД ,
по всем а , затем раскроем скобки и выполним поглощения. Каждый
член полученной д.н.ф. (от переменных-номеров) дает тупиковую д.н.ф.
Пример. Для функцпп Д пусть простые имиликанты занумерованы
следующим образом:
Ку = ЖД'2 Ку> = ЯДЖг К3 = ДЖз К4 = ХуХз К$ = Х2Х3 Kfy = Дж.3-
Отбор имиликант, обращающихся в 1 на каждом пз б наборов дает
следующее
001 - 3V6	010 - 2V5	100 - 1V4
011 - 2V3	101 - 1V6	ПО - 4V5.
- 144 -
Раскрывая скобки в выражении
(3 V 6)  (2 V 5)  (1 V 4)  (2 V 3)  (1 V 6)  (4 V 5) ,
получаем
1  2  5  б V 1  2  3  4 V 3  4  5  б V 1  3  5 V 2  4  б .
Членам полученной д.н.ф- соответствуют тупиковые формы (4.22)—
(4.26).
Метод карт Карно.
Этот метод, применимый для функций от 3-5 переменных, исполь-
зует более простую наглядную интерпретацию задачи минимизации.
Таблица функции от 4 переменных /2(^'1, яд, ж.з, яц) компактно запи-
сывается в форме матрицы 4x4 (’’карты”), как это показано на рисунке
4.21.
	X 3Z4			
Х2	00	01	11	10
00	1	1	0	1
01	1	1	0	1
11	0	1	1	0
10	1	1	1	1
Рнс. 4.21. Карта Карно.
Следует обратить внимание на порядок, в котором выписываются
комбинации пар нулей н единиц для обозначения строк н столбцов та-
блицы: 00,01,11,10. При таком порядке пары в соседних рядах отли-
чаются одним разрядом, это относится н к первой (00) н последней
(10) строке - они так же соседние (то же н для столбцов). Такую карту
удобнее было бы рисовать на поверхности тора (баранки), на плоскости
мы рисуем ее разрез, сделанный по границе между последней'н первой'
строкой н между последним н первым столбцом.
Принцип интерпретации здесь такой же, как в случае куба: каждой
функции сопоставляется подмножество клеток, в которых эта функция
- 145 -
равна единице. Прп этом элементарным конъюнкциям соответствуют
некоторых правильно расположенные специальные подмножества кле-
ток.
Конъюнкции ранга соответствует одна клетка
Конъюнкции ранга 3 соответствует пара соседних клеток
- 146 -
Конъюнкции ранга 2 соответствуют клетки,
образующие горизонтальный или вертикальный ряд,
либо подматрицу размера 2x2.
Ж2Ж4
Ж2Ж4
Конъюнкцпп ранга 1 (пз одной буквы) соответствуют 8 клеток пз
двух соседних рядов (вертикальных или горизонтальных).
Для построения минимальной или близкой к ней дизъюнктивной
нормальной формы функцпп /(жд, жд, ж.з, Ж4) ее таблицу заносят в
карту п находят по возможности экономное покрытие множества еди-
ничных клеток рассмотренными выше специальными подмножествами
клеток, соответствующими конъюнкциям.
Пример. Для функцпп ^(жд, жд, жд, жд) заполненная карта пока-
зана на рпс.4.21. Можно выделить следующие специальные подмноже-
ства клеток
- 147 -
X1Ж4
Ж2Ж4
Их объединение дает все единичные клетки функцпп /2  Поэтому
/2(^'1, Ж'2, Ж.З, Ж4) = T1T4 V T3T4 V T1T4 V T2T4 .
- 148 -
Глава 5
Конечные автоматы
5.1. Определение конечного автомата
Рассмотренные выше схемы пз функциональных элементов не дают
полного представления о работе дискретного преобразователя инфор-
мации такого, например, как ЭВМ или какой-либо ее узел, поскольку не
учитывается тот факт, что реальные устройства работают во времени.

y(t)
Рис. 5.1
По сравнению с СФЭ конечный автомат является более точной мо-
делью дискретного преобразователя информации, однако, как и лю-
бая модель, понятие конечного автомата связано с рядом упрощающих
предположений.
Во-первых, предполагается, что вход (выход) автомата в каждый
момент времени может находиться в одном пз конечного числа раз-
личимых состояний. Это приводит, например, к тому, что еслп у ре-
ального преобразователя входной сигнал представляет собой непрерыв-
ную величину, то для описания такого преобразователя с помощью мо-
дели конечного автомата нужно разделить диапазон изменения сигнала
на конечное число уровней и произвести квантование. В формальном
определении автомата, которое дается ниже, конечный набор состоя-
ний входа или выхода автомата называется, соответственно, входным
п выходным алфавитом, отдельные состояния — буквы этого алфавита.
Во- вторых, предполагается, что время изменяется дискретно. Это
означает, что состояния входа и выхода устройства отмечаются только
в определенные моменты времени, образующие дискретную последова-
тельность И, t'i,    ,tn     Каждый момент времени однозначно опре-
деляется его индексом, поэтому с целью упрощения будем считать, что
- 149 -
время t принимает значения 1,2,3, ... ,п, .... Временной промежуток
[п,п+ 1] называется тактом.
С учетом сказанного работа автомата представляется следующим
образом. На вход поступают сигналы
ж(1), т(2), . .., х(п),. . . х(г) G X, X—входной алфавит; (5-1)
Это приводит к появлению на выходе сигналов
у(2),..., у(п),... y(i) 6 Y, Y—выходной алфавит; (5-2)
Выходная последовательность (5.2) определенным образом завпспт
от входной (5.1). Эта завпспмость определяется внутреннпм устрой-
ством автомата. Рассмотрим ее подробнее.
Заметим, что работу СФЭ также можно рассматривать во вре-
мени. Прп этом y(t) = /(ж(/)), т.е. выход схемы полностью определя-
ется состоявшем входа в тот же момент временп п не завпспт от значе-
ний входа в предыдущие моменты временп. Это можно выразпть так:
СФЭ не обладает памятью, попользовав поступпвшпй на нее спгнал,
она тут же его ’’забывает”. Автомат представляет собой устройство
с памятью, т.е. выход автомата в момент временп t определяется
не только входом ж(/), но п предысторпей H(t), сформпрованной
спгналамп
x(t — 1), х(1 — 2), . . . т(1).
Запомпнанпе предысторпп осуществляется следующим образом: во вну-
тренней структуре автомата пмеется ряд состояний', входной' спгнал
изменяет состояние, а выходной спгнал завпспт не только от входа, но
п от текущего состояния.
Будем обозначать состояние автомата в момент временп t буквой
</(/). Тогда работа автомата в некотором такте выглядпт так:
-	поступает входной спгнал ж(/) ;
-	выдается выходной спгнал y(t), завпсящпй от входного п от вну-
треннего состояния автомата;
-	автомат переходпт в новое состояние </(/+!), завпсящее от теку-
щего состояния q(t) п поступпвшего входного сигнала.
Дадпм теперь формальное определенпе автомата.
- 150 -
Определение автомата
Конечным автоматом называют пятерку объектов
А = (X,Y,Q,6, А),
где
X — конечное множество {жi, . . ., хп }, называемое входным
алфавитом', каждый символ ж, описывает одно пз возможных
состояний входа;
Y — конечное множество {т/i,..., Ут}, называемое выходным
алфавитом-, элементы этого множества описывают возможные со-
стояния выхода;
Q —конечное множество {qi, . . ., qr}, называемое алфавитом
внутренних состояний',
д — функция, <5 : X х Q —> Q ; таким образом, функция <5
каждой паре ’’вход-состояние” ставит в соответствие состояние, ее
называют функцией переходов автомата;
А — функция, А : X х Q —> Y ; таким образом, функция
А каждой паре ’’вход-состояние” ставит в соответствие значение
выхода, ее называют функцией выходов автомата.
Закон функционирования автомата определяется следующим обра-
зом : если на автомат А , находящийся при t = 1 в состоянии </(1),
поступает входная последовательность x(t), t = 1,2,..., то автомат
изменяет своп состояния в соответствии с функцией <5 п вырабатывает
выходные сигналы в соответствии с функцией А :
q(t+ 1) = 6(x(t),q(ty) ,
y(t) = А(ж(/), q(t\).	(5.3)
t = 1,2,...
Способы задания автомата
Поскольку функцпп д п А определены на конечном множестве п
принимают значения также пз конечного множества, то пх задают прп
помощи таблиц.
- 151 -
Пример. Зададим автомат следующим образом: X = {жi, х?, хз},
У = [д, у2] , Q = {ц1,Ц2,цз}. Функции <5 и А определим с помощью
табл. 5.1 и 5.2 соответственно.
Таблица 5.1
ВХОД	состояние		
	91	92	9з
Xl	'/2	92	9з
Х2	91	9з	9з
Хз	91	92	91
Таблица 5.2
ВХОД	состояние		
	91	<12	9з
Xl	У1	У2	У2
Х2	У2	У1	У2
Хз	У2	У2	У1
Табл. 5.1 носит название таблицы переходов, табл. 5.2 — та-
блицы выходов. Еслп известна последовательность сигналов на входе
автомата, то с помощью таблиц переходов и выходов однозначно опре-
деляется выходная последовательность.
Вместо таблиц для задания автомата можно использовать более на-
глядный способ — диаграмму переходов-выходов. Она представляет со-
бой ориентированный граф (точнее, мультпграф), в котором каждому
внутреннему состоянию автомата соответствует вершина. Переходы
автомата нз состояния в состояние изображаются стрелками, на стрел-
ке пишутся входной символ, вызывающий данный'переход, н выходной'
символ, вырабатываемый автоматом.
Рнс. 5.2
- 152 -
Для рассмотренного выше примера автомата диаграмма переходов-
выходов будет выглядеть так, как показано на рпс. 5.2.
Пример. Требуется постропть автомат, который работал бы следую-
щим образом: в каждый такт на вход автомата поступают очередные
двопчные разряды слагаемых, автомат вырабатывает соответствую-
щий двопчнып разряд пх суммы.
Из условпя примера вытекает, что X = {00,01,10,11}, а У =
{0, 1} . Так как необходимо запоминать налпчпе плп отсутствие пе-
реноса, то в качестве Q можно взять Q = {0, 1} ; автомат будет
находиться в состоянпп 1, еслп прп сложенпп предыдущих разрядов
возникает перенос, п в состоянпп 0, еслп переноса не возникает. Диа-
грамма переходов-выходов автомата показана на рпс. 5.3.
00 | 0
01 | 1
10 | 1
Рпс. 5.3
5.2. Некоторые вопросы синтеза автоматов
Ио аналогпп с задачей синтеза схем пз функциональных элементов
можно поставить задачу синтеза для автоматов: пмеется набор базис-
ных автоматов
{Л,...,А};
(каждый представлен в неограниченном количестве экземпляров); как
путем пх соедпненпя собрать автомат А с наперед заданным функци-
онированием ?
Здесь, однако, возникает серьезное препятствпе. Допустим, напрп-
мер, что нужно прпсоедпнпть выход автомата А} = (A'i, УД, Qi, <5i, АД
к входу автомата А^ = (АД, Уг, Q2, <Д, As). Тогда необходимо, чтобы
выполнялось условпе У[ С Х2, пначе второй автомат ”не поймет”
сигналы, поступающие на него с первого. Это прпводпт к запутанной
сптуацпп, когда некоторые соедпненпя возможны, а некоторые нет, п
задача неоправданно усложняется.
- 153 -
Чтобы преодолеть это препятствие, вводится понятие структур-
ного автомата, в котором все алфавиты (входной, выходной и алфавит
внутренних состоянии) кодируются двоичными словам. Рассмотрим
это подробнее.
Пусть М = {я1,...,ар} — конечное множество нз р элементов,
а {О, I}77 — множество двоичных слов длины тг, где 2" >_р. Про-
извольное инъективное отображение ф : X —> {О, I}77 будем называть
кодированием множества X двоичными словами.
Пусть А = (X, Y, Q, 8, А) —любой автомат. Произведем кодиро-
вание его алфавитов:
________*_______~ У Q
Ж1	. . .фи, = У1 рп   -Шр. = т 1/1	<7ц . . .СГщ = ОД
(217 > п)
Ут 1 Ут 1 • • • Ут ц — Ут
Qr (Тг1 . . . (У г р = (У}
> т)
№ > г)
Будем обозначать закодированные вход, выход н состояние авто-
мата в момент времени ^соответственно, ф(1ф,у(1ф и <т(/). Тогдазакон
функционирования автомата (5.3) будет записываться в виде
?(/+1) = A (i;(/),?(/)} ,
i)-(f) = л	.
(5-4)
Отображение А, которое паре двоичных слов ставит в соответ-
ствие двоичное слово, определяется следующим образом: пусть ф =
<т = <Tj и d(xi,qj) = qp. Тогда А(^,<т)) = ар. Аналогично опреде-
ляется функция Л. Чтобы построить таблицы функции А и Л ,
надо в таблицах переходов и выходов автомата заменить все символы
нх кодами.
Полученный после кодирования автомат называют структурным;
автомат в смысле основного определения параграфа 1 называют иногда
абстрактным. Будем считать, что структурный автомат имеет к дво-
ичных входов н р двоичных выходов. Внутреннее состояние автомата
задается двоичным словом длины р . На рисунке 5.4 показаны автомат
А н соответствующий ему структурный автомат.
- 154 -
—
<Tjl .	 ajp	CN Г Г ‘
			 l]kv
Рис. 5.4
Переход к структурному автомату обеспечивает два важных для
синтеза преимущества.
1. Теперь все входы и выходы совместимы, так как через них пе-
редается двоичная информация. Аналогично определению СФЭ можно
дать определение схемы, составленной нз структурных автоматов. Мы
не будем давать общего определения, рассматриваемые далее схемы
имеют простую структуру, не сильно отличающуюся от СФЭ.
2. Если соотношения (5.4) записать ”в координатах”:
<Т1(/ + 1) = Ai(6(6,   ,6(6, Мб,  ,Мб) ;
ap(t + б = М(6(6>    >6(6, Мб,    > Мб) ; zt-
(5 5
М6 = Л1 (6(6,   МЛ6,М6,   ,М6) ;
Мб = М (6(6,   ,6(6>сг1(6,   - ,М6),
то видно, что аргументы н значения функций Ai,. . ., Д.р, Ai,. . ., Л;,
могут принимать только два значения 0 н 1, то есть все перечисленные
функции — булевы. Итак,
закон функционирования структурного автомата
задается системой булевых функций.
Элементарные автоматы
Так же как это было сделано в случае булевых функций, выделим
простейшие автоматы (структурные) н дадим нм название.
Заметим сначала, что рассмотренные в параграфе 4.4 функцио-
нальные элементы укладываются в понятие автомата. Можно считать,
что функциональный элемент имеет только одно внутреннее состояние,
- 155 -
поэтому его выход зависит только от входа. Говорят также, что функ-
циональный элемент — это автомат без памяти.
Перейдем к автоматам с двумя состояниями. Рассмотим структур-
ный автомат, имеющий один двоичный вход £ н один двоичный выход
г), совпадающий с внутренним состоянием: г) = <т :
£----- а
Рнс. 5.5
(Автомат, выход которого зависит только от состояния, называ-
ется автоматом Мура, они подробнее рассматриваются в параграфе
6.2).
Для задания автомата, показанного на рнс.5.5, достаточно задать
его таблицу переходов (таблица выходов не нужна). Она имеет следу-
ющий вид
Таблица 5.3
ВХОД	состояние	
	0	1
0	*	*
1	*	*
Вместо звездочек надо расставить нули н единицы. Это можно
сделать 16 способами. Однако, не все они приемлемы. Допустим, на-
пример, что в первом столбце таблицы 5.3 оба элемента нули. Такой
автомат, оказавшись в состоянии 0, более нз него не выходит, то есть
фактически будет работать как функциональный элемент. Анализ ана-
логичных ситуаций показывает, что для того чтобы получился авто-
мат, не сводящийся к автомату без памяти, надо потребовать, чтобы в
каждом столбце таблицы 5.3 встречались бы н ноль н единица. Таких
таблиц 4, они приведены ниже (табл. 5.4 — 5.7).
- 156 -
Таблица 5.4
ВХОД	состояние	
	0	1
0	0	0
1	1	1
Таблица 5.5
вход	состояние	
	0	1
0	0	1
1	1	0
Таблица 5.6
вход	состояние	
	0	1
0	1	0
1	0	1
Таблица 5.7
вход	состояние	
	0	1
0	1	1
1	0	0
Автомат, представленный таблицей 5.7, получается пз автомата
5.4, еслп переобозначить два его внутренних состояния: 0 ь-> 1, 1 ь-> О,
то же справедливо для автоматов 5.5 и 5.6. Таким образом, имеется
только два простейших автомата.
Автомат, задаваемый таблицей 5.4, называется задержкой нлн
D-трнггером. Как видно нз таблицы, состояние, в которое устана-
вливается автомат, совпадает с символом на входе. Это состояние по
предположению н есть значение выхода, таким образом
+ 1) = a(t + 1) =	.	(5.6)
то есть автомат действительно задерживает сигнал на 1 такт.
Автомат, задаваемый таблицей 5.5, называется триггером со счет-
ным входом нлн Т-трнггером. Как видно нз таблицы, состояние авто-
мата меняется на противоположное, если на вход поступает 1, и оста-
ется без изменения, если на вход поступает 0. Следовательно,
=	=	.	(5.7)
Если в некоторый момент времени Т-трнггер находится в состоянии 0,
то это значит, что в предшествующие моменты времени на вход авто-
мата поступило четное количество единиц (считаем, что в начальный
момент времени автомат находится в состоянии 0); если Т-трнггер
находится в состоянии 1, то количество поступивших на вход единиц
нечетно. Таким образом, Т-трнггер ’’считает” количество единиц на
входе, но так как он имеет всего 2 состояния, то н считает он до двух.
- 157 -
Замечание. Физическая реализация триггеров такова, что возникают
два выхода: прямой и инверсный. Поэтому ниже мы будем изображать
D-трнггер н Т-трнггер так, как показано на рнс.5.6. Если поменять
местами прямой н инверсный выходы, то нз D-трнггера получится
автомат, задаваемый таблицей 5.7, а нз Т-трнггера — автомат, зада-
ваемый таблицей 5.6.
D
Рнс. 5.6
Задача о полноте автоматного базиса
Набор структурных автоматов
{Л,...,Л}
(5.8)
будем называть полным (нлн автоматным базисом), если путем соеди-
нения базисных автоматов (5.8) (каждый автомат можно использовать
столько раз, сколько нужно) можно построить любой наперед заданный
структурный автомат.
Значительные усилия математиков были посвящены тому, чтобы
получить аналог теоремы Поста для автоматов: найти условия, при
выполнении которых система (5.8) будет полной. В 1964 г. М.П.Кратко
доказал несуществование алгоритма, который, исходя нз какого-либо
задания набора (5.8), отвечал бы на вопрос полная это система нлн нет.
Что означает несуществование алгоритма, мы рассмотрим в главе 7,
где дадим формальное определение алгоритма.
Так как общего критерия полноты не существует, представляют
интерес варианты теоремы о полноте, когда полнота устанавливается
при дополнительных предположениях о системе (5.8).
Рассмотрим наиболее популярный нз них.
- 158 -
Вариант теоремы о полноте. Канонический метод синтеза
Теорема. Система автоматов (5.8), содержащая
1) полный набор функциональных элементов;
2) D-триггер (или Т-триггер),
является полной.
Для доказательства теоремы рассмотрим произвольный структур-
ный автомат А, заданный соотношениями (5.4), и опишем его схему
нз указанных в теореме автоматов, называемую канонической струк-
турой. Каноническая структура показана на рпсунке 5.7.
Ш    dfi
Рпс. 5.7
Она состопт пз двух частей.
Левая половпна называется запомпнающей частью. Она составлена
пз р триггеров (на рпсунке для примера взяты D-трпггеры). Набор
состояний этпх триггеров образует состоянпе автомата: еслп в неко-
торый момент времнп t
°”1(^) —	   , Cp(t) —
то это означает, что автомат А в момент временп t находится в
состоянпп а).
Правая половпна называется комбинационной частью. Она пред-
ставляет собой схему пз функциональных элементов. Входами этой
схемы являются
1) двопчное слово ( =	— входной спгнал автомата А ;
- 159 -
2) двоичное слово <7 = од . . . сгр — текущее внутреннее состояние
автомата А.
Выходами комбинационной части являются
1) двоичное слово rj = щ . . ,г)р — выходной сигнал автомата А. Они
реализуются ио формулам (5.5) для функции Л1,. . ., Л;, ;
2) двоичное слово тг = tti . . . ~кр, которое поступает на входы тригге-
ров в запоминающей части и, таким образом, управляет памятью
автомата.
Рассмотрим подробнее как формируются сигналы управления па-
мятью. В каждый момент времени t эти сигналы должны переводить
автомат нз состояния <т(/) в состояние <т(/ + 1). Так как
?(1) = <71 (1) . . .<Tp(t)	?(f + 1) = <Tl(f + 1) . . . <7 p(t + 1),
то дело сводится к тому, чтобы изменить состояние каждого триггера
<7;(f) -> <Ti(t + 1), i = 1, . . .р .
Используемые нами D- нлн Т-трнггеры обладают следующим свой-
ством: для любой пары состояний <7, а' существует входной сигнал,
переводящий автомат нз состояния <7 в состояние а'. Обозначим
этот сигнал через тг(<т, <т'). Имеем для D-трнггера: тгд(<т, <т') = ст',
(состояние, в которое устанавливается D-трнггер, равно входному сиг-
налу). Для Т-трнггера: тгт(<т, <т') = <т ф <т', (при <7 = <т' на вход надо
подать 0, чтобы состояние не изменилось, при <7	<т' на вход надо
подать 1, чтобы триггер ’’перевернулся”).
Итак, тг, = 7r(<7i(t), (ii(t + 1), i=l,...,p нлн в векторной форме
тг = Тг(<7(1), <r(t + 1)) .	(5.9)
Выразим в соотношении (5.9) величину <f(t + 1), исходя нз закона
функционирования автомата (5.4)
тг = тг ^ст(1), Д ^(1), ст(1)^ = И ^(1), ст(1)^ .	(5-Ю)
Соотношение (5.10) показывает, что сигналы управления памятью
являются функциями (булевыми) от тех же переменных, что н выход
автомата.
- 160 -
Остается заметить, что поскольку в базис входит полная совокуп-
ность функциональных элементов, то при помощи них можно реализо-
вать любую систему булевых функций. Теорема доказана.
Пример
На конвейере, по которому двигаются детали двух типов А и
В, установлен автомат, задачей которого является такая сортировка
деталей, чтобы после прохождения мимо автомата они образовывали
группы АВВ. Неподходящую деталь автомат сталкивает с конвейера.
Пусть, например, по конвейеру движется последовательность
ААВВВВАВААВАВАВ...
Тогда автомат столкнет 2-ю, 5-ю,б-ю,9-ю, 10-ю, 14-ю ... детали, в резуль-
тате чего нх последовательность примет требуемый вид
А ВВ АВ В АВ В ...
Требуется построить схему такого автомата, используя Т-трнггер
н элементы ”11” ,”НЛП” ,”НЕ”.
Синтез автомата естественным образом разбивается на этапы.
1° . Сначала построим абстрактный автомат А = (X, Y, Q, <5, А).
Входными данными для нашего автомата является информация о том,
какая деталь проходит в данный момент по конвейеру, поэтому можно
считать, что X = {Л, В}. Результатом работы автомата является либо
сталкивание (С) детали либо ее пропуск (П), будем поэтому считать,
что Y = {С,П}. Внутренние состояния, как это обсуждалось выше
(см. определение автомата) нужны для запоминания каких-либо фак-
тов о входной последовательности; в данном примере автомат должен
помнить какую часть группы АВВ он уже сформировал. Положим
Q = {q,qA,<lAB}- По мере формирования группы автомат циклически
перемещается по этим состояниям, не изменяя состояния при поступле-
нии неподходящей детали. В итоге приходим к диаграмме переходов-
выходов автомата, показанной на рнс. 5.8.
- 161 -
2° . Кодирование.
В следующих трех табличках приведен один пз многих возможных
вариант кодирования множеств X, Y, Q. Разрядам кодовых слов даны
обозначения, которые будут нсполвзоватвся н для обозначения сигналов
в схеме автомата.
3° . Конкретизация
Каноническая структура разрабатываемого автомата показана на
рнс. 5.9.
Рнс. 5.9
- 162 -
Выходы СФЭ тг 1, 7Г2 н г) являются булевыми функциями от пере-
менных а?- Найдем эти зависимости сначала в форме таблиц, по
которым далее составим формулы.
Составление таблиц функции ту(С fi, <72), тгДС fi, <72) и '’’Ь сг2)
происходит так. Пусть, например, £ = 0, од = 0, <72 = 0. В соответ-
ствии с нашим кодированием это означает, что автомат находится в
состоянии q (его код 00), а на вход поступает А. По диаграмме
переходов-выходов автомата (рнс. 5.8) находим, что выход автомата
— П, при этом он переходит в состояние q^. Так как П закодирован
единицей, то 7?(0, 0, 0) = 1. Сигналы управления памятью должны из-
менить состояния триггеров 00 (состояние абстракного автомата q )
на состояние 01 (состояние абстракного автомата q ), то есть состо-
яние 1-го триггера не меняется, а 2-го меняется на противоположное.
Следовательно,
ТгДО, 0, 0) = 0 , тг2(О, 0, 0) = 1 .
Рассуждая аналогичным образом для остальных комбинации значении
С <71, <72, приходим к таблице 5.8.
Таблица 5.8
£	О’!		д	o’!		7Г1	^2
0	0	0	1	0	1	0	1
0	0	1	0	0	1	0	0
0	1	0	*	*	*	*	*
0	1	1	0	1	1	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	1	1	0
1	1	0	*	*	*	*	*
1	1	1	1	0	0	1	1
Звездочки в 3-й и 7-й строках таблицы возникают из-за того, что
слово <71 <72 = 10 не использовалось при кодировании состояний —
этому слову не соответствует никакое состояние автомата. Булевы
функции ту(С <71, <72), 7Г1(С <71, <72) и лд(С <71, <72) на указанных наборах не
определены, в связи с чем называются частично определенными. Для
выполнения каких-либо действий с частичной функцией (в частности,
нам надо представить ее формулой) ее тем нлн иным способом доопре-
деляют, то есть заменяют звездочки нулями и единицами. Для функ-
- 163 -
ций, описывающих работу автомата, допустимы любые доопределения,
так как при работе автомата ситуаций, которым соответствуют звез-
дочки, не возникнет. Этот факт можно использовать, выбирая для
звездочек такие значения, которые приводят к более простому пред-
ставлению функций формулами.
4° . Представление функций выхода автомата н функций управле-
ния нанятые формулами.
Используя расмотренные в главе 4 методы (геометрическую ин-
терпретацию, карты Карно), строим по возможности экономное пред-
ставление функций <71, <Т2), 7Г1(^, <71, <Т2) II 7Г2 (£, <71, <72) формулами В
базисе V,&,— :
Ц = <,Т2 V £<72
7Г1 = £<72
7Г2 = ^СТ2 V ^<71 .
5° . Реализация СФЭ н окончательная схема автомата.
Окончательная схема показана на рнс. 5.10.
Рнс. 5.10
- 164 -
5.3. Функциональное описание автомата
В этом параграфе решается такой вопрос: какую функцию реа-
лизует конечный автомат? Напрпмер, функциональный элемент реали-
зует булеву функцию, СФЭ — систему булевых функций, а как описать
с функциональной стороны конечный автомат?
Если наблюдать только вход н выход автомата (такой подход к изу-
чению объекта носит название ’’метод черного ящика”), то, очевидно,
будет обнаружено следующее: на вход автомата поступают побуквенно
слова, составленные нз букв входного алфавита, результатом работы
автомата являются появляющиеся на выходе слова, составленные нз
букв выходного алфавита. Далее мы так н будем рассматривать ко-
нечный автомат - как преобразователь слов - н попытаемся выяснить
какие именно преобразования он может выполнять.
Обозначения.
Алфавитом называют любое конечное множество
{ X х , X 2 , . . ., т п } ,
элементы этого множества яд, яд, . . ., хп — это буквы. Рассмотрим да-
лее декартово произведение Хк. Элементы этого множества, то есть
упорядоченные наборы х, составленные нз к элементов множества X
(то есть букв),
Ж   X 2 г 32 2 2    X i д, ,
называют словами длины к в алфавите X.
Замечание. Слова записываются так же, как в естественном языке,
а не как требуется в определении декартова произведения. Например,
ah, а не (а, 6). Ясно, что это просто условность.
Имеет смысл ввести в рассмотрение пустое слово, в котором нет
нн одной буквы (к = 0). Оно обозначается А.
Множество всех слов в алфавите X обозначается X*. Имеем
X* = A U X U X2 U ... U Хп U . . .
Длину слова х будем обозначать £(£). Например,
ДА) = о Д£) = к & г е хк.
- 165 -
Пусть £i = XitXi2 . . .Xip и £д = XjtXjr2 . . .Xjq - два слова в ал-
фавите X. Слово, полученное приписыванием слова £д к слову £j
обозначается х-ух^ :
Замечание. Приписывание слова к слову часто рассматривают как
операцию на множестве X* и называют конкатенацией. Нетрудно про-
верить такие свойства этой операции:
а)	ассоциативность: £1(£2£.з) = (£1£'2)ж.з;
б)	существование нейтрального элемента ( Л ): Л£ = £Л = £
Ясно также, что эта операция некоммутативна.
Словарные операторы
Пусть X и Y — два алфавита, X* и У* — соответствующие
множества слов. Отображение
Lp : X* —> У*, х у = </?(£)
называется словарным оператором.
Рассмотрим несколько примеров словарных операторов. Во всех
примерах Х = У = {0,1}, то есть аргументами и значениями опера-
торов будут двоичные слова.
Пример 1. Оператор ip-[ сопоставляет каждому слову его первую
букву:
y?i(a-ia2 . . . а„) = оц .
Пример 2. Оператор ср? производит в слове-аргументе замену ка-
ждого нуля на единицу н каждой единицы на нуль:
— 0'10'2    Оп
Пример 3. Оператор у?з переписывает каждое слово справа-налево :
   &п) — ^п^п — 1   -0'1 .
- 166 -
Пример 4. Оператор у?4 определяется следующим образом:
<р4(а]_а2    ап) = А[32    Рп
где
А = «1
А = a-i Ф 0'2
А = Q'i Ф а2 Ф аз
А — 0'1 Ф 0'2 Ф    Ф О'п .
Словарный оператор, реализуемый автоматом
Пусть дан автомат А = (X, Y, Q, <5, А). По определенпю автомата
<5(ж, q) — это состоянпе, в которое переходит автомат пз состояния q,
когда на его вход поступает символ ж;
А(ж, q) — это символ на выходе автомата, находящегося в состоянпп q,
в момент, когда на его вход поступает символ х.
Обе функцпп определены на множестве X х Q. Для дальнейшего
удобно определить аналогичные функцпп с более широкой областью
определения X* х Q, полагая
<5(2, q) — это состоянпе, в которое переходит автомат пз состояния q,
после того как на его вход поступит слово аГ;
X(x,q) — это слово, появляющееся на выходе автомата, на который в
исходном состояния q подается слово х.
Формальное определение функций 8(x,q) п X(x,q) можно дать,
применяя индукцию по длине слова х. (Таким же методом доказывается
большинство приводимых ниже теорем).
Начальный шаг. Сначала полагаем А(Л, </) = Л п 8(K,q) = q. Теперь
нашп функцпп определены для слов длпны 0.
Индукционный шаг. Предположим, что функцпп S(x,q) п X(x,q)
определены для всех слов х, длпна которых не превосходит п — 1.
Рассмотрим пропзвольное слово длпны п, пусть его первой буквой
будет буква х, такпм образом, рассматрпваемое слово пмеет впд хх,
где £(х) = п—1. Определяем <5(xx,q) п X(xx,q) по формулам:
<5(xx,q) = <5(x,<5(x,q)) .	(5-11)
- 167 -
X(xx,q) = X(x,q)X(x, 8(x,q() .	(5.12)
Из формул (5.11) и (5.12) вытекает, что новые функции <5(ж, </)
и X(x,q) полностью определяются функциями 8(x,q) и X(x,q), за-
дающими закон функционирования автомата, и фактически являются
суперпозициями этих функции. Например, для слова х = abed, со-
гласно (5.11), имеем
<5(2, q'j = 8(abcd, q) = 8(bed, 8(a, q)) =
= 8 (cd, 8(b, 8(a, q))) = 8(d, 8(c, 8(b, 8(a, </)))).
Заметим, что, в силу (5.11), выражение 8(cd, 8(b, 8(а, q))) в этой це-
почке формул совпадает с выражением 8(cd,8(ab,q)). Следовательно,
8(abcd, q) = 8(cd, 8(ab, q)). Рассуждая аналогичным образом для произ-
вольных слов Xi и 2'2, можно вывести нз (5.11) и (5.12) следующие
соотношения:
8(£iX2,q) = 8(x2,8(£i,q)) ,	(5-13)
X(xiX2, q) = X(x-i, q)X(x2,8(x-i, q)) .	(5-14)
Выделим одно нз состоянии автомата q± G Q. Будем называть его
начальным и считать, что в момент времени t = 1 автомат находится
в состоянии qi.
Словарным оператором, реализуемым автоматом А, назовем
отображение
Ал : X* -> У*, х е-> у = рА(х),
определяемое следующим образом:
Аа(х) = Х(х, г/i) .	(5.15)
Словарный оператор рА описывает как автомат преобразует по-
даваемые на его вход слова. Поставим вопрос : каждое ли преобразо-
вание слов можно реализовать на автомате ? Более точно этот вопрос
формулируется так:
пусть р : X* —> У* — словарный оператор; существует ли авто-
мат А такой, что <рА = р ?
- 168 -
Отрицательный ответ на этот вопрос очевиден : например словар-
ный оператор из приведенного выше примера 1, нельзя реализовать
автоматом, так как из определений (5.11) и (5.15) вытекает, что слова
х н </?а(ж) имеют одну н ту же длину. Отметим этот факт как первое
свойство словарного оператора.
Свойство 1.	£(</?(£)) = 1(х), х G X* .
Рассмотрим далее некоторое слово xq £ X* н совокупность всех
слов, имеющих общее начало хо :
{хох | х 6 X*} .	(5.16)
Для оператора, реализуемого автоматом А, будем иметь
1рА(хох) = \(хох, г/1) = А(£о, <71)А(ж, й(£0, г/Д) .
Следовательно, совокупность значений оператора на словах вида
(5.16) имеет вид
{УоУ I У С У*},	(5.17)
где через уо обозначено слово Д(жо,<71)-
Итак, чтобы словарный оператор ip можно было реализовать авто-
матом, он должен отображать слова с общим началом в слова с общим
началом:
Свойство 2.	y?(£fj£) = уоу, х G X*, уо = р(хо) .
Словарный оператор р, обладающий свойствами 1 н 2, называ-
ется детерминированным. Название связано с философским термином
’’детерминизм” н отражает в применении к автомату тот факт, что
в данный момент времени t действия автомата полностью опреде-
ляются входными воздействиями, полученными до этого момента (то
есть ж(1), ж (2), .. ., т(Д ) н ”не зависят от будущего” (то есть от сим-
волов х (/ + 1), х (/ + 2), . . .).
Из приведенных выше примеров свойством 2 не обладает словар-
ный оператор у?з : первая буква выходного слова становится известной
- 169 -
только после того, как будет получено все слово, то есть надо ’’загля-
дывать в будущее”.
Для формулировки третьего ограничения на словарный оператор,
реализуемый конечным автоматом, необходимо ввести новое понятие.
Пусть у? — детерминированный оператор, а £q — некоторое
слово. Остаточным оператором оператора ср, порожденным словом
£о, называется словарный оператор ср$0 : X* —> У*, действующий по
правилу:
= У, если ‘Р(хох') = уоу.	(5.18)
Корректность этого определения вытекает нз свойства 2. (См. (5.16) н
(5.17)). Правило (5.18) можно сформулировать так: чтобы найти образ
слова х при отображении ps0, припишем к нему слева слово £ о, най-
дем образ полученного слова при отображении ср н удалим в полученном
слове первые 7(£о) букв.
Пз определения остаточного оператора (5.18) получаем следующее
соотношение
у?£1(£2£) = у?£1(£2)у?£1£2(£) .	(5.19)
Действительно, нз равенства у?(£х£2£) = уру-ру следует по опреде-
лению (5.18), что
у?£1(£2£) = уру н у?£1£2(£) = ?).
При х = Л, это дает
У’гДжз) = Th 
Пз трех последних равенств между словами н получаем (5.19).
Замечание. Остаточный оператор порожденный пустым словом
Л, очевидно, совпадает с ср.
Рассмотрим, что представляют собой остаточный оператор для
словарного оператора, реализуемого автоматом. Для слов (5.16), име-
ющих общее начало xq, имеем
срА(хох) = А(£о£, 41) = А(£о, 41)А(£, <5(£0, г/Д).
Отсюда
(Xa)s0(£) = А(£Д(£0,41)) .
- 170 -
Заметим, что J(£o,</i) —это одно из состояний автомата А, напри-
мер, <5(2о, </j) = qi. Следовательно,
(Aa)s0(£) = Л(£,г/г) .	(5.20)
Итак, для каждого остаточного оператора (^a)x(s можно указать со-
стояние автомата (ц такое, что
ЬЦ1')
будет выходом автомата, установленного в состояние (р, на вход кото-
рого подано слово х. Так как состояний конечное число, то приходим
к следующему ограничению:
Свойство 3. Оператор у? имеет конечное число остаточных операторов
Замечание. Из (5.20) следует, что число различных остаточных опе-
раторов (ра)х0 не больше, чем число состояний автомата А.
Словарный оператор, обладающий свойствами 1—3, называется
ограниченно-детерминированным. Мы доказали следующую теорему.
Теорема. Словарный оператор, реализуемый конечным автоматом,
является ограниченно-детерминированным.
Обратная теорема
Будем говорить, что автомат А реализует словарный оператор
р, если срА = ср.
Теорема. Для каждого ограниченно-детерминированного словарного
оператора существует реализующий его конечный автомат.
Доказательство. Пусть р : X* —> У* ограниченно-детерминирован-
ный словарный оператор. Будем обозначать через г(р) число различ-
ных остаточных операторов словарного оператора р. Допустим что,
г(р) = г, и пусть
Ai, А2, , Аг (ау = а)
совокупность всех остаточных операторов оператора р. Поскольку
каждый остаточный оператор порождается некоторым словом то £
X*, множество слов разобьется на г классов
X* =GiUG2U...UGr,	(5.21)
- 171 -
где Ci = {ж | </?£ = ifii}. Удобно обозначать класс, в который входит
слово £, через С(£). Имеем
(5.22)
Напрпмер, С'(Л) = C'i, так как остаточный оператор, порождаемый
пустым словом — это сам оператор ср.
Установим следующее свойство разбиения (5.21):
Vt G X(C'(£i) = С'(т2) => С(х-[х) = С'(т2ж)),
(5.23)
означающее, что еслп два слова входят в один и тот же класс, то после
приписывания к ним любой буквы новые слова будут также пз одного
класса. Для доказательства, в соответствии с (5.22), проверим, что
p£lX = А£2х- В силу свойства (5.19) остаточных операторов для любых
х Е X п £ G X*
<рХ1(хх) = <рХ1 (х)<Рх1Х(х)
ср£,(х£) = ср£2(х)ср£2х(£) 
Слова, стоящие в левых частях этих соотношений совпадают, так как
= ср£гр, по той же причине совпадают слова p£l(x) и ср£2(х) в
правой части. Следовательно, cp£lX(x) = <р£2х(х) для любых £ £ X*
то есть
C'(£it) = С{х^х).
Перейдем к построению автомата
Aq — (Хо, Yq, Qo, <5о, Ао),
реализующего оператор ср.
Так как ср : X* —> У*, то полагаем Xq = X, Yq = Y. В качестве
состояний автомата возьмем классы разбиения (5.21):
Q0 = {C(£) | ££%*} = {СД С'2,..., ГС} .
Функцию переходов автомата Aq определим следующим образом:
$о(х, С(£)) = С(£х).
(5-24)
- 172 -
Это определение можно расшифровать так: чтобы определить в
какое состоянпе (класс) переходит автомат пз данного состояния С,
при поступлении входа х, выбираем в классе С любое слово х,
приписываем к нему букву х п смотрим в каком классе оказывается
слово хх. На основанпп свойства (5.23) можно утверждать, что это
определение корректно : класс, в котором будет находиться слово хх,
не зависит от того какое будет выбрано слово х в классе С.
Еслп использовать соотношение (5.13) для функцпп переходов, то
соотношение (5.24) по пндукцпп можно распространить на слова:
<50(жг, С(х)) = С(££1).	(5.25)
(Например, для х-у = ху имеем
<$о(£1, С(£)) = S0(xy, С(£)) = <5а(у, <50(х, С-'(х))) =
= 60(у, С'(хх)) = С'(хху) = С(££1)).
Наконец, завершая построение автомата Aq, полагаем
Ао(х, С'(х)) = ifis(x) .	(5.26)
Покажем, что <рАо = ср. Для этого нужно убедиться, что для
каждого слова х Е X*
Аа0(£) = а(х) .	(5.27)
Установим (5.27) индукцией по длине слова х.
Еслп £(х) = 1, то есть слово состоит пз одной буквы, то
У’Ао(ж) = А0(т,С'1) = у?л(ж) = р(х) .
(В этой выкладке использовано (5.15) п (5.26), а также тот факт, что
Ле с\).
Пусть (5.27) установлено для всех слов длпны п — 1. Рассмотрим
произвольное слово длпны п п пусть последней буквой этого слова
будет буква х, то есть слово имеет вид хх, где £(х) = п — 1. Имеем
срАо(хх) = X0(xx,C-q) = Ао(£, C'i)A0(t, <50(£, C'i)).
- 173 -
Мы использовали соотношение (5.14) для функции выходов. По пред-
положению индукции Ао(£, Ci) = <рд0(х) = </?(£) На основании (5.25)
<$o(£,C'i) = С'(х). Следовательно,
^А0(жж) = у?(£)А0(т, С(х)) = ср(х)ср£(х) = ip(xx) .
(В этой выкладке использовано определение (5.26) функции Ао и свой-
ство (5.19) остаточных операторов).
Теорема 2 доказана.
Пример. Убедимся, что словарный оператор 74 нз примера 4 является
ограниченно-детерминированным, найдем его остаточные операторы н
построим автомат, реализующий <74.
Пусть £о = 7172   - 7fc> ® = a'ia'2    an ~ двоичные слова н
(y?4)£0(Q'lQ'2   «„) = PiP'l   - Рп 
По определению остаточного оператора это означает, что
7^(7172    7^Q;1Q;2   'ап) — ^1^2   -fikPlP?    Рп у
то есть
<	51 = 71
<	^2 = 71 Ф 72
<	5fc = 71 Ф 72 Ф    Ф 7fc	„о,
(5.28
Pi = 71 ® 72 ®    ® 7fc	®ai
Р2 = 71 Ф 72 Ф    Ф 7k	Ф ai	Ф 0'2
Рп = 71 ® 72 ф    ф 7fc	Ф 0'1	ф 0'2 Ф	... Ф оп	.
Группа формул (5.28) представляет	собой	определение оператора
(^4)£о :
1) если 71 ф 72 Ф . . . Ф 7п = 0, то
Р1 = 0'1
А> = 0'1 ф О2
Рп = 0'1 ф 0'2 Ф . . . Ф О'п ,
- 174 -
то есть (у?4)£о =
2) если 7х ф 72 ф . . . ф 7„ = 1, то
А = 1 ф ai
А> = 1 Ф 0'1 Ф 0'2
Рп = 1 Ф 0'1 Ф 0'2 Ф . . . Ф О'п .
Это новый словарный оператор. Он действует так: сначала к слову
х применяется оператор ср, затем в полученном слове ср(х) произ-
водится пнверспя: едпнпцы заменяются на нулп, нулп - на едпнпцы.
Обозначим этот словарный оператор <^4.
Итак, оператор р4 пмеет два различных остаточных оператора:
р4 п ср4. Следовательно, оператор р4 - ограниченно-детерминирован-
ный.
Перейдем теперь к построению автомата, реалпзующего ср4. Мно-
жество всех входных слов разобьем на два класса X* = C'o U C'i, где
Со = {7172    7„ | 71 Ф 72 Ф    Ф 7„ = 0},
С\ = {7172    7n | 71 Ф 72 Ф    Ф 7п = 1} 
Слова пз первого класса порождают остаточный оператор ср4, пз вто-
рого — ср4. Полагаем
Q = {Co,Ci}.
Легко заметить, что Со состопт пз всех слов, в которых четное ко-
личество едпнпц, а С\ — пз всех слов, в которых количество едпнпц
нечетно. Поэтому,
-	еслп слово х £ Со, то слово £0 £ Со, а слово х! £ С\ ;
-	еслп слово £ £ C'i, то слово £0 £ С\, а слово £1 £ Со-
Следуя построению в доказательстве теоремы, полагаем
<	5(0, Со) = Со, <5(1, Со) = С\, <5(0, С\) = С\, <5(1, С\) = Со.
Наконец, определяем функцию выходов:
А(т, Со) = ср4(х) = х, Х(х, C'i) = <р4(х) = х, х £ {0, 1} .
Построенный автомат реализует словарный оператор ср4.
- 175 -
Минимизация автомата
Построенный при доказательстве последней теоремы автомат Aq,
обладает тем свойством, что число его состояний (будем обозначать
число состояний автомата А через р(А) ) равно числу различных
остаточных операторов словарного оператора ср:
р(А0) = г(ср) .	(5.29)
Каждый остаточный оператор реализуется в некотором состоянии ав-
томата: задаваемое остаточным оператором преобразование слов мож-
но выполнить, установив автомат в подходящее состояние н подавая
на него входные слова (см. 5.20). Отсюда вытекает, что у любого
автомата А, реализующего данный ограниченно-детерминированный
оператор ср, число состояний не меньше, чем г (ср):
ср а =р^ р(А) > г(ср).	(5.30)
Автомат с наименьшим числом состояний, реализующий данный
ограниченно-детерминированный' оператор ср. называется минималь-
ным автоматом оператора ср.
Сравнивая (5.29) н (5.30), приходим к выводу, что автомат Aq,
построенный при доказательстве теоремы 2, минимальный.
Если Ai — другой минимальный для того же оператора ср авто-
мат, то количество его состояний также будет равно г(ср) н каждому
нз них будет однозначно соответствовать некоторый остаточный опе-
ратор epi. Переобозначив состояния автомата А} по правилу : если в
состоянии q реализуется остаточный оператор epi, то заменяем обо-
значение q на Ci, мы, как нетрудно проверить, получим автомат Aq.
Отсюда вытекает
Теорема Минимальный автомат единственен с точностью до обо-
значений состояний.
Замечание. Пз вышеизложенного вытекает такой признак минималь-
ности автомата: автомат будет минимальным, если для любых двух
его состояний q н q' реализуемые в этих состояниях остаточные
операторы
х ь-> Х(х, q) н х ь-> Х(х, q')
- 176 -
различны.
Рассмотрим следующую ситуацию. Пусть задан некоторый авто-
мат А. Он реализует некоторый ограниченно-детерминированный опе-
ратор у? = ifiji, но, вообще говоря, не нанлучшнм образом: число состо-
яний в автомате А может оказаться больше минимально необходимого,
то есть количества различных остаточных операторов г(<р). Требуется
по автомату А построить минимальный автомат оператора <р, реали-
зуемого автоматом А. Эта задача носит название задачи минимизации
автомата. Изложим алгоритм ее решения.
Пусть А = (X,Y,Q,8, X). В процессе работы алгоритма строятся
разбиения множества Q состояний автомата А на непересекающнся
классы:
(Я) Q = С\ U С2 U ... U Ст.
На очередном шаге алгоритма происходит измельчение предыдущего
разбиения, то есть каждый класс нового разбиения входит в один нз
классов предыдущего. Классы разбиения, полученного после заверше-
ния алгоритма, н будут состояниями минимального автомата.
1-й шаг. Состояния автомата q н q' отнесем к одному классу,
если
Vt е X (А(х, q) = А(х, q')) .	(5.31)
Полученное разбиение обозначаем (ДО):
(Я^) Q = C(11> ucf’ U-.-uCfJ.
Здесь н далее начальное состояние автомата будем относить в первый
класс.
i + 1-й шаг. Пусть на г-ом шаге построено разбиение (R1^)'-
(Я^) Q = C'P А Ср U...UC<‘’.
Состояния автомата q н q', отнесем к одному классу нового разбие-
ния, если выполнены следующие два условия
1) q н q' входят в один класс разбиения {R^p,
2) для каждого входного символа х состояния i(x,q) н i(x,q')
входят в один класс разбиения (Rpy
- 177 -
Будем обозначать через C(q) класс, в который входит состояние
q. Тогда условия 1) н 2) запишутся так:
1) C{q) = C{q')-
2) \/х (C{8{x,q)) = C(8(x,q')).
Алгоритм заканчивает работу после того, как на некотором шаге
к не произойдет дальнейшего измельчения разбиения, то есть ока-
жется, что (Rk+1‘) = (7?fc). Это последнее разбиение обозначим просто
(Я) :
(Я) Q = Ci U С'2 U ... U Сг.
Тот факт, что алгоритм закончил работу на разбиении (R) можно
выразить как следующее свойство разбиения (R) :
С'(</) = C(q') => Vt (С'(Й(т, q)) = С(6(х, q')) .	(5.32)
Строим теперь автомат Aq = (Aq, Yq, Qo, <5q, Aq) следующим обра-
зом:
-	входной н выходной алфавиты такие же как у исходного авто-
мата А: Хо = X, Yo = Y;
-	Qo = {C'i, С'2, . . ., C'r} — классы разбиения (Я);
-	функцию переходов Йо определим соотношением
60(x,C(q)) = C(6(x,q)).	(5.33)
Иными словами, чтобы найти в какое состояние переходит авто-
мат Aq нз текущего состояния-класса при входе х, берем в этом
классе любое состояние q н находим в какое состояние й(т,</) пере-
ходит при входе х исходный автомат А. Класс, в который входит
<5(х, q), (согласно (5.32), этот класс не зависит от выбора состояния q
в текущем состоянии-классе) н будет новым состоянием автомата Aq .
Так как при поступлении на вход слова х автомат А нз состоя-
ния q переходит в состояние <$(£,</), то
ШС’(?)) = СШ<	(5.34)
- 178 -
Наконец, завершая построение минимального автомата, определим
его функцию выходов Aq соотношением
А0(Ж,С'(Д) = А(Ж,Д,	(5.35)
то есть в качестве выходного символа автомата Aq в состоянии C(q)
прп входе х берется выходной символ автомата А, равный А(т,</),
где 9 — произвольное состояние пз C'(q). Независимость результата
от выбора состояния в классе C'(q) вытекает из того, что разбиение R
является измельчением разбиения R1'1^ , которое строилось так, чтобы
выполнялось условие (5.31): все состояния одного класса дают одни и
тот же выход при данном входе.
Автомат Ао построен. Докажем, что он реализует тот же словар-
ный оператор, что н автомат А н его минимальность.
Индукцией по длине слова установим, что £ X*
A(2,<Zi) = А0(£,С'1) .	(5.36)
Для слов, состоящих нз одной буквы х = х равенство (5.36) вы-
текает нз определения (5.35) функции выходов До (напомним, что
qi G 6'1). Пусть (5.36) верно для всех слов длина, которых не превосхо-
дит п— 1, возьмем произвольное слово длины п н пусть его последней
буквой будет буква х, то есть слово имеет вид хх, где £(£) = п — 1.
Тогда в силу соотношения (5.12) для функции выхода,
А0(£т,С'1) = А0(£,С1)А0(тД(£,С(г/1)))
н А(£т, </i) = А(£, </1)А(т, <$(£, </i)) .
По предположению индукции Ао(£, 6'1) = A(£,</i). Покажем, что
Ао(тДо(£, С'(<л))) = А(т,<5(£, гл)).
Согласно соотношению (5.34), <Д(£, 6'(</i))) = 6'(<5(£, </i)). Поэтому,
Ао(тДо(£, C'(r/i))) = А0(т, С'(<5(£, г/i))) = А(т, <$(£, г/Д)
(последнее равенство на основании определения (5.35) функции выходов
автомата До).
- 179 -
Равенство (5.36) доказано.
Для доказательства минимальности автомата Aq воспользуемся
признаком, сформулированным выше: минимальный автомат в разных
состояниях реализует разные словарные операторы. Покажем, что еслп
классы С и С различные, то найдется слово £ такое, что
Ао(£, С) Ао (£, С).
Пусть q н q' состояния автомата А нз классов С н С" соот-
ветственно, то есть С = C(q) , а С = C(q'). Напомним, что С н
С — классы разбиения R , построенного на Ar-ом шаге описанного
выше алгоритма. Так как состояния q н q' входят в разные классы
этого разбиения, найдется входной символ такой, что состояния
q) н 8(xi1,q1') принадлежат разным классам разбиения
н, следовательно, найдется входной символ ж;2 такой', что состояния
<5(т;1, й(т;2,г/)) = й(т;1т;2,г/) н й(т;1,6(xir2,q'y) = 6(х^х^2, q')
принадлежат разным классам разбиения	Продолжая это по-
строение, мы найдем слово
i 1 % i 2 • • • % i к. —1
такое, что состояния
6(xilXi2 . . .Xik_l,q) н 6(xilXi2 . . .xik_l,q')	(5-37)
входят в разные классы разбиения ДТ. Последнее означает, что для
некоторого входного символа xtk выход автомата А в первом нз со-
стояний (5.37) не совпадает с его выходом во втором. Следовательно,
А(ж; х ж;2 . . . х2к_х, q)	А(т'21т-22 . . . х^к_к q )
нлн
Ао(жх х жХ2 ... Х{к-1, С (*?)) 7- Aq(ждхжХ2 ... х2к_х, С (</ )) ,
то есть словарные операторы, реализуемые автоматом Aq в состояниях
C(q) н C(q’), различны.
Тем самым доказана минимальность автомата Aq.
- 180 -
Глава 6
Формальные языки и автоматы
6.1. Регулярные языки
В предыдущей главе мы рассматривали конечное множество
{ Т 1, Т 2 , ..., Т п }
как алфавит и ввели множество всех слов в алфавите X :
X* = A U X U X2 U . . . U Хк U . . .
Языком L будем называть произвольное подмножество
L С X*,
то есть любое множество слов.
Интересно сравнить это определение с понятием языка в обиход-
ном понимании этого слова. На первый взгляд естественный язык (рус-
ский, английский и т.п.) удовлетворяют этому определению: имеется
алфавит, язык состоит пз слов. Однако, естественный язык предста-
вляет собой объект, который постоянно изменяется, развивается; по
поводу некоторых слов возникают споры : является ли данное слово
словом пз русского языка пли нет? Данное выше определение вводит
язык как точный объект - подмножество, следовательно, должно быть
задано правило однозначно решающее входит лн некоторое слово в это
подмножество, то есть в язык нлн нет. Чтобы подчеркнуть это раз-
личие, языки, удовлетворяющие данному нами определению называют
формальными. Формальным является, например, любой язык програм-
мирования. Когда компилятор, например Сн-компилятор, читает текст
программы, в котором имеются ошибки (пропущена точка с запятой, не
закрыта скобка н т.п.) он отвергает такой текст как слово, не входящее
в язык Сн.
Набор правил образования слов формального языка называют его
грамматикой. В зависимости от сложности этих правил формальные
- 181 -
языки делятся на ряд классов. Далее мы рассмотрим один пз наиболее
простых классов языков - регулярные языки - и выявим их непосред-
ственную связь с конечными автоматами.
Рассмотрим совокупность языков с одним и тем же алфавитом и
введем три операцпп над этими языками:
1)	Объединение
L = LiU £2
( L состоит пз всех слов, входящих в L\ пли в £2).
2)	Произведение (конкатенация)
L = L1 L'i = {£ = x-yi'i | £i £ £i, ж2 G /<>}
( L состоит пз всевозможных слов, получающихся приписыва-
нием к слову нз языка L\ слова нз языка £2).
3)	Итерация
L* = Л U L U L2 U . . . U Lk U . . .
( £* состоит нз всевозможных слов, получающихся приписы-
ванием друг к другу нескольких слов нз языка L : в L*
входят
-	пустое слово;
-	все слова нз языка £;
-	слова, полученные приписыванием к слову нз L еще какого-
нибудь слова нз L ( L2)-
-	слова, полученные приписыванием к слову нз L2 еще какого-
нибудь слова нз L ( L3 );
-	и так далее.
Языки {Л}, {ti}, {т2}, . . ., {тп}, состоящие нз одного однобуквен-
ного слова (либо только нз пустого слова) назовем элементарными.
Язык называется регулярным, если его можно построить нз элемен-
тарных с помошью конечного числа применений операций объединения,
произведения н итерации.
Примеры.
(Для простоты обозначаем элементарный язык {а} просто а).
1.	а* = {Л, а, аа, ааа, аааа, .. .}.
- 182 -
2.	X* = (га U ж2 U . . . U ж„)*.
3.	Пусть язык L над двоичным алфавитом X = {0, 1} состоит
из всех слов (двоичных), в которых встречается комбинация
ПОП. Тогда
L= (0U 1)*11011(0 U 1)* .
4.	L состоит нз всех двоичных слов, в которых количество еди-
ниц четно. Тогда
L= (О U 10*1)* .
6.2.	Автоматы Мили и Мура
Автомат называется автоматом Мура (Е.Н.Moore), если функция
выходов автомата зависит только от состояния (не зависит от входного
символа) :
А(т, q)=p(q).	(6.1)
Автоматы, удовлетворяющие определению, данному в первом пара-
графе, (выход — функция от входа и состояния) называют автоматами
Милн (G.К.Mealey). Таким образом, автомат Мура - это частный слу-
чаи автомата Милн. Имеет место, однако, следующая теорема.
Теорема.Для любого автомата Мили можно построить эквивалент-
ный ему автомат Мура.
Прежде чем доказывать это утверждение заметим, что в случае
автоматов Мура влияние входного символа на выход задерживается на
одни временной такт:
q(t + 1) = <5(к,/)
y(t + 1) =	+ 1)) =	.
В частности, это проявляется в том, что в 1-м такте выход автомата
Мура будет всегда одним и тем же: г/(1) = p(<h), и мы не будем при-
нимать его во внимание, считая, что автомат перерабатывает входное
слово
т(1)т(2) . . . т(1)
в выходное
гу(2)гу(3) . . . у{1 + 1).
- 183 -
Именно так и определим словарный оператор, реализуемый автоматом
Мура.
Доказательство теоремы. Пусть автомат Мили А = (X, Y, Q,8, А)
имеет п входных символов и s состояний':
А' — { X х , X 2 ,    , X п }
Q = {?1Л2,   -,qs}
п реализует ограниченно-детерминированный оператор ср. Эквива-
лентный автомат Мура М = (X, Y, Qm , &м, Р ) будем строить следую-
щим образом. В число состояний автомата М включим все состояния
автомата А, обозначив их </oi, 402,   , ^Os, соответственно, и, кроме
того, для каждой пары (xi,yj) G X х Q включим в Qm состояние
rjij. Еслп работу автоматов А и М рассматривать параллельно, то
автомат М будет находиться в состоянии у,j, когда на автомат А в
состоянии rjj поступает символ Xi. В соответствии с этим выходную
функцию автомата М определим так:
= А(тг,^) (1 < г < n) , (1<)<Д
p(yoj) определяем произвольно (1 < j < .s) .
Таким образом, новый автомат имеет s + ns состояний.
Определим, наконец, функцию переходов автомата М следующим
образом:
8м , Qdj) — Qij
^M(xi,qjk) = qu, еслп для автомата A 8(xj,qk)=qi (6.3)
(1 < i < п, 1 < j < п, 1 < k < s, 1 < £ < .s).
Связь между функциями 8 м и J описывается в следующей лемме.
Лемма. Пусть xxi — произвольное слово, оканчивающееся буквой
Xi. Если 8(х,ук) = ук, то 8M(xxi,yok) = <це.
Лемма доказывается индукцией по длине слова х. Для слов, со-
стоящих пз одной буквы утверждение леммы совпадает с определением
(6.3). Пусть лемма верна для всех слов х, длина которых не превосхо-
дит t — 1. Рассмотрим слово xXjXi длпны t. Пусть
8(x,yQ = ye, 8(xj,yQ = ут, тогда 6(xxj,yk) = ут .
- 184 -
По индуктивному предположению
8 м (xxj, 40/г) — 'Ijz 
Следовательно,
8м (xx‘j Xi, 4ofc) — 8м	, 8м (,ХХ‘j , 4ofc) ) —	— Qim 
Лемма доказана.
Убедимся теперь, что автоматы А и М реализуют один и тот
же словарный оператор, то есть, что ipА = рм-
Снова применяем пндукцпю по длпне слов. Для однобуквенных слов
пмеем
Рл(хг) = X(xi,qi) .
Автомат М, в начальный момент установленный в состояние 401,
сначала под действием входа xt перейдет в состояние <$м(жг,401),
равное qn, (см.(6.3)), п в следующем такте выдаст выход
В сплу (6.2)
= А(т;, <7i),
поэтому <рА(Хг) = Рм(Хг)-
Пусть рА п рм совпадают на всех словах, длпна которых не
превосходит t — 1, рассмотрим слово xxi длины t. Пмеем
pA(xxi) = X(xxi, qA) = Х(х, qA)X(xi, 8(х, 41)) .	(6.4)
По предположению пндукцпп
Х(х, г/i) = рА(х) = рм(х) .	(6.5)
Пусть 8(x,qA) = qm- Тогда
X(xi, 8(x,qA) = X(xi,qm) = p(qim) .	(6.6)
По предыдущей лемме
8м(хх{, 4oi) = qim .	(6.7)
- 185 -
Подставляя (6.5), (6.6) и (6.7) в (6.4), получаем
ipA(xxi) = А(£,г/1)А(т;,<5(£1,г/1)) = ^M(i)/«(fim) =
= ^м{х)^м{&м{хх1, гуси)) = ifM{xxi).
Теорема доказана.
6.3.	Автомат Мура как распознаватель
Рассмотрим автоматы Мура с двумя выходными символами 0 и 1.
Такой автомат будет для некоторых слов выдавать в конце слова вы-
ход 1, будем считать, что автомат ’’узнал” это слово, для остальных
слов выход равен нулю (это слово автомат ” не распознал”). Тем самым
определяется некоторый язык, состоящий нз слов, распознаваемых ав-
томатом.
Так как выход автомата Мура полностью определяется состоянием,
то множество состояний можно разбить на два класса так, что в состо-
яниях нз класса F выход равен 1, а в состояниях нз класса Q\F выход
равен 0. Таким образом, если слово х перевело автомат в состояние
нз множества F, то автомат распознает слово, в противном случае -
нет. Такое положение позволяет, вообще не рассматривать выходы н
определить автомат-распознаватель следующим образом.
Автоматом-распознавателем будем называть пятерку
А = (X,Q,8,qi,F) ,
где X —входной алфавит, Q —множество состояний, <5 —функция
переходов, 41 — одно нз состояний, выделенное как начальное,
F С Q — совокупность состояний, объявленных как заключительные
(если автомат, на вход которого подано некоторое слово, оказывается
в одном нз состояний нз F, то будем говорить, что он распознал слово
на входе).
С каждым автоматом-распознавателем свяжем распознаваемый нм
язык:
£(А) = {£ | 8(х, 4i) е F},
- 186 -
то есть язык £(А) состоит из всех слов, которые переводят автомат
А из начального состояния qi в одно из заключительных (в любое
состояние нз множества F).
Пример. А = (X, Q, S, qi, F), где X = {0, 1}, Q = {1, 2}, F = {1}, а
функция переходов задается таблицей
ВХОД	состояние	
	1	2
0	1	2
1	2	1
Вход 0 не изменяет состояния автомата, вход 1 - изменяет состо-
яние. Поэтому слова, переводящие автомат нз состояния 1 в это же
состояние — это слова с четным количеством единиц. Следовательно,
£(А) —это язык, рассмотренный выше в примере 4 параграфа 1.
Далее мы устанавливаем, что языки, распознаваемые конечным ав-
томатом — это регулярные языки н только они.
6.4.	Теорема анализа
Теорема. Язык, распознаваемый автоматом, является регулярным.
Для доказательства определим рекуррентно семейство языков .
Индексы i н j - это номера состояний: 1 <_ г <_s, ' Ti T-s> гДе
s — количество состояний автомата. Индекс k, по которому ведется
рекурсия, изменяется от 0 до s.
Язык состоит нз всех символов входного алфавита (однобу-
квенных слов), которые переводят автомат нз состояния qt в состояние
qj, то есть нз всех таких Xk, что 8(xk,qi) = qj. При i = j в язык
включаем еще н пустое слово. Таким образом, каждый нз языков
состоит нз конечного числа однобуквенных слов (н еще, быть может,
пустого слова) н, следовательно, является регулярным.
Пример. Для автомата А нз предыдущего примера
= AuO, L^ = l, = 1,	= A U 0.
- 187 -
Остальные языки семейства определим рекуррентно:
т(к)  	1) г (fc — 1) / j-(k-1) \ * г (fc — 1)
- L*J U Ltk \Lkk ) Lk j	(ggj
к = 1, 2, . . ., s; i = 1, 2, . .., s; j = 1, 2, . .., s .
Из формулы (6.8) вытекает, что все языки — регулярные.
Продолжение примера. Для автомата из параграфа 3 имеем по
формуле (6.8)
£0 = 0*, £0 = 0*1, £.0 = 10*, £.О = Ли 0 U 10*1.
Например,
£22} = L22 U L21 (Ln ) * L12 = {л и О} U 1 (Л U 0) * 1 = л и о и О U 10* 1 .
Чтобы охарактеризовать языки рассмотрим множество Wij
всех слов, переводящих автомат из состояния Qi в состояние Qj :
Wij = {х I J(£, (Ji) = qj} .
Пуств x = x^x^ . . .x^ одно из таких слов. При переходе пз (ц в qj
автомат проходит промежуточные состояния
= ^Ц.й)
'	(6.9)
= 3(xiLxi2   xir_L,(li) 
Определим W^ как подмножество слов нз Wij, для которых при
переходе нз с/, в (jj номера промежуточных состоянии'не превосхо-
дят к:
21 < k,j2 <к,..	< к.
Из определения непосредственно вытекает, что
£(0) = Ж(0) с ж(1) с ... с с с ... с w(s) = Ж, .
2J	2J _ 2J _	_ 2J	_ 2J _	_ 2J	2 J
- 188 -
Лемма. L^ = W^.
ZJ	ZJ
Лемма доказывается индукцией по к.
При к = 0 определение ж/0"1 (запрещаются в качестве промежу-
х	Г (°)
точных все состояния) совпадает с определением языка .
Пусть = ж/^ для t < к — 1 . Чтобы убедиться в спра-
r(fc) тлЖ)
ведлнвостн равенства L- = применим стандарное рассуждение
’’равнообъемностн”: каждое слово нз левой части входит в правую, и
наоборот.
Допустим, что х £	. Тогда, в силу определения (6.8),
НЛН	\Lkk ) Lk3 
В первом случае по предположению индукции	= ж/^
Так как С ж/,^, то х £	.
Во втором случае x представляется в виде произведения подслов
X — £ 0 £ 1 • •  р р 1 ,
таких что
жо G L,k ’xrGLkk для v = 1, . . .,р и хр+1 £ Lkj <
Снова используя предположение индукции, заключаем, что
1° слово £о переводит автомат нз состояния гр в состояние
rjk, таким образом, что номера промежуточных состояний не
превосходят к — 1;
2° каждое нз слов х-р . . ., хр переводит автомат нз состояния q/.
в состояние q/., при этом номера промежуточных состоянии
не првосходят к — 1;
3° слово £р-|-1 переводит автомат нз состояния qk в состояние
qj так, что номера промежуточных состоянии'не превосходят
к - 1.
- 189 -
Следовательно, слово х переводит автомат пз (ц в qj так, что
номера промежуточных состояний не превосходят к, то есть £ £ иДС
Обратно, пусть х £	. Предположим, что средн промежуточ-
ных состояний (6.9) состояние qk встречается ровно р раз, так что
номера остальных промежуточных состояний не превосходят к — 1.
При р = 0 имеем
х £	С .
При р > 0 слово х можно разбить на подслова
•Р - «I Q «I 2 • • • J) J) —|- X )
так, что выполняются условия 1°—3°. Следовательно,
ж0 £ Wg-1"1, £r £	для v = 1,... ,р н £р+1 £ wg-1"1
Z Л.	п, п,	х	I '	п, J
нлн, используя предположение индукции,
~ г-	~ г-	1	~ г- r(k-l)
xOeLlk xr £ Lkk для v = 1, . . .,p н xp+1 £ Lkj >,
то есть x £ Ltk (Lkk Lk] CL^’.
Лемма доказана.
Для доказательства теоремы анализа остается заметить, что
ВД = и 4Д
Эта формула представляет язык L(A) в виде объединения регулярных
языков, следовательно, язык L(A) — регулярный.
Теорема доказана.
6.5. Регулярные языки и источники
Источником Q над алфавитом X будем называть ориентирован-
ный граф, в котором
1) выделены два непустых подмножества вершин: вершины нз
первого подмножества называются начальными, вершины нз
второго - конечными.
2) каждой дуге приписана либо некоторая буква нз алфавита X,
либо пустое слово.
- 190 -
Дугу, которой приписана буква х, будем называть’’дугой ж” нлн
” к-дугой”, дугу, которой прпппсано пустое слово — пустой дугой.
С псточнпком Q можно связать некоторый язык L(Q), определи-
мый следующим образом. Рассмотрим всевозможные путп в Q, начи-
нающиеся в какой-либо начальной вершине п заканчивающиеся в какой-
либо пз конечных. (Напомним, что прп перемещенпп по путп требуется
соблюдение ориентации: начало очередной дуги совпадает с концом
предыдущей). Для каждого такого путп выппшем подряд все буквы,
встречающиеся на его дугах — получптся некоторое слово. Совокуп-
ность всех получаемых такпм образом слов п образует язык L(Q).
Будем называть этот язык языком, порождаемым источником Q.
Замечание. Про путь п связанное с нпм слово х £ L(Q) будем гово-
рить: ’’путь порождает слово 2” п называть такой путь 2-путем.
Замечание. Два псточнпка называют эквивалентными, еслп онп поро-
ждают одни п тот же язык. Для каждого псточнпка можно постропть
эквивалентный псточнпк с одной'начальной'п одноп 'конечноп вершп-
ной: для этого к множеству вершпн данного псточнпка нужно присо-
единить еще две, первую объявить начальной п провестп пз нее пустые
дуги во все вершпны, бывшие начальными в псходном псточнпке, вто-
рую объявить конечной п провестп в нее пустые дуги пз всех вершпн,
бывших конечными в псходном псточнпке.
Повторяя для псточнпка доказательство теоремы анализа, легко
убедиться, что порождаемый псточнпком язык — регулярный. Имеет
место обратная теорема.
Теорема. Для каждого регулярного языка существует порождающий
его источник.
Доказательство. Согласно определенпю, регулярный язык — это
язык, который можно получпть пз элементарных, применяя конечное
чпсло раз операцпп объедпненпя, пропзведенпя п птерацпп. Поэтому
для доказательства теоремы достаточно проверпть, что
1° элементарные языкп порождаются псточнпком;
2° еслп каждый пз двух языков порождается псточнпком, то можно
постропть псточнпк, порождающий объедпненпе языков;
3° еслп каждый пз двух языков порождается псточнпком, то можно
постропть псточнпк, порождающий' пропзведенпе языков;
- 191 -
4° если язык порождается источником, то существует источник поро-
ждающий итерацию языка.
Проверим 1°—4°, выбирая каждый раз в качестве порождающего
язык источника источник с одной'начальной'н однон'конечнон верши-
ной (это возможно, согласно сделанному выше замечанию) н обозначая
эти вершины буквами В н Е, соответственно.
1°. Непосредственно проверяется (так как имеется всего один путь
нз В в Е), что изображенные на рнс. 6.1 источники порождают
элементарные языки.
®----------->®
a) L = {Л}
Ж 2
®---------------1>®
a) L = {ж,}
Рнс. 6.1. Источники, порождающие элементарные языки
2°. Пусть L = L^Lq н для языков Еу н Lq построены порожда-
ющие их источники Q\ н Qq. Начальные н конечные вершины этих
источников обозначим Bi,Ei н В2, Eq, соответственно. Источник
Q, порождающий язык L строится следующим образом :
-	источники Qi н Qq объединяются (то есть объединяются
множества вершин н множества дуг Qi н Qq );
-	добавляются две новые вершины :
В - нз нее проводятся пустые дуги в В, н в Bq н
Е - в нее проводятся пустые дуги нз Ei н нз Eq ;
-	В объявляется начальной, а Е - конечной вершиной нового
источника.
- 192 -
Рис. 6.2. Источник, порождающий объединение языков.
Из построения вытекает, что каждый путь между вершпнамп В п
Е в новом источнике представляет собой либо путь между п Ei,
в начало п в конец которого добавлена пустая дуга, лпбо путь между
В2 п Е2, в начало п в конец которого добавлена пустая дуга. Отсюда
L(Q) = £(Qi)U L(Q2) = EjU L2.
3°. Пусть L = LiL2 и для языков L\ и L2 построены, порожда-
ющие пх источники Qi и Q2. Начальные и конечные вершпны этих
источников обозначим В у, Ei п В2, Е2, соответственно. Источник
Q, порождающий язык L строптся следующим образом :
-	источники Qi п Q2 объединяются;
-	пз вершпны Ei проводится пустая дуга в В2 ;
объявляется начальной, а Е2 — конечной вершпной
нового псточнпка.
Рпс.6.3. Источник, порождающий пропзведенпе языков.
Из построения вытекает, что каждый путь между вершпнамп В п
Е в новом псточнпке будет состоять пз трех частей: путь между п
- 193 -
Ei, пустая дуга и путь между В? п Е^. Порождаемое такпм путем
слово пмеет впд £ = £д£2, где £д — слово, порождаемое частью
путп от Bi до Ei, £2 — слово, порождаемое частью путп от В2
до Е2, то есть слово £j порождается псточнпком Qi, а слово £2
— псточнпком Q2. Наоборот, еслп взять любые два слова £ Е Li п
£2 G L2, то согласно определенпю языка, порождаемого псточнпком,
первому пз слов будет соответствовать некоторый путь от Bi до Ei,
а второму — путь от В2 до Е2. Добавление пустой дуги от Ei до
В2 даст путь в новом псточнпке, порождающий £i£j2. Отсюда
L(Q) = {£ = T1T2 | £1 G Li, £2 G L2} = L1L2 
4°. Пусть L = (£1)* п для языка Li построен порождающий его
псточнпк Qi с начальной вершпной Bi п конечной Ei. Псточнпк
Q, порождающий язык L строптся следующим образом :
-	добавляются две новые вершпны :
В - пз нее проводятся пустые дуги в Bi п в Е
Е - в нее проводится пустая дуга пз Ei .
-	пз вершпны Ei проводится пустая дуга в Bi (’’зацпклпва-
нпе”) ;
-	вершпна В объявляется начальной, Е — конечной вершпной
нового псточнпка.
Рпс.6.4. Псточнпк, порождающий птерацпю языка.
Совокупность путей между вершпнамп В п Е в новом псточнпке
можно оппсать следующим образом :
- 194 -
-	путь по пустой дуге (порождает пустое слово);
-	путп, проходящие через Еу, не содержащие ”циклической”
дугп пз Ei в Bi - очевидно, что этп путп порождают слова
пз £i;
-	путп, к раз проходящие через ’’циклическую” дугу (к >_1)~
этп путп порождают слова впда £ = x-yXQ . . .£k, где £[ £
Ly, xq G Ly, . . . хк £ Ly, то есть слова пз языка Lk.
Итак, язык, порождаемый построенным псточнпком
£(Q) = Л и £1 и и ... и Ьк и ... = (£1)* .
Теорема доказана.
Замечание. Введенпе пустых дуг в приведенных выше построенпях
необходимо, чтобы избежать так называемых ’’ложных” путей. Иапрп-
мер, в случае 3° можно попытаться обойтпсь без пустой дугп Еу—Bq,
просто склепвая этп вершпны в одну вершпну. Однако, в таком псточ-
нпке может возникнуть путь, проходящий'
-	пз By в С по источнику Qy ;
-	далее пз С в С по источнику Qq ;
-	еще раз пз С в С по источнику Qy ;
-	ПЗ С' В Eq ПО ПСТОЧНПКу Qq
Порождаемое такпм путем слово, вообще говоря, не входпт в язык
£1£2.
В конкретных случаях, еслп нет опасностп вознпкновенпя ложных
путей, пустые дугп можно удалять.
6.6.	Детерминизация источника и теорема синтеза
Пусть А = (X, Q, <5, qy, F) — автомат-распознаватель. Его диа-
грамму переходов можно рассматривать как псточнпк: это ориенти-
рованный граф, в котором каждой дуге прпппсана буква пз входного
алфавита X. Объявляя вершпну qy начальной, а вершпны пз множе-
ства F конечными, мы, очевидно, получпм псточнпк Q такой, что
порождаемый псточнпком язык совпадает с языком, распознаваемым
- 195 -
автоматом. Источник Q, однако, весьма специального вида. Еслп
входной алфавит X автомата А состоит пз п букв, X = {ад, . . ., к„},
то в источнике Q
D1) нз каждой вершины выходят ровно п дуг, так что для каждой
буквы нз X имеется помеченная этой буквой дуга;
D2) нет пустых дуг.
Для удобства дальнейших формулировок мы будем называть источ-
ник, удовлетворяющий ограничениям D1) н D2), детерминированным.
Иаооборот, каждый детерминированный источник можно рассмат-
ривать как диаграмму переходов некоторого автомата-распознавателя.
Язык, порождаемый детерминированным источником, совпадает с язы-
ком, распознаваемым соответствующим ему автоматом.
Имеет место теорема, назывемая теоремой детермнннзацнн.
Теорема. Для .любого источника существует эквивалентный ему де-
терминированный источник.
Доказательство. Иусть Q произвольный источник н {у±, . . ., ys}
- множество его вершин. В качестве множества вершин детермини-
рованного источника Q./. эквивалентного Q, мы будем брать так
называемые замкнутые подмножества вершин Q. Иодножество вер-
шин
? = {(Jii >	   > l7u)
источника Q назовем замкнутым, если вместе с каждой вершиной оно
содержит все вершины, в которые нз данной'ведут пустые дуги:
у € у н (у, (/'(-пустая дуга => у' £ у .
Если дано произвольное подмножество вершин, то после добавления к
нему всех вершин, которые можно достичь нз данных, двигаясь по пу-
стым дугам, получится замкнутое подмножество вершин. Будем назы-
вать его замыканием исходного подмножества.
Иусть {</}- совокупность всех замкнутых подмножеств. Замкну-
тое подмножество Д, содержащее начальную вершину уi источника
Q (то есть замыкание подмножества {</i},) объявляем начальной вер-
шиной нового источника. Конечными объявляем все замкнутые под-
множества, содержащие по крайней' мере одну нз конечных вершин ис-
точника Q. Отметим также, что средн вершин нового источника есть
- 196 -
вершина, соответствующая пустому подмножеству, ее будем обозна-
чать 0.
Перейдем к определению дуг в источнике Qd- Пусть q £ Qd вер-
шина, х —буква алфавита X. Рассмотрим все ж-дуги источника Q,
начала которых расположены в вершинах множества q. Замыкание
множества нх концов является вершиной источника Qd, обозначим
эту вершину qx. Вершину q соединяем ж-дугой с вершиной qx. Если
нн одна нз вершин нз подмножества q~ не является началом ннкакон '
ж-дугн, проводим ж-дугу нз q в вершину 0. Наконец, для каждой
буквы ж £ X проводим ж-петлю нз 0 в 0. Очевидно, в резуль-
тате такого построения условия D1) н D2) будут выполнены, то есть
получится детерминированный источник.
Для доказательства эквивалентности источников Q н Qd необ-
ходима следующая лемма.
Лемма. Пусть ж — слово, q — вершина источника Qd- х-
путъ по источнику Qd из начальной вершины <Д в вершину q
существует в том и только в том случае, когда q состоит из всех
вершин источника Q, к которым в этом источнике ведут х-пути
из начальной вершины q^.
Лемма доказывается индукцией по длине слова ж. Если ж = ж (ж £
X), то утверждение леммы вытекает нз правила проведения дуг в ис-
точнике Qd : ж-дуга нз qi в q проводится, если q — замкнутое
подмножество, содержащее концы всех ж-дуг с началом в qi, дру-
гими словами q состоит нз всех вершин, к которым ведут ж-путн нз
вершины </1.
Допустим, что лемма верна для всех слов длины k — 1, рассмотрим
произвольное слово длины k с последней буквой ж, то есть слово,
имеющее вид жж (Дж) = к — 1).
Предположим, что вершина q соединена жж-путем с начальной
вершиной . Обозначим предпоследнюю вершину этого пути через
<р> : эта вершина соединена ж-путем с начальной (<Д), а нз нее вы-
ходит ж-дуга в вершину q. Пспользуя предположение индукции, по-
лучаем, что q состоит нз тех н только тех вершин источника Q, в
которые ведут ж-путн нз q±. По определению дуг в источнике Qd
вершина q — это совокупность всех вершин, в которые ведут ж-дугн,
начинающиеся в вершинах, образующих множество <р> (плюс, быть
- 197 -
может, пустые дуги). Следовательно, q состоит нз всех вершин ис-
точника Q, в которые ведут тж-путп по источнику Q нз начальной
вершины.
Обратно, пусть х состоит нз всех вершин источника Q, в кото-
рые ведут жж-иутн по источнику Q нз начальной вершины. Обозначим
через </2 подмножество вершин источника Q, в которые ведут ж-иутн
нз <71. Это подмножество замкнуто, поэтому <72 является вершиной
источника Qd- Так как £(£) = к — 1, то по предположению индукции
в источнике Qd имеется ж-иуть нз начальной вершины в вершину <72.
Рассмотрим вершину, в которую нз <72 ведет ж-дуга в источнике Qd-
Из только что изложенного вытекает, что эта вершина будет состоять
нз всех вершин источника Q, в которые ведет жж-иуть нз <71. Сле-
довательно, это вершина х. Итак, в источнике Qd имеется ж-дуга от
<72 До <7, а, значит, н жж-иуть от <71 до <7'.
Лемма доказана.
Эквивалентность источников Q н Qd просто следует нз леммы.
Сотношенне L(Q) С L(Qd) вытекает нз следующего рассуждения.
Пусть х Е L(Q), тогда в источнике Q существует ж-иуть нз <71
в одну нз конечных вершин <7. Рассмотрим замкнутое подмножество
<7, состоящее нз всех вершин, к которым в источнике Q ведут х-
путн нз <71. Это подмножество содержит вершину <7 н, следовательно,
будет одной нз конечных вершин источника Qd- Тогда по предыдущей
лемме к этой вершине имеется ж-иуть в источнике Qd, следовательно,
х 6 L(Qd).
Соотношение L(Qd) С L(Q) вытекает нз следующего рассужде-
ния.
Пусть х £ L(Qd)- Тогда существует т-путь нз <71 в одну нз
конечных вершин <7 источника Qd- Так как вершина <7 — конечная,
то в подмножество <7 будет входить по крайней мере одна нз конечных
вершин <7 источника Q. Ио лемме имеется ж-иуть нз <71 в <7;
следовательно х £ L(Q).
Итак, L(Q) н L(Qd) состоят нз одних н тех же слов. Теорема
детермнннзацнн доказана.
- 198 -
Из теоремы о порождении регулярного языка источником и тео-
ремы детермнннзацнн легко вытекает следующая основная теорема.
Теорема, (теорема синтеза). Для каждого регулярного языка можно
построить автомат, распознающий этот язык.
Для построения автомата строим вначале источник, порождающий
язык, а затем эквивалентный ему детерминированный" источник, то
еств автомат.
Теоремы анализа н синтеза дают еще одну характеристику возмож-
ностей конечного автомата: конечный" автомат распознает некоторое
множество слов тогда н только тогда, когда это множество предста-
вляет собой регулярный язык.
6.7.	Языки И ГРАММАТИКИ
Изучая регулярные языки, мы определяли нх как подмножества
слов, получающиеся путем естественных операции': приписывания слов
друг к другу н объединения. Более естественный способ определения
языка — задание его с помощью свода правил словообразования нлн
грамматики.
В грамматике G, определяющей формальный язык L(G) над
алфавитом А имеются два непересекающнхся множества символов
(букв):
-	множество А букв основного алфавита, называемых терминаль-
ными ;
-	множество N нетерминальных, вспомогательных символов.
Нетерминальные символы называются также синтаксическими пе-
ременными нлн грамматическими понятиями.
Слова языка порождаются при помощи правил, в которых исполь-
зуются вспомогательные символы. С формальной стороны, правило —
это пара слов нлн элемент декартова произведения
(Я U ЛрЛфУи А)* х(ЯиА)*.
Правила записывают в виде
а —> [3,
- 199 -
где а — слово нз терминальных и нетерминальных символов, в кото-
ром по крайней мере один символ нетерминальный, а (3 — любое слово
в алфавите N U А.
Содержательно, правило означает возможность подстановки вме-
сто слова а слова (3 :
пп
Грамматикой называется четверка G = (N, А,Р, ,5'), в которой
N — конечное множество, алфавит нетерминальных симво-
лов;
А — конечное множество, алфавит терминальных символов
( А А Я = 0);
Р — конечное подмножество декартова произведения (N U
A)* N(N U Л)* х (Я U Л)* - набор правил грамматики G;
,5' — символ нз N, объявленный начальным.
Пример 1. Gi = ({Л, ,5'}, {0, 1}, Р, ,5'), где Р состоит нз следующих
правил :
Р :	S 0Л1
ОЛ 00Л1
Л —> Л (Л— пустое слово) .
Грамматика определяет язык рекурсивно, путем задания множе-
ства выводимых в данной грамматике слов. Множество выводимых
слов задается следующим образом :
1) ,5' — выводимое слово;
2) если слово ускд — выводимое слово, н средн правил грамма-
тики имеется правило а —> (3, то слово -'/(38 также выводимое.
Обозначим через 1(G) множество всех слов, выводимых в данной
грамматике ( 1(G) С U Л)*). Более отчетливо состав множества
1(G) выявляется через понятие вывода в грамматике G.
- 200 -
Последовательность слов 71,72, ••• ,7w в алфавите N U А назы-
вается выводом слова А в грамматике G, еслп
1) 7i = S, yN = S;
2) каждое слово 7, (2 < i < N) получается пз слова 7,- (j < г)
прпменененпем одного пз правил грамматики, то есть слова
7j и 7; имеют вид
7j = 7 «7'
7г = 7'^7"
и в множестве Р правил грамматики имеется правило а —> (3.
Слово А называется выводимым, еслп для него можно построить
вывод.
Основное определение.
Множество всех выводимых в грамматике G слов, составленных
только пз терминальных символов, называется языком, определяемым
грамматикой G.
Язык, определяемый грамматикой G, обозначается L(G). Имеем
L(G) С 1(G) С (Я U Л)* и L(G) = 1(G) П Л* .
Продолжение примера 1. В грамматике Gi все выводы легко про-
сматриваются:
.5', 0Л1, 00Л11,..., 00 ... ОЛП ... 1, 00 ... 011... 1.
(Первое правило нз Р применимо только в начале, третье — только
в конце, то есть ’’внутри” цепочки вывода применимо только второе
правило). Следовательно,
L(Gr) = {01,0011,000111,...}
Пример 2. Go, = ({Е,Т, F}, {а,+,*,(,)}, Р, Е) , где Р состоит нз
следующих правил:
Р :	E^rE + T	T->T*F	F (Е)
Е^Т	Т F	F а .
- 201 -
Вот пример вывода в грамматике G? :
Е, Е + Т,Т + Т, F + Т,а + Т,а + Т*Е, а + Е*Е, а + а*Е, а + а*а .
Если на последнем шаге вместо шестого воспользоваться пятым
правилом, то получится слово а + а*(Е). Повторяя для него уже по-
строенный вывод (начиная с Е) , получим слово а + а*(а + а*а). Можно
убедиться, что язык L(G) состоит нз всевозможных правильных ариф-
метических выражении.
Классификация грамматик и языков.
Грамматики можно классифицировать по виду нх правил. Для
упрощения последующих обозначений будем употреблять большие ла-
тинские буквы для нетерминальных символов, малые — для терминаль-
ных н греческие буквы для слов.
Пусть
G = (N, А, Р, S) -
грамматика. Грамматика называется
(1)	право.линейной, если каждое правило в Р имеет вид
А —> хВ нлн А —> х (A G N, В Е N, х Е А) .
(2)	контекстно-свободной, если каждое правило в Р имеет вид
А^а (А Е N,a Е (Я U Л)*) .
(3)	контекстно- зависимой нлн неукорачнвающен, если каждое
правило в Р имеет вид
а -Е Д, где Да) < ДД) .
( £ — длина слова).
(4)	Грамматика общего вида без каких-либо ограничений на пра-
вила.
Язык, который можно задать грамматикой одного нз этих типов н
нельзя задать грамматикой младшего по иерархии типа, носит соответ-
ствующее название: праволннейный язык, контекстно-свободный язык
(нлн КС-язык), контекстно-зависимый н язык общего вида.
Определенные выше четыре типа грамматик н языков называют
иерархией Хомского.
- 202 -
Праволпнейные языки .
Теорема. Язык является праволинейным тогда и только тогда, когда
он регулярный.
Доказательство состоит из двух частей.
1)	Праволинейный язык регулярен.
Пусть L = L(G) , где G = (N, А, Р, S) — праволпнейная грамма-
тика. Напомним, что каждое правило в грамматике G имеет вид
либо А —> хВ ,
либо А —> х
(Р1)
(Р2)
(большие буквы — нетерминальные, малые — терминальные).
Построим источник I следующим образом:
1.	Вершинами I являются элементы множества N плюс еще
одна конечная вершина, которую обозначим Z. Начальной
вершиной источника объявим вершину ,5'.
2.	Для каждого правила вида (Р1) проведем дугу нз вершины А
в вершину В. Этой дуге припишем букву х.
3.	Для каждого правила вида (Р2) проведем дугу нз вершины А
в конечную вершину Z. Этой дуге припишем букву х.
Каждому ж-путн в источнике I от вержнны ,5' до вершины
В соответствует вывод слова хВ в грамматике G ( ж-путн от
,5' до вершины Z соответствует вывод слова х) и, наоборот. Это
утверждение без труда устанавливается индукцией по длине слова х.
Следовательно,
£(7) = L(G).
Так как L(G) порождается источником, то он — регулярный.
2)	Регулярный язык праволннейный.
Для доказательства этого утверждения достаточно убедиться в
том, что элементарные языки являются праволнненнымн, а примене-
ние операций объединения, произведения и итерации к праволннейным
языкам снова дает праволннейный’ язык.
- 203 -
Элементарные языки.
Очевидно, язык, состоящий только из буквы х, порождается грам-
матикой с однпм правилом ,5' —> х, язык, состоящий только пз пустого
слова Л, порождается грамматикой с однпм правилом ,5' —> Л.
Объединение.
Пусть языкп Li = L(Gi) п £2 = L(G2) порождаются праволпней-
нымп грамматпкамп
Gj = (Ж, A, Z3!, ,S'i) п G2 = (Лф ДР2,,$'2).
Будем считать, что Л) A W2 = 0, этого всегда можно добпться
переобозначенпем вспомогательных символов. Построим грамматику
G = (N, А,Р, S) следующим образом. Множество вспомогательных
символов грамматпкп G включает в себя вспомогательные символы
обепх грамматик плюс новый символ ,5' : N = U Af2 U {.S'}. Правила
грамматпкп G включают в себя все правила обепх грамматик плюс
два новых правила : S —> ,S'i п S —> ,S'2.
Каждый вывод в грамматике G пмеет одну пз следующих форм:
S', .S'i, вывод в грамматике Gi слова х х
вывод в грамматике Gi слова х
вывод в грамматике G2 слова у
Наоборот, каждому выводу в грамматике Gi(G2) соответствует
вывод в грамматике G первой (соответственно, второй) формы.
Следовательно, £(G) = £1 U £2, то есть объедпненпе праволпней-
ных языков является праволпнепным языком.
Произведение.
Пусть языкп £1 = £(Gi) п £2 = £(G2) порождаются праволпней-
нымп грамматпкамп
Gj = (Аф Л, Pi,,S'i) п G2 = (JV2,A,P2,S2) JV-j. П N2 = 0.
Построим грамматику G = (N, А,Р, ,5ф следующим образом. Мно-
жество вспомогательных символов грамматпкп G включает в себя
вспомогательные символы обепх грамматик : N = A/j U N2. Правила
грамматпкп G включают в себя все правила грамматпкп Gi п правила
грамматпкп G2, преобразованные следующим образом:
- 204 -
правила грамматики G? оставлены без изменения;
правила грамматики Gi типа (Р1) оставлены без изменения;
каждое правило грамматики G\ типа (Р2), то есть правило
вида А —> х заменено на правило А —> ж,8'2.
Каждый вывод терминального слова в грамматике G имеет сле-
дующую форму:
Вывод в гр-ке Gi слова х.
По новым правилам вывод
закончится словом х,$2
Вывод в гр-ке G2 слова у
Все слова в этом выводе
имеют приставку х
Наоборот, пусть имеются два вывода: слова х в грамматике Gi и
слова у в грамматике G2. Тогда, объединяя эти выводы и приписывая
слово х к каждому слову пз второго вывода, получим вывод слова ху
в грамматике G.
Итак, L(G) = L1L2, то есть произведение праволнненных языков
является праволнненным языком.
Итерация
Иусть язык L = L(G\) порождается праволнненнон грамматикой
Gj = {NX,A,PX,S) .
Построим грамматику G = (N, А,Р, S) следующим образом: N =
#1, правила грамматики G включают в себя все правила грамматики
Gi, преобразованные следующим образом:
-	правила типа (Р1) оставлены без изменения;
-	каждое правило А —> х типа (Р2) заменено на правило А —> х,$;
-	добавлено новое правило ,5' —> Л.
Описывая, как в предыдущих разделах, все возможные выводы в
грамматике G, убеждаемся, что L(G) = L*. Следовательно, итерация
праволнненного языка праволнненна.
Теорема доказана.
- 205 -
О нерегулярных языках
Выше мы всесторонне рассмотрели регулярные языки и выяснили,
что
1)	это языки, которые строятся пз букв операциями объединения,
пропзведенпя и итерации;
2)	это языки, порождаемые источниками;
3)	это языки, распознаваемые конечными автоматами и, наконец,
4)	это языки, определяемые праволпнейнымп грамматиками.
Нерегулярные языки в явном виде пока не встречались. Приведем
пример нерегулярного языка.
Пример. Пусть £C{OU1}* состоит пз всевозможных двоичных слов
четной длпны и таких, что в левой' половине слова все символы нули,
а в правой — единицы. Слово, состоящее пз п нулей, за которыми
следуют п единиц будем обозначать 0"1".
L = {01, ООП, 000111, ..., 0"1",...}
Допустим, что L —регулярный. Тогда можно построить порожда-
ющий его псточнпк, причем, согласно теореме детерминизации можно
считать, что в этом источнике нет пустых дуг. Рассмотрим путь по
источнику, порождающий слово 0"1", где п выбрано большим, чем
количество вершин источника.
На участке путп, порождающем левую половину слова и состоя-
щем, следовательно, пз 0-дуг, некоторая вершина повторяется дважды,
то есть имеется петля. Значит, наряду с рассматриваемым путем мы
имеем путп, получающиеся пз него добавлением TV-кратного обхода
петли. Этп путп порождают слова, не входящие в L, так как каждый
дополнительный обход петли нарушает баланс между количеством ну-
лей п единиц в слове. Таким образом, не существует источника, поро-
ждающего L, то есть L — нерегулярный язык.
Рассматриваемый язык можно задать при помощи грамматики Gi
пз примера 1 в начале этого паранрафа. Однако, такое задание явно
неудачное, так как грамматика Gi — грамматика общего вида. На
самом деле, легко видеть, что язык L контекстно-свободный : соот-
- 206 -
ветствующая грамматика состоит из правил
,5'	041
А 041
4 —> Л .
Контекстно-свободные (КС) языки образуют следующую группу
по сложности в иерархии языков. Они играют главную роль при описа-
нии языков программирования высокого уровня (С, Паскаль, Фортран
и др.). Дело в том, что с помощью регулярных языков можно описать
только простейшие элементы программного текста: идентификаторы,
различного рода константы. Уже для описания арифметических вы-
ражении требуется КС-язык (См. выше пример 2). Такие элементы
программы как цпклы, условные переходы и др. могут быть описаны
в рамках КС-языка.
Конечный автомат распознает слова регулярного языка, для КС-
языка такую же роль играет, так называемый' автомат с магазинной'
памятью пли МП-автомат. Неформальное описание МП-автомата сле-
дующее.
МП-автомат, кроме элементов обычного конечного автомата имеет
потенциально бесконечную стековую память. В каждый момент вре-
мени действия МП-автомата определяются входным символом, внут-
ренним состоявшем п символом на вершине стека. Самп же действия
состоят в выдаче выхода, перехода в новое состоянпе п работе со сте-
ком, то есть лпбо в проталкпванпп некоторого символа в стек, лпбо в
пзвлеченпп пз стека.
В качестве примера рассмотрим, как распознает МП-автомат при-
веденный выше нерегулярный язык {0"1" | п = 1,2,3,...}. Пока на
входе нулп, автомат проталкивает пх в стек, прп появленпп едпнпц
пропзводпт пзвлеченпе пз стека. Еслп после прохождения слова, стек
оказывается пустым, МП-автомат относпт слово к языку (распознает),
в остальных случаях — нет.
- 207 -
Глава 7
Элементы теории алгоритмов
7.1.	О ПОНЯТИИ АЛГОРИТМА
В настоящее время в математике имеется строгое определение ал-
горитма как некоторого формального объекта. В этой главе рассма-
тривается это определение и некоторые связанные с ним вопросы.
Точное определение алгоритма явилось итогом тысячелетнего раз-
вития математики. На протяжении веков понятие алгоритма остава-
лось описательным н разъяснялось примерно так.
Алгоритм — это четкая система правил оперирования над неко-
торыми объектами, которая после некоторого числа шагов приводит к
достижению поставленной цели. Система правил (инструкций) такова,
что если вручить ее разным исполнителям, не знакомым с сутью задачи,
то они, следуя инструкциям, будут действовать одинаково н придут к
одному результату.
Примеры алгоритмов хорошо известны. Когда школьник младших
классов решает примеры на сложение н вычитание, умножение ’’стол-
биком” н деление ’’уголком”, он всякий раз исполняет некоторый алго-
ритм. С этим примером связано н происхождение слова ’’алгоритм”. В
12 в. в Европе появился латинский перевод трактата математика 9 в. нз
Хорезма, подписанный аль-Хорезмн. С помощью этой книги европейцы
познакомились с десятичной' системой' счисления н искусством счета в
ней. От имени автора трактата н образовалось слово ’’алгоритм”.
С развитием математических знаний происходило накопление раз-
нообразных алгоритмов: разложения натурального числа на простые
множители, извлечения квадратного корня, решения квадратного урав-
нения, решения линейной системы н много других. В своей основе по-
нятие алгоритма при этом не изменялось, приобретая, однако, все боль-
шую отчетливость. Постепенно выявлялись общие черты, характерные
для понятия алгоритма. Перечислим нх.
Дискретность.
Любой алгоритм состоит нз отдельных шагов. На каждом шаге
происходят определенные преобразования некоторой системы величин:
- 208 -
в начале алгоритма эту систему образуют исходные данные, в конце —
результаты работы алгоритма.
Детерминированность.
Система величин, получаемая на каждом шаге алгоритма одно-
значно определеяется величинами, полученными на предыдущих шагах.
Элементарность шагов.
Преобразования системы величин на каждом шаге алгоритма дол-
жны быть простыми: нх может выполнить исполнитель, не знакомый с
существом решаемой задачи, н даже некоторое автоматическое устрой-
ство.
Результативность.
Если на некотором шаге преобразование системы величин не опре-
делено (например, приходится делить на нуль), то должно быть явно
указано, что считать результатом работы алгоритма в таком случае.
Массовость.
Исходные данные для работы алгоритма можно выбирать нз неко-
торого потенциально бесконечного множества.
Со временем в математике накопился ряд проблем, для которых не
удавалось найти алгоритма нх решения, н имелись серьезные основания
предполагать, что такого алгоритма нет. В связи с этим возникла не-
обходимость определения алгоритма как некоторого математического
объекта таким образом, чтобы для одних задач этот объект можно
было строить, а для других задач доказывать, что такого объекта не
существует. Именно, так обстоит дело для таких математических по-
нятий как предел, интеграл н др.: несуществование предела нлн ненн-
тегрнруемость какой-либо функции мы можем устанавливать только
благодаря наличию строгого, формального определения.
Уточнение понятие алгоритма было сделано в 30-х годах 20-го сто-
летня в работах сразу нескольких математиков. Определения алго-
ритма, построенные в этих работах, сильно различаются по форме, но
все они замечательным образом оказываются эквивалентными, то есть
фактически определяется одно н то же.
- 209 -
Остановимся, в общих чертах на том, как строится уточнение по-
нятия алгоритма.
В первую очередь уточняется, что является объектом действия ал-
горитма. Примеры показывают, что природа этих объектов весьма
разнообразна. В математических алгоритмах объектом действия ал-
горитма являются наборы чисел, функций того нлн иного типа, ма-
трицы и прочие математические объекты. Экс-чемпион мира по шах-
матам М.М.Ботвинник разрабатывает алгоритм шахматной игры —
здесь объектом действия алгоритма являются шахматные позиции. Ал-
горитмы, по которым работают разнообразные технические системы
управления (летательным аппаратом, станком с программным управле-
нием, роботом и т.п.), в качестве входных данных используют показа-
ния различных приборов, сигналы от датчиков, информацию о положе-
нии тех нлн иных переключателей'.
Можно заметить, однако, что в каждой нз ситуаций применения
алгоритмов, они работают не с реальными объектами, а с нх изобра-
жениями. Эти изображения представляют собой слова в некотором ал-
фавите, а работа алгоритма состоит в определенном преобразовании
этих слов. Например, алгоритм сложения в десятичной системе счисле-
ния можно рассматривать как переработку слов вида ”1945+23106” в
алфавите нз 10 цифр и знака ”+” в слова в том же алфавите
71428 + 22847 => 94275 .
Аналогично, шахматный алгоритм перерабатывает слова типа
Б.Кре1,Фс13; Ч.КрЬ4
в слово такого же типа, скажем, Ф15. Входные и выходные сигналы си-
стемы управления могут быть записаны в виде длинного набора чисел
и булевых значений (0,1), что также представляет собой слово в подхо-
дящем алфавите.
Рассматривая алгоритмы нз самых разных областей человеческой
деятельности, можно убедиться, что описанная выше схема универ-
сальна, и принять в качестве постулата такой факт:
.любой алгоритм представляет собой преобразование слов в не-
котором алфавите в слова в том же алфавите, то есть сло-
варный оператор.
- 210 -
Убедительным подтверждением этого постулата является следую-
щий факт: когда алгоритм исполняется на компьютере, внутри ком-
пьютера, с логической точки зрения, не происходит ничего, кроме пре-
образования двоичных слов.
После того, как уточнен объект действия алгоритма, необходимо
выделить преобразования слов (словарные операторы), которые можно
рассматривать как алгоритмы. Как говорилось выше, это было сделано
разными, но как выяснилось, эквивалентными способами. Основные нз
этих способов следующие:
а)	рекурсивные функции;
б)	машины Тьюринга;
в)	нормальные алгорифмы А.А.Маркова.
Далее мы подробно рассмотрим определение Тьюринга.
7.2.	Машины Тьюринга
Машина Тьюринга — это некоторая абстрактная конструкция,
имитирующую, по замыслу автора, процесс исполнения алгоритма с
карандашом н бумагой.
Машина Тьюринга состоит нз трех частей.
1° . Лента, разделенная на ячейки. В каждый момент работы машины
в каждой ячейке ленты может находиться один нз символов алфа-
вита
А = {ai,..., ат} ,	(7.1)
который называют алфавитом ленты. Один нз символов алфавита
ленты выделен н соответствует пустой ячейке (в которую еще ни-
чего не записано), далее он обозначается большой греческой буквой
лямбда: А. В любой момент работы машины Тьюринга использу-
ется лишь конечное число ячеек ленты, но если нх не хватает, к
ленте приставляются пустые ячейки. В связи с этим говорят, что
лента потенциально бесконечна.
2° . Управляющая головка, которая перемещается по ячейкам ленты.
В каждый момент времени головка находится против определенной
- 211 -
ячейки ленты и воспринимает записанный в ней символ. Управля-
ющая головка представляет собой конечный автомат с множеством
внутренних состояний
{?1, ,?/} 	(7.2)
Входом в этот автомат является символ в обозреваемой ячейке,
таким образом, (7.1) — это входной алфавит управляющей головки.
Выход описывается так: в зависимости от текущего состояния н
обозреваемого символа на ленте головка
-	переходит в новое состояние;
-	печатает новый символ (вместо того, который воспринимает);
-	перемещается по ленте влево (£) , вправо (Я), нлн остается
в той же ячейке (Г7).
3° . Программа машины Тьюринга — набор инструкций вида
Qi Qk R ,
(7.3)
означающих, что если головка в состоянии ср воспринимает сим-
вол aj, то происходит ее переход в состояние qi~, на ленте печа-
тается символ а/ н головка перемещается направо по ленте.
Средн состояний головки (7.2) выделено одно начальное н одно нлн
несколько заключительных. Работа машины Тьюринга происходит так:
на ленту записывается некоторое слово (в алфавите А ), головка в
начальном состоянии устанавливается на правый символ слова. Далее
машина ’’запускается в работу”, то есть в соответствии с программой
происходят переходы в новые состояния, движение по ленте н изменения
записанных там символов. При переходе в заключительное состояние
происходит остановка машины н записанное в этот момент слово на
ленте считается результатом пререработкн исходного слова.
Приведем несколько примеров. Во всех примерах мы будем предпо-
лагать, что алфавит ленты состоит нз символов 0,1 н Л. Этот алфавит
будем называть стандартным. Пспользуя кодирование (как это дела-
лось в параграфе 5.2) любой алфавит можно свести к стандартному.
Поэтому, всюду далее мы будем предполагать, что у всех рассматрива-
емых машин Тьюринга один н тот же алфавит ленты (стандартный).
- 212 -
Пример 1. Машина ” + 1” имеет два состояния: начальное qi и за-
ключительное, которое здесь н в дальнейших примерах мы для нагляд-
ности будем обозначать восклицательным знаком. Программа машины
” + 1” содержит следующие инструкции
41	0	—>	!	1	U
41	1	->	г/i	0	£
41	Л	—>	!	1	U
(7.4)
Чтобы выяснить как эта машина перерабатывает двоичные слова,
будем по-тактно выписывать содержимое ленты н указывать против
какого символа находится головка. Например,
начало 1-й такт 2-й такт
91	91	!
1	0	1
1	0	0
1	1	0
нлн
начало 1-й такт 2-й такт 3-й такт
41	91	91	!
1	1
1	0
Л	0	0
1	0	0
Нетрудно убедиться, что если на ленте написать двоичное разло-
жение числа п , 71 = 0,1,2,..., установить головку в состоянии 41 на
младший разряд н последовательно выполнять инструкции (7.4), то по-
сле остановки машины (в результате перехода в состояние ”!”) на ленте
будет написано двоичное разложение числа п + 1.
Пример 2. Машина ” —> ” с программой
41 0
91 1
41 Л
—> 4i 0R
-> 41 1 R
! Л L
(7-5)
не изменяя написанного на ленте слова, устанавливает головку против
крайнего правого символа слова.
Меняя R н L получим машину машину ” <— ”, выходящую на
крайний левый символ слова.
Пример 3. Машина ” — 1” имеет три состояния: начальное 41
н два заключительных — ! н !!. Если в начальный момент на ленте
написано двоичное разложение положительного числа п, то машина
- 213 -
” — 1” преобразует его в двоичное разложение числа п — 1, если
в начальный момент на ленте написано двоичное разложение нуля, то,
обнаружив это, машина останавливается в состоянии !!. Вот программа
этой машины.
qL 0 -> г/i 1 L
41 1	!	О U	(7.6)
41 Л —> 42 Л R
42 1 —> 42 Л R
42 Л —> !! Л Г/
Примеры работы машины ” — 1” :
начало
91
2-й такт
I
1	1	0
1-й такт
91
1	1	1
начало 1-й такт 2-й такт
91	91	91
4-й такт 5-й такт
42	!!
0	0
0	1
Л	1	1
3-й такт
?2
1	1
Л	1
Операции над машинами Тьюринга
1. Последовательная обработка. Пусть имеются две машины Тьюринга:
головка машины Mi имеет г + 1 внутреннее состояние
41, . . .,4г-1,4г, ! ;
головка машины М2 имеет s внутренних состояний
91,  ..,qs-i,qs =! 
Тогда можно построить машину, работающую следующим образом:
сначала слово, записанное на ленту в начальный момент, обрабатыва-
ется машиной Mi ; после перехода Mi в заключительное состояние
слово, записанное на ленте в этот момент времени, начинает обраба-
тываться машиной М2. Работа новой машины заканчивается после
перехода машины М2 в свое заключительное состояние.
- 214 -
Для построения этой машины надо проделать такие действия.
1) Переобозначить состояния машины М2,
добавляя г к пн-
Дексу:
91
Чг + -1
qs
?r+s-i qr+s
2) Заменить в программе машины М \ восклицательный знак
на </r+i п дописать к измененному таким образом тексту
программы машины М \ программу машины М2 (с переобо-
значенными состояниями).
Работа построенной машины будет состоять пз двух этапов: так
как множества состояний первой п второй машины после переобозначе-
ния не пересекаются, то на первом этапе будут исполняться инструкции
только первой машины до тех пор, пока головка не окажется в состо-
янии qr+i_. По построению это состоянпе соответствует заключитель-
ному состоянию машины М\, это означает, что машина М \ завер-
шила обработку слова. С другой стороны </r+i — начальное состоянпе
второй машины, таким образом, в рассматриваемый момент времени
мы имеем слово на ленте — результат работы первой машины п ма-
шину М2 в начальном состоянии. Далее будут исполняться только
инструкции машины М2 до ее остановки.
Естественно обозначить построенную машину так, как на блок-
схемах алгоритмов изображают последовательное выполнение двух дей-
ствий
____]___
Mi
I
М2
Пример 4. Соединяя машины ” + 1” п ” —> ” , получим машину, кото-
рая после прибавления 1 возвращает головку на правый символ резуль-
тата. Программа новой машины получается в результате соединения
программ (7.4) п (7.5) описанным выше способом:
- 215 -
qi	0	—>	</2	1	U
41	1	->	4i	О	£
41	Л	—>	42	1	U
42	О	—>	42	OR
42	1	—>	42	1	R
42 Л -д ! Л L
2. Условный переход. Пусть имеются три машины Тьюринга:
машина М имеет г + 2 внутренних состояния
41,..., 4r-i, qr,!,!! ,
среди которых два заключительных,
машина имеет s внутренних состояний
41,..	,,4s_i,4s =! .
машина М? имеет р внутренних состояний
41, . . ., qp-y,qp =! .
Тогда можно построить машину, работающую следующим образом:
сначала записанное на ленту слово обрабатывает машина М. В зави-
симости от хода обработки машина М может остановиться либо в
состоянпп ”!”, либо в состоянпп В первом случае образовавше-
еся на ленте слово далее обрабатыватся машиной М\, во втором —
машиной М2.
Для построения этой машины надо проделать такие действия.
1)	Переобозначить состояния машины М\, добавляя г к ин-
дексу:
41		Ч- Ч-
4- ...	4-	4-
4г+1	...	4г-н-1 qr+s
2)	Переобозначить состояния машины М2, добавляя г + s к
индексу:
41	qP-i	чР
		
qr+s+i 	  qr+s+P-i	4r + s+P
- 216 -
3)	Заменить в программе машины М восклицательный знак на
</г+1, два восклицательных знака на qr+s+i, и дописать к
измененному таким образом тексту программы машины М
программы машин М \ и М2 (с переобозначенными состоя-
ниями).
Как и выше, на первом этапе работы новой машины будут испол-
няться инструкции только машины М, до тех пор, пока головка не
окажется в состоянии ryr_|_i пли qr+s+i. По построению эти состояния
соответствуют заключительным состояниям машины М, это озна-
чает, что машина М завершила обработку слова. На втором этапе
будут исполняться инструкции одной нз машин М\ нлн М2, так как
множества нх состояний не пересекаются.
Будем называть построенную машину машиной условного перехода
н изображать ее так, как это показано на рнс.7.1.
Рнс. 7.1	Рнс. 7.2
В качестве одной нз машин М \ нлн М2 может быть взята сама
машина М. Тогда возникает цикл: машина М работает до тех пор,
пока не будет выполнено некоторое условие, в результате чего машина
М перейдет в состояние ”!!” н произойдет выход нз цикла (см. рнс.7.2).
Блок-схема даже очень сложного алгоритма состоит нз фрагмен-
тов, рассмотренных нами типов: последовательное выполнение каких-
то действий нлн проверка условия н переход в зависимости от его вы-
полнения нлн невыполнения. Поэтому представляется убедительным
формулируемый в следующем параграфе тезис о том, что любой ал-
горитм можно исполнить на подходящей машине Тьюринга. В пользу
этого тезиса говорит н такой факт: на самом низком уровне компьютер
выполняет только две операции — либо складывает двоичные числа (см.
схему двоичного сумматора в параграфе 4.4), либо пересылает двонч-
- 217 -
ные слова нз одного места в другое. В качестве следующих двух при-
меров рассмотрим как выполнить этп операции на машине Тьюринга.
Пример 5. Построим машину ” + ”, которая работает следующим
образом: еслп в начальный момент на ленту поместить двоичные раз-
ложения целых неотрицательных чисел т н п, разделив нх пустой'
ячейкой, н запустить машину в работу, то после остановки машины на
ленте будет написано двоичное разложение числа т + п.
Цикл работы машины ” + ” описывается следующим образом:
нз правого слова вычитается 1 (для этого используется машина ” —
1” ), затем головка перемещается на левое слово н прибавляет к нему
единицу (для этого используется машина ” + 1” ), после этого головка
перемещается на правое слово н цикл повторяется. Работа машины
закончится, когда машина ” — 1” перейдет в состояние ”!!”, в этот
момент правое слово равно нулю, следовательно, левое — т + п.
Машину ” + ” можно ’’собрать”, используя рассмотренные опера-
ции над машинами Тьюринга, нз рассмотренных в примерах 1-3 про-
стейших машин ” + 1” , ” —> ” , ”	— 1” . К ним надо только добавить
машины, перескакивающие (при движении головки влево н вправо) че-
рез пустую ячейку, разделяющую числа. Эти машины, которые мы
обозначим Л <— н —> Л получаются нз машин <— н —> заменой
одной буквы в заключительной инструкции. Например, для машины
—> инструкция <71 Л —>!Л£. заменяется на </i Л —>!ЛЯ. Для другой
машины R заменяется на L.
На рнс. 7.3 показана блок-схема машины ”+” н построенная по ней
программа. Фрагменты окончательной программы, соответствующие
отдельным машинам нз блок-схемы, разделены чертой.
- 218 -
91	0 -	<11	1	L
91	1 -	£ <1з	0	и
91	Л -	£ <12	Л	R
92	1 -	£ <12	Л	R
92	Л -	1	Л	и
<13	0 -	£ <1з	0	L
9.3	1 -	£ <1з	1	L
<13	Л -	£ <14	Л	L
<14	0 -	£ <15	1	и
<14	1 -	£ <14	0	L
<14	Л -	£ <15	1	и
95	0 -	£ <15	0	R
<15	1 -	£ <15	1	R
<15	Л -	£ <16	Л	R
<16	0 -	£ <16	0	R
<16	1 -	£ <16	1	R
<16	Л -	£ <11	Л	L
Рпс. 7.3
Примерб. Построим машину ” сору” которая переносит написанное
на ленте слово на другой участок ленты, напрпмер, слева от данного
слова через пробел.
Цикл работы машины ” сору” описывается следующим образом:
очередной разряд копируемого слова заменяется пробелом и запоми-
нается переходом в соответствующее состояние. После этого головка
перемещается к левому краю записи на ленте и пишет там запомненный'
символ, перемещается обратно до пробела на месте стертого символа,
восстанавливает символ, после чего цикл повторяется для следующего
символа.
Головка машины ’’сору” имеет следующие состояния
</1 — начальное;
q“ , а £ {0,1} головка находится в этом состоянии прп перемеще-
нии влево по копируемому слову;
(1з > а {ОД} головка находится в этом состоянии прп перемеще-
нии влево по копии;
</4 , а £ {0,1} головка находится в этом состоянии прп перемеще-
нии вправо по копии;
^5 , а £ {0, 1} головка находится в этом состоянии прп перемеще-
нии вправо по копируемому слову;
! — заключительное;
- 219 -
В нижеследующем тексте программы применяется такое сокраще-
ние: инструкцию вида
о ^ ...
надо заменить на 4 инструкции, получающиеся, еслп вместо а и 1
подставить 00,01,10 и 11:
(Ji 0 -> ...	1 -> ... (ji 0 -> ... (ji 1 -> ... .
<11	а -	<12	А	L
	р -	<12	Р	L
<12	А -	<?3	А	L
<12	А -	<13	А	L
<?3	Р ~	<7з	Р	L
<?3	А -	<14	а	R
<14	Р ~	<14	Р	R
<14	А -	<15	А	R
<15	Р ~	<15	Р	R
<15	А -	<11	а	L
<11	А -	4. 1	А	и
7.3. Точное определение алгоритма.
Алгоритмически неразрешимые проблемы
Примеры построения машин Тьюринга можно продолжать, убе-
ждаясь всякий раз, что для того пли иного алгоритма можно построить
подходящую реализующую его машину. Напрпмер, немного изменяя
машину ”+” (заменив блок ” + 1” на ”+” и добавив некоторые начальные
действия), можно построить машину для умножения. Взяв произволь-
ный вычислительный' алгоритм, можно разложить его на простейшие
шаги, составить объединяющую эти шаги блок-схему и по ней собрать
машину Тьюринга, как это сделано в примере сложения двоичных чи-
сел.
Возвращаясь к рассмотрениям параграфа 7.1, напомним, что там
мы пришли к выводу, что алгоритм — это словарный'оператор и оста-
валось только выделить те операторы, которые следует считать алго-
ритмами. Дадим теперь нужные определенпя.
- 220 -
Пусть А — алфавит,
/ : А* A\'x^y = f{'x) -
словарный оператор.
Словарный оператор f называется вычислимым по Тьюрингу, если
существует машина Тьюринга с алфавитом ленты A U {Л}, которая
работает следующим образом: еслп на ленту записать произвольное
слово х G А*, установить головку на правый символ слова и запустить
машину в работу по ее программе, то после остановки машины на ленте
будет написано слово /(2).
Одно пз возможных определений алгоритма — следующее:
алгоритм — это словарный оператор, вычислимый по Тьюрингу.
Алгоритмически неразрешимые задачи
Определение алгоритма, по-существу, состоит в том, что если ра-
нее это понятие существовало на неточном, интуитивном уровне, то
теперь ему сопоставлен некоторый точно определенный объект — про-
грамма машины Тьюринга. Фактически программа представляет со-
бою слово в некотором алфавите н можно себе представить, что, ана-
лизируя какую-либо проблему, мы придем к выводу о несуществовании
указанного слова, тем самым к алгоритмической'неразрешимости про-
блемы. Далее приводится несколько примеров алгоритмически нераз-
решимых проблем.
Первый результат об алгоритмической неразрешимости был полу-
чен в 1947 г. независимо друг от друга А.А.Марковым н Э.Л.Постом
по проблеме равенства в полугруппах.
1.	Проблема равенства в полугруппах
Полугруппой нлн ассоциативной системой называют множество, на
котором определена одна ассоциативная бинарная операция.
Важным примером полугруппы является рассматривавшаяся в па-
раграфе 5.3 совокупность X* всевозможных слов в алфавите
А — , X х , X 2 ,   , xnJ,	( I. I)
- 221 -
вместе с операцией приписывания слов друг к другу (конкатенация).
X* называется свободной полугруппой с п образующими. Свобод-
ная полугруппа с одной образующей х состоит, очевидно, пз слов
{Л, х, х1, . . ., хп, . . .} и изоморфна полугруппе неотрицательных целых
с операцией сложения.
Отправляясь от свободной полугруппы, можно строить новые по-
лугруппы прп помощи так называемых определяющих соотношений.
Пусть
ai = ф,.. ,,ак = Ьк -	(7.8)
произвольная конечная совокупность пар слов пз X*. Элементарным
преобразовавшем называется переход от слова хару к слову xlpy
плп обратно, то есть замена в некотором слове произвольного вхожде-
ния одного пз слов какой-лпбо пары (7.8) на другое слово пз этой же
пары. Два слова пз X* называются эквивалентными, еслп от одного
можно перейтп к другому конечным чпслом элементарных преобразова-
ний. Легко убедиться, что мы пмеем дело, действительно, с отношением
эквпвалентностп (т.е с рефлексивным, спмметрпчным п транзптпвным
отношением), поэтому X* распадается на классы эквивалентных эле-
ментов. Обозначим класс, в который входпт слово х через [ж] п опре-
делим произведение классов как произведение соответствующпх языков
(см. параграф 6.1). Тогда пмеет место соотношение [ту] = [т][у], пз
которого вытекает, что совокупность классов вместе с введеннноп'опе-
рацией умноженпя образует полугруппу. Про нее говорят, что это по-
лугруппа с образующпмп (7.7) п определяющпмп соотношенпямп (7.8).
Проблема равенства слов в полугруппе заключается в отысканпп
алгоритма, выясняющего для любой пары слов эквивалентны онп плп
нет.
Пример Пусть определяющпе соотношения следующие
XiXj = XjXi , 1 < i < j < n .
Составом слова x назовем вектор <т(2) = (,5д, . . ., sn), где s, — ко-
личество букв Xi в слове, i = 1, . . ., п. Элементарные преобразования
не изменяют состав, с другой стороны, каждое слово можно прпвестп
в впду
- 222 -
в котором буквы стоят в алфавитном порядке. Отсюда вытекает, что
два слова эквивалентны в том и только в том случае, когда они имеют
одинаковый состав, что н дает алгоритм распознавания эквивалентно-
сти для данной полугруппы.
А.А.Марков н Э.Л.Пост построили примеры полугрупп, для кото-
рых алгоритма распознавания равенства (эквивалентности) не суще-
ствует. В дальнейшем число таких примеров значительно увеличилось.
Одним нз наиболее впечатляющих является пример Г.С.Центнна: полу-
группа с образующими {a, b, с, d, е} н определяющими соотношениями
ас = са ad = da be = ch hd = dh
eca = ce edb = de cca = ccae ,
имеет неразрешимую проблему равенства слов.
2.	Проблема полноты автоматного базиса
В параграфе 5.2 была сформулирована задача о полноте автомат-
ного базиса: задан набор структурных автоматов
Ах,..., Аг ,	(7.9)
требуется выяснить можно лн путем нх соединения построить любой
наперед заданный автомат.
Эта задача близка к задаче полноты системы функциональных эле-
ментов (нлн системы булевых функций), которая решается при помощи
теоремы Поста (параграф 4.3). Учитывая терминологию этой главы,
можно сказать, что теорема Поста дает алгоритм для проверки пол-
ноты системы функциональных элементов.
Замечание. Нетрудно представить как алгоритм проверки полноты
по теореме Поста выполнить на машине Тьюринга. На ленту записыва-
ются таблицы заданных функций, таблица функции от п переменных
будет двоичной строкой длины 2" (предполагается естественный по-
рядок наборов значений переменных). Например, если исследуемая си-
стема функций состоит нз дизъюнкции, конъюнкции н отрицания, но
начальное состояние ленты таково
- 223 -
0	1	1	1	л	0	0	0	1	л	1	0
Машину Тьюринга для проверки полноты можно построить пз пяти
машин, проверяющих условия теоремы Поста. Машина, проверяющая,
что в системе есть функция, не сохраняющая ноль, просто двигается по
написанным на ленте словам и ищет слово, у которого первый символ
единица. Машина, проверяющая самодвопственность, выясняет сим-
метрию слова относительно его середины. Более сложными являются
проверки линейности и монотонности, однако, и здесь можно постро-
ить подходящие машины, используя процедуры, описанные в параграфе
4.3.
В виду большого сходства задач о полноте для функциональных
элементов п для автоматов, в теченпп нескольких десятилетии”усплпя
многих математиков былп направлены на то, чтобы получпть крите-
рий полноты автоматного базпса. В 1964 г. М.II.Кратко установпл
алгоритмическую неразрешимость задачп о полноте автоматного ба-
зпса. Этот результат, еслп пметь в впду данное выше определенпе
алгоритма, означает, что не существует машины Тьюринга, работаю-
щей следующим образом. Еслп на ленту машины поместить оппсанпя
автоматов (7.9) п запустпть машпну в работу, то машпна остановится в
состоянпп !, еслп спстема (7.9) полная п в состоянпп !!, еслп эта спстема
неполная.
3.	10-я проблема Гпльберта
В 1900 г. на II Международном Конгрессе математиков корпфей
математпкп, немецкий математик Давпд Гпльберт выступил с докла-
дом ” Математпческпе проблемы”. В нем он сформулпровал 23 про-
блемы, ’’исследование которых может значптельно стпмулпровать раз-
витие наукп”, что впоследствпп полностью подтвердплось. Десятая пз
этпх проблем называется ’’Задача о разрешпмостп дпофантова уравне-
нпя” п занпмает в докладе несколько строк:
Пусть задано диофантово уравнение с произвольными не-
известными и целыми рациональными числовыми коэффициен-
тами. Указать способ, при помощи которого возможно после
конечного числа операций установить, разрешимо ли это урав-
нение в целых рациональных числах.
- 224 -
Диофантовым называют уравнение вида
Pn(xL,..., хт) = 0 ,	(7.10)
в котором Рп — многочлен n-ой степени от т переменных с целыми
коэффициентами:
Рп (,Х 1 , . . . , Хт) —	,    Лт *^1 . . . Хт
^1+	+ &т<П
Уравнения названы диофантовыми в память греческого матема-
тика 3 в. Диофанта, который рассмотрел некоторые типы таких урав-
нений. Вклад в исследование диофантовых уравнений внесли многие
велнкне математики: Эйлер, Ферма, Лагранж, Гаусс. Ими так же
изучались отдельные классы диофантовых уравнений. Например, Ла-
гранж полностью решил вопрос отыскания решений уравнения (7.10)
при п = т = 2. Однако, вопрос, поставленный Гильбертом, общего
характера: речь идет об алгоритме, отвечающем на вопрос о разреши-
мости для произвольного многочлена произвольной'степени.
В 1900 г. точного определения алгоритма не было, как уже гово-
рилось выше, оно появилось в 30-х годах 20 в., поэтому в постановке
задачи подразумевалось ее положительное решение: ’’способ, при по-
мощи которого возможно после конечного числа операции'установить,
разрешимость диофантова уравнения в целых числах” рано нлн поздно
будет найден.
После опубликованных в 60-х годах глубоких результатов по деся-
той проблеме Гильберта американских математиков М.Девиса, Х.Пут-
нама н Ю.Робинсон появились серьезные основания считать, что алго-
ритма, о котором говорит Д.Гильберт, не существует.
В 1970 г. Ю.И. Матнясевнч доказал этот факт.
В заключении рассмотрим пример задачи, для которой алгоритми-
ческая неразрешимость устанавливается путем несложных рассужде-
ний.
4.	Проблема остановки машины Тьюринга
Так как набор инструкций (7.3) машины Тьюринга может быть
достаточно произвольным, возможны такие ситуации, когда машина
- 225 -
работает без остановки, то есть не переходит в заключительное состо-
янпе. Рассмотрим, например, машину с программой
0 —> !	1 U
41 1 -> 41 О L
41 Л -> 4i	1 L
Эта программа получена нз программы машины ” + 1” (см. выше
пример 1) небольшим изменением последней инструкции. Машина с дан-
ной программой будет работать следующим образом: если в начальном
слове на ленте есть нули, то дойдя до первого нз них машина остано-
внттся; если начальное слово состоит нз одних единиц, то головка будет
без остановки перемещаться влево.
Можно сформулировать такую массовую проблему: для данной ма-
шины Тьюринга н данного слова выяснить остановится лн машина, на-
чав работу с правого символа этого слова нлн нет (проблема оста-
новки). Покажем, что не существует алгоритма для решения этой про-
блемы, убедившись, что предположение о существовании алгоритма ве-
дет к противоречию.
В самом деле, если существует алгоритм для решения проблемы
остановки, то можно построить машину Тьюринга ”S”, работающую
следующим образом. В начальный момент на ленту машины ”S” запи-
сывается два слова. Первое представляет собой программу какой-либо
машины Тьюринга М, второе слово а, (отделенное от первого пу-
стой ячейкой) — это слово, для которого надо выяснить остановится
лн на нем машина М нлн нет. Далее машина ”S” работает по своей
программе н заканчивает работу в состоянии !, если выяснит, что ма-
шина М на слове а остановится. Если же машина М на слове а не
останавливается, то машина ”S” закончит работу в состоянии !!.
Замечание. Программа машины М н начальное слово записываются
на ленту машины ”S”, вообще говоря, в закодированном виде. Можно,
например, считать, что у машины ”S” стандартный алфавит ленты н
использовать для кодирования известный ASCII-код, отводя под ка-
ждый символ группу нз 8 ячеек ленты.
Построим теперь машину ”Т” по блок-схеме, показанной на рнс.
7.4.
- 226 -
Рис. 7.4
Машины Mi и М2 имеют следующие программы
Mi	М2
41	0	—>	г/i	0	£	41	0	—>	!	1	ГУ
41	1	->	4i	1	L	41	1	->	!	1	U
41	Л	—>	41	Л	L	41	Л	—>	!	Л	Г/
то есть машина Mi независимо от воспринимаемого символа движется
влево, а машина ,1/2 сразу же (в 1-м такте) останавливается.
Рассмотрим теперь как будет работать наша гипотетическая ма-
шина ”Т”, если на ее ленту написать ее собственную программу. Со-
гласно блок-схеме рнс. 7.4, сначала это слово будет скопировано п го-
ловка установлена на крайний правый символ. После этого начинает
работу машпна ”S”, прп этом на ленте такпе исходные данные: про-
грамма машины ”Т” п слово, которое было наппсано на ее ленту в на-
чальный момент. Машпна ”S” решпт проблему остановки для данной
сптуацпп. Однако, здесь мы сталкиваемся с такпм протпворечпем: оба
ответа на вопрос остановптся плп нет машпна ”Т” неправильные. Дей-
ствительно, еслп ”Т” останавливается, то машпна ”S”, выяснпв это,
перейдет в состоянпе !, после чего начинает работу машпна М\, без
остановки двигающая головку влево. Еслп предположпть, что машпна
”Т” не останавлпвается, то машпна ”S”, выяснпв это, перейдет в со-
стоянпе !!, после которого машпна ,1/2 сразу же останавлпвается.
Единственным псточнпком этого протпворечпя является предположе-
ние о существованпп машины ” S”, что п доказывает несуществованпе
алгоритма, решающего проблему остановки.
- 227 -
Библиографический список
1.	Яблонский С.В. Введение в дискретную математику. М. :”Наука”,
1986 г., 384 с.
2.	Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика
для инженера. М.: Энергоатомпздат, 1988 г., 480 с.
3.	Глаголев В.В. Основы теории систем. Методы дискретной мате-
матики: учебное пособие. Тула, ТулПи, 1987 г., 90 с.
4.	А.Ахо,Дж.Ульман, Теория синтаксического анализа, перевода н
компиляции. Том 1, Синтаксический анализ. М.: ”Мнр”, 1978 г.,
612 с.
5.	В.Дж.Рейуорд-Смнт. Теория формальных языков (вводный курс).
М. : ’’Радио н связь”, 1988 г., 128 с.
6.	П.С.Новиков. Элементы математической логики. М.: Фнзматгнз,
1959 г.,400 с.
7.	Э.Мендельсон. Введение в математическую логику. М.: ’’Наука”,
1984 г., 320 с.
8.	А.II.Мальцев. Алгоритмы н рекурсивные функции. М.: ’’Наука”,
1965 г., 391 с.
9.	А.А.Зыков. Теория конечных графов. Новосибирск: ’’Наука”, 1969
г., 543 с.
10.	М.Холл. Комбинаторика. М.: ”Мнр”, 1970 г., 424 с.
- 228 -
Оглавление
Предисловие.................................................3
Глава 1. Теоретико-множественное введение...................4
1.1	Основные понятия и обозначения........................4
1.2	Операции над множествами. Булевы тождества............6
1.3	Алгоритм для проверки теоретико-
множественных тождеств...................................9
1.4	Декартово произведение ..............................14
Глава 2. Элементы комбинаторики............................16
2.1	Принципы подсчета....................................16
2.2	Принцип включений-исключений.........................23
2.3	Рекуррентные соотношения ............................26
2.4	Производящие функции.................................37
Глава 3. Теория графов.....................................46
3.1	Основные определения ................................46
3.2	Связность графов.....................................51
3.3	Цикломатика графов...................................59
3.4	Транспортные сети....................................74
3.5	Сетевые графики......................................89
Глава 4. Булевы функции....................................93
4.1	Булевы функции ......................................93
4.2	Представление булевых функций формулами..............99
4.3	Критерий полноты.Теорема Поста..................... 107
4.4	Схемы нз функциональных элементов.................. 125
4.5	Дизъюнктивные нормальные формы..................... 135
Глава 5. Конечные автоматы............................... 149
5.1	Определение конечного автомата..................... 149
5.2	Некоторые вопросы синтеза автоматов................ 153
5.3	Функциональное описание автомата................... 165
- 229 -