Магия чисел и фигур. Занимательные материалы по математике - Трошин В.В.

Магическая треугольная призма
Магический тор

Угадывание в таблице суммы закрытых чисел

Автор: Трошин В.В.

Теги: математика логика учение с увлечением учащимся средних и старших классов увлекательное путешествие в магический мир чисел и фигур

ISBN: 978-5-903050-91-8

Год: 2007

Похожие

Увлекательная наука математика

Занимательная математика в рассказах для детей

Занимательная математика

Занимательная арифметика. Загадки и диковинки в мире чисел

Текст

ЗАНИМАТЕЛЬНЫЕ МАТЕРИАЛЫ ПО МАТЕМАТИКЕ
ШНПЯШВ &ШЩШ
шапшшвщщ
ИЗДАТЕЛЬСТВО

Серия «Учение с увлечением»
В.В. Трошин
Занимательные материалы по математике
Москва
«Глобус»
Магия чисел и фигур

ББК 22.1
М12
Автор-составитель:
В.В. Трошин
М 12 Магия чисел и фигур. Занимательные материалы
по математике / авт.-сост. В. В. Трошин. - М.: Глобус,
2007. - 382 с: ил. (Учение с увлечением)
ISBN 978-5-903050-91-8
Сборник предлагает учителям математики, учащимся
средних и старших классов, всем любителям
математики и логики увлекательное путешествие в магический
мир чисел и фигур. Книга хорошо иллюстрирована,
содержит большое количество различных нестандартных
задач, числовых головоломок и интересные сведения
для расширения кругозора.
Сборник станет занимательным собеседником своим
читателям, послужит помощником в расширении
математического кругозора, развитии логического
мышления, пространственных представлений и выработке
математической интуиции.
Включение занимательных материалов данного
сборника в учебный процесс непосредственным
образом отразится на повышении успеваемости учащихся.
ISBN 978-5-903050-91 -8 © Составление, оформление.
Трошин В.В., 2007
©ООО «ГЛОБУС», 2007

Оглавление
Оглавление
Предисловие 5
Глава 1. Кросс-суммы 9
Кросс-суммы 11
Задачи (1-80) 15
Глава 2. Магические квадраты 45
История 47
Те ория 53
Задачи (1-12) 57
Как самому составить магический квадрат 61
Метод Баше 61
Узоры магических линий 62
Метод де ла Лубера 64
Диагональный метод 67
Метод окаймления 70
Метод де ла Ира 71
Разнообразие квадратных таблиц чисел 73
Симметрические квадраты 73
Совершенные квадраты 74
Квадраты из непоследовательных чисел 78
Магические квадраты из простых чисел 80
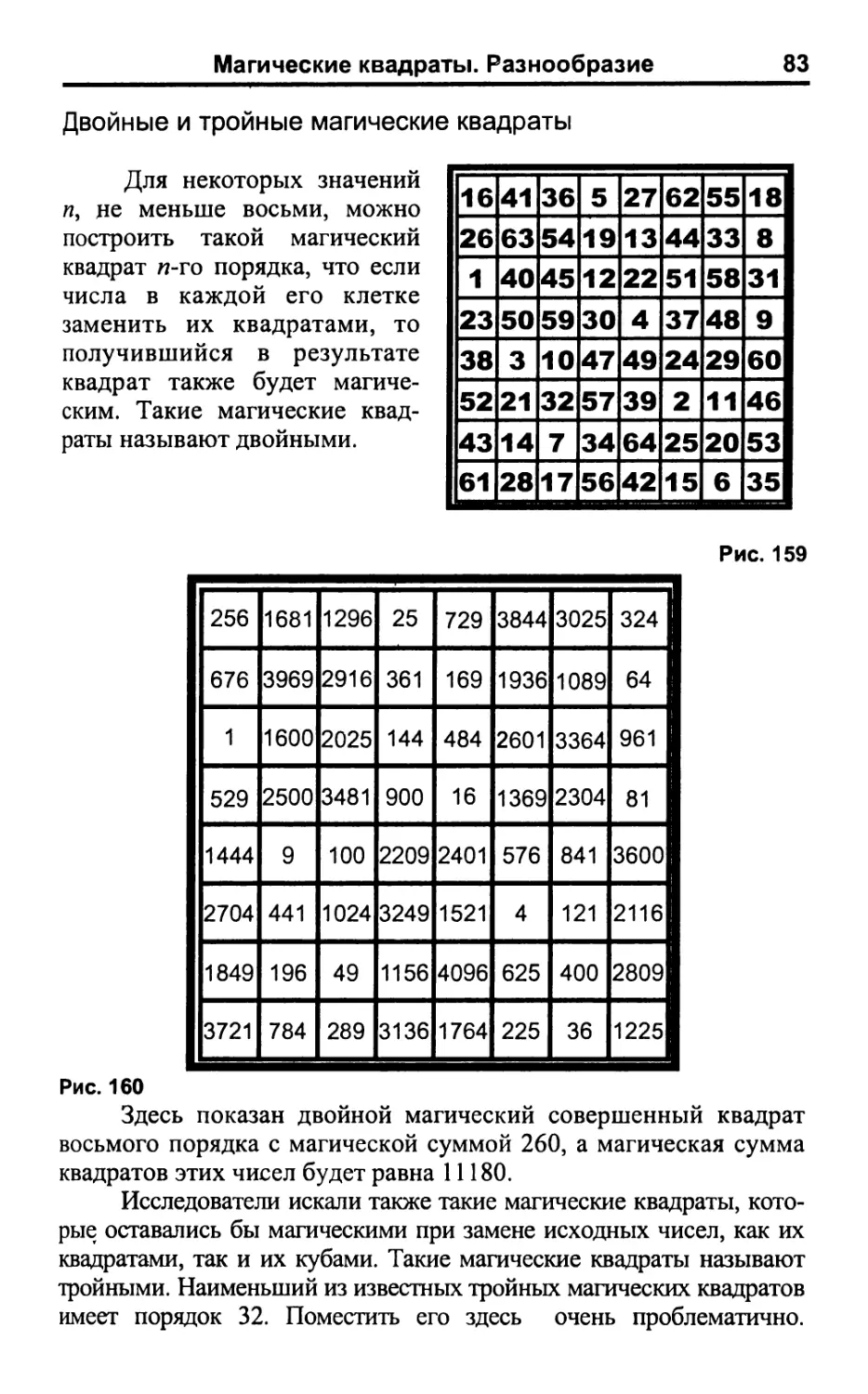
Двойные и тройные магические квадраты 83
Задачи(13-45) 84
Латинские квадраты 93
Греко-латинские квадраты 96
Задачи (46-71) 101
Квадромагический числовой квадрат 106
Мультипликативные магические квадраты 107
Глава 3. Магическое разнообразие 109
Конфигурации из магических квадратов ...., 111
Задачи (1-2) 113
Магическое кольцо и магический круг 114
Магический шестиугольник 118
Магический прямоугольник 121
Магический треугольник 122
Магические трехмерные тела 124
Проекционный магический куб 124
Магические кубы 126
Магический параллелепипед 128
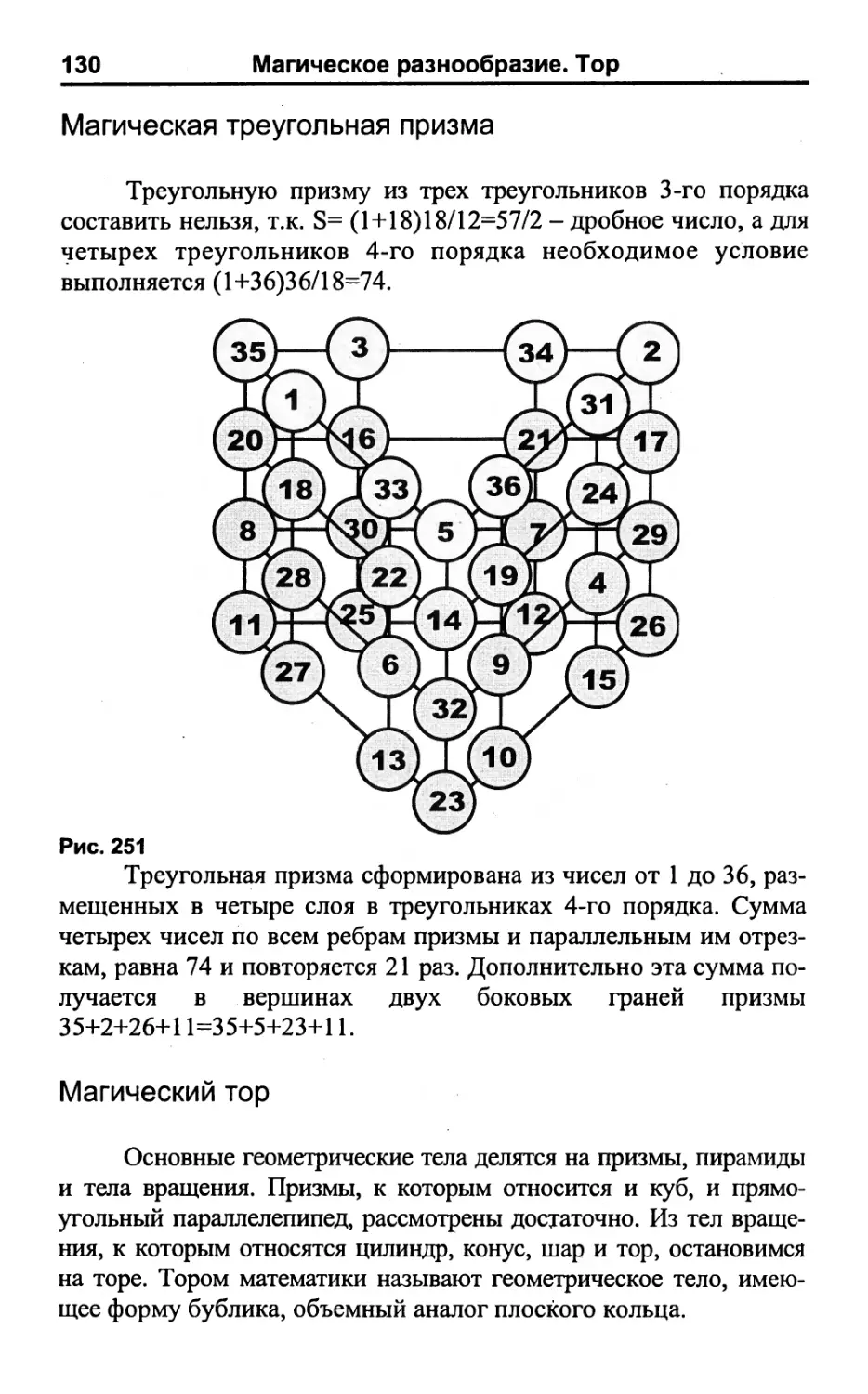
Магическая треугольная призма 130
Магический тор 130
Правильные многогранники 132
Задачи (3-17) 134
Четвертое измерение 139
Задача (18) 145

Оглавление
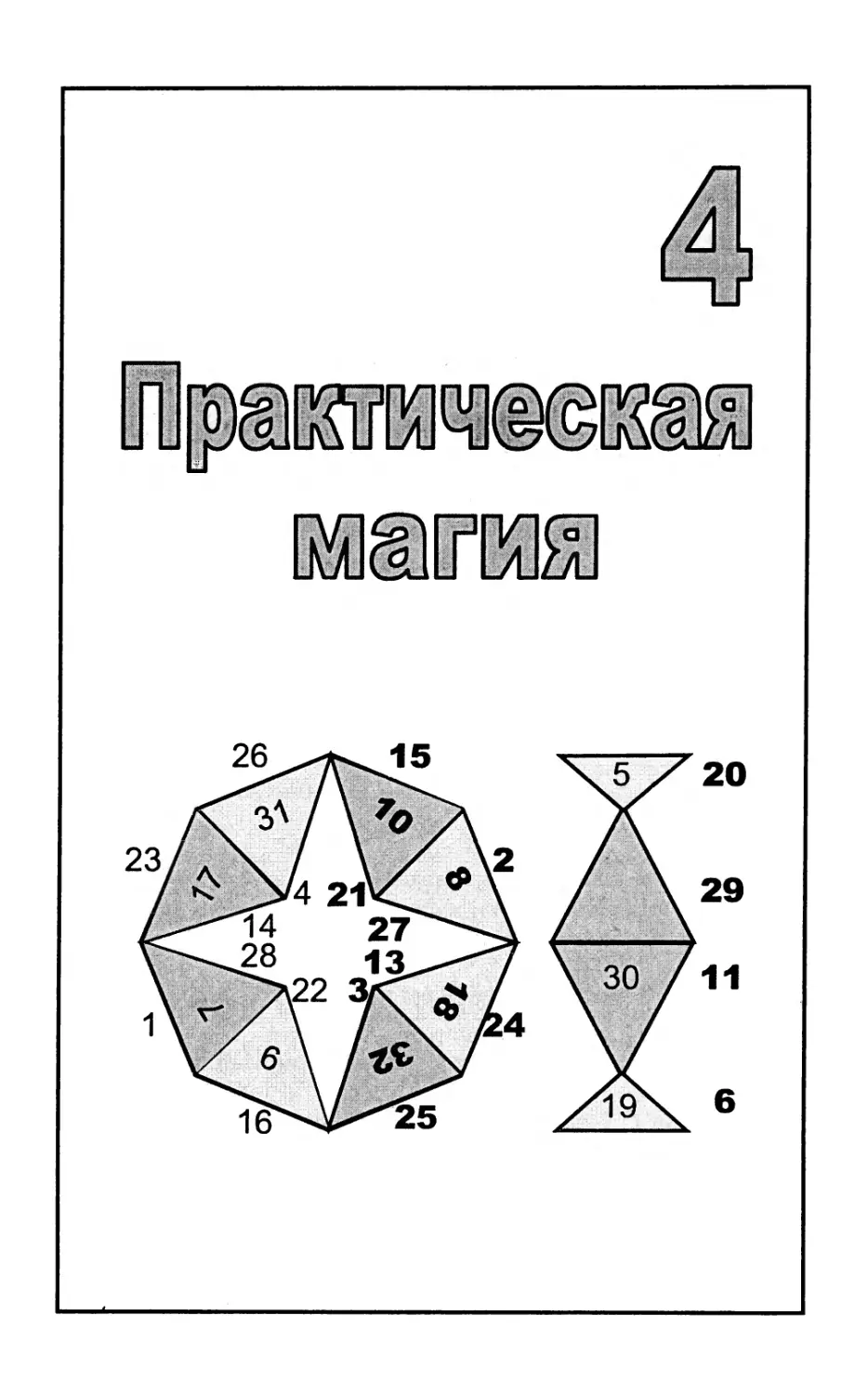
Глава 4. Практическая магия ; 147
Магические таблицы для угадывания чисел 149
Угадывание чисел с помощью карточек 150
Угадывание чисел на шестиугольнике 159
Волшебный квадрат 160
Фокусы с настенным календарем 163
Чудесный квадрат 167
Угадывание в таблице суммы закрытых чисел 168
Плоско-магический куб 172
Магический цветок 174
Магический гексафлексагон 176
Магическое кольцо тетраэдров 178
Фокусы с игральными костями 179
Фокусы с домино 183
Фокусы с картами 186
Быстрый счет 188
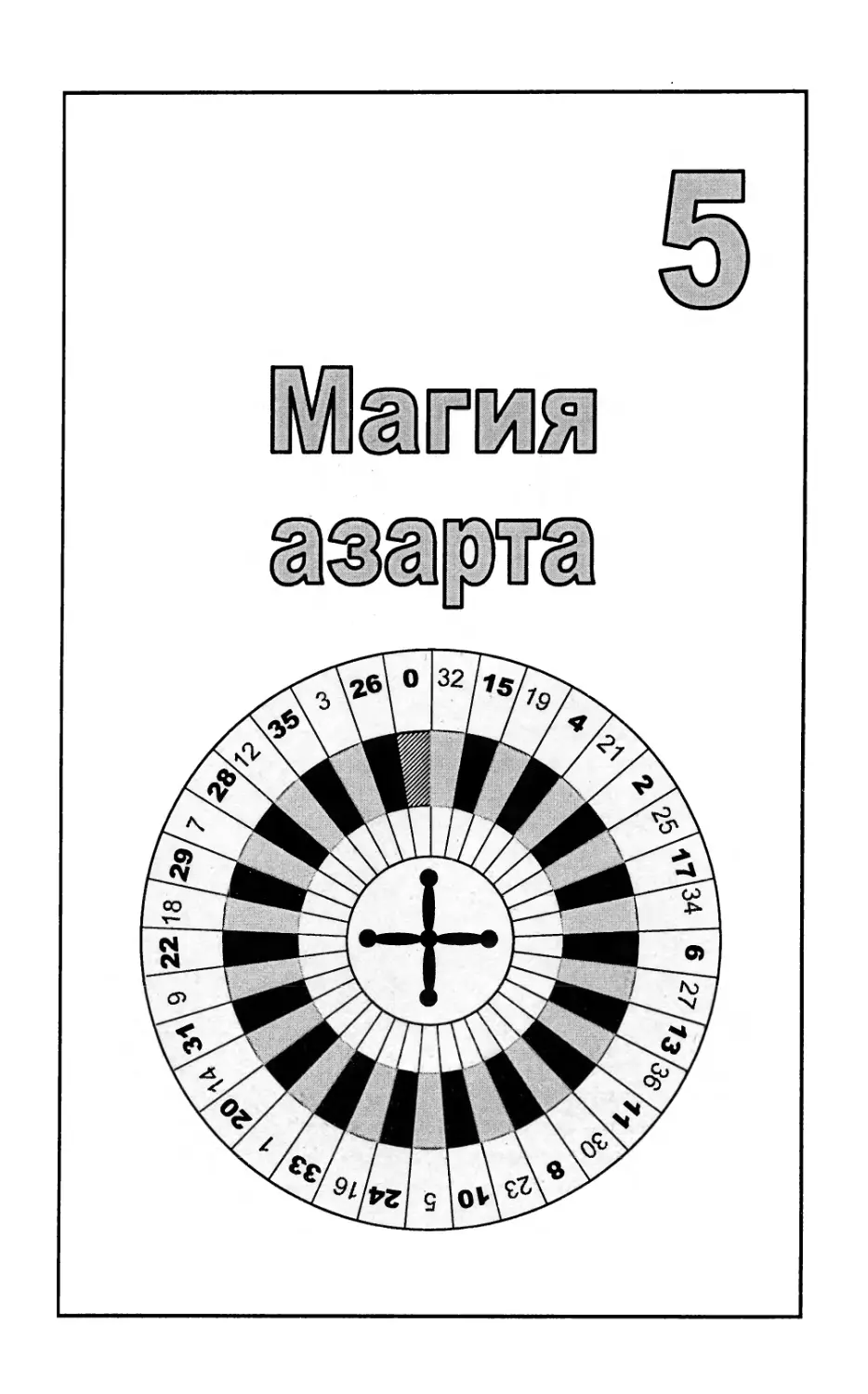
Глава 5. Магия азарта 191
Игральные кости 195
Домино 208
Игральные карты 211
Рулетка 216
Лотереи 225
Числовые игры 230
Головоломка «15» 233
Задачи (1-36) 234
Глава 6. Числовые фантазии 241
Задачи (1-141) 243
Математические равенства 250
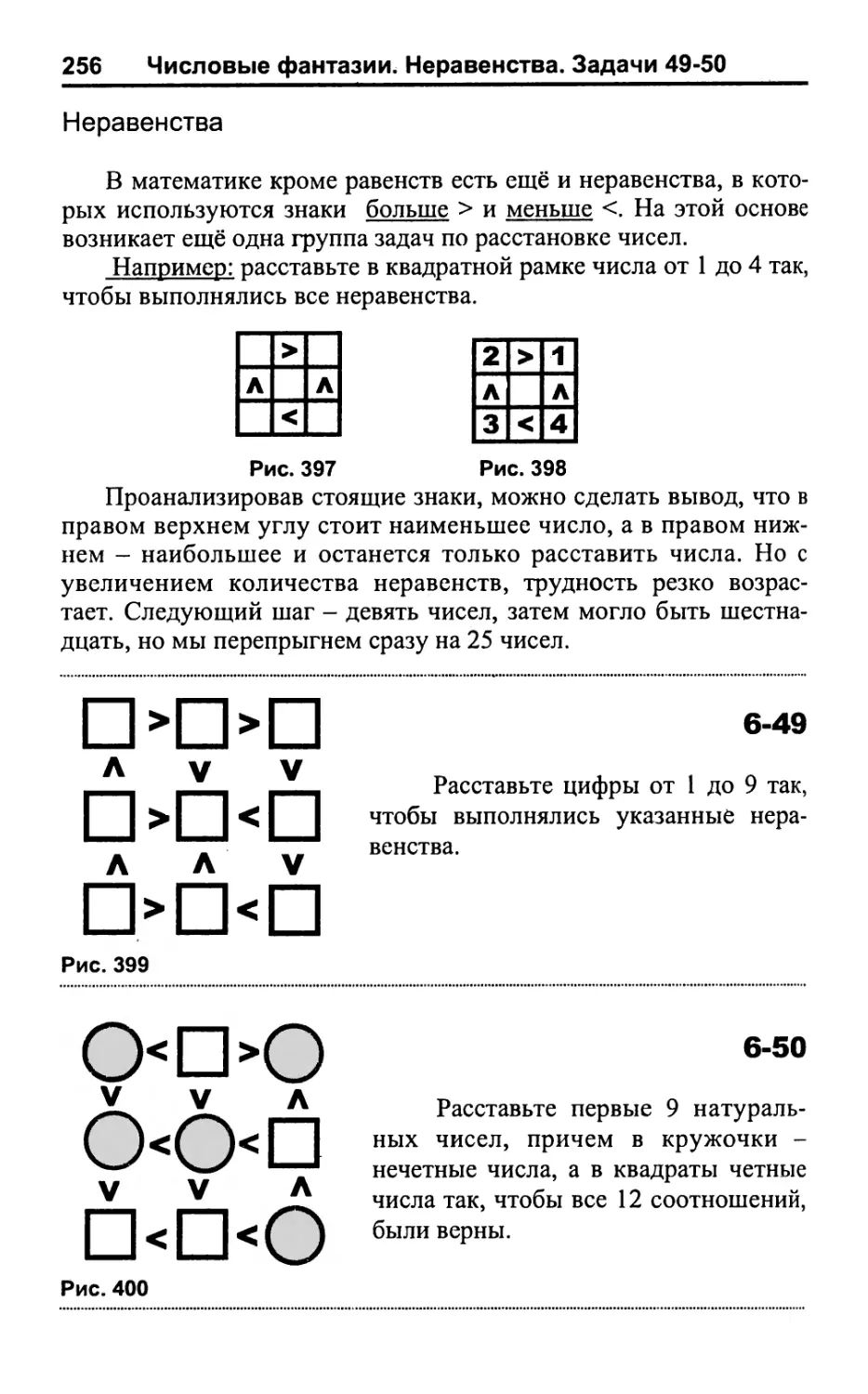
Неравенства 256
Пересечение чисел 257
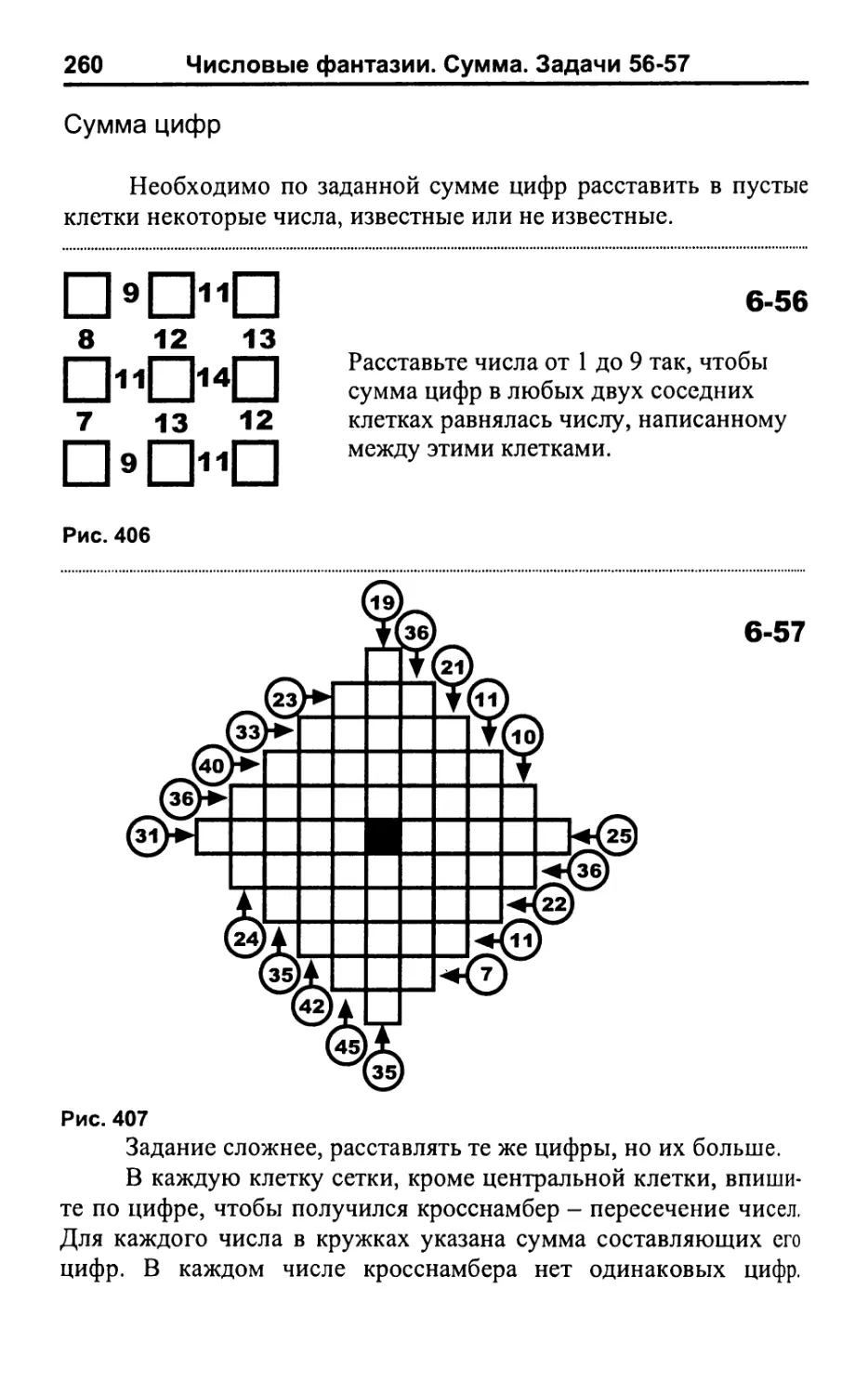
Сумма цифр 260
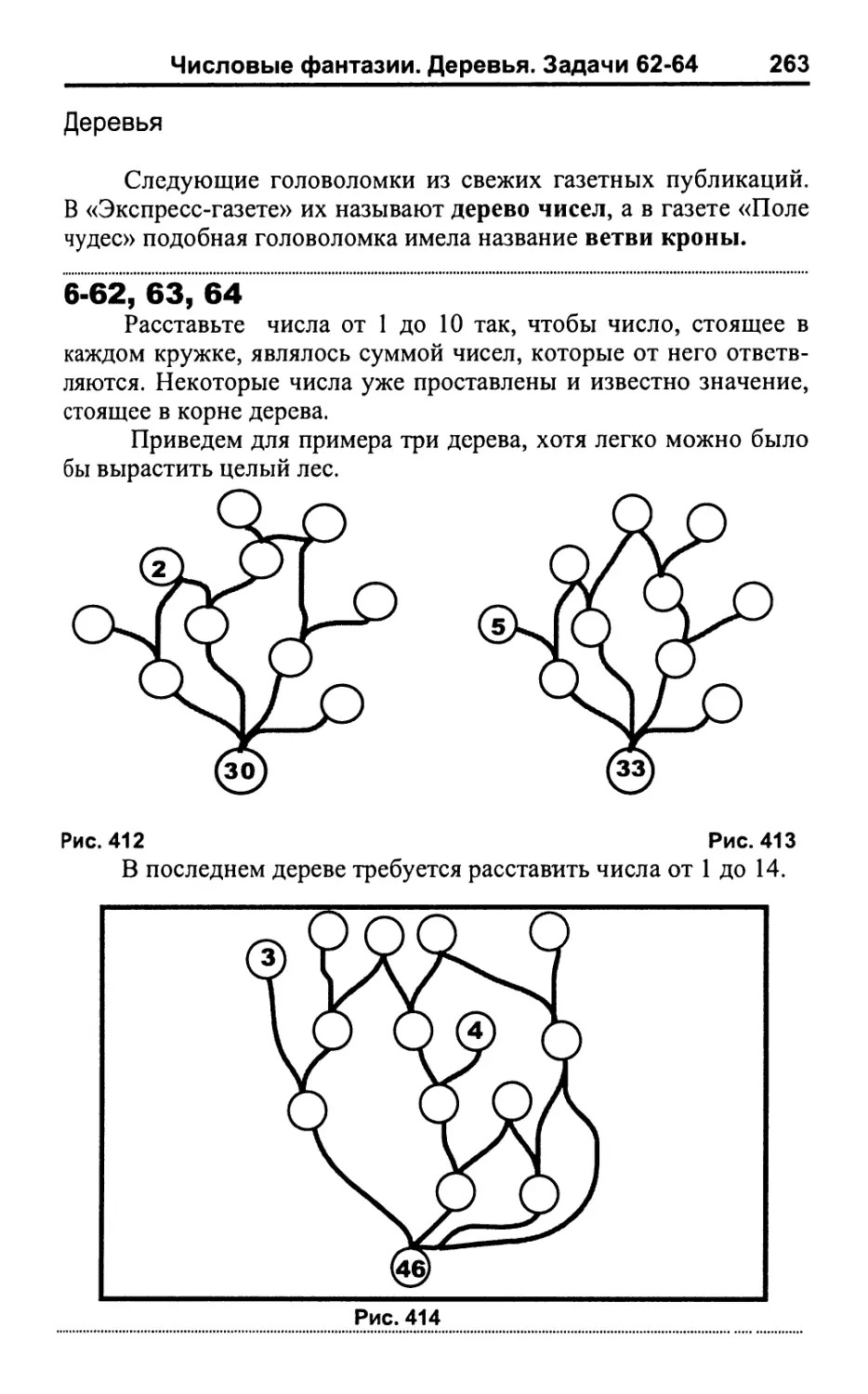
Деревья 263
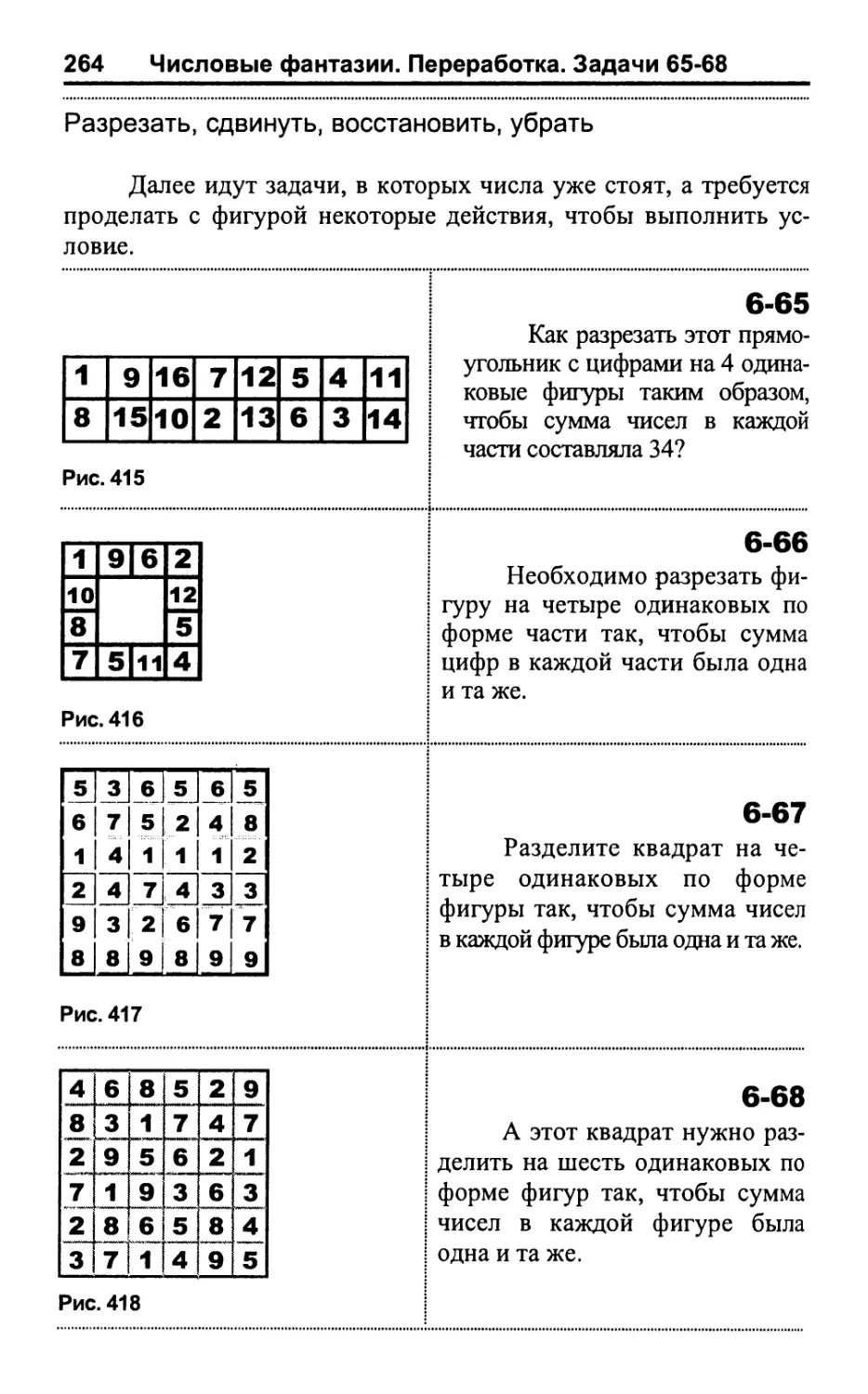
Переработка 264
Стрелки 270
Сапер 271
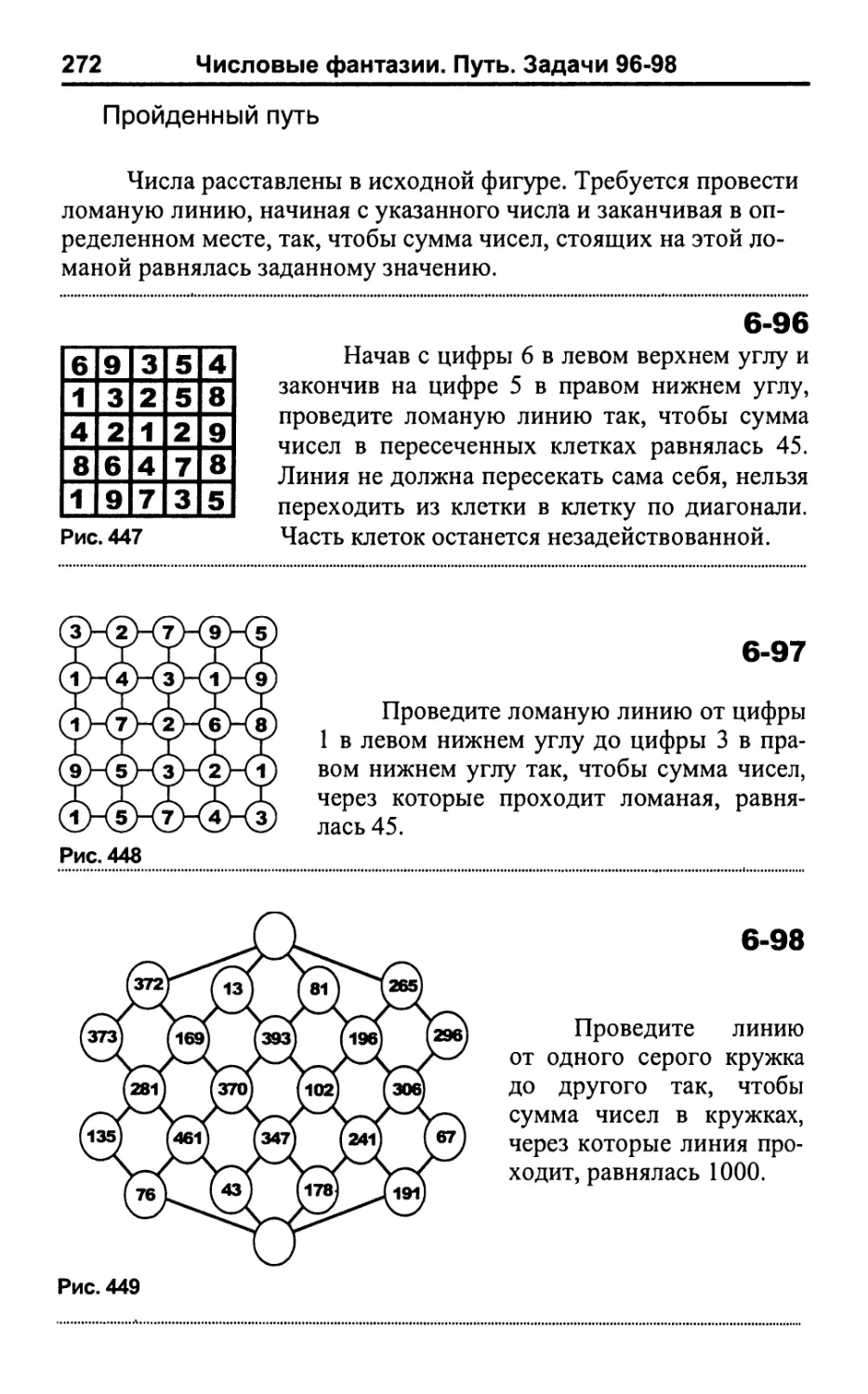
Пройденный путь 272
Поиск закономерности 276
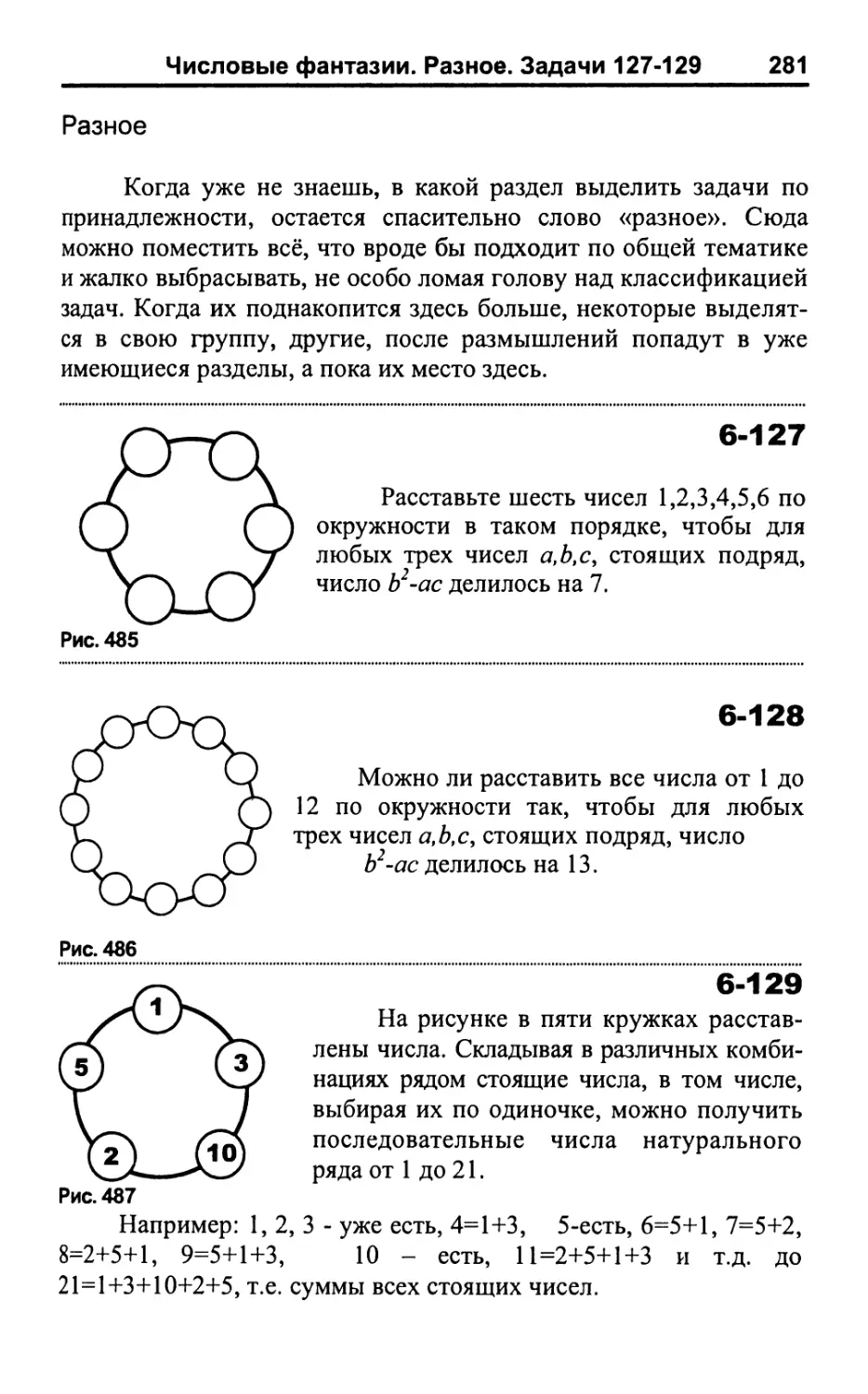
Разное 281
Рисование по-японски 286
Справочные материалы 295
Ответы и решения 297
Справочные таблицы 369
Литература 371
Персоналии 373

Предисловие
Всё наше достоинство заключено в
мысли. Не пространство и не время, которых мы не
можем заполнить, возвышают нас, а именно она,
наша мысль.
Блез Паскаль
ПРЕДИСЛОВИЕ
ХАОС И ПОРЯДОК
В соответствии с библейскими представлениями,
первоначально мир представлял собой сплошной хаос, то есть зияющую
бездну, наполненную туманом и мраком. В русском языке это
слово понимается как полный беспорядок. Потом за дело принялся
Бог, он же Создатель, и упорядочил всё, начиная с элементарных
частиц, сотворив за определенное время мир, где порядок
побеждает хаос. И увидел Бог, что это хорошо, когда есть порядок.
Отсюда идет наше понимание порядка, как божественного
проявления, созидательного начала, в противоположность хаосу,
беспорядку, как порождению темных разрушительных сил.
Чтобы человек понял значение порядка, пришлось Богу прибегнуть к
крайним мерам - подвергнуть человека наказанию: пожизненной
ссылке из Эдема и рядом других, мягко выражаясь, неудобств.
И вот теперь всю свою жизнь человек наводит порядок,
вокруг себя, а беспорядок как будто сам по себе, так и
продолжает проявляться то там, то здесь. Попробуйте месяц совсем не
убирать в квартире, и вы поймете, что такое хаос. Пыль
проникнет через любые окна и ляжет слоем, на кухне возникнут горы
немытой посуды, в ванной появятся ворохи грязного белья. Вещи
по всей квартире, как ни старайся класть их на свои места,
окажутся не там, где вы надеетесь их найти, путаница в бумагах и
книгах, залежи ненужного мусора и хлама. Это, почувствовав,
что вы с ним не боретесь, из тьмы поднимается хаос. Ведь чтобы
был порядок, нужно затрачивать на его наведение время и
энергию, а хаос возникает сам, там, где лень и апатия.
Порядок - это гармония, постичь которую, дано не
каждому. Периодическая таблицы химических элементов Д. И.
Менделеева, стихи А. С. Пушкина, музыка Людвига ван Бетховена -

Предисловие
" примеры достижения человеком в своих творениях истинной
гармонии. Бог, сотворив мир, сказал, что это хорошо. Александр
Сергеевич выразился о своем творчестве по-человечески просто:
«Ай-да Пушкин, ай-да сукин сын!», понимая вторичность своей роли,
как выразителя уже существующей в мире красоты и гармонии.
Мир нашего бытия в целом стабилен, хотя в природе не все
идеально и окончательно гармонично с точки зрения человека.
Постоянно прорывается хаос в виде землетрясений, смерчей,
наводнений, эпидемий, падающих метеоритов и прочих
катаклизмов, пугающих людей. Взаимоотношение порядка и хаоса,
как нельзя лучше, иллюстрирует философскую концепцию
единства и борьбы противоположностей. Быть может, в этом есть своя
необходимость, пока не доступная нашему пониманию.
Создав персональный компьютер, приученный к порядку,
человек предусмотрел в операционной системе Windows корзину
для мусора, куда отправляются ненужные файлы, периодическое
проведение чистки дисков с их последующей дефрагментацией,
т.е. упорядочением файлов - положительный пример стремления
к порядку. Пример другого плана - Internet: изначально благое
дело, превращающееся в неконтролируемую международную
свалку нужной и не нужной, а порой вредной и опасной,
информации. Каждый маньяк может бесконтрольно «сливать» сюда всё,
что пожелает, не заботясь о последствиях доступа к этой
информации других людей.
Какую бы область деятельности мы ни взяли, борьба хаоса
и порядка продолжается. С одной стороны - добро, порядок,
гармония, Бог, с другой - зло, хаос, разрушение, Дьявол.
Даже во время отдыха, в играх, человек моделирует борьбу
порядка и хаоса. Расставит в определенном порядке кегли или
городки, а потом разбивает их, идет от порядка - к хаосу. Или,
наоборот, из хаоса рассыпанных пазлов собирает целостную
картинку, из костяшек домино выкладывает упорядоченную
цепочку, раскладывает карточный пасьянс.
Расставить фигуры по правилам - с этого начинаются
шахматы, шашки, нарды и многие другие игры; и далее,
передвигать их, опять-таки по правилам и с определенной целью.
Расставить, найти каждому элементу свое место, из
множества хаотичных расположений, единственное и неповторимое
- вот цель игры «пятнадцать», цель поворотов кубика Рубика.
Бросание кубиков в некоторых играх привносит элемент
случайности в чистую логику мышления, добавляет азарт,
благодаря непредсказуемости последствий нарушения порядка.

Предисловие
Почти все газеты печатают для развлечения своих
читателей кроссворды, последнее время переходят на сканворды,
которые немного легче. Что нужно в них делать? Вспомнить,
найти и расставить слова в сетке, в соответствии с их
определениями. Слово расставить становится ключевым в наших
развлечениях, стремление к порядку в людях изначальное, Богом данное.
В свою очередь, решение кроссвордов упорядочивает нашу
память, слова расставляются в ней по невидимым полочкам,
сортируются по отраслям знаний, по алфавиту, по своей длине.
Память любителя кроссвордов постепенно превращается из
огромной россыпи различных слов в аккуратный архив с
полочками, папочками, указателями.
В этой книге хотелось собрать под одной обложкой -
головоломки и игры, связанные с расстановкой не слов, а чисел.
Числа не нужно вспоминать, чаще всего, они заранее даны,
требуется расставить их по определенному принципу. В дело
включается не память, а логическое мышление.
Красив сам по себе натуральный ряд чисел: 1, 2, 3, 4, 5, 6,...
Он демонстрирует упорядочение по возрастанию в чистейшем
виде. Принцип построения следующей цепочки чисел не так
очевиден: 1,1, 2, 3, 5, 8,13, 21,..., хотя они тоже стоят не хаотично:
каждое число, начиная с третьего, равно сумме двух
предшествующих. Этому ряду натуральных чисел, имеющему свое
историческое название - ряд Фибоначчи, присуща своя логика и
красота, постижение которой возможно только при
целенаправленном изучении. В одной из последующих глав книги
будут специально рассмотрены задачи, связанные с поиском
закономерности в различных числовых последовательностях,
подобных ряду Фибоначчи. Но начнем мы с числовых построений с
заранее заданным условием расположения чисел. Мы будем
строить эту книгу на трех китах:
• натуральные числа вместе с ноликом (который
строго математически к ним не относится),
• простейшие плоские геометрические фигуры и
объемные тела,
• и слово расставить (или наоборот - разрушить).
Количество подобных головоломок, разнообразие идей,
которые лежат в их основе, порой просто удивляет.

8 Предисловие
Восхищает неограниченность полёта фантазии
человеческого разума, способного творить даже с минимальным
исходным материалом.
Вот перед вами этот первоначальный материал для
творчества и торжества человеческой мысли:
0,1,2,3,4,5,6,7,8,9...
Рис.1
На этой основе можно создавать математические
развлекательные задания наподобие кроссвордов.
В этом простом, но абстрактном мире есть своя красота и
гармония: красота симметрии, гармония упорядоченности,
разнообразие, гарантированное бесконечностью и первого, и второго
ряда, и глубина мысли, обеспечиваемая разумом человеческим,
которым движет извечное любопытство.
Оставим в стороне океан других чисел: дробных,
иррациональных, комплексных и гиперкомплексных (а есть и такие),
забудем про аксиомы и теоремы, - только натуральные числа и
самые простые фигуры, но не по отдельности, а в различных
соотношениях и комбинациях. Еще нам понадобится понимание
основных математических действий. Вот и весь необходимый
багаж знаний, чтобы читать эту книгу и решать собранные в ней
головоломки.
Это не учебник, хотя некоторые теоретические сведения
читатель получит. В большей степени это сборник головоломок и
игр, объединенных одной узкой темой, но с широким охватом
разнообразия отображения этой темы в различных задачах,
опубликованных как в старых книгах, так и в современной
периодической печати. Никто и ничто не заставляет их решать, кроме
собственного интереса и любопытства. И есть два пути: решить
самому или, на крайний случай, заглянуть в ответы, которые
приводятся в конце, иногда с подробным объяснением. Только
имейте в виду, что каждая самостоятельно решенная задача - это ваша
маленькая победа над хаосом, ваш вклад в гармонизацию мира и
собственное совершенствование.

Историю цивилизации можно выразить в
шести словах: чем больше знаешь, тем больше можешь.
Э. Абу (1828-1885) - французский писатель
Знание того, какими вещи должны быть,
характеризует человека умного; знание того, каковы
вещи на самом деле, характеризует человека
опытного; знание же того, как их изменить к лучшему,
характеризует человека гениального.
Д. Дидро (1713-1784) - французский философ
Знание - это абсолютная ценность нашего
мира. Необходимо учиться, необходимо познавать.
Непознаваемого - не существует, мы можем говорить
лишь о том, что существует непознанное.
М. Горький (1868-1936) -русский писатель
Нужны умные, образованные люди: по мере
приближения человечества к лучшей жизни число
этих людей будет увеличиваться, пока не составит
большинства.
А. П. Чехов(1860-1904) -русский писатель
Весь смысл жизни заключается в бесконечном
завоевании неизвестного, в вечном усилии познать
больше.
Э. Золя (1840-1902) - французский писатель

Кросс-суммы
11
КРОСС-СУММЫ
Числа и фигуры могут объединиться, например, в такую
композицию
4
3
8
9
5
1
2
7
6
4
3
8
9
5
1
2
7
6
Рис. 2
Девять чисел натурального ряда расставлены в клетках
квадрата. Можно ли сразу сказать, что это красиво? Вряд ли.
Красота здесь не внешняя, а содержательная, внутренняя. Чтобы
ее понять требуется напряжение мысли, нужно посчитать суммы
трех чисел в каждой строчке, в каждом столбце и по каждой из
двух диагоналей. Оказывается, сумма во всех восьми случаях
одна и та же, равная 15.
=15
=15
=15
лг и и II v>
* 15 « 15 *
Выходит в огромном количестве различных расположений
девяти чисел в клетках квадрата можно найти такое удивительное
по своему содержанию. От хаоса различных, ничем не
примечательных вариантов расположения - к своеобразному и редкому
упорядочению.
История происхождения подобных квадратов уходит в
глубь тысячелетней истории человечества. Естественно, в те
древние времена, когда даже отдельным числам приписывались
магические свойства, подобные числовые построения не могли
назвать иначе как волшебные или магические квадраты.
К магическим квадратам вернемся отдельно, в следующей
главе, а пока рассмотрим более простые, но и более разнообразные
расположения чисел с постоянными суммами.

12
Кросс-суммы
Именно в этой области существует большое количество
занимательных задач простых по условию и полезных для ума.
Для пересекающихся рядов чисел с одинаковыми суммами
отечественный математик и популяризатор науки Борис Ана-
стасьевич Кордемский ввел определение кросс-суммы, по
аналогии с кроссвордами (от английского cross - пересекаться,
скрещиваться). Таким образом, кросс-суммы - это
пересекающиеся ряды чисел с одинаковыми суммами. Словосочетание
немного неблагозвучное из-за трех букв «с», идущих подряд.
Можно было бы назвать их по-русски: числовые пересечения с
одинаковыми суммами, но получается более громоздко. Кроме
того, нужно отдать долг вежливости по отношению к мэтру
отечественной занимательной математики, автору «Математической
смекалки», на книгах которого воспитывалось наше поколение.
Начнем с простейшего расположения чисел в одну строчку
и один столбец с пересечением:
Рис.4
Можно ли расставить числа от 1 до 5 так, чтобы сумма
трех чисел в строчке и трех чисел в столбце была одна и та же?
Ответ дается в приведенной схеме:
Рис.5
Число 3 в центр, а по краям равноудаленные от центра пары
чисел. Это не единственное решение. Сумма 1+2+3+4+5=15,
нечетная. Число, стоящее на пересечении, входит как в сумму
чисел строки, так и в сумму чисел столбца, и мы должны
прибавить его к 15 и, поделив на два, вычислим кросс-сумму. Значит,
чисцо на пересечении обязательно нечетное, но это может быть 1,
3, 5. Отсюда получим другие решения, с суммой равной 8 или 10.

Рис. 6
Кросс-суммы
2
3
1
4
5
2
1
5
4
3
13
Еще возможны перестановки крайних чисел, не влияющие
на сумму, но дающие дополнительные решения.
Убеждаемся, что вариант с одним пересечением достаточно
легкий и допускает несколько решений с различными кросс-
суммами. Увеличение количества чисел в строчках и столбцах, а
также сдвиг пересечения не усложняют задачу.
Ш25
89
Рис.7
Лучше всего, если задача имеет единственное решение, его
и найти труднее и удовлетворение от такой головоломки больше.
Увеличивая количество пересекающихся числовых рядов, мы
усложняем подобные задачи и уменьшаем количество
возможных решений. Для примера рассмотрим пересечение двух строчек
и двух столбцов по 6 клеток, уже более близкое к кроссвордной
сетке. Расставить требуется числа от 1
до 20, так чтобы суммы в двух строчках
и двух столбцах были одинаковые.
Четыре числа будут стоять на
пересечении и одновременно входить в две
суммы.
Следите за методикой решения.
Находим сумму данных чисел:
Рис. 8 1+2+3+...+20=210. Она дает при делении
на 4 (2 строки + 2 столбца) остаток 2. Значит и сумма четырех
чисел, стоящих на пересечениях, должна давать при делении
на 4 остаток 2, так как они учитываются дважды. Только тогда
общая сумма будет делиться на 4 и можно определить кросс-
сумму, а затем уже расставить числа.

14
Кросс-суммы
10
9
5
1
6
19
3
20
11
15
12
13
7
2
8
17
4
18
16
14
Рис. 9
Мы можем поставить в клетках
пересечений числа 1, 2, 3, 4, (1+2+3+4=10) и
кросс-сумма получается (210+10)/4=55.
Расставить оставшиеся числа это уже дело
техники, причем снова обращаем
внимание на равноудаленные от концов ряда,
они дают одинаковую сумму. Получаем
одно из множества решений.
Увы, снова решение не единственное. В
пересечениях можно поставить четверки чисел: (1, 2, 3, 8),(1, 2, 3, 12), (1,
2, 3, 16), (1, 2, 3, 20) - это не меняя первые три цифры. Можно
поменять их, можно переставлять числа в готовом решении.
Общий вывод: задача не сильно усложнилась, количество
решений очень большое. Нужно искать другие конфигурации
числовых рядов, иные пересечения, чтобы уменьшить количество
решений. Так возникли задания, аналогичные кроссвордам: есть
кросс-сетка, только расставить в ней нужно не слова, а некоторые
числа, чтобы получить требуемый результат. Друг от друга
головоломки с кросс-суммами отличаются набором используемых
чисел, исходной фигурой и количеством пересекающихся
числовых рядов, но имеют практически одинаковую формулировку:
расставьте числа так, чтобы . Их красота определяется
симметрией расположения, а сложность вообще понятие
субъективное. На то они и головоломки, чтобы не иметь общего правила
решения, каждый раз требуется особый подход, новые
размышления, но из любой решенной задачи можно и нужно что-то взять
для себя на будущее, если не метод, так хотя бы опыт. Для
удобства задачи сгруппированы по исходной фигуре: круги,
треугольники, квадраты, многоугольники и т. д. Это позволяет
попытаться выделить, для некоторых групп задач, общие подходы
к решению. Ваша стратегическая цель - это не просто решить
задачу, а постараться выделить полезные идеи, интересные методы.
И ещё одно замечание по построению книги. Можно взять
пять задач, к каждой придумать длинную и увлекательную
литературную историю, дать запоминающееся название и отвести на
них несколько страниц книги. Здесь принято иное решение:
показать максимум вариантов, не пять, а пятьдесят или больше, но
убрать лишние слова - только номер задачи и её условие.
Примечание: при решении головоломок удобно
пользоваться бочонками от настольной игры лото, на которых стоят
цифры от 1 до 90. Передвигать бочонки на столе гораздо проще,
чем делать записи на листе бумаги, а потом их стирать.

Задачи 1-3
15
Окружности
1-1
Расставьте числа от 1 до 9
в кружочки фигуры так, чтобы
сумма трех цифр по каждой
прямой составляла 15.
Рис. 10
1-2
Расставьте десять
последовательных натуральных
чисел в кружочки фигуры так,
чтобы сумма любых трех
чисел по каждой прямой,
составляла 42.
Рис.11
1-3
Расставьте числа от 1 до 19
в кружочки фигуры так, чтобы
сумма любых трех чисел на
одной прямой равнялась 30.
Рис.12

16
Задачи 4-6
I
Рис. 13
1-4
Расставьте числа от 1 до 8
так, чтобы суммы чисел по
прямым и окружностям были
одинаковыми.
1-5
Расставьте числа от 1 до 10
в маленькие кружочки так,
чтобы суммы чисел в четырех
больших кругах были равными.
Рис. 14
J
1-6
Расставьте 9 натуральных
последовательных чисел так,
чтобы равнялись 60 суммы по
4 малым и одной большой
окружности, а также в
вершинах центрального квадрата.
Рис.15

Задачи 7-9
17
1-7
Расставьте числа от 1 до 16
так, чтобы суммы по 4-м
радиусам и 4-м окружностям
равнялись 34.
1-8
Расставьте числа от 1 до 8
так, чтобы сумма чисел на
каждой окружности была
одной и той же.
1-9
Расставьте числа от 1 до 25
так, чтобы сумма чисел по
пяти радиусам и по пяти
окружностям равнялась 65.
Рис.16
Рис.17
Рис.18

18
Задачи 10-12
Рис. 19
1-10
Расставьте числа от 1 до 6
в маленькие кружочки так,
чтобы сумма четырёх чисел на
любой окружности равнялась
14.
Рис.20 1-11
Расположите цифры от 1 до 9 в отделах пересекающихся
олимпийских колец так, чтобы сумма чисел в любой паре колец
(таких пар - четыре) была равна 22. Есть два различных решения.
Рис.21 1-12
Расставьте числа от 1 до 17 в маленьких кружках так,
чтобы сумма четырёх чисел по каждой большой окружности была
одна и та же.

Задачи 13-15
19
Треугольники
1-13
Расставьте в кружочки J
числа от 1 до 6 так, чтобы сумма
чисел вдоль каждой стороны
треугольника равнялась 12.
Г
Рис.22
1-14
Расставьте цифры от 1 до 9
так, чтобы сумма их по каждой
стороне треугольника
составляла: а). 20
б). 17.
Рис.23
1-15
Расположите в кружках
числа от I до 7 так, чтобы
сумма чисел по каждой
прямой, содержащей три круга,
была одна и та же.
Рис.24

20
Задачи 16-18
Рис. 25
1-16
Расставьте числа от 1 до 9
так, чтобы сумма четырех
чисел в 3-х треугольниках со
стороной 2 была одинаковой.
Какие значения может
принимать сумма?
Рис.26
Рис.27
1-17
Расставьте числа от 1 до 10
так, чтобы сумма чисел,
расположенных по периметру
каждого из 3-х маленьких
треугольников равнялась: 28 или
29, или 30 и так до 38
включительно.
1-18
Расставьте числа от I до 6
так, чтобы сумма чисел по
сторонам большого треугольника
равнялась 11, а сумма чисел по
углам выделенных 3-х малых
треугольников равнялась 10.
!

Задачи 19-21
21
!
1-19
Расставьте числа от 1 до 7
так, чтобы сумма трех чисел на
каждой прямой была
одинаковой.
1-20
Расставьте числа от 1 до 15
так, чтобы по Периметру
каждого из четырех треугольников
сумма была одинаковой.
Рис. 28
Рис.29
1-21
Расставьте числа от 1 до 9
в кружочках так, чтобы сумма
чисел вдоль каждой стороны
большого треугольника и в
вершинах трех темных,
выделенных треугольников,
равнялась 20.
Рис. 30

22
Задачи 22-23
1-22
Числа от 1 до 10 расположены так,
что сумма их в каждой группе из
четырех малых треугольников, образующих
большой треугольник, равна 22. Таких
пересекающихся больших
треугольников четыре. Расставьте эти числа иначе,
так, чтобы сумма равнялась: 18 или 20,
или 24, или 26.
Рис. 31
7
\
Рис.32 1-23
Каждый из этих трёх концентрических треугольников
содержит 9 кружков. В некоторых уже проставлены цифры.
Заполните остальные 18 кружков, принимая во внимание
следующее:
• цифры от 1 до 9 должны быть в каждом треугольнике;
• сумма четырёх цифр на каждой стороне любого треугольника
равна 20;
• сумма трёх цифр в каждом из 9 рядов, отмеченных стрелками
равна 15.

Задачи 24-26
23
Квадраты
1-24
Расставьте числа от 1 до
16 таким образом, чтобы
сумма пяти чисел каждого ряда
(2-х вертикальных и 2-х
горизонтальных) равнялась 41 (или
42, или 43, или 44).
Рис. 33
1-25
Расставьте числа от 1 до 9
так, чтобы суммы чисел в
вершинах любого квадрата, из шести
представленных на рисунке, были
равны между собой.
Рис. 34
1-26
Подберите 13 натуральных
чисел, из них 11 различных, а 2
одинаковых и впишите их так,
чтобы сумма трех чисел в каждом
ряду вдоль линий равнялась 20.
Рис. 35

24
Задачи 27-29
Рис. 36
1-27
Расставьте числа от 1 до 11
так, чтобы сумма трех чисел на
каждом из десяти отрезков
была одна и та же.
Рис. 37
1-28
Расставьте числа от 1 до 16
так, чтобы сумма чисел вдоль
контуров всех квадратов была
одинаковой и равнялась 68.
Рис. 38
1-29
Числа от 1 до 12
расставьте в кружках фигуры так, чтобы
сумма чисел в вершинах
каждого закрашенного квадрата
равнялась 30.

Задачи 30-32
25
1-30
Расставьте числа от 1 до 12
так, чтобы сумма чисел в
вершинах каждого из пяти
квадратов и по четырем прямым была
одинаковой.
"Г
Рис. 39
1-31
Расставьте числа от I до 8
так, чтобы сумма чисел в
вершинах каждого четырехугольника
(2-х квадратов и 4-х трапеций)
равнялась 18.
Рис. 40
1-32
Расставьте числа от 1 до 11 так, чтобы сумма трех чисел на
каждой прямой была одинаковой.
Рис. 41

26
Задачи 33-35
Рис. 42
1-33
Расставьте в кружках
числа от I до 8 так, чтобы сумма
чисел в вершинах каждого
белого треугольника равнялась 12, а
в вершинах серого треугольника
и квадрата - по 11.
Рис. 43
1-34
Расставьте в клетки
фигуры: пять чисел 20,
три числа 15,
три числа 10
и шесть чисел 5 так,
чтобы сумма вдоль каждой
прямой линии равнялась 55.
г
1-35
В кружочки фигуры расставьте
числа от 1 до 13 так, чтобы сумма
четырех чисел, расположенных в
вершинах всех 11 квадратов,
была постоянной.
Рис.44

Задачи 36-38
27
Многоугольники
1-36
Расставьте числа от 1 до
10 так, чтобы сумма трех
чисел по любой стороне
пятиугольника была одна и та
же.
1-37
Расставьте числа от 1 до 19
так, чтобы сумма вдоль
каждой стороны и вдоль каждого
радиуса равнялась: а).22
б).23.
1-38
Расставьте числа от 1 до 13
так, чтобы равнялись 39 суммы
шести чисел по периметру
каждого шестиугольника, пяти
чисел вдоль любой оси
симметрии, пяти чисел по
периметру каждого большого
треугольника.
Рис. 45
Рис. 46
Рис. 47

28
Задачи 39-41
Рис. 48
1-39
Расставьте числа от 1 до 13
так, чтобы сумма 3-х чисел по
каждой из девяти линий
равнялась 21.
Рис. 49
1-40
Расставьте числа от 1 до
19 так, чтобы сумма чисел,
расположенных в вершинах
всех правильных
шестиугольников (их 9) была постоянной.
!.
1-41
Расставьте числа от 1 до 14
так, чтобы три числа на
каждой из сторон семиугольника
в сумме давали 19.
Рис. 50

Задачи 42-44
29
1-42
Расставьте числа от 1 до 13 так,
чтобы сумма чисел в вершинах
четырех пятиугольников была
одинакова.
Рис. 51
1-43
Расставьте числа от 1 до 24
включительно так, чтобы в
каждом из семи шестиугольников
сумма чисел была одинаковой.
г
1-44
Расставьте числа от 1 до 25
так, чтобы в каждой однотонной
группе из пяти кружков и в
каждой из пяти окружностей сумма
была равна 65.
Рис. 52
Рис. 53

30
Задачи 45-47
Звезды
Рис. 54
Рис. 55
| 1-45
|
| Можно ли в кружках звезды
1 расставить 10 различных,
натуральных чисел так, чтобы суммы
4-х чисел вдоль каждой из пяти
прямых равнялись 24?
1-46
Расположите первые 11
натуральных чисел так, чтобы сумма
4-х чисел в вершинах каждого из
5 секторов равнялась 25.
|
1
1-47
Расставьте числа от 1 до 15 так,
чтобы сумма чисел в вершинах
| звезды и по контуру 5-ти окруж-
| ностей была равна 40.
Рис. 56

Задачи 48-50
31
1-48
Расставьте числа от 1 до 12
так, чтобы суммы четырех
чисел по каждой прямой и
сумма чисел в вершинах звезды
равнялись 26.
!
Рис.57
1-49
Расставьте числа от 0 до 12
так, чтобы суммы четырех
чисел в вершинах всех шести
ромбов равнялись 30.
1
Рис. 58
1-50
Расставьте числа от 1 до 14
так, чтобы сумма чисел в
любых четырех кружках,
лежащих на одной прямой,
равнялась 30.
Рис. 59

32
Задачи 51-53
1-51
Расставьте числа от 1 до 15
так, чтобы сумма четырех чисел
в каждом из семи секторов-
ромбов была равна 30.
1-52
Расставьте числа от 1 до 16
так, чтобы сумма 4-х чисел на
сторонах каждого квадрата и в
вершинах каждого квадрата
равнялась 34.
•!
1-53
Расставьте числа от 1 до 16
так, чтобы сумма 4-х чисел вдоль
каждой прямой равнялась 34.
Рис. 62

Задачи 54-56
33
Разные фигуры
__
Впишите в каждый
маленький треугольник числа от
1 до 16 так, чтобы сумма чисел
в любом из шести больших
треугольников, состоящем из 4-х
маленьких и вплетенных друг в
друга, равнялась 34.
1-55
Расставьте числа от 1 до 8
так, чтобы сумма чисел в
вершинах каждого из 4-х
треугольников равнялась сумме чисел в
вершинах квадрата.
Рис. 63
I
1-56
Расставьте числа от 1 до 8 так,!
чтобы сумма трех чисел в верши-!
нах каждого светлого треуголь-1
ника равнялась 13, а в вершинах!
каждого темного треугольника
равнялась 14.
Рис. 64
Рис. 65
2 Трошин

34
Задачи 57-59
1-57
Расставьте числа от I до 9
так, чтобы сумма чисел,
стоящих в вершинах каждого из
семи, изображенных на рисунке
треугольников, была одна и та
же.
1-58
Расставьте числа от 1 до 11
| так, чтобы сумма чисел в
вершинах каждого квадрата была
одна и та же.
1-59
Расставьте числа от 1 до 12
•; так, чтобы они составляли одну
! и ту же сумму в 4-х кружках, в
| 4-х треугольниках, в 4-х квад-
I ратах, в 2-х центральных
j строчках и 2-х центральных
| столбцах.
Рис. 68

Задачи 60-62
35
1-60
Расставьте числа от 1 до 12
так, чтобы суммы чисел на
каждой из 6-ти прямых, на
каждой из 3-х окружностей,
в вершинах каждого из 3-х
ромбов были равны.
1-61
Расставьте числа от 1 до 21
так, чтобы сумма чисел по
каждой из трех окружностей была
равна 60, не считая и не
используя три уже поставленных
числа.
I
1-62
Расставьте числа от 1 до 18
так, чтобы суммы чисел,
расположенных по каждой
окружности и по вертикальным прямым,
были равны 57. Совокупности
же верхних и нижних чисел
должны образовывать 2
магических квадрата.
Рис. 69
Рис. 70
Рис. 71

36
Задачи 63-65
Рис. 72
Рис. 73
г
I
I
I
1-63
Расставьте в кружки 12
последовательных простых
чисел от 3 до 41 так, чтобы
суммы 3-х чисел в вершинах
каждого из 4-х
треугольников были равны. При этом
суммы чисел по каждой
окружности также равны, но
другому числу.
1-64
| Расставьте числа от 3 до 13
I так, чтобы суммы чисел,
I расположенных по всем
! прямым равнялись 25.
1-65
Впишите в маленькие
кружочки числа от 1 до 16 так,
чтобы в каждой части квадрата,
ограниченной дугой, сумма
! семи чисел составляла 60, а
| сумма четырех чисел в цен-
| тре была равны 30.
Рис. 74

Задачи 66-68
37
1-66
Цифры написаны на
карточках и разложены в два ряда, как
показано на рисунке.
Поменяйте местами две карточки
так, чтобы сумма четырёх
чисел в каждой строке была
одной и той же.
1-67
Расставьте цифры от 1 до 7
в окружностях так, чтобы сумма
цифр на любой линии была
одна и та же.
Рис. 76
1-68
Расставьте числа от 1 до 10
в семь областей, образованных
пересечением этих
геометрических фигур, выполняя
следующие требования:
• Сумма чисел, охваченных
кругом, квадратом или
треугольником, должна равняться 30;
Рис. 77
• Сумма чисел, расположенных вне круга, или квадрата, или
треугольника, должна равняться 25.
(В некоторых областях будет стоять не одно число, но может
быть и пустая область).

38
Задачи 69-70
1-69
Начав от стрелки и
двигаясь к центру, расставьте цифры
от I до 8 в порядке возрастания
в кружках так, чтобы на каждом
из четырёх радиусов сумма
цифр оказалась равной 9.
Некоторые кружки оставляете
пустыми. Есть шесть решений.
Рис. 78
Рис.79 1-70
На каждой из трех спиралей нужно расставить в кружках
цифры от I до 7. Одиннадцать из них уже стоит.
Поставьте остальные так, чтобы сумма цифр на любой из
сторон треугольника, образованного кружками, равнялась 32.

Лирическое отступление 39
Подход к построению книги у меня получается как у
хозяйки угощающей своих гостей: на стол выставляются
внешне красивые блюда, «вы их сначала попробуйте, дорогие
гости, и, если понравится, я скажу, из чего они сделаны и кому
полезны».
Начнем с полезности. На стадии создания книги мне
приходилось со многими спорить о востребованности подобной книги.
Основной аргумент оппонентов - то, что интересно одному
увлеченному человеку, не обязательно заинтересует многих. Поэтому
для себя я сразу очертил круг людей, которых может
заинтересовать подобный сборник головоломок.
Во-первых, это преподаватели математики, которые
получат готовый материал для использования на уроках, но
в большей степени для внеклассной работы. Эта книга - готовый
курс для кружковых занятий в течение целого учебного года.
Вторая группа потенциальных читателей - ученики,
увлекающиеся математикой. Их не так много, как, например,
увлекающихся курением. Минздрав постоянно предупреждает,
что курение вредно для здоровья, а курят многие, потому что
кроме Минздрава о них «думают» тысячи табачных фабрик.
Если кто-то в противовес подумает о детях, которым не хватает
пищи для пытливого ума, у которых горят глаза при виде
интересной задачи, никому от этого хуже не будет. В каждом
классе как минимум один такой ребенок есть, остается, чтобы
умный учитель направил его на путь истинный, посоветовал что
читать, как развивать свои способности дальше.
К третьей многочисленной группе потенциальных читателей я
отношу людей, имеющих избыток свободного времени, которое
можно или «убить» или провести более-менее с толком. Поезд
дальнего следования, зона долгого заключения, больница
неопределенного лежания, временная безработица или пенсия, в конце
концов. Здесь вынужденный избыток времени, наличие навязчивых
мыслей и переживаний, которые лучше заглушить положительными
эмоциями.
Посмотрите на красивую картинку, попробуете решить задачу,
отвлекитесь от окружающего, отдохните. А если вы решите задачу
самостоятельно, то вам обеспечен всплеск эмоций, который не
сравнится ни с какими витаминами.
Второй вопрос к «хозяйке» - из чего это сделано? Ответ,
мне кажется, ясен уже из того, что попробовали.

40 Лирическое отступление
Винегрет, сборная солянка, ассорти - вот слова,
описывающие процесс и состав приготовления. Плюс ко всему хозяйские
предпочтения и некоторая доля вкуса, о котором, как известно,
не спорят. Я не называю себя автором, хотя некоторые задачи
составлял сам, но чаще перефразировал уже известные,
продолжил мысль там, где другой автор остановился, перенес какую-то
идею на новый материал, просто перепечатал подходящую по
теме задачу. Затем нарисовал на компьютере в программе
Macromedia FreeHand все рисунки и, главное, собирал 25 лет
разбросанные по книгам, журналам, газетам задачи,
систематизировал, решал и просеивал. Поэтому, я автор-составитель этой
книги, хранитель мудрости многих людей.
Относительно дозировки материала. Здесь собрано около
300 задач, которые можно использовать для проведения
ежедневной гимнастики ума. Многие люди, думающие о своем
здоровье, делают по утрам физическую зарядку, но не менее полезна
зарядка умственная. Решите одну задачку в день, введите этот
ритуал в распорядок дня и через год ваш умственный потенциал
неминуемо возрастет, что положительно отразится на всей вашей
жизни и деятельности.
Наконец, как это употреблять? Вариантов много и они
зависят от конкретной ситуации. Кто-то будет решать как
кроссворд в газете, вписывая простым карандашом числа и стирая их,
если не подходят. Учитель изготовит крупный рисунок и фишки с
числами к нему, чтобы можно было решать у
демонстрационной магнитной доски. Человек, трепетно относящийся к
книгам, перечертит рисунок на тетрадный листок, и будет решать
на нем. Я уже упоминал об удобстве использования бочонков от
игры лото с готовыми цифрами. Их можно расставлять,
передвигать на любой плоской поверхности.
Кроме лото есть еще распространенные настольные игры,
которые в той или иной степени основаны на числах. Это
игральные кости, игральные карты и домино. Для наших задач они
представляют собой готовые фишки с изображением чисел, их
остается только расставлять в соответствии с условием. Поэтому
нельзя обойти вниманием такие замечательные игры,
выдержавшие испытание временем, запреты и гонения. В каждой главе
будут задачи, связанные по тематике с этими играми.
Кросс-суммам подходит домино, которым и закончим эту главу.

Задачи 71-73
41
Кросс-суммы из косточек домино
Обычный набор для игры в домино содержит 28 фишек от
«0-0» до «6-6». Каждая фишка или кость, как их чаще называют,
разделена на два квадратика. Из этих 56 квадратиков восемь
«пустых», восемь содержат 1 очко, восемь - 2 очка и т. д.
•
•
•
•
• •
• •
•
::
•
•
•
•
•
•
ч
•
• •
• •
Рис. 80
4
2_
5
И
6
4"
1
1-71
Четыре кости домино можно выбрать так,
чтобы из них составился квадрат с равной суммой
очков по каждой стороне и с пустой клеткой внутри.
Образец с суммой 11 вы видите на рисунке. Такой
квадрат правильнее назвать рамкой, ведь он имеет
пустоту внутри. Рис. 81
Есть много задач для домино, на составление таких рамок с
равными суммами по четырем сторонам.
Можно ли из полного набора домино составить одновременно
семь таких квадратов? Не требуется, чтобы сумма очков по каждой
стороне получалась у всех квадратов одна и та же: важно, чтобы
квадрат имел на своих четырех сторонах одинаковую сумму очков.
1U72
Переставьте эти кости домино так, чтобы
сумма очков по каждой стороне рамки
равнялась 17.
Рис. 82
1-73
Из всех костей домино выложите одну квадратную рамку,
соблюдая правила игры (т. е. прикладывая кости друг к другу
одинаковыми значениями) так, чтобы сумма очков по каждой
стороне была одна и та же. Какая может быть эта сумма?

42
Задачи 74-76
1-74
Из полного комплекта домино
уберите дубль 3, дубль 4, дубль 5 и
дубль 6, они не потребуются.
Теперь сложите из оставшихся 24
костяшек 3 квадратные рамки так,
чтобы суммы очков по каждой
стороне каждой рамки равнялись не
15, как на этом рисунке, а 12.
Доминошный принцип
прикладывания костяшек соблюдать не
требуется.
Рис...83
1J75
Из 28 костей домино выложите четыре рамки разных
размеров так, чтобы сумма очков вдоль каждой стороны каждой
рамки равнялась 13. Прикладывать косточки друг к другу
одинаковыми значениями не обязательно.
•
•
У.
• •
X
•
• г**
• •
• •
•
•
Рис. 84
1-76
Из прлного комплекта домино
сложите две рамки, одну в другой,
чтобы суммы очков вдоль каждой из
восьми сторон совпадали.
Исследуйте, в каких пределах может меняться
значение этой суммы. В этой задаче
вы не обязаны прикладывать кости
друг к другу согласно обычному
правилу домино. Рис. 85
I I I
I I I
МММ!

Задачи 77-79
43
1-77
Уложите 24 кости
домино в виде рамки,
изображенной на
рисунке, так, чтобы суммы
очков вдоль всех
прямых были равны. При
этом в тех местах, где
кости соприкасаются
гранями как при игре в
домино, на них должны
быть одинаковые
цифры.
Как влияет на
кросс-сумму выбор
четырех отбрасываемых костей?
—
II I
II I
I I
—
=
II I
JL
I I
—
Рис. 86
1-78
Уложите все 28
косточек домино в
соответствии с рисунком и так, чтобы
сумма очков вдоль каждой
прямой была равна 25.
Косточки не обязательно
прикладывать друг к другу
одинаковыми значениями.
Рис. 87
1-79
Разложите полный комплект костей домино в виде семико-
нечной звезды по 4 косточки в каждом луче так, чтобы:
1. в центр выходили половинки с 0, 1, 2, 3, 4, 5, 6 очками,
2. на концах лучей также были все очки от 0 до 6,

44
Задачи 79-80
3. в каждом луче
косточки
укладывались
согласно принципу
домино -
одинаковыми
половинками друг к
другу,
4. суммы очков на
косточках
домино во всех лучах
были равными.
Рис. 88
1-80
Разложите полный комплект костей домино в виде восьми-
лучевой звезды с лучами из трех и четырех костяшек
попеременно так, чтобы:
1. в центр
выходили половинки с
1, 2, 3, 4, 5, 6
очками и две
«пустышки»,
2. в каждом луче
косточки
укладывались
согласно принципу
домино -
одинаковыми
половинками друг к
другу,
3. каждый луч
должен
содержать 21 очко.
Рис. 89

Наиболее существенное и наиболее благородное
из всего присущего нам - это разум.
Г. Мабли (1709-1785) - французский мыслитель
Разум человеческий владеет тремя ключами,
открывающими все: цифрой, буквой, нотой. Знать,
думать, мечтать. Все в этом.
В. Гюго (1802-1885) - французский писатель
Нет ничего чудеснее человеческого мозга, нет
ничего более изумительного, чем процесс мышления,
ничего более драгоценного, чем результаты научных
исследований.
М. Горький (1868-1936) -русский писатель
Свойство мудрого человека состоит в трех
вещах: первое - делать самому то, что он советует
другим, второе - никогда не поступать против
справедливости и третье - терепеливо переносить
слабости людей, окружающих его.
Л. Н. Толстой (1828-1910) -русский писатель
Самое меньшее благо в жизни - это богатство;
самое большое - мудрость.
Г. Лессинг (1729-1781) - немецкий мыслитель

Магические квадраты. История
47
Высшее назначение математики - находить
порядок в хаосе, который нас окружает.
Норберт Винер
Определение 1: магический квадрат — это последовательность
чисел от 1 до п2, расположенных по клеткам разграфленного
квадрата так, что суммы чисел во всех строках, столбцах и по
обеим диагоналям квадрата имеют одно и то же значение,
называемое магической суммой.
Определение 2: порядком магического квадрата называется
число клеток п, примыкающих к его стороне.
История
Говорить люди умели раньше, чем научились фиксировать
сказанное. И простейшие вычисления с использованием условных
единиц в виде пальцев, палочек, камешков, узелков появились
еще до того, как люди смогли записать это. Но доказательно судить
о том, что и когда научился делать человек в своем развитии, мы
можем только на основе дошедших до нас вещественных и
письменных источников.
Точно можно утверждать, что история магических
квадратов начинается в древнем Китае. В ранних литературных
сочинениях, написанных там еще до нашей эры, появляются
упоминания о некой схеме «ло-шу», которую «мудрые берут за
образец». Изображение
магического квадрата в виде связанных
кружков встречается в более
позднем трактате мыслителя Чжу
Си. Вот как эффектно он
выглядел там:
Черные кружки - это четные
(женственные) числа, белые -
нечетные (мужественные) числа.
Рис. 90
фооооооооо^

48
Магические квадраты. История
Существует несколько легенд о происхождении этого
первого магического квадрата, часто называемого «ло-шу». Скорее
всего, это просто выдумки, потому что я знаю несколько
абсолютно разных толкований, которые даются со ссылками на
различные древние книги, но противоречат друг другу. Поэтому
останавливаться на изложении чьих-то фантазий не будем, но
пальму первенства в этом открытие оставим за Китаем.
Так выглядит этот квадрат в обычной
числовой форме, и именно он был показан в
первой главе книги. В дальнейшем, занимаясь
магическими квадратами, китайские математики
рассматривали квадраты не только третьего, но
и более высоких порядков, придумали правила
для их построения.
Рис. 91
В древнеиндийских надписях и трактатах встречаются
изображения магических квадратов четвертого порядка.
4
3
8
9
5
1
2
7
6
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
7
2
16
9
12
13
3
6
1
8
10
15
14
11
5
4
Рис. 92 Рис. 93
Второй из этих квадратов сохраняет свойство быть магическим
и после того, как его строки или столбцы циклически перемещаются,
соответственно сверху вниз или слева направо. Иначе говоря, если
сделать плоский непрерывный ковер с узором из таких квадратов, то,
вырезав любую его часть из 4 строк и 4 столбцов, получаем снова
магический квадрат.
Из Индии сведения о магических квадратах перешли к арабам.
Арабы были знакомы с квадратом третьего порядка в VIII веке, а в
XII веке его описал в своих сочинениях Ибн Эзра, испанский еврей,
принявший мусульманство. Мусульмане очень благоговейно
относились к квадратам пятого порядка с цифрой I в середине, считая
это изображение символом единства Аллаха. В Европе о магических
квадратах узнали благодаря византийскому писателю Э. Мосхопу-
лосу, жившему в Константинополе в начале XV века.

Магические квадраты. История
49
Редкостью является использование магического квадрата в
изобразительном искусстве, а не в литературном или научном
произведении. Впервые это сделал немецкий художник Альбрехт
Дюрер (1471-1528), выпустивший в 1514 году гравюру
«Меланхолия», на которой в правом верхнем углу есть изображение
магического квадрата четвертого порядка. Причем два числа в
середине нижней строки указывают на год создания гравюры -
1514. Этот факт говорит об умении в то время составлять
магические квадраты с определенным заданным расположением
некоторых чисел. Говорят, что гравюра А.Дюрера послужила толчком
для знаменитых пророчеств его современника Мишеля
Нострадамуса (1503-1566).
Рис. 94

50 Магические квадраты. История
Известный немецкий гуманист Корнелий Генрих Агриппа
(1486-1535) построил магические квадраты порядков 3, 4, 5, 6, 7,
8, 9 - он связал их с семью астрологическими «планетами» -
Сатурном, Юпитером, Марсом, Солнцем, Венерой, Меркурием, и
Луной. Слово планеты взято в кавычки потому, что Луна и
Солнце, как известно, проходят по другим категориям небесных тел. В
Западной Европе в средние века магические квадраты были
достоянием представителей алхимии и астрологии. Серебряные
пластинки с выгравированными магическими квадратами носили как
амулеты, предохраняющие от чумы и других бед и поветрий. От
суеверных представлений древних китайцев, индусов,
европейских алхимиков и астрологов эти числовые квадраты и получили
свое необычное для математики название - «магические» квадраты.
Иногда по отношению к ним употребляется слово «волшебные», но
значительно реже, чем «магические».
В наш просвещенный век снова в почете астрологи, колдуны
и магистры магии. Один из современных колдунов, Магистр Белой
магии Юрий Лонго предлагал через газету «Комсомольская
правда» бесплатно выслать Магический Квадрат, который
поможет избавиться от финансовых трудностей, невезения, проблем в
любви. Очень много мистических словоизлияний, посвященных
магическим квадратам и магическим свойствам чисел, можно
найти в Интернете. Например, на одном из сайтов, открытом при
поиске материала по квадратам, прочитал высказывание:
«Обычно в церемониальной магии используются семь квадратов Силы,
которые называются Совершенной Силой, или квадратами
Планетарных Разумов. Эти древние знания содержат в себе
Числовой Цветок Жизни». Почти все слова пишутся с большой буквы,
чтобы придать вес бессодержательному потоку. Это написал не
древний алхимик, в манускрипте гусиным пером, а современный
человек с помощью компьютера и разместил на собственном сайте.
Можно и так использовать свои знания. Но что-то мешает
мне разложить на столе свою коллекцию головоломок, завесить
окна шторами, зажечь свечи и под невнятное бормотание
вычерчивать суеверным согражданам магические квадраты,
«избавляющие от всего плохого и притягивающие все хорошее». Вместо этого
пишу, возможно «пособие» для будущих Магистров разных магий.
В мистику ударяться не будем, но ради общего развития и
удовлетворения любопытства посмотрим на магические квадраты
Корнелия Агриппы. Это не просто красиво внешне, но и
содержательно с точки зрения математики. Увы, цвет фона и цифр
указан отдельно ввиду черно-белого издания книги.

Магические квадраты. История
51
Сатурн
(черный-белый)
Юпитер
(синий-оранжевый)
АЛ
I
13
Рис. 96 Рис. 97
Солнце
(желтый-пурпурный)
19
18
25
36
32
14
29
27
16
2022 21
10
33
3435
28
15
8
23 24
17
26
30
13
12
31
Рис. 99
Меркурий
(оранжевый-синий)
Марс
(красный-зеленый)
8
49
41
17
5859
15
23
145253
2244
3234352928
4026 2737 363031
47462021
4519
62
11
63
10
И
4
17
10
23
?4
12
5
18
6
7
25
13
1
19
20
8
21
14
2
3
16
9
22
15
Рис. 98
Венера
(зеленый-желтый)
Рис. 100
Луна
(пурпурный-желтый)
377829702162 13 545
6 3879 307122631446
47 7 39 80 31 72 23 55 15
1648 8 40813264 2456
571749 9 417333 65 25
265818 50 1 4274 3466
6727 5910 51 2 43 75 35
366819 6011 52 3 4476
772869 2061 12 53 4 45
Рис. 101
Рис. 102

52
Магические квадраты. История
Представим в виде таблицы данные семи квадратов:
И
п
т
1
16
25
36
49
64
81
п
8
45
136
325
666
1225
2080
3321
nS
15
34
65
111
175
260
369
я х а. у
? ч Ь S*
1М !
^» Н я ^
U 5 3
10
17
26
37
59
65
82
20
34
52
74
100
130
164
т S
I ё
40
102
208
470
600
910
1312
Величины, стоящие в столбцах, имеют определенную связь
друг с другом, которую можно выразить рядом математических
формул. Этому посвящен следующий раздел.
Составление магических квадратов было делом не только
астрологов или бездельников, ищущих забавы. Теорию их
разрабатывали многие выдающиеся математики. В 1654 году
французский ученый Блез Паскаль написал трактат, полностью
посвященный магическим квадратам. В дальнейшем к теории
магических квадратов обращались многие выдающиеся
математики. Она находит применение в ряде важных математических
вопросов. Выводы теории магических квадратов используются в
одном из методов решения систем уравнений со многими
неизвестными и даже в современной квантовой механике. В теории
квантования моментов количества движения, используется так
называемая таблица Редже, которая представляет собой
магический квадрат 3x3, составленный из произвольных чисел.
А любителям математики составление квадратов служило
хорошей гимнастикой ума и одно время столь же процветало,
как увлечение кроссвордами в наши дни. Особо усердным хватало
терпения, чтобы составить, например, квадрат 43-го порядка с
числами от 1 до 1849. Один только факт: в 1838 году, когда о
магических квадратах было известно намного меньше, чем теперь, во
Франции был напечатан трактат на эту тему, состоящий из трех
объемных томов. Однако полного описания всех возможных
магических квадратов не получено и до сего времени.

Магические квадраты. Теория
53
Теория
1. Формула магической суммы
Для каждого числа п , где п - порядок магического квадрата,
значение магической суммы S можно определить по формуле,
которую легко вывести.
Во-первых: сумма чисел в каждой строке равна S, а строк
всего п, значит, сумма всех чисел магического квадрата равна n-S.
Во-вторых: последовательность чисел от 1 до п2
представляет собой арифметическую прогрессию, сумма которой
вычисляется по формуле:
ем n-S=
или 5=
. Приравнивая эти два значения,
получали2+1) п3+п
или 5
2 2 2
Таким образом, если число п задано, то число S можно
подсчитать по формуле.
п
S
3
15
4
34
5
65
б
111
7
175
8
260
9
369
10
505
2. Магический квадрат второго порядка не существует
В этом легко убедиться испытанием. Учитывая симметрию
квадрата, абсолютно безразлично, в какой из четырех углов мы
поставим 1, допустим в левый нижний угол. В расположении
чисел по одной диагонали возможны три варианта:
Рис.103
Какое бы теперь число мы ни поставили в левый верхний
угол, суммы чисел в первой строке и первом столбце будут
разными. Вывод: магический квадрат второго порядка не существует.

54
Магические квадраты. Теория
Х2
Хз
У*
У»
Z1
Z2
z3
Рис.104
3. Существует только один магический квадрат 3-го порядка
Представим квадрат 3x3 в общем виде и выясним, какими
могут быть эти девять чисел.
Из формулы магической суммы следует, что
при w=3, £=15. Просуммируем числа второй
строки, второго столбца и обеих диагоналей.
В эту сумму каждое число, кроме у2, входит
по одному разу, а число у2 - четыре раза.
*2 +У2 +Z2 +У1 +у2 +УЗ +*/ +У2 +?3 +*3 +У2 +Z/=4S=60
Перегруппируем слагаемые:
x1+y1+zI+x2+y2+z2+x3+y3+z3+3y2=60
1+2+3+4+.. .+9+3^=60
3^2=15, у2=5.
Однозначно в центре может стоять только число 5.
Число 9 не может стоять в углу. Если, например, xj=9, тогда z3—\
(xI+y2+z3=9+5+z3=l5).
9+y/+z/=15, yi+zi=6, yi<6 и z/<6
9+x2+x3=l5jc2+x3=6, x2<6 и х3<6
Но у нас осталось только три
Рис. 105 Г*3!**! * I числа меньше шести: 2, 3, 4.
Получили противоречие. Следовательно, число 9 должно
находиться в середине строки или столбца (но не в центре
квадрата, там уже стоит число 5).
Квадрат примет вид
9
Х2
*|
У1
5
У»
Zi
Z2
1
х,
Хг
9
5
1
Zi
Zs
Рис. 106
Число 7 не может стоять в одной строке с числом 9, так как
тогда сумма чисел этой строки больше 15. Число 7 не может
стоять в одной строке с числом 1, так как тогда третье число в этой
строке должно быть также семеркой. Выходит, что число 7 не
может стоять в углу и автоматически определяет
противолежащее число, это будет число 3.
х,
7
Хз
9
5
1
Zi
3
Z3
Рис.107
Осталось определить на свои места числа 2, 4, 6, 8. Из них в
одной строке с 9 могут стоять 2 и 4, а в одной строке с 1 - 6 и 8.

Магические квадраты. Теория
55
Кроме того, число 8 не может стоять в одном столбце с
числом 7, так как 8+7 уже равно 15. Значит х3=6, z3=8, */=2, z/=4.
В результате получаем квадрат уже известный нам.
Как видим из наших рассуждений, других вариантов
расстановки просто нет. Все видимые модификации магического
квадрата 3-го порядка получаются в результате поворотов или
симметричных отображений. Таких модификаций всего восемь:
повороты на 90°, 180°, 270° и для каждого, включая исходный
квадрат, - его зеркальное отражение.
4
3
8
8
3
4
9
5
1
1
5
9
2
7
6
6
7
2
2
9
4
4
9
2
7
5
3
3
5
7
6
1
8
8
1
6
6
7
2
2
7
6
1
5
9
9
5
1
8
3
4
4
3
8
8
1
6
6
1
8
3
5
7
7
5
3
4
9
2
2
9
4
Рис. 108
Чтобы оценить уникальность магического квадрата третьего
порядка подсчитаем общее количество разных квадратов,
которые можно составить из чисел от 1 до 9. В математике такие
расположения чисел называются перестановками из п элементов.
Есть формула для подсчета количества различных перестановок.
Представим себе, что клетки квадрата пронумерованы некоторым
образом. В первую клетку мы изначально можем поставить
любое из девяти, имеющихся у нас чисел (9 вариантов заполнения
первой клетки). Во вторую клетку теперь можно поставить любое
из восьми оставшихся чисел, т.е. для каждого из 9 вариантов
заполнения первой клетки, имеется 8 вариантов заполнения второй,
а всего 9-8=72 различных сочетания двух чисел. В третью клетку
можно поставить любое из оставшихся семи чисел и различных
сочетаний трех чисел получается 72-7=504. Продолжая
рассуждать аналогично, мы получаем окончательную цифру
9-8-7-6-5-4-3-2-1=362 880. В это число попадают и все 8
модификаций магического квадрата, полученных от поворотов и
симметрии. Подобные рассуждения позволяют вывести общую формулу
для числа перестановок из п элементов
Рп=п-(п-1)-(п-2) ...-3-2-1 т
Таким образом, чтобы узнать, сколько перестановок можно
составить из п элементов, нужно перемножить все натуральные
числа от 1 до п. Такое произведение обозначается коротко п!
(читается п -факториал). Эти знания могут пригодиться.

56 Магические квадраты. Теория
4.Общее число магических квадратов
Мы уже доказали, что магического квадрата второго порядка
не существует и можно составить единственный магический
квадрат третьего порядка, если не считать его отражения и
повороты. На очереди - квадрат четвёртого порядка. Оказалось, что с
возрастанием порядка, количество различных магических
квадратов увеличивается очень резко. Несимметричных магических
квадратов четвертого порядка существует 880, с учетом
поворотов и отражений это число увеличивается до 7040.
Используя формулу для числа перестановок из п
элементов, мы теперь можем, ради любопытства, посчитать, сколько
всего существует различных квадратов 4-го порядка из чисел от 1
до 16 (вместе с немагическими).
16-15-14-...-3-2-1=20 922 789 880 000
Не смотря на то, что различных магических квадратов 4-го
порядка уже приличное количество - 880, относительно общей
цифры возможных квадратов их уникальность во много раз
выше, чем у единственного квадрата 3-го порядка.
20 922 789 880 000/7040»362 880/8
2 971 987 200»45 360
По последним данным для магических квадратов пятого
порядка существует 275 305 224 возможных вариантов.
Установление формулы для вычисления общего числа различных
магических квадратов более высокого порядка - это одна из труднейших
задач занимательной математики и на данный момент она не
решена. Даже развитие компьютерной техники с миллионами
операций в секунду не очень-то продвинуло людей в этом вопросе.
Порядок
Число
квадратов.
2
0
3
1
4
880
5
275 305 224
6
???
Естественно встает вопрос - как самому составить
магический квадрат четвертого или более высокого порядка?
Правила составления есть, но они, давая вам знания, убьют
интерес к этой теме. Так в свое время возник и пропал интерес к
кубику Рубика. Тысячи людей крутили его в руках, пытаясь
собрать, но как только узнавали готовый алгоритм сборки,
откладывали кубик в сторону и больше к нему не возвращались.
Поэтому не будем перегружать читателей математической
теорией и сменим на время вид деятельности, порешаем задачи.

Магические квадраты. Задачи 1-4
57
2-1 Антимагический квадрат
Есть интересная игра под названием «перевертыши». По
правилам этой игры, каждое понятие заменяется
противоположным по смыслу, насколько это возможно. Следуя принципу,
«Черная луна тайги» означает «Белое солнце пустыни».
Соответственно магический квадрат превратится ...в «антимагический»,
у которого все восемь сумм - по столбцам, строчкам и
диагоналям будут различные.
Расставьте числа от 1 до 9 в клетках квадрата так, чтобы все
8 сумм были различны.
2-2, 2-3, 2-4 Неполный магический квадрат
Итак, мы установили, что магический квадрат третьего
порядка существует только один. Что дальше? Можно добавить
клеток и перейти к четвертому порядку (это ещё впереди), а
можно наоборот - вырезать одну клеточку. Есть три принципиально
различных способа это сделать, соответственно, получается три
задачи с различным расположением вырезанной клетки.
Рис.109
Рис.110
Расставьте цифры от 1 до 8 в клетках
неполного кЬадрата так, чтобы магическая
сумма чисел, стоящих вдоль горизонталей и
вертикалей равнялась 12.
Во всех трех заданиях нужно расставить
числа от 1 до 8, но во втором магическая
сумма должна получиться ещё по большой
диагонали.
В третьем примере магическая сумма
должна получиться по всем направлениям,
включая и обе диагонали.
Рис.111

58
Магические квадраты. Задачи 5-6
2-5 Шутливый квадрат
6
Рис.112
В центре квадрата 3x3 стоит число 6. В
остальные клетки квадрата нужно вписать
оставшиеся цифры от 1 до 9 (кроме уже занятой
цифры 6) так, чтобы сумма в двух верхних
строчках, в двух боковых столбцах, по двум
главным и по четырем коротким диагоналям
была равна 18, и чтобы в каждой клетке стояли
разные цифры.
Квадрат в этой задаче магический только на Ул, так как из
восьми сумм, только шесть равны между собой, но в нем есть
одна большая хитрость, ради которой и приводим его здесь.
Когда в школе, изучив формулу решения квадратного
уравнения, мы решаем одно за другим десять, двадцать квадратных
уравнений - это не задачи, это механическая работа. Настоящая
задача та, в которой есть оригинальный прием, идея, хитрость.
Учиться мыслить нужно на нестандартных задачах.
2-6
Квадрат с довеском
8
8
Е
Удалять клетки дело не хитрое,
пойдем другим путем - добавим
четыре клетки, в которых уже стоят
восьмерки. Требуется заполнить пустые
клетки цифрами от 1 до 8 так, чтобы
сумма чисел в вертикальных и
горизонтальных рядах равнялась 20.
Каждая цифра используется один
раз, кроме цифры 8.
Рис.113
Магические квадраты - это не только развлечение, но и
серьезный раздел математики. Чтобы вы в этом убедились,
приведем в качестве примера три задачи с очень «крутыми»
формулировками. Можете их пропустить, чтобы они не отпугнули от
дальнейшего чтения книги, но ради интереса прочитайте хотя бы
как звучат задания, узнаете мудрёные новые слова, которые можно
при случае ввернуть в разговоре ради прикола.

Магические квадраты. Задачи 7-9 59
2-7 Определитель магического квадрата
Пусть S - сумма всех элементов магического квадрата
третьего порядка, составленного из целых чисел, a D -
определитель этого квадрата, если последний рассматривать как матрицу.
Докажите, что D/S- целое число.
Как видите, чтобы решить эту задачу нужно знать, что
такое матрица и определитель матрицы, а это уже высшая алгебра.
2-8 Пандиагональный гетероквадрат
Математики, забавляющиеся магическими квадратами,
чтобы придать солидность своему занятию, квадрат названный нами
«антимагическим» умудрились назвать - пандиагональный
гетероквадрат. Не знаю, кто это сделал, но закручено сильно.
Пандиагональный гетероквадрат - это такое расположение
первых п2 натуральных чисел в виде квадрата, при котором
никакие две суммы чисел, расположенных вдоль любой строки,
столбца или диагонали (прямой или ломаной), между собой не
совпадают.
Существует ли такое п, при котором эти 4-п сумм
совпадают с последовательными целыми числами?
Примечание: под ломаной диагональю понимается любое
подмножество, содержащее п чисел, которые окажутся
расположенными на одной прямой диагонали двух приставленных друг к
другу одинаковых квадратов.
2-9 Гномон - магические квадраты
Квадрат 3x3 называется гномон-магическим, если суммы
чисел, составляющих квадраты 2x2, которые остаются после
удаления из исходного квадрата одного из четырех уголков
(гномонов), равны между собой.
Покажите, что у гномон-магического квадрата третьего
порядка суммы чисел, стоящих на двух диагоналях, равны между
собой. Сохраняется ли это свойство для более высоких порядков?
Мы совершили небольшой экскурс в серьезную
математику, где не только суммы чисел считают, но и доказывают
некоторые утверждения. Но если вы это пропустили, никто в «гномон»,
т.е. в угол, вас не поставит, спокойно продолжайте читать дальше.

60
Магические квадраты. Задачи 10-12
2-10
Крест из квадратов
Рис.114
На рисунке изображен крест,
составленный из четырех квадратов
3x3. Какое число нужно поставить в
центральную клетку, чтобы суммы
трех больших вертикальных
столбцов, трех горизонтальных строк и
каждого из квадратов 3x3 были
равны 30? Из условия понятно, что числа
могут повторяться. Выполните такое
же задание для сумм 48 и 66. Какая
сумма получится, если в центральную
клетку поставить цифру 5?
2-11
1
15
10
8
14
4
5
11
7
9
16
2
12
6
3
13
Неправильный магический квадрат
На рисунке изображен магический
квадрат, составленный из чисел от 1 до 16 с
магической суммой 34. Предположим, что
вам запрещено использовать числа 2 и 15,
но вместо этого вы можете повторить
любые два числа, уже использованные ранее.
Как следует расположить числа,
чтобы в новом квадрате магическая
сумма по-прежнему равнялась 34. Какими
числами заменить 2 и 15?
Рис.115
2-12
Сколько раз по 66?
1
30
4
31
8
27
5
26
29
2
32
3
28
7
25
6
Этот магический квадрат составлен
из непоследовательных чисел, но любой
вертикальный, горизонтальный ряд, обе
диагонали и даже любые четыре
смежные клетки дают в сумме 66.
Попробуйте сосчитать, сколькими
различными способами вы сможете в
этом квадрате получить сумму 66?
Рис.116

Магические квадраты. Составление
61
Как самому составить магический квадрат
Квадрат 3x3 мы заполняли, следуя определенным
логическим рассуждениям, находя для каждого числа единственно
возможное место его расположения. Это была «штучная» работа.
Квадратов четвертого порядка 880, не считая модификаций, и
здесь разных подходов к составлению должно быть тоже много,
не говоря уже о высших порядках.
Метод Баше для квадратов нечетного порядка
Самый простой прием составления магических квадратов
нечетного порядка придумал в XVII веке французский математик
Клод Гаспар Баше. Он применим и к квадрату 3x3 , но нет
смысла снова его составлять, поэтому изучение метода Баше начнем с
квадрата пятого порядка.
1. Квадрат дополняется вспомогательными клетками с
четырех сторон «лесенкой» или «террасами» как показано на
рисунке 117.
2.Последовательные числа от 1 до п2 выписываются ряд за
рядом в направлении, параллельном одной из диагоналей
квадрата.
3.Числа, оказавшиеся за рамками квадрата, нужно ввести
внутрь. Для этого «террасы» мысленно вдвигаем в квадрат
так, чтобы они примкнули к противолежащим сторонам
квадрата (Рис. 118).
1
2
6
3
7
11
4
8
12
16
5
9
13
17
21
10
14
18
22
15
19
23
20
24
25
1
2
6
3
7
11
8
12
4
16
9
13
5
17
21
14
18
10
22
15
19
23
20
24
25
Рис.117
Рис.118

62
Магические квадраты. Составление
3
20
7
24
11
16
8
25
12
4
9
21
13
5
17
22
14
1
18
10
15
2
19
6
23
Вот какой квадрат 5-го порядка
получается в итоге. В нем можно узнать
повернутый магический квадрат Марса.
Способ Баше очень прост, на практике
его можно применять для построения
нечетных квадратов сколь угодно высокого
порядка, но он дает только один из множества
возможных вариантов.
Рис.119
В этом месте сделаем небольшое лирическое отступление,
переводящее красоту чисел в красоту линий, а затем вернемся к
рассмотрению других способов составления магических квадратов.
Узоры магических линий
Американский архитектор Клод Ф. Брэгдон обнаружил,
что, соединив в порядке возрастания чисел центры клеток
магического квадрата ломаной линией, в большинстве случаев
получается изящный узор. Для квадратов больших порядков можно
соединять клетки только с четными или только с нечетными
числами. Полученные таким образом «магические линии», Брэгдон
использовал как образцы рисунков для тканей, книжных
обложек, архитектурных украшений и декоративных заставок.
Вот примеры подобных орнаментов из магических линий.
Для придания узору завершенности, соединим в конце последнее
число с первым.
4
3
8
9
5
1
2
7
6
Рис. 120
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис. 121

Магические квадраты. Составление
63
3
20
7
24
11
16
8
25
12
4
9
21
13
5
17
22
14
1
18
10
15
2
19
6
23
Рис. 122
Интересный узор можно получить, если соединять
линиями (не обязательно прямыми) все группы чисел, образующих при
сложении магическую сумму.
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис. 123
1
9
12
20
23
15
18
21
4
7
24
2
10
13
16
8
11
19
22
5
17
25
3
6
14
Рис. 124

64
Магические квадраты. Составление
Вернувшись снова к способу Баше для составления
магических квадратов, можно увидеть общие черты в узорах
магических линий в квадратах разного порядка, составленных этим
методом. Сравните характер линий уже показанных квадратов
третьего и пятого порядка, с построенным теперь квадратом
седьмого порядка.
10
41
16
15 4?
22
28
11
17
В
23
2
12
18
24
30
13
19
25
31
13
43
1*5
20
26
32
14
38
27
33
39
21
44
28
34
40
16
46
35
42
47
48
49
Рис. 125
Каждый метод построения магических квадратов имеет
свой характерный рисунок линий. Изучая другие методы, вы
убедитесь в этом.
Метод де ла Лубера для квадратов нечетного порядка
Еще один, довольно простой, способ составления
магических квадратов нечетного порядка в одних книгах называется
индийским (якобы его знали в Индии ещё до нашей эры). В
других, авторство признается за А. де ла Лубером, который служил
посланником французского короля Людовика XIV в Сиаме (ныне
Таиланд) в период 1687-1688 г.г.
Этот способ определяется следующими правилами:
1. В середине верхней строки пишут 1, а в самом низу
соседнего справа столбца — 2.
2. Следующие числа пишут по порядку в диагональном
направлении вправо вверх.
3. Дойдя до правого края квадрата, переходят к крайней левой
клетке ближайшей вышележащей строки.

Магические квадраты. Составление
65
4. Дойдя до верхнего края квадрата, переходят к самой нижней
клетке соседнего справа столбца. (Дойдя до правой верхней
угловой клетки, переходят к левой нижней, если она не
занята, иначе см. правило 5.)
5. Дойдя до уже занятой клетки, переходят к клетке, лежащей
непосредственно под последней заполненной клеткой.
6. Если последняя заполненная клетка находится в нижнем
ряду квадрата, переходят к самой верхней клетке в том же
столбце.
1
2
3
4
1
2
-3
4
10
\
«4
Щ—.
1
7
\
\
17
23
4
10
11
24
5
6
12
18
1
7
13
19
25
8
14
20
21
2
15
16
22
3
9
Рис. 126
Магические линии у квадратов, составленных этим
способом, отличаются от линий метода Баше, но и те, и другие
симметричны относительно центра квадрата.
17
23
4
10
11
24
5
6
12
18
1
7
13
19
25
8
14
20
21
2
15
16
22
3
9
Рис. 127
Рис.128
3039
38
47
46
13
21
22
14
23
31
48
8
16
1524
32
40
9
1726
25
33
41
49!
10
18
34
42
43
19
2729
35
44
11
28
37
3645
12
20

66
Магические квадраты. Составление
Если число клеток квадрата не делится на 3, можно
начинать составление квадрата не по правилу 1, а по другому правилу.
Единицу можно написать в любой клетке диагонального ряда,
идущего от средней клетки крайнего левого столбца к средней
клетке самой верхней строки квадрата. Все последующие числа
вписываются согласно правилам 2-5.
Это замечание дает возможность составить по индийскому
способу не один, а несколько различных квадратов.
19
25
1
7
13
21
2
8
14
20
3
9
15
16
22
10
11
17
23
4
12
18
24
5
6
18
24
5
6
12
25
1
7
13
19
2
8
14
20
21
9
15
16
22
3
11
17
23
4
10
Рис. 129
Одновременно с построением квадратов будем теперь
время от времени вычерчивать их магические линии, которые дают
схематическую картинку для быстрого установления симметрии
в расположении чисел или отсутствия таковой.
Рис.130
Квадраты по-прежнему магические, но симметрия, а с ней и
красота, магических линий потеряна.
Магические квадраты порядка двойной четности
Рассмотрев два метода построения нечетных магических
квадратов, пора перейти к четному порядку. Но начнем с
квадратов, порядок которых число кратное четырем, их называют
квадратами порядка двойной четности. Для изучения
следующих методов построения возьмем квадрат четвертого порядка,
чтобы за количеством чисел не потерять содержание.

Магические квадраты. Составление
67
Диагональный метод
X
5
9
US
2
и®
14
3
ц
15
8
12
5
9
2
НИ
14
3
fl®
(В
15
US
8
12
и
Рис. 131
1. Выпишите все числа от 1 до п2 по порядку в строках
квадрата.
2. Числа, стоящие в диагональных клетках, поменяйте
местами с числами симметрично стоящими к ним
относительно центра квадрата.
Эти правила применимы для построения магического
квадрата любой двойной четности. Только обмену подлежат
числа, стоящие на диагоналях, каждого из квадратов 4x4,
составляющих большой квадрат. Но центром симметрии по-прежнему
является центр большого квадрата.
ч
9
17
25
33
41
49
si
2
т
26
34
42
50
58
3
11
13
27
35
43
51
59
'&
1?
20
28
36
44
52
60
X
13
21
29
?1;
45
5J3
И
6
22
30
38
46
54
62
7
15
31
39
ш
55
63
8
16
24
32
46
48
56
64
9
17
4® 26
41
8
55
4746
£2 34
4915
58
з киот
М1213
27
35
22
114
59
2021
37
29
52
36
28
44 45
53
6
43
30
38
19
-0-0
50
4S2
31
39
10
62 63
Рис. 132
Рис.133

68
Магические квадраты. Составление
Безымянный метод
Этому методу никто не умудрился дать название или, на
крайний случай, своё имя, поэтому оставим его безымянным.
1. Впишите в квадрат карандашом все числа от 1 до 16 по
порядку. В полученном квадрате диагональные ряды дают
одинаковую сумму равную 34, т. е. как раз ту, которая должна
быть в магическом квадрате четвертого порядка (см.
таблицу). Но строки и столбцы имеют другие суммы.
2. Разделите данный квадрат на четыре одинаковых
квадратика меньшего размера.
3. В левом верхнем квадратике
обведите кружком половину
всех чисел так, чтобы в каждом
столбце и каждой строке этого
<| квадратика была отмечена
ровно половина входящих в них
чисел. Это можно сделать
различными способами.
4. В правом верхнем квадратике
обведите числа симметричные
2 относительно вертикальной оси
тем, которые были отмечены в
о левом верхнем квадратике.
Л 5. Теперь поменяйте местами,
отмеченные, симметричные
относительно центра квадрата,
числа.
По правилу 3 мы могли
отметить другие числа в верхнем левом
5 квадратике, причем при порядке 4 есть
всего два варианта, а при порядке
квадрата 8 - вариантов выполнения
правила 3 значительно больше.
1
5
9
13
2
6
10
14
3
7
11
15
4
8
12
16
1
13
#
f ^\
ы
4
s)
ft
16
1
12
8
13
14
6
10
3
15
7
11
2
4
9
5
16
Рис.134

Магические квадраты. Составление
69
Магические квадраты порядка простой четности
Рассмотрим метод построения магических квадратов и-го
порядка при п=2(2т+1)9т.е. п=6, 10, 14, 18, ...
1. Разделим исходный квадрат на четыре
равных квадрата А, В, С, D.
Рис.135
2. Построим в квадрате А по методу де л а Лубера магический
квадрат из чисел от 1 до п2/4. Аналогичные магические
квадраты построим в квадратах D (от п2/4 до п2/2), С (от
2 до Зп2/4\ В (от Зп2/4+1 до п2).
А
В
С
D
3. В средней строке квадрата А возьмем m клеток от
середины строки к левому краю, а в каждой из оставшихся строк
возьмем m клеток, ближайших к левому краю квадрата А;
числа в этих клетках поменяем местами с числами в
соответствующих клетках квадрата В.
4. Возьмем числа в клетках каждого из т-1 правых крайних
столбцов квадрата С и поменяем их местами с
соответствующими числами квадрата D.
Получившийся в результате квадрат будет магическим.
Проиллюстрируем эти правила при п=в и п=№ .
8
3
4
35
30
31
1
5
9
28
32
36
6
7
2
33
34
29
26
21
22
17
12
13
19
23
27
10
14
18
24
25
20
15
16
11
35
3
31
8
30
4
1
32
9
28
5
36
6
7
2
33
34
29
26
21
22
17
12
13
19
23
27
10
14
18
24
25
20
15
16
11
Рис. 136
Построении магического квадрата 6-го порядка:
А (1-9); D (10-18); С (19-27); В (28-36), п=6^ /и=1-> т-1=0,
поэтому правило 4 не применяется.

70
Магические квадраты. Составление
Построение магического квадрата 10-го порядка:
17
23
4
10
11
92
98
79
85
86
24
5
6
12
18
99
80
81
87
93
1
7
13
19
25
76
82
88
94
100
8
14
20
21
2
83
89
95
96
77
15
16
22
3
9
90
91
97
78
84
67
73
54
60
61
42
48
29
35
36
74
55
56
62
68
49
30
31
37
43
51
57
63
69
75
26
32
38
44
50
58
64
70
71
52
33
39
45
46
27
65
66
72
53
59
40
41
47
28
34
92
98
4
85
86
17
23
79
10
11
99
80
81
87
93
24
5
6
12
18
1
7
88
19
25
76
82
13
94
«0
8
14
20
21
2
83
89
95
96
77
15
16
22
3
9
90
91
97
78
84
67
73
54
60
61
42
48
29
35
36
74
55
56
62
68
49
30
31
37
43
51
57
63
69
75
26
32
38
44
50
58
64
70
71
52
33
39
45
46
27
40
41
47
28
34
65
66
72
53
59
А (1-25), D (26-50), С (51-75), В (76-100),
п=Ю ->т=2
Рис. 137
Метод окаймления магических квадратов
Этот метод построения магических квадратов
произвольного порядка придумал Френикл. Для построения магического
квадрата w-ro порядка, сначала строят, тем или иным способом,
магический квадрат(л-2)-го порядка. Затем добавляют к каждому
его числу некоторое целое число т, вычисляемое по
определенной формуле и, наконец, окаймляют полученный квадрат рамкой
из оставшихся чисел, причем так, чтобы квадрат, к которому мы
в результате придем, был магическим.
Этим способом из квадрата 3-го порядка можно
последовательно получить магические квадраты 5-го, 7-го, 9-го и т.д.
порядков, т.е. квадраты любого нечетного порядка. Подобным
образом из квадрата четвертого порядка можно последовательно
получить все квадраты четного порядка.
Рассмотрим конкретный пример. Возьмем за основу
единственный магический квадрат третьего
порядка и построим магический квадрат 5-го
порядка, а затем 7-го порядка.
^2
Вычислим по формуле w=2w-2=8.
Рис.138

Магические квадраты. Составление
71
23
22
ii
8
7
1
12
11
16
25
2
17
13
9
24
20
10
15
14
6
19
4
21
18
3
Добавим к каждому числу этого
квадрата w=8, тогда сумма чисел в каждой
строке, в каждом столбце и на каждой диагонали
станет равной iS/=(w2+1)(w-2)/2=39. Из чисел
ряда (1,..., 25) остались 1, 2, 3,..., 8 и
дополнительные к ним 25,24,..., 18 (1, 2,..., 2и-2 и п2у
Рис.139
Эти числа размещают в 4(w-l)=16 граничных клетках таким
образом, чтобы дополнительные числа стояли на противоположных
концах каждой строки, каждого столбца и каждой диагонали - это
позволяет обеспечить равенство суммы Sn=(n2+l)-n/2 чисел вдоль
каждого направления. Остается только добиться, чтобы сумма
чисел и вдоль каждой из граничных линий была равна той же
самой величине, но такое их расположение легко получить
простым перебором. Хотя для расположения чисел в граничных
клетках были предложены различные правила, попробуйте
увидеть их сами из приведенных примеров.
Продолжим для w=7, 2л-2=12.
23
22
5
а
7
1
12
11
16
25
2
17
13
9
24
20
10
15
14
6
19
4
21
18
3
7
12
11
10
1
35
34
17
20
19
2
13
24
23
28
37
3
14
29
25
21
36
32
22
27
26
18
В
31
16
33
30
15
9
5
6
4
46
45 35
44 34
11
10
17
12 20
19
49
13
24
23
28
48
1432
29
25
21
3736
47
42
22
27
26
18
41
31
16
15
40
6
33 43
30 38
39
Рис. 140
Синтетический метод Ф. де ла Ира
Метод Ф. де ла Ира (1640-1718) основан на двух
первоначальных квадратах. На рисунке 141 показано, как с помощью этого
метода строится квадрат 5-го порядка. В клетки первого квадрата
вписываются числа от 1 до 5 так, что число 3 повторяется в
клетках главной диагонали, идущей вправо вверх, и ни одно число не
встречается дважды в одной строке или в одном столбце. (О таких
квадратах речь еще впереди). То же самое мы проделываем с
числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь
повторяется в клетках главной диагонали, идущей сверху вниз.

72
Магические квадраты. Составление
1
2
5
4
3
2
5
3
1
5
4
3
1
2
3
1
2
5
3
1
2
5
10
20
15
0
5
5
10
20
15
0
0
5
10
20
15
15
0
5
10
20
20
15
0
5
10
11
22
20
4
8
7
15
24
18
1
5
9
13
21
17
19
3
6
12
25
23
16
2
10
14
Рис. 141
Поклеточная сумма этих двух квадратов образует
магический квадрат. Этот метод используется и при построении
квадратов четного порядка.
Составные магические квадраты
Если известен способ построения квадратов порядка т и
порядка и, то можно построить квадрат порядка тхп. Суть этого
способа показана на рисунке. Здесь т = 3 и п = 3. Исходный
квадрат 3-го порядка (с числами, помеченными штрихами)
строится методом де ла Лубера. В клетку с числом Г (центральную
клетку верхнего ряда) вписывается квадрат 3-го порядка из чисел
от 1 до 9, также построенный методом де ла Лубера. В клетку с
числом 2' (правую в нижней строке) вписывается квадрат 3-го
порядка с числами от 10 до 18; в клетку с числом З1 — квадрат из чисел
от 19 до 27 и т.д. В результате мы получим квадрат 9-го порядка.
Такие магические квадраты называются составными.
3'
т
9
6"
Т
2
71
6668
67
26
21
22
35
30
31
6469
72
19
23
27
28
32
36
70
65
24
25
20
33
34
29
8
44
39
40
80
75
76
9
37
41
73
77
81
6
42
4538
78
79
74
534651
4850
495447
6255
435759
17
13
5863
10
1214
18
52
60
61
56
15
16
11
Рис. 142
Так как квадрата 2-го порядка не существует, то этим
методом можно построить квадраты порядков 3x3=9, 3x4=12,
3x5=15, 4x4=16, 3x6=18, 4x5=20, 3x7-21 и т.д.

Магические квадраты. Разнообразие
73
Разнообразие квадратных таблиц чисел
Так как общее количество магических квадратов, начиная с
четвертого порядка очень велико, особое внимание привлекают
построения квадратов, удовлетворяющих кроме основных
условий (т.е. равенство сумм чисел по строкам, столбцам и двум
диагоналям) тем или иным дополнительным условиям.
Симметрические квадраты
Определение. Если в магическом квадрате п-го порядка
сумма любых двух чисел, расположенных симметрично
относительно центра квадрата постоянна и равна п2+1, то он
называется симметрическим (или связанным).
Таковым является квадрат 4-го порядка, изображенный на
гравюре «Меланхолия» немецкого художника Альбрехта Дюрера.
16+1=10+7=6+11=4+13=42+1=п2+1
ш
5
Ш
4
3
10
6
15
2
11
7
14
13
®
12
Рис. 143
Дополнительное условие позволяет выделить в квадрате
много групп из четырех чисел помимо строк, столбцов и главных
диагоналей, сумма которых также равна магической постоянной
квадрата 34. Таковы, например, четыре числа, расположенные в
вершинах всего квадрата (16+13+1+4), четыре числа в вершинах
каждого квадрата 3-го порядка (16+2+7+9, 3+13+12+6,
5+11 + 14+4, 10+8+1+4) и четыре числа в каждом из маленьких
квадратов 2x2, расположенных в углах большого квадрата
(16+3+10+5, 2+13+8+11, 9=6+15+4, 7+12+1+14).
Симметрическими будут все квадраты, построенные по
методу де ла Лубера и все квадраты порядка двойной точности,
построенные по диагональному методу. Вместе с тем доказано,
что симметрических магических квадратов порядка простой
четности (/7=6; 10; 14...) не существует. Особо обратите
внимание на 6-ой порядок, в магических квадратах он часто не
поддается тем операциям, которые возможны для других порядков.

74
Магические квадраты. Разнообразие
Совершенные квадраты
Определение. Магический квадрат называется
совершенным, если условие равенства сумм кроме обычных двух диагоналей
квадрата дополнительно распространяется на распадающиеся на
части или «ломаные» диагонали.
Такие магические квадраты получили
много разных названий: многодиагональные,
пандиагоналъные, изящные, а чаще их
называют «дьявольские».
О «ломаных» диагоналях мы уже
упоминали в задаче 2-8. «Ломаную» диагональ
можно восстановить, если поставить рядом
два одинаковых квадрата.
Магический квадрат не теряет своего
«совершенства», если над ним производить
следующие преобразования:
1. особую перестановку клеток по
следующей схеме:
X
н
/
10
yi
8
3
X
13
у
/
Ж
X
Рис. 144
№
Н
tf
В*
л.
Б
с
f
t
2.
3.
4.
Поворот на 90°, 180°, 270° Рис. 145
Отражение
Его можно разрезать на две части вдоль линий,
разделяющих любые две соседние строки или два
соседних столбца, а затем эти две части поменять
местами.
Путем одного горизонтального разреза и одного
вертикального разреза и описанного переноса любой элемент квадрата
можно поместить в любую заранее заданную клетку.
Единственный магический квадрат третьего порядка не
совершенный, а из 880 магических квадратов четвертого порядка
совершенных - 48. Известно также, что совершенных магических
квадратов пятого порядка 3600 и более 6,5 миллиардов
совершенных квадратов 8-го порядка. Совершенных квадратов порядка
простой четности (п=6; 10; 14...) не существует. Не везет этой
простой четности на качество. Вот такие исключения и приводят
к мистическим воззрениям на некоторые числа.

Магические квадраты. Разнообразие
75
Совершенные квадраты пятого и седьмого порядка
Рис. 146
7
13
19
25
1
20
21
2
8
14
3
9
15
16
22
11
17
23
4
10
24
5
6
12
18
26
44
20
38
14
32
1
21
39
8
33
2
27
45
9
34
3
28
46
15
40
4
22
47
16
41
10
35
48
17
42
11
29
5
23
36
12
30
6
24
49
18
31
7
25
43
19
37
13
Рис. 147
Чтобы построить эти совершенные квадраты, мы можем
поставить 1 в любую клетку. Затем, выполняя посяедовательные
шаги, подобные ходу коня - одна клетка вправо и две клетки
вверх, вписываем по порядку числа 2, 3, 4, 5,... в каждую клетку
до тех пор, пока не придем в уже занятую клетку. Тогда, подобно
шахматной ладье, делаем ход на одну клетку вниз - и так
продолжаем, пока не заполним весь квадрат. Причем, выходя при
очередном шаге через верхнюю или правую границы квадрата,
возвращаемся в него, соблюдая количество клеток шага,
соответственно через нижнюю или левую границы.

76
Магические квадраты. Разнообразие
Развлечения Бенджамина Франклина
Составлением магических фигур, причем не только
квадратов, увлекался в свободное время американский общественный
деятель, дипломам ученый Бенджамин Франклин (1706-1790).
Ему принадлежат интересные находки в этой области. Приведем
для примера два его достижения в области «квадратостроения»:
квадраты 8-го и 16-го порядка. В дальнейшем рассмотрим,
созданные им магические круги.
52
14
53
•
61
3
ZmLm
nn
63
1
4
pi
Ж
59
v
1
2
64
5б!
15
49|
l±o
[46
^1
кл»
41
18
29
35,
28
ц
33
36
30
3^
|27
34
1»
4S
19
44
^4
Рис. 148
Магическая сумма этого квадрата равна 260, но он
обладает рядом дополнительных свойств:
а Сумма чисел в каждой половине любой строки и в
каждой половине любого столбца равняется 130, что
составляет половину магической суммы
а Четыре числа, стоящие в углах, в сумме с четырьмя
числами, стоящими ё центре квадрата, дают 260
а Если разбить данный квадрат 8x8 на квадратики 2x2,
то в каждом из них сумма чисел будет равна 130
а В любом прямоугольнике 2x4 сумма чисел равна 260
а Сумма чисел по наклонному ряду, идущему от числа
16 вправо-вверх до числа 10, а далее по наклонному
ряду, идущему от числа 23 вправо-вниз до числа 17
равна 260. То же самое верно для каждого ряда из
восьми чисел, параллельного описанному. Это
свойство сохраняется для таких же ломаных,
построенных от любой из трех оставшихся сторон квадрата.

Магические квадраты. Разнообразие
77
Еще более удивителен квадрат 16x16, который. Франклин
составил за один вечер. Он по праву гордился своим творением
и писал, «что этот квадрат является самым магически-
магическим из всех магических квадратов, составленных когда-
либо каким-либо магом».
200
58
198
60
201
55
203
53
205
51
207
49
196
62
194
64
217
39
219
37
216
42
214
44
212
46
210
48
221
35
223
33
232
26
230
28
233
23
235
21
237
19
239
17
228
30
226
32
249
7
251
5
248
10
246
12
244
14
242
1G
253
3
255
1
8
250
6
252
9
247
11
245
13
243
15
241
4
254
2
256
25
231
27
229
24
234
22
236
20
238
13
240
29
227
31
225
40
218
38
220
41
215
43
213
45
211
47
209
36
222
34
224
57
199
59
197
56
202
54
204
52
206
50
208
61
195
63
193
72
186
70
188
73
183
75
131
77
179
79
177
68
190
66
192
89
167
91
165
88
170
86
172
84
174
82
176
93
63
95
161
104
154
102
156
105
151
107
149
109
147
111
145
100
158
98
160
121
135
123
133
120
138
118
140
116
142
114
144
125
131
127
129
136
122
134
124
137
119
139
117
141
115
143
1'3
132
126
130
128
153
103
155
101
152
106
150
108
148
110
146
112
157
99
159
97
168
90
166
92
169
87
171
85
173
83
175
81
164
94
162
96
185
71
187
69
184
74
182
76
180
78
178
80
89
67
191
65
Рис. 149
Магическая сумма равна 2056.
Если вырезать в листе бумаги квадратное отверстие 4x4 и
наложить этот лист на большой квадрат так, чтобы 16 чисел
большого квадрата попали в прорезь, то сумма этих чисел будет
одна и та же, равная 2056, куда бы мы ни передвигали наш лист с
прорезью по большому квадрату. Этому же значению равны
суммы вдоль ломаных, как и в квадрате 8-го порядка, от 64 до 52
вверх-вправо и от 77 вниз-вправо до 65, а также по ломаным
параллельным этой й полученным из них поворотами на 90°, 180°, 270°.

78
Магические квадраты. Разнообразие
Магические квадраты из непоследовательных чисел
Классические магические квадраты строятся для
последовательных чисел от 1 до п2, но магическим называется также
квадрат, построенный из любых других чисел, если только
сохраняется равенство сумм по строкам, столбцам и двум
главным диагоналям. Натуральный ряд чисел - это строгий порядок,
магический квадрат - это четкая закономерность, выбирая другие
числа для его составления, насколько мы свободны в своем
выборе, допустим ли здесь полный хаос или есть определенные рамки?
Последовательные числа натурального ряда, являются
арифметической прогрессией с первым членом, равным единице
и разностью равной единице. Обобщая, легко доказать, что
магический квадрат, например, третьего порядка можно составить из
9 порядковых членов любой арифметической прогрессии с
первым членом а и разностью d, т. е. фактически построить его
исходя первоначально из двух чисел (a, d). Магическая сумма в
этом случае определяется по формуле S=3-(a+4-d). Расставить
члены прогрессии по клеткам квадрата можно по методу Баше.
Возьмем, для примера, а=5, d=2, соответствующий ряд чисел:
5, 7,9, 11,13,15,17, 19,21, образует следующий магический квадрат.
11
9
19
21
13
5
7
17
15
Рис. 150
А можно ли составить магический квадрат из чисел не
являющихся членами одной арифметической прогрессии?
Наиболее общее утверждение о существовании магического
квадрата третьего порядка из непоследовательных чисел звучит
так: для существования магического квадрата из 9 попарно
различных чисел необходимо и достаточно, чтобы данные числа
имели вид:
а, а+п, а+2-п, a+d, a+n+d, a+2-n+d, a+2-d, a+n+2-d, a+2-n+2-d.
Особенностью этих чисел является то, что их можно
рассматривать как три разных арифметических прогрессии с одной и
той же разностью d или же, как три разные прогрессии с одной и
той же разностью п. Рамки расширились, но порядок остался!

Магические квадраты. Разнообразие
79
Доказательством достаточности условия существования
магического квадрата из представленных чисел является сам
такой квадрат, составленный
по методу Баше.
Доказательство второй
части утверждения, о
необходимости, уже развлечением
не назовешь, и приводить
здесь его мы не будем. Для
дотошных читателей: см.
журнал «Математика в
школе» 4-5.1992 г. Рис.151
Показанный квадрат однозначно определяется тремя
числами. Можно записать его несколько иначе, если исходить из
заранее заданной магической суммы. Магический квадрат третьего
порядка можно составить с любой, заданной магической суммой,
при условии, что это число делится на три. Если магическая
сумма равна 3-я, то квадрат однозначно определяется тр£мя числами
а, Ь, п, причем числа а и b вы выбираете сами. Клетки квадрата
заполняются в соответствии с формулами.
a+d+2n
a+2d
a+n
а
a+d+n
a+2d+2n
a+2d+n
a+2n
a + d
a
4n-2a-b
a+b-n
b
n
2n-b
3n-a-b
2a+b-2n|
2n-a
Рис.152
Правда, выбирая произвольные числа а ,Ь можно выйти в
область отрицательных чисел, ведь в формулах есть вычитание.
У рассмотренного квадрата имеется много дополнительных
свойств, в частности: суммы квадратов чисел первой и последней
строки равны между собой. Такое же равенство справедливо для
первого и последнего столбцов. Это можно доказать
аналитически:
a2+b2+(3-n-a-b)2 = (a+b-n)2+(2-п-Ь)2+(2'П-а)2, далее
проверьте равенство, раскрыв скобки, сами.
Если внимательно присмотреться, то можно отыскать и
другие интересные равенства в этом квадрате.

80
Магические квадраты. Разнообразие
Магические квадраты из простых чисел
В квадрате, составленном из арифметической прогрессии
(5, 2) случайно оказалось шесть простых чисел, а если сделать это
не случайностью?
Определение. Натуральное число называется простым,
если оно делится только на единицу и само на себя.
Также как магический квадрат диковинка среди множества
квадратных числовых таблиц, простые числа - изюминки среди
множества натуральных чисел. Естественно возникает желание
совместить эти два понятия, т.е. попробовать составить
магический квадрат не из последовательных чисел, а только из одних
простых. Первый подобный квадрат встречается в книгах
известных мастеров головоломок Сэма Лойда и Генри Дьюдени. Кто из
них был первым, вопрос спорный и для нас не главный.
67
13
31
1
37
73
43
61
7
Рис. 153
Магическая сумма равна 111, с меньшей суммой из
простых чисел магического квадрата нет. Однако простые числа в
квадрате не последовательные.
В показанном далее квадрате четвёртого порядка
пропущены простые числа 43, 59, 61, 67.
3
53
17
29
71
11
13
7
5
37
41
19
23
1
31
47
Рис. 154
Возникает вопрос: можно ли построить магический
квадрат из последовательных нечетных простых чисел? Простое
число 2 нельзя использовать, т.к. с ним не получится магический
квадрат. (Как вы думаете почему?)
В 1913 году Дж. Н. Манси составил квадраты из простых
чисел 5-го, 6-го,..., 12-го порядка и только в последнем добился,
чтобы простые числа шли без пробелов в их ряду.

Магические квадраты. Разнообразие
81
Манси доказал, что наименьший магический квадрат из
последовательных простых чисел должен иметь порядок 12.
Вот этот магический квадрат, составленный из 144 первых
простых нечетных чисел. S=4514.
1
89
97
223
367
349
503
229
509
661
659
827
823
83
227
653
379
359
523
491
199
101
673
3
821
211
103
499
521
353
233
373
73
643
677
7
809
79
107
197
383
647
337
487
541
239
683
5
811
641
193
109
241
389
547
461
347
691
71
13
797
631
557
113
467
331
397
251
191
701
67
11
19
619
719
563
257
317
421
443
181
127
61
787
29
709
727
479
263
311
17
464
569
131
47
769
313
617
607
173
269
409
401
137
577
179
59
773
31
53
139
761
167
307
271
439
571
613
743
419
23
43
757
587
601
293
431
457
163
277
733
149
37
739
281
157
599
449
433
283
593
151
41
751
Рис.155
Все, показанные здесь магические квадраты из простых
чисел, имеют существенный математический недостаток - в них
входит единица, которая, строго говоря, не является простым
числом. Это побуждает математиков продолжать поиски более
совершенных вариантов.
В настоящее время найдено более 100 арифметических
прогрессий из 9 и более простых чисел. Из членов каждой такой
прогрессии можно составить магический квадрат, например:
829
619
1669
1879
1039
199
409
1459
1249
Рис.156

82
Магические квадраты. Разнообразие
Здесь я/=199, d=2lO, сумма трех чисел по всем
направлениям равна 3117.
В 1969 году математик S. С. Root (США) нашел
арифметическую прогрессию из 16 простых чисел, первый член которой
aj=2 236 133 941, разность d=223 092 870. Получается следующий
квадрат с суммой 15 637 321 864.
2 236 133 941
4 690 155 511
3 797 784 031
4 913 248 381
5 359 434 121
3 351 598 291
4 243 969 771
2 682 319 681
5 136 341 251
3 574 691 161
4 467 062 641
2 459 226 811
2 905 412 551
4 020 876 901
3 128 505 421
5 582 526 991
Рис.157
А вот какой интересный магический квадрат из простых
чисел был опубликован в журнале «Математика в школе» в 1995
году. Его автор Берколайко С. Т. назвал свое произведение
«Великолепная семерка».
Это не просто магический квадрат 7x7 из простых чисел, он
содержит в себе магический квадрат 5x5, который, в свою
очередь, содержит в себе магический квадрат 3x3.
Все эти квадраты имеют общее центральное число 3407.
Все 49 чисел, входящие в квадрат оканчиваются цифрой 7 и
представимы в виде ЗОп +17.
1847
2267
2897
3557
4337
4817
4127
6257
1427
947
4157
5717
4767
557
6197
5987
2357
4397
3467
827
617
3677
5927
4517
3407
2297
887
3137
1307
1667
3347
2417
4457
5147
5507
1877
2027
5867
2657
1097
5387
4937
2687
4547
3917
3257
2477
1997
4967
Рис. 158
С. Т. Берколайко принадлежит авторство теоремы о
необходимости и достаточности существования магического квадрата
их 9 попарно различных чисел и множество других находок в
этой области занимательной математики.

Магические квадраты. Разнообразие
83
Двойные и тройные магические квадраты
Для некоторых значений
и, не меньше восьми, можно
построить такой магический
квадрат п-го порядка, что если
числа в каждой его клетке
заменить их квадратами, то
получившийся в результате
квадрат также будет
магическим. Такие магические
квадраты называют двойными.
16
26
1
23
38
52
43
61
41
63
40
50
3
21
14
28
36
54
45
59
10
32
7
17
5
19
12
30
47
57
34
56
27
13
22
4
49
39
64
42
62
лл
51
37
24
2
25
15
55
33
58
48
29
11
20
6
18
8
31
9
60
46
53
35
Рис. 159
256
676
1
529
1444
2704
1849
3721
1681
3969
1600
2500
9
441
196
784
1296
2916
2025
3481
100
1024
49
289
25
361
144
900
2209
3249
1156
3136
729
169
484
16
2401
1521
4096
1764
3844
1936
2601
1369
576
4
625
225
3025
1089
3364
2304
841
121
400
36
324
64
961
81
3600
2116
2809
1225
Рис.160
Здесь показан двойной магический совершенный квадрат
восьмого порядка с магической суммой 260, а магическая сумма
квадратов этих чисел будет равна 11180.
Исследователи искали также такие магические квадраты,
которые оставались бы магическими при замене исходных чисел, как их
квадратами, так и их кубами. Такие магические квадраты называют
тройными. Наименьший из известных тройных магических квадратов
имеет порядок 32. Поместить его здесь очень проблематично.

84
Магические квадраты. Задачи 13-15
Сделаем очередной перерыв на решение занимательных задач.
2-13
Центрированный квадрат
В центре магического квадрата пятого
порядка, составленного по методу Баше или
методу окаймленных квадратов, стоит число
13. Но это не обязательный факт, в центре
может стоять любое число от 1 до 25, и это
подтверждается одним уникальным по
своим свойствам квадратом, который мы
покажем в разделе ответов и решений.
Рис. 161
А пока, составьте магический квадрат пятого порядка, у
которого в центре стоит число 1.
2-14 Условный квадрат
1
Можно ли построить магический квадрат
пятого порядка из чисел от 1 до 25, если
размещать в выделенных клетках только нечетные
числа, а в остальных четные?
Рис. 162
2-15 Матрешка из магических квадратов
20
14
58
65
64
10
56
55
31
46
33
48
47
27
30
50
38
43
42
32
52
57
29
45
41
37
53
25
28
60
40
39
44
22
54
71
35
36
49
34
51
11
26
68
24
17
18
72
62
Рис. 163
Внешний квадрат является
магическим квадратом седьмого
порядка с суммой 287, внутри него
магический квадрат пятого
порядка с суммой 205 и самый
маленький магический квадрат третьего
порядка имеет магическую сумму
123.
Заполните теперь пустые
клетки некоторыми числами от 1
до 83 так, чтобы в целом
получился магический квадрат 9-го
порядка с магической суммой 369.

Магические квадраты. Задачи 16-20
85
2-16 Квадрат из четырех цифр
1234
1234
1234
1234
1234
1234
1234
1234
1234
Рис.164
Квадрат третьего порядка составлен
из одного числа 1234. Задача в том, чтобы
составить и разместить девять различных
четырехзначных чисел из тех же самых
четырех цифр так, чтобы они образовали
правильный магический квадрат. При этом все
вместе числа должны содержать по девять
экземпляров каждой из цифр 1, 2, 3, 4.
2-17 Квадрат с двойным набором цифр
Расставьте цифры от I до 8, используя
каждую цифру дважды, так, чтобы сумма в
любом горизонтальном, вертикальном и двух
диагональных рядах, а также по углам
большого квадрата, а также в любом квадрате,
образованном четырьмя клетками, а также в углах
любого квадрата, образованного девятью
клетками равнялась 18.
Рис. 165
2-18
Магический квадрат третьего порядка составлен из
произвольных чисел. Докажите, что в любом случае магическая сумма
делится на 3.
2-19
Можно ли в каждую клетку квадрата 5x5 вписать
некоторые числа (допускаются и отрицательные) так, чтобы:
1. сумма четырех чисел в каждом квадрате 2x2 была
отрицательна, а сумма чисел во всем квадрате 5x5
была положительна;
2. сумма чисел в каждом квадрате 2x2 была
отрицательна, а в каждом квадрате 3x3 положительна?
2^20
Можно ли составить квадратную таблицу 100x100 из чисел
так, чтобы сумма чисел, стоящих в каждом столбце, была
положительна, а сумма чисел, стоящих в каждой строке, была
отрицательна?

86
Магические квадраты. Задачи 25-28
2-21
10
32
2
4
15
16
7
10
8
11
6
13
20
15
1
В пустые клетки расставьте числа от I до
32 так, чтобы сумма чисел в каждой строке и
каждом столбике равнялась 60.
Рис. 166
2-22
31
34
7
2
8
1
32
33
30
35
6
3
5
4
29
36
Рис. 167
2-23
Сейчас в этом полупустом квадрате
любой ряд, кроме диагоналей, в сумме
дает 74.
Впишите в пустые клетки оставшиеся
числа из последовательности 1, 2...35, 36,
чтобы получился магический квадрат с
суммой 111.
Расставьте в белых клетках квадрата
все числа от 30 до 54 включительно так,
чтобы сумма чисел в каждом из семи
горизонтальных рядов и семи вертикальных
рядов равнялась 150, а сумма чисел вдоль
каждой из двух диагоналей равнялась 300.
Рис. 168
2-24 Квадрат-оборотень
Некоторые цифры, если их определенным образом
написать, при повороте на 180° не изменяются (1,8) или превращаются
друг в друга (6, 9). Основываясь на этом можно составить
магический квадрат, который не теряет смысла и остается магическим
при повороте его на 180°. Попробуйте составить такой квадрат-
оборотень четвертого порядка из чисел: И, 16,18,19, 61, 66, 68, 69,
.Ё?..М?...?.?.» .?..?.> .?.!> .?.£> .?..?>.??: Ш.Римечанис: I- обозначает единицу).

Магические квадраты. Задачи 25-28
87
2-25, 26, 27
В следующих трех магических
квадратах из непоследовательных чисел каждой
буквой зашифрована цифра от 0 до 9. Требуется
расшифровать магические квадраты так,
чтобы магическая сумма по горизонталям,
вертикалям и диагоналям равнялась:
1. в первом квадрате 1446
(подсказка, КТО473); Рис.169
2. во втором квадрате 1515 (подсказка, БУГ=602);
3. в третьем квадрате 1167 (подсказка, ЕДА=380).
КТО
РКА
ТРИ
ТОК
КАР
РОМ
РОВ
ТУЗ
КВУ
БУГ
ТУЦ
КУБ
ЦУМ
ПУП
НУТ
ГУЛ
МУН
ЛУК
ВДА
НИИ
СЕВ
сон
вду
НЕТ
НОС
СВЕ
ЕУД
Рис.170
Рис. 171
2-28
Однажды придворный математик получил сразу все свое
жалование за год серебряными талерами и, сложив из монет 9
неравных столбиков, расположил их в виде магического
квадрата. Королю затея придворного математика понравилась, но он
посетовал на то, что ни в одном столбике число талеров не было
простым. На это придворный математик заметил, что если бы
король добавил к его жалованию еще 9 талеров, то он смог бы
увеличить число монет в каждом столбике на 1, и тогда все 9
чисел стали бы простыми. Король, будучи любителем математики,
посчитал. Оказалось именно так, как сказал придворный
математик. Король собрался уже добавить к жалованию 9 талеров, как в
дело вмешался шут. Он взял по одной монете из каждого столбика,
и число оставшихся талеров в каждом столбике оказалось
простым. Более того, 9 новых чисел по-прежнему составляли
магический квадрат. Девять лишних талеров шут оставил себе. Сколько
талеров в год получал придворный математик? Восстановите в
числах всю картину задачи.

88
Магические квадраты. Задачи 29-32
2-29
Рис. 172
14
11
5
■■■■■
4
■■■■■
7
11
6
6
10
10
15
|7
|з
12|
5
16
8
13
1
12
El
И
|13
4
9
1
8
Восстановите из 10 деталей два различных магических
квадрата четвертого порядка.
2-30
Используя отрицательные числа, составьте квадрат третьего
порядка, у которого сумма чисел по всем столбикам и строчкам
равна нулю.
2-31
Расставьте в клетках квадрата 4x4 целые числа не равные
нулю так, чтобы сумма чисел в вершинах всех квадратов 2x2,
3x3, 4x4 была равна нулю.
Для составления магических квадратов можно использовать
распространенные настольные игры, в которых фигурируют в той
или иной степени числа: карты, домино, лото. Колоду карт в 52
листа можно считать четырьмя наборами чисел от 1 до 13, где
туз=1, валет=11, дама=12, король=13, а остальные карты в
соответствии с цифрой. Кость домино можно рассматривать как одно
целое, тогда все они будут символизировать числа от 0 (пусто-
пусто) - до 12 (шесть-шесть) или же каждую половинку как
отдельный элемент с цифрами от 0 до 6, это специально
подчеркивается в условии конкретной задачи.
Магические квадраты из колоды карт
2-32
Возьмите из колоды 9 карт так, чтобы из них можно было
составить магический квадрат третьего порядка с наибольшей
возможной для карточных номиналов магической суммой.
Аналогичную задачу поставим для квадратов 4-го, 5-го, 6-го и 7-го порядков. В
каком из них будет достигнута самая большая магическая сумма?

Магические квадраты. Задачи 33-35
89
Магические квадраты из бочонков лото
Ранее мы уже упоминали, что бочонки игры «Лото» от 1 до
90 очень удобно использовать для решения большинства задач,
рассматриваемых в этой книге, так как их можно двигать,
раскладывать, переставлять. Поэтому отдельные задачи для них нужны
только для иллюстрации практического удобства работы с этим
материалом. Вообще эту книгу нужно бы пускать в продажу с
коробочкой фишек, типа бочонков лото, в придачу (нагрузку).
2-33
Задача для иллюстрации
этого факта: переставьте бочонки
лото с цифрами так, чтобы сумма
чисел по рядам и диагоналям
равнялась 70.
Рис. 173
2-34, 2-35
В обеих задачах необходимо поставить вместо знаков
вопроса некоторые бочонки лото, чтобы получились магические
квадраты 5-го порядка.
Рис. 174
Рис. 175

90
Магические квадраты. Задачи 36-39
Магические квадраты из домино
2-36
Если считать половинку кости
домино за отдельный квадратик, то
выложить из них квадрат 3x3 нельзя.
Такой «квадрат» можно построить,
если считать всю кость, как единое
целое.
Сначала тренировочное задание.
Поменяйте местами 2 пары косточек
домино так, чтобы сумма очков в
каждом из трех вертикальных и трех
горизонтальных рядов стала равна 15.
4
О
2
2
2
3
5
1
3
1
1°
5
2
4
4
1
|з
3
Рис. 176
2-37
Из 7 костяшек домино, содержащих половинку «пусто», добавив
ещё 2 произвольные кости, сложите магический квадрат третьего
порядка с магической суммой 12.
2^38
Постройте магический квадрат третьего порядка, используя
все 7 костяшек, содержащих «шестерки» и еще две
произвольные. Чему равна его магическая сумма? Будет ли она
максимально возможной для магического квадрата 3-го порядка, если
составлять его из любых 9 косточек домино, взятых из полного
комплекта?
2-39
Отберите все костяшки, содержащие «пусто» и «единицы» -
их 13 штук. Добавьте к ним из оставшихся ещё 3 кости и сложите
из всех 16 костяшек квадрат 4x4 с магической суммой 18.
Первая серия задач с домино, предполагала использование
костяшек как единого целого, без деления на половинки.
Последующие задачи составлены с учетом того, что каждая половинка
кости выступает как самостоятельная единица построения
магического квадрата. Во всех задачах игнорируется основной
принцип игры домино: приставление костяшек друг к другу
половинками с одинаковым количеством очков.

Магические квадраты. Задачи 40-42
91
2-40
Выберите из полного набора 8 костей домино и сложите из
них магический квадрат четвертого порядка, считая суммы
половинок.
2-41
Из 56 половинок домино большой квадрат не сложить. Но
можно сложить такой прямоугольник 7x8, что семь пустых
квадратиков образуют последний столбец, а оставшаяся часть
представляет собой квадрат 7x7.
О
0
О
О
0
О
0
Рис.177
Сложите кости домино так, чтобы этот квадрат был
магическим, с суммой очков по горизонталям, вертикалям и двум
диагоналям равной 24. Суммируются очки половинок костей.
2-42
Из 18 костей домино, считая за отдельный элемент
половинку кости, можно сложить магический квадрат 6-го порядка с
магической суммой равной «чёртовой дюжине», числу 13.
Кстати, это наименьшая из возможных сумм для квадрата из 18
костей домино, есть и другие варианты.
Составляя магические квадраты с разными суммами,
определите, какая сумма максимальная для набора из 18 костей?
Кстати между магическими квадратами из костей домино с
минимальной и с максимальной суммой есть интересный
алгоритм перехода, превращающий один из них - в другой без каких
бы то ни было вычислений и размышлений.

92
Магические квадраты. Задачи 43-45
2-43
Изменим немного формулировку предыдущей задачи.
Нужно выбрать 18 костяшек домино и расположить их в виде
квадрата так, чтобы ни одно число не повторялось дважды ни в
одной строке, ни в одном столбце. Пустышка рассматривается
как число, поэтому на шесть вакантных мест имеется семь
претендентов. Из-за этого в простом варианте суммы по рядам не
обязательно совпадают. Можно ли решить эту задачу,
предварительно убрав из полного набора все кости с пустышками? Тогда в
квадрате получатся одинаковые суммы по строкам и столбцам.
2-44
Квадраты нечетного порядка из домино сложить
невозможно и самый большой квадрат четного порядка, который можно
сложить - это 6x6. Из полного комплекта домино можно
выложить три квадрата: 2x2, 4x4, 6x6 одновременно.
Квадрат 2x2 магическим быть не может, а вот как обстоит
дело с двумя другими, попробуйте выяснить.
Можно ли разложить все косточки домино в три квадрата
(2x2, 4x4, 6x6) так, чтобы магическим был:
• средний из них;
• или большой квадрат;
• или оба средний и большой?
2Ё45
По схеме, изображенной на
рисунке, из все 28 костей домино
сложите магический квадрат с
прямоугольным отверстием в
центре. Сумма очков по всем
восьми строчкам, восьми
столбцам и двум диагоналям должна
равняться 21. Часть косточек уже
стоит на своих местах.
2
5
5
2
6
2
II
1
1
II
1
0
_5
0
3
_5
0
Рис. 178

Магические квадраты. Латинские
93
1
7
3
5
3
5
1
7
5
1
7
3
7
3
5
1
Латинские квадраты
Определение. Латинским квадратом называется
квадратная таблица, состоящая из п различных чисел, всех по п раз,
расположенных так, что в каждой строке и в каэк:дом столбце
каждое число встречается только один раз.
Отсюда следует вывод, что в латинском
квадрате суммы по строкам и столбцам
равные, а по диагоналям - не обязательно тацие
же.
Определение. Латинский квадрат
называется диагональным, если все элементы
каждой диагонали попарно различны (так
же, как элементы каждой строки и каж-
Рис. 179 дого столбца).
Изучением латинских квадратов много занимался великий
математик Леонард Эйлер(1707 - 1783), который дал им это
название. Решая задачи в общем виде, он вместо конкретных чисел
писал в клетках квадрата латинские буквы.
Составить латинский квадрат гораздо проще,
чем магический. В первой строке выписываем
числа в порядке возрастания, во второй - со
сдвигом вправо на одно место, возвращая последнее
число на первое место в строке и т.д. Получится
самый примитивный латинский квадрат.
Рис.180
Этим методом мы получаем простой, не диагональный
латинский квадрат, один из великого множества. Есть более
изощренный способ составления латинского квадрата для
значений п=р-1, где /7-простое число, т.е. п =4, 6, 10, 12, 16 и т.д.
Пронумеруем строки квадрата сверху
вниз и столбцы слева направо числами от 1
до п . На пересечении строки с номером а и
столбца с номером Ъ поставим остаток от
3 I з I 6 | 2 I 5 11 |4 | деления произведения аЬ на р. Так как но-
4 имГгПгТбТз! мера строк и столбцов положительные
числа не делящиеся на р, то в клетках квадрата
будут стоять числа от I до п. Докажем, что в
каждой строке стоят различные числа.
Рис.181
1
4
3
2
2
1
4
3
3
2
1
4
4
3
2
1
12 3 4 5 6
1
2
3
4
5
6
2
4
6
1
3
5
3
6
2
5
1
4
4
1
5
2
6
3
5
3
1
6
4
2
6
5
4
3
2
1

94
Магические квадраты. Латинские
Доказательство ведем методом от противного: пусть в строке
а стоят два равных числа, например, в столбцах сие, это означает,
что числа ас и ае имеют равные остатки при делении на/? и их
разность а(с-е) делится на р. Но оба сомножителя отличны от нуля и
по абсолютной величине меньше р. Следовательно, получили
противоречие, р - простое число и делимость не может иметь место.
Доказательство для столбцов повторяется слово в слово.
Второй метод дал нам снова не диагональный квадрат.
Третий алгоритм составления латинских квадратов. Пусть
12 3 4 5 п ~ пРоизвольное натуральное число и к-
натуральное число, не имеющее общих с п
делителей, больших единицы. Поместим на
пересечении строки с номером а и столбца с
номером Ъ остаток от деления на п числа ак+Ь.
Если остаток равен 0 то в соответствующую
клетку поместим число п. Доказательство, что
подобным методом будет построен латинский
квадрат аналогично предыдущему. На этот
3
5
2
4
1
4
1
3
5
2
5
2
4
1
3
1
3
5
2
4
2
4
1
3
5
n=5,k=2
1
2
2
1
Рис. 182 раз повезло, квадрат оказался диагональным.
Введя определение и рассмотрев примеры построения
латинских квадратов, уместно поставить вопрос об их количестве
в зависимости от порядка.
Существует два латинских квадрата
второго порядка. Причем они симметричны как
сиамские близнецы.
Для определения количества квадра-
Рис. 183 тов третьего порядка, сначала построим один
специфический, из которого все остальные получаются
перестановками строк и столбцов. Впишем числа 1, 2, 3 в порядке
возрастания в первую строчку и в первый столбик, заполнение
оставшихся четырех клеток происходит однозначно. Из
полученного квадрата перестановкой столбцов получается 6 различных
расположений цифр, и при каждом расположении
столбцов перестановкой второй и третьей строк -
еще две модификации. Итак, существует всего
6-2=12 различных латинских квадратов 3-го порядка.
Рис. 184
Если для квадрата 4-го порядка мы выпишем цифры по
аналогии в первую строчку и в первый столбец в порядке
возрастания, то остальные клетки заполнить однозначно уже не удается,
получается четыре различных варианта.
1
2
3
2
3
1
3
1
2

Магические квадраты. Латинские
95
1
2
3
4
2
3
4
1
3
4
1
2
4
1
2
3
1
2
3
4
2
.
1
3
3
1
4
2
4
3
2
1
1
2
3
4
2
1
4
3
3
4
1
2
4
3
2
1
1
2
3
4
2
1
4
3
3
4
2
1
4
3
1
2
Рис.185
Четыре столбца можно переставить между собой 24
способами, а при фиксированном расположении столбцов вторую,
третью и четвертую строчки можно переставить 6 способами.
Поэтому, начиная с каждого показанного размещения можно
получить 144 латинских квадрата, а всего латинских квадратов
четвертого порядка насчитывается 576.
Количество латинских квадратов быстро растет с
увеличением порядка. Известно, что существует не менее
латинских квадратов размером пхп. Действительно, каждая
строка латинского квадрата это некоторая перестановка из п
элементов, число таких перестановок равно п!, но для конкретного
квадрата нам нужно только п различных перестановок из общего
их количества. Вся тонкость подсчетов в том, что эти п
перестановок, должны соответствовать определению латинского квадрата,
т.е. не могут быть любыми из nl. Точное значение этого количества
известно только для малых п.
На следующем рисунке показаны два латинских квадрата
4x4, обладающие интересной особенностью: если один квадрат
наложить на другой, то все пары получившихся чисел оказываются
различными.
и
2
3
4
2
И
4
3
3
4
И
2
4
3
2
и
и
3
4
2
2
4
3
И
3
и
2
4
4
2
И
3
ии
23
34
42
22
114
43
34
33
4U
112
24
44
32
21
ИЗ
Рис.186

96
Магические квадраты. Латинские
Перейдем от конкретных чисел к буквам. Шестнадцать
клеток в одном квадрате заполним латинскими буквами а, Ь, с, d
так, чтобы получился латинский квадрат, а клетки второго
квадрата заполним греческими буквами а, Д у, &
Если наложить квадраты друг на друга, то получится, что
каждая латинская буква появляется один и только один раз в
паре с каждой греческой буквой.
а
b
с
d
Ь
а
d
с
с
d
а
b
d
с
Dd
а
а
Г
8
Р
Р
8
г
а
г
а
Р
8
8
Э
а
Y
aajb^
ьг
с8
dp
а8
dy
са
су
da
ар
Ь8
d«
сЭ
Ьх
ау
Рис. 187
Два или более латинских квадратов, которые можно так
попарно скомбинировать друг с другом, называются
ортогональными, а получившийся комбинированный квадрат принято
называть греко-латинским.
Греко-латинские квадраты
Определение. Квадратная таблица, в каждой ячейке
которой расположены различные пары чисел так, что первые и
вторые компоненты этих пар образуют в отдельности
латинские квадраты, называется греко-латинским квадратом.
Таким образом, для получения греко-латинского квадрата
нужно составить два латинских ортогональных квадрата и
наложить их друг на друга. Вся трудность заключена именно в поиске
ортогональных латинских квадратов.
В последние годы жизни Леонард Эйлер написал обширное
«Исследование магических квадратов нового типа». Он впервые
поставил задачу отыскания ортогональных латинских квадратов в
следующей формулировке.
«Среди 36 офицеров поровну уланов, драгунов, гусаров,
кирасиров, кавалергардов и гренадеров и, кроме того, поровну
генералов, полковников, майоров, капитанов, поручиков и
подпоручиков. Причем каждый род войск представлен офицерами
всех шести рангов. Можно ли выстроить этих офицеров в каре
6x6 так, чтобы в любой колонне и любой шеренге встречались
офицеры всех рангов и всех родов войск?»

Магические квадраты. Латинские
97
1
2
2
1
2
1
1
2
12
21
21
12
Сформулировав задачу, Эйлер не смог найти её решение, но
он доказал, что ортогональные пары латинских квадратов
существуют для всех нечетных значений п и для таких четных
значений п, которые делятся на 4. В частности он решил подобную
задачу для 25 офицеров пяти рангов и пяти родов войск.
Эйлер выдвинул гипотезу, что для остальных значений п,
т.е. если число п при делении на 4 дает в остатке 2,
ортогональных квадратов не существует.
Для «=2в первой клетке может
стоять I или 2 и этим определены все
остальные клетки. Разных вариантов
Рис. 188 получается только два, но они не ортогональны.
В 1901 году французским математиком Гастоном Тарри
было доказано, что ортогональных квадратов размером 6x6 не
существует. Доказательство было проведено очень трудоемким
методом полной индукции, т.е. перебором всех возможных
вариантов и пар квадратов.
Следующий неизученный случай и=10 оказался уже
слишком сложным для такого исследования и находился за пределами
возможностей даже появившихся к тому времени ЭВМ. В 1959
году машина SWAC , проработав 100 часов, не нашла ни одной
пары ортогональных квадратов 10-го порядка, но в том же году
группе математиков удалось составить греко-латинский квадрат
10-го порядка и тем самым через 177 лет опровергнуть гипотезу
Эйлера. Далее процесс пошел быстрее, да и скорости ЭВМ
возрастали день ото дня, и вскоре были найдены греко-латинскис
квадраты 14, 18, 22
порядка.
Вот тот квадрат
10-го порядка,
опровергнувший гипотезу
Эйлера.
Рис. 189
00
86
95
59
73
68
37
14
21
42
47
11
80
96
69
74
08
25
32
53
18
57
22
81
90
09
75
36
43
64
76
28
67
33
82
91
19
40
54
05
29
70
38
07
44
83
92
51
65
16
93
39
71
48
17
55
84
62
06
20
85
94
49
72
58
27
66
03
10
31
34
45
56
60
01
12
23
77
89
98
61
02
13
24
35
46
50
88
97
79
52
63
04
15
26
30
41
99
78
87

98
Магические квадраты. Латинские
В каждой клетке левая цифра (от 0 до 9) относится к
первому латинскому квадрату, а правая цифра - ко второму. Обратите
внимание, что квадратик 3x3 в правом нижнем углу, тоже греко-
латинский: как самоцвет в оправе.
Изменение порядка расположения строк и столбцов не
влияет на свойства греко-латинского квадрата. Если один квадрат
получается из другого перестановкой строк или столбцов, то эти
два квадрата не различаются. В связи с этим возникло
предположение, что все квадраты 10-го порядка содержат подквадрат 3-го
порядка, но позднее нашлось много квадратов, не обладающих
таким свойством.
Магические линии греко-латинского квадрата (если их
провести) не обладают симметрией и скорее напоминают
изображение броуновского движения частиц.
Если каждой цифре от 0 до 9 поставить в соответствие свой
цвет, то показанный выше квадрат 10-го порядка можно было бы
красочно представить в следующем виде, если бы не черно-белое
издание книги.
Рис. 190

Магические квадраты. Латинские
99
Совершенствование компьютеров и искусства программистов
привели к отысканию сотни новых греко-латинских квадратов 10-го
порядка, но так и не удалось найти трех взаимно ортогональных
латинских квадратов 10-го порядка.
Раньше было доказано, что максимальное число взаимно
ортогональных латинских квадратов п-го порядка равно и-1. Если
найдено п-\ таких квадратов, то они называются «полным
набором». Квадрат третьего порядка имеет полный набор из двух
ортогональных квадратов, полный набор квадрата четвертого
порядка содержит 3 квадрата, 5-го порядка 4 квадрата. Но не
обязательно они есть.
Определение. Латинский квадрат, не имеющий
ортогонального себе квадрата, называется нерасширяемым.
Квадрат 6-го порядка не имеет не только полного набора,
но даже взаимно ортогональной пары. Зато полные наборы 7-го,
8-го, 9-го порядков существуют.
Поэтому 10-ый порядок является наименьшим, для
которого пока не выяснено, можно ли найти полный набор. В настоящее
время решение этой задачи программисты с компьютерами не
осилили. Хотя время бежит так стремительно, что пока я печатаю
эти строки, возможно где-то и кто-то уже решил задачу. В
качестве иллюстрации понятия, приведем полный набор
ортогональных квадратов пятого порядка.
0
1
2
3
4
1
2
3
4
0
2
3
4
0
1
3
4
0
1
2
4
0
1
2
3
0
2
4
1
3
1
3
0
2
4
2
4
1
3
0
3
0
2
4
1
4
1
3
0
2
0
3
1
4
2
1
4
2
0
3
2
0
3
1
4
3
1
4
2
0
4
2
0
3
1
0
4
3
2
1
1
0
4
3
2
2
1
0
4
3
3
2
1
0
4
4
3
2
1
0
Рис.191
Греко-латинские квадраты сейчас широко применяются при
планировании экспериментов в биологии, медицине, социологии,
в тех случаях, когда нужно одновременно рассмотреть зависимость
четырех переменных величин. Как в задаче Эйлера с офицерами:
колонна, шеренга, род войск и звание - вот четыре переменные
величины, каждая из которых может принимать п значений.
Применительно, к сельскому хозяйству использование греко-латинских
квадратов позволяет, с минимальной затратой времени и средств,
проводить опыты по селекции. Допустим, нужно испытать 7
сортов пшеницы и 7 видов удобрения, при этом свести к минимуму
отклонения, вносимые неоднородностью состава почвы.

100 Магические квадраты. Латинские
Пшеничное поле разбивается на клетки, чтобы получился
квадрат 7x7, Удобрения распределяются в соответствии с
латинскими буквами, а сорта пшеницы высеваются в соответствии с
греческими буквами специально составленного греко-латинского
квадрата 7-го порядка. Первые две переменные - это координаты
участка, третья - вид удобрения, четвертая - сорт пшеницы. В
результате за один эксперимент испытываются 7 видов
удобрения, 7 сортов пшеницы, исключается неоднозначность,
порожденная изменением состава почвы. Далее следует статистическая
обработка результатов.
Греко-латинский квадрат является при этом схемой
эксперимента, ячейка квадрата совсем не обязательно должна быть
участком земли. Главное, что она характеризуется двумя
координатами: номер строки и номер столбца. Например, в медицине
проведение исследования нескольких лекарственных средств
может проходить так:
строкам соответствует п возрастных групп испытуемых,
столбцам - п весовых категорий пациентов, латинские буквы - п
лекарственных препаратов, греческие буквы - п стадий болезни
(или и-различных заболеваний). Всё это в соответствии со схемой
греко-латинского квадрата и-го порядка, причем любого из
имеющихся. Только помните, что греко-латинских квадратов
шестого порядка не существует.
Получается очень интересная особенность, объединяющая
магические квадраты различных видов, но одного и того же
шестого порядка:
■ греко-латинских квадратов не существует;
■ симметрических магических квадратов не
существует;
■ совершенных магических квадратов не существует.
Снова и снова эта исключительность шестого порядка!
Пытаясь хоть как-то восполнить этот природный пробел,
американский математик К. Планк разработал метод построения
совершенных и симметрических магических квадратов порядка п
простой четности для чисел, которые являются почти
последовательными. Для квадрата порядка п он использовал числа от 1 до
п2+3, пропуская «среднее число» (]/2)п2+2 и какие-либо два других
четных числа, сумма которых равна п2+4. В частности можно
выбросить из последовательного ряда числа, кратные (%)и2+1. При
таких условиях можно построить и совершенный, и
симметрический квадраты шестого порядка. Возникнет желание, попробуйте
это сделать самостоятельно, у нас же еще одна серия задач.

Магические квадраты. Задачи 46-49
101
2-46
Сколькими различными способами можно
закрасить клетки квадрата 3x3 в красный, зеленый
и синий цвет, чтобы в каждой строке й в каждом
столбце встречались клетки всех цветов.
Варианты, переводимые один в другой с помощью
поворотов, не считаются различными.
■
■
■
С 3
■
■
■
■
2-47
Пятью разными цветами нужно
раскрасить 25 клеток квадрата так, чтобы не было
соседних клеток одного цвета. Соседними
считаются как клетки, имеющие общую
сторону, так и расположенные рядом по
диагонали
Рис. 192
Рис. 193
е
А
2-48
Можно ли заполнить табличку 4x4
цифрами 1,2,3,4, обвести их рамками четырех
типов (квадрат, круг, треугольник, ромб) и
раскрасить их в четыре цвета так, чтобы
одновременно выполнялись все следующие условия:
Рис. 194
а) в каждой строке и в каждом столбце должны встречаться
все цифры, все цвета и все типы рамок;
б) каждая цифра должна быть раскрашена по одному разу
каждым цветом;
в) рамка каждого типа должна содержать по разу каждую
цифру и каждый цвет?
2-49
В квадрате 4x4 требуется расставить числа 1,
2,3,4, 5 так, чтобы ни в одном столбце, ни в одной
строке и ни на одной диагонали не было двух
одинаковых цифр. Дополнительное условие: сумма
всех чисел должна быть максимально возможная.
Какая сумма достижима?
Рис. 195

102
Магические квадраты. Задачи 50-58
2-50, - , 2-55
Латинские магические квадраты
В каждый из квадратов необходимо вписать цифры от 1 до
4 так, чтобы в каждой строке, в каждом столбце и в каждой
выделенной фигуре из 4 клеток все цифры были различны.
1
2
J
Рис
НИ
I
.196
I I
Щ
т
i
19
1
I
9
Рис. 200
Рис. 201
2-56
В латинский квадрат 5-го порядка
необходимо вписать цифры от 1 до 5 так, чтобы в
каждой строке, в каждом столбце и по второй
диагонали все цифры были различны.
1
2
2
1
3
5
4
4
5
Рис. 202
2-57
Данная вариация латинского квадрата
содержит в себе «основное» и «диагональное»
условия. Кроме того, между всеми соседними
клетками, сумма чисел в которых равняется 6,
проведена граница.
1
3
4
Рис. 203
2-58
Квадрат 5x5 заполнен некоторыми числами
(положительными и отрицательными) так, что в каждой строке произведение
чисел отрицательно. Докажите, что хотя бы в одном столбце
произведение чисел тоже отрицательно.

Магические квадраты. Задачи 59-63
103
2-59, 2-60
В этой вариации головоломки латинский квадрат 5-го
порядка разбивается на 5 связных областей, каждая из которых
состоит из 5-ти клеток. И помимо основного условия добавляется
требование, чтобы в каждой, выделенной одним цветом, фигуре
из 5 клеток все цифры были различны.
Рис. 204
Рис. 205
2-61
Расположите цифры от I до 9 в
квадрате так, чтобы в каждой строке,
в каждом столбце и в каждом
одноцветном квадрате все цифры
встречались по одному разу.
Рис. 206
8
9
5
3
4
6
1
6
9
2
1
3
7
1
3
5
6
7
2
7
5
8
7
4
2
2-62, 2-63
Расставьте цифры от 1 до 6 в клетки квадратов так, чтобы в
каждой строке, в каждом столбце и каждой выделенной фигуре
из шести клеток все цифры были различны.
5
6
1
2
6
6
5
3
3
1
6
2
3
1
4
6
4
4
1
4
5
6
2
6
2
3
5
Рис. 207
Рис. 208

104
Магические квадраты. Задачи 64-67
2-64
1
1
Сколько единиц можно расставить в
клетках квадрата так, чтобы сумма в
каждом из рядов, включая и все диагональные,
оказалось не более двух. Две единицы уже
стоят на главной диагонали, значит, на нее
уже ставить нельзя.
Рис. 209
2-65 Задача Эйлера о шахматном короле
1
и,
64
1
Нужно обойти шахматным
королем всю шахматную доску, начав путь
с клетки 1 и закончив замкнутый
маршрут в клетке 64, последовательно
нумеруя при этом пройденные клетки так,
чтобы в итоге номера клеток
образовали магический квадрат 8-го порядка.
Рис.210
2-66
Задача Баше
Эту задачу аббат Баше, оставивший след не в истории религии,
а в математике, опубликовал в своей книге, вышедшей во
Франции в далеком 1692 году.
Из 16 карт тузов, королей, дам и валетов всех четырех
мастей, требуется сложить квадрат так, чтобы ни в одном ряду, ни в
одном столбце, ни на одной из двух больших диагоналей не было
двух карт, совпадающих по значению или по масти.
2-67
Квадрат 6x6 состоит из 36 не закрашенных клеток. Нужно
закрасить 12 клеток так, чтобы после этого в каждом столбике и в
каждой строке осталось по одинаковому числу не закрашенных клеток.

Магические квадраты. Задачи 68-71
105
2-68 Задача Эйлера
Среди 25 офицеров поровну драгунов, гусаров, кирасиров,
кавалергардов и гренадеров и, кроме того, поровну генералов,
полковников, майоров, капитанов и поручиков, причем каждый
род войск представлен офицерами всех пяти рангов.
Нужно выстроить офицеров в каре 5x5 так, чтобы в любой
колонне и любой шеренге встречались офицеры всех рангов и
родов войск.
2-69, 2-70
Игральные кубики
Перед вами 81 грань кубиков (вид сверху). Необходимо
закрасить 27 кубиков так, чтобы в каждом вертикальном и
горизонтальном ряду осталось по 6 из них с неповторяющимися гранями.
Для примера одна грань уже закрашена, осталось закрасить 26.
•
•
• •
•
•
•
•
It
• •
:t
• •
•
•
rf
• •
• •
•
It
• •
•
• •
• •
т
•
• •
•
•
•
• •
• •
!!
\
It
• •
•
• •
• •
•
• •
к
9
9
9
It
• •
• •
•
•
•
• •
•
•
•
•
• •
• •
• •
•
• •
• •
•
•
•
•
It
I t
• •
• •
•
• f
\
• •
• •
•
• •
• •
• •
•
• f
•
•
•
•
11
• •
• •
• •
•
•
\
11
• •
• •
•
•
•
•
•
11
• •
•
• f
•
•%
• •
tx
• •
11
• •
•
V
ч
•
•
tt
\
•
• •
• •
•
• •
• •
•
9 9
9
9
\
•
•
t t
• •
•
It
• •
• •
•
•
•
•
•
•
•
•
•
• •
• •
•
•
9 9
9
9
9 9
9 9
гг
9 9
9
9
9
9
9
9
9
гг
9
9
9
9 9
9 9
9
9 9
9
9 9
9
9 9
H
9
9
9 9
9 9
9
9 9
•
•
•
t t
• •
•
•
•
•
• •
•
• •
• •
• •
• •
•
• •
•
• •
•
• •
•
•
•
•
• •
t t
Рис.211
Рис. 212
2-71
В квадрате 4x4, показанном на
рисунке, в каждом столбике, каждой
строчке и на главных диагоналях обведите по
одному числу так, чтобы общая сумма
обведенных чисел равнялась 32.
11
4
12
14
16
7
2
9
1
10
15
6
5
13
8
3
Рис.213

106
Магические квадраты. Разные
Квадромагический числовой квадрат
Показанный на рисунке квадрат 4-го
порядка не является магическим в обычном
понимании этого слова, т.к. суммы чисел по
строчкам и столбцам получаются разные.
Если же посчитать сумму четырех чисел в
любом выделенном из него квадратике 2x2
(назовем его подквадрат 2-го порядка), то получим
одно значение равное 34.
Рис. 214
Определение. Числовой квадрат п-го порядка (п>2)
называется квадромагическим, если сумма четырех чисел в любом его
подквадрате 2-го порядка одна и та же.
Не трудно установить, что у квадрата п-то порядка можно
выделить (и-1)2 подквадратов 2-го порядка.
Построить квадромагический квадрат очень просто.
Расставим числа от 1 до п2 по
порядку в клетках
квадрата, предварительно
закрашенных в шахматном
порядке. Числа, стоящие
на закрашенных клетках,
оставим на своих местах,
а каждое, из стоящих на
белых клетках, поменяем
Рис. 215 местами с центрально-симметричным ему числом.
Вот и всё! Получается квадромагический квадрат, причем этот
метод универсален и применим для
построения квадромагического
любого порядка.
Выведем формулу для магической
суммы квадрата п-то порядка. Выделим в
квадрате п-то порядка подквадрат 2-го
порядка. Пусть в его вершинах стоят числа
a,b,c,d. Числа а и Устоят на закрашенных
Рис. 216 клетках, значит, они соответствуют номерам
этих клеток. Числа Ъ и с стоят на белых клетках, значит они
равны числам центрально-симметричным номерам а+\ и d-l , значит
b=n2-(a+\)+\=n2-a, c=n2-(d-\)+\ , т.к. клетке с номером к
центрально-симметрична клетка п2-к+\. Таким образом:
S=a+b+c+d=a+n2-a+n2-d+2=2(n2+\).
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
1
20
11
10
21
24
7
14
17
4
3
18
13
8
23
22
9
12
19
2
5
16
15
6
25
S=52
1
a
с
3
b
d
2
n2
квадрата

Магические квадраты. Разные
107
Мультипликативные магические квадраты
В заключение этой главы нужно сказать ещё об одной
разновидности квадратных таблиц чисел. О квадратах, в которых
натуральные неповторяющиеся числа расставлены так, что
произведение чисел в каждой строке, в каждом столбце и по обеим
диагоналям одинаковое. Естественно, их отличие от
традиционных магических квадратов, позволяет отнести их к
«нетрадиционным» меньшинствам.
Самый простой способ построения подобного квадрата
состоит в использовании известного правила умножения
степеней: при перемножении степеней с одинаковым основанием
основание остается то же, а показатели складываются. Берем
традиционный магический квадрат третьего порядка и
рассматриваем его числа как показатели степени некоторого основания,
например, числа 2. В результате образуется квадрат с
одинаковыми произведениями.
4
3
8
9
5
1
2
7
6
24
2з
2е
29
25
21
22
27
2е
16
8
256
512
32
2
4
128
64
Рис.217
Постоянное произведение по всем рядам и двум диагоналям
этого квадрата равно 32768.
Таким образом, любой магический квадрат с постоянной
суммой можно превратить в некоторый квадрат с постоянным
произведением.
Усовершенствуя этот способ построения
мультипликативного магического квадрата, можно построить подобный квадрат
из членов произвольной геометрической прогрессии,
определяемой двумя числами а и q, где а - первый член геометрической
прогрессии, q - её знаменатель.
Расставляем члены прогрессии a, aq,
aq2, aq3,...,aq8 в сетку квадрата по методу
Баше.
Получается магический квадрат с
по312
aq
acf
aq3
aq"
aq4
aq2
aq5
a
aq'
у
стоянным произведением P=a3q12.
Рис.218

108
Магические квадраты. Разные
Ещё одна схема построения квадрата получается
почленным слияниям двух исходных квадратов с разным основанием
степеней.
а
а2
1
1
а
а
а2
1
а2
1
Ь2
Ь
Ь2
b
1
b
1
b2
Рис. 219
Постоянное произведение Р=а3Ь3
Заменяя а=2, Ь=3, получим квадрат с
произведением 216.
а
аЪ2
b
2
36
3
b2
ab
а2
9
6
4
cfb
1
atf
12
1
18
Рис. 220
Эта глава начиналась с самого древнего магического
квадрата, и заканчивается тоже квадратом, только
«нетрадиционным». У кого-то может возникнуть вопрос: зачем нужна сейчас
эта древность, в век информатизации, электроники, компьютеров?
Ответ прост: космонавтам, управляющим сложнейшей техникой,
нужны физические упражнения не меньше, чем простому
древнегреческому воину, хотя их разделяют тысячелетия развития
цивилизации. Точно так же развитие ума человека требует
ежедневных мыслительных упражнений. В обоих случаях сущность
подобных основополагающих занятий мало изменилась, если
меняется, то в большей степени внешняя форма. Для тела полезен
бег, будь он по пересечённой местности от Марафона до Афин
или на специальном тренажере космической станции. Для мозга
полезно решать задачи, и головоломка, придуманная средневековым
аббатом, не менее полезна для ума современного человека, чем
занятия на персональном компьютере. «Упражнения, друзья, дает
больше, чем хорошее природное дарование» - сказал
древнегреческий философ Протагор из Абдеры, живший более двух тысяч лет
назад. Разве изменили века истинность этого утверждения?

Для того чтобы творить великие дела, нужно
жить так, как будто и умирать не придется.
Л. Вовенарг (1715-1747) - французский писатель
Жизнь так широка и многостороння, что в ней
человек всегда найдет досыта всего, искать чего
чувствует сильную и истинную потребность.
Н. Г. Чернышевский (1828-1889) - русский мыслитель
В нас живут труд, силы тех, кто жил до нас.
Пусть в свою очередь будущие поколения смогут
жить благодаря нашему труду, благодаря силе наших
рук и нашего ума. Лишь в этом случае мы достойно
выполним свое назначение.
Ж. Фабр (1823-1915) - французский ученый
Стараться оставить после себя больше знаний и
счастья, чем их было раньше, улучшить и умножить
полученное нами наследство - вот над чем мы
должны трудиться.
Д. Дидро (1713-1784) - французский философ
Как басня, так и жизнь, ценится не за длину, а
за содержание.
Сенека -римский философ

Магическое разнообразие. Квадраты 111
- Как построить квадрат?
- Нужно просто отрезать у круга углы!
Из разговора
Столько написано о магических квадратах, что просто
обидно становится за другие плоские геометрические фигуры и
объемные тела. Цель настоящей главы - покинуть квадратные
рамки, посмотреть какие ещё магические фигуры можно сделать
в плоскости и вырваться в пространство - перейти к объемным,
трехмерным геометрическим объектам. Но вначале еще немного
о магических квадратах, точнее об их объединениях.
Конфигурации из магических квадратов
В предыдущей главе мы рассматривали магические квадраты
всевозможных видов, меняли накладываемые условия, меняли
состав используемых чисел. Получались квадраты
симметрические и совершенные, двойные и тройные, латинские и греко-
латинские, из непоследовательных чисел и квадромагические, но
все время только квадраты. Два небольших шажка в сторону, если
проанализировать, мы сделали в задачах. Первый в задаче 2-15,
когда нужно было составить матрешку из магических квадратов:
квадрат 3-го порядка внутри квадрата 5-го порядка, тот внутри
квадрата 7-го порядка и т. д. Этот процесс можно продолжать до
бесконечности, используя метод окаймления магических квадратов.
Второй шаг: при решении задачи 2-13 получился «назикский»
квадрат, который тоже можно было продолжать в плоскости до
бесконечности, и любой участок 5x5 этого числового ковра
представлял собой магический квадрат. Продолжая идти в этом
направлении мы можем получить различные красивые
конструкции объединяя определенным образом несколько магических
квадратов в одно целое.
На следующей странице изображены четыре магических
квадрата 4-го порядка, объединенные в один квадрат так, что
сумма чисел в каждой клетке, составленной из четырех
разноцветных треугольников равна 34, т.е. магической сумме квадрата
4-го порядка. Треугольники каждого цвета составляют отдельные
магические квадраты, вырезанные из «назикского» квадрата.

112
Магическое разнообразие. Квадраты
\15/
6Ж1
\14/
Ж
1ЗДЙ4
\10/
1S&8
4JHO
\tl/
1JH1
\з/
1<W3
\1б/
5Ж3
\2/
11JH6
\13/
8Ж2
412/
13Ж7
Расчеты показывают,
что объединить 4 квадрата
4-го порядка можно:
(Кстати, если бы их
расположить в четыре слоя друг
над другом, получился бы
магический куб, но это я уже
забегаю вперед). А вот три
квадрата 4-го порядка нельзя
объединить подобным
образом [(1+16)- 16-3]У(16-2)=51/2 -
получается дробное число
Рис. 221 для искомой суммы. Можно
объединить 6 квадратов 4-го порядка, сумма получится равной
51. В журнале «Квант» было опубликовано несколько подобных
изысканий Е. Кривошеева. Например, на следующем рисунке
показано объединение четырех магических квадратов 5-го
порядка с суммой в квадратной клетке равной 52 .
[(1+25)-25-4]/2-25=52
1оЩч6
У™\
Ж
У^23\
20^4
У^9\
^К22
Ж-
ул*\
Ж
^К19
^\
>/25\
^К23
23^4
1
Рис. 222

Магическое разнообразие. Задачи 1-2
113
3-1,3-2
Попробуйте объединить три или пять магических квадратов
пятого порядка. Предлагаем готовые конструкции для записи чисел.
Рис. 223
Рис. 224

114
Магическое разнообразие. Кольцо и круг
При построении последней конструкции можно
воспользоваться «назикским» квадратом из ответа к задаче 2-13.
Несколькими примерами мы указали вам одно из возможных
плоских направлений развития «квадратомагии», дальнейшее
движение зависит от желания, усидчивости и фантазии читателя.
Теперь настало время сделать операцию обратную той, что
вынесена в эпиграф данной главы: убрать углы у квадрата.
Магическое кольцо и магический круг
Представим себе, что магический квадрат нарисован на
некой эластичной пленке, которую можно подвергать любым
деформациям - растягивать произвольным образом, скручивать
и т. д. Для преобразования возьмем совершенный квадрат пятого
порядка и превратим его в магическое кольцо следующим
образом:
1
9
12
20
23
15
18
21
4
7
24
2
10
13
16
8
11
19
22
5
17
25
3
6
14
В
Отрезок ВС изгибаем и
превращаем в окружность так, чтобы
точка В совпала с точкой С;
Отрезок AD растягиваем и также
закручиваем, чтобы эта вторая
окружность имела значительно
больший диаметр.
Рис. 225
В результате преобразований перед нами магическое кольцо,
в котором суммы чисел по каждому из радиусов (бывшие
строчки), по каждой концентрической окружности (бывшие столбцы) и
по каждой спирали (бывшие диагонали) будут равны между собой.
Специально взят совершенный квадрат, у которого равенство
сумм сохраняется не только по главным, но и по ломаным
диагоналям, которые становятся спиралями. Причем спирали можно
закручивать по часовой стрелке или против часовой стрелки, все
равно сумма остается прежней. Вот такое простое
преобразование привело к красивым последствиям, наглядно представленным
на следующей странице.

Магическое разнообразие. Кольцо и круг
115
AD
Рис. 226
Поговорим еще раз о творчестве американского
общественного деятеля и ученого Бенджамина Франклина, страстного
любителя составления магических квадратов и изобретателя
магических кругов. Он сам признавался, что этим занятием он
скрашивал себе скучные часы на службе в Законодательном
Собрании штата Пенсильвания. Кстати, именно его портрет красуется
на 100 долларовой купюре, популярной у наших сограждан.
Два примера, составленных им магических квадратов 8-го
и 16-го порядка, мы уже рассмотрели, настало время посмотреть
на его магический круг. Круг содержит числа от 12 до 75 и число
12 повторяется в центре фигуры. Суммы чисел по восьми радиусам,
включая каждый раз центральное число, по восьми
концентрическим кольцам, но опять-таки прибавляя центральное число,
наконец, по 24 окружностям с центрами в точках А, В, С, D (с
центральным числом) все равны между собой, а именно, равны 350.
Если внимательно изучить этот магический круг, то станет ясно,
что принцип его построения аналогичен тому, каким мы только
что получали магическое кольцо.

116
Магическое разнообразие. Кольцо и круг
В основе построения круга лежит магический квадрат
восьмого порядка, составленный Франклином.
Только в нем переставлены местами некоторые строки и
столбцы, но так, что это не повлияло на его свойства.
+ 11 =
31
33
24
42
22
44
29
35
18
48
25
39
27
37
20
46
15
49
8
58
6
60
13
51
2
64
9
55
11
53
4
62
63
1
56
10
54
12
61
3
50
16
57
7
59
5
52
14
47
17
40
26
38
28
45
19
34
32
41
23
43
21
36
30
44^
35]
*3
33
55
40
46
29
59
*6
50
38
48
31
57
26
60
n
69
*4
62
13
75
20
Ц
64
>s
74
12
67
&
65
23
72
14
61
27
[68
16
63
25
58
^
37
49
39
56
30
45
4*
52
34
54
32
47
41
Рис. 227
Магическая сумма такого квадрата равна 260, но если
каждое число увеличить на 11, сумма будет 260+88=348.
Деформируем этот квадрат описанным методом и, чтобы
центр не пустовал, ставим туда число 12, округляя тем самым
сумму до 350. У магического квадрата Б. Франклина было
дополнительное свойство - равенство сумм по ломаным линиям,
составленным из двух «полудиагоналей». Это свойство дало
дополнительные 24 окружности с центрами в точках А, В, С, D.
Поняв это можно превратить в магический круг и большой
квадрат Б. Франклина, но это требует огромного труда,
усидчивости и аккуратности. Кстати, оригинал его магического круга,
выполненный в цвете, был продан на аукционе в частную
коллекцию, т.е. принес какую-то материальную выгоду автору.
За соответствие рисунка, который приведен здесь, тому
оригиналу не ручаюсь, потому что выполнял его с черно-белой
копии малого формата сначала в цвете, а потом вынужден был
снова превратить в черно-белый.
То, что здесь названо магическим кольцом, кто-то может
назвать магической спиралью; ломаные диагонали совершенного
квадрата превратились в спирали и суммы чисел на спиралях равны.

Магическое разнообразие. Кольцо и круг 117
Рис. 228
Принцип получения и магического кольца, и магического
круга Франклина один и тот же - деформация магического
квадрата. Отличий только два: первое - исходные квадраты обладают
разными дополнительными свойствами и второе - у круга не
пустует центральная окружность, там стоит число 12, которое
участвует во всех суммах.
«Муз и наук единство в Красоте.
Она живёт в скульптурах и гипотезах».
Эти слова написал профессор О. Боксер. Магический круг,
в котором внешняя гармония линий и цвета сливается с красотой
математического содержания, служит иллюстрацией этого
утверждения. Эта фигура красива в многоцветье, но, увы,
донести цвет до читателя не удается. Задержите своё внимание,
задумайтесь о чём-то добром и хорошем, отбросьте мелочные
проблемы перед вечным.

118 Магическое разнообразие. Шестиугольник
Магический шестиугольник
Интересно устроено человеческое мышление. На
протяжении тысячелетий люди увлекались составлением и исследованием
магических квадратов, причем наряду с рядовыми любителями
головоломок этим занимались великие умы математической науки.
Усложнение задачи шло в направлении увеличения порядка
квадрата и расширения накладываемых условий. Появились
квадраты симметрические, совершенные или дьявольские,
двойные и тройные, но за квадратные рамки никто никак не мог
вырваться. Только в начале XX века возник вопрос: почему
только квадрат, а не шестиугольник, например?
В 1910 году Клиффорд У. Адаме принялся за поиски
магического шестиугольника.
Задача формулируется так: молено ли натуральные числа от 1
до п расставить в п ячейках шестиугольника так, чтобы суммы
всех чисел в каэюдом ряду в трех направлениях были бы равны
между собой?
Наименьший шестиугольник, имеющий более одной ячейки,
состоит из семи ячеек.
По аналогии с порядком квадрата
можно сказать, что это шестиугольник
второго порядка, так как к любой стороне
шестиугольника примыкают две ячейки.
Угловая ячейка А входит в два ряда АС и
АВ. Если бы суммы А+В и А+С были
равны, то в ячейках В и С должны стоять оди-
Рис. 229 наковые числа. Это противоречит условию
задачи, следовательно, магический шестиугольник второго
порядка составить нельзя. Невозможность существования
магического шестиугольника второго порядка следует ещё из того,
что сумма чисел 1+2+3+...+7=28 не делится на 3 (количество
рядов по любому из трех направлений).
Идем дальше, увеличивая порядок. Шестиугольник третьего
порядка состоит из 19 ячеек и имеет по пять рядов в трех
направлениях. Магическая сумма должна быть равна
(1+2+...+19)/5=190/5=38. Но возможность условно вычислить
предполагаемую магическую сумму ещё не является
доказательством того, что магический шестиугольник третьего порядка
существует, его еще построить нужно!

Магическое разнообразие. Шестиугольник 119
Клиффорд Адаме занимался
решением этой задачи в свободное
время на протяжении 47 лет и,
наконец, решил её.
Вот пример завидного
упорства в достижении поставленной
цели! Потом лист с записью
решения куда-то потерялся и 5 лет он
пытался воспроизвести решение
ещё раз, пока не отыскал
потерянную бумажку.
Адаме отослал решение
известному популяризатору мате-
Рис. 230 матики Мартину Гарднеру, а тот
передал его для анализа специалисту по комбинаторным задачам
Чарльзу Триггу. Тригг доказал, что не существует более ни
одного магического шестиугольника любого порядка, т.е. это
решение уникально.
Есть аналогия с магическими квадратами: второго порядка
не существует, а третьего порядка только единственный
экземпляр, если не считать симметричные отображения. Но дальше
аналогия закончилась, квадратов с увеличением порядка все больше
и больше, а шестиугольников кроме одного нет вообще, хоть как
увеличивай порядок.
Независимо от Адамса в 1958 году такой же шестиугольник
опубликовал в «Математической газете» Том Винере.
Доказательство невозможности существования магического
шестиугольника выше третьего порядка Тригг начал с вывода
формулы магической суммы S для шестиугольника w-го порядка.
Для вывода этой формулы достаточно знать, как вычисляется
сумма членов арифметической прогрессии, и уметь оперировать
не конкретными значениями порядка, а абстрактным обобщением
в виде п. Итак, вычислим магическую сумму шестиугольника п-
го порядка.
Во-первых, выразим через п количество рядов в
шестиугольнике, идущих в каком-то одном направлении. Наглядно мы
уже убедились, что у шестиугольника 2-го порядка 3 ряда, 3-го
порядка - 5 рядов и далее, при увеличении порядка на единицу,
количество рядов увеличивается на два. Эта зависимость
выражается формулой: количество рядов равно 2пЛ.

120
Магическое разнообразие. Шестиугольник
Во-вторых, подсчитаем количество чисел в шестиугольнике
п-го порядка. В первом ряду (и в последнем) п чисел, во втором
(и предпоследнем)-^ 1 , в третьем (и втором от конца) п+2 ,...,
наконец, в среднем, самом длинном, 2л-1.
Сложим все эти выражения:
2(п+(п+1)+(п+2) + ..Л(2п-2))+2п-1=(Зп-2)(п-1)+(2п-1)=Зп2-Зп+1
Так как числа начинаются с 1, то количество чисел совпадает с
последним числом, т.е. Зп2-Зп+1 -это и количество чисел, и
последнее число в шестиугольнике п-ro порядка. Чтобы найти
магическую сумму, остается сложить все числа и поделить на
количество рядов в одном направлении.
S=[l+(3n2-3n+l)]-(3n2-3n+l)/W2n-l)]=^
Затем, используя методы решения диафантовых уравнений, Тригг
показал, что это выражение принимает целые значения лишь при
п=\ или п=3. Доказательство единственности решения для
шестиугольника третьего порядка он провел перебором всех
возможных вариантов. Сейчас это можно перепроверить с помощью
компьютера, что и было сделано. Перебрав все комбинации
чисел, ЭВМ установила единственность магического
шестиугольника третьего порядка.
Как меняются времена: задача, над которой К. Адаме бился
почти полвека, в 1979 году была предложена простым советским
школьникам в детском физико-математическом журнале
«Квант», как обычная рядовая задача.
Пора показать этот исторический и уникальный магический
шестиугольник, на случай если вы сами еще не решили эту задачу.
Рядом линиями показана симметрия в расположении чисел.
Рис. 231

Магическое разнообразие. Прямоугольник 121
Итак, магический шестиугольник существует, причем в
единственном варианте, цель достигнута и одновременно вопрос
исчерпан. Что же делать дальше, полюбоваться этим уникумом и
всё? Примитивный подход. Фантазии ума ограничений быть не
может. Вспомните квадрат без одной клетки. Перенесем эту идею
на шестиугольник и снова простор для головоломок: построить
магический шестиугольник с одной или несколькими
незаполненными ячейками, или же убирая некоторые числа из
натурального ряда, составить магический шестиугольник из
непоследовательных чисел. Именно так была поставлена задача в журнале
«Наука и жизнь» и читатели нашли много решений, причем не
только третьего порядка, но и вышеч Задачи сгруппированы в
конце данной главы, пока же продолжим мыслить в направлении
разнообразия форм магических фигур.
Магический прямоугольник
Квадрат - это прямоугольник, у которого все стороны равны.
А если стороны не равны, то, разбивая прямоугольник на
квадратные клетки, получим разное количество клеток в строчке и в
столбике. В таком случае невозможно добиться равенства сумм
по всем строчкам и столбцам одновременно. Ослабим
требования, назовем магическим прямоугольник, у которого суммы
чисел по всем строчкам равны между собой и отдельно равны
между собой суммы чисел по всем столбцам, т.е. у
прямоугольника будет две магические суммы, одна для строчек, другая для
столбцов.
Назвать - назвали, а можно ли его построить?
Начнем проверку с прямоугольника 2x3 (2 строчки,
3 столбика). Сумма чисел 1+2+3+4+5+6=21, делится
на 3, но не делится на 2, а значит, эти числа нельзя
распределить по двум строчкам так, чтобы сумма
Рис. 232 чисел была одинаковой.
Продолжим поиск. Прямоугольник 2x4 должен содержать
числа от 1 до 8. Сумма 1+2+...+8=36, делится и на количество
строчек, и на количество столбиков. Разбив числа на пары с
одинаковой суммой, легко получаем магический прямоугольник 2x4.
Можно сделать первые выводы. Необходимое условие его
существования - сумма расставляемых чисел должна делиться и
на количество строчек, и на количество столбиков.
ш

122
Магическое разнообразие. Треугольник
Кроме того, отношение сумм
по строчкам и по столбикам равно
отношению количества столбиков к
количеству строчек.
1
8
4
5
7
2
6
3
= 18
= 18
и
9
и
9
и
9
и
9
15
6
3
4
7
13
5
8
11
2
10
12
14
9
1
Рис. 233
Перейдем к размеру 3x4. 5=1+2+...+12=78 не делится на 4,
пролетаем не задерживаясь к размеру 3x5.
1+2+...+15=120, делится и на 3, и на 5, прямоугольник возможен.
= 40
II
24
Рис. 234
Ставим задачу в общем виде. Числа от 1 до пк требуется
разместить в прямоугольнике из п строк и к столбцов так, чтобы
образовались две магические суммы: Sj= (l+nk)k/2 для каждой
строчки и S2=(l+nk)n/2 для каждого столбца, тогда этот
прямоугольник будем называть магическим. Необходимое условие для
построения такого прямоугольника выяснено, существование
доказано двумя примерами, дальнейшее в ваших руках.
Магический треугольник
Простейший многоугольник - это треугольник. Если
первые п натуральных чисел расположить в форме треугольника так,
что образуется одна и та же сумма вдоль каждой из его сторон, то
такой числовой треугольник называют магическим.
Как видите, понятие «магичности» в
треугольнике свелось к кросс-суммам и задачам,
уже рассмотренным в соответствующей главе.
Пример магического треугольника на
рисунке. По аналогии с квадратами, такой
треугольник назовем магическим
треугольником 3-го порядка, т.к. по каждой стороне
треугольника стоят три числа.
Рис. 235

Магическое разнообразие. Треугольник
123
8=12
Магические квадраты конкретного порядка могли
отличаться только расположением чисел, а магическая сумма была
для них одна, жестко определенная по
формуле для каждого порядка.
Магические треугольники одного порядка
различаются не только расположением чисел, но
и магической суммой.
Основной недостаток магического
треугольника - его внутренняя пустота, числа
стоят только по сторонам, в отличие от
полностью заполненного квадрата,
прямоугольника, шестиугольника. Возникает
желание его «уплотнить».
Рис. 236
Реализация этого желания приводит вот к такому,
например, магическому уплотнённому
треугольнику из чисел от 1 до 15.
Для внешнего треугольника
£,=1+6+13+3=3+4+14+2=2+5+15+1
=23, для внутреннего треугольника
&=7+11+9=9+10+8=8+12+7=17.
Кроме того, он имеет равные
дополнительные суммы:
^=3+13+9+4=6+1+7+15=14+5+
8+2=29
£,=3+7+8=2+9+7=1+9+8=18
^=3+11+10=2+10+12=1+11+12=24 Рис.237
55=9+10+11=8+10+12=7+11+12=30
5t=13+11+12+5=15+12+10+4=6+11+10+14=41
^=3+13+5+2=2+14+6+1=1+15+4+3=23
5Р=3+13+15+5+4=1+6+4+14+15=2+14+13+6+5=40
Этот треугольник был напечатан в журнале «Математика в
школе». Его автор Ф. Ф. Егоров высказал предположение, что из
чисел 1-15 можно сформировать около 30 различных
уплотненных магических треугольников, обладающих суммами
указанного вида. В данном случае получается два больших вложенных
треугольника, не считая образующихся маленьких, а можно ведь
увеличить количество элементов в такой «треугольной
матрешке». Попробуйте поискать в этом направлении. Человеческая
мысль по предназначению никогда не должна стоять на месте.

124 Магическое разнообразие. Проекционный куб
Магические трехмерные тела
Настала пора покинуть плоскость и выйти в наш
трёхмерный мир. На смену плоским фигурам приходят объёмные
геометрические тела, и они тоже могут быть магическими.
Проекционный магический куб
Промежуточное положение между плоскими магическими
квадратами и объемным магическим кубом отведем объемным
конструкциям, плоские проекции которых являются магическими
квадратами. Из курса школьного черчения каждый помнит о трех
проекциях геометрических тел: вид спереди, вид сверху и вид
слева. Большой куб разбит на 64 маленьких кубика. Заполнены из
них только 16, по 4 кубика в четыре слоя, в соответствии с
прилагаемыми плоскими рисунками. Каждая из трех проекций
объемного построения - это магический квадрат 4-го порядка. Они
показаны отдельно. К сожалению, на рисунке не все кубики
просматриваются, они перекрывают друг друга. Такую модель
хорошо бы покрутить в руках или в виртуальном пространстве.
Рис. 238
Рис. 239

Магическое разнообразие. Проекционный куб 125
1
ill
■
ш
щ
ш
й
I
12
4
10
13
7
Рис. 240
Книга все больше становится похожей на альбом красивых
(жаль что не цветных) геометрических рисунков, но не могу
отказаться от соблазна показать аналогичную конструкцию
проекционного магического куба 5-го порядка.
Рис. 241
1
6
15
19
23
2
п
tan
*
Рис. 242
Рис. 243
19
16
12
23
15
1216
15
т
25
19
23
1
! 23
19
Ж

126
Магическое разнообразие. Куб
Магические кубы
Если уж от квадрата переходить к пространственным
объектам, то первым на очереди должен быть куб.
Магический куб инго порядка состоит из последовательных
чисел от 1 до п3 , расположенных в форме куба таким образом,
что сумма чисел в каждой строке, в каждом столбце, в каждом
ряду и по каждой из 4-х диагоналей одна и та же и равна
(п3+1)п/2. Эту сумму в кубе можно получить Зп2+4 способами.
Для построения магических кубов можно обобщить методы,
которые использовались для построения магических квадратов.
Мы не будем делать этого, а просто приведем несколько
примеров, чтобы вы убедились воочию в существовании подобных
объектов.
Рис. 244
Магический куб третьего порядка, представленный в форме
пространственной решетки, с суммой 42.
Такое изображение магического куба довольно сложное,
поэтому его можно показать упрощенно, как набор из нескольких
плоских слоев. Что мы и сделаем для демонстрации совершенно-
То магического куба 4-го порядка.

Магическое разнообразие. Куб
127
60
13
56
3712
20
41
61
8
32 49
21
36
25
48
7
50
11
62
26
47
22
35
55
2
59
14
42
31
38
19
57
16
53
4
40
17
44
29
9
64
5
52
24
33
28
45
6
51
10
63
27
46
23
34
54
3
58
15
43
30
39
18
Рис. 245
На схеме показано как эти слои располагаются в кубе, но, к
сожалению, все числа здесь не
рассмотришь.
Наконец, еще один пример
магического куба 4-го порядка, который
получается разрезанием на четыре
части магического квадрата 8-го порядка.
Каждый слой этого куба является
магическим квадратом, что, в общем-то,
не обязательно. По определению
магического куба, только 4 его диагонали
должны давать магическую сумму, про
диагонали слоев это не сказано.
Рис. 246
/ -ж /&&/*&/«*&
&*/
У
г/
Рис. 247
1
62
52
15
32
35
45
18
8
59
53
10
25
38
44
23
61
2
16
51
36
31
17
46
60
7
9
54
37
26
24
43
48
19
29
34
49
14
4
63
41
22
28
39
56
11
5
58
20
47
33
30
13
50
64
3
21
42
40
27
12
55
57
6

128
Магическое разнообразие. Параллелепипед
Рассматривая плоские магические фигуры, мы не ограничились
только квадратом, а ввели понятия магического прямоугольника,
треугольника и т.д. Перейдя к трехмерным пространственным
объектам, не будем ограничиваться кубом, а продолжим аналогию
и рассмотрим магический параллелепипед, магическую
треугольную призму, т.е. насколько фантазии хватит.
Магический параллелепипед
Прежде, чем расставлять числа в форме прямоугольного
параллелепипеда, нужно проверить, а возможно ли их расставить
так, чтобы выполнялось условие равенства сумм по всем трем
направлениям, хотя бы по отдельности.
Допустим, мы хотим построить параллелепипед из
прямоугольников 2x3, взятых в два слоя. 2x3x2=12, поэтому
потребуются числа от 1 до 12. S = (1+12)6=78. В двух слоях вместе,
четыре строчки, а число 78 на 4 не делится, следовательно, такой
размерности магический параллелепипед построить заведомо
нельзя. Этого и следовало ожидать, ведь прямоугольник 2x3 тоже
нельзя было построить. Однако прямоугольник 2x4 построили
легко, попробуем построить из таких прямоугольников
параллелепипед 2x4x4. 2x4x4=32. S= (1+32)16=3316=528.
Эта сумма делится на количество строчек (8), на количество
рядов(16) и на количество столбцов (8), т.е. необходимое условие
выполнено. Осталось расставить числа так, чтобы добиться
равенства сумм по строчкам и столбцам из четырех чисел - 66, а
по рядам из двух чисел - 33. Способ расстановки понятен из схемы:
Рис. 248
Получается прямоугольный параллелепипед, рисунок
которого показан на следующей странице. С другой стороны, этот
параллелепипед можно рассматривать, как два квадрата 4-го
порядка, расположенные в два слоя.

Магическое разнообразие. Параллелепипед
129
К сожалению, они не
магические, т.к. равенство сумм по
диагоналям не выполняется, но по
определению магического
параллелепипеда этого не требуется,
достаточно равенства сумм по
трем направлениям, причем по
отдельности. Этим простым
примером доказываем сам факт
существования магических
параллелепипедов. Теперь можно
продолжить поиск магических
параллелепипедов других
размерностей, каждый раз,
предварительно проверяя, чтобы сумма
всех входящих в него чисел
делилась на количество горизонтальных строчек, Рис. 249
на количество горизонтальных рядов и на количество
вертикальных столбцов.
В следующем примере магический параллелепипед
сформирован из чисел от 1 до 45, размещенных тремя слоями в пря-
моугольниках 3x5. В
Sr( 1+45)3/2=69
повторяется 32 раза: вдоль 15
параллелей ребру АВ,
вдоль 15 параллелей
ребру AAj и вдоль двух
диагоналей AQ
(6+23+40) и DB!
(25+23+21), а вторая
магическая сумма
повторяется 9 раз вдоль
параллелей ребру AD (и
еще дополнительно по
двум «разломанным»
диагоналям
21+7+23+39+25=40+7+
+23+39+6.
5 Трошин
результате одна магическая сумма
Рис. 250

130 Магическое разнообразие. Тор
Магическая треугольная призма
Треугольную призму из трех треугольников 3-го порядка
составить нельзя, т.к. S= (1+18)18/12=57/2 - дробное число, а для
четырех треугольников 4-го порядка необходимое условие
выполняется (1+36)36/18=74.
Рис. 251
Треугольная призма сформирована из чисел от 1 до 36,
размещенных в четыре слоя в треугольниках 4-го порядка. Сумма
четырех чисел по всем ребрам призмы и параллельным им
отрезкам, равна 74 и повторяется 21 раз. Дополнительно эта сумма
получается в вершинах двух боковых граней призмы
35+2+26+11=35+5+23+11.
Магический тор
Основные геометрические тела делятся на призмы, пирамиды
и тела вращения. Призмы, к которым относится и куб, и
прямоугольный параллелепипед, рассмотрены достаточно. Из тел
вращения, к которым относятся цилиндр, конус, шар и тор, остановимся
на торе. Тором математики называют геометрическое тело,
имеющее форму бублика, объемный аналог плоского кольца.

Магическое разнообразие. Тор
131
Соответственно и получить его можно, используя.методику
образования кольца из квадрата.
Возьмем магический квадрат 4-го порядка и проделаем с
ним следующие преобразования: свернем его в трубку, затем
растянем её и изогнем так, чтобы она превратилась в тор
(предполагается, что квадрат сделан из эластичного материала,
позволяющего делать любые деформации).
7
2
16
9
12
13
3
6
1
8
10
15
14
11
5
4
Рис. 252
Все строки, столбцы и диагонали квадрата превратились в
замкнутые кривые. Начав двигаться из любой клетки и сделав из
нее два шага по диагонали в любом из 4-х направлений, мы всегда
окажемся в одной и той эке клетке. Эту клетку называют
«антиподом» той, из которой мы вышли. Суммы чисел в любых двух
клетках, являющихся антиподами по отношению друг к другу,
равны 17. Любая замкнутая полоска из 4-х клеток,
расположенных вдоль меридиана, параллели или диагонали, содержит числа,
сумма которых равна 34, магической сумме исходного квадрата.
Эта же сумма получается, если взять любую «квадратную
заплату» на поверхности тора, состоящую из 4-х клеток.
В качестве исходного можно взять любой другой
магический квадрат, в частности более высокого порядка, но слишком
толстенький тор получится.
Процесс можно продолжить и рассматривать далее основные
геометрические тела. Остались абсолютно неохваченными
пирамиды, к которым прямой путь от треугольников, цилиндр,
образуемый движением окружности параллельно оси. Есть над чем
подумать, в свободное время. Мы рассмотрели часть призм, а
именно: куб, прямоугольный параллелепипед, треугольную
призму. Но с позиции красоты и совершенства более интересны
правильные многогранники, у которых равны между собой все
ребра и все грани являются равными правильными многоугольниками.

132
Магическое разнообразие. Многогранники
Правильные многогранники
Всего существует пять правильных многогранников, одним
из которых является куб или гексаэдр, поэтому было бы интересно
рассмотреть остальные с точки зрения расстановки чисел и
равенства сумм, причем числа можно ставить в вершинах или на
гранях, наконец, на ребрах многогранников.
Сведения о правильных многогранниках представим в виде
таблицы.
Многогранник
Тетраэдр
Гексаэдр (куб)
Октаэдр
Додекаэдр
Икосаэдр
Рис
253
254
255
256
257
Вершины
4
8
6
20
12
Ребра
6
12
12
30
30
Грани
4
6
8
12
20
Рис. 253
Рис. 254
Рис. 255
Рис. 256
Рис. 257

Магическое разнообразие. Многогранники
133
Кстати, есть интересная формула, связывающая количество
вершин, граней и ребер у всех правильных многогранников,
формула Эйлера: В-Р+Г=2.
Самый известный и распространенный многогранник — это
куб. Он встречается во многих играх и головоломках. Грани куба
можно пронумеровать цифрами от 1 до 6 так, что сумма пар
чисел на противоположных гранях будет равна 7. Размеченный
таким образом куб называется игральной костью и используется
во многих играх, например, нардах. Вершины куба можно
пронумеровать числами от 1 до 8 так, что сумма четырех чисел на
каждой из шести граней куба будет одна и та же.
При решении некоторых задач уместно пространственные
головоломки превратить в плоские, аналогичные рассмотренным
в главе «Кросс-суммы», для этого необходимо заменить
многогранники их проекциями на плоскость. Методика получения плоской
проекции многогранника
состоит в следующем:
берем проволочную
модель многогранника и
освещаем её точечным
источником света.
Расположив необходимым
образом многогранник,
источник света и
плоскость экрана, получим
теневое изображение
проекции многогранника
на плоскость.
Рис. 258
Придумывание головоломок с многогранниками чем-то
напоминает развешивание гирлянд из лампочек перед праздником.
Берется какой-то многогранник, и вдоль его вершин или рёбер
развешиваются гирлянды кружочков, а потом ставится вопрос:
можно ли расставить числа от 1 до и так, чтобы выполнялось
некоторое условие. Многогранники - это красивейший раздел
стереометрии, кроме пяти правильных есть ещё 13 полуправильных
или архимедовых тел, звёздчатые многогранники и масса других.
Поле деятельности обширно и с точки зрения «магичности» еще
мало распахано, в отличие от квадрата. Но пора переходить от
готовых построений непосредственно к головоломкам.

134
Магическое разнообразие. Задачи 3-5
3-3
Впишите числа от 1 до 19, исключая
одно из них, в желтые кружочки так, чтобы
сумма чисел в каждом ряду по каждому из
трех направлений, была одна и та же.
Исключая разные числа, можно получать
разные значения магической суммы.
Рис. 259
3-4
Решите предыдущую задачу с иным расположением
незаполненного красного кружка, а если хватит энтузиазма, то
перенесите условие на шестиугольник четвертого порядка.
Рис. 260
Рис. 261
Рис. 262
3-5
Расставьте числа от 1 до
19 так, чтобы сумма чисел в
ряду, состоящем из трех
кружков, равнялась бы 22, сумма
ряда из 4-х кружков была бы
равна 42, а сумма ряда из пяти
кружков составляла бы 62.
Рис. 263

Магическое разнообразие. Задачи 6-10 135
3-6
Первые восемь натуральных чисел можно расставить в
прямоугольнике 2x4 так, что сумма чисел в верхней строке равна
сумме чисел в нижней строке, а суммы чисел в столбцах также
равны между собой. Мы убедились в этом.
Можно ли расставить подобным образом:
а), первые 10 ,
б), первые 12 натуральных чисел?
3-7
Попробуйте построить магический прямоугольник для
других значений п и к , например, п=А и к=6. (Необходимое условие
выполняется, но является ли оно достаточным?)
3-8
Прямоугольник разбит на клетки 1x1 см. Внутри каждой
клетки написано число. Известно, что сумма всех чисел в каждой
горизонтальной строчке равна 1, а в каждом вертикальном столбике
равна 2. Может ли площадь прямоугольника равняться 1986 см2 ?
3-9
В задаче 14 из первой главы нужно было построить
магический треугольник 4-го порядка с суммой а). 20, б). 17.
Усложним требования: докажите, что магическая сумма у треугольника
4-го порядка может принимать значения 17, 19, 20, 21, 23 и
никаких других, и постройте треугольники, обладающие каждой из
возможных сумм.
3-10
Среди магических треугольников 4-го порядка с суммой 20
есть один, который можно назвать двойным магическим
треугольником, т.к. у него равны между собой и суммы квадратов
чисел, стоящих на сторонах. Он обладает ещё рядом свойств:
равенством сумм для треугольников 3-го порядка и для
внутренних пятиугольников. Найдите такой уникальный треугольник,
если он у вас ещё не встречался.

136
Магическое разнообразие. Задачи 11-13
3-11
В кружочки этого куба впишите
числа от 1 до 8 так, чтобы сумма чисел
по шести граням куба и по двум
диагональным плоскостям равнялась 18.
Рис. 264
3-12
Попробуйте составить магические параллелепипеды другой
размерности, нежели те, что были показаны. Особенно
интересно, если все три измерения будут разными, можно ли составить
такой магический параллелепипед?
3-13
Рис. 265
Оставшиеся числа от 1 до 27 нужно расставить в кружочках
так, чтобы сумма трех чисел по любому из 37 отрезков равнялась 42.

Магическое разнообразие. Задачи 14-16 137
3-14
Можно ли грани правильного многогранника
пронумеровать числами от 1 до п (где п - число граней) так, чтобы сумма
чисел соответствующая граням, сходящимся в одной вершине,
была бы одна и та же для всех вершин многогранника?
3-15
Можно ли ребра правильного многогранника
пронумеровать числами от 1 до п (где w-число ребер) так, чтобы сумма
чисел соответствующих ребрам, сходящимся в одной вершине,
была бы одна и та же для всех вершин многогранника?
3-16
Можно ли вершины правильного многогранника
пронумеровать числами от I до п (где п- число вершин) так, чтобы сумма
чисел соответствующих вершинам каждой грани была бы одинакова?
Рис. 266 Рис. 267
Красиво выглядят объемные модели, но можно сделать
упрощение и заменить их, как уже было сказано, плоскими
проекциями. Причем куб уже рассмотрен, и задача распадается на
четыре отдельных головоломки.
3-16-1
Можно ли цифры от I до 4
расставить в кружках фигуры так, чтобы суммы
трех чисел в вершинах каждого из 4-х
треугольников были одинаковыми?
\j
Рис. 268

138
Магическое разнообразие. Задачи 16-17
3-16-2
Расставьте числа от I до 6 в кружках
фигуры так, чтобы суммы трех чисел в
вершинах каждого из восьми
треугольников были одинаковыми.
Рис. 269
3-16-3
Расставьте числа от 1 до 12 в
кружках фигуры так, чтобы сумма
трех чисел в вершинах каждого из
двадцати треугольников была одна и
та же.
Рис. 270
3-16-4
Расставьте некоторые числа от
I до 25 в кружках фигуры так, чтобы
сумма пяти чисел в вершинах
каждого из двенадцати пятиугольников
была одна и та же.
Рис. 271
3-17
Углы плоских граней многогранника упорядочены
следующим образом: если «-число плоских углов многогранника, то
каждый из них обозначается одним и только одним из чисел
1,2,...и. Можно ли расставить эти числа так, чтобы во всех гранях
суммы чисел, соответствующих углам данной грани были равны?
Докажите, что такая расстановка возможна для куба и не
возможна для других правильных многогранников.

Магическое разнообразие. Четвертое измерение 139
Четвертое измерение
Прекрасный храм математической науки строится из
кирпичиков, основными из которых являются «числа» и «фигуры».
Только в узко конкретных задачах эти понятия могут
присутствовать по отдельности; стоит рассмотреть более широкий вопрос
и уже одно без другого не существует.
В основу этой книги положено понятие суммы чисел, мы
постоянно подсчитывали сумму чисел по рядам, столбцам,
строчкам, диагоналям, и постоянно перед нами были различные
фигуры, по клеткам, кружочкам, ячейкам, которых расставлялись
числа. Соединяли числа последовательно и получали
«магические» линии, вырывались из рамок квадрата и попадали в рамки
других плоских фигур и пространственных тел.
А раз так, то уже сознательно поговорим о размерности
пространства и попробуем замахнуться на четвертое измерение.
Для человеческого разума это большая нагрузка, мы живем в
трехмерном пространстве, поэтому нужен постепенный подход.
Одномерная Страна - это прямая линия. Чтобы в стране
был порядок, нужна центральная власть, нужны законы и должна
быть концепция развития общества, иначе говоря, цель - куда
идти в своем развитии.
Рис. 272
Так создается на прямой система координат. Центральная
власть - это точка 0, начало отсчета; общие законы
символизируются введением единичного отрезка, которым всё измеряется;
направление положительного развития указывается с помощью
стрелки. Судя по всему, это общество тоталитарное, потому что
те, из кого всё строится, а именно - точки, имеют нулевую
размерность. Это даже хуже, чем быть «винтиком». Хотя у каждой
точки есть свой паспорт, а грубо говоря, - номер или её
координата. Причем по координате точки сразу можно судить о её
близости к центральной власти, к кормушке, к началу координат.
Все как в человеческом обществе. Начало отсчета выбирается
произвольно, как и единичный отрезок. Начало отсчета - это
тоже точка, следовательно, имеет нулевую размерность как все
точки, но её выбрали и этим всё сказано и предопределено.

140 Магическое разнообразие. Четвертое измерение
Точки объединяются в коллективы, получается ещё два вида
объектов: отрезки и лучи. Они могут входить один в другой, или
частично пересекаться, или вообще не иметь общих точек. Лучи
могут иметь разное направление, как партии в нашем обществе,
левое или правое. Отрезки «беспартийные», у них нет
направления, но они отличаются длиной. Отрезок - это объект единичной
размерности. Можно продолжать аналогию с человеческим
обществом, но прогресс требует перехода от тоталитарного
общества с одним диктатором во главе к демократическому
обществу. Попробуем и мы перейти к двумерному пространству.
Представим себе, что один из отрезков единичной длины
вырвался из одномерного общества, т.е. из прямой. Вырываются
обычно самые умные представители, поэтому естественно
предположить, что он интуитивно будет двигаться в направлении
перпендикулярном к прямой, чтобы подальше удалиться. Но мы,
руководя процессом со стороны, не дадим ему уйти дальше, чем на
единицу длины. В процессе своего движения этот единичный
отрезок «опишет» плоскую двумерную фигуру - единичный квадрат.
УД
т х
Рис. 273
В плоскости система координат состоит уже не только из
точки 0, начала отсчета, но и «двухпалатного парламента» - двух
взаимно перпендикулярных единичных отрезков. Каждой точке
плоскости теперь ставятся в соответствие две координаты.
Разнообразие объектов, населяющих плоскую страну, возрастает: точки,
получив две координаты, так и остались с нулевой размерностью,
далее одномерные отрезки и лучи, причем лучи могут иметь
бесчисленное множество направлений, наконец, новые двумерные
объекты - треугольники, квадраты и другие четырехугольники,
многоуголыпжи, правильные и неправильные, окружности и эллипсы.
Это многообразие уже требует значительного времени на
изучение их свойств и характеристик.

Магическое разнообразие. Четвертое измерение 141
Одна из характеристик - числовая. У одномерных отрезков -
это длина, у двумерных объектов - площадь. В нашу задачу не
входит задерживаться в плоскости, мы изучаем процесс перехода
от одной размерности к другой, пора в трехмерный мир.
Продолжение процесса состоит в движении единичного
квадрата в направлении перпендикулярном к плоскости, в которой он
содержится. В процессе движения квадрат «описывает» объемное
тело - единичный куб. Появляется третье направление движения
- ось Z, перпендикулярная к двум предыдущим. Каждая точка
трехмерного пространства характеризуется тремя координатами,
а трехмерные объекты - своим объемом. Трехмерный
геометрический мир изучает стереометрия.
Что мешает нам продолжить движение мысли и объектов?
Только одно: мы не знаем,
какое направление
перпендикулярно к трем осям Ox, Oy,Oz
одновременно; в нашем
трехмерном пространстве такого
направления нет. Но ведь с
точки зрения квадрата на
плоскости, не знающего другого мира,
у него тоже не было в его
двумерном мире третьего
направления перпендикулярного к
двум другим. А у отрезка на
прямой не было даже понятия
Рис. 274 перпендикулярности. Двигали их мы,
потому что из своего трехмерного пространства видели, как и
куда нужно идти. Здесь напрашивается такая аналогия: человек,
как существо мыслящее легко разбирается с объектами живой
природы, стоящими ниже его на эволюционной лестнице: от
одноклеточных до приматов. О том же, что стоит выше, о Боге -
люди строят догадки, чувствуют, что-то там есть, но представить и
понять не могут, единственно считая себя созданными «по образу и
подобию». Очень хорошо сказал Александр Мень, обладавший
энциклопедическими познаниями: «К сознательной вере человек
приходит только через большие знания». Кстати, теория
происхождения органической жизни на Земле, предложенная академиком
Опариным А. И., настолько шаткая и молодоказательная, что тоже
требует не понимания, а фанатичной веры.

142 Магическое разнообразие. Четвертое измерение
Итак, мы верим в наличие этого четвертого направления Ow,
перпендикулярного всем трем осям Ox, Oy, Oz, и сдвигаем
единичный куб в этом направлении на расстояние равное единице.
Фигура, которую «опишет» куб в результате такого сдвига, есть
четырехмерный единичный гиперкуб или тессеракт. Не буду
даже пытаться изобразить это, чтобы не сбивать правильную
мысль заведомо неправильным изображением. Можно
продолжить рассуждения по аналогии с предыдущими шагами и
рассмотреть предполагаемые свойства этого, недоступного
взору объекта.
В каждой вершине гиперкуба сходятся четыре взаимно
перпендикулярных ребра. Выбрав одну из вершин гиперкуба за
начало координат, а сходящиеся в ней ребра за оси координат, мы
сможем поставить в соответствие каждой точке четырехмерного
пространства упорядоченную четверку чисел, координаты этой
точки. Аналитическая геометрия позволяет обращаться с этими
упорядоченными четверками чисел так же, как в планиметрии
обращаются с парами чисел, а в стереометрии - с
упорядоченными тройками чисел.
Когда мы сдвигали квадрат, то из четырех вершин квадрата
получали 8 вершин куба, к четырем ребрам квадрата в начальном
положении добавились 4 ребра квадрата в конечном положении и
4 ребра, произведенных вершинами при движении, т.е. ребер
стало 12. Квадрат представляет собой одну грань, при движении,
каждое из четырех ребер образовало ещё четыре грани и шестая
грань - это конечное положение квадрата. Повторим эти
рассуждения для движения куба.
Сосчитав каждую вершину трехмерного куба дважды, в её
начальном и конечном положении, найдем, что у гиперкуба
имеется 16 вершин. Каждая вершина трехмерного куба, двигаясь,
производит единичный отрезок - одно из ребер гиперкуба, Всего
таких ребер столько, сколько вершин у трехмерного куба, т.е. 8,
плюс ещё 12 ребер трехмерного куба в начальном положении и
ещё 12 ребер в его конечном положении. Итого: у гиперкуба 32
ребра. Каждое из 12 ребер куба при движении образует одну грань,
всего 12, и к ним нужно добавить 6 граней трехмерного куба в
начальном положении и столько же в конечном. Граней будет 24.
Трехмерный куб ограничен двумерными гранями, а одномерные
отрезки образуют только его скелет. Четырехмерный гиперкуб
ограничен трехмерными кубами, а 24 двумерные грани - это его скелет.

Магическое разнообразие. Четвертое измерение 143
К шести кубам, порожденным гранями исходного куба, следует
добавить ещё два: исходный куб в начальном и конечном
положении. Таким образом, у четырехмерного гиперкуба имеется 8
трехмерных кубических граней, они-то и ограничивают гиперкуб,
образуя его гиперповерхность.
Нагрузку мыслям дали, теперь попробуем загрузить глаза. В
одной из предшествующих задач, мы заменяли правильные
трехмерные многогранники их проекциями на двумерную плоскость,
освещая каркас многогранника точечным источником света.
Также можно сделать проекцию гиперкуба в трехмерное
пространство. Естественно, это вполне конкретный трехмерный
объект, который можно и посмотреть и потрогать руками, если
сделать его объемную модель, но в книге, на плоском листе, мы
можем изобразить только проекцию на плоскость трехмерной
модели, которая в свою очередь служит трехмерной проекцией
четырехмерного гиперкуба. Вот такое двойное упрощение
истинной сущности этого объекта. Выглядит это так.
Рис. 275

144 Магическое разнообразие. Четвертое измерение
Для удобства сведем все полученные сведения в таблицу
Объект
Точка
Отрезок
Квадрат
Куб
Гиперкуб
Размерн.
простр.
0
1
2
3
4
Проекция на
пространство
меньшей
размерности
Нет
Точка
Отрезок
Квадрат
См. рис.
Вершин
1
2
4
8
16
Ребра
0
1
4
12
32
Грани
0
0
1
6
24
Кубы
0
0
0
1
8
Гип.куб
0
0
0
0
1
Вернемся к магии чисел и их расстановке в узлах
различных фигур. Новый объект - проекция гиперкуба.
16 клеток совершенного магического квадрата 4-го порядка
можно сопоставить с 16 вершинами гиперкуба в соответствии с
показанным рисунком. Сумма чисел, стоящих в 4-х вершинах
каждой из 24 квадратных граней гиперкуба, будет равна 34.
Числа, стоящие на противоположных концах диагоналей гиперкуба,
дают в сумме 17, только нужно правильно понять, какой отрезок
на проекции соответствует диагонали гиперкуба.
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис. 276
Рис. 277
Первая четырехмерная фигура, точнее её проекция в
трехмерное пространство, и сразу получилось расставить
числа в вершинах по «магическому» принципу. В четырехмерном
пространстве могут быть представлены аналоги всех наших
трехмерных геометрических тел. Рассмотрим еще один объект
- четырехмерный аналог тетраэдра, называемый пентатоп.

Магическое разнообразие. Четвертое измерение 145
Если центр равностороннего треугольника соединить
отрезками прямых с вершинами, то получится проекция на
плоскость каркаса правильного тетраэдра. Точно так же, соединив
отрезками прямых центр тетраэдра с четырьмя вершинами, мы
получим проекцию на трехмерное пространство каркаса пентатопа.
У него имеется 5 вершин, 10
ребер, 10 треугольных граней и 5
«клеток» в форме тетраэдра,
ограничивающих его поверхность. На
проекции мы видим четыре маленьких
клетки - тетраэдра и один большой.
В самом пентатопе, если он
правильный, все клетки конгруэнтны, т.е.
одинаковые.
Рис. 278
ЗИ8
Попробуйте сами составить задачу на расстановку чисел,
используя трехмерную проекцию пентатопа и действуя по
аналогии с ранее рассмотренными задачами.
Заканчиваем краткую экскурсию по экспонатам
«магической кунсткамеры». Перед нашим взором прошли плоские
фигуры и объемные геометрические тела, а наше воображение,
возможно, позволило представить тела четырехмерные, увидеть
которые не может глаз, но может мысль. Как всякий музей, эта
кунсткамера постоянно пополняется новыми экспонатами,
которые приносит человеческая изобретательность и фантазия.
Для направления поисков, приведу на следующей странице
рисунки некоторых геометрических объектов, о которых я ещё не
знаю, можно ли их рассматривать в контексте этой книги и
предлагаю пофантазировать читателям. В качестве напутственных
слов, уместно привести высказывание человека, оставившего
свой след в истории цивилизации.
«Никогда не прекращайте вашей самообразовательной
работы и не забывайте, что, сколько бы вы ни учились,
сколько бы вы ни знали, знанию и образованию нет ни
границ, ни пределов». Это слова русского писателя и библиографа
Николая Александровича Рубакина.

146
Магическое разнообразие. Перспективы...
г
Рис. 279
Усечённая пирамида
Рис. 281
Цилиндр
Рис. 280
Ромбический додекаэдр
...!
Рис. 282
Звездчатый октаэдр
Рис. 283
Кубооктаэдр
Рис. 284
Ромбокубооктаэдр

Нет таких отдаленных явлений, познания
которых нельзя было бы достичь, и нет таких
таинственных явлений, которые нельзя было бы понять.
Р. Декарт (1596-1650) - французский математик
Незнание природы является корнем тех
неизвестных сил, перед которыми так долго трепетал,
человеческий род, и тех суеверных вероучений,
которые были источником всех его бедствий.
77. Гольбах (1723-1789) - французский философ
Чем больше мы познаем неизменные законы
природы, тем все более невероятными становятся
для нас чудеса.
Ч. Дарвин (1809-1882) - английский ученый
Чудо так же бессмысленно, недопустимо для
разума, как немыслимо, например, деревянное
железо или круг без окружности.
Л. Фейербах (1804-1872) - немецкий философ
Суеверие проходит с успехом цивилизации.
В. Г. Белинский (1811-1848) -русский философ

Практическая магия. Таблицы
149
Народ, зараженный суеверием, становится
добычей шарлатанов всякого рода.
77. Буаст
Название этой главы в какой-то степени шутка, но оно
объясняется тем, что здесь собраны элементы магии чисел и фигур,
которые можно использовать на практике. Речь идет не об
изготовлении талисманов с магическими квадратами, хотя в наше
время целителей и экстрасенсов, может быть и это пошло бы на
ура. Просто, описанные здесь предметы, можно изготовить и с
их помощью показать фокус, выступить на школьном вечере или
на встрече друзей, повеселить или удивить своих знакомых. Для
такой практической работы, кроме умной головы, потребуются
умелые и аккуратные руки и желание перерисовать, вырезать,
склеить. Начнем с некоторых числовых таблиц, с помощью
которых можно продемонстрировать друзьям свои удивительные
математические способности.
Магические таблицы для угадывания чисел
I
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
II
8
9
10
11
12
13
14
15
24
25
26
27
28
29
30
31
II
4
5
6
7
12
13
14
15
20
21
22
23
28
29
30
31
IV
2
3
6
7
10
11
14
15
18
19
22
23
26
27
30
31
V
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
Рис. 285

150 Практическая магия. Таблицы
Эта таблица, состоящая из чисел от 1 до 31, выписанных
определённым образом в пяти столбцах, отличается специфическим
магическим свойством. Отвернитесь от таблицы и предложите
своему приятелю или зрителям вашего трюка задумать любое
число от 1 до 31, и пусть вам только скажут, в каких столбцах
встречается задуманное число. По этим сведениям вы можете
назвать его безошибочно. Например, вам скажут, что задуманное
число находится в 1 и 5 столбцах таблицы. Для отгадывания вам
нужно хорошо знать степени числа 2.
2°=1, 2!=2, 22=4, 23=8 , 24=16.
Первому столбцу соответствует 24=16, второму 23=8, ... ,
пятому 2°=1. Вам нужно в уме сложить числа, соответствующие
названным столбцам, в данном случае 16+1=17.
Секрет основан на кодировании чисел в двоичной системе
счисления. Каждое из чисел от 1 до 31 переведено в двоичную
запись и расставлено в таблице в соответствии с этим кодом.
Например, 27 = 16+8+2+1 - 24+23+22+2° = (11011)2, эта запись
означает, что число 27 нужно поставить в 1, 2, 4, и 5 столбики
нашей таблицы при её создании, а в третьем - не ставить.
Основываясь на том же принципе можно составить таблицу
крупнее, из чисел от 1 до 63. В этом случае в ней будет шесть
столбцов, первому будет соответствовать значение 25=32,
второму 24=16 и т.д. Эти числа как раз стоят в первой строчке таблицы.
Вам остается только их хорошенько запомнить, чтобы потом на
таблицу не смотреть. Сама таблица не умещается на текущей
странице, и мы вынуждены перенести её на страницу 152.
Угадывание чисел с помощью карточек
Второй вариант фокуса, основанный на том же принципе
двоичного кодирования, выглядит несколько иначе. С его
помощью демонстрируется угадывание задуманного числа от 1 до 63.
Для демонстрации применяются шесть специальных
перфорированных карточек, на каждой из которых имеется 35 чисел,
расположенных на первый взгляд «бессистемно», и пять отверстий. Зритель
просматривает все карточки и передает фокуснику те из них, на
которых имеется задуманное им число. Вам остается сложить их
стопкой и сверху положить свою магическую карточку с отверстиями.

Практическая магия. Карточки
151
Теперь, чтобы получить задуманное число, вам нужно
сложить числа, видимые сквозь отверстия и сообщить
результат зрителям.
Отверстия на вашей карточке соответствуют местам,
на которых расположены «ключевые числа» - степени двойки, а
на каждой из шести карточек отверстия сделаны в тех же
местах, что и у вас, кроме одного, где проставлено «ключевое
число». В этом варианте вам не нужно запоминать степени
числа два, они видны в окошках.
54
29
56
31
62
23
28
49
18
61
19
24
58
50
17
55
57
63
20
59
22
31
27
48
30
52
26
21
16
27
51
52
60
53
25
45
29
13
46
43
63
8
24
15
27
11
12
41
10
57
60
44
31
58
30
40
26
9
59
47
25
62
61
14
12
42
62
56
27
28
39
53
43
60
36
63
40
32
48
54
57
44
50
38
46
55
59
56
45
43
42
52
61
41
51
58
47
49
59
42
33
62
35
58
37
5
37
22
23
45
47
63
36
28
44
29
39
53
30
12
54
21
61
46
62
47
13
55
14
15
28
20
4
60
63
52
7
31
6
38
11
10
14
26
54
38
3
23
62
63
6
50
51
35
59
47
30
43
31
27
2
35
26
19
7
39
42
55
58
11
15
46
18
22
43
33
3
15
57
53
49
7
5
27
31
1
29
47
17
51
19
9
25
21
63
15
45
55
43
23
35
33
61
59
11
39
13
41
51
37
Рис. 286
Первый комплект карточек для угадывания числа.

152
Практическая магия. Таблицы
I
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
II
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
III
8
9
10
11
12
13
14
15
24
25
26
27
28
29
30
31
40
41
42
43
44
45
46
47
56
57
58
59
60
61
62
63
IV
4
5
6
7
12
13
14
15
20
21
22
23
28
29
30
31
36
37
38
39
44
45
46
47
52
53
54
55
60
61
62
63
V
2
3
6
7
10
11
14
15
18
19
22
23
26
27
30
31
34
35
38
39
42
43
46
47
50
51
54
55
58
59
62
63
VI
1
3>
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53
55
57
59
61
63
Рис. 287
Таблица для отгадывания задуманных чисел от 1 до 63.

Практическая магия. Карточки
153
Угадывание задуманного числа по карточкам -2
Фокус с угадыванием задуманного числа, настолько
древний, что для него существует большое количество вариантов,
отличающихся внешне, но основанных на одном и том же
принципе двоичного кодирования. В очередном варианте имеется
семь различных по размерам карточек, на которых выписаны
некоторые числа из интервала от 1 до 100. Для удобства зрителей
на каждой карточке числа упорядочены по возрастанию, так их
легче искать, и удобно распределены по строчкам. Вы даете
карточки зрителю и просите, задумав число, вернуть вам, только те,
на которых оно есть. Развернув карточки веером, вы немедленно
называете задуманное число. Для этого вам всего-навсего нуэюно
найти сумму первых чисел на возвращенных карточках.
Есть более эффектный вариант этого фокуса. Нужно
окрасить карточки в семь цветов радуги: К, О, Ж, 3, Г, С, Ф и
запомнить ключевые (первые) числа для каждого цвета. Тогда вам даже
не нужно брать карточки в руки, пусть только зритель покажет
вам цвет отобранных карточек.
красная
1
11
21
31
41
51
61
71
81
91
3
13
23
33
43
53
63
73
83
93
5
15
25
35
45
55
65
75
85
95
7
17
27
37
47
57
67
77
87
97
9
19
29
39
49
59
69
79
89
99
оранжевая
фиолетовая
2
11
22
31
42
51
62
71
82
91
3
14
23
34
43
54
63
74
83
94
6
15
26
35
46
55
66
75
86
95
7
18
27
38
47
58
67
78
87
98
10
19
30
39
50
59
70
79
90
99
64
71
78
81
88
91
98
65
72
79
82
89
92
99
66
73
80
83
90
93
100
67
74
84
94
68
75
85
95
69
76
86
96
70
77
87
97

154
Практическая магия. Карточки
4
12
21
31
44
52
61
71
84
92
5
13
22
36
45
53
62
76
85
93
желтая
6
14
23
37
46
54
63
77
86
94
7
15
28
38
47
55
68
78
87
95
20
29
39
60
69
79
100
30
70
16
21
27
31
48
51
57
61
80
81
87
91
17
22
28
49
52
58
62
82
88
92
голубая
18
23
29
50
53
59
63
83
89
93
19
24
30
54
60
84
90
94
20
25
55
85
95
26
56
86
зеленая
8
11
24
31
40
56
61
72
88
91
9
12
25
41
57
62
73
89
92
10
13
26
42
58
63
74
90
93
14
27
43
59
75
94
15
28
44
60
76
95
29
45
77
30
46
78
47
79
СИНЯЯ
32
41
48
51
58
61
96
33
42
49
52
59
62
97
34
43
50
53
60
63
98
35
44
54
99
36
45
55
100
37
46
56
38
47
57
39
40
Рис. 288. Второй комплект карточек для угадывания числа

Практическая магия. Карточки
155
Угадывание задуманного числа по карточкам - 3
Для угадывания с помощью специальных карточек чисел от
I до 255, набор состоит из 8 карточек.
красная
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53
55
57
59
61
63
65
67
69
71
73
75
77
79
81
83
85
87
89
91
93
95
97
99
101
103
105
107
109
111
113
115
117
119
121
123
125
127
129
131
133
135
137
139
141
143
145
147
149
151
153
155
157
159
161
163
165
167
169
171
173
175
177
179
181
183
185
187
189
191
193
195
197
199
201
203
205
207
209
211
213
215
217
219
221
223
225
227
229
231
233
235
237
239
241
243
245
247
249
251
253
255
оранж.
2
3
6
7
10
11
14
15
18
19
22
23
26
27
30
31
34
35
38
39
42
43
46
47
50
51
54
55
58
59
62
63
66
67
70
71
74
75
78
79
82
83
86
87
90
91
94
95
98
99
102
103
106
107
110
111
114
115
118
119
122
123
126
127
130
131
134
135
138
139
142
143
146
147
150
151
154
155
158
159
162
163
166
167
170
171
174
175
178
179
182
183
186
187
190
191
194
195
198
199
202
203
206
207
210
211
214
215
218
219
222
223
226
227
230
231
234
235
238
239
242
243
246
247
250
251
254
255

156
Практическая магия. Карточки
Если делать их тоже цветными, то для восьмой карточки
оставим серый цвет. Преимущество этих карточек в том, что они
одинаковые по размеру. Принцип угадывания тот же самый.
желтая
4
5
б
7
12
13
14
15
20
21
22
23
28
29
30
31
36
37
38
39
44
45
46
47
52
53
54
55
60
61
62
63
68
69
70
71
76
77
78
79
84
85
86
87
92
93
94
95
100
101
102
103
108
109
НО
111
116
117
118
119
124
125
126
127
132
133
134
135
140
141
142
143
148
149
150
151
156
157
158
159
164
165
166
167
172
173
174
175
180
181
182
183
188
189
190
191
196
197
198
199
204
205
206
207
212
213
214
215
220
221
222
223
228
229
230
231
236
237
238
239
244
245
246
247
252
253
254
255
зеленая
8
9
10
11
12
13
14
15
24
25
26
27
28
29
30
31
40
41
42
43
44
45
46
47
56
57
58
59
60
61
62
63
72
73
74
75
76
77
78
79
88
89
90
91
92
93
94
95
104
105
106
107
108
109
ПО
111
120
121
122
123
124
125
126
127
136
137
138
139
140
141
142
143
152
153
154
155
156
157
158
159
168
169
170
171
172
173
174
175
184
185
186
187
188
189
190
191
200
201
202
203
204
205
206
207
216
217
218
219
220
221
222
223
232
233
234
235
236
237
238
239
248
249
250
251
252
253
254
255

Практическая магия. Карточки
157
Имея современную технику, вы можете их отсканировать из
этой книги, сделать в цвете и распечатать на цветном принтере.
голубая
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
синяя
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
96
97
98
99
100
101
102
103
104
105
106
107
108
109
ПО
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255

158
Практическая магия. Карточки
фиолет.
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
серая
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
Рис. 289
Третий комплект карточек для угадывания числа.

Практическая магия. Шестиугольник
159
Угадывание чисел на шестиугольнике
Для демонстрации потребуется изготовить двусторонний
числовой шестиугольник в соответствии с рисунком.
Попросите кого-либо задумать любое число, стоящее в лучах
шестиконечной звезды и сказать в каком луче оно находится. Вам
на эту сторону смотреть не обязательно. Затем вы просите
повернуть шестиугольник обратной стороной с концентрическими
окружностями и сказать вам, в каком ряду оно на этой стороне.
Узнав это, вы называете задуманное число, посмотрев
предварительно на шестиугольник.
Рис. 290
Секрет заключается в следующем. Все числа, которые на
одной стороне расположены в первом луче звезды, на другой
стороне расположены на первой окружности от центра.
Соответственно числа второго луча - на второй
окружности от центра и т.д. Следовательно, цифра, названная
вам первой, указывает номер окружности от центра, а вторая
цифра - номер ряда на стороне, которую вы видите. Это
позволяет вам сразу назвать задуманное число. Например, задумали
число и сказали, что оно находится на шестом луче. Это же
число на обороте оказалось в четвертом ряду. Значит, вам
нужно назвать число из четвёртого ряда, стоящее на шестой
окружности считая от центра - это число 6.

160
Практическая магия. Волшебный квадрат
23
8
3
18
13
21
6
1
16
11
25
10
5
20
15
24
9
4
19
14
22
7
2
17
12
Рис. 291
Волшебный квадрат
Этот квадрат не является
магическим в традиционном понимании, суммы
чисел по строчкам и столбцам не будут
равными, но у него своя система в
расположении чисел и, как следствие, свое
интересное свойство. Если взять любые
пять чисел, но так, чтобы из каждой
строчки и из каждого столбца выбрано
было только одно число, то сумма их
будет всегда постоянной. Чтобы отличать
этот квадрат от традиционного магического
квадрата, назовем его волшебным.
С ним можно показать следующий фокус. Нарисуйте
квадрат на школьной доске, так, чтобы потом легко было стирать
ненужные числа. Попросите зрителя назвать любое из чисел,
записанных в квадрате. Обведите это число, а все остальные из
этого столбика и этой строчки сотрите. Повторите эту процедуру
ещё три раза, и у вас останется не обведенным только одно число.
Обведите его. Когда вы сложите все пять чисел, у вас получится
65. И это не случайность. Вы можете предсказать заранее, что
сумма будет равна 65, какие бы числа зрители не выбирали.
Хотя со стороны будет казаться, что есть свобода выбора, но
результат предопределен поставленными условиями, и общая
сумма неизбежно будет равна числу 65. И это будет повторяться
каждый раз, когда вы будете показывать этот математический
фокус. Производимый эффект зависит от того, как вы обыграете
этот фокус. Можно заранее демонстративно записать
«некоторое» число на карточке, запечатать ее в конверт и отдать на
хранение кому-то из зрителей, а в конце фокуса попросить открыть
конверт и зачитать, что там написано. Это применимо, если вы
демонстрируете фокус однократно. Если вы планируете провести
процедуру выбора чисел несколько раз, то, во-первых, не нужно
стирать числа ряда и строчки, а придумайте как их временно
закрывать (например, магнитная доска и т. д.) и во-вторых, по-
другому обговорить эффект фокуса. Можно сказать, что вы
обладаете силой внушения и будете каждый раз внушать зрителям,
чтобы набрали сумму чисел 65 и они не смогут вам противиться.

Практическая магия. Волшебный квадрат
161
3 15 4 2
Секрет волшебного квадрата раскрывается поразительно
просто. Он представляет собой таблицу сложения, образованную
двумя рядами чисел I, 2, 3, 4, 5 и 0, 5, 10, 15, 20. Сумма всех этих
чисел равна 65.
Чтобы получить этот квадрат, нужно
выписать в клетки квадратной таблицы
последовательные числа от 1 до 25, а затем,
переставить местами некоторые строчки и
столбцы, нарушив тем самым
последовательность, но, не изменив сути этого
квадрата, как таблицы сложения двух рядов чисел.
20
5
О
15
10
2321
8
18
6
16
1311
25 2422
10
2019
1514
17
12
0
3
6
1
1
4
7
2
2
5
8
3
3
6
9
Рис. 292
Самый простой квадрат,
обладающий таким же свойством, получается, если
выписать подряд последовательные числа
от 1 до 9, начиная с верхнего левого угла,
получится таблица сложения для двух
наборов чисел 1, 2, 3 и 0, 3, 6.
Сумма любых трех чисел, взятых
по одному из каждого столбца и каждой
Рис. 293 строчки, всегда будет равна 15. Интересно
отметить, что эта сумма совпадает с магической суммой квадрата
данного порядка. Для квадратов с нечетным порядком она равна
произведению числа, стоящего в центральной клетке и порядка
квадрата.
Если нумерацию клеток начать с числа а>1 и продолжить
по порядку, то сумма окажется равной: S =
п +п
п -п
+ап. С помощью этой формулы можно легко найти,
каким должно быть число в левом верхнем углу квадрата любых
размеров, чтобы получалась заранее заданная сумма. Выразим а
S-
п -п
из формулы суммы а =
Обозначим
п -п
п
= М„1Л подсчитаем значение этого числа
для самых распространенных квадратов.

162
Практическая магия. Волшебный квадрат
При и=3, М3=12, п=4, Мг=ЗО, л=5, Мз=60, п=6, М^=\05. Для
каждого порядка сумма чисел квадрата не должна быть меньше М„,
чтобы избежать отрицательных чисел.
Теперь вы готовы показать ещё более эффектный фокус.
Попросите кого-нибудь назвать порядок квадрата п (например,
от 3 до 6), затем любое число, но только задайте ограничение -
пусть оно будет больше Мп (которое знаете вы, но не зрители), и
вы можете быстро вычертить квадрат, дающий заданную сумму.
При этом ваши действия заключаются в следующем. Вы
отнимаете от названной суммы число Мп и делите на порядок квадрата
л, получается первое число а. Оно может получиться дробным,
тогда пишите его в виде обыкновенной дроби или смешанного
числа, каждое следующее число больше на единицу. Чтобы ещё
больше запутать зрителей, расставьте числа в квадрате не по
порядку. Выберите последовательность расположения чисел в
строке и повторяйте её при переходе от одной строчки к другой,
например:
3 столбик, 1 ст., 4 ст., 2 ст.,
и так по каждой строке. Заполнив одну строчку, можете
переходить к любой другой.
Рассмотрим действия на конкретном числовом примере.
Пусть задан квадрат 5-го порядка. Попросите назвать число
больше 60. Допустим это 124, тогда я=(124-60)/5=12,8.
Расставляем числа в таком порядке: берём строки 3, 1, 2, 5, 4 и в каждой
строке идем в той же последовательности по столбцам: 3, 1, 2, 5, 4.
Получаем следующий квадрат.
Если вы не хотите иметь
дело с дробными числами, но
получить при этом заданную
сумму, то можете отбросить
дробную часть, но при этом ко
всем числам одной строки
(например, второй) прибавить
по 4, компенсируя тем самым
потерю 4/5 у каждого числа.
18,8
23,8
13,8
33,8
28,8
19,8
24,8
14,8
34,8
29,8
17,8
22,8
12,8
32,8
27,8
21,8
26,8
16,8
36,8
31,8
20,8
25,8
15,8
35,8
30,8
Рис. 294

Практическая магия. Календарь
163
18
27
13
33
28
19
28
14
34
29
17
26
12
32
27
21
30
16
36
31
20
29
15
35
30
Перестановка строк и
столбцов не меняет свойств
квадрата, но делает его более
загадочным.
Пользуясь этим приемом,
вы можете послать
нестандартное поздравление своему
другу ко дню рождения или на
Новый год, составив
волшебный квадрат, сумма в котором
будет равна количеству лет или
предстоящему году. Нужно же
Рис. 295 как-то разнообразить нашу
повседневную жизнь, скрашивая её такими незамысловатыми мелочами.
Фокусы с настенным календарем
На принципе, подробно рассмотренном выше, строятся
несколько фокусов «быстрых вычислений», использующих
большой настенный календарь за любой год.
Фокус- предсказание
Предупредив зрителей, что вы обладаете даром прорицания
и умеете производить в уме быстрое сложение нескольких чисел,
попросите кого-то обвести на настенном календаре в любом
месяце любой квадрат из 16 чисел. Бегло взглянув на обведенную
фигуру, вы записываете на листке предсказание, кладете его в
конверт и отдаете на хранение зрителю. Затем просите зрителя
выбрать любое число в этом квадрате, обвести его кружком и
вычеркнуть все числа, находящиеся в той же строчке и том же
столбце, что и только что обведенное число. В качестве второго
числа зритель может обвести кружком любое число, оставшееся
незачеркнутым. После этого он должен вычеркнуть все числа,
стоящие в одной строчке и в одном столбце со вторым
обведенным числом. Так же выбирается третье число, а соответствующие
строчка и столбец вычеркиваются.

164
Практическая магия. Календарь
В результате этих операций останется незачеркнутым одно-
единственное число. Его тоже зритель должен обвести кружком
и посчитать сумму четырех чисел, выбранных абсолютно
случайным образом.
ПН
ВТ
СР
чт
пт
СБ
ВС
1
X
3
X
X
6
7
8
X
X
X
12
13
14
15
16
X
X
X
20
21
22
X
X
25
X
27
28
29
30
31
Рис. 296
В финале вы эффектно предлагаете достать из конверта
листок и убедиться, что на нем заранее вами была написана
именно эта сумма.
Чтобы это сделать, вам нужно было сложить два числа,
находящихся на двух диагонально противополоэюных углах
квадрата (безразлично какая пара из двух возможных берется) и
найденную сумму удвоить.
Сумма чисел, выбранных по одному из каждой строки и
каждого столбца квадрата, равна сумме чисел на диагонали.
Эта последняя есть сумма четырех членов арифметической
прогрессии с разностью 8 и равна, в силу известной формулы,
удвоенной сумме первого и последнего членов.
Фокус с нахождением суммы
Вы снова просите кого-либо из зрителей обвести на
настенном календаре в любом месяце квадрат, содержащий 16 чисел.
Взглянув на него ровно одну секунду, вы отворачиваетесь
от календаря, закрываете глаза, глубокомысленно обхватываете
лоб рукой и называете сумму всех чисел, попавших в этот
квадрат. Все внешние эффекты нужны вам только для того, чтобы
чуть-чуть потянуть время, необходимое вам для умножения
суммы двух чисел, стоящих на противополоэюных концах любой
диагонали, обведенного квадрата, на восемь.

Практическая магия. Календарь
165
Чтобы их выхватить взглядом секунды хватит, а,
отвернувшись и закрыв глаза, вы имеете возможность произвести
вычисления.
Рис. 297
ПН
ВТ
СР
чт
пт
СБ
ВС
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Вычисления вслепую
Каждый следующий номер должен быть менее трудоемок
для зрителей, чтобы не переутомить их и, вместе с тем, более
эффектен. На этот раз вы вообще не смотрите на календарь и
стоите, повернувшись спиной к зрителям, а один из них по
вашему распоряжению выбирает на настенном календаре любой месяц
и обводит на нем какой-нибудь квадрат, содержащий 9 чисел. Вы
просите самую малость: назвать наименьшее из чисел, попавших
в квадрат, чтобы через пару мгновений назвать сумму этих девяти
чисел. Объяснение ваших действий. Нужно прибавить к
названному числу 8 и результат умножить на 9.
Если - т наименьшее число в указанном квадрате, то весь
квадрат имеет вид
т
т+1
т+2
т+7
т+8
т+9
т+14
т+15
т+16
Рис. 298
Й сумма всех чисел квадрата равна 9-т+72=9-(т+8).

166
Практическая магия. Календарь
ПН
ВТ
СР
чт
пт
СБ
ВС
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Рис. 299
Вычисления для данного примера:
(8+8)-9=144 и гораздо длиннее 8+15+22+9+16+23+10+17+24=144
Фокус с отмеченными датами
Если посмотреть на настенный календарь, то числа
большинства месяцев располагаются в пять столбиков, очень редко
они стоят в шесть столбцов, это когда первое число приходится
на субботу или воскресенье и совсем редкое явление может быть
в феврале не високосного года, начинающегося с понедельника,
тогда числа умещаются всего в четыре столбика.
Предложите зрителю выбрать на настенном календаре
любой месяц, в котором числа занимают пять столбиков, и
обвести кружком по своему выбору по одной дате в каждом из пяти
столбцов. При этом на протяжении всего фокуса вы стоите
спиной к календарю и не видите манипуляций зрителя.
Далее вы просите зрителей сообщить вам некоторые не
числовые сведения необходимые для подсчета суммы обведенных
чисел:
• каким днем недели начинается выбранный месяц;
• на какие дни недели приходятся выбранные пять чисел.
После чего сообщаете «вслепую» сумму пяти обведенных
чисел. Математическое обоснование ваших способностей, а
точнее вычислений заключается в следующих рассуждениях.

Практическая магия. Чудесный квадрат
167
|пн
II вт
II ср
№]
|| пт
СБ
ВС
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Рис. 300
Сумма чисел в строке, которая начинается первым числом
месяца, всегда равна 75 (1+8+15+22+29), за исключением
февраля не високосного года. Каждое отмеченное число в следующей
строке увеличивает эту сумму на единицу, в следующей за ней
строке на 2 и т.д.; каждое отмеченное число в предыдущей
строке уменьшает сумму на 1, в предшествующей ей строке на
2 и т.д. Пусть, например, вам сообщили, что первое число
месяца приходится на четверг, а обведены один понедельник, две
среды, один четверг и суббота. Ваши вычисления в уме должны
выглядеть так: 75-3 -1-1+2=72.
Чудесный квадрат
Слово «магический» у нас занято, «волшебный» тоже,
поэтому для следующего фокуса назовем квадрат «чудесным».
Велик и могуч русский язык!
В клетках квадрата написаны числа
от 1 до 16 вразбивку. Один из ваших
товарищей задумывает любое из написанных
чисел. Далее вы объясняете, что при
каждом вашем прикосновении указкой к
числам заданного квадрата, ваш товарищ
должен в уме прибавлять к задуманному
числу единицу и сказать «стоп», как
только досчитает до двадцати. Вы начинаете, ударяя Рис. 301
указкой, показывать числа и, когда ваш товарищ говорит «стоп»,
указка останавливается на задуманном числе.
3
7
11
2
5
1
14
9
8
12
4
16
10
15
6
13

168 Практическая магия. Таблицы
Получается, как будто он сам вам выдал задуманное число.
Секрет ваших действий: первые три числа показываете
наугад, но четвертое число должно быть 16, пятое 15 и т.д.,
пока не услышите команду «стоп». Надеюсь, вы поняли
математическую основу фокуса.
Можно увеличить квадрат, взяв 5x5. Соответственно и
прибавлять по единице, задумавшему число, придется до 30, а вам,
начиная с пятого шага, вести обратный отсчет: 25, 24 и т.д.
Угадывание в таблице суммы закрытых чисел
Показав в фокусе с календарем, что вы умеете складывать
числа, едва взглянув на них, можете пойти дальше и
продемонстрировать, как вы складываете числа, которых вообще не видите.
Для этого имеется несколько специальных числовых таблиц.
Причем, внешняя степень сложности ваших действий возрастает
при переходе от одной таблицы, к другой. Хотя невидимые
зрителям вычисления в уме, не так уж и сложны.
В каждой таблице разные числа расставлены по
определенному принципу и к ней прилагается алгоритм действий
демонстратора фокуса, который и нужно запомнить, а далее -
дело техники и вашего умения художественно обставить
демонстрацию с необходимым словесным оформлением.
В демонстрационной таблице 10x10 записаны разные числа.
Попросите кого-нибудь из присутствующих закрыть заранее
приготовленной непрозрачной полоской картона любые четыре
клетки, не имеет значения, вертикальных или горизонтальных.
Размеры полоски должны этому соответствовать, а как её крепить
на таблице, придумайте сами. (Например, можно повесить таблицу
на магнитной доске, а с обратной стороны картонки приклеить
небольшой плоский магнит). Вы поворачиваетесь к таблице,
когда числа уже закрыты и называете их сумму.
Секрет в таблице. Она составлена так, что сумма любых
пяти рядом стоящих чисел по горизонтали или по вертикали
равна 65. Чтобы назвать сумму закрытых чисел, нужно от 65
отнять число, стоящее рядом с полоской, или любое из двух, если
полоска не касается края таблицы.

Практическая магия. Таблицы
169
Таблица 1
18
10
22
14
1
18
10
22
14
1
12
4
16
8
25
12
4
16
8
25
6
23
15
2
19
6
23
15
2
19
5
17
9
21
13
5
17
9
21
13
24
11
3
20
7
24
11
3
20
7
18
10
22
14
1
18
10
22
14
1
12
4
16
8
25
12
4
16
8
25
6
23
15
2
19
6
23
15
2
19
5
17
9
21
13
5
17
9
21
13
24
11
3
20
7
24
11
3
20
7
Рис. 302
В таблице-2 записаны 75 произвольных чисел, только форму
она имеет прямоугольную, а пластинка из картона закрывает сразу
три горизонтальных ряда Чисел, оставляя открытым только один
уголочек, который как раз и нужен для нашего фокуса.
Полоску важно изготовить так, чтобы её можно было
повернуть в плоскости, но нельзя было бы перевернуть обратной
стороной. Например, для крепления картонки на таблицу, сделать
на тыльной стороне резиновые присоски. В этом случае её можно
положить так, что вырез будет сверху справа или снизу слева. В
любом случае, закрытыми оказываются 14 чисел, а вы обязуетесь
назвать сумму всех трех рядов, т.е. всех 15 чисел. Ваши действия
по угадыванию суммы немного различаются в зависимости от
расположения выреза.
Когда накрывают картонкой три ряда чисел и вырез на ней
смотрит вверх, то отгадчик видит левое верхнее число трех
рядов чисел. Все 15 чисел подобраны так, что если слоэюитъ цифры
двузначного числа, которое видно в вырезе картонки, и
полученную сумму поставить между цифрами этого числа, то
образуется трехзначное число, которое и будет суммой 15 чисел.

170
Практическая магия. Таблицы
Обратите внимание, таблица составлена так, что нижнее
число правой колонки на 9 единиц меньше левых верхних чисел
для каждых трех строк, накрываемых полоской. Поэтому
достаточно к известному нижнему правому числу прибавить 9, и
сумма будет равна любому верхнему числу. Значит, когда картонка
расположена вырезом вниз, вы предварительно прибавляете к
видимому числу 9, затем, считаете сумму цифр полученного
числа, ставите её между цифрами и называете трехзначное
число.
Таблица 2
22
18
31
41
54
63
72
71
81
80
90
61
45
2
50
18
36
10
1
99
35
20
122
37
28
ПО
29
19
1
20
15
6
7
3
24
37
30
29
71
10
32
60
98
3
14
25
8
1
2
24
5
32
46
19
8
128
39
55
1
18
20
12
13
9
22
32
45
54
63
62
72
71
81
52
36
Рис. 303

Практическая магия. Таблицы
171
Таблица 3
17
28
30
22
5
13
17
34
52
68
60
52
30
18
7
9
2
15
20
37
13
1
2
1
8
40
20
7
30
22
46
94
44
1
28
45
17
6
22
9
16
9
3
15
32
80
115
40
20
16
9
50
27
14
9
18
23
1
19
122
29
5
1
2
7
15
58
10
9
7
32
38
40
16
11
20
13
5
10
26
30
27
38
26
18
12
25
38
65
67
68
56
43
17
15
13
15
14
28
41
■ 1
Рис. 304
Ваше совершенство не знает границ: в таблице снова сто
различных чисел, а пластинка из картона закрывает сразу пять
рядов клеток, оставляя открытыми только две угловых клетки.
Закрываются ряды по горизонтали, но пластинку можно
перевернуть обратной стороной, и тогда открыты два других угла. Фокус
аналогичен предыдущему, вы называете сумму теперь уже
двадцати пяти чисел, из которых видите только два. Порядок ваших
действий: нужно сложить два числа, которые видны, и эту
сумму умножить на 10. Всё остальное за вас сделал тот, кто
придумал расположение чисел в таблице.

172
Практическая магия. Плоско-магический куб
Плоско-магический куб
Кубик, который предлагается изготовить, отличается от
определения магического куба, данного в предыдущей главе..Все
шесть плоских граней этого кубика представляют собой
магические квадраты 4-го порядка, составленные из чисел от 1 до 96,
отсюда название плоско-магический, а объемность в данном
случае второстепенна.
Интересен принцип одновременного составления шести
магических квадратов из одной последовательности чисел.
Нужно пронумеровать грани кубика и разбить числа от 1 до 96 на 12
интервалов по восемь чисел. Затем, в соответствии со схемой
заполнения (серые стрелки) и нумерацией граней,
в клетки квадратов вписываются числа: 1-
я грань 1-8, 2-я грань 9-16, ... , 6-я грань 41-48.
Обратно возвращаемся, выписывая числа по
симметричной схеме (черные стрелки): 6-я грань
49-56, 5-я грань 57-64, ... , 1-я грань 89-96.
Магические квадраты на гранях этого кубика
Рис. 305
Рис. 306
хороши настолько, что
магическую сумму, в данном
случае 194, можно получить
25-ю способами на каждой
грани (4 строчки + 4 столбца
+ 2 главные диагонали + 9
квадратов 2x2 + 6 ломаных
диагоналей). Значит, на всем
кубике число 194 получается
150-ю способами! Заполнить
грани числами и склеить
кубик можно в соответствии с
разверткой (см. рис. 307).
Для красоты можно сделать грани разноцветными, а размеры - в
соответствии с аудиторией, чтобы его хорошо было всем видно.
Кубик склеен, он красив и интересен, а что дальше?

Практическая магия. Плоско-магический куб
173
Фокус с ним основан на том, что число 194 получается при
сложении четырех чисел на любой грани множеством способов.
Ваши зрители не могут знать магическую сумму заранее, да и
много ли людей знает о магических квадратах вообще. Ваша
задача эффектно обыграть это. Например, возьмите какую-
нибудь книгу стихов и выучите заранее стихотворение на 194
странице. Во время демонстрации фокуса вы вручаете зрителям
эту книгу и кубик (словесную аранжировку о ваших
способностях, о памяти или магических свойствах кубика придумайте
сами, но обязательно скажите, что на гранях кубика выписаны
числа от 1 до 96 без повторений).
Вы предлагаете зрителям выбрать любую из шести граней,
а на ней любой столбик строчку или диагональ из четырех чисел,
или любой квадратик 2x2 и, сложив эти числа, открыть книгу на
соответствующей странице.
Именно это многообразие вариантов выбора вызывает
удивление, когда вы начинаете читать наизусть стихотворение,
написанное на этой странице.
Насладитесь эффектом, который произведет ваш номер с
кубиком, но никогда не показывайте фокус дважды в одной
аудитории. Даже если смените книгу, получив снова сумму 194,
зрителей начнут терзать смутные догадки и удивление пойдет на
убыль. Истинный маг должен держать зрителей в постоянном
напряжении мысли: «а как это делается»?
Развертка для изготовления плоско-магического кубика
\
f X
87
82
11
14
12
13
88
81
86
83
10
15
9
16
85
84
95
90
3
6
79
74
19
22
63
58
35
38
4
5
96
89
20
21
80
73
36
37
64
57
94
91
2
7
78
75
18
23
62
59
34
39
1
8
93
92
17
24
77
76
33
40
61
60
Ч
71
66
27
30
28
29
72
65
70
67
26
31
25
32
69
68
55
50
43
46
44
45
56
49
54
51
42
47
41
48
53
52
Рис. 307

174
Практическая магия. Магический цветок
Магический цветок
Каждый лепесток такого цветка - это магический квадрат
5-го порядка. Лепестков может быть 3, 5, 7 -зависит от вашего
желания и трудолюбия, но лучшим вариантом будет цветик-
семицветик, напоминающий о чудесах из детской сказки.
Начнем с минимального количества - трех лепестков. Числа
от 1 до 75 по определенной схеме записываются в клетки
квадратов. Магическую сумму можно просчитать заранее
(1+75)/2-75/15=190.
Таким образом, на любом лепестке сумма пяти чисел по
Рис. 308
любому горизонтальному, вертикальному или диагональному
ряду равна 190 и вы это знаете. Напишите это число на листке,
положите в конверт и заклейте, конверт отдайте заранее зрителю
сидящему на 1 месте в 9 ряду. Демонстрируя фокус, предложите
одному из зрителей выбрать любой лепесток, любой ряд из пяти
чисел на нем и сложить их. Первая цифра покажет место, вторая
ряд, где сидит зритель, который знает, сколько получилось в
результате сложения, пусть он распечатает конверт.
Цветок с тремя лепестками показан на рисунке, но для
красоты мы добавили к нему ещё три лепестка без чисел.

Практическая магия. Магический цветок
175
Хотя, можно было написать на них, например, ещё раз
числа использованных трех квадратов, только отобразив их
симметрично.
Интереснее будет цветок с пятью лепестками, и мы
обсудим, как его сделать. Пять магических квадратов заполняются
числами от 1 до 125. Схема похожа на заполнение граней кубика,
но немного сложнее. Кстати, куб с квадратами 5-го порядка на
гранях и последовательными числами от 1 до 150 сделать нельзя.
Как вы думаете, почему?
Итак, лепестки пронумеруем, числа разбиваем на группы по
5 чисел, т.е. 1-5, 6-10,...,121-125. Всего 25 групп по пять чисел.
Для определения последовательности заполнения лепестков
понадобится любой магический квадрат 5-го порядка, в котором
расставим числа по рядам в порядке возрастания и поменяем
ряды местами.
' 3 9 15 16 22
2 8 14 20 21
1 7 13 1925
5 6 12 18 24
4 10 11 17 23
Рис. 309
В качестве схемы заполнения берем латинский квадрат 5-го
порядка и записываем числа в лепестки таким образом: в 1-ый
лепесток записываем числа 1-5 в соответствии с красными
числами в латинском квадрате, во 2-ой - числа 6-10 по красной
схеме и т. д., все лепестки по красной схеме. Затем заполнение
пойдет по зеленой схеме латинского
квадрата, а порядок лепестков будет в
соответствии с номером группы чисел, который
берется из модификации магического
квадрата, т.е. 6-ая группа - 5-ый лепесток,
7-ая группа - 1-ый лепесток, далее 2-ой,
3-ий, 4-ый. Переходим на синюю схему
латинского квадрата и лепестки в порядке:
4-ый, 5-ый, 1-ый, 2-ой, 3-ий. Далее
фиолетовая и черная схемы. Магическая сумма
у такого цветка равна 315.
Рис.310
3
20
7
24
11
16
8
25
12
4
9
21
13
5
17
22
14
1
18
10
15
2
19
6
23
1
2
3
4
5
7
8
9
10
6
13
14
15
11
12
1925
20
16
17
18
21
22
23
24
12 3 4 5
1
3
5
2
4
2
4
1
3
5
3
5
2
4
1
4
1
3
5
2
5
2
4
1
3

176 Практическая магия. Гексафлексагон
(Сумму всех чисел от 1 до 125 делим на количество рядов в пяти
квадратах, т.е. на 25). Для цветика-семицветика сумма будет
равна 440, проверьте это. Все действия по аналогии с пятью
лепестками, несамостоятельно!
Магический гексафлексагон
Флексагоны - это многослойные многоугольники, сложенные
из полосок бумаги, которые обладают удивительным свойством:
при перегибании особым образом их наружные поверхности
прячутся внутрь, а ранее скрытые поверхности выходят наружу.
Отечественных читателей с ними познакомил Мартин Гарднер в
серии книг по занимательной математике, выпущенной
издательством «Мир». Изобрел флексагоны Артур Стоун ещё в 1939 году,
но, спросите сейчас наугад нескольких своих знакомых, и вряд ли
кто-то имеет о них представление. Школьная программа по
математике слишком насыщена материалом, слишком серьезна,
стремится к развитию логического и абстрактного мышления, на
занимательность времени не остается, а жаль. Сколько в
математике красоты и занимательности, за какой вопрос ни возьмись -
это удивительный мир. Для подробного изучения флексагонов
отсылаем к книгам Мартина Гарднера, а здесь познакомимся
только с одним образцом, который называется гексагексафлек-
сагон. Произнесите это слово, оно. производит впечатление уже
своим звучанием. По-гречески «гекс» означает шесть, по-
английски flex - складываться, сгибаться. Полная расшифровка
означает шестиугольник с шестью поверхностями, который
может складываться.
Чтобы сложить гексагексафлексагон берут полоску бумаги,
разделенную на 19 равносторонних треугольников. На рисунке
эта полоска изображена с лицевой (1-2-3) и обратной (4-5-6)
стороны. Цифры проставьте карандашом, чтобы потом можно было
их стереть. Они означают номер поверхности, к которой относится
каждый треугольник и нужны, чтобы правильно свернуть эту
полоску. Делая магический флексагон, мы позднее заменим их
другими числами. Хорошенько прогните полоску по всем линиям
сгиба в обе стороны, тогда готовый флексагон лучше
раскрывается. Как свернуть флексагон ясно из рисунков.

Практическая магия. Гексафлексагон
177
III
Рис.311
а Полоску складывают так, чтобы треугольники
обратной стороны, имеющие одинаковые цифры,
оказались наложенными друг на друга: 4-4, 5-5, 6-6.
а Перегнув по линиям аЪ и cd, получим шестиугольник.
□ Треугольники без цифр, стоящие на концах ленты
после сгибания склеивают между собой.
После склеивания, на одной поверхности шестиугольника
стоит цифра 1, на другой - 2. Когда подсохнет клей, попробуйте
раскрыть другие поверхности. Взявшись за два смежных
треугольника, сжимаем шестиугольник по их общей стороне и
подгибаем противоположный угол флексагона. При этом он как-
бы раскрывается другой поверхностью наверх. Берясь за разные
углы шестиугольника и, перегибая наугад, вы сможете увидеть
все шесть поверхностей. Осталось сделать его магическим. Для
этого понадобится любой магический квадрат шестого порядка.
На каждой из шести поверхностей флексагона выпишем в
треугольники, образующие шестиугольник, шесть чисел поочередно
из шести строчек магического квадрата. Обязательно поставьте точку
внизу и цифры 6, чтобы в дальнейшем не путать её с цифрой 9, т.к.
при раскрытии поверхностей, ориентация треугольников в
шестиугольнике может быть разная. Теперь, как бы мы его ни крутили,
сумма чисел на любой поверхности равна 111.
Удлиняя цепочки треугольников, можно делать флексагоны
с 9-ю, 12-ю и более поверхностями. Для их заполнения не
достаточно одного магического квадрата 6-го порядка и потребуется,
показанный ранее, метод, аналогичный заполнению граней
плоскомагического куба и лепестков магического цветка.

178
Практическая магия. Кольцо тетраэдров
Магическое кольцо тетраэдров
Мы уже говорили о пяти правильных многогранниках, их
еще называют Платоновыми телами, Есть ещё полуправильные
или архимедовы тела. Кристаллы в природе имеют форму
различных многогранников, красоту которых человек всегда ценил.
В поэзии есть такое понятие «венок сонетов», когда 15
сонетов связаны между собой одной темой и переходящими из
одного в другой строчками, например Corona Astralis у
Максимилиана Волошина. Венок - это нечто гибкое и, в тоже время,
связанное. А можете вы представить себе изгибаемые
многогранники или венок из тетраэдров? Вполне, между прочим, реальные
вещи; в математике своя поэзия и красота.
Два математика Дж. М.Андреас и Р. М. Сталкер независимо
друг от друга открыли интересное семейство изгибаемых
многогранников, гранями которых служат грани тетраэдров,
соединенных между собой в циклическом порядке по определенным парам
противоположных ребер так, что получается фигура наподобие
кольца из тетраэдров. Рассмотрим такое кольцо их восьми
тетраэдров, которое можно изготовить, используя показанную развертку.
Рис.312
На развертке проставим числа от 1 до 32, чтобы после
склеивания получилось магическое кольцо тетраэдров. Четыре
числа на четырех гранях каждого тетраэдра дают в сумме 66.
Восемь соответствующих граней, взятых по одной от каждого
тетраэдра, например, на виде спереди 31+10+8+18+32+9+7+17
(или внутренне кольцо граней 4+21+27+13+3+22+28+14), дают в
сумме 132; то же самое можно получить, если взять 8 граней
спирально обвивающихся вокруг кольца. Кольцо изгибается и его
можно полностью выворачивать.

Практическая магия. Кольцо тетраэдров
179
1
11
6
Если вы в ладу со своими руками, попробуйте склеить
модель из 10
тетраэдров, она еще краси- 26 ^ф^ 15
вее. Развертку
можно сделать по
аналогии, поняв
принцип
расстановки чисел.
Кстати, эти
модели красивы сами по
себе настолько, что
наличие на них
чисел может нарушать
гармонию своим излишеством.
Рис.313
Всё описанное выше: таблицы, карточки, гексафлексагоны
и т.д., требовали специального изготовления. В арсенале любого
мага, кроме специальной аппаратуры, есть и обыденные предметы,
с которыми он демонстрирует свои «уникальные» возможности.
Затронем, хотя бы краешком, фокусы с игральными костями,
костяшками стандартного набора игры домино и игральными
картами. Все эти игровые атрибуты связаны напрямую с числами.
Количество очков на кубике и костяшках домино - это числа,
игральные карты тоже имеют определенное числовое значение.
Фокусы с игральными костями
Атрибутом нескольких числовых фокусов служат игральные
кости. Для демонстрации можно изготовить их в увеличенном
масштабе, чтобы за процессом могли наблюдать зрители,
присутствующие при вашем выступлении. Игральная кость имеет форму
кубика, на гранях которого нанесены точки, количество которых
соответствует числам 1, 2, 3, 4, 5, 6, причем соблюдается
«принцип семерки»: числа на противоположных гранях в сумме дают
семь (1-6 2-5, 3-4). Ориентация первых трех чисел
показана на рисунке, остальные по «принципу
семерки». Такая игральная кость соответствует
существующему стандарту.
Рис. 314

180
Практическая магия. Игральные кости
Угадывание суммы невидимых чисел
Показывая этот фокус, повернитесь спиной
демонстрационному столику и попросите кого-либо
из зрителей составить вертикальным столбиком в
произвольном порядке три игральные кости, а затем
сложить числа на пяти невидимых гранях. На двух
соприкасающихся гранях верхней и средней костей,
на соприкасающихся гранях средней и нижней
костей и на нижней грани нижней кости. Как только
зрители сложили эти числа, вы на мгновение
поворачиваетесь якобы для того, чтобы дать платок,
которым следует накрыть кости.
На самом деле нужно успеть за это мгновение
увидеть цифру на верхней грани верхнего кубика. После чего вы
без труда называете полученную зрителями сумму.
Секрет основан на стандарте расстановки чисел
игральной кости: сумма чисел на любой паре противоположных граней
равна семи. Значит нужно от 21 отнять число, стоящее на
верхней грани, это и будет искомая сумма чисел на пяти
невидимых гранях. То обстоятельство, что зрители складывают
числа на соприкасающихся гранях соседних кубиков, а не на
противоположных гранях одного кубика служит маскировкой
применения этого принципа.
Угадывание суммы выпавших очков
Рис. 315
Рис. 316
Вы поворачиваетесь спиной к зрителям и просите одного из
них бросить на стол три игральные кости. Затем предлагаете
зрителю сложить три выпавших числа, взять любую из трех костей и
прибавить число на нижней её грани к только что полученной
сумме. Потом снова бросить эту же кость и выпавшее число
опять прибавить к сумме. Поворачиваясь к зрителям, вы
акцентируете их внимание на том, что вам не может быть известно,
какую из трех костей бросали заново, и какое число стояло у нее

Практическая магия. Игральные кости 181
на нижней грани перед этим. Затем вы собираете кости,
встряхиваете их в руке, подносите к уху, и тут же правильно называет
конечную сумму. Объяснение фокуса. Прежде чем собрать
кости, нужно быстро сложить числа на верхних гранях и добавив к
сумме семерку, получите конечную сумму.
Отгадывание выпавшего числа очков на 2 костях
Следующие два фокуса связаны с позиционным способом
записи чисел. Не глядя на стол, на котором лежат игральные
кости, вы просите одного из зрителей бросить две игральных кости и
запомнить выпавшие числа. Затем зрителю предлагается:
• выбрать одно из этих двух чисел и умножить его на 5;
• к произведению прибавить 7;
• затем удвоить полученную сумму;
• и, наконец, прибавить к ответу второе число.
Узнав полученное таким образом число, вы сообщаете,
какие числа выпали на каждой из двух костей.
Для этого, мысленно вычитаете из названного числа 14 и
получаете двузначное число, две цифры которого равны двум
исходным числам. В самом деле, допустим, выпали числа аи Ъ.
Нам важно, что каждое из них меньше 10. В результате
проделанных операций получаем: 5-а, 5-а+7, 10-а+14, lO-a+b+14.
Таким образом, если из окончательного ответа вычесть
14, то останется двузначное число, цифры в котором
соответствуют исходным числам.
Отгадывание выпавшего числа очков на 3 костях
На этот раз вызовите зрителя посмышленее, так как
вычислений придется сделать больше. Зритель бросает три кости, вы
демонстративно на стол не смотрите. Затем просите зрителя:
• число, выпавшее на одной из костей, умножить на два;
• к полученному произведению прибавить пять;
• и результат снова умножить на пять;
• число, выпавшее на второй кости прибавить к
предыдущей сумме и результат умножить на десять;

182
Практическая магия. Игральные кости
• наконец, к последнему числу прибавить значение,
выпавшее на третьей кости.
Зритель сообщает полученный результат, и вы немедленно
можете назвать три выпавших числа.
Объяснение фокуса. От названного результата вычислений
нужно отнять 250. Три цифры полученной разности и будут
искомыми числами, выпавшими на трех костях. Над
математической стороной объяснения фокуса подумайте сами.
Кубики с трехзначными числами
Если вы захотите показать этот фокус, то придется
предварительно потрудиться, так как нужны не стандартные игральные
кости, а кубики с трехзначными числами на гранях.
На гранях пяти кубиков должны быть расставлены числа в
соответствии с приведенной таблицей.
I
483
285
780
186
384
681
II
642
147
840
741
543
345
III
558
855
657
459
954
756
IV
168
663
960
366
564
267
V
971
377
179
872
773
278
Рис.317
Спросите у зрителей: сколько секунд потребуется, чтобы
сложить в уме пять трехзначных чисел? Пригласите самого
грамотного, пусть он бросит на стол эти пять кубиков. Взглянув на
цих, запишите на доске ответ и спокойно дождитесь, пока зритель
посчитает сумму. Разрыв во времени должен быть ощутимым.
Чтобы получить эту сумму вам нужно сложить только
последние цифры пяти трехзначных чисел, это сделать совсем не
трудно. Сразу идите к доске и записывайте это число, если оно
однозначное, поставьте перед ним ноль. Затем вычтите в уме
полученное число из 50 и поставьте найденную разность перед
вычитаемым.

Практическая магия. Домино
183
На доске будет записано четырехзначное число, которое и
будет искомой суммой пяти трехзначных чисел, выпавших на
кубиках. Допустим, выпали числа: 285, 741, 657, 663, 971. Сумма
последних цифр равна 17. Вычитаем 50-17=33, в ответе будет
число 3317.
Усильте полученный эффект, продемонстрировав такой же
фокус на другом комплекте из семи кубиков с трехзначными
числами на гранях.
Вся разница ваших действий будет в том, что сумму
последних цифр нужно вычесть из 70, а остальное все аналогично
предыдущему варианту.
Соответственно и подбор чисел на гранях другой. Он
показан в следующей таблице.
I
523
424
721
325
622
820
II
258
555
357
456
951
753
III
784
982
289
883
685
388
IV
346
742
643
841
940
544
V
116
215
512
611
413
710
VI
336
732
138
930
732
435
VII
578
776
479
677
875
974
Рис.318
Цепочка домино с разрывом
Для следующего фокуса используется стандартный набор
из 28 косточек для игры домино.
Перед демонстрацией вы записываете на листочке некое
предсказание, кладете листок в конверт и отдаете одному из
зрителей на хранение. Затем, высыпаете на стол косточки домино
лицевой стороной с точками вверх и перемешиваете их. Одному
или двум зрителям предлагается выложить все косточки в цепочку,
прикладывая одинаковые концы друг к другу, как это делается при
обычной игре в домино. Раскладка может делаться, начиная с
любой косточки. После окончания раскладки вы обращаете
внимания на число очков на каждом из концов цепи и просите
зрителя, . которому вначале передали конверт, зачитать ваше
предсказание. Оказывается, там записаны именно эти два числа.

184
Практическая магия. Домино
Фокус можно повторять, причем каждый раз будут
предсказываться другие числа.
В этом фокусе нужна ловкость рук и немного жульничества.
Перед началом демонстрации, вы должны изъять и спрятать
незаметно одну косточку из комплекта, только не дубль. Вряд ли
найдется дотошный зритель, который пересчитает, сколько
косточек высыпано на столе. Число очков на концах этой
косточки записываете в предсказание. Фокус получается потому,
что любая цепочка, составленная из всех 28 косточек домино,
имеет одинаковое число на концах, т.е. фактически может
быть замкнутой. Отсутствующая косточка и будет
замыкающей, поэтому она показывает числа очков на месте разрыва
Чертова дюжина
Для этого фокуса нужны 13 косточек домино, которые
выкладываются в ряд лицевой стороной вниз. Объясняете зрителям
их действия: когда вы отвернетесь, кто-то из зрителей
передвигает по одной любое количество косточек (от одной до двенадцати)
с левого конца ряда на правый. Покажите, как именно это делать,
передвинув одну за другой две косточки с левого края на правый.
Затем вы отворачиваетесь, можете даже уйти в другую комнату.
Когда вам скажут, что дело сделано, берете со стола одну
косточку, и количество очков на ней оказывается равным числу
перемещенных косточек.
Косточки вылоэ/сены не произвольно, а подобраны
специальным образом. Суммы очков на них должны последовательно
равняться всем целым числам от 0 до 12, нуль представлен
двойной пустышкой. Расставьте их с учетом того, что перед
демонстрацией вы сами передвинете две косточки с левого края на
правый край. Вот как выглядит лицевая сторона «заряженного»
ряда (зритель ее не видит!). Тогда, после ваших перестановок,
первой слева будет стоять двойная пустышка.
• •
•••
• •
• •
• •
:•
!!
•
•
•
• •
• •
•
::
Ч
• •
Ч
• •
ч
• •
::
• •
й
Л
Рис. 319

Практическая магия. Домино
185
Если зритель передвинет одну косточку - слева останется
косточка с единицей, передвинет семь косточек - слева
останется косточка с суммой очков равной семи.
Следовательно, ваша задача перевернуть крайнюю левую
кость и посмотреть сумму очков на ней. Если это окажется
двойная пустышка, значит, зрители подшутили над вами и не
двигали ни одной кости.
Демонстрируя фокус второй раз, вы должны знать,
сколько очков было после первого показа на левой кости, например
семь. Возвратившись, берете уже не крайнюю левую кость, а
отсчитываете седьмую справа и ее открываете.
Так было перед второй демонстрацией фокуса:
• •
• •
••
• •
л
•
::
• •
• •
л
::
• •
::
::
• •
•
•
•
Ч
• •
• •
::
Рис. 320
Допустим, зритель передвинул на этот раз 10 косточек,
тогда получится ряд:
• •
• •
::
Ч
• •
Ч
• •
ч
::
•
• •
•
•
::
• •
::
•
•
•
Ч
Рис. 321
Для третьей демонстрации вам нужно мысленно
сообразить, какая теперь косточка крайняя слева.
Перекладывание косточек домино
Если вы не планируете дважды показывать фокус с
перекладыванием косточек домино с одного края ряда на другой, то
можете построить более длинный ряд.
Зрителям будет предложено переложить с левого края ряда
на правый край, не нарушая очередности, не более 12 косточек. В
этом варианте фокуса не демонстрируйте, как это делать, а сразу
приготовьте для зрителей «заряженный» ряд косточек. Оснозная,
приготовленная часть ряда будет выглядеть как на рис. 322.

186
Практическая магия. Карты
•
•
•
••
• •
::
• •
••
• •
::
л
л
л
::
и
::
Рис. 322
Левее этих косточек можете положить ещё 7 любых, доведя
общее количество до ровного счета 20, а можете положить левее
основного ряда ещё 12 косточек, получится ряд в 25 косточек.
Но, и в том, и в другом случае, когда вы будете угадывать
количество передвинутых косточек, нужно взять тринадцатую
косточку справа и посмотреть сумму очков на ней. При длине ряда
в 25 косточек, нужная вам будет как раз средняя.
Фокус с четырьмя картами
Нужно заметить, что отношение к картам постоянно
негативное. Считается, что детям нельзя играть в карты, а в домино
можно. В нашу задачу не входит выяснять, почему это так,
поэтому перейдем к делу. Стандартная колода содержит 52 карты.
Нас интересуют числовые значения карт. Обычно туз
приравнивается к 1, далее от 2 до 10 в соответствии с номиналом, валет -
11, дама- 12 и король- 13.
Колода карт тасуется зрителем, после чего демонстратор
фокуса кладет ее себе в карман и просит назвать любую карту.
Надо быть шулером, чтобы сразу достать эту карту из кармана,
но показать карту этой же масти и вытащить из кармана карты,
дающие в сумме значение названной карты - это фокуснику под
силу. Обсудим, как это сделать на практике.
Без жульничества в картах мало что обходится,
может поэтому такое к ним отношение. Вот и в этом фокусе
заранее прячут в карман трефового туза, червовую двойку,
четверку пик и восьмерку бубен, запоминая их порядок.
Перетасованная колода опускается в карман так, чтобы отобранные
карты остались сверху. Числовые значения карт образуют ряд
степеней двойки: 1=2°, 2=2*\ 4=22, 8=23. Работая ранее с
таблицами, мы уже убедились, что, комбинируя эти четыре карты,
молено получить в сумме любое число от 1 до 15. Первой вы
достаете карту требуемой масти. Если она не нужна в числовой
комбинации, то ее откладывают в сторону, в противном случае

Практическая магия. Карты 187
вы демонстрируете масть и сразу начинаете подсчет очков,
добирая следом нужные карты.
С вероятностью 4/52=1/13 могут назвать отложенную вами
карту. Тогда вы покажете высший класс, достав сразу нужную
карту. Но такое бывает редко. Если же был назван, например,
червовый валет, то нужно достать первой двойку черв, говоря
при этом - вот нужная масть и два очка. Затем достаете восьмерку
и туза, суммируя очки, получаете 11, это значение имеет валет.
Циклическая перестановка
Зрителю выдаются пять карт красной масти, имеющие
числовые значения 2, 3, 4, 5, 6. Показывающий раскладывает на
столе лицевой стороной вверх шесть карт черной масти,
образующих число 142857, Зритель тасует свои карты и, вытянув
одну из них, кладет ее лицевой стороной вверх под рядом черных
карт. Теперь зритель должен на доске или с помощью карандаша
и бумаги (но не с микрокалькулятором) посчитать произведение
этих чисел. Пока он занят этим делом, демонстратор собирает
свои карты и кладет их на стол кучкой лицевой стороной вниз.
После того как зритель выполнит умножение, попросите его
открыть ваши карты, раскладывая их лицевой стороной слева
направо. Шестизначное число, которое при этом получится должно
совпадать с результатом, полученным зрителем, если никто из
вас двоих не ошибся.
Фокус основан на том, что при умножении «циклического
числа» 142857 на любое из чисел от 2 до б, получается число,
составленное из тех же цифр, но с круговой их перестановкой.
Вам нужно только собрать карты в определенном порядке, не
привлекая к этому внимания. Например, зритель достал карту
со значением 4. Вы сразу умножаете 4- 7=28, последняя цифра 8.
Ваши карты лежат лицевой стороной вверх. Начните собирать
их с карты 8, двигаясь влево, положите 8 на 2, потом их вместе
на 4, затем так же стопкой на 1. Далее переносите всю стопку
на 7 и, двигаясь по-прежнему влево, на 5. Остается перевернуть
стопку карт лицом вниз. Восьмерка окажется внизу, раскрывая
карты слева направо, зритель выложит число 571428, которое
соответствует результату умножения. Циклическое число
142857 представляет собой период десятичной дроби,
полученный при делении единицы на простое число 7.

188
Практическая магия. Быстрый счет
В завершении разговора - парочка фокусов без всякой
предварительной подготовки и с минимумом реквизита, только
школьная доска и мел. Засучив рукава, чтобы подчеркнуть только
ловкость рук, как это обычно делал знаменитый Арутюн Акопян.
Хотя, если быть точным, наша специфика предполагает ловкость
ума, причем, обратите внимание, мы ничуть не уходим в сторону
от темы «расставьте числа.. .так, чтобы...».
Быстрый счет
Попросите одного из зрителей написать на доске любые два
натуральных числа одно под другим. Затем предложите ему
построить столбик из десяти чисел так, чтобы каждое следующее
число равнялось сумме двух предыдущих. Третье число
получается сложением двух первоначально записанных, четвертое - как
сумма второго и третьего и т. д. Во время всех вычислений
демонстратор стоит спиной к доске. Когда все десять чисел
выписаны в столбик, поворачиваетесь, подводите черту под
столбиком чисел и, не задумываясь, записываете их сумму.
Чтобы получить эту сумму, нужно четвертое снизу число
умножить на 11, что гораздо прощ$ сделать, чем
действительно складывать между собой десять чисел.
Ряд чисел, полученных по описанному правилу (каждое
число, начиная с третьего, равно сумме двух предыдущих)
называется обобщенным рядом Фибоначчи. Посмотрите ход всех
вычислений в общем виде и на конкретном числовом примере.
1
2
3
4
5
6
7
8
9
10
а
Ь
а+Ь
а+2Ь
2а+ЗЬ
За+5Ь
5а+8Ь
8а+13Ь
13а+21Ь
21а+34Ь
55а+88Ъ
\\=55а+Ш
13
21
34
55
89
144
233
377
610
987
2563
+233
233
2563

Практическая магия. Быстрый счет 189
Чтобы быстро умножить число на И нужно в разряде
единиц записать последнюю цифру числа, затем сложить цифру
единиц с цифрой десятков и записать последнюю цифру суммы,
затем сложить цифру десятков с цифрой сотен (и добавить к ней
единицу, если предыдущая сумма была больше десяти) и т.д.,
передвигаясь справа налево.
Получение заданной суммы
В начале демонстрации попросите зрителя из зала назвать
любое пятизначное число, желательно сложнее, т.е. с разными
цифрами. Расскажите сразу о том, что будет происходить дальше.
Между фокусником и зрителем организуется поединок, они по
очереди пишут числа одно под другим на доске. Задача
фокусника получить в сумме названное число, поэтому он оставляет за
собой право написать первое число и подвести черту под
столбиком цифр в любой момент. Задача зрителя всячески мешать ему,
он может писать любые числа, но только четырехзначные.
Рассмотрим действия исполнителя фокуса на конкретном
примере. Допустим, названо число 35 678. Отбросьте первую
цифру, сложите ее с оставшимся числом и запишите полученное
число первым: 5681. Теперь попросите зрителя записать ниже
четырехзначное число, для нас абсолютно все равно какое, пусть
3497. Третье число вы пишете быстро, но не наугад, а под каждой
цифрой, написанной зрителем, пишется ее дополнение до
девятки. Тогда последняя пара чисел дает в сумме 9999. Чтобы
получить требуемую сумму вам остается написать со зрителем еще
две пары чисел, он произвольных, а вы по правилу дополнения.
Подведите черту, и пусть зритель, сложив числа, убедится, что не
смог помешать вам в осуществлении задуманного.
35 678 —► 5681
3497
6502
7524
2475
1955
8044
35678
Первое число вы пишете по одному и тому же правилу,
убрав левую цифру и прибавив ее к оставшемуся числу.

190 Практическая магия. Быстрый счет
Это действие добавит к каждой паре единичку и превратит ее
сумму из 9999 в 10 000, поэтому количество пар чисел равно
первой цифре в названном зрителем пятизначном числе. Если
назовут пятизначное число с первой цифрой 9, вот тогда придется
повозиться: кроме первого числа вам со зрителем придется
написать еще 9 пар чисел, а всего будут суммироваться 19 чисел. Писать
долго, но скорость сложения от этого не меняется.
Этот фокус можно показать в другой, упрощенной
интерпретации. Вы пишете на доске многозначное, например, шестизначное
число. Важно только чтобы число единиц в этом числе было больше
двух. Под вашим числом пишет зритель свое число с таким же
количеством цифр. Потом снова вы и т.д. В определенный момент
подводите под столбиком чисел черту и мгновенно записываете
сумму этих чисел. Принцип записи ответа обратный предыдущему
варианту. За основу берется первое, записанное вами число.
Количество пар чисел, которые вы писали на пару со зрителем,
отнимается от числа единиц первого числа и приписывается спереди слева.
На этом закончим краткий курс «практической магии», чтобы
не ввергнуть вас в искушение бросить все свои дела и заняться
частной магической практикой. Описывая различные
математические фокусы, я постоянно думал о школе, которой отдал тридцать
лет своей жизни. О том, как можно использовать все, что есть в этой
книге, на школьном математическом вечере, а что-то даже на уроке,
когда чувствуешь, что ослабевает внимание учащихся и их желание
учится. Для детей игровые моменты в учебном процессе -
первейший стимул внимания и активности. Хотелось бы надеяться, что
собранные здесь материалы помогут бедному учителю в его
подвижническом труде. Никто из современных деловых людей и
чиновников разных рангов не поймет учителя. Его унижают
мизерной зарплатой, а он упорно готовится к урокам и идет на них без
опозданий. Его лишают наглядных пособий, а он что-то вырезает из
бумаги, клеит, раскрашивает, чтобы интереснее провести урок. На
него свысока смотрят обеспеченные родители учеников, а он ласково
гладит по головке их избалованных детей и старается сделать иХ
добрее. Ему хамят некоторые ученики, а он всеми силами души
пытается отыскать в них что-то хорошее и, зацепившись за это,
выправить человека. А что будет, если такие люди переведутся,
вымрут как мамонты? Уцелеет ли тогда человеческое общество?

Благоразумен тот, кто не печалится о том, чего
не имеет, и, напротив, рад тому, что имеет.
Демокрит (460-370 до //. э.) - древнегреческий философ
Постейший способ не нуждаться в деньгах - не
получать больше, чем нужно, а проживать меньше,
чем можно.
В. О. Ключевский (1841-1911) -русский историк
Кто умеет довольствоваться малым, тот богат.
К Гольдони (1707-1793) - итальянский драматург
Тот, кто оставляет все на волю случая,
превращает свою жизнь в лотерею.
Г. Фулер (1608-1661) - английский писатель
Величайшей заслугой человека остается,
конечно, то, что он как можно больше определяет
обстоятельства и как можно меньше дает им
определять себя.
И. Гёте (1749-1832) - немецкий мыслитель

Магия азарта 193
Отрицание случайного не может
превратить случайное в необходимое, оно остается и
играет центральную роль в познании
окружающего нас мира.
Академик Б.В.Гнеденко
Порядок и закономерность не исчерпывают всего
многообразия окружающего нас мира. Огромную роль в происходящих
событиях играет случай. Каждый из нас - результат случайного
слияния двух хромосом. Только после этого вступают в силу
законы Менделя, начинается взаимодействие доминантных и
рецессивных генов и определяется, что получилось. Порядок
нужно наводить, а хаос возникает сам по себе. Таланту нужно
помогать, а бездарность пробьется сама. Так и случай всегда
позаботится о себе сам и внесет в нашу жизнь с одной стороны
хаос, а с другой - разнообразие в закономерное течение жизни.
Но нельзя сравнивать случай с хаосом и бездарностью,
случайность - это не всегда негативное явление. Счастливчик,
выигравший в лотерею, будет всю жизнь благодарить этот случай.
Случайно происходящие мутации живых организмов приводят с
равной вероятностью к положительным или отрицательным
изменениям. Посвятив столько времени решению задач по
расстановке чисел, иначе говоря, по наведению порядка, нельзя
обойти вниманием роль случая, и рассмотрим мы это на
примерах различных числовых игр, придуманных человеком за свою
многовековую историю. В задаче все статично, есть неизменное
условие и нужно добиться его выполнения. Даже имея
стабильные начальные условия, игра предполагает динамику, изменение
ситуации на каждом шагу, множественность исходов в любой
позиции. Шахматы, шашки, начинаясь с одинаковой расстановки
фигур, имеют большое число возможных шагов на каждом этапе.
Но случаю в них места нет, только логические размышления,
просчет на несколько шагов вперед. Разве что «случайный»
зевок, означающий, что игрок не заметил один из возможных
ответных шагов противника и ухудшил свое положение.

194 Магия азарта
Большинство игр с домино и картами начинается
перемешиванием и последующей раздачей, поэтому случайной является
уже начальная позиция игры. Если в ходе игры приходится брать
еще одну карту из колоды или кость домино, то ее выбор тоже
случайный. Еще больше случайности в тех играх, где каждый
очередной ход начинается с бросания кубиков, например в нардах.
Рамки нашей темы предполагают рассмотрение игр,
связанных с числами. Числа есть на игральных кубиках,
костяшках домино, картах, лотерейных билетах, колесе рулетки и т. д.
Интересно, что каждый из этих атрибутов породил множество
различных игр, со своими, особыми правилами. Простое
описание карточных игр занимает целые энциклопедии, о количестве
различных лотерей можно судить по витринам киосков,
распространяющих билеты, немного меньше игр в домино и кости.
Естественно, в рамках обзора мы сможем коснуться только
некоторых игр по каждому разделу, избранных на свой вкус.
Еще один аспект игр со случайностью, это присутствие
азарта игрока. Психологи утверждают, что в основе игр у детей
лежит дух соперничества, состязания, а стремление испытать
риск, получить денежное вознаграждение появляется у взрослых
на основе жизненного опыта. Азартные игроки на вопрос чем
объясняется их страсть к играм, отвечают по-разному: тренировка
интеллекта, необъяснимое возбуждение, стремление доказать
свое превосходство над силами случая. Желание получить
незаработанные деньги, сорвать куш, стараются не афишировать.
Хотя о каком развитии интеллекта можно говорить в любой
лотерее или игре в рулетку, когда от человека ничего не зависит. Но
сильные эмоциональные переживания здесь налицо и не только
при выигрыше. Я сам несколько раз покупал билеты одной из
лотерей. Потом, сидя перед телевизором, смотрел проведение
тиража и вычеркивал цифры. Надежда выиграть и яркие эмоции:
иногда положительные, иногда отрицательные, но в
определенных границах, присутствуют и поддерживают интерес.
Неприятное отрицательное чувство я пережил, когда в моем билете было
вычеркнуто всего только три цифры, а кто-то уже взял джек-пот
в 11 миллионов. Больше лотерейные билеты не покупаю, чтобы
не испытывать подобного чувства.
Описывая различные игры, постараемся коснуться
математических вопросов, связанных с просчетом вероятности того или
иного исхода, используя элементы теории вероятности.

Магия азарта. Игральные кости 195
Игральные кости
Из множества настольных игр, придуманных людьми,
игральные кости, очевидно, самый древний атрибут. Подобно
магическому квадрату, первоначальное их назначение опять-таки
магия, гадание. Наши доисторические предки, бросая кости,
пытались с их помощью толковать будущее. Название «кости» не
случайно, так как до создания искусственной кости в виде кубика,
действительно использовалась таранная кость овцы, так
называемый астрагал. Бросали две таких кости одновременно - правую и
левую, каждая из которых могла лечь одной из четырех сторон
вверх. Каждое их положение трактовалось по-своему.
На каком-то этапе развития из атрибута гадания кости
превратились в инструмент азартных игр. Для этого неизвестные
мастера стали изготавливать игральные кости из дерева, камня,
из бивня слона и т.д. История убедительно свидетельствует, что
азартные игры с игральными костями появились задолго до
строительства пирамиды Хеопса, т.е. за 3000 лет до нашей эры
они уже были. В различных музеях мира хранятся образцы
древнеегипетских, древнегреческих, римских, китайских игровых
костей. Чаще всего они имели форму кубика с выемками на
гранях, обозначающими числа от 1 до 6. Хотя есть образцы в виде
других многогранников: прямой призмы с различным
количеством боковых поверхностей; кубооктаэдра с 14 гранями; в виде
призматического волчка и другие. До наших дней не вышли из
употребления игральные кости в виде кубика, остальные
хранятся как музейные экспонаты. Преимущества кубической формы
игральной кости имеют вполне резонные объяснения:
• только правильный многогранник обеспечивает полное
равноправие всех граней;
• из пяти существующих в природе правильных
многогранников куб легче всего изготовить;
• он перекатывается легко, но не слишком. Тетраэдр
перекатывается труднее, а, додекаэдр и икосаэдр настолько близки
по своей форме к шару, что быстро укатываются.
Западный стандарт требует, чтобы сумма чисел на
противоположных гранях равнялась семи: 6-1,5-2, 4-3. Существует
только два различных способа нумерации костей, причем один из
них является зеркальным отображением другого и, более того,
все современные игральные кости нумеруются одинаково.

196 Магия азарта. Игральные кости
Если держать кубик так, чтобы были
видны три числа 1, 2 и 3, то цифры будет
расположены в порядке, обратном движению часовой
стрелки.
Почему эти игры были именно азартными,
то есть предполагали какие-то ставки в игре,
деньги или вещи, которые можно было
Рис. 323 выиграть или проиграть?
Наверное, потому, что при бросании игральной кости не
требовалось думать - подбросил и отдался на волю случая. Если
не подсластить это действие возможностью сорвать куш, то
другого смысла в бестолковом бросании костей попросту нет. В
отличие, например, от шахмат, где сам длительный процесс
борьбы умов приносит удовлетворение, люди с удовольствием
играют без дополнительных стимулов, и то уже не всегда.
Азартные игры с игральными костями, как это ни странно
звучит, принесли пользу науке, послужили толчком к развитию
комбинаторики и математической теории вероятностей. Эта
теория начиналась с исследования различных видов азартных игр, с
целью установления закономерностей в случайных событиях,
определения вероятности выигрыша или проигрыша. В борьбе со
случайностью эти знания ничего не изменяют, но могут
предостеречь, дать возможность реально оценить свои шансы на
выигрыш, а уж тогда решать: ввязываться в игру или благоразумно
отказаться. Знание шахматных дебютов, шахматной теории,
будет полезно в самой игре и может привести к победе, а знание
теории вероятностей ни на игральную кость, ни на шарик в
американской рулетке не подействует, вы останетесь наедине со
случайностью. Хотя интересно все-таки знать, что и случайность
имеет свои закономерности.
Игры в кости, могут проходить с различным количеством
бросаемых одновременно костей. Начнем с одной кости.
Игра примитивная
Примитивная игра с одной костью состоит в том, что
игроки поочередно бросают её и побеждает тот, у кого выпадет
большее число очков. При равенстве очков, игроки повторяют бросок.
Вряд ли кого заинтересует такая игра, поэтому такая процедура
используется чаще не для самой игры, а при жеребьевке в каких-
то других играх или делах.

Магия азарта. Игральные кости 197
Но даже этот простой вариант позволяет нам потренировать
свое логическое мышление. В истории развития математического
аппарата азартных игр было много случаев неправильной логики,
которые приводили к неверным результатам. Рассмотрим
подобный пример.
При подбрасывании одного игрального кубика вероятность
появления единицы равна 1/6. При втором подбрасывании -
тоже. Значит, если провести два броска, то вероятность появиться
единице хотя бы один раз (при первом броске или при втором)
равна 1/6+1/6=1/3. Рассуждая аналогично, получается, что для
шести бросков вероятность выпадения 1 хотя бы один раз из
шести равна единице (1/6-6=1), т.е. является достоверным
событием. Мы можем применить эти рассуждения к любому из чисел
от 1 до 6, и сделать вывод, что каждое число при проведении
шести бросков, обязательно выпадет. С другой стороны опыт
подсказывает нам, что это не так. Бросьте кость шесть раз и вряд
ли, каждое из возможных чисел, выпадет ровно по разу. В чем
ошибочность рассуждений?
Высказывание: «единица выпала хотя бы один раз при двух
бросках» на самом деле распадается на несколько различных
событий:
• выпала в первый раз и не выпала во второй (1/6-5/6) или
• не выпала в первый раз и выпала во второй (5/6-1/6) или
• выпала в первый раз и во второй тоже (1/6-1/6).
Соответствующая вероятность подсчитывается как
5/36+5/36+1/36-11/36, что немножечко меньше чем 1/3.
Для шести бросков подсчет лучше начать по-другому.
Вероятность того, что 1 не выпала при одном броске 5/6, при двух
бросках 5/6-5/6, соответственно вероятность, что 1 не выпала при
шести бросках равна(5/6)6. А значит вероятность, что она выпала
хотя бы раз в шести бросках равна 1-(5/6)6 = 0,66510.
Игра с дополнением
Первый игрок бросает кость и складывает число, выпавшее
на верхней грани, с любым числом на одной из четырех боковых
граней. Его соперник складывает все остальные числа на трех
боковых гранях. Нижняя грань в расчеты не принимается. Затем
второй игрок бросает кость, и они проводят аналогичные подсчеты.
Выигрывает тот игрок, у которого после бросков обоих игроков,

198 Магия азарта. Игральные кости
будет больше итоговая сумма. К слепому случаю добавилась
маленькая возможность для выбора самим игроком одного из
боковых чисел, хотя, что там выбирать - нужно брать наибольшее.
К тому же еще в уме числа сложить придется, получается, что
добавили мышление.
Перевороты кости
Для этой игры опять-таки нужна одна игральная кость.
Первый игрок называет любое число от 1 до 6, а второй бросает
кость. Затем они по очереди переворачивают кость через её ребро
в любую сторону на четверть полного оборота. К числу очков,
названных первым игроком, прибавляется число очков,
выпавших на верхней грани после бросания кости и после каждого её
поворота. Выигрывает тот из игроков, которому удается при
очередном повороте достичь суммы 25 очков или вынудить
противника при следующем повороте превзойти 25 очков.
Всего на третьем шаге, оставаясь с одной игральной
костью, мы пришли к необходимости серьезно думать.
Какое число должен назвать первый игрок, чтобы выиграть
с наибольшими шансами?
Игры с двумя костями были настолько популярны на
протяжении веков, что у них есть свои исторические названия и
определенная терминология.
Азар
Название игры происходит от арабского выражения
«аз-захр» - «игральные кости».
Игрок, выступающий в роли банкомета, ставит против
остальных участников, число которых неограничено, на то, что
ему удастся с помощью двух костей выбросить одно из
следующих чисел: пять, шесть, семь, восемь или девять. Противники, в
свою очередь, обязаны уравнять его ставку.
Загаданное банкометом число называется «мейн». Если
после его броска выпадает «мейн», то банкомет получает все
деньги, поставленные на кон. Такой удачный ход получил
название «ник». Если же выпадает какое-то иное число, его называют
«чане», то для банкомета еще не все потеряно.

Магия азарта. Игральные кости
199
Он обязан продолжать бросать кости до тех пор, пока вновь не
выбросит «чане» - тогда он выиграл, или выпадет «мейн» - тогда
он проиграл и должен выплатить деньги.
В казино имел распространение азар с бросанием трех
костей и иными правилами, о нем поговорим позже.
Крэпс
Игра «Крэпс» одна из популярнейших в Америке.
Изобретена в IX веке черными невольниками с берегов Миссисипи.
Игрок бросает две кости и подсчитывает сумму выпавших очков.
Он сразу же выигрывает, если эта сумма равна 7 или 11, и
проигрывает, если она равна 2, 3, или 12. Всякая другая сумма - это его
«пойнт». Если в первый раз выпадает «пойнт», то игрок бросает
кости ещё, до тех пор, пока он или выиграет, выбросив свой
«пойнт», или проиграет, получив сумму очков, равную 7.
Проведем некоторые размышления по поводу бросания
двух игровых костей. Для начала посчитаем вероятности для
полного числа очков на двух костях. Будем считать, что одна из
них белого цвета, а вторая - черная. Это немаловажная деталь в
рассуждениях, так как мы должны различать кости, а,
следовательно, и такие варианты возможных исходов, как (3,5) и (5,3).
Подбрасывание двух костей имеет 36 равновероятных исходов,
которые мы обобщили в виде таблицы.
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
б
7
8
9
10
11
12
В клетках таблицы указаны получаемые суммы очков. На
основе первой таблицы модно просчитать распределения
вероятностей получения определенной суммы очков при
подбрасывании двух игральных костей. Эти значения оформим таблицей 2.

200
Магия азарта. Игральные кости
Е
Р
2
1
36
3
2
36
4
3
36
5
4
36
б
5
36
7
6
36
8
5
36
9
4
36
10
3
36
11
2
36
12
1
36
Здесь нижняя строка обозначает вероятность появления
соответствующей суммы очков. Таблица позволяет подсчитать
вероятность выигрыша после первого броска
Р(7)+Р(11 )=6/3 6+2/3 6=8/3 6=2/9
Вероятность проигрыша после первого броска равна
Р(2)+Р(3 )+Р( 12)= 1 /3 6+2/3 6+1 /3 6=4/3 6= 1 /9
Таким образом, теория говорит, что вероятность выигрыша при
первом броске в 2 раза больше вероятности проигрыша, но еще
больше (2/3) составляет вероятность того, что игра не
остановится на первом броске, а будет продолжена. Попробуйте сами
провести исследование вероятности при первом броске «пойнт»
снова его выбросить в дальнейшей игре.
Попытай счастья
Это азартная игра с тремя игральными костями. В неё часто
играют в игорных домах и во время народных гуляний на
ярмарках или карнавалах. На прилавке лежат шесть квадратов,
помеченных цифрами 1, 2, 3, 4, 5, 6. Игроки делают стандартные
одинаковые ставки на один из номеров, после чего
подбрасываются три игральные кости. Если номер играющего выпадает на
одной, двух или трех костях, то за каждое появление этого номера
игроку выплачивается первоначальная ставка, при этом
возвращаются и его собственные деньги. Игроки, чей номер не выпал
ни разу теряют ставку. Игрок может ставить на несколько
номеров одновременно, но каждая ставка рассматривается отдельно.
Игра проста и увлекательна. Только необразованность
объясняет то, что ее обошли вниманием наши «лохотронщики», ведь
никакого криминала.
Предположим для простоты, что на каждый номер положена
единичная ставка. Игра безобидна только в случае, когда все три
выпавших номера различны. Тогда, получив на шесть номеров
шесть ставок, игорный дом расплачивается этими деньгами с
тремя удачливыми игроками, отдавая им Три выигранных ставки

Магия азарта. Игральные кости 201
возвращая три поставленных. В этом случае организаторы игры
ничего не имеют, а только перераспределяют деньги между
везучими и проигравшими. Так будет всегда, когда выпадают три
различных номера, но не всегда будут выпадать все разные номера.
Предположим теперь, что после подбрасывания костей
выпало ровно два одинаковых номера. Из шести полученных ставок
три отдадут игроку, чей номер выпал дважды (с учетом
возвращаемой ставки) и две - игроку, чей номер выпал один раз.
Получается, что при таком раскладе одна ставка остается у игорного дома.
Наконец, пусть на всех трех костях выпал один и тот же
номер. Тогда один игрок получает четыре ставки, три
выигранных и одну возвращаемую, а игорному дому остаются уже две
ставки игроков.
Рассмотрим вероятность этих случаев. Пусть игральные
кости различаются по цвету, например, красная, зеленая и синяя.
Они мбгут выпасть 6-6-6 = 216 способами.
Легко просчитать последний случай, когда выпадают три
одинаковых номера. Число таких вариантов всего 6, так как
красная кость может выпасть любой из 6 граней, а зеленая и синяя
только той единственной, которой уже выпала красная кость.
Определим, сколькими способами могут выпасть три
различных номера. Для красной кости имеется 6 различных
вариантов, для зеленой - только 5, потому что номер, выпавший на
красной кости, не должен повторяться, аналогично рассуждая,
синяя кость может выпасть только одной из 4 граней. Итого 6-5-4
= 120 вариантов.
Отсюда следует, что в 90 случаях выпадают два
одинаковых номера (216 - 126 = 90).
Вероятность получения ставки игорным домом равна
(120/216)0 +(90/216)1 + (6/216)2 = 102/216.
Это означает, что количество единичных ставок игроков,
остающихся в игорном доме приблизительно равно половине
проведенных игр и никаких потерь. При таком раскладе выгодно
работать круглосуточно.
Теперь рассмотрим эту игру с точки зрения игрока. Из 216
равновероятных исходов он выигрывает только в 91 случае и
проигрывает в 125. Откуда мы взяли цифру 91?
Допустим, игрок поставил на «единицу». Один из 216
исходов - это когда выпадают все три единицы; из 90 случаев с двумя
одинаковыми цифрами третья часть включает в себя единицу; из
120 вариантов с тремя различными числами единица входит в
половину. Итого: 1+30+60=91.

202 Магия азарта. Игральные кости
Эта вероятность существенно отличается от вероятности
выигрыша для игорного дома. Хотя цифры 102/216 и 91/216 не
очень сильно различаются, но для игорного дома они означают
неминуемую прибыль, а для игрока более вероятный проигрыш,
чем выигрыш.
Сложнее будут вычисления, если игрокам разрешить делать
не фиксированные, а произвольные ставки на различные числа.
При таких правилах есть вероятность, что на начальном этапе
игорный дом вложит какую-то сумму в игру, когда маленькие
ставки проигравших игроков не покрывают большую ставку
выигравшего, но если игра длится достаточно долго, то организатор
игры может надеяться получить 7,8% от каждого поставленного
игроками доллара. Попробуйте вывести эту цифру самостоятельно.
Три кости
Сначала каждый игрок называет некоторое число от 3 до
18 . Бросают три кости. Выигрывает тот игрок, у которого сумма
выпавших очков равняется числу, названному им перед игрой.
Определим шансы игрока в зависимости от названного им
числа. Три игральные кости подбрасывают над столом и считают
сумму, очков выпавших на верхних гранях. Сколько различных
исходов возможно для одного подбрасывания кубиков?
Каждый кубик может показать на верхней грани одно из
шести чисел: 1, 2, 3, 4, 5, 6. Комбинируя 6 расположений первого
кубика с шестью расположениями второго, получим 6-6=36
вариантов для двух кубиков. Каждое из этих 36 расположений двух
кубиков в сочетании с одним из 6 расположений третьего кубика
дают 36-6=216 сочетаний по 3 числа.
Одинаковы ли вероятности появления у каждой суммы от
наименьшей (1-3) до наибольшей (6-3)? Сравним, например,
вероятности получения сумм 9 и 10. На первый взгляд
вероятности одинаковы. Три кубика формируют 6 троек чисел, дающих в
сумме 9 - (6, 2, 1), (5, 3, 1), (5, 2, 2), (4, 1, 1), (4, 3, 2), (3, 3, 3), и
столько же формируют троек чисел с суммой 10 - (6, 3, 1), (6, 2, 2),
(5,4, 1), (5, 3,2), (4, 4, 2), (4, 3,3).
Чтобы не допустить ошибки в рассуждениях, предположим,
что наши кубики окрашены, например, по системе RGB, т. е.
красный, зеленый и синий. Тогда первая тройка чисел, дающая
сумму 9, фактически распадается на шесть объективно различных

Магия азарта. Игральные кости
203
вариантов: (6, 2, 1), (6, 1, 2), (2, 1, 6), (2, 6, 1), (1, 2, 6), (1, 6, 2). В
этой записи на первом месте стоит число, выпавшее на красном
кубике, на втором месте число, выпавшее на зеленом и на
третьем - выпавшее на синем кубике. Если в тройке чисел, дающих
нужную сумму, два числа одинаковые, то с учетом раскраски
получается три различных расклада. Например, - (5, 2, 2), (2, 5, 2),
(2, 2, 5). При трех одинаковых числах, перестановки не создают
различающихся случаев и возможен только один вариант.
Вот теперь подсчитаем число случаев, дающих сумму 9, с
учетом индивидуальности кубиков: 6+6+3+3+6+1=25.
Аналогичный подсчет для суммы 10 дает результат: 6+3+6+6+3+3=27.
Пусть не намного, но при броске трех игральных костей
вероятность появления суммы 10 больше, чем вероятность суммы 9.
Таким образом, можно посчитать вероятности появления
каждой из возможных сумм от 3 до 18. В итоге все 216
возможных исходов распределятся по своим суммам.
Первым, кто правильно провел подобные рассуждения, был
знаменитый ученый Галилео Галилей.
Азар в три кости
Эта игра распространена в казино и, следовательно, в ней играет
казино в лице крупье против игроков, делающих ставки.
Рис. 324

204 Магия азарта. Игральные кости
Стол для игры имеет специальную разметку, для того,
чтобы игроки могли делать ставки на различный исход при броске
трех костей. Положив фишку на любую из 6 комбинаций в поле
Raffles, игрок тем самым делает ставку на то, что на всех трех
костях одновременно выбросят именно это число очков. В случае
удачи его ожидает выигрыш в соотношении 180:1. Поставив на
поле Any raffle, игрок выигрывает, если после броска на всех трех
костях будет одинаковое число очков, но не важно какое
конкретно. Выигрыш выплачивается в соотношении 30:1. На поле
Low (мало) выигрывают, когда сумма выпавших очков не более
10. На поле High (много) - когда сумма очков не меньше 11.
Выигрыш на Even (чёт) и Odd (нечет) выплачивается в том случае,
если выпадает любое четное или соответственно нечетное число.
Но если полученное число складывается из трех одинаковых
цифр, это означает проигрыш игрока. Кроме этих ставок, есть
ставки на конкретную сумму очков, «на числа». На разметке
стола видно, в каком соотношении производится выплата выигрыша
при ставке на то или иное число. Соотношения разные и зависят
от вероятностей выбрасывания каждой суммы.
Не будем повторять расчеты вероятностей для броска трех
костей, отметим только, что при любой ставке соотношение,
выплачиваемое игроку, меньше того, которым оно должно быть исходя
из теории. В поле Raffles истинное соотношение равняется 215:1,
а значит, казино оставляет себе 162/з % от суммы выигрыша. На
каждом поле свой процент, остающийся у казино. Как это
посчитать мы наметили в обсуждении предыдущей игры, а вы, при
желании можете довести расчеты до конца. Тем самым вооружить
себя знаниями, главное из которых - выигрывает всегда казино.
Покер
Для игры необходимо иметь пять игральных костей
стандартного вида. Кости бросают из рук или из любого стакана на
ровную поверхность. В игре могут участвовать два и более игроков.
Цель игры - выполнение определенных фигур с максимальным
количеством очков. Первым броском производится жеребьевка
очередности хода между игроками. Начинает игрок, набравший
наибольшее количество очков, и далее по убыванию очков. Набор
фигур состоит из двух программ: обязательной и произвольной.

Магия азарта. Игральные кости 205
Обязательная программа: единицы, двойки, тройки,
четверки, пятерки, шестерки. (Нужно выбросить не менее 3-х костей
конкретного достоинства).
Произвольная программа:
• одна пара (1п) - 2 кости одного достоинства;
• две пары (2п) - 2 кости одного достоинства и 2 кости
другого достоинства;
• любая тройка (3) - 3 кости одного достоинства;
• малый стрит (LS) - 5 костей достоинством 1, 2, 3, 4, 5;
• большой стрит (BS) - 5 костей достоинством 2, 3, 4, 5, 6;
• фул (F) - 2 кости одного достоинства и 3 кости другого
достоинства;
• каре (С) - 4 кости одного достоинства;
• покер (Р) - 5 костей одного достоинства;
• шанс (Sh) - 5 костей любого достоинства.
Выполнение фигур начинается с обязательной программы.
Фигуры произвольной программы можно выполнять только
после окончания обязательной программы. Порядок выполнения
фигур в программах - произвольный. При каждом ходе игрок
имеет право на три попытки для выполнения одной из фигур.
После первого броска он оставляет кости, необходимые для
задуманной фигуры, а в следующих попытках выбрасывает
оставшиеся для получения желаемого результата. При любой из
трех попыток можно начинать выполнение другой фигуры в
зависимости от ситуации. Результаты ходов записываются в
специальную, заранее расчерченную, таблицу (см. стр. 206).
После выполнения каждого хода обязательной программы
могут возникнуть следующие варианты:
1. Выпали 3 кости одного достоинства: тогда в
соответствующей клеточке таблицы ставится знак «+», отмечающий
выполнение фигуры;
2. Выпало менее 3 костей одного достоинства: в таблицу
заносится отрицательный результат, равный числу костей,
недостающих до трех, умноженному на их достоинство (при двойках
2, при тройках 3 и т.д.);
3. Выпало более 3 костей одного достоинства: в таблицу
записывает положительный результат, равный числу костей сверх
трех, умноженному на их достоинство.

206
Магия азарта. Игральные кости
4. Не выпало ни одной кости нужного достоинства: тогда в
таблице указывается отрицательный результат, равный
достоинству желаемой кости, умноженному на 3.
Каждый участник может выполнить комбинацию только по
одному разу. Например, если у одного из участников вторично
выпадает обязательная комбинация «четверки», и возможно с
лучшим результатом, то он не может снова занести этот результат
в таблицу, а должен выполнять одну из оставшихся комбинаций.
Имена игроков
1
2
3
4
5
6
Промежуточный итог
1н
2п
3
LS
BS
F
С
Р
Sh
Итого:
А
В
С
д
После обязательной программы подводится промежуточный
итог. Очки каждого игрока суммируются. Если итог равен нулю
или больше, то добавляется премия 50 очков.
При выполнении фигуры произвольной программы с
первого броска сумма очков её удваивается, кроме шанса. Если при
выполнении хода не удалось выбросить нужную фигуру, то по
желанию игрока в таблице вычеркиваются очки за любую уже
выполненную фигуру. При выполнении покера дается премия 50
очков. Игра заканчивается заполнением всех клеточек таблицы.
Очки каждого игрока суммируются, далее производится расчет.

Магия азарта. Игральные кости
207
Из очков конкретного игрока вычитается среднее
арифметическое суммы всех игроков. Положительный результат - это
выигрыш, отрицательный - проигрыш.
Покажем пример заполнения таблицы с подсчетом очков
для одного из игроков и комментариями к процессу игры.
Имена игроков
1
2
3
4
5
6
Промежуточный итог
1н
2п
3
LS
BS
F
С
Р
Sh
Итого:
А
+1
-4
+
+4
+
+
51
10
18
30
15
-
27
24
ПО
21
306
выбросил 4 кости по «1»
выбросил только 1 кость «2»
выполнил 3 кости по «3»
выбросил 4 кости по «4»
выполнил
выполнил
+1+50 премия
две «5», но не с первого
две «3» и две «6», не сразу
три «5» с первого броска
выполнил, не сразу
не выполнил F или С, или Р
5+5+5+6+6
3-4-2, если сразу, или 6-4
6-5-2 с первого +50 премия
1+3+5+6+6
Эта игра представляет собой вариант карточного покера.
Причем здесь описан покер с обычными костями, а существуют
специальные покерные кости, на гранях которых нанесены
карточные символы: девятка, десятка, валет, дама, король и туз.
Итак, мы рассмотрели несколько игр в кости, показали
некоторые методы вычислений вероятностей отдельных исходов.
Есть еще вариант крэпса для казино со своей разметкой стола,
популярная игра пассе ди и множество других. Но покер, как мне
кажется, самая интеллектуальная из игр в кости, поэтому на нем
закончим разговор об этой группе азартных числовых игр.
Игральные кости дали основной толчок для развития
комбинаторики и теории вероятностей. А занимались теоретическими
исследованиями игр в кости такие великие математики как Тарта-
лья и Галилей, Ферма и Паскаль, оставившие свои имена в
науке в связи с другими крупными открытиями и исследованиями.

208
Магия азарта. Домино
Домино
•
•
•
• •
• •
•
::
••
\
• •
• •
::
• •
Игра «домино» родом из древнего Китая, где называлась
«костяные таблички», и своим происхождением обязана более
старой игре в кости. На китайских табличках, как и на костях, не
было нулевого очка. Оно появилось в Европе, куда «костяные
таблички» завез Марко Поло, и где их значительно упростили,
присвоив им другое название. Стандартный комплект домино из
28 костей разного достоинства значительно сложнее простой
игральной кости, и уж если с игральными костями существует
много игр, то о домино нужно писать отдельную книгу. В эту
книгу вошли бы не только различные доминошные игры, но и
большое количество разнообразных головоломок с костяшками
домино. Поэтому здесь упомянем обзорно только минимум игр.
Традиционное домино
Играют от 2 до 4 человек. Для двух сдают по 7 косточек,
для трех или четырех - по 5. Остальные косточки остаются в
закрытом резерве, которой называют «базар». Начинает игрок,
выкладывающий дубль 6-6. Следующие игроки выставляют
костяшки с соответствующими очками с любой стороны цепочки, а
при отсутствии таковых тянут из резерва, сколько потребуется.
Если и резерва уже нет, то пропускают ход. Если вначале ни у
кого нет дубля 6-6, то игра начинается с 5-5 или 4-4 и т.д., при
отсутствии дублей заходят с кости, имеющей наибольшее число
очков (например, 6-5).
Игра заканчивается когда:
• один из игроков выложит последнюю костяшку;
• весь резерв выбран, а к выкладке нечего доложить, игра
заблокирована. Эта ситуация называется «рыба».
Выигравшему игроку, в качестве выигрыша, записывается
сумма очков всех костяшек, оставшихся на руках проигравших.
При «рыбе», выигрывает игрок, имеющий на руках
наименьшее число очков. В выигрыш ему записывается разность
очков. Обычно игра идет до 100 очков.

Магия азарта. Домино
209
Блиц
Играют от 4 до 8 игроков. Для четверых сдают по 7 косточек,
для пятерых - по 5, для шестерых и семерых - по 4, для восьмерых
- по 3 косточки домино. Оставшиеся косточки в игре не участвуют.
Начинают игру с дубля 0-0 или ближайшего к нему. Каждый
из игроков в свой ход может выложить сразу любое количество
косточек, прикладывая их друг к другу в соответствии с правилами
традиционного домино, даже все, если расклад позволяет это
сделать. Выигрыш подсчитывается как в традиционном домино.
Севастополь
Четыре игрока берут по 7 косточек. Игра открывается
дублем 6-6. При первых ходах каждый игрок обязательно начинает
одну из четырех сторон выкладки, как показано на рисунке.
•
•
•••
•
• •
::
• •
• •
•
III
• •
• •
Рис. 325
В дальнейшем ходы делаются на произвольную сторону,
куда позволяют имеющиеся косточки. Выигрывает тот, кто
первым выложит косточки из рук. Подсчет очков как в
традиционном варианте, т.е. выигравшему записывается сумма очков всех
косточек, оставшихся на руках проигравших. Игра продолжается
до 100 очков.
Матадор
В эту игру играют от двух до четырех участников, Если
игроков два или три, то они получают по шесть косточек, если
четыре - по пять. Игрок, начинающий игру определяется
жребием, следующие ходы делаются по часовой стрелке.

210
Магия азарта. Домино
Начинающий выкладывает любую кость. Особенностью
этой игры является то, что приставляют косточки друг к другу не
одинаковым числом очков, как в предыдущих играх, а так, чтобы
сумма приставленных половинок обязательно равнялась семи. К
единице приставляют шесть, к двойке - пять и т.д.
Косточки, сумма половинок которых составляет семь очков, а
также «пусто-пусто», называются матадорами (см. рис. 326). К
нулевой половинке можно приставлять только матадоры, которые
кладутся поперек цепочки. Матадоры можно использовать как
обычные кости, кроме «пусто-пусто», тогда их кладут вдоль
цепочки. Если невозможно сделать ход из-за отсутствия
подходящей косточки на руках, можно взять кость из резерва (базара), но
только одну.
V
•
•••
•р
Рис. 326
Рис. 327
Игра заканчивается только тогда, когда нет косточек в
резерве, и на руках отсутствуют косточки необходимые для
продолжения игры. Подсчитывают очки как в традиционном домино
и играют до 100 очков.
Игры в домино в качестве азартных, дающих возможность
делать ставки просуществовали до начала двадцатого века. В
наше время домино просто настольная и даже детская игра.
Существуют разновидности домино с картинками для детей
детсадовского возраста. В школе придумали химическое домино и
математическое домино, т.е. используют его модификации на
уроках в качестве наглядного учебного пособия. Какой учитель
допустит, чтобы на перемене ученики «резались» в карты, а
домино есть в каждой школьной игротеке. Видимо свою
«благородную» окраску домино получило за счет малого влияния
случайного фактора (только при первоначальном перемешивании),
относительно неторопливого развития игровой ситуации и
отсутствия острых моментов в процессе игры. Поэтому теперь положение
домино среди многообразия игр ближе к шашкам и шахматам.

Магия азарта. Игральные карты 211
Игральные карты
История различных игр уходит в настолько далекое
прошлое, что сейчас трудно установить чей-то приоритет в
изобретении тех, или иных игр. Это только в последние пару столетий,
когда стала работать патентная система, изобретения обязательно
патентуются их авторами, чтобы сохранить за собой приоритет, а
значит и денежную компенсацию за использование изобретения.
Поэтому теперь мы четко знаем, что игру «пятнадцать» придумал
Сэм Лойд, а «кубик Рубика» создал венгерский изобретатель Эр-
не Рубик. О происхождении более древних игр можно говорить с
той или иной степенью достоверности. Поэтому о происхождении
игральных карт можно высказать следующие предположения.
Эволюция игр шла от игральных костей к «костяным табличкам»
домино, а от них к совсем плоским игральным картам. Больше
всего фактов говорит о том, что и карты тоже пошли из Китая.
Именно там раньше других стран в обороте появились бумажные
деньги, на которых изображались императоры, их жены,
губернаторы провинций и сановники рангом пониже. Причем банкноты
служили не только для денежных взаимных расчетов, но и для
азартных игр.
В Европу карты попали, скорее всего, от арабов, которые в
основном использовали их в качестве магических атрибутов для
предсказания судьбы. Как видим, древняя магия лежит в основе и
магических квадратов, и игральных костей, и игральных карт.
Объяснение этому самое простое, из всех направлений различных
наук мы взялись за самый древний пласт знаний, когда носителями
знаний были жрецы, одновременно выполнявшие миссию
предсказателей и толкователей предстоящих событий. Там где
конкретных знаний не хватало, на помощь жрецам приходила мистика,
основанная на эксплуатации «темноты» остального населения.
Игральные карты можно рассматривать, как прямоугольники
с изображенными на них цифрами и фигурами, и карты с
картинками тоже имеют свой числовой эквивалент, но для них он
может меняться в зависимости от конкретной игры. На этом
основании карты могут полноправно присутствовать в этой книге,
ведь они отвечают всем её требованиям: наличие чисел, фигур и
необходимость расставлять, а по своей азартности они рядом с
игральными костями, рулеткой и лотереями.

212 Магия азарта. Игральные карты
Различных карточных игр ещё больше, чем игр в домино, а
если добавить к ним не меньшее количество пасьянсов,
раскладываемых в одиночку, множество фокусов с картами, то
становится ясно - это тоже материал для отдельной книги. Правда, с
этим вопросом дело обстоит лучше всего, за последнее время
выпущено достаточное количество книг, посвященных
игральным картам. Раньше на это был относительный запрет, а когда
стало можно - поток хлынул.
Среди всех игр, рассмотрим несколько, в которых
используется числовое значение карт, и которые показывают
процессуальное разнообразие карточных игр. Кроме того, чтобы быть
последовательным, я выбрал игры, в названии которых
фигурирует некоторое число.
Девятка
Обычно используется колода из 36 карт, можно играть и
колодой из 52 карт. Количество игроков 3, 4 или 6. При игре
вдвоем исход предопределен раскладом карт и поэтому игра
теряет всякий интерес. Перетасованная колода раздается
полностью всем игрокам поочередно по одной карте. Цель игры - как
можно быстрее выложить все свои карты и помешать, если можно,
сделать это партнерам. Первым ходит тот, кому выпала девятка
бубен (некоторые начинают с девятки треф, поэтому обсудите
этот вопрос заранее). Карты раскладываются в четыре
горизонтальных ряда по мастям, в обе стороны начиная от девяток. Карту
можно положить на соответствующее ей место только в том
случае, если выложена предыдущая по достоинству карта с
восходящей или нисходящей стороны. Девятки можно выкладывать в
любое время. За десяткой идут валет, дама, король, туз. Ходят
игроки по очереди, выкладывая за один ход только одну карту. (В
некоторых разновидностях игры разрешается, как в блице
домино выкладывать сразу несколько карт, если они есть на руках).
Если у игрока нет необходимых карт, он пропускает ход.
Побеждает тот, кто первым выложит все свои карты.
Игру можно усложнить, если ввести подсчет штрафных
очков, которые начисляются проигравшим в зависимости от
стоимости оставшихся на руках карт. Или же делать
определенные ставки в банк, начиная игру. Этим ее можно превратить в
игру азартную, т.е. требующую выплаты победителю.

Магия азарта. Игральные карты 213
Тринадцать
Используется колода в 52 карты. Игра основывается на
случайности и разыгрывается механически. Число игроков не
ограничено. Первым банкометом становится тот, кто вынет самую
младшую карту. Потом банк переходит от одного к другому, по
очереди. Игра ведется таким образом. Банкомет кладет в банк
определенную сумму, которой ограничивается общая сумма
ставок остальных игроков. Ставят, в этих пределах, любые суммы,
причем право ставки, прежде всего, принадлежит левому соседу,
а затем переходит (на оставшуюся свободную сумму) в том же
направлении дальше, по очереди. Деньги должны лежать на
столе, перед каждым игроком.
После этой операции банкомет начинает игру. Из хорошо
перетасованной и снятой колоды, лежащей перед ним на столе,
крапом вверх, он выкладывает карты одну за другой и
произносит: открывая первую карту - «Двойка», вторую - «Тройка»,
третью - «Четверка», четвертую - «Пятерка», пятую -
«Шестерка», шестую - «Семерка», седьмую - «Восьмерка», восьмую -
«Девятка», девятую - «Десятка», десятую - «Валет»,
одиннадцатую - «Дама», двенадцатую - «Король», тринадцатую - «Туз».
Если банкомет во время этого перечня не отгадает ни одной
карты, то есть не вскроет ту, которую называет, то игроки
забирают банк, деля его между собой пропорционально своим
ставкам. Далее банкует игрок, сидящий слева. Он перетасовывает
карты, дает снять и ведет игру в том же порядке. Если и он не
отгадал ни одной карты, банк переходит к следующему и т.д.
Если банкомет во время перечня угадал карту, например
«пятерку», он останавливает перечисление, забирает себе все
ставки игроков и продолжает игру. Дождавшись, когда игроки
сделают новые ставки, он начинает перечень снова с «Двойки».
Если еще раз повезет, он продолжает банковать до тех пор, пока не
проиграет. Тасовать карты после каждого раза он не имеет права,
это разрешено только тогда, когда выйдет вся колода и ему
приходится снова отгадывать. Банкомет обязан открывать карты не
торопясь, и по одной складывать их на стол в ровную кучку.
Банкомету предоставляется право оставлять выигранные деньги в
банке, т.е. удвоить его. Но рекомендуется всегда снимать взятые с игроков
ставки, иначе банкомет, выигравший несколько раз, в конце концов,
все-таки останется в убытке, ведь он обязан играть до проигрыша.

214 Магия азарта. Игральные карты
Двадцать одно
Число игроков два и более. Рекомендуется колода из 52
карт, хотя часто играют и в 36. Стоимость карт от 2 до 10 в
соответствии с достоинством, валет - 2, дама - 3, король - 4, туз —11,
два туза считаются за 21 очко. Выигрывает тот, у кого при наборе
карт окажется в сумме 21 очко или выпадает два туза. Если не
набрано 21 очко, то выигрывает тот, у кого на руках больше
очков, но не более 21.
Первый банкир разыгрывается на картах до туза, далее бан-
кование передается по кругу налево.
Банкир перетасовывает карты и дает снять, игроку сидящему
справа. После этого он назначает банк от рубля и выше, деньги
кладутся на стол. Банкир раздает всем игрокам, начиная слева по
одной карте в закрытом виде, последнюю берет себе и вскрывает
её, показывая всем. Первая карта сдается сверху колоды,
остальные - снизу. После сдачи всем первой карты, банкир берет одну
карту снизу и кладет ее сверху колоды картинкой вверх, чтобы в
дальнейшем она отделяла колоду от сыгранных карт.
Игрок, получивший карту, не вправе отказываться от игры,
пока не разыгран данный «банк». Он называет сумму денег, на
которую хочет сыграть данный тур, но не превышающую сумму
денег в банке. Затем игрок просит у банкира ещё одну карту, если
в двух картах мало очков, просит ещё. Играющий имеет право
остановиться на любом количестве очков и просить банкира
набирать себе. Игрок, набравший ровно 21 очко или двух тузов,
сразу предъявляет их и забирает из банка свой выигрыш. Банкир
в этом случае себе не набирает и карту не меняет. Если у игрока
перебор, т.е. больше 21 очка, он обязан сразу предъявить карты и
заплатить долг в банк. Игрок, набравший меньше 21 очка, ждет
результата набора банкира.
Банкир набирает очки в открытую. Если набралась сумма из
17 очков - «казна», добирать больше он не вправе, при любом
другом количестве очков - можно продолжить набор. Когда
банкир останавливает набор очков, он предлагает игроку вскрыть
карты для подсчета. У кого больше очков, тот и выиграл. При
одинаковом количестве очков выигрывает банкир. Проигравший
игрок добавляет в банк свой проигрыш, а банкир кладет
отыгранные карты поверх колоды рубашкой вверх, берег себе снизу
карту и продолжает игру со следующим игроком.

Магия азарта. Игральные карты 215
Банк собирается до «стука», суммы денег втрое
превышающей первоначальную ставку банкира. Начиная с объявления
«стука» проходит последний тур игры, после чего банкир
забирает все оставшиеся деньги себе, если они есть.
Если банк сорван раньше, карты для банкования
передаются следующему игроку слева.
Сто
Хотя карты в школе запрещены, но эта игра тренирует
умение считать, запоминать числа, и доступна ученикам 1-2
класса.
Число участников 2, 3, 4, 6 или 9. Колода из 36 карт.
Количество очков: от шестерки до десятки в соответствии с указанным
достоинством, валет - 2 очка, дама - 3, король - 4, туз - 11 очков.
Сдающий перетасовывает карты и раздает всю колоду по одной
карте поочередно всем участникам. Игрок, сидящий слева от
сдатчика, начинает игру с произвольной карты. К стоимости
сыгранной карты второй игрок прибавляет стоимость своей карты,
которую кладет сверху и сообщает всем участникам общую
сумму. Каждый следующий участник поступает аналогично: кладет
сверху любую карту и называет общую сумму. Игрок, перешедший
рубеж 100 очков, проиграл и наказывается таким количеством
штрафных очков, на какое превысил 100. Если кто-то из
участников сумел достичь ровно 100 очков, он выиграл и получает 5
очков премиальных, которые может вычесть из своих штрафных.
Игра продолжается до достижения кем-либо из игроков заранее
договоренного предела штрафных очков.
Мы рассмотрели, скажем так, простенькие карточные игры.
Солидные игры, такие как покер, преферанс, бридж требуют
специального изучения и недюжинных интеллектуальных
способностей. По игре бридж проводятся международные
соревнования, чемпионаты мира и командные первенства. Бридж относят
к спортивным играм, наряду с такими играми как шахматы,
шашки, го, рэндзю, реверси. В карточных играх, чем они сложнее, тем
меньше влияние случайного фактора раздачи и большее значение
приобретает память игрока на карты, стратегия и тактика его
игры. Так что зря на них были такие гонения. Дело не в
инструменте, а в том, как его использовать.

216 Магия азарта. Рулетка
Рулетка
Слово «рулетка» происходит от французского слова,
означающего - «колесо, ролик». Принцип крутящегося колеса со
стрелкой, которое при остановке после вращения занимает
случайное положение, лежит в основе не только азартных игр, но и
процесса жеребьевки. В древности этому служили щит,
сбалансированный на острие меча или колесо от колесницы. Этот
принцип лежит в основе «колеса фортуны», которое представляет
собой вертикально укрепленный вращающийся круг с
нанесенными на него цифрами. Игроки делают ставки на то, какое число
окажется против стрелки после остановки колеса. Рулетка из этого
же семейства игр, только вместо стрелки-указателя маленький
шарик из слоновой кости. Это азартная игра в чистейшем виде.
Игрок только делает ставки и отдается на волю случая, от него
больше ничего не зависит, остается только следить за бегом
шарика, который и решит судьбу игрока.
Стол для игры в рулетку содержит два основных элемента:
рулеточное колесо и игровое поле, на котором делаются ставки.
Колесо в европейской рулетке имеет 36 номеров от 1 до 36
и один особый номер - нуль или «зеро». ( Американская рулетка
имеет 38 радиальных гнезд). Тридцать шесть номеров
расположены по кругу, без какого бы то ни было видимого порядка и
попеременно окрашены в красный и черный цвет. Нуль - не
красный и не черный, он обычно окрашен в зеленый или
каштановый цвет. Рулетка устроена так, чтобы номера выпадали
случайным образом, т.е. чтобы никакие, один или несколько из них,
не имели предпочтения перед другими и не выпадали чаще
остальных. Для этого она изготовлена и установлена с очень
большой точностью. Сама игра в рулетку ведется одним, двумя или
тремя крупье - в зависимости от типа стола (с одним или с двумя
игровыми полями). Единственное преимущество игрового стола с
двумя полями, расположенными по обе стороны от самой
рулетки, состоит в том, что он вмещает вдвое большее число
участников, которые в свою очередь, имеют возможность сделать больше
ставок. Крупье - это представители администрации казино. Один
из крупье раскручивает колесо рулетки, вбрасывает шарик,
сгребает специальной лопаточкой фишки проигравших и подвигает
фишки тем, кому улыбнулась удача. Его коллеги
рассортировывают фишки по достоинству, следят за ходом игры и соблюдением
участниками установленных правил игорного заведения.

Магия азарта. Рулетка
217
Рис. 328
Колесо европейской рулетки
Прелюдией к игре обычно служит обмен денег на фишки-
«кеш ченч». Игровые фишки каждого игрока имеют свой цвет.
Перед началом каждой партии крупье произносит фразу:
«Делайте ваши ставки», приглашая участников к игре.
Играющий в рулетку может делать некоторую ставку «на
номера», «на простой шанс» и «на сложный шанс»,
соответственно располагая свои фишки на внутреннем или на внешнем
секторе игрового поля.
1. На внутреннем секторе.
Рис. 329
а). Ставка на один номер - фишка помещается
внутри клетки с одним из 37 номеров, включая и поле
«зеро». Называется эта комбинация «стрейт an», т.е.
максимум и в случае удачи выплачивается выигрыш 35:1.

218
Магия азарта. Рулетка
Рис. 330
Игровое
1
4
7
10
13
16
19
22
25
28
31
34
2ТО1
поле рулетки
^\
0
2
5
8
11
14
17
20
23
26
29
32
35
;2ТО1|
3
6
9
12
15
«
21
24
27
ЭО
33
ж
2ТО1
Й
I II
см
Q
СО
ш
S
(>
0
ODD
8
1

Магия азарта. Рулетка
219
35:1
11:1
Рис. 331
Другой вариант игрового поля рулетки с указанием
относительных выплат при определенных ставках.

220
Магия азарта. Рулетка
5(]>6
Рис. 332
Рис. 333
Рис. 334
Рис. 335
Рис. 336
б). Ставка на два номера называется «сплит».
Размер выигрыша 17:1.
в). Ставка на три номера - «стрит»,
Размер выигрышу 11:1.
г). Ставка на четыре номера - «каре».
Размер выигрыша 8:1.
д). Ставка на шесть номеров -
«сикслайн». Размер выигрыша 5:1.
При желании можно сделать сразу
несколько ставок на номера или их
комбинации, причем соответствующую
группу номеров можно выбирать любым
способом.
Рис. 337
В первой комбинации «звезда» шесть фишек расположены
так, что при выпадении числа 5, дают возможность суммарного
выигрыша 114:1.
Во второй комбинации «ковер» восемнадцать фишек при
выпадении числа 5 дают выигрыш 156:1

Магия азарта. Рулетка 221
2. На внешнем секторе.
а). Ставка на 12 номеров «дюжину» или «дазен» делается в
боковом секторе на числа от 1 до 12, или от 13 до 24, или от 25 до
36. Размеры выигрыша 2:1.
б). Ставка на 12 номеров одной из вертикальных колонок -
«калам» делается в нижней части избранной колонки. Размеры
выигрыша 2:1.
в). Ставка на 24 номера, фишка ставится на границе двух
дюжин в боковом секторе или в нижней части колонок. Размер
«выигрыша» 0,5:1. Теоретически это возможно сделать, но
понять зачем сразу ставить на проигрыш - трудно.
Все вышеперечисленные ставки были «на номера» и «на
сложный шанс». Внешний сектор включает в себя также ставки
на «простые шансы» - «симпл ченс». Простых шансов всего
шесть:
• красное и черное - «руж» и «нуар»,
• чет и нечет - «пэр» и «импэр» или «even» и «odd»,
• «пасс» («большие» номера - от 19 до 36) и «манк»
(«малые» номера-от 1 до 18),
выигрыш на которые соответствует 1:1.
Нуль не является ни красным, ни черным; ни четным, ни
нечетным; он не входит ни в пасс, ни в манк.
Когда выпадает «зеро», ставки на номера и сложные шансы
проиграны, а ставки на простые шансы блокируются (попадают в
«тюрьму»). При этом можно:
1. либо ждать следующего раза; если в следующий раз
выпадает простой шанс, на который была сделана ставка, то
поставленная сумма без всякого выигрыша возвращается
игроку; если же этого не произошло, то ставка окончательно
теряется;
2. либо сразу после выпавшего нуля потребовать у банкира
возвращения половины сделанной ставки.
Рулетку вращает крупье, один раз в одном направлении,
следующий в другом при этом шарик запускается каждый раз в
направлении противоположном вращению колеса. На своем пути
шарик встречает препятствия, вследствие чего, даже если бы
крупье вращал рулетку все время строго одинаково, путь,
который проделывает шарик, всегда был бы чисто случайным и

222 Магия азарта. Рулетка
обеспечивал бы строгую независимость результата от манеры
вращения. Именно по этим причинам случай и только случай
определяет, какой номер выпадет в очередной раз.
Когда шарик начнет замедлять свое вращение, крупье
объявляет: «Ставки сделаны, спасибо», Все поставленные после этих
слов фишки считаются опоздавшими и снимаются с поля. Теперь
никто не имеет права дотрагиваться до ставок. Если игрок
попытается поставить или убрать свою фишку, то ему будет сделано
вежливое предупреждение. Если и оно не подействует, то его
фишки не будут приняты к оплате.
Наконец с легким стуком шарик скатывается в одно из
гнезд и замирает на месте. Крупье ставит на соответствующий
номер игрового поля специальную форму для обозначения
выигрыша («долли») и объявляет результат: «Одиннадцать, черное,
нечетное, манк». И начинается чистка поля, то есть убираются
все проигравшие фишки. Затем происходит выплата. Вначале она
идет на внешнем секторе, а затем на внутреннем.
Следует отметить еще один важный факт: величина ставок
в рулетке ограничена как снизу, так и сверху. Причем если
нижняя граница чаще всего одинакова для всех видов ставок, то
верхняя граница строго обусловлена видом ставки. Но эти
значения зависят от страны, от конкретного казино, от инфляции
валюты и т. д. Поэтому называть какие-то числа просто бесполезно.
Несколько характерных деталей. У крупье не должно быть
на руке часов, чисто психологический фактор, и либо
отсутствуют, либо зашиты карманы. Кроме крупье за столом присутствует
инспектор, который внимательно следит за ходом ставок и в
кризисной ситуации старается объективно решить все споры.
Математический анализ игры в рулетку показывает, что
выплачиваемые проценты отличаются от истинных, естественно,
в пользу казино. (См. таблицу на стр. 223). Кроме того, сектор
«зеро» - постоянный выигрыш заведения. Все это вместе
позволяет процветать игорным заведениям. Поэтому самая разумная
стратегия - не играть в рулетку вообще. Зная все это, люди
продолжают посещать казино и играть. Почему? Многие
приходят не выигрывать, а тратить деньги, покупать за них острые
ощущения. Те же, кто надеется на выигрыш, опираются на тот
факт, что даже при длительной игре, когда казино выигрывает
наверняка, из сотни игроков двадцать или около того окажутся в
выигрыше и надеются попасть в двадцатку счастливчиков.

Магия азарта. Рулетка
223
Ставка
На один номер
На два номера
На три номера
На четыре номера
На шесть номеров
на 12 номеров
На простые шансы
На 24 номера
выплачиваемый %
35:1
17:1
11:1
8:1
5:1
2:1
1:1
'/2:1
истинный %
36:1
17,5:1
П'/з:1
8,25:1
5'/6:1
2'/12:1
1'/18:1
И/ .1
/13.1
Пристрастие к азартным играм часто проявляется как
болезнь сродни алкоголизму. Причем одни люди ей подвержены,
другие имеют некий иммунитет. Поэтому, рассказывая об
азартных играх, считаю своим долгом присовокупить некоторые советы,
типа обращения Минздрава на пачках сигарет.
• Научитесь отходить от стола, будучи в выигрыше.
Установите себе определенную разумную сумму, которую
хотелось бы выиграть, и при ее достижении прекращайте игру.
• Научитесь проигрывать. Так же как при выигрыше тут
необходимо иметь определенную границу, до которой
можно проигрывать. Достиг ее - прекращай игру, даже
если еще остались деньги.
• Никогда не играй на ставки, которые тебе не по карману.
Возможный проигрыш не должен повредить вашему
бюджету.
• Радуйтесь при выигрыше и не огорчайтесь при
проигрыше. Даже небольшой выигрыш, с которым вы покидаете
казино, даст вам хорошее настроение.
• Разумный игрок, который играет лишь от случая к случаю
и подвергает себя лишь ограниченному риску.
Теория и разум подсказывают нам, что результат какой-то
конкретной партии, не может оказывать влияния ни на
предыдущие, ни на последующие результаты. Шарик рулетки или шарики
лототрона не имеют памяти, для них каждый бросок - это новое
независимое событие. Тем не менее, люди придумывают
множество систем или стратегий игры. Большинство таких систем

224 Магия азарта. Рулетка
основано на учете результатов предыдущих игр, т.е. исходит из
наличия «памяти» у шарика рулетки или лототрона в различных
лотереях. Есть системы, которые опираются на математические
знания. Наиболее простая из математических стратегий - это
стратегия Д'Аламбера. Она состоит в следующем. Возьмем в
качестве условной единицы для начала игры 1 доллар. Ставим 1
доллар на красное.
Если выпадает выигрыш, то данная серия игры окончена и
в следующей раз снова начинают игру ставкой -1 доллар на красное.
Если выпадает проигрыш, то в следующий раз ставят 2
доллара на красное. Если выпадает красное, то выигрыш за две
игры составит 2-1=1 доллар и серия считается законченной. Новая
серия начинается по-прежнему ставкой 1-го доллара на красное.
Если второй раз выпадает проигрыш, то в третий раз на
красное ставят 4 доллара. При каждом проигрыше ставка
удваивается, и так поступают до тех пор, пока не выпадет выигрыш.
Если мы проиграем п раз подряд и выиграем на (п+1)-й раз, то
итог игры составит: -1 -2-22-23-...-2n"l +2П= 1, т.е. выигрыш снова
составит 1 доллар. Эта стратегия оказалась бы беспроигрышной,
если бы ставки не были ограничены, и игрок обладал достаточно
большим капиталом. Но и в случае благоприятного исхода,
каждая серия игры приносит всего только 1 доллар выигрыша.
Верхние ограничения ставок в казино разные. Если
предположить, что это 1000 долларов, то играя по стратегии Д'Аламбера
мы можем довести ставку максимум до 512 долларов, следующее
удвоение превысит ограничение. Другими словами мы можем в
одной серии сыграть до 10 раз. Вероятность не проиграть в серии
из десяти игр, равна
l-(75/i48)10=l- 0,00112= 0,99888.
Но если все-таки с вероятностью 1:895 мы проиграем во
всех десяти играх серии, то проигрыш составит 1023 доллара. С
увеличением числа сыгранных серий вероятность не проиграть
убывает и возрастает преимущество казино.
Заокеанские атрибуты роскошной жизни - казино и рулетка,
символы Лас-Вегаса и Монте-Карло прописались теперь и в
нашей стране, живущей в еще неопределенном политологами
общественном строе. Вроде бы уже не социализм, но и не
капитализм, хотя тенденции развития явно капиталистические и
происходит это независимо от народа. Поэтому нужно быть готовым к
«прелестям» жизни, ранее скрываемым за железным занавесом.

Магия азарта. Лотереи 225
Лотереи
Лотерея (итал. lotteria, восходит к франкскому hlot —
жребий), форма добровольного привлечения средств населения
путём продажи лотерейных билетов, при которой часть
привлечённых средств разыгрывается в виде денежных или вещевых
выигрышей. Первая из известных лотерей, где проходила именно
продажа билетов, а количество и размер денежных призов были
установлены заранее, состоялась в 1466 году в Брюгге (Бельгия).
С тех пор различные виды лотереи получили распространение
практически во всех цивилизованных странах. Причем, не смотря
на явно азартный характер этой игры, различные виды лотереи
проводились даже в СССР и странах социализма на
государственном уровне. Вспомните денежно-вещевые лотереи, лотерею
ДОСААФ, «Спортлото». Объясняется это тем, что лотереи
служили хорошим пополнением государственного бюджета страны.
В 1960 году американцы посчитали, сколько денег потрачено на
призы в одном тираже советской денежно-вещевой лотереи.
Вышло всего 10 000 долларов, по их меркам сумма
незначительная, а для советского человека выигрыш машины считался
заоблачной мечтой.
С точки зрения азартных развлекательных игр любая
лотерея, в конечном счете - это раздача призов победителям. Таким
образом, сама идея лотереи чрезвычайно проста, хотя здесь не
применима ни одна из математических систем. Причина в том,
что любой из билетов или шаров с точки зрения математики имеет
одинаковые шансы на выигрыш по сравнению со всеми
остальными. Но, как и в большинстве азартных игр, основанных на
принципе случайности, этот неоспоримый факт никогда не
останавливал энтузиастов.
Генуэзская лотерея
В прошлые века процветала так называемая генуэзская
лотерея, сохранившаяся в некоторых странах до сих пор. Суть её
заключалась в следующем. Участники лотереи покупали билеты,
на которых стояли числа от 1 до 90. Можно было купить билет с
одним числом или сразу с двумя, тремя, четырьмя и пятью
числами. В день розыгрыша лотереи из мешка, содержащего жетоны
с числами от 1 до 90, вынимали пять жетонов.

226 Магия азарта. Лотереи
Выигрывали те участники лотереи, у которых все числа на
билете были среди тех пяти чисел, что достали из мешка.
Например, если из мешка достали номера 3, 24, 38, 57, 88, то выиграют:
• билеты с одним числом, содержащие по одному из этих
чисел;
• билеты с двумя числами, содержащие любые два из этих
чисел и т. д.
Но не выиграет билет с двумя числами 5, 38 или билет с тремя
числами 3,38, 60, потому что в них не все числа выигрышные.
Распределение выигрышей подчинялось правилам:
• если участник лотереи покупал билет с одним числом, то
он получал при выигрыше в 15 раз больше стоимости
билета;
• если с двумя числами («амбо»), то в 270 раз больше;
• если с тремя числами («терн»), то в 5 500 раз больше;
• если с четырьмя числами («катерн») - в 75 000 раз
больше;
• а если с пятью числами («квин»), то в 1 000 000 раз
больше, чем стоимость билета.
Стремясь обогатиться, люди чаще ставили на «амбо» или
«терн», интуитивно полагая, что это золотая середина. Но лотерея
была рассчитана так, чтобы в выигрыше оставались ее
устроители. Наверное, это главный принцип для всех лотерей, казино и
финансовых пирамид. К сожалению, когда человек охвачен
желанием легко обогатиться, то почему-то ни вековой
общественный, ни личный опыт его не учат и не останавливают.
Применим комбинаторику и теорию вероятностей, чтобы
посчитать соотношение счастливых исходов лотереи к общему
числу её исходов при различных способах игры.
Для подсчета общего числа исходов лотереи применим
формулу комбинаторики для сочетаний по пять произвольных
элементов из 90 заданных элементов.
Определение: к-сочетаниями из п элементов называют
всевозможные к-расстановки, составленные из этих п элементов и
отличающиеся друг от друга составом, но не порядком элементов.
Число ^-сочетаний, которые можно составить из п элементов,
обозначают через Сп и вычисляют по специальной формуле

Магия азарта. Лотереи 227
Ск = - ,гдрп!=п-(п-1)-(п-2)-(п-3)-...-3-2-1.
" (п-к)\к\
90!
С59о= = 43 949 268
85!5!
Рассмотрим случай, когда участник купил билет с одним
номером. Во скольких случаях он выиграет? Для выигрыша
необходимо, чтобы один из вынутых номеров совпал с номером
на билете. Остальные 4 номера могут быть любыми. Но эти 4
номера выбираются из оставшихся 89. Поэтому число
благоприятных комбинаций выражается формулой
С489=(89-88-87-86)/(1-2-3-4)=2 441 626
Отсюда следует, что отношение числа благоприятных исходов к
общему числу комбинаций С489/ С59о=1/18
Это означает, что примерно один из 18 игроков, купивших
билеты с одним числом может рассчитывать на выигрыш и
получить в 15 раз больше стоимости одного билета. В то время как
стоимость ещё трех проданных и не выигравших билетов осядет
в карманах устроителей лотереи. Мы сказали слово «примерно»,
потому что вероятность есть вероятность и ожидаемые значения
тем ближе к формулами, чем больше количество игроков.
Теперь подсчитаем вероятность выигрыша при игре на
«амбо», т.е. на два номера. Нужно чтобы два загаданных номера
вошли в число вынутых из мешка, а остальные три могут быть
любыми из оставшихся 88 чисел. Следовательно, по аналогии,
число благоприятных исходов вычисляется по формуле
С388=(88-87-86)/1-2-3
Отношение числа благоприятных исходов к общему их числу
С388/ С590=(4'5)/(90-89)=2/801
Это значит, что примерно двое из 801 игроков, купивших
билеты с двумя числами, могут рассчитывать на выигрыш,
который составит на двоих 540 стоимостей одного билета. Простое
вычитание показывает, что стоимость 261 билета остается у
организаторов.
Дальнейшие рассуждения показывают ещё большую
невыгодность для игрока покупать билеты с большим количеством
чисел. В игре на «терн» выигрывает 1 из 11 748, в игре на
«катерн» - 1 из 511 038 и в игре на «квин» - 1 из 43 949 268. Платят
же выигравшим лишь в 5 500, 75 000 и 1 000 000 раз больше. Но
ничего другого и не следовало ожидать, лотерея
перераспределяет деньги проигравших между организаторами и выигравшими.

228 Магия азарта. Лотереи
Денежно-вещевая лотерея, проводившаяся в нашей стране,
трудно поддается вероятностному анализу из-за сложности самой
системы. Билеты часто распределялись по организациям, стоили
30 копеек и покупались не из азартных побуждений, а потому что
так нужно было стране. Моему сокурснику, например, повезло:
купив пару билетов, навязанных в день зарплаты, он выиграл
«Жигули». Поэтому факт существования таких выигрышей могу
засвидетельствовать, хотя сам никогда везунчиком не был.
Первая лотерея в нашей стране, связанная с азартом - это
«спортлото». Игрок сам принимал участие в процессе, зачеркивал
числа в своем билете, в определенный срок отсылал отрывную
часть билета в отделения организации этой лотереи. Наряду с
синими почтовыми ящиками по всей стране висели желтые ящики
«спортлото». Здесь уже присутствовали все элементы азартной
игры, многие люди придумывали свои системы вычеркивания
чисел, потом отсылали купон, ждали результатов - были
определенное время в состоянии надежды на выигрыш. К тому же
существовало две системы игры «6 из 49» и «5 из 36». Самый
большой выигрыш получался при угадывании всех чисел, но
были и меньшие выигрыши при угадывании, например, 3-х чисел.
Используя выше показанную формулу комбинаторики для
числа сочетаний, можно посчитать количество всех вариантов
для обеих систем спортлото:
С649= 13 983 816 С536=376 992.
Получается, что система «5 из 36» имеет в 37 раз большую
вероятность выигрыша. Когда я получил эту цифру, то сам себе
не поверил и еще раз пересчитывал, уж слишком большая разница.
Во времена ажиотажного пика спортлото я работал на заводе
и воочию видел распространение этой игры в рабочей среде.
Создаваемые системы игры грешили обычной ошибкой -
предположением о зависимости очередного тиража от предыдущих.
Некоторые энтузиасты просчитывали частоту выпадения каждого
числа за большие промежутки времени, примерно за год, и,
увидев к концу года, что какие-то числа выпадали реже, зачеркивали
их. Были и консерваторы, которые с упорством дятла били в один
и тот же набор чисел из тиража в тираж. В тоже время, мало кто
задавался подсчетами соотношения проигранных и выигранных
денег за определенный период.
Существующие сейчас лотереи «Русское лото», «Золотой
ключ» и подобные им, имеют в своей основе другой принцип.

Магия азарта. Лотереи 229
Участие человека в игре сводится только к покупке билета
и просмотру самого тиража, транслируемого в прямом эфире.
Никакой системы придумывать не нужно, да нет и самой
игры, есть только желание выиграть.
Интересен сам принцип игры, Билет лотереи включает в
себя две карточки по образцу старинной игры наших бабушек -
лото. Карточка представляет собой прямоугольную таблицу 3x9, в
каждой строчке которой проставлены 5 чисел, таким образом,
всего в карточке 15 чисел. Числа в карточке проставлены не
произвольным образом. Рассмотрим одну строчку таблицы - в ней 9
клеточек. В первой клетке может стоять число от 1 до 9, во
второй от 10"до 19, в третьей от 20 до 29, ..., в последней от 80 до 90.
Но стоять будут числа только в каких-то пяти клетках.
Существует С59=126 вариантов выбрать пять клеток из девяти для
заполнения. Для первой клетки имеется 9 вариантов выбора конкретного
числа, для последней - 11, а в остальных по 10. Получается, что
различных вариантов заполнить только одну строчку карточки
лотереи С59-Ю5= 12 600 000. Количество различных сочетаний из
этих строчек по три, чтобы получить карточку 3x9 вообще
умопомрачительное число. Но главная сложность анализа этой игры
в том, что карточка заполнена по новому, в сравнении со
спортлото, принципу, а лототрон продолжает выбрасывать шарики по
старому принципу, т.е. любой от 1 до 90. Для тех же пяти чисел у
лототрона С59о= 43 949 268 вариантов. Это означает, что набора
чисел Л, 2, 3, 4, 5 ни в одной строчке билетов лотереи в принципе
быть не может, а лототрон или мешок с бочонками лото
способны выдать подобную комбинацию. Поэтому вероятность выиграть
джек-пот в «Золотом ключе», закрыв строчку с первых пяти чисел
равна 1: 43 949 268. В «Русском лото» для получения джек-пота
нужно с первых пятнадцати шаров закрыть одну карточку,
вероятность такого события 1: 2,7 квадриллиона. Можете проверить
по формуле С159о - это число с пятнадцатью нулями в конце. На
самом деле все не так грустно, потому что из 90 шаров или
бочонков в игре участвуют в среднем 85, а иногда и больше,
поэтому малая вероятность выиграть джек-пот покрывается большим
количеством других выигрышей. Кроме того, наличие большого
количества мелких выигрышей поддерживает постоянный
интерес к лотереям, а чисто психологически, получив небольшую
сумму в качестве выигрыша, человек чаще всего тратит ее на
покупку новых билетов той же лотереи.

230
Магия азарта. Числовые игры
Теперь рассмотрим описание нескольких, как
малоизвестных, так и широко известных игр, связанных с расстановкой
чисел на различных фигурных полях.
Числовые игры
Игра '
1
1
8*
б'
-7
3*1
>
Л
1
Рис. 338
Эта игра для двоих. В
элементарном исполнении, поле для
игры можно обвести на тетрадном
листе в клетку. Игра начинается на
любом квадратике, в который
первый игрок ставит число 1. Далее,
противники по очереди ставят
последовательные числа
натурального ряда, переходя на соседний по
горизонтали, вертикали или
диагонали свободный квадрат.
Получается, что первый игрок ставит нечетные числа, а
второй - четные. Можно делать это ручками разного цвета.
Проигрывает тот, кто не сможет сделать очередной ход. Пример
партии, в которой первый игрок выигрывает на 11 ходу, изображен на
рисунке.
Для этой игры можно изготовить специальное поле такого
размера, чтобы в качестве фишек использовать бочонки от игры
лото. При достижении определенного навыка игры, когда это
поле в 41 клетку станет тесновато, его можно увеличить до 61 или
даже 85 клеток. Бочонков лото как раз хватит.
Французская числовая игра
Играют вдвоем. Реквизит игры: квадратное поле 5x5 и
специальные полоски с цифрами от 1 до 5, по пять полосок у
каждого игрока. Для одного игрока - черные числа на белом фоне, а
для второго негативное изображение - белые цифры на черном
фоне. Партия обязательно состоит из четного количества игр, так
как игрок, делающий второй ход, имеет преимущество в 15 очков.

Магия азарта. Числовые игры
231
I—I
-
л-
3
-
1
2
3
4
5
4SBSBSRL
ПППП1
Рис. 339
Начинающий выкладывает на доску по своему выбору одну
полоску в своём направлении (по цвету краёв поля). Соперник
выкладывает свои полоски в перпендикулярном направлении и
также не может менять его в ходе игры.
Каждый игрок стремится закрыть самые большие цифры на
полосках противника.
В конце каждой игры, когда выложены все полоски, под-
считывается и записывается сумма незакрытых цифр у каждого
игрока. Выигрывает тот, у кого в конце партии, т.е. после четного
количества игр, сумма цифр, оставшихся незакрытыми, будет
больше.
Итальянская числовая игра
Для игры нарежьте из плотной бумаги 52 небольшие
карточки и на каждой из них напишите по одному числу: на четырех
карточках - 1, на четырех - 2 и т.д. Последним написанным
числом будет 13. Количество играющих не ограничено. Каждый
игрок берет себе ручку, листок бумаги в клетку и очерчивает
квадрат 5x5. Ведущий берет стопку приготовленных карточек с
числами, перемешивает их, затем открывает первую карточку и
объявляет написанное на ней число. Каждый из играющих
записывает это число в одну из клеток своего квадрата. После того
как число вписано исправлять ничего уже нельзя. Затем ведущий
открывает следующую карточку и объявляет число, а игроки
вписывают его в любую из свободных клеток и т. д. Игра
прекращается, когда будут заполнены все 25 клеток. Дальше
начинается самое интересное - подсчет очков по специальной системе.

232
Магия азарта. Числовые игры
Цель игры не просто бездумно ставить числа куда придется,
а разместить их так, чтобы набралось наибольшее количество оч-
ков в соответствии со следующей таблицей:
Комбинация чисел
два одинаковых числа
две пары одинаковых чисел
три одинаковых числа
три одинаковых числа и два других
одинаковых числа
четыре числа
пять последовательных чисел, но не
обязательно по порядку
расположенные
три раза по 1 и два раза по 13
числа 1, 10, 11, 12, 13, но не
обязательно по порядку расположенные
четыре единицы
строка
или
столбец
10
20
40
80
160
50
100
150
200
диагональ
20
30
50
90
170
60
ПО
160
210
Проницательный читатель, наверное, догадался, что
первоначально эта игра велась колодой из 52 игральных карт, отсюда и
повторение на карточках каждого числа по четыре раза и
числовые значения: туз - 1, далее от 2 до 10 в соответствии с картой,
валет - 11, дама - 12, король - 13. Поэтому самая большая
стоимость - четыре туза в ряд. Есть этой игре что-то от покера. Просто в
таком варианте игра была адаптирована для нежных детских душ
и могла проводиться даже в школе, как обучающая счету и
логическому мышлению.
На рисунке
показано примерное
заполнение клеток и
произведен для него подсчет
очков. Общая сумма равна
570.
Рис. 340
20
1
1
7
1
7
80
2
10
2
13
2
40
5
12
13
5
7
10
3
3
3
11
3
160
4
12
4
13
12
20
50
10
-
10
10
160

Магия азарта. Числовые игры
233
Головоломка «15»
Перед вами знаменитая головоломка - игра «15». В плоской
квадратной коробке располагаются 15 фишек с числами от 1 до
15. Одно свободное место позволяет передвигать эти фишки, не
вынимая из коробки.
Рис. 341
У этой головоломки есть автор - американский
изобретатель и популяризатор науки Сэмюэль Лойд. Время появления его
игры и известного всем кубика Рубика разделяют примерно 100
лет. Массовое увлечение венгерским кубиком еще у всех в
памяти, а популярность игры «15» в свое время была не меньшей. Это
первая в истории головоломка, имевшая всемирный успех,
которому в немалой степени способствовало напечатанное в газетах
объявлении о призе в тысячу долларов за решение следующей
задачи.
В исходном состоянии фишки расположены по порядку за
исключением двух последних 14 и 15, которые переставлены
местами. Передвигая фишки, но, не вынимая их из коробки,
нужно найти способ поменять местами номера 15 и 14 так, чтобы все
фишки стояли по порядку.
Помещая это объявление, Лойд знал, что ничем не рискует,
так как задача, предложенная им, неразрешима. Но когда он
пошел в патентное бюро оформить изобретение, то чиновник,
узнав об отсутствии решения опубликованной задачи, отказывался
выдавать патент на конструкцию игры, не имеющей решения.
Изобретатель не стал спорить и тут же придумал для своей
головоломки несколько «корректных» задач, которые можно решить
за определенное число ходов.

234
Магия азарта. Задачи 1-3
Самыми известными стали три задачи Лойда.
5-1
Из того же исходного положения,
расставить фишки по порядку так, чтобы
свободное поле было в верхнем левом
углу. Лучшее из известных решений - 44
хода.
Рис. 342
5-2
Из стандартного исходного
положения с переставленными фишками 15 и
14, повернуть коробку на 90° и в таком
положении расставить все фишки по
порядку в соответствии с рисунком. Лучшее
решение - 39 ходов.
Рис. 343
5-3
Передвигая фишки из исходного
положения, показанного на рисунке к
первой задаче, составить из них
магический квадрат, у которого сумма чисел,
стоящих в любом столбце, в любой
строке и на двух диагоналях, равнялась
бы 30? Для облегчения задачи мы его
вам показываем, остается только
передвигать фишки. Лучшее решение - 50
ходов.
Рис. 344
Придумано и множество других задач с этой игрушкой.

Магия азарта. Задачи 4-5
235
Интерес к ней не пропадает совсем еще и потому, что
остается нерешенной одна проблема: до сих пор не разработан метод,
позволяющий найти самый короткий путь перехода от одной
перестановки к другой. Поэтому для каждой задачи можно
указать только кратчайшее из найденных решений, но нет гарантии,
что не существует еще более короткое.
Находились люди, которые все-таки «решали» головоломку
Лойда, причем на глазах у зрителей, но они, конечно,
жульничали. Перед игрой углы фишек немного закруглялись так, чтобы
при перемещении номера 6 и 9 можно было незаметно
поворачивать. В процессе перестановки меняют местами фишки 14 и 15, 6
и 9. Но фишки 6 и 9 при движении незаметно поворачивают на 180°.
Таким способом «пари» у Лойда можно «выиграть» за 27 ходов.
От знаменитой числовой головоломки Сэма Лойда
совершаем плавный переход к серии задач, касающихся азартных игр,
рассмотренных в этой главе.
5-4 Перемещение чисел
Возможно, эта головоломка появилась раньше игры «15»,
принцип у них одинаковый - передвижение фишек с числами,
используя свободное пространство. Задача тоже одинаковая: из
нарушенной последовательности вернуться к натуральному ряду,
начиная с единицы. Имеется целых четыре свободных клетки,
куда можно ставить фишки в процессе передвижения, нельзя
только вынимать фишки из плоскости.
I®
'3s
s6)
Рис. 345
5-5
В головоломке «15» из правильного расположения,
передвигая фишки, составьте магический квадрат, у которого сумма
чисел, стоящих в любом столбце, любой строке и на любой из
двух диагоналей, равнялась бы 30. Желательно сделать это за
наименьшее число передвижений фишек.

236
Магия азарта. Задачи 6-11
5-6 Перемещение чисел-2
Используя четыре свободных клетки, восстановите
расположение фишек по возрастанию от 1 до 13. Фишки можно
передвигать на свободные места, но нельзя выходить из плоскости и
за рамки игрового поля.
ЙШ8)
[в)
8
9)
Рис. 346
5-7
Какова вероятность, что при броске стандартного игрального
кубика выпавшее число очков простое?
5-8
Сколько в среднем раз нужно бросить игральную кость,
чтобы появилась шестерка?
5-9
Три кубика сложены в столбик.
Найдите сумму чисел на всех
невидимых гранях кубиков, помня о том,
что сумма очков на
противоположных гранях равна семи.
Рис. 347
5-10
Бросают п стандартных игральных костей. Сколько может
получиться различных результатов, если результаты,
отличающиеся лишь порядком очков, считаются одинаковыми?
5-11
Грани каждой из двух нестандартных игральных костей
помечены числами О, I, 3, 7, 15, 31. Сколько различных сумм
можно получить при метании этих костей?

Магия азарта. Задачи 12-18 237
5-12
Игральную кость, на гранях которой изображены цифры О,
I, 2, 3, 4, 5, бросают до тех пор, пока общая сумма выпавших очков
не превзойдет 12. Чему, скорее всего, будет равна эта сумма?
5-13
Грани каждой из трех нестандартных игральных костей
помечены числами 1,4, 13, 40, 121, 364. Сколько различных сумм
может получиться при их метании?
5-14
Приготовьте два кубика с нестандартными наборами чисел
на гранях: у одного - 0, 1, 2, 4, 5, 6, у другого - 1, 1, 1, 4, 4, 4.
Первый кубик трижды бросаете вы, второй - трижды ваш друг.
Кто из вас должен в среднем чаще получать за три
подбрасывания сумму очков, большую чем 9?
5-15
Разрешается трижды бросить игральный кубик (1, 2, 3, 4, 5, 6)
или кубик (1, 1, 1, 6, 6, 6). Каким кубиком лучше играть, чтобы с
большей вероятностью набрать в сумме не менее 15 очков?
5-16
Бросают шесть стандартных игральных костей. Во скольких
случаях они дадут один вид очков? Два вида? Три вида? Четыре
вида? Пять видов? Шесть видов? Все кости считаются
различными друг от друга, например окрашенными в шесть разных цветов
5-17
Нестандартный набор домино состоит из костей от (0-0) до
(п-п). Показать, что число домино с суммой очков на половинках
п-г равно числу домино с суммой очков п+г. Найдите это число и
общее количество всех костей домино в таком наборе.
5-18
При игре в домино 4 игрока делят поровну 28 костей.
Сколькими различными способами они могут это сделать?

•
•II •
•
•
238 Магия азарта. Задачи 19-23
5-19
Рис. 348
Изображенные здесь две костяшки домино расположены
таким образом, что, объединяя между собой группы очков,
непосредственно прилегающие друг к другу, можно получить все
числа от I до 9 включительно. (Числа I, 2, 3 - есть
непосредственно, 4=1+3, 5=3+2, 6=3+3, 7=1+3+3, 8=3+3+2, 9=1+3+3+2).
Попытайтесь расположить 4 костяшки домино так, чтобы
аналогичным образом получить любое число от 1 до 23
включительно. Костяшки не обязаны располагаться одинаковым числом
очков друг к другу, как в игре.
5W2O
Сколькими способами из 28 костей домино можно выбрать
две кости так, чтобы их можно было приложить друг к другу
(т.е. чтобы какое-то число очков встречалось на обеих костях).
5-21
Из хорошо перетасованной колоды на стол последовательно
выкладываются карты одна рядом с другой в ряд лицевой
стороной наверх. После чего аналогичным образом выкладывается
вторая колода, так что каждая карта первой колоды лежит под
картой из второй колоды, каково среднее число совпадений
нижней и верхней карты?
5-22
Сколькими способами можно выбрать из полной колоды
карт по одной карте каждой масти? То же самое при условии, что
среди вынутых карт нет ни одной пары одинаковых, то есть двух
королей, двух дам и т.д.
5-23
Сколькими способами можно выбрать из полной колоды
карт, содержащей 52 карты, по одной карте каждой масти так,
чтобы карты красных мастей и карты черных мастей
образовывали пары (например, дамы пик и треф, короли червей и бубен).

Магия азарта. Задачи 24-30 239
5-24
Из колоды, содержащей 52 карты, вынули 10 карт. Во
скольких случаях среди этих карт окажется хотя бы один туз? Во
скольких случаях ровно один туз? Во скольких случаях не менее
двух тузов? Ровно два туза?
5-25
Из хорошо перетасованной колоды в 52 карты, содержащей
четыре туза, извлекают сверху карты до появления первого туза.
На каком месте в среднем появляется первый туз?
5-26
Сколькими способами можно разделить колоду из 36 карт
пополам так, чтобы в каждой половинке было по два туза?
5-27
Сколькими способами можно выбрать из полной колоды,
содержащей 52 карты, 6 карт так, чтобы среди них были все четыре масти?
5-28
Сколькими способами можно вынуть 4 карты из полной
колоды так, чтобы были 3 масти? Так, чтобы были 2 масти?
5-29
Три игральные карты из одной колоды выложены в ряд на
стол вверх рубашкой. Справа от короля находится дама или
двойка. Слева от дамы лежит дама или двойка. Слева от карты
червовой масти лежит карта пиковой масти или двойка. Справа
от карты пиковой масти лежит карта пиковой масти или двойка.
Назовите карты, выложенные на стол.
5-30
Сколькими способами можно раздать колоду в 52 карты 13
игрокам по 4 карты каждому игроку? Та же задача с условием,
что каждый имеет по одной карте каждой масти. Та же задача при
условии, что один игрок имеет карты всех четырех мастей, а все
остальные - карты одной и той же масти.

240 Магия азарта. Задачи 31-36
5-31
Из колоды в 52 карты Герман извлекает наугад три карты.
Найти вероятность того, что это будут тройка, семерка и туз?
5-32
Перетасовали четыре карты - две красной масти и две
черной - и разложили их в ряд картинкой вниз. Выберем наугад две
карты. Какова вероятность того, что обе карты окажутся одного цвета?
5-33
Карты в колоде пронумерованы последовательно числами
от I до 7, а затем тщательно перетасованы. Из колоды случайным
образом вынимаются последовательно 5 карт. Какова вероятность
того, что номера этих карт будут идти в возрастающем порядке?
5-34
Человеку, находящемуся в Лас-Вегасе, нужны 40 долларов,
в то время как у него имеется только 20 долларов. Он решает
играть в рулетку согласно одной из двух стратегий: либо поставить
все свои 20 долларов на «чет» и закончить игру сразу же, если он
выиграет или проиграет, либо ставить на «чет» по одному
доллару до тех пор, пока он не выиграет или не проиграет 20 долларов.
Какая из этих двух стратегий лучше?
5-35
Браун всегда ставит I доллар на номер 13 в рулетке. Чтобы
отучить Брауна от игры в рулетку его друг спорит с ним на 20
долларов, утверждая, что Браун останется в проигрыше после 36
игр. Имеет ли смысл Брауну принять такое пари?
5-36
В денежной лотерее выпущено 100 000 билетов.
Разыгрываются 2 выигрыша по 5000 рублей, 8 по 1000 рублей, 170 по 100
рублей, 350 по 50 рублей и 750 выигрышей по 10 рублей.
Требуется составить таблицу распределения вероятности выигрыша
для владельца одного лотерейного билета и вычислить
«справедливую» цену билета.

4
1
1
3
3
1
3
1
1
3
з| I
зЫ
1М 1
э|
1
1
3
5 ~~И
11 Щ
1
1
1
3
5
9
3
7
1
1
-III-
■ t
I 1 1
1
2
3
■■■■■
т г
p г
1
ц
х
"Г

Величие народа не измеряется его
численностью, как величие человека не измеряется его
ростом; единственной мерой служит его умственное
развитие и его нравственный уровень.
В. Гюго (1802-1885) - французский писатель
В человеке заложены безграничные источники
творчества, иначе бы он не стал человеком. Нужно
их освободить и вскрыть, ставя человека в
подходящие общественные и материальные условия.
А. Н. Толстой (1883-1945) -русский писатель
Умственные занятия оказывают на человека
такое благотворное влияние, какое солнце оказывает
на природу; они рассеивают мрачное настроение,
постепенно облегчают, согревают, поднимают дух.
В. Гумбольдт (1767-1835) - немецкий ученый
Главное не в том, чтобы накопить как можно
больше знаний, - главное в том, чтобы это знание,
великое или малое, принадлежало тебе, явилось бы
детищем твоих собственных свободных усилий.
Р. Роллан (1866-1944) - французский писатель

Числовые фантазии. Задачи 1-2
243
Последняя глава книги практически не содержит
теоретических сведений, а целиком отводится задачам. Знаменитое
высказывание Козьмы Пруткова: «Нельзя объять необъятное» с
полным основанием можно отнести к миру головоломок. Начнем
мы с задач, содержащих фразу - расставьте числа ... так,
чтобы..., постепенно видоизменяя отдельные элементы
формулировки. На ваших глазах пройдет превращение головоломок,
похожих на кросс-суммы в примеры японского рисования по
клеточкам, где уже по заранее расставленным числам рисуется
фигура. Но и это, надо думать, не всё, так как фантазия
человеческого сознания безгранична.
Этот раздел книги наиболее собирательный, здесь есть
задания из старинных учебников, и рядом с ними те, которые вы
встретите сегодня в газетах и журналах. Стремления составителя
были в упорядочении этого множества, сглаживании переходов в
логической цепочке и в желании донести до читателя свое
восхищение коллективным человеческим разумом.
6-1
Расставьте числа от 1 до 9
так, чтобы сумма чисел в
вершинах малого треугольника
равнялась квадрату одного из
этих чисел, сумма чисел по
окружности- кубу того же
числа, а сумма чисел по контуру
большого треугольника - сумме
квадрата и куба этого числа.
Рис. 349
6-2
I I I 1 1 1 1 I 1 I 1
Рис. 350
Расставьте все десять цифр 0, 1,2, 3,4, 5, 6, 7, 8, 9 в таком
порядке, чтобы получившееся число делилось на все числа от 2 до 18.

244
Числовые фантазии. Задачи 3-7
1 I I I I I I 1 ТТЛ
6-3
Рис. 351
Составьте из всех десяти цифр от 0 до 9 такое десятизначное
число, что число из двух его первых цифр делится на 2, из трех
первых цифр делится на 3 и т. д. до того, что само число делится на 10.
игл
6-4
Рис. 352
Заполните пустые клетки так, чтобы сумма чисел, стоящих
в любых трех подряд идущих клетках, равнялась 15.
1 И
1 1»
1
6-5
Рис. 353
Расставьте некоторые числа в пустые клетки так, чтобы
сумма любых трех соседних чисел была одна и та же, а сумма
всех чисел равнялась 200.
Рис. 354
Рис. 355
6-6
Расставьте цифры от 1 до 8 так,
чтобы в горизонтальных рядах
получились числа, являющиеся квадратами, а
сумма чисел, расположенных в
центрально-симметричных кружках была
одна и та же.
6-7
На концах пяти диаметров
расположите числа от 1 до 10 так, чтобы сумма
любых двух соседних чисел равнялась
сумме двух противоположных им чисел.

Числовые фантазии. Задачи 8-11
245
6-8
Можно ли все 10 цифр от 0 до 9
расставить по окружности так, чтобы
сумма любых трех из них, идущих
подряд, не превышала: а) 13, б) 14,
в) 15?
Рис. 356
6-9
Числа.1,2, 3, 4, 5, 6, 10, 12, 15,20,
30 расставьте так, чтобы
произведение любых трех чисел, лежащих в
трех кружках на одной прямой, было
равно 60.
6-10
Расставьте числа от I до 8 в
клетках прямоугольника так, чтобы
любые два последовательных числа
не были соседями по горизонтали,
вертикали или диагонали.
Рис. 357
1234 678
•!
Рис. 358
6-11
Расставьте числа от 1 до 7 так,
чтобы в любом из двух соседних
(соединенных прямой) кружках
находились числа, не являющиеся
«соседями» в натуральном ряду чисел.
Рис. 359

246
Числовые фантазии. Задачи 12-16
-{
Рис. 360
6-12
Расставьте числа от I до 8
так, чтобы числа в кружочках,
соединенных отрезками,
отличались не меньше чем на 2.
6-13
6-14
6-15
Рис. 361
Рис. 362
Рис. 363
Расставьте числа от 1 до 13 (некоторые из них уже стоят на
своих местах) в клетки фигуры так, чтобы в клетках, имеющих
общую сторону, числа отличались, по крайней мере, на 3.
6-16
В кружках фигуры
расставлены числа от 1 до 18.
Докажите, что найдется отрезок,
на концах которого стоят числа
с разностью, большей трех.
Рис. 364

Числовые фантазии. Задачи 17-20
247
6-17
В 25 клеточек нужно вписать
как можно больше различных чисел
от 1 до 25, соблюдая при этом одно
условие: разница между числами в
квадратах, соединенных линиями,
должна быть не менее 10. На
чемпионате мира по головоломкам
удалось вписать все числа, кроме тройки.
А как получится у вас?
I
6-18
Расставьте числа от 1 до 10 так,
чтобы сумма чисел в любых двух
соседних кружках не делилась ни на
3, ни на 5, ни на 7.
6-19
Можно ли в кружках звезды
расставить десять натуральных
различных чисел так, чтобы суммы
четырех чисел вдоль каждой из пяти
прямых были нечетными?
6-20
Заполните прямоугольник
цифрами так, чтобы в каждом
горизонтальном ряду стояло
четырехзначное число, делящееся на 92, а в
каждом вертикальном ряду -
трехзначное число, также делящееся на 92.
Рис. 365
Рис. 366
Рис. 367
Рис. 368

248
Числовые фантазии. Задачи 21-25
Рис. 369
6-21
Расставьте цифры от 1 до 9 так, чтобы
три, образовавшихся в горизонтальных
рядах, числа были точными квадратами.
Рис. 370
6-22
Заполните квадрат цифрами так, чтобы
по краям и диагоналям в любом направлении
читались квадраты натуральных чисел
(цифры могут повторяться).
Рис. 371
6-23
Расставьте цифры от 1 до 9 так, чтобы
в 3-х горизонтальных рядах и каждом из 5-
ти вертикальных столбцов получались
различные квадраты натуральных чисел.
Некоторые цифры могут повторяться.
.;
Рис. 372
6-24
Расставьте числа от 1 до 9 так, чтобы
пять чисел, запись которых получается по
горизонтальным прямым, были бы
квадратами целых чисел.

.пгп
II I II
6-25
Расставьте цифры от 0 до 9 так, чтобы
по горизонталям получилось четыре
квадрата натуральных чисел. Сколько решений
имеет эта задача?
Рис. 373

Числовые фантазии. Задачи 26-30
249
6-26
Запишите в клетках фигуры, изображенной на рисунке,
цифры от 1 до 9 с повторением так, чтобы во всех вертикальных
и горизонтальных полосках из трех клеток стояли различные
трехзначные числа, яв- ' ' ' ' ' ' """"
ляющиеся полными
квадратами.
Рис. 374
6-27
Рис. 375
Расставьте цифры 1, 3, 5, 7 и 9 так, чтобы произведение
двузначного числа, образованного двумя цифрами, на число,
образованное двумя другими цифрами, минус последняя цифра
равнялось числу, составленному из повторений одной и той же
цифры.
6-28
ГП»П1 МММ
Рис. 376
Два сомножителя составлены из всех цифр от 1 до 9 так,
что их произведение - целое число. Какие два числа
перемножаются?
6-29
Рис. 377
Впишите в клетки цифры от 1 до 9, каждую по одному разу,
так, чтобы произведение оказалось наибольшим.
2 18
Рис. 378
Из девяти цифр от 1 до 9
составьте квадрат таким образом, чтобы
трехзначные числа, стоящие в первой
и второй строках, в сумме давали
третью строку. Один из примеров
решения показан на рисунке, но он не
единственный.
2
4
6
1
3
5
8
9
7

250 Числовые фантазии. Равенства. Задачи 31-34
4
5
9
3
О
1
6
3
2
6-31
Поменяйте местами две цифры
так, чтобы в каждой строке
образовались два новых пятизначных числа,
причем одно - в два раза больше
второго.
Рис. 379
Математические равенства
Большая группа задач содержит кроме клеток, в которые
нужно вписать числа, ещё и знаки математических действий и в
этом случае основное требование к расстановке чисел -
выполнение полученного равенства. Арифметические действия в таких
примерах выполняются слева - направо и сверху - вниз в порядке
ях следования, без принятого приоритета умножения и деления
над сложением и вычитанием.
ММ ИШ>1
6-32
Рис. 380
Расставьте числа от 1 до 9 так, чтобы выполнялось
равенство в натуральных числах.
1=П-П=П+П=
1—1 6-33
Рис.381
Расставьте цифры от 1 до 9 так, чтобы выполнялись все равенства.
6-34
ММ 1-ГГП=ГГП
В каждом из четырех ра-
| | | | +1 | | | = | | | | ""| венств расставьте все цифры от
0 до 9 без повторений так, что-
I I I I I . I I = I I I I I I бы равенства были верными и
все 12 чисел, входящих в них
были бы разными.
Mill 1--1_LUJ=
Рис. 382

Числовые фантазии. Равенства. Задачи 35-38 251
6-35
Расставьте цифры от 0 до 9 так,
чтобы все равенства были верными.
п*п=п
п»п=гп
Рис. 383
6-36
Расставьте числа от 1 до 10
так, чтобы выполнялись указанные
действия и равенства.
:□ + □=□
□
■□♦□■□
Рис. 384
6-37
Расставьте цифры от 1 до 9 так,
чтобы результат арифметических
действий в каждой строке, в каждом
столбце (сверху вниз) и по обеим
диагоналям (слева направо) равнялся 10.
+ + + - х
Рис. 385
6-38
Вставьте недостающие числа
так, чтобы выполнялись все равенства.
-ПВ
+ X
и и
Рис. 386

252 Числовые фантазии. Равенства. Задачи 39-41
П-Ш=П+
=П
Рис. 387
6-39
В пустые клетки
проставьте числа от 1 до 9 так,
чтобы последовательно слева
направо и сверху вниз
выполнялись все действия и
равенства.
. ■ ■ + .
+ +
Рис. 388
6-40
Вставьте
недостающие числа так, чтобы
последовательно слева
направо и сверху вниз
выполнялись все действия и
равенства.
|12|:
|12|х
|12|х
N-
|12|:
+
-
X
■
■
=
12
X
-
■
■
■
■
-
-
■
■
+
X
12
-
■
■
-
+
x
X
+
■
■
-
12
+
+
+
X
+
=
X
-
■
■
+
12
s
12
■M
= |12|
6-41
Впишите в пустые
клетки цифры от 0 до 9 с
повторением некоторых
цифр так, чтобы
выполнялись все равенства.
Рис. 389

Числовые фантазии. Равенства. Задачи 42-44 253
(£42
+
-
=
13
X
+
+
+
13
ч l+
+l Is
-I I-
-
+
13
X
-
■
■
-
+
13
-
X
+
X
-
=
13
■
■
+
X
X
+
13
-
-
т
т
+
=
13
«I |+| I»
-I I+I |:
-I hi I +
+
+
=
13
o|ia|
■м
=фз|
Рис. 390
Пустые клетки нужно заполнить числами от 1 до 11 так,
чтобы в каждой строке и каждом столбце все числа были разными, а
все 11 равенств - верными.
До сих пор мы расставляли в свободные клетки или кружки
различные числа. Сначала вычисляли только суммы этих чисел,
постепенно ввели остальные математические действия вплоть до
возведения в степень. Теперь делаем следующий шаг: числа уже
стоят, а требуется расставить знаки математических действий так,
чтобы равенства были верны. Маленькое изменение условия и
получается новая серия задач. Вот так движется мысль, всегда
вырываясь за ограничивающие рамки и барьеры.
6-43
Из = И:
Рис. 391
Расставьте между клетками с числами знаки математических
действий, в том числе и скобки, с таким расчетом, чтобы
получилось верное равенство.
6-44
Расставьте в пустые клетки
математические знаки +, - , х , : , = так, чтобы по
трем строчкам и по трем столбцам
получились верные арифметические равенства.
Действия выполняются по порядку их
следования.
Рис.392
I*
I9
8
1
3
4
3
8
7
4
3
9
3
2
2
8
6
8
4
3
■I
з|
2I

254 Числовые фантазии. Равенства. Задачи 45-46
6"45 т*т*т*т*т*ы=га
9 * 8
3*5 * 12 =|1;
8 46
7 4945=11
Рис. 393
В этих арифметических примерах вместо звездочек (*) нужно
проставить знаки + или - так, чтобы получилось четыре верных
равенства.
6-46
Вставьте в пустые квадраты знаки четырёх различных
математических операций так, чтобы каждый раз в результате получалась
тысяча. Выполнять действия необходимо в порядке их следования,
т.е. не нужно отдавать приоритет умножению и делению.
|18|
1936
| 550
568
M
203
|21| 13
I I504
I I22I
I hi
1618 |
I M
I 11(
I I24
|11|
I4I
M
Э1
I
313
= |1000
107
5
103
9
168
8
=|юоо;
730
=
1000|
236
= |1000|
70| =
1000|
9
s
1000|
Рис. 394
Решая задачу, в которой требовалось расставить числа так,
чтобы получилось верное равенство, рано или поздно, кто-то
подумал: «почему расставляем числа, а не наоборот - знаки
математических действий между имеющимися числами?»
Была бы идея, а воплотить её в конкретную головоломку -
это уже дело техники, логики и затраченного времени.

Числовые фантазии. Равенства. Задачи 47-48 255
Затем кто-то второй, проанализировав ситуацию, решает, что
можно усложнить задачу, если оставить пустые места и для
некоторых чисел, и для знаков математических действий. Третий
мыслитель, осмотрев с высоты своего роста стол, на котором
лежит книга с подобными головоломками, думает: «Почему
составители зациклились на плоскости, ведь можно придумать
пространственную аналогию задачи». Очередной любитель
головоломок скептически скажет: «Всё равенства и равенства, а в
математике решают и неравенства!» Так и идёт процесс,
появляются новые идеи, новые задачи и конца этому не должно быть
в силу бесконечности самой природы и неисчерпаемой
любознательности человека. Перед вами воплощение последних трех идей:
• расставлять в пустые клетки и числа, и знаки
математических действий одновременно;
• сделать пространственный вариант подобной задачи;
• использовать знаки неравенства в соотношении между
расставляемыми числами.
6-47
С учетом уже имеющихся цифр и
арифметических знаков заполните
пустые клетки так, чтобы все равенства
были верны.
8
-
=
9
-
4
5
=
6
+
6
3
=
1
=
=
=
=
3
8
=
Рис. 395
6-48
На каждой из граней куба
некоторые клетки заполнены
числами и знаками
арифметических действий. Ваша задача
в том, чтобы заполнить пустые
клетки так, чтобы все
равенства были верны.
18Х =
X. Х7Х
ЧЛ XX
+ ч
ч
ч
ч
ч
ч
^х х*х х*
4
ч
ч
s
II
ч
V
X.
3
я
21
ч
= X X \3\
■
■
-
я
=
я
=
9
я
Рис. 396

256 Числовые фантазии. Неравенства. Задачи 49-50
Неравенства
В математике кроме равенств есть ещё и неравенства, в
которых используются знаки больше > и меньше <. На этой основе
возникает ещё одна группа задач по расстановке чисел.
Например: расставьте в квадратной рамке числа от 1 до 4 так,
чтобы выполнялись все неравенства.
Л
>
<
Л
2
Л
3
>
<
1
Л
4
Рис. 397 Рис. 398
Проанализировав стоящие знаки, можно сделать вывод, что в
правом верхнем углу стоит наименьшее число, а в правом
нижнем - наибольшее и останется только расставить числа. Но с
увеличением количества неравенств, трудность резко
возрастает. Следующий шаг - девять чисел, затем могло быть
шестнадцать, но мы перепрыгнем сразу на 25 чисел.
□>□>□
Л V V
□>□<□
Л Л V
□»□<
Рис. 399
6-49
Расставьте цифры от I до 9 так,
чтобы выполнялись указанные
неравенства.
ото
V V Л
ООП
V V Л
П<П<О
6-50
Расставьте первые 9
натуральных чисел, причем в кружочки -
нечетные числа, а в квадраты четные
числа так, чтобы все 12 соотношений,
были верны.
Рис. 400

Числовые фантазии. Неравенства. Задачи 51-53 257
6-51
6-52
2
V
Л
V
Л
>
<
>
<
<
Л
Л
Л
Л
<
<
>
>
>
V
V
V
Л
>
<
<
<
>
Л
V
V
V
<
>
>
<
<
V
V
Л
V
V
Л
Л
V
<
<
>
>
<
V
V
Л
Л
>
<
<
<
>
Л
V
V
V
<
>
>
>
<
Л
V
V
Л
<
>
<
<
3
V
Л
V
V
Рис. 401 Рис. 402
Эти две головоломки отличаются как одно квадратное
уравнение от другого: небольшие внешние различия и
одинаковый метод решения.
В пустые клетки расставьте цифры от 1 до 5 так, чтобы
выполнялись все неравенства и любая цифра встречалась по каждой
горизонтали и вертикали строго один раз.
6-53
Расставьте числа от 1 до 25
таким образом, чтобы выполнялись
неравенства, и каждое число
использовалось только один раз.
V
V
Л
V
>
<
>
<
>
Л
V
Л
V
>
<
>
>
>
Л
V
Л
V
>
<
>
>
>
Л
V
Л
V
>
<
>
<
>
Л
V
Л
V
Рис. 403
Пересечения чисел
Среди множества головоломок с расстановкой чисел есть в
точности похожие своим внешним видом на кроссворды, они
имеют кроссвордную сетку, только не нужно ничего вспоминать,
числа, которые требуется вписать в сетку, уже перечислены,
остается только чистое мышление: как их расставить.
В разных изданиях их называют по разному, в зависимости
от фантазии составителей: цифрокросс, числобус, кросснамбер,
кому как нравится. Приведем примеры таких «числопересечений».

258 Числовые фантазии. Пересечения. Задача 54
6-54 ' ' '
Рис. 404
В колонках даны числа, которые необходимо разместить в
кроссворднои сетке по кроссвордным правилам. Одно число уже
стоит на месте, следующие начинайте связывать с ним.
19581
1034
2146
3491
4159
5873
5884
7597
8325
14937
22536
35728
46024
51673
63215
70537
73909
77150
85442
98361
158709
179003
286136
291628
354750
419454
451301
503275
537336
620835
718419
796975
860642
902514
942082
947567
1048073
2241694
2753198
2823945
4692038
4977802
5308170
6645816
7110254
7566793
7624205
9313528

Числовые фантазии. Пересечения. Задача 55 259
6-55
Задание аналогичное предыдущему, только сетка совсем
пустая и нет числа, с которого начинать заполнение. Его
придется определять самостоятельно. Если вы внимательно рассмотрите
таблицу чисел, то увидите одно число, отличающееся чем-то от
других, с него и начните заполнение сетки.
Рис. 405
12
29
37
56
79
88
90
91
239
409
445
584
597
616
619
713
720
777
972
983
1157
1199
2254
2657
3816
3972
4337
4473
4502
5067
5840
6111
6292
6363
6387
6854
6979
7625
7947
7955
9303
9329
9567
9833
23175
28019
29905
51003
52936
82221
83364
377812
480802
732664
827339
959567
2004865
3362372
3919273
6219023
7010000
8018813
90701180

260
Числовые фантазии. Сумма. Задачи 56-57
Сумма цифр
Необходимо по заданной сумме цифр расставить в пустые
клетки некоторые числа, известные или не известные.
П9П111
8 12 13
□1О4П
7 13 12
ООП
Рис. 406
6-56
Расставьте числа от I до 9 так, чтобы
сумма цифр в любых двух соседних
клетках равнялась числу, написанному
между этими клетками.
6-57
Рис. 407
Задание сложнее, расставлять те же цифры, но их больше.
В каждую клетку сетки, кроме центральной клетки,
впишите по цифре, чтобы получился кросснамбер - пересечение чисел.
Для каждого числа в кружках указана сумма составляющих его
цифр. В каждом числе кросснамбера нет одинаковых цифр.

Числовые фантазии. Сумма. Задачи 58-59
261
6-58
Заполните клетки цифрами
от 1 до 9 так, чтобы выполнялись
следующие условия:
• сумма каждой четверки
цифр равнялась числу,
записанному в центральном
квадратике;
• эти четыре цифры различны
между собой и
записываются по ходу часовой стрелки
в возрастающем порядке за
минимальной цифрой.
Рис. 408
6-59
Рис. 409
Заполните шесть пустых звёздных дисков числами.
В трёх дисках числа уже стоят, это поможет вам понять
закономерность, на основе которой путем сложения, по 36 числам
«парящим» в лучах всех девяти звезд, определяются центральные числа.

262 Числовые фантазии. Сумма. Задачи 60-61
6-60
В этом задании нужно расставить числа так, чтобы суммы
цифр по указанным направлениям совпадали с теми числами,
которые стоят рядом со стрелками.
14
31
10
7
12
31
м
4
14
13
24
24
14
13
►
14
т
►
24
8
►
14
т
►
9
36
24
16
2J
т
23
т
7
18
21
5
►
13
24
18
13
24
14
21
9
10
►▼
22
6
37
38
▼
2?
7
27
т
15
12
22
22
17
13
17
11
20
т
11
17
т
19
24
25
11
▼
3
43
20
т
30
т
*
15
10
▼
9
▼
8
▼
10
▼
14
Рис.410
А
Рис.411
О
О
о
0000
6-61
Начав с окружности,
помеченной буквой А, расставьте
семь последовательных чисел в
порядке возрастания в семи
окружностях. Другой набор из 12
последовательных чисел
расположите в квадратах так, чтобы
суммы чисел в горизонтальных и
вертикальных рядах
прямоугольника были равны числам в
соответствующих окружностях.

Числовые фантазии. Деревья. Задачи 62-64
263
Деревья
Следующие головоломки из свежих газетных публикаций.
В «Экспресс-газете» их называют дерево чисел, а в газете «Поле
чудес» подобная головоломка имела название ветви кроны.
———-™
Расставьте числа от 1 до 10 так, чтобы число, стоящее в
каждом кружке, являлось суммой чисел, которые от него
ответвляются. Некоторые числа уже проставлены и известно значение,
стоящее в корне дерева.
Приведем для примера три дерева, хотя легко можно было
бы вырастить целый лес.
Рис.412 Рис.413
В последнем дереве требуется расставить числа от 1 до 14.
Рис. 414

264 Числовые фантазии. Переработка. Задачи 65-68
Разрезать, сдвинуть, восстановить, убрать
Далее идут задачи, в которых числа уже стоят, а требуется
проделать с фигурой некоторые действия, чтобы выполнить
условие.
1
8
9
15
16
10
7
2
12
13
5
6
4
3
11
14
Рис.415
!
6-65
Как разрезать этот
прямоугольник с цифрами на 4
одинаковые фигуры таким образом,
чтобы сумма чисел в каждой
части составляла 34?
1
10
8
7
9|б
5|и
2
12
5
4
Рис.416
6-66
Необходимо разрезать
фигуру на четыре одинаковых по
форме части так, чтобы сумма
цифр в каждой части была одна
и та же.
6
1
I
9
8
3
7
4
Z
3
8
6
5
1
JL
2
9
: 2
1
6
8
*
4
1
3
7
9
5
8
2
T
7
9
Рис.417
6-67
Разделите квадрат на
четыре одинаковых по форме
фигуры так, чтобы сумма чисел
в каждой фигуре была одна и та же.
J
4
8
2
_7_
\
3
6
3
9
1
8
7
8
1
5
9
6
1
5
7
6
3
5
4
2
4
2
6
8
9
9
7
1
3
4
5
6-68
А этот квадрат нужно
разделить на шесть одинаковых по
форме фигур так, чтобы сумма
чисел в каждой фигуре была
одна и та же.
Рис.418

Числовые фантазии. Переработка. Задачи 69-74 265
6-69
Разделите квадрат на четыре
одинаковые части, но так, чтобы произведения чисел
в каждой выделенной части были равны.
8
5
6
3
7
0
4
0
6
1
7
6
6
4
7
5
1
1
2
7
2
9
4
0
1
9
1
0
7
9
2
2
6
4
2
6
Рис.419
6-70
Разделите квадрат на четыре
одинаковые части, но так, чтобы произведения чисел
в каждой выделенной части были равны.
Обратите внимание, что в этом квадрате нет
нулей, а это существенно меняет задачу.
4
8
1
7
2
3
1
5
9
6
8
7
8
2
3
5
1
6
3
7
6
2
4
9
9
4
1
4
6
2
5
7
3
8
5
9
Рис. 420
6-71
Разделите этот квадрат четырьмя
прямыми линиями так, чтобы в
образовавшихся девяти частях суммы чисел были
равны между собой.
819
12
179
3
15
516
6
114
18
112
413 7
Рис. 421
6-72, 73, 74
Каждое из трех круговых полей, показанных на следующей
странице, содержит одинаковый набор цифр, расставленных как
бы беспорядочно. Вам предлагается:
• двумя прямыми разделить первый круг на 3 части, чтобы
сумма цифр в любой из них равнялась 20;
• двумя прямыми разделить второй круг на 4 части, чтобы
сумма цифр в любой из них равнялась 15;
• тремя прямыми разделить оставшийся круг на пять частей,
чтобы сумма цифр в любой из них равнялась 12.

266 Числовые фантазии. Переработка. Задачи 75-77
Рис. 422
Рис. 423
Рис. 425 Рис. 426
Сумма всех чисел, изображенных на циферблате часов,
равна 78. Разделите циферблат:
• двумя прямыми линиями на три части так, чтобы сумма чисел
в каждой части была одинаковая;
• кривыми линиями на 4 неравных части так, чтобы сумма
чисел в каждой из них равнялась 15.
Сдвинуть
6
3
7
3
6
8
4
1
1
2
3
2
9
4
5
4
2
3
0
5
О
1
4
1
5
14
2
6
1
5
1
9
3
15
5
О
Рис. 427
6-77
Горизонтальные ряды чисел нужно
сдвинуть относительно друг друга
влево и вправо по горизонтали так,
чтобы получилось десять
вертикальных рядов цифр, сумма которых в
каждом вертикальном ряду была бы
равна пятнадцати. Дня решения
головоломки можно выписать ряды чисел
на полоски бумаги и передвигать их.

Числовые фантазии. Переработка. Задачи 78-80 267
Восстановить
6-78
Восстановите
рассыпавшийся
квадрат так, чтобы
получилось пять
чисел. Каждое из
них должно один
раз появиться по
горизонтали и один раз по вертикали.
9
3
5
1
8
3|5
8
6
0
1
4
Т
|б|7
8|б|
0
И [4
2
7
о
л
1
Рис. 428
6-79
0
Рис. 429
Соберите из элементов тримино квадрат 7x7 так, чтобы по
строчкам и столбцам получалась одинаковая сумма, равная 150.
Ноль уже стоит на своем месте.
Зачеркнуть, убрать
Расставлять числа - это одно дело, а зачеркивать их -
совершенно противоположное. Разнообразие, которого мы
добиваемся, требует рассмотрения и таких задач.
6-80
Рис. 430
Какое наименьшее число клеток с цифрами можно
вычеркнуть, чтобы оставшиеся цифры образовали, не меняя их порядок,
квадрат целого числа? Какие вычеркнуть?

268 Числовые фантазии. Переработка. Задачи 81-84
6-81
3
4
1
5
8
3
9
8
2
6
8
1
5
2
6
3
9
Рис. 431
На 9 карточках выписаны цифры от 1 до 9, и каждая
встречается по три раза. Оставьте только три карточки, чтобы сумма
цифр любого горизонтального ряда в них равнялась 15. При этом
должны остаться все цифры от 1 до 9 по одному разу.
111
777
999
Рис. 432
6-82
Вы видите здесь три числа, подписанные
одно под другим. Нужно зачеркнуть шесть цифр так,
чтобы оставшиеся числа составляли в сумме 20.
111
333
+ 555
777
999
Рис.433
6-83
Зачеркните девять цифр так, чтобы
оставшиеся числа составляли в сумме ПИ.
3
1
9
6
2
9
2
7
8
5
7
4
1
1
3
5
2
3
7
8
6
8
2
4
5
6-84
Зачеркните лишние цифры так,
чтобы в каждом ряду по горизонтали и по
вертикали сумма чисел составляла 15.
Рис. 434

Числовые фантазии. Переработка. Задачи 85-87 269
6-85
Из приведённых 16 чисел
оставьте только четыре: по одному
в каждом горизонтальном,
вертикальном ряду и на главных
диагоналях, причем так, чтобы сумма
оставленных чисел оказалась рац-
ной 32. Остальные числа можно
просто закрасить, для этого
рисунок сделан негативным.
11 Не
Рис. 435
6-86
Закрасьте шесть единиц из
клеток квадрата так, чтобы
оставшиеся десять были распределены в
четырёх строках и четырёх
столбцах в соответствии с условием:
должна быть четная сумма в
каждом горизонтальном и
вертикальном ряду, а также в двух
диагоналях. Решение не единственное.
Рис. 436
6-87
Закрасьте 24 цифры из
шестидесяти четырёх так, чтобы в
каждом горизонтальном и каждом
вертикальном ряду осталось по пять
неповторяющихся цифр.
Рис. 437

270
Числовые фантазии. Стрелки. Задачи 88-91
Снова требуется расставить, но не числа и не знаки
математических действий, а...стрелки.
В пустых клеточках по краям квадрата расставьте стрелки
(вертикальные, горизонтальные и диагональные) так, чтобы
числа внутри квадрата указывали, сколько стрелок направлено на
соответствующую клетку. Каждая стрелка должна указывать хотя
бы на одну клетку.
Пример решения:
Первым делом определяемся с числом 6. На
него могут быть направлены 2 вертикальных
стрелки, 2 горизонтальных и только 2
диагональных. Как раз, сколько нужно, ни больше, ни меньше.
Автоматически решился вопрос с цифрой 2,
расставив стрелки для шестерки, мы попали и на двойку
Рис. 438. Остаются без стрелок две клетки в правом нижнем
углу. Только одна стрелка должна попасть на единицу, этим все
решается с оставшимися двумя стрелками.
6-88, 89, 90, 91
\
6
2
t
/
4
1
t
\
4
5
3
6
2
3
2
3
3
4
0
3
0
3
1
3
2
3
2
2
2
5
2
4
3
Рис.439
3
5
4
3
3
1
4
4
1
2
3
3
1
4
1
4
3
3
2
6
2
5
2
4
2
4
2
2
3
3
4
0
0
1
4
4
1
0
1
3
2
2
2
1
2
6
3
5
4
3
Рис.440
1
2
3
3
1
2
1
4
3
2
1
5
3
6
2
1
1
6
2
2
3
5
4
7
3
Рис. 441
Рис. 442

Числовые фантазии. Сапер. Задачи 92-95
271
Сапер
Игра «Сапер» стала известна в компьютерном варианте, как
стандартное приложение к операционной системе Windows. Хотя
может быть представлена как логическая головоломка на бумаге.
На бумаге удобнее тем, что при неправильном ходе вы не
«взорвётесь», а спокойно его сотрёте и продолжите дальше решать
головоломку.
6-92, 93, 94, 95
На поле расположены мины, в одной клетке не более одной.
В клетках с цифрами мин нет. Каждая цифра показывает, сколько
мин находится в соседних с ней (и по диагонали тоже) клетках.
Восстановите расположение мин.
Рис. 443
4
1
1
2
4
3
1
1
2
2
1
2
2
1
2
2
1
2
2
3
3
1
2
2
2
2
3
3
3
1
1
2
1
2
2
2
1
1
2
2
2
1
2
3
3
2
3
1
2
2
1
2
4
4
1
3
1
1
3
2
3
Рис.444
3
1
4
4
3
2
1
1
2
2
4
3
4
4
3
1
4
4
3
4
1
1
1
2
5
1
2
2
1
1
2
1
1
3
2
1
4
5
4
2
1
4
2
1
2
1
1
1
3
1
2
2
2
3
3
1
2
2
3
2
1
1
1
4
1
2
1
1
3
3
3
1
1
1
1
2
2
2
1
1
Рис. 445
Рис. 446

272
Числовые фантазии. Путь. Задачи 96-98
Пройденный путь
Числа расставлены в исходной фигуре. Требуется провести
ломаную линию, начиная с указанного числа и заканчивая в
определенном месте, так, чтобы сумма чисел, стоящих на этой
ломаной равнялась заданному значению.
6-96
Начав с цифры 6 в левом верхнем углу и
закончив на цифре 5 в правом нижнем углу,
проведите ломаную линию так, чтобы сумма
чисел в пересеченных клетках равнялась 45.
Линия не должна пересекать сама себя, нельзя
переходить из клетки в клетку по диагонали.
Часть клеток останется незадействованной.
6
1
4
8
1
9
3
2
6
9
3
2
1
4
7
5
5
2
7
3
4
8
9
8
5
Рис. 447
6-97
Проведите ломаную линию от цифры
I в левом нижнем углу до цифры 3 в
правом нижнем углу так, чтобы сумма чисел,
через которые проходит ломаная,
равнялась 45.
6-98
Проведите линию
от одного серого кружка
до другого так, чтобы
сумма чисел в кружках,
через которые линия
проходит, равнялась 1000.
Рис. 449

Числовые фантазии. Путь. Задачи 99-101
273
6-99
Необходимо пройти от числа 3 в
левом верхнем углу до числа 3 в правом
нижнем углу, двигаясь только по
горизонтали или по вертикали так, чтобы
общая сумма набранных чисел равнялась
ПО. А по какому пути будет набрана
наименьшая сумма?
3
1
2
7
9
1
3
4
3
6
4
5
6
7
8
9
1
2
4
6
8
8
3
5
9
1
7
6
5
9
4
2
4
7
8
1
3
6
3
3
Рис. 450
6-100
Нужно найти такой путь от
цифры I в верхнем левом углу до
цифры 9 в нижнем правом углу,
чтобы сумма всех чисел была равна
100. Двигаться можно только
вправо и вниз.
А
1
2
3
4
5
6
7
8
9
А
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
Рис. 451
6-101
Рис. 452
Необходимо пройти от левого серого кружка до правого,
набрав при этом сумму: а) 250, б) 350.

274
Числовые фантазии. Путь. Задачи 102-104
6-102
Пройдите путь от вершины к
основанию, переходя из каждой клетки в одну
из расположенных под ней, и наберите по
дороге заданную сумму: а) 35, б) 45, в) 55.
л?1?14?1?7?1.
|5|7|9|2|4|9|3|
Рис. 453
|в|4|3|7|
1111
Г6Г8|719Т115|
1^ви]5^б17|
|8|7|1|5|8|9|5|3|1|
|4|6|5|9|8|7l6f5T8T9l
6-103
Пройдите путь от вершины
пирамиды к основанию,
переходя из каждой клетки в одну из
расположенных под ней, и
наберите заданную сумму: а) 40,
б) 50, в) 60.
Рис. 454
6-104
Из всех шести вершин звезды
нужно пройти к центру через
ворота с числами, по пути производя с
ними любые арифметические
действия, но рассчитать их так, чтобы,
придя в центр, результатом
вычислений каждый раз получалось
число 7 , стоящее в центре.
Рис. 455
В каждом из лабиринтов нужно найти путь к центру, пройдя
по которому наберем в сумме число, стоящее в центре лабиринта.

Числовые фантазии. Лабиринты. Задачи 105-108 275
6-105
Рис.
6-106 50
Рис. 457
Рис. 458
^W^ 25 ^ь_^ 30 ^^J
6-107
6-108
Рис.459

276
Числовые фантазии. Закон. Задачи 109-111
Поиск закономерности
Большая часть чисел уже стоит на своих местах, остается
заполнить пустые места, но как? В заданиях не указано точное
требование к расстановке чисел и необходимо, рассматривая
имеющиеся числа, понять закономерность, которой они
подчиняются, и в соответствии с ней заполнить пустоты. Работа чистой
логики. Обычно исходные числа связаны какими-то
арифметическими действиями. Например:
Рис. 460
Из первой пары чисел можно получить соотношение
32-15=17, т. е. нижнее число на 17 больше верхнего. Проверяем,
справедливо ли это соотношение для других пар чисел:
38-21=17 и 52-35=17, значит, это и есть искомая закономерность.
Недостающее число 43+17=60.
Сначала формулируется гипотеза, затем она проверяется и,
наконец, применяется для определения недостающего числа или
чисел.
|Щ12|15|1в| |141б|15|7|
6-109
Рис. 461
Определите закономерность, которая связывает первое
число в четверке с тремя остальными, проверьте её на второй
четверке и примените для определения недостающего числа.
6-110,6-111
Если вы найдете закономерность, которой подчиняются
тройки чисел в первых двух кругах, то написать недостающее
число в нижнем секторе третьего круга уже несложно. Какое же
эт число?
Рис. 462
Рис. 463

Числовые фантазии. Закон. Задачи 112-114
277
6-112
В каждом из следующих кругов закономерность своя. Ищите
её либо в соотношении чисел противолежащих секторов, либо в
чередовании чисел по кругу.
X
/ 7
V 13
X
5
\
/
21
?
\
10
X
26 \
14/
У
к
1 3
V 5
X
^-
2
\
/
8
?
/
\
13
X
34 1
21 1
у
X
1 6
V 4
X
?
\
/
3
9
/
\
36
X
16 \
30/
У
Рис.464
Рис. 465
Рис. 466
Рис. 467
6-113
Найдите закономерность получения среднего числа из
крайних в верхней строчке и впишите недостающее число в
нижней строке. Закономерность в каждом задании разная.
196
325
25
324
137
188
893
300
263
915
12
17
56
16
21
16
29
27
43
56
Рис. 468
Рис. 469
Рис. 470
Рис. 471
6-114
Числа в квадратах расположены в соответствии с
определенной закономерностью (для каждого квадрата своей).
Установите закономерность и назовите число, которое следовало бы
вписать в пустую клетку.
4
8
10
9
5
3
20
14
3
4
5
12
16
20
6
8
Рис. 472
Рис. 473
Как видите, во многих задачах на поиск закономерности
меняется рисунок, но остается неизменным задание - найти
закономерность, связывающую проставленные числа и заполнить
пустые места. Поэтому в нескольких однотипных задачах,
показанных далее, не будем каждый раз повторять условие, а
приводим только соответствующий рисунок

278 Числовые фантазии. Закон. Задачи 115-121
6-115
Рис. 474
Рис. 475
6-116
Рис.476
6-117
[91 Гм1 [б! \Т\
Г20| Г13|
6-119
rial Г?1
Рис.479
6-121
2
-
Л4
Й-
Г
-Е
5
3-
5
-ч
13
I 9
"Л—
Ti7
Рис. 480

Числовые фантазии. Закон. Задачи 122-126
279
6-122
Рис. 482
Рис. 483
6-125
Соедините карточки с цифрами
в один ряд из 15 клеток так, чтобы в
получившейся последовательности
обнаружилась строгая числовая
закономерность.
Рис. 484
7
4
3 0
6 3
10
[col
5 | 9
Если в Библии «в начале было слово», то в математике
можно сказать - в начале был натуральный ряд чисел:
1,2,3,4,5,6,7,8,9,10,....
Из натуральных чисел можно построить и другие числовые
последовательности. В связи с чем возникают интересные
логические задачи определения закономерности построения того или
иного ряда чисел.
6-126
В каждом из перечисленных числовых рядов нужно
установить закономерность, которой подчиняются числа, и написать два
следующих числа: а) 5,10,15, 20, 25, 30, _, _

280 Числовые фантазии. Закон. Задача 126
б) 3,7,11,15,19, 23, _,_
в) 6, 9,12,15,18, 21, _,_
г) 1,2,4,8,16,32,_,_
д) 1,1,2,3,5,8,13, 21,34, _,_
е) 1,7,13,19,_,_
ж) 3,2,6,5,9,8,_,_
з) 5,3,7,3,9,3,_,_
и) 1,4,7,10,13,_,_
к) 3,4,12,5,6,30,_,_
л) 4,3,8, 7,16,15, _,_
м) 4,5,7,10,14,_,_
н) 3,4,6,9,13,18,_,_
о) 1,4,9,16,25,_,_
п) 4,8,10, 20, 22,44, _,_
р) 4,5,8,9,12,13,_,_
с) 1,8,27,64,_,_
т) 7,17,37,77,157,317, _,_
у) 1, 2,3,4, 5, 6, 7, 8, 9,1, 0,1,1,1, 2, 1, _, _
ф) 1,11, 21,1211,111221,312211,13112221, _,
х) 101,112,131,415, _, _
ц)

Числовые фантазии. Разное. Задачи 127-129
281
Разное
Когда уже не знаешь, в какой раздел выделить задачи по
принадлежности, остается спасительно слово «разное». Сюда
можно поместить всё, что вроде бы подходит по общей тематике
и жалко выбрасывать, не особо ломая голову над классификацией
задач. Когда их поднакопится здесь больше, некоторые
выделятся в свою группу, другие, после размышлений попадут в уже
имеющиеся разделы, а пока их место здесь.
6-127
Расставьте шесть чисел 1,2,3,4,5,6 по
окружности в таком порядке, чтобы для
любых трех чисел а,Ь,с, стоящих подряд,
число Ь2-ас делилось на 7.
Рис. 485
Рис. 486
6-128
Можно ли расставить все числа от I до
12 по окружности так, чтобы для любых
трех чисел а,Ь,с, стоящих подряд, число
Ъ2-ас делилось на 13.
6-129
На рисунке в пяти кружках
расставлены числа. Складывая в различных
комбинациях рядом стоящие числа, в том числе,
выбирая их по одиночке, можно получить
. (101 последовательные числа натурального
' * ' ряда от 1 до 21.
Рис.487
Например: 1, 2, 3 - уже есть, 4=1+3, 5-есть, 6=5+1, 7=5+2,
8=2+5+1, 9=5+1+3, 10 - есть, 11=2+5+1+3 и т.д. до
21=1+3+10+2+5, т.е. суммы всех стоящих чисел.

282
Числовые фантазии. Разное. Задачи 129-130
Рис. 488
Попробуйте в шести кружках,
соединенных в кольцо, расставить^ числа так,
чтобы они и их суммы с рядом стоящими
числами образовывали натуральный ряд,
т.е. последовательность 1,2,...N.
Возможны различные решения и соответственно
получаются непрерывные отрезки ряда
натуральных чисел различной длины.
Естественно, чем большего значения удастся достичь, тем
лучше. В своё время эта задача предлагалась в журнале «Наука и
жизнь» и читатели присылали различные решения, в том числе
рассчитанные на компьютере.
6-130
Математический знак бесконечности, представляет собой
восьмёрку, лежащую на боку. В данном случае, он сложен из 31
четырёхугольной плитки. Плитки пронумерованы таким образом,
начиная с центрального «нулевого» квадрата: делается один шаг
и ставится число I, делается два шага и ставится число 2 и т. д.
Движение должно идти по петле с пересечением в
«нулевом» квадрате в направлении стрелок. Нельзя ставить число на
уже пронумерованную плитку дорожки, но этого и не придется
делать, если правильно рассчитано количество плиток в
восьмёрке. Существует не более двадцати подобных фигур с числом
плиток в пределах миллиона.
Попытайтесь построить ближайший меньший и ближайший
больший варианты головоломки.
Рис. 489

Числовые фантазии. Разное. Задачи 131-132
283
В старых книгах каждая задача имела свою литературную
трактовку, а не только изложение математической стороны
вопроса. Вот примеры подобных головоломок в художественном
изложении.
6-131
6
9
6
9
9
6
9
6
Рис.490
Обманутый хозяин
Хозяин устроил в своем погребе шкаф в
форме квадрата с девятью отделениями. Среднее
отделение он оставил свободным для пустых
бутылок, а в остальных разложил 60 бутылок
масла так, что в каждом угловом отделении их
было по 6, а в каждом среднем - по 9. Таким образом,
на каждой стороне квадрата было по 21 бутылке.
Слуга заметил, что хозяин проверяет число бутылок, только
считая их по сторонам квадрата и следя за тем, чтобы на каждой
стороне квадрата было по 21 бутылке. Тогда слуга унес 4 бутылки,
а остальные расставил так, что вновь получалось по 21 на каждой
стороне. Хозяин пересчитал бутылки и подумал, что бутылок
остается то же число, просто слуга переставил их. Слуга
воспользовался оплошностью хозяина и снова унес 4 бутылки, расставив
остальные. Так он повторял, пока было возможно. Спрашивается,
сколько раз слуга брал бутылки и как их расставлял в каждом
случае? Сколько всего бутылок смог унести?
1
7
1
7
7
1
7
1
6-132
Задача об обманутом хозяине имеет
вариант с другим начальным количеством бутылок и
другим их первоначальным раскладом. Слуга
остается тот же и уносит за один раз по 4
бутылки, пока это возможно. Восстановите
расклад бутылок по отделениям после каждой
очередной кражи.
Рис.491

284 Числовые фантазии. Разное. Задачи 133-134
6-133
Расстановка часовых
Квадратный бастион имел по углам круглые башни.
Комендант расставил 16 часовых так, как показано на рисунке, по 5
человек с каждой стороны. Пришел
полковник и распорядился расставить солдат так,
чтобы с каждой стороны их было по 6.
Затем с проверкой нагрянул генерал и
приказал разместить по 7 солдат с каждой
стороны. Каждый раз комендант обошелся тем
же количеством часовых, только менял их
расстановку. Каково было их расположение
в двух последних случаях?
Рис. 492
6-134
В наше время любой кассовый фильм обязательно получает
продолжение до тех пор, пока сборы перестанут окупать
производство. В «докиношную» эпоху, люди развлекались, решая
головоломки. И точно также, каждая интересная задача могла
иметь несколько разных вариантов, трактовок. Вот иное
представление задачи о бастионе.
Неприятель окружил бастион, который обороняли 40
бойцов. Командир расставил их так, что вдоль каждой стены, считая
и башни, стояло 12 защитников. После первой атаки
обороняющиеся недосчитались четырёх человек, но командир расставил
оставшихся так, что по-прежнему с каждой стороны их было по
12. Новая атака унесла жизни ещё четырёх человек, но когда
рассеялся дым, с каждой стороны бастиона
оставалось 12 бойцов. Во время третьей
атаки были убиты ещё четверо, только
неприятель не заметил этого - с каждой стороны
бастиона его снова обороняли 12 человек.
Видя бесполезность своих действий, и неся
большие потери, враг отступил.
Восстановите картину обороны бастиона, а именно,
расположение бойцов после каждой атаки.
Рис. 493

Числовые фантазии. Оцени фигуру. Задачи 135-136 285
Оцени фигуру
Каждой фигуре соответствует одна цифра от 1 до 9. Суммы
цифр по горизонталям и вертикалям проставлены, Определите,
какая цифра стоит за каждой фигурой.
6-135
44
42
36
43
41
27
27
22
28
27
®
22
29
24
В
в
*
и
®
Рис. 494
6-136
38
39
37
43
40
23
ш
то
30
СИ)
то
32
СИ)
-*-
22
«
СИ)
26
м
то
*■
СЙ)
20
ей)
19
*
ш
то
25
?
м
то
ш
ш
то
i3
ей)
if
Рис. 495

286 Числовые фантазии. Рисование по-японски
Рисование по-японски
Правила японского письма лишают наших восточных
соседей возможности разгадывать кроссворды и сканворды на родном
языке, и они придумали своеобразное «рисование по-японски»,
которое вполне соответствует духу этой страны. Подобное
развлечение требует логического мышления, расчета и приносит
эстетическое удовлетворение красотой полученных результатов.
Сейчас этот вид головоломок распространился и в нашей стране
под не правильным названием «японские кроссворды».
Кроссворд - это пересечение слов, которых здесь нет и в помине, но
есть сетка из клеточек, которые нужно закрасить в соответствии с
имеющимися числами.
Мы рассмотрим три вида рисования по-японски, которые
отличаются методом использования данных в условии чисел.
1. Традиционное рисование по-японски
В традиционном японском рисовании по клеточкам картинка
зашифрована с помощью чисел, расположенных слева и сверху
от сетки. Каждое число указывает, сколько клеточек подряд нужно
закрасить в этой строке или столбце. Если в строке или столбце
стоит два или сразу несколько чисел, значит, закрашивать
придется не подряд, а по фрагментам, каждый из которых по величине
соответствует своему числу. Фрагменты идут в том же порядке,
что и числа, и отделяются друг от друга пробелами как минимум
в одну клетку. Определение величины этих пробелов и есть
главная сложность в подобном рисовании.
Рассмотрим на простом примере основные тонкости
разгадывания традиционных японских рисунков. Во-первых, при
решении удобно использовать два контрастных карандаша,
например, черный и желтый, Черным закрашиваем клетки рисунка, а
желтым - промежутки между фрагментами, отмечая те клетки,
которые остаются пустыми и мы это уже установили. Закрашивание
клеток, в которых заведомо будет пусто, очень облегчает
разгадывание картинки.
1. В первую очередь следует обратить внимание на большие
числа. Так, в пятой сверху строчке стоит число 9 и клеток в
каждой строке ровно 9, значит, всю строчку можно закрасить.

Числовые фантазии. Рисование по-японски
287
Следующее по величине число 5 в
девятой строке. Как бы ни
располагался фрагмент из пяти клеток в
данной строчке, центральная
клетка обязательно будет закрашена.
2. Переходим к вертикалям. В
пятом столбце слева стоит число 9,
это значит, что центральные 6
клеток можно сразу закрасить. В
шестом столбике расположение
фрагментов полностью
определилось. В четвертом столбце можно
однозначно определить две клетки
из пятиклеточного фрагмента.
Рис. 496 Клетки, которые заведомо останутся
не закрашенными, отмечаем серым (лучше желтым) цветом,
чтобы к ним уже не возвращаться. Так мы отметим две клетки в
шестом столбце; в третьем и седьмом стоят только единицы и
можно окаймить уже закрашенные клетки. В последнем столбце
известна одна клетка из трехклеточного отрезка, а значит две
клетки сверху и пять снизу - заведомо пустые.
1
1
з"
3
1
2
I
3
4
3
]Г
1
3
5
1
3
1
3
1
1
1
3
1
1
1
1
1
3
5
1
9
1
3
7
■
1 1
т
1 1
1
1
■
1
2
1
3
1
2
1
з"
3
1
2
3
4
3
1
3
5
1
3
1
3
1
1
1
3
1
1
1
1
■
I I I
3| |3|1
5|э|т|1
■
I ■
■ ■ ■
■ ■■
■ ■
ш
1
1
1
3
1
1
3
3
1
2
3
4
3
1
3
1
1
3
1
1
1
I I I
3| |3|1
5|9|7|1
ш
JE
■ I
1
2
3
□
1
1
3
5
1
3
1
^^■^
■■ ■
■ ■
■
I I П
Рис. 497 Рис. 498
3. Возвращаемся к строчкам. Закрасить можно одну клетку
во второй строке и закончить отрезок в шестой. Но много клеток
выходят из игры, до них не дотянутся фрагменты или, как в
восьмой строке - все уже определено. Отметим их серым цветом.

288
Числовые фантазии. Рисование по-японски
Рис. 499
4. Снова просматриваем вертикали.
В первом столбце определяется трехкле-
точный отрезок, во втором можно
закрасить две клетки из трех, в четвертом,
пятом и шестом полностью определить
фрагменты, в последнем дорисовать одну
клетку. И отмечаем серым (желтым)
пустые клетки. Далее процесс состоит в
попеременном просматривании ситуации
по строчкам и столбикам с
закрашиванием нужных клеток в черный цвет, а
пустых - в серый (желтый).
6-137 Восстановите картинку по её числовой записи. Рис. 500
4
3
3
5
2
2
7
2
4
4
2
7
7
7
2
2
16
7
4
3
12
3
5
7
20
20
20
4
8
11
14
7
6
6
6
5
5
4
4
3
4
5
6
6
5
4
2
1
1
2
22
го
5
5
2
6
2
7
3
15
4
1«
5
13
5
3
1
7
6
2
3
6
6
1
5
5
6
1
5
5
4
2
3
6
4
3
1
7
4
12
4
15
5
1*
5
2
7
6
2
6
6
5
6
2
5
6
4
1
12
1
11
1
9
1
6
2

Числовые фантазии. Рисование по-японски
289
Рисование по-японски не ограничивается черно-белыми
рисунками. По аналогии можно числами зашифровать цветной
рисунок. В этом случае каждое определяющее число слева и
сверху от рабочего поля головоломки стоит в клетке
соответствующего цвета. Основное отличие в том, что разноцветные
фрагменты не обязательно должны отделяться друг от друга пустыми клетками,
а могут стоять и слитно, т.е. мевду ними пустые клеточки могут быть,
а могут и не быть. Но между соседними блоками одного цвета
обязательно должна быть как минимум одна пустая клетка.
Решать цветные головоломки интереснее, хотя с точки зрения
логики немного проще, чем черно-белые, но эстетическое
удовольствие при завершении работы значительно выше. Посмотрев на такой
рисунок, так и хочется написать стихотворение в стиле «хокку».
Ввиду черно-белого издания книги, планируемый на это место
цветной рисунок приходится заменить еще одним черно-белым, но вы
не огорчайтесь, сейчас выходит много периодических изданий с
японскими рисунками.
6-138
2
2
1
1
1
1
ill
11
4
hi1
1I1
11
1
1
1
8
8
3
1
1
1
3
3
3
1
1
*
4
4
4
12
1
3
3
1
8
1
1
1
3
1
1
3
4
1
1
1
1
1
8
8
1
8
25
2
2
1
25
25
3
1
1
10
2
4
3
3
2
5
3
4
3
3
2
2
4
4
2
1
2
2
2
1
7
2
3
1
2
2
3
3
2
2
3
1
2
3
3
3
2
1
2
1
2
1
1
3
3
2
2
1
3
1
2
1
1
3
3
2
1
2
1
2
2
7
2
1
2
2
2
8
4
2
2
2
2
2
1
2
4
3
1
2
2
5
2
4
3
10
Рис. 501

290
Числовые фантазии. Рисование по-японски
2. Японская мозаика
Названия, которые мы здесь даем различным видам
рисования по-японски, чисто условные. Например, следующий вид
головоломок в некоторых периодических изданиях называют
филлипинскими кроссвордами. Но мы не будем выяснять, кому
принадлежит приоритет их изобретения: «восток - дело тонкое».
Правила рисования следующие:
1. Все числа расположены не по краям, как в традиционном
варианте, а внутри самой сетки. Каждое число, кроме 1, имеет свою пару.
2. Клетки с цифрой 1 просто закрашиваются. Остальные пары
чисел соединяются прямой или ломаной линией, количество
клеток в которой должно равняться числам на её концах. Эти
линии из клеток тоже закрашивается.
3. Линии, соединяющие пары, могут преломляться и идти как в
вертикальном, так и в горизонтальном направлении, но не по
диагонали. Кроме того, они не могут пересекаться и
проходить через одни и те же клетки.
Рассмотрим простой пример, чтобы понять порядок
разгадывания рисунка.
7
6
5
4
4
5
1
6
3
3
1
1
1
6
6
3
3
2
3
2
2
7
2
3
3
3
2
2
2
2
2
2
1
2
1
1
2
7
6 5
i"
4
4
_
6
_
т
В
71
j
jjjj
s
3
3
Рис. 502
Рис. 503
• Начните решение с закрашивания всех клеток,
содержащих цифру 1.
• Затем соедините всегда стоящие рядом клетки с цифрами 2.
Эти этапы выполняются механически, без вмешательства
интеллекта.
• Следующие этапы мыслительные. Это проведение более
сложных линий, которые могут быть прямыми или ломаными.
Лучше идти по мере возрастания чисел, т.е. 3,4, ....

Числовые фантазии. Рисование по-японски
291
Рис. 504
Рис. 505
6-139
Попробуйте свои силы в разгадывании японской мозаики.
4
4
2
2
2
2
12
12
3
3
5
5
9
9
1
9
4
4
4
2
1
8
16
10
6
6
4
2
3
3
16
8
6
3
3
8
8
4
8
8
6
8
6
5
4
1
3
9
3
3
5
9
10
3
6
3
3
3
1
3
3
5
2
2
8
9
6
6
з|
2
2
1
2
2
2
2
5
6
3
2
7
4
2
2
1
5
8
5
2
2
2
1
3
2
2
2
7
6
6
2
2
4
7
6
1
2
2
2
7
6
3
3
5
6
4
4
6
5
1
8
8
8
14
4
4
4
5
8
3
5
4
4
8
9
4
4
6
4
3
9
4
6
16
2
2
4
5
6
1
6
3
1
5
5
5
4
1
|2
4
4
2
2
1
10
6
3
5
1
4
1
4
16
14
4
4
4
2
2
2
15
2
3
3
10
3
4
5
2
15
7
4
4
4
3
3
2
2
3
3
1
3
3
7
5
3
5
2
2
3
3
4
4
4
5
4
2
2
1
5
5
4
5
11
4
11
4
5
6
3
3
2
5
3
4
5
5
5
5
7
3
3
2
3
6
6
6
1
2
5
б
3
3
7
3
1
2
3
2
2
Рис. 506

292
Числовые фантазии. Рисование по-японски
3. Логическая икебана
Этот вид головоломок является родственником
компьютерной игры «Сапёр», о которой мы ранее уже упоминали. Только
здесь мы не мины ищем, а закрашиваем клетки в соответствии с
числами. Правило простое: цифры указывают, сколько
примыкающих клеток (считая и ту, в которой стоит цифра) должно быть
закрашено. Краткость правила не соответствует сложности, а
приводит к тому, что труднее указать общий порядок решения
головоломки. Можно только дать минимальные рекомендации.
9
5
4
3
6
4
4
5
4
4
2
5
0
5
2
5
3
5
4
4
2
6
6
4
4
4
6
3
6
5
5
4
9
5
4
3
6
4
4
5
4
4
2
5
0
5
2
5
3
5
4
4
2
6
6
4
4
4
6
3
6
5
5
4
Рис. 507 Рис. 508
• Как и в традиционном варианте, здесь удобно использовать
карандаши двух цветов и начать с закрашивания жёлтым
(серым) цветом клеток с цифрой 0 и вокруг неё. Хотя нуля
может и не быть.
• Далее ищем цифру 9 и закрашиваем её, вместе со всеми
прилегающими клетками, черным цветом.
• Всё остальное сводится к рекомендации смотреть, думать,
искать, закрашивать.
■
9
4
3
4
4
1
2
5
2
5
3
5
4
4
2
4
4
4
3
6
5
4
Рис. 509
Рис. 510

Числовые фантазии. Рисование по-японски
293
Рис.512
Закрасьте рисунок.
0
0
3
0
4
5
4
0
0
0
0
5
4
5
0
3
0
4
5
0
3
2
4
0
0
3
3
3
0
0
3
3
3
0
3
3
4
0
5
6
0
0
4
2
4
5
5
4
3
5
3
3
3
2
0
2
3
5
5
4
2
3
4
0
4
5
3
3
3
0
3
0
4
4
0
3
3
3
2
3
4
3
3
5
3
4
2
0
0
3
3
4
4
3
4
2
2
5
3
2
3
3
3
2
3
3
3
2
3
2
2
3
5
4
3
2
3
3
0
3
4
3
3
2
2
0
3
3
3
2
0
2
0
0
0
0
Рис.513
Процесс верстки книги накладывает свои fpeбoвaния не
только на расположение текста и рисунков на странице, но порой
и на количество материала. Сейчас,можно бы и завершить
изложение, но считается лучше, если глава закончится на четной
странице, а заголовок следующего раздела пойдет на нечетной.
Поэтому разрешите предложить вам еще одно задание
традиционного японского рисования по клеточкам.

294
Числовые фантазии. Рисование по-японски
6-141
2
2
2
2
3
2
5
1
1
1
3
2
2
1
2
2
4
6
1
6
2
Ю
4
2
2
3
4
2
2
2
1С
8
2
6
2
4
5
7
3
1
2
3
3
6
1
5
2
1
2
1
2
3
2
1
2
1
2
1
1
2
1
1
3
3
1
1
2
1
2
2
3
6
5
3
3
3
1
2
7
5
2
Рис. 514
И пусть в конце стоит фраза Сократа, которая настраивает
на продолжение процесса мышления: «То, что я понял -
прекрасно. Думаю, таково же и то, чего я не понял».

Книга - великая вещь, пока человек умеет ею
пользоваться.
А. А. Блок (1880-1921) -русский поэт
Учитесь читать - это, может быть, гораздо
труднее, чем вы воображаете. Учитесь быть
разборчивым в вашем чтении, читать добросовестно и с
величайшим для вас доступным вниманием все, к чему
вы питаете действительный интерес.
Т. Карле иль (1795-1881) - английский писатель
Общение с книгой - высшая и незаменимая
форма интеллектуального развития человека.
А. Твардовский (1910-1974) -русский поэт
Чтение книг - это лишь начало дела.
Творчество жизни - вот цель.
Н. А. Рубакин (1882-1946) -русский писатель

Ответы и решения. 1 (1-3)
297
Ответы и решения
Бросая в воду камешки, смотри на круги,
ими образуемые; иначе такое бросание будет
пустою забавой.
Козьма Прутков
Глава 1. Кросс-суммы
1-1
Рис.515
1-2
Рис.516
1-3
Рис.517

298 Ответы и решения. 1 (1-3)
1-1. Выпишем числа из условия первой задачи в ряд по
возрастанию:
1,2,3,4,5,6,7,8,9.
Числа, равноудаленные от краев этого ряда, имеют одинаковую
сумму 1+9=2+8=3+7=4+6=10. Ставим эти числа попарно на
концах диаметров, а центральное число ряда - 5, ставим в центр
фигуры. Подобное расположение дает одно решение задачи.
Другие решения получаются, если изменить порядок следования
чисел 1, 2, 3, 4 по окружности. Число 5 неизменно остается в
центре, а числа 6, 7, 8, 9 - неразрывно связаны со своей парой.
1-2. Выпишем все пары натуральных чисел, дающие в сумме 21.
1+20=2+19=3+18=4+17=5+16=6+15=7+14=8+13=9+12=10+11
Таких пар всего десять, нам нужно выбрать из них пять пар,
состоящих из последовательных чисел натурального ряда
1-3. Задача отличается от первой только количеством чисел.
Что полезного дало нам решение этих задач? Основная
мысль: если взять отрезок последовательных чисел
натурального ряда, то числа, равноудаленные от концов отрезка, имеют
одинаковую сумму. (Причем не обязательно чтобы отрезок
начинался с единицы).
В истории математики существует легенда, которую часто
соотносят с кем-нибудь из великих математиков, желая
подчеркнуть его одаренность еще в школьные годы. Однажды учитель
математики, чтобы немного отдохнуть на уроке, задал учащимся
сложную, как он полагал, работу: сложить все числа от I до 1000.
Но один из учеников дал ответ уже через минуту. Он использовал
выделенную нами закономерность: числа равноудаленные от
концов числового ряда, имеют одинаковую сумму
1 + 1000=2+999=3+999=.... Всего таких пар 500, значит общая
сумма 500x1001=500500.
В общем случае так вычисляется сумма членов
арифметической прогрессии, простейшим примером которой является
натуральный рад чисел:
Эту формулу вы изучали на уроках математики в средней школе.

Ответы и решения. 1 (4-9)
299
Рис. 518
Рис.519
1-6
1-7
Рис. 520
Рис. 521
1-8
1-9
Рис. 522!
Рис. 523

300
Ответы и решения. 1 (10-12)
1-10
Рис. 524
Рис. 525
1-12
Рис. 526
Обзор ответов на задачи 1-4...Ы2 показывает, что каждый
раз сначала приходится считать сумму всех чисел, потом искать
какими числами может быть образована искомая кросс-сумма и,
только после этого, искать возможную их расстановку в узлах
заданной фигуры.
В некоторых из задач 1-4...1-12 можно снова увидеть пары
чисел равноудаленных от концов числового ряда, и
просматривается некоторая симметрия в их расположении. За счет
перестановки чисел в таких парах можно получить другие решения,
отличающиеся от показанных. Например, в задаче 1-4 допускается
перестановка чисел в парах; в задаче 1-5 можно, оставив на
местах красные числа, переставить черные в двух «тройках» и
получить новое решение; в задаче l-l l второе решение получится
одновременной перестановкой таких пар чисел: 2-6, 3-7, 4-8, 5-9.
Относительно полноты ответов в дальнейшем подход будет
разный, экономя пространство, минимально мы показываем одно
из решений задачи, т.е. только ответ, но возможно и полное
исследование задачи, с указанием всех допустимых решений.

Ответы и решения. 1 (13)
301
1-13.
Решение задачи не представляет особой сложности.
Подбором находим, какие тройки, составленные из заданных чисел
(1, 2, 3, 4, 5, 6), дают в сумме число 12.
6+5+1=6+4+2=6+4+3=12
Других троек различных чисел, удовлетворяющих условию
задачи, не существует. Числа 4, 5, 6 одновременно входят в две
суммы, поэтому их нужно расположить в угловых кружочках, а
затем расставить оставшиеся числа 1, 2, 3 на сторонах
треугольника. Так получается решение поставленной задачи.
Но остановились мы на ней подробно, чтобы изучить
обобщенный вариант этой задачи: «расставить числа от 1 до 6 так,
чтобы сумма чисел вдоль каждой стороны треугольника была
одна и та же», не указывая конкретное значение суммы.
Когда в угловых клетках стоят наибольшие из заданных чисел: 4,
5, 6, то и кросс-сумма получается максимальная. Что будет, если
в угловых клетках поставить числа 1, 2, 3?
Кросс-сумма для каждого варианта устанавливается так:
сумму чисел, стоящих в углах удваиваем и складываем с суммой
оставшихся чисел, после чего делим на количество сторон.
[(1+2+3)-2+(4+5+6)]/3=9 - это минимальная из возможных кросс-
сумм в обобщенной задаче. Легко установить, что возможны и
промежуточные значения кросс-суммы: 10 и 11. Расставить числа
по местам для каждого варианта не составляет особого труда.
Рис. 527
Рис. 529|

302
Ответы и решения. 1 (14-15)
1-14
Рис. 531 Рис. 532
В условии задачи заданы только два варианта кросс-суммы:
20 и 17. Для каждого мы приводим по одному решению, хотя
есть и другие варианты. Попробуйте самостоятельно провести
исследование обобщенной задачи, найти все возможные значения
кросс-суммы и решения для них. Такая тренировка может
пригодиться в серьезной умственной работе.
1-15
Задача допускает аналитическое решение используя
системы уравнений с несколькими переменными. Обозначим искомую
кросс-сумму трех чисел S, а неизвестные числа сверху вниз и
слева направо: xi, x2, х3, х4, х$, Хб,х7, тогда:
Сумма всех чисел равна I+2+...+6+7=28. Она образуется: с одной
стороны - числом xj и суммой двух троек, с другой стороны -
суммой выделенных трех троек чисел без лишних 2- xj. Получаем
систему уравнений (
Рис. 533
2S=28
3S-2xi=28
Решая систему двух уравнений с
двумя неизвестными, получим:
xj=4,S=\2.
Одну переменную величину,
например х2, выбираем произвольно из
оставшихся чисел 1, 2, 3, 5, 6, 7, а
другие неизвестные находим из
уравнений, получая каждый раз новое
решение. С учетом осевой симметрии
получается 12 различных
решений задачи.

Ответы и решения. 1 (16-19)
303
1-16
Сумма может принимать
подряд все значения от 17 до 23 и
зависит от чисел, входящих
одновременно в два треугольника (они выделены
красным цветом). Все вычисления
аналогичны задаче 1-13.
Рис. 534
1-17
Не хочу занимать пространство книги всеми 11 решениями.
Приведу только два с наименьшей и с наибольшей суммами.
Надеюсь, опыт, полученный при решении предыдущих задач,
поможет вам довести исследование до конца.
28
38
Рис. 535
Рис. 536
1-18
1-19
Рис. 537
Рис. 538

304
Ответы и решения. 1 (20-23)
1-21
Рис. 539
Рис. 540
1-22
S=18
\
/
S=24
\
/
\
9
8
\
.4
1
6
у
2
ч9
'8
.5
4,
5^
'6
7
10
7 /
ю\
\
2 /
\
\
Рис. 541
Рис. 542
Рис. 543
Рис. 544
Ss20
\
/
S-26
\
/
\
7
у
Л
6
\
2
v
Л
3
4
'л >
10
ч5/
\9 /
2
Л
у
5 /
\
\
4/
\
1-23
Рис.545

Ответы и решения. 1 (24-28)
305
1-24
11-25
S=41
3
4
1
5
9
10
16
12
8
2
7
11
6
15
14
13
Рис. 546
Рис. 547
1-27
Рис. 548
Рис. 549
1-28
Рис. 550
Рис. 551

306
Ответы и решения. 1 (29-34)
1-29
1-30
1-31
Рис. 552 I
1-32
Рис. 553

Ответы и решения. 1 (35-37)
307
1-35
Показав ответы на задачи с
квадратами, подчеркнем еще раз, что не
всегда мы приводим все возможные
решения. Когда-то у вас получится
иное решение, проверьте его
правильность вычислениями сумм.
Рис. 558
1-36
Числа 1, 2, 3, 4, 5 ставим в соответствии с красной линией
через один угол по часовой стрелке, затем в пустые промежутки
против часовой стрелки ставим числа 6, 7 ,8, 9, 10. Сумма чисел
по каждой стороне в этом варианте равна 14.
Другое решение (с суммой 19), получится, если числа 6, 7,
8, 9, 10 разместить первым способом, а
оставшиеся - вторым.
Еще два решения (с суммами 16 и
17)можно получить этим же методом
расстановки, но, разбивая числа на четные и
нечетные, а пятое и шестое решения имеют
такие же суммы, но более сложное
построение. Попробуйте найти их
самостоятельно. Рис. 559
1-37
Рис. 560
Рис. 561

308
Ответы и решения. 1 (38-41)
1-38
1-39
Рис. 562
1-40
Рис. 563
1-41
Рис. 564
Рис. 565
В задаче 1-39 если сложить все 9 троек чисел, то 12 чисел
войдут в эту сумму дважды, а центральное число трижды.
(1+2+3+...+11+12+13)-2=182. В зависимости оттого, какое число
будет поставлено в центр, общая сумма может изменяться от 183
(в центре 1), до 195 (в центре 13). Из них только 189 (в центре 7)
делится на 9 (количество линий). Поэтому значение суммы 21
можно было не говорить заранее, оно получается в процессе
решения единственно возможное.
Метод решения задачи 1-41 аналогичен методу,
описанному для задачи 1-36. Первое решение имеет сумму 19. Если по
красному пути расставлять числа 1, 3, 5, 7, 9, 11, 13, а затем
оставшиеся четные числа, то получится другое решение с суммой 22.

Ответы и решения. 1 (42-45)
309
Если в приведенных решениях, заменить каждое число
разностью между 15 и этим числом, то получаются два решения с
суммами 26 и 23 соответственно.
1-42
Рис. 566
1-43
Рис. 567
1-44
1-45
Рис. 568
Рис. 569
Задача 1-45 позволяет провести целое исследование.
Приведем только его выводы:
• другое решение получается заменой чисел в парах 1-6, 2-10,
3-9,4-8,5-12;
• наименьшая сумма, удовлетворяющая условию -24, далее
следуют 26, 28 и другие только четные числа.

310
Ответы и решения. 1 (46-51)
1-46
1-47
Рис. 570
;...
Рис. 571
1-48
1-49
1-50
Рис. 572 !
Рис. 573
1-51
Рис. 574
Рис. 575

Ответы и решения. 1 (48-50) 311
1-48
У этой задачи возможны варианты, когда сумма четырех
чисел по всем прямым остается равной 26, но отличается от
суммы чисел в вершинах звезды. Сумма чисел, стоящих в шести
вершинах может равняться любому четному числу от 24 до 54
включительно, кроме 28 и 50. Причем количество решений не
одинаково для разных сумм при вершинах. В частности, для
суммы 26, существует 12 решений: 6 основных и 6 дополнительных,
получаемых из основных заменой каждого числа на разность
между 13 и эти числом. Остается масса вопросов для
самостоятельного исследования:
• почему сумма чисел при вершинах не может равняться 28 и 50?
• сколько различных решений существует для каждого значения
суммы чисел при вершинах?
• возможны ли другие варианты значений суммы четырех чисел
по каждой прямой?
1-49
Существуют модификации этой задачи:
• Требуется расставить числа от 1 до 13 так, чтобы сумма
четырех чисел в вершинах всех шести ромбов была одна и та же.
Как это проще всего сделать? Какое значение может
принимать эта сумма?
• Расставьте 13 последовательных чисел так, чтобы все шесть
сумм четырех чисел в вершинах ромбов были равны 1977.
Известно, что в центре стоит число 496. Какой ближайший
календарный год можно поставить в условие подобной задачи?
Например, при сумме 2002 в центре должно стоять число 503, а
отрезок последовательных чисел берется от 493 до 505.
1-50
Относительно семиконечной звезды известный мастер
головоломок Генри Дьюдени утверждал, что существует 56
решений задачи, а редактировавший его книгу корифей занимательной
математики Мартин Гарднер сделал примечание о
существовании 72 решений. Конечно, ни тот, ни другой не могли привести
исчерпывающий перечень решений. Это может сделать только
каждый для себя, если хватит терпения, желания и усидчивости.

312
Ответы и решения. 1 (52-56)
Рис. 576 Рис. 577
Для случая восьмиконечной звезды известно 112 различных
решений. Если вместо каждого числа поставить разность между
числом 17 и этим числом, то получится второе решение. Казалось
бы, решений огромное количество, какой смысл брать подобные
задачи? Однако, когда пытаешься найти хотя бы одно из 112
решений, начинаешь понимать, что это не так-то просто. Количество
решений и легкость нахождения хотя бы одного из них не всегда
однозначно связаны. Зная решение для одной из восьмиконечных
звезд, можно получить решение для другой. Для этого внимательно
присмотритесь к двум рисункам, и вы сможете вывести алгоритм
перестановки чисел, связывающий решения внешне различных
задач.
1-54
1-55
Рис. 578
Рис. 579
Рис. 580

Ответы и решения. 1 (57-62)
313

314
Ответы и решения. 1 (63-68)
1-63
Рис. 587
1-65
.{
1-66
Рис. 589
1-64
Рис. 588
1
3
|2
I4
7
5
8
6
Рис. 590
1-67
1-68
в с
в
А
Е
Рис. 591
Рис. 592

Ответы и решения. 1 (69-70)
315
Задача 1-66 требует комментария, потому что решается
нестандартно. Сумма всех цифр, входящих в задачу равна 39 (прот
пущена цифра 6) и не делится на 2. Поменять местами нужно
цифры 8 и 9, но дополнительно «девятку» перевернуть,
превратив в «шестерку» и тогда все получится.
1-69
Остальные решения этой задачи
можно условно записать так:
12-3-4—56-7-8
1.2-3-4—5-67-8
1.23-4—5-6-7-8
1.-2-3-4—5678
1234—5-6-7-8
Рис. 593
1-70
Рис. 594

316
Ответы и решения. 1 (71-73)
1-71
0
1
2
|о
1
3
0
0
4
LgJ
о
2
«I
6
3
1
О
5
1
2
4
1
J^
6
2
з"
5
3
2
4
4
О
6
5
5
6
О
6J
3
4
6
6
4
з|
5
1
3
2
5.
2
6 1
Е
3 4
Рис. 595
При составлении квадратов нужно пользоваться
следующим правилом. Если общая сумма очков на выбранных четырех
костях равна, например, 7 как в первом квадрате из примера, а вы
хотите, чтобы сумма вдоль каждой стороны равнялась 3, то сумма
очков в четырех углах вычисляется так: 4-3-7=5. Это правило
необходимо для правильной ориентации костей в «четверках».
1-72
Правило из предыдущей задачи
применимо и здесь. Сумма всех очков на 4-х костях
равна 51. Требуемая сумма по сторонам 17,
значит, сумма очков в угловых клетках
должна быть 17-4-51=17
Рис. 596
1-73
На рисование подобной рамки жалко места в книге,
поэтому просто перечислим какие кости стоят, начиная с левого
верхнего угла с обходом по часовой стрелке: 2-1, 1-5, 5-5, 5-4, 4-4, 4-2,
2-0, 0-6, 6-4,4-1, 1-1, 1-3, 3-3, 3-4, 4-0, 0-0, 0-1, 1-6, 6-6, 6-5, 5-2, 2-
2, 2-6, 6-3, 3-0, 0-5, 5-3, 3-2. В этом варианте решения сумма
очков по сторонам равна 44. Сумма очков на косточках полного
набора домино - 168. В угловых клетках стоят 2, 0, 4, 2, сумма
которых 8. Расчеты дают 44-4-168=8.
Выходит, если допустить теоретически, что во всех угловых
клетках стоят пустые половинки, то сумма по сторонам может
равняться минимум 42, а если в угловых клетках шестерки, то
максимум - 48. Но можно ли сделать это практически, соблюдая
принцип домино при выкладывании большой рамки?

Ответы и решения. 1 (74-77)
317
1-74
Сумма всех оставшихся очков равна 132. Разделите сначала
все костяшки на три кучки по 44 очка в каждой. Если мы хотим,
чтобы сумма очков по каждой стороне равнялась 12-ти, необходимо
добиться, чтобы сумма очков, стоящих по четырем углам, в каждой
рамке равнялась 4. Потому что 12-4-44=4. Остальное получается
методом проб и ошибок. Причем можно перекладывать отдельные
кости из одной кучки в другую, если на них равное число очков.
•
• •
7.
•••II
•••II
Ч
V
•••
•••
9
V
X
•
• •
•
ч
IE
• •
• «Г •
• •
*.
• #
• •
Ч
•
3[Х
• •
ч
Х1Г •
•
ч
Рис. 597
1-75
0
6
5
1
0
1
2
1
5
1
0
5
3
2
3
2
2
0
3
3
0
1
4
4
4
0
1
б|б
2|4
1
6
1
3
2
4
6
3
0
5|4
б|2
0
2
6
5
6
4
3
4
5
3
5
5
Рис. 598
1-76
2
1
5
5
0
4
2
3
0
0
3
5
4
1
5
1
0
3
4
4
3
6
2
4
3
5
6
2
6
5
2
6
2
3
2
6
3
0
6
4
6
5
1
1
4
0
3
4
2
1
1
5
0
6
0
Рис. 599
1-77
5
3_
3
0
0
2_
2"
6
3
1 1|1
0|0Ц0|5
6
1|1|2
6
0^
0
4
5
2_
~2
2
1|5||5|4
6|4|4|2
2|3|3|3
4
1
0
4
4^
4"
3
Рис. 600

318
Ответы и решения. 1 (78-80)
1-78
1-79
6
5
6
1
0
2
2
2
1
2
1
4
5
4
3
3
6
1
ю|со
0
1
5
6
4
0
5
5
4
0
2
5
5
4
4
0
м|ео
0
611
б|о
1
3
3
6
1
4
2
0
3
3
2
4
6
Рис. 601
Рис. 602
1-80
3|2|2|010[4|41б
0[0|0|5|5|4|4|3
Рис. 603

Ответы и решения. 2 (1-5)
319
Глава 2. Магические квадраты
2-1 Антимагический квадрат
14
1
2
4
5
7
8
3
6
9
= 9
= 15
= 21
и
7 20 18 17
Возможны и другие решения, но такие
квадраты мало кого интересовали в отличие
от магических, поэтому, сколько различных
решений не известно. Логично
предположить, что неупорядоченность встречается
гораздо чаще упорядоченности.
Рис. 604
Неполный магический квадрат
2-2 2-3
2-4
7
3
2
5
1
6
8
4
5
1
6
7
3
2
8
4
7
2
3
4
8
5
6
1
Рис. 605
Рис. 606
Рис. 607
Магическая сумма у неполного квадрата равна 12 при
любом расположении выброшенной клетки. В неполном ряду такая
сумма может быть образована только двумя парами чисел: 5 и 7,
8 и 4. Находим допустимое расположение для этих пар,
остальные числа расставить уже несложно.
2-5 Шутливый квадрат
1+1+1
3 + 3
/
6
2+4
8
3
6
9
12
6
12
3
6
9
18 30 18
= 18
= 18
= 30
Рис. 608

320
Ответы и решения. 2 (6-8)
1
1
6
2-6 Квадрат с довеском
Ответ на рисунке и некоторые замечания. По
аналогии с неполным квадратом интересно бы
исследовать на возможность получения
магических сумм всевозможные варианты квадрата,
у которого одна клетка вырезана и приставлена
в другом месте.
8
8
8
Рис. 609
Рис.610
2-7 Определитель магического квадрата
Пусть N=S/3 - магическая сумма данного
квадрата. Тогда N= (x1+y2+z3)+(x2+y2+z2)+(x3+y2+z1)-
(x1+x2+x3)-(zI+z2+z3)=3y2, S=9y2
Отсюда, складывая строки и столбцы определителя,
выносим за знак определителя произведение 9у2= S.
Xi
Х2
Хз
У<
У*
Уз
Zi
Z.2
Рис.611
D =
Xi
Х2
Х3
У"
У*
Уз
Zi
Z2
z3
Xi yi Zi
X2 У2 Z2
3y23y23y2
xi у. Зу2
*>* Зу,
Зу2Зу29у2
=3
•Зу2
Xi yi
Хг Уз
1 1
У2
1
Значит D кратно S и D/S целое число. Что и требовалось доказать.
2-8 Пандиагональный гетероквадрат
Если мы сложим все числа, стоящие в каждой строке,
каждом столбце и на двух диагоналях, то при этом каждое
число войдет в сумму четырежды. Следовательно, полученная
общая сумма равна
4-[п2-(п2+1)/2]=2п2-(п+1)
Если бы существовало такое к , что 4п сумм представляли бы собой
последовательные числа от к до к+4п-1 включительно, то общая
сумма равнялась бы 2п-(2к+4п-1). Приравнивая между собой
полученные выражения, приходим к равенству
n-(n2+l)=2k+4n-L

Ответы и решения. 2 (9-11)
321
Но слева стоит четное, а справа - нечетное число. Следовательно,
нужного к не существует ни при каком и, а это значит, что ни при
каком п наши суммы не совпадают с 4п последовательными
целыми числами. Ответа красивее, чем в задаче 2-1 не получится.
2-9 Гномон-магические квадраты
Пусть гномон-магический квадрат имеет вид как на рис. 104.
В соответствии с определением
Из равенства первых двух сумм, находим, что
Из равенства двух вторых сумм получаем
yi+zi= y3+z3 или zrz3=y3-yi.
Следовательно, Xj-x3= zj-z3 или Xj+z3=x3+zj. Прибавив к обеим
частям последнего равенства у2, получим требуемое утверждение.
Это свойство не распространяется на квадраты 4-го порядка, но
углубляться в исследование не станем.
2-10 Квадрат из крестов
Для суммы 30 ответ
приведен на рисунке. Для построения
квадрата с суммой 48 в центре
ставится число 4, и квадрат
заполняется числами 4, 5, 6, 7; для суммы
66 - числа 6 - 6, 7, 8, 9 по такой же
схеме. Если в центр поставить
число 5 и расставить по схеме
числа 5. 6, 7, 8, то получится
сумма 57 (при изменении
центрального числа на I сумма меняется на 9).
Рис.612
2-11 Неправильный магический квадрат
Числа 2 и 15 в сумме дают 17, значит и
заменяющие их числа должны иметь сумму 17. В
данном решении повторяются числа 7 и 10.
2
5
2
3
4
3
4
3
4
2
3
4
5
2
5
4
3
2
5
4
3
2
2
2
3
4
5
2
3
4
5
2
5
4
3
2
4
3
4
3
4
3
2
5
2
1
13
8
12
10
10
3
11
9
5
16
4
14
6
7
7
Рис.613

322
Ответы и решения. 2 (12-13)
2-12
4 строки, 4 столбца, 2 главных диагонали, 6 ломаных
диагоналей, 9 квадратов 2-го порядка, четыре угловых клетки в 4-х
квадратах 3-го порядка и 1-ом исходном, четыре угловые клетки
в прямоугольниках 2x4 и 3x4 -10 вариантов. Всего - 40 вариантов.
Немного обобщим мысли навеянные последними задачами.
У каждого понятия, явления есть противоположность: черное -
белое, порядок - хаос, равенство - неравенство, сложение -
вычитание. Одно и то же содержание, можно по-разному выразить
внешне. Например, число «три» можно записать любой цифрой
3=1+1+1=2+2/2= и т.д. Эти рассуждения интересны с философской
точки зрения, но могут далеко увести нас от математики, поэтому
продолжим разбор решений задач.
2-13 Центрированный квадрат
9
3
12
21
20
9
3
12
21
20
9
3
12
21
20
11
25
19
8
2
11
25
19
8
2
11
25
19
8
2
18
7
1
15
24
18
7
1
15
24
18
7
1
15
24
5
14
23
17
6
5
14
23
17
6
5
14
23
17
6
22
16
1С
4
12
22
16
10
4
13
22
16
10
4
13
9
3
12
21
20
9
3
12
21
20
9
3
12
21
20
11
25
19
8
2
11
25
19
8
2
11
25
19
8
2
18
7
15
24
18
7
1
15
24
18
7
1
15
24
5
14
23
17
6
5
14
23
17
6
5
14
23
17
6
22
1С
1С
4
12
22
16
ю
4
13
22
16
10
4
13
9
3
12
21
20
9
3
12
21
20
9
3
12
21
20
11
25
19
8
2
11
25
19
8
2
11
25
19
8
2
18
7
1
15
2'
1*
7
1
1!
24
18
7
1
15
24
5
14
23
17
6
5
14
23
17
6
5
14
23
17
6
22
16
10
4
13
22
16
10
4
13
22
16
10
4
13
Рис. 614
Этот квадрат, составленный из девяти одинаковых
магических квадратов 5-го порядка с цифрой 1 в центре называется на-
зикским квадратом (в честь Назика - места в Индии) и является
единственным правильным квадратом с уникальным свойством.

Ответы и решения. 2 (14-19)
323
Передвигая по его поверхности пустую квадратную рамку
размерностью 5x5 можно выделить магический квадрат 5-го порядка
с любым числом от 1 до 25 в центральной клетке!
2-14 Условный квадрат
2-15 Матрешка из магических
квадратов
18
24
6
12
22
16
10
4
14
20
2
8
Рис. 615
2-16 Квадрат из четырех цифр
5
1
4
76
7
74
67
66
69
80
20
14
58
65
64
10
56
2
59
55
31
46
33
48
47
27
23
73
30
50
38
43
42
32
52
9
61
57
29
45
41
37
53
25
21
3
28
60
40
39
44
22
54
79
63
71
35
36
49
34
51
11
19
12
26
68
24
17
18
72
62
70
13
81
78
6
75
8
15
16
77
2243
3141
1342
1341
2242
3143
3142
1343
2241
1
4
7
6
7
6
1
4
2
3
8
5
8
5
2
3
Рис.616
2-17 Квадрат с двойным
набором цифр
S=6726
Рис.617
2-18
Рис.618
Выше уже было сказано, что произвольность в выборе чисел
для составления магического квадрата 3-го порядка ограничена. Эти
9 чисел должны быть членами трех арифметических прогрессии,
только тогда из них можно составить магический квадрат (рис.
151). Откуда следует, что магическая сумма кратна трем:
S=(a+d+2n)+a+(a+2d+n)=3a+3d+3n=3-(a+d+n).
2-19
На рисунке показан один из ответов на
первую часть вопроса, а вторая часть остается для
самостоятельных раздумий, должна же быть
какая-то тайна. Рис. 619
1
-4
1
-4
1
1
-4
1
-4
1
1
1
1
1
1

324
Ответы и решения. 2 (20-28)
2-20 Нет. Сумма всех чисел в таблице может быть выражена,
как итоговая сумма всех сумм по столбцам или как итоговая
сумма всех сумм по строкам. Естественно, она не может быть в
одном случае отрицательной, а в другом положительной.
2-21
2-22
2-23
10
14
32
2
4
15
16
7
10
8
11
6
13
20
15
1
Рис. 620
31
34
7
2
8
1
32
33
30
9
35
6
3
5
■
4
29
36
Рис. 621
30
41
37
42
49
48
53
44
35
39
32
54
50
46
43
36
40
31
47
52
51
33
38
34
45
Рис. 622
2-24
96
88
61
19
II
69
86
98
89
91
18
66
68
16
99
81
2-25
18
66
91
89
99
81
16
68
86
98
69
II
61
19
88
96
473
248
725
734
482
230
239
716
491
Рис. 623
Рис. 624
2-26
2-27
Рис. 625
602
107
806
709
505
301
204
903
408
Рис. 626
380
155
632
641
389
137
146
623
398
2-28
1350 талеров.
191
197
59
17
149
281
239
101
107
192
198
60
18
150
282
240
102
108
193
199
61
19
151
283
241
103
109
Рис. 627

Ответы и решения. 2 (29-32)
325
2-29
14
1
12
7
11
8
13
2
5
10
3
16
4
15
6
9
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис. 628
2-30
6
-16
10
-11
12
-1
5
4
-9
Рис.629
2-31
1
-1
1
-1
-1
1
-1
-1
1
1
Рис. 630
2-32
К
в
D
В
D
К
D
К
В
13
11
12
11
12
13
12
13
11
S=36
Рис. 631
6
13
2
11
5
13
1
9
10
12
2
2
5
10
11
2
1
11
9
7
10
8
7
13
4
12
1
6
4
3
9
8
12
8
7
3
13
8
9
7
6
5
10
3
6
5
4
11
12
11
13
8
8
5
9
7
5
10
11
8
13
9
8
11
5
13
11
6
7
7
12
12
6
7
12
6
9
10
10
13
9
12
9
6
5
S=54 max
11
13
12
6
9
11
7
10
13
10
9
9
8
12
13
S=51
11
12
10
12
6
I
9
10
11
8
13
10
12
11
13
11
13
10
12
12
10
13
11
13
11
12
10
5=45
S=51
Рис. 632

326
Ответы и решения. 2 (33-38)
2-33
2-34
Рис. 633
Рис. 634
2-35
2-36
4
О
3
3
2
3
О
5
3
1
5|1
2
4
4
1
2
2
Рис. 635
Рис. 636
2-37
2-38
S=12
S=24
Рис. 637
3
О
6
2
1
О
2
О
4
О
6
О
6
1
О
О
5
О
6
1
6
О
6
5
6
6
6
2
3
1
3
2
6
4
6
3
Рис. 638

Ответы и решения. 2 (39-42)
327
2-39
-18
2-41
3I2
511
5I4
1|1
3I4
6I6
116
112
315
613
6|5
215
412
212
416
313
1 14
4I4
6I2
1 Ю
5I5
6
4
0
О
1 |0
ЗЮ
2|0
5J0
3
О
Рис. 639
Рис. 640
2-40
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Для магического квадрата 4-го
порядка, составленного, учитывая
половинки костей, магическая сумма может
принимать значения от минимального,
равного 5 (см. рис.) до максимального -
равного 19. Этот разброс зависит от
конкретного выбора 8 костей из полного их
набора. Если в показанном квадрате,
каждое число заменить его дополнением
Рис. 641 до 6, то получится магический квадрат с
максимальной суммой 19.
2-42
Алгоритм перехода указан
в предыдущей задаче - каждое
число заменить его дополнением
до 6. В этот раз максимальная
сумма получится 23.
• •
• •
•
•
•
•
•••
• •
• •
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
• •
• •
•
•
•••
•••
•
•
•
•
• •
• •
•
Рис. 642

328
Ответы и решения. 2 (43-45)
2-43
Ни в одной строке или столбце
одно и то же число не повторяется
дважды, но каждый раз
присутствуют шесть чисел из семи. А вот
возможен ли вариант без пустышек
- это предстоит вам самостоятельно
выяснить, ответа не даем
принципиально до следующего издания
книги.
• •
• •
:•:
•
•
•••
•••
• •
•
•
•
•
•
•
•
•
• •
• •
•
• •
• •
• •
•
• •
• •
•••
•••
•
X
Рис. 643
2-44
а). Средний квадрат можно сделать магическим, ответом служит
задача 2-40, остается только разложить оставшиеся косточки на
квадраты 2x2 и 6x6 без какого-то порядка.
б). Большой квадрат тоже можно сделать магическим (см. 2-41), а
остальные выложить в произвольном порядке.
в).
3
2
6
1
5
2
5
0
3
|з|
|2|
0
|в
I1
Is
4
|1
I4
з
2
4
6
2
2
5
О
2
3
2
4
4
6
1
5
3
1
4
3
0
1
0
6
6
Рис. 644
2-45
2
1
1
5^
4~
1
2
5
3
3
о]
1
1
4
3
5
4
6
6
2
4
2
4
и
Т]
2]
6
3
6
3
5
1
0
3
4
6
2
3
0
2
3
5
6
0
5
0
3
0
3
5
6
4
0
0
Рис. 645

Ответы и решения. 2 (46-49,64,71)
329
2-46
Прежде всего, существуют три расположения, которые
отличаются между собой цветом центрального квадратика.
Казалось бы, различные расстановки остальных квадратиков вокруг
центрального, при ближайшем рассмотрении, переходят друг в
друга в результате поворотов и, следовательно, различными не
являются. Итак, разных только 3.
2-47
Рис. 647 Рис. 648
Обе задачи сводятся к составлению латинских квадратов.
В 2-47 это просто латинский квадрат, в котором вместо цифр
стоят различные цвета. Дополнительное требование, чтобы
одинаково закрашенные квадратики не касались даже по диагонали,
достигается циклическим сдвигом следующей строки на 2 клетки
вправо. В 2-48 нужно найти три попарно ортогональных
латинских квадрата 4x4 (один дает цвет, другой - фигуры, третий -
цифры). У квадрата 4-го порядка ортогональных как раз - три.
2-49
2-64
2-71
4
5
1
3
3
2
4
5
5
1
3
2
2
4
5
1
1
1
1
1
1
1
1
1
1
1
1
11
4
12
14
16
7
2
9
1
10
15
6
5
13
8
3
S=50
Рис. 649
S=12
Рис. 650
Рис. 651

330
Ответы и решения. 2 (50-59)
2-50
Рис. 652
2-53
в
в
D
а
в
п
в
ияшш
Рис. 655
2-51
Рис. 653
2-54
Рис. 656
2-52
Рис. 654
2-55
Рис. 657
2-56
1
3
5
2
4
3
2
4
5
1
4
5
3
1
2
5
1
2
4
3
2
4
1
3
s
Рис. 658
2-57
5
3
2|
4
3
1
И
2
5
4
2
5
1
2
5
1|
4
3
1
5
3
2
Рис. 659
2-59
1
3
2
4
5
5
4
1
2
3
4
2
5
3
1
3
1
4
5
2
2
5
3
1
4
Рис. 660
2-58
В каждой строке нечетное число отрицательных чисел, а
всего 5 строк, следовательно, общее количество отрицательных
чисел в квадрате - нечетное. Нечетное число нельзя представить в
виде суммы пяти четных чисел, значит, хотя бы в одном столбике
будет нечетное число отрицательных чисел.

Ответы и решения. 2 (60-65)
331
2-60
шшшл
Щ3 D
2 5 4
ш
I
ft
5
в
5
4
——
2
1
Рис. 661
2-61
7
8
9
5
1
2
3
6
4
3
5
2
9
4
6
1
8
7
6
4
1
8
7
3
5
9
2
1
9
8
7
6
4
2
5
3
5
7
6
2
3
9
8
4
1
2
3
4
1
8
5
6
7
9
9
2
3
6
5
7
4
1
8
4
1
5
3
9
8
7
2
6
8
6
7
4
2
1
9
3
5
Рис. 662
2-62
2-63
5
3
1
6
2
4
4
1
2
3
6
5
2J6
6j4~
4[3
5
1
3
2
5
1
1
5
6
4
3
2
3
2
5
1
4
6
6
3
2
1
5
4
5
4
3
6
1
2
2 |1
1
4
5
3
5
6
2
4
6 3
4
6
5
3
2
1
3
2
1
6
5
Рис. 663
Рис. 664
2-65
61
60
12
13
20
21
37
36
62
11
59
14
19
38
22
35
63
58
10
15
18
23
39
34
64
57
9
16
17
24
40
33
1
8
56
49
48
41
25
32
2
7
55
50
47
42
26
31
3
54
6
51
46
?7
43
30
4
5
53
52
45
44
28
29
I
?
L
I
L
?
L
^4
v>
/\
4>
f~
v_
1
T
-4
J
/—
1
т
4-
^4
"4
Л
s/
I
s
J
1
)
s
J
Рис. 665

332
Ответы и решения. 2 (66-70)
2-66
2-67
к
■■г
в
*
т
А
К
д
т
Д
*
к
к
А
в
Рис. 666
Рис. 667
2-68
1
□
ц
5
D
I 3 I 4
4
о
В
D
3
ш
2
D
Задачи 2-66 и 2-68 сводятся к
построению греко-латинских квадратов,
как совмещения двух ортогональных
латинских квадратов. К ответу задачи 2-
68 требуется дать пояснение. Чтобы не
усложнять рисунок изображением
майоров-кавалергардов, условимся, что
цветом закодировано одно из пяти
воинских званий, а цифрами - род войск.
Рис. 668
2-69
2-70
Рис. 669
Рис. 670

Ответы и решения. 3 (3-4)
333
Глава 3. Магическое разнообразие
3-3
S=36
(-10) S=37
Рис. 671
3-4
S=36
(-10)
(-3)
Рис. 672
Рис. 673
Классический магический шестиугольник Адамса имеет
магическую сумму 38, т.к. сумма всех чисел от 1 до 19 делится на
5 рядов, получается (1+19)-19/2=190, 190/5=38. Отсюда можно
сделать вывод, что строя шестиугольник 3-го порядка с одой
пустой ячейкой, можно выбрасывать только числа кратные 5, а
именно: 5, 10, 15. Соответственно возможны варианты с
магическими суммами 37, 36 и 35. Для двух сумм варианты ответов
показаны. Данные рассуждения не зависят от месторасположения
пустой ячейки. Для шестиугольника 4-го порядка с одной пустой
ячейкой возможны магические суммы: 100, 99, 98, 97, 96, т.к.
сумма всех чисел равна (1+37)-37/2=703 и на 7 рядов из меньших
сумм делятся только700 (-3), 693 (-10), 686 (-17), 679 (-24), 672
(-31). Кроме того, возможны красивые варианты с большим
количеством симметрично расположенных пустых ячеек.

334
Ответы и решения. 3 (5-9)
3-5
Задача имеет много
решений, но среди них есть одно,
получаемое из шестиугольника
Адамса путем простого
преобразования. Нужно в каждой
ячейке написать разность
между числом 20 и числом,
стоящим в ячейке.
Рис. 674
3-6
а). Нельзя, можно только при
четных п>4
б). См. рис. 234.
1
12
11
2
3
10
9
4
8
5
7
6
Рис. 675
3-7 Это задание выполняется только самостоятельно!
3-8
Пусть в прямоугольнике п строк и к столбцов. Тогда должны
выполняться следующие соотношения: п=2-к, я7с=1986=2-3-331.
В разложении 1986 на множители число 331 простое. Отсюда
ясно, что решения нет.
3-9
Сумма чисел от 1 до 9 равна 45. Если в угловые клетки
поставить три самых маленьких числа из этого набора (1,2, 3), то
кросс-сумма по каждой стороне будет равна (45+6)/3=17 - это
минимальное значение. Если в угловые клетки поставить самые
большие числа из набора (7, 8, 9), то кросс-сумма будет равна
(45+24)/3=23. - это ее максимальное значение. Исходя из этих
рассуждений, для каждой суммы находим числа, которые
должны стоять в угловых клетках, а остальные расставить совсем не
трудно. Ответы для сумм 17 и 20 даны в задаче 1-14, остаются
суммы: 19, 21, 23. Для четных сумм 18 и 22 решения нет.

Ответы и решения. 3 (10-13)
335
Рис. 676
Рис. 677
Рис. 678
3-10
3-11
Рис. 679
Рис. 680
3-12 Это задание выполняется только самостоятельно!
3-13
Рис. 681

336
Ответы и решения. 3 (14-16)
3-14
Допустим, мы пронумеровали грани правильного
многогранника числами от I до п. Если в каждой вершине
многогранника сходятся m граней, то искомая сумма должна быть равна
(1+п)т/2. Отсюда следует, что либо т - четно, либо п - нечетно.
Для всех правильных многогранников п - число четное, и только
у октаэдра в вершинах сходится четное число граней (4). Таким
образом, задача разрешима только для октаэдра. Грани октаэдра
можно пронумеровать так, чтобы сумма чисел, соответствующая
граням, сходящимся в одной вершине, была равна 18 для всех
шести вершин. Это можно сделать тремя существенно
различными способами, каждый из которых имеет два варианта. Решения
изобразим схематически в плоской интерпретации.
3-15
У правильных многогранников количество граней,
сходящихся в одной вершине, совпадает с количеством ребер,
сходящихся в ней. Поэтому рассуждения при решении предыдущей
задачи можно полностью перенести на эту задачу. Решение есть
только для октаэдра, но нужно нумеровать подобным образом не
грани, а ребра.
3-16-1
Группируя числа I, 2, 3, 4 в суммы по три, можно получить
следующие суммы 4+3+2-9, 4+3+1=8, 4+2+1=7, 3+2+1=6. Все
суммы разные и других вариантов нет. Следовательно, задача не
имеет решения. К аналогичному выводу мы придем, если
посмотрим на треугольники ABC и ABD. Равенство сумм в этих
треугольниках возможно только при C=D.

Ответы и решения. 3 (16)
337
Рис. 683 Рис. 684
Вот если дополнительно установить по кружочку на каждое
ребро фигуры, то мы получим конструкцию как в задаче 1-17,
только там не требовалось равенство суммы по большому
треугольнику, а только по трем маленьким (в реальной объемной
модели они все одинаковые).
3-16-2
Рис. 685 Рис. 686
Рассмотрение треугольников ABC и ABD, показывает, что
решения с данными условиями быть не может. Возможно
решение при двойном наборе цифр I, 2, 3. Кроме того, можно попро^
бовать поместить еще по кружочку на каждое ребро и
расставлять числа от 1 до 18.
з-16-з
Наличие треугольников с одной общей стороной и разными
третьими вершинами не позволяет решить задачу и для третьей
модели. Горький опыт последних трех задач приводит нас к
важному выводу: красота фигуры не гарантирует существование
решений. Зная это заранее, я все-таки оставил эти примеры именно
для демонстрации прискорбного факта о трудности
придумывания новых задач, даже по аналогии с десятками похожих.

338
Ответы и решения. 3 (16-18)
3-16-4
Специальное
послабление в условие, позволяет
выбросить пять чисел
последовательного ряда, а остальные
расставлять в вершинах
додекаэдра. В частности
решение получается, если
выбросить числа I, 7, 13, 19, 25.
Рис. 687
3-17
У куба шесть граней по 4 плоских угла. Сумма чисел
I +2+... +23 +24=300, тогда сумма номеров одной грани должна
быть равна 50 (300/6=50). Можно пронумеровать плоские углы
таким образом: (1, 2, 23, 24), (3, 4, 21, 22), (5, 6, 19, 20),
(7,8, 17, 18), (9, 10, 15, 16),(11,12, 13, 14).
У тетраэдра 12 плоских углов на 4 гранях. Сумма номеров
78 не делится на 4. У октаэдра 24 плоских угла на 8 гранях.
Сумма номеров 300 не делится на 8. У додекаэдра 60 плоских углов
на 12 гранях. Сумма номеров 1830 не делиться на 12. У икосаэдра
60 плоских углов на 20 гранях. Сумма номеров 1830 не делится
на 20. Таким образом, задача имеет решение только для куба.
3-18
Рис. 688
Можно попробовать расставить 15
чисел в 5 вершинах и на 10 ребрах
проекции пентатопа так, чтобы сумма 10
чисел в каждом из 5 тетраэдров была
одна и та же. Числа, стоящие в вершинах
входят сразу в 4 тетраэдра, а на ребрах -
в 3 тетраэдра. Этот факт нужно
учитывать при вычислении кросс-суммы.
Пробуйте, может быть получится.

Ответы и решения. 5 (1-6) 339
Глава 5. Магия азарта
5-1
В ответе записана очередность передвижения фишек в
решении за 44 хода: 14, 11,12, 8, 7, 6, 10, 12, 8, 7, 4, 3, 6, 4, 7, 14,
11, 15, 13, 9, 12, 8, 4, 10, 8, 4, 14, 11, 15, 13, 9, 12, 4, 8, 5, 4, 8, 9,
13, 14, 10,6,2, 1.
Решение за 39 ходов: 14, 15,10, 6, 7, 11,15, 10, 13, 9, 5, 1, 2, 3,
4, 8,12,15,10,13,9,5,1,2, 3,4, 8,12,15,14,13,9,5,1,2,3,4, 8, 12.
5-3
Магический квадрат удается получить за 50 ходов: 12, 8, 4,
3, 2, 6, 10, 9, 13, 15, 14, 12, 8,4, 7, 10, 9, 14, 12, 8, 4, 7, 10, 9, 6, 2, 3,
10, 9, 6, 5, 1, 2, 3, 6, 5, 3, 2, 1, 13, 14, 3, 2, 1, 13, 14, 3, 12, 15, 3.
5-4 Клетки пронумеруем числами от 1 до 10, а три
свободные сверху - 11, 12,'13. В каждом ходе на первом месте указан
номер фишки, а на втором месте - клетка, в которую фишка
передвигается. Порядок движения следующий: 2-1, 3-2, 4-3, 5-11,
6-4, 7-5, 8-6, 9-7, 1-13, 9-10, 8-9, 1-12, 7-13, 6-8, 5-7, 1-11, 4-12, 3-
6, 2-5, 1-1,2-2, 3-3,4-4, 5-5, 6-6, 7-7, 8-8, 9-9.
5-5
В сравнении с задачей 5-3 здесь решение короче, всего 37
ходов: 15, 14, 10,6,7,3,2,7,6,11,3,2,7,6, 11, 10, 14,3,2, 11,10,
9, 5, 1, 6, 10, 9, 5, 1, 6, 10, 9, 5, 2, 12, 15, 3.
5-6
Пронумеруем клетки горизонтального ряда числами от 1 до
13, две нижние клетки - 14, 16, две верхние клетки - 15, 17.
Иногда, передвигаясь, фишка проходит сразу несколько пустых
клеток. Для сокращения записи написан номер фишки и
конечная клетка ее передвижения. Решение содержит 60 таких
комплексных шагов: 6-14, 8-4, 7-5, 9-15,10-6,11-7, 12-16, 13-17, 2-8, 1-
9, 13-13, 1-17,2-12, 12-11,1-16, 11-17, 10-10,9-9, 1-15,7-16,8-8,6-7,
1-14, 5-15, 4-6, 3-5, 1-1, 3-2, 4-3, 5-14, 6-4, 8-15, 7-5, 9-6, 10-7, 11-16,
12-8, 2-17, 12-12, 11-11, 2-16, 10-17, 9-10, 8-9, 2-15, 7-16, 6-8, 5-7, 2-
14,4-15,3-6,2-2, 3-3,4-4,5-5,6-6,7-7, 8-8,9-9,10-10.

340 Ответы и решения. 5 (7-13)
5-7
Так как данному событию благоприятствуют три
элементарных исхода: 2, 3, 5 из шести возможных, то вероятность равна 0,5.
5-8
В среднем шесть раз. С одной стороны очевидно, но
существует строгое доказательство этого факта, которое мы не приводим.
5-9
Сумма всех очков на 3-х кубиках (1+2+...+6)-3=63. Сумма
очков на видимых гранях 1+3+4+5+4+6+2=25. Получается, что
сумма невидимых очков равна 38.
5-10
При броске кости разбиваются на группы по числу
выпавших очков. Поэтому нам надо найти число способов разбить п
костей на 6 групп. Это число равно С5п+5- (Число способов
разбить п неразличимых вещей на г различных групп, причем
допускаются пустые ячейки, равно CMn+r-i).
5-11
Из условия задачи видно, что различные броски дают
одинаковую сумму, только если они получаются друг из друга перестановкой
костей. Поэтому число различных сумм равно С26+6=21.
5-12
Рассмотрим предпоследний бросок. После этого броска
сумма очков может быть равна 12, 11, 10, 9 или 8. Если она равна
12, то после последнего броска итоговая сумма очков может с
равными шансами принимать значения 13, 14, 15, 16 или 17.
Аналогично, если эта сумма равна 11, то итоговая сумма может с
равными шансами принимать значения 13, 14, 15 или 16.
продолжая рассуждения далее, убеждаемся, что наиболее вероятное
значение итоговой суммы очков равно 13.
5-13
По аналогии с задачей 5-11 получаем ответ С36+2С26+6=56.

Ответы и решения. 5 (14-19)
341
5-14
Распределения сумм для первого кубика симметричны
относительно 9, а для второго относительно 7,5, поэтому вы чаще
будете получать сумму очков, большую 9.
5-15
Лучше играть вторым кубиком.
5-16
Один вид очков будет в 6 случаях. Два вида - 930 случаев,
три вида - 10800 случаев, четыре вида - 23400, пять видов -
10800, шесть видов - 720 случаев. Сумма всех этих вариантов б6.
5-17
Поставим в соответствие каждой кости (р, q) кость (п-р, n-q).
Если p+q=n-r, то (n-p)+(n-q)=n+r . Значит, число костей с
суммой очков п-r равно числу костей с суммой очков п+r. Общее
число всех костей домино равно C2n+i-
5-18
Раздел костей выполним следующим образом. Сначала
выложим все 28 костей домино в один ряд. Число всех возможных
перестановок из 28 костей равно 28! Потом первый игрок берет
себе первые 7 костей, второй - вторую семерку костей, третий -
следующие 7 костей и четвертый забирает остаток.
Любая перестановка первых 7 костей не меняет дела,
игроку неважен порядок костей в этой семерке, аналогично и по
отношению к другим игрокам. Значит (7!)4 перестановок костей не
меняют результата дележа. Отсюда следует, что число способов
раздела костей домино между четверкой игроков равно 28!/(7!)4.
Это число приблизительно равно 4,7-1015.
5-19
•
•
•
•
•
•
•
•
Рис. 689
Попробуйте найти лучшее решение, позволяющее получить
из цепочки 4-х костяшек все числа от 1 до29.

342 Ответы и решения. 5 (20-25)
5-20 Сначала выберем одну кость. Это можно сделать 28
способами. При этом в 7 случаях кость окажется дублем, а в 21
случае - костью с различными числами очков на половинках. В
случае первого дубля, вторую кость можно выбрать шестью
способами. Во втором же случае вторую кость можно выбрать 12
способами. По правилу произведения в первом случае получается
7-6= 42 варианта, а во втором 21-12=252 варианта. В итоге по
правилу суммы, получаем 294 способа выбора пары.
5-21
Если в колоде 52 карты, то каждая карта с вероятностью
1/52 занимает место, уже занятое такой же картой. Так как общее
число возможных мест для каждой карты равно 52, то среднее
число совпадений равно 52-(1/52)=1. Таким образом, в среднем
происходит только одно совпадение. Если бы колода содержала п
карт, то среднее число совпадений по-прежнему равнялось бы 1.
5W22
Получаем размещения с повторениями из 13 карт по 4.
Всего 134=28 561 способ. Если среди карт не должно быть пар, то
имеем размещения без повторений, их число A4i3=17 160.
Так как достаточно выбрать одну черную карту и одну
красную карту, то получается 132=169 способов выбора.
5^24
Общее число способов взять 10 карт равно С|052. Число
способов, при которых не будет выбран ни один туз, равноС|048.
Поэтому хотя бы один туз будет в С1О52- С|048 случаях. Ровно один
туз в С!4-С948 случаях, не менее двух тузов в С|052-С|048-4С949
случаях и ровно два туза в С24С848 случаях.
5-25 Четыре туза делят колоду на 5 частей, каждая из которых
содержит от 0 до 48 карт. Если два туза лежат подряд, то длина
соответствующего куска колоды равна нулю. Аналогично
нулевую длину имеют части колоды, которые находятся до первого
туза, если он лежит сверху и за четвертым тузом, если он
является последней картой в колоде. Согласно принципу симметрии
средняя длина каждой части равна 48/5=9,6. Последующей
картой должен быть туз, который является, таким образом, в
среднем 10,6 картой.

Ответы и решения. 5 (26-29) 343
5-26
4 туза можно разделить по два 4!/(2!)3=3 способами, а
остальные 32 карты 32!/[(16!)22!] способами. Так как эти
разбиения можно двумя способами комбинировать друг с другом,
получаем 3-32!/(16!)2 способов разбиения.
5^27
Сначала выберем по одной карте каждой масти. Это можно
сделать 134 способами. После этого выберем еще две карты. Если
они разных мастей, то это можно сделать С24122=864 способами.
Комбинируя эти способы с различными способами выбрать
первые 4 карты и учитывая возможность перестановки порядка
выбора двух карт одной масти, получаем 216134 способов. Если
новые две карты имеют одну и ту же масть, то получаем
4C2i2=264 способов выбора. По тем же соображениям это
приводит к 88-134 способам выбора всех карт. Окончательно
получается 304134 способов.
5Й28
4 карты из полной колоды можно вынуть С452 способами.
Ровно 3 масти будут в А24(С! 1з)2С21з=518 184 случаях - мы
выбираем отсутствующую и повторяющуюся масти А24 способами^
после чего выбираем две карты повторяющейся масти C2i3
способами и по одной карте еще двух мастей (С\3)2 способами. Ровно
две масти будет в С24(С2]3)2+А24С\3С\3= 81 120 случаях. Это
возможно либо если имеем по две карты двух мастей, либо одна
карта одной масти и три - другой. В первом случае нужно
выбрать две масти и по две карты каждой из этих мастей, а во
втором выбрать первую и вторую масти (здесь уже играет роль
порядок мастей), а потом взять три карты первой и одну карту
второй масти.
Двум первым условиям задачи удовлетворяют только две
раскладки карт: КДД и ДКД (К - король, Д - дама). Двум
последним условиям также удовлетворяют только две раскладки
и ФУф. Всем четырем условиям удовлетворяют 4 варианта
размещения карт: КФдФд¥~Кфд¥дФ-ДФкФд¥~ ДФК^ Дф.
Последний вариант нужно отбросить, поскольку в нем две

344 Ответы и решения. 5 (30-34)
Три оставшихся набора содержат одни и те же три карты. Мы
можем с уверенность назвать их, но указать в какой
последовательности они лежат, мы не можем. С уверенностью можно утвер-
.щатьЛиетоилет
5-30 Колоду можно сдать 13 игрокам 52!/(4!)13 способами.
Если каждый должен иметь по одной карте каждой масти, то для
каждой масти получаем перестановку из 13 карт. Поскольку
перестановки мастей не зависят друг от друга, то по правилу
произведения получаем (13!)4 способов. В третьем случае один
игрок может выбрать по карте каждой масти 134 способами.
После этого оставшиеся 12 карт каждой масти можно
разделить на 3 группы 12!/[(4!)33!] способами, а все оставшиеся карты
(12!)4/[(4!)|2(3!)4] способами. Эти группы можно раздать 12
игрокам 12! способами. Учитывая, что игрок, имеющий все масти,
может быть выбран 13 способами, получаем для третьего случая
ответ (13!)5/[(4!)12(3!)4].
5-31 Вероятность этого события 0,0029.
5-32 Вероятность равна 1/3. Если составить список всех 24
равновероятных перестановок из 4-х карт, то, выбрав две любые
позиции (например, 1-ю и 3-ю), вы обнаружите 8 случаев, когда
карты будут соответствовать друг другу по цвету.
5-33 Нас интересует только порядок вынутых карт. Всего
существует 5! перестановок из пяти чисел, поэтому искомая
вероятность равна 1/120.
5-34 Ставка 20 долларов сразу, дает игроку вероятность
выигрыша 18/38-0,474. (Речь идет об американской рулетке, в
которой 38 секторов, два из которых «зеро»). Вычисление
вероятности выигрыша при осторожной игре по доллару за одну
партию производится по специальной формуле
PJ У .Ьа^.о,,,,
1_ A** 67,7-1
18
Итак, осторожная игра уменьшает шансы игрока на
выигрыш вчетверо по сравнению со смелой игрой.

Ответы и решения. 5 (35-36), 6 (1-3)
345
5-35
Если Браун выиграет хоть один раз за 36 игр, он не
потерпит убытка. Вероятность проиграть все 36 раз равна
(36/38)36=0,143. Есть смысл Брауну принять пари.
5-36
Xi
Pi
5000
0,00002
1000
0,00008
100
0,0017
50
0,0035
10
0,0075
0
0,9872
С,=0,1 +0,08+0,17+0,175+0,075=0,6 рублей.
Глава 6. Числовые фантазии
6-1
Рис. 690
6"2 |2|4|3|8|1|9|5|7|6|0|
|3|7|8|5|9|4|2|1|6|0|
|4|7|5|3|8|6|9|1|2|0|
14|8|716|3|9|1|512|О1
Рис. 691
6-3 |3|8|1|6|5|4|7|2|9|0|
Рис. 692
6-2
Независимо от расположения цифр число делится на 3 и 9,
т.к. на них делится сумма всех цифр. На последнем месте
обязательно стоит ноль и тогда число делится еще на 2, 5, 6, 10, 15 и
18. Если предпоследняя цифра любая четная, то дополнительно
число делится на 4 и 12. Остается рассмотреть только делимость
на 7, 11, 13, 16 и 17. Можно продолжить этот процесс, но самое
лучшее - взять микрокалькулятор и провести вычисления на нем.
Подсчитываем наименьшее общее кратное искомого числа:
НОК=2-3-2-5-7-2-3-1ИЗ-2-17=12252240. Затем подбираем
наименьшее число, при умножении НОК на которое получается
десятизначное число 8212 252 240=1 004 683 680.

346
Ответы и решения. 6 (4-7)
Затем проводим чисто механическую работу -
последовательно прибавляем НОК к этому числу, до тех пор, пока все цифры
числа не станут разными. Можно конечно для перебора составить
простенькую компьютерную программу. Всего получается четыре
различных решения.
6-3 Сразу можно поставить ноль на последнее место, а цифру 5
на пятое. Очевидно, что на четных местах стоят четные числа.
Далее можно снова использовать метод полной индукции, что
означает перебор всех возможных вариантов. Получается всего
32 варианта для первых трех цифр, чтобы трехзначное число
делилось на 3. В каждом из них проверяем четвертую цифру, с
которой четырехзначное число будет делиться на 4.
Затем проверяем шестую цифру и делимость на 6. На седьмой
цифре произойдет большой отсев и останется только 6 вариантов,
а на восьмой цифре останется единственное решение.
6-4
1б|5|4|б|5|4|б|5|4|б|5|
х+у=9
Рис. 693
6-5
И 7|20|13|17|20|13|17|20|1
Рис. 694
6-6
6-7
Рис. 695
Рис. 696

Ответы и решения. 6 (8-13)
347
6-7 Если на концах одного диаметра поместить числа л:/ и yl9
а на концах соседнего х2 и y2i то по условию Xj+x2=yj+y2 или
Хгу1=у2-х2, т.е. разности противоположно расположенных чисел
должны быть равны между собой. Для решения задачи нужно
разбить числа от 1 до 10 на пять пар с одинаковой разностью
чисел в каждой паре. Возможны две группы пар,
удовлетворяющих этому условию:
• с разностью равной 1 (1-2, 4-3, 5-6, 8-7, 9-10),
• с разностью равной 5 (1-6, 7-2, 3-8, 9-4, 5-10).
Расположив эти числа по кругу получаем два основных решения,
все остальные (всего 48) варианты достигаются различными
перестановками пар чисел с одного диаметра на другой.
6-8
а).- б), нет; в), см. рис.
6-9
6-11
Рис. 697
6-10
2
4
6
1
8
5
3
7
Рис. 700
Рис. 701
Рис. 702

348
Ответы и решения. 6 (14-18)
6-14
Рис. 703
6-15
Рис. 704
6-13
Начинаем с двух ячеек, расположенных между числами 12
и 2. Там могут стоять цифры 5, 6, 7, 8, 9. Из них нужно выбрать
две, имеющие разность не менее трех. Получаются варианты 8-5,
5-8, 9-6, 6-9, 5-9, 9-5. Поставив один из вариантов, подбираем
остальные цифры вокруг числа 12. Для оставшихся чисел смотрим,
в какую клетку их можно ставить. Проходят не все варианты, при
некоторых не удается дальнейшее заполнение и приходится
начинать сначала, с другой пары.
«-те
Каждое число в этой фигуре
соединено как минимум с тремя другими. Для
«единицы» допустимые пары (т.е. с
разностью не больше трех): 1-2, 1-3, 1-4; для
«двойки» 2-1, 2-3, 2-4, 2-5. поэтому
некоторый фрагмент фигуры однозначно будет
выглядеть как на рисунке. Следовательно,
Рис. 705 не зависимо от конкретных мест цифр 1 и 2,
третье соединении «двойки» будет неминуемо давать разность >3.
6-17
6-18
Рис. 706
Рис. 707

Ответы и решения. 6 (17-25)
349
6-17 Показываем известное решение без одной цифры 3.
6-19 Нельзя, так как, с одной стороны, сумма полученных по
пяти прямым нечетных чисел должна быть нечетна, а с другой
стороны, в эту сумму каждое из вписанных в кружочки чисел
входит ровно 2 раза, и, следовательно, эта сумма должна быть четной.
6-20
6-21
6-22
3
6
8
4
6
0
9
2
0
6
4
4
3
5
7
6
2
8
1
9
4
1
2
1
2
2
2
1
2
1
Рис. 708
Рис. 709
Рис. 710
6-22 Из таблицы квадратов натуральных чисел выписываем
трехзначные квадраты, читаемые в обе стороны: 121, 144, 169,
441, 484, 676, 961. С повторениями можно построить семь
разных квадратов, кроме показанного, это следующие квадраты:
484 676 121 144 484 441
888 777 444 248 444 842
484 676 484 144 121 441
6-23
9
Рис.711
(£25
6-24
Рис.712
1
3
7
9
6
8
0
4
2
5
■
3
1
6
Г 8 | 4
0
2
5
Рис.713
Рис.714

350
Ответы и решения. 6 (26-37)
6-26
8
4
1
8
1
4
4
6
4
9
6
1
2
2
5
6
2
7
5
7
6
_2_
1
9
6
Рис.715
6-27
39-57-1=2222
6-28
6-29
64-3,921875=251
763-852-941=611 721 516
6-30
+273 .327
546 +654
819 981
Есть и другие решения.
6-31
2
5
9
8
0
1
6
3
7
4
6-32 4396:157=28
Есть много других решений.
Рис.716
6-34
6-33
56:8=9-2=3+4=1-7
849+753=1602
7039-4=28156
27504:9168=3
6-35
6-36
00 = И+[Ц=
6-37
х
+ + + - х
I ♦
Рис.717
Рис.718
Рис.719

Ответы и решения. 6 (38-42)
351
6-38
+ х -
: [б1=|12
+ |Т| + РП = |ТТ|
и и и
|зо| |Т
Рис. 720
+ +
: х
В S
6-39
+ - +
Рис. 721
6-40
: : + -
+ + + +
Рис. 722
6-41
|12|:
|12|х
|12|х
|12|-
|12|:
6
+
2
-
2
X
2
■
1
=
12
X
-
■
■
■
■
-
8
-
4
■
■
2
+
2
X
3
12
-
■
■
-
+
X
5
X
2
+
2
:
1
-
0
12
+
+
+
X
+
1
X
2
-
2
■
■
2
+
12
12
= M
= |12|
= |12|
■M
= |12|
Рис. 723
6-42
8
+
10
-
5
13
-
X
+
3
+
9
+
1
ss
MB
13
: |s| +
-t-161:
x|9|-
11
-
4
+
6
=
13
X
-
■
■
7
-
2
+
8
13
-
X
+
4
X
5
-
7
=
13
■
■
+
X
10
X
1
+
3
13
-
-
-
6
■
■
3
+
11
13
xl2
-In
-|ю
+ |9|x
+ |7|:
:|2| +
1
+
8
+
4
13
= |13|
= |13|
Рис. 724

352
Ответы и решения. 6 (43-49)
Одно из возможных решений. Рис. 725
6-44
!•
8
-
1
=
3
+
4
3
8
7
4
X
3
-
9
=
3
2
2
8
6
=
8
:
4
X
3
•I
з|
Рис. 726
6-45
Рис. 727
6-46
[18| + |21| ; |3|х| 101 |- |313| = |Ю00|
|936 |- | 504 | ; |24| + |107 |х|8 | =|1ОО0|
| 550 | : |22|х|111-|5|»|730|=|1000[
|568| ; |71| + |4 |х 1103|-| 236 | = )f 000|
[24|+|618|х[15| : |Э[-
| 203 |- |65| х |64[ + 1168 I : I 9 | = |Ю00|
6-47
7
+
8
-
6
=
9
—
—
+
-
4
+
7
-
5
=
6
+
+
-
+
6
—
2
-
3
=
1
=
=
=
=
9
+
3
-
8
=
4
Рис. 728
Рис. 729
6-48
+ s
Рис. 730
S
ч
S
ч
S
^х х^х х*х
4
s
+
4
s
II
ч
л
з\
3
+
18
=
21
= х.
X
■
■
-
1 Хх X
3
+
3
■-
6
=
=
зх
9
+
6
=
15
6-49
л v v
i^fihS
Л Л V
Рис. 731

Ответы и решения. 6 (50-54)
353
6-50
®<[§
V V
®<®
V V
Рис. 732
6-51
Л
6]
Л
2
V
1
л
5
V
3
л
4
>
<
>
<
<
1
л
2
л
3
л
4
л
5
<
<
>
>
>
5
V
4
V
2
V
1
л
3
>
<
<
<
>
3
л
5
V
4
V
2
V
1
<
>
>
<
<
4
V
3
V
1
л
5
V
2
Рис. 733
6-52
6-53
4
V
1
л
2
л
5
V
3
<
<
>
>
<
5
V
3
V
1
л
2
л
4
>
<
<
<
>
1
л
5
V
4
V
3
V
2
<
>
>
>
<
2
л
4
V
3
V
1
л
5
<
>
<
<
>
3
V
2
л
5
V
4
V
1
21
V
15
V
10
Л
14
V
5
>
<
>
<
>
19
Л
20
V
9
Л
25
V
4
>
<
>
>
>
18
Л
22
V
8
Л
12
V
3
>
<
>
>
>
17
Л
23
V
7
Л
11
V
2
>
<
>
<
>
16
Л
24
V
6
Л
13
V
1
Рис. 734
Рис. 735
6-54
Рис. 736

354
Ответы и решения. 6 (55-58)
Рис. 737
6-57
Рис. 739
Рис. 740

Ответы и решения. 6 (59-64)
355
6-59
Рис. 741
6-61
6
-2
5
-1
4
7
8
3
О
2
9
1
©©©©
Рис. 743
6-63
6-60
14
31
10
7
12
31
4
14
13
24
24
14
13
►3
►6
►4
14
►3
►3
►8
24
8
Л
►4
14
Л
►3
►2
►3
9
7
2
0
36
24
1
9
'1
0
9
16
V
6
6
2
23
4
7
3
'9
7
18
J5
5
5
21
5
1
4
13
8
9
6
18
6
3
2
>7
13
24
9
>6
14
21
5
>7
8
1
9
10
Ч
9
22
6
!
0
>5
17
38
8
'8
7
6
25
7
1
►2
27
5
1
'9
1
0
2
'9
15
12
1
6
22
22
V
2
7
13
17
13
1
4
11
20
ь
4
'9
1
11
17
*7
8
19
24
25
►7
>6
3
5
'4
11
2
з
43
7
8
9
.7
►7
20
►со
4
1
8
4
30
5
4
'1
6
7
3
15
£
9
10
3
7
9
3
8
0
2
10
£
4
14
8
Рис. 742
6-62
Рис. 745
Рис. 744
Рис. 746

356
Ответы и решения. 6 (65-76)
6-65
6-66
6-67
8
9 1«7 12
15|iO|2|i3|
11
14
Рис.747
6-68
1
10
8
7
9
5
6
11
2
12
5
4
Рис. 748
4
8
2
7
2
3
6
3
9
1
8
7
8
1
5
9
6
1
5
7
6
3
5
4
2
4
2
6
8
9
9
7
1
3
4
5
6-69
5
6
1
2
9
8
3
7
4
4
3
8
6
5
1
7
2
9
5
2
1
4
6
8
6
4
1
3
7
9
5
8
2
3
7
9
Рис. 750
6-71
8
5
6
з
7
(о)
4
(о)
6
1
7
6
А,
4
i
1
2
7
({И
1
9
1
(о)
7
9
2
2
6
4
2
6
Рис. 749
Рис. 751
6-72
4
8
1
7
_г]
3
1
5
9
6
8
7
8
[2
3
[гГ
1
в
3
7
[б
ЕЕ
4
9
6-70
9
4
fi
4
|б
_2J
5
р7
3
8
5
9
Рис. 757
Рис. 758

Ответы и решения. 6 (77-86)
357
6-77
1*
I"
6
1
6
2
4
5
3
3
9
3
0
2
1
0
1
2
3
4
5
5
4
3
2
1
0
1
5
4
5
14J9|
1|6|15
Рис. 759
6-78
6
7
2
4
9
7
1
4
8
3
2
4
7
6
5
4
8
6
О
1
9
3
5
1
8
Рис. 760
6-79
15
5
2
8
49
43
28
9
35
32
14
17
2
41
46
13
5
19
26
37
4
11
16
21
О
29
34
39
3
38
24
31
20
12
22
44
23
18
36
8
15
6
22
20
48
42
1
7
10
6-80
134 689=3672
Вычеркнуты: 2, 5, 7.
6-81
—
—
—
—
7_
4
—
1
5^
2
Рис. 761
6-84
3
1
9
2
2
8
5
7
4
1
3
5
3
7
8
2
5
Рис. 762
6-82
011
+ 000
009
20
6-83
100
000
+ 005
007
999
1111
111
030
+ 000
070
900
1111
011
330
+ 000
770
000
1111
101
303
+ 000
707
000
1111
6-85
6-86
Рис. 763
Рис. 764
Рис. 765

358
Ответы и решения. 6 (87-93)
6-87
5 4 2
5 13
3 1 254
3 2 14 5
24 13
4 3 5 2 1
Рис. 766
6-88
ч
/
\
->
/
1
4
5
3
6
2
t
3
2
3
3
4
t
0
3
О
3
1
+
3
2
3
2
2
\
I
2
5
2
4
3
t
4-
Рис. 767
6-89
ч
ч
-•>
\
4
2
2
3
3
ч
4
О
О
1
4
4
1
О
1
3
\
ч
2
2
2
1
2
1
6
3
5
4
3
t
Рис. 768
6-90
ч
k
3
5
4
3
3
1
4
4
1
2
3
3
1
4
1
/
4
3
3
2
6
t
|
2
5
2
4
2
\
*-
^»
/
-4-
Рис. 769
6-91
s
1
2
3
3
1
/
2
1
4
3
2
\
I
1
5
3
6
2
/
\
1
1
6
2
2
3
5
4
7
3
I
Рис. 770
6-92
6-93
Г 1
к. А
□
к. А
■
1
1
2
г ч
к А
г ~л
к А
□
г л
к ^
3
Г 1
к. А
1
т
2
Г 1
к J
2
1
Г.'-. Ч
к.' Л
2
Р-
1
I
2
к J
г ^
к А
' Л
J-- А
г л
к. А
I
1
2
"гп
3
3
1
Г; Ч
к. J
2
2
Г 1
L j
Г ч
к J
2|ф|
2
Г "ЧГ .1
к J к '' А
3
3 1
3ИМ
•
2
1
2
2
Г "1
к J
2
1
1
I
к. ■" А
2
Г .4
к J
2
2
Г 1
к J
1
1
2
Г 1
к А
3
3
Г 1
к ''.А
2
3
Г 1
к ^
1
2
Г ^
к -i
г ч
к ^
г ч
к А
Г -Л
к А
Г 1
к. А
2
1
I
И!
Щ
п
1
Шз
Шг
|з|з
Рис. 771
Рис. 772

Ответы и решения. 6 (94-100)
359
6-94
6-95
и
и
к. Jk. A
ЕШ
' Л
к. А
г\
2
1
I
1
к. А
г Л
к. J
2
Г 1
к. J
4
В
г ч
к. л
4
Г ч
к л
Г ч
к. ^
4
к. J
L-
Г ^
к. ^
3
•
1
4
W Jk.
4|
И
1
1
I
И
К2|
3-1
ГР
щ
\л\
k J
1
2
I
1
□□□□qb: :еш
: :□□: ]н::
к. jk. jk jk. jEJ
□QD
::: □■
BIBQB
D
■
■
В
■
■
■
D
■■а: т п
■■DBQD
V El
a ]H
DDD
■■□
■□ :
Рис. 773
Рис. 774
6-96
6
1
4
8
1
9
3
2
6
9
3
2
1
4
7
5
5
2
7
3
4
8
9
8
5
6-97
6-99
3
4
5
7
8
9
1
2
4
6
8
3
9
5
9
4
4
7
8
1
3
Рис. 776
Рис. 777
6-100
1
1
1
2
3
4
5
6
7
8
8
9
9
9
9
9
9
Рис. 778
Рис. 779

360
Ответы и решения. 6 (101-103)
6-101
Рис. 780
Рис. 781
6-102
6-103
S=60
i i
II»! II II.
IN»! II II
Рис. 782
,ГЖ1,
,1 I |»| I L
,1 I I I l?l IJL
■ I I I I I I»IJJ-
I I I I I \П ГГП
Рис. 783
В задачах раздела «Пройденный путь» (6-96...6-103)
каждый новый маршрут имеет свою сумму, поэтому их можно
использовать в конкурсах с несколькими участниками. Для этого
заранее нужно посчитать суммы по нескольким различным
маршрутам и дать их в качестве заданий. Для самостоятельного
исследования будет интересно выяснить, сколько различных
маршрутов возможно в каждой из задач и какие при этом можно
получить суммы. В частности попробуйте найти варианты с
минимальной или максимальной из возможных сумм. Задачи можно
изменять не только в отношении требуемых сумм, но и
придумывая другие фигуры расположения чисел. Важно выделить саму
идею: в некотором расположении чисел, найти путь, пройдя по
которому можно получить заранее заданную сумму чисел. От
условия «расставьте числа так, чтобы получилась заданная
сумма», мы пришли к условию «пройдите числа так, чтобы получилась
заданная сумма», вот и все изменения, а каков результат!

Ответы и решения. 6 (104-122)
361
6-104
Варианты ответов: 1-5-2-3=7; 2-8:4+3=7; 3+7-6+3=7;
(4+1)-2-3=7; 5+8-9+3=7; 6+10-12+3=7.
6-105 50+30+25+8+20+3=136
В задачах с лабиринтами мы покажем только по одному
варианту ответа, не задаваясь целью установления полного их
количества. Кроме того, условие каждой задачи можно было бы
расширить и допустить к рассмотрению все математические
действия, а не только сложение.
6-106 4+2+3+2+4=15
6-107
6-108 ^
6-109 11=12+15-16, 14=6+15-7 -► ;c=8+10-7=11
__™__ ___^
6-112' 41ЕЩГп1и5ГТ7:З^Й[
5-2=10,7-2=14, 13-2=26 -► 21-2=42
2+3=5, 3+5=8, 5+8=13, 8+13=21, 13+21=34 ^21+34=55
3.as.9.r4.-.4=.1.6,.5-.6=3.0...-»..x=36;6=d
6-113 25=1+9+6+3+2+4 -»jc=3+2+5+1+3+7=21
300=(263-188)-4 -+ *=(915-893)-4=88
56=(12+16)-2
6-114 20=4:2+9-2, 14=8:2^-2^ ^10:2+3-2=11
^^2j4jJM+lMzi3E^9^il>
6-115 ^y^lMiilii?±
6-116 7=5+2, 10=7+3, 14=10+4, 19=14+5 -+ д^=19+6=25
6-117 Го=(9+Гз+Г7)-(15+14)^
6-1"1"8 .^^——~————^
6-119 Аналогичная закономерность, jc=11.
6-120 20=9+l 1. 11=^Ъ 12=4+? ~*X=?.+9.=U
6-121 20=2+4+8+6, 24=3+5+9+7 -* д:=5+9+17+13=44
6-122 Начиная с нижнего лепестка по часовой стрелке числа
.?.д..ЗЛ.5,. 7 умножаются.^

362 Ответы и решения. 6 (123-126)
6-123 10=(8±9
6-124 Сумма двух, ниже..стоящих^
6:125 uMj^^
6-126 а) 35,40 (+5) 6)27,31 (+4)
в) 24,27 (+3) г) 64,128 (-2)
д) 55, 89 (каждое число, начиная с третьего, равно сумме
двух предыдущих, ряд Фибоначчи)
е)25,31 (+6)
ж) 12,11 (две арифметические прогрессии d=3, tf/=3, bj=2)
з) 11, 3 (на нечетных местах арифметическая прогрессия
а/=5, d=2, на всех четных местах число 3)
и) 16,19 (+3)
к) 7,8,56 (два числа натурального ряда,
затем их произведение)
л) 32, 31 (на нечетных местах -2, на четных -2+1) -
м) 19,25 (+1, +2, 4-3, ...)
н)24,31 (4-1, 4-2,4-3, ...)
о) 36,49 (квадраты натуральных чисел)
п) 46, 92 (на четных местах удвоение чисел,
на нечетных 4-6,4-12,4-24, ...)
р) 16,17 (два числа натурального ряда пишутся,
следующие два - пропускаются)
с) 125, 216 (кубы натуральных чисел)
т) 637,1277 (первая часть числа получается по правилу
•24-1 ив конце дописывается цифра 7)
у) 3,1, 4 (числа натурального ряда, только между всеми
цифрами ставится запятая)
ф) 1113213211, 31131211131221 (каждое следующее число
описывает предыдущее, только словесная запись переведена в
цифры, например, описание последнего числа заданного в
условии: одна единица одна тройка две единицы три двойки одна
единица или И 13 21 32 И)
х) 161, 718 (числа 10, 11, 12, ... объединены в группы
по три цифры)
ц) 5, 2 (чередование цифр чисел я=3,14159... и
^=2,718228....)

Ответы и решения. 6 (127-131) 363
6-127
По часовой стрелке расставлены остатки от
деления на 7 чисел 3°, З1, З2, З3, З4,35.
6-128 J^^IX Л&^
tfo) (?) Gj Qo)
Рис. 785 Рис. 786
В первом решении по часовой стрелке выписаны остатки от
деления на 13 последовательных степеней двойки: 2°, 21, 23, ...,2м.
Во втором решении точно так же выписаны остатки от
деления на 13 последовательны степеней числа 6.
"6-129
Рис. 787 Рис. 788
Из условия ясно, что N больше 1+2+3+4+5+6=15, но меньше
26-1=63. Приводим здесь два решения из журнала «Наука и жизнь».
6-130 [б] [|]
Ближайшие варианты содержат 15 и 63 [з] Yq\ [4]
плитки, а минимальный - 7 плиток с числами от fgl ГГ"|
О до 6. Остальные получаются по рекуррентной '—' '—'
формуле 2-n+l, т.е. 7,15, 31, 63,127 и т.д Рис. 789
6-131
Каждый раз слуга брал по одной
бутылке из каждого среднего
отделения и еще по одной
бутылке добавлял в угловые отделения. Рис. 790
Всего он взял 16 бутылок за четыре раза.

364
Ответы и решения. 6 (132-137)
6-132
2
5
2
5
5
2
5
2
3
3
3
3
3
3
3
3
4
1
4
1
1
4
1
4
Рис. 791
6-133
6-134
'2) 2 |
2
2
r3^ 1 i
1
3
r-r-i
3
1
->.
3,
Рис.792
4
^ 4 (
A) 4 <s
4
4
5
2
5
^ 2 (
) 2 {
s\
2
Рис. 793
6-135
6
г
9
♦
2
©
8
О
4
3
®
5
п
7
г-
1
*
8
4
9
7
1
»
5
•О
3
d6
6
2
Рис. 794
6-136
Рис. 795
6-137
Рис. 796
3
3
5_
2
2
7
г"
4
4
2
7_
7
7
2
2_
|6
7_
4
3
12
3
_5
7_
20
20
20
4
8
И
14
7
6
6
6
5
5
4
4
3_
4_
5"
в
в
5
j
5
1
5
Е
2
6
2
7
3
15
4
15
_
I
5
13
5|6|6|6|4|4
3|2|1|1|2|з
1 |з | 5 | 5 |3 11
7
II
1 1
i
I
1
i
i
6|5|5
;
;
6
|
7
4
13
II
j
4
15
_
5
15
5
2
7
_
6
2
6
i
6
5
_
I
6
2
5
I
6
4
1
_
12
1
_
11
1
-
!
1 i
9
1
6
2
j
I
I
1

Ответы и решения. 6 (138)
365
6-138
Рис. 797
Если вас заинтересовало рисование по-японски, то сейчас
выпускается много газет и журналов, специально посвященных
этому виду головоломок. Традиционное рисование по-японски с
подзаголовком японский кроссворд вы найдете, прежде всего, в
изданиях под знаком 777 таких как журналы «То яма, то канава»
и «Сикоку-сикоку», издаваемых ЗАО «Логос-Медиа». Несколько
журналов выходит с подзаголовком японские сканворды,
названия у них тоже выдержаны в японском стиле: «Сакэ», «Анимэ».
Практически во всех газетных киосках они есть.

366
Ответы и решения. 6 (139)
6-139
Рис. 798
Японскую мозаику можно найти в газете «Кимоно-то не-
дошито», тоже из серии изданий «Три семерки». В журнале «Са-
кэ» этот вид головоломок называется филиппинские сканворды.
Но в этих двух изданиях японская мозаика встречается в
единичных экземплярах, как дополнение к традиционному рисованию
по-японски. Издательский дом «Мир новостей» выпускает
сборники «Филиппинские сканворды», целиком посвященные тому,
что здесь названо японской мозаикой.

Ответы и решения. 6 (140)
367
6-140
Рис. 799
Логическая икебана - это совсем свежее явление в мире
рисования по-японски и пока что встречается только в газете
«Кимоно-то недошито».
Сейчас для любителей головоломок наступило благодатное
время, потому что многие периодические издания целиком
посвящены различным интеллектуальным забавам, правда в
большей степени имеют не математический, а кроссвордно-
сканвордный уклон. Как любитель со стажем порекомендую,
прежде всего «Загадочную газету». Она интересна широтой охвата
различных видов головоломок. Газета «Русский кроссворд» хоть
и не имеет отношения к математике, но в ней много интересных
заданий с точки зрения развития логики. Из-за дороговизны
подписки немного ушли в тень солидные журналы «Наука и жизнь»,
«Квант», «Математика в школе».

368
Ответы и решения. 6 (141)
6-141
2
2
2
3
Т
1
2
5
1
1
3~
2~
2
1
2
2
4
6
1
6
2
Ю
3
1
2_
3
3
6
1
5
2
1
2
1
2
3
■
н
_■
4 ^^^^|
Г
ил
8
2_
6
2
4
■
н
■
■
V
п
■
2
1
2
1
2
1
1
■
1
■
■
1
1
■
J
■
2
1
1
3
3
1
1
■
1
■
■
п
1
J
■
■
2
1
2
2
3
6
5
3
2.
■I
3
1
2.
mr
■T
JT
2
!l
■_
1
J
1
Рис. 800
В этой книге дважды я обращался к творчеству мудрого
человека Бенджамина Франклина, который, занимаясь серьезной
политикой, одновременно увлекался составлением магических
квадратов и окружностей. На этой странице уместно будет
привести его высказывание: «Любишь ты жизнь? Тогда не теряй
времени; ибо время - ткань, из которой состоит жизнь».

Таблица основных рисунков
369
Таблица основных рисунков
№
2,91
90
92
96
97
98
99
100
101
102
137
143
146
147
149
153
155
159
160
179
187
189
190
214
220
226
228
231
234
235
241
244
245
259
251
252
253
254
255
256
257
содержание
Магический квадрат 3-го порядка
«Ло-шу»
Магический квадрат 4-го порядка
Магический квадрат Сатурна (3-го порядка)
Магический квадрат Юпитера (4-го порядка)
Магический квадрат Марса (5-го порядка)
Магический квадрат Солнца (6-го порядка)
Магический квадрат Венеры (7-го порядка)
Магический квадрат Меркурия (8-го порядка)
Магический квадрат Луны (9-го порядка)
Магический квадрат 10-го порядка
Симметрический магический квадрат 4-го порядка
Совершенный магический квадрат 5-го порядка
Совершенный магический квадрат 7-го порядка
Магический квадрат Франклина 16-го порядка
Магический квадрат из простых чисел 3 порядка
Магический квадрат из простых чисел 12 порядка
Двойной магический квадрат 8-го порядка
Латинский квадрат 4-го порядка
Греко-латинский квадрат 4-го порядка
Греко-латинский квадрат 10-го порядка
Греко-латинский квадрат 10-го порядка в цвете
Квадромагический числовой квадрат
Мультипликативный магический квадрат
Магическое кольцо
Магический круг
Магический шестиугольник
Магический прямоугольник 3x5
Магический треугольник
Проекционный магический куб 5-го порядка
Магический куб 3-го порядка
Магический куб 4-го порядка
Магический параллелепипед 3x3x4
Магическая треугольная призма
Магический тор
Тетраэдр
Гексаэдр (куб)
Октаэдр
Додекаэдр
Икосаэдр
стр.
11,48
47
48
51
51
51
51
51
51
51
70
73
75
75
77
80
81
83
93
96
97
98
106
108
115
117
120
122
122
125
126
127
129
130
131
132
132
132
132
132

370
Таблица основных рисунков
275
278
280
282
283
284
307
311
312
323
328
330
331
338
339
341
614
Проекция гиперкуба
Проекция пентатопа
Ромбический додекаэдр
Звездчатый октаэдр
Кубооктаэдр
Ромбокубооктаэдр
Развертка плоско-магического куба
Магический гексагексафлексагон
Развертка магического кольца тетраэдров
Стандартная игральная кость
Колесо европейской рулетки
Игровое поле рулетки
Поле числовой игры -1
Французская числовая игра
Головоломка «15»
«Назикский» магический квадрат
143
145
146
146
146
146
173
177
178
196
217
218
219
230
231
233
322

Литература 371
Список литературы, использованной в процессе
подготовки данного сборника
Литература указана в алфавитном порядке, а не по
количеству содержащегося в ней материала по теме. В мире
занимательной литературы я бы выделил трех титанов - это Яков
Исидорович Перельман, Борис Анастасьевич Кордемский и
Мартин Гарднер. Они сделали в деле популяризации науки больше,
чем все остальные авторы занимательных книг вместе взятые.
Поэтому я решил после этого списка книг поместить краткие
жизнеописания классиков занимательной литературы (о
современных авторах сведений не нашел). С одной стороны -
классиков нужно знать в лицо, и не только в художественной
литературе. С другой стороны, возможно, это приведет к
пониманию их особенности, отличия от других людей, даст
возможность увидеть, как росли и развивались эти люди, как они
пришли к играм и головоломкам, а с ними в литературу.
1. Азартные и интеллектуальные игры: универсальный
справочник /сост. М. Захаров. - Челябинск: Аркаим, 2004.
2. Антропова Т. Рулетка. Статья в журнале
«Интеллектуальные игры», 1993.
3. Болл У., Коксетер Г. Математические эссе и развлече-
ния.-М.:Мщ>, 1986.
4. Болховитинов В.Н., Колтовой Б.И., Лаговский И.К. Твоё
свободное время: Занимательные задачи, опыты, игры. -
Д.:ВАП, 1994.
5. Вайкс Алан Энциклопедия азартных игр.- М.: «Ефрат»,
1994.
6. Виленкин Н. Я. Комбинаторика. - М.: Наука, 1969.
7. Гарднер М. Математические головоломки и развлечения.
-М.:Мир, 1971.
8. Гарднер М. Математические досуги.- М.: Мир,1972.
9. Гарднер М. Математические новеллы.- М.: Мир, 1974.
10. Гарднер М. Математические чудеса и тайны.- М.:
Наука, 1978.
11. Дьюдени Г.Э. 520 Головоломок.- М: Мир, 1975.
12. Игры: Энциклопедический сборник. (Сост. В. А. Черно-
земцев). - Оренбургское кн. издательство, 1995.
13. Кордемский Б. А. Математическая смекалка.

372 Литература
- Гос. изд. технико-теоретич. лит-ры, - М,1954.
14. Кордемский Б. А. Математика изучает случайности. -
М.: Просвещение, 1975.
15. Лойд С. Математическая мозаика.- М: Мир, 1980.
16. Лучшие в мире загадки: Сборник (Сост. Н. Н. Курлов) -
Минск.: ООО «Попурри», 2003.
17. Минский Е. М. От игры к знаниям: Пособие для
учителя.- М.: Просвещение, 1987.
18. Milos Zapletal Kniha hlavolamov,- Mlade Leta, Bratislava,
1987.
19. Мочалов Л. П. Головоломки: Кн. для учащихся.- М.:
Просвещение, 1996.
20. Оре О. Приглашение в теорию чисел. Биб-ка «Квант».
Вып. З.-М.: Наука, 1980.
21. Перельман Я.И. Занимательные задачи и опыты.- Гос.
изд. Детской Литературы. Москва, 1959.
22. Rudiger Thiele. Die gefesselte Zeit.- Urania-Verlag, Leipzig,
1984.
23. Werner Hirte. Unzere Spiele.- Verlag fiir die Frau, Leipzig,
1971.
Также использованы материалы многих периодических
изданий, начиная от уже несуществующей «Пионерской правды», до
совсем не детской «Экспресс-газеты».

Персоналии 373
Персоналии
Баше Гаспар Клод де Мезириак (Bachet C.-G.) (1581-1638)
- французский ученый, любитель математики и поэт. Его книга
«Problemes plaisans et delectables», изданная впервые в 1612 году,
многократно переиздавалась и переводилась на другие языки. На
русском языке есть только один несовершенный перевод,
названный «Игры и задачи, основанные на математике» (Спб.- 1877), он
является библиографической редкостью.
Некоторые задачи книги Баше взяты из сочинений Алкуина,
Пачоли из Бурго, Тартальи, Кардано, какие-то имеют восточное
происхождение. Определенные заимствования присущи всем
научно-популярным книгам. Их главное достоинство - это
увлекательная и доступная пропаганда знаний, а не стремление к
закреплению приоритета в каких-то направлениях науки или
открытиях. Книга Баше способствовала росту интереса к
математике. В течение веков многочисленные подражатели во многих
странах черпали из нее материалы для своих сборников
«развлекательных математических задач».
Гарднер Мартин (GARDNER Martin) (1914) -
американский писатель и популяризатор науки.
Рис. 801
Мартин Гарднер родился в 1914 году в семье геолога. В 1935
году, еще обучаясь в университете, опубликовал небольшую
брошюру о фокусах, которыми он интересовался с детства. В 1936
году закончил философский факультет Чикагского университета.

374 Персоналии
В это же время он был автором и редактором литературного сту
денческого журнала. После защиты диплома, стал помощникол
редактора газеты в родном городе. В 1941 г. он записывается i
военно-морской флот США и до конца второй мировой войнь
служит сигнальщиком на эсминце, совершающем патрулирова
ние в водах Северной Атлантики. Уволившись с военной службы
Гарднер занялся написанием фантастических рассказов для
журнала «Esquire». В 1947 году он переехал в Нью-Йорк, надеясь
хоть там прорваться на издательский рынок. Но все время ем>
приходилось балансировать на грани нищеты. Только счастливый
случай - открытие детского журнала «Humpty Dumpty», в
котором он работал с первого выпуска, - позволили ему утвердиться в
журналистской среде. Он становится достаточно популярным
детским писателем.
В середине 50-х годов Гарднер на досуге сочиняет статью о
гексафлексагонах, которая неожиданно меняет всю его жизнь.
Статья попадает в редакцию журнала «Scientific American» и
издатель совместно с редактором приглашают Гарднера для личной
беседы. Они предлагают ему стать постоянным ведущим раздела
математических развлечений «Mathematical Games»
(«Математические игры»). Символично, что начальные буквы этих слов
совпадают с его инициалами. «Математические игры» быстро стали
наиболее популярным разделом журнала. Гарднер признавал свое
сравнительно неглубокое математическое образование, но
расценивал этот факт как преимущество, которое позволяло ему
ощущать все сложности математических проблем и в доступной
форме доносить их до читателя. Мартин Гарднер - автор
множества занимательных задач и головоломок из самых различных
областей математики.
На русский язык переведены его книги: "Теория
относительности для миллионов", "Математические чудеса и тайны",
"Математические головоломки и развлечения", "Математические
досуги". "Математически новеллы» и др.

Персоналии 375
Дьюдени Генри Эрнест (DUDENEY Henry Ernest) (1857-
1930) - английский изобретатель головоломок и популяризатор
науки.
Рис. 802
Генри Эрнест Дьюдени родился 10 апреля 1857 года на юге
Англии, в графстве Суссекс. Его дед был простым пастухом и
большим любителем математики, которую он изучал
самостоятельно, а в последствии даже преподавал, став школьным
учителем в небольшом городке Льюис, неподалеку от Лондона.
Учителем был и отец Генри. Самому Дьюдени также не довелось
изучать математику в колледже. Как и его дед, он был
талантливым самоучкой. Его стихией была «игра» в самом широком
понимании этого слова от подвижных игр до игр разума и игры на
музыкальных инструментах. Он с увлечением играл в шахматы,
на бильярде, в крикет, был пианистом и органистом, руководил
церковным хором, переложил все произведения Вагнера для
фортепиано. Составление и решение головоломок было для Дьюдени
не просто профессией, но и призванием, делом жизни. Если
интересная идея приходила ему в голову за обедом, он мог в
задумчивости рисовать геометрические фигуры прямо на скатерти.
Важную роль в жизни Г.Дьюдени сыграло дружеское
соперничество с другим известным мастером головоломок - американцем
Сэмом Лойдом. Дьюдени и его заокеанский коллега вели
оживленную переписку и даже, по признанию самого Дьюдени,
заключили неофициальное соглашение об обмене идеями. В
образовавшемся «трансатлантическом тандеме» Г. Дьюдени
часто исполнял роль генератора идей, тогда как Сэм Лойд был

376 Персоналии
особенно силен в «беллетризации» задач и придумывании
броских названий.
На протяжении 20 лет Г. Дьюдени вел раздел математических
развлечений в ежемесячном журнале Strand Magazine. Им
написаны книги:
• «Кентерберийские головоломки» - 1907;
• «Математические развлечения» - 1917;
• «Лучшие головоломки со всего света» - 1925;
• «Современные головоломки» - 1926;
Уже после его смерти изданы книги «Занимательные задачи и
головоломки» - 1931; «Копи головоломок» - 1935; на русском
языке: «520 гловоломок» - М.; Мир, 1975, «Кентерберийские
головоломки». - М.; Мир, 1979.
Кордемский Борис Анастасьевич (1907-99) - русский
математик, методист, кандидат педагогических наук (1956), доцент
(1957), популяризатор занимательной математики.
Родился Борис Анастасьевич в семье сельских учителей.
Окончив в 1924 году среднюю школу начал работать на курсах
для малограмотных рабочих Средне-Азиатской железной дороги.
Начиная с 17 лет, он преподавал математику почти во всех типах
учебных заведений: средней школе, школе рабочей молодежи,
ремесленном училище, даже в балетной школе при Большом
театре (1год), в Военной академии связи, в Военной академии
химической защиты (33 года), МИСИ (5 лет). Этот путь стал
возможным потому, что по счастливому стечению обстоятельств
в 1926 году Борис Анастасьевич стал студентом физико-
математического отделения педфака МГПУ им В.И.Ленина и
окончил его в 1930 году. После усиленной самостоятельной
подготовки в 1957 году защитил кандидатскую диссертацию, и ему
было присвоено звание доцента кафедры высшей математики.
Овладевшее Борисом Анастасьевичем с молодых лет стремление
к творчеству в жанре занимательной математики имело своим
началом выполнение полученного от Физматгиза в 1949 году
задания по редактированию и обновлению книги «Занимательная
геометрия» Я.И. Перельмана, подготавливаемой к седьмому
изданию. Процесс создания дополнений в стиле Перельмана
настолько увлек Кордемского, что им был собран материал для

Персоналии 377
большой самостоятельной книги «Математическая смекалка».
Книга была издана Физматгизом в 1954 году и имела большой
успех и в дальнейшем переиздавалась более десяти раз. С
большим интересом были встречены и другие книги, созданные Б.А.
Кордемским. Более тридцати лет Борис Анастасьевич вел
рубрику «Занимательная страница» в журнале «Математика в школе».
Его интересные статьи и любопытные заметки можно было найти
в журналах «Квант» и «Юный техйик», «Наука и жизнь». Он
автор свыше 70 статей и книг по занимательной математике:
• «Очерки о математических задачах на смекалку»
(1958),
• «Математика изучает случайности» (1975),
• «Увлечь школьников математикой» (1981),
• «Великие жизни в математике» (1995),
• , «Удивительный мир чисел» (совместно с А.А. Аха-
довым) (2 изд., 1996),
• «Геометрия помогает арифметике» (2 изд., 1994;
совместно с А.И. Островским),
• «Удивительный квадрат» (2 изд., 1994; совместно с
Н.В. Русалевым).
• Подготовил к печати книгу «Математические завле-
калки» (2000).
Лойд Сэмюэль (LOYD Sam) (1841-1911) - американский
изобретатель головоломок и популяризатор науки.
Рис. 803

378 Персоналии
Лойд родился в Филадельфии. Его отец, состоятельный
торговец недвижимостью, переехал в Нью-Йорк, где юный Сэм до
17 лет посещал школу. В семье Лойдов большой любовью
пользовались шахматы. Естественно, что Сэм к 10 годам уже умел
неплохо играть в шахматы. 14 апреля 1855 году в газете «Нью-
Йорк сэтерди курир» была опубликована первая шахматная
задача Лойда. В том же году он напечатал еще несколько задач. Когда
в 1856 году газета «Фрэнк Леслис иллюстрейтид ньюспейпер»
провела первый в США конкурс составления шахматных задач,
Лойд завоевал призы по разделам трех- и четырехходовок.
Период 1856-1860 гг. был самым продуктивным для Лойда. Он
напечатал за это время около 300 задач. В 1868 году вышел из печати
сборник «Американские шахматные орешки». Он содержал
свыше 2400 задач, принадлежавших 231 автору. Лойду уделено
наибольшее место - здесь помещено свыше 350 его задач. Но после
выхода сборника Лойд забросил композицию на многие годы.
Его внимание было обращено на математические головоломки и
всевозможные трюки, которым он умел придать удивительную
пикантность и оригинальность. В области математических задач,
ребусов, различных игр Лойд преуспел не меньше, чем в
шахматных задачах. Еще в детстве Лойд отличался любовью к шуткам,
каламбурам, он умел подражать любому музыкальному
инструменту, показывать фокусы на пальцах. Его исключительная
любознательность, сообразительность, математическая даровитость
позволили ему еще в юношеском возрасте придумать ряд
интересных задач и головоломок, получивших вскоре широкую
известность. В юности он придумал головоломку с вырезанием из
картона, которая принесла ему огромный коммерческий успех. В
90-х годах Лойд вел колонку головоломок в газете Brooklyn Daily
Eagle, а с начала нового века вплоть до самой смерти ему
принадлежала ежемесячная страничка головоломок в журнале
Woman's Home Companion.
Самая знаменитая из игр Лойда - широко распространенная и
у нас игра «15». Лойд изобрел ее в 1878 году, и она сразу
получила известность не только в Америке, но и Европе. Большое число
головоломок Лойда собрано в сборнике «Стрэнд» (1908 г.). В
1912 году, уже после смерти Лойда, вышла из печати красочно
оформленная книга для детей «Головоломки Сэма Лойда».

Персоналии 379
После смерти Лойда его сын Сэм Лойд-младший продолжал
вести колонки головоломок своего отца. Сын посмертно издал
несколько сборников головоломок Лойда-старшего, из которых
наиболее признанным стал «Cyclopedia of Puzzles» -
«Энциклопедия головоломок», впервые опубликованный в 1914 году. Эта
книга остается и сегодня самым большим и восхитительным
сборником головоломок, когда-либо собранных под одной
обложкой.
Перельман Яков Исидорович (22 ноября 1882, г. Белосток -
16 марта 1942, Ленинград), российский популяризатор науки,
создатель жанра «занимательная наука».
Рис. 804
Его отец работал счетоводом на суконной фабрике, а мать
преподавала в начальных классах. В 1890 году Яков пошел
учиться в первый класс начальной школы, а 18 августа 1895 года
поступил в Белостокское реальное училище - единственное
среднее учебное заведение города. Деятельность Я. И. Перельмана
как популязатора науки началась еще в школьные годы. Свой
первый очерк «По поводу ожидаемого огненного дождя» Я. И.
Перельман опубликовал 23 сентября 1899 г. в «Гродненских
губернских ведомостях» еще учеником Белостокского реального
училища. В 1901-1909 гг. Перельман учится в петербургском
Лесном институте и начинает сотрудничество с редакцией
журнала «Природа и люди» (с 1904 г. по 1917 г. ответственный
секретарь редакции).

380 Персоналии
Начиная с первой публикации «Столетие астероидов» в 1901,
Перельман за 17 лет работы в редакции журнала «Природа и
люди» (еженедельный журнал «Природа и люди» существовал с
1889 по 1917) опубликовал на его страницах более 500 статей,
очерков и заметок. По инициативе Перельмана с 1908 журнал
выпускал в качестве бесплатного приложения сборник «Мир
приключений», включавший в себя лучшие произведения
зарубежных мастеров приключенческого, детективного и научно-
фантастического жанра. Первая книжка сборника вышла в свет в
1910 и имела такой успех, что «Мир приключений» продолжал
выходить и после закрытия журнала до 1928 года.
С 1908 г. Перельман приступает к работе над «Занимательной
физикой», первая часть которой выходит в 1913 году. Небывалый
успех книги окрыляет автора ив 1916 он выпускает вторую часть
«Занимательной физики». Эта книга возвестила о рождении
нового жанра — «Занимательной науки».
Занимательная наука, по Я. И. Перельману, «не берется
популяризировать все на свете, всю науку в полном ее объеме».
Борясь с верхоглядством, она, прежде всего, сосредотачивает
внимание на основах науки и восполняет пробелы школьного
образования. Вторая особенность занимательной науки состоит в
том, что ее приемы побуждают мысль читателя работать. Для
этого занимательная наука стремится к тому, чтобы «привычная
мысль, давно знакомое явление показывалось с новой,
необычной, подчас неожиданной, стороны. Новизна подстрекает
интерес, а интерес помогает сосредоточить внимание и будит работу
мысли.
Я. И. Перельман был членом редколлегии созданного по его
предложению научно-популярного журнала «В мастерской
природы. В «Мастерской природы» опубликовано более 150 статей и
заметок Перельмана.
В начале 1920-х годов Перельман много и успешно трудился
на педагогическом поприще. Но подлинным учителем миллионов
он стал в период с 1918 по 1942, когда им были написаны
основные произведения. Библиография Перельмана насчитывает более
1000 статей и заметок, опубликованных им в различных
изданиях. И это помимо 47 научно-популярных, 40 научно-
познавательных книг, 18 школьных учебников и учебных посо-

Персоналии 381
бий. Вслед за "Занимательной физикой" им были написаны
"Занимательная арифметика", "Занимательная алгебра",
"Занимательная астрономия", "Занимательная геометрия",
"Занимательная механика". Популяризацией науки занимались
многие литераторы задолго до Перельмана, но только ему
удалось достигнуть в этом деле таких вершин.
15 октября 1934 в Ленинграде открылся уникальный
культурно-просветительный центр «Дом занимательной науки». В
четырех отделах ДЗН (астрономии, физики, математики и географии)
было собрано более 350 крупных экспонатов. Кроме того,
несколько сот диапозитивов, карт, рисунков, приборов и т.п.
«мелких» экспонатов были вмонтированы в стены, висели на стендах,
лежали на столах. ДЗН отличался от обычных музейных
экспозиций полным отсутствием запретительных надписей типа «Руками
не трогать!». Наоборот, надписи радушно приглашали:
«Трогайте!» Я. И. Перельман был одним из пионеров космонавтики,
состоял в переписке с К. Э. Циолковским, был членом президиума
ЛенГИРДа, участвовал в разработке первой советской противо-
градовой ракеты, переписывался с СП. Королевым по вопросам
пропаганды «космических» знаний.
В блокадном Ленинграде читал лекции для воинов
Ленинградского фронта и Краснознаменного Балтийского флота. Голод
и холод блокадного Ленинграда медленно подтачивал силы
пожилого человека. 16 марта он также скончался ot голода в
осажденном Ленинграде.
По далеко не полным данным, с 1913 года книги Перельмана
только на русском языке переиздавались более 300 раз тиражом
почти 15 миллионов экземпляров. Кроме того, его книги
печатались на многих других языках нашей планеты.
Яков Исидорович Перельман не совершил никаких научных
открытий, ничего не изобрел в области техники. Он не имел
никаких ученых званий и степеней. Но он был предан науке и нес
людям радость общения с наукой.
Франклин Бенджамин (Franklin, Benjamin) (1706-1790),
американский государственный деятель и ученый. Родился в
Бостоне 17 января 1706. Учился в местной школе до 10 лет, работал в
свечной мастерской и типографии. В 17 лет переехал в Фила-

382 Персоналии
дельфию. В 1727 основал собственное дело, в 1729-1748 издавал
«Пенсильванскую газету», в 1732-1758 - ежегодник «Альманах
бедного Ричарда».
Рис. 805
Франклин самостоятельно изучил французский, испанский,
итальянский языки, латынь. В 1727 организовал дискуссионный
клуб «Джунто», в 1731 основал первую в Америке публичную
библиотеку. Франклин в 1752 провел знаменитый эксперимент с
воздушным змеем, благодаря которому стал известен как ученый.
Из этого эксперимента впоследствии родилась идея громоотвода,
а затем общая теория электрических явлений и связанная с ней
новая терминология (понятия положительного и отрицательного
электричества, проводника, батареи и т.п.). Франклин объяснил
принцип действия лейденской банки и роль диэлектриков,
явление растекания капель масла по поверхности воды и эффект
увеличения скорости звука в воде. Изобрел «электрическое колесо»
и лампу для уличных фонарей, В 1743 Франклин основал
Американское философское общество, в 1751 - Пенсильванский
университет. Поддерживал концепцию естественных и
неотъемлемых прав человека. Отстаивал идеи разума, свободы и
демократии, организовал первую в Америке публичную
библиотеку (1731), Американское философское общество (1743),
Филадельфийскую академию (1751), ставшую основой
Пенсильванского университета.
Был избран членом 2-го Континентального конгресса. Стал
советником генерала Дж. Вашингтона и членом комитета по
выработке Декларации независимости. В течение десяти лет служил
делу независимости колоний и формированию нового
государства - Соединенных Штатов Америки.
Умер Франклин в Филадельфии 17 апреля 1790.

Заключение 383
Заключение
В заключение приведу слова классика, Льва Николаевича
Толстого: «Чем больше человек дает людям и меньше требует
себе, тем он лучше; чем меньше дает другим и больше себе
требует, тем он хуже».
Смею вас заверить, что в процессе деятельности
целенаправленного характера можно развивать любые свои задатки: в
физическом совершенствовании своего тела посредством занятий
спортом, в отношении органов чувств - в развитии слуха,
глазомера, тактильной чувствительности посредством тренировок, так
и в отношении мозга, памяти и сообразительности посредством
регулярного решения различных задач и головоломок. Сделал
утреннюю гимнастику, почистил зубы - реши какую-нибудь
задачу из подходящего сборника, хотя бы из этого. Тогда
гармоничное развитие вам обеспечено. Успехов вам, дорогие читатели,
на этом пути самосовершенствования.
Автор-составитель будет благодарен тем неравнодушным
читателям, которые найдут время и возможность сообщить свое
мнение о данном сборнике по электронному адресу
troww(a)krn.ru.

Серия «Учение с увлечением»
Трошин Владимир Валентинович
МАГИЯ ЧИСЕЛ И ФИГУР
Занимательные материалы по математике
Ответственный за выпуск А. /7. Пашкович
Редактор А. П. Пашкович
Компьютерная верстка и корректура авторские
Дизайн обложки А.А. Попукалова
ООО «Глобус»
(оптовые поставки учебной литературы)
Тел./факс: (495) 937-63-84; (8442) 266-398
e-mail: globus-kniga@mail.ru
сайт: www.globus-kniga.ru
Заказ «Книга-почтой»:
105318, г. Москва, а/я «Профкнига»
Тел. (495) 740-78-37, 727-06-67;
e-mail: zakaz@profkniga.ru
Подписано в печать 01.08.07. Формат 60x90 1/16. Печать офсетная.
Бумага газетная. Гарнитура «Arial».
Усл. печ. л. 24. Тираж 5.000 экз. Заказ № 19650.
Отпечатано ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru

V
° (Зисюзса
Я©.-'Л ИЗ Й
Автор
Трошин Владимир Вале
Учитель математики и информатики
работы в школе. Отличник npoceei
занимательными, математическими гс
нестандартными задачами на развитие
пространственного мышления.
Автор книг «Слова и числа», «Занимательные задан
спичками» и публикаций на методические темы в журна
«Наука и жизнь», «Школа и производство».
Сборник предлагает учителям математики, учащимся средних и
старших классов, всем любителям математики и логики
К увлекательное путешествие в магический мир чисел и фигур. Книга
хорошо иллюстрирована, содержит большое количество различных
нестандартных задач, числовых головоломок и интересные сведения
9 * 9
для расширения кругозора.
Сборник станет занимательным собеседником своим читателям,
послужит помощником в расширении математического кругозора,
развитии логического мышления, пространственных представлений и
выработке математической интуиции.
Включение занимательных материалов данного сборника в учебный
процесс непосредственным образом отразится на повышении
успеваемости учащихся.