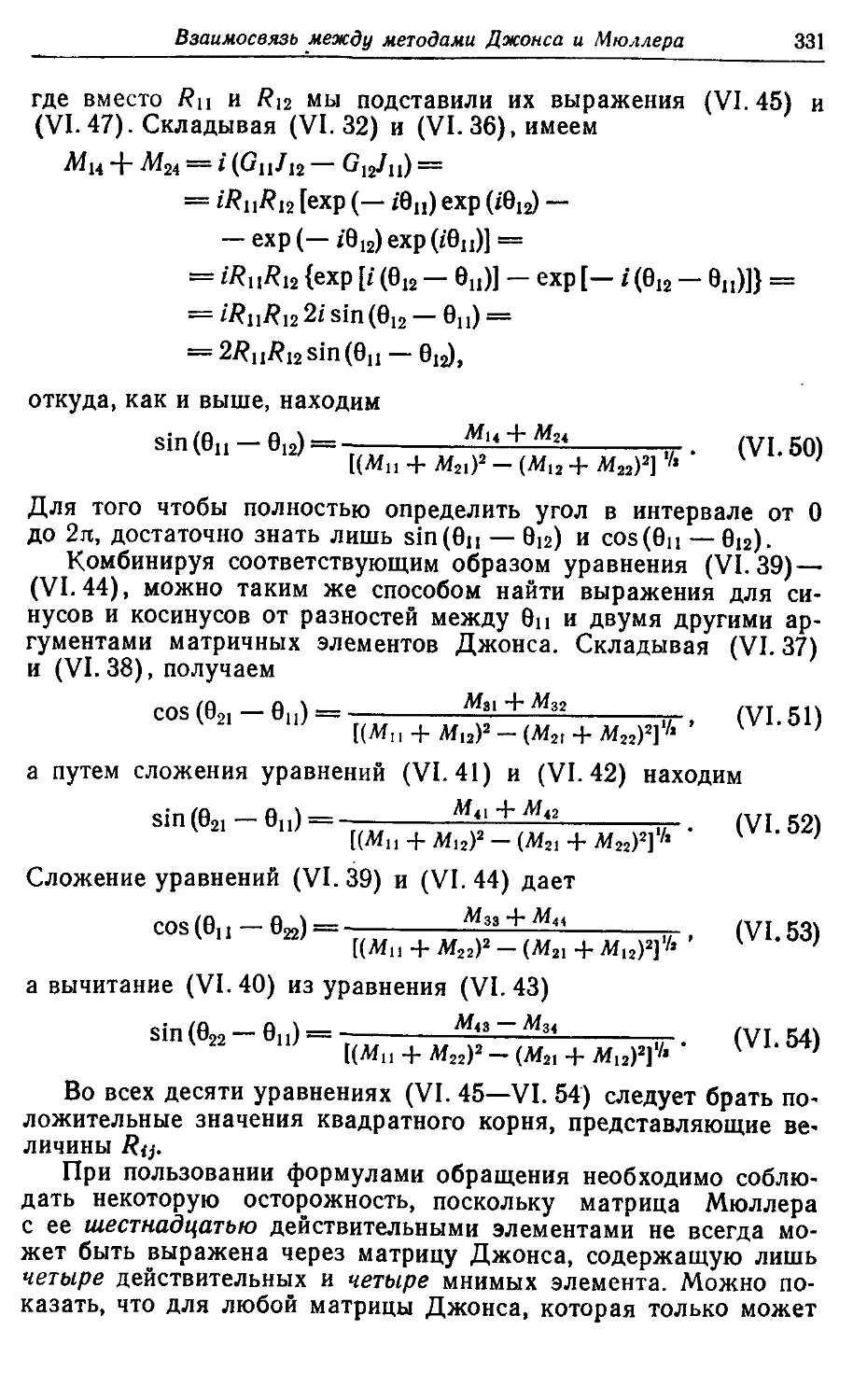Автор: Джеррард А. Бёрч Дж.М.
Теги: применение оптики в целом электротехника оптика лазерная оптика
Год: 1978
Текст
А.ДЖЕРРАРД
ДЖ.М.БЁРЧ
^*
ВВЕДЕНИЕ
В МАТРИЧНУЮ
ОПТИКУ
Перевод с английского
канд. физ.-мат. наук
А. И. Божкова и Д. В. Власова
Под редакцией
канд. физ.-мат. наук
В. В. Коробкина
ИЗДАТЕЛЬСТВО „МИР"
МОСКВА 1978
INTRODUCTION TO
MATRIX METHODS IN OPTICS
A. Gerrard
University of Bath
J. M. Burch
National Physicail Laboratory, Teddington
A Wlley-lntorscloiicu Publication
John Wlli'y Л Sons
London ¦ Now Yoik • t'.yilnoy • I ш onto
УДК 535.8+621.375.826
Книга представляет собой вводный курс по использованию
элементарных матричй«х методов в современной оптике. Наряду
с общими вопросами в ней рассмотрены многочисленные примеры
применения матриц для расчета линзовых систем и оптических
резонаторов, а также параметров лазерных пучков, поляризаци-
поляризационных характеристик и т. д.
Написанная вр&ётйн язйкОЯ и~ не* требующей знания диффе-
дифференциального и интегрального исчисления, книга' является доступ-
доступной широкому кругу читателей. Она представляет безусловный
интерес для студентов и аспирантов, изучающих оптику, а также
для научных работников н инженеров, прямо или косвенно свя-
связанных с лазерной оптикой.
Редакция литературы по физике
Copyright © 1975, by John Wiley & Sons, Ltd.
All Rights Reserved. Authorised translation from
the English, language edition published by John
Wiley & Sons, Ltd.
Д M1.o" -p 53-78 © Перевод на русский язык, «Мир», 1978
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 5
ПРЕДИСЛОВИЕ АВТОРОВ 12
ГЛАВА 1. ВВЕДЕНИЕ В МАТРИЧНОЕ ИСЧИСЛЕНИЕ 19
§ 1. Вводные замечания 19
§ 2. Перемножение матриц 22
§ 3. Нулевые матрицы 26
§ 4. Единичные матрицы 27
§ 5. Диагональные матрицы 28
§ 6. Многократное умножение . 28
§ 7. Сложение и вычитание матриц 29
§ 8. Транспонированные матрицы 30
§ 9. Определители 31
§ 10. Деление н обращение матриц 33
§ 11. Приведение матрицы к диагональному виду 35
§ 12. Собственные значения и собственные векторы унимодулярных
матриц 2X2 36
ГЛАВА 2. МАТРИЧНЫЕ МЕТОДЫ В ПАРАКСИАЛЬНОЙ ОПТИКЕ 40
§ 1. Введение 40
§ 2. Матрицы преобразования лучей 42
§ 3. Матрица перемещения У 44
§ 4. Матрица преломления Я 48
§ 5. Матрица преобразования лучей для оптической системы . . .51
§ 6. Матричное описание свойств оптической системы 54
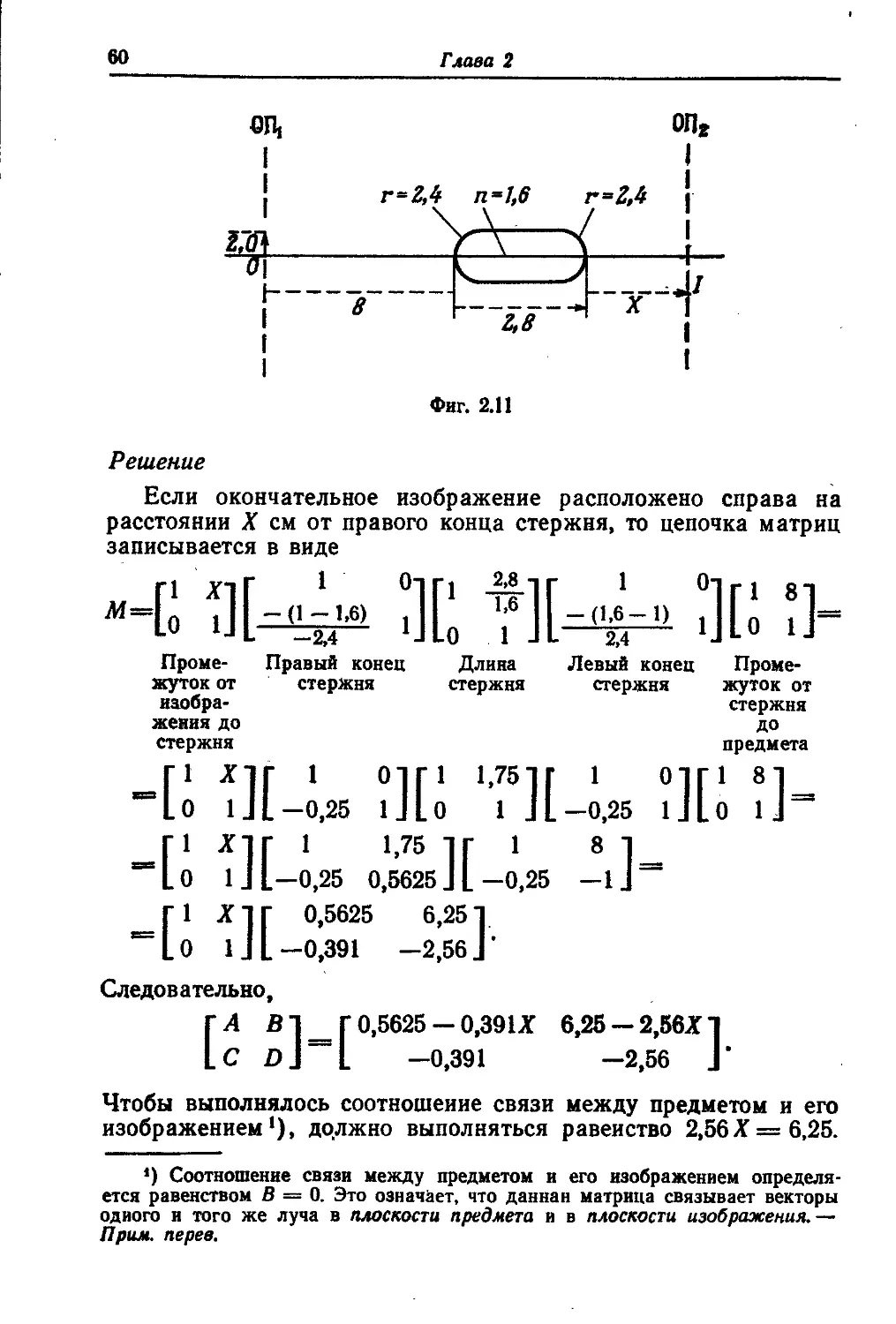
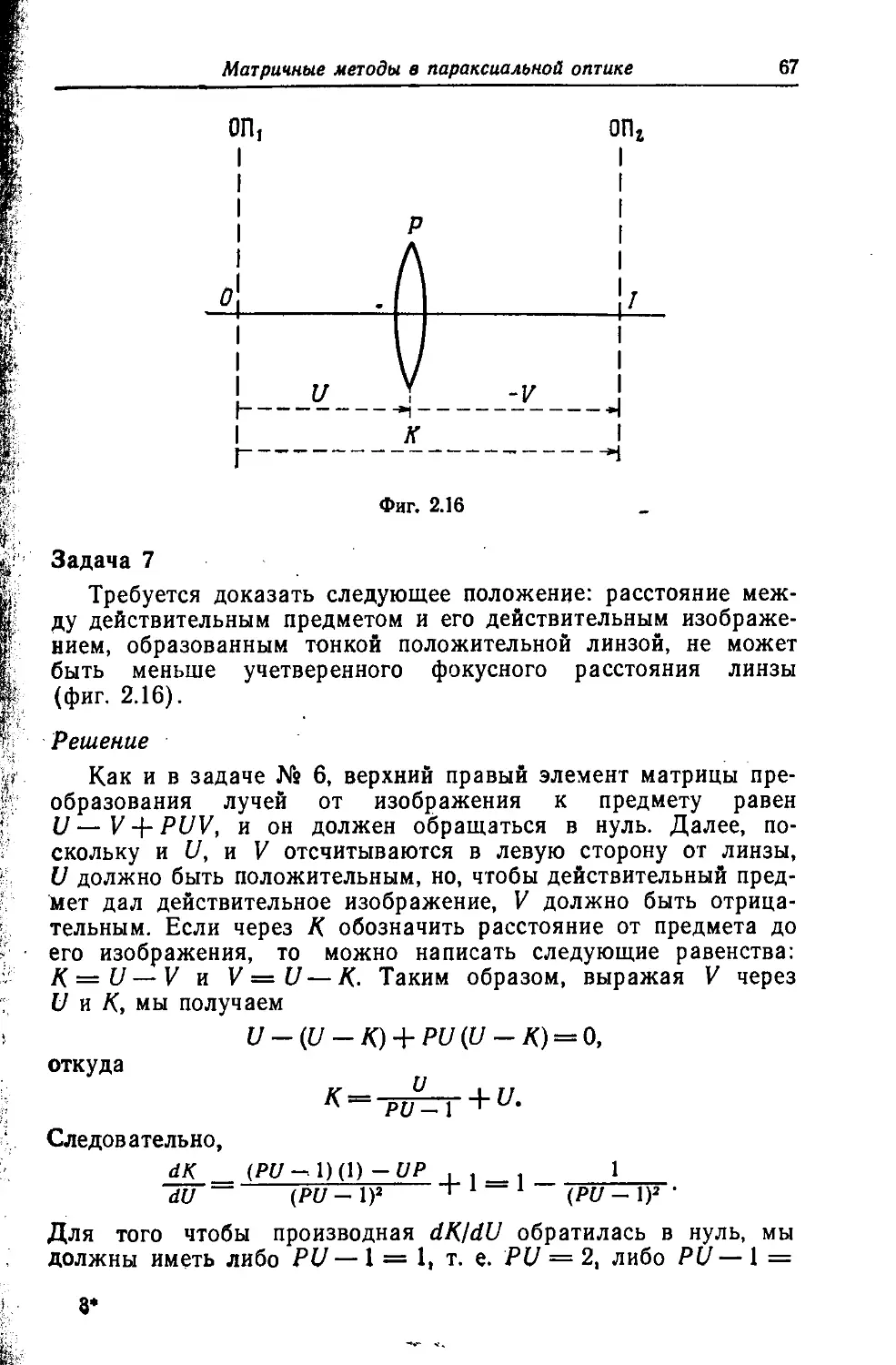
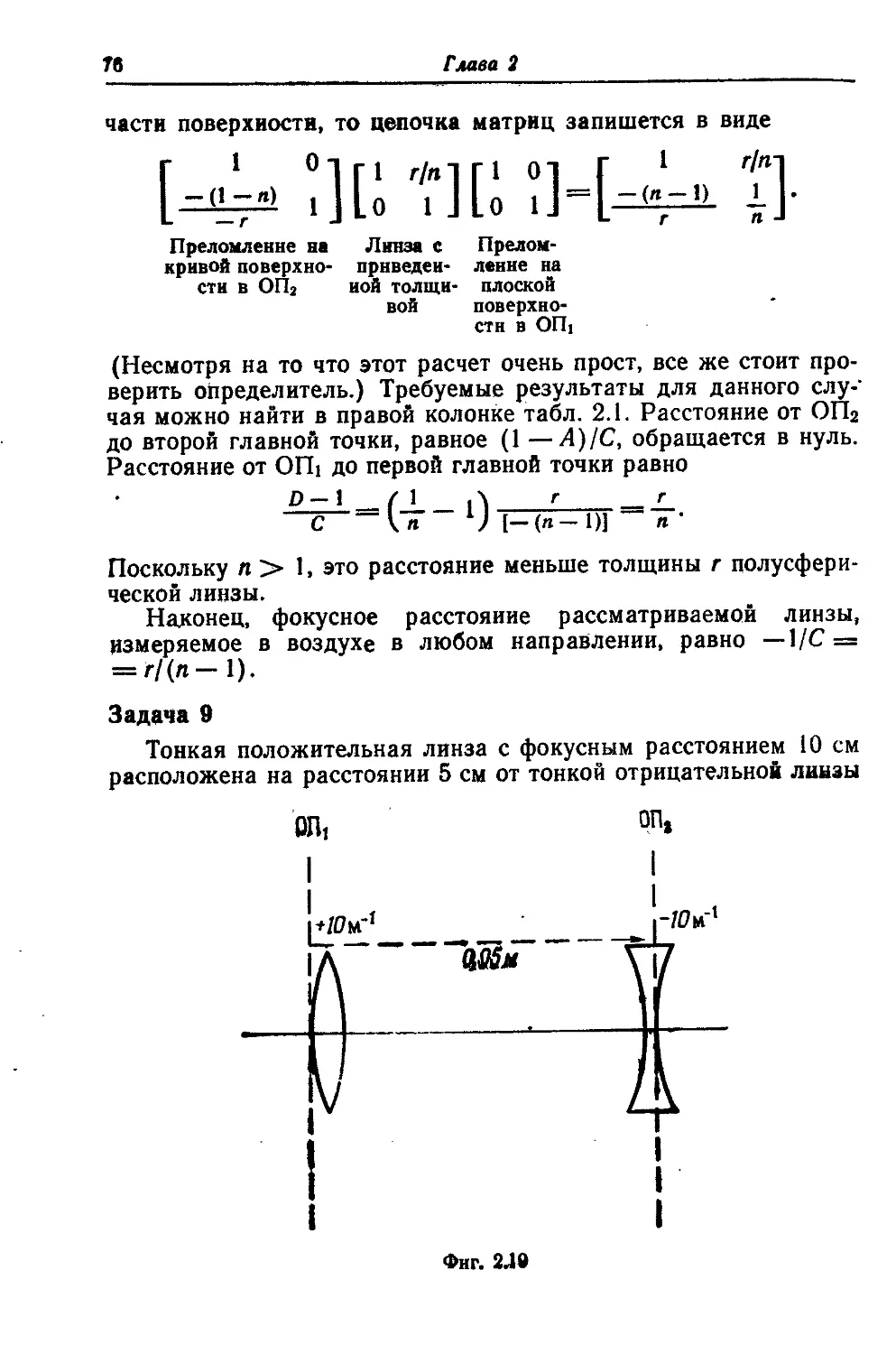
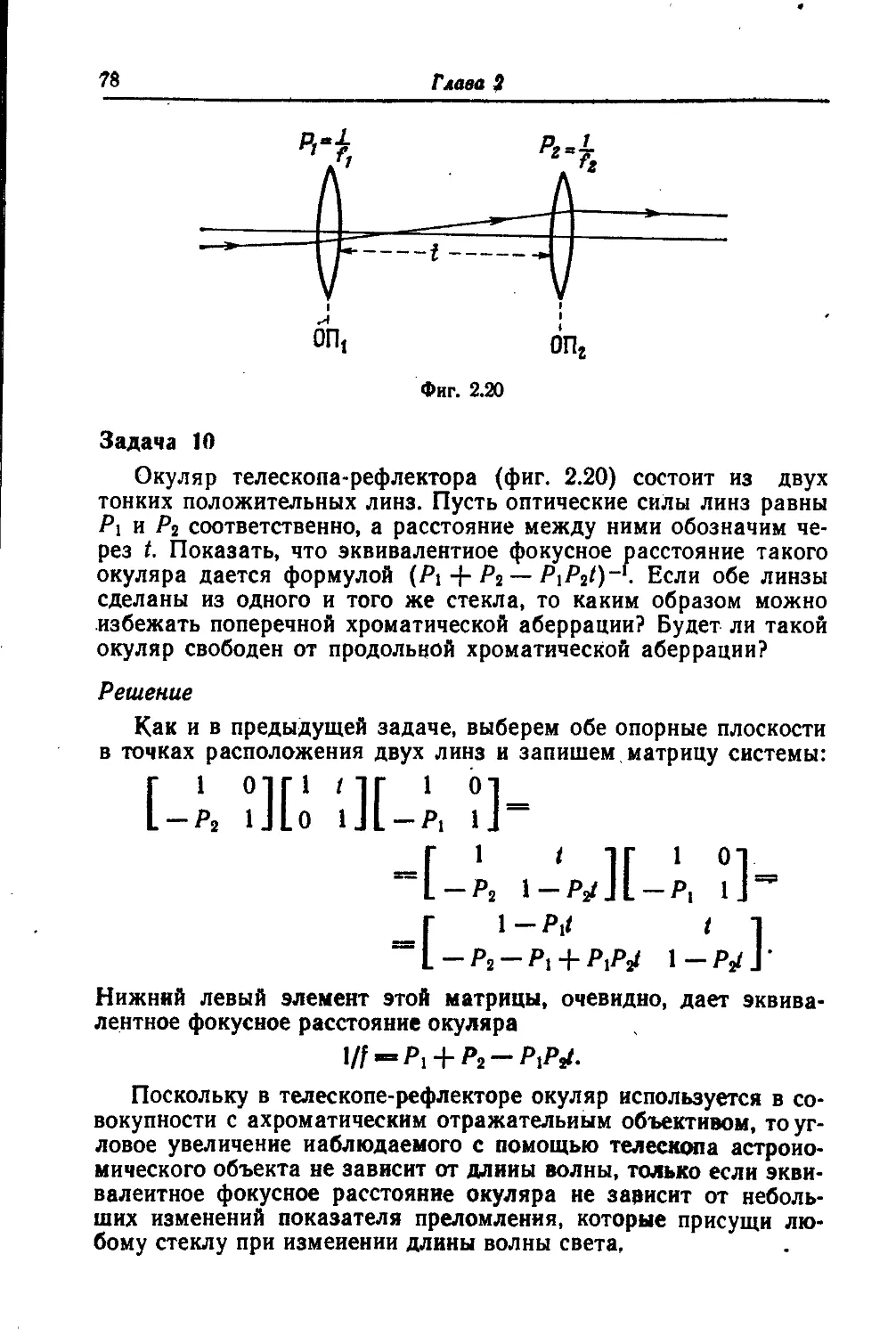
§ 7. Задачи, иллюстрирующие матричный подход 58
§ 8. Экспериментальное определение элементов матриц оптической
системы 68
§ 9. Расположение кардинальных точек системы 70
§ 10. Дополнительные задачи 75
§ 11. Обобщение метода преобразования лучей иа случай отражаю-
отражающих систем 81
ГЛАВА 3. ОПТИЧЕСКИЕ РЕЗОНАТОРЫ И РАСПРОСТРАНЕНИЕ
ЛАЗЕРНОГО ПУЧКА 91
§ 1. Сводка результатов, полученных для параксиальных систем,
формирующих изображение 91
340 Оглавление
§ 2. Описание процесса распространения волн иа языке геометриче-
геометрической оптики 94
§ 3. Разрешающая сила, этандю и принцип неопределенности . . . 105
§ 4. Матричное описание оптического резонатора 112
§ 5. Различие между устойчивыми и неустойчивыми резонаторами . 122
§ 6. Распространение гауссовых пучков и комплексный параметр
пучка 130
§ 7. Расчет параметров пучка, излучаемого лазером 136
§ 8. Применение правила ABCD для согласования мод 147
§ 9. Матрицы преобразования лучей в лннзоподобной среде с квадра-
квадратичным законом изменения показателя преломления 164
§ 10. Иллюстративные задачи 174
ГЛАВА 4. ИСПОЛЬЗОВАНИЕ МАТРИЦ ДЛЯ ОПИСАНИЯ СОСТОЯ-
СОСТОЯНИЯ ПОЛЯРИЗАЦИИ СВЕТА 190
§ 1. Поляризованный свет — методы получения и анализа 190
§ 2. Использование параметров Стокса для описания поляризации
света 200
§ 3. Использование матрицы Мюллера для преобразования вектора
Стокса 204
§ 4. Экспериментальное определение элементов матрицы Мюллера и
столбца Стокса 213
§ 5. Использование метода Джонса для преобразования столбцов
Максвелла 217
§ 6. Экспериментальное определение элементов матрицы Джонса и
столбца Максвелла 222
§ 7. Наглядные примеры использования матриц Джонса и матриц
Мюллера 230
ГЛАВА 5. РАСПРОСТРАНЕНИЕ СВЕТА В КРИСТАЛЛАХ . . . .247
§ 1. Вводные замечания 247
§ 2. Представление операций над векторами в матричной форме . . 247
§ 3. Диэлектрические свойства анизотропной среды 252
§ 4. Распространение плоских волн в одноосном кристалле 255
§ 5. Волны Гюйгенса в одноосном кристалле 263
ПРИЛОЖЕНИЕ I. АПЕРТУРНЫЕ СВОЙСТВА ЦЕНТРИРОВАННОЙ
СИСТЕМЫ ЛИНЗ 267
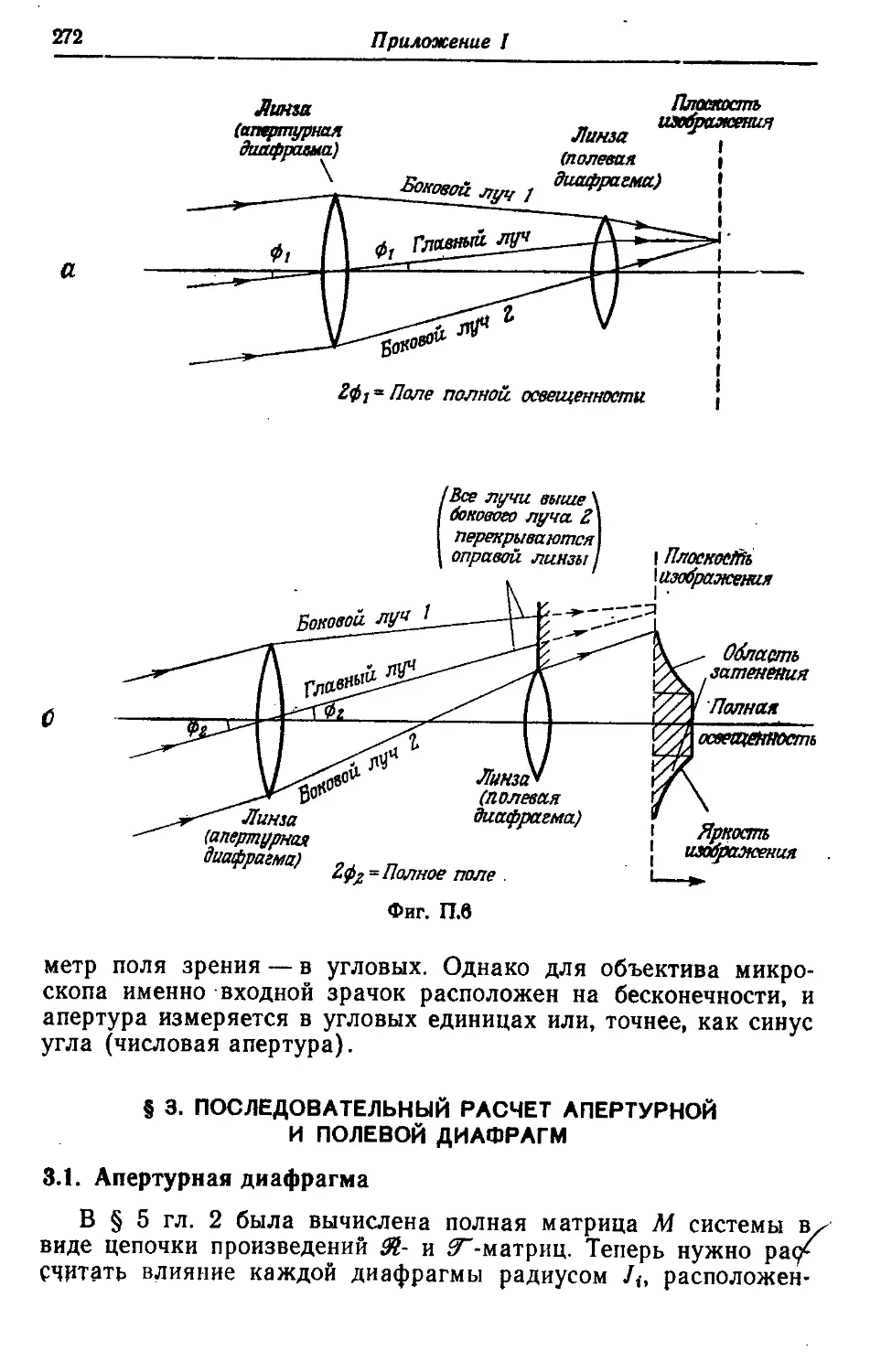
§ 1. Диафрагмы, ограничивающие апертуру 267
§ 2. Диафрагмы, ограничивающие поле зрения 270
§ 3. Последовательный расчет апертурной и полевой диафрагм . . . 272
§ 4. Определение полей освещенности 276
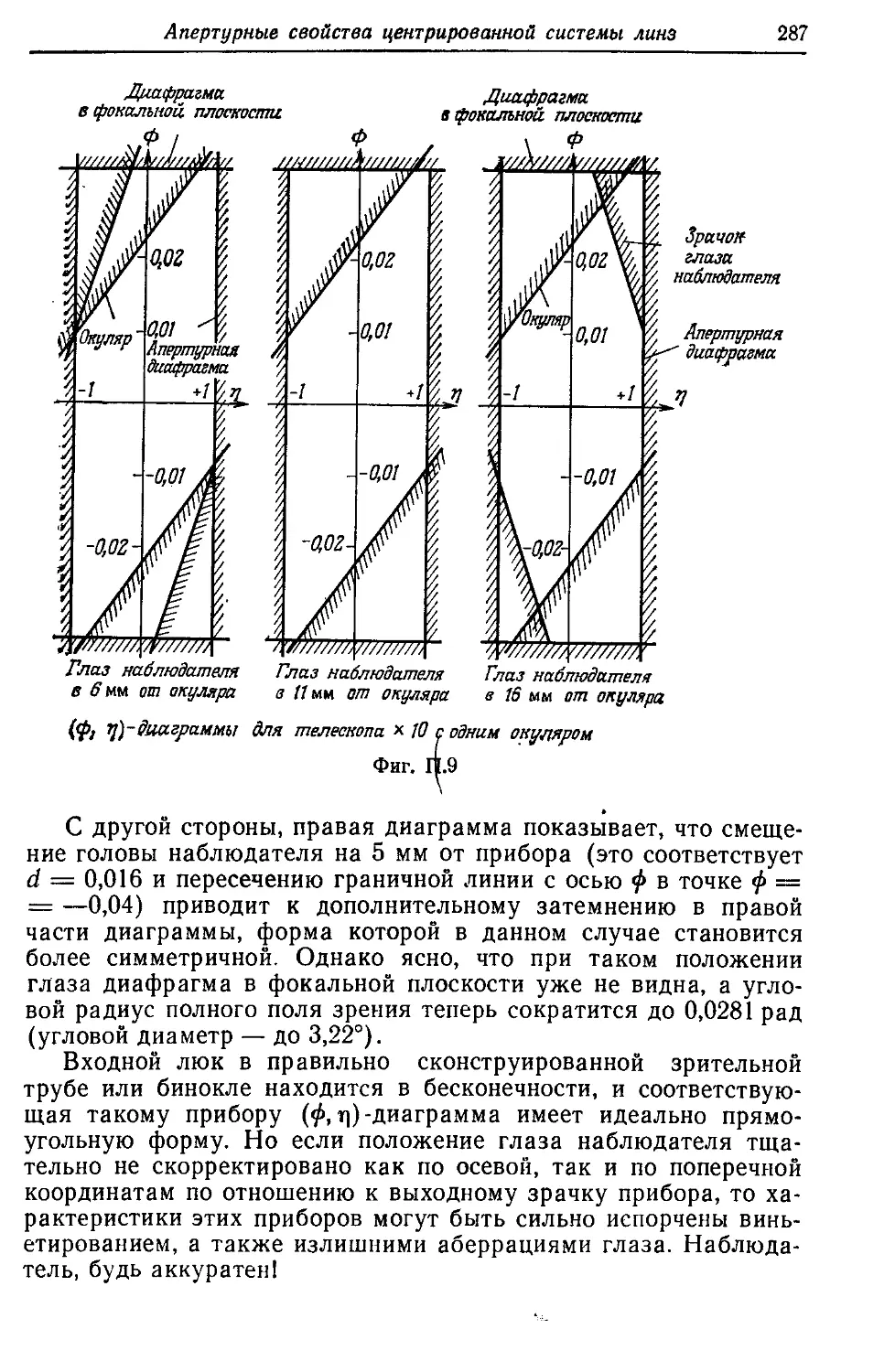
§ 5. Пример 281
Оглавление 341
ПРИЛОЖЕНИЕ II. МАТРИЧНОЕ ОПИСАНИЕ ЦЕНТРОВКИ И ЮСТИ-
ЮСТИРОВКИ ОПТИЧЕСКОЙ СИСТЕМЫ 288
§ 1. Применение расширенных матриц 3X3 288
§ 2. Перемножение расширенных матриц 289
§ 3. Влияние расстройки оптического резонатора 291
ПРИЛОЖЕНИЕ III. СТАТИСТИЧЕСКИЙ ВЫВОД ПАРАМЕТРОВ
СТОКСА 293
ПРИЛОЖЕНИЕ IV. ВЫВОД МАТРИЦ МЮЛЛЕРА 302
§ 1. Поляризатор 302
§ 2. Полуволиовая пластинка (оптическая ось составляет угол 9 с
осью х) 305
§ 3. Четвертьволновая пластинка: Общий случай ориентации (оптиче-
(оптическая ось составляет угол в с осью х) 307
§ 4. Произвольная фазовая пластинка (вызывающая в обыкновенном
луче отставание по фазе иа б), оптическая ось которой состав-
составляет угол 9 с осью х 313
ПРИЛОЖЕНИЕ V. ПОЛУЧЕНИЕ МАТРИЦ ДЖОНСА 319
§ 1. Поляризатор типа пленочного поляроида 319
§ 2. Матрица Джонса прибора, вызывающего произвольную фазовую
задержку 321.
ПРИЛОЖЕНИЕ VI. ВЗАИМОСВЯЗЬ МЕЖДУ МЕТОДАМИ РАСЧЕТА
ДЖОНСА И МЮЛЛЕРА 324
§ 1. Введение 324
§ 2. Вывод соотношения между векторами Стокса и Максвелла . . . 324
§ 3. Представление «матричных сэндвичей» через элементы матриц
Мюллера и Джонса 326
§ 4. Попарное сравнение «матричных сэндвичей» в двух методах рас-
расчета 327
§ 5. Выражения для элементов матрицы Мюллера через элементы
матрицы Джонса 329
§ 6. Получение выражений для элементов матрицы Джойса через
элементы матрицы Мюллера 329
БИБЛИОГРАФИЯ И ЗАКЛЮЧЕНИЕ 333
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 336
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Лазеры применяются уже почти два десятилетия, и сфера их
использования быстро расширяется. Замечательные свойства
лазерного луча находят многочисленные, порой самые неожи-
неожиданные применения в научных исследованиях, технических раз-
разработках, а также в различных отраслях промышленности.
В связи с этим быстро растет число специалистов самых разно-
разнообразных профилей, которым так или иначе приходится рабо-
работать с лазерами, а также конструировать простейшие оптические
системы фокусировки и преобразования лазерных пучков. Не-
Несмотря на обилие монографий и обзорных статей по квантовой
электронике, лазерной технике и приложениям лазерных систем,
книга А. Джеррарда и Дж. М. Бёрча- является, по-видимому,
наиболее удачным пособием для изучения основ практической
лазерной оптики как для студентов, так и для широкого круга
ученых и инженеров, использующих лазерное излучение в раз-
различных целях.
Прежде всего отметим, что книга написана очень простым,
почти популярным языком и, вообще говоря, не требует от
читателя даже знания дифференциального исчисления, не го-
говоря уже о более сложных и тонких вопросах математической.^
физики, физической оптики и квазиоптики. С другой стороны;
ни в коем случае нельзя сказать, что содержание книги три-
тривиально. Напротив, в ней собраны и систематизированы весьма
эффективные методы расчета, включающие многочисленные
классические и хорошо известные результаты по поляризацион-
поляризационной и геометрической оптике наряду с более поздними резуль-
результатами квазиоптики, оптики гауссовых пучков и теории опти-
оптических резонаторов.
Столь удачное сочетание простоты и в то же время эффек-
эффективности матричных методов, изложенных в книге, стало
возможным благодаря целому ряду обстоятельств.
Во-первых, дифракционная теория распространения гауссо-
гауссовых пучков в квазиоптическом приближении как в свободном
пространстве, так и через системы идеальных линз (а также
в средах с параболическим распределением показателя прелом-
преломления) может быть сформулирована на простом матричном
языке с помощью правила ABCD, введенного Когельником
[1, 2]. Самое удивительное состоит в том, что эта формулировка
Предисловие редактора перевода
использует матрицы, которые уже более ста лет известны в гео-
геометрической оптике. По сути дела, задача распространения
лазерных пучков сведена к простейшей и давно решенной задаче
распространения лучей в геометрической оптике. Проводя ана-
аналогию между оптикой и механикой (геометрическая оптика —
механика Ньютона, квазиоптика — волновая, или квантовая, ме-
механика), можно сказать, что правило ABCD в принципе по-
позволяет построить точное решение уравнения Шредингера для
частицы в свободном пространстве на основе решения элемен-
элементарной задачи классической механики. Таким образом, совер-
совершенно естественно, что формулы, полученные с помощью пра-
правила ABCD, при А,—>0 в полном согласии с принципом соответ-
соответствия переходят в формулы геометрической оптики (см. гл. 3,
стр. 157).
Во-вторых, матричные методы расчета оптических систем во
многом аналогичны широко известным методам, которые уже
давно используются в инженерной практике при расчетах при-
приборов в диапазоне СВЧ и электрических схем на основе четы-
четырехполюсников. В рамках этих методов полная матрица системы
записывается в. виде произведения матриц составляющих ее
элементов, которых, например в оптике, формирующей изобра-
изображение, всего два: 1) преломляющая или отражающая оптиче-
оптическая поверхность и 2) оптический промежуток, измеряемый
приведенным расстоянием вдоль оптической оси между двумя
такими поверхностями. С помощью этих матриц можно решать
(в квазноптическом приближении) многочисленные практически
важные задачи лазерной оптики, например вычислять пара-
параметры резонаторов лазеров по заданным параметрам пучка
на выходном зеркале и решать обратную задачу согласования
оптических систем лазерной оптики, рассчитывать линзовые
оптические волноводы, оптимальную фокусировку лазерного
излучения на мишень и т. д.
Нередко в лабораторной практике возникает вопрос: с какой
точностью и в каких случаях лазерный пучок можно считать
гауссовым? Известно, в частности, что при использовании спе-
специальным образом сконструированных лазеров с эффективной
селекцией поперечных и продольных мод резонатора можно
получить пучок, конфигурация которого чрезвычайно близка к
гауссовой практически на любом расстоянии от лазерного источ-
источника. Большинство же лазеров, используемых на практике, излу-
излучает многомодовые пучки, которые с большей или меньшей точ-
точностью могут быть описаны линейной суперпозицией функций
Эрмнта — Гаусса [3]. Применение правила ABCD часто оправ-
датю даже в случае многомодовых лазеров, поскольку, согласно
[3J, радиус кривизны волнового фронта одинаков для всех мод
резонатора и перетяжки всех мод такого пучка совпадают как
Предисловие редактора перевода
внутри резонатора, так и при внешней фокусировке. Тем не ме-
менее на практике желательно иметь хотя бы грубые критерии,
позволяющие устанавливать, можно ли пучок данного конкрет-
конкретного лазера считать гауссовым.
Кроме того, никогда не мешает проверить, насколько пара-
параметры пучка на выходном зеркале лазера соответствуют рас-
расчетным значениям (см. табл. 3.2, гл. 3). Существует много при-
причин, которые могут вызвать отклонения истинных значений
параметров лазерных пучков от расчетных; это термические
линзоподобные неоднородности, часто возникающие в активной
среде, неоднородность профиля коэффициента усиления по сече-
сечению лазерного усилителя, разъюстировка лазерного резонатора,
аберрации, дифракция на малых апертурах и т. д. Следует отме-
отметить, что в ряде случаев (например, для резонаторов с двумя
плоскопараллельиыми зеркалами) формулы, приведенные в
табл. 3.2, вообще неприменимы. Таким образом, очевидно, что
в лабораторной практике очень важно уметь непосредственно
измерять геометрические характеристики лазерных пучков в со-
соответствии с конкретно решаемой задачей.
К сожалению, в данной книге вопрос об измерении геометри-
геометрических параметров лазерных пучков практически не рассмотрен,
хотя в четвертой главе, а также во второй подробно описаны
экспериментальные методы измерения буквально всех парамет-
параметров, используемых в приведенных там расчетах. Мы попытаемся
здесь хотя бы частично восполнить этот пробел, описав по край-
крайней мере самые простые методы экспериментального измерения
геометрических параметров лазерных пучков. Речь идет об из-
измерении полуширины гауссова пучка:
>l] A)
и радиуса кривизны волнового фронта такого пучка
4^> B)
где 20 и до© — радиус дифракционной расходимости (конфокаль-
(конфокальный параметр) пучка и радиус перетяжки пучка. Эти параметры
связаны между собой соотношением 20==яа|/Л. Следовательно,
для полного описания геометрии гауссова пучка необходимо за-
задать или измерить два независимых параметра.
Наиболее прямой метод измерения геометрических парамет-
параметров гауссова пучка предложен Пирсоном и др. в работе [4] и
основан на измерениях радиуса пучка w{z) в двух точках оси г.
Предисловие редактора перевода
При этом радиус дифракционной расходимости пучка следует
искать по формуле
C)
где Z\ — nw2(zi)/K и Ri — радиус кривизны волнового фронта
пучка в точке Z\, который, как показано в работе [4], опре-
определяется действительным положительным корнем уравнения
R ;L\ - LXL2 + z\, 2) + R\ BL?Zi, 2) + R\ U\ - h\l2 + 2l\z\, 2) +
+ /?iBLK2) + /-fzb = 0, D)
где L2 = пш2B2)/Я и ZiJ = Zi — z2. Вычислив Ri и te;(z"i), можно
найти положение перетяжки пучка, а также все его остальные
параметры, необходимые для корректной постановки экспери-
эксперимента.
Следует отметить, что этот метод несовершенен; среди его
недостатков — сложность вычислений (а именно — решение
уравнения четвертой степени) и необходимость прямого или
косвенного построения кривой почернения фотопленки для изме-
измерения полуширины пучка. Поскольку речь идет о лазерных пуч-
пучках, для которых использование стандартных многоступенчатых
ослабителей существенно затруднено дифракцией и интерферен-
интерференцией, построение кривой почернения фотопленки требует опре-
определенной сноровки. Кроме того, для проведения сколько-нибудь
точных измерений сам ослабитель часто необходимо предвари-
предварительно калибровать на длину волны излучения лазера. Поэтому
для лазерных пучков проще строить кривую почернения без мно-
многоступенчатых ослабителей, используя, например, известное рас-
распределение интенсивности в дифракционной картине щели. Од-
Однако можно вообще обойтись без непосредственного построения
кривой почернения фотопленки, если применить метод отражаю-
отражающего клина или эквивалентный ему метод заданного ослабления
пучка. При этом заранее предполагается, что пучок является
гауссовым. Согласно этим методам, лазерный пучок несколько
раз репродуцируют на фотопленку (если луч обладает доста-
достаточно большой энергией, то для измерений можно использовать
ожоги на заовеченной фотопленке или фотобумаге), каждый раз
с известным ослаблением D^ В методе отражающего клина
ослабление интенсивности пучка Dt можно рассчитать по фор-
формулам Френеля.
Пусть в t-м эксперименте оптическая плотность фильтра
равна Di = ln(l/ti). Тогда следует измерять радиусы rt пятен
на пленке, соответствующих определенному уровню почерне-
почернения. При этом поток энергии S/, необходимый для реализации
Предисловие редактора перевода
данной степени почернения, определяется выражением
W^\. E)
Логарифмируя это выражение, получим линейную зависимость
г] от Dit причем наклон прямой равен A/2) w2(z). Таким об-
образом,
Используя метод отражающего клина, необходимо следить за
тем, чтобы радиус дифракционной расходимости пучка был су-
существенно больше толщины клина, с тем чтобы все отраженные
пучки имели одинаковую полуширину при попадании на пленку.
Недавно был предложен иной метод [5], существенно более
простой с точки зрения вычислений и не требующий ни прямого,
ни косвенного фотометрирования. В этом методе лазерный луч
пропускают через тонкую плоскопараллельную прозрачную пла-
пластину (толщина пластины должна быть много меньше предпо-
предполагаемого радиуса дифракционной расходимости пучка) под
некоторым углом ф. При отражении от пластины возникают два
параллельных пучка приблизительно равной интенсивности, оси
которых смещены друг относительно друга на расстояние
d sin Bф)
0 ~~ V«2 — sin2 (Ф) '
где d — толщина пластины, ф — угол падения, п — показатель
преломления материала плоскопараллельной пластины. Легко
показать (читателю предлагается проделать это самостоятельно,
используя выражение для амплитуды гауссова пучка, приведен-
приведенное в гл. 3, стр. 131), что распределение интенсивности в интер-
интерференционной картине представляет собой систему эквидистант-
эквидистантных интерференционных полос, растояние между которыми Ах
однозначно связано с радиусом кривизны волнового фронта R
выражением
Таким образом, для того чтобы измерить радиус кривизны
пучка R в данной точке оси г, необходимо всего лишь измерить
в соответствующей плоскости расстояние Ах между максиму-
максимумами интерференционной картины. Иными словами, параметры
пучка можно найти, измерив радиус кривизны волнового фронта
пучка R(zi) и R(z2) в двух точках на оси z. Все дальнейшие
вычисления очень просты (точно такая же задача решается §
10 Предисловие редактора перевода
п. 8.3 гл. 3, стр. 160); в частности, положение перетяжки пучка
определяется соотношением
Zn (Rl-2z1)-(R2-2z2) '
а радиус дифракционной расходимости
На практике удобно направить пучки, отраженные от плооко-
параллельной пластины, вдоль оптической скамьи и, передвигая
рейтер с фотопленкой по скамье, репродуцировать на пленку
(без всяких дополнительных объективов и линз!) распределение
интенсивности в интерференционной картине в нескольких точ-
точках оси г. Первый признак «высокого качества» пучка — это
эквидистантность ') и прямолинейность полос интерференционной
картины, свидетельствующие о параболичности волнового фрон-
фронта. Для получения количественных данных следует обработать
совокупность измеренных значений радиусов кривизны волно-
волнового фронта пучка /?,-= R(Zi), используя стандартные методы
математической статистики. При этом можно с высокой точно-
точностью вычислить параметры лазерного пучка, а также при жела-
желании ввести количественный критерий его гауссовости.
В заключение сделаем краткое замечание по поводу терми-
терминологии, используемой в настоящей книге. Практически боль-
большинство специальных оптических терминов вводится с обстоя-
обстоятельными и подробными пояснениями, так что во всех случаях
читателю нетрудно усвоить смысл и назначение данного опре-
определения. Однако в ряде случаев при переводе мы столкнулись
с английскими терминами, которым соответствуют несколько
различных толкований, и с терминами, не имеющими русских
эквивалентов и не получившими достаточно широкого распро-
распространения в советской технической и научной литературе. Во
всех таких случаях мы старались использовать наиболее употре-
употребительные термины, максимально отражающие физический
смысл введенной характеристики.
Следует особо отметить четкое и наглядное определение
важной физической характеристики оптических приборов —
«этандю». Эта величина равна полному световому потоку, про-
проходящему через прибор при отображении плоского бесконечно
протяженного светящегося объекта единичной яркости, располо-
расположенного в плоскости входного люка прибора. Вообще говоря,
эту характеристику в советской литературе (см., например, [6])
иногда называют светосилой или «геометрическим фактором
') Гауссово распределение амплитуды в пучках может, вообще говоря,
приводить к некоторой неэквидистаитности полос (~ 5%). Подробнее этот
вопрос рассмотрен в [5].
Предисловие редактора перевода 11
прибора». К сожалению, часто термин «светосила» используют
для обозначения других энергетических характеристик прибора,
в частности относительного отверстия (см., например, [7]) или
квадрата этой величины [8], либо предпочитают вообще не поль-
пользоваться им [9]. Для того чтобы избежать неопределенности в
этом важном вопросе, при переводе, следуя авторам книги, мы
оставили специальный термин «этандю» (франц. etendue) '). От-
Отметим, что в отечественных справочниках и каталогах оптиче-
оптических приборов (см., например, [6]), как правило, приводятся
данные по относительному, или действующему, отверстию при-
прибора, угловой величине поля зрения (для спектральных прибо-
приборов— угловой размер выходной или входной щели и соответ-
соответствующие фокусные расстояния объективов) и ряд других харак-
характеристик, используя которые, этандю всегда можно вычислить.
Отметим, наконец, что комментарии и примечания к рус-
русскому изданию книги мы старались сделать лишь в самых
необходимых случаях, хотя многие вопросы лазерной оптики, в
частности нелинейной оптики, оставшиеся за рамками книги
или затронутые весьма поверхностно (например, самофокуси-
самофокусировка и пробой прозрачных диэлектриков), к настоящему вре-
времени подробно изучены. Хотя знакомство с этими вопросами
было бы весьма полезно для читателя, интересующегося лазер-
лазерной техникой, достаточно подробное их рассмотрение лишило
бы книгу ее основного достоинства — простоты и наглядности
изложения, которые, как мы надеемся, обеспечат ей широкую
читательскую аудиторию в нашей стране.
В. В. Коробкин
ЛИТЕРАТУРА
1. Kogelnik H., Appl. Opt., 4, 1562 A965).
2. Kogelnik H., Li Т., Proc. IEEE, 54, 1312 A966) [имеется перевод: Когель-
ник. Ли, Резонаторы и световые пучки лазеров, ТИИЭР, т. 54, № 10, (95)
1966].
3. Марк узе Д., Оптические волноводы, «Мир», М., 1974; см. также: Гонча-
ренко А. М., Гауссовы пучки света, «Наука и техника», Минск, 1977.
4. Pearson I. E., McGill Т. С, Kurtin S., Yariv A., Journ. Opt. Soc. Amer.,
59, 1440 A969).
5. Власов Д. В., Коробкин В. В., Серов Р. В., Квантовая электроника (в пе-
печати), 1978.
6. Нагибина Н. М., Прокофьев В. К., Спектральные приборы и техника спек-
спектроскопии, «Машиностроение», Ленинград, 1967, стр. 36.
7. Борн. М., Вольф Э., Основы оптики, «Наука», 1970.
8. Яворский Б. М., Детлаф А. А., Справочник по физике, «Наука>, М., 1965.
9. Шишловский А. А., Прикладная оптика, Физматгиз, М., 1961.
*) Этот термин впервые ввел Конн и в настоящее время его широко ис-
используют в зарубежной литературе в качестве важнейшей характеристики
светосилы оптических приборов.
ПРЕДИСЛОВИЕ АВТОРОВ
Наша цель при написании настоящей книги состояла не
столько в том, чтобы изложить некоторые новые результаты,
сколько в том, чтобы расширить и систематизировать использо-
использование простых матричных методов в процессе преподавания
оптики студентам университетов и технических вузов. Многие
из этих методов давно известны, однако они не нашли пока
достаточно широкого признания. Мы полагаем, что пришло вре-
время активно использовать матрицы в лекционных курсах по
оптике. Наша уверенность в этом частично основывается на том,
что матрицы сейчас широко используются и изучаются в учеб-
учебных заведениях, и многие студенты уже почувствовали эконо-
экономичность и элегантность применения матричных методов для ра-
расчета систем, когда целый ряд соотношений между входными и
выходными параметрами .системы можно представить с помо-
помощью одной лишь матрицы.
Кроме того, более чем за десятилетие оптика обогатилась
методами, развитыми в других дисциплинах, таких, как физика
микроволн и теория электрических цепей. Хотя студент техниче-
технического вуза может быть новичком в оптике, однако матричные
методы должны быть хорошо известны ему из лекций по теории
электрических фильтров или передающих линий. Мы считаем,
что он без особого труда будет воспринимать курс оптики, в ко-
котором вместо нагромождения узкоспециальных, исторически
сложившихся концепций используются методы, уже изученные
им по другим дисциплинам.
Другой барьер, который матричные методы, по-видимому,
позволят преодолеть, — это традиционное классическое деление
оптики на два раздела: геометрическую оптику и физическую
оптику. Современная оптика переступает все границы, и студент
может разделить наше удовольствие, поняв, что матрица преоб-
преобразования лучей, полученная из чисто геометрических сообра-
соображений, почти точно предсказывает картину дифракции гауссова
пучка как при его возбуждении в лазерном резонаторе, так и
при распространении его через некоторую оптическую систему.
Такая универсальность матричных методов доставила бы, на-
наверное, огромное удовольствие самому Гауссу!
Надеясь, что матричные методы помогут навести мосты
между различными направлениями оптики и другими дисципли-
Предисловие авторов 13
нами, мы сочли необходимым устранить какие-либо несоответ-
несоответствия в номенклатуре. Из нескольких предложенных разными
авторами типов матриц преобразования лучей нами были вы-
выбраны матрицы, данные Синклером (Оптический институт, Ро-
честер, шт. Нью-Йорк). Согласно Синклеру, в рассмотрение
вводятся только унимодулярные матрицы, построенные в полном
соответствии с методом ynv, а также с современными простей-
простейшими методами расчета оптических резонаторов. В отличие от
номенкл но о ост
\ еЦ" яТ° «""-««-о. е»„0Ч(>ртССмИе воо
Р
НИС-К СОН.ТТнН. п
тьнянеотттнтдха1
14 Предисловие авторов
Другие аспекты, которые остались за рамками книги, но которые
было бы весьма уместно рассмотреть в курсе более высокого
уровня,— это матрицы когерентности Вольфа и использование
матриц 3X3 и 4 X 4 для описания отражения от ряда зеркаль-
зеркальных поверхностей, ориентированных различным образом, как это
имеет место, например, в отражающей призме.
Первая глава книги предназначена для тех, кто не знаком
с матричной алгеброй. Основные положения, алгебры прямо-
прямоугольных матриц, а также правила их сложения и перемножения
рассмотрены с использованием большого количества численных
примеров. В параграфе, посвященном квадратным матрицам,
для простоты описываются матрицы 2x2. После введения
транспонированных матриц и определителей, мы обсуждаем
методы обращения матриц. Это позволяет в какой-то, степени
рассмотреть вопрос о приведении матриц к диагональному виду.
Глава заканчивается описанием методов возведения матриц в
n-ю степень (без привлечения теоремы Сильвестра)?. ¦
Вторая глава посвящена методам формирования изображе-
изображения в параксиальном приближении в центрированных оптиче-
оптических системах. Задавая луч двумя параметрами—высотой на
оптической оси й оптическим направляющим косинусом, мы по-
показываем, каким образом можно использовать матрицу преобра-
преобразования лучей, чтобы описать изменения этих параметров при
распространении луча через оптическую систему»; Для образо*
вания эквивалентной матрицы тонкой линзы, толстой линзы или
полной оптической системы используются два основных типа
Матриц, которые комбинируются соответствующим образом.
Одна из них описывает эффект простого оптического промежутка
(перемещение луча в свободном пространстве), а другая —про-
—прохождение луча через одну из преломляющих поверхностей. По-
Показано, каким образом можно вывести свойства оптической си-
системы из ее матрицы и, наоборот, как экспериментально можно
определить матричные элементы полной матрицы системы.
В конце данной главы мы обобщили понятие матрицы преобра-
преобразования лучей и ввели матрицы отражения, аналогичные мат-
матрицам,'описывающим преломление. Материал иллюстрируется
практическими примерами. В приложении к этой главе даны
методы расчёта апертурных характеристик оптических систем.
В первой части гл. 3 проанализированы и сведены в таблицу
результаты, полученные в первых двух главах, которые затем
используются для описавяя радиуса кривизны волнового фронта,
длины оптического пути н этандю. Затем мы рассмотрели опти-
оптические резонаторы и показали, каким образом можно описать
полный проход луча между зеркалам» резонатора с помощью
одной эквивалентной матрицы. Для того чтобы рассмотреть мно-
многократные прохождения луча через резонатор, мы привели эту
Предисловие авторов 15
матрицу к диагональной форме и нашли, что в случае «неустой-
«неустойчивого» резонатора как собственные значения, так и собствен-
собственные векторы этой матрицы действительны, причем первые опре-
определяют потери луча за проход вследствие ухода части энергии
из резонатора, а последние — радиус кривизны самовоспроизво-
самовоспроизводящегося волнового фронта.
В случае устойчивого лазерного резонатора как собственные
значения, так и собственные векторы комплексны, причем пер-
первые определяют сдвиг фазы пучка за проход, а вторые интер-
интерпретируются на основе введенного Когельником комплексного
параметра кривизны, что позволяет найти не только расходи-
расходимость, но также и размер пятна гауссова пучка, генерируемого
лазером. Кроме того, если решается задача согласования мод,
в которой мы должны учесть дифракцию лазерного пучка при
распространении его вне резонатора, то такую задачу довольно
просто решить, используя матрицы преобразования лучей. Глава
заканчивается кратким описанием возможностей применения
развитых выше методов для описания линзоподобной среды.
В приложении обсуждаются также вопросы использования рас-
расширенных матриц для описания эффектов, связанных с несовер-
несовершенствами юстировки оптической системы.
В гл. 4 мы рассматриваем два альтернативных матричных
метода, используемых при решении задач поляризационной оп-
оптики. Рассмотрев предварительно различные состояния поляри-
поляризации света, мы вводим вначале параметры Стокса и матрицы
Мюллера 4X4, которые позволяют решать задачи для поляри-
поляризованного и неполяризованного света. Обсуждая эти результаты,
мы приводим многочисленные практически важные примеры по-
подобных расчетов, а также показываем, каким образом пара-
параметры Стокса и элементы матрицы Мюллера можно измерять
экспериментально. Матрицы Мюллера поляризационных прибо-
приборов, наиболее часто используемых на практике, сведены в со-
йтветствующие таблицы, а подробности вывода таких матриц
описаны в приложении.
Далее таким же образом описан метод Джонса с использо-
использованием комплексных матриц 2X2, который часто оказывается
более удобным при работе с полностью поляризованным светом.
Материал излагается так, что при желании читатель может
ограничиться изучением либо метода Джонса, либо метода
Мюллера.
В других приложениях к этой главе рассмотрены статистиче-
статистическая интерпретация параметров Стокса и полный анализ связи
между матричными элементами матрицы Джонса и соответ-
соответствующими элементами матрицы Мюллера.
Глава 5 посвящена применению матричных методов для
описания процессов распространения света в одноосных
16 Предисловие авторов
кристаллах. Хотя последняя тема является более сложной и пред-
предполагает знание некоторых основ электромагнитной теории, од-
однако она не связана с содержанием предыдущей главы и ее
можно изучать отдельно. Мы надеемся, что читатель самостоя-
самостоятельно сможет восстановить детали, опущенные в этой главе,
обратившись к библиографии, приведенной в конце книги.
Наконец, поскольку главы настоящей книги были задуманы
главным образом, чтобы дать студентам основные представле-
представления и проиллюстрировать применение матричных методов ра-
расчетов, многие разделы оптики остались за рамками книги. На-
Насколько полезным окажется изложенный материал студенту в
его дальнейшей практической деятельности?
Из числа окончивших вуз студентов лишь небольшая часть
будет заниматься конструированием и производством оптиче-
оптических приборов. Для них мы отмечаем, что на практике задачи
по поляризационной оптике встречаются не очень часто, а учет
оптических эффектов первого порядка в большинстве случаев
является тривиальным; действительно сложные задачи возни-
возникают либо при использовании ЭВМ для расчета аберрации тре-
третьего и более высоких порядков, либо при решении более кон-
конкретных вопросов во время производства и сборки систем.
Однако на каждого профессионального оптика приходится
большое количество других специалистов, которые так или
иначе используют готовое оптическое оборудование, а также со-
собирают достаточно сложные оптические системы из простых
элементов. В частности, речь идет о специалистах, занятых в
области научных исследований, а также в новых направлениях
промышленности, использующих оптоэлектронику и лазерную
технику. Более того, сюда можно также включить специалистов,
работающих в традиционных конструкторских бюро, связанных
с разработкой механических систем. Здесь мы имеем в виду
не только измерения фотоупругих характеристик объектов и
широко используемые методы оптического контроля и юсти-
юстировки деталей, но также и последние достижения в области
лазерной голографии и интерферометрии порошков. Наступило
время, когда оптические методы измерений можно применить
при решении большого круга задач, и специалист обычно дол-
должен самостоятельно вникать в основные вопросы оптики. В го-
лографических методах неразрушающих испытаний при иссле-
исследовании вибраций или при анализе картины напряжений иссле-
исследуемая деталь может иметь столь сложную форму, что не будет
никакого смысла в попытках создать хорошо скорректирован-
скорректированное изображение такой детали на широкой плоской поверхно-
поверхности. Следовательно, умело используя простейшие линзы, можно
сэкономить деньги (как, впрочем, и устранить многократные
внутренние отражения); однако мы надеемся, что, прежде чем
ГЛАВА 1
ВВЕДЕНИЕ В МАТРИЧНОЕ ИСЧИСЛЕНИЕ
§ 1. ВВОДНЫЕ ЗАМЕЧАНИЯ
В настоящей книге мы рассмотрим, какие преимущества дает
применение некоторых простых идей матричной алгебры в зада-
задачах построения оптического изображения и в поляризационных
задачах. Содержание этой главы предназначено главным обра-
образом тем читателям, которые недостаточно знакомы с матрицами
и определителями. Поэтому материал излагается на элементар-
элементарном уровне и охватывает только то, что необходимо для пони-
понимания остальной части книги.
Матрицы ввел в 1857 г. математик Кэли как удобную крат-
краткую запись систем линейных уравнений. Действия над матри-
матрицами несколько отличаются от действий над обычными числами,
но их правила были вскоре найдены и разработаны. Матричные
методы привлекли большой интерес физиков в 1920 г., после того
как Гейзенберг дал матричную формулировку квантовой меха-
механики. Использовались они и в различного рода инженерных рас-
расчетах, но в оптике стали применяться совсем недавно.
Вандермонд еще в 1771 г. ввел определители, которых мы
будем касаться в меньшей степени. Сперва они назывались «эли-
минантами», поскольку возникали при решении уравнений ме-
методом последовательного исключения. В большинстве тех опти-
оптических задач, с которыми мы будем иметь дело, все определи-
определители равны единице, и это обстоятельство обеспечивает удобную
проверку отдельных этапов вычислений.
Рассмотрим теперь, каким образом возникает понятие мат-
матрицы. Предположим, что мы имеем пару линейных уравнений:
U = Ax + By,
V = Сх + Dy,
где А, В, С и D — известные постоянные, а х н у — переменные
величины. Эти уравнения позволяют вычислить U и V, если
известны х и у. Во многих случаях оказывается удобным отде-
отделить постоянные от переменных. При этом два уравнения можно
Предисловие авторов 17
эти линзы будут собраны с использованием соответствующих
матриц преобразования или без них, читатель данной книги не
забудет проверить каждую из них на приборе для визуализации
внутренних напряжений в стекле!
Один из авторов книги, Дж. М. Бёрч, выражает признатель-
признательность Научно-техническому фонду штата Нью-Йорк, благодаря
которому он проработал год в качестве приглашенного лектора в
Оптическом институте Рочестерского университета. Он также
признателен целому ряду сотрудников Рочестерского универси-
университета, и в особенности Дугласу К. Синклеру, за обсуждение
некоторых аспектов теории матриц преобразования лучей.
I Академия наук СССР
j Куйбышевский филиал
Физического института |
Б И Б Л И О Т Е К Я й
20_ Глава 1
записать в виде одного соотношения следующим образом:
оно имеет тот же самый смысл, что и пара уравнений. Каждая
из групп символов, заключенная между парой вертикальных
скобок, рассматривается как единое целое и называется матри-
[у] ¦ И
цей. Величины I I и I I представляют собой матрицы-столб-
матрицы-столбцы, или, что то же самое, векторы-столбцы, поскольку каждый
из них содержит лишь один столбец.
В общем случае матрица образует прямоугольную таблицу
символов, записанных в виде строк и столбцов. Матрица
[Л В1
I r n I, которая состоит из двух строк и двух столбцов, назы-
называется квадратной матрицей второго порядка. Матрица-строка,
или вектор-строка, записывается в виде [Р Q]; в ней отдельные
символы — матричные элементы — расположены горизонтально
на одной строке. Матрица, состоящая из одного-единственного
элемента, представляет собой обычное число, или скалярную
величину.
Если каждой матрице поставить в соответствие определенный
символ, то два уравнения можно записать гораздо более кратко,
а именно:
Гх1 [Wl
здесь С] — матрица-столбец I , С2 — матрица-столбец \„ J
[Л В1
a S — квадратная матрица I _ ~ I.
Предположим теперь, что U и V связаны в свою очередь с
другой парой переменных L и М, скажем, посредством другой
пары линейных уравнений
которую мы запишем в виде
гр Q-||-{/
Ltf
или
Ы и
введение в матричное исчисление 21
С3 — матрица-столбец 1дЛ, а К — матрица I.
Конечно, мы можем выразить L и М через я и у, подставляя
U и V в уравнения, определяющие L и М. Таким образом,
здесь
или
L = (РА + QC) х + (РВ + QD) у,
М = {RA + ТС) х + (RB + TD) у.
Эти уравнения можно записать в матричном виде:
LlTPA + QC PB + QD1 Гх1
м\ ~ LRA + TC RB + TD\ \_уУ
или
[PA + QC PB + QD1
где F обозначает матрицу ^Д _^тс ^в_^ TDj . Но, с другой
стороны, можно написать
Теперь, если бы это было уравнение в обычной алгебре, мы
могли бы, изменив просто местоположение скобок, переписать
его в виде
Тогда KS называлось бы произведением К a S.
Кроме того, сравнивая уравнения, связывающие Ci и С3,
можно было бы написать
з i и Сз=*
Следовательно,
F KS
и можно было бы сказать, что F представляет собой произведе-
произведение К на S.
В матричном исчислении мы хотели бы поступать таким
же образом, однако в таком случае необходимо определить про-
произведение двух матриц, поскольку в обычной алгебре определено
лишь произведение обычных чисел.
22 Глава 1
§ 2. ПЕРЕМНОЖЕНИЕ МАТРИЦ
Определим матричное произведение так, чтобы описанный
выше формализм мог быть перенесен из обычной алгебры в ал-
алгебру матриц. Таким образом, будем называть матрицу F про-
произведением матрицы К на матрицу S, причем
ГР Q1 ГА В1 _ Г PA + QC РВ + QD1
Ь? Т] 1С d1~LRA + TC RB + TD1'
Рассматривая структуру матрицы в правой части этого равен-
равенства, нетрудно понять правило ее получения.
Левый верхний элемент новой матрицы стоит в первой строке
и в первом столбце. Для того чтобы его получить, нужно взять
первую строку матрицы К, т. е. [Р Q], и первый столбец матри-
[А1
r I , и умножить друг на друга их соответствующие
элементы (первый элемент строки на первый элемент столбца),
образуя произведения РА и QC, а затем сложить эти произведе-
произведения: РА + QC.
Элемент в первой строке и втором столбце матрицы F обра-
образуется аналогичным способом из элементов первой строки мат-
матрицы К и второго столбца матрицы S. Элемент матрицы F,
стоящий во второй строке и первом столбце, образуется из
второй строки матрицы К и первого столбца матрицы 5. И, на-
наконец, элемент во второй строке и втором столбце матрицы F
получается из второй строки матрицы К и второго столбца мат-
матрицы 5.
В некоторых приложениях оказывается удобным использо-
использовать обозначения для элементов матриц с помощью индексов.
Например, запишем матрицу-столбец А в виде
¦М-
где нижний индекс указывает на местоположение элемента в
столбце. Квадратную матрицу 5 можно написать следующим
образом:
-E
здесь первый индекс указывает номер строки, а второй — номер
столбца, на пересечении которых расположен данный элемент.
В индексных обозначениях произведение двух квадратных мат-
матриц К и S, записываемых как
] и 5=
/C21 A22J LS2i 022
Введение в матричное исчисление
23
равно F = KS, причем матрица F принимает вид
>Ц "Г Al2"J2I All«Jl2 "l Al2'
- Л221 А212 "г А22'
ИЛИ
-2 2
Zj KuS{i 21 KuSi2
3»2
Отсюда следует общая формула для любого элемента мат-
матрицы:
FRT =
где FRT — элемент матрицы F в /?-й строке и Т-м столбце; обо-
обозначения для матриц К и 5 аналогичны. (Используемый здесь
знак суммирования означает, что повторяющийся индекс i про-
пробегает последовательно все возможные значения; этот индекс
иногда опускают.)
До сих пор мы рассматривали матрицы размером «два на
два» BX2) и столбцы размером «два на один» BX1); но
матричное представление является значительно более общим.
В настоящей книге нам потребуются квадратные матрицы раз-
размером 2X2, ЗхЗи4Х4, столбцы 2Х1,ЗХ1и4Х1и строки
размером 1X2, 1 X 3 и 1X4. Все эти матрицы определяются
таким же образом. Например, пусть имеется система четырех
уравнений с четырьмя неизвестными:
Запишем ее в матричном виде либо как
К\1 Kl2 К\3 Кц
^21 А 22 А*23 А 24
П ^~* V Т? ТГ ТТ
&л Аз1 Аз2 Азз Аз4
Ml A 42 А 43 А 44
либо в более сокращенной форме:
В = К А,
24
В этом случае R-й. элемент матрицы-столбца В дается выра-
выражением
Заметим, что мы применили изложенное выше правило по-
получения элементов произведения матриц, поместив А на место
матрицы S, а В — на место матрицы F; однако, поскольку А я В
представляют теперь матрицы-столбцы размером 4X1. второй
индекс Т в матрицах F я S принимает единственное значение,
равное 1. Поэтому запись можно упростить:
4
R IM R
(где В и А являются, очевидно, векторами).
Это правило для перемножения матриц весьма важно, и мы
будем часто им пользоваться. Необходимо, чтобы читатель осно-
основательно познакомился с ним, прорешав множество конкретных
примеров. В качестве иллюстраций приведем следующие при-
примеры:
2Л .
Если
[1 31 Г2 61
5 7] И Hi -4J'
то
ГAХ2) + (ЗХ1) AХ6)+ЗХ(-4)]_
LEX2) + GX I) EX6) + 7X(-4)J
[2 + 3 6 + (-12I Г 5 —6
10 + 7 30 + (—28) J 1.17 $
но
RA=I I=
L(lXl) + (-4X5) A X 3) + (—4 X 7)J
[2 + 30 6+421 Г 32 481
1-20 3-28j==L-19 -25j'
Нетрудно видеть, что матрицы АВ и ВА сильно отли-
отличаются друг от друга. При перемножении матриц должен
соблюдаться порядок сомножителей: равенство АВ = ВА
здесь не справедливо. Таким образом, произведение матриц
некоммутативно.
Введение в матричное исчисление 25
2.2
Если
ГЗ 1 41 Г-Б-1
:= 2 1 б и d = \ з ,
Li з 4J L iJ
то
CD = \
(l
Г-
= -
L-
-16 + 3+4-j Г-8
10 + 3 + 6 =
5 + 9 + 41
При получении произведения DC мы должны сначала умно-
умножить элементы первой строки матрицы D на элементы первого
столбца матрицы С. Но в первой строке матрицы D есть только
один элемент [—5], в то время как в первом столбце I 2 мат-
матрицы С — три элемента. Поэтому это произведение записать
невозможно. Мы можем перемножить две матрицы С и D тогда
и только тогда, когда число столбцов в первом сомножителе
(матрице С) такое же, как число строк во втором сомножителе
(матрице D); при этом матрицы С и D называются согласован-
согласованными в смысле умножения и можно получить произведение CD.
2.3
Пусть даны матрицы
? = [3 1 4] и F =
Тогда мы можем написать
Г1 5 91
2 4-3.
L6 1 3J
(ЗХ9)-AХ
[C + 2 + 24) A5 + 4 + 4) B7-3+12)] =
[29 23 36].
26 Глава 1
Если поменять порядок сомножителей, то нельзя получить прот
изведенне FE, поскольку F содержит три столбца, а Е — только
одну строку.
2.4
Пусть
# = [3 1
6] и К~> 4 .
Если в качестве первого сомножителя взять матрицу Я, а в ка-
качестве второго — матрицу К, то эти матрицы являются согласо-
согласованными, поскольку Н состоит нз трех столбцов, а К — из трех
строк. Тогда произведение
представляет собой обычное число.
Рассмотрим, что произойдет, если умножать К на Н. В атом
случае матрицы опять согласованы, так как в К содержится
один столбец, а в Н — одна строка. Таким образом,
•2-|[3 1 6]
КН-
'-Id
Г2ХЗ 2X1 2X61 Гв 2 12-1
= 4X3 4X1 4X6 = 12 4 24 .
L7X3 7X1 7X6J L21 7 42J
.7X3 7X1 7X6-
Следовательно, для рассмотренной пары матриц произведе-
произведение НК есть простое число, а произведение КН — квадратная
матрица размером 3X3.
§ 3. НУЛЕВЫЕ МАТРИЦЫ
Если
О 0
7 11
2J
(или любая квадратная матрица второго порядка), то произве-
Г0 01
дения и LM, и ML записываются в виде I I . Матрица
I I называется нулевой матрицей второго порядка. Нулевые
Введение в матричное исчисление
27
матрицы обычно обозначаются символом 0 и выполняют ту же
роль, что и 0 в обычной алгебре.
Нулевой матрицей 0 может быть любая квадратная или
прямоугольная матрица (любого размера), в которой все эле-
элементы равны нулю. При умножении любой матрицы, имеющей
в качестве первого или второго сомножителя нулевую матрицу
(согласованной формы), мы получаем нулевую матрицу.
§ 4. ЕДИНИЧНЫЕ МАТРИЦЫ
4.1
Если
Г °1
Lo и
]•
то
т. е. мы
'-[
Г1 01
получаем снова матрицу Q. Матрица I n , I
имеет сле-
следующее свойство: любая матрица из двух строк, умноженная на
нее слева, и любая матрица из двух столбцов, умноженная на
нее справа, в результате остаются неизменными. Такую матрицу
мы называем единичной матрицей второго порядка.
Другие примеры единичной матрицы, как правило, обозна-
обозначаемой символом /:
единичная матрица 3X3
Г1 О 01
О 1 0 .
Lo о и
единичная матрица
4
Х4
- 1
0
0
-0
0
1
0
0
0
0
1
0
о-
0
0
1 -
и т. д.
Единичная матрица порядка п имеет п строк и п столбцов.
Все ее элементы — нули, за исключением элементов, располо-
расположенных на главной диагонали, которая проходит от верхнего
левого элемента до нижнего правого; все диагональные эле-
элементы равны единице.
28 Глава 1
§ б. ДИАГОНАЛЬНЫЕ МАТРИЦЫ
Единичная матрица — это частный случай диагональной мат-
матрицы; последняя определяется как квадратная матрица, в кото-
которой все недиагональные элементы равны нулю. Элементы на
главной диагонали могут иметь любые значения. Например,
матрицы
ОТ Г3 ° °
и
0 I
являются диагональными.
Если перемножаются две диагональные матрицы, то порядок
сомножителей не имеет значения, причем умножение выпол-
выполняется очень просто и в результате получается также диагональ-
диагональная матрица.
5.1
Если
то
АВ^ВА-
[а, 001 р, ООП
0 а2 0 и В=0 620,
0 0 а3Л Lo 0 &Н
Га.Ь, 0 0 I
0 аф2 0 .
L 0 0 OobsJ
(Следует заметить, что в этом примере для матричных элемен-
элементов мы использовали алгебраические символы вместо арифмети-
арифметических величин. Как и в обычной алгебре, мы можем использо-
использовать их, чтобы выразить один из параметров через другой.)
§ 6. МНОГОКРАТНОЕ УМНОЖЕНИЕ
Если мы хотим найти произведение трех матриц L, М и N,
то мы можем поступить двумя способами:
1) можно найти произведение (MN) и затем умножить его
слева на L;
2) можно найти произведение (LM) и затем умножить его
справа на N.
При условии, что мы сохраняем порядок расположения мат-
матриц, эти два способа дают одинаковый результат. Таким обра-
образом, L(MN) = (LM)N. Как и в обычной алгебре, оба эти резуль-
результата обозначим LMN.
Введение в матричное исчисление 29
6.1
Пусть
1
Г 1 31 Г 2 1 1 Г 1 2 1
=U 2J- M=L3 J и Л'=Ь 3J-
Тогда можно написать
9 71 Г 48 34
48 34
[б2 46
что было установлено выше.
Таким образом, хотя произведение матриц не обладает свой-
свойством коммутативности, тем не менее ассоциативный закон, для
него справедлив. Обобщая этот закон на большее число матриц,
нетрудно показать, что для произведения четырех матриц
PQRS = P(QR)S = (PQR)S и т.д.
§ 7. СЛОЖЕНИЕ И ВЫЧИТАНИЕ МАТРИЦ
При условии, что две матрицы М и Л' имеют одинаковое
число строк и столбцов, их сумма (или разность) получается
простым сложением (или вычитанием) любых двух соответ-
соответствующих матричных элементов. Если Р = М + N, то Р,^ =
= Mjk + jtyjfc. Поскольку все элементы пулевой матрицы 0 равны
нулю, мы можем написать М + 0 = М и М — М — 0. Матрицы
подчиняются дистрибутивному закону: А (В -f- С) = Л5 -J- ЛС.
7.1. Численный пример
Пусть
2 01 Г 3 О "I Г-1
A B = U 2J И И 2
Тогда можно написать
2 0"|Г2
i 1 JLs 2
01 Г-2 21 Г4 2
J [ J [ 3
30 Г лам 1
Из сказанного ранее ясно, что если мы одну и ту же матрицу
сложим саму с собой К раз, то каждый из матричных элементов
окажется умноженным на одно и то же число (или скалярную
величину^ X. Такую операцию называют иногда умножением
матрицы на скаляр. Тот же результат можно получить перемно-
перемножением матриц, если умножить матрицу справа или слева на
диагональную матрицу KI, все диагональные элементы которой
равны к.
Итак, мы рассмотрели правила умножения, сложения и вы-
вычитания матрнц. Может быть также полезной операция деления
одной матрицы на другую, и в данной книге мы нередко будем
пользоваться парой квадратных матрнц второго порядка, любая
из которых является обратной по отношению к другой. Однако,
прежде чем перейти к рассмотрению этой темы, мы кратко
обсудим транспонирование матриц и познакомимся с понятием
определителя.
| 8. ТРАНСПОНИРОВАННЫЕ МАТРИЦЫ
Матрнца, полученная в результате замены строк на соответ-
соответствующие столбцы в некоторой матрице А, называется транспо-
транспонированной матрицей по отношению к Л н обозначается Лт.
Если матрица А имеет m строк и я столбцов, то транспониро-
транспонированная к Ней матрица Лт состонт из п строк и m столбцов..
8.1 ,
Если
: ГЗ 41 т гз 21
I. то А =*\А jj.
8.2
Если
8.3
Если
-а
С«*[5 7
то В
И, то
-[3 1 4].
Введение в матричное исчисление 3!
Существует важная теорема об умножении транспонирован-
транспонированных матриц: Матрица, транспонированная по отношению к про-
произведению двух матриц, равна произведению их транспонирован-
транспонированных матриц, выполненному в обратном порядке. Таким образом,
8.4
Если
то
13 191 т Г13 41
Г1 31 Г4 11
С другой стороны,
,т Г1 б1 т Г4 31
А =1з 7J и в =li ej-
откуда получаем
т т Г13 41
В А =Ll9 47
(читателю полезно проверить эти произведения).
Следует отметить, что если А и В — прямоугольные матрицы,
которые являются согласованными, только когда при умножении
А предшествует В, то матрицы Вт и Лт будут согласованными,
только когда при умножении этих матриц Вт стоит впереди Лт,
как того и требует приведеиная выше теорема.
Используя ассоциативное свойство матричного умножения,
нетрудно показать, что
(АВС)Т = ((АВ) С)Т = СТ (АВ)Т = СТВТАТ,
и аналогично для произвольного числа матриц
(ABCDEF)T = FTETDTCTBTAT и т. д.
§ 9. ОПРЕДЕЛИТЕЛИ
Для любой квадратной матрицы существует единственное
число или величина, которая называется ее определителем.
Определитель матрицы М обозначается либо прямыми
Глава I
линиями, между которыми записываются элементы матрицы,
либо просто знаком det(Af). Таким образом,
ц М12 М13
Определитель матрицы М
= det(Af).
М21 М&,
Af31 M32
В случае квадратной матрицы большого порядка п правило
вычисления определителя является довольно сложным; оно
включает суммирование очень большого числа попеременно по-
положительных и отрицательных n-кратиых произведений матрич-
матричных элементов; даже для п = 4 требуется выполнить 4! = 24
операции умножения!
Однако в настоящей книге мы будем рассматривать только
определители матриц размером 2X2. Правило для их вычисле-
вычисления очень простое: нужно найти произведение двух элементов
на главной диагонали (верхнего левого и нижнего правого) и
вычесть из него произведение остальных двух элементов.
CD
имеем
Таким образом, для^латрицы Р
А В
det(P)= n
где А, В, С я D — обычные числа или скалярные величины.
9.1
Бели
Г1 31
12 9J'
то
— 6*=3.
Мы можем сформулировать следующую теорему об опреде-
определителях: Определитель произведения двух квадратных матриц
равен произведению их определителей.
9.2
Если
и если
, то
-42- 15 = 27,
Таким образом, (det Р) X Idet Q) = B7) X (—2) == —54.
Введение в матричное исчисление 33
С другой стороны, если мы найдем произведение двух квад-
квадратных матриц:
Г 15 241
PQ = 2fi OR I' то мы снова ПОЛУЧИМ
det (PQ) = ( 1 б X 38) — B4 X 26) = 570 - 624 = —54.
Эту теорему можно обобщить на любое число матриц:
det (PQRST и т. д.) = det (P) det (Q) det (Д) det (S) det (Г) и т. д.
Этот факт удобно использовать для проверки правильности вы-
выполнения операции произведения матриц.
Следует отметить, что, хотя для квадратных матриц произ-
произведение PQ в общем случае не является тем же самым, что
произведение QP, эти два произведения имеют одинаковые оп-
определители. Иными словами, для определителей порядок пере-
перемножения матриц не имеет значения.
9.3
В примере 2.1 мы нашли, что если
2 6
1то
Г 1 31
Ms 7J
5 —61 Г 32 48
П 2\, но BA = [_l9 _25
В этом случае
detD?)=10+102=H2, det(BA)= —800 + 912 =
и, конечно,
Некоторые квадратные матрицы имеют определитель, рав-
равный нулю. Такие матрицы называются вырожденными1). Почти
все матрицы, которые мы будем рассматривать в настоящей
книге, являются невырожденными2), т. е. их определители от-
отличны от нуля.
§ 10. ДЕЛЕНИЕ И ОБРАЩЕНИЕ МАТРИЦ
В обычной арифметике, если мы хотим разделить некоторый
набор чисел на одно и то же число k, то часто бывает более
удобным найти число {k)~l, ему обратное, и использовать его
в качестве множителя. Точно так же, если мы хотим разделить
некоторые матрицы на квадратную матрицу М, полезно решить
•) Или особенными. — Прим. ред.
г) Их еще называют неособенными. — Прим. ред.
2 Зак. 774
34 Глава 1
задачу нахождения матрицы, обратной матрице М. Оказы-
Оказывается, что если матрицу М не вырождена, то существует одна
и только одна обратная ей матрица R, обладающая тем свой-
свойством, что как произведение (MR), так и произведение (RM)
равны единичной матрице / того же порядка. Эту матрицу
удобно обозначить через М~1. Матрицу М~Л можно умножать
на некоторую матрицу слева, и мы имеем ВМ~\ или справа, т.е.
М~1В, причем это будут различные операции.
Правило нахождения обратной матрицы называется обраще-
обращением матрицы, и для матриц большого порядка оно довольно
сложно. Это правило состоит в том, чтобы иайти присоединен-
присоединенную матрицу, транспонировать ее, а затем разделить на опре-
определитель.
Здесь мы, однако, будем име-ть дело только с обращением
матриц 2X2, что является предельно простой процедурой.
В этом случае присоединенная матрица получается простой
взаимной заменой диагональных элементов с одновременным
изменением знака правого верхнего и левого нижнего элемен-
элементов.
Таким образом, для матрицы
А В~\
' D
можно сразу написать
Затем найдем матрицу, транспонированную по отношению
к adj (Л1),
1
-С А
и, наконец, разделим каждый ее элемент на определитель
Заметим, что определители всех трех приведенных выше мат-
матриц одинаковы.
10.1
Корректность описанной выше процедуры мы проверим сле-
следующим образом:
А В 1 Г D -
JU
Г (AD - ВС) (- АВ + В А)
-[(CD-DO (-BC + AD)
(где / — единичная матрица).
Введение в матричное исчисление 35
Большинство необходимых нам матриц размером 2X2, ко-
которые придется обращать, имеют определитель, равный единице.
Для таких матриц, называемых иногда унимодулярными, пра-
правило обращения можно сформулировать совсем просто: Чтобы
обратить унимодулярную матрицу 2X2, нужно поменять ме-
местами элементы, расположенные на главной диагонали, и изме-
изменить знаки двух других элементов, оставляя эти элементы на
Своих местах.
Таким образом, если
ГА t
М = [с D.
то
м-1
-Г D
-[-с
"Никаких вычислений здесь производить не надо!
И, наконец, точно так же, как и для транспонированных мат-
матриц, чтобы получить матрицу, обратную произведению несколь-
нескольких матриц, мы должны перемножить в обратном порядке мат-
матрицы, обратные отдельным сомножителям:
{PQRSy'^S-'R-'Q-'p-1 и т. д.
Чтобы убедиться в этом, запишем произведение
(PQRS)(S~iR~iQ~iP~1) н найдем, что центральные звенья це-
цепочки, начиная с SS-1 = /, образуют последовательность еди-
единичных матриц, которые, свертываясь, дают в качестве оконча-
окончательного результата одну единичную матрицу.
§ 11. ПРИВЕДЕНИЕ МАТРИЦЫ К ДИАГОНАЛЬНОМУ ВИДУ
Иногда возникает необходимость выполнять одно за другим
умножение на одну и ту же невырожденную матрицу М. При
этом оказывается удобным найти диагонализирующую матри-
ЧУ') F, т. е. такую, что
где Л — диагональная матрица, a F-1 — матрица, обратная к F.
Если мы допустим, что такие матрицы F и Л существуют, то, по-
поскольку F~lF = I, квадрат матрицы М равен
М2 = ММ = (FAF~*) (FAF~*) — FAIAF'* — FA1/7.
') Под диагоиализирующей матрицей далее понимается матрица, преобра-
преобразующая исходную к диагональному виду, — Прим. ред.
а*
36 Глава 1
Аналогично,
М3 = ММ2 = (FAF-*) (FA'F-1) о
В общем случае
MN = FANF~\
Таким образом, если преобразование к диагональному виду
найдено, то N-я степень исходной матрицы получается простым
возведением диагональной матрицы в N-ю степень, причем все,
что мы должны сделать, — это заменить каждый f-fi диагональ-
диагональный элемент А* величиной "кг.
Диагональные элементы %\, hi, ..., кг, ... матрицы А назы-
называют характеристическими^ корнями илн собственными значе-
значениями исходной матрицы W, а отдельные столбцы диагонализи-
рующей матрицы F называют соответственно ее характеристи-
характеристическими векторами, или собственными векторами.
Чтобы разобраться в этом несколько глубже, выделим из
квадратной матрицы F ее r-й столбец FT. Последнее можно сде-
сделать, умножив F справа на вектор-столбец Ст, в котором г-й
элемент равен 1, а остальные — нулям.
Что произойдет, если мы умножим матрицу М на вектор-стол-
вектор-столбец FT — FCr? Мы имеем
MFr = (FAF-1 j (FCr) = FAC, *= FrXr = XrFr
(поскольку %r — скаляр). Иными словами, при умножении мат-
матрицы М на вектор Рг мы получаем тот же самый вектор, умно-
умноженный на скаляр V Вектор-столбец Fr называют r-м собствен-ч
ным вектором матрицы М, а К — соответствующим r-м собствен-
собственным значением. Для матриц 2 X % & в дальнейшем мы будем
приводить к диагональному виду лишь такие матрицы, суще-
существуют только два собственных вектора F\ и F2 и два собствен-
собственных значения A,i и "h%.
(Кроме того, если матрицу М рассматривать вторым сомно-
сомножителем, а не первым, то можно получить собственные векторы
в виде векторов-строк, которые в этом случае будут выделяться
как строки из обратной матрицы F~l. В дальнейшем мы будем
использовать со.бственные векторы только в виде столбцов.)
§ 12. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ УНИМОДУЛЯРНЫХ МАТРИЦ 2x2
Если мы хотим привести квадратную матрицу М к диаго-
диагональному виду, то следует начинать с определения собственных
значений Я.ь %2, ... и т. д. Для этого обычно решают характери-
характеристическое уравнение матрицы:
Введение в матричное исчисление 37
Однако в случае унимодулярнрй матрицы 2X2 более поучи-
И тельно сделать это, исходя из первоначальных понятий. Дана
6. Г А В 1
J, матрица М = I _ I, требуется найти диагонализирующую
матрицу F и диагональную матрицу Л, такие, что М = FAF~l
и, следовательно, Л!/7 = FA. Перепишем последнее уравнение
в развернутом виде и получим необходимое условие:
-[Лс Ж
м'-[Лс Ж"
где (AD — BC)= 1, так как det(M)= 1. В результате умноже-
умножения имеем
+ BFai AFa + BFa-l_rFuKi Fl2k2l
+ DF2i CFu + D/^J —L^i ^22^2 J'
Поскольку требуется, чтобы матрицы в левой и правой частях
были одинаковыми, мы можем записать четыре отдельных урав-
уравнения, которые получаются приравниванием соответствующих
элементов правой и левой матриц:
^,1 + ^81 = ^11*,, A.1)
A.2)
A.3)
A.4)
Разделив уравнения A.1) и A.2) на F2U мы можем исключить
отношение (Fn/F2\) и получить
i.FnIF2x) = В/(Л, - А) = (Я, - D)/C.
Следовательно,
(Я
Аналогично, разделив уравнения A.3) и A.4) на Р& и исклю-
исключив (F12/F22), находим
(Fa/Fri = В/(Я2 - А) = (Я2 -
Следовательно,
Таким образом, Х\ и Я2 удовлетворяют одному и тому же
уравнению
{X-A)(X-D)-BC = Q. A.5)
det (Я/ —
(k-A)(k-D)-BC=*O.
38 Глава I
Хотя это решение не совсем строгое, нетрудно заметить, что
полученное уравнение эквивалентно упомянутому выше харак-
характеристическому уравнению. Действительно,
(А, - А) -В
= - С (k-D)
Согласно условию, det(Af) = (AD — flC) = 1, и характернче-
ское уравнение для двух значений к можно упростить:
tf — (A + D)k+ 1=0. A.6)
Отсюда сразу видно, что два решения ki и X.j должны удовле-
удовлетворять равенствам ki + А* ¦*» А + D и АД* = 1. Решая квадрат-
квадратное уравнение, находим
4]. A.7)
(Решение ki определяется этим выражением с положительным
знаком перед корнем, а Яг — с отрицательным знаком перед кор-
корнем.)
Величину А -f- D, т. е. сумму диагональных элементов, назы-
называют следом, или шпуром, матрицы. Если след А + D принимает
значение от 2 до —2, то два собственных значения удобно пере-
переписать в виде функций угла 9, выбирая его так, чтобы он изме-
изменялся в пределах от 0 до я. Таким образом, можно записать
A -J- D = 2 cos в. Тогда мы получаем следующие равенства:
А,! = cos 8 + i sin в = exp (t"8),
k2 = cos в — i sin в = exp (— Щ,
где exp обозначает экспоненциальную функцию, а (У
Наоборот, если А + D больше 2 или меньше —2, то мы мо-
можем выбрать такую положительную величину /, что A -J- D =
= 2chf [или —2ch(—t), если величина A-\-D отрицательна].
При этом собственные значения записываются в виде
ki = exp(t) [или — ехр@, если A + D отрицательна],
Л2 = ехр(— f) [или — ехр (*-*), если A + D отрицательна}.
12.1
Чтобы завершить процесс приведения матрицы к диагональ-
диагональному виду, мы должны теперь определить диагоналнзирующую
матрицу F и ей обратную матрицу F~l. Отметим, что нами уже
определены отношения
(Fu/Fal) - (X, - D))C = ВДЯ, - А), A.8)
A). A.9)
Введение е матричное исчисление 39
Фактически это дает нам два важных соотношения, которые
определяют с точностью до скалярного множителя вид двух соб-
собственных векторов
Если мы теперь произвольно положим, что как Fn, так и F22
принимают значение С, то мы получим одну из возможных форм
/^матрицы:
P-\F" F^l[(^-D) (А,-ЯП
IF« F2J~l С С У
определитель которой
det (F) = {FnFn) - (Fl2F2l) - С (Я, - Я,).
При желании мы могли бы преобразовать матрицу F к уни-
мрдулярномувиду, разделив каждый ее элемент на^\/С(Х1 — А2),
но это необязательно. Обратной к ней матрицей являет-
[С (D — Aj) 1
— С (к —D)\
делится на скалярную величину C(A.i — Х2).
;• Итак, окончательное преобразование, приводящее матрицу
Я диагональному виду, имеет вид
[
Г(Я.,-0) (А,2 - D) 1 Г X, 0 -|Г С (D-X2)l
А 81— 1 С С JLo X2}l-C (Xi-fl)J
J " '
С Z)J " С(Я,-х,) ' ' AЛ
где AD — ВС=1, a A,i и Я,2 таковы, что А,^ = I и J
— A + D.
12.2
Читатель может проверить, что тройное произведение матриц,
приведенное выше, действительно удовлетворяет указанным
соотношениям. Следует заметить также, что если элемент С
в исходной матрице обращается в нуль, то собственные векторы
Должны определяться выражениями B/fa — А) и B/(ta — A).
Тогда получим
в в л г х, о I т2 -А) — в I
— /4)JLO XJ ЦА — Xi) BJ /f ц\
С D\ = -В(Х,-Х2) • (М1)
(Очевидно, если и С, и 5 обращаются в нуль, то матрица М уже
приведена к диагональному виду!)
I Bl_\.(h-A) (Xt
С
ГЛАВА 2
МАТРИЧНЫЕ МЕТОДЫ
В ПАРАКСИАЛЬНОЙ ОПТИКЕ
§ 1. ВВЕДЕНИЕ
В данной главе мы рассмотрим, каким образом можно при-
применить матрицы для описания геометрического построения изо-
изображений в центрированной системе линз, т. е. в системе, со-
состоящей из последовательности сферических преломляющих по-
поверхностей, центры которых расположены на одной оптической
оси. Все полученные ниже результаты справедливы лишь в рам-
рамках двух главных приближений.
Первое из них представляет собой основное допущение всей
геометрической оптики и состоит в том, что длина волны света
считается пренебрежимо малой и что распространение света
можно описывать с помощью отдельных лучей, а не на языке
волновых фронтов. (В гл. 3 мы еще вернемся к этому вопросу,
когда будем обсуждать распространение гауссова пучка, кото-
который наилучшим образом, каким только позволяет природа, ап-
аппроксимирует одиночный луч света.) Путем построения Гюй-
Гюйгенса можно показать, что в свободном пространстве световые
волны распространяются вдоль направления нормалей к волно-
волновым фронтам. Понятие геометрического луча представляет собой
идеализацию этой волновой нормали. Последнюю на языке век-
векторов можно рассматривать либо как вектор Пойнтинга электро-
электромагнитного поля, либо как градиент некоторой скалярной функ-
функции (эйконала), которая описывает фазу волнового возмуще-
возмущения. Из этих представлений следует принцип наикратчайшего
оптического пути Ферми, которому подчиняется каждый луч.
Суть этого принципа заключается в следующем. Если мы рас-
рассмотрим окрестность любого небольшого участка траектории
луча, то луч выбирает такой путь между двумя точками, кото-
который соответствует минимуму времени, затрачиваемому» на про-
прохождение расстояния между этими точками.
Второе наше приближение состоит в том, что мы будем рас-
рассматривать лишь параксиальные лучи, — лучи, которые при сво-
своем прохождении через оптическую систему остаются близкими
к ее оси симметрии и почти параллельными ей. Тогда для сину-
синусов и тангенсов любых углов, образуемых этими лучами с опти-
Матричные методы в параксиальной оптике 41
ческой осью, можно использовать первый порядок разложения
в ряд. Следовательно, эффекты третьего порядка, такие, как
сферическая аберрация или кома (сферическая аберрация на-
наклонных пучков), а также астигматизм, кривизна поля и дистор-
сия, выпадают из поля зрения нашего анализа. Однако продоль-
продольной и поперечной хроматической аберрации мы немного кос-
коснемся.
Оптику параксиальных изображений часто называют гаус-
гауссовой оптикой, поскольку именно Карл Фридрих Гаусс в 1840 г.
заложил ее основы. В своем классическом труде «Dioptrische
Untersuchungen» Гаусс показал, что свойства любой системы
линз полностью определены, если известны шесть ее кардиналь-
кардинальных точек: две фокальные точки, две узловые точки, соответ-
соответствующие единичному угловому увеличению, и две главные точ-
точки, соответствующие единичному линейному увеличению. Гаусс
в этой статье дал рецепты для экспериментального определения
положений этих точек и итерационные методы их вычисления
через радиусы кривизны поверхностей, расстояния между этими
поверхностями и показатели преломления входящих в системы
оптических материалов. Формулируя итерационный метод, Гаусс
составил систему двух линейных совместных уравнений, выра-
выражающих в явном виде соотношения между высотой и углом
луча на выходе оптической системы с высотой и углом соответ-
соответствующего луча на входе. Однако в те времена матричный фор-
формализм не был известен, и Гаусс воспользовался алгоритмом,
который он заимствовал у Эйлера, для того чтобы выразить че-
четыре коэффициента в своих уравнениях в удобной для вычис-
вычислений форме. (Используемые Гауссом выражения — сокращен-
сокращенная запись непрерывных дробей — называется теперь скобками
Гаусса. Они никоим образом не потеряли своего значения, по-
поскольку почти точно такой же экономный порядок вычислений
используется в современном «ynv» методе.)
В настоящей главе будет показано, что матрицы дают другой
способ проведения вычислений такого типа. Впервые в оптике
матрицы применил, по-видимому, Сэмпсон [4] около шестидеся-
шестидесяти лет тому назад, но широко использоваться они стали лишь
недавно. Первыми книгами по матричным методам в оптике
были монографии Э. Л. О'Нейла [6] и В. Брауэра [7]. В течение
последующих двух лет появились статьи Холбэча [8] и Ричардса
[9] в Americay Journal of Physics, в которых обсуждались мат-
матричные методы, однако имелись несогласия по поводу того, в
какой последовательности должны выполняться вычисления.
В 1965 г. Когельник опубликовал работу [11], в которой было
предложено важное обобщение метода, в результате чего мат-
матрицу преобразования лучей оказалось возможным использовать
щ TOjihKQ для описания геометрической оптики параксиальны*
*2 Глава 2 -
лучей, но также и для описания распространения лазерного пуч-
пучка света с дифракционным углом расходимости. Мй отложим
рассмотрение пучков света и резонаторов до следующей главы,
однако работа Когельннка оставила столь сильный след в ли-
литературе, что мы, как это сделал недавно Синклер [10], тоже бу-
будем пользоваться во всех своих матричных вычисленных схемой
Когельника.
§ 2. МАТРИЦЫ ПРЕОБРАЗОВАНИЯ ЛУЧЕЙ
Обсудим теперь прохождение параксиального луча через цент-
рированную систему линз. Введем общепринятую в современной
оптике систему декартовых координат: ось Ог, совпадающую с
оптической осью системы, а также с главным направлением,
вдоль которого распространяются лучи света, направим слева
направо; ось Оу будем считать расположенной в йлоекос?и
страницы н направленной вверх, а ось Ох перпендикулярной
этой плоскости и направленной от читателя. В Данной главе мы
не будем рассматривать сагиттальные лучи. Таким образом, бее
наше внимание будет уделено получению лучей, лежащих в пло-
плоскости yz в непосредственной близости от оси Ьг.
Траектории луча, поскольку он проходит через различные
преломляющие поверхности системы, будет состоять из после-
последовательности прямых линий. Каждая из этих прямых опреде-
определяется координатами одной принадлежащей ей точки и углом,
который составляет данная прямая линия с осью Ог. Выберем
заранее любую плоскость z = const, перпендикулярную оси Ш$
н назовем ее опорной плоскостью (ОП). Тогда луч можно опре*
делить по отношению к опорной плоскости двумя параметрами:
высотой, на которой этот луч пересекает опорную плоскость, и
углом, который он составляет с осью Oz. Угол v измеряется в
радианах н считается положительным, если он соответствует
вращению против часовой стрелки от положительного найраб-
леиня оси z к направлению, в котором свет распространяется
вдоль луча (фиг. 2.1).
Хотя мы и могли бы попытаться описать все лучи, участвую-
участвующие в вычислениях, по отношению к одной-единственной опор-
опорной плоскости (например, взять в качестве ОП плоскость 2*»
= 0), однако на практике оказывается гораздо более удобный
на каждом этапе расчета выбирать новую ОП. Это означает,
что параметры луча непрерывно переносятся с одной ОП на дру-
другую, по мере того как мы рассматриваем различные элементы
системы. Однако если требуется выполнить полный расчет си-
системы в целом, то возникает вопрос о полной матрице преобра-
преобразования лучей, которая преобразовывала бы все необходимы?
Матричные методы в параксиальной оптике
43
Фиг. 2.1
параметры луча от выбранной нами входной ОП непосредствен-
непосредственно к выбранной выходной ОП.
Мы уже отмечали, что по отношению к любой ОП положе-
положение луча можно определить с помощью высоты у и угла v этого
луча. Однако для проведения расчетов более удобно заменить
угол луча v соответствующим ему оптическим направляющим
косинусом nv (или, точнее говоря, п sin v), где п — показатель
преломления среды, в которой распространяется луч. Согласно
закону Снеллиуса, оптический направляющий косинус (обозна-
(обозначим его буквой V) остается неизменным при пересечении гра-
граничной поверхности двух оптически различных сред. (Хотя при-
применение оптических направляющих косинусов V = nv может
показаться громоздким, однако в большинстве случаев для рас-
рассматриваемых оптических систем исходная и конечная ОП рас-
расположены в воздухе, и вычисления усложняются незначительно;
кроме того, такой расчет сильно упрощается для систем с пло-
плоскопараллельными поверхностями, и вдобавок все используемые
в вычислениях матрицы оказываются унимодулярными.)
Поскольку луч проходит через систему преломляющих линз,
то для исследования его поведения необходимо рассмотреть
только два основных процесса:
1) Перемещение между двумя преломляющими поверхно-
поверхностями— оптический промежуток. На таком участке пути луч,
предоставленный самому себе, просто проходит по прямой ли-
линии от одной преломляющей поверхности к другой. Область
между поверхностями характеризуется ее толщиной t и показа-
показателем преломления п среды, через которую проходит луч.
2) Преломление на граничной поверхности между двумя об-
областями с различными показателями преломления. Для того
44 Глава 2
чтобы определить величину отклонения прошедшего луча, необ-
необходимо знать раднус кривизны преломляющей поверхности и
два значения показателя преломления граничащих сред.
В следующнх двух параграфах мы рассмотрим, каким обра-
образом эти два основных процесса влияют на значения величин у
и V луча, проходящего от одной опорной плоскости к другой,
между которыми расположен оптический элемент. Вначале луч
пересекает ОГЬ и имеет на ней значения параметров у{ и Vi,
затем он проходит через оптический элемент и, наконец, дости-
достигает ОПг, на которой он характеризуется высотой у2 и углом
W Мы ищем уравнения, устанавливающие связь величин у2 и
V2 с величинами у\ и V\ и свойствами оптического элемента,
расположенного между опорными плоскостями.
Нетрудно установить, что уравнения для наших двух оптиче-
оптических элементов (преломляющая поверхность и оптический про-
промежуток) являются линейными, и, следовательно, их можно
записать в матричной форме:
причем матричные элементы таковы, что определитель (AD —
— ВС) равен единице.
С другой стороны, если нам понадобится рассмотреть такой
случай, когда луч проходит через систему в обратном направ-
направлении, то матричное уравнение обращается и принимает вид
•yii г D -в~\[У2
Таким образом, каждому элементу оптической системы мож-
можно поставить в соответствие свою унимодулярную матрицу пре-
преобразования лучей. Для того чтобы получить общую матрицу
преобразования лучей, описывающую всю оптическую систему
в целом, следует перемножить в правильной последовательно-
последовательности все матрицы элементарных перемещений и преломлений,
встречающихся в системе. Такая система может представлять
собой все что угодно, начиная от единственной тонкой линзы и
кончая сложной оптической системой.
§ 3. МАТРИЦА ПЕРЕМЕЩЕНИЯ Г
На фиг. 2.2, а и б приведены два примера распространения
лучей, проходящих слева направо путь t между двумя опор-
опорными плоскостями. Очевидно, что угол, под которым распро-
распространяются лучи, остается тем же самым на протяжении всего
Матричные методы в параксиальной оптике
45
ОП;
перемещения, в то время как его расстояние до оси г меняется.
На фиг. 2.2, а показан случай, когда величины и у, и v являются
положительными, а на фиг. 2.2, б — случай, когда у положи-
положительна, а угол v отрицателен. Для ясности углы v на обеих фи-
фигурах даны в увеличенном масштабе; в действительности мак-
максимальные значения величины v для параксиальных лучей не
превышают 0,1 (одной десятой радиана, или около 6°). При
этом погрешность вычислений в приближении параксиальной
оптики оказывается менее 1%. В случае фиг. 2.2,а мы имеем
у2. RP = RQ + QP = TS + SQ tg (Z PSQ) = ух +/ tg («,) = ух +tvu
а в случае фиг. 2.2,6 —
у2 = RP = RQ - PQ = TS - SQ tg U PSQ) =
(Переход к параксиальному приближению означает замену tg о
или sin и на и с пренебрежнмо малой ошибкой.) Мы уже отме-
отмечали, что наша матрица перемещения предназначена для опера-
операций с такими параметрами луча, как высота луча и оптический
направляющий косинус (или величина V), а не просто его угол
v. Таким образом, если п — показатель преломления среды
4й_ Глава 2
между ОП1 и 0П2, то приведенное выше уравнение нужно пере-
переписать в виде
У2 = Ух + {tin) (no,) = 1 г/, -f TV,,
где Т = Щп)—приведенная толщина оптического промежутка.
Из диаграмм (фиг. 2.2, а и б) нетрудно заметить, что V\ и v2
равны друг другу. Следовательно, для нового оптического на-
направляющего косинуса V2 можно написать уравнение
Полученные нами два уравнения теперь можно записать в
матричной форме:
М-Р ПМ-
iv2] Lo iJU,J
Таким образом, перемещение луча вправо описывается мат-
матрицей
¦-[I
о
в которую в качестве матричного элемента входит приведенное
расстояние 7. Определитель этой матрицы det(^~), очевидно,
равен единице."
3.1. Составные слои и плоскопараллельные пластины
Следует отметить, что если мы произвольным образом раз-
разделим Оптический промежуток t на два примыкающих друг к
другу промежутка U и t2, имеющих одинаковые коэффициенты
преломления п, то мы получим две последовательные матрицы
Ti
¦ И ?Г,=
где 7, = (tjn), Тг = (Ш) и U + h = t.
Если затем перемножить &~\ и &~г в произвольном порядке,
то, как и должно быть, получим
О 1
поскольку 7i + 72 =3 Т.
Аналогичная ситуация возникает и в тех случаях, когда оп-
оптический промежуток общей толщиной t состоит из нескольких
различных слоев, каждый из которых характеризуется собствен-
Матричные методы в параксиальной оптике 47
ной толщиной ti и собственным показателем преломления tii.
При условии что все граничные поверхности являются плоскими
и перпендикулярными оси z, высота луча и оптический направ-
направляющий косинус будут оставаться неизменными иа каждой
граничной поверхности. Отсюда следует, что можно не опасаться
ошибок в написании матриц преломления, ибо любая из них
есть просто единичная матрица I . I. которую можно не учи-
учитывать. (Данное утверждение мы проверим в следующем па-
параграфе.)
Таким образом, для получения общей матрицы, описываю-
описывающей действие оптического промежутка в целом, при условии, что
каждый i-й слой характеризуется собственной приведенной тол-
толщиной Tt = (ti/tii), все отдельные матрицы перемещения нужно
перемножить друг с другом. Как мы уже показали, эти матрицы
перемещения обладают полезным свойством — их произведение
ие зависит от порядка их умножения. Величина Т в результи-
результирующей матрице равна сумме значений 7\ исходных отдельных
матриц-сомножителей:
П 7У1Г1 7-,-|Г1 Г,"! Г1 Г.1 П 1.ТП
Lo i До 1 До 1 J ••: Lo I J |_о 1 -Г
Давайте посмотрим, что означает с точки зрения оптики тот
факт, что матрицы перемещения дают один и тот же результат,
в каком бы порядке они не были взяты. Если смотреть через
набор плоскопараллельных пластинок в направлении, перпенди-
перпендикулярном их плоскостям, то, сдвигая эти пластинки или даже
меняя их местами, можно повлиять на количество отраженного
света, но геометрия передаваемого ими изображения будет ос-
оставаться точно той же самой.
[Когда мы говорим, что плоскопараллельная стеклянная пла-
пластинка с показателем преломления п и толщиной t имеет приве-
приведенную толщину (tin), мы этим термином отражаем определен-
определенное физическое явление. Действительно, если смотреть на пред-
предмет через пластинку, то свет идет к нам дольше, чем в ее отсут-
отсутствие, но предмет, несомненно, кажется расположенным ближе.
Замена слоя воздуха перед наблюдателем на слой стекла такой
же толщины зрительно приближает к нему наблюдаемый мир
на расстояние (t/l)— (t/n)=t(n — 1)/п, приблизительно равное
одной трети толщины пластинки. Для погруженных в воду пред-
предметов коэффициент (п—\)/п составляет лишь около 'Д, однако
истинная глубина t может оказаться значительной — даже мед-
медведю, хватающему своей лапой рыбу из воды, необходимо знать
об оптическом уменьшении толщины!]
48
Глава 2
§ 4. МАТРИЦА ПРЕЛОМЛЕНИЯ 31
Рассмотрим теперь вопрос о том, как действует на распро-
распространение лучей кривая поверхность, разделяющая две области
с показателями преломления П\ и Пч- Радиус кривизны поверх-
поверхности считается положительным, когда центр кривизны располо-
расположен справа от поверхности. На фиг. 2.3 приведена поверхность
положительной кривизны, причем показатель преломления Пг
среды, находящейся справа от нее, больше, чем показатель пре-
преломления П\ среды, находящейся с левой стороны от нее. Луч,
показанный на фигуре, также имеет положительные значения
величин у и V на обеих сторонах поверхности.
Как и на фиг. 2.2, углы здесь даны в увеличенном масштабе.
Поэтому проходящая через вершину преломляющей поверхности
ОП] кажется расположенной на заметном расстоянии от ОП2,
проходящей через точку пересечения луча с этой поверхностью.
Однако в случае параксиальных лучей расстояние между этими
двумя плоскостями равно r(l—cos а) и, следовательно, прене-
пренебрежимо мало, поскольку, согласно предположению, а, так же
как и V\, и V2, — малый угол. Отсюда мы имеем уъ = у\.
Применяя закон Снеллиуса к нашей диаграмме, мы можем
написать
rtj sin /j = rt2 sin /2»
или в параксиальном приближении
Но по теореме о внешнем угле треугольника
h = vl-\-a = vi-\-yi/r и i2 = v2 + о = v 2 + yjr.
\
Фиг. 2.3
Матричные методы в параксиальной оптике 49
Следовательно,
(о 1 + yi/r) = п2 (v2 + yjr),
или
Vi + riiyi/r = V2 + n^iA".
Таким образом, переписывая эти уравнения в матричной фор-
форме, окончательно получаем
Величину (n2 — /ii)/r обычно называют оптической силой по-
поверхности.
Мы получили матрицу преломления
•-[
-(п2-щ)/г
для конкретного случая, когда все величины являются положи-
положительными. Однако тщательный анализ показывает, что матрица
0L правильно описывает преломление луча и в других случаях,
т. е. если поменять местами граничащие среды, или изменить
знак кривизны поверхности, или иметь отрицательные величины
у или V.
Рассмотрение важного случая отражающей поверхности мы
отложим на конец настоящей главы. Что касается преломляю-
преломляющих поверхностей, то, если луч проходит через плоскую прелом-
преломляющую поверхность, для которой радиус кривизны г равен бес-
бесконечности, и, следовательно, ее оптическая сила {п% — n-i)/r
обращается в нуль, мы приходим к тривиальному случаю еди-
единичной матрицы преломления. В предыдущем параграфе мы
уже использовали это обстоятельство, когда свертывали друг
с другом матрицы перемещения нескольких плоскопараллель-
плоскопараллельных пластинок.
4.1. Тонкая линза
Аналогичное свертывание матриц преломления возможно и
в случае нескольких преломляющих поверхностей, когда они
расположены близко одна от другой, так что оптические проме-
промежутки между ними пренебрежимо малы (матрица перемещения
через такой промежуток вырождается в единичную матрицу).
Если кривизна каждой t-й преломляющей поверхности равна rit
а показатели преломления прилегающих к ней сред м< и tii+i со-
соответственно, то ее оптическую силу можно записать в виде
50 Глава 2
Pi — (tii+i — rti)/ri. Тогда общая матрица системы тонких линз
не будет зависеть от того, в каком порядке скла-
складываются друг с другом оптические силы отдельных линз.
Читателю предлагается самостоятельно проверить равенство
-p, IJL—я,
Например, матрица преломления одиночной тонкой линзы
одна и та же для всех путей луча. Ее оптическая сила дается
выражением
Р = Р1 + Р2 = (п- 1)/г, + A - п)/г2 = (п- 1) A/г, - 1/г2) = 1/f.
Оптическая сила обычно выражается в диоптриях A/м), а
фокусное расстояние / и радиусы кривизны г\ и г2 измеряются
в метрах.
В общем случае, если нужно рассчитать систему, состоящую
из ряда тонких линз с заданными фокусными расстояниями.,
удобно каждое фокусное расстояние /,¦ заменить на соответ-
соответствующую ему оптическую силу />< = 1//<. Тогда матрица пре-
преломления (-й линзы имеет вид
_Г * °1_Г 1 °1
i~Y-Pi \\~i-\m и'
Мы уже показали, что наиболее просто свертывается в еди-
единую матрицу либо последовательность ^"-матриц, либо после-
последовательность ^-матриц. Однако в общем случае может быть
произвольный порядок следования 31 и ^"-матриц; поэтому
нужно тщательно следить за тем, в каком порядке они появ-
появляются. Умножение любой матрицы преломления на любую
матрицу перемещения* не коммутативно. Например,
Л-р Ли ЛЛ-р (i-
тогда как
']
Мы видим, что вторая матрица отличается от первой: матрич-
матричные элементы на главной диагонали поменялись местами.
Матричные методы в параксиальной оптике 51
§ б. МАТРИЦА ПРЕОБРАЗОВАНИЯ ЛУЧЕЙ
ДЛЯ ОПТИЧЕСКОЙ СИСТЕМЫ
5.1. Нумерация опорных плоскостей
Рассмотрим распространение параксиальиого луча через оп-
оптическую систему, состоящую из п преломляющих поверхностей,
разделенных (п— 1) промежутками. Из конструктивных сообра-
соображений удобно выбрать в качестве первой — входной — опорной
плоскости плоскость ОПЬ расположенную на расстоянии da
слева от первой преломляющей поверхности. ОП2 и ОП3 в таком
случае помещают непосредственно слева и справа от первой
преломляющей поверхности; ОЩ и ОП5— с обеих сторон от
второй поверхности и т. д., до тех пор пока мы не дойдем до
последних плоскостей ОП2п и ОГЬп+ь расположенных по левую
и правую стороны от n-й поверхности. Конечную — выходную —
опорную плоскость ОП2п+2 следует поместить на расстоянии йь
справа от этой последней преломляющей поверхности. Далее мы
попытаемся получить общую матрицу преобразования лучей М,
которая позволит нам непосредственно преобразовывать вектор
Г У\ Л Г У2П+2 "I .
входного луча I „ I в вектор выходного луча I ., I (см.
фиг. 2.4).
5.2. Нумерация матриц
Следующий шаг состоит в том, чтобы выписать матрицы пе-
перемещения или преломления, соответствующие каждому из оп-
оптических элементов, расположенных между различными опор-
опорными плоскостями. Перемещаясь по схеме (фиг. 2.4) слева на-
направо, присвоим каждой матрице порядковый номер, т. е. за-
запишем Mi, M2, ..., М2п+и причем присваиваемый каждой мат-
матрице оптического элемента номер должен совпадать с номером
опор«ой плоскости, расположенной слева от элемента. Таким
образом, если обозначить вектор луча I v I. проходящего че-
через r-ю опорную плоскость, как Кг, то для преобразования пара-
параметров луча из ОПГ в ОПг+1 можно написать следующее рекур-
рекуррентное соотношение: Kr+i = МТКТ\ аналогично Кт = MT^iKr-i
и т. д.
Входная
опорная
плоскость
Совокупности поверхностей (n-J)
Выходная
опорная
плоскость
К-матрицы—
Цепочка матриц
Me
-Т-матрицы -
плоскостей— 01-
2n M2n-t мз мг Mt) Ki
2п МгпЧ M3M2Mt) -
произведение матриц, умноженных в обратном порядке
Фиг. 2.4
Матричные методы в параксиальной оптике 53
5.S. Расчет параметров выходного луча
по заданным параметрам входного луча
Используя повторно это рекуррентное соотношение, а также
ассоциативное свойство умножения матриц, находим
{M2n+iM2n) Ш2п-ХК2п-\) =
= {M2.n+iM2nM2n-lM2n-2 ...
Следовательно, K2n+2 = MKi, где М представляет собой произ-
произведение всех матриц, взятых в нисходящем порядке номеров:
М = (М2п+1М2пМ2п-1М2п-2М2п-3 ... МЪМ2МХ).
Здесь важно отметить, что в этих уравнениях отдельные мат-
матрицы стоят в обратном порядке по сравнению с принятой для
них нумерацией. Было бы полезно зрительно представлять себе
такой порядок как порядок, который видит наблюдатель, если
он смотрит назад от выходной опорной плоскости по направле-
направлению к источнику света. Кроме того, этот же порядок уместно
сохранять при написании уравнения, если уж мы решили начать
с вектора выходящего луча; тогда последующие матрицы можно
рассматривать как звенья математической цепочки, которая
приведет нас назад к входу системы.
5.4. Расчет входного луча по данному выходному лучу
Если мы хотим исходить из первых принципов, то для реше-
решения этой задачи мы должны обратить каждую из отдельных
матриц, а затем воспользоваться обращенным рекуррентным со-
соотношением Кг= М71Кг+\. При этом мы получим
/С, = МТ1Кг = МГ1М21Кз = (Л1 Г'МГ'МГ'МГ1 • • • Afo+i) К2П+2.
(Здесь звенья цепочки оказываются расположенными в возра-
возрастающем порядке номеров, но каждое из них представляет со-
собой обращенную матрицу.)
Однако, как правило, мы будем иметь уже рассчитанную об-
общую матрицу М и можем приступать прямо к обращению урав-
уравнения /Сгп+2 = MKi с тем, чтобы получить Ki = M-lK2n+2-
В итоге мы получим тот же результат, поскольку, как было по-
показано в § 10 гл. 1, матрица, обратная по отношению к произ-
произведению матриц, равна произведению обратных матриц-сомио-
жителей, взятых в обратном порядке.
84 Глава 2
5.5. Получение общей матрицы М
Свойство ассоциативности позволяет по разному организо-
организовать вычисление общей матрицы, представляющей собой произ-
произведение отдельных матриц. Однако, если мы имеем дело более
чем с тремя матрицами, то для облегчения расчетов можно
предварительно разбить все произведение на пары матриц. Мат-
Матрицу для произведений типа 9№Г можно выписать почти сразу,
поскольку в этом случае требуется вычислить только четвертый
матричный элемент A—РТ). По мере того как продвигается
вперед вычисление длинной цепи матриц, целесообразно время
от времени проверять, равен ли единице определитель результи-
результирующей матрицы, полученной к данному моменту. Если он ока-
окажется не равным единице, это означает, что где-то в процессе
вычислений была допущена ошибка, ибо все Я- и ^"-матрицы
сами по себе унимодулярные.
Как только будет найдена общая матрица М всей оптиче-
оптической системы, о всех промежуточных выкладках и элементах
расчета можно забыть и перенумеровать входную опорную пло-
плоскость, а именно обозначить ее ОП2. (Теперь преобразование па-
параметров луча через всю систему от входной ОП] до выходной
ОПа можно выполнить за один прием.)
Однако в некоторых случаях часть оптической системы мо-
может быть отделена от другой промежутком переменной длины.
Вследствие этого лучше было бы рассчитать отдельно обе из-
известные части системы, а затем получить общую матрицу всей
системы, связав две вычисленные матрицы через матрицу
I . . I, соответствующую оптическому промежутку с перемен-
переменной толщиной t Тогда четыре элемента общей матрицы будут
просто линейными функциями от /.
Кроме того, на практике нередко сложный набор лииз при-
применяется в ситуациях с переменными расстояниями до объекта
и до изображения. В этих случаях также приходится сначала
вычислить отдельно матрицу для известной центральной части
оптической системы.
f $. МАТРИЧНОЕ ОПИСАНИЕ СВОЙСТВ
ОПТИЧЕСКОЙ СИСТЕМЫ
Предположим, что мы нашли численные значения матричных
элементов матрицы М сложной оптической системы и что урав-
уравнение К% = Af/Ci в развернутом виде записывается следующим
образом:
Матричные методы в параксиальной оптике
55
Фиг. 2.5
где AD — ВС = 1. Для того чтобы лучше уяснить себе смысл
четырех величин А, В, С к D, рассмотрим, что произойдет, если
одну из них положить равной нулю.
а) Если D = О, то уравнение для V2 принимает вид К2 =
= Су\ ¦+¦ OVi = Суь Это значит, что все лучи, выходящие
из одной и той же точки у\ входной опорной плоскости,
выйдут из выходной опорной плоскости под одним и тем
же углом Vi = Cyi к оси системы независимо от того, под
каким углом V\ эти лучи входили в систему. Отсюда сле-
следует, что входная плоскость OFli должна быть первой
фокальной плоскостью снстемы (фиг. 2.5).
б) Если 5 = 0, то уравнение для у2 записывается следую-
следующим образом: у2 = Ayi-{-0Vi= Ayi. Это значит, что все
56
Глава 2
лучи, покидающие точку О (с координатой у{) на пло-
плоскости ОПь пройдут через одну и ту же точку / (с коор-
координатой у2) на плоскости ОП2. Следовательно, точки О
и / являются соответственно точкой-объектом и точкой-
изображением, а плоскости OIli и ОПг— сопряженными
плоскостями. Кроме того, в данных условиях величина
Л =» Уг1у\ дает увеличение системы (фиг. 2.6).
в) Пусть С = 0, тогда Уг = DVi. Это означает, что все лучи,
которые входят в систему параллельно друг другу (на-
(например, под углом Vi к оптической оси), на выходе опти-
оптической системы дадут также параллельный пучок лучей,
но относительно оси его угол распространения изменится
и станет равным У2- Такая система линз, которая преоб-
преобразует параллельный пучок лучей в параллельный же, но
распространяющийся под другим углом, называется афо-
кальной или телескопической системой. В этом случае ве-
величина (niDJn2) = (v2/vi) представляет собой угловое
увеличение оптической системы (фиг. 2.7).
г) В случае А = 0 уравнение для у2 записывается в виде
y2 = BVi. Это значит, что лучи, входящие в систему под
одним и тем же углом Vi, пройдут через одну и ту же
точку (с координатой у2) на выходной плоскости ОПг.
Таким образом, система собирает пучок параллельных лу-
лучей в фокус в точках, расположенных на плоскости ОПг,
т. е. ОПг является второй фокальной плоскостью оптиче-
оптической системы (фиг. 2.8).
д) Наконец, нужно помнить, что если какая-либо из вели-
величин А или D в матрице преобразования лучей обращается
в нуль, то условие AD — ВС = 1 требует, чтобы выпол-
выполнялось равенство ВС = —1. Аналогично если в нуль обра-
обращается В или С, то А должно быть величиной, обрат-
обратной D.
«г. 3,7
Матричные методы в параксиальной оптике
57
Фиг. 2.8
На том основании, что В обращается в нуль, когда в качестве
опорных плоскостей выбраны оптически сопряженные плоско-
плоскости, и что А или A/D) в этом случае дает поперечное увеличе-
увеличение, можно построить экспериментальный метод для нахождения
ОП
on on
Фиг. 2.9
58 Глава 2
матричных элементов оптической системы, причем не требуется
ни расчленения ее на отдельные части, ни измерения параметров
ее отдельных компонент. Мы опишем этот метод ниже после
применения матричного подхода к решению некоторых задач.
Вообще говоря, если только величина V не равна нулю, луч
обязательно пересекает оптическую ось в какой-либо точке.
Координата г этой точки относительно данной точки, в кото-
которой луч имеет высоту у и угол v = V/n, равна —y/v = —ny/V.
Точка пересечения расположена слева от опорной плоскости в
случае, когда величины у и V либо обе положительны, либо
обе отрицательны (фиг. 2.9).
§ 7. ЗАДАЧИ, ИЛЛЮСТРИРУЮЩИЕ МАТРИЧНЫЙ ПОДХОД
Задача 1
Левый конец длинного цилиндрического стержня из органи-
органического стекла с показателем преломления 1,56 имеет форму
выпуклой полированной сферической поверхности радиусом
2,8 <ш. Предмет в виде стрелки длиной 2 см расположен в воз-
воздухе на оси стержня на расстоянии 15 см от крайней точки этой
поверхности (фиг. 2.10). Требуется определить положение и раз-
размер изображения внутри стержня.
Решение
Выберем в качестве единицы измерения длины см для обеих
матриц 91 и 9~ и будем решать задачу следующим образом. За-
ОП, 0П2
\
1
2~d\o
1
1
1
1
Радиус
(
\
15 ^
=2,8
X
1
1
1/
T
I
1
1
1
n-1,56
Фиг. 2.10
Матричные методы в параксиальной оптике 59
пишем Я-матрицу оптической поверхности:
г ы i-f
L — («а — «,)/г lJ L(-l,56+l)/2,8 lj L-0,2 i
Если изображение находится на расстоянии X см справа от
вершины преломляющей поверхности, то цепочка матриц в на-
направлении от изображения назад к предмету имеет вид
Х/п1[ 1 01Г 1 15
1 Л-0,2 iJlo l
Промежу- Преломляю- Промежу-
Промежуток от щая ток от
изображе- поверхность поверх-
ння до ностн до
поверх- предмета
ности
_Г1 Х/1,56-1 Г 1 15-|_Г1-Х/7,8 15-^/0,78-j
~L0 I J L-0,2 —2 J~~L -0,2 -2 J
Проверка
det(AJ) = (AD - ВС) = -2 + W3.9) -f 3 - (X/3,9) = 1.
Чтобы выполнялось соотношение, связывающее предмет с его
изображением, верхний правый элемент В должен быть равен
нулю:
15-w=°. х==п>7'
Таким образом, изображение находится внутри стержня на рас-
расстоянии 11,7 см от вершины сферической поверхности. Попереч-
Поперечное увеличение дается либо величиной А, либо величиной 1/D
и равно —0,5. Следовательно, изображение представляет собой
перевернутую стрелку размером @,5-2) см = 1 см.
Задача 2
Оба конца стеклянного цилиндрического стержня длиной
2,8 см имеют форму выпуклой сферической поверхности радиу-
радиусом 2,4 см. Предмет в виде стрелки длиной 2 см помещен на оси
стержня в воздухе на расстоянии 8 см от левого конца стержня
(фиг. 2.11). Требуется найти положение и размер окончатель-
окончательного изображения.
60
Глава 2
Фиг. 2.11
Решение
Если окончательное изображение расположено справа на
расстоянии X см от правого конца стержня, то цепочка матриц
записывается в виде
Проме-
Промежуток от
изобра-
изображения до
стержня
Правый конец
стержня
Длина
стержня
Левый конец
стержня
Проме-
Промежуток от
стержня
до
предмета
¦к
Г1 Х1Г 0,5
10 1 J L —0,2
01Г1 1.751Г 1 01Г1 81
lJLo I J L —0,25 lJLO lj
6,251
-2,56 J'
1,75
-0,25 ULO 1 JL-0,25
Х1Г 1 1,75 1Г 1 81
1 JL-0,25 0,5625 JL-0,25 -1 J
0,5625
i,391
Следовательно,
ТА fi-J Г 0,5625 -0,391* 6,25-2,56*1
1С Dj~[ -0,391 -2,56 J"
Чтобы выполнялось соотношение связи между предметом и его
изображением1), должно выполняться равенство 2,56* =6,25.
•) Соотношение связи между предметом и его изображением определя-
определяется равенством В = 0. Это означает, что даннан матрица связывает векторы
одного и того же луча в плоскости предмета и в плоскости изображения.—
Прим. перев.
Матричные методы в параксиальной оптике
61
оп,
Фиг. 2.12
Следовательно, X = 2,44 см (справа от стержня). Увеличение
1/D =—1/2,56 = —0,39. Следовательно, изображение стрелки
перевернуто и его размер равен B-0,39) см = 0,78 см.
Задача 3
Параллельный пучок света проходит через прозрачный сфе-
сферический шарик диаметром 2 см из органического стекла, пока-
показатель преломления которого равен 1,4 (фиг. 2.12). В какой точ-
точке за шариком свет соберется в фокус?
Решение
Если мы выберем выходную опорную плоскость ОП2 распо-
расположенной на расстоянии X см справа от шарика, то цепочка
матриц запишется в виде
[I
I
Воздуш-
Воздушный
промежу-
промежуток
X
Правая
поверхность
Г1 XIГ 0,
L0 lJL-0,
Г 0,429-
L -0,
2
1,4
О 1
Промежуток
между
поверх-
поверхностями
429 1,429
°ь
Левая
поверхность
571 0,429 J ~
0,429-0,571* 1,429 + 0,429X1
J
1
0,429 J
Г Л В1
[.С D\-
Глава 3
Чтобы параллельный пучок света собрался в фокус в ОП2, мат-
матричный элемент А должен быть равен нулю:
0,571* = 0,429, Х = 0,75.
По-другому такой же результат можно получить непосредствен-
непосредственно из матрицы для шарика
0,429 1,4291
-0,571 0,429 J'
Поскольку У1 — 0, мы имеем
ГА В1ТУ11
lc dJLo J
Следовательно, расстояние, на котором луч I "й I пересечет ось,
равно —пу^Уг = —AJC справа от шарика, т. е. 0,429/0,571 =
в 0,75 см.
Замечание
Этот расчет относится только к центральному параксиаль-
параксиальному участку пучка лучей — остальная часть пучка даст сфери-
сферическую аберрацию.
Зшдача 4
Диапозитив размером 5 см расположен на расстоянии 3 м от
экрана (фиг. 2.13). Каково должно быть фокусное расстояние
линзы н где ее следует поместить, чтобы даваемое этой линзой
изображение диапозитива на экране имело размер 100 см?
Дщщвшпиа
0П,
3-Х.
L--.P
Э&ан
Фиг. 2.13
Матричные методы в параксиальной оптике 63
Решение
Хотя размеры предмета и изображения даны в сантиметрах,
в данном случае для вычисления матричных элементов более
удобно использовать метры. Потребуем, чтобы линза была тон-
тонкой и положительной (собирающей). Оптическую силу Р этой
линзы будем измерять в обратных метрах. Предположим, что
мы поместили линзу на расстоянии X метров от щели и C — X)
метров от экрана. Произведение матриц, соответствующее це-
цепочке элементов от экрана до щели, записывается в виде
Промежуток Линза Проме-
от экрана жуток от
до линзы линзы
до щели
П г-xiT 1 х 1
Lo 1 М-р 1-рх\
Следовательно,
Г Л ВI _ Г 1 - ЗР + РХ X + C - X) A - РХ) 1
[с Dj —L -р 1-рх J
Одиночная линза всегда дает перевернутое действительное изо-
изображение действительного предмета; поэтому увеличение сле-
следует взять со знаком минус, т. е. —100/5 = —20. Следовательно,
в приведенной выше матрице имеем А = 1/D = —20 и В=0,
т. е. выполняется соотношение связи между предметом и его
изображением. Поскольку D = \ — РХ — —0,05, то из равен-
равенства 5 = 0 находим
В = X — 0,05 C — X) — 0.
Следов ательно,
1,05* = 0,05-3, откуда Хж 0,15 м.
Уравнение для D теперь принимает вид
1 — 0,15Р== — 0,05, так что Р
Таким образом, фокусное расстояние линзы составляет
A/7) м « 14 см.
Ответ
Линза должна иметь положительное фокусное расстояние,
равное 14 см, и располагаться на расстоянии 15 см от диапози-
диапозитива.
64
Глава 2
Фиг. 2.14
Задача 5
Положительная (собирающая) линза с фокусным расстоя-
расстоянием +8 см установлена на расстоянии 6 см слева от отрица-
отрицательной (рассеивающей) линзы с фокусным расстоянием
—12 см. Слева от положительной линзы на расстоянии 24 см
от нее помещен предмет высотой 3 см иа оси системы. Тре-
Требуется найти положение изображения и его размер (фиг. 2.14).
Решение
При решении задачи будем пользоваться метрами и диоп-
диоптриями. Оптическая сила положительной линзы равна +100/8 =
=s-f-12,8 диоптрий, а для отрицательной линзы (—100/12) =
= —8,33 диоптрий. Предположим, что изображение находится
на расстоянии X метров справа от отрицательной линзы. Тогда
цепочку матриц от изображения к предмету можно записать в
виде
1 ХЛ Г 1 01Г1 0,061 Г 1 01Г1 0,241
0 1JL8.33 lJLo I JL—12,6 lJLo 1 J
Проме-
Промежуток от
изобра-
изображения
до отри-
отрицательной
лиизы
Отрица-
Отрицательная
линза
Промежуток
между
линзами
1
12,5
Положитель-
Положительная линза
Промежуток
от положи-
положительной
линзы до
предмета
*1Г1 0,061 Г 1 0,241
lj 1.8,33 1,5 JL-12,5 -2 J
Матричные методы в параксиальной оптике
65
Следовательно,
Г
d\ 1
- 1 X -I Г 0,25
.0 1 J L—10,42
,25-10,42* 0,
. -10,42
0,12
12-
-1
]
X
Для того чтобы выполнялось соотношение связи между пред-
предметом и его изображением, мы должны положить В = 0,12 —
— X = 0, откуда находим X = 0,12 м. Увеличение 1/D = —1.
Следовательно, конечное изображение перевернуто, а его вы-
высота равна 3 см. Расположено это изображение справа от от-
отрицательной линзы на расстоянии 12 см от нее.
Задача 6
Слева от тонкой линзы на расстоянии U от нее находится
предмет, изображение которого образуется на расстоянии V
слева от той же самой линзы (фиг. 2.15). Затем предмет сме-
смещают вдоль оптической оси влево на небольшое расстояние dU.
Требуется определить соответствующее смещение изображения
dV. Величина dV/dU называется продольным увеличением. По-
Показать, что продольное увеличение равно квадрату поперечного
увеличения.
Решение
(Заметим, что если формируется действительное изображение,
то величина V будет иметь отрицательное значение; однако не-
независимо от того, является ли тонкая линза положительной или
огь
Фиг. 2.15
S Зак. 774
W . Глава 2
отрицательной, существует такое положение предмета на оси
линзы, при котором его изображение является мнимым, т. е.
величина V становится положительной. Заметим также, что и
в этой, и в следующей задачах через V обозначено расстояние
от линзы до изображения, а не оптический направляющий ко-
косинус.)
Цепочка матриц от изображения к предмету записывается
в виде
Промежуток Линза Промежу-
от изобра- ток от
жеиия до линзы до
лиизы') предмета
1 -К1Г 1 V 1 П+PV U-V + PUV
Р Л —PU
ir 1 U 1 П +
JUp \-риГ1 ~,
Для того чтобы удовлетворить соотношению связи между пред-
предметом и его изображением, нужно приравнять нулю правый
верхний элемент и— V -\-PUV последней матрицы. Следова-
Следовательно, ,•¦•¦:' :;: .:..•¦'•¦ - • •
и
. Vc= ,
Y 1 - PU ш
Дифференцируя это выражение, подучаем
{\->Р(ГЦ\)+УР
Как видно из правого нижнего элемента полученной матрицы,
величина 1/A —PU) представляет собой поперечное увеличение,
квадрат которого совпадает с нашим выражением для dV/dU.
Для поперечного увеличения можно найти и другие выражения,
а именно A+PV) и V/U. (Следует заметить, что в процессе
получения данного решения мы определили основное соотноше-
соотношение между Р, U и V для тонкой линзы. Поскольку U— V+
-f- PUV = О, то, разделив это выражение на UV н выполнив со-
соответствующие преобразования, мы придем к хорошо известной
формуле линзы
и v r f •
где f — фокусное расстояние лиизы.)
•) Здесь V имеет отрицательный знак, поскольку это расстояние отсчи-
тывается вдоль оси z в отрицательном направлении.
Матричные методы в параксиальной оптике
67
Г"
Фиг. 2.16
Задача 7
Требуется доказать следующее положение: расстояние меж-
между действительным предметом и его действительным изображе-
изображением, образованным тонкой положительной линзой, не может
быть меньше учетверенного фокусного расстояния линзы
(фиг. 2.16).
Решение
Как и в задаче № б, верхний правый элемент матрицы пре-
преобразования лучей от изображения к предмету равен
U—V + PUV, и он должен обращаться в нуль. Далее, по-
поскольку и U, и V отсчитываются в левую сторону от линзы,
U должно быть положительным, но, чтобы действительный пред-
предмет дал действительное изображение, V должно быть отрица-
отрицательным. Если через К обозначить расстояние от предмета до
его изображения, то можно написать следующие равенства:
K=U—V и V=U—К. Таким образом, выражая V через
U и К, мы получаем
U - (U - К) + PU (U - К) = О,
откуда
А—PU_l +U.
Следов ательно,
dK _ (PU-^l)Q) -UP ¦ i _i _
dU ~ (PU-\y +
1
(PU - \J •
Для того чтобы производная dK/dU обратилась в нуль, мы
должны иметь либо PU — 1 = 1, т. е. PU = 2, либо PU— 1 =
68 Глава 2
*=—1, т. е. PU = O (тривиальный случай). Поскольку по пред-
предположению и Р, и U являются положительными величинами, то
для дальнейшего анализа случая PU = 2 необходимо рассмот-
рассмотреть вторую производную
d*K d_ Г -1 I _ - (-2) Р 2Р
dU* ~ dU Y (PU - IJ J ~* (PU - l)s ~~ (PU - l)s '
В случае PU = 2 знаменатель этого выражения равен единице,
а числитель положителен. Стало "быть, производная cPK/dU2
положительна, и величина К должна проходить через минимум.
Подставляя в выражение для К значение U = 2/Р, находим
где f = 1/Р — фокусное расстояние линзы.
§~8. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
ЭЛЕМЕНТОВ МАТРИЦ ОПТИЧЕСКОЙ СИСТЕМЫ
Рассмотрим положительную систему линз, помещенную в
воздушное пространство. Прежде всего выберем две удобно рас-
расположенные опорные плоскости системы: одну, ОП], у входной
поверхности оптической системы и другую, ОП2, у выходной по-
поверхности. Первую из них назовем входной опорной плоскостью,
а вторую — выходной опорной плоскостью. Матричные элемен-
элементы А, В, С и D должны удовлетворять уравнению
А В-\[У1
С i
Г у 21 Г
UJ-L
Предмет известной величины будем помещать на различных
расстояниях слева от ОП1 и регистрировать величину и положе-
положение получающегося каждый раз действительного изображения.
В общем случае смещение в положительном направлении
вдоль оси z от предмета к ОП] обозначим через R, а смещение
в положительном направлении вдоль оси г от ОП2 к действи-
действительному изображению — через S. Мы будем смещать предмет
таким образом, чтобы величины R и S каждый раз оставались
положительными.
Цепочка матриц преобразования лучей от плоскости изобра-
изображения назад к плоскости предмета имеет вид
_Г1 S1TA ДТП /П Г1 S1\A AR +
М~[о 1J L С olio lJ^Lo lJ|_C CR + ,
A + SC AR + B + S(CR + DI
С CR + D ]'
Матричные методы в параксиальной оптике 69
Относительно этой матрицы нам известно, что ее определитель
равен единице и что ее верхний правый элемент в силу соотно-
соотношения связи между предметом и его изображением равен нулю.
Верхний левый элемент A+SC общей матрицы представляет
поперечное увеличение, а нижний правый элемент CR-\-D ра-
равен величине, обратной поперечному увеличению, которую мы
будем обозначать через а.
Величины, которые можно экспериментально измерить, — это
расстояния R и S и отношение высоты предмета к высоте изо-
изображения, равное а = CR + D. (Следует заметить, что если
изображение перевернуто, как часто бывает на практике, то а
отрицательно.)
Если значения а, измеренные при нескольких расстояниях
R, представить в виде графика зависимости от R, то получим
прямую, пересекающую ось а при а = D, тангенс угла которой
равен С. Таким образом определяются величины С и D.
Приравнивая в матрице М верхний правый элемент нулю,
получаем AR + В «=—S(CR + D)*=—Sec = р, где мы ввели
новую величину р, численные значения которой нам известны.
Если теперь построить график зависимости р от R, то величина
А будет определять наклон соответствующей прямой, пересекаю-
пересекающей ось р в точке р = В. После того как все четыре матричных
элемента будут найдены, следует удостовериться в том, что
определитель AD — ВС приблизительно равен единице.
8.1. Отрицательная система линз
Если система, параметры которой нужно измерить, является
рассеивающей (отрицательной), то приходится использовать до-
дополнительную линзу, для того чтобы образовать действительное
изображение, размер и местоположение которого справа от ОП]
заданы. Путем подбора подходящего диапазона отрицательных
значений R можно получить действительное изображение справа
от ОП2 и измерить его величину. Однако эта методика весьма
неудобна.
8.2. Иммерсионные системы
Экспериментальное определение параметров иммерсионных
оптических систем, которые характеризуются тем, что в них
слева от ОП] находится среда с показателем преломления пи
а справа от ОШ — среда с показателем преломления п2, яв-
является весьма сложной процедурой. Однако что касается мат-
матричного описания системы, то все, что необходимо сделать, —
это заменить расстояния R и S там, где они встречаются, на-
например в матрицах перемещения, их приведенными значениями
70
Глава t
R/щ и S/n2. Когда вычисляется новая, с учетом этой подста-
подстановки, матрица преобразования лучей от изображения к пред-
предмету, ее нижний правый элемент по-прежиему будет соответ-
соответствовать измеряемому значению величины а.
§ 9. РАСПОЛОЖЕНИЕ КАРДИНАЛЬНЫХ ТОЧЕК СИСТЕМЫ
Предположим, что для данной системы либо путем расчета,
либо экспериментально с помощью описанного выше метода мы
ГА В1
нашли матрицу М = I _ _. I. которая связывает параметры
луча в выбранной выходной плоскости ОП2 с его параметрами
во входной плоскости ОПь Относительно этих опорных плоско-
плоскостей будем искать местоположение двух фокальных точек, глав-
главных плоскостей единичного поперечного увеличения и сопря-
сопряженных (или узловых) плоскостей единичного углового увели-
увеличения. Возьмем самый общий случай. Предположим, что пх и
яг— соответственно показатели преломления сред, расположен-
расположенных слева и справа от системы.
а) Рассмотрим сперва луч, входящий в оптическую систему
параллельно оптической оси на высоте у\ (фиг. 2.17а). В соот-
соответствии с принятыми в гауссовой оптике допущениями такой
луч появится на той же самой высоте во второй главной пло-
плоскости #2, выходя из которой он резко меняет направление
своего распространения таким образом» чтобы пройти через вто-
вторую фокальную точку F2. Для этого луча v\, а следовательно, и
Vi равны нулю. Тогда из матрицы преобразования лучей мы
имеем в плоскости ОП2 уч » Аух и»;» К»/«2 = Cyi/n2.
Пусть U — смещение, измеряемое в положительном направле-
направлении оси г от ОП3 к Ft, тогда должно выполняться следующее
соотношение: t2 = —уз/оц = -~ПяА/С, которое дает местоположе-
местоположение второго фокуса.
Фиг.
Матричные методы в параксиальной оптике
71
Фиг. 2.176
Рассматриваемый луч выходит из второй главной плоскости
И2 в точке с вертикальной координатой у\. Следовательно, если
определить второе фокусное расстояние /2 как смещение от Н2
до F2, то оно должно быть равно /2 = —yi/v2. Поэтому /2 =
= —П2У\1Су\ = —п2/С, и тем самым определяется второе фокус-
фокусное расстояние.
Следовательно, смещение от ОП2 до второй главной плоско-
плоскости равно s2 = t2 — f2 = п2(\ —А) 1С.
б) Рассмотрим теперь луч, который входит в оптическую си-
систему под углом V\, проходя через первый фокус F\ (фиг. 2.176).
Направление распространения этого луча резко изменяется при
пересечении им первой главной плоскости Н\\ он становится па-
параллельным оптической оси системы и, следовательно, пересе-
пересекает ОП2 под углом у2 = О (стало быть, и V2 = 0).
Следовательно, можно написать V2 = Су\ -f- Dn\V\ = 0 и
ух = —DntVi/C. Из фиг. 2.176 видно, что смещение t\ фокуса
F\ от ОП] дается выражением t\ = —yi/vi = niD/C. Таким об-
образом определяется положение первого фокуса.
Мы уже упоминали, что в первой главной плоскости у-коор-
дината этого луча должна быть равна у2 = Аух + Bti\V\. По-
Поэтому, определив первое фокусное расстояние f\ как смещение
F\ от #ь мы должны иметь /i = y2/v\ = —DArii/C + Вщ =
= —ni(AD — BC)/C. Вспомнив, что (AD — BC)=\, оконча-
окончательно получаем выражение для первого фокусного расстояния,
а именно f\ = —п\\С.
Следовательно, величина s\ = U + /1 = n{(D— I)/С пред-
представляет собой смещение первой главной плоскости #i относи-
относительно ОП].
в) В заключение нам нужно определить две узловые точки
системы L\ и L2. Эти точки характеризуются следующим свой-
свойством: любой луч,, входящий в систему под углом wi и проходя-
проходящий через точку L\, появится на выходе системы как луч, выхо-
выходящий из точки L2, причем выходящий луч будет составлять с
Глава 2
Фиг. 2.17в
осью системы угол v2 = V\ (фиг. 2.17в). Обозначим через р\ и
р2 соответственно смещения точки L\ от OFIi и точки L2 от ОГЬ.
Цепочка матриц, связывающая в обратном направлении вторую
узловую точку L% с первой узловой точкой Llt записывается в
виде
[;
О 1
Промежу-
Промежуток от L2
до ОП2
Проме-
Промежуток от
ОП2 до
ОП,
d\U i J-
Промежуток
от ОП1
до L\
Рг/«2 IT A
i JLc
Л + (/72С/«2) -
0
Cpjm +
J
(Заметим, что при записи этого выражения мы использовали
приведенные смещения и что в матрице У для оптического про-
промежутка от ОП1 до узловой точки L\ стоит —/7i, а не pi.)
Обозначим только что полученную матрицу через ф и пусть
у0 и i>o являются параметрами луча на входе в плоскости узло-
узловой точки Lu а уз и из — параметрами этого же луча на выходе
из плоскости узловой точки L2. Тогда можно написать следую-
следующие уравнения:
Уз
ФиУо + Фп
n2v3 = у3 = ф21у0 + ФпУо
Однако если Li и L8 — узловые точки и у0 = 0, то независимо
от величины v0 мы должны иметь у3 = 0 и и3 = v0. А эти
Матричные методы в параксиальной оптике
73
Таблица 2.1
Описываемый параметр
системы
Первый фокус
Первое фокусное рас-
расстояние
Первая главная точка
Первая узловая точка
Второй фокус
Второе фокусное рас-
расстояние
Вторая главная точка
Вторая узловая точка
Измеряемый
от до
ОП, F,
Fi Нг
ОП1 Hi
On, Li
ОП2 F3
#2 Ft
ОП2 tf2
ОП2 L2
Функция от матричных
элементов
ntD/C
-/ii/C
я, (D-!)/C
(Dm - п2)/С
— п2А/С
-п2/С
п2 A - А)/С
(яд - Ап2)/С
Частный
случай
п,=п,=1
D/C
-1/С
(D-\)IC
ф-1)/С
-А/С
-1/С
A-Л)/С
A - А)/С
равенства выполняются, только если фм = 0 и ^22A1/12) = 1.
иными словами, если матрица ^ представляет собой матрицу
преобразования луча от предмета до изображения с поперечным
(линейным) увеличением 1/фа = (щ/щ).
Из уравнения фчч =• («2/11) вытекает равенство р\ = (Z)rti —
— п2)/С. Подставляя его в условие фи = 0, в конечном счете по-
получаем р2 = («1 — Ап2)/С.
Для удобства вычислений все эти результаты мы свели в
таблицу (см. табл. 2.1).
Из правой колонки табл. 2.1 видно, что узловые точки совпа-
совпадают с главными точками системы в том случае, когда система
находится в воздухе (случай, наиболее часто встречающийся на
практике). Такое совпадение узловых и главных точек обуслов-
обусловлено тем, что для погруженной в воздух оптической системы
условия для единичного углового увеличения и единичного ли-
линейного увеличения одинаковы. Кроме того, оба фокусных рас-
расстояния равны одной и той же величине —1/С. (В тех случаях,
когда показатель преломления среды отличается от единицы, мы
имеем дело с приведенным фокусным расстоянием, которое так-
также равно —1/С.)
Чтобы сделать наш элементарный анализ параксиальных
преломляющих систем полным, выясним, как будет выглядеть
матрица
ГА В1
1С D}'
если преобразование луча рассматривать не
между OFli и ОП2, а между а) двумя главными плоскостями или
0) двумя фокальными плоскостями системц.
Ti Глава 2
a} Для промежутка между двумя главными плоскостями ма-
матрица преобразования луча записывается в виде
1 — D
С
1
От Нг до ОПг От ОП2 От ОП,
до ОП, до Hi')
1
Тк t №
[здесь мы учли, что (AD — ВС)=== 1\ Таким образом, для про-
промежутка между двумя главными плоскостями матрица прелом-
преломления совпадает с матрицей преломления тонкой линзы, опти-
оптическая сила которой Р *= —С =s= 1/f. Как и следовало ожидать,
существует соотношение связи между предметом в плоскости
€шi н его изображением в плоскости ОП2 с единичным коэффи-
коэффициентом поперечного увеличения.
б) Для промежутка между двумя фокальными плоскостями
матрица преобразоиания луча записывается следующим обра-
образом:
Г1 -A/ClfA В-1Г1 -D/C-I
Lo i lie d\[o i Г
От F2 до ОП, От ОП, От Olli до Ft')
до OHi
_Г1 -А1С1ГА -1/С1 ГО -1/С1 ГО /1
~Lo 1 lie о j^U о J^l-i// oJ'
Эта матрица описывает хорошо известный результат: высота
луча во второй фокальной плоскости зависит только от угла
луча в первой фокальной плоскости, в то время как угол луча
во второй фокальной плоскости зависит только от высоты луча
в первой. Кроме того, если расстояние z\ от предмета до пер-
') Заметим, что здесь происходят изменение знака,
Матричные методы в параксиальной оптике
75
вой фокальной плоскости, измеряемое влево от фокуса Fi, запи-
записать в виде yi/V\, а расстояние z2 от изображения до второй фо-
фокальной плоскости — в виде yilV2, то сразу можно получить, что
(y2/V2) = — /2 (уравнение Ньютона).
Кроме того, как и следовало ожидать, равенство нулю диаго-
диагональных элементов матрицы отражает тот факт, что OIli и ОП2
совпадают с фокальными плоскостями системы. Если эквива-
эквивалентные фокусные расстояния не изменяются при таком преоб-
преобразовании матрицы, то матричный элемент С остается тем же
самым и, для того чтобы матрица оставалась унимодулярной, ее
правый верхний элемент должен быть равен —1/С
§ 10. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
Задача 8
Стеклянная полусфера радиусом г используется в качестве
линзы (показатель преломления стекла п). Через эту полусферу
проходит пучок лучей, почти совпадающих по направлению с ее
оптической осью. Показать, что если полусфера обращена пло-
плоской поверхностью в левую сторону, то вторая главная точка сов-
совпадает с точкой пересечения выпуклой поверхности с осью (с ее
вершиной). Показать также, что первая главная точка располо-
расположена внутри линзы на расстоянии г/п от плоской поверхности и
что фокусное расстояние линзы равно г/(п — 1) (фиг. 2.18).
Решение
Если опорные плоскости поместить одну на плоской поверх-
поверхности полусферы, а другую параллельно ей в вершине выпуклой
Фиг. 2.18
76 Глава 2
части поверхности, то цепочка матриц запишется в виде
1 0
o 1JL0 ij=L^T^- U'
Преломление на Линза с Прелом-
кривой поверхно- приведен- ление на
стн в ОП2 ной толщи- плоской
вой поверхно-
поверхности в ОП1
(Несмотря на то что этот расчет очень прост, все же стоит про
верить определитель.) Требуемые результаты для данного слу
чая можно найти в правой колонке табл. 2.1. Расстояние от ОП
до второй главной точки, равное A —А)/С, обращается в нуль
Расстояние от OIli до первой главной точки равно
Поскольку п > 1, это расстояние меньше толщины г полусфери-
полусферической линзы.
Наконец, фокусное расстояние рассматриваемой линзы,
измеряемое в воздухе в любом направлении, равно —1/С =
= f/(n-l).
Задача 9
Тонкая положительная линза с фокусным расстоянием 10 см
расположена на расстоянии 5 см от тонкой отрицательной линзы
г/Ом
Фиг. 2Л8
Матричные методы в параксиальной оптике 7?
с фокусным расстоянием —10 см (фиг. 2.19). Требуется найти
эквивалентное фокусное расстояние всей системы и положение
фокусов и главных плоскостей.
Решение
Предположим, что положительная линза расположена в ле-
левой части системы, а опорные плоскости совпадают с плоско-
плоскостями линз. Выражая расстояния в метрах, а обратные фокус-
фокусные расстояния в диоптриях, находим матрицу системы
Г 1 01 Г 1 0,05 I Г 1 01 _ Г 1 0,05 I Г 1 0 у
М==1Ю 1 J L 0 1 JL-10 1 J== L Ю 1,5 JL-10 1J
Отрица- Промежуток Положитель-
тельная между лин- иая лииза
линза зами в ОП]
в ОП2
Следовательно,
Г Л ВI _ Г 0,5 0,05 I
1С dJ = L-5 1,5 J
Проверяя определитель, имеем (AD — ВС) = @,5) A,5) +
-+- E) @,05) = 1. Используя снова результаты, приведенные в
табл. 2.1, приходим к выводу, что фокусное расстояние рассма-
рассматриваемой комбинации линз должно составлять —1/С =
= +0,2 м = 20 см (оптическая сила = +5 диоптрий).
Первый фокус расположен на расстоянии D/C = —0,3 м
вправо от ОПь т. е. на расстоянии 30 см в левую сторону от
тонкой положительной линзы. Поскольку фокусное расстояние
системы, как мы нашли, равно 20 см, то первая главная пло-
плоскость должна располагаться слева в 10 см от положительной
линзы. (Согласно формуле, приведенной в табл. 2.1, мы полу-
получаем, что расстояние вправо от ОП: до #i равно (D— 1)/С =
= 0,5/(-5) м.)
Второй фокус расположеи справа от ОПг (от отрицательной
линзы) на расстоянии —А /С =« —0,5/(—5) = 0,1 м = 10 см. Те-
Теперь либо непосредственно, либо путем применения формулы
A —А)/С находим, что вторая главная плоскость системы рас-
расположена на расстоянии 10 см слева от отрицательной линзы,
или в 5 см слева от положительной линзы.
Оптическая система такого типа в действительности пред-
представляет собой довольно грубый пример телеобъектива, у кото-
которого фокусное расстояние больше, чем габаритный размер объ-
объектива и расстояние до плоскости сфокусированного изображе-
изображения.
Глава $
Фиг. 2.20
Задача 10
Окуляр телескопа-рефлектора (фиг. 2.20) состоит из двух
тонких положительных линз. Пусть оптические силы линз равны
Pi и />2 соответственно, а расстояние между ними обозначим че-
через /. Показать, что эквивалентное фокусное расстояние такого
окуляра дается формулой (Pi -f Р2 — P\Pst) -'. Если обе линзы
сделаны из одного и того же стекла, то каким образом можно
избежать поперечной хроматической аберрации? Будет ли такой
окуляр свободен от продольной хроматической аберрации?
Решение
Как и в предыдущей задаче, выберем обе опорные плоскости
в точках расположения двух линз и запишем матрицу системы:
-Pi i
ULo
Г 1 t -IT 1 О
^1-р2 i-p^JL-p, i
_ Г 1 — Pit t I
~ L - p2 - P\ + Р№ i - Pit J •
Нижний левый элемент этой матрицы, очевидно, дает эквива-
эквивалентное фокусное расстояние окуляра
Поскольку в телескопе-рефлекторе окуляр используется в со-
совокупности с ахроматическим отражательным объективом, то уг-
угловое увеличение наблюдаемого с помощью телескопа астроно-
астрономического объекта не зависит от длины волны, только если экви-
эквивалентное фокусное расстояние окуляра не зависит от неболь-
небольших изменений показателя преломления, которые присущи лю-
любому стеклу при изменении длины волны света.
Матричные методы в параксиальной оптике 79
Как было показано в § 4 настоящей главы, оптическая сила
Р любой тонкой линзы равна произведению величины п — 1 на
геометрический фактор G. В рассматриваемом случае G пред-
представляет собой разность кривизн двух поверхностей. Таким об-
образом, для комбинации линз можно написать следующее выра-
выражение:
1= (п - 1) (О, + G2) - (п - IJ GXGJ.
Вычислим производную этого выражения по п:
и приравняем ее нулю. В результате получаем
, , . Oi + О» 1 Г 1 | 1 I
1 ~~ 2 (п - 1) GiGt = 2 L (л - 1) G2 "*¦ (п - 1) О, J
Это условие лежит в основе классических приборов — окуляра
Гюйгенса и окуляра Рамсдена.
К сожалению, хотя при выполнении этого условия мы и из-
избегаем ошибки, связанной с поперечной хроматической аберра-
аберрацией (т. е. с зависимостью увеличения от длины волны), од-
однако нельзя быть уверенным в том, что окуляр не вносит про-
продольных искажений. Согласно табл. 2.1, первый фокус рассма-
рассматриваемой системы должен быть расположен на расстоянии
D/C слева от ОПь Хотя мы уверены в том, что знаменатель С
в величине D/C не зависит от небольших изменений в показателе
преломления п, но, очевидно, в отношении числителя, который
равен D = 1 — /У = 1 — (п — l)G2t, этого сказать нельзя. Сле-
Следовательно, при наблюдении звезды с помощью такого окуляра
положение его фокуса при настройке на максимальную резкость
должно слегка изменяться в зависимости от длины волны.
(Необходимо помнить, что кроме рассмотренных здесь вопро-
вопросов, связанных с хроматической аберрацией, которые можно изу-
изучить в рамках параксиальной оптики, сферическая аберрация
таких простых окуляров, существующая даже для параксиаль-
параксиальных пучков, может оказаться нежелательной в случае примене-
применения последних в ньютоновском отражательном телескопе с ма-
малым отношением фокусных расстояний.)
Задача 11
Стеклянная линза толщиной 3 см вдоль оси имеет выпуклую
входную поверхность с радиусом кривизны 5 см и вогнутую вы-
выходную поверхность с радиусом кривизны 2 см. Первая поверх-
поверхность расположена слева и граничит с воздухом, а вторая —
80
Глава 2
Радауб2 си.
Фиг. 2.21
справа от нее и граничит с жидкостью, показатель преломления
которой п = 1,4. Требуется найти положения фокусов, главных
и узловых точек, а также вычислить фокусные расстояния си-
системы, считая показатель преломления стекла равным 1,5
(фиг. 2.21).
Решение
Прежде всего, как обычно, запишем матрицу системы, а за-
затем воспользуемся результатами, приведенными в табл. 2.1. На-
Напомним, что в данном случае нужно пользоваться центральной
колонкой таблицы. Если опорные плоскости выбрать располо-
расположенными вблизи первой и второй поверхностей линзы и взять
в качестве единицы измерения длины сантиметр, то матрица си-
системы запишется в виде
1
1
Вогнутая поверхность
линзы, погруженная
в жидкость
Линза
Выпуклая поверх-
поверхность лннзы
^"Lо,о5 lJLo iJL-o,i ij Lo,o5 l.iJL—o,i ij*
Следовательно,
М = 1С /> J ^ L — 0,06 1,1
Матричные методы в параксиальной оптике
81
Проверка:
det (M) = @,8) A,1) + B) @,06) = 1.
Вспоминая, что по условию задачи п\ = 1, а Пз = 1,4, и исполь-
вуя данные из табл. 2.1, получаем следующие решения:
Входная сторона системы: п\ = 1
Кардинальная точка
Положение кардинальной точки
справа от ОП,, см
Первый фокус F\
Первая главная точка Н\
Первая узловая точка L\
Первое фокусное расстояние
D 1,1
С — 0,06 ""
Р-\ Ojl
С
" (- 0,06)
-п2 1,1-1,4
-18,3
— 1,67
+ 5,0
- 0,06
i = — 1/С = —1/(— 0,06) =
= + 16,7 см (оптическая сила + 6 диоптрий)
Выходная сторона системы: л2 = 1,4
Кардинальная точка
Положение кардинальной точки справа
от ОП,, см
-п2А (-1,4) @,8)
С — 0,06
п2(\-А) _ A,4) A -0,8)
С - 0,06
п, - Ап2 1-A,4) @,8)
С = -0,06
+ 18,7
= — 4,67
+ 2,0
Второй фокус f2
Вторая главная точка Н2
Вторая узловая точка L2
Второе фокусное расстояние [2 = — п2/С =«(—1,4)/(—0,06) = + 23,3 см.
В рассмотренной оптической системе узловые точки L\ и Z-2 сов-
совпадают, причем расположены они в общем центре кривизны обе-
обеих сферических поверхностей.
§ 11. ОБОБЩЕНИЕ МЕТОДА ПРЕОБРАЗОВАНИЯ ЛУЧЕЙ
НА СЛУЧАЙ ОТРАЖАЮЩИХ СИСТЕМ
До сих пор, отчасти для того чтобы упростить рассмотрение,
наше обсуждение параксиальных систем ограничивалось систе-
системами, содержащими лишь преломляющие поверхности. Однакд
82
Глава 2
в тех случаях, когда нужно добиться улучшения эксплуатацион-
эксплуатационных характеристик оптических приборов, не считаясь с затра-
затратами на их изготовление, целесообразно использовать катадноп-
трическиё системы. Кроме того, в следующей главе для изуче-
изучения оптических резонаторов нам придется рассмотреть отра-
отражающие поверхности. Исходя из этого, займемся обобщением
нашего метода иа случай отражающих поверхностей.
Существует одно основное правило, которое позволит нам
решить эту задачу с помощью уже описанных лучевых векторов
и 0~- и ^-матриц. Оно формулируется следующим образом: во
всех случаях, когда световой луч распространяется в отрица-
отрицательном направлении оси г, показатель преломления среды, че-
через которую он проходит, нужно брать со знаком минус. Рас-
Рассмотрим теперь, как действует это правило отдельно на лучевые
векторы, ЗГ- и ^-матрицы.
11.1. Лучевые векторы
При интерпретации данных, описываемых вектором-столб-
\ V 1
дом луча 1 у I, следует помнить, что величина Vjn, а не V оп-
определяет геометрический угол наклона v луча относительно оп-
оптической оси. Например, когда луч отражается от плоской по-
поверхности, перпендикулярной оптической оси, как показано на
фиг. 2.22, то его направление меняется на противоположное н
Фиг. 2.22. Отражение от плоской поверхности.
Для лучей, распространяющихся ¦ отрицательно»! направлении оси *, показатель прелом-
преломления меняет знак. Матрицы преобразовавня лучей между плоскостями имеют вид
п«-{о ij> M»-Lo l J*
**-W « J"Le «J-
f
\ Матричные методы в параксиальной оптике 83
¦' знак угла v изменяется, но то же самое происходит и с показа-
показателем преломления для луча, распространяющегося назад.
В результате величина оптического направляющего косинуса
остается неизменной. Это означает, что закон отражения, соот-
соответствующий закону преломления Снеллиуса в параксиальной
оптике, уже содержится в утверждении о том, что при пересече-
пересечении любой точки плоского зеркала или плоской отражающей по-
Г у* 1 Г yi 1
верхности I „ I = I у I. К обсуждению этого вопроса в об-
общих чертах мы еще вернемся при рассмотрении 52-матриц.
11.2. ^"-матрицы
Для лучей света, распространяющихся через оптический про-
промежуток от плоскости z = Z\ до плоскости z = z2, длина про-
промежутка z2 — Z\ будет положительной, если луч идет в положи-
положительном направлении оси г, и отрицательной для лучей, распро-
распространяющихся в отрицательном направлении этой оси. Кроме
того, в последнем случае показатель преломления среды нужно
считать отрицательным, так что приведенная длина промежутка,
равная отношению двух отрицательных величин, останется поло-
положительной. Следовательно, при условии, что цепочка матриц вы-
вычисляется в обычном порядке, т. е. начиная с выхода системы и
кончая ее входом, значения приведенныхрасстояний Т в различ-
различных ^"-матрицах всегда будут положительными.
11.3. ^-матрицы
Используем теперь 52-матрицы для описания действия как
лреломляющих, так и отражающих поверхностей. Чтобы вычис-
вычислить оптическую силу Р отражающей кривой поверхности, пре-
преобразуем формулу Р= (п2 — П\)/г, заменив в ней показатель
преломления п2 второй среды на отрицательное значение пока-
показателя преломления п той среды, в которую погружен отража-
отражатель и в которой распространяется луч после своего отражения.
Таким образом, мы получим Р = —2п/г, и 52-матрица запишет-
Г 1 °
ся в виде [ 2ф 1
Важно помнить здесь, что радиус кривизны зеркала, так же
как и поверхности линзы, считается положительным, если его
центр кривизны расположен справа от его поверхности. Этот
случай, например, осуществляется, когда зеркало выпуклой сто-
стороной обращено влево, т. е. лучи отражаются от него в отрица-
отрицательном направлении оси z. Как и в случае рассеивающей лин-
линзы, оптическая сила такого выпуклого (рассеивающего) зер-
84
Глава 2
кала считается отрицательной, и, следовательно, нижний левый
элемент Я-матрицы будет положительным.
Заметим, что если это же зеркало повернуть так, что его вы-
выпуклая часть будет обращена вправо, то следует поменять знаки
радиуса кривизны г и показателя преломления п среды, в кото-
которую это зеркало погружено; при такой операции матрица оста-
останется неизменной. Оптическая сила Р рассеивающего (выпук-
(выпуклого) зеркала всегда отрицательна, в то время как оптическая
сила собирающего (вогнутого) зеркала всегда положительна.
11.4. Последовательность плоских поверхностей
Как и в случае преломления, отражение от плоской поверх-
поверхности, радиус кривизны г которой равен бесконечности, очевид-
очевидно, описывается тривиальным образом, т. е. единичной матри-
матрицей. Следовательно, если свет отражается назад или вперед по-
последовательностью плоскопараллельных плоскостей, перпенди-
перпендикулярных оптической оси, то, как и прежде, можно свернуть
друг с другом различные ^-матрицы, суммируя приведенные
толщины всех оптических промежутков, на которые разбивается
система опорными плоскостями. Если цепочка матриц вычис-
вычисляется обычным путем, т. е. начиная от выхода системы назад
ко входу, то все эти приведенные толщины дадут положитель-
положительный вклад в общую приведенную толщину. Так, например, в
случае, когда световой луч выходит из плоскопараллельной
стеклянной пластинки (толщина пластинки /, показатель пре-
преломления стекла п) после 2k внутренних переотражений, то дей-
действие этой пластинки можно представить в виде комбинации ис-
Г 1 '/
ходной ff-матрицы перемещения I n . с возведенной в сте-
степень 2k ^-матрицей «отражения» I Q ^ I (фиг. 2.23). Не счи-
считая ослабления луча после каждого отражения, его параметры
Фиг. 2.23. Многократное отражение света в пластинке.
Точки /t. It, h Щ U представляют манные изображения точки О, обусловленные внутрен-
внутренними переотражениями.
Матричные методы в параксиальной оптике 85
на выходе пластинки будут такими же, как если бы свет про-
прошел один раз через такую пластинку, толщина которой в
B& + 1) раз больше рассматриваемой.
В заключение этой главы вычислим полную матрицу простой
катадиоптрической системы.
Задача 12
а) Луч света входит слева в стеклянный шар радиусом г
(фиг. 2.24). Показатель преломления стекла п. Когда он дости-
достигает правой граничной поверхности шара, некоторые из его лу-
лучей отражаются назад и опять появляются с левой стороны
шара. Требуется найти матрицу преобразования лучей для это-
этого случая, причем в качестве опорной плоскости следует взять
плоскость, примыкающую слева к поверхности шара.
б) Преобразовать полученную матрицу к опорной плоско-
плоскости, проходящей через центр шара. Объяснить результат и по-
подробно разобрать случай п « 2.
Решение (а)
Цепочка матриц относительно опорной плоскости, примыкаю-
примыкающей слева к поверхности шара, записывается в виде
°1Г1
1J[0
2г/п1Т 1 0
Последнее прелом- Переме- Отражение от
ление на левой по- щенне че- правой по-
поверхности шара рез шар верхности
после отра-
отражения
Г1
[0
Г1 2r/n
х[0
Перемеще- Начальное прелом-
ние черва ленив на левой по-
шар до от- верхностн
ражения
После перемножения этих матриц получаем
п - 4
м
I —*
пг
Проверка
[я-« ~4Г 1
п
-2B-я) д-4 Г
пг я -I
j i. /1» tl — 8я + 16 16 — 8я ,
det(M) = -2 jjs 1.
Глава 2
п=2 (шар " является
рвпрорефлектерт)
Фнг. 2J24
Решение (б)
Если мы хотим преобразовать найденную матрицу М к мат-
матрице, рассматриваемой относительно опорной плоскости, распо-
расположенной на расстояния t слева от левой поверхности шара, то
действие промежутка (т. е. удлинения пути) между новой и ста-
старой опорными плоскостями учитывается добавлением одной и
той же ^"-матрицы I ' 'Гц обоих концах цепочки матриц.
Одиакб «ели опорная плоскость сдвигается вправо, то вообра-
воображаемый пути оптического луча •укорачивается. Для того чтобы
перенести опорную плоскость в центр шара, матрицу М нужно
И -гЛ
умножить слева неправа на I Q .1.
Таким образом, матрица преобразования лучей относительно
центра шара записывается в виде
Очевидно, det (Af,) = 1.
Матричные методы в параксиальной оптике 87
При интерпретации этого результата следует соблюдать не-
некоторую осторожность. Равенство нулю правого верхнего эле-
элемента матрицы указывает на то, что центр шара отображается
сам на себя (как и должно быть в случае любой последователь-
последовательности отражений или преломлений в системе с одним центром).
Но поскольку верхний левый элемент матрицы говорит о том,
что поперечное увеличение равно не -{-1, а —1, то главные пло-
плоскости системы не проходят, как можно предполагать, через
центр рассматриваемого шара.
Для значений показателя преломления в интервале от 1 до
2 эквивалентное фокусное расстояние системы —1/С будет по-
положительным, а так как 1 — D = 2, то главные плоскости си-
системы будут отстоять справа от центра шара на два фокусных
расстояния.
Наконец, в случае л = 2 матричный элемент С обращается
в нуль и система становится афокальной, т. е. такой, у которой
Г-1 О "I
матрица преобразования лучей имеет вид! п .1. Это озна-
означает, что хотя поперечное увеличение у2/у\ = А все еще и ос-
остается равным —1, тем не менее угловое увеличение, как было
показано в § 6 настоящей главы, равно
(поскольку для обращенного луча п2 = —«i). Следовательно,
данный луч покидает шар с противоположным по знаку значе-
значением своей координаты у и уходит на бесконечность обратно
в том же направлении, откуда он пришел. Аналогичным свой-
свойством отражать лучи в обратном направлении обладает оптиче-
оптический элемент другой формы — кубический уголковый отража-
отражатель (каждая поверхность которого обращает один из трех на-
направляющих косинусов луча). (Иначе устроен отражатель типа
«кошачий глаз» — сферическая бусинка с высоким значением
показателя преломления. Этот отражатель не требует юсти-
юстировки; он одинаково хорошо работает в качестве переотража-
переотражателя почти в любом направлении. В настоящее время такие
отражатели нашли широкое применение при изготовлении ретро-
рефлекторов'). Вследствие эффектов сферической аберрации
выбор п = 2 не обязательно дает лучшие фотометрические
свойства.)
*) Ретрорефлектором называется устройство, отражающее луч строго в
обратном направлении, независимо от ориентации этого устройства относи-
относительно падающего на него луча. — Прим. мрев.
Глава 2
11.5. Случай совпадающих опорных плоскостей
При вычислении отражающей системы часто оказывается
удобным выбирать входную и выходную опорные плоскости
расположенными при одном и том же значении координаты г.
Такой ситуации отвечает определенная симметрия, и в получае-
получаемой при этом матрице преобразования лучей элементы А и D
на главной диагонали всегда совпадают. Читатель, наверно,
заметил, что так оно и было в только что рассмотренной задаче.
Чтобы показать, что и в обшем случае это справедливо, мы
воспользуемся принципом обратимости светового луча.
Выберем общую опорную плоскость на некотором удобном
расстоянии слева от отражающей оптической системы и пред-
представим себе, что произвольно выбранный пробный луч I v I,
распространяющийся в положительном направлении оси z, воз-
вращается как отраженный луч I v I в отрицательном направ-
лении оси z, причем, как обычно, \ v I = I ^ r> 11 v I •
Требуется доказать, что А = D.
Гу21
Теперь возьмем этот отраженный луч I v I и пошлем его
назад вдоль траектории, так чтобы он образовал второй пробный
луч
(фиг. 2.25). Поскольку соглашение о знаке относится
Отражающая
ошпичсския
система
Фиг. 2,25
Матричные методы в параксиальной оптике
к показателю преломления п, знак величины V для этого луча
изменится на противоположный. Следовательно,
Kl-UHi _?][?.]¦
Падая на отражающую поверхность, этот второй пробный луч
даст второй отраженный луч:
vi\ Lc dJLfiJ Ic dJLo -
A В-1Г1 0-.ГЛ В1ГЙ
JL JL JL
YA В-1Г1 0-.Г
Lc dJLo -iJL
c
Но поскольку любая траектория луча может быть обращена,
второй отраженный луч должен повторить (в отрицательном
направлении оси г) весь путь нашего первоначального луча
. Инымн словами,
Учитывая все эти преобразования, получаем
c
ГУ1
01ГЛ В-.Г1 ОТГЛ В1ГУ1
-iJLc dJLo -iJL JL
A BIT А В
_c -d\L-c -d
(A2-BC) B(A-D)iryi
-C(A-D) (D2-BC) Rv
Поскольку последнее уравнение должно быть справедливым
[У\ 1
I,
то вычисленная матрица должна сводиться к единичной мат-
матрице. Так как AD — ВС = 1, это может быть тогда и только
тогда, когда диагональные элементы матрицы А и D равны
друг другу. Это обстоятельство обеспечивает полезный способ
проверки при расчетах общей матрицы для катадиоптрических
систем.
вв -..!*¦•¦.; Глава $
Авторам выражают благодарность администрации издатель-
издательства McGraw-Hill Book Company, любезно разрешившей ис-
использовать в настоящей книге опубликованные задачи 3 (на
стр. 42), И 8 J3 (на стр. 43) и 10 и 11 (на стр. 60) нз моногра-
монографии : JenUm $nct White, Fundamentals of Optiks 3rd ed., 1957
(Copyright 1937 and 1950 by the McGraw-Nitl Book Company,
Inc. Использовано по разрешению McGraw-Hill Company.), a
также д-ру Хьюстону и администрация издательства Longmans,
(jreen and Сб., любезно разрешившим яслользовать опублнко-
вайные задачи 2 (на стр. 48), 12 (на стр. 31) и 9 (на стр. 49) из
монографии: R. A. Houston, Treatise on Light, 5th ed., 1928.
ГЛАВА 3
ОПТИЧЕСКИЕ РЕЗОНАТОРЫ
И РАСПРОСТРАНЕНИЕ
ЛАЗЕРНОГО ПУЧКА
Один из наиболее приятных сюрпризов современной оптики
состоит в той легкости, с которой методы геометрического пре-
преобразования лучей можно приспособить для описания генерации
и распространения лазерного луча. Для того чтобы ознако-
ознакомиться с этими методами, нам придется использовать некоторые
положения волновой теории; мы постараемся объяснять эти
положения непосредственно по ходу изложения материала и на-
надеемся, что настоящую главу смогут прочесть даже те, кто не
знаком с основами физической оптики. Отправным пунктом
нашего рассмотрения будут матрицы и лучевые векторы, опи-
описанные в предыдущей главе.
§ 1. СВОДКА РЕЗУЛЬТАТОВ, ПОЛУЧЕННЫХ
ДЛЯ ПАРАКСИАЛЬНЫХ СИСТЕМ,
ФОРМИРУЮЩИХ ИЗОБРАЖЕНИЕ
Ниже в табл. 3.1 приведены матрицы преобразования лучей,
соответствующие восьми наиболее часто встречающимся опти-
оптическим элементам.
Для оптических систем, которые представляют собой комби-
комбинации этих наиболее часто встречающихся элементов, необхо-
необходимо перемножать соответствующие матрицы, не забывая при
этом соблюдать порядок их расположения: расчет необходимо
ГА В1
ГА В1
производить от выхода к входу системы. Если I r n I — мат-
матрица системы, полученная в результате всех преобразований, то
следует проверить, равен ли ее определитель единице, а затем
использовать ее в уравнении преобразования луча
d\{v
MM
1
2
3
4
Onenke
*
Перемещеняе в свободном про-
странегве (•? -матрица/
Преломление на одной поверхности
(Я-матрица)
Отражение от охноя поверхности
(см. § 11 гл. 2)
Тонкая лннза в воздухе (фокусное
ОаССТОЯНИе L аавпштсжая шля Р\
Оптическая схема
i "• 1
1
|
Г
on, о
1 '
1 ;
ЛЬ
on, опг
' д < ттД^ЧЯОР рвССВЮ$Вш&'/
Ш] 0П2
М«траца
1 — («2 -
u
г ,
Таблица 8J
вреобраюваввя лучей
//ЯП
0
О"!
'/-I
[i
1
-
J
С
•Г р jj
101
р ij
1 i «1
о
8
Преобразование луча между двумя
главными плоскостями системы
линз в воздухе (фокусное расстоя-
расстояние /)
Преобразование луча между фо-
фокальными плоскостями системы линз
в воздухе (фокусное расстояние f)
Преобразование луча между двумя
сопряженными плоскостями опти-
оптической системы (поперечное увели-
увеличение т и фокусное расстояние /)
Афокальная система с поперечным
увеличением tn
Ft
—\-
ОП,
н,
on,
0П2
-1// и-я J
г о л
L-1// oj
[-
т
Uf Urn.
р» о
Lo i/»
94
Глава S
§ 2. ОПИСАНИЕ ПРОЦЕССА РАСПРОСТРАНЕНИЯ ВОЛН
НА ЯЗЫКЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
По-видимому, здесь полезно уточнить некоторые вопросы,
рассмотренные в начале предыдущей главы. Как было впервые
показано Гюйгенсом, распространение света лучше всего опи-
описывать, используя понятие волнового фронта. Если мы будем
рассматривать световые волны, излучаемые точечным источни-
источником, то волновые фронты расходящихся волн можно предста-
представить себе как во.лны, разбегающиеся по поверхности пруда от
брошенного камня. По мере удаления от источника радиус
кривизны расходящихся волн постепенно увеличивается. Поме-
Помещая в какой-либо точке на пути этих волн положительную лин-
линзу, можно заставить их сходиться в некоторой другой точке,
которую называют изображением. С другой стороны, если
использовать более слабые линзы, то можно получить колли-
мированный световой пучок, в котором волновые фронты яв-
являются относительно плоскими. Если мы внесем какие-либо
ограничения или-препятствия на пути распространения волновых
фронтов, то тем самым нарушим их структуру и получим неко-
некоторую дифракционную картину; в отсутствие же таких препят-
препятствий световая энергия распространяется в направлении нор-
нормали к волновым фронтам.
Понятие геометрического луча является идеализацией
свойств таких волновых нормалей. При условии что из рассмот-
рассмотрения исключается фокальная и околофокальная области, лучи
и соответствующие им волновые фронты можно представить
себе как взаимно ортогональные семейства прямых линий и
кривых поверхностей.
У
Характерный
J-L'JJ
I I Г ' '
I I ' I I /
I I I I I
*¦ в
фронты
Фиг. 34
ОП
Оптические резонаторы и распространение лазерного пучка 95
В том случае, когда волновой фронт можно считать сфери-
сферическим, его форма полностью определяется векторами лучей
двух пересекающихся нормалей к волновому фронту. Кроме
I того, если известно, что центр кривизны сферического волнового
i фронта расположен в некоторой точке на оптической оси, то до-
| статочно задать всего лишь один дополнительный параметр,
; чтобы полностью определить его местоположение.
¦,; Вернемся теперь к нашей геометрической модели лучей; од-
h нако вместо того, чтобы рассматривать отдельные лучи, обсе-
обсеем щим нашу модель, введя понятие пучка лучей, связки или се-
f мейства лучей, исходящих из одной и той же точки. В качестве
примера на фиг. 3.1 показаны несколько параксиальных лучей,
расходящихся от некоторого точечного объекта О\, расположен-
расположенного на оси на расстоянии гх слева от опорной плоскости ОП].
Для всех членов этого семейства отношение высоты луча у\
к лучевому углу vi равно п, т. е.
Если теперь рассматривать каждый из лучей в этом пучке
как нормаль к волновому фронту, то полученный таким образом
волновой фронт будет сферическим, причем его центр кривизны
будет расположен в точке О{ на расстоянии гх слева от ОПь1 по-
поскольку лучи в нашем пучке распространяются слева направо
в положительном направлении оси г, то волновые фронты, свя-
связанные с этим пучком, должны расширяться и расходиться.
При определении кривизны волнового фронта для удобства
будем считать ее положительной, когда волна расходится, и ис-
использовать для радиуса кривизны «приведенное значение»
R = (r/n) = (y/V). Использование приведенных значений дает
следующее преимущество: в тех случаях, когда световой пучок
пересекает плоскую границу раздела двух сред, значение R для
соответствующего волнового фронта остается неизменным. (Эта
инвариантность связана с тем, что для каждого луча, пересе-
пересекающего такую границу, как высота у луча, так и оптический
направляющий косинус V остаются постоянными.) Для сфери-
сферического фронта, центр которого расположен на оси, и данной
опорной плоскости значение R является единственным парамет-
параметром, который полностью определяет форму волнового фронта.
Рассмотрим теперь, как меняется значение параметра (y/V),
или R, для пучка лучей при прохождении его через оптическую
систему. Из матрицы преобразования лучей получаем непосред-
непосредственно два уравнения:
Оптические резонаторы и распространение лазерного пучка
97
Для описания такого луча можно использовать как вход-
входные, так и выходные значения у и V, однако обычно предпочи-
предпочитают иметь дело с высотой луча на входе у\ и высотой луча на
выходе у2. Посмотрим теперь, каким образом можно использо-
использовать матрицу преобразования луча при получении выражения
эйконала W(yuy2) для полного оптического пути пучка между
двумя опорными плоскостями.
Если нам известны только значения у\ и у2, характеризующие
луч, тем не менее можно получить соответствующие значения Vi
и V2, решая систему совместных уравнений
относительно
V2 = Cy1+DVl
и V2. Очевидно,
Уг — ¦
vi g—- и v2=*\
Поскольку AD — ВС — 1, получаем
V2— д .
Следовательно, точка пересечения входящего в систему луча
с оптической осью (точка О\) расположена на расстоянии /?i =
= yJVi =Byi/(y2 — Ayi) от плоскости ОПь Аналогично точка
пересечения выходящего из системы луча с оптической осью
(точка О2) расположена на расстоянии /?2 слева от ОП2, причем
Rz^yzlVi^Byn/iDyi — y!) (фиг. 3.2).
Теперь представим себе, что рассматриваемые нами входя-
входящий и выходящий лучи являются элементами пучков лучей, рас-
расходящихся из точки Oi в пространстве предметов и из точки О2
в пространстве изображений соответственно. Очевидно, точка
02 есть изображение точки Oi, и мы можем использовать тео-
а
Фиг. 3.2
4 Зак, 774
98 Глава S
рему Мал юса, которая утверждает, что в любой стигматической
системе, формирующей изображение, оптический путь, измеряе-
измеряемый вдоль луча, одинаков для всех лучей, исходящих из данной
точки предмета, — иными словами, сферическая волна, исходя-
исходящая из точки Ои возбуждает другую сферическую волиу, сходя-
сходящуюся в точке Ог.
Однако, если мы рассматриваем луч, распространяющийся
прямо вдоль оси из точки О\ в точку О2, то, как показано на
фиг. 3.2, его оптический путь равен [ni{O\Q\)~п2(О2<?2) + К].
где К представляет собой полный оптический путь, измеряемый
вдоль оси от OFli до ОП2. Полный оптический путь от точки О\
до точки О2, проходящий через Pi и Р2, по теореме Малюса дол-
должен быть таким же, а именно равным приведенному выше выра-
выражению в квадратных скобках. Для того чтобы получить расстоя-
расстояние между Л и Р2, из полного пути нужно вычесть величину
ti\- (OiPi) и прибавить величину «2» (О2Р2). Таким образом,эйко-
образом,эйконал для полного оптического пути между Pi и Р2 запишется
в виде
W (уи yi) = [К - л, (О,Р, - 0&х) + П2(О2Р2 - O2Q2)].
Выражения в круглых скобках определяют стрелы прогиба
дуги волновых фронтов сферических волн, достигающих опорных
плоскостей OFli и ОП2. Если для радиусов кривизны каждого
волнового фронта использовать приведенное значение" R = г/п,
те выражение tfftR = ш/*/2г будет определять как геометриче-
геометрическую стрелу прогиба волнового фронта, так и показатель пре-
преломления среды, в которой распространяется волна- Таким об-
образом, получаем
"*" 2B J —[# + 2В _Г
Напомним, что К — это полный оптический путь \n(z)dz,
причем интегрирование проводится вдоль оси между ОП1 и ОП2.
Поскольку величина К ие зависит от у\ и #2> то она должна иг-
играть важную роль при расчетах интерферометра, когда возни-
возникает необходимость сравнивать два различных оптических пути.
Для многих вычислений, включающих расчет оптической
дифракции, обычно представляет интерес зависимость W от по-
поперечных координат у\ и у2. Предположим, что нам задана ком-
комплексная функция Ai(yi), которая характеризует амплитуду и
фазу световой волны на входной плоскости ОПь и мы хотим
вычислить соответствующую комплексную амплитуду Л2(#2), оп-
определяющую световую волну на выходной плоскости.
Оптические резонаторы и распространение лазерного пучка 99
Ограничиваясь рассмотрением одномерной задачи и прене-
пренебрегая небольшой поправкой, связанной с медленно меняющи-
меняющимися эффектами наклонного падения1), с помощью принципа
Гюйгенса — Френеля можно получить следующее уравнение
дифракции:
-=У-O1 J Л,(у,)ехр[-^1Р(у„ ya)]dyi.
В этом выражении постоянная величина (—i/XB)'i' является
нормирующим множителем, который необходим для того, чтобы
размерности правой и левой частей совпадали, и который учиты-
учитывает ослабление волны в выходной плоскости в том случае, если
В очень велико. Поскольку аналогичные вычисления должны
быть проведены и для х-координаты, то в итоге получаем, что
амплитуда обратно пропорциональна первой степени В, а интен-
интенсивность подчиняется известному закону обратных квадратов.
(Короче говоря, точечный источник, расположенный в плоскости
ОПь дает изображение на расстоянии B/D слева от ОП2 с попе-
поперечным увеличением 1/D; следовательно, в нормирующий мно-
множитель должен входить только матричный элемент В.)
Рассматривая подынтегральное выражение, мы видим, что
вклад, который вносит каждый элемент OFIi в амплитуду волны
в ОПг, определяется аргументом комплексного экспоненциаль-
экспоненциального множителя, а именно фазовым углом <f>, равным оптиче-
оптическому пути W, деленному на длину волны А, й умноженному на
2л. Чтобы понять, как строится этот интеграл, его можно пред-
представить себе как сумму большого числа малых векторов, скла-
складываемых с учетом соответствующих фазовых углов ф на диаг-
диаграмме Аргана. Если все эти векторы складываются графически
таким образом, что начало каждого следующего вектора совме-
совмещается с концом предыдущего, то вектор, соединяющий начало
первого вектора с концом последнего, определяет результирую-
результирующую амплитуду в выходной плоскости, а квадрат длины этого
вектора — результирующую интенсивность волны.
Рассмотрим теперь несколько простых примеров построения
функции эйконала между двумя опорными плоскостями.
2.2. Распространение пучка через воздушный промежуток
толщиной t
В данном случае матрица записывается в виде
ГА В1 Г1 ,1
1С D] LO lj-
*) Имеется в виду параболическое параксиальное приближение. — Прим.
перев.
100 Глава 3
Подставляя эти матричные элементы в выражение эйконала,
имеем
{Если при вычислениях использовать непосредственно теорему
Пифагора, то точное расстояние дается выражением [t2 + (t/2 —
— yiJ]4'- Однако для параксиальных лучей, проходящих через
две плоскости, отношение (у2— У\)№ должно быть мало, так что
наше приближение вполне справедливо.}
Подставляя полученное выше выражение для эйконала в
уравнение дифракции, можно решить задачу о дифракции Фре-
Френеля. Например, если на ОП] падает плоская волна единичной
амплитуды, причем половина- ОП] закрыта поглощающим кли-
клином с острым краем, то мы имеем следующие условия на входе:
4i(«/i)= 1 при ух > 0 и Ах(ух) = О при ух < 0. Тогда распреде-
распределение амплитуды в затененной части ОП2 дается выражением
Интегралы, входящие в это выражение, называются интегра-
интегралами Френеля; в графическом представлении на диаграмме Ар-
Гана онн образуют спираль Корню.
Поскольку выражение эйконала для оптического промежутка
является функцией только разности у2— ух, новое распределе-
распределение амплитуды A2(y2), определяемое дифракционной формулой,
можно рассматривать как свертку исходного распределения
амплитуды Ах(ух) и члена с квадратичным законом изменения
фазы, определяемым эйконалом; А2(у2) иногда называют тене-
теневым преобразованием амплитуды Ах(ух). Преобразования та-
такого типа играли важную роль в ранних работах Габора^ по
«одномерной» голографии.
2.3. Преобразование пучка между двумя
фокальными плоскостями линзы
В этом случае матрица ABCD имеет вид
ГА В1 Г 0
1С О] l-l/
l/f
Оптические резонаторы и распространение лазерного пучка 101
Поскольку А = D = 0, выражение эйконала записывается сле-
следующим образом:
где К—оптический путь между двумя фокальными точками.
Для любого заданного значения у\ этот эйконал дает линей-
линейную зависимость в выходной плоскости, — другими словами, то-
точечный источник, смещенный от оси на расстояние у и возбуж-
возбуждает по другую сторону линзы плоскую волну, волновой фронт
которой имеет наклон dW/dy2 = —(yjf) рад.
Подставляя последнее выражение эйконала в уравнение ди-
дифракции, мы находим, что, поскольку квадратичные фазовые
члены отсутствуют, этот случай соответствует дифракции Фра-
унгофера. Соотношение между А^(у[) и A^iyi) представляет со-
собой преобразование Фурье:
А* («,) = {^-У \ А, Ы exp [*L {К - Jf)] dVl «
— оо
- (ж)" «р (т5-) j * w «р (- » Т) *¦¦
— оо
Если, например, на ОП] падает плоская волна единичной ам-
амплитуды и в плоскости ОП! имеется щелевая апертура, которая
пропускает только центральную часть пучка, т. е. а > у\ >
>¦ —а, то амплитуда, возбуждаемая в ОП2 (где в приближении
геометрической оптики свет фокусировался бы в точку), дается
выражением
Вследствие дифракционных эффектов световые волны в фо-
фокальной плоскости линзы дают изображение конечного размера.
Распределение интенсивности h(yi), которое в действительности
мы будем наблюдать в изображении, записывается в виде
(и \ — А (и\ А* (и ~\ — (^-\ Г si" УяаугЦК) I»
\Уг) - А2 {У2) А2 [У2) — \-Jf) [ BПау21!%) \ •
Когда уъ мало, выражение в квадратных скобках стремится
к своему максимальному значению, равному единице, поскольку
.. / sin г \ ,
hm ( 1 = 1.
102
Глава S
Пяратвршю
Распределение
UHnWHVUBHOCtTIU
ortt
Фиг. 3.3
Таким образом, при когерентном, освещении яркость в центре
изображения пропорциональна квадрату ширины щели. Это обу-
обусловлено двумя факторами: увеличение ширины щели ие только
Вызывает увеличение потока энергии через линзу, но также
уменьшает дифракционное размытие изображения. В следую-
следующем параграфе мы рассмотрим вопросы, связанные с разре-
разрешающей силой оптической системы, но из приведенной выше
формулы для интенсивности очевидно, что яркость дифракцион-
дифракционной Мартины Фраунгофера спадает до нуля в том случае, когда
аргумент синуса становится равным ±я, т. е. когда #2 =¦
-=±(fV2a) (фиг. 3.3).
Для этого значения «Лг из выражения эйконала получаем, что
ширина щели Bа) в плоскости OIli в точности равна одной
длине волны. Все возможные в пределах 2я фазы дают прибли-
приблизительно равноценные вклады, и таким образом происходит пол-
полное взаимное погашение волновых возмущений. Если мы попы-
попытаемся наглядно представить себе эту ситуацию с помощью
диаграммы Арпана, то обнаружим, что для у2 = 0 в результате
суммирования всех элементарных векторов получается прямая
лнння; однако по мере увеличения у2 мы получим кривую, кото-
которая замкнется в исходную точку, образуя замкнутую окруж-
окружность при у2 = ± (fV2a). Длина хорды каждой из этих кривых
(учитывая, что 2а представляет собой длину, измеряемую вдоль
кривой), равная результирующей амплитуде поля, дается вы-
выражением [2asinBnay2/fX)]lBnay2/fk), а радиус кривизны —
выражением }Х/2лу2 (фиг. 3.4).
2.4. Оптические системы с В = 0
Если в матрице преобразования лучей В = 0, то опорные
плоскости ОГЬ и ОПз должы быть оптически сопряжены, т. е.
существует только одно значение у2, для которого можно по-
построить траекторию луча для данного значения у\. Таким обра-
образом, не удивительно, что функция эйконала, полученная нами,
Мнимая ось
Начальная
точка
Конечная
точна
Действительная
ось
Случай Г-уг=О
Мнимая" ось
Мнимая ось
Начальная тг конечная Начальная
точки, совпадают точка
О
Случай 2: ^=fc
Действительная
ось
^i/bfA \ Конечная
' г | \ точка
Случай J:
Действительная
ось
Фиг. 3.4. Векторное суммирование интеграла \ ехр I —~~- dy\. '
—а
Случай 1—фазовый угол остается равным нулю для всех построенных векторов; случай 2—фазовый угол монотонно увеличи-
увеличивается от начального значения —я до конечного значения +п; случай 3—фазовый угол монотонно увеличивается от —я/4 до
+я/4.
Если фазовый угол изменяется от — Ф до + *, то радиус кривой длины 1а должен быть равен а/Ф. а длина хорды 2 (а1Ф) sin #—
-2а (sin Ф/Ф) (см. случай 3). Из подынтегрального выражения следует, что в общем случае * =»2naj/i/fА, рад.
»04 Глава 3
расходится; она не может дать правильного ответа на не имею-
имеющий смысла вопрос. Для того чтобы рассмотреть этот случай,
мы должны использовать эйконал, который является функцией
других переменных, например у\ и V\, а не у\ и у*
При вычислении эйконала W(t/i, V\) в этом специальном слу-
случае мы будем использовать упрощенную матрицу преобразова-
преобразования лучей
[т 0
-1// 1/т.
приведенную под номером 7 в табл. 3.1 для систем, формирую-
формирующих изображение.
Рассматривая, как и прежде, характерный луч, можно запи-
записать такое же выражение для эйконала, а именно
но теперь нужно представить произведение #2^2 через у\ и У\.
Следовательно,
Отметим, что в данном случае зависимость от Vx исчезает
и эйконал является функцией только от у\\ это непосредственно
следует из теоремы Малюса — время, которое необходимо свету
для того, чтобы пройти от некоторой точки предмета у\ до точки
изображения в плоскости ОПг, одинаково для всех лучей, исхо-
исходящих из точки предмета, т. е. для лучей с произвольными зна-
значениями параметра V\.
В некоторых случаях, например при обработке оптического
изображения, может потребоваться система, очень точно пере-
передающая изображение. При этом конструктору иногда нужно до-
добиться исчезновения квадратичных членов в эйконале посред-
посредством применения афокальных изображающих систем; однако
при этом должны быть также учтены эффекты аберрации треть-
третьего порядка, и поэтому производство таких линз становится до-
довольно дорогим.
Функция эйконала, которую мы до сих пор рассматривали,
вводилась по отношению к двум раздельным опорным плоско-
плоскостям. Там, где это возможно, ее предпочтительно определять как
функцию, симметричную относительно высоты луча в двух опор-
опорных плоскостях. В случае двумерной поперечной картины, т. е.
при учете второй поперечной координаты (нормальной к пло-
плоскости фигуры) эйконал W(xit уи х2, у%) зависит от четырех па-
Оптические резонаторы и распространение лазерного пучка 105
раметров. Если зафиксировать положение плоскости OOi в точ-
точке z = 0 и ввести опорную плоскость ОПг, которая первона-
первоначально совпадает с ОПь а затем постепенно удаляется от нее
в положительном направлении оси г, то можно построить более
общую трехмерную функцию эйконала W(xuyux,y,z). Для то-
точечного источника, расположенного в точке (хи у\) в OFIi, вол-
волновые фронты, возбуждаемые в произвольной области про-
пространства, представляют собой поверхности, на которых значе-
значение функции W остается постоянным: локальный градиент ска-
скалярной функции W является трехмерным мгновенным вектором,
определяющим не только направление луча, в котором распро-
распространяются волны, но также и скорость изменения фазы волны
с расстоянием.
В начале данного параграфа мы показали, как правило
ABCD позволяет нам проследить за распространением одно-
однозначно определяемых волновых фронтов пучка лучей, в частно-
частности пучка лучей от идеального точечного источника. Тем не ме-
менее, как мы показали при исследовании эйконала, эффекты раз-
размытия, связанные с дифракцией Фраунгофера, не позволяют
световой волне образовывать идеальное точечное изображение.
Следовательно, вблизи фокуса очень малйе значения R, пред-
предсказываемые правилом ABCD, в действительности могут ока-
оказаться глубоко ошибочными.
В следующем параграфе мы рассмотрим более детально ог-
ограничения, в рамках которых можно определять направление
светового луча. Эти ограничения важны не только для обычного
некогерентного света, но также и для пространственно когерент-
когерентного света, возбуждаемого внутри лазерного резонатора.
§ 3. РАЗРЕШАЮЩАЯ СИЛА,
ЭТАНДЮ И ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ
Поскольку длина волны света неисчезающе мала, изобра-
изображение, образуемое сходящимся пучком лучей, никогда не яв-
является точкой; это — пятно, конечный размер которого опреде-
определяется дифракцией Фраунгофера. В предыдущем параграфе
мы нашли, что параллельный пучок света, проходящий через
щель шириной 2а, фокусируется линзой с фокусным расстоянием
/ так, что яркость центрального пятна спадает до нуля на рас-
расстоянии от его центра, равном 0,5fX/a. В случае круглой апер-
апертуры диаметром 2а вычисление дифракционного интеграла при-
приводит к аналогичному выражению, только вместо синуса появ-
появляется функция Бесселя второго порядка. Центральное пятно
этого распределения называют диском Эйри, причем радиус, на
106 Глава 3
котором яркость спадает до нуля, равен 0,61/Л/а, т. е. примерно
на 22% больше, чем в случае квадратной апертуры шириной
2а. Чем больше апертура, тем меньше размер изображения, ра-
разумеется, при условии, что линза идеальна и все типы аберраций
отсутствуют.
Если оптическая система дает ограниченные дифракцией изо-
изображения двух точечных источников одинаковой яркости, то
обычно говорят, что изображения «вполне разрешены», если
центр одного из них совпадает с первым темным кольцом дру-
другого.
а) В случае правильно сконструированного телескопического
объектива диаметром d расстояние между изображениями
в фокальной плоскости равно \,22fkjd, а угловое расстоя-
расстояние между двумя источниками l,22X/d рад.
б) Для объектива микроскопа главная диафрагма, опреде-
определяющая разрешающую силу, расположена в задней фо-
фокальной плоскости, так что, когда мы смотрим со стороны
предмета, входной зрачок системы оказывается в беско-
бесконечности. Если обозначить через 0 угловой радиус этой
диафрагмы, то для малых 0 наименьшее разрешаемое рас-
расстояние в плоскости предмета равно 0,61А./в. В действи-
действительности величина 6 может быть довольно большой, и
поэтому часто необходимо использовать более точное вы-
выражение 0,61X/sin6 или 0,61A/nsin6 в том случае, когда
образец погружен в иммерсионную среду с показателем
преломления п. Величину п sin 6 обычно называют число-
числовой апертурой (Ч. А.) объектива микроскопа. (Эту вели-
величину можно рассматривать как максимально возможное
значение V для луча, исходящего из точки предмета, рас-
расположенной на оптической оси.)
с) Для объектива фотоаппарата диаметром d, разрешение
которого ограничено дифракцией и фокальным отноше-
отношением f/d = F, наименьшее разрешаемое расстояние в пло-
плоскости изображения дается формулой А«/ = 1.22FX. На-
Например, линза с фокусным расстоянием F/6, освещаемая
зеленым светом, полностью разрешает изображения ли-
линий или точек, отстоящих друг от друга на расстоянии
4 мкм. (Эта формула получена для светящихся объектов
или для некогерентного освещения. Чтобы достигнуть та-
такого же разрешения в случае когерентного света, может
оказаться необходимым использование бокового освеще-
освещения.) Однако для «вполне разрешенных» изображений
характерное расстояние разрешения приближается к
8 мкм, и даже для пространственных частот, соответствую-
соответствующих 125 штрихам на миллиметр, расчет модуляции пе-
Оптические резонаторы и распространение лазерного пучка 107
редаточной функции показывает, что контраст миры')
будет воспроизводиться с ослаблением на 50% по сравне-
сравнению с оригиналом.
Рассмотрим теперь задачу отображения модели точечного
источника — обскуры — хорошо скорректированным коллиматор-
ным объективом с фокальным отношением F. Такая постановка
задачи моделирует наблюдение «искусственной звезды». Даже
если диаметр обскуры меньше длины волны света, ее кажущий-
кажущийся угловой размер, определяемый по расходимости света, про-
прошедшего через коллиматор, равен l,22K/d рад и соответствует
линейному размеру l,22XF ее изображения в фокальной плоско-
плоскости коллиматора. Таким образом, разумно использовать обскуру,
диаметр которой близок к указанному выше размеру, — любое
уменьшение размеров приводит к неоправданной потере боль-
большого количества света без какого бы то ни было улучшения его
направленности. Свет, падающий на обскуру, обычно представ-
представляет собой сфокусированное изображение какого-либо яркого
источника: солнца, циркониевой дуги, газонаполненной вольфра-
вольфрамовой лампы накаливания и т. п. Не будем, однако, забывать,
что при фокусировке лазерного луча на ту же самую диафрагму
можно получить значительно более высокую яркость изображе-
изображения.
Для некоторых задач светотехники, например в прожекто-
прожекторах, желательно использовать световые лучи, угловая расходи-
расходимость которых существенно превосходит расходимость, обуслов-
обусловленную дифракцией. В этом случае основные преимущества ла-
лазерного луча теряются и лучше выбрать подходящий источник
некогерентного света.
Для того чтобы описать направленность светового пучка, вы-
выберем опорную плоскость, расположенную на некотором, удоб-
удобном для вычислений расстоянии R справа от источника света.
Если Умакс — максимальное значение угла, охватываемого кол-
коллиматором, то для любого луча, исходящего из центра источ-
ника, можно записать лучевой вектор в виде I v I, где
— ^макс <г V ^ Умако- Мы можем рассматривать семейство та-
таких лучей как основную часть светового пучка.
Рассмотрим теперь какой-либо другой луч, проходящий че-
через опорную плоскость с компонентами лучевого вектора у' и
V'. Оценим теперь, сколько «масштабов, разрешаемых оптиче-
') Оптическая мира представляет собой набор моделей решеток с различ-
различным числом штрихов на миллиметр. Миры применяются для эксперименталь-
экспериментального измерения предельной разрешающей способности оптических систем, фор-
формирующих изображение. — прим. перев.
108 Глава 3
ской системой», укладывается между этим пробным лучом и
центральным лучом пучка.
Для того чтобы проследить за распространением света в об-
обратном направлении до плоскости источника, необходимо умно-
умножить лучевой вектор на (отрицательную) матрицу перемеще-
Г1 — Д1
ния I „ .1. При этом мы найдем, что величина у, соответ-
соответствующая точке источника, из которой вышел наш пробный луч,
дается выражением {/-—RV. Разделив полученное, выражение
на дифракционный радиус 0,61 Я/Умакс, получим безразмерное
отношение (</'УМакс — /?У'УМакс)/0,61А,. Последнее выражение
можно переписать в виде
I . .IV
„, I вместе с
вектором крайнего луча центрального пучка для получения мат-
матрицы 2X2 нового типа. Определитель этой матрицы позволяет
установить, принадлежит ли пробный луч исходному семейству
лучей. Если это так, то поскольку два вектор-столбца характери-
характеризуются одним и тем же отношением y/V, то определитель обра-
обращается в нуль. Если же пробный луч «принадлежит другому
пучку лучей», то определитель имеет конечное, отличное от нуля
значение, и если оно существенно больше 0,61 А,, то пробный
луч характеризует световой пучок, параметры которого отли-
отличаются на измеряемую величину от параметров центрального
пучка лучей.
На Данном этапе важно понять, что величина ^того опреде-
определителя зависит лишь от того, какую именно пару лучей мы вы-
выбрали, и не зависит от выбора опорной плоскости. По сути дела
мы задаем вопрос: какую часть дифракционной ширины состав-
составляет расстояние между выбранными двумя лучами, если их
продолжить до плоскости источника? Мы свяжем полученный
определитель с величиной, называемой инвариантом Лагранжа,
и покажем, что ее постоянство следует из закона сохранения
энергии. Однако, чтобы доказать, что эта величина остается
постоянной при переходе от одной опорной плоскости к следую-
следующей, мы можем положиться на тот факт, что, всякий раз как
с помощью унимодулярной матрицы преобразования лучей осу-
р. *ч
ществляется переход от матрицы I , I в одной опорной
плоскости к матрице I T/ vi I в другой опорной плоскости,
I У О '! I
2
Оптические резонаторы и распространение лазерного пучка 109
матричные элементы могут меняться, однако определитель дол-
должен оставаться постоянным для любой опорной плоскости. В ча-
стности, если два выбранных нами луча I „ I и I „, I при-
принадлежат одному и тому же световому пучку, то этот определи-
определитель равен нулю. В противном случае он будет иметь постоян"-
ное значение, отличное от нуля.
Если мы выберем два луча, отличающиеся друг от друга
настолько, насколько это возможно, то значение рассматривае-
рассматриваемого определителя дает нам для любой заданной оптической си-
системы меру числа различных оптических путей, по которым свет
может пройти через систему. В таких расчетах удобно исполь-
использовать понятия входного люка, или полевой плоскости, системы
и ее входного зрачка. (Эти понятия определены в приложе-
приложении I). Мы выберем следующие два луча первый — главный —
луч, который проходит через край поля зрения системы и центр
входного зрачка, и второй — боковой — луч, который проходит
через центральную точку поля зрения и крайнюю точку входного
зрачка.
Пусть входной зрачок радиусом а2 расположен справа на
расстоянии Ь от входного люка радиусом сц; тогда в опорной
плоскости, совпадающей с плоскостью поля зрения системы, лу-
чевои вектор главного луча записывается в виде I ., I, a
Г 0
крайнего луча — в виде I ., I. Используя эту пару лучевых
[а\ 0 "I
— ai/o що J
Разделив, как и прежде, найденную величину на 0,61Я, получим
безразмерный параметр a^/OfilbX, представляющий собой по-
половину полного числа линий, которые рассматриваемая изобра-
изображающая система может разрешить в отсутствие всех типов абер-
аберраций.
Вместо того чтобы рассматривать изображение линий, раз-
разделенных расстоянием 0,61ХЬ/а2 и прочерченных вдоль диаметра
полевой диафрагмы, обратимся к двумерной картине. Пусть по-
полевая диафрагма имеет радиус аи а радиус изображения точки
мы выберем равным 0,3Xb/a2; тогда полное число вполне разре-
разрешаемых элементов источника составляет па\/п @,ЗХЬ/аЛ2 или
(приблизительно) п2а\аЦЬ?'к2.
Точное значение этого числа зависит от того, какой мы вы-
выберем критерий разрешения или контрастности изображения.
Окончательное выражение для полного числа разрешаемых але-
ПО Глава 3
ментов можно записать в виде
где А — площадь, освещаемая пучком лучей в плоскости изо-
изображения, a Q — телесный угол, под которым виден выходной
зрачок из центра выходного люка.
Произведение Аи иногда определяют как инвариант Лагран-
жа. Тот факт, что эта величина остается постоянной при пере.-
ходе от одной плоскости изображения к другой, непосредствен-
непосредственно следует из общего вида матрицы преобразования лучей
Г « о 1
I _ i/f 1/ I изображающей системы. Поперечное увеличение
т всегда обратно угловому увеличению, так что когда величина
А преобразуется при прохождении через оптическую систему в
т*А, новое значение телесного угла становится равным Q/m2.
Для систем, формирующих изображение и предназначенных
для работы при низких уровнях, освещенности, а также для мно-
многих приборов, таких, как спектрографы и монохроматоры, про-
произведение Аи представляет собой важную и полезную величину,
определяющую световую энергию, которая может быть принята
и передана оптической системой. Поскольку термин «инвариант
Лагранжа» является не совсем понятным, используют более на-
наглядные названия этого произведения. В настоящее время широ-
широкое распространение получил термин «этандю» (французское
слово etendue), введенный Конном •).
Предположим теперь, что изображающая система освещает-
освещается протяженным источником однородной яркости, «яркостную
силу» которого можно представить как мощность излучения,
равную S ватт на квадратный метр в телесный угол, равный
1 ср. Тогда полная мощность излучения в ваттах, попадающего
от источника в оптическую систему, равна SAQ; если в оптиче-
оптической системе лиизы идеально прозрачны, то световой поток бу-
будет сохраняться при переходе от одной плоскости изображения
к другой и вся мощность излучения от источника пройдет через
систему иа ее выход.
Выше мы установили, что, если этандю разделить на Я2, то
получится безразмерное число, определяющее максимальное ко-
количество разрешаемых структурных элементов объекта, которое
может быть передано изображающей оптической системой, ра-
работающей в условиях, когда разрешение ограничивается ди-
дифракцией. Необходимо подчеркнуть, что лишь очень небольшое
*) В английском языке существует несколько терминов, соответствующих
эффективной светосиле прибора, в частности, «пропускная способность»
(throughput) или «светозахват» (light grasp). — Прим. ред.
Оптические резонаторы и распространение лазерного пучка 111
число оптических систем, предназначенных для работы с неко-
герентным светом, дает такое разрешение и, как правило, линзы
больших размеров используются в основном для увеличения яр-
яркости изображения, а не для увеличения разрешающей силы.
Однако в астрономических камерах новейших типов выполнена
тончайшая коррекция внеосевых аберраций, при этом поле зре-
зрения прибора может состоять из 108 разрешаемых элементов изо-
изображения.
С развитием лазерных источников света было разработано
несколько типов оптических систем, предназначенных для ра-
работы с когерентным освещением, причем в каждой из них важ-
важную роль играет параметр /Ш/?А Например, при оптической об-
обработке информации это число обычно называют пространствен-
пространственно-частотным произведением; оно определяет эффективное чис-
число независимых параллельных каналов, которые реализуются
в данном процессоре для передачи информации. Поскольку все
эти каналы работают одновременно, использование оптических
систем таит в себе, очевидно, огромные потенциальные преиму-
преимущества по сравнению с системами, в которых вся информация
обрабатывается последовательно.
Другим примером служит фотографическая пластинка с мел-
мелкозернистой эмульсией, используемая в голографии или для фо-
фотографирования модовой картины лазера. Если площадь пла-
пластинки 100 мм2 и она освещается световым пучком с телесным
углом, равным 1 ср, то на нее можно записать порядка 10ю
вполне различимых элементов даже в том случае, когда инфор-
информация записывается в течение времени экспозиции всего лишь
порядка нескольких наносекунд. Если ту же самую информацию
передавать по телевизионной системе с полосой по видеосигналу
около 10 МГц, то для записи такого количества информации
потребуется время порядка 15 мин.
Довольно парадоксальным кажется то, что лазерный свет,
позволяющий получить очень большие пространственно-частот-
пространственно-частотные произведения, зависит от генерационных характеристик оп-
оптических резонаторов, для которых произведение AQ/X2 жестко
ограничено и не превышает единицы. Такое ограничение вво-
вводится специально при установке пространственного фильтра, при
этом в процессе генерации возбуждается только одна строго
определенная стоячая волна: генерация происходит на одной по-
поперечной моде.
При расчете оптических резонаторов обычно используют па-
параметр а\пч1ЬК который мы уже рассматривали выше; этот па-
параметр называется числом Френеля N. Двумерное пространст-
пространственно-частотное произведение AQ/J численно равно квадрату
величины лЛ?. Для типичного гепш-неонового лазера низкой
мощности длина резонатора Ь может быть порядка 300 мм, а ра-
112 Глава 8
диус разрядной трубки а = 0,5 мм. В случае длины волны
633 нм число Френеля N составляет @,5) @,5) 10е/ C00) F33) «
да 1,3.
В принципе, если рассматривать разрядную трубку как про-
пространственный фильтр, то от одного конца резонатора к другому
может проходить порядка дюжины вполне разрешаемых свето-
световых пятен; для генерирующего лазера такое распределение из-
излучения может быть нежелательным, но, к счастью, в лазере
осуществляется естественная селекция мод, и только централь-
центральное пятно обладает минимальными дифракционными потерями
и характеризуется самовоспроизводящейся модовой картиной.
Рассмотрением геометрии этой модовой картины мы и будем за-
заниматься в следующих параграфах настоящей главы.
§ 4. МАТРИЧНОЕ ОПИСАНИЕ ОПТИЧЕСКОГО РЕЗОНАТОРА
Основная функция оптического резонатора, о чем мы кратко
упомянули в предыдущем параграфе, состоит в том, чтобы при-
придать световым волнам, излучаемым лазером, строго определен-
определенную форму или модовую картину. Специалисты в области кван-
квантовой электроники при разработке таких источников света дол-
должны учитывать три следующих важных аспекта:
а) Необходимо выбрать подходящую среду для лазера, та-
такую, чтобы вынужденное излучение при переходе с верх-
верхнего лазерного уровня на нижний соответствовало желае-
желаемой области спектра.
б) Активйую среду, которая поглощает свет на заданной
длине волны, необходимо превратить в усиливающую сре-
среду с требуемым коэффициентом усиления. Обычно это до-
достигается с помощью «иакачки», которая позволяет се-
селективно поглощать энергию таким образом, чтобы обе-
обеспечить «инверсную населенность» между двумя энергети-
энергетическими уровнями.
в) Чтобы превратить полученный таким образом усилитель
света в генератор, необходимо ввести оптическую обрат-
обратную связь так, чтобы свет многократно проходил через
усилитель. При условии что усиление превышает полные
потери излучения в резонаторе, возникает самоподдержи-
самоподдерживающаяся генерация, начинающаяся с естественной спон-
спонтанной эмиссии, которая всегда присутствует в инверти-
инвертированной активной среде. Во всяком случае, для боль-
большинства лазеров непрерывного действия результирующая
картина стоячих световых волн автоматически становится
стабильной при уровнях мощности, определяемых ско-
скоростью, с которой требуемая энергия накачки поступает
в усилитель.
Оптические резонаторы и распространение лазерного пучка 113
При изложении материала в данной главе мы будем считать
само собой разумеющимся, что проблемы выбора активной сре-
среды и накачки уже решены. Предположим, что лазерный усили-
усилитель цилиндрической формы представляет собой, например,
стеклянный стержень или газоразрядную трубку и имеет одно-
однородный коэффициент усиления по всему сечению. Кроме того,
будем считать, что активная среда не вносит никаких аберраций
и никаких других изменений в форму волновых фронтов, кото-
которые в ней усиливаются. Хотя последнее предположение является
идеализацией реальной ситуации, оно довольно близко соответ-
соответствует действительности, в частности, во многих газовых лазе-
лазерах низкой мощности, а также в некоторых лазерах на неодимо-
вом стекле и в лазерных системах на красителях.
Поскольку рассматривается способ создания оптической об-
обратной связи (см. п. «в»), мы пренебрежем многочисленными,
играющими важную роль, нестационарными (переходными)
процессами, которые могут возникать в реальной ситуации, и ис-
исследуем распространение света в лазере в стационарном режиме
генерации, когда потери на один проход резонатора полностью
возмещаются усилением активной среды. Другой аспект, кото-
который мы также будем предполагать заданным, — это процесс се-
селекции аксиальных мод, который строго фиксирует интервалы
между модами, поскольку световые волны, прошедшие через ре-
резонатор и совершившие «полный проход», должны иметь ту же
фазу, что и в начале. Все, что мы будем здесь рассматривать,
можно сформулировать в виде следующего вопроса: «Что про-
происходит с поперечным распределением амплитуд световых волн
при их распространении внутри резонатора?»
Чтобы ответить на этот вопрос, нам нужно знать геометрию
оптического резонатора. В подавляющем большинстве лазерных
систем свет многократно проходит интервал между двумя тор-
торцевыми зеркалами. Существуют также кольцевые лазеры, в ко-
которых свет циркулирует по замкнутому пути либо по часовой,
либо против часовой стрелки. Но такие системы используются
достаточно редко, и мы рассмотрим их позже.
На фиг. 3.5 показано схематически устройство типичного ла-
лазерного резонатора. Усиливающий стержень лазера имеет длину
L и помещается между двумя отражающими зеркалами, рас-
расстояние между которыми равно Ъ. Поскольку лазерный стер-
стержень эквивалентен плоскопараллельной пластине, матрица пе-
перемещения луча, соответствующая оптическому промежутку ме-
между двумя зеркалами резонатора, содержит приведенную длину
™ b-L . L , (n-l)L
Т'=——+т=Ь
где п — показатель преломления активной сред-ы лазера.
114
Глава 3
ОП
±
I 0 I,
Лащятйуеятвающии
стержень
Выход
Излучения
Фиг. 3.5. Схема лазерного резонатора.
3,—полностью отражающее зеркало; 3,—частично отражающее зеркало.
Прежде чем выписывать полную матрицу преобразования лу-
лучей, описывающую эту систему, остановимся кратко на назначе-
назначении частично прозрачного зеркала, расположенного в правой ча-
части системы. Обычно это зеркало называют «выходным зерка-
зеркалом», поскольку оно позволяет выводить нужную часть энергии,
накопленной в резонаторе, и таким образом использовать эту
энергию для различных целей. Выбор коэффициента, отражения
выходного зеркала вполне напоминает проблему, с которой
встречаются хлеборобы, когда необходимо сохранить часть зер-
зерна для того, чтобы получить урожай в следующем году. При
очень высоком коэффициенте усиления, которым, например, об-
обладает неодимовый лазер, иногда бывает достаточно, чтобы это
зеркало отражало всего лишь 10% падающей энергии, в то вре-
время как остальные 90% покидают лазерный резонатор. Напротив,
в гелий-неоновых лазерах коэффициент усиления очень мал, и из
резонатора удается вывести не более чем 1% энергии. По этой
причине в таких лазерах возбудить генерацию удается, только
применяя многослойные диэлектрические зеркала с высокими
коэффициентами отражения и поверхностью очень высокой чи-
чистоты.
Поскольку мы будем интересоваться конфигурацией свето-
световых волн, излучаемых через выходное зеркало лазера, удобно
расположить ОП1 на поверхности частично отражающего зер-
зеркала и рассматривать исходный луч I „ I, который падает на
в положительном направлении оси г после выхода из уси-
усилителя. Та часть энергии луча, которая отражается от выход-
выходного зеркала, после отражения распространяется в обратном на-
направлении, проходит через усилитель к левому зеркалу системы,
затем возвращается и вновь проходит через усилитель к выход-
выходному зеркалу.
Оптические резонаторы и распространение лазерного пучка Пб
Если теперь расположить вторую опорную плоскость ОПг та-
таким образом, что она будет совпадать с ОПь то можно записать
полную матрицу преобразования лучей М, связывающую эту
«пару» опорных плоскостей и представляющую «полный про-
проход» через резонатор.
Обозначая оптические силы двух торцевых зеркал как Р\ и
Р2, мы можем записать, что
p2-|_ri r-ir- 1 o-iri г-|г
ivj Lo iJL-л iJLo 1JL-
B
l-PJ
1 р
P2 iJLf.
Jl-PlT-2P2T + PiP2T2 ТB-Р1ТIГу1
L -Pi~P2 + P>P2T JI
Ш
Проверив теперь равенство определителя этой матрицы единице,
мы фактически имеем достаточно информации для расчета од-
одного прохода или многократных проходов луча через резонатор.
Для того чтобы рассчитать изменение параметров луча вслед-
вследствие N последовательных полных проходов через резонатор,
нужно возвести полную матрицу преобразования лучей М в N-ю
степень. С этой целью используем методы диагонализации мат-
матрицы, описанные в §§ 11 и 12 гл. 1. Мы ищем преобразование,
приводящее исходную матрицу к диагональному виду:
где
pi 0 1
L о %2 J
— диагональная матрица, причем
Для того чтобы найти собственные значения Ki и Хг, рассмо-
рассмотрим след А + D матрицы М, при этом получим
А + D = A - Р(Г - 2Р2Т + Р^Т2) + A - Р,Г) =
Следуя в точности процедуре, описанной в § 11 гл. 1, ищем
теперь значения 6 или t, такие, что
либо Л + О =
тогда hx = eiQ, К2 = е~ю;
116 / ' ¦ Глава 3
либо A -f D -ш 2 ch t = 4 ch2 (t/2) — 2,
тогда ^ = 0*, Я2 = е~';
либо e«fe Л + 0 = - 2ch(-0 = — 4sh2(-*/2) — 2,
тогда Xi = — e{, X^ = — e~*.
Чтобы решить, какая из этих трех альтернатив реализуется, нам
необходимо вычислить всего лишь произведение A — Т1г{)(\ —
— Tjr2) и установить соответственно, лежит ли величина этого
произведения в интервале между 0 и 1 или она больше 1, или
меньше 0.
Как было показано в § 12 гл. 1, если К\ и Х2 являются соб'
А В1
ГА В1
„ ~ I,
ственными значениями унимодулярной матрицы
то отношение компонент одного собственного вектора равно
(Я.1 — D)/C, а другого (%2 — D)/C.
В соответствии с приведенным выше рассмотрением эти отно-
отношения являются значениями,у/V, или значениями R луча, рас-
распространяющегося через резонатор без изменения. Если внутри
резонатора существует волновой фронт с такой кривизной, то он
будет самовоспроизводиться. Это очень важное следствие, кото-
которое впоследствии мы будем обсуждать.
- Для тех, кто предпочитает не пользоваться методами диа-
гонализации, описанными в гл. 1, заметим, что те же самые
результаты можно получить, используя непосредственно пра-
правило ABCD. Если значение R луча при прохождении резонатора
остается неизменным, то мы сразу получим два уравнения:
о "«- AR> + в я о _ о
Исключая Ri, находим следующее квадратное уравнение отно-
относительно R\\
)
Его решения записываются в виде
d (A — D)db У(Л - DJ + 4ДС" [А + D ±^/(А + D)* - 4 ] - 2D
/?, = ^ = ^ г-
Нетрудно проверить, что эти решения, определяющие значение
R, совпадают с отношениями компонент собственных векторов
{Xi — D)/C и (%i — D)IC, полученных методом диагонализацин.
Прежде чем рассмотреть подробно роль этих отношении, об-
обратимся к некоторым другим возможным типам резонаторов, для
которых бывает полезно выписать матрицу преобразования лу-
лучей, :
Оптические резонаторы и распространение лазерного пучка
117
имеет вид
пРичем для плоского зеркала она ста-
ста4.1. Другие возможные типы отражателей
На фиг. 3.6 схематически показаны два различных типа ре-
трорефлекторов, которые иногда используют вместо глухого зер-
зеркала резонатора. Напомним, что для такого зеркала матрица
Г 1 °1
I nil'
новится единичной матрицей.
а) Чтобы описать действие отражателя типа «кошачий глаз»,
выберем опорную плоскость совпадающей с первой фо-
фокальной плоскостью линзы. Если мы рассмотрим преобра-
преобразование параметров луча при его прохождении от этой
плоскости до плоского зеркала, расположенного во второй
фокальной плоскости, а затем его прохождение в обрат-
обратном направлении, то получим полную матрицу
M=l-Uf oJLo lJL-i/f oJ = L о -ij-
Следовательно, в отличие от плоского зеркала отража-
отражатель типа «кошачий глаз» обращает значения как пара-
параметра у, так и параметра V. Изменение знака величины
V = п sin v обусловлено изменением знака показателя
преломления п, т. е. изменением геометрического направ-
направления луча при повороте его на 180° относительно перво-
первоначального направления распространения.
б) Как хорошо известно, точно такими же свойствами обла-
обладает уголковый отражатель, который обращает все три
направляющих косинуса луча в произвольно выбранной
декартовой системе координат. Если выбрать опорную
\L
ОП
-M
u -iJ
-
f 4
Фиг. 3.6. а — отражатель типа «кошачий глаз», М = _. I;
б — уголковый отражатель, Af
Г-1 --1
J ft I.
L о -l J
118 Глава 8
плоскость так, что она пройдет через вершину прямого
угла отражателя, то матрица преобразования лучей запи-
[-1 01
n —ll для У~ и ^"значеиий. а также
для соответствующих х- и (/-значений, когда измерения
производятся в плоскости (х, г), нормальной к плоскости
фигуры.
Если уголковый отражатель выполнен в форме стек-
стеклянной призмы, то следует также учесть прохождение
света через слой стекла толщиной t от вершины уголко-
уголкового отражателя до входной поверхности. При этом пол-
полная матрица, вычисленная относительно опорной плоско-
плоскости, совпадающей с входной поверхностью отражателя,
имеет вид
и Г1 '/"ll"-1 °1Р '/ Г ~211
M==Lo 1 JL о —1 JLo л Г1 о -
В точности такая же матрица описывает изменение у-
и V-зиачений при отражении от прямоугольной призмы,
ребро которой перпендикулярно плоскости (y,z), однако
в этом случае матрица преобразования соответствующих
х- и [/-значений будет такая же, как и для плоского глу-
глухого зеркала. При этом очевидно, что матрицы преобра-
преобразования луча в плоскости (х, г) и в плоскости (у, г) бу-
будут различны.
4.2. Системы с изломом оптической оси (фиг. 3.7)
Существует несколько причин, по которым целесообразно ис-
использовать лазерные резонаторы с изломом оптической оси, со-
соединяющей торцевые зеркала резонатора:
а) Торцевые поверхности твердотельного лазерногр усили-
усилителя или окошки газоразрядной трубки часто ориенти-
ориентируют под углом Брюстера, чтобы устранить паразитное
отражение света и обеспечить линейную поляризацию ла-
лазерного луча.
б) С целью осуществления селекции заданной длины волны
в резонатор часто вводят дополнительно преломляющую
призму, поверхности которой ориентированы под углом
Брюстера.
в) Излом оптической оси при отражении вносят также для
сокращения размеров системы или для того, чтобы осу-
осуществить модуляцию добротности Q лазера с помощью
быстро вращающейся призмы и получить режим генера-
генерации одного или нескольких гигантских импульсов.
Оптические резонаторы и распространение лазерного пучка
119
Полностью Частично
отражающее Окна, впаянные под углом пропускающее
зеркало / Брюстера \ зеркало
' Газовый лазерный. \
усилитель \
\ -^ \Ц Выход
а
Твердотельный лазерный
усилитель
60°-пршма
Выходное
зеркало
Вращающееся
зеркало
для модуляции
добротности
в
Резонансный
,, . . отражатель
Усиливающий стержень г
» \ Двухинпульсный
~^^ отражатель
Фиг. 3.7
г) Как уже отмечалось выше, оптическая ось резонатора мо-
может несколько раз менять направление вследствие отра-
отражений и(или) преломлений и образовывать таким обра-
образом замкнутый оптический путь. Иногда в такие системы
устанавливают оптический вентиль, который пропускает
излучение только в одном направлении и таким образом
препятствует образованию стоячих волн. Однако в боль-
большинстве кольцевых лазеров (фиг. 3.8) используются одно-
одновременно оба направления циркуляции излучения; при
этом разность их оптических частот, измеряемая методом
гетеродинирования, является функцией абсолютного вра-
вращения платформы, на которой установлен резонатор.
В результате получается «лазерный гироскоп», который
можно использовать в качестве очень чувствительного
инерциального гироскопа.
Для всех таких систем специфика расчета состоит в том, что
мы должны просчитать одиночный ход луча, распространяюще-
распространяющегося первоначально вдоль оптической оси одной из прямолиней-
120
Глава 3
Частично
отражающие
пластины
Детектор 1
Детектор Z
Фиг. 3.8
ных секции резонатора, а затем проследить его распространение
через другие секции. При этом мы вычисляем матрицы, соответ-
соответствующие оптическим промежуткам приведенной толщины Т (ма-
(матрицы перемещения) и преломляющим поверхностям с задан-
заданными оптическими силами Р (матрицы преломления), которые
встречаются на пути луча. Если одна из отражающих поверхно-
поверхностей расположена под углом к оптической оси резонатора и не
является плоской, то возникает астигматизм, причем оптическая
сила /^.определяющая распространение лучей в плоскости (у, г),
будет больше, чем оптическая сила Рх для плоскости (х, г). При
этом понадобятся две различные матрицы Му и Мх, чтобы опи-
описать изменение величин у и V, а также х и U при полном про-
проходе через резонатор.
4.3. Эффекты неправильной юстировки
При проведении этих вычислений предполагалось, что все
элементы резонатора установлены и ориентированы таким обра-
образом, что реализуется идеальная юстировка резонатора. При этом
луч, распространяющийся вдоль оптической оси одной из сек-
секций резонатора с лучевым вектором I 11 после полного одно-
однократного прохода через резонатор будет также распространять-
распространяться вдоль оптической оси этой же секции, т. е. по тому же пути.
Оптические резонаторы и распространение лазерного пучка 121
На практике, однако, небольшая неустранимая ошибка юсти-
юстировки каждого элемента резонатора может приводить к неболь-
небольшому поперечному смещению луча Ау и к небольшому угловому
смещению AV, в результате чего луч после прохода через резо-
резонатор пойдет по новому пути, несколько отличному от первона-
первоначального.
Поскольку рассмотрение эффектов неправильной юстировки
требует использования расширенных матриц преобразования лу-
лучей размером 3X3, то соответствующие расчеты мы приведем
отдельно в приложении II. Здесь же дадим лишь краткий пере-
перечень основных результатов таких расчетов:
а) Если нам заданы остаточный сдвиг и угловая ошибка для
каждой t-й опорной плоскости, то нетрудно вычислить ре-
результирующие ошибки Ау и AV, которые связаны с пол-
полной матрицей преобразования лучей в резонаторе и кото-
которые учитывают совместно все отдельные ошибки юсти-
юстировки.
б) При условии что след А + D этой матрицы не равен +2,
можно найти новую эффективную ось, такую, что луч,
распространяющийся вдоль нее, после полного прохода
через резонатор пойдет точно по тому же пути. Высота г/о
и угол Vo этого нового эффективного луча даются выра-
выражениями
(l-Z?)Ay + BAF у
Уо = 2-A-D И Vo== 2-A-D '
Применяя эти результаты к простому резонатору, образован-
образованному двумя зеркалами, след матрицы которого мы уже вычис-
вычислили, найдем, что новая эффективная ось существует лишь для
таких схем резонаторов, для которых не выполняется соотноше-
соотношение
О-?)('-*)-'•
Это равенство справедливо либо при Т = Г\ + г% (в этом случае
зеркала расположены концентрично), либо когда как Г\, так и
Г2 оба обращаются в бесконечность (система типа Фабри — Пе-
Перо с плоскими зеркалами), либо когда Г = 0 (однако в этом
случае не остается места для лазерного усилителя!)
Для всех других типов резонаторов величина 2 — A—D не
обращается в нуль и центры кривизны обоих торцевых зеркал
расположены в различных точках оси резонатора. Следователь-
Следовательно, даже если они слегка смещены от оси z, соединяющая их
линия все же будет принадлежать параксиальной области си-
системы и будет новой эффективной осью системы. Хотя конструк-
конструктор, рассчитывающий лазер, даже не знает точного положения
122 Глава 3
эффективной оси, но если эта ось существует, то в процессе ре-
регенеративного усиления ее положение будет найдено лазерным
излучением автоматически. Однако следует помнить, что при до-
достаточно большом нарушении юстировки зеркал и ограниченной
величины этандю системы, что обычно имеет место, существен-
существенную роль начинает играть виньетирование, которое вносит допол-
дополнительные потери энергии в резонаторе из-за частичного пере-
перекрытия света диафрагмами системы.
Для лазеров, работающих в непрерывном режиме, предпо-
предпочтительно использовать резонатор, для которого не выполняется
условие А + D = 2, так что оптическая ось резонатора, переме-
перемещаясь, может до некоторой степени компенсировать нарушение
юстировки системы. Однако если для генерации гигантского им-
импульса применяется вращающееся зеркало, то имеет смысл ис-
использовать резонатор, чувствительный к нарушению юстировки;
это гарантирует генерацию коротких импульсов, поскольку воз-
возбуждение лазера будет происходить лишь в тот момент, когда
излучение, отраженное вращающейся призмой, пройдет по един-
единственному направлению, для которого в резонаторе осуществ-
осуществляется обратная связь.
§ 0. РАЗЛИЧИЕ МЕЖДУ УСТОЙЧИВЫМИ
И НЕУСТОЙЧИВЫМИ РЕЗОНАТОРАМИ
Как было показано в предыдущем параграфе, обычно не со-
составляет труда вычислить матрицу преобразования лучей, аде-
адекватно описывающую геометрию оптического резонатора. Вы-
Вычислив след матрицы А + А можно затем найти собственные
значения ki и Аа, а также отношения компонент соответствую-
соответствующих им собственных векторов (Ki — D)/C и (Я,а — D)/C.
Напомним, что для значений следа А + А лежащих в интер-
интервале —2-т- +2, собственные значения записываются в виде eie и
e~ie, т. е. в виде комплексных чисел, расположенных на окруж-
окружности единичного радиуса. Во избежание неоднозначности будем
считать, что значения в находятся в интервале я > в > 0. Вне
этого интервала собственные значения записываются в виде е* и
е-' или, для отрицательной ветви, как —е* и —ег%, т. е. являются
действительными числами, не равными единице. Каким образом
можно интерпретировать эти различные с математической точки
зрения свойства и каким образом это различие сказывается на
распространении луча в резонаторе?
Рассмотрим вначале численный пример. Резбнатор, показан-
показанный на фиг. 3.9, состоит из двух зеркал, причем одно из них, вы-
выпуклое, имеет радиус 8 м и расположено на расстоянии 1 м от
плоского выходного зеркала. Используя выражение для матри-
Оптические резонаторы и распространение лазерного пучка
123
В этой плоскости
пучок сужается
? этой плоскости пучок
становится широким.
М
-1м
U, 25 2,25
Щ25 1,25
1
г
W
1
ОП
Л^ + 2
Лг-+Уг
Ri
*г
L
- -J
Фиг. 3.9
цы полного прохода, полученное в § 4 настоящей главы, для
расчета рассматриваемой системы подставим в нее значения
Т = 1,0, Pi =*= — 0,25 и Р2 = 0 соответственно в метрах и диопт-
диоптриях. В результате получаем матрицу, описывающую проход
луча через резонатор в направлении от выходного зеркала и об-
обратно к нему:
Г 1,26 2,251
M==L0,25 1,25 J
След этой матрицы А + D — 2,5. Чтобы найти собственные зна-
значения, предположим, что t — действительное положительное чис-
число. Тогда получим %\ = 2 и А,2 = 0,5. Следовательно, соответст-
соответствующие отношения компонент собственных векторов равны
(A,j —D)/C =+3 и (h2 — D)/C = —3. Согласно нашей интер-
интерпретации, эти отношения представляют собой радиусы кривизны
волновых фронтов1). Первое отношение определяет сфериче-
сферическую волну, исходящую из точки, смещенной на 3 м влево от
выходного зеркала, а второе — сферическую волну, сходящуюся
в точку, смещенную на 3 м вправо от него.
Рассмотрим теперь один из лучей, принадлежащих пучку,
расходящемуся из точки 5. Пусть его лучевой вектор записы-
') Точнее говоря, втн отношения соответствуют приведенным радиусам
#, 2 = п, i/я, где я — показатель преломления среды. Однако в данном слу-
случае имеется в виду свободное пространство, т. е. л =¦ 1, и, следовательно, Ri, i
совпадает с фактическими радиусами кривизны волновых фронтов. — Прим.
ред.
124 Глава Я
Г 0,031
L 0,01 J •
вается, например, в виде I n n« I • Этот луч проходит достаточно
близко к оптической оси системы. Поскольку лучевой вектор яв-
является одним из собственных векторов матрицы М, найдем, что
после одного полного прохода он принимает вид
Г °.°31
I ... I,
го.озяп
Lo.ouJ
так как ему соответствует собственное значение2.
Новый луч также принадлежит исходному пучку, однако он сме-
смещен от оптической оси на расстояние, в два раза большее, чем
расстояние от оси, которое имел исходный луч. После п проходов
через резонатор смещение луча от оси увеличится в 2" раз и
будет увеличиваться до тех пор, пока его путь не перекроет одна
из диафрагм системы.
Чтобы более ясно представить себе, что происходит в этом
случае, преобразуем нашу матрицу к новой «паре» опорных пло-
плоскостей, совпадающих друг с другом и расположенных в точке
S, из которой пучок лучей расходится. Умножая справа и слева
матрицу М на соответствующие ^"-матрицы, получаем
Г1 -31 Г 1,25 2,251 Г 1 31 Г 1 -31 Г 1,25 6 1 _
10 1 J L 0,25 1,25 J L 0 1 J Lo 1 J L 0,25 2j =
г 0,5 01
L0,25 2J-
Поскольку матричный элемент в правом верхнем углу матрицы
равен нулю, полученная нами матрица представляет изобра-
изображающую оптическую систему. При каждом проходе луча через
резонатор любое распределение, существующее в плоскости S,
будет сжиматься по оси у и расширяться по соответствующей
угловой координате V в два раза (или в общем случае в A,i =
= е* раз).
С другой стороны, если перейти к опорной плоскости, прохо-
проходящей через точку L (фиг. 3.9), то получим матрицу
Г 2 0 1
I о 25 0 5 1' К0Т0Рая' напротив, дает расширение по оси у и
сжатие по соответствующей угловой координате V.
Таким образом, с точки зрения геометрической оптики пучок
лучей произвольного первоначального вида (например, спонтан-
спонтанное излучение) в результате многократных прохождений через
резонатор сконцентрируется в очень небольшой центральной об-
области плоскости 5 и, напротив, сильно расширится в плоскости
L. Как правило, процесс расширения ограничивается диафраг-
Оптические резонаторы и распространение лазерного пучка 125
мами, установленными в плоскости L, однако сжатие пучка в
плоскости S происходит вплоть до дифракционного предела,
определяемого максимальными значениями параметра V, допу-
допускаемыми системой.
Вместо частично отражающего выходного зеркала конструк-
конструкторы, создающие лазерные системы, нередко используют зер-
зеркала, центральная область которых является полностью отра-
отражающей. При этом излучение, выходящее из резонатора, имеет
форму кольца и возникает за счет радиального расширения пуч-
пучка, а именно выходят те лучи, которые в результате последнего
прохода через резонатор выходят из него, минуя плоское зер-
зеркало (фиг. 3.9). Хотя этот пучок довольно быстро расходится,
его расходимость является дифракционной, так что такой пучок
можно коллимировать или вновь сфокусировать в небольшое
пятно, используя дополнительную оптическую систему.
Резонатор с запланированными потерями энергии, который
мы рассмотрели выше, обычно называют «неустойчивым». Во-
Вообще говоря, этот термин в данном случае не совсем уместен,
поскольку волновой фронт плавно и достаточно быстро изме-
изменяет свою форму, воспроизводя значения R, определяемые соб-
собственным вектором; тем не менее при каждом полном проходе
резонатора соответствующий пучок лучей расширяется, причем
«потери» каждого рассматриваемого отдельно пучка возрастают
до тех пор, пока его лучи вообще не покинут систему. Поскольку
радиальное расширение пучка происходит как по оси х, так и по
оси у, то в центральную область выходного зеркала после ка-
каждого прохода пучка через резонатор возвращается четвертая
часть исходной энергии, поэтому необходимо использовать ла-
лазерный усилитель, который давал бы за два прохода усиление,
равное по меньшей мере четырем (или в общем случае равное
)J\ = e2t), и таким образом поддерживал бы непрерывную гене-
генерацию лазера.
На первых порах конструкторы лазерных систем предпочи-
предпочитали не использовать резонаторы неустойчивого типа, поскольку
для реализации таких систем необходим лазерный усилитель с
высоким коэффициентом усиления. Огромное преимущество ре-
резонатора неустойчивого типа состоит в том, что при больших
пространственных масштабах с очень большим числом Френеля
он позволяет получить высоконаправленное излучение на вы-
выходе и в то же время он не чувствителен к незначительным из-
изменениям юстировки. В будущих конструкциях сверхмощных
промышленных лазерных систем будут, по-видимому, преобла-
преобладать различные типы неустойчивых резонаторов. Для СО2 лазе-
лазеров, работающих в инфракрасном диапазоне на длине волны
10,6 мкм, в качестве внешних дополнительных оптических си-
систем, возможно, выгоднее использовать вместо линз зеркалй, и
126
Глава 3
Плоскости
Фиг. ЗЛО
тогда кольцевая структура пучка не приведет к каким бы то ни
было дополнительным неудобствам.
Возможны и другие реализации резонаторов неустойчивого
типа, для которых не составляет труда получить на выходе кол-
лимированный пучок. На фиг. 3.10, а и б для иллюстрации при-
приведены два таких резонатора, каждый из которых образован
двумя зеркалами и представляет собой афокальную систему
с увеличением, отличным от единицы.
Система, показанная на фиг. 3.10, а, образована вогнутыми
зеркалами с оптическими силами Pi = +1.6 и Р% = +3, кото-
которые разделены интервалом длиной Т = 1. Полная матрица та-
такой системы имеет вид М-
Г-2 0,5-1
1 0 -0,6 J
След этой матрицы
равен —2,5, а собственные значения, очевидно, Х| = —2 и Xj =¦
= —0,5. Для первого собственного значения отношение компо-
компонент собственного вектора (Ki — D)/C обращается в бесконеч-
бесконечность, поскольку С =з 0 для этой афокальной системы. Для вто-
второго собственного значения это отношение, определяемое форму-
формулой (X» — D)[C, имеет неопределенное значение, однако исполь-
Оптические резонаторы и распространение лазерного пучка 127
зование другого выражения, а именно В/(к2 — А) (см. п. 12.1
гл. 1), дает второе возможное значение R = '/з- В этой системе
существуют две оптически сопряженные плоскости, одна из ко-
которых расположена на бесконечности, а вторая проходит через
общий фокус двух зеркал. В процессе многократных переотра-
переотражений внутри резонатора пучок будет расширяться в плоскости,
расположенной в общей фокальной точке, и сжиматься к ди-
дифракционному пределу в плоскости, расположенной на бесконеч-
бесконечности. Коэффициент усиления, необходимый для возбуждения
лазерной генерации, в точности такой же, какой и в предыдущем
примере.
Однако для лазеров высокой мощности эта конструкция ре-
резонатора имеет серьезный недостаток: при распространении в
положительном направлении оси г излучение фокусируется в
точке L, расположенной внутри резонатора, а значительная кон-
концентрация энергии (мощности) в этой области почти наверняка
приведет к пробою диэлектрика (воздуха или активной среды)
и возникновению плазмы. Поэтому лучше использовать теле-
телескопическую систему с положительным увеличением, показан-
показанную на фиг. 3.10,6. В этом случае мы имеем Pi = +0,5, Pi =
= —1 и Т=\. Следовательно, М = I . ле I, а след
L 0 0,5 J
матрицы А + D = 2,5, как и в первом примере. Наибольшее
значение R, характеризующее излучение на выходе резонатора,
равно
Другое отношение компонент собственного вектора равно
в _ 1,5 _ ,
Х3 — А 0,5 — 2,0
Следовательно, плоскость L смещена на 1 м вправо от выход-
выходного зеркала и фактически проходит через общий фокус двух
зеркал. Поскольку наш луч распространяется в положительном
направлении оси г, он будет концентрироваться в ограниченное
дифракцией пятно в плоскости S, расположенной в бесконечно-
бесконечности. Поперечное сечение луча в плоскости L увеличивается до
тех пор, пока это позволяют диафрагмы, установленные в си-
системе.
Все примеры, рассмотренные до сих пор, касались резонато-
резонаторов с запланированными потерями, или резонаторов неустойчи-
неустойчивого типа. Наибольшее собственное значение е' определяет по-
поперечное увеличение (квадратный корень из этого собственного
значения дает усиление при двойном проходе, которое необхо-
необходимо для поддержания лазерной генерации). В то же время дей-
действительный собственный вектор, определяемый отношением
128 Глава 3
Pi'0,2 p^
ijf-Г 0g800 0,65T 1 1 _Л ллл .* л СПИ!
M-L/7 год л л?? A-O,ffOO -O,OUOl
a
oin
? SI
Фиг. 3.11
(e{ — D)/C или другим выражением В/(е{ — А), предсказывает
значение геометрического радиуса кривизны волнового фронта
излучаемой лазером волны.
Рассмотрим теперь геометрию резонатора устойчивого типа.
Резонаторы такого- типа всегда используют в маломощных ге-
гелий-неоновых газовых лазерах, которые имеют очень низкий ко-
коэффициент усиления. Два примера таких резонаторов показаны
на фиг. 3.11.
Резонатор, приведенный на фиг. 3.11, а, образован двумя во-
вогнутыми зеркалами, каждое из которых имеет радиус кривизны
10 м, причем расстояние между зеркалами равно 34 см. Запи-
Записывая соответствующие числа в метрах и диоптриях с точностью
до третьего десятичного знака после запятой, имеем Р\ =г Ра =
= +0,200 и Т в 0,340. Теперь вычислим матрицу
Г 0,800 0,6571
М - L -0,386 0,932 J • Ее след Л + Д = 1,732 - 2cos 9 «гсе-
видно, в этом случае в == 30°). Поскольку в лежит в диапазоне
углов 0—180°, то для собственных значений получаем е±1в =
= cos 0 ± / sin 8 = 0,866 ± 0,500 L Следовательно,, отношение
(комплексное) компонент собственного векторе равно
f."
', Оптические резонаторы и распространение лазерного пучка 125
' Для конкретной геометрии системы, которую мы выбрали,
I угол 6 равен (почти точно) 30°, или я/6 рад. Отсюда непосред-
\ ственно следует, что для двенадцати полных проходов через ре-
¦ зонатор матрица преобразования лучей равна единичной мат-
| рице. Используя преобразование F, введенное в § 11 гл. 1 для
в диагонализации матрицы, получаем
здесь
o
Следовательно, какой бы параксиальный луч в резонаторе
мы ни выбрали, после двенадцати полных проходов через резо-
резонатор его направление совпадет с первоначальным. В этом
смысле мы имеем устойчивый резонатор, в котором все лучи
после некоторого количества проходов воспроизводятся и ни
один из собственных лучей не удаляется от оси и не выходит из
системы.
Как мы сейчас увидим, нет никакой необходимости проекти-
проектировать резонатор с каким-либо заданным значением 6 — любое
значение 0 дает стабильный режим генерации в том смысле, что
потери излучения вследствие ухода лучей из резонатора отсут-
отсутствуют. Однако на примере второго резонатора, схема которого
показана на фиг. 3.11,6, можно понять необходимость исполь-
использования комплексных отношений, характеризующих собственные
векторы. Второй резонатор — это пример идеально устойчивого
«полуконфокального» оптического устройства, в котором Р\ = 1,
Г 0 11
Р2 = 0 и Т = 1. Тогда матрица М = I. I, а ее след А +
-f- D = 0 = 2cos 0 (очевидно, в этом случае 6 = 90°). Собст-
Собственные значения равны e±ini2 = ±t, а отношения компонент соб-
собственных векторов равны (±t — 0)/(—1) = =Ft (в этом случае
они чисто мнимые). Нетрудно установить, что для полученной
матрицы М выполняются следующие соотношения:
М2
Г—1 01
= 1 _ _ 1 I n M* = I. При двойном проходе луча резо-
резонатор эквивалентен хорошо известному конфокальному резона-
резонатору, а в случае четырех проходов каждый параксиальный луч
повторяет свою первоначальную траекторию.
Ниже будет показано, что при конструировании лазерных си-
систем обычно наиболее важную роль играет комплексное отноше-
отношение компонент собственного вектора, а не само собственное зна-
значение. Однако для полноты изложения мы приведем формулу,
которая позволяет сразу вычислить результирующую матрицу
для любого устойчивого резонатора при «-кратном проходе.
5 Зак. 774
tdO Глава 3
Пусть М — унимодулярная матрица с собственными значе-
значениями e±ie. Тогда мы можем написать
[81п(д+1N — DsinnB
С
sin в sinO
Этот результат, известный как теорема Сильвестра, можно ис-
использовать для любого значения 9 и любого целого значения п.
(Заменяя тригонометрические функции от 6 соответствующими
гиперболическими функциями от t, этот же результат можно ис-
использовать для вычисления n-кратного прохода луча через не-
неустойчивый резонатор.)
Студенту, которому необходимы навыки работы с теоремой
Муавра, можно рекомендовать вывести полученную выше фор-
формулу непосредственным вычислением с использованием проце-
процедуры диагонализации, описанной в § 12 гл. 1:
как
L С С Л 0 «_-и]|.-С ete~D J
в ас sine \ •
По-видимому, следует проверять также следующие положения:
а) Если в формулу Сильвестра подставить л = 1, то, по-
ГЛ В1
скольку 2 сое 8 во А ¦+• D, мы получим М = I _ _. I,
и требуется.
б) Подставляя пвш—1, имеем обратную матриду
i Г D -fil
в) Если л0 является числом, кратным 2я, то мы получаем
единичную матрицу.
§ 6. РАСПРОСТРАНЕНИЕ ГАУССОВЫХ ПУЧКОВ
И КОМПЛЕКСНЫЙ ПАРАМЕТР ПУЧКА
На этой стадии нашего обсуждения устойчивых резонаторов
необходимо ввести понятие «гауссова пучка». Это термин, кото-
который используется для описания пучка когерентногомизлучения с
дифракционной расходимостью, "энергия которого остается со-
сосредоточенной в приосевой области и быстро спадает на пери-
периферии в соответствии с гладкой функцией Гаусса;. Такой пучок
в действительности представляет собой наиболее близкое при-
приближение, которое допускает дифракция, к одиночному лучу
или пучку параксиальных лучей. По мере развития этой обла-
Оптические резонаторы и распространение лазерного пучка 131
сти исследований было обнаружено, что концепция гауссовых
пучков, введенная в чисто математическом смысле, позволяет
теперь гораздо более детально и полно описывать свойства оп-
оптических систем на языке так называемой «гауссовой оптики» ').
Как было показано Когельником и рядом других авторов,
детальное описание распространения гауссова пучка в свобод-
свободном пространстве нетрудно получить из волнового уравнения.
Вблизи оптической оси распределение амплитуды А(г, г) «фун-
«фундаментальной гауссовой моды» дается выражением
В этом выражении член 2nz/X описывает изменение фазы
вдоль направления распространения пучка, а ф представляет со-
собой небольшое дополнительное изменение фазы, которое зави-
зависит от z в соответствии с формулой tg^«= (Az/ita^). (Заметим,
что здесь X — длина световой волны, а не собственное значение.)
Коэффициент при г2 содержит мнимую и действительную ча-
части, каждая из которых играет важную роль для рассмотрения,
проводимого в данной главе. Действительная часть 1/до2 указы-
указывает на то, что в радиальном направлении модуль амплитуды из-
изменяется как функция Гаусса ехр(—r2/w2). Таким образом, ве-
величина до определяет «радиус пятна», или расстояние, на кото-
котором амплитуда света уменьшается в е раз, а яркость или интен-
интенсивность излучения — соответственно в е2 раз по сравнению с цен-
центральной областью пучка. Мнимая часть —2ni/2KR описывает
квадратичное изменение фазы волнового фронта в радиальном
направлении, причем величина /? представляет собой в обычном
смысле радиус кривизны поверхности постоянной фазы волны,
распространяющейся в положительном направлении оси г.
Вследствие эффекта дифракции гауссов пучок при распро-
распространении в свободном пространстве медленно расширяется и
расходится, так что радиус пятна до и радиус кривизны волно-
волнового фронта R являются медленно меняющимися функциями ко-
координаты г. Решая волновое уравнение в таком приближении,
получаем законы изменения этих двух параметров вдоль оси
пучка:
') В курсах квантовой механики показано, что гауссов волновой пакет
обладает минимальной неопределенностью, и, следовательно, из всех возмож-
возможных профилей именно пучки с гауссовым профилем обладают самой высокой
направленностью. — Прим. ред.
132
Глаёа 3
Дальняя зона
Ближняя мня
контур пучка
по уровню¦(%*)
Энергетический профиль
, гауссова пучка г=-гв
г-0
Фиг. 3.12
Асимптоты
Поверхности
постоянной ф/ш
На фиг. 3.12 показано поведение этих»величин в плоскости
(у, г), а в табл. 3.2 — значения различных параметров и соот-
соответствующие формулы. Как мы увидим ниже, кривая, опреде-
определяющая уровень постоянной интенсивности пучка или его ра-
радиус, на котором квадрат амплитуды уменьшается в ё2 раз, пред-
представляет собой гиперболу. В точке г = 0 (перетяжка пучка)
она имеет минимальное расстояние от оси г, равное w0. Ее асим-
асимптоты расположены под углом V3 — ± (Я,/яоH) к оси г.
Вблизи перетяжки гауссова пучка поверхности постоянной
фазы являются плоскостями, щ в точках ± z0 == ± яа^/А. их кри-
кривизна достигает максимального значения. Центральную область
длиной 2г0, в которой сечение пучка остается практически по-
постоянным, иногда называют «ближней зоной» («ближним по-
полем»), а область, в которой происходит асимптотическое расши-
расширение, — «дальней зоной».
Таблица SJ2
Параметр
.«
R(z)
Я(г)
V,
Значение
Радиус пучка, определяемый
по уровню 1/е2
Радиус кривизны поверхно-
поверхностей постоянной фазы
Комплексный параметр кри-
кривизны
Радиус дифракционной расхо-
расходимости пучка
Асимптотический угол расхо-
расходимости пучка
• (ж)-
«(.)-
1
Формула
Юо| 1 + Г —-j | 1 *
*[f+(*¦*)']
ш 1 . А
Л (г) ' я[т(г)]2
t
Оптические резонаторы и распространение лазерного пучка 133
Параметр wQ/w, стоящий в выражении для амплитуды перед
экспонентой, показывает, что вблизи перетяжки, или фокуса,
пучка напряженность электрического поля больше, чем в даль-
дальней зоне, где пучок существенно расширяется. Однако полная
энергия, переносимая пучком, остается постоянной для всех зна-
значений z (при условии, что среда не является поглощающей или
усиливающей). В радиальном интервале, ограниченном гипербо-
гиперболической поверхностью, на котором интенсивность пучка умень-
уменьшается в е2 раз, сосредоточено 86% всей падающей энергии.
Уравнения, приведенные выше и определяющие зависимость
радиуса пятна w(z) и радиуса кривизны R(z) от z, хотя они и
громоздки, позволяют нам вычислить особенности распростране-
распространения гауссова пучка в свободном пространстве или при прохо-
прохождении его через оптический промежуток конечной длины. Ин-
Интуитивно понятно, что если гауссов пучок проходит через тон-
тонкую линзу или поверхность р оптической силой Р, то радиус
пятна остается неизменным, а расходимость пучка 1/R умень-
уменьшается в соответствии с формулой (\/R) — Р.
Удобный метод, позволяющий одновременно следить за обои-
обоими этими параметрами луча, получается, если их скомбиниро-
скомбинировать и образовать новую величину, которую назовем комплекс-
комплексным параметром кривизны q(z). Вместо того чтобы записывать
в выражении для амплитуды пучка коэффициент при г2 как
(l/w2) — Bni/2XR), мы напишем просто —2ni/2Xq, где q может
быть комплексным числом.
Из этого определения немедленно следует, что
q R nw* '
Действительная часть величины l/q определяет расходимость по-
поверхности постоянной фазы, а мнимая часть пропорциональна
l/w2 и характеризует степень концентрации энергии в приосевой
области пучка.
Подставляя этот новый параметр в выражения для R(z) и
w(z), записанные выше, нетрудно убедиться, что при распро-
распространении в свободном пространстве справедливо равенство
q(z) = qo-\-z, где qo = (iX/nwfy~l представляет собой значение
q в области перетяжки пучка (т. е. при z = 0). Следовательно,
в случае распространения пучка через оптический промежуток
толщиной Т имеем q^ = q\ -f- Т, т. е. точно такую же формулу,
как и для действительных значений R.
В случае преломления на тонкой линзе или на поверхности
с оптической силой Р мы имеем четыре уравнения. Согласно оп-
определению, два из них записываются в виде
1 \ , I А* 1 1 , (Л
____ ^__ 1 ___^_ тя ___ i | ___^
134 Глава 3
Третье уравнение I/R2 = 1/Ri— Р описывает расходимость пуч-
пучка, и, наконец, четвёртое уравнение а>2 = Wi представляет собой
условие постоянства радиуса пятна при прохождении тонкой
линзы. Объединяя эти уравнения, находим \/q2 = l/<7i — Р. Та-
Таким образом, мы снова получаем, что уравнение, определяющее
Преобразование комплексного параметра q, в точности такое же,
как и для действительного значения R.
Хотя предыдущие рассуждения опираются на формулы, ко-
которые мы привели без доказательства, они показывают, что мы
можем преобразовывать комплексный параметр кривизны q
точно таким же образом, как и параметр R, используя при этом
либо ?Г-матрнцы, либо Л-матрицы, либо, разумеется, их любую
комбинацию. Кроме того, если известна общая матрица всей оп-
оптической системы, мы можем использовать правило ABCD: При
этом получим комплексный параметр кривизны на выходе опти-
оптической системы:
В § 7 настоящей главы мы покажем, что комплексные зна-
значения отношения компонент собственного вектора для устойчи-
устойчивого резонатора, смысл которых до сих пор оставался неопре-
неопределенны^ можно идентифицировать со значениями параметра
q Основной -гауссовой моды, генерируемой в данном резонаторе,
при использовании соответствующих апертур и достаточного уси-
усиления активной среды лазера.
6.1. Проверка правила ABCD для гауссовых пучков
Прежде всего попытаемся показать, используя уравнение ди-
дифракции, рассмотренное в § 2, что если q\ описывает гауссов пу-
пучок в плоскости ОПь то на выходе в плоскости ОПг мы получим
другой гауссов пучок, определяемый параметром
Запишем общее одномерное уравнение дифракции
Подставляя сюда амплитуду гауссова пучка
Оптические резонаторы и распространение лазерного пучка 135
"? и 1!:яользуя выражение для эйконала
имеем
r Г
ni ША
Для вычисления этого интеграла сделаем следующие две под-
подстановки:
w==-lB и ТС5Г +U = -"?-•
Тогда интеграл принимает вид
ехр у — -^-J exp Bя/у| v) dyu
Это хорошо известная формула преобразования Фурье, причем
значение интеграла равно sexp (—nv2s2). Переходя к исходным
обозначениям, получим
A
Записывая
в виде
f — l
X»p[
(<
V
ч'Л
^ t
\Aqi+Bj
величину
ADq,
+ BD-
(ri
Ufa
exp
n
(-J) 1
г 2Я2В У
(Л<7, + В)
u пи
-1 -I1/»
1 ^^
г -^^,
л^. + в
В (Cqi + D)
A4l+B '
получаем окончательное выражение:
136 Глава 3
В § 8 настоящей главы мы покажем, что комплексную вели-
величину [qi/(Aqi-\-В)]1/; стоящую перед экспонентой, можно пред-
представить в виде [(Wi/w2) exp (#i2)]'/j, где ш2 — действительное
число, равное радиусу пятна пучка, а фи — действительное чис-
число, определяющее фазовый сдвиг, возникающий при распростра-
распространении пучка между двумя опорными плоскостями. (Кроме того,
конечно, имеется очень большой набег фазы всего пучка, опре-
деляемой постоянной величиной \ ndz, которую мы опустили
в выражении для эйконала.)
Рассмотрим теперь подробнее показатель экспоненты, заклю-
заключенный в квадратные скобки, и покажем, что ои имеет квадра-
квадратичную зависимость от ц$, характерную для гауссова пучка.
Приравнивая показатель экспоненты величине Bni/k) (y^2q2),
мы находим, что q2 — комплексный параметр кривизны гауссова
пучка в выходной опорной плоскости — действительно дается
выражением
Выше мы провели вычисления для одномерного случая, т. е.
фактически для цилиндрических волн. Однако любую гауссову
функцию, которая описывает амплитуду сферической волны, мо-
можно представить в виде произведения двух независимых одно-
одномерных цилиндрических волновых функций.
Таким образом, если мы умножим амплитуду А%{у%) на сб-
ответствующую амплитуду, зависящую от координаты х, то по-
получим для сферической волны следующее выражение:
где Ш|И»2- два различных радиуса пятна, а
„ . Aqt + В
— значение q в опорной плоскости, расположенной на выходе
системы.
§ 7. РАСЧЕТ ПАРАМЕТРОВ ПУЧКА, ИЗЛУЧАЕМОГО ЛАЗЕРОМ
Мы будем теперь рассматривать комплексное отношение
компонент собственного вектора для устойчивого резонатора как
значение q, которое определяет геометрию гауссова пучка, гене-
Оптические резонаторы и распространение лазерного пучка 137
рируемого в системе, если она работает в режиме возбуждения
основной моды.
В соответствии с результатами, полученными в § б, если
ГА В1
I . п I — матрица, описывающая резонатор, и если ее два
собственных значения равны exp(±i&), то значения q, сохра-
сохраняющиеся при полном проходе резонатора, даются выраже-
выражениями
<7= е*Р(±^6)-,Р ^ ИЛи (что эквивалентно) i?°= е
причем я > 0 > 0. Обращая второе уравнение и учитывая, что
cos 8 = (А + D)/2, имеем
1 _ ехр (± /9) — A cos 6 — А {sin 6 _ D — A i sin 8
q ~ В = В ^ "В 2В ± В '
Но в соответствии с определением
1 ш 1 . /Я
""° R "¦" лда2 '
Приравнивая в последних двух выражениях их действительные
и мнимые части друг другу, получаем
JL Р—.А
R = 2В
и, в зависимости от того, какое берется собственное значение,
Я ±sin8
яда2 В
Можно показать, что отрицательная величина w2, отвечаю-
отвечающая второму собственному значению, соответствует нереальному
случаю, когда энергия пучка должна была бы сильно возрастать
при удалений'от оси. Отбрасывая это решение и оставляя только
первое собственное значение h = ехр(+/в), находим основную
моду гауссова пучка, радиус пятна которого дается выражением
w = (ЯВ/я sin 0) ч>. Поверхности постоянной фазы этого пучка
имеют кривизну R = 2B/(D — А). Разумеется, значение функ-
функции, входящей в полученное выше выражение, можно вычислить
непосредственно через матричные элементы, что дает
Другой метод расчета параметров гауссова пучка основан на
преобразовании выражения для q. Выделим в нем мнимую и
действительную части. С одной стороны, мы имеем
_ ехр (+ гб) — Q A — D , i sin 6
Ч— Q ^ 2G +~Т~'
Таблица ЗЛ
СВЯЗЬ МЕЖДУ МАТРИЦЕЙ РЕЗОНАТОРА И ЕГО ОПТИЧЕСКИМИ СВОЙСТВАМИ
Матрица, описывающая полип»проход через резонатор» имеет вид!" Г|, где AD — BC
п все матричные элементы действительны.
Неустойчивые системы
Расематрпаеиое евоймво
Устоятавые еасммы
A + D
A + D
> 1, условие неустойчивого
резонатора (положитель-
(положительная ветвь) ' '
< — 1, условие неустойчивого
резонатора (отрицатель-
(отрицательная ветвь) ~ -
След матрицы
, условие устойчивого
резонатора
здесь
Главное собствен^» значение
(t берется положительным, а 9-
в интервале 0 -н я)
i.i — ехр (Л) — cos 8 -М sin в;
здесь
1
Радиус крмшаим R
¦ gg *
D-A
Отношение компонент собственного
вектора
А0
Комплексный параметр кривизны |
"Г"
в
&—А
2В
1 , IX
+
Для генерации необходимо, чтобы уси-
усиление эа полный проход (в двумерном
случае) превышало exp Bt). Приведен-
Приведенные выше формулы определяют радиус
кривизны волнового фронта на выходе
системы
Параметры гауссова пучка
1. Радиус кривизны
2. Расходимость волнового фронта
3. Радиус пучка
4. Положение перетяжки
5. Радиус пучка в перетяжке
6. Конфокальный параметр пучка
7. Половина угла расходимости
в дальней зоне (в радианах)
Параметры гауссова пучка находим I
уравнения для \/q:
измеряются в вы-
выходной опорной
плоскости
Из уравнения для q получим
A-D
2С
(влево от опорной пло-
плоскости),
— XsinO \'Л
ЯША
-sin6
го'
яшо "~ zo "~ V
Хорошая, при условии что число Фре-
Френеля системы достаточно велико и хва-
хватает усиления
Селекция мод
Проявляется лишь при малых числах
Френеля
') Там, где в формулах имеются два звака, верхний знак соответствует положительной ветви, а нижний—отрицательной ветви.
*) Необходимо тщательно сладить аа обозначениями и не путать длину волны Я, с главным собственным значением, которое обозна-
обозначено символом Я.,.
140 Глава S
С другой стороны, как было показано в предыдущем параграфе,
если <70 = — /яш^/Я, есть значение параметра q в перетяжке гаус-
гауссова пучка, то для опорной плоскости, расположенной на рас-
расстоянии z справа от перетяжки, мы получим (используя пра-
правило ABCD для оптического промежутка длиной z)
Сравнивая эти два выражения для значения q в выходной
опорной плоскости, находим, что перетяжка пучка располагает-
располагается на расстоянии (А —D)/2C слева от опорной плоскости и что
минимальный радиус пятна (соответствующий перетяжке) равен
— Я sine у/.
-(:
Расстояние яп^/К иногда называют конфокальным параметром
пучка и обозначают Zo1). Его можно вычислить по формуле
sine
В табл. 3.3 сведены результаты, которые мы только что об-
обсудили, а также соответствующие соотношения, полученные на-
нами для неустойчивого резонатора. Однако, прежде чем рассма-
рассматривать конкретные примеры их использования, обратим внима-
внимание на ряд вопросов, связанных с дискриминацией мод.
Во-первых, если устойчивый резонатор сконструирован так,
что действующие диафрагмы достаточно малы и, следовательно,
число Френеля сравнимо с единицей, то потери энергии вслед-
вследствие дифракции на краях диафрагмы чрезвычайно малы и нет
никакой гарантии, что при включении лазерного усиления будет
генерироваться только основная гауссова мода. В самом деле,
в некоторых газовых лазерах усиление в разрядной трубке не-
несколько увеличивается вблизи стенок трубки, так что сущест-
существует большая вероятность возбуждения поперечных мод выс-
высшего порядка.
Во-вторых, математики могут заметить, что если число Фре-
Френеля достаточно мало и потери, возникающие на диафрагме при
любом полном проходе резонатора, достаточно велики, то соб-
собственные моды резонатора должны были бы описываться вытя-
вытянутыми сфероидальными функциями. Однако практически рас-
распределение амплитуды на выходе лазера все же с достаточно
большой степенью точности описывается гауссовой функцией.
') В отечественной литературе эту величину принято называть радиусом
дифракционной расходимости пучка, поскольку на этом расстоянии за счет
дифракции площадь пятна станоаатся в два раза больше, чем в перетяжке. —
Прим. перев.
Оптические резонаторы и рйспространение лазерного пучка \4\
которую для получения мод высших порядков следует умножить
на полином соответствующего порядка (в частности, для прямо-
прямоугольной апертуры — на полином Эрмита, а для круглой — на
обобщенный полином Лагерра). При условии, что полиномы нор-
нормированы правильно, для вычисления значений q, характери-
характеризующих гауссову функцию по-прежнему можно использовать
правило ABCD.
vВ-третьих, даже если поперечный размер резонатора ограни-
ограничен таким образом, что возбуждается только основная гауссова
мода, все же могут возникать трудности, связанные с вырожде-
вырождением. Мы проиллюстрируем это обстоятельство, рассматривая
два резонатора, описанные в § 5 настоящей главы.
Для первого резонатора (см. фиг. 3.11, а) мы вычислили ма-
Г 0,800 0,657 П
трицу системы, т. е. М — \ __Q 3g6 0 932 I ' пРичем 9 = я/6.
Следовательно, в этом случае sin 0 = 0,5. Подставляя эти циф-
цифры в формулы, приведенные в табл. 3.3, находим
2@,657)
А 0,932 — 0,800 '
(Волновой фронт на выходе резонатора имеет ту же самую кри-
кривизну, что и поверхность выходного зеркала.)
п х Г @,633) A0-6) @,657) T/j - 1С ,„_4 псп
Радиус пятна w = \—— я/05)—J ==5,15- 10 м»0,52 мм
(значение, вполне соответствующее небольшому лазеру).
п 0,800 — 0,932 _ ,_,
Положение перетяжки z= /_0звбН2) = 0,171 м
(перетяжка смещена на 17 см влево и располагается в центре
резонатора).
о я Г(— 0.633) A0~6) @,5) T/j
Радиус перетяжки до0 = I я /_0 386) — I ~
= 5,11 • 10~4 MgaO,51 мм
(это значение почти равно радиусу пятна на выходном зеркале,
так что внутри резонатора гауссов пучок имеет практически по-
постоянное поперечное сечение).
„ , „ яE,11-Ю-4J , оп
Конфокальный параметр пучка z0 = —i—-7—rsr = 1,30 м.
@,633) A0 )
Ближняя зона пучка простирается от его перетяжки, смещенной
на 17 см влево от выходного зеркала, до расстояния 1ДЗ м
вправо. В этой плоскости радиус пятна увеличится до л/2 до0
Глава 8
P,-Q2 Т'ОМ РгжО,г
Ъ I й
-*¦ z
Диаметр Гауссов
перетяжка 1,02мм профит
а
' Т'ыгп
?-*¦ s
Диаметр
пертяжт О
Фиг. 3.13
(т. е. его значение будет 0,7 мм), а радиус кривизны волнового
фронта R «= 2*0 » 2,6 м (фиг. 3.13, а).
Половина угла расходимости в дальней зоне ==
Приведенные выше цифры соответствуют одной из вполне
реальных конструкций небольшого гелий-неонового газового ла-
лазера. Они показывают, что гауссов пучок в точности воспроиз-
воспроизводит себя после каждого прохода резонатора.
Предположим теперь, что мы ввели в тот же самый резона-
резонатор центральный гауссов пучок, радиус пятна и радиус кривизны
которого R имеют значения, слегка отличающиеся от приведен-
приведенных выше. В этом случае полной воспроизводимости пучка уже
не будет, но после шестикратного полного прохода резонатора,
поскольку мы выбрали собственное значение, соответствующее
В = я/6 (и поскольку эта мода симметрична), опять получим
исходный пучок.
Если резонатор характеризуется большим числом Френеля,
то гауссов пучок последнего типа может циркулировать беско-
бесконечно долго, Однако .если апертуры двух торцевых зеркал неве-
/ Оптические резонаторы и распространение лазерного пучка 143
лики, то минимальные потери на краях апертур будут у того
пучка, радиус пятна которого остается постоянным при каждом
его проходе через резонатор. На практике устойчивая генерация
в режиме основной моды обычно достигается в тех случаях, ког-
когда 9 точно делится на я или 2я.
Другой пример, в котором реализуется такая же ситуация,
представляет собой полуконфокальный резонатор — вторая ус-
устойчивая система, рассмотренная в § б настоящей главы. Для
этой системы матрица, описывающая полный проход, имеет вид
О 11
I • , а главное собственное значение равно е+19 = еЫ12 =
= I, так что sin 9=1.
В этом случае А = D. Следовательно, радиус кривизны R
волнового фронта на выходе равен бесконечности, а поскольку
z = 0, то перетяжка гауссова пучка расположена непосред-
непосредственно в плоскости выходного зеркала. Конфокальный пара-
параметр z0 = 1 м, и формулы для ш и ад0 позволяют вычислить ра-
радиус пучка (фиг. 3.13,6)
/ a.\'/j @,633• ю~6 V7* л лп ln-4 n ,е
^¦jj-l = 1 ——jj ) =4,49 -10 м fa 0,45 мм.
Поскольку этот радиус перетяжки почти такой же, как и в пре-
предыдущем примере, половина угла расходимости пучка в даль-
дальней зоне будет порядка 0,4 мрад. Если предположить, что ла-
лазерная трубка в 3 раза длиннее, чем в предыдущем примере, то
можно ожидать увеличения мощности пучка более чем в 3 раза,
однако, по всей вероятности, эта мощность распределится по
большему числу аксиальных мод, чем в случае лазера с более
коротким резонатором.
Мы не собираемся обсуждать здесь подробно методы селек-
селекции аксиальных мод. Однако существует простая формула, кото-
которая выражает зависимость частоты данной оптической моды не
только от расстояния между зеркалами и номера аксиальной
моды, но также и от поперечных индексов моды и от действую-
действующего собственного значения е'9. Для более подробного ознаком-
ознакомления с этими вопросами читателю следует обратиться к ра-
работе Когельника с сотр. (см. литературу в конце книги).
Прежде чем рассматривать вопросы согласования мод, мы
должны вернуться к вопросу, упомянутому в предыдущем пара-
параграфе, а именно рассмотрим сдвиг фаз фц, возникающий у гаус-
гауссова пучка при распространении его от одной опорной плоско-
плоскости до другой, используя правило ABCD. В общем случае этот
набег фазы может привести к изменению яркости и, следова-
следовательно, напряженности поля в центральной области пучка.
Рассмотрим сперва гауссов пучок, радиус перетяжки кото-
которого ш0 мал и сравним с %. Для достаточно большого диапазона
144 Глава 9
углов (dtk/nwo рад) волновой фронт световой волны, достигаю-
достигающей плоскости ОПь можно считать сферическим с радиусом Ri.
Мы можем представить это геометрически как пучок лучей, так-
также расходящихся из точки, расположенной в области перетяжки.
Для некоторого луча, принадлежащего данному пучку и распро-
распространяющегося под углом Vi к оси, можно записать лучевой век-
вектор I т/ I t который в выходной плоскости преобразуется к
виду
Г RiV»! rARlVl + BVll
L V2 }'=lcRlVl+DVir
При условии что в оптической системе отсутствует поглоще-
поглощение, весь световой поток, попадающий на ОПь целиком пройдет
через ОП2. В частности, доля энергии, прошедшая через круг
радиусом у\ = R\V\ в плоскости ОПь должна пройти через круг
в плоскости ОПг, радиус которого у% = AR\V\ -\~ BV\. Таким об-
образом, очевидно, если мы будем рассматривать эту задачу в
двух измерениях, то энергию (яркость) в приосевой области
можно найти, умножая плотность потока света на «фактор пло-
площади» [Ri/(ARi + В)]2, а амплитуду электрического поля сле-
следует умножить на R\/(AR\ + В) или, в одномерном случае, — на
W( + )]
Как было показано выше, если область перетяжки гауссова
пучка не слишком мала, то удовлетворительное формальное опи-
описание пучка можно получить при условии, что мы рассматри-
рассматриваем любое отношение y/V не как действительное значение R, а
как комплексное значение q. Однако очень сложно найти какую-
либо разумную интерпретацию комплексных значений как для
у-, так и для У-значений. Тем не менее, как было показано в
§ 6 настоящей главы, множитель qJ(Aqi + В) наглядно свиде-
свидетельствует о том, что эти значения обязательно появляются в
процессе решения уравнения дифракции. При этом мы устано-
установили, что модуль этого комплексного множителя определяет от-
отношение wifwt, соответствующее отношению t/ifyt, рассмотрен-
рассмотренному выше, а аргумент фц определяет фазовый сдвиг всего пуч-
пучка (в дополнение к значительно большему набегу фазы 2яЛД).
Чтобы проверить, что
I "l \=(WlY
I Aq, + В | V и* ) '
воспользуемся обращенной формой правила ABCD:
1 IX _ 1 Су, + D __ С + Р1дх
7?
Aqx+B
Оптические резонаторы и распространение лазерного пучка 145
Умнол^я числитель и знаменатель последнего выражения на
число, комплексно сопряженное знаменателю, и записывая зна-
знаменатель в исходной форме A -f- B/q\, получаем
1 i% _ (с + ?>//?1 + а/)/яю|!)(л + в//?1
Т2 лЩ, \А+В/Й1\2
Приравнивая мнимые части этого уравнения, имеем
iX iX (DA+DBIRX-CB-DBIR{) iX j ]
nw\ nw\ | A + B/q{ |2 nw\
(здесь мы учли, что определитель AD — ВС =1). Следователь-
Следовательно, в окончательном виде формула преобразования размера
пятна записывается следующим образом:
(JSLY
V W2 )
или (что эквивалентно)
В частном случае, когда гауссов пучок совершает полный
проход через оптический резонатор, комплексный множитель
qi/(Aqi -j- В) по-прежнему позволяет нам найти преобразование
размера пятна или набег фазы. Но если мы выберем значение
цх так, что оно совпадет с собственным значением рассматривае-
рассматриваемого резонатора, т.е. (eie — D)/C = B(eie — А), то величина
qi/(Aq] + В) будет равна просто e~ie. Хотя, как и следовало
ожидать, размер пятна не меняется, остается фазовый сдвиг, ко-
который определяется собственным значением резонатора eie.
(При соответствующей ситуации для неустойчивого резонатора
в нем не происходит никакого фазового сдвига, но значение у
умножается на действительное собственное значение е*, т. е. на
поперечное увеличение системы.)
В большинстве оптических приборов небольшой фазовый
сдвиг, возникающий одновременно для всех лучей пучка, как
правило, не играет существенной роли. Однако регулярное по-
повторение фазового набега внутри лазерного резонатора приво-
приводит к небольшому смещению оптической частоты излучения на
выходе системы. Корреляция фазового сдвига такого рода мо-
может, кроме того, потребоваться при очень точных интерфероме-
трических измерениях длины, в особенности при использовании
излучения в инфракрасном или микроволновом диапазонах.
Здесь следует сделать два небольших замечания относитель-
относительно учета оптических эффектов, которые могут давать выходное
зеркало и его подложка. В большинстве случаев используются
146 Глава 3
частично отражающие вогнутые поверхности. Если предполо-
предположить, что такая поверхность имеет кривизну, то, за исключе-
исключением тех случаев, когда прозрачная поверхность подложки так-
также имеет кривизну и полностью компенсирует влияние кривизны
частично отражающей поверхности, зеркало будет действовать
как слабая линза (обычно рассеивающая). Эта линза не будет
оказывать никакого влияния на форму волны, возбуждаемой
внутри резонатора, но будет изменять значение Я пучка, выхо-
выходящего из него. Однако если сделать прозрачную поверхность
выходного зеркала слегка выпуклой, то на выходе можно полу-
получить гауссов пучок, который слабо сходится. В таком случае
вся ближняя зона пучка будет находиться вне резонатора и мо-
может быть пригодна для внешнего использования (без примене-
применения какой бы то нн было дополнительной оптической системы
для согласования мод; такие системы мы обсудим в следующем
параграфе).
Кроме того, ва исключением тех случаев, когда прозрачная
поверхность выходного зеркала скошена под достаточно боль-
большим углом или на нее нанесено высококачественное просветляю-
просветляющее покрытие, интерференционные эффекты, обусловленные про-
прозрачной поверхностью и основной частично отражающей по-
поверхностью зеркала, нередко приводят к возникновению полос
или кольцевых структур в сечеиии пучка на выходе оптической
системы. Для лазерных систем с высоким коэффициентом усиле-
усиления, по-вндимому, конструировать резонатор лучше таким обра-
образом, чтобы выходное зеркало было плоским; при этом требуе-
требуемая оптическая обратная связь может быть обусловлена обеими
поверхностями зеркала, действующего как резонансный отража-
отражатель. В этом случае характеристики выходного излучения «сгла-
«сглаживаются» и улучшаются.
Разумеется, можно использовать более строгий подход' к
проблеме одномодовой лазерной генерации. Например, если мы
будем использовать теорию Гюйгенса — Френеля, то найдем, что
распределение амплитуды А (у) световых воли на выходе из ре-
резонатора должно удовлетворять интегральному уравнению вида
Ядро этого уравнения К (у,«/') представляет собой (комплекс-
(комплексную) симметричную функцию, которая описывает ие только фа-
фазовые сдвиги, возникающие при полном проходе резонатора, но
также и эффекты, связанные с ограничением сечения пучка ко-
конечными апертурами системы. Потери, вносимые апертурами,
должны, безусловно, компенсироваться усилением, обеспечивае-
обеспечиваемым активной средой лазера.
Оптические резонаторы и распространение лазерного пучка 147
Простые решения, которые обсуждались в данном парагра-
параграфе, получены в действительности при условии, что эффектами,
связанными с действием конечных апертур, можно пренебречь,
а функцию К(у,у') можно заменить ехр[Bш'Д) W(y, у')], где
W — обычная функция эйконала, описывающая полный проход.
Это приближение дает полезные результаты в двух случаях:
1) для устойчивого резонатора с числом Френеля N, близким
к единице, и 2) для неустойчивого резонатора с большим чис-
числом Френеля и постоянным коэффициентом усиления.
Однако если рассматриваются резонаторы, которые рабо-
работают на границе между устойчивым и неустойчивым режимами
генерации [например, плоскопараллельный резонатор или резо-
резонатор с концентрическими зеркалами, для которого (A-\-D)/2
имеет номинальное значение, равное единице], то формулы, по-
полученные в этом приближении, следует использовать с предо-
предосторожностью. В таких случаях, по-видимому, необходимо ре-
решать точную дифракционную задачу: однако даже такая поста-
постановка задачи может оказаться бесполезной, если в системе при-
присутствуют оптические аберрации или фазовые искажения, обус-
обусловленные накачкой. При этом необходимо рассматривать так-
также всевозможные динамические (переходные) и нелинейные
процессы, которые могут развиваться в реальных лазерных си-
системах. В большинстве случаев получить генерацию в режиме
одной моды достаточно трудно.
§ 8. ПРИМЕНЕНИЕ ПРАВИЛА ABCD ДЛЯ СОГЛАСОВАНИЯ МОД
Хотя лазеры представляют собой очень специфические ис-
источники света, они уже широко используются в разнообразных
приложениях. Поэтому исследователь, работающий с лазером,
рано или поздно обнаружит, что ему необходимо преобразовать
форму гауссова пучка, который выходит из резонатора, в соот-
соответствии с конкретной постановкой эксперимента. В некоторых
случаях для этого можно рекомендовать готовые, имеющиеся в
продаже приспособления, например, расширитель пучка; в дру-
других случаях достаточно использовать обычную линзу. В данном
параграфе мы покажем, как решаются задачи такого рода, свя-
связанные с преобразованием пучков.
Однако сначала рассмотрим задачи, которые возникают при
последовательном соединении классических оптических систем,
формирующих изображение. Предположим, например, что при-
приближающаяся комета или вспышка сверхновой звезды привлек-
привлекли широкий общественный интерес; тогда инженерно-техниче-
инженерно-техническому персоналу на телевидении может понадобиться временно
совместить телевизионную камеру с используемым астрономиче-
астрономическим телескопом.
Ш Глава i
Для того чтобы такое совмещение не приводило к существен-
существенному ухудшению качества изображения, вторая оптическая си-
система должна иметь этандю, по крайней мере большую или рав-
равную по величине этандю первой системы, и если требуется каче-
качественное изображение деталей, то необходимо, чтобы простран-
пространственно-частотное произведение для второй системы было таким
же, как и для первой. Если эти условия выполнены и если вы-
выходной люк телескопа и входной люк телевизионной камеры
расположены в бесконечности, то необходимо всего лишь убе-
убедиться в том, что входной зрачок камеры совпадает по размерам
н совмещен по оси с выходным зрачком телескопа. (Виньетиро-
(Виньетирование, которое, вероятно, возникает, если эти требования не вы-
выполнены, обсуждается в приложении I.)
Представим себе, что имеется более сложная ситуация, когда
этандю двух оптических систем хотя и совпадают, но размеры
их люков и зрачков отличаются друг от друга и сами они рас-
расположены в различных точках оси г (хотя и не в бесконечно-
бесконечности) .
Для выяснения апертурных свойств первой системы выберем
плоскость ОП) так, чтобы она находилась сразу за последней
оптической поверхностью этой системы, но таким образом, что-
чтобы она ие совпадала ни с выходным зрачком,, ни с выходным
люком системы. Предположим, что выходной зрачок расположен
на расстоянии R\ слева от плоскости ОП1; обозначим через Vi
максимальный угол луча, проходящего из центра выходного
зрачка к краю выходного люка. Очевидно, в плоскости ОП) со-
ответствующии лучевой вектор имеет вид v
Если выходной люк расположен на расстоянии R\ слева от
плоскости ОПь a V\ — максимальный угол, под которым рас-
распространяется луч, идущий из центра выходного люка к краю
выходного зрачка, то соответствующий лучевой вектор анало-
аналоI уУ
гично записывается в виде
L v, у
Как отмечалось в § 3 настоящей главы, этандю первой си-
системы определяется детерминантом матрицы, образованной эти-
этими двумя крайними лучевыми векторами. Эта матрица имеет
вид
fVi*i УМ]
Рассматривая теперь вторую оптическую систему, определим
ее свойства аналогичным образом, причем плоскость ОПг рас-
расположим на некотором, удобном для вычислений, расстоянии
Оптические резонаторы и распространение лазерного пучка 149
перед первым элементом системы. Если входной зрачок си-
системы смещен на расстояние R2 влево от ОПг, то луч, проходя-
проходящий через центр входного зрачка и край входного люка, должен
описываться лучевым вектором I „ I , где Кг — максималь-
максимальный угол, допускаемый входным люком системы. Таким же об-
V2 J
разом получим лучевой вектор , , характеризующий луч,
L V2 J
идущий из центра входного люка, расположенного на расстоя-
расстоянии /?2 слева от опорной плоскости ОПг, к краю входного
зрачка. (Будем считать, что как R2, так и /?2 могут принимать
отрицательные значения.)
Оба лучевых вектора, определенных таким образом, можно
записать в виде матрицы выходящего луча:
V2R2
Определитель этой матрицы дает этандю второй оптической си-
системы. В проводимых здесь вычислениях мы должны предполо-
предположить, что det(S2) = det(Si). (На практике, если вторая оптиче-
оптическая система представляет собой камеру с переменной апертур-
ной диафрагмой, очень полезно в конечном счете приоткрыть
апертурную диафрагму второй системы чуть больше, чем это
необходимо для точного согласования.)
Чтобы достичь точного согласования этих двух систем, ме-
между ОП) и ОПг нужно поместить дополнительную оптическую
систему, матрица которой М должна удовлетворять следующему,
матричному уравнению:
где S\ и S2 — матрицы, определенные выше.
Считая, что определитель матрицы Si не обращается в нуль,
можно умножить обе части этого матричного уравнения на об-
обратную матрицу S~l. В результате получаем выражение для М
в явном виде:
м = s2st1=s2
или, если полностью выписать матричные элементы,
А
С
V[ -
160
Глава 3
Чтобы исключить параметр V из приведенного выше выра-
выражения, удобно ввести величину т, характеризующую угловое
увеличение VgJVu которое показывает, во сколько раз увеличи-
увеличивается угол луча, проходящего через центр выходного зрачка
системы 1, по сравнению с углом луча, проходящего через центр
входного зрачка системы 2. Поскольку линейное увеличение об-
обратно угловому увеличению, то т можно записать также как
следующее отношение:
Радиус выходного зрачка системы 1
Радиус входного зрачка системы 2 '
Аналогичным образом определим величину т' = VjVi как
угловое увеличение люка. Но мы должны здесь сделать следую-
следующее замечание, а именно: чтобы обе величины этандю были оди-
одинаковы, должно существовать соотношение, связывающее т и
т'. Мы имеем
det(S,) =
Vi
Следовательно,
Учитывая эту связь между т и т', мы можем теперь запи-
записать
М
ТА В1
[с d\
mVl
Если перемножить эти две матрицы и разделить каждый эле-
элемент полученной матрицы на стоящую в знаменателе скалярную
величину ViV'i(Ri—Rt), то мы получим у
М
Г
с
B
mR3 —
m RXR2 —
/?,-/?
т
mRl — mR\
Таким образом, каждый из элементов А, В, С и D полностью
определен, и задача теперь состоит в том, чтобы построить опти-
оптическую систему, отвечающую такой матрице. Здесь мы обсудим
только тот случай, когда коэффициенты, характеризующие уве-
Оптические резонаторы и распространение лазерного пучка
151
личение зрачка и люка т и т', имеют одинаковые значения.
В этом случае элемент С, очевидно, обращается в нуль, и, сле-
следовательно, требуется афокальная система с угловым увеличе-
увеличением т. Тогда искомая матрица принимает вид
I
к :i-[f
т
Матрица афокальной системы с угловым увеличением т,
описывающая преобразование луча между двумя оптически со-
сопряженными опорными плоскостями, в соответствии с табл. 3.1
Г 1//п 0 1
записывается в виде I I . Однако если эту матрицу ум-
умножить справа и слева на соответствующие ^"-матрицы, то мы
можем выбирать значения В произвольно, в частности так, что-
чтобы выполнялись определенные условия:
Г1 /2-]Г1//и 0-1Г1 tnrl/tn (hm+ti/m)-]
Lo 1J L 0 mJLo 1J L 0 m J "
В практических целях мы смещаем либо афокальную систе-
систему, либо, если это возможно, вторую оптическую систему вдоль
оптической оси на такое расстояние, что
ty
т
т
(Поскольку в нашей установке мы имеем два свободных пара
метра t\ и /2, осуществить это смещение нетрудно.)
Ниже дано схематическое представление такой ситуации:
Система 1 0П} ^Согласующая оптическая система | 0Пг Система 2
В&д
\ri$?!$cu№al ^фокальная система
I емыа | ¦'¦ '
Выход
"t
0
i
X
w
0
0
m
1
0
h
1
(Замечание. Если в процессе вычислений окажется, что tt или
Ц должно быть отрицательным, то целесообразнее использовать
152 Глава 8
афокальную систему с отрицательным увеличением. При этом
значения t все же останутся отрицательными, но сопряженные
плоскости системы расположатся более удачно, и опасность тога,
что OIli нли ОГЬ окажется внутри согласующей системы, будет
меньше. При использованин такой системы необходимо помнить,
что результирующее изображение будет перевернутым!
Кроме того, хотя матричные методы могут оказаться весьма
полезными при решении подобных задач, они не являются па-
панацеей. Инженеру, конструирующему оптическую систему, необ-
необходимо использовать весь опыт, уже накопленный в этой обла-
области. Он должен, например, изучить опыт использования полевых
лннз, а также то, каким образом преобразуется изображение в
оптической системе перископа подводной лодки или в системах
оптической обработки информации.)
Рассмотрим теперь более простую, на наш взгляд, задачу
из этой области, а именно преобразование и формирование ла-
лазерных пучков нужной формы, в частности, такой, которая необ-
необходима для согласования с некоторой системой, внешней по от-
отношению к лазеру. Такая задача может возникнуть для лазеров
любого уровня мощности.
Например, мощность гелий-неонового газового лазера изме-
измеряют в милливаттах, и такой лазер обычно используют для ин-
терферометрических измерений и для юстировки, иногда на
очень больших расстояниях. Он также используется в качестве
источника света для испытания оптических систем или для за-
записи и восстановления голограмм. Лазеры средней мощности,
которая измеряется в ваттах, используются в голографии, в си-
системах связи и в хирургии глаза, как источники накачки для
лазеров на красителях, а также в устройствах, в которых бы-
быстрое сканирование луча используется для записи и считывания
информации. Когда мы входим в диапазон «высоких» мощно-
мощностей, то появляются новые применения, такие, как сварка и ме-
механическая обработка, импульсная голография и светолокация
(включая светолокацию луны). Более мощные лазеры, работаю-
работающие в импульсном режиме, используются для экспериментов в
нелинейной оптике и для исследования плазмы. Сфокусирован-
Сфокусированные лучи сверхмощных лазеров позволяют получить темпера-
температуру порядка нескольких миллионов градусов, что в принципе
позволяет зажечь термоядерную реакцию. (В некоторых экс-
экспериментах лазерный импульс может длиться всего 10~" с,
однако пиковая мощность может при этом достигать 1018 Вт!) ')
•) В настоящее время строятся гораздо более мощные установки — до
2-Ю14—1015 Вт в импульсе Например, проектная мощность установки УМИ—35,
создаваемой в лаборатории колебаний ФИАН'а, составляет 2-10й Вт (подроб-
(подробнее см. тезисы докладов конференции по нелинейной оптике, состоявшейся в
Тбилиси в 1976 г.). — Приц. реф.
Оптические резонаторы и распространение лазерного пучка 153
Когда мощность лазерного луча достигает мегаваттного уро-
уровня, в диэлектрической среде, через которую проходит этот луч,
может произойти пробой (например, в воздухе, в стекле, в жид-
жидкости и т. д.). При этих интенсивностях часто развивается явле-
явление самофокусировки, но даже и при мощности в несколько ки-
киловатт необходимо учитывать тепловые эффекты, обусловлен-
обусловленные прохождением лазерного луча через среду, если только она
не является идеально прозрачной. Мы ограничимся здесь рас-
рассмотрением лучей низкой и средней мощности, для которых пе-
перечисленные выше эффекты не играют, существенной роли.
Однако следует заметить, что даже лазер мощностью
~ 1 мВт может существенно повредить глаз неосторожного на-
наблюдателя. Инструкции по лазерной технике безопасности в
большинстве случаев гарантируют достаточно надежную за-
защиту. Каждый специалист, работающий с лазером, должен не-
неуклонно соблюдать требования этих инструкций. Смотреть непо-
непосредственно на узкий лазерный луч так же неразумно, как и
разглядывать солнце невооруженным глазом.
В большинстве задач согласования мод гауссов пучок, вы-
выходящий из лазера, имеет круговое сечение и должен быть на-
направлен в некоторую внешнюю оптическую систему, которая
также обладает круговой симметрией. Однако иногда требует-
требуется преобразовать пучок с круговым поперечным сечением в пу-
пучок с существенно эллиптическим сечением, и наоборот. При ус-
условии, что оси х и у выбраны так, что они совпадают с большой
и малой осями такого эллипса, последнее преобразование выпол-
выполнить совсем просто. Для этого необходимо определить как вдоль
оси х, так и вдоль оси у отдельные параметры луча q и соответ-
соответствующие матрицы преобразования луча. В действительности
нам нужно провести два независимых вычисления для каждой
переменной х и у, а затем можно определить амплитуду элек-
электрического поля в любой точке (х, у, z) как произведение двух
функций ехр[Bш'Д) (y2/2qy)] и ехр [Bш/Я) (x2/2qx)]. Следова-
Следовательно, действительные части величин l/qx и l/qy определяют
главные значения радиусов кривизны волновых фронтов, и если
они не совпадают, то пучок должен обладать астигматизмом и
в общем случае иметь эллиптическое сечение. Аналогично если
мнимые части этих величин различны, то линии равной энер-
энергии, характеризующие распределение энергии в сечении пучка,
уже не будут окружностями, а приобретут форму эллипса.
Таким образом, здесь достаточно будет рассмотреть только
одномерную задачу или задачу для систем, обладающих ак-
аксиальной симметрией. В этом случае в произвольной плоскости,
перпендикулярной оси z, гауссов пучок полностью определяется
значением его комплексного параметра q, который имеет две
степени свободы.
164 Глава 8
Постараемся теперь определить параметры оптической си-
системы, которая преобразует одно заданное значение параметра
ц в другое. Вспоминая, что определитель матрицы преобразова-
преобразования луча должен быть равен единице, мы имеем одно действи-
действительное и одно комплексное уравнения для четырех действи-
действительных матричных элементов А, В, С и D:
Поскольку значение,параметра q гауссова пучка всегда со-
содержит мнимую часть, то в первом уравнении можно выделить
отдельно действительную и мнимую компоненты. Следовательно,
в действительности мы имеем три уравнения, поэтому матрич-
матричные элементы искомой матрицы определены неоднозначно (ис-
(исключение составляет редко встречающийся на практике случай,
когда нам нужно также определить набег фазы <j>\z =а=
= arg[(/4</i -\-B)/qi] вдоль оптической оси между двумя опор-
опорными плоскостями).
Тот факт, что один из параметров задачи остается свобод-
свободным, играет чрезвычайно важную роль при выборе соответ-
соответствующей согласующей системы; если, например, в распоряже-
распоряжении конструктора имеется ограниченный набор линз, то, ис-
используя свободу выбора одного параметра, можно сконструиро-
сконструировать согласующую систему на одной из этих линз. ,
8.1. Оптические системы преобразования луча
Начнем с рассмотрения двух простейших типов преобразова-
преобразования, а именно тех, которые описываются одной ^"-матрицей или
одной ^-матрицей.
Если ОП2 отделена от ОП] воздушным промежутком толщи-
толщиной Т, то, используя правило ABCD, мы сразу получаем
п 1' qi + Т п 4Г
Иными словами, действительная часть параметра q, значение г
которой описывает положение перетяжки пучка, увеличивается
на величину Т, а мнимая часть —iz0 остается без изменения.
Следует напомнить, что Zo — это конфокальный параметр пучка,
равный пхшЦХ, где а»0 — радиус перетяжки пучка.
Рассмотрим теперь преобразование луча тонкой линзой,
имеющей оптическую силу Р. Используя обращенную форму
правила ABCD, получаем.
.. 1 = Сд,+Р ^ -Рд, + 1 _ 1 п
цг Aq, +B q, qx
Оптические резонаторы и распространение лазерного пучка 155
В этом случае действительная часть величины \lq, описывающая
расходимость 1/R, уменьшается на оптическую силу линзы, а
мнимая часть iX/nw2, определяющая локальный радиус пучка w,
остается неизменной. (Прозрачная линза изменяет форму вол-
волнового фронта пучка, но не меняет его энергию.,)
В редких случаях входной пучок уже имеетч подходящий ра-
радиус перетяжки и радиус пучка, и в качестве согласующей си-
системы достаточно использовать либо просто оптический проме-
промежуток, либо одну линзу с нужным фокусным расстоянием. Од-
Однако более распространен случай, когда требуется, чтобы си-
система согласования мод содержала по меньшей мере одну 9~-
матрицу и одну 52-матрицу.
Если линзе предшествует оптический промежуток, то его
толщину нужно выбрать таким образом, чтобы по достижении
линзы пучок уже имел требуемый диаметр; при этом линза дол-
должна обеспечить желаемую сходимость или расходимость вол-
волнового фронта. Если же первой устанавливается линза, то ее не-
необходимо выбрать так, чтобы новый гауссов пучок имел требуе-
требуемый радиус перетяжки, а толщину последующего оптического
промежутка следует взять такой, чтобы эта перетяжка распола-
располагалась на заданном расстоянии от ОПг-
Для использования этих методов мы должны уметь выбирать
линзы с нужным фокусным расстоянием, при этом полезными
могут оказаться наборы линз вроде тех, которые применяют оку-
окулисты. Однако иногда возникают трудности, связанные с тем,
что получаемая в расчетах толщина оптического промежутка
оказывается либо отрицательной, либо чересчур большой. В не-
некоторых случаях, для того чтобы получить более удобное при-
приспособление, можно использовать вторую линзу. В других слу-
случаях удовлетворительное решение можно найти, выбирая линзу
с соответствующим фокусным расстоянием и устанавливая ее
так, что справа и слева от нее имеются два оптических проме-
промежутка, каждый из которых представляет собой свободный па-
параметр. •
Для описания такой системы с двумя оптическими промежут-
промежутками мы будем использовать безразмерные ^-параметры, кото-
которые являются мерой отношения расстояния от ОП] до первой
фокальной плоскости и расстояния от второй фокальной плоско-
плоскости до ОП2 к фокусному расстоянию линзы. Таким образом, мат-
матрица системы записывается в виде
ТА ВТ Г 1 g2fir 0 / Г 1
[с d\ lo i JL-i// oJLo
-i// -
gi
_[1 ft/If 0 / 1 Г-ft f(l-
Lo i JL J
156 Глава 3
Перетяжка входящего Перетяжка выходящего
пучка пучка
i
i
t
о
Фиг. 3.14
Г/ й^1
[oil
ол2
Во многих случаях при изучении геометрии входящего и вы-
выходящего пучков удобно использовать в качестве параметров
размер и положение перетяжки пучка. Рассмотрим здесь слу-
случай, когда две опорные плоскости совладают с двумя перетяж-
перетяжками пучка (фиг. 3.14). Следовательно, как входящий, так и» вы-
выходящий пучки характеризуются чисто мнимыми параметрами
щ. Таким образом, можно написать Ц\ = —/zOi и q* =* —iZo% где
положительные действительные величины Zoi и Z02 определяют
соответствующие конфокальные параметры пучка. Применяя
для этих величин правило A BCD, получаем
(~ ga) (~ 'Zoi).+ / 0 - gigs) feaZpi -f / A - gift)
Умножая обе части этого уравнения на знаменатель f g
который не равен нулю, и выделяя мнимую и действительную
части, окончательно получаем
Поскольку как zOi, так и Zoa — положительные величины, то
из второго уравнения следует, что gi и ?г должны иметь один и
тот же знак; поэтому произведение gig2 также положительно.
Из первого уравнения имеем, что когда перетяжка пучка пере-
переходит таким образом из ОП1 в ОПг, то среднегеометрическое ве-
величин zOi и Z02 не может никогда превышать фокусного расстоя-
расстояния употребляемой линзы. В случае симметричной оптической
системы, для которой g\ = ?2 = g, справедливо следующее ра-
равенство: zoi = z02 = ze = /A — g2)'/».
Мы уже показали, что если радиус перетяжки гауссова пуч-
пучка сделать очень небольшим, то расходимость пучка становится
Оптические резонаторы и распространение лазерного пучка 157
значительной, причем угол расходимости близок к углу асимпто-
асимптотической расходимости \/nw0, и пучок становится похожим на
семейство сферических волновых поверхностей, расходящихся из
точки, в которой расположена перетяжка пучка. По мере при-
приближения к этому геометрооптическому пределу как гоьтак и zO2
становятся очень малыми, и в соответствии с первым уравне-
уравнением член 1 — gig2 стремится к нулю. Следовательно, g2 при-
приближается к величине, обратной gi, в полном соответствии с
уравнением Ньютона для отрезков, измеряемых ot точек распо-
расположения классического объекта и изображения до первого и
второго фокусов линзы соответственно.
Второе уравнение можно переписать, представив его через
отношение радиусов перетяжек:
^02 _fO2 &2_
Wl\ Z01 Si '
В геометрооптическом пределе, т. е. при условии, что g2 =
= 1/Яь величину g2 можно рассматривать как поперечное уве-
увеличение Доо2/о>оь которое имеет изображение области перетяжки.
Однако, за исключением этого предельного случая, нет ос-
оснований рассматривать процесс преобразования пучка как
обычный процесс получения оптического изображения. Рассмо-
Рассмотрим, например, простой случай, когда перетяжка входящего
пучка расположена в первой фокальной плоскости; следователь-
следовательно, g\ = 0. Можно было бы ожидать, что «изображение пере-
перетяжки пучка» появится в бесконечно удаленной точке простран-
пространства изображений. На самом деле, однако, как следует из вто-
второго уравнения, величина g2 тоже обращается в нуль, так что
перетяжка выходящего пучка располагается во второй фокаль-
фокальной плоскости линзы. В этом случае конфокальные параметры
пучка связаны соотношением z0iZ02 = f2-
(Говоря на понятном для оптика языке, волна во второй фо-
фокальной плоскости представляет собой дальнюю зону или фраун-
гоферову дифракционную картину входного пучка; обычно та-
такая картина наблюдалась бы на бесконечности, но линза пере-
переносит это изображение во вторую фокальную плоскость. С ма-
математической точки зрения распределения амплитуд в этих двух
плоскостях всегда связаны между собой преобразованием
Фурье, и поскольку первая функция представляет собой дей-
действительную гауссову функцию, у которой отсутствует квадра-
квадратичный сдвиг фазы, то вторая функция также должна быть дей-
действительной.)
Если конфокальный параметр входного пучка гО1 равен фо-
фокусному расстоянию /, то z02 также равен f и мы имеем систему,
в которой геометрия пучка воспроизводится. Такую систему мо-
158 Глава 3
-4—
Фиг. 3.15. Передающая оптическая система (линзовый волновод) с четырьмя
последовательно расположенными элементами.
жно использовать в качестве передающей оптической системы '),
как показано на фиг. 3.15. Если в этой системе устранить погло-
поглощение и потери на отражение, то ее можно использовать в каче-
качестве системы оптической связи между какими-либо двумя точ-
точками. Для лазерного пучка с длиной волны 800 нм, передавае-
передаваемого с минимальным размером перетяжки 10 мм, конфокальный
параметр пучка равен (я-10~4)/(8-10—7) « 400 м. Передающая
система, таким образом, должна состоять из очень слабых линз
(с оптической силой 1/400 диоптрий), каждая диаметром
~ 100 мм, расположенных (вдоль прямой линии!) с интерва-
интервалами 800 м.
Кроме того, существует еще один случай, достаточно просто
описываемый матричным методом, в котором перетяжка выход-
выходного пучка точно совпадает с геометрическим изображением пе-
перетяжки входного пучка. Х;
Как мы знаем, в этом случае параметры qx и q% должны быть
мнимыми, и для системы, осуществляющей отображение одной
опорной плоскости иа другую, матрица преобразования лучей
Г m 0 I
записывается в виде I ... .. I , где m — поперечное уве-
увеличение. Используя затем правило ABCD, получаем
+ 0
Сразу очевидно, что это уравнение справедливо только в том
случае, если знаменатель является действительной величиной;
а поскольку Zoi представляет собой с необходимостью действи-
действительное положительное число, то фокусное расстояние системы
f должно быть бесконечно велико. Следовательно, мы имеем
афокальную систему, обладающую этим специальным свойст-
свойством. При желании можно записать матрицу такой системы в
виде произведения двух матриц «фокальных плоскостей»:
I — 1/f 0 J И L—\lrnf О I" ри ЭТ0М в системе Фактиче-
Фактически осуществляется двойное преобразование Фурье, на первой
стадии которого перетяжка исходного пучка, расположенная в
'} Или линзовый волновод. — Прим. ред.
Оптические резонаторы и распространение лазерного пучка
159
Перетяжка входящего
пучка
Перетяжка выходящего
Положение
промежуточной
перетяжки
система/
увеличениям *2
0Пг
Фиг. 3.16
первой фокальной плоскости, отображается в промежуточную
фекальную плоскость, а затем в следующую фокальную пло-
плоскость, расположенную на выходе системы (фиг. 3.16). (Мы ви-
видим из фигуры, что, хотя радиус перетяжки уменьшился вдвое,
расходимость пучка увеличилась в два раза.)
До сих пор в этом разделе мы рассматривали случаи, когда
параметры q входного и выходного пучков известны; и правило
ABCD позволяет нам определить, какого типа должны быть оп-
оптические системы, чтобы осуществить заданное преобразование
параметров пучка. Обсудим теперь две задачи, которые не-
несколько отличатся от предыдущей, а именно будем считать, что
система, используемая для преобразования пучка, задана, но
параметры q входного и выходного пучков определены непол-
неполностью.
8.2. Получение максимально узкой перетяжки пучка
Пусть имеются: а) лазер, излучающий гауссов пучок с ра-
радиусом перетяжки wQ\ и соответствующим конфокальным пара-
параметром пучка 20, = ядо^/Л, и б) оптическая система, матрица
преобразования которой от OFIi до ОП2 записывается в виде
ТА В1
I I . Оптическая система установлена на подвижном рей-
рейтере, так что расстояние от нее до лазера можно свободно ме-
менять. Каков минимальный радиус пятна а»02. измеряемый в пе-
перетяжке пучка, выходящего из ОП2, и каким образом размер
этого пятна зависит от расстояния гх между перетяжкой вход-
входного пучка и положением ОП?
Решение
(Очевидно, в этом случае параметр q входного пучка дается
выражением q\ = Z\ — izO\, а параметр q выходного пучка за-
160 Рлава 3
писывается в виде
^ Л<7,+Д = (Aql+B)(Cq*
Cqx+D (C
(здесь * обозначена комплексно сопряженная величина). Остав-
Оставляя только мнимую часть этого выражения, мы получаем
- Mzqi (Сг. + D) + (Azi +
=
_ — izpi [ACz{ +AD — ACzi — ВС] — tzoi
~~ ~~
(Czt + Df + С2^01 ~~ (CZl + Df
(выражение в квадратных скобках равно единице).
Если теперь заменить z01 на яш^/А,, a z02 на яш^/Я, то окон-
окончательный результат имеет вид
В том случае, когда наша оптическая система состоит из од-
одной линзы с фокусным расстоянием /, причем ОП] и ОП2 распо-
расположены в фокальных плоскостях, матрица преобразования луча
записывается в виде
\А в-] г о Г
1С 1
и, следовательно,
ш2
Для получения минимального радиуса перетяжки пучка обычно
выбирают линзу с коротким фокусным расстоянием, а также,
как это ни парадоксально, отодвигают линзу от лазера на такое
расстояние Z\, которое значительно больше конфокального па-
параметра пучка z01 = яаУ2,/Я. Отдвигая линзу от лазера, мы уве-
увеличиваем радиус пятна пучка на линзе, и до тех пор, пока апер-
апертура линзы не переполняется, мы получаем более острую фоку-
фокусировку пучка и более высокую концентрацию энергии в фокусе
линзы. В пределе радиус перетяжки пучка определяется соот-
соответствующей числовой апертурой (в данном случае Я/I)
') Предельное минимальное значение радиуса перетяжки пучка после
идеальной линзы, имеющей диаметр D и фокусное расстояние /, легко найти,
пользуясь неравенством^ Гейзенберга, или принципом неопределенности, кото-
который в этом случае имеет внд woAk ^ 1 или X/nwo ^ D/f, откуда w0 ^
^ }X/nD. — Прим. перев.
Оптические резонаторы и распространение лазерного пучка 161
Общее выражение, только что полученное нами, можно рас-
рассматривать как формулу преобразования радиусов перетяжки
пучка:
fO2
(CZl+DJ+C*z2m
m
Этоувыражение почти совпадает с формулой преобразования
радиуса пятна пучка, которое мы получили в § 7 настоящей гла-
главы, приравнивая только мнимые части выражения для l/q.
В обращенном виде формула преобразования радиуса пятна
пучка записывается в виде
W,
в
п
8.3. Нахождение параметров гауссова пучка
по двум заданным радиусам кривизны
Гауссов пучок распространяется через оптический промежу-
промежуток шириной d между ОП1 и ОП2. Все что нам известно, — это
радиус кривизны R\ волнового фронта в ОП] и радиус кривизны
R2 волнового фронта в ОП2. Требуется отыскать остальные па-
параметры пучка, в частности, размер и положение перетяжки, а
также радиусы пятен пучка в ОП1 и ОП2.
Решение
Полагая qx = Z\ — iz0, из правила ABCD имеем qi = q\ +
+ d = (Zi + d) — iz0. Если оба эти выражения обратить, то по-
получим следующие формулы:
qx
И
1 ... 1 _ (г. + Ю + «гп ^ 1 .
q2 B, +d)- iZQ (Z, + df + z\ /?2 ЯВ^
Оставляя в этих выражениях только действительные части,
из C.2) получаем
^ 2 = 2,^ + ^, C.3)
а из C.1)
zf + z^z,/?,. C.4)
Вычитание уравнения C.4) из C.3) дает
2*,d + d2 = d/?2 + г, (Яа-/?,),
6 Зак. 774
162 Глава 3
откуда находим
d № -
Zl —25+ /е, _ j?a ¦ ld'0)
Чтобы получить формулу для zq, подставим выражение C.5)
для Z\ в уравнение C.4) и после небольших алгебраических вы-
выкладок найдем
^i № - d) (Ы •+-/?! — &) - rf2 № - df _
Bd + *i-*2J
(«2 - d) B dRx + /?J - ^,^2 - dR2 + d2)
Это выражение можно упростить и записать в виде
jfr^ _ d{R2d){R1 + d){d + RlR2)
Zo Я2 ~~ {Id + R\- R2J ' *¦ }
Для того чтобы получить формулу для W\, мы используем
мнимую часть выражения C.1):
[здесь мы использовали соотношение C.4)]. Обращая это вы-
выражение и подставляя соответствующие величины, определяе-
определяемые формулами C.5) и C.6), находим
n2w\ d2 (R2 - df R] Bd + R{~ R,2f
X2 Bd + Ri- R2)'1 d (R2 - d) (Ri +d)(d + Rl~ R3) "
Следовательно,
X2d (R9 - d) R2,
Ш\ n1 (Ri +rf){d + ^! -R3) ¦ W-'t
Для получения w2 поступим аналогичным образом, исполь-
используя только теперь мнимую часть выражения C.2):
[здесь мы использовали уравнение C.3)]. Обращая это выраже-
выражение и подставляя соответствующие величины, определяемые фор-
формулами C.5) и C.6), окончательно находим
w* = *Ч/?2 - dMrf + *¦ -/?af t3"8)
Оптические резонаторы и распространение лазерного пучка
163
Наконец, для расстояния z2 (измеряемого от перетяжки пуч-
пучка до ОПг) получаем
<3-9>
Найденное нами решение физически реализуемо, только если
все величины wPQ, w\ и а|, определяемые соответственно форму-
формулами C.6), C.7) и C.8), положительны. Например, при распро-
распространении в свободном пространстве невозможно, чтобы пучок,
первоначально расходящийся, начал затем сходиться.
Поскольку геометрия гауссова пучка остается той же самой,
даже если он распространяется в противоположном направлении,
то выражения, полученные выше, можно использовать для ре-
решения соответствующей задачи согласования гауссова пучка с
резонатором. Если зеркала, обращенные внутрь резонатора
своими сферическими поверхностями с радиусами кривизны
т\ = —R\ и г2 = #2, соответственно расположены в ОПх и ОПг,
то волновые фронты гауссова пучка совпадают с каждой из по-
поверхностей зеркал. Следовательно, пучок будет бесконечное чис-
число раз отражаться от поверхностей зеркал (фиг. 3.17). Пара-
Параметры пучка, вычисленные Нами выше, соответствуют основной
моде рассматриваемого оптического резонатора. (Заметим, од-
однако, что поскольку вогнутая поверхность зеркала, расположен-
расположенного в ОПь обращена вправо, радиус кривизны этого зеркала гх
следует брать с противоположным знаком по сравнению с тем
случаем, когда пучок распространяется в положительном напра-
направлении оси г.)
Поверхности постоянной
Г
Дополнительные aepgcuta
о радиусами rr я Г}
Фиг. 3.17. Распространение гауссова пучка между двумя зеркалами.
Если иа пути гауссова пучка поставить два зеркала, поверхности которых совпадают
с поверхностями постоянной фазы такого пучка, то возможно образование картины стоя-
стоячих волн.
в*
164 Глава 8
§ 9. МАТРИЦЫ ПРЕОБРАЗОВАНИЯ ЛУЧЕЙ
В ЛИНЗОПОДОБНОЙ СРЕДЕ С КВАДРАТИЧНЫМ ЗАКОНОМ
ИЗМЕНЕНИЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
До сих пор в этой книге мы рассматривали аксиально-сим-
аксиально-симметричные системы, которые состоят всего лишь из двух основ-
основных элементов: оптического промежутка (интервала свободного
пространства) и преломляющих или отражающих поверхностей.
Последние можно рассматривать как нарушение непрерывности
на границе раздела между двумя средами с различными, но по-
постоянными показателями преломления. Каждый из этих элемен-
элементов легко можно идентифицировать и полностью описать с по-
помощью соответствующей 9"- или 32-матрицы.
Однако иногда возникают ситуации, когда показатель пре-
преломления в данной среде не является постоянным, а представ-
представляет собой медленно меняющуюся функцию координат х, у, г.
По-видимому, наиболее простому случаю, который мы кратко
обсудим в настоящем параграфе, соответствует среда с «линзо-
подобным распределением» показателя преломления, т. е. когда
показатель преломления п квадратично изменяется с расстоя-
расстоянием от оптической оси Ог и имеет цилиндрическую симметрию
относительно этой оси. Мы покажем, что при распространении
параксиального пучка света через среду с таким распределением
показателя преломления «параболический» профиль удерживает
излучение в ограниченной области пространства вблизи оптиче-
оптической оси.
Следует заметить, что такое, представление не является чем-
то новым: его обсуждал пятьдесят лет тому назад Р. Вуд в сво-
своей книге «Физическая оптика», но рассмотрение этого вопроса
стало особенно важным в последнее время по следующим двум
причинам.
Первая из них связана с постоянно растущей необходи-
необходимостью создания эффективных передающих систем для оптиче-
оптических линий связи. Было выполнено несколько исследований того,
как можно создать линзоподобное распределение показателя
преломления: например, в газовой среде посредством создания
соответствующих температурных градиентов внутри наполнен-
наполненной газом трубы или в твердом теле посредством точно контро-
контролируемого процесса диффузии примесей внутрь оптического во-
волоконного волновода.
Вторая причина — это то, что при использовании мощного ла-
лазерного луча такое распределение показателя преломления воз-
возникает в среде автоматически. При мегаваттных уровнях мощно-
мощности, достигаемых в импульсных лазерах, нелинейное изменение
показателя преломления среды даже на очень небольшую вели-
Оптические резонаторы и распространение лазерного пучка 165
чину вызывает эффект самофокусировки либо внутри, либо вне
лазерного резонатора. Эти эффекты приводят к нежелательному
пробою или разрушению прозрачной диэлектрической среды, а
также к искажению геометрии лазерного пучка ').
Для того чтобы описать такое распределение показателя пре-
преломления, рассмотрим следующее выражение:
Здесь по — значение показателя преломления п на оптической
оси, а множитель а можно рассматривать как величину, обратно
пропорциональную характерному масштабу, на котором показа-
показатель преломления п уменьшается в два раза по сравнению с его
значением на оси (в этом случае характерный размер вводится
гипотетически, поскольку практически рассматривается лишь
параксиальная область, в которой абсолютное изменение пока-
показателя преломления мало). (В реальных системах существует
только приосевая область такого параболического распределе-
распределения показателя преломления, причем даже на самом краю си-
системы величина а2г2, как правило, очень мала — меньше чем
0,01.)
Конечно, показатель преломления может как увеличиваться,
так и уменьшаться пропорционально квадрату расстояния от
оси; в общем случае нам необходимо предполагать, что пара-
параметр а может быть мнимым. (Квадратичный закон изменения
поглощения или усиления в среде также можно описать, исполь-
используя комплексное представление параметра а.)
Чтобы найти матрицу преобразования лучей, которая описы-
описывает оптические свойства такого распределения, рассмотрим бес-
бесконечно тонкий слой среды, заключенной между плоскостями
z = z0 и г = 20 + 6г. Такой слой можно рассматривать не толь-
только как оптический промежуток с приведенной толщиной 8г/п0,
но также как участок, который вносит неоднородную задержку,
определяемую следующим образом:
W{x,y) = [n (х, y)-no]6z = -±. поа2 (х2 + г/2) бг.
Если сравнить эту неоднородную задержку с задержкой, вно-
вносимой очень слабой тонкой линзой с оптической силой Р, а имен-
именно —Р (х2 + У2) /2, то мы обнаружим, что оптическая сила эк-
•) Для, световых пучков существует понятие критической мощности, т. е.
мощности, при приближении к которой эффекты самофокусировки начинают
играть важную роль. Для гауссовых пучков Я„р = спо/йпц/г2, где с — ско-
скорость света, «о — показатель преломления среды, я2 — нелинейная добавка
к показателю преломления, a k — волновое число. Более подробно явление
самофокусировки рассмотрено, в частности, в обзоре: В. Н. Луговой,
А. М. Прохоров, УФН, т. III, вып. 2, 203 A973). — Прим. ред.
166 Глава 8
вивалентной бесконечно тонкой линзы должна определяться вы-
выражением Яэкв = поа26г.
Следовательно, для того чтобы описать оптические свойства
такого тонкого слоя, мы должны использовать две матрицы:
ЬгК 1
Г\ и
Очевидно, существует четыре различных способа, с помощью
которых можно записать пронзведние этих двух матриц. На-
Например,
2)
Кроме того, мы можем представить одну из этих матриц в виде
двух матриц и умножить вторую матрицу на эти матрицы слева
и справа соответственно. Таким образом, получим
3) М (Ьг) = Т (вг/2) Я (Ьг) Г(Ьг/2)
и
4) М (Ьг) = Ж (вг/2) T{bz) & (вг/2).
Как мы увидим ниже, все эти четыре альтернативы дают
один и тот же окончательный результат. Здесь мы рассмотрим
лишь первую и третью комбинации матриц (случаи 1 и 3).
Случай 1
Мы имеем
JU J L J
Т Г1-
J — L -
Используем следующие подстановки:
/С = ало, 8 = 2 arcsin (а Ьг/2), или а Ьг = 2 sin (9/2).
Следовательно,
2 cosG-I Bsin(9/2))//Cl
— 2/С sin (9/2) 1 J
Теперь проверим, равен ли определитель втой матрицы единице,
и отметим, что ее след равен 2 сое 0, т. в. ев собственные значе-
значения записываются в виде e±ib.
Оптические резонаторы и распространение лазерного пучка 167
Построив эту «бесконечно малую», или «инфинитезималь-
ную», матрицу M(bz), возведем ее теперь в р-ю степень, где р —
очень большое число. При этом мы получим матрицу преобра-
преобразования лучей для слоя конечной толщины t = pbz. Для этой
цели используем теорему Сильвестра, рассмотренную нами в
§ 5 настоящей главы. Если М = _ I — унимодулярная
матрица с собственными значениями е±гв, то
[sin(p + 1)9 — DsinpQ В sin pQ -i
sin 6 sin 8 I
С sin pQ D sin рв — sin (p — 1) 8 I"
sin fl «in fl J
Подставляя вместо матричных элементов В, С и D найден-
найденные нами выражения, получаем
[sin рв cos8 + cos p8 sin 8 — sin /?8 2 sin pQ sin (8/2) -i
sin 8 /Csin8 I
— 2/C sin (8/2) sin /?8 sin /?B — sin p8 cos 8 + cos p& sin 8 "
sin 8 sin 8 -•
о _ sin pQ A — cos 8) sin p6 -i
sin8 К cos (8/2)
- * sin p9 „„„„q i sin p9(l -cosB) '
cos (8/2) COS/rtH jjj^ J
Если теперь предположить, что 6z -> 0, а р -* со таким обра-
образом, что их произведение рбг = t остается постоянным, то па-
параметр 9 также будет стремиться к нулю, но произведение
pQ = at останется неизменным. Следовательно, в полученной
выше матрице параметр A — cos 9) /sin 9 пренебрежимо мал, а
cos (9/2) -> 1. Таким образом, окончательно имеем
[cosp9
— KsinpQ cospQ
Прежде чем обсуждать оптические свойства, вытекающие из
полученного решения, покажем, что при использовании в каче-
качестве исходной инфинитезимальной матрицы другой альтерна-
альтернативной формы мы получим такую же матрицу M(t).
НИ Глава 8
Случай 8
В этом случае наша инфинитезимальная матрица записы-
записывается в виде произведения трех сомножителей:
Используя те же параметры б и К., что и прежде, перепишем
эту матрицу в виде
fl2sin2(9/2) 2sy2)(l-sln2(9/2)I
fl
L —
г
L
2/С sin (9/2) 1 - 2 sin2 (9/2) J
cos9
-2/Csin(9/2) cos 9
(Следует заметить, что диагональные элементы этой матрицы
такие же, как и в предыдущем случае 1; определитель- матрицы
также равен единице, а собственные значения имеют вид в**8.)
Снова используя теорему Сильвестра, получаем
М (р Ьг) =* Мр =
[sin p8 cos 8+cos p8 sin 8— sin p8 cos 8 sin 8 cos (8/2) sin p8 -i
sin 8 К sin 8
— 2/C sin (8/2) sin p8 cos8sinp8—sinp8cos8 +cosp8sin8 1°*
sin8 sind -I
[cospO cos{QI2)^jp-]
-*%* COSP9 J"
cos Г8/2) K J
cos (8/2)
В пределе 9—»• 0 опять-таки cos (9/2) = 1. Таким ббразом,
матрица M(t), как и в предыдущем случае, принимает оконча-
окончательный вид:
г cospe My
L —/Csinp9 cosp9J L —
cosafJ
Начиная с этого момента мы будем использовать данную
матрицу M{t) для описания оптических.характеристик среды
Оптические резонаторы и распространение лазерного пучка 169
любой протяженности как сколь угодно большой, так и беско-
бесконечно малой. За исключением множителя ап0, эта матрица в
точности совпадает с матрицей поворота и обладает тем же свой-
свойством, а именно, что M(t{)M(t2) = M(t2)M(t\) = M(ti -f t2).
С помощью теоремы Сильвестра нетрудно установить, что
{M(t)}N = M(Nt); последнее равенство справедливо даже в том
случае, когда N не является целым числом.
Беглый взгляд на эту матрицу показывает, что она обладает
свойством периодичности: через каждый интервал t = 2я/а она
обращается в единичную матрицу. Посередине такого интер-
интервала она напоминает матрицу афокальной системы с увеличе-
увеличением — 1 и на интервале t = я/2а она имеет ту же форму, что и
матрица линзы с оптической силой К — поа, записанная для
двух фокальных плоскостей. Используя эту матрицу, рассмот-
рассмотрим теперь более детально путь геометрооптического луча (или
распространение гауссова пучка) в такой среде.
9.1. Распространение параксиальных лучей
Пусть входная опорная плоскость ОП0 расположена в точке
ж = 0, а выходная опорная плоскость 0П2 может свободно пе-
перемещаться вдоль оси z на любое удобное нам расстояние *.
Для любого заданного входного луча I „ I можно записать
матрицу в ОПг
cos (az) sin ^°*
in(az) cos(az).
Если, например, входной луч распространяется параллельно
оси на высоте г/о и, следовательно, Vo = 0, то
у (г) = г/0 cos (az)
и
V (z) = — уфф. sin (az).
Для величины v (z) = V (г)/«о имеем
v (z) = — уоа sin (az)
(очевидно, v(z) = dy(z)/dz).
Следует заметить, что на тех расстояниях z, на которых от-
отрезок я/2а укладывается точно нечетное число раз, «/-коорди-
«/-координата этого луча обращается в нуль независимо от высоты у0, кб-
ТОрую луч имел во входной опорной плоскости. На расстояниях
же z, на которых отрезок я/2а укладывается точно четное число
раз, в нуль обращается параметр луча v и луч вновь распро-
распространяется параллельно оптической оси.
170
Глава 3
y*t/ocos'a.a
t'O
Zm\
г>0
Фиг. 3.18. Геометрический путь пучка (углы для наглядности показаны в уве-
увеличенном масштабе).
Следовательно, в соответствии с геометрической моделью
входной пучок параллельных лучей периодически фокусируется
в точку, а затем снова расходится на интервалах Дг = л/а. Этот
случай представлен на фиг. 3.18.
Однако из-за дифракции фокусировка пучка в точках пере-
пересечения оси никогда не бывает совершенной. Если ут — макси-
максимальный радиус пучка в точке г = 0, то максимальное значение
V в «фокальной области» z = я/2а будет равно Vm = ПоаУщ',
как было показано в § 3, следует ожидать, что диаметр пучка в
этой точке по крайней мере равен 0,61К1Ут=0,(з\Х/(пеа.ут). Сле-
Следовательно, произведение диаметров пучка в точках г = /йя/а
иг= B/ге -\- 1)я/2а приближенно равно Bуп) (Qfilk)} (поаут),
или \,22К/поа. Это существенное ограничение, а лучи, показан-
показанные на фиг. 3.18, представляют собой геометрическую идеализа-
идеализацию реальной картины.
9.2. Распространение гауссова, пучка
Чтобы проследить за распространением гауссова пучка в
линзоподобной среде, нам нужно лишь применить правило
ABCD, причем коэффициенты А, В, С и D представляют собой
известные функции координаты г, которые были получены выше.
Таким образом, если <7о — комплексный параметр входного пуч-
пучка в плоскости г = 0, то
Точно так же, если нас интересует только зависимость ра-
радиуса пятна w от расстояния, которое прошел пучок в среде, то
Оптические резонаторы и распространение лазерного пучка 171
можно использовать формулу преобразования радиуса пятна
пучка:
В том случае, когда перетяжка входного пучка расположена
в точке z = 0, мы сразу можем написать w @) = w0 и l/q0 =
= /Я,/яшо> так что
Эта формула показывает, что (за исключением случая, ког-
когда А,2 = я2а2ПоИ)о) радиус пучка колеблется между двумя экс-
экстремальными значениями: одно из них существует npHsin(az) =
=» 0 и его значение в точности равно w0, а другое при sin2(a2)=-
= 1. В последнем случае w (z) = wQ (%/nanowfy = (X/nanQwQ\
Если nanowl > X, то второе экстремальное значение соответ-
соответствует перетяжке пучка (как показано на фиг. 3.19, о). Если же
яал^до* < X, то это значение является максимальным
(фиг. 3.19,6). Наконец, если nanowl==X, то коэффициент при
sin2(az) обращается в нуль и радиус пучка остается постоян-
постоянным, равным своему первоначальному значению, на любом рас-
расстоянии z (фиг. 3.19, в). Очевидно, в этом случае входной пучок
в точности согласован с основной гауссовой модой такой си-
системы с линзоподобным распределением показателя преломле-
преломления. Радиус пучка этой фундаментальной моды дается выраже-
выражением wf = (Х/лащ)'1', а соответствующее значение параметра q
на входе равно q0 = — inwf/X = — i/an0.
Конечно, можно было бы получить это выражение для пара-
параметра q непосредственно, вычисляя отношение компонент соб-
собственных векторов матрицы M(z), а именно
„_ Я1 - Д _ еш - cos (az) ?_
^° С — ап0 sin (az) апй '
Следует заметить, что, даже если входной пучок не согласо-
согласован с основной модой, произведение максимального и минималь-
минимального диаметров пучка в процессе колебаний всегда остается по-
постоянным и равным
172
Глава S
wf-(X/min0)Vt
*~a
w0 • Wf (пучок на входе z=0 согласован
правильно)
н -7
2я
9*0
Фиг. 3.19
Последнее выражение находится в полном согласии с выра-
выражением, вычисленным раньше для однородного пучка по фор-
формуле Эйри. Однако это согласие до некоторой степени случай-
случайно, поскольку при определении диаметра пучка использовались
различные критерии.
Рассматриваемая нами тема весьма многогранна. Например,
в системах газовых линз коэффициент а часто не является по-
постоянной величиной, а медленно меняется в направлении рас-
распространения пучка. Существуют также системы, в которых ко-
коэффициент а представляет собой чисто мнимую величину. В этом
случае среда ведет себя приблизительно так же, как и неустой-
неустойчивый резонатор бегущей волны. Если ввести величину а =а ta,
то распределение показателя преломления запишется в виде
а матрица, описывающая распространение пучка в среде, дается
выражением
J *-
— ащвЪаг chaz
«Отрицательное» линзоподобное распределение показателя
преломления такого типа можно создать в среде (правда, на от-
Оптические резонаторы и распространение лазерного пучка 173
носительно больших временных масштабах) излучением лазера
непрерывного действия. Если пучок переносит энергию порядка
нескольких килоджоулей, то нагревание среды вследствие оста-
остаточного поглощения стремится уменьшить ее показатель прелом-
преломления в приосевой области. Этот эффект, обратный эффекту са-
самофокусировки, обычно называют «тепловой линзой». Для сре-
среды с заданным коэффициентом поглощения начальное увели-
увеличение температуры зависит не только от интенсивности и вре-
времени действия пучка, но также и от его радиуса; причем если
рассматривается распространение пучка в атмосфере, то необ-
необходимо учитывать еще целый ряд сложных эффектов, вызывае-
вызываемых ветром, турбулентностью и конвекцией.
Как следует из последнего замечания, вряд ли можно ожи-
ожидать, что матрица преобразования лучей позволит решить все
проблемы, возникающие при исследовании сред с непрерывным
распределением показателя преломления. Матричные методы
применимы только в том случае, когда распределение является
линзоподобным, а геометрия пучка близка к гауссовой.
По-видимому, есть еще одна причина, в связи с которой стои-
стоило рассмотреть линзоподобную среду в настоящей главе. Мы
полагаем, что это очень поучительный пример, который может
вдохновить студента на поиски аналогий, существующих между
оптикой и другими разделами физики. В данном случае мы
имеем в виду аналогию с теорией электрических цепей.
Переход, который мы делали, от системы, содержащей ко-
конечное число линз, к системе с непрерывным распределением по-
показателя преломления, во многом аналогичен переходу от много-
многозвенного фильтра (который состоит из индуктивностей и емко-
емкостей) к непрерывной передающей линии. В более общем смысле
собственное значение, которое позволяет оптику установить, яв-
является ли резонатор устойчивым или нет, в теории связи опре-
определяет фазовый сдвиг или затухание электрического сигнала;
отношение компонент собственного вектора, определяющее в оп-
оптике значения R или q автомодельной волновой картины, в тео-
теории связи аналогично отношению напряжение/ток — повторному
импедансу. С момента изобретения лазера поиски таких анало-
аналогий часто оказывались весьма плодотворными. Однако необхо-
необходимо всегда тщательно анализировать как физическое различие
аналогий, так и их подобие!
В последнем параграфе настоящей главы мы рассмотрим не-
несколько задач; они позволят нам резюмировать основные ре-
результаты, изложенные выше. В конце книги помещен список ли-
литературы для дальнейшего изучения проблем, связанных с мат-
матрицами преобразования лучей.
174 Глава 3 '
f 10. ИЛЛЮСТРАТИВНЫЕ ЗАДАЧИ
Задача 1
Дана герметически изолированная оптическая система. Тре-
Требуется найти элементы матрицы преобразования лучей!
Mo —, r n
L Co '-'и
Единственное изменение, которое вы можете сделать, »то доба-
добавить к системе одну или две тонкие оптические линзы с извест-
известными оптическими силами Pi и Лг- Эти линзы можно распола-
располагать как на входе, так и на выходе системы. Единственными уст-
устройствами для проведения измерений являются удаленный ис-
источник с заданным угловым размером и катетометр. Они позво-
позволяют измерять эквивалентное фокусное расстояние / ¦=» -~\/С
для каждой из четырех возможных комбинаций.
Показать, что по четырем измеренным значениям С: Со, Си
Cg и С12 можно записать решение для искомой матрицы в виде
Со —- w Си + С»~-1
[
С
о
Решение
В том случае, когда к системе добавлены обе линзы, моди-
модифицированная матрица преобразования лучей, очевидно, прини-
принимает вид
[А12 ?12]_Г 1 ОТГЛо ЛоТГ 1 0]
LC12 D,J~L-P2 lJLCo DoJL-Pi U =
Во"!
= В° 1
, L -Р2 (Ао - BoPt) + (Со - DoPi) - P2BQ + Do J "
Следовательно, когда установлены обе линзы, измеренное
значение параметра С дается выражением
Сis ^B Dw\Pi ~~ DqPi ~~ «о* % т Со»
Если была установлена только одна передняя лииза, то мы дол-
должны положить Рг = 0. Тогда получаем
С,
Оптические резонаторы и распространение лазерного пучка 175
Если же установить лишь одну заднюю линзу, то следует поло-
положить Pi = 0, и тогда мы имеем
Таким образом, требуемые решения записываются в виде
л с0 — с2 -. с0 — С]
ЛО Р. ' ^0 р, "
Gn ~~ C»2 r\ t^O "~~ *¦*! •¦ D ^12 "г" ^0 "~~ С* 1 "~~ ^
В экспериментальном методе, который мы обсудили выше,
необходимо использовать всего лишь две вспомогательные лин-
линзы. С другой стороны, если в распоряжении имеется несколько
тонких линз, то, заменяя их друг другом, можно осуществить це-
целую серию измерений параметра С в зависимости от различ-
различных оптических сил Pi и Рг. Поскольку в любом случае С =
= В0Р1Р2 — A)?*i — Л0Р2 + Со, то полную матрицу системы мо-
можно записать через частные производные следующим образом:
¦ дС дгС
L ь° дР,
(Почти сто лет назад этот результат получил, правда в несколь-
несколько иной форме, Л. Пендлбери и привел его в своей книге «Лин-
«Линзы и линзовые системы в гауссовом приближении»1).
Задача 2
Рассмотрим два связанных сферических волновых фронта и
соответствующие им пучки лучей, исходящие из двух отдельных
изображений точек 0 и 0', расположенных на оси системы. Пусть
крайние лучи в этих двух пучках характеризуются в заданной
ру
I v I и I v, I.
опорной плоскости лучевыми векторами
Требуется показать, что в плоскости, в которой эти два край-
крайних луча пересекутся (площадь, освещаемая при этом обоими
пучками, будет одинакова), разность стрел прогиба волновых
[У У' Л
V V Г
Показать также, что, если лучевой вектор одного крайнего
\уЛ . \~уЛ
луча I у I заменить на соответствующий вектор I _ у J луча,
распространяющегося в направлении зеркального отображения
') Pendlebury L., Lenses and Systems of Lenses Treated after the Manner
of Gauss, Deighton and Bell, Cambridge, 1884, pp. 55, 91.
17в
Глава-Я
Плоскость
п-1
a
S'
Вторая плЬскость
пересечения
Фиг. 3.20
первого луча относительно оптической оси, то можно найти дру-
другую плоскость, в которой площади, освещаемые обоими пучками,
будут одинаковы. Вычислить разность стрел прогибов волнового
фронта в этой второй плоскости пересечения лучей и дать физи-
физическое объяснение того, почему знак этой разности меняется на
противоположный.
Решение
а) На фиг. 3.20, а показан вектор I у I лУча, выходящего
из точки О, и второй вектор
луча, выходящего из точки
О'. Чтобы найти плоскость, в которой эти два луча пересекают-
пересекаются, будем искать ^"-матрицу, которая, будучи умножена на лу-
лучевые векторы первого и второго лучей, а именно
[о Ti][v]. и [о !][*']•
дает два лучевых вектора с одинаковыми значениями у.
Оптические резонаторы и распространение лазерного пучка 177
Иными словами, потребуем, чтобы
y + TV=y' + TV.
Отсюда находим
/Очевидно, величина Т будет конечной, только если V Ф V.)
В плоскости пересечения лучей, расположенной на расстоянии Т
справа от заданной опорной плоскости, частное значение у опре-
определяется выражением
У(у-у') _ уУ-у'У .
У "т"
— V ~~ V — V
следовательно, два лучевых вектора в плоскости пересечения лу-
лучей записываются в виде
уУ'-у'У -1 г уУ'-у'У
V } ¦ [ V
Поскольку параметры V различны, то два сферических вол-
волновых фронта, связанные с этими двумя лучевыми векторами,
должны иметь различные радиусы кривизны и различные про-
прогибы. В § 2 настоящей главы было показано, что прогиб волно-
волнового фронта равен половине произведения значений у п V. Сле-
Следовательно, для разности прогибов можно написать следующее
выражение:
S' — S = Прогиб О'-волны — Прогиб О-волны =
Мы увидим, что именно вторая волна, исходящая из точки
О', имеет большую расходимость и больший прогиб волнового
фронта. Следовательно, поскольку V > V, то определитель дол-
должен быть положительным (относительно любой опорной пло-
плоскости).
б) На фиг. 3.20,6 показан случай, когда вектор! v [заменен
на вектор I v I, соответствующий зеркальному лучу. Но-
Новая плоскость пересечения расположена на расстоянии
(— у — У'I(У' + V) справа от опорной плоскости, — другими
словами, на расстоянии (y + y')/(V+ V) слева от нее.
Общее значение у, соответствующее этой точке пересечения,
равно (—yV' + y'V)/(V'+V), причем прогиб О'-волны, ис*о-
178 Глава 8
дящей из точки О', больше, чем прогиб волны, исходящей из точ-
точки О, на величину
Таким образом, мы получили тот же определитель, но с проти-
противоположным знаком.
Как видно из фигуры, когда О'-волна Достигает плоскости
пересечения, она еще не достигла осевой точки СУ и, очевидно,
является сходящейся. Расходимость О-волны, с Другой сто-
стороны, несколько больше, чем в области пересечения, показанной
на фиг. 3.20, а.
Следует обратить внимание на то, что для любой ограничен-
ограниченной сферической волны, распространяющейся в воздухе вдоль
направления оси г, скорость изменения прогиба 5 с расстоянием
z сохраняется постоянной. Если V описывает предельный луче-
лучевой угол (Ч. А.), то эта скорость дается выражением
_±
dz ~ dz\2
l_y (dy\__l_v2
2V \dz)~ 2V '
Следовательно, для двух волн, рассматриваемых в этой за-
задаче,
Расстояние Az между двумя плоскостями пересечения опреде-
определяется формулой
га«["у г]
у v V + V
V'3 V1 '
Таким образом, для изменения разности прогибов имеем
Как мы уже вычислили, при замене луча на его зеркальное ото-
отображение происходит симметричное изменение значения этого
определителя от —'/г до Ч-'/г-
Студенту полезно проверить тот факт, что подобная формула
увеличения прогиба применима и к распространению гауссовых
пучков. Если прогиб вычисляется по отношению к контуру 1/е2,
то его значение равно S =» (%12п) (z/zo), где г— расстояние от
перетяжки пучка, а г0 *** n8%fk — радиус дифракционной расхо-
расходимости пучка. Если считать, что V геометрического пучка лу-
лучей Соответствует углу А./яа»<ь т- е- асимптотическому углу рас-
Оптические резонаторы и распространение лазерного пучка 179
ходимости гауссова пучка, то применима та же самая формула
dS/dz = С/2) V2 даже в непосредственной близости от перетяжки
пучка.
Задача 3
В линейном резонаторе лазера на красителе полностью от-
отражающее зеркало, расположенное слева, обладает оптической
силой Pi, а зеркало, расположенное справа на выходе, имеет
оптическую силу Р2. Внутри резонатора находится несколько
линзовых элементов, причем матрица преобразования луча от
левого зеркала к правому не является уже простой матрицей
перемещения. Если обозначить эту матрицу через М =
А, Е
Г
1
. , то можно показать, что матрица полного про-
v>o Uq j
хода, вычисленная относительно правого зеркала, должна иметь
вид
ГА В]_ГА> В0]Г 1 0]ГА) А>]Г 1 °
1С D J ~~ L CQ Do J L - Pi 1 J L Co A> J L - P2 1
Решение
В данной задаче нам нужно рассмотреть прямое и обратное
распространение луча через внутрирезонаторную оптическую си-
систему. Для наглядности эту систему можно представить в виде
цепочки 31- и ^"-матриц, произведение которых, взятое для луча,
распространяющегося слева направо, дает полную матрицу
ГА> Во]
I I. Нам нужно доказать, что если та же цепочка мат-
L t>o *A) J
риц записана в обратном порядке, то после перемножения полу-
[Оо Во]
1Со А)_Г
диагональных элемента, причем ни един из элементов не меняет
знака.
Ниже мы покажем, что это можно доказать методом матема-
математической индукции, используя при этом тот факт, что для про-
произвольно выбранных 31- и ^"-матриц матричные элементы А и
D всегда имеют одно и то же значение. Однако предпочтитель-
предпочтительнее сначала доказать это положение, привлекая оптические ме-
методы.
Предположим, что все оптические элементы нашей системы
целиком размещены на достаточно короткой оптической скамье.
[У\ 1
v I, распространяющий-
распространяющийся в направлении +z, а также соответствующий выходной луч
чится результат . . I, т. е. меняются местами два главных
180
Глава 3
oh,
I
Оптическая
система
0П,
ОП.5
i
i
2-*-
0П,'
vmuiota
ипяоаьпшщ)
У
tr
гташот
ш-жт
0П,
i
oh;
Фиг. 3.21
Гй1 ГА) Во1Г?.1
I = I •> n 111/ Г также распространяющийся в напра-
.Со Do.
влении +z. На фиг. 3.21,6 показана новая геометрия системы,
которая получается, если всю оптическую скамью повернуть во-
вокруг оси х на 180°, так что ось у и ось г изменят свое направле-
направление на противоположное, и лишь одна ось х останется без изме-
изменения.
Обозначим компоненты лучевых векторов в новых у'- и z7»
осях штрихованными величинами. Теперь мы можем также из-
изменить на противоположное направление первоначального вы-
выходного луча по отношению к системе и использовать его в ка-
качестве нового входного луча (фиг. 3.21,в). Вследствие обрати-
обратимости световых лучей новый выходной луч будет совпадать со
старым входным лучом и будет распространяться направо, как
показано на фиг. 3.21. В каждом из этих случаев значения V
Оптические резонаторы и распространение лазерного пучка 181
останутся неизменными, однако знаки у будут обращены. Та-
Таким образом, имеем
га-га-г: ли
га-га-г;
Вспоминая, что с помощью инверсии исходной матрицы мож-
можно написать следующее соотношение:
А> -В0
-Co . aq
В01Гу2-\
q JLf2J'
мы объединим все эти три уравнения и получим, наконец, новое
соотношение, связывающее вход и выход новой системы:
1 °1[ D° -
Это выражение дает матрицу преобразования лучей для оп-
оптической системы, развернутой на 180°, так что порядок распо-
расположения всех линзовых поверхностей и оптических промежут-
промежутков, которые проходит свет, обращен. Такая матрица очень по-
похожа на обратную матрицу.^однако, как и следовало ожидать,
элемент Со, определяющий эквивалентную оптическую силу,
остался тем же самым.
Доказательство методом математической индукции
Пусть матрица М записывается в виде
М1М2М№... Mi... Mn,
где каждая матрица Мг является унимодулярной и такой, что
оба ее диагональных элемента Л,- и D,- равны друг другу. Пусть
Мв соответствует «обратному» произведению матриц:
Мв = Мп... Mi ... MtM3M2Mi.
182 Глава 3
Требуется доказать, что
«А* ВЛ
Рассмотрим цепочку матриц
[—1 01 Г-1 0
Q ^М = Ма... М^.. МзММу Q
... М( ... Мп.
Если мы сначала вычислим произведение трех центральных
матриц, то получим
Mll 0 lJ^^Lc, dJL 0 lJLc, пг
t Btir-Аг -В,
, z),Jl c, z)
x{D,-Ax) Щ-Bf, У
Но, поскольку A\ = J3i, a 4jDi — B,^ = 1, #та матрица приво-
Г-1 01
дится к виду Г _ . |, т.е. к той же центральной матрице, что
и раньше.
Продолжая эту процедуру, находим
и т. д., так что окончательно получаем
[-1 от г—i от
о iJ*H о J
Умножая теперь левую часть этого равенства иа
-•Г °1
М \ п . |, а правую часть на эквивалентное выражение
г D -ЛГ-1 01
1-С All 0 1J'
i o-ir d -fl-ir
о lJL-c ar
d -fl-ir-i о
о i
Оптические резонаторы и распространение лазерного пучка 183
Отсюда получаем требуемый результат:
Задача 4
Для резонатора, рассмотренного в задаче 3, показать, что
матрица полного прохода может быть записана также в виде
Г Л в'1г •
-p2
где Pz — оптическая сила выходного зеркала.
Какие значения Р2 допустимы, чтобы данный резонатор был
устойчивым? Если использовать одно из этих значений, то чему
будет равен радус кривизны волнового фронта пучка, испускае-
испускаемого лазером в процессе генерации?
Решение
Аг В/
Мы увидим в дальнейшем, что матрица
D-0
Аг
представляет собой наиболее общую форму унимодулярной мат-
матрицы, у которой два элемента, расположенные на главной диа-
диагонали, одинаковы. В данном случае она описывает преобразо-
преобразование луча, выходящего из ОП2 в направлении —г и возвра-
возвращающегося в ту же опорную плоскость. Это преобразование
включает совместное действие внутрирезонаторной оптической
системы и левого зеркала — полной катадиоптрической системы.
В конце § 11 гл. 2 мы-доказали, что такая матрица всегда имеет
одинаковые матричные элементы А и D.
Для того чтобы подтвердить это, не обращаясь к доказатель-
доказательству, проведенному в § 11 гл. 2, перемножим тройную цепочку
матриц, полученных в задаче 3. В результате имеем
ГА До]Г
Lc0 aJl-
Pi
[с
V
О]Г?>о Во
lJLCo a
о В01Г
о AJLCo-
oDq -f- BoCo —
2Co?>o — D\
1
Do
-PXD
B0D0P,
IP,
B° ] =
A - BoP\ J
2AoBo — Д
BoCo + AA> —
1
J'
Если обозначить теперь матричные элементы на главной диа-
диагонали A0D0 -\- В0С0 — B0D0Pi через Аг, а элемент 2А0В0 —
184 Глава S
расположенный в правом верхнем углу матрицы, через Вт, то
можно получить искомую форму матрицы. (Мы опускаем здесь
простую проверку унимодулярности полученной матрицы, хотя
это всегда рекомендуется делать.)
Перемножая две оставшиеся матрицы, получаем матрицу
полного прохода:
Г '
1С 1
Для того чтобы эта матрица описывала устойчивый резона-
резонатор, ее след А + D должен иметь значения в интервале 2 -. 2.
Записывая это условие в виде 2 > BАГ— ВгР2) > —2, мы на-
находим, что Рг должно изменяться в пределах от 2(ЛГ+ \)/Вг до
2(Ar-l)/Br.
Если, например, мы имеем наиболее простой тип резонатора,
который состоит только из плоского зеркала, расположенного
на приведенном расстоянии Т, то Ат = 1, Вг = 2Г и Рг должно
находиться в интервале 2/Г Ч- 0. Другими словами, выходное
зеркало может быть вогнутым, но не выпуклым, и его радиус
кривизны должен быть меньше, чем Г (в случае г2 = Т имеем
резонатор с полусферическим зеркалом).
Теперь мы обратимся к рассмотрению более общего типа
резонатора. Если условие устойчивости выполняется, то радиус
кривизны гауссова пучка, излучаемого через выходное зеркало
резонатора, когда лазер работает в режиме основной моды,
дается выражением (см. § 7 настоящей главы)
D 2В 2ВГ 2
^^ D-A ~~ Ar-(Ar-BrP2) Z*"K=S''2
(радиус кривизны выходного зеркала). Иначе говоря, с точки
зрения физики явления генерируется такая волновая мода, в ко-
которой фаза на выходном зеркале постоянна.
Для любой системы с линейными резонаторами, работаю-
работающими в устойчивом режиме, это условие постоянной фазы удо-
удовлетворяется на обоих торцевых зеркалах, и внутри резонатора
во всем пространстве образуется четкая картина стоячих волн.
В неустойчивом режиме генерации, когда часть энергии поки-
покидает резонатор в радиальном направлении, данное условие не
выполняется,
\
Оптические резонаторы и распространение лазерного пучка 185
Если нам необходимо знать не только радиус кривизны, но
также и радиус пятна гауссова пучка, возбуждаемого в резона-
резонаторе, мы можем получить последнюю величину непосредственно,
используя довольно утомительную процедуру вычислений, опи-
описанных в § 8 настоящей главы (см. фиг. 3.17). Однако, по всей
вероятности, лучше составить сначала матрицу полного прохода,
а затем вычислить ее собственные функции. Действуя таким об-
образом, мы получим две полезные проверки: во-первых, проверим
факт устойчивости резонатора и, во-вторых, выясним, согла-
согласуется ли полученное значение R с заданной формой выходного
зеркала.
Задача 5
Требуется рассчитать короткий лазер с отпаянной трубкой на
двуокиси углерода для генерации на одной частоте и достаточно
низком уровне мощности. Из предварительных соображений
предполагают, что он должен быть построен на основе устойчи-
устойчивого резонатора длиной 50 см и иметь на выходе пучок парал-
параллельных лучей. Предполагается также, что 8 (фазовый угол в
выражении для собственного значения) должен быть равен од-
одному радиану. Какую кривизну зеркала вы считаете оптималь-
оптимальной для такой системы и какого диаметра трубку (приблизи-
(приблизительно) необходимо выбрать?
Решение
Поскольку мы имеем дело с устойчивым резонатором, то,
чтобы на его выходе был коллиМированный пучок, мы должны
использовать плоское выходное зеркало. Следовательно, в стан-
стандартную матрицу для резонатора, образованного двумя зерка-
зеркалами, мы можем подставить значения Т = 0,5 и Pi = 0, выра-
выражая соответствующие единицы измерения в метрах. При этом
получим (см. § 4 настоящей главы)
Г Л ВI _ Г 1 - Р{Г — 2Р2Т + Р{Р2Т2 ТB — Р1Т)
1С dJ^L -P1-P2 + P1P2T 1-PiT
-Л 1-4
Как и следовало ожидать, два элемента, расположенные на
главной диагонали, одинаковы и, кроме того, матрица унимо-
дулярна. Теперь мы найдем Р\, исходя из условия А + D =
= 2 — Р\ = 2 cos 9, где угол 9 = 1 рад. Следовательно, Р{ =
= 0,92 и /"! = 2/Pi = 2,17 (радиус кривизны в метрах).
186 Глава 3
При этом значении кривизны зеркала матрица полного про-
прохода численно записывается 9 виде
TAB! Г 0,54 0,771
1С Z)J -0,92 0,54 J *
Необходимо отметить, что вплоть до этого момента мы не
принимали во внимание длину волны лазерного излучения. Од-
Однако, чтобы выбрать диаметр трубы, мы должны знать геомет-
геометрию основной гауссовой моды, которая будет возбуждаться в
процессе генерации.
Используя формулу для радиуса перетяжки w0, находим
- A, sin 6 у/. Г A0,6) A(Г6) @,842) V i па m-3 i ,в
Па!—) =[ @,92) (я) J -1.76.10 м-1.76 мл.
Для конфокального параметра пучка z0 имеем
Следует заметить, что если тот же резонатор использовать
для лазера, работающего в видимой области спектра, то радиус
перетяжки пучка w0 будет приблизительно в четыре раза мень-
меньше, однако конфокальный параметр пучка z0 останется тем же.
Чтобы найти подходящий размер диаметра разрядной труб-
трубки, нам необходимо учесть, что на другом конце резонатора луч
будет несколько шире. Радиус пятна в этой области опреде-
определяется формулой
W ss= Wq I I -\ s- I =1 14Ш»О'
V 4)
Вследствие такого небольшого расширения пучка его макси-
максимальный диаметр, измеренный на уровне 1/е2, почти точно равен
4 мм.
В большинстве газовых лазеров, чтобы уменьшить дифрак-
дифракционные потери и учесть некоторую неизбежную расстройку,
диаметр разрядной трубки делают по крайней мере в два раза
больше диаметра пучка, определяемого на уровне 1/е2. В случае
лазера на двуокиси углерода стенки разрядной трубки могут вы-
вызывать нежелательные наклонные отражения, а также способ-
способствовать некоторому охлаждению газа, вызывая при этом увели-
увеличение коэффициента усиления. Кроме того, полный газовый объ-
объем может также быть важен с точки зрения продолжительности
работы отпаянной системы.
В рассматриваемом случае разумно выбрать разрядную
трубку с внутренним диаметром 10 мм; однако, по-видимому,
лучше использовать трубку большего диаметра, применяя диа-
диафрагму диаметром 10 мм.
Оптические резонаторы и распространение лазерного пучка 187
Входной Г/
луч L0
У {Разрушение может произойти
\Щ * точке X, если иажтьзшкя
импульсный лазер)
Задача 6
Как показано на фиг. 3.22, коллимированный лазерный пу-
чок диаметром 2 см фокусируется простой стеклянной плоско-
-выпуклой линзой с оптической силой 10 диоптрий и толщиной
вдоль оптической оси 1 см. Показатель преломления материала
линзы 1,5. Используя параксиальную оптику, вычислить поло-
положение любого сфокусированного изображения, образованного в
результате внутренних отражений пучка от поверхностей линзы.
Рассмотреть те изображения, которые образуются внутри стек-
стеклянной линзы.
Если поверхности линзы не просветлены и сферические абер-
рации и эффекты самофокусировки пренебрежимо малы, то на
сколько интенсивность света в фокусе превышает интенсивность
исходного параллельного пучка?
Решение
Обозначим через 31\ и 91% матрицы, соответствующие прелом-
лению луча на первой и второй поверхностях. Пусть Щ и Ж2 —
соответствующие матрицы отражения (здесь мы имеем в виду
отражения с внутренней стороны стеклянной линзы). Наконец,
пусть задана матрица ZT, соответствующая перемещению пучка
через слой стекла толщиной 1 см.
Матрица преобразования параметров луча на первой и вто-
рой поверхностях линзы без учета внутренних отражений запи-
записывается в виде
С другой стороны, если луч распространяется в направлении
+2, испытав п внутренних отражений, то матрица преобраэо-
188 Глава 3
вания лучей принимает следующий вид:
Для рассматриваемой линзы, поскольку ее вторая поверх-
поверхность плоская, обе матрицы #2 и Я'2 сводятся к единичной мат-
матрице /. Следовательно, полученную выше матрицу можно запи-
записать в более простом виде:
Используя в качестве единицы измерения длин сантиметры,
мы видим, что Г\ = 5. Таким образом,
*-¦ - °
,¦
]=V 2/3l
o i J Lo i J-
Подставляя эти матрицы в цепочку Мп, получаем
м /Т1 2/з1Г 1 °1Г1 ^lVF1 2/з1Г 1 °
^-Uo I JL-0,6 IJ Lo и; Lo i J L—o,i i
/Ti 7з1Г i 2hT\n Г 0,9333 2/з1
"ILo i JL-o,6 0,6V L -o.i i J
Г 0,6 1,06671" Г 0,9333 7з1
"L-0,6 0,6 J L -0,1 i J'
Поскольку нас интересует лишь п-е изображение, можно не-
непосредственно использовать теорему Сильвестра. Однако в этом
случае лучше воспользоваться последовательным методом вы-
вычислений. Для каждых значений г/,- и Vu взятых из последова-
последовательности многократных отражений, мы можем найти соответ-
соответствующее значение Rt; если Ri лежит в интервале 0,67 ч- 0, то
это означает, что рассматриваемый луч появился в фокусе, по-
после того как он последний раз прошел через толщу стекла лин-
линзы. С другой стороны, если R лежит в интервале 0 -. 0,67, то
луч соберется в фокусе, после того как он отразится от плоской
поверхности линзы и пройдет вновь через толщу стекла.
Проводя вычисления по этой схеме и используя крайний луч
р
находим прежде всего, что
г/о 1 Г 0,933
JL
o.
/?о ¦" — 9.33 (положение нормального сфокусированного изображения)}
Оптические резонаторы и распространение лазерного пучка 189
ГУ{ 1 _ Г °'6 1>06671Г °'9331 _ Г0>45331
UJ-L-0,6 0,6 JL — 0,1 J L— 0,62 J'
Ri = — 0,731 (лишь незначительно меньше, чем —0,67);
Г у21 _ Г 0,6 1,0667 1 Г 0,4533 П _ Г - 0,390 П
L K2J ""L — 0,6 0,6 J L — 0,62 J ~ L — 0,644 J'
R2 = 0,606 (внутри стекла);
Г #3 I Г 0,6 1,0667 1 Г -0,390 1 Г -0,921-1
L Кз J ~ L — 0,6 0,6 J L — 0,644 J ~ L — 0,152 J'
R3 = 6,06 и т. д.
(Заметим, что, когда рассматриваемый нами луч проходит че-
через фокус, его значение у меняет знак.)
Поскольку значения R, которые мы вычисляем, представляют
собой приведенные радиусы, то положение сфокусированного
изображения или «точка Бойза», которая получается после двух
внутренних отражений, будет располагаться на расстоянии
nR2 = 0,909 см слева от плоской поверхности, т. е. приблизи-
приблизительно на расстоянии 1 мм от выпуклой передней поверхности.
Для непросветленных поверхностей с показателем преломле-
преломления 1,5 доля падающей мощности, отраженной в случае нор-
нормального падения, составляет 0,04. Следовательно, в сфокусиро-
сфокусированном изображении, которое мы рассматриваем, полная мощ-
мощность будет равна всего лишь @,04L мощности входного пучка.
С другой стороны, если размер изображения ограничен дифрак-
дифракционной расходимостью, то его радиус уменьшится от исходного
значения, равного 1 см, до 0,61А,/Ч. А., или в данном случае до
0,61А,/0.644. (Заметим, кроме того, что значения V вычисляются
с учетом показателя преломления среды.)
Если мы предположим, что длина волны лазерного излуче-
излучения соответствует излучению гелий-неонового лазера, то увели-
увеличение интенсивности в центре этого изображения, усредненное
по площади диска Эйри, будет равно приблизительно
@,04L(V2J/@,61ЯJ = 710. (В случае гигантских импульсов,
излучаемых рубиновым или неодимовым лазером, это число мо-
может быть несколько меньше, поскольку длина волны излучения
больше, но все же достаточно большим, чтобы вызвать диэлек-
диэлектрический пробой с катастрофическими последствиями для этой
вполне пригодной в других ситуациях линзы.)
ГЛАВА 4
ИСПОЛЬЗОВАНИЕ МАТРИЦ
ДЛЯ ОПИСАНИЯ СОСТОЯНИЯ
ПОЛЯРИЗАЦИИ СВЕТА
§ 1. ПОЛЯРИЗОВАННЫЙ СВЕТ -
МЕТОДЫ ЕГО ПОЛУЧЕНИЯ И АНАЛИЗА
Предполагается, что читатель знаком с понятием поляризо-
поляризованного света в объеме, который обычно излагается в элемен-
элементарных курсах оптики. Будем считать известным, что для произ-
произвольного электромагнитного излучения осциллирующие компо-
компоненты электрического и магнитного полей направлены под пря-
прямым углом1друг к другу и перпендикулярно направлению рас-
распространения. В настоящей главе, как и в предыдущих, будем
использовать правую систему координат, ось Ог которой парал-
параллельна направлению распространения света. Рассматривая проб-
проблемы поляризации излучения, мы исключим из рассмотрения
магнитное поле и будем интересоваться в основном ориентацией
вектора электрического поля в плоскости ху, перпендикулярной
направлению распространения. Мы начнем с рассмотрения раз-
различных методов получения поляризованного света, а также ме-
методов его исследования и анализа. Прежде всего рассмотрим
два крайних случая.
Самые обычные источники света, такие, как солнце и элек-
электрическая лампа накаливания, испускают некогерентный и не-
поляризованный свет. Он представляет собой хаотическую су-
суперпозицию почти бесконечного числа независимых возмущений,
каждое из которых характеризуется собственным направлением
распространения, оптической частотой и состоянием поляриза-
поляризации. Возникает вопрос: насколько велико число этих «состоя-
«состояний», или «мод поля излучения»?
Относительно поперечных мод мы показали в предыдущей
главе, что для источника площадью А, излучающего в телесный
угол Q, число различных направлений распространения дается
выражением AQ/K2; например, для истопника площадью 1 см2,
излучающего в полусферу, это число будет порядка 108. Кроме
того, если наблюдать за некоторым тепловым источником света
в течение времени около 1 с, то нетрудно показать, что в спектре
излучения такого источника можно выделить, по крайней мере
теоретически, более 1014 различных частотных компонент. На-
Напротив, если мы будем рассматривать поляризацию электромаг-
Матрицы для описания состояния поляризации света 191
нитного волнового поля, то обнаружим, что число независимых
ортогональных состояний равно всего лишь двум\
Иногда говорят, что неполяризованный свет представляет со-
собой случайную смесь «всех сортов» поляризаций. Однако более
правильно было бы сказать, что, как бы мы ни старались ана-
анализировать неполяризованный свет, выбирая любые ортогональ-
ортогональные пары состояний, мы никогда не обнаружим, что какое-либо
из этих состояний имеет преимущество перед другим. Если бы мы
могли проводить наблюдения достаточно быстро, то нашли
бы, что «мгновенное» состояние поляризации очень быстро про-
проходит через все возможные комбинации выбранной нами пары
состояний, причем процесс этот носит статистический (случай-
(случайный) характер. В большинстве случаев состояние поляризации
изменяется приблизительно 1012 раз в секунду, так что мы на-
наблюдаем усредненное состояние поляризации.
По-видимому, сказано уже достаточно, для того чтобы по-
понять, что, хотя неполяризованный свет легко получить, описать
его математически или в рамках какой-либо модели достаточно
трудно. (Это обстоятельство обсуждается более подробно в при-
приложении III.)
Обратимся теперь к противоположному случаю, а именно к
случаю полностью когерентного света, с которым человек столк-
столкнулся сравнительно недавно, исследуя генерацию одномодового
лазера. Хотя лазер представляет замечательный триумф чело-
человеческой мысли, излучаемый им свет является наиболее простым
состоянием, которое только может существовать. Рассмотрим
плоскую волну с угловой частотой со, которая распространяется
со скоростью с в направлении Ог. Поскольку мы знаем, что ко-
колебания вектора электрического поля Е перпендикулярны на-
направлению распространения волны, то его можно определить
через дс-компоненту Ех с амплитудой Н и «/-компоненту Ev с ам-
амплитудой К. Таким образом, можно написать
и
(Обычно договариваются обозначать временную зависимость в
этой комплексной экспоненте в виде ei@( или е~ш. В настоящей
главе мы будем использовать первое обозначение.)
192 Глава 4
Пусть А представляет собой разность фаз фу — fx- Обозна-
Обозначим через i и j единичные векторы, направленные вдоль осей
Ох и Оу соответственно. Тогда эти два выражения можно объ-
объединить, записав поле в векторной форме:
Е (х, у, г, 0 = (Я? + /Се'дj) ехр { / [со (t - -J ) + фх] }.
С другой стороны, более удобно использовать для целей на-
нашей книги то, что поле можно записать в виде следующего век-
вектора-столбца:
В приведенном выше выражении отсутствует зависимость от*
и у, поскольку рассматривается плоская волна, т. е. волна бес-
бесконечной протяженности в плоскости, перпендикулярной напра-
направлению распространения. (С хорошей точностью эту волну мож-
можно получить, если выбрать точку наблюдения на большом рас-
расстоянии ') от лазерного источника или рассматривать излучение
при значительно более низких частотах от непрерывно работаю-
работающего радиопередатчика.)
ГЯе'**1 Г Я 1
Вектор-столбец вида I , или I „ (Д обычно назы-
называют вектором Максвелла или вектором Джонса2). В нашей
книге мы будем использовать в основном первое название. Как
будет показано в дальнейшем, „столбец Максвелла полностью
описывает состояние поляризации любого светового пучка, кото-
который полностью поляризован. Нетрудно заметить, что если в рас-
рассматриваемой когерентной плоской волне либо К, либо Я об-
обращается в нуль, то поперечные колебания должны быть поля-
поляризованы либо в вертикальной, либо в горизонтальной плоско-
плоскости. Если обращается в нуль разность фаз fv — <f>x = А, то мы
имеем линейно-поляризованный свет, а если Я = К при А =
= л/2, то свет обладает круговой поляризацией. В общем же
случае говорят, что свет поляризован эллиптически.
Если такое геометрическое описание поперечных колебаний
трудно себе представить, то полезной может оказаться следую-
следующая модель. Допустим, мы следим за движением в .««/-плоскости
небольшой заряженной частицы, которая одновременно притя-
*) В частности, необходимо выбрать расстояние много большим, чем
го = яа»д/Я, где Wo — радиус перетяжки пучка, а X — длина волны излуче-
излучения лазера. — Прим. ред.
2) В ряде случаев, с тем чтобы подчеркнуть матричную форму записи
этих векторов, мы будем использовать термин «столбец», — Прим. ред.
Матрицы для описания состояния поляризации света
193
Фиг. 4.1. Фигуры Лиссажу, соответствующие параметрическим уравнениям
х = cos со/ и у = cos (со/ + Д).
гивается к началу координат слабой пружинкой и в то же вре-
время удаляется от него под действием осциллирующего вектора
электрического поля. Если выбрать начало отсчета времени так,
что фх = 0, и измерять расстояние между частицей и началом
координат в соответствующих единицах, то мгновенные коорди-
координаты х и у пробной частицы, характеризующие ее смещение от
начала координат, будут изменяться со временем в соответствии
с выражениями
х = Я cos (at)
и
Отсюда следует, что при изменении величины at на 2я (а
это может происходить по крайней мере 10м раз в секунду) пе-
перемещение пробной частицы за один цикл имеет вид простой фи-
фигуры Лиссажу, как показано на фиг. 4.1. (Разумеется, такие фи-
фигуры очень просто получить при гораздо более низких частотах
на экране обычного осциллографа; для этого необходимо подать
на входы его усилителей вертикального Y и горизонтального X
отклонения луча два синусоидальных сигнала одной и той же
звуковой частоты. Если ^-отклонение луча задавать таким спосо-
способом, чтобы можно было получить «ЛГY-дисплей», то отсчет вре-
времени не играет роли.)
7 За к. 774
194 Глава 4
Каждая из этих фигур описывает положение конца осцилли-
осциллирующего вектора электрического поля. Для того чтобы исследо-
исследовать их геометрию, следует прежде всего исключить параметр
at из приведенной выше пары уравнений. Однако, прежде чем
перейти к этой процедуре, рассмотрим некоторые промежуточ-
промежуточные состояния светового поля между полностью когерентными и
полиостью некогерентными состояниями.
Существует два основных способа, с помощью которых мож-
можно получить частично когерентный свет:
а) Сначала рассмотрим лазер. В некоторых научных экспе-
экспериментах полная когерентность лазерного пучка может
вызвать затруднения, поскольку она дает нежелательные
эффекты интерференции, дифракции или «пятнистости»
поля. Обычно «квазитепловой» свет получают, посылая
лазерный пучок через прибор, разрушающий когерент-
когерентность, например, через быстро вращающийся стеклянный
матированный рассеиватель.
б) Однако в подавляющем большинстве случаев частично ко-
когерентный свет получают, посылая некогерентный свет от
обычного теплового источника через некоторую комбина-
комбинацию оптических, спектральных и поляризационных фильт-
. ров.
Простейшим типом оптического фильтра является узкая диа-
диафрагма. Она ограничивает расходимость светового пучка путем
весьма неэффективного процесса гашения почти всего света, ко-
который на нее падает; при~~этом проходит только центральная
часть пучка с существенно уменьшенной величиной этандю. По
такому же принципу действует спектральный фильтр. Им мо-
может быть либо кусок окрашенного стекла, либо монохроматор с
призмами или решетками, либо интерференционный прибор.
В любом случае он ограничивает спектр частот светового пучка
только путем гашения светового потока вне узкой полосы длин
волн.
Если пытаться ограничить обычный свет таким образом, что-
чтобы получить свет, близкий по направленности и спектральной
чистоте (монохроматичности) к лазерному, то в фильтрах те-
теряется практически вся начальная энергия светового потока. До
изобретения лазера свет, используемый в оптической лаборато-
лаборатории, мог быть либо направленным, либо монохроматическим.
Оба эти качества одновременно реализовать было невозможно.
В случае когда в эксперименте требуется полностью поляри-
зованный свет, возможна более эффективная фильтрация; по-
поскольку исходный свет распределен всего лишь между двумя
состояниями поляризации, то при фильтрации теряется всего
лишь половина энергии.
Матрицы для описания состояния поляризации света 195
Один из наиболее эффективных типов поляризующих фильт-
фильтров (поляризаторов) основан на использовании свойства двой-
двойного лучепреломления в одноосных кристаллах типа кальцита.
Разработанные первоначально поляризаторы, такие, как призма
Николя, впоследствии были заменены более совершенными ти-
типами поляризаторов, например поляризатором Глана — Фуко,
которые пропускают желаемую плоскополяризованную компо-
компоненту излучения с эффективностью, ограниченной в основном
потерями на отражение; другая же плоскополяризованная ком-
компонента, подлежащая гашению, устраняется практически пол-
полностью с помощью эффекта полного внутреннего отражения. Но
при использовании таких призм падающий свет должен быть
приблизительно коллимированным.
Столь же высоко эффективны в широком диапазоне длин
волн и апертур различные типы поляризационных фильтров, вы-
выпускаемых фирмой «Поляроид корпорэйшен». Например, поля-
поляризационный фильтр этой фирмы типа HN-32 пропускает около
32% падающего на него видимого света, причем доля нежела-
нежелательной компоненты поляризации составляет 1/10 000.
В лабораторной практике в любом случае для получения пол-
полностью поляризованного света удобно использовать либо лазер,
либо один из рассмотренных выше типов поляризационных
фильтров. Конечно, существуют и другие способы и ситуации, в
которых та или другая степень поляризации света получается
естественным образом, например, это происходит в тех случаях,
когда свет отражается под косым углом от полированной про-
прозрачной поверхности или рассеивается под углом ~90° ансамб-
ансамблем рассеивающих частиц очень малого размера. (В астрономии
или в лабораторной практике может встретиться ситуация, ко-
когда свет излучается в присутствии мощных, ориентированных в
пространстве электрических и магнитных полей; при этом возни-
возникает либо общая для всех длин волн степень поляризации, либо
степень поляризации, сильно зависящая от длины волны.)
В большинстве этих случаев фильтрация не бывает полной и
получается лишь частично поляризованный свет. В следующем
параграфе будет показано, что «степень поляризации» такого
светового пучка может быть описана с помощью его параметров
Стокса. При анализе свет можно рассматривать как смесь двух
полностью поляризованных и независимых пучков неравной ин-
интенсивности, состояния поляризаций которых взаимно ортого-
~нальны.
1.1. Плоскополяризованный свет
Представим себе теперь, что неполяризованный свет с по-
помощью поляроида (поляризационного светофильтра) становится
плоскополяризованным. Колебания вектора электрического поля
7*
lj» Глава j
происходят теперь сугубо в одном направлении в ^-плоскости,
перпендикулярно направлению распространения, Плоскость, со-
содержащую это направление и направление распространения Qz,
будем называть плоскостью колебаний1). Возникает вопрос: ка-
каким способом можно определить ориентацию этой плоскости?
Для большинства поляризаторов плоскость колебаний прохо-
проходящего света — плоскость пропускания — указывается жирной
прямой линией или стрелкой с двойным концом; если поляроид
имеет квадратную форму, то плоскость пропускания обычно па-
радлельца одной щ сторон квадрата. (Однако в некоторых ла-
лабораториях предпочитают использовать также 45° срезы!)
Первую полезную проверку можно провести, анализируя с
помощью поляризатора свет, отраженный под некоторым углом
от гладкой горизонтальной порерхности, например от полиро-
полированного стола. Поляризатор вращается в своей собственной пло-
плоскости до тех пор, пока отраженный свет почти полностью не по-
гасится. Поскольку известно, что отраженный свет поляризован
в основном горизонтально, плоскость пропускания нашего поля-
поляризатора в пределах нескольких градусов совпадает с верти-
вертикалью,. Таким образом, можно смело нанести в этом направле-
направлении обозначение плоскости пропускания — линию РР'.
Для того чтобы более точно установить ориентацию э!той
предварительно проведенной линии или проверить, правильно
ли была нанесена линия на готовом поляризаторе, можно посту-
поступить следующим образом. Поляризатор устанавливают на гори-
горизонтальную оптическую скамью так, что линия РР' располагает-
располагается строго вертикально (или горизонтально). Затем ставят вто-
второй поляризатор либо со стороны лампы, либо со стороны на-
наблюдателя и вращают этот второй поляризатор до тех пор, пока
не получат минимальную интенсивность проходящего света.
Не трогая второго поляризатора, следует развернуть первый
поляризатор вокруг оси, перпендикулярной направлению распро-
распространения света, на угол 180° и ориентировать его таким обра-
образом, чтобы линия РР' имела ту же ориентацию, что и в преды-
предыдущем случае. Если и в этом случае РР' совпадает с истинной
плоскостью пропускания поляризатора, то поле зрения вновь
окажется темным; но если через поляризаторы проходит значи-
значительная часть света, то следует повернуть первый поляризатор
на несколько градусов до такого положения, когда поле зрения
вновь станет темным. Затем наносят вторую линию на поляри-
') В литературе встречаются два термина: плоскость колебаний и пло-
плоскость поляризации. В старых справочниках и книгах плоскостью поляриза-
поляризации называют плоскость, проведенную через векторы Н и К, а плоскостью
колебаний-г-плоекоеть, содержащую Е в К. В последние годы в литературе
отождествляют эти два термина, подразумевая при этрм плоскость Е, К. Мы
также не будем делать различий между этими терминами. — Прим. ред. .
Матрицы для описания состояния поляризации света 197
затор, и истинное положение плоскости пропускания поляриза-
поляризатора будет находиться между двумя отметками.
Откалибровав таким образом поляризатор, можно опреде-
определить угол 8, образованный плоскостью колебаний исследуемого
света и горизонтальной осью х. Выражения, описывающие вза-
взаимно перпендикулярные компоненты электрического вектора,
имеют вид
Ех = A cos 6 cos (со/ + ^>)
и
Еу = A sin 6 cos {<ot + ^>).
(Эти выражения аналогичны тем, которые мы уже использовали
д^ля описания полностью когерентного лазерного пучка; однако
здесь рассматривается свет, характеризуемый целым диапазо-
диапазоном различных направлений и частот, причем амплитуда А и
фаза 9 осциллирующего поля не являются в действительности
постоянными. Они представляют собой функции пространствен-
пространственных и временных координат и быстро флуктуируют случайным
образом около своих средних значений. Расстояние и время, для
которых эти величины можно считать приблизительно постоян-
постоянными, иногда называют длиной когерентности и временем коге-
когерентности пучка. Точнее говоря, для каждой точки л#-плоскости,
перпендикулярной направлению распространения, мы можем на-
написать следующее равенство:
ГЕХ1 fcose
[еу\(Х' y) = [sinQ
> У' 0cos{©/ + *(*, у, ()}.
Однако следует заметить, что, поскольку рассматривается
столбец Максвелла, флуктуации происходят только в скалярном
множителе, который изменяет обе компоненты одинаковым об-
образом. В большинстве случаев фаза ф и ее флуктуации несуще-
несущественны, а величину А (х, у, t) можно заменить среднеквадра-
среднеквадратичным значением, которое мы будем обозначать А.)
Рассмотрим теперь снова движение нашей гипотетической
малой заряженной частицы. Под действием электрического поля,
описываемого этой синхронной парой векторов, ее смещение
дается уравнениями
х = A cos 6 cos (at + ф) и у — A sin 6 cos (cot + ф).
Умножая первое уравнение на sin 6, а второе на cos 0, сразу по-
получаем для поперечного смещения уравнение х sin В = у cos 0,
т. е. в плоскости колебаний движение частицы является прямо-
прямолинейным,
198 Глава 4
1.2. Эллиптически поляризованный свет
Для получения эллиптически поляризованного света плоско-
поляризованный пучок обычно пропускают через фазовую пла-
пластинку, вырезанную из одноосного кристалла. Как будет пока-
показано в гл. 5, такая пластинка вносит разность фаз между двумя
компонентами электрического вектора, параллельной и перпен-
перпендикулярной выделенному направлению в кристалле. Это направ-
направление называется оптической осью кристалла. Луч, в котором
колебания электрического вектора параллельны направлению
оптической оси кристалла, называют необыкновенным (Я-луч
или Я-колебания), а луч, в котором колебаняя электрического
вектора перпендикулярны направлению оптической ос,и, назы-
называют обыкновенным (О-луч или О-колебания) '). Для большин-
большинства фазовых пластинок (если они сделаны из отрицательного
одноосного кристалла) показатель преломления для Я-луча
меньше, чем для О-луча, и в этом случае оптическую ось кри-
кристалла называют быстрой осью. При маркировке ориентации
фазовой пластинки лучше всего нанести линию на оправке, ко-
которая параллельна быстрой оси. (Чтобы проверить правиль-
правильность маркировки, можно использовать тот же самый метод
проб и ошибок, описанный нами для случая определения ориен-
ориентации поляризатора, а именно фазовая пластинка испытывается
в двух положениях между двумя скрещенными поляризато-
поляризаторами.)
Будем предполагать, что фазовая пластинка, которую мы ис-
используем, расположена таким образом, что ее оптическая ось
параллельна оси х, а толщина фазовой пластинки такова, что
она создает положительный сдвиг фаз на угол А радиан О-луча
относительно Я-луча. (В этом случае быстрая ось повернута на
90° относительно оси х). Компоненты электрического вектора
световой волны, прошедшие через фазовую пластинку, опреде-
определяются теперь выражениями
х = A cos 8 cos at и у = A sin 8 cos (at + А).
Если исключить отсюда at, то получим уравнение, связывающее
х- и «/-компоненты электрического вектора световой волны, про-
прошедшей через фазовую пластинку:
*2 2xycosA ¦ уг _„Лпзд
A2 cos2 9 A2 sin 9 cos 9 ^ A2 sin2 9 ьш "»
или, обозначая И = А cos 8 и К = A sin 8, имеем
2*ycosA ¦ i JL — cjn2 A-
y у
Н2 НК + К2
•) В соответствии с первыми буквами английских слов extraordinary (не-
(необыкновенный) и ordinary (обыкновенный). — Прим. перев.
Матрицы для описания состояния поляризации света 199
здесь Я — компонента электрического вектора во входном пуч-
пучке, параллельная оси х, а К — соответствующая компонента, па-
параллельная оси у. Возводя в квадрат и складывая эти компо-
компоненты, находим, что Я2 4- Л = А2 — квадрат амплитуды коле-
колебаний электрического вектора на входе фазовой пластинки. Эта
величина пропорциональна энергетическому потоку исходной
волны. Мы ее будем называть интенсивностью и обозначать /
(по-видимому, более правильно было бы называть эту величину
освещенностью).
Рассмотрим теперь некоторые частные случаи последнего
уравнения. Если А = 0, т. е. фазовая пластинка отсутствует, то
cos А = 1, a sin А = 0, и наше уравнение принимает вид
х2 2ху . у2
н2 нк "*¦ к2 ~~ •
т. е.
.я
или
JL — JL
х Н ¦
Данное соотношение в точности описывает плоскополяризован-
ную исходную волну. Предположим теперь, что мы имеем дело
с полуволновой пластинкой, для которой А = я, так что sin A =
= 0, a cos А = — 1. В результате получим соотношение, анало-
аналогичное предыдущему, за исключением лишь того, что знак пра-
правой части изменится на противоположный, а именно
i—f
Это означает, что отношение смещений, параллельных двум
осям, такое же, как и в предыдущем случае, но противоположно
по знаку, так что, когда х достигает своего максимального поло-
положительного значения, у достигает своего максимального отрица-
отрицательного значения, и наоборот. Таким образом, волна остается
плоскополяризованной, но колебания теперь происходят под уг-
углом 9 к оптической оси, т.е. полуволновая пластинка повора-
поворачивает плоскость колебаний на угол 29.
Рассмотрим теперь случай А = я/2, т. е. так называемую
четвертьволновую пластинку. Поскольку при этом cos А = 0, а
sin А = 1, то уравнение, связывающее х- и «/-компоненты, при-
принимает вид
~Н2"^~КГ =
Это хорошо известное уравнение эллипса, ориентированного
таким образом, что его большая и малая оси параллельны соот-
соответственно осям х и у. Полуось, параллельная оси х, равна Я, а
200 Глава 4
полуось, параллельная оси у, равна К. Если 9 = 45°, то Н = К
и наше уравнение записывается следующим образом:
о ¦ о А
X2 + y2 = ~2~.
При этом говорят, что свет поляризован по кругу.
Если полностью поляризованный луч света проходит через
поляризатор, который медленно поворачивают на угол 360°, то
различие между линейной, эллиптической и круговой поляриза-
поляризациями нетрудно обнаружить экспериментально. Линейной поля-
поляризации соответствуют две различные ориентации поляризатора,
при которых свет будет полностью гаситься. В случае эллипти-
эллиптической поляризации должны наблюдаться два минимума и два
максимума интенсивности, но в минимуме не будет полного га-
гашения света. В случае же круговой поляризации света яркость
все время остается постоянной.
Эллиптическая и круговая поляризации бывают правой или
левой в зависимости от направления вращения электрического
вектора. Для состояния с правым вращением фазовый угол А,
на который колебания по оси у опережают колебания по оси х,
должен лежать в пределах от 0 до я. В этом случае конец век-
вектора электрического поля описывает эллиптическую траекторию,
вращаясь по часовой стрелке с точки зрения наблюдателя, рас-
рассматривающего источник света из точки -\-z (см. фиг. 4.1).
§ 2. ИСПОЛЬЗОВАНИЕ ПАРАМЕТРОВ СТОКСА
ДЛЯ ОПИСАНИЯ ПОЛЯРИЗАЦИИ СВЕТА
Исходное уравнение, полученное исключением at из уравне-
уравнений для х- и «/-составляющих колебания электрического вектора,
определяет эллипс более общего типа, причем его полуоси не
параллельны осям х и у. Чтобы найти ориентацию и отношение
осей эллипса, в этом случае целесообразнее применить более
тонкий математический аппарат, чем мы использовали до сих
пор. Для чистого состояния поляризации, описываемого величи-
величинами Н, К и Д, определим следующие четыре параметра Стокса:
/ = я2 + К2 = Л2,
Q = H2— K2 = A2cos2Q — Л2 sin2 6 = Л2 cos 26 =/cos 26,
U = 2НК cos A = 2 (Л cos 6) (Л sin 9) cos A = Л2 sin 26 cos A =
= /sin 26 cos A,
V =
С помощью элементарных алгебраических преобразований мож-
можно показать, что для полностью поляризованного пучка света
Матрицы для описания состояния поляризации света 201
р == Q2 -f U2 -f- V2. Физический смысл этих величин мы рассмо-
рассмотрим ниже. В соответствии с определениями этих величин имеем
1 1 V* V^
H—jV + Q), К =j{I — Q), sin A = 4tf2/c2 = /2 _ q2 •
Таким образом, уравнение, описывающее колебания, принимает
вид
2л;2 АЦху ¦ 2у2 _ V2
I+Q Р — Q2 ~*~ / — Q /2 — Q2 '
ИЛИ
2у2 (/ + Q) ,
у2 у2 I у2
Введем следующие величины:
P^litzL G
Г yi ' и
В новых обозначениях наше уравнение записывается в виде
Проще всего найти ориентацию и отношение осей эллипса
следующим образом. Перепишем наше уравнение в полярных
координатах, причем если точка с координатами (R, ф) соответ-
соответствует точке с декартовыми координатами (х, у), то х = R cos ф,
у = R sin ф, и уравнение принимает вид
PR2 cos2 ф - 2GR2 cos ф sin ф + FR2 sin2 ф=1.
Используя хорошо известные формулы для cos 2ф и sin 2ф,
получаем
PR2 A + cos 2ф)/2 — GR2 sin 2ф + /="#2 A - cos 2ф)/2 = 1.
Обозначая здесь 2ф = р и 2/Я2 = W7, находим следующее выра-
выражение для W^:
И7 = (Р +/г) _ 2G sin р + (Р - .F) cos р.
На концах большой и малой осей эллипса R принимает соот-
соответственно максимальное и минимальное значения, и, следова-
следовательно, W также имеет соответственно минимум и максимум. Та-
Таким образом, значения р, соответствующие осям эллипса, опре-
определяются корнями уравнения dW/d$ = 0:
dW/d$ = - 2G cos p — (Р — F) sin p.
Следовательно, если а является значением р на оси эллипса, то
можно написать
, sina 20
tga~ cosa — f-P'
Это соотношение определяет два возможных значения а.
202 Глава 4
Последовательные значения угла, для которых тангенс имеет
одну и ту же величину, отличаются на я; поэтому если <ц — наи-
наименьшее, ао2- наибольшее значение а из интервала 0 -4- 2я, то
а2 = aj + я, так что sin a2 = —sin си и cos a2 = —cos сц. Сле-
Следовательно, если W\ и И?2 — соответствующие значения перемен-
переменной 2/R2, то можно написать соотношение
Л| №, (Р + F) — 2G sin a, +. (P — F) cos a,
R^ W2 (P + F) — 2G sin a2 + (Я - F) cos a2 '
Подставляя в это соотношение параметры Стокса, находим,
что наименьший угол а/2, который одна из осей эллипса состав-
составляет с осью х, дается выражением
2G U , па .
p-p — -q = tg 2е cos д-
При этом отношение квадратов длин малой и большой осей по-
после небольших преобразований записывается в виде
Ц2) _ 1 — УA — sin2 29 Sin2 А)
V
/ + V(Q2 + U2) 1 + V(l — sin2 26 sin2 Л)
Полученные нами соотношения можно проверить эксперимен-
экспериментально, используя два поляроида, фазовую пластинку и фото-
фотоэлемент.
Эти соотношения связывают параметры Стокса одной пло-
скополяризованной волны с соответствующим столбцом Макс-
Максвелла. В то же время параметры Н и К определяют амплитуды
колебаний вектора электрического поля, которые при оптиче-
оптических частотах нельзя наблюдать непосредственно. Параметры
Стокса связаны линейно с непосредственно измеряемыми с по-
помощью фотоэлемента энергетическими характеристиками — они
определяются реально измеряемой интенсивностью или раз-
разностью интенсивностей. (Такие измерения мы обсудим в § 4 на-
настоящей главы.)
Исходя из этого различия, сформулируем два важных след-
следствия, которые можно применять в тех случаях, когда мы сме-
смешиваем два или более пучка, состояния поляризации которых
известны, и хотим предсказать поляризацию полученной смеси,
а) Если смешиваемые волны взаимно когерентны, то необхо-
необходимо складывать соответствующие столбцы Максвелла, с
тем чтобы получить стоЛбец Максвелла смеси. (Этот слу-
случай, соответствующий сложению амплитуд, реализуется
главным образом, когда пучки выходят из полностью ком-
компенсированного интерферометра или получены от одного
лазерного источника.)
Матрицы для описания состояния поляризации света
203
б) Если же смешиваемые волны взаимно некогерентны, то
следует складывать их векторы Стокса, с тем чтобы полу-
получать вектор Стокса смеси. Этот случай соответствует сло-
сложению интенсивностей и встречается гораздо чаще, чем
предыдущий случай, например всегда, когда мы имеем
дело с неполяризованным или лишь с частично поляризо-
поляризованным светом. При этом эффективные значения Н, К и
Д определяются средними статистическими значениями,
полученными за конечный интервал времени наблюдения.
Математический анализ данного случая рассмотрен в при-
приложении III.
В приложении III показано, что для полностью поляризован-
поляризованного света всегда справедливо равенство I2 = Q2 -f- U2 + V2, а
для полностью неполяризованного света три компоненты Q, U и
V обращаются в нуль и остается только один параметр интен-
интенсивности /.
Частично поляризованный свет можно характеризовать сте-
степенью поляризации Р. Эта величина равна положительному зна-
значению корня квадратного из отношения (Q2 + U2-\- V2)/I2. Для
любого физически реализуемого светового пучка значение пара-
параметра Р лежит между нулем и единицей.
При желании частично поляризованный свет можно разло-
разложить на два независимых луча, один из которых будет пол-
полностью поляризован, а другой полностью деполяризован. Оче-
Очевидно, это разложение имеет вид
О
О
О
Однако во многих случаях удобнее использовать другое раз-
разложение на два полностью поляризованных луча с противопо-
противоположными состояниями поляризации. При условии что Р не об-
обращается в нуль, получаем
¦ / -
Q
и
-V
- PI -
Q
и
-V -
-I -
Q
и
-V -
0 + Р)
2Р
-PI-,
Q
и
-V -
, A-Я)
"т" 2/>
¦ PI -]
-Q
— и
у _
где
Если Р = 0, то свет полностью деполяризован и его можно
рассматривать как смесь двух лучей равной интенсивности с
произвольными, но ортогональными состояниями поляризации.
204 . Глава 4
Здесь следует отметить, что для полностью поляризованного
луча единичной интенсивности параметры Q, U и V могут при-
принимать любое действительное значение между 1 и —1 при усло-
условии, что сумма квадратов этих величин остается равной 1. Если
рассматривать эти три величины как координаты в декартовой
системе, то получим пространственное представление, в котором
точка пространства (Q, U, V), соответствующая произвольному
состоянию поляризации, расположена на сфере единичного ра-
радиуса — сфера Пуанкаре. На такой сфере, очевидно, точки (Q,
U, V) и (—Q,—U,—V), соответствующие противоположным со-
состояниям поляризации, лежат на противоположных концах диа-
диаметра. (Существует множестбо проблем поляризационной оп-
оптики, для которых сфера Пуанкаре дает наглядное геометриче-
геометрическое представление, однако здесь мы не будем подробно обсу-
обсуждать эти проблемы.)
§ 3. ИСПОЛЬЗОВАНИЕ МАТРИЦ МЮЛЛЕРА
ДЛЯ ПРЕОБРАЗОВАНИЯ ВЕКТОРА СТОКСА
Рассмотрим теперь применение матричных методов для вы-
вычислений параметров поляризации. Четыре параметра Стокса,
определяющие состояние поляризации луча, можно рассматри-
рассматривать как элементы матрицы размером 4 X 1. Такую матрицу бу-
будем называть столбцом (или вектором) Стокса и обозначать S:
с
Q
и
(В разных книгах параметры Стокса обозначают по-разному,
например как /, М, С, S или Pq, Р\, Pi, Рг- В настоящей глаЬе
мы будем использовать для обозначения столбца Стокса про-
прописную букву S, напечатанную жирным шрифтом, чтобы отли-
отличить ее от сокращенного обозначения 5 функции синус. Для обо-
обозначения эрмитово сопряженных величин мы будем использо-
использовать буквы с чертой внизу.)
Покажем, что для приборов любого типа (поляроидной плен-
пленки, плоскость пропускания которой образует произвольный угол
с осью; фазовой пластинки с произвольным запаздыванием и
произвольной ориентацией быстрой оси; пластин, поворачиваю-
поворачивающих плоскость поляризации, роль которых могут играть некото-
некоторые органические жидкости) параметры Стокса для выходя-
выходящего из прибора луча являются линейными функциями четырех
Матрицы для описания состояния поляризации света
205
параметров Стокса входного луча. Таким образом, можно на-
написать следующие соотношения:
I2 = MnIi + Mh
Q2 = Af2i/i + M2<
U2 = M31Ii + M3,
V2 = Af41/, + M*
2Qi + M13Ui -
iQ\ + Mat/, -
2Q, + /Mast/, -
,q, 4. MbC/, -
\-M2iVu
\- M^Vu
h Л144У,.
Здесь параметры Стокса, отмеченные индексом 1, относятся к
входному лучу, а индексом 2 — к выходному лучу. Величины Ms
с двумя нижними индексами описывают только характеристики
прибора и его ориентацию. Эти четыре уравнения можно запи-
записать в матричном виде:
-Mil
M
2i
M
i2
-Л п
или
S2 = MS,
Здесь Si — столбец Стокса для входного луча, a S2 — столбец
Стокса, характеризующий выходящий из прибора луч, и М —
матрица 4X4, описывающая ориентацию и характеристики при-
прибора. Последнюю матрицу, характеризующую прибор, назы-
называют матрицей Мюллера в честь автора, который впервые ее
ввел. Таким образом, если луч проходит через ряд последова-
последовательно расположенных приборов, мы можем определить пара-
параметры луча на выходе, зная только параметры входного луча и
характеристики приборов, через которые он проходит.
В табл. 4.1 приведены матрицы Мюллера, характеризующие
различные наиболее часто употребляемые приборы. Выражения
для столбцов Стокса и столбцов Максвелла при различных со-
состояниях поляризации света можно найти в приложении III.
Используя данные, приведенные в табл. 4.1, выполним не-
несколько простых вычислений. Эти вычисления мы используем
для описания фотоупругого эффекта, который широко исполь-
используется для анализа напряжений при моделировании объектов ь
строительной и инженерной практике. Физическое проявление
фотоупругого эффекта заключается в следующем. Если пластин-
пластинку из прозрачного материала, например из стекла или пласт-
пластмассы, сжимать в направлениях, параллельных ее поверхности,
Твбшца 4,1
МАТРИЦЫ МЮЛИБРА ДДЯ ИДЕАЛЬНОГО'ЛИН1ВЯЯОГО ПОЛЯРИЗАТОРА. ФАЗОВЫХ ПЛАСТИНОК
для лянвяно-полда>1|эов*шкн-о света, поворота осей
» ФАЗОВОЙ ПЛАСТИНКИ ДЛЯ ШЯЧСУЛЯРНОЛОЛЯРИЗОВАННОГО СВЕТА
Тип прибора I)
9—0
Произвольны! угол
Идеальный Mutu-
вый поляризатор,
0|Ш«ШПрОВ
вод углом i
-1
I
0
.0
1
1
0
о
0
0
0
0
о-
0
0
«_
т
10
1 во
±1 0
00
0
оо
1 0
00
-10 0
ЮО
000
00 9
Г 1 С, 5, 0
С2 Cf С252 О
.00 0 0,
" _/•*» Oft
S»««in 26
Чет»ерти<мво»м
вдастшщи, быст-
быстрая «с€ которой
Ор*я«» под
Полуьоляомя I
стнюса. быстде
ось жотороА <^в*
вятяромна * мж
углом 0
-1
0
0
lo
-ю
0 1
оо
1
10
0
1
0
0
0
0
-1
0
0
-1
0
or
1
0_
0"
#
-1_
о
0
.0
¦1
0
6
.0
0
0
0
*1
0
_1
о"
0
0
0
1
0
0
i
0
0
=F1
: 0
0
Ч 0
; о
-1
-loo о-
0 10 0
0 0 0-1
Lo о Г оJ
Г1 0 0 0
10 1 0 0
100-1 О
Lo о о-1.
1
0
0
0
1
0
0
0
0
с\
с,
S,
0
с4
s4
0
0
dS,
s» si.
-с,
о o-
54 0
—C40
0 -1
о ¦
-s,
ct
0.
C« —coe46
S4 - sin 48
Фазовая пластинка
с разностью фаз б,
быстрая ось кото-
которой ориентирована
под углом в
-1
0
0
_0
0
1
0
0
0
0
р
— и
0
0
р
¦) Угол в—угол орнеитации плоскости пропускания поляризатора или быстрой оси фазозоя пластинки для линейно-поляризованного
•света относительно оси Ох.
Замечание: здесь мы использовали сокращения В*»cos 8 и n«=sln9.
Переход к новой системе координат, получаемой при
повороте старой системы вокруг оси Ох на угол в
или действием фазовой пластинки для циркулярио-
поляризованного света, которая замедлиет волну
•с левой круговой поляризацией иа 26 рад.
1-1 ОООП
10 С, S, 0 I
I 0 -S, С, 0 I
L0 0 0 1 J
Обозначим эту матрицу поворота через R @); с ее по»
можно преобразовывать матрицу Мюллера для произв
поляризационного прибора (или целой системы), ориентиро-
ориентированного иод углом Ф, в соответствующую матрицу для того же
прибора (или системы) с новой ориентацией 9+^. При этом
формула преобразования записывается в виде
=./? (- в) М (¦) R (в).
Если целую систему, состоящую из нескольких поляризационных приборов, необходимо развернуть иа некоторый угол, то, используй
унитарность преобразовании поворота, можно значительно сократить выкладки. Однако в случае одного пробора целесообразнее исполь-
использовать матрицу из соответствующего столбца этой таблицы. (Методы вычнсленая таких матриц даны в приложении IV.)
208 Глава 4
то она работает как фазовая пластинка, причем ее оптические
оси параллельны поверхности. Этот эффект исследовали Керр,
Брюстер, Филон, Коукер и др. Они обнаружили, что законы фо-
фотоупругости можно сформулировать наиболее просто следую-
следующим образом: 1) направление оптической оси в любой точке пла-
пластинки совпадает с направлением напряжения в этой точке и
2) запаздывание обыкновенного луча по сравнению с необык-
необыкновенным лучом, выходящим из произвольной точки пластинки,
пропорционально величине напряжения в этой точке. Если за-
запаздывание по фазе измерять в радианах и обозначить его через
о, то второй закон можно записать следующим образом:
б = csd; '
здесь s — напряжение в точке, d — толщина пластинки и с —
постоянная, называемая фотоупругим коэффициентом, который
зависит только от материала пластинки и длины волны. Таким
образом, если определены направление оптической оси и разность
фаз в каждой точке нагруженной пластинки, то можно най-
найти распределение напряжений. Зная картину распределения на-
напряжений, которая возникает в некоторой модели под действием
заданных деформаций, мы можем вычислить, используя про-
простую пропорцию, напряжения в геометрически подобном иссле-
исследуемом объекте. Следует считать, что напряжения в модели и в
истинной структуре пропорциональны. Это позволяет избежать
длинных и громоздких вычислений.
Изложим теперь теорию этого метода на основе матриц
Мюллера.
Модель помещается между двумя поляроидными пленками,
или поляроидами, плоскости пропускания которых скрещены под
прямым углом так, что если модель отсутствует, то свет пол-
полностью гасится. Однако сначала вместо описанной схемы рас-
рассмотрим несколько более общую, в которой плоскости пропуска-
пропускания поляроидов ориентированы произвольным образом. Для про-
простоты исследуем случай, когда оптическая ось фазовой пластин-
пластинки горизонтальна, что, впрочем, не приводит к какой-либо по-
потери общности наших выводов. Предположим, что фазовая пла-
пластинка вносит разность фаз б между обыкновенными и необык-
необыкновенным лучами, причем первый распространяется более мед-
медленно. Предположим также, что первый поляроид, через кото-
который проходит свет, ориентирован так, что его плоскость пропу-
пропускания составляет угол а с горизонтальной осью Ох, а второй
поляроид, расположенный за фазовой пластинкой, ориентиро-
ориентирован под таким углом, что его плоскость пропускания образует
с осью Ох угол у. причем у отсчитывается от оси по часовой
стрелке, т. е. в общепринятых обозначениях он является отри-
Матрицы для описания состояния поляризации света
209
цательным углом — у. Будем считать, что на первый поляроид
падает пучок неполяризованного света интенсивностью 1\. Ис-
Используя матрицу Мюллера, вычислим интенсивность света, про-
прошедшего через второй поляроид. Проведем эти вычисления в три
этапа. Сначала для первого поляроида. Если свет на выходе
первого поляроида описывается столбцом Стокса S2, то, ис-
используя матрицу Мюллера для поляроида, его можно записать
в виде
1
cos 2а
sin 2а
0
cos 2а
cos2 2а
sin 2а cos 2а
0
sin 2а
cos 2а sin 2а
sin2 2а
0
h '
/1 cos 2а
/j sin 2а
0 -
2
- 1 -
cos 2а
sin 2а
- 0 -
0-
0
0
0-
г/i-i
0
0
-0 -
Затем пропустим луч, прошедший первый поляроид, через
фазовую пластинку. Столбец Стокса луча после фазовой пла-
пластинки обозначим через S3. Для того чтобы вычислить S3, нужно
умножить S2 на матрицу Мюллера, соответствующую фазовой
пластинке, а именно:
и
2
Л
2
- 1
0
0
-0
|-
__
0
1
0
0 -
1
0
0
cos б
-sin 6
-
cos 2а
sin 2а cos 6
- sin 2а
sin 6 -
0 -
0
sin б
cos б -
г 1
cos 2а
sin 2а
- 0
•
(Отметим, что в процессе этих матричных вычислений любой
скалярный множитель вроде 1\ можно произвольно записывать
как с одной, так и с другой стороны матрицы.) Наконец, луч,
прошедший фазовую пластинку, пропустим через второй поля-
поляроид, после которого он будет описываться столбцом S4. Чтобы
210
Глава 4
вычислить S4, нужно умножить S3 на матрицу Мюллера вто-
второго поляроида. Таким образом,
1 cos 2у
cos 2y cos2 2y
— sin 2y — sin 2y cos 2y
0 0
— sin 2y 0
— sin 2y cos 2y О
sin2 2Y 0
О 0_
1
cos 2a
sin 2а cos 6
— sin 2а sin 6
1 + cos 2y cos 2а — sin 2y sin 2а cos 6
cos 2у + cos2 2у cos 2а — sin 2y cos 2y sin 2a cos 6
—sin 2y — sin 2y cos 2y cos 2a + sin22y sin 2a cos 6
0
Первый элемент вектора S4 равен /4 — интенсивности луча на
выходе из' системы. Теперь рассмотрим специальный случай,
когда первый и второй поляроиды скрещены, т. е. их плоскости
пропускания перпендикулярны одна другой, так что в отсут-
отсутствие рассмотренной нами выше модели происходит полное га-
гашение света. Это значит, что a -f- у = 90°, следовательно, 2а +
+ 2у = 180°, так что sin 2у = sin 2a и cos 2y = —cos 2a. Вы-
Выражение для интенсивности света на выходе системы получается
после некоторых небольших преобразований и записывается в
виде
/4 == 1 A _ cos2 2a — sin2 2a cos 6) -?- = 4" h sin2 2a sin2 F/2).
Интенсивность /4 обращается в нуль, во-первых, если sin 2a = 0,
т. е. когда a = 0 или 90°, или, иначе говоря, когда оптическая
ось фазовой пластинки параллельна плоскости пропускания
того или другого поляроида. Это условие позволяет найти кри-
кривые, называемые изоклинами, по которым можно определить на-
направление напряжения в любой точке.
Во-вторых, интенсивность /4 обращается в нуль, если
sin F/2) = 0, т. е. когда 6/2 = 0, я, 2я или любому другому
числу, кратному я. Отсюда можно найти напряжение в любой
точке, поскольку оно пропорционально 6. Кривые, вдоль кото-
которых sin F/2) обращается в нуль, называются изохроматами.
Одновременное присутствие изоклин и изохромат на экране мо-
может усложнить анализ изохромат.
Часто желательно устранить изоклины, что можно осущест-
осуществить, используя две четвертьволновые пластинки, устанавливае-
устанавливаемые следующим образом. Одна четвертьволновая пластинка по-
помещается между первым поляризатором и моделью, причем ее
быстрая ось образует угол 45° с горизонталью и проходит через
Матрицы для описания состояния поляризации света
211
первый и третий квадранты. Другую четвертьволновую пластин-
пластинку располагают сразу после модели таким образом, чтобы ее
быстрая ось также проходила под углом 45° к горизонтали, но
через второй и четвертый квадранты; следовательно, в общепри-
общепринятых обозначениях угол ориентации второй пластинки следует
считать равным —45°.
Покажем теперь, что при использовании этих двух четверть-
четвертьволновых пластинок интенсивность света на экране зависит
только от сдвига фаз, вносимого фазовой пластинкой, и не зави-
зависит от ее ориентации. Предположим для простоты, что пло-
плоскость пропускания первого поляроида горизонтальна, а вто-
второго — вертикальна. При наблюдении изохромат это условие
практически всегда можно выполнить.
Направим на первый поляроид пучок неполяризованного све-
света, для которого все параметры Стокса, за исключением h, рав-
равны 0. Записывая матрицу Мюллера, соответствующую поля-
поляроиду, получаем, что столбец Стокса для луча, прошедшего пер-
первый поляроид, имеет вид
-1
1
0
-0
1
1
0
0
0
0
0
0
о-
0
0
0-
r/i-i
0
0
-0 -
1
~~ 2
-/.-1
/,
0
-0 -
Далее луч проходит через четвертьволновую пластинку, быстрая
ось которой повернута на угол -(-45° относительно оси х. Ис-
Используя соответствующую матрицу Мюллера из табл. 4.1, полу-
получаем столбец Стокса, описывающий свет с правой круговой по-
поляризацией:
-1
0
0
-0
0
0
0
1
0
0
1
0
о-
-1
0
0-
r/i-i
/l
0
-0 -
1
~~ 2
¦/l
0
0
-h
Затем пропустим луч через фазовую пластинку, которая создает
разность фаз б и быстрая ось которой ориентирована под некото-
некоторым неизвестным углом 6. В табл. 4.1 приведена матрица Мюл-
Мюллера, соответствующая такому прибору. В ней для краткости
cos 2в и sin 28 обозначены через Сг и S2, a cos б и sin б обозна-
обозначены через р и ц соответственно. В этих обозначениях столбец
212
Глава 4
Стокса дли луча на выходе фазойой пластинки
о
Sill
0
CAO-P)
si + pc2
— С2ц
0
P _
/Г
0
0
в/,
После того как пучок пройдет через вторую четвертьволновую
пластинку с быстрой осью, ориентированной под углом —45° от-
относительно оси х, его столбец Стокса запишется в виде
1
2
- 1
0
0
-0
0
0
0
-1
0
0
1
0
On
1
0
0-
- 52ц/,
p/,
Наконец, после прохождения через поляроид, плоскость пропу-
пропускания которого вертикальна, выходящему из системы пучку со-
соответствует столбец Стокса следующего вида:
1 -1 0 От
-1 10 0
0 0 0 0
0 0 0 0J
1 1
Т
&б—1Г' -в"
1
о
о
0
о
Интенсивность светового пучка на выходе системы описывается
первым элементом столбца Стокса S6) а именно:
Теперь мы видим, что интейСибность выходного пучка Опреде-
Определяется только интенсивностью Л входного пучка и разностью
фаз б, вносимой фазо&ой пластинкой, и совсем не зависит от угла
Матрицы для описания состояния поляризации света
213
йриеитации фазовой пластинки 0. Таким образом, изоклины, ко-
1-орые зависят от ориентации пластинки, исчезнут и останутся
только йзохроматы.
Иногда линейный поляризатор и четвертьволновая пластин-
пластинка, ориентированная под углом +45 или —45°, изготавливаются
совместно на одной и той же пленке, и такая комбинация назы-
называется поляризатором с правовращающей и левовращающей
круговыми поляризациями. При использовании такого фильтра
Необходимо проявлять особую осторожность, чтобы не устано-
установить его «задом наперед». (Студенту весьма полезно, выполняя
вычисления, которые были проведены выше, рассчитать эффект,
связанный с перестановкой первого поляроида на место первой
четвертьволновой пластинки.)
Метод вычислений, рассмотренный выше, заключается в том,
что последовательно получают столбцы Стокса. Хотя можно
было бы найти тот же самый результат и другим путем, а имен-
именно перемножая все матрицы Мюллера 4X4, но вычисления
здесь оказываются значительно более громоздкими. Однако если
использовать соответствующие программы для расчетов на ЭВМ,
приведенные в приложении VII, то это неудобство становится
несущественным. (Следует заметить, что если исходный неполя-
ризованный луч со столбцом Стокса
о
о
LO J
заменить поляризо-
поляризованным лучом
то большинство эффектов, связанных с со-
состоянием поляризации входного пучка, погашаются первым по-
поляризатором; единственное различие, которое при этом возник-
возникнет, состоит в том, что в последующих этапах расчета величина
h заменяется на h + Qi.)
§ 4. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
ЭЛЕМЕНТОВ МАТРИЦЫ МЮЛЛЕРА И СТОЛБЦА СТОКСА
Теперь мы сделаем небольшое отступление и опишем ме-
методы, с помощью которых можно экспериментально находить
параметры Стокса для любого светового пучка и матрицы Мюл-
Мюллера для произвольного оптического прибора. (См. также § 8,
гл. 2, где были описаны методы экспериментального определе-
определения элементов матрицы преобразования луча для оптических си-
систем, формирующих изображение.)
214
ГлавЧ 4
Во-первых, нам необходимо научиться измерять параметры
Стокса для произвольного луча. Предположим, что мы можем
измерять непосредственно интенсивность пучка, используя, ска-
скажем, фотоэлемент, а затем определять параметры Стокса путем
наблюдения за изменениями этой интенсивности при прохожде-
прохождении пучка через различные приборы. Как обычно, предположим,
что пучок распространяется горизонтально в направлении Ог
и что ось Оу расположена в вертикальной плоскости, а ось Ох —
в горизонтальной. В общем случае, для того чтобы определить
путем измерений полный столбец Стокса, необходимо провести
следующие шесть измерений интенсивности.
1. На пути пучка устанавливается поляроидная пленка так,
что плоскость пропускания ее параллельна оси Ох. Поля-
Поляроид пропускает интенсивность Еи которая пропорцио-
пропорциональна квадрату амплитуды вектора электрического поля,
параллельного оси Ох, т. е. Я2 в наших прежних обозна-
обозначениях. Таким образом, Е\ = Я2.
2. Затем поляроидную пленку поворачивают до тех пор, пока
ее плоскость пропускания не станет вертикальной, т. е. па-
параллельной оси Оу. Теперь поляризатор пропускает интен-
интенсивность Е2, пропорциональную квадрату «/-компоненты
вектора электрического поля, т. е. Е% = К2 в наших преж-
прежних обозначениях. Далее, исходя из определения парамет-
параметров Стокса, находим
/ = #2 + К2 = ?, + ?2 и Q = tf2-.K2 = ?,-E2.
3. Исходный пучок пропустим теперь через поляроид, пло-
плоскость пропускания которого образует угол 45° с горизон-
горизонталью и проходит через первый и третий квадранты. Ис-
Используя полученную выше матрицу Мюллера, соответст-
соответствующую поляроиду, находим столбец Стокса для пучка,
прошедшего через поляроид:
-1
0
1
-0
0
0
0
0
1
0
1
0
о-
0
0
0-
-/ -1
Q
и
-V -
1
"~ 2
rl + U-
0
/ + ?/
- 0 -
Таким образом, интенсивность Е3 пучка, прошедшего че-
через поляроид, равна ('/г) (/+ U).
4. Пропустим теперь исходный пучок через поляроид, пло-
плоскость пропускания которого также образует угол 45° с го-
горизонталью, но проходит через второй и четвертый квад-
квадранты, так что угол удобно рассматривать как — 45°. Если
вычислить матрицу Мюллера для поляроида при таком
значении угла ос, то получим столбец Стокса для пучка,
Матрицы для описания состояния поляризации света
215
прошедшего через поляроид, в следующем виде:
1
2
- 1
0
-1
- 0
0
0
.0
0
—1
0
1
0
о-
0
0
0-
- / -1
Q
и
-V .
1
— 2
- I-U-
0
-I + U
0 -
Интенсивность пучка на выходе этого поляроида равна
Е4 = Gг) (/ — Щ. После вычитания ?4 из Е3 имеем
Таким образом, на данном этапе мы определили три из четы-
четырех параметров Стокса. Для того чтобы измерить четвертый па-
параметр, на пути пучка установим четвертьволновую пластинку
так, чтобы ее быстрая ось была горизонтальна. Используя мат-
матрицу Мюллера для четвертьволновой пластинки, получаем стол-
столбец Стокса для пучка, прошедшего через эту пластинку:
rl 0 0 От г/т Г /т
0
0
0
1
0
0
0
0
-1
0
1
0-
Q
и
-V -
Q
V
TJ
5. Пучок, прошедший через четвертьволновую пластинку,
пропустим затем через поляроид, ориентированный также,
как и при третьем измерении. В этом случае столбец Сток-
Стокса имеет вид
1
2
- 1
0
1
-0
0
0
0
0
Интенсивность
1
0
1
0
0-
0
0
0-
пучка
/
Q
V
--U
на
-
-
1
~ 2
выходе
- / + V -
0
I + V
- 0 -
•
поляроида
6. Пучок, вышедший из четвертьволновой пластинки, пропу-
пропустим теперь через поляроид, ориентированный как в чет-
четвертом измерении. Столбец Стокса получается тогда сле-
следующим образом:
1
2
те
- 1
0
-1
- 0
нсивн
0
0
0
0
эсть
-1
0
1
0
о-
0
0
0-
равна Е
-
= (
/ -I
Q
V
и -
1
~~ 2
l/2)(I-V
• I —
0
— 1 +
0
V-
V
-
216
Глава 4
Для того чтобы определить первый элемент в двух послед-
последних столбцах Стокса, вычтем интенсивность Е6 из Е$. В резуль-
результате получаем V= Е5 — ?6. Таким образом, мы измерили все
четыре параметра Стокса для исходного пучка.
Посмотрим теперь, каким образом можно использовать эти.
результаты для определения элементов матрицы Мюллера лю-
любого оптического прибора, пропуская через прибор пучки света
с различными состояниями поляризации и измеряя параметры
Стокса выходящего пучка.
Предположим, что для исходного пучка столбцом Стокса яв-
является Si, а для пучка, прошедшего через систему, $2 и что мат-
матрица Мюллера равна Т. Следовательно, мы имеем S2 = TSi,
т. е.
hi
и2
-fJ
-A
E
J
-N
В
F
К
P
С
G
L
R
D-
H
M
S -
r/i -
Qi
Vi
LFi-
Пропустим теперь пучки света четырех различных типов поля-
поляризации через прибор по очереди и измерим описанными выше
методами параметры Стокса для выходного пучка.
1. Пропустим сначала через прибор неполяризованвый свет.-
Пусть его интенсивность равна а; тогда h *= <*, а <Эь Ui
и Ft все равны нулю, как следует из формул, приведенных
выше для случая неполяризованного света- При этом урав-
уравнения записываются в виде
/2 = Аа, т. е. А = /$/д,
Q2*=Ea, т. е. E — QJa,
U2 = Ja, т. е. / = С/г/а,
2. Пусть на прибор поступает пучок плоскополяризованного
света, плоскость поляризации которого параллельна оси
Ох. В этом случае интенсивность h == Qi и равна, скажем,
Р, a U\ и V\ равны нулю. Следовательно, если обозначить
столбец Стокса для пучка, прошедшего через эту систему,
как S3, то уравнения принимают вид
В = 13/й- А.
т. е.
т. е. F =
т. е. К =
т. е. Р = Ка/Р —
Матрицы для описания состояния поляризации света 217
3. Пусть затем через прибор проходит пучок света с правой
круговой поляризацией, для которого Л =* V\ = ш, a Qi и
Ui равны нулю. Следовательно, если обозначить столбец
Стокса в этом случае как S4, то можно написать следую-
следующие уравнения:
/4 = (Л + 0)ю, т. e. D = /4/co — A,
Qt = {E + H)a, т.е. H = QJ<a-E,
U4 = (J + М) со, ' т. е. М = UJa - J,
V4 = {N + S)<o, т.е. S^VJa-N.
4. Пропустим теперь через прибор линейно-поляризованный
свет, плоскость поляризации которого составляет угол 45°
с осью Ох и проходит через первый и третий квадранты
Для этого пучка Л = U\ = ц, в то время как Qi и V\ рав-
равны нулю. Следовательно, если обозначить столбец Стокса
луча, прошедшего через систему, как Ss, то получим урав-
уравнения
/8 = (Л + С)|1, т.е. С = /5/ц-
Q5 = (? + G)n, т.е. G =
t/6 = (/ + Z.)|i, т.е. L = U^-J,
Vt = {N + R)\i, т. е. R^VsIvl-N.
В каждом из полученных уравнений неизвестный элемент
матрицы Мюллера выражается через измеряемые интенсивно-
интенсивности и вычисленные ранее элементы матрицы Мюллера. С по-
помощью этой схемы, следовательно, можно определить все
шестнадцать элементов матрицы Мюллера, характеризующей
прибор.
§ 5. ИСПОЛЬЗОВАНИЕ МЕТОДА ДЖОНСА
ДЛЯ ПРЕОБРАЗОВАНИЯ СТОЛБЦОВ МАКСВЕЛЛА
Наряду с развитым выше методом Мюллера существует иной
метод вычислений, с помощью которого можно решать задачи
для полностью поляризованного света. Этот метод был развит
Джонсом. Во многих отношениях он проще метода Мюллера,
поскольку в нем вместо матриц 4X4 используются матрицы
2X2. Но элементы этих матриц в некоторых случаях комплекс-
комплексны, и, кроме того, метод Джонса имеет существенный недоста-
недостаток, поскольку он оперирует с величинами, которые нельзя не-
непосредственно измерять в эксперименте. Однако в используемых
в этом методе матрицах не имеется никаких лишних элементов,
218 Глава 4
и любая матрица Джонса, которая может быть написана, соот-
соответствует по крайней мере в принципе физически реализуемому
прибору.
Для многих задач поляризационной оптики оба метода вы-
вычислений являются одинаково пригодными. Но если свет лишь
частично поляризован, то следует выбрать метод Мюллера; с
другой стороны, если необходимо учесть интерференционные эф-
эффекты или в системе используется когерентный лазерный свет,
то метод Джонса является более полезным.
(При написании настоящей главы мы попытались в отдель-
отдельных параграфах изложить оба метода вычислений; следователь-
следовательно, для читателя, интересующегося только одним методом, опи-
описание другого метода можно просто пропустить. Однако, изу-
изучая оба метода, вдумчивый студент получит более глубокое
представление о различии, которое существует между когерент-
когерентным и некогерентным светом и соответствующими методами вы-
вычислений в оптике. Между областями, в которых применимы эти
два метода, существует промежуточная область, требующая
дальнейшего исследования.)
В рамках метода Джонса оперируют не с параметрами Сток-
са, пропорциональными интенсивности пучка, а со столбцом
Максвелла, элементы которого определяют амплитуды и фазы
поперечных компонент электрического вектора. При построении
этого метода вычислений будем считать, что справедливо сле-
следующее положение: для приборов, через которые проходит по-
поляризованный свет, компоненты вектора электрического поля
луча, прошедшего через прибор, линейно связаны с компонен-
компонентами вектора электрического поля исходного луча, и матрица,
связывающая компоненты прошедшего луча с компонентами ис-
исходного луча, позволяет нам описать характеристики прибора.
Точно так же, как и в случае метода Мюллера, составим таб-
таблицу матриц Джонса для приборов различных типов. (Способы
их получения даны в приложении V, и поскольку оба эти ме-
метода вычислений тесно связаны друг с другом, взаимосвязь ме-
между ними обсуждается в приложении VI.)
В § 1 настоящей главы мы уже видели, что любые попереч-
поперечные колебания, соответствующие произвольному полностью по-
поляризованному возмущению, можно представить в виде вектора
Максвелла. Для плоской волны, распространяющейся в направ-
направлении оси Oz, электрическое поле можно рассматривать как дей-
действительную часть комплексного вектора
[Я-
Матрицы для описания состояния поляризации света 219
В большинстве случаев зависимость параметров луча от вре-
гМени и координаты г можно вынести из столбца в качестве ска-
скалярного множителя. Таким образом, мы имеем
: Полезное правило для вычисления интенсивности пучка со-
I стоит в следующем: вектор Максвелла умножается слева на ком-
I плексно сопряженный ему транспонированный вектор — опера-
j ция, которую иногда называют произведением скобок. При этом
: получаем
[Exl [Hexp(ij>x)-\
EXJ = [ЯехР(- Ц>х) *ехр(- ВД [Ке?{™ J =
(модуль скалярного множителя равен единице).
Если рассматривается одна световая волна, иногда можно
не учитывать абсолютную фазу колебаний и задавать ее произ-
произвольно, например положить фазу х-компоненты равной нулю.
Кроме того, во многих случаях нет необходимости учитывать аб-
абсолютную амплитуду, при этом ее также можно вынести из столб-
столбца и записать в виде скалярного множителя. Для пучка еди-
единичной интенсивности должно выполняться условие Я2 -f- К2 =
= 1; следовательно, можно написать Я = cos 8 и К = sin 9.
С помощью такого «нормированного» вектора Максвелла можно
записать выражение для исходной волны в следующем виде:
[COS 6
Это выражение содержит все необходимое для описания пол-
полностью когерентной плоской монохроматической волны. Как уже
отмечалось выше, его можно также использовать для описания
частично когерентного излучения, однако при этом необходимо
помнить, что амплитуда А и фаза ф являются случайными функ-
функциями, которые остаются более или менее постоянными лишь
в ограниченной области пространства, измеряемой как поперек
пучка, так и вдоль направления его распространения. Чем выше
когерентность, тем больше объем этой области и тем меньше,
в соответствии с принципом неопределенности Гейзенберга, неоп-
неопределенность вектора импульса, связанного с каждым фото-
фотоном, — на классическом языке неопределенность длины волны и
направления распространения.
Хорошо известен экспериментально установленный факт, ко-
который состоит в том, что при оптических частотах отклик среды
220 Глава 4
на воздействие электромагнитного поля почти точно линеен. Ра-
Разумеется, существуют и нелинейные оптические эффекты, но для
того чтобы нх наблюдать, необходимо использовать лазерный
источник света и работать при очень высоких напряженностях
электрического поля.
Следовательно, можно ожидать, что если вектор
?,=
является столбцом Максвелла луча, входящего в некоторый по-
поляризационный прибор, то столбец Максвелла луча, выходящего
из прибора, можно записать в виде вектора Е2, а именно
где
Этот вектор можно записать как произведение матриц:
/„ /,21 Г Я,е'*
/21 /JL
Г
L
(В общем случае четыре элемента квадратной матрицы яв-
являются комплексными числами и зависят только от характери-
характеристик прибора.)
Следует заметить, что в приведенных выше выражениях для
большей общности мы использовали два различных фазовых
угла ф и \|э в каждом из столбцов Максвелла. Поскольку нас ин-
интересует состояние поляризации луча, существенна лишь раз-
разность фаз \|э — ф = Д, которая может принимать любое значе-
значение. Но в действительности никогда нельзя быть уверенным в
том, что если для входного луча фазовый угол ф\ = 0, то соот-
соответствующий фазовый угол ф% лс-компоненты луча на выходе из
прибора также равен нулю. Сразу после того, как столбец Мак-
Максвелла для выходного луча был найден, его совсем нетрудно
умножить на любой желательный фазовый множитель.
Исходя из написанного выше уравнения, теперь можно по-
построить метод Джонса. Матрица, состоящая из четырех элемен-
элементов /s, называется матрицей Джонса / прибора, так что матрич-
матричное уравнение в окончательной форме имеет вид
Предположим, что у нас имеются два прибора, матрицы
Джонса которых равны соответственно /а и ^&-
fCOHCA ЙЛЯ ИДЕ>
фазовой пластинки для линейно-поляризованного света,
поворота осей и фазовой пластинки для циркулярно-поляризованного света •)
Тип прибора
6=0
е=± я/4
е=я/2
Произвольный угол 6
Идеальный линей- Г 1 0 "I
ный поляризатор, L 0 о J
ориентированный
под углом 8
Четвертьволновая Г1 0
пластинка, быст- \_q —i
й
2 L
±1 1
гоо-1
Lo 1J
Г-101
L о 1J
Г С? C.S.1
Lc,s, s? J
C\-iS\
C1Sl
i + o-i
. .- ... - ^±A +i) A -i) J
рая ось которой
ориентирована под
углом 8
В случае 9 = ± я/4 матрицу можно умножить на ein^4; при этом получим —pr I
- iC\
± i
I
U
Полуволновая пла- Г1 01 Г 0 ± 1 1
стинка, быстрая |_ о I J L ±1 0 J
ось которой ори-
ориентирована под
углом 8
Фазовая пластинка Г1 0 "| ) Г (е-'в_|_|) ± (j _e-rt)
с разностью фаз б, Q -(& Т . п -16\ ( -« , ,\
быстрая ось кото- L и е J г L±(l— е ш) (е 1О + 1)
рой ориентирова-
ориентирована под углом 8
') Угол в—угол ориентации плоскости пропускания поляризатора или быстрой оси фазовой пластннкн для лннейно-полярнзованного
света относительно оси Ог; Ci=cose; Si = sin6, Сг=соз2в, Sj = sin29.
г—1 o-i гс2 s2i
L о и Ls2 -c2j
-| Ге-'во1 Г <
L 0 1J \п
C,S, A - в"
;?]
Переход к новой системе координат, получаемой при пово-
повороте старой системы координат вокруг оси Ох на угол 6 или
действием фазовой пластники для циркулярно-поляризоваи
яого света, которая замедляет волну с левой круговой поля-
поляризацией на 29 рад.
г с, s,-|
L-s, c,J
Обозначим эту матрицу поворота через R (в); с ее помощью
можно преобразовать матрицу Джойса для произвольного
поляризационного прибора (илн целой системы), ориентиро-
ориентированного под углом ф, в соответствующую матрицу для того же
прибора (нлн системы) с новой ориентацией 6+*. При этом
формула преобразования запишется в виде /F + *) =
= R (- 6) J (ф) R (В).
Если целую систему, состоящую нз нескольких поляризационных пр(нборов, необходимо развернуть на некоторый угол, то, используя
унитарность преобразования поворота, можно значительно сократить выкладки. Однако в случае одного прибора предпочтительнее
использовать матрицу нз соответствующего столбца этой таблицы. (Методы вычисления таких матриц, а также некоторые замечания по
поводу их нормировки приведены в приложении V.)
222 Глава 4
Пропустим пучок света последовательно через каждый из
двух приборов. Пусть вектор Максвелла для входного пучка ра-
равен Е\, для пучка на выходе первого прибора Е2 и на выходе
второго прибора Es. Тогда, используя наше предположение, мы
можем написать следующие соотношения:
Подставляя первое соотношение во второе, получаем
(здесь мы использовали свойство ассоциативности матриц). Та-
Таким образом, мы видим, что если пучок света проходит ряд по-
последовательно установленных приборов, то параметры пучка на
выходе такой системы вычисляются путем перемножения соот-
соответствующих этим приборам матриц Джонса. (Такое же самое
правило мы использовали для матриц преломления и перемеще-
перемещения в гауссовой оптике и для матриц Мюллера.)
Для удобства решения задач в табл. 4.2 представлены мат-
матрицы Джонса различных наиболее часто используемых поляри-
поляризационных приборов.
§ 6. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ
МАТРИЦЫ ДЖОНСА И СТОЛБЦА МАКСВЕЛЛА
Рассмотрим теперь методы измерения вектора Максвелла
для любого пучка света, поляризованного либо линейно, либо
эллиптически, и методы, с помощью которых можно найти экс-
экспериментально матрицу Джонса произвольного прибора. Эти
методы характеризуются тем, что пучки света пропускают через
прибор, различные поляроиды и фазовые пластинки, а затем из-
измеряют интенсивность пучка на выходе каждого элемента си-
системы.
Сначала займемся измерением вектора Максвелла. Предпо-
Предположим, что он определяется выражением
Следовательно, интенсивность равна
Единицу измерения интенсивности выберем таким образом,
чтобы исследуемый пучок света имел единичную интенсивность.
Матрицы для описания состояния поляризации света 223
Сначала пропустим пучок через поляризатор, плоскость про-
пропускания которого горизонтальна, т. е. параллельна оси Ох. Век-
Вектор Максвелла для пучка на выходе поляризатора равен
Г1 °1ГЯ
Lo оJL/с
exp(*A)J LO
Следовательно, интенсивность lx = H2 и соответственно
# = VA> где 1\ — измеряемая интенсивность прошедшего све-
светового пучка.
Теперь пропустим исходный пучок через поляризатор, пло-
плоскость пропускания которого вертикальна (параллельна оси Оу);
при этом вектор Максвелла принимает вид
О 01ГЯ 1 ГО
Отсюда находим, что интенсивность /2 = К2, т. е. К = ^Jh-
Затем пусть пучок проходит через поляризатор, плоскость
пропускания которого составляет угол 45° с осью Ох и распола-
располагается в первом и третьем квадрантах. Для такого поляриза-
поляризатора матрица Джонса записывается следующим образом:
Г/г '/.IIP П
Lv* v»J 2Li и'
п
а вектор Максвелла становится равным
1 1 J L/Cexp(/A).
' Умножая комплексно сопряженный транспонированный вектор
Максвелла на исходный вектор, находим интенсивность
h = (У*) Ш2 + И К {ехр (*А) + ехр (- /А)} + Я2).
Далее, пропустим луч через поляризатор, плоскость пропуска-
пропускания которого образует угол 45° с осью Ох, но располагается во
втором и четвертом квадрантах, так что 8=—45°. При этом век-
вектор Максвелла запишется в виде
_1Г 1 -МГЯ 1 = 1Г Я-/Сехр(/А)-1
2L-1 I J L /С ехр (/A) J 2 L-tf + *exp(«A)J
и интенсивность равна
U = (У.) (Н2 - НК {ехр (US) + ехр (- /А)} + К2).
Следовательно,
I, ~ h = (Vi) 2HK {ехр (/А) + ехр (- /А)} =
= НК (cos А + / sin A + cos А — / sin А) = ЧНК cos A.
224 Глава 4
Поскольку Я и /С уже известны, из этого уравнения получаем
значение cos Д. Однако А все еще может быть и положительным,
и отрицательным. Таким образом, существует неопределенность
в знаке разности фаз. Для того чтобы разрешить эту неопреде-
неопределенность, найдем sin A.
Пропустим теперь исходный пучок через четвертьволновую
пластинку, быстрая ось которой горизонтальна. Учитывая, что
для четвертьволновой пластинки б = 90° и что 6 = 0, находим
матрицу Джонса для четвертьволновой пластинки:
[1 ОТ
о -,]•¦
соответствующий вектор Максвелла определяется следующим
образом:
Г1 °1ГЯ Ы н 1
LO —/JL/Cexp(/A)J L —iKexp(iA)J'
Пусть затем пучок после четвертьволновой пластинки проходит
через поляризатор, плоскость пропускания которого образует
угол 45° с осью Ох. При этом вектор Максвелла определяется
выражением
1 lJL-i/Cexp(/A)J 2|_Я-17СехрAД)_Г
а интенсивность пучка на выходе равна
/5 = (i/2) (Я2 - ШК {ехр (гД) - ехр (- tA)} + /С4) ==
= Ш (Я2 - 2Я/С sin A + /С2).
Далее, пропустим пучок, прошедший четвертьволновую пла-
пластинку через поляризатор, плоскость пропускания которого об-
образует угол —45° с осью Ох. Для вектора Максвелла тогда
имеем
11Г Я "I jj Я + 1
1 J L — г/Сехр(*Д)J *1-Н-~1
Ц 1 -11Г Я "I jj Я + 17Сехр(/А)-|
2 L-1 J L J 1
а для интенсивности находим
/6 * G2) (Я2 - /ЯЛ {ехр {- /А) - ехр (*Д)} + А») =
Следовательно,
/6_/5
Таким образом, мы нашли величину, которая определяет sin A.
Записывая условие sin2 Д + cos2 Д = 1, находим значение Д.
I Матрицы для описания состояния поляризации света 225
5 — ——
: Теперь мы полностью определили вектор Максвелла для исход-
исходного пучка.
(При проведении описанных выше измерений необходимо
учитывать то, что поляризатор никогда не бывает идеальным,
т. е. никогда не пропускает весь свет даже в том случае, когда
луч поляризован в плоскости пропускания поляризатора. Если,
например, использовать поляроид марки HN32, то ток фотоэле-
фотоэлемента, полученный при измерении величин /, 12, ¦.., h, будет
приблизительно на 64% меньше, чем соответствующие теорети-
теоретические значения для идеального поляризатора. Точное значение
потерь для данного поляризатора должно быть определено не-
непосредственно в процессе измерений путем пропускания через
него неполяризованного света и измерения прошедшей интен-
интенсивности по крайней мере для двух ориентации плоскости про-
пропускания поляризатора.)
Опишем метод, с помощью которого можно найти матрицу
Джонса произвольного прибора посредством измерений интен-
интенсивности. Предположим, что матрицу Джонса можно записать
в виде
у Г7» 7и"| ГЯп + Л'и Yn + lYul
L ^21 "^22 J L X2i + lY21 Х22 + lY22 J
Rl2exp(iQl2)l
J
Г
L
ex
(Элементы матрицы Джонса могут, конечно, быть комплекс-
комплексными, и мы записали матрицу Джонса как в декартовых, так
и в полярных координатах.)
1. Пропустим через прибор линейно-поляризованный пучок
света единичной интенсивности, плоскость поляризации которого
параллельна оси Ох. Следовательно, вектор Максвелла этого
входного пучка записывается в виде
После прохождения пучка через прибор его вектор Максвелла
принимает вид
Г/» МГП Г'
L/21 /22 J L О J ~" L /21 J "
1.1. Пропуская затем пучок через поляризатор, плоскость
пропускания которого горизонтальна, получаем вектор Макс-
Максвелла
Г1 <ПГ/п1 Г/и!
Lo 0JL/21J Lo J'
8 Зак. 77-1
И6 Глава 4
При этом интенсивность пучка на выходе дается выражением
h — Л/и = {Хп - iYu) (Хц + iYu) = Х2и + Y\x mm /?h-
1.2. Пучок, прошедший через прибор, пропустим теперь че-
через поляризатор, плоскость пропускания которого вертикальна.
При этом вектор Максвелла принимает вид
го <пг/„1 го -.
Lo iJUJ UJf
а интенсивность /з = /?ii-
2. На прибор падает пучок линейно-поляризоваиного света
единичной интенсивности, плоскость поляризации которого па-
параллельна оси Оу, а вектор Максвелла равен
На выходе этого прибора пучку соответствует вектор Максвелла
Г/и /ulfO] Г'12]
2.1. Пучок, вышедший из прибора, падает затем на поляри-
поляризатор, плоскость пропускания которого горизонтальна; при этом
вектор Максвелла для выходного пучка дается выражением
[1 О "I П У12 ~| Г/ц
о oJL/22-l lo
Интенсивность /4=*=/?12.
2.2. Теперь пучок, вышедший из прибора, пропустим через
поляризатор, плоскость пропускания которого вертикальна, и
получим соответствующий вектор Максвелла для выходного
пучка:
го о -1 г /12 -I _ г о -1
LO IJL/22J L/22-T
ИнтеНСИВИОСТЬ /5 =#22.
Таким образом, мы нашли все четыре элемента матрицы
Джонса. Осталось лишь иайти фазовые углы для этих матрич-
матричных элементов.
3. Пропустим теперь через прибор пучок света единичной
интенсивности с правой круговой поляризацией; при этом имеем
Н*=К и
откуда
Матрицы для описания состояния поляризации света 227
Для света с правой круговой поляризацией Д = я/2, так что
ехрО'Д) = i- Следовательно, вектор Максвелла для входного
пучка равен
На выходе из прибора пучок описывается вектором Максвелла
следующего вида:
_ДЛ/п ЛЛПТ ДГ'п
V2 L/21 /22JLJ V2 ii2l
3.1. Затем пропустим пучок через поляризатор, плоскость
пропускания которого горизонтальна, так что вектор Максвелла
определяется следующим образом:
1_ П Oir/n + f/ul _^Г/„ + |7,21
V2 Lo oJL/21 + «/22J V2 L О J
V2L о
и - Y12) + i (Yn + Xl2)
0
1
J-
Интенсивность пучка на выходе поляризатора получим, умно-
умножая эту матрицу на комплексно сопряженную ей транспониро-
транспонированную матрицу. Таким образом,
/б = С/2) {(*u - Yi2f + (Yn + Xi2f].
Отсюда находим
2/в = ^п — 2^11^12 + Y\2 + ^u + 2Y
Следовательно, подставляя известные значения 1г и Л, полу-
получаем
21^-h-U _^ 2(Yl2Xl2-
V/гЛ R11R12
= 2 (sin 8n cos 812 — cos 8U sin 8i2) =
= 2 sin (9,, - 812)
(здесь мы использовали соотношения между декартовой и по-
полярной формами записи элементов матрицы Джонса).
3.2. А теперь пучок с выхода прибора пропустим через поля-
поляризатор, плоскость пропускания которого вертикальна. Тогда
для вектора Максвелла имеем
1 ГО 01Г/„ + */,21 _^_Г О
V2 LO lJUi + ^J V2
8*
228 Глава 4
Для интенсивности получаем
h = G2) {(Х21 - У»? + (У21 + Xnf).
Следовательно,
2/ 7-/3-/5 = 2 sjn (Q2) _ g^
V/з'б
(Здесь и далее в данном параграфе мы опускаем большое коли-
количество подробных выкладок. Читателю полезно проделать их са-
самостоятельно.)
Теперь мы знаем синусы углов (8ц— 612) и F21 — 822), од-
однако все же остается некоторая неопределенность, поскольку
sin (я — 6) = sin в.
Для полного определения углов нам нужно знать также коси-
косинусы этих углов.
4. Пропустим через прибор пучок линейно-поляризованного
света единичной интенсивности, плоскость поляризации которого
составляет угол 45° с осью Ох. Для этого пучка Н = K=l/->/2
и Л = 0, так что ехр(г'Д) = 1, а его вектор Максвелла равен
После прохождения пучка через прибор его вектор Максвелла
принимает вид
-LI" МГ1!^—Г'п+М
V2 L/21 /22 J L 1 J V2 L /2, + /22 J '
4.1. Пусть пучок света проходит затем через поляризатор,
плоскость пропускания которого горизонтальна. Вектор Макс-
Максвелла выходного пучка определяется выражением
1 Г1
2 Lo
V2 Lo 0JL/21+/22J V2 L 0
а интенсивность
/8 - (Vf) {(XH + Xl2f + {Yn + Yl2f)-
Используя преобразования, аналогичные приведенным выше,
находим
4.2. Пропустим теперь луч, вышедший из прибора, через по-
поляризатор, плоскость пропускания которого вертикальна. Тогда
Матрицы для описания состояния поляризации света 229
?: для вектора Максвелла имеем
1 ГО
_
V2 LO 1
21 + /22J V2 L/21 + /22J
а для интенсивности
/э = (Vt) KX2l + Хъ? + (Y2l
Теперь мы знаем полностью углы F11 — 812) и @21 — 622).
(Следует проверить результаты измерений, используя тот факт,
что сумма квадратов синусов и косинусов, полученных в про-
процессе измерений, должна приблизительно быть равна единице.)
Для того чтобы завершить нашу работу, необходимо устанввить
евязь между этими углами, т. е. нам необходимо получить соот-
соотношение, связывающее угол 9ц либо с бгь либо с Вгг- Это можно
сделать, пропустив через прибор пучок света, линейно-поляризо-
линейно-поляризованного в горизонтальной плоскости, так что (см. п. 1) вектор
Максвелла на выходе этого прибора запишется в виде
¦/„
Г/и]
U.J
Затем пропустим этот пучок через поляризатор, плоскость про-
пропускания которого ориентирована под углом 45° к оси Ох. Тогда
для вектора Максвелла имеем
if1 2 I Г 7^ 1 = ± Г 7Н
2Li 1JL/2J 2L/u
Пусть теперь пучок света с выхода прибора падает на другой
поляризатор, плоскость пропускания которого горизонтальна.
В этом случае вектор Максвелла принимает вид
JJ1 ОI Г /и + /21 "I = j_ Г /„ + /21 "I
По oJU, + /2.J 4 о J-
Как и в п. 4.1 или 4.2, для интенсивности получаем
/ю = СЛ) (№i + X2tJ + (Yu + Y2Xf),
так что
4/ ^-/3==2со
Пропустим теперь пучок с выхода прибора, вектор Максвелла
которого равен
230 Глава 4
через четвертьволновую пластинку с быстрой осью, расположен-
расположенной вертикально. На выходе этой пластинки пучок имеет сле-
следующий вектор Максвелла:
г1 oir'""ur»i
L0 iJUJ L/21-Г
Затем с выхода пластинки направим пучок на поляризатор, пло-
плоскость пропускания которого ориентирована под углом 45 к оси
Ох. Для вектора Максвелла тогда получаем
if1 ЧГ /»i_±r/»
Hi lJUJ U/n
а для пучка, прошедшего через поляризатор, плоскость пропу-
пропускания которого горизонтальна, вектор Максвелла принимает вид
Uo oJl/u + *72iJ U о J
Аналогично тому, как это было сделано в п. 3.1 и 3.2, для интен-
интенсивности имеем
так что
4'"vra''-2sin(9"-6">-
Угол (Оц — 02i), таким образом, определен однозначно, и, сле-
следовательно, известна разность между 6ц и тремя остальными
углами.
Как было показано в § 5, мы можем выбрать значение од-
одного из углов 0S произвольным, т. е. положить, например, 0ц =
= 0. Это означает, что остальные три угла, соответствующие
элементам матрицы Джонса, известны; таким образом, мы опре-
определили всю матрицу.
§ 7. НАГЛЯДНЫЕ ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ
МАТРИЦ ДЖОНСА И МАТРИЦ МЮЛЛЕРА
Пример 1
Источник испускает плоскополяризованный свет единичной
интенсивности, который затем проходит через идеальный линей-
линейный поляризатор. Доказать, что интенсивность света, прошед-
прошедшего через поляризатор, равна cos2 0, где 0 — угол поворота по-
поляризатора, измеряемый от положения максимального пропу-
пропускания. Пусть поляризатор установлен так, чтобы полностью
погасить проходящий луч; затем между источником н первым
поляризатором ставят второй поляризатор.
Матрицы для описания состояния поляризации света 231
Показать, что в этом случае часть света может проходить
через оба поляризатора и что интенсивность проходящего света
пропорциональна sin2 2<f>, где <f> — угол поворота второго поляри-
поляризатора, измеряемый от положения, при котором происходит пол-
полное гашение луча света.
Решение
Для решения этой задачи воспользуемся как методом Джон-
Джонса, так и методом Мюллера.
Сначала применим метод Джонса. Пусть падающий пучок
света линейно-поляризован в горизонтальной плоскости, так что
его вектор Максвелла имеет вид
-[.']¦
Матрица Джонса поляризатора, плоскость пропускания которого
образует угол 9 с осью Ох, записывается в виде
[cos2e sine cos ei
«inecose sin2e _r
следовательно, для пучка, прошедшего через поляризатор, век-
вектор Максвелла будет равен
cos2e sinecoseirtfir #cos2e
nOcosO sin2e J L
irtfir #
J L 0 JLttsi
Интенсивность прошедшего пучка мы найдем, умножая век-
вектор Максвелла этого пучка слева на комплексно сопряженный
ему транспонированный вектор, как было описано выше. Для
удобства записи матрицы, комплексно сопряженной данной мат-
матрице М, заменим обозначение М*т одним эрмитовым символом
М. Используя такое обозначение, для интенсивности имеем
c°s
4#cosesinej
— Я2 cos4 в + Я2 cos2 в sin2 в = Я2 cos2 в (cos2 в + sin2 9) =
= #2cos2e.
При решении этой частной задачи начальная интенсивность Я2
заранее полагалась равной единице.
Предположим, что пучок проходит через другой поляризатор,
плоскость пропускания которого вертикальна, так что соответст-
соответствующая матрица Джонса имеет вид
ГО О]
Lo ij-
232
Глава 4
Вектор Максвелла луча на выходе поляризатора тогда опреде-
определяется следующим образом:
го о
Lo l
#cos2e
#cos0sin9
Для получения интенсивности вектор Е3 умножается слева на
транспонированный комплексно сопряженный ему вектор:
.[О Ясо.вв1пв][Ясо8°в8!пв]-
= H2cos4sitfQ>
Нг sin2 29
Таким образом, существуют четыре ориентации промежуточного
поляризатора, при которых происходит полное гашение пучка
света.
Теперь решим ту же самую задачу, используя метод Мюл-
Мюллера. Пусть исходный пучок света является также линейно-по-
линейно-поляризованным, причем его плоскость поляризации параллельна
оси Ох. Вектор Стокса для такого пучка имеет вид
г И
1
О
L0J
Умножая этот вектор Стокса на матрицу Мюллера поляриза-
поляризатора, плоскость пропускания которого повернута на угол 0 отно-
относительно оси Ох, находим вектор Стокса для пучка, прошедшего
через первый поляризатор:
1
т
-1
с2
s2
-О
с2
с2
S2C2
О
s2
C2S2
si
О
о-
0
0
0-
¦ 1-
1
0
-0-
1
~~ 2
- н
с2
s2-
-с, -1
f S2C2
0
Интенсивность на выходе поляризатора равна
A + cos 20)/2 = 2 cos2 @/2) = cos2 9.
Теперь пропустим исходный пучок через поляризатор, плоскость
пропускания которого вертикальна: 0 = 90°. Умножая вектор
Матрицы для описания состояния поляризации света
233
1
т
г 1
1
0
- 0
-1
1
0
0
0
0
0
0
0-1
0
0
0-
1
2
г 1
с2
s2
_
+ С2 -|
+ cl
+ s2c2
0
1
в 4
Стокса падающего луча на соответствующую матрицу Мюллера,
имеем на выходе поляризатора следующий вектор Стокса:
rl-Cb
Cl-l
0
• 0
а интенсивность пучка на выходе равна A — С|)/4 =¦ Sl/4 =>
= sin2B6)/4.
Пример 2
Три поляризатора установлены последовательно, так что пу-
пучок света по очереди проходит через каждый из них. Найти от-
отношение интенсивностей прошедшего света к падающему, если
плоскость пропускания первого поляризатора вертикальна, пло-
плоскость пропускания второго повернута на угол 12° вправо от
вертикали, если смотреть на источник света, и плоскость про-
пропускания третьего поляризатора повернута на угол 12° влево от
вертикали.
Решение
Мы решим эту задачу, используя параметры Стокса и мат-
матрицы Мюллера, поскольку метод Джонса нельзя применять при
решении задач с участием неполяризованного света. Сначала
рассмотрим неполяризованный свет, для которого вектор Стокса
имеет вид
гИ
0
0
LOJ
Пропустим сперва этот пучок через поляризатор, плоскость про-
пропускания которого вертикальна, т. е. 8 = 90°. Тогда для вектора
Стокса на выходе получаем
1
2
г _ 1
— 1
0
- 0
—1
1
0
0
0
0
0
0
о-
0
0
0-
-1-
0
0
-0-
}
~ 2
г
—1
0
- 0-
(Поскольку теперь мы имеем вертикально поляризованный
луч света, то, начиная с этого этапа вычислений, можно исполь,-
234
Глава 4
зовать далее метод Джонса, учитывая тот факт, что 50% интен-
интенсивности входного пучка были поглощены в первом поляриза-
поляризаторе.)
Затем пучок проходит через второй поляризатор, плоскость
пропускания которого повернута на угол 12° вправо от верти-
вертикали, так что 0 = 90°— 12° = 78°. При этом получим cos B0) =
= —0,91 и sin B8) = 0,41. Для пучка света, прошедшего через
второй поляризатор, вектор Стокса находим умножением век-
вектора Стокса для пучка на выходе первого поляризатора на мат-
матрицу Мюллера второго поляризатора:
1
2
г 1
-0
0
- 0
,91
,41
-0
0
-0
0
,91 ? ?-!
,83 ? ?
,37 ? ?
0 0-
1
2
- 1-
— 1
0
- 0-
1
4
Г 1,91
-1,74
0,77
- 0
Следует заметить, что в матрице Мюллера несколько матричных
элементов заменены вопросительными знаками. Это связано с
тем, что вектор Стокса для пучка на входе поляризатора содер-
содержит всего лишь два не равных нулю элемента, расположенных в
верхней части столбца; следовательно, элементы в двух правых
столбцах матрицы Мюллера будут умножаться на нулевые эле-
элементы вектора Стокса, давая нули. Поскольку результат никак
не будет зависеть от значений этих элементов, нет смысла рас-
расписывать их в процессе вычислений.
Наконец, пучок проходит через последний поляризатор, пло-
плоскость пропускания которого повернута на угол 12° влево отно-
относительно вертикали, т. е. 0 = 102°, cosB0) = —0,91 и sinB0) =
= —0,41. Вектор Стокса луча, прошедшего через систему, опре-
определяется выражением
г 1 -0,91 -0,41
? ? ?
L?
Таким образом, интенсивность пучка на выходе системы равна
3,17/8 = 0,396 (интенсивность исходного пучка принимается
равной единице). Здесь снова мы заменили вопросительными
знаками все матричные элементы в нижних трех строках мат-
матрицы Мюллера. Это можно сделать в силу того, что нас интере-
интересует только интенсивность пучка, прошедшего через поляриза-
поляризатор, поэтому нет смысла вычислять все остальные элементы век-
вектора Стокса, за исключением первого.
1
4
- 1
-1
0
- 0
,9И
,74
,78
1
~ 8
¦з,
17-
?
?
Матрицы для описания состояния поляризации света
235
.Пример 3
Рассмотрим пучок эллиптически поляризованного света с
правым вращением плоскости поляризации, описываемый выра-
выражениями
= Hcosa>l
и y =
Найти угол, который образуют оси этого эллипса с осью Ох,
и отношение длин осей эллипса.
Решение
Считая интенсивность пучка / = 1, в обычных обозначениях
имеем Я = cos 0 и К = sin 0; следовательно, параметры Стокса
записываются в виде
/=1, Q = cos20, ?/ = sin20cosA, V = sin20sin A.
Предположим, что теперь луч проходит через поляризатор, пло-
плоскость пропускания которого образует угол а с осью Ох. Вектор
Стокса для пучка на выходе этого поляризатора имеет вид
- 1 cos 2a sin 2a 0 -i
1
cos 28
sin 20 cos A
-sin 20 sin A
- 1 + cos 20 cos 2a + sin 20 cos A sin 2a -i
Таким образом, если положить 2а = р, то можно показать, что
интенсивность пучка, прошедшего через поляризатор, прямо про-
пропорциональна величине
Е = 1 + cos 20 cos p + sin 20 cos A sin p.
При вращении поляризатора значения р меняются и соответст-
соответствующим образом меняется интенсивность. Когда плоскость про-
пропускания поляризатора совпадает с одной из осей эллипса, ин-
интенсивность становится либо максимальной, либо минимальной.
Следовательно, мы можем найти ориентацию осей эллипса, при-
приравнивая нулю производную интенсивности по р. Эта производ-
производная дается выражением
dE/d$ = — cos 26 sin p -f sin 26 cos Д cos p.
236 Глава 4
Максимум или минимум интенсивности имеет место в точках,
где dE/dfi обращается в нуль, т. е. когда
Если найти два решения этого уравнения относительно вели-
величины 2а, различающихся на 180°, то соответствующие значения
а будут различаться на 90°. Эти значения и определяют ориен-
ориентацию осей эллипса. Обозначая одно решение а, а другое а1,
получаем
aI=a + 90°,
т. е.
p>=2aI=p+180°.
Следовательно,
sin р1 = — sin р и cos р1 = — cos p.
Интенсивность пучка, прошедшего через поляризатор, угол ори-
ориентации которого соответствует второму решению, равна
?' = 1 — cos 29 cos p — sin 29 cos A sin p.
Таким образом, отношение интенсивностей, которое равно отно-
отношению квадратов осей эллипса, записывается в виде
_Е|_ 1 — (cos 29 cos ft + sin 29 cos Д sin ft)
~Ё 1 + (cos 29 cos P + sin 29 cos Д sin P) "
Используя известные значения tg p, получаем значения cos p и
sin p. Подставляя их в это уравнение и производя соответствую-
соответствующие упрощения, получаем окончательный результат:
?' _ 1 - V(l - sin2 29 sin^Aj
Е ~~ 1 + V(l-sin229sin2A) '
Читателю рекомендуется в качестве упражнения решить эту
задачу методом Джонса. Попутно мы получили некоторые ре-
результаты относительно геометрических характеристик эллипса,
которые достаточно трудно получить обычными геометрическими
методами.
Пример 4
Эллиптически поляризованный свет пропускают через чет-
четвертьволновую пластинку, а затем через поляризатор. Свет пол-
полностью гасится, когда быстрая ось пластинки и плоскость пропу-
пропускания поляризатора образуют с горизонталью углы 30 и 60°
соответственно. Углы отсчитываются в одном и том же направ-
направлении. Найти ориентацию эллипса и отношение его осей.
Матрицы для описания состояния поляризации света 237
Решение
Если подставить данные значения углов в стандартные фор-
формулы матриц Джонса для поляризатора и четвертьволновой пла-
пластинки, то получим матрицу системы, состоящей из четвертьвол-
четвертьволновой пластинки, и установленного последовательно за ней поля-
поляризатора:
Чл/з" з J 4 L л/з" A + о 1-з/ J
л/з~A-01
з-з; J
Поляризатор Четвертьволновая пластинка
Пусть вектор Максвелла для входного пучка имеет вид
Г 1
Принимая интенсивность этого пучка равной единице, имеем в
принятых обозначениях
Следовательно, вектор Максвелла принимает вид
[cos 9 I
sin9exp(t'A) J"
Поскольку свет на выходе системы гасится, то оба элемента век-
вектора Максвелла для пучка, прошедшего через систему, должны
быть равны нулю, т. е.
3 + / УЗ"A-О1Г cos9
3 J L
"A-О1Г cos9 "I Г ° I
-3t J L sin 9 exp (*Д) J L 0 J "
Предположим теперь, что мы имеем квадратную матрицу 2X2,
умноженную на такой вектор, что в результате получается нуле-
нулевой вектор-столбец:
[с ШЫо°]
Иными словами, АХ + BY = 0 и СХ + DY = 0.
Считая, что для эллиптически-поляризованного света ни X,
ни Y не обращаются в нуль, из этих уравнений мы сразу полу-
получаем
Х_ J___?.
Y ~ А С '
238 Глава 4
В нашей задаче
УA-0 и л =
откуда
в _ Уз"A-<) _ Уз (i-j)(i + t) (Уз~)B) _ Уз"
А З + j C + /)A+0 2 + 4/ 1+2/ '
(Рекомендуем читателю самостоятельно проверить наше реше-
решение, доказав, что D/C имеет то же самое значение.) Следова-
Следовательно,
cose _ х _ в _ Уз~
sin в ехр (/Д) ~~ Y ~~ А ~~ — 2/ — 1 '
Таким образом, обращая последнее равенство, имеем
sin 8 cos A + I sin 8 sin A — 2t — 1
cos в Уз"
Приравнивая действительные части, получаем
tg8cosA =
а приривнивая мнимые части, —
tg8sinA=—
Далее разделим второе уравнение на первое и сократим tg 9.
В результате находим
tg Д = sin Д/cos А = 2,
откуда
Д = 63°26', cos Д = 0,447.
Уравнение, полученное выше приравниванием действительных
частей, дает
^9== A,7327@,446) 1.292.
ИЛИ
9 = -52о16'.
Используя формулы, полученные в предыдущей задаче,
tg 2а = tg 29 cos Д
._ ,., 1 + УA — sin2 26 sin2 Д)
(Отношение осейJ = —¦—/ ,
1 _VA — sin229sin2 Д)
находим, что а' = 30° (угол между_малой осью эллипса и осью
Ох), а длины осей относятся как -\/3 : 1 •
Пример 5
Пучок света с правой круговой поляризацией падает нор-
нормально на а) четвертьволновую пластинку и б) на пластинку с
Матрицы для описания состояния поляризации света 239
фазовым сдвигом Х/8. Будем считать, что быстрые оси обеих
пластинок вертикальны. Описать состояние поляризации света
после каждой пластинки.
Решение
В случае циркулярно-поляризованного пучка света компо-
компоненты Н и К равны. Для правополяризованного света разность
фаз между компонентами А = 90°, и, следовательно, нормиро-
нормированный вектор Максвелла записывается в виде
¦ (cos я/2+ t sin я/2).
Матрицу Джонса для четвертьволновой пластинки, быстрая ось
которой вертикальна, можно записать следующим образом:
1
О
Следовательно, вектор Максвелла на выходе четвертьволновой
пластинки определяется выражением
[.
2 LO i \[i J 2 L —1 J'
Второй элемент этого вектора является действительным числом,
так что для пучка на выходе sin А должен быть равен нулю,
т. е. А = 0 или я. Поскольку действительная компонента отри-
отрицательна, А должно быть равно я. Таким образом, К== Н = 1.
Следовательно, прошедший через пластинку свет становится ли-
линейно-поляризованным, причем плоскость поляризации образует
угол —45° с осью Ох и проходит через второй и четвертый квад-
квадранты.
Для пластинки К/8 разность фаз между обыкновенным и не-
необыкновенным лучами равна 45° и cos б = sin б = 1/д/2. В этом
случае 0 = 90° и матрицу Джонса можно записать в виде
1 0
0 {l
Вектор Максвелла для пучка на выходе дается выражением
2 О
V2~V
Вычисляя отношение действительной и мнимой частей второй
компоненты, получаем tgA = —1, и, следовательно, Д= 135°,
240 Глава 4
sinA= l/-^2~, a cosA= — 1/V2~« Подставляя эти значения в
матрицу, мы имеем Н = К = 1. Записывая уравнение эллипса
в стандартной форме
х* 2ху Л , у2 . 2\
tj2 ~~" // is COS ?Л -\ J72~ Sill ?Af
находим
_^ Чху . у2 ___ .
I2 Ы • V2 I2 ~ '
т. е.
Поскольку А может принимать значения в интервале 0—180°,
свет поляризован эллиптически с правым вращением.
Пример 6
Волна, описываемая выражениями
х = A cos (оо/ + я/4) и г/= Л cos оо/,
падает на поляризатор, который вращают до тех пор, пока ин-
интенсивность света, прошедшего через него, не становится макси-
максимальной.
а) Как в этом случае ориентирована плоскость пропускания
поляризатора?
б) Вычислить отношение интенсивностей пучков, прошедших
через поляризатор, ориентированный в первом случае
так, как описано выше, а во втором случае так, что его
плоскость пропускания параллельна оси Оу.
Решение
Мы можем найти интенсивность прошедшего луча для про-
произвольной ориентации поляризатора, используя либо матрицы
Мюллера, либо матрицы Джонса. Согласно методу Мюллера,
мы имеем
Следовательно,
/==2Л2, Q = 0, U = 2A2cosnf4, v = — 2A2 sin (я/4).
Пропустим луч через поляризатор, ориентированный под углом
9, и найдем его интенсивность на выходе. Следует заметить, что
нужно использовать только первую строку матрицы Мюллера
поляризатора. Результирующая интенсивность равна
2Л2
0
i = G2I1 cos 26 sin 26 0]
V2 A2
Матрицы для описания состояния поляризации света 241
Очевидно, это выражение имеет максимум, когда sin 26 = 1, т. е.
когда 6 = 45°, причем максимальное значение интенсивности
равно
(
Когда плоскость пропускания поляризатора параллельна оси
Оу, т. е. 6 = 90°, и, следовательно, sin 26 = 0, интенсивность
равна А2. Таким образом, мы имеем следующее отношение ин-
тенсивносте»:
1,707: 1.
Если для вычисления интенсивности мы хотим использовать ме-
метод Джонса, сначала нужно написать вектор Максвелла для
входного пучка, а именно
\А 1-лГ1 1
Uexp(-nt/4)J L exp (-/я/4) J-
После прохождения света через поляризатор, ориентированный
под углом 6, вектор Максвелла принимает вид
[cos26 sin6cos6ir I I
cos 6 sin 6 sin2 8 J L exp (— in/4) J ~
[cos2 6 + sin 6 cos 6 exp (— in/4) 1
sin 8 cos 6 + sin2 6 exp (— /я/4) J'
Как и обычно, найдем интенсивность пучка, умножая этот век-
вектор Максвелла на комплексно сопряженный ему транспониро-
транспонированный вектор. При этом
И 1тенсивность =
=Л2 [cos2 6+sin 6 cos 6 exp (+/л/4) sin 8 cos 6+sin2 6 exp (+/л/4)] X
[cos28 + sin6cos6exp(—m/4)
sin 6 cos 6 + sin2 6 exp (— in/4) J'
что приводит нас к результату, полученному выше, а именно
Пример 7
Эллиптически-поляризованный свет с правым вращением
плоскости поляризации описывается эллипсом, характеризуемым
большой осью Н и малой осью К- Этот световой пучок проходит
через поляризатор, плоскость пропускания которого ориентиро-
ориентирована под углом а относительно большой оси эллипса,
242 Глава 4
Доказать, что интенсивность пучка, прошедшего через по-
поляризатор, дается выражением
/ = Н2 cos2 a + К2 sin2 а.
Решение
Если считать, что большая ось эллипса горизонтальна, то
вектор Максвелла для падающего пучка можно записать в виде
|_/(ехр(ш/2),
[См. состояние поляризации типа 4 в приложении III.] Умножая
этот вектор на матрицу Джонса поляризатора, находим вектор
Максвелла на выходе поляризатора:
[cos2 a sin Э cos а "j Г Я "j Г Н cos2 а -f iK sin а cos а "I
sinacosa sin2a J L iK J L #sinacosa + iK sin2a J'
Произведение вектора Максвелла на комплексно сопряженный
ему транспонированный вектор дает интенсивность:
[Н cos2 a — iK sin a cos a Я sin a cos a — iK sin2 a] X
Г Н cos2 a + iK sin a cos a
L H sin a cos a + iK sin2 a J'
После умножения и упрощения полученного выражения найдем
искомый результат.
Интересно отметить, что этот результат легко проверить экс-
экспериментально, используя для измерения интенсивности фото-
фотоэлемент; таким образом, мы получаем прямое подтверждение
теорий эллиптически-поляризованного света. Эти результаты
можно также получить, хотя и не столь просто, рассматривая
геометрию эллипса в соответствующих координатах. [Для пучка
света с левым вращением плоскости поляризации вычисления
полностью аналогичны, за тем лишь исключением, что знаки при
всех мнимых частях (перед i) меняются на противоположные.
Однако, поскольку мы ищем произведение сопряженных векто-
векторов, эти мнимые члены исчезают.]
Пример 8
Требуется построить теорию фотоупругости, используя век-
векторы Максвелла и матрицы Джонса.
Решение
Для решения этой задачи удобно рассматривать поляриза-
поляризаторы, ориентированные под углами 45 и —45° (в обычных обо-
обозначениях) относительно оси Ох. Предположим, что для исход-
исходного пучка света Н = К =. 1 (следовательно, интенсивность
Матрицы для описания состояния поляризации света
243
равна 2 единицам). Исходный луч считаем линейно-поляризо-
линейно-поляризованным. Таким образом, его вектор Максвелла имеет вид
[!]¦
Для первого поляризатора 0 = 45°, т. е. cos 9 = sin 8 = 1/д/2 >
и матрица Джонса записывается в виде
г'л /21 _j_г 1 п
L'/2 72.1 2Li и-
Для второго поляризатора 0 = — 45°, т. е. cos 8 =
a sin9 = — l/V2 , и матрица Джонса принимает вид
Г
v2 V2
i
2L-i
(Эта матрица приведена в табл. 4.2). Используя формулу для
линейной фазовой пластинки, чтобы описать изменение состоя-
состояния поляризации света, проходящего через какую-либо точку
исследуемого образца, можно найти вектор Максвелла для вы-
выходного пучка:
—И
tJx
Второй
поляризатор
sin2aexp(—гб) cos a sin a {1 — exp(— /6)}
cosasina{l — exp(—/6)} sin2a + cos2aexp(—/6) J ^
Фазовая пластинка
Г
L
cos2a
Первый Исходный
поляри- луч
затор
После перемножения получим
С/2) (cos2a) {1 _ехр(-Й)}[ _{ ] = G [ _
Для того чтобы найти интенсивность прошедшего пучка света,
как уже отмечалось выше, нам необходимо умножить вектор
Максвелла на комплексно сопряженный ему транспонированный
вектор:
Интенсивность =
GG
[1 — !11 _ j I =
2GG.
244 Глава 4
Это выражение можно преобразовать к виду
Интенсивность = 2 cos2 2а sin2 F/2) = /.
Поскольку интенсивность исходного пучка света /0==2, то
/ = /0 cos2 2a sin2 F/2).
Следует заметить, что данное выражение для интенсивности
отличается от формулы, полученной с помощью матриц Мюл-
Мюллера; здесь вместо sin2Ba) мы получили cos2Ba). Это обус-
обусловлено тем, что вместо вертикальной и горизонтальной ориен-
ориентации плоскостей пропускания поляризаторов были выбраны
направления +45 и —45°. Обращение в нуль cos2Ba) теперь
означает, что оптическая ось фазовой пластинки параллельна
какой-либо из плоскостей пропускания поляризатора. Рассмо-
Рассмотрим теперь, что происходит при введении в систему четверть-
четвертьволновых пластинок. Поскольку оси пластинок перпендикулярны
и ориентированы под углом 45° относительно плоскостей пропу-
пропускания поляризатора, одна из них должна быть горизонтальна,
а другая вертикальна. Если направить быструю ось первой чет-
четвертьволновой пластинки вертикально, то 6 = 90°, cos 0 = 0,
sin 0 = 1, 6 = я/2 и следовательно, exp(ifi) = i. Используя эти
значения и соответствующую матрицу из табл. 4.2, находим мат-
матрицу четвертьволновой пластинки:
Г1 0] Г-/ 01
L о / J или> п°-другому. [ о 1J •
Для второй четвертьволновой пластинки 0 = 0, так что cos 9 =
= 1, sin 0 = 0 и матрица записывается в виде
0] Г1 01
jj или, по-другому, |^0 _fJ.
Используя тот же самый исходный пучок света, находим вектор
Максвелла на выходе системы:
E 2 | 1 1 'I П 1 I I л> о (л -ib\ r.2 i ^2-lb I X
Второй Вторая Сдвиг фаз 6, угол в
поляризатор Я/4-пла-
стинка
x[J Ж !][
Первая Первый Исходный пучок,
Х/4-пла- полярн- линейно-поляри-
стинка затор зованный под углом 45"
Матрицы для описания состояния поляризации света 245
В использованной выше матрице для фазовой пластинки
sin в обозначен через Si, a cos 9 — через С\. На следующей ста-
стадии вычислений мы упрощаем выражения на обоих концах мат-
матричной цепи и подставляем е~*в = р — щ, где р = cos б, а
ц = sin б. В результате получаем
Г с? + s?p - ;s?ji с& A - р) + /c,s,n I г in
L c,s, (i - р) + idSm s? + с?р - /cfr J L i J
2 L — t i J L
1
(c,s, - c,s,p + c?ii) + i (s? + c?p + c,s,ii) J ¦
Выполняя оставшиеся операции умножения, получаем для
вектора Максвелла луча, прошедшего через систему, следующее
выражение:
j_ Г {- $2 A - Р) - С2ц} +1 {С2 A - р) - S2»} 1
2 L {S2 (I - р) + С2ц} +1 {- С2A - р) + S2ii} J
(здесь С2 = cos 26, aS2 = sin 29).
Следует заметить, что компоненты этого вектора Ех и Еу
с точностью до знака одинаковы — это с необходимостью выте-
вытекает из того факта, что исследуемый луч проходит через поля-
поляризатор, установленный под углом —45°. Умножая каждый эле-
элемент вектора на комплексно сопряженный ему вектор, находим
интенсивность пучка на выходе системы:
I - G2) {S2 A - Р) + С2ц}2 + С/2) {S2ti - С2 A - р)}2 =
Это выражение можно преобразовать к виду
/ = 2sin2F/2)
(независимо от значения 9). Поскольку интенсивность исходного
пучка / = 2, то записывая формулу /„ых = /вх sin2 F/2), мы по-
получаем тот же самый результат, что и при использовании метода
Мюллера.
С нашей точки зрения, при анализе когерентной суперпози-
суперпозиции нескольких пучков предпочтительнее использовать для вы-
вычислений чисто действительные числа в соответствии с методом
Мюллера.
Один из авторов, А. Джеррард, приготовил ряд программ
как на АЛГОЛе, так и на ФОРТРАНе для решения многих за-
задач поляризационной оптики. Читатели, желающие получить
246 Глава 4
копии этих программ, могут обратиться к нему непосредственно
в университет Bath, с тем чтобы он выслал копии программ н,
возможно, соответствующие перфокарты или магнитные пленки
с программами для использования их в ЭВМ.
Авторы выражают признательность за разрешение использо-
использовать следующий печатный материал:
Администрации издательства «Longmans, Green and Co> и
оксфордской экзаменационной комиссии за задачу 4 из книги:
R. S. Longhurst, Geometrical and Physical Optics, 1957, p. 546,
547; администрации издательства «Addison — Wesley Publishing
Co. Ltd.» за задачи 6.4 и 6.7 из книги: Bruno Rossi, Optics, 1957,
p. 307, 308.
ГЛАВА 5
РАСПРОСТРАНЕНИЕ СВЕТА
В КРИСТАЛЛАХ
§ 1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Хорошо известно, что при прохождении пучка света через не-
некоторые кристаллы возникает явление двойного лучепреломле-
лучепреломления. Это явление заключается в том, что после прохождения
кристалла луч света разделяется на два луча с различной по-
поляризацией. Двойное лучепреломление можно описать, восполь-
воспользовавшись френелевским обобщением построения Гюйгенса,
т. е. путем введения двух волновых фронтов Гюйгенса, сферои-
сфероидального и сферического, причем необыкновенная волна харак-
характеризуется сфероидальным фронтом, а обыкновенная волна —
сферическим. Существование сферического и сфероидального
фронтов можно объяснить, обратившись к электромагнитной
теории света и принимая во внимание тот факт, что диэлектри-
диэлектрическая проницаемость кристалла является не скалярной величи-
величиной, а тензором, компоненты которого можно записывать в виде
матрицы.
Для того чтобы понять, как возникает это явление, не обра-
обращаясь к тензорному анализу, прежде всего представим обыч-
обычные операции векторного анализа в матричной форме. Затем,
учитывая кристаллический характер среды, через которую рас-
распространяются электромагнитные волны, получим уравнения
Максвелла в матричной форме. И в заключение решим эти ура-
уравнения, из чего будет ясно видно, что они приводят к наблюдае-
наблюдаемому поведению света в кристаллах. При выполнении этой про-
программы ограничимся случаем одноосного кристалла.
§ 2. ПРЕДСТАВЛЕНИЕ ОПЕРАЦИЙ НАД ВЕКТОРАМИ
В МАТРИЧНОЙ ФОРМЕ
2.1.
Вектор V с компонентами V\, V2 и Уз по осям х, у и г соот-
соответственно, записывается в виде
248 Глава б
где i, j и к — единичные векторы вдоль положительных направ-
направлений осей х, у и г соответственно.
Определим четыре матрицы — две строчные и две столбце-
вые матрицы следующим образом:
В
У 2 Уз] (транспонированная
относительно V)
А=\ j |, Л'-р j k].
к
Равенство, определяющее вектор V, можно теперь написать в
виде
или
V = [F, V2 V3]\ j =V*A.
2.2.
Скалярное произведение можно представить следующим об-
образом. Допустим, мы имеем другой вектор, скажем
где
U
run
иЛ = и*А,
luJ
U
\и3
причем ит = [и{ U2 U3].
Тогда скалярное произведение вектора U на вектор V равно
и. v=v • и=и {Ух + u2v2 + u3v3.
Это скалярное произведение можно записать в любом виде:
либо как
\их и2 и3}\ v2\ =
Распространение света в кристаллах 249
либо как
[Vi V2 V3] I
U3-
2.3
Векторное произведение двух векторов можно записать сле-
следующим образом:
V X U = i (V2U3 - V3U2) + j (V3U1 - V,t/3) + k (VlU2 - V2UX) =
= V1(-]U3 + kU2) + V2(ii
Это выражение можно записать в виде
Wx V2 V3]\ it/3-kt/, =[F, V2 V3)X
1 г о +k -j-i run
X -k 0 +1 \U2 =
L + j -i oJ luJ
где
Г 0 +k -jl
a= -k 0 +i
L+i -i OJ
¦ + ]
(аналогично V X U = f/TaTV, где aT — транспонированная мат-
матрица a),
Г 0 -k +м
aT = + k 0 — i =-a.
L-i +1 OJ
+
Далее нам потребуются матрицы, каждый элемент которых
является не скалярной величиной, а дифференциальным опера-
оператором, например частной производной д/дх. Пользуясь такими
операторами, нужно помнить, что, хотя для них и выполняется
дистрибутивный закон, т. е.
они не подчиняются коммутативному закону. Так, например,
если U зависит от х, то Ud(V)/dx — это не то же самое, что
d(UV)/dx.
Выразим теперь градиент скалярной величины, скажем ф,
дивергенцию и ротор вектора V в матричном обозначении.
250 Глава 5
2.4
Градиент скалярной величины ф определяется следующими
равенствами:
Гдф/дх1
grad ф — 1 дф/дх + j дф/ду + к дф/dz = [i j к] дф/ду =-
д/дх
где
¦д/дх-1
Q--
д/ду\ и G?=ld/dx д/ду д/дг].
a/5«J
2.6
Дивергевдия вектора V дается выражением
*'* ixix*. л/д,. л/л~1 \ у | __ ntw
2.6 ¦
Ротор вектора V определяется следующими соотношениями:
rot V = i (dVJdy - dVJdz) + j (dVi/дг -
+ k(dVJdx-dVi/dy)*=*
k] dVJdz-dVJdx
Г 0 -д/dz +а/^-|ГК,-|
к] + д/dz О - д/дх \\v2\
\- — д/дц +д/дх О JLkJ
А= +
+д/дх
где
О -д/дг +ё/ду!
д/dz 0 - д/дх .
д/ду +д/дх О J
Воспользуемся теперь матричным методом для доказатель-
доказательства некоторых хорошо известных тождеств.
Распространение света в кристаллах 251
2.7.
Если divV = 0 (скаляр), то 0 = GTV (см. п. 2.5), а
grad div V = grad 0 = ЛТО0 (см. п. 2.4), или
\д/дх-1
grad div-V = ATGGTV = Лт д/ду [д/дх д/ду д/дг] V =
Ld/dzJ
Vd2/dx2 Р/дхду tf/
= Лт д2/ду дх tf/dy2 д2/ду dz\v= ATMV.
Ltf/dzdx д2/дгду d2/dz2 J
(Путем прямой проверки можно убедиться в том, что Мт = М.)
2.8
В матричной форме вектор V имеет вид ATV (см. п. 2.1). Его
ротор (обозначим его через С) равен ATAV, т. е. в матричном
представлении равен произведению ЛТЛ на вектор V, причем
множитель Лт является матрицей, стоящей слева в одном из
матричных представлений вектора V (см. п. 2.1). Таким об-
образом,
T = rot rot V = rot С = ЛТЛ (АV) ¦
Г 0 — д/dz +д/ду!Г О
= ЛТ +д/дг О —д/дх +д/дг
\--dldu 4- д/дх О Л-Л/Л»
О -д/dz +д/ду1
/д 0 — д/дх W=
д/ О J
-д/ду +д/дх О J
[ - д2/ду2 +д2/дхду +д2/дхдг
+ д2/дхду -д2/дг2 — д2/дх2 +д2/дгду
д2/дхдг +д2/дудг
= ЛТ(Л1-
здесь
- д2
L =
L)
V;
д2
0
0
4?г О О
JL.J.JL о
ду2 + дг* U
262 Глава 5
2.9.
Пусть 6 — любая скалярная функция координат х, у, г.
Тогда
rot(i4TG9) (см. п. 2.4)==ЛтАОв (см. п. 2.6)-
[О -д/дг + д/ду 1 Гд/дх1
+ д/дг 0 — д/дх I д/ду в =
— д/ду +д/дх О J Ld/dzl
[-tf/dzdy + tf/dydzl ГОТ
+ д2/дгдх-д2/дхдг в = Лт О 6 = 0;
-дР/дидх + дР/дхди! Ln J
дР/дхду!
2.10
ditV diHTAK) (см. п. 2.6) = GTAF (см. п. 2.5)
[О -д/дг +д/ду
+
[
+
—
[
+ д/дг 0 -
д/ду +д/дх О
ili- i (** i д* \ ( -* i I*
dydz дгду) \дхдг~дгдх) Кдхду ~ дудх
= [0 0 0]F=0.
f а ДИЭЛЕКТРИЧЕСКИЕ СВОЙСТВА АНИЗОТРОПНОЙ СРЕДЫ
3.1. Матричная форма уравнений Максвелла и вывод общего
волнового уравнения для электрического поля
Предполагается, что читателю знакомы физические идеи и
положения, которые приводят к уравнениям Максвелла, а также
векторная форма этих уравнений. Пользуясь системой обозна-
обозначений, введенной в предыдущем параграфе, четыре уравнения.
Максвелла можно записать в матричной форме следующим об-
образом:
div D = 0 -> GTD = 0 (см. п. 2.5), F.1)
(Магнитные свойства среды предполагаются изотропными, так
что из равенства нулю div В следует равенство нулю div H.)
rotE = --If-»ЛТД? = --!?¦ (см. п. 2.6), E.3)
? -§-. E.4)
Распространение света в кристаллах 253
Найдем теперь общее волновое уравнение для электрического
поля. Будем предполагать синусоидальный характер зависимо-
зависимости от времени всех векторов поля; в частности, напряженность
электрического поля дается выражением
S = Е sin (со/ + 8),
где со — угловая частота, а 8 — фазовый угол. В таком случае
-2J- = соЕ cos (Ш + 8)
и
d^ = - со2Е sin (со/ + 8) = -
dt2
Следовательно, двойное дифференцирование по времени экви-
эквивалентно умножению на —со2.
3.2. Вывод волновых уравнений в матричном виде
Из уравнения E.3) имеем
¦[I].
Взяв rot от обеих частей этого равенства и замечая, что порядок
дифференцирования можно менять, получаем
Л*Д (Д?) = - Л*Д (i|) = - М*Д (-fr) (см. п. 2.6) =
[для получения предпоследнего выражения мы использовали
уравнение E.4)].
Следовательно,
Лт(М-1)? = цсо2ЛтО (см. п. 2.8).
До сих пор наше исследование носило общий характер, и его
результаты можно применить к любой среде. Рассмотрим теперь
волны, распространяющиеся в анизотропной среде. Это озна-
означает, что диэлектрическая проницаемость К не является обыч-
обычной скалярной величиной и уравнение D = КЕ неприменимо.
Теперь каждая компонента величины D зависит от всех трех
компонент Е и уравнение D = КЕ принимает вид
D2 = K21E1 + ^22^2 + К2ъЕ3,
Рз — Кз\Е\ + К&Е2 + К33Е3.
254 Глава 5
В матричной форме эта система уравнений записывается сле-
следующим образом:
ИЛИ
где К — квадратная матрица. Кроме того, исходя из закона со-
сохранения энергии, можно показать, что матрица К симметрична
и путем соответствующего выбора координатных осей может
быть приведена к диагональному виду, в котором все недиаго-
недиагональные элементы матрицы обращаются в нуль. Будем считать,
что такая операция выполнена; тогда соотношение между D и
Е запишется в виде
Заметим, что теперь нам достаточно иметь лишь один индекс
для обозначения элементов квадратной матрицы.
Введем в рассмотрение следующее упрощающее предположе-
предположение: будем считать, что две величины из трех /Cs равны друг
другу. В дальнейшем мы увидим, что это соответствует одноос-
одноосному кристаллу. Допустим, что Кг равно Кз- В окончательном
виде наше соотношение выглядит следующим образом:
Волновое уравнение теперь принимает вид
А1(М - L) Е = цюМт#?,
где ц и ю — постоянные величины, и поэтому удобно ввести их
в матрицу #. Определим новую матрицу S:
т. е.
5,
0
0
0
s2
0
0
0
s.
]-l
0
L о
0 1
©2#3J
Распространение света в кристаллах 255
Введем еще одну матрицу Р = М — L:
д2
( ё! EL
V ду2 дг2
ду2 дг2 ) дх ду
д2
(__ j_
дхду \ дх2 дг2)
д2 д2
дх дг ду дг
f д2 д2 \
\ дх2 ду2) _
Таким образом, волновое уравнение принимает вид
AT{S-P)E = 0. E.6)
Мы получили общую форму волнового уравнения для Е. Пока-
Покажем теперь, как можно найти Н по известному значению Е. Это
нам потребуется в дальнейшем. Напишем одно из уравнений
Максвелла:
rotE
—?~ »¦?• *--(*)$•*¦*•
Так как дифференцирование по времени сводится к умножению
на со и увеличению фазы на л/2, то интегрирование по времени
должно привести к делению на а и вычитанню из фазы л/2. Сле-
Следовательно, если опустить фазовый множитель, то можно напи-
написать
Теперь применим этот формализм для исследования распро-
распространения плоских волн в кристалле.
§ 4. РАСПРОСТРАНЕНИЕ ПЛОСКИХ ВОЛН
В ОДНООСНОМ КРИСТАЛЛЕ
Читателю, вероятно, известно, что в таком кристалле почти
вдоль всех направлений могут распространяться две плоские
волны с различными скоростями, но в направлении оптической
оси может распространяться только одна волна. Там, где суще-
существуют две волны, они всегда поляризованы под прямым углом
относительно друг друга. Обыкновенная волна, которая соответ-
соответствует сферическому волновому фронту Гюйгенса, всегда поля-
поляризована так, что колебания вектора электрического поля про-
происходят в направлении, перпендикулярном главной плоскости1).
') Главная плоскость одноосного кристалла определяется как плоскость,
натянутая на оптическую ось кристалла и направление распространения
луча. — Прим. ред.
256 Глава 5 .
Необыкновенная волна, которая соответствует эллипсоидаль-
эллипсоидальному волновому фронту Гюйгенса, поляризована таким образом,
что колебания поля в ней происходят в главной плоскости. Ниже
мы выведем все эти результаты, пользуясь развитой выше мат-
матричной формой уравнений электродинамики. Сначала рассмо-
рассмотрим два выделенных направления распространения воли: вдоль
оптической оси кристалла и перпендикулярно к ней.
4.1. Первый частный случай, когда плоский волновой фронт
распространяется параллельно оптической оси кристалла
- Рассмотрим волновые фронты, для которых значения Е и Н
однородны вдоль плоскостей, перпендикулярных оси х, т. е. оси,
связанной с конкретным значением Ki — диагонального элемен-
элемента матрицы диэлектрической проницаемости. По определению,
для этих волн все производные по у и 2 равны нулю; следова-
следовательно, матрица Р принимает вид
0 0 0
[00 ОТ
0 -Р/дх2 0 ,
0 0 — д*/дх2 J
-О 0 -&/дх2-
и волновое уравнение для Е записывается следующим образом:
[5, О О I
О S2-\-dP/dx2 О \Е = 0.
О О S2 + <37<5*2-I
После умножения этих матриц получаем
\S1E1 + j ( S2E2 + ^) + к (S2?3 + -ff1) = 0.
В этом уравнении при i стоит лишь один член; следовательно,
Ех должно быть равно нулю. Иными словами, вектор Е не имеет
составляющей вдоль оси х, т. е. вдоль нормали к волновому
фронту, так что в данном случае поле Е является полностью по-
поперечным.
Выражая S2 через Kz и учитывая, что умножение на —ю2 эк-
эквивалентно двойному дифференцированию по времени /, полу-
получаем (приравнивая нулю по отдельности у- и г-компоненты ле-
левой части приведенного выше уравнения)
д3Е2
Сравнивая полученное выражение с общеизвестной формой вол-
волнового уравнения
д2Ф 1 дЧ
дх2 ~ V2 д? '
Распространение света в кристаллах 257
можно показать, что у- и дг-компоненты поля Е распространяют-
распространяются вдоль оси х как волны со скоростью \j-*J\\Ki-
Пользуясь установленным для Я общим выражением, а так-
также учитывая тот факт, что величина Е\ и все производные по у
и г теперь равны нулю, находим
ГО 0
H=ibAT\° ' °
L0 +д/дх 0
1 Г 1дЕз I It дЕ* 1
цш L ' дх "г дх J"
Из этого уравнения для Я видно, что а) ^-компонента поля Я
отсутствует; иными словами, Я, как и Е, полностью поперечно;
б) если ?г = 0, то Я направлено строго вдоль оси у, тогда как
если Е3 — 0, то Н направлено вдоль оси г (пп. «а» и «б» гово-
говорят о том, что поля Е и Я взаимно перпендикулярны); в) для
волн, распространяющихся без изменения волнового фронта, ко-
колебания дЕг/дх должны распространяться с той же самой ско-
скоростью, что и волна Е2; то же самое относится и к составляю-
составляющей ?3- Следовательно, как у-, так и z-компонента поля Я рас-
распространяются с той же самой скоростью, что и поле Е, т. е. со
скоростью l/Vn^2- Таким образом, в этом направлении ско-
скорости распространения обыкновенной и необыкновенной волн
совпадают. Это согласуется с хорошо известным фактом, что
для волн, распространяющихся вдоль оптической оси одноос-
одноосного кристалла, двойное лучепреломление отсутствует.
4.2. Второй частный случай распространеиия плоской волиы
через одноосный кристалл
Рассмотрим плоские волновые фронты, перпендикулярные
оси z, так что все производные по х и у равны нулю. Поскольку
величины 52 и S3 равны друг другу, то из соображений симмет-
симметрии следует, что рассуждения, аналогичные приведенным выше,
могут быть проведены и для волновых фронтов, перпендикуляр-
перпендикулярных оси у, с той лишь разницей, что у и z всюду просто поме-
поменяются местами. Так как div H = 0 и производные по х и у, со-
согласно предположению, равны нулю, то dHJdz = 0; следова-
следовательно, Я3 также равно нулю, поскольку мы рассматриваем поля
без постоянной составляющей; иными словами, в данном случае
поле Я является полностью поперечным. Матрица Р имеет вид
9 Зак. 774
268 Глава 5
а уравнение E.6) записывается следующим образом:
[Si+o^/az2 о on
О Sz + tf/dz* О ? = 0,
О 0 sJ
т. е.
Здесь снова при к имеем только один член; следовательно, Е3 =
= 0. Это означает, что у поля Е отсутствует z-компонента, т. е.
Е, подобно Н, является опять чисто поперечным полем. Прирав-
Приравнивая остальные два члена нулю, подставляя значения 5i и Sa
и учитывая, что умножение на —юя равносильна двойному диф-
дифференцированию по времени, получаем следующие два уравне-
уравнения:
и
д*Е2 „ д*Е2
Сравнивая эти уравнения с общим волновым уравнением, мы
видим, что Е\ и ?$ представляют собой плоские волны, распро-
распространяющиеся вдоль оси г, но с разными скоростями: волиа Е\
имеет скорость 1/Уц/Сь а скорость волны ?g равна l/Vj*^2-
Таким образом, волна Е% распространяется с точно такой же
скоростью, что и волны Е2 и Е3 в случае распространения по-
последних вдоль оси х. Следовательно, мы имеем две волны, по-
поляризованные под прямым углом друг к другу и распростра-
распространяющиеся вдоль оси г с различными скоростями. Оказывается,
??з связано с обыкновенным волновым фронтом, а Е\ — с не-
необыкновенным. Снова воспользуемся общим выражением для Н
и тем обстоятельством, что производные по х и у, а также Е3
равны нулю. Таким образом, имеем
Г 0 -д/дг О-Ц-ЕП
H==TZb * Ч \+dJdz 0 0 \\Е2 \,
L о о оJL оJ
откуда
Для того чтобы форма волны не менялась, производная дЕ2/дг
должна иметь ту же скорость распространения, что и Е2, а
d ту же скорость, что Е\. Следовательно, а) поле Н не
Распространение света в кристаллах
239
имеет z-компоненты, т. е. является чисто поперечным; б) ско-
скорости распространения лг-компоненты поля И и «/-компоненты
поля Е одинаковы. (Это обыкновенная волна.); в) «/-компонента
поля Н распространяется с той же скоростью, что и лг-компо-
нента поля Е. (Это необыкновенная волна.) Таким образом,
обыкновенная и необыкновенная волны поляризованы под пря-
прямым углом относительно друг друга.
4.3. Более общий случай распространения плоских волн
в одноосном кристалле
Допустим, что поле Е постоянно вдоль плоскостей, парал-
параллельных оси у (подобных плоскости а на фиг. 5.1), так что все
производные по у равны нулю. Пусть эти плоскости образуют
угол Э с положительным направлением оси х, так что угол ме-
между нормалью к этим плоскостям и осью х равен Э — я/2 = р.
Все производные от ? и Я по направлениям, лежащим в плоско-
плоскости а, будут равны нулю. Так, на фиг. 5.1 dE/dq = 0.
Выражения для производных по направлению, которые мож-
можно найти, например, в [37, стр. 63; 38*], записываются следую-
следующим образом:
дх
дг
дп
дп
— cos В , +sin0-^- sinB-r—
д
дп
Фиг. 6.1
9*
tf/dzdxl
0
— tfjdx2 J
260 Глава S
Следовательно, для матрицы Р имеем
dPfiz2 0
О {—дР/дх2 —,
дР/дхдг 0 —tf/dx2
- sin2 p {tf/dn2) 0 sin P cos p (dW) "I
О —&1дп2 О
-sinpcosp^/att2) 0 — cos2?^^2) J
и общее уравнение для ? принимает вид
Г S, + sin2 pCW) 0 — sin p cos p {дР/дп*) 1
Ат| 0 a2/d«2 + S2 . О ? = 0,
о s2+cos2e(az/a«2) J
-L
откуда
i (sin2 р ^- + ЗД - sin p cos р
Приравнивая коэффициент при j нулю, получаем волновое урав-
уравнение для Е2, совпадающее с уравнением, приведенным в п. 4.1,
за исключением лишь того, что в данном случае в это уравнение
входит вторая производная по п, а не по х. Это означает, что
у-компонента поля Е распространяется вдоль нормали со ско-
скоростью l/Vn#2» не зависящей от направления нормали. Данная
компонента является частью "обыкновенного волнового фронта,
и ее скорость, только что найденная, совпадает со значением
скорости, полученным в пп. 4.1 и 4.2. Теперь уже нельзя считать
поле Е чисто поперечным, т. е. что вектор Е лежит в плоскости а
(разумеется, ^-компонента поля Е расположена в плоскости а
просто в силу выбора направления оси у). Если абсолютную ве-
величину вектора Е обозначить как |?|, то
Здесь F — величина компоненты поля Е в плоскости хг.
Удобно оперировать с поперечной и продольной составляющими
компоненты F. Обозначим их, скажем, А и С соответственно. Ис-
Используя известные формулы преобразования координат при по-
повороте координатных осей (см., например, [37, стр. 6, 38*]),
имеем
?i = 4cosp — Csinp, ?3 = 4si
Распространение сеета в кристаллах 261
В общем уравнении для Е приравняем нулю коэффициент при i
и подставим написанные выше выражения для Ех и Ег. После
простых преобразований полученного таким образом соотноше-
соотношения имеем следующее уравнение:
S, A cos р — SiC sin p — sin р -—¦ = 0.
В результате приравнивания нулю коэффициента1 при к находим
cos р-|^- + S2A sin P + S2C cos p = 0.
Исключая А из этих двух последних уравнений (посредством ум-
умножения первого из них на S% sin р, а второго — на Si cos p и
последующего вычитания одного из другого), приходим к ура-
уравнению
-g- (S, cos2 p + S2 sin2 p) + SiSzC = 0.
Подставляя вместо St и S2 их выражения через ц и Ks и учиты-
учитывая то, что умножение на —со2 равносильно двойному дифферен-
дифференцированию по времени, получаем
д2С 1 д2С 1 д2С
дп2 cos2 р/ц/С2 + sin2 р/ц/Ci dt2 N2 dt2 '
Сравнивая это уравнение со стандартной формой волнового урав-
уравнения, нетрудно установить, что плоские волны поля Е распро-
распространяются со скоростью N в направлении, определяемом уг-
углом р. (Если р = 0, то N= l/УиДг, тогда как при Р = я/2
ЛГ xs 1/^n/Ci- Эти простые результаты согласуются с выводами,
полученными в пп. 4.1 и 4.2.)
Теперь найдем магнитное поле, используя формулу
Поскольку все производные по у равны нулю, эту формулу мо-
можно записать в виде
О — д/dz О 1[Ег
+ d/dz О
О + д/дх
или
О 1ГЕП
-д/дх Е2
о JLf3-
„ / 1 \ Г , дЕ2 . ( дЕ, дЕ3\,.дЕ
2
262 Глава 5
Отсюда, применяя формулу дифференцирования по направле-
направлению, получаем
Компонента поля Н в плоскости xz равна (дЕ2/дп)[—i sin р -f-
+ k cos p]. Скорость распространения этой компоненты такая же,
как и для дЕ2/дп, т. е. такая же, как и для поля Е, а именно
1/л/\хК2, причем для всех направлений распространения ско-
скорость одна и та же. Таким образом, это поле Н является Я-
частью обыкновенной волны и она перпендикулярна Е-части
обыкновенной волны. Можно видеть, что поле Я чисто попе-
поперечно. Действительно, тангенс угла ф, который поле Я образует
с осью х, дается выражением
= ^-компонента Н = +си|, = _
«-компонента Н — sin р
Следовательно,
так что направления, определяемые углами ф и р, перпенди-
перпендикулярны друг другу. Далее, «/-компонента поля Н равна
s'mfi(dEi/dn)—cos $(дЕз/дп). После подстановки сюда выра-
выражений для Е\ и Еа через А и В получаем —дВ/дп. Таким обра-
образом, Я-компонента распространяется с той же самой скоростью,
что и В, и, следовательно, представляет собой Я-часть необык-
необыкновенной волны.
Поскольку поле направлено вдоль оси у, то оно перпендику-
перпендикулярно как электрическому полю, так и направлению распро-
распространения волны. Иными словами, поле Н является попереч-
поперечным как в обыкновенной, так и в необыкновенной волне.
Найдем теперь величину D. Поскольку наше рассмотрение
связано с анизотропным кристаллом, то нельзя считать, что D и
Е имеют одно и то же направление. Из полученного выше ура-
уравнения получаем
3D ,„ лтлн
—— rottl— Л ДЯ —
Г 0 - д/дг
= ЛТ +д/дг О
L 0 +д/дх
1 f. дН2
О 1ГЯП
-д/дх Н2\
О J L Я, J
дх
Распространение света в кристаллах 263
Так как нам известно, что дифференцирование по времени t
эквивалентно умножению на со и на фазовый множитель, то ком-
компоненты поля D пропорциональны соответствующим компонен-
компонентам dD/dt, причем ^-компонента поля D лежит в плоскости вол-
волнового фронта. Для угла S, который компонента поля D в пло-
плоскости xz составляет с положительным направлением оси х,
имеем
, ^ z-компонента D дН2/дх cos ft (дН2/дп) ,
g jc-компонента D ~~ — дН2/дг ~ — sin р (дН2/дп) Ctg Р
(здесь мы использовали формулу для производной по направле-
направлению) . Следовательно,
tgStgp=-l,
так что компонента поля D в плоскости xz лежит в плоскости
волнового фронта. Это означает, что поле D, подобно Н, яв-
является чисто поперечным. (То же самое относится и к В, кото-
которое равно Н, умноженному на скалярную величину ц.) Послед-
Последнее утверждение, очевидно, справедливо как для обыкновенной,
так и для необыкновенной волны. Таким образом, и в обыкно-
обыкновенной, и в необыкновенной волне обе величины D и Н попе-
поперечны, однако поле Е может и не быть поперечным.
§ 5. ВОЛНЫ ГЮЙГЕНСА В ОДНООСНОМ КРИСТАЛЛЕ
Мы показали, что скорость N плоского волнового фронта,
нормаль к которому составляет угол р с осью х, дается выраже-
выражением
где V\= \1\ьК2 — квадрат скорости волновых фронтов, бегущих
вдоль оси х, a V\= l//x/Cj — квадрат скорости волновых фрон-
фронтов, распространяющихся вдоль оси z.
В анизотропной среде энергия волнового возмущения пере-
перемещается вместе с волновым фронтом. Поток энергии направ-
направлен не вдоль нормали к волновому фронту, а вдоль вектора
Пойнтинга. Таким образом, если рассмотреть точечный источ-
источник (излучающий волны Гюйгенса) в среде, то для каждого ин-
интервала времени найдется некоторое направление вектора Пойн-
Пойнтинга, двигаясь вдоль которого энергия достигнет точки пересе-
пересечения вектора Пойнтинга с соответствующим волновым фрон-
фронтом. Рассмотрим лучевую поверхность, определяющую распре-
распределение энергии возмущений, испущенных источником одновре-
одновременно по различным направлениям, спустя короткий интервал
264
Глава В
Фиг. 6.2
времени порядка одной пикосекунды. Эта поверхность будет оги-
огибающей всех плоских волновых фронтов, соответствующих раз-
различным направлениям распространения (фиг. 5.2).
Точка пересечения Q данного волнового фронта (спустя
одну пикосекунду после прохождения через начало координат)
с собственной нормалью (проведенной через точечный источник
под углом р к оси х) имеет координаты N cos р, N sin p (N из-
измеряется в метрах за пикосекунду). Наклон волнового фронта
равен tg 0 = —ctg p. Следовательно, уравнение, описывающее
волновой фронт, имеет вид
z — N sin р = — ctg р (х — N cos P),
или
=±=tf. F.8)
Уравнения для волновых фронтов, соответствующих иным
направлениям, имеют такую же форму и отличаются друг от
друга лишь различными значениями угла р и, следовательно, ве-
величины N. Для того чтобы найти огибающую этих волновых
фронтов, исключим из уравнения E.8) угол р и продифферен-
продифференцируем его по р (см., например, [37], стр. 171—174; [38*]). Диф-
Дифференцируя уравнение E.8) по р, имеем
dN (V2 — V2)
Pip v 2N u F.9)
{здесь мы использовали определение величины N). Умножим
уравнение E.8) на sin p, а уравнение E.9) на cos p и сложим их:
Распространение света в кристаллах
265
Если же уравнение E.8) умножить на cos p, а уравнение E.9)
на sin p и вычесть одно из другого, то получим
Подставим сюда выражения для dN/dfi через
выразим через р. Тогда можно написать
V\ sin P
K2cos|
и р, а затем N2
Из этих равенств имеем
cos2 р =
/4 •
sin2p =
После подстановки выражения для
шения принимают вид
и упрощений эти соотно-
соотноtg2p=
Исключая из этих равенств tg2 p, после несложных преобразова-
преобразований окончательно получаем
^2 1" „2 ~ 4 •
Это уравнение описывает пересечение поверхности необыкновен-
необыкновенных лучей (волн Гюйгенса) с плоскостью Oxz.
Поскольку мы показали, что скорость обыкновенной волны
не зависит от направления распространения, фронт обыкновен-
обыкновенной волны Гюйгенса представляет собой сферу радиусом
Vi — I/vVAV Параллельная оси х полуось эллипса, описываю-
описывающего необыкновенную волну Гюйгенса, имеет длину V\. Это озна-
означает, что волновые фронты обыкновенной и необыкновенной волн
. 5,3,
ПРИЛОЖЕНИЕ I
АПЕРТУРНЫЕ СВОЙСТВА
ЦЕНТРИРОВАННОЙ СИСТЕМЫ ЛИНЗ
Матричные методы, изложенные в гл. 2, позволяют провести
расчет положения и увеличения изображения, даваемого оптиче-
оптической системой, однако вопрос о резкости изображения остается
открытым. Дефекты резкости протяженного оптического изо-
изображения, получаемого в системе с достаточно большой апер-
апертурой, за исключением самых простых оптических систем, необ-
необходимо рассчитывать, используя теорию аберраций третьего и
даже более высоких порядков. Тем не менее все же остается
одна проблема, которую можно решить в рамках приближения
первого порядка, а именно задача определения того, каким об-
образом ограничители системы, ее конечные апертуры, реально
ограничивают резкость формируемого изображения.
Любая линза системы имеет конечный диаметр, однако во
многих случаях ограничители представляют собой реальные диа-
диафрагмы с непрозрачными краями, вводимые в систему специаль-
специально; они могут служить, например, для задержки прямого света,
рассеянного внутренней поверхностью трубы или предшествую-
предшествующими экранами, как это имеет место в коронографе. Иногда для
фильтрации пространственных частот используют диафрагмы
малого диаметра или обскуры.
Вероятно, читатель уже встречался с такими терминами, как
апертурная диафрагма, зрачки и люки оптической системы. Од-
Однако ради полноты изложения мы дадим здесь точные опреде-
определения этих технических понятий.
§ 1. ДИАФРАГМЫ, ОГРАНИЧИВАЮЩИЕ АПЕРТУРУ
Рассмотрим систему, которая отображает плоскость, содер-
содержащую точечный объект О на оси системы, на плоскость изо-
изображения, содержащую точечное изображение источника на оси
в точке / (фиг. П.1). Из всего пучка лучей, исходящих из точки
О, только центральная часть лучей достигнет точки изображе-
изображения /; остальные будут обрезаны либо краями линз, либо края-
268
Приложение I
Апертурная
диафрагма
Линза 1
а
Лита 2
-Апертурная диафрагма:
для источника в точке Q
I
Линза 1
Линза 8
Фиг. П.1
ми любых других апертур оптической системы. Среди всех диа-
диафрагм будет одна такая, которая максимальным образом огра-
ограничивает размеры пучка и таким образом определяет конус лу-
лучей, проходящих через систему. Именно эту фактически дейст-
действующую диафрагму называют апертурной диафрагмой, или ири-
ирисовой диафрагмой.
На фиг. П.1, а роль апертурной диафрагмы выполняет пер-
первая линза, а на фиг. П.1, б вторая линза обрезает часть света,
проходящего через первую линзу, и таким образом действует
как апертурная диафрагма. На фиг. П.2 показаны два примера,
когда предмет расположен на бесконечности; в обоих случаях
вопреки ожиданиям лучи проходят так, что эффективной апер-
апертурной диафрагмой является линза большего диаметра.
С обеих сторон системы можно построить действительные
или мнимые изображения реальной апертурной диафрагмы.
Входным зрачком системы называют изображение апертурной
диафрагмы, образованное всеми линзами системы, которые встре-
встречаются на пути светового пучка до того, как он достигнет апертур-
апертурной диафрагмы, т. е. изображение апертурной диафрагмы, которое
можно увидеть, глядя на систему слева') (см. фиг. П.З). Выход-
') Или изображение апертуриой диафрагмы в пространстве предметов.—
Прим. черев.
Апертурные свойства центрированной системы линз
269
Апвртурная
диафрагма
Апергпурния
диафрагма
Фиг. П.2
ной зрачок — это изображение апертурной диафрагмы, образо-
образованное линзами системы, которых свет достигает после прохо-
прохождения апертурной диафрагмы, т. е. изображение, которое мож-
можно увидеть, глядя на систему, изображенную на фиг. П.З, справа.
С точки зрения устранения паразитного света иногда выгод-
выгодно размещать апертурную диафрагму перед первой линзой си-
системы, причем в этом случае входной зрачок системы совпадает
[Мнимое
изображение)
Входной
зрачок
{Действительное
изображение)
Выходной
зрачок
Апертурная диафрагма
в компаунд- микроскопе
Фиг. П.З
270
Приложение 1
с апертурной диафрагмой. Однако существуют причины (как ме-
механические, так и оптические), по которым переменную апертур-
ную диафрагму, используемую, например, в объективе фотоап-
фотоаппарата, размещают где-либо внутри оптической системы. Часто
выгодно сконструировать систему так, чтобы входной или вы-
выходной зрачок располагался на бесконечности. Такую схему при-
применяют, в частности, в проекторах, где необходимо сравнивать и
измерять размеры изображений, или в системах преобразования
изображения. Такие системы называют телецентрическими в
пространстве соответственно предметов или изображений. Афо-
кальные системы могут быть телецентрическими с обеих сторон.
Поскольку входной зрачок отображается первой частью си-
системы на апертурную диафрагму, а второй частью- системы —
на выходной зрачок, любой луч из пространства предметов, рас-
распространяющийся под некоторым углом к оптической оси, но
идущий через центр входного зрачка, будет проходить через
центр выходного зрачка в пространстве изображений. Такой луч
мы будем называть главным лучом, или кардинальным лучом.
(Поскольку входной зрачок не обязательно совпадает с первой
главной плоскостью системы, главный луч, определенный выше,
не обязательно проходит через главные точки системы.)
§ 2. ДИАФРАГМЫ, ОГРАНИЧИВАЮЩИЕ ПОЛЕ ЗРЕНИЯ
Отыскав положение и размер апертурной диафрагмы для
данной плоскости предмета и соответствующие выходной и вход-
. ной зрачки, попытаемся теперь определить размеры поля зре-
зрения, видимого в пространстве предметов оптической системы.
Для этого рассмотрим вначале всевозможные главные лучи, ко-
которые исходят из различных точек плоскости предмета и прохо-
проходят через центр входного зрачка.
Полевая диафрагма — это оправа линзы или апертура, огра-
ограничивающая размер пучка главных лучей, проходящих через
Входной и выходной люки на бесконечности
Линза
(апертурная
диафрагма)
Конус главных
лучей
Полевая
диафр
Выходной
зрачок
Входной,
зрачок
Фиг. П.4
Апертурные свойства центрированной системы линз
271
Линза 1
Изображение полевой,
диафрагмы в лише 1
(Входной люк)
Линза Z
Палевая Изображение палевой
диафрагма диафрагму в линзе 2
^н (Выходной люк)
Фиг. П.5
центр выходного зрачка в пространство изображений (фиг. П.4).
Входным люком (иногда его называют входным окном) системы
называют изображение полевой диафрагмы, видимое со стороны
входа системы. Выходной люк — это изображение полевой диа-
диафрагмы, видимое со стороны выхода системы (фиг. П.5). В пра-
правильно сконструированных системах входной и выходной люки
располагаются в плоскости предмета и в плоскости изображе-
изображения соответственно.
Если точечный предмет расположен в плоскости входного
люка, то лучи, которые из него исходят, равномерно освещают
входной зрачок, а следовательно, и выходной зрачок. Для про-
протяженных предметов однородной яркости такое положение
входного люка дает протяженное изображение также однород-
однородной яркости, вплоть до резкой границы поля зрения, соответст-
соответствующей краю выходного люка.
Однако если полевая диафрагма расположена неправильно
или кроме апертурнои диафрагмы используются дополнительные
диафрагмы, то в плоскости изображения получается освещен-
освещенная область с затененными краями. Таким образом, имеется
поле полной освещенности (фиг. П.6, а), окруженное частично
затененной областью, которые вместе называют полным полем.
По мере того как рассматриваемая точка изображения переме-
перемещается, через затененную область, часть поверхности выходного
зрачка (в процентах), заполненная светом, уменьшается от
100% на краю поля полной освещенности до 0 на краю полного
поля (фиг. П.6, б). Когда изображение формируется при ча-
частично затененном выходном зрачке, говорят, что имеет место
виньетирование.
Обычно телескоп или камера сконструированы так, чтобы
отображать предмет, расположенный на бесконечности. При
этом апертуру прибора измеряют э линейных единицах, а диа-
272
Приложение I
Линза
(апертурнал
диафравып.)
Боковой
Линза
(полевая
диафрагма.)
Плоскость
изображения
а
Пале полной освещенности
/Все лучи выше \
I бокового луча. Е\
перекрываются]
\ оправой линзы]
I ПлоскосШ
\ изображения
Линза
(апертурная
диафрагма)
Линза*
(полевая
диафрагма)
Полное тле .
Фиг. П.в
Область
затенения
' Яркость
' изображения
метр поля зрения — в угловых. Однако для объектива микро-
микроскопа именно входной зрачок расположен на бесконечности, и
апертура измеряется в угловых единицах или, точнее, как синус
угла (числовая апертура).
§ 3. ПОСЛЕДОВАТЕЛЬНЫЙ РАСЧЕТ АПЕРТУРНОИ
И ПОЛЕВОЙ ДИАФРАГМ
3.1. Апертурная диафрагма
В § 5 гл. 2 была вычислена полная матрица М системы
виде цепочки произведений Я- и ^"-матриц. Теперь нужно ра
считать влияние каждой диафрагмы радиусом /<, расположен
Апвртурные свойства центрированной системы линз 273
ной в соответствующей промежуточной опорной плоскости
С этой целью мы разорвем матричную цепочку и воспользуемся
только той ее частью, которая связывает ОП< с ОПр Тогда соот-
соотношение связи между промежуточным лучевым вектором Ki и
входным лучевым вектором К\ записывается в виде
Ki = Mi-iMi-2 •. .M3M2MiKi = LtK\.
Здесь через L{ обозначено произведение последовательности
матриц (Aff_iAff_2... M3M2Mi). Нам нужно будет вычислить L-
матрицы для каждой из диафрагм системы, ио их вычисление не
составит особого труда, поскольку они представляют собой часть
цепочки уже определенной полной матрицы системы М. Элемен-
Элементы матрицы Li будем обозначать как {Ьи)и (Li2)< и т. д.
Рассмотрим луч, выходящий из точки предмета О, располо-
расположенной на оси системы на расстоянии R слева от ОП(. Пусть
V — угол, под которым этот луч распространяется относительно
оси системы. Тогда в плоскости ОП1 его лучевой вектор имеет
вид
R
Высота этого луча в промежуточной опорной плоскости
дается выражением
RVl [R
J F[1 OIL^J
где V как скалярный множитель вынесен из матрицы. После
выполнения операции перемножения матриц отсюда получаем
Если луч из точки предмета, расположенной на оси системы,
должен пройти через диафрагму в плоскости ОП*, то макси-
максимально допустимый угол V, который мы можем выбрать для
него, должен соответствовать такому углу, для которого у{ равно
± J{ — радиусу диафрагмы в ОП,-.
[Примечание. В этом приложении мы в основном будем иметь
дело с промежуточными опорными плоскостями, однако иногда
будем рассматривать и выходную опорную плоскость. Там, где
необходимо отличать выходную опорную плоскость от второй
промежуточной опорной плоскости ОП2, будем обозначать пер-
первую из них как ОПг (с полужирным индексом 2)].
Обозначим максимальный лучевой угол через Кмакс (*у Для
него можно написать
v ±Jl
274 Приложение I
Если это вычисление повторить для всех диафрагм и оправ линз
системы, то среди них найдется такая диафрагма (например, в
плоскости ОП,), которая дает наименьшее значение Умано т. е.
такую величину УМакс(«). которая меньше любой другой вели-
величины VMaKc(i)- Таким образом, диафрагма в плоскости ОП« яв-
является апертурной диафрагмой системы, причем ее радиус ра-
равен /8.
В тех случаях, когда расстояние R до плоскости предмета
очень велико или даже равно бесконечности, в приведенном вы-
выше расчете нужно использовать высоты лучей у во входной пло-
плоскости (угол луча, определяемый как y/R, стремится к нулю
при R -* оо). (С другой стороны, если плоскость OIli сама по
себе является плоскостью предмета, так что R обращается в
нуль, необходимо применить прежний метод, в котором V ис-
используется как удобная переменная.) В таком случае находим
У1 = П 0] Lt [ JR ] = у \(Ln)t + (Li2){/R].
Следовательно, уШЛКС «) — наибольшее значение координаты у
луча во входной плоскости, при котором луч еще проходит через
диафрагму в ОП*, дается выражением
*/«акс (|) — ± *
При R -*¦ оо получаем
Утке (О —
(L|i).
Снова апертурная диафрагма находится в той плоскости, кото-
которая обусловливает наименьшее значение координаты «/„акс-
Положение и размер входного и выходного зрачков опреде-
определяются тем же методом, что и в задачах 1 и 2 гл. 2. Если вход-
входной зрачок расположен на расстоянии Е\ слева от ОПь то мат-
матрица преобразования от плоскости апертурной диафрагмы 0П8 в
обратном направлении к входному зрачку будет иметь вид
г Г1
Чо
Для двух сопряженных плоскостей расстояние Е\ должно быть
равно —(Li2/Ln)s, и отношение радиуса входного зрачка к ра-
радиусу апертурной диафрагмы /3 имеет величину |l/(Ln),|.
Аналогично если выходной зрачок расположен на расстоянии
?? справа от выходной опорной плоскости ОШ, то матрица пре-
Апертурные свойства центрированной системы линз 275
образования лучей от выходного зрачка назад к апертурной диа-
диафрагме будет определяться выражением
Г1 Е21
Lo IJ
Qs,
где Qs представляет собой часть матричной цепочкн между 0П8
н выходной плоскостью ОГЬ.
Следовательно, для сопряжения выходного зрачка с апертур-
апертурной диафрагмой должно выполняться равенство Е2 =
= —(Qi2/Q22)s; отсюда отношение радиуса выходного зрачка к
радиусу апертурной диафрагмы /s имеет величину |l/(Qs2)e|-
(Вообще говоря, лишь две из этих Q-матриц будет необхо-
необходимо вычислять: одну — для выходного зрачка и одну — для
выходного люка. Поскольку L-матрицы уже будут известны, то
нет необходимости производить умножение на вторую половину
матричной цепочки. Для каждой t-й опорной плоскости мы
имеем QiLt = М, так что Qt = NILT1 н нужно провести лишь од-
одну дополнительную операцию перемножения матриц.)
3.2. Полевая диафрагма
Определив ограничения, налагаемые апертурной диафрагмой,
расположенной в s-й опорной плоскости, возьмем в качестве
пробного входного луча главный луч, проходящий под углом V
через центр входного зрачка. Поскольку входной зрачок нахо-
находится на расстоянии Е\ слева от OIli, то вектор этого входного
луча записывается в виде I I, а его высота Уг в t-и опор-
опорной плоскости определяется выражением
у \ = V[l 0]Lt[ j'J.
Если главный луч должен пройти через диафрагму в t-й пло-
плоскости, то допустимый максимальный угол, который он может
иметь на входе системы, равен
'макс (») == i J г F- 1 == -'-- с // 5 i it Г~ •
м 01Z.I ' ^l(LU)l + (Ln)i
Заметим, что, поскольку речь идет об исходной плоскости апер-
апертурной диафрагмы ОП8, знаменатель этого выражения обра-
обращается в нуль, так как величина Е\ была уже определена рав-
равной — (Ll2lLn)s.
276 Приложение I
Выберем теперь наименьшее значение Умакс из всех получае-
получаемых по этой формуле значений и назовем диафрагму в соответ-
соответствующей опорной плоскости (скажем, ОП?) полевой диафраг-
диафрагмой. (У одних систем полевая диафрагма оказывается располо-
расположенной перед апертурной диафрагмой, у других — после, так
что не следует придавать особого значения тому, что по алфа-
алфавиту буква s стоит после /.}
Определение размеров и положения входного и выходного лю-
люков производится точно так же, как и для зрачков, только те-
теперь матрицы рассматриваются относительно плоскости ОП/, а
не ОП8. Входной люк расположен слева от ОП] на расстоянии
F\, где F\ =—(Li2lL\\)f. Отношение радиуса входного люка к
радиусу полевой диафрагмы // равно \l/(Lu)f\. Выходной люк
расположен справа от ОПг на расстоянии F%, где F% =
= —(Q12/Q22)/, a Qf = MLyK Отношение радиуса выходного
люка к радиусу полевой диафрагмы // равно 11/(Q22)/|-
В окончательном виде максимально допустимый угол, изме-
измеряемый со стороны входа (предмета) для главного луча, дается
выражением
v ±Jf 1 (Lll)*/f
l'макс (поле)— El (Lu)f + (Ll2)f ~ * (LI2)f (Lu)s - (Ln)f (Ln)s '
[Здесь мы учли, что Е\ = — (
§ 4. ОПРЕДЕЛЕНИЕ ПОЛЕЙ ОСВЕЩЕННОСТИ
Хотя эффекты влияния апертурных диафрагм проявляют-
проявляются именно на выходе (в плоскости изображения) системы, мы
будем относить все эти эффекты обратно к сопряженной плоско-
плоскости предмета, расположенной на входе системы.
4.1
В правильно сконструированной оптической системе входной
люк совпадает с плоскостью предмета. При этом мы имеем
Следовательно, поле освещенности имеет резкую границу, ра-
радиус которой равен произведению величины Кмако (поле) на рас-
расстояние (Е\ — Fi) = (Е\ — /?) между входным зрачком и пло-
плоскостью предмета. Подставляя выражения, полученные для
VWkc (поле), ?i и Fu находим
Vмакс (поле) X (^1 — ^l) == ТЦ~\7Ш
Апертурные свойства центрированной системы линз 277
(Это выражение согласуется с приведенным выше выражением
для радиуса входного люка).
В случае расположения входного люка перед или после пло-
плоскости предмета радиус области освещения в плоскости пред-
предмета (наблюдаемого через оптическую систему) становится чет-
четко определенным лишь только при подходящей диафрагме, сво-
сводящей эту область до небольшого центрального пятна. Проеци-
Проецируя входной люк на плоскость предмета, мы пользуемся мас-
масштабным множителем (?1—R)/(Ei — F\) и для радиуса поля
зрения, вне которого центральная область входного зрачка бу-
будет затемнена, получаем
(Ln)f
Если в этом выражении R -> оо, то получаем угловой размер
поля освещенности, равный
(Ex r-Ft) (in)/ "
4.2
Однако до тех пор, пока используются малые апертурные
диафрагмы, область полутени или виньетирования может быть
значительной и возникает необходимость разделять понятия
«полное поле» и «поле полной освещенности».
Простейшим примером такого случая является система, в ко-
которой имеются лишь две диафрагмы, одна из них — апертур-
ная, а другая — полевая диафрагма (но не сопряженная с пло-
плоскостью предмета). В таком случае искомые радиусы полей
различной освещенности получаются путем проведения пары
боковых лучей, проходящих соответственно через нижнюю и
верхнюю точки апертурной диафрагмы и через верхнюю точку
полевой ХиаФРагмы- Обычно этот расчет удобно проводить в
пространстве предметов, пользуясь вычисленными значениями
размера и положения входного зрачка и входного люка.
Если помимо апертурной диафрагмы имеется большое коли-
количество полевых диафрагм, такой процедуры может оказаться не-
недостаточно, и обычный подход состоит в построении диаграмм
некоторого вида. Одна из возможностей заключается в том, что-
чтобы построить изображение всех полевых диафрагм в простран-
пространстве изображений; каждая k-я полевая диафрагма даст свое соб-
собственное изображение на расстоянии —(Li2/L\i)k слева от ОПь
а их радиусы в пространстве предметов будут равны |/а/(?ц)а|-
После того как получены эти результаты, мы сможем для
любой выбранной точки освещенного поля строить диаграмму
278
Приложение I
виньетирования, в которой все изображения диафрагм проеци-
проецируются на входной зрачок, с тем чтобы указать, какая доля по-
последнего остается незатемненной. Однако может потребоваться
несколько диаграмм такого типа.
4.3
Другой метод состоит в использовании (у, tj) -диаграммы, в
которой через у обозначена высота пересечения лучом плоскостн
предмета, а через tj — отношение высоты луча к радиусу зрачка
для одного и того же луча, пересекающего входной зрачок (или,
что равнозначно, любой сопряженный зрачок). (См. фиг. П.7.)
На диаграммах такого типа каждый луч описывается не ли-
линией, а «лучевой точкой» с координатами у, ц. На такой диа-
диаграмме действие каждой k-й диафрагмы можно представить в
виде полосы с параллельными краями ahy -f- bhx\ = ±ch, цен-
центральная линия которой проходит через начало координат. Луч,
проходящий через k-ю диафрагму, описывается точкой внутри
этой полосы. В определенных выше обозначениях ширина k-й
полосы равна 2сА/д/(а| + b\), a тангенс угла, который она со-
составляет с осью г), равен —bh/ah, т. е. отношению (со знаком ми-
минус) отрезка, отсекаемого одним краем полосы на оси у, к от-
отрезку, отсекаемому этим же краем на оси tj.
Полевая У
виафрааха Л
Допалнитетная^
Дополнительная л
диарраст ^&
Входной зрачок
Фиг. П.7
Апертурные свойства центрированной системы линз 279
Апертурное ограничение, обусловленное апертурной диафраг-
диафрагмой (s-й диафрагмой), описывается граничными линиями г\ =
= ±1; очевидно, через апертурную диафрагму нельзя пропу-
пропустить луч на расстоянии от оси, большем чем радиус этой диа-
диафрагмы. Для всех диафрагм, за исключением апертурных, об-
область на т]-оси от т] = +1 до т] = —1 по определению должна
оставаться незатемненной.
Для того чтобы определить границы затемнения, обусловлен-
обусловленные каждой из оставшихся диафрагм, возьмем какой-либо луч,
описываемый двумя параметрами у и ц, и вычислим затем его
последовательные /(-величины. Такой луч начинается в точке,
расположенной на расстоянии R слева от ОП1; высота его иад
оптической осью равна у. Затем этот луч проходит через вторую
точку во входном зрачке на расстоянии Е\ = —(L\2/Lu)s слева
от ОП[ и на высоте т)/8/Aц)в над оптической осью, поскольку
величина /s/(^u)s равна радиусу входного зрачка. Наклон та-
такого луча определяется выражением
V i[Js/(Lii)s — У __
(L)l(L) + R
Следовательно, в плоскости ОП] лучевой вектор запишется в
виде
*!~Lo lJLvJ-L v J-UJ-
Высота луча в k-й опорной плоскости, определяемая вектором
К\ этого входного луча, дается выражением
Ун =.П/0] I*Ki = (Ln)k (У + RV) + {Ln)kV,
а условие, что он пройдет через край k-n диафрагмы радиусом
Л, записывается в виде \уь\ = /&. Подставляя сюда полученные
выше значения для уь и V, после некоторых преобразований
получим следующее основное уравнение для двух граничных ли-
линий на {у, ц)-диаграмме:
У Un)k (Ll2)s - {L
Это уравнение по форме совпадает с приводимым выше уравне-
уравнением
М = ± cfe.
Таким образом, коэффициенты ah, bh и ch можно вычислить не-
непосредственно через данные для L и J. Затем можно провести
построение граничных линий на (i/, rj)-диаграмме либо путем со-
единения точек пересечения на двух осях, либо (если малость
280 Приложение I
коэффициентов а или Ь вызывает затруднения) с помощью упо-
упомянутых выше соотношений между тангенсами.
В простейшем случае, когда имеется одна полевая диафраг-
диафрагма, не сопряженная с плоскостью предмета, (у,г\) -диаграмма
представляет собой параллелограмм. Однако по мере того, как
добавляются новые диафрагмы, граничные линии все больше и
больше обрезают центральную незатемненную область, и в ре-
результате может получиться весьма сложная фигура. Как пока-
показано на фиг. П.7, по величине общей протяженности диаграммы
вдоль ^-направления легко определить диаметр полного поля.
Если необходима большая точность, то можно рассчитать у-ко-
ординату точки персечения двух подходящих пересекающихся
граничных линий, но в таком случае может потребоваться учет
аберраций третьего порядка. Диаметр поля полной освещенно-
освещенности соответствует такому отрезку на оси у, симметричному отно-
относительно у = 0, при параллельном переносе которого вдоль оси
г\ его длина сохраняется. Полевой диафрагмой всегда является
та диафрагма, которая определяет высоту диаграммы вдоль цен-
центральной оси у, т. е. поле для главных лучей.
Для оптических систем, подобных объективам фотоаппара-
фотоаппаратов или телескопам, в которых предмет находится на большом
расстоянии от объектива, всегда имеет смысл вводить вместо ли-
линейного размера поля у соответствующий ему угловой размер
ф = yJR. Поэтому уравнение для двух граничных линий на
(ф, г\) -диаграмме принимает вид
ЯФ Un)k (Ll2)s - {Ln)k (LM)J + т)/, [(Ll2)k + R (LM)J =
В пределе бесконечно больших значений величины R получается
несколько более простое уравнение:
Ф Рп)* (Ln). ~ (I12)* (in)J + Л/, (in)* = ± h (in)..
Следует заметить, что если принято решение строить каждую
граничную линию по методу пересечений, то большая часть тре-
требуемых расчетов должна быть выполнена уже при первоначаль-
первоначальном определении апертурной и полевой диафрагм.
Например, для того чтобы найти апертурную диафрагму, для
каждой диафрагмы рассчитывают максимально допустимые зна-
значения угла Умакс (г) или высоты г/макс (г) луча, исходящего из осе-
осевой точки у = 0 в плоскости предмета. Если каждое из этих
значений разделить соответственно на УМакс м и умакс (s) (значе-
(значения в плоскости апертурной диафрагмы), то полученное в ре-
результате отношение можно использовать для определения иско-
искомого отрезка на оси г\. Аналогично, для того чтобы определить
Апертурные свойства центрированной системы линз
281
полевую диафрагму, мы пользовались главными лучами, для ко-
которых ц = 0, и для каждой диафрагмы рассчитывали макси-
максимально допустимый угол. Если плоскость предмета находится в
бесконечности, то каждый из этих углов непосредственно можно
рассматривать как искомый отрезок на оси ф. Однако в случае
(г/, т])-диаграммы необходимо умножать каждый угол УМакс«)
на величину Е\ — R = —R— {LulLx\)s, для того чтобы полу-
получить из него высоту луча в плоскости предмета.
Ниже все эти моменты будут проиллюстрированы на числен-
численном примере, которым мы и заключим данное приложение.
§ б. ПРИМЕР
Простой астрономический поисковый телескоп состоит из
объектива диаметром 30 мм с фокусным расстоянием 100 мм, ус-
установленного конфокально с однолинзовым окуляром диаметром
5 мм и фокусным расстоянием 10 мм. В общей фокальной пло-
плоскости имеется апертура диаметром 6,5 мм.
а) Найти апертурную и полевую диафрагмы, а также угло-
угловое поле зрения этого прибора.
Линза объектива.
Входной зрачок
on
[tnocKOcmi вЫхоЭнога
зрачка
Диафрагма
0П31
Окуляр
0,015 м
ОП,
0.003Z5 ы
0П5
0,0025ы
|оп6
Р" + 10 диоптрий—
аи*
Р=+100 диоптрий
0,0Ы
Фиг. П.8
282 Приложение I
б) Где должен находиться глаз наблюдателя, если диаметр
зрачка глаза составляет 4 мм? Что произойдет с полем зрения,
если наблюдатель приблизит свой глаз на 5 мм ближе к оку-
окуляру или, наоборот, отодвинет его на 5 мм дальше от окуляра?
Решение
Поскольку плоскость предмета находится в бесконечности,
то нет смысла использовать ее как опорную плоскость. Как по-
показано на фиг. П.8, возьмем в качестве ОП: и ОПг плоскости,
расположенные по обе стороны от линзы объектива, в качестве
ОПз — общую фокальную плоскость, а для ОП4 и ОП5 выберем
плоскости по обе стороны от окулярной линзы. Для того чтобы
ответить на вопрос (б), нам потребуется еще одна опорная пло-
плоскость ОП6, которую мы будем располагать на расстоянии 5 мм
либо до, либо после выходного зрачка.
5.1
Прежде всего вычислим полную матрицу М, начиная вычис-
вычисления от ОП6 назад к ОПь выписывая L-матрицы справа в про-
процессе вычисления. Поскольку каждая Lj-матрица записывается
в виде произведения M,_iMj_2... М2Ми то ее можно рассматри-
рассматривать как произведение матрицы M,_i на соответствующую Lt-\-
матрицу (этот расчет приведен на стр. 283). Прежде чем идти
дальше, проверим, равны ли единице определители всех этих
матриц. Анализ полной матрицы М подтверждает, что она опи-
описывает афокальную систему с угловым увеличением —10. Ясно
также, что если ^=0,011 A1 мм), то плоскости ОП1 и ОП6 бу-
будут сопряженными.
Вычислив L-матрицы, перейдем к построению таблицы I. 1,
где для каждой опорной плоскости перечисляются три величины,
которые понадобятся нам в дальнейшем, а именно: радиус диа-
Таблица 1.1
ДАННЫЕ, НЕОБХОДИМЫЕ ДЛЯ РАСЧЕТА АПЕРТУРНЫХ ЭФФЕКТОВ
В СИСТЕМЕ ЛИНЗ
Опорная плоскость Ofli ОП3 ОП( ОП,
Радиус диафрагмы Jt 0,015 0,00325 0,0025 0,002
(Lu)i I 0 -0,1 -0,1
(Li2)i 0 0,1 0,11 0,ll-10d
Апертурные свойства центрированной системы линз 283
фрагмы Jt и матричные элементы (Lu)i и (Ь\2){. Используя в
$ качестве единиц измерения метры и диоптрии, мы имеем:
| L—матрицы
; Положение Линза фокусное Фокусное Линза ' |о ij
=. глаза окуляра расстояние расстояние объектива
наблюдателя d окуляра объектива (простейший случай)
М= Ms Mi, M, Мг Aft = L2
Г1 <*] Г 1 ol["i о,оЛ Ti о,Л Г1 ol ^ = Г 1 °]
: Lo ij L-ioo lJLo i J Lo ij L-Ю ij г L-io J
M
M
Г. ,1Г. oir. ИГ. l'o,h/
Lo ij L-юо 1JL0 i J L-io ij
p. d\ Г l о1Г-о,1 о,ill yf Г-од о,ill
Lo lJ.L-ioo iJL-io 1 J L0 *¦ J
[T и./ i-
-o.i (o,n-iod)\w Г-од (o.ll-
Z« =
. О -Ю J L ° -1
-loj L о -io
5.2. Определение апертурной диафрагмы
/ Поскольку предмет находится в бесконечности, то апертур-
ная диафрагма будет соответствовать минимальному значению
величины
i/макс (/) =1 Ji/(Ln)t I-
Полученные значения могут быть записаны в виде еще одной
дополнительной строки табл. I. 1:
Опорная плоскость
1 '¦ 1
Умаксш (L]]). 1
on,
0,015
ОПз
00
оп4
0,025
on,
0,02
284 Приложение I
Наименьшее значение величины умакс (,•> помещено в рамку, т. е.
в данном случае роль апертурной диафрагмы играет оправа лин-
линзы объектива вблизи OFIi. Поскольку OFli находится иа одном
из концов системы, апертурная диафрагма одновременно яв-
является входным зрачком. Что касается местоположения выход-
выходного зрачка, то ясно, что матрица Qi совпадает с матрицей М,
так как L\ в точности равна единичной матрице. Следовательно,
мы получаем Е^ = —(AWAl^) = —d-\- 0,011. Но сама по себе
ОП6 расположена на расстоянии d справа от окулярной линзы,
а это означает, что выходной зрачок или диск Рамсдена нахо-
находится справа от линзы окуляра на расстоянии 11 мм. Радиус вы-
выходного зрачка равен | /i/Af221 = 0,0015. Мы уже знаем, что в
том случае, когда глаз наблюдателя расположен правильно, т. е.
d = 0,011, то зрачка его собственного глаза диаметром 4 мм
вполне достаточно, чтобы воспринять весь поток света из выход-
выходного зрачка прибора диаметром 3 мм. Однако допустимые от-
отклонения от этого положения глаза наблюдателя составляют
всего лишь ±0,5 мм.
5.3. Определение полевых диафрагм
Для того чтобы определить, какая из опорных плоскостей
выполняет функции полевой диафрагмы, рассмотрим главный
луч, проходящий через центр входного зрачка под максимально
возможным углом зрения V. Запишем параметры этого луча в
виде еще одной строки табл. 1.1:
Опорная плоскость
V h
1«акси) (Lll)|
on,
00
(апертурная
диафрагма)
on,
0,0325
ОП4
| 0,0227
on.
0,002
0,11-lOd
@0, если
<*-* 0,011)
Если не учитывать влияние положения глаза наблюдателя в
плоскости ОП6, то мы видим, что в данном случае именно оправа
окуляра в ОГЦ, а не диафрагма в фокальной плоскости ОПз дол-
должна рассматриваться как полевая диафрагма.
Входной люк системы находится на расстоянии F\ =
= —(Li2/LiiL = -f—1,1 м слева от объектива, расположенного
в ОПь Его радиус составляет \JJ(Ln)i\ = 0,025 м (т. е. диа-
диаметр равен 5 см). Поскольку роль полевой диафрагмы играет
оправа последней линзы системы, то она же является и выход-
выходным люком, поэтому нет необходимости проводить еще какие-
либо расчеты.
Апертурные свойства центрированной системы линз 285
(Заметим, что когда оправа линзы играет роль диафрагмы,
то при расчете вносимого ею затенения вместо двух опорных
плоскостей можно обойтись одной из них. Матрица промежутка
между линзами такова, что она оставляет неизменными элемен-
элементы Ln и Z-12-)
5.4. Определение поля зрения прибора
Поскольку входной люк, к сожалению, не совпадает с пло-
плоскостью предмета, расположенной в бесконечности, следует ожи-
ожидать появления эффектов виньетирования. Так же как и в п. 4.1,
проецируя входной люк на плоскость предмета, получаем угло-
угловой размер поля зрения, соответствующий конусу главных лу-
лучей. Значение этого углового размера равно
0,0025
= п nm n =0,0227 рад
[полученное значение занесено в приведенную выше таблицу
(см. колонку ОП4) для Умакс (г)]- (Здесь / = 4.)
Чтобы определить влияние виньетирования, построим (Ф,ц)-
диаграмму. Для каждой k-k диафрагмы граничные линии, соот-
соответствующие полю предмета на бесконечности, определяются
следующим уравнением:
Ф [(Ln)h (Lu). - (Li2)k (LM)S] + т|/, (Lu)k = ±Jk (Ln)s.
Поскольку для рассматриваемого прибора s = 1 — апертурная
диафрагма расположена перед ним, — мы можем сразу же поло-
положить (Lu)s = 1 и (Li2)s = 0. В результате получаем простое
уравнение /
Это означает, что одна из граничных линий соединяет точку
[ф == 0, л = Jh/Js(Lu)k] с точкой [ф ~ — /ft/(Li2)ft, л = 0], а дру-
другая проходит параллельно ей на таком же расстоянии, но с дру-
другой стороны от начала координат.
Следует заметить, что, помимо деления на нормировочный
множитель г/макс («) = h, мы уже вычислили для каждой диа-
диафрагмы все необходимые для построения отрезков данные. От-
Отрезки на оси ф перечислены в п. 5.3, а данные, полученные в
п. 5.2, после деления на /s = 0,015 и расстановки знаков опре-
определяют отрезки на оси у\:
Опорная плоскость ОП, ОПа ОП4 ОП,
Отрезки вдоль оси т) 1 оо —1,667 —1,333
286 Приложение I
Далее, пользуясь этими значениями для отрезков, мы строим
(ф, т]) -диаграммы, как показано на фиг. П.9. На средней диа-
диаграмме, которой по предположению соответствует правильное
положение глаза наблюдателя перед выходным зрачком, основ-
основное действие окуляра, ограничивающее поле зрения, изобра-
изображается параллелограммом. Лишь самые вершины этого парал-
параллелограмма отсекаются линиями ф = ±0,0325, которые пред-
представляют действие диафрагмы, расположенной в фокальной пло-
плоскости. Для визуальных наблюдений это кеплеровское устрой-
устройство крайне неудовлетворительно, поскольку свободной от винье-
виньетирования остается лишь небольшая центральная область поля
зрения. Именно по этой причине все астрономические окуляры
оборудованы полевой линзой, которая помогает перенести изо-
изображение апертурной диафрагмы в приосевую область окуляр-
окулярной линзы. (Ситуация совершенно меняется, когда телескоп ис-
используется в перевернутом виде в качестве расширителя луча
маломощного лазера. Такое устройство могло бы с успехом при-
применяться с предельно малой диафрагмой в фокальной плоскости,
работающей, как фильтр пространственных частот.)
Либо из диаграммы, либо путем вычисления значений ф для
подходящих точек пересечения получаются следующие угловые
радиусы для поля предмета на бесконечности:
Угловой
Радиус, рад диаметр,
град
Поле полной освещенности 0,0091 1,04
Поле зрения для главных лучей 0,0227 2,60
Полное поле 0,0325 3,72
Поскольку система работает как телескоп X Ю, то углы,
стягиваемые полями зрения в пространстве изображений, будут
в десять раз больше. Однако для лучей, распространяющихся
под углом 0,2 рад к оси, параксиальное приближение становится
неточным. Можно ожидать, что расхождения между действи-
действительными и номинальными значениями будут составлять 1 или
2%, если окуляр не был изготовлен по ортоскопической схеме.
5.5. Влияние положения глаза наблюдателя
На левой диаграмме фиг. П.9 двумя дополнительными гранич-
граничными линиями иллюстрируется влияние смещения глаза наблю-
наблюдателя от нормального положения на 5 мм ближе к окуляру.
[Для d = 0,006 граничная линия пересекается с осью ф в точке
0,002/@,11 — lOcf) =0,04.] В этом случае дополнительного за-
затемнения не происходит, так как условия наблюдения и, в част-
частности, поле зрения, определяются диаметром окуляра.
Апертурные свойства центрированной системы линз
287
Диафрагма
е фокальной плоскости
Диафрагма
в фокальной плоскости
Зрачок
глаза
А наблюдателя
Апертурная
диафрагма
Глаз наблюдателя
от окуляра
Глаз наблюдателя Глаз наблюдателя
в Ими от окуляра в 16 мм от окуляра
(<р, 1})-диаграммы для телескопа *¦ 10 с одним окуляром
Фиг. П.9
С другой стороны, правая диаграмма показывает, что смеще-
смещение головы наблюдателя на 5 мм от прибора (это соответствует
d = 0,016 и пересечению граничной линии с осью ф в точке <f> =
= —0,04) приводит к дополнительному затемнению в правой
части диаграммы, форма которой в данном случае становится
более симметричной. Однако ясно, что при таком положении
глаза диафрагма в фокальной плоскости уже не видна, а угло-
угловой радиус полного поля зрения теперь сократится до 0,0281 рад
(угловой диаметр — до 3,22°).
Входной люк в правильно сконструированной зрительной
трубе или бинокле находится в бесконечности, и соответствую-
соответствующая такому прибору (ф,ц) -диаграмма имеет идеально прямо-
прямоугольную форму. Но если положение глаза наблюдателя тща-
тщательно не скорректировано как по осевой, так и по поперечной
координатам по отношению к выходному зрачку прибора, то ха-
характеристики этих приборов могут быть сильно испорчены винь-
виньетированием, а также излишними аберрациями глаза. Наблюда-
Наблюдатель, будь аккуратен!
ПРИЛОЖЕНИЕ II
МАТРИЧНОЕ ОПИСАНИЕ
ЦЕНТРОВКИ И ЮСТИРОВКИ
ОПТИЧЕСКОЙ СИСТЕМЫ
§ 1. ПРИМЕНЕНИЕ РАСШИРЕННЫХ МАТРИЦ 3X3
В случае идеальной центрированной оптической системы мы
имели возможность пользоваться матрицей преобразования лу-
лучей размером 2X2, чтобы представить однородные уравнения
в виде
u;H
Однако в реальной системе положение оптической оси в опор-
опорной плоскости ОП2 может быть смещено относительно своего
предполагаемого положения на небольшое расстояние Ауи на-
например из-за того, что плоскопараллельное окно слегка накло-
наклонено и больше не образует прямого угла с осью г. Во многих
случаях направление оптической оси также строго не выдержи-
выдерживается, и она слегка отклоняется от своего предполагаемого
идеального направления на небольшой угол ДУь Этот же эф-
эффект может иметь место и в том случае, когда «плоскопарал-
«плоскопараллельная» пластинка имеет немного клиновидную форму или ког-
когда оптический центр одной из линз слегка смещен от оси.
В этих случаях в приведенные выше два уравнения должны
быть добавлены постоянные члены Ayi и АУ\. В результате наша
система уравнений становится неоднородной. Мы можем, если
хотим, описать преобразование луча уравнением
г*1
Yv2\ Y
Но теперь вектор выходного луча нельзя получить путем про-
простого умножения матрицы системы на вектор входного луча. Од-
Однако существует несколько искусственный метод, который и в но-
новых условиях позволит нам сохранить это важное свойство мат-
матричного умножения: для этого мы будем использовать «расши-
«расширенные матрицы» 3X3. Чтобы уяснить, как образуются такие
Матричное описание центровки и юстировки
289
матр; цы, запишем оба наших уравнения преобразования одно
под другим, а затем добавим к ним снизу третье «фиктивное»
уравнение, которое на первый взгляд кажется совершенно три
виальным:
Эти уравнения можно переписать следующим образом:
#2
v2
1
=
A
С
0
В
D
0
Ay\
AVX
1
II У
Г
1 1
Нетрудно проверить следующее утверждение: если I _ I -
унимодулярная матрица, то и расширенная матрица 3X3 будет
унимодулярной. Поскольку два элемента добавленной снизу
строки равны нулю, а третий элемент этой строки равен -f-1, то
определитель расширенной матрицы 3X3 должен остаться тем
же, что и у исходной матрицы 2 X 2.
§ 2. ПЕРЕМНОЖЕНИЕ РАСШИРЕННЫХ МАТРИЦ
Рассмотрим оптическую систему, полная матрица которой
дается перемножением всех матриц цепочки обычного вида, т. е.
матриц 2X2:
М = МпМп-х ... Мг ... М3М2Ми
», ГЛ' В' 1 I
где Мг — I r п I — унимодулярная матрицу, описывающая
преобразование луча от г-н промежуточной опорной плоскости к
(г + 1)-й. Предположим, что у каждой матрицы Мт имеются до-
дополнительные малые члены Ayr, AVr, учитывающие возмуще-
возмущения, которые необходимо ввести в рассмотрение.
Следовательно, нам придется рассматривать соответствую-
соответствующую цепочку расширенных матриц 3X3, которым мы присвоим
символы Ли JCz и т. д. Можно написать
«Я
здесь
ГА, Вг Ауг1
Mr=ACr Dr AVr
Lo о 1 J
i/210 Зак, 774
290 Приложение И
Рассмотрим теперь умножение двух таких матриц:
[А2 В2 Ау21ГЛ, В, Ayt I
С2 D2 AV2 С, Di A7, =
О 0 1 JLO 0 1 J
= С2Л! +ДА C2Bx + D2Di C2A#1 + D2AV1 +AK2
Loo l
Если внимательно проанализировать элементы матрицы произ-
произведения, то обнаружим, что левый верхний квадрат этой мат-
матрицы, состоящий из четырех элементов, полностью совпадает с
результатом перемножения двух матриц 2X2:
_ Г А2 В21 ГЛ, В, I
2 ' LC2 ZJ J LCj DJ"
Что же касается остальных элементов, то те из них, которые
расположены в третьей строке, малоинтересны, но два верхних
элемента третьего столбца могут рассматриваться как новые
эффективные величины Ау и AV для двух матриц, взятых вме-
вместе. Обозначая эти величины Ay2i и AF2i и вынося их из только
что вычисленной матрицы Ж2Ж\, путем прямой проверки нахо-
находим, что
Д#21 1 ,
Действуя точно так же для образования произведения
ЛгЖ2Жх = Л3 (M2Jti), получаем
д1/21
и аналогично
А#4321
Если, как и в приложении I, обозначить результирующую мат-
матрицу произведения цепочки матриц, начинающейся с матрицы
Матричное описание центровки и юстировки 291
' Мп и заканчивающейся матрицей Мг, через Qr, то эффективные
значения Ау и А У полной матрицы М = МпМп-х.. .M2Mi мож-
\ но записать в следующем виде:
Эффек-
] тивные
С другой стороны, поскольку Qr+\Lr+\ = M и Qr+i = MLr+1, этот
же результат можно выразить иначе, а именно через L матрицы:
Эффек-
Эффективные
Примеры вычисления различных L-матриц обсуждались в
приложении I.
Полную матрицу системы теперь можно записать следующим
образом:
JC--
ГА В Ау
\с D AV
Loo 1 -
здесь А, В, С и D — элементы обычной полной матрицы преоб-
преобразования лучей М, а Ау и АУ—полные поправочные члены,
рассчитанные выше.
§ 3. ВЛИЯНИЕ РАССТРОЙКИ ОПТИЧЕСКОГО РЕЗОНАТОРА
Допустим, что полная расширенная матрица М, которую мы
вычислили, описывает результат одногопцлного прохода луча в
оптическом резонаторе. Очевидно, что-^йуч^ описываемый векто-
о-
ром I 0 I в ОП] и распространяющийся ниже оптической оси.
1:1
[Ау
AV
1
f который имеет иной путь.
Чтобы в этой ситуации найти новую эффективную оптическую
ось, попытаемся отыскать такой входной луч I У о I, который в
7«И>*
892
Приложение II
точности повторяет сам себя, т. е. является собственным векто-
вектором матрицы JL. Очевидно, в этом случае должно выполняться
соотношение
Уо
[А В . Ay "I Гу0 1 Гу0-
C D AF Ko = \VO
0 0 1 JL 1 J Ll .
Выполняя умножение, получаем
Ay0 + BV0 +
y0,
т. е. снова тривиальный результат. Преобразуя первые два ура-
уравнения, находим
Следовательно,
(
AV
-А)
-С
A
—
A
В
-D)
-В
-D)
A
(\ -A
— C
-A)
-C
)
A
Ду
AV
— fi
-D)
{l-D)Vo =
И Ип =
Определитель в знаменателе равен A — Л) A — D) — ВС =
= 2 — А — D, так как AD — ВС = 1. При условии, что вели-
величина 2 — А — D не равна нулю, получаем решение
Уо== 2-Л-О ' Vo== 2-A-D
Это решение можно записать в матричной форме:
Некоторые приложения этого результата в случае простого ре-
резонатора из двух зеркал рассмотрены в § 4 гл. 3.
ПРИЛОЖЕНИЕ III
СТАТИСТИЧЕСКИЙ ВЫВОД
ПАРАМЕТРОВ СТОКСА
В этом приложении мы рассмотрим задачу определения со-
состояния поляризации светового луча, который представляет со-
собой сумму большого числа независимых осциллирующих вкла-
вкладов.
В § 3 гл. 4 мы определили параметры Стокса для заданного
единственного полностью поляризованного возмущения через
амплитуды и фазы поперечных компонент электрического поля
Ех = Не1*
где Я и К — действительные положительные амплитуды, а раз-
разность фаз ф — ф = А. В этих обозначениях определяющие ура-
уравнения записывались в виде
I = H2 + K2, Q = H2-K\ U = 2HKcosA и F = 2tftfsinA.
Первый параметр / представляет собой интенсивность. Напом-
Напомним обычный прием вычисления этой величины из вектора элек-
электрического поля путем образования произведения скобок
I
Если в этом соотношении заменить каждую матрицу на эр-
митово-сопряженную, то получим новое произведение, которое
не является скалярной величиной, а представляет собой эрми-
эрмитову матрицу 2X2:
Последнюю матрицу иногда называют матрицей когерентности.
Видно, что каждый элемент этой матрицы можно записать с по-
10 Зак, 774
294 Приложение III
мощью четырех действительных параметров Стокса. Обозначая
матрицу когерентности через Z, можно написать
+ Q U — iV
U-iVl
I-Q У
В любой эрмитовой матрице 2X2 два диагональных эле-
элемента обязательно должны быть действительными, а два не\-
диагональных элемента — комплексно сопряженными. Следова-
Следовательно, при выборе элементов для Z-матрицы мы имеем только
четыре степени свободы, и существует одна и только одна Z-
матрица, которая соответствует четырем действительным элемен-
элементам столбца Стокса.
Займемся теперь вычислением Z-матрицы,
Z =
в случае, когда поперечные компоненты электрического поля
представляют собой суперпозицию большого числа N отдель-
отдельных возмущений. Предположим, что каждое r-е возмущение мо-
можно представить в виде произведения вектора Максвелла
Г* 1
IK/*' J
на временной множитель exp(iat), который берется
одним и тем же для всех /V возмущений.
[Здесь следует, по-видимому, отметить два момента. Во-пер-
Во-первых, можно учесть тот факт, что каждое r-е волновое возмуще-
возмущение распространяется в несколько отличном от другого направ-
направлении и имеет слегка отличающуюся оптическую частоту, и счи-
считать фг и \рг — быстро меняющимися функциями времени и ко-
координат в плоскости ху. Во-вторых, читатель должен обратить
внимание на то, что во многих учебниках зависимость от вре-
времени в случае электромагнитной волны описывается в виде ком-
комплексной экспоненты с отрицательным знаком перед мнимым по-
показателем экспоненты: ехр(—iatt).]
Воспользовавшись принципом суперпозиции для электро-
электромагнитных полей, для вектора Максвелла, соответствующего ре-
результирующему электрическому полю, получим следующее вы-
выражение:
г
Статистический вывод параметров Стокса
295
Таким образом, соответствующая Z-матрица имеет вид
г N
- N N N N
? Нге1фг ? Hse-l*s ? Hrel*r ?
r s r s
N N N N
? к/*г ? Hf»' ? к*»' ?
Для дальнейших вычислений нам нужно сделать следующие три
предположения:
а) Предположим, что наша основная цель при вычислении
Z-матрицы заключается в том, чтобы определить значения че-
четырех параметров Стокса — действительные числа, которые
можно сравнить с числами, полученными непосредственно из
фотоэлектрических измерений. Однако в процессе таких изме-
измерений мы должны собрать энергию света, переносимую ограни-
ограниченной областью светового луча за конечный период времени
наблюдения, и измеренные таким образом величины будут соот-
соответствовать усредненным во времени и в пространстве элемен-
элементам приведенной выше Z-матрицы. Получающуюся при таком
усреднении Z-матрицу будем обозначать \Z).
б) Будем также предполагать, что колебания вдоль оси х и
вдоль оси у всех jV волновых возмущений «взаимно когерентны».
Это означает, что наблюдается усредненная интенсивность излу-
излучения, в которую каждое волновое возмущение дает независи-
независимый вклад, и, следовательно, полная наблюдаемая интенсив-
интенсивность есть сумма интенсивностей отдельных г и s возмущений.
Что касается колебаний вдоль оси х, когда имеются одновре-
одновременно два волновых возмущения '), то интенсивность излучения
дается выражением
/ = (и р~'фг 4- //_/>"'*«) (н р1фг 4- Hj>14>s\ =
= Щ + Щ + 2HfHs cos (фг - ф$) = lr + ts + 2HrHs cos (фг - фз).
Отсюда следует, что если два волновых возмущения взаимно
некогерентны, то усредненное значение интерференционного
члена или взаимной интенсивности должно ёыть близ-
близким к нулю, т.е. BHrHs cos (фг — ф8)) == 0. Так 1<ак обе вели-
•) Термином «волновое возмущение» электромагнитного поля автор на-
называет цуг электромагнитных волн, испускаемый одним атомом или одной
молекулой в одном акте спонтанного излучения. — Прим. ред.
10*
296 Приложение III
чины Н положительны и ради простоты они могут рассматри-
рассматриваться как неизменные за время наблюдения и по пространству,
занятому лучом света, то равенство нулю этого члена означает,
что разность фаз фт — фв претерпевает большое число полных
периодов изменения и в любой данный момент времени с рав-
равной вероятностью может принимать любое значение в интер-
интервале 0 — 2л. При этом мы можем сказать, что все усред-
усредненные члены, такие, как (cos($r— Ф$)), (ехр [i(j>r — Ф*)\) и
(ехр [—1(фг — Фв)]), пренебрежимо малы.
По аналогичным соображениям для составляющей поля
вдоль оси у мы находим, что (ехр [i(tyr — ф«)]) = 0 и
(ехр [—i(tyr— 4j?s)]^ = 0. Разумеется, существует одно важное
исключение из этого правила: при г = s все приведенные выше
выражения равны не нулю, а единице.
в) Наконец будем предполагать, что у каждого отдельного
r-го волнового возмущения разность фаз r|v — фт = Лг есть по-
постоянная величина. Иными словами, хотя сама по себе фаза фг
и испытывает за время наблюдения большое число циклов
изменения, однако ее поведение во времени в точности одно-
одновременно повторяется фазой \jjr. Следовательно, r-е возму-
возмущение можно рассматривать как произведение вектора Макс-
н
р
Г нт Л
ц I и
L Are T J
велла ц I и быстро меняющегося фазового множителя
L Л|-б т J
ехр(фг). Отсюда следует, что при усреднении выражений
(ехр [±»(фг — Фв)]) мы получаем либо нуль, либо ехр(±(Д)
в зависимости от того, имеем ли мы дело со случаем г Ф s или
со случаем г = s.
Воспользовавшись этими тремя допущениями, теперь можно
выполнить процедуру усреднения Z-матрицы. В результате
имеем
" Е Е HrHs (ехр [/ {фт - ф,)] > Е Е НrK. (exp [i (фг - *,)]
Г S Г S
N N N N
Г S Г S
Поскольку, как мы видели, каждый фазовый множитель при
усреднении обращается в нуль, кроме случая г = s, то можно
исключить двойное суммирование и получить
r N N
Статистический вывод параметров Стокса 297
Таким образом, мы получили важный результат, состоящий
в том, что когда складываются взаимно иекогерентные волно-
волновые возмущения, то усредненная Z-матрица суммарного волно-
волнового возмущения равна сумме Z-матриц отдельных возмущений.
Аналогично каждый из четырех параметров Стокса суммарного
волнового возмущения равен сумме соответствующих параме-
параметров отдельных возмущений:
N N N N
1=1,1» Q=T,Qr, u=Zur, v = Zvr.
г г г г
Отсюда следует, что если известны параметры Стокса каж-
каждого отдельного волнового возмущения или с помощью законов
статистики можно предсказать их наиболее вероятные значения,
то параметры оптического луча в целом можно получить непо-
непосредственным суммированием. Можно поступить и наоборот:
начать сразу с определения элементов (усредненной) Z-мат-
рицы, а затем воспользоваться формулами
U = Zl2+Z2U V = I (Z12 — Z21).
Заканчивая это приложение, приведем несколько конкретных
примеров Z-матриц и столбцов Стокса для некоторых типов све-
световых пучков и соответствующие векторы Максвелла, которые
в большинстве случаев также описывают состояния пучков. Пе-
Перечисленные ниже вектор-столбцы нормированы так, что каж-
каждый из них описывает луч с интенсивностью, равной единице.
Тип 1: Неполяризованный свет
В этом случае все величины Нт и Кт положительны и имеют
одинаковые среднеквадратичные значения: Н2 = К,2- С другой
стороны, разности фаз Аг не будут иметь выделенного значения,
поэтому возникающие при суммировании по многим волновым
N N
возмущениям величины ?ехр(/Дг) и ?ехр(— /Дг) будут весь-
г г
ма малы по сравнению с N.
Таким образом, Z-матрица принимает вид
Гя2 о 1 г '/2 о 1
о ipj-'[o J-
298
Приложение III
где
I = N(H2 + К2) = 2NH2 = 2NK2.
Очевидно, соответствующий Z-матрице нормированный на
Г
О
единичную интенсивность столбец Стокса есть
О
. Разумеет-
Разумеется, для света рассматриваемого типа не существует вектора
Максвелла.
Тип 2а: Свет, поляризованный вдоль оси х
В этом случае все К равны нулю, так что Z-матрица имеет
вид
Г NH2 0
L О О
o o
Если свет типа 2а получается в результате прохождения света
типа 1 через (идеальный) линейный поляризатор, то интенсив-
интенсивность поляризованного света составляет лишь половину интен-
интенсивности _падающего на_поляризатор света, собственно вместо
NH2 -f NX* мы имеем NH2.
Г 1
Столбец Стокса для такого света записывается в виде
1
О
LO J
(пучок нормирован на единичную интенсивность), а соответст
вующий вектор Максвелла есть I I.
Тип 26: Свет, поляризованный вдоль оси у
В этом случае все величины Н равны нулю и Z-матрица
имеет вид
ГО 0 1 _Г0 01
Соответствующие ей нормированные столбец Стокса и вектор
П
Максвелла записываются следующим образом:
-1
0
0 J
Статистический вывод параметров Стокса
299
Тип 2в: Плоскополяризованный свет, плоскость поляризации
которого составляет угол 6 с осью х
Такой свет можно получить, если пропустить свет типа 1 че-
через поляризатор, плоскость пропускания которого составляет
с осью х угол 6. Введем новые координаты х', у' таким образом,
чтобы ось х' лежала в плоскости пропускания поляризатора.
Для поперечных составляющих поля в этих координатах все
величины Кг' обращаются в нуль. Обозначим каждую остав-
оставшуюся величину Н/ через Лг, тогда поперечные составляющие
в исходной системе координат х, у будут иметь вид
Нг = Лг cos 6, Кг = К sin 6,
причем Дг = 0. Таким образом, для Z-матрицы получаем
г- N N
ЦЛ? cos2 6 ? Л2-cos 6 sin 6
4 cos в sin в ? Л2-sin2 6
NA2\ .
Lsi
cos2 в sin в cos в "I
sin 9 cos в sin2 9 J "
Соответствующие нормированные столбцы Стокса и Максвелла
записываются в виде
1 ¦
cos 26
sin 26
• 0
и
Г cos 61
L sinG J'
Тип 2г: Свет, поляризованный под углом —6 к оси х
Все результаты для этого случая получаются путем подста-
подстановки —9 вместо 9 во все выражения для света типа 2в. Это
приводит только лишь к изменению знака перед синусом, пй*
этому имеем
1
cos 26
— sin 26
0
Г cos 6 "I
L — sine _г
Тип 3: Свет с круговой поляризацией
Рассмотрим сначала свет типа 2в при 6=п/4 D5°), так что
cos 29 = 0, a sin 28 = 1. Если такой луч пропустить через чет-
четвертьволновую пластинку, быстрая ось которой ориентирована
300
Приложение III
вдоль оси х, то на выходе пластинки составляющая поля по
оси у отстанет по фазе на я/2 от составляющей поля по оси х.
Следовательно, каждое r-е волновое возмущение будет иметь
левую круговую поляризацию, для которой Аг = — я/2. По-
Поскольку cos 9 = sin 0= 1/д/2, для Z-матрицы имеем
7-1
^ ~~ 2
г
N
=4_1 []¦
Поэтому соответствующие столбцы Стокса и Максвелла запи-
" П
сываются в виде
О
о
и w[-tl
Если повернуть четвертьволновую пластинку на 90° так,
чтобы ^-составляющая поля опережала по фазе на я/2 х-состав-
ляющую этого поля, то разность фаз Дг = + я/2 и на выходе
пластинки получится свет с правой круговой поляризацией. Нор-
Нормированные столбцы Стокса и Максвелла для такого света
имеют вид
vr L / J
Тип 4: Эллиптически-поляриэованный свет, когда оси эл-
эллипса параллельны осям х и у
Как и при рассмотрении света типа 3, предположим, что свет
типа 2в пропускается через четвертьволновую пластинку, уста-
установленную так, что ее быстрая ось параллельна оси х. Однако
теперь возьмем луч, линейно-поляризованный не под углом
8 = 45°, а под произвольным углом 0 к оси х.
В этом случае для Z-матрицы имеем
г- N N
Z =
N N
-tZ ^2sin9cos8 ?
Г Г
cos2 9 i sin 8 cos 81
— »sin 8 cos 8 sin2 8 I'
Статистический вывод параметров Стокса
301
и L-*sin
Следовательно, для этого света с левой эллиптической поля-
поляризацией нормированные столбцы Стокса и Максвелла будут
записываться соответственно в виде
1
cos 29
О
— sin 28-1
Как и в случае света типа 3, если четвертьволновую пла-
пластинку повернуть на 90°, то на выходе этой пластинки мы бу-
будем иметь свет с правой эллиптической поляризацией. Такому
свету соответствуют следующие нормированные столбцы Стокса
и Максвелла:
1
cos 28
0
sin 29 -
Г cos9
LisineJ
J
ПРИЛОЖЕНИЕ IV
ВЫВОД МАТРИЦ МЮЛЛЕРА
§ 1. ПОЛЯРИЗАТОР
Пусть плоскость пропускания линейного поляризатора (на-
(например, пленочного поляроида или призмы Николя) составляет
угол 9 с осью х в произвольной прямоугольной системе коорди-
координат. Введем следующие обозначения: Сх = cos 9, С2 = cos 29,
Si = sin 9 и S2 = sin 29, а общий вид матрицы запишем в виде
ГХ В Т D-i
Е F О Н
J К L М
LN P R S J
(Эту матрицу Z размером 4 X 4 не следует путать с комплекс-
комплексной матрицей когерентности Z размером 2X2, введенной
в приложении III).
а) Прибор, поляризующий неполяризованныи свет под углом
9 к оси х, преобразует свет типа 1 в свет типа 2в (см. перечень
параметров Стокса в приложении III). (В дальнейшем мы бу-
будем использовать символ W = 1/2, где / — интенсивность непо-
ляризованного входного пучка света.) Следовательно, мы имеем
W (Столбец Стокса для света типа 2в) =
= Z X 21F (Столбец Стокса для света типа 1),
- w -
wc2
ws2
- 0 -
—а.
-X
Е
J
-N
В
F
К
Р
Т
G
L
R
D -1
Я
М
S -
- 2W-
0
0
- 0 -
т. е. W = 2WX + 5-0 + Т-0 + D-0, WC2 = 2WE + ..., WS2 =
= 2WJ + .... 0 = 2WN -\- .... (Многоточием в этих суммах
обозначены члены, равные нулю.) После сокращения W полу-
получаем 2Х =•!, X = 1/2. Аналогично Е = С2/2, J = S2/2, N = 0.
Вывод матриц Мюллера
303
б) Свет, поляризованный под углом 0 к оси х, при прохожде-
прохождении через прибор остается без изменения, т. е. прибор преобра-
преобразует свет типа 2в в свет типа 2в. В этом случае
W -j
wc2
ws2
0 -
Г k
C2/2
Ss/2
- 0
В
F
К
P
T
G
L
R
D -
H
M
S -
- w
wc2
ws2
- 0
откуда
W = Г/2 + BWC2 + TWS2 + D-0,
WC2 = WCs/2 + FWC2 + GWS2 + H • 0,
= WSz/2 + KWC2 + LWS2 + Af • 0,
0 = 0-0 + PWC2 + RWS2 + S-0.
(IV. 1)
(IV. 2)
(IV. 3)
(IV. 4)
Из уравнения (IV. 4) следует, что РС2 = — RS2 для всех зна-
значений С2 и S2. Полагая С2 = 0, имеем R = 0, а полагая S2 = О,
имеем Р = 0. Уравнение (IV. 1) дает равенство ВС2 + TS2=1/i,
которое нам понадобится ниже.
в) Свет с амплитудой А, поляризованный вдоль оси Ох, пре-
преобразуется прибором в свет с амплитудой Лсо8 0 = ЛСь по-
поляризованный под углом 0 к оси Ох. Для исходного луча Н2 =
= Л2, К = 0, так что / = Q = Л2, U = V = 0. Компонента вы-
выходного луча вдоль оси Ох равна АС2, а вдоль оси Оу она
равна ACiSi. Следовательно, Я2 = Л2С1, K2 = A2C\S2, А = 0.
Из этих выражений получаем / = А2С2, Q = А2С2С2, U = A2C2S2,
V = 0 (как для света типа 2в). Таким образом, сокращая
всюду Л2, имеем
cis2
7.
С2/2
S2/2
0
S
F
К
0
г
G
Z.
0
D-
Н
м
S -
1
0
-0-
откуда
г2- 1
О, О — О1 ?г — —тг- .
= C1S,BC2-1) =
S0C0
304
Приложение IV
Подставляя в уравнение (IV. 1) выражение для В, находим
Следовательно, T J
г) Рассмотрим свет с круговой поляризацией и амплитудой
А (радиус круга). Амплитуды компонент, параллельных оси
Ох и оси Оу, обе равны А, так что (см. столбец Стокса для
света типа 3) / = 2А2, Q = ?/ = 0 и V = 2А2. Прибор преоб-
преобразует такой свет в линейно-поляризованный под углом 0 к оси
Ох с амплитудой А. Следовательно, Я = ACt, К = AS^, Д = О,
откуда / = A2, Q = А2(С?-5?) = Л2С2, U = 2ACl-AS1 • 1 =A2S2,
V = 0, т. е. получаем свет типа 2в. Исключая А2, находим
откуда
1 -|
c2
s2
0 -
г k
Сг/2
Sa/2
- 0
1 = 1 +
(
C2/2
C^/2
C2S2/2
0
20,
-2Я
S2/2
G
L
0
0-1
Я
M
S -
- 2
0
0
-2
0 = 0,
0,
0 = 2S, S = 0.
Уравнение (IV. 2) с учетом известного выражения для F дает
GS2 = CJ2 - q/2 = (CJ2) A - Cf) = C2S|/2,
G =
а из уравнения (IV. 3) с учетом известных выражений для К и
AJ имеем
LS2 = S2/2 - S2Cl/2 = A - С*) SJ2 = &J2,
L = Sl/2.
Таким образом, матрица Мюллера поляризатора записывается
в виде
1
2
1
c2
52
0
C2
q
ОД
0
ОД*
0
0-
0
0
0_
Вывод матриц Мюллера
305
§ 2. ПОЛУВОЛНОВАЯ ПЛАСТИНКА
(ОПТИЧЕСКАЯ ОСЬ СОСТАВЛЯЕТ УГОЛ в С ОСЬЮ х)
Этот прибор создает сдвиг фазы на я A80°) между обыкно-
обыкновенным и необыкновенным лучом, прошедшим через него. Бу-
Будем считать, что он увеличивает фазу необыкновенной волны
на я по отношению к фазе обыкновенной волны. Геометриче-
Геометрический эффект пластинки состоит в том, что она поворачивает
плоскость колебаний плоскополяризованного света на угол 26,
где 6 — угол между плоскостью пропускания и оптической осью.
При этом энергия света не поглощается, а плоскость колебаний
поворачивается относительно оптической оси так же, как при
зеркальном отражении.
Пусть матрица прибора имеет вид
Г W В Y D-\
Е F G Н
К L М N
Р R X Т Л
Далее будем использовать следующие сокращенные обозначе-
обозначения: Сх = cos 8, С2 = cos 26, С4 = cos 46, Sx = sin 6, S2 =
= sin 20, S4 = sin 40.
а) Прибор преобразует (без потери интенсивности) свет еди-
единичной интенсивности, плоскость колебаний которого содержит
ось х, в свет, плоскость колебаний которого составляет угол 20
с осью х, т. е. этот прибор преобразует свет типа 2а в свет типа
2в; только при этом в столбце Стокса для света типа 2в вме-
вместо 6 мы имеем 26. Таким образом, /= 1, Q — {c\ — S2), U =
= 2S2C2, V = 0. Следовательно,
г 1 т
1
0
L-0-
1 -|
С 2 — S2
2S2C2
0
- W
Е
К
-Р
В
F
L
R
Y
G
М
X
Н
N
Т -
откуда получаем
W + B=l,
Е -(- F = С2
(IV. 5)
(IV. 6)
(IV. 7)
(IV. 8)
306
Приложение IV
б) Прибор не воздействует на неполяризованный свет, т. е.
свет типа 1 преобразуется в свет типа 1. Следовательно,
-1-
0
0
-0-
1
- w
Е
К
-Р
В
F
L
R
Y
G
М
X
D-
Н
N
Т -
Г1-
0
0
-0-
т. е.
Отсюда, используя равенства (IV. 5)—(IV. 8), имеем
F = С2 — 5г = С4,
в) Свет, плоскость колебаний которого составляет угол 8
с осью х, при прохождении через прибор остается без измене-
изменения, т.е. свет типа 2в преобразуется в свет типа 2в. Таким
образом,
-1 -J
c2
s2
LO -
г 1
0
0
-0
0
r2 C2
C2 — O2
2C2S2
0
Y
G
M
X
1
H
N
T -
Г "
c2
s2
-0 .
откуда
С2 == \С2 — S%) L>2 "T" Go2t
G = [С2 - A - 251) C|]/S2 = 2S2C2 = S4,
г) Рассмотрим свет с правой круговой поляризацией (типЗ).
После прохождения света через прибор его интенсивность
остается неизменной, а разность фаз Д, первоначально равная
п/2, становится равной Зя/2, или, что эквивалентно, равной
—п/2. Это соответствует окружности, описываемой в противо-
противоположном направлении, так что Я2 и /С2 остаются без измене-
изменения. По-прежнему cos Д = 0, но теперь sin Д = — 1. Таким об-
образом, для параметров Стокса имеем / = 2А2, Q = О, U = О,
Вывод матриц Мюллера
307
V = —2Л2 в полном соответствии с левым столбцом Стокса
для света типа 3. Следовательно, исключая 2А2, получаем
откуда
A
0
0
-—1 -
-1
0
0
-0
0
г2 я2
С<2 — -~>2
2C2S2
0
0
2СгО2
о2 __ р2
0
D-
н
N
Т -
- 1 -
0
0
-1 -
= 1+2),
= о,
1=7\
Г —— 1.
Таким образом, матрица полуволновой пластинки имеет вид
l 0 0 От
0 С4 S4 0
0 S4 -С4 0
L0 О О -U
§ 3. ЧЕТВЕРТЬВОЛНОВАЯ ПЛАСТИНКА:
ОБЩИЙ СЛУЧАЙ ОРИЕНТАЦИИ
(ОПТИЧЕСКАЯ ОСЬ СОСТАВЛЯЕТ УГОЛ в С ОСЬЮ х)
В случае отрицательного одноосного кристалла ^-колебания
в плоскости оптической оси распространяются быстрее, чем
О-колебания'). Предположим, что пластинка имеет толщину,
при которой О-волна отстает по фазе на л/2 относительно
?-волны. Пусть С\ = cos 6, Si = sin 6, С2 = cos 26, S2 = sin 26.
Запишем матрицы Мюллера в общем виде:
W В Y D-i
Е F G Я
К L М N
\-Р R X Т-1
а) Неполяризованный свет остается без изменения после
прохождения через прибор, т. е. свет типа 1 преобразуется в свет
') Напомним, что автор называет ?-волной необыкновенную, а О-волиой
обыкновенную волну. — Прим. ред.
308
Приложение IV
типа 1. Следовательно,
¦ 1 -1
0
0
-0-
Г*"
0
0
-0-
w
Е
К
Р
В
F
L
R
Y
G
М
X
D-i
Н
N
Т -
- 1-1
0
0
-0 -
1
-W-
Е
К
-Р -
откуда
W = 1,
? = 0,
Р = о! \
б) Прибор не изменяет состояния поляризации света, поля-
поляризованного вдоль оптической оси под углом 8 к оси х, т. е. свет
типа 2в преобразуется в свет типа 2в. (Для удобства будем
считать интенсивность равной единице.) Следовательно,
- 1 1
- 1 В Y Dn
- 1 л
откуда
с2
s2
о J
0
0
-0
F
L
R
G
М
X
1
с2
s2
о
н
N
т.
c2
S2
-0 -
= 1 + ВС2 + Г5
= FC2 -I- GS2,
— LCt + MS*,
+ XS
2»
FC2
LC2
- RC2
2
+ GS2
+ MS2
I Vp
-
f
(IV. 9)
(IV. 10)
(IV, 11)
(IV. 12)
в) Чтобы исследовать действие прибора на колебания, па-
параллельные оси х, очень удобно пользоваться матрицами пово-
поворота. Эти матрицы преобразуют координаты точки в одной
плоской прямоугольной системе в координаты этой же точки
в системе координат, повернутой на угол 8 относительно пер-
первоначальной пары осей (фиг. П. 10). В соответствии с фиг. П. 10
имеем
Ti = #sin(a — 8), х =s R cos (8 + to),
tj = R sin a cos 8 — 7? cos a sin 8, x=*R cos 0 cos © — R sin 0 sin <o,
rj = ycos0 — xsin0, * = !cos8 — TjsinO,
1 = 7? cos (a — 0), у = R sin (8 + ©),
I = # cos a cos 8 + R sin a sin 8, у = R sin 8 cos © + /?cos0sina>,
| — x cos 0 + у sin 0, у = | sin 0 + ц cos 0.
Вывод матриц Мюллера
309
Фиг. П. 10.
В матричном виде эти уравнения записываются в виде
[cos 8 sin 8 "I Г х 1 Г х 1 Г cos 8 — sin 8
— sin9 cos8jLf/J И Lf/J Lsin0 cos9
Теперь оптическая ось направлена вдоль оси ?, так что колеба-
колебания в ?-луче происходят вдоль оси ^, а в О-луче — вдоль оси г\.
Исходное колебание определяется выражениями
= Asinpt, у = 0.
Следовательно,
?-колебания 1
С\ S| Г Л sin р/ "I Г ACi sin pt "I
колебания J |_ — Si С, J |_ О J = [_ — AS, sin/rtj
ТЕ,
10-
В фазовой пластинке О-колебания отстают по фазе на л/2:
in (pi — y) = sin ptcos \ — cos pt sin -y = — cos pt.
[
sin I
Таким образом, на выходе фазовой пластинки имеем
?-колебания "| Г АС\ sin pt "j
О-колебания J |_ AS\ cos pt J'
Для того чтобы найти параметры Стокса, нам нужно знать Н
и К, т. е. составляющие выходного колебания вдоль осей х и у.
Используя опять матрицы поворота, получаем
Г,1 ГС, -bVTACrslnpfl
lyl LS, cJLAS.cosp/J
_ f C\ sin pt-S\ cos pt I r Cf -SMrsinp/T
= A L S,C, sin pt +SlC1 cos pt\~ Ls,C, SiCi J L cos pt J'
310 Приложение IV
Теперь положим х = Н sin {pt + ф), у = К sin (pt + р), так что
Н и К являются составляющими результирующего колебания
вдоль осей хну, а А = р — ф представляет собой разность фаз
между этими составляющими. Следовательно,
х = Н sin pt cos ф + Н cos р/ sin ^>,
у = К sin р/ cos р + ft cos pf sin p,
или
[х I Г Я cos ^> Я sin ф "I Г sin p* "I
t/J = L^cosp /Csinp JLcosp/ J'
[x~\
I получается из
fsinp/ /
I I двумя различными способами. В этих двух уравне^
Гх 1
ниях, для того чтобы получить один и тот же столбец I
[sinpt I
I. должны совпадать, т. е
(полагая для простоты А = 1) мы должны иметь следующие
равенства:
Г Н cos ф НзтфТГ С* -Sf
L J=LiC, S,C,
Sfj
Умножим теперь справа каждую из этих равных друг другу
матриц на транспонированные им матрицы (транспонированная
матрица получается путем замены строк и столбцов в исходной
матрице, т. е. транспонированная к - „I матрица имеет вид
А С
ГА В1
к - „I
в dJ>- Этодает
Н cos ф Н sin ф I Г Н cos ф К cos p
/Ccosp ^sinpJL^sin^ /Csinp J
c\
U, .JL-s? s
Отсюда получаем
tcty
H2 //Kcos(*-p)-ir Ci + S\ CtSxitf-Sfil
2SfC? J*
(С? — S?)
312 Приложение IV
г) Действие прибора на свет с правой круговой поляриза-
поляризацией и интенсивностью, равной 2 единицам, для которого (пер-
(первоначально) х = cos tat, y = — sin ш/. Как и в случае (в),
имеем Я = К = 1, Л = я/2, / = V = 2, Q = ?/ = 0. Мы мо-
можем написать
[| 1 Г С, S, "I Г cos©/ I Г С, cosш — S, sinшП
Л J ~~ L — S, С, J L — sin art \ ~ L — S, cos at — С, sin at J '
В пластинке О-колебания вдоль оси ц отстают по фазе на д/2:
sin {at — л/2) = — cos со/, cos (at — п/2) = sin at.
Таким образом, на выходе пластинки
[I "I Г Сх cos at — S, sin со/ 1 Г— S, СЛГвтш^Т
¦П J ~ L — Si sin и/ + Ci cos ш/J ^ L — St C, J L cos at J '
Следовательно, окончательные значения для х и «/ даются сле-
следующим соотношением:
С, -Snr-S, С,
JL-
l Ci J L — S, C, J L cos at
Итак, на выходе пластинки, как и в случае (в), имеем
Г Я cos <f> H sin <j> "I Г sin at 1
L/CcosP К sin p J L cos tat J
— О, — 1^,0, ^i^i-T
Опять, так же как в случае (в), умножим в последнем равен-
равенстве матрицы 2X2 справа на транспонированные им матрицы.
В результате получаем
г я2 як cos д I Г q-^c.s. + s2 q-s\
L Я/С cos Д К2 J L q-S2 С2 + 25,С,Н
Следовательно,
/ . Я2 + /С2 = 2С? + 2S? = 2,
Q = Я2 — К2 = —4C,S, = —2S2,
U = 2НК cos A = 2 (С? - S?) = 2С2,
Вывод матриц Мюллера
313
Таким
образом,
г 2 1 Г 1
— 2S2
2С2
- 0 -
0
0
-0
В
F
L
R
Y
G
М
X
D-
Н
N
т .
-2
0
0
L2
-2 + 2Z)
2Н
2N
2Т
Отсюда следует, что D = 0, Н = — S2, N — С2 и Т = 0.
Следовательно, матрица Мюллера для четвертьволновой пла-
пластинки имеет вид
о
1
о
о c2s2
с\
о
C2S2
si
Lo S, —Co
О
-s2
с2
о
§ 4. ПРОИЗВОЛЬНАЯ ФАЗОВАЯ ПЛАСТИНКА (ВЫЗЫВАЮЩАЯ
В ОБЫКНОВЕННОМ ЛУЧЕ ОТСТАВАНИЕ ПО ФАЗЕ НА б),
ОПТИЧЕСКАЯ ОСЬ КОТОРОЙ СОСТАВЛЯЕТ УГОЛ 6 С ОСЬЮ х
Запишем матрицу Мюллера
rW
Z =
Е
К
-Р
в общем виде:
В
F
L
R
Y
G
М
X
D-
Н
N
Т -
•
Пусть Ci = cos Э, С2 = cos 20, Sx = sin 0, S2 = sin 20, 0 =
= cos Д, ц = sin A.
а) Неполяризованный свет после прохождения через прибор
остается без изменения, т. е. свет типа 1 преобразуется в свет
типа 1. Следовательно,
-1 -
0
0
-0-
Е
К
LP
В
F
L
R
Y D-
G Н
М N
X Т -
- 1 -
0
0
-0 -
1
-W-
Е
К
-Р -
?=0,
Р ==0.
б) Любые колебания вдоль оптической оси прибора остаются
без изменения после прохождения света через прибор, т. е. свет
И Зак, 774
314
типа 2в преобразуется
Г 1 1
С2
S2
- 0 -
Таким образом
- 1
0
0
-0
J
в
F
L
R
Приложение У
V
в свет типа 2в:
Y
G
М
X
D-
Н
N
Т -
Г 11
с2
s2
- 0 -
¦ 1 + ВС2
FC2 +
LC2 +
L RC2 +
+ Г52-|
GS2
MS2
XS2 -
•
LC2 + MS2 = S2, RC2 + XS2 = 0.
в) Воздействие прибора на колебания единичной амплитуды
вдоль оси х. Для такого колебания х = sin at, у = 0, / = Q =
= 1, U = V = 0. Рассмотрим повернутую систему координат,
описанную выше в связи с четвертьволновой пластинкой. Если
^-колебания описываются координатой |, а О-колебания — ко-
координатой т], то | = С\ sin at, ц = — Si sin cot.
После прохождения фазовой пластинки О-колебания отстают
по фазе на б относительно f-колебаний. Следовательно, на вы-
выходе пластинки
т] = — Si sin {at — б) = — Si sin at cos б + Si cos at sin 6,
I =Cisinco/.
Таким образом, результирующие составляющие вдоль осей хну
можно записать в виде
де! Г С, — Si Г
#J LSi Ci JL —
Sipsinco*+ S^cosco/
— S?ncosart
sin at — SjCipsin at + SiCi\i cos at
"j _
J
LS,C,(l-p)
где p = cos б, а ц = sin 6.
Кроме того, для четвертьволновой пластинки, если,
ном счете, х == Я sin (<at -\- <f>) и у = К sin(cof + a), т
= a — ф, можно написать следующее соотношение:
Г*! ГЯсов^ Я sin ^> Г sin со/ 1
L у J =X L К cos a К sin a J L cos at J '
Таким образом,
в конеч-
конеч.е. Д =
L/Ccosa
Вывод матриц Мюллера
315
Умножая каждую матрицу на ее транспонированную, как и
прежде, получаем
Я2
cos Ь
К2
1 + 25?С2р + 51 S2C2 (I — р)/2
S,C,(l-p)/2 2SfCf(I — Э)
]•
Это дает/=Я2+Я2=1, Q—Д8'—/С*=|Р,
= S2C2A—-p), так что (из равенства /2 = Q2 + ?/2 + V2) имеем
F2 = S2n2. Отсюда следует, что У равно либо +52ц, либо
— S2(i. Для того чтобы выбрать правильный ответ, рассмотрим
снова равенство
iC,(l — p) S,C,
Приравнивая друг другу определители этих двух матриц, на-
находим
НК (sin a cos ф — cos a sin ф) =
= iiStd (С? + S?p) + iitfd A - p) = nS,C,.
Отсюда сразу получаем
HK sin (a — #)-=S,C,n.
Следовательно,
V = 2Я/С sin A = 2Я/С sin (a — ?) = 2S,C,n = S2(i.
Таким образом,
-
п
"О2С2
_
1
+ s2p
(i-P)
Soil
Г 1
0
0
-0
в
F
L
R
Y
G
М
X
D-
Н
N
Т .
- 1 -
1
0
-0 -
-1 +
F
L
- R
откуда
= 52C2(l-p), R =
Из этих равенств, учитывая четыре окончательных выражения,
приведенных в п. «б», получаем
0, G =
-p),
г) Действие фазовой пластинки на пучок света с круговой
поляризацией, для которого х = cos at, у = —sin at, а пара-
параметры Стокса имеют вид B, 0,0,2). Так же, как и в п. «в», пе-
перейдем к осям I и т), одна из которых параллельна, а другая
перпендикулярна оптической оси пластинки, и рассмотрим вы-
U*
316 Приложение IV
зываемое пластинкой отставание по фазе на б О-колебаний от-
относительно ^-колебаний, а затем снова вернемся к старым осям
х и у. В результате имеем
Гх1 ГС, -5,]Г1 01Г С, Sjir 0 lirsinfi)/]
UJ LS, С, JU pJL-5, cJL-1 oJLcosarfJ"
TCi —^S, — SiP"ir — Si С,1ГsincD/ I Г sin со/1
LSi + цС, CjPJL-C! -S1JLcos(ad==GLcos(ad'
Точно так же, как и в п. «в», нужно умножить матрицу, связы-
[х "I Г sin ш/ I
I и I I. на ее транспонированную.
В данном случае удобно воспользоваться широко известной тео-
теоремой матричной алгебры относительно транспонирования про-
произведения матриц (см. § 8 гл. 1). Обозначим операцию транс-
транспонирования правым верхним индексом Т. Нетрудно проверить,
что (ЛВ)Т = (В)Т(Л)Т, т.е. матрица, транспонированная по
отношению к произведению двух матриц, равна произведению
отдельных транспонированных матриц, но в обратном порядке.
Таким образом, (АВ) (ЛВ)*= (А) (В) (В)тD)т=» (А) (ВВРЦАI1
(поскольку матричное произведение ассоциативно).
Применяя это свойство к матрице G, получаем
rc,-ns -s^-ir-s, сп
^LSj + ^C, Сф JL-C, -SjX
Г-Si -СЛГС-nS, S, + |iC,1
XL с, -s,JL -s,p c,p J"
В этом произведении перемножение двух средних матриц дает
Г1 ОТ
единичную матрицу I . I > которую можно не учитывать.
В результату перемножения двух других матриц после упро-
щаюЩих преобразований получаем
г 1 _ Ц52 + цС2 I
L J
Как и прежде, эта матрица должна быть равна матрице
Я2 НК cos A I
К* У
Таким образом / = Я2 + К2 = 2, Q = H'l — K2=x —2]iS2, U =
= 2НК cos A = 2цС2. Равенство Я = Q2 + U2 + V2 приводит
к V2 ш* 4pJ, но величина V может быть равной либо ^2р, либо
Вывод матриц Мюллера
317
—2р. Чтобы дать однозначный ответ, снова приравняем друг
другу найденные нами две матрицы 2X2, которые связывают
[л: I Г sin to/ I
I и I , I ¦ Это равенство
записывается в виде
L/C
cosa
-5,р1Г-5, С, 1
C,pJL —С, — 5,J"
Приравнивая определитель левой матрицы в этом равенстве
произведению определителей матриц, стоящих в правой части
равенства, получаем
НК (sin a cos ф — cos а sin ф) =
= (C?p-npi
Отсюда сразу же следует
HKsin(a — ф) = $, т. е. V =
Таким образом,
2
,C,) {S\ + C\) = p.
-2[iS2
2цС2
2P
- 1
О
О
В
F
Y D
G Н
L М N
LO R X Т-1
-2-
0
0
-2 -
г2
0
0
-0
+
+
4-
+
2D-i
2Я
W
2Т -
откуда D = О, Я = — ц52, W = цС2, Т = р. Следовательно, ма-
матрица фазовой пластинки в общем случае имеет вид
Замечания
- 1
0
0 5
-0
0
Г2 4- S2
2С>2 V * —
S2H
р
Р)
С
2^2
s2
—
0
A
-f-
с
-р)
2^
о -
-52ц
С2ц
Р -
1. Из последней матрицы можно получить матрицы для пло-
плоскопараллельной стеклянной пластинки, полуволновой и чет-
четвертьволновой пластинок путем подстановки в нее конкретных
значений, а именно 6 = 0, л, п/2 соответственно (см. табл. 4.1
в §3 гл. 4).
2. Для того чтобы поменять местами в правом столбце cos at
Г ° !
и sin at, была введена матрица I ,
318 Приложение IV
Г i 01
3. Матрица I . I описывает отставание по фазе на о
Lfi рJ
О-волны относительно ?-волны. Так же, как и в п. «в>, мы за-
записываем
д0 фазовой
пластинки
и
Si С, "I Г Sin (Of "I „осле фазовой
+ рС, цС, - PS, J L COS <at J пластинки
Эта матрица получается из предыдущей матрицы путем замены
Ы иа (со/ — б) в выражении для х\. Кроме того,
ri o-irs, с«1 Г 5, с, -I
U pJLc, -s,J L^Si + pc, nc,-ps,_r
ПРИЛОЖЕНИЕ V
ПОЛУЧЕНИЕ МАТРИЦ ДЖОНСА
/
§ 1. ПОЛЯРИЗАТОР ТИПА ПЛЕНОЧНОГО ПОЛЯРОИДА
а) Сначала рассмотрим идеальный линейный поляризатор,
плоскость пропускания которого горизонтальна, т. е. парал-
параллельна оси х. Такой прибор позволяет пройти лишь колебаниям
поля, параллельным оси х, так что в общих уравнениях, описы-
описывающих свойства идеального оптического прибора, имеем Я2 =
= #i и Кч = 0 независимо от того, какими являются величины
Н\ и /Сь Таким образом, имеем следующие уравнения:
О = /2,# 1 + /22#i ехр (/А,)
для всех значений Яь К\ и Ai. Положим К\ = 0. Тогда получаем
Я, = /ц#ь т. е. /ц = 1 и 0 = /2i#i для всех Я,, т. е. /2, = 0.
Положим теперь Hi = 0. Тогда приходим к уравнениям 0 --
= JiaKi exp(«Ai) и 0 =/22/Ci exp(t'Ai) для всех К\ и Аи т.е.
/12 = /22 = 0.
Таким образом, матрица Джонса для этого идеального поля-
поляризатора имеет вид . Конечно, в действительности пленка
поляроида вызывает некоторое ослабление даже для преимуще-
преимущественной плоскости колебания, и ее толщина достаточна для
того, чтобы привести к запаздыванию сигнала по крайней мере
порядка нескольких сотен длин волн. В некоторых случаях, на-
например при расчете интерферометра, приведенную выше ма-
грицу необходимо умножать на комплексную скалярную вели-
величину, которая описывает комплексный амплитудный коэффи-
коэффициент пропускания поляризатора. Если в рассмотрении исполь-
используется лишь один вектор Максвелла, то вряд ли необходима
информация относительно абсолютного значения фазы колеба-
колебаний. Однако часто оказывается удобным данную матрицу
Джонса привести к более простой или более симметричной
форме путем умножения ее на подходящий фазовый множитель.
Напоимер, указанную выше матрицу с одинаковым правом
Г — 1 (И [i 01
можно представить в виде I . . или .
32 О
Приложение V
Колебание
Плоскость
в пропускания
х
Фиг. П.11.
Нетрудно также показать, что поляризатор с вертикальной
плоскостью пропускания, т. е. параллельной оси у, может быть
го 01 г о о п
описан матрицей Джонса вида I . I или, например, I _ 1ф I.
б) Рассмотрим теперь поляризатор более общего вида, т. е.
такой, плоскость пропускания которого составляет угол О
с осью х (фиг. П. 11). Предположим, что на этот поляризатор
падает плоскополяризованная волна, плоскость колебаний ко-
которой составляет угол а с осью х. Допустим, что амплитуда
этой волны равна А; тогда по определению Х\ = A cos a,
а У! = A sin а. Через прибор пройдет лишь составляющая ко-
колебаний, параллельная плоскости пропускания поляризатора.
Амплитуда этой составляющей дается выражением
U = A cos (а — 6) = A cos а cos G + A sin а sin G = Xi cos 6 + Y\ sin G,
a проекции ее на ось х
Х2 = U cos G = Xi cos2 G + Y, sin G cos G
и на ось у
У2 = U sin G = Xi cos G sin G + ^i sin2 6.
Два последних уравнения можно записать в матричной форме
21 Г cos2G sinGcos6ir
IY2 J^LsinGcosG sin2G JIT
Следовательно, матрица прибора имеет вид
cos2 G sin 9 cos G I
sin G cos 9 sin2 6 J'
[
Получение матриц Джонса 321
§ 2. МАТРИЦА ДЖОНСА ПРИБОРА,
ВЫЗЫВАЮЩЕГО ПРОИЗВОЛЬНУЮ ФАЗОВУЮ ЗАДЕРЖКУ
Рассмотрим кристаллическую пластинку, оптическая ось ко-
которой составляет угол а с осью х. Предположим, что в этой
пластинке фаза обыкновенной волны — составляющей поля, пер-
перпендикулярной оптической оси, — отстает на б по отношению
к фазе необыкновенной волны, т. е. колебания вдоль оптической
оси. Прибор/ такого типа не вносит каких-либо изменений в век-
вектор Максвелла для плоскополяризованной волны с колебаниями
вдоль оптической оси. Допустим, что амплитуда волны равна А;
тогда, как было показано в предыдущем параграфе, посвящен-
посвященном поляроидам, ее составляющие записываются в виде A'i =
= A cos аи Y\ = A sin а. Поскольку прибор на эту волну не
влияет, компоненты прошедшей волны останутся такими же, как
на входе прибора, т. е. Х2 = A cos аи У2 = A sin а.
Подставляя эти выражения в общее уравнение, описываю-
описывающее действие оптического прибора, находим
A cos а —У, 1^4 cosa-f /i2<4sina,
A sin a = J2\A cos a -f J^A sin a.
Из этих уравнений сразу получаем
sin a I — Ju J2\
tga =
cos a /i2 I — /2
(отсюда следует, что cos a не должен обращаться в нуль). Рас-
Рассмотрим теперь действие прибора на пучок плоскополяризован-
ного света с амплитудой А, в котором плоскость колебаний
параллельна оси х. Для этого луча вектор Максвелла записы-
записывается в виде
-ш-
Теперь нужно рассмотреть компоненты исследуемой волны,
параллельные и перпендикулярные оптической оси. Для того
чтобы их определить, используем матрицы поворота, введенные
при получении матрицы Мюллера для четвертьволновой пла-
пластинки. В результате имеем
Г Компонента, параллельная оптической оси
L Компонента, перпендикулярная оптической оси
Ну.]-
[cos a sin a "] Г A "] Г A cos a
— sin a cos a J L 0 J L — A sin a J"
Компонента, перпендикулярная оптической оси, отстает теперь
по фазе на б, т.е. V\ умножается на ехр(—гб). Таким образом,
322 Приложение V
матрица для компонент, параллельной и перпендикулярной оп-
оптической оси, принимает вид
?/21Г Лсоз(а)
J L
_Г Лсоз(а) I
L-/lsin(a)exp(-/6) J
Вернемся теперь к первоначальным осям. Чтобы сделать это,
воспользуемся снова матрицей поворота, однако на этот раз
нам нужно совершить обратный переход от осей U и V к перво-
первоначальным осям X и У. Таким образом, получаем окончатель-
окончательный вид вектора Максвелла
[cos (a) — sin (a) 1 Г A cos (a)
sin (a) cos (a) J [_ — A sin (a) exp (— /6) J ~~
[A cos2 (a) + A sin2 (a) exp (— ib) "I
A cos (a) sin (a) — A sin (a) cos (a) exp (— ib) J
_ Г {cos2 (a) + sin2 (a) exp (- ib)} A1
L cos (a) sin a {1 — exp (— ib)} A J *
С другой стороны, можно записать
Следовательно, сравнивая выражения для Е2, находим
/п = cos2 (a) + sin2 (a) exp (— ib)
и
/21 = cos (a) sin (a) {1 — exp (— ib)}.
Используя здесь два полученных выражения для tg a, после
простых преобразований получаем
/12 = sin (a) cos (a) {1 — exp (— ib)}
и
/22 = sin2 (a) + cos2 (a) exp (— ib).
Таким образом, матрица Джонса для фазовой пластинки об-
общего вида с произвольной ориентацией записывается в виде
cos2 (a) + sin2 (a) exp (— ib) cos (a) sin (a) {1 — exp (— ib)}
cos (a) sin (a) {1 — exp (— ib)} sin2 (a) + cos2 (a) exp (
-ib) \
В качестве упражнения читателю предлагается доказать, что
матрица Джонса простого вращателя, т. е. прибора, который
поворачивает плоскость колебаний линейно-поляризованного
Получение матрац Джонса 323
света на угол 9 против часовой стрелки (это, например, осуще-
осуществляется некоторыми органическими жидкостями), имеет вид
Г cos 0 — sin 0 "j
cos 0 J *
Вообще говоря, если / представляет собой матрицу Джонса,
вычисленную для некоторого частного прибора, то новая ма-
матрица для того же прибора, но повернутого на угол 9, дается
тройным~матричным произведением
Для того чтобы закрепить это полезное правило, читателю
полезно убедиться самостоятельно в том, что приведенная выше
матрица для линейного вращателя плоскости поляризации на
произвольный угол 9 равна произведению следующих матриц:
Tcos0 — sine Г 1 0 "|Г cos0 sin9 "j
Lsin0 cosoJLo e-'*JL—sin0 cos0j"
В табл. 4.1 (см. § 5 гл. 4) приведены такие матрицы для неко-
некоторых частных случаев. Нужно отметить, что именно азимут
быстрой оси (направление наиболее быстрого распространения
волны) конкретизирует каждый отдельный случай, так что
в случае волновой пластинки, вырезанной из отрицательного од-
одноосного кристалла, значения б относятся к отставанию по фазе
для обыкновенной волны.
ПРИЛОЖЕНИЕ VI
ВЗАИМОСВЯЗЬ МЕЖДУ МЕТОДАМИ
РАСЧЕТА ДЖОНСА И МЮЛЛЕРА
§ 1. ВВЕДЕНИЕ
Поскольку и матрица Мюллера, и матрица Джонса описы-
описывают свойства оптических приборов и для полностью поляризо-
поляризованного света результаты, полученные тем и другим методом,
всегда совпадают, то между этими двумя методами расчета
должна существовать тесная связь. Паркес показал, используя
матрицы когерентности Винера, что элементы матрицы Мюл-
Мюллера для конкретной системы можно выразить через элементы
матрицы Джонса той же системы. Цель этого параграфа со-
состоит в том, чтобы показать, что это можно сделать в рамках
формализма матриц Джонса и Мюллера. Кроме того, мы полу-
получим формулы обратного перехода от одной матрицы к другой
и вычислим действительную и мнимую части матрицы Джонса
по известной матрице Мюллера (при условии, что матрица
Мюллера описывает физически реализуемый поляризационный
прибор).
§ 2. ВЫВОД СООТНОШЕНИЯ МЕЖДУ ВЕКТОРАМИ СТОКСА
И МАКСВЕЛЛА
Покажем теперь, что все параметры Стокса можно выразить
через вектор Максвелла и через транспонированный ему ком-
комплексно сопряженный вектор и некоторые постоянные матрицы
2X2, которые мы определим в этом параграфе.
В общем случае вектор Максвелла луча записывается в виде
[11 -¦
к С\\ Г ^го тРанспониРованный вектор принимает
вид вектор-строки [Я /Cexp(tA)]. Комплексно сопряженный ему
вектор при этом равен [Я /Сехр(—?А)]. (Этот вектор можно на-
назвать эрмитово сопряженным по отношению к вектору Е. Обо-
Обозначим его, как и в § 7 гл. 4, через Е.)
Следовательно (используя матричное умножение), имеем
а) ЕХЕ=[Н
Взаимосвязь между методами Джонса и Мюллера 325
[поскольку exp(tA)exp(—iA) = 1]. Мы получили первый пара-
параметр Стокса луча, т. е. /. Ниже между Еи? будет введена еди-
1 0
Г1 01
! . . I;
ничная квадратная матрица! . . I; назовем ее Ль Разумеется,
введение матрицы А\ не может повлиять на конечный резуль-
результат расчета. Таким образом, мы можем написать
Г 1 01 Г 1 01 Г Я
б)ЕХ[0 _\ХЕ ЕХ[ \х[
Все это можно записать в виде
EX4»X? = Q, (VI. 2)
где
Г01
в)ЕХ[1
[/Сехр(/Д)
Я
НК ехр (/А) + НК ехр (- /А) =
Я/С (cos A + i sin A + cos A — i sin A)
Это можно записать в виде
EXA3XE = U, (VI .3)
где
О —/ 1 ГО —/ 1 ГЯ
]ЯЕХ[ JxU
326 Приложение VI
[ — iK exp (гД) 1
/Я J=
= — ШК exp (/Д) + iHK exp (- /Д) =
HK {— i (cos Д + / sin Д) + / (cos Д — / sin Д)} =
HK{— /cosA — i2
(здесь мы учли, что i2 = — 1). Запишем это в виде
r EXA4XE = V, (VI. 4)
где
-Г ~Ч
i~L/ oj-
(Приведенные только что уравнения (VI. 1 — VI. 4) позволяют
представить каждый из четырех параметров Стокса в виде
«матричного сэндвича». Три матрицы Лг, Л3 и Л4 тесно связаны
со спиновыми матрицами Паули.)
§ 3. ПРЕДСТАВЛЕНИЕ „МАТРИЧНЫХ СЭНДВИЧЕЙ"
ЧЕРЕЗ ЭЛЕМЕНТЫ МАТРИЦ МЮЛЛЕРА И ДЖОНСА
3.1. Использование матричных элементов Мюллера
Первое уравнение, определяющее матричные элементы Мюл*
лера, записывается в виде
/, = М„/о + М12Q0 + Ml3U0 + MUVO.
Воспользовавшись выражениями, полученными в § 2, для пара-
параметров Стокса через элементы вектора Максвелла, можем за-
записать
+ (Af 13 X Eo X А3 X Ео) + (Ми X Ео X Л4 X ?о) =
= Eo X [М,И, + М12А2 + М13А3 + Af „Л,] X Ео.
Подставляя выражения для Л-матриц и производя упрощающие
преобразования, последнее уравнение можно записать в виде
[М „ + М12 Af 13 — Ш14
Остальные три определяющих уравнения для матричных эле-
элементов Мюллера получаются в таком же виде, за исключением
нижнего индекса в матрице Л„ расположенной слева, и первого
Взаимосвязь между методами Джонса и Мюллера 327
нижнего индекса у элементов матрицы МЯ{. Таким образом,
[ЛГ31 + M32 М33 — Ш34
«:;+«¦*, *?-*.
[Af4, + M42 Af« — Ш441
м;+ш;4 Af41_AfJx*'- <vL8>
3.2. Использование матричных элементов Джонса
Для матрицы Джонса определяющим уравнением является
Ei = JEQ. Переходя к эрмитово сопряженным матрицам в обоих
частях этого уравнения, получаем Ei = (Матрица, эрмитово со-
сопряженная для JEq). Далее, транспонированное произведение
двух сомножителей есть произведение двух транспонированных
сомножителей, взятых в обратном порядке, т. е. (Транспо-
(Транспонированная АВ) — (Транспонированная 5)Х (Транспонирован-
(Транспонированная А). Поскольку операция перехода к эрмитово сопряженной
матрице просто эквивалентна комплексному сопряжению транс-
транспонированной матрицы, то аналогичная теорема имеет место и
для эрмитово сопряженных матриц. Таким образом, (Эрмитово
сопряженная матрица JE0) = (Эрмитово сопряженная матрица
^о) X (Эрмитово сопряженная матрица /), т.е. Ei = Ео X J-
Следовательно (вставляя единичную матрицу А\ в соответ-
соответствии с последними соотношениями), имеем
Е, X Л, X Я, = (Ео X J) X А, X (/ X Ео) =
(здесь мы воспользовались свойством ассоциативности матрич-
матричного умножения). Аналогично можно получить следующие ра-
равенства:
Е.ХЛгХЯ^ЕоХ^ХЛХ-ОХЯо, (VI. 10)
Е^ЛзХЯ^ЕоХиХЛзХ-ОХЯо, (VI. 11)
Е1Х^Х^1 = ЕоХиХ^Х/)Х?1о. (VI. 12)
§ 4. ПОПАРНОЕ СРАВНЕНИЕ „МАТРИЧНЫХ СЭНДВИЧЕЙ"
В ДВУХ МЕТОДАХ РАСЧЕТА
Левые части уравнений (VI. 5) и (VI. 9) совпадают; следо-
следовательно, должны быть равны между собой и правые части.
И в том и в другом случае в правой части стоит Ео X (Неко-
(Некоторая матрица) Х^о- Поскольку обе правые части этих двух
328 Приложение VI
уравнений равны между собой, то должны быть равны друг
другу и матрицы, «зажатые» между Ео и Ео. То же самое можно
сказать и относительно «зажатых» матриц в уравнениях (VI. 6)
и (VI. 10), в уравнениях (VI. 7) и (VI. 11), а также в уравне-
уравнениях (VI. 8) и (VI. 12).
«Зажатой» матрицей в уравнении (VI. 9) является матрица
(JX^iX-О- Матрица J получается транспонированием мат-
матрицы /, в которой затем каждый матричный элемент заменяется
на соответствующий ему комплексно сопряженный элемент. По-
, га. м
скольку транспонированной к матрице /= . [является
[h\ h\~\ Г Gn G21 "I
j . I, то J = I „ „ I, где элементы Gs опре-
•42 >>22 J L <-f12 Cr22 J
деляются как комплексно сопряженные элементы /s.
Таким образом, в (VI. 9) «зажатая» матрица имеет вид
rGu G21 "I Г 1 ОТГ/п /12-|_
Lg12 G^JlO lJL/2. /22J
[Gn/ц + G2i/2i GM/i2 + G21/221
G12/n + G22/21 G12/i2 + G22/22 J '
Каждый элемент последней матрицы теперь можно приравнять
соответствующему ему элементу «зажатой» матрицы в уравне-
уравнении (VI. 5). Следовательно,
Mn + Mu = Gn]n + GnJn, (VI. 13)
М13 - Ши = Gn/12 + G21/22, (VI. 14)
Ml3 + Шм = G12/n + G22/2,, (VI. 15)
М„ - М12 = G12/12+ G22/22. (VI. 16)
Действуя точно так же с другими парами «зажатых» матриц,
из уравнений (VI. 6) и (VI. 10) получаем
М21 + М22 = G,,/,, - G21/21, (VI. 17)
Ми - Ш24 = Gn/12 - G2i/22; (VI. 18)
М2г + Ш24 = G12/u - G22/21> (VI. 19)
М21 - М22 = G13/12 - G^; (VI. 20)
из уравнений (VI. 7) и (VI. И)
^3i + M32 = G11/21 + G2l/11, (VI. 21)
M33-/M34 = Gn/22 + G21/12; (VI. 22)
Мзз + Ш,4 = О12/21 + О22/и, (VI. 23)
М31 - М32 = G12/22 + O22/i2; (VI. 24)
^ Взаимосвязь между методами Джонса и Мюллера 329
и из уравнений (VI. 8) и (Vi. 12)
Mi{ + Mi2 = i{G2{Jn-GnJn), ' (VI. 25)
Mi3 - iMH = i (G21/12 - G,,/22); (VI. 26)
М4з + Ш44 = / (GrJu - G12J2l), (VI. 27)
M4I - M42 = i (G22/12 - G12/22). (VI. 28)
§ 5. ВЫРАЖЕНИЯ ДЛЯ ЭЛЕМЕНТОВ МАТРИЦЫ МЮЛЛЕРА
ЧЕРЕЗ ЭЛЕМЕНТЫ МАТРИЦЫ ДЖОНСА
Теперь нетрудно выразить матричные элементы Мюллера че-
через матричные элементы Джонса. Для этого нужно только сло-
сложить или вычесть одно из другого соответствующие пары урав-
уравнений, входящие в набор (VI. 13—VI. 28). Таким образом,
A3+16) M11 = (Gn/n + G21/21 + G12/12 + G22/22)/2, (VI. 29)
A3 - 16) М12 = (GnJn + G21/21 - G12/12 - G22/22)/2, (VI. 30)
A4 + 15) Afl3 = (G,,/12 + G21/22 + G12/u + G22J21)J2, (VI. 31)
A5 - 14) Afи = i (On/12 + G2lJa - G12/u - G22/21)/2, (VI. 32)
A7 + 20) ^21 = (Gu/11 + G12/12-G21/21-G22/22)/2, (VI. 33)
A7_20) M22 = (G,1/1, + G22/22-G21/21-G12/l2)/2> (VI. 34)
A8 + 19) M2. = (G12/u + G,,/12 - G^Jv - G21/22)/2, (VI. 35)
A9 - 18) ^24 = i (G,,/12 + GvJk - G,,/^ - G12/u)/2, (VI. 36)
B1 + 24) M31 = (G11/21 + G22/n + G,^ +G22/12)/2, (VI. 37)
B1-24) M32 = (G11/21 + G21/11-G12/22-G22/12)/2) (VI. 38)
B2 + 23) M33 = (Gn/22 + G21/, + G12/ , + GE/n)/2, (VI. 39)
B3 - 22) M34 = / (Gu/22 + G21/12 - G12/21 - G22Jn)/2, (VI. 40)
B5 + 28) M41 = i (G21/n + G22/l2 - Gn].n - G12/22)/2, (VI. 41)
B5 - 28) M42 = i(G21/u + G12/22 - G,,/21 - G22/12)/2, (VI. 42)
B6 + 27) M43 = I (G2I/12 + G22/n - Gn/22 - G12/21)/2, (VI. 43)
B7-26) M44 = (G22/11 + G,,/22 - G12/2, - G21/12)/2. (VI. 44)
Эти выражения полностью совпадают с выражениями, данными
Паркером.
§ 6. ПОЛУЧЕНИЕ ВЫРАЖЕНИЙ ДЛЯ ЭЛЕМЕНТОВ
МАТРИЦЫ ДЖОНСА ЧЕРЕЗ ЭЛЕМЕНТЫ МАТРИЦЫ МЮЛЛЕРА
Элементы матрицы Джонса в общем случае комплексны, и
нужно находить выражения как для действительной, так и для
мнимой частей этих элементов. При выводе оказывается удоб-
330 Приложение VI
ным пользоваться полярным представлением комплексных мат-
матричных элементов, т. е. комплексное число, например X + iY,
записывать в виде Rexp(iQ), где R = -у/Х2 + Y2, a tg 8 = Y/X.
Следовательно, комплексно сопряженное число X — iY записы-
записывается как /?ехр(—1'8). Таким образом, вместо /ц имеем
/?uexp(t6n) и т. д. Следовательно, G,,/,, = {/?,, ехр(— «в,,)} X
Х{/?1|ехр(г9|1)} = /?21 и т. д.
Складывая уравнения (VI. 13) и (VI. 17), имеем
Ми + М21.+ М„ + Мп = 2GUJU =
Следовательно,
Rn = {(М„ + М21 + М12 + М^/2}1': (VI. 45)
Аналогично, вычитая (VI. 17) из уравнения (VI. 13), получаем
#2i = {{М,, + М12 - Af2I - Л^уг}*. (VI. 46)
Складывая уравнения (VI. 16) и (VI. 20), приходим к
#.2 = {{Ми - Af,2 + М2| - Afa)y2}%. (VI. 47)
Вычитая (VI. 20) из (VI. 16), получаем
/?22 = {{Ми - Мп - М21 + М22)/2}'Л. (VI. 48)
Таким образом, мы нашли модули матричных элементов
Джонса. Что касается аргументов, то достаточно определить
разности между одним из них, выбранным произвольно, и
остальными тремя аргументами. Дело в том, что увеличение на
одну и ту же величину аргументов всех четырех элементов мат-
матрицы Джонса означает просто прибавление этой величины к at
в правых частях уравнений (VI. 1) и (VI. 2), т.е. введение до-
добавочной фазы <f>, что, как уже отмечалось, никоим образом не
сказывается на интенсивностях.
Складывая уравнения (VI. 31) и (VI. 35), имеем
М13 + М23 = GnJl2 + Gi2/n =
= #iifli2[exp(— 1"е„)ехр(*812)] -f
+ Ri2Rn [exp(- Ш|2) exp (»„)] =
= RnRl2 {exp [/ (8,, - 6I2)] + exp [- / (8,, - в12)]} =
= /?,,/?I2 2 cos (e,,-
Следовательно,
cos(9,, - 912) =
Взаимосвязь между методами Джонса и Мюллера 331
где вместо Rn и /?J мы подставили их выражения (VI. 45) и
(VI. 47). Складывая (VI. 32) и (VI. 36), имеем
Мм + М2А = / (С„/и - С12/п) =
— iRnRit [ехр (— Ю„) ехр (#12) -
-ехр(-/812)ехр(г8п)] =
= iRuRl2 {ехр [t(Ba - в,,)] - ехр[- /(в„ - в,,)]} =
= //?11/?122fsin(G12-Gu) =
—в12),
откуда, как и выше, находим
sin(G,,-G12) = Mi*+ Mi* г. (VI. 50)
[(А*„ + М? (M + М?\ Ч* v '
Для того чтобы полностью определить угол в интервале от 0
до 2л, достаточно знать лишь sin(Gn — 8i2) и cos(Gn — Gi2).
Комбинируя соответствующим образом уравнения (VI. 39) —
(VI. 44), можно таким же способом найти выражения для си-
синусов и косинусов от разностей между 8ц и двумя другими ар-
аргументами матричных элементов Джонса. Складывая (VI. 37)
и (VI. 38), получаем
cos(821-en) = М31 + М32 (VI. 61)
[(М„ + М„)»-(А*„ + А*„)*]* V }
а путем сложения уравнений (VI. 41) и (VI. 42) находим
sin(G21-Gu) = М*1 + М*2 jr.. (VI. 52)
V [(А*„ + А*„)«-(А*„ + А*я)Ч* У '
Сложение уравнений (VI. 39) и (VI. 44) дает
cos (в„- 6^) = Мм + М4< (VI. 53)
а вычитание (VI. 40) из уравнения (VI. 43)
sinF22-6u) = Mt3-M3t (VI. 54)
Во всех десяти уравнениях (VI. 45—VI. 54) следует брать по-
положительные значения квадратного корня, представляющие ве-
величины Яц.
При пользовании формулами обращения необходимо соблю-
соблюдать некоторую осторожность, поскольку матрица Мюллера
с ее шестнадцатью действительными элементами не всегда мо-
может быть выражена через матрицу Джонса, содержащую лишь
четыре действительных и четыре мнимых элемента. Можно по-
показать, что для любой матрицы Джонса, которая только может
332 Приложение VI
быть выписана, существует физически реализуемый поляриза-
поляризационный прибор и, стало быть, существует соответствующая ему
матрица Мюллера. С другой стороны, если шестнадцать произ-
произвольно выписанных чисел образуют матрицу Мюллера, то мо-
может оказаться, что нельзя решить уравнения (VI.45—VI.54),
не получив мнимых значений для величин, которые по опреде-
определению должны быть действительными, т. е. для величин R и раз-
разностей фаз 6. Даже в том случае, когда все подкоренные выра-
выражения положительны, уравнения могут предсказать недопусти-
недопустимые пары значений для косинусов и синусов, сумма квадратов
которых не равна единице. Так происходит, например, если рас-
рассматривается матрица Мюллера для «идеального деполяриза-
деполяризатора», у которого Мц = 1, а все остальные элементы равны
нулю. Без процесса усреднения по времени деполяризовать
вбл^у невозможно; прибор физически нереализуем, и для него
не существует матрицы Джонса.
БИБЛИОГРАФИЯ И ЗАКЛЮЧЕНИЕ1*
Поскольку данная книга является введением в матричные методы в оп-
оптике, то в заключение мы обязаны дать некоторые рекомендации относительно
дальнейшего изучения матричных методов с точки зрения применения их в
оптике. Ниже дана краткая библиография B6 наименований) специально
отобранной литературы, в которой затронутые в нашей книге вопросы изло-
изложены более подробно. Кроме того, в конце списка даны 10 ссылок на лите-
литературу по тем аспектам теории матриц, которые хотя и ие обсуждались, но
использовались').
СПЕЦИАЛЬНАЯ ЛИТЕРАТУРА
Матричные методы
1. Coulson Л., Introduction to Matrices, Longmans Green, London, 1965.
2. Aitken A. C, Determinants and Matrices, Oliver and Boyd, Ltd., Edinburgh,
1939.
3. Bellman R., Introduction to Matrix Analysis, McGraw-Hill, New York, I960,
Матрицы в параксиальной оптике
4. Sampson R. Л., A new treatment of optical abberations, Phil. Trans. Roy.
Soc, 212, 149—185 A913).
5. Smith Т., On tracing rays through an optical system, Proc. Phys. Soc,
London, 27, 502 A915); 57, 286 A945).
6. O'Neill E. L, Introduction to Statistical Optics, Addison-Wesley, Reading
Mass., 1963 (имеется перевод: Э. О'Нейл, Введение в статистическую
оптику, «Мир», М., 1966).
7. Brouwer W., Matrix Methods in Optical Instrument Design, W. A. Benja-
Benjamin, Inc., New York, 1964.
8. Halbach K., Matrix representation of Gaussion optics, Amer. Journ. Phys.
32,90 A964).
9. Richards P. /., Conventions in matrix algebra, Amer. Journ. Phys., 32, 890
A964).
10. Sinclair D. C, Image-forming Optics, Notes for 1971 Summer School on
Contemporary Optics, University of Rochester, New York, 1971.
Оптические резонаторы и гауссовы пучки
11. Kogelnik H., On the propagation of Caussian beams of light through lens-
like media including those with a loses or gain variation, Appl. Opt. 4,
1562 A965).
12. Kogelnik H., Li Т., Laser beams and resonators, Proc. IEEE, 54, 1312
A966); Appl. Opt. 5, 1550 A966) [имеется перевод: Когельник, Ли, Резо-
Резонаторы и световые пучки лазеров, ТИИЭР, т. 54, № 10, 95 A966)].
') Звездочкой отмечена литература, добавленная при переводе, — Прим.
ред.
334 Библиография и заключение
13. Siegnnm А, ?., Unstable optical resonators for User implications, Proc.
IEEE, 53, 1312 A965),
14. Siegman Л. ?., Stabilising output with unstable resonators, Laser Focus,
7, 42 (May 1971).
15. Yamamoto S., Makimoto Т., On the ray transfer matrix of a tapered lens-
like medium, Proc. IEEE, 59, 1254 A971) [имеется перевод: С, Ямамото,
Т. Макимото, О матрице передачи лучей в конусной лпнзоподобной сре-
среде, ТИИЭР, т. 59, № 8, 144 A971)].
16. Arnaud J. A., Modes in helical gas Lenses, Journ. Opt. Soc. Amer., 61,
751 A971).
17. Chester A, N., Mode selectivity and mirror misalignment elfects in un-
unstable laser resonators, Appl. Opt., 11, 2584 A972).
18. Ernst G. J., Witteman W. J., Mode structure of active resonators, IEEE
Journ. Quant, Electr., QE-9, 911 A973).
Матрицы в поляризационной оптике
19. Stokes G. Q., Trans. Cambr. Phyl. Soc, 9, 399 A8521,
20. Shurcliff W. A., Polarized Light: Production and Use, Harvard Univ. Press,
1962.
21. Jones R. C, Journ. Opt. Soc. Amer. 46, 126 A956).
22. O'Neill E. L., Introduction to Statistical Optics, Addison — Wesley, Reading,
Mass., 1963 (имеется перевод: Э. О'Нейл, Введение в статистическую оп-
оптику, «Мир», М., 1966).
23. Parke N. G., Journ. Math, and Phys., 28, 131 A949).
24. Born M., Wolf E., Principles ol Optics, 4th End., Pergamon Press, 1970,
p. 544—545 (имеется перевод: М. Бори, Э, Вольф, Основы оптики, «Нау-
«Наука», М.. 1970).
25. McMaster W. H., Matrix representation of polarization, Rev, Mod. Phys.,
33, 8 A961).
26. Simmons J. W., Guttman M. /., States Waves and Photons, A Modern
Introduction to Light, Addison — Wesley, Reading, Mass., 1970.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА ПО СМЕЖНЫМ ВОПРОСАМ
27. Braae R., Matrix Algebra for Electrical Engineers, Pitman, London, 1963.
28. Lewis W. E., Pryce D. G., Application of Matrix Theory to Electrical Engi-
Engineering, Spon, London, 1965.
29. Stavroudis O. N., The Optics of Rays, Wavefronts and Caustics, Academic
Press, New York and London, 1972.
30. Herzberg M, Modern Geometrical Optics, Interscience Publishers Inc., New
York, 1958.
31. Harrold I. //., Matrix algebra for ideal lens problems, Journ. Opt. Soc.
Amer., 44, 254 A954)-
32. Hopkins R. E-, Mirror and Prism System, в книге «Applied Optics and
Optical Engineering» (ed- R. Kingstake), vol. Ill, ch, VIII, Academic Press,
London and New York, 1965.
33. Born M., Wolf E., Principles of Optics, 4th End., Pergamon Press, 1970,
p. 51—70 (имеется перевод: М. Борн, Э. Вольф, Основы оптики, «Наука»,
AL, 1970). Здесь приведены характеристики матрми для слоистой среды.
34. Abeles F., Transmission of Light by a system of alternate layers, Compt.
rend,, 226, 1808 A948).
35. Welford W. Т., Thin film optics, Vacuum, IV, 3 A954).
36. Gamo H, .Matrix Treatment of Partial Coherence, в книге «Progress in
Optics» (ed. E. Wolf), vol. Ill, ch. Ill, North Holland, Amsterdam, 1964.
Библиография и заключение 335
37. Courant R., Differential and Integral Calculus, vol. 2, Blackie and Son,
London and Glasgow, 1936.
38*. Фихтенгольц Г. М., Курс Дифференциального и интегрального исчисления,
т. И, «Наука», М., 1966.
39*. Гантмахер Ф. Р., Теория матриц, «Наука», М., 1966.
40*. Гельфанд И. М., Лекции по линейной алгебре, «Наука>, М., 1966.
Для тех, кто имеет дело с расчетом призм или тонкопленочиой оптикой,
будет особо полезным изложение матричных методов в книгах [32—35].
Читателям, которым доставляет удовольствие изучение элегантной и ак-
актуальной теории, мы рекомендуем обратиться к обсуждению вопросов ча-
частичной когерентности н матриц когерентности, которое содержится в рабо-
работах [22, 24—26 н 36].
Наконец, тем, кто имеет желание самостоятельно продвинуться немного
вперед, мы могли бы предложить в качестве первого шага заняться днагоиа-
лнзацией некоторых поляризационных матриц из гл. 4, а затем проинтерпре-
проинтерпретировать полученные в результате собственные векторы. Проделавшие это
могут найти несколько экспериментальных ситуаций, в которых полученные
ими собственные векторы имеют важное значение, особенно в лазерной
оптике.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аберрация 16, 104
— астигматизм 40, 119, 153
— сферическая 41
— хроматическая 41, 79
ABCD правило 96, 105, 134,
140, 170
Апертура 105, 106
— числовая (Ч. А.) 106, 178,
189
Аргана диаграмма 100, 102,
104
Афокальная система 56
Ближняя зона 132, 133
Боковой луч 109
Брюстера угол 118, 119
Вектор луча 57, 82
Вектор-столбец 20, 24
Вектор-строка 20
Взаимная когерентность волн
202
Виньетирование 277, 278, 285,
287
Волновое уравнение в матрич-
матричной форме 254
Волны Гюйгенса в одноосном
кристалле 263
Входной зрачок 109, 148, 247,
275
— люк 108, 109, 149, 150, 276,
285, 287
Выходной зрачок 148, 274, 286
— люк 148, 150, 275, 287
Гауссова оптика 70
Гауссова амплитуда 9, 13, 131
— расходимость 132
Гауссов комплексный пара-
параметр 15, 122, 135, 137
— пучок 130—132
Геометрическая оптика 40
Геометрический луч 40
— фактор 10
Гюйгенса окуляр 79
Гюйгенса — Френеля принцип
99
Дальняя зона 132, 133
Джонса вектор 192
— матрица 319
— метод 217
Диаграмма (у, ц) 278, 280
— (ф, г)) 280, 285
Диафрагма апертурная 105,
272, 274, 283
— полевая 270, 275
Длина когерентности 197
Изоклина 210
Изохромата 210
Кардинальные точки 70, 81
Катодиоптрическая система 82,
85
Конфокальный параметр пучка
139, 141, 154, 156, 158
Корню спираль 100
Предметный указатель
337
Лагранжа инвариант ПО
Лазерный резонатор 114
— гироскопЛ19
Линза полевая, см. Диафрагма
полевая
— тепловая 173
— тонкая 48, 49
Линзовый волновод 158
Линзоподобная среда 15, 164,
173
Максвелла вектор 192.
— столбец 192
— уравнения 252
Малюса теорема 98, 104
Матрица 19, 20, 41
— вырожденная (особенная)
33
— диагонализирующая 35, 37,
38
— диагональная 28
— единичная 27
— инфенитезимальная 167, 168
— невырожденная (неособен-
(неособенная) 33
— нулевая 26
— обратная 34
— перемещения 44, 45, 49, 51,
108
— поворота осей 206, 221
— преломления 48, 51
— преобразования лучей 42,
51, 97, 288
— присоединенная 34
— Я 83, 272
— след 38
— собственные векторы 36
— — значения 36
— транспонированная 14, 30,
310,316
— Т 83, 272
— унимодулярная 35, 36, 54,
130
— фазовой пластинки 206, 221
— характеристическое уравне-
уравнение 36, 37
— эрмитово сопряженная 293,
327
Матричные элементы 20, 28
Метод отражающего клина 8
— ynv 13, 41
Мира оптическая 107
Модуляция добротности 118
Мюллера матрица 13, 15, 206,
212, 302, 304, 324
— метод 214
Обскура 107
Объектив 78, 286
Определитель 14, 19, 31, 33,
317
Оптическая сила 49, 64, 79, 83
Оптический вентиль 119
— направляющий косинус 14,
43,45
— промежуток 6, 14, 46, 113,
120, 155
— путь 98, 119
— фильтр 194
Отражатель 117, 118
— уголковый 87, 117, 118
Параксиальная оптика 40, 83
Параксиальное приближение
13, 48, 286
Параксиальный луч 40, 42, 45,
48, 51
Паули матрица 326
Перетяжка пучка 7, 10, 138
Пластинка фазовая 198, 206,
221, 307, 309
— полуволновая 199, 206, 221
— четвертьволновая 199, 206,
221, 313
— плоскопараллельная 9, 10
Плоская волна в одноосном
кристалле 255—263
338
Предметный указатель
Плоскость колебаний 196
— опорная 42, 51, 58, 88
— пропускания 196
— сопряженная 274
— фокальная 55, 73, 286
Пойнтинга вектор 40
Показатель преломления 41,
43,47
Поле зрения 277, 285, 286
— освещенности 277, 286
Поляризатор 195, 302, 319
— поляроидная пленка (поля-
(поляроид) 204, 208, 319
Поляризационный фильтр 194
Поляризация круговая 192, 200
— линейная 191, 195
— эллиптическая 192, 200
Преломляющая поверхность 6,
14, 42, 43, 49
Приведенное расстояние 46
Приведенный радиус 47, 48
Пробой прозрачных диэлектри-
диэлектриков И, 127, 153, 189
Пространство изображений 97
— предметов 97
Пространственно-частотное
произведение 111, 148
Пуанкаре сфера 204
Радиус дифракционной расхо-
расходимости 7—10, 132, 138, 142,
153
— кривизны волнового фронта
7—10, 131, 132
— перетяжки 7, 132, 139, 151,
161
Разрешающая сила 105
Рамсдена диск 79, 284
Резонатор неустойчивый 15,
125, 130, 145
— устойчивый 15, 128, 130
Сагиттальный луч 42
Самофокусировка 11, 153, 164,
187
Светосила 10, 110
Сильвестра теорема 130, 167,
168
Сложение амплитуд 202
Снеллиуса закон 48, 83
Степень поляризации 203
Стокса вектор 203
— параметры 200
Телеобъектив 77
Телескоп 147, 286
Телескопическая система 56
Увеличение поперечное 73
— продольное 65
— угловое 148, 286, 56, 87
Узловые точки 71—73, 81
Фокусное расстояние 50, 63, 66,
73, 75, 77
Френеля интеграл 100
— число 111, 139, 140, 147
Эйконал 97, 98, 99, 100—102,
135
Эйри диск 105, 189
Этандю 10, 11,45, 105, 122, 148,
149
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 5
ПРЕДИСЛОВИЕ АВТОРОВ 12
ГЛАВА 1. ВВЕДЕНИЕ В МАТРИЧНОЕ ИСЧИСЛЕНИЕ 19
§ 1. Вводные замечания 19
§ 2. Перемножение матриц 22
§ 3. Нулевые матрицы 26
§ 4. Единичные матрицы 27
§ 5. Диагональные матрицы 28
§ 6. Многократное умножение . 28
§ 7. Сложение и вычитание матриц 29
§ 8. Транспонированные матрицы 30
§ 9. Определители 31
§ 10. Деление н обращение матриц 33
§ 11. Приведение матрицы к диагональному виду 35
§ 12. Собственные значения и собственные векторы унимодулярных
матриц 2X2 36
ГЛАВА 2. МАТРИЧНЫЕ МЕТОДЫ В ПАРАКСИАЛЬНОЙ ОПТИКЕ 40
§ 1. Введение 40
§ 2. Матрицы преобразования лучей 42
§ 3. Матрица перемещения У 44
§ 4. Матрица преломления Я 48
§ 5. Матрица преобразования лучей для оптической системы . . .51
§ 6. Матричное описание свойств оптической системы 54
§ 7. Задачи, иллюстрирующие матричный подход 58
§ 8. Экспериментальное определение элементов матриц оптической
системы 68
§ 9. Расположение кардинальных точек системы 70
§ 10. Дополнительные задачи 75
§ 11. Обобщение метода преобразования лучей иа случай отражаю-
отражающих систем 81
ГЛАВА 3. ОПТИЧЕСКИЕ РЕЗОНАТОРЫ И РАСПРОСТРАНЕНИЕ
ЛАЗЕРНОГО ПУЧКА 91
§ 1. Сводка результатов, полученных для параксиальных систем,
формирующих изображение 91
340 Оглавление
§ 2. Описание процесса распространения волн иа языке геометриче-
геометрической оптики 94
§ 3. Разрешающая сила, этандю и принцип неопределенности . . . 105
§ 4. Матричное описание оптического резонатора 112
§ 5. Различие между устойчивыми и неустойчивыми резонаторами . 122
§ 6. Распространение гауссовых пучков и комплексный параметр
пучка 130
§ 7. Расчет параметров пучка, излучаемого лазером 136
§ 8. Применение правила ABCD для согласования мод 147
§ 9. Матрицы преобразования лучей в лннзоподобной среде с квадра-
квадратичным законом изменения показателя преломления 164
§ 10. Иллюстративные задачи 174
ГЛАВА 4. ИСПОЛЬЗОВАНИЕ МАТРИЦ ДЛЯ ОПИСАНИЯ СОСТОЯ-
СОСТОЯНИЯ ПОЛЯРИЗАЦИИ СВЕТА 190
§ 1. Поляризованный свет — методы получения и анализа 190
§ 2. Использование параметров Стокса для описания поляризации
света 200
§ 3. Использование матрицы Мюллера для преобразования вектора
Стокса 204
§ 4. Экспериментальное определение элементов матрицы Мюллера и
столбца Стокса 213
§ 5. Использование метода Джонса для преобразования столбцов
Максвелла 217
§ 6. Экспериментальное определение элементов матрицы Джонса и
столбца Максвелла 222
§ 7. Наглядные примеры использования матриц Джонса и матриц
Мюллера 230
ГЛАВА 5. РАСПРОСТРАНЕНИЕ СВЕТА В КРИСТАЛЛАХ . . . .247
§ 1. Вводные замечания 247
§ 2. Представление операций над векторами в матричной форме . . 247
§ 3. Диэлектрические свойства анизотропной среды 252
§ 4. Распространение плоских волн в одноосном кристалле 255
§ 5. Волны Гюйгенса в одноосном кристалле 263
ПРИЛОЖЕНИЕ I. АПЕРТУРНЫЕ СВОЙСТВА ЦЕНТРИРОВАННОЙ
СИСТЕМЫ ЛИНЗ 267
§ 1. Диафрагмы, ограничивающие апертуру 267
§ 2. Диафрагмы, ограничивающие поле зрения 270
§ 3. Последовательный расчет апертурной и полевой диафрагм . . . 272
§ 4. Определение полей освещенности 276
§ 5. Пример 281
Оглавление 341
ПРИЛОЖЕНИЕ II. МАТРИЧНОЕ ОПИСАНИЕ ЦЕНТРОВКИ И ЮСТИ-
ЮСТИРОВКИ ОПТИЧЕСКОЙ СИСТЕМЫ 288
§ 1. Применение расширенных матриц 3X3 288
§ 2. Перемножение расширенных матриц 289
§ 3. Влияние расстройки оптического резонатора 291
ПРИЛОЖЕНИЕ III. СТАТИСТИЧЕСКИЙ ВЫВОД ПАРАМЕТРОВ
СТОКСА 293
ПРИЛОЖЕНИЕ IV. ВЫВОД МАТРИЦ МЮЛЛЕРА 302
§ 1. Поляризатор 302
§ 2. Полуволиовая пластинка (оптическая ось составляет угол 9 с
осью х) 305
§ 3. Четвертьволновая пластинка: Общий случай ориентации (оптиче-
(оптическая ось составляет угол в с осью х) 307
§ 4. Произвольная фазовая пластинка (вызывающая в обыкновенном
луче отставание по фазе иа б), оптическая ось которой состав-
составляет угол 9 с осью х 313
ПРИЛОЖЕНИЕ V. ПОЛУЧЕНИЕ МАТРИЦ ДЖОНСА 319
§ 1. Поляризатор типа пленочного поляроида 319
§ 2. Матрица Джонса прибора, вызывающего произвольную фазовую
задержку 321.
ПРИЛОЖЕНИЕ VI. ВЗАИМОСВЯЗЬ МЕЖДУ МЕТОДАМИ РАСЧЕТА
ДЖОНСА И МЮЛЛЕРА 324
§ 1. Введение 324
§ 2. Вывод соотношения между векторами Стокса и Максвелла . . . 324
§ 3. Представление «матричных сэндвичей» через элементы матриц
Мюллера и Джонса 326
§ 4. Попарное сравнение «матричных сэндвичей» в двух методах рас-
расчета 327
§ 5. Выражения для элементов матрицы Мюллера через элементы
матрицы Джонса 329
§ 6. Получение выражений для элементов матрицы Джойса через
элементы матрицы Мюллера 329
БИБЛИОГРАФИЯ И ЗАКЛЮЧЕНИЕ 333
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 336