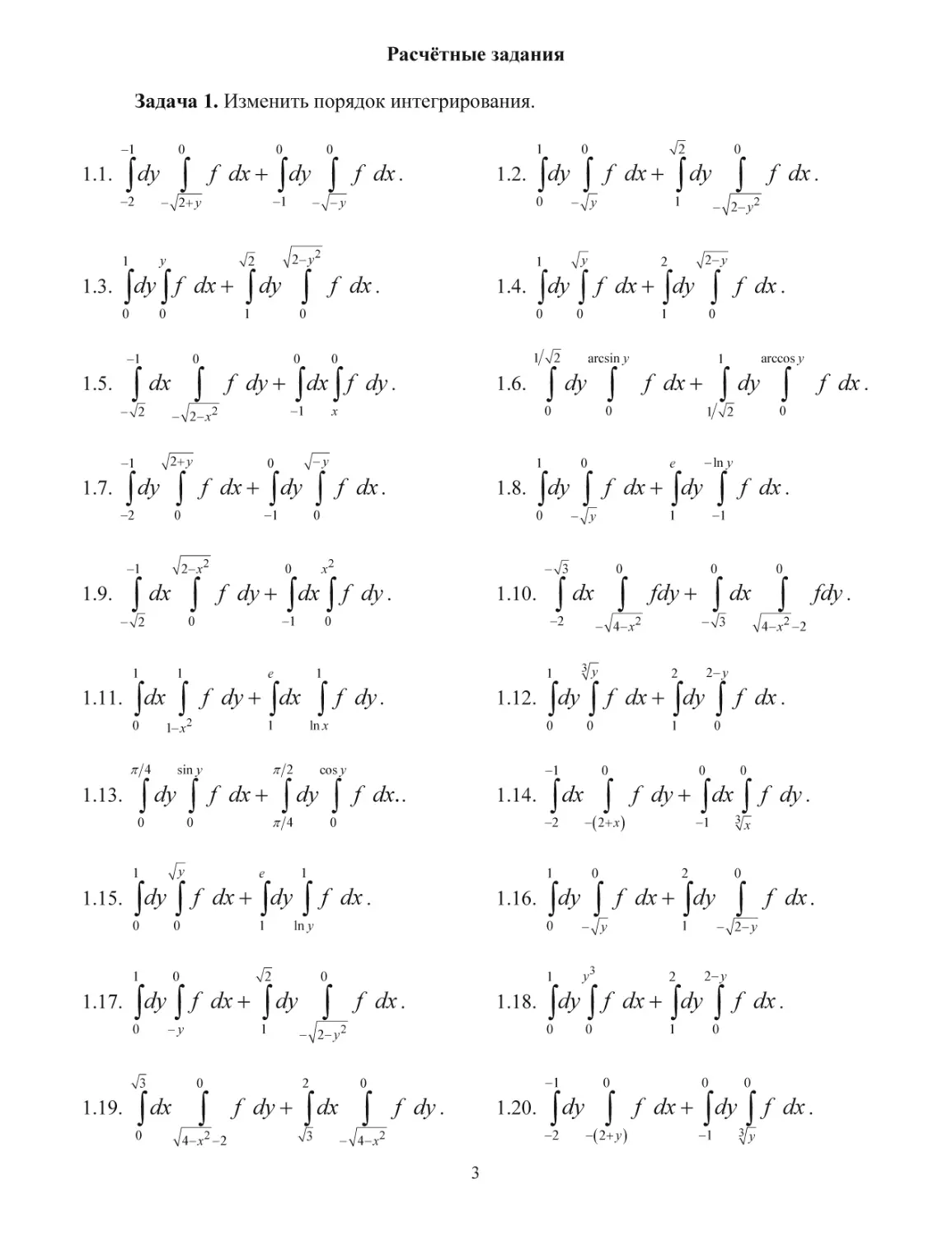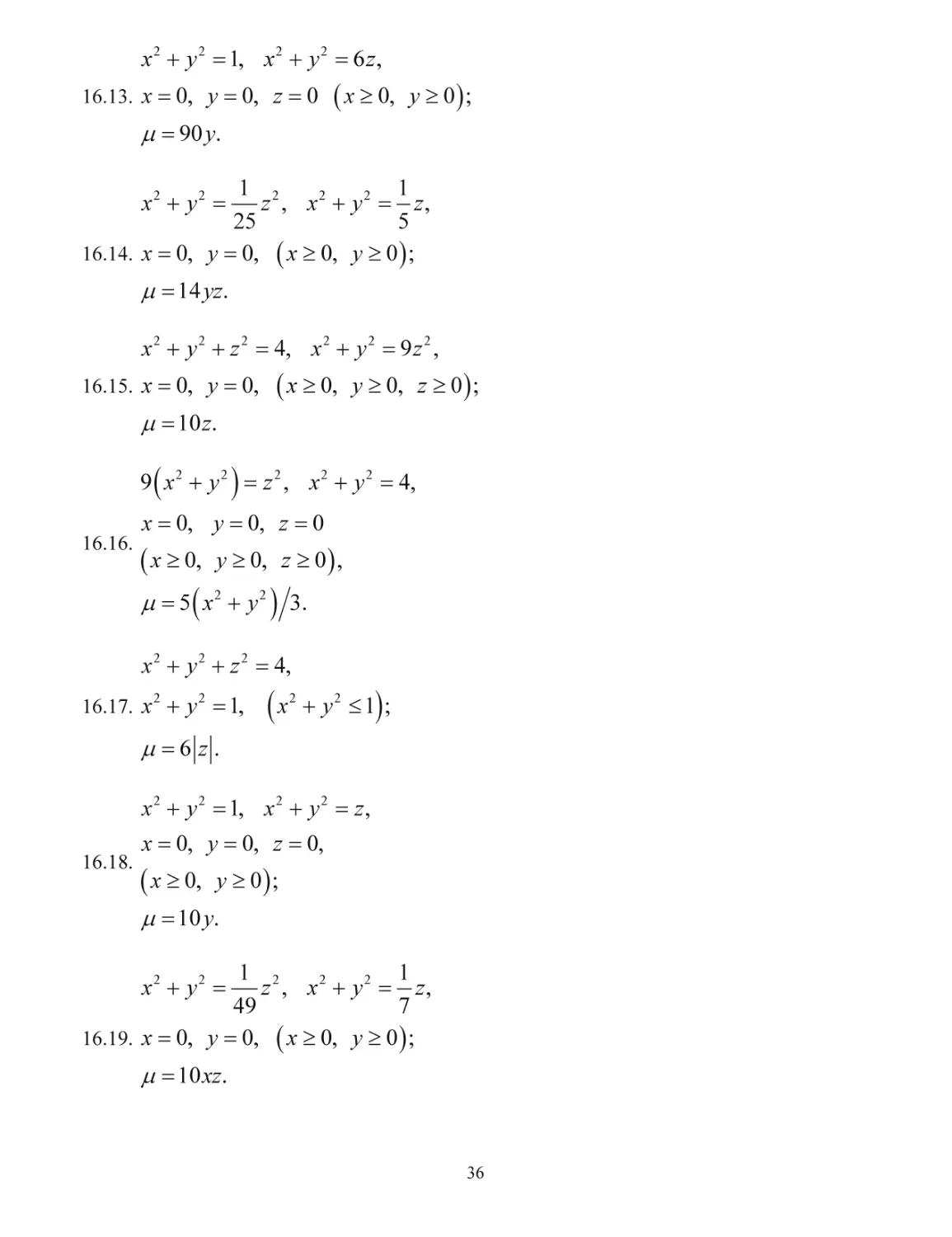Текст
1
VII
. КРАТНЫЕ ИНТЕГРАЛЫ
Теоретические вопросы
1.
Определение
двойного и тройного интегралов.
Их геометрический и физический
смысл.
2.
Основные свойства двойных и тройных интегралов.
3.
Теорема о среднем для двойного и тройного интегралов.
4.
Вычисление двойных интеграл
ов двумя последовательными интегрированиями
(случай прямоугольной области).
5.
Вычисление двойных интегралов двумя последовательными интегрированиями
(общий случай).
6.
Замена переменных в двойном интеграле.
7.
Якобиан, его геометрический смысл.
8.
Двойной интеграл в
полярных координатах.
9.
Тройной интеграл в цилиндрических координатах.
10.
Тройной интеграл в сферических координатах.
Теоретические упражнения
1.
Пользуясь определением двойного интеграла, доказать, что
222
0
mn
xyR
xydxdy
,
если
m
и
n
-
натуральные числа, и, по меньшей мере, одно из них нечетно.
2.
С помощью теоремы о среднем найти
222
2
0
1
lim,
R
xyR
fxydxdy
R
,
2
где
,
fxy
-
непрерывная функция.
3.
Оценить интеграл
2222
2222
000
222
000
,
xyzR
dxdydz
xyzR
xxyyzz
,
т.е. указать, между какими значениями заключена его величина.
4.
Вычислить двойной интеграл
,
D
fxydxdy
,
если область
D
-
прямоугольник {
,
axbcyd
}, а
,,
xy
fxyFxy
.
5.
Доказать равенство
bd
Dac
fxgydxdyfxdxgydy
,
если область
D
-
прямоугольник {
,
axbcyd
}.
6.
Доказать формулу Дирихле
000
,,
axaa
y
dxfxydydyfxydx
,
0
a
.
7.
Пользуясь форму
лой Дирихле, доказать равенство
000
y
aa
dyfxdxaxfxdx
.
8.
Какой из интегралов больше
111
000
,,
dxdyfxyzdz
или
1
11
000
,,
xy
x
dxdyfxyzdz
,
если
,,0
fxyz
?
3
Расчё
тные задания
Задача 1.
Изменить порядок интегрирования.
1.1.
1000
21
2
yy
dyfdxdyfdx
.
1.2.
2
1020
01
2
y
y
dyfdxdyfdx
.
1.3.
2
2
12
0010
y
y
dyfdxdyfdx
.
1.4.
2
12
0010
yy
dyfdxdyfdx
.
1.5.
2
1000
1
2
2
x
x
dxfdydxfdy
.
1.6.
12
arcsinarccos
1
000
12
yy
dyfdxdyfdx
.
1.7.
2
10
2010
yy
dyfdxdyfdx
.
1.8.
ln
10
011
y
e
y
dyfdxdyfdx
.
1.9.
22
120
010
2
xx
dxfdydxfdy
.
1.10.
22
3000
2
3
442
xx
dxfdydxfdy
.
1.11.
2
111
01ln
1
e
x
x
dxfdydxfdy
.
1.12.
3
2
12
0010
y
y
dyfdxdyfdx
.
1.13.
42
sincos
0040
.
yy
dyfdxdyfdx
.
1.14.
3
1000
221
x
x
dxfdydxfdy
.
1.15.
11
001ln
y
e
y
dyfdxdyfdx
.
1.16.
1020
01
2
yy
dyfdxdyfdx
.
1.17.
2
1020
01
2
y
y
dyfdxdyfdx
.
1.18.
3
2
12
0010
yy
dyfdxdyfdx
.
1.19.
22
3020
0
3
424
xx
dxfdydxfdy
.
1.20.
3
1000
221
y
y
dyfdxdyfdx
.
4
1.21.
11
001ln
y
e
y
dyfdxdyfdx
.
1.22.
22
122
0010
xx
dxfdydxfdy
.
1.23.
42
sincos
0040
xx
dxfdydxfdy
.
1.24.
2
1000
1
2
2
y
y
dyfdxdyfdx
.
1.25.
3
122
0010
xx
dxfdydxfdy
.
1.26.
22
32424
000
3
xx
dxfdydxfdy
.
1.27.
1020
01
2
xx
dxfdydxfdy
.
1.28.
2
122
0010
xx
dxfdydxfdy
.
1.29.
2
2
12
0010
yy
dyfdxdyfdx
.
1.30.
122
0010
xx
dxfdydxfdy
.
1.31.
22
34024
200
3
xx
dxfdydxfdy
.
Задача 2.
Вычислить.
2.1.
2233
2
1216;
: 1, , .
D
xyxydxdy
Dxyxyx
2.2.
2233
2
948;
: 1, , .
D
xyxydxdy
Dxyxyx
2.3.
2233
3
3
3696;
: 1, , .
D
xyxydxdy
Dxyxyx
2.4.
2233
3
3
1832;
: 1, , .
D
xyxydxdy
Dxyxyx
2.5.
2233
2
3
2748;
: 1, , .
D
xyxydxdy
Dxyxyx
2.6.
(
)
(
)
.
0
,
,
1
:
;
32
18
2
3
3
3
2
2
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
y
x
D
5
2.7.
2233
3
1832;
: 1, , .
D
xyxydxdy
Dxyxyx
2.8.
2233
3
2748;
: 1, , .
D
xyxydxdy
Dxyxyx
2.9.
22
2
43;
: 1, , .
D
xyxydxdy
Dxyxyx
2.10.
22
2
129;
: 1, , .
D
xyxydxdy
Dxyxyx
2.11.
22
3
3
89;
: 1, , .
D
xyxydxdy
Dxyxyx
2.12.
22
3
3
2418;
: 1, , .
D
xyxydxdy
Dxyxyx
2.13.
(
)
(
)
.
0
,
,
1
:
;
27
12
3
2
2
2
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
xy
D
2.14.
(
)
(
)
.
0
,
,
1
:
;
18
8
2
3
2
2
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
xy
D
2.15.
22
3
49
;
511
: 1, , .
D
xyxydxdy
Dxyxyx
2.16.
22
3
4
9;
5
: 1, , .
D
xyxydxdy
Dxyxyx
2.17.
33
2
2448;
: 1, , .
D
xyxydxdy
Dxyxyx
2.18.
33
2
624;
: 1, , .
D
xyxydxdy
Dxyxyx
2.19.
33
3
3
416;
: 1, , .
D
xyxydxdy
Dxyxyx
2.20.
33
3
3
416;
: 1, , .
D
xyxydxdy
Dxyxyx
2.21.
(
)
(
)
.
0
,
,
1
:
;
16
44
3
2
3
3
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
xy
D
2.22.
(
)
(
)
.
0
,
,
1
:
;
176
4
3
3
3
3
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
xy
D
2.23.
33
3
4;
: 1, , .
D
xyxydxdy
Dxyxyx
2.24.
33
3
4176;
: 1, , .
D
xyxydxdy
Dxyxyx
6
2.25.
2244
2
25
6;
3
: 1, , .
D
xyxydxdy
Dxyxyx
2.26.
2244
2
925;
: 1, , .
D
xyxydxdy
Dxyxyx
2.27.
2244
3
3
50
3;
3
: 1, , .
D
xyxydxdy
Dxyxyx
2.28.
2244
3
3
925;
: 1, , .
D
xyxydxdy
Dxyxyx
2.29.
(
)
(
)
.
0
,
,
1
:
;
150
54
3
2
4
4
2
2
ᄈ
-
=
=
=
+
x
x
y
x
y
x
D
dxdy
y
x
y
x
D
2.30.
(
)
(
)
.
0
,
,
1
:
;
9
2
3
5
5
ᄈ
-
=
=
=
-
x
x
y
x
y
x
D
dxdy
y
x
xy
D
2.31.
2244
3
54150;
: 1, , .
D
xyxydxdy
Dxyxyx
Задача 3
. Вычислить.
3.1.
/2
;
: ln2, ln3, 2, 4.
xy
D
yedxdy
Dyyxx
3.2
.
2
sin ;
2
: 0, , .
2
D
xy
ydxdy
x
Dxyy
3.3.
cos ;
: /2, , 1, 2.
D
yxydxdy
Dyyxx
3.4.
2/4
;
: 0, 2, .
xy
D
yedxdy
Dxyyx
3.5.
sin ;
: /2, , 1, 2.
D
yxydxdy
Dyyxx
3.6.
2
cos ;
2
: 0, 2, y2.
D
xy
ydxdy
Dxyx
3.7.
2
4;
1
: ln3, ln4, , 1.
2
xy
D
yedxdy
Dyyxx
3.8.
2
4sin ;
: 0, , .
2
D
yxydxdy
Dxyyx
7
3.9.
cos2 ;
1
: , , , 1.
22
D
yxydxdy
Dyyxx
3.10.
2/8
;
: 0, 2, .
2
xy
D
yedxdy
x
Dxyy
3.11.
12sin2 ;
: , , 2, 3.
42
D
yxydxdy
Dyyxx
3.12.
2
cos ;
: 0, , .
D
yxydxdy
Dxyyx
3.13.
/4
;
: ln2, ln3, 4, 8.
xy
D
yedxdy
Dyyxx
3.14.
2
4sin2 ;
: 0, 2, 2.
D
yxydxdy
Dxyyx
3.15.
2cos2 ;
: , , 1, 2.
42
D
yxydxdy
Dyyxx
3.16.
2/2
;
: 0, 2, .
xy
D
yedxdy
Dxyyx
3.17.
sin ;
1
: , 2, , 1.
2
D
yxydxdy
Dyyxx
3.18.
2
cos2 ;
: 0, , .
22
D
yxydxdy
x
Dxyy
3.19.
4
8;
11
: ln3, ln4, , .
42
xy
D
yedxdy
Dyyxx
3.20.
2
3sin ;
2
42
: 0, , .
33
D
xy
ydxdy
Dxyyx
3.21.
cos ;
: , 3, 12, 1.
D
yxydxdy
Dyyxx
3.22.
2/2
;
: 0, 1, .
2
xy
D
yedxdy
x
Dxyy
3.23.
sin2 ;
: 2, 32, 12, 2.
D
yxydxdy
Dyyxx
3.24.
2
cos ;
: 0, , 2.
D
yxydxdy
Dxyyx
8
3.25.
/3
6;
: ln2, ln3, 3, 6.
xy
D
yedxdy
Dyyxx
3.26.
2
sin ;
2
: 0, , .
D
xy
ydxdy
Dxyyx
3.27.
cos2 ;
: 2, 32, 12, 2.
D
yxydxdy
Dyyxx
3.28.
2/8
;
: 0, 4, 2.
xy
D
yedxdy
Dxyyx
3.29.
3sin ;
: 2, 3, 1, 3.
D
yxydxdy
Dyyxx
3.30.
2
cos ;
2
: 0, 2, 2.
D
xy
ydxdy
Dxyyx
3.31.
6
12;
: ln3, ln4, 16, 13.
xy
D
yedxdy
Dyyxx
Задача 4.
Вычислить.
4
.1.
2
2 ;
0, 1, ,
0, 1.
xy
V
yedxdydz
xyyx
V
zz
4.2.
2
sin ;
2, , z1,
0, 0, 0.
V
xzxyzdxdydz
xy
V
xyz
4.3.
2
ch2 ;
0, 2, y4,
0, 2.
V
yxydxdydz
xyx
V
zz
4.4.
22
8 ;
1, 2, z1,
0, y0, 0.
xyz
V
yzedxdydz
xy
V
xz
4.5.
2
sh3 ;
1, 2, y0,
0, 36.
V
xxydxdydz
xyx
V
zz
4.6.
2
cos ;
1, , z2,
0, 0, 0.
V
yzxyzdxdydz
xy
V
xyz
9
4.7.
2
2
cos ;
4
0, 1, y2,
0, .
V
yxydxdydz
xyx
V
zz
4.8.
2
sin ;
4
1, 2, z4,
0, 0, 0.
V
xyz
xzdxdydz
xy
V
xyz
4.9.
2
;
0, 2, y4,
0, 1.
xy
V
yedxdydz
xyx
V
zz
4.10.
2
2 ;
1, 1, z1,
0, y0, 0.
xyz
V
yzedxdydz
xy
V
xz
4.11.
2
ch2 ;
0, 1, y,
0, 8.
V
yxydxdydz
xyx
V
zz
4.12.
2
shxyz ;
2, 1, z1,
0, 0, 0.
V
xzdxdydz
xy
V
xyz
4.13.
22
;
0, 2, y2,
0, 1.
xy
V
yedxdydz
xyx
V
zz
4.14.
2
cos ;
3
3, 1, z2,
0, 0, 0.
V
xyz
yzdxdydz
xy
V
xyz
4.15.
2
2
cos ;
2
0, 1, y,
0, 2.
V
xy
ydxdydz
xyx
V
zz
4.16.
2
2 shxyz ;
1, 1, z1,
0, 0, 0.
V
xzdxdydz
xy
V
xyz
4.1
7.
2
2
cos ;
0, 1, y2,
0, .
V
yxydxdydz
xyx
V
zz
4.18.
2
2 sh2xyz ;
2, 12, z12,
0, 0, 0.
V
xzdxdydz
xy
V
xyz
4.19.
2
sh2 ;
1, , y0,
0, 8.
V
xxydxdydz
xyx
V
zz
4.20.
2
xyz
sin ;
2
1, 4, z,
0, 0, 0.
V
xzdxdydz
xy
V
xyz
1
0
4.21.
2
ch ;
0, 1, y,
0, 2.
V
yxydxdydz
xyx
V
zz
4.22.
2
chxyz ;
1, 1, z1,
0, 0, 0.
V
yzdxdydz
xy
V
xyz
4.23.
2
sin ;
2
2, , y0,
0, .
V
xxydxdydz
xyx
V
zz
4.24.
2
cos ;
9
9, 1, z2,
0, 0, 0.
V
xyz
yzdxdydz
xy
V
xyz
4.25.
2
sin ;
1, 2, y0,
0, 4.
V
xxydxdydz
xyx
V
zz
4.26.
2
xyz
ch ;
2
2, 1, z2,
0, 0, 0.
V
yzdxdydz
xy
V
xyz
4.27.
2
ch3 ;
0, 2, y6,
0, 3.
V
yxydxdydz
xyx
V
zz
4.28.
2
2 ch2 ;
1
, 2, z1,
2
0, 0, 0.
V
yzxyzdxdydz
xy
V
xyz
4.29.
2
sin4 ;
1, 2, y0,
0, 8.
V
xxydxdydz
xyx
V
zz
4.30.
2
8 ;
2, 1, z2,
0, y0, 0.
xyz
V
yzedxdydz
xy
V
xz
4.31.
2
sh ;
2, 2, y0,
0, 1.
V
xxydxdydz
xyx
V
zz
11
Задача 5.
Вычислить.
5.1.
;
: 10, 0, 1,
, 0.
V
xdxdydz
Vyxyx
zxyz
5.2.
4
;
x
1
348
: 1,
348
0, 0, 0.
V
dxdydz
yz
xyz
V
xyz
5.3.
22
15 ;
: , 1,
0, 0, 0.
V
yzdxdydz
Vzxyxy
xyz
5.4.
22
34 ;
: , 0, 1,
5, 0.
V
xydxdydz
Vyxyx
zxyz
5.5.
3
12 ;
: 9, 0, 1,
, 0.
V
xdxdydz
Vyxyx
zxyz
5.6.
3
2754 ;
: , 0, 1,
, 0.
V
ydxdydz
Vyxyx
zxyz
5.7.
;
: 15, 0, 1,
, 0.
V
ydxdydz
Vyxyx
zxyz
5.8.
5
;
x
1
1683
: 1,
1683
0, 0, 0.
V
dxdydz
yz
xyz
V
xyz
5.9.
22
3 ;
: 10, 1,
0, 0, 0.
V
xydxdydz
Vzyxy
xyz
5.10.
22
1530 ;
: z3, z0,
, 0, x=1.
V
xzdxdydz
Vxy
yxy
5.11.
3
48 ;
: , 0, 1,
, 0.
V
zdxdydz
Vyxyx
zxyz
5.12.
3
12 ;
: 36, 0, 1,
, 0.
V
xdxdydz
Vyxyx
zxyz
12
5.13.
21 ;
: , 0, 2,
, 0.
V
xzdxdydz
Vyxyx
zxyz
5.14.
6
;
x
1
1083
: 1,
1083
0, 0, 0.
V
dxdydz
yz
xyz
V
xyz
5.15.
22
3 ;
: 10, 1,
0, 0, 0.
V
xydxdydz
Vzxxy
xyz
5.16.
22
6090 ;
: , 0, 1,
, 0.
V
yzdxdydz
Vyxyx
zxyz
5.17.
105
;
33
: 9, 0, 1,
, 0.
V
xdxdydz
Vyxyx
zxyz
5.18.
918 ;
: 4, 0, 1,
, 0.
V
zdxdydz
Vyxyx
zxyz
5.19.
2
3 ;
: 2, 0, 2,
, 0.
V
ydxdydz
Vyxyx
zxyz
5.20.
4
;
1
246
: 1,
246
0, 0, 0.
V
dxdydz
xyz
xyz
V
xyz
5.21.
2
;
: 103, x1,
0, 0, 0.
V
xdxdydz
Vzxyy
xyz
5.22.
22
812 ;
: , 0, 1,
32, 0.
V
yzdxdydz
Vyxyx
zxyz
5.23.
6312 ;
: , 0, 1,
, 0.
V
ydxdydz
Vyxyx
zxyz
5.24.
22
;
: , 0, 1,
3060, 0.
V
xydxdydz
Vyxyx
zxyz
13
5.25.
5
;
1
6416
: 1,
6416
0, 0, 0.
V
dxdydz
xyz
xyz
V
xyz
5.26.
;
: , 0, 2,
, 0.
V
xyzdxdydz
Vyxyx
zxyz
5.27.
2
;
: 103, x1,
0, 0, 0.
V
ydxdydz
Vzxyy
xyz
5.28.
22
3
5 ;
2
: , 0, 1,
15, 0.
V
z
xdxdydz
Vyxyx
zxyz
5.29.
22
4 ;
: 202, x1,
0, 0, 0.
V
xydxdydz
Vzxyy
xyz
5.30.
6
;
1
835
: 1,
835
0, 0, 0.
V
dxdydz
xyz
xyz
V
xyz
5.31.
2
;
: 3, 0, 2,
, 0.
V
xzdxdydz
Vyxyx
zxyz
14
Задача 6.
Найти площадь фигуры, ограниченной данными линиями.
6.1.
3, 4, 3, 4.
x
yxyeyy
6.2.
22
36, 636.
xyxy
6.3.
222
72, 6 0.
xyyxy
6.4.
2
8, 2.
xyxy
6.5.
3
, 8, 3, 8.
x
yyeyy
x
6.6.
1
, , x16.
22
x
yy
x
6.7.
2
5, 4.
xyxy
6.8.
222
12, -6 0.
xyyxy
6.9.
22
12, 2312, 0 0.
yxyxxx
6.10.
33
, , x9.
22
yxy
x
6.11.
22
24, 23, 0 0.
yxyxxx
6.12.
sin, cos, x0, 0.
yxyxx
6.13.
2
20, 8.
yxyx
6.14.
22
18, 3218.
yxyx
6.15.
2
32, 4.
yxyx
6.16.
2, 5, 2, 5.
x
yxyeyy
6.17.
222
36, 32 0.
xyyxy
15
6.18.
3, 3, 4.
yxyxx
6.19.
22
636, 36, 0 0.
yxyxxx
6.20.
2
254, 52.
yxyx
6.21.
, 1, 16.
yxyxx
6.22.
2, 7, 2, 7.
x
yxyeyy
6.23.
2
27, 6.
xyxy
6.24.
22
72, 6, 0 0.
xyxyyy
6.25.
22
6, 66.
yxyx
6.26.
33
, , x4.
22
yxy
x
6.27.
sin, cos, x0, 0.
yxyxx
6.28.
1
, 6, 1, 6.
x
yyeyy
x
6.29.
3, 3, 9.
yxyxx
6.30.
2
11, 10.
yxyx
6.31.
222
12, 6 0.
xyxyx
16
Задача 7.
Найти площадь фигуры, огран
иченной данными линиями.
7
.1.
22
22
20,
40,
3, 3.
yyx
yyx
yxyx
7.2.
22
22
40,
80,
0, 3.
xxy
xxy
yyx
7.3.
22
22
60,
80,
3, 3.
yyx
yyx
yxyx
7.4.
22
22
20,
40,
0, .
xxy
xxy
yyx
7.5.
22
22
80,
100,
3, 3.
yyx
yyx
yxyx
7.6.
22
22
40,
80,
0, .
xxy
xxy
yyx
7.7.
22
22
40,
60,
, 0.
yyx
yyx
yxx
7.8.
22
22
20,
100,
0, 3.
xxy
xxy
yyx
7.9.
22
22
60,
100,
, 0.
yyx
yyx
yxx
7.10.
22
22
20,
40,
3, 3.
xxy
xxy
yxyx
7.11.
22
22
20,
40,
3, 0.
yyx
yyx
yxx
7.12.
22
22
20,
60,
3, 3.
xxy
xxy
yxyx
7.13.
22
22
40,
60,
3, 0.
yyx
yyx
yxx
7.14.
22
22
20,
80,
3, 3.
xxy
xxy
yxyx
7.15.
22
22
20,
60,
3, x0.
yyx
yyx
yx
7.16.
22
22
20,
40,
0, 3.
xxy
xxy
yyx
17
7.17.
22
22
20,
100,
3, 3.
yyx
yyx
yxyx
7.18.
22
22
20,
60,
0, 3.
xxy
xxy
yyx
7.19.
22
22
40,
100,
3, 3.
yyx
yyx
yxyx
7.20.
22
22
20,
60,
0, .
xxy
xxy
yyx
7.21.
22
22
20,
40,
, 0.
yyx
yyx
yxx
7.22.
22
22
20,
40,
0, 3.
xxy
xxy
yyx
7.23.
22
22
60,
80,
, 0.
yyx
yyx
yxx
7.24.
22
22
40,
80,
0, 3.
xxy
xxy
yyx
7.25.
22
22
40,
80,
, 0.
yyx
yyx
yxx
7.26.
22
22
40,
80,
3, 3.
xxy
xxy
yxyx
7.27.
22
22
40,
80,
3, 0.
yyx
yyx
yxx
7.28.
22
22
40,
60,
3, 3.
xxy
xxy
yxyx
7.29.
22
22
20,
100,
3, 0.
yyx
yyx
yxx
7.30.
22
22
60,
100,
3, 3.
xxy
xxy
yxyx
7.31.
22
22
40,
80,
3, 0.
yyx
yyx
yxx
18
Задача
8.
Пластинка
D
задана ограничивающими ее кривыми,
-
поверхностная
плотность. Найти массу пластинки.
8
.1.
2
2
: 1, 0, 4 0;
7.
Dxyyxy
xy
8.2.
2222
22
: 1, 4,
0, 0 0, 0;
.
Dxyxy
xyxy
xyxy
8.3.
2
2
: 1, 0, 4 0;
725.
Dxyyxy
xy
8.4.
2222
22
: 9, 16,
0, 0 0, 0;
25.
Dxyxy
xyxy
xyxy
8.5.
2
2
: 2, 0, 2 0;
782.
Dxyyxy
xy
8.6.
2222
22
: 1, 16,
0, 0 0, 0;
.
Dxyxy
xyxy
xyxy
8.7.
2
2
: 2, 0, 2 0;
726.
Dxyyxy
xy
8.8.
2222
22
: 4, 25,
0, 0 0, 0;
23.
Dxyxy
xyxy
xyxy
8.9.
2
2
: 1, 0, 4 0;
3.
Dxyyxy
xy
8.10.
2222
22
: 1, 9,
0, 0 0, 0;
.
Dxyxy
xyxy
xyxy
8.11.
2
2
: 1, 0, 0;
36.
Dxyyxy
xy
8.12.
2222
22
: 9, 25,
0, 0 0, 0;
2.
Dxyxy
xyxy
yxxy
8.
13.
2
2
: 2, 0, 2 0;
23.
Dxyyxy
xy
8.14.
2222
22
: 4, 16,
0, 0 0, 0;
23.
Dxyxy
xyxy
yxxy
8.15.
2
2
1
: , 0, 8 0;
2
73.
Dxyyxy
xy
8.16.
2222
22
: 9, 16,
0, 0 0, 0;
25.
Dxyxy
xyxy
yxxy
19
8.17.
2
2
: 1, 0, 4 0;
72.
Dxyyxy
xy
8.18.
2222
22
: 1, 16,
0, 0 0, 0;
3.
Dxyxy
xyxy
xyxy
8.19.
2
2
: 2, 2, 0 0;
742.
Dxyxyy
xy
8.20.
2222
22
: 1, 4,
0, 0 0, 0;
2.
Dxyxy
xyxy
xyxy
8.21.
2
2
: 2, 0, 2 0;
74.
Dxyyxy
xy
8.22.
2222
22
: 1, 9,
0, 0 0, 0;
2.
Dxyxy
xyxy
xyxy
8.23.
2
2
: 2, 0, 2 0;
728.
Dxyyxy
xy
8.24.
2222
22
: 1, 25,
0, 0 0, 0;
4.
Dxyxy
xyxy
xyxy
8.25.
2
2
: 1, 0, 4 0;
63.
Dxyyxy
xy
8.26.
2222
22
: 4, 16,
0, 0 0, 0;
3.
Dxyxy
xyxy
xyxy
8.27.
2
2
: 2, 0, 2 0;
46.
Dxyyxy
xy
8.28.
2222
22
: 4, 9,
0, 0 0, 0;
4.
Dxyxy
xyxy
yxxy
8.29.
2
2
1
: , 0, 2 0;
2
49.
Dxyyxy
xy
8.30
.
2222
22
: 4, 9,
0, 0 0, 0;
2.
Dxyxy
xyxy
yxxy
8.31.
2
2
1
: , 0, 16 0;
4
1692.
Dxyyxy
xy
20
Задача 9.
Пластинка
D
задана неравенствами,
-
поверхностная плотность. Найти
массу пластинки.
9
.1.
22
2
: 41;
.
Dxy
y
9.2.
22
: 1942;
2
0, ;
3
.
Dxy
yyx
yx
9.3.
22
2
: 9251;
0;
.
Dxy
y
xy
9.4.
22
2
: 9251;
0;
718.
Dxy
y
xy
9.5.
22
3
: 144;
0, 2;
8.
Dxy
yyx
yx
9.6.
22
6
: 91;
0;
7.
Dxy
x
xy
9.7.
22
4
: 41;
4.
Dxy
y
9.8.
22
: 1494;
x0, 32;
.
Dxy
yx
xy
9.9.
22
: 11644;
0, 2;
.
Dxy
xyx
xy
9.10.
22
3
: 491;
0, 0;
.
Dxy
xy
xy
9.11.
22
33
: 41;
0, 0;
6.
Dxy
xy
xy
9.12.
22
3
: 1425;
x0, 2;
.
Dxy
yx
xy
9.13.
22
22
: 941;
.
Dxy
xy
9.14.
22
7
: 161;
0, 0;
5.
Dxy
xy
xy
9.15.
22
37
: 41;
0, 0;
30.
Dxy
xy
xy
9.16.
22
: 1943;
2
0, ;
3
.
Dxy
yyx
yx
21
9.17.
22
4
: 251;
0;
7.
Dxy
y
xy
9.18.
22
43
: 91;
0;
35.
Dxy
y
xy
9.19.
22
2
: 491;
.
Dxy
x
9.20.
22
3
: 1169;
0, 4;
.
Dxy
yyx
yx
9.21.
22
8
: 91;
0;
11.
Dxy
x
xy
9.22
22
:14165;
0,2;
.
Dxy
xyx
xy
.
9.23.
22
: 1945;
x0, 23;
.
Dxy
yx
xy
9.24.
22
5
: 491;
0, 0;
.
Dxy
xy
xy
9.25.
22
4
: 4251;
.
Dxy
x
9.26.
22
53
: 41;
0, 0;
15.
Dxy
xy
xy
9.27.
22
3
: 14936;
3
x0, ;
2
9.
Dxy
yx
xy
9.28.
22
9
: 1001;
0, 0;
6.
Dxy
xy
xy
9.29.
22
39
: 161;
0, 0;
105.
Dxy
xy
xy
9.30.
22
5
: 19162;
4
0, ;
3
27.
Dxy
yyx
yx
9.31.
22
5
: 1163;
x0, 4;
.
Dxy
yx
xy
22
Задача 10.
Найти объ
ё
м тела, заданного ограничивающими его поверхностями.
10
.1.
162, 2,
0, 2.
yxyx
zxz
10.2.
5, 53,
0, 553.
yxyx
zzx
10.3.
22
2, , 0,
0, 15.
xyyxy
zzx
10.4.
2, ,
12, 0.
xyyx
zyz
10.5.
202, 52,
0, 12.
xyxy
zzy
10.6.
52, 56,
5
0, 3.
6
xyxy
zzy
10.7.
22
2, , 0,
0, 30.
xyxyx
zzy
10.8.
2, ,
125, 0.
xyxy
zxz
10.9.
172, 22,
0, 12.
yxyx
zxz
10.10.
53, 59,
0, 539.
yxyx
zzx
10.11.
22
8, 2, 0,
0, 1511.
xyyxy
zzx
10.12.
4, 2,
3, 0.
xyyx
zyz
10.13.
55
, ,
618
5
0, 3.
18
xyxy
zzy
10.14.
192, 42,
0, 2.
xyxy
zzy
10.15.
22
8, 2, 0,
3011, 0.
xyxyx
zyz
10.16.
4, 2,
35, 0.
xyxy
zxz
10.17.
63, 3,
0, 3.
yxyx
zxz
10.18.
55
, ,
618
5
0, 3.
18
yxyx
zzx
23
10.19.
22
18, 3, 0,
0, 511.
xyyxy
zzx
10.20.
6, 3,
4, 0.
xyyx
zyz
10.21.
73, 23,
0, 3.
xyxy
zzy
10.22.
53, 59,
0, 539.
xyxy
zzy
10.23.
22
18, 3, 0,
0, 1011.
xyxyx
zzy
10.24.
6, 3,
45, 0.
xyxy
zxz
10.25.
15, 15,
0, 151.
yxyx
zzx
10.26.
22
50, 5,
0, 0, 311.
xyyx
yzzx
10.27.
8, 4,
3, 0.
xyyx
zyz
10.28.
162, 2,
2, 0.
xyxy
zyz
10.29.
15, 15,
0, 151.
xyxy
zzy
10.30.
22
50, 5,
0, 0, 611.
xyxy
xzzy
10.31.
172, 22,
0, 12.
xyxy
zzy
24
Задача 11.
Найти
объём
тела, заданного ограничивающими его поверхностями.
11.1.
22
2
2,
54, 0.
xyy
zxz
11.2.
2222
22
, 4,
, 0.
xyyxyy
zxyz
11.3.
22
22
82,
64,
0 0.
xyx
zxy
zz
11.4.
22
2
40,
8, 0.
xyx
zyz
11.5.
2222
22
6, 9,
, 0,
0 0
xyxxyx
zxyz
yy
11.6.
22
22
62,
36,
0 0.
xyy
zxy
zz
11.7.
22
2
2,
94, 0.
xyy
zxz
11.8.
2222
22
2, 5,
, 0.
xyyxyy
zxyz
11.9.
22
22
220,
4,
0 0.
xyy
zxy
zz
11.10.
22
2
4,
10, 0.
xyx
zyz
11.11.
2222
22
7, 10,
, 0,
0 0
xyxxyx
zxyz
yy
11.12.
22
22
82,
64,
0 0.
xyy
zxy
zz
11.13.
22
2
2,
134, 0.
xyy
zxz
11.14.
2222
22
3, 6,
, 0.
xyyxyy
zxyz
11.15.
22
22
62,
36,
0 0.
xyx
zxy
zz
11.16.
22
22
22,
4,
0 0.
xyy
zxy
zz
25
11.17.
22
2
4,
12, 0.
xyx
zyz
11.18.
2222
22
8, 11,
, 0,
0 0
xyxxyx
zxyz
yy
11.19.
22
22
42,
16,
0 0.
xyx
zxy
zz
11.20.
22
2
4,
4, 0.
xyy
zxz
11.21.
2222
22
4, 7,
, 0.
xyyxyy
zxyz
11.22.
22
22
42,
16,
0 0.
xyy
zxy
zz
11.23.
22
2
20,
174, 0.
xyx
zyz
11.24.
2222
22
9, 12,
, 0,
0 0
xyxxyx
zxyz
yy
11.25.
22
22
220,
4,
0 0.
xyx
zxy
zz
11.26.
22
2
4,
6, 0.
xyy
zxz
11.27.
2222
22
10, 13,
, 0,
0 0
xyxxyx
zxyz
yy
11.28.
22
22
22,
4,
0 0.
xyx
zxy
zz
11.29.
22
2
2,
214, 0.
xyx
zyz
11.30.
2222
22
5, 8,
, 0.
xyyxyy
zxyz
11.31.
22
2
20,
254, 0.
xyx
zyz
26
Задача 12.
Найти
объём
тела, заданного ограничивающими его поверхностями.
12.1.
2
22
22
52, 7,
372,
375.
yxy
zyx
zyx
12.2.
22
22
22
52, 47,
495,
195.
yxyx
zxy
zxy
12.3.
2
22
22
52, 3,
31,
35.
xyx
zxy
zxy
12.4.
22
22
22
23, 76,
116,
316.
xyxy
zxy
zxy
12.5.
2
22
22
68, 2,
1,
5.
yxy
zxxy
zxxy
12.6.
22
22
22
51, 31,
23,
53.
yxyx
zxy
zxy
12.7.
2
22
22
59, 4,
44,
42.
xyx
zxxy
zxxy
12.8.
2
22
22
61, 5,
2,
24.
yxy
zxxy
zxxy
12.9.
22
22
22
51, 31,
26,
16.
xyxy
zxy
zxy
12.10.
2
22
22
37, 4,
26,
36.
xyx
zxy
zxy
12.11.
2
22
22
53, 2,
2361,
2362.
yxy
zxyy
zxyy
12.12.
22
22
22
5, 3,
458,
158.
yxyx
zxy
zxy
12.13.
2
22
22
35, 2,
216,
816.
xyx
zxy
zxy
12.14.
22
22
22
2, 43,
162,
161.
xyxy
zxy
zxy
27
12.15.
2
22
22
21, 1,
53,
56.
yxy
zxy
zxy
12.16.
22
22
22
2, 43,
2,
1.
yxyx
zxy
zxy
12.17.
2
22
22
41, 3,
71,
72.
xyx
zxy
zxy
12.18.
22
22
22
76, 23,
385,
285.
xyxy
zyx
zyx
12.19.
2
22
22
12, 1,
22,
21.
yxy
zxyy
zxyy
12.20.
22
22
22
7, 82,
3125,
2125.
yxyx
zyx
zyx
12.21.
2
22
22
23, 5,
194,
494.
xyx
zxy
zxy
12.22.
2
22
22
34, 7,
523,
123.
yxy
zxy
zxy
12.23.
22
22
22
52, 47,
423,
123.
xyxy
zxy
zxy
12.24.
2
22
22
25, 3,
525,
225.
xyx
zxy
zxy
12.25.
2
22
22
35, 2,
35,
15.
yxy
zxy
zxy
12.26.
22
22
22
35, 64,
210,
210.
yxyx
zxy
zxy
12.27.
2
22
22
42, 6,
41,
44.
xyx
zxyy
zxyy
12.28.
22
22
22
32, 45,
479,
179.
xyxy
zxy
zxy
12.29.
2
22
22
25, 3,
24,
14.
yxy
zxy
zxy
12.30.
22
22
22
23, 76,
156,
356.
yxyx
zxy
zxy
28
12.31.
2
22
22
27, 5,
123,
423.
yxy
zxy
zxy
Задача 13.
Найти
объём
тела, заданного ограничивающими его поверхностями.
13.1.
22
22
9,
92.
zxy
zxy
13.2.
22
22
152,
172.
zxy
zxy
13.3.
22
22
4,
255.
zxy
zxy
13.4.
22
22
64, 1,
60
внутри цилиндра.
zxyz
xy
13.5.
22
22
16
,
9
2.
zxy
zxy
13.6.
22
22
3,
10.
zxy
zxy
13.7.
22
22
25,
99.
zxy
zxy
13.8.
22
22
100, 6,
51
внутри цилиндра.
zxyz
xy
13.9.
22
22
212,
232.
zxy
zxy
13.10.
22
22
16,
6.
zxy
zxy
13.11.
22
22
9,
80.
zxy
zxy
13.12.
22
22
81, 5,
45
внутри цилиндра.
zxyz
xy
13.13.
22
22
1,
32.
zxy
zxy
13.14.
22
22
6,
16.
zxy
zxy
29
13.15.
22
22
36,
63.
zxy
zxy
13.16.
22
22
64, 4,
39
внутри цилиндра.
zxyz
xy
13.17.
22
22
144,
18.
zxy
zxy
13.18.
22
22
32,
52.
zxy
zxy
13.19.
22
22
9,
35.
zxy
zxy
13.20.
22
22
49, 3,
33
внутри цилиндра.
zxyz
xy
13.21.
22
22
36,
9.
zxy
zxy
13.22.
22
22
9,
22.
zxy
zxy
13.23.
22
22
16,
15.
zxy
zxy
13.24.
22
22
36, 2,
27
внутри цилиндра.
zxyz
xy
13.25.
22
22
49,
.
zxy
zxy
13.26.
22
22
12,
28.
zxy
zxy
13.27.
22
22
9,
8.
zxy
zxy
13.28.
22
22
25, 1,
21
внутри цилиндра.
zxyz
xy
13.29.
22
22
64,
12.
zxy
zxy
13.30.
22
22
92,
112.
zxy
zxy
13.31.
22
22
36,
3.
zxy
zxy
30
Задача 14.
Найти
объём
тела, заданного ограничивающими его поверхностями.
14
.1.
22
212,
242.
zxy
zx
14.2.
2
2
1011,
2120.
zxy
zx
14.3.
22
83,
163.
zxy
zx
14.4.
2
2
2201,
4038.
zxy
zx
14.5.
22
414,
428.
zxy
zx
14.6.
2
2
2813,
5659.
zxy
zx
14.7.
22
323,
364.
zxy
zx
14.8.
2
2
461,
128.
zxy
zx
14.9.
22
24,
82.
zxy
zx
14.10.
2
2
2213,
4744.
zxy
zx
14.11.
22
241,
481.
zxy
zx
14.12.
2
2
2181,
3634.
zxy
zx
14.13.
22
161,
321.
zxy
zx
14.14.
2
2
3011,
6061.
zxy
zx
14.15.
22
262,
522.
zxy
zx
14.16.
2
2
211,
45.
zxy
zx
14.17.
22
21,
41.
zxy
zy
14.18.
2
2
2612,
5052.
zxy
zx
14.19.
22
301,
601.
zxy
zy
14.20.
2
2
1611,
3233.
zxy
zx
31
14.21.
22
218,
236.
zxy
zy
14.22.
2
2
2411,
4849.
zxy
zx
14.23.
22
223,
344.
zxy
zy
14.24.
2
2
241,
86.
zxy
zx
14.25.
22
46,
124.
zxy
zy
14.26.
2
2
3213,
6764.
zxy
zx
14.27.
22
283,
563.
zxy
zy
14.28.
2
2
4141,
2824.
zxy
zx
14.29.
22
220,
240.
zxy
zy
14.30.
2
2
813,
1619.
zxy
zx
14.31.
22
101,
120.
zxy
zy
Задача 15.
Найти
объём
тела, заданного неравенствами.
15
.1.
222
2222
149,
,
353
0.
xyz
xyxy
z
xy
15.2.
222
2222
464,
,
153
30.
xyz
xyxy
z
xy
15.3.
222
22
464,
, 0.
3
3
xyz
xyx
zy
15.4.
222
22
436,
, 0.
63
3
xyz
xyx
zy
15.5.
222
22
136,
, 33.
99
xyz
xy
zxyx
15.6.
222
22
25100,
, 33.
99
xyz
xy
zxyx
32
15.7.
222
22
149,
0,
24
, 3.
3
xyz
xy
z
x
yyx
15.8.
222
22
25121,
0,
24
, 3.
3
xyz
xy
z
x
yyx
15.9.
222
2222
464,
,
353
0.
xyz
xyxy
z
xy
15.10.
222
2222
16100,
,
153
30.
xyz
xyxy
z
xy
15.11.
222
22
16100,
, 3.
3
3
xyz
xyx
zxy
15.12.
222
22
1664,
,
63
3.
3
xyz
xy
z
x
yx
15.13.
222
22
449,
, 0, 3.
99
xyz
xy
zyyx
15.14.
222
22
36121,
, 0, 3.
99
xyz
xy
zyyx
15.15.
222
22
464,
0,
24
3, .
3
xyz
xy
z
x
yxy
15.16.
222
22
36144,
0,
24
3, .
3
xyz
xy
z
x
yxy
15.17.
222
2222
981,
,
335
0.
xyz
xyxy
z
yx
15.18.
222
2222
36144,
,
315
03.
xyz
xyxy
z
yx
33
15.19.
222
22
36144,
, 3.
3
3
xyz
xyx
zxy
15.20.
222
22
36100,
,
63
3.
3
xyz
xy
z
x
yx
15.21.
222
22
964,
,
99
, .
33
xyz
xy
z
xx
yy
15.22.
222
22
49144,
,
99
, .
33
xyz
xy
z
xx
yy
15.23.
222
22
981,
0,
24
0, .
3
xyz
xy
z
x
yy
15.24.
222
22
49169,
0,
24
0, .
3
xyz
xy
z
x
yy
15.25.
222
2222
16100,
,
335
0.
xyz
xyxy
z
yx
15.26.
222
2222
64196,
,
315
03.
xyz
xyxy
z
yx
15.27.
222
22
64196,
, 0.
3
3
xyz
xyx
zy
15.28.
222
22
64144,
, 0.
63
3
xyz
xyx
zy
15.29.
222
22
1681,
,
99
0, 3.
xyz
xy
z
yyx
15.30.
222
22
64169,
,
99
0, 3.
xyz
xy
z
yyx
34
15.31.
222
22
16100,
0,
24
0, .
3
xyz
xy
z
x
yy
Задача 16.
Тело
V
задано ограничивающими его поверхностями,
-
плотность.
Найти массу тела.
16
.1.
22222
22
64, 4,
0, 0 0, 0,
54.
xyzxy
yzyz
xy
16.2.
22222
22
4, 1,
1, 0 0;
4.
xyzxy
xyxx
z
16.3.
2222
1, 2,
0, 0, 0 0, 0;
10.
xyxyz
xyzxy
x
16.4.
22222
164
, ,
497
0, 0, 0, 0;
80.
xyzxyz
xyxy
yz
16.5.
222222
1, 4,
0, 0, 0, 0, 0;
20.
xyzxyz
xyxyz
z
35
16.6.
22222
22
36, 1,
0, 0 0, 0,
5
.
6
xyzxy
xzxz
xy
16.7.
22222
22
16, 4,
4;
2.
xyzxy
xy
z
16.8.
2222
4, 8,
0, 0, 0 0, 0;
5.
xyxyz
xyzxy
x
16.9.
22222
42
, ,
255
0, 0, 0, 0;
28.
xyzxyz
xyxy
xz
16.10.
222222
4, ,
0, 0, 0, 0, 0;
6.
xyzxyz
xyxyz
z
16.11.
22222
22
25, 4,
0, 0, 0
0, 0, 0,
2.
xyzxy
xyz
xyz
xy
16.12.
22222
22
9, 4,
4, 0 0;
.
xyzxy
xyyy
z
36
16.13.
2222
1, 6,
0, 0, 0 0, 0;
90.
xyxyz
xyzxy
y
16.14.
22222
11
, ,
255
0, 0, 0, 0;
14.
xyzxyz
xyxy
yz
16.15.
222222
4, 9,
0, 0, 0, 0, 0;
10.
xyzxyz
xyxyz
z
16.16.
22222
22
9, 4,
0, 0, 0
0, 0, 0,
53.
xyzxy
xyz
xyz
xy
16.17.
222
2222
4,
1, 1;
6.
xyz
xyxy
z
16.18.
2222
1, ,
0, 0, 0,
0, 0;
10.
xyxyz
xyz
xy
y
16.19.
22222
11
, ,
497
0, 0, 0, 0;
10.
xyzxyz
xyxy
xz
37
16.20.
222222
4, 4,
0, 0, 0, 0, 0;
10.
xyzxyz
xyxyz
z
16.21.
22222
22
16, 1,
0, 0, 0 0, 0, 0,
5.
xyzxy
xyzxyz
xy
16.22.
222
2222
16,
4 4;
.
xyz
xyxy
z
16.23.
2222
4, 4,
0, 0, 0 0, 0;
5.
xyxyz
xyzxy
y
16.24.
22222
, ,
0, 0, 0, 0;
35.
xyzxyz
xyxy
yz
16.25.
222222
1, ,
0, 0, 0, 0, 0;
32.
xyzxyz
xyxyz
z
16.26.
22222
22
, 4,
0, 0, 0
0, 0, 0,
52.
xyzxy
xyz
xyz
xy
16.27.
22222
22
9, 4,
4, 0 0;
2.
xyzxy
xyzz
z
38
16.28.
2222
1, 3,
0, 0, 0
0, 0;
15.
xyxyz
xyz
xy
x
16.29.
22222
42
, ,
497
0, 0, 0, 0;
20.
xyzxyz
xyxy
xz
16.30.
222222
16, 9,
0, 0, 0, 0, 0;
5.
xyzxyz
xyxyz
z
16.31.
22222
22
4, 1,
0, 0 0, 0,
10.
xyzxy
yzyz
xy