Автор: Попов А.М. Богацкая А.В.
Теги: физика квантовая механика атомная физика электромагнитные волны квантовая система
Год: 2021
Текст
А.В. Богацкая, А.М. Попов
ОСНОВЫ АТОМНОЙ ФИЗИКИ
И ТЕОРИИ ВЗАИМОДЕЙСТВИЯ
СВЕТА И ВЕЩЕСТВА
Москва, 2021
3
Оглавление.
Введение 9
Глава 1. Основы формализма квантовой механики............................ 11
1.1. Волновая функция и нестационарное уравнение Шредингера......... 11
1.2. Определение средних по квантовому состоянию значений и дисперсии
импульса и координаты частицы....................................... 14
1.3. Операторы физических величин и их свойства..................... 17
1.4. Собственные значения и собственные функции оператора импульса и
z-проекции момента импульса......................................... 20
1.5. Собственные значения и собственные функции оператора квадрата
момента количества движения......................................... 21
1.6. Собственные состояния оператора Гамильтона. Стационарное
уравнение Шредингера................................................ 26
1.7. Спин........................................................... 28
1.8. Коммутатор..................................................... 31
1.9. Соотношения неопределенностей.................................. 34
1.10. Многочастичная квантовая система. Понятие о матрице плотности. 36
1.11. Движение волновых пакетов. Предельный переход к классической
механике............................................................ 39
1.12. Представления Шредингера и Гейзенберга........................ 42
1.13. Пространственная четность состояний........................... 43
1.14. Симметрия волновой функции относительно их перестановки
местами. Тождественность микрообъектов. Бозоны и фермионы. Принцип
Паули............................................................... 44
1.15. Сложение моментов количества движения......................... 47
Приложение 1.1. Атомная система единиц.............................. 49
Задачи к Главе 1.................................................... 51
Глава 2. Стационарные состояния квантовой системы........................ 54
2.1. Свободное движение частицы..................................... 54
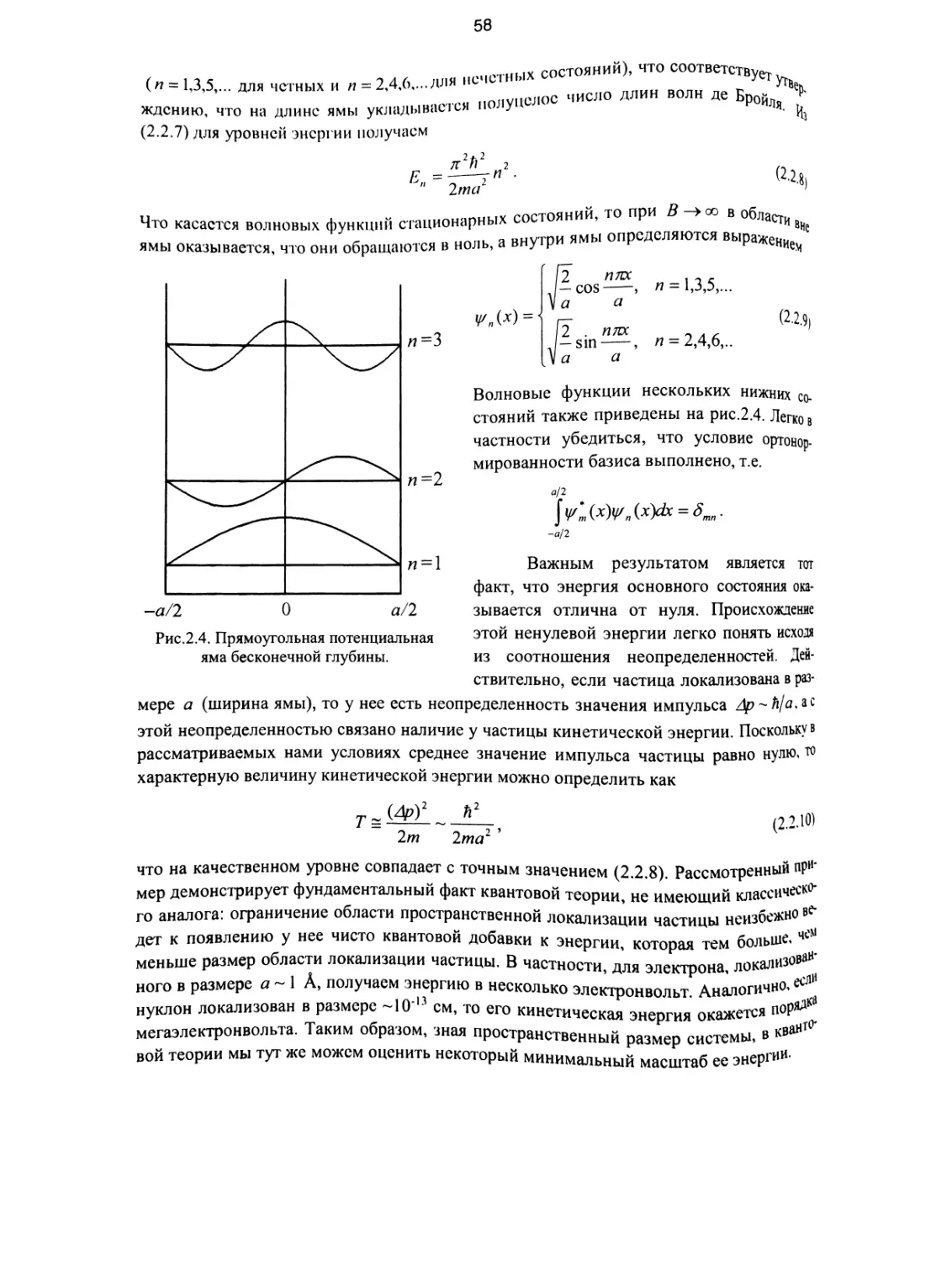
2.2. Частица в прямоугольной потенциальной яме конечной глубины..... 55
2.3. Туннелирование................................................. 60
2.4. Приближенное решение стационарного уравнения Шредингера.
Стационарная теория возмущений...................................... 62
2.5. Периодический потенциал. Зонная структура спектра.............. 66
Задачи к Главе 2.................................................... 67
Глава 3. Гармонический осциллятор........................................ 69
3.1. Стационарные состояния......................................... 69
3.2. Нестационарные состояния....................................... 74
3.3. Когерентные состояния и переход к классическому описанию....... 75
3.4. «Сжатый» вакуум................................................ 80
3.5. Трехмерный изотропный гармонический осциллятор................. 82
3.6. Операторы рождения и уничтожения квантов. Возбуждения как
частицы............................................................. 83
Задачи к Главе 3.................................................... 85
4
Глава 4. Атом водорода......................................................
4.1. Общая постановка задачи..........................................
4.2. Движение в центрально-симметричном поле.......................... 88
4.3. Задача Кеплера................................................... 90
4.4. Переход к классическому описанию................................. 95
4.5. Модель атома Бора................................................ 97
4.6. Систематика состояний атома водорода. Базисы n,£,me,ms и .. 99
4.7. Релятивистские поправки. Тонкая структура спектра атома водорода. 102
4.8. Сверхтонкая структура спектра атома водорода.....................
4.9. Изотопические эффекты в атомах...................................
114
4.10. Мюонный атом водорода...........................................
4.11. Экситон Ванье - Мотта...........................................
Прило жение 4.1. Структура энергетического спектра атома водорода.... 116
Задачи к Главе 4......................................................
Глава 5. Простейшие многоэлектронные системы................................ 119
5.1. Вариационный метод............................................... 119
5.2. Приближение самосогласованного поля.............................. 121
5.3. Атомные оболочки и подоболочки. Электронная конфигурация......... 123
5.4. Атомы щелочных металлов.......................................... 124
5.5. Атом гелия....................................................... 129
5.6. Отрицательный ион водорода....................................... 139
Приложение 5.1. Момент количества движения в многоэлектронном атоме.. 141
Задачи к Главе 5...................................................... 143
Глава 6. Общие принципы описания многоэлектронных атомов.................... 144
6.1. Заполнение атомных оболочек электронами.......................... 144
6.2. Термы многоэлектронных атомов.................................... 145
6.3. Тонкая структура терма. Состояния................................ 150
6.4. Различные типы связи моментов в многоэлектронном атоме........... 152
6.5. Основные термы атомов. Правила Хунда............................. 155
6.6. Сверхтонкая структура спектров многоэлектронных атомов........... 158
6.7. Атом в электрическом поле. Эффект Штарка......................... 159
Задачи к Главе 6...................................................... 161
Глава 7. Строение молекул................................................... 163
7.1. Невозможность существования молекул в классической физике........ 163
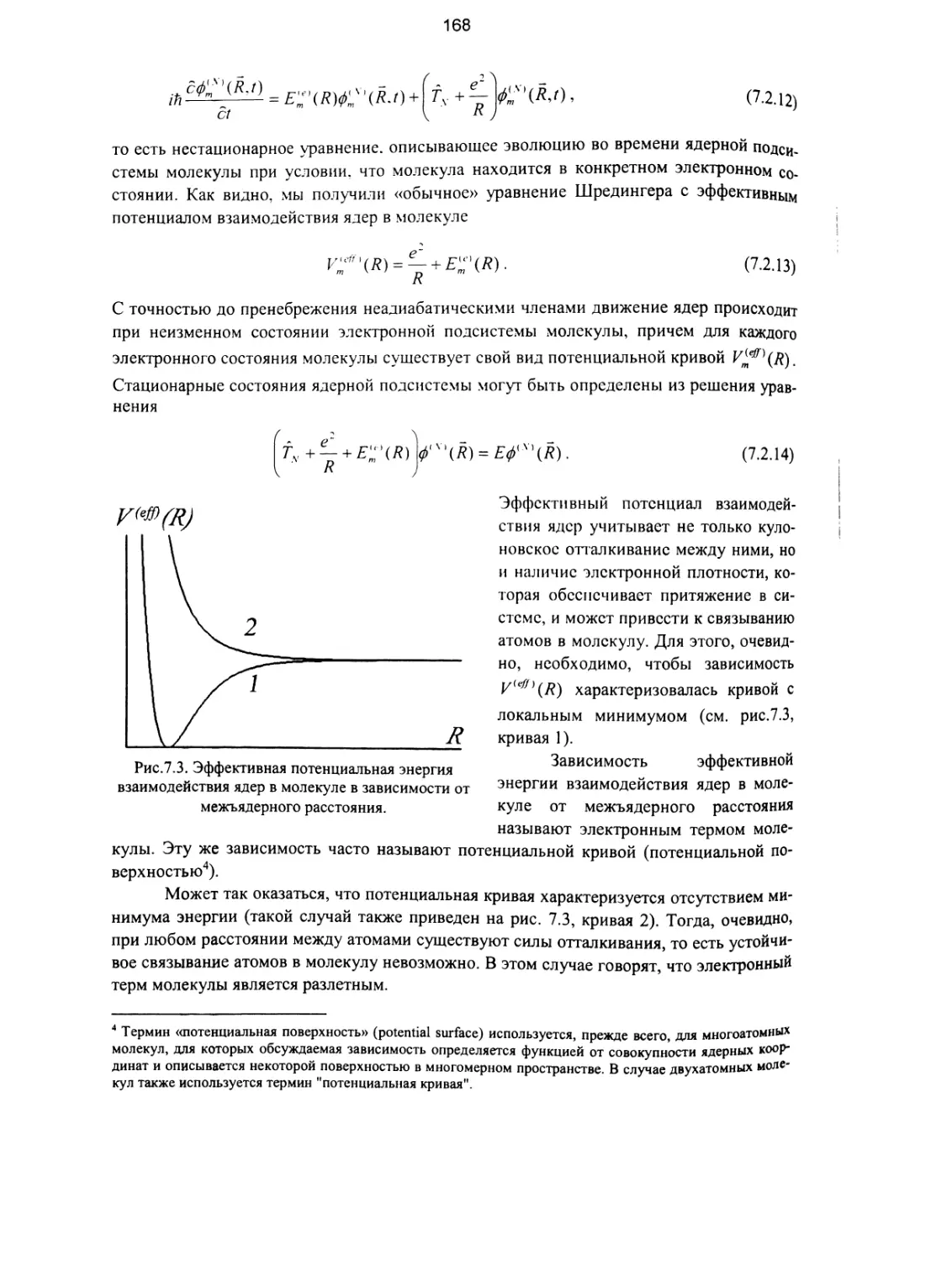
7.2. Адиабатическое приближение....................................... 164
7.3. Молекулярный ион водорода........................................ 169
7.4. Молекула водорода. Теория Гайтлера - Лондона..................... 174
7.5. Насыщение химических связей. Валентность......................... 177
7.6. Метод линейной комбинации атомных орбиталей (ЛКАО).
Ковалентная полярная и ионная связи................................... 179
7.7. Основы систематики электронных состояний двухатомных молекул..... 181
7.8. Ядерная подсистема молекулы...................................... 184
7.9. Изотопические эффекты в молекулах................................ 192
Задачи к Главе 7............................... 193
Глава 8. Основы полуклассической теории взаимодействия света и вещества. 194
8.1. Постановка задачи. Электрическое дипольное приближение........... 194
5
8.2. Две формы записи оператора взаимодействия квантовой системы с
электромагнитным полем: с!Е - и рЛ - калибровки.................. 196
8.3. Нестационарная теория возмущений............................ 200
8.4. Вероятность перехода. Первый порядок теории возмущений...... 202
Задачи к Главе 8................................................. 207
Глава 9. Электромагнитные переходы в атомах и молекулах................ 208
9.1. Понятие о правилах отбора................................... 208
9.2. Спектральные серии атома водорода.щелочных металлов......... 211
9.3. Электромагнитные переходы в многоэлсктронных атомах......... 214
9.4. Электромагнитные переходы в двухатомных молекулах........... 219
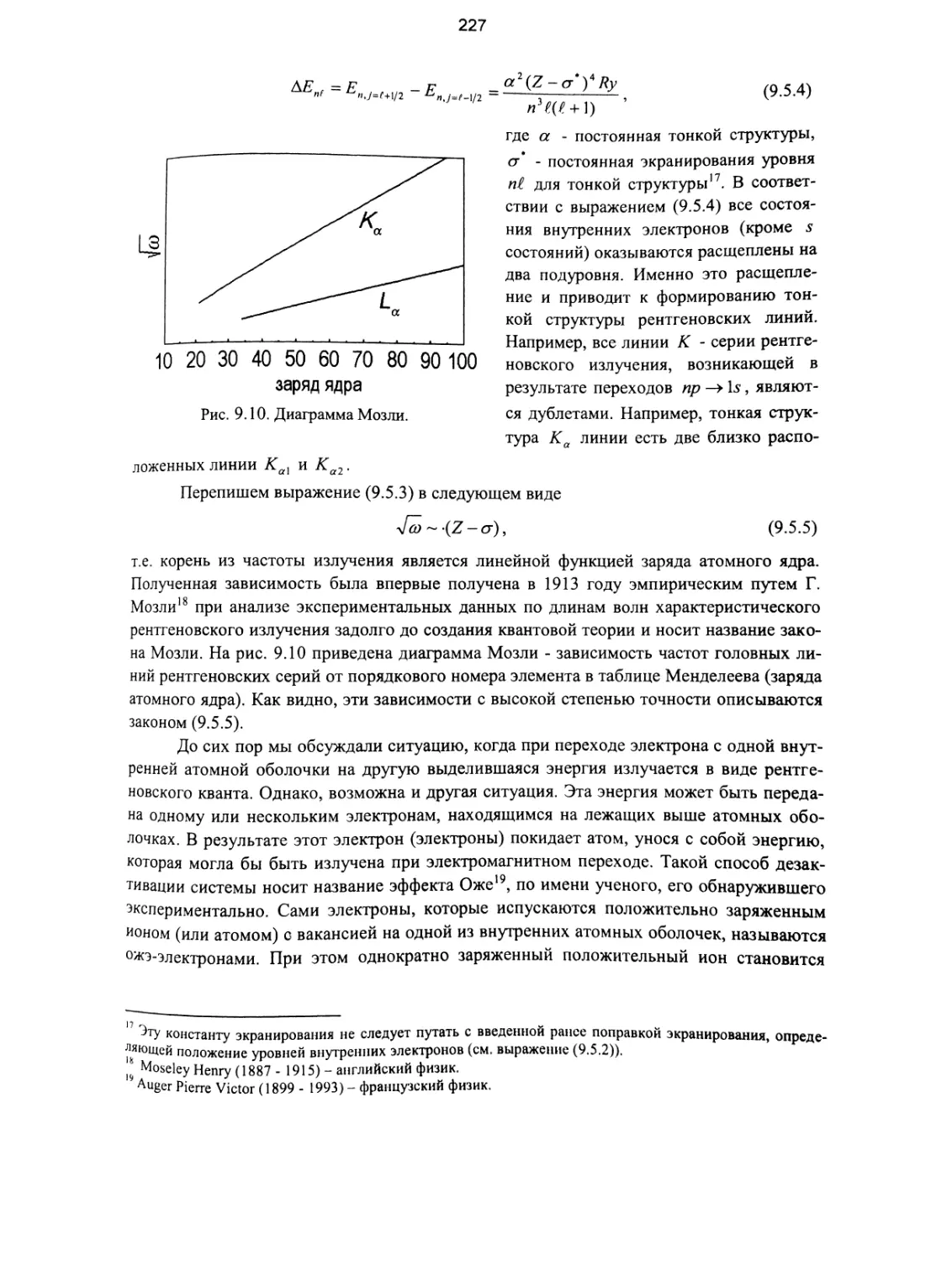
9.5. Переходы внутренних электронов в атомах. Характеристическое
рентгеновское излучение. Эффект Оже.............................. 224
Задачи к Главе 9................................................. 228
Глава 10. Полуклассическая теория взаимодействия света с веществом.
Точно решаемые задачи.................................................. 230
10.1. Двухуровневая система в поле электромагнитной волны........ 230
10.2. Гармонический осциллятор в поле электромагнитной волны..... 234
10.3. Свободный электрон в электромагнитном поле. Состояния Волкова.... 238
Задачи к Главе 10................................................ 240
Глава 11. Многофотонные процессы....................................... 241
11.1. Второй порядок нестационарной теории возмущений............ 241
11.2. Двухфотонные переходы...................................... 243
11.3. Высшие порядки теории возмущений........................... 245
11.4. Рамановские переходы А - типа. Комбинационное и релеевское
рассеяние........................................................ 245
11.5. Динамический эффект Штарка................................. 247
11.6. Диаграммы Фейнмана......................................... 249
Задачи к Главе 11................................................ 252
Глава 12. Квантовая система в поле электромагнитной волны. Переходы
между состояниями континуума........................................... 253
12.1. Основы квантовомеханической теории столкновений. Борновское
приближение...................................................... 253
12.2. Рассеяние на потенциале Юкавы. Резерфордовское рассеяние... 257
12.3. Рассеяние электронов на атомах во внешнем электромагнитном поле.
Вынужденный тормозной эффект..................................... 258
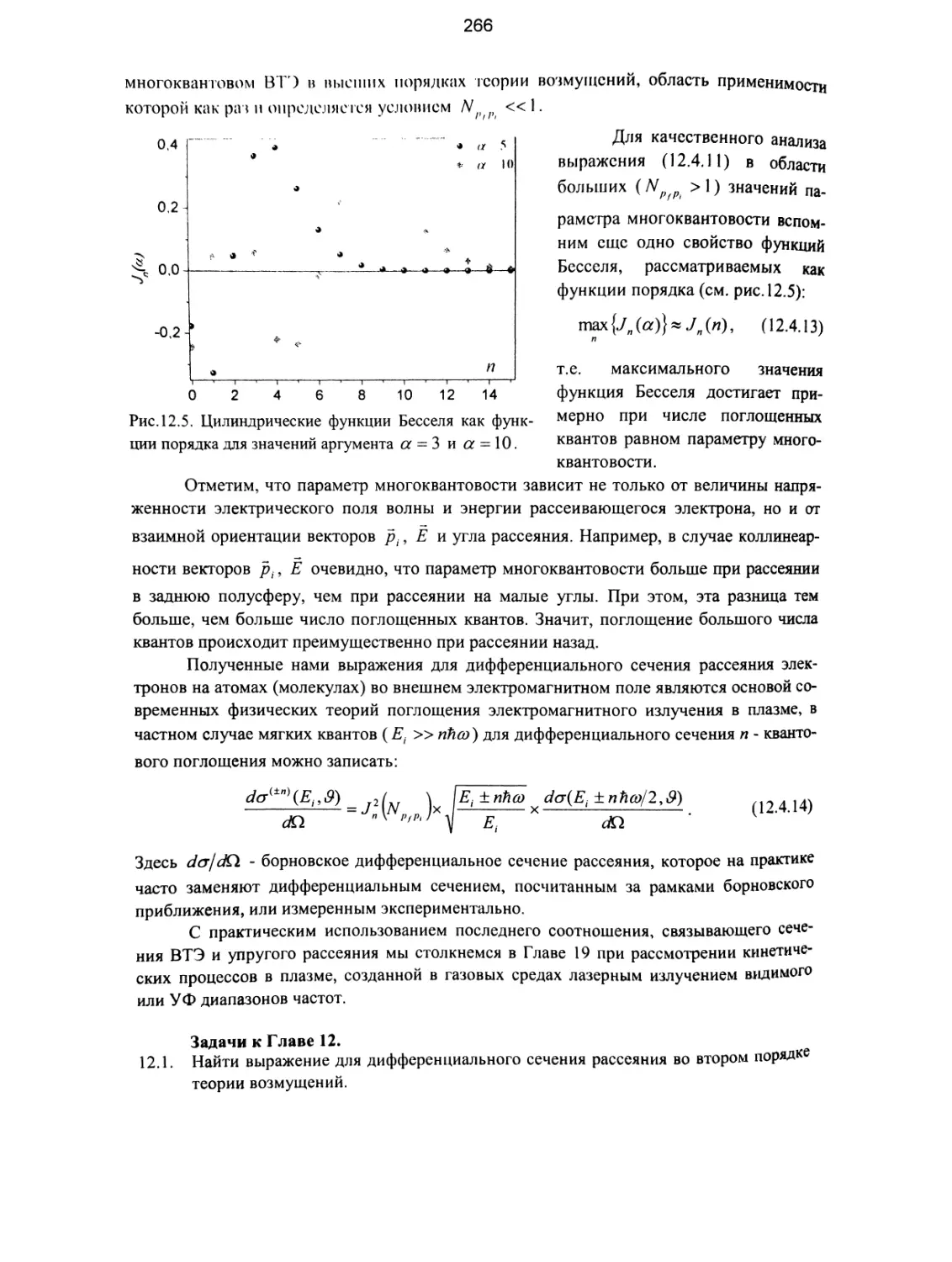
12.4. Многоквантовый вынужденный тормозной эффект. Теория Бункина -
Федорова......................................................... 262
Задачи к Главе 12................................................ 266
Глава 13. Фотоионизация атомов......................................... 268
13.1. Первый порядок теории возмущений. Одноквантовый фотоэффект. 268
13.2. Многоквантовый фотоэффект.................................. 270
13.3. Надпороговая ионизация атомов.............................. 271
13.4. Туннельная ионизация атомов оптическим полем............... 274
13.5. Теория фотоионизации Келдыша............................... 277
13.6. Эффект стабилизации атомов в сильном поле излучения........ 281
Задачи к Главе 13................................................ 290
6
Глава 14. Квантовая теория взаимодействия света с веществом............. 291
14.1. Разложение поля на осцилляторы............................. 292
14.2. Электромагнитное поле, как квантовый объем................. 294
14.3. Классическое электромагнитное поле в квантовой i сории..... 297
14.4. «Сжатый» свет................................................ ^98
14.5. Взаимодействие атомной системы с квантовым электромагнитным
_ .... 290
полем. Спонтанные переходы..............................
14.6. Спонтанные переходы и естественная ширина спектральной линии. 305
14.7. Формула Планка............................................... ^10
14.8. Лэмбовский сдвиг атомных уровней............................. 311
14.9. Аномальный магнитный момент электрона........................ 317
14.10. Стационарный и нестационарный эффекты Казимира.............. 318
14.11. Спонтанное излучение атомов в сильном лазерном поле......... 320
14.12. Квантовая электродинамика в микрополости.................... 328
Приложение 14.1. Расчет вероятности спонтанного перехода 2р -> 1s в
водородоподобном ионе............................................ 332
Задачи к Главе 14.................................................. 333
Глава 15. Распространение электромагнитных волн в диэлектрических и
проводящих средах........................................................ 335
15.1. Общая постановка задачи...................................... 335
15.2. Отклик атома на внешнее поле: классическая модель............ 337
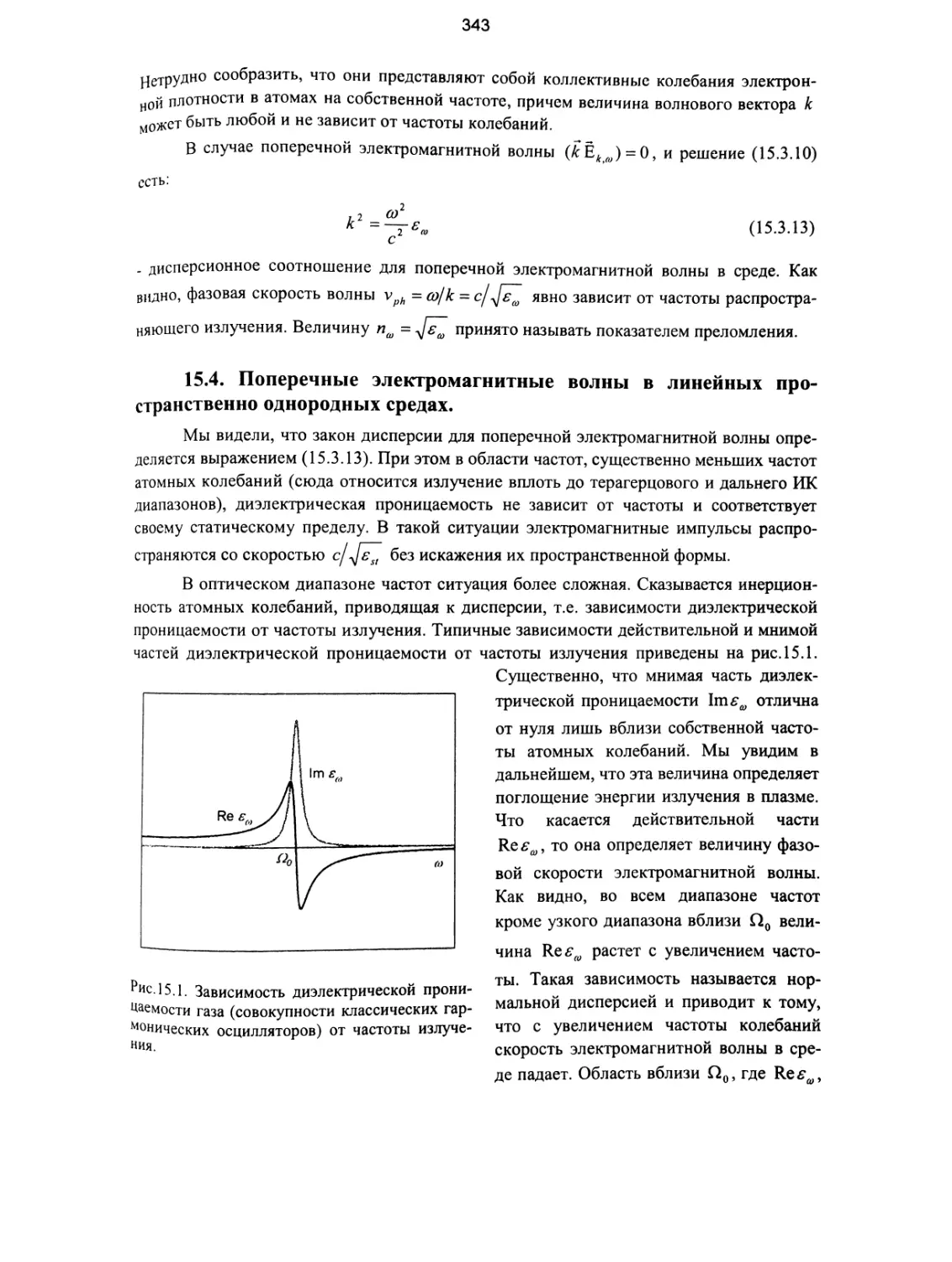
15.3. Анализ волнового уравнения. Общие замечания.................. 341
15.4. Поперечные электромагнитные волны в линейных пространственно
однородных средах................................................... 343
15.5. Отклик атома на внешнее поле: квантовомеханическая модель.... 345
15.6. Нелинейные атомные восприимчивости высших порядков........... 348
15.7. Плазма: отклик на внешнее воздействие........................ 352
15.8. Прохождение электромагнитной волны через границу раздела двух
сред................................................................ 356
15.9. Прохождение электромагнитной волны через границу раздела двух
сред. Случай наклонного падения..................................... 359
15.10. Теория Друде металлов........................................ 360
15.11. Поверхностные электромагнитные волны......................... 362
Приложение 15.1. Вычисление функции отклика на внешнее электрическое
поле для классического осциллятора с затуханием и плазмы............ 365
Приложение 15.2. Правило сумм....................................... 366
Задачи к Главе 15................................................... 366
Глава 16. Кинетическая теория распространения электромагнитных волн в
плазме.................................................................... 368
16.1. Кинетическое уравнение Больцмана для электронной компоненты
плазмы в поле электромагнитной волны................................ 368
16.2. Уравнение Больцмана в двучленном приближении и функция отклика
на внешнее поле............................... 371
16.3. Комплексные диэлектрическая проницаемость и проводимость
плазмы в кинетической теории. Показатель преломления и коэффициент
поглощения................. -57л
7
16.4. Продольные волны............................................ 376
16.5. Усиление электромагнитного излучения в плазме в условиях се
сильной нсравновссности........................................... 376
16.6. Разряд в электроотрицательных газах, поддерживаемый электронным
пучком, как среда для усиления электромагнитного излучения........ 381
16.7. Эффект усиления как отрицательная абсолютная проводимость и
движение электронов в плазме в направлении против действующей на них
силы............................................................ 383
Приложение 16.1. Интеграл упругих столкновений для уравнения
Больцмана......................................................... 384
Задачи к Главе 16................................................. 386
Глава 17. Свободный электрон в поле электромагнитной волны. Дипольное
приближение и релятивистские эффекты.................................... 387
17.1. Электрон в электромагнитном поле. Пределы применимости
дипольного приближения............................................ 387
17.2. Удержание электрона полем стоячей световой волны. Сила Гапонова -
Миллера........................................................... 388
17.3. Рассеяние света на удвоенной частоте........................ 390
17.4. Давление света.............................................. 392
Задачи к Главе 17................................................. 395
Глава 18. Пробой газов излучением оптической частоты.................... 396
18.1. Электрон в поле электромагнитной волны. Обратный тормозной
эффект. Классическое рассмотрение................................. 396
18.2. Баланс энергии электронов в плазме.......................... 401
18.3. Элементарная теория оптического пробоя...................... 403
Задачи к Главе 18................................................. 408
Глава 19. Кинетическая теория оптического пробоя 409
19.1. Уравнение Больцмана для функции распределения электронов по
энергиям в поле электромагнитной волны в двучленном приближении. 409
19.2. Баланс энергии электронов в плазме.......................... 412
19.3. Условия применимости двучленного приближения................ 415
19.4. Неупругие столкновения...................................... 416
19.5. Влияние неупругих соударений с атомами на вид энергетического
спектра электронов................................................ 421
19.6. Квантовое кинетическое уравнение............................ 423
Задачи к Главе 19................................................. 426
Глава 20. Основы нелинейной оптики...................................... 428
20.1. Уравнения Максвелла в нелинейной среде...................... 428
20.2. Приближение медленно меняющихся амплитуд (ММА).
Распространение пучка света в линейной пространственно неоднородной
среде.............................................................
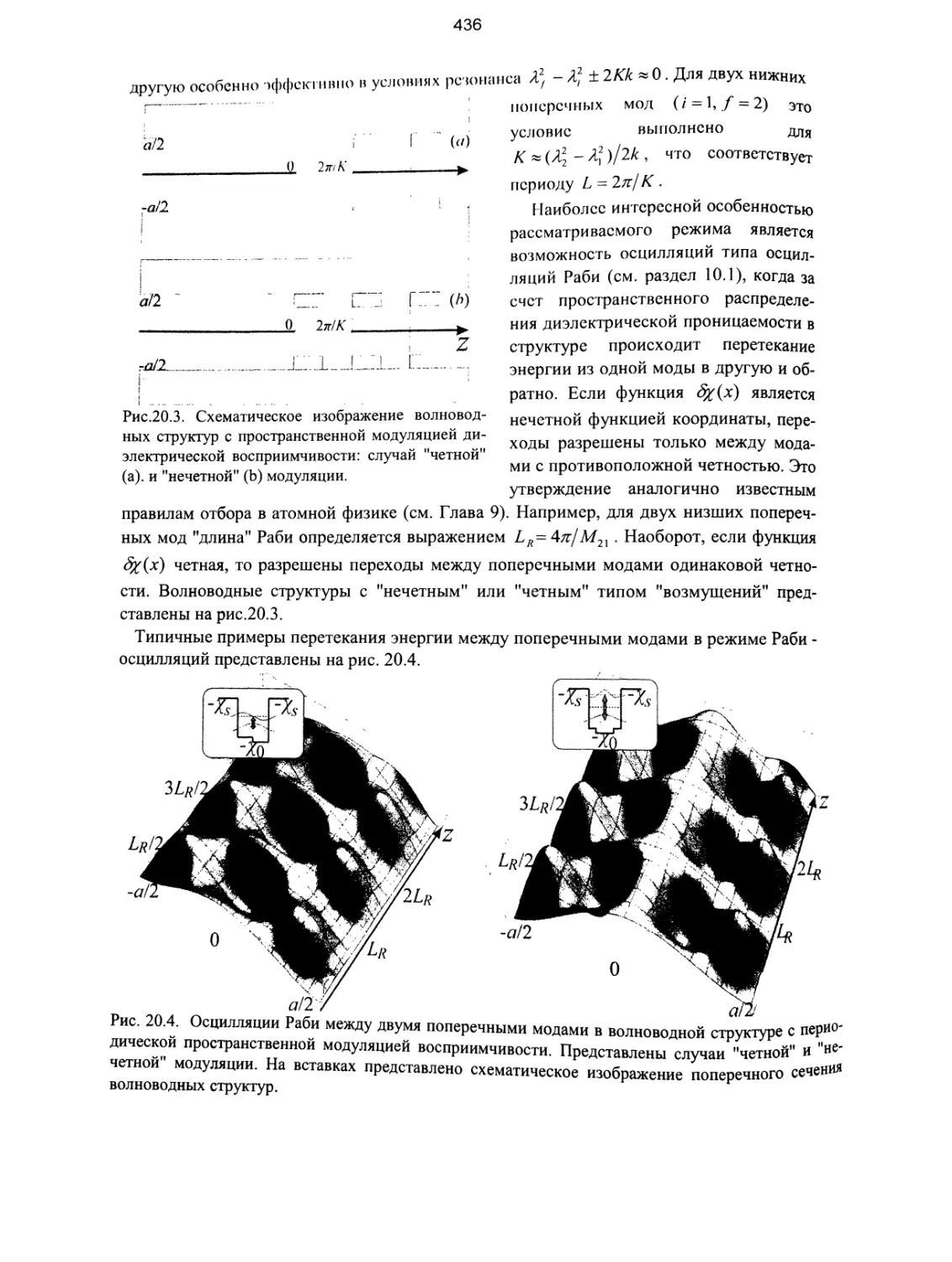
20.3. Распространение электромагнитных волн в волноводных структурах.. 433
20.4. Самофокусировка и самодефокусировка излучения в нелинейной
среде.............................................................
20.5. Генерация оптических гармоник............................... 439
20.6. Параметрическое преобразование частоты...................... 443
8
20.7. Генерация терагерцового излучения.......................... 445
20.8. Спонтанное и вынужденное комбинационное рассеяние света... 446
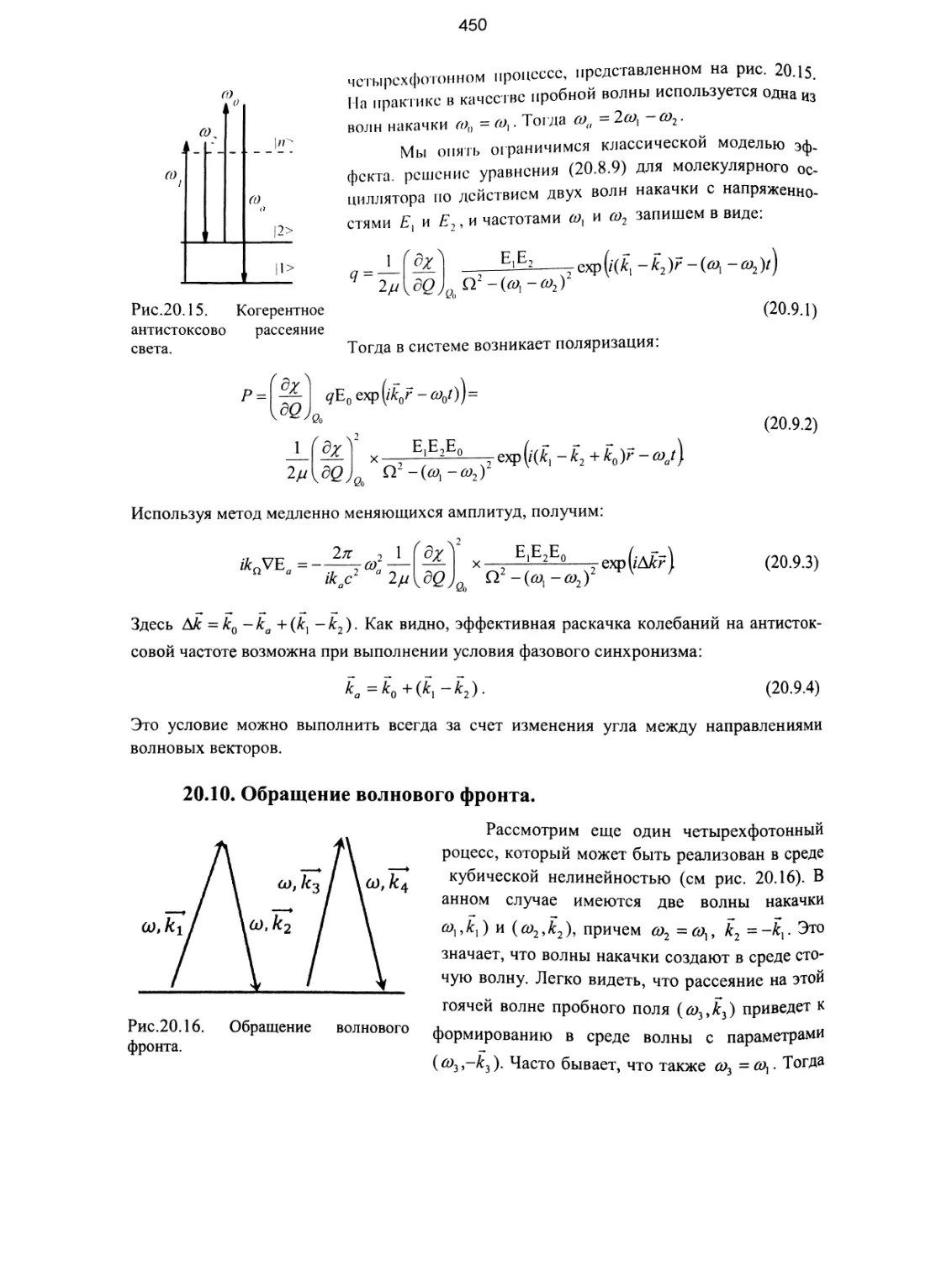
20.9. Когерентное антистоксово рассеяние света (КАРС)............ 449
20.10. Обращение волнового фронта................................ 450
Задачи к Главе 20................................................ 451
Глава 21. Основы физики лазеров........................................ 453
21.1. Спонтанные и вынужденные переходы. Сечение фотопоглощения. 453
21.2. Распространение резонансного излучения в двухуровневой среде.
Эффект насыщения.................................................. 457
21.3. Трех- и четырехуровневые схемы накачки..................... 459
21.4. Динамика лазерной генерации в приближении скоростных уравнений.
Стационарный режим работы........................................ 461
21.5. Динамика лазерной генерации в приближении скоростных уравнений.
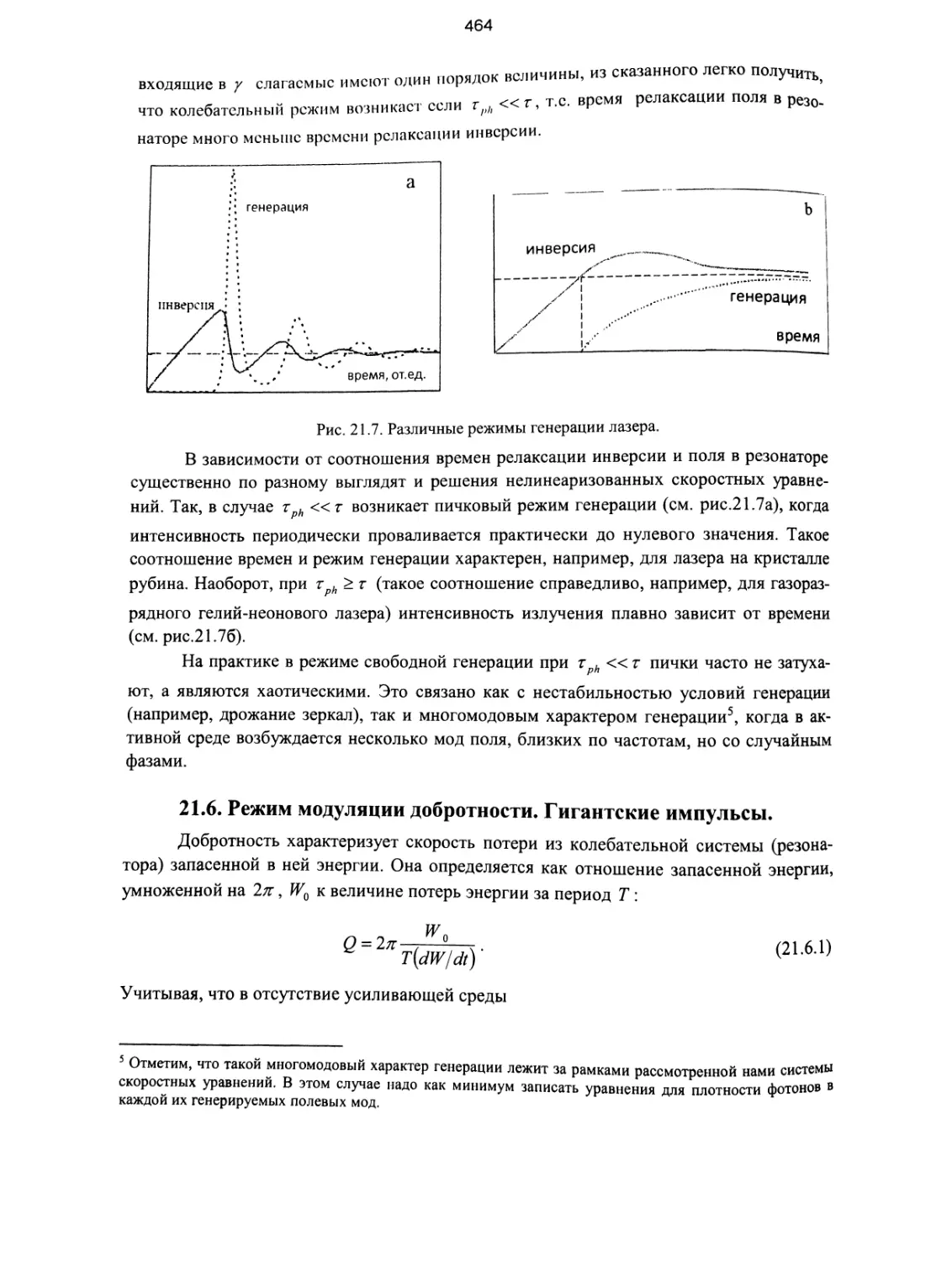
Нестационарный режим работы лазера............................... 463
21.6. Режим модуляции добротности. Гигантские импульсы........... 464
21.7. Синхронизация мод и генерация ультракоротких импульсов..... 466
21.8. Генерация фемто- и аттосекундных импульсов................. 470
21.9. Некоторые лазеры........................................... 472
Рубиновый лазер.............................................. 472
Неодимовый лазер............................................. 473
Гелий-неоновый лазер......................................... 474
СО2 - лазер.................................................. 476
Газодинамический СО2 - лазер................................. 479
Химические лазеры............................................ 479
Химический и электроразрядный кислород - йодный лазеры....... 480
Эксимерные лазеры............................................ 481
Рентгеновские лазеры......................................... 482
Лазер на свободных электронах................................ 484
Задачи к Главе 21................................................. 486
Справочные материалы.................................................... 433
Дополнительная литература............................................... 505
9
Введение.
Практически вес явления вокруг нас относятся к миру электромагнитных явлений.
В конечном счете особенности этого мира определяются законами движения электронов в
атомах, взаимодействием атомов друг с другом и внешними электромагнитными полями.
За рамками нашего внимания при этом остаются эффекты, обусловленные гравитацией,
которые, как правило, малосущественны в лабораторных масштабах, а также явления в
мире атомных ядер и частиц, определяемые короткодействующими сильным и слабым
взаимодействиями. Поэтому в основе описания подавляющего большинства наблюдаемых
нами явлений лежит теория строения вещества на микроскопическом уровне атомно-
молекулярных масштабов. Такая теория микроскопического строения вещества впервые
была создана Г. Лоренцом* (1895) на основе синтеза классической механики и
электромагнитной теории Максвелла применительно к описанию движения элементарных
зарядов в веществе и процессов поглощения (испускания) ими электромагнитных волн.
Фундаментальной основой теории Лоренца являлось представление об атоме, в котором
электрон совершает гармонические колебания. Это представление как раз соответствовало
модели атома Томсона1 2, предложенной в 1904 году.
В начале XX века стало ясно, что для описания свойств света и вещества
традиционных классических представлений недостаточно. В противном случае
невозможно объяснить ни устойчивость атомов и излучаемые ими спектры, ни
многочисленные эксперименты, в которых световой пучок ведет себя как совокупность
частиц (фотонов), в то же время оставаясь волновым полем. Несколько позже выяснилось,
что электроны (и все другие частицы) проявляют также и волновые свойства, причем
длина волны, соответствующая частице (длина волны де Бройля3), определяется
импульсом частицы. Новая теория, позволяющая описать строение вещества на
микроскопическом уровне (квантовая механика), была создана во второй половине
двадцатых готов прошлого века в работах Гейзенберга4, Шредингера5, Дирака6, Борна7 и
ряда других ученых. Оказалось, что использование квантовой теории для описания
вещества совместно с классической теорией для описания электромагнитного поля (так
называемая полуклассическая теория) позволяет корректно описать подавляющее
большинство явлений в окружающем нас мире. Казалось даже, последовательная теория,
описывающая и поле, и вещество с позиций квантовой механики, представляет
практический интерес только в задачах, когда число квантов поля, фотонов, невелико, или
1 Lorentz Hendrik Antoon (1853 - 1928) - нидерландский физик - теоретик, Нобелевская премия (1902) «В
знак признания исключительных услуг, которые они оказали науке своими исследованиями влияния
магнетизма на явления излучения», совместно с П.Зееманом.
2 Thomson Joseph John (1856 - 1940) - английский физик, Нобелевская премия (1906) «За теоретические и
экспериментальные исследования прохождения электричества через газы».
3 De Broglie Louis (1892 - 1987) - французский физик- теоретик, Нобелевская премия (1929)" За открытие
волновой природы электронов".
4 Heisenberg Werner Karl (1901 - 1976), немецкий физик - теоретик, Нобелевская премия (1932) «За создание
квантовой механики, применение которой привело, помимо прочего, к открытию аллотропических форм
водорода».
5 Schroedinger Erwin (1887 - 1961) - австрийский физик - теоретик, Нобелевская премия (1933) «За открытие
новых продуктивных форм атомной теории»
6 Dirac Paul Adrien Maurice (1902 - 1984) - английский физик - теоретик, Нобелевская премия (1933),
совместно Э. Шредингером.
7 Bom Мах (1882-1970) - немецкий физик - теоретик, Нобелевская премия (1954) "За фундаментальные
исследования по квантовой механике, особенно за статистическую интерпретацию волновой функции".
10
даже равно нулю, а поле находится в состоянии электромагнитного вакуума. С другой
стороны, экспериментальное обнаружение неклассических состоянии электромагнитного
поля, содержащих большое количество квантов и несущих макроскопически большую
энергию, привело к необходимости рассмотрения взаимодействия таких полей с
веществом за рамками полуклассического подхода.
Предлагаемое пособие содержит изложение основных положении квантовой
механики в объеме, достаточном для построения квантовой теории атомов и простейших
молекул, а также изложение основ полуклассической теории взаимодействия света с
веществом, и ее использования для описания взаимодействия электромагнитного
излучения с отдельными атомами (молекулами), с газовыми и плазменными средами,
включая задачи нелинейной оптики и физики лазерной генерации. Кроме того,
сформулированы основные идеи рассмотрения электромагнитного поля, как квантового
объекта, и построения последовательной квантовой теории взаимодействия света и
вещества.
Авторы считают своим приятным долгом выразить благодарность всем
сотрудникам кафедры атомной физики, физики плазмы и микроэлектроники физического
факультета МГУ а также отдела микроэлектроники НИИЯФ МГУ, участвовавшим в
обсуждении материалов пособия на различных этапах его подготовки. Особую
признательность авторы выражают А.С. Ковалеву и С.С. Красильникову, без
продолжительных дискуссий с которыми написание данного пособия бы было
невозможно.
Пособие издано при финансовой поддержке Научно-образовательной школы
«Фотоника и квантовые технологии. Цифровая медицина».
11
Глава 1. Основы формализма квантовой механики.
В данной Главе мы рассмотрим общие принципы описания квантовомеханиче-
скнх систем в объеме, достаточном для построения простейших физико-математических
моточен атомов, молекул и газовых сред, а также их взаимодействия с внешними элек-
тромагнитными полями. Как правило, изложение будет основано на так называемом ко-
ординатном представлении Шредингера.
1.1. Волновая функция и нестационарное уравнение Шредингера.
В квантовой теории состояние объекта (для нас это чаще всего будет один или
некая совокупность атомных электронов) будем описывать волновой функцией, как
функцией пространственных координат и времени. В случае одночастичной системы
запишем ее в виде ^(г,/). При этом квадрат модуля волновой функции \yf(r,C^ есть
плотность вероятности обнаружить частицу в точке с координатой г в момент времени
1:
р(г,Г) = |^(г,0|1 2. (1-1.1)
Естественно полагать, что где-то в пространстве частица достоверно существует. По-
этому волновая функция должна удовлетворять следующему условию нормировки
]У(г,/)|2<73г = 1.
V
(1.1.2)
Здесь интеграл берется по области определения волновой функции, как правило, это все
бесконечное пространство. Таким образом, состояния частицы должны описываться
функциями с интегрируемым квадратом модуля.
В общем случае движение частицы массы т в произвольном потенциальном по-
ле K(r,z) описывается нестационарным уравнением Шредингера.
й —= -—vV + r(F,O^(r,/).
д/ 2т
(1.1.3)
Здесь Й = 1.0545887 • 10 27 эрг*с - постоянная Планка'. Часто используют также постоян-
ную Планка, умноженную на 2к: h = 2лЙ = 6,626176 -10“ эрг*с.
Как видно, уравнение Шредингера (1.1.3) является уравнением первого порядка
по времени. Поэтому для его решения необходимо задать одно начальное условие, а
именно, волновую функцию в некоторый начальный (например, нулевой) момент вре-
мени
W(r,t = 0) = ^/0(г)
(1.Е4)
Тогда, зная волновую функцию системы в начальный момент времени, проинтегрировав
(1.1.3), мы сможем определить волновую функцию в любой наперед заданный момент
времени.
1 Planck Max Karl Ernst Ludwig (1858- 1947) немецкий физик - теоретик, лауреат Нобелевской премии
(1918) «В знак признания услуг, которые он оказал развитию физики своим открытием квантов энергии».
12
Нестационарное уравнение Шредингера сеть основное уравнение квантовой ме-
ханики и фактически приходи г на смену классическим уравнениям Ньютона. Состояние
микрообъекга в квантовой теории описывасзся волновым полем, у/ - функцией. Вся ин-
формация. копирую мы можем узна й, о сис теме, содержи гея в сс волновой функции.
Отметим, что в квантовой теории используются и состояния с волновыми функ-
циями. которые нс удовлетворяют условию квадратичной интегрируемости (1.1.2). При-
мером такого состояния является волна де Бройля, соответствующая частице с опреде-
ленным значением импульса р :
= схр у Р?
V п
(1.1.5)
Поскольку для этой волны |^(r)|2 = 1 , го нормировочный интеграл, очевидно, расходит-
ся.
Конечно, к реальному состоянию частицы плоская волна прямого отношения не
имеет. Любой физический процесс происходит, может быть, и в макроскопически боль-
шой, но ограниченной области пространства. Поэтому мы можем утверждать, что состо-
яние частицы с точно определенным значением импульса принципиально невозможно, а
волновая функция вида (1.1.5) не описывает никакого состояния реального физического
объекта. С другой стороны, если волновой пакет достаточно широкий, т.е. его простран-
ственной размер много больше длин волн де Бройля его образующих, приближение
плоской волны часто оказывается очень удобным с математической точки зрения. Рас-
смотрим вопрос о нормировке таких функций на примере состояния (1.1.5). Для просто-
ты ограничимся одномерным случаем. Будем считать, что состояние в виде плоской
волны
(х) = Лехр ~ рх
1 Та
(1.1.6)
( А = т/1/L - нормировочная константа, индекс « р » указывает, что это состояние с им-
пульсом р) задано на отрезке х е (-£/2,£/2). Мы полагаем, что L велико и в даль-
нейшем перейдем к пределу L
Рассмотрим значение следующего интеграла
Z./2
-L/2
(1.1.7)
Вычисление интеграла (1.1.7) дает
sin Д££/2
ML/2
(1.1.8)
Здесь Дк = (р- p')/h. При /Ус 0 в пределе L —> оо получаем, что / —> 0, т.е. волновые
функции состояний с различными значениями импульса становятся ортогональны друг
другу. В случае Лк s 0 получаем, что 1 = 1 для любого конечного сколь угодно большо-
го значения £, т.е. условие нормировки (1.1.2) оказывается выполненным. Указанная
13
процедура может быть использована при решении конкретных задач, однако не совсем
удобна, так как в исходной функции (1.1.6) появился нормировочный размер L. Поэто-
му обычно поступают немного иначе. Пусть нормировочная константа Л = 1. Тогда вы-
числение интеграла (1.1.7) в пределе L -> со даст
, f 'k .. sinA^Zz/2
/ = hm exp - (p - p)x ar = hm---------------= 2rtho( p- p ).
1 J ' ™ &k/2
Мы здесь использовали известные соотношения lim sin^6ac? =лЗ(х), 6(ах) = S(x)l\d.
х
Отсюда возникает условие нормировки на 6 - функцию:
(х)^р (x)dx = д(р-р'),
(1.1.9)
где
(1.1.10)
В трехмерном случае аналогично получаем
f (r)4sp {r)d3r = д(р-р')> (1.1.11)
причем
^(?)=^ехр(г?)- (,112)
Условие нормировки на 3 - функцию используется в квантовой теории всякий раз, ко-
гда волновая функция не может быть нормирована согласно условию (1.1.2).
Получим теперь одно очень важное свойство, которому удовлетворяют волновые
функции, являющиеся решениями нестационарного уравнения Шредингера в произ-
вольном потенциальном поле. Запишем для этого еще раз уравнение Шредингера
V> + (1.1.13)
ot 2т
а также уравнение, комплексно сопряженное ему:
-й^ = --УУ+И(г,()/(гЛ (1.1.14)
ot 2т
Умножим (1.1.13) на ^*(г,/), (1,1.14) на ys(r,t), а затем вычтем одно из другого. Полу-
чим:
(1.1.15)
или
14
h v(y/*Vy/ y/Vy/ ).
2 m i
(1.1.16)
Вспоминая, mix'» |v'(r’./)| ~ pU'd) - пжнносгь вероятности, перепишем (1.1.16) в виде
( + div j = 0,
Р/
где введено обозначение
-^-(у/’Vy/ -yAV*).
2mi
(1.1.17)
(1.1.18)
Уравнение типа (1.1.17) хорошо известно в различных областях физики. В частности, в
электродинамике оно является математическим выражением закона сохранения элек-
трического заряда, причем р есть плотность электрического заряда, a j - плотность
электрического тока. Уравнение (1.1.17) означает, что электрический заряд не исчезает и
не появляется, а только перетекает из одной точки пространства в другую. Аналогичное
уравнение в гидродинамике (р - плотность жидкости, j - поток массы) означает закон
сохранения массы. Поэтому естественно в квантовой теории величину j назвать векто-
ром плотности тока вероятности. Полученное нами уравнение непрерывности (1.1.17)
означает, что плотность вероятности в квантовой теории перетекает из одной простран-
ственной точки в другую подобно заряду в электродинамике, или массе в гидродинами-
ке.
Отметим, что полученные соотношения являются общими и не зависят от кон-
кретного вида потенциального поля, в котором движется частица. Для нас было важным
только требование, чтобы потенциальная функция К(г,/) была вещественной. Легко по-
казать, что введение в теорию комплексного потенциала может быть использовано дм
описания процесса рождения или гибели частицы, причем скорость рождения (гибели)
будет определяться мнимой частью потенциала ImK(r,/).
1.2. Определение средних по квантовому состоянию значений и
дисперсии импульса и координаты частицы.
Начнем обсуждение вопроса о вычислении квантовомеханических средних с
определения среднего значения пространственной координаты частицы. В данном слу-
чае среднее значение можно определить исходя из вероятностного смысла волновой
функции. Величина
</Hz(/) = |v/(F,/)|\/3r
(12.1)
есть вероятность обнаружить частицу в момент времени t в элементе объема dyr вбли-
зи точки с координатой г . Поэтому среднее по квантовому состоянию значение коорди-
наты частицы определяется по формуле
= j^(rj)|2</V я J ^’(Г,/)Г^(Г,Г)^3Г .
(1.2.2)
15
Здесь скобки ( ) означают процедуру усреднения по квантовому состоянию системы.
Выражение (1.2.2) легко расписать для каждой из проекций радиус-вектора x,y,z.
Например, для а - проекции имеем:
= |а|у/(/~,/)|2 dyr = |у/‘ (г ,t)xy/(r J)dy г. (1.2.3)
Рис. 1.1. Измерение координаты микрочастицы
Отмстим, что речь идет о принципиально новом способе усреднения, отличном от
усреднения по времени или по ансамблю частиц. В нашем случае усреднение проводит-
ся по квантовому состоянию одной микрочастицы в фиксированный момент времени.
Важно отмстить, что определить экспериментально это среднее по квантовому состоя-
нию значение координаты нс так просто. Действительно, в микромире процедура изме-
рения влияет на протекание изучаемого физического процесса. Поэтому после измере-
ния волновая функция системы оказывается уже иной. Эта ситуация на примере измере-
ния х - координаты частицы проиллюстрирована на рис. 1.1. Сплошная кривая соответ-
ствует величине |^(х)|2 до измерения.
Пусть в результате измерения мы об-
наружили частицу где-то вблизи точки
с координатой х}. Новая волновая
функция системы оказывается локали-
зована около этой точки (штриховая
кривая) и описывает уже совсем дру-
гое состояние частицы, которое воз-
никло после измерения. Поэтому, если
мы хотим определить среднее значе-
ние координаты в заданном состоянии,
мы должны позаботиться о том, что
каждый раз снова приготавливать это состояние после очередного измерения.
На практике обычно подразумевается, что имеется большое количество идентич-
ных невзаимодействующих квантовых систем, например, сгусток из N электронов2
(N »1). Тогда при измерении координат каждого из них мы получаем распределение
значений, определяемое квадратом модуля волновой функции, а по этому распределе-
нию в соответствии с выражением (1.2.2) или (1.2.3) определим среднее значение коор-
динаты электронного сгустка.
Введем еще дисперсию среднего значения координаты, характеризующую раз-
брос измеряемых значений относительно среднего значения. Определим дисперсию сле-
дующим образом
= ^(х-(х))2^ = (х2 -2х(х) + (х)2^ = ^х2^-(х)". (1-2.4)
Здесь символом ( ) всюду также обозначена интегральная операция типа (1.2.2).
Например:
(1.2.5)
2 При этом принципиально важно, чтобы взаимодействие между электронами было пренебрежимо мало.
16
- среднее значение квадрага координаты частицы.
Перейдем к обсуждению вычисления среднего значения и дисперсии импульса
частицы в некотором заданном состоянии у/(х). Вспомним, что мы знаем состояния, в
которых импульс частицы точно определен. Это плоская волна де Бройля
I ( ' I
^(л)=жсхрЬИ-
(1.2.6)
Представим ^(х) в виде линейной суперпозиции состояний с определенными
значениями импульса у/р(х}. Считая, что величина измеряемого импульса «пробегает»
непрерывный набор значений, имеем:
И*) = [CpVpdP- (L2-7)
Величина |Ср |2 есть плотность вероятности того, что при измерении у частицы будет
обнаружено значение импульса, равное р, а |Ср | dp есть вероятность измерить значе-
ние импульса в интервале от р до p + dp.
С математической точки зрения представление (1.2.7) есть разложение функции
^(х) в интеграл Фурье. Поэтому величина Ср может быть найдена с помощью обратно-
го преобразования Фурье:
i
h
(1-2.8)
Теперь легко определить среднее значение импульса в состоянии ^(х). Поскольку |Ср |
есть плотность вероятности импульсного распределения, то по аналогии с определением
(х) запишем
{р) = \р\Ср\2 dp.
Для вычисления (р) перепишем (1.2.9) в виде
(1.2.9)
(р) = f f dpdp'pC*p,CpS{p - /У),
(1.2.10)
а затем воспользуемся интегральным представлением для 5 - функции
(1.2.11)
Подставляя (1.2.11) в (1.2.10) и, затем, меняя местами порядок интегрирования, получим
{р} = f dx f С*, exp
(1.2.12)
Очевидно, первый вложенный в (1.2.12) интеграл есть просто у/*(х). Второй интеграл
легко сводится к производной от волновой функции:
17
Г/^ (i Ф .* ду/
b'VW=“'V (1-2-13)
Поэтому окончательно для (р) получаем
(p)=$y/\x)(pi//(x))dx, (1.2.14)
где введено обозначение
p^-ihd/dx. (1.2.15)
Аналогично для дисперсии значения импульса можно записать
DP ={р2)-(р)2, (1.2.16)
где квадрат среднего значения импульса определяется выражением
(р2) = р2\Ср\2dp = ^*(x{-h2 ^-}dx = ^\x)p2y/(x)dx. (1.2.17)
k Vх )
1.3. Операторы физических величин и их свойства.
Итак, полученные в предыдущем разделе выражения для средних значений коор-
динаты и импульса можно записать единым образом, если ввести операторы координаты
х и импульса рх:
x^(r,/) = x^(f,/), (1-3.1)
РхЧ^г^ = -т^у/(г,Р), (1.3.2)
ох
т.е. оператор х - проекции координаты есть просто умножение на величину х, а опера-
тор импульса есть (с точностью до постоянного множителя - ih) оператор дифференци-
рования по координате. Аналогичные соотношения можно записать и для двух других
проекций. Поэтому в общем случае для оператора импульса можно записать
£ = (1.3.3)
А теперь сделаем важное обобщение. Каждой физической величине, введенной в клас-
сической механике, в квантовой механике ставится в соответствие оператор этой вели-
чины. При этом соотношение между величинами в классической механике в квантовой
механике переносится на операторы. Например, оператор кинетической энергии есть
I 52 I Н - й\г
2т 2т 2т дх2 ду2 dz2) 2т
(1-3.4)
оператор потенциальной энергии есть также оператор умножения на потенци-
альную функцию К(г,/):
18
Важную роль в квантовой механике играет оператор полной энергии. Его также назы
вают оператором Гамильтона3 или гамильтонианом
Н = Т +¥ = - — V2 + К(г,/). (1.3.5)
2m
Введенный нами оператор Гамильтона позволяет записать нестационарное уравнение
Шредингера (1.1.3) в более компактном виде
,/Л = Яч,. (13-б)
dt
Построим еще оператор момента количества движения. Поскольку в классиче-
ской механике L = [г х р], то для операторов имеем
L = -ih[r х V], (1.3.7)
Рис. 1.2. Сферическая система
координат.
или для каждой из компонент:
Lx = -ih(y d/dz-z д/ ду),
Ly = -ih(z д/дх-х д/ dz\
Lz = -ih(xд/ду- уд/дх).
(13.8)
Для нас будет важен еще оператор квадрата момента ко-
личества движения
L2=L2x+L2y+L2.
(1.3.9)
В ряде задач нам будет удобно использовать сфе-
рическую систему координат. Поэтому приведем выра-
жения для некоторых из введенных нами операторов в
сферической системе координат. Напомним, что в этой системе вместо тройки чисел
x,y,z, задающих декартовы координаты, используются модуль радиус-вектора г и два
угла в и (р (см. рис. 1.2). Здесь мы приведем выражения для оператора Лапласа
1 д2 1
= -7Тг + —гДе
г dr г v
1 д ( . п д А 1 д2
—-----sin#— +—-----------
sin 0 д0\ д0) sin2 0 д(р
- угловая часть оператора Лапласа, а также для операторов z - проекции момента коли-
чества движения и квадрата момента количества движения:
Lz=-ihd/d(p, Ь2=-П2Ьв<р.
У нас есть универсальный рецепт вычисления средних значений. Если некоторой
физической величине А поставлен в соответствие оператор А, то среднее значение фи-
зической величины А в некотором квантовом состоянии, описываемом функцией
,t), можно определить по формуле:
Hamilton William Rowan (1805 - 1865) -ирландский математик и физик - теоретик.
19
(A(t)) = |^‘(г,/)т4^(г,/)<73г, (1.3.10)
Дисперсию величины А , характеризующую разброс результатов возможных измерений
относительно среднего значения, можно вычислить как
(1.3.П)
Все операторы, введенные нами, являются линейными операторами, действующими в
пространстве функций с интегрируемым квадратом £2.
Легко видеть, что если состояние у/ является собственным для оператора А, т.е.
AVa =aVa
(1.3.12)
(здесь а - собственное значение, соответствующее функции \ то в этом состоянии
физическая величина А принимает точно определенное значение. Действительно, опре-
делим среднее значение
(А) = J = 4 y/'ay/ad3r = а,
(1.3.13)
т.е. среднее значение величины совпадает с собственным значением оператора. По-
скольку в рассматриваемом случае = а2, то дисперсия величины А в собственном
состоянии оказывается равна нулю, т.е. физическая величина имеет точно определенное
значение, равное собственному значению оператора А .
Собственные значения всех операторов физических величин должны принимать
только действительные значения. Из этого требования следует свойство эрмитовости
операторов физических величин. Неэрмитовы операторы тоже используются в кванто-
вой механике, однако таким операторам не могут быть поставлены в соответствие изме-
ряемые физические величины.
Таким образом, в квантовой теории важное значение приобретает задача на соб-
ственные значения и собственные функции операторов различных физических величин.
Набор собственных значений образует спектр оператора, который может быть как дис-
кретным, так и непрерывным. Соответствующий набор собственных функций образует
полную систему, то есть произвольное состояние системы у/ может быть представлено
в виде разложения в ряд по собственным функциям какого-либо оператора А
(1.3.14)
п
причем это разложение однозначно и
единственно. Набор функций
} всегда может
быть выбран ортонормированным:
= где
0,
Smn = *
1,
т Ф п,
т = п.
(1.3.15)
В (1.3.15) интегрирование ведется по всей области определения волновой функции си-
стемы. Разложение (1.3.14) и условие ортонормированности (1.3.15) записаны для слу-
20
чая оператора Л с дискретным спектром. В случае непрерывного спектра следует запи-
сать
у/ - j Cni//Itda, (1.3.16)
J Vх Лх« V = -1/') • (1.3.17)
Прежде чем рассмотреть несколько конкретных примеров задач на собственные
значения и собственные функции для операторов физических величин, остановимся еще
на физическом смысле разложения (1.3.14). Величина =|С„| есть вероятность того,
что при измерении физической величины, соответствующей оператору А, будет изме-
рено значение А„, соответствующее собственной функции у/п. Аналогично, если речь
идет о физической величине, спектр оператора которой является непрерывным, величи-
ну dw = |С, |2 da следует трактовать, как вероятность при измерении величины А , обна-
ружить ее значение в интервале (а, а + da).
Сами коэффициенты разложения Сп или Са (их часто называют амплитудами
вероятности) легко определить по известной волновой функции. Умножая (1.3.14) на
у/*т и интегрируя по всей области определения функции с учетом (1.3.15) найдем
(1.3.18)
Аналогично в случае непрерывного спектра имеем
(1.3.19)
1.4. Собственные значения и собственные функции оператора
импульса и z-проекции момента импульса.
Рассмотрим задачу
PXVP = PVP-
(1.4.1)
Здесь индекс «р » указывает на принадлежность функции ц/ р собственному значению
равному р. Используя явное выражение для х - проекции оператора импульса, получим
I z I
WP = ехр -Р* ,
U J
(1.4.2)
т.е. плоскую волну де Бройля. Отметим, что оператор импульса есть пример оператора с
непрерывным спектром, а условие нормировки (1.1.9) тождественно условию (1.3.17).
Рассмотрим еще одну задачу:
41//... = L^i.;»
или в сферической системе координат
- ihdy/, /д(р- LtwL .
(1.43)
(1.4.4)
21
Интегрируя (1.4.4), находим
V/, =cxpH-Lz^ . (1.4.5)
к Л )
Все выглядит очень похожим на решение задачи на собственные значения и собствен-
ные функции для оператора импульса. Однако есть одно существенное отличие. В рас-
сматриваемом нами сейчас случае существует дополнительное условие - условие пери-
одичности волновой функции, как функции полярного угла. Действительно при измене-
нии угла <р на 2/г волновая функция не должна измениться, то есть
y/L (<р) = i//L; (<р + 2л-). (1.4.6)
Из (1.4.6) находим
expf—L -2яг | = 1. (1.4.7)
)
Очевидно, равенство (1.4.7) справедливо при строго определенных значениях Lz
L:-mh, т = 0,±1,±2,... (1.4.8)
Мы получили, что оператор z - проекции момента количества движения имеет чисто
дискретный спектр, возможные значения Lz оказываются кратными постоянной Планка,
а квантовое число т (его называют магнитным квантовым числом) как раз и определяет
величину проекции момента. Теперь, с учетом условия нормировки, мы можем записать
нормированные собственные функции оператора Lz:
= —j==vxp(irn(p\ т = 0,±1,±2,...
х/2л-
(1.4.9)
1.5. Собственные значения и собственные функции оператора
квадрата момента количества движения.
Эта задача, как мы увидим позже, имеет особое значение для квантовых систем,
характеризующихся центральной симметрией. Это, прежде всего, атом, в том числе и
многоэлектронный. Часто и ядерные состояния оказывается возможным описывать в
приближении центральной симметрии системы.
В сферической системе координат оператор квадрата момента с точностью до по-
стоянной совпадает с угловой частью оператора Лапласа
£2=-й2а^=-й2
( 1 д ( . п д ) 1 д
-------sin/9— 1 + —-------
^sin0d0\ дО) svn2 0 д(рг
(1.5.1)
Решение задачи на собственные значения и собственные функции для угловой
части оператора Лапласа
А,/(0,<р) + ЛГ(0,р) = О
(1.5.2)
22
хорошо известно4: Y(m, причем собственное значение Л = +1) • Здесь f. - любое целое
неотрицательное число, т.е. f = 0,1,2,..., а т для каждого пробегает целочисленный
набор значений от - f до f : т = 0,±1,±2,...± С, всего 2?. + 1 значений.
Следовательно, для оператора квадрата момента количества движения имеем.
= + (1-5.3)
т.е. сферическая функция Y(m определяет состояние с точно определенным значением
квадрата момента количества движения, причем
L2 = Гг2^ + 1). (1-5.4)
Свойства сферических функций хорошо изучены. Общее представление для Y(m
имеет следующий вид
Y(m(0,<p) = Р({п,}(cos6>)exp(zw^) , (1.5.5)
где (cos 0) - присоединенный полином Лежандра. В частном случае т = 0 присо-
единенные полиномы превращаются в обычные полиномы Лежандра Р( (cos 0). Приве-
дем явные выражения для первых нескольких сферических функций (без учета норми-
ровки):
Yoo(0,(p) = l,
У1О(0, (р) = cos 0, у; ±1 (6», (р) = sin(0) exp(±z» ,
Y2,0 (<?, (р) = | (3 cos2 (6») -1), У2 ±1 (0, ф) = 3 sin(0) cos(6>) exp(±z<p),
^2,±2 (^» $0 = 3 sin2 exp (±2z (p).
Некоторые свойства сферических функций, а также полиномов Лежандра и присоеди-
ненных полиномов обсуждаются в разделе Справочные материалы.
Нетрудно видеть, что сферические функции являются также собственными функ-
циями оператора z - проекции момента количества движения с собственным значением
mh. Действительно
k (#, <Р) = Y(m (О, <Р) = hm Y(m (0, (р),
д(р
поэтому квантовое число т определяет величину Lz в состоянии, описываемом функ-
цией Y(m. Таким образом, мы нашли состояния, в которых величина квадрата момента и
его z - проекции имею точно определенные значения. Такие состояния описываются
сферическими функциями Ybn(0,<p), при этом
L2 =Й2^ + 1), Lz = mh, (1.5.6)
причем z? = 0,1,2,..., m = 0,±l,±2,...±
4 А.Н. Тихонов, А.А. Самарский «Уравнения математической физики», М.: Наука, 1972, с.671
23
Введенные нами сферические функции удовлетворяют следующему условию
нормировки
J= W.., •
Здесь
4л- (1 + |/и|)!
2^ + 1 (£-|/и|)!
(1-5.7)
В дальнейшем нам будет удобно использовать нормированные на единицу сферические
функции, т.е.
(1.5.8)
Такие функции отличаются от введенных ранее умножением на численный множитель
2^ + 1 (I- ^)!
4л- (Т + |ти|)!
. В дальнейшем мы сохраним для этих функций то же обозначение Yfm .
Таким образом, мы построили состояния квантовомеханической системы с точно
определенными значениями £2 Lz. Заметим, что мы можем построить и состояния, в
которых величина квадрата момента определена точно, в то время как величина z - про-
екции точно не определена. Например, это состояния
(1-5.9)
т
Что касается двух других проекций момента количества движения, то в рассмат-
риваемых нами состояниях они не имеют точно определенного значения5. В этом смыс-
ле в квантовой теории вектор момента импульса не имеет строго определенного направ-
ления в пространстве. Точно известны лишь его длина и проекция на одну из осей
(например, ось z )6. Можно показать, что для любого состояния Y(m(0,<p) средние значе-
ния двух других проекций равны нулю:
(Lx) = {Ly) = 0. (1.5.10)
Вычислим теперь дисперсии (l2x^ и Полагая, что вследствие симметрии задачи
эти дисперсии равны между собой, и используя очевидное соотношение
^) + (L2y) + L^L\
получим
(i2) = (i2) = ^-(^ + l)-m2). (1.5.11)
5 Это утверждение справедливо для всех состояний с ненулевым значением орбитального квантового чис-
ла. В случае £ = 0 все три проекции орбитального момента имеют точно определенное значение, равное
нулю.
6 Можно, конечно, построить набор состояний с заданной величиной проекции момента на любую ось,
например, на ось х. В этом случае проекция на ось z не будет иметь точно определенного значения.
24
Как видно, максимальное значение дисперсии измеряемых зна юни“ х у проекций
момента импульса реализуется для состояния с Lz = 0, а минимальное для состояния с
максимально возможной величиной L. = . В этом случае.
В случае ( »1 для состояния Y(f имеем
180
Рис. 1.3. Угловые распределения плотности ве-
роятности для 5 - и р - состояний.
Поскольку, как уже отмечалось, в этом
состоянии = = то в предель-
ном случае к »1 и т = £ реализуется
почти классический случай: вектор мо-
мента имеет определенное направление в
пространстве (направлен вдоль оси z ).
Договоримся теперь о следующей
терминологии. Квантовое число £ будем
называть орбитальным квантовым числом. Оно задает значение квадрата момента коли-
чества движения. Обычно состояния с различными значениями I обозначают буквами
латинского алфавита. Состояние с £ — Q называют s -состоянием, с = 1 - р -
состоянием, I = 2 - d -состоянием, I - 3 - f -состоянием, и далее по латинскому алфа-
виту:
1 = 0, 1, 2, 3, 4, 5,...
s, р, d, f, g, h,...
Например, когда говорят о р -электроне, то это означает, что электрон находится в со-
стоянии с орбитальным квантовым числом равным единице.
Величина = |У^(<9,^)|2 определяет угловое распределение электронной
плотности в состоянии с заданным I. Как видно, это распределение характеризуется ак-
сиальной симметрией. Распределения угловой плотности для 5 - и р - состояний с раз-
личными z- проекциями момента (ди = 0,±1) приведены на рис. 1.3. Аналогичные рас-
пределения для d - состояний с различными значениями проекций углового момента
приведены на рис. 1.4.
Отметим еще одно важное свойство состоянии с заданным квадратом орбиталь-
ного момента. Эти состояния характеризуются определенной пространственной четно-
стью. Действительно, инверсия координаты г > — г означает, что сферические коорДИ'
наты точки (г,0,<р) преобразуются в (г,л — 0у(р + л), Поскольку сферическая функция
7^(0,^) обладает свойством
(1.5.13)
25
то все состояния с четным значением орбитального квантового числа (5, d, g,...) харак
теризуются положительной четностью, а состояния с нечетным значением £ (p,f, h,...) -
отрицательной четностью.
В случае, если речь о заряженной
частице, например, электроне, с орби-
тальным моментом количества движения
неразрывно связан магнитный момент.
Для построения оператора этого момента
найдем связь между физическими вели-
чинами, механическим и магнитным мо-
ментом, существующую в классическом
механике. Проще всего это сделать, рас-
сматривая случай круговой орбиты (см.
рис. 1.5). Действительно, запишем выра-
жение для магнитного момента
p = -iS. (1.5.14)
с
Здесь i --е/Т - ток в атоме, Т = 2я/бУ -
Рис. 1.4. Угловые распределения плотности
вероятности для d - состояний.
круговая частота обращения электрона вокруг ядра, a S = лг2 - площадь контура, охва-
тываемого током (вектор 5 направлен по нормали к поверхности и образует с направле-
нием обтекания контура правовинтовую систему). Учитывая также, что орбитальный
момент количества движения частицы есть
Рис. 1.5. Орбитальный механический и
магнитный моменты электрона.
£ = [г*р],
из (1.5.14) получим
р —
P = -—-L. (1.5.15)
2mc
Как видно, вектора L и Д направлены в противо-
положные стороны, что обусловлено отрицатель-
ным зарядом электрона. Величину ejlmc называ-
ют гиромагнитным отношением. Гиромагнитным
отношением (или g - фактором) часто также
называют безразмерную величину отношения
магнитного и механического моментов частицы (взятых по модулю):
g
е/2тпс
(1.5.16)
Переход к квантовой теории осуществляется просто. Та связь между величинами, кото-
рая существует в классической теории, в квантовой теории переносится на операторы.
Таким образом, мы можем ввести новый оператор - оператор магнитного момента ча-
стицы
26
л <'-5.17)
2тс
тт /» _ t f гл/лр w 11 и и магнигного момента*
Нас прежде всего будет интересовать опера тор z - проекции
(1.5.18)
2тс
Нетрудно видеть, что состояния с точно определенным значением z - проекции орби-
тального момента одновременно характеризуются точным значением z - проекции маг-
нитного момента, причем
с •
eh
Р(. =~^—т
2тс
Здесь т( =0, ±1, ±2,... - магнитное квантовое число7. Величина fiB — eh/2mc
характерное значение атомного магнитного момента и носит специальное
магнетон Бора. Численное значение /ив = 0.927 • 1О-20 эрг/Гс.
Модуль магнитного момента электрона может принимать значения
(1.5.19)
определяет
название -
(1.5.20)
здесь (. = 0,1,2,... - орбитальное квантовое число.
В заключение раздела отметим, что механический момент в квантовой механике
удобно измерять в единицах постоянной Планка, а магнитный момент (если мы говорим
об электроне) - в магнетонах Бора.
1.6. Собственные состояния оператора Гамильтона. Стационар-
ное уравнение Шредингера.
Рассмотрим теперь задачу на собственные значения и собственные функции опе-
ратора Гамильтона (мы полагаем, что потенциальное поле является стационарным):
Ну/ = Еу/, (1.6.1)
или
й2 2
- — vy/ + V(r)y/ = Ey/. (1.6.2)
2т
Эта задача на собственные значения и собственные функции имеет отдельное название -
стационарное уравнение Шредингера. Задача чрезвычайно разнообразна: в зависимости
от конкретного вида потенциала, определяющего в гамильтониан, спектр может дис-
кретным или непрерывным, может быть и так, что есть и дискретные уровни энергии, и
континуум одновременно. Ниже мы познакомимся с решениями задачи (1.6.1) для ряда
квантовых систем.
Знание набора собственных состояний оператора Гамильтона оказывается полез-
ным для решения нестационарного уравнения
7 Чтобы не путать массу электрона с магнитным квантовым числом мы в дальнейшем, как правило, маг-
нитное квантовое число будем обозначать символом .
27
/л^-zfy. (1.6.3)
dt
Пусть, в начальный (нулевой) момент времени система находится в некотором состоя-
нии 0(г):
И'\' = 0) = ^(г). (1.6.4)
Будем искать решение уравнения (1.6.3) в виде разложения в ряд по собственным функ-
циям {у/,(г)} оператора Гамильтона8:
= (1.6.5)
п
Здесь Сп - некоторые постоянные коэффициенты разложения. Подставляя разложение
(1.6.5) в уравнение (1.6.3), получим:
П У “Z )
Учитывая теперь, что у/п есть собственное состояние оператора Гамильтона с собствен-
ным значением Еп, перепишем (1.6.6) в виде
_ ( #г А
УС„ ih^--EnTn =
И ПИ т п v /
п \ dt )
(1-6.7)
Очевидно, это равенство возможно, если выражение, стоящее в скобках равно нулю. То-
гда получаем
TW = T(' = O).expl-i£,/
(1.6.8)
Коэффициенты разложения Сп определим по волновой функции начального состояния.
Для нулевого момента времени из (1.6.5) имеем
№) = '£с^(г'). (1.6.9)
откуда находим
Сп =
(1.6.10)
причем Тп (t = 0) = 1. Поэтому в окончательном виде решение нестационарного уравне-
ния (1.6.3) с начальным условием (1.6.4) записывается в виде
Vlf, /) = £ Спу„ (г) expf- £ А (1.6.11)
п \ * )
8 Такое разложение всегда возможно и является единственным вследствие полноты указанного набора.
Мы здесь для простоты полагаем, что спектр оператора Гамильтона является чисто дискретным.
28
Таким образом, знание базиса собственных функций оператора Гамильтона действ
тельно легко позволяет получить аналитическое решение начальной задачи0.
Рассмотрим теперь важный частный случай. Пусть в начальный момент врсмС(1
система находится в одном из собственных состояний гамильтониана i//n. Тогда, оЧс
видно, общее решение нестационарного уравнения (1.6.3) запишется в виде
I z г
^('',') = ^„('')ехр •
V п 7
(1-6.12)
Выражение (1.6.12) описывает эволюцию собственного состояния оператора Гамильтона
во времени. Отметим, что в рассматриваемом случае = \y/(f ,/)| = \у/п(г)|2 и Не За
висит от времени. Поэтому собственные состояния оператора Гамильтона называют
стационарными состояниями. В таких состояниях плотность вероятности обнаружить
частицу в различных точках пространства не меняется со временем. Не меняются во
времени и средние значения физических величин, рассчитанные по общим квантовоме-
ханическим правилам9 10. В дальнейшем, работая с функциями y/\(r), будем помнить, что
это пространственные части волновых функций стационарных состояний системы. Пол-
ные волновые функции стационарных состояний содержат еще и временную часть и
определяются с помощью (1.6.12).
1.7. Спин.
Совокупность опытных фактов, о которых мы будем говорить позже, приводит к
выводу, что помимо орбитального механического момента у частиц существует еще и
собственный механический момент, называемый спином11. В частности, говорят, что
спин электрона равен 1/2. Это означает, что проекция спина (собственного) механиче-
ского момента электрона на некоторую выделенную ось (например, ось z) составляет
±Й/2:
S: = msh = ±й/2.
(1.7.1)
При этом, как и для орбитального момента, проекции спина на два других направления
не имеют определенного значения, а их средние значения оказываются равны нулю.
С математической точки зрения спиновому движению электрона надо поставить в
соответствие еще одну (четвертую) степень свободы, причем соответствующая «коор-
дината», описывающая спиновое движение, принимает всего два возможных значения.
Тогда наиболее естественно задать состояния с проекцией спина на выделенную ось г в
9 Данное утверждение справедливо только если оператор Гамильтона не зависит от времени. Если это не
так, то, строго говоря, стационарных состояний у квантовой системы нет, и задача о ее временной эволю-
ции системы является существенно более сложной.
10 При этом, конечно, мы полагаем, что оператор физической величины А не зависит от времени.
11 Попытка классической трактовки спина заключается в рассмотрении электрона, как некоторого шарика
(например, с размером, равным классическому радиусу электрона) вращающегося вокруг собственно
оси. Такая картина, однако, не может быть признана удовлетворительной. Даже если распределить зар
по экватору шарика, окажется, что угловая скорость его вращения должна быть слишком большой: лине ♦
нал скорость на экваторе превысит скорость света. Спин следует рассматривать, как такое же «вро*Де
ное» свойство электрона, как, например, масса или заряд.
29
виде двухрядных столбцов: например, состоянию с проекций спина на ось z, равной
+ Й/2, ставится в соответствие столбец
а состоянию с S, = -h/2 - столбец . В
дальнейшем такие спиновые состояния электрона мы будем обозначать функциями
Z(w< =1/2) и =-1/2):
(1.7.2)
Произвольное спиновое состояние электрона, очевидно, есть столбец
. Это состоя-
ние можно представить в виде суперпозиции двух базисных состояний (1.7.2):
(1.7.3)
Здесь |а|“ определяет вероятность того, что при измерении будет обнаружена величина
проекции, равная +1/2 (в единицах Й ), а |/7|2 - есть вероятность того, что при измерении
будет обнаружена величина проекции, равная -1/2. При этом, естественно,
1«Г+И2=1-
Наша задача теперь определить операторы спина S = (s„$,S,), которые дей-
ствуют в пространстве спиновых функций. Очевидно, такие операторы - матрицы раз-
мера 2 х 2. Их можно записать в следующем виде:
(1-7.4)
где
(1.7.5)
Матрицы (1.7.5) называются матрицами Паули12 и представляют собой основу матема-
тической теории спина.
Проверим, прежде всего, что введенные нами состояния (1.7.2) действительно яв-
ляются собственными состояниями оператора z - проекции спина с собственными зна-
чениями Sz = ±Й/2. Действительно:
/о
йГ i
<0
ЙГОЛ
2lL
(1.7.6)
- ГоА
т.е. =±l/2) = ±^z(m, =±1/2).
12 Pauli Wolfgang (1900 - 1958) - физик -теоретик, Нобелевская премия (1945) «За открытие принципа за-
прета, названного его именем».
30
Ведем теперь оператор квадрата спинового момента S .
4 \v '/
Здесь I - единичная матрица. Следовательно,
52/(етЛ. =±1/2) = |й2/(шл. =±1/2) = /725(5 + 1)z(wv =±1/2), (1.7.8)
где квантовое число 5 = 1/2.
Таким образом, наши состояния %(ms = 1/2) и = — 1/2) являются собствен-
ными состояниями одновременно для операторов Sz и S2.
Мы уже говорили, что произвольное спиновое состояние электрона (как и любой
частицы со спином 1/2), очевидно, может быть описано столбцом
а
где а и /3 .
комплексные числа, причем |а|2 + |/?|2 =1- Нетрудно убедиться, что такое состояние яв-
ляется собственным состоянием оператора S2 с собственным значением Й25(5 + 1), од-
нако, в общем случае, не является собственным для оператора Sz. При этом физический
смысл коэффициентов а и ft заключается в том, что квадраты их модуля определяют
вероятности обнаружить проекции спинового момента на ось Z, равные + 1/2 и -1/2
соответственно.
Обсудим еще вычисление среднего значения проекции спина на любую из коор-
динатных осей в заданном состоянии
. Очевидно, поступать надо так:
(1.7.9)
где i = x,y,z - любая из координатных осей.
Можно ожидать, что наличие спина (собственного механического момента ча-
стицы) приведет к существованию у частицы и собственно магнитного момента. Это
действительно так, но эксперименты показали, что величина гиромагнитного отношения
для спинового момента электрона в два раза больше, чем для орбитальногот.е. мы
можем записать
fis=~—S. (1.7.10)
тс *
13 С теоретической точки зрения наличие у электрона собственного механического момента (спина) явля-
ется прямым следствием релятивистского волнового уравнения Дирака. Из этого уравнения также следу-
ет, что величина гиромагнитного отношения для спинового момента ровно в два раза больше, чем для ор*
витального момента. Следует, однако, иметь в виду, что уравнение Дирака было получено в 1928 году, т'е'
позже, чем эти факты были установлены экспериментально.
31
В этом случае для g - фактора находим g = 2 |4. Что касается состояний с заданными
проекциям момента на выделенную ось z = 1/2) и /(wt — —1/2), то нетрудно ви-
деть. что в этих состояниях величина z - проекции магнитного момента электрона со-
ставляет .
Собственные механические моменты существуют и у других частиц. Например,
протон и нейтрон это также частицы со спином 1/2. И с математической точки зрения
можно ввести точно такие состояния, как и для электрона, описывающие их спиновые
свойства. Однако с собственными магнитными моментами частиц (протона и нейтрона)
оказывается сложнее. Эксперименты показывают, что g - факторы для протона и
нейтрона равны gp « 5.58 и g «-3.82 соответственно14 15, а сами z - проекции магнитных
моменты равны
^=2.79/^, д, =-1.91/^,
= eh/2mpc - ядерный магнетон, тр - масса протона. Как видно, собственные магнит-
ные моменты нуклонов примерно на два три порядка меньше чем у электрона. Заметим,
также, что нейтрон, являясь незаряженной частицей, характеризуется ненулевым значе-
нием собственного магнитного момента.
1.8. Коммутатор.
Выше мы говорили, что физическая величина имеет точно определенное значе-
ние, если соответствующее состояние является собственным состоянием оператора этой
физической величины. Обсудим теперь вопрос, при выполнении каких условий сразу
две физических величины могут быть измерены точно в одном и том же состоянии?
Прежде чем ответить на этот вопрос, введем новое понятие коммутатора двух
операторов А и В . Определим коммутатор [л, в] следующим образом
[л,2?]= АВ-ВА. (1.8.1)
Если коммутатор [Л,Д] равен нулю, то говорят, что операторы коммутируют. В против-
ном случае операторы некоммутативны.
Рассмотрим несколько примеров. Займемся вычислением коммутатора операто-
ров х - проекций импульса и координаты [х,рд]. Для этого подействуем коммутатором
(это новый оператор, действующий в пространстве Ь2) на некоторую волновую функ-
цию y/(x,y,z). Получим:
[х,А^(х,у,г)
I '
= -/Й х-----------— (х у/) = /Й у/(х, у, z).
(1-8.2)
В результате имеем [х,^д] = /Й, т.е. операторы не коммутируют. С другой стороны, по-
скольку х, у и z - независимые переменные, легко показать, что коммутатор операто-
14 Более правильно было бы определить g - фактор, как g = -2, подчеркивая, что направления магнитного и
механического моментов противоположны, но мы сохраним стандартное обозначение.
15 Здесь знак “минус“ у нейтрона означает, что его магнитный момент направлен против спина (как и у
электрона), в то время как магнитный момент протона сонаправлен спину.
32
ров различных проекции импульса и коорлииагы равен у Р Р,
Сформулируем теперь важную теорему'6. Д- ^Тоника!
набор,,, собственных функций в там и
означает, что если коммутатор двух операторов отличен от , сУЩествует
стояний, в которых две физических величины, соответствующие данным °пераТОр^
могут быть точно определены одновременно. И, наоборот, если коммутатор равен нуЛ[0
можно найти общие собственные функции двух операторов, а, следовательно, суще,
ствуют состояния, в которых две физических величины могут^ ыть определены точн0
одновременно. Например, как мы уже видели, операторы одной и той же проекции им-
пульса и координаты не коммутируют между собой. Это означает, что не существу^
таких состояний, в которых соответствующие величины заданы точно одновременно.
В качестве еще одно примера рассмотрим операторы квадрата момента количе-
ства движения его проекции за данные оси. Мы видели, что собственные функции опе-
ратора L2 являются одновременно и собственным функциями оператора Lz. Это позво-
лило определить состояния, в которых величины Z2 и Lz точно определены. С другой
стороны, нетрудно видеть, что операторы Z2 и Lz коммутируют:
[л2Л]=о.
(1.8.3)
Вычисление коммутаторов, как правило, существенно проще, чем определение
собственных функций. Важно, что правила коммутации операторов позволяют безоши-
бочно предсказывать результат, даже когда собственные функции операторов неизвест-
ны. В качестве примера рассмотрим серию коммутаторов различных компонент проек-
ции момента количества движения .
\tX’Ly\=ihLz, \ty,Lz\=ihLx,
|Zzz, Lx j ihLy.
(1.8.4)
To есть все три проекции момента количества движения попарно не коммутируют меж-
ду собой. С другой стороны, квадрат момента количества движения коммутирует с каж-
дой из проекций:
[£2,Д]=0,где i = x,y,z
(1.8.5)
Правила коммутации (1.8.4), (1.8.5) в значительной мере определяют специфические
черты момента количества движения в квантовой механике. Мы можем найти состояния
с точно определенными значениями квадрата момента и одной из его проекций (напри-
мер, на ось z). Две другие проекции момента оказываются в таком состоянии точно не
определены, и мы можем говорить лишь о вероятности измерения того или иного значе-
ния этих проекций.
Посмотрим теперь на коммутаторы спиновых операторов , Sv., S: и S: • Оче-
видно, квадрат спина, являясь фактически единичной матрицей, коммутирует с любой из
матриц Паули, определяющих проекции спина, т.е.
16 Доказательство этой теоремы можно найти в любом учебнике пп -
17 Соответствующие коммутаторы легко вычисляются в дек™™ антовои механике-
пуляются в декартовой системе координат.
33
[.S’’,*V, jw 0. где / - г,y.z.
С' другой стороны, вычисляя
ПОЛУЧИМ
Г, Л ] й2
4
(18.6)
(1.8.7)
т.е. соотношение эквивалентное (1.8.4). Вычисляя попарно коммутаторы для других
проекция спина, также получим
|£Л]='Ч- <18-8’
Мы видим, что для спинового и орбитального моментов количества движения
действуют одни и те же правила. В частности, существует такой набор состоянии, в ко-
торых точно одновременно определены квадрат орбитального момента и его проекция
на одну из осей (наиболее удобно выбирать ось z) [} и L. То же самое относится и к
спину: мы нашли состояния, которые можно также характеризовать точно определен-
ными значениями S2 и Sz. В этом смысле работа с дифференциальными операторами,
описывающими орбитальный момент и его собственные функции в пространстве Lz,
оказывается совершенно аналогична матричной алгебре с матрицами Паули, действую-
щими в пространстве двухрядных столбцов.
Отметим, также, что поскольку операторы орбитального момента и спина дей-
ствуют в различных пространствах, все их компоненты попарно коммутируют между
собой. Следовательно, можно построить, например, базис состояний, в которых точно
определены квадраты орбитального и спинового моментов частицы, а также их проек-
ции на одну из осей.
Рассмотрим еще правила коммутации операторов орбитального момента н спина
для важнейшей задачи атомной физики - движения частицы в центрально симметрич-
ном поле, в частности, в кулоновском потенциале. В центрально симметричном поле по-
тенциальная энергия зависит лишь от удаления от центра и не зависит от угловых коор-
динат. Представляя оператор Гамильтона в виде
А Й2 Г72 I// ч Й2 1 дг L~ ... .
// = -—V2 + K(r) = --------+ -—y + K(r),
2т 2т г дг 2тг
и учитывая выражения для операторов квадрата момента и его z - проекции
L2 = -Й2Д^=-Й2
fl д ( . п д £
-------SIH# 1 + ,
Vsin#d#v (Ю) sin2#
Lt =-ihd!d<p,
легко показать, что
34
I/7J/J-0. •' u.8.9)
- млммсгписй мы можем найти стационарные СОст
то сеть в потенциале с центральной с момента количества движения
ння с точно определенными значения ч_|1Исанный выше гамильтониан не *
проекцией на „«деленную ось е. Поскольку«писан
от спина, то. например, для электрона стаи Р =1/2 или т =z~\i^ в₽и’
зовать определенным значением проекции спина на ос ,
-.ч'.шенис квадрата спина уже точно опоет»
мы говорим об одноэлсктроннои системе, з 1еде.
но. поскольку S’2 = Л2л(л’ +1) = (3/4)Й2 •
Сформулированные нами утверждения играют Р°ль в «Га-
гике стационарных атомных состояний. С некоторыми допущениями аналогична, С11.
стсматика используется для характеристики нуклонов в атомн др
1.9. Соотношения неопределенностей.
ЛВУХ физических величин не коммутируют, то не
Мы видели, что если операторы двух ц»
ы видсл ’ v J 6 Физических величины могут одновременно при-
существует состоянии, в которых оое ф
J у n„OUMa R такой ситуации можно говорить о средних за-
нимать точно определенные значения. от у
F . п X,мирских величин В случае, если коммутатор рассмат-
чениях и дисперсии каждой из физических величин. у
„„.шшпми ппепатооу как это имеет место, например, для
риваемых операторов кратен единичному оператору,
операторов импульса и координаты
ДАг]=/й’
дисперсии физических величин оказываются связанными соотношением неопределен-
ности.
Не ограничивая общности рассмотрения, остановимся на случае состояний, удо-
влетворяющих условиям (х) = (р) = 0. Рассмотрим неотрицательный функционал на мно-
жестве функций с интегрируемым квадратом
2
EV \ Г . Jv'
W) = I аху/(х) + -~
< dx
(1.9.1)
Перепишем функционал в виде:
F(</) = а2 [ х2 |</(х)|2 dx + f dx +
± dx dx
Очевидно, что
/, = а2 (х2} = a2 Dx,
00 I1
1 f • d u/ , 1 /
35
It = a |.v-‘-|y/(x)|2t/x = -«||y/(x)|2t/x = -a .
-'*> ' -f)A
Поэтому условие неотрицательности функционала /г0//) приобретает вид:
F\a) = a2Dx -a + Djh2 £0. (1.9.2)
Для того, чтобы полученный квадратичный (по а) трехчлен был неотрицательным при
любых значениях а , его дискриминант Д = 1 -4DX Dp/К1 должен быть меньше нуля, т.
е. должно быть выполнено условие
О,Л„>Л74. (1.9.3)
Полученное соотношение называют соотношением неопределенностей для импульса-
координаты. Для произвольного вида волновой функции произведение дисперсий им-
пульса и координаты не может быть меньше, чем й2/4.
Определим вид волновой функции, которая минимизирует соотношение неопре-
деленностей, т.е. найдем состояние, для которого величина произведения DxDp оказы-
вается минимальной. Функционал F(^) обращается в нуль только если выполнено
условие
аху/(х) + ^- = 0,
dx
отсюда для волновой функции, минимизирующей соотношение неопределенностей, по-
лучаем
j/(x)~exp(-ax2),
т. е. гауссов волновой пакет, ширина которого определяется параметром а .
Вводя понятия неопределенностей координаты и импульса Дх = -/5? и
Дрх = ^Dp , мы можем записать соотношение неопределенностей в виде
ДхДрЛ>Й/2, (1.9.4)
или просто
&х Дрх £ Й .
В общем случае такие же соотношения мы можем записать для двух других проекций
импульса и координаты
AyApv>h, (1.9.5)
С другой стороны, никаких ограничений на определение различных проекций, напри-
мер, х - проекция импульса и у - координаты, не возникает.
Мы видели ранее, что импульс частицы связан с волновым вектором соотноше-
нием p-hk. Поэтому соотношения неопределенностей для импульса и координаты
можно записать и таким образом:
36
Av ЛА\ £ I. Дг M,. ~ 1 •
В таком виде соотношения неопределенностей нам хорошо знако по волновой тСо_
рни. Действительно, если имеется пространственный волновой паке! размера Аг , то0н
имеет спектральную ширину в пространстве волновых векторов А г /Ах. Как резудь_
тат, возникает дифракционное расплывание волнового пакета.
Отмстим, что в волновой теории известно и друг ос соотношение связь частот,
нои ширины спектра сигнала Ave его длительностью г .
A v г ~ I.
Вспоминая связь частоты и энергии Е = tico, получаем соотношение неопределенностей
для энергии - времени
АЕ т ~ti.
(1.9.7)
Обычно в квантовой теории это соотношение трактуется следующим образом. Если не-
которое состояние живет конечно время г, то его энергия может определена лишь с
точностью до соотношения неопределенностей &Е ~ h/т. Более конкретно с этим
утверждением мы познакомимся в Главе 14 при рассмотрении излучательных процессов
в атомах.
Часто соотношения неопределенностей позволяют на качественном (оценочном)
уровне решать большое число квантовомеханических задач, не прибегая к громоздким
вычислениям.
1.10. Многочастичная квантовая система. Понятие о матрице
плотности.
До сих пор мы рассматривали движение одной частицы в произвольном потенци-
альном поле. Остановимся теперь на некоторых особенностях многочастичных кванто-
вых систем. Мы ограничимся случаем двухчастичной квантовой системы, поскольку
обобщение на случай многих частиц делается элементарно.
Введем волновую функцию системы из двух частиц у/(г\, г2), находящихся в не-
котором внешнем потенциальном поле. Величина p{rx,r2} = |v'(rl,r,)|2 представляет со-
бой двухчастичную плотность вероятности, т.е. плотность вероятности того, что одна из
частиц находится в точке с координатой г,, а вторая - с координатой г2. При этом веро-
ятность обнаружить одну из частиц в некоторой точке пространства получается путем
интегрирования двухчастичной плотности по координате другой частицы. Например,
Pi(O = J|^(F,F2)|2€/3r2
(1.10.D
есть плотность вероятности обнаружить первую частицу в точке с координатой г . Ана-
логично, интегрируя по первой координате, получим одночастичную плотность вероат
ности для второй частицы:
(1.10.2)
37
Рассмотрим теперь задачу на собственные значения и собственные функции опе-
ратора Гамильтона двухчастичной системы. Пусть оператор Гамильтона системы запи-
сывается в виде
Н 0-. Г-2) = Н, (г,) + Н2 (г2) + У12 (г2),
(1.10.3)
где
Й,^ = Т, + К(г,) (1.10.4)
- гамильтониан i - той частицы ( / = 1,2 ), включающий в себя ее кинетическую энергию,
а также взаимодействие с внешним потенциальным полем, а также ' межча-
стичное взаимодействие.
Например, если мы рассматриваем простейший многоэлектронный атом, атом
гелия, то в одночастичный гамильтониан (1.10.4) входит кинетическая энергия электро-
на и взаимодействие электрона с ядром, а оператор Г12(^, г2) описывает межэлектронное
взаимодействие.
Стационарные состояния двухчастичной системы могут быть найдены из стацио-
нарного уравнения Шредингера
(1.10.5)
Казалось бы, каждый из электронов должен характеризоваться своей волновой функци-
ей ^(ъ), поэтому решение уравнения (1.10.5) следует искать в виде произведения од-
ночастичных функций
= (1.10.6)
Тогда, в частности, из выражений (1.10.1) и (1.10.2) получим уже привычные для нас со-
отношения
А(П) = |^1(^)Г и Р2(^) = к2(':2)Г • (1.10.7)
Однако, мы сейчас покажем, что факторизация двухчастичной волновой функции на
произведение двух одночастичных возможна лишь в случае невзаимодействующих
между собой частиц. В противном случае введение одночастичных функций в многоча-
стичной квантовой системе оказывается невозможным. Действительно, подставим раз-
ложение (1.10.6) в уравнение (1.10.5). Учитывая, что операторы и Н2 действуют в
подпространствах функций, зависящих от 7] и г2 соответственно, получим
(/2(Д</|)+^1(^2У/2)=(£'“ ^12^1^2- (1.10.8)
Разделив все теперь на произведение > получим
= + (1.10.9)
V. Vi
Если К) 2 (г;, г2) е 0, то левая и правая части в (1.10.9) зависят от координат только первой
и только второй частицы соответственно. Следовательно,
38
^L = £, и S^ = e2 = e-e,, (1.1O|
V, Vi
где £, „ Ег - некоторые постоянные величины. В результате получаем два одно^
ных уравнения Шредингера, а Е, и Е, имеют смысл энергий стационарных состоя^
первой и второй частицы соответственно. Если частицы взаимодействуют между собой,
то есть Й]2(^2)#о, факторизация (1.10.6) оказывается невозможной. ОдночастиЧНь|’
функции в системе взаимодействующих между собой частиц ввести нельзя.
Однако, в квантовой теории многочастичных систем (многоэлектронные атомы,
электронная подсистема твердого тела, атомное ядро) широко используется понятие од.
ночастичного состояния и одночастичной волновой функции. Эти понятия могут быть
введены лишь приближенно, в случае если взаимодействие между объектами достаточно
мало, или, например, в рамках концепции самосогласованного поля. Основная идея этой
концепции заключается в следующем. Мы выделяем одну из частиц, например, один из
атомных электронов, и рассматриваем его движение в потенциале, созданном ядром
плюс всеми остальными атомными электронами. Так поочередно поступаем для каждого
электрона. В результате каждый из электронов характеризуется своей одноэлектронной
волновой функцией, которая через электростатический потенциал зависит от волновых
функций одноэлектронных состояний всех остальных электронов. В теории многоэлек-
тронных атомов такой подход был развит Д. Хартри18 в 1928 году, и будет обсуждаться
нами при изучении строения многоэлектронных атомов. В теории атомного ядра пред-
ставление о самосогласованном поле лежит в основе так называемой одночастичной
оболочечной модели.
Отметим, что если речь идет о системе одинаковых (тождественных) частиц,
например, электронов, то представить полную волновую функцию системы в виде про-
изведения одночастичных волновых функций оказывается не всегда возможно даже в
отсутствие взаимодействия между частицами. Более подробно на этом «парадоксе» мы
остановимся в Разделе 1.14 при обсуждении принципа тождественности микрообъектов.
Таким образом, мы видели, что в системе взаимодействующих объектов ввести
одночастичные волновые функции, строго говоря, невозможно. Поскольку любой из ма-
териальных объектов взаимодействует со своим окружением, то фактически мы неиз-
бежно придем к выводу, что для его описания необходимо ввести волновую функцию
Вселенной. Бессмысленность такого подхода очевидна. Например, если хотим описать
один из атомов, образующих газовую среду, то необходимо учесть его взаимодействие с
другими атомами, со стенками сосуда, в котором он находится. Атомы, образующие со*
суд, в свою очередь взаимодействуют между собой, а также с поверхностью, на которой
сосуд находится, и т.д. Мы можем говорить о волновой функции некоторого объекта
только в приближении отсутствия взаимодействия с его окружением. А как быть, если
это взаимодействие с окружением необходимо учесть? Оказывается, в этом случае
удобно ввести новое понятие - матрицу плотности.
Представим себе, что у нас есть некоторая квантовая система (например, атом),
характеризующаяся совокупностью координат q, взаимодействующая со своим окрУ'
18 Hartree Douglas (1897-1958) - английский физик - теоретик.
39
жснисм (будем называть это окружение термостатом), описываемым совокупностью ко-
ординат Q (см. рис. 1.6). Тогда для описания полной системы «атом + термостат» можно
ввести волновую функцию Ч'(д,£>). В отсутствие взаимодействия атома с термостатом
полная волновая функция системы представима в виде
= (1.10.11)
Если нас интересует эволюция атома, взаимодей-
ствующего со своим окружением, то волновая
функция ^{q^Q) не факторизуется на сомножи-
тели. В тоже время изучать динамику полной си-
стемы чаще всего не представляется возможным.
Введем понятие матрицы плотности, описываю-
щей состояние атома, с помощью следующего
соотношения
Рис. 1.6. К введению понятия матрицы = j 4х (q,Q,ty¥(q',Q,t)dQ. (1.10.12)
плотности. Квантовая система и тер-
мостат. Как видно, введенная нами матрица плотности
зависит только от координат исследуемого объ-
екта и не зависит от координат термостата. Диагональный элемент этой матрицы
p(q,q'= q,t) имеет смысл плотности вероятности обнаружить у атомной подсистемы
координаты q . Чтобы убедиться в этом, рассмотрим предельный случай отсутствия вза-
имодействия атомной подсистемы и термостата, используя факторизацию (1.10.11) по-
лучим
p(q,q'= q,l) = J'V’(q,Q,t)'V(q,Q,t)dQ = (6.^(6.WQ = \V(q,tf ,
то есть обычное выражение для плотности вероятности.
Существенно, что в некоторых приближениях, описывающих взаимодействие
квантовой системы с термостатом, для матрицы плотности может быть получено за-
мкнутое уравнение (уравнение Неймана19), которое не содержит координат термостата.
В квантовой теории состояния, которые не могут быть описаны в терминах вол-
новой функции и требуют введения матрицы плотности, принято называть смешанными
состояниями. В случае, если введение волновой функции возможно, то говорят о чистых
состояниях квантовой системы.
1.11. Движение волновых пакетов. Предельный переход к класси-
ческой механике.
Как мы уже отмечали, в квантовой механике у частицы отсутствует понятие тра-
ектории движения. В каждый момент времени ее состояние задается некоторым волно-
вым пакетом, имеющим конечную область пространственной локализации. Мы теперь
обсудим условия, при выполнении которых квантовомеханическое движение может
19 von Neumann John (1903 - 1957) - венгерский и американский математик и физик.
40
быть описано в классическом пределе и возникает предогавле Д нии Микро^^
окта по классической траектории.
Докажем прежде всею справедливоетт» следующего утверждения теорема
фоста20). Основное уравнение классической механики, апис ывающее (вижение Цасгпицы^
потенциальном поле Г (г)
= р = (1.11 ।
di 1
в квантовой теории справедливо для усредненных по квантовому состоянию велцц^
т.с.
где
(,Р) = Ji//'(r,l)pt//(r,t)d,r ,
У У} = J
Докажем это утверждение. Дифференцируя (1.11.3) по времени, получим
d/_х t(dy z ,d.z Л,3 с( дух*
т\д)=1 d г = \
at J < dt dt J \ dt
pyx + yx* p(dyx/dt) d3r .
(1.11.2)
(1-U.3)
(1-11.4)
(1.11.5)
Выражения для производных по времени от у/ и ух* возьмем из уравнения Шредингера
dt dt *
Тогда получим
4& = Т^)“ WPHv^r = f (ух*Нрух - ух*^Нух\3г = у [ух* [н, ptyd'r.
at п * ЛУ п J
(1.11.6)
Здесь мы воспользовались свойством эрмитовости оператора Гамильтона
Вычисляя коммутатор операторов Н и f>
[A>J=[p.^J=/rtvr,
окончательно получим
j((p) = -J ys'lyv^r = -(VK) = (1.11.7)
Таким образом, теорема Эренфеста доказана.
Уравнение Эренфеста (1.11.7) по форме совпадает с уравнением классической
механики. Это совпадение будет выглядеть еще более полным, если доказать следующее
утверждение (см. задачу 1.12)
20 Ehrenfest Paul (1880 - 1933) — австрийский и нидерландский физик - теоретик
41
d(r\ / / . Г a а] I
-7^ = т(^ [Я’г У/} = — (р)> (1.11.8)
си п\ т
то есть производная по времени от среднего значения координаты частицы равна сред-
нему значению скорости (р}[т. С учетом соотношения (1.11.8) уравнение (1.11.7) мож-
но переписать в виде
<72(г) 1 . .
=---(VK . (1.11.9)
dt т
Казалось бы, для определения средних значений физических величин достаточно ре-
шить классические уравнения движения. На самом деле это не так. Уравнение (1.11.9) не
может быть непосредственно использовано для решения задач динамики, так как для
определения средних значений необходима информация о волновой функции системы,
которая должна быть получена из решения уравнения Шредингера. Рассмотрим, однако,
случай, когда величина среднего по квантовому состоянию значения импульса частицы
существенно превышает его неопределенность Ар, т.е.
(р}»4>~Л/а, (1.11.10)
а - начальная ширина волнового пакета. В такой ситуации перемещение частицы за не-
которое время t
L = (Р)*1т
окажется много больше, чем неопределенность координаты частицы (ширина пакета)
Ах ~ , обусловленная расплыванием волнового пакета во времени
L»Ax(t),
т.е. можно приближенно считать, что частица характеризуется определенным значением
координаты, совпадающим с положением «центра тяжести» пакета [х(1)^.
Для того чтобы из (1.11.9) следовал классический закон движения для (*(/)),
необходимо также выполнение условия
{F(x)} = F({x)),
то есть среднее значение силы должно совпадать с величиной силы в «средней» точке.
Последнее условие, очевидно, выполнено, если на размере Ах, определяющем ширину
волнового пакета, величина Г(х) почти не меняется, т.е. потенциальная функция есть
плавная функция координаты
|УК|«Г(х)/Лх. (1.11.11)
Таким образом, условием перехода к классическому описанию движения микрообъекта
является его движение с большой скоростью (см. условие (1.11.10)) в плавно меняю-
щемся в пространстве силовом поле (см. (1.11.11)).
42
1.12. Представления Шредингера и 1 ейзеибер
„н.мгиспия средних значений физических
Уравнения (1,11.7). (1.11.1» Л"« ’ ’ ,)ависИМОсти от времени позв<)ЯяJ*4
чин (конкретно, импульса и коорди.ш< > „ Мы можсм рассматривать '
новому взглянуть на формальное нос рос₽ зависящих от времени (таки *
отношения, как уравнения движения для опер 1 ие о^
раторы называются гейзенберговскими)
с/ Л i [л -
V = 7 И'Р(;
dt h
имея в виду, то средние значения наблюдаемых величин вы желаются обычным обрд.
зом. как интегралы вида
а волновые функции считаются заданными и независящими от времени. При этом к
уравнениям движения для операторов (1.12.1) необходимо задать начальные условия,
которые, очевидно, имеют вид
PG(t = 0) = P
dt ° лL
з
-ihv, rG(t = o) = f
то есть в начальный момент времени операторы заданы «обычными» соотношениями,
введенными ранее. Такие независящие от времени операторы принято называть шредин-
геровскими операторами.
Можно показать, что уравнения вида (1.12.1) справедливы для любого введенного
нами ранее квантовомеханического оператора F .
2р0 =1[Я,#О], (1.12.3)
dt h
где в начальный момент времени
FC(/ = O) = F.
Фактически, речь идет о возможности перехода от одной квантовомеханической
картины описания движения в микромире к другой. В «обычной» шредингеровской кар-
тине введенные нами операторы не зависят от времени, а эволюция системы определя-
ется изменением во времени волновой функции. В картине Гейзенберга во времени из
меняются операторы, сама же волновая функция определяется начальным условием за-
дачи. Можно показать, что эти две картины (или, как принято говорить, эти два пред-
ставления) эквивалентны друг другу. Какое из них использовать — это вопрос удобства.
В качестве простейшего примера использования представления Гейзенберга Р»с'
смотрим задачу о свободном движении частицы. В этом случае из (1.12.3) имеем ЗР”'
нения
Учитывая начальные условия (1.12.2), получим
43
Л(О = Р = -^, rG(t) = r+ — р.
(1.12.5)
Из (1.12.5) сразу же следует, среднее значение импульса не меняется во времени и сов-
падает с начальным. Что касается среднего значения координаты, то она изменяется по
линейному закону движения. Эти же результаты, естественно, следуют и из (1.11.9). От-
метим, что переход к представлению Гейзенберга часто оказывается удобен, когда необ-
ходимо определить лишь низшие моменты распределений физических величин, в то
время как информация об эволюции волновой функции системы не требуется.
1.13. Пространственная четность состояний.
В этом разделе мы познакомимся с еще одной важной физической величиной, ха-
рактеризующей квантовомеханическую систему, а именно, с пространственной четно-
стью (или просто четностью) состояния. Определим оператор четности Р следующим
образом
РИг) = И-г). (1-13.1)
А теперь рассмотрим задачу на собственные значения оператора четности:
Р^(г) = 2^(г) (1.13.2)
Подействуем на соотношение (1.13.2) оператором четности еще раз:
Р(Р|/(г)) = Р(Я^(г)) = ЛРуЛг) = Л2у/(г) .
С другой стороны, из (1.13.1) имеем
Р(/>(г)) = РСУ^-г)) = И?) •
Поэтому Л2 = 1, или для собственного значения оператора четности Л = ±1, т.е. из
(1.13.1), (1.13.2) следует, что
И“':) = ±И':), (1.13.3)
Мы получили, что собственные функции оператора четности должны быть либо четны-
ми, либо нечетными функциями координаты. Ранее мы видели, что инверсия координа-
ты г —> -г означает, что сферические координаты точки (г, 0, (р) преобразуются в
(г, л - 0, (р + я). Поскольку сферическая функция Ytm {0, ср} обладает свойством
У(т(я-0,<р += Y(m(0,(p),
то в состояния с заданным квадратом момента количества движения обладают и опреде-
ленной честностью, определяемой значением орбитального квантового числа Л = (-!)*,
а сам оператор квадрата момента коммутирует с оператором четности:
(1.13.4)
44
Особый интерес представляет возможность введения четности стационарных со
мильГ” СИСТСМЬ1, 410 возможно, оператор четности коммутирует с оператор^41’!’
1\-
[А«]=0. (1.13.5)
Легко видеть, что последнее возможно, сели потенциальная функция И(г) является
ной функцией координаты = И(—г) • Ниже при анализе энергетических спектр^
ряда конкретных модельных систем мы увидим, как использование понятия четности
упрощает анализ конкретных систем. В частности, еще не решая задачу об энергети^.
ских состояниях в кулоновском потенциале, мы можем сказать, что существует набор
стационарных состояний, характеризующихся четными или нечетными волновыми
функциями, причем четность состояния определяется значением орбитального кванто-
вого числа.
1.14. Симметрия волновой функции относительно их перестанов-
ки местами. Тождественность микрообъектов. Бозоны и фермионы.
Принцип Паули.
Теперь мы познакомимся еще с одним видом симметрии волновой функции в
многочастичной квантовой системе, состоящей из ансамбля тождественных частиц
(например, электронов). Речь идет об операции перестановки частиц местами. Для про-
стоты будем считать, что у нас имеется система из двух частиц (электронов), описывае-
мая волновой функцией ^(^, £2) (здесь £ и £2 - совокупности координат первой и вто-
рой частицы). Введем оператор перестановки частиц местами
= (1-14.1)
Рассмотрим задачу на собственные значения и функции оператора перестановки
Рр(£„&) = Лр(£„{2). (1.14.2)
Подействуем на левую и правую части (1.14.2) оператором перестановки еще раз
РУй.Й) = Р(Р^ ,&) = ,£). (1-14.3)
С другой стороны, из (ХО. 14.1) имеем
то есть 22 = 1, или 2 = ±1 - собственные значения оператора перестановки. В системе
одинаковых частиц (например, электронов) оператор Гамильтона коммутирует с опера'
тором перестановки. Таким образом, собственные функции оператора Гамильтона
должны быть симметричным 2 = 1 и, или антисимметричным Л = —I относительно пе
рестановки частиц местами:
и^^2) = ±^2,^). (1-14-4)
Утверждение (1.14.4) является математической формулировкой принципа тождеств
ности микрообъектов: волновые функции И£»£2) и описывают одно и то*е
состояние двухчастичной системы.
45
Рассмотрим важный частный случай - систему двух невзаимодействующих ча-
стиц. В этом случае волновая функция системы ^(^,^2) может быть представлена в ви-
де произведения одночастичных функций
И£,Л) = ^,(£.Ш£)- (1.14.5)
Выражение (1.14.5) не удовлетворяет принципу тождественности. Перестановка частиц
местами ведет к другому состоянию • Однако, из двух введенных одноча-
стичных функций у/, (£) и j/, (£) можно построить две комбинации, удовлетворяющие
необходимым свойствам симметрии. Одна из них является симметричной
V'S (£) ^2 ) = (^1 )^2 (£ ) + (<2 >2 )) >
а другая - антисимметричной относительно перестановки электронов местами
Л £) = ^ (^! (£, >2 >2 (£ )) •
(1.14.6)
(1.14.7)
Наиболее важным свойством полученных состояний является то, что даже в отсутствие
взаимодействия в общем случае волновая функция системы тождественных частиц не
может быть представлена в виде произведения одночастичных функций, то есть
^(Л,(^И<,)*^(^)^(^). (1.14.8)
Состояния, для которых выполнено условие (1.14.8). называются перепутанными (от ан-
глийского «entanglement» - перепутывание) и лежат в основе многих современных при-
ложений квантовой теории, включая квантовые компьютеры и квантовую телепортацию.
До сих пор мы рассматривали лишь систему из двух частиц. Обобщение на слу-
чай Af - частичной системы делается элементарно. Волновая функция системы из N
частиц должна быть симметрична или антисимметрична относительно перестановки
любой пары частиц местами:
..£...г>....^.) = ±и^.-^,..4„-^). (1-14.9)
В частном случае невзаимодействующих частиц правильная (то есть удовлетворяющая
принципу тождественности) антисимметричная волновая функция N - частичной си-
стемы может быть записана в виде
Г1(£) —
^(4л ) пгт
yINl
^(£1) ^2(^2) ••••
(1.14.10)
Здесь (£) - «обычные» одночастичные волновые функции. Многочастичная волновая
функция, записанная в виде (1.14.10), называется детерминантом Слэтера21. Перестанов-
ка частиц местами означает перестановку пары столбцов в определителе (1.14.10). Хо-
:| Slater John Clarke (1900 - 1976) - американский физик - теоретик.
46
рошо известно, что при такой перестановке определитель Вол,
новая функция (1.14.10) действительно является антисимм но пере.
становки любой пары частиц местами.
Итак, мы видели, что с математической точки зрения принцип тождественно^
частиц означает свойство симметрии: волновая функция системы частиц должна быц,
либо симметрична, либо антисимметрична относительно перестановки частиц местами.
А какой из этих случаев реализуется в природе? Оказывается о а. ричем симметрии,
ная волновая функция описывает совокупность частиц с целым спином s 0,1,2,...), а
антисимметричная - совокупность частиц с полуцелым спином (5 1/2,3/2,...). Таким
образом, спин оказывается важнейшей характеристикой, описывающей свойства сим-
метрии частиц.22
Помимо электронов к числу частиц с полуцелым спином относятся протон и
нейтрон, мюон (их спин - тоже 1/2) и многие другие частицы. Целым спином характери-
зуются, например, фотон, нейтральный и заряженные пионы (тг ,/г ), частицы - кванты
переносчики слабого взаимодействия (1F*,Z0 - бозоны) и другие частицы. Понятие
спина может быть введено и для составного объекта в случае, если энергия связи этого
объекта значительно превышает его энергию взаимодействия с окружающим миром.
Например, энергия связи атомных ядер на много порядков превышает энергию взаимо-
действия ядра с электронной оболочкой атома. Это позволяет рассматривать ядро как
единый объект и ввести понятие спина ядра. Аналогично, если в газе или жидкости
энергия взаимодействия атомов (молекул) мала по сравнению с их внутренней энергией
(потенциалами ионизации и (или) диссоциации), то можно говорить о спине атома или
молекулы.
Из рассмотренных свойств симметрии волновой функции системы частиц с оче-
видностью следует принцип Паули. Две частицы с полуцелым спином не могут нахо-
диться в одном и том же квантовом состоянии. Действительно, пусть у/{ (£) = С?) •
Тогда
^(^^2) = ^(^1(^>1(^2)-^1(^>1(^))=0,
(1.14.11)
т.е. такое состояние невозможно. Этот принцип (известный также как принцип запрета
Паули) был сформулирован В.Паули еще до создания квантовой механики на основе
анализа атомных спектров.
В рамках приближения самосогласованного поля стационарные состояния атом*
ных электронов задают некоторым набором квантовых чисел. Поэтому можно утвер-
ждать, что в атоме не может быть двух электронов, характеризующихся одним и тем
же набором квантовых чисел.
Как мы увидим в дальнейшем, принцип Паули необходим для понимания строе-
ния электронных оболочек атомов. В более широком плане принцип тождественности
22 Надо иметь в виду, что здесь речь идет о полной волновой функции системы, включающей ее спиновую
часть. Например, если мы говорим о системе из двух фермионов, в частности электронов антисиммет-
ричную относительно перестановки частиц местами волновую функцию можно построить в виде произве-
дения антисимметричной пространственной части, и симметричной спиновой или наоборот. И наобороЬ
спиновой симметричной части должна тогда соответствовать асимметричная пространственная часть.
47
оказывается принципиально важен при описании систем многих частиц и отвечает за
возникновение многих макроскопических квантовых эффектов.
1.15. Сложение моментов количества движения.
Представим себе, что в атоме имеется совокупность электронов, каждый из кото-
рых может быть охарактеризован определенным значением орбитального и магнитного
квантовых чисел23. Поэтому естественно встает вопрос о значении суммарного момента
количества движения электронов в атоме. При этом, в зависимости от ситуации, речь
может идти как о нахождении суммарного орбитального или спинового момента сово-
купности электронов, так и о сложении моментов различной природы.
В данном разделе на примере сложения орбитальных моментов количества дви-
жения двух частиц (электронов) мы рассмотрим общую постановку задачи о сложении
моментов количества движения двух частиц. При этом мы будем полагать, что правила,
полученные нами, будут справедливы для сложения моментов любой природы (напри-
мер, орбитального и спинового моментов электрона, спиновых моментов двух электро-
нов, орбитального момента одного электрона и полного механического момента другого
электрона и т.д.).
Итак, пусть имеются два невзаимодействующих электрона, характеризующихся
совокупностью орбитальных и магнитных квантовых чисел £х,тх и £2,т2 соответ-
ственно24. Это значит, что состояние двухэлектронной системы представимо в виде
(/(1,2) = (1>^2 (2) = 1I,, тх) • 112, т2). (1.15.1)
Здесь аргументы «1» и «2» означают совокупность координат первого и второго элек-
трона. При заданных значениях £х и £2 полное число таких состояний -
(2Л+1Х24+1).
Введем операторы полного момента и полной проекции момента количества
движения
£ = Lz=£2X+£z2, (1.15.2)
Здесь и далее при рассмотрении многоэлектронных систем мы будем использовать ма-
лые буквы для обозначения момента (проекции момента) конкретного электрона, а
большие - для обозначения тех же величин, характеризующих всю совокупность атом-
ных электронов.
Нетрудно установить следующие коммутационные соотношения для введенных
А А
нами операторов. Поскольку операторы и 12 действуют в различных подпростран-
ствах, то
] = 0, [?;,?„]= О, i,у = 1,2.
Мы здесь неявно используем приближение самосогласованного поля, т.к. подразумеваем возможность
введения одноэлектронных состояний.
В этом разделе, чтобы не загромождать формулы, величину z - проекции орбитального момента мы
будем обозначать как т , а не т(.
48
Кроме того, нетрудно показать, что
Z?.??j=O. / = 1,2-
Также, каждый из операторов квадрата момента коммутирует со своей проекцией. Од.
нако,
' = |'2' (1-15.3)
Это означает, что помимо набора квантовых чисел и р р зующихСОн
стояние двухэлсктронной системы, можно ввести и другой набор, а именно .
Г,л,ЛWt, где квантовые числа L и М,, определяют квадрат полного момента двух
электронов и величину его проекции на ось z. При этом в состоянии с заданным пол-
ным моментом L величины z - проекции моментов каждого из электронов не могут
быть определены точно. Таким образом, мы имеем два набора базисных функций, опи-
сывающих состояние двухэлектронной системы
и . (1.15.4)
Мы хотим определить набор значений, которые могут принимать суммарный момент L
него z - проекция ML в состоянии |^1,/и1)-|^2,/и2) •
Поскольку |/'1,/'2,ДЛ/£) есть собственная функция оператора L:, то
= (1.15.5)
С другой стороны
41 Л > '«I ) • 1^ 2 , ^2 ) = lz *" 2z ) 1»^1) ' I 2 > ^2 ) =
Az|^uwi) + ^2z|^2’w2) = ^(^1 + w2)|^i,W]) -|^2,ги2) . (1.15.6)
Сопоставление (1.15.5) и (1.15.6) дает
. (1.15.7)
Полученное правило сложения проекций момента количества движения позволяет ре-
шить вопрос о максимальном и минимальном значении полного орбитального момента в
состоянии Как видно из (1.15.7), максимальное значение проекции
полного орбитального момента есть
ml = t, + е2.
Поскольку максимально возможное значение магнитного квантового числа равно орби-
тальному квантовому числу, мы приходим к выводу, ЧТО максимальное значение полно-
го орбитального момента есть
^ПВХ “ 1 + G •
49
Такое значение соответствует ситуации, когда вектора и «параллельны» друг дру-
гу. Минимальное же значение L соответствует случаю, когда вектора и /2 «антипа-
раллсльны»25. Для этого случая
=ki -Ц-
rmn I I 21
Таким образом,
|^i - £ 2| < £ < + ^2, через единицу,
или
£ = ^+^2, е, + £2-1, ^+^2-2, ...,|^-^2| + 1, (1.15.8)
всего (2^ 2 +1) или (2^ । +1) значений. Нетрудно видеть, что, как и следовало ожидать,
полное число состояний в базисе |€р€2,£,Л/д) также равно (2^ + 1)(2j?2 +1). Действи-
тельно (мы полагаем, что £х > /2):
14 (2(Л+^2) + 1) + (2(Л-^) + 1)
(2L +1) = —Z—LkJ------12—/ pg 2 +1) = (2/, +1)(2^ 2 +1).
2
Отметим еще раз, что сформулированное правило (1.15.8) справедливо при сложении
моментов любой природы.
Рассмотрим несколько примеров.
1. Пусть имеются два электрона, один из которых находится в р, а другой в -
d состоянии. Определить возможные значения полного орбитального момента. В рас-
сматриваемом случае £х =1, ^2=2. Поэтому, в соответствии с (1.15.8), находим
L = 1,2,3, то есть возможны Р, D и F состояния26.
2. Определить возможные значения полного спинового момента двух электронов.
Поскольку 5] = s2 =1/2, то, очевидно, 5 = 0, 1. Про эти два случая иногда говорят, что
спины параллельны, или антипараллельны друг другу.
3. Электрон в атоме находится в состоянии с орбитальным моментом, равным
£. Определить значение полного механического момента j = £ + s . По правилу (1.15.8)
находим, что для s - состояния квантовое число j = 1/2, для состояний с ненулевым ор-
битальным моментом j = £ ± 1/2.
Приложение 1.1. Атомная система единиц.
Всюду в тексте мы использовали абсолютную (гауссову) систему единиц, которая
выглядит наиболее удобной и естественной для описания мир электромагнитных явле-
25 Слова «параллельны» и «антипараллельны» здесь взяты в кавычки, поскольку даже в состоянии с мак-
симально возможной величиной проекции момента количества движения вектор момента направлен под
углом к оси квантования (ось z ), что формально делает невозможным существование параллельной (ан-
типараллельной) ориентации векторов 11 и 12 в пространстве.
26 Заглавные латинские буквы Р, D, F здесь использованы, чтобы показать, что речь о суммарном орби-
тальном моменте совокупности электронов.
50
НИЙ. Однако, а мире .„„„„„-молекулярных масштабов - ™
называемой атомной системой единиц, а которой та юн й , лостояц.
ных Г, (постоянная Планка). п, (масса электрона), е ’"’'*’**
_ 27 Пия ПОСТООСНИЯ ЗТ0МН0И СИСТСМЫ единиц цо
безразмерными и приняты за единицу . Для пос । ц нац
будс достаточно знаний из боровской модели атома.
Будем изменять пространственную координату в оровс их радиуСах
<70 -h2/me2 »0.529 А.
Мы знаем, что потенциальная энергия (по модулю) на первой боровской орбще
есть — е2/а^ = me*/h2 «27.2 эВ. Это и есть единица, в которых мы будем измерЯТь
энергию: - Ry = -meA/2h2 . Следовательно, энергия основного состояния атома водор0.
да равна -1/2.
За единицу скорости естественно принять значение электрона на первой боров-
ской орбите va = e2/h = ac (а - постоянная тонкой структуры). Отсюда, в частности,
получаем, что скорость света в атомных единицах равна 1/а «137.
А как ввести атомную единицу времени? Очевидно, надо найти отношение атом-
ной единицы координаты и атомной единицы скорости: получим
= — = -^-«2.42-10 ” с.
va те
Атомная частота есть соа= \/та ~ 4.13-1016 с’1.
Определим теперь атомные единицы измерения напряженности электрического
поля и интенсивности электромагнитного излучения. За значение атомной напряженно-
сти естественно принять величину напряженности электрического поля на первой бо-
ровской орбите Еа = е/а2 «1.715 107 абс. ед. CGSE = 5.15 109 В/см. Тогда атомная ин-
тенсивность излучения 1а = сЕ2/%я « 3.5 • 1016 Вт!см2.
Запишем теперь нестационарное уравнение Шредингера для атомной системы в
поле электромагнитной волны в атомной системе единиц.
.. ди/ Й2 д2и/
ih— =--------v +
dt 2т дх2
eExy/(x,t)
Переходя к атомным единицам
~ > Х = Х/а0 ’ Е = Е/Ея,
получим
й ду/ Й2 д2у/ _ ~
откуда 27
27 В связи со сказанным эту систему единиц часто называют системой
систему единиц иногда называют системой Хартри. мои
единиц е = h = т = 1 • Эту
51
1 (*-*о)
,ду/ 1 д2у/ ~~ .
dt 2 Зх2
Последнее уравнение и есть уравнение Шредингера в атомных координатах.
Задачи к Главе 1.
1.1 Волновая функция частицы в некоторый момент времени определяется
выражением
1 ( 1 х2
^(*) =-р==ехр .
VoX I 2й J
Определить средние значения и дисперсии координаты и импульса частицы в
этом состоянии.
1.2. Решить предыдущую задачу для состояния частицы, описываемого волновой
функцией ^(х) = —----- • exp(ikQx} exp
yjay/я
1.3. В основном состоянии атома водорода волновая функция имеет вид
\|/(г) = у4ехр(-г/а0), г - удаление электрона от притягивающего центра,
aQ=ti2lme2 - боровский радиус, А - нормировочная константа. Определить
средние значения кинетической и потенциальной энергии электрона.
1.4. Определить собственные значения и собственные функции оператора кинетической
энергии Тх =р2х/1т.
1.5. Может ли так быть, что в одном и том же состоянии импульс и полная энергия
имеют точно определенные значения?
1.6. Доказать справедливость следующих коммутационных соотношений для оператора
момента количества движения
|Д,,£,]=<Я4, [Д,4]=0.
1.7. Доказать, что в центрально симметричном потенциале можно найти стационарные
состояния, которые характеризуются точно определенными значениями квадрата
и z- проекции момента количества движения.
1.8. Состояние частицы определяется волновой функцией
у/(х) = . * • exp (ikox) • exp
у1ау[л
Определить плотность вероятности распределения импульса JV(p).
1.9. Волновая функция системы как функция полярного угла ф задается выражением
(А - нормировочная константа):
а) у/((р) = A cos (р,
б) у/((р) = y4sin2 <р,
в) = А(1 + sin(<p) cos(0>)),
2
Глава 2. Стационарные состояния квантовой системы.
Мы уже говорили, что стационарные состояния квантовой системы - это
ственные состояния оператора Гамильтона, т.е. состояния с точно определенным зцачс
нием энергии. В этом разделе мы рассмотрим ряд простейших задач об определеНйи
уровней энергии и волновых функций стационарных состояний частицы в потенциалу
ном поле.
2.1. Свободное движение частицы.
Рассмотрим простеншхто задачу об определении стационарных состояний сво-
бодной частицы для случая одномерного движения. Гамильтониан такой системы есть
а стационарное уравнение Шредингера записывается в виде
Здесь Е - собственное значение оператора Гамильтона, а индекс «Е» у функции подчер-
кивает ее принадлежность к собственному значению Е. Вводя к2 = 2mE/h2 >0. пере-
пишем (2.1.2) в виде
=0.
откуда получаем, что собственному значению Е соответствуют две функции
exp(zA’.v),
ехр(-/Лх),
E = H'k-/2m.
(2.1.3)
Никаких ограничений на значение волнового вектора к не возникает, т.е. система имеет
непрерывный спектр.
Найденные функции стационарных состояний совпадают с введенными ранее
собственными функциями оператора импульса. Состояния (2.1.3) одновременно явля^
ся собственными состояниями оператора импульса, соответствующими собственный
значениям р = . Это не удивительно: поскольку оператор импульса и оператор ки-
нетической энергии (в рассматриваемом случае операторы Гамильтона и кинетической
энергии тождественны) коммутируют между собой, то можно найти состояния, в коп>
рых обе физические величины энергия (кинетическая) и импульс имеют точно опрела
ленные значения.
Как видно, существует два разных состояния, которые соответствуют одном? *
тому же значению энергии. Такие состояния называются вырожденными. Кратность в
рождения в рассматриваемом случае равна двум. Отметим, что наличие вырождения
системе позволяет построить неограниченное число состояний с одним и тем же
нием энергии. Действительно, любая линейная комбинация базисных функций (2-Ь-^
55
(2-1.5)
Ч'е
= A exp(ikx) + В cxp(-ikx) (2.1.4)
дает состояние с тем же точно определенным значением энергии Е. В частности, может
быть удобен другой набор базисных состояний
sin(Ax),
cos(Zrx).
Отмстим при этом, что состояния (2.1.5) (как и состояния (2.1.4) в случае, если оба ко-
эффициента А и В отличны от нуля) уже не являются состояниями с точно определен-
ным значением импульса.
2.2. Частица в прямоугольной потенциальной яме конечной глу-
бины.
Рассмотрим теперь задачу об определении стационарных состояний частицы в
прямоугольной потенциальной яме конечной глубины. Пусть потенциал задан в следу-
ющем виде:
[б, |х|<а/2,
V(x) = \ 11 7
|К0, |х|>а/2.
(2.2.1)
Рис.2.1. Прямоугольная потенциальная
яма конечной глубины.
Запишем стационарное уравнение Шредингера в каждой из областей непрерывности по-
тенциала (см. рис. 2.1)
« тттт h2 . TZ г
области 1,Ш -------y + = Еу/,
2т dx
яп h2 d2y/
2т dx2
Мы должны рассмотреть две возможности:
Е < Ио, что соответствует связанному состоянию
частицы в яме, и Е > Ио, что соответствует ин-
финитному движению частицы в пространстве.
Более подробно остановимся на случае
связанных состояний частицы в яме Е < Ко. Вве-
дем к 2 = 2mE/h2 и к2 = 2zn(K0 - £)/й2 . Обе
введенные величины являются положительными.
Тогда в каждой из областей непрерывности по-
тенциала уравнение Шредингера имеет вид
области ЦП у/” -к2!// = Ъ,
область II + к2у/ = 0.
Решения этих уравнений запишем в виде
область I
область II
(х) = ехр(-лх) + Bt ехр(кх),
у/и (*)= А и sin(^x) + Вц cos(Ax),
(2.2.2)
56
область III УЛ// (•*) = Л/z + Вт exPt**) •
Волновая функция должна удовлетворять условию квадратичной интегрируемости f[Q
этому необходимо потребовать, чтобы коэффициенты A, — Bfll —0. Остается четыре *
>ффнциснта В,. А„ ,А,„ , для которых из условий непрерывности волновой фунКц
и се первой производной* легко получить четыре уравнения.
Однако, можно существенно упростить решение задачи, если учесть, что в рас
сматривасмом нами случае стационарные состояния характеризуются определение
четностью. Поэтому из набора функций (2.2.2) мы должны выделить решения, характс
ризующисся определенной четностью. Рассмотрим сначала систему четных волновые
функций, т.е. функций, не меняющих свой знак при инверсии координаты </(х) =
Очевидно, соответствующие решения имеют вид
область! ул(х) = В, ехр(лх),
область II (х) = В„ cos(Ax),
область III у/т (х) = А1П ехр(-лх).
При этом Bt = Ат. «Сшивая» функции и первые производные в точке разрыва потенци-
ала х = а/2, найдем* 2
Рис.2.2. Определение уровней энергий четных
состояний в прямоугольной потенциальной яме.
Вп cos(ka/2) = Аш ехр(-кп12),
-кВп s\n(ka/2) = -кАш ехр(-ка/2).
Поделив одно уравнение на другое, и,
учитывая, что к = ^2mV0/h2 -к1,
получим
ка- tg(ka/2) = J-~^a--(ka): .
N h~
(2.2.4)
Полученное уравнение есть уравне-
ние для определения энергетического
спектра системы. Будем анализиро-
вать решение уравнения (2.2.4) гра-
фически. Корни уравнения могут
быть определены как абсциссы точек
пересечения функции /(£) = £/g(£/2) и дуги окружности Z>(£) = V^"?
£ — ка) радиуса >Гв — -У2/иК0а /й (см. рис.2.2). Как видно, хотя бы один корень ур4®"
нения, т.е. одно четное связанное состояние всегда существует. С увеличением радиус®
окружности (глубины ямы, или ее ширины) число связанных состояний возрастает.
« С физической точки зрения эти условия означают требование непрерывности вектора плотности то*8
вероятности в точках разрыва потенциала.
2 Условия непрерывности в точке х = - а/2 дают такие же соотношения.
57
Аналогичным образом легко рассмотреть случай нечетных состояний
^(_Y) =-y/(.v). Запишем для этого случая решения стационарного уравнения Шредин-
1'сра в виде
область 1
область П
область П1
(2.2.5)
y/f(x) = В, сяр(кх),
у/„ (х) = В„ sin(Zrx),
у/И1 (х) = Лт ехр(-лх),
причем В, = -Ат . Так же как и в предыдущем случае из условия непрерывности функ-
ции и се первой производной получаем уравнение для определения значений энергии
нечетных состояний
JlmV.a2 ч2
—~-------(ка)2 .
(2.2.6)
(2.2.7)
Рис.2.3. Определение уровней энергий нечетных
состояний в прямоугольной потенциальной яме.
Структуру энергетического спектра, получающегося из решения уравнения (2.2.6), ил-
люстрирует рис.2.3. В рассматривае-
мом случае, если яма достаточно
мелкая, связанного состояния может
и не быть. Из графика видно, что
условием его возникновения является
неравенство
2wFoa2 2
----------;— - п
h2
При дальнейшем увеличении радиуса
окружности >[в появляются новые
связанные состояния, характеризую-
щиеся нечетной волновой функцией.
Сопоставление рис.2.2 и 2.3 показы-
вает, что четные и нечетные состоя-
ния чередуются: основное состояние
является четным, следующее состоя-
ние - нечетное, потом - снова четное и т.д.
Важной особенностью рассматриваемой задачи является то, что структура спек-
тра определяется параметром В = 2mV0a2/h2. Например, если глубина ямы увеличилась
в 4 раза, а ее ширина уменьшилась в два раза, общее число связанных состояний и их
относительное расположение по энергиям остается неизменным. Глубокой ямой мы бу-
дем считать яму, в которой имеется большое число состояний, т.е. В »1.
Отметим также, что решение задачи о яме бесконечной глубины является пре-
дельным случаем полученного нами решения для ямы конечной глубины при выполне-
нии условия В -> оо. Действительно, из данных, представленных на рис.2.2 и 2.3, видно,
что в этом случае корни уравнения соответствуют точкам
ка = пл
(2.2.7)
58
м.птиых состояний), что соответствует w
(и = 1,ЗЛ... для четных и п = 2.4.6.... для "L число длин волн де Бройл, *►
ждснию, что на длине ямы укладывается п У
(2.2.7) для уровней энергии получаем
/Г 2/Г и2
------п .
2та
Что касается волновых функций стационарных состояний, то при В —>оо в области^
ямы оказывается, что они обращаются в ноль, а внутри ямы определяются выражений
Рис.2.4. Прямоугольная потенциальная
яма бесконечной глубины.
п = 1,3,5,...
п = 2,4,6,..
(22.9)
Волновые функции нескольких нижних со-
стояний также приведены на рис.2.4. Легко в
частности убедиться, что условие ортонор-
мированности базиса выполнено, т.е.
о/2
-о/2
Важным результатом является тот
факт, что энергия основного состояния ока-
зывается отлична от нуля. Происхождение
этой ненулевой энергии легко понять исходя
из соотношения неопределенностей. Дей-
ствительно, если частица локализована в раз-
мере а (ширина ямы), то у нее есть неопределенность значения импульса Ap-h/ал^
этой неопределенностью связано наличие у частицы кинетической энергии. Поскольку в
рассматриваемых нами условиях среднее значение импульса частицы равно нулю, то
характерную величину кинетической энергии можно определить как
Г~СФ)2 п2
2т 2та2 ’
(2.2.Ю)
что на качественном уровне совпадает с точным значением (2,2.8) Рассмотренный при-
мер демонстрирует фундаментальный факт квантовой теории, не имеющий классик
го аналога: ограничение области пространственной локализации частицы неизбежно ве-
дет к появлению у нее чисто квантовой добавки к энергии, которая тем больше, че»
меньше размер области локализации частицы. В частности, для электрона, локализо^
ного в размере а ~ 1 А, получаем энергию в несколько электронвольт Аналогично, если
нуклон локализован в размере-10 ’ см, то его кинетическа! энергия окажется пор^
мегаэлектронвольта. Таким образом, зная пространственный размер системы, в
вон теории мы туг же можем оценить некоторый минимштьный масштаб ее энергии.
59
На рис. 2.5 пред-
ставлены волновые функ-
ции стационарных состо-
яний в потенциальной яме
конечной глубины, со-
держащей всего два уров-
ня (один четный и один
нечетный). Важной осо-
бенностью этих волновых
Рис.2.5. Волновые состояний функции стационарных в прямо- функций является ненуле-
угольной потенциальной яме конечной глубины. вая вероятность обнару-
жить частицу в области классически запрещенного движения, то есть для значений ко-
ординаты |д'| > а/2. Эту вероятность можно определить как
w = 2 J|^(x)|2tZr.
а/ 2
Как видно, чем ближе энергия состояния к величине Ио, тем медленнее убывает волно-
вая функция в области классически запрещенного движения, и тем больше величина w.
В заключение этого раздела остановимся на случае Е > Ио, соответствующего
инфинитному движению частицы. Решение стационарного уравнения Шредингера мож-
но найти аналогично случаю, рассмотренному выше. При этом оказывается, что это ре-
шение существует для любого значения энергии, т.е. инфинитному движению частицы
соответствует непрерывный энергетический спектр, причем стационарные состояния
также двукратно вырождены: каждому значению энергии можно поставить в соответ-
ствие два разных состояния, характеризующихся различной пространственной четно-
стью.
На этом примере отметим важную закономерность. Всякий раз, когда движение
системы ограничено некоторой пространственной областью у системы возникает дис-
кретный энергетический спектр, и, наоборот, если движение инфинитно, энергетический
спектр является сплошным. Возникает континуум состояний. При этом волновые функ-
ции состояний континуума (в простейшем случае, рассмотренном нами, это волны де
Бройля) не могут быть нормированы на единицу в соответствии с условием
поскольку на бесконечности волновая функция таких состояний не стремится к нулю,
хотя и остается ограниченной. Можно показать, что условие нормировки на J - функ-
цию является общим условием нормировки состояний непрерывного спектра. Как мы
уже отмечали, невозможность удовлетворить условию квадратичной интегрируемости
означает, что стационарные состояния в континууме не могут быть реализованы. На
практике состояние частицы в этом случае может быть представлено как волновой па-
кет, составленный из состояний континуума и обладающий некоторой энергетической
шириной.
60
2.3. Туннелирование.
Мы видели, что в квантовой теории с некоторой
можным нахождение частицы в области классически запрещено о XT Та °с°'
бенность приводит к возникновению существенно неклассиче кта тунНед^
рования (просачивания) частицы через область классически запрещенного движения.
Качественно понять происхождение такого эффекта можно на основе анализ
рассмотренной выше задачи о стационарных состояниях частицы в потенциальной яме
конечной глубины. Мы видели, что в области классически запрещенного движения вод.
новая функция, описывающая состояние частицы, отлична от нуля, причем
у/(х) ~ ехр(-кх),
где х - удаление частицы от классической точки поворота, а к y2w(K0 E}f ft Это
значит, что плотность вероятности обнаружить частицу в области классически запре-
щенного движения (под барьером) на глубине d есть
(2__________
~~E)d
(2.3.1)
Если рассматривать частицу в яме, от-
деленной от области инфинитного дви-
жения потенциальным барьером конеч-
ной ширины d (см. Рис.2.6), то интуи-
тивно ясно, что выражение (2.3.1) опре-
деляет вероятность проникновения
(туннелирования) частицы через потен-
циальный барьер. Величину D называ-
ют также туннельной проницаемостью
(прозрачностью) барьера.
Нетрудно обобщить полученный
произвольной формы (см. рис. 2.7). Пусть
циальный барьер, описываемый функцией
Рис.2.6. Проникновение частицы в область клас-
сически запрещенного движения.
результат на случай потенциального барьера
поток частиц с энергией Е налетает на потен-
Е(х), слева, причем Е < тах(К(х)). Тогда с
классической точки зрения частицы дошли бы до точки с координатой (классическая
точка поворота) и отразились бы от потенциального барьера. Квантовомеханическое
Рис. 2.7. К вопросу об определении
вероятности туннелирования.
просачивание частиц в подбарьерную об-
ласть приводит к тому, что с ненулевой
вероятностью они могут оказаться в ДРУ'
гой области классически разрешенного
движения (х > х2), т.е. протуннелировать
через барьер. По аналогии с (2.3.1) для ве
роятности этого процесса запишем
( 2 ЛХ
D ~ ехР -- 142m(V(x)-E)dx , (2-3>2)
I Ч )
где интеграл берется по области классиче
61
ски запрещенного дннження. Очевидно, в частном случае потенциального барьера пря-
моугольной формы выражение (2.3.2) переходит в (2.3.1). Как видно из (2.3.2), вероят-
ность туннелирования экспоненциально сильно зависит or ширины потенциального ба-
рьера и ст высоты (точнее высоты потенциала в области классически запрещенного
движения). Также видно, что вероятность туннелирования быстро убывает с ростом мас-
сы частицы. Именно последнее обстоятельство приводит к тому, что туннелирование
практически никогда нс наблюдается для макроскопических объектов.
Наши рассуждения являются, конечно, нестрогими и нс позволяют определить, в
том числе, прсдэкспонснциальный множитель в выражении (2.3.2). В общем случае вы-
ражение (2.3.2) может быть получено в рамках так называемого квазиклассического
приближения в квантовой механике.
Туннельный эффект представляет собой несомненно загадочное явление с точки
зрения классической механики. Казалось бы, вероятность обнаружить частицу в области
классически запрещенного движения противоречит закону сохранения энергии, по-
скольку величина кинетической энергии заведомо положительна. Однако, надо иметь в
виду, что в каждый момент времени состояние частицы описывается у, - функцией,
волновым полем, причем это состояние заведомо не характеризуется точно определен-
ными значениями кинетической и потенциальной энергии. Экспериментальное обнару-
жение частицы в подбарьерной области, очевидно, предполагает измерение ее коорди-
наты с достаточно высокой точностью, что неизбежно ведет к изменению волновой
функции системы и сопровождается изменением ее энергии. Важно понимать, что пред-
ставление о туннелировании, как о процессе, в ходе которого некоторое время частица
находится в подбарьерной области, неверно. Такой ситуации соответствовало бы рас-
пределение плотности вероятности |^|2, отличное от нуля только в области классически
запрещенного движения в течение некоторого конечного интервала времени. На самом
деле область локализации частицы в процессе туннелирования всегда значительно
больше ширины потенциального барьера, поэтому представление о том, что частица
находится в подбарьерной области, не соответствует действительности ни для какого
момента времени.
В то же время эффект подоб-
ный квантовомеханическому тунне-
лированию хорошо известен в оптиче-
ских явлениях. Рассмотрим явление
прохождения световой волны через
среду с кусочно-непрерывным показа-
телем преломления, например, систе-
му стеклянных пластинок (I и И), раз-
деленных вакуумным зазором Ш (см.
рис.2.8). Показатель преломления
стекла п »1.5 и заведомо больше, чем
в вакуумном зазоре. Поэтому при па-
дении электромагнитной волны из оп-
тически более плотной среды (стекло)
на оптически менее плотную (вакуум)
ш____
^яннв
Рис.2.8. Оптический аналог туннельного эффекта
(прохождение пучка света через систему стеклян-
ных пластин, разделенных вакуумным зазором).
62
при определенных условиях (угол падения превышает некоторый кри ический) возн^
ет явление полного внутреннего отражения. Свет целиком отражается ог гРаницыраз^
ла. однако в оптически менее плотной среде возникает осциллирующее во времени поде
экспоненциально спадающее но мере удаления вглубь от границы раздела. При больц^
ширине вакуумного зазора наличие второй стеклянной плас г инки никак не скажете^
процессе отражения от границы раздела. Однако, если вакуумный зазор является лоста.
точно узким (его ширина не должна существенно превышать глубины проникновения
электрического поля в вакуум), то в пластинке II тем не менее возникнет волновое поле,
распространяющееся вглубь от границы раздела. Рассмотренный эффект полностью
аналогичен эффекту квантовомсханичсского туннелирования. Вакуумный зазор оказы-
вается эквивалентен потенциальному барьеру конечной ширины, экспоненциально убы-
вающее электрическое поле - экспоненциально убывающей волновой функции в обла-
сти классически запрещенного движения, а проходящая световая волна через систему
«стекло — вакуум - стекло» - протуннелировавшей через барьер частице.
2.4. Приближенное решение стационарного уравнения Шрединге-
ра. Стационарная теория возмущений.
Часто бывает, что при анализе спектра и волновых функций стационарных состо-
яний гамильтониан системы можно представить в виде суммы двух слагаемых:
H = HQ+V, (2.4.1)
где HQ - главная (невозмущенная) часть гамильтониана, а V - сравнительно малая до-
бавка, называемая возмущением. Будем также считать, что мы знаем решение задачи
=Епу/п.
(2.4.2)
В рассматриваемой ситуации естественно ожидать, что собственные значения и соб-
ственные функции гамильтониана Н будут близки к решению задачи (2.4.2). Наша за-
дача - найти в такой ситуации приближенное решение задачи
(я0+^Х = ^„. (2.4.3)
Сформулированная задача является широко распространенной. Например, Но - атом-
ный гамильтониан, учитывающий кинетическую энергию электрона и его кулоновское
взаимодействие с ядром, а И описывает взаимодействие с внешним статическим элек-
трическим или магнитным полем.
Случаи невырожденного спектра.
Общий подход к решению задачи (2.4.3) заключается в следующем. Будем искать
энергии стационарных состояний и соответствующие им волновые функции в виде
= Е„ + == у,п + > (2.44)
где поправки £Е„ и к уровням энергии и волновым функциям стационарных состо-
яний полагаются малыми.
63
Подставляя представление (2.4.4) в
ко первого порядка малости, получим:
уравнение (2.4.3), и учитывая слагаемые толь-
+ HQdv/n + V^n = Е/У/ „ + + Е„3у/п
(2.4.5)
Для получения поправки к уровню энергии 8Еп домножим уравнение (2.4.5) на у/* и
проинтегрируем по всей области определения волновой функции. Получим
Ж” = -E,)fyndT. (2.4.6)
Покажем теперь, что второй интеграл в (2.4.6) обращается в нуль. Поскольку набор
функций {</„} образует полный базис, то возможно представление поправки к
функции в виде3
т
(2.4.7)
Тогда второе слагаемое в (2.4.6) преобразуется к виду
/у.(я„ -(Е„ -Е„W„d- = О
т
и равно нулю в силу условия ортогональности собственных функций гамильтониана
Но. Таким образом, для поправки к уровням энергии окончательно получаем
(2.4.8)
т.е. дополнительная энергия может быть вычислена как среднее значение энергии воз-
мущения, вычисленной на невозмущенных волновых функциях. Выражение (2.4.8) сим-
волически также записывают в виде:
= (2.4.9)
Интеграл вида (2.4.8) называют матричным элементом оператора V . Как видно, в дан-
ном случае речь идет о диагональном элементе, а в общем случае вся совокупность эле-
ментов Vmn образует матрицу оператора возмущения V.
Вычислим теперь поправки к волновым функциям стационарных состояний <5у/п.
Умножая (2.4.5) на у/'к (ktn) и интегрируя по всей области определения волновой
функции, получим
(2.4.10)
Здесь = ^kVy/ndT - недиагональный матричный элемент оператора возмущения V,
построенный на волновых функциях невозмущенного состояния. Подставляя в (2.4.10)
функцию 8у/ п в виде разложения (2.4.7), получим
^=^/(£я-^),
„тп гпектпа оператора Гамильтона является дискретным,
здесь для простоты мы полагаем, что спектра операми»
64
...лмпго состояния имеет вид:
т.е. поправка к волновой функции н-ю сгапио
| / л ' J л *
Л..иПгп стационарного состояния записывав
а полная волновая функция п -го возмущен ®тся
в виде
V. + "
П к
Про выражение (2.4.12) иногда говорят, что возмущение «подмешивает >к л му стацио-
нарному состоянию другие стационарные состояния нсвозмушенного гамильтониана.
Таким образом, выражения (2.4.8) (или (2.4.9)) и (2.4.12) дают решение постав-
ленной нами задачи в первом порядке теории возмущении.
Полученные нами выражения позволяют сформулировать условия применимости
полученных результатов. Необходимо потребовать, чтобы поправки к положению энер-
гетических уровней и волновым функциям были малыми. Это, очевидно, возможно при
выполнении условий
V..«\E.-Et\,Vh,«\E,-Ek\, (2.4.13)
т.е. матричные элементы оператора возмущения должны быть малы по сравнению с раз-
ностью невозмущенных энергий данного уровня и любого другого уровня системы. Не-
равенства (2.4.13), фактически, можно рассматривать как условия малости оператора
возмущения V по сравнению с невозмущенным гамильтонианом Но.
Может так оказаться, что поправка к положению энергетического уровня в пер-
вом порядке теории возмущений оказывается равной нулю. Тогда необходимо рассмат-
ривать влияние возмущения во втором порядке малости. Проводя рассуждения, анало-
гичные приведенным выше, нетрудно получить
8£2) =2К|7(Д,-*.)- (2.4.14)
к*п
Мы пришли к выводу, что поправки к уровням энергии и волновым функциям зависят
не только от величины возмущения, но и от структуры энергетического спектра. В част-
ности, если спектр оказывается вырожденным, то наши поправки оказываются беско-
нечно велики даже при сколь угодно малой величине оператора ш>зму ।1|ення. Поэтому
фактически рассмотренная схема может быть использована лишь для систем с невырож-
денным энергетическим спектром. Этот случай теории возмущений мы рассмотрим ни-
же. Из сказанного выше ясно, что «перемешивание» группы вырожденных состояний
оказывается существенным при любой величине возмущения.
Случаи вырожденного спектра.
Рассмотрим теперь вариант теории возмущений для случая наличия выро*®’*'
ных состояний. Пусть имеется N . кратно вырожденный уровень с энергией Е- СМ*
65
ватсльно. для некоторого невозмущенного гамильтониана /7(| мы имеем набор состоя-
ний V7»' ,г ~ N' характеризующихся одним и тем же значением энергии Е, то есть
Нпу/п=Еу/п. (2.4.15)
Пусть на систему воздействует некоторое возмущение, характеризуемое оператором V.
Определим поправки к энергии различных состояний
обусловленные воздействием возмущения:
+ =(£+ж,Ж- <2-416)
Мы уже знаем, что для вырожденных состояний даже малое возмущение вызывает
сильно перемешивание невозмущенных состояний. Поэтому будем искать решение за-
дачи (2.4.16) в виде
V.=Yc^k- (2.4.17)
к
Подставляя (2.4.17) в (2.4.16), с учетом (2.4.15) получим
Yck(Evk+Vvk)<E + ttS£ckll,k <2-4'18)
к к
Умножая (2.4.18) на одну из собственных функций у/ и интегрируя по всей области
определения функций, получим
<2-4-19)
к
Здесь 8пк - символ Кронекера.
Таким образом, мы получили систему линейных уравнений определения коэффи-
циентов разложения в (2.4.17). Условием ее нетривиальной разрешимости является ра-
венство нулю детерминанта
пк
= 0.
(2.4.20)
Уравнение (2.4.20) представляет собой алгебраическое уравнение степени N относи-
тельно поправки к энергии невозмущенного уровня . В общем случае это уравнение
имеет N корней, если все эти корни различны, то исходный уровень расщепляется на
jV подуровней с различными значениями энергии еп = Е + 8Еп. Про такую ситуацию
говорят, что возмущение снимает вырождение в системе. Может оказаться, что среди
корней уравнения (2.4.20) имеются кратные корни. В таком случае говорят, что вырож-
дение в системе снимается частично.
Может так оказаться, что собственные функции невозмущенного оператора Га-
мильтона Но являются одновременно и собственными функциями оператора возмуще-
ния V. В этом случае
то есть матрица оператора возмущения является диагональной в выбранном нами б^
се. В этом случае решение уравнения (2.4.20) сеть
SE„={v.,\V\V^^\i'\nXl = V'"” (2.4.21;
что совпадает с выражением (2.4.9), полученным для случая невырожденного уровня.
В последующих разделах мы рассмотрим несколько примеров использования
теории возмущений для анализа ряда конкретных физических систем.
2.5. Периодический потенциал. Зонная структура спектра.
В этом разделе мы на качественном уровне рассмотрим формирование энергетц.
ческого спектра в периодическом потенциале, который является простейшей моделью
кристалла. Мы уже отмечали, что атом создает для электронов некоторую потенциаль-
ную яму. Рассмотрим теперь одномерную цепочку атомов, расположенных друг от друга
на некотором расстоянии d. Если величина d много больше характерного атомного
размера, то мы имеем совокупность изолированных атомов. Если же мы сближаем ато-
мы так, что расстояние между ними оказывается порядка атомного размера, то электрон,
находящийся в какой-либо из ям, начинает "чувствовать" наличие ям - соседей. Харак-
терный вид потенциала V(x) в такой системе имеет вид, изображенный на рис.2.10.
Пусть изолированный атом характеризуется некоторой системой энергетических уров-
ней. Очевидно, электрон, локализованный первоначально в одной из потенциальных ям,
может протуннелировать в соседние ямы. Поэтому время жизни электрона в конкретной
яме т оказывается конечным и определяется длительностью процесса туннелирования.
Но тогда в силу соотношения неопределенностей для энергии - времени
ДЕ г ~ h,
энергия состояния оказывается точно не определена: энергетический уровень размыва-
ется и превращается в энергетическую зону шириной ЛЕ. Отметим также, что прове-
денные рассуждения показывают, что электрон в периодическом потенциале принадле-
жит не конкретному атому, а делокализован по всей цепочке атомов. Очевидно, чем вы-
ше положение исходного энергетиче-
ского состояния в спектре исходного
изолированного атома, тем больше ве-
роятность туннелирования, и, следова-
тельно, тем больше ширина энергети-
ческой зоны. Таким образом, мы при-
ходим к выводу о существовании зон-
ной структуры энергетического спектра
кристаллов. Дискретные атомные уров-
ни превращаются в разрешенные энер-
гетические зоны, разделенные друг от
друга запрещенными зонами (см.
рис.2.9). Иногда зоны, созданные двумя
_______d
-------
Рис.2.9. Периодический потенциал. Зонная стрУ*
тура спектра.
67
различными атомными уровнями, могут перекрываться, создавая единую разрешенную
энергетическую зону. Зоны, полностью заполненные электронами, называют валентны-
ми, частично заполненные или пустые - зонами проводимости. Если при нулевой темпе-
ратуре в отсутствие внешних воздействий в кристалле имеется не полностью заполнен-
ная зона (т.е. в зоне проводимости присутствуют электроны), то такой образец является
металлом. Если зона проводимости является пустой, то в зависимости от ширины за-
прещенной зоны, разделяющей верхнюю валентную зону и нижнюю зону проводимости,
образец называют диэлектриком или полупроводником. Например, в кристалле алмаза
(широкозонный диэлектрик) ширина запрещенный зоны составляет 5 эВ, в кристалле
кремния (типичный полупроводник) — 1.1 эВ. С повышением температуры (мы, конечно,
говорим о диапазоне температур, не превышающих пороговые значения, при которых
происходит разрушение кристаллической структуры) в полупроводниках в зоне прово-
димости появляются электроны, которые приводят к способности полупроводника про-
водить электрический ток. Поскольку число электронов в зоне проводимости экспонен-
циально растет с температурой, можно ожидать, что зависимость собственной проводи-
мости полупроводникового материала от температуры также будет экспоненциальной4.
Задачи к Главе 2.
2.1.
2.2.
2.3.
2.4.
2.5.
Частица массы т находится в одномерной бесконечно глубокой прямоугольной
потенциальной яме шириной а. Написать волновые функции хотя бы двух со-
/Х7\
стоянии, в которых среднее значение энергии частицы равно (£) =-—.
та
Частица массы т находится в основном состоянии в одномерной бесконечно
глубокой прямоугольной потенциальной яме шириной а. Найти значения рх,
которые могут быть измерены в этом состоянии. Какова вероятность их измере-
ния? Чему равно среднее значение величины рх ?
оо х < О,
Частица массы т находится в одномерном потенциале V(x) = < О, 0 < х < а.
/о, х > а.
Определить, сколько связанных состояний находится в яме в следующих случа-
ях: а) Коа2 = 75Й2/?и,б) VQa2 = h2/m.
Определить энергию нижнего стационарного состояния частицы в одномерной
прямоугольной потенциальной яме конечной глубины в случаях: а)
2mV0a2/й2 «1, б) 2mV0a2/й2 »1 (Ко - глубина потенциальной ямы, а - ее
ширина).
Дейтрон имеет энергию связи Е = 2.23 МэВ, среднее расстояние между прото-
ном и нейтроном а = 210~13 см, возбужденного состояния у дейтрона нет. Ис-
пользуя эти данные, оценить глубину потенциальной ямы поля ядерных сил.
4 Мы использовали здесь термин «собственная проводимость», поскольку на практике полупроводники
часто легируют, вводя некоторое количество примесных атомов, энергетически уровни которых располо-
жены в запрещенной зоне исходного полупроводника. В зависимости от того, где они располагаются
(близко к валентной зоне, или зоне проводимости) возникают полупроводники р или п типа, проводимость
которых может быть значительной уже при комнатных температурах и определяется, прежде всего, уров-
нем легирования.
Глава 3. Гармонический осциллятор.
В >той главе рассмотрим одну из важнейших задач квантовой теории гармони-
ческий осциллятор. Приближение гармонического осциллятора для описания атомно-
молекулярных систем широко использовалось еще в классической физике электромаг-
нитных явлений. Болес того, мы увидим, что в квантовой теории отклик атома на срав-
нительно слабые внешние электромагнитные поля подобен отклику осциллятора на
внешнее поле. Задача об осцилляторе широко используется для описания колебательных
спектров молекул, в различных задачах физики твердого тела. Оказывается, в ряде слу-
чаев и самосогласованный потенциал, создаваемый совокупностью нуклонов в атомном
ядре, также можно рассматривать в приближении гармонического осциллятора. Прин-
ципиально важно, что свободное электромагнитное поле может быть представимо в виде
совокупности полевых мод, каждая из которых является гармоническим осциллятором.
Поэтому квантовая теория электромагнитного поля - это прежде всего квантовая меха-
ника гармонического осциллятора, а взаимодействие атома с полем излучения - это вза-
имодействие двух осцилляторных систем. Наконец, мы увидим, что по своим свойствам
состояния квантового гармонического осциллятора в ряде случаев наиболее близки к
состояниям осциллятора классического. Поэтому анализ соотношения рассмотрения
квантовомеханической и классической задач о гармоническом осцилляторе частот важен
и интересен с точки зрения соотношения квантового и классического подходов и пони-
мания особенностей предельного перехода к классической теории.
3.1. Стационарные состояния.
Начнем с анализа стационарных состояний системы. Для этого рассмотрим зада-
чу о собственных значениях и собственных функциях оператора Гамильтона. Пусть по-
тенциальная энергия системы записывается в виде
V(x) -тсо2хг jl,
где ы - частота колебаний. Тогда гамильтониан гармонического осциллятора имеет вид
Й2 d2 та>2х2
2т dx2 2
(3.1.1)
Наша задача заключается в определении собственных функций и собственных значений
оператора Н :
Й2 d2y/
2т dx2
2 2
та) х
4-------
2
или
1^2 Й2 Й2 /
(3.1.2)
Для того, чтобы удовлетворить условию квадратичной интегрируемости на бесконечно-
сти (х —> ±оо) волновая функция должна стремиться к нулю.
70
Уравнение (3.1.2) удобно обещо .мерить. Вводя новые безразмерные ко
^.т/<, изверг,но ,..= С/Л-„ = ^МгМ.еренишемОЛ.г^ *
^т-ь2+';W> = 0' (3.1.з,
Начнем решение задачи с анализа асимптотического поведения волной функции прц
<7 —>±оо. При больших значениях £ последним слатаемым в ( можно пренебр^
то есть:
(3.14,
Это уравнение имеет асимптотику
у/ ~ехр(-£2/2).
Действительно у/" = (£2 — 1)ехр(—£2/2), т.е. для |<^|»1 уравнение (3.1.4) оказывается
выполненным. Будем поэтому искать решение уравнения (3.1.3) в виде
^) = v©exp(-f2/2), (3.1.5)
где v(£) - некоторая новая неизвестная функция, не меняющая асимптотику функции
^(£) на бесконечности. Подставим представление (3.1.5) в уравнение (3.1.3). Тогда учи-
тывая, что
= "77 (О' “ £0 ехР (“ £72)) = (v* “ v - 2^' + <2 v)exp (- f /2),
d£
для функции v(£) получим новое уравнение
v"-2&' + (s-Y)v = 0. (3.1.6)
Будем искать решение уравнения (3.1.6) в виде полинома конечной степени £, т.е.
(3.1.7)
v(^> = £>,<*
£=0
Как мы увидим позже, попытка найти решение (3.1.6) именно в виде полинома, а небес*
конечного ряда, связана с необходимостью сохранить правильное асимптотическое по*
ведение волновой функции на бесконечности. Подставляя разложение (3.1.7) в уравне-
ние (3.1.6) и собирая члены при одинаковых степенях £, получим:
+ 2)(к + ])ак+2 -]-2к)ак)^к =0. (зЛ‘8)
к-0
Поскольку это равенство должно удовлетворяться при любом значении получаем
следующее рекуррентное соотношение связывающее коэффициенты полинома;
_ 2*-(«-1) ?19)
“‘-’ЖГ2' (
к •
71
Если известны коэффициенты ап и at, то остальные можно найти с помощью (3.1.9).
ряд будет конечным, если па некотором слагаемом с номером п коэффициент ап обра-
тится в ноль. Из (3.1.9) имеем, что это возможно если
= 2п +1,
п.пн переходя к размерным единицам
=Йщ(и + 1/2), и = 0,1,2,... (3.1.10)
Условие обрыва ряда не может быть выполнено одновременно и для четных и для не-
четных членов разложения. Поэтому полином (3.1.9) должен содержать только четные,
или только нечетные степени , т.е.:
а0 —>а2 —>а4 —>..., aj=a3=... = 0,
или
а\ ~>аз ~^as ~=а2 = ... = 0.
Последнее утверждение можно было сделать сразу и искать разложения вида (3.1.6) по
четным или нечетным степеням £. Это следствие того, что в рассматриваемом случае
оператор четности коммутирует с оператором Гамильтона.
Таким образом, задача решена. Выражение (3.1.10) определяет энергетический
спектр гармонического осциллятора, а волновые функции представимы в виде (3.1.5),
где функции у(£) есть полиномы, которые легко построить с помощью соотношения
(3.1.9). При этом значения коэффициентов а0 и ах должны быть определены из условия
нормировки волновой функции.
Если бы мы искали решение уравнения (3.1.6) в виде бесконечного ряда, то для
больших значений к мы бы получили связь между коэффициентами (см. (3.1.9)):
2
ак+2 № . ак •
к
Такая связь между коэффициентами возникает при разложении функции
оо Е*
ехр<^2) = JL(W’
то есть приводит к тому, что волновая функция на бесконечности неограниченно возрас-
тает.
Полиномы, коэффициенты которых удовлетворяют рекуррентному соотношению
(3.1.9), хорошо известны в математике и называются полиномами Эрмита1. Приведем
явные выражения для первых нескольких полиномов:
HQ (£) = 1, Я. (£) = 2£, Н2 (£) = 4£2 - 2, Н.«) = 8<3 - Щ. (3.1.11)
Все они являются либо четными, либо нечетными функциями £. Значит, в нашем случае
стационарные состояния опять характеризуются определенной четностью. Об этом
' Hermite Charles (1822 - 1901) - французский математик.
72
„ ПРГК0 видеть, что оператор четности
можно было догадаться, конечно, заранее, •
мутирует с гамильтонианом. СПОСоб построения полиномов Эп
Часто бывает удобно использовать ДРУ ^РМи.
та:
Я„(^) = (-|)"ехР(4'2)^7схР('^
Выпишем также условие ортонормированности полиномов.
= <ЗЛ.13)
Эти и некоторые другие свойства полиномов Эрмита более подробно обсуждаются в
разделе Справочные материалы.
Условие (3.1.13) позволяет записать удовлетворяющие условию нормировки вол-
новые функции стационарных состояний гармонического осциллятора
(/„(*) = (3.1.14)
где нормировочный множитель Nn - определяется как
’ F- (3-1.15)
yl2nnlay/n
Перейдем теперь к обсуждению свойств полученного решения. Прежде всего от-
метим, что энергетический спектр осциллятора строго дискретный, как и у всякой си-
стемы совершающей финитное движение. Энергия основного состояния осциллятора2
отлична от нуля: существуют так называемые нулевые колебания, их энергия оказывает-
ся равна
Ео = ha>l2,
и это минимально возможное значение энергии осциллятора.
Происхождение нулевых колебаний нетрудно понять на основе соотношения не-
определенностей Гейзенберга. Дей-
ствительно, локализация частицы в об-
ласти размером Ах ведет к появлению
У нее кинетической энергии
Т ~ й2/2т(Дх)2. С другой стороны ДЛ*
частицы с такой областью простран-
ственной локализации, находящейся в
осцилляторном потенциале, величина
потенциальной энергии будет состав
лять та)2 (Ах)2/2. Минимум пол-
ной энергии Е = Т + V достигается ДЛ*
вполне определенной пространствен
ной ширины волнового пакет3
Рис.3.1. Уровни энергии и волновые функции
гармонического осциллятора.
2 Это состояние часто называют вакуумным состоянием осциллятора.
73
= jh/ma> Для минимально возможного значения энергии осциллятора при этом по-
лучаем ^n,in = ^с0‘ Это значение всего в два раза отличается от точного значения энер-
гпн нулевых колебаний осциллятора.
Отметим, что основное состояние осциллятора - это гауссов волновой пакет, мы
видели, что для такого состояния произведение дисперсий импульса и координаты ока-
зывается минимально возможным. В этом смысле такое состояние наиболее близко к
состоянию классической частицы, когда значения импульса и координаты известны точ-
но одновременно.
На рис.3.1 приведено положение нескольких нижних энергетических уровней ос-
циллятора. Для этих же состояний на рис.3.2 представлены распределения плотности
Рис.3.2. Распределения плотности вероятности
для нижних стационарных состояний
гармонического осциллятора.
вероятности |^(х)|2. Важной особенно-
стью энергетического спектра является
его эквидистантность, т.е. энергетиче-
ское расстояние между любой парой
уровней одинаково
Еп - Е„ , = ti(D.
п п—1
При этом, так же как и в ранее рассмот-
ренных задачах, существует ненулевая
вероятность обнаружить частицу в об-
ласти классически запрещенного дви-
жения.
Необходимо отметить, что, хотя
энергия возбужденного состояния ос-
циллятора может быть весьма велика, средние значения координаты и импульса частицы
оказываются равны нулю. В этом легко убедиться прямым вычислением интегралов
(х) = , (р) = (x)py/(x)dx.
В этом смысле все стационарные состояния соответствуют неподвижной частице. Более
того, как мы уже ранее отмечали, распределение плотности вероятности |у/|2 также не
зависит от времени. Однако, средние значения кинетической и потенциальной энергии
отличны от нуля. Действительно3,
(Г) =(р2/2т) =^-\y/*np2y/ndx = ^-{ri + \l2),
" ' /п 2mJ 2
1у)п=(тю2х2/2\ =^-^x2v„dx = ^-(n + \l2).
При этом для квантовомеханических средних оказывается выполненным равенство
средних значений кинетической и потенциальной энергии
(3.1.16)
Эти интегралы легко вычисляются с учетом формул, приведенных в Справочных материалах.
74
знакомое нам но классической механике. Однако, под « R „ , ?!?СИ,Се Ре^
идет об усреднении по периоду колебательного движения. . ) поду^
для квантовомсханических средних.
Для различных практических приложений также гасго )ьв ет важным вычИСЯе
ние в диагональных и недиагональпых матричных элементов oi операторов
справок мы придем их значения для п = 1,2,3,4:
(х2)„„ = о2(и + 1/2), (х2)„,„2 =а2(« + >/2)
=а’3((« + 1)/2)3'2,(х2)„„, = о33(и/2)3/2,
U’),„„3=a3V(„ + 3)(„ + 2)(n + l)78, (х’)„„_з=а37«(«-1)("-2)/8, (3.|.|7)
(х4)„„=«4|(''2+п + 1/2),
(х4)„„2 =a4(« + 3/2)7(„ + 2)(„ + l), (х4)„„.2 =a4(n-l/2)^(„-l),
(х4)„„4 =a'yl(n + 4)(и + 3)(п + 2)(н +1)/16 , (х4)„ „.4 = a4 п(и -1)(л - 2)(н - 3)16
3.2. Нестационарные состояния.
Перейдем к анализу нестационарных состояний осциллятора. Как «увидеть» ко-
лебания частицы (волнового пакета), аналогичные классическим колебаниям? Для отве-
та на эти вопросы рассмотрим самый простой случай. Пусть в начальный момент време-
ни состояние частицы описывается волновой функцией, которая является суперпозицией
двух нижних стационарных состояний осциллятора:
^(х, t = 0) = (^0 (х) + у/х (х)).
(3.2.1)
Тогда, в соответствии с общим способом решения нестационарного уравнения Шредин-
гера, рассмотренным в Главе 2, волновая функция системы, удовлетворяющая нестацио-
нарному уравнению Шредингера и описывающая эволюцию состояния во времени, за-
пишется виде
1
. Зой
1---
2
7 1 I 7 \ ( • 6* ) z \ I
^(х,/) = -5= ^0(х)ехр +^,(х)ехр -i
у/2 V v 2 J L
(3.2.2)
Для плотности вероятности p(x,t) получаем
p(x,o = ku,/)|2 ф0(х)|2 +1Их)|2 +^>iWc0S(ur (3.2.3)
Первые два слагаемых в (3.2.3) не зависят от времени и дают некоторое статичен
распределение плотности вероятности, однако третье слагаемое показывает, 4W яс-
ность вероятности в системе перетекает из одной пространственной области в ДРУ^'
75
причем это перетекание происходит с частотой колебаний классической частицы. Чтобы
еше более полно установить аналогию с классикой, найдем среднее значение координа-
ты частицы:
Г । 1 2 1 \
= Jvp(.x,/)<&' = J А 2^/()(л)| + 2^/1(л')|2 +hW^i(x)coscut \jx = х0| cos^X , (3.2.4)
где
A'oi = J (x)dx = а/42 = ^/2та) .
Мы получили, что частица совершает колебательное движение с частотой классических
колебаний и амплитудой х01 = Jh/2mco .
3.3. Когерентные состояния и переход к классическому описанию.
Среди бесконечно большого числа нестационарных состояний осциллятора осо-
бый интерес представляет так называемое когерентное состояние осциллятора. Как мы
увидим в дальнейшем, по своим свойствам это состояние наиболее близко к классиче-
ским представлениям о гармоническом осцилляторе, как об объекте совершающим ко-
лебательное движение по закону
х = х0 cos(cX + ф).
Рассмотрим следующее состояние частицы в гармоническом потенциале
1
(аЛ-)'/2
(3.3.1)
Такое состояние, очевидно, описывает гауссов волновой пакет с шириной, равной ши-
рине основного (вакуумного) состояния осциллятора, но характеризующийся средним
значением импульса (р} = /?0. Состояние (3.3.1) не является стационарным, однако, как
и любое другое состояние, оно может представлено в виде суперпозиции стационарных
состояний:
^о(а) = ЕС^"(х)-
п
Для коэффициентов разложения имеем
1 / j \
С, = r--Jtf.Wexp\~р„х-(х/а)2 . (3.3.2)
J ауМ2 п\ J
Используя представление полином Эрмита в виде (3.1.12) и выполняя замену перемен-
ных % = х/а, перепишем (3.3.2) в виде:
1 f (i у ыр(-£2) „
С= ,—=Jexp (333)
Ул-2"и!J Vй '
Выполняя п • кратное интегрирование по частям, перепишем (3.3.3) в виде
76
lJ i pJ' рх 4 U.
Выражение (3.3.4) сводится к интегралу Пуассона, в результате получим
сп = (Ров/м)" ехр[“ ’
>!п\ < 4Й )
или
<33,4)
^3.5)
|сд[2 =~ехр(-Л), (3.3.6)
где Л = (А67)2/2/р .
Распределение (3.3.6) представляет собой распределение Пуассона, причем
метр А представляет собой среднее число квантов по распределению, то есть
пара-
(п) = £и|С„|2 =Л. <3-3'
п
Вычисление среднего от квадрата числа квантов4 5 (п2^ дает
(«2) = Я2+Я. (3.3.8
Вычисляя дисперсию числа квантов по распределению (3.3.6), найдем
Dn={n2)-{n)2 ={п). (3.3.9
При этом относительная неопределенность числа квантов в когерентном состоянии есть
дп = &п/(п) = JeTI(и) = 1/yf(n).
Как видно, при больших (п) эта величина оказывается мала.
Рассматриваемое нами нестационарное состояние принято называть когерентным
состоянием гармонического осциллятора. Средняя но квантовому состоянии энергия
этого состояния связана со средним числом квантов очевидным соотношением’
(Е) = £M„ + 1/2)|С„|2 = +1/2).
п
(3.3.10)
Остановимся теперь на изучении воем
заданного в виде (3.3.1). Представляя решение6ТеГ Э®°ЛЮЦИИ КО|ерентного состояния,
в виде разложения по собственным состояния тационарного уравнения Шредингера
(3.3.4), получим М гамильт°ниана и используя выражение
И*4) =
1 Х"1 1 ( п2 2 2 \
J НЛх^СХР ---4 |ехр(-+ 1/2у).
4 Утверждения (3.3.7) и (3.3.8) доказываются в любом vu^
и3ишмарев <<кУрс теории вероятностей и матемя^ П° теории вероятностей, например. К)-
во МГУ, 1983 математической статистики доя физиков». М- №'
5 Здесь мы используем условие Сп 2 = 1.
77
Перегруппировывая слагаемые
\ayj7r "
ip0aexp(icot)Y (
------------I //„(x/a)exp -
2 2
Р0О
2 ।
, --icotll ,
4Й2 2a2
и учитывая известное разложение
ехр(-Л2+2ЛП = Х^Я,,(£),
и!
получим
1
exp — х/а-
2 \
-----SindtW
п
exp — i cot/2 —
2 2
рпа р^а .
—— cos cot + , sin 2cot
Ъ 4Й2
(3.3.11)
Решению (3.3.11) соответствует распределение плотности вероятности (см. рис.3.3)
1
exp - х/а-
Роа
—— sinft#
h
(3.3.12)
координата
Рис.3.3. Когерентное состояние осциллятора.
Нетрудно видеть, что в рассмотренном случае средние значения координаты и импульса
осциллируют по гармоническому закону
{x(t)) = ^-sincDt}
(p(t)} = PoCOS6yr’
(3.3.13)
78
снижения для частицы с начальными значеНи
совпадающему с классическим законом дви соответственно. Действитель
ми импульса и координаты ранными пулю и и ти(ьиого движения "°,
вспоминая, что а2 -tl/mco, замечаем, что амнли у Иы
есть д*0 = pjtnco, что и соответствует классической ieop „MnneiIMtt
я ч м ч 1 показывает, что в процессе осцилляции сохраняй
Явный вид выражения (3.3.12) показыва , „ ег0 ширина
ся не только начальная гауссова форма ВО,"«1В СОСТОяния осциллятора не
дисперсии координаты и импульса для когср ; своим тачениям *
от времени и равны соответственно — а / £> ир
ном (вакуумном) состоянии. Если квантовые неопределенности координаты и импШса
малы по сравнению с их амплитудными значениями
а « х0, й/а « Ро ’
(3.3.14)
то фактически движение волнового пакета сводится к движению материальной точки, с
нулевой начальной координатой и начальным значением скорости, равным p^fm (см.
выражения (3.3.13)). Поскольку неравенства (3.3.14) фактически эквиваленты условию
(л) »1, то можно сказать, классическая картина движения возникает для когерентного
состояния осциллятора с большим средним числом квантов.
Выражения (3.3.13) заметно проще получить из уравнений движения для опера-
торов импульса и координаты в представлении Гейзенберга. Действительно, для одно-
мерного гармонического осциллятора уравнения (1.12.3) для гейзенберговских операто-
ров импульса и координаты имеют вид
Л 2л/\ d ж . .
— Pg= xG (/), — xG = pG (t)/m.
at
Решая эту систему линейных уравнений, получаем
. „ 1 Л .
xG (t) = x- cos ал +-р sin ал,
та>
Pg (0 = Р'008 ~ так. ‘ sin cot.
(3.3.15)
Здесь х, р «обычные» операторы импульса и координаты в шредингеровском пред-
ставлении. Для определения квантовомеханических средних подействуем операторами,
заданными через (3.3.15), на волновую функцию вида
Г z 1 А
рехР -Ах--((х-х„)/а)г .
(3.3.16)
Для этого состояния {х} — Xq , (j)} — р0. Тогда из (3.3.15) сразу получаем:
(х(/)) = х0 • cos cot + -— р0 • sin cot,
mco (З.З.П)
(р(0) = р0 • cos z# - • sin ал. В *
В частное™, если =0 a a2 что соответствует состоянию (3.3.1), из (3.3.1’)
получаем найденное нами ранее решение (3.3.13).
79
Аналогично из (3.3.15), (3.3.16) находим дисперсии координаты и импульса в за-
висимости от времени
2
D,(/) = ycos!« + ±L_L^.sinI
z 2а т со
/)2 2
= 2^ 'cos! ая + — т2ш2 sin2 tol.
(3.3.18)
в частности, если а2 = Л/ти, из (3.3,18) имеем = D, = ^/2а> , т0 есть для к0.
герентного состояния осциллятора дисперсии координат и импульса не меняются во
времени. Этот результат был уже нами получен в рамках представления Шредингера.
Однако, рассматриваемый пример является иллюстрацией того, что конкретную задачу
можно решить, проще переходя к представлению Гейзенберга.
Итак, мы видели, что движение волнового пакета, подобное движению классиче-
ской частице в осцилляторном потенциале, возникает только в нестационарном состоя-
нии. В этом смысле стационарные состояния являются чисто квантовыми и не имеют
аналога в классической механике.
Можно, однако, попытаться сопоставить квантовомеханические плотности веро-
ятности, соответствующие стационарным состояниям, и распределение вероятности об-
наружить классический осциллятор в некотором определенном положении в случайный
момент времени. Пусть классическая частица совершает колебательное движение по за-
кону
х = х0 cos cot.
Тогда в интервале координат (х,х + dx) частица находится в течение времени dt
(33.19)
dt = -пт =----7— ----- •
И хой?д/1-(х/хо)2
Поскольку частица проходит все возможные значения своего положения за половину
периода, то вероятность обнаружить ее в интервале (x,x + dx) есть
dW = — =------
Г «о
Как видно, максимальная вероятность для классического осциллятора достигается вбли-
зи точек поворота. Это понятно: вблизи точки поворота скорость частицы мала, и по-
этому она там долго находится. Величина
В некотором смысле является классической плотностью вероятности и может быть сопо-
ставлена с квантовомеханическим значением |«/(x)|\ Зависимости р1((х) и |(Kx)|2, со-
ответствующие состояниям с определенным значением энергии, представлены на
рис.3.4. Как видно, для малых квантовых чисел поведение кривых существенно различ-
но. Однако для больших и (для сильно возбужденных состояний) усредненная кривая
80
и квантовомеханического осциллятора Хор
для распределения плотности веройп 1ИЛЛятора-
согласуется с кривой для классичсско! рассмотренное соответствие доСт
Следует, однако, отметить eu.e не имеют классического ”
условно. Стационарные состояния ква ^^^cHM0CTH координаты и импульса Hae^
Для классической частицы мы имеем з панические средние (х} и (р\ Не
1гняНТОВОМеха”г* ' / v
времени х(/) и р(,). в то время к стационарного состояния». В рассматр ’
от времени и равны нулю для лю вероятности также равна нулю, то
нами стационарных состояниях плотность одНО^ точки пространства в дпу^
отсутствует перетекание плотности вероят оническими колебаниями классичеЛ
Такая картина не имеет ничего общег° как и с колебаниями квантового волной
частицы в осцилляторном ™Те”р^та в виде суперпозиции некоторого количеств
пакета, который всегда можно предел *ва
стационарных состояний системы.
/7=0
/7=1
/7=2
/7=6
Рис.3.4. Классические и квантовые распределения плотности вероятности.
3.4. «Сжатый» вакуум.
Среди нестационарных состояний гармонического осциллятора в настоящее вре-
мя большой интерес представляют собой так называемые «сжатые» состояния осцилля-
тора и, в частности, состояние «сжатого» вакуума.
«Сжатые» состояния осциллятора описываются волновой функцией вида
^о(х) = -г=^=ехр(/са)ехр(- х2/2(яД)2) (3.4.1)
у] fay/л
~ h/mto), зависящей от двух параметров сс и /3. Очевидно, случай <2 = 0, Д=1со-
ответствует основному (вакуумному) состоянию осциллятора, а случай а*0, /М ‘
когерентному состоянию. Особенностью состояния, описываемого волновой функцией
вида (3.4.1), является то, что при Д «1 дисперсия координаты оказывается существен-
но меньше, чем в вакуумном или когерентном состояниях Dx = а2Д2 /2 . Для дисперсии
6 Следует оговориться. Именно основное состояние - .„ирскоп-1
осциллятора) по своим свойствам наиболее близко к состоя°нию Данном случае’ гаР“ маним»’*'
ным значением энергии. Действительно, в классической классического осциллятора с #
соответствует ситуация, когда частица покои"!С°СТ0ЯНИЮ ‘
В квантовой теории основному состоянию соответствуйг°илноГ'"°И ~ ими Сач'”*”'
ми координаты и импульса, делокализованной У волновой пакет с нулевыми средними з»
определенности значений координаты и импульса ?ИЗИ НЭЧаЛа К00Рдинат- С точностью до ^^ко-
лебаний) такое состояние как раз соответствует - ” В03ника1°Щей вследствие этого энергии нулей
сгице, «лежащей» на дне потенциальной ямы-
81
импульса имеем Dp = Л‘/(2«2/?2), что, наоборот, существенно превышает величину
дисперсии, соответствующей вакуумному или когерентному состояниям. При этом, ко-
нечно. удовлетворяется соотношение неопределенностей
ОдО„=л74.
Для анализа изменения средних значений импульса и координаты, а также их дисперсий
опять удобнее воспользоваться представлением Гейзенберга. Из выражений (3.3.18) сле-
дует. что в процессе временной эволюции состояния (3.4.1) дисперсии координаты х и
импульса р осциллируют с удвоенной частотой электрического поля, так что через по-
ловину периода возникнет состояние с Dx = а2/(2Д2) и Dp = Й2Д2/(2а2). В этом смыс-
ле «сжатые» состояния с параметрами р и 1/Д оказываются физически эквивалентны-
ми. Параметр К = р (если р > 1), или К = \/р (если р < 1) мы будем называть парамет-
ром «сжатия» состояния осциллятора.
Среди «сжатых» состояний гармонического осциллятора особый интерес пред-
ставляет в состояние «сжатого» вакуума. Это состояние описывается функцией (3.4.1) с
параметрами а = О и Д 1, то есть отличается от основного (вакуумного) состояния
лишь шириной распределения величины х:
<Psgv(x) =
1
^Рал/я
ехр(-х2/2(аД)2)
(3.4.2)
Хотя средние значения импульса и координаты в этом состоянии также равны нулю для
любого момента времени, энергия состояния «сжатого» вакуума в случае Д«1 или
Р »1 оказывается велика. Действительно, вычисляя по волновой функции (3.4.2) вели-
чину средней по квантовому состоянию энергии
(£) = ^(/?2/2 + 1/(2/?2)),
(3.4.3)
и вводя среднее число квантов поля в произвольном состоянии поля с помощью соот-
ношения
(£) = Я<а((л) + 1/2), (3.4.4)
из (3.4.3) и (3.4.4) получим связь коэффициента «сжатия» со средним числом квантов
= (3.4.5)
4
Разложение состояния «сжатого» вакуума» W по стационарным состояниям дает
= (3.4.6)
п
Отличными от нуля оказываются только четные члены разложения, а все нечетные ко-
эффициенты равны нулю, в частности, |С0| = 1/-J1 + (и) (см. задача 3.8).
82
Рис.3.5. Распределения по числу квантов для когерентного
состояния (1) и состояния «сжатого» вакуума (2) гармони-
ческого осциллятора.
Распределения |q р
числу квантов для когерен
го состояния и состояния
того» вакуума для спЛ**4
числа квантов (п) = log '
ставлены на рис.3.5. ДИсг_
ерсци
числа квантов в когерер
состоянии и в состоянии «е^
того вакуума» есть - / \
/ " \л/ и
О"' = 2Й2+Н) соответ,
ственно. При больших значки
ях имеем Dsq»jy*
есть в сжатых состояниях ано-
мально велика вероятность об-
наружить число квантов, суще.
ственно отличающееся (как в большую, так и в меньшую сторону) от среднего значения.
Сжатые состояния сейчас широко рассматриваются в квантовой оптике, неклас-
сические как состояния моды электромагнитного поля. Более подробно этим вопросом
мы познакомимся в Главе 14.
3.5. Трехмерный изотропный гармонический осциллятор.
Рассмотрим структуру энергетического спектра частицы в трехмерном изотроп-
ном гармоническом потенциале V(r) = mco2r2/2. Запишем стационарное уравнение
Шредингера для данной задачи:
Й2 ТП(О2Г2 п
----А^-1--------у/= Еу/. (3.5.1)
2m 2
Поскольку г2 = х2 + у2 +z\ гамильтониан данной задачи в декартовой системе коорди-
нат представим в виде суммы гамильтонианов Я(г) = Ях(х)+ ЯДу) + Я, (z) одномер-
ных гармонических осцилляторов, описывающих колебания частицы вдоль каждой из
осей. Это, в свою очередь, позволяет разделить переменные в уравнении Шредингера и
искать решение в виде:
И*, у, z) = у/х (х)у/у (y)y/z (z). (3.5.2)
Тогда решение уравнения Шредингера сводится к решению трех независимых ура»не'
ний, описывающих динамику одномерного гармонического осциллятора. Для одномер-
ного гармонического осциллятора известны и волновые функции, и энергии стационар*
ных состояний. Поэтому
Е = Е,+ Еу + EZ = Йй)(и, + пу +п,+ 3/2)=й<у(л + 3/2), I3'5’3’
83
</(х, у, z) = Nni Nn> Nn= Нп(х/ а)НПу {у I d)Hn (z / a) exp ( -| ((r / a)2 L (3.5.4)
где я = nx + ny + nz, nx,ny,nz — О, 1, 2, целые неотрицательные числа, a = y/h/ma>>
- полином Эрмита, Nn =^2"n\a-jn} 1 - нормировочная константа.
Таким образом, произвольное состояние трехмерного изотропного гармоническо-
го осциллятора задается тройкой чисел {их,яу,иг}, определяющих число квантов коле-
баний вдоль каждой из осей. Основное состояние {0,0,0} характеризуется энергией ну-
левых колебаний ЗЙ<у/2. Все уровни энергии, кроме основного, являются вырожденны-
ми. Например, кратность вырождения состояний с энергией 5Й<у/2 равна трем, по числу
возможных одноквантовых возбуждений осциллятора {1,0,0}, {0,1,0}, {0,0,1}. Найдем в
общем случае кратность вырождения п - го энергетического уровня трехмерного гармо-
нического осциллятора. Для заданного значения п кратность вырождения уровня равна
числу возможных комбинаций трех чисел пх, пу и п., сумма которых равна п . Найдем
сначала число перестановок при фиксированном значении пх. Оно равно числу возмож-
ных значений пу (или, что то же самое, п.). Число пу при заданном пх может меняться
в пределах от 0 до п - пх, т.е. принимает n - nx +1 значение. Следовательно, число ком-
бинаций при фиксированном пх равно n-nx -1. Суммируя это выражение по пх, нахо-
дим кратность вырождения п -го уровня gn:
z i\2 1 z i\ (и +1)(/? + 2)
gn = +1) = (л + 1) --w(w + l) = -------
nx--0
(3-5.5)
Отметим, что задача о стационарных состояниях трехмерного осциллятора может быть
также решена и в сферической системе координат. В этом случае стационарные состоя-
ния характеризуются заданными значениями квадрата орбитального момента его проек-
ции на заданную ось z. В общем случае волновые функции стационарных состояний
выражаются через вырожденную гипергеометрическую функцию7.
3.6. Операторы рождения и уничтожения квантов. Возбуждения
как частицы.
В этом разделе рассмотрим еще один очень удобный способ описания гармониче-
ского осциллятора. Заметим, прежде всего, что если измерять координату в единицах
и = y/h/nia), а импульс в единицах ра = y/hma>, гамильтониан гармонического осцилля-
тора можно представить в виде8
g 3. Флюгге. «Задачи по квантовой механике», т.1, М.: Меркурий Пресс (2000) с.177-177
Симметрия этого выражения относительно импульса и координаты позволяет утверждать, что выраже-
Ния (3.1.17) для матричных элементов операторов координаты х" справедливы также и для операторов
Импульса рп с заменой величины а на р0.
84
Н = Ал?
2
где х „ р = -/<’/Л- - безразмерные оператор1» «0^""“™ и ИМПуЛЬСа' В'*ч
операторы
с - —7= V* ~ /э
V2
Поскольку Г = Х(с + С ) >. р = 4= (С - С'), в представлении операторов с, g.
V2 /72
репишем гамильтониан осциллятора в виде
Пе.
2
Рассмотрим коммутационное соотношение для операторов С и С
[с, С+1= - Гх + ip,х - z^]== -7i х,р +1 *]= “z‘k л1
L J 2L 2 4
1.
Поэтому находим CC+ = C+C + \. В результате выражение для гамильтониана (3.6.3)
переписывается в виде:
7/ = /ку(с+С + 1/2). (3.6.4)
Зная собственные функции гармонического осциллятора, мы видим, что
С+С</„ = пу/п, (3.6.5)
то есть оператор п = С+С можно назвать оператором числа квантов.
Для выяснения смысла оператора С подействуем этим оператором на соотноше-
ние (3.6.5)
СС*С^,=(С*С+!)<>„ =«6^,
откуда получаем:
й(С,^) = (и-1)(С^„). (3.6.6)
Отсюда видно, что состояние Су/ п есть собственное состояние числа квантов, но соот*
ветствующее индексу и — 1, то есть оператор С состояние у/п переводит в состояние
^л_1. Аналогично легко увидеть, что
й(су.)=(я+1)сх,
то есть оператор С+ переводит состояние в состояние . Прямым вычисление»
легко показать, что
сч/„ = ,, су„ = , (3.б-7)
85
СТИЧ
^пленный формализм позволяет несколько 11п .
PaCV чсеком осцилляторе. Эквидистантность сиектп’ °Му И'И ЯЯНУ"’ на задачу о тар-
..,,„я ос.и.лля-.-ор(. как отде)1Ы1ыс Р-и^РИ- кванты
С „жлевпя и уничтожения квантов. " С °Пера'
П’1„|Т1'ВОЙ теории шскгромагнитного поля- мола ш "°'‘X‘W рсали ,уется’ 11ап₽имер’
" К' с,,ныс состояния этой моды . кванты -н„ ’ 1 аРмо||и,,еский осциллятор, а
1Нйб)*' nnnonnti млп ’ 'ЯектРома|нитного поля, фотоны. Стацио-
|]ipiibie состояния полевой моды - ЭТО состояния с определенным числом фотонов, а
кя;1ссичсскому электромагнитному полю соответствует когерентные состояния полевой
моды с точно неопределенным, но ольшим средним числом квантов. Аналогично, нор-
мальные коле ания крис галди 1еской решетки можно представить в виде особых "ча-
фононов, являющихся квантами возбуждения нормальных мод.
Задачи к Главе 3.
3.1. Определить средние значения кинетической и потенциальной энергии в произ-
вольном стационарном состоянии линейного гармонического осциллятора.
3.2. Волновая функция частицы, находящейся в осцилляторном потенциале
у = тсо2 х2 / 2, имеет вид
a) И*) = Ах2 ехр(-|(х/а)2); б) ^(х) = Ах3 ехр(--(х/а)2); а = у/Ъ/тй).
Определить, какие значения энергии и с какой вероятностью в этих состояниях
могут быть измерены.
3.3. Определить энергетический спектр и волновые функции стационарных состоя-
ний системы связанных линейных гармонических осцилляторов с гамильтониа-
ном Н = Нх + Н2 + а(хх — х2)2, где Н. = Т. + тсо/х2 / 2 - гамильтониан гармони-
ческого осциллятора с частотой а>0, а - константа связи. Также решить задачу
по теории возмущений, полагая связь между осцилляторами слабой.
3.4. Определить уровни энергии одномерного ангармонического осциллятора
U = то)2х2/2 + ах4. Ангармоническую добавку считать малой.
3.5. Определить энергии стационарных состояний заряженной частицы, находящейся
в гармоническом потенциале U = тй)2х2/2, в присутствие внешнего однородно-
3.6.
3.7.
3.8.
го постоянного электрического поля.
Волновая функция частицы, находящейся в гармоническом потенциале, в мо-
мент времени t = 0 определяется выражением
ф(х) = J2/3 • -г2== • (1 + х/а)ехр[ -1(х/а)2 ,
у/ау/я '
где аг = Определить среднее значение координаты частицы, как функ-
цию времени.
Воспользовавшись теоремой
начального состояния средние
Эренфеста, показать, что для произвольного
значения координаты и импульса (х(0) и (р(0)
удовлетворяют классическому закону движения.
Для состояния «сжатого» вакуума со средним число
квантов равным (п) найти
вероятность обнаружить осциллятор в основном состо
87
Глава 4. Атом водорода.
В этом главе мы подробно остановимся на анализе простейшего атома - атома во-
дорода. Мы рассмотрим не только кулоновское взаимодействие электрона с ядром, но и
магнитные эффекты, возникающие в результате наличия собственных магнитных мо-
ментов электрона и ядра, приводящие к возникновению тонкой и сверхтонкой структу-
ры атомных спектров, а также учтем эффект конечной массы атомного ядра. Существует
три изотопа атома водорода, собственно, водород, ядром которого является протон, а
также тяжелый водород - дейтерий (его ядро, дейтрон состоит из протона и нейтрона) и
сверхтяжелый водород - тритий (его ядро, тритон, состоит из протона и двух нейтронов).
Различие в массах, размерах и в величине магнитных моментов ядер приводит к изото-
пическим эффектам: положение энергетических уровней у изотопов одного и того же
химического элемента оказывается различным.
4.1. Общая постановка задачи.
Простейший атом, атом водорода, состоит из ядра (протона) и "вращающегося
вокруг него" электрона. Это означает, что волновая функция системы есть 'Р(Ре,Лу,0,
где ге - координата электрона, RN - координата ядра (протона). Будем считать, что вза-
имодействие между частицами определяется лишь относительной координатой
р = rc-RN, то есть V(re, RN ) = V(re - RN ). Покажем, что волновая функция системы в
этом случае представлена в виде произведения волновых функций, описывающих отно-
сительное движение частиц и движение центра масс. Действительно, гамильтониан двух
взаимодействующих частиц с массами т и MN имеет вид:
2т
(4-1.1)
где производные берутся по координатам электрона и ядра соответственно. Перейдем от
описания системы при помощи радиус-векторов отдельных частиц к векторам относи-
тельного движения и положения центра масс:
r=re-Rn,
mre + MnRn
m + MN
(4.1.2)
Выражая производные по старым координатам через производные по новым
8 _ 8 8R 8_ёг_ 8 _ 8 8R { 3 дг ,
8r, 8R 8г, + 8г dr, ’ oR., 8R 8RN 8f dR,
придем к гамильтониану системы в новых переменных. Поскольку энергия взаимодей-
ствия между частицами зависит только от относительного расстояния между ними, то
гамильтониан будет иметь вид:
Н = Hg (R) + нг (г) = - — + (4л -3)
88
HBVX частиц (электрона и
Здесь M = m + MN - полная масса Д У Пр
А = тМ. /(т + A/v) - приведенная масса.
пмгтрмы представим в виде суммы гами
Таким образом, гамильтониан си лтнпсительно nnvr ™ ИльТоци
пвмженис частиц относительно друг друга а Ч.
нов, один из которых описывает движен а др^
движение атома, как единого целого.
Для такого гамильтониана в уравнении Рсд Тся
провести разделение переменных, что также приводит к ф и волновой фу?
ции системы на волновую функцию, описыва щу ей сц^
как целого и движение частицы приведенной массы относительно центра масс. уЧ(?*
вая, что масса электрона много меньше массы протона (и олее тяжелых ядер), имее^
т.е. приведенная масса с хорошей точностью совпадает с массой свободного электрОн.
и мы можем говорить о движении электрона в атоме вокруг практически неподвц^^
ядра.
4.2. Движение в центрально-симметричном поле.
В этом разделе рассмотрим важнейшую задачу атомной физики - определение
стационарных состояний частицы в центрально-симметричном, в частности, кулонов-
ском потенциале. Эта же задача важна и в физике атомного ядра, поскольку в первом
Рис.4.1. Сферическая система координат,
электрона с атомным ядром с зарядом
приближении нуклоны в ядре создают цен-
тральный самосогласованный потенциал, в ко-
тором можно рассматривать однонуклонные
состояния.
Итак, пусть поле внешних сил описыва-
ется центральным потенциалом V = К(|г|), по-
тенциал зависит лишь от удаления частицы от
силового центра. В частном случае
y = (4.2.1)
г
такой потенциал описывает взаимодействие
Z.
Для задач с центральной симметрией удобно использовать сферическую систем)
координат, в которой положение частицы описывается длиной радиус-вектора г я
мя углами 0 и (р (см. рис.4.1). Запишем поэтому стационарное уравнение Шредингера
виде:
~ + = ЕчЛг&ср). (4,2‘2)
Прежде чем приступить к решению задачи на собственные значения (4.2.2), вспои*®*
что в случае поля с центральной симметрией оператор Гамильтона коммутируйс
ратором квадрата момента количества движения L2 и оператором его z - прое*"*1111
Кроме того, коммутируют и операторы L1 и Д. Следовательно, в произвольном
89
трально с м поле можно найти такие состояния, в которых сразу три физиче-
ских величи , нно энергия, квадрат момента количества движения и его проекция
на ось~ - I определенные значения. Именно к нахождению таких состояний
мы сейчас дм. ри этом найденные нами решения задачи (4.2.2) будут справед-
ливы для лю ого центрального поля. Затем более подробно мы остановимся на особен-
ностях решения задачи для случая кулоновского потенциала (4.2.1).
Наличие центральной симметрии потенциала позволяет искать решение задачи
(4.2.2) методом разделения переменных
^(г, 6, (р) = R(r)Y(0, <р), (4.2.3)
где соответственно R(r) - радиальная, a Y(0,<p) - угловая волновые функции. Подста-
вим разложение (4.2.3) в уравнение (4.2.2). Получим:
" Ь У{в' ~r ^rR(r^ ~ V) + V(r)R(r)Y(fi,<р) = ER(r)Y(6, (») ,
откуда после несложных преобразований находим:
~ Ин)+(Е - F0)=
R(r)dr2 й2 Y(e,(p)
Левая часть уравнения (4.2.4) зависит только от радиальной координаты, в то время как
правая — только от совокупности угловых координат. Следовательно, каждая из частей
уравнения есть некоторая константа Л. Тогда имеем
-berY(e,<p) = ZY(0,'p). (4.2.5)
Решение задачи (4.2.5) мы уже обсуждали в разделе 1.5: это сферические функции Y(m.
Как мы уже отмечали, с физической точки зрения уравнение (4.2.5) представляет собой
задачу на собственные значения оператора квадрата момента количества движения:
£2^=й2/(£ + ОДт, (4.2.6)
С учетом решения задачи для угловой части оператора Лапласа, из (4.2.4) получим урав-
нение для радиальной волновой функции R(r):
Й2 1 d2
2т г dr2
Вводя новую функцию
(4.2.4)
+ = ER(r).
2mr
(4.2.7)
u(r) = rR(r),
получим
+ (r)„(r) = W),
2т dr
(4.2.8)
где
, ч й2Г(* + 1)
^(r)=m+
® 2mr
(4.2.9)
90
(л имеем обычное одномерное уравнение Цтп
Таким образом, для функции «( ) +|)/w называют цен '’Х
но с эффективным потенциалом. Д в03никает и в решении класс *
тенциалом. Точно такое же слагаемое^ поле. Именно
ХиХ7чеа“™ЦЧуо™ЦЦеЫнтра, препятствуя се падении, нг‘ СИЛ°В°Й «етР » слу^Ч
убывает более плавно, чем — 1
вблизи начала координат потенциал ( ) У • Квацт0
ито квадрат момента количества движеи,
специфика заключается только в том, Ния Пр
мает строго определенный дискретный на ор значен
Как видно, вследствие цененной симметрии задачи эффективный „0
V.„ (К) не зависит от магнитного квантового числа. Это означает, что состояния с
ным I, но различными т , описываются одним и тем же радиальным волновым ура
нием. Следовательно, такие состояния характеризуются одинаковыми радиол*
волновыми функциями и имеют совпадающий набор энергетических уровней. Таким
образом, состояния с заданным , но различными т , оказываются вырождены по пр0.
екции орбитального момента, причем кратность вырождения g - 2£ +1. Это очень ва*.
ная особенность решения задачи (4.2.2) в произвольном центрально-симметричном поле
^ + 1) (4.3.1)
4.3. Задача Кеплера.
Перейдем теперь к более подробному обсуждению случая кулоновского потенци-
ала (задача Кеплера1). В этом случае эффективный потенциал, в котором происходит ра-
диальное движение частицы, записывается в виде
г 2тг
Графики функций для различных зна-
чений £ приведены на рис.4.2. Для 5 -
состояний эффективный потенциал
совпадает с кулоновским, для состоя-
ний с ненулевым моментом в области
малых г возникает центробежный ба-
рьер, тем больший, чем больше значе-
ние орбитального квантового числа.
Наша задача теперь проанали-
зировать решение радиального уравне-
ния (4.2.8) с потенциалом (4.3.1). Ре-
шение задачи можно искать как в области отрицательных значений энергии Е < ®
при Е > 0. Мы ограничимся рассмотрением только случая Е < 0, соответствую111^
связанному состоянию частицы в кулоновском потенциале. В случае положите^
значения энергии возникает непрерывный энергетический спектр. Решение УР^е
(4.2.8) можно найти для любого Е > 0
' Kepler Johannes (1571 - 1630) - немецкий математик, астроном.
91
Обсзразмсрнм уравнение (4.2.8). Вводя £ = г/„() и г = |£|/Яу (здесь
а{} =Ъ‘1”'е* «0.529-10 к см - боровский радиус, Ry^h’/lmal -me^lh2 «13.606 эВ -
ридберг), перепишем уравнение (4.2.8) в виде
2Z
^2"(s) <V + 1) (27 А
-------
V s >
(4.3.2)
установим, прежде всего, асимптотическое поведение радиальной волновой функции
;/(^) в области больших значений £ —> оо. В этой области уравнение (4.3.2) имеет вид
откуда находим
w(£ -> оо) ~ ехр(- 4е^). (4.3.3)
С другой стороны, в области малых £ (£ —>0) наиболее существенным оказывается
центробежный потенциал. Поэтому в этой области имеем\
ита_^)и(,).о.
Ограниченное в точке % = 0 решение этого уравнения имеет вид
«(£) ~ • (43.4)
С учетом асимптотик (4.3.3) и (4.3.4) решение радиального уравнения (4.3.2) будем ис-
кать в виде
M© = ^Mv©exp(-^), (4.3.5)
где а = 4ё. При этом функция v(£) должна быть полиномом конечной степени пг:
rir
к=0
Как и в случае гармонического осциллятора, это условие может быть выполнено лишь
для строго определенных значений £, определяемых из условия
nr +£ + \ = Zl4e • (4-3.6)
Здесь пг = 0,1, 2,...- степень полинома и называется радиальным квантовым числом. Из
(4.3.6) получаем
Вводя главное квантовое число п = nr +£ +1, перепишем (4.3.7) в виде
Z2Ry
(4.3.8)
92
Здесь п принимает положительные целочисленные значения п 1,2,3,... При
но, что значения орбитального квантового числа изменяются в следующих пред
( = 0,1, 2,..., п ~ 1. При этом состояния с различными f , принадлежащими оДН0Му
же значению п, оказываются вырожденными, т.е. в случае кулоновского поля возниц
дополнительное «случайное» вырождение по орбитальному квантовому числу, у^
вая также вырождение уровней по проекции орбитального момента, легко °преде
кратность вырождения состояний с данным значением главного квантового числа П
g = g(2f + l) = /72.
Г-0
Таким образом, основное состояние 15 является невырожденным, состояния 2s и 2^
имеют одинаковую энергию, кратность вырождения равна четырем (существует
р состояния, отличающихся значением маг-
нитного квантового числа). Далее имеется
набор состояний 3s, Зр и 3d (их всего де-
вять - одно 5 -, три р - и пять d -состояний),
также имеющих одинаковое значение энер-
гии. Энергетическая диаграмма нижних со-
стояний в атоме водорода (или водородопо-
добном ионе) приведена на рис.4.3.
Вернемся теперь к обсуждению ради-
Рис.4.3. Диаграмма энергетических уровней
атома водорода.
альных волновых функций в задаче Кеплера.
Полиномы v(<f), через которые выражается
решение уравнения (4.3.2) называются обобщенными полиномами Лагерра2, и их свой-
ства хорошо изучены в математике. Эти полиномы могут быть определены как
= exp(0f ’ exp(-f)).
(4.3.10)
Тогда общее выражение для радиальной волновой функции 7?лДг) имеет следующий
вид:
RAr} = Nni - И exp
Zr^
naQ>
L^(2Zr/na0)
(4.3.10
где нормировочный коэффициент Nn( определяется из условия нормировки.
Таким образом, задача об определении волновых функций стационарных состоя
ний решена. Волновая функция частицы в центрально симметричном поле характеризу
ется тремя квантовыми числами п,£,тп и может быть представлена в виде
в случае кулоновского поля радиальные функции связанных состояний
представимы в виде (4.3.11). При этом квантовые числа могут принимать следую^
набор значений
2 Laguerre Edmond Nicolas (1834-1886) - французский математик.
93
п = 1, 2, 3,..., (> = о, I 2 и 1
’ , А.W = -/\-/? +jv.
, „.нповочный коэффициент /V . должен К. .....
lIopM'1! ,,е д жсн оьнь определен из условия:
JlVArfml /"2tZrdD = l. (4.3.13)
С учетом представления (4.3.12), поскольку мы договорились использовать нормиро-
ванные на единицу с ерические функции, условие нормировки радиальных функций
записывается в виде
ОС
JX2z(r)r2 Jr = 1. (4.3.14)
О
Здесь мы учли, что обобщенные полиномы Лагерра являются действительными функци-
ями.
Не обсуждая решение задачи в области энергий Е > 0, запишем общее представ-
ление для волновой функции континуума в виде
1^Еет (г, 0, (р} = RE( (r)Y(m (0,<р), (4.3.15)
где индекс Е означает принадлежность функции к собственному значению, равному
Е. При этом сами волновые функции континуума нормируются на 8 -функцию соглас-
но условию
/ (r)REt (r}r2dr = 8(Е-Е'). (4.3.16)
О
Приведем явные выражения для радиальных волновых функций нескольких ниж-
них энергетических состояний:
Ь R{ о (г) = liZ/a^ )3/2 ехр (- Zr/a0),
2s Я20(г) = 2(Z/2a0)3/2(l-Zr/2tz0)exp(-Zr/2a0),
2/? R21 (г) = 2= (Z/2a0 )3/2 • Zr/2я0 • exp (- Zr/2a0),
3s J?30(r) = 2(Z/3a0)3/2fl-|zr/a0+^(Zr/a0)2 |exp(-Zr/3a0),
\ 3 27 J
3p J?31(r) = ^-(Z/3a0)3/2(Zr/a0)fl-|zr/a0>|exp(-Zr/3a0),
9 \ о J
3d R32 (r) = —4= (Z / 3a0)3z 2 (Zr / a0)2 exp (-Zr / 3a0).
27V10
Графики функций k, а также 2s и 2p состояний приведены на рис.4.4. Важной осо-
бенностью рассмотренных нами состояний является то, что все состояния с отличным от
нуля орбитальным моментом обращаются в нуль в начале координат, причем, чем боль-
ше значение орбитального момента, тем больше электронная плотность оказывается
«отжата» от ядра центробежным потенциальным барьером. Для 5 - состояний потенци-
альный барьер отсутствует, в результате волновая функция оказывается отлична от нуля
94
что именно структура 5 - состояний а.
в начале координат. Это приводит к тому, цйпичи 01сазЫь
Z- - ^Апиплстям потенциала вблизи Центральной
ется наиболее чувствительной к особенное uan-runv п КЛ<1Г, - 011 Т°Чь
-глбнаоужить частицу в малой обпо Ч|(и
поскольку существует ненулевая всроя I нос гь РУ Ласти пп ’
у у у у ' ,,„ОР|,И о таких состояниях атомный
странства вблизи силового центра. Факти щеки Электр0
некоторой вероятностью может оказаться внутри атомною ядр , то делает нсобХо с
мым учитывать его неточечность при точном расчете положения s уровней, g
нейшем мы рассмотрим целый ряд эффектов, обусловленных, в конечном счете, .
особенностью состояний с нулевым значением орбитального момента.
Рис.4.4. Радиальные волновые функции атома водорода.
Выпишем в явном виде также волновую функцию 1 s состояния электрона в водо-
родоподобном ионе с зарядом Z. Принимая во внимание, что нормированная сфериче-
ская функция s - состояния есть
У00(^(Р) = -1=
л/4д-
получим
JZ3
— exp(-Zr/a0).
яа0
Как найти вероятность обнаружить электрон на некотором расстоянии от ядра?
Для ответа на этот вопрос вспомним, что величина
p(?)6/V = |^ta(F)|2dV
(4.3.17)
представляет собой вероятность обнаружить частицу в элементе объема dyr вблизи
точки г . Если нас интересует только удаление от центра, но не интересует направление,
под которым определяется вероятность, мы должны проинтегрировать (4.3.17) по всем
углам, оставив зависимость только от радиальной координаты:
P(r)dr = J|^„ta(F)|2dQ.r2^,
откуда с учетом (4.3.15) для радиальной плотности вероятности получаем
Р(г) = г2Я2Дг). (4.3.18)
Распределения радиальной электронной плотности вероятности для Is, 2s и 2р
яний приведены на рис.4.5. Как видно, геометрический фактор приводит к тому, Ра'
95
опьная плотность вероятности в точке г-О
диаль ~ / — О обращается ноль для всех, в том числе и
стоянии. При этом простои пасчот
5-tOt * ст доказывает, что наиболее вероятное удаление
.к-тпона от ядра в водородоподобном un»n о „„
м ионе в основном состоянии определяется выра-
жением
1 ~ ,
в частности, в атоме водорода наиболее вероятное удаление электрона от ядра равно бо-
ровск-ому радиусу.
Рис.4.5. Радиальные распределения плотности вероятности в атоме водорода.
Стационарные состояния, определяемые функциями иногда называют
квантовыми орбитами. В квантовой химии вместо слова орбита используют понятие ор-
битали. Фактически атомная или молекулярная орбиталь - это некоторое стационарное
состояние электрона в атоме или молекуле, характеризуемое определенным значением
энергии и волновой функцией, являющейся решением стационарного уравнения Шре-
дингера.
4.4. Переход к классическому описанию.
Рассмотрев квантовомеханическую теорию строения атома, обсудим теперь во-
прос, как в рамках волновой картины увидеть предельный переход к классическому
атому, в котором происходит движение электрона по некоторой траектории вокруг
атомного ядра? Для ответа на этот вопрос вспомним о квантовомеханическом векторе
плотности тока вероятности, введенном нами в Главе 1:
J = —
2mi
который что в сферической системе координат имеет следующие проекции (см. рис.4.6)
_ д _ 1 д 1 д
V = ег — + ее “7TZ + е<? —•
дг гдб v г sin# дер
Принимая во внимание, что радиальные волновые функции и присоединенные полино-
мы Лежандра являются действительными функциями, находим, что только (р - компо-
нента тока вероятности отлична от нуля. Это означает, что в стационарном состоянии в
96
„имением магнитного квантового числа3 вок
атоме для состоянии с ненулевым зна Лдр5
циркулирует ток вероятности
!- cxp(im,<p) + cxp(/m,«>)— ехр(_,„ \
д(р С(р '*>
Ьт? I2
. /z
°’ 2z?zz-sin(#)z
Рассмотрим теперь сильно возбужденное
ми квантовыми числами f и т(
(( = п — 1, т( = (. = л — 1 )• Для этого
случая угловое распределение плотно-
сти вероятности имеет вид
pW~\v,,d\ ~|/>''(С0И2 ~sin2'W'
При больших значениях I данное рас-
пределение оказывается «плоским», то
есть ток циркулирует вокруг ядра в
плоскости z = 0, учет радиального рас-
пределения Л2>и_,(г) приводит к тому,
что этот ток локализован преимуще-
ственно в области, удаленной на расстояние п а0 от ядра. Учитывая, что для больших
значений ( орбитальный момент L , выражение (4.4.1) можно переписать в виде
М । |2
mrs'm(0)
состояние
,/<р
(И » 1) с максимально возмп-х,
v 'КНьь
Рис.4.6. К вычислению плотности тока в атоме.
р - плотность вероятности, a v — L/mr - скорость движения по орбите. Таким образом,
рассматриваемое нами состояние представляет собой кольцевой ток, циркулирующий
вокруг ядра, и по своей структуре напоминает кольцо Сатурна. Движение вокруг ядра
хорошо локализованного пакета получится, если мы рассмотрим суперпозицию большо-
го числа состояний с различными значениями п и £, но такими, что все они удовлетво-
ряют соотношению € ~ п »1. То есть классическая картина движения получается для
волнового пакета, образованного из большого числа стационарных состояний с высоки-
ми квантовыми числами.
Отметим, что самыми «неклассическими» являются 5 - состояния электрона в
атоме, то есть состояния с нулевым значением орбитального момента Действительной
классической точки зрения в таких состояниях траектория электрона в атоме является
отрезком прямой и проходит через точку сингулярности потенциала В рамках кванто-
вой теории соотношение неопределенностей не допускает существование траектории
электрона в атоме, и в состоянии с нулевым орбитальным моментом электрон описыва-
ется сферически симметричной волновой функцией, локализованной вблизи притягн»»’
3 Здесь во избежание путаницы в обозначениях
магнитное квантовое число обозначено как
97
ioiucr° центра, р юризующсйся нулевым значением вектора плотности тока веро-
ЯТНОС™-
4.5. Модель атома Бора.
Рассмотрим следующий приближенный метод решения стационарного уравнения
Шредингера. Для простоты ограничимся одномерным случаем
Й2 d2\y
^^ + r<xW) = £y/(x).
Перепишем его в виде
- Й 2 = 2tn(E - У(*)>(*) = рг (*>(*).
Здесь р(х) — yj2m(E — ^(х)) - «обычный» классический импульс частицы.
Будем искать решение уравнения (4.5.1) в виде
И*) = ехр ^(х) ,
ул )
где ф(х) - некоторая новая неизвестная функция. Подставляя представление (4.5.2) в
уравнение (4.5.1), получим
(12ф 2
~Л~^ = Р «•
(4.5.1)
(4.5.2)
(4.5.3)
Переход к классическому пределу предполагает малость второго слагаемого в левой ча-
сти уравнения (4.5.3). В этом случае имеем
dfijdx = р(х),
откуда
(4-5.4)
В случае, если движение частицы носит периодический характер, в силу однозначности
определения волновой функции имеем
J p(x)dx = 2яиЙ, л = 1,2,3,... (4.5.5)
Перепишем условие (4.5.5) для случая движения по круговой орбите (см. рис.4.7)
p = mv = const, dx = rd(p.
J p(x)dx = mvrj dtp = 2nmvr,
(4.5.6)
4 Фактически обсуждаемый метод представляет собой так называемое квазиклассическое приближение в
квантовой механике.
98
откуда получаем условие квантования
количества, впервые предложенное Н t
1913 году задолго до создания квант0
рии: В°й
L и = (4.5Л)
„ квантовое условие Бора напом„.
Отметим, чт чи на собственные значение
нает решение 0 не допускает нулевой
для оператор»
проекции "°”™” условие Бора совместно с
классическим уравнением движения электрона на круговой орбите
v2 Ze2
т— - ——
дает следующие выражения для радиусов орбит, скоростей движения и разрешенных
уровней энергии (п = 1, 2, 3,...)
Й2 п2 П2
те2 Z ° Z
те4 Z2
2Й2 п2 '
(4.5.8)
(4.5.9)
(4.5.10)
Здесь а = e2/hc = 1/137 - постоянная тонкой структуры.
Сопоставляя полученные выражения с результатами квантовомеханического рас-
смотрения, замечаем, что в отличие от модели Бора в квантовой теории существуют со-
стояния с нулевым значением орбитального момента, что в принципе невозможно в
классической задаче о движении электрона в кулоновском поле.
В заключение этого раздела остановимся на понятии «круговой» орбиты в кван-
товой механике. В классической теории существует целый набор орбит с одинаковой
энергией, но различными значениями орбитального момента. Случаю круговой орбиты
соответствует состояние с максимальным значением величины момента импульса. Ана-
логично, в квантовомеханической теории атома водорода круговой орбите соответствуя
состояние с максимальным I, т.е. I = п -1. На «круговой» орбите дисперсия радиальной
координаты является минимальной. Действительно, вычислим эту величину
М'-’НЛ
где
5 Bohf Niels (1885-1962) - датский физик - теоретик, Нобелевская премия по физике (1922) "За заслуг»в
исследовании строения атомов и испускаемого ими излучения".
99
□с
/ 2 \ f 4 n2
V' М'- -МОЛ-, 0= jr’Rl(r)dr. (4.5.11)
О
цнто-ралы (4.5.11) могут быть вычислены аналитически для произвольного состояния
0-2^.(3"2 <v + l)), (гг) = +1 _3^(^ + l)),
Поэтому
D- =^(«2('’2 +2W0 + 1)2).
Очевидно, минимальное значение Dr достигается для £ = п -1: Dr = а^п2(2п + 1)/4Z2 ,
а относительная неопределенность радиальной координаты
Zlr _ 1
0 (г) у[2п + \ '
Для больших значений п эта неопределенность стремится к нулю, что соответствует
фиксированному удалению электрона от ядра, характерному для круговой орбиты. При
этом состояние с максимально возможным значением проекции момента количества
движения т = = п — 1 характеризуется почти точно определенным направлением век-
тора L в пространстве, что еще больше сближает представления о квантовомеханиче-
ских и классических электронных орбитах. Состояния с т = f' — n — 1 называют цирку-
лярными состояниями. Именно они являются аналогом круговых орбит в классической
теории.
4.6. Систематика состояний атома водорода. Базисы n,£,m(,ms и
Мы видели, что стационарное состояние электрона в произвольном центрально-
симметричном поле определяется тремя квантовыми числами - п, т( (главным, орби-
тальным и магнитным), причем энергия состояния в общем случае зависит от двух чисел
п, £. При этом для кулоновского потенциала возникает дополнительное "случайное" вы-
рождение по орбитальному квантовому числу. Введение в теорию спинового момента
электрона означает появление еще одного квантового числа ms, определяющего проек-
цию спина на заданную ось z. Поэтому состояние электрона в атоме водорода (и в лю-
бом потенциале с центральной симметрией) характеризуется четырьмя квантовыми чис-
лами
Рассмотренная выше процедура сложения моментов количества движения позволяет нам
ввести и другой набор квантовых чисел, а именно
100
В отсутствие взаимодействия между “‘’"“Сказанных наборов и характеризовав
литературе принято использовать вгоро числами n,t,j . Записываете.,
ционарныс состояния атома водорода к <
1 я ииЖНИС
ti( г Например, основное состояние - |л,/2,
Рис. 4.8. Диаграмма энергетических уровней атома водорода.
7 и s оба этих набора равноценм
«Ы. &
ч.
возбужденные состояния .
2/?з/2- Все послел
три состояния в рассматп
смых нами приближен/
являются вырожденный
Кроме того, каждое из
состояний содержит Наб^
подуровней с различны^
значениями квантового числа
т, (т, Kero
2j+l значений). Энерг^.
ческая диаграмма уровней
атома водорода с введенны-
ми обозначениями приведена на рис. 4.8.
Введенные нами два набора квантовых чисел, n,£,Tn(,ms и n,t, j,rrij, которыми
можно описать состояние электрона в атоме водорода, естественно описываются совер-
шенно разными волновыми функциями. Что касается первого набора то со-
стояние с заданными этим набором квантовыми числами есть у/пЬП( (г) %(ms), где первый
сомножитель представляет собой «обычную» координатную волновую функцию, а вто-
рой - спиновую. Например, состояние электрона с главным квантовым числом л = 2,
единичным орбитальным моментом ^ = 1, нулевым значением проекции орбитального
момента на ось z и проекций спина на ту же ось равной +1/2 описывается функций
Т(г,о-) = Л21(г)У;0(^^)х
(4.6.1)
о
Аналогично, состояние
ГоА
Т(г,о-) = /г21(г)У10(^,^)х
характеризуется той же самой пространственной волновой функций, однако, значение
проекции спинового момента в этом случае есть -1/2 В случае
T(r,a) = -^/?21(r)x uv
имеем 2р состояние, в котором с вероятностью 1/2 z-проекция орбитального момен”
равна 1, а проекция спина +1/2, и с такой же вероятностью 1/2 z-проекция орбит^
го момента равна -1, а проекция спина есть -1/2
А как построить волновые функции с зяпо,». п лирвиД110’
функции с заданными значениями j,m^ ОчеВ
волновые функции ЭТИХ СОСТОЯНИЙ МОГУТ 6kiTL
гут оыть представлены в виде линейных комо»
101
ций функций (4.6.1) и (4.6.2), Прежде всего построим операторы /2 и jz. Вспоминая
, .пажения для матриц Паули, получим
^<+1/2 0
.° <~1/2,
(4.6.3)
и
< +< +3/4
у2 = ? + s2 + 2ls =
?+3/4
(4.6.4)
Используя выражения (4.6.3) и (4.6.4), легко убедиться, что, например, волновые функ-
ции 2Ру2 состояния представимы в виде
о ’
= 1/2> = Я2,
/°у
2У,о(0,р)
(4.6.5)
Л >
|2р, J = 3/2, = -3/2) =
Для состояния 2рх/2 аналогично можно получить
х
X
,W.
0
= -^^21W
foY
и=
Г,о(^р) '
(-л/2У,,(ад/
('0'1
X
= 4Л2.('-)
WJ
Г 4iY^e,<p)
(4.6.6)
1
X
Легко убедиться непосредственной подстановкой, что все построенные функции (4.6.5)
и (4.6.6) удовлетворяют соотношениям
102
Мы знаем, что с орбитальным механическим и спиновым моментами эЛСКТп
связаны соответствующие магнитные момсшы. Пали шс у атомного электро^
магнитных моментов приводит к возникновению 1ак называемого спин ~ °РбитадЬн
взаимодействия, которое мы до настоящего времени нс рассматривали. Значит, лри 9
числении положения энергетических уровней в снскгрс агома водорода при записиг'
мильтониана системы мы не учитывали слагаемое, описывающее спин - орбиту
взаимодействие, и наши предыдущие расчеты нуждаются в уточнении. Оказывав
энергия спин — орбитального взаимодействия весьма мала по сравнению с энерг^
электростатического взаимодействия электрона с атомным ядром. Поэтому поправку,
уровням энергии будут малы и могут быть найдены в рамках теории возмущений.
4.7. Релятивистские поправки. Тонкая структура спектра атома
водорода.
Мы знаем, что с орбитальным механическим и спиновым моментами электрона
связаны соответствующие магнитные моменты. Наличие у атомного электрона этих
магнитных моментов приводит к возникновению так называемого спин - орбитального
взаимодействия, которое мы до настоящего времени не рассматривали. Значит, при вы-
числении положения энергетических уровней в спектре атома водорода при записи га-
мильтониана системы мы не учитывали слагаемое, описывающее спин - орбитальное
взаимодействие, и наши предыдущие расчеты нуждаются в уточнении. Оказывается,
энергия спин - орбитального взаимодействия весьма мала по сравнению с энергией
электростатического взаимодействия электрона с атомным ядром. Поэтому поправки к
уровням энергии будут малы и могут быть найдены в рамках теории возмущений.
Самый простой взгляд на природу спин — орбитального взаимодействия заключа-
ется в попытке представить его как взаимодействие двух магнитных моментов, один из
которых связан с орбитальным, а другой — со спиновым движением электрона. В этом
случае энергия взаимодействия может быть оценена как
Г
Такая оценка не вполне обоснована. Действительно, выражение для диполь - дипольн
го взаимодействия вида (4.7.1) получается в предположении, что характерное рас^т
ние г между пространственными областями, в которых локализованы токи, создаю^
магнитные моменты, существенно больше размера этих областей (рис. 4.9). В
случае это не так. Эти пространственные размеры совпадают по порядку величины и**
гут быть оценены как а. - боровский радиус. Более строгое рассмотрение природ сП\
- орбитального взаимодействия будет дано позже. А сейчас оценим величину энерг“"'
помощью выражения (4.7.1). Полагая, что ц, = ч = я/Щс и г z а„, полУчИ“
103
(4.7.2)
" u()
zv = e2 fa - постоянная тонкой
ГДе ir
^•ктуры- ^ак видно’ энергия
ч1ИН - орбитального взаимодей-
егвия примерно на четыре поряд-
к-а меньше, чем энергия электро-
статического взаимодействия электрона с ядром, что позволяет решать задачу об учете
с|1|1Н . орбитного взаимодействия в атоме по теории возмущений
С Другой стороны, ВСПОМНИМ Что cimnnoT ^снии.
/ _ ’ рость электрона на первой боровской орбите
определяется vjc-a, а, следовательно, учет релятивистской связи кинетической
энергии И импульса частицы
- Jp2c2 + т2с4 - тс2 (4.7.3)
даст также добавку порядка a Ry в энергию системы. Действительно, разлагая выраже-
ние в ряд по малому параметру р/тс, получим
Т = тс2f ^1 + (р/тс)2 -11 = тс2 Г1 +1 (p/wc)2 -1 (р/тс}4 +... -1^1« Р— -
' \ 2 8 ) 2т 2тс2
= Т„-Та2/2тс2. (4.7.4)
Здесь первый член разложения дает «обычную» нерелятивистскую энергию То = р2 /2ги,
а второй - релятивистскую поправку. Учитывая, что в атоме водорода То =Ry, для по-
правки получаем
<5Т = Ry2/2тпс2 ~ a2Ry,
(4.7.5)
т е. величину порядка энергии спин - орбитального взаимодействия. Таким образом, обе
поправки имеют релятивистскую природу и должны быть учтены одновременно. Учет
этих поправок приводит к возникновению так называемой тонкой структуры спектра
атома водорода, причем величина тонкого расщепления определяется квадратом посто-
янной тонкой структуры6.
После проведенных качественных рассуждений перейдем к последовательному
рассмотрению обеих поправок в рамках квантовомеханической теории возмущений. Бу-
дем рассматривать водородоподобный ион с зарядом Z. Невозмущенный гамильтониан
Этой системы имеет вид
А,/- — (4.7.6)
770 _ 7о г *
Наша задача найти поправки к уровням энергии, обусловленные релятивистскими эф-
Фатами.
^Тс,°ла происхождение названия - постоянная тонкой структур
104
<- гпячИ ИМПУЛЬСЗ И энергии ЭЛектРОцд
1) Учет релятивистекои^^язилм^------ ----
.г 1Испгип электрона, обусловленной реляти
Начнем с учета поправки к эн I
начнем с учма i пспсход к квантовой механике означал.
связью энергии и импульса электрона. I MPMniv onorm аег>Чт0 н
ражение (4.7.4) приобретает смысл соотношения между операторами. Хг
-^/2^ , которая с физической точки зрения представляет собой релятИВИСТс
правку к кинетической энергии электрона, мы будем трактовать как оператор во,м
ния <57. Тогда поправка к положению энергетических уровней может быть запис^
виде
kET = (п£\$Г\пЛ =--^—In^iH.+Ze2/^2 | nf\.
т \ / Ъпс2 ' ' (4.7.
Учитывая, что \ntj есть собственные функции гамильтониана 7/0, из (4.7.7) получу
Д£г =-—1^, +2E,„Ze- < 1/r >+Z2e4(l/r2)).
(4.7.Si
Здесь
E^-Z^Ry/n2 (4И|
- уровни энергии невозмущенного гамильтониана, а знак ( } означает квантовомехани-
ческое усреднение по состоянию \ ntj. Учитывая, что7
l^=\R^rdr^, ^ = /Л2(^ =
z2
ц3а02(£ + 1/2)
(4.7.10i
(здесь Rn( (г) - радиальная волновая функция водородоподобного атома), получим
, _^2/2 77
п
^4-1/2 4и/
(4.7.111
где Ent определяется формулой (4.7.9). Как видно, поправка растет как четвертая сте-
пень Z и быстро уменьшается с увеличением главного квантового числа. Важно,
учет релятивистской поправки снимает «случайное» вырождение по орбитальному
менту. Все уровни смещаются вниз по энергии, причем уровни с большим значение
орбитального квантового числа испытывают меньшее смещение, чем уровни с малым
взаимодействия . к Р вписать вЫраж ’ ИМенно спин - орбитальное »=*
Действии, как о взаимп - °™ечал°еь, прело опеРат°ра спин - орбите^1"'
-содействии двук магнн^ ° ~ **
полей не вполне удоалетворател11'11
’ Эта интегралы вычисляются аналитически с учетом свойств обобщенных полиномов ЛагеРР3
105
.и - орбитальное взаимодействие можно г...,.
СП‘п1очаюшийся во взаимодействии собственно!™“фИВаТЬ КЭК Рсля™вистский эФФект’
3аК’ мм полем, возникающим в собственной , Маи,и,ного момента электрона с маг-
Н,|1Н woHiiCM В этой системе отп СИсгсме отсчета, определяемой орбиталь-
нЫМ лв1,жснпсм. uicicmc отсчета ядро с зарядом Ze дВИЖСТСЯ вокруг .„на и
.o i iaCT магнитное ноле Н , которое мы можем записать я виде
(4.7.12)
где = р;/ электРостатическое поле, создаваемое атомным ядром. Фактически выра-
жение (4.7.12) есть формула преобразования полей в нерелятивистском случае при пере-
ходе из одной системы отсчета в другую8. Поэтому выражение для энергии спин - орби-
тального взаимодействия мы можем записать в виде
Vts = -(д н\
(4.7.13)
где А - тс $ ' собственный магнитный момент электрона. В дальнейшем нам будет
удобно выражать спиновый и орбитальный механический моменты в единицах постоян-
ной Планка, поэтому выражение для Д перепишем в виде
Д=-2//а?. (4.7.14)
Подставляя в (4.7.13) выражения (4.7.12) и (4.7.14), получим
Vts = “(Д#) =
сг
Учитывая, что 7 = [f,mv\ и выражая орбитальный момент также в постоянных Планка,
окончательно для энергии спин - орбитального взаимодействия получим
= 4/4 4(^4
г
Переход к квантовой механике означает замену физических величин соответствующими
операторами. Поэтому имеем выражение для оператора энергии спин — орбитального
взаимодействия
Правильное выражение для этого оператора (оно может быть получено в рамках реляти-
вистской теории Дирака) отличается от приведенного выше ровно в два раза:
<4-7Л5)
8 н ппм пеПеходе из одной инерциальной системы отсчета в
а самом деле выражение (4.7.12) справедли р ающуюся систему координат. С этим обстоя-
ли не может быть использовано при переходе во BPa^ ^^пин _ орбитального взаимодействия,
™ЬСТВОМ связана необходимость введения поправки в энергию
называемой поправкой Томаса — Френкеля.
106
Дополнительный множитель («2») называю! поправкой Томаса9 10 ф
нсйшего нам будет удобно переписи 1 ь оператор спин орби7алы1п^СНКС;,я1й в
виде: ’°'0 взаИМоА,
Чь'
.----1,
г 2
* у г я пкНОГО И СПИНОВОЮ MOMCHTOR
где f1, s2 - операторы квадрата орбшальною мюв, у .
квадрата полного механического момента электрона / ~. Напомним, что
моменты выражаются в единицах постоянной Планка. Для определения попрайк
ложению энергетического уровня нам надо теперь посчитать величину матриц^ ,г
мента оператора Vfs в базисе собственных функций невозмущенного гамильтониан
Прежде чем перейти к вычислению соответствующего матричного w
вспомним, что в атоме водорода (на самом деле - для электрона в любом центру
симметричном потенциале) мы сумели построить два различных набора базисных ф?1!„
ций \n,£,mf ,ms''j и \n,£,j,m^. Какой из них нам сейчас следует использовать?Замети',
^ппя были введены для атома в предположении, что спин - орбиту,
что эти два набора Наличие спин - орбитального взаимодействия в атоме Ме-
взаимодействие отсутствует. Наличие спин н ~ к
тт поте итп полный атомный гамильтониан п Пц+у не к».-.
няет ситуацию. Легко видеть, что полным а
„ _ нппекпии орбитального и спинового моментов. А значит.:
мутирует с операторами величины точно не определены, т.е. стационара
стационарном состоянии атома э
состояние не может быть охарактеризовано набором квантовых чисел
же время легко убедиться, что полный атомный гамильтониан коммутирует с оператс-
рами у2 и jz. На этом основании мы приходим к выводу, что в присутствие спин-
битального взаимодействия мы должны работать в базисе состояний w,^,j,wJ.Ton
учитывая, что
J21«, Л J, mj ) = у(У +1)| n,£J, т j),
£21 n,£, j, tn} } = £(£ +1) n, £, J, mj } ,
i21j,m. ) = s(s +1)| n,£, j,m.},
запишем выражение для поправки к энергии состояния, обусловленной учетом спи»
орбитального взаимодействия, в виде
= zAj^(j(j+l)-^ + l)-s(i + l)), 14Л'
/l\flD2zxj ./ з Значе1*111
где (—) — J -~кп1(г)аг - усредненное по квантовому состоянию значение 1/г
этого интеграла также известно:
9 Thomas Llewellyn Hilleth (1903 -1992) - британский и американский физик - теоретик.
10 Френкель Яков Ильич (1894 - 1952) - советский физик-теоретик.
107
/±\ =__________£
V / /r'n’ftV + r
учитывая, что ,v = 1/2
ТогД^ ?
(4.7.18)
№..
, j = ( ± 1/2, из (4.7.17) получим
a2Z2
-------Е.
п
a2Z2
п
nf
Е ( *
П( Й(Ги/2)’
(4.7.19)
Лч1НчагеЛьный ответ получается, если просуммировать обе поправки
№п( = &ЕТ + Д£& = 1 _
п <7 + 1/2 4я>
(4.7.20)
формула (4.7.20) называется формулой тонкой структуры (формулой Дирака) и описы-
вает релятивистские поправки в положение энергетических уровней в спектре водоро-
доподобного иона.
С точки зрения теоретической физики полученная формула является разложени
ем по параметру aZ решения упавнем™ р у является разложени-
Уравнения Дирака для частицы в кулоновском поле Од-
нако. на самом деле ситуация оказывается несколк™ п
_ сколько более сложной. Во-первых, следует
считать, что спин-орбитальное взаимодействие еипАе». - wicayci
/ лаим°Деиствие существует лишь в состояниях с ненуле-
вым значением орбитального квантового чиепя м R J
,л - 1ОЧ мангового числа, и, стало быть, для 5 - состояний выра-
женис (4.7.19) использовано быть не может. Во-вторых, при анализе уравнения Диршса
помимо рассмотренных двух поправок возникает еще одна, описываемая оператором
^л =^т~4лг7(Р), (4.7.21)
и называемая поправкой Дарвина11. Поскольку при г = 0 отличны от нуля только волно-
вые функции 5 - состояний, поправка Дарвина только для них дает отличный от нуля
вклад:
А£я=^М^.(г = 0)|г.
(4.7.22)
7^
Учитывая, что \i//ns (0)12 = ——-, из (4.7.22) получим
яайп
a2Z4
№D=-~r-Ry. (4.7.23)
Складывая полученную поправку с поправкой (4.7.11), для s - состояний получим
a2Z4< 3>
Д£„-Д£г+Д^- яз
Г. ------------ - - Аидик - теоретик и математик.
Darwin Charles (1887 - 1962) - англиискии физик
108
Полученное выражение совпадает с (4.7.20) для случая € 0. Это означает, форму^
Дирака может быть использована для любых значений орбитального квантового числа
Как видно, спин — орбитальное взаимодействие приводит к расщеплению уровне^
по значению полного механического момента атома. Уровень с большим значение^
j = £ + 1/2 лежит выше, чем уровень с меньшим значением j = £ — 1/2. Такая ситуацця
имеет понятную физическую интерпретацию. Величина энергии спин - орбитального
взаимодействия определяется скалярным произведением Vfs ~ (£?)• Если вектора £ и $
«параллельны» друг другу (т.е. у = £ +1/2), величина энергии Vfs оказывается положи-
тельной. Наоборот, при «антипараллельной» ориентации векторов скалярное произведе-
Рис. 4.10. Тонкая структура спектра атома водорода.
определена с помощью формулы Дирака:
ние меняет знак, и энергия К от-
зывается отрицательной. Заметим
однако, что вырождение снимается
частично. В соответствии с нашей
теорией состояния с различными
значениями £, но одним и тем же
значением j (например, 2$1/2 и
2р1/2) оказываются по-прежнему вы-
рожденными.
Общий вид спектра атома во-
дорода с учетом тонкой структуры
приведен на рис. 4.10. Как видно, все
уровни с ненулевым значением орби-
тального момента расщепились
надвое (стали дублетами). Величина этого дублетного расщепления может быть легко
SE = ЛЕ„,(у = ( +1/2)-&Е„,(j = f-1/2) = •
(4.7.24)
В частном случае для дублета 2р|/23/2 в атоме водорода имеем Ж = а2Т?у/16 ® 4.5 10’5
эВ. Это максимальная величина тонкого расщепления в атоме водорода. Как видно из
(4.7.24), она быстро убывает с увеличением главного и орбитального квантового чисел.
4.8. Сверхтонкая структура спектра атома водорода.
Мы уже отмечали, что нуклоны, так же как и электрон, обладают спином - соб-
ственным механическим моментом количества движения: протон и нейтрон являются
фермионами, их спин равен 1р=1п=\1'2. Поэтому, спин ядра атома водорода
IH =1 -i/2, спин ядра атома дейтерия ID =1 (в дейтроне спины протона и нейтрона
«параллельны» друг другу). Наличие ненулевого магнитного момента нуклонов, связан-
ное с их спином, приводит к дополнительному взаимодействию в атомах, приводящего к
так называемому сверхтонкому расщеплению атомных уровней. Поскольку собственные
магнитные моменты нуклонов примерно на три порядка меньше, чем магнитный момент
электрона, величина этого расщепления примерно на три порядка меньше величины
тонкого расщепления.
109
В качсовс примера чуть более подробно остановимся „а сверхтонкой структуре
основного состояния атома водорода . В „ом случае полнь.й механический м^Хт
"ZZTZMOMC"Ty —° -лектрона. а спин ядра опре-
ЛС"Я о он 7 ! / ТОМ П°ЭТОМУ Квантояос "Р"—
два зна юн . 1 если спины электрона и протона «параллельны» и А - 0 я случае
.антипараллсльнои» ориентации спинов. В соответствии с тгим приходим к выводу, что
сверхтонкая структура основного состояния атома водорода состоит из двух компонент.
ровсдсм теперь количественный расчет сверхтонкой структуры основного со-
стояния атома водорода. В этом состоянии электрон описывается сферически симмет-
ричной дикцией у/1г(?) с нулевым значением орбитального момента. Поэтому возник-
новение сверхтонкой структуры можно рассматривать как результат взаимодействия
спинового магнитного момента поотоня п г . Гг
а про юна цр с магнитным полем Я, создаваемым элек-
тронным спином:
Для магнитного момента имеем Д, = Sp^Nlp. Что касается магнитного поля Н, то
вычислим его исходя из следующих соображений. Электрон создает в пространстве рас-
пределенный магнитный момент (намагниченность), определяемую выражением
М(г) = -2^д|^15(г)|2х5, (4.8.1)
где s - вектор спина электрона. В соответствии с общими правилами электродинамики t
с вектором намагниченности связан ток намагничения
7 = cro^ = -2^fefx[n-5]>
dr
где n = r/r - единичный вектор, «смотрящий» по радиус-вектору. Тогда, вычисляя маг-
нитное поле, созданное током намагничения в точке нахождения протона (в начале ко-
ординат)
Н(г = 0) = - [ЬЩ/’г, (4.8.2)
cJ г
получим
Я(0) = -2дд J= -2//в|^ь(0)|2 у х?,
откуда
И = -fifH = (4.8.3)
Рассматривая последнее выражение как оператор, и, принимая во внимание, что
(0)|2 = 1/(яОо), для оператора сверхтонкого взаимодействия получим
Г = (4Л4)
3 V 7
110
Вводя вектор полного механического момсн ia а тома Л - 7„ + V , и учитывая также, ЧТо
(ХфУ 1 - '
для дополнительной энергии состояния с учетом взаимодействия (4.8.4) получим
Д£, = - g, (Л Г + I )-/„(/„ + । )-•'•(' + I» = (F(F + I) - 3/2),
3 а0 -5 ао
где квантовое число суммарного механического момента атома принимает два значения
F = 0,1. а Iр =5 = 1/2. Для разницы энергий между компонентами сверхтонкой струну,
ры с F = 0 и F = I получаем:
ЗЕ — ЗЕГ_\
_ FnFb
=° о ° Р 3
3 <70
(4.8.5)
Это и есть величина сверхтонкого расщепления основного состояния атома водорода
Длина волны перехода между компонентами F = 0 и F = l лежит в радиочастотном
диапазоне и составляет А = 21.1 см, что соответствует частоте перехода 1420 Мгц. Из-
лучение атомов водорода на этой длине волны широко используется в современной ра-
диоастрономии при изучении пространственного распределения атомарного водорода во
Вселенной.
Поскольку величина расщепления s - состояний определяется значением квадра-
та модуля волновой функции в начале координат, мы можем легко предсказать зависи-
мость величины расщепления от номера главного квантового числа 5 - состояния и за-
ряда ядра водородоподобного иона:
6E~Z3ln3 .
Эти зависимости подтверждаются экспериментально.
Аналогичные расчеты могут быть легко проведены и для тяжелых изотопов водо-
рода (см. задачу 4.16). При этом надо учесть, что в дейтроне спины протона и нейтрона
«параллельны» друг другу, а, следовательно, магнитные моменты противоположно
направлены. Что касается ядра атома трития, то в нем спины нейтронов направлены в
противоположные стороны и компенсируют друг друга. Следовательно, как и у атома
водорода, магнитный момент ядра определяется наличием магнитного момента у прото-
на. Поэтому можно ожидать, что величины сверхтонкого расщепления в водороде и три-
тии совпадают. Эксперимент подтверждает это предсказание. Длина волны перехода
между компонентами сверхтонкой структуры основного состояния атома трития
А = 19.8 см.
4.9. Изотопические эффекты в атомах.
Изотопы - это атомы одного и того же химического элемента, ядра которых име-
ют различное число нейтронов. Например, мы уже говорили, что существуют три изото^
па атома водорода - собственно, водород, тяжелый водород (дейтерий) и сверхтяжелы*1
водород (тритий). Ядро тяжелого изотопа (дейтрон) состоит из протона и нейтрона, ядр°
сверхтяжелого изотопа (тритон) - из протона и двух нейтронов. Различие в свойствах
111
ядер приводит к некоторому отличию положения энергетических уровней - изотопиче-
скому эффекту.
Один из таких эффектов мы рассмотрели в предыдущем параграфе. Протон и
дейтрон имеют различные магнитные моменты, а, следовательно, положение энергети-
ческих уровней в атомах водорода и дейтерия с учетом сверхтонкой структуры несколь-
ко отличается.
Другой эффект связан с конечной массой атомного ядра. Действительно, мы ви-
дели, при последовательном рассмотрении системы "ядро + электрон" возникает задача
о движении в пространстве атома как единого целого, в то время как относительное
движение электрона вокруг ядра описывается приведенной массой, которая, впрочем,
близка к массе свободного электрона. Учесть конечность массы атомного ядра легко:
для этого всюду в теории вместо массы электрона т надо использовать приведенную
массу /л = тМ/(т + М), где М - масса атомного ядра. Тогда, учитывая, что т/М «1,
выражение для энергии п -го стационарного состояния в водородоподобном ионе, запи-
шем в виде
п Tt,?- 2 ~ 2 1
2п п п \
т
~М;
(4-9.1)
Поэтому, например, выражения для потенциалов ионизации всех трех изотопов
водорода можно записать в виде:
I (4.9.2)
где М - масса каждого из ядер. Как видно, учет конечной массы протона приводит к не-
большому изменению потенциала ионизации по сравнению с расчетами, выполненными
в приближении бесконечно тяжелого ядра. В первом приближении можно считать, что
массы дейтрона и тритона превосходят массу протона соответственно в два и три раза.
Поэтому для разницы потенциалов ионизации изотопов водорода и дейтерия имеем
п ( т т \ т о , Л_4 D
ID-IHaRy-----7— =Ry-^—«2.7-ю Ry,
тп 2т„ 2тп
Аналогично, для изотопа трития получим
„ гп т ) п 2т , 4
IT-IH^Ry-------— =Ry~—-3.6-10 Ry.
Т н z \т„ Зт„ Зта
(4.9.3)
(4.9.4)
Существует и еще одна причина изотопического сдвига атомных уровней. Она
обусловлена конечным размером атомного ядра, и, как мы увидим, даже на качествен-
ном уровне не может понятна из классических соображений. В качестве примера рас-
смотрим вопрос о влиянии конечного размера атомного ядра на положение энергетиче-
ских уровней в водородоподобном ионе с зарядом Z. Действительно, при определении
энергетического спектра водородоподобных ионов с зарядом Z до сих пор мы исходили
из предположения, что ядро является точечным. На самом деле ядро имеет конечный
размер (порядка 1013 см для легких ядер и ~10'12 см - для тяжелых). В результате потен-
циальная энергия взаимодействия электрона с ядром описывается формулой
T „Р выпажсние для энергии взаимодействия может быть записа.
лишь приближенно. Точное выражени
НО в виде
£/(,-) =-е<р(г), ( ,9-6)
где - электростатический потенции создаваемый ядром в пространстве. Распреде.
ление <p(r) удовлетворяет уравнению Пуассона
= №л)
где функция определяется распределением заряда в атомном ядре. Вследствие ма.
ости размера ядра по сравнению с размером области локализации электронной
' сыпать что (4 9 5) и (4.9.6) дают близкие распределения и
В0ЛН°^:Хе“ разХа ядра на положение уровней можно по теории возму-
щений. Рассматривая в качестве невозмушенного атомного гамильтониана оператор
запишем полный гамильтониан водородоподобного иона в виде
Здесь в качестве оператора возмущения выступает разность между потенциальной энер-
гией взаимодействия электрона с реальным и точечным ядром:
дТ = Р(г) - V(r) = -eqtf) + Ze1 /г .
Запишем выражение для поправки к энергетическому уровню:
= |УлД';)|2£Г(Р)473г.
(4.9.8)
Рис. 4.11. Электростатический потенциал,
создаваемый атомным ядром.
Мы будем считать, что распределение заряда в атомном ядре является сферически сим-
метричным, то есть р(г) = р(|г|). Вид функ-
ций V(r) и -е(р(г) для этого случая приве-
ден на рис.4.11. Как видно, вне ядра выраже-
ния (4.9.5) и (4.9.6) совпадают, и интеграл в
(4.9.8) берется по объему атомного ядра, то
есть смещение энергетического уровня обу-
словлено тем, что с некоторой вероятностью
электрон может быть локализован внутри
атомного ядра. При этом существенно, что
неточечность ядра приводит к тому, что по-
тенциальная яма становится более мелкой по
сравнению с моделью точечного ядра. Следо-
вательно, величина возмущения > 0, и уровни должны сместиться вверх относитель-
но невозмущенного положения.
113
следствие малости размера атомного ядра по сравнению с обла-
стью локализации электронной волновой функции ««0/Z), можно считать, что в
области гр рования значение электронной волновой функции практически посто-
янно и определяется величиной = 0). Поэтому перепишем (4.9.8) в виде
^Еп( - -е\^п( (0)|2 J(p(r) _ Ze/r)d\. (4.9.9)
Принимая во внимание поведение радиальных волновых функций вблизи точки г = О
-/,(£*()) и Я„,(0)*0,
находим, что в нашем приближении будут смещены только s - состояния. Все состоя-
ния с ненулевым значением орбитального момента останутся несмещенными, то есть
Так получилось потому, что центробежный потенциальный барьер отжимает электрон
от центра и делает вероятность обнаружить его внутри атомного ядра исчезающее ма-
лой. Что касается s - состояний, то для них центробежный барьер отсутствует, и элек-
трон с некоторой вероятностью может быть обнаружен внутри атомного ядра, что и
приводит к смещению уровней с нулевым значением орбитального момента.
Для вычисления интеграла (4.9.9) воспользуемся следующим тождеством
V2(r2)=6.
С учетом (4.9.10) перепишем (4.9.9) в виде
(4.9.10)
ns
= f V2 Р \<Р<Г) ~ Ze!•
(4.9.11)
или, интегрируя по частям:
=-|<К(0)Г Р2 V2Wr)-Ze/r)rf3r.
(4.9.12)
1
Учтем теперь, что V2
= 4/rJ(r), и г2 3(f) = 0. Тогда из выражения (4.9.12) найдем
= ^^К(°)Г Jr2p(r)d3r = ^e^ris(ofZeR2, (4.9.13)
О у
где R2 = — I*r2p(r)d2r - протонный среднеквадратичный радиус ядра. Поскольку
ZeJ
з
2
^3„3 ’
для поправки к уровню энергии ns окончательно находим
(4.9.14)
4 R2 1
3 а0 п
114
Как видно, поправка быстро убывает с увеличением главного квантового числа, Что
зано с уменьшением вероятности обнаружить электрон виугри ядра по мере увеличе?
п. Дальнейшее уточнение полученного результата зависит от конкретного вида фуцк
ции. описывающей распределение плотности заряда внутри ядра. Например, в слу^
равномерного распределения заряда
Ze
~ , л -JX Г) 3
(4 3)д7?,у
- const
— 7 3 п 7
имеем R = — л Г
5
Итак, учет конечного размера ядра привел к смещению s - уровней вверх относи-
тельно их положения, рассчитанного в приближении точечного ядра. Уровни с ненуле-
вым значением орбитального момента остались несмещенными. Таким образом, «слу.
чайное» вырождение по орбитальному моменту оказалось частично снятым. Величина
смещения в атоме водорода чрезвычайно мала. Например, для основного состояния ато-
ма водорода, полагая, что для протона12 R « 0.8 • 10“13 см, из (4.9.14) находим
4 R1
5£15=- —^3-10-’>,
3 <70
однако, поправка быстро растет с увеличением заряда ядра. Поскольку различные изо-
топы одного и того же химического элемента имеют несколько отличающиеся размеры
ядра, то положение s - уровней у них несколько отличается. Рассматриваемый нами эф-
фект оказывается тем существенней, чем тяжелее ядро атома.
4.10. Мюонный атом водорода.
Рассмотрим еще одну интересную водородоподобную систему - мюонный атом
водорода. В этой системе вокруг протона (или дейтрона, тритона) вращается не элек-
трон, а отрицательно заряженный мюон. Эта частица по своим свойствам очень похожа
на электрон, но тяжелее электрона в 207 раз: тпр = 207т. Кроме того, частица неста-
бильна, время ее жизни составляет « 2.2 мкс. Это очень много, почти бесконечно
много по масштабам атомного времени. Рассматривая эту систему аналогично тому, как
выше был рассмотрен атом водорода, получим, выражение для характерного размера
системы
а, =^/тме2 = а0/207 «2.5-10’11 см,
а потенциал ионизации (в пренебрежении эффектами, связанными с конечной массой
ядра, а также тонкой и сверхтонкой структурой)
= ^е4/2Й2 = 207Ry « 2.8 кэВ.
Учет движения атомного ядра приводит к некоторому изменению рассчитанного значе
НИЯ
См., например, И.М.Капитонов «Введение в физику ядра и частиц», М.: УРСС, (2002), с.23-24.
115
Л, «(I “ т,, /М)х 207Ry * 186/<y « 2.5 кэВ.
Система оказывается очень компактной, и именно это обстоятельство вызывает к ней
интерес. Мюонные атомы могут образовывать молекулы также как и обычные атомы.
При этом расстояние между ядрами оказывается порядка размера "орбит" мюонов, обра-
зующих химические связи13. Поэтому, если характерное расстояние между атомами во-
дорода в обычной молекуле водорода составляет величину порядка ангстрема, то в мю-
онной молекуле это расстояние на два порядка меньше. Это делает мюонные молекулы
водорода интересными с точки зрения проблемы ядерного синтеза. Оказывается, при
расстоянии между дейтронами (или дейтроном и тритоном), достигаемом в мюонной
молекуле, возможна туннельная реакция синтеза
d + d^He+n,
сопровождающаяся выделением большого количества энергии. При этом не требуется
разогрева вещества и создания высокотемпературной плазмы, а сам мюон в реакции не
участвует, выступая в роли своеобразного катализатора (отсюда название - мюонный
катализ ядерного синтеза). Принципиальная возможность такого способа осуществления
управляемой термоядерной реакции была продемонстрирована в экспериментах группы
JI. Альвареца14 в 1956 году.
4.11. Экситон Ванье - Мотта.
В данном разделе рассмотрим еще одну систему, которую можно описать в рам-
ках нашей модели. Известно, что в полупроводниках перенос зарядов осуществляется
свободными электронами (носители п типа) и дырками (носители р типа), являющи-
мися положительно заряженными вакансиями в кристаллической решетке. В полупро-
воднике электрон и дырка могут объединяться в экситон - электрически нейтральное
образование, аналогичное атому водорода (экситон Ванье15-Мотта16).
Считая, что в среде с диэлектрическою проницаемостью £ электрическое поле
заряда ослабляется в е раз, получим выражение для характерного размера, определяю-
щего волновую функцию экситона (р - приведенная масса системы электрон - дырка):
aex=E-ti/ ре2 =ай^Е(рг’ / р}. (4.11.1)
Энергия связи электрона и дырки в экситоне есть
т — у /?v
* ex Л 212 2 ♦
2е ft е m
В выражениях (4.11.1) и (4.11.2) гп есть эффективная масс полупроводника17.
(4.11.2)
13 Строение простейших молекул мы будем обсуждать более подробно в Главе 7.
14 Alvarez Luis Walter (1911 - 1988) - американский физик - экспериментатор, Нобелевская премия (1968)
«За открытие множества резонансных состояний, ставшее возможным благодаря использованию водород-
ных пузырьковых камер и анализу данных».
15 Wannier Gregory Hugh (1911 - 1983) - швейцарский физик.
16 Mott Nevill Francis (1905 - 1996) - английский физик, Нобелевская премия (1977) «За фундаментальные
теоретические исследования электронной структуры магнитных и неупорядоченных систем».
17 В твердых телах (кристаллах) движение электрона можно рассматривать как движение свободной ча-
стицы, обладающей некоторой эффективной массой.
116
Для наиболее используемого в современной микроэлектронике полупроводника (v-
ния) значение диэлектрической проницаемости ~ 12, а эффективные массы Электр^'
нов и дырок одинаковы т* 0.25т. Поэтому ц = т /2 ® 0.125щ. Следовав
асх ~100t7() и / ., «8.68x10 '/?г «0.018 эВ. Как видно, экситон представляет собой
босвязанную систему, что приводи! тому, что он может наблюдаться лишь ппи п
доста-
точно низких температурах.
Отмстим, размер экситона существенно превышает межатомное расстояние в
шетке, что позволяет использовать макроскопический параметр - диэлектрическую
ницаемость.
ПРИЛОЖЕНИЕ 4.1. СТРУКТУРА ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
АТОМА ВОДОРОДА’8.
На прилагаемом рисунке приведены экспериментальные данные по положению
k, 2s и 2р уровней атома водорода. Помимо рассмотренных ниже эффектов тонкого и
свертонкого расщепления на представленных данных виден также лэмбовский сдвиг 1$
2s уровней атома водорода. Видно, что эти уровни смещены относительно своего по-
ложения, которое предсказывается теорий Дирака. Как результат снимается вырождение
состояний 2s и 2р, которое имеет место в теории Дирака.
2466 THz
— — 1Sj/2 from Dirac theory
18 По данным MJ.Eides, H.Grotch, V.A.Shelyuto // Physics Reports, V.342, P.63-261, (2001)
117
Возникновение лэмбовского сдвига атомных состояний есть фундаментальный
факт взаимодействия атома с так называемым электромагнитным вакуумом, является
убедительным доказательством его существования, и будет рассматриваться нами в Гла-
ве 14. Заметим, что величина лэмбовского сдвига существенно превышает величину
сверхтонкого расщепления. Что касается эффекта, связанного с конечным размером
протона, то он оказывается пренебрежимо мал. Однако, современные прецизионные из-
мерения лэмбовского сдвига позволяют одновременно увидеть в том числе и вклад в по-
правку уровней энергии, обусловленный конечным размером протона.
Задачи к Главе 4.
4.1. Определить средние значения модуля скорости, кинетической и потенциальной
энергии электрона в основном состоянии атома водорода.
4.2. Определить среднее и наиболее вероятное удаление электрона от ядра в атоме
водорода, находящемся в состояниях Is, 2s и 2р.
4.3. Нарисовать радиальные волновые функции и распределения плотности вероятно-
сти обнаружить электрон на расстоянии г от ядра в атоме водорода, находящим-
ся в состояниях с главным квантовым числом п — 4.
4.4. В сферической системе координат электрон в атоме водорода характеризуется
волновой функцией ^/(г,(9,<р) = (^2д, + ^2д +2^2 0 0)/Тб , здесь у/п f m - волновая
функция стационарного состояния с квантовыми числами п, £ ,т. Какие, и с какой
вероятностью значения энергии, квадрата момента количества движения и его z -
проекции могут быть измерены в этом состоянии?
4.5. В начальный (нулевой) момент времени состояние электрона в атоме водорода
задано волновой функцией у/(г) = (у/15 + 42y/2s)/ VI , здесь и y/2s - волновые
функции стационарных состояний. Какие, и с какой вероятностью значения энер-
гии могут быть измерены в этом состоянии? Как зависит от времени распределе-
ние плотности вероятности обнаружить частицу в различных точках простран-
ства.
4.6. Угловая часть волновой функции некоторой системы в сферических координатах
определяется выражением (А - нормировочная константа):
а) у/(0, <р) = A sin(20) cos(<p),
б) у/(0, (р) = A cos(#)(l 4- sin((9) sin(<p)).
Какие значения квадрата момента количества движения и с какой вероятностью
могут быть измерены в этом состоянии? Каковы среднее значение и дисперсия
величины £2?
4.7. Доказать, что в состоянии описываемом сферической функцией У(т(0,ф) средние
значения х - и у - проекций орбитального момента равны нулю.
4 8. Определить вектор плотности тока вероятности для циркулярного состояния
(mt = £, £ = п-\) атома водорода. Полученное выражение сравнить с классиче-
ской величиной электрического тока, создаваемого электроном в атоме водорода,
движущимся по круговой орбите.
119
Глава 5. Простейшие многоэлектронные системы.
В этой Главе мы сформулируем общие принципы описания многоэлектронных
атомов и рассмотрим строение простейших из них, а именно атомов щелочных метал-
лов, а также гелия и гелиеподобных ионов. В общем случае волновая функция такой си-
стемы есть где £(. (/ = 1,...,Z) - совокупность координат всех атомных элек-
тронов. Мы уже отмечали, что взаимодействие между электронами делает невозможным
введение одноэлектронных волновых функций. Поэтому для описания стационарных
состояний атома с Z электронами, вообще говоря, необходимо решать стационарное
уравнение Шредингера в 3Z - мерном пространстве. Такая задача не может быть решена
точно даже для случая Z = 2, поэтому необходимо искать приближенные подходы к
решению задачи.
Простейший подход к решению задачи о строении электронной оболочки много-
электронных атомов заключается во введении одноэлектронных волновых функций и
представлении полной волновой функции в виде их произведения. Мы видели, что такие
одноэлектронные функции могут быть построены, если пренебречь межэлектронным
взаимодействием по сравнению с взаимодействием электронов с атомным ядром, а затем
попытаться учесть межэлектронное взаимодействие по теории возмущений. Такой под-
ход мы используем в дальнейшем для описания простейшего многоэлектронного атома
- атома гелия. Однако, интуитивно ясно, что для нейтральных атомов суммарная энер-
гия межэлектронного взаимодействия и взаимодействия электронов с ядром имеют один
порядок величины, а, значит, точность расчетов, проведенных по теории возмущений,
окажется низкой1. Поэтому в данной главе мы рассмотрим и другой подход, также при-
водящий к возможности построения волновой функции многоэлектронного атома в виде
произведения одноэлектронных функций. С физической точки зрения этот подход бази-
руется на приближении самосогласованного поля, о котором мы упоминали в Главе 1, а
с математической - на вариационном методе решения задач на собственные значения и
собственные функции оператора Гамильтона.
5.1. Вариационный метод.
В этом разделе остановимся на краткой формулировке вариационного метода
приближенного решения стационарного уравнении Шредингера. Покажем, что функци-
онал вида
J(f«) = (5.1.1)
заданный на множестве функций с интегрируемым квадратом, при дополнительном
условии нормировки
1 Сказанное относится к нейтральным атомам. В случае тяжелых многозарядных ионов расчеты по теории
Восмущений могут иметь заметно более высокую точность.
J///* (Д'>/z( Д')</Д ~ I
характеризуется экстремумом на функции <//(Д), совпадающей с решением
ного уравнения Шредингера
^•1.2)
стаииоцар.
/Л// £<//. (5]3)
Как известно, необходимым условием экстремума функционала (5.1.1) при дополни
тельном условии (5.1.2) является равенство нулю вариации
<>'(./(!//)-= 0.
(5.1.4)
где Л - неопределенный множитель Лагранжа. Раскрывая вариацию в (5.1.4), получим
откуда с учетом эрмитовости Гамильтониана (у/ Нбу/^ = !^Ну/ бу/^
бу/ Ну/ - Ху/) +(Ну/ - Ху/ бу/) = О.
имеем
(5.1.5)
Поскольку равенство (5.1.5) должно выполняться для произвольной бу/ , получим
Ну/ -Ху/ ,
то есть стационарное уравнение Шредингера, причем множитель Л имеет смысл энер-
гии системы.
Таким образом, экстремум функционала (5.1.1) при дополнительном условии
(5.1.2) достигается на функции, являющейся решением стационарного уравнения Шре-
дингера. Покажем теперь, что абсолютный минимум функционала (5.1.1) при дополни-
тельном условии (5.1.2) совпадает с энергией основного состояния системы. Действи-
тельно, произвольное состояние системы у/(£) может быть представлено в виде линей-
ной суперпозиции собственных состояний гамильтониана Н:
п
а функционал энергии J(^) имеет вид
У(ул) = (!/Д|((/)=^С„сДу/,.|ДД) = ^£„|сД, (5-1-6)
пуп' \ п
где Еп - энергия состояния у/п. Поскольку Еп>Е{ (п = 1,2,3,...), из (5.1.6) имеем
J(y/) > £], то есть абсолютный минимум функционала энергии совпадает с энергией ос-
новного состояния £,.
При определении вариационным методом энергии возбужденных состояний по
мимо (5.1.2) в качестве дополнительных условия надо требовать ортогональности иско
мой функции уже найденным волновым функциям низших состояний.
В рассмотренном виде вариационный метод полностью эквивалентен задаче
стационарное уравнение Шредингера. При приближенном решении уравнения ШреДиН
121
гера ищется экстремум функционала (5.1.1) на некотором множестве функций, являю-
щихся подпространством пространства функций с интегрируемым квадратом. Качество
решения оказывается тем лучше, чем ближе точная волновая функция к тому классу
функций, на котором минимизируется функционал. Из сказанного ясно, что для успеш-
ного решения задачи вариационным методом оказывается крайне важным хотя бы в об-
щих чертах представлять себе, как устроена «правильная» волновая функция системы.
5.2. Приближение самосогласованного поля.
Многоэлектронный атом, как правило, рассматривают в приближении самосогла-
сованного поля Хартри. Как уже отмечалось ранее (см. Глава 1), основная идея этого
подхода заключается в следующем. Состояние каждого из электронов описывается сво-
ей волновой функцией ^ (£,.), которая определяется из одночастичного уравнения Шре-
дингера, описывающего движение i -го электрона в самосогласованном потенциале, со-
зданным ядром плюс всей совокупностью электронов, кроме заданного. При этом суще-
ственно, что самосогласованный потенциал сохраняет центральную симметрию, поэто-
му оказывается возможным выделение угловой части одноэлектронной волновой функ-
ции и введение квантовых чисел п,£,те, характеризующих координатную волновую
функцию. Кроме того, спиновое состояние электрона характеризуется квантовым чис-
лом ms, то есть в приближении самосогласованного поля возникает тот же самый набор
квантовых чисел, который мы использовали при описании состояния одноэлектронного
атома2.
Более подробно рассмотрим эту схему на примере двухэлектронного атома (ато-
ма гелия, или гелиеподобного иона с зарядом Z ). Пусть состояние одного из электронов
описывается функцией ), а второго - у/2(г2}. Тогда каждый из электронов создает в
пространстве электростатический потенциал, определяемый как
(5-2.1)
где А(^) = е|(У/('; )Г
- плотность заряда, создаваемая в пространстве каждым из электро-
нов. Поэтому самосогласованный потенциал, в котором движется каждый их электро-
нов, имеет вид
т 2 Ze
(?,)=-— + еЧ>2 (Г,) , /2(<) ft ) = -— + ) •
Г] Г2
а уравнения самосогласованного поля записываются в виде
(f2 + j/w>(?2)^2(':2)=£'2^(?2)-
(5.2.2)
(5.2.3)
(5.2.4)
2 Сказанное нуждается » некотором уточнении. Как мы увидим в дальнейшем. в тяжевых системах крайне
«манное нуждается в некими 3 взаимодействие. В этом случае состояние атомного элек-
существенным оказывается спин-орбитальное взаимодеичви у
трона правильнее характеризовать квантовыми числами и, /
122
Полученные уравнения (5.2.3) и (5.2.4) известны как уравнения Хартри. Наща3а^
дача теперь показать, что уравнения Хартри эго лучшее в классе произведения одно,
электронных функций приближение к решению л очной задачи с i амильтонианом
1
= H|(r,)+ /72(г2) + i- -1 • (5.2.5)
Г1 Г21 7
А Ze2 - е2
Здесь Н.(Е) = Т-----(/ = 1,2) - «обычный» одночастичныи гамильтониан, а ---__
' МГ
энергия межэлектронного взаимодействия.
Итак, будем искать минимум функционала энергии с гамильтонианом (5.2.5) в
классе функций
^(/5,г2) = (У1(7))^2(г2), (5.2.6)
представимых в виде произведения волновых функций каждого конкретного электрона:
ft >2 (^2 )| Д + Н2 + V} 2>2 (г2)} - )у/2 (г2) | ^ (/• )у/2 (Р2)) .
Варьируя этот функционал, например, по функциям ^(а)) и ^/2(г2) соответственно, по-
лучим
(^) = ,
-f2l
H2W2 (h)+(^1(^1)
2(^2) = E2y/2(^2).
(5.2.7)
(5.2.8)
Полная энергия двухэлектронной системы есть
£ = ^1 + E2-{y/l(ri)y/2(r2)
^1 (r})y/2(r2)},
где последнее слагаемое учитывает тот факт, что энергия межэлектронного взаимодей-
ствия в сумме Е} + Е2 учтена дважды.
Как видно, система уравнений (5.2.7) и (5.2.8) совпадает полученными ранее ин-
туитивным путем уравнениями Хартри (5.2.3) и (5.2.4). Строгий вывод уравнений Харт-
ри из вариационного принципа был выполнен В.А.Фоком3. Отметим, что полученные
уравнения Хартри не удовлетворяют принципу тождественности. Введенная нами пол-
ная волновая функция системы двух электронов (5.2.6) не является ни симметричной, ни
антисимметричной относительно перестановки электронов местами. Фактически вместо
(5.2.6) надо использовать функции вида
, г2) = у= (а- >2 (г2) ± i//x (f2 )^2 (^)),
V **
3 В. А. Фок (1898 - 1974) - советский физик - теоретик.
123
симметрированные относительно перестановки электронов местами. Модификация
уравнений самосогласованного поля Хартри с целью удовлетворить принципу тожде-
ственности была также выполнена В.А.Фоком. Поэтому в современной литературе по
атомной физике приближение самосогласованного поля известно также как метод Харт-
ри - Фока. Следует иметь в виду, что эффективность использования метода Хартри или
Хартри - Фока для описания структуры многоэлектронного атома в значительной мере
обусловлена тем, что существенной частью самосогласованного потенциала является
потенциал взаимодействия электрона с атомным ядром, а энергия межэлектронного вза-
имодействия, как правило, меньше. Это позволяет в ряде случаев (особенно при каче-
ственном анализе атомной структуры) существенно упростить задачу и рассматривать
структуру многоэлектронного атома в рамках теории возмущений, выбирая в качестве
нулевого приближения приближение невзаимодействующих электронов.
В заключение этого раздела заметим, что приближение самосогласованного поля
также широко используется в теории атомного ядра с целью построения волновой функ-
ции системы в виде произведения однонуклонных функций. В теории ядра приближение
самосогласованного поля лежит в основе одночастичной оболочечной модели ядра. В
рамках этой модели каждый из нуклонов движется в потенциальном поле, создаваемым
всеми остальными нуклонами кроме выделенного. Однако, точность такого приближе-
ния в ядерной физике оказывается заметно хуже. Это связано с тем фактом, что, в отли-
чие от атома, в ядре отсутствует некий единый центр, который определяет главную (су-
щественную) часть взаимодействия частиц в системе. Поэтому при построении теории
ядра помимо приближения одночастичной модели ядерных оболочек широко использу-
ются модели коллективного движения нуклонов. Наиболее известной моделью такого
вида является капельная модель ядра4.
5.3. Атомные оболочки и подоболочки. Электронная конфигура-
ция.
Принцип Паули оказывается ответственным за существование оболочечной
структуры атомов и многообразие их свойств. Если бы не принцип запрета, все электро-
ны заняли основное состояние с минимальной энергией. Как мы уже отмечали, состоя-
ние атомного электрона может быть задано с помощью набора из четырех квантовых
чисел , причем не может быть двух электронов, у которых эти наборы кванто-
вых чисел совпадают. В результате, по мере увеличения числа электронов, они должны
занимать состояния со все более высокими значениями главного и орбитального кванто-
вых чисел.
Договоримся о следующей терминологии. Атомной оболочкой (слоем) мы будем
называть совокупность электронов с одинаковым значением главного квантового числа.
Оболочки принято обозначать буквами латинского алфавита. Оболочку, соответствую-
щую п = 1, называют АГ - оболочкой. Далее используют последующие буквы латинского
алфавита L, М, ... Атомной подоболочкой мы будем называть совокупность электронов в
атоме с одинаковыми значениями главного и орбитального квантовых чисел. Очевидно,
4 Более подробно с этими вопросами можно познакомиться в И. М. Капитонов Введение в физику ядра и
частиц, М.; УРСС (2002), с.ЗО
124
число мест в подоболочке определяется набором различных значении и „ ад,
данного Г и равно 2(21 + I) - Для данного значения п главного квантового числа ор6и.
тальное число может принимать „ различных значений. Например. К - оболочка сосТОИт
из единственной подоболочки 1г. L - оболочка ( » — 2 ) состоит из двух подоболочек 2s
и 2/7, и так далее. Общее число мест в оболочке - 2н‘. Суммируем все вышесказанное в
следующей таблице:
и 1 2 3 4
оболочки К L м N
подоболочки 1s 2s, 2р 3s, Зр, 3d 4s, 4р, 4d, 4f
число мест 2 2. 6 2, 6, 10 2, 6, 10, 14
Электроны, которые находятся в одной подоболочке, называются эквивалентными.
Распределение электронов по оболочкам и подоболочкам называется электронной
конфигурацией. Принято следующее обозначение электронной конфигурации: записы-
ваются обозначения подоболочек, в которых имеются электроны, и справа вверху ука-
зывается их количество. Например, имеется конфигурация kv‘25‘2/?3. Эта запись озна-
чает, что имеется семь электронов, два из них находятся на К - оболочке (значит, эта
оболочка является полностью заполненной), на L - оболочке находится пять электронов,
из них два - в 2s и три - в 2р - подоболочках. При этом 2s -подоболочка также является
полностью заполненной, а в 2р - подоболочке имеется еще три свободных места. Рас-
смотренная конфигурация соответствует атому азота, причем электроны в этой конфи-
гурации занимают состояния с минимальным значением энергии.
Отметим, что задание электронной конфигурации позволяет грубо оценить энер-
гию атома. Фактически мы учли энергию взаимодействия атомных электронов с ядром и
некоторую часть энергии электростатического взаимодействия электронов друг с дру-
гом. Для лучшего понимания общих принципов, используемых для описания строения
электронных оболочек многоэлектронных атомов, мы сначала рассмотрим ряд простей-
ших многоэлектронных систем. К простейшим системам мы относим, во-первых, атомы
щелочных металлов, содержащие единственный электрон сверх полностью заполненных
оболочек и подоболочек, а, во-вторых, двухэлектронную систему - атом гелия и ге-
лиеподобные ионы. Затем эти принципы будут обобщены на случай атомов с произ-
вольным числом электронов.
5.4. Атомы щелочных металлов.
К атомам щелочных металлов относятся литий Li, натрий Na, калий К, руби-
дий Rb и цезий Cs. Это элементы, которые стоят в первой группе таблицы
Д.И.Менделеева5, и имеют по одному электрону во внешней оболочке атома. В качестве
примера приведем электронные конфигурации для атомов лития и натрия:
Li-. \s22s,
Na -. ls22s22p63s.
5 Менделеев Дмитрий Иванович (1834 - 1907) - русский химик.
125
Рис.5.1. Строение атома щелочного металла.
У более тяжелых атомов щелочных метал-
лов (калий К, рубидий Rb и цезий Су)
внешний электрон находится в 4s, 5s и
6s гтодоболочках соответственно.
Внешний электрон находится до-
статочно далеко по сравнению с осталь-
ными электронами, образующими атом-
ный остов. Поэтому в первом приближе-
нии можно считать, что внешний электрон
движется в поле остова, состоящего из яд-
ра с зарядом Z и Z -1 атомных электро-
нов. Полный заряд остова оказывается
единичным, однако, по сравнению с атомом водорода он не является точечным, а рас-
пределен по размеру порядка боровского радиуса (размер остова). Схематически такая
структура атома щелочного металла изображена на рис.5.1. На расстояниях, превышаю-
щих размер атомного остова, очевидно, потенциал совпадает с потенциалом поля точеч-
ного заряда, наоборот, вблизи атомного ядра экранирующее действие остова пропадает,
и потенциал определяется зарядом атомного ядра Z . В общем виде это потенциал мож-
но задать как
r(r) = -Z<(r)e2/r, (5.3.1)
Рис.5.2. Эффективный потенциал, создаваемый
атомным остовом в атоме щелочного металла.
где - эффективный заряд, учи-
тывающий степень экранировки ядра
атомным остовом. Конкретный вид
функции Z^r(r) определяется распре-
делением заряда по атомному остову,
однако, при любом распределении за-
ряда она должна удовлетворять следу-
ющим условиям
(5.3.2)
Качественный вид распределения потенциала, в котором движется внешний атомный
электрон, приведен на рис.5.2. Как видно, потенциальная яма для этого электрона ока-
зывается глубже, чем для электрона в атоме водорода, а, значит, уровни сместятся вниз
по оси энергий. Качественный анализ ситуации можно провести в рамках теории воз-
мущений аналогично тому, как мы рассматривали смещение атомных уровней, обуслов-
ленное конечным размером атомного ядра (см. Глава 4). Отличие заключается в знаке и
величине эффекта. Учет конечного размера ядра делал потенциальную яму, в которой
Движется атомный электрон, менее глубокой - в результате энергия уровней возрастала.
Сейчас ситуация обратная. Более существенным является то, что размер атомного осто-
126
ва на несколько порядков больше радиуса атомного ядра и составляет величину порЯДКа
боровского радиуса. Как следствие, происходит не только смещение 5 - уровней, но ц
состояний с ненулевым значением орбитального момента. Если воспользоваться теорией
возмущений, то величину сдвига уровней в атоме щелочного металла относительно их
положения в атоме водорода можно определить как
= J (г) • W)''2^, (5.3.3)
где и, t квантовые числа внешнего электрона, = — (Z^ (г) — 1)в /г, а интеграл факти-
чески берется по размеру остова. Вычисление интеграла должно быть проведено для
конкретного вида функции Мы ограничимся лишь общими соображениями.
Наибольшая величина поправки к энергии будет наблюдаться для 5 - состояний, т.к, для
этих состояний отсутствует центробежный потенциальный барьер, и электрон с
наибольшей вероятностью может оказаться внутри остова. По мере увеличения орби-
тального квантового числа центробежный потенциал возрастает, что приводит к умень-
шению вероятности обнаружить электрон внутри остова. В результате положение уров-
ня оказывается все ближе к положению аналогичного уровня в атоме водорода. Расчет
показывает, что с учетом конечного размера атомного остова положение энергетических
уровней в атомах щелочных металлов можно описать следующей формулой:
Е„,=~, КУл (5.3.4)
где Anf - квантовый дефект, зависящий от квантовых чисел п и I. Спектр получился
водородоподобным. Отметим также, что учет неточечности кулоновского центра привел
к снятию «случайного» вырождения по величине орбитального момента.
Для проведения более точных расчетов следует еще учесть поляризацию атомно-
го остова внешним электроном. Поляризация остова приводит к появлению у остова
наведенного дипольного момента и к дополнительному взаимодействию типа «заряд -
диполь»). С учетом эффекта поляризации взаимодействие электрона с атомным остовом
может быть записано в виде:
2 2
И(г) = -—(5.3.5)
г г
Здесь постоянная Ct фактически определяет величину наведенного дипольного момен-
та. Радиальное уравнение Шредингера для функции un( (г) = rRn( (г) записывается в виде
+ (5.3.6)
где
(5.3.7)
127
Как видно, поляризационная добавка к эффективному потенциалу не меняет его вида6.
Поэтому, вводя эффективное орбитальное квантовое число £*, мы можем записать эф-
фективный потенциал (5.3.7) в обычном виде:
^(r)=-£i+w±i).
г 2тг2
Здесь £*(£ +1) = £(£ + 1)-2С,. Отсюда находим
£* =-1
2
Вспоминая, что решение уравнения Шредингера
виде(Глава 4)
£ + 1/2
с потенциалом (5.3.7) записывается в
Еп(
Ry
(53.8)
(/?,. - радиальное квантовое число), введем квантовый дефект7 в соответствии с выраже-
нием Дг = С} /(£ +1/2). Тогда выражение для энергетического спектра также может быть
записано в виде
Ry
(5.3.9)
Как видно, с увеличением орбитального момента величина квантового дефекта падает, и
в пределе больших £ мы переходим к спектру атома водорода. Такая зависимость кван-
тового дефекта от орбитального квантового числа обусловлена наличием центробежного
потенциального барьера, который возрастает с увеличением £. Как уже отмечалось, в
общем случае величина квантового дефекта зависит не только от орбитального, но и от
главного квантового числа, хотя зависимость от главного квантового числа является
слабой и ею часто пренебрегают.
Данные по величинам квантового дефекта основных состояний атомов щелочных
металлов в состояниях с различными значениями орбитального момента приведены в
таблице8. В той же таблице приведены значения потенциалов ионизации тех же атомов.
Как видно из данных, представленных в таблице, величины квантовых дефектов, обу-
словленные неточечностью остова, существенно превышают по величине значения «по-
ляризационных» дефектов. Отметим также, именно возрастание размера атомного осто-
ва у тяжелых атомов щелочных металлов приводит к увеличению квантовых дефектов
атомных состояний по мере увеличения заряда ядра.
6 Это утверждение, конечно, не справедливо для состояний с нулевым значением орбитального момента.
Для s - состояний решение уравнения (5.3.6) с потенциалом (5.3.7) требует отдельного рассмотрения.
Иногда в литературе вводят поправку Ридберга — —Д^. В этом случае в знаменателе выражения
(5-3.9) знак меняется на противоположный.
Знаком «*» в таблице помечены квантовые дефекты, при расчете которых поправка, связанная с конеч-
ным размером остова, доминирует.
128
Элемент Л/ д/ Потенций" -Ионизации эп
и 0.412* 0.041 0.002 0.000 537^-
Na 1.373* 0.883* 0.010 0.001 ТГГ""
К 2.230* 1.776* 0.146* 0.007 Тз2 "
Rb 3.195* 2.711* 1.233* 0.012
Cs 4.131* 3.649* 2.448* 0.022 3~89
ия, эВ В заключение, в качестве примера, приведем диаграмму
у Р f энергетических уровней атома натрия (см. рис.5.3), наглядно ил-
7$ 12 1/2-3/2 5d}2.5 2 Sfs2,7 2 6s" 5p^2 люстрирующую отмеченные выше особенности спектров атомов ще- лочных металлов. Нижнее состоя-
^S12 ние атома натрия - 3^1/2. Выше по
I 2.3 2 энергии лежит дублет Зр1/23/2, еще
3d)2S! выше - дублет 3 J3/2t5/2. Положение
^S12 этого дублета практически не от- личается от положения уровней с п = 3 в атоме водорода9. В резуль- тате оказывается, что уровень 4sv, лежит по энергии даже ниже, чем
1/2,3/2 34у2,5/2 > но выше, чем 3/?1/2 3/2. Та- кое же расположение s, р и d - состояний реализуется и для более высоких значений главного кван- тового числа. На диаграмме указа- ны также f - состояния, суще- ствующие для п > 4. В дальнейшем мы увидим, что именно такое рас- положение энергетических уровней
3S определяет последовательность за-
1'2 Спектр энергетических уровней атома натрия. полнения атомных оболочек и под- оболочек в многоэлектронных ато-
ление этих и вышележащих дублетов обусловлено спин - орбитальным взаимодействием и в Д^
еле не рассматривается.
129
5.5. Атом гелия.
Перейдем теперь к рассмотрению простейшей двухэлектронной системы — атома
гелия и гелиеподобных ионов. Основные идеи этого рассмотрения затем на качествен-
ном уровне будут использованы для анализа многоэлектронных систем.
Запишем гамильтониан нашей системы в виде (обозначение координат см. на
рис.5.4):
H = Hi+H2+Vi2, (5.5.1)
где
Н, =f, +VV?н =t +V —
' 1 1 2m ' 2m -’ л
- гамильтонианы, учитывающие взаимодействие каждого из электронов с ядром,
И12 = £2/ri2 " межэлектронное взаимодействие. Наша задача - найти собственные значе-
ния и собственные функции гамильтониана (5.5.1), т.е. решить следующее стационарное
уравнение Шредингера
Г~? Ъ) = Е г2) (5.5.2)
\ Здесь волновая функция определена в шестимерном
\ s' 1 пространстве. В общем случае такое уравнение не
\ s' может быть решено аналитически.
Для решения задачи (5.5.2) можно использо-
вать приближение самосогласованного поля. Однако,
Рис.5.4. для качественного анализа проблемы мы поступим
еще проще. Будем искать приближенное решение, воспользовавшись теорией возмуще-
ний. В качестве возмущения будем рассматривать оператор межэлектронного взаимо-
действия Г12. Такое приближение правомерно, если ядро имеет достаточно большой за-
ряд, и энергия взаимодействия каждого из электронов с ядром значительно превышает
энергию межэлектронного взаимодействия. В случае атома гелия (Z = 2) указанные
энергии имеют один порядок величины. Поэтому рассчитывать на хорошее согласие с
экспериментальными данными будет трудно, и мы сможем провести анализ структуры
системы лишь на качественном уровне.
Итак, в нулевом приближении имеем уравнение Шредингера для невозмущенно-
го гамильтониана
[Д (г,) + Н2 (r2 )р(^, r2) = £(0V(^, г2). (5.5.3)
В уравнении (5.5.3) переменные легко разделяются, и волновая функция </(гиг2) пред-
ставляется в виде произведения одноэлектронных функций
Ип Л) = (п )^2 ) • (5.5.4)
Здесь функции ^(л) и </2(г2) удовлетворяют одночастичному уравнению Шредингера
/ = 1,2.
130
Энергия системы в нулевом прнбиижении ecu. ( умма >нсргий каждого из электронов, т0
есть
л"" /:, । л,
I-
>
)
"х
Г5.5.5)
Здесь и, и п, - Еплвныс квантовые числа каждою и? шскгроиов. В частности, для Ос_
новного состояния системы в нулевом приближении имеем
/?'" =-27'Ry.
Вспомним, однако, что для системы тождественных частиц волновая функция
должна быть или симметрична, или антисимметрична относительно перестановки их
местами. Поэтому вместо волновых функций вида (5.5.4) мы должны рассматривать их
симметризованные комбинации:
^(.o(zL^2) = ^(v/i('l)y/2(?2)±Vzl(':2)V'2('i))- (5.5.6)
Казалось бы, электроны являются фермионами, поэтому мы должны выбрать антисим-
метричную функцию у/А(г\,г2). Однако, мы забыли про спиновую часть волновой функ-
ции: полная волновая функция системы есть произведение пространственной и спино-
вой волновых функций
^1 , £>) = г2 )^(а,, а2), (5.5.7)
где %(уу},о-2) " спиновая волновая функция системы из двух электронов. Антисиммет-
ричной относительно перестановки электронов местами должна быть полная волновая
функция Этого можно достичь двумя способами: пространственная часть
волновой функции является симметричной, а спиновая - антисимметричной, и, наобо-
рот, пространственная часть - антисимметричной, а спиновая - симметричной. Запишем
поэтому
^2 ) = (П , Г2 )х.< (0-1 ^2 ) ’
^(£1) = Va (П» Г'1 )Xs (О-p сг2).
Построим теперь «правильные», то есть симметризованные относительно пере-
становки электронов местами спиновые волновые функции системы из двух электронов.
В общем случае эта система может иметь следующие ориентации спинов:
n, U, ,1Т, U,
которым соответствуют следующие спиновые функции
Здесь индексы «1» и «2» обозначают соответственно спиновые состояния первого и вто-
рого электронов. Как видно, первая и четвертая из волновых функций являются снимет
ричными относительно перестановки электронов местами. Две оставшихся функции не
131
переходят при перестановке друг в друга, то есть не удовлетворяют принципу тожде-
ственности. Однако, из этих состояний легко построить две симметризованные должным
образом комбинации, а именно
одна из которых является симметричной, а другая — антисимметричной относительно
перестановки электронов местами.
Итак, мы имеем всего четыре спиновых состояния системы двух электронов, из
них три описываются симметричными и одно — антисимметричной функциями. Полу-
ченные три симметричных волновых функции образуют набор состояний с проекцией
суммарного спина на выделенную ось z равной Ms = 0,±1. На этом основании мы
приходим к выводу, что это триплет состояний с полным спином 5 = 1. Что касается
единственного антисимметричного состояния, то для него Ms = 0 и, следовательно, это
состояние имеет полный спин 5 = 0. Соберем теперь все полученные данные вместе:
Zs(o-i,o-2) = |^, 5 = 1, Ms=l,
Zs(<7pOj = -^(jU) + |^ 5 = 1, Ms=0,
Zs(o-i>o-2) = |^\ S = l> Ms=-L,
= s = o, ms=o,
(5.5.8)
Договоримся о терминологии. Величину 25 + 1 будем называть мультиплетностью. В
рассматриваемом нами случае системы из двух электронов имеем значения 25 + 1 = 1 и
25 +1 = 3, т.е. набор синглетных и триплетных состояний.
Таким образом, мы показали, что полная волновая функция двухэлектронного
атома должна строиться в виде
(°Ъ ^2 ) >
причем в этом случае мы имеем синглетное состояние (5 = 0), или
для триплетного состояния (5 = 1).
Мы получили принципиально важный результат. Хотя оператор спина нигде не
стоит в гамильтониане, пространственные части волновых функции стационарных со-
стояний явно зависят от спина и описывают совершенно различные распределения элек-
тронной плотности в атоме. Как мы увидим в дальнейшем, учет межэлектронного взаи-
модействия приведет к тому, энергия стационарных состояний в одной и той же конфи-
гурации также будет зависеть от спинового состояния электронов, хотя гамильтониан
системы и не зависит от спина.
132
Для дальнейшего рассмотрения важно заметить следующее обстоятельство. Orie-
ратор Гамильтона (5.5.1). учитывающий электростатическое взаимодействие между
Л2 (~ ~ У
электронами, коммутирует с квадратом иодного момента системы L — I + £2 :
Доказательство этого факта приведено в Приложении 5.1. Это значит, что мы можем по-
строить стационарные состояния системы, являющиеся одновременно состояниями с
точно определенным квадратом полного орбитального момента. Аналогично, можно
ввести квантовое число S, определяющее суммарный спиновый момент совокупности
атомных электронов.
Проиллюстрируем сказанное конкретными примерами.
Рассмотрим, прежде всего, основное состояние атома гелия. Пусть оба электрона
находятся в наинизшем энергетическом состоянии, т.е. п} = п2 = 1 и £х =^2 =0. Это
означает, что задана электронная конфигурация И2. Пространственная часть волновой
функции в этой конфигурации может быть записана в виде
(5.5.9)
Как видно, в такой конфигурации удается построить только симметричную относитель-
но перестановки электронов местами пространственную функцию (у(^,г2). Значит, спи-
новая часть волновой функции должна быть обязательно антисимметричной, т.е. полный
спин системы должен быть равен нулю, а триплетное состояние в такой конфигурации
оказывается невозможным.
Перейдем теперь к рассмотрению конфигурации, когда один из электронов нахо-
дится в возбужденном состоянии, например пх =1, п2 = 2 и £х = ^2 = 0. Следовательно,
задана конфигурация 1525. В этой конфигурации из одноэлектронных волновых функ-
ций и y/2s(г2) мы можем построить симметричную и антисимметричную про-
странственную комбинации
Vs Л ) = -j= (y/Xs ft )y/2s (r2) + ft2 )y/2s ft)),
V
V7, ('i > 'i) = (r} >21 (r2) - Hl, (r2 )H2, (^)),
(5.5.10)
(5.5.11)
Очевидно, полный орбитальный момент в этих состояниях равен нулю. Однако, полный
спин в этих состояниях различен. Состояние (5.5.10) должно быть синглетным, а состоя-
ние (5.5.11) - триплетным.
Мы уже говорили, что стационарные состояния можно охарактеризовать значе-
нием полного спинового S и полного орбитального L момента. Если заданы суммарные
значения L и S всей совокупности атомных электронов, то говорят, что задан атомный
терм. Записывается так:25+1L. Величина 2S +1 называется мультиплетностью терма.
В рассматриваемом нами случае конфигурации 1525 принадлежат два терма S и
3S. Спиновые и пространственные части волновых функций этих термов задаются
133
функциями (5.5.8) и (5.5.10), (5.5.11) соответственно. Конфигурации l.v2, как мы видели,
принадлежит единственный терм ‘S.
В общем случае конфигурации \snf., соответствующей одноэлектронному воз-
бужденному состоянию а гома гелия, ситуация совершенно аналогична. Этой конфигу-
рации также принадлежат два терма, например, для f. = 1, 1Р и 1Р.
Пока мы не учитываем электростатическое взаимодействие электронов друг с
другом, энергии атомных термов совпадают и определяются электронной конфигураци-
ей, которая в нашем приближении учитывает лишь взаимодействие электронов с ядром.
Воспользовавшись теперь теорией возмущений, определим поправки к энергиям стаци-
онарных состояний, связанные с электростатическим взаимодействием электронов:
АЕ = (г„г2У,2(Т-,r2,r2yr,d'r2. (5.5.12)
Остановимся, прежде всего, на поправке к энергии основного состояния. В этом случае с
учетом (5.5.9) в первом порядке теории возмущений получим
А£’ = • (5.5.13)
In-rzl
Полученному выражению можно придать наглядный физический смысл. Если ввести
величину р(г) = ф/"15(г)|2 - плотность заряда в пространстве, создаваемая отдельным
электроном, то (5.5.13) переписывается в виде
Ag= (5.5.14)
С точки зрения классической электродинамики это есть не что иное, как электростатиче-
ская энергия взаимодействия двух распределенных зарядов10. Вычислим этот интеграл
для основного состояния
-cxpl-Zr/aJ.
Используя известное разложение 1/|^ — г21 по сферическим функциям
4ZT у 1 ^2
Г, M^ + ltn }
/ V
4л-у 1 (г,
г2 ^2£ + 1[г2,
Yfm (^1 ’ W (^2 »^2 )>
у;т^^)у(т(02,(р2\
Гу > г,,
г, <г2
(5.5.15)
(здесь (^,^) и (02,<р2) полярный и азимутальный углы векторов г( и г>) и учитывая,
что функции s - состояний являются сферически симметричными, а
10 Собственно, именно выражение типа (5.5.14) позволяет трактовать величину р(г) = е|^(г)|2, как объ-
емную плотность заряда, создаваемую электроном в пространстве, и говорить о «размазанном» электроне.
На самом деле электрон является точечным и неделимым, а размазана плотность вероятности обнаружить
ег° в различных точках пространства.
134
J ) „„((). ФИЛ> - J Г,,,, (0. ФП»^ <P>^ = <Ш * 0, m * 0),
получим, что При интегрировании ио угловым координатам первого и второго электро-
на в сумму по < и т даст ненулевой вклад только слагаемое с = 0 , т = ():
'> , у.
Г -- - exp(-2Zr2 / <70 )<Vr2 +
J !•
» А
Jr2exp(-2Zr2/a0)Jr2
ехр(-ч,)^ц1
А
схр(-;2 Ж + f <2 схР(-£2 )^2
ч /
5Ze2 5
-----= — ZRy,
8«о 4
(5.5.16)
Тогда выражение для полной энергии основного состояния имеет вид
E = -(2Z2 ~^Z)Ry.
(5.5.17)
Как и следовало ожидать, с увеличением заряда ядра относительный вклад энергии меж-
электронного взаимодействия убывает, и применение теории возмущений оказывается
все более обоснованным. В частном случае атома гелия ( Z = 2) из (5.5.16) имеем
Е = -5.5Ry * 74.8 эВ.
Полученная энергия представляет собой энергию двухэлектронной системы. Если
учесть, что энергия удаления электрона из водородоподобного иона гелия составляет
47?у, то получаем, что энергия удаления одного из электронов из атома гелия, т.е. его
потенциал ионизации есть I = 1.57?у « 20.4 эВ. Экспериментально измеренное значение
составляет » 24.6 эВ, т.е. мы вычислили эту величину примерно с 20%- ой точно-
стью. Очень неплохо для первого порядка теории возмущений в рассматриваемом слу-
чае.
В возбужденных состояниях расчет энергии межэлектронного взаимодействия
проводится несколько сложнее. Для конфигурации lsn£, например, имеем:
^EsiA} »^2)| d rxd r2 —
Г12
If Ifr'i, (r2) ± V'lv (r2 Wn( (n )Г dyrxdV2 = C ± A. (5.5.18)
Здесь
c = JK ft Г Kfc Г рАтт dyr\dyr2
Ki-'bl
- обычная кулоновская энергия взаимодействия двух «размазанных» электронов,
э
А = [ У'ь Й К Й V,’, (п) dyt\dyr,
I'i -Г>|
- так называемая обменная энергия. Обменная энергия не имеет наглядного классиче-
ского истолкования. Это тоже часть электростатической энергии взаимодействия дву*
электронов, связанная со свойствами симметрии волновой функции относительно перс*
135
становки электронов местами, то есть с принципом тождественности микрочастиц. При
этом мы помним, что знак «+» в (5.5.18) соответствует симметричной пространственной
волновой функции, то есть антисимметричной спиновой (синглетному терму). И, наобо-
рот. знак «-» соответствует антисимметричной пространственной функции и симмет-
ричной спиновой (триплетному терму). Оба интеграла в (5.5.18) имеют положительное
значение. Следовательно, триплетный терм характеризуется меньшим значением энер-
гии, чем синглетный. С физической точки зрения такая ситуация понятна. В случае сим-
метричной пространственной функции (5 = 0, спины антипараллельны) электроны
находятся ближе друг к другу, и потому энергия их взаимодействия больше, чем для
триплета, когда пространственная волновая функция антисимметрична, и электроны
находятся дальше друг от друга. Таким образом, электростатическое взаимодействие
электронов привело к тому, что термы, принадлежащие одной и той же конфигурации,
стали обладать различной энергией, причем ниже по энергии оказался триплетный терм.
Общая схема расщепления приведена на рис.5.5. Отметим еще раз, что расщепление
конфигурации на термы при учете электростатического взаимодействия электронов обу-
Рис.5.5. Расщепление двухэлектронной конфигурации
на термы с учетом электростатического
взаимодействия электронов.
словлено, в конечном счете, принципом тождественности микрочастиц, т.е. свойствами
симметрии волновой функции отно-
сительно перестановки электронов
местами.
Обратим внимание на, каза-
лось бы, парадоксальный результат.
В гамильтониан рассматриваемой
системы (5.5.1) спин никак не вхо-
дит, однако энергия терма явно за-
висит от спина. Так получилось в результате влияния свойств симметрии функции отно-
сительно перестановки электронов местами на пространственное распределение элек-
тронной плотности, а, следовательно, и на энергию состояний системы.
В качестве примера остановимся чуть подробнее на расчете энергии термов кон-
фигурации 1525 'S' и 35.
В нулевом приближении невзаимодействующих электронов энергии синглетного
и триплетного термов равны между собой и записываются в виде простой суммы энер-
гий одночастичных состояний и y/2s:
Ет =Е„+Е2а.
Если заряд ядра равен Z, то соответствующая энергия нулевого приближения равна
£'"» =-Z2/?y(l + l/4) = -^Z2«y,
при этом энергия связи возбужденного электрона (потенциал ионизации) есть
I = Z2Ry/4.
Найдем поправку к энергии, которая обусловлена электростатическим взаимо-
действием электронов, в первом порядке теории возмущений. Для расчета кулоновского
и обменного интегралов опять воспользуемся выражением (5.5.15) и учтем, что любое
слагаемое в сумме за исключением нулевого, будучи проинтегрировано по угловым ко-
136
ординатам электрона, находящегося в s-состоянии, даст нулевой вклад в интеграл Q
учетом свойства оргонормированпосги сферических функций угловые интегралы легко
вычисляются, и мы получаем следующие выражения для кулоновского и обменного Иц
тегралов:
7 У 7 '
= — f f + — JR1\s(£)£2^J
"(J 0 0 *0 0 £
7 2 £
4,2. = — J «„ (£)^. (f (>7)ЯЬWrfdT!
о 0
Ze2 r , r
+----J /?„ [£)R„(£)f dtf Rh (if)R2, frW
a() 0 £
Здесь 7?ls(£) = 2exp(-£) и Я2л (£) =-^=l l--£lexp(-£/2) - обезразмеренные радиаль-
v2 \ )
ные части волновых функций соответствующих состояний атомов водорода.
Вычисляя значение каждого из интегралов, имеем:
34 32
С, 2v = — ZRy = \\A13B и Лн2, =---ZRy = \A93B.
’'2' 81 729
В случае Z = 2 (атом гелия) это приводит к следующим значениям энергии термов
1^25 ‘S и 1525 35:
3097
энергия триплета: - Ry = -4.2487?у « -57.80 эВ,
2969
энергия синглета: =-4.0737?у ~-55.41 эВ,
64
величина расщепления: Ry « 2.39 эВ.
Учитывая, что энергия связи второго электрона есть 47?у « 54.42 эВ, получаем, потенци-
ал ионизации терма 3»У есть 0.248/?у ~ 3.38 эВ, а терма 'S - 0.073Ry « 0.99эВ.
Экспериментальные значения соответствующих потенциалов ионизации - 4.77 эВ
и 3.98 эВ соответственно. Такое соотношение между расчетными и экспериментальны-
ми данными не может считаться удовлетворительным. Физическая причина отсутствия
удовлетворительного согласия заключается в следующем. В отличие от основного со-
стояния водородоподобного иона, отделенного большим энергетическим интервалом от
возбужденных состояний, энергии невозмущенных конфигураций 15пС близки между
собой. Как следствие, для расчета поправок на кулоновскую энергию межэлектронного
взаимодействия первого порядка теории возмущений оказывается недостаточно.
Покажем теперь, как можно улучшить точность расчетов структуры уровней
нашей системы. Не прибегая к уравнениям теории самосогласованного поля, обсудим
возможность расчета основного состояния атома гелия вариационным методом.
Из расчета по теории возмущений мы видели, что межэлектронное взаимодей'
ствие уменьшает энергию связи системы. Этот факт можно рассматривать как частич-
ную экранировку поля ядра вторым электроном. Поэтому можно представить себе вол-
137
новую функцию двухэлектронной системы ^(Г|,г2) как произведение одноэлектронных
волновых функций задачи Кеплера в поле ядра с эффективным зарядом Zeff :
H»',,'-2,Z?(r)-^.exP(-Zer(rl +r2)/a„).
/U40
(5.5.19)
Будем искать минимум функционала энергии на множестве функций вида (5.5.19), рас-
сматривая Zeff как вариационный параметр. Легко видеть, что при Zeff = Z функция
(5.5.19) является собственной функций гамильтониана двухэлектронной системы с «вы-
ключенным» межэлектронным взаимодействием. Поэтому учет этого взаимодействия
должен привести к некоторому уменьшению величины Z^ по сравнению с Z .
Функционал энергии (5.1.1) в рассматриваемом случае имеет вид
Ze2 Ze2
е2
(5.5.20)
и фактически является функцией параметра Zeff. Вычисление интегралов, входящих в
(5.5.20), дает
^,r2,Ze#)
Ze1
Ze1
2
ИП, r2, г,# )} = -4ZZeffRy,
^,r2,Z^ = ^ZeffRy.
Поэтому
J(Z^ = 2(Z^-IZZ^Z^Ry. (5.5.21)
Из условия минимума dJ/dZ^ =0 получаем
Z^=Z-5/16. (5.5.22)
Как видно, каждый из электронов действительно «чувствует» уменьшенный заряд.
Например, в гелии (Z = 2) функция (5.5.19) соответствует приближению двух невзаи-
модействующих электронов, движущихся в поле ядра с зарядом Z^ ~ 1.7 . Подставляя
(5.5.22) в (5.5.21), найдем для энергии основного состояния атома гелия
£ = -2Z^y. (5.5.23)
В частности для Z = 2 имеем Е = -5.695ф, для энергии удаления внешнего электрона
(потенциал ионизации атома гелия) I = 1.695Лу « 23.1 эВ. Наше приближение оказалось
ближе к экспериментальным данным, чем расчет по теории возмущений.
Подводя итог обсуждению строения двухэлектронной квантовой системы, нари-
суем диаграмму энергетических термов атома гелия (см. рис.5.6). На этой диаграмме
138
ы термы, соответствующие только одноэлектронным возбуждениям (конфигу.
W), числа на диаграмме задают значение главного квантового числа возбуж-
электрона. Отметим, что все термы являются синглетами, или триплетами. Ос-
ерм 'S принадлежит конфигурации Lv2. В этой конфигурации это единствен-
:. Во всех остальных конфигурациях \snf имеется по два терма, причем в пре-
юй конфигурации все триплетные термы лежат ниже по энергии. Нижний воз-
>ш терм атома гелия - в конфигурации . Его энергия возбуждения -
) 19.8 эВ.
1s2
Рис.5.6. Спектр атома гелия.
ак мы увидим в дальнейшем, электромагнитные переходы между термами раз-
иультиплетностей запрещены (так называемый "запрет интеркомбинаций"). Пе-
{аблюдаются только среди синглетов и среди триплетов. Это привело к тому,
время даже считалось, что существует две формы гелия, каждая из которых ха-
уется своим оптическим спектром.
о сих пор мы рассматривали только одноэлектронные возбуждения в атоме ге-
кду тем есть и другой набор состояний, когда оба электрона являются возбуж*
[ (так называемые дважды возбужденные состояния). Например, пусть оба элек-
ходятся в состоянии 2s, т.е. мы имеем электронную конфигурацию 2s1 Оче‘
той конфигурации принадлежит единственный терм *5. Однако, какова его
относительно основного терма 'S конфигурации к2? Как видно из данных,
139
представленных на рис.5.6, энергия возбуждения электрона из состояния с п — 1 в состо-
яние с и = 2 в атоме гелия составляет примерно 20 эВ. Поэтому энергия дважды воз-
бужденного состояния оказывается порядка 40 эВ, то есть даже больше потенциала од-
ноэлектронной ионизации. Это значит, что возможен так называемый процесс автоиони-
зации
Яе(252)->Яв+(15) + е,
т.е. ионизация атома может происходить самопроизвольно без дополнительного ввода
энергии в систему. Вопрос лишь в том, какова вероятность такого процесса и сколько
времени будет жить атом в дважды возбужденном состоянии.
В заключение этого раздела отметим, что среди химических элементов по своим
спектрам на гелий оказываются похожи атомы, у которых на внешней оболочке нахо-
дится два 5 - электрона. Это, прежде всего, атомы бериллия Be (электронная конфигу-
рация ls'2?) и магния Mg (электронная конфигурация ls22s22p63.y2).
5.6. Отрицательный ион водорода.
Чуть подробнее остановимся на еще одной двухэлектронной системе - отрица-
тельном ионе водорода. Эта квантовая система представляет собой протон, вокруг кото-
рого «вращаются» два электрона. Экспериментально известно, что потенциал ионизации
отрицательного иона водорода составляет I н~ » 0.75 эВ, т.е. I « 0.0557?у. Поскольку
энергия связи оставшегося электрона есть Ry, энергия основного состояния рассматри-
ваемой нами системы есть £'(ехр) « —1.0557?у. Отметим, что возбужденных связанных со-
стояний отрицательный ион водорода не имеет.
В рамках подходов, рассмотренных выше, постараемся теперь описать квантовую
систему теоретически. Фактически наша задача сводится к применению полученных
выше результатов для случая Z = 1.
Попытаемся сначала использовать теорию возмущений. При этом, поскольку па-
раметр малости (отношение энергии межэлектронного взаимодействия к энергии взаи-
модействия электрона с ядром) в такой ситуации отсутствует, ожидать удовлетвори-
тельных результатов вряд ли стоит. Используя выражение (5.5.17) при Z = 1, найдем для
энергии основного состояния £ = -(2-5/4)Лу = -0.75ф>. Как мы уже отмечали, полу-
ченное значение есть энергия двух электронов в поле протона. При этом энергия удале-
ния электрона из атома водорода есть Ry. Следовательно, для потенциала ионизации
(энергии отрыва одного из электронов) имеем Iн. =-0.25ф, т.е. отрицательную вели-
чину! Это означает, что в рамках рассмотренного варианта теории возмущений связан-
ного состояния двух электронов в поле протона быть не может. Наша теория оказалась
не способна даже на качественном уровне описать рассматриваемый объект.
Попытаемся теперь использовать вариационный метод с пробной функций вида
(5.5.19), где, как и раньше, в качестве варьируемого параметра выступает эффективный
заРяд ядра Ze# . Из (5.5.22) при Z = 1 немедленно получаем Z^ = Z -5/16 = 11/16, отку-
да для энергии основного состояния найдем (см. (5.5.23)):
E^-lZ^Ry «-0.945ф.
140
Этот результат также совершенно неудовлетворителен. Потенциал ионизации также по-
лучается отрицательным, т.е. связанного состояния в системе быть не должно. Это озна-
чает, что, хотя пробная волновая функция вида (5.5.19) удовлетворительно описывает
атом гелия, она не может быть использована для описания отрицательного иона водоро.
да. Строение этих, на первый взгляд очень похожих квантовых систем, является прин-
ципиально отличным.
Попытаемся, используя вариационный метод, построить пробную функцию ина-
че, чем это было сделано при анализе атома гелия. Обратим внимание, прежде всего, на
то, что первый и второй потенциалы ионизации в отрицательном ионе водорода (они со-
ставляют 0.75 эВ и 13.6 эВ) отличаются почти в 20 раз. В то же время для атома гелия их
отношение составляет * 2.2. Такое различие наталкивает нас на мысль, что характерные
удаления каждого из электронов от ядра в отрицательном ионе водорода существенно
различны. Можно предположить, что отрицательный ион водорода - эта система с «вы-
толкнутым» электроном. Тогда пробную функцию двухэлектронной системы имеет
смысл выбрать в виде
^^2) = ЛЦтехР("г|/а1)Хл1ТехР(_г2/а2)- (5.5.24)
у ла, у ла2
Мы будем полагать, что а2 > ах, т.е. второй электрон является внешним - «вытолкну-
тым». При этом естественно ожидать, что для внутреннего электрона ах ~aQ (а0 - бо-
ров ский радиус).
Попытка улучшить приближение (5.5.24), несомненно, возможна. В частности,
наша волновая функция не удовлетворяет принципу тождественности микрообъектов и
должна быть должным образом симметризована относительно перестановки электронов
местами. Более важным представляется другое обстоятельство. Наша функция не учи-
тывает так называемые электронные корреляции, которые крайне существенны в систе-
ме, где энергии межэлектронного взаимодействия и взаимодействия электронов с ядром
сравнимы между собой. Действительно, электроны отталкиваются друг от друга. Поэто-
му естественно ожидать, что они с большей вероятностью будут находиться по разные
стороны от ядра (т.е. движение электронов является скоррелированным). Наша функция
(5.5.24) совершенно не учитывает это обстоятельство: вероятности обнаружить оба
электрона по одну, или по разные стороны от ядра равны межу собой. Учет межэлек-
тронных корреляций предполагает, что пробная волновая функция должна быть пред-
ставлена в более сложном виде, чем (5.5.24): она должна зависеть не только от уже вве-
денных нами вариационных параметров, но и быть некоторой функцией угла пред-
ставляющего собой угол между радиус-векторами каждого из электронов. При этом
пробная функция должна достигать максимума при значении «9 = л- (электроны нахо-
дятся по разные стороны от ядра) и - минимума при значении <9 = 0 (электроны нахо-
дятся по одну сторону от ядра). Такая функция была предложена С.Чандрасекаром “ в
1944 году:
11 Chandrasekhar Subrahmanyan (1910 - 1995) - американский астрофизик и физик - теоретик, Нобелевская
премия (1983) «За теоретические исследования физических процессов, играющих важную роль в строении
и эволюции звёзд».
141
уsr2at3a^eXp( Г'/а' ~f2/a2)+Q*p(-fi/a2 -r2/«,))x(1 + -r2|),
и известна как функция Чандрасекара. Как видно, последний сомножитель обеспечивает
малость функции в области rt « г2, т.е. учитывает наличие межэлекзронных корреляций,
функция Чадрасекара есть функция трех варьируемых параметров (а,, а2 и С) и обес-
печивает удовлетворительное согласие расчетных и экспериментальных данных. При
этом оказывается, что at « aQ а а2 » Зя0, т.е. внешний («вытолкнутый») электрон нахо-
дится на расстоянии, примерно в три раза превышающем удаление от ядра внутреннего
электрона, а внутренний электрон находится примерно на таком же расстоянии от ядра,
как и в атоме водорода. Поэтому приближенно отрицательный ион водорода можно
представить себе как нейтральный атом водорода, вокруг которого «вращается» еще
один электрон.
Отметим также, что рассмотренная нами функция Чандрасекара находится за
рамками приближения самосогласованного поля Хартри (Хартри - Фока), поскольку
наличие корреляционного сомножителя не позволяет рассматривать ее как некоторую
комбинацию одноэлектронных функций.
В заключение заметим, что попытка представления духэлектронной волновой
функции в виде (5.5.24) возможна и для атома гелия и других гелиеподобных систем.
Соответствующие расчеты, однако, показывают, что в этом случае «выталкивания» од-
ного из электронов не возникает, и энергетически оказывается более выгодным состоя-
ние, когда оба электрона характеризуются одинаковым удалением от ядра. Что касается
корреляционного сомножителя, то его роль быстро убывает с увеличением заряда атом-
ного ядра.
Приложение 5.1. Момент количества движения в многоэлектрон-
ном атоме.
Покажем, что в атоме при наличии кулоновского взаимодействия между электро-
нами сохраняется полный орбитальный момент количества движения. Рассмотрим га-
мильтониан двухэлектронного атома с учетом взаимодействия между электронами
Н = Н, +H2+Vi2,
(П5.1)
где , Н2 - одноэлектронные гамильтонианы, учитывающие взаимодействие каждого
из электронов с ядром, И12 = е2/г12 - оператор межэлектронного взаимодействия. Пока-
жем теперь, что оператор квадрата полного орбитального момента системы
л а а2
L2 = I + ^2 I коммутирует с оператором Гамильтона (П5.1), то есть в стационарных
состояниях системы квадрат полного момента системы имеет точно определенное зна-
чение. Для доказательства утверждения нам достаточно убедиться, что коммутатор
L,H =0.
(П5.2)
142
Очевидно, оператор L коммугирует с каждым из одночастичных гамильтонианов, вхо-
дящих в (П5.1). Поэтому нам достаточно удостовериться, что
L,\/rn = 0. Рассмотрим
равенство
где f - произвольная дифференцируемая функция.
Для одной из компонент, например, .v - компоненты момента, имеем
-Z у,--------2, —— /((.Г,
= 2/(у|Д2 — -
Из соображений симметрии следует, что
2 ’ /(Г122 )] = ~2/(У1Z2 - 21У2 )f' ) •
Объединяя два последних равенства, получаем
к’Ж)]=°-
(П5.3)
Аналогично, получаем, что равенство (П5.3) справедливо и для двух других компонент
полного момента, т.е.
ДЖ) =0.
Выбирая /(^) = 1/7^ , заключаем, что Л,1/г12
= 0.
Поэтому окончательно имеем L,H =0. Поскольку в рассматриваемых услови-
ях оператор Гамильтона явно не зависит от спина, имеем также S,H =0, где
S = + ?2 - оператор полного спинового момента двух электронов.
Полученные утверждения справедливы и для произвольного количества электро-
нов. Поэтому в многоэлектронном атоме при учете электростатического взаимодействия
между электронами можно найти стационарные состояния с точно определенными зна-
чениями орбитального и спинового моментов электронной оболочки. Набор таких со-
стояний образует атомный терм.
Задачи к Главе 5.
5.1. Атом щелочного металла можно рассматривать, как одноэлектронную систему, в
которой единственный электрон движется в поле атомного остова, представляющего
ядро с зарядом Z и совокупность Z -1 электронов. Оценить размер атомного остова
атома лития (Z = 3), считая, что по объему остова отрицательный заряд распределен
равномерно. Потенциал ионизации атома лития I. = 5.37 эВ.
144
Глава 6. Общие принципы описания многоэлектронных
атомов.
Попытаемся использовать теперь данные, полученные при рассмотрении струк-
туры атомов щелочных металлов и атома гелия, для построения качественной картины
строения многоэлектронного атома с произвольным числом электронов.
6.1. Заполнение атомных оболочек электронами.
Рассмотрим, прежде всего, очередность заполнения электронных оболочек и под-
оболочек в многоэлектронных атомах. Казалось бы, энергия одноэлектронных состоя-
ний в атоме определяется, прежде всего, значением главного квантового числа п. А,
следовательно, атомные оболочки и подоболочки должны заполняться по мере увеличе-
ния главного квантового числа. То есть одноэлектронные состояния в оболочке, соот-
ветствующей п = 4, начнут заполняться электронами, только если все три оболочки с
п = 1,2,3 будут полностью заполнены. Однако, как мы видели при изучении спектров
атомов щелочных металлов, в многоэлектронных атомах энергия одноэлектронного со-
стояния зависит также и от значения орбитального квантового числа. Состояния с глав-
ным квантовым числом и и нулевым значением орбитального момента «проваливают-
ся» вниз так, что их энергия оказывается даже меньше, чем энергия d - состояний, соот-
ветствующих квантовому числу п -1. Именно эта закономерность лежит в основе пра-
вила заполнения электронных оболочек и подоболочек в многоэлектронных атомах
(правило Маделунга1 * (1936)). Это правило утверждает, что
1) из двух подоболочек ниже по энергии располагается та, для которой величина
п +Ц. оказывается меньшей.
2) Если для каких-либо двух подоболочек значения сумм п +1 совпадают, то
ниже по энергии лежит подоболочка с меньшим значением п .
В соответствии со сформулированными утверждениями имеем:
п + £: 1 2 3 4 5 6 7
Is 2s 2р 3s Зр 4 х 3d Ар 5s Ad 5р 6s Af 5d 6p 7s
Z 1 3 5 11 13 19 21 31 37 39 49 55 57 72 82 87
В последней строке Z означает заряд ядра атома, у которого начинается заполнение
указанной подоболочки. Таким образом, 4х и 5х подоболочки должны заполняться
раньше, чем 3d и Ad соответственно. Еще более интересно, что 4/ подоболочка ока-
зывается лежащей по энергии выше сразу трех подоболочек с большим значением глав-
ного квантового числа (5х, 5р и 6s). На качественном уровне справедливость указан-
ного выше порядка заполнения подоболочек подтверждается периодическим законом
Д.И.Менделеева. Поскольку за химические свойства элементов отвечают электроны
внешних не полностью заполненных оболочек, то по известным химическим свойствам
1 Madelung Erwin (1881 - 1972) - немецкий физик - теоретик. Сформулированное правило иногда также
называют правилом Клечковского по имени Клечковского В.М., переоткрывшего его в 1951 году.
145
того или иного эл е13за можно судить о его электронном строении. Например, близость
химических свойств а и К (щелочные металлы, Z= ll, 19) фактически подтверждает,
что в атоме калия внешний электрон занимает место в 4s подоболочке, а не в 3d. О том
ж-с свидетельствует и схожесть химических свойств атомов магния (Z = 12) и кальция
(Z = 20). Заполнение внутренней 4/ подоболочки должно приводить к схожести хими-
ческих свойств соответствующих элементов. Действительно, элементы с Z = 57-71 об-
разуют семейство лантанидов с близкими химическими свойствами. Следует, однако,
иметь в виду, что энергии электронов в 4s и 3d подоболочках близки2. Поэтому для ря-
да элементов происходит «перепрыгивание» электрона из 4s подоболочки в 3d. Такие
особенности распределения электронов по близко расположенным подоболочкам можно
предсказать только в результате количественных квантовомеханических расчетов.
6.2. Термы многоэлектронных атомов.
При рассмотрении двухэлектронного атома (атома гелия) мы видели, что в преде-
лах одной конфигурации \sn£ существуют два терма, характеризующихся различным
полным спиновым моментом совокупности атомных электронов3. Волновые функции
термов обладают отличающейся пространственной симметрией, что приводит к разным
значениям среднего удаления электронов друг от друга и, как следствие, разной вели-
чине энергии электростатического взаимодействия электронов. В результате электрон-
ная конфигурация расщепляется на термы. При этом величина энергетического расщеп-
ления термов определяется, как мы видели, обменной частью кулоновского интеграла
межэлектронного взаимодействия.
Аналогичная ситуация реализуется и в атомах, содержащих произвольное число
электронов. В каждой электронной конфигурации можно построить определенное коли-
чество термов, характеризующихся заданными значениями полного орбитального
l=
и полного спинового момента
5=22,
1
всей совокупности атомных электронов. В отсутствие электростатического взаимодей-
ствия электронов все атомные термы, принадлежащие одной и той же конфигурации,
вырождены Учет такого взаимодействия приводит к снятию вырождения, причем вели-
чина расщепления определяется пространственной структурой волновой функции терма
и зависит от мультиплетности терма, хотя спин и не входит в оператор межэлектронного
взаимодействия. ,
В качестве примера рассмотрим задачу о построении волновых функции термов
конфигураций из двух эквивалентных и двух неэквивалентных р - электронов пр2 и
npri р.
3 Же СИТуаЦИЯ имеет место и ДЛЯ конфигурации, могут отличаться и значением суммар-
в общем случае термы, принадлежащие заданной конутур у J
н°го орбитального момента.
146
Полная волновая функция системы может быть представлена в виде произведе-
ния пространственной и спиновой волновых функций
Т( . £) = , /у Ж, ст,), (6.2.1)
причем она должна быть антисимметричной относительно перестановки электронов ме-
стами. Это значит, что пространственная часть волновой функции является симметрич-
ной, а спиновая - антисимметричной, или, наоборот, пространственная часть - антисим-
метричной, а спиновая - симметричной:
Ч7^ , £) = ips (г}, г2 )/< ’ (6.2.2)
Ч^, £) = у/А > 'У ’ ^2) • (6.2.3)
Набор спиновых волновых функций с требуемыми свойствами симметрии был ранее по-
строен и имеет следующий вид
/5(сг1,сг2) = |ТТ^, 5 = 1, Ms=l,
ZJ(<7l,cr,) = -J=-(|U) + |iT^ 5 = 1, Ws=0,
/5(<Т,,<Т2) = |4J^, 5 = 1, Ms =-l,
= 5 = 0, .W, =0,
Три симметричных волновых функции образуют набор состояний с суммарным спином
5 = 1 и проекцией на выделенную ось z равной Ms = 0, ± 1. Антисимметричное состо-
яние, образует синглет, для него 5 = 0 и Ms = 0.
Наша задача теперь из одноэлектронных волновых функций вида
^(г) = 7?я1(г)У1т (#,$?) построить пространственные волновые функции двухэлектронной
системы с различной симметрией.
Начнем с построения симметричной относительно перестановки электронов ме-
стами пространственной волновой функции. Нетрудно видеть, что для тх = т2 = т
симметричные волновые функции записываются в виде
<Ps (fi Л) = Лп, (^ )Яя1 (г2) • (Ц, <рх )Yim (02, (р2), т = 0, ± 1. (6.2.4)
Кроме того, возможны еще три симметричных состояния, которые построены из функ-
ций с тх &т2. Эти состояния имеют следующий вид
Л ) = Rn\ (Г1 )ЛИ1 (Г2 ) • frl 1 (0. )^10(^2 ) + ^101 (#2 ^2 )) > (6-2-5)
WS ('i Л ) = Rnl (г1 )Rm (r2 ) - ^ (^ 1 (3, (Pi )K1_, (#2 > ^2 ) + ^-1 (<?., (Pi , (6>2 ,<Рг )) > (6-2
Ps ('i , r2) = Rnl (r( )Rni (r2) • -J= (y; 0 (0,, <px )У1_1 (6>2 ,<p2) + r,., ((9,, <рх )У10 (02, <p2)). (6.2.7)
147
Таким образом, имеется всего шесть симметричных относительно перестановки коорди-
нат электронов местами функций с величиной суммарной проекции орбитального мо-
мента М = т}+т2 соответственно равной Л/ = 0,±2 (см. (6.2.4)) и Л/ = 0,±1 (см.
(6.2.5) - (6.2.7)). Поскольку мы имеем состояние с М = 2, значит у нас имеется XD -
терм. Это терм включает в себя пять волновых функций с М = 0,± 1,±2. Остается еще
одна волновая функция с М = 0. Ее следует отнести к терму 'S
Справедливость полученного решения может быть проверена непосредственно
действием оператора L =1 +£2 1 на построенные волновые функции. Действитель-
но, введем обозначения
| L = 2, М = ±2) = У|±, (0,, <р, )У[±] (02, ; (6.2.8)
|z = 2,M = ±i) = .-b(y1±,(e,,(p,)y;„(^,p2)+y,0(e„1?>,)y,11((?2>%)), (6.2.9)
|ЛУ = 0), = ^о(^1>«’1Л1о(е2.«’2). (6.2.10)
|W = 0)2 =--^(y;1(e1,(Z>,)^_1(02,?J2) + y;_,(01,(i21)y;l(e2,(i,2)). (6.2.11)
Для вычисления результата действия оператора Z? на состояния (6.2.8-11) запишем опе-
ратор L2 в виде L2 = I +~£2 I =22 + 2(/\Д2г +^1Л^2х + Л_/2>-)- Прямым вычисле-
нием (его можно провести в декартовой системе координат) нетрудно проверить, что
функции \L = 2,М = ±2) и \L = 2,М = ±1) являются собственными функциями операто-
ра £2, соответствующими квантовому числу суммарного момента L = 2. То есть эти
функции действительно являются компонентами D - терма, соответствующие проекци-
ям М = ±1,± 2. Что касается функции D - терма, соответствующей проекции М = 0, то
можно убедиться, что она является линейной суперпозицией состояний |Л/ = 0^ и
\М = 0)2, причем
|А = 2,М = 0) = ^=(|М = 0\+|Л/ = 0)2). (6.2.12)
*v 2
Аналогично, для S - терма имеем
|1 = 0,)И = 0) = -Мм = 0),-|Л/ = 0)2) (6.2.13)
V 2
Подведем теперь итоги: в конфигурации пр2 имеются синглетные термы 5 и 'О. Со-
ответствующие им волновые функции записываются в виде
| ' (г, )Я„, (г2) • IL = °. М = 0) |Т4) -1 ГТ)) (6.2.14)
148
| L = 2, M = ±2)
11 d) = Rl:l Oi )/?„, O': ) IL = 2, M = ± О x (| U) | И)).
(6.2.15)
| L = 2, M = 0)
теперь построению пространственных функций, принадлежащих триплетным
термам, т.е. являющихся антисимметричными относительно перестановки электронов
местами. Мы можем построить всего три таких состояния.
А ^2 ) = ('1 (>2 ) ' (Г, | КМ ^2 ) - У10(^1 )У1 . (02 ^2 )) ’
VхА (^1 Л ) = (Г1 )^1 (Г2 ) ‘ (^11 (#1 ’ ^1 )К ^2 ’ ^2 ) ~ К (^1 ’ ^1 I (^2 ’ ^2 )) ’ (6-2-16)
Va (^1 Л ) = К (Г1 )^>1 (Г2 ) ’ (^10 (#1 > <Р1 КМ ’ ^2 ) “ К (6*1, ф\ )У) 0 (^2 > ^2 )) •
Аналогично предыдущему случаю можно убедиться, что функции
\b — \,М — ±1^ — •~^(У)±1 )^io(^2 ’^2) W ’^1 )У|±1 (^2 ’^2 ))’
|Л = 1,М==0) = ~(У1|(^1,^ДУ1_1(^2,^2)-У1_1(^,^|)^1(^2,^2)).
(6.2.17)
(6.2.18)
есть собственные функции оператора L2, соответствующие значению орбитального
квантового числа L = 1. Таким образом, имеем триплетный терм 3Р, которому принад-
лежат следующие волновые функции
]l = \,m = +\}
\L = 1,M = 0)
(6.2.19)
Итак, волновые функции всех термов 15, 'D и 3Р построены. Других термов с пра-
вильными свойствами симметрии построить не удается. Таким образом, в системе двух
эквивалентных р электронов существуют термы синглеты '5, 'D и триплет 3Р.
Перейдем теперь к анализу конфигурации двух неэквивалентных р - электронов,
для определенности конфигурации 2рЗр. Здесь ситуация оказывается отличной, и по-
мимо термов S, D и Р мы можем построить еще и волновые функции термов *Р, ,
3D. Действительно, в конфигурации неэквивалентных электронов у нас возникает до-
полнительная «степень свободы». Мы можем выбирать не только угловые, но и ради-
альные функции в виде симметричной или антисимметричной комбинации одноэлек-
тронных радиальных функций4:
4 В конфигурации двух эквивалентных р электронов радиальная волновая функция была заведомо сим-
метричной.
149
91 s (П, r2) = (Л2. (Л) i (r2) + R,, (П )Л,1 )),
91 A (Г. , r2) = -^ (R2 > (n )*3 i(r2) - Я3, (>> )R1, <r2 )).
(6.2.20)
(6.2.21)
роэтОму возможны следующие комбинации
функций’ образующих атомный терм:
радиальной, угловой и спиновой волновых
T(^,^2) = 91(rl,r2)|L,M)Z(a1,a2)
О
2)
S S А
Sas
'S, 'D,
3Р.
Эти две комбинации мы уже рассмотрели. Соответствующие функции задаются выра-
жениями (6.2.14,15,19), в которых в качестве радиальной функции стоит симметризо-
ванная комбинация (6.2.20). Однако теперь появляются еще две комбинации, в которых
радиальная волновая функция является антисимметричной, а симметрия угловой и спи-
новой функций совпадают.
> &) = Wj] , r2 )| £, , <т2)
3) A S S
4) А А А.
Легко видеть, что в случае 3) реализуются термы 3S, 3Z), а в случае 4) - 'Р. Волновые
функции, принадлежащие этим термам есть:
(6.2.22)
(6.2.23)
(6.2.24)
Таким образом, в рассматриваемом случае неэквивалентных р электронов реали-
зуются следующие термы
'S, lP, 'D,
3S, 3Р> 3D.
(6.2.25)
150
Полученный результат можно записать короче: ' SPD, SPD, или так SPD. Итак, в
рассматриваемой конфигурации существует шесть термов, характеризующихся различ-
ными значениями энергии.
Причину полученного результата нетрудно понять и на основе принципа Паули,
который собственно и является проявлением свойств симметрии волновой функции
тождественных частиц - фермионов относительно их перестановки местами. Действи-
тельно, оба электрона не могут иметь совпадающие наборы квантовых чисел. В случае
неэквивалентных электронов главные квантовые числа принимают различные значения.
Поэтому при определении возможных значений L и S принцип Паули автоматически
соблюдается. Если электроны эквивалентные, т.е. квантовые числа п и ( обоих элек-
тронов совпадают, при построении термов необходимо учесть невозможность совпаде-
ния квантовых чисел т, и т, обоих атомных электронов. Это приводит к тому, что
часть термов, которые мы нашли в конфигурации прп' р, нс реализуется в конфигурации
пр2.
В заключение отмстим, что в системе двух эквивалентных электронов удается
построить функции с правильной симметрией только для четных L + S.
6.3. Тонкая структура терма. Состояния.
Вспомним теперь о спин орбитальном взаимодействии в атоме. Это взаимодей-
ствие приводит к появлению тонкой структуры терма: терм расщепляется на группу со-
стояний - мультиплет, число компонент которою определяется числом возможных ори-
ентаций векторов L и S в пространстве, то сеть числом возможных значений квантово-
го числа J, задающего величину механическою момента всей электронной оболочки
атома. Таким образом, терм в заданной конфигурации это совокупность состояний с
заданными значениями L и S. Для обозначения состояния многоэлектронного атома
принято следующее обозначение
Например, в конфигурации npri р возможны следующие состояния
’50, % ’D2, X 3Д,2.3- (6.3.1)
Полное число состояний, принадлежащих конфигурации, оказалось равно десяти.
Легко видеть, что число состояний в терме есть min((25 + l),(2L + l)). В случае
Е > 5 их 25 +1, то есть мультиплетность указывает число компонент мультиплета,
например, термы Р и D действительно состоят из трех компонент. В противополож-
ном случае L < S число компонент терма равно 2L +1 и не совпадает с мультиплетно-
стью. Например, терм 35, хотя и называется триплетным, но состоит всего из одной
компоненты. Что касается синглетных термов, то они всегда состоят из единственной
компоненты, то есть для них понятия терма и состояния совпадают.
Иногда введенные нами обозначения состояний многоэлектронного атома ис-
пользуют и для атома водорода и других одноэлектронных атомов (например, атомо®
щелочных металлов), указывая еще и значение главного квантового числа. Например*
151
основное состояние атома водорода можно обозначить так: 1 2S1/2. Следует отметить,
что такое обозначение несет избыточную информацию: мультиплетность одноэлектрон-
ной системы всегда равна двум.
рассмотрим теперь тонкую структуру терма чуть более подробно. По аналогии с
атомом водорода оператор спин - орбитального взаимодействия можно записать в виде
VLS = A(LS), (6.3.2)
где А - константа связи, являющаяся на самом деле некоторым оператором в простран-
стве радиальных волновых функций многоэлектронного атома. Используя теорему ко-
синусов, перепишем оператор (6.3.2) в виде
VLS=^(j2-L2-S2).
Учитывая, что квантовые числа L, S и J задают точно определенные значения орби-
тального спинового и полного механического момента электронной оболочки атома, то
вычисляя матричный элемент от оператора спин — орбитального взаимодействия полу-
чим
Е} = + 1)-Z(L + 1)-S(S + 1)).
Тогда расстояние между соседними компонентами мультиплета определяется как
Нормальный мультиплет
Обращенный мультиплет
------J=2
Рис.6.1. Тонкая структура терма.
8Е, -Е,-Е, } = AJ. (6.3.3)
Последнее соотношение называют правилом интер-
валов Ланде5, а сам мультиплет - нормальным (если
А > 0) и обращенным (при А < 0).
В качестве примера рассмотрим тонкую
структуру терма 3Р, состоящего из трех состояний
(J = 0,1,2). С учетом правила Ланде получаем
(Е2 -Е})/(Е{ -Ео) = 2/1. Сама картина расщепления
для нормального и обращенного мультиплетов, пока-
зывающая положение состояний относительно не-
смещенного терма, приведена на рис.6.1. Экспери-
ментальные данные по мультиплетному расщеплению могут быть использованы для
определения константы связи в энергии спин — орбитального взаимодействия. Следует
иметь в виду, что задача о вычислении энергии спин - орбитального взаимодействия на
самом деле является значительно более сложной. Помимо собственно энергии взаимо-
действия спинового и орбитального моментов электронов надо учитывать также взаи-
модействия типа «спин - спин» и «спин - чужая орбита». Соответствующие этим взаи-
модействиям операторы должны быть добавлены к выражению (6.3.2). Эти слагаемые,
оказывается, наиболее существенны для легких атомов .
* Lande Alfred (1888 - 1976) - немецкий физик - теоретик.
Более подробно см. И. И. Собельман, «Введение в теорию
атомных спектров», М. Наука, (1977), §19.
152
6.4. Различные типы связи моментов в многоэлектронном атоме.
До с,IX пор мы предполагали, что электростатическое взаимодействие электронов
в атоме значительно больше еппн-орбитального взаимодействия. Именно возможность
нс учитывать спин орбитальное взаимодействие позволило ввести термы, в которых
величины квадратов орбитального и спинового моментов совокупности атомных элек-
тронов могут быть определены точно. Эти орбитальный и спиновый моменты совокуд.
ности атомных электронов определяются как
Однако такая схема построения атомных термов (ее называют приближением LS- связи’)
реализуется не всегда.
Для того чтобы убедиться в этом, вернемся к нашему анализу строения двухэлек-
тронной квантовой системы (гелиеподобного иона с зарядом Z). Сравним по порядку
величины энергии электростатического и спин - орбитального взаимодействия электро-
нов в такой системе. Действительно, при расчете энергии электростатического взаимо-
действия электронов в атоме гелия мы видели, что эта величина (см. 5.5.16) есть
Еее - ZRy.
(6.4.1)
Линейная зависимость от заряда ядра связана с тем, что с увеличением Z радиусы элек-
тронных орбит уменьшаются, т.е. электроны оказываются ближе друг к другу. С другой
стороны, при вычислении энергии спин - орбитального взаимодействия в атоме мы по-
лучили
ELS~Z4a2Ry.
Сравнивая (6.4.1) и (6.4.2), находим, что при
Z > Z* = а~2/3 z Т1
(6.4.2)
энергия спин — орбитального взаимодействия уже больше, чем энергия электростатиче-
ского взаимодействия. Значит, в тяжелых гелиеподобных ионах (Z > 27) энергия спин-
орбитального взаимодействия уже превышает энергию электростатического отталкива-
ния электронов. В таком случае при изучении строения электронной оболочки атома
надо сначала учитывать спин - орбитальное взаимодействие, а уже затем - электроста-
тическое.
Сделанная нами оценка справедлива для гелиеподобного иона, т.е. иона, содер-
жащего всего два электрона. В многоэлектронных системах за счет частичной экрани-
ровки ядра электронами внутренних оболочек энергия спин — орбитального взаимодей-
ствия оказывается существенно меньше оцененной по (6.4.2) величины. Можно пока-
зать , что в многоэлектронных атомах эта энергия имеет порядок величины
ELS~Z2a2Ry,
Говорят также о нормальной связи, или о связи Рессела - Саундерса
Л. Д. Ландау, Е. М. Лифшиц Квантовая механика. Нерелятивистская теория, §72, М.: Наука, (1974)
153
то есть для внешних атомных электронов энергия спин-орбитального взаимодействия
растет как квадрат заряда атомного ядра и в тяжелых атомах оказывается порядка Ry.
На практике это приводит к тому, что в тяжелых атомах приближение LS количествен-
но выполняется не очень хорошо, и атомные термы лишь приближенно можно характе-
ризовать значениями полного орбитального и полного спинового моментов L и S .
Рассмотрим другой способ построения атомных термов, который реализуется при
EIS » ^ее • В этом случае энергией электростатического взаимодействия атомных элек-
тронов можно пренебречь. Тогда состояние каждого из электронов конфигурации харак-
теризуется квантовыми числами В случае если заданы значения квантового числа
j всей совокупности атомных электронов в заданной конфигурации (j = 1,...,Z), то го-
ворят, что задан атомный терм в приближении jj - связи. Этот терм принято обозначать
так
Последующий учет электростатического взаимодействия электронов ведет к расщепле-
нию терма на группу состояний, число которых определяется количеством значений
квантового числа J, задающего возможные значения полного механического момента
электронной оболочки атома
i
Состояние в приближении jj - связи принято обозначать так
В качестве примера определения возможных термов и состояний в схеме jj - связи рас-
смотрим следующие конфигурации.
Пусть имеется гелиеподобный ион, электронная конфигурация которого есть
!.$ пр. В приближении LS - связи (как мы видели, это приближение справедливо для не
слишком больших Z ) в этой конфигурации имеются термы
1Р, 2Р
и состояния
*р 3Р
•*0,1,2 •
Триплетный терм состоит из трех состояний, для синглета понятия терма и состояния
тождественны.
В случае тяжелых систем (например, гелиеподобный ион урана U ) расчет
энергий и волновых функций системы в той же конфигурации 15 пр должен проводиться
в приближении jj связи. Вычисляя моменты j каждого их электронов, найдем jx =1/2,
Л = 1/2,3/2. Поэтому имеем в этом приближении следующие термы
1 П Г1 31
2’2/ [2’2]
154
и состояния
/1
(2 ’ 2) u ’
Как видно, полное число состояний в конфигурации не зависит от вида используемого
приближения.
Рассмотрим еще один пример. Пусть имеется конфигурация из двух неэквива-
лентных р - электронов. Требуется определить термы и состояния в приближении jj .
связи. Для решения этой задачи поступим следующим образом. Определим возможные
значения полных механических моментов каждого из электронов: у, =1/2,3/2,
j2 = 1/2,3/2. Поэтому получаем следующие термы
Этим термам соответствуют следующие состояния
Полное число состояний в конфигурации равно десяти и нс зависит от схемы построе-
ния термов (см. (6.3.1)).
Отметим, что для нейтральных атомов в чистом виде приближение jj - связи не
реализуется никогда, и для атомных термов и состояний часто используют обозначения,
принятые для LS - связи. Следует, однако, иметь в виду, что такие обозначения доста-
точно условны, так как с учетом спин - орбитального взаимодействия оператор Гамиль-
тона не коммутирует с операторами квадратов суммарного орбитального и спинового
моментов атомных электронов, то есть в стационарном состоянии эти величины не име-
ют точно определенных значений. Приближение jj - связи часто используют при расче-
те спектров многозарядных ионов, а также в физике атомного ядра, где спин - орбиталь-
ное взаимодействие играет заметно более важную роль, чем в атомной физике.
Бывает, в атомах возникают и другие виды связей. Например, в сильно возбуж-
денных атомах, когда один из атомных электронов (его квантовые числа I и s) нахо-
дится далеко от атомного остова, электростатическое взаимодействие этого электрона с
электронами остова оказывается слабым и меньше, чем спин-орбитальная связь между
электронами остова. Как пример, такая ситуация типична для возбужденных состояний
тяжелых инертных газов. В результате для электронов остова реализуется нормальная
связь, и остов характеризуется полным моментом j = Г + S*. Здесь L* и 5* задают ор-
битальный и спиновый моменты остова. В дальнейшем учитывается электростатическое
взаимодействие остова с внешним электроном, приводящее к формированию момента
К = j + 7, а затем взаимодействие магнитных моментов, связанных с К и s . В резуль-
тате формируется полный момент J = К + s = (j + 7) + s . Такой способ сложения мо-
ментов носит название /Т - связи. Обозначают так:
155
Проиллюстрируем сказанное на примере атома ксенона. Состояние с наинизшей
5НСР,„СЙ » ксенона находитс" » конфигурации 5/', и это Рассмотрим воз-
(5У*ДенИС атома кс^нона’ к°™ один из электронов перемещен в более высокую оболоч-
ку - & ПРИ лиж®нии связи соответствующие этой конфигурации состояния
обозначаются так 1/2 L1/2]0.i и 5р Р3/2 [3/2]12. Всего имеем четыре состояния.
Отмстим, что в приближении LS связи для данной конфигурации получаются , 3Р012
тоже четыре состояния.
В заключение раздела заметим, что в приближении LS связи цепочка понятий
«электронная конфигурация терм — состояние» фактически отражает иерархию взаи-
модействий в многоэлектронном атоме «взаимодействие электронов с ядром - электро-
статическое взаимодействие электронов - спин - орбитальное взаимодействие». В
случае ф ~ связи последовательность интенсивности взаимодействий другая: «взаимо-
действие электронов с ядром — спин - орбитальное взаимодействие - электростатиче-
ское взаимодействие электронов».
Всюду в дальнейшем мы будем использовать только приближение LS - связи.
6.5. Основные термы атомов. Правила Хунда.
Мы видели, что для конкретной электронной конфигурации можно построить
набор атомных термов, обладающих различной энергией. Аналогично, терм расщепля-
ется на группу состояний (мультиплет), образующий тонкую структуру терма. Часто
оказывается важным определить основной терм и основное состояние по данной элек-
тронной конфигурации. Для определения основного терма, принадлежащего данной
конфигурации, существуют простые правила. Эти правила были получены эмпириче-
ским путем в 1925 году еще до создания квантовой механики и известны как правила
Хунда9. Правила заключаются в следующем:
1) ниже по энергии лежит тот терм, у которого мультиплетность является макси-
мальной,
2) при равенстве мультиплетностей двух или более термов минимальной энерги-
ей обладает терм с максимальным значением суммарного орбитального момента конфи-
гурации.
Физический смысл этих правил заключается в том, что в состоянии с максималь-
ными значениями S и L электроны локализованы дальше друг от друга, а потому их
энергия электростатического взаимодействия оказывается минимальной, а, следователь-
но, соответствующий терм основным. Справедливость этого утверждения при анализе
термов двухэлектронной конфигурации lsn£ мы проверили непосредственно.
в качестве примера использования правил Хунда обратимся еще раз к электрон-
ам конфигурациям из двух неэквивалентных и двух эквивалентных р - электронов. В
ПеРВ0м случае (см 6 2 25) мы должны, очевидно, выбрать терм 'D, во втором - SP.
Важно, однако что правила Хунда легко позволяют построить основной терм,
Да*е не зная всех термов конфигурации. Прежде, чем продемонстрировать, как это де-
^Und Friedrich Hermann (1896 - 1997) - немецкий физик - теоретик.
156
лается, докажем, что полный орбитальный и полный спиновый моменты полностью за.
полненной (замкнутой) атомной подоболочки раны нулю, то есть терм такой конфигу.
рации есть '5.
Конфигурацию s2 мы уже подробно исследовали при изучении основного состо-
яния атома гелия. Поэтому рассмотрим теперь конфигурацию пр (такая конфигурации
соответствует атомам инертных газов — Ne, Аг, Кг, Хе и Rri). Действительно, в соответ-
ствии с принципом Паули в атоме не может быть двух электронов с одинаковыми кван-
товыми числами. Для эквивалентных электронов два квантовых числа, главное и орби-
тальное, уже совпадают. Поэтому совокупность шести электронов должна иметь отли-
чающиеся наборы квантовых чисел /и, и . Каждое из этих квантовых чисел может
принимать значения mf = 0, ±1 и ms = ±1/2. Поэтому единственно возможная комбина-
ция этих квантовых чисел, не нарушающая принцип Паули, есть
т( 1 0 -1 1 0 -1,
ms 1/2 1/2 1/2 -1/2 -1/2 -1/2.
Суммарные проекции орбитального и спинового моментов количества движения
ML = ^mf и Ms = ^ms могут принимать только нулевые значения, а, значит, и сами
моменты L и S равны нулю, т.е. мы имеем терм '5. Аналогично, в nd подоболочке
имеется десять мест, и мы можем расположить в ней десять электронов лишь задействуя
все возможные значения т, и ms. Поэтому получим ML = Ms = 0, а, следовательно, и
L = S = Q.
Для определения основного состояния в терме используют правило Ланде (его
иногда включают в правила Хунда), согласно которому, если атомная подоболочка за-
полнена менее чем наполовину, наименьшую энергию имеет состояние с минимальным
значением J (нормальный мультиплет), если же атомная подоболочка заполнена более
чем наполовину, то наименьшую энергию имеет состояние с максимальным J (обра-
щенный мультиплет).
Рассмотрим теперь элементы второго периода таблицы Менделеева (от лития до
неона) и, воспользовавшись сформулированными правилами, определим у них основные
термы и основные состояния.
Атом лития, конфигурация 1s2 2s.
На внешней оболочке имеется единственный s - электрон. Поэтому имеем терм
2 S и состояние2 5^.
А том бериллия, конфигурация 1s2 2s2. Атом имеет полностью заполненные обо-
лочки. Поэтому его терм - '5 и состояние .
Атом бора, конфигурация Is22s2 2р. На внешней оболочке имеется единствен-
ный р - электрон. Поэтому имеем терм 2Р. Терм состоит из двух состояний - 2 Д/гл? ’
Подоболочка заполнена меньше чем наполовину, потому мультиплет нормальный, ос-
новное состояние - 2 Pi/2
157
Атом \<лерода, конфигурация ls22.v22p2. Мы уже рассматривали эту задачу, од-
нако сейчас определим терм непосредственно по правилам Хунда. Имеем два электрона,
поэтому максимально возможный спин 5 = 1, т.е. основной терм будет триплетом. Те-
перь мы должны выбрать максимально возможное значение L у двух эквивалентных р
. электронов- При этом мы должны не нарушить принцип Паули. Рассмотрим возмож-
ные значения квантовых чисел, описывающих состояния электронов
п £ mf ms
2 111/2
2 10 1/2
Мы выбирали эти числа так, чтобы сначала получить максимально возможное значение
проекции орбитального момента. Имеем тах(Л/£) = 1, Поэтому L = max(ML) = 1, то
есть основной терм есть 3Р. Терм состоит из трех состояний 3Р012. Основным является
Ро. Выше по энергии лежат сначала терм '£>, а потом *5. Волновые функции, принад-
лежащие всем этим термам, были построены в разделе 6.2.
Атом азота, конфигурация \s22s22p3. Направим спины всех трех электронов в
одну сторону. Поэтому 5 = тах(Л/5) = 3/2, т.е. мы имеем квартетный терм. Составим
теперь таблицу из квантовых чисел электронов
п £ т( ms
2 111/2
2 10 1/2
2 1 -1 1/2
Для того, чтобы направить все три спина в одну сторону, мы вынуждены использовать
все три значения квантового числа т(. В результате L = шах(Л/£) = 0, т.е. основной
терм есть 4 5, основное состояние 453/2.
Атом кислорода, конфигурация \s22s22p\ Теперь мы уже не можем направить
все спины в одну сторону (см. таблицу)
п £ те ms
2 111/2
2 10 1/2
2 1 -1 1/2
2 1 1 -1/2
Теперь мы имеем два нескомпенсированных спина, т.е. основной терм будет триплет-
ным. Кроме того суммарный орбитальный момент равен орбитальному моменту послед-
него четвертого электрона, т.е. L = 1. В результате имеем основной терм 3Р. В данном
случае р -подоболочка заполнена больше чем наполовину. Поэтому по правилу Ланде
°сновным будет состояние 3Р2
158
фтора, конфигурация 1<2?2/Л Здесь удобно рассуждать следук>щИм
образом. Следующий за фтором атом неона имеет полностью заполненную р,
подоболочку, и. следовательно, нулевые значения орбитального и спинового моментов.
Значит, 2р' представляет собой «дырочную» конфигурацию, где момент всей конфигу.
рации равен моменту недостающего электрона — «дырки». Поэтому аналогично конфи-
гурации 2р' (атом бора) имеем основной терм ‘Р. Мультиплет является обращенным,
поэтому основное состояние сеть 'Л 2
На атоме неона (его терм 'S) заканчивается второй период таблицы Менделеева
и начинается третий, в котором происходит заполнение Зли Зр подоболочек. Основные
термы и состояния этих элементов такие же, как у элементов второго периода.
6.6. Сверхтонкая структура спектров многоэлектронных атомов.
При анализе спектра атома водорода мы уже говорили, что помимо тонкой струк-
туры спектра, обусловленной наличием спин - орбитального взаимодействия в атоме,
существует еще и сверхтонкая структура, обусловленная, взаимодействием магнитных
моментов атомного электрона и атомного ядра. В случае многоэлектронных атомов речь
идет о взаимодействии магнитного момента электронной оболочки атома и магнитного
момента ядра, обусловленного как наличием спинов нуклонов, так и орбитальным дви-
жением нуклонов в ядре. Универсальную оценку на энергию это взаимодействия сделать
достаточно просто. Считая, что суммарный магнитный момент электронной оболочки
атома порядка магнетона Бора, а магни тный момент ядра порядка ядерного магнетона,
получим для энергии взаимодействия
бг2Яу~1(Г6 эВ. (6.6.1)
«о
С другой стороны, по аналогии со спин - орбитальным взаимодействием мы можем за-
писать оператор взаимодействия, приводящего к возникновению сверхтонкого расщеп-
ления, в виде
К,, =.В(Л), (6.6.2)
А А
где J и I - операторы полного механического момента электронной оболочки атома и
спина ядра, В - константа связи, ее численное значение может быть оценено по формуле
(6.6.1). Величина энергии (6.6.2) зависит от ориентации векторов J и 1 в пространстве
относительно друг друга. Число таких ориентаций определяется квантовым числом F,
определяющим значение суммарного механического момента атома F = J + 7. Из об-
щих правил сложения моментов число различных значений F определяется как
min{(2J + 1),(27 + 1)}. Это и будет число компонент сверхтонкого расщепления.
Введем оператор полного механического момента атома F = J + 7. Действуя
аналогично случаю тонкого расщепления, перепишем оператор (6.6.2) в виде
159
для дополнительной энергии атомного состояния \L,S,J), обусловленной нШи-
1 сМ оператора сверхтонкого взаимодействия, получим
ЧН1
=y(7r(^ + l)-J(J + l)-Z(/ + l)),
где квантовые числа F, J и I задают точно определенные значения полного механиче-
ского момента атома, механического момента электронной оболочки атома и спин ядра.
qepKO видеть, что расстояние между соседними компонентами сверхтонкой структуры
атомного состояния мультиплета определяется выражение аналогичным (6.3.3):
= Ef - Ef_x = BF. (6.6.3)
Последнее соотношение называют правилом интервалов Ланде для сверхтонкой струк-
туры. При этом константа связи В оказывается всегда положительной.
Еще одной причиной смещения атомных уровней является наличие у многих ядер
электрического квадрупольного момента, обусловленного отличием их формы от сфе-
рической. Как правило, этот эффект следует учитывать, прежде всего, для тяжелых ато-
мов (Z »1).
Отметим, что спины и магнитные моменты, а также электрические квадруполь-
ные моменты атомных ядер различных изотопов одного и того же химического элемента
имеют разные значения. Поэтому оказывается различной и их сверхтонкая структура
(как по величине расщепления, так и по числу компонент). В этом смысле сверхтонкая
структура также является одним из проявлений изотопических эффектов в атомных
спектрах. Это означает также, что по характеру сверхтонкого расщепления часто оказы-
вается возможным определить спин и магнитный момент атомного ядра, т.е. методами
атомной радиоспектроскопии исследовать свойства атомных ядер.
6.7. Атом в электрическом поле. Эффект Штарка.
В этом разделе рассмотрим влияние слабого однородного статического поля на
стРУктуру энергетического атома и его спектральных линий. Мы увидим, что в резуль-
тате такого воздействия происходит сдвиг и расщепление атомных уровней, причем
наблюдаемые особенности эффекта в многоэлектронных атомах и атоме водорода суще-
ственно отличны друг от друга.
Эффект Штарка в многоэлектронных атомах (квадратичный эффект).
Для упрощения задачи будем рассматривать атом в одноэлектронном приближе-
НЧ считая, что имеется единственный электрон, который движется в центральном, но,
в°°61де говоря, некулоновском потенциале. Оператор взаимодействия атомного элек-
Г*)°На с внешнем электрическим полем запишем в виде (ось z направим вдоль электри-
'CCKU'O поля):
V = -Зг =-d,e, (6.7.1)
160
,Г опсоатор электрического дипольного момента атома.
гдсг/ = -е> -оператор эл 1 стационарные состояния электрона
В центрально-симметричном поле атом
ц р ,иппгни F кратность вырождения которых равна
ш (/-) характеризуются уровнями энергш ,,f, Р
" ! и определяется числом возможных значений проекции орбитального момента на
о’сь - Все эти состояния характеризуются определенной четностью (-1) . Поэтому все
матричные элементы дипольного оператора вида = 0. Следовательно, в пер-
вом порядке теории возмущений электрическое поле не влияет на положение атомного
уровня. Рассмотрим поэтому второй порядок теории возмущении. Для поправки к уров-
ню энергии получим
\{n('m\d. \ri Е w')| 2
/---------------- х £
Г - Е
ntn. ^nhn
('*(,
m'tm
SE{'}
UJ^ nlm
(6.7.2)
Как видно, величина сдвига уровней растет как квадрат электрического поля, поэтому
рассмотренный эффект называют квадратичным эффектом Штарка10. Общее выражение
(6.7.2) допускает упрощение для случая центрально-симметричного поля атома. Мы ви-
дели, что матричный элемент дипольного оператора (n£m\d 2\ri Е т'} отличен от нуля
лишь в случае Г = £ ± 1, т' = т. Поэтому
О £ F 1 •' 1 (6-7.3)
n'tn, ^n(m ^п'Гт
\(n^m\d, \n'
Величину %ntm = --------------— принято называть статической поляризуемостью
Л'*и, Еп'('т ~ Еп1т
Г=(±1
атома. В частности, для атома, находящегося в .у - состоянии, получим
|(га|^2|и>,ге = 0)|2
X„s = 2^
n'p,m=0 ns
(6.7.4)
Выражения (6.7.2), (6.7.3) показывают, что во втором порядке теории возмущений уро-
вень с заданными квантовыми числами п и I расщепляется на несколько подуровней.
Их количество определяется числом значений модуля магнитного квантового числа /я,
то есть t +1. При этом состояния с заданными т и — т остаются вырожденными, то
есть внешнее электростатическое поле лишь частично снимает вырождение по проекции
орбитального момента.
Смещение и расщепление атомных уровней можно наблюдать по спектральному
составу излучения атомов, помещенных в электрическое поле. Такие исследования были
проведены И. Штарком в 1913 году.
Johannes (1874-1957) немецкий физик. Нобелевская премия (1919) «За открытие эффекта Допле-
ра в каналовых лучах и расщепления спектральных линий в электрическом поле (эффект Штарка)»
161
Эффект Щтарка в атоме водовода (линейный эффект).
Отдельно остановимся на рассмотрении эффекта Штарка в атоме водорода. Как
мы увидим, наличие «случайного» вырождения по орбитальному квантовому числу при-
водит к качественно иной картине расщепления и, прежде всего, к линейной по полю
величине расщепления уровней. С физической точки зрения этот результат возникает
вследствие наличия стационарных атомных состояний с ненулевым электрическим ди-
польным моментом, характерных только для атома водорода. Действительно, любая су-
перпозиция состояний с заданным значением п и различными значениями (. в атоме во-
дорода является стационарным состоянием, однако не характеризующимся определен-
ным значением четности. Как следствие в этом состоянии атом обладает отличным от
нуля статическим дипольным моментом.
Математически расчет штарковского расщепления в атоме водорода надо прово-
дить в первом порядке теории возмущений с учетом «случайного» вырождения энерге-
тического спектра. Например, для уровня с п = 2 имеем четыре вырожденных состояния
25, 2p,w = 0, 2/?,/n = l, 2р,т = -1. Тогда уравнение (2.4.20), определяющее поправки к
уровню энергии, возникающие при наложении слабого электрического поля, имеет вид
ЗЕ ^.2 0 0
К21 ж 0 0
= о,
0 0 ЗЕ 0
0 0 0
(6.7.5)
где К21 =Г12 =-e£(zy/2 Q(r)y/2s(r)d3r = -^[R2 (r)R2s(r)r3dr = -3e£a0, а0 - боров-
J V3 J
ский радиус. Решение уравнения (6.7.5) дает четыре корня, 8ЕХ 2 - ±3esaQ и <5Е3 4 = 0.
Последние два корня, соответствующие состояниям 2р,т ± 1, показывают, что эти со-
стояния не смещаются и остаются вырожденными.
Задачи к Главе 6.
6.1. Сколько компонент имеет тонкая структура нижнего возбужденного состояния ато-
ма натрия (Z=l 1). Оценить величину расщепления.
6.2. Воспользовавшись теорией возмущений, в рамках приближения LS связи опреде-
лить энергию основного состояния атома гелия и гелиеподобных ионов.
6.3. В рамках теории возмущений оценить потенциалы ионизации атома Не и гелиепо-
добного иона урана .
6.4. В приближении самосогласованного поля Хартри каждый из электронов в атоме
движется в электростатическом поле, создаваемом ядром с зарядом 2 и совокупно-
стью Z-1 электронов. Считая, что плотность заряда, создаваемая в пространстве
электроном есть 4/(г,/)|2, получить уравнения для волновой функции, описываю-
щей 152р конфигурацию атома гелия.
163
Глава 7. Строение молекул.
7.1. Невозможность существования молекул в классической фи-
зике.
В данном разделе мы рассмотрим общие принципы квантовомеханического опи-
сания молекулярных систем, основные особенности электронного строения молекул,
подходы к описанию движения ядерной подсистемы молекулы, а также основы система-
тики молекулярных состояний двухатомных молекул.
Образование молекул - эффект чисто квантовый, необъяснимый с точки зрения
представлений классической физики. При этом, на первый взгляд, существование моле-
кул остается непонятным даже если каждый атом в отдельности рассматривать кванто-
вомеханически. Действительно, рассмотрим возможность образования простейшей мо-
лекулярной системы - , состоящей из двух протонов и одного электрона. Будем счи-
тать, что у нас имеется атом водорода в основном состоянии (1s). Пусть на расстоянии
R от атома находится протон. Для того чтобы образование молекулы было возможно,
между атомом водорода и протоном (хотя бы в некотором диапазоне изменения величи-
ны R) должны возникнуть силы притяжения. Для определения силового поля рассчита-
ем электростатический потенциал, который создает атом водорода в пустом простран-
стве. При этом будем полагать, что электрон создает в пространстве распределенную
плотность заряда
р(г) = -е|^1, (г)|2 = —~ ехр (- 2г/а0), (7.1.1)
где г - удаление электрона от «своего» протона, а0 - боровский радиус. Тогда с учетом
сферической симметрии волновой функции
тростатического потенциала, создаваемого
атомом водорода, записывается в виде
1 d1
- — (г(р{г)) = -4тг(еЗ(г) + р(г)). (7.1.2)
г аг
Первый член в правой части (7.1.2) учиты-
вает наличие атомного ядра. Решение урав-
нения (7.1.2) с учетом (7.1.1) имеет вид (см.
рис. 7.1)
<p(r) = - 1 + — ехр(-2г/я0). (7.1.3)
Как видно, между атомом водорода и про-
тоном возникает короткодействующий, но
отталкивающий потенциал. Энергия взаимодействия протона с атомом водорода e<p(R)
возрастает по мере приближения протона к атому водорода: отталкивание возникает при
приближении протона на расстояния R<a0. Казалось бы, это означает, что образование
1s состояния уравнение Пуассона для элек-
Рис.7.1. Электростатический потенциал,
создаваемый атомом водорода в пространстве
164
молекулы Н: невозможно1. Что конкретно не было учтено в наших рассуждениях? к
ответу на этот вопрос мы вернемся позже, а пока перейдем к обсуждению общих прин-
пипов квантовомеханического описания молекулярных систем.
7.2. Адиабатическое приближение.
При описании общих принципов мы для простоты ограничимся рассмотрением
только двухатомых молекул. Запишем гамильтониан простейшей двухатомной молеку-
лярной системы - молекулярного иона водорода Н2 (обозначения см. на рис.7.2):
Н = Не+Т\+f2+e2/R . (7.2.1)
Здесь Не - Те + И - электронная часть гамильтониана, Те - кинетическая энергия элек-
э э
в"
трона. Ve =---------- энергия взаимодействия электрона с протонами, rt и г2 - удале-
'1 >2
ние электрона от первого и второго протонов соответственно, Т,, Т2 - кинетическая
энергия ядер, R = Я, - R2 - межъядерное расстояние. Стационарные состояния системы
могут быть определены из решения уравнения Шредингера
Рис.7.2. Молекулярный ион во-
дорода.
НФ(г, R,, R2) = ЕФ(г, R} ,R2). (7.2.2)
Здесь г - удаление электрона от начала координат.
Дальнейшее рассмотрение нам будет удобно прово-
дить в системе координат, связанной с центром масс
молекулы. Пренебрегая массой электрона m по срав-
нению с массой ядра М, введем координату центра
2
масс
Й = (Д + Я,)/2
и координату относительного движения
R = R2-R}.
Тогда координаты и R2 каждого из ядер определя-
ются как
R} = ^-R/2,
R2 = W + R/2.
(7.2.3)
1 На самом деле малое притяжение в системе все-таки существует. Поляризация протоном электронной
оболочки атома приводит к появлению у него небольшого дипольного момента, который приводит к воз-
никновению сил притяжения. Это так называемые силы Ван-дер-Ваальса. Они малы и не приводят к обра-
зованию химической связи между атомами. Болес подробно - см. Раздел 7.8.
2 Мы здесь предполагаем, что массы ядер атомов, образующих молекулу, равны Л/( = М2 = М .В слу-
чае, если массы ядер являются различными, для 91 имеем 91 = (л/^! 4- M2R2^/{Ml + Л/2).
165
Получим выражение для кинетической энергии ядер в системе координат, связанной с
снТром масс. Учитывая, что
= ______— = д
dR{ 2 дй 8R И dR2~ 2 ан +
а также
dj _i g2 | < а2 = 1 а2 а2 а2
ад2 4 ай2 ад2 айая’ ая2 ~4ай2+ая2+айая’
получим
f+f - д2 *г д2 = п2 а2 Й2 а2 (724)
4М ай2 М dR2 2(2М) ай2 2// SR2’
где ц = М/2 - приведенная масса молекулы. Таким образом, мы получили, что полный
гамильтониан молекулы представим в виде
Я(г,Я,Й) = Te+Ve(r,R}
п2 a2 |g2>| h2 а2
2ц dR2* R) 2(2М) ай2 ‘
(7.2.5)
Здесь г - координата электрона, отсчитываемая от центра масс молекулы, при этом
r^r+R/2, 72=r-R/2. (7.2.6)
Полученное выражение означает, что полный гамильтониан молекулы H(r,R,&) можно
представить в виде суммы гамильтонианов двух подсистем, одна из которых определя-
ется совокупностью координат, описывающих относительное движение электронов и
ядер в молекуле, а другая - координатой центра масс молекулы . Значит, волновая
функция стационарного состояния молекулярной системы Ф(г,7?,93) может быть пред-
ставлена в виде произведения волновых функций, описывающих ее структуру и движе-
ние как целого, которое может быть очень различным в зависимости от внешнего потен-
циального поля. В простейшем случае свободного движения мы можем записать:
Ф(г, Я,Й) = ^(г,^) • ехр(/ХЙ),
где второй сомножитель определяет волновую функцию свободного движения молекулы
как целого в пространстве, К - волновой вектор молекулы. Вся информация о внутрен-
ней структуре молекулы содержится в функции Т(г,Л), которая является собственной
Функцией гамильтониана
Д(г,Я) = 7', + КДг,Я)-^-ЛГ + ^-. (7.2.7)
2// ОК К
Решение задачи на собственные значения и собственные функции гамильтониана
(7.2.7) обычно проводят в адиабатическом приближении (приближении Борна - Оппен-
166
геймера3). Суть этого приближения заключается в следующем. Молекула состоит из
двух подсистем — электронной (легкой) и ядерной (тяжелой). Движение электронов про»
исходит с существенно большей скоростью, чем движение ядер. Поэтому приближенно
можно считать, что движение электронов происходит при неподвижных ядрах. При рас.
смотрении же ядерной подсистемы мы будем полагать, что электронная подсистема
успевает подстроиться под мгновенное положение ядер.
Это означает, что в гамильтониане (7.2.7) удобно выделить часть, соответствую-
щую электронной подсистеме молекулы
и найти стационарные состояния этого гамильтониана
(t + Г (г, Я))Х (г, к) = («X1 (?,Я). (7.2.8)
Здесь и электронная волновая функция молекулы и энергия п -ого
стационарного состояния электронной подсистемы молекулы, зависящие, в том числе,
от ядерной координаты, как от параметра. Решая (7.2.8) мы получаем полный набор
электронных состояний молекулы и их энергий, зависящих, в том числе, и от расстояния
между ядрами.
Волновую функцию молекулы, являющуюся решением нестационарного уравне-
ния Шредингера с гамильтонианом (7.2.7), удобно представить в виде линейной комби-
нации собственных функций гамильтониана электронной подсистемы
W, Л.о = (Я.'X’ (к «), (7-2.9)
где ^<Л,)(Я,/) - коэффициент разложения полной волновой функции Т(г,Я,/) по базису
электронных состояний. Как мы увидим в дальнейшем, этот коэффициент разложения
есть волновая функция ядерной подсистемы молекулы, соответствующая п - ому стаци-
онарному состоянию электронной подсистемы. Получим:
удф^К,!)
Г St
е2
~R
N
п
Здесь
(7.2.10)
t д2
N dR2
- оператор кинетической энергии ядерной подсистемы.
Умножая (7.2.10) на одну из собственных функций
электронной координате, с учетом (7.2.8) получим
dt
(r,R) и интегрируя по
= E^(R^\R,f) + Тн + е-
к
тп
8-^ + В фт . (7.2.11)
тпгп v
oR
п К
^K'(R,t) + Y 4
п
3 Oppenheimer Robert (1904 - 1967) - американский физик - теоретик.
167
Здесь
л,„ В =_Rtv/<.^yw^r
PJ dR mn 2//J / m ( } d
. так называемые неадиабатические члены, обеспечивающие переходы между электрон-
ными состояниями (термами) молекулы, а функция = е2/Я + £^(Я) имеет
смысл потенциальной энергии взаимодействия ядер в т -ном электронном состоянии
молекулы.
Наша задача теперь показать, что неадиабатические члены малы по сравнению с
другими слагаемыми, входящими в (7.2.11). Слагаемое е2 /R в (7.2.11) имеет величину
порядка Ry, поскольку характерное значение межъядерного расстояния 7? ~ а0 (а0 -
боровский радиус). Такое же значение имеет и величина электронной энергии .
Ь 2 *2
Оценивая неадиабатические члены как ------- и В-------, получим А-----Rya0,
ш
В----Ry • Поэтому соответствующие слагаемые в (7.2.11) малы по сравнению с каж-
М
дым из членов е2/?? и . Однако, слагаемое определяющее кинетическую энергию
ядер также содержит множитель М"*. Поэтому необходимо сравнить неадиабатические
слагаемые с величиной TN ~ Р2/ZM (Р - импульс ядерной подсистемы). Будем считать,
что ядра колеблются вблизи положения равновесия 7?0, поэтому их потенциальную
энергию взаимодействия можно представить в виде
V{eff} (R) « + - Г(е#)" (Я = Ro) х (R - Ro)2.
2
Определим масштаб амплитуды колебаний <5R = R — RQ из предположения, что при гар-
монических колебаниях величины кинетической и потенциальной энергии осциллятора
равны, то есть Р2/1М * ^V{eff}'\R^8R2 . С другой стороны, из соотношения неопреде-
ленностей имеем Р ~Ti/8R, откуда находим
en I
XD ~ 4 ------------------- ~ 4 --
VW
о»
тогда
Т №-Ry.
" 2М 2M6R2 VM
Эта величина мала по сравнению с характерной энергией электронной подсистемы, од-
нако, она все же больше неадиабатических членов в (7.2.11) в отношение g =
раз.
Пренебрегая неадиабатическими членами в уравнении (7.2.11), получим
168
/Л £<1^0 = £.,>(R> (д.,) + fv + e к' ’(Я,r),
m x ' т m
Ct
(7.2.12)
R
то есть нестационарное уравнение, описывающее эволюцию во времени ядерной подси-
стемы молекулы при условии, что молекула находится в конкретном электронном со-
стоянии. Как видно, мы получили «обычное» уравнение Шредингера с эффективным
потенциалом взаимодействия ядер в молекуле
IC"(R}= Ec,(Ry (7.2.13)
IX
С точностью до пренебрежения неадиабатическими членами движение ядер происходит
при неизменном состоянии электронной подсистемы молекулы, причем для каждого
электронного состояния молекулы существует свой вид потенциальной кривой
Стационарные состояния ядерной подсистемы могут быть определены из решения урав-
нения
2 \
Tx+^- + E^(R) 4'"(R) = E<f"(R).
R J
(7.2.14)
Рис.7.3. Эффективная потенциальная энергия
взаимодействия ядер в молекуле в зависимости от
межъядерного расстояния.
Эффективный потенциал взаимодей-
ствия ядер учитывает не только куло-
новское отталкивание между ними, но
и наличие электронной плотности, ко-
торая обеспечивает притяжение в си-
стеме, и может привести к связыванию
атомов в молекулу. Для этого, очевид-
но, необходимо, чтобы зависимость
yi(^f)(R) характеризовалась кривой с
локальным минимумом (см. рис.7.3,
кривая 1).
Зависимость эффективной
энергии взаимодействия ядер в моле-
куле от межъядерного расстояния
называют электронным термом моле-
кулы. Эту же зависимость часто называют потенциальной кривой (потенциальной по-
верхностью4).
Может так оказаться, что потенциальная кривая характеризуется отсутствием ми-
нимума энергии (такой случай также приведен на рис. 7.3, кривая 2). Тогда, очевидно,
при любом расстоянии между атомами существуют силы отталкивания, то есть устойчи-
вое связывание атомов в молекулу невозможно. В этом случае говорят, что электронный
терм молекулы является разлетным.
4 Термин «потенциальная поверхность» (potential surface) используется, прежде всего, для многоатомных
молекул, для которых обсуждаемая зависимость определяется функцией от совокупности ядерных коор-
динат и описывается некоторой поверхностью в многомерном пространстве. В случае двухатомных моле-
кул также используется термин "потенциальная кривая".
169
1таК’ rKn?n nnuf. рые ИТОГИ' ^Ри Рассмотрении структуры молекулы в рам-
ках адуа атиче лижения необходимо сначала решить задачу на собственные
учения и с0 сгпвенные ункции для гамильтониана электронной подсистемы молеку-
лы. В качестве решения получаются набор собственных функций и собственных значе-
ний. параметрически зависящих от расстояния между ядрами в молекуле. Далее мы
уоэкем построить на ор электронных термов молекулы (каждому электронному со-
стоянию молекулы соответствует конкретный вид зависимости V(e/f\R~)) и проанали-
зировать задачу о пространственном строении молекулы и особенностях движения
ядер &1Я каждого из термов.
Рассмотрим теперь более подробно электронное строение ряда простейших моле-
хулярных систем.
7.3. Молекулярный ион водорода.
Приближенную электронную волновую функцию основного состояния молеку-
лярного иона водорода будем искать в виде суперпозиции двух невозмушенных функ-
ций водородного атома5 (обозначения см. на рис. 7.4):
И^Л) = а^(г,) + ^ь(г2).
(73.1)
е
Рис.7.4. Координаты электронной
и ядерной подсистем Н2 .
Здесь f] и г2 - удаление электрона от каждого из
протонов, каждая из этих величин выражается через
переменные г и R . Приближение (7.3.1), очевидно,
выполнено для больших межъядерных расстояний
R » а0. Однако, для нас в дальнейшем существен-
но, что представление волновой функции электрона
в молекуле (молекулярной орбитали) в виде линей-
ной комбинации атомных волновых функций
(атомных орбиталей) приводит к правильным ре-
зультатам, хотя бы и на качественном уровне, для
произвольного соотношения параметров R и а0.
Вследствие тождественности ядерных центров естественно предположить, что
вероятности обнаружить электрон около каждого из них равны между собой, то есть
|а|2 = |^|2. Отсюда ясно, что функция y/(r,R) представима в виде симметричной, или
антисимметричной комбинации атомных функций6
P(r,R) = С‘(Я)к,Л?, (7.3.2)
где С1 (7?) - нормировочная константа, определяемая из условия
ЦуЛ (Л Я)рг = {v'Pr.R^O.R)) = I (7.3.3)
5 Зго приближение иногда называют приближением разъединенных атомов.
Здесь координаты и г2 связаны с координатами Г и Л соотношениями (7.2.6).
170
Вычисление интеграла (7.3.3) дает
(<” <«))'(<>,. ('i О+<(",. (':г )КМ)=1,
откуда находим
(7?) = -^-^=,
V2 Vl±.S'(/?)
(7.3.4)
где S(tf) = (yz,Дг- )|yzu (Л)) - интеграл перекрытия. Учитывая, что
для интеграла перекрытия можно получить7
R 1
5(Я) = 1 + — + -
«о з^,
R
ехр(-Я/а0).
(7.3.5)
В случае R » а0 волновые функции каждого из центров локализованы в различных об-
ластях пространства, и интеграл перекрытия обращается в ноль. Как мы увидим в даль-
нейшем, в связанном состоянии молекулы R ~ а0, и притяжение между ядрами возника-
ет именно вследствие перекрытия атомных волновых функций.
Теперь мы можем определить энергию электронной подсистемы:
£(е)(7?) = ^±(гД)|Яе|^±(Я,А)) =
(с± (Л))2 (rx) ± y/Xs (г2)\те - — - — |y/Xs (fx) ± y/Xs (r2)). (7.3.6)
Г1 Г2
Вводя для сокращения записи обозначения
I1)
перепишем выражение (7.3.6) в виде
1 f 2 2 2 1
2 2 2 2 1
+ (2|-^|2) + (1|-^|O±(1|-^|2)±(2|-^|1) . (7.3.7)
'1 r2 '2 Г2 J
Легко видеть, что слагаемые в фигурных скобках попарно равны между собой. Прини-
мая во внимание, что
2 2
(1 It - -10 = £„ И (1 It - -12) = Е„ (112) = Е,,Е(Я),
Г\ Г2
где Els - энергия основного состояния атома водорода, перепишем (7.3.7) в виде
7 См., например, А. С. Давыдов «Квантовая механика», М.: Наука, (1978), §130.
171
~Т±5(Д)~~
(7.3.8)
гЛС введены следующие обозначения а ? ?
I /' 'I 5 *2
и г связаны соотношениями (7.2.6):
. кулоновская энергия взаимодействия распределенного электронного заряда с «чужим»
протоном в данном случае, электрона, «распределенного» около центра «один» со
«вторым» протоном),
^(Х) - ОI - е /г212) = -j y/Xs ) — c/V
- так называемый обменный интеграл, обязанный своим происхождением тому, что в
молекуле единственный электрон оказывается «размазан» сразу по обоим центрам. Для
дальнейшего существенно, что оба интеграла принимают отрицательное значение. Оба
интеграла могут быть вычислены аналитически8
V(R) =
R \
1- 1 + — ехр(-2Я/а0)
R
W(R} =
ао >
ехр(-Л/а0)
Выражение для эффективной потенциальной энергии взаимодействия ядер в молекуле9
Рис.7.5. Электронные термы молекулярного
иона водорода.
запишем теперь в виде
R ls 1±S(£)
(7.3.9)
Полученные электронные термы
приведены на рис.7.5. Как видно, в со-
стоянии на кривой, соответствующей
симметричной волновой функции, воз-
никла потенциальная яма, свидетель-
ствующая о возможности образования
связанного состояния молекулы. Анализ
выражения (7.3.9) показывает, что воз-
никновение'притяжения между ядрами в системе обусловлено обменным членом «'(Л),
то есть связано с делокализацией атомного электрона сразу по двум ядерным центрам.
Наоборот в случае электронного состояния, описываемого антисимметричной функци-
ей, связанное состояние не возникает, а электронный терм является разлетным. Расчеты
Методика вычисления этих интегралов
также обсуждается в монографии: А. С. Давыдов «Квантовая ме-
ханика», М.: Наука, (1978), §130.
Эту энергию часто принято отсчитывать от уровня
172
для связанного состояния дают значение для равновесного межъядерного расстояния
(положение минимума на потенциальной кривой Vun(R)) R =2aQ, и глубину потен-
циальной ямы ~ 2.6 эВ.
Заметим, что если предположить, что S(R) = 0, то есть электрон сосредоточен
около одного из протонов (тогда, конечно, JV(R) = 0) для электронного терма
получаем
2 2 /
(R) = — + K(R) = — 1 + — cxp(-2/?/tz0),
(7.3.10)
R R
а,
то есть полуклассический результат, с которого
мы начинали обсуждение физики моле-
Рис. 7.6. Схематический вид электронной
волновой функции в симметричном состоя-
нии
Возникновение в системе притяже-
ния или отталкивания в зависимости от вида
симметрии электронных волновых функций
можно проиллюстрировать с помощью сле-
дующих картинок. Рассмотрим структуру
электронных волновых функций, описыва-
ющих симметричное и антисимметричное
состояние молекулы //2+. Для симметрич-
ного состояния вид функции у/+ в зависи-
мости от межъядерного расстояния схема-
тически приведен на рис. 7.6. На больших
расстояниях (R » а0) волновые функции
не перекрываются, при уменьшении рассто-
яния наблюдается перекрытие атомных
волновых функций. При этом отрицатель-
ный заряд оказывается сосредоточен в обла-
сти между ядрами, что и обеспечивает воз-
никновение связанного состояния.
Аналогично, случай антисимметричного состояния у/ представлен на рис. 7.7.
На расстояниях R»а0 мы также имеем суперпозицию двух неперекрывающихся
функций, однако, в отличие от предыдущего случая одна из этих функций принимает
отрицательные значения. Поскольку распределение электронной плотности определяет
ся квадратом модуля волновой функции на больших расстояниях электронные плотно-
сти в симметричном и антисимметричном состояниях практически совпадают. Однако,
при R ~ а0 ситуация меняется. Антисимметричное состояние характеризуется нулевым
значением электронной плотности в точке равноудаленной от обоих ядер. В результате
формируется такое распределение отрицательного заряда, которое не может компенси-
ровать кулоновское расталкивание ядер, и возникает разлетный молекулярный терм.
173
Рис.7.7. Схематический вид электронной
волновой функции в антисимметричном со-
стоянии Н~>
нию вопроса, с которого начали изучение
нии «из бесконечности» протона к атому
Еще более наглядно распределение
отрицательною заряда в молекулярном
ионе водорода в зависимости от симметрии
состояния можно видеть из данных, пред-
ставленных на рис.7.8. На этом рисунке
изображены линии уровня, соответствую-
щие равной электронной плотности в состо-
яниях и у/~. Симметричное состояние
характеризуется преимущественной локали-
зацией электронной плотности между атом-
ными ядрами. В случае антисимметричного
состояния расстояние между «центрами тя-
жести» отрицательных зарядов, локализо-
ванных около каждого из протонов, оказы-
вается больше межъядерного расстояния.
Как следствие, симметричная волновая
функция описывает связанное состояние
молекулы, в антисимметричном состоянии
связанного состояния не возникает.
Вернемся теперь к обсужде-
физики молекул. Как и почему при приближе-
водорода в системе все-таки возникает притя-
жение, несмотря на то, что нейтральный атом водорода создает в пространстве коротко-
действующий положительный потенциал, который, казалось бы, приводит к возникно-
вению сил отталкивания?
Рис.7.8. Распределения электронной плотности в симметричном и
антисимметричном состояниях молекулярного иона водорода.
Оказывается, дело в явлении туннелирования (см. рис. 7.9). При сближении про-
бное между собой, электрон, который первоначально находится около одного из них,
оказывается способен протуннелировать в другую потенциальную яму. В результате
Электронная плотность окажется распределенной сразу по двум ядерным центрам, что,
174
Рис. 7.9. Образование химической связи как результат
туннелирования электрона от одного атома к другому.
как мы видели, и может обеспе
чить возникновение сил притя
жения в системе. Таким образом
в конечном счете, именно явле-
ние туннелирования обуславли-
вает возможность связывания
атомов в молекулы, то есть, обра-
зование молекул - это чисто
квантовый эффект, который не
может быть понят вне рамок
квантовой теории.
Такой случай обобществ-
ления электронов характерен и
для многоатомных молекул, ко-
гда образующие химическую
связь электроны делокализованы
сразу по многим ядерным цен-
трам. Предельным случаем такой
ситуации является кристалл,
представляющий собой фактически одну макромолекулу, где электроны могут быть де-
локализованы по макроскопически большому объему.
7.4. Молекула водорода. Теория Гайтлера - Лондона.
Рассмотрим теперь более сложную задачу - образование молекулы из двух
нейтральных атомов водорода. Эта задача была решена в 1927 году В. Гайтлером10 и
Ф.Лондоном11.
Пусть имеется протон «Л» и протон «В», расстояние между ними - R. Введем те-
перь координаты электронов так, как показано на рис.7.10. При этом мы условно будем
предполагать, что электрон «1» принадлежит протону «А», электрон «2» - протону «5».
Тогда гамильтониан электронной подсистемы молекулы водорода запишется в виде:
н = нА+нв+и,
где
. е2 - е2
н„=т,—, н,=т2-^~
ГА\ ГВ2
- гамильтонианы атомов водорода с центрами в
точках «А» и «В» соответственно,
. е2 е2 е2
U —
Г12 ГВ1 ГА2
- энергия взаимодействия электронов между со-
Рис. 7.10. Молекула водорода.
10 Heitler Walter Heinrich (1904 - 1981) - немецкий физик - теоретик.
11 London Fritz Wolfgang (1900 - 1954) - немецкий физик - теоретик.
175
бой, а также каждого из эпонов с «чужим» протоном (элек-
трона ((1» с протоном «В» электрона «2» с „ротоном (<Л))) в У„рибл и>£ении
/>2 ~ ° Риближсние соответствует двум удаленным друг от друга ато-
мам водорода) величина U может рассматриваться как возмущение. В качестве нулево-
o’ приближения мы будем рассматривать гамильтониан + /7„ представляющий со-
бой гамильтониан двух нсвзаимодеиствуютиу ятлпп п
’•’° ** снующих атомов водорода. В этом случае с учетом
ппинципа тождественности волновая Лункпия е
11Р” ®и функция системы может быть выбрана в виде:
VI + 5
(7.4.2)
=7у ИМ2) -^2)<}-Д=,
V1-?
(7.4.3)
где
“ /—ге;ф(“гл1/яо)> ^i2) =-r=exp(-rfi2/a0)
V^o д/^о
- волновые функции 15 состояния атома водорода, S - интеграл перекрытия, выражение
для которого может быть записано в виде
5=Нм2) И2)<)=(^а И2))=(Ип И))2
Легко видеть, что (и/^ ty/g / есть не что иное, как интеграл перекрытия, который мы
вычисляли при изучении электронной подсистемы Н2 (см- выражение (7.3.5)).
Таким образом, пространственную электронную волновую функцию молекулы
водорода можно представить в виде симметричной или антисимметричной относительно
перестановки электронов местами комбинации одноэлектронных функций водородного
атома. Поскольку полная волновая функция электронной подсистемы молекулы есть
произведение пространственной и спиновой волновых функций, мы понимаем, что сим-
метричной пространственной функции (7.4.2) соответствует антисимметричная спино-
вая функция (то есть такое состояние является синглетным), и, наоборот, антисиммет-
ричной пространственной функции (7.4.3) соответствует симметричная спиновая волно-
вая функция (это означает, что состояние является триплетным). Для энергии невозму-
Щенного состояния системы, очевидно, имеем
£(°) = + £<2) = -2Ry .
Вычислим теперь поправку к энергии невозмущенной двухатомной системы,
обусловленные действием оператора U :
/ 2 2 2 \
&Et = Iw1 и и/1 \ = -Д—5 f ’ ± V'Wl -— ~— — dr,dr,,
V V / 2(1 ± S) 1 Vi? r‘> r<‘)
Че интеграл берется no совокупности координат первого и второго электронов. Вычис-
ление дает:
176
Рис. 7.11. Электронные термы молекулы водорода.
Здесь
(7.4.4)
{/(Ю = ЯИТИ2)| UdT\dr2
- «обычная» кулоновская энергия вза-
имодействия электронов с «чужим»
протоном и друг с другом,
обменный интеграл, который возника-
ет вследствие учета свойств симмет-
рии волновой функции относительно
перестановки электронов местами.12
В соответствии с (7.2.13) выра-
жение для эффективной потенциаль-
ной энергии взаимодействия ядер в
молекуле имеет вид
R \ + S(R)
(7.4.5)
В выражении (7.4.5) также часто удобно за нулевой уровень энергии выбрать величину
-2Ry, соответствующую энергии двух удаленных друг от друга атомов водорода. По-
лученные в этом случае зависимости V{l’,n(R) приведены на рис. 7.11. Оба слагаемых
И(7?) и W(R) являются отрицательными. Поэтому на кривой, соответствующей сим-
метричной относительно перестановки электронов местами пространственной функции
(в этом случае спины электронов антипараллельны, и полный спин 5 = 0), возникает
потенциальная яма, свидетельствующая о возможности связанного состояния молекулы.
Антисимметричной пространственной волновой функции (в этом случае полный спин
двух электронов 5 = 1) соответствует разлетный терм: атомы водорода отталкиваются
друг от друга. Мы получили важный результат: химическая связь, приводящая к связы-
ванию атомов в молекулу, возникает в результате спаривания электронов - образованию
электронных пар, с полным спином равным нулю. Такая связь называется ковалентной
(гомеополярной). С физической точки зрения притяжение между атомами возникает в
результате того, что в синглетном состоянии электроны находятся преимущественно в
области между атомными ядрами, в результате кулоновское отталкивание ядер с избыт-
ком компенсируется притяжением ядер к расположенной между ними электронной
плотности. В триплетном состоянии (5 = 1) принцип Паули препятствует нахождению
электронов в одной области пространства. В результате между атомными ядрами возни
кает минимум электронной плотности, а, следовательно, силы отталкивания. Минимум
на потенциальной кривой, соответствующей синглетному терму, в рамках рассматрива
12 Оба интеграла, кулоновский и обменный, могут быть вычислены аналитически.
177
s теории достигается для значения R - 0 «ч Л и.
еМ01’ 1 ° А. Фактически, эта величина определя-
ет равновесное Ра"' оянис между ядрами в молекуле. Экспериментально измеренное
знаЧснис равновесного межъядерного расстояния в молекуле водорода равно * 0.74
Л. и на качественном уровне хорошо согласуется с предсказанием теории Гайтлера -
Лондона-
7.5. Насыщение химических связей. Валентность.
Повторим еще раз. наличие в оболочке атома электронов с нескомпенсированны-
.мн спинами приводит к возможности спаривания электронов, обладающих противопо-
ложно направленными спинами и принадлежащих различным атомам, что приводит к
возникновению сил притяжения между атомами и возникновению химической связи.
Теперь легко понять хорошо известное из курса химии свойство насыщения химических
связей: если в образовавшейся молекуле «свободных» (несларенных) электронов уже
нет, то дальнейшее присоединение атомов к ней уже невозможно. По этой причине с
очевидностью невозможно образование молекул Н3, НеН и т.п.
Способность атома образовывать определенное количество химических связей с
другими атомами называют валентностью. Очевидно, валентность определенного хими-
ческого элемента определяется числом неспаренных электронов на внешней оболочке
атома и равна 2S - удвоенному спину атома.
Остановимся теперь на нескольких примерах, иллюстрирующих сказанное.
Рассмотрим невозбужденный атом азота. Электронная конфигурация в этом слу-
чае есть l?2s22p3. В соответствии с правилами Хунда основной терм атома - 4S, то
есть полный спин атома S = 3/2, а валентность равна 3. Действительно, химическое со-
единение 7У/73 (аммиак) подтверждает сделанный вывод. Атом азота устанавливает три
связи с тремя атомами водорода, то есть является трехвалентным.
В качестве следующего примера определим валентность атома кислорода (элек-
фонная конфигурация 1522s22/>4). Мы видели, что по правилам Хунда основной терм
есть 3Р, то есть S = 1, а валентность равна 2. Справедливость сделанного заключения
подтверждается, например, существованием молекулы Н2О.
Рассмотрим, наконец, атом углерода. Казалось бы, по электронной конфигурации
Ь22.$-22р2 определяем основной терм 3Р, то есть S = 1, на основании чего делаем вы-
вод о двухвалентности атома углерода. Действительно, в ряде химических соединений
У1 лсрод выступает как двухвалентный элемент. В качестве примера можно указать мо-
лекулу окиси углерода СО (в этом случае речь о двойной связи между атомами углеро-
да и кислорода). Однако, значительно чаще углерод выступает как четырехвалентный
Бемент. Простейшим примером химического соединения, в котором валентность атома
У'лерода равна 4, является молекула метана CW4. Другой не менее известный пример
Двуокись углерода СО2. В этой молекуле атом углерода образует две двойные связи
с атомами кислорода. Что мы не учли и в чем причина нашей ошибки? Оказывается, уг-
ЛСР<>Д вступает в химические реакции из возбужденного состояния ’5,, принадлежаще-
178
го конфигурации \s22s'2p3. Спины всех четырех электронов оказываются неспаренны,
ми, и валентность углерода в этом состоянии равна 4. Энергия возбуждения состояния
(2.sy>3)"S2 из основного состояния (2.v22/?2)3равна 4.19 эВ. Для того чтобы образова-
ние молекулы было, тем не менее, энергетически выгодным, необходимо, чтобы энергия
химической связи, выделяющаяся при присоединении дополнительных атомов, превы-
шала энергию, затрачиваемую на возбуждения атома углерода в квинтетное состояние
5S2. В случае молекулы метана СН4 энергия связи С — Н составляет *4.5 эВ, поэтому
энергия, которая выделяется при присоединении дополнительных атомов водорода, су-
щественно превышает энергию, затрачиваемую на возбуждение атома углерода.
В качестве еще одного примера, подтверждающего справедливость наших кван-
товомеханических представлений о строении молекул, имеющего, в том числе, большой
практический интерес, упомянем также о существовании так называемых эксимерных
молекул13. Из сказанного выше очевидно, что атомы инертных газов Не, Ne, Аг, Кг,
Хе не могут образовывать химических соединений. Действительно, все электронные
подоболочки этих элементов являются замкнутыми, и неспаренных электронов в них
нет. Однако, это утверждение является справедливым лишь для основного состояния.
Если атом инертного газа перевести в возбужденное состояние, то у него появится сразу
два неспаренных электрона, поэтому такой атом уже может образовывать химические
соединения. Для определенности рассмотрим атом ксенона Хе. В основном состоянии
(5р6)'5о он действительно химически инертен. Однако, в возбужденных состояниях
конфигурации 5p56s атом Хе имеет два не-
спаренных электрона и может выступать либо
как одновалентный, либо как двухвалентный
химический элемент, то есть образовывать мо-
лекулы, которые могут существовать лишь в
электронном возбужденном состоянии. Такие
молекулы хорошо известны (например, XeF*,
XeF2 , ХеО , Хе2) и называются эксимерными
молекулами. Как мы уже отмечали, их важ-
нейшим свойством является то, что, если каж-
дый из атомов находится в основном состоя-
нии, образование химической связи является
невозможным, то есть основной электронный Рис.7.12. Термы эксимерной молекулы,
терм молекулы является разлетным. Типичный вид электронных термов эксимерной
двухатомной молекулы представлен на рис.7.12. Эксимерные молекулы представляют в
настоящее время большой интерес в лазерной физике, поскольку относительно легко
позволяют достичь инверсной населенности на переходе из возбужденного состояния в
основное.
13 Эксимер - от английского «excited dimer» - возбужденный димер.
179
7.6. Метод линейной комбинации атомных орбиталей (ЛКАО).
ковалентная полярная и ионная связи.
Детальное рассмотрение образования химических связей в молекулах — предмет
«вантовой химии. Один из основных подходов, который при этом используется, это по-
строение электронной волновой функции в молекуле (молекулярной орбитали) в виде
линейной комбинации атомных волновых функций (атомных орбиталей). Отсюда назва-
ние метода - ЛКАО.
Рассмотрим какую-либо двухатомную молекулу, например, молекулу водорода
//,. Тогда волную функцию каждого из электронов в молекуле мы представим в следу-
ющем виде
И2)~^2) + ^2).
Здесь «1» и «2» означают координаты первого и второго электрона, а функции у л и у/в
обозначают волновые функции атомных электронов, центрированные около ядер «А» и
«В». Тогда для молекулярной орбитали имеем:
^(1,2) = И0И2) - +v'!;V!?n V«2)- (7.6.1)
В полученном выражении первые два слагаемых описывают ситуацию, когда электроны
находятся вблизи различных ядер, третье слагаемое соответствует ситуации, когда оба
электрона находятся около центра «Л», а четвертое - когда оба электрона находятся
около центра «В». Удобно ввести подгоночные параметры
^(1,2) - Ve ’+ ‘ V)/’ • (7.6.2)
В случае а = 1, ft = 6 = 1 имеем симметризованную комбинацию атомных орбиталей,
которая соответствует модели Гайтлера - Лондона. Однако возможно построение и дру-
гих молекулярных орбиталей. Например, при ft = 1, а = 8 = 0 мы получаем случай, ко-
гда оба электрона локализованы около центра «А». Аналогично при 8 = 1, а = Р = 0 оба
электрона локализованы около центра «В». В такой ситуации молекула существует в ви-
де совокупности двух ионов - отрицательно и положительно заряженного, то есть реа-
лизуется ионный тип связи. В качестве промежуточного случая может реализоваться
также ковалентная полярная связь, когда электронная плотность распределена по двум
ядерным центрам, но смещена к одному из них. Из общих соображений ясно, что для
гомоядерных молекул (молекул, состоящих из двух одинаковых атомов), например, Нг,
О,, N,, р2} будет возникать ковалентная связь. Ионный тип связи характерен для ато-
мов, один из которых имеет сравнительно небольшой потенциал ионизации (например,
атом щелочного металла), а другой - большой потенциал ионизации для своего отрица-
тельного иона (галогены). Типичный пример соединения с ионной связью - молекула
NaCl, которая в связанном состоянии существует в виде Na+ +СГ. В качестве примера
молекулы с ковалентной полярной связью укажем на молекулу НС1, в которой проис-
ходит частичное смещение электронной плотности от атома водорода к атому хлора.
180
С теоретической точки зрения в рассматриваемом приближении задачей кванто
вой химии является расчет волновой функции электронов в молекуле, то есть вычисле
ние параметров а , /3. 8. наилучшим образом описывающих распределение электрон
ной плотности, и определение типа связи. Обычно эта задача решается вариационным
методом, подробно рассмотренным нами в Главе 5.
Рассмотренные нами общие принципы описания молекул позволяют хотя бы и на
качественном уровне понять структуру многих молекул. Обычно электронные орбитали
рисуют как линии уровня углового распределения электронной плотности. В качестве
примера 5- и -электронные орбитали приведены на рис.7.13. Тогда общая структура
двухатомной молекулы, химическая связь в которой обусловлена спариванием двух 5-
s - орбиталь
Рис. 7.13. Электронные s - и р - орбитали.
7.15). Такой тип связи возникает, например,
sp- или двух р -электронов пред-
ставлена на рис. 7.14. Все приведен-
ные случаи являются примерами ст -
связи и реализуются, в частности, в
молекулах Н2, НС!, С12. При пере-
крытиии р - электронных орбиталей
может возникать и другой тип связи
- так называемая я - связь (см. рис.
в молекуле бензола и в других ароматиче-
ских углеводородах.
Рис. 7.14. Схема образования ст-связи.
Остановимся теперь на во-
просе о пространственном строении
простейших многоатомных молекул.
Рассмотрим, прежде всего, молекулу
воды Н2О. В этой молекуле два не-
спаренных р -электрона атома кис-
лорода образуют ковалентные по-
лярные связи с s -электронами ато-
мов водорода. В результате про-
странственная структура молекулы
имеет вид, представленный на рис.
7.16. Молекула оказывается нелинейной, причем, казалось бы, угол между направлени-
ями на атомы водорода должен составлять 90°. На самом деле этот угол равен 105°. При-
чина этого заключается в следующем. Ковалентная связь О — Н является полярной,
центр электронной плотности смещен к атому кислорода. В результате на атомах водо-
рода возникает некоторый положительный заряд, приводящий к расталкиванию атомов
водорода друг от друга и увеличению угла между направлениями связей до 105°. Анало-
гичную молекуле воды пространственную структуру имеют и молекулы F2O, ChO,
При этом углы между направлением связей в этих молекулах составляют 100°, 115° и 92
соответственно.
В качестве следующего примера рассмотрим молекулу аммиака НН2. Атом азота
имеет три неспаренных р - электрона, каждый из которых образует ст -связь с атомом
181
воД°Рода’ Молекула имеет форму треугольной
пирамиды, в вершине которой расположен атом
азота-
Несколько более сложная ситуация имеет
меСто для молекулы метана СН4. Мы уже гово-
рили, что в химические реакции атом углерода
вступает, как правило, из квинтетного состояния,
принадлежащего конфигурации 2s2p3. Поэтому
на первый взгляд кажется, что одна из связей
С-Н в молекуле метана должна быть выделена
и характеризоваться длиной и энергией связи, от-
личными от трех других. Однако, многочислен-
ные экспериментальные данные позволяют
Рис. 7.15. Схема образования тг-связи.
утверждать, что в молекуле метана все четыре
химических связи эквивалентны. Этот
факт можно понять на основе пред-
положения о гибридизации орбита-
лей.
В рамках этого предположе-
ния вместо волновых функций 2s и
2р состояний атома углерода в рас-
смотрение вводятся состояния, кото-
рые являются суперпозицией s- и
р -состояний:
Такая орбиталь называется гибрид-
ной, а процесс ее образования назы-
Рис. 7.16. Молекула воды. вается sp3 - гибридизацией. Гибри-
дизация электронных орбиталей атома углерода позволяет объяснить свойства молекулы
метана и многих других органических соединений.
7.7. Основы систематики электронных состояний двухатомных
молекул.
Геометрия многоатомной молекулы в общем случае бывает достаточно сложной
и различной уже даже для трехатомных молекул. Поэтому общих принципов системати-
ки состояний много- и даже трехатомных молекул не существует. Поэтому в этом разде-
ле мы рассмотрим только основы систематики электронных состояний только двух-
атомных молекул.
Напомним, что в многоэлектронных атомах систематика состояний базируется на
концепции самосогласованного поля, в соответствии с которой каждый атомный элек-
трон движется в центрально-симметричном поле и потому характеризуется точно опре-
деленным значением квадрата момента количества движения. Систематика проводится
по значениям полного орбитального и полного спинового моментов электронной обо-
182
лочкк Кроме ТОГО, в приближении LS связи, которое достаточно хорошо работает
большей части периодической таблицы элементов, операторы квадратов полного орби-
тального и полного спинового моментов совокупности атомных электронов и
коммутируют с оператором Гамильтона. Поэтому существуют стационарные состояния
системы, в которых квадраты орбитального и спинового моментов всей совокупности
атомных электронов также имеют точно определенные значения. Именно эти квантовые
числа, L и 5, и используются для систематики состояний многоэлектронных атомов,
задавая атомный терм в заданной электронной конфигурации.
В молекулах такой подход оказывается неприменимым. Хотя при изучении стро-
ения многоэлетронной молекулы мы также базируемся на приближении самосогласо-
ванного поля, потенциал, в котором движется каждый из электронов, не характеризуется
центральной симметрией, оператор квадрата орбитального электронного момента кон-
кретного электрона не коммутирует с электронным гамильтонианом молекулы
/V2]* °,
то есть в стационарных состояниях квадрат орбитального момента точно не определен.
С другой стороны, в двухатомной молекуле потенциал характеризуется аксиальной
симметрией. Это значит, что гамильтониан электронной подсистемы коммутирует с
оператором проекции момента количества движения на ось молекулы (ось z)
АЛ]=0.
Поэтому в двухатомной молекуле стационарные состояния электронов можно охаракте-
ризовать точно определенным значением проекции орбитального момента на межъядер-
ную ось. Состояния электронов в оболочке обозначаются в соответствии со схемой:
проекция момента - Л = |тг| =0, 1, 2, 3 ...
состояние электрона - ст, п, 8, (р
Здесь квантовое число т( определяют проекцию орбитального момента электрона на
ось молекулы.
Что касается всей электронной оболочки молекулы, то в пренебрежении спин-
орбитальным взаимодействием наличие аксиальной симметрии также приводит к тому,
что гамильтониан электронной подсистемы коммутирует с оператором проекции сум-
марного момента количества движения электронов на ось молекулы (ось z )
k>ij=o.
Это значит, что можно построить набор стационарных состояний электронной подси-
стемы молекулы, в которых величина проекции суммарного орбитального момента
электронов на ось молекулы определена точно. Возможные значения этой проекции есть
Lz=MLh, ML = 0,±1,±2,...
Таким образом, мы можем ввести квантовое число А = \ML \ = 0,1,2,
характеризующее
электронную структуру молекулы. Принято использовать следующую терминологию.
Состояния с А = 0 называют S состояниями молекулы, А = 1 - П состояниями, А = 2
Д состояниями:
183
Л 0 12 3
Е П Д ф
Состояния с более высокими значениями квантового числа Л встречаются крайне ред-
ко. Для состояний с Л * 0 квантовое число ML принимает два возможных значения
д^=+Л, все эти состояния оказываются двукратно вырождены. Это вырождение
называется Л - удвоением. Что касается Е - термов, то они не вырождены. Однако, сле-
дует различать Z - термы, волновая функция которых меняет, или не меняет знак при
отражении системы относительно плоскости, проходящей через ось молекулы. В первом
случае говорят о Е - термах, а во втором (знак волновой функции не меняется) - о Е+ -
термах. Кроме того, двухатомные гомоядерные молекулы, т.е. образованные двумя оди-
наковыми атомами, обладают еще и центром симметрии относительно точки, делящей
пополам линию, соединяющую ядра. Поэтому гамильтониан системы не меняется при
замене знака координат всех электронов в молекуле. Оператор этого преобразования
также коммутирует с оператором орбитального момента, и, в частности, с его проекций
на ось молекулы. Поэтому состояния с определенным Л можно еще разделять по их
четности - волновая функция четных состояний g (от немецкого gerade - четный) не ме-
няет свой знак, нечетных u (ungerade) - изменяет его. Четность состояния принято ука-
зывать слева внизу от Л: например, Yg, Пи.
Помимо квантового числа Л , электронная оболочка характеризуется квантовым
числом S, определяющим значение суммарного спина всей совокупности электронов
молекулы. Поэтому электронный терм14 молекулы принято обозначать следующим об-
разом
25+1Л, например, 'I, 3П, 2Д.
Чаще всего основным термом двухатомной молекулы является терм 1Z+, а если
молекула гомоядерная, то 1Z*. Однако, бывают и исключения, например, основной терм
молекулы кислорода О2 - 3S~.
Рассмотрим теперь вопрос о том, какие молекулярные термы могут образовать
два атома, находящиеся в определенных состояниях, характеризующихся заданными
квантовыми числами (ДЛ) и (L2,S2). Если атомы находятся далеко друг от друга, то
проекция орбитального момента каждого из них на любую ось, и в том числе на ось мо-
лекулы может принимать следующие значения:
Следовательно, проекция суммарного орбитального момента на ось молекулы будет
Равна Л= М, + М,
Ч L2
Кроме того, значение полного спина электронной оболочки мо-
лекулы определяется спиновыми моментами каждого из атомов
*------ --------------------
Как и для атома, электронный терм молекулы состоит из группы состояний, которые являются вырож-
денными с точностью до учета спин - орбитального взаимодействия в электронной оболочке молекулы,
однако, не будем касаться вопросов, связанных с изучением тонкой структуры электронных термов.
184
S |.К, 5\|.|5‘, 5, 4 I-!-S J
R качос1вс примера опре лечим молекулярные термы, которые могут образовать две
ма Ro iopoла. няхо чяшнеся а основном состоянии. Поскольку основное состояние
жпороза есть 5. то есть лая обоих атомов, образующих молекулу 5, „
W, - М, 0. то находим Л Л/,, < М,. ”0 и 5-0,1. Поэтому возможны синглет,
ный и трип чет ный L -термы: L и £ Именно эти два терма и были получены имея рв-
нее при рассмотрении молекулы водорода в рамках метода Гайтлера Лондом. При
этом синглетный терм описывает связанное состояние молекулы, а триплетный являвцл
разлетным.
Рассмотрим еще один пример. Какие молекулярные термы могут образовать две
атома, термы которых ‘S и ‘ Р (например, два атома водорода, один из которых нахо-
дится в возбужденном р - состоянии)? Поскольку в этом случае =0. ML =0,±1,
то квантовое число А принимает два возможных значения А = 0.1. то есть возможны I
и П термы, каждый из которых может быть либо синглетным, либо триплетным. В ито-
ге имеем:
’Z, ’П, ’Z, 3П.
Легко сообразить, два последних терма являются разлетными. Как уже отмечалось, ос-
Рнс.7.17. Электронные термы двухатомной молеку-
лы. Атомные термы ?$ и гР.
новным термом является, как прввм*
ло, 1Z. Характерная картинка, соот-
ветствующая рассматриваемой ситу-
ации, приведена на рис.7.17. На
больших .межъядерных расстояниях
(R » а0) молекулярные термы вы-
рождены и соответствуют двум
невзаимодействующим атомам в со-
стояниях 2S и Р. При сближении
атомов в зависимости от их кванто-
вых чисел ML и W5 энергия эдем-
тронной подсистемы молекулы «ДО
зывается различной, что и приводит
к расщеплению термов (см. рис. 7.17).
7Л. Ядерная подсистема молекулы.
Кам мы уже товорнлн, в рамках адиабатического приближения полная попил ват
функция молекулы представляется в виде
где волновая функция электронной под с истомы есть решение задачи на соб-
ственные значения и собственные функции для оператора Га м инэлектронной под*
системы, а ядерная волновая функция определяется из задачи
185
= (78Л)
гДс V электронный терм молекулы15. Решив задачу для электронной подсисте-
мы. МЬ1 получаем на ор электронных термов. Для каждого из них теперь можно постро-
ить набор ядерных состоянии.
Выборе для определенности одно какое-либо электронное состояние молекулы
и перейдем к изу ению ядерного движения16. Будем искать решение уравнения (7.8.1) в
виде
0(Л,)(Я) = ф(Я)У(О)? (7.8.2)
где & есть совокупность угловых координат, определяющих положение молекулярной
оси в пространстве. Вспоминая, что оператор кинетической энергии ядерного движения
есть
Й2 А
2^ R
(Дл, " радиальная и угловая части оператора Лапласа, у. - приведенная масса моле-
кулы), перепишем (7.8.1) в виде
1 ( ft2 Л 1 й2
_ ^_Дл+^>(Д)]ф(Д)-_—ДПУ(Й) = £. (7.8.3)
Очевидно, уравнение (7.8.3) допускает разделение переменных, причем для угловой ча-
сти волновой функции имеем
-Й2ДОУ = ЯУ. (7.8.4)
Мы получили уравнение на собственные значения и собственные функции угловой ча-
сти оператора Лапласа, описывающего угловой момент ядерного вращения. Решение
этой задачи хорошо известно: это сферические функции У7М(П), а квадрат вращательно-
го момента ядер есть
J2 =Й2У(/ + 1).
Здесь J = 0,1,2,... - вращательное квантовое число.
Учитывая решение задачи (7.8.4), из уравнения (7.8.3) получим
( t,2 Й2
_ д я + (Л) + J(J +1) Ф(Л) = -ЕФ(Я).
1и " 2/Л2 )
(7.8.5)
15 Для дальнейшего существенно, что эффективная энергия взаимодействия ядер в молекуле зависит лишь
°'г абсолютного значения межъядерного расстояния, но не от ориентации оси молекулы в пространстве.
16 Мы будем считать, потенциальная кривая V(eff}(R) характеризуется минимумом, т.е. у молекулы име-
йся связанные состояния и ядерная подсистема имеет, в том числе, дискретный энергетический спектр. В
случае разлетных термов спектр ядерных состояний только непрерывный. Такую ситуацию мы анализа-
Р°вать не будем.
186
Таким образом, радиальное движение ядер (для дискретного спектра речь идет об их ко-
лебатсльном движении) происходит в потенциале
U(R) = \R} + +1),
2/z/c
то есть для каждого конкретного значения J возникает свой потенциал в котором
надо рассматривать радиальное движение ядер. Особенности движения в этом потенци-
але зависяз от структуры электронного терма . Однако, ниже мы покажем, что
второе слагаемое, обусловленное вращательным движением ядер, дает при не слишком
больших значениях вращательного квантового числа малый вклад в потенциал (/(7?).
Поэтому в этом слагаемом приблизительно можно считать, что R « /?(), где Ro - равно-
весное значение межъядерного расстояния, соответствующее минимуму функции
Г,</7’(/?). Тогда
U(R)^rl,i/}(R) + E',o'\ (7.8.6)
где
= h , ./(./ + 1) (7.8.7)
2/2/?,;
п о А?2
- энергия вращательного движения ядер. Величину В =------------- называют вращательной
2///?0
постоянной. Отмстим также, чю. вводя момент инерции молекулы относительно оси,
проходящей через центр масс молекулы / = pR^, выражение для вращательной посто-
янной мы можем также переписать в виде В = /г/(2/). Как видно из (7.8.7) вращатель-
ная постоянная определяет характерную величину энергии ядерного вращения в моле-
кулах.
С учетом сделанных предположений мы можем рассматривать колебательное и
вращательное движение ядер в молекуле независимо друг от друга и записать теперь
уравнение, описывающее колебательное движение ядер в молекуле
Г й2 >
- — Д л + K(t#) (R) Ф(Я) = Е(у‘Ь)Ф(Я). (7.8.8)
Здесь E{vtb) - энергетический спектр колебательного движения ядер, который получается
из решения задачи (7.8.8). Полная энергия ядерного движения есть
Е = E(vib) + Е(го,)
Вблизи положения минимума потенциальную функцию (R) можно разложить в ряд
Тейлора, ограничившись приближением гармонического осциллятора
Г(R) = (Яо) + ft*" V
(7.8.9)
187
ГДе
(7.8.10)
, _ d2V(eff}
dR2
. постоянная квазиупругой силы. В таком приближении спектр собственных значений
задачи (7.8.8) представляет собой спектр гармонического осциллятора17
= Ю(у + 1/2).
Здесь = у/к/Р' ~ частота колебаний молекулы, v = 0,1, 2,... - колебательное квантовое
число. Реально оказывается, что приближение гармонического осциллятора для ядерных
колебаний справедливо лишь для небольших значений колебательного квантового чис-
ла.
Таким образом, для небольших значений колебательного и вращательного кван-
товых чисел энергию ядерной подсистемы можно записать в виде
Е = M2(v +1/2) + BJ{ J +1).
Оценим характерную величину энергии колебаний и вращений молекулы. Мы видели,
что для вращательного движения
Е{го,} "
~ 2/J?2 '
Поскольку Rq = а0 и Я2/(2та^) = Ry, для энергии вращений получаем
£(ro/) ~ m_Ry
А
Оценим теперь масштаб энергии колебательного движения: E{v,b) = hCl = ^h^k/ (л . Пола-
гая, что к =------—
dR2
y(efT)
= —— = Ry lai , получим
R = R. Ro
£<vib)
Принимая во внимание, что характерная энергия электронной подсистемы молекулы
Е<е> ~ Ry, находим следующее соотношение между характерными значениями энергии
электронной, колебательной и вращательной энергии молекулы
£-(*) . £<»"*) . ^Ot) _ j
(7.8.11)
Обычно w/xz-lO"4. Поэтому характерная энергия колебательного кванта hQ ~ 0.1 эВ.
Для вращательной энергии В ~ Ю"3 эВ. Значения энергии колебательного кванта и вра-
щательной постоянной для ряда двухатомных молекул приведены в таблице. Как видно,
"Мы здесь полагаем, что энергия отсчитывается от положения минимума (R„).
188
с увеличением массы молекулы энергия колебательного кванта Ю и вращательная по-
стоянная убывают.
молекула R„.\ Ml, эВ В, эВ
Я, 0.7412 0.5456 7.54-10’3
1.098 0.2925 2.48-10^
о2 1.207 0.1959 1.79-ПГ4
а2 1.988 0.0694 3.03-10’5
Чуть более подробно остановимся на рассмотрении колебательного движения
ядер. До сих пор мы рассматривали только приближение гармонического осциллятора
для потенциальной кривой V{efr\R). В рамках такого приближения спектр колебатель-
ных состояний является эквидистантным. Однако, реально такое приближение работает
лишь для первых нескольких состояний. Для более высоких состояний существенен эн-
гармонизм молекулярных колебаний. Реальная потенциальная кривая постепенно рас-
ширяется, что приводит к сгущению колебательных уровней энергии.
Проиллюстрируем все вышесказанное на примере электронного терма молекулы,
допускающего следующую удобную аппроксимацию:
^(Я) = Ф,;/Я!-2RJR). (7.8.12)
Легко видеть, что здесь 7?0 есть положение минимума потенциальной кривой (равновес-
ное расстояние между ядрами в молекуле), a D - глубина потенциальной ямы, опреде-
ляющая энергию диссоциации молекулы. Для ядерной волновой функции имеем урав-
нение
й2 (р А
~V2y + D —£--2 — у = Еу/.
2а I R2 R Г
Отделяя угловую часть волновой функции y/(R) =
ции %(R) получим
R
I р[
2a dR2 R2
Ro\ h2J(J + 1)
R Г
(7.8.13)
YJM(O,(p), для радиальной функ-
(7.8.14)
Здесь J - вращательное квантовое число. Вводя эффективное квантовое число J* с по-
/j2J*(j’+l) h2J(J + \\
мощью соотношения -----------~ — DR2 + ~ /7 8 141
ш, v п ш^ппл , полученное уравнение (7.оД*7
сведем к виду уравнения для радиальной волновой функции в задаче Кеплера, которое
можно решить в приближении квантового дефекта (см. Раздел 5.4). Для уровней энергии
получим
109
2Л2
р *
(7.8.15)
v •' б. колс^а1сльное квантовое число (оно в данном случае аналогично радиаль-
ном' квантовому числу в задаче об атомных спектрах), а Д, Л 1^*1 > 1/2)2
2 V Л*
квантовый дефект.
Считая, что v, J «2/zD/^/ft2 (не слишком сильное колебательное и вращатель-
ное возбуждение), и разлагая знаменатель в (7.8.15) в ряд относительно точки
jlpDR^Iti2 для уровней энергии Ev j получим
EvJ =~D + M2(v +1/2) + В(J +1/2)2 - 3B(v +1/2)2 - — (J + 1/2Хv +1/2).
________ hQ,
где Q = y2Z)/xzK02 - частота молекулярных колебаний, В = h2/ipR^ - вращательная по-
стоянная. В полученном выражении второе и третье слагаемые дают энергию колеба-
тельного и вращательного движения, четвертое - учитывает ангармонизм колебаний, а
пятое дает поправку к энергии, связанную с влиянием колебаний и вращения ядер друг
на друга. Как видно, членом, описывающим связь колебаний и вращений можно прене-
бречь в силу В « М2. В то же время энергия вращательного движения молекулы оказы-
вается порядка энергии ангармонического члена.
Удобной аппроксимацией вида потенциальных кривых различных молекул явля-
ется потенциал Морзе18:
V{efn (R) = D[1 - ехр(- а(Л - /?0))f.
Нетрудно видеть, что точка R = Ro соответствует положению минимума потенциальной
кривой (равновесное межъядерное расстояние), а величина D - глубину потенциальной
ямы, которая с точностью до энергии нулевых колебаний определяет энергию диссоциа-
ции молекулы. Разложение выражения (7.8.16) в ряд Тейлора вблизи положения равно-
весия дает
(7.8.16)
Г(<)(Л) = Ра2(/?-Л0)2,
то есть гармоническое приближение, причем частота колебаний оказывается равна
V V
Точное решение стационарного уравнения Шредингера для частицы в потенциале Мор-
зе*9 дает следующее выражение для энергетического спектра системы
е:л> =ЛП(у + 1/2)-^-
(7.8.17)
'* Morse Philip (1903 -1985) - американский физик.
Ьолее подробно см. Л. Д. Ландау, Е. М. Лифшиц Квантовая механика. Нерелятнвистская теория, М.:
НауКа> (1974), с.96-97
190
Рис. 7.18. Энергетический спектр состояний в
потенциале Морзе.
Величину K = h£l/4D называют по-
стоянной энгармонизма, обычно
к = 10’2 ч-Ю-3. Характерный вид по-
тенциальной кривой Морзе и энерге-
тический спектр в таком потенцииале
представлены на рис.7.18. Как мы и
ожидали, происходит сгущение энер-
гетических состояний к границе коле-
бательного континуума, причем число
состояний дискретного спектра оказы-
вается конечным. Действительно, по-
лагая, что максимальное значение
энергии колебательного уровня в дис-
кретном спектре есть D, из (7.8.17)
легко для максимального значения колебательного квантового числа получаем
D
Vmax 2к 2Ш
Еще одной часто используемой аппроксимацией потенциальных кривых является
потенциал Леннарда-Джонса20, известный также как потенциал «шесть - двенадцать»:
Г^’(7?) = Г0
(7.8.17)
Положение минимума на кривой (7.8.17) достигается в точке R глубина потен-
циальной ямы есть Ио /4. Этот потенциал с успехом используется для описания взаимо-
действия атомов инертных газов и описывает силы притяжения Ван-дер-Ваальса, обу-
словленные взаимодействием наведенных атомных дипольных моментов, которые на
малых расстояниях сменяются интенсивным отталкиванием. Типичное значение глуби-
ны потенциальной ямы, возникающей при взаимодействии атомов друг с другом, со-
ставляет величину порядка 0.01 эВ, а равновесное расстояние между атомами ~ Зч-4 А.
Таким образом, образование молекулярных комплексов типа Аг2, Хе2, обусловленное
силами Ван-дер-Ваальса, возможно лишь при низких температурах.
Покажем, что вне зависимости от сил, приводящих к образованию химической
связи, между любыми21 атомами (молекулами) на больших (по сравнению с атомным
размером) расстояниях действуют слабые силы притяжения, известные как силы Ван-
дер-Ваальса22. Казалось бы, дальнодействующий характер сил между атомами может
быть обусловлен их диполь-дипольным взаимодействием (или взаимодействием диполь
- наведенный диполь). Однако, все атомы (кроме атома водорода) в стационарных со-
20 Lennard-Jones John Edward (1894 - 1954) - английский физик - теоретик.
21 Доказательством этого является тот факт, что при низких температурах любой газ переходит в конден-
сированное состояние, то есть его атомы удерживаются друг возле друга силами притяжения.
22 van der Waals Johannes Diderik (1837 - 1923) - голландский физик. Нобелевская премия (1910) «За рабо-
ту, посвящённую уравнению состояния газов и жидкостей».
181
стояниях характеризуются нулевым значением литюлмюго момента, а потому сил взаи-
мплсйстяия между удаленными атомами вотиюигть не лояжно Как мы увидим, универ»
сйпьнмЙ характер этих сил имеет чисто квантовую природу я обуежжлмн нулевыми ко»
„ебяниями атомных дипольных моментов
рассмотрим следующую модель Пусть имеются две агтома (линейных остишшгто
ря). удаленных друг от друга на расстояние R. Пусть колебания электронов проиежоягг
в направлении прямой, со»
Р»------------------—________ fc< елтипошей атомы, i х, в
х, - нх смешения опюсаь
г. »
<у -^Э---------------—-------- х* - дельно положения раяшммь
, сия (рис 7.19\ причем
ряс 7.19 Модель мполь-дипольного вми^лейепт, * Пуст,
частота колебаний атомных электроне. Запишем ткпетшальнун, QtKmat ,
виде
е2 е2 е2 е3 2е2х,х2
----------------+ — 4.---------а------1_1 в----L-L
R-x} R + x2 R Л-х, + х2 R3 R3
Таким образом, в рассматриваемом случае взаимодействие атомов
взаимодействия двух диполей. Для функции Гамильтона имеем:
и 1 . 1 -a ma^xl -e3x.x,
Н--тх} +—*-+-тх, +—-a-i-2—V-1.
2 2 2 2 2 R3
Вводя новые координаты
(7.8.18)
(7.8J9)
перепишем функцию Гамильтона в виде
, maiil . । .-.1 .
Н =
-п')
вЗ
или
(7 8.20)
^Ь1 получили функцию Гамильтона двух независимых осцилляторов с частотами
6>t •
\ Htf^R
Разлагая корень в ряд до второго порядка малости, имеем
f е2 е* 1
2 Й411 I i « а “ _ 2 4 I ‘
^чки зрения квантовой теории основное состошис систем двух осцилляторов штп»
^Ризуется энергией
192
Е — Е _ + Е _ = h ctr jl + h (0_ /2 — hcDf) 1
2m2cD40Re
(7.8.21)
Мы видим, что энергия системы зависит степенным образом от межъядерного расстоя-
ния. причем потенциал взаимодействия (притяжения) есть
U(R) = —
R
(7.8.22)
Это и есть потенциал, описывающий ван-дер-ваальсовское взаимодействие. Мы видим,
что в конечном счете это взаимодействие обусловлено наличием нулевых колебаний
атомных дипольных моментов.
В заключение отметим, что потенциал Леннарда-Джонса на больших расстояниях
между атомами как раз и описывает силы Ван-дер-Ваальса.
7.9. Изотопические эффекты в молекулах.
В этом разделе мы коротко обсудим некоторые особенности изотопического
смещения энергетических уровней в молекулах. Наиболее существенной причиной изо-
топического смещения атомных состояний является различие в массах атомных ядер
изотопов одного и того же элемента. Но даже в этом случае мы видели, величина изото-
пического смещения невелика, и пропорциональна отношению массы электрона к массе
атомного ядра. Если говорить об электронных уровнях молекул, изотопический сдвиг
будет также мал. Однако, совсем другая ситуация возникает при анализе колебательно -
вращательной структуры молекулярных состояний. Действительно, квадрат частоты мо-
лекулярных колебаний есть отношение постоянной квазиупругой силы (ее величина
определяется электронным строением молекулы) к приведенной массе: Q = 7^/А • При-
веденные массы различных молекулярных изотопов могут значительно отличаться друг
от друга. Например для изотопов молекулярного водорода и дейтерия Н2 и D2 приве-
денные массы отличаются в два раза и составляют тр/2 и тр соответственно (jnp -
масса протона). Следовательно, отношение колебательных квантов молекул Н2 и D2
есть
« 72 .
В других, более тяжелых молекулах относительная величина изотопического сдвига
меньше. Назвать такой изотопический сдвиг малым эффектом нельзя.
Аналогичная ситуация возникает и с изотопическим смещением вращательных
состояний молекулы. Для двухатомным молекул структура вращательного спектра
определяется значением вращательной постоянной В = h2/2^R2 (здесь R - равновесное
межъядерное расстояние). Как видно, для рассматриваемых выше молекул Н2 и Д ве'
личина вращательной постоянной отличается вдвое, что приводит к существенному Ра3'
линию во вращательных спектрах молекул.
194
Глава 8. Основы полуклассической теории
взаимодействия света и вещества.
В этом разделе мы рассмотрим основы построения общей полуклассической
теории взаимодействия электромагнитного излучения с веществом. Это означает, что
вещество (атомы, молекулы или их совокупность, атомное ядро, электронная
подсистема твердого тела) будут рассматриваться с позиций квантовой теории, в то
время как электромагнитное поле будет описываться классически. Оказывается, в
рамках такой теории можно описать подавляющее большинство электромагнитных
явлений в окружающем нас мире. В Главе 14 обсудим построение последовательной
квантовомеханической теории электромагнитных явлений, когда и поле и вещество
описываются с позиций квантовой механики. Такая теория несомненно нужна для
описания взаимодействия очень небольшого количества фотонов с веществом. Но, как
мы увидим, существуют и достаточно интенсивные электромагнитные поля,
содержащие макроскопически большое число фотонов, которые не могут описаны в
рамках классической теории электромагнитного поля. Изучением взаимодействия таких
неклассических интенсивных полей с веществом занимается квантовая оптика. Более
подробно такие вопросы будут рассмотрены в Главе 14.
8.1. Постановка задачи. Электрическое дипольное приближение.
Для определенности в этой главе будем говорить о воздействии классического
поля излучения на атом, но фактически, как уже отмечалось, в качестве квантовой
системы может выступать и атомное ядро, и молекула, и электронная подсистема
твердого тела. Пусть атомная система описывается гамильтонианом Но, причем будем в
дальнейшем считать, что мы знаем набор собственных значений и собственных функций
атомного гамильтониана у/п и Еп, удовлетворяющих уравнению
Н^п=Епу/п,
Ноу/Е = Еу/Е,
(8.1.1)
где у/ п и у/Е - волновые функции стационарных состояний дискретного и непрерывного
спектров, принадлежащие собственным значениям Еп и Е соответственно.
Электромагнитное поле мы можем описать векторами напряженности
электрического и магнитного полей, как функций пространственной координаты и
времени Е(г,г) и H(r,z), удовлетворяющие уравнениям Максвелла. В важном, но
частном случае, мы будем говорить о плоской линейно поляризованной
электромагнитной волне с частотой со, напряженности электрического и магнитного
полей в которой записываются в виде
Ё(г,/) = Ёо cos(£r -cot),
H(r,f) = Но cos(#f — ay).
Здесь к = со]с.
Со стороны поля волны на атомный электрон действует сила Лоренца
195
F = eE + - [v x H
c
М» будем считать, что поле достаточно слабое, и электрон остается нерелятивистским'.
поскольку в электромагнитной волне в вакууме |Ё0| = |й0|, то магнитная и электрическая
части силы Лоренца связаны соотношением
yL«-Sa = l/137«l,
Fei с
(8.1.2)
поэтому магнитной частью силы Лоренца можно пренебречь, и считать, что на атомный
электрон воздействует только электрическое поле волны. Будем также считать, что
длина волны воздействующего излучения Я, = 2я/к заметно больше характерного
размера квантовой системы, т.е.
(8-1.3)
Для атома в качестве оценки размера а следует использовать боровский радиус. Это
означает, что для излучения оптического диапазона частот условие (8.1.3) также хорошо
выполняется. Следовательно, при выполнении условия (8.1.3) электрическое поле вопны
можно считать пространственно однородным.
Если же мы захотим рассматривать взаимодействие рентгеновского излучения с
энергией квантов ~10 кэВ (А,~1 А), то необходимо учитывать пространственную
неоднородность поля электромагнитной волны.
Таким образом, если условия (8.1.2) и (8.1.3) выполнены, можно говорить, что
наша система находится в пространственно однородном изменяющемся во времени
электрическом поле. Такое приближение принято называть электрическим дипольным
приближением (длинноволновым приближением) для взаимодействия квантовой
системы с электромагнитным полем. Его суть заключается в возможности пренебречь
действием магнитного поля волны на атомную систему и в возможности не учитывать
пространственное изменение напряженности электрического поля волны на характерном
размере системы.
Условия применимости электрического дипольного приближения, как правило,
выполнены достаточно широко. Например, оно выполнено при анализе взаимодействии
Y • излучения с атомными ядрами. Действительно, характерная энергия нуклонов в
атомных ядрах составляет величину порядка нескольких МэВ, т.е. нуклоны являются
нерелятивистскими (энергия покоя нуклона ~ 1000 МэВ). Для энергий у - квантов
£ --- I t 0 МэВ соответствующие длины волн составляют X - КГ10 -10 " см, что также
больше размера атомного ядра R.. - 10 13 10 см.
Фактически электрическое дипольное приближение является первым членом
«ультипольного разложения энергии взаимодействия квантовой системы с полем
«лучения. Учет высших членов разложения по параметрам v/c и а/Х по теории
“«лущений приводит к магнитному дипольному и электрическому квадрупольному
'^^„огозарядных ионах элеюроны являются изначальнопоэтому в этом
’Учае все наши дальнейшие рассуждения, вообще говоря, не сир
196
приближениям. Всюду в дальнейшем мы будем работать только в рамках
электрического дипольного приближения, пренебрегая мультиполями высших порядков
8.2. Две формы записи оператора взаимодействия квантовой
системы с электромагнитным полем: dE - ирА - калибровки.
Наша задача теперь - записать оператор взаимодействия квантовой системы с
классическим электромагнитным полем. Для этого, как всегда при построении
квантовомсханических операторов, запишем классическое выражение для энергии
заряженной частицы в электромагнитном поле.
В классической электродинамике показывается, что в произвольном
электромагнитном поле функция Гамильтона заряженной частицы есть
( е - V
р-- -A(r,t)
Н(r,p,t) =---С-~------+ eg>(r,t), (8.2.1)
2т
где (p(r,f) и A(r,t) - скалярный и векторный потенциалы электромагнитного поля,
связанные с напряженностями электрического и магнитного полей следующим образом:
= . 1 сА _
Е(г,/) =-----— - V^,
с dt
H(r,/) = rot А.
(8.2.2)
Свободное электромагнитное поле удобно описывать в кулоновской калибровке
потенциалов
divA = 0, (8.2.3)
полагая, что скалярный потенциал тождественно равен нулю. Тогда напряженности
электрического и магнитного полей определяются как
1 дЛ
Е = -- —, H = rotA. (8.2.4)
с dt
В квантовой теории функция Гамильтона частицы (8.2.1) превращается в гамильтониан
частицы, взаимодействующей с электромагнитным полем. В кулоновской калибровке
тогда имеем
(8.2.5)
Перепишем (8.2.5) в виде
Я = + + (8.2.6)
2т 2тс 2тс
Отметим, что поскольку векторный потенциал есть функция пространственной
координаты, то, вообще говоря, рА^Ар. Вычисление коммутатора [Д А] дает
197
[A ^ = pA-A^~ihdivA.
no^WMV ДЛЯ КУЛОНОВСКОЙ КалиброВКИ [Д JI = 0 u ffil a,
1*° к J и и (б.2.6) мы можем переписать в виде
LJ — ^~А -
О = --------ПЛ а . j2
2м тсР 2тс2 ' (8.2.7)
Как видно, оператор
(8.2.8)
(г, f) = —~ рА + А2
тс 2тс2
мы можем назвать оператором взаимодействия квантовой системы с электромагнитным
полем.
Динамика квантовой системы в этом случае описывается уравнением
Шредингера
dy/(r,f) ft2 _2 z_
1П Tt 4'(r>6 + WpA(rd)v(r,f).
(8.2.9)
В дипольном приближении, которое предполагает нерелятивистский характер
квантовой системы, а также, малость ее размера по сравнению с длиной волны
излучения, мы должны пренебречь зависимостью векторного потенциала от
пространственной координаты и считать, что векторный потенциал зависит только от
времени А = A(t). В этом случае магнитное поле обращается в ноль, а электрическое
поле волны становится пространственно однородным.
Существует и другая форма записи оператора взаимодействия квантовой системы
с полем электромагнитной волны, справедливая в дипольном приближении
Ж^(г,/) = -^Е(0,
(8.2.10)
где d = er - оператор дипольного момента. Мы покажем сейчас, что две этих формы
оператора взаимодействия эквивалентны друг другу, и с помощью некоторого
унитарного преобразования2 = Sy/(r,t) от уравнения Шредингера с оператором
взаимодействия W . можно перейти к уравнению Шредингера с оператором
РА
взаимодействия WdE.
Действительно, пусть (/„,(?,,) - решение уравнения Шредингера (8.2.9) с
потенциалом (8.2.8). Введем новую функцию |/Л.(г,/) = 5|/^(г,1), где
= ехр
i eA(t)r\ ~
----. Тогда
h с ;
f i eA(t)r\ Л
=s'vdE(f,t)=exp(j“V~’°
(8.2.11)
Уни гарным называется оператор, для которого SS
= 7, где / - единичный оператор.
198
Подставим выражение (8.2.11) в уравнение (8.2.8). Учитывая, что
(^ = ехр[^^Ъю?^(М),
к с ) \h С ) с )
[ /Э - - Л(,)Т ехр(- V(?.') = expU W )V2^£ (?,/),
I с J Ц? С ) V1 С J
а также
.. д ( ( i еА(1)Г} J f е Ai7 л7ш (7 nLxnf * еЛ(/Н
Ц Дл с /•" J I а с ) ^л с )
для функции (//^(т7,/) получим:
/й ДЦМ =_^v;^(?7) + ^(FiZXffi(?iZ)j (8.2.12)
ot 2т
где
Л р д
= ~A(i)r = ~dE(t).
с
Таким образом, в дипольном приближении эквивалентность записи операторов
взаимодействия квантовой системы с полем электромагнитной волны (8.2.8) и (8.2.10)
доказана. Эти два представления иногда называют выражениями для оператора
взаимодействия в рА- и с/Е- калибровках, или в калибровках скорости и длины. Какой
из калибровок пользоваться при решении конкретной задачи, как правило, это вопрос
удобства. Важно, однако, понимать, что, если волновая функция является лишь
приближенным решением уравнения Шредингера, использование калибровок длины и
з
скорости может приводить к разным результатам .
Выше мы молчаливо предполагали, что речь идет об одноэлектроннои
(одночастичной) квантовой системе. В случае многочастичной системы под дипольным
моментом следует понимать величину d = rt , где сумма берется по всем частицам
i
(электронам) системы. Если мы говорим о многоэлектронном атоме, то под мы
понимаем координату атомного электрона (начало координат совмещено с атомным
ядром). Для простоты мы будем работать в одноэлектронном приближении. В случае
многоэлектронной системы это приближение основано на концепции
самосогласованного поля, позволяющего ввести одноэлектронные волновые функции.
При этом, как мы увидим в Разделе 9.3, в слабых полях можно ограничиться
рассмотрением воздействия поля всего на один атомный электрон.
В заключение отметим, что представление взаимодействия в виде (8.2.8)
справедливо только в дипольном приближении. Вне рамок дипольного приближения
необходимо всегда использовать оператор взаимодействия в виде (8.2.8).
3 Более подробно см. М.О. Скалли, М.С. Зубайри Квантовая оптика, М.: Физматлит, (2003), с. 147
199
Прежде чем перейти к решению уравнения (8.2.9) или (8.2.12), описывающего
динамику кв ан о системы во внешнем электромагнитном поле в дипольном
приближении, * сопоставим энергии взаимодействия, которые входят в полный
гамильтониан Н, а именно энергию взаимодействия атомного электрона с внешним
эдектр°магнитным п°лем W и энергию его взаимодействия с атомным ядром V ~ е2/а0
(д0 - боровский радиус). Полагая, что дипольный момент атома есть величина порядка
’ получим W ~ ея0Е. Как видно, для значений напряженности поля
Е«е/а02
(8.2.13)
величина дополнительной энергии, обусловленной воздействием внешнего
электромагнитного поля, мала по сравнению с внутриатомной энергией. В таких
условиях воздействие внешнего поля волны можно рассматривать как малую поправку и
учесть по теории возмущений. Условие (8.2.13) имеет простой физический смысл.
Величина Ео, = е/а^ «5-109 В/см есть внутриатомное значение напряженности
электрического поля. Поэтому решение задачи по теории возмущений возможно, если
напряженность поля волны существенно меньше внутриатомного значения. Для
электромагнитных волн чаще задают не значения напряженности поля, а величину
интенсивности излучения / = cEq/8^. Поэтому условие (8.2.13) как условие
применимости теории возмущений по взаимодействию квантовой системы с полем
электромагнитной волны можно переписать в виде
at ’
(8.2.14)
где 1а1 =сЕ2а1/8я - так называемое атомное значение интенсивности. Как видно из
определения, это такая интенсивность излучения, амплитуда напряженности
электрического поля волны в котором равна напряженности поля внутри атома Еа/.
Оценка атомной интенсивности дает 1а1 ~ 3.5 • 1016 Вт/см2.
Полученное значение весьма велико. В долазерную эпоху (до 60-х годов
прошлого века) такие интенсивности казались принципиально недостижимыми.
Использование режима модуляции добротности позволило в первой половине 60-х годов
XX века получить интенсивности ~1О10 - Ю12 Вт/см2. Освоение этого диапазона
интенсивностей привело к открытию широкого круга эффектов и развитию нового
раздела физики - нелинейной оптики. Однако, соответствующие значения
интенсивностей на много порядков меньше атомного значения и, следовательно, задача
о воздействии таких оптических полей на атомную систему может быть рассмотрена в
Рамках теории возмущений. В середине 80-х годов прошлого века в лазере на кристалле
титаната сапфира (Ti: Sapphire) были получены импульсы фемтосекундной
Длительности, в которых были достигнуты потоки энергии излучения порядка Iat.
Использование техники усиления так называемых чирпированных импульсов,
200
предложенной Ж.Муру4 ношолило еще существенно увеличить интенсивность
ватерного излучения (вплоть до 10м-К)22 Вт/см2) н получить напряженности
электрического поля в волне многократно превышающие внутриатомное значение.
Мы начнем анализ проблемы с рассмотрения случая слабых (по критериям 8.2.13
- 8.2.14) электромагнитных полей, воздействие которых на атом может быть учтено по
теории возмущений. Потом рассмотрим некоторые подходы к решению задач за
рамками теории приближений по параметрам (8.2.13 - 8.2.14), однако в предположении
что дипольное приближение остается справедливым.
8.3. Нестационарная теория возмущений.
Как мы уже отмечали, общая задача об эволюции атомной системы в поле
электромагнитной волны в дипольном приближении предполагает решение
нестационарного уравнения Шредингера (8.2.9) или (8.2.12). В этом параграфе мы будем
пользоваться калибровкой длины. Будем полагать, что в начальный момент времени
(Г = 0) система находится в некотором стационарном состоянии невозмущенного
атомного гамильтониана Но, то есть
= 0) = ул(г),
(8.3.1)
где у/. - одна из функций, удовлетворяющих стационарному уравнению Шредингера
(8.1.1), принадлежащая дискретному спектру5. Система собственных функций атомного
гамильтониана Но является полной, это означает, что волновая функция произвольного
состояния </(?,/) может быть однозначно представлена в виде линейной комбинации
собственных функций невозмущенного гамильтониана:
(8.3.2)
Здесь первое слагаемое означает суммирование по всем состояниям дискретного спектра
атома, а второе - интеграл по состояниям континуума. Учитывая разложение (8.3.2), мы
можем переписать начальное условие (8.3.1) в виде
с,(/ = 0) = г„,
О,
л
п Z,
п = Z,
СДг = 0) = 0,
(8.3.3)
то есть в начальный момент времени лишь один из коэффициентов разложения отличен
от нуля. Отметим, что разложение (8.3.2) фактически определяет физический смысл
решения, которое мы ищем. Поскольку коэффициенты разложения С„(Г) и CE(f) есть
амплитуды вероятности обнаружить систему в момент времени t в п -ном стационарном
состоянии дискретного спектра и в состоянии континуума с энергией Е, то наше
4 Mourou Gerard Albert (род. 1944) - французский физик. Нобелевская премия по физике (2018) "За метод
генерации высокоинтенсивных ультракоротких оптических импульсов". Более подробно о получении
импульсов предельно короткой длительности будет рассказано в Главе 21.
5 Могут быть, конечно, заданы и другие начальные условия, когда, например, в начальный момент
времени электрон находится в состоянии континуума.
201
решение означает, что в процессе внешнего воздействия в системе возникнут переходы
между состояниями атомного гамильтониана, причем их вероятность будет
определяться квадратом модуля коэффициента разложения |С„(/)|2 и |С£(/)|2. При этом
вероятности |С„ (0| будут определять вероятности возбуждения конкретных состояний,
а |С£(0| " плотность вероятности перехода в состояние континуума с энергий Е
(эффект фотоионизации).
Подставляя разложение (8.3.2) в уравнение (8.2.12), получим
Учитывая, что у/п и у/Е есть собственная функция атомного гамильтониана, перепишем
полученное в виде
ехР| ~ ГEJ | + JЛЕехрГ- {Et
„at \ fl ) J dt \ h )
(8.3.4)
XCn^n ex₽f-+
„ I Й J
Г A f Z I
[C£HV£exp —Et dE.
J V h )
Умножим теперь (8.3.4) на комплексно сопряженную волновую функцию какого-либо
атомного состояния y/*f(r)exp[(i/fi)Eft) и проинтегрируем по всей области определения
функций. Тогда, используя условие ортогональности собственных функций оператора
Гамильтона, получим
/й^ = 2Сл(^/|^^„)ехр(/й)/„0 + |С£(^/|^|^)ехр(/^0^> (83.5)
UZ п
где (^/|ИГ|^Я) = (/|ИГ|«) = И7„ =^y/}Wy/ndT, (у f\w\y/Е} = {f\W\E} = WfE =^y/*fWy/Edr
- матричные элементы оператора W, связывающие состояния дискретного и
непрерывного спектров системы, (Ofn={Ef-En)/hi со^ =(Еf - Ey/h
соответствующие частоты перехода.
Теперь получим уравнения для коэффициентов, описывающих заселение
континуальных состояний. Умножая (8.3.4) на комплексно сопряженную волновую
функцию состояния континуума у/Е(г)exp((z/ft)Et), аналогично найдем
= ^Сп^Е |^|</л)ехр(йУ£л/) + Jc£.(^£ |^£.}exp(/a)££./)J£'. (8.3.6)
п
Система уравнений для коэффициентов разложения по базису собственных
Функций (8.3.5) и (8.3.6) тождественна исходному уравнению Шредингера (8.2.12). Мы
будем решать эту систему приближенно в рамках нестационарной теории возмущений.
Представим амплитуды вероятности Сп в виде ряда теории возмущений
202
Г - Г’'0' _L Г'(|) J- Г(~} -i- С — Г,(0) 4- Г'(1) 4- Г(2) 4- /л -
<-„=Cn +c„ +c„ +•••’ 4: -c/-; +CA- +C/J +- (8.3.7)
причем каждый последующий член ряда много меньше предыдущего. В качестве малого
параметра будем рассматривать возмущение W. В нулевом порядке малости мы
рассматриваем решение в отсутствие действия возмущения. Тогда, очевидно,
Подставляя (8.3.7) в (8.3.5-6) и удерживая члены только первого порядка малости
получим для случая f
dC('}
ih-!- = (w Иу/, )exp(i®,/),
dt, (8.3.8)
ih—T~ = {^E H^)exp(zTa£/),
at
Тогда выполняя интегрирование по времени, в первом порядке теории возмущений
получаем
= - | [^(Oexp(z7zy)<7r,
™ о
. , (8-3.9)
се}(1) = ~7 f ^f,(/)exp(zzy/;z)t7z.
* о
Фактически, выражение (8.3.8) является решением поставленной задачи и определяет
амплитуду вероятности перехода из начального состояния |z'^ в конечное состояние
дискретного |/) или непрерывного |Е) спектра системы за время t под действием
возмущения W(г,t).
Дальше легко записать уравнения для амплитуд во втором порядке теории
возмущений
t/C(2)
|^1^„)ехР(/бУ/^) +|pK|^£.)exp(ztwy£,/)t7E',
at п (8.3.10)
dCw -
|^K)exP(/ftW) + |Иг|^£,)ехр(/щ££7)йЕ",
ul n
где C*n и C£? определяются как решение уравнений (8.3.8). Далее, решив задачу во
втором порядке теории, несложно записать общие выражения для третьего и более
высокого порядков.
8.4. Вероятность перехода. Первый порядок теории возмущений.
Получим теперь выражение для вероятности перехода из начального состояния
|z) в конечное состояние |/) дискретного спектра под действием электромагнитного
поля E = E0cos6rf . Используя оЕ - калибровку для оператора взаимодействия атома с
полем волны, из выражения (8.3.8) получим
203
Cf * р. J&(t)cxp(ja)nf)dt = i——- Jcos(zwZ)exp(/7w/)/)t/Z.
Здесь dfl - матричный элемент оператора дипольного момента. Полученный интеграл
легко вычисляется. Учитывая, что
cos cot = — (exp(i(Dt) + exp(-/<yf)),
получим
<’>(Z)=[ expQ'(^-^)o-i
f 2h l /(бУ^-й?)
ехрОХбУд +<y)/)-l
/(бУу, + (D)
(8.4.1)
Отметим, что частота перехода со^ = (Е^ — E.^lh может быть как положительной, так и
отрицательной. Если Е; > Е.то есть переход идет с поглощением энергии, то > 0.
И, наоборот, если переход идет с испусканием энергии, то сол < 0. В любом случае
видно, что процесс идет эффективно только вблизи резонанса, когда частота внешнего
поля примерно совпадает с частотой перехода <у«|й)у7|. Для определенности будем
рассматривать переход с поглощением энергии поля. Тогда вблизи резонанса вторым
слагаемым в (8.4.1) можно пренебречь по сравнению с первым:
Г(1)/Л_ .^Ё0Гexp(z(<yyj-ty)Z)-P
С' Г ) --- I
f 2Й i((Ofl-(D) J
Вводя величину Д<у = cofl-co - отстройка от резонанса, перепишем выражение для
амплитуды вероятности в виде:
гт(/, - ЛЁ° cxnf
С/ (0 -, м exp^ 2 J Дй;/2 .
(8.4.2)
Возводя по модулю в квадрат, найдем выражение для вероятности электромагнитного
перехода из начального состояния |/‘) в конечное состояние |/) за время t. Считая поле
линейно поляризованным и направляя ось z вдоль вектора поля волны, получим
sin 2(ДдХ/2)
(Дй)/2)2
(8.4.3)
Здесь dfi - z -компонента оператора дипольного момента системы.
Резонансное приближение, которым мы воспользовались для получения (8.4.3) в
литературе известно как приближение вращающейся волны, или RWA (от
английского Rotating Wave Approximation).
Проанализируем полученное выражение. Прежде всего, отметим, что теория
возмущений является применимой при выполнении условия Р« 1, то есть
204
I. (8.4.4)
Фактически )то условие задат о1раничсиис сверху на допустимую напряженность поля
элекзромагннтной волны. Однако, по предельное шачснис интенсивности определяется
в том числе о гс тройкой oi резонанса, и если эта отстройка оз резонанса мала, то
формально теория возмущений можез оказаться неприменимой уже в достаточно
слабых полях. Действительно, в случае точного резонанса из (8.4,3) находим
Ы Ео ( sin Лм//2 V 2 ~ р
4/)? Л Л^/2~)
т.е. вероятность неограниченно возрастает во времени. Условие Рft « 1 выполнено
лишь на ограниченном интервале времени. Аналогичная ситуация формально возникает
и в отсутствие точного резонанса при выполнении условия Ля/ « 1. Таким образом, в
общем случае возможность использования теории возмущений по взаимодействию
атома с электромагнитным полем ограничена как величиной интенсивности излучения,
так и длительностью воздействия.
В важном частном случае на больших временах (формально, при t —>оо), но для
малых вероятностей перехода, используя известное представление для 8 - функции
sin2 at
lim-----— = л8(a),
at
из (8.4.3) нетрудно получить
КГЕо
Ргм =
т.е. на больших временах вероятность перехода растет линейно по времени. Это
позволяет нам ввести вероятность перехода в единицу времени
И/fl Ел 2тг |^Г I Ел
= рл /' = 4/р • 2^^/) - 6У) = — —— 8(Е, - £, - tuo). (8.4.5)
Как видно, полученное выражение можно интерпретировать в том смысле, что переход
из начального состояния |/) конечное |/^ сопровождается поглощением кванта
электромагнитного поля hco. При этом, переход оказывается возможен только в случае
Et = £, л-hco.
Аналогично, в случае если конечное состояние лежит ниже но энергии, мы бы получили
Ej = Ej - ha).
Последние два соотношения представляют закон сохранения энергии при поглощении
(испускании) кванта поля. При этом существенно, что электро магнитное поле является
классическим, и использованное нами понятие квантов поля является достаточно
205
умозрител Дискретный характер поглощения энергии поля возникает лишь
вследствие дискретной структуры атомных уровней.
Поле воздействующей на атом электромагнитной волны нам будет удобнее
характеризовать интенсивностью излучения Z = cEq/8^. Поэтому выражение (8.4.5)
можно переписать в виде:
_ 4;г2КГ
•1 • #(а>л - со). (8.4.6)
При использовании соотношения (8.4.6) возникает формальная трудность. Как следует
понимать соотношение с 8 -функцией? В данном случае мы подразумеваем, что
выражение (8.4.6) должно быть проинтегрировано по частотам, то атом "видит" не
совсем монохроматическое излучение. Полагая, что интенсивность излучения может
быть представлена в виде
1 = J,
где 70 - спектральная плотность интенсивности излучения, перепишем (8.4.6) в виде
4л"2КГ г
=----~2----co)d(o.
СП J
Интеграл с 8 - функцией элементарно вычисляется, в результате имеем
(8-4.7)
то есть вероятность перехода определяется значением спектральной интенсивности
излучения на частоте перехода.
Напомним, что dfi в выражении (8.4.7) есть матричный элемент z - компоненты
дипольного оператора. Поскольку d2 = d2 + d2y + d2z и для сферически симметричной
системы (атом) d2 = d2/3, выражение (8.4.7) обычно записывают в виде
о! |2
4д’2
^=-гУ-4=«Л- <8-4-8>
Здесь
- коэффициент Эйнштейна вынужденного перехода . Как видно из (8.4.9),
8/1 = 8,/
‘ Отметим, что коэффициент Эйнштейна В „ иногда вводят как коэффициент пропорциональное™ между
вероятностью перехода и спеяральной плотностью энергии электромагнитного поля на частоте перехода
Р„ - Соответствующее выражение может быть легко написано, если учесть что /„ = сра.
206
В рассмотренном выше случае мы фактически предполагали, что поле
электромагнитной волны включается мгновенно в момент времени / = 0. Между тем, в
реальности существует конечная длительность включения электромагнитного поля
которая, как правило, многократно превышает его период колебаний7. В этом смысле
можно говорить об адиабатически плавном включении поля волны.
Будем считать, что поле медленно нарастает по экспоненциальному закону от
t = —оо:
Е(т) = Ео схр( Л/) cos cot, Л > 0,
(8.4.10)
предполагая затем переход к пределу Л—>0. Тогда для амплитуды вероятности
перехода С^п(/) запишем:
d Е г
С(? (/) = i fi ° I ел' cos(cot) ехр( icofit}dt,
откуда вычисляя интеграл, получим
C<l)(z) = ^B
f 2Й
-со- id}t} exp(i(cofl +со- id)t)
(cofl - со id) (cofl + со- id)
(8.4.11)
(8.4.12)
Рассматривая полученное выражение вблизи резонанса со»со(мы полагаем, что
со> 0, то есть речь идет о поглощении излучения), имеем
Eq exp(22z)
4Й2 (oofl — со)1 + Л2
(8.4.13)
Введем вероятность перехода в единицу времени как
„ d
пт —
22
2 = И—1 lim-------—------ = l_ZLL_pi2^(щ, - cd), (8.4.14)
4Й2 ^(сор-СО}1 +d2 4Й2
что в точности соответствует выражению (8.4.5).
Таким образом, мы получили, что в первом порядке теории возмущений
приближения мгновенного и адиабатически плавного включения поля дают одинаковые
выражения для вероятности перехода в единицу времени8.
Отметим также, что в рассматриваемом случае результаты расчета вероятности
перехода в dE- и рА - калибровках совпадают. Для доказательства этого утверждения
7 Исключение составляют появившиеся в последние годы лазерные импульсы предельного короткой
длительности, вплоть до одного - двух периодов оптических колебаний. При изучении взаимодействия
таких импульсов с атомно-молекулярными системами оба приближения (и мгновенного и адиабатически
плавного включения) оказываются неприменимы, и надо учитывать конкретный вид функции,
описывающей напряженность электрического поля в волне.
8 Такое совпадение, однако, получается лишь в первом порядке теории. В более высоких порядках (в
частности, уже во втором) приближения мгновенного и адиабатически плавного включения поля приводят
к различным результатам.
207
найдсм связь матричных элементов операторов импульса
1/7 И — Л
I” -------------------------------р ,
т
и координаты. Учитывая, что
и
</|1й-4> = (/|№-гН|#> = (Е, - Е,)z
получим Ра - imcOflZfl. Также поинимла ВЛ п
о внимание соотношение между амплитудами
векторного потенциала и напряженно™ .
л -eF /й> имеем п™ пРяженности электрического поля в плоской волне
A^-ctjco имеем следующее соотношение
w шение, связывающее матричные элементы
взаимодействия в различных калибровках:
е ооп
= а ~ ~е Eoz,.
тс со
Тогда с учетом 6 -функции в выражении (8.4.5) (или (8 4 14))
эквивалентность калибровок в рассматриваемом случае.
сразу же получаем
Задачи к Главе 8.
8.1.
Электрон находится в бесконечно глубокой прямоугольной потенциальной яме в
основном состоянии. Определить вероятность перехода за импульс в первое
возбужденное состояние под действием лазерного импульса гауссовой формы
Z ~ X
Е = Ео ехр
t2
2Т2 ;
cos(d>0/‘). Считать, что д)от»1, Как и почему
вероятность возбуждения зависит от длительности лазерного импульса?
8.2. Сформулировать правила отбора для заряженной частицы, находящейся в
одномерной прямоугольной бесконечно глубокой потенциальной яме.
8.3. Определить вероятности переходов и = 1—»и = 3 в атоме водорода в линейно и
циркулярно поляризованном поле с частотой со = щ31.
208
Глава 9. Электромагнитные переходы в атомах и моле-
кулах.
9.1. Понятие о правилах отбора.
Рассмотренная теория взаимодействия квантовой системы с электромагнитным
полем позволяет сформулировать правила отбора - указать соотношения между кванто-
выми числами начального и конечного состояний, для которых электромагнитный пере-
ход оказывается возможен (разрешен). Общий подход к решению проблемы ясен. Если
d г, = е\у/^гу/^г * 0,
(9.1.1)
то переход является разрешенным, наоборот, если d fl = 0, то говорят, что переход за-
прещен. Действительно, в этом случае согласно полученным результатам вероятность
перехода оказывается равна нулю даже в сильном электромагнитном поле. Следует, од-
нако, иметь в виду, что все сказанное выше относится только к электрическому диполь-
ному приближению, причем в низшем порядке теории возмущений. Поэтому запрещен-
ный в электрическом дипольном приближении переход может быть разрешен в высших
порядках мультипольного разложения, например, как электрический квадрупольный или
магнитный дипольный переход. Может также оказаться, что он разрешен в более высо-
ких порядках теории возмущений по дипольному приближению. Поэтому, понятие «за-
прещенный переход» не означает реально, что такой переход невозможен в принципе.
Скорее всего, он маловероятен по сравнению с переходами, разрешенными в первом по-
рядке теории возмущений в электрическом дипольном приближении.
Рассмотрим несколько примеров формулировки правил отбора для различных
квантовых систем.
Линейный гармонический осциллятор.
Получим правила отбора для переходов в линейном гармоническом осцилляторе.
Рассмотрим матричный элемент
□о
(9.1.2)
где
V. =Л'Л»®ехр(-^2/2), N„ = (72"n!V^) ', £ = z/a, а = .
Для вычисления матричного элемента (9.1.2) воспользуемся рекуррентным соотношени-
ем для полиномов Эрмита (см. Справочные данные):
(й = (й+!//„,( J). (9.1.3)
Подставляя (9.1.3) в (9.1.2), получим
Z
со
тп
= MmNna jНт(£)[ пН,^ (£) +1 /7н+1 (^|ехр(-^.
(9.1.4)
209
учитывая свойство ортогональности полиномов
грзл отличен от нуля только в случае
Эрмита, замечаем, что последний инте-
го есть электромагнитные переходы возможны
гармонического осциллятора. Поскольку
только между парой соседних состояний
w = п ± 1,
Е„+у ~Еп = ha>,
то эффективное взаимодействие осциллятора с внешним электромагнитным полем воз-
можно лишь в случае совпадения частоты осциллятора с частотой внешнего поля.
Проведем конкретные вычисления матричного элемента zn+}n. В этом случае из
(9.1.4) имеем
00 /
гп+1.» = N„+iNna + |ехр(-£2)б7£ =
-00 \ )
= [Е1а. (9.1.5)
2 2Nn+x V 2
В частности, для переходов между основным и нижним возбужденным состояниями по-
лучаем:
zl0=a/V2. (9.1.6)
Сопоставляя (9.1.5) и (9.1.6), найдем
~^ = 4п + \, (9.1.7)
*10
то есть вероятность перехода между уровнями с номерами осциллятора п и п +1 оказы-
вается в п +1 раз больше, чем между парой нижних состояний.
Центрально-симметричное поле.
Сформулируем теперь правила отбора для заряженной частицы в центрально-
симметричном поле. Эта задача имеет принципиально важное значение для атомной фи-
зики, поскольку атом представляет собой систему с центральной симметрией. Вспом-
ним, что волновая функция стационарного состояния системы в этом случае записыва-
ется в виде
| п, I, mt) = R„t (г)Y>т( •
Наша задача теперь рассмотреть следующие матричные элементы
(и,4 m(\x,y,z\ri,£' ,mf'). (9.1.8)
Вспомним, что
х = rsin(0)cos^,
< у - rsin(0)sin^,
z = г cos О,
210
- COS (р 2/7 cos (p
|ехр(-/>и<.<р)« sin <р >cxp(zz;z, '(p)d<p = j cxp(z(m/-mj^> sin <p >d(p —> <
0 1 0 1
а также
Ylm (/?,</>) = (costf)cxp(zm^) •
Тогда при вычислении матричных элементов (9.1.8) возникнут следующие интегралы
fexp(i(m/-m, ±1)^
)d<p.
Первый из и полученных интегралов отличен от нуля, если = +1, второй - при
т,'=т(. Таким образом, получаем следующее правило отбора по магнитному кванто-
вому числу т(:
Лт( = 0,±1, (9.1.9)
т.е. при электромагнитных переходах в дипольном приближении магнитное квантовое
число либо изменяется на единицу, либо не меняется.
Аналогичным образом решается вопрос о правилах отбора по орбитальному
квантовому числу: используя рекуррентные соотношения для присоединенных полино-
мов Лежандра (здесь тп > 0)
cos 0 Р^ (cos 0) = (cos 0) + (cos 0) ,
(см. Справочные данные) для матричного элемента оператора z - проекции дипольного
момента легко получить
Г=^±1, (9.1.10)
т.е. при электрическом дипольном переходе орбитальное квантовое число изменяется на
единицу. Аналогичное правило отбора получаются и для х, у - компонент дипольного
момента.
Правилам отбора (9.1.9), (9.1.10) можно придать простой физический смысл. Если
считать, что в процессе перехода происходит излучение (поглощение) кванта электро-
магнитного поля (фотона), спин которого равен единице, соотношение (9.1.10) пред-
ставляет собой закон сохранения момента количества движения в системе «атом + элек-
тромагнитное поле». Фотон уносит единичный момент. Что касается проекции, то она
может не менять своего значения, или также измениться на единицу. При этом можно
показать, что случаю Дт( = 0 соответствует испускание линейно поляризованных фото-
нов, а случаю Дт( = ±1 - фотонов с круговой поляризацией.
Что касается возможных значений изменения главного квантового числа, то нам
следует рассмотреть радиальный интеграл:
оо
о
Это интеграл оказывается отличным от нуля при произвольных значениях квантовых
чисел. Поэтому никаких ограничений на изменение главного квантового числа нет:
211
Ли -любое. (9.1.11)
Совокупность условий (9.1.9) - (9.1.11) и составляют правила отбора для переходов в
центрально- симметричном поле, в частности в атоме водорода.
Для формулирования полного набора правил отбора в атоме водорода а также в
произвольном одноэлсктронном атоме1 необходимо еще учесть наличие спинового ме-
ханического момента электрона. Поскольку оператор взаимодействия с электромагнит-
ным полем в дипольном приближении не зависит от спиновых переменных системы, мы
можем записать
/Н=0, Лу = о. (9.1.12)
Последнее утверждение для одноэлектронного атома является лишним, поскольку в
этом случае всегда 5 = 1/2. Сформулируем еще правила отбора для изменения полного
механического момента атома j и его проекции mj. Поскольку т j — mf + ms, то из
(9.1.9) и (9.1.12) получаем
= Лте + Ams = 0,±1. (9.1.13)
Для квантового числа j из правил отбора для орбитального и спинового моментов по-
лучаем
4 = 0,±1. (9.1.14)
Важно что, несмотря на то, что излученный фотон уносит единичный момент, оказыва-
ется возможным и случай 4 = 0- Такая ситуация реализуется в результате того, что из-
меняется взаимная ориентация векторов 7 и s в пространстве так, что величина полно-
го механического момента атома остается неизменной.
9.2. Спектральные серии атома водорода щелочных металлов.
Рассмотрим на основе сформулированных правил отбора совокупность разре-
шенных электромагнитных переходов в атоме водорода. Остановимся сначала на пере-
ходах в основное состояние 151/2. В соответствии с правилом отбора по орбитальному
моменту переход возможен только из возбужденных р - состояний с произвольным
значением главного квантового числа. Все р - состояния являются дублетами
(у = 1/2,3/2). В соответствии с правилом отбора по j переход в 151/2 разрешен с обоих
компонентов дублета прхМ2 • Указанные переходы образуют серию Лаймана2 в спектре
атома водорода («р1/23/2 Цг )• Первую линию любой серии принято называть голов-
ной. Линии серии Лаймана принято обозначать буквой L, номера линий в серии обозна-
1 Под одноэлектронным атомом в данном случае мы понимаем любой атом, у которого сверх полностью
заполненных оболочек и подоболочек имеется единственный электрон. При этом подразумевается, что
рассматриваются переходы, связанные с изменением состояния именно этого электрона. Например, атом
алюминия (электронная конфигурация 15 2 252 2/76 352 3/>1) имеет один р электрон сверх полностью
заполненных подоболочек. Электромагнитные переходы, связанные с изменением состояния этого внеш-
него электрона могут быть также рассмотрены в одноэлектронном приближении.
2 Layman Theodore (1874 - 1954) - американский физик - экспериментатор.
212
да.
Рис.9.2. Тонкая структура головной линии
серии Бальмера.
чаются буквами латинского алфавита.
Все линии серии являются дублетами и
лежат в ультрафиолетовой части спек-
тра. На рис.9.1 приведены две линии серии
La,Lp. В частности головная линия се-
рии Лаймана La есть переход
2.Р1/2.3/2 ^1/2 •
Рассмотрим теперь совокупность
переходов на уровень п = 2 со всех бо-
лее высоких энергетических состояний.
Все эти переходы лежат в видимой ча-
сти спектра и образуют серию Бальме-
ра3. В соответствии с правилами отбора
возможны следующие переходы
пр —> 2s,
< ns ^>2р, п>3.
nd -» 2р.
Линии этой серии принято обозначать
буковой Н. Более подробно остановим-
ся на анализе тонкой структуры голов-
ной линии серии Бальмера. Она форми-
руется следующими переходами (см.
рис.9.2); Зрц2'3/2 ~~^2S\/2, 3s^2
Зб73/2 —> 2/7^2 з/2 j 3<У5/2 2р3/2 • Отметим,
что с нижней компоненты дублета 3d3/2
возможны переходы на обе компоненты
дублета 2р, в то время как для верхней компоненты дублета 3d5l2 правило отбора по j
разрешает переход лишь на верхнюю компоненту дублета 2р3/2. Как видно, возникает
семь линий. Однако, если учесть вырождение состояний nsl/2 и npV2 а также пр3/2 и
nd3/2, получим, что длины волн переходов 3sI/2 -+2pi/2, 3pV2 ->2s1/2 и 3d3/2 -*2px/2,
Зр3/2 ~>‘^s\i2 попарно совпадают. Поэтому в приближении, основанном на релятивист-
ской теории Дирака, тонкая структура На линии имеет пять компонент. Следует иметь
в виду, что более точный анализ спектра водородоподобных ионов показывает, что вы-
рождение nsl/2 и пр1/2 состояний по квантовому числу j также снимается. Снятие вы-
рождения обусловлено так называемым лэмбовским сдвигом атомных уровней. Этот
эффект будет рассмотрен в Главе 14. Величина лэмбовского сдвига существенно мень-
ше, чем тонкое расщепление. Поэтому, чтобы экспериментально обнаружить наличие
3 Balmer Johann Jakob (1825 - 1898) - швейцарский физик и математик.
213
семи компонент На линии, требуется спектральный прибор с большей разрешающей
способностью.
В общем случае спектр излучения, испускаемого водородоподобным ионом при
перех0Де электрона из состояния п в состояние тп (в пренебрежении тонкой структу-
рой) определяется выражением:
= „>т (9.2.1)
\jn п J
формула (9.2.1) известна как обобщенная формула Бальмера и описывает всю совокуп-
ность частот в спектрах водородоподобных систем. В частности, случаи nt = 1 и т = 2
дают серии Лаймана и Бальмера соответственно. Выражение (9.2.1) часто записывают
для длин волн переходов
1 = Я.У Г 1____О
2лйс\т2 и2 J
п>т,
(9.2.2)
ние в область все больших т сильно
где RH = Ry/lithe = 109737 см'1 - постоянная
Ридберга. Общая схема энергетических уровней
атома водорода и соответствующих спектраль-
ных серий приведена на рис. 9.3. На нем обозна-
чены четыре линии серии Лаймана La,LpiLr,Ls
и три линии серии Бальмера На,Нр,Нг. Две
первых линии серии Пашена4 также представле-
ны на рис. 9.3.
Переходы на более высокие конечные
состояния (т > 3) лежат в инфракрасной, а за-
тем и в радиочастотной частях спектра. В част-
ности, переходы на уровень т = 4 со всех более
высоких п = 5,6,7,... составляют серию Брэкета,
на уровень т = 5 - серию Пфунда (п = 6,7,8...),
на уровень т = 6 - серию Хэмфри (п = 7,8,9...),
на уровень т = '1 - серию Хансена - Стронга
(л = 8,9,10,...).
Все эти серии носят имена ученых, впер-
вые идентифицировавших соответствующие
спектральные линии. Отметим, что продвиже-
затрудняет измерения5, в частности серии Хэмфри
и Хансена - Стронга были обнаружена только в 50-х годах XX века. В настоящее время
в астрофизической плазме наблюдают переходы между уровнями атомарного водорода с
квантовыми числами, превышающими значения п,т> 100. Такие сильно возбужденные
< Paschen Friedrich (1865 - 1947) - немецкий физик - экспериментатор.
$ Одна из причин этого - быстрое уменьшение вероятности перехода с увеличением длины волны спек-
тральной линии. Причину этого мы будем обсуждать при изучении квантовой теории электромагнитных
Переходов.
214
состояния атома называют ридберговскими состояниями, их изучение представляет как
прикладной, так и общефизический интерес.
Мы уже говорили о том, что атомы щелочных металлов, на внешней оболочке ко-
торых находится единственный электрон, являются водородоподобными. Поэтому их
спектральные серии во многом похожи на спектральные серии атома водорода. Тем не
менее отсутствие «случайного» вырождения по орбитальному моменту вносит свою
специфику в формирование спектров этих элементов, к рассмотрению которой мы сей-
час перейдем. В качестве примера на рис. 9.4 приведены спектральные серии, возника-
ющие при электромагнитных переходах в атоме натрия. Основное состояние атома
натрия - З2^. Переходы в это состояние со всех выше лежащих Р - состояний обра-
зуют основную или главную серию:
энергия, эВ
5.12-------
77 ^/2,3/2 —*^1/2 ’ П — 3 •
Все линии этой серии имеют дублет-
ную структуру. Аналогично, переходы
п *^1/2 ~^3 -^/2,3/2 ’ п — 4
образуют резкую серию в спектре
атома натрия. Очевидно, все линии
резкой серии также являются дублета-
ми. Далее имеем серии
n2D^32P, п>3,
n2F-+32D, п>4,
которые называются диффузной и
фундаментальной сериями6. Нетрудно
видеть, что тонкая структура линий
этих серий состоит из трех компонент.
Названия серий «главная»,
«резкая», «диффузная» «фундамен-
тальная» в англоязычной литературе
звучат как “principle”, “sharp”,
“diffuse” и “fundamental”. Собственно
первые буквы в названиях этих серий
исторически и были использованы для
систематики атомных состояний по
величине углового момента.
9.3. Электромагнитные переходы в многоэлектронных атомах.
До сих пор мы рассматривали электромагнитные переходы в так называемых од*
ноэлектронных атомах, т.е. в системах, имеющих один электрон, связанный с атомным
остовом более слабо, чем остальная совокупность атомных электронов. В такой ситуа-
6 Фундаментальную серию называют также серией Бергмана.
215
пни —' “J*' сс,сс’веннь,м рассмотрение проблемы электромагнитных пере-
ходов в о ном при унижении. Однако, покажем сейчас, что одноэлектронные
переходы доминируют и в случае, если на пипи1ипн л , У е
11 1 J ’ VVJ,H ,fa внешней атомной оболочке имеется совокуп-
ность эквивалентных электронов
Для определенности рассмотрим двухэлектронную конфигурацию nf1 и возмож-
ный переход из нес в конфигурации В приближении самосогласованного поля
(1.„ раздал 5.2) запишем мазричный элемент дипольного оператора:
Ой
i=l,2
v'„,<tri )dfdr:
(9.3.1)
Проводя элементарные вычисления, получим
=е\~^2 ) ± (^2 (^))п +
4('"’гЪ ) ± v'.;.(?2(Г,))?2 v'„,(/ )V'„ (Г2 )d?,dr2 =
4= IriP dx ±1п”Г dx n£\s(.e + (и"Г ±(и’Г d2 nA?,J=
(9.3.2)
ri£'\dx |л^(1 ± \)5rt + t"\dx |zj^(1 ± 1)£„
Как видно, матричный элемент дипольного оператора состоит из совокупности матрич-
ных элементов одноэлектронных переходов t -> Р и t —> Р ’, откуда следует, что орби-
тальное квантовое число только одного из электронов может измениться на единицу, т.е.
в нашем приближении возможны только одноэлектронные переходы. При этом состоя-
ние второго электрона не меняется. Кроме того, мы видим, что в случае изменения сим-
метрии пространственной волновой функции относительно перестановки электронов
местами (такой ситуации соответствует знак в (9.3.2)) матричный элемент перехода
обращается в нуль. Мы знаем, что за симметрией относительно перестановки электронов
местами стоит суммарный спин электронной конфигурации. Значит, следствием (9.3.1)
является сохранение полного спина при электромагнитном переходе: Д5 = 0.
Теперь несколько обобщим полученное. Действительно, дипольный оператор,
который отвечает за электромагнитный переход, является нечетной функций координат,
то есть меняет свой знак при замене г -> -г . Это означает, что атомные термы, между
которыми происходит переход, должны обладать различной пространственной четно-
стью. Это правило отбора известно как правило Лапорта7. В одноэлектронном атоме это
правило выполняется автоматически, поскольку четность волновой функции определя-
ется как Р = (-1)' и действует правило отбора At = ±1. В многоэлектронном атоме чет-
ность терма есть
/> = (-1)В. (9.3.3)
7 Laporte Otto (1902-1971) - американский физик.
216
где алгебраическая сумма берется по всей совокупности атомных электронов8. Поэтому
для того, чтобы определить, удовлетворяется ли правило Лапорта, необходимо знать ор-
битальные квантовые числа всей совокупности атомных электронов, то есть фактически
необходимо знать электронную конфигурацию. Четность терма в справочной литературе
часто указывают с помощью маленькой буквы «о» (от английского «odd» — нечетный),
которая пишется справа вверху относительно символа терма L. Например, обозначе-
ние ''Р° показывает, что речь идет о триплетном терме с отрицательной четностью. Если
буква «о» отсутствует, то четность терма считается положительной. Отметим, что все
термы в пределах одной конфигурации характеризуются одинаковой четностью. Это
означает, что в дипольном приближении переходы между термами одной конфигурации
запрещены правилом Лапорта.
В случае если переход разрешен правилом Лапорта (которое показывает, разре-
шен ли переход между электронными конфигурациями), можно сформулировать следу-
ющие правила отбора, которые определяют, разрешен ли переход между термами задан-
ных конфигураций. Эти правила имеют следующий вид:
AL = 0,±1,
Л5 = 0.
Правило отбора по спину часто называют запретом интеркомбинаций. Отметим что, в
отличие от одноэлектронной атомной системы, суммарный орбитальный момент элек-
тронной оболочки многоэлектронного атома может и не меняться при переходе
(AL = 0). С физической точки зрения это связано с тем, что в многоэлектронном атоме
при излучении фотона, уносящего единичный момент, может произойти переориентация
орбитальных моментов отдельных атомных электронов так, что суммарный орбиталь-
ный момент электронной оболочки не меняется.
Кроме того, укажем еще правило отбора, указывающее разрешенные переходы
между атомными состояниями.
Д7 = 0,±1 .
Это правило имеет точно такой же вид, как и в одноэлектронном атоме. При этом до-
полнительно необходимо учесть, что переход J = 0 —> J = 0 (так называемый «0-0 - пе-
реход») является запрещенным. Этот запрет связан с невозможностью удовлетворить
закону сохранения момента количества движения, когда в начальном и конечном состо-
янии у атома момент отсутствует, а в системе появился фотон, несущий единичный мо-
мент.
В качестве примера использования сформулированных правил отбора рассмот-
рим возможные переходы в спектре атома гелия (см. рис. 9.5). Основное состояние ато-
ма гелия '50 в конфигурации Is". Это состояние характеризуется положительной четно-
стью. Четными являются и все термы (и состояния) в конфигурации В2л . В этой конфи-
гурации имеются термы 1 и 3S. Переходы из этих термов в терм конфигурации В" за-
8 В полностью заполненной подоболочке число электронов всегда является четным, то есть многоэлек-
тронная волновая функция подоболочки всегда характеризуется положительной четностью. Следователь
но, в выражении типа (9.3.2) суммирование фактически следует проводить по орбитальным квантовым
числам электронов, находящимся в не полностью заполненных подоболочках.
217
преШены правилом Лапорта. Кроме того, переход запрещен таКже по
СП"Впепеход из которых °^°ЩИе атомные состояния являются долгоживущими. Состоя-
НИЯ пять метастяб все ниже лежащие состояния является запрещенным, приня-
т0 называть метастабильнымн’. Все термы конфигурации 1з2р являются нечетными.
Поэтому правило Лапорта разрешает переходы в термы конфигураций 1з> и 1з2з. Од-
нако, из три етного терма ls2p( Р) возможен только переход в триплетный терм
ls2s( 5”), ремя как из синглетного терма рассматриваемой конфигурации возмож-
ны переходы в синглетные термы обоих ниже лежащих конфигураций Is2 и 152s :
Ь2р('Р)
b2(’S).
Отметим, что поскольку в одноэлектронных возбужденных состояниях атома гелия чет-
ность конфигурации и суммарный орбитальный момент определяются орбитальным
квантовым числом возбужденного электрона, для атома Не оказывается возможным
также использовать правила отбора, сформулированные нами для переходов в одноэлек-
тронных атомах.
Рис.9.5. Разрешенные переходы в спектре гелия.
9 Метастабильные состояния представляют большой интерес в различных областях физики, химии и био-
логии поскольку они могут являться резервуаром, в котором можно запасать энергию. Например, воз-
буждение метастабильных состояний в газовом разряде широко используется в процессе накачки газовых
лазеров.
218
Рассмотрим еще одни пример использования правила Лапорта для определения
разрешенных атомных переходов. Пусть у нас имеется атом углерода. Терм с минималь.
ной энергией принадлежит конфигурации 1л’2<2р;. Эта конфигурация характери-
зуется положительной четностью. Рассмотрим еще несколько конфигураций атома угле-
рода, а именно
l.v2 2.V2 2рЗх
\s22s22p3p
1.<Г 2.v‘ 2p3d
Для первой конфигурации возможные значения L — 1, S — 0,1, т.е. возможны
термы 13 Р.
Для второй конфигурации L = 0,1,2, S = 0,1, а, следовательно, ]SPD, 3SPD.
Для третьей: L = 1,2,3, S = 0,1 и термы: }PDF, 3PDF.
Теперь перейдем к вопросу о переходах между найденными термами и основным
термом атома углерода 3 Р (согласно правилам Хунда именно этот терм обладает мини-
мальной энергией в конфигурации 2/?2). Согласно правилу Лапорта, переходы могут
происходить только между термами, принадлежащими конфигурациям с различной чет-
ностью. Легко видеть, что конфигурации 1) и 3) являются нечетными, в то время как
конфигурация 2) является четной. Таким образом, из всех термов конфигурации
1522?2рЗ/? переход в основное состояние будет запрещен.
Согласно еще одному правилу отбора реализуется т.н. запрет интеркомбинаций
AS = 0, таким образом, переходы в указанный терм возможны только из триплетных
термов.
Правило отбора по суммарному орбитальному квантовому числу Д£ = 0,±1 при-
водит нас к заключению, что переход с терма 3F в основной терм основной конфигура-
ции также запрещен.
В итоге возможными остаются три перехода:
(l?2?2p3s) 3Р—> (ls22s22p2) 3Р,
(ls22s22p3d) 3PD -> (1?2?2р2) 3Р.
В пределах одной электронной конфигурации все переходы запрещены правилом
Лапорта.
На рассмотренном примере удобно еще раз проиллюстрировать очередность
применения различных правил отбора. Так, наиболее грубо состояние электронной обо-
лочки атома задается электронной конфигурацией. Мы видели, что фактически правило
Лапорта и определяет возможность перехода между различными конфигурациями. В
рамках одной конфигурации, как правило, существует несколько термов, характеризу-
ющих более точно структуру электронной оболочки. На этом уровне возникают правила
отбора между термами заданных конфигураций AS = 0, AL = 0,± 1. Возможна и даль-
нейшая конкретизация: терм характеризуется тонкой структурой - это группа состояний
219
(мультиплет) с различными значениями квантового числа J. Если мы хотим проанали-
зировать число компонент тонкой структуры перехода между двумя термами, мы вос-
пользуемся правилом отбора zV = 0,± 1.
В заключение раздела отметим еще раз, что сформулированные правила отбора
являются приближенными. Они получены для электрического дипольного приближения
в первом порядке теории возмущений по дипольному взаимодействию. Кроме того, в
многоэлектронных атомах запрещенные переходы могут происходить вследствие того,
что приближение LS - связи, в рамках которого эти правила отбора сформулированы,
является недостаточно точным. Фактически, в этом случае квантовые числа L и S вве-
дены лишь приближенно, поскольку стационарное состояние атома не может быть оха-
рактеризовано точно определенными значениями L и S. Именно такая ситуация харак-
терна для тяжелых атомов, например, для атома ртути, у которого линия с нарушением
интеркомбинационного запрета является почти такой же интенсивной, как и переходы
без изменения спина.
9.4. Электромагнитные переходы в двухатомных молекулах.
Рассмотрим применение построенной нами теории для описания электромагнит-
ных переходов в двухатомных молекулах. Мы видели, что в электрическом дипольном
приближении вероятность перехода пропорциональна квадрату матричного элемента
дипольного момента, связывающего начальное и конечное состояние системы. Наша за-
дача теперь заключается в том, чтобы конкретизировать полученные ранее результаты и
сформулировать правила отбора для электромагнитных переходов в молекулах.
Запишем, прежде всего, выражение для оператора дипольного момента системы.
В отличие от атомарной, в молекулярной системе полный дипольный момент складыва-
ется из электронного дипольного момента d{e) и дипольного момента ядерной подси-
стемы D(N}. Для дипольного момента ядерной подсистемы запишем
D(N) = eRx+eR2.
Здесь Rt и R2 - координаты каждого из ядер атомов, образующих молекулу. Переходя
от и R2 к координате центра масс молекулы
^ = (M,R1 + M2R2)/(MX +М2)
н М2 - массы атомов, образующих молекулу) и координате относительного дви-
жения R = R2 - R,, имеем
Dm = 2еЙ + еЛ'~^; Д. (9.4.1)
+ м2 v ’
в системе координат, связанной с центром масс (9? — 0) для дипольного момента ядер-
ной подсистемы получим
Dm=eM' MJ-R.
М, + Л/2
(9.4.2)
220
Как видно, для гомоядерных молекул ( Л/, = Л/2) ядерный дипольный момент равен ну-
лю, то есть внешнее электромагнитное иоле не оказывает прямого воздействия на ядер-
ную подсистему молекулы. Этот результат выглядит совершенно естественным. По вто-
рому закону Ньютона ускорение атомных ядер, связанное с воздействием на них элек-
трического поля волны, есть гЁ/Л/, (z = 1,2). Поэтому при равенстве масс входящих в
молекулу атомов, сила действующая на них, оказывается одинаковой, а, следовательно,
ускорение R = 0, то есть воздействие на ядерную подсистему молекулы отсутствует.
Поэтому в дальнейшем, при формулировке правил отбора для электромагнитных пере-
ходов в молекуле, будем различать случай гомо- и гетероядерных молекул.
В рамках приближения Борна — Оппенгеймера волновые функции начального и
конечного состояния молекулы представимы в виде:
Тогда для матричного элемента оператора дипольного момента запишем:
dfl + D(7V)|4z/) = (4z/|J(e)|%) + ('P/|D(yv)|'P/). (9.4.3)
Рассмотрим теперь правила отбора для переходов в гомо- и гетероядерных моле-
кулах. Остановимся, прежде всего, на переходах в пределах одного электронного терма
(без изменения электронного состояния молекулы). Такие переходы называют колеба-
тельно-вращательными. В этом случае индексы «i» и «f » у волновой функции элек-
тронной подсистемы совпадают. Тогда учитывая, что в гомоядерных молекулах ядерный
дипольный момент отсутствует, а матричный элемент электронного дипольного момен-
та (у/.е) = 0, мы приходим к следующему выводу. В гомоядерных молекулах
колебательно-вращательные переходы в пределах одного электронного терма запреще-
ны. В гетероядерных молекулах ситуация другая. Во-первых, существует прямое воз-
действие электрического поля волны на ядерную подсистему молекулы, а кроме того
молекула может обладать электрическим дипольным моментом в стационарном состоя-
нии10 d(^(R) = ,R) d(e} (г, R)^. В результате из (9.4.3) получим:
dj, = (Я)| ФГ (R)) + (уу (Л>iО' (Я)} (9.4.4)
Обычно матричный элемент электронного дипольного момента системы плавно зависит
от ядерной координаты и почти не меняется на размере области локализации ядерной
волновой функции. Поэтому в силу условия ортогональности функций ядерной подси-
стемы молекулы, принадлежащих одному электронному терму,
окончательно получаем:
10 При наличии ковалентной полярной или ионной связи, характерной для гетероядерных молекул, рас-
пределение электронной плотности смещено относительно центра масс молекулы, что и приводит к появ-
лению электронного дипольного момента в стационарном состоянии.
221
(9-4.5)
то есть вероятность колебательно-вращательных переходов в гстероядерных молекулах
определяется матричным элементом дипольного момента ядерной подсистемы молеку-
цьт Учитывая, что угловые части ядерных функций ф{^} и есть сферические функ-
ции. получаем правило отбора по вращательному квантовому числу:
AJ = J f — J/ = ± 1.
Что касается правила отбора по колебательному квантовому числу, то в приближении
гармонических колебаний молекулы, очевидно:
Av = vf - v. = ±1.
Следует, однако, иметь в виду, что вследствие существенного ангармонизма молекуляр-
ных колебаний это правило легко нарушается даже в дипольном приближении.
Перейдем теперь к рассмотрению электромагнитных переходов между различ-
ными электронными состояниями молекулы. При таких переходах автоматически изме-
няется и состояние ядерной подсистемы молекулы. Поэтому обычно говорят об элек-
тронно - колебательно - вращательном переходе. Такие переходы возможны как в гомо-,
так и в гетероядерных молекулах. Вследствие ортогональности электронных волновых
функций (y/(fe)(r,R) i//.e)(r,R)^ = 0 из (9.4.3) получим:
dfi = \d(e) + D(N) | %) = p(e) | T.) = j(R))*d{f (Ж(Ю (R)dR , (9.4.6)
где
df (R) = j (ул<'> (f,R))' (r, R)dr
(9.4.7)
- матричный элемент электронного дипольного момента системы, который параметри-
чески зависит от межъядерного расстояния. Полученное выражение имеет очень про-
стой физический смысл. Матричный элемент электронного дипольного момента, кото-
рый в атомах есть некоторое число, в случае молекулярной системы зависит от межъ-
ядерного расстояния и должен быть дополнительно усреднен по ядерной координате.
При анализе матричного элемента (9.4.7), описывающего электронно -
колебательно - вращательный переход, следует иметь в виду, что до сих пор мы не при-
нимали во внимание наличие спина электронной подсистемы молекулы и оперировали
только координатной частью волновой функции. Мы помним, что полная волновая
функция системы может быть построена, как произведение координатной и спиновой
части волновой функции, причем симметричной относительно перестановки электронов
местами координатной части соответствует антисимметричная спиновая часть и наобо-
рот. Как следствие этого утверждения, возникает правило отбора по спину - запрет ин-
теркомбинаций:
AS = 0, (9.4.8)
то есть, как и в атомах, переходы разрешены между термами одинаковой мультиплетно-
сти. Аналогично, из (9.4.7) нетрудно получить правило отбора по квантовому числу Л,
определяющего проекцию электронного орбитального момента на ось молекулы:
222
Л4=0,±1. (9.4.9)
В размене 7 7 мы видели, что электронные термы характеризуются определенными свой-
ствами симметрии относительно смены знака электронных координат молекулы. Они
могу!' либо четными (g), либо нечетными (м). Поскольку оператор электронного ди-
польного момента является нечетным, то возможны переходы только с изменением чет-
ности:
u-+g. (9.4.10)
Кроме того, для состояний с А = О (L - термы) имеется дополнительное квантовое чис-
ло, определяющее четность состояния относительно отражения в плоскости, проходя-
щей через ось молекулы, что приводит к дополнительному правилу отбора.
Z+-»Z+,
(9.4.11)
Перейдем теперь к формулировке правил отбора для квантовых чисел, характери-
зующих ядерную подсистему. Следствием правила (9.4.9), при анализе правила отбора
по вращательному квантовому числу помимо сформулированного выше условия
(Д/ = ±1) возникает возможность перехода без изменения вращательного квантового
числа. В случае А/ = 0 излучаемый фотон уносит момент из электронной подсистемы
молекулы. Поэтому окончательно для электронно - колебательно - вращательных пере-
ходов запишем
Д/ = 0,±1. (9.4.12)
Мы уже отмечали, что матричный элемент электронного дипольного момента молекулы
(9.4.7), как правило, является плавной функцией. Поэтому величину d^} (R) = d0 = const
можно вынести из-под знака интеграла в (9.4.6). Тогда получим
(9.4.13)
то есть матричный элемент перехода пропорционален интегралу перекрытия ядерных
волновых функций, описывающих начальное и конечное состояние ядерной подсистемы
и принадлежащих различным электронным термам молекулы. Интеграл перекрытия
называют фактором Франка" — Кондона11 12, квадрат его модуля определяет вероятность
заселения колебательных уровней электронного терма молекулы, в которое происходит
электронно - колебательно - вращательный переход. Физический смысл полученного
выражения заключается в следующем. Можно предполагать, что электромагнитный пе-
реход происходит при неизменном межъядерном расстоянии, причем вероятность этого
перехода максимальна, если ядерные волновые функции начального и конечного состо-
яний локализованы в одной и той же области пространства, что обеспечивает макси-
мально возможное значение фактора Франка - Кондона. Сформулированное утвержде-
ние называют принципом Франка и Кондона.
11 Franck James (1882 - 1964) - немецкий и американский физик. Лауреат Нобелевской премии по физике
(1925) "За открытие законов соударения электрона с атомом"
12 Condon Edward Uhler (1902 - 1974) - американский физик. Фактором Франка - Кондона иногда называ-
ют также квадрат модуля введенного нами интеграла перекрытия.
223
Рис.9.6. Электромагнитный переход между двумя
электронными состояниями молекулы.
Случай хорошо «вложенных» термов.
Рассмотрим несколько при-
меров, иллюстрирующих принцип
Франка Кондона. На рис. 9.6
изображены два электронных терма
молекулы, причем для них равно-
весные межъядерные расстояния и
колебательные кванты примерно
совпадают13. Тогда при переходе с
одного терма на другой значение
колебательного квантового числа
меняться будет незначительно. При
этом переход с одного терма на
другой надо рисовать в виде верти-
кальной линии, соединяющей клас-
сические точки поворота, если пе-
реход осуществляется между воз-
бужденными колебательными со-
стояниями молекулы. Если же пе-
реход происходит между основны-
ми колебательными состояниями
молекулы, то его следует изобра-
жать линией, проведенной при равновесном значении межъядерного расстояния14. Дру-
гая ситуация представлена на рис. 9.7. В этом случае равновесные расстояния между яд-
рами различны. Как видно, в такой ситуации при переходе с терма на терм происходит
Рис.9.7, Электронно-колебательный переход
в двухатомной молекуле.
существенное изменение колеба-
тельного квантового числа, описы-
вающего состояние молекулы. При
этом переходы «1» (возбуждение) и
«2» (излучение) иллюстрируют
возможность колебательного воз-
буждения молекулы, осуществляе-
мое через выше лежащий электрон-
ный терм. В гомоядерных молеку-
лах, где переходы в пределах одно-
го электронного терма запрещены,
такой способ возбуждения колеба-
тельных состояний молекулы элек-
тромагнитным полем оказывается
единственным.
Про такие термы говорят, что они хорошо вложены дру! в друга.
14 Эю связано с тем, что в возбужденных колебательных состояниях квадрат модуля ядерной волновой
Функции достигает максимального значения вблизи классических точек поворота, в то время как для ос-
новного колебательного состояния максимальное значение плотности вероятности соответствует положе-
нию равновесия.
224
В качестве еще одного примера на рис.
рис.9.8 приведена картинка, иллюстриру.
юшая процесс фотоионизации молеку-
лы Х2. Равновесное межъядерное рас-
стояние в молекулярном ионе Х2
больше, чем в молекуле Х2. Посколь-
ку переход с терма на терм происхо-
дит при неизменном межъядерном
расстоянии, минимальная энергия
кванта /гео, необходимая для фо-
тоионизации системы оказывается су-
щественно больше потенциала иони-
зации /, (см. рис. рис.9.8).
Рис.9.8. Ионизация двухатомной молекулы.
9.5. Переходы внутренних
электронов в атомах. Характеристическое рентгеновское излучение.
Эффект Оже.
До сих пор мы рассматривали электромагнитные переходы, связанные с измене-
нием состояния внешних (валентных) электронов в атомах или молекулах. Длина волны
излучения для таких переходов лежит в оптическом диапазоне частот15. Остановимся
теперь на переходах, связанных с изменением состояния внутренних атомных электро-
нов. В этом случае возникает характеристическое рентгеновское излучение. Как мы уви-
дим в дальнейшем, энергия таких квантов рентгеновского излучения может достигать
десятков кэВ.
В отличие от оптических спектров, которые являются индивидуальными для
каждого конкретного элемента, рентгеновские спектры различных элементов похожи
друг на друга. Это связано с тем, что изменение количества электронов во внешней
атомной оболочке кардинальным образом сказывается на энергетическом спектре си-
стемы. В то же время внутренние атомные электроны находятся, прежде всего, в потен-
циале, создаваемом атомным ядром, который лишь частично экранируется электронной
оболочкой. Поэтому их энергия плавно меняется с изменением заряда ядра, однако каче-
ственных перестройки спектра не происходит.
Тот факт, что электроны, находящиеся на внутренних атомных оболочках, «чув-
ствуют», прежде всего, кулоновский потенциал атомного ядра -Ze2 /г, а учет межэлек-
тронного взаимодействия может быть сделан в рамках теории возмущений, означает
возможность описания внутренних атомных электронов в одночастичном приближении,
причем их волновые функции и положение энергетических уровней являются водородо-
подобными. Обычно для описания энергетического спектра внутренних атомных элек-
тронов используют приближение эффективного заряда:
15 Под оптическим диапазоном частот мы понимаем инфракрасную, видимую и ультрафиолетовую часть
спектра излучения. Характерная величина кванта излучения в оптическом диапазоне составляет от долей
электрон-вольта до нескольких электрон-вольт.
225
Е —-Ю-72 КУ
п2£е0=---Т
П п
(9.5.1)
Здесь w И ( - главное и орбитальное квантовые числа атомного электрона, находящего-
ся на внутренней оболочке, ап( - постоянная экранирования. Например, для электрона,
находящегося на К оболочке, crliS ~ 1, что означает частичную экранировку поля ядра
другим электроном, находящимся на К - оболочке16. При переходе к оболочкам, соот-
ветствующим большим значениям главного квантового числа (L,M- оболочки) вели-
чина постоянной экранирования возрастает за счет увеличения числа внутренних элек-
тронов, причем тем сильнее, чем больше значение орбитального момента рассматривае-
мого электрона. Однако, для нас важно, чтобы было выполнено условие <jnf « Z.
Пусть каким-то образом был удален один из электронов, находящийся на АГ -
оболочке многоэлектронного атома. Например, этого можно достичь, воздействуя на
атомы электронным пучком с энергией в несколько сотен килоэлектронвольт, или облу-
чая их рентгеновским или у - излучением с длиной волны, достаточной для удаления
электрона из К - оболочки. Тогда оказываются возможными переходы на К - оболочку
с более высоких атомных оболочек. Так возникает К - серия рентгеновского
Рис. 9.9. Серии характеристического рентгеновского
излучения.
излучения (см. рис. 9.9). При этом
номера линий в серии обозначают
буквами греческого алфавита,
например, переход с £ - на К - обо-
лочку формирует АГа линию рент-
геновского излучения, с М — на К -
оболочку - АГр -линию, и так далее.
Аналогично, если была создана
электронная вакансия на L - обо-
лочке атома, то переходы из распо-
ложенных выше атомных оболочек
образуют L серию рентгеновского
излучения. Затем идет М - серия
характеристического рентгеновско-
го излучения (см. рис. 9.9). Номера
линий в этих сериях также обозна-
чают буквами греческого алфавита.
Используя выражение (9.5.1) для энергии внутреннего электрона в атоме, мы можем
легко найти общее выражение для частот квантов характеристического излучения, свой-
ственных элементу с заданным зарядом ядра Z:
(Z-cr,)^
п1 )
ha>-Ry
(Z-Q-,)2
«.2
(9.5.2)
Заметим, что в тяжелых атомах при вычислении поправки стболее существенным является учет
СПин-орбитального взаимодействия, чем электростатического взаимодействия атомных электронов.
226
Здесь <7] и <т, есть постоянные ’экранирования для нижнего и верхнего состояний, меж-
ду которыми совершается переход с испусканием рентгеновского кванта. Как мы уже
отмечали, эти поправки достаточно малы по сравнению с зарядом ядра, поэтому часто
оказывается удобным ввести эффективную постоянную а сразу для обоих состояний.
Тогда выражение (9.5.2) мы можем переписать в виде:
ha) = Ry (Z-a)2
(9.5.3)
В таком виде выражение для возможных значений частот характеристического рентге-
новского излучения фактически совпадает с обобщенной формулой Бальмера, опреде-
ляющей спектральные закономерности в атоме водорода и водородоподобных ионах.
В выражении (9.5.3) случай пх =1, п2 > 2 соответствует К -серии рентгеновского
излучения, аналогично = 2, п2 > 3 - L -серии, пх = 3, п2 > 4 - М -серии. В частности
из (9.5.3) получаем, что энергия рентгеновского кванта Ка - линии есть
3
Ка
1\СХ у| •' х Л '
1
и с точностью до постоянной экранирования <зк »1 совпадает с выражением для энер-
гии кванта головной линии серии Лаймана в водородоподобном ионе. Аналогично, для
Ла -линии рентгеновского излучения имеем
h(»La =^Ry<Z~^L)2-
Jo
Численное значение постоянной экранирования <jl может быть определено либо экспе-
риментально, либо из квантовомеханических расчетов электронной структуры много-
электронного атома. Мы можем лишь ожидать, что 2 < < 9. Нижняя граница диапа-
зона определена из предположения, что в экранировку ядра вносят вклад только два
электрона, находящихся на К -оболочке, а верхняя граница соответствует предположе-
нию, что в экранировку вносят вклад все электроны К - и L -оболочек.
До сих пор мы рассматривали структуру энергетических уровней внутренних
атомных электронов без учета спин-орбитального взаимодействия. Рассмотрим теперь
тонкую структуру рентгеновских спектров, возникающую вследствие спин-
орбитального взаимодействия. Как уже отмечалось, внутренние электроны взаимодей-
ствуют прежде всего с атомным ядром, в то время как в первом приближении межэлек-
тронным взаимодействием можно пренебречь. Тогда для анализа тонкой структуры
можно использовать формулу Дирака, где вместо реального заряда ядра использовать
некоторый эффективный заряд, учитывающий экранирующее действие других атомных
электронов. Как и в атоме водорода, состояние внутреннего электрона в многоэлектрон-
ном атоме можно описать четырьмя квантовым числами В отсутствие спин-
орбитального взаимодействия состояния с различными j = ± 1/2 оказываются вырож-
денными. Учет спин-орбитального взаимодействия приводит к снятию вырождения по
квантовому числу j: В соответствии с формулой Дирака для величины расщепления
уровня с заданными п и £ можно записать:
227
^Enf En,j=t+\i2
-E
a2(Z - cr*Ry
n4(£ + V)
(9.5.4)
n,j=f-\/2
заряд ядра
Рис. 9.10. Диаграмма Мозли.
где а - постоянная тонкой структуры,
ст* - постоянная экранирования уровня
п(. для тонкой структуры17. В соответ-
ствии с выражением (9.5.4) все состоя-
ния внутренних электронов (кроме s
состояний) оказываются расщеплены на
два подуровня. Именно это расщепле-
ние и приводит к формированию тон-
кой структуры рентгеновских линий.
Например, все линии К - серии рентге-
новского излучения, возникающей в
результате переходов пр —> 15, являют-
ся дублетами. Например, тонкая струк-
тура Ка линии есть две близко распо-
ложенных линии Ка{ и Ка2.
Перепишем выражение (9.5.3) в следующем виде
Л ~ (Z - ст),
(9-5.5)
т.е. корень из частоты излучения является линейной функцией заряда атомного ядра.
Полученная зависимость была впервые получена в 1913 году эмпирическим путем Г.
Мозли18 при анализе экспериментальных данных по длинам волн характеристического
рентгеновского излучения задолго до создания квантовой теории и носит название зако-
на Мозли. На рис. 9.10 приведена диаграмма Мозли - зависимость частот головных ли-
ний рентгеновских серий от порядкового номера элемента в таблице Менделеева (заряда
атомного ядра). Как видно, эти зависимости с высокой степенью точности описываются
законом (9.5.5).
До сих пор мы обсуждали ситуацию, когда при переходе электрона с одной внут-
ренней атомной оболочки на другую выделившаяся энергия излучается в виде рентге-
новского кванта. Однако, возможна и другая ситуация. Эта энергия может быть переда-
на одному или нескольким электронам, находящимся на лежащих выше атомных обо-
лочках. В результате этот электрон (электроны) покидает атом, унося с собой энергию,
которая могла бы быть излучена при электромагнитном переходе. Такой способ дезак-
тивации системы носит название эффекта Оже19, по имени ученого, его обнаружившего
экспериментально. Сами электроны, которые испускаются положительно заряженным
ионом (или атомом) с вакансией на одной из внутренних атомных оболочек, называются
ожэ-электронами. При этом однократно заряженный положительный ион становится
Эту константу экранирования не следует путать с введенной ранее поправкой экранирования, опреде-
ляющей положение уровней внутренних электронов (см. выражение (9.5.2)).
|9 Moseley Henry (1887 - 1915) - английский физик.
Auger Pierre Victor (1899 - 1993) - французский физик.
228
двукратно заряженным. Схематически
испускание кванта рентгеновского из-
лучения и ожэ - электрона представле-
но на рис. 9.11. Нетрудно видеть, что
эффект Оже представляет собой явле-
ние автоионизации иона с электронной
вакансией на внутренней атомной обо-
лочке. На практике испускание рентге-
новского кванта и эффект Оже являют-
ся конкурирующими процессами дез-
активации начального сильно возбуж-
денного состояния квантовой системы.
Какой их этих процессов является бо-
Рис. 9.11. Конкурирующие процессы: испускание
рентгеновского кванта и оже-электрона.
лее вероятным, заранее не очевидно.
Количественный расчет вероятности Оже - эффекта и в более широком смысле процесса
автоионизации является достаточно сложным и лежит за пределами наших квантовоме-
ханических возможностей.
Задачи к Главе 9.
9.1. Учитывая наличие тонкой структуры, определить длины волн головных линий
серии Лаймана и серии Бальмера в спектре атома водорода.
9.2. Спектральные линии каких серий могут возникнуть при возбуждении атомов
натрия и калия в состояние 5s ?
9.3. Сколько компонент имеют линии диффузной серии в атомах щелочных метал-
лов?
9.4. Какие излучательные переходы возможны после возбуждения атома гелия в со-
стояния, принадлежащие конфигурации ls3d ?
9.5. Определить все возможные термы атома углерода для электронных конфигура-
ций Is22s22pl4€ (2 - любое возможное орбитальное квантовое число). Указать
все возможные электромагнитные переходы между термами заданных конфигу-
раций и основным термом конфигурации ls22s22p2.
9.6. В условиях предыдущей задачи схематически изобразить тонкую структуру ли-
ний возникающих переходов.
9.7. Оценить величину тонкого расщепления Ка линии характеристического рентге-
новского излучения атома ртути (Z = 80).
9.8. Найти величину расщепления рентгеновского дублета Ка1 и Ка2 атомов молиб-
дена. Константа экранирования для тонкой структуры в L - оболочке ст’ » 3.5.
9.9. Определить число компонент тонкой структуры головной линии L - серии рент-
геновского излучения.
9.10. Определить оператор дипольного момента для ядерной подсистемы молекул Нг+
и HD+. Показать, что в гомоядерных молекулах в дипольном приближении элек-
тромагнитные переходы в пределах одного электронного терма запрещены.
9.11. В двухатомной молекуле происходит электромагнитный переход из основного
колебательного состояния возбужденного электронного терма на нижележащий
230
Глава 10. Пол у классическая теория взаимодействия све-
ла с веществом: Точно решаемые задачи.
В Главе 8 в рамках полуклассической теории был развит общий подход к рас-
смотрению задачи об эволюции квантовой системы в поле электромагнитной волны. Мы
видели, что поле электромагнитной волны вызывает переходы между различными ста-
ционарными состояниями квантовой системы. При этом эти переходы идут с макси-
мальной вероятностью, если частота воздействующего поля близка к частоте перехода в
какое-либо атомное состояние. Это позволяет существенно упростить задачу и, если по-
ля не очень сильные, фактически рассматривать задачу в приближении всего двух уров-
ней. Особняком стоит задача о гармоническом осцилляторе поле электромагнитной вол-
ны. В данном случае приближение двухуровневой системы не может быть использова-
но: условие резонанса оказывается выполненным сразу для любой пары соседних состо-
яний.
Кроме того, оказывается, что решение задачи об эволюции свободного электрона
в поле электромагнитной волны тоже имеет точно аналитическое решение.
Все эти задачи будут рассмотрены в данной главе.
10.1. Двухуровневая система в поле электромагнитной волны.
В этом разделе рассмотрим динамику двухуровневой системы в резонансном
электрическом поле. Будем считать, что энергии
— ------- 2) Е-у атомных состояний есть Ех и Е2 (Е2> £,) и на
flO) систему воздействует резонансное поле
£(/) = EQ cos cot с частотой <59, <w21 = (Е2 -E^h
- частота перехода. Будем считать, что нам также
известны волновые функции состояний |1) и |2)
^т (см. рис. 10.1).
Представляя волновую функцию атома в
Рис. 10.1. Двухуровневая система. виде линейной суперпозиции атомных состояний
ИО = Сх (/)| 1) ехр(~ Ext) + С2 (/)| 2) ехр(-— E2t),
п h
запишем систему уравнений для амплитуд вероятностей С, (/) и С, (г) в виде
dC
ih = -d2 ,E0Cj cos ал • exp (/To, /),
dC
ih = -dX2E0C2 cos ал • ехр(-/бУ2,/).
Здесь J2I = d\2 = (2|t7|l) - матричный элемент оператора дипольного момента.
(10.1.1)
(10.1.2)
Рассмотрим случай точного резонанса: со = а>21. Тогда, используя приближение
вращающейся волны (см. Раздел 8.4), перепишем (10.1.2) в виде:
231
'Л = -frh/2)c„
'С, =-(Q„/2)c2. (10Л'3)
Здесь введено обозначение Qs =</2|Е0/й - частота Раби '
Из системы уравнений (10.1.3) легко получаем:
С,+(П=/4)С, =0,
откуда
С, =Лсо80д//2 + В8тПЛ//2,
С2 =£4sinQ^/2-ificosQs//2. (Ю.1.4)
Пусть в начальный момент времени волновая функция задана в виде:
ф{г = 0) = a )| 1)+р )| 2). (10.1.5)
Здесь сс, Р действительные числа, причем а2 + р2 =1, и %р - соответствующие им
фазовые множители. Из начальных условий С,(/ = 0) = А = aexp(i£a),
C2(t = 0) = -iB = рexp(i<!;p) находим
C,(Z) = exp(/^)(acos(Q^/2)+^exp(^)sm(Q^/2)), 1
C2(/) = exp(z£j(/«sin(Q*//2) +Дехр(^)соз(рд//2)).
Здесь £ = - разность фаз между начальными значениями амплитуд базисных со-
стояний. Как видно, эта величина может оказаться существенной при изучении динами-
ки системы во времени, в то время как сама фаза , казалось бы, может быть выбрана
произвольно. Действительно, для населенностей состояний как функции времени полу-
чим
|С,(/)|2 =а2 cos2(fV/2) + р2 8т2(ПЛ//2)-2аДсо8(а^/2)8ш(П^/2)8т^,
|С, (/)|2 = а2 sin2 (Пя//2)+Р2 cos2 (ПЛг/2)+2аРcos(dRt/2)sin(Q.Rt/2)sin %.
При этом, конечно, |С,(Г)|2 + |С2(/)|2 = а2 + р2 =1. Выражения (10.1.6) и (10.1.7) показы-
вают, что в процессе внешнего воздействия двухуровневая система переходит из одно
состояния в другое и обратно. Этот процесс известен как осцилляции Раби.
Более подробно остановимся на важном частном случае, когда ct = 1, а р = 0 (си-
стема находится в начальный момент времени в основном состоянии. Тогда имеем (см.
рис. 10.2):
|C,(Z)|2 =cos2(n.r/2), |C(Z)|2 =sin2(Q,Z/2).
Мы видим, что в условиях резонанса вероятность перехода оказывается не мала даже в
слабых полях. Система с вероятностью равной единице переходит в возбужденное сос-
1 Rabi Isidor (1898-1988) - американский физик, Нобелевская премия по физике (1944) «За резонансный
метод измерений магнитных свойств атомных ядер».
232
0.0 0.5 1.0 1.5 2,0
Q//2;r
Рис. 10.2. Осцилляции Раби.
гоянис при произвольных, СКОЛЬ
угодно слабых интенсивностях воз-
действия. Время такого перехода
есть величина и возрастает
по мерс уменьшения напряженности
поля волны. Отмети также, что рас-
смотренный ранее в Главе 8 режим
теории возмущений реализуется при
выполнении условия £lRt«1, и при
разложении в ряд по этому парамет-
ру полученные выше выражения пе-
реходят в соотношения Главы 8.
Что касается волновой функции системы, то она может быть записана в виде:
y/(z) = cos(QflZ/2p}exp(“£1/) + zsin(Q/?//2)|2)exp(--^£'2/) =
Л z
z
(10.1.8)
2
В таком представлении волновая функция выглядит как суперпозиция не двух, а четы-
рех состояний (их называют квазиэнергетическими), энергии которых равны
Е. у = Е. ± ЛИ» /2. Схема воз-
1,2 1,2 л
сказать, как будет выглядеть спектр излучения такой
Рис. 10.3. Квазиэнергетические состояния и формирова-
ние триплета Моллоу.
никающего расщепления пред-
ставлена на рис. 10.3. Суще-
ственную перестройку энерге-
тического спектра системы
внешним электромагнитным
полем принято называть "оде-
ванием" атома. Рассмотренное
нами представление "одетого"
двухуровневого атома в виде
совокупности квазиэнергетиче-
ских состояний позволяет пред-
системы. Очевидно, кроме одной
линии на частоте атомного перехода а>21 появятся еще сателлиты с частотами д)21 ±ОЙ-
Т.е. вместо одной линии возникнет триплет, известный как триплет Моллоу. Более по-
дробно вопросы излучения одетых внешним электромагнитным полем систем буду1
рассматриваться в Главе 14. Здесь мы лишь отметим, что переход к представлению че-
тырех квазиэнергетических состояний является достаточно условным, т.к. размерность
пространства базисных функций не зависит от наличия или отсутствия взаимодействия
и в рассматриваемом нами случае по-прежнему равна двум.
233
Покажем теперь, что задача о двухуровневой системе в резонансном поле имеет
точное аналити 1ССК0С решение и для произвольной огибающей электромагнитного им-
пульса Ео(О-
Пусть импульс задастся в следующем виде
Е(0 = E0/(/)cos<yr,
где f (О ‘ огибающая импульса, причем max {/'(/)}= 1, а частота поля совпадает с часто-
той перехода со — б>21. Тогда уравнения для амплитуд заселения состояний (10.1.3) за-
пишутся в виде:
'С, =-(П«/2)/(ОС2.
причем C}(t —оо) = 1, C2(t —со) = 0. Здесь O.R = d^E^/ti и соответствует макси-
мальному значению поля в импульсе. Вводя новые функции u(t) = С\ (/) + С2 (/) и
v(r) = С] (/) - С2 (/), получим
откуда
w(r) = exp Ij f(t)dt , v(/) = exp - i j f(t)dt .
k 2 -00 J k 2 -00 J
В результате получим:
с(0 = «Ю+2^ = соЛк =
2 I 2 4 / 2 k 2 - )
(10.1.10)
В случае мгновенного включения импульса с прямоугольной огибающей
решение (10 1.10) переходит в полученное ранее.
Рассмотрим важные частные случаи полученного решения. Пусть
бран так, что
импульс вы-
00
234
Тогда к концу импульса |С,(оо)|2 = 1, |С2(-<< = 0, т.е. атом вернулся в исходное состоя-
ние. Такие импульсы называются 2л - импульсами, которые распространяются в среде
практически без потерь энергии. Если же
QR ]/(^ = л,
то, наоборот |С,(оо)|2 = 0, |С2(оо)|2 = 1, и воздействующее поле инвертирует атом, пере-
водя его в возбужденное состояние. Это л - импульс.
10.2. Гармонический осциллятор в поле электромагнитной вол-
ны.
В этом параграфе рассмотрим еще одну систему, динамика которой в поле волны
также может быть рассмотрена аналитически вне рамок теории возмущений. Речь идет
о квантовом гармоническом осцилляторе. В каком-то смысле данная система представ-
ляет собой противоположный случай рассмотренному выше приближению двухуровне-
вой системы. Действительно, в условиях, когда частота воздействующего поля в) совпа-
дает с частотой осциллятора а)() условие эквидистантности его спектра обеспечивает
наличие резонанса между любой парой соседних состояний, делает невозможным ис-
пользование двухуровневого приближения для любых значений интенсивности воздей-
ствующего поля на достаточно больших временах.
Итак, запишем уравнение для гармонического осциллятора в присутствии резо-
нансного поля электромагнитной волны Е(/) = Ео cos ал :
dt
й2 d2y/
2т dx2
та>2х2
Т~
у - dE(t)y/.
(10.2.1)
+
Здесь d = ex - дипольный момент.
Пусть в начальный момент времени (t = 0) система находится в основном состо-
янии с энергий Eq = Й&>/2 и характеризуется волновой функцией ^0(х). Будем искать
решение (10.2.1) в виде
И*, О = X Сп СО ехР (- i +1/2)/), (10.2.2)
77=0
где </„(*) - волновая функция п -ного стационарного состояния с энергией
Е„ =ha)(n + \/2). Подставляя (10.2.2) в (10.2.1), аналогично разделу 8.3 получим систему
уравнений для коэффициентов разложения Сп (/):
(10.2.3)
2 Обратим внимание: здесь и ниже в этом разделе надо различать массу частицы (электрона) и индекс,
определяющий стационарное состояние осциллятора, также обозначенный буквой т. Мы полагаем, что
это не вызовет затруднение у читателя.
235
учитывая, чт р д матричных элементов dmn только два отличны от нуля, а именно
= еаd =
V 2 т~1'т еу 2 ’
(здесь а = y[h/ma>) из (10.2.3) получим:
.^.dCm _ еЕоа z -- --------------- ч
~^/2 008 ^C'"+’+1 е5Ф(~/й*) + С^ЛехрО^)). (10.2.4)
Используя приближение вращающейся волны перепишем (10.2.4) в виде:
dC_ . еЕпа ! .---- _ \
dt + (10.2.5)
причем в начальный момент времени Cm(t = 0) = дт0.
Рассмотрим сначала поведение системы для достаточно малых моментов времени
t, таких, что для всех т выполнено условие Ст « Ст_}, т.е. вероятность заселения всех
состояний, кроме начального (нулевого) мала и быстро убывает с ростом номера т . То-
гда перепишем (10.2.5) в виде:
(10'2-6)
Система уравнений (10.2.6) интегрируется элементарно
откуда с учетом начальных условий для Ст получим:
k 2А J>/2 ’
,eEoaY 1 ,з
1 2h J д/23-23
(10.2.7)
Сш(/) =
/ 2Й )
Полученное решение, очевидно, справедливо на временах, удовлетворяющих условию
еЕоа/ <<1
2Л
(10.2.8)
Г „ £ оттиАЫИИ по высокой частоте (приближение вращающейся вол-
L Другой стороны, об усреднении по bww
н . /^1/л) Сопоставление этих двух условии дает:
Ды) можно говорить, если t » Ч® •
236
е2Е2
4т аг
(Ю.2.9)
В левой части неравенства стоит величина колебательной энергии свободного электрона
в поле волны с частотой со. Таким образом, теория возмущений справедлива, если вели-
чина колебательной энергии электрона в поле волны мала по сравнению с энергий кван-
та.
Будем искать общее решение задачи (10.2.5) в виде:
С„,(/) = (шГ-_=©(/),
V2'" -т\
(Ю.2.10)
где а = еЕоа/(2й), а ©(/) - неизвестная функция. Подставляя (10.2.10) в (10.2.5) полу-
чим
Г .1 (т@ + Z©) = ia
>!2т -т\
\т + 1 . (/а)"”1 Г'1
2т+1 -(т + 1)!
т-1 -(т-1)'-
откуда
2
Поскольку &(t = 0) = 1, из (10.2.11) получим ©(/) = exp(-zz2Z2/4), а
(10.2.11)
0 2 4 6 8 10 12 14 16 18
Рис. 10.4. Квантовый осциллятор в резонансном
электромагнитном поле. Моменты времени соот-
ветствуют значениям т = 1, 2, 5,10.
СМ
ехр(-«2/2/2). (10.2.12)
^2m-rnl
Для вероятности заселения различных
состояний в зависимости от времени
получим
|с„(')| =—-ехр(-й), (10.2.13)
т\
где m=(at)2/2. Распределения |Ст|*
для различных значений т представ-
лены на рис. 10.4.
Полученное распределение есть
распределение Пуассона3, причем па-
раметр этого распределения задает
среднее значение числа квантов в зави-
симости от времени. Выражения
(10.2.12) и (10.2.13) означают, что под действием резонансного поля возникает коге-
t ,7J~^
рентное состояние осциллятора, средняя энергия которого изменяется по закону
Е = hco(m(t) + \/2)
(10.2.14)
3 Poisson Simeon Denis (1781 - 1840) - французский математик и физик.
237
„ возрастает по параболическому закону. Вспоминая, что а = еЕоа/(2Л) и а =
для средней энергии получим
E(t\ _ е2Е^2 ha)
(} ^г+т- <10-215>
Зторой член ~ сумме представляет энергию нулевых колебаний (энергию начально-
го состояния , а первый энергию, набранную от поля волны. Заметим, что в эту вели-
чину не входит постоянная Планка, и это верный признак того, что полученное выраже-
ние для набора энергии осциллятором в поле волны (с точностью до энергии нулевых
колебаний) справедливо и в классической теории. Выражение (10.2.15) позволяет
утверждать, что амплитуда колебаний осциллятора линейно возрастает во времени, при-
чем значение этой амплитуды х0(/) можно найти из соотношения:
та>2х2 _ е2Е^2
2 8m
откуда
еЕ0
хо ~ э •
2тй)
Аналогично, для амплитудного значения импульса получим:
еЕ0/
А= —
(10.2.16)
(10.2.17)
При этом, если амплитудные значения х0 и р0 существенно превышают квантовые не-
определенности координаты и импульса в основном состоянии
р0 » y/hma), х0 » д/й/та),
(10.2.18)
то движение частицы будет происходить по классическому закону. Легко видеть, что
условия (10.2.18) эквивалентны неравенству т »1. Мы еще раз увидели, что с точки
зрения квантовой механики - классический осциллятор - это когерентное состояние
квантового осциллятора с большим средним число квантов.
Для определения средних по квантовому состоянию значений координаты
и импульса (/?(/)) можно воспользоваться выражением для волновой функции (10.2.2) с
вычисленными нами значениями коэффициентов разложения. Однако, мы поступим
проще, воспользовавшись теоремой Эренфеста (см. Глава 1). На основании теоремы
Эренфеста можно утверждать, что эти средние значения определяются из классических
Уравнений движения. Поэтому:
= A!sinnf. =
2md)
(10.2.19)
При этом ширина волнового пакета во времени не меняется и соответствует ширине ос-
новного (вакуумного) состояния (см. рис. 10.5).
238
координата
Рис. 10.5. Гармонический осциллятор в резонансном поле электромаг-
нитной волны.
10.3. Свободный электрон в электромагнитном поле. Состояния
Волкова.
В данном разделе рассмотрим эволюцию свободного электрона в поле электро-
магнитной волны. В данном случае нам будет удобнее решать задачу в рА - калибровке
потенциала взаимодействия.
Уравнение Шредингера для свободного электрона запишем в виде:
,й^2)= 1 (10.3-1)
ot 2т \ с )
Здесь векторный потенциал поля зависит лишь от времени, что означает использование
дипольного приближения. Пусть в начальный момент времени (t = 0) электрон характе-
ризуется функцией:
= 0) = (г) = —I—-expfip/l (10.3.2)
(2лЯ) )
т.е. в начальный момент времени электрон характеризовался импульсом р0.
Будем искать решение уравнения (10.3.1) в виде разложения по собственным
функциям оператора импульса:
= (10.3.3)
Подставляя (10.3.3) в (10.3.1), получим:
239
Из (Ю-3.4) находим:
- \pL e -1 e2
V2w me 2mc2
Л2 Vp(r)cPp.
(10.3.4)
e -Z
p--A(t) dt .
с У
(10.3.5)
0
По условию (10.3.2) в начальный момент времени
Ср(' = О) = £(р-ро).
(10.3.6)
Поэтому из (10.3.3) получаем:
.,,. 1 j • t -1 Л х 2 А
v (10Л7)
Полученная волновая функция известна как функция Волкова (волковская функция), а
состояния электрона в поле плоской электромагнитной волны часто называют волков-
скими состояниями4. В частном случае А = 0 они естественным образом переходят в
плоские волны де Бройля (стационарные состояния свободного электрона). Если же
A(t) есть некоторая функция времени, состояние является нестационарным.
Волковские функции получены нами в рА - калибровке. Перейти к dE - калиб-
ровке можно с помощью унитарного преобразования:
V'dE(r>t) = Syr A(r,t) = expf-1. (10.3.8)
l й c )
Например, для монохроматического поля А = Ад sin cat
Ё(/) = = --Ад cos cot (10.3.9)
с dt с
(здесь амплитуды электрического поля и векторного потенциала связаны соотношением
Ао =сЕд/со}. Тогда:
1 I _
(2л/о3/2’еДЧА
V"\r,t) =
X . t , / \2 \
еЕп sin ал _ i г 1 ( - е - . 1 .
-----5------ г — — рп----------En sin аЛ I dt
а> ) й 2<°---------------------° J
(10.3.10)
Для уяснения физического смысла полученного выражения вспомним, что плоская вол-
на де Бройля (10.3.2) описывает состояние электрона с заданным импульсом р0. Вол-
ковское состояние (10.3.10) есть тоже плоская волна. Поэтому мы приходим к заключе-
нию, что она описывает состояние с импульсом
4 По имени Д М Волкова впервые рассмотревшего задачу об электроне в поле электромагнитной волны
(Д.м. Волков Электрон в поле плоских неполяризованных электромагнитных волн с точки зрения урав-
нения Дирака ЖЭТФ 7, 1286-1289 (1937)). Найденные нами состояния являются нерелятивистским пре-
делом общих волковских состояний.
240
(4L sin
---------
a)
(10.3.11)
Состояние нестационарное: для вычисления среднего значения энергии воспользуемся
стандартными правилами квантовой теории:
(E(t)) = ^/,, )|/7р'/) J = ih\^y/(Vtdyr.
(Ю.3.12)
Вычисляя полученный интеграл с учетом явного выражения для волковской функции
(10.3.10), получим:
р0-~ Eosina* = — - g —sin^ +-----------у sin2 cot. (10.3.13)
co J 2m mco 2mco
Полученные выражения для импульса и энергии в точности соответствуют результатам,
полученным в классической теории (см. Глава 18). В частности, если усреднить выраже-
ние (10.3.13) по времени, получим
2 2р2
+ (10.3.14)
2т 4та>
т.е. в поле электромагнитной волны к энергии поступательного движения добавляется
еще и колебательная энергия электрона.
Совпадение результатов квантовомеханических и классических расчетов не слу-
чайно. Этот результат является прямым следствием теоремы Эренфеста.
Задачи к Главе 10.
10.1. Сформулировать условия применимости приближения двухуровневой системы
для случая воздействия на нее резонансного поля электромагнитной волны.
10.2. Определить средний по квантовому состоянию дипольный момент двухуровнево-
го атома, находящегося в резонансном электромагнитом поле. Считать, что в
начальный момент времени атом находится в основном состоянии.
10.3 Энергия перехода между состояниям двухуровневого атома равна щ21=1 эВ.
Импульс имеет гауссову форму с полушириной т=1 пс. При какой пиковой ин-
тенсивности этот импульс будет 2я - импульсом?
10.4. Доказать, что среднее по квантовому состоянию значение координаты квантового
осциллятора в поле электромагнитной волны может быть определено из класси-
ческих уравнений движения осциллятора в поле.
10.5. На квантовый осциллятор с частотой со воздействует импульс резонансного
электромагнитного поля. Определить среднее значение и дисперсию энергии ос-
циллятора в зависимости от времени. В начальный момент осциллятор находится
в основном состоянии. Считать, что поле включается мгновенно.
10.6. Свободный электрон находится в слабом электромагнитном поле. Определить его
волновую функцию, соответствующую режиму теории возмущений.
10.7. Система из двух взаимодействующих электронов находится в поле электромаг-
нитной волны. Получить общее уравнение для волновой функции их относитель-
ного движения.
241
Глава 11. Многофотонные процессы.
В данной шанс мы рассмотрим воздействие электромагнитного поля на кванто-
вую систему в высших порядках теории возмущений. Такое рассмотрение предполагает,
что электрическое поле волны по-прежнему существенно меньше внутриатомного. Мы
видели, что результат, полученные в первом порядке нестационарной теории возмуще-
ний можно трактовать, как поглощение (испускание) фотона с частотой со, причем это
процесс идет эффективно, если частота поля близка к частоте какого-либо атомного пе-
рехода щ » <у2| • Теперь мы покажем, что в высших порядках теории возмущений возни-
кают процессы многоквантового поглощения (испускания). Во втором порядке - двух-
квантовые переходы, в третьем - трехквантовые, в п - ном порядке - п - квантовые пе-
реходы. При этом в условиях применимости теории возмущений вероятность п - фо-
тонных переходов мала, и убывает с увеличением числа поглощенных квантов.
11.1. Второй порядок нестационарной теории возмущений.
До сих пор мы рассматривали процесс взаимодействия электромагнитного излу-
чения с квантовой системой в первом порядке теории возмущений по дипольному взаи-
модействию. Рассмотрим теперь второй порядок теории, полагая, что условия примени-
мости дипольного приближения по-прежнему выполнены. Как и раньше, будем считать,
что атомная система в начальный момент времени находится в одном из состояний дис-
кретного спектра ул с энергией Et. Оператор взаимодействия квантовой системы с
электромагнитным полем запишем в виде:
= (11.1.1)
Представляя решение нестационарного уравнения Шредингера
= (11.1.2)
dt
в виде комбинации собственных функций невозмущенного гамильтониана Но *:
у/(г, е) = ^сп (г) е*р[ “ Д (11.1.3)
п ' '
получим систему уравнений для коэффициентов разложения
л— = (11.1.4)
dt п
Представляя амплитуды вероятности Сп в виде ряда юории возмущений
СЛ=С™ + С1,)+С")+.... (11.1.5)
И подставляя (11.1.5) в (11.1 -4), получим для случая f ф i.
1 Для сокращения длины записи мы полагаем здесь, что знак суммы означает, в том числе, и интегрирова-
ние по состояниям континуума.
242
/7) 4 (''+ •’L + с'1’ + G',2’ + -)\,/// W(/z7V) •
(If н
Удерживая в левой и правой частях уравнения члены одинакового порядка малости, по-
лучим:
и, 7'7 = У C,%/f Iw'lv/Jcxpf/®,,/). (11.1.6)
dt „
Поэтому, решив задачу в первом порядке теории возмущений, легко получить решение
второго порядка, и так далее: по It - тому порядку легко определяются коэффициенты
разложения к 4-1 порядка.
Будем предполагать адиабатически плавный характер включения поля. Тогда,
выполняя интегрирование по времени, в первом порядке теории возмущений получаем.
С1” (Г) = -7 jWfi(t)&^(icDflt)dl =
df-Ej ехр(/(бУ/; -6w)Z) expCz'C^ +co)t)'
2/? (a>fl-a)) (d)fl+a)) }
(11.1.7)
Подставляя (11.1.7) в (11.1.6), во втором порядке теории возмущений получим
С}2)(z) = ZX /4fe2'~x f (ехР~(О~+ exP(z(^# +&- W))
(11.1.8)
х (~ + ехр(/(й?л/ + fl))/) V
I (*>„,-*>) (*>„,+<”) )
где X -малый параметр, обеспечивающий адиабатически плавное включение поля при
Амплитуда (11.1.8) содержит четыре слагаемых, которые мы рассмотрим пооче-
редно и независимо друг от друга. При этом учтем очевидное соотношение
®fn + *4 = •
В выражении для амплитуды перехода (11.1.8) содержатся слагаемые
d d Ed j '
71 = zZ ^2 ° x 7) _ x x J exp(z(^ - - iX)t}dt, (11.1.9a)
Л v /)/ / _(4)
72 = Z'Ex x j cxp(/(rw/; + Ito - iAWt, (11.1.96)
71 —; V dfndnfio f 1 1 r
= ^777+77^) Jx 1ехр(,(й,й' (11'L9B)
При вычислении вероятности перехода для каждого из написанных выше выражении
должен быть найден квадрат модуля. Действуя способом, аналогичным тому, который
был использован при выводе выражения для вероятности перехода в единицу времени в
первом порядке теории возмущений (см. (8.4.13), (8.4.14)), получим из (11.1.9а) и
(11.1.96):
243
Г'
Г 4»?
х2яЛЧ-м
v ‘^Q'o ।
2/ 1Л? *------------
" («>„,+«>)
2
(11.1.10)
X + 2го).
и ученные выражения означают, что пспехлпм
1в переходы происходят при выполнении условия:
Е/=^+2Лщ, (11.1.11)
H.1H
£/=^-2ЛбУ. (11.1.12)
Последние два соотношения представляют закон сохранения энергии при поглощении
(испускании) энергии поля. То есть во втором порядке теории возмущений мы получили
возможность двухквантового поглощения (испускания). Такие переходы мы будем
называть двухфотонными. Отметим, что процесс двухфотонного поглощения (испуска-
ния) представляет собой элементарный акт взаимодействия атомной системы с полем
электромагнитной волны и не может быть представлен как последовательное поглоще-
ние (испускание) сначала первого, а потом второго фотона.
В свете вышесказанного выражение (11.1.9в) соответствует случаю, когда один
фотон был испущен, а другой поглощен, в результате энергия атомной системы осталась
неизменной. На физическом смысле этой ситуации мы остановимся несколько позже.
Отметим также, что при вычислении вероятности перехода с помощью (11.1.8)
возникают перекрестные слагаемые вида Re(/1 х 12*). Можно показать, что на больших
временах воздействия вклад этих слагаемых в вероятности перехода оказывается прене-
брежимо мал, и может не приниматься во внимание.
11.2. Двухфотонные переходы.
Таким образом, мы показали, что во втором порядке теории возмущений в атом-
ной системе под действием внешнего электромагнитного поля возникают процессы
двухквантового поглощения (испускания). Легко видеть (см. выражение (11.1.10)), что
вероятность двухфотонного процесса пропорциональна квадрату интенсивности излуче-
ния
Сопоставление вероятностей двухфотонного и однофотонного поглощения дает (см. вы-
ражения (8.4.5) и (11.1.10))
и'у,. J lg7a<o
(Е/Е„У,
(11.2.1)
Е„ - введенное ранее характерное значение внутриатомного поля. Как и ожидалось, мы
"бучили, что в условиях применимости теории возмущений вероятности двухфотон-
нь'х переходов должны быть значительно меньше, чем однофотонных. Поэтому в доста-
точно слабых полях двухфотоиные переходы надо принимать во внимание, если по ка-
244
кой-.табо причине (закон сохранения энергии, правила отбора) однофотонные переходы
оказываются невозможными.
Остановимся более подробно на
1/> структуре выражения (11.1.10), описываю-
--------------- щего вероятность двухфотонного поглоще-
ния (испускания). Суммирование в этом
выражении формально идет по всему бес-
. конечному набору стационарных состояний
__________________________атомного гамильтониана. Эти состояния
(к________________________принято называть промежуточными2. Од-
нако, может так оказаться, что некоторое
состояние из этого набора удовлетворяет
условию (для определенности мы говорим о
двухквантовом поглощении):
Е . -Е, « hco.
Рис. 11.1. Двухфотонное поглощение. "
В этом случае слагаемое с номером п оказывается резонансно большим и вносит опре-
деляющий вклад в сумму по промежуточным состояниям (см. рис. 11.1). В таком случае
в (11.1.10) из всей суммы можно выделить оно слагаемое и приближенно записать
d .d . Е; j
fn П I 1
----------- X -----------
4А2 {со. -со)
х 2nS{cDfl -2а>).
(11.2.3)
Сформулируем теперь правила отбора для двухфотонных переходов в атомах.
Как следует из выражений (11.1.10), такие переходы оказываются возможны, если хотя
бы одно слагаемое из суммы по промежуточным состояниям отлично от нуля. Вспоми-
ная правила отбора для электрических дипольных переходов, полученные в первом по-
рядке теории возмущения: Af. = ±1, заметим, что орбитальные квантовые числа началь-
ного |/) и промежуточного состояний должны отличаться на единицу. По той же
причине орбитальное квантовое число конечного состояния |/) должно отличаться на
единицу от орбитального квантового числа промежуточного состояния состояний |«)-
Поэтому имеем:
=Л,±1 =
< ±2.
В результате для двухфотонных переходов получаем:
zU = 0,±2.
(11.2.3)
2 Термин «промежуточное состояние» возникает как результат формальной интерпретации выражений
(11.1.10), как переходов, происходящих в две стадии: | /) -> | п) -> | /), т.е. из | j) в | /) через промежуточ-
ное состояние | л).
245
Замшим, ЧТ Р ’ РазРешеннЬ1е как однофотонные, оказываются запрещенными во
вТором пор озмущений, и, наоборот, переходы, разрешенные как двухфо-
тонные. оказываются запрещены в первом порядке теории возмущений.
11.3. Высшие порядки теории возмущений.
В этом разделе проведем на качественном уровне рассмотрение процесса воздей-
ствия на атомную систему внешнего электромагнитного поля в высших порядках теории
возмущений. Из общей структуры уравнения (11.1.6), описывающего процесс взаимо-
действия в произвольном порядке теории возмущений, можно сделать вывод, что в к -
том порядке теории возмущений возникнут многофотонные процессы к -того порядка,
вероятность которых будет пропорциональна к -той степени интенсивности
w(k) ~1к.
В частности, оказываются возможны про-
цессы многофотонного поглощения и ис-
пускания квантов поля, удовлетворяющие
закону сохранения энергии
Ef = Е, ± khco.
При этом в общем случае в к -том порядке
теории возмущений будет возможен про-
цесс с поглощением т фотонов и испуска-
нием к-т фотонов. Примеры такого рода
процессов для случая к = 5 приведены на
рис. 11.2.
11.4. Рамановские переходы Л - типа. Комбинационное и релеев-
ское рассеяние.
Рассмотрим теперь случай воздействия на атомную систему двухчастотного ла-
зерного поля
Ё = Ё, cos a\t + Ё2 cos co2t.
В первом порядке теории возмущений мы получим процессы поглощения или
испускания квантов hox или hd)2. Во втором порядке помимо двухквантовых процессов
С поглощением (испусканием) квантов to, или Л®, появятся и процессы, удовлетворя-
ющие следующему закону сохранению энергии.
Ef =Et +hcox + h(D2,
Ef =EX -H(ox -Яа>2.
(11.4.1)
Для вероятности таких переходов нетрудно получить
4/Г
и,(2> = у, (5ДМД) , (УМЙ)
" “ 4/г +
2
ТбЦ Тй)2). (11.4.2)
246
Рис.11.3. Двухфотонное поглощения в случае
двухчастотного воздействия.
При этом случай использования знаков «-»
соответствует вероятности двухфотонного
поглощения, а знаков «+» - двухфотонного
испускания. Это тоже процессы двухкван-
тового поглощения (испускания), когда
поглощаются (испускаются) кванты из
различных полевых мод (см. рис.11.3), При
этом первый член в (11.4.2) описывает ам-
плитуду перехода в промежуточное состо-
яние под действием поля £, и, затем, в ко-
нечное - под действием поля Е2. Второе
слагаемое, наоборот, соответствует ампли-
туде перехода в промежуточное состояние
под действие поля Е2, и, затем, в конечное
под действием поля Ej.
Однако, помимо процессов (11.4.1), возможны и процессы, когда квант поглоща-
ется из одной моды (например, <w,) и испускается в другую (й?2). Для определенности
будем считать, что сох > со2:
Е f = Ej+ha>x-ha>2. (11.4.3)
Для вероятности такого процесса имеем:
(^E2)(d„,E,) 1
-------------х__________
4Й2
, (^Ё,)(<Ё2) 1
-|-----------х--------
4Й2 (ч(+®2)
х -(Оу+аъ).
Рис. 11.4. Рамановские переход А - типа.
(11.4.4)
Схема такого процесса приведена на рис. 11.4.
При этом первый член в выражении (11.4.4)
описывает сначала поглощение кванта и
затем испускание h(o2, а второй - сначала ис-
пускание hco2 и затем поглощение ha\. Важно
отметить, что, как всегда в квантовой теории,
складываются не вероятности, а амплитуды
вероятностей переходов.
Аналогично может быть рассмотрен
процесс с поглощением ййа и испусканием
ha){ (см. рис.11.5):
Ef = Et + hco2 -ha\.
(11.4.5)
Рассматриваемые двухфотонныс переходы иногда называют процессами Л - типа, по*
скольку их графическое изображение (см. рис. рис. 11.4 и 11.5) напоминает греческую
букву «ламбда». С физической точки зрения они интересны тем, что матричные элемеН"
247
ты (И-4.4) описывают процесс комбинационного (или рамановского3) рассеяния. Суть
этого эффекта заключается в том, что при облучении какого-либо вещества электромаг-
нитным излучением частоты соо в спектре рассеянного света (помимо несмещенной ча-
стоты) появляются сателлиты с частотами со = со ± Q, Где Q - собственная частота ко
лебаний среды. В рассматриваемом нами слу-
чае, очевидно, £l = cofl - частота перехода
между состояниями |/) и |/). В теории ком-
бинационного рассеяния компоненту, соот-
ветствующую поглощению hco{ и излучению
hco2 (> а>2)’ принято называть стоксовой
компонентной. В случае же, если атом пере-
ходит в нижележащее состояние, говорят об
антистоксовой компоненте комбинационного
Рис. 11.5. Рамановские переходы Л - типа.
рассеяния.
Правила отбора для комбинационно-
активных (разрешенных) переходов были сформулированы выше: ДИ = 0,± 2 .
|л>
1>
Может оказаться, что частоты
<У] = со2, однако речь идет о разных модах
излучения, отличающихся, например,
направлением распространения, задаваемым
вектором к . В этом случае переход будет
идти если конечное состояние совпадает с
начальным, т.е. |/) = |/), а, фактически энер-
Рис. 11.6. Релеевское рассеяние.
рассеянием называют также рассеяние
гия поля передаваться из одной моды в дру-
гую. Описываемый процесс есть релеевское4
рассеяние света (см. рис. 11.6). Релеевским
света без изменения длины волны на частицах,
неоднородностях или других объектах, когда частота рассеиваемого света существенно
меньше собственной частоты рассеивающего объекта или системы. В рассматриваемом
нами случае речь идет чаще всего о рассеяния света на молекулярных (нулевых) колеба-
ниях.
11.5. Динамический эффект Штарка.
Остановимся теперь на случае двухфотонного перехода в монохроматическом
поле, соответствующего случаю, когда один фотон поглощается, а другой испускается.
Амплитуда такого процесса определяется интегралом (11.1.9в). Полагая, что конечное
состояние l/*) совпадает с начальным |/^, из (11.1.8) и (11.1.9) получим:
3 По имени индийского физика Ч. Рамана (1888 - 1970), одного из авторов открытия комбинационного
Рассеяния света (1928). Нобелевская премия по физике (1930) присуждена Ч. Раману «За работы по рассе-
янию света и за открытие эффекта, названного по его имени».
4 По имени Релея (John Strutt Rayleigh (1842-1919)- британский химик и механик). Нобелевская премия по
Физике (1904) за открытие аргона.
248
или
и
(11.5.1)
Тогда атомная волновая функция может быть представлена в виде.
где
«(1 + C,(2)(r)X(r)exp
^(C'/’+Cf )у/ДЕ)ехрГ-^Е/]«
1 у KJ
4 „ h (щ2-^2)
у р2 — Хю р2
— д ’
(11.5.2)
- линейная атомная поляризуемость.
Как видно, во втором порядке теории возмущений волновая функция начального
состояния изменяется под действием поля электромагнитной волны, причем величину
ЗЕ, можно рассматривать как поправку к уровню энергии Е,. Этот сдвиг уровня энер-
гии в высокочастотном (оптическом) поле называют динамическим эффектом Штарка.
На качественном уровне понять происхождение динамического эффекта Штарка
можно исходя из следующих соображений. Атомный электрон, поглощая и испуская
фотоны внешнего поля, на какое-то время приобретает дополнительный импульс, в ре-
зультате чего он как бы дрожит на свой «квантовой орбите». Как результат, «видимый»
размер атомного ядра определяется амплитудой дрожания, тем большей, чем больше
амплитуда воздействующего поля. Неточечность атомного и ядра и есть причина сме-
щения атомных уровней, которая была подробно нами рассмотрена в Разделе 4.9.
В случае со -> 0 (статический предел) выражение (11.5.2) может быть переписано
в виде:
SEi =-УЬ1кхС2
П1
(под Е здесь понимается эффективное значение напряженности поля волны
E = E0/V2 ), фактически совпадающее с результатом (6.7.3), полученным для штарков-
ского сдвига в постоянном электрическом поле. Величина шгарковского сдвига атомных
уровней в сильных электромагнитных полях, вообще говоря, не мала и может быть со-
поставима с квантом поля tuo и даже превышать его.
В случае если начальное (основное) состояние |/‘) связано е континуумом много-
фотонным переходом (в такой ситуации все сон1 > 0 и со < соп1), как видно из (11.5.2), ве-
личина штарковского сдвига отрицательна, то есть в поле волны происходит увеличение
потенциала ионизации. С другой стороны, можно показать, что для высоковозбужден-
249
них (ридберговких) состояний величина штарковского сдвига положительна и оказыва-
ется примерно равна
2
« xEj (Ц.5.3)
4 т со
Величина (11.5.3) представляет собой колебательную энергию свободного элек-
трона в поле волны с частотой со. Это значение представляет собой дополнительную
энергию, на которую смещаются энергетические уровни атомного континуума (штар-
ковский сдвиг континуума). Как видно, штарковский сдвиг ридберговских состояний
совпадает со штарковским сдвигом уровней в континууме. В результате эффективный
потенциал ионизации атома оказывается равен
continuum ! |^|Ер । е2Ер (Ц.5.4)
‘ ' 4 4т со1
| 1 и возрастает линейно по интенсивности излуче-
J ния. Как правило, штарковский сдвиг границы
4 А континуума существенно больше штарковского
х I сдвига связанных состояний с потенциалом
м п м ионизации больше, чем энергия кванта.
Отмеченная особенность приводит к ин-
а п тересному физическому эффекту - закрытию
-I----------------каналов ионизации5 в сильных электромагнит-
ных полях. Сущность этого явления заключает-
Рис. 11.7. Закрытие каналов ионизации. ся в следующем. Например, в слабом поле иони-
зация атома может происходить в результате поглощения п квантов поля. Такой про-
цесс возтможен, если nhco > Ir Однако, с увеличением интенсивности излучения значе-
ние потенциала ионизации возрастает (см. (11.5.4)) и при некоторой интенсивности из-
лучения оказывается, что nhco < . В таком случае фотоионизация возможна уже как
п +1 - фотонный процесс, ап- фотонный канал закрывается. Схематически явление за-
крытия канала ионизации представлено на рис. 11.7: трехфотонная ионизация при неко-
тором значении интенсивности сменяется четырехфотонной, а затем и пятифотонной.
Более подробно процесс фотоионизации атомов, в том числе многофотонной, бу-
дет рассмотрен в Главе 13.
11.6. Диаграммы Фейнмана.
В этом разделе мы остановимся на графическом способе изображения амплитуд
рассматриваемых нами многофотонных процессов, позволяющих по картинке легко за-
писать выражение для конкретного процесса любого порядка многофотонности. Такие
графические изображения называют диаграммами Фейнмана6 и широко используются в
квантовой электродинамике для рассмотрения электромагнитных процессов в различ-
5 Это явление было экспериментально обнаружено группой П. Агостини (Р. Agostini) в 1988 году.
6 Feynman Richard Phillips (1918 - 1988) - американский физик - теоретик, Нобелевская премия (1965) "За
Фундаментальные работы по квантовой электродинамике, имевшие глубокие последствия для физики
элементарных частиц".
250
ных порядках теории возмущений. Диаграммы, которые мы рассмотрим ниже, являются
нсрслятивисгскнм приближением введенных Фейнманом диаграмм.
Начнем наше рассмотрение с первою порядка теории возмущений. В этом случае
имеется всего два процесса поглощение, либо испускание кванга hco. Амплитуды этих
процессов пропорциональны выражению:
г(|) ~
z ~ 2ft ’
|f> |f>
- dfiE
п> н>
Рис. 11.8. Элементарные диаграммы, опи-
сывающие процесс поглощения (слева) и
испускания (справа) кванта поля.
(11.6.1)
а энергии начального и конечного состоя-
ний связаны соотношением Е= Е: ± ft<y
Поставим в соотношение двум этим ам-
плитудам элементарные диаграммы (см.
рис. 11.8). Сплошная вертикальная линия
соответствует состоянию атомного элек-
трона, а пунктирная линия - фотону. При
этом, если последняя находится слева от
вертикальной линии, то речь идет о его
поглощении, а если справа - то испускании. Узлу диаграммы соответствует множитель
^Е.
Перейдем к рассмотрению процессов второго порядка. Мы видели, что их всего
четыре: поглощение (испускание) двух квантов поля и поглощение, а затем испускание
кванта. Или наоборот - сначала испускание, а потом поглощение кванта. Эти процессы
описываются соответственно амплитудами (11.1.9а-в), причем выражение (11.1.9в) опи-
сывает оба процесса без изменения энергии состояния. Соответственно, мы можем
нарисовать четыре диаграммы, каждая из которых описывает один из перечисленных
процессов (см. рис. 11.9).
Рис. 11.9. Диаграммы Фейнмана, описывающие процессы второго порядка.
Помимо уже знакомых нам выражений, которые надо сопоставить узлам каждой
из диаграмм dnjE (причем индексы у матричного элемента соответствуют обо-
значениям состояний после и до поглощения/испускания кванта), появляется промежу-
точная линия, описывающая «промежуточное» состояние электрона между актами взаи-
модействия. В случае, в этом акте взаимодействия речь шла о поглощении фотона, то
этому «промежуточному» состоянию надо поставить в соответствие множитель
1/(<уя/ -6У)’ если же фотон испускался - то 1/(о>и/ + а>). Кроме того надо помнить, что по
всем промежуточным состояниям |и) выполняется суммирование. С учетом сказанного,
например, первой и третьей диаграмме надо поставить в соответствие амплитуды:
251
C<2) ~ V^E°x<y«'Eo I
' “др------------ХГ~------’ (11.6.2)
4141 как раз и соснвстсшус! амплитуде (11.1.9а) и первому слагаемому в (11.1.9в). Для
второй п четвертой диаграмм, соответственно, имеем:
г^./ьЕох</Ео ]
L ТГг---------х---------.
" 4Л (О)п1 + со)
(11.6.3)
При ЭТОМ мы помним, что конечные | /^ состояния, входящие в амплитуды (11.6.2) для
случая двухквантового поглощения и процесса поглощения испускания кванта, раз-
личны. То же самое замечание относится и двум процессам, описываемых амплитудами
(1.6.3).
При вычислении вероятностей надо помнить, что если конечные состояния, куда
происходит переход из заданного начального состояния 1ty, совпадают, то надо склады-
вать именно амплитуды, а не вероятности процессов, чтобы не потерять процесс интер-
ференции амплитуд возможных переходов.
Рис. 11.10. Процессы третьего поряд-
ка, соответствующие трехфотонному
поглощению (слева) и испусканию
(справа).
А что будет в третьем порядке теории
возмущений? Легко сообразить, что полное
число различных процессов будет равно вось-
ми: два из них - процессы трехквантового по-
глощения и трехквантового испускания. Также
возможны процессы поглощения двух квантов
поля и испускания одного, и, наоборот, по-
глощения кванта поля и испускания двух.
Каждый из двух последних процессов описы-
вается совокупностью трех амплитуд. Все воз-
можные амплитуды процессов представлены
на рис. 11.10 и рис. 11.11.
На рис. 11.10 представлены диаграммы для процессов трехфотонного поглощения
и испускания. Им соответствуют следующие амплитуды процессов:
d/п&о х ^Ео х 4Л у_____________1________
8й3 (cont^2co)(a)ki^coY
(11.6.4)
причем знак «минус» соответствует процессу поглощения квантов, а «плюс» - испуска-
нию. При этом в множителях в знаменателе фактически стоит разница энергии перехода
в промежуточное состояние из начального и суммарной энергии поглощенных (испу-
щенных) квантов. Например, при переходе |/> ->|*> поглощается (испускается) один
квант, а при переходе |/) -> \к) -» |п) поглощается (испускается) уже два кванта поля.
Рассмотрим теперь следующую серию процессов третьего порядка (см.
Рис. 11.11). На верхних диаграммах приведены случаи, когда два кванта поглощаются и
один испускается (таких диаграмм, очевидно, гри), а на нижних - случаи поглощения
Двух квантов и испускания одного (еще три диаграммы). Соответствующие им амплиту-
ды записываются в виде:
252
lf> <i,,E lf>^
1п> rl .£ |п>И^ 6 - - |n>
1к> г<’\ lk> lk> !
. d,.E
li> li> li>
|f> dfnE
|П> dn<E
lk> dE
- О *
li>
1
\\&d*E
...
Ii> 11
Рис. 11.11. Процессы третьего порядка, соответствующие по-
глощению (испусканию) двух и испусканию (поглощению)
одного кванта поля).
d Х ^иА;Е0 X <УЪЕО ( 1 11
-----------------------х------------------------1---------------1--------------
8Й ЦбУ„, -2бУ)(^. -CD) CDni{CDti-(D) (Dni{(Dti^(D))
dfr^0 Х dnkE0 Х dki^0 ( 1 1 1
--------------------X---------------1-------------1------------------
8Й [aJjD^ - CD) (Dj^ + cd) ((Dni+2a))(£Dh+(D)J
Существенно, что здесь также необходимо учитывать интерференцию различных ам-
плитуд перехода в одно и то же конечное состояние.
Еще раз отметим в заключение, что рассмотренная техника позволяет легко пи-
сать выражения для амплитуд любого порядка многофотонности.
Задачи к Главе 11.
И1‘ —ичХТп’ НаХ0ДЯЩИЙСЯ в основном состоянии Is, воздействует моно-
ветствует пепехоплГ счастот^и Удвоенное значение которой примерно соот-
будут пои этом возб™ ~^П9 о ' главное квантовое число). Какие состояния
зации излучения ассмотРеть случай линейной и круговой поляри-
мента удобно выбпятк НИС случае линейно поляризации ось квантования мо-
* ЯВДОЛЬ ВСКТ0Ра ПОЛЯРиза^и электрического поля волны.
Р^прХне“нь: °СЬ КВаНТ0ВаНИЯ М0МСНта вдоль направления
1 L2' XPaTyZ°BaTb ПРаВИЛа °Тб0Ра ДЛЯ фотонных и четырехфотонных перехо-
‘' -3- °”, “еЛИЧИНУ Ш'1арК0ВС,<0Г<’ сдвига 1 s состояния атома водорода в поле ти-
таи-сапфирового лазера (ha, =1.55 эВ) с интенсивностью 10|4Вт/см2 Длятого же
значения интенсивности определить штапковский ' Д
114 Наоисоват! лиятям.п , .. 1 гарковскии сдвиг границы континуума.
Хессов соответствующие им амплитуды для четыхфотонных
253
Глава 12. Квантовая система в поле электромагнитной
волны- Переходы между состояниями континуума.
В предыдущих разделах мы познакомились с электромагнитными переходами
мсжл> различными состояниями дискретного спектра квантовой системы, а также пере-
ходами из дискретного спектра в непрерывный. Последние описывают процесс фо-
тоионизации, в о щем случае многоквантовый. В этом разделе мы остановимся на пере-
ходах между состояниями непрерывного спектра, индуцированных внешним полем. С
физической точки зрения такие переходы описывают процесс рассеяния частицы (элек-
трона) на некотором потенциале при наличии внешнего электромагнитного поля. По-
этому обсуждение таких переходов мы начнем с краткого знакомства с квантовомехани-
ческой теорий столкновений.
12.1. Основы квантовомеханической теории столкновений. Бор-
цовское приближение.
Рассмотренная ранее в Главе 8 нестационарная теория возмущений дает возмож-
ность рассматривать, в частности, столкновения атомных частиц друг с другом и сфор-
мулировать некоторые общие положения квантовомеханической теории рассеяния. В
данном разделе мы для простоты будем говорить о рассеянии электрона на некотором
В классической теории
столкновений вводится понятие
дифференциального сечения рас-
сеяния dcr(ff) = 2pdp как отно-
шения числа частиц dN, рассеян-
ных на потенциале на угол «9 в
элемент телесного угла
d£l = 2;rsin( «9)^.9, к налетающему
на рассеивающий центр потоку
частиц J (см. рис. 12.1):
потенциальном центре.
Рис. 12.1. К понятию дифференциального сечения рас-
сеяния частиц на потенциале конечного радиуса дей-
ствия а.
В квантовой теории мы по-
ступим аналогичным образом. Бу-
дем считать, что из бесконечности на рассеивающий центр налетает поток частиц с
энергией Е, = р‘ /2т. Такой поток частиц задается функцией
| р,) = (г, О = expjjr (р/ - £,0) О 2-1 -2)
Мы изменили здесь нормировку волновой функции по сравнению с использованной ра-
нее в Главах 1 и IО В выражении (12.1.2) волновая функция нормирована так, что задает
в пространстве поток частиц, движущихся в направлении импульса р„ причем концен-
254
трация частиц в потоке равна единице в единичном объеме. Всюду в этой главе мы бу-
дем использовать такую нормировку.
В результате рассеяния1 (взаимодействия с потенциальным центром И(г)) проис-
ходит переход из состояния | pt в некоторое другое состояние | р}. В этом смысле про-
цесс рассеяния можно описать как переход \р^ —>|р') П°Д действием оператора
описывающего взаимодействие электрона с потенциальным центром.
Мы будем рассматривать взаимодействие V(?) как возмущение и воспользуемся
развитой ранее нестационарной теорией возмущений. Следовательно, наша задача со-
стоит в том, чтобы проанализировать решение нестационарного уравнения Шредингера:
= +mV(r./) (12.1.3)
Ct
„ h2
(здесь Ho =-----V2 - оператор кинетической энергии, который и представляет собой
2т
невозмущенный гамильтониан) с начальным условием (12.1.2). Отметим, прежде всего,
что использование теории возмущений предполагает малость энергии взаимодействия с
рассеивающим центром по сравнению с кинетической энергией налетающих частиц, т.е.
V «Е = р2 /2т. Другими словами, мы отраничсны случаем рассеяния быстрых частиц.
Используя разложение функции y/(f.t) по собственным функциям невозмущен-
ного гамильтониана //(|
y/(rj) = \tp(j}4/p(rj)cl'p,
из (12.1.3) получим:
i^Cr(t)Vp(rj)d'p = \Cp(t)V(f)Vp(r,l)dip. (12.1.4)
Умножим теперь (12.1.4) на комплексно сопряженную волновую функцию какого-либо
состояния атомного состояния р< (г,t) и проинтегрируем по всей области определения
функций. Тогда, используя условие ортогональности функций iyp(r,t)
/ I \ Г fz А Л/ \
(pz|.p) = Jexp т(Р-Р/)': Р '•хехр \-(Ef-E)t =(2^S(p-p ), (12.1.5)
получим
dC . >з
Я^=1СЛР'^Р')^- <121-б)
Заметим, что по своему физическому содержанию система уравнений (12.1.6) аналогич-
на системе уравнений (8.3.5) — (8.3.6), полученной нами при описании взаимодействия
квантовой системы с полем электромагнитной волны.
1 Мы предполагаем, что на больших расстояниях от рассеивающего центра его потенциал достаточно
быстро спадает и его влияние на волновую функцию пренебрежимо мало. Оказывается, такая не выполня-
ется для кулоновского потенциала.
255
Будем решать систему (12.1.6) приближенно в рамках нестационарной теории
возмущений. Представим амплитуды вероятности С в виде ряда теории возмущений::
^=^+^'4^+..., (12.1.7)
причем каждый последующий член ряда много меньше предыдущего. В нулевом поряд-
ке малости мы рассматриваем решение в отсутствие действия возмущения. Тогда, оче-
видно.
С™(/) = (2лй)]/25(р-Д),
где р, - импульс начального состояния системы. Подставляя (12.1.7) в (12.1.6) и удер-
живая члены только первого порядка малости, получим для случая f i :
dCw „ j3 п 1
Выполняя интегрирование по времени, в первом порядке теории возмущений получаем
=4 . (12.1.8)
Полученное выражение является решением поставленной задачи и определяет амплиту-
ду вероятности перехода из начального состояния | в конечное состояние | pf в ре-
зультате рассеяния на силовом центре К(г).
При изучении рассеяния наибольший интерес представляет значение амплитуды
при t —> оо. В этом случае из (12.1.8) имеем
=4 dr =~2т
(12.1.9)
Здесь
Vpp = [^(ОехрГуСД-Pf)r}d3r= [Г(г)ехр(-^г>/3г (12.1.10)
J \п )
- матричный элемент от потенциала, построенный на координатных частях волновых
функций свободного электрона до и после рассеяния, a q = (pf -p^/h - переданный
импульс (в единицах постоянных Планка). Дельта - функция в выражении (12.1.10) вы-
ражает закон сохранения энергии - переходы возможны только в такие состояния, для
которых Ef = Еу, или р2 = р2, т.е. модуль импульса в процессе рассеяния не изменяет-
ся. Такое рассеяние называют упругим. В рассматриваемом случае величина переданно-
го импульса зависит лишь от угла рассеяния & и может быть записана в виде (см. рис.
12.2):
q = 2к sin(»9/2), к = pt /Л.
Для вычисления вероятности перехода в соответствии с общими правилами квантовой
Механики надо найти квадрат модуля амплитуды (12.1.9). Однако, в этот момент возни-
256
Рис. 12.2. Диаграмма импульсов
при упругом рассеянии.
кает формальная «неприятность»: в выражении появ-
ляется квадрат дельта-функции, что обусловлено бес-
конечной длительностью процесса взаимодействия.
Эту формальную трудность обычно преодолевают сле-
дующим образом2:
S2(Ef-Ei} = d(Ef-Ei)d(0} =
1 т/2 т
6(Ef~E!)x——- fd^-x^-E,)’
1 2тш _//2 2тиг
где Т - очень большое, но конечное время взаимодей-
ствия. Тогда для плотности вероятности перехода в
единицу времени получаем:
w
ргр,
(12.1.11)
Из выражения (12.1.11) для вероятности рассеяния в интервал конечных значений им-
пульса dpf и телесный угол d£l получаем
г г
dW(9) = Jx>„,„ip}dp/ dn = — j\vpil,
S(p}/lm - p. /2m) P'^ x dn,
(2тт)
или
dWW = \\pj- p/) x dn.
п (2яи)
(12.1.12)
Выражение (12.1.12) задает величину вероятности перехода в единицу времени. В тео-
рии столкновений процесс рассеяния принято описывать не вероятностью dW(ff), а се-
чением процесса d<j(ff). Для этого начальную волновую функцию перенормируем на
единичную плотность потока вероятности
vPl(r,t}^> J— x>EPi (rd}.
Тогда, учитывая, что -p?)p2fdpf = д/2, получим:
d<j(&} _ ш2
d£l
jV(f) exp(-iqr)d2r2.
(12.1.13)
Выражение (12.1.13) описывает дифференциальное сечение рассеяния на потенциале
К(г), полученное в первом порядке теории возмущений. В теории рассеяния такой под-
ход называют борцовским приближением. Фактически, в борцовском приближении
дифференциальное сечение рассеяния определяется образом Фурье потенциала.
2 А.С. Давыдов Квантовая механика, М. Наука, (1973).
257
Ь1Ра v может быть использовано для произвольного (в том числе,
нецентрально ^тенциэда. ® частном случае, если потенциал обладает сферической
симметрией, т.е. г 0), выражение (12.1.13) может быть упрощено. Выбирая ось
- вдоль вектора q, перепишем выражение для матричного элемента Vp/p в виде
V(^ = VP/P, = fr(r)exp(-iqr)d3 4r =
J Г(г) exp (- iqr cos 0)r2dr sin(0)dW(p = 4л j Г (г) rdr,
о q
а значит
dcr(&) 4т2 г singr
^\V(r)grdr
(12.1.14)
Интеграл в выражении (12.1.14) формально берется по всему бесконечном пространству,
а реально по радиусу действия потенциала а. Если при этом выполнено условие qa «1
(очевидно, речь идет о медленных электронах), то приближенно можно записать
dcr(S) _ 4т2
|К(г)г2б/г ,
о
(12.1.15)
то есть в области малых энергий рассеяние оказывается изотропным и не зависящим от
энергии рассеиваемой частицы3. Наоборот, для быстрых частиц (да»1) основной
вклад в интеграл (12.1.14) вносит узкий конус углов к/р.^. Вне этого конуса углов
под интегралом (12.1.14) стоит быстро осциллирующая функция singr, и интеграл ока-
зывается малым.
Интегрируя дифференциальное сечение рассеяния по углу, получаем полное се-
чение рассеяния:
(12.1.16)
J dQ.
Во многих практических приложениях кинетической теории, физики плазмы (более по-
дробно, см. Главы 15, 16, 18, 19) часто бывает нужно вычислять так называемое транс-
портное сечение рассеяния, определяемое как:
а =f(l_cos0)^^dn. (12.1.17)
J Л 2
12.2. Рассеяние на потенциале Юкавы. Резерфордовское рассея-
ние.
В качестве примера использования полученных результатов рассмотрим рассея-
ние электронов на потенциале Юкавы .
3 При этом условия применимости борновского приближения должны быть выполнены.
4 Yukawa Hideki (1907 - 1981) - японский физик - теоретик, Нобелевская премия (1949) «За предсказание
существования мезонов на основе теоретической работы по ядерным силам».
258
Рис. 12.3. Угловая зависимость дифференциально-
го сечения рассеяния на потенциале Юкавы.
;/(г) = _£-ехр(-Лг). (12.2.1)
В первом приближении это удачная
аппроксимация потенциала, описыва-
ющего взаимодействие электрона с
нейтральным атомом, параметр
а = можно рассматривать как ра-
диус действия потенциала. Вычисляя
матричный элемент
И(^ = 2A:sin(«9/2)) =
4яе2 f
------exp(-Zr)sin(^r)dr’
Я 1
получим
4 ле2
Ш = ~~2-------г- (12.2.2)
Л +q
Для дифференциального сечения рассеяния имеем (а0 - боровский радиус):
^(9) _ т2 . .2 = 4
Щ я2(Л2+<72)2 ’
(12.2.3)
Вид функции (12.2.3) для различных значений параметра ка приведен на рис. 12.3 и
наглядно иллюстрирует случаи рассеяния медленных и быстрых частиц.
В важном частном случае Л —> 0 из (12.2.2) получаем
4 ле2
^) = —(12-2.4)
Я
откуда
d<4&) .41 е4 1
dn al q‘ (pl/2т)2 sin4 .9/2 '
Последнее выражение дает дифференциальное сечение рассеяния в кулоновском поле
И(г) = -е2/г и описывается формулой Резерфорда5, полученной в классической теории
столкновений. Мы получили, что для кулоновского рассеяния квантовая и классическая
теории дают одинаковый результат для дифференциального сечения рассеяния. При
этом важно, что выражение (12.2.5) может быть получено в квантовой теории точно, вне
рамок борновского приближения.
12.3. Рассеяние электронов на атомах во внешнем электромаг-
нитном поле. Вынужденный тормозной эффект.
В данном разделе мы рассмотрим процесс рассеяния электронов на атоме (потен-
циальном центре) в присутствии поля электромагнитной волны. Эта задача принципи-
5 Rutherford Ernest (1871 - 1937) - английский физик. Нобелевская премия по химии (1908) «За проведён-
ные им исследования в области распада элементов в химии радиоактивных веществ».
259
зльно важна во многих разделах физики. Мы увидим, что в результате такого рассеяния
возникает возможность поглощения или испускания кванта поля.
Из классической электродинамики хорошо известно, что частица, двигаясь с
ускорением, излучает. Поэтому при рассеянии электронов на атомах возникает так
называемое тормозное излучение. Если такое рассеяние происходит во внешнем элек-
тромагнитном поле, то процесс излучения может стать вынужденным. Кроме того, ока-
зывается возможным и поглощение энергии внешнего поля волны (так называемый об-
ратный тормозной эффект). В дальнейшем оба упомянутых процесса - вынужденное
тормозное испускание и обратный тормозной эффект мы будем называть вынужденным
тормозным эффектом (ВТЭ). Наша задача в данном разделе — построить квантовомеха-
ническую теорию ВТЭ. Сопоставление с классической теорией ВТЭ будет рассмотрено
в Разделе 17.1.
Как и раньше, будем считать, что электрон рассеивается на некотором потенциа-
ле К(г), который мы будем рассматривать как возмущение. Такое приближение накла-
дывает дополнительные ограничения на параметры воздействующего поля. Действи-
тельно, в таком подходе мы не учитываем воздействие поля на атомные электроны, ко-
торое может приводить к ионизации, возбуждению или поляризации атома. Будем также
считать, что воздействие поля электромагнитной волны на электрон можно описать в
электрическом дипольном приближении. В данном разделе нам будет удобнее восполь-
зоваться рА -калибровкой для описания взаимодействия квантовой системы с внешним
электромагнитным полем. Считая поле достаточно слабым, оператор взаимодействия
представим в виде:
тс
где р - оператор импульса, A(t) - векторный потенциал поля электромагнитной волны.
Мы не будем учитывать квадратичную по векторному потенциалу добавку к оператору
взаимодействия, которая в рассматриваемом ниже случае несущественна. В дальнейшем
мы полагаем A(f) = Ао sin(ftX).
Уравнение для эволюции электрона запишем в виде:
+К(г) + Й'(г,^.О. (12.3.1)
dt
где как и раньше Н =-—V2 - оператор кинетической энергии. Начальное условие
запишем в виде (12.1.2). Раскладывая решение задачи (12.3.1) по собственным функциям
невозмущенного гамильтониана Нй
y/(f,t) = jCp(t)i//p(r,t)d3p,
получим систему уравнений для коэффициентов разложения СДг) в следующем виде:
Л = 1СР (р, |И(Р) + р) (12.3.2)
260
Легко видеть, что в первом порядке теории возмущений рассматриваемые нами как ма-
лые поправки К(г) и JV(r,t) изменяют состояние электрона независимо друг от друга.
При этом рассматриваемое возмущение V(/*) описывает процесс рассеяния, а слагаемое
позволит описать воздействие поля волны на свободный электрон. Очевидно,
влияние электрического поля волны на процесс рассеяния можно получить лишь во вто-
ром порядке теории возмущений. Используя результаты, полученные в Главе 11, ддя
амплитуды вероятности перехода в некоторое конечное состояние во втором порядке
теории возмущений можно записать:
(12.3.3)
где амплитуда есть (см. выражение (12.1.8))
с"’(/) = 4 j' lf'! +р''
(12.3.4)
Подставляя (12.3.4) в (12.3.3) и выполняя интегрирование по времени, получим:
1 j3 ( V W
. \ 1 I Г “ Р Р,Р РР.
й (2лй)1/2 f (2лй)’ [ Е - Е, - ha)
W V 1
PfP рр, 1
£-Е,. )21
(12.3.5)
-(E/-Ei-hco)t dt.
\.h J
Здесь введены следующие обозначения
Vp(p = f^('“)exp(^(p-pA)rVr,
у
_ fGV) jexpf_ 1 (- pyузг = £(4^) x (2^)3_ p )
me J V й ) me }
(12.3.6)
(12.3.7)
При записи (12.3.5) учитывались только слагаемые, соответствующие воздействию на
квантовую систему сразу двух возмущений К(г) и FT(f,r); вторые порядки, соответ-
ствующие только упругому рассеянию и воздействию поля на свободный электрон опу-
щены. Также следует иметь в виду, в (12.3.5) записаны только слагаемые, соответству-
ющие временному множителю ехр(—icut^, входящему в зависимость векторного потен-
циала от времени. По аналогии с записанным выражением легко записать еще два слага-
емых, соответствующих множителю exp(zTar). Как будет видно из дальнейшего, запи-
санные слагаемые описывают процесс поглощения кванта поля при рассеянии электрона
на атоме, а опущенные нами - процесс испускания.
Вычисление интеграла по импульсам в (12.3.5) с учетом (12.7) проводится эле-
ментарно:
С| +тАгК Ы>> -• (,23-8)
' h (Irfi)1 Imcy-hco Ef-E^ ' J
261
Поскольку входящий в полученное выражение интеграл дает дельта-функцию, соответ-
сТВуюшую закону сохранения энергии Ef = Ej +ha>, и учитывая, что амплитуда элек-
трического поля волны Ёо = а^/с, перепишем (12.3.8) в виде:
С',2’(/ -> оо) = 2л- —~gi2
2mW (2лй)3/2
х 8(Ef - Е. - йбу).
(12.3.9)
Таким образом, полученное выражение задает амплитуду вероятности перехода
IA)-ИАа) пРи рассеянии электрона на потенциальном центре в присутствии поля
электромагнитной волны с поглощением кванта йсо. Повторяя рассмотренную ранее
процедуру перехода от вероятности перехода | Д) —> | Д- к сечению дифференциально-
го рассеяния, получим:
= (eE0(pf-p.)^ xPj_* т2
dfl 2mhaj2 J Х р. Х 4тг2Й4
|к(г)ехр(-/<Д)<73г ,
(12.3.10)
где р2 - р2 ±2mha>, при этом «плюс» («минус») соответствуют процессам поглощения
(испускания) кванта поля.
Выражение (12.3.10) есть общее выражение для сечения однофотонного вынуж-
денного тормозного эффекта, полученное в низших порядках теории возмущений по
рассеивающему потенциалу и по взаимодействию с полем электромагнитной волны. По-
следний сомножитель в (12.3.10) по своей структуре полностью эквивалентен (12.1.13) и
потому иногда интерпретируется как дифференциальное сечение упругого рассеяния.
Тогда величина
«' = Кй/2?
(здесь Npfpi
~Pi)
mhco2
- так называемый параметр многоквантовости) может быть
интерпретирована как вероятность поглощения (испускания) кванта при рассеянии. В
этом смысле говорят, что сечение ВТЭ факторизуется на сечение упругого рассеяния и
Рис. 12.4. Диаграмма импуль-
сов при рассеяния электрона
на потенциале с поглощением
кванта поля.
сомножитель, определяющий вероятность поглощения
(испускания) кванта. При этом, как и следовало ожидать,
в первом порядке теории возмущений по взаимодействию
с полем волны величина этой вероятности оказалась про-
порциональной квадрату поля, т.е. интенсивности излу-
чения.
Заметим, что параметр многоквантовости зависит,
в том числе, и от угла рассеяния. При рассеянии назад (на
углы близкие к /г) параметр многоквантовости больше,
чем при рассеянии на малые углы. Это означает, что ве-
роятность поглощения кванта поля зависит от угла рассе-
яния и достигает максимума в случае <9 = тт.
Отметим, что, хотя последний сомножитель в
262
(12.3.10) и выглядиг как дифференциальное сечение упругого рассеяния, он на самом
деле нс является лаковым. Действительно, для случая упругого рассеяния величина пе-
реданного импульса </ определяется выражением (см. рис. 12.4)
Tig = yj p2t - 2/?z/;. cos .9 = д/2р2(1-COS19) = 2/?z sin(i9/2), (12.3.Ц)
где <9 - угол рассеяния. В случае рассеяния с поглощением кванта поля имеем
= у1р'г + р,2 - 2р, [г cos £ = J2/?2 ((\ + mfid)/ р*)- ^\ + Imhco/p? cos"#), (12.3.12)
что не совпадает угловой зависимостью (12.3.11). В случае мягких фотонов
(Асу « р2/im) выражение (12.3.12) представимо в виде
hq = 2
2т ^- + hd)/2 sin(i9/2).
l 2т
(12.3.13)
Сопоставление (12.3.11) и (12.3.13) показывает, что в случае мягких фотонов дифферен-
циальное сечение ВТЭ с поглощением кванта действительно выражается через сечение
упругого рассеяния
da\S) _(NPfPl\ . [Ei+ha) d<y{Ei+h(ol2,&)
dQ. Д 2 J \ Ei X dQ.
причем сечение упругого рассеяния должно быть взято в точке £) + Й&>/2.
Аналогично, для случая испускания кванта найдем:
d<5~(19) _ fPfPj \р. - ha) d<y{Ei -ha>/2,<9)
dQ. 2 J XV~Д X ‘
(12.3.14)
(12.3.15)
12.4. Многоквантовый вынужденный тормозной эффект. Теория
Бункина - Федорова.
Естественно ожидать, что в высших порядках теории возмущений по взаимодей-
ствию с полем волны возникнут процессы многофотонного поглощения (испускания)
квантов поля. Оказывается, однако, что задачу о многофотонном ВТЭ проще рассмот-
реть за рамками теории возмущений по взаимодействию квантовой системы с полем
электромагнитной волны, оставаясь при этом в рамках теории возмущений по рассеива-
ющему потенциалу (т.е. в борновском приближении теории рассеяния). Такое рассмот-
рение было проведено Ф.В. Бункиным6 и М.В. Федоровым7 в 1965 году и известно как
теория Бункина - Федорова.
Прежде всего вспомним, что задача об эволюции состояния свободного электрона
в поле электромагнитной волны имеет точное решение. Это волковские состояния
рассмотренные нами в Главе 10. Тогда решение общей задачи (12.3.1) можно
6 Бункин Федор Васильевич (1929 - 2016) - советский и российский физик.
7 Федоров Михаил Владимирович (р. 1940) - советский и российский физик - теоретик.
263
’^Г^вНО)^ ° П° ПЛ°СКИМ волнам Де Бройля, а по волковским функциям
t,/'"(f,/) = exp Г
CO
r-L J_
ft о 2tn
co
(12.4.1)
вторые точно Учитывают воздействие поля волны U£. ™ «
1 «юля волны на свободный электрон
(12.4.2)
Подставляя (12.4.2) в нестационарное уравнение Шредингера (12.3.1), получим:
* I ( + С" ^~\d>P = К (Я + У(Г»^р .
(12.4.3)
Здесь Н - гамильтониан свободного электрона в поле электромагнитной волны, запи-
санный в рА - или dE - калибровке, а функция Волкова нормирована согласно условию:
Pf
^} = ^ys(p-pf).
h
Учитывая, что
т----—
dt
из (12.4.3) получим для коэффициентов разложения Cp(t):
dCп . , . . .уз
zft---- = f С (r, t) V (r) y/p (r, •
dt J PVPf V ’ 7 V >\YP v '/(2яй)3
(12.4.4)
Решая эту систему уравнений в первом порядке теории по рассеивающему потенциалу, с
с учетом того, что С^0)(/) = (2лй)3/2^(р-Д) найдем:
(12.4.5)
где y/(p}(r,t) - начальное волковское состояние электрона до рассеяния, также нормиро-
ванное на одну частицу в единице объема.
Проанализируем матричный элемент атомного потенциала (12.4.5), построенный
на волковских волновых функциях. Легко видеть, что этот матричный элемент имеет
вид:
|К(р)|= JV(r)exp(-iqr)d3r хI(t) = V(q)*l(Z) ,
(12.4.6)
Че q = . переданный импульс, a 1(f) есть некоторая функция времени. За-
стим также, что вычисление матричного элемента (12.4.6) приводит к одинаковому от-
ветУ в рА - и dE - калибровках.
Остановимся теперь на вычислении временной части интеграла (12.4.6).
264
е р-
— Ьо sin a)t
со
( \2\
в -
Д — Ео sin ах dt
У а ) ) )
eE0(pf-pi)
тсо
(12.4.7)
t + ia cos cot exp(-ia).
Здесь
mhaP
Вспоминая, что
exp (z a cos cot) = (/)” Jn (a) exp (-in cot),
(здесь J n(a) - цилиндрическая функция Бесселя) перепишем выражение (12.4.7) в виде:
х ' ( D2
7(Z) = exp(-za)^(z)V„(a)exp
п\ 2т
п=-
Pi
2т
-nhco t •
(12.4.8)
Тогда вычисление интеграла по времени в (12.4.4) в пределе t —> оо дает:
2
п2 „2
Pf Pi
2т
I
-7 J £(0Ч(«)ехр 7 t dt = -2m^(i)nJn(a)S
n)J ]Ji(2m 2т ) J \2т
— rihco .
Полученный результат показывает, что при упругом рассеянии в присутствие поля излу-
чения энергии электронов до и после рассеяния связаны соотношением
^ = ^- + пЬсо, и = 0, ±1, ±2,... (12.4.9)
2т 2т
т.е. в процессе рассеяния электрон может поглощать или испускать различное количе-
ство квантов. В частности, случай п = 0 соответствует упругому рассеянию в поле,
п = ±1 - поглощению (испусканию) одного фотона, п = ±2 - двух фотонов, и т.д. Для
вычисления вероятности надо найти квадрат модуля полученной амплитуды. Этот во-
прос и возникающая проблема, обусловленная необходимостью интерпретации квадрата
d - функции решается также, как и в разделе 12.1. В результате для вероятности перехо-
да Pt Р/ получим:
с '
- = = (12.4.10)
Как и в предыдущих разделах вместо вероятности нам удобно ввести величину диффе-
ренциального сечения рассеяния вынужденного тормозного эффекта:
da(±n\&)
сК1
' eEQ(pf-Pi)
mhco2
Pf т2
х-^-х—
Pi 4л-2Й4
j V(r)exp(-iqr)d2r
(12.4.11)
265
„..ueM последнее слагаемое в (124 in ™ с
при4 v • . 11) по структуре аналогично выражению для бор-
цовского дифференциального сечения в теории рассеяния.
Отметим еще раз, что полученный результат является точным с точки зрения уче-
та взаимодействия сво одного электрона с полем электромагнитной волны и потому
учитывает электромагнитные переходы в любом порядке многофотонности. Однако, он
основан на борновском приближении по рассеивающему потенциалу, т.е. мы предпола-
гаем, что рассеиваемый электрон является быстрым. Это условие накладывает дополни-
тельное ограничение на величину поля: с ростом интенсивности излучения возрастает
вероятность испускания большого числа квантов, что может приводить к нарушению
условий применимости борцовского приближения.
Фундаментальный результат, полученный нами, заключается в том, что в рамках
теории Бункина - Федорова дифференциальное сечение рассеяния электрона на атомном
потенциале в присутствии поля электромагнитной волны факторизуется на два сомно-
жителя, один из которых определяется параметрами потенциала и может быть интерпре-
тирован как борновское дифференциальное сечение рассеяния, а другой (квадрат функ-
ции Бесселя) - задает вероятность поглощения (испускания) определенного числа кван-
тов. При этом аргумент бесселевой функции
N -CboiPf-PJ
р,р' mhco1
есть не что иное как введенный выше параметр многоквантовости (см. раздел 12.3), ко-
торый определяет область применимости теории возмущений. В случае, если N «1,
вероятности многофотонных процессов малы, и доминируют процессы однофотонного
поглощения (испускания), в случае N' > 1 оказываются существенными процессы
многофотонного поглощения (испускания). При этом, поскольку
Л„(а) = (-1)яЛ(а),
вероятности и поглощения и испускания п квантов описываются формально одним и
тем же выражением. Следует, однако, иметь в виду, что параметр многоквантовости,
стоящий в аргументе функции Бесселя принимает различные значения для случая ис-
пускания и поглощения фотонов даже при одинаковой геометрии рассеяния. Поэтому
эти вероятности различны.
Рассмотрим этот вопрос несколько подробнее. Пусть параметр многоквантовости
удовлетворяет условию NptP «1 Учитывая разложения функции Бесселя в ряд при
малых значениях аргумента (см. Справочные материалы).
(12.4.12)
находим, что дифференциальное сечение рассеяния остается таким же, как и при отсут-
ствии поля сечение однофотонного поглощения/испускания определяется уже получен-
ной нами в рамах теории возмущений формулой (12.3.10). Оказывается, учет многофо-
тонных процессов с использованием (12.4.12) есть ничто иное, как решение задачи о
266
многоквантовом ВТ ) в высших порядках теории возмущений, область применимости
которой как раз и определяется условием /V « I.
Для качественного анализа
выражения (12.4Л) в области
больших (NpfPt > 1) значений па-
раметра многоквантовости вспом-
ним еще одно свойство функций
Бесселя, рассматриваемых как
функции порядка (см. рис. 12.5):
max {.7п (а)} ~.7/«), (12.4.13)
п
т.е. максимального значения
функция Бесселя достигает при-
Рис.12.5. Цилиндрические функции Бесселя как функ-
ции порядка для значений аргумента а = 3 и а = 10.
мерно при числе поглощенных
квантов равном параметру много-
квантовости.
Отметим, что параметр многоквантовости зависит не только от величины напря-
женности электрического поля волны и энергии рассеивающегося электрона, но и от
взаимной ориентации векторов Е и угла рассеяния. Например, в случае коллинеар-
ности векторов , Е очевидно, что параметр многоквантовости больше при рассеянии
в заднюю полусферу, чем при рассеянии на малые углы. При этом, эта разница тем
больше, чем больше число поглощенных квантов. Значит, поглощение большого числа
квантов происходит преимущественно при рассеянии назад.
Полученные нами выражения для дифференциального сечения рассеяния элек-
тронов на атомах (молекулах) во внешнем электромагнитном поле являются основой со-
временных физических теорий поглощения электромагнитного излучения в плазме, в
частном случае мягких квантов (Д » riheo) для дифференциального сечения п - кванто-
вого поглощения можно записать:
da{±n\Ei,S)
d£l
\ Е;±пйо) da-(Ei ±nha>/2,&)
)X X dQ
(12.4.14)
Здесь der/dCl - борцовское дифференциальное сечение рассеяния, которое на практике
часто заменяют дифференциальным сечением, посчитанным за рамками борцовского
приближения, или измеренным экспериментально.
С практическим использованием последнего соотношения, связывающего сече-
ния ВТЭ и упругого рассеяния мы столкнемся в Главе 19 при рассмотрении кинетиче-
ских процессов в плазме, созданной в газовых средах лазерным излучением видимого
или УФ диапазонов частот.
Задачи к Главе 12.
12.1. Найти выражение для дифференциального сечения рассеяния во втором порядке
теории возмущений.
268
Глава 13. Фо’юиони'шция атомов.
В ДЛННОЙ 1 IJHHC МЫ pacCMOipHM переходы ИЗ дискретного спектра В континуум под
действием элскгромт ни moi о ноля. 1акис переходы представляют собой фотоионизацию
квантовой системы Мы начнем анализ процесса фотоионизации в рамках нестационарной
зеорнн возмущений. Напомним, чю 1акос рассмотрение предполагает, что электрическое
поле волны по-прежнему сушесзвснио меньше внутриатомного. При этом, как всегда, в п
- ном порядке теории возмущений возникают и - квантовые переходы, т.е. в общем
случае фотоионизация можез носить многоквантовый характер, а, следовательно, т.н.
красная граница фотоэффекта, обнаруженная в опытах по фотоэлектрическому эффекту и
являющаяся одним из наиболее убедительных доказательств квантовых свойств
излучения, носит достаточно условный характер. Если фотоионизация невозможна как
однофотонный процесс, она возможна в высших порядках теории возмущений. Однако, в
условиях применимости теории возмущений вероятность п - фотонной ионизации часто
пренебрежимо мала. Мы также рассмотрим несколько моделей фотоионизации вне рамок
теории возмущений. Во-первых, это теория Келдыша1, основанная на том, что волновые
функции свободного электрона в поле электромагнитной волны (волковские функции)
позволяют учесть точно (вне рамок теории возмущений) воздействие поля волны на
конечное состояние электрона в процессе фотоионизации. Во-вторых, это ряд моделей,
предсказавших новое интересное физическое явление - стабилизацию атома сильном поле
относительно фотоионизации. Суть этого заключается в уменьшении вероятности
фотоионизации атома (или в насыщении это величины на уровне меньшем единице) при
увеличении интенсивности излучения выше некоторого критического значения,
называемого порогом стабилизации.
13.1. Первый порядок теории возмущений. Одноквантовый
фотоэффект.
Как и раньше, будем считать, что мы знаем решение задачи на собственные
функции атомного гамильтониана. Пусть в начальный момент времени (/ = 0) система
находится в одном из состояний дискретного спектра а практике чаще всего это
основное состояние. Рассмотрим теперь случай перехода из начального состояния
дискретного спектра в конечное состояние континуума \Е) = у/Е(г) под действием поде
Е(/) = Ёо cos i£t. В первом порядке теории возмущений, полагая, что поле включается
мгновенно, для амплитуды перехода запишем:
J р I
С") (/) = / J cos(ftX) ехр( . (13.1Л)
" о
Здесь =(£-£/)/Й = (£ + //)/Л - частота перехода, /, - энергия связи (потенций
ионизации) начального состояния. Из (13.1.1) находим:
1 Келдыш Леонид Вениаминович (1931 - 2016) - советский и российский физик - теоретик.
269
C‘n(r) =
J
2Й
CXp(/(ft)fl - (i))t) - I ! СХр(/'(щ/,7 + й>)/) -1
^C0EI ~ to) Цй)® + (О)
(13.1.2)
Заметим, если энергия кванта воздействующего поля превышает потенциал ионизации
в пеРВ0М слагаемом (13,1.2) возникает полюс, который "вырезает" некоторое
значение энергии куда и пойдет переход. Второе слагаемое ни при каких условиях не
имеет "полюсной особенности, и всегда меньше чем первое. Поэтому, будем учитывать
вклад только первого слагаемого, получим:
</аЕо sin2((<ua-а>)</2)
4Л2 ((а>в - ®)/2)2
(13.1.3)
Для вычисления вероятности фотоионизации полученное выражение надо
проинтегрировать по всем возможным состояниям континуума:
^(') = J|c“Wp£. (13.1.4)
Для проведения дальнейших рассуждений будем считать, что изначально электрон
находится в 5 - состоянии. Тогда конечное состояние электрона в континууме есть
состояние с единичным моментом t = 1. Направляя ось z вдоль направления
электрического поля волны и учитывая угловую зависимость волновой функции р
состояния, мы приходим к выводу, что угловое распределение фотоэлектронов
характеризуется зависимостью ~cos20, О - угол между направлением вылета по
отношению к оси z. Выполняя интегрирование по углу вылета электрона с учетом
(r,0|cos^roo) = 1/7з , получим:
W ГЛ Е° 1 Г|а>Г /7\|2 ^V/^) j£.
(13.1.5)
где
9?(£) = е j (r)Rs (r)r3dr (13.1.6)
- радиальный матричный элемент дипольного оператора, взятый на функциях начального
$ состояния дискретного спектра y/s и конечного состояния- континуума REp. Полагая,
что матричный элемент 91(£') является плавной функцией энергии и делая замену
переменных ^ = (Е + 1,-h(d)t/2h, получим:
=
^•)2E2rfSln2^x^
4Й2 3’. е
(13.1.7)
Здесь Е* взято в точке максимума подинтегральной функции. Если энергия кванта
больше потенциала ионизации то есть £ (7^ Й<у)г/2Й <0, интеграл в
выражении (13.1.7) равен я и для вероятности ионизации в единицу времени получаем:
270
2>r|W)|42
= = ’ (13.1,8)
где энергия конечного состояния определяется выражением Е =hco—I.. Полученное
выражение представляет собой закон Эйнштейна для фотоэффекта. Если же haxl.^
интеграл (13.1.7) обращается в нуль, то есть фотоионизация невозможна. Это так
называемая красная граница фотоэффекта, обнаруженная еще в конце XIX-ого века: для
наблюдения атомного фотоэффекта необходимо, чтобы энергия кванта света превышала
энергию связи электрона в атоме.
13.2. Многоквантовый фотоэффект.
Рассмотрим теперь переход электрона из начального состояния дискретного
спектра в конечное состояние континуума в высших порядках теории возмущений. Мы
знаем, что п -ном порядке теории возмущений возможно п -квантовое поглощение. При
этом, если энергия кванта меньше чем потенциал ионизации атомного состояния, и
одноквантовый фотоэффект невозможен, может быть выполнено условие для
двухквантового (2Й<у> I,), а в общем случае - п -квантового (пйщ>//) фотоэффекта. В
этом смысле красной границы фотоэффекта не существует. Нетрудно догадаться, что
процесс многоквантового фотоэффекта требует гораздо более сильных полей, чем поля,
необходимые для одноквантового фотоотрыва электрона от атома. Поэтому в несильных
полях процессы высших порядков практически нс идут, что и проявляется в виде
существования красной границы фотоэффекта.
Вакуумная камера
Рис. 13.1. Схема опытов Делоне по наблюдению многоквантового фотоэффекта.
Потенциалы ионизации большинства атомов составляют 10 - 15 эВ, энергия квантов
излучения видимого диапазона частот ~2 эВ. Поэтому ионизация атомов оптическим
излучением возможна лишь в результате многофотонного поглощения и стала возможна
лишь с созданием лазерных источников излучения, позволивших получить в середине 60-
х годов XX века интенсивности ~10|0-1012 Вт/см2. Экспериментально многоквантовый
271
атомный фотоэффект ыл обнаружен в 1964 году Н.Б.Делонс2 с сотрудниками (см.
рис. 13 О- экспериментах, выполненных в Физическом институте АН СССР,
на6.’нодя-пась мног ©квантовая ионизация атомов ксенона в поле излучения рубинового
лазера = 1 78 эВ)- Поскольку потенциал атома ксенона равен I, = 12.13 эВ, то для его
ионизации необходимо поглощение W = [/,//&£»]+j =7 квантов поля, а вероятность
фотоионизации должна быть пропорциональна седьмой степени интенсивности
излучения. Именно такая зависимость и была обнаружена в экспериментах Н.Б.Делоне.
Позже степенная зависимость фотоэффекта от интенсивности излучения была
многократно получена для различных атомов и для различных частот лазерного
излучения.
Более подробно остановимся на описании двухквантового фотоэффекта. Пусть
энергия кванта электромагнитного излучения йсо меньше потенциала ионизации атома
tico < 11 (11 — ~Ef )• Мы видели, что в таком случае в первом порядке теории фотоэффект
невозможен. Пусть, однако, выполнено условие 2ha>> I.. Тогда оказывается возможным
переход в состояние континуума с энергией:
Е = 2ha>-I..
(13.2.1)
в результате поглощения двух квантов поля. Для амплитуды вероятности
рассматриваемого перехода аналогично выражению (11.1.9а) запишем
’(2) _ • X ' Еп^
Е " „ 4Й2
Г 1
J 4Й2 (соЕЧ-а>)
1
х t
dE' х Jexp(z(<»s -2a>-iA)f)dt.
J -Ю
Здесь, как и ранее при рассмотрении высших порядков теории возмущений, мы также
полагаем, что поле включается адиабатически медленно. При этом слагаемое с суммой
содержит переходы через промежуточные состояния дискретного спектра, а интегральный
член - описывает переходы через промежуточные состояния континуума. Вычисляя
вероятность двухфотонной ионизации в единицу времени, найдем:
W.
юп
у ^En^ni 1 _|_ f ^ЕЕ'^ЕЧ 1_______
„ 4Й2 (бУл/-й>) 4Й2 (й)£7-д?)
х Ер х 2лй,
(13.2.2)
где энергия конечного состояния определяется выражением E — 2tico—. Оказывается,
что если речь не идет о возникновении промежуточного резонанса со ® coni, второе
(интегральное) слагаемое в (13.2.2) доминирует.
Как и следовало ожидать, вероятность двухквантовой ионизации оказалась
пропорциональна квадрату интенсивности излучения. Отметим, что угловое
распределение фотоэлектронов при двухквантовом фотоэффекте уже другое. Для
Двуфотонных переходов справедливы правила отбора Дг = 0,±2. Например, если
начальное состояние электрона было состоянием с нулевым орбитальным моментом, то
Фотоэлектрон будет либо в s, либо в d - состоянии.
1 Делове Николай Борисович (1926 - 2008) - советский и российский физик - экспериментатор.
272
13.3. Нйдпорогопая ионизация атомов.
Отмстм. 'ио с формальной гочки зрения выражение (13.2.2) описывает
вероятность двххкшшговой фоюнонтацин также и в гом числе в случае, когда
одноквантовый процесс также разрешен. В такой ситуации двухквантовый фотоэффект
приводит к явлению наднороговой ионизации поглощению числа квантов сверх
минимально необходимого дня перехода электрона в континуум.
Рис.)3.2. Спектры надпороговой ионизации.
Остановимся на явлении надпороговой
ионизации атомов несколько подробнее.
Пусть фотоэффект возможен в У -том
порядке теории возмущений, т е. переход в
континуум в континуум происходит в
результате поглощения У квантов поля.
Однако, возможно и поглощение большего
числа фотонов - У +1, У+ 2,.., л,.. при
условии, что минимально необходимое для
перехода в континуум число фотонов равно
N. Это поглощение избыточного по
сравнению с минимально необходимым числа
фотонов называется надпороговым
поглощением. В условиях применимости
теории возмущений естественно ожидать, что
вероятность надпорогового поглощения мала
по сравнению с вероятностью поглощения
минимально необходимого числа квантов для
фотоионизации, причем можно ожидать, что
вероятности надпорогового поглощения
убывают с увеличением числа надпороговых
фотонов в соответствии соотношением
(Л+Л)
(13.3.1)
где п - число надпороговых фотонов.
Для экспериментального обнаружения надпороговой ионизации атомов можно
регистрировать энергии образующихся фотоэлектронов. Энергетический спектр
электронов в условиях надпороговою поглощения должен состоять из рада пиков,
отстоящих друг от друга на величину кванза ноля Лш. Именно такие спектры
фотоэлектронов были зарегистрированы впервые в 1979 году группой П. Агостини3 при
изучении ионизации атомов ксенона излучением Nd лазера (Л = 1064 им, Лее =1.17 эВ) с
интенсивностью 1012 - 1013 Вт/см2 (см. рис. 13.2). В рассматриваемом случае ионизация
происходит в результате И-квантового фотоэффекта. Поэтому пики в энергетическом
спектре фотоэлектронов соответствуют поглощению 11, 12, ... фотонов. Эксперименты
показали, что с ростом интенсивности излучения количество пиков в спектре
3 Agostini Pierre - французский физик - экспериментатор.
273
фоюэлектронов eoapaciaci, что свидетельствует об увеличении вероятности
надпоро! ового noi лощения. Существенно также, что при превышении некоторого
критического значения интенсивности (для данных, представленных на рис. 13.3 - 2.6 1012
Bi/см ) вероятное^ noi лощения избыточного количества фотонов оказывается даже
больше. >см минимально необходимого для ионизации числа квантов. При дальнейшем
росix' инюнснвносги излучения наиболее вероятным оказывается все большее количество
поглощенных фотонов. Так, при интенсивности излучения / = 4.5 1012 Вт/см2
доминируют пики, соответствующие поглощению 2-г 4 надпороговых фотонов. Более
того, оказывается, что с увеличением напряженности лазерного излучения положение
пиков постепенно смещается в область меньших энергий, хотя расстояние между ними
по-прежнему равно энергии кванта. При дальнейшем увеличении интенсивности
излучения первый пик (соответствующий N - фотонному поглощению) достигает
нулевой энергии и исчезает. Говорят, что происходит закрытие канала ионизации, а сама
ионизация становится N +1 - фотонной. Эффект закрытия каналов ионизации атома
сильным лазерным полем был обнаружен в 1988 году. При дальнейшем возрастании
интенсивности излучения может закрыться и N+1 - фотонный канал ионизации.
лазерного излучения при
фотоионизации атома сильным
полем.
В рассматриваемом случае соотношение (13.3.1)
оказывается конечно несправедливым. Несправедливым
оказывается и теоретический подход к описанию процесса
ионизации, основанный на малости отношения
напряженности поля электромагнитной волны к
внутриатомному электрическому полю. Последовательное
описание явления надпороговой ионизации требует
выхода за рамки теории возмущений и будет рассмотрено
в одном из следующих разделов.
Отметим при этом, сопоставление малости
величины поля волны по сравнению с внутриатомным
полем не вполне справедливо, если речь о переходах в
континууме. В этом случае поле надо считать сильным
если дополнительная энергия, которую электрон
приобретает в поле волны (колебательная энергия
Ее =е2Ео/4етй)2) оказывается больше чем энергия кванта
fia) f т.е. критерий сильного поля можно записать в виде:
£ = Ее/Ъсо = е2Ъ\/4тНа>3 >1.
Параметр £ называют параметром Риса4, например для
Nd лазера (йй) = 1.17 эВ) получаем область сильных полей />10” Вт/см2, что на
несколько порядков меньше внутриатомной интенсивности. Таким образом, в сильных
электромагнитных полях, когда доминирует процесс надпороговой ионизации, в
континууме заселяется набор состояний континуума вблизи энергий
Еп »(N +
(13.3.2)
4 Reiss Howard (p. 1929) - американский физик - теоретик.
274
где N - минимально необходимое число квантов для ионизаций, а п - номер
надпорогового пика. В достаточно сильном лазерном поле электронный волновой пакет
образовавшийся при фотоионизации, совершает колебательное движение в области
родительского остова. При этом возможен процесс фоторекомбинации электрона обратно
в основное состояние с испусканием кванта с энергией, кратной частоте лазерного поля
(см. рис. 13.3)
= haklk 4-1). (13.3.3)
Здесь к > ктп - минимальное целое нечетное число, превышающее (или равное) N
Существенно, что излучаются только нечетные гармоники частоты ионизующего поля.
Это обусловлено четностью атомных состояний, правилами отбора, в соответствии с
которыми четность атомного состояния меняется при переходе с излучением кванта.
Легко видеть, что состояния в континууме имеют четность, противоположную четности
начального состояния только при поглощении нечетного числа фотонов.
Детальный анализ рекомбинационного излучения показывает, что в спектре
гармоник образуется плато - определенное число гармоник характеризуется примерно
одинаковой интенсивностью излучения. На данном примере мы сталкиваемся с еще
одним механизмом возникновения нелинейного процесса преобразования частоты
лазерного поля. При ионизации газа сильным полем возможно излучение большого числа
гармоник примерно с одинаковой интенсивностью. При этом анализ такой генерации надо
проводить за рамками разложения поляризации по степеням поля. Такие задачи обычно
относят к экстремальной нелинейной оптике.
13.4. Туннельная ионизация атомов оптическим полем.
К задаче об ионизации атома полем электромагнитной волны можно подойти и с
другой стороны. Мы знаем, что если атом помещен в статическое поле, то в результате
туннельного эффекта возможен его выход из потенциальной ямы в область инфинитного
движения - ионизация атома в электростатическом поле. Можно себе представить, что
примерно также будет происходить ионизация и в переменном, но достаточно медленно
меняющемся во времени поле. Мы пока оставим в стороне вопрос, что значит "медленно
меняющее во времени" поле. Понятно, что этот вопрос неразрывно связан с понятием
времени туннелирования электрона через
потенциальный барьер. Четкого определения
этого времени нет. Поэтому вопрос о
применимости статической теории
туннелирования к высокочастотным полям
мы отложим.
Пусть, И(гл,г) есть атомный
потенциал (>1 = - совокупность
координат электрона в направлении,
Рис. 13.4. Туннельная ионизация атома в
переменном поле.
перпендикулярном действию электрического
поля волны). Тогда с учетом внешнего
переменного поля потенциал, в котором движется атомный электрон, может быть
представлен в виде
275
Г(г±,2,/) = Ko(rL,z)-eE(/)z.
(13.4.1)
jvlbi полагаем, что напряженность поля волны изменяется по гармоническому закону:
Е(/) = Е0 cos at.
В результате барьер конечной проницаемости попеременно возникает то слева от атома,
то справа (см. рис. 13.4), причем время, на которое барьер открывается, составляет
величину порядка половины периода электромагнитной волны. Если электрическое поле
является низкочастотным", то процесс туннелирования происходит практически также
как в статическом поле. Аппроксимируя потенциальный барьер треугольной формой, и
считая, что туннелирование происходит в направлении электрического поля волны,
используя выражение для вероятности туннелирования через потенциальный барьер,
полученное в Главе 2 (см. выражение (2.3.2)), мы можем получить выражение для
мгновенной вероятности туннелирования в виде (см. задачу 13.2)
w,.(/)~exp(-4Ea/3|E(0|).
(13.4.2)
J2mlj
Здесь Еа =----—
еп
- характерное значение поля внутри атома5, - потенциал ионизации.
Нам теперь необходимо провести усреднение выражения (13.4.2) по половине периода
колебаний электрического поля волны:
4ЕО
ЗЕ0 cos £
(13.4.3)
Если поле является слабым (Е0«Еа), то подинтегральная функция имеет острый
максимум, т.е. ионизация происходит лишь в узком временном интервале вблизи момента
соответствующий максимуму поля волны (£ = 0).
Проведем поэтому вычисление интеграла методом перевала. Разлагая
подинтегральную функцию в ряд вблизи точки максимума £ = 0, получим
4ЕД (1 + 472)
3£„
— ехр(-4Ео/ЗЕ0
ТС
Д Д exp(-4E„/3Ej
) У2л-уЕа
(13.4.4)
Как видно, в туннельном режиме вероятность ионизации зависит
экспоненциальным образом от амплитуды напряженности электрического поля волны (см.
Рис. 13.5). Экспериментально туннельная ионизация атомов инертных газов в поле
излучения мощного СО2 лазера (длина волны % = 10.6 мкм) впервые наблюдалась в 1985
году в экспериментах С.Л.Чина6. При этом существенно, что рассмотренный туннельный
механизм фотоиоионизации реализуется, в том числе, в инфракрасном диапазоне частот.
5 Легко видеть, что это значение напряженности по порядку величины есть как раз напряженность поля на
первой боровской орбите в атоме водорода.
6 Chin See Leang (р. 1942) - канадский физик - экспериментатор.
276
Заметим, что при помещении атома в поле (в том числе высокочастотное)
происходит понижение высоты барьера (см. рис. 13.4) и при превышении некоторого
порога ионизация становится надбарьерной (см. задачу 13.8).
Рис. 13.5. Зависимость вероятности
ионизации от амплитуды электрического
поля волны в туннельном режиме.
Следует заметить, что туннелирование в
высокочастотном поле тем не менее
существенно отличается от своего
статического аналога. Действительно, при
туннелировании в высокочастотном
(инфракрасном) поле на электрон, вышедший
из-под барьера, действует изменяющаяся во
времени сила со стороны электрического поля
волны, которая «толкает» электрон обратно к
родительскому центру. В результате, при
определенных значениях фазы электрического
поля волны в момент туннелирования,
электрон может вернуться к родительскому
остову и перерассеяться на нем. Можно
показать, что максимально возможное
значение энергии электрона, возвращающегося к родительскому центру, составляет
Е^ «3.17 х(7 где Uр = 4тсо2 - колебательная энергия свободного электрона в
поле электромагнитной волны. Эффект перерассеяния электрона на родительском ионе в
процессе туннельной ионизации атома в сильном низкочастотном поле излучения был
впервые рассмотрен П. Коркумом7 в 1993 году и является основой для рассмотрения
различных эффектов, возникающих при ионизации атома в сильном лазерном поле.
Например, для излучения неодимового лазера (Х = 1.06 мкм) с интенсивностью ЗхЮ14
Вт/см2 получаем, «110 эВ. Рассеяние электрона с такой энергией на родительском
ионе может приводить к его ионизации и образованию двукратно заряженных ионов,
испусканию квантов жесткого ультрафиолетового и мягкого рентгеновского излучения8.
Именно с последним процессом (тормозное испускание коротковолнового излучения при
перерассеянии электрона на родительском остове) связан прогресс в генерации импульсов
аттосекундной длительности (1 ас = 1018 с). Впервые импульсы аттосекундной
длительности были получены в 2001 году. В настоящее время длительность предельно
короткого электромагнитного импульса составляет 67 ас9 *.
В заключение этого раздела обсудим на качественном уровне возможность
описания статической формулы (13.4.2) для описания явления туннелирования в
переменном поле. Будем исходить из предположения, что за время движения электрона
через барьер т его форма не должна существенно измениться, т.е. сот «1. Считая, что
электрон движется со скоростью v~ jljm, а ширина барьера а-Ц/еЕ^, получим
7 Corkum Paul (р. 1943) - канадский физик - экспериментатор.
8 Этот процесс испускания жестких квантов по своей сути эквивалентен процессу испускания гармоник при
надпороговой ионизации атома. Их единая физическая суть будет рассмотрена позже.
9 Импульс такой длительности получен в 2012 году в университете Центральной Флориды группой проф-
Чанга.
277
г ~ 7^^ЛЕо • Тогда условие
записывается в виде
применимости
теории статического туннелирования
еЕ0
(13.4.5)
13.5. Теория фотоионизации Келдыша.
В предыдущих разделах мы рассмотрели два подхода к задаче об ионизации атома
в сильном электромагнитном поле: один из них - многоквантовый фотоэффект, другой -
туннельная ионизация. Если в рамках теории возмущении говорить о многоквантовом
фотоэффекте имеет смысл в достаточно высокочастотных полях, когда число
необходимых для вырывания электрона их атома сравнительно невелико, то туннельный
механизм, обобщая формулы статической задачи о туннелировании, наоборот, требует
низкочастотного поля.
Казалось бы, эти два механизма существенно разные по своей природе и при
определенных значениях параметров могут конкурировать между собой.
В этом разделе мы рассмотрим основные положения теории ионизации атомов в
сильном поле, предложенной Л.В.Келдышем в 1964 году, которая вне рамок теории
возмущений по взаимодействию электрона с полем волны рассматривает переходы атома
из дискретного спектра в континуум. В рамках этого подхода мы увидим, что туннельная
ионизация и многоквантовый фотоэффект - это два разных предельных случая такого
перехода.
Как и раньше, будем считать, что мы умеем решать задачу на собственные
значения и функции атомного гамильтониана::
^о^„(г) = (^ + ^(г)Х(г) = ^„(г) (13.5.1)
Будем полагать, что в начальный момент времени атом находится в основном состоянии
V.,(г), его потенциал ионизации /, = -Ео. Эволюция атома в поле волны описывается
Л 1 6
нестационарным уравнением Шредингера
Л = Hap(r, t) - t), (13.5.2)
dt
В дальнейшем мы полагаем, что Ё(/) = Ёо cos at .
Будем искать решение уравнения (13.5.2) в виде:
( i "l
^(г,/) = ^(г)е>Ф --Egt\ + 3y/(ri),
(13.5.3)
ГДе ^(г,/) - волновая функция электрона в континууме. Мы полагаем, что все
Возбужденные состояния в дискретном спектре остаются ненаселенными. Также будем
СЧИтать, что [|<5^(г,/)|2d3r «1. Подставляя (13.5.3) в уравнение (13.5.2), получим:
(13.5.4)
278
Волновую функцию электрона в континууме представим в виде разложение по функция
Волкова:
IM
=j ср (/>;'’ (г, Об/3 р •
Учитывая, что функции Волкова удовлетворяет уравнению
ду/;,Г)(оо
dt
(13.5.5)
(13.5.6)
из (13.5.4) получаем:
(13.5.7)
Здесь первое слагаемое описывает переход из начального связанного состояния в
состояния волковского континуума, это и есть процесс фотоионизации. Второе слагаемое
в (13.5.7) описывает переходы между различными состояниями волковского континуума,
обусловленные взаимодействием с атомным потенциалом. С физической точки зрения это
и есть эффект перерассеяния фотоэлектрона на родительском ионе. Мы ограничимся
сейчас рассмотрением только прямого процесса фотоионизации:
dC(t)
ih—^
dt
(13.5.8)
откуда
z г (i
С (?) = — dt' cos cot'x exp — If
Вычисление интеграла (13.5.9) позволяет вычислить |С(t)\
фотоэлектронов по импульсам и полную вероятность ионизации
^.(?) = {|С/?)|2б/3р.
(13.5.9)
распределение
(13.5.10)
Проанализируем матричный элемент (ifp(r,f)dE0 ^g(r)^ • Его координатная часть есть:
9?(г) = еЕ0
/ _ А
-P(t)r y/g(r)d r = eE(}x
Л 7
Здесь P(f) = p-(eEja>)s\ncot - импульс электрона в континууме - фактически
определяется фурье-образом начального связанного состояния электрона в атоме.
В свою очередь, временная часть матричного элемента
^')(г,/)б/Е0</к
есть
3(Z) ~ cos cot х exp — /7 х
IЙ J
- Г ——gE0 sin cot /со) Вычисляя интеграл в экспоненте,
hl 2т J
получим с точностью до несущественного фазового множителя:
279
/^(r/fek^-cosftxxexpfif/ +_£2eo , P2\ eE0P , e2Ej . o J
И'' 1 1 / ь ' 7ZTT + T~ t------— coscot---^sin2cot .
' <4 4m co 2m) mco Kmco2 )
Легко видеть, что матричный элемент а Др ,,z r-A а
есть периодическая функция
времени. а, следовательно, может быть разложена во временной ряд Фурье
И’(г,/)|Ж„Iv^(г)} ~ cos<иXехрАр, + -^L + pLY|ху L (р)ехр(-и<й),
IX 4«® 2'"J ।
(13.5.10)
где Ln(p) коэффициент Фурье-разложения, определяемый видом волновой функции
связанного состояния. Для амплитуды Cp(t—>оо), учитывая в (13.5.10) слагаемое,
пропорциональное cos cot, получаем:
Ср (t^)~mx ^(Ьп+] (р) + Ln_x (р)~) х //. + -^L + ^-- Ппа
п I 4wty 2т
(13.5.11)
Для расчета вероятности ионизации, чтобы избежать квадрата 8 -функции, надо
воспользоваться тем же приемом, что и в разделе 12.1. Для вероятности ионизации в
единицу времени получим
f и 2 2
^(p))“Z|(Wp) + A,-i(£))|2 *4 Л + —”*<» • (13.5.12)
27? „ 4 т со 2т )
Проанализируем полученное выражение. Прежде всего, мы видим, что при
фотоионизации преимущественно образуются электроны с энергиями
Еп = ^- = nhco-Ii--^7. (13.5.13)
” 2т ' 4тсо2
Мы видим, что спектр фотоэлектронов образует эквидистантную последовательность
пиков с интервалом энергий hco, причем в качестве эффективного потенциала ионизации
атома выступает величина
е2Е2
I=I,+ XX. (13.5.14)
4т со
Фактически, выражение (13.5.13) предсказывает и явление надпороговой ионизации, и
эффект закрытия каналов ионизации. С ростом напряженности электрического поля
волны положение энергетических пиков смещается в сторону меньших энергий. Закрытие
первого канала ионизации, соответствующего поглощению минимального числа квантов
поля (= [/,/hcol+l), происходит при интенсивности излучения
2 2
J = (13.5.15)
8тг 2ле
Отметим, что на практике изменение энергии ионизации атома в поле волны определяется
также и изменением энергии начального (основного) атомного состояния (динамический
эффект Штарка), однако, как правило, штарковский сдвиг связанных состояний
280
существенно меньше сдвига границы континуума. Исключение составляют лишь
ридберговские состояния, штарковский сдвиг которых совпадает со сдвигом границы
континуума.
Для определения полной вероятности ионизации выражение (13.5.12) должно быть
проинтегрировано по импульсам фотоэлектронов. Ответ дает:
27 I
W\ - ехр-----Г(у) , Г (у) = arshy - у
I hco
2
2
Здесь
афтГ,
еЕ0
(13.5.16)
(13.5.17)
Келдыша. Заметим, что параметр Келдыша с точностью до численного
порядка единицы совпадает с введенным ранее параметром (13.4.5),
- параметр
множителя
интуитивно определяющим условие возникновения оптического туннелирования.
Рассмотрим важные частные случаи.
1) Параметр Келдыша у »1. Как видно, этот случай реализуется для высоких частот и
относительно слабых полей. Учитывая, что у2=///(2£е) (Ее = e2E2J 4тсо2 -
колебательная энергия электрона в поле волны), получаем, что в рассматриваемом случае
7(. »Ее, т.е. штарковский сдвиг границы континуума несущественен. Тогда, учитывая,
что
arsh у = 1п(у + 7/2 +1) * In 2/,
получим
Wt - ехр
27
hco
arsh у-у ----т
' 1 + 2/
ехр
hco
ехр(-/hco)* (4/) 1,/Гм
Учитывая, что 4у2=2^/Ее, N = I/ha>
атома, находим:
- число квантов, необходимое для ионизации
W( ~exp(-Ij/hco)x
g2Ep
8wd?2/,
(13.5.18)
ионизации пропорциональна N -ной степени
соответствует рассмотренной выше теории
что вероятность
излучения, что
Мы получили,
интенсивности
многоквантового фотоэффекта.
2) Параметр Келдыша у «Л. Поскольку 7 =It+Ee =Ii(l + Ee/Ii) = Ie(l + ^
arshy «у-у3 /б +..., Г(у) ® 4/ /3 +...., имеем:
2
27 .
W: -exp - arshy-y
hco
ехр -
hco 3
_ а
ЗЕП
2
/ = ехр -
(13.5.19)
281
где Е<-= "TF-
(13.4.2) характерное значение напряженности поля внутри
ат()М>1- Как | '*. ’ три у << | вероятность ионизации нс зависит от частоты, и
рппсывастся формулой для туннельной ионизации.
01 мет нм. что разложение параметра Келдыша в ряд до более высокого порядка
малости дзет.
г 4 Е А
И' -exp
\ ь0
(13.5.20)
В туннельном пределе вероятность ионизации растет с увеличением частоты излучения.
Таким образом, теория Келдыша единым образом описывает процесс
фотоионизации атома и показывает, что характер этого процесса различен в различных
частотных диапазонах и определяется значением параметра у (параметр Келдыша). В
области у «1 можно говорить о туннельной ионизации атома в оптическом поле, при
у »1 ионизация происходит как многоквантовый фотоэффект.
В настоящее время теория фотоионизации Келдыша, известная также как
приближение сильного поля (SFA - Strong Field Approximation), активно развивается и
является основой современных исследований по ионизации атомов в сильных
электромагнитных полях. В частности, учтены кулоновские поправки к волновым
функциям электрона в континууме, а также эффект перерассеяния электрона в
континууме на родительском атомном остове.
13.6. Эффект стабилизации атомов в сильном поле излучения.
Суть эффекта стабилизации заключается в повышении устойчивости атома по
отношению к ионизации при превышении интенсивности излучения некоторого
порогового значения. Вероятность ионизации начинает убывать, или выходит на
некоторое стационарное значение с ростом интенсивности излучения. Понятно, что
эффект стабилизации должен рассматриваться вне рамок теории возмущений и учитывать
существенную перестройку
внешним полем атомных
состояний.
Мы рассмотрим два
механизма стабилизации - стаби-
лизацию Крамерса - Хеннебергера
(ее еще называют адиабатической
стабилизацией) и интерференцион-
ную стабилизацию.
1) Адиабатическая стабилиза-
ция.
Для понимания сути эффекта
представим себе, что атом
находится в очень сильном
высокочастотном поле,
Связанный электрон
\
Кулоновский I
потенциал
Сильное лазерное поле:
Свободные осцилляции
Совместное воздействие
на электрон кулоновского
потенциала и поля волны
Крамерса
Хеннебергера
Рис. 13.6. Формирование атома Крамере» - Хеннебергера. превышающем напряженность
282
поля внутри атома. Тогда в уравнении Шредингера, описывающего временную эволюцию
такого атома
/7? ° 1') = - ^- V V + И,/)-tZE(Z>(r,Z) (1з 6 п
dt 2т }
в нулевом приближении можно "выкинуть" член, описывающий взаимодействие
электрона с атомным остовом. Электрон будет совершать почти свободные колебания.
Качественно стабилизацию можно объяснить тем, что при больших значениях
напряженности электромагнитного поля амплитуда колебаний электрона, вызванных этим
полем, существенно превышает характерный размер исходной атомной системы. Поэтому
электрон можно считать практически свободным, что приводит к невозможности
поглощения (или испускания) энергии от поля и уменьшению вероятности ионизации.
Именно малая связь с атомным остовом в максимуме лазерного импульса, характерная
для почти свободного электрона, приводит, в конечном счете, к неионизации системы.
Это проявляется в значительном восстановлении заселенности исходного атомного
состояния к концу лазерного импульса. Качественно, такая ситуация представлена на рис.
Рис. 13.6. Движение электрона в рассматриваемом случае удобно изучать в
неинерциальной системе отсчета, связанной со свободно осциллирующим в поле волны
свободным электроном. В этой системе координат10 атомный электрон "видит"
осциллирующий атомный потенциал:
|-f + 0, (13.6.2)
d
где re (t) есть решение уравнения
z/2r
^-> = еЁ(/)/т, (13.6.3)
at
a E(z) = Ео cos ах есть осциллирующее электрическое поле лазерного импульса. Считая
поле линейно поляризованным и направляя ось z вдоль вектора поляризации, перепишем
(13.6.2) в виде:
/Й——= [т + V(r -eza(l-cos (f, t), (13.6.4)
dt
где а = ёЕй1та>2 - амплитуда колебаний свободного электрона в поле электромагнитной
волны. Отметим, что при мгновенном включении поля точка, относительно которой
качается атомный потенциал, смещена на величину а относительно начала координат.
Таки образом, задача об атоме в поле электромагнитной волны сводится к задаче об
атомном электроне в осциллирующем потенциале. Нетрудно видеть, что потенциал,
стоящий в уравнении (13.6.2) есть периодическая функция времени, а, следовательно,
может быть разложен в ряд Фурье:
V(r-eza(l- cos я#)) = Г(К/У) (г±, z) + (r±, z) exp (ш <yf). (13.6.5)
л*0
10 Это так называемая система координат Крамерса (по имени Крамерса Х.А. (1894-1952) - нидерландского
физика -теоретика).
283
Нулевая гармоника разложения
(КН 1
Г )0*±,z) = jK(F-e2a(l-cos<ar))df (13.6.6)
о
представляет собой некоторый новый статический потенциал (потенциал Крамерса -
Хеннебергера), а совокупность гармоник K„(r±,z)exp(w6X)
। 2лг/<у
PZ"(,±’Z) = 2^ 1Г^~^а0~СО8^))ехр(-ш^)47/ (13.6.7)
может быть рассмотрена как
возмущение, которое вызывает
переходы между стационарными
состояниями атома Крамерса
Хеннебергера (КХ). В сильных полях,
соответствующих режиму
стабилизации, потенциал КХ имеет
характерный двухъямный характер
(см. Рис. 13.6, 13.7), причем расстояние
между ямами равно удвоенной
амплитуде колебания свободного
электрона в поле электромагнитной
волны. Как результат, стационарные
состояния атома в потенциале КХ
приобретают дихотомическую
структуру, когда в основном состоянии
плотность вероятности оказывается
делокализована по обоим ямам (см.
Рис.13.8).
Преимущество выбранного
базиса проявляется в том, что в случае
сильных полей гармоники КХ
Рис. 13.7. Характерный вид потенциала Крамерса -
Хеннебергера. Расстояние между максимумами
равное удвоенной амплитуде колебаний свободного
электрона. Для лучшей визуализации нарисована
поверхность -K^(Fx,z).
потенциала можно рассматривать как возмущение, и реальное поведение системы
незначительно отличается от решения задачи со стационарным потенциалом КХ
^.z).
Расчеты показывают, что явление стабилизации возникает при
интенсивностях излучения превышающих пороговое значение, определяемое из условия
a = eEjin(D2 >а0
(13.6.8)
Кроме того, говорить о почти свободных колебаниях атомного электрона в поле волны
можно лишь для в случае, когда I~ потенциал ионизации атома Крамерса -
Хеннебергера).
Интересно отметить, что если речь идет о потенциале конечного радиуса действия
(такие потенциалы описывают отрицательные ионы в одноэлектронном приближении), то
число связанных состояний в КХ потенциале может нарастать с увеличением лазерной
интенсивности. Действительно, обычно отрицательные ионы характеризуются
284
Рис. 13.8. Структура волновой функции
электрона в атомном потенциале и в
двухямном потенциале КХ. Расстояние
между максимумами волновой функции в
КХ потенциале примерно равно удвоенной
амплитуде колебаний свободного электрона.
единственным связанным состоянием, а
перестройка атомного потенциала в КХ
потенциал может привести к появлению
дополнительных состояний в дискретном
спектре.
2) Интерференционная стабилизация.
Этот механизм был впервые предсказан и
изучен М. В.Федоровым и может
реализовываться при ионизации
высоковозбужденных (ридберговских).
Мы знаем, что у любого атома
положение высокоэнергетичных уровней
описывается формулой En=-Ry/n2, где
п » 1 - главное квантовое число, значение
которого в лабораторных экспериментах
может достигать
Расстояние между соседними ридберговскими уровнями есть
нескольких десятков.
Д = Е.„ - Е, = 2Яг/„’ .
Для определенности выделим какую либо
пару соседних состоянии (их энергии
обозначим Еп и ЕяЧ) и будем считать,
что в начальный момент времени атом
находится в одном из них. Будем считать,
что а атом воздействует поле с частотой
а>, причем tico»А. Каждое их этих
состояний связано с континуумом
однофотонным переходом. В достаточно
слабых полях переходы в континуум из
этих двух состояний происходят
независимо. Однако в сильных полях в
результате когерентного перезаселения
континуума в результате рамановских
переходов А - типа и
переходов с ионизационно уширенных
уровней11 в одни и те же состояния
континуума происходит интереференция
Рис. 13.9. Интерферирующие переходы в
континуум.
последующих
” В электромагнитном поле энергетические уровни атома несколько размываются. Это следствие
соотношения неопределенностей для энергии - времени: энергетическая ширина уровня Г определяется
обратным временем его жизни, т.е. скоростью ионизации. В результате ридберговские уровни могут
оказаться перекрытыми. Это в свою очередь делает возможными двухфотонные переходы Л - типа, в
которых один фотон поглощается атомной системой, а другой - излучается, что приводит к когерентному
перезассп^нию совокупности близкорасположенных ридберговских состояний.
285
амплитуд, которая может носить деструктивный характер, что приводит к подавлению
процесса ионизации.
Действительно, рассмотрим квантовую систему, состоящую из двух близко
расположенных по энергии состояний и континуума. Полная волновая функция такой
системы может быть представлена в виде:
V/О',/) = ^Ск (/)exp(-z£\///j)^(f) + ^CE(t)cxp(-iEt/ti)y/F(r)dE. (13.6.9)
Подставляя (13.6.9) в нестационарное уравнение Шредингера, аналогично (8.3.5) и (8.3.6)
получим систему уравнений для амплитуд:
}exp(/®21z) + |с£(|К2|Й>£)ехр(-/®£2()<Ж, (13.6.10)
'7i^L = C2(v'iWv'2)exp(-I®:,l/) + jc£((/]|»'|(1/£)exp(-/®£l/)Iy£, (13.6.11)
ffl^ = ZCX^M^)e4>('®&O + fC£.(!/£|lF|(y£.)e;q)(/®££.OJ£'. (13.6.12)
Здесь W = —dE0 cos ax. Полагая что со»са2Л, мы можем пренебречь сильно
нерезонансными переходами между состояниями дискретного спектра. Пренебрежем
также переходами между состояниями континуума. Тогда получим:
= f ^(^ul^ol^JexpH^u -co)t)dE, (13.6.13)
at 2J
=_1 ^Ся(|/£|йЕ0|^я)е2ф(|(®э, -а>У). (13.6.14)
dt 2 Л=12
Будем искать решение системы уравнений (13.6.13), (13.6.14) в виде:
С„ = Ап exp(iEnt/fi),CE = ЛЕ ехр(/(£ -hcd)t/h). (13.6.15)
Получим
/йД,-ЕпАп = -(E0/2)J AE(f)dnEdE, (13.6.16)
ihAE-(E-ho)AE=-(E()/2)^AAt)dEtl. (13.6.17)
n-1,2
Запишем формальное решение второго из полученных уравнений в виде:
Л£(/) = -^ехр(-/(£’-^^)/Ж-Ео)|е^(/(£”;’")/'/^ЕЛ^/'^Л'- (13.6.18)
Подставляя (13.6.18) в (13.6.16), получим:
ihAn-EnAn =___^Е2|^£^я£|^'ехр(/(Е'-Лй))(/'-О/Л)^А(^)^£>1 • (13.6.19)
Мы будем считать, что матричный элемент dEn есть плавная функция энергии и потому
может быть вынесен из под знака интеграла по энергии в некоторой точке, например,
£ = Йй)-|Е,|.
286
f
Тогда с учетом (<//•. ехр(/(/< /ко)(/’ /)/Л) - 2flW ~') имеем
О
М л;л,- + 4/Л;>4).
~ ~i 1 'о(<А/г.i^i ^ir.^Ei^2)
03.6.20)
(13.6.21)
(13.6.22)
Таким образом, мы получили систему уравнений для амплитуд населенностей состояний
дискретного спектра, взаимодействующих между собой через континуум12. Будем
считать, что diF - d2F = D. Тогда, тогда вводя обозначение Г =/г|£)|2 EjJ/л .
ионизационная ширина, перепишем (13.6.20) в виде
iAt-(E,/^A, =-/(Г/2)(4+А).
,Л:-(£г/Л)Л=-/(Г/2)(4+Лг)
Будем искать решение системы уравнений в виде:
Я„(/) = ЯПехр(-гХ), и = 1,2.
Тогда получим однородную систему уравнений для коэффициентов В, и В2
(Г-(Е,/Ю)В, = -£(Г/2)(В,+Вг\
(/-(£2/й))Я; =-'|(Г/2)(5,+BJ
нетривиальное решение которой возможно, если ее определитель равен нулю:
(/ - (£, /»)Хг - (Е, /f») +i у (2/ - (£, + Е2 )/») = 0.
Решение квадратного уравнения (13.6.23) дает
1 _1 ^1 + ^2 ± 1(^2 ~^1)' р2
Ч » V л= J-
При Г<<(Е2 имеем
f=Ejh-ir/2t Г ^Е2/П-1Г/2,
(13.6.23)
(13.6.24)
т.е. в слабом поле мы получаем два несмещенных уровня энергии с временем жизни
~1/Г. С увеличением интенсивности воздействующего поля ситуация меняется. При
Г »(Е2 -E^/fi (перекрытие ионизационных ширин) из (13.6.24) находим:
£dA_/r
2Л 2Л 4А2Г
12 Процедура получения таких уравнений была предложена М В. Федоровым (1989) и известна
адиабатическое исключение континуума.
287
Detector
|«*> ;i,z
Atom beam
Рис.13.11. Схема эксперимента по
наблюдению явления стабилизации..
Рис. 13.10. Действительные и мнимые части квазиэнергий в зависимости от ионизационной
ширины исходных состояний.
Мы получили два вырожденных уровня с энергией (Ех + Е2)12, однако, с существенно
разными временами распада: скорость распада одного из этих состояний падает с
увеличением интенсивности излучения. Это и есть эффект стабилизации атома в сильном
поле.
Графики зависимостей действительной и мнимой частей квазиэнергий
приведены на рис. 13.10 и подтверждают сказанное. Как видно, при небольших
интенсивностях излучения положение уровней примерно соответствует исходному, а их
ионизационная ширина оказывается пропорциональна интенсивности. При превышении
интенсивностью некоторого порогового значения, определяемого из условия
Г»(Е2 -Ех)/1г (т.е. из условия перекрытия ионизационных ширин), спектр атомной
системы кардинально перестраивается: формируются два вырожденных состояния, одно
из которых оказывается устойчивым по
отношению к ионизации.
Учитывая, что дипольный матричный
элемент связывающий ридберговские состояния и
континуум13 dEn ~ 1/(а//2 и /3) и
А = £„+1 -Еп -Х/п3, получаем, что пороговая
интенсивность интерференционной стабилизации
не зависит от номера главного квантового числа и
растет с частотой излучения по закону Г ~й)1(уз.
Этот закон близок к тому, который характерен для
КХ стабилизации и потому не может
использоваться в экспериментах для уточнения механизма эффекта в конкретной
ситуации.
Коротко обсудим эксперименты, в которых наблюдалось явление стабилизации
атомов в сильном поле излучения. Типичная схема экспериментальной установки
приведена на рис.13.11. Обычно формируется пучок атомов, который подвергается
User
beam
13 Такая оценка для матричного элемента получается в квазиклассическом приближении.
288
воздействию излучения лазера. Детектор анализирует состав пучка, подвергшегося
лазерному воздействию, что позволяет определить вероятность ионизации атомов, а в
ряде случаев и вероятности возбуждения различных состояний.
0.8
0.6
0.4
0.2
О
0 12 3
Так, на рис. 13.12 приведены результаты
эксперимента по ионизации ридберговских состояний
атомов бария (Z = 56), приготовленных в состоянии
6s lid ' D2. Это состояние приготавливалось в результате
двухфотонного возбуждения основного состояния атома
бария 6.у2 '50. Для этого использовался лазер на
красителе с длиной волны 553.7 нм для возбуждения
промежуточного состояния 6s6p }Р°, с последующим
возбуждением вторым импульсом на длине волны 420.39
нм состояния 6s lid ]D2. Основной ионизующий импульс
Рис. 13.12. Экспериментальное
наблюдение явления стабили-
зации атомов в сильном поле.
излучения имел длину волны 620 нм и длительность 0.25 -
2.7 пс. Как видно, при заданной энергии импульса в
области длительностей импульса меньше 1.5 пс
наблюдается уменьшение выхода ионов с уменьшением длительности, т.е. увеличением
интенсивности излучения. Очевидно, эти данные свидетельствуют об уменьшении
вероятности ионизации с ростом интенсивности излучения. Действительно, в области
однофотонной ионизации вероятность ионизации атомов пропорциональна величине
F = 1т (энергия импульса, приходящаяся на квадратный сантиметр), где интенсивность
излучения а т -длительность импульса14 и потому не зависит при фиксированном F не
должна зависеть от длительности импульса. Эксперимент показывает, что это не так. При
повышении интенсивности выше некоторого значения (и одновременном уменьшении
длительности импульса) наблюдается
демонстрирует эффект стабилизации.
Остановимся также на
экспериментах группы X. Мюллера15
(1996 г.), убедительно подтвердивших
существование эффекта стабилизации
ридберговских атомов. В этих
экспериментах исследовалась ионизация
атомов неона в возбужденном
циркулярном состоянии 2p55g,w = 4
лазерным импульсом длительностью 90
фс с длиной волны 2 = 620 нм (йщ = 2.0
эВ). Исходное состояние 2p55g,m = 4
приготовлялось импульсом излучения
УФ лазера с длиной волны Л = 286 нм в
результате пятифотонного возбуждения
уменьшение вероятности ионизации, и
100 200
интенсивность, ТВ/см2
Рис. 13.13. Зависимость вероятности ионизации
5g,пт-4 состояний атома неона от интенсивности
лазерного излучения.
14 Величина F, измеряемую в Дж/см2, в англоязычной литературе известна как fluence.
15 Muller Harm - нидерландский физик теоретик и экспериментатор.
289
атомов Ne в основном состоянии. С некоторой задержкой относительно импульса,
возбуждающего взомы в ридберговское состояние, на систему воздействовал основной
импульс сильного поля с интенсивностью в диапазоне 10й-ЗЮ1'’ Вт/см2, ионизующий
рндбер! чзвекне атомы. Для точного определения доли ридберговских атомов,
прононнзованных основным пульсом, с некоторой задержкой относительно него на
систему воздействовал зондирующий лазерный импульс, относительно невысокой
интенсивности и длительности г ~ 5 нс. Этот импульс ионизовывал все оставшиеся
нспрононизованными возбужденные атомы.
Независимое измерение сигналов с фотоэлектронного детектора позволяло
определить количество электронов, рожденных каждым импульсом, и определить
вероятность ионизации атома сильным полем в зависимости от интенсивности излучения.
На рис. 13.13 приведены полученные данные по образованию ионов под действием
основного и зондирующего лазерных импульсов в зависимости от интенсивности
основного импульса. Как видно, при значениях интенсивности выше 5 1013 Вт/см2
вероятность ионизации атомов остается примерно постоянной и существенно меньшей
единицы, что и свидетельствует о достижении режима стабилизации: более 70% всех
ридберговских атомов остаются неионизованными во всем исследуемом диапазоне
интенсивностей.
главное квантовое число
Рис. 13.14. Распределение возбужденных атомов
Не по значениям главного квантового числа
после облучения импульсом Ti-Sa лазера
петаваттной интенсивности.
Хорошо известны также
эксперименты, выполненные в Институте
Макса Борна в Берлине группой У.
Эйхмана16. В этих экспериментах
исследовался процесс ионизации атомов
гелия излучением 30-фемтосендного
импульса титан - сапфирового лазера
( ha) = 1.55 эВ) петаваттной
интенсивности. Несмотря на такие
гигантские значения интенсивности
излучения было обнаружено, что в
широком диапазоне интенсивностей до
10% общего числа атомов остаются в
неионизованных возбужденных
состояниях со значениями главного
квантового числа около п = 6-10 (см.
рис. 13.14). В данном случае в процессе
воздействия лазерного поля на атом помимо ионизации происходит также многофотонное
возбуждение ридберговских состояний, которые оказываются устойчивыми по
отношению к ионизации.
С практической точки зрения эффект стабилизации может представлять интерес
как один из способов создания инверсной населенности в протяженных плазменных
каналах, созданных излучением высокоинтенсивных лазеров и последующей генерации
когерентного излучения различных частотных диапазонов от ТГц и ИК до вакуумного
Ультрафиолета. С другой стороны, остаточная населенность неионизованных атомов
16 Eichmann Ulli - немецкий физик экспериментатор.
290
должна приниматься во внимание при анализе отклика среды на внешнее воздействие, что
существенно при исследованиях филаментации излучения в экстремально сильных полях,
когда приближение разложения отклика по степеням поля уже не работает.
Задачи к Главе 13.
13.1. Определить интенсивности излучения Nd лазера (ЙбУ = 1.17 эВ) и его второй
гармоники, при достижении которой происходит закрытие каналов ионизации.
13.2. Получить выражение (13.4.2) для вероятности туннельной ионизации атома
электрическим полем.
13.3. В рамках теории ионизации Келдыша определить зависимость вероятности
туннельной ионизации от частоты излучения.
13.4. Определить пороговые значения интенсивности излучения, при которых для атомов
аргона (потенциал ионизации 15.76 эВ) будет происходить смена механизма
ионизации (многофотонного на туннельный). Оценки провести для излучения COi
(7z<w = 0.12 эВ), Ti-Sa (hco = 1.55 эВ), iAKrF(Jta> = 5.0 эВ) лазеров.
13.5. Показать, что в "слабых" электромагнитных полях, когда амплитуда колебаний
свободного электрона a = eEjma>2 много меньше характерного атомного размера
энергия основного состояния в потенциале совпадает с энергий состояния в
исходном атоме с учетом штарковского сдвига уровня.
13.6. Оценить величину порога интерференционной стабилизации ридберговских
состояний атома водорода для излучения Ti-Sa (йгу = 1.55 эВ), и KrF (Й<у = 5.0 эВ)
лазеров.
13.7. Оценить величину порога адиабатической стабилизации (стабилизации КХ)
отрицательного иона водорода (потенциал ионизации 0.75 эВ) в поле излучения Ti-
Sa (ha> = 1.55 эВ), и KrF (ha> = 5.0 эВ) лазеров.
13.8. Оценить интенсивность лазерного излучения, при достижении которой происходит
подавление барьера для выхода электрона из атома водорода, и ионизация
становится надбарьерной.
291
Глава 14. Квантовая теория взаимодействия света с ве-
ществом.
Рассмотренная нами полуклассичсская теория взаимодействия электромагнитно-
iv поля с веществом позволила нам описать широкий круг' различных процессов. Одна-
Kv, в некотором смысле она является нс вполне удовлетворительной. Действительно, ос-
новной результат полуклассической теории заключается в том, что под действием внеш-
него электромагнитного поля, описываемого в рамках классической теории, между ста-
ционарными состояниями атомного гамильтониана происходят переходы, вероятность
которых (в единицу времени) определяется выражением (см. Раздел 8.4):
Здесь 1 п, - спектральное значение интенсивности на частоте перехода, dft - матричный
элемент дипольного оператора, связывающий начальное состояние |/) и конечное |/).
В отсутствие внешнего воздействия (= 0) переходы не происходят. Это выглядит со-
вершенно естественным. Полный гамильтониан системы совпадает с атомным, и общее
решение нестационарного уравнения Шредингера имеет вид:
И?, /) = (г) exp - Ett ,
V п )
то есть система неограниченно долго будет оставаться в начальном стационарном состо-
янии с точно определенным значением энергии Е,. Однако, мы знаем, что даже для изо-
лированного атома время жизни в возбужденном состоянии конечно. Рано или поздно
он испускает квант и переходит в нижележащее состояние. Опыт подсказывает, что у
атома, строго говоря, существует единственное стационарное состояние - основное.
Процесс испускания кванта света атомом в отсутствие внешнего воздействия называют
спонтанным переходом (распадом). Мы должны признать, что существование спонтан-
ных переходов противоречит развитой нами полуклассической теории и, прежде всего,
понятию стационарного состояния.
Что именно принципиально важное не было учтено? Ответ на это вопрос заклю-
чается в следующем. До сих пор атом мы описывали квантовомеханически, а электро-
магнитное поле - в рамках классических представлений. Действительно, электромаг-
нитное поле мы описывали функциями Ё(г,/) и Н(г,/), которые определяются из ре-
шения уравнений Максвелла. Нам необходимо построить теперь квантовую теорию
электромагнитного поля, а затем рассмотреть задачу о взаимодействии двух подсистем -
атома и электромагнитного поля с позиций квантовой механики. При этом старая по-
луклассическая теория должна оказаться частным случаем новой, когда состояние элек-
тромагнитного поля, как квантового объекта, может быть описано в классическом пре-
деле. Естественно, при таком последовательном квантовом подходе можно ожидать по-
явления нового круга эффектов, существование которых непонятно в рамках традици-
онного полуклассического подхода. Последовательную квантовую теорию взаимодей-
ствия электромагнитного излучения с веществом называют квантовой электродинами-
292
кой. В общем случае w ре.оппчк гская теория. Мы же ограничимся рассмотрением ос-
нов короля ГПВПС ГСКОЙ КВ1ШГОВОЙ ЭЛСК1рОДИ1ШМИКИ.
14.1. Разложение поли на осцилляторы.
Рпоомогрим свободное электромагнитное иоле в некотором объеме. Произволь-
ное состояние этого поля оппсывасгся уравнениями Максвелла.
(14.1.1)
Наша задача сейчас показать, что эго поле можно представить в виде совокупности бес-
конечного числа полевых мод, каждая их которых представляет собой гармонической
осциллятор. Не ограничивая общности рассмотрения будем считать, что электромагнит-
ное поле находится в кубическом объеме с зеркальными стенками (размер стенки куба
Тогда в кулоновской калибровке потенциала
divA = O (14.1.2)
напряженности электрического и магнитного полей определяются как:
1 Д4
Е = -- —, H = rotA, (14.1.3)
с dt
а сам векторный потенциал удовлетворяет волновому уравнению
71 2Л--^^4 = 0. (14.1.4)
с2 dt2
Будем искать решение этого уравнения в виде разложения по стоячим волнам (полевым
модам)2:
= 2XoJu(')cos(£ar), (14.1.5)
м
где к - волновой вектор стоячей волны, ел - единичный вектор поляризации. С учетом
(14.1.5) выражения для напряженностей электрического и магнитного полей имеют вид:
Ё(г, Г) = - - £ ел акЛ (Г) cos(^ г), (14.1.6)
С к,л
Н(г,О = -£[£хёл }/w(/)sin(^r). (14.1.7)
к.А
1 При изучении электромагнитных явлений в свободном пространстве размер куба может быть выбран
достаточно большим, так чтобы на временах рассмотрения конкретного процесса волновое возмущение,
распространяясь в пространстве со скоростью света, не достигало границ нашего объема. В этом смысле
оказываются произвольными размер и геометрическая форма нашего объема, а также тип стенок.
2 Вместо разложения по стоячим волнам часто используют эквивалентное ему разложение по бегущим
волнам.
293
Подставляя разложение (14.1.5) в уравнение (14.1.4), получим, что аи (/) удовлетворяют
уравнению гармонического осциллятора:
+ (14.1.8)
причем сок=кс. Аналогичное уравнение нетрудно получить и для величины
’ определяющей напряженность электрического поля в моде с волновым
вектором к и состоянием поляризации Л :
d2e
-^ + <^=0- (14-1.9)
Вычисление энергии электромагнитного поля в объеме L3 дает:
и/ f Е + Н , L ^-1
W = ----------dV =------> —-------(14.1.10)
J 8л- 8яс ft 2
Здесь мы учли, что
jcos2(^f)JK = Jsin2(^Ar)t7K = £3/2, |со8(£дг)со8(£'Л.r)dV = 0.
Таким образом, выражение (14.1.10) показывает, что энергия свободного элек-
тромагнитного поля представима в виде суммы слагаемых, соответствующих энергии
гармонического осциллятора, каждое из которых соответствует определенной полевой
моде. Поэтому про разложение (14.1.5) часто говорят как о разложении поля на осцилля-
торы. Число полевых мод в (14.1.5) или (14.1.10) бесконечно велико. В этом смысле об
электромагнитном поле говорят, как о системе с бесконечно большим числом степеней
свободы. Отметим также, что все осцилляторы независимы и не взаимодействуют между
собой. Этот результат - следствие линейности уравнений Максвелла.
В дальнейшем для определенности выберем какую-либо одну степень свободы с
волновым вектором к и заданным состоянием поляризации. Запишем энергию для этой
моды в виде:
L3 а2+со2а2
W =----7---------
8яг2 2
(14.1.11)
где a(t) и £*(/) определяют значения векторного потенциала и напряженности электри-
ческого поля в выбранной полевой моде3. Сравнивая выражение (14.1.11) с выражением
Для энергии «обычного» гармонического осциллятора
тх2
та)2х2
+-------
2
(14.1.12)
замечаем, что векторный потенциал а фактически играет роль «координаты» полевого
осциллятора, а электрическое поле е - «импульса», при этом величину £3/(8лс2) по
Эти величины в квантовой оптике иногда называют квадратурными компонентами электрического поля
в°лны.
294
своему смыслу можно назвать «массой» полевой моды. Сходство выражений (14.1.Ц)и
(14.1.12) можно сделать еще более полным, если перейти к безразмерным переменным
Введем безразмерные координату и импульс в соответствии с соотношениями:
V = х/х*, р = р/р*,
где х* = yjTi/nico, р* = yl'hma). Тогда, в безразмерных переменных выражение для энер-
гии (14.1.12) переписывается в виде4:
W = hco^ *Х (14.1.13)
и представляет собой функцию Гамильтона одномерного гармонического осциллятора.
Аналогично, обезразмеривая векторный потенциал а = а/а и напряженность электри-
ческого поля £ = £/г* на величины5
/4лйбУ , /4лйй>
= ^пОгт^ = } —(14.1.14)
получим выражение для функции Гамильтона некоторой полевой моды:
g2 + 2?2
H = h(D-----. (14.1.15)
Заметим, что в силу симметрии функции Гамильтона относительно замены импульса на
координату и наоборот, мы можем считать, что в выражении (14.1.15) электрическое по-
ле имеет смысл координаты, а векторный потенциал - импульса.
14.2. Электромагнитное поле, как квантовый объект.
Таким образом, мы показали, что произвольное состояние электромагнитного по-
ля в некотором объеме может представлено в виде совокупности полевых мод - гармо-
нических осцилляторов, не взаимодействующих между собой. Эти осцилляторы можно
рассматривать в рамках классической теории, а можно с позиций квантовой механики.
Переход от классической теории к квантовой осуществляется заменой соответствующих
величин операторами. Поэтому, аналогично тому, как нами были введены операторы
импульса и координаты
х —> х, р —> p = -i д/дх,
мы можем ввести полевые операторы е и а :
£->£, а —> а =-id/де . (14.2.1)
Можно ввести полевые операторы и иначе:
а—> а, £ —> е = -idjда. (14.2.2)
4 Отметим, что хотя в этом параграфе мы и остаемся в рамках классической теории, обезразмеривание У*е
проводится на величины импульса и координаты, вытекающие из квантовомеханических соображений.
5 Величины f* и а* мы выбираем, учитывая, что минимальная энергия осциллятора равна h(t)/2.
295
фактически задание нелепых операторов в виде (14.2.1) и (14.2.2) означает выбор £ -
или " представления, аналогичного координатному и импульсному представлениям в
теории "обычного" осциллятора. Тогда, с учетом (14.1.15):
-ЛЛ/'2+"2 - Ьй)( д2
п „ем- па> ~— = —------~т + £ =----------- + а2 (14.2.3)
2 2 де2 J 2 ( ffi2 J
. оператор Гамильтона (гамильтониан) свободного электромагнитного поля* 6. Построен-
ные операторы действуют в пространстве функций с интегрируемым квадратом, в слу-
чае .*>' - представления - это ф(е^)^ причем физический смысл волновой функции, опи-
сывающей квантовое состояние полевой моды, заключается в следующем: величина
|^(£.0| есть плотность вероятности измерить значение напряженности электрического
поля равным £ в момент времени t.
Дальнейшее построение квантовой теории электромагнитного поля осуществля-
ется просто. Все ранее сказанное про гармонический осциллятор мы должны отнести
теперь к полевой моде. В частности, имеем стационарное уравнение Шредингера для
7 v»
определения стационарных состоянии моды электромагнитного поля:
Нлмф„(.е) = Е^^).
Таким образом, отдельная мода поля характеризуется набором стационарных состояний
с энергиями
Е[п =М^ + 1/2),
где к имеет смысл числа квантов поля (фотонов) в стационарном состоянии | к} = фк (f).
В частности, имеем основное состояние поля, электромагнитный вакуум, как состояние
с нулевым числом квантов к = 0. Это состояние характеризуется дисперсией напряжен-
ности электрического поля (в размерных единицах) Ds =£ц/2. Распределение плотно-
сти вероятности получить при измерении значение напряженности £ в этом состоянии
есть:
|^(г)|2 = -Lexp(-r2), (14.2.4)
а энергия поля равна энергии нулевых колебаний Йй)/2 и отлична от нуля. Мы уже от-
мечали, что полевых мод бесконечно много. Поэтому даже если все полевые моды нахо-
дятся в основном (вакуумном) состоянии, то полная энергия поля (электромагнитного
вакуума)
= £й<а/2 (14.2.5)
оказывается неограниченно велика. Для нас это обстоятельство является несуществен-
ным, поскольку в дальнейшем мы будем вычислять изменение энергии поля при перехо-
----—
6 В дальнейшем для сокращения записи для обозначения безразмерных переменных поля мы будем ис-
пользовать СИМВОЛЫ £ И а .
в квантовой оптике эти состояния обычно называют фоковскнми по имени В. А. Фока, впервые введше-
Го их в рассмотрение.
296
лс из одного состояния 1. другое. Фактически бесконечное значение (14.2.5) мы будем
использовать в качестве уровня отсчет )нср!ии .
Распределение плотности вероятности в произвольном стационарном состоянии
полевой моды к записывается в виде:
2 /<!Ул
(14.2.6)
Здесь Н/, - полином Эрмита. Хотя энергия поля в стационарном состоянии может быть
весьма велика, среднее по квантовому состоянию значение напряженности оказывается
равным нулю, а дисперсия Dt(k) = +1/2).
Отметим, что электромагнитное поле в любом стационарном состоянии пред-
ставляет собой чисто квантовый объект. Среднее по квантовому состоянию значение
напряженности £ в произвольном стационарном состоянии оказывается равным нулю
И к =|ф*(^)Г^ = о,
а значит равно нулю и среднее значение силы, действующей на электрический заряд.
Кроме стационарных (фоковских) состояний существует огромное количество
нестационарных состояний полевой моды, однако, все такие состояния могут быть пред-
ставлены в виде суперпозиции стационарных состояний:
0(£,f) = ^бб^(б-)ехр(-7бэ(& +1/2)/). (14.2.7)
к
Здесь |<zj2 определяют вероятность обнаружить поле в А:-том стационарном состоянии,
то есть в состоянии содержащем к фотонов. При этом естественно, что выполнено
условие = 1. В этом смысле, как правило, приходится иметь дело с состояниями
к
с неопределенным числом фотонов. Мы можем, однако, ввести среднее число фотонов в
произвольном нестационарном состоянии с помощью соотношения:
W = • (14.2.8)
к
Средняя энергия полевой моды связана со средним числом фотонов в ней соотношени-
ем:
(£7<z’) = »«X<A) + l/2).
Остановимся на еще одном важном свойстве электромагнитного поля. Мы знаем,
что операторы импульса и координаты не коммутируют между собой8 9:
[£,£] = /.
Поэтому нельзя найти такие состояния, в которых обе эти величины имеют точно опре*
деленные значения. Поскольку в квантовой теории электромагнитного поля операторы
а иё эквивалентны операторам х, р , то
8 Проблема на самом деле существует, если вспомнить о теории гравитации.
9 Мы здесь используем безразмерные единицы.
297
[a,f] = z.
учитывая, что напряженность магнитного поля в выбранной нами моде А ~ а, то мы
приходим к выводу, что в квантовой теории одновременно точно определить значения
напряженностеи электрического и магнитного полей невозможно. При этом, конечно,
речь пдет измерении напряженностей полей в одной и той же полевой моде.
Для дальнейшего наиболее важно еще раз подчеркнуть следующее. Электромаг-
нитное поле, как квантовый объект, существует всегда. Основным состоянием электро-
магнитного поля является вакуумное состояние. Это такое состояние, когда во всех по-
левых модах отсутствуют фотоны. А значит, невозможно исключить взаимодействие
атомной системы с всегда окружающим ее внешним электромагнитным полем. Это
утверждение справедливо и в том случае, если это поле находится в основном (вакуум-
ном) состоянии. Исключить взаимодействие атома с окружающим его электромагнит-
ным вакуумом принципиально невозможно. Как мы увидим в дальнейшем, именно вза-
имодействие атомной системы с электромагнитным вакуумом ведет к появлению спон-
танных переходов и ряду других эффектов, из которых мы достаточно подробно обсу-
дим лишь так называемый лэмбовский сдвиг атомных уровней.
Повлиять на взаимодействие с электромагнитным вакуумом тем не менее можно.
Структура полевых мод зависит от размера и конкретной геометрии той области, в кото-
рой электромагнитное поле существует. Выбирая размер полости с зеркальными стен-
ками достаточно малым, а также меняя геометрию этой полости, мы можем существенно
перестраивать спектр полевых мод и, тем самым, интенсивность взаимодействия атома,
находящегося в полости, с окружающим его электромагнитным вакуумом. Задачи такого
рода являются предметом исследования квантовой электродинамики в полости, области
науки, интенсивно развивающейся в последние годы.
14.3. Классическое электромагнитное поле в квантовой теории.
А что такое классическое электромагнитное поле с точки зрения квантовой тео-
рии? Для ответа на вопрос вспомним о когерентных состояниях гармонического осцил-
лятора. Мы видели, что при большом среднем числе квантов именно такие состояния
описывают состояния осциллятора, близкие к классическим. Поэтому можно утвер-
ждать, что классическое электромагнитное поле — это когерентное состояние полевой
моды с большим средним числом квантов {к} »1 •
В Главе 3 мы видели, что когерентное состояние осциллятора характеризуется
пуассоновским распределением вероятностей по стационарным (фоковским) состояни-
ям. Например, распределение
« 'U/V2M41 (14-зл)
паст распределение Пуассона (3.3.6) для |«. Г с параметром (к) = г; /2. Тогда для волно-
в°й функции
ф^ = ^акФк<^
298
с распределением запишем:
0(/г) = 1 схр(-/;,74)£ ;:к„/2)* //Д4’)схр(-^72). (14.3.2)
у/тг k к\ 7
Учитывая, что
^2 = схр(-А' + 2А4).
АО*.
(здесь Л = £,/2) получим
<*(*) = -U схр(- £2 /2 + £а£-£2/2) = -^е^(-(£-£а)2/2), (14.3.3)
V я- Мтг
т.е. гауссовым волновой пакет с шириной, соответствующей вакуумному состоянию, и
центрированный около координаты £а. Эволюция во времени состояния (14.3.3) приво-
дит к классическому «закону движения»10 для напряженности электрического поля,
• cos at = sa cos at. В практически важном случае (к) »1 квантовой не-
определенностью величины £ можно пренебречь. При этом энергия поля и интенсив-
ность излучения оказываются пропорциональны среднему числу квантов в моде (А:) и
связаны с величиной напряженности 7) соотношениями, справедливыми в классиче-
ской электродинамике11.
14.4. «Сжатый» свет.
До середины 80-ых годов прошлого века казалось, что учет квантового характера
света дает лишь малые поправки к тем явлениям, которые описываются неквантовыми
уравнениями Максвелла. Прежде всего, квантовый характер поля надо принимать во
внимание, когда число фотонов в исследуемой системе невелико. Если же энергия поля
макроскопически велика, то для описания физических процессов можно пользоваться
так называемым полуклассическим подходом, когда вещество (среда) описываются
квантовомеханически, а поле - классически. Фактически, в основе такого подхода лежит
представление, что макроскопически интенсивные электромагнитные поля представля-
ют собой когерентные состояния полевых мод. Однако, помимо когерентных состояний
полевой моды существует бесконечное количество других состояний с большим сред-
ним числом квантов, которые по своим свойствам весьма отличны от когерентных со-
стояний, соответствующих классическому случаю. В настоящее время наиболее экспе-
риментально изученными являются так называемые сжатые состояния, и, в частности,
состояние сжатого вакуума.
С математической точки «сжатый» свет описывается как состояние полевой моды
вида (3.4.1). При этом особый интерес с физической точки зрения вызывают состояния,
10 Это утверждение проще всего доказать с использованием теоремы Эренфеста.
11 Более подробно о классическом электромагнитном поле с точки зрения квантовой теории можно,
например, посмотреть в: М. О. Скалли, М. С. Зубайри «Квантовая оптика», глава 2, М.: Физматлит, (2003)-
299
близкие к состояниям «ежаlol о» вакуума (3.4.2), Практический интерес к таким «сжа-
тым» состояниям о условлен 1ем, чго при больших значениях среднего числа квантов
дисперсия пюла квантов в «сжатых» состояниях аномально велика по сравне-
нию с диспсрсиси числа квантов в когерентном состоянии (см. Глава 3). Следовательно,
в «сжатых» состояниях аномально велика вероятность обнаружить число квантов, суще-
ственно отличающееся (как в большую, так и в меньшую сторону) от среднего значения.
Поэтому в таких полях можно ожидать, например, существенного увеличения вероятно-
стей многофотонных процессов по сравнению с классическими электромагнитными по-
лями той же интенсивности.
Существенной особенностью состояния "сжатого" вакуума является также нали-
чие ненулевых вероятностей обнаружить только четное число фотонов в полевой моде.
Как результат, среднее по квантовому состоянию значение напряженности электриче-
ского поля оказывается равным нулю. А значит, равно нулю и среднее значение силы,
действующей на атомный электрон со стороны электрического поля волны. В такой си-
туации динамика электронного волнового пакета должна быть существенно отличной от
той, что наблюдается в классических электромагнитных полях. Фактически, речь идет о
новом макроскопическом квантовом эффекте — чисто квантовом (неклассическом) со-
стоянии электромагнитного поля, содержащем, тем не менее, большое количество кван-
тов. И, хотя в настоящее время экспериментально достигнутые степени «сжатия» лазер-
ного излучения сравнительно невелики, по-видимому не существует физических огра-
ничений, которые не позволят в будущем генерировать высокоинтенсивные поля весьма
далекие по своим свойствам от классического электромагнитного поля. Это означает,
что полуклассическая теория (среда - квантовая, электромагнитное поле - классиче-
ское), которая ранее с успехом использовалась для описания процессов взаимодействия
мощного электромагнитного излучения с веществом, должна быть заменена последова-
тельной квантовой теорией, когда и среда, и электромагнитное поле описываются кван-
товомеханически. При этом старая полуклассическая теория оказывается частным слу-
чаем новой, когда состояние электромагнитного поля, как квантового объекта, может
быть описано в классическом пределе.
Экспериментально сжатые состояния электромагнитного поля получают в про-
цессе спонтанного параметрического рассеяния света (СПР).
ha = Й(й>/2) + Й(й>/2), hk(co) = 2^(гд/2),
когда оба кванта образующихся в процессе СПР попадают в одну и ту же моду. Легко
видеть, что в такой ситуации в рассеянном пучке будут присутствовать состояния толь-
ко с четным числом фотонов, что и является характерным признаком сжатия12.
14.5. Взаимодействие атомной системы с квантовым электромаг-
нитным полем. Спонтанные переходы.
Наша задача теперь - построить последовательную квантовую теорию взаимодей-
ствия атома с полем излучения. При этом, в отличие от рассмотренного ранее полуклас-
^ьйёГподробно см., например" В. П. Быков «Основные особенности сжатого света», УФН, т.161, №10,
300
сичсского подхода, и атом и электромагнитное поле будут рассматриваться как кванто-
вые объекты. Общий подход к решению проблемы заключается в следующем. Мы име-
ем две подсистемы, атом и электромагнитное поле, взаимодействующие между собой.
Атомная подсистема описывается гамильтонианом Но (например, это гамильтониан во-
дородного атома), гамильтониан полевой подсистемы есть
А Э А 2
й (14.5.1)
field z
где сумма берется по всем полевым модам. Будем по-прежнему считать, что знаем набор
собственных функций и собственных значений атомного гамильтониана:
(14.5.2)
Здесь верхний индекс « а » указывает на принадлежность собственного значения к
спектру атомного гамильтониана. Стационарные состояния полевого гамильтониана
также известны. Это есть набор осцилляторных функций и соответствующих им
собственных значений {е/*}, каждое из которых определяется числом квантов поля
(фотонов) в конкретной моде электромагнитного поля. Что касается взаимодействия
атома с электромагнитным полем, то в общем случае энергию взаимодействия можно
записать в виде (см. Раздел 8.2)
Q — (А —
=-----рА +------А2. (14.5.3)
тс 2тс
Здесь р - импульс электрона, а А - векторный потенциал электромагнитного поля. При
переходе к квантовой теории и импульс и, векторный потенциал следует заменить на
соответствующие операторы, действующие в пространстве атомных и полевых коорди-
нат13. В не слишком сильных полях квадратичным слагаемым по полю можно прене-
бречь: поэтому для оператора взаимодействия двух квантовых подсистем, атома и поля,
запишем14:
W =——[рА]. (14.5.4)
тс\ )
Здесь р = -ihV, а векторный потенциал определяется выражением:
= (14.5.5)
к Л
где акЛ - векторный потенциал, соответствующий моде а апогт - нормировочная
константа, определяемая (14.1.14). Напомним, что операторы акЛ и ёкл являются сопря-
женными друг другу подобно операторам импульса и координаты в "обычном" коорди-
13 Напомним, что при построении полуклассической теории взаимодействия света и вещества векторный
потенциал и напряженность поля волны описывались "обычными" функциями времени.
14 Мы здесь, как более общее, используем рА - представление для оператора взаимодействия. В ряде слу-
чаев в дальнейшем там, где это удобнее, будет использоваться adE- представление.
301
яатном пространстве. В lac I пости, если состояние полсиой молы задано а е. - представ-
ПС,(.Н1. ТО "о =-"W-
Переход к квантовой теории означает замену соответствующих величин на опе-
1ЙП,ры. Поэтому
W = (14.5.6)
Полный гамильтониан системы «атом + электромагнитное поле» есть:
Н = HQ+H fteld+W. (14.5.7)
Принципиально важным моментом является следующий. Полный гамильтониан зависит
от совокупности атомных и полевых координат и не может быть представлен в виде
суммы гамильтонианов атома и электромагнитного поля. А, следовательно, невозможно
ввести и атомные, и полевые волновые функции стационарных состояний. Такие функ-
ции могут быть введены лишь приближенно, если в (14.5.6) пренебречь взаимодействи-
ем атомной и полевой подсистем. Действительно, в этом случае полная волновая функ-
ция системы «атом + электромагнитное поле» '{'(г, факторизуется на произведе-
ние атомной и полевых волновых функций:
W.k.}) = ^(?)ПА(гы) • (14.5.8)
Здесь знак означает произведение, которое берется по волновым функциям всех по-
левых мод. Взаимодействие атома с окружающим его электромагнитным полем будем
учитывать по теории возмущений15. Тогда, раскладывая полную волновую функцию си-
стемы «атом + электромагнитное поле» по базису функций (14.5.8), в рамках нестацио-
нарной теории возмущений мы получим, что оператор взаимодействия W вызывает пе-
реходы между различными состояниями (14.5.8).
Мы ограничимся лишь первым порядком теории возмущений. Поэтому мы мо-
жем провести рассмотрение для взаимодействия лишь одной полевой моды с атомной
системой, а полученный результат затем просуммировать по различным модам электро-
магнитного поля. Будем считать, что начальное состояние системы
то есть в начальный момент атомная система характеризуется состоянием у/, (г), а неко-
торая полевая мода содержит kj квантов поля. Конечное состояние системы есть
где к, - число квантов в конечном состоянии палевой моды. Записывая выражение дм
“мплитуды вероятности перехода в первом порядке теории возмущений, получим:
11 Везможноеп, использования теории возмущений при описании взаимодействия атома с внешним злек-
^магвитиым полем в конечном счете обусловлена тем, что постоянная тонкой структуры а « 1. Обое-
°вание этого факта мы получим в разделе 14.12.
302
с\"(1) = ^и.......+ (14.5.9)
Time ’ к ft J
Здесь Et и Et - энергия конечного и начального состояний атомной подсистемы. При-
нимая во внимание, что операторы d и акЛ действуют соответственно в подпростран-
ствах атомной и полевой подсистем, перепишем (14.5.9) в виде:
с'Л') = Г^а....»O’,i^yA,l<’u|Ar)jexp(/(-(y,,+»«(/</-к, (14.5.10)
time х 'о
Здесь р а - матричный элемент оператора импульса, связывающий атомные волновые
функции начального и конечного атомного состояний, (^>kf - полевой матричный
элемент, a cojf =(Е^ -Еf)/h - частота атомного перехода. Учитывая, что pfl = inuofirfl
(гГ1 - матричный элемент оператора координаты, <г>/; = -о)1Г), а также свойства матрично-
го элемента полевого оператора аи, можно утверждать, что в конечном состоянии чис-
ло фотонов будет на единицу отличаться от к, то есть kf = /с, ± 1.
Рассмотрим для определенности переход с испусканием кванта. Тогда из (14.5.10)
получим:
Q 0) = —L-------------L—I exp V(-^ + o)k^t)dt =
he Jo
_ cc>ifanorm^\Фь) /.. , \sin(Aft#/2)
he Ага/2
Здесь dj) = erfi - матричный элемент дипольного момента, А<у = со^ , a>if > 0, по-
скольку переход происходит в нижележащее состояние. Как видно, квант испускается
только в том случае, если частота атомного перехода близка к частоте полевой моды.
Учитывая явное выражение для матричного элемента полевого осциллятора
(А+1|аы|А) = Л+1/2,
для вероятности перехода в заданную моду получим:
] a>ifanorm sin2 (Дй^/2)
2й2с2 (Дбу/2)2
(14.5.11)
(* + 1).
Наиболее интересным следствием полученного результата является обстоятель-
ство, что переходы в нижележащее состояние возможны, в том числе, в случае если мо-
да поля не содержит фотонов (к = 0), то есть находится в вакуумном состоянии. Такие
переходы называют спонтанными. В этом случае вероятность перехода есть:
\ '/| &ПОГП1 sin2(Aa#/2)
2h2 а>2кЛ (Длу/2)2
(14.5.12)
303
Здесь нормировочные константы апогт и е связаны соотношением Еппгт-й\;апогт1с-
Для того чт°бы получить полную вероятность спонтанного перехода, выражение
(14.5.12) надо просуммировать по всем полевым модам, куда произошел переход. По-
скольку для достаточно большого нормировочного объема спектр полевых мод можно
считать плотным, сумму по модам можно заменить интегралом по :
of dЧ 3 2Z? г , (
21 /о х ~ 7-. 1 I I d£l.
J(2^) (2л-) с J J
(14.5.13)
Поэтому
I |2
п/ _V«sP°n' -_______гл! f 2 2 sin2(AftX/2) , t , „
f‘ ^Pfi 4я-3с3 2/12 J £norm(Dlf ’ (ДбУ/2)2 dC°kX/C°S
(0- - угол между радиус-вектором и вектором поляризации ех). Выполняя интегрирова-
ние по углам jcos2 Q^dQ. = 4тг/3, и учитывая выражение (14.1.14), получим:
I , |2
nz 2Г Я 2f sin2(A<5#/2)
Wft = ~ 7ГТ —T-2- d(OkK .
’rMc’ 1/1 a (A®/2)2
Основой вклад в полученное выражение дает узкий интервал частот вблизи частоты пе-
рехода (Djf. Поэтому приближенно имеем:
w _2гМ „з fsin2(A^/2)
' л-ЗЙс’ Д®/22
(14.5.14)
Здесь мы воспользовались значением интеграла:
fsin2<*
1^г^ = ж-
-00 9
Из (14.5.14) найдем выражение для вероятности спонтанного перехода в единицу време-
ни:
(14.5.15)
Зпс
Величину Afl принято называть коэффициентом Эйнштейна спонтанного перехода.
В случае, если число фотонов в некоторой моде велико (к »1), то переходы
идут преимущественно с испусканием кванта в именно в эту заселенную моду. При
этом вероятность такого перехода оказывается пропорциональна спектральной интен-
сивности на частоте перехода, что соответствует результатам рассмотренной ранее по-
луклассической теории.
Легко видеть, что введенные нами коэффициенты Эйнштейна спонтанного и вы-
нужденного переходов связаны между собой соотношением.
Л„=^В,. (14.5.16)
7С С
304
Ранее мы сформулировали правила отбора для электромагнитных переходов в атомах.
Переход называется разрешенным, если он возможен в дипольном приближении в пер-
вом порядке нестационарной теории возмущений. Мы видели, что в полуклассической
теории для этого необходимо, чтобы d ft Ф 0. Как видно из (14.5.15) и (14.5.16), такие же
правила отбора существуют и для спонтанных переходов.
Итак, мы получили важный результат. Рассматривая электромагнитное поле как
квантовую систему, мы показали, что даже если поле находится в основном (вакуумном)
состоянии, происходит взаимодействие этого вакуумного поля с атомной системой, в
результате чего атом «спонтанно» переходит в нижележащие энергетические состояния.
Величина т = А представляет собой время жизни атома относительно спонтанного пе-
рехода с уровня |/) на уровень \f) Оценим характерную величину коэффициента Эйн-
штейна спонтанного перехода в оптическом диапазоне частот16. Считая, что d^ ~ еа0
(а0 - боровский радиус), из (14.5.15) получим:
А-----те~сг- -----1-------------1 со. «со.. (14.5.17)
пс \ Л J п а0 у Л J
Здесь Л - длина волны перехода. co:l = Ry/h -в2/(a^h) - атомная частота (характерная
частота обращения электрона вокруг атома). Полагая что со~соа1, выражение (14.5.17)
можно переписать также в виде А - odcoit. где а - постоянная тонкой структуры. Мы
приходим к выводу, что электрон успевает совершить много (порядка 106 - 107) оборо-
тов вокруг атомного ядра, прежде чем испустит квант света. Численная оценка для
Й(У«10 эВ (£а - линия в спектре атома водорода) дает А ~ 1О10 с'1, или для времени
жизни уровня г ~ 1О~10 с. Отметим, что оценка времени падения электрона на ядро, вы-
полненная в рамках классической электродинамики (см. задачу 14.5), дает аналогичный
результат. На качественном уровне результаты, полученные в рамках квантовомехани-
ческого и классического подходов, совпадают. Однако, физическое содержание этих ре-
зультатов существенно различно. Классическая теория оказывается неспособной объяс-
нить устойчивое существование электронной оболочки атома.
Как видно из (14.5.16), скорость распада пропорциональна кубу частоты перехо-
да. Этот результат также имеет естественное классическое истолкование. Действитель-
но, в соответствии с классической электродинамикой энергия, излучаемая в единицу
времени осциллирующей частицей, пропорциональна четвертой степени частоты
W ~ со4. С другой стороны, в рамках квантовомеханического подхода имеем W ~ hco- А,
где А - вероятность испускания кванта hco. Сопоставляя эти выражения, имеем А ~ со2,
что соответствует (14.5.16).
На основании полученных результатов, в частности, можно сделать вывод, что в
рентгеновском диапазоне частот времена жизни состояний существенно меньше, чем в
оптическом диапазоне. Наоборот, в радиочастотном диапазоне они оказываются очень
16 Точный расчет коэффициента Эйнштейна спонтанного перехода 2р—> 1j можно найти в Приложении
14.1.
305
велики- Например, для Я ~ 1 см из (14.5.16) имеем т ~ 1()н с (несколько лет!). Это озна-
.ист. что спонтанными переходами в различных радиофизических приложениях практи-
'ки всегда можно пренебречь.
Отмстим, чю полученное выражение для времени жизни возбужденного состоя-
ния относительно спонтанного распада (14.5.16) может быть с успехом использовано и в
я1срноп физике для оценки времени жизни возбужденных ядерных состояний относи-
1г'льно процесса у - излучения. Например, оценивая величину ядерного дипольного мо-
мента как d ~ eRN (/?л ~ 10 —10 см - размер атомного ядра) для длины волны у -
кванта А - Ю'0 см (Ъа>г ~ 1 МэВ) из (14.5.17) получим г ~ Л1 ~ ИГ14 — 1016 с. Отме-
тим. что именно быстрые спонтанные распады в рентгеновском и у диапазонах являют-
ся главным препятствием на пути создания источников когерентного индуцированного
излучения в этих диапазонах частот.
До сих пор мы говорили лишь о разрешенных переходах. Что касается запрещен-
ных переходов, то их вероятности, как правило, на четыре — пять порядков меньше.
14.6. Спонтанные переходы и естественная ширина спектральной
линии.
Остановимся на еще одной важной стороне полученных нами результатов. Мы
видели, что взаимодействие атомной системы с электромагнитным вакуумом (нулевыми
колебаниями электромагнитного поля) привело к появлению спонтанных переходов.
Время жизни атома в возбужденном состоянии оказывается конечным и определяется
коэффициентом Эйнштейна спонтанного перехода:
У
Вспомним про соотношение неопределенно-
1 стей «энергия - время» АЕ • т ~ Й . Если систе-
ма живет конечное время, то ее энергия точно
У не определена. Возбужденные атомные состо-
яния не могут иметь точно определенного зна-
чения энергии, атомные уровни оказываются
«размытыми», имеющими конечную ширину
(см. рис. 14.1). Для ширины атомного состоя-
ния, очевидно, имеем:
Рис. 14.1. Ширина спектральной линии. ДЕ~Й/г. (14.6.1)
Часто для ширины уровня вводят и другую ве-
личину у = де/Й . Тогда последнее соотношение можно переписать в виде у = 1/г.
Поскольку атомные уровни уширены, то энергия кванта, испускаемого при пере-
воде между парой состояний, также не имеет точно определенного значения. Испускае-
мая спектральная линия имеет конечную ширину. Эту ширину, обусловленную спон-
танными переходами, принято называть естественной шириной линии. Как результат,
возникает некоторое распределение фотонов по частотам, которое принято называть
Формой линии.
306
Рассмотрим более подробно вопрос о форме линии, возникающей при спонтан-
ном переходе из некоторого возбужденного атомного состояния |1) в основное |0^ в ре-
зультате взаимодействия с электромагнитным вакуумом. Будем считать, что в началь-
ный момеш времени (/ ~0) атом находится в состоянии |l), а вся совокупность поле-
вых мод в вакуумном состоянии. Амплитуду вероятности этого события обозначим как
(',„(/). В процессе эволюции системы во времени атом перейдет в состояние |0), в не-
которой полевой моде Л = ,/<л,ёл} появится один фотон. Амплитуда вероятности это-
го события есть Сох(г). Раскладывая полную волновую функцию системы «атом + по-
ле» по базису вида (14.5.8), получим систему уравнений для коэффициентов С10(/) и
<7С0,
/й----
dt
•ft
т-------
dt
= Q0^ ехРО(^л
(14.6.2)
= ЕСо.Л* ехр(-/(бУЛ -6У1ОУ),
где Wx = - — (/501ё. )х а- о х а0 - матричный элемент оператора взаимодействия атомной
тс
системы с полевой модой, связывающий начальное и конечное состояния17,
со]0 = (£"] - £0)/h - частота перехода между атомными состояниями.
Будем искать решение для амплитуды начального состояния Сх 0 (/) в виде
С10(0 = ехр(-х/2), (14.6.3)
то есть в виде экспоненциального убывания во времени вероятности обнаружить систе-
му в возбужденном состоянии |С, 0(z)|2 = ехр(~х). При этом величина т = у"1 есть время
спонтанного распада. Подставляя (14.6.3) в первое из уравнений (14.6.2), получим:
Ом -й>|0 + /y/2)i)dt = -i~. (14.6.4)
л о * 1(а>л-й)хо+1у/2)
Подставляя (14.6.4) во второе из уравнений (14.6.2), получим:
- /Й ~ехр(-yt/2) = £W* ехр(- i(a>A - 0)//^- ~ ^10 + 1 И,
2 л ^Й (бУл-<ц0 + ///2) )
или
_ifir = у W71-схр(-/(^ -а>1и+///2)гЛ (И 6 5)
2 л h ( (й>л-<Уц) + /7/2) )
В большом нормировочном объеме А' спектр полевых мод является плотным. Поэтому
от суммирования в (14.6.5) можно перейти к интегрированию (см. (14.5.13)):
17 Здесь для сокращения записи индекс Л подразумевает также и различные направления волнового векто-
ра фотона.
307
Выполняя iihtci рнрованис ио угловой координате, получим:
1 - exp (- i(g)A + iy/2)t)
("л -«>io + />/2)
(14.6.6)
/
где _ 2С2 |й)J | X norm/’ а плотность полевых мод определяется выражением
\г, - 2^,3 ’ Полученное соотношение есть уравнение для величины у. Нас интересу-
ет его решение на больших временах t »\/\у\. Будем также считать, что |/| « го10.
Как видно из (14.6.6), выражение для у получается комплексным
у = Re/ + /1т/.
Поскольку
^1,о (0 = exP(_X/2) = exp(-Re—х/)ехр(-/1т—х/), (14.6.7)
2 2
скорость распада состояния определяется действительной частью /, а величина мнимой
части может рассматриваться как добавка к энергии возбужденного атомного состояния
Е} =ЕХ +Йх1т//2. (14.6.8)
Это так называемый лэмбовский сдвиг уровня, который более подробно будет обсуж-
даться ниже. Рассматривая интеграл (14.6.6) в пределе больших времен, получим:
Z
-W, ( 1
Im//2=f—— ------
ЗЙ2 I й), -й).
(14.6.9)
где мы учли, что cos(ft> — a\0)t является быстро осциллирующей функций частоты и по-
тому вклад в интеграл (14.6.9) не дает.
Для действительной части Re / получаем
D 2 f W 2( Sin(^-^o)'L dM
Re / = —у Wx ------------ ^о>аа>л •
3/z J t J
(14.6.10)
Учитывая, что
, Г x )2 x KI2 2
me
т 3
Nu = _L. замечаем, что в подинтегральном выражении (14.6.10) имеется резонанс-
ная кривая, определяемая множителем sin((tVi ~ — <Цо)» показывающая, что
основной вклад в интеграл (14.6.10) вносит узкий набор частот вблизи «ец0. Поэто-
му (14.6.10) можно переписать в виде:
308
2 In- 1? м f
Rc/~ Md/Vl
УЬ 11 «Ц с»; )
где вынесенные in пол niiTcipajin функции взяты я точке (ft, Учитывая, что
г sill г .t
I —- я. получим:
Rcr=„ 1К < (14.6.11)
Зпс
что тождественно выражению (14.5.15).
Из выражения (14.6.6) видно, что в подинтегральном выражении полюс возникает
только для действительной части величины /. Поэтому Re/» 1т/ и в дальнейшем
под у мы будем понимать только действительную часть этой величины.
Рассмотрим теперь конечное состояние системы, определяемое коэффициентами
Со(т —> со). Из (14.6.4) найдем
|с рЖ_______________!_______
1 “л| я2 (^-®,«)2+/74’
что фактически определяет распределение по энергии фотонов в конечном состоянии, то
есть форму линии излучения. Форму линии удобно ввести в нормированном виде:
= ------^7—г-- (14.6.12)
2я-(й>-й)10) +/ /4
Такая кривая называется лоренцевой и удовлетворяет условию нормировки:
f g(co -a)}Q)da} = ^-\ --1-----— do> = 1
J 2zrJ (бУ-й>10) +/ 4
При этом ширина линии есть скорость спонтанного перехода из состояния |1) в состоя-
ние |0).
Понять происхождение естественного уширения линии и возникновение лорсн-
цевой формы линии можно и в рамках классической электродинамики. Действительно,
рассматривая атом, как классический осциллятор с затуханием, мы получили уравнение
движения атомного электрона в виде:
г + )г + а)цГ =0, (14.6.13)
где / = 2^2Шо /Зшс’ - классическая постоянная затухания. Решение этого уравнения заг
писывается в виде:
г(0 з г0 ехр(- х/2)соа(7«^ -/г/4 О •
Спектральный состав излучения определяется фурье-комнонетной ускорения электрона-
1 ~1а..|2, (14.6.14)
309
гДе
_ 1 f 2 _ 2
°" ’ 757-1 Г(')*-'Л’Й fF(0exp(-ia*y/,
v2zrJ
I13 (14.6.14) при условии у « получим:
” <14-615’
где I о jlvd® полная интенсивность излучения осциллятора. Как видно, выражения
(14.6.15) и (14.6.12) дают один и тот же результат для формы линии излучения.
В частности, для гармонического осциллятора для скорости спонтанного распада
нижнего возбужденного состояния имеем:
l^oil = е2
h
2тсо}й
и, следовательно,
А = у = — ^10
1 3 he3 та) Зтс3
что тождественно совпадает с величиной классической постоянной затухания, описыва-
ющей время релаксации энергии колебаний классического гармонического осциллятора.
В случае, если атом может перейти из начального состояния |z^ в целый набор
нижележащих конечных состояний, то для времени жизни i -го состояния следует запи-
сать:
г = ^Л-, (14.6.16)
1Л»
f
где сумма берется по всем конечным состояниям, в которые возможен переход.
Для ширины уровня тогда имеем:
где уj - парциальная ширина уровня, связанная с переходом | —> | _/").
Если переход происходит в основное атомное состояние , ширина атомной ли-
нии определяется шириной верхнего энергетического уровня. Если же оба состояния |1)
и 12), между которыми происходит переход, имеют конечные ширины, то можно пока-
зать, ЧТО ширина спектральной линии есть сумма ширин состоянии (см. Рис. 14.2), т.е.
/ = /) +/2-
имеет точно определенное значение энергии,
то единственное состояние в атоме, которое име
310
Оценим характерное значение есте-
ственной ширины атомных уровней. Посколь-
ку для разрешенных переходов в оптическом
диапазоне частот r~10~8- 1О’10 с, то
~ Й/г ~ 10 5 —10”7 эВ. Эта величина на
много порядков меньше энергии атомного пе-
рехода, поэтому атомная линия является узкой,
а степень монохроматичности излучения весь-
ма высока. Такие распадающиеся во времени
состояния в квантовой теории называют квази-
стационарными. Мы видели, что их можно
охарактеризовать комплексным значением
Рис. 14.2. Ширина спектральной линии.
энергии Е-Игу/2 и записать волновую функцию в виде:
। i
ys(r,t) = ^(r)exp —(E-ihyliy
I h
' i I
ехр —Et ехр(-^/2).
(14.6.17)
Тогда |(у(г ,/)|2 ~ ехр(-^), что и описывает распад состояния на временах порядка 1/у.
Помимо естественного уширения существуют и другие механизмы уширения
атомных линий. В газовых средах наиболее важными являются доплеровский и столкно-
вительный механизмы уширения19, которые, как правило, приводят к значительно боль-
шей ширине линий по сравнению с естественной. В твердых телах (кристаллах), где
атом находится в электрическом поле, создаваемом атомами-соседями по кристалличе-
ской решетке, возникает штарковское уширение линий, обусловленное внутрикристал-
лическим полем. Поэтому в экспериментах наблюдать естественную ширину атомной
линии достаточно трудно.
Рис. 14.3. Спонтанные и вынужденные переходы
между состояниями квантовой системы.
14.7. Формула Планка.
Установив связь между вероятно-
стями спонтанных и вынужденных пере-
ходов, мы можем теперь из первых прин-
ципов получить распределение энергии
по спектру равновесного электромагнит-
ного излучения (формула Планка).
Действительно, рассмотрим двух-
уровневую систему, находящуюся в со-
стоянии термодинамического равновесия
(см. Рис. 14.3). Населенности состояний
|1) и |2) есть соответственно У, и N2. Под действием поля излучения в системе идут
переходы между уровнями. В состоянии равновесия населенности и N2 не зависят
от времени. Поэтому мы можем записать.
19 Более подробно об этих механизмах можно прочитать, например, в монографии: С.А.Ахманов,
С.Ю.Никитин «Физическая оптика», М.: МГУ, (1988), часть II, лекция 6.
311
- W2#l2/n, + N2AV}. (14.7.1)
Поскольку = #12, то из (14.7.1) получаем:
7 — ^l2 1
rt’ ^12^ж-г
g состоянии термодинамического равновесия
^/TV, = ехр(-7ЬД/,Г), (14.7.2)
где het) - энергия перехода между состояниями, Т - температура. Подставляя (14.7.2) в
(14.7.1) и учитывая выражение, связывающее коэффициенты спонтанного и вынужден-
ного переходов (14.5.16), получим:
т _ 1_______ha?_____
лг2с2 ехр(йй)ДдТ)-1' (14.7.3)
Учитывая связь между спектральной плотностью и спектральной интенсивностью излу-
чения 1(0 = сра, перепишем (14.7.3) в виде:
_ 1 ЙбУ3
Ра> 7г2с3 &xf>(ha>/kBT}-\ (14.7.4)
Полученный результат есть формула Планка для распределения объемной плотности
энергии по спектру равновесного электромагнитного излучения. Фактически, мы сумели
получить это выражение из первых принципов, рассматривая взаимодействие атомной
системы с полем излучения.
Отметим, что в историческом плане проведенные нами рассуждения соответ-
ствуют работе А.Эйнштейна 1917 года. В этой работе задолго до создания квантовой
теории электромагнитного поля, опираясь на выражения для статистических распреде-
лений (формулы Больцмана и Планка), А.Эйнштейн обосновал необходимость суще-
ствования спонтанных переходов и установил связь между вероятностями вынужденных
и спонтанных переходов, то есть соотношение между коэффициентами Л12 и В12.
14.8. Лэмбовский сдвиг атомных уровней.
Рассмотрим еще один эффект, обусловленный взаимодействием электромагнит-
ного вакуума с атомной подсистемой - так называемый лэмбовский сдвиг. При обсужде-
нии тонкой структуры спектра атома водорода мы видели, что в соответствии с теорией
Дирака для одного и того же значения главного квантового числа уровни с различным
значением /, но одинаковым значением полного механического момента j, например,
2sV2 и 2р1/2, являются вырожденными. Оказывается, взаимодействие атомного электро-
на с вакуумным электромагнитным полем снимает это вырождение. Уровень 25^2 сме-
лется вверх относительно своего положения, предсказываемого формулой Дирака, в то
вРемя как положение уровня 2р1/2 практически не изменяется (см. Рис. 14.4). Экспери-
312
п
п-1
Рис. 14.4. Лэмбовский сдвиг 2s состояния
атома водорода.
ментально лэмбовский сдвиг атомных
уровней был впервые обнаружен в 1947
году в опытах Лэмба20 и Ризерфорда21.
Опыты Лэмба - Ризерфорда.
Мы сначала коротко обсудим ос-
новные идеи опыта Лэмба - Ризерфорда, а
затем на качественном уровне проведем
анализ явления. Схема экспериментальной
установки по наблюдению лэмбовского
сдвига приведена на рис. 14.4. Нейтраль-
ные невозбужденные атомы водорода вы-
летают из печки (П) и подвергаются дей-
ствию пучка электронов, в котором элек-
тронным ударом происходит возбуждение
атомных состояний 2s1/2 и 2р1/23/2. Атомы
водорода H(2pV23/2) в результате радиационного перехода быстро переходят в основное
состояние ls1/2. Состояние 2sV2 является долгоживущим (метастабильным), поскольку
переход 2s V2 —>к1/2 в дипольном приближении запрещен. В результате атомы H(2s]j2)
долетают до детектора (Д) и отдают электронам детектора свою энергию возбуждения
(«10.2 эВ). Получившие энергию электроны покидают детектор, и включенный в цепь
гальванометр (Г) начинает показывать электрический ток. Величина электрического то-
ка в цепи детектора оказывается пропорциональной переданной энергии, то есть числу
метастабильных атомов водорода H(2s[i2). По пути к детектору пучок атомов водорода
пролетает через область СВЧ поля, частота которого может перестраиваться. При совпа-
дении частоты поля с частотой переходов 2s1/2 ->2р1/2 или 2sV2 —>2рлз оказываются
возможны вынужденные переходы в 2р - состояние, что приводит к быстрому спонтан-
ному переходу в основное состояние. В результате метастабильные атомы не долетают
до детектора и сигнал с него пропадает. Таким образом, оказывается возможным точно
измерить положение уровня 2si/2 относительно дублета 2р1/2 у2. Эксперимент показал,
что расстояние между компонентами дублета 2р1/2 3/2 составляет величину 10950 МГц в
соответствии с теорией Дирака22, а уровень 2sl/2 сдвинут вверх примерно на 1058 МГц
относительно нижней компоненты дублета 2р1/2>3/2.
Качественный анализ лэмбовского сдвига.
Перейдем теперь к обсуждению физических причин возникновения лэмбовского
сдвига. Мы уже отмечали, что при строгом анализе строения квантовомеханической си-
20 Lamb Willis (1913 - 2008)- американский физик, Нобелевская премия (1955) «За работы по аномальному
магнитному моменту электрона»
21 Retherford Robert (1912 - 1981) американский физик.
22 В энергетических единицах это значение равно осгRy/16.
313
^лы вообще говоря, необходимо учитывать ™
стемь, у ать се взаимодеиствие с электромагнитным
вакуумом. Взаим д и твие атомного электрона с вакуумными полями ведет не только к
спонтанным переходам, но и к энергетическому сдвигу уровней23. С физической точки
зрения флуктуирующие вакуумные поля оказывают дополнительное воздействие на
электрон, приводя к его «дрожанию» на орбите. В системе отсчета, связанной с электро-
ном. «дрожащим» оказывается атомное ядро. В результате электрон «видит» его как не-
точечный о ъект. анее мы уже обсуждали (см. Раздел 4.7) влияние конечного размера
ядра на положение энергетических уровней атома. В рамках рассматриваемой модели
лэмбовский сдвиг имеет точно такую же природу, только под размером ядра нам следует
подразумевать амплитуду «дрожания» электрона на орбите. Мы видели, что учет про-
странственной структуры радиальных волновых функций ведет к тому, что неточеч-
НОСТЬ атомного ядра приводила к сдвигу вверх только 5 - состояний. Поэтому мы ожи-
даем, что взаимодействие атомного электрона с вакуумным электромагнитным полем
также приведет к сдвигу вверх атомных состояний с нулевым орбитальным моментом.
Изложенные выше качественные соображения постараемся теперь облечь в мате-
матическую форму. Запишем уравнение, описывающее «дрожание» электрона орбите
под действием вакуумных полей:
т& = eEvac (14.8.1)
Здесь описывает отклонение электрона от равновесной орбиты. Считая электрон не-
релятивистским, и учитывая, что
cos(®“') ’
к, А
нтересно, что и в классической теории сила радиационного трения ведет не только к затуханию коле-
аний атомного осциллятора, но и к изменению его частоты. Это изменение частоты излучения в некого-
смысле является классическим аналогом лэмбовского сдвига (см. выражение (14.6.13)).
314
запишем решение уравнения (14.8.1) в виде:
, С — COSy69^
<*' = / Г
т к,Л 0}кЛ
(14.8.2)
Определим теперь величину среднего (по времени) квадрата отклонения электрона от
равновесной траектории:
(14.8.3)
Здесь екл - амплитудное значение вакуумного электрического поля в полевой моде. Эту
величину мы уже вычисляли (см. выражение (14.1.14)):
_ /4лйбУи
Еи
Поэтому
• (14.8.4)
' ' т L
В случае, если объем 1} достаточно большой, спектр полевых мод является достаточно
плотным и в (14.8.4) от суммы можно перейти к интегралу
1 V of d'k _ 1 f 2 ,
гЗ X 2J п чЗ “ 2 3 J •
Zj (2тг) 7С с
В результате получаем:
= = la>a2t^u (14.8.5)
' ' лт с 3 сокл 7ihc\mc) 3 сокл я 3 а>кл
Полученный интеграл расходится и на верхнем и на нижнем пределе. Для устранения
расходимости необходимо ограничить спектр полевых мод, взаимодействующих с элек-
троном. В качестве граничных частот выбирают24:
. 2 1 2 2 Z2
= тс , = - а тс —,
2 п
откуда для квадрата амплитуды дрожания окончательно находим:
' 1 я Z а
Как видно, амплитуда дрожания достаточно мала: ^(<5г)2^ ~«3/2а0 ~6-1О"4яо «ао
Поэтому эффект окажется существенным только для $ - состояний. Используя результа-
24 Первое из этих ограничений предполагает, что электрон в атоме остается нерелятивистским. Низкоча-
стотное ограничение предполагает, что вакуумные поля приводят именно к эффекту «дрожания» на оро”
те. Поэтому частота «дрожания» должна быть больше частоты обращения вокруг атомного ядра. Б°лее
подробно см. А.А.Соколов, И.М.Тсрпов, В.Ч. Жуковский: «Квантовая механика», §21, М.: Наука, (1979)-
315
тЫ расчета смещения у уровней, обусловленные конечным размером ядра (см. выра-
жение (4.9.14)), получим величину лэмбовского сдвига ns состояния
74
~a3Ry.
Более точные вычисления были проведены Бете25 в 1947 году:
и хорошо согласуются с экспериментальными данными, полученными Лэмбом и Ризер-
фордом. Как видно, в тяжелых водородоподобных ионах величина лэмбовского смеще-
ния уровней быстро возрастает.
Отметим также, что в атоме водорода максимальная величина лэмбовского сдви-
га наблюдается для основного 15 - состояния. Как и следует из формулы Бете (14.8.6),
величина лэмбовского сдвига 15 состояния примерно в восемь раз больше, чем для 2s -
состояния. Однако, измерить это смещение гораздо более трудно чем смещение 2s -
уровня. Это связано с тем, что промерять положение 15 - уровня также приходится от-
носительно положения дублета 2р^2^2. Относительная точность таких измерений
должна быть примерно на пять порядков выше, чем в опытах Лэмба — Ризерфорда. Экс-
перименты такого уровня стали возможны лишь с развитием лазерной техники в сере-
дине 80-ых годов XX века и были проведены Т. Хэншем26.
Опыты Хэнша.
Остановимся коротко на опытах Т. Хэнша, позволивших измерить лэмбовский
сдвиг 15 состояния атома водорода. Значение разницы энергий между уровнями 151/2 и
251/2 можно определить, измеряя точное значение длины волны света, вызывающего
двухфотонный переход 15V2 -э-251/2 (Л «2430 А). Поскольку уровень 2sl/2 является ме-
тастабильным, его радиационная ширина крайне мала. В результате теплового движения
атомов и связанного с ним эффекта Доплера происходит расстройка частоты воздей-
ствующего излучения и частоты перехода. Экспериментально эту проблему решают ме-
тодом так называемой двухфотонной бездоплеровской спектроскопии. Схематически
такой способ спектроскопии представлен на рис. 14.6. Фотоны поглощаются атомом сре-
ды из двух пучков, распространяющихся навстречу друг другу .
В результате с точностью до релятивистских эффектов происходит компенсация
эффекта Доплера. Действительно, с учетом эффекта Доплера закон сохранения энергии
ДЛЯ атома, движущегося со скоростью v под углом 0 к оси, вдоль которой распростра-
няются навстречу друг другу лазерные пучки частоты о, записывается в виде.
“ Bethe Hans (1906 2005) - физик - теоретик, Нобелевская премия (1967) «За вклад в теорию ядерных
Р^ЦИЙ и особенно за открытие цикла термоядерных реакций, являющихся источником энергии звезд»
’ Hansch Theodor Wolfeane (о 1941) - немецкий физик - экспериментатор, Нобелевская премия (2005)
развитие прецизионной леерной спектроскопии, включая технологию оптически-частогных гребе-
” Организовать такую схему экспериментально очень легко. Достаточно направить лазерный пучок на
еРкало и наблюдать эффект поглощения в падающем и отраженном пучках.
316
Г?<у(1 + - cos 0) + hco(\ - - cos 0) = 2ft co = E2s - Eis.
Измерение частоты перехода 15lz2 —> 2s1/2 позволяет прямо измерить расстояние между
уровнями. Однако, полученный результат завязан на точное значение постоянной Рид
берга, входящей в выражение
для длины волны (или частоты)
* • ** " перехода. Поэтому точное значе-
' ' У* е --------------- " ние энергии перехода
• ’f’ - ' 1^1/2 определяется сопо-
-------- * ставлением с длиной волны дру.
* "——** ------------ того перехода, а именно длиной
Рис. 14.6. Схема двухфотонной бездоплеровской
спектроскопии.
волны перехода Н р линии. Дей-
ствительно, в нерелятивистском
приближении мы имеем
--= Е —г—т = —к>
Лнр l22 42J 16
то есть кнр = 4л/а . Положение всех подуровней, соответствующих п = 2 и и = 4 про-
мерено экспериментально с высокой степенью точности. Поэтому по отклонению от ра-
венства Лнр = 4Л£а оказывается возможным точно измерить положение уровня Ц/2.
В экспериментах использовался лазер на красителях с длиной волны Л « 4860 А,
а также на удвоенной частоте. Экспериментально измеренное значение сдвига 1$ уровня
составило AE](Jxp) =8161 ±29 МГц, теоретические расчеты дают =8149.43 ±0.08
МГц.
В последние годы большой интерес вызывают эксперименты по измерению лэм-
бовского сдвига атомных уровней в тяжелых многозарядных ионах. Этот интерес обу-
словлен тем, что в таких системах величина сдвига уже не мала (см. задачу 14.7), и для
его расчета необходимы существенно более точные методы расчета квантовой электро-
динамики28, учитывающие высокие члены разложения по параметру aZ, когда этот па-
раметр уже не является малым и оказывается порядка единицы, aZ ~ 1.
Лэмбовский сдвиг в спектре водорода и размер протона.
Интерес к прецизионным расчётам и измерениям лэмбовского сдвига в атоме во-
дорода связан не только с возможностью проверки предсказаний квантовой электроди-
намики со все более высокой степенью точности, но и с возможностью определения по-
правок к положению энергетических уровней, не связанных непосредственно со взаимо-
действием атомного электрона с электромагнитным вакуумом. В частности, помимо
лэмбовского сдвига и сверхтонкой структуры, в положение основного состояния атома
28 Современная теория взаимодействия атомно - молекулярных систем с электромагнитным полем (кваН
товая электродинамика) строится как ряд теории возмущений по параметру aZ, который, как
является малым, что обеспечивает возможность при расчете эффектов ограничиться очень неоол
количеством членов ряда.
317
водороДа вносит вклад нсючсчность прогона. Эта поправка была нами определена в
разделе 4.7 и для 2s состояния атома водорода составляет
I Г 2
=--~Ry, (14.8.7)
6 ап
= ljr2p(?*v’r
вJ
где г„
определяется плотностью распределения заряда в протоне по ра-
iiivcy • Для современного экспериментального значения радиуса протона
= v 0-87 Ф (1 Ф (Ферми)— 10'13 см) величина сдвига уровня 2s составляет 0.146
уГи и почти на четыре порядка меньше величины лэмбовского сдвига уровня. Однако,
достигнутая в настоящее время точность ~2 кГц позволяет в принципе определить ради-
ус протона с погрешностью 0.01 Ф. Такая точность почти в два раза лучше, чем точность
определения радиуса протона в экспериментах на ускорителях по упругому электрон —
протонному рассеянию.
С другой стороны, для современной теории сильных взаимодействий (квантовой
хромодинамики) точный расчет структуры протона и, в том числе, его радиуса, является
такой же фундаментальной проблемой, как и задача о строении атома водорода для не-
релятивистской квантовой теории. Поэтому прецизионные измерения радиуса протона
методами современной атомной физики позволяют проверить предсказания квантовой
хромодинамики.
Мы уже говорили о том (см. Раздел 4.10), что помимо обычного атома водорода,
существует и его мюонный аналог, в котором вместо электрона по орбите «вращается»
мюон, отрицательно заряженная частица, по своим свойствам очень похожая на элек-
трон, но обладающая массой в 207 раз больше электронной. Из-за разницы в массах ра-
диус мюонной орбиты приблизительно в 200 раз меньше, он существенно ближе к про-
тону, и точное положение его энергетических уровней намного сильнее зависит от
структуры протона. Измерив лэмбовский сдвиг уровней мюонного атома водорода,
можно независимо определить и размеры протона. Такие эксперименты впервые были
выполнены в 2010 году29. Оказалось, что «мюонные» эксперименты привели к значению
гр * 0.84 Ф, что примерно на 4 процента меньше результата, полученного традицион-
ными «немюонными» методами. При этом полученная разница значительно выше по-
грешностей эксперимента. В чем причина обнаруженных отличий и каков «истинный»
размер протона в настоящее время неясно.
14.9. Аномальный магнитный момент электрона.
Остановимся на еще одном эффекте, обусловленным взаимодействием квантовой
системы с окружающим ее электромагнитным вакуумом. Речь идет о так называемом
аномальном магнитном моменте электрона. Ранее мы говорили, что (Раздел 1.7), что
магнитный момент, связанный со спиновым движением электрона, равен магнетону Бо-
Ра, то есть гиромагнитное отношение (или g ~ фактор) для спинового движения ровно в
Два раза больше, чем для орбитального движения. С теоретической точки зрения этот
-—-
Pohl et al Nature 466, The size of the proton, Nature 466, p. 213-216 (2010)
318
результат является прямым следствием релятивистского уравнения Дирака, описываю-
щсто частицы со спином 1/2. Однако, расчеты показывают, что если учесть взаимодей-
ствие элек трона с окружающим его электромагнитным вакуумом, то g - фактор элек-
трона оказывается несколько больше двух. Возникает так называемый аномальный маг-
нитный момент электрона. В соответствии с современными расчетами величина магнит-
ного момента электрона равна
( сс аг
= ^в 1+ — -0.32848 —+ ..
2я- Д'2
где (jlib - магнетон Бора, ot - постоянная тонкой структуры). Экспериментально отличие
g -фактора для электрона от двойки было обнаружено И. Раби в 1947 году при измере-
ния интервалов сверхтонкой структуры уровней энергии водорода и дейтерия. Получен-
ное в настоящее время экспериментальное значение есть
А„р »1.0011596521869/;,,
Utheor
1.001159652236//e,
(14.9.1)
14.10. Стационарный и нестационарный эффекты Казимира.
проводящие незаряженные
пластины
Высокочастотные моды
Рассмотрим еще один физи-
ческий эффект, предсказанный X.
Казимиром30 в 1948 году, и дока-
зывающий реальность существова-
ния электромагнитного вакуума и
его взаимодействия, в том числе, с
макроскопическими объектами.
Суть этого эффекта заключается во
взаимном притяжении проводящих
незаряженных тел, возникающих за
счет наличия электромагнитного
вакуума (см. рис. 14.7). Чтобы на
качественном уровне понять при-
чину возникновения эффекта, рас-
смотрим две параллельные незаря-
женные идеально проводящие пла-
стины большой площади 5, распо-
ложенные на близком расстоянии
L (L «Vs ). Такая система фак-
Рис. 14.7. Эффект Казимира. В отличие от свободного
пространства в области между пластинами присут-
ствуют только "высокочастотные" полевые моды.
тически представляет собой незаряженный конденсатор. Ранее мы видели, что плот-
ность числа полевых мод определяется объемом рассматриваемой системы. С уменьше-
нием объема плотность числа полевых мод уменьшается. В результате, с уменьшением
расстояния между проводящими пластинами число полевых мод в объеме между ними
уменьшается, то есть плотность энергии поля в объеме между платинами убывает, в то
время как плотность энергии поля в свободном пространстве остается неизменной, что и
30 Casimir Hendrik (1909 - 2000) - нидерландский физик.
319
црцвеч»v к возникновению силы притяжения. Численный расчет показывает, что сила
междх незаряженными проводящими пластинами определяется выражени-
Puc.l4.S. Схема установки по наблюдению эффекта
Казимира.
f (14.10.1)
( 240Л
Например, для единичной площади
£ = 1 см2 и расстояния L = 1 мкм
имеем Fc«1.3xl0"2 дин. Это мак-
роскопическая величина. На рассто-
яниях порядка I0'6 см (сотни харак-
терных атомных размеров) давление,
создаваемое силами Казимира, ока-
зывается сравнимым с атмосферным.
Казимировские силы между
двумя параллельными металличе-
скими пластинами впервые были измерены в 1957 году. Проведенные эксперименты31
дали качественное подтверждение теоретического результата (14.10.1) для силы притя-
жения. Пластины в данной работе изготавливались из хрома и размещались на расстоя-
нии L = 0.5 -ь 2 мкм друг от друга. За счет действия сил Казимира растягивалась уравно-
вешивающая их пружина, в результате чего изменялась емкость конденсатора С (см.
схем) эксперимента на рис. 14.8). Измерение емкости С, в свою очередь, позволяло
определять силы притяжения F между пластинами начиная со значений ~ 10-4 дин. Экс-
перименты по измерению сил Казимира с тер пор неоднократно повторялись для объек-
тов различной формы, в том числе ди-
электрических. В настоящее время
наличие эффекта можно считать
надежно экспериментально установ-
ленным и находящимся в количе-
ственном согласии с предсказаниями
квантовой электродинамики.
Помимо рассмотренного нами
эффекта Казимира (его еще называют
стационарным эффектом Казимира)
существует и динамический (нестаци-
онарный) эффект Казимира, предска-
занный в 1970 году американским фи-
зиком Дж. Муром. Им было рассмот-
Рис.14.9. Схема опыта по наблюдению динамиче-
ского эффекта Казимира.
Рено состояние полевых мод, изначально находящихся в вакуумном состоянии, в поло-
сти, ограниченной двумя сближающимися или расходящимися плоскопараллельными
3еРкалами, и показано, что в такой ситуации будет происходить рождение фотонов из
ВакУума. Однако, для генерации фотонов в сколь-нибудь заметных количествах, зеркала
Должны иметь релятивистскую скорость.
31 ^Рагпаау, М. j. Attractive Forces between Flat Plates // Nature. 1957. Vol. 180, no. 4581. P. 334—335
320
Экспериментально динамический эффект Казимира был обнаружен в 2011 году
шведским ученым К. Уилсоном вместе с коллегами из Австралии и Японии. Схема их
экспериментальной установки приведена ни рис. 14.9. Рождение фотонов из вакуума
происходило около волновода из алюминия, подключенного к сверхпроводящему кван-
товому интерферометру (СКВИД32). Экспериментаторы изменяли индуктивность конту-
ра интерферометра, пропуская через него магнитный поток, осциллирующий с частотой
порядка 11 ГГц. Колебания индуктивности сказывались на эффективной длине волново-
да, которая осциллировала с релятивистской скоростью (около четверти скорости рас-
пространения электромагнитных волн в волноводе). Волновод, как и ожидалось, излучал
фотоны, «извлеченные из вакуума», спектр которых соответствовал теоретическим
предсказаниям.
14.11. Спонтанное излучение атомов в сильном лазерном поле.
Развитие лазерных технологий привело к появлению широкого круга новых за-
дач, связанных со взаимодействием высокоинтенсивного лазерного излучения с веще-
ством. При изучении атомной динамики в высокоинтенсивных лазерных импульсах
спонтанные переходы в атомах, обусловленные взаимодействием квантовой системы с
электромагнитным вакуумом, обычно не рассматриваются. Это обусловлено малостью
взаимодействия атома с вакуумными модами поля по сравнению с взаимодействием с
высокоинтенсивным лазерным полем. Кроме того, длительность фемтосекундных ла-
зерных импульсов на несколько порядков меньше характерного времени спонтанных
переходов (10'9-10‘7 с), т.е. спонтанные переходы просто не успевают происходить на
временах воздействия. С другой стороны, любой процесс вынужденного испускания
квантов начинается со спонтанного фона излучения. Поэтому для корректного описания
излучения различных частотных диапазонов из лазерной плазмы, созданной высокоин-
тенсивным фемтосекундным лазерным импульсом, по крайней на начальных этапах
спонтанное испускание квантов атомом должно также приниматься во внимание. При
этом существенно, что атом может быть существенно перестроен ("одет") лазерным по-
лем. В такой ситуации спектр спонтанной эмиссии позволит также судить о структуре
атомных уровней "одетого" атома.
Мы уже знаем, что в "стандартной" квантовой механике, спонтанных переходов
нет, полуклассическая теория способна описать только вынужденные внешним полем
переходы. Однако, в рамках полуклассической теории, когда атомная динамика рас-
сматривается квантовомеханически, а поле излучения - в соответствии с классическими
законами, можно попытаться рассмотреть спонтанное следующим образом: спонтанное
излучение определяется средним по квантовому состоянию дипольным моментом си-
стемы, эволюционирующей в поле электромагнитной волны
^(0 = -ej|^(r,0|2rc/3r, (14.11.1)
Если внешнее поле является достаточно слабым, т.е. его величина много меньше внут-
риатомных полей, задача об эволюции атома в поле может быть решена по теории воз-
мущений. Как результат, получается разложение поляризационного отклика по степеням
32 SQUID - superconducting quantum interference device.
321
rra fcM. Глава 20). В сильных полях когпя
’ огда теория возмущении оказывается неприме-
1А,лй для изучения атомной динамики и
ни*10 ’ 101 и определения поляризационного отклика
обычно используют теории типа Келдыша (см. Глава 13), известные как приближение
сильного поля s rong ie approximation), или же методы численного интегриро-
вания уравнения Шредингера.
Однако правомерность использования ппП1,.,„.,п
кования полуклассического подхода для анализа
спонтанного излучения сильно возбужденных атомлп D
„О, если предположить, что атом в начальный мп ЫВает сомнения' Действитель-
ном состоянии, то его дипольный момент Л” На“ДИТСЯ В некот0Р°« вовбуж-
равен нулю, и в соответствии с законами кпя/ ННЫИ в соответствии с (14.11.1)
будет. Нетрудно видеть, что в полуклассичесХпо0” ЭЛеКТр0ДИНамики имения не
атомными состояниями, обладающими ненулевой Переходы возможны между
процессе воздействия сильного поля основное В частности’ если в
ходы в него, рассчитываемые в рамках полуклягг Я™е аТ°Ма опУстошается, то пере-
данными. С другой стороны, из рассмотоХо” К0Г° ПОДХ0Да ока1ываю™ подав-
Р ь, из рассмотренной выше квантовоэлекгродинамической
теории спонтанных переходов ясно, что их вероятность не зависит от наличия населен-
ности состояния, в которое идет переход. В связи с вышесказанным мы остановимся
чуть подробнее на анализе спонтанных переходов в квантовой системе в присутствии
сильного поля электромагнитной волны. Наш подход будет основан на учете взаимо-
действия атома с совокупностью мод квантованного поля, находящихся в вакуумном
состоянии, в первом порядке теории возмущений, в то время как взаимодействие с ла-
зерным полем, которое полагается классическим, рассматривается вне рамок теории
возмущений.
Будем полагать, что мы знаем решение уравнения, описывающего динамику
квантовой системы во внешнем классическом поле:
dt
(14.11.2)
при условии, что в начальный момент времени атом находился в некотором стационар-
ном (или нестационарном) состоянии дискретного спектра или континуума ф(г):
, t = 0) = ф{г). (14.11.3)
Здесь Но = Hal(r) + W(r,t) ; Hat(r) - атомный гамильтониан, а
W = -—А(£)р + ———^- (14.11.4)
тс 2тс
• взаимодействие с полем волны в дипольном приближении, A(f) = J0(z)sindX - вектор-
иый потенциал классического лазерного поля, а р = -—/Л V - оператор импульса.
Мы будем считать, что изначально все моды поля находятся в вакуумном состоя-
Нии |{о}) и начальная волновая функция нашей системы есть
^Mau},Z = O) = 0(r)x|{o}}, где {акЛ} есть совокупность координат полевых мод. Об-
322
щая задача об эволюции "одетого" атома, взаимодействующего с электромагнитным ва-
куумом. записывается в виде:
,71-|,(Г- '• - = (/7„(/) + /), + К},/) (14.11.5)
dt
Здесь Н f - гамильтониан совокупности полевых мод, а Г(г,{<як}) -оператор взаимодей-
ствия атома с квантованными полевыми модами. Уравнение (14.11.5) будем решать по
теории возмущений, рассматривая У(г, {<7Ы}) как малое возмущение.
Тогда волновая функция нулевого приближения, не учитывающая взаимодей-
ствие с совокупность квантованных мод, записывается в виде:
0х|{0}), (14.11.6)
то есть факторизуется на атомную и полевую части.
Мы будем искать решение уравнения (14.11.5) в виде:
Ч-(г, К V) = Ч-<“>(г, К },Z) + <w, К }S), (14.11.7)
причем <Я'«Ч/(0). Подставляя (14.11.7) в (14.11.5), удерживая члены только первого
порядка малости, получим:
дЗ^(Г,{аи},8) = }? z) + рр<о> (?> 0 (14.! 1.8)
причем начальное условие имеет вид: <УР(г, {акл }, t = 0) = 0.
Вспомним, что в начальный момент времени все полевые моды находились в ва-
куумном состоянии. Следовательно, в первом порядке теории возмущений функция
будет содержать однофотонное возбуждение в одной из полевых мод:
<yP(f,{a„},r) = X<^u(?.Cx{°,0,....1„,0,...0,0} (14.11.9)
куЛ
Здесь - электронная волновая функция, соответствующая появлению фотона в
моде {к,Л}. Взаимодействие атома с полевыми модами запишем в виде:
= =--£(^КиАп (14.11.10)
к,Л ТПС кЛ
где акЛ - оператор векторного потенциала в моде {Л,Л}, екЛ - вектор поляризации, а
апогт = ) - введенная ранее нормировочная константа, L3 - нормировоч-
ный объем. Подставляя (14.11.9) в (14.11.8), с учетом линейности уравнения Шрединге-
ра получаем уравнение для волновой функции <5y/u(r,/), соответствующей однофотон-
ному возбуждению заданной полевой моды:
/Й х х /) х exp(1сокЛt), (14.11.11)
dt тс V2
323
причем
в начальный момент времени
^и(^/ = 0) = 0.
(14.11.12)
Заметим, что уравнение (14.11.11) является неоднородным уравнением Шредин-
гера для ФУНКЦИИ Sy/ кЛ(1 ,1) с источником в правой части, описывающим появление фо-
тона заданного типа.
Таким образом, мы имеем систему уравнений (14.11.2), (14.11.11) с начальными
условиями (14.11.3) и (14.11.12), которая описывает динамику квантовой системы в ла-
зерном поле с учетом спонтанного излучения фотонов с различными к, Л. Очевидно, что
выражение
^(O = f|^u(r,/)|2i73r
(14.11.13)
задает вероятность излучить фотон типа в зависимости от времени, а величина
к
(14.11.14)
определяет полную вероятность испустить фотон (любой частоты и поляризации) при
переходе i -> f.
В случае если спектр полевых мод полагается плотным, в (14.11.14) суммирова-
ние может быть заменено интегрированием:
к,Л
d3k 2L3 f 2 j f 1гл
2L -------г = —— а)^й)кЛ dQ..
J(2;r) 8/r3c3j J
(14.11.15)
В результате для вероятности спонтанного распада с появлением фотона в спектральном
интервале частот (а), со + da>) получим:
р
W„dct) = 6)2 dc0 х ,
Зя- с
(14.11.16)
где определяется выражением (14.11.13). Заметим, что в выражение (14.11.16) не
входит нормировочный объем, поскольку WkX ~\/l? . Фактически, это означает, что хо-
тя с увеличением нормировочного объема растет число полевых мод, с которыми взаи-
модействует квантовая система, одновременно уменьшается интенсивность взаимодей-
ствия с каждой из мод, локализованных во все большем объеме пространства.
Поскольку мы рассматриваем задачу в первом порядке теории возмущений,
Должны быть выполнено условие J W^dto«1, т.е. вероятность испускания фотона мала
н Двуквантовыми спонтанными переходами можно пренебречь. В фемтосекудном диа-
пазоне длительностей лазерного импульса это условие легко выполнено.
Для более глубокого понимания физики спонтанного излучения в сильном лазер-
ном поле, когда спектр атома может быть существенно перестроен, разложим волновые
Функции Sy/,t) по базису стационарных состояний свободного атома.
324
(14.11.17)
8^,1) = ^С,"."1<оя(иехр'"-
n
Квадраты модулей коэффициентов разложения (14.11.17) |C^f имеют смысл вероят-
ностей обнаружить атом в состоянии \п) при условии, что был испущен фотон в моду
{м}.
Заметим прежде всего, что в отсутствие внешнего классического поля наша тео-
рия совпадает с моделью, рассмотренной в разделе 14.5. Действительно, в этом случае
W = о и гамильтониан Н0 есть гамильтониан атомной системы. Тогда, если в началь-
ный момент времени атом находится в стационарном состоянии, описываемом волно-
вой функцией ^9,(г), с энергией Еп решение уравнения (14.11.2) записывается в виде:
п
(14.11.18)
Подставляя (14.11.18) в (14.11.11) и разлагая волновую функцию 8y/u(r,t) по стацио-
нарным состояниям атомного гамильтониана (см. 14.11.17), получим:
^C;W)(Z)^Xr)expf-^E,I^ = -^^x-^x^XF)||xe^(z^Z)-
п \ h J тс ^2 у п )
Умножая полученное соотношение на ^(r)expl
и интегрируя по всей области
определения функции, получим:
zAC}U)(Z) =
kxPfi) anorm <-f ч ч
------х —7=- х exP(z(^w - COif )t) .
тс V2
(14.11.19)
Интегрируя (14.11.18), получим для амплитуды вероятности испустить фотон и
перейти в состояние (pf (г):
С<И1 {() = ^Арг.ёа) х / sin(Afflt/2)
ч/2Й V 7 Дш/2 ’
(14.11.20)
где сок) еду отстройка от резонанса, а со^ — (Ej —Е ^) / й > 0 поскольку мы рас-
сматриваем переход в нижележащее по энергии состояние. Суммируя по всем полевым
модам, в которые был испущен фотон (см. (14.5.13)), и вспоминая связь матричных эле-
ментов импульса и координаты33, получим для вероятности излучения кванта за время Z:
ш г/ч 2 f 8ш2(Дщ//2) ,
(14.11.20)
33 Фактически эта связь матричных элементов импульса и координаты и приводит к тому что конечное
выражение выглядит так, как будто оно было получено в </Е калибровке взаимодействия с модами кванто-
ванного поля.
= Afi =
325
(14.11.21)
откУ88,
Как и раньше, получаем:
,4^ У5КС полученное ранее выражение для коэффициента Эйнштейна спонтанного
перехода.
Спонтанные релеевское и комбинационное рассеяние света.
Мы уже обсуждали процессы релеевского и комбинационного рассеяния в разде-
1]С 11.4. Мы видели, что эти процессы - суть двухфотонные переходы, когда поглощается
квант классического электромагнитного поля и затем переизлучается в другую моду,
рели речь идет о спонтанном процессе, эта мода изначально находится в вакуумном со-
стоянии, а в рамках полуклассической теории процесс оказывается невозможен. Одна-
ко. в рамках развитого подхода мы теперь можем рассмотреть эти процессы.
Пусть внешнее лазерное поле достаточно слабое и для анализа электронной ди-
намики мы можем ограничиться первым порядком теории возмущений. Тогда, полагая,
что в начальный момент времени атом находится в состоянии р), волновая функция
атомной системы может быть записана в виде:
= (Pi(r)exp
+S Wv* (?) ехР (~ Т Ej\’
n*i I й )
где
C(D(Z) = 4Д (ey$(i(coni-co)t) t ехр(/(й>я,. + й>)0>
"° 2Й (Ч,.-д>) (Ч/ + д)) )
(14.11.22)
(14.11.23)
Подставляя (14.11.22) и (14.11.23) в (14.11.11), мы получаем уравнение для амплитуды
вероятности найти атом в состоянии | а фотон в моде {к, Л}:
(14.11.24)
п Д/ Z n^i
Второе слагаемое в правой части (14.11.24) описывает рождение фотона типа {&,!}, в то
время как первое определяет эволюцию атомной волновой функции в классическом поле
после рождения фотона заданного типа. Здесь мы пренебрежем описанием этой эволю-
ции. Тогда из (14.11.24) получаем:
2 V (^ fn^kA Х^я/Го)
с/ (/->оо) > —------?=----
погт% 2л/2Й
2
х2я£(£г -£, -Йа>+Й<г>и)хг (14.11.25)
Полученное выражение задает вероятность излучения стоксовой компоненты спонтан-
Н01 о комбинационного рассеяния с переходом атома в конечное состояние | j ) и излу-
чением фотона с частотой
^Ь1 полагаем здесь, что поле включается адиабатически медленно.
2
327
(14.11.30)
2[~sin2(ft?u -fo2,)r/2)
2 4 cos2 (Qr /2)t + —n-2(^u 6,21 ±n*Xi2-2
(^-^21) /4 (<yu -бУ2| ±Ой)2/4
sin2(^-^.)^2)1sin2 z sin2(^A-*>2l ±Олу/2)
-бУ21)2/4 R (бУм -й>21 ±QJ2/4
и задает излучение фотонов в некоторой полосе частот вблизи а>кЛ = a>,a>±£lR, соответ-
ствуюшее Раби - осцилляциям атомных амплитуд. Вероятность испускания фотона
{£ /} есть WkA (0 = |Cj(W) | +|С^Л)|2 и представлена на Рис. 14.10а для некоторой дли-
тельности лазерного импульса. Как мы и ожидали, исходная линия расщепляется на три
линии, возникает триплет Моллоу. Интенсивность центральной линии в два раза больше
п0 сравнению с линиями-сателлитами на частотах сокЛ =a> + QR. При этом ширина ли-
ний определяется длительностью воздействия: с увеличением длительности лазерного
импульса линии сужаются.
Казалось бы, рассчитать спектр излучения квантовой системы, "одетой" полем
можно и иначе, определив ее дипольный момент, усредненный по квантовому состоя-
нию
d(t) = ef |^(r, /)| 2rd3r, (14.11.31)
предполагая затем спектральное разложение дипольного момента
d(f) = f,
2тг J
определяющее спектральную интенсивность излучения в соответствии с
полуклассической теорией, рассмотренной нами в Главе 9:
Рис. 14.10. Спектры спонтанного излучения двухуровневой квантовой системы в резонансном
Поле- Квантовоэлектродинамический (а) и полуклассический (б) расчеты. В начальный момент
времени атом находится в нижнем состоянии.
Расчеты интенсивности излучения по формуле (14.11.32) с учетом решения уравнения
Шредингера (14.11.27) представлены на рис. 14.106 и дают результат принципиально от-
328
личный от полученного в рамках квантовой электродинамики, центральный пик отсут-
ствует, а в спектре наблюдаются только два сателлита. Исчезновение центральной линии
обусловлено деструктивной интерференцией амплитуд переходов между квазиэнергети-
ческими состояниями, соответствующими переходу на несмещенной частоте (см.
Рис. 10.3). Однако, квантовая электродинамика, подтвержденная многочисленными экс-
периментами, показывает, что центральная линия в спектре доминирует.
14.12. Квантовая электродинамика в микрополости.
До сих пор мы рассматривали взаимодействие свободного атома с электромаг-
нитным вакуумом. В таком случае спектр полевых мод оказывается плотным и в реаль-
ности атом взаимодействует с неограниченно большим числом полевых мод. Однако
можно себе представить ситуацию, когда атом находится в микрорезонаторе или поло-
сти малых размеров, так что спектр полевых мод оказывается существенно разрежен.
Действительно, частота низшей моды колебаний в идеальном металлическом резонаторе
есть
а> = лс/L,
(14.12.1)
где L - размер резонатора. Например, для резонатора микронных размеров имеем
а> ~ 1015 с1, что соответствует энергии кванта ~ 1 эВ. В такой ситуации может оказаться,
что атом может эффективно взаимодействовать всего с несколькими, или даже одной
полевой модой (см. рис. 14.11). В результате
динамика атома будет существенно отлич-
ной от динамики атома в свободном про-
странстве. В качестве примера динамики
квантовой системы в микрорезонаторе рас-
смотрим случай гармонического осцилля-
тора, взаимодействующего всего с одной
полевой модой, причем частоты осциллято-
ра и полевой моды совпадают между собой.
Запишем полный гамильтониан си-
стемы:
Н = H0(x) + Hf(e) + V(x,e),
2
-+х2
Рис. 14.11. Моды резонатора и атомная ли-
ния.
(14.12.2)
ниан атомной, Hf(e) = ha>—
2
д2
де2
где Я0(х) = Йд>—
2
гамильтониан полевой
гамильто-
подсистемы,
2
V(x,s) = Axe - оператор взаимодействия подсистем. Все выражения записаны в безраз-
мерных единицах. Атомная координата обезразмерена на х0 = yjh/met), полевая - на
епогт = = Т4Й <у4/(#2с3) • Здесь размер резонатора равен половине длины вол-
ны полевой моды. Тогда константа связи в операторе взаимодействия подсистемы есть:
329
(14.12.3)
= exQ£norm = ha)xA = hcox — Ja-^-,
я V тс
где 6Г = ^2/йс ‘ постоянная тонкой структуры. Считая, что ho-а2 тс2, получаем, что
кОнстанта связи подсистем А ~ а3/2, а вероятность перехода w~ А2 -а3. Малость по-
стоянной тонкой структуры обеспечивает "слабость" электромагнитного взаимодействия
(слабую связь атомной и полевой подсистем) и возможность применять для анализа вза-
имодействия подсистем теорию возмущений.
Эволюция системы, описываемой гамильтонианом (14.12.2), однако, может быть
рассмотрена точно. Действительно, делая замену переменных:
£ = —7=-, 4 = —^, (14.12.4)
V 2 v 2
или
£ + 7 %-г)
Х = -1=-, £ = ?-у=!-,
V2 у/2
мы преобразуем гамильтониан (14.12.2) к виду:
/7О) = ЙяД
„ if 82 i2-’!1
) 2l dr)2 \ 2
(14.12.5)
С математической точки зрения выполненное преобразование координат - это поворот
осей на 45 градусов. Как видно, в повернутых координатах переменные и г/ разделя-
ются, и гамильтониан оказывается представим в виде суммы гамильтонианов двух
невзаимодействующих осцилляторов:
1 ( rfi А 1 (
= р + (1 + ^2 + - + (1~/IW2 • (14.12.6)
2^ 5^г j )
Вводя новые переменные £ =^V1 +Л и 7 =7?V1-Л , преобразуем гамильтониан
(14.12.6) к виду:
1 ( ~ А 1 ( л2 А
Д(?,7) = ю 1 + -—р + 72 , (14.12.7)
где
= ahh + A, = (Оу!\-А (14.12.8)
определяют частоты нормальных мод колебаний в системе. Стационарные состояния
гамильтониана (14.12.7) хорошо известны. Их энергии есть
Е =ЮД/и + 1/2) + Ю„(п + 1/2), т,п = 0,1,2,.... (14.12.9)
Соответствующие волновые функции:
Л) = NmNnHm^}Hn(ri^-^2 +72)/2), (14.12.10)
Nn - нормировочные коэффициенты.
330
Отмстим, что при наличии взаимодействия между подсистемами все полученные
стационарные состояния системы "атом 4- мода поля" являются перепутанными: волно-
вая функция нс может быть факторизована на произведение функций атомных и поле-
вых состояний. Особое внимание обратим на основное состояние системы Его
энергия есть Епт = (М1, 4- liQ^/2 и также отличается от суммарной энергии состояний
свободного атомного состояния и вакуумной энергии полевой моды, равной tico. Мы
видели, однако, что константа связи А весьма мала. Поэтому это отличие мало и, как
видно из (14.12.9), возникает лишь во втором порядке разложения в ряд Тейлора по па-
раметру А.
В дальнейшем с учетом малости взаимодействия атомной и полевой подсистем
будем полагать, что £ = £ и // = /у. Пусть в начальный момент атом находится в воз-
бужденном состоянии | п = 1), а полевая мода в вакуумном, и рассмотрим временную
эволюцию такой системы. Очевидно, в исходном базисе начальное состояние есть
ys(x, е, t = 0) = у/] (х)(£) = NqН\ (х)Н0 (£) ехр(-(х2 4- £•2) / 2). (14.12.11)
В "повернутом" базисе состояние (14.12.11) записывается в виде:
Ъ t = 0) = -±= (£>0 (7) + y/Q (£>, (т/)),
(14.12.13)
т.е. в суперпозиции двух нижних возбужденных одноквантовых состояний. Тогда в про-
извольный момент времени волновая функция системы "атом 4- мода поля" есть:
7,0 = (^i (£>0 (7) exp(-zQ^) + у/й (&у/, (77) expHQ^exp (- i(Q + &„)!/2).
Преобразование к исходному базису дает:
( 1 / . \
1 UJ + (O)exp(-zQ^)
y/(x,£,f) = —
/2 1
+ -77(^1 (О - (O)exp(-zQ,/)
ИЛИ
^(x, = — / *
21^4- </0(x>, {£ )(exp(-/nf0 - exp(-/Q,/
exp(-/(Q,
+ ^t/2\
(14.12.14)
Проекция (14.12.14) на начальное состояние определяет вероятность обнаружить атом в
исходном состоянии:
W1O НМх’*’/)Их’*’' = °))|2 = ||e*P(-tfV) + exp(-/Q„/)|2 =
= (14- cos(Q^ -Q )/)/2 = cos2fb
I 2 )
Учитывая, что константа связи А « 1, имеем:
331
+ A - л/l — J ййИ,
откуда
Рис. 14.12. Взаимодействие атома с одномодовым ваку-
умным полем.
2| . . . - ,
wl0 =cos А—t .(14.12.15)
Как видно, в системе вместо
спонтанного распада наблю-
даются биения: энергия
атомной подсистемы перете-
кает в полевую и обратно
(см. рис. 14.12), причем ча-
стота этих биений определя-
ется разностью частот нор-
мальных мод колебаний
= CL - = hcoA, то есть
значением константы связи.
Например, если Й<у«1 эВ, а
А = 10^*, для частоты бие-
ний имеем ~10и с'1.
Рассмотренная картина явления напоминает классическую картину биений в си-
стеме двух связанных осцилляторов. На рис. 14.13 приведен пример такой системы: свя-
занные пружинкой математические маятники, имеющие совпадающие частоты. В такой
системе имеются нормальные моды колебаний, соответствующие синфазным и проти-
вофазным колебаниям маятников, имеющие отлича-
ющиеся частоты. В случае, если в начальный момент
времени лишь один из маятников выведен из поло-
жения равновесия (такая ситуация предполагает воз-
буждение обоих нормальных мод), то в системе воз-
никают биения, а энергия, запасенная в системе, пе-
ретекает от одного маятника к другому.
При увеличении объема резонатора возрастает
число полевых мод, с которыми атом эффективно
взаимодействует. В результате энергия, изначально
запасенная в атомной подсистеме, распределяется по
полевым модам и не возвращается обратно. Хорошей
классической моделью такого взаимодействия явля-
ется совокупность связанных маятников, из которых
один (атомный осциллятор) связан со всеми други-
ми, моделирующими полевые моды (см. рис. 14.14).
При этом полевые моды не связаны между собой
(линейность уравнений Максвелла), а могут обмени-
ваться энергией только через атом.
-лпнпяяяп-
э i
Рис. 14.13. Связанные маятники.
Нормальные моды колебаний.
332
Рис. 14.14. Классическая модель взаимодействия атома с полевыми модами. Атом связан со все-
ми модами электромагнитного поля, моды поля не связаны между собой. Жирным выделена
связь атома с резонансными модами.
Приложение 14.1. Расчет вероятности спонтанного перехода 2р ->
1s в водородоподобном ионе.
Вероятность спонтанного перехода в единицу времени в электрическом диполь-
ном приближении определяется коэффициентом Эйнштейна Afi, который может быть
вычислен как
А _ 4й?3 U I2
где
= e\^*f{r}ry/i(r)d2r.
Заметим, что состояние 2р в водородоподобном ионе является вырожденным по проек-
ции орбитального момента. Из центральной симметрии задачи следует, что вероятность
спонтанного перехода не должна зависеть от магнитного квантового числа, а из того, что
оператор электрического дипольного момента не зависит от спина, следует и спиновая
независимость вероятности спонтанного перехода. Таким образом, при вычислении ко-
эффициента Эйнштейна нам достаточно рассмотреть переход из состояния с одним
значением mt, например, =0 в ls-состояние. Матричный элемент оператора ди-
польного момента может быть найден как
& я 2л
dА = 4 (r)^2P (r )r3 t/r J sin 0de\4ф^(0, Tlo(0, (р)ёг,
0 0 0
где er = — = ёхыпОю&ф + ёу$\п0$Улф + ёгсв$0 - единичный вектор в направлении ра-
г
диус-вектора. Соответствующие радиальные и угловые части волновых функций для во-
дородоподобного иона выглядяг следующим образом:
333
>00«^)------7~ ♦ У)о(0,0>) = J-— COS/9,
х/4;г У 4/г
\^71
Л1,(Н = J—г cxP(~Zr/a0),
V °о
„ , ч 1 Zr , „
Я2 - J—y — exp (-Zr / 2ап).
2 у 6а0 а0
Из трёх слагаемых в интеграле по углам в d отлична от нуля только z-компонента.
Подставляя в выражения для d волновые функции и произведя интегрирование, полу-
чим:
Частота перехода есть cd = (1 -\/22)Z2Ry/Й = 3Z2Ry/tfi. Подставим полученные
значения в формулу для Afi:
Д 4^4 с _ 29 з 4 Ду
^-(.зГ <3«“z У'
Для атома водорода (Z = 1) имеем Afl « 6.28x108 с’1, или г = А~' »1.6x1О9с. Отметим,
что классическая теория качественно правильно описывает время жизни атома в воз-
бужденном состоянии, в том числе, зависимость вероятности перехода от заряда ядра
(~ Z4) (см. задача. 14.5).
Задачи к Главе 14.
14.1. Показать, что состояние фсоЬ(е) = -4=ехр(-(£-<£\, )2 /2) полевой моды характе-
ризуется пуассоновским распределением по числу квантов со средним значением
W = ^/2-
14.2. В дипольном приближении определить вероятности спонтанных переходов меж-
ду стационарными состояниями частицы с зарядом е в гармоническом потенци-
але.
14.3. В дипольном приближении определить вероятности спонтанных переходов меж-
ду различными стационарными состояниями электрона в одномерной бесконеч-
но глубокой прямоугольной потенциальной яме.
14.4. Найти отношение вероятностей спонтанных переходов 3d -+2р и Зл->2р в
водородоподобном ионе с зарядом ядра Z.
14 5. Определить время падения электрона на ядро в классической теории. Показать,
что если начальная энергия электрона порядка Ео * -Ry ~ -а'тс\ то в рамках
/ з у 1
классического подхода получим г~(а о>а1) , что соответствует выражению
(14.5.17).
335
Глава 15. Распространение электромагнитных волн в ди-
электрических и проводящих средах.
До сих мы рассматривали воздействие на среду как совокупность атомов задан-
ного электромагнитного поля. В то же время ясно, что заряды в среде, которые приходят
в движение под действием внешнего поля, создают некоторый поляризационный отклик,
который изменяет воздействующее на среду поле. В этом разделе мы сформулируем
общие основы подхода, позволяющего учесть такой поляризационный отклик. Понятно,
цдо наша теория должна будет базироваться на совместном рассмотрении уравнений
Максвелла, описывающих эволюцию электромагнитного поля в пространстве и уравне-
ний. описывающих среду и ее отклик на внешнее электромагнитное поле. Эти уравнения
могут быть получены в рамках различных моделей, базирующихся как на классической
теории, так и на квантовой механике. Ниже мы рассмотрим некоторые из таких моделей,
описывающих газообразные и плазменные среды. Как и раньше, мы будем считать, что
электромагнитное поле не слишком сильное и условия применимости дипольного при-
ближения выполнены. Мы также не будем рассматривать среды, обладающие большим
собственным магнитным моментом, как например, ферромагнетики. Это означает, от-
клик среды на внешнее электромагнитное поле определяется лишь электрической его
компонентой и является пространственно локальным, т.е. определяется электрическим
полем в той же пространственной точке.
15.1 . Общая постановка задачи.
Будем исходить из общей системы уравнений Максвелла:
й 1Ж 4я- ......
rotH = —— + — j, (15.1.1)
с dt с
divE = 4 яр,
JrvH = 0.
Здесь E(r,z) и Н(г,/) - напряженности электрического и магнитного полей в волне, а
p(r,t) и j(г,t)есть плотности зарядов и токов, создаваемых полем в среде. С физиче-
ской точки зрения это токи и заряды, создаваемые за счет воздействия поля волны на
атомные электроны. Как всегда, при рассмотрении сплошной среды (не имеет значения,
это газ, или конденсированное состояние) в качестве плотностей зарядов и токов мы бу-
дем понимать соответствующие величины, усредненные по физически "бесконечно" ма-
лому объему, т.е. объему, в котором находится тем не менее большое количество эле-
ментарных носителей заряда. Возможность использовать дипольное приближение озна-
чает, что обе эти функции определятся лишь напряженностью электрического поля
Ё(г,/) и не зависят от напряженности магнитного поля Н(г,/).
Вместо двух функций p(r,t) и j(r,t) часто оказывается удобно ввести одну -
вектор поляризации P(r,t) или дипольный момент единицы объема среды, такой что
336
p(r,P) = -divP(T-,Pp ~j(r,t} = dP(r,f)/dt. (15.1.2)
Как и положено, из (15.1.2) следует закон сохранения электрического заряда:
др)dt + div j =0. (15.1.3)
Используя понятие вектора поляризации, систему (15.1.1) можно переписать в виде:
- 1 ан
rot Е =------,
с dt
- 1 dD
rot Н =------
с dt
div D = 0, div Н = 0.
(15.1.4)
Здесь введен новый вектор D = Ё + 4лР, называемый вектором электрической индук-
ции.
Для получения волнового уравнения из системы (15.1.4) воспользуемся известной
формулой векторного анализа:
rot rotE - grad divE- V2E.
Тогда из (15.1.4) нетрудно получить:
V2E-grad div Ё = (15.1.5)
с2 dt2
В вакууме, когда плотности токов и зарядов равны нулю, D = E, из (15.1.5) получаем
обычное волновое уравнение:
^41^ 05.1.6)
Наиболее известным решением этого уравнения является плоская монохроматическая
волна с частотой со и волновым вектором к :
E(r,Z) = Ё0 exp(z(£r-йЖ)), (15.1.7)
где к - волновой вектор, указывающий направление распространения волны. Подстав-
ляя (15.1.7) в (15.1.6), получаем дисперсионное соотношение
к = со/с. (15.1.8)
Как результат фазовая скорость волны в вакууме равна с и не зависит от частоты излу-
чения (дисперсия отсутствует). В случае, если начальное волновое поле представляет
собой импульс конечной протяженности, то решение волнового уравнения (15.1.6) мож-
но найти в виде фурье разложения по плоским волнам (15.1.7). Действительно, раскла-
дывая начальный импульс Е(.(г) в интеграл фурье
Ea(<u) = f Д(г)ехр(-/Л(<у)г)^3г, (15.1.9)
получим общее решение уравнения (15.1.6) в виде:
337
Ё(г,0 = fехР(a>)r ~ a)f)\ico.
(15.1.10)
Отметим, что для плоской электромагнитной волны условие divE = /(лЁ) = 0
означает ее поперечность, т.е. вектора к и Ё ортогональны друг другу. Как видно, в
спучае распространения электромагнитной волны в среде, вообще говоря, div Ё 0, т.е.
плоская волна может иметь продольную компоненту поля.
Для анализа распространение электромагнитной волны в среде в рамках уравне-
ния (15.1.5) нам теперь нужно получить уравнения для плотностей токов и зарядов, со-
здаваемых полем волны. Т.е. нам теперь надо построить некоторую модель среды, опи-
сывающую отклик на внешнее электромагнитное поле. Мы сейчас остановимся на самой
простейшей модели газовой среды, как совокупности отдельных не взаимодействующих
между собой атомов. Причем первоначально каждый их этих атомов будем рассматри-
вать в рамках классической механики.
15.2 . Отклик атома на внешнее поле: классическая модель.
В рамках классической теории атом (атомный электрон) можно рассматривать
как гармонический осциллятор с некоторой частотой Qo:
f + Q*r=0, (15.2.1)
где Qo лежит, как правило в инфракрасном, оптическом или ультрафиолетовом диапа-
зонах частот. Тогда, если атом находится в поле электромагнитной волны, в условиях
применимости дипольного приближения динамику атомного электрона можно описать в
так:
f+ = еЁ(/)/ти, (15.2.2)
где Ё(/) - электрическое поле волны в точке нахождения атома, как функция времени,
/и - масса электрона. Отметим, что Ё(/) - вообще говоря, произвольная функция време-
ни.
Будем искать решение уравнения (15.2.2) методом разложения в интеграл Фурье:
r(t) = — cy3p(-i(t>t)da). (15.2.3)
2 л J
Учитывая что
Ё(/) = —(Ё^ехр^йУ^щ, (15.2.4)
2 лJ
и подставляя (15.2.3), (15.2.4) в уравнение (15.2.2), для фурье- компоненты дипольного
момента атома получим:
= e2E„/m(Q20 - а)2) = • (15.2.5)
Здесь
338
=e2/m(Qo-^2)
(15.2.6)
- линейная атомная восприимчивость (поляризуемость). Линейная - поскольку видно,
что индуцируемый полем дипольный момент пропорционален величине поля. Отметим
наличие резонанса при совпадении частоты поля с частотой собственных колебаний си-
стемы. Также важно, что в низкочастотной области (<w«£20) величина восприимчиво-
сти не зависит от частоты: х'™ ~ е2/wQq , в то время как на высоких частотах
(<y»Q0) x'"gh &-ег / та>2 и неограниченно убывает по абсолютному значению с по-
вышением частоты. Последнее утверждение достаточно очевидно: на предельно высо-
ких частотах электрон практически не успевает сместиться из положения равновесия,
что приводит к очень маленькому значению наведенного полем дипольного момента.
Для нахождения отклика атома на произвольный импульс Ё(?) имеем:
J(Z) = er(t) = \da &$(-iayt)da) = exp(-zTyr)ita).
2лJ 2лJ
Учитывая, что Ё^ = jE(t)exp(ica)dt, перепишем (15.2.7) в виде:
(15.2.7)
= у-JХшЁа exp (- icot)d(o = у- Jх(о (- ~ Ё(Г )<*' = f Z(z ~ •
(15.2.8)
Здесь
Ж(г) = (15.2.9)
2лJ
- функция отклика функция на импульсное воздействие, связанная с введенной атомной
восприимчивостью Ха> через преобразование Фурье. Во всех интегралах, записанных
выше, стоят бесконечные пределы интегрирования. Делая замену г = t-f в (15.2.8), по-
лучаем:
00
d(t)= ^x(^(t-T)dr.
—00
(15.2.10)
Как видно, дипольный момент атома в момент времени t определяется электрическим
полем волны во все другие моменты времени, вклад которых задается функцией отклика
Х(г). Вследствие принципа причинности (причина всегда предшествует следствию), мы
говорим только о предыдущих моментах времени, т.е. ^(т<0) = 0, а интеграл в
(15.2.10) берется только по положительному значению переменной. В дальнейшем мы
увидим, что зависимость атомного дипольного момента от запаздывающего аргумента
приводит к дисперсии, т.е. зависимости фазовой скорости волны от частоты.
Отметим, что полученное выражение (15.2.10) автоматически следует из линей-
ной связи da = Ха^о) и не зависит от конкретного выражения для % • Следовательно,
оно справедливо для любых атомных моделей, классических или квантовомеханических,
приводящих к линейной связи атомного дипольного момента с электрическим полем.
339
Для определения физического смысла функции отклика рассмотрим воздей-
ствие на атом предельного короткого 8 - образного электромагнитного импульса
W) - Подставляя эту функцию в (15.2.10), получим:
<*(') ~ Z(') .
т.е функции Z(r) определяет отклик атома на 8 - образное воздействие, обладающее
бесконечно широким "белым” спектром.
Что касается макроскопического дипольного момента среды, то в случае если мы
имеем дело с достаточно разреженным газом, макроскопический дипольный момент
есть просто сумма дипольных моментов отдельных атомов:
P = Nd,
где .V есть концентрация, а дипольный момент атома определяется формулой (15.2.10).
Если среда пространственно однородна ( tV = const), то получим:
(15.2.11)
о
Мы вычислим теперь временную функцию отклика /(т) для модели классиче-
ского гармонического осциллятора. Из выражений (15.2.6) и (15.2.9) найдем:
2тп Д, - со1
Вычисление этого интеграла проведем методом теории вычетов (см. Приложение 15.1):
2
-----sinQnr,
mQ0 0
0,
(15.2.12)
(15.2.13)
/(г) =
В частности, это означает, что в качестве отклика на 8- воздействие в системе возника-
ют незатухающие колебания на собственной частоте £20.
В качестве примера вычислим теперь наведенный полем дипольный момент для
случая мгновенного включения электрического поля волны:
Ё(/) = Р° C°Sd*’ Г"°’ (15.2.14)
1 [0, t < 0.
В этом случае
? - е2Ё '
«/(/) = J z(r)E(/ - r)dr = —
о
Особое внимание обратим на то, что, вследствие (15.2.14) верхний предел интегрирова-
ния соответствует текущему моменту времени t. Учит ывая, что
sin х cos у ~ (sin(.v - у) + sin(x 4- у)) / 2,
- J sin(Qor) cos (o(t - r)dг. (15.2.15)
о 0
,r> (15.2.15) получим:
340
d(t) ‘ 1 ° ([sin((£i0 o)r ♦ „¥)+ sin((Q0 + ft,)r - ft*)]c/r, (15.2.16)
2ш£2п n
откуда:
</(/)- <J'° ? (cos ft* cosQ0/). (15.2.17)
?h(Q0 ft) )
Таким образом, мгновенное включение (толчок) приводит как возбуждению вынужден-
ных колебаний на частоте поля, так и собственных колебаний, которые имеют незату-
хающий характер.
Полученное решение нс применимо, если частота поля совпадает с собственной
частотой колебаний со = Qo. В этом случае (15.2.16) переписывается в виде:
d(t) =----— Г [sin(Q0/) + sin(2Q0r-Q0/)]<7r, (15.2.18)
2wQ0 Jo
откуда
е2Ё
<7(0 =---2-1 sin Qof. (15.2.19)
2wQ0
Дипольный момент атома нарастает во времени.
До сих пор наша модель атома не учитывала потери энергии на излучение и свя-
занное с этим фактором затухание колебаний. С учетом радиационного торможения
атомного осциллятора запишем уравнение движения в виде:
г + )f + £l20r = (15.2.20)
где у = 2е2/?о /Зтс3 - классическая постоянная затухания, определяющая время затуха-
ния атомных колебаний. В оптическом диапазоне частот у ~ 10 s т Ю4 с*1.Общее решение
уравнения (15.2.20) также легко найти с помощью преобразования Фурье. Для фурье -
компоненты индуцированного внешним полем атомного дипольного момента находим:
< = егш = e2Ejm(Q20-(o2 -//69) = /^, (15.2.21)
откуда
_ е2 1
т (Qq - со2 - /у<у)
(15.2.22)
Выражение (15.2.22) обобщает полученное ранее соотношение (15.2.6). Как видно, в
данном случае восприимчивость оказывается комплексной величиной, и, как мы увидим
в дальнейшем, мнимая часть восприимчивости отвечает за поглощение энергии элек-
тромагнитной волны в плазме.
Вычисление функции временного отклика /(г) в данном случае проводится ана-
логично предыдущему случаю и приводи! к результату (см. Приложение 15.1):
341
е2 г exp (-/шт)
2лт -со2 - iyco
12 с \
е I Ут • гл
---exp smfir,
’/и(1 Ч 2 )
О, т < О.
т > О,
(15.2.23)
Здесь Q = v^o-/2/^- Отметим, что в отличие от спектральной функции (15.2.22)
функция отклика (15.2.23) остается вещественной. Однако, в рассматриваемом случае на
временах t»\/yстремится к нулю. Система обладает конечным временем памяти и
"забывает" на временах > 1/у предисторию своей эволюции.
15.3. Анализ волнового уравнения. Общие замечания.
Вернемся теперь к волновому уравнению (15.1.5), описывающему распростране-
ние электромагнитной волны в среде. Мы будем считать, что среда является простран-
ственно однородной, т.е. концентрация атомов среды постоянна по объему (N = const):
1 Г) 00
V2E-grad divE = ——D(r,t)-E(r,t) + ^7iN^-т)с1т . (15.3.1)
c dt n
В рассматриваемых нами приближениях уравнение оказывается линейным, а вектор ин-
дукции D определяется как интегральный, но линейный функционал от воздействую-
щего поля.
Прежде, чем перейти обсуждению решения уравнения (15.3.1), обсудим основные
свойства функции Характерные частоты колебаний атомов лежат, как правило, в
видимой или ультрафиолетовой частях спектра. В случае колебаний молекул речь идет
об инфракрасном диапазоне частот, условие у « Qo всегда выполнено. Поэтому, если
мы рассматриваем излучение с частотами со « Qo (сюда попадает излучения вплоть до
терагерцового диапазона частот) выражение (15.2.22) для атомной восприимчивости
можно переписать в виде
Z*, = —гт = Xs, = const, (15.3.2)
wQ0
что соответствует своему статическому пределу. В этом пределе диэлектрическая про-
ницаемость является действительной величиной и не зависит от частоты излучения. Ес-
ли спектральная ширина импульса попадает в интервал, где = %st, при вычислении
Функции отклика Х(т) выражение (15.3.2) можно "продлить" на весь диапазон частот.
Тогда из (15.2.9)) получаем %(т) = %st 8(т) и
P(r,t) = NXs^(r,t). (15.3.3)
отсутствие дисперсии связь между наведенным дипольным моментом и полем полу-
Чилась локальной. В этом случае вектор индукции D связан с вектором напряженности
Электрического поля соотношением:
D(F,t) = (\ + 4nNxsl)E(r,t) = sstE(r,t), (15.3.4)
342
где с = 1 + 4zcV/sf - статическая диэлектрическая проницаемость.
Линейность связи /.) и Ё позволяет искан» решение волнового уравнения (15.3.1)
в виде суперпозиции отдельных частотных гармоник
Ё(/\/) = — f Ё„,(г)ехр(- i(ui)da). (15.3.5)
2л-J
Подставляя (15.3.5) в (15.3.1), получим:
V2 Ёт (г) - grad div Ём (г) = (1 + 4лМ%ы )Ё„ (г). (15.3.6)
с
Мы учли здесь, что Рда(г) = У/(УЁ<у(г). Введем обозначение:
£ю = 1 + = 1 +
4ne2N 1
т Q2 - со2 - iyco
(15.3.7)
- комплексная диэлектрическая проницаемость. Тогда для спектральной компоненты
поля имеем линейное уравнение, описывающее его пространственную структуру:
V^Jr) - grad divEJr) + — ^ЕДг) = 0. (15.3.8)
с
Решение уравнения (15.3.8) будем искать плоской волны, распространяющейся вдоль
оси z:
Ёш(г) = Ё4.„Иф(Лг). (15.3.9)
Тогда получим:
~ — — — бу2 —
* 2Ек.„-к(кЕк.„) = — £eEt.„=0, (15.3.10)
С
здесь ЁА й, - амплитуда плоской волны с волновым вектором к . Уравнение (15.3.10) ли-
нейное, поэтому произвольный вектор Ёл а можно представить в виде суммы двух ком-
понент:
Ё,.«, =Ё4\ + Ё1.„, (15.3.11)
перпендикулярной и параллельной волновому вектору к .
В случае продольной компоненты поля ЩЁ‘А J = Л2Ё^ а>, и нетривиальное ре-
шение возможно только если £ш = 0. Такое решение невозможно в низкочастотном
(статическом) пределе. Учитывая, что для атомов Qo »у, и кроме того, при не слиш-
ком высоких концентрациях атомов £10 » Q’ = yl4ne2N/m, получаем, что продольные
волны возможны на частотах
(15.3.12)
343
НетруДн0 сообразить, что они представляют собой коллективные колебания электрон-
ной плотности в атомах на собственной частоте, причем величина волнового вектора к
может быть любой и не зависит от частоты колебаний.
В случае поперечной электромагнитной волны (АЁЛ(И) = О, и решение (15.3.10)
есть:
,2 со2
к = (15.3.13)
с
. дисперсионное соотношение для поперечной электромагнитной волны в среде. Как
видно, фазовая скорость волны vph = a>/k = cl явно зависит от частоты распростра-
няющего излучения. Величину пш = принято называть показателем преломления.
Рис. 15.1. Зависимость диэлектрической прони-
цаемости газа (совокупности классических гар-
монических осцилляторов) от частоты излуче-
ния.
15.4. Поперечные электромагнитные волны в линейных про-
странственно однородных средах.
Мы видели, что закон дисперсии для поперечной электромагнитной волны опре-
деляется выражением (15.3.13). При этом в области частот, существенно меньших частот
атомных колебаний (сюда относится излучение вплоть до терагерцового и дальнего ИК
диапазонов), диэлектрическая проницаемость не зависит от частоты и соответствует
своему статическому пределу. В такой ситуации электромагнитные импульсы распро-
страняются со скоростью с/без искажения их пространственной формы.
В оптическом диапазоне частот ситуация более сложная. Сказывается инерцион-
ность атомных колебаний, приводящая к дисперсии, т.е. зависимости диэлектрической
проницаемости от частоты излучения. Типичные зависимости действительной и мнимой
частей диэлектрической проницаемости от частоты излучения приведены на рис. 15.1.
Существенно, что мнимая часть диэлек-
трической проницаемости отлична
от нуля лишь вблизи собственной часто-
ты атомных колебаний. Мы увидим в
дальнейшем, что эта величина определяет
поглощение энергии излучения в плазме.
Что касается действительной части
ReffJ, то она определяет величину фазо-
вой скорости электромагнитной волны.
Как видно, во всем диапазоне частот
кроме узкого диапазона вблизи О0 вели-
чина Re£f(, растет с увеличением часто-
ты. Такая зависимость называется нор-
мальной дисперсией и приводит к тому,
что с увеличением частоты колебаний
скорость электромагнитной волны в сре-
де падает. Область вблизи Qo, где Re<^,
344
наоборот, убывает с увеличением частоты называется областью аномальной дисперсии.
Таким образом, общее решение для плоской монохроматической волны, распро-
страняющейся в среде в направлении оси z, мы можем записать в виде.
E(z,Z) = ЁА „ exp(i(kz-cot)) = Ёкп) exp(i((a>/c)riт z - eot)) х ехр(-(а>/с)п (0 z). (15.4.1)
Здесь п = Je = и' +in" - комплексный показатель преломления. Как видно, его дей-
ствительная часть определяет изменение фазовой скорости распространения волны и
оказывается равной:
vph = с!п\- (15.4.2)
Что касается мнимой части показателя преломления, то ее величина определяет погло-
щение электромагнитной волны в среде. Действительно, амплитуда поля волны меняет-
ся по закону:
Eflmp(z) = Еатр х е?ф(-(су/с)и"<а z) = Ёатр х exp(-z/<5„) , (15.4.3)
где =с1((оп"ш) - глубина проникновения поля в плазму, часто называемая толщиной
скин-слоя. Учитывая, то поток энергии излучения I пропорционален квадрату поля, по-
лучаем:
Z(z) = /0 х exp(-2(<y/c)w"d, z) = /0 х exp(-^z),
(15.4.4)
где Io =I(z = G) - начальный поток энергии, а = 2(щ/с)л"(У - коэффициент поглоще-
ния электромагнитного излучения. Как видно, коэффициент поглощения и толщина
скин-слоя связаны соотношением = 2/6^ .
Для дальнейшего анализа используем полученное нами выражение для диэлек-
трической проницаемости (15.3.7). Выделяя действительную и мнимую части, найдем:
1 , л х, . 4яг2У Q2 - со2 + iya>
£.й = 1 + 4лУу = 1 +------------------
<9 ™ ® 2x2 2 2 *
т (Q; -а>2)2 + у2а>2
(15.4.5)
В газовых средах при давлениях порядка атмосферного (N —10'^ сги'^) в оптическом
диапазоне частот вне резонанса второе слагаемое всегда много меньше единицы. Поэто-
му:
1 ! 2ne2N О.20-а>2 + iyg>
т (Qj -со2)2 +у2а>2 ’
(15.4.6)
откуда:
co/c)^N_______
т (О2-6У2)2 •
(15.4.7)
В условиях резонанса a»~Q0 ситуация обратная, второе слагаемое в (15.4.5) много
больше единицы и
А* = 2(й)/с)п"ш = 2(a)/с)
V туа>
(15.4.8)
345
При этом ширина линии поглощения оказывается ~ 1// .
Рассмотрим теперь движение волнового пакета в среде с заданным законом дис-
персии к(а>). В этом случае из выражения (15.1.10) получим
J Ё* ехр(/(Л(ш)г - а*)\ко, (15.4.9)
где Ед. fl> - спектральный состав импульса в начальный (нулевой) момент времени. Если
считать, что спектр импульса достаточно узкий (а волновой пакет, наоборот, является
пространственно протяженным), то можно считать, что в пределах ширины спектра
функция к(а>) плавно меняется с частотой. Тогда:
Л(о>) « к(й)0) + dk/da^ w=aJb х (щ - &>0 ).
Здесь - центральная (несущая) частота импульса. Для поля получим:
1 ^+Дй> _ ( ( dk \
E(z,Z)~ — Г £Д£)ехр i — z-t (й>-
щ0) б/о» х ехр (/(Аох
(15.4.10)
интеграл берется по ширине спектра излучения. Как видно из (15.4.10), пакет в про-
странстве перемещается со скоростью
1
8 dk/ da> ’
(15.4.11)
называемой групповой скоростью. Отметим, что эта величина в общем случае является
комплексной. Действительная ее часть определяет скорость перемещения в простран-
стве волнового пакета, как единого целого, причем с неизменяющейся формой. Понятно,
что данное приближение соответствует лишь достаточно протяженным по пространству
пакетам (с узким спектром), что позволяет разлагать функцию к(й)) только до первого
порядка малости. Отметим также, что в области аномальной дисперсии выражение
(15.4.11) также часто нельзя использовать для определения скорости перемещения па-
кета в пространстве.
Выражение (15.4.11) удобно также переписать в виде:
v =---------------. (15.4.12)
8 nbj+a>dnJdcD
Вне зоны поглощения функция является действительной, а дисперсия нормальной.
Это означает, что vg < vph.
15.5. Отклик атома на внешнее поле: квантовомеханическая мо-
дель.
Рассмотрим теперь вычисление отклика среды на внешнее поле с позиции кван-
товой механики. Мы также будем рассматривать среду, как совокупность отдельных
атомов, находящихся первоначально в основном состоянии и не взаимодействующих
между собой. В этом случае эволюция атомной системы во времени может быть найдена
346
из решения нестационарною уравнения Шредингера для атома в поле электромагнитной
волны. Пусть у/('".') - волновая функция, описывающая атомную систему. Тогда опре-
делим величину среднего по квантовому состоянию дипольного момента атома с помо-
щью соотношения:
(d(t)^ = eji/(r,t)ry/(r,t)d3r, (15.5.1)
где волновая функция удовлетворяет нестационарному уравнению Шредингера:
/Й^ = (д,+Й'(?,/))/(?,0. (15.5.2)
dt
где HQ - атомный гамильтониан, a fV(r,t) описывает взаимодействие атома с полем во-
лы в дипольном приближении. В dE - калибровке тогда запишем:
PF(r,/) = -^E(/),
где d — ёг - оператор дипольного момента атома, Е(/) = Ео cos ojt - вектор напряженно-
сти электрического поля волны. Пусть поле волны является линейно поляризованным, а
атом в начальный момент времени находится в стационарном (основном) состоянии | .
Представляя общее решение задачи (15.5.2) в виде разложения по собственным
функциям атомного гамильтониана
С i \
= - — Ent\
(здесь у/п (г) - собственная функция атомного гамильтониана с собственным значением
£„), и решая полученную систему уравнений для коэффициентов разложения Cn(t) в
приближении адиабатического включения внешнего поля, в первом порядке нестацио-
нарной теории возмущений, найдем (см. Раздел 8.4):
^,Ё0 (ехр(/(й)„,.-(ц)0 + ехррХ^ + юуЙ
2й (<Dni-cD) (а)„,+й>) J*
с<°(0 = -
2Й
(15.5.3)
Здесь dni - (у/п |d\ i//l } - матричный элемент оператора дипольного момента, а
Ч/ = (Еп ~Ei)/h ~ частота перехода между уровнями р) и . Тогда волновая функция
атома, подвергающегося воздействию электромагнитного поля с частотой со, может
быть представлена в виде:
_ I /
4'(rd) = V'i(f)exp\--Eit +
S (О ехр (- Ent
n*i V Й
(15.5.4)
где С^(0 определяется выражением (15.5.3). Подставляя (15.5.4) в (15.5.1) и учитывая,
что дипольный момент атома в произвольном стационарном состоянии равен нулю, то
есть d„„ = ly/„ d у/
л) = 0, получим:
347
d(t) = J (F)r (r) d'r' x
exp(z(ft?ni -a)t)
< (ч,-*>)
откуда
ло=S
n*i
К|2Ё0Г exp(-iGJt) + ехр(/йХ)л
2Й U^-'y) (Ч,+^)у
+ CjC.
у» KJ 2шт-
— h
хЕ0 cos erf.
(15.5.5)
Здесь \dj\ =е2|гя/|2 - квадрат модуля проекции матричного элемента дипольного мо-
мента на направление магнитного поля (здесь и далее мы полагаем, что это ось z). Вид-
но, как и в случае классического осциллятора, дипольный момент оказался пропорцио-
нален полю электромагнитной волны. Поэтому коэффициент пропорциональности
КГ
Л co2ni - со1
(15.5.6)
естественно назвать линейной атомной восприимчивостью (поляризуемостью) атома.
Заметим, что полученное выражение (15.5.6) подобно выражению для восприим-
чивости гармонического осциллятора в классической теории (см. выражение (15.2.6)).
Действительно, если рассматривать задачу в первом порядке теории возмущений по вза-
имодействию атома с полем электромагнитной волны, атом ведет себя как совокупность
гармонических осцилляторов с набором частот {&>„,}• Это утверждение становится осо-
бенно наглядным, если в спектре частот атомных переходов {<уп/} выделить какую-либо
конкретную частоту и положить се равной частоте классического осциллятора Qo. То-
гда для отношения квантовомеханической и классической восприимчивостей получим:
fni
, (classic)
со
(15.5.7)
h(2mconl)
Величина fn. называется силой осциллятора атомного перехода и является безразмерной
величиной, часто близкой по своему значению к единице. В частности, для линейного
гармонического осциллятора сила осциллятора, связывающая основное 10) и первое воз-
бужденное 11) состояния, равна единице. Это означает, что восприимчивости квантово-
механического и классического осцилляторов одинаковы и по отношению к внешнему
электромагнитному полю квантовомеханический и классический осцилляторы ведут се-
бя одинаково. Отметим, что значение силы осциллятора может быть и отрицательным.
Если переход идет из возбужденного состояния в нижележащее, то <оя1 < 0 и, следова-
тельно f <0
Сформулируем еще одно важное свойство, которому удовлетворяют силы осцил-
ляторов, известное как правило сумм:
(15.5.8)
п
348
то есть сумма сил осцилляторов переходов из заданного состояния во все возможные*
тождественно равна единице (см. Приложение 15.2). Например, для гармонического ос-
циллятора утверждение, что /|0 = 1 автоматически означает, что силы осцилляторов пе-
реходов во все остальные возбужденные состояния равны нулю.
Выражение (15.5.6) позволяет определить диэлектрическую проницаемость раз-
реженного газа:
^=1 + 4^»=1 + ^~S^“7’ (15Л9)
определяющую оптические свойства среды и являющуюся обобщением выражения
(15.3.7) на квантовомеханический случай.
Таким образом, с точки зрения квантовой механики атом представляет совокуп-
ность осцилляторов с некоторым известным набором частот, соответствующим частотам
переходов (oni. При этом величина fni может интерпретироваться как число классиче-
ских атомных осцилляторов с собственной частотой a>ni, принадлежащих одному атому.
Казалось бы, такая классическая трактовка полученного выражения (15.5.6) в случае
многоэлектронного атома вполне возможна: в атоме имеется совокупность электронов,
которые осциллируют на разных, но в том числе, и совпадающих частотах. Тогда можно
было бы ожидать, что силы осцилляторов должны принимать целые значения 1, 2, 3,...,
соответствующие числу атомных электронов с данной собственной частотой. Экспери-
мент не подтверждает сделанное утверждение: как правило силы осцилляторов прини-
мают дробные значения, меньшие единицы. Более того, атом водорода, в котором име-
ется единственный электрон, также имеет набор частот и соответствующих им сил ос-
цилляторов. Объяснить эту сторону рассматриваемого нами явления с позиций класси-
ческой физики оказывается невозможным.
С другой стороны, наше квантовомеханическое рассмотрение не содержит эф-
фекта затухания колебаний и, потому, в узком диапазоне частот вблизи резонанса
coni ~ не может быть использовано. Мы видели, что затухание достаточно легко вве-
сти в классической теории, как некоторую тормозящую силу, действующую на осцилля-
тор. В квантовой теории это существенно более сложный вопрос, который требует вве-
дения квантовых представлений об электромагнитном поле. Эту проблему мы обсужда-
ли в Главе 14.
В заключение, подчеркнем еще раз, что с точки зрения квантовой механики в
первом порядке теории возмущений атом может рассматриваться как совокупность тар-
монических осцилляторов с набором частот conj. Полученный нами результат позволяет
понять почему, хотя бы и на качественном уровне, классическая модель атома как ос-
циллятора до сих пор используется для описания оптических свойств среды.
15.6. Нелинейные атомные восприимчивости высших порядков.
В этом разделе рассмотрим квантовомеханический подход к вычислению поляри-
зуемости атома в поле электромагнитной волны в высших порядках теории возмущений.
1 Если у квантовой системы имеются и состояния непрерывного спектра, то в (15.5.8) под суммированием
подразумевается в том числе и интегрирование по состояниям континуума.
349
Как и раньше, среднее по квантовому состоянию значение дипольного момента
аТома определим с помощью соотношения:
(t/(O) = -eJ^‘(r,Ory/(r,Z)673r, (15.6.1)
где волновая функция y/(r ,t) удовлетворяет нестационарному уравнению Шредингера
(11.1-2) Пусть поле волны является линейно поляризованным и вектор напряженности
электрического поля направлен вдоль некоторого направления п, в начальный момент
времени атом находится в стационарном (основном) состоянии |/). Представляя общее
решение задачи (11.1.2) в виде разложения по собственным функциям атомного гамиль-
тониана, перепишем (15.6.1) в виде:
Остановимся на втором порядке теории возмущений. Удерживая только члены второго
порядка малости, для дипольного момента получим:
= Х^с/2)(0ехр(-/бУ7г/)+^^^лл.С^(Г)С^’(0ехр(-/бцп„./) + сг. (15.6.2)
f п п
Здесь коэффициенты разложения C^l)(t) определяются выражением:
С(»(/) = ЁЛ]Гехр(/(й?л/-й>)/) । ехр(/(й)л/ + ш)/Й (15 6 3)
2Ъ { (*>„,-*>) (а>п1+(О) )'
а С^2)(/) может быть записано в виде:
с<2 = у (л/лЁорл,.ЁоУ Qxp(i(cofl -2co)t) + е^ф(/(^+2й))0 2^„,.exp(/ay)>
f 4Й2 [{cofi-2co){coni-co) (cofi + 2co)(coni + co) со^со^-со2) /
(15.6.4)
Это выражение легко получается после интегрирования (11.1.8) в пределе А—>0. Под-
ставляя (15.6.4) и (15.6.3) в (15.6.2), получим:
п,п'
ИДИ
exp(-2z&tf)
ехр(2/7аг)
2(0
П1
k (a>fl - 2co){(Oni - со) (cofi + 2й))(бУл, + со) cofi (co2ni - со2)
vxp(-2icot) | ехр(2/й>Г) t 2co^(oni + co2
(со„, + СО)(й>„, - со) (со„, - со)(соп1 + со) {со2. - со2 ){co2ni -со2)
(da (0) = zS/2zy)Ef Е£ cos 2cot 4- Х^{со = °)E?EJ ’
(15.6.5)
гДс, как и раньше, компоненты а, /3, у = х, у, z, а по повторяющимся индексам произво-
дится суммирование, а Х^(2со) и Х^г(со = 0) - квадратичные восприимчивости кван-
350
товой системы на удвоенной частоте воздействующего поля и на нулевой частоте, явля.
ющиеся тензорами третьего ранга. Для этих восприимчивостеи имеем.
d(a}d(P}d{r} ( 1 1 | .
2Гг {(сог,-2со)(сот-со) (cofl+2co)(coni + со))
d(a}d(P}d{r} ( 1 1
nr 2ti- {(соГ1+оо)(соп1-со) (со^-со)(соп!+со))
Xafr(<» = 0) = £
d(a} d(p} d{r> ( 1 1
Ufi afn Uni ________1________!______*______ _|_
2h 2 0) fi (COni - CD) CDft (coni + co)J
y ( 1 + 1__________________________________________________'
2/?2 {(cofl + co)(conl-cd) (cofi -co)(conj + co)?
(15.6.6)
Итак, во втором порядке теории возмущений получается, что воздействие на сре-
ду периодической силы с частотой со вызывает в среде колебания дипольного момента
на частотах, не совпадающих с частотой воздействующего поля. Конкретно возникают
колебания дипольного момента на удвоенной частоте, а также статическая поляризация.
Полученные нами квадратичные восприимчивости характеризуются тензорами третьего
ранга и лежат в основе рассмотрения простейших нелинейно-оптических эффектов - ге-
нерации второй гармоники и оптического детектирования. Полученные зависимости
компонент тензора от частоты излучения носят резонансный характер. Эти резонансы
проявляются, например, если частота воздействующего поля близка к разрешенного ча-
стоте перехода в какое-либо состояние. В этом случае в суммах по всем промежуточным
состояниям часто можно ограничиться слагаемыми, дающими резонансный вклад.
Можно показать, что для квантовой системы с центрально симметричным потен-
циалом (атом) все компоненты тензора квадратичной восприимчивости равны нулю (см.
задача 15.9). Поэтому отмеченные выше эффекты, возникающие в среде с квадратичной
нелинейностью, обычно наблюдают в нелинейных анизотропных кристаллах. Более по-
дробно эти эффекты будут рассмотрены в Главе 20.
В высших порядках теории возмущений возникают восприимчивости более вы-
соких порядков. Например, в третьем порядке возникают кубические восприимчивости
2f(3)(3tw) и > (со), описывающие возникновение колебаний дипольного момента на
утроенной частоте, а также на частоте поля. Величина ^(3)(За>) определяет возможность
генерации третьей гармоники воздействующего излучения, а величина /(3)(л>) фактиче-
ски вносит нелинейную добавку (добавку, зависящую от величины поля) в показатель
преломления среды на частоте воздействующего поля. В случае, если /(3)(д>) > 0, то в
области сильного поля показатель преломления возрастает, поле само создает себе соби-
рающую линзу. В результате может возникнуть самофокусировка излучения.
Расчет восприимчивости третьего порядка, приводящий к эффекту самовоздей-
ствия, приводит к следующему выражению для компонент тензора восприимчивости
четвертого ранга:
351
(15.6.7)
Аналогично, для восприимчивости /3)(3<у) можно получить
...» н,.Л_ к- ! !
* ' 4»’ [(^±3«Хч,±2«Хч,±<<
v г_________j_________
мх 4Й3 |_(й?л.. + а>\й)^ ± 2й>Хч, ± <у)_
(15.6.8)
В выражениях (15.6.7) и (15.6.8) всего шесть и четыре слагаемых соответственно, в
скобках используются либо верхние, либо нижние знаки. Легко показать, что в средах с
центральной симметрией потенциала тензор кубической восприимчивости отличен от
нуля. При этом его компоненты, отличные от нуля, связаны определенными соотноше-
ниями (ем. Справочные материалы), а вектор поляризации "смотрит" по направлению
электрического поля волны.
Рассмотренный нами способ вычисления атомных восприимчивостей различных
порядков лежит в основе подхода вычисления поляризационного отклика среды как раз-
ложения по степеням поля и широко используется в современной нелинейной оптике.
Заметим еще раз, что этот подход базируется на квантовомсханической теории возму-
щений, то сеть фактически предполагает малость электрического поля в волне по срав-
нению с внутриатомным значением. Как уже отмечалось, современная лазерная техника
позволяет получать напряженность поля в волне сравнимую с внутриатомной и даже
превышающую ее. В таких полях традиционно используемый метод вычисления атом-
ных восприимчивостей оказывается неприменимым. Универсальных подходов к вычис-
лению отклика в таких сверхсильных световых полях в настоящее время не существует.
Понять происхождение нелинейных восприимчивостей можно и в рамках класси-
ческой механики. Мы видели ранее, что в пределах применимости первого порядка
кван говомсханической теории возмущений атом фактически представляет собой сово-
купность классических осцилляторов с различными весовыми множителями, известны-
ми как сила осциллятора. Поэтому кажется естественными, что в более сильных полях,
когда амплитуда колебаний атомного электрона уже не мала, рассматривать его как ан-
гармонический осциллятор.
В качестве примера, рассмотрим движение атомного электрона в центрально-
симметричном потенциале:
2 2
u{r) = '^V_ + pr44. (15.6.9)
2
352
Уравнение движения для а томного электрона в ноле электромагнитной волны запишется
в виде:
Г + СО^Г = COS (О! - — г1 Г . (15.6.10)
т т
Мы полагаем энгармонизм атомного осциллятора слабым. Поэтому рассмотрим задачу
(15.6.10) в рамках теории возмущений. Будем искать решение задачи в виде.
r(t) = rw (/) + r"’ (/) + ..., (15.6.11)
где
г(0)(/) =--—— cos cot (15.6.12)
Ш(6УО2-6У2)
- полученное ранее решение для гармонического осциллятора, причем | гП)(/) |«^ г(0) |.
Подставляя (15.6.12) в (15.6.11), получим уравнение для г(|):
Fl,’+®02r"’ (15.6.13)
ГЛ
Учитывая, что cos3 cot = cos(3fiX) + 3 cos(6tf), получим, что:
Р ^3ЕрЁ0 (СО8(ЗйХ)ЗСОЗ^Й
Г V/ 3Z 2 2\3 2 П 2 2 2 ’
т т(со0 -со ) -9<у <а0 -со J
т.е. возникают колебания на частоте поля и на утроенной частоте. Как видно, мы можем
теперь ввести кубические восприимчивости:
Г (ЗбУ) = ~Р -^-—2-------------2 3 2 2 ,
т (со0 - со ) (cOq -9со )
(15.6.15)
X°\co) = --3fi f (15.6.16)
т (coQ - со )
Эти поляризуемости резонансно возрастают, когда частота внешнего поля близка к ча-
стоте атомного осциллятора, величина ^(3)(Зй>) также имеет резонанс на утроенной ча-
стоте. Однако, по структуре выражений они отличны от квантовомеханических анало-
гов.
15.7. Плазма: отклик на внешнее воздействие.
Рассмотрим в качестве среды ионизованный газ, плазму, и определим ее отклик
на внешнее электромагнитное поле. В качестве модели плазмы рассмотрим элементар-
ную модель, которую будем использовать при изучении лавинной ионизации и оптиче-
ского пробоя (см. Глава 17). Будем считать, все электроны одинаковы, их концентрация
равна пе. Кроме того задана эффективная частота столкновений с нейтральными атома-
ми, или молекулами v = NalrvT = const, где N - концентрация нейтральных частиц, сг,г
- транспортное сечение рассеяния, a vT - тепловая скорость движения электронов. Урав-
нение движения для электрона в этом случае можно записать в виде:
353
v + vv =eE(/)/w.
(15.7.1)
Здесь Ё(/) электрическое поле электромагнитной волны. Как и прежде, мы полагаем,
чт0 условия применимости дипольного приближения выполнены.
Аналогично случаю атомного осциллятора, рассмотренного в разделе 15.2, пред-
ставляя электрическое поле волны в виде разложения по частотам
CD
для фурье-компоненты скорости движения электрона в плаз-
ме. получим:
еЁ
у = —_s____
m(v-ia))
(15.7.2)
В частности, в статическом поле имеем v = eE/wy = //еЕ, /ле=е!ту - подвижность
электрона в плазме.
Тогда, учитывая, что направленное движение электронов в плазме создает элек-
трический ток, получим для его спектральной компоненты:
- - е\ е
/ = еп v =--------— Е .
J со "е со / . х со
miy-iat)
(15.7.3)
Ток в плазме в рамках нашей модели оказался пропорционален электрическому полю
волны. Это утверждение известно, как закон Ома2, а коэффициент пропорциональности
в соотношении (15.7.3) между плотностью тока и напряженностью поля называется про-
водимостью
(15.7.4)
z . \ '
m(y -i со)
Учитывая, что скорость электрона связана с его смещением соотношением v = г , а, сле-
довательно, = — icor^, для фурье - компоненты наведенного дипольного момента
найдем:
(15.7.5)
5 - - /•
а = er = — е v,Jico =-----------~
°> а 0)1 m{(O + iv}(O
Получаем, что в рамках нашей модели поляризуемость (восприимчивость) электронного
газа есть:
е2
%01 m(a) + iv)(o
В частном случае отсутствия столкновений
е2
Xш 2
та)
(15.7.6)
(15.7.7)
2 Ohm Georg Simon (1789 - 1854) - немецкий физик.
354
- поляризуемость свободного электрона. Легко видеть, чю эго выражение может быть
получено из модели атомного осциллятора (см. (15.2.22), если в последнем положить
= 0 и / = v. Такое же значение восприимчивости получается в высокочастотном
пределе и у атома. Действительно, если частота поля существенно превышает частоты
всех атомных переходов, то с учетом правила сумм из (15.5.6) получим:
vKI ^(°,и _ g2 у fni _________________-___.
(а h h «)2,-со2 тсо2 ^{-соЦсо2 тсо2'
(15.7.8)
В частности, из (15.7.8) мы получаем, что поляризуемость высоковозбужденных (рид-
берговских) атомов равна поляризуемости свободного электрона.
Переходя от восприимчивости (15.7.6) к диэлектрической проницаемости элек-
тронной компоненты плазмы, получим:
(15.7.9)
Нетрудно видеть, что введенные нами функции проводимости (15.7.4) и диэлектриче-
ской проницаемости плазмы (15.7.9) связаны между собой соотношением:
6У
4жт
= l + z--
CD
(15.7.10)
Вводя обозначение сор = ^Але2пе1 т - плазменная (ленгмюровская3) частота колебаний,
выражение (15.7.9) перепишем в виде:
2 2
69
£ = 1-------___[_ у__?____
*бУ 1 2 2^/2 2\
СО + V (со +V )со
В частном важном случае бесстолкновительной плазмы имеем:
(15.7.11)
(15.7.12)
Для показателя преломления имеем пш — -^£ш . Например, для слабоионизованной плаз-
мы (сОр « со,у):
со2у
1 + 1----,
2(а>2 + v2)ty
(15.7.13)
т.е. действительная часть показателя преломления п'(0 близка к единице, а коэффициент
поглощения
\ 4ж2л у
/'«, = ‘ . (15.7.14)
тс(со + v ) 4
Например, для слабоионизованной плазмы с концентрацией электронов «е»Ю12
см'3, W ~ 2.5 • 1019 см'3 и излучения СО? лазера (длина волны - 10.6 мкм) для длины про-
3Langmuir Irving (1881-1957) - американский химик, лауреат Нобелевской премии по химии 1932 года «за
открытия и исследования в области химии поверхностных явлений».
355
(Sera излучения получим f til = 1/;/o) ~ IO4 + 1(Г см. To есть такая плазма является практи-
к1, прозрачной средой, нс влияющей на параметры лазерного пучка.
В случае бссстолкновитсльной плазмы все определяется соотношением частоты
11(у1Я н плазменной частоты колебаний. Если со> а)р, то пт -п'м и волна в плазме рас-
пространяется с фазовой скоростью xfph~ . Отмстим, что фазовая ско-
рость волны является сверхсветовой. Однако, групповая скорость волны в этом случае
оказывается меньше скорости света, причем v Avx - с1.
В противоположном случае о)<сор имеем пт -п"м, и распространение волны в
плазме невозможно. Как мы увидим в дальнейшем, элскгромаг нитное излучение в этом
случае отражается от плазмы. Концентрацию электронов, разделяющую эти два режима,
н соответствующую а) = сор, называют критической концентрацией. Как видно,
"сг =~Г~2-
(15.7.15)
Например, для излучения СО2 лазера ncr »1019 см'3.
Подводя итог сказанному, мы показали, что свойства плазмы можно описывать
одной из функций, комплексной проводимостью <уш , или диэлектрической проницаемо-
стью £ш, связанных между собой соотношением (15.7.10). Нетрудно видеть, что, ис-
пользуя связь (15.7.10), мы можем ввести понятие проводимости и для диэлектрической
среды. В этом случае мы фактически вместо введенного вектора поляризации, описыва-
ющего свойства среды, введем понятие тока поляризации с помощью соотношения
j = cP[dt.
Покажем, однако, в случае проводящей среды использование понятия именно
комплексной проводимости оказывается более удобным. Действительно, обсудим воз-
можность рассмотрения отклика на внешнее немонохроматическое поле. Из линейной
связи проводимости плазмы и электрического поля волны для произвольного
немонохроматического поля мы получаем
= j сг(г)Ё(г,/ - T)dr, (15.7.16)
о
где функция отклика <т(г) связана с проводимостью соотношением аналогичным
(15.2.9):
сг(т) = —- [crwexp(-/6wr)t/tv, (15.7.17)
Счисление (15.7.17) проводится также с помощью теории вычетов и дает (см. Прило-
жение 15.1);
е2гг гехр(-Уй)г) .
----L _13-------->- Jo) = <
2лт v-ico
'•Cl
е2пе
т
0,
(15.7.18)
356
Как видно, "глубина памяти" системы в нашей модели определяется эффективной часто-
той столкновений, и гок в плазме сохраняется на временах порядка ~ 1/v после выклю-
чения электрического поля волны. Для физики взаимодействия фемтосекундных лазер-
ных импульсов с плазмой эго могут быть существенные времена.
С другой стороны, мы можем по-прежнему ввести функцию отклика.
1г / \ rexp(-tcor) .
у(г) = — f у ехр(- iarcjdco = --— ---------— “бУ
z 2;rJ Zrnn* (co + tv)co
(15.7.19)
Это выражение легко получить из функции х(т) •> полученной для гармонического ос-
циллятора с затуханием при устремлении его собственной частоты к нулю и замене
у —> v. В результате:
/(т) = — (l-cxp(-vr)), т>0. (15.7.20)
т v
В отличие от функции сг(г) полученная функция не стремится к нулю с увеличением
времени, т.е. глубина памяти системы по времени оказывается неограниченно велика.
Это может быть очень неудобно при проведении численных расчетов. С физической
точки зрения такой результат понятен. Полученный результат возникает за счет того,
что на нулевой частоте (статическое поле) поляризуемость плазмы, как совокупности
электронов, неограниченного возрастает во времени, в то время как функция сг^ при
стремлении частоты к нулю не имеет особенностей и стремится к своему статическому
пределу: сг^ = сг0 = e2ne/mv.
В качестве примера найдем функцию отклика сг(г) для случая мгновенного
включения поля с частотой со:
Ёо cos cot,
А
^>0,
/<0.
В этом случае
00 е2п Ё z
7(0 = J <т(т)Е(/ - г)<Уг = —Пе -0 j exp (-vr) cos co(t - =
0 m о
е2и v - / ч
——2 тг Ео (cos cot - exp(-vr) 1
m(co r
(15.7.21)
Как и ожидалось, установление стационарного режима наступает на временах t > 1/у . В
частности, для статического поля
- е п - / \
7(0 = -^Е0(1 -ехр(-и))= <т0Е0(1-ехр(-и)).
(15.7.22)
15.8. Прохождение электромагнитной волны через границу разд©"
ла двух сред.
До сих пор мы рассматривали распространение электромагнитных волн в про-
странственно однородной среде. Теперь остановимся на вопросе о прохождении плоской
357
дектр01^агнитн0^ волны через границу раздела двух сред, причем для простоты будем
читать, чт0 волна палает нормально к границе раздела. Будем считать границу раздела
езкоЙ, з сами среды пространственно однородными. Тогда мы можем записать решение
Елового уравнения в каждой из сред (см. Раздел 15.4) с учетом того, что на границе
раздела тангенциальные компоненты векторов напряженности электрического и маг-
нитного полей должны быть непрерывны.
Выберем систему координат так, как показано на рис. 15.2. Плоскость z = О есть
граница раздела сред, и из области z < 0 (вакуум) на границу раздела падает монохро-
матическое линейно поляризованное излучение с частотой а): Ё(г,/) = Ё(г)ехр(—ia/t). В
области z > 0 имеем среду с показателем преломления п(0. В среде I (вакуум) имеем две
Рис. 15.2. Нормальное падение волны
на границу раздела двух сред.
волны - падающую с амплитудой Ео и отражен-
ную с амплитудой Ег; в среде II - имеем прошед-
шую волну, ее амплитуда Е, .Запишем условия не-
прерывности компонент поля на границе раздела
(z = 0). Полагая, что электрическое поле обладает
только х- компонентой, запишем:
ЕО+ЕГ=Е,. (15.8.1)
Здесь мы предположили, что вектор электрическо-
го поля волны при отражении не изменил свой
знак. Запишем теперь условие непрерывности для
компонент магнитного поля. Из уравнения Макс-
велла
го/Ё(г) = /-Н(г) (15.8.2)
с
для тангенциальной у - компоненты магнитного
поля получим Н = -/(с/й>)ЗЕ/&, на границе раздела тангенциальная компонента поля
является непрерывно дифференцируемой функцией. Учитывая, что 5E/Sz ~ АЕ ~ идаЕ, а
также тот факт, что для отраженной волны волновой вектор меняет свой знак, получим.
Е0-Ег =«<аЕ/.
(15.8.3)
Разрешая уравнения (15.8.1) и (15.8.3) относительно амплитуд отраженной и прошедшей
волны получим:
е'=_2Ле“’
(15.8.4)
Как видно из (15.8.4), в случае, если среда на которую падает излучение является опти-
чески более плотной (пш > 1), вектор электрического поля волны действительно не ме-
няет свое направление, а вектор магнитного поля, наоборот, меняет. Так бывает не все-
*Да: в случае падения на оптически менее плотную среду ситуация обратная. В отражен-
358
ной волне именно вектор Ё изменяет свой знак. В частности, мы видели, что плазма ча-
сто является оптически менее плотной средой по сравнению с неионизованным газом.
Вводя коэффициенты отражения и прохождения излучения от границы раздела,
как отношение потоков отраженной и падающей волны, получим
и
|Е,.|2 _ я„-12 _«-l)2+(»"J;
|е„|! «„+' <<.+'г
«)2|е,|2 4(«'„);
|Е„|2 (<+1)2 У '
(15.8.5)
(15.8.6)
Легко видеть, что R + Т = 1.
В качестве примера рассмотрим нормальное падение электромагнитной волны с
частотой а) на бесстолкновительную плазму, характеризующуюся диэлектрической
проницаемостью (15.7.12). Мы уже отмечали, что в зависимости от соотношения часто-
ты падающего поля и плазменной частоты а)р показатель преломления является или чи-
сто действительной, или чисто мнимой величиной. В случае, если концентрация элек-
тронов превышает критическое значение (15.7.15), т.е. о)<а)р, п'ш = 0, следовательно,
R = 1 - излучение полностью отражается от плазмы. При этом в плазме поле спадает по
экспоненциальному закону с глубиной проникновения 6 = с/yja)2 - со2 . В случае
со«а>р толщина скин-слоя не зависит от частоты падающего излучения и равна
8 = с/й)р. Наоборот, при а)>сор имеем «"^ = 0 и ri а = а)2р / а)2 . В этом случае
)2
«+1)2
- излучение частично проходит сквозь границу раздела. Заметим, что если
со» сор, то Т »1 - За)214й>2 близко к единице, а отражение почти отсутствует.
Эффект отражения электромагнитного излучения от плазмы со сверхкритической
концентрацией электронов может быть использован для определения электронной кон-
центрации. Плазменный объект облучается излучением, частота которого может плавно
изменяться во времени (см. рис. 15.3). Действительно, в этом случае при совпадении ча-
стоты зондирующего поля с частотой плазменных колебаний происходит смена режима,
и прохождение сквозь плазменный объект электромагнитного излучения сменяется его
отражением, или наоборот.
Рис. 15.3. Диагностика электронной плотности в плазме по отражению электромагнитного
излучения.
359
15.9. Прохождение электромагнитной волны через границу разде-
ла двух сред. Случай наклонного падения.
В данном разделе рассмотрим случай наклонного падения электромагнитной
оПны на границу раздела двух сред. Как и раньше, будем полагать что плоскость z - О
сеть граница раздела сред, и из области z < 0 (вакуум) на границу раздела падает моно-
хроматическое линейно поляризованное излучение с частотой (о\
gp-/) = Ё(г:)е)ф(-/йХ). В области z<0 имеем среду с показателем преломления рав-
ным единице, области z > 0 - п. В среде I имеем две волны - падающую с амплитудой и
отраженную с амплитудой; в среде II - имеем прошедшую волну. Специфика данного
спучая по сравнению с нормальным падением заключается в том, что существуют две
разные геометрии рассматриваемой задачи (см. Рис. 15.4). В одном случае вектор Ё ле-
жит в плоскости границы раздела сред. Такая волна называется волной Е - типа или ТЕ
волной. В другом случае в плоскости границы раздела лежит вектор Н и такая волна
называется волной Н - типа или ТМ волной4. Специфика случая ТМ - волны заключает-
ся в том, что электрическое поле волны имеет нормальную к поверхности компоненту
электрического поля и вызывает появление токов, нормальных к поверхности, что при-
водит к возникновению поверхностных зарядов.
Оба случая ТЕ и ТМ волны могут быть рассмотрены подобно тому, как это было
сделано выше для нормального падения волны на границу раздела5.
Например, для случая ТЕ волны, падающей под углом 0О к нормали к поверхно-
сти, для коэффициента отражения RTE и прохождения ТТЕ получаем
^ис. 15.4. Наклонное пяление электромагнитной волны на границу раздела двух сред. Случай
(слева) и ТМ (справа) поляризаций поля.
английского: transverse electric (ТЕ) и transverse magnetic (ТМ).
Р-С- Ландсберг Оптика, М.: Наука (1976), с.471-479.
360
(15.9.1)
2sin /90 cos#,
sin(/?0 + 0,)
Здесь 0t - угол, под которым в среде распространяется преломленный луч. Его величина
определяется из соотношения:
sin 0. ,,
----L = /. •
/) ' а>
sin v(}
Для случая ТМволны формулы получаются другими:
2 т М-
' П: №
(15.9.2)
R -M-
Ы
sin 2#0 - sin 2#,)
sin 2#0 + sin 2#,)
2sin<90 cos#,
sin(#0 + 0,) cos(#0 + 0t)
(15.9.3)
2
Здесь 0Q - угол падения, 0t - угол преломления.
В случае нормального падения 0t = #0 = 0 различие между ТЕ и ТМ волнами
пропадает. Раскрывая неопределенность в выражениях (15.9.1) и (15.9.3) с помощью
(15.9.2), получим:
что соответствует выражению (15.8.5).
15.10. Теория Друде металлов.
До сих пор говоря о плазме, мы и имели в виду ионизованный газ. Однако, анало-
гичные соображения могут быть использованы для рассмотрения электронного газа в
металлах, или полупроводниках. Действительно, известно, что в идеальных кристаллах
электроны, находящиеся в зоне проводимости, двигаются как свободные, но с некоторой
эффективной массой, которая часто близка к массе свободного электрона. Наличие нере-
гулярностей решетки, а также ее тепловых колебаний приводит к эффекту рассеяния
электронов и их торможению, подобно тому, как это происходит при столкновениях
электронов в газах с атомами и молекулами. Теория, которую мы использовали для опи-
сания электродинамических свойств газовой плазмы применительно к электронному га-
зу в металлах, была создана еще в 1900 году П. Друде6 и носит его имя. Значения пара-
метров, определяющих величину диэлектрической проницаемости электронного газа в
некоторых металлах, приведены в Таблице 15.1. Типичные значения плазменной часто-
ты электронного газа в металле составляют (Dp < 1016 с’1. Эта величина соответствует
ультрафиолетовому диапазону частот. Что касается полупроводников, то значение плаз-
менной частоты определяется как уровнем легирования, так и его типом, т.к. эффектив-
ные массы носителей заряда в случае р - легирования (дырочная проводимость) как пра-
вило больше, чем в случае п - легирования (электронная проводимость). Типичные зна-
чения частоты рассеяния в металлах составляют v ~ 1014 с1. Указанные значения плаз-
6Drude Paul (1863-1906) - немецкий физик.
361
^елной частоты и частоты столкновений определяют диапазоны частот электромагнит-
ного излучения, в которых металлы ведут себя существенно по разному. Так, диапазон
& << v « сор мы будем называть низкочастотным. Сюда, в частности, относится радио-
частотное излучение и излучение вплоть до ТГц и дальнего ИК диапазонов. Случай
примерно соответствует ИК - УФ диапазону частот, и в том числе види-
мой части спектра (излучение оптического диапазона частот, именно в этом диапазоне
находятся источники интенсивного лазерного излучения). И, наконец, случай
г « сор «со - это высокочастотное излучение (вакуумный ультрафиолет и рентгенов-
ское излучение).
Таблица 15.1. Проводимость и подвижность носителей заряда в металлах.
Вещество Статическая про- водимость, 1017 с"1 <т = e^njmv Подвижность, CGSE, це ~e/mv Эффективная масса (в массах свободного электрона)
А1 2.8 3690 0.97
' Си 5.0 9600 1.0
Ag 5.4 16800 -
Zn 1.4 5250 0.85
Sn 0.8 51 -
Представленные данные по проводимости и подвижности зарядов позволяют в конечном счете
определить значение плазменной частоты и частоты столкновений в металле.
Из общего выражения
йГ co2„v
£ = 1----, , + i —;--j—
(О~ +V* (а?2+У2)й>
(15.10.1)
можно перейти к следующим частным случаям:
со2
1) Низкочастотное излучение £ш * i—— - диэлектрическая проницаемость чисто мнимая.
COV
Для показателя преломления имеем: ri=n"=coply/2vco.
2) Оптическое излучение
£<° я
CD у
___£. 1-/— . Действительная часть диэлектрической
со2 V со)
проницаемости сильно отрицательная, мнимая мала по сравнению с ней. Для показателя
преломления имеем: п'= co2pv f2co2 ,п"= сор/co-
co2 co2pv ( со2р (( co2pv
3) Высокочастотное излучение £ш ~1 у + * у ’ а п а> ~ 1— 2^2 > п а>~ ви^“
но, п'ш % 1 и и" «1 Как результат, излучение распространяется со скоростью света и
почти без поглощения. Частота излучения много выше частоты плазменных колебании,
поэтому металл становится прозрачным для излучения. Здесь необходима важная ого-
ворка. Для зашиты высокочастотного рентгеновского и у излучения обычно исполь-
зуют тяжелые металлы, обычно свинец. Поглощение такого излучения в них определи-
362
ется нс свободными элск1рош1ми. о коюрых мы говорили до сих пор, а электронами на
внутренних оболочках томов, имеющих энергии связи порядка энергии квантов пада-
ющего излучения.
15.11. Поверхностные электромагнитные волны.
В данном разделе мы рассмотрим особый класс решений уравнений Максвелла,
так называемые поверхностные электромагнитные волны (ПЭВ). ПЭВ - это волна, вол-
новой вектор который лежит в плоскости границы раздела двух сред, а величина поля
(электрического и магнитного) экспоненциально затухает вглубь каждой из сред (см.
рис. 15.5). Будем считать, что плоскость z = 0 является границей раздела сред, характе-
ризующимися различными значениями диэлектрической проницаемости
s2, z > 0.
(15.11.1)
Будем также считать, что вектор напряженности магнитного поля лежит в плоскости
границы раздела (такая волна называется волной Н - типа), и направим ось у вдоль
вектора Н (см. рис. 15.5). Как мы увидим, вектор Ёбудет иметь компоненту вдоль вол-
нового вектора к , т.е. волна будет частично продольной. В данном случае нам будет
удобнее анализировать процесс распространения волны, решая уравнение для напря-
женности магнитного поля Н. Полагая волновое поле монохроматическим,
Е,Н ~ exp(-zTut), запишем волновое уравнение в виде:
2 69 2
V Н(х, z) + £-(z)—Н(х, z) = 0. (15.11.2)
С
Что касается напряженности электрического поля, она может быть найдена потом из
уравнения
Рис. 15.5. Поверхностная электромагнитная волна.
Будем искать решение уравнения (15.11.2) в каждой из сред в виде:
363
(15.11.4)
11! ( V, 7.) ~ 11 exp(Ikx I- A", z).
11 и (л\ “) - ll0 cxp(//<\ k2z).
I цч'ь '"° обеспечивает экспоненциальное затухание поля вглубь каждой из
V|H'ч । loneгпилмя (15.11,4) в (15.11.2), получим:
A ’ I а; -гг;,(</?/с2) = 0,
-к2 I k-j +е2(ю1/с1)аО.
(15.11.5)
Дцч функций (15,11.4) непрерывность тангенциальной компоненты магнитного поля
пыиопвеиа автоматически. Что касается непрерывности тангенциальных компонент век-
ivpii ю из (15.11.3) имеем:
1 ан
1 ан„
(15.11.6)
= 0 я2 dz z = 0 ’
о । к\,ца
к\£2 +к2£{ =0.
(15.11.7)
Поскольку АрА-, >0, выполнение (15.11.7) возможно лишь если диэлектрические про-
ницаемости сред имеют противоположные знаки. Для определенности будем считать,
чю 0, < 0. Подставляя ,к2 из (15.11.5) в (15.11.7), получим дисперсионное вы-
ражение для поверхностной электромагнитной волны:
ГУ / g|g2
е I е 2
с у £2 - с у е2 + е!
(15.11.8)
Волновой вектор должен быть действительной величиной. Отсюда получаем, что ди-
vicKгрнчсские проницаемости сред должны удовлетворять соотношению |f2| > .
До сих пор мы предполагали, что £, и е2 - действительные. Однако, выражение
(15.11.8) верно и в общем случае комплексных значений диэлектрических проницаемо-
vicii. В этом случае условие существования поверхностной электромагнитной волны
имеет вид:
Rc6-2<0, |Re6’2| > Re Яр
(15.11.9)
Отметим прежде всего одно важное свойство поверхностной электромагнитной
,""iiii,i. Эта волна является частично продольной: вектор электрического поля имеет
компоненту, как перпендикулярную волновому вектору к , так направленную вдоль к .
^с1’Ц'1В1Г1сл|,ц(), из уравнения
rot H(r) ^~i~ E(r)
|,0||У'шм:
364
(15.11.10)
с (. ан .. ai । )
a.v J
С \\(x,z)(-e7ik + ех/с),
а)
где к вычисляется в соответствующей области пространства.
Насколько реально найти среды, вдоль Гранины раздела которых может распро-
страняться поверхностная электромагнитная волна? Это легко. Одной из них может
быть воздух (вакуум) с ~ 1. другой - металлическая поверхность. Мы уже обсуждали,
что формула (15.10.1) может быть, в том числе, использована для описания свойств
электронного газа в твердых телах и, в частности, в металлах. При этом для металлов
значение плазменной частоты cDp ~ Ю'^’с1, а частоты столкновений v ~ 5 • 10 3 с *. Тогда,
например, в видимом и ИК диапазонах частот (tw~1015 с1) действительная часть ди-
электрической проницаемости сильно отрицательна (|Res2| ~ 100 » £, ~ 1), т.е. сформу-
лированное нами условие возможности существования поверхностной волны заведомо
выполнено.
В качестве примера подробнее рассмотрим структуру ПЭВ на границе раздела
"металл - вакуум". В этом случае
(15.11.11)
При этом
^2 =^2 -^1.2(^2A2)-
2 2
й? <у V
Учитывая, что е2 * —у + i -^г-
CD CD
со2
, получим:
«х ^й)1!(сй)р), к2 ~CDp/c,
и
к ®
( 2 >
CD . CD .CDV
— 1 +---y + Z---у .
с 2®р J
(15.11.12)
Обратные значения кХг2 определяют глубину проникновения ПЭВ вглубь каждой из
сред. 12 ®с/сор,£\ ~с/сор-(cDpfcDf ~ 10(И2. Мнимая часть волнового вектора определя-
ет длину пробега ПЭВ вдоль границы раздела:
^яэд=(1тЛ)’'
CD CDV
Для использованных выше параметров отсюда получаем доли сантиметра.
На практике поверхностные электромагнитные волны часто возникают на по-
верхности металлического расплава, возникающего при облучении поверхности металла
мощным лазерным излучением в различных задачах лазерной обработки материалов. В
такой ситуации волны уносят энергию из области пятна фокусировки излучения, огра-
ничивая в конечном счете локальность лазерного воздействия.
365
Отметим, что мы рассматривали поверхностную электромагнитную волну Н - ти-
с в плоскости границы раздела лежал вектор напряженности магнитного поля вол-
П Казалось бы, можно также попытаться построить решение в виде волны Е - типа,
а в плоскости границы раздела лежит вектор Е. Оказывается, однако, что поверх-
постные волны Е - типа не существуют (см. задача 15.5).
Приложение 15.1. Вычисление функции отклика на внешнее
электрическое поле для классического осциллятора с затуханием и
плазмы.
Проведем вычисление функции отклика, заданной выражением
Z(r) =
2лгп ДПд - аг- iya>
Для этого рассмотрим контурный интеграл в комплексной плоскости а> (см. рис. 15.6).
Замкнем контур в нижней полуплоскости. Внутри контура находятся два полюса перво-
го порядка в точках бэ12 = —z’//2±Q, Q = д/Qq — /2/4 . Поскольку мы выбрали обход
контура по часовой стрелке, то:
ехр(-/щг) , п лг ехр(-/щт)
, >-----da) = Im > res - т
Q; -iya-о) а> + iya>-щ
& = ^1,2
Рис. 15.6. К вычислению функции отклика гармонического осциллятора.
Учитывая, что интеграл по удаленной полуокружности равен нулю, в результате
Г1°лучим искомый ответ. В частном случае ответ для осциллятора в отсутствие затуха-
Ний получается при / —> 0. Аналогичным образом вычислим функцию отклика плазмы
На внешнее поле (см. Рис. 15.7):
366
P \ П'/l J /
1 v - do) =
o) + i v
е'п г схр(- i(t)T) . -e‘ ,1e fexl
—c ’A. d(t)--i ♦
2;nn , v — id) 2zzw
2 (> П
^res(cxp(-M,r) . = - ^exp(-vr).
v ' ]n) = -iv tn
Рис. 15.7. К вычислению функции отклика плазмы.
Приложение 15.2. Правило сумм.
Докажем сформулированное в Разделе 15.5 правило сумм = 1, где сила ос-
п
к,|2
циллятора определяется выражением fni = —-—1---(см. (15.5.7)). Действительно:
A/(2wiwnj.)
п п ” п ”
1 I j г л
— 2-1 ft 'ZniZin + ZniZln> ~ 2-SP nlZ т ~ ZniPin) = ~Т £^(ZinPni ~ PinZni) = — ТрАкл’
п tn in п п „ п
Здесь мы учли, что матричные элементы импульса и координаты связаны соотношением
pni = imconiznl. Принимая во внимание, что коммутатор [гр] = /Й, получим
п
п
Задачи к разделу 15.
15.1. Определить зависимость коэффициента поглощения электромагнитного излучения
металлической поверхностью от частоты в ИК, видимом и УФ диапазоне частот.
368
Глава 16. Кинетическая теория распространения элек-
тромагнитных волн в плазме.
При рассмотрении распространения электромагнитных волн в плазме в Главе 15
мы исходили из элементарной модели плазмы, основанной на том, что все электроны в
плазме одинаковые и характеризую гея одним и тем и тем же значением скорости (энер-
гии), определяемым электрическим нолем волны в данной пространственной точке.
Кроме того, мы предполагали, что частота столкновений электронов с атомами является
постоянной величиной, нс зависящей от их энергии, а в качестве соударений рассматри-
вали только упругие столкновения с атомами (молекулами). Каждое из этих предполо-
жений является существенным упрощением, обоснованность которого изначально со-
вершенно не очевидна. Прежде всего, отмстим, что в реальности сечения упругого рас-
сеяния на атомах (молекулах) имеют совершенно разные зависимости для различных
газовых сред, а предположение v = const и вытекающая из этого предположения зави-
симость транспортного сечения рассеяния <jtr ~ 1/v (v - скорость электрона) не реализу-
ется ни в одном из газов. Кроме того, неупругие столкновения, которые происходят, как
правило, заметно реже чем упругие, характеризуются заметно большими потерями энер-
гии электронов. В такой ситуации, даже если в начальный момент времени все электро-
ны и характеризовались одним и тем же значением энергии, в процессе эволюции они
"расплываются" по энергиям. Как результат, приближение одинаковых электронов теря-
ет свою обоснованность. Альтернативный подход основан на кинетической теории
Больцмана, когда состояние электронного газа описывается функцией распределения
электронов по скоростям. В данном разделе мы рассмотрим подход к вычислению от-
клика плазмы, основанный на кинетическом уравнении Больцмана1. В частности, мы
выясним, в каких условиях может быть использован ранее рассмотренный подход, бази-
рующийся на элементарной теории. Мы также рассмотрим эффекты, связанные с суще-
ственной неравновесностью энергетического спектра электронов в плазме, и в, в частно-
сти, возможность усиления электромагнитного поля в плазме.
16.1. Кинетическое уравнение Больцмана для электронной ком-
поненты плазмы в поле электромагнитной волны.
Будем исходить из кинетической теории, базирующейся на кинетическом уравне-
нии Больцмана. Будем полагать, что плазма по объему является пространственно одно-
родной, и слабоионизованной, так что межэлектронные соударения не являются доми-
нирующими. Также будем считать, что воздействующее на плазму поле волны является
достаточно слабым, что позволяет воспользоваться дипольным приближением. В этом
случае кинетическое уравнение Больцмана может быть записано в виде2:
a/(v,Z) eE(0W,/)
-------L2 = St(f} (16. 1.1)
ot т dv
1 Boltzmann Ludwig (1844-1906) - австрийский физик - теоретик, основатель статистической механики и
молекулярно-кинетической теории.
2 Здесь в уравнении явно учитывается отрицательный знак заряда электрона.
369
Здесь ,/(v»z) " Фунхиия распределения электронов по скоростям (ФРЭС), Ё(/) - элек-
1ричес1<ос поле элскэромагни i ной волны (напомним, что в дипольном приближении за-
1)11симос,ь1<) напРяжснносги поля 01 пространственной координаты можно пренебречь,
В03ДСЙС1ВИС поля волны на исследуемую систему является пространственно локальным),
Slij•) - интеграл столкновений, описывающий изменение ФРЭС в результате упругих
и iicynpyi их столкновений электронов с атомами (молекулами), ионами и друг с другом,
функция распределения по скоростям нормирована согласно условию’
f/(v,/)</3v = l. (16.1.2)
Рис. 16.1. Сферическая система координат.
Будем считать воздействующее на плазму
поле линейно поляризованным и направим
ось z вдоль направления вектора Ё. Перехо-
дя в сферическую систему координат
у = \у,О,ф] и учитывая, что в этой системе
координат
д _ д _ 1 d _ 1 d
dy dy в у дв 9 vsin# д(р
(16.1.3)
(здесь } - орты сферической системы
координат, см. рис. 16.1), перепишем (16.1.1)
в виде:
dt w \ dv
sin# df(y,t)y
у dO >
= W).
(16.1.4)
Как видно, в случае линейно поляризованного поля, в уравнение не входит дифференци-
рование по азимутальному углу ф. Это означает, что если начальная функция f(y,t — 0)
имеет осевую симметрию и не зависит от ф, такая зависимость и нс появится в процессе
ее эволюции во времени.
В дальнейшем нам будет удобно вместо переменной # перейти к переменной
cos#:
dt
df sin 0 df(y,t)
cos и — +-------—------~
dy у и)
= W).
(16.1.5)
еЕ(р
т
Нс конкретизируя пока вид интеграла столкновений, перейдем к решению уравнения
(16.1.5). В условиях аксиальной симметрии задачи будем искать ее решение в виде раз-
ложения ФРЭС по полиномам Лежандра3:
Av,0,/) = /„(v>() + /,(v,z)coS^+/2(v,o|(3cos^-1) + ... = ZA(v,/)/>,(cos^). (16.1.6)
X, tl
Legendrc Adrien-Marie (1752 - 1833) - французский математик.
370
Основные свойства полиномов Лежандра даны в Справочных материалах.
Мы понимаем, что электрическое поле волны, воздействуя на электроны и раска-
чивая их вдоль оси z , создаст асимметрию углового распределения электронов по ско-
ростям. Однако, если эта асимметрия невелика (интуитивно ясно, что в случае высоко-
частотного поля это означает, что направленная скорость колебательного движения
электронов существенно меньше хаотической тепловой скорости движения электронов),
в разложении (16.1.6) мы можем ограничиться всего двумя первыми членами разложе-
ния:
f (V, 0, /)» /0 (V, /) + (V, /) cos 0. (16.1.7)
Представление функции распределения по скоростям в виде симметричной (изотропной)
части /0(у,/) и малой анизотропной добавки /^(v,/) принято называть двучленным при-
ближением. Помимо уже упоминавшегося ограничения на величину напряженности по-
ля воздействующего излучения, для использования этого приближения необходимо так-
же потребовать, чтобы начальная функция распределения была слабоанизотропной и
могла быть представлена в виде (16.1.7).
Прежде чем перейти к решению уравнения (16.1.5) в рамках двучленного при-
ближения, обсудим физический смысл гармоник /0(г,/) и f}(y,f). Интегрируя функцию
ftyj) по угловым значениям переменной, мы можем найти функцию распределения по
абсолютным значениям скорости:
F(y,t)v2dv = ^f(v,t)cKlxv2dv = 4^f0(v,t)v2dv. (16.1.8)
Как видно, нулевая гармоника функции распределения по скоростям задает распределе-
ние по абсолютному значению скорости. Что касается условия нормировки для fQ(y,f),
то оно имеет вид:
$f0(v,t)v2dv = l/47r. (16.1.9)
С функцией распределения по модулю скорости неразрывно связана функция
распределения электронов по энергии (ФРЭЭ). Действительно, делая замену перемен-
ных Е = mv2/2 и принимая во внимание, что v2dv = yj'l/m3 х 4Ес1Е, функция
«(^0 = ^f0(y[2E/m,t) (16.1.10)
есть распределение электронов по энергиям, нормированное согласно условию;
QO
fn(E,t)JEdE = l. (16.1.11)
О
Величина n(JEyt)y!~E есть плотность электронов с энергией Е. Средняя энергия электро*
нов по спектру, очевидно, может быть вычислена как
00
= \n(E,t)E,ftdE. (16.1.12)
О
371
Рассмотрим теперь физический смысл гармоники формирующей анизо-
тропию ФРЭС под действием внешнего поля. Вычислим плотность тока в плазме;
,7(О = -еи<.|у/(у,/)<У3у. (16.1.13)
Здесь л,. - концентрация электронов. Очевидно, изотропная часть функции распределе-
ния нс даст вклада в электрический ток, а анизотропная добавка создает ток в направле-
нии электрического поля волны (ось z):
j: (Г) = -епе J v cos2 (0)/ (у, t}dyу = - j у3/ (v)dv. (16.1.14)
Мы учитывали, что Joos dQ = ^тг/З. Таким образом, первая гармоника ФРЭС определя-
ет создаваемый в плазме ток. Отметим, что полученное утверждение вследствие условия
ортогональности полиномов Лежандра
[ Рп (cos 0)Рт (cos 0) sin 0d0 = < ’ _ п*т,
о [1/л/2л + 1, п = т.
является общим и не связано с двучленным приближением. Понятно, что для вычисле-
ния функции отклика на внешнее электромагнитное поле нам необходимо найти /,(v,0,
т.е. решить уравнение Больцмана.
16.2. Уравнение Больцмана в двучленном приближении и функ-
ция отклика на внешнее поле.
Получим теперь систему уравнений для гармоник /0(v,Z) и /,(v,/). Для этого
умножим поочередно уравнение (16.1.5) на нулевой и первый полиномы Лежандра и
проинтегрируем по угловым координатам скорости электрона. Получим:
^^=|^^у7,(у,о+а.
д‘ 3mv (16.2.1)
а/, (у, 0 еЕ(1)5/0
dt т dv 1
Здесь а = Д-|л(/)Л2, a =^fcosOTSr(/)dn.
Для дальнейшего анализа системы уравнений (16.2.1) нам необходимы знания об
интеграле столкновений. Для краткого анализа всех возможных столкновений электрона
с атомами, влияющими на ФРЭС, выделим конкретно упругие столкновения. Эти столк-
новения происходят наиболее часто, сечения упругих столкновений, как правило, на
°Дин - два (и более) порядка больше сечений неупругих столкновений. С другой сторо-
ны, доля теряемой электроном энергии в упругих соударениях мала, она составляет ве-
личину 8е1 ~ 2т/М (здесь М - масса атома или молекулы). В этом смысле для анализа
изменения энергии электронов (или абсолютного значения их скорости) как правило
Ва*ны именно неупругие столкновения. С другой стороны, изменение направления век-
372
тора скорости и изотропизация функции распределения определяются упругими столк-
новениями. В Главе 15 мы видели, что скорость направленного движения электрона дей-
ствительно забывается за одно "эффективное" столкновение, определяемое транспорт-
ной частотой рассеяния. В то же время релаксация энергии происходит, как правило,
значительно медленнее, за больше количество "эффективных столкновений. Следова-
тельно, в уравнении для /Ду,/) достаточно учесть только упругие столкновения, а в
уравнении для /Ду,/) определяющая роль будет принадлежать неупругим столкновени-
ям электронов с атомами (молекулами). Вычисление упругого интеграла столкновений,
входящего в уравнение для асимметричной части ФРЭС, приведено в Приложении 16.1:
2i =-^(v)Z(v>0, (16.2.2)
где vtr (у) = N(jtr (v)v - эффективная (транспортная) частота рассеяния, <т1г - транспорт-
ное сечение рассеяния, N - концентрация атомов (молекул). Тогда систему (16.2.1) пе-
репишем в виде:
О’
(16.2.3)
dt 3mv2 dv 1
c/Xv,/) z ч еЕ(,
dt т
Для решения этой системы уравнений необходимо задать начальные распределения
/0(г,/) и /Ду,/). Естественно считать что в начальный момент времени (/ = 0 или
t = -оо) функция распределения изотропна, т.е. fx = 0.
Не накладывая никаких ограничений на вид функции, задающей электрическое
поле в зависимости от времени, можем написать формальное решение второго из урав-
нений (16.2.3), удовлетворяющее нулевому начальному условию:
/ДьО = —ехр(-у,Ду)/)х [ ехр (y,r (у)/' )Е(/') dt'. (16.2.4)
т -00 dv
Подставляя (16.2.4) в (16.1.14), и меняя местами порядок интегрирования по скорости и
по времени, для наведенного в плазме тока получим:
Л (О = v3/, (y)dv = j сг(г,/ - г)Е(/ - T)dv , (16.2.5)
о
где функция сг(г,/ —г) есть функция отклика на внешнее воздействие и задается выра-
жением:
сг(т,/-г)
4л??2ле
Зт
Г зГ
Г--------exP(~^(v)r)^.
(16.2.6)
Полученное нами выражение для тока (16.2.5) по структуре напоминает выражение
(15.6.16), полученное ранее в рамках элементарной теории. Ток в плазме также записы-
вается в виде функционала от поля, взятого в том числе и в запаздывающие моменты
времени. Однако, следует иметь в виду, что полученное нами выражение гораздо слож-
373
и в том числе, содержит новую физику за рамками рассматриваемой ранее элемен-
^ноЙ теории. Прежде всего отмстим, что сама функция отклика стала функций двух
Нумеитов, она неявно, через симметричную часть функции распределения, также зави-
уг запаздывающего аргумента, т.е. от прсдистории эволюции /0. Еще более важно
С1П '
)С; мы понимаем, что функция распределения электронов зависит от приложенного
fonfl Как? Для этого надо решать систему уравнений (16.2.3), и мы этого пока не дела-
1И Но интуитивно ясно, что чем сильнее воздействующее поле, тем более "горячей" при
прочих равных условиях является электоонняя
функция отклика зависит от напряженности поля < ПЛазмы' Если так’ то сама
оказывается нелинейным функционалом поля Сп* * ЗНаЧИТ возникаю1йий в плазме ток
частоте будут вызывать колебания тока на частота^°не сов К°ЛебаНИЯ П0ЛЯ На 0ДИ0Й
ика на частотах, не совпадающих с частотой падаю-
щего поля с последующим переизлучением на этих частотах. Таким, образом, в рамках
кинетической теории, плазма, вообще говоря, оказывается нелинейной средой.
Рассмотрим, однако, пока простейшие случаи. Во - первых, предположим, что
распространяющееся в среде поле достаточно слабое и не влияет на свойства среды, т.е.
на функцию распределения по электронов энергиям. В этом случае связь тока и поля за-
дается через линейный функционал вида (15.6.16) с функций отклика:
4®2«„ г 3
------ v
Зт J
о-0(г) =
dv j
(16.2.7)
а функция /0 (v) является стационарной. При этом сам вид функции отклика определя-
ется как зависимостью транспортной частоты от скорости (энергии) электрона, так и
конкретным выражением для симметричной части функции распределения электронов
по скоростям.
Рассмотрим теперь важный частный случай. Пусть транспортная частота столк-
новений не зависит о скорости (энергии) электрона уДу) = у0 = const. Тогда для функ-
ции отклика (16.2.7) получаем:
z . 4яЕ2« . f 3f zir->o\
<т0(г) = ——-exp(-vor)Jv-----— py. (16.2.8)
3m J \ ov )
Тогда, вычисляя полученный интеграл по частям, учитывая, что на при v->oo функция
7o(v) ~>0 и принимая во внимание условие нормировки (16.1.9), из (16.2.8) получим:
откуда
в^п
сг0(т) =—-ехр(-иог). (16.2.9)
т
Мы видим, что в этом случае функция отклика не зависит от конкретного вида распре-
деления электронов по скоростям. Более того, полученная функция отклика совпала с
т°й, что была получена в рамках элементарной модели (см. (15.6.18)). Это означает, что
374
в рассматриваемом случае элементарная модель правильно описывает электродинамиче-
ские свойства плазмы. Фурье - преобразование функции отклика
= j сг(,(г)ех|э(/7дт>/г = ^77;
(16.2.10)
дает проводимость плазмы на частоте со. Зная функцию отклика (16.2.9) или (16.2.10),
мы можем описывать процессы распространения электромагнитной волны.
Однако, мы уже отмечали, что случай v/r(v) = v0 = const на практике не встреча-
ется у атомов ни одного из газов. Это означает, что рассмотренная нами кинетическая
теория отклика на внешнее воздействие может давать результаты, отличные от предска-
заний элементарной модели. Остановимся на этом вопросе подробнее.
16.3. Комплексные диэлектрическая проницаемость и проводи-
мость плазмы в кинетической теории. Показатель преломления и ко-
эффициент поглощения.
Для качественного понимания ситуации рассмотрим сначала самый простой слу-
чай: пусть имеется монохроматическая волна Е = Ео exp(-zTtf). Вычисляя для этого слу-
чая возникающий в плазме установившийся ток, найдем:
jz (/) = j сг0 (r)E(Z - т) dr = j <т0 (т + Г)Е(г)б/т =
о о
_ 4ле2ле
3m
— e?qj(-v/r(v)/)jexp((-z6y + vfr)T)47rxE0 =
vfr+z<w
2
Р_
I J ” , .,2
О
—-— ovxE0 cxp(-zo>/).
Как видно, величина
г .з y,r+ico( df0(y^
3 J cd1 + v 1dv j
(16.3.1)
есть комплексная проводимость плазмы на частоте со. Легко также получить выражение
для комплексной диэлектрической проницаемости
3 J со' + у2
(16.3.2)
В случае v,r =const это выражение совпадает с (15.6.11), полученном в элементарной
теории. Подчеркнем еще раз, что эти выражения получены для стационарного во време-
ни распределения электронов по модулю скорости (энергии). Эти же выражения, однако,
можно использовать и в случае плавного во времени изменения /0, однако при этом
важно выполнение условия |с/0/д/|« cof{].
375
Полученные выражения позволяют определить рефракционную способность
плазмы, а также коэффициент поглощения (или усиления) излучения. Например, для
слабоионизованной плазмы сор <<a>,vlr имеем:
3 ® dv
(163.3)
а коэффициент поглощения:
2а> „ 4лег', 4 лгу2
и = — п =----------" =_____р.
с с Зс J (йг 4- V2
vAv) ( dfQ(y)
k/y.
dv I
(163.4)
Для справки приведем полученные выражения и для представления спектра элек-
тронов через энергетическое распределение п(Е):
—---j
3 о® +vi
dEJ
dE,
(16.3.5)
(16.3.6)
3 с j zy2 + ид dE )
Здесь ФРЭЭ нормирована согласно условию j п(Е)уГЁ<1Е = 1.
Полученные выражения носят весьма общий характер, конкретные значения па-
раметров зависят от вида распределения электронов по скоростям, которое может быть
различным в различных физических ситуациях, и, в том числе, как уже отмечалось, за-
висеть от величины интенсивности распространяющегося в плазме излучения. В этом
случае плазма оказывается нелинейной средой. Обычно, даже в неравновесной плазме
выполнено условие df /dv < 0. Поэтому плазма оказывается оптически плотной средой
по сравнению с неионизованным газом, а > 0 если только в плазме есть столкнове-
ния. Однако, для количественного определения обсуждаемых электродинамических ха-
рактеристик надо знать распределение электронов по скоростям, т.е. решить предвари-
тельно кинетическое уравнение Больцмана.
В простейшем случае функция распределения электронов по скоростям является
максвелловской и характеризуется температурой Т:
( У/2
/«м= Л:
Напомним, что эта функция нормирована согласно условию Jv f M(y)dv — \/4л. Учиты-
вая, ЧТО dfMldv = -{mv/T)fM{v-), из (16.3.3) и (16.3.4) получим:
ы зт J а> +vt
mv
~2Т
4лтсо2р г 4 уДу)
ЗТс со2+v/r
376
16.4. Продольные волны.
В этом разделе мы несколько подробнее остановимся на рассмотрении в рамках
кинетической теории продольных электромагнитных волн в плазме. В Разделе 15.6 мы
видели, что такие волны - это ленгмюровские колебания плазмы, удовлетворяющие дис-
персионному соотношению = 0. Тогда в рамках кинетической теории получаем.
4^ , ^-jyjco
3 JV co2+v2r
a/o(v)
dv
(16.4.1)
dv = 0.
В случае v,r = const из (16.4.1) получаем:
€ =1_____
(1-i—) = 0,
co
т.е уравнение которое уже обсуждалось в рамках элементарной теории (см. раздел 15.6).
Его решение в области vtr «со есть со — сор —ivtr/2. Рассмотрим теперь приближенное
решение уравнения (16.4.1). Разлагая подинтегральное выражение в ряд по малому па-
раметру v/co, получим
(16.4.2)
3 J со + vfr < dv J
Тогда получим:
со
^7ССО~ f (
---^[^ivjco+tvjco')1)
Представляя со « сор + 6, получим
2 + -
6
(16.4.3)
Здесь означают усреднение по функции распределения электронов по скоро-
, . lf,
стям =—J v /0 (v) dv. Как
видно, первое слагаемое в (16.4.3) фактически эквива-
лентно результату элементарной теории, в то время как второе слагаемое может как уве-
личивать (в случае возрастания транспортной частоты рассеяния с увеличением скоро-
сти), так и уменьшать (в противоположном случае) скорость затухания плазменных ко-
лебаний.
16.5. Усиление электромагнитного излучения в плазме в условиях
ее сильной неравновесности.
Мы видели (см. (16.3.5), (16.3.6)), что электродинамические характеристики
плазмы существенным образом зависят от конкретного выражения для транспортного
сечения и вида энергетического спектра электронов. Мы уже отмечали, что обычно даже
в неравновесной плазме величина dn/de<$, что обеспечивает положительные значения
377
обоих интегралов (16.3.5), (16.3.6). Однако, представим себе ситуацию, когда в энерге-
Тйческом спектре электронов имеется область энергий в которой производная дп/де > О
(см РиС> 16'2)' Такая ситуация может рассматриваться как наличие инверсной населен-
ности в распределении электронов по энергетическим состояниям, т.к. в некотором
энергетическом интервале плотность числа электронов возрастает с энергией. Нетрудно
видеть, что соответствующая область энергий вносит отрицательный вклад в интеграл
(16.3.6), уменьшая величину коэффициента поглощения. Вопрос, который представляет
существенный интерес, заключается в том, может ли в итоге коэффициент поглощения
быть отрицательным, т.е. плазма оказаться усиливающей средой? Очевидно, это воз-
можно, если энергетический диапазон с инверсией в ФРЭЭ будет вносить определяю-
щий вклад в интеграл (16.3.6). Для более детального анализа ситуации перепишем вы-
ражение (16.3.6) в следующем виде:
_ 2 7 ( g„
3 с Jo®2+^1 дЕ
2<f
3 c J
d ( E~/2vlr
dE{ а2 + у2
n(E}dE. (16.5.1)
Рис. 16.2. ФРЭЭ с областью инверсии.
Как видно, режим отрицательного поглоще-
ния (усиления) может быть достигнут, если в
некотором интервале энергий
d ( E3/2vlr У
dc[“)2+v2r>
(16.5.2)
причем именно этот интервал дает опреде-
ляющий вклад в интеграл (16.5.1).
Проанализируем отдельно случаи
низких (щ«у,г) и высоких (щ»у/г) ча-
стот.
В низкочастотном случае из (16.5.2) имеем
rf(£3/2/v,r)M<0, или учитывая, что
= No-".(N - концентрация атомов или молекул среды), найдем:
d
ds\atr(E))
<0,
(16.5.3)
т.е. в области инверсии спектра электронов транспортное сечение должно расти с энер-
гией быстрее, чем по линейному закону.
В высокочастотном случае (а)» ) получаем d{E^2vtr (Е))/dE < 0, откуда
^-(£2<7,,(£))< 0,
dE
(16.5.4)
транспортное сечение должно убывать быстрее, чем квадрат энергии.
Насколько реально выполнение таких условий? Оказывается, реально. Например,
Условие возможности усиления низкочастотного излучения (16.5.3) легко выполняется
378
для тяжелых инертных газов (крип тон, ксенон) благодаря минимуму Рамзауэра4 5 в сече-
нии транспортного рассеяния (см. рис. 16.3).
Рис. 16.3. Транспортные сечения рассеяния элек-
тронов на атомах аргона (1), ксенона (2).
Интервалы энергий с растущим
транспортным сечением рассеяния
ссть и в ряде других газов, в частности
в азоте (см. рис. 16.4). Что касается
выполнения условия "высокочастот-
ного" усиления (16.5.4), то оно выгля-
дит более экзотическим. Как правило,
такое резкое убывание сечения не
свойственно явлению электрон - атом-
ного (молекулярного) рассеяния. В ка-
честве примера выполнения условия
(16.5.4), однако, можно привести зави-
симость аДЕ) в аргоне где условие
"высокочастотного" усиления выпол-
няется также благодаря эффекту Рам-
зауэра но уже, наоборот, в области ма-
лых энергий (0.12 - 0.23 эВ).
Отметим еще раз: условия (16.5.3) или (16.5.4) являются необходимыми, но недо-
Рис.16.4. Транспортное сечение рассеяния элек-
тронов на молекулах азота.
статочными для возникновения эффекта
усиления. Необходимо, чтобы обсужда-
емый интервал энергий вносил главный
вклад в интеграл (16.5.1). Этому усло-
вию удовлетворить достаточно легко:
например, интересующего нас вида
распределения электронов по энергиям
формируются при ионизации газа до-
статочно коротким лазерным импуль-
сом в пределе многоквантового фото-
эффекта (рис. 16.5). Действительно, в
процессе многоквантовой ионизации
формируется набор фотоэлектронных
пиков с энергиями
(16.5.5)
где Q - частота ионизующего газ излучения, /( - потенциал ионизации атома (молеку-
лы), а К = К^п,К^п +1, Кпт +2,... - число поглощенных лазерных квантов, которое в
соответствии с законом Эйнштейна для фотоэффекта должно превышать минимальное
число К^п > • Если длительность ионизующего лазерного импульса меньше
4 Ramsauer Carl (1879-1955) - немецкий физик.
5 При записи (16.5.5) мы пренебрегли штарковским сдвигом основного состояния и континуума, что ока-
зывается часто возможным при умеренных значениях интенсивности излучения.
379
вреМенИ Релаксации ЭНСРГИИ электронов (при атмосферном давлении и если в области
иОцизаиионных пиков возможны только упругие столкновения, это время составляет
с) мЫ получаем фотоионизационную плазму с ФРЭЭ, имеющую области инверсии.
Например, среду, пригодную для усиления низкочастотного излучения (<w< vzr)
Рис. 16.5. Спектр фотоэлектронов в плаз-
ме ксенона, созданный импульсом KrF
легко получить при ионизации ксенона
(Л *12.13 эВ) импульсом ультрафиолетового
импульса KrF лазера (Ю = 5.0 эВ) субпикосе-
кудной длительности. При интенсивностях из-
лучения ~ Н^’-Ю12 Вт/см2 доминирующим
процессом будет процесс трехфотонной иони-
зации, который приводит к образованию фото-
электронного пика в области энергий
Ео «2.87 эВ, как раз попадающего
в область растущего с энергий транспортного
сечения (см. рис. 16.6). Считая пик достаточной
узким (для спектрально ограниченного им-
пульса длительностью 100 фс его ширина со-
ставляет ~ 0.1 эВ), мы можем приближенно считать его форму S - образной:
п(Е)4Ё = 3{Е-Ей).
Тогда из (16.5.1) получим:
2 Г 1 d ( E3/2vlr '
3 с Je dE{jo2 +v2r j
+ y2)-(2/3)£(Jy<r/J£)(y2 -cd2)
c (ft>2+v2)2
Полученные выражения показывают,
что при достаточно быстром нарастании
с энергией транспортного сечения ко-
эффициент поглощения становится от-
рицательным, т.е. плазма оказывается
усиливающей средой. Величину
кш=-/л(0 мы будем называть коэффи-
циентом усиления электромагнитного
излучения в плазме. В области CD«vtr
выражение для коэффициента поглоще-
ния существенно упрощается:
^Ис- 16.6. R возникновению усиления излучения
8 Фотоионизационной плазме в инертных газах.
Как и ожидалось, в пределе низких ча-
Пот усиление возможно если транспортное сечение нарастает с энергией быстрее, чем
по линейному закону.
380
Обычно при атмосферном давлении величина транспортного сечения составляет
порядка 012 с’1. Значит, такая плазма может быть использована для усиления радиоча-
стотного излучения вплоть до терагсрцового диапазона частот. Для усиления излучения
в терагерцовом диапазоне следует поднимать давление до нескольких атмосфер.
Отметим теперь еще одну важную особенность неравновесного фотоионизацион-
ного плазменного канала, созданного ультракоротким лазерным импульсом. Мы видели
ранее, что плазма является оптически менее плотной средой по сравнению с неионизо-
ванным газом. Такой результат получается как в элементарной модели, так и в рамах
кинетической теории, если функция распределения электронов по энергиям не имеет ин-
тервалов с инверсией (см. (16.3.5)). Однако, рефракционные свойства плазмы, определя-
емые действительной частью показателя преломления (см. (16.3.5)), тоже зависят от
наличия инверсии в энергетическом спектре электронов. Действительно, из (16.3.5) по-
лучаем:
(16.5.7)
Аналогично условию (16.5.2) полу-
чим:
d ( Е2'2
dE , со2 + v2
(16.5.8)
В низкочастотном случае (со « v*) из
(16.5.8) имеем:
d Е'/4
ds[crlr(E)
(16.5.9)
т.е. в области инверсии спектра элек-
тронов транспортное сечение должно
Рис.16.7. Распространение СВЧ излучения в плаз-
менном волноводе скользящих мод. 0 - угол пол-
ного внутреннего отражения.
расти с энергией быстрее, чем по закону сг,г ~ Ех14. Это условие оказывается даже более
мягким, чем сформулированное ранее условие (16.5.3), необходимое для возникновения
эффекта усиления. Что касается высокочастотного случая (со » ), то, очевидно, вы-
полнение условия (16.5.8) невозможно.
Таким образом, если основной вклад в интеграл, определяющий действительную
часть показателя преломления (16.5.7) вносит область энергий, удовлетворяющая усло-
вию (16.5.9), плазма окажется более плотной средой по сравнению с неионизованным
газом. В рассмотренном нами ранее случае фотоионизационной плазмы, созданной
субпикосекудным УФ лазерным импульсом в приближении 6 - образного энергетиче-
ского спектра электронов получим:
, 1 Г 4Ev„dvJdE\
2<а2+и,Д 3 <y2+v2 I
(16.5.10)
381
Очевидно, плазма становится оптически более плотной если слагаемое, стоящее в скоб
ках, больше единицы. В низкочастотном пределе:
(16.5.11)
Выполнение условия (16.5.9) ведет к возможности использования неравновесного плаз-
менного канала, созданного УФ лазерным импульсом, как волновода для распростране-
ния СВЧ импульсов. Процесс распространения СВЧ излучения в таком плазменном ка-
нале схематически изображен на рис. 16.7 и основан на эффекте полного внутреннего
отражения на границе с оптически менее плотной средой, которой в данном случае яв-
ляется неионизованный газ. При этом, если выполнено более жесткое условие (16.5.3),
импульс СВЧ излучения в канале может еще и усиливаться в процессе распространения.
Для плазмы при атмосферном давлении такой режим распространения с усилением мо-
жет быть реализован для диапазона частот вплоть до субтерагерцового.
Рис. 16.8. Пространственная структура СВЧ (1) и
лазерного (2) импульсов в заданный момент
времени. Пунктирные линии показывают области
усиления и показателя преломления, большего
единицы, в плазменном канале.
Схематически процесс распространения
и усиления субтерагерцового импульса
в неравновесном плазменном канале,
созданном импульсом УФ лазера, пред-
ставлен на рис. 16.8. Фемтосекундный
лазерный импульс, распространяясь в
газе, создает за собой пространствен-
ный след - область усиления, протя-
женность которой определяется време-
нем релаксации энергетического рас-
пределения. То же самое касается фо-
кусирующих свойств плазменного ка-
нала, однако протяженность зоны кана-
лирования обычно оказывается больше.
Для наиболее эффективного усиления
радиочастотного импульса в такой си-
туации удобно реализовать режим, ко-
гда импульсы движутся в среде один за
Другим, так что радиочастотный импульс постоянно находится в зоне усиления, создава-
емой лазерным импульсом.
16.6. Разряд в электроотрицательных газах, поддерживаемый
электронным пучком, как среда для усиления электромагнитного из-
учения.
В этом разделе мы рассмотрим еще один способ создания инверсной населенно-
сти в низкотемпературной слабоионизованной плазме, который можно использовать для
Усиления в ней электромагнитного излучения. Как мы видели, необходимыми условия-
ми для этого является наличие интервала энергий с инверсией энергетического спектра
электронов в области где т ранспортное сечение рассеяния возрастает с энергий. При
382
этом необходимо, чтобы данный интервал
r vnent энергий вносил определяющий вклад в инте-
а' а'"е гралы, определяющие электродинамические
р1 " 1 • 1 . свойства плазмы. Все эти условия, оказывает-
[ production J ся, могут быть выполнены для несамостоя-
тельного разряда, поддерживаемого электрон-
ным пучком, в смеси тяжелого инертного газа
Рис. 16.9. Области рождения и гибели и газа? МОЛекулы которого обладают свойством
электронов в разряде._______________электроотрицательности (т.е. молекулы, кото-
рые имеют устойчивые отрицательные ионы).
К числу таких молекул относятся, например, О2, F2, CI2, SF6, CCU и многие дру-
гие. В несамостоятельных разрядах в смесях, содержащих электроотрицательные приме-
Рис. 16.10. Сечение прилипания электро-
нов к молекулам фтора.
си, происходит интенсивная гибель электронов в результате процесса прилипания, а
рождение электронов обусловлено ударной ионизаций быстрыми электронами пучка.
При этом гибель электронов в процессе при-
липания происходит в области малых энергий
- как правило, долей электронвольта (см.
рис. 16.9). В то же время вторичные электроны,
возникающие при ионизации пучком, в сред-
нем имеют существенно большую энергию. В
такой ситуации возникает спектр электронов,
характеризующийся инверсией, которую мож-
но использовать для усиления электромагнит-
ного излучения, подобрав смесь газов так, что-
бы в области инверсии транспортное сечение
росло с энергией. Это легко сделать, например,
в смеси Хе.Тг со сравнительно невысокой кон-
центраций молекул фтора, так, чтобы молекулы фтора обеспечивали эффективную ги-
бель электронов в области малых энергий (см. рис. 16.10). Скорость рождения вторичных
электронов Qb{E') при ионизации атомов газа быстрым электронным пучком при каче-
ственном рассмотрении может быть ап-
проксимирована выражением:
2 Г Е
£л(£) = ?х—- 1-—- , (16.6.1)
JXe К. * Хе )
в области энергий 0 < Е < 1Хе (1Хе - по-
тенциал ионизации атома ксенона) и
Qb (Е) = 0 вне этого интервала. Спектр
рожающихся электронов нормирован со-
гласно условию
^Qb(E)dE = q. (16.6.2)
Типичные виды ФРЭЭ, полученные
в таком разряде при давлении в смеси 4
Рис. 16.11. Стационарные ФРЭЭ в плазме
смеси Хе:р2 для концентраций молекул F2 (в
см’3) 4х1015 (1), 8х1015 (2) and 1.6Х1016 (3).
383
атмосферы и различных концентрациях молекул фтора в смеси, представлены на рис.
|6.Н Как ВИЛНО' они харнктсризуются областью инверсии в диапазоне энергий, соот-
рс1х,'тву*о1пнх растущему гранспоргному сечению рассеяния электронов на атомах ксе-
нона. чго н может бы ть использовано для усиления радиочастотного излучения. Отме-
нно. ЧТО в отличие ог фоюнонизационных пиков, существующих лишь на временах ре-
кгксацнч спектра, определяемых в ксеноне упругими потерями энергии, полученные
распределения могуг бьпь реализованы в непрерывно горящем разряде и пригодны для
усиления достаточно длинных импульсов излучения.
16.7. Эффект усиления как отрицательная абсолютная проводи-
мость и движение электронов в плазме в направлении против действу-
ющей на них силы.
Рассмотренное нами усиление электромагнитного излучения в неравновесной
плазме предполагает, что часть энергии, запасенной в плазме, передается электромаг-
нитному полю, т.е. сама плазма остывает, если в ней распространяется электромагнит-
ное излучение. Так всегда бывает при усилении излучения в среде с инверсной населен-
ностью в дискретном спектре. Атомы, которые находились в возбужденных состояниях,
переходят в нижележащее состояние, отдавая энергию электромагнитному полю. Анало-
гично и при наличии инверсии в континууме: электроны плазмы отдают часть свой
энергии усиливаемому полю и "охлаждаются". С этой точки зрения эффект усиления
выглядит парадоксальным. При воздействии на плазму, характеризующуюся изначально
изотропной по углам функцией распределения по скоростям, при приложении поля со-
вокупность электронов начинает двигаться в сторону, противоположную действующей
на них силе. В статическом поле такой эффект фактически означает возникновение от-
рицательной абсолютной проводимости. В рамках элементарной теории такой эффект
невозможен: направленная (дрейфовая) скорость движения электронов всегда направле-
на вдоль действующей на электроны силы. Возможно ли наблюдать эффект отрицатель-
ной абсолютной проводимости в рамках кинетической теории? Оказывается, да. В ки-
нетической теории такой эффект возможен.
Для обсуждения возможности такой ситуации вернемся к системе уравнений для
гармоник функции распределения и рассматривая для простоты случай
статического поля с напряженностью Е:
(16.7.1)
»2=^Av7,(v,/)+a.
dt 3mv dv
a/.(v,/) z A eEdf0
7|V - + vlr(v)Ji(v,/) = ——•
" m dv
Считая как обычно что время релаксации к стационарному распределению электронов
"о >нер, ии (по модулю скорости) гораздо больше, чем время установления направлен-
1101 о движения, определяемое ./i(v,/), запишем.
mv„ dv
(16.7.2)
384
Подставляя (16.7.2) в уравнение для /()(v,/), получим:
(16.7.3)
Полученное уравнение может быть легко представлено в виде уравнения диффузии в
пространстве скоростей с направленным потоком. Действительно, вводя функцию
F(y)= У’/о(v)> п учитывая, что d/0/dv = д(у/0)/dv- , преобразуем (16.7.3) в виду:
dF(v,t)_ dJv
dt dv
(16.7.4)
QP" e2E2v
где J =—D-------\-UF - поток в пространстве скоростей, Dv =—:— - коэффициент
dv Зт vlr
диффузии, U = Dv /v - дрейфовая часть потока. Представим себе, что у нас имеется уз-
кий фотоэлектронный пик в спектре /0 (v). Как мы видим, влияние электрического поля
энергия
Рис. 16.12. К объяснению механизма эффекта
усиления излучения в неравновесной плазме.
сводится к направленному движению
электронов в сторону больших энергий,
сопровождающееся одновременным диф-
фузионным расплыванием пика. Пусть в
области существования пика транспортное
сечение (и транспортная частота) доста-
точно быстро возрастают с энергией элек-
тронов. (см. рис. 16.12). Следовательно
пик фотоэлектронов находится в области
падающего с энергией (скоростью) коэф-
фициента диффузии Dv. В такой ситуации
"медленные" электроны пика (с энергиями
Е < Ео, Eq - положение начального мак-
симума ФРЭЭ) характеризуются большим
коэффициентом диффузии, в то же время
для быстрых электронов Е > Ео коэффициент диффузии оказывается маленьким. В ре-
зультате фотоэлектронный пик становится асимметричным, расплываясь преимуще-
ственно в область меньших энергий (см. рис. 16.12). Как результат, "центр тяжести" пи-
ка смещается в область меньших энергий. Еще раз отметим, что такой эффект возможен
только для случая коллективной динамики электронов, что оказывается невозможным в
рамках элементарной теории.
Приложение 16.1. Интеграл упругих столкновений для уравнения
Больцмана.
В упругих соударениях существенно изменяется направление движения электро-
на, в то же время его энергия почти не меняется. Действительно доля потери энергии в
одном упругом столкновении есть ~ 2т/М (т, М - массы электрона и атома соответ-
385
ствснно). поэтому в первом приближении мы будем считать, что в упругом столкнове-
нии происходит лишь разворот вектора скорости на некоторый угол, в то время как аб-
оЛ1отная величина скорости остается неизменной.
Рис. 16.13. К вычислению инте-
грала упругих столкновений.
Запишем изменение числа электронов, имеющих
скорость v и движущихся в направлении & = {в,<р}, в
результате упругого рассеяния на атомах (молекулах) с
концентрацией У:
= yvf П . (П.16.1)
u «12
Здесь интеграл по £2* означает учет переходов во все
возможные направления движения, а -» £2 )
d£2
дифференциальное сечения рассеяния, соответствующее
переходу £2 —> £2'. Аналогично, для переходов в конус
направлений <7£2 вблизи £2 из всех других направлений
запишем:
г б/<т(£2'->£2)
----- J (v, £2 )d£2 d£2' .
(П.16.2)
Тогда интеграл упругих столкновений есть Qel =S+-S_. Учитывая, что
da(Q -> £2') = €/сг(£2'-> £2) _ Ja(v, &)
J£2 ” d£2 d£2
есть дифференциальное сечение рассеяния, а угол В между направлениями £2 и £2' (см.
рис. 16.13), получим
Ste, = Nv\n{f(y,n’)-f(y,Cl))^p-dn'.
В двучленном приближении для случая осевой симметрии
/(v,£2) = f(y,d) = /0(v) + /(v)cos0, где угол В - угол между вектором скорости и
направлением электрического поля до рассеяния. Аналогично
/(v,£2') = /(v,^) = /0(v) + ЛОО008#'- Здесь угол В' - угол между вектором скорости и
направлением электрического поля после рассеяния. Тогда
= Wv/|(v)Jn,(coS^cos^)^^. (П.16.3)
Теперь вычислим интеграл, входящий в уравнение для первой гармоники функции рас-
Пределен ия:
2, = ~Jcos(0)SU/)^ = Nv/,(v)x А Цс°^ (cos0'-cos0)^^dnun.
(П.16.4)
386
Вычисление интеграла проведем следующим образом. Введем систему координат так,
как показано на рис. 16.14. Ось z направим вдоль вектора v , а ось х так, чтобы вектор
напряженности электрического поля волны лежал в плоскости xz. Тогда очевидно, что
dO'=sini9aW<p, где 0 - угол рассеяния. Воспользовавшись известной формулой6 *
Рис. 16.14. Система координат для расчета
интеграла упругих столкновений.
cos0'= cos0cos«9 + sin0 sin .9 cos
получим
21 =-^v/(v)x
— f cos2 0 d£l f (1 - cos dQ,'
4^Jo Jn d&'
= -Nvatr(v),
(П.16.5)
где a<r(v) = £(l-cos<9)
dcr(v,&)
d£l
dQ.
транс-
портное сечение рассеяния. Вспоминая, что
эффективная (транспортная) частота столкно-
вений есть у* = Ntjfr (v)v, окончательно полу-
чим:
2i =-Mv)/i(v)-
(П.16.6)
Задачи к Главе 16.
16.1 Определить скорость затухания ленгмюровских колебаний в плазме в газе, в кото-
ром сечение упругого рассеяния не зависит о энергии электрона.
16.2. Плазма характеризуется максвелловской ФРЭЭ с температурой Т. Получить вы-
ражения для показателя преломления и коэффициента поглощения излучения ча-
стоты со в плазме. Сравнить с результатами элементарной теории.
16.3. Оценить величину коэффициента поглощения (усиления) радиочастотного излуче-
ния с 69 = 2x10” с’1 в плазме аргона, криптона и ксенона, созданной в результате
многофотонной ионизации атомов ксенона фемтосекундным импульсом KrF - лазе-
ра. Давление газа равно атмосферному, концентрация электронов - 1011 см'3. Транс-
портные сечения рассеяния электронов на атомах - см. рис. 16.6.
16.4. Определить условия, при которых плазма, созданная при многофотонной иониза-
ции газа фемтосекундным лазерным импульсом, будет являться оптически более
плотной средой по сравнению с неионизованным газом.
16.5. Определить условия, при выполнении которых в плазме возможно усиление высо-
кочастотного излучения (со»vtr).
6 Эта формула, в частности, является следствием теоремы сложения для сферических функций (см. раздел
Справочные материалы).
387
Глава 17. Свободный электрон в поле электромагнитной
родни. Дипольное приближение и релятивистские эффекты.
17.L Электрон в электромагнитном поле. Пределы применимости
11|Польн°го приближения.
Уравнение движения свободного электрона в поле электромагнитной волны в
0QU1CM виде имеет вид.
~ = еЁ(г, Z) +1 [v Н(7, /)], (17.1.1)
где р - импульс электрона, Е(г,/) - электрическое поле волны, v - скорость электрона,
Н(г./) - магнитная часть поля волны.
В дипольном приближении мы не учитываем релятивистские эффекты, т.е.
v!c«1 • Кроме того, естественно предположить, что ае «Л, т. е. амплитуда
осцилляций электрона много меньше длины волны излучения. Это значит, что
рассматривая движение электрона, можно считать поле волны пространственно
однородным Е(г,Г) <-> Е(/) . Тогда уравнение (17.1.1) упрощается:
^ = еЁ(() (17.1.2)
at
Полагая, что в начальный момент времени (t = 0) электрон покоится, а
Е(/) = Ео cos(atf + (р), (<р - начальная фаза), запишем решение в виде:
v(/) = —-(sin(tf)/ + <р)-sin^). (17.1.3)
ТПй)
Как видно, электрон совершает колебательное движение (амплитуда колебаний по
скорости ve =еЕ0/тсо - колебательная скорость свободного электрона) и дрейфовое со
скоростью vd = ve sin (р, причем величина дрейфовой скорости определяется начальной
фазой поля волны. В частности, при (р = 0 ("косинусный" импульс) дрейфовое движение
отсутствует, при (р = л/2, наоборот, дрейфовая скорость максимальна и равна
колебательной. Мы видим, что мгновенное включение вызывает "толчок" электрона, его
интенсивность определяется начальной фазой.
Интегрируя (17.1.3) по времени еще раз получим:
бЕ / \ о
r(Z) = fn +—(cos 69 —cos(69/ и-<^>))-/xsinp. (17.1.4)
° таг
Здесь г0 . начальная координата электрона, величина ае -еЕ0/та)2 - амплитуда
к°лебательного движения. Типичные зависимости смещения электрона в направлении
л^ля волны от времени представлены на рис. 17.1. Заметим, что условия vr/c«l и
« Л в нашем случае эквивалентны друг другу, т.е. дипольное приближение означает
388
Рис. 17,1. Смещение электрона во времени
при мгновенном включении для начальной
фазы 0 (пунктир) и тг/2 (сплошная кривая).
пренебрежение релятивистскими
эффектами.
Рассмотрим теперь рЯд
релятивистских поправок, возникающих в
первом порядке малости по параметру v/c
Мы видели при этом, что MbJ
одновременно должны учитывать как
действие магнитной компоненты силы
Лоренца на электрон, так и
пространственную неоднородность
электрического поля волны. При этом
если ограничиваться первым порядком
малости, выражение для импульса
электрона можно по-прежнему записать в
нерелятивистском виде: р = ту
Релятивистские поправки здесь надо учитывать, начиная с членов, квадратичных по
параметру v/c.
17.2. Удержание электрона полем стоячей световой волны. Сила
Гапонова - Миллера.
Покажем, что стоячая электромагнитная волна создает для электрона
потенциальную яму (ловушку), в которой при определенных условиях электрон может
удерживаться.
Поле стоячей электромагнитной волны запишем в виде:
E(r,/) = E0(r)cos6W/, (17 2 1)
Н(г, /) = Но (г) cos ал.
Отметим, что в стоячей электромагнитной волне колебания векторов Ё и Н сдвинуты
по фазе на тг/2.
Запишем уравнение движения:
mr =eE0(r)cosatf+ -|г H0(r)sinftX|. (17.2.2)
с J
Будем искать решение задачи по теории возмущений:
г(0 = Е(0)(/) + г(|)(/) + ..., (17.2.3)
где г(0)(/) - решение уравнения движения в дипольном приближении, а г(1)(/) учитывает
поправки первого порядка малости по v/c. Решение для г(0)(г) с начальными условиями
r(/ = O) = ro, r(t = 0) = 0 имеет вид:
?<»>(,) = £^sin<u(> ?1">(о = ?о+^ф(1-С08й*) <17-2-4’
389
н описывает колебательное движение электрона вблизи начального положения г0.
Пе;1Сгавляя полученное в уравнение движения и удерживая члены только первого
порядка малости по г/с, получаем:
+ г "')=<!• „ (0 _ cos nX)'lcos + [Е й f- ]sin2 м
\ J тссо J
Отмстим, что во втором слагаемом мы полагаем поля пространственно однородными и
взятыми в начальной точке г0, т.к. соответствующее слагаемое уже имеет первый
порядок малости по v/c. Разлагая амплитуду электрического поля волны в ряд Тэйлора
вблизи начально! о положения г0, получим уравнение для поправки первого порядка :
п”Л" =-^-?(E0V)E0 _ (1 — cos лд) cos бэ/+ ———уfe0(f0),H0(r0)]sin* 2 cot. (17.2.5)
wrw z'o mca>
Усредним полученное уравнение по
воспользуемся уравнениями Максвелла
Ёо(;“о) и Н0(г0):
высокочастотным колебаниям, а также
для установления связи между функциями
го/Е0 = —Но.
С
Тогда:
=-------^-((E0V)E0 + го(Ё0,ЁД_ =---------- V(Ej/2) . (17.2.6)
2m со r0 2m co
Это уравнение можно переписать в виде:
Рис. 17.2. Потенциальный рельеф,
создаваемый для свободного электрона
полем стоячей электромагнитной волны.
тЁ(|) = F = -VU,
,, е2Ё»<л)
где U =------SL3- - потенциальное поле,
AmcD2
созданное стоячей электромагнитной волной.
Полученную силу называют силой Миллера1
или силой Гапонова2-Миллера. Например, для
волны 60(z) = 3cos(£z) имеем яму
£/(z) = —cos2 kz, глубина которой
4тсо2
определяется величиной колебательной энергии
электрона. Таким образом, стоячая волна может
Удерживать электроны, энергия которых меньше высоты потенциальной ямы (см. рис.
17.2).
Идея использовать ловушки такого типа, созданные высокочастотными
электромагнитными полями, для удержания плазмы была высказана в конце 50х годов
прошлого века.
' Миллер Михаил Адольфович (1924-2004) - советский и российский физик - теоретик.
2 Гапонов - Грехов Андрей Викторович, род. 1926 - советский и российский физик.
390
А что будет, если волна бегущая? Тогда потенциальный рельеф будет
перемещаться в прое гране гве ео скоростью света, и удержание заряженных частиц будет
невозможно. Однако, если замедлить элсктромаг нитную волну каким-либо образом так,
чтобы фазовая скорость волны была меньше скорости света, частицы могут
удерживаться потенциальным рельефом, двигаясь вместе с ним. При этом, если
начальная скорость частицы меньше фазовой скорости элскгромагнитной волны, будет
наблюдаться ускорение частиц, в противном случае, частицы наоборот будут отдавать
энергию волне, усиливая се. Такой принцип усиления элскгромагнитной волны (как
правило СВЧ диапазона частот) реализован в лампе бегущей волны (ЛБВ), схема
Рис. 17.3. Схематическое изображение лампы бегущей волны, как усилителя СВЧ излучения.
Принцип действия лампы бегущей волны основан на механизме взаимодействия
электронного потока с полем бегущей электромагнитной волны, замедленной с
помощью спиральной системы. На рисунке схематично представлено устройство ЛБВ.
Электронная пушка формирует электронный пучок с определенным сечением и
интенсивностью. Скорость электронов определяется ускоряющим напряжением и
должна превышать скорость распространения электромагнитной волны вдоль
спиральной системы. Соленоид служит для предотвращения расплывания пучка и
удержания его в заданной области пространства.
17.3. Рассеяние света на удвоенной частоте.
Перейдем теперь к рассмотрению другого эффекта, который возникают при учете
релятивистских поправок в уравнении движения электрона. Мы знаем, что под
действием поля волны с частотой со электрон совершает колебания на этой частоте и
переизлучает энергию в пространство (рассеяние света). Покажем теперь, что учет
релятивистских эффектов приводит к возникновению колебаний электрона на удвоенной
частоте воздействующего излучения и, следовательно, к переизлучению энергии на
удвоенной частоте. В это смысле релятивизм свободного электронного газа выступает
как одна из причин возникновения нелинейных эффектов в плазме.
Как и раньше, запишем уравнение движения для свободного электрона в поле
волны в виде:
391
(17.3.1)
даберем систему координат следующим об1)азом
распространения волны, ось г направим по элеХоиис/ На"РаВИМ ВДОЛЬ на"Р—
будет направлена по вектору магнитного по™ в ₽ичесК0«У полю волны, тогда ось у
я. Вспоминая, что
ez
о
= -ёхУ2Н + ёгглН,
перепишем (17.3.1) в проекциях на оси координат:
еЕ
= —
т
* mvy = О,
е
ст
vzH,
(17.3.2)
е
v2 = — V
ст
н.
Как видно, в направлении магнитного поля сила не действует, зато действие магнитной
составляющей силы Лоренца приводит к появлению ускорения в направлении
распространения электромагнитной волны.
Будем решать задачу по теории возмущений, взяв за нулевое приближение
решение задачи в дипольном приближении. Полагая, что Ё(/) = ехЕ0 cos cot, получим:
v(0) _ s|n
та)
Тогда в первом порядке по у/с для движения вдоль оси z получим:
vz(t) = f—^lsin(<wr)H0 cos cotdt, (17.3.3)
' cm ma)
откуда
L 1 e2E2 1 e2E2 , . 1 v
v: (0 = |--r-2- s’n =-------5—?- (1 - cos 2cot) = —- • ve (1 - cos 2cot). (17.3.4)
0 2 m O)c 4 m a) c 4 c
Здесь ve - введенная ранее колебательная скорость электрона. Как видно, полученная
величина действительно имеет первый порядок малости по параметру vjc. Мы не
Учитываем здесь пространственную структуру поля волны, т.к. соответствующая
поправка имела бы уже второй порядок малости. Как видно, по оси z колебания
происходят на удвоенной частоте, а, следовательно, и излучение происходит на
Удвоенной частоте. Возникает нелинейный эффект - сила действующая на частоте а)
привела к колебаниям на удвоенной частоте. Кроме того, как видно из (17.3.4),
Говенное включение поля волны приводит также к дрейфовому движению, которое в
Данн°м случае присутствует и для "косинусного" импульса. Как результат, траектория
Движения электрона является вытянутой восьмеркой (см. рис. 17.4). Отметим при этом,
392
что усредненная но периоду колебаний сила, действующая в направлении
распространения электромагнитной волны равна нулю.
Сравним теперь интенсивности излучения
. £ Л осциллирующим электроном на фундаментальной
/v</с частоте и частоте второй гармоники, учитывая, что
интенсивность дипольного излучателя есть:
]]/_____________*•* / = 1^\, (17.3.5)
—-------------------* Vе /
/ ;. где d = ev - дипольный момент системы. На
/Ну частотах со и 2<у имеем соответственно:
. 1 ve
da~vx =vecocoscot; d2o) ~ vz =- — vecosm2cot,
c
Рис. 17.4. Траектория движения
свободного электрона в поле
электромагнитной волны.
откуда:
(17.3.6)
Отметим, что в высших порядках теории возмущений появляются и более высокие
гармоники За», 4а>,.... Однако, следует иметь в виду, что анализ в высших порядках
теории является более сложным. Нам в том числе необходимо учитывать
релятивистскую связь импульса со скоростью электрона.
17.4. Давление света.
Рассмотрим еще один релятивистский эффект, возникающий при движении
свободного электрона в поле электромагнитной волны. Речь идет о давлении света.
Экспериментально световое давлении было обнаружено в экспериментах П.Н.Лебедева3
в 1901 году. Давление света наиболее легко объяснить с точки зрения световых квантов,
которые несут импульс, передаваемый некоторому объекту (поверхности, частице) при
взаимодействии. Мы покажем сейчас, тем не менее, что эффект светового давления по
своей природе является чисто классическим, и никакого отношения к квантовой теории
не имеющим.
Что мы не учли при рассмотрении выше и электрической и магнитной
компоненты силы Лоренца? Есть еще одна сила, которую надо принять во внимание при
движении электрона с ускорением. Это сила радиационного трения. Известно, что эта
сила определяется выражением:
= (17.4.1)
Сила радиационного трения возникает как следствие того, что электрон в поле волны
движется с ускорением и теряет энергию, т.е. испытывает торможение. Если считать, что
электрон движется по почти гармоническому закону, то г = -со2г, следовательно
3 Лебедев Петр Николаевич (1866—1912) - русский физик - экспериментатор.
393
2е2а)2 л _ - _ 2е2а)2
г ~ ',т> ’ ГДе Y Зтс3 ~ КЛассичсская постоянная затухания. В таком
приближении сила радиационного трения фактически является силой "вязкого трения",
пропорциональной скорости. Если классическая постоянная затухания мала по
сравнению с частотой воздействующего излучения, затухание можно учитывать как
ма.пую поправку порядка у/a) по отношению в силе, действующей на электрон со
стороны электрического поля волны.
Выберем систему координат аналогично тому, как это было сделано в разделе
17.3- Для Движения электрона по оси х в нулевом порядке по релятивистским эффектам
имеем теперь следующее уравнение:
еЕ
vv + yvx - —- cos ajt .
m
Решение записываем в виде:
vx(0 = —п sin + — cos |.
та) I a) J
(17.4.2)
Первое слагаемое в выражении для скорости по оси х - полученное ранее выражение, не
учитывающее силу радиационного трения, а второе - малая поправка (порядка //©),
описывающее колебание х- компоненты скорости электрона синфазно с электрическим
полем волны. Именно эта малая величина и приведет к появлению силы светового
давления. Действительно, найдем теперь усредненное выражение для vz за период поля
с учетом найденной поправки (отметим, что первое слагаемое в выражении для vx
отвечает за колебания вдоль оси z на удвоенной частоте, которые при усреднении по
периоду дают 0):
(v \ = -1 е еЪ1У_1 _8rf gL
г Т ст' х Т 2 ст та) а) 2 ст2а)2 Зтс3 Зс4т3 Зс с4т3
Здесь означают усреднение по времени, a I = cEq/8tt - интенсивность излучения.
Ненулевое ускорение по оси z означает наличие силы, действующей на электрон в
направлении распространения электромагнитной волны, которая и называется силой
светового давления. Как видно, эта сила не зависит от частоты излучения и определяется
формулой:
(17.4.3)
Здесь г =е2/тс2 «2.82-10’13 см
классический радиус электрона,
томсоновское сечения рассеяния.
Эффект светового давления тесно связан с эффектом Комптона4: рассеяние
Фотона на свободном электроне, при котором частота рассеянного фотона смещается в
c°mpton Arthur Holly (1892 - 1962) - американский физик, Нобелевская премия (1927) "За открытие
Ффекта, названного его именем".
394
красную сторону, а электрон приобретает импульс отдачи, в среднем в направлении
распространения электрического поля электромагнитной волны свет оказывает
давление на электрон. При сопоставлении эффекта светового давления (явление чисто
классическое!) и эффекта Комптона (эффект существенно квантовый) следует иметь в
виду, что эффект Комптона наблюдается при рассеянии жестких единичных квантов
электромагнитного поля, в то время как классическое рассмотрение предполагает
наличие огромного количества достаточно мягких квантов, одновременно
взаимодействующих с электроном. При этом движение электрона в направлении
распространения электромагнитной волны, возникающее под действием силы светового
давления, приводит к "покраснению" воздействующего излучения (эффект Доплера), а
следовательно, и к смещению в "красную" часть спектра рассеянного излучения (см.
рис. 17.5). Действительно, движение в направлении распространения электромагнитной
волны со скоростью V. приводит к сдвигу частоты "наблюдаемого" электроном
излучения: со* = а>(1 -vz/с). Здесь со* - частота излучения в собственной системе
отсчета. На этой частоте и происходит переизлучение энергии. При этом наблюдаемая в
исходной лабораторной системе отсчета частота излучения зависит от угла наблюдения
в по отношению к направлению распространения рассеянного света и определяется
выражением:
сон = бу(1-vz/c)(\ + vz/cxcos<9) « со(1 —vz/cx(l-cos#)). (17.4.4)
Рис. 17.5. Световое давление и эффект Комптона.
То есть сдвиг длины волны АЛ,
наблюдаемый под углом 0 к
направлению распространения
рассеянного света, характеризуется
зависимостью АЛ ~ (vz /с)(1 - cos #),
такой же как и в квантовой теории, а
сама величина сдвига растет во времени
по мере увеличения скорости движения
электрона под действием силы светового
давления.
Рассмотрим теперь возникновение силы светового давления с энергетических
позиций. Свободный электрон, взаимодействуя с полем электромагнитной волны,
забирает у нее энергию, а следовательно, и импульс, поскольку объемные плотности
энергии W и импульса Р электромагнитного поля бегущей волны связаны
соотношением W = Рс. При этом при рассеянии энергия, поглощаемая электроном,
переизлучается обратно в пространство. А импульс переизлученного поля оказывается
равным нулю. Это означает, что электрон приобретает импульс в процессе рассеяния.
Скорость изменения этого импульса и определяет силу светового давления (см.
рис. 17.6).
Действительно, переизлученная электроном энергия определяется выражением:
dW _2е2
dt Зс3
2е2 ( еЕ0 V
Зс3 тп ?
2
COS
cot.
(17.4.5)
395
Рис. 17.6. Возникновение силы светового давления.
Тогда, усредняя по высокочастотным колебаниям для импульса, передаваемого
электрону получим:
г _dpe_\dW _ е4 * * * * * с2 18л- г4 т
Свд' rlt г Л О 2 4 ^0 2 2^’ (17.4.6)
dt с dt 3m с с 3 m с
т.е. тот же ответ, что и в предыдущем подходе.
Отметим, что сила светового давления определяется лишь интенсивностью
излучения и не зависит от частоты электромагнитного излучения.
Задачи к Главе 17.
17.1. Какие ускорения и скорость приобретет электрон под действием силы светового
давления в импульсе неодимового лазера (длина волны Л = 1064 нм) с
интенсивностью I = Ю10 Вт/см2 и длительностью г = 1 нс? Сопоставить величину
силы давления с силой радиационного трения и силой, действующей на электрон со
стороны поля волны?
17.2. Оценить напряженность электромагнитного поля волны частоты 69 = 10 с1, с
помощью которой можно удерживать плазму с температурой 1 кэВ.
17.3. Определить диапазон частот, в котором классическая постоянная затухания
существенно меньше частоты излучения у «art
396
Глава 18. Пробой юзов излучением оптической частоты.
До сих пор при рассмотрении процесса распространения электромагнитного
излучения в плазменных средах мы полагали, что степень ионизации газа не изменяется
во времени. Это означает, что электромагнитное поле является достаточно слабым, или
импульс излучения коротким, так что процессами ионизации атомов (молекул) среды
можно пренебречь. Заметим, что процесс ионизации среды в интенсивном поле
излучения может происходить различными способами. Во-первых, речь может идти о
непосредственной фотоионизации атомов (молекул) среды электромагнитным полем.
Такой процесс может осуществляться в зависимости от конкретных условий в
многофотонном или туннельном режиме, и был рассмотрен в Главе 13. Однако,
независимо от конкретного механизма ионизации, при постоянной интенсивности
излучения число фотоэлектронов нарастает линейно по времени. Существует и другой
механизм ионизации: ионизация атомов (молекул) электронным ударом. В этом случае
свободный электрон в плазме набирает энергию в поле волны, и, в случае, если его
энергия оказывается больше потенциала ионизации атомов (молекул), ионизует их. В
таком случае говорят об ионизации электронным ударом. В результате в газе
оказывается возможным развитие электронной лавины. При этом концентрация
электронов во времени возрастает по экспоненциальному закону. Поэтому на практике
часто оказывается, что начальные затравочные электроны возникают в результате
прямой фотоионизации среды излучением1, а последующее размножение электронов и
формирование плазменного образования с достаточно высокой концентрацией
электронов есть результат лавинной ионизации. В данной главе рассмотрим эффект
лавинного пробоя газа излучением оптического диапазона частот.
(18.1.1)
18.1. Электрон в поле электромагнитной волны. Обратный
тормозной эффект. Классическое рассмотрение.
При анализе движения свободного электрона в поле электромагнитной воины (см.
раздел 17.1), мы видели, что электрон не набирает энергию от поля. Действительно,
полагая, что в начальный момент времени (/ = 0) электрон покоится, а
E(z) = Ео cos(ztf + (р), мы получаем, что скорость электрона равна:
еЁ / .
~ (sin(&>/ 4- (р) - sin (р),
та) 7
а, следовательно, для энергии имеем:
. mv2(t) е2Е20 2
' 2 — 2та>2 81П + + <Р + 2sin(ftX + ^>)sin^>) .
Усредняя полученное выражение по высокочастотным осцилляциям, получим:
, р2Г2
{E(t)) = -^(] + 2sin2p).
4та)
(18.1.2)
1 Затравочные электроны также могут появится в результате фотоионизации примесей с маленьким
потенциалом ионизации. г
397
величину Е,-е!Е2 *„/4та> будем называть колебательной энергией электрона в поле
0опны Ьак видно, при попадании электрона в поле волны его энергия складывается из
двух слагаемых, соответствующих колебательному и дрейфовому движению. Однако,
она нс Растет в0 времени. При интенсивностях излучения порядка 1О10 Вт/см2 (эта
величина типична для пробоя газов изучением видимого диапазона частот) величина
колебательной энергии на несколько порядков меньше потенциала ионизации (см. задача
18.1).
Учтем теперь эффект столкновений с нейтральными атомами (молекулами).
Уравнение движения электрона мы можем теперь записать в виде*.
mv = еЁ(() + 7го„ (18.1.3)
где ./,<,/ " сила’ действующая на электрон в плазме со стороны атомов (молекул). Эта
сила является случайной и должна быть усреднена по большому числу столкновений.
Поскольку масса электрона на несколько порядков меньше массы атома
(молекулы): т/ М «1, будем
р’> считать, что абсолютное значение скорости электрона при
9 ° । н\ 1 " 1 1 1 1 столкновении не изменяется. Происходит лишь поворот вектора скорости на некоторый угол &2. Схематически этот
Рис. 18.1. К вычислению силы, действующей на процесс представлен на рис. 18.1.
электрон со стороны атомов в плазме. Изменение импульса в направлении движения электрона
есть &р = -wv(l - cos . Интервал времени между столкновениями есть r = l/y, v -
частота столкновений. Предполагая, что величина импульса Др теряется электроном
непрерывно в течение времени т, получаем усредненное по времени значение силы
действующей на электрон, возникающей за счет столкновений:
= — mv(l - cos i9)v. (18.1.4)
Здесь "черта” означает усреднение по большому числу соударений. Введем
эффективную частоту столкновений
v = у(1 - cos «9). (18.1.5)
Как видно, столкновения приводят к возникновению действующей на электрон
Тормозящей силы, причем в рассматриваемом приближении эта сила есть сила вязкого
трения, пропорциональная скорости. Тогда уравнение движения (18.1.3) запишется в
виде:
v + .
(18.1.6)
2 Мы здесь имеем в виду только упругие столкновения, которые не сопровождаются изменением
“«Утреннего состояния атома (молекулы), например в результате ее возбуждения.
398
На практике яьлепие еижкновепия жектроиа с атомом (молекулой) принято
характеризовать шшкящпм о, угла .9 дифференциальным сечением рассеяния da/dn
(см. Глава 12). Интегрируя но возможным углам рассеяния, мы можем получить полное
сечение рассеяния и частоту упругих столкновений:
<7с1 = |((/<т/<Л2)гЛ2, и ~ Мсте1 v, (18.1.7)
здесь Л' - концентрация атомов (молекул). В Разделе 12.1 мы обращали внимание, что
часто удобно ввести транспортное сечение рассеяния:
сгг,. = j(l - cos dQ.)dQ..
(18.1.8)
В случае изотропного рассеяния de!d£l = const понятия транспортного и упругого
сечений совпадают. Нетрудно видеть, что введенная нами эффективная частота
столкновений есть не что как транспортная частота
veff =v„. =Ncrlry. (18.1.9)
В рамках нашей предельно упрощенной модели мы будем полагать, что транспортная
частота не зависит от энергии электрона.
Общее решение уравнение (18.1.6) с нулевым начальным условием v(r = 0) = 0 и
функцией Ё(/) = Ёо cos(<5/ + (р) запишем в виде:
v(z) =----—— (cdsin(69/ + <р) + vtr cos(cot + ^))----—— exp(-y„./)(^ysm (р + cos(р).
т(а> 4- vtr) т(й) 4- v*)
(18.1.10)
В частном случае отсутствия столкновений мы получаем результат, уже рассмотренный
в Главе 17. В общем случае также зависимость v(z) содержит "колебательное" и
"дрейфовое" слагаемые, также зависящие от начальной фазы <р. Однако, на временах
t»\/vtr "дрейфовое" слагаемое затухает: в результате столкновений забывается
начальная фаза поля, и остается только колебательное движение. Отметим также, что в
результате наличия столкновений у электрона появляется составляющая скорости,
изменяющаяся во времени синфазно изменению поля волны. Мы увидим в дальнейшем,
что именно этот факт приведет к поглощению энергии поля волны электроном.
Отметим, что часто удобно выражение (18.1.10) переписать в комплексном виде:
Р(/) = m(^+vdV" + '®)eXp(-''(<U'+ *>» - + /®)exp(i(»),
niyuj ' *tr j m\o) + vtr)
(18.1.Н)
а Ё(/) = Ёо ехр(-/(йХ + (рУ).
Найдем теперь энергию, набираемую полем волны при столкновениях ({ ) скобки
означают усреднение по времени):
dt
2 in 2
e K,vlr
2m{(o2 4-y2) ’
(18.1.12)
= е^Ё(/)р(Г)^ =
399
Здесь мы использовали, что (cos2 (cos(^)sin(^)) = 0. При использовании
,0мплексного представления величин тот же результат получается в результате
Ь щенения формулы (ЯВ) = (1/2Же(ЛВ*).
Как видно, именно столкновения приводят к набору энергии электроном в поле
родны При этом в каждом столкновении в среднем электрон приобретает энергию
е2Е2
ДЕ =-----.
2т(со + у*)
(18.1.13)
0 оптическом диапазоне частот и в газах при атмосферном давлении (vtr ~1012 с'*)
выполнено условие со»vtr. В этом случае набираемая энергия равна удвоенной
колебательной энергии электрона в поле волны. С учетом (18.1.12) также заметим, что
максимальная скорость набора энергии электроном достигается при выполнении условия
(О = Vfr
Полученный результат позволяет нам определить коэффициент поглощения
электромагнитного излучения в плазме. Действительно, полагая, что концентрация
электронов в плазме равна пе, мы заключаем, что энергия, поглощаемая в единице
объема есть:
П‘^Г= ° 7 ZE°”,V,,2 , (18.1.14)
dt ' ' 2т(со +v2)
С другой стороны эту же энергию можно записать как , где - коэффициент
поглощения излучения с частотой со, I - интенсивность излучения. Учитывая, что
/ = сЕр/8д-, из (18.1.14) получим (см. также Главу 15):
4лг2кеУ„,
тс(со2 + v2)
(18.1.15)
Полученные выше результаты получены при усреднении скорости изменения
энергии электрона по большому числу столкновений. Проведем теперь более детально
анализ конкретного столкновения и покажем, что в зависимости от фазы скорости
электрона в момент столкновения энергия от поля может как поглощаться, так и
испускаться.
Пусть перед столкновением электрон характеризуется скоростью:
v(/) = vr +VeCOS6X,
ьде vr,ve - скорости поступательного и колебательного движения. Для простоты здесь
Мы рассматриваем случай, когда векторы скоростей коллинеарны друг другу. Величина
С1<орости в момент столкновения t* определяется фазой ср = cot* и может изменяться в
нределах от vT - ve до vT + ve. Мы здесь полагаем, что ve « vT ? При столкновении
>Го условие, как правило, выполнено в полях оптического диапазона частот, соответствующих явлению
Этического пробоя газов.
400
скорость электрона практически нс меняется по величине, однако изменяется ее
направление. При этом новое значение поступательной скорости как раз равно
значению скорости в момент столкновения, в процессе движения к этой скорости снова
добавляется скорость колебательного движения. Поэтому изменение энергии,
соответствующей поступательному движению сеть:
ДЕ = ~(Vf + Ve C0S ф) - mVT /2 ~ mVTVe C0S^ ’ (18.1.16)
и изменяется в пределах ±mvTvc. Таким образом, электрон может и терять, и поглощать
энергию, причем порциями гораздо большими чем величина колебательной энергии.
Усреднение по большому количеству столкновений приводит к тому, что в среднем
электрон набирает энергию от поля порциями порядка колебательной энергии.
Отметим, что такая картина обратного тормозного эффекта напоминает
квантовомеханическое рассмотрение явления. Электрон может и поглощать и набирать
энергию при рассеянии на атомах в поле волны, однако, в отличие от классической
теории поглощение происходит порциями riheo, п = ±1,±2,...(более подробно см. Раздел
12.4). Интуитивно ясно, что если mvTve то речь идет о многофотонном
поглощении, дискретная структура поглощаемой энергии становится незаметна, и можно
пользоваться классической теорией. Наоборот, в случае mvTve < hco применять
классическую теорию нельзя: величина поглощаемой энергии не может быть меньше
энергии кванта. В этом случае надо использовать квантовомеханический подход.
При рассмотрении квантовомеханической теории вынужденного тормозного
эффекта мы видели, что вероятность процесса многофотонного поглощения
определяется параметром многоквантовости
N = (18.1.17)
тпа>
где ф - изменение импульса электрона в процессе рассеяния. Считая, что 8р ~ р = mvT
(т.е. изменение импульса электрона порядка импульса, соответствующего его
поступательному движению), из (18.1.17) получаем:
eEnmvT mvTv
N------(18.1.18)
тпа> Тио
т.е. отношение характерной величины классического набора в величине набора энергии
в квантовой теории.
Таким образом, действительно, если параметр многоквантовости N »1, можно
использовать классическую теорию ВТЭ, при N <1 надо пользоваться квантовой
теорией. Как видно, классическая теория работает лучше в области сильных и
сравнительно низкочастотных полей.
Ниже при анализе нагрева электронной компоненты плазмы мы будем
пользоваться классической теорией, считая что условие W »1 выполнено. Как правило,
при рассмотрении задачи о пробое газов лазерным излучением такой подход применим
вплоть до ближнего ИК диапазона частот.
401
18.2. Баланс энергии электронов в плазме.
Мы видели, что при столкновении с атомом (молекулой)
п0Глошает энергию порядка колебательной. С другой стороны,
происходит и потеря энергии. Рассматривая столкновение _
(электрон, его энергия Е) и М (атом, мы полагаем его неподвижным) легко
чт0 доля энергии переданная от электрона к атому в одном столкновении, есть
---—£(l-cos .9),
М
в поле волны электрон
в каждом столкновении
двух частиц массы т
показать,
(18.2.1)
где & угол рассеяния. Тогда, очевидно, получаем уравнение для скорости
набора/потери энергии электроном в поле волны:
dE _ e2EoV„ 2т
— '------------------у/
dt 2т(й)2 +у^) М 1
(18.2.2)
Решение этого уравнения, соответствующее начальному условию £(/ = 0) = 0,
записывается в виде (график зависимости представлен на рис. 18.2:
dE _ М /
dt 2m2m(a>2+v2) **
(18.2.3)
Здесь vE - обратное время релаксации энергии к равновесному значению, равному
М е2Ед
2т 2т(а>2 + у2)
(18.2.4)
Рис. 18.2. Нагрев электронов в плазме полем
электромагнитной волны.
Фактически Е^ - это та максимальная
энергия, до которой поле может нагреть
электроны плазме при наличии только
упругих соударений.
Отметим, что время релаксации
энергии оказывается на несколько порядков
меньше, чем время релаксации импульса.
Действительно, в случае импульса это время
равно т » v~l, т.е. электрон "забывает” свой
начальный импульс практически за одно
столкновение. Изменение энергии,
напротив, в одном столкновении очень
мало.
До сих пор мы говорили только об упругих столкновениях электронов в плазме.
Однако, помимо упругих столкновений электрон в плазме испытывает еще и неупругие
столкновения. В атомарных газах это, прежде всего, возбуждение электронных
состояний, в молекулярных еще и возбуждение колебательных и вращательных
состояний. Также это процесс ионизации. Неупругие соударения достаточно редки, их
сечения, как правило, существенно меньше сечений упругого рассеяния. Кроме того, они
характеризуются ненулевым порогом по энергии. Например, в гелии порог возбуждения
402
нижнего электронного состояния составляет 19.82 эВ. до этого значения энергии
электрон испытывает лишь упругие столкновения. При этом потенциал ионизации атома
гелия равен 24.59 эВ. Похожая ситуация рсапизустся и в других инертных газах (см.
Таблица 18.1).
Таблица 18.1.
газ j Энергия возбуждения нижнего электронного ; состояния. эВ Потенциал ионизации, эВ
Не 19.82 24.59
Ne 16.62 21.56
Аг 11.55 15.76
Кг 9.92 14.00
Хе 8.44 12.13
В молекулярных газах роль неупругих потерь энергии на возбуждение
существенно выше прежде всего за счет наличия низколежащих колебательных
состояний, которые, как правило, составляют доли электронвольт. (См. Таблица 18.2)
Таблица 18.2.
газ Энергия возбуждения нижнего колебательного состояния, эВ Потенциал ионизации, эВ
н2 0.54 15.43
n2 0.29 15.58
о2 0.20 12.08
f2 0.11 15.69
С12 0.069 11.48
Формально для учета неупругих столкновений в уравнении для скорости
изменения энергии электрона в поле волны в правую часть (18.2.3) можно ввести члены
вида — , где сумма берется по всем неупругим каналам с потенциалом
к
возбуждения Гк, а частота конкретного неупругого процесса столкновений vk
от нуля только если (Е) >Гк. В таком виде уравнение для набора энергии
dE _ g ___________.
dt 2т(а>2+v^) М V,r к**
сложно для аналитического решения. Поэтому часто в (18.2.5) потери
описывают одним членом:
dE e2E20vtr
отлична
(18.2.5)
энергии
(18.2.6)
где - усредненная по всевозможным процессам средняя доля потери энергии в одном
столкновении. Если столкновения чисто упругие, то 5eff - 2т/М. В молекулярных
403
газах, где роль неупругих соударений особенно велика, как правило 8# =10 3 -10"1. В
случае существенного вклада в баланс энергии неупругих процессов выражение
перепишется в виде:
__1 е2Е*
5eff Ъп((£>г + У2) ’
(18.2.7)
18.3. Элементарная теория оптического пробоя.
Целью нашего рассмотрения является определение порога лавинной ионизации в
газе, т.е. величины поля, необходимого для начальной стадии развития оптического
пробоя, и анализ зависимости порога пробоя от типа газа, давления, а также от
параметров воздействующего лазерного излучения (частота излучения, длительность
импульса, размер пятна фокусировки).
Баланс электронной плотности ие(г,/) в некотором пространственном объеме,
занятом лазерным излучением, определяется решением уравнения диффузионного типа:
= (18.3.1)
ot
Здесь D - коэффициент диффузии электронов, у,. - частота ионизации атомов (молекул)
среды электронным ударом, Q(ne) - слагаемое, описывающее гибель частиц в
различных процессах.
Остановимся прежде всего на определении частоты ионизации и зависимости
этой величины от интенсивности электромагнитного излучения. В рамках
рассмотренной выше элементарной теории нагрева электронного газа электрон может
набрать энергию, достаточную для ионизации атомов молекул лишь при выполнении
условия:
1 е2Е2
Е ______°____
^2^+у2)
(18.3.2)
Здесь /. - потенциал ионизации. Фактически, условие (18.3.2) позволяет определить
минимальное значение поля, при превышении которого лавинное размножение
электронов в газе в принципе возможно. В частном случае, когда мы учитываем только
упругие потери энергии, условие (18.3.2) можно переписать в виде:
М е2Ер
2тл 2w(<y2 + V2) ‘
(18.3.3)
Их (18.3.2) и (18.3.3) видно, что чем меньше потенциал ионизации и чем больше масса
атома, тем легче электрону набрать необходимую для ионизации энергию. То есть
можно ожидать, что необходимые для пробоя напряженности поля растут с увеличением
потенциала ионизации газа и уменьшением массы атомов. Мы также отмечали, что в
оптическом диапазоне частот при давлениях порядка атмосферного выполнено условие
404
Отсюда заключаем. чю порог ланинной ионизации / ~ Е2, ~ а>2, т.е. растет
квадратично с час го гой излучения.
Определим час го 1 у ионизации у следующим образом. Пусть условие (18.3.2)
выполнено. Будем гакже считан», чго электрон, набрав энергию достаточную для
ионизации атома (молекулы) электронным ударом, мгновенно ионизует атом. Тогда
приближенно можно записать:
v = _L^ = J_____. (18.3.4)
' 7, dt I, 2т(а>2+v2.)
Что касается гибели электронов, то туг возможны различные процессы. В атомарных
газах это прежде всего процесс тройной рекомбинации4:
А+ +2е —> А + е.
Этот процесс характеризуется константой скорости5 (3Т »-JT / т (e2/Tj-Т-4'5 (Т -
температура электронов) и описывается слагаемым в (18.3.1):
Qr = ~^тпеп+ ~ ~Ртп\ •
Мы здесь учли свойство квазинейтральности плазмы, полагая, что концентрации ионов
и+ и электронов равны. В молекулярных газах диссоциация часто идет по другому
механизму, когда выделяющая в ходе реакции энергия идет на диссоциацию молекулы6:
7^2 + £ —А + А .
При этом один из атомов часто оказывается в возбужденном состоянии. Этот процесс
характеризуется константой скорости (3D и описывается слагаемым в (18.3.1):
QT = -PD”en+ ~ ~PD^e •
Возможен еще и процесс фоторекомбинации, когда энергия уносится квантом
электромагнитного излучения:
Л+ +е —> А + Ьсо.
В этом случае
Qph =~Р
Не вдаваясь в сравнительный анализ того или иного процесса рекомбинации, отметим,
что на начальных этапах развития лавины, когда концентрация электронов как правило
крайне мала, процессами рекомбинации можно пренебречь. Рекомбинация часто
определяет именно тот уровень концентрации заряженных частиц, на котором
лавинообразное размножение электронов останавливается.
4 Ион представляет для электрона потенциальную яму, поэтому третье тело необходимо, чтобы
рекомбинирующий электрон мог передать ему свою избыточную энергию.
5 Смирнов Б.М. "Физика слабоионизованнго газа", М.: Наука (1978), Глава 4, с.250.
6 Такая рекомбинация называется диссоциативной.
405
В этом смысле с точки зрения влияния на процесс развития лавины более важное
зипчсннс имеет процесс прилипания. Этот процесс реализуется только в
^дектроотрннательных газах, т.е. в газах, в которых атомы А (молекулы А2) имеют
усгоп'|пвыс отрицательные ионы А (А2). К таким газам относятся, например,
(Х./г .СЛ.С/74о57**, и многие другие газы. Прилипание может быть также тройным, или
ассоциативным. Например, в случае диссоциативного прилипания
А2 + с —А 4- А
происходит распад молекулы на отрицательный атомарный ион и нейтральный (он
может быть в возбужденном состоянии) и в уравнении (18.3.1) появляется слагаемое:
Qa =-va”e’
где - частота прилипания. Важно, что слагаемое линейно по концентрации
заряженных частиц, поэтому оно может оказаться существенным в том числе и на
ранних этапах развития электронной лавины.
Остановимся теперь на диффузионном слагаемом в (18.3.1). Формально,
диффузия не приводит к гибели электронов, однако, в результате процесса диффузии
электроны тоже исчезают из объема, занятого электромагнитным излучением. Оценивая
диффузионный член DV2ne
п
перепишем тогда уравнение (18.3.1) в виде:
dnAt)
= ~D^ + Vine ~ Vane • (18.3.5)
at Л.
Здесь Л есть величина порядка радиуса перетяжки светового пучка. Величину
г, = D/Л2 имеет смысл назвать частотой диффузии, т.к. rD=vdl есть характерное
время диффузионного ухода электронов из фокального объема.
Общее решение уравнения (18.3.5) записывается в виде:
«е(0 = пе0 exp((v, - va -vd)t). (18.3.6)
Здесь пе0 - начальная концентрация электронов. Как видно, условием лавинного
размножения электронов является неравенство:
(18.3.7)
Это условие будем называть стационарным критерием пробоя. В электроположительных
газах частота прилипания равна нулю, и частота ионизации должна превышать частоту
Диффузии.
Критерий пробоя (18.3.7) соответствует условию, когда излучение фактически
является непрерывным. Однако, в случае достаточно коротких лазерных импульсов
Давина должна развиться в условиях ограниченного времени, на временах не больше
Длительности импульса. Сформулируем критерий пробоя для этого случая. Будем
считать, что пробой произошел, если концентрация электронов в плазменном
образовании возросла с начальной пе0 (часто лавина начинается с одного единственного
электрона) до конечной и*. Эта величина может быть оценена по-разному. Например,
406
она может соогветсгвовап. полной ионизации газа или концентрации электронов,
которая установится в шкпме в резуш.тото включения процесса рекомбинации. Если
лавина начинасз развива!вся с сдинс!венного начального электрона, то в качестве
оценки для конечной концентрации часзо выбирают п ~ И) см . Последняя оценка
определяется гем фактом, что указанную концентрацию электронов в фокальном объеме
достаточно легко зарегистрировать экспериментально. Чуть позже мы увидим, что
выбор того пли иного значения конечной концентрации тлскгронов не оказывает
существенного значения на величину порогового ноля для развития электронной
лавины. Тогда, считая, что длительность импульса есть тр, получим, что лавина в газе
развилась, если выполнено условие:
v,-vo-v,> —ln(„7^0).
тр
(18.3.8)
Условие (18.3.8) будем называть нестационарным критерием пробоя. Как видно, в
длинных импульсах (формально тр —> оо) нестационарный критерий (18.3.8) переходит в
стационарный (18.3.7). Очевидно, нестационарный критерий может приводить к
повышению величины порогового поля в коротких импульсах, что связано с
необходимостью размножения электронов в условиях ограниченного интервала времени,
величина А = 1п(«7ие0) есть число поколений электронов в лавине и очень слабо зависит
от конкретных значений начальной и конечной концентрации электронов.
Действительно, например, для пео=1 см'3, и*=1013 см’3 имеем
А = 1п(1013) «13*2.303 «30. При ие0=1 см'3, и*=1019 см’3 находим Л «43. Может
оказаться, что начальная концентрация электронов достаточна велика - ~1013 см’3. Такая
ситуация реализуется, например, при оптическом пробое в плотных парах металла,
образующихся при нагреве и испарении металлической поверхности в поле лазерного
излучения. Тогда, если п = 1019 см'3, получаем А = 1п(106) «6*2.303 »14. Как видно, во
всех этих совершенно различных случаях число поколений электронов в лавине
составляет один порядок.
Прежде чем перейти к оценкам величин пороговых полей, отметим, что в
зависимости от конкретной физической ситуации диффузия электронов в начальном
плазменном образовании может быть разной. Если лавина начинает развиваться со
считанного количества электронов (или даже единственного электрона) диффузия
электронов будет свободной. Если начальная концентрация электронов достаточно
велика (такая ситуация может реализоваться, например, при пробое в плотных парзх
металла), диффузия может быть амбиполярной. В этом случае электроны и ионы в
плазменном образовании удерживаются вместе плазменным электрическим полем и
диффундируют совместно. Очевидно, коэффициент амбиполярной диффузии Da
существенно меньше, чем свободной. Можно показать, что7 8
7 Такая рекомендация, в частности, содержится в монографии Ю.П. Райзера "Лазерная искра и
распространение разрядов", М.: Наука, (1974)
8 С явлением амбиполярной диффузии можно подробно познакомиться, например, в монографии Райзера
Ю.П. "Физика газового разряда", М.: Наука, (1992)
407
D-“D<(' + W. (18.3.9)
rjc p . коэффициент ионной диффузии, a т, и Т, - температурь, электронной и ионной
,^систем. В частном случае равенства температур Т„ =7;, получаем, что коэффициент
амбиполярной диффузии Da = 2D,. Для того чтобы определить характер диффузии
^тронов, необходимо сравнить размер области, занимаемой электронами (в
рассматриваемой задаче это размер области фокусировки излучения Л) и величину
дебаевского радиуса в плазме t D = . В случае 1„ » Л диффузия электронов
носит свободный характер, в противоположном «Л - амбиполярный. Отметим, что
при развитии лавины характер диффузии может измениться. Если на начальных стадиях
развития лавины она была свободной, то в процессе увеличения электронной
концентрации может стать амбиполярной. Очевидно, для оценки порогового поля
пробоя в этом случае надо использовать значение коэффициента диффузии,
соответствующее начальному плазменному образованию, т.к. именно на ранних этапах
размножения электронов определяется, сможет развиться лавина, или нет.
Остановимся теперь на пороге зависимости порога оптического пробоя газа от
давления р. Будем считать, что атомы (молекулы) газа не обладают свойством
электроотрицательности, т.е. va = 0. Будем считать, что лазерный импульс достаточно
длинный, и порог развития пробоя контролируется скоростью диффузии электронов из
фокального объема. При низких давлениях естественно ожидать, что (o»vtr. Поэтому:
Рис. 18.3. Зависимость порога пробоя в газе от
Давления.
1 e2E2v[r у Р у;
2та>2 Л2 З^Л2'
(18.3.10)
Здесь у2 - квадрат тепловой скорости
движения молекул. Поскольку уг - р,
из (18.3.10) получаем, что пороговое
поле пробоя обратно пропорционально
давлению Elh~\/p. При высоких
давлениях, наоборот, v№ »ш.
Следовательно, для порога пробоя
имеем:
/, 2m г,, Л2 Зг„Л! ’
(18.3.11)
откуда получаем обратную зависимость Ел~р. Общий график зависимости приведен
на рис. 18.3. Минимальный порог пробоя реализуется при таком значении давления, что
й>=и„. Отметим, что в оптическом диапазоне частот мы практически всегда находимся
на левой (убывающей) ветви полученной зависимости. Например, даже для частоты СОг
лазера условие v,r « со выполняется при давлениях порядка ста атмосфер. Правая ветвь
кривой на рис 18 3 реализуется для разрядов СВЧ диапазона частот. При понижении
давления можно получить горение СВЧ разряда с параметрами, соответствующими
408
левой ветви рассматриваемой зависимости. Такой СВЧ разряд низкого давления будет
очень похож на оптический разряд.
Заканчивая обсуждение проблемы вычисления пороговых полей в рамках
элементарной теории, отмстим, что в рамках рассматриваемого подхода оценки
пороговых полей получаются, как правило, завышенными. Это связано с тем, что в
нашем подходе каждый из электронов, чтобы ионизовать газ, должен набирать энергию,
равную потенциалу ионизации атома (молекулы). На самом деле, на практике
оказывается, что развитие лавины возможно, когда энергией, достаточной для
ионизации, обладает лишь сравнительно небольшая доля электронов, находящаяся в
высокоэнергетичной части функции распределения по энергиям. Такой подход к
определению порога пробоя должен базироваться на кинетической теории и будет
рассмотрен нами в Главе 19. При этом окажется, что частота ионизации зависит от
напряженности электрического поля волны заметно более сильно, по
экспоненциальному, а не параболическому закону.
Задачи к Главе 18.
18.1. Оценить величину колебательной скорости и энергии электрона в лазерном поле
рубинового лазера (ЙбУ = 1.78 эВ) с интенсивностью 1О10 Вт/см2.
18.2. В рамках элементарной теории оптического пробоя определить зависимость порога
развития электронной лавины от массы атома и его потенциала ионизации.
18.3. Оценить порог пробоя в Не излучением Nd лазера при тр = 10 нс, г = 0.01 см, р = 1
атм. Как порог пробоя зависит от размера пятна?
18.4. Какой характер, свободный или амбиполярный, будет носить диффузия электронов
в плазме с концентрацией электронов пе =1О10 см‘3 и температурой электронов
Т = 1 эВ? Размер плазменного образования ~ 0.01 см.
18.5. При воздействии излучения СОг - лазера (диаметр пятна фокусировки ~ 1мм) на
поверхность алюминия образуется пар с температурой Т=2740 К при атмосферном
давлении. Оценить пороговую интенсивность оптического пробоя.
409
Глава 19. Кинетическая теория оптического пробоя.
Рассмотренная ранее модель оптического пробоя газов, базирующаяся на
элементарной модели, предполагает, что все электроны одинаковы. Это значит, что
каждый из них должен набирать энергию, достаточную для ионизации атомов (молекул)
газа. Фактически это означает, что энергия электронной компоненты плазмы
оказывается порядка потенциала ионизации. Однако, эксперименты показывают, что
средняя электронов в плазме разряда оказывается заметно меньше потенциала
ионизации. Следовательно, только небольшая часть электронов обладает ионизующей
способностью. В такой ситуации для вычисления скорости ионизации надо знать
функцию распределения электронов по энергиям (ФРЭЭ), т.е. основываться на
кинетической теории.
19.1. Уравнение Больцмана для функции распределения
электронов по энергиям в поле электромагнитной волны в двучленном
приближении.
Вернемся к рассмотрению задачи о функции распределения электронов по
скоростям (см. Глава 16). Мы видели, что в двучленном приближении
/(v,<9,z)«/0(v,/) + /1(v,/)cos^, (19.1.1)
(19.1.2)
и для гармоник функции распределения справедлива следующая система уравнений:
^^=^T^-v2/(v,o+e„,
dt 3mv dv
^ + v,r(v)Z(v,,) = ^5
dt m dv
Здесь E(/) - напряженность электрического поля волны, Qo - интеграл неупругих
столкновений. При этом при выводе выражения для интеграла упругих столкновений
(Приложение 16.1) полагалось, что в таких столкновениях происходит лишь разворот
вектора скорости на некоторый угол, в то время как абсолютная величина скорости не
изменяется.
При анализе этой системы уравнений будем учитывать, что время релаксации
гармоник /o(v,O и /(у,/) к своим стационарным распределениям существенно
Различно. Асимметричная добавка релаксирует на временах ~ и,;1, в то время как
как симметричная часть /„(у,Г), определяющая распределение по модулю скорости (или
по энергии), на временах ~ (W/2m)v,;'. Поэтому, записывая общее решение второго из
Уравнений (19.1.2) в виде:
Z(v,/) = exp(-v,r(v)Z)x |exp(v,r(v)/')
a/0(v,f) eE(f)
dt' + C(v) ,
m
(19.1.3)
и вынося из под знака интеграла dfQ/dv, получим.
410
,/;(v./) = cxp(-r„(r)/)x
<’ d/^’J ) f }•(/')cxp(^„(v)/')6//' + C'(v) .
m <7v
(19-1.4)
Здесь C(r) - начальное распределение. Считая, что
Eocxp(-/ftX), /^0,
вд = (о. '<«
из (19.1.4) получим:
f(v,t) =____-------^ol^exp(-/fiX) + C(v)exp(-v/r(v)/). (19.1,5)
1 ’ w(v,r - /69) dv
Функция C(v) определяется из начальных условий. Однако видно, что на временах,
превышающих у”’, мы получаем установившуюся связь между /^(v,/) и f0(v,t).
j\(y,t) =---—------"V’~exp(-/<??Z). (19.1.6)
m(ytr -ia>) dv
В частном случае статического поля имеем:
Z(V,<)= еЬ"
mvtr dv
(19.1.7)
Подставляя (19.1.6) в первое из уравнений (19.1.2) и усредняя по высокочастотным
осцилляциям, получим уравнение для нулевой гармоники f0 (у, t):
Sf0(y,t)
dt
(19.1.8)
В случае постоянного поля аналогично имеем:
df0(y,t) = е2Е2 d
dt 3m2v2 dv
dv
о-
(19.1.9)
Переходя от функции распределения по модулю скорости /0(у,Г) к функции
распределения по энергиям n(e,t) с нормировкой f n(EttyjEdE = 1, из (19.1.8) получим:
дп(Е,Г)4Ё
dt
_еТ; д ( Е3,2у,г СП
Зт dE\a>2+v2r dE;
(19.1.Ю)
Замечая, что
£1/2 _ 1
dE~ dE 2^ЕП'
перепишем (19.1.10) в виде:
411
dn(JE,t)J£ dJE
St ~ дЕ +^0’ (19.1.11)
ГДС
Л = "°£ ~дГ + n^U'DE= —*Е = Л(Е)Е, U = A/2. (19.1.12)
Как видно, наше уравнение есть уравнение диффузии в пространстве энергий, причем
поток JE включает в себя как диффузионную, так и дрейфовую части. Выражения для
/X и U представляют собой коэффициент диффузии электронов и скорость дрейфа в
энергетическом пространстве.
Отметим, что увидеть диффузионно-дрейфовый характер кинетического
уравнения можно было из очень простых соображений. При анализе набора электроном
энергии в поле электромагнитной волны мы видели, что электрон либо поглощает, либо
испускает энергию порциями &E~tnvevT (ve, vT- колебательная и тепловая скорости
электрона соответственно) примерно с равной вероятностью, и при этом в среднем
набирает энергию порядка колебательной за одно столкновение. Тогда, оценивая
коэффициент энергетической диффузии электронов как
De = (ДЕУ/2? = (ДЕ)\г/2 = ^Еу,г,
та
а скорость дрейфового движения вверх по оси энергий:
е2Е2
U = 2Ev = Q v
2та)
получим для случая а>»vlr выражения с точностью до численного множителя
совпадающие с (19.1.2).
Понимание того факта, что движение электронов в пространстве энергий носит
диффузионно-дрейфовый характер, позволяет теперь легко ввести в уравнение член,
описывающий упругие потери энергии. Действительно, по аналогии с дрейфовым
слагаемым в потоке JE, описывающим набор энергии электроном, введем в поток еще
одно слагаемое, описывающие движение вниз по энергетической оси.
j D Э^ + п^Ёи-пУЁи,,. (19.1.13)
£ 8Е
где (У ^~Ev Отметим что добавленное (и угаданное) слагаемое является точным, в
М
случае если энергия тяжелых частиц (атомов, молекул) равна нулю. Если же учитывать
максвелловское распределение по скоростям (с газовой температурой Т,) тяжелой
компоненты плазмы, выражение для потока (19.1.13) следует переписать в виде:
j--DES-H^ + n4EU-{n + Tg^\4EUd. (19.1.14)
Е Е дЕ к дЕ)
412
Как видно, учет конечного значения газовой температуры приводит к увеличению
коэффициента энергетической диффузии. Однако, в задачах о лавинной ионизации газов
в поле излучения это увеличение, как правило, несущественно.
Обсудим теперь коротко условия применимости диффузионного приближения.
Мы уже говорили, что возможность ограничиться всего лишь двумя членами в
полиномиальном разложении предполагает, что все последующие гармоники функции
распределения/’^2(v)« /0(v), /;(v). Мы, однако, используем более строгое условие
fx (v)« /о(г). Как видно из (19.1.6), в высокочасто гном поле (со » vfr):
_£Ео А = 2к/л. (19.1.15)
тсо dv тсо vT vr
Поэтому условием малости первой гармоники является условие ve «vr, т.е.
колебательная скорость электрона мала по сравнению с тепловой (средней по
распределению скоростью). Аналогично, в низкочастотном (в том числе постоянном)
поле из (19.1.7) имеем:
= \/о, (19.1.16)
mv,r dv mv,r vT vdr
(vdr =eE0/mvtr - дрейфовая скорость электрона), т.е. дрейфовая скорость движения
много меньше тепловой.
С увеличением воздействующего на плазму поля колебательная (и дрейфовая)
скорости движения электрона, очевидно, возрастают. Однако, одновременно и плазма
становится более горячей, т.е. возрастает и характерная скорость теплового движения.
Поэтому ограничения применимости двучленного приближения, вытекающие из
соотношений (19.1.15) и (19.1.16), требуют дополнительного анализа.
19.2. Баланс энергии электронов в плазме.
Мы видели, что в рамках элементарной теории баланс энергии электрона в поле
волны определяется уравнением:
dE ^2EqV 2m
---=--------——-------
dt 2m(<y2+v2) М
(19.2.1)
Поскольку в элементарной теории все электроны обладают одной и той же энергией, это
означает, что их функция распределения по энергиям является 8 - образной:
п(Е,1)4Е ~ 8(Е-Е*), где Е* определяется из решения уравнения (19.2.1).
Рассмотрим теперь вопрос о нагреве электронной компоненты плазмы в рамках
кинетической теории. Учитывая, что средняя по спектру энергия электронов есть
{E(t)) = jn(E,t)jEdE,
(19.2.2)
дифференцируя (19.2.2) по времени, получим:
dt J dt J \ dE)
(19.2.3)
413
0ыполняя интегрирование по частям с учетом того, что Je(E ->оо) ->о , получим:
Jt{E(t)) = \jE(E,t)dE.
упоминая, что
е2Е2
— __Z0
Е Зт
t<y2+v2 дЕ)
~Е*\,п = -А(Е)Е3'2 E331v п ,
М BE М
найдем:
(19.2.4)
где (...) означает результат усреднения по функции распределения.
Как видно, в частном случае, когда vtr = const, имеем:
d{E} g2EpVfr 2m(F\v
dt 2m(co2+v2r) ' ,r'
(19.2.5)
т.е. уравнение элементарной теории, причем полученный результат не зависит от
конкретного вида ФРЭЭ. Если же vtr const, динамика во времени средней становится
зависящей как от конкретной зависимости транспортного сечения рассеяния от энергии,
так и от вида ФРЭЭ, изменяющейся во времени.
Для более детального анализа ситуации остановимся на решении кинетического
уравнения Больцмана. Будем считать, система находится в достаточно медленно
изменяющемся во времени поле с несущей частотой а), таком что ФРЭЭ является
квазистационарной, т.е. dn/ct~Q. Ранее мы видели, что характерное время релаксации
энергии электрона к равновесному значению есть тЕ ~ (М/Ъп^. Это означает, что
амплитуда электрического поля волны меняется плавно на временах порядка тЕ. Тогда
приблизительно можно считать, что
cJE/dE = 0,
т.е. JE = const. Учитывая, что функция распределения задана на полубесконечной оси
энергий, мы получаем JE = 0, т.е.
е2Е^ Г E3,2vlr '
Зт + v2 j
dn 2т „3/2 л
— + — Е ’ у.гп = 0,
dE М
(19.2.6)
откуда
п(Е) = С ехр
2m\^+vl>dE
М е2Ец /Зт
(19.2.7)
Здесь постоянная интегрирования С определяется из условия нормировки.
Рассмотрим случай vtr = const. Тогда:
414
Таким образом, в отсутствие нсуиругих noicpb в слу iac vtr const функция
распределения электронов по энергиям оказывается максвелловской, а, следовательно,
параметр этого распределения Т можно назвать температурой. Нормированная функция
распределения есть
п(Е)уГЁс1Е = Т}4е dE, (19.2.9)
dxT"~
а средняя по спектру энергия
М е2Ео
{Е} = (3/2)Т =
2m 2m(co2 + v2)
(19.2.10)
Обратим внимание, что эта величина совпадает с энергией, которую электроны
набирают в поле волны в рамках элементарной теории!
Отметим еще один важный результат: в случае, если гу »max{i//r(E')} (такая
ситуация характерна именно для оптического диапазона частот) из (19.2.7) получаем, что
функция распределения всегда является максвелловской с температурой
Тк М g2Eo
2m 3mсо2
Рассмотрим еще один важный частный случай: пусть от энергии электрона не
зависит величина транспортного сечения рассеяния ст1г = const. В этом случае
постоянной оказывается длина свободного пробега электронов Я = 1/Ncrtr (N -
концентрация атомов), а транспортная частота оказывается пропорциональна скорости
электрона v(r =v/Л = ^2Е/тЛ2 . Тогда вычисление интеграла в (19.2.7) дает:
п(е) = С ехр
2т со2 Е + Е2/тХ
~М е2Е2/Зт
= Сехр
Ех Е2
(19.2.11)
р М е2Е2
где Ех=——^
2т эта>
— еЕ0Я - параметры распределения. Распределение (19.2.11)
называют распределением Маргенау. Как видно, параметр Ех определяется
колебательной энергией электрона в поле волны, а параметр Е^ - энергией, набираемой
свободным электроном на длине пробега, еЕ0Я. В низкочастотном (tw«imx{v,r(£)}) и,
в частности, в статическом случае распределение Маргенау переходит в распределение
Дрювестейна:
п(е) =
2
^/2Г(3/4)
ехр(-£2/£2).
(19.2.12)
415
Здесь Еп ^^еЕ0Л т.н. дрювесгсйновская энергия, Г - гамма-функция. Средняя
энергия электронов по дрювсстсйовскому распределению сеть:
п. в отличие от случая максвелловского распределения (19.2.10), растет линейно по
ПОЛЮ.
Рис. 19.1. Распределения Максвелла и
Дрювестейна для случая ED = Т — 3 эВ.
Логарифмы функций распределения
Максвелла и Дрювестейна, соответствующие
одной и той же средней по спектру энергии
электронов, представлены на рис. 19.1. Как
видно, в области высоких энергий
(Е > {Ё} ~T,£d) количество электронов по
дрювестейновскому распределению существен-
но меньше чем по максвелловскому. Это
понятно: в области больших энергий частота
транспортного рассеяния в случае crtr = const
растет с энергией, поэтому в низкочастотных
полях (со« vlr) коэффициент диффузии электронов в пространстве энергий падает с
увеличением энергии электронов. Этот факт и приводит к более быстрому спаданию
количества электронов в высокоэнергетической части спектра.
19.3. Условия применимости двучленного приближения.
Вернемся к вопросу о пределах применимости двучленного приближения. Ранее
мы показали, что условием его применимости заведомо является условие малости
колебательной (или дрейфовой) скорости движения электрона по сравнению со
скоростью теплового движения. Теперь, имея простейшие решения кинетического
уравнения, рассмотрим вопрос чуть подробнее.
Будем считать, что поле имеет оптическую частоту, поэтому tt>»max{yfr(£')}, а
следовательно функция распределения является максвелловской с температурой,
определяемой выражением:
„ А/ е2Е2
----------т.
2m 3 m со
Вычисление средней по распределению скорости теплового движения дает.
VT = (у) = 72/w jn(E)EdE =^Т/лт\ехр( -= ^Т/лт , (19.3.1)
или
I 8 М еЕ0 IМ
V, =.--~----->>V<>
у Зтг 2m mco v 2m
416
т.е. скорость теплового движения оказывается всегда много больше колебательной
скорости. Аналогичная ситуация возникает и для слу !ая дрювейстеновского
распределения (см. задача 19.3).
Казалось бы. полученный результат означает, что двучленное приближение
справедливо всегда, вне зависимости от величины электрического поля в плазме.
Однако, следует иметь в виду, что мы нс учитывали нсупругие потери энергии. Мы
видели, что нсупругие столкновения, будучи сравнительно редкими по сравнению с
упругими, слабо влияют на скорость релаксации направленного движения электронов в
плазме. Поэтому они не окажут существенного влияния на расчет дрейфовой скорости
движения. В то же время, такие соударения крайне существенны при определении
энергетического баланса. Увеличение напряженности поля в плазме безусловно
приводит к увеличению энергии теплого движения, что в свою очередь приводит к
увеличению неупругих потерь энергии электроном. Как результат, скорость теплового
движения возрастает заметно медленнее, чем это описывается выражением (19.3.1), что
и приводит к нарушению условия применимости двучленного приближения.
19.4. Неупругие столкновения.
До сих пор все рассмотрение проводилось без учета влияния неупругих
столкновений на функцию распределения электронов. Однако, уже и в таком
приближении можно высказать некоторые соображения о зависимости скорости
возбуждения или ионизации различных атомных состояний от параметров
воздействующего на газ излучения (частоты и напряженности поля в волне).
Будем считать, что сечение ионизации в зависимости от энергии налетающего
электрона описывается известной формулой Томсона (- потенциал ионизации атома):
Е<1^
(19-4.1)
Рис. 19.2. Сечение ионизации атома в
зависимости от энергии налетающего
электрона, полученное по формуле Томсона.
Вид зависимости crf(£) приведен на
рис. 19.2 и качественно правильно описывает
реальные зависимости сечений ионизации и
возбуждения электронных состояний от
энергии для многих атомов. Отметим, что
вблизи порога процесса сечение линейно
зависит от энергии, превышающей порог:
максимальное значение сечения достигается
для энергии Е = 11 , а в области больших
I
энергий <jj ~\/Е. Квантовомеханические
расчеты в этой области дают at ~ 1п( Е)/Е.
Предположим, что функция распределения электронов является максвеллловской
с температурой
417
м с2е;
2т Зтсо2
Такая ситуация реализуется в оптическом диапазоне частот вне зависимости от видя
гранспортного сечения рассеяния. Тогда величина константы скорости ионизации есть:
к, = = ^]0{(E)n(E)EdE.
h
(19.4.2)
Считая, что выполнено условие Т «I., из (19.4.2) получим:
ле4
7 E-I
\-—Lexp(<~ElT)EdE.
Делая замену переменных % = (Е-1^[Т, получим:
8Т ле4
лпг I2
00
exp(-Z,/r)J<ехр(-£)(1 + ,
О
откуда:
, яг4 , г _
к>=~7Гу— 1 + 2т ехР(~Л/г)~
— exp(-Z;./T).
лт
(19.4.3)
Как видно, зависимость скорости ионизации от амплитуды поля волны оказывается
экспоненциальной. Аналогичный результат (экспоненциальная зависимость от величины
поля) получается и для дрювестейновского распределения (см. задача 19.6).
Рассчитанная величина константы скорости ионизации (или возбуждения)
является, конечно, завышенной. Учет влияния неупругого процесса на ФРЭЭ приводит к
уменьшению числа электронов в области энергий, превышающих порог процесса, что и
приводит к уменьшению константы скорости по сравнению с полученным значением.
Для более детального рассмотрения неупругих процессов в рамках кинетического
уравнения рассмотрим выражения для соответствующих интегралов столкновений.
Рассмотрим прежде всего интеграл неупругих столкновений, описывающий
процесс возбуждения атомных состояний (или электронных состояний в молекулах).
Представим себе процесс возбуждения атомного состояния электронным ударом, причем
порог процесса есть Г:
А + е —> А* +е
Ис -19.3. К вычислению интеграла
НеУпругих столкновений для процесса
в°збуждения
атомных состояний.
Тогда уход электронов из области энергий Е
(Е>Г) есть -v*(Е)п(Е)у[Ё, где v* - частота
возбуждения (см. рис. 19.3). С другой стороны, в
область энергий Е приходят электроны,
которые до столкновения с атомом имели
энергию E + I . Соответствующее слагаемое
есть + у (Е +1 )п(Е +1 )у1е+7 . Вспоминая
418
связь частоты возбуждения и сечения возбуждения, подучим следующее выражение для
ннтс1рала столкновений:
N 2 ( <т'(/<)/;( Л’)Е ♦ t/‘M(7; + /*)(£+/ )),
V /и
(19.4.4)
где /V - концентрация атомов в разряде, гг (Л) - сечение возбуждения атомного
состояния. На практике, у любого атома имеется целый набор возбужденных состояний,
поэтому в (19.4.4) надо взять сумму по всем возбужденным состояниям, которые следует
принять во внимание.
В молекулярных газах кроме возбуждения электронных состояний существенным
является также возбуждение колебательных состояний. Энергия колебательных квантов
различных молекул, как правило, — 0.1- 0.3 эВ. Например, для молекулы азота энергия
возбуждения нижнего колебательного состояния основного электронного терма
равна /гИ «0.29 эВ. Выражение для "колебательного" интеграла столкновений
записывается в виде, аналогичном (19.4.4), причем сумму надо брать по определенному
числу сечений колебательного возбуждения молекулы. Существенно отметить, тем не
менее, что зависимость сечений колебательного возбуждения, как правило, существенно
отличается от аналогичной зависимости для электронного возбуждения. Например, для
молекул азота сечения колебательного возбуждения отличны от нуля лишь в области
энергий от 1.7 до 4 эВ, оставаясь пренебрежимо малыми вне этого интервала.
Процесс прилипания (диссоциативного) есть:
.^2 + е —А + .
В этом случае в ходе рассматриваемого процесса происходит исчезновение электрона.
Электроны с некоторой вероятностью, определяемой частотой прилипания уДЕ),
исчезают из области энергий Е, но никогда не появляются в этой области. Поэтому:
&(«) = -^(Я)и(£)7£ = -N j-a„(E)n(E)E.
N т
(19.4.5)
Здесь сга - сечение прилипания.
Рассмотренный нами процесс прилипания позволяет по аналогии включить в
кинетическую теорию и процесс диффузии электронов. Это тоже исчезновение
электронов с заданной энергией, которое происходит с частотой диффузии vd = D/A2
(здесь D = v2/'iVtr - коэффициент диффузии электронов, Л - размер области занимаемой
плазмой). Следовательно
ваМ = «(£). (19.4.6)
Зоти/г(Е)А
На практике часто еще приходится иметь дело с так называемыми ударами
второго рода, или сверхупругими столкновениями1 Под этим термином скрывается
процесс девозбужения атомов электроны ударом:
1 От английского "superelastic collisions".
419
Л' + е > А + е,
p(jC 19.4. К вычислению интеграла неупругих
столкновений для процесса девозбуждения
атомных состояний.
столкновений, очевидно, запишется в виде:
схематически предел явленный на
рис. 19.4, в результате которого электрон
приобретает дополнительную энергию,
равную потенциалу возбуждения.
Очевидно, это процесс является
обратным по отношению к процессу
возбуждения атома. Интеграл
Q\n) = N‘ -(-а1 (Е)п(Е)Е + а\Е-Г)п(Е-/*)(Е-Г)). (19.4.7)
Здесь <г*(Е) - сечения девозбуждения атома электронным ударом с порогом Г, а -
концентрация соответствующих возбужденных атомов. Очевидно, удары второго рода
могут оказаться существенны только когда в газе присутствует значительное количество
возбужденных атомов, которые могут образоваться, например, в процессе горения
разряда. Заметим, что сечение девозбуждения некоторого атомного состояния связано с
сечением его возбуждения соотношением детального баланса (см. Задача 19.1):
о-\£) = СТ,(£ + /’)^-. (19.4.8)
Е
Ионизация. Рассмотрим еще интеграл столкновений, описывающий процесс
ионизации:
А + е А+ + 2е.
Легко сообразить, что член описывающий
уход электронов из области энергий £
।________। у__________ (мы полагаем здесь, что эта энергия
О I, Е Е + 1> превышает потенциал ионизации) есть
-у\Е)п(Е)4Ё, где у,(£) - частота
Рис. 19.5. Вычисление интеграла столкновений тт л__
ионизации. Что касается слагаемого,
для процесса ионизации.
которое описывает появление электронов
с энергией £, то ситуация несколько более сложная (см. рис. 19.5). Действительно, при
ионизации атома (молекулы) электроном с энергией £' энергия E'-It распределяется
между двумя электронами, первичным и вторичным2 * *, по некоторому вероятностному
закону, определяемому двойным дифференциальным сечением ионизации
d<Jl(E\E)/dE, определяющим вероятность появления электрона с энергией £ при
Условии, что начальная энергия налетающего электрона была равна £'. При этом
. (Е1 £)
величина сг(£')= Г ——’—dE дает полное сечение ионизации электронным ударом.
' 7 J dE
2 Электроны являются тождественными частицами, однако в данном случае обычно полагают, что
первичный электрон - это электрон с большей энергией, а вторичный, т.е. вылетевший из атома, - с
меньшей.
420
Как результат, интеграл столкновений, соответствующий процессу ионизации,
записывается в виде:
2,(и) = nJ1(-(Ti(Е)п(Е)Е + 2 [ ,E±n(J?)E'dE' . (19.4.9)
dE )
Двойка перед интегралом возникает в результате того, что любой из двух электронов
(первичный или вторичный) может в результате ионизации приобрести энергию равную
Е. Записанный интеграл столкновений оказывается достаточно сложным. Однако в
задачах, когда функция распределения достаточно быстро спадает в области энергий,
превышающих потенциал ионизации, энергия обоих рождающихся электронов невелика
(много меньше потенциала ионизации). Поэтому на практике оказывается, что реальное
распределение энергии между первичным и вторичным электронами практически никак
не влияет на вид формирующейся ФРЭЭ. Поэтому, в зависимости от удобства, можно
предположить, что энергия между электронами распределяется поровну, или
равновероятно по интервалу (0, £'-/,).
Наконец, коротко обсудим влияние межэлектронных столкновений на вид ФРЭЭ,
формирующейся в разряде. Прежде всего, очевидно, что электроны, имея одинаковые
массы, эффективно обмениваются энергией при столкновениях между собой. Интеграл
межэлектронных столкновений может быть записан в стандартной больцмановской
форме3 и обращается в нуль для максвелловской ФРЭЭ. Это означает, при
определяющей роли электрон- электронных столкновений в формировании ФРЭЭ
функция распределения будет максвелловской. Наша задача сейчас оценить, при каких
степенях ионизации плазмы межэлектронные столкновения надо принимать во
внимание. Скорость потерь энергии электроном в упругих столкновениях есть — Evea>
М
где = vtr - частота электрон-атомных столкновений. В случае электрон - электроных
(е-е) соударений аналогично для скорости потерь имеем Е vee. Сопоставляя записанные
выражения, получим, что е-е соударения надо принимать во внимание, если степень
ионизации плазмы a = njN превышает значение:
2т сг1г
~М аее{Е} ’
(19.4.10)
где аее - резерфордовское сечение рассеяния. Как видно, е-е соударения оказываются
существенными при уже невысокой степени ионизации плазмы на уровне Ю^-ИО”5.
При этом, поскольку <уее ~\/Е2, максвеллизация спектра оказывается более
существенной в области небольших энергий, а по мере возрастания степени ионизации
начинается максвеллизация в высокоэнергетичной части спектра.
Мы рассмотрели проблему необходимости учета столкновений, когда в газе
доминируют упругие потери энергии. Такая ситуация часто реализуется, например, в
плазме инертных газов. В молекулярных газах, где средняя доля потери энергии
3 Е. М. Лифшиц, Л. П. Питаевский "Физическая кинетика", М: Наука, (1979), §3
421
электроном в столкновениях заметно выше, межэлектронныс соударения в области
энергий электронов Е можно не учитывать вплоть до значений
< v V
“ Е «„(Е)'
(19.4.11)
Здесь и о\. - энергия колебательного кванта и сечение колебательного возбуждения
соответственно. Например, при характерных значениях IjE-О.ОЗ и crjcr^ ~ 0.003
п0Лучаем, что е-е соударения несущественны вплоть до а < 10’3.
19.5. Влияние неупругих соударений с атомами на вид
энергетического спектра электронов.
Рассмотрим теперь влияние неупругих столкновений (возбуждения электронного
состояния с порогом I ), причем будем считать, что средняя по спектру энергия мала по
сравнению с потенциалом возбуждения. Будем рассматривать стационарный случай,
cnjdt = 0, а частота электромагнитного поля много больше транспортной частоты. В
таких предположениях кинетическое уравнение записывается в виде:
(19.5.1)
dE
тле поток в пространстве энергий определяется выражением:
J = -^Lv {Е)Е3’2 — v (Е)п(Е)Е3/2.
Е Зта)2 ,r dE М ,г
Мы будем полагать, что функция распределения быстро спадает за порогом неупругого
процесса. Поэтому в области энергий, превышающих I , запишем:
Поток в пространстве энергий
К
Неупругое
столкновение
Рис. 19.6.
упругого столкновения на ФРЭЭ.
анализу влияния
Q‘(n)^-v\E)n(E)jE ,
а в области энергий Е<1* неупругие соударения
отсутствуют. Поскольку в процессе возбуждения
электроны «прыгают» в область малых энергии
(£«/*), приближенно можно считать, что они
появляются с нулевой энергией, т.е. могут быть
описаны как поток через границу (см. рис. 19.6).
Таким образом, будем решать уравнение (19.5.1)
раздельно в каждой из областей:
I £</*
II Е>1*
(19.5.2)
(19.5.3)
В области I имеем:
422
Общее решение этого уравнения есть
(19^
Здесь Со - нормировочная константа. В частном случае Jo =0 получается решение, не
учитывающее неупругис потери энергии, тогда Т - температура распределения. При
этом величина потока 70 определяется видом функции п(Е} за порогом возбуждения:
Jo = j v\E)n(E)jEdE. (19.5.5)
/’
Проанализируем ФРЭЭ за порогом возбуждения. В области действия неупругих потерь
мы можем пренебречь упругими потерями энергии. Тогда перепишем уравнение (19.5.3)
в виде:
— -^^vtr(E)E312—
dE{3ma)2 ' dE}
Мы уже предполагали, что функция достаточно быстро убывает с энергией. Для
упрощения будем также считать, что v*(E > Г) = v*0 = const. Тогда (19.5.6) перепишем в
виде:
-у*(Е)и(Е)л/Ё = 0. (19.5.6)
Зтй)2 dE2
v.n{E) = 0.
Решение этого уравнения, удовлетворяющее условию п{Е —> оо) —> 0, есть:
Рис. 19.7. Бимаксвелловская функция
распределения электронов.
п(Е) ~ ехр(-кЕ'),
где
I v* 3
^~^/г(/*)4ГЕе'
Функция распределения тоже имеет
максвелловский вид, но с "температурой"
Т = \/к. Таким образом, в условиях
рассматриваемой задачи функция распределения
имеет бимаксвелловский характер, причем
отношение "температур" определяется
соотношением:
Т* _ 2m 1зу(г(Г) Г
Т М у 4 у0* Ее
Для характерных значений 2m/M~10^> v/r/v‘~100, /*/Х~Ю4 находим т'/Т^ОЛ,
т.е. температура "хвоста" функции распределения существенно меньше температуры
низкоэнергетичной части. При этом с увеличением напряженности поля
электромагнитной волны отношение Т*/Т убывает. Характерный вид бимаксвелловскоЙ
функции распределения представлен на рис. 19.7.
423
19.6. Квантовое кинетическое уравнение.
До сих пор при рассмотрении кинетики электронов в плазме мы пользовались
классической теорией вынужденного тормозного эффекта (ВТЭ), в рамках которой
электрон может набирать или поглощать энергию от поля при столкновениях с атомами
порциями
ДЕ* = mvTve,
где vf,v7 - скорости теплового и дрейфового движения электрона соответственно. С
другой стороны, с точки зрения квантовой теории hco есть минимальная порция
энергии, которую может поглотить электрон. Поэтому в условиях
^^<£^27
й)
классическая теория заведомо неприменима и нам необходимо пользоваться квантовой
теорией ВТЭ.
Вспомним результаты, полученные в Разделе 12.4. В рамках теории Бункина -
Федорова дифференциальное сечение рассеяния электрона с начальной энергией Е на
атоме в присутствии внешнего электромагнитного поля с частотой со описывается
формулой:
dcr(±n\E,9) _ z2/\; V, /Е±«Лй> dcr(E±nhco/2,«9)
d& v p'pJ N E dQ.
(19.6.1)
где & - угол рассеяния. N = —- параметр многоквантовости, a op - изменение
p<'' mhco'
импульса при рассеянии. Оценивая величину изменения импульса при рассеянии как
8р ~~ р, получим:
дг еЕоЕ = eEQvT/(o
PfP‘ rntico2 ha>
т.е. физический смысл параметра многоквантовости — это отношение величины
поглощаемой энергии в рамках классической теории к величине кванта (квантовому
набору энергии). С учетом свойств функций Бесселя, рассмотренных в Разделе 12.4, мы
видим, что случаю большого значения параметра многоквантовости N»1
соответствует классической набор энергии, Наоборот, случай доминирования
одноквантовых переходов (Л^< 1) не может быть описан в рамках классической теории.
Поэтому более подробно остановимся именно на процессах одноквантового поглощения
и испускания. Дпя одноквантовых переходов выражение (19.6.1) перепишем в виде:
<fo-(±1)(Е,Г ~ ] х I& х d(T(E±ha)/2,^)
55 2mhco2 J V Е dQ.
(19.6.2)
Здесь Е = рг1'2т, E + hco = р]/2т.
424
Для вычисления вероятности поглощения кванта нам надо проинтегрировать
(19.6.2) по углу .9 между векторами начального импульса р и импульса после
рассеяния р . Кроме того, полученное полное ссчснис ВТЭ зависит от ориентации
импульса pf относительно направления поля Е. Поэтому при описании ансамбля
электронов, имеющих изотропное распределение по скоростям, полученное сечение
должно быть также усреднено по углу О - углу между векторами р и Е. Тогда для
частоты столкновения с поглощением (испусканием) кванта поля получим выражение:
W\E) = Ny/2E/mxcT(±,)(E), (19.6.3)
где
сг(±1)(£) = —
4^-J 'J t/Q
e2Ej lE±fai> 1 f a-, f n 2dcr(E±ti(o/2,&)
—, - x.-----------dCLk/Q (p f cos 0f- p cos 0) —1--------------.
4m2h2co4 V E 4л-J '£ f f dQ.
Рис. 19.8. Геометрия процесса рассеяния
электрона на атоме во внешнем поле.
Здесь внутренний интеграл определяет
сечение однофотонного поглощения
(испускания) кванта поля, а внешний -
усреднение полученного сечения по
начальной ориентации импульса электрона.
Ориентация векторов и углы между ними
обозначены на рис. 19.8. При этом углы 0f и
О связаны соотношением:
cos#z = cos# cos«9 + sin 0 sin & cos^>.
Учтем, что dQ. = sin & d& dep. Тогда для
случая изотропного сечения рассеяния
получаем:
fdtl(pf cos 0f - p cos #)2 (j? ± 2) x (1 p2 + p2 cos2 .
n J
Следовательно,
o-(±,)(£) = ~ 4 x ± йш/2) x (E ± hco/2^ I, (19.6.4)
t'KlCil Ct) ]/ £
где I - интенсивность излучения.
Для вероятностей поглощения/испускания имеем:
№\Е) = NplEthaMm х —~a,r(Е± Й<у/2)х (Е ± Ы2)х I. (19.6.5)
3 men со
Отметим важное свойство полученного выражения:
И/+(Е-Йбу) = ^'(Е), (19.6.6)
425
г.с. вероятность перехода hj состояния с энергией E-ha) с поглощением кванта равна
вероятности перехода из состояния с энергией Е с испусканием кванта.
Теперь мы можем записать ключевые слагаемые в квантовом кинетическом
уравнении, описывающие взаимодействие электронов с полем излучения. Напишем
уравнение баланса для электронов с энергией Е. Уход электронов из области энергий Е
в результате поглощения или испускания кванта есть (E) + W~(E))n(E)J~E. С
другой стороны, в область энергий Е приходят электроны, которые до столкновения с
атомом имели энергию E — hco и поглотили квант поля, а также электроны, имевшие
энергию E + hco, но испустили квант поля. Соответствующее слагаемое есть
II (£ - — Tiaj)yjе — tico + W (£ 4- ha>)n(£ + e + hco . Схематически все эти
процессы представлены на рис. 19.9. Как результат, имеем кинетическое уравнение в
виде
= -(»'*(£) + №(Е))п(Е)4Ё + W\E-h<o)n{E-
Й ______ (19.6.7)
+ IV (Е + ha>)n(E4- ha>yjE + ha) + ^- — (ylr(E)E3/2n(E,t)}+ Q(ri).
M dE
Рис. 19.9. Процессы, определяющие
взаимодействие электрона с полем
электромагнитной волны.
Существенное отличие ФРЭЭ, полученных путем
решения квантового кинетического уравнения от
тех, которые соответствуют классическому
уравнению, есть результат скачков по оси энергии
на величину кванта ha), который в видимом и тем
более ультрафиолетовом диапазоне составляет
несколько эВ. Как результат, электрон всего за
несколько столкновений с поглощением кванта
поля способен набрать энергию, необходимую
для ионизации атомов (молекул) среды. Поэтому
можно ожидать, что с ростом энергии кванта зависимость порога пробоя Ith не будет
соответствовать классическому закону Ilh ~ а)2. Действительно, экспериментальные
данные показывают, что уже в ближнем ИК и в видимом диапазоне эта зависимость
существенно более плавная (Ith ~ со), а в УФ диапазоне частот наблюдается понижение
порога пробоя с увеличением частоты излучения. Более того, например, для эксимерного
KrF -лазера ha> = 5 эВ, величина кванта больше ширины области эффективных потерь
энергии на колебательное возбуждение молекулы азота (интервал энергий примерно от 2
до 4 эВ): поглотив всего один квант поля, электроны перепрыгиваю эту область и
оказываются в области энергий, где колебательные потери несущественны.
Отметим еще одну особенность спектров электронов, формируемых в полях
видимого и УФ диапазона частот (см. рис. 19.10). В условиях квантового характера
поглощения энергии поля ФРЭЭ могут приобретать немонотонную зависимость от
энергии, обусловленную "прыжками" электронов по оси энергий на величину кванта
hco. Фактически, такая немонотонность ФРЭЭ по своей природе аналогичная пичковому
характеру спектра фотоэлектронов, образующихся в газе в результате процесса
надпороговой ионизации.
426
Рис. 19.10. Структура нестационарной ФРЭЭ,
формирующейся в результате вынужденного
тормозного эффекта.
В заключение этого раздела
отмстим, что в условиях, когда величина
кванза много hm меньше средней По
спектру энергии электронов4, движение
электронов по оси энергий также в
сущности носит диффузионный характер
К такому квантовому уравнению диффу3ии
нетрудно перейти в уравнении (19.6.7)
разлагая функции n(E±hco,t) и
W^E + ha)) в ряд Тейлора по малому
параметру tic»j Е. Отметим, однако, что
такое уравнение не будет являться
классическим пределом квантовой теории.
Для перехода к классическому уравнению
Больцмана, как мы отмечали, необходим
учет процессов многофотонного поглощения (испускания) энергии при рассеянии
электрона на атоме.
Задачи к Главе 19.
19.1. Определить связь сечения возбуждения и сечения девозбуждения («удары второго
рода») атома электронным ударом. Считая, что сечение возбуждения определяется
формулой Томсона (см. (19.4.1), вместо потенциала ионизации подставить
потенциал возбуждения) получить выражение для сечения девозбуждения.
19.2. В рамках кинетической теории получить уравнение для средней по спектру энергии
электронов в плазме, находящейся в поле электромагнитной волны с частотой to, в
случае сг(Е) = сг0 = const. Неупругие процессы не учитывать.
19.3. Считая, что спектр электронов является стационарным, получить уравнение для
средней по ФРЭЭ энергии электронов в плазме разряда, поддерживаемой
постоянным электрическим полем. Сопоставить случаи v(E) = у0 = const и
сг(£) = а0 = const. Неупругие процессы не учитывать.
19.3. Считая энергетический спектр электронов установившимся, определить величину
скорости дрейфа электронов в плазме, поддерживаемой постоянным
электрическим полем, в случаях у(£) = у0 = const и сг(Е) = <т0 = const. Неупругие
процессы не учитывать. При каких условиях дрейфовая скорость меньше тепловой
(Vdr « Утр
19.4. Получить выражение для проводимости плазмы, поддерживаемой постоянным или
высокочастотным электрическим полем, в случае сг(£) = сг0 = const. Неупругие
процессы не учитывать.
19.5. Показать, что в оптическом диапазоне частот в отсутствие неупругих соударений в
газе атмосферного давления ФРЭ является максвелловской.
4 Мы полагаем при этом, что параметр многоквантовости остается малым и доминируют процессы
однофотонного поглощения (испускания).
428
Глава 20. Основы нелинейной оптики.
Мы видели, что отклик среды на внешнее электромагнитное поле существенно
зависит от интенсивности воздействия. В достаточно слабых полях, в которых воздей-
ствие поля на среду можно рассматривать в первом порядке квантовомеханической тео-
рии возмущений, отклик оказывается линейным: в среде возникает поляризация на ча-
стоте воздействующего поля. Если же рассматривать воздействие электромагнитного
поля на среду в высших порядках теории возмущений, среда оказывается нелинейной:
отклик среды оказывается более сложной функцией поля. При рассмотрении задачи во
втором порядке теории возмущений возникает квадратичный по полю отклик (более по-
дробно - см. Главу 11), в третьем порядке - кубический, и так далее: в п - порядке теории
возмущений наведенный в среде дипольный момент оказывается пропорционален п -
ной степени напряженности электрического поля волны. Фактически, такая процедура
поиска отклика есть его разложение по степеням поля. Физической ее основой является
применимость квантовомеханической теории возмущений к анализу динамики атомной
системы в поле волны. Как правило, это означает, что напряженность электрического
поля в волне существенно меньше внутриатомного значения. В этом смысле такие поля
являются слабыми. На практике, нелинейные эффекты возникают при интенсивностях
излучения ~ 10'° -1012 Вт/см2, которые стали доступны для эксперимента в первой поло-
вине 60-х годов прошлого века с созданием лазерных источников излучения и получе-
нием генерации в режиме модуляции добротности. Мы уже отмечали, что современная
лазерная техника достигла возможностей получать поля, напряженность поля волны в
которых существенно превышает атомные значения. В таких сверхатомных полях тео-
рия возмущений конечно неприменима, а потому оказывается невозможным и представ-
ление поляризации среды в виде разложения по степеням поля. Такая область интенсив-
ностей относится к так называемой экстремальной нелинейной оптике и не будет рас-
сматриваться в данной главе. В этой главе мы рассмотрим лишь несколько самых про-
стых эффектов, определяемых квадратичными и кубическими членами разложения по-
ляризации среды по степеням поля.
20.1. Уравнения Максвелла в нелинейной среде.
Мы будем исходить из волнового уравнения в среде (15.1.5), полученного нами в
Главе 15:
У2Ё(г, г) - grad div E(r,t) = . (20.1.1)
с дг
Здесь вектор D(r,t) = E(r,f) + 4xP(r,t) - вектор электрической индукции, a P(r,t) - век-
тор поляризации среды, являющийся функцией напряженности электрического поля
волны. В линейной среде наиболее общая связь между вектором поляризации P(r,t) и
напряженностью электрического поля волны задается функционалом:
00
ра 0 = JXa/ffip (г,1 . (20.1.2)
о
429
11 Д!,1Ик HtuiiKi»! <x, // обоiiupunoi лекпрюны оси координат, и ио повторяющимся
ик ц.я <) MMiipoiuuiHc. В отличие от Главы 15, функция отклика от-
щн'по'” омами с|хды. При этом спектральные компоненты поля и вектора
„.пи uihhh связаны соотношением:
ц0’’ ч
(20.1,3)
! (с спек 1р«оп»ная и временная функции отклика связаны между собой соотношением:
I г
Z<«//(r):: _ I Za//(<w)cxp(- i(or)da),
(20.1.4)
j* Ztt/7(r)exp(/<yT)c/r.
р общем случае линейные свойства среды описываются тензором диэлектрической вос-
приимчивости (поляризуемости) второго ранга хар(со). Однако, для пространственно
и ютройной среды тензор представим в виде /„^(й>) = /(<у)х j (I - единичная матрица),
и вектор поляризации "смотрит" вдоль направления поля волны.
А как записать общее выражение для поляризации в среде, наведенной полем, в
рамках разложения функции отклика по степенями поля? Обобщая (20.1.2.), напишем,
JC 00 ЭД
/’,(^.4 = J Xa/f^P^d ~T^T + j[ XaPY^\^2^/}(^^-T^r(r^-T2)dTxdT2 +
О 0 0
Л' ос ос
JJ JXa}irAT\’г2>T№p{r,t - Tj)E/r,t - т2)ЕДг,/ -T3)dT{dT2dT3 +...
о о о
(20.1.5)
Первый член в этой сумме описывает линейную по полю поляризацию, а все последую-
щие - нелинейную (квадратичную, кубичную и так далее, более высоких порядков). От-
метим, что во все члены входит эффект памяти, поляризация в момент времени t опре-
деляется электрическим полем, в том числе, в предыдущие моменты времени. За выра-
жением (20.1.5) стоит квантовомеханическая теория возмущений, поэтому каждый по-
следующий член разложения (20.1.5) существенно меньше предыдущего.
Как и в случае линейной функции отклика, для нелинейных членов нам удобно
ввести их спектральные представления1:
= , (20.1.6)
zXK®,.®,) = /• (20.1.7)
В разделе 11.6 мы видели, что во втором порядке теории возмущений связь меж-
ДУ спектральными компонентами вектора поляризации и поля задается в виде:
/£=z^(+®.+®)E»E»> P^,=Xa}r(+0i-C0^'E,..< (20.1.8) (20.1.9)
(199‘|СС |1одр°б1ю см. Н.И. Коротеев, И.Л. Шумай "Физика мощного лазерного излучения", §3.2, М. Наука,
430
т.е. монохроматическое поле с частотой со вызывает в среде поляризацию на удвоенной
частоте, а также статическую поляризацию. Мы увидим в дальнейшем, что за этими вы-
ражениями стоят эффекты генерации второй гармоники и оптического детектирования.
Среды с отличными от нуля компонентами тензора восприимчивости третьего ранга
называют средами с квадратичной нелинейностью. Мы видели, что в изотропных
средах все компоненты этого тензора обращаются в ноль.
В третьем порядке теории возмущений для свойств среды аналогично имеем.
(20лл°)
= Z^(®. е: . (20.1.11)
Первое их этих выражений описывает появление нелинейной поляризации на утроенной
частоте воздействующего поля, в то время как второе - поляризацию на частоте поля.
Следовательно, первое из этих выражений ответственно за генерацию третьей гармони-
ки в среде с кубической нелинейностью, а второе - за эффекты самовоздействия светово-
го пучка, например, эффект самофокусировки. В отличие от эффектов второго порядка,
эффекты третьего порядка могут наблюдаться и в пространственно изотропных средах.
В этом случае свойства среды описываются скалярными функциями частоты /(3)(<у) и
Х(3)(Зсо).
В дальнейшем при рассмотрении нелинейных эффектов мы будем полагать, что
электромагнитные импульсы достаточно длительные, и, следовательно, обладают высо-
кой степенью монохроматичности, так что в пределах его спектральной ширины линей-
ную и нелинейные восприимчивости можно считать постоянными величинами.
Будем также считать, что
4/гуЁ*0. (20.1.12)
Это условие выполнено, если на размере порядка длины волны излучения свойства сре-
ды практически не изменяются. Тогда волновое уравнение (20.1.1) может быть записано
в виде
Здесь мы явно выделяем линейную P(r ,t) и нелинейную Р^пГ> (r,f) части поляризации.
20.2. Приближение медленно меняющихся амплитуд (ММА). Рас-
пространение пучка света в линейной пространственно неоднородной
среде.
Начнем с задачи о распространении светового пучка в среде, линейная восприим-
чивость которой является функцией пространственных координат, но не зависит от ча-
стоты излучения. Тогда, вводя понятие диэлектрической проницаемости
^7) = 1 + 4^(F),
перепишем (20.1.13) в виде:
431
V’p.(r,z)„ j (I , 4zrZ(f))''’ (20.2.1)
l»\ им iHKrtib pi nit ii нс уравнения (20.2.1) n виде линейно поляризованного пучка света,
pin iipoi граняющи ося вдоль осн z с плавно меняющейся по пространству амплитудой:
h(r,/) = 1,’0(г)схр(/(Лг-ох)), (20.2.2)
где А =- «>/е. Приближение медленно меняющейся амплитуды (ММА) означает, что
|VE0|«ArE0. (20.2.3)
Получим теперь уравнение для медленно меняющейся амплитуды £0(г). Вычисляя
ЭЕ ( ЭЕ„ / ч
— = ikЕо + —2- exp (l(kz - tut)),
cL у dz )
Э2Е
&2
'-k2E{} + 2ik^
I ° dz )
exp(i(kz-tot))
(здесь в силу условия (20.2.3) мы пренебрегли слагаемым d2E0/o!z2), найдем:
V2E
(20.2.4)
Здесь Vx = д2/дх2 +д2/ду2 - оператор Лапласа по координатам, лежащим в плоскости
перпендикулярной направлению распространения пучка. Дифференцирование выраже-
ния (20.2.2) по времени дает:
= -tu2E0 exp (i(kz - а*)). (20.2.5)
Тогда из уравнения (20.2.1) с учетом (20.2.4) и (20.2.5), получим:
^^ = -|vlE„ + Z7(r1>z)E0. (20.2.6)
dz 2
Здесь z;(r±,z) = -2я^2/(гх,г), а вектор г± = {х,у}.
Уравнение (20.2.6) с математической точки зрения эквивалентно нестационарно-
му уравнению Шредингера:
й = - *1 V>(rx, Z) + К(Г±, z>(rt, 1). (20.2.7)
dt 2т
Задача о временной эволюции волновой функции двумерной системы оказывается ана-
логична задаче о вычислении стационарного распределения амплитудного значения
напряженности электрического поля в пространстве при распространении электромаг-
нитной волны в среде. При этом координата z, вдоль которой распространяется свето-
вой пучок, аналогична времени в квантовой теории, а функция rj(ritz), определяемая
линейной поляризуемостью среды, имеет смысл потенциала К(г1,/). В частности, если
432
z- ч / \ /пп э ал Ti-пиийпрнтна задаче о свободном движении ча-
?;(r±,z) = 0 (вакуум), то задача (20.2.6) эквивалента мда ча
стицы. Отметим, что среды с показателем преломления п - 4s > 1 (для таких сред
2” > 0) в оптике называются фокусирующими. Область пространства, в которой Z > 0,
образует в пространстве собирающую линзу, обеспечивающую фокусировку излучения.
В квантовой механике такой области пространства (% > 0) можно поставить в соответ-
ствие притягивающий потенциал V < 0. Наоборот, среды с и — <1 (Z < 0) образуют
в пространстве рассеивающую линзу и называются дефокусирующими, в квантовой ме-
ханике таким средам соответствует отталкивающий потенциал V > 0.
В качестве важного частого примера остановимся еще на распространении пучка
света в свободном пространстве. В этом случае волновое уравнение имеет вид.
& 2 1
(20.2.8)
и эквивалентно уравнению Шредингера для движения частицы в свободном простран-
стве. Считая, что начальное состояние частицы описывается волновым пакетом некото-
рой пространственной протяженности R (с точки зрения оптики это ширина пучка све-
та в некотором сечении z = 0), легко видеть, что будет наблюдаться его дифракционное
расплывание. Оценим, исходя из (20.2.8) , пространственный размер L, на котором про-
исходит дифракционное уширение пакета. Оценивая члены в (20.2.8) как 5Е0/&~Е0/£
и V]E0 ~Ео/R2, найдем:
L*kR2. (20.2.9)
Размер L в оптике принято называть дифракционной длиной. Учитывая, что длина вол-
ны изучения 2 = 2л/к, перепишем (20.2.9) в виде:
L « 2яЯ(Я/Л) .
(20.2.10)
Как видно, расплывание светового пучка определяется параметром R/Л.
В случае начального гауссового профиля распределения электрического поля в
световом пучке с плоским волновым фронтом
Eo (r±, z = 0) = А ехр (- r2/2R2)
(20.2.11)
решение уравнения (20.2.8) может быть найдено аналогично тому, как решается задача о
движении свободного волнового пакета в квантовой механике2 и записывается в виде:
, exp(-r.2/2a2(z)) , , ( Z г2 \
°' ’Z) l + ,'(z/£) eXp(/fe) СХР( ' ~L 7^ J ’ <20-2'12)
где L = kR2 -дифракционная длина, a a2(z) = Л2(1+ z/i) - радиус пучка на удалении z
от начальной точки. Как видно, при z = L, площадь сечения пучка возрастает вдвое.
2 В.В. Балашов, В.К. Доливов "Курс квантовой механики" М.: МГУ, (1982), параграф 16
433
20.3. Распространение электромагнитных волн в волноводных
структурах.
В этом разделе мы рассмотрим распространение электромагнитных волн в ди-
электрических волноводных структурах с переменным по длине волновода профилем
показателя преломления. Такие структуры в настоящее время представляют интерес для
различных оптоэлектронных устройств обработки и передачи информации. С другой
стороны, такая задача интересна как одно из проявлений оптико-механической анало-
гии. Мы покажем, что такое распространение электромагнитной волны в волноводе с
математической точки зрения аналогично эволюции квантовой системы под действием
изменяющегося во времени возмущения.
Мы уже видели, что в рамках приближения медленно меняющихся амплитуд рас-
пространение вдоль оси z линейно поляризованной электромагнитной волны
Е(г,/) = E0(r)exp(f(fcz —ях)) описывается уравнением:
., ЭЕП 1 9
'*-^ = -TVlE0+7(ri,z)E0. (20.3.1)
u/X' X*
Здесь <!_={*, у} совокупность координат, перпендикулярных оси волновода, и
rj{r ,г) = -2лк2 %(r±,z) = -k2 (£’(r±,z)-l)/2, £(rx,z) - диэлектрическая проницаемость
структуры. Уравнение (20.3.1) есть не что иное как нестационарное уравнение Шредин-
гера (20.2.7).
Наш анализ мы проведем для планарной структуры, когда восприимчивость сре-
ды зависит только от одной перпендикулярной координаты (7j = rj(x)) и не зависит otz.
Такая ситуация может реализована в гетероструктуре, сформированной из набора ди-
электрических слоев с различной восприимчивостью при условии, что излучение рас-
пространяется вдоль структуры.
Рассмотрим структуру с заданным профилем х(х), таким что эта функция достигает
минимума в центре структуры (х = 0) и возрастает к ее краям. Такая структура является
оптическим волноводом и может использоваться для транспортировки пучка света,
остающегося локализованным в пространстве.
Общее решение нестационарного уравнения Шредингера (20.2.7) в потенциале,
независящем от времени, можно найти как линейную суперпозицию изначально засе-
ленных стационарных состояний с амплитудами Сп:
^(х,0 = ^С„^(х)ехр(-/£„//Й). (20.3.2)
Здесь энергии и волновые функции стационарных состояний могут быть найдены из ре-
шения стационарного уравнения Шредингера:
-—+ V(x) V (х) = E„q>, (х). (20.3.3)
2т dx )
По аналогии с квантовой механикой будем искать решение задачи (20.3.1) в виде:
( I2 \
E0(x,z) = (х)ехр -I’^z I, (20.3.4)
п X /
434
где 7?,(х) и Л„ удовлетворяют задаче на собственные значения, подобной (20.3.3).
dx2
+ Алк2 /(х) + Л2 R„ (х) = 0
(20.3.5)
Решение задачи (20.3.5) позволяет найти набор поперечных мод в пучке, распространя-
ющемся в z - направлении. Полученные собственные функции Rn(x) мы будем норми-
ровать согласно условию:
|Я,/(х)|'б& = -14-
071
(20.3.6)
Здесь 30 - нормировочная константа, которая может быть выбрана произвольно, a Lo
нормировочная длина. Общее решение (20.3.4) задает пространственное распределение
электрического поля при распространении волны вдоль оси z. При этом, если восприим-
чивость зависит также от z - координаты, в системе окажутся возможными переходы
между поперечными модами, подобные переходам между стационарными состояниями
Рис.20.1. Трехслойная планарная структура. Цен-
тральный слой характеризуется диэлектрической вос-
приимчивостью, большей чем внешние слои. Такая
структура эквивалентна прямоугольной потенциаль-
ной яме конечной глубины и может использоваться
для демонстрации пространственных осцилляций
классического пучка света. Для наблюдения таких
осцилляций можно присоединить волновод к Y-
сплиттеру (его начальная часть соответствует S'-
плоскости на вставке) с двумя детекторами D\ и Z>2.
рассматриваемая "потенциальная яма" является
в квантовой системе, подвергаемой
внешнему нестационарному воз-
действию.
В качестве простейшей струк-
туры рассмотрим совокупность
трех диэлектрических слоев, при-
чем центральный слой имеет шири-
ну а и восприимчивость > 1, в то
время как два внешних слоя харак-
теризуются восприимчивостью
близкой к единице %s»1 (см.
рис.20.1). С точки зрения квантовой
механики такая структура подобна
прямоугольной потенциальной яме
конечной глубины, в которой может
находится некоторое число стацио-
нарных состояний - поперечных
мод электромагнитного поля. Если
достаточно глубокой, задача (20.3.5)
имеет решение:
где хе(-а/2,а/2) и
30/>/8я- • cos(«za/a), п = 1,3,5,...,
S0/V8tt • sin(H7zr/a), п = 2,4,6,...,
(20.3.7)
Л2 « -4я£2/0 + (пл/а)2. (20.3.8)
Эти поперечные моды устойчивы по отношению к дифракционной расходимости
пучка. Тем не менее, суперпозиция различных поперечных мод приводит к определен-
435
пространственным колебаниям пучка и перестройке его пространственной структу-
Ь1 (рис. 20.2). Если изначально заполнены только две низшие поперечные моды, про-
странственный период этих колебаний будет определяться выражением:
L « 4Л<я2/Зд- .
(20.3.9)
Однако, величиной поля в поперечных модах достаточной легко управлять. Для этого
можно использовать волноводную структуру, диэлектрические параметры которой зави-
сят также от z-координаты, например, параметры центрального диэлектрического слоя
Рис.20.2. Колебания пучка при распространении
вдоль волноводной структуры для случая первона-
чально заселенных двух низших поперечных мод.
«Потенциальный» рельеф, а также структура поля
в двух нижних поперечных модах приведены на
вставке.
(его толщина или восприимчивость)
слегка модулированы в направлении
z. В этом случае мы можем предста-
вить восприимчивость структуры
%(х, z) в виде
^(х, z) = /0 (х) + (х, z), (20.3.10)
где первый член определяет парамет-
ры рассматриваемой ранее структуры,
а второй - возмущение, задающее про-
странственную модуляцию ее свойств,
например, по гармоническому закону:
Z1(x,z) = #(x)cos(Xz), (20.3.11)
причем <^f(x)< %0(х), а К - волновое
число, задающее пространственный
период структуры. Это возмущение
будет вызывать перетекание энергии
между поперечными модами подобно тому, как внешнее воздействие, например, свет,
вызывает переходы между атомными состояниями. Подставляя разложение (20.3.4) в
волновое уравнение (20.3.1) и учитывая, что R„(x) есть решение задачи на собственные
значения (20.3.5), получим систему уравнений:
(20.3.12)
которая подобна той, что получается в задаче о квантовых переходах в атоме под дей-
ствием электромагнитного поля (см. Глава 8). Здесь
Mfl = • 2лк jЯ* (х)#(х)Я„(x)dx.
Ограничиваясь первым порядком теории возмущений, получим:
dCj(z) j ( i 2 ->2 ।
—J----= — Mft exp — (2y - Д ± 2Kk)z ,
dz 2 \2k J
(20.3.13)
(20.3.14)
Гдс R, означает начальную моду поля. Как видно, перетекание энергии с одной моды в
436
другую особенно эффективно в условиях резонанса -% ±2Кк*0. Для двух нижних
—.----------- ' поперечных мод (/=!,/" = 2) это
! । условие выполнено для
а/2 п n t.' “ К «(Aj- Л?)/2£, что соответствует
_____________ 0 2т К 2
периоду L = 2л/К .
-а!2
i
i
а/2
.-д/2.________________....____
Г
!
I ..... ...
Наиболее интересной особенностью
рассматриваемого режима является
возможность осцилляций типа осцил-
ляций Раби (см. раздел 10.1), когда за
счет пространственного распределе-
ния диэлектрической проницаемости в
структуре происходит перетекание
энергии из одной моды в другую и об-
ратно. Если функция <%(х) является
Рис.20.3. Схематическое изображение волновод-
ных структур с пространственной модуляцией ди-
электрической восприимчивости: случай "четной"
(а), и "нечетной" (Ь) модуляции.
нечетной функцией координаты, пере-
ходы разрешены только между мода-
ми с противоположной четностью. Это
утверждение аналогично известным
правилам отбора в атомной физике (см. Глава 9). Например, для двух низших попереч-
ных мод "длина" Раби определяется выражением ГЛ=4яг/М21 . Наоборот, если функция
<fy(x) четная, то разрешены переходы между поперечными модами одинаковой четно-
сти. Волноводные структуры с "нечетным" или "четным" типом "возмущений" пред-
ставлены на рис.20.3.
Типичные примеры перетекания энергии между поперечными модами в режиме Раби -
осцилляций представлены на рис. 20.4.
Lr!
-а/
-а!2
Рис. 20.4.
„ Осцилляции Раби между двумя поперечными модами в волноводной структуре с перио*
дическои пространственной модуляцией восприимчивости. Представлены случаи "четной” и "не-
четной модуляции. На вставках представлено схематическое изображение поперечного сечения
волноводных структур.
Lr/
437
20.4. Самофокусировка и самодефокусировка излучения в нели-
нейно»» среде.
Мы уже огмечали, ’но в среде с кубической нелинейностью возможен эффект са-
мо1Ю<тейс1вня - возникасг нелинейная поляризация на частоте воздействующего на сре-
ty поля волны. Будем считать, что среда является пространственно однородной, зависи-
мостью линейной восприимчивости от частоты можно пренебречь. Тогда волновое
уравнение (20.1.13) можно переписать в виде:
е2
(20.4.1)
Здесь <<; —1 + 4^’ \ Будем искать решение уравнения (20.4.1) в приближении медленно
меняющихся амплитуд (20.2.2), к = /с. Аналогично предыдущему получим:
'к ~ 1 - 2M2Z(”E;E0 (20.4.2)
OZ Z
Здесь /(3) - кубическая восприимчивость среды на частоте распространяющегося поля.
Полученное уравнение принято называть нелинейным уравнением Шредингера, причем
величина
(/(rJ = -2^2y3)Ej(rJ
(20.4.3)
играет роль потенциала в квантовой теории. При этом первое слагаемое в правой части
(20.4.2) ответственно за дифракционное расплывание пучка. Случай /<3) >0 соответ-
ствует возникновению "потенциальной ямы", т.е. среды к которое распространяющееся
поле создает само себе собирающую линзу. Именно в такой среде возможно возникно-
вение эффекта самофокусировки излучения. Если же /(3) < 0, то электрическое поле
волны ведет к уменьшению показателя преломления и формирует рассеивающую линзу
для излучения. Возникает явление самодефокусировки излучения, когда расходимость
пучка оказывается больше дифракционной. В рамках микроскопической теории кубиче-
ские поляризуемости, отвечающие за эффект самовоздействия могут быть рассчитаны с
помощью выражения (11.6.7).
Оценка на пороговую интенсивность излучения, при достижении которого возни-
кает режим самофокусировки излучения может быть сделана на основании качественно-
*о анализа уравнения (20.4.2). Очевидно, для достижения режима самофокусировки из-
лучения фокусирующая способность линзы, наведенной в среде и определяемой вторым
слагаемым в правой части (20.4.2), должна превосходить дифракционную расходимость
лучка, т.е. должно быть выполнено условие:
Z/C
(20.4.4)
*4с /( _ характерный поперечный размер пучка, а х >0. Учитывая что
^ = ^2сЕ2/8л- - мощность светового пучка, условие (20.4.4) приобретает вид:
438
(20.4.5)
Важной особенностью полученного результата является предсказание того факта, цТо
порог самофокусировки определяется нс интенсивностью, а полной мощностью излу-
чения. Так получилось полому, что для фиксированной мощности излучения при увели-
чении поперечного размера пучка интенсивность излучения надает, а, следовательно
уменьшается и фокусирующая способность наведенной в среде собирающей линзы. С
друпзи стороны, уменьшается и дифракционная расходимость пучка. Как результат, по-
рог возникновения самофокусировки нс изменяется.
дифракция
Лазер
самофокусировка
излучения
нелинейная
среда
Рис.20.5. Движение пучка света в условиях самофокусирующей среды.
Эффект самофокусировки излучения впервые был предсказан Г.А. Аскарьяном3 в
1962 году и впервые наблюдался экспериментально в 1965 году при распространении
сфокусированного пучка рубинового лазера мощностью ~20 МВт в органических жид-
костях. В газовых средах, в том числе воздухе, пороговая мощность самофокусировки
обычно составляет несколько гигаватт, для твердотельных сред - несколько мегаватт.
Характерный вид распространения светового пучка в нелинейной фокусирующей
среде представлен на рис.20.5.
На практике эффект самофокусировки излучения приводит к возрастанию интен-
сивности излучения светового пучка, что приводит к интенсивной ионизации среды и
формированию филамента - ярко светящегося плазменного канала, который неразрывно
связан с распространяющимся пучком. Заметим, что свободные электроны, образующи-
еся в канале, вносят отрицательный вклад в показатель преломления среды. Поэтому,
как правило, именно свободный электронный газ, возникающий в процессе филамента-
ции, ограничивает нарастание интенсивности в канале. Свой вклад в ограничение пре-
дельной интенсивности излучения в филаменте может также внести накопление возбуж-
денных (ридберговских) атомов, которые также могут уменьшать фокусирующие свой-
ства среды. В случае, если мощность светового пучка существенно (на порядок и более)
3 Аскарьян Гурген Ашотович (1928 - 1997) - советский и российский физик - теоретик.
439
превышает пороговое значение мощности возникновения фокусировки, как правило
возникает режим множественной филаментации, когда в процессе самофокусировки из-
учения образуется сразу большое количество светящихся плазменных каналов.
20.5. Генерация оптических гармоник.
Перейдем теперь к вопросу о генерации гармоник распространяющегося в среде
излучения. Например, процесс генерации третьей гармоники возможен в среде с кубиче-
ской нелинейностью, где помимо отклика на частоте воздействующего поля возникает
еще отклик на утроенной частоте /(3)(Зщ). Выражение
для этой восприимчивости, полученное в рамках кван-
товомеханической теории возмущений, можно найти в
Главе 11. Здесь отметим, что эта восприимчивость от-
лична от нуля также в средах, атомы которых характери-
зуется центральной симметрией. Отметим, что за про-
цессом генерации третьей гармоники стоит четырехфо-
тонный процесс, соответствующий поглощению трех
квантов поля частоты со и испусканию одного кванта
частоты Зсо (см. рис. 20.6).
Анализ процесса раскачки на утроенной частоте
будем проводить также в рамках метода медленно ме-
Рис. 20.6. Генерация третьей няющихся амплитуд. Будем считать, что в среде распро-
гармоники. страняется интенсивная волна с частотой со (волна
накачки) и относительно слабая волна, возникающая в результате преобразования волны
накачки в третью гармонику (см. рис. 20.7):
Ё(г,/) = ЁДг^ехрО^г - cot) + Ё3а,(г,t)exp(ik3o)z -3cot). (20.5.1)
Здесь кш = п(а>)(со/с), к3а = п(3со)(3со/с) - линейные показатели преломления на часто-
Лазерное
излучение.
нелинейная среда
тах со и Зсо соответствен-
но. Мы будем считать, что
эффективность преобразо-
вания невелика, так что
E3(V « E(t). В такой ситуа-
Рис.20.7. Схематическое изображение процесса генерация тре-
тьей гармоники.
ции анализ можно прово-
дить в приближении задан-
ной волны накачки, т.е. ам-
плитуда поля Е^ не зависит от z - координаты. Тогда для амплитуды генерируемого на
Утроенной частоте поля E3ty получим:
- За.).
oz L С Ul
Здесь нелинейная поляризация задается полем волны накачки
Е3„(г,0 = /(3)(3<y)E3JfJexp(/(3V-3cot).
(20.5.2)
(20.5.3)
440
Подставляя (20.5.3) в (20.5.2). получим
_ lv,|: ..2'r(.3w))Z'”(3w)i:,’„cxp(/(3*„,-*JJz). (20.5.4)
/Л'<” (-)- 2 ' М"’ <’
Будем считать. что пучок накачки достаточно широкий, так что его дифракционной рас-
ходик,ость,о можно пренебречь. Тогда уравнение легко интегрируется, и в предположе-
нии. что на входе в среду (с = 0) поде третьей гармоники отсутствует, E,„,(z 0)-0,
получим:
Е,„(--) = /-±^(3«,)=/3’(3«))Е’ jexp(/(3A„-kv„)z)dz. (20.5.5)
Отсюда
Е3„(--) = , (20.5.6)
с к3а> м
Ак = к. -Зк . Для интенсивности излучения третьей гармоники получаем:
Зео со
(Д£/2)2
/3.(z)=^|^(Z)|2=^^(Wk3’(3«)|24xsin2(MzZ21
8я с с к3(0
(20.5.7)
Рис. 20.8. Генерация третьей гармоники. Фа-
зовый синхронизм.
График зависимости I3eo(z) от отстройки
ДА: = к3ео -Зкш представлен на рис. 20.8.
Как видно, наиболее эффективно процесс
генерации происходит в условиях выпол-
нения условия фазового синхронизма
^„=3i„. (20.5.8)
Условие фазового синхронизма с физиче-
ской точки зрения означает закон сохране-
ния импульса - импульс фотона третьей
гармоники равен трем импульсам волны
накачки. Условие (20.5.8), очевидно, мож-
но переписать в виде:
и(3й>) = и(су),
(20.5.9)
т.е. показатели преломления на частотах волны накачки и третьей гармоники должны
быть равны.
Насколько реально выполнение этого условия? В Главе 15 мы видели, в области
нормальной дисперсии показатель преломления растет с увеличением частоты. Поэтому
вне зависимости от вида кривой и(щ) одна из частот, или волны накачки, или третьей
гармоники, должна находиться в области аномальной дисперсии. На рис. 20.9 приведен
случай, когда в области аномальной дисперсии находится частота третьей гармоники.
Это означает, что одна из этих волн находится в зоне поглощения, а, следовательно, эф-
441
Re «а,, ЬпПю l-J
Зш
442
Рис. 20.11. Фазовый синхронизм
обыкновенной н необыкновенной
волн в анизотропном кристалле.
Действительно, ВСПОМНИМ, ЧТО В ОДНООСНЫХ
крис-1 аллах присутствует так называемый эффект
двойного лучепреломления.4 В таком кристалле мо-
гут распространяться две волны, обыкновенная, и
необыкновенная, причем скорость распространения
обыкновенной волны одинакова по веем направле-
ниям кристалла, а необыкновенной - зависит от
направления, причем вдоль некоторого направления
(оптическая ось кристалла) совпадает по величине
со скоростью обыкновенной волны. Поверхности
фазового фронта от некоторого точечного источника
излучения с частотой со, находящегося на поверх-
ности кристалла, образуют полусферы для обыкно-
венной волны, и полуэллипсоиды вращения для необыкновенной, (см. рис. 20.11). Такие
же поверхности образуют и фазовые фронты от точечных источников с частотой 2<у.
Поскольку мы полагаем, что обе частоты излучения находятся в области нормальной
дисперсии, то /?(2<у) > и(бу), а фазовая скорость волны для удвоенной частоты оказыва-
ется меньше, чем для волны накачки. Может так оказаться, что под некоторым углом к
оптической оси кристалла 0С фазовая скорость необыкновенной волны частоты со равна
фазовой скорости обыкновенной волны на частоте 2со. Именно такая ситуация пред-
ставлена на рис. 20.11. Это означает, что для достижения эффективного преобразования
волны накачки во вторую гармонику необходимо вырезать нелинейный кристалл так,
чтобы обе волны, накачки и второй гармоники, распространялись вдоль строго опреде-
ленного направления, обеспечивающего достижение режима фазового синхронизма. За-
метим при этом, что угол вс обеспечивает выполнение условия фазового синхронизма с
частотами волн, которые участвуют в процессе. Например, если мы хотим использовать
тот же кристалл для реализации процесса дальнейшего повышения частоты
2со + 2со —»4бУ, то угол 0с, необходимый для такого преобразования, будет уже другим.
Чувствительность процесса преобразования частот к углу 0С является принципиально
важной, поскольку обеспечивает высокую селективность избранного нелинейного про-
цесса и позволяет обеспечить его высокую эффективность. В частности, в нелинейных
кристаллах достаточно легко обеспечить эффективность преобразования копны накачки
во вторую гармонику на уровне, превышающем 50%.
Отметим еще важный эффект оптического детектирования (оптического выпрям-
ления) - в среде с квадратичной восприимчивостью возникает наведенное статическое
электрическое поле, пропорциональное квадрату электрического поля воздействующего
излучения. По величине этого поля можно судить об интенсивности лазерного излуче-
ния.
Среди кристаллов, которые используются в нелинейных процессах преобразова-
ниях частоты, наиболее известны: KDP - дигидрофосфат калия (КН2РО4), ВВО - р-борат
бария (р-ВаВ2О4), КТР - титанил-фосфат калия (КТ1ОРО4) и ниобат лития LiNbCh.
4 С.А. Ахманов, С.Ю. Никитин "Физическая оптика", М.: МГУ, (1988), Лекция 21
443
20.6. Параметрическое преобразование частоты.
Посмотрим на процессы, которые могут происходить в среде с квадратичной не-
.щнсйностью. несколько шире. Представим себе, что на такую среду падает двухчастот-
нос livn’MCHHc:
Ё(Г) = Ё„,| cos(ftV - kf) + ЁЛ2 cos(ru2r - k2r). (20.6.1)
3 iccb А। = co}/c, k2 =n{co2)cD2/c - волновые вектора, соответствующие частотам
, и <у, • Легко видеть, что в среде с квадратичной нелинейностью помимо уже обсуж-
давшихся раньше эффектов возникновения поляризации на удвоенных частотах а)х и
к а также статической поляризации возникнет еще и поляризация на суммар-
ен разностной частоте со = а\ ±<о2. Рассматривая задачу в приближении медленно ме-
няющихся амплитуд, легко показать, что эти процессы будут идти эффективно только
при выполнении условия фазового синхронизма, которое будет записываться в виде:
к (со) = к\ (й>]) + к2 (гу2). (20.6.2)
Условие фазового синхронизма (20.6.2) оказывается выполнить заведомо проще, чем
(20.5.13). Возможность использовать неколлинеарную геометрию пучков снимает доста-
точно жесткое условие на связь между показателями преломления: для каждой пары ча-
стот гУ] и а>2 можно подобрать подходящую геометрию пучков так, чтобы условие син-
хронизма было выполнено. С точки зрения квантовой теории света соотношение (20.6.2)
означает закон сохранения импульса в процессе преобразования двух квантов Йгц и
hd)2 в один квант ha>.
Падающий
Кристалл Инфракрасное излучение
Рис. 20.12. Спонтанное параметрическое рассеяние света в нелинейном кристалле.
Возможен и обратный процесс - распад в нелинейной среде кванта hco на два
кванта меньших частот Йгу, и ha>2 (так называемая бифотонная пара), но так что
°-> = а\+а)2. Такой процесс называют спонтанным параметрическим рассеянием света
(СПР). Эффект спонтанного параметрического рассеяния был предсказан в 1966 году
Д Н. Клышко5. Схематически он представлен на рис. 20.12. При этом для различных пар
частот ГУ) и гу2 условия фазового синхронизма могут быть записаны в виде:
5 Клышко Давид Николаевич (1929-2000) - советский и российский физик.
444
<ш((О) = CO{ n(co}) cos <9j + O)2n(a>2) cos &2, ^0.6 3)
co} к(<y,) sin i9, = (o2n(a>2) sin <92,
где углы i9j и <9, - это углы вылета фотонов ho)} и hco2 по отношению к направлению
движения фотона tico. В частном случае можег оказаться, что частоты и (о2 совпа-
лают, ®, =<у2 =®/2. Тогда, очевидно, 6>, = Э7 =9, причем угол 9 определяется из
условия:
/?(бд) = /7(<у/ 2) cos <9. (20.6,4)
При этом, хотя испущенные фотоны имеют одно и то же значение частоты, они находят-
ся в разных полевых модах, так как отличаются направлением волнового вектора. Мо-
жет оказаться и так, что оба фотона испущены в одну и ту же моду. Тогда условие
(20.6.4) трансформируется в
п(со) = п(а>/ 2),
что эквивалентно условию фазового синхронизма (20.5.13), а сам процесс является об-
ратным по отношению к генерации второй гармоники.
В настоящее время спонтанное параметрическое рассеяние с излучением обоих
квантов в одну и ту же моду представляет большой интерес в связи с возможностью ге-
нерации неклассических, так называемых "сжатых" состояний электромагнитного поля
(см. также Раздел 14.4).
Заметим, однако, что полуклассическая теория взаимодействия света с веществом
не позволяет, строго говоря, рассмотреть процесс спонтанного параметрического рассе-
яния. В отсутствие начального затравочного поля на частоте а\ <а> процесс преобразо-
вания частоты бУ —> 6У] + <у2 не начнется, нужно некоторое слабое начальное поле. Вве-
дение в систему такого поля с частотой со} сделает процесс параметрического рассеяния
вынужденным. И, более того, из всевозможного набора частот, которые могут возник-
нуть при параметрическом рассеянии, выделит дополнительно именно частоту а>2, та-
кую, что со} + а>2 = со. Что касается именно процесса спонтанного параметрического
рассеяния, то для его последовательного рассмотрения необходимо рассмотрение взаи-
модействия квантовой системы с электромагнитным вакуумом6, что делает необходи-
мым построение квантовой теории электромагнитного поля (более подробно см. Главу
14).
20.7. Генерация терагерцового излучения.
Представим себе, что в среде с квадратичной нелинейностью распространяется
две волны с такими частотами и со2, что Q = — со2 лежит в терагерцовом диапа-
зоне частот (см. рис.20.13). Тогда в случае коллинеарного распространения волн накачки
(ось z) в среде возникнет поляризация:
7п(^0 = /2)(^ = й>1 -^2)El(r)E2(r)exp(/(^1 -k2)z-(n}-ct)2)t). (20.7.1)
Это замечание справедливо при изучении любых спонтанных переходов в квантовых системах.
445
здесь Е, и Е, - амплитуд,,, „„„ей накачки „а частотах и соответственно. Проде-
|1ьда|Я преобразования, аналогичные тем, что были выполнены при рассмотрении гене-
V.11HH второй гармоники, получаем УПЙНИеиип пг.а 1 vMlnpvnnn icnc
Р*11 ,П11ЛО,й»м, УР ЖС ЛЛЯ мсдлснно меняющейся амплитуды
нопя герагерцовои волны: 7
I 2
~дГ ~ ~ 2 Vj Е° ~7rQ2Z(2)(Q = (Ц -й>2)Е|Е2 схр(/(Ао -(А( -k2))z), (20.7.2)
гас волновой вектор терагерцового поля. Тогда, пренебрегая дифракционной рас-
ходимостью волн накачки и генерируемого терагерцового импульса, имеем:
1пм = ^|Е„(а-)Г = — 4^(П)4Ь(2)(Я)Г/,Л X
8л- с с2к„ 'I 1 2 (М/2)2 ’
(20.7.3)
Рис.20.13. Генерация терагерцового
излучения в среде с квадратичной
нелинейностью.
где АА - кп-(кх -к2), а /, 2 =cE^2/8^. Как и в
случае генерации гармоник, процесс может быть
эффективен, если выполнено условие фазового
синхронизма и кп = кх — к2. На практике обе ча-
стоты берутся из одного достаточно короткого им-
пульса. Его длительность должна быть порядка не-
скольких пикосекунд.
Процесс генерации терагерцового излуче-
ния можно организовать и в среде с кубической
нелинейностью. С одной стороны, кубическая не-
линейность среды меньше чем квадратичная, по-
этому, казалось бы, процесс генерации должен
быть менее эффективным. С другой стороны, в рассматриваемом случае средой, в кото-
рой происходит генерация, может быть газ, в том числе воздух, что с одной стороны су-
щественно упрощает условия выполнения эксперимента (не требуется подбирать анизо-
тропный кристалл с заданными свойствами), а с другой - в газовой среде оказывается
возможным проводить эксперименты в области существенно более высоких напряжен-
ностей полей накачки, не опасаясь радиационного повреждения и разрушения кристалла
при высоких лучевых нагрузках.
Для генерации терагерцового излучения в газовых средах в настоящее время
обычно используют импульсы титан-сапфирового (TiSa) лазера фемтосекундой дли-
тельности (ЙбУ] «1.55 эВ) и его второй гармоники (Йй)2 «3.15 эВ). Тогда низкочастот-
ное терагерцовое поле возникает в процессе смешения:
^«2^-^. (20.7.4)
Типичные интенсивности излучения составляют ~10* Вт/см“, что одной стороны, делает
процесс генерации на кубической нелинейности достаточно эффективным, а с другой
стороны, в условиях ультракороткого фемтосекундного воздействия еще не приводит к
полной ионизации атомов (молекул) среды. При этом ширина спектра терагерцового
сигнала определяется спектральной шириной TiSa импульса и его второй гармоники.
Для спектрально ограниченных импульсов их ширина ~ 2/г/г. Например, для им-
446
пульсов длительностью —100 фс мы получаем спектральную ширину генерации
1013 Гц. Такая ширина генерации соответствует всего нескольким периодам коле-
баний поля в терагерцовом диапазоне частот, поэтому, в экспериментах по лазерной ге-
нерации ТГц излучения удастся получать импульсы предельно короткой длительности,
вплоть до одного периода поля.
Существует и другой механизм генерации ТГц излучения из плазмы, созданной
ультракороткими лазерными импульсами. Этот механизм обусловлен возникновением
плазменных колебаний электронного газа с высокой концентрацией, возникающих при
фотоионизации атомов (молекул) среды двухцветным лазерным полем (обычно выби-
раются частоты со и 2<z>). Действительно, в таких лазерных импульсах существует
асимметрия электрического поля волны, воздействующего на атомы, причем величина
этой асимметрии определяется соотношением фаз колебаний поля волны на частотах,
образующих двуцветный импульс. Как результат, в процессе ионизации фотоэлектроны
вылетают преимущественно в некотором направлении, создавая колебаний электронной
плотности на плазменной частоте. При значениях концентрации электронов в плазме на
уровне 1015- 1016 см’3, легко достигаемых в современных экспериментах. Эти колебания
происходят как раз в терагерцовом диапазоне частот.
20.8. Спонтанное и вынужденное комбинационное рассеяние све-
та.
Эффект комбинационного рассеяния (КР) света был обнаружен в 1928 году Г.С.
Ландсбергом7 и Л.И. Мандельштамом8 в Советском Союзе и практически одновременно
и независимо Ч. Раманом9 и К. Кришнаном10 в
Индии. Теоретическое предсказание КР было
сделано раньше - в 1923 году в работе А. Сме-
кала11. В англоязычной литературе КР обычно
называют рамановским рассеянием. Как уже
отмечалось, суть этого эффекта заключается в
возникновении в спектре рассеянного некото-
рым веществом света (кристаллами в экспери-
ментах Ландсберга - Мандельштама и жидко-
стями в экспериментах Рамана - Кришнана) по-
мимо несмещенной частоты сателлитов с часто-
тами со = со{} ± Q, где <г>0 - частота падающего
излучения, а О собственная частота колебаний среды. Принято называть частоты
- О и (Oq + Г2 стоксовой и антистоксовой компонентами рассеяния соответственно.
При этом сама несмещенная частота есть результат релеевского рассеяния, (см.
-П <э0 +Q
Рис.20.14. Комбинационное рассеяние
света.
7 Ландсберг Григорий Самуилович (1890 - 1957) - советский физик.
8 Мандельштам Леонид Исакович (1879 - 1944) - русский и советский физик, один из основателей отече-
ственной научной школы радиофизики.
9 Raman Chandrasekhara Venkata (1888-1970) - индийский физик.
10 Krishnan Kariamanikkam Srinivasa (1898-1961) - индийский физик.
11 Smekal Adolf (1885-1959) - австрийский физик.
447
рцс.20.14). Отмстим, что КР в сущности единственный нелинейный эффект, который
был экспериментально открыт в долазерцую эпоху.
В настоящее время КР широко используется в задачах спектроскопии. Зная
спектр рассеянною стнала, часто оказывается возможным определить строение иссле-
дусмого всщсс1ва, сю атомарный состав или пространственную структуру. Может быть
и наоборот. если строение рассеивающего объекта известно, по сигналу КР можно ис-
i тсловать динамику протекающих физико-химических процессов, например, определять
ысслснности различных возбужденных состояний и их изменение во времени.
С точки зрения квантовой теории и релеевское, и комбинационное рассеяние
представляют собой двухфотонные переходы, когда квантовая система поглощает квант
внешнего поля, а затем испускает его и переходит обратно в исходное (релеевское рас-
сеяние) или ниже/вышележащее по энергии состояние (комбинационное рассеяние).
Двухфотонные переходы такого типа были рассмотрены нами в Главе 11. Следует, од-
нако. иметь в виду, что в Главе 11 рассматривалась ситуация, когда оба поля, обеспечи-
вающих двухфотонный переход рамановского типа, уже существуют. На практике это
не так. Рассеянного поля изначально нет, а потому в полуклассической теории нет и
1Вухфотонного перехода. Здесь мы имеем дело с общей проблемой полуклассической
теории взаимодействия света с веществом, которая не "видит" т.н. спонтанные перехо-
ды. происходящие как бы "в отсутствие" внешнего воздействия. Более подробно физику
возникновения спонтанного излучения мы рассмотрели в Главе 14. Здесь отметим, что
всякий раз, когда возникает излучение на некоторой частоте, которое отсутствовало в
системе, оно может появиться только в результате спонтанного процесса и находится
вне рамок нашей полуклассической теории. В полной мере эти слова относятся и к гене-
рации гармоник оптического излучения. Если мы хотим увидеть самый начальный этап
их зарождения, нам необходимо научиться рассматривать спонтанные переходы.
При рассмотрении КР мы сейчас ограничимся классической моделью явления.
Будем считать, что у нас есть некоторая молекула, которая характеризуется поляризуе-
мостью , где Q есть совокупность ядерных координат. Пусть Qo есть равновесное
значение, причем = x(Qo) = 0> т.е. в невозбужденном состоянии молекула не имеет
дипольного момента. Тогда для дипольного момента молекулы во внешнем поле с ча-
стотой со мы можем записать:
P(t) = %E(t)= Zo+ —
(2«-а)+- ею »
a J '5Q
(?(/)E0coscar. (20.8.1)
Здесь <?(/) = Q(t)-Q0 = qQ cos О/ - малые колебания молекулы вблизи положения равно-
весия, которые мы будем считать гармоническими, Q - это частота молекулярных коле-
баний. Из (20.8.1) для дипольного момента получим:
<7оЕо (cos(tf) + Q)r + cos(ft) - Q)/).
(20.8.2)
Как видно, колебания дипольного момента происходят как раз на комбинационных ча-
стотах со±Г2, а, следовательно, на этих частотах и происходи! переизлучение энергии.
Интенсивность излучения молекулярного диполя есть (мы полах аем, что Q «со).
448
(20.8.3)
Введем сечение комбинационного рассеяния <тял как отношение поглощаемой (и пере-
излучасмой) мощности к падающему потоку энергии:
(20.8.4)
В рассматриваемом приближении сечения рассеяния на стоксовой и антистоксовой ком-
понентах равны между собой и определяются в том числе амплитудой колебательного
движения. Если считать колебания молекулы классическими, то амплитуда колебаний
q0 связана температурой среды Т соотношением:
_т
2
(20.8.5)
Здесь /7 - приведенная масса. Однако, при температурах порядка комнатных, величина
колебательного кванта ЙГ2 »Т. В такой ситуации речь идет о рассеянии на нулевых
колебаниях осциллятора, амплитуду которых можно оценить как qQ = . Тогда для
сечения КР получаем:
RS ~
W ~ 2тгй со4 (д%
cE’/fcr “ П [88Ja
(20.8.6)
Видно, что сечение КР пропорционально четвертой степени частоты. Этот вывод под-
тверждается экспериментом. С другой стороны, в рассмотренной модели получились,
что интенсивности стоксовых и антистоксовых компонент излучения одинаковы. В
квантовой теории КР, основанной на рассмотрении двухфотонного перехода, ситуация
другая: стоксова компонента возникает в результате возбуждения квантовой системы, а
антистоксова - в результате девозбуждения (см. рис. 11.4 и 11.5). В такой ситуации от-
ношение интенсивностей антистоксовой 1а и Is стоксовой компонент оказывается про-
порционально населенности возбужденного и невозбужденного состояний и при термо-
динамическом равновесии с температурой Т есть:
Is/Ia *ехр(-МЦГ). (20.8.7)
Здесь ЙО - энергия возбуждения (девозбуждения) системы при переходе. Например, для
молекулы азота (ЙО-0.29 эВ) при комнатной температуре (Г-0.025 эВ) отношение
интенсивностей стоксовой и антистоксовой компонент рассеяния будет около пяти по-
рядков величины. Переход к классической картине наступает при высоких температурах
(Т > ЙО), когда наблюдается выравнивание населенностей состояний.
С увеличением интенсивности волны сигнал КР возрастает линейно по интенсив-
ности. При определенном значении интенсивности волны накачки с частотой со в среде
возбуждается достаточно интенсивная волна на стоксовой частоте <ц-О, такая, что в
449
среде начинается резонансная раскачка колебаний под действием двух волн - исходной
8ОЯНЬ' накачки и стоксовой компоненты КР. Действительно, запишем функцию Рамиль-
тона молекулы-осциллятора в поле электромагнитной волны:
(20.8.8)
где последний член описывает взаимодействие наведенного диполя с внешним электро
магнитным полем. Из (20.8.8) получаем уравнение движения:
q = -Q.2q +
-------- Е2(/).
2^qJ&
(20.8.9)
В случае если Е(Г) Ео cos cot + Ео cos(<d О)/, поле волны содержит компоненту на ча-
стоте собственных колебаний, что и приводит к резкому росту амплитуды молекуляр-
ных колебании и сигнала комбинационного рассеяния. Процесс КР становится вынуж-
денным. Впервые вынужденно комбинационное рассеяние (ВКР) наблюдалось в 1962
году при распространении в нитробензоле импульса рубинового лазера, генерировавше-
гося в режиме модуляции добротности. Мощность сигнала ВКР достигала 1/5 от мощно-
сти излучения накачки.
Казалось бы, ВКР, как и спонтанное комбинационное рассеяние, может очень
эффективно использоваться в различных спектроскопических приложениях. Однако это
не так. Дело в том, что ВКР требует значительно более высоких интенсивностей излуче-
ния (на уровне 1010 Вт/см2), что, с одной стороны, резко увеличивает полезный сигнал,
но, с другой стороны, может существенно перестраивать исследуемую систему. Кроме
того, как правило, при примерно таких же значениях интенсивности в среде возникают и
другие нелинейные эффекты, самофокусировка излучения, вынужденное рассеяние
Мандельштама - Бриллюена (рассеяние на акустических колебаниях среды) и другие не-
линейно-оптические процессы. Как результат, возможности ВКР для спектроскопии
среды сильно ограничены. Однако, существует специальный метод, который позволяет
эффективно использовать ВКР для целей спектроскопии. Это так называемый метод
КАРС - когерентное антистоксово рассеяние света.
20.9. Когерентное антистоксово рассеяние света (КАРС).
В данном разделе мы рассмотрим схему ВКР, которая используется в задачах
спектроскопии - когерентное антистоксово рассеяние света * (КАРС). Другое название
метода - активная спектроскопия когерентного рассеяния (АСКР). Идея метода заключа-
ется в резонансной раскачке молекулярных колебаний с помощью двух относительно
слабых лазерных полей накачки. Их частоты сох и со2, причем — й>2 ® Q - частота ко-
лебаний среды. Через сильно возбужденную систему распространяется пробное лазер-
ное поле с частотой со§, которое и используется для формирования сигнала на антисток-
совой частоте соа = б?0 +(^ -а>2). С квантовомеханической точки зрения речь идет о
12 в англоязычной литературе CARS (Coherent Anti-Stokes Raman Spectroscopy).
450
OK
CD
О
CD
1
четырехфотонном процессе, представленном на рис. 20.15.
На пракI икс в качсстве пробной волны используется одна из
волн накачки соп — Щ То1да сог1 — 2д>| со2-
Мы опять ограничимся классической моделью эф-
фскта. решение уравнения (20.8.9) для молекулярного ос-
циллятора по действием двух волн накачки с напряженно-
стями £, и Е2, и частотами со, и а>2 запишем в виде:
= _L f ------ ехр (/(£, - )г - (й>! - со2)/)
(20.9.1)
Рис.20.15. Когерентное
антистоксово рассеяние
света.
Тогда в системе возникает поляризация:
(20.9.2)
Используя метод медленно меняющихся амплитуд, получим:
х Г^1Е2Е0
Q2 -(щ, -<у2)2
(20.9.3)
Здесь Лк = к0 -ка +(к} -к2). Как видно, эффективная раскачка колебаний на антисток-
совой частоте возможна при выполнении условия фазового синхронизма:
ka=k+(k}-k2). (20.9.4)
Это условие можно выполнить всегда за счет изменения угла между направлениями
волновых векторов.
20.10. Обращение волнового фронта.
Рис.20.16. Обращение волнового
фронта.
Рассмотрим еще один четырехфотонный
роцесс, который может быть реализован в среде
кубической нелинейностью (см рис. 20.16). В
анном случае имеются две волны накачки
и (со2,к2), причем д>2 =бур к2 =-к{. Это
значает, что волны накачки создают в среде сто-
чую волну. Легко видеть, что рассеяние на этой
гоячей волне пробного поля (д>3,£3) приведет к
формированию в среде волны с параметрами
(д>3к3). Часто бывает, что также д>3 = Тогда
451
все четыре волны характеризуются одинаковой частотой, но отличаются направлениями
волновых векторов к . Этот процесс называют обращением волнового фронта (ОВФ).
Нетрудно понять, что в рассматриваемом процессе две волны накачки в среде создают
своеобразное зеркало, которое формирует отраженное поле: волновой вектор отражен-
ной волны меняется на про швопололожный. В случае падения на среду пробной волны
с произвольным волновым фронтом при ее отражении происходит восстановление вол-
ны о же самым волновым фронтом, но при этом волна распространяется в обратном
направлении. Рассмотренный процесс позволяет осуществлять коррекцию волнового
фронта: при прохождении через среду волновой фронт обычно искажается. Но при об-
ратном распространении волны, полученной в результате ОВФ, происходит восстанов-
пение волнового фронта. Важно только, чтобы за время распространения волны "туда и
обратно" параметры среды не успели существенно измениться. Отметим, что при отра-
жении от обычного зеркала волны, распространяющейся в z - направлении, изменяется
на противоположную только
при обратном проходе происходит не
одна из компонент волнового
зеркало ОВФ
Рис.20.17. Двухпроходный усилитель,
использующий коррекцию волнового
фронта при ОВФ.
вектора: kz -» -kz. Поэтому
восстановление, а дополнительное искажение
фронта.
Явление ОВФ может использоваться,
например, для формирования высокоинтен-
сивных лазерных пучков высокого качества с
помощью мощных, но неоднородно усилива-
ющих сред. Организация двухпроходного ре-
жима усиления позволяет компенсировать на
обратном проходе возникшие при проходе
пучка "туда" фазовые искажения и сформиро-
вать усиленный пучок с исходным волновым
фронтом (см. Рис.20.17).
Задачи к Главе 20.
20.1 Через кювету длины L, заполненную молекулярным водородом при комнатной
температуре, распространяется две электромагнитных волны с частотами а)х и со2
и интенсивностями Ц и /2, причем гц - й>2 ® £10 (/20 - частота колебательного
кванта молекулы). Определить интенсивность сигнала на антистоксовой частоте на
выходе из кюветы. Считать, что волновые вектора обоих волн (кх и к2) коллине-
арны друг другу.
20.2. На среду с квадратичной нелинейностью падает волна накачки с частотой а)0 и ин-
тенсивностью 10 и пробная волна с частотой со = а>0/2. В рамках приближения
медленно меняющихся амплитуд записать уравнение, описывающее раскачку в
среде волны с частотой а> = со0/2 (вынужденное параметрическое рассеяние).
20.3. На среду воздействуют два лазерных импульса с частотами а\ и «1а\, причем
частота сог близка к разнице энергий основного и одного из возбужденного атом-
ных состояний. Рассмотреть процесс четырехволнового смешения
453
Глава 21. Основы физики лазеров.
В этом разделе мы познакомимся с основными пп
генерации, и основными режимами работы лаз Ринципами получения лазерной
жСнии скоростных уравнений. Также коротко бСРНЫХ источник°в излучения в прибли-
здания инверсии в твердотельных и гачпик^ о УДУТ рассмотРсны основные методы со-
1 «ииых средах.
шения1Л‘ СП°НТаННЬ,е И переходы. Сечение фотопогло-
в„делХРп^ "°™ Глава 8) „н
переходы между стационарными состояниями квантоиой си
стсмы, причем вероятность перехода в единив рпр. квантовой си-
верехода в единицу времени wfi из некоторого начального
состояния |1) В конечное состояние |2) определяется выражением:
4я-2|е721|2
(21.1.1)
Здесь d2l - матричный элемент дипольного оператора, связывающий начальное и ко-
нечное состояния, - спектральное значение интенсивности воздействующего излуче-
ния на частоте перехода со = су21 , коэффициент
в _4*К|2
- коэффициент Эйнштейна вынужденного перехода. Мы отмечали, что В21 = В{2, то есть
переходы с поглощением и испусканием энергии атомом равновероятны. Считая, что
плотности атомов в состояниях |1} и |2^ есть Nl и N2 соответственно, мы можем запи-
сать уравнение баланса
^- = И,2,ЛГ,-и,,г^=-В21/.(^-^) = -В2ЛДУ,
at
где AV = N2 -Nx - разность населенностей состояний. Поскольку для населенности
справедливо уравнение
dNx _ dN2 дм
dt dt 21 ш ’
(21.1.2)
(21.1.3)
для AV получим:
(21.1.4)
dt
Ранее мы видели, что взаимодействие электрона с так называемым электромаг-
нитным вакуумом ведет к появлению спонтанных переходов. Атом, находящийся в воз-
454
бужденном состоянии |2), «самопроизвольно» испускает квант и переходит в состояние
11), причем вероятность этого перехода в единицу времени есть
Величину Л12 принято называть коэффициентом Эйнштейна спонтанного перехода.
Очевидно, величина г = 1/Л)7 есть время жизни возбужденного состояния относительно
спонтанного распада в состояние |1^. Легко видеть, что введенные нами коэффициенты
Эйнштейна спонтанного и вынужденного переходов связаны между собой соотношени-
ем:
(21.1.6)
Отметим, что введение в теорию спонтанных переходов означает очень важный
факт: возбужденные состояния атома более не являются стационарными, они живут ко-
нечное время, а, следовательно, их энергия точно не определена. Уровни свободного
атома размыты и имеют определенную ширину у«А/г, которая носит название есте-
ственной ширины линии. На практике, .ня атомов, находящихся в газовых средах, как
правило, ширина атомной линии заметно больше естественной и определяется другими
механизмами уширения - столкновитсльным или допплеровским. В твердых телах атом
находится в узлах кристаллической решетки и чувствует электрическое поле соседних
атомов - возникает штарковскос уширение линии. Часто ширина линии излучения опи-
сывается лоренцевой формой линии1
У
g(d)-<y0) =
2л- (<У-6УО)2 + у2/4
(21.1.7)
Здесь <у0 - центр линии, а у - ее ширина. При этом кривая нормирована согласно усло-
вию ^g((D-(oQ)dco = 1. В случае естественного уширения у = Л12, для других механиз-
мов уширения, как правило, ширина линии Av
Рис.21.1. Атомная линия и спектр воздеиству юн^егр излучения
1 Такая форма линии реализуется не только для естественной ширины линии, но и для столкновительного
уширения и полевого уширения кристаллическим полем в хорошо упорядоченных кристаллах.
455
При записи выражений (21.1.1) - (21.1.4) мы полагали, что атомная линия беско-
нечно узкая (атомные состояния имеют точно определенные значения энергии), а линия
^действующего излучения имеет некоторый спектр конечной ширины. Сейчас мы по-
нимаем, что на самом деле атомная линия тоже имеет конечную ширину, причем эта
ширина может оказаться как больше, так и меньше ширины спектра воздействующего
излучения (см. рис.21.1). В задачах физики лазерной генерации, о которых мы будем го-
ворить в этой главе, ширина линии воздействующего излучения (ширина линии генери-
руемого лазерного излучения) будет существенно меньше ширины атомной линии,
определяющей ширину полосы усиления активной среды лазера. В такой ситуации мы
можем считать, что спектральная интенсивность излучения описывается 8 - функцией
1ю=Ц8(со-со^
а вместо выражения для AN = N2-NX в выражениях (21.1.3), (21.1.4) стоит величина
Ду/2
ДЛ^=^х- , , . ,
я (а>-а>0)2 + (Ду)2/4
(21.1.8)
где определяет величину разности населенностей на частоте воздействующего из-
лучения. Тогда вместо (21.1.4) имеем:
dNN
-^ = -2B2xIANa. (21.1.9)
Учитывая, что при переходе атома из состояния |2) в состояние |1) в системе испуска-
ется один фотон, а величина разности населенностей меняется на две единицы, мы мо-
жем записать следующее уравнение для числа фотонов:
dnnh
= (21.1.10)
dt
или, учитывая, что интенсивность излучения есть I = cha>* nph,
— = chaB2lIANg(a-co0). (21.1.11)
dt
Будем считать, что частота излучения совпадает с частотой центра линии а = 69О. Тогда,
учитывая связь коэффициентов спонтанного и вынужденного переходов, а также, что
g(0) = 2/(д- Д v), из (21.1.11) получим:
ту 2 2 о 0^ А
^ = cha^-Ax2INN— = c^-^-NNI = caphNNI, (21.1.12)
dt ha я-Ду 2л-Дг
где
(21.1.13)
"‘гл-ди
' сечение фотопоглощения (в центре линии).
Делая замену переменных х — ct, перепишем уравнение (21.1.12) в виде.
456
б// 1 б// Z X г КТ \ J
- = -
dx с dt
решение которого есть
7(.г) = /(, ехр(he).
(21.1,14)
Здесь к =o~ph(N2 — Nx). В состоянии термодинамического равновесия Mt > N2, поэтому
по мере распространения в среде интенсивность излучения уменьшается, а величину
pi = — к = <yph(N} — /V2) можно назвать коэффициентом поглощения. Однако, в случае
если N2 > N} (такой случай называют инверсией, или инверсной населенностью), среда
оказывается способна усиливать излучение, введенная нами величина к есть коэффи-
циент усиления.
Таким образом, мы получили важнейший результат. Для получения эффекта из-
лучения в системе нам необходимо организовать наличие инверсии. Однако, наличие
положительного коэффициента усиления еще недостаточно для получения генератора.
Для получения генерации еще нужна положительная обратная связь, в лазерной технике
ее роль выполняет резонатор (см. рис.21.2). Будем считать, что активная среда имеет
длину L, а коэффициенты отражения зеркал 7?,
Зеркала оптического резонатора
Рис.21.2. Вычисление порога генерации.
и R2 соответственно. Предположим, что
на входе в усиливающую среду
интенсивность излучения равна
/0. Тогда при проходе через уси-
литель, отражении от зеркал, по-
вторном проходе через усилитель
и еще одном отражении от второго
зеркала интенсивность излучения
составит:
I = /0 exp(kL)R2 exp(kE)Rx.
Если I > /0, в системе начнется
раскачка колебаний. Поэтому по-
лучаем выражение для порога ге-
нерации
RXR2 ехр(2££), > 1,
или
к >-L|n(l/(A,^)),
(21.1.15)
Если зеркала одинаковы (Rx =R2 = R), то
к > 11п(1/Я).
Если коэффициент отражения зеркал близок к единице, то принимая во внимание, что
1п(1/Я) = - In Л = -1п(1+ (•/?-!))«1 -7?, получим:
457
L (21.1.16)
величина есть длина пробега фотона в резонатопе с vu^
риалах, а р назоре с учетом переотражения на
(21.1.17)
г — L
с(1 - R)
активное время жизни фотона в резонаторе относительно потерь „а зеркалах Без-
,слов„о. кроме потерь на зеркалах есть и другие механизмы потерь излучения (рассея-
ние на неоднородностях в активной среде, поглощение), но часто именно потери на зер-
калах оказываются наиболее существенными. Если, как это часто бывает, только одно из
зеркал частично пропускает излучение, а второе является глухим, выражение (21 1 17)
надо переписать в виде:
2£
С учетом потери излучения на зеркалах уравнение для временной динамики ин-
тенсивности излучения мы можем записать в виде:
~ . (21.1.19)
Аналогичное уравнение мы можем записать и для плотности числа фотонов в резонато-
ре:
= caph(N2 - Nx) nph - nph/Tph. (21.1.20)
Для дальнейшего анализа процесса генерации нам необходимо получить уравнение,
описывающее изменение во времени величины разности населенностей AN = N2-N{.
Отметим, что для раскачки генерации в системе величина инверсии должна быть больше
некоторого порогового значения AN*, определяемого выражением:
AV’ =-----!---. (21.1.21)
ph? ph
Фактически, нам теперь необходимо обсудить возможные способы создания ин-
версии. На практике они весьма многочисленны. Но наиболее распространенными яв-
ляются оптическая накачка (обычно используется в твердотельных лазерах) и накачка
газовым разрядом (такой способ получения инверсии характерен для газовых лазеров).
Мы для определенности будем говорить об оптической накачке.
21.2. Распространение резонансного излучения в двухуровневой
среде. Эффект насыщения.
Рассмотрим процесс распространения в среде излучения, такого что его частота
совпадает с частотой перехода атома из основного в одно из возбужденных состояний.
458
Тогда уравнение для величины разности населенноег и состояний ДУ N2 запи-
шем в виде:
(21.2.1)
Здесь первое слагаемое описывает взаимодействие с полем излучения, причем мы пола-
гаем. что ширина спектра излучения существенно меньше ширины атомной линии, а его
частота совпадает с центральной частотой перехода. Второе слагаемое описывает про-
цесс релаксации населенностей к равновесному значению ДУ0 > которое определяется,
например, температурой среды. Длительность этого процесса - f . Мы полагаем, что ин-
тенсивность излучения 1 = chcoxn/)h задана и не меняется во времени. Стационарное
решение уравнения (21.2.1) есть
&N = AN,—Ц—, (21.2.2)
1 + //Л
где = ha>/(2<j hT) - интенсивность насыщения.
вынужденные
Рис.21.3. Эффект насыщения.
Если система
в начальный момент
времени находилась
в состоянии равно-
весия, то ДУ0 < 0.
Следовательно ве-
личина ДУ остается
отрицательной и для
любой интенсивно-
сти воздействующе-
го излучения. При
этом в пределе
больших интенсивностей I»Is величина разности населенностей стремится к нулю,
оставаясь отрицательной. Фактически это означает выравнивание населенностей (эф-
фект насыщения)- в сильных полях N2 » N}, а, следовательно, коэффициент поглоще-
ния в такой системе стремится к нулю с увеличением интенсивности излучения, остава-
ясь, тем не менее, слабоположительным.
В оптическом диапазоне частот, когда величина кванта порядка нескольких элек-
трононвольт, в отсутствие излучения практически всегда можно считать, что все атомы
находятся в основном состоянии. Следовательно = -N{. При значении 1 =
ДУ = ДУ0/2. Это означает, что одна четвертая часть атомов перешла в возбужденное
состояние. Вид зависимости (21.2.2) для этого случая приведен на рис.21.3.
Подведем итог. Во-первых, мы видим, что среда становится оптически прозрач-
ной для резонансного излучения (эффект насыщения можно использовать для создания
самопросветляющихся фильтров). Во-вторых, воздействуя на двухуровневую систему,
оказывается невозможно получить в ней инверсную населенность.
459
Оценим характерное значение интенсивное™ излучения в оптическом диапазоне
„ас-гот. в предположении, что релаксация разности населенностей происходит в резуль-
,,,тс спонтанного распада верхнего состояния. Тогда ширина линии Ди = Л12, и сечение
фртопо) лощения есть сг/)Л ~ Л/2/г ~ 10 см. А, следовательно, для интенсивности
пасышсния, полагая ^12 Ю с > имеем 75 ~1 —10 Вт/см2. Это очень небольшие вели-
мины, н0 они соответствуют излучению очень высокой степени монохроматичности, со-
ответствующему центру линии. Заметим также, что для резонансного излучения сечение
поглощения очень велико, видимый таким излучением "размер" атома на два порядка
больше его реального размера.
21.3. Трех- и четырехуровневые схемы накачки.
Мы видели, что в двухуровневой системе невозможно получить инверсную насе-
ленность оптическими методами. В 1955 Н.Г. Басов2 и А.М. Прохоров3 предложили ме-
тод создания инверсии населённостей с помощью вспомогательного излучения на дру-
гой (более высокой) частоте -- трёхуровневую схему накачки (см. рис. 21.4). В этом слу-
чае излучение возбуждает рабочие атомы среды из основного состояния |1) в состояние
|3), откуда потом атом достаточно быстро (в твердотельных лазерах это обычно без-
излучательный переход) релаксирует в верхнее рабочее состояние 12). В такой схеме при
достаточно большой интенсивности пучка накачки возникает инверсия на переходе
2) -> 11), которая и может быть использована для получения генерации. Именно такой
3
2
I Л/З
Быстрый распад
Долгоживущий
уровень
Л/г
И/21 Т
Ni
V1/12 - И/21
метод получения инверсии был реализован в
первом лазерном источнике света (лазер на
кристалле рубина) Т.Мейманом4 в 1960 году.
Получим уравнение для инверсной
населенности в лазере, работающем по трех-
уровневой схеме накачки. Обычно переход
|3) —>|2) происходит достаточно быстро, по-
этому можно считать, что N3 « 0, а излучение
Рис.21.4. Трехуровневая схема накачки.
накачки сразу переводит атомы в состояние
|2). Учитывая уравнение (21.2.1), запишем
= 2WN. - 2ccrph£N nph--------- (21.3.1)
dt T
Здесь W - мощность накачки, определяющая скорость возбуждения атомов из основного
состояния в состояние ]3>, 2V, - концентрация атомов в основном состоянии. Множите-
2 Басов Николай Геннадьевич (1922-2001) - советский физик, лауреат Нобелевской премии (1964) сов-
местно А.М. Прохоровым и Ч. Таунсом "За фундаментальные работы в области квантовой электроники,
которые привели к созданию генераторов и усилителей на лазерно-мазерном принципе ~
Прохоров Александр Михайлович (1916 - 2002) - советский физик, лауреат Нобелевской премии (1964)
совместно Н.Г.Басовым и Ч.Таунсом.
Maiman Theodore (1927-2007) - американский физик.
460
ли "2" в правой части (21.3.1) учи. ь.ва.от тот факт, что при переходе одного атома из |1)
в |2) или обратно инверсия изменяется па две единицы. У {игывая, гго Л/( +А2 _ дг* _
полная концентрация рабочих атомов, а /V ? - -/V, — A/V, для /V, полу зим.
В результате, поскольку ДЛ/0=- NK, для инверсной населенности и плотности числа
фотонов в резонаторе в приближении трехуровневой схемы накачки получим следую-
щую систему скоростных уравнений:
z/лл/ AN + N к
-— = IV(N - ДА) - 2caphbN пph-----------,
dt т (21.3.2)
—р~ = cVpiAN nph “ " ph Л Ph
at
Здесь г и rph - время релаксации инверсии и время жизни фотона в резонаторе. Вели-
чина nph связана с внутрирезонаторной интенсивностью излучения соотношением
I = chajnph. Величина выходной интенсивности излучения есть (1 — R)I.
Легко сообразить, что для полу-
чения инверсии в трехуровневой схеме
накачки в возбужденное состояние надо
перевести более половины всех рабочих
атомов среды. Это требует большого
подвода энергии, что ведет к сильному
разогревы среды, и нарушению условий
генерации. Поэтому лазеры, работаю-
щие по трехуровневой схеме накачки (в
их числе лазер на кристалле рубина)
обычно дают генерацию только в им-
пульсном режиме.
Часто более удобной оказывается
четырехуровневая схема генерации,
представленная на рис. 21.5. Аналогич-
но случаю трехуровневой схемы верхнее рабочее состояние 12) заселяется через проме-
жуточное состояние |3), причем переход |з) —>|2) полагается быстрым, так что А3 »0.
VV
И/12
МММ» Л/з
Быстрый распад
Долгоживущий
уровень
№
И/21
N1
Быстрый распад
— N.
И/12 = И/21
Рис.21.5. Четырехуровневая схема накачки.
3
2
1
S
В отличие от трехуровневой схемы нижний рабочий уровень |1) тоже является возбуж-
денным, так что его начальная населенность практически равна нулю. При этом состоя-
ние |1) выбирается так, чтобы его распад в основное состояние атома |g) был быстрым,
так что в процессе генерации можно приближенно считать, что N{ » 0. В этом случае
величина инверсной населенность есть просто величина населенности верхнего рабочего
уровня ДЛ/ « N2, и уравнение для величины инверсии в системе может быть записано в
виде:
461
^ = 1Г(^-ЛА)-сгт„^
0 рассматриваемой ситуации, поскольку нижний рабочий уровень является пустым, для
лучения положительного коэффициента усиления достаточно перевести в возбужден-
ное состояние даже небольшое количество атомов. Поэтому скорость накачки W может
онть значительно меньше, чем для лазера, работающего по трехуровневой схеме. Как
правил0' <<: • В таком приближении система скоростных уравнений для четырех-
•повневой схемы накачки имеет вид:
d&N ... AN
—— = WNg и,,„—
dn .
= cvphbN nph - nph/Tph.
(21.3.3)
Наиболее существенным отличием этой системы уравнений от (21.3.2) является нулевое
значение разности населенностей в равновесном состоянии AN() = 0, а также отсутствие
множителя "2" в слагаемом, описывающем изменение инверсии при вынужденных пере-
ходах. Последнее обстоятельство понятно: в случае трехуровневой схемы испускание
одного фотона ведет к изменению инверсии на две единицы, для четырехуровневой схе-
мы ситуацию другая: испускание фотона ведет к изменению инверсии на единицу.
Как уже отмечалось, четырехуровневая схема как правило требует меньших ин-
тенсивностей накачки, что обуславливает возможность организации как импульсного,
так и непрерывного режима работы. К числу лазеров, работающих по такой схеме, отно-
сится, например, неодимовый лазер, дающий генерацию в ближнем ИК диапазоне частот
(длина волны излучения 2 = 1.06 мкм, или ha> = 1.17 эВ).
21.4. Динамика лазерной генерации в приближении скоростных
уравнений. Стационарный режим работы.
В этом разделе на основе скоростных уравнений рассмотрим динамику лазерной
генерации. Всюду ниже будем считать, что исходно среда находится в основном состоя-
нии.
Рис.21.6. Зависимость внутрирезонатороной интенсивности излу-
чения от мощности накачки.
Начнем с рас-
смотрения стационарно-
го режима. Уравнение
для плотности числа фо-
тонов в резонаторе оди-
наково в случае трех- и
четырехуровневой схем
накачки. Его стационар-
ное решение получается,
если выполнено равен-
ство
(с<тм^-уг,А)лм=0,
(21.4.1)
462
откуда находим, что в стационарном режиме величина инверсной населенности должна
быть равна пороговому значению AN = 1/(с<трЛг/,Л). Еще одно решение соответствует
nph = 0. Это значит, что если в начальном момент времени фотонов не было, то генера-
ция не разовьется. Мы не будем обсуждать данную ситуацию. Она скорее свидетель-
ствует о неполноте модели. Некоторое небольшое число фотонов в системе всегда воз-
никнет за счет фона спонтанного излучения, возникающего при возбуждении верхнего
рабочего состояния. Эти начальные фотоны можно ввести в модель с помощью началь-
ного условия nph(t ~ 0) = п0.
Определив, что инверсия в стационарном режиме генерации равна своему поро-
говому значению, нетрудно рассчитать плотность числа фотонов и внутрирезонаторную
интенсивность излучения. Например, для четырехуровневой схемы накачки из (21.3.3)
получаем:
= nphcaph£sN*,
откуда видно, что мощность накачки должна превышать пороговое значение
W>W' . (21.4.2)
г N
При мощностях накачки больших порогового значения с учетом выражения для порого-
вого значения инверсии получим:
nP*=WNgrph----— • (21.4.3)
Как видно, число фотонов в резонаторе возрастает по линейному закону с увеличением
мощности накачки (см. рис.21.6). Такая же зависимость возникает и от плотности атомов
среды.
В случае трехуровневой схемы накачки ситуация выглядит несколько иначе. По-
роговое значение инверсии по-прежнему определяется выражением (21.1.21). Тогда
плотность числа фотонов в резонаторе определяется из соотношения:
» » ДУ* + N
W(Ng - ДУ ) - 2caphW nph---------*- = 0,
т
откуда получаем выражение для пороговой мощности накачки W , при превышении ко-
торой возможна генерация:
, 1 N + ДУ*
W =-----------г- (2144)
vNg-^N 7
Обычно выполнено условие AN* « Ng. Поэтому W* «(1 + 2^/N^/t. Как видно, эта
величина действительно много больше, чем пороговая мощность накачки для четырех-
уровневой схемы (см. (21.4.2)).
463
21-5. Динамика лазерной генерации в приближении скоростных
уравнении. Нестационарный режим работы лазера.
В этом разделе мы для определенности будем рассматривать четырехуровневую
схему накачки. Тогда уравнения для инверсной населенности и плотности числа фото-
нов в резонаторе имеют вид:
= -ссгДУ и Л- —,
е7лрЛ Т (21.5.1)
— = cophNN nph-nph/rph.
3 качестве начальных условий будем полагать, что AN(t = 0) = 0, a nph(t = 0) = п0, т.е. в
системе имеется некоторое начальное число фотонов, например, как результат спонтан-
ного фона излучения.
Система (21.5.1) является нелинейной. Поэтому общее аналитическое решение
получить невозможно, и мы ограничимся качественными рассуждениями. Прежде всего
рассмотрим режим, близкий к стационарному. В этом случае
ДУ = ДУ* + <5V, причем ДУ* = \/(cophrph), 8N « AN*,
"/,/> = , причем = WNт h--------—, дп « п™.
Тогда запишем:
d3N rlr.r , (0) еч AN + 3N
—— = JVNg -со ph(ДУ + <W) {n{p}h + 3ri)---,
= со- h (ДУ* + <5У)(л^ + дп) - («^ + дп)/Tph.
dt
Удерживая члены только первого порядка малости, получим линеаризованную систему
скоростных уравнений:
~~ = + l/r)<W - 3n/Tph,
dt (21.5.2)
— = cahn™8N.
dt ph
Отсюда получаем уравнение колебаний для инверсии 3N.
(0)
^+(СО-Х’+1А)—+^^да = 0. (21.5.3)
dt1 ” " ’ dt rph
Полученное уравнение есть уравнение осциллятора с затуханием и допускает как перио-
дические (осцилляторные) решения, так и апериодические, в зависимости от соотноше-
ния параметров / = co-phn(pl + \/т и О = yjco-phnph ]тph . Так, в случае у « Q реализуют-
ся затухающие колебания вблизи стационарного значения инверсии и плотности фото-
нов, а у > Q - апериодический режим выхода на стационарные значения. Считая, что
464
входящие в у слагаем,..с имеют один иорядок величины, из сказанного легко получить,
что колебательный режим возникает если г„„ «г, т.е. время релаксации поля в резо-
наторе много мсныпс времени релаксации инверсии.
Рис. 21.7. Различные режимы генерации лазера.
В зависимости от соотношения времен релаксации инверсии и поля в резонаторе
существенно по разному выглядят и решения нелинеаризованных скоростных уравне-
ний. Так, в случае Tph «т возникает пичковый режим генерации (см. рис.21.7а), когда
интенсивность периодически проваливается практически до нулевого значения. Такое
соотношение времен и режим генерации характерен, например, для лазера на кристалле
рубина. Наоборот, при rph > т (такое соотношение справедливо, например, для газораз-
рядного гелий-неонового лазера) интенсивность излучения плавно зависит от времени
(см. рис.21.76).
На практике в режиме свободной генерации при т h « т пички часто не затуха-
ют, а являются хаотическими. Это связано как с нестабильностью условий генерации
(например, дрожание зеркал), так и многомодовым характером генерации5, когда в ак-
тивной среде возбуждается несколько мод поля, близких по частотам, но со случайным
фазами.
21.6. Режим модуляции добротности. Гигантские импульсы.
Добротность характеризует скорость потери из колебательной системы (резона-
тора) запасенной в ней энергии. Она определяется как отношение запасенной энергии,
умноженной на 2л-, FF0 к величине потерь энергии за период Т:
Q = 2it—,—2—г.
T(dW/dt)
(21.6.1)
Учитывая, что в отсутствие усиливающей среды
Отметим, что такой многомодовый характер генерации лежит за рамками рассмотренной нами системы
скоростных уравнений. В этом случае надо как минимум записать уравнения для плотности фотонов в
каждой их генерируемых полевых мод.
465
Ил = Илоехр(-//грЛ),
где rpb = 2L/c0- ~ К) ~ время жизни фотона в резонаторе (мы здесь полагаем, что одно из
зеркал является идеально отражающим, а другие потери пренебрежимо малы), получим:
2caL
Q = =
Р c(l-R)
Пороговое значение инверсии, при достижении которой в активной среде начитается
раскачка генерации есть:
1-1q I
т.е. чем больше добротность резонатора, тем про-
ще получить генерацию. С другой стороны, воз-
буждаемая генерация препятствует дальнейшему
росту инверсной населенности и повышению ин-
тенсивности излучения в резонаторе. В связи с
этим для повышения интенсивности излучения
можно на этапе накачки резко уменьшить доброт-
ность резонатора (достичь этого можно проще все-
го, убрав одно из зеркал, или поместив внутрь ре-
зонатора поглощающий элемент). В этом случае
пороговое значение инверсии существенно возрас-
тет, а, следовательно, в активной среде удастся за-
пасти значительно большее количество энергии.
Например, если убрать одно из зеркал, то время
жизни фотона в резонаторе упадет до величины
T*ph=2L/c. При значении коэффициента отраже-
ния зеркала R » 0.98 (такие значения типичны для
лазерных резонаторов), это означает, что доброт-
Рис.21.8. Формирование гигантского
импульса в режиме модуляции доб-
ротности. Стрелочкой обозначен мо-
мент "включения" добротности резо-
натора.
ность резонатора упала в 5U раз, во столько же раз
возрос уровень порогового значения инверсии. Идея модуляции добротности заключает-
ся в том, что при достижении с "выключенным" зеркалом некоторого значения инверсии
AN »&N* = l/(ccrphTph) снова "включить" резонатор. В результате получится, что зна-
чение инверсии существенно выше порогового значения для возбуждения генерации и в
системе разовьется "гигантский" импульс, интенсивность в котором много больше ин-
тенсивности свободной генерации. Схематически такая ситуация представлена на рис.
21.8. В некоторый момент времени tQ (он обозначен стрелочкой) "включается" доброт-
ность резонатора, а формируемый гигантский импульс скидывает излучение практиче-
ски до нуля. После этого добротность следует опять выключить, что приведет к новому
нарастанию инверсии до высокого значения и последующему формированию следую-
щего гигантского импульса.
Динамика развития гигантского импульса может быть описана следующей систе-
мой уравнений (сравнить с (21.3.3)):
466
,/ЛЛ' = AW п,л.
Л
= га,,,AN
dt
(21.6.2)
с начальными условиями
ДУ(/ = /с?) = AN, п(( =tL))-ntt.
Мы предположили, что в процессе развития гигантского импульса всеми процессами,
кроме вынужденного „спускания, можно пренебречь. Учитывая, что в рассматриваемом
приближении \N + „P„ = AN = const, из (21.6.2) получим для плотности фотонов:
= с ст,,/((AN -пph) nph.
dt
(21.6.3)
Интегрирование этого уравнения дает:
(21.6.4)
Как видно, время развития гигантского импульса составляет величину tg ~ 1/(ccr^AN).
Обычно на практике это время составляет величину порядка 10-30 нс.
Отметим, что режим модуляции добротности, впервые реализованный в 1961 го-
ду, позволил получить интенсивности в оптическом диапазоне частот на уровне 1ОВ * 10 * -
1012 Вт/см2.
Обсудим теперь экспериментальные методы реализации режима модуляции доб-
ротности. Модуляция добротности может организована как в активном, так и в пассив-
ном режимах. Исторически первой была осуществлена активная модуляция добротно-
сти. Режим активной модуляции добротности проще всего реализовать механическим
воздействием на одно из зеркал резонатора, например, путем его вращения вокруг своей
оси. (см. рис. 21.9). В этом случае может быть организован режим получения гигантских
импульсов с периодом следования равным частоте вращения зеркала.
вращающееся
зеркало зеркало
фильтр
Рис. 21.9. Активная и пассивная модуляция добротности.
В случае пассивной модуляции добротности свойства резонатора резко изменя-
ются под действием процессов, непосредственно происходящих в самой активной среде.
Например, внутри резонатора помимо активной среды помещается самопросветляю-
щийся фильтр (см. рис.21.9). Такой самопросветляющийся фильтр может работать на
467
эффекте нась,,1*сния (см> Р«»Дел 21.2). При малых значениях интенсивности фильтр,
,ич роенный на частоту генерации, поглощает падающее на него излучение, как резуль-
. - добротность резонатора мала. По мере роста инверсной населенности в системе,
условленной воздействием накачки, на выходе из рабочей среды растет фон спонтан-
излучения. Как результат, при превышении некоторого порогового по интенсивно-
ц| фона значения фильтр насыщается и просветляется, что приводит к резкому возрас-
),)Н11Ю добротности резонатора. Формируется гигантский импульс. После того, как ин-
нерсня населенности в активной среде пропала, а, следовательно, пропал и фон излуче-
ния. поглощающие свойства фильтра восстанавливаются, он снова становится непро-
данным для излучения. Добротность резонатора опять резко убывает. В таком режиме
работы частота следования гигантских импульсов определяется скоростью накачки ак-
тивной среды до уровня, способствующего просветлению фильтра.
21.7. Синхронизация мод и генерация ультракоротких импульсов.
До сих при анализе лазерной генерации мы предполагали, что все фотоны в си-
стеме одинаковые. На самом деле часто ситуация более сложная и лазерная генерация
происходит на некоторой совокупности мод с различными частотами, попадающими в
позосу усиления активной среды, а рассмотренная выше модель относится, скорее, к
режиму одномодовои генерации.
продольные моды резонатора
Av - с/2/.
частота
спектр генерации
Рис.21.10. Модовый состав лазерной генерации.
Остановимся чуть подробнее на
модовом составе излучения и на физи-
ческих эффектах, к которым приводит
этот модовый состав. Будем считать,
что мы имеем дело с резонатором, об-
разованным двумя плоскими зеркала-
ми, расположенными на расстоянии L
друг от друга. Тогда в этом резонаторе
могут существовать стоячие волны,
длины волн которых удовлетворяют
соотношению:
мЛ„/2 = £, п = 1,2,3,...
или
Ч =«т- (21.7.1)
Lj
Как видно, плоскопараллельный резо-
натор образует эквидистантный спектр
с межмодовым расстоянием
= (21.7.2)
Например, для длины L = 100 см име-
ем &D »109 с'1. Рассмогренные нами
468
моды - это так называемые продольные моды резонатора.
С другой стороны, полоса усиления (ширина линии усиления) Ди обычно удо.
влетворяет условию 2/rAi' »<\о , то есть на ширине линии усиления укладывается
много (по крайней мерс несколько) продольных мод резонатора, на которых и возбужда-
ется генерация (см. рис.21.10). Например, ширина линии усиления рубинового лазера
Д1'«10" с1, это означает, что при длине резонатора 100 см лазер может генерировать
излучение на нескольких сотнях продольных мод. В случае лазера на неодимовом стекле
Д v ч? 1012 с’1 - число продольных мод на ширине линии усиления измеряется уже тыся-
чами. В газовых лазерах линии усиления заметно уже, и такие лазеры генерируют на от-
носительно небольшом числе продольных мод. Например, ширина линии усиления в ге-
лий - неоновом лазере всего Дг « 109 с1, при метровой длине резонатора получится все-
го 6 продольных мод. Именно в таких лазерах, вводя в резонатор диспергирующий эле-
мент, наиболее просто получить режим одномодовой генерации.
Представим себе, что генерация в лазере происходит на .V (N »1) мод в преде-
лах от некоторой минимальной wmjn до максимальной птх:
E(/) = ^E'”’exp(I4' + %)- (21.7.3)
п
Фазы различных мод <рп случайны. Поэтому, когда мы вычисляем интенсивность излу-
чения, это есть просто суммарная интенсивность отдельных мод:
/(/) ~ |Е(/)|2
2E‘0lexp(i®„l + ^) ~52|е'„'"|2 ,
п п п
(21.7.4)
где 1п - интенсивность излучения в п - моде.
Совсем другая ситуация получается, если колебания во всех модах сфазированы,
т.е. все д>п =ф0. Такой режим называют синхронизацией мод. Для упрощения дальней-
шего анализа будем полагать, что амплитудные значения поля во всех модах одинаковы.
Проводя суммирование, получим:
ад = Ео exp(z7ymjn/ + ^)£ехр(/ад =
N _ (21.7.5)
Ео ехр(/^п/ + ^)£ехр(ш&>/) = Ео ехр(/^пГ + ^)--
п~о 1 —exp(z«y/)
или, переходя к интенсивности излучения:
Z(/)~E2(/)
s'\n\N8cDt/2)
sin2(&y//2)
(21.7.6)
График полученной зависимости приведен на рис.21.11. Видно, что пиковые значения
интенсивности составляют =Л^2/0 (/0 - интенсивность излучения в каждой из мод),
в то время как в отсутствие синхронизации имеем 1 = Мо. В случае если 7V~ 100, речь
идет о стократном увеличении интенсивности по сравнению со средним уровнем сво-
бодной генерации. С другой стороны, как видно из (21.7.6), в режиме синхронизации
469
мод возникает последовательность ультракоротких
торых т/; определяется из условия
импульсов (УКИ), длительность ко-
Рис.21.11. Последовательность ультракоротких
импульсов, получаемая в режиме синхронизации
мод.
ММг„/2)_
2
откуда тр Inl^NScij). Учитывая, что
N6oj = Ай? = 2яД v - ширина линии
усиления, получаем, что длительность
пичка УКИ
~1/Ди
(21.7.7)
определяется шириной линии усиле-
ния. Для получения коротких импуль-
сов необходимо иметь широкую поло-
су усиления. Например, для лазера на
неодимовом стекле Ду ~ 1012 с’1, это означает, что в режиме синхронизации мод мы мо-
жем получим импульсы длительностью порядка 1 пс. Отметим, что в рассматриваемом
режиме пространственная протяженность каждого импульса стр ~ 0.03 см. Поэтому
пространственная структура поля в резонаторе состоит из совокупности коротких им-
пульсов «бегающих» в резонаторе от зеркала к зеркалу.
С другой стороны, частота следования пичков УКИ также определяется из выра-
жения (21.7.6): временной интервал между пичками Т есть
зеркало
Рис.21.12. Пассивная синхронизация мод в лазере.
2
откуда Т = 2л1&о и определяет-
ся расстоянием между соседними
продольными модами, т.е. дли-
ной резонатора.
Каким образом можно
осуществить синхронизацию
экспериментально? Оказывается,
существуют способы пассивной и активной синхронизации мод. В случае активной син-
хронизации в резонатор дополнительно вводятся потери, изменяющиеся во времени по
закону ~ cos(&y/), где 8а> есть межмодовое расстояние. В случае активной синхрониза-
ции в резонатор вводится дополнительный элемент — самопросветляющиися фильтр (см.
рис. 21.12). Короткий импульс, взаимодействуя с фильтром, «открывает» его на время
своего прохождения и при этом несколько укорачивает длительность импульса. После
прохождения импульса фильтр опять «закрывается». При многократном прохождении
через фильтр длительность импульса сокращается и формируется УКИ. Можно пока-
зать, что такое сокращение импульса на спектральном языке и есть синхронизация фаз
различных мод излучения.
470
21.8. Генерация фемто- и ап осекундных импульсов.
Мы видели, что для генерации импульсов предельно короткой длительности
нужны среды с большой полосой усиления. Предельная длительность импульса - это
просто обратная спектральная ширина линии усиления.’
Уникальным но своим свойствам лазерным кристаллом, позволяющим генериро-
вать импульсы фемтосекундной длительности, является титанат сапфира (Ti-Sapphire),
ширина линии поглощения в котором достигает Av ~ 101 с *. Это означает, что в таком
кристалле можно получать импульсы длительностью до 10 фс. Отметим, что именно с
широким использованием этого кристалла для генерации излучения связан прогресс в
области генерации фемтосекундных лазерных импульсов и сверхатомных интенсивно-
стей излучения.
Спектральную ширину лазерного импульса можно расширить искусственно, а
затем сжать импульс до предельно коротких длительностей в оптическом компрессоре.
Рассмотрим этот вопрос чуть подробнее. Пусть лазерный импульс
Е = Ео exp(z(£z- йХ)
(здесь к = п со/с, п - показатель преломления) распространяется в среде с квадратичной
нелинейностью. В такой среде показатель преломления можно представить в виде
п = п0 +п21, где п0 - линейная часть показателя преломления, п2 определяет нелиней-
ную добавку, I - интенсивность излучения. Тогда дополнительный набег фазы волны за
счет нелинейности на длине L составляет
А^?(/) = — n2I(t)L,
с
а добавка к частоте волны есть
dt с dt
Оценивая dl/dt^I^r? (Zo -
амплитуда импульса, т - его
длительность), получим для
уширения спектра:
Агу ~ ,
с тр
откуда определим предельное возможное сжатие такого импульса:
^(min) ~ 2 Д' ~ 'iTUCTр
р Асо ton2I0L ‘
В роли сжимающего объекта (оптического компрессора) выступает диспергирующая
среда, в качестве которой, например, могут быть использованы две призмы (или две ди-
фракционных решетки), так как показано на рис. 21.13. В такой системе за счет различия
6 Отметим, что это утверждение соответствует квантовомеханическому соотношению неопределенностей
для энергии - времени.
Кристалл представляет собой окись алюминия с примесью ионов титана Тр+.
длинный лазерный
импульс компрессор
Рис.21.13. Простейшая схема оптического компрессора.
471
скоростях движения спектральных компонент пакета (мы полагаем, что дисперсия яв-
ится нормальной) обеспечивается их совмещение по времени на выходе их оптическо-
ч1 компрессора, ЧТ° И позволяст получить импульс предельно короткой длительности,
^.прсссия ,1МПУЛЬСОВ титан-сапфирового лазера позволяст получить импульсы дли-
'пьностыо вплоть до одного периода оптических колебаний (т/; ~ 2 фс). Очевидно, та-
11С импульсы обладают шириной спектра порядка несущей частоты излучения.
А как можно получать импульсы аттосекундной длительности? Отметим прежде
,сго. чт0 такие импульсы уже не могут быть оптическими, т.е. соответствовать види-
мому диапазонУ частот- Действительно, для длительности импульса субфемтосекундно-
г0 диапазона, например тр ~ 100 ас, имеем ширину спектра 2лДр ~ 6-1016 с'1,
фактически это означает, что такой импульс имеет энергию квантов в несколько десят-
ое электровольт, т.е. лежит уже в рентгеновском диапазоне частот.
Обший принцип получения в экспериментах импульсов аттосекундной длитель-
ности очень похож на рассмотренный способ получения ультракоротких импульсов в
сжиме синхронизации мод. Мы видели, что генерация на совокупности продольных
мод резонатора в режиме синхронизации позволяла получать импульсы длительностью
г ~ , где 8а> - частотный интервал между соседними модами, a N - число
мод С другой стороны, мы видели, что в процессе надпороговой ионизации атомов в
сильных полях в континууме заселяются состояния с энергий, отстоящей от основного
состояния на целое число квантов ионизующего лазерного поля hto. Величина
оказывается порядка отношения колебательной энергии электрона в поле волны к энер-
гии кванта ~ Ее/hco, Ее = е2Е2 /4щщ2, Ео - амплитуда поля в падающей волне.
lg4
=(2и+1)б>
1ЙИЙ..
мк/ м зп 40 во
Номер гармоники
Рис.21.14. Излучение высоких гармоник лазерного излучения и генерация аттосекундных им-
пульсов.
Для частоты излучения титан-сапфирового лазера (Йй> = 1.55 эВ) и интенсивно-
сти излучения - З Ю15 Вт/см2 получаем N-ЮО, т.е. в континууме заселены состояния
С энергий вплоть до ~ 150 эВ. Электроны с такой энергий фактически совершают коле-
бательное движение в области нахождения родительского иона и с некоторой
стью могут испустить квант в процессе перерассеяния и рекомбинации в исхо^зное со-
стояние (см рис.21.14). Легко видеть, что в таком процессе правила отбора разрешают
472
испускание только нечетных гармоник воздействующего излучения (2п + 1)фу цри
этом важно, что в области высоких гармоник (практически вплоть до ) интенсив-
ность излучения гармоник практически одинакова, причем фазы напряженностей полей
излучаемых гармоник близки между собой (см. рис.21.14). В такой ситуации возникает
временная последовательность импульсов длительностью тр со). Для приве-
денных выше параметров имеем г ~ 30 ас.
21.9. Некоторые лазеры.
В этом разделе мы кратко рассмотрим реализацию рассмотренных выше общих
принципов на примере ряда конкретных лазерных схем, отличающихся типами актив-
ных сред (кристаллические и аморфные твердые тела, газы и плазма), способами накач-
ки (оптическая накачка, возбуждение в газовом разряде, химические реакции) и др. Кон-
кретно мы остановимся на рассмотрении рубинового и неодимового лазеров, гелий -
неонового лазера и лазера на молекулах СОг, эксимерных лазерах на галогенидах инерт-
ных газов и ряд других.
кристалл рубина
лампа накачки
непрозрачное
зеркало
Блок питания
лампы
Рубиновый лазер.
Лазер на кристалле
рубина (оксид алюминия
AI2O3, в котором ионы
алюминия А13+ частично
заменены ионами хрома
Сг34, массовая доля хрома
примерно 0.05%) историче-
ски был первым лазерным
источником излучения. Ге-
нерация была получена в
1960 году Т.Мейманом. Ла-
зер работает по трехуров-
невой схеме, в нем реали-
зована оптическая накачка
от лампы-вспышки. Общий
вид кристалла и схема
накачки представлены на
рис. 21.15. Кристалл имеет
две полосы поглощения в
Рис.21.15. Общий вид рубинового лазера и схема рабочих зеленой части спектра, ко-
уровней. торые и используются для
накачки верхнего рабочего уровня иона Сг3+ (3<У3 2О). Переход на верхний рабочий
уровень осуществляется в результате беизлучательной релаксации (характерная дли-
тельность этого процесса ~5 • 10 8 с). Переход с верхнего рабочего уровня в основное
состояние Сг34 (3<У3 4F) соответствует длине волны излучения 2 = 0.69 мкм (ЙбУ = 1.78
эВ). Время спонтанного перехода составляет 3 10 3 с, а ширина рабочего перехода (она
473
определяется внутрикристаллическим полем8) Ди~Ю" с’1. Линия излучения лежит в
аСНой области видимого спектра.
КР Как мы уже отмечали, лазер, работающий по трехуровневой схеме, генерирует в
1)Мпульсном режиме. Типичная длительность свободной генерации, которая происходит
в пичковом режиме, достигает ~1 мс. В режиме модуляции добротности формируются
гигантские импульсы длительностью 10-20 нс, их мощность достигает 10-50 МВт. В ре-
жиме синхронизации мод пиковая мощность в импульсе длительностью ~10 пс рання
нескольким гигаваттам.
Неодимовый лазер.
Неодимовый лазер, работающий на длине волны Я = 1064 нм (энергия кванта
}ict)= 1-17 эВ — ближний ИК диапазон) — еще один типичный представитель твердотель-
ных лазеров с оптической накачкой, работающий по четырехуровневой схеме. Это об-
стоятельство позволяет достаточно легко осуществлять как импульсную, так и непре-
рывную генерацию.
Существуют две основных разновидности неодимовых лазеров - лазер на неоди-
мовом стекле и лазер на кристалле иттрий-алюминиевого граната (YAG) Y3AI5O12. В
первом случае ионы Nd3+ находятся в стекле (аморфное вещество), во втором случае они
внедрены в кристаллическую матрицу. Этот факт приводит к существенной разнице:
ширина линии усиления в лазере на стекле заметно больше, чем в лазере на гранате
(ДА = 30 нм и 0.7 нм соответственно). Как результат, в лазере на стекле можно получить
заметно более короткие импульсы излучения в режиме синхронизации мод. В то же
время, коэффициент усиления в лазере на гранате оказывается больше по величине.
В Nd YAG лазере уровень
легирования составляет порядка
одного процента: ионы Nd3+ (кон-
фигурация 4/3) замещают в мат-
рице ионы Y3+. Обычно накачка
системы осуществляется излучени-
ем ксеноновой или криптоновой
ламп на длинах волн 0.73 и (или)
0.80 мкм (см. рис.21.16), откуда си-
стема безизлучательно на временах
~10’7 с переходит на верхнее рабо-
чее состояние 4F, откуда идет ра-
бочий переход в состояние 41. От-
метим, что оба эти состояния рас-
Шеплены внутрикристаллическим полем на ряд подуровней. Время релаксации инверсии
на этом переходе составляет ~0.23 мс.
Типичные параметры Nd: YAG -лазера оказываются следующими: в непрерыв-
ном многомодовом режиме выходная мощность до 200 Вт, в импульсном лазере с боль-
0,8 мкм
безизлучательно
1,06 мкм
03
X
0,73 мкм та
X
та
быстрая релаксация
v = 2 -103 см1
Рис.21.16. Упрощенная схема переходов в неодимо-
' Искажение центральной симметрии атомного потенциала кристаллическим полем делает в значительной
мере условными квантовые числа полного орбитального момента, которые мы использовали для обозна-
чения атомных состояний.
474
шой скоростью повторения импульсов (50 Г..) средняя выходная мощность порядка 500
Вт, в режиме модулированной добротное™ максимальная выходная мощность д0 50
МВт. в режиме синхронизации мод длительность импульса до 20 пс. При этом лазер на
стекле позволяет получить импульсы длительностью до 1 пс.
Как в импульсном, так и в непрерывном режиме КПД при накачке газоразрядным
лампами составляет около 1-3 %. Заметим, что в настоящее время оказывается возможно
накачивать неодимовый лазер излучением диодных (полупроводниковых) лазеров, дли-
на волны излучения которых совпадает с длиной волны поглощения накачки (0.8 мкм).
В этом случае КПД генерации более чем на порядок больше и может достигать 50 Л.
Гелий-неоновый лазер.
Остановимся теперь на принципах работы газового лазера на электронных пере-
ходах на примере гелий-неонового лазера. Этот лазерный источник излучения был впер-
вые реализован в 1960 году А. Джаваном9 в инфракрасной части спектра (Л = 1.15 мкм)
и несколько позднее (А. Уайт10 11, 1962 г.) в видимой части спектра (Я = 0.632 мкм). От-
метим прежде всего, что в газовых средах оптическая накачка неэффективна. Атомные
линии чрезвычайно узки по сравнению с полосами поглощения в кристаллах, поэтому
широкополосный спектр от ламп-вспышек оказывается практически непригоден11. По-
этому в случае возбуждения газовых сред обычно используют электрический разряд, где
возбуждение состояний атомов или молекул вызывается электронным ударом. Именно
такой способ возбуждения и используется в газовом лазере на смеси гелия и неона.
элемент
стеклянная ооолочка
Рис.21.17. Схема гелий - неонового лазера.
Общая схема гелий - неонового лазера представлена на рис. 21.17. Разряд в смеси
гелия и неона заживают в стеклянной колбе (обычно соотношение компонент в смеси Не
: Ne = 5-15 : 1, давление газа < 1 Торр). Торцы стеклянной колбы образуют зеркала, одно
из которых как правило глухое, а другое пропускает порядка одного процента падающе-
го на его излучения. Принцип работы лазера понятен из следующей схемы уровней (см.
рис. 21.18). В разряде электронным ударом возбуждаются метастабильные состояния
атома гелия в конфигурации k 2s 1,3£ с энергиями возбуждения 19.81 и 20.51 эВ для
’Javan АН (1926 - 2016) - американский физик азербайджанского происхождения.
White Alan David (1923 - 2020) - американский физик.
11 Здесь надо сделать оговорку. В настоящее время для возбуждения лазерной среды часто используют
излучение другого лазера, имеющего достаточно узкую спектральную линию. В этом случае возможно и
оптическое возбуждение газообразной среды.
475
триплета и синглета соответственно. В атоме неоия
„„энергии этим состояниям в конфи^ациях 2р~^5 S™™'
на временах порядка нескольких микросекунд оказывается во С°°ТВеТСТВСННО' П°ЭТОМу
ной передачи возбуждения зможен процесс рсзонанс-
Не + Ne-+He+Ne .
Рис.21.18. Схема уровней в гелий - неоновом лазере.
Таким образом происходит заселения верхних рабочих состояний. Нижнее рабочее со-
стояние атома неона принадлежит конфигурации 2р53р. При этом переход
2р~ 5s —> 2/?5 Зр дает красную линию Я = 0.63 мкм, переход 2р5 4s -> 2р5 Зр - линию
в инфракрасной части спектра 2 = 1.15 мкм. Из нижнего рабочего состояния атом быст-
ро спонтанно переходит в состояние 2р5 3s. Казалось бы, далее происходит переход в
основное состояние атома неона 2р6 XS. Однако это состояние населено, поэтому ис-
пускаемый квант не покидает разрядный объем, а многократно перепоглощается в нем.
Излучение оказывается пленено, в итоге населенность начинает накапливаться в состоя-
нии 2р5 3s, что губительно может сказаться на генерации. В реальности атомы в состо-
янии 2р5 3s диффундируют к стенкам разрядной трубки и при столкновении с ней дез-
активируются (говорят, что происходит тушение на стенках). Время диффузии опреде-
ляется давлением газа и радиусом разрядной трубки. Для успешной работы лазера диа-
метр трубки не может быть большим (~ 1 см). Типичная выходная мощность лазерной
генерации в непрерывном режиме варьируется от 1 до 100 мВт.
Как мы уже отмечали, спектральная ширина полосы излучения гелий-неонового
лазера мала и составляет ~ 109 с1. Её значение определяется главным образом доплеров-
476
ским уширением ................... „сна. Узость линии усиления
легко получки, олиомодовую iviicpimiiio. что важно в таких пракгичсс риложениях
как интерферометрия, голография, спектроскопия.
- лазер.
Остановимся теперь еще на
одном газоразрядном лазере - лазере на молекулах
углекислою газа. Этот лазер работает в дальнем
ИК диапазоне частот, длина волны излучения -
2-10.6 мкм, энергия кванта tico = 0.12 эВ. Это
самый длинноволновый лазер, имеющий доста-
точно высокую выходную мощность излучения.
Обычно, для получения генерации разряд зажи-
гается в смеси СО2 : : Не. При этом генерация
Рис.21.19. Моды колебаний молекулы
СО2.
идет на колебательных уровнях молекулы угле-
кислого газа, азот служит как резервуар энергии,
откуда она передается на верхний рабочий уро-
вень СО2, гелий используется как буферный газ
для повышения устойчивости горения разряда и
отвода энергии из разрядного промежутка. В за-
висимости от режима работы лазера (непрерыв-
ный или импульсный режим с длительностями
импульсов генерации в милли-, микро- или нано-
секундном диапазоне) соотношение компонент в
разрядной смеси выбирается различным, однако
объемная концентрация гелия оказывается самой
высокой, а углекислого раза самой низкой. Кон-
центрации COi и N2 в смеси обычно составляют
5—20 %.
Для понимания общих принципов работы
лазера рассмотрим схемы колебательных уровней молекул азота и СО2. Молекула СО2
является линейной и имеет три моды колебаний - симметричную, асимметричную и де-
формационную (см. рис.21.19). В общем случае состояние колебательного возбуждения
молекулы СО2 можно задать тремя квантовыми числами [v1, v2, v3 ], где Vj, v2, v3 задают
число квантов колебаний в симметричной, деформационной и асимметричной модах со-
ответственно12. Например, состояние [1,0,0] соответствует одноквантовому возбуждение
симметричной моды, а [0,2,0] - двухквантовому возбуждению деформационной моды.
Что касается молекулы азота, то он имеет единственную колебательную моду, причем
для основного терма X '2* величина колебательного кванта Йй> = 0.29 эВ. Схема рас-
положения колебательный уровней молекул азота и диоксида углерода продетавпены на
рис. 21.20. Наиболее существенно, что величина колебательного кванта молекулы азота
12 Такое представление оправдано для достаточно небольших степеней колебательного возбуждения, ко-
гда справедливо приближение гармонических колебаний и межмодовым обменом энергии можно прене-
бречь.
477
,фактически точно совпадает с анергией возбуждения асимметричной моды колебаний
молекулы СО2. В разряде происходит эффективное заселение колебательных состояний
молекул азота, эксперимен т показывает, что в рассматриваемых смесях до 90% энергии,
„олводнмои к разряду, идет на возбуждение колебательной подсистемы молекулы азота,
откуда в процессе
N2(X"L,V^ i)+co2[o,o,o]-> Wi(A'T,v = 0) + CO,[0,0.|]
она передастся на верхний рабочий уровень лазера. Генерация возможна на переходах
[0.0J] [1,0,0] и [0,0,1] —> [о,2,о] молекулы СО2 и соответствует длинам волн 10.6 и 9.6
мкм соответственно. При этом коэффициент усиления на переходе между асимметрич-
ной и симметричной модами больше. Для быстрого опустошения нижнего рабочего со-
стояния [1,0,о] крайне существенно, что энергии состояний [1,0,0] и [0,2,0] близки между
собой (так называемый резонанс Ферми). Поэтому релаксация в основное состояние
идет через деформационную моду колебаний.
Отметим, что СО2 лазер обладает большим КПД, до 20-30%, от энергии вложен-
ной в разряд. Это обстоятельство делает СО2 лазер востребованным в практических
приложениях, где требуется большая энергия (мощность) пучка. Это, прежде всего, за-
Рис.21.20. Схема колебательных уровней молекул углекислого газа и
азота, поясняющая принцип работы СО2 лазера.
дачи, связанные с ла-
зерной обработкой
материалов. Однако,
для высокой мощно-
сти излучения необ-
ходим большой энер-
говклад в среду, при-
чем для качества вы-
ходного пучка этот
энерговклад должен
быть осуществлен
равномерно по объе-
му. Однако, в разря-
дах с высоким энер-
говкладом и большим
рабочим объемом
развиваются различ-
ного рода неустойчи-
вое™, приводящие к контракции - стягиванию разряда в ярко светящийся шнур (дуго-
вой разряд) с равновесной плазмой, нагретой до высокой температуры, и непригодный
для усиления излучения.
В качестве примера рассмотрим механизм возникновения одной из таких не-
устойчивостей. Предположим, что в некоторой области разрядного объема произошла
, Т ппкяпьно повысилась. Тогда выравнивание давления
флуктуация и температура газа Tg локально повысил
п н.и^рмию в этой области пространства плотности газа N, и
приведет к локальному понижению в ли
поперт™ Е/N (Е - напряженность электрического по-
следовательно, к возрастанию параметра ъ/zv i н
478
ля), определяющего скорость ионизационного размножения электронов. Локальное воз-
растание электронной НЛО1НОС1П. в свою очередь, способсгвусг увеличению энерговы-
делення (?и дальнейшему локальному возрастанию температуры газа. Как результат та-
кой нонизационно - персгревной неустойчивости, разряд конграг ируст. Схема описан-
ных выше процессов предо гаилена на следующей диаграмме.
7; Т -> n i > E//v Т >пе T •
Для подавления развивающейся неустойчивости необходимо разорвать на каком-то
участке возникающую положительную обратную связь. Это можно сделать, заменив са-
мостоятельный разряд на несамостоятельный, когда поддержание электронной плотно-
сти обеспечивается внешним ионизатором (это может электронный пучок или УФ излу-
чение от внешнего источника излучения), а приложенное к разрядному промежутку поле
нужно для обеспечения энерговклада в среду. В таком разряде локальное возрастание
температуры, приводящее к увеличению параметра Е/.У, уже не приводит к росту ско-
рости ионизации, что и приводит к повышению устойчивости горения разряда. Действи-
тельно, несамостоятельные разряды заметно более устойчивы по отношению к контрак-
ции, что и обеспечивает их достаточно широкое применение для накачки мощных газо-
вых лазеров, несмотря на существенное усложнение и удорожание установки. Тем не
менее, такие разряды тоже подвержены развитию неустойчивостей, которые существен-
но затрудняют создание мощных электроионизационных13 лазеров. В частности, в рас-
сматриваемом случае перегревная неустойчивость развивается по следующему меха-
низму:
Рис.21.21. Контракция разряда, развивающая-
ся из приэлектродных областей. Отчетливо
видны катодные пятна, которые являются ис-
точником токопроводящих каналов, прорас-
тающих в объем плазмы.
7?->w4<-»at->2T->rT.
о <5
В данном случае локальное уменьшение
плотности среды ведет к возрастанию про-
водимости плазмы, и, как следствие, уве-
личению энерговыделения и дальнейшему
росту температуры газа.
Часто контракция разряда развива-
ется из приэлектродных областей (катод-
ных пятен) в виде горячих хорошо прово-
дящих каналов, прорастающих в объем
плазмы (см. рис.21.21).
Крайне существенным в мощных
лазерах, особенно работающих на колеба-
тельных переходах молекул, является про-
блема отвода тепла от рабочего объема.
Это связано как с тепловым заселением
нижнего рабочего состояния в лазерной
системе, так и со скоростью релаксации
13 Электроионизационными лазерами принято называть лазеры с несамостоятельным разрядом, лазеры с
самостоятельным разрядом называют электроразрядными.
479
Ы11,й VT релаксации),
™ Рассмотрим еще одни ™„ СО, лазера,
‘Х’рах. где инверсия обр.т1уется "к,Исчст\>£1аждсС1СНН"СТИ РС''Ь ° га'!одинамичсских
•п н н у я за счет охлаждения потока газа на выходе из сопла.
область формирования
Рис.21.22. Принципиальная схема газодинамического СО2 лазера.
Именно в таких лазерах, работающих в непрерывном режиме, достигнуты мощности ге-
нерации до 1 МВт. Принципиальная схема газодинамического СО2 лазера представлена
на рис. 21.22. Нагретый газ из камеры выдувается через сопло и попадает в резонатор,
образованный зеркалами, расположенными вдоль торцов потока. При выдувании газа
через сопло происходит его охлаждение. При этом температура нижнего рабочего уров-
ня «следит» за газовой температурой и быстро убывает вдоль потока, температура верх-
него рабочего состояния соответствует температуре колебательного резервуара молекул
азота и падает медленно, на временах, соответствующих скорости процесса VT - релак-
сации. Характерная зависимость населенностей верхнего и нижнего рабочего состояний
в лазере при движении газа вдоль по потоку представлена на рис. 21.23 и демонстрирует
возникновение инверсной населенности.
Химические лазеры.
Эти лазеры интересны для нас способом накачки активной среды. Инверсная
населенность в данном случае получается в ходе протекания химической реакции, по-
скольку образующееся вещество получается в колебательно возбужденном состоянии.
В качестве примера рассмотрим принципы работы лазеров на галогенидах водо-
рода. Наиболее известным среди них является HF лазер, генерирующий в диапазоне
длин волн Я «2.7-3.2 мкм (средний ИК диапазон). Поддержание генерации основано
на протекании цепной реакции, которая запускается процессом фотодиссоциации моле-
кулы фтора
14 Более подробно с различными видами неустойчивостей, развивающихся в объеме плазмы и приводящих
к контракции разряда можно познакомиться в монографии Е.П. Велихов, А.С. Ковалев, А.Т. Рахимов
«Физические явления в газоразрядной плазме», М.. Наука, 1987
480
Рис.21.23. Распределение населенностей
верхнего и нижнего рабочего состояний
в газодинамическом СО2 лазере.
/<, + Ъо> —> I7 + F .
Далее запускаются реакции:
Г+//2 н>//Г‘ +// + £,,
I / + F2 —> 1IF + F + Q2.
Обе реакции идут с выделением энергии
(Ci ~ 1 -4 эВ/молскула, Q2 & 4.25 эВ/молекуда).
При этом в ходе реакции молекулы HF образу.
10'гся в колебательно возбужденном состоянии с
преимущественным заселением состоянии с ко-
лебательным квантовым числом v = 4 —6, при-
мерно 66% выделяющейся энергии идет в коле-
батсльное возбуждение молекул. Реакция само-
поддерживающаяся и может продолжаться до
полного выгорания реагирующих компонентов.
Однако, нагрев смеси, возникающий в ходе протекания
химической реакции, ведет к
ускорению процесса колебательной релаксации, что может приводить к срыву генера-
ции. Для генерации в непрерывном режиме обычно необходима прокачка газа.
Аналогичным образом работает и НС1 лазер. Процесс фотодиссоциции молекул
хлора:
ci2+hcD-+ci + a.
Далее протекают реакции:
С1 + Н2 -+НС1 + Н-Ci,
h+cl -+hci+ci+q7.
В отличие от предыдущего случая, одна из этих реакций идет с поглощением энергии,
что приводит к более низкой эффективности возбуждения колебательных состояний.
Генерация излучения в этом случае происходит в области длин волн Л 3.8 мкм.
Химический и электроразрядный кислород - йодный лазеры.
Остановимся теперь еще на одном источнике когерентного излучения, который
реализован в настоящее время и как химический лазер и как электроразрядный. Кон-
кретно, мы рассмотрим лазер на смеси кислорода и йода. В качестве резервуара энергии
выступают молекулы кислорода в метастабильном синглетном состоянии <92(tf'Ag)>
энергия возбуждения « 0.98 эВ, время жизни ® 45 мин. Эта энергия близка к энергии
тонкого расщепления основного терма атома йода 5р5 2/у23/2, которая равна «0.94 эВ.
Поэтому в процессе
О2 (а 'дг ) + I(2P3/2) -> О2 (X ) + 1СР1/2)
идет заселение верхнего рабочего состояния, а генерация возникает на переходе
Я^з/г) _>^(2^/2) + ЙбУ.
481
Длина волны излучения Л = 1.315 мкм и достаточна близка к длине волны неодимового
лазера.
Таким образом, для получения генерации важной задачей является получение
синглетного кислорода. В первоначальном варианте химического кислород - йодного
лазера кислород в состоянии а получался в ходе химической реакции молекулярно-
го хлора С12 с раствором перекиси водорода Н2О2 и гидроксида калия КОН. Даль-
нейшее подмешивание к синглетному кислороду молекулярного йода приводило к его
диссоциации и возбуждению в верхнее рабочее состояние. Существенным недостатком
химического варианта кислород - йодного лазера является токсичность веществ, исполь-
зуемых в генераторе синглетного кислорода. Несколько позже был реализован и элек-
троразрядный вариант кислород - йодного лазера, в котором синглетный кислород нара-
батывается в газовом разряде. Обычно в качестве разрядных сред используются смеси
Аг : О2, О2:Не, (Х'СО.Аг, О2:Н2:Аг.
Выходная мощность кислород-йодного лазера в непрерывном режиме достигает
единиц мегаватт, в импульсном - от сотен гигаватт до единиц тераватт.
Эксимерные лазеры.
В разделе 7.5 мы уже обсуждали коротко возможность существования эксимер-
ных молекул: это молекулы, которые в основном электронном состоянии имеют разлет-
Рис.21.24. Электромагнитные переходы между
термами эксимерной молекулы. Значения
hci)G,hco\ha)" соответствуют центру линии
усиления активной среды, её красной и фиолето-
вой границам, Д<у - ширина линии усиления.
ные термы, в то время как в возбужден-
ных электронных состояниях в системе
существует притяжение. Например,
электронные подоболочки атомов
инертных газов являются замкнутыми.
Однако, в возбужденном состоянии у
них появится сразу два неспаренных
электрона, поэтому такие атомы уже
могут образовывать химические соеди-
нения. Для определенности рассмотрим
атом ксенона Хе. В возбужденных со-
стояниях конфигурации 5p56s он име-
ет два неспаренных электрона и может
выступать либо как одновалентный, ли-
бо как двухвалентный химический эле-
мент и образовывать молекулы, кото-
рые могут устойчиво существовать
лишь в возбужденном состоянии. Такие
эксимерные молекулы хорошо извест-
ны, например, XeF*, XeF2 , ХеО*, Хе\, и могут быть использованы для получения ла-
зерной генерации. Типичный вид электронных термов эксимерной двухатомной молеку-
лы и возможных электромагнитных переходов между ними представлен на рис.21.24.
Образование эксимерных молекул достаточно эффективно происходит в разрядах высо-
кого давления в смесях, содержащих атомы инертных газов.
482
Поскольку нижнее состояние лазерного перехода в эксимерном лазере опустоша-
ется в результате разлёта атомов эксимерной молекулы, характерное время которого *-
Ю>2 с, что значительно меньше времени радиационного распада верхнего состояния ла-
зерного перехода, в среде, содержащий эксимерные молекулы, можно получить усиле-
ние на переходах между возбуждённым связанным и основным разлётным термами эк-
симерной молекулы.
Первый эксимерный лазер (1970 г.) генерировал вынужденное излучение с дли-
ной волны 172 нм, возникающее на димерах ксенона (Хег). образующихся в процессе
прохождения пучка электронов через ксенон15. В настоящее время наиболее широко ис-
пользуются электроразрядные лазеры на галогенидах инертных газов. Такие лазеры яв-
ляются наиболее эффективными источниками когерентного излучения ультрафиолето-
вого диапазона частот. Основные процессы, которые обеспечивают создание инверсии и
получение генерации на примере KrF лазера приведены ниже:
F-, + е —> F + F.
Кг + с —> Кг + <?.
Кг + F + М -> KrF’ + Л/.
В последней реакции третье тело забирает на себя избыток энергии.
Длины волн наиболее распространенных лазеров приведены в таблице. Ширина
линии усиления лазерного перехода в эксимерных лазерах аномально велика, что связа-
но с разлётным характером нижнего терма перехода. Характерные значения параметров
лазерных переходов для наиболее распространенных эксимерных лазеров представлены
в таблице.
Таблица. Параметры некоторых эксимерных молекул.
Эксимерная молекула Длина волны излучения, нм Ширина линии усиления, нм
ArF 193.3 7
KrCl 222.0 7
KrF 248.4 15
XeCl 308.0 12
XeF 351.1 25
Рентгеновские лазеры.
До сих пор мы говорили о лазерных источниках излучения в оптическом диапа-
зоне частот. Обсудим теперь основные проблемы создания источников когерентного из-
лучения в рентгеновской части спектра. Основная проблема заключается в высокой ча-
стоте излучения. Мы помним, что вероятность спонтанного распада уровня пропорцио-
нальна кубу частоты излучения А} 2 ~ а>3, поэтому в рентгеновском диапазоне частот
время жизни возбужденного состояния на несколько порядков меньше, что существенно
затрудняет получение инверсии и положительного значения коэффициента усиления.
Оценим зависимость коэффициента усиления в активной среде от частоты усиливаемого
15 Лазер был запущен в ФИАН в лаборатории Н.Г.Басова
483
излучения. Действительно, считая, что нижнее рабочее состояние является ненаселен
ным, для коэффициента усиления запишем
k = N2^P^
где N, - населенность верхнего рабочего уровня лазера. Его максимальную населен-
ность оценим как N2 — где время релаксации инверсии определяется скоростью
спонтанного распада г ~ 1/Л12. Учитывая, что в рентгеновском диапазоне частот ширина
линии усиления определяется скоростью спонтанного распада, Д v = Л12, а следователь-
но, сечение фотопоглощения есть о-рЛ = Л2/2;гх(Л12/Д v) « 22/2лг, для зависимости ко-
эффициента излучения от частоты получим:
к = N2°Ph ~ ~ .
^12
Заметим, что в оптическом диапазоне частот зависимость коэффициента усиления от ча-
стоты заметно более плавная к ~ а>~2 (см. задача 21.10).
Еще одной проблемой на пути получения лазерного источника излучения рентге-
новского диапазона частот является проблема создания зеркал, отражающих излучение.
Рис.21.25. Схема уровней неоноподобного иона селена и схема эксперимента по получению
плотной плазмы при воздействии мощного лазерного импульса на селеновую нить.
Ниже мы рассмотрим первую экспериментальную реализацию лазерного источ-
ника излучения в мягком рентгеновском диапазоне частот, выполненную П. Хагельстей-
ном16 в 1985 году. Инверсная населенность была получена в неоноподобном ионе селена
&?24+ на переходе 2s2 2р5 Зр -+2s2 2р5 3s (длина волны перехода 2 «205 А или
ftco а 68 эВ) с последующим быстрым спонтанным распадом в основное состояние
2s2 2р6 (}S). При этом заселение верхнего рабочего состояния происходит в результате
рекомбинации электронов из континуума в процессе разлета плотной плазмы, созданной
в результате взрыва селеновой нити в поле мощного лазера (см. рис.21.25).
Взрыв селеновой нити происходил в ходе ее облучения излучением второй гар-
моники Nd лазера (энергия импульса ~ 2 кДж, длительность « 450 пс), сфокусирован-
16 Hagelstein Peter (1945) - американский физик и инженер - электрик.
Селеновая фольга
484
ным цилиндрической линзой в пятно размером 1.2 х 0.02 см . Величина интенсивности в
фокальном пятне достигает ~1014 Вт/см2. Взрыв фольги приводит к образованию плазмы
с температурой ~ 1 кэВ и плотностью ~ 5 • 1О20 см 3. При ее разлете и остывании и обра-
зуется инверсия17 *. Энергия импульса рентгеновского излучения составила 0.1 мкДж.
Это значит, что КПД преобразования оптического излучения в рентген составила ~ Ю10.
Лазер на свободных электронах.
В этом разделе мы рассмотрим еще один способ генерации, который позволяет
продвинуться в область рентгеновского излучения, а именно лазер на свободных элек-
тронах.
Рис.21.26. Движение пучка электронов в магнитном ондуляторе:
1 - магнитная система, 2 - релятивистский электронный пучок, 3 -
диаграмма излучения.
Представим себе,
что у нас имеется элек-
тронный пучок (энергия
электронов Е), проле-
тающий через последо-
вательность конденсато-
ров, в которых направ-
ление электрического
поля попеременно меня-
ется на противополож-
ное. Такая система назы-
вается электростатиче-
ским ондулятором. Лег-
ко видеть, что под дей-
ствием электростатиче-
ского поля электрон,
двигаясь внутри ондулятора, будет совершать колебания в плоскости перпендикулярной
направлению его движения (частота этих колебаний определяется периодом ондулятора
£0 и скоростью энергией электрона), а, следовательно, излучать энергию. На практике
обычно используют магнитные ондуляторы, в которых качание электронного пучка обу-
словлено разнонаправленно действующим магнитным полем (см. рис.21.26). Если пери-
од ондулятора равен £0, а скорость электрона - у, то частота излучения будет равна
й>0 = 2яу/£0 . Например, для Lo = 1 см получим, что частота колебаний лежит в радиоча-
стотной части спектра. Однако, полученная формула несправедлива в нерелятивистской
области. Если пучок электронов движется с релятивистской скоростью, то вследствие
лоренцева сокращения дины он «видит» изменение периода структуры
= // = д/1 “ (*7c2)Lq . Тогда в системе отсчета, связанной с электроном, частота из-
лучения будет равна
• 2л$с
а> =——г^а)йГ.
А)
17 Важно, что тройная рекомбинация электронов преимущественно идет в высоковозбужденные состоя-
ния.
485
Здесь P = vjc. При переходе обратно в лабораторную систему отсчета необходимо
учесть допплеровский сдвиг частоты. При наблюдении излучения в узком конусе в
направлении распространения пучка получим
= (1 + fi)Py2a^ » 2у2а>0.
Например, для у = 103 (такое значение релятивистского фактора соответствует энергии
пучка Е = уте2 = 500 МэВ) мы получаем частоту излучения а> ~ 106 х10“ ~ 1017c'’, что
соответствует энергии фотонов ~ 100 эВ. Отметим, что в релятивистской области даже
некогерентное излучение будет характеризоваться узкой диаграммной направленности
генерируемого излучения.
лазерный пучок
электронный пучок
рентгеновское излучение
Рис.21.27. Рассеяние пучка электронов на движущейся навстречу световой волне.
А можно ли еще увеличить частоту излучения, не меняя энергию пучка электро-
нов? Да, можно! Для этого надо уменьшать размер структуры, с которой взаимодейству-
ет пучок. Реально размер ондулятора сделать еще меньше уже практически невозможно.
Но ондулятор можно заменить на поле электромагнитной волны, распространяющейся
навстречу электронному пучку. Действительно, электрическое поле волны мощного ла-
зера может эффективно раскачивать электронный пучок, заменяя ондулятор. Схематиче-
ски такой процесс представлен на рис. 21.27. В этом случае «наблюдаемая» релятивист-
ским электроном частота поля волны в собственной системе отсчета есть
1 + £ о
6У = а)0 - ~ 2уй)0.
С точность до комптоновского сдвига частоты18 в рассеянном свете при наблюдении из-
лучения в направлении движения пучка получим
ш = ш 1-^- « 4/2®о,
т.е. повышение частоты также определяется квадратом релятивистского фактора. Если
использовать в качестве мощного лазерного излучения пучок от СОг лазера
(Яо =10.6мкм, Ййэо »0.12 эВ), то при /~103 в рассеянном назад свете19 мы получаем
энергии фотонов ~ 105 - 106 эВ.
18 Эти сдвигом можно пренебречь, если энергия кванта поля в собственной системе отсчета много меньше
энергии покоя электрона, т.е. выполнено условие « тс2 .
19 Этот процесс иногда называют обратным комптоновским рассеянием.
488
Справочные данные
Основные физические постоянные
Скорость снега в вакууме
Гравитационная постоянная
Постоянная Больцмана
Заряд электрона
Масса электрона
Энергия покоя электрона
Масса протона
Энергия покоя протона
Отношение масс протона и электрона
Объемная постоянная Стефана-Больцмана
Поверхностная постоянная Стефана-
Больцмана
Постоянная Планка
Постоянная Ридберга (для бесконечной
массы ядра)
Постоянная Ридберга (для атома водорода)
Ридберг
Боровский радиус
Классический радиус электрона
Комптоновская длина волны электрона
Постоянная тонкой структуры
Магнетон Бора
Ядерный магнетон
с = 2.998 -1010 см/с
G = 6.67-10 н см’/г.с2
/< = 1.381 • 10 16 эрг/град
с = 4.803 10 10 абс. ед.
т = 0.911 -10 27 г
тс2 =0.511 МэВ
М = 1.673 -10’24 г
Мс2 = 938.28 МэВ
М/т = 1836.15
а = 7.57 • 10-’5 эрг/(см3 град4)
сг = 5.67 -10"5 эрг/(с.см2.град4)
h = 1.0546 10 27 эрг.с
h = 6.626 IO'27 эрг.с
R = 109737 см’1
RH =109677 см’1
Ry = me^2h2 =13.606 эВ
а0 = Й2/те2 = 0.529 • 10 8 см
ге=е2!тс2 = 2.82-10~13 см
Ле = 2rth!тс = 2.426-10“'0 см
a ^e2/hc = 1/137.036
Ao = eh!2mc = 0.927 • 1020 эрг/Гс
Мы =ей/2Л/с = 5.051-10"24эрг/Гс
Некоторые интегралы
<Т2/б, 77 = 1,
Л x"dx _ 2.405, /7 = 2,
И' -1 Iл-4/15, 77 = 3,
24.9, т? = 4.
Интеграл Пуассона
fexp(-x2)<fr = Ттг.
Г -функция Эйлера Г(р) = jxp~'e~xdx.
Г(р +1) = рГ(р), Г(2) = Г(1) = 1, Г(1/2) = , Г(л +1) = и!,
Jxn exp(-x)tfr = 77!, 77 > 0 - целое,
о
4.
Формула Стирлинга
F(z + 1) = zF(z) « >/2fl-exp(zlnz-l)- 1т
1
12z
Полиномы Эрмита.
1. Общее выражение для полиномов Эрмита: Нп (х) = (-1) ” е*2 (е~х2
dxn
В частности, Яо (х) = 1, Н} (х) = 2х, Н2 (х) = 4х2 - 2, Н3 (х) = 8х3 - 12х.
Полиномы Эрмита Нп (х) являются решениями уравнения Эрмита:
d2u du
—-~2х-----\-2nu = 0
dx2 dx
и могут быть представлены в виде
[Я/2] /_ 1\т
нп(х) = и\У—L12—
^,т<(п-2ту.
(2х)"-2"
2. Нормировка и ортогональность
JНт (х)Нп (х) ехр(-х2 )dx = 2n п\4л<5тп .
3. Рекуррентные соотношения для полиномов Эрмита
1 z ч dHAx) . „ . .
хНп (х) = пНп_х (х) + - Ня+1 (х), — - 2-пНп_\ (х).
4. Экспоненциальная производящая функция
490
ехр(2л7 - Г) = J Я„ (л ).
5. Асимптотическое поведение при больших значениях п
. 2” ( И+ 1^1 ( Л ]
е "Н„(х) ~ -т=Г ------ cos ху/2п-п — .
у!я < 2 ) V 2)
6. Полиномы Эрмита как собственные функции преобразования Фурье.
г{ехр(-х2 /2)Ни(л')}=7” ехр(-£2 /2)Я„(£),
где
. +оо
F{/W} = .— | exp (ikx) f {x)dx.
л/2я- t,
Полиномы Лежандра.
1. Общее выражение
1 df
2^\dx(
/>(х) =
(х2-1/.
Присоединённые полиномы Лежандра определяются как (здесь всюду тп > 0 )
т т
Р,м(х) = (1-х2Г'2^Р,(х),
ах
р^ (х) = _L (1 - х2 )"'2 -22L (х2 -1)'.
' 2'Я dx‘-m
Присоединённые полиномы Лежандра Р/т) (х) являются решениями уравнения
Лежандра:
Z-. « du (.... т2 \
(1-х2)—--2х------h £(£ + l)----- и = 0.
J dx2 dx I/ l-x2J
2. Ортогональность
f Р<т} (xtP^ (x)dx = 2(^ + m)! <?t,.
3. Рекуррентное соотношение
xPl"’(x) = (~m + i pM w + I+m pM( )
2^ + l ' 2m
Сферические функции (сферические гармоники).
I. Определение: Ylm (0, (р) = I I)? в(Р»в ^CQS
V 4л- (€+|ш|)!
491
Сферические гармоники собственные функции угловой части оператора Лапласа &в<р:
2. Ортонормированность:
/7 2л-
jsina/^\d<pYlnl(04<p')Yt'm,(0,<p) -8tt.Smjn..
о о
3. Теорема сложения
Если х и у - два единичных вектора, задаваемых в сферической системе координат
направлениями (0^) и (02,$?2),то
Р У) = ^7—j- Z W ’ <Рх (#2 ’Ч>2 ) .
+ 1 т=_г
где Ре (х • у) - полином Лежандра степени £.
4. Разложение :—-—г по сферическим функциям
—Хтт-'l У'Лв^<Р^Г„(02^2\ Г1>Г2<
1 _ I г' 2^ + 1 Vi J
I' 2' —Г'<Г2-
I r2 ^2( + 1{г2]
Здесь (0,,^) и (#2,^2) ‘ полярный и азимутальный углы векторов j- и г2.
5. Разложение плоской волны по сферическим функциям
ехр(ikr) = 4л£ £i(j( (kr)Y*m (0к, <рк )Ytm(0,(р),
/=0 т=-£
где 0к ,(рк и 0, <р - углы, задающие ориентацию векторов к и г в пространстве,
j( (£) - сферическая функция Бесселя.
Явные выражения для нескольких сферических функций
ум(М = Р-;
V 4л
У, 0 (0, <р) = cos(0), У,. ±, (0, <₽) = Л- sin^e"9, Y2.„ (0, <р) = JГ| (з cos2 (0) -1)
V 4л V о71 V 471 \ X
К2,±1(0>^) = ^^^(3sin(0)cos(0)e±I^), Y2±2(0,<p) = J^|-(3sin2(6>)e±2/^).
492
Цилиндрические функции Бесселя.
1. Определения.
Функция Бесселя
2 т »а
т
J . ч = у_____V" И____ '
~}т\Г(п1 + а + 1)12 J
а - порядок функции Бесселя.
Функции Бесселя являются решениями уравнения Бесселя
2 d и du 1 2 \ п
х —- + л-----h (х - а )и = 0.
^,.2 Л.. v
Функция Неймана (функция Бесселя второго рода):
Y = Ja{x)cos{a7v)-J a{x)
sin(a^)
В случае целого а выражение следует понимать как предел по а .
Функция Инфелъда (модифицированная функция Бесселя первого рода):
Функция Макдональда (модифицированная функция Бесселя второго рода):
к = я-/а(х)-/а(х)
2 sm(cr^)
В случае целого а выражение следует понимать как предел по а .
2. Интегральные представления:
" О
1 °°
Ка (х) = — ]*ехр(-х ch T)ch(ar)dr.
71 о
3. Асимптотическое поведение.
а) Малые значения аргумента при неотрицательных значениях порядка, 0 < х « Va+1:
— (1п(х/2) + /),
Г(а)Г2Г
а = О,
493
б) Большие значения аргумента, х » а2 -1/4
4 формулы Якоби-Ангера
exp (iz cos ф) = ^i”Jn (z) е?ф {in ф\
5. Теорема сложения
00
(Z1 + Z2 ) ~ (Zl )^п-к (z2 )•
£=-оо
6. Сферические функции Бесселя
и+1 /2 (Х) ’
л+1/2 (Х) •
Сферические функции Бесселя jn (х) являются радиальными частями решений
уравнения Гельмгольца для шара:
2 d2u _ du , 2 , ...
х —- + 2х-----F (х2 — п{п + 1))м = 0.
Л(х) = (-х)"
п
sin X
n„(x) = -(-x)n
и
COS X
и
В частности
z ч sin(x) cos(x)
Ji (*) = —г--------—
( ч cos(x) z ч cos(x) sin(x)
no(x) =------nx{x) =----------------------
494
Оператор Лапласа:
1.
в декартовых координатах
д~и/ д~ш д~у/
дх2 dv* dz^
2. в цилиндрических координатах
1 д . дуг 1 д2у/
г дг дг г д(р
д2у/
3. в сферических координатах
„2 1 й2 I г,. „Зу/ I д\
V w = —— (г(//) + —------------(sin0-----)+ 7 . ?
г дг2 г2 sin# д0 дв г sin 0 д(р
Волновые функции стационарных состояний водородоподобного иона
1. Общий вид
(г,<Р) = (r)Ytm (0, <р),
где Y£m(0,(p) - сферические функции,
2?^ (г) - радиальные части волновых функций.
3/2
Л„,(г) = -
2 l(»-l-l)!c-zrM„
п2 }((п+ ОС’
2Zr
2,X,(2Zr/ao),
Z - заряд ядра атома, а0 - боровский радиус,
Z2^Li (*) -обобщённые полиномы Лагерра, определяемые как
л:(х)=е-х-’£г(х’+'е-).
В частности
£?О) = 1, Z?(x) = l-x, Zj(x) = -1,
^2 (х) = 2 - 4х + X2 , l}2 (х) = -4 + 2х, L22 (х) = 2 ,
1^ (х) - 6 -18х + 9х2 - х3, £3 (х) = -18 +18х - Зх2,
£з(х) = 18-6х, £^(х) = -6.
2. Выписанные в таком виде, радиальные части волновых функций подчинены условию
нормировки
/|л«Дг)|2г2^ = 1.
о
495
Несколько первых радиальных частей волновых функций водородоподобного иона:
Д10(г) = 2(Z /а0)372 exp(-Zr/а0),
R20 (г) = 2(Z / 2я0 )3 7 2 (1 - Zr / 2а0) exp (-Zr / 2а 0,
д;1(г) =-j=(Z / 2а0)”2 Zr/2а0 exp(-Zr / 2а0) ,
(г) = 2(Z / За0 )5'2 Г1 -1 Zr / a„ + ^- (Zr / a„) 2j exp (-Zr / 3u„),
^4i(r) = i^(Z/3a0)3/2(Zr/a0)^l-|zr/a0^exp(-Zr/3a0),
v (r) = —(Z / 3a0)3 7 2 (Zr / a0)2 exp (-Zr / 3a0).
32 27J10
496
Массы, размеры, потенциалы ионизации, спектроскопические характеристики
элементов периодической системы.
Атом- ный номер Элемент Сим- вол Атом- ная масса Электрон- ная конфи- гурация Осно- вной терм Средний радиус, ед. a0 Потенциалы ионизации, (эВ)
I II
1 Водород Н 1.008 15 2S 1.5 13.599 -
2 Гелий Не 4.003 Is2 ]s 0.927 24.588 54.418
3 Литий Li 6.940 2s 2S 3.874 5.392 75.641
4 Бериллий Be 9.013 2s2 's 2.649 9.323 18.211
5 Бор В 10.81 2p 2P 2.205 8.298 25.155
6 Углерод С 12.011 ?-p2 3P 1.743 11.260 24.384
7 Азот N 14.007 Ip3 4S 1.447 14.534 29.602
8 Кислород О 16.00 2P4 3P 1.239 13.618 35.118
9 Фтор F 19.00 2ps 2P 1.085 17.423 34.971
10 Неон Ne 20.179 2p6 's 0.965 21.565 40.964
11 Натрий Na 22.990 3s :S 4.209 5.139 47.287
12 Магний Mg 24.305 3s2 !s 3.253 7.646 15.035
13 Алюминий Al 26.98 ?>P 2P 3.434 5.986 18.829
14 Кремний Si 28.09 ip2 3P 2.788 8.152 16.346
15 Фосфор P 30.974 3p3 4S 2.369 10.487 19.726
16 Сера S 32.06 3p4 3P 2.069 10.360 23.338
17 Хлор Cl 35.453 Зр5 2P 1.842 12.968 23.814
18 Аргон Ar 39.948 3p6 's 1.663 15.760 27.630
19 Калий 39.10 45 2S 5.244 4.341 31.626
20 Кальций Ca 40.08 4s2 ]s 4.218 6.113 11.872
21 Скандий Sc 44.96 3d4s2 2d 3.96 6.562 12.800
22 Титан Ti 47.90 3d2 4s2 3F 3.766 6.74 13.58
23 Ванадий V 50.94 3d3 4s2 4F 3.607 6.74 14.66
24 Хром Cr 51.996 3d54s 7S 3.843 6.767 16.498
25 Марганец Mn 54.94 3d5 4 s2 6S 3.349 7.434 15.640
497
'^26 Железо Fe 55.85 3d6 4s2 5D 3.242 7.870 16.188
""27 Кобальт Со 58.93 3d7 4s2 4F 3.144 7.864 17.083
"^28 Никель Ni 58.70 3$4s2 3F 3.055 7.637 18.169
""29 Медь Си 63.55 3dI04s 2S 3.331 7.726 20.292
Ho Цинк Zn 65.38 3d104s2 's 2.898 9.394 17.965
Hl Галлий Ga 69.72 4s24p 2P 3.424 5.999 20.515
^2 1 Германий Ge 72.59 4s24p2 3P 2.904 7.899 15.934
33 1 Мышьяк As 74.92 4s24p3 4S 2.561 9.789 18.589
Г34 I Селен Se 78.96 4s24p4 3P 2.309 9.752 21.16
35 Бром Br 79.904 4s24p5 2P 2.112 11.814 21.81
" 36 H Криптон Kr 83.80 4s24p6 's 1.952 14.000 24.359
37 Рубидий Rb 85.47 5s 2S 5.632 4.177 27.28
38 Стронций Sr 87.62 5s2 ]s 4.633 5.695 11.030
39 Иттрий Y 88.91 4d5s2 2d 4.300 6.217 12.24
40 Цирконий Zr 91.22 4d25s2 3F 4.078 6.634 13.13
41 Ниобий Nb 92.91 4d*5s 6D 4.207 6.759 14.32
42 Молибден Mo 95.94 4(f5s 7S 4.079 7.092 16.16
43 Технеций Tc [98] 4d55s2 6S 3.650 7.28 15.26
44 Рутений Ru 101.1 4cf5s 5f 3.877^ 7.366 16.76
45 Родий Ro 102.91 4 cP 5 s 4F 3.795 7.46 18.08
46 Палладий Pd 106.4 4d10 's 1.533 8.336 19.43
47 Серебро Ag 107.88 4d105s 2S 3.656 7.576 21.484
48 Кадмий Cd 112.41 Ad^Ss2 3S 3.237 8.994 16.908
49 Индий In 114.82 5s25p 2P 3.778 5.786 18.870
50 Олово Sn 118.69 5s25p2 3P 3.286 7.344 14.632
51 Сурьма Sb 121.75 5s25p3 4S 2.952 8.608 16.53
52 Теллур Те 127.60 5s25p4 3P 2.701 9.010 18.6
53 Иод I 126.90 5s25p5 2P 2.502 10.451 19.131
54 Ксенон Xe 131.30 5s25p6 !S 2.338 12.130 21.21
55 Цезий Cs 132.91 6s 2S 6.30 3.894 25.08
56 Барий Ba 137.33 6s2 ———5 !s 5.25 5.212 10.004
57 Лантан La 138.91 5^6? 2D 4.93 5.577 11.06
498
58 Церий Се 140.12 4f5d6s2 ‘G 4.88 5.539—
59 Празеодим Рг 140.9 4f6s2 4I 5.06 5.473 ~Tol5~
60 Неодим Nd 144.24 4f6s2 5I 5.01 5.526 ~ТотГ
61 Прометий Pm [145] 4f6s2 6H 4.96 5.582
62 Самарий Sm 150.4 rffis2 7F 4.91 5.644~ ~ТГ07'
63 Европий Eu 151.96 4f6s2 8S 4.86 5.670 ~VL24~
64 Г адолиний Gd 157.25 4f5d6s2 9d 4.58 6.150 IZOF
65 Тербий Tb 158.93 4/bs2 6H 4.77 5.864 11.52
66 Диспрозий Dy 162.50 4f°6s2 5I 4.73 5.939 11.67
67 Г ольмий Ho 164.93 tf^s2 4I 4.69 6.022 11.80“"
68 Эрбий Er 167.26 4f26s2 3H 4.65 6.108 11.93
69 Тулий Tm 168.93 4/36s2 2f 4.61 6.184 12.05
70 Иттербий Yb 173.04 4f46s2 's 4.57 6.254 12.76
71 Лютеций Lu 174.97 4f45d6s2 2d 4.27 5.426 12.97
72 Г афний Hf 178.49 Sd^s2 3F 4.08 6.454 13.78
73 Тантал Ta 180.95 ScPbs2 4F 3.94 7.89 14.47
74 Вольфрам W 183.85 5d*6s2 5D 3.82 7.98 15.08
75 Рений Re 186.21 Scfbs2 6S 3.72 7.88 15.73
76 Осмий Os 190.2 5<P6s2 5d 3.62 8.73 16.34
77 Иридий Ir 192.2 5d76s2 4f 3.53 9.05 16.91
78 Платина Pt 195.09 5cf6s 3D 3.72 8.96 18.563
79 Золото Au 196.97 5d106s 2S 3.70 9.226 20.56
80 Ртуть Hg 200.59 5d106s2 }s 3.33 10.438 18.756
81 Таллий T1 204.37 6 s2 6p 2P 3.92 6.108 20.428
82 Свинец Pb 207.21 6s26p2 3P 3.42 7.417 15.032
83 Висмут Bi 208.98 6s26p3 4S 3.08 7.285 16.69
84 Полоний Po [209] 6s26p4 3P 8.417 17.18
85 Астат At [210] 6s26p5 2P - 9.224 19.10
86 Радон Rn [222] 6s26p6 's 2.54 10.749 20.99
87 Франций Fr [223] 7s 2S - 4.073 20.02
88 Радий Ra 226.03 7s2 's - 5.279 10.147
89 Актиний Ac 227.03 6d7s2 2d - 5.17 11.04
499
^90 Торий То 232.04 6d27s2 3 5.00 6.08 11.90
^91 Протактиний Ра 231.04 Sfadls2 4K 5.35 5.89 11.46
Уран и 238.03 Sfadls* TL 5.08 6.194 11.63
^93 Нептуний Np 237.05 5fbdls2 6L - 6.266 11.80
Плутоний Pu [244] 5/7? 7F 5.18 6.06 11.19
"^9? Амерций Am [243] 5/7? •s 5.99 12.15
9(Г Кюрий Cm [245] 5fbdls2 9d 6.02 12.36
^"97 Берклий Bk [247] Sfls* SH 6.23 12.57
L^98 Калифорний Cf [249] 5j,07s2 5I 6.30 11.83
99 Эйнштейний Es [254] 5/'7s2 4I 6.42 11.98
"100 Фермий Fm [253] Sfls2 3H 6.50 12.14
—101 Менделевий Md [255] 5/37s2 2f 6.58 12.29
" 102 Нобелий No [255] 5f47s2 's 6.65 12.45
103 Лоуренсий Lr [257] Sf46d7s2 2d 4.312 14.00
104 Резерфордий Rf [261] 6d27s2
“ 105 Дубний Db [262] 6d37s2
106 Сиборгий Sg [263] 6J7s
107 Борий Bh [262] 6d57s
108 Хассий Hs [264] 6Jls
109 Мейтнерий Mt [266] 6d77s
Примечания.
1) В квадратных скобках указаны массовые числа наиболее устойчивых изотопов данного
элемента.
2) Основные термы всех элементов заданы в приближении LS связи. Это приближение
нарушается для тяжелых атомов, поэтому представленные данные для тяжелых атомов
достаточно условны.
3) Под средним радиусом атома понимается среднее удаление валентного электрона от
атомного ядра. Эта величина рассчитывалась по формуле
00
= р3|^|2^г,
о
где одноэлектронная радиальная волновая функция была получена путем разложения в ряд
по базису слэтеровских атомных орбиталей.
500
Параметры некоторых двухатомных молекул.
Моле- кула Основной электрон- ный терм Потенциал ионизации, эВ Равновесное межъядер! юе расстояние, А Колебате- льный квант, эВ Вращатель- ная посто- янная^*^, эВ Энергия диссоци- ации, эВ
н2+ 2E 29.9 1.06 0.285 3.70(-3) 2.649
Н2 ’e 15.426 0.741 0.545 7.55(-3) 4.48
n2 ’e 15.580 1.098 0.293 2.48(-4) 9.76
О2 -e 12.077 1.207 0.196 1.79(-4) 5.12
f2 'E 15.686 1.417 0.141 1.10(-4) 1.38
С12 ’E 11.48 1.988 0.069 2.08(-5) 2.50
Br2 ’E 10.56 2.281 0.040 1.01 (-5) 1.97
I2 ’S 9.4 2.666 0.027 4.64(-6) 1.54
L12 ’E 5.15 2.67 0.044 8.35(-5) 1.03
НС1 'E 12.74 1.275 0.371 1.30(-3) 4.43
HBr 'E 11.62 1.414 0.329 1.04(-3) 3.75
HI '27 10.38 1.609 0.287 7.98(-4) 3.06
LiH 'E 7.85 1.595 0.174 9.34(-4) 2.43
Na2 'E 4.90 3.077 0.020 1.92(-5) 0.75
NaCl 'E 8.92 2.361 0.045 2.71(-5) 4.3
CO ‘E 14.014 1.128 0.269 2.40(-4) 11.09
NO 2n 9.264 1.151 0.237 2.12(-4) 6.50
OH 2n 13.18 0.971 0.464 2.34(-3) 4.40
CN 2e 14.20 1.172 0.257 2.36(-4) 7.75
CH 2n 10.9 1.120 0.355 1.76(-3) 3.45
(*} Число 3.70(-3) следует читать как 3.70 • 10~3.
501
Длины волн и силы осцилляторов переходов некоторых атомных переходов.
Атом_ Переход Длина волны, A Сила осциллятора
"'н l.v —> 2р 1215.7 0.416
Lv —> Зр 1025.7 0.079
kv —> 4р 972.5 0.029
2s —>3р 6562.7 0.435
2р —>35 6562.9 0.0136
2р —> 3d 6562.8 0.696
2s —> 4р 4861.29 0.103
2р —> 45 4861.35 0.0030
2р —> 4d 4861.33 0.122
Не \s2(xS)^>\s2p(xP) 584.3 0.276
is2('S')->is3x1/’) 537.0 0.0734
522.2 0.030
1525(’S) -> ls2p(x Р) 20581.3 0.376
1525(,S)->153p(’P) 5015.7 0.151
1525(’5) -> ls4p(xP) 3964.7 0.14
1525(3S) -> ls2p(3P) 10830 0.539
ls2sCS)^is3p(3P) 3888.6 0.0645
\s2s(3S)-^ls4p(3P) 3187.7 0.023
Li 251/2 “* ^P\/2 6707.91 0.251
2s^2 —> 2p3/2 6707.76 0.502
2P\/2 ~* ^S\/2 8126.23 0.115
2Рз/2 ~3Sy2 8126.45 0.115
Na 35(/2 —» 3/?|/2 5895.9 0.324
35j/2 —> 3/?3/2 5889.9 0.648
ЗЛ’1/2 —> 4/>!/2 3303.9 0.051
35|/2 —> 4py2 3302.9 0.102
^P\/2 ~* ^1/2 22084.0 0.167
^A/2 “* ^5l/2 22057.0 0.335
К 45i/2 -> 4/>1/2 7699.0 0.347
451/2 -> 4p3/2 7664.9 0.684
4/>|/2 ~* ^Л’1/2 12434.3 0.051
4A/2 ^Л1/2 12523.0 0.102
502
Rb 5.V|/; —> 5/?|/2 7947.6 0.363
^•S'l/2 “> ^/;.V2 7800.23 0.726
5/?|/2 -> 6.v1/2 13237.3 0.187
5 /Л/2 -> 6‘S'l/2 13667.0 0.364
Cs 6.S’|/2 —> 6/2,/2 8943.5 0.394
5.v1/2 -> 6p3/2 8521.2 0.814
6p}/2 -> 7.y1/2 4593.2 0.00284
^P\/2 —* 7Py2 45554.4 0.0174
Be 2s2 -+2s2p('P) 2348.61 1.36
2s2p(]P)-^2s3sCS) 8254.1 0.13
2s2p(} P)-^2s3d('D) 4572.7 0.19
2s2p(3 P)—>2s3s(3S) 3321.2 0.034
2s2p(3 P)—>2s3d(3D) 2494.6 0.16
2s2pCP)^2p2CP) 2650.6 0.466
В 2s2 2 p —> 2s235 2497.4 0.11
2s22p-*2s23d 2089.3 0.24
2s23s^2s23p 11661 1.07
2s22p^2s2p2(2D) 2089.3 0.24
2s22p ^2s2p2CS) 1573.5 0.16
Mg 3s2 ->3s3pCP) 2852 1.2
3s2 ->3s3p(3P) 4571.1 2.6 10^
Al 3s23X42)^35245(2S1/2) 3944.0 0.15
3?3X23’3/2)^3?4X2s]/2) 3962.0 0.15
3?3X2P3/2)^3524rf(2D3/2.5/2) 3092.0 0.23
3?3/2(2^2)^3.v24rfr2Z'),2) 3089.0 0.22
•сциллятора перехода i —> f (J, f - совокупности квантовых чисел начального и
ого состояний атома) определяется с помощью следующего выражения
F 2
f‘ g, 3te2 71 ’
- частота перехода, d# - матричный элемент дипольного момента атома, g{ — 2J
эсть вырождения начального состояния (J - квантовое число полного механического
а атома). Вероятность перехода в единицу времени из состояния р) в состояние \f)
1яется выражением
503
2е2лЛ
РреМЯ
жизни относительно спонтанного перехода состояния |/) определяется как
, сумма берется по всем ниже лежащим состояниям.
Метастабильные состояния атомов.
Атом Состояние Энергия возбуждения, эВ Время жизни, с
' Н 2s 10.20 0.142
Не ls2s(3S) 19.82 6 Ю5
\s2s?S) 20.61 0.038
N 2p3CD5/2) 2.384 6-104
2p3Cd3/2) 2.385 1.4 Ю5
2p\2P) 3.58 13
О 2p\'D2) 1.97 110
2p\'S) 4.19 0.8
504
Ненулевые компоненты тензора квадратичной восприимчивости в кристаллах с
определенной симметрией1
класс симметрии решетки международное обозначение (2) Тензор %аРг Число ненулевых компонент тензора^
моноэдрический 1 ххх хуу xzz xyz xzy xzx xxz xxy xyz yxx yyy yzz yyz yzy yzy yxz yxy yyx zxx zyy zzz zyz zzy zzx zxz zxy zyx 27
ромботетраэдрический 222 0 0 0 xyz xzy 0 0 0 0 0 0 0 0 0 yzx yxz 0 0 0000000 zxy zyx 6
ромбо-пирамидальный mm2 0 0 0 0 0 xzx xxz 0 0 0 0 0 yyz yzy 0 0 0 0 zxx zyy zzz 0 0 0 0 0 0 7
моноклинно- доматический ш xxx xyy xzz 0 0 xzx xxz 0 0 0 0 0 yyz yzy 0 0 уху yyx ^xx zyy zzz 0 0 zzx zxz 0 0 14
Ненулевые компоненты тензора кубической восприимчивости в изотропной среде.
Тензор кубической восприимчивости содержит 81 компоненту. Число отличных от
нуля компонент зависит от типа симметрии кристалла. В изотропных средах выполнены
следующие условия для ненулевых компонент тензора (все остальные компоненты равны
нулю)2:
лххх = ууууу = zzzz
yyzz = zzyy = zzxx = xxzz = xxyy = yyxx
yzzy = zyyz = zxxz = xzzx = xyyx = yxxy
yzyz = zyzy = zxzx = xzzx = xyxy = yxyx
xxxx = xxyy + xyxy + xyyx
1 Здесь введены обозначения XXX =
2 Аналогично xxxx = > W = /X
.(2)
xyz и так далее.