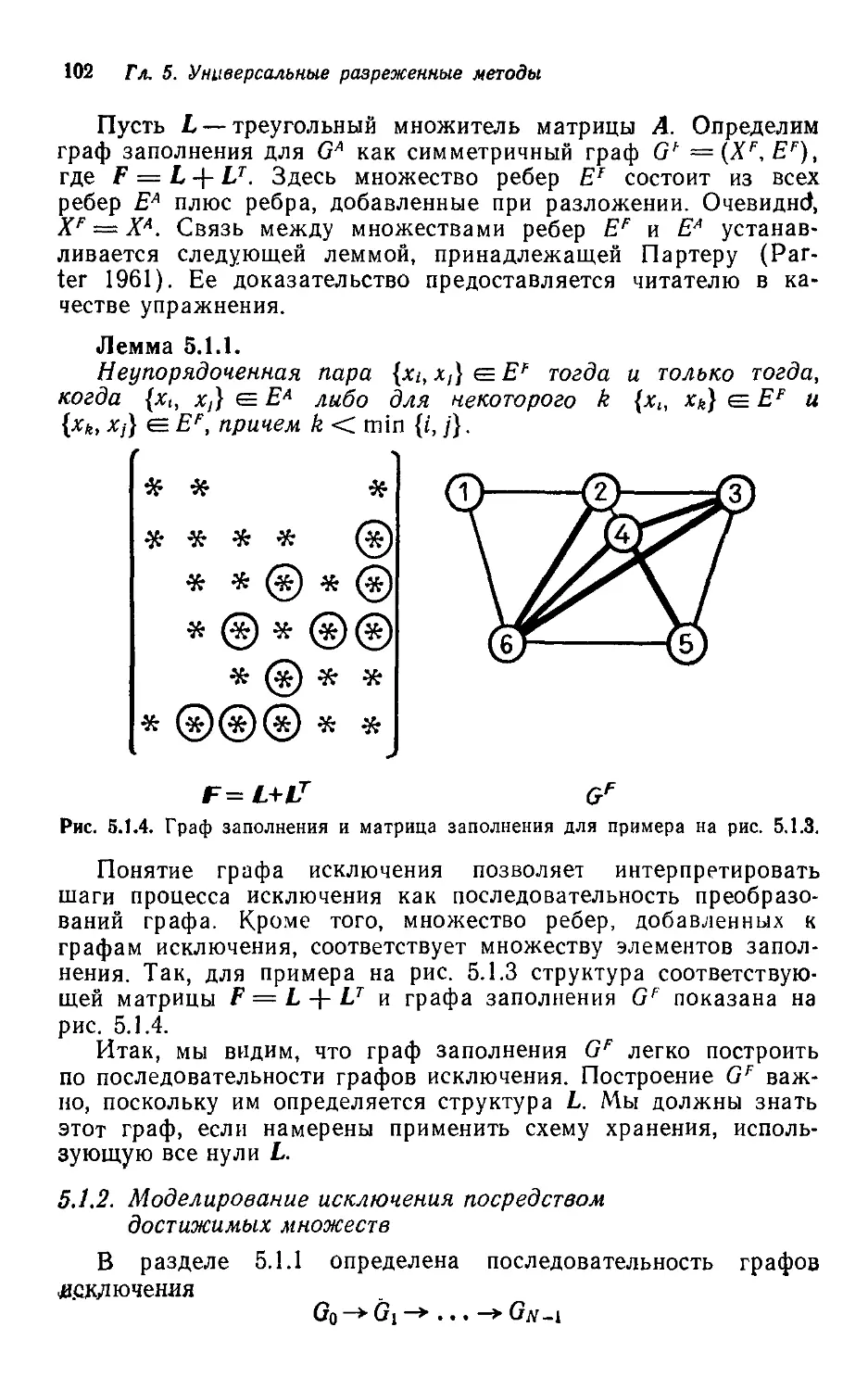
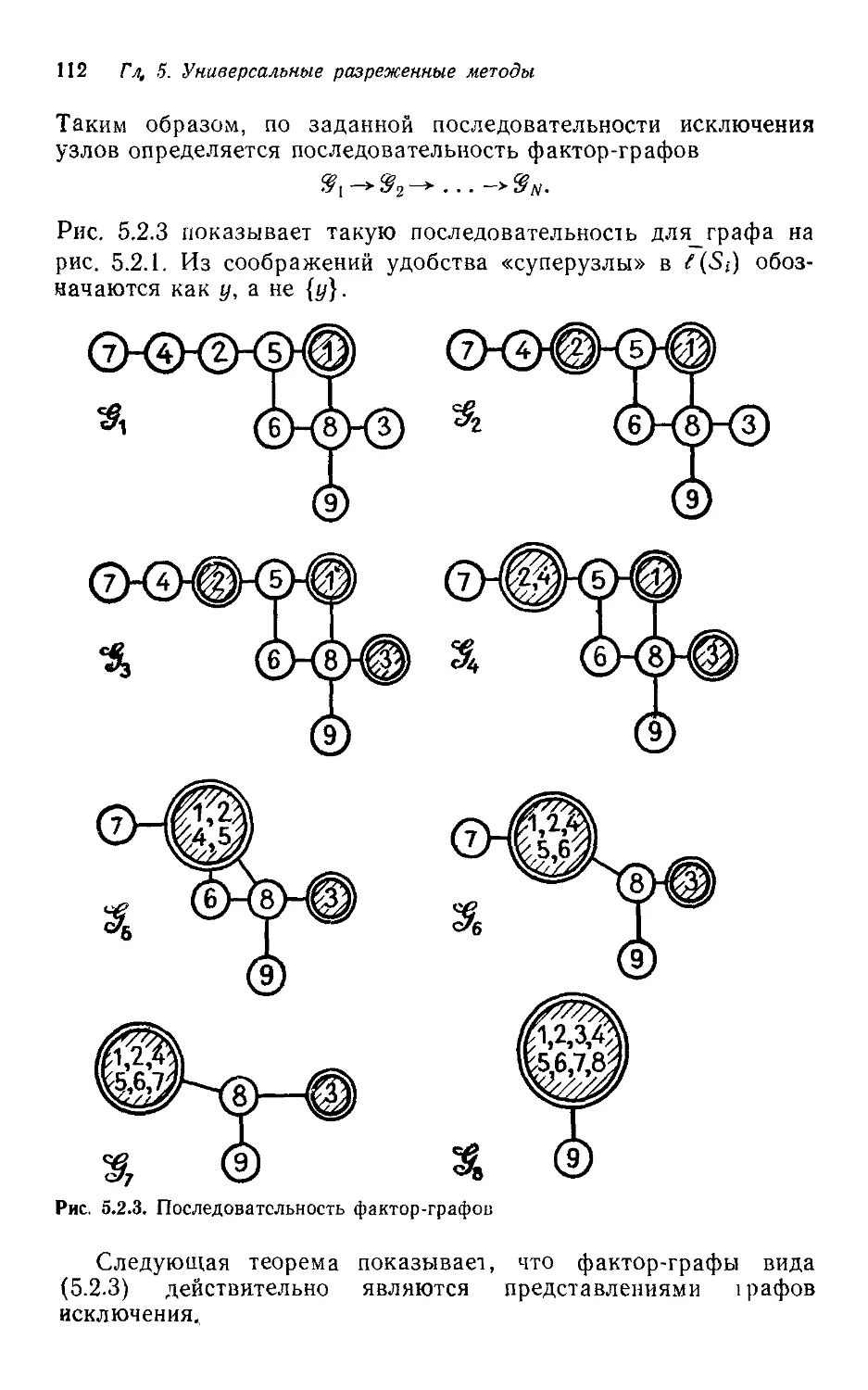
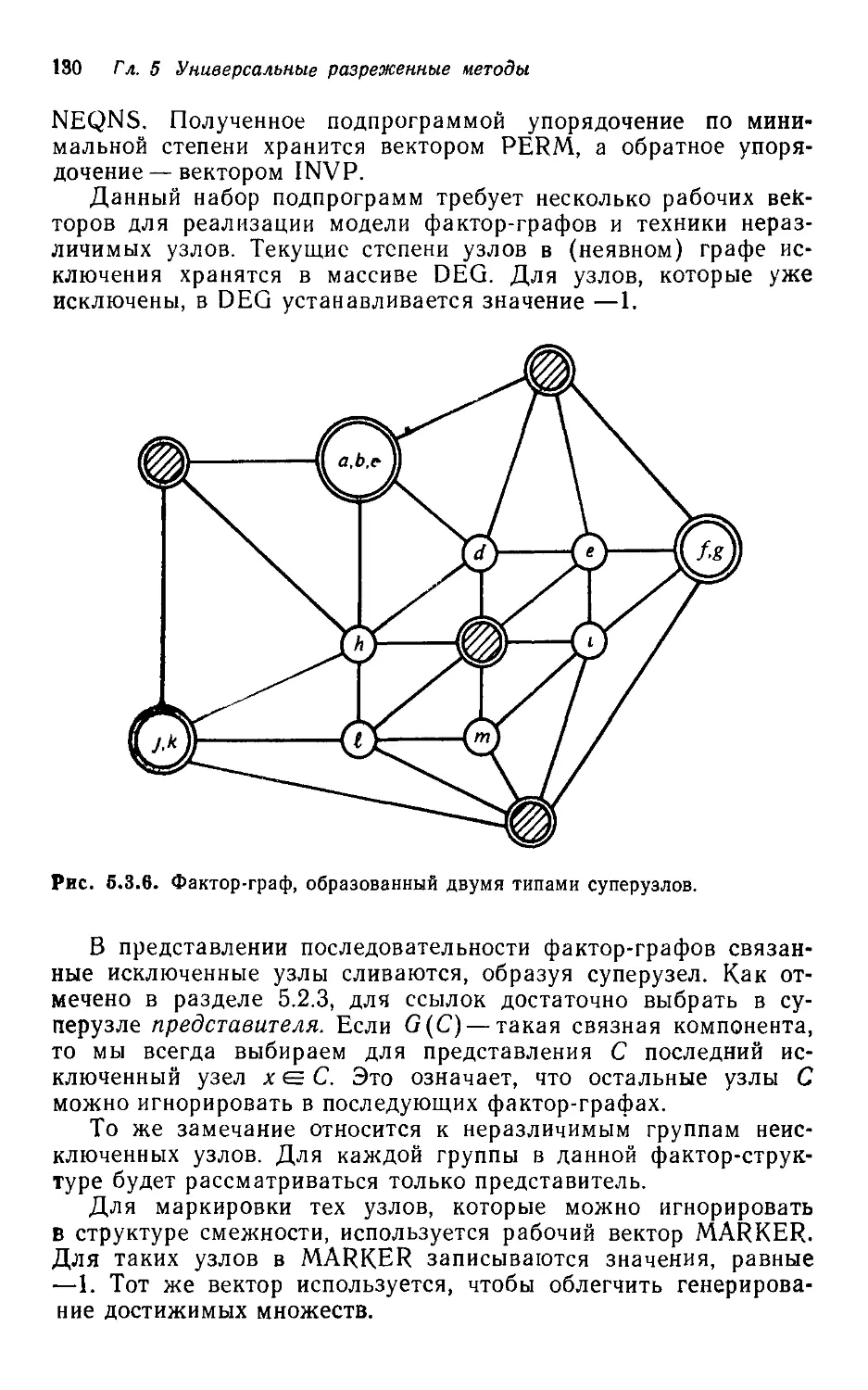
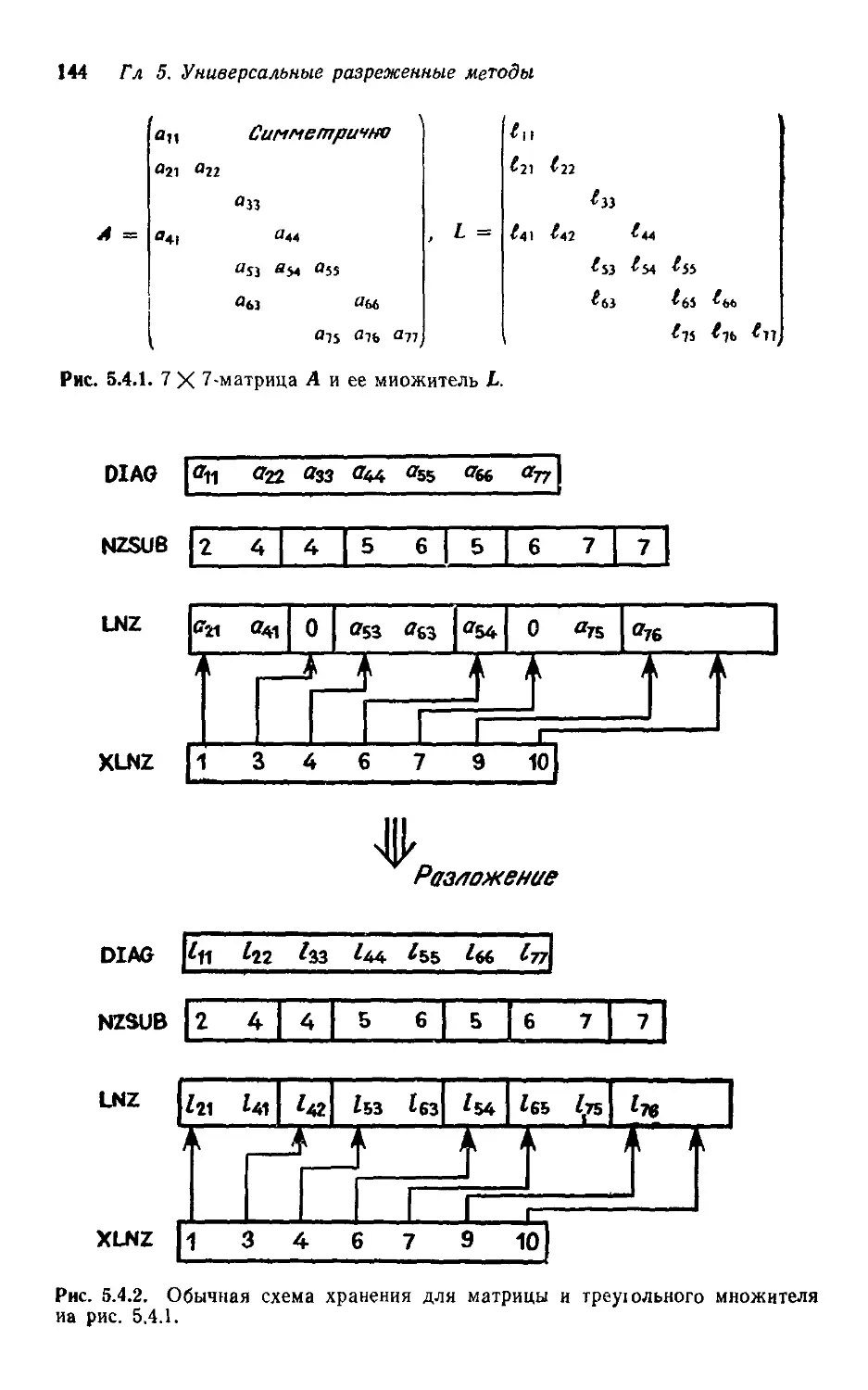
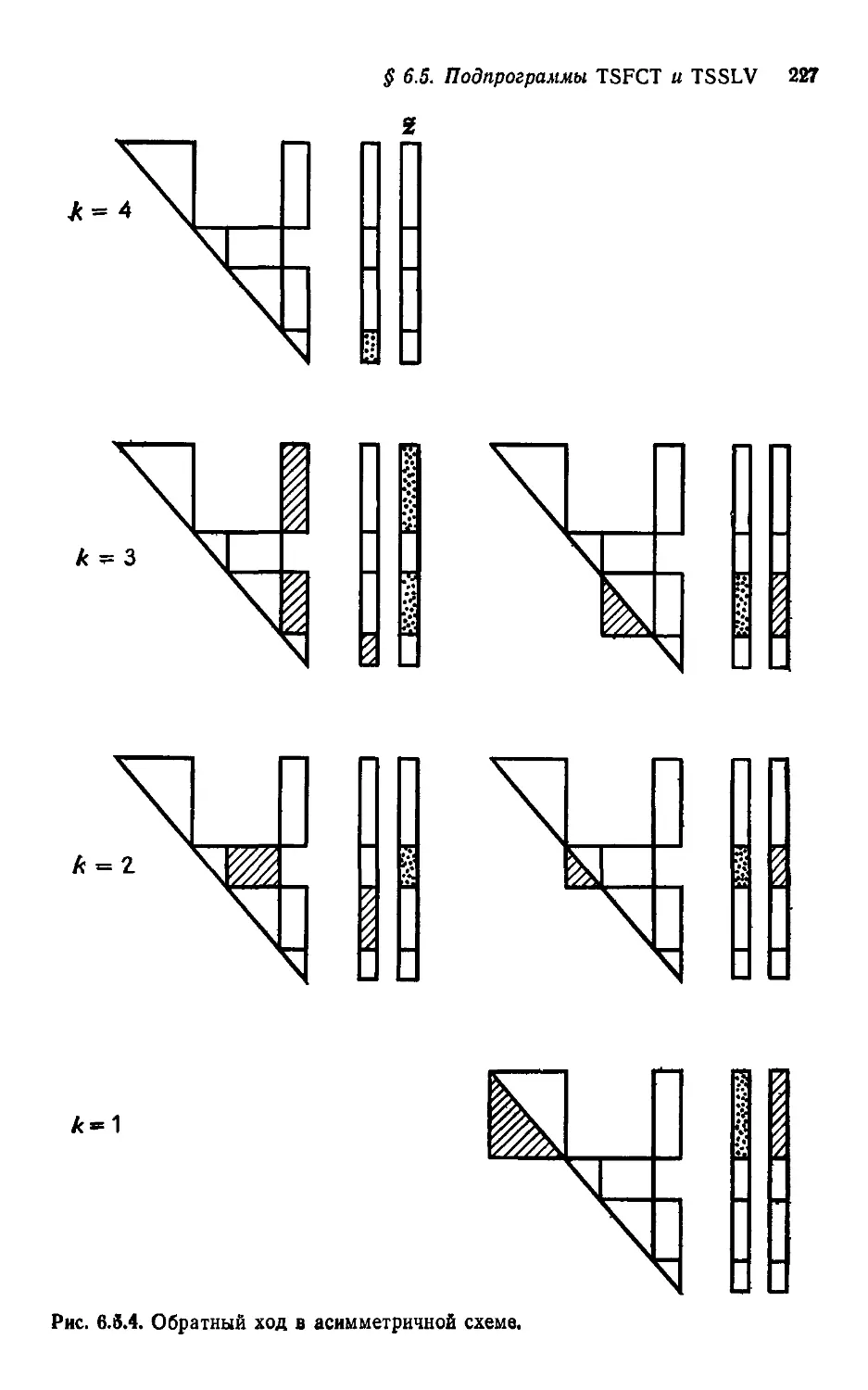
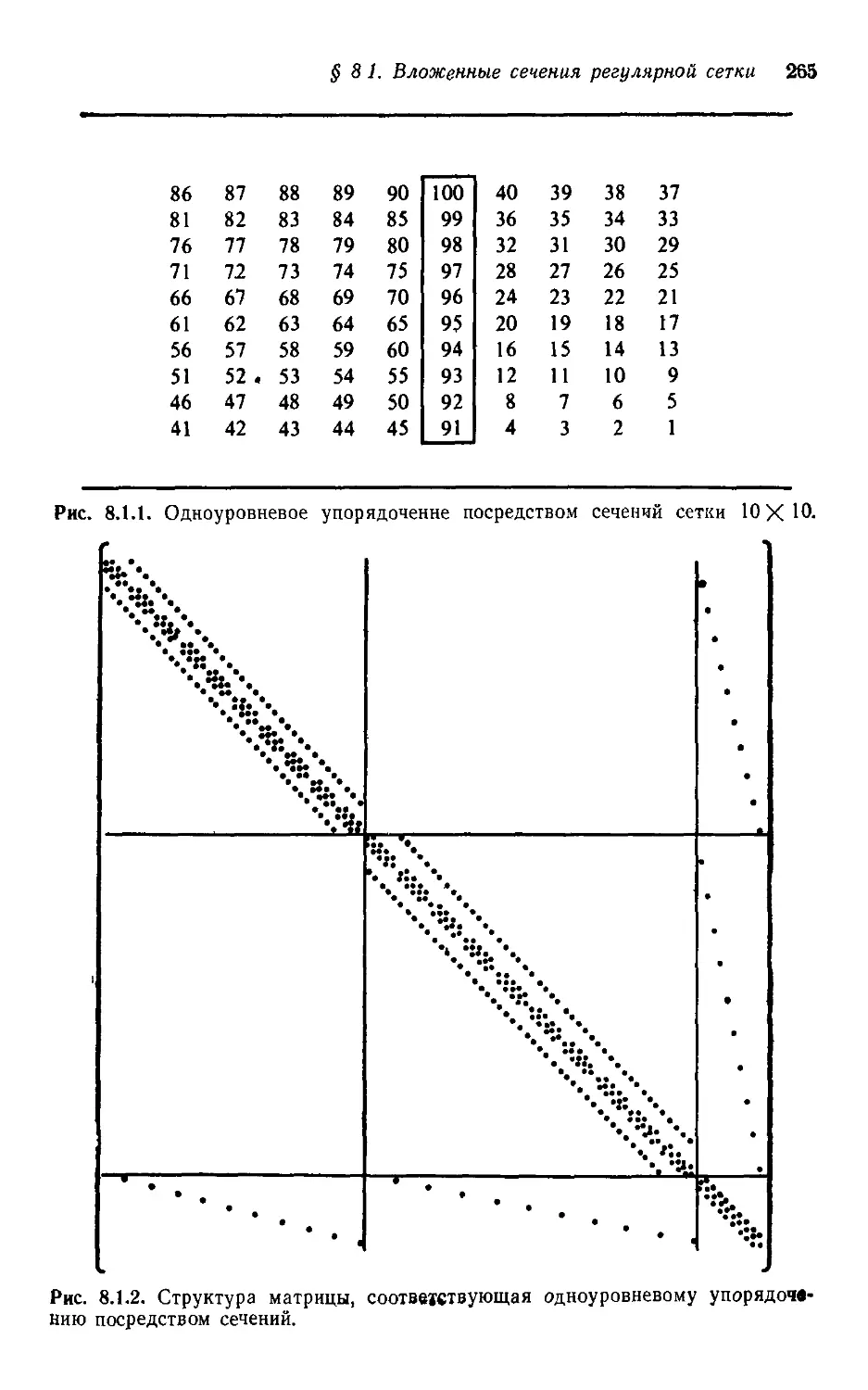
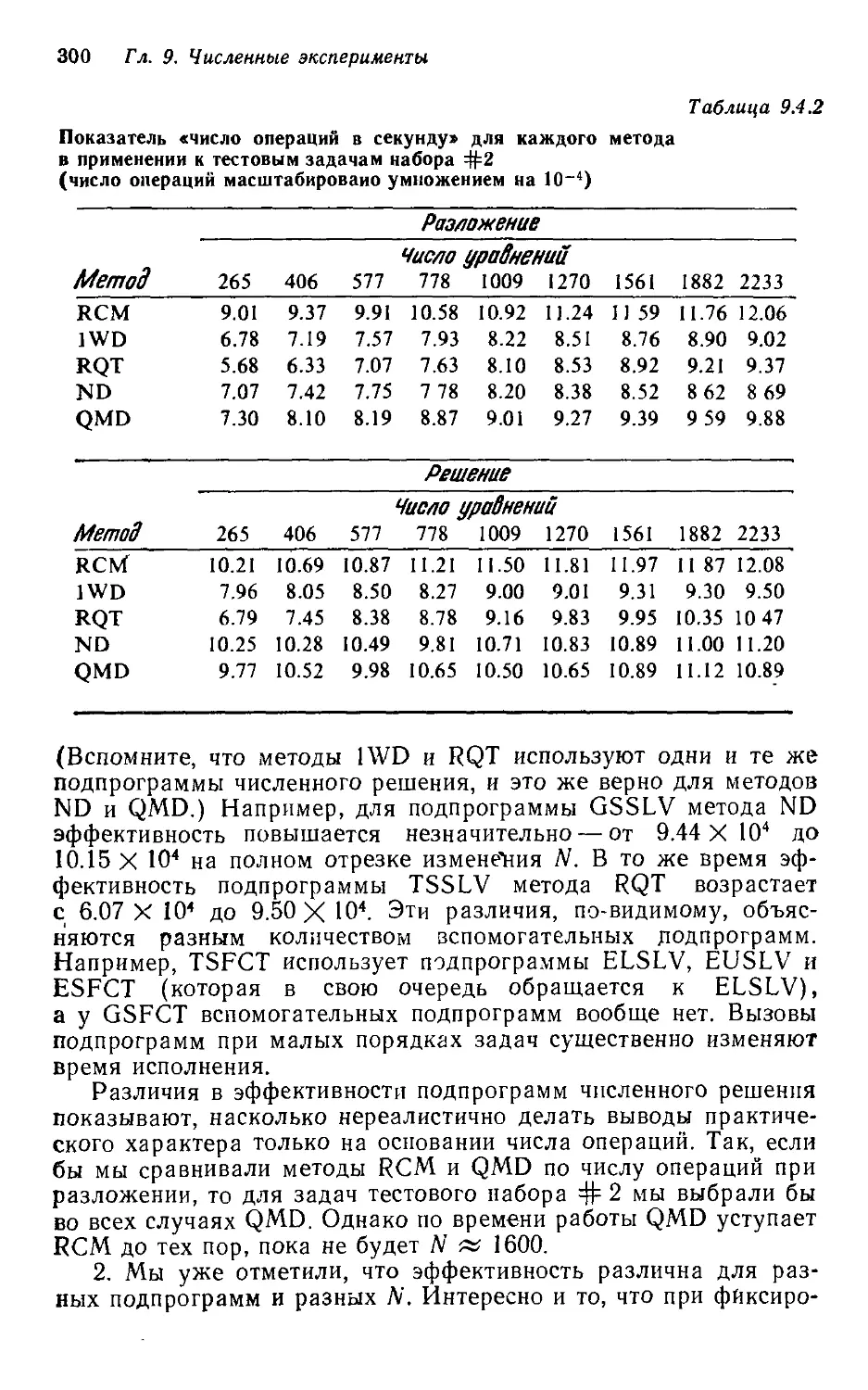
Текст
Alan George
University oj Waterloo
Waterloo, Ontario
Joseph W-H Liu
Computer
Solution
of Large Sparse
Positive
Definite
Systems
Prentice-Hall, Inc,
Englewood Cliffs,
New Jersey 07632
1981
А. Джордж
Дж.Лю
Численное
решение
больших
разреженных
систем
уравнений
Перевод с английского
X Д. Икрамова
Москва
«Мир»
1984
ББК 22.193
Д42
УДК 512.8 + 518.12
Джордж А, Лю Дж.
Д42 Численное решение больших разреженных систем урав-
уравнений: Пер. с англ. — М.: Мир, 1984. — 333 с, ил.
В книге известных американских математиков-вычислителей описаны все
основные методы решения разреженных положительно определенных линейных
систем Впервые в монографической литературе излагаются алгоритмы параллель-
параллельных и вложенных сечений, разработанные А Джорджем и предназначенные для
систем метода конечных элементов Включены тексты фортранных программ,
реализующие описанные методы
Для математнков-прикладников, для всех, кто связан с решением разрежен-
разреженных линейных систем, для студентов и аспирантов факультетов прикладной ма-
математики
1702070000-051
Д 041@1)—84 37~84' Ч> ' ББК 518
Редакция литературы по математическим наукам
ф 1981 by Prentice Hall, Inc., Englewood Cliffs, N.J,
© Перевод на русский язык, «Мир>, 1984
От переводчика
Книга американских математиков Джорджа и Лю посвящена
вопросам машинной реализации метода Холесского для решения
линейных систем с симметричными положительно определен-
определенными матрицами. Системы предполагаются разреженными; в то
же время, как правило, допускается использование только опе-
оперативной памяти. При таком серьезном ограничении повышение
порядка решаемых систем возможно лишь за счет максималь-
максимальной эксплуатации их разреженности.
Центральная проблема в методах исключения — это способ
выбора главных элементов. Для систем общего вида обычно
принимается компромисс между требованием численной устойчи-
устойчивости процесса и желанием по возможности сохранить разре-
разреженность матрицы. При этом использование разреженности
основывается исключительно на структуре матричного графа,
в то время как выбор по устойчивости зависит от числовых зна-
значений элементов. Отсюда следует, что для класса систем общего
вида с различными матрицами одинаковой структуры априор-
априорный выбор порядка исключения, вообще говоря, невозможен.
Иначе обстоит дело в симметричном положительно опреде-
определенном случае. Здесь численная устойчивость обеспечена при
любом порядке исключения, что позволяет подчинить выбор
главных элементов единственной цели — наиболее полному ис-
использованию разреженности.
В книге представлены — и реализованы в виде фортранных
подпрограмм — все основные современные подходы к обработке
разреженных структурно симметричных систем: методы, ориен-
ориентированные на уменьшение профиля; методы, основанные на
локальной минимизации заполнения (алгоритм минимальной
степени); блочные методы; -наконец, методы сечений для конеч-
ноэлементных систем. В каждый из названных методов, либо в
теоретическую разработку, либо в практическую реализацию,
авторы внесли собственный значительный вклад. В особенности
это относится к Алану Джорджу — одному из ведущих амери-
американских экспертов по разреженным матрицам. Имя Джорджа
известно советским специалистам главным образом в связи с
разработанным им оригинальным алгоритмом упорядочения
плоских конечноэлементарных графов. В нашей литературе этот
6 От переводчика
алгоритм обычно называют методом гнездовых или крестовых
сечений (разбиений). В предлагаемом переводе принят третий
вариант названия — алгоритм вложенных сечений Этим терми-
термином, по-видимому правильнее всего отражающим существо ме-
метода, я обязан В. Д. Чубаню
Книга адресована широкому кругу читателей — вычислителей
и инженеров, — занимающихся решением больших разреженных
систем. Она может составить основу спецкурса для студентов
факультетов прикладной математики. Для понимания мате-
материала достаточно скромной математической подготовки — зна-
знания вводного курса линейной алгебры и языка Фортран.
Можно сказать без преувеличения, что книга Джорджа и Лю
отражает самый передовой уровень математического обеспече-
обеспечения в данной области. Советскому читателю она принесет боль-
большую пользу.
X. Икрамов
Предисловие
Назначение этой книги — ввести читателя в важную практи-
практическую задачу машинного решения больших разреженных систем
линейных уравнений. У этой проблемы много граней —от фун-
фундаментальных вопросов, касающихся внутренней сложности не-
некоторых задач, до менее точно определенных вопросов, связан-
связанных с построением эффективных структур данных и составле-
составлением машинных программ. Чтобы ограничить объем книги и
при этом не пожертвовать подробностью изложения, мы решили
сузить ее предмет случаем симметричных положительно опреде-
определенных систем уравнений. Такие системы возникают очень часто
в различных областях науки и инженерных приложениях По
тем же причинам мы ограничиваемся разбором только одного
конкретного метода в рамках каждого общего подхода к реше-
решению больших разреженных положительно определенных систем.
Например, среди многих методов приближенной минимизации
ширины ленты матрицы мы выбрали лишь один, который в на-
нашей практике показал себя достаточно хорошо. Наша цель —
познакомить читателя с важнейшими идеями, а вовсе не предло-
предложить метод, который обязательно будет самым эффективным
для интересующей его конкретной задачи. Мы надеемся, что,
ознакомившись с книгой, читатель сможет вынести обоснован^
ные суждения относительно применимости и полезности изла-
излагаемых в ней идей и методов решения разреженных систем.
Характеристики алгоритмов для разреженных матриц могут
очень сильно зависеть от качества их машинной реализации;
сложность же реализации весьма различна для разных алго-
алгоритмов. Поэтому, хотя анализ алгоритмов для разреженных
матриц с помощью карандаша и бумаги полезен, он отнюдь не
достаточен. Мы считаем, что изучение и использование подпро-
подпрограмм, реализующих такие алгоритмы, является существенной
составной частью хорошего вводного курса в эту важную об-
область научных вычислений Исходя из этого, мы включили в
книгу листинги фортранных подпрограмм и их подробное обсуж-
обсуждение. В Приложении А описана процедура доводки подпро-
подпрограмм до состояния, при котором они полностью готовы к вводу
в машину.
Мы благодарны Мэри Уонг за превосходное качество пере-
перепечатки первоначального варианта рукописи, а Энн Трип де Рош
8 Предисловие
и Эзер Пант — за терпеливость при печатании многочисленных
переделок. Мы признательны также многим нашим студентам
за помощь в устранении ошибок, содержавшихся в ранних вер-
версиях книги. Особой благодарности засл>живают Хамза Рашваи
и Эсмонд Нг, тщательно проверившие ее окончательный вариант.
Написание книги заняло у нас много времени, которое иначе
принадлежало бы нашим женам и детям. Мы благодарим своих
жен за терпение и понимание и посвяшаем эту книгу им.
Алан Джордж
Джозеф Лю
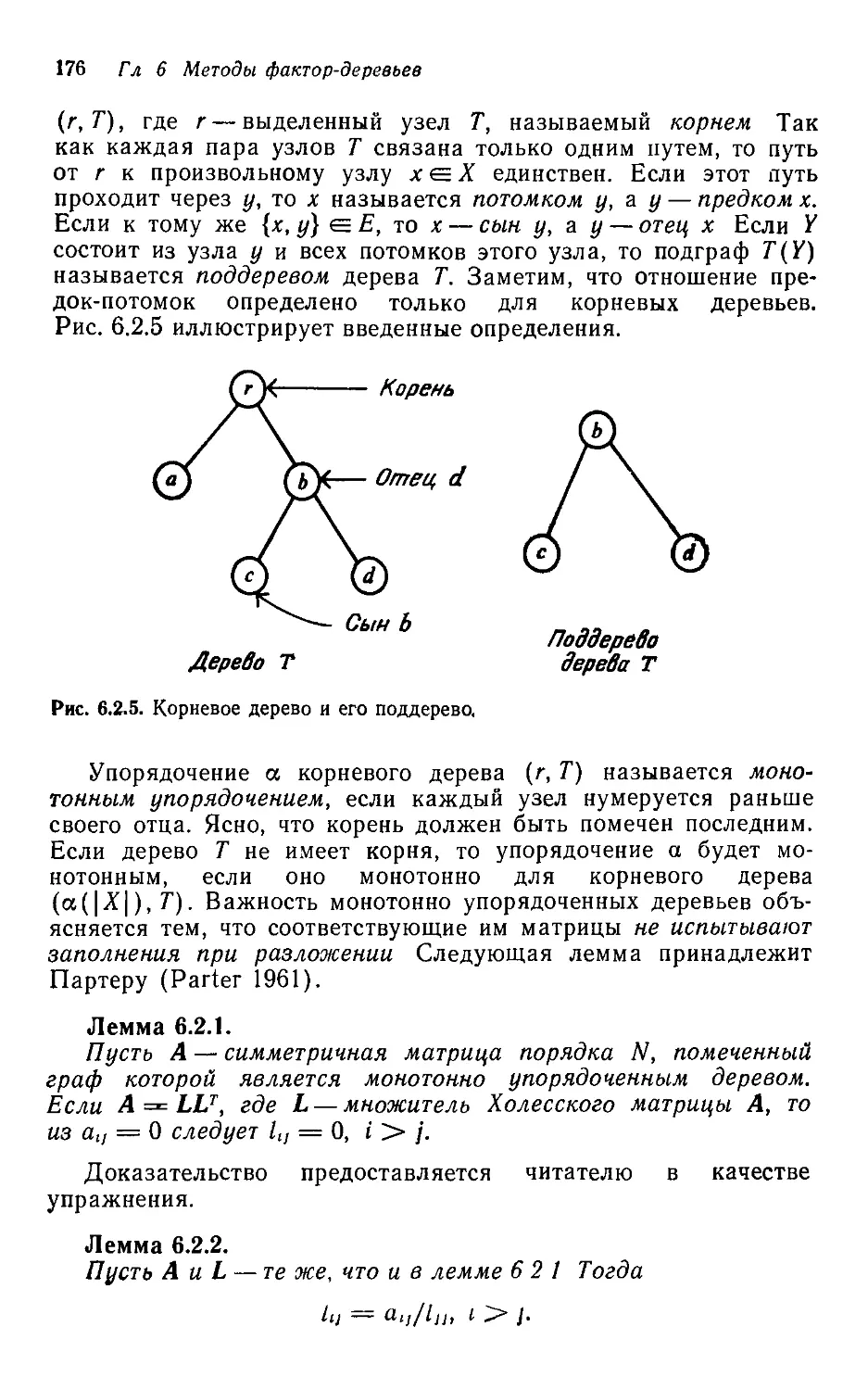
/. Введение
§ 1.0. Об этой книге
В нашей книге речь идет об эффективных машинных методах
для решения больших разреженных систем линейных алгебраи-
алгебраических уравнений. Предполагается, чго читатель усвоил начала
линейной алгебры и знаком со стандартными матричными обо-
обозначениями и операциями. Полезно было бы и знакомство с тер-
терминологией теории графов, однако оно не является обязатель-
обязательным, поскольку все необходимые понятия и обозначения будут
введены там, где они нужны.
Это книга о вычислениях, и в ней содержится ряд фортран-
ных подпрограмм, предназначенных для изучения и использо-
использования. Поэтому читатель должен хотя бы в некоторой мере
владеть Фортраном, а в идеальном случае иметь доступ к вы-
вычислительной машине, с тем чтобы пропускать программы, ис-
использующие подпрограммы из этой книги. Успешность алгорит-
алгоритмов для разреженных матриц, возможно, более, чем в какой-
либо другой области вычислений, зависит от качества их
машинной реализации, т. е. машинной программы, исполняю-
исполняющей алгоритм. Реализация этих алгоритмов связана с использо-
использованием довольно сложных схем хранения, и степень сложности
весьма различна для разных алгоритмов. Некоторые алгоритмы,
очень привлекательные «на бумаге», совсем не таковы на прак-
практике вследствие усложненности и неэффективности их реализа-
реализации. Другие, теоретически не столь красивые алгоритмы могут
оказаться более практичными, поскольку их реализация проста
и требует лишь очень небольших «накладных расходов».
По этим и другим причинам, которые прояснятся позднее,
мы включили в книгу фортранные подпрограммы, реализующие
многие из обсуждаемых в ней алгоритмов. Мы приводим также
результаты некоторых численных экспериментов, иллюстрирую-
иллюстрирующие отмеченные выше проблемы реализации и дающие чита-
читателю некоторую информацию о времени и памяти, необходимых
для вычислений с разреженными матрицами на типовой ма-
машине. Подпрограммы были тщательно оттестированы; они напи-
написаны на машинно-независимом подмножестве Фортрана (Ryder
1974) и без каких-либо изменений они должны правильно рабо-
работать для большинства машинных систем. Они будут полезным
10 Г Л 1 Введение
дополнением к библиотеке любого вычислительного центра, вы-
выполняющего научные расчеты. У авторов можно пол>чшь запи-
записанные на ленту копии подпрограмм вместе с тестовыми зада-
задачами, обсуждаемыми и используемыми в главе 9.
Мы надеемся, что эта кнша будет полезна по крайней мере
в двух отношениях. Во-первых, она может служить учебником
для студентов-старшекурсников и аспирантов факультетов при-
прикладной и вычислительной математики, а также инженерных
специальностей. Упражнения в конце каждой главы имеют
целью проверку усвоения материала читателем, указание на-
направлений дальнейшего исследования и конкретных важных
задач. Некоторые упражнения требуют использования и/или
модификации составленных нами программ, поэтому желательно
иметь доступ к машине, оснащенной для работы на Фортране,
с необходимыми программами в библиотеке.
Книга должна послужить также полезным справочником для
научных работников и инженеров, которым приходится решать
задачи с большими положительно определенными матрицами.
Несмотря на специальность рассматриваемого класса задач,
существенная часть (а возможно, и большинство) линейных си-
систем, возникающих в научных и инженерных расчетах, обладает
этим свойством Это достаточно большой класс для того, чтобы
заслуживать отдельного рассмотрения. Вдобавок, как мы уви-
увидим позже, решение задач с большими, разреженными положи-
положительно определенными матрицами коренным образом отличается
от решения задач общего вида.
§ 1.1. Метод Холесского и проблема упорядочения
Все методы, обсуждаемые в книге, основаны на единствен-
единственном численном алгоритме, известном как метод Холесского, —
симметричном варианте гауссова исключения, скроенном для
симметричных положительно определенных матриц. Мы опре-
определим этот класс матриц и детально опишем метод в § 2.1.
Предположим, что система уравнений, которую нужно решить,
есть
Ах = Ь, A.1.1)
где А— N~X.N симметричная положительно определенная ма-
матрица коэффициентов, Ь — вектор длины N, называемый правой
частью, а х — вектор-решение длины N, компоненты которого
должно вычислить. Применение к А метода Холесского приво-
приводит к треугольному разложению
A = LLT, A.1.2)
1*де L — нижняя треугольная матрица с положительными диаго-
диагональными элементами. Матрица М называется нижней (верх-
§ 1.1 Метод Холесского и проблема упорядочения 11
ней) треугольной, если ¦ т,/ = 0 для i <C j (i > j). Верхний ин-
индекс Т указывает на операцию транспонирования. В § 2.1 мы
покажем, что разложение A.1.2) всегда существует, если А сим-
симметрична и положительно определена.
Подставляя A.1.2) в A.1.1), имеем
LLTx = b. A.1.3)
Замена у = Ux показывает, что х можно получить, решая тре-
треугольные системы
Ьу = Ь A.1.4)
и
LTx = y. A.1.5)
В качестве примера рассмотрим задачу
4
1
2
j_
2
2
1
2
0
0
0
2
0
3
0
0
2
0
0
0
2
0
0
0
16
' 1
Х\
х2
*3
*4
7
3
7
-4
-4
A.1.6)
Множитель Холесского для матрицы коэффициентов системы
A.1.6) выглядит так:
2
0.50
1
0.25
1
0.50
-1
-0.25
-1
1
-0.50
-2
0.50
-3
Решая систему Ly = Ь, получаем
3.5
2.5
6
-2.5
-0.50J
О
A.1.7)
12 Г л I Введение
Затем, решая систему Ux = у, находим
2
2
1
-8
-0.50,
Этот пример иллюстрирует наиболее важный факт, относя-
относящийся к применению метода Холесского для разреженной
матрицы А: матрица обычно претерпевает заполнение Это зна-
значит, что L имеет ненулевые элементы в позициях, где в нижней
треугольной части Д стояли нули.
Предположим теперь, что мы перенумеровали переменные в
соответствии с правилом x,-*-xs-t+\, /= 1, 2, ..., 5, и переупо-
переупорядочили уравнения так, чтобы последнее стало первым, второе
снизу — вторым сверху и так далее, пока, наконец, бывшее пер-
первое уравнение не станет последним. Мы получим тогда эквива-
эквивалентную систему уравнений П. 1.8)
16
0
0
0
2
0
5.
8
0
0
т
0
0
3
0
2
0
0
0
т
1
2
х
2
2
1
4
х
*з
х4
=
-4
-4
7
3
7
A.1.8)
Должно быть ясно, что эта перенумерация переменных и пере-
переупорядочение уравнений равносильны симметричной переста-
перестановке строк и столбцов Д, причем та же перестановка приме-
применяется к Ъ. Эту новую систему обозначим через Хх = }>. При-
Применяя к ней, как и прежде, метод Холесского, мы разложим Д
в произведение LU, где (с точностью до трех значащих цифр)
4 О
О 0.791
0 0 L.73
0 0 0 0.707
,0.500 0.632 1.15 1.41 0.129,
§ 1.1 Метод Холесского и проблема упорядочения 13
»»• * <
** » • *
» •• * *
• •* «в
* * * * *
• * * * *
• • **
• * * * t
• • •
• * •*
* * * *
• ***
**•
* •*
***
* *
* * *
* • •
* *
* *
***
** *
Рис. 1.1.1. Структура ненулевых элементов матрицы Л порядка 35.
• * *
* *
*****
*****
**
Рис. 1.1.2. Структура ненулевых элементов множителя Холесского L для мат-
матрицы, устройство которой показано на рис. 1.1.1.
14 Гл 1 Введение
• • * *
• ф • •
ф ф ф *
* ф ф *
• • ф * •
• * • • •
ф ф ф ф *
• * ф *
* ф* *
* ф • • *
• ф ф • •
• ф • • ф
ф • •
> • * ¦ •
• • • • *
ф * ф ф ф
ф *• 4 *
• *ф •
ф •• ф ф
ф *** ф
ф • • ф •
• фф *
ф • ф ф
• ф ф • •
• • • ф •
* • * * •
• • Ф А
Ф * *
• • Ф Ф
Ф • • Ф
Ф * Л
Рис. 1.1.3. Структура матрицы А', симметричной перестановки
устройство которой показано на рис. 1.1.1.
матрицы Л,
* Ф • Ф
Ф Ф Ф
Ф Ф
Ml*
фффф ф ф
ф* фф
• фф
ф ф
* ф ф
• ф ф ф
Рис. 1.1.4. Структура L\ множителя Холесского матрицы А\ чье устройство
показано на рнс. 1.1.3.
§11. Метод Холесского и проблема упорядочения 15
Решая Ly = b и LTx = у, получим решение ж, которое есть
всего лишь переупорядоченная форма х. Важнейший момент
состоит в том, что переупорядочение уравнений и переменных
привело к треугольному множителю L, который разрежен в
точности в той мере, что и нижний треугольник А. Хотя на
практике редко удается достигнуть столь полного успеха, для
• *
* *
* * *
• • *
• *
• *
* • • •
* • • • •
* * * *
• * * *•
* • • • •
* • • • •
• • • * *
• • * • *
¦ * • •
* * •
* * * * *
* *
* * ••
> * * *
* * • * *
* •
* *
Рис. I.I.5. Структура матрицы 4", симметричной перестановки матрицы Л,
устройство которой показано на рис 1.1.1.
большинства задач с разреженными матрицами разумное упо-
упорядочение строк и столбцов матрицы коэффициентов может
дать огромное сокращение заполнения и, следовательно, эконо-
экономию машинного времени и памяти (при условии, конечно, что
разреженность используется). Исследование алгоритмов, кото-
которые автоматически выполняют этот процесс переупорядоче-
переупорядочения,— один из главных предметов этой книги наряду с иссле-
исследованием эффективных численны* методов и схем хранения
разреженных множителей L, предоставляемых этими переупо-
переупорядочениями.
Приведенный выше матричный пример 5X5 иллюстрирует
основные характеристики разреженного исключения и эффект пе-
переупорядочения. Чтобы лучше прочувствовать эти вопросы, рас-
рассмотрим пример несколько большего порядка; соответствующая
16 Га I Введение
ему структура нулей-ненулей приведена на рис. 1.1.1. Раскла-
Раскладывая эту матрицу в произведение LU, получим структуру!
указанную иа рис. 1.1.2. Очевидно, что матрица при ее тепереш-
теперешнем упорядочении нехороша для разреженного исключения, по-
поскольку она претерпевает значительное заполнение.
Рисунки 1.1.3 и 1.1.5 демонстрируют структуру двух сим-
симметричных перестановок А' и А" матрицы А, устройство которой
*
• •• *
• • *»*
** * ••••
• •• » *
• • * >•
• • * *
• * > >
** •• •*
* *
* •• ••• ** *
*•• *** *» **
**
Рве. 1.1.6. Структура L", множителя Холесского матрицы А", чье устройство
показано на рис. 1.1.5.
было показано на рис. 1.1.1. Матрица А' приведена к так назы-
называемой ленточной форме, обсуждаемой в главе 4. Матрица А"
упорядочена так, чтобы уменьшить заполнение; метод получе-
получения этого типа упорядочения является предметом главы 5.
Число ненулевых элементов в L, L' и L" равно соответственно
369, 189 и 177.
Как показывает наш пример, некоторые упорядочения могут
вести к весьма существенным сокращениям заполнения или
ограничить его определенными областями L, которые допускают
удобное хранение. Эта задача отыскания «хорошего» упорядо-
упорядочения, называемая в дальнейшем «проблемой упорядочения»,
занимает центральное место при решении разреженных подо-
жнтельно определенных систем.
$ 1.2. Положительно определенные задачи 17
§ 1.2. Положительно определенные и неопределенные матричные
задачи
В этой книге мы будем иметь дело исключительно со слу-
случаем, когда А симметрична и положительно определена. Как
уже было отмечено, существенная часть линейных систем, воз-
возникающих в научных и инженерных расчетах, обладает этим
свойством, и проблема упорядочения для них решается иначе
и проще, чем для разреженной матрицы А общего вида. В по-
последнем случае необходима для обеспечения численной устойчи-
устойчивости та или иная форма выбора главного элемента, т. е. пере-
перестановки строк и/или столбцов (Forsythe 1967). Таким образом,-
при заданной А обычно получают разложение для РА или PAQ,
где Р и Q —матрицы перестановок соответствующих размеров.
(Заметим, что умножение на Р слева переставляет строки 4, а
умножение на Q справа переставляет столбцы А.)
Эти перестановки определяются в процессе разложения пу-
путем компромисса между (обычно конкурирующими) требова-
требованиями численной устойчивости и разреженности (Duff 1974).
Различные матрицы, хотя бы они и имели одинаковую струк-
структуру нулей-ненулей, обычно приводят к различным Р и Q и,
следовательно, имеют множители с различной структурой раз-
.реженности. Другими словами, для разреженных матриц общего
вида, как правило, нельзя предсказать, где произойдет заполне-
заполнение, пока не начались собственно вычисления. Тем самым мы
вынуждены пользоваться какой-либо схемой динамического хра-
хранения, в которой память для заполнения выделяется в ходе вы-
вычислений.
С другой стороны, симметричное гауссово исключение (т. е.
метод Холесского или один из его вариантов, описываемых в
главе 2), в применении к симметричной положительно опреде-
определенной матрице, не требует перестановок (выбора главных эле-
элементов) для поддержания численной устойчивости. Поскольку
РАРТ также симметрична и положительно определена при лю-
любой матрице перестановки Р, это значит, что можно симметрич-
симметрично переупорядочить А, во-первых не заботясь о численной устой-
устойчивости и, во-вторых, до начала реального численного разло-
разложения.
Эти возможности, обычно отсутствующие в случае матрицы
А общего вида, имеют важнейшие практические последствия.
Раз упорядочение можно определить до начала разложения, то
можно определить также и местоположение заполнения, кото-
которое произойдет при разложении. Поэтому способ хранения L
можно выбрать до реального численного разложения, так же
как и зарезервировать место для элементов заполнения. Вычис-
Вычисления затем проводят при структуре хранения, остающейся ста-
статичной (неизменной). Таким образом, три задачи- 1) выбор
18 Гл. 1 Введение
надлежащего упорядочения; 2) формирование подходящей схемы
хранения; 3) реальные вычисления — могут быть разделены как
самостоятельные объекты исследования и как разные модули
программного обеспечения. Ситуация изображена на рисунке.
Найти
перестановку
Р
Сформировать
структуру
данных для L, где
РАРТ = LLT
Выполнить
вычисления
Эта независимость задач имеет ряд отчетливых преиму-
преимуществ. Она поощряет модульность при составлении математ»-
ческого обеспечения и, в частности, позволяет кроить метод
хранения по мерке данного этапа. Например, применение спи-
списков для хранения матричных индексов может быть вполне
приемлемо при реализации алгоритма упорядочения, но реши-
решительно неудобно для реального хранения матрицы или ее мно-
множителей. Точно так же уверенность в возможности использовать
при факторизации статичную схему хранения позволяет выбрать
метод, очень эффективный в смысле требований к памяти, ко-
который, однако, потребовал бы катастрофических накладных рас-
расходов, если бы схему хранения пришлось менять в процессе
разложения. Наконец, во многих инженерно-конструкторских
приложениях приходится решать большое количество различных
задач с положительно определенными матрицами, имеющих
одинаковую структуру. Ясно, что упорядочение и формирование
схемы хранения нужно выполнить лишь однажды; поэтому же-
желательно, чтобы эти этапы были изолированы от реальных вы-
вычислений.
В многочисленных практических ситуациях возникают ма-
матричные задачи, хотя и несимметричные, но имеющие симме-
симметричную структуру; при этом можно показать, что применение
к ним гауссова исключения не требует выбора главных элемен-
элементов для обеспечения численной устойчивости. Почти все идеи
и алгоритмы, описываемые в книге, непосредственно приложимы
к этому классу задач. Некоторые указания на то, как это можно
сделать, даны в упр. 4.5.1 главы 4.
§ 1.3. Итерационные и прямые методы
Численные методы для решения систем линейных уравнений
распадаются на два больших класса: итерационные и прямые.
Типичный итерационный метод состоит из выбора начального
§ 1.3. Итерационные и прямые методы 19
приближения *A> к х и построения последовательности *B),
жC), ..., такой, что lim x{t) = х. Обычно для вычисления х('+1)
нужны лишь Л, b и одно или два предыдущих приближения.
В теории при использовании итерационного метода мы должны
выполнить бесконечное число арифметических операций, чтобы
получить х, но на практике мы прекращаем итерацию, когда,
с нашей точки зрения, очередное приближение достаточно близ-
близко к х С другой стороны, при отсутствии ошибок округления
прямые методы позволяют вычислить решение за конечное число
арифметических операций.
Какой класс методов лучше? На этот вопрос нельзя ответить
безусловно; ответ зависит от того, какой смысл мы вкладываем
в слово «лучше», а также от конкретной решаемой задачи или
класса задач. Итерационные методы привлекательны с точки
зрения требований к машинной памяти, поскольку их реализа-
реализация в типичном случае требует хранения лишь Л, Ь, ж"' и еще,
может быть, одного или двух векторов. В то же время при раз-
разложении матрицы Л она обычно претерпевает некоторое запол-
заполнение, так что матрица заполнения1) F = L -\- U имеет нену-
ненулевые элементы в тех позициях, где в А стояли нули. Поэтому
реализация прямых методов часто требует большей памяти, чем
реализация итерационных. Реальное отношение очень сильно
зависит от решаемой задачи и от используемого упорядочения.
Сравнение прямых и итерационных методов с точки зрения
вычислительной работы еще более затруднено. Как мы видели,
выбор упорядочения в огромной степени влияет на количество
арифметической работы при использовании гауссова исключе-
исключения. Число итераций, выполняемых итерационной схемой, сильно
зависит от характеристик Л и от подчас деликатной проблемы
регистрации, посредством вычисляемых величин, момента, когда
х<'> «достаточно близок» к х.
В некоторых ситуациях, например, при конструировании не-
некоего механического устройства или моделировании какого-ни-
какого-нибудь разворачивающегося во времени явления приходится
решать много систем уравнений с одной и той же матрицей
коэффициентов. В этом случае стоимость прямой схемы может
по существу совпадать со стоимостью решения треугольной си-
системы при известном разложении, поскольку стоимостью един-
единственного разложения, отнесенного ко всем системам, можно
пренебречь В этих ситуациях часто верно и то, что число ите-
итераций, требуемых итерационной схемой, очень невелико, по-
поскольку имеются хорошие начальные векторы хA).
После этих замечаний должно быть ясно, что пока вопрос
о том, какой класс методов следует использовать, не поставлен
1) В оригинале — the filled matrix — Прим. перев.
20 Гл 1 Введение
в очень узком и хорошо определенном контексте, ответ на него
или слишком сложен или вообще невозможен. Причина, почему
в этой книге рассматриваются лишь прямые методы, та, что по
итерационным методам уже имеется несколько отличных спра-
справочных книг (Varga 1962, Young 1971); в то же время авторам
не известна сравнимая книга по прямым методам для больших
разреженных систем. Вдобавок существуют ситуации, когда
можно очень убедительно показать, что прямые методы намного
предпочтительней, чем любая мыслимая итерационная схема.
2, Вводные сведения
§ 2.0. Введение
В этой главе мы исследуем основной численный алгоритм,
используемый во всей книге для решения симметричных поло-
положительно определенных матричных задач. Этот метод, извест-
известный как метод Холесского, кратко обсуждался в § 1.1 Ниже
мы докажем, что для положительно определенных матриц раз-
разложение всегда существует, и изучим несколько способов, кото-
которыми могут быть организованы вычисления Хотя математически
и (обычно) численно эти способы эквивалентны, они разли-
различаются порядком, в котором вычисляются и используются
коэффициенты. Эти различия важны при машинной реализации
метода. Будут выведены также выражения для числа арифмети-
арифметических операций, требуемых методом.
Как было указано в § 1.1, при применении метода Холесского
к разреженной матрице А она обычно претерпевает некоторое
заполнение, так что множитель Холесского L имеет ненулевые
элементы в позициях, где в А стояли нули. При некоторой
матрице перестановки Р мы можем вместо А разложить в про-
произведение LU матрицу РАРТ, и в соответствии с тем или иным
критерием L может оказаться много привлекательнее, чем L
В § 2.3 мы обсуждаем некоторые из этих критериев и показы-
показываем, как факторы, обусловленные практической реализацией,
усложняют сравнение различных методов.
2.0.1. Обозначения
Предполагается, что читатель знаком с элементарной тео-
теорией и свойствами матриц; см., например, {Stewart 1973). В этом
параграфе мы опишем матричные обозначения, используемые
в книге.
Для обозначения матриц используются жирный курсив и про-
прописные буквы. Элементы матрицы обозначаются курсивными
строчными буквами с двумя индексами. Например, пусть
А — Л/Х iV-матрица. Ее элемент (i, /) обозначается через а,/.
Число N называется порядком матрицы А.
22 Гл. 2 Вводные сведения
Вектор обозначается жирной строчной буквой, а его компо-
компоненты — строчными буквами с одним индексом. Например,
v =
— вектор длины N.
Для данной матрицы А ее t-я строка и г-й столбец обозна-
обозначаются через А(» и А*< соответственно. Если А симметрична, то
Аи = А*, для i = 1, ..., N.
Для единичной матрицы порядка N, т. е. для матрицы, у ко-
которой на диагонали стоят единицы, а вне диагонали — нули,
используется обозначение In-
В анализе разреженных матриц часто приходится подсчиты-
подсчитывать число ненулевых элементов вектора или матрицы. Мы
пользуемся символом *](?) для числа ненулевых коэффициентов
в Q, где символ П замещает название вектора или матрицы.
Очевидно,
Часто приходится упоминать о числе элементов в множестве 5;
это число обозначается через \S\.
Пусть f(n) и g(n)—функции независимого переменного п.
Будем писать
если для некоторой константы К и всех достаточно больших п
\ш\<к-
Мы скажем, что f(n) есть, самое большее, величина порядка
g(n). Это полезное обозначение в анализе разреженных матрич-
матричных алгоритмов, поскольку часто интерес представляют лишь
доминирующие члены в оценках арифметики и количества не-
ненулевых элементов.
112
Например, если / (п) — -г п3 + -^ п2 — у п, то можно написать
Для достаточно больших п относительный вклад членов уп2
и (~тп) несуществен.
Выражения типа выписанной выше f(n) возникают при под-
подсчете числа арифметических операций или количества ненуле-
§ 2.1. Алгоритм разложения 23
вых элементов и являются часто результатом довольно слож-
сложных суммирозалнй. Поскольку обычно мы интересуемся лишь
главным членом, то очень распространенный прием упрощения
таких подсчетов состоит в замене знака суммы на символ инте-
интеграла. Например, для больших п
п
Bn + k) (n — k) ~ ^ Bn + k) (n — k) dk.
k-i о
Упражнения
N
2.0.1. Вычислить непосредственно сумму V i2 (N — i), а затем найти ее
1-х
приближенное значение, используя интеграл, как указано в конце параграфа.
2.0.2. Вычислить непосредственно сумму
N JV-i+1
а затем с помощью двойного интеграла приближенное значение.
2.0.3. Пусть А и В — разреженные матрицы порядка N. Показать, что
число умножений, необходимых при вычислении С = АВ1), равно
N
2.0.4. Пусть S — разреженная М X ^-матрица. Показать, что для вычис-
вычисления ВТВ достаточно
I M
умножений.
2.0.5. Обычная схема хранения разреженного вектора такова' имеются
основной массив, содержащий значения всех ненулевых компонент вектора, и
вспомогательный массив, хранящий индексы этих компонент. Пусть и и v —
два разреженных вектора порядка N, хранимых таким образом Рассмотреть
задачу вычисления скалярного произведения w = uTv.
а) Если индексные векторы упорядочены по возрастанию (или убыва-
убыванию), показать, что для вычисления скалярного произведения достаточно вы-
выполнить О(т](и) +r)(t>)) сравнений
б) А если индексы размещены случайным образом'
в) Как бы вы организовали вычисления, если бы индексы были разме-
размещены случайно, но у вас в распоряжении находился рабочий вещественный
массив длины N с нулевыми компонентами?
§ 2.1. Алгоритм разложения
2.1.1. Существование и единственность разложения
Симметричная матрица А называется положительно опре-
определенной, если хтАх > 0 для всех ненулевых векторов х. Такие
') В соответствии с определением произведения матриц — Прим перев.
24 Гл. 2. Вводные сведения
матрицы появляются во многих приложениях; в типичном слу-
случае произведение хтАх представляет энергию некоторой физи-
физической системы, которая положительна для любой конфигура-
конфигурации х. В положительно определенной матрице А диагональные
элементы всегда положительны, поскольку
где е — г-й характеристический вектор, все компоненты которого
равны нулю, кроме j'-й, равной единице. Это обстоятельство бу-
будет использовано в доказательстве следующей, теоремы о раз-
разложении, принадлежащей Холесскому (Stewart 1973).
Теорема 2.1.1.
Если А — N X N симметричная положительно определенная
матрица, то существует и единственно ее треугольное разложе-
разложение LLT, где L — нижняя треугольная матрица с положитель-
положительными диагональными элементами.
Доказательство. Будем проводить доказательство индукцией
по порядку матрицы А. Очевидно, что утверждение справедливо
для матриц порядка 1, так как ац — положительное число.
Предположим, что утверждение верно для матриц порядка
N — 1. Пусть А — симметричная положительно определенная
матрица порядка N. Ее можно представить в блочной форме
—1.
где d — положительный скаляр, а Н — матрица порядка
Блочную матрицу можно записать как произведение
Vd~
1 О
О Н
о
Здесь Н = Н — j-- Ясно, что матрица Н симметрична. Она
будет и положительно определена, потому что для любого нену-
ненулевого вектора х порядка N— 1
ХТУ
d '
d vT
v H
1 xTv
d
X
L J
=xtHx.
§2.1 Алгоритм разложения 25
откуда следует хтНх > 0. По предположению индукции, Н имеет
треугольное разложение LhLh, причем диагональ Lh положи-
положительна. Поэтому А может быть разложена в произведение
0
Vet
VJ 0
1
0
0
LH
i
1
0
0
lS
A
-1
о
LLT-
Доказательство единственности множителя
читателю.
Применяя результат теоремы к матрице
'4 8
получим множители
представляется
/
\
/2 0W2 4N
V4 зДо зл
Здесь уместно отметить, что существует другое разложение
симметричной положительно определенной матрицы, тесно свя-
связанное с рассмотренным (Martin 1971). Поскольку множ-итель
Холесского имеет положительные диагональные элементы, то
можно вычленить из L диагональную матрицу DI/2, что дает
L = tD{'2 и
A = LDLT B.1.1)
В рассмотренном выше примере это разложение таково:
/1 0W4 04/1 24
V2 1 ДО 9 ДО 1/
Такое разложение столь же легко получить, как и первоначаль-
первоначальное, и при этом не потребуется извлекать квадратные корни
(см. упр. 2 1.4). Мы не используем его п этой книге, потому что
при некоторых обстоятельствах оно приводит к неприятной
асимметрии в вычислениях с блочными матрицами
2.1.2. Вычисление разложения
Теорема 2.1.1 гарантирует существование и единственность
множителя Холесского для симметричной положительно опреде-
определенной матрицы, однако порядок и способ реального вычисле-
вычисления элементов множителя L могут быть различными. В этом
26 Гл. 2. Вводные сведения
параграфе мы исследуем некоторые возможные методы вычис-
вычисления L. Наличие разных вариантов дает необходимую гибкость
при выборе схемы хранения разреженного матричного множи-
множителя L
Конструктивное доказательство теоремы 2.1.1 подсказывает
вычислительную схему для построения множителя L. Это алго-
алгоритм в так называемой форме внешних произведений. Схему
можно описать на матричном языке шаг за шагом следующим
образом:
Г> #,j
1 О
1 О
о я,
L?
'/v-i
B.1.2)
О
1 О О
О d2 vj
О v2 Я2
1 О
О I
— v2v2r
О О Я2 -
1 О
О
= ?г2-Аг^2»
/v-
.v-г
An-i =LnInI>n-
§ 2.1. Алгоритм разложения 27
Здесь для значений i от 1 до N dt есть положительный ска-
скаляр, v, — вектор длины N — i, a H, — положительно определен-
определенная симметричная матрица порядка N — i.
После N шагов алгоритма имеем
А = L\Lj ... LnLn . • • LiL\ = LL .
Можно показать (см. упр. 2.1.6), что
L = Lt + L,+ ...+LN-(N-l)IN. B.1.3)
Таким образом, i-й столбец L есть в точности i-fi столбец Li.
В этой схеме вычисляются один за другим столбцы ?-_В то
же время каждый шаг требует модификации подматрицы Н, по-
посредством внешнего произведения fifj/d,. Результатом яв-
является Н,, т. е. как раз та матрица, которую остается разло-
разложить. Порядок обращения к элементам А в процессе разложе-
разложения изображен на рисунке.
Дальнейших
обращении
не требуется
Изменяемая часть
Разлагаемый столбец
Другая формулировка процесса разложения — это метод
окаймления. Пусть матрица А представлена в виде
М
причем уже получено симметричное разложение LMLTM ведущей
главной подматрицы М порядка N—1. (Почему М положи-
положительно определена?) Тогда разложением А будет
wT
/До t )
где
B.1.4)
B.1.5)
и
/ = (s — wrw)V».
(Почему число s — wTw положительно?)
28 Гл. 2. Вводные сведения
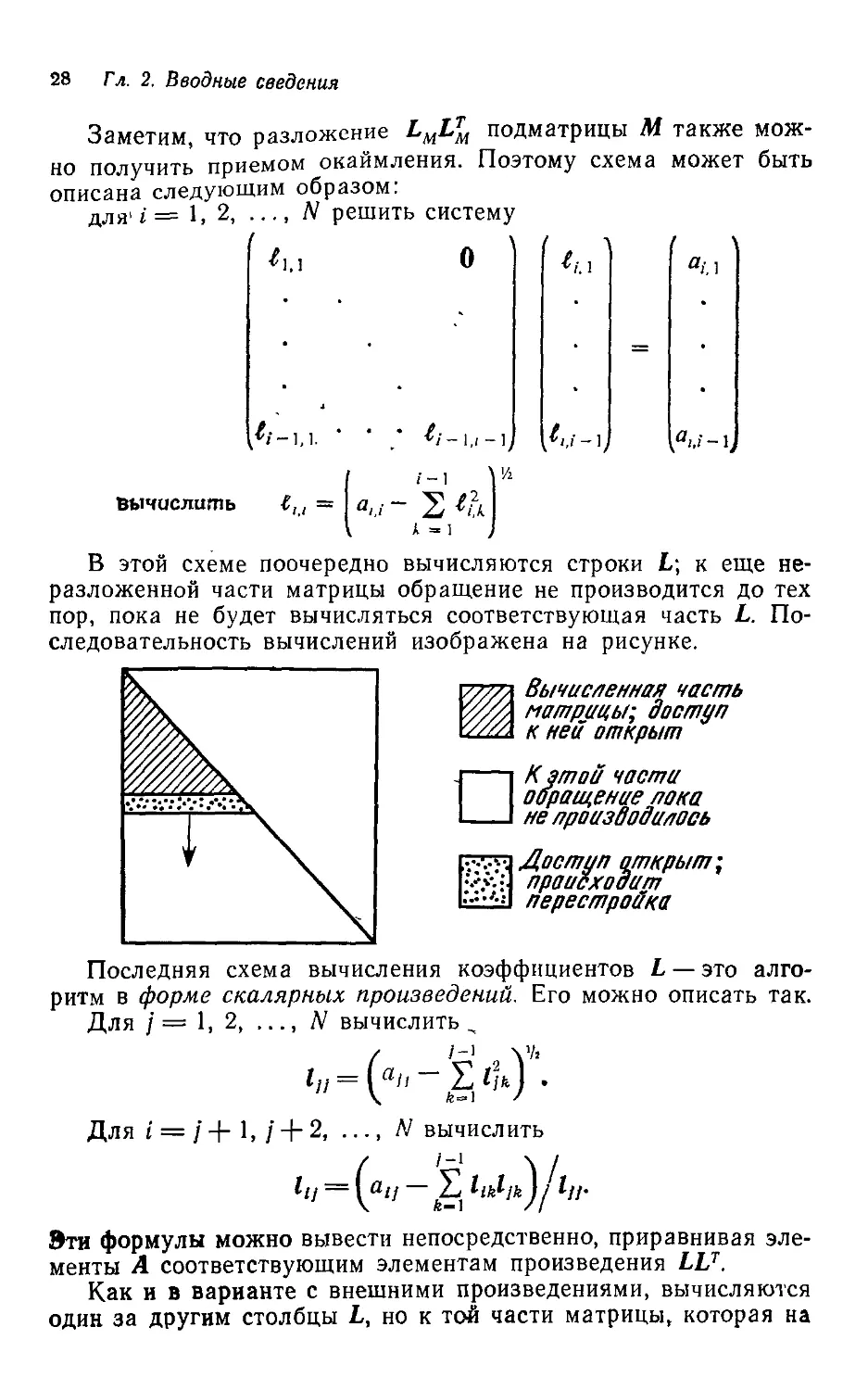
Заметим, что разложение LMLTM подматрицы М также мож-
можно получить приемом окаймления. Поэтому схема может быть
описана следующим образом:
для. i= \, 2, ..., N решить систему
'1,1
О
//-1.1.
Вычислить
аи
В этой схеме поочередно вычисляются строки L; к еще не-
разложенной части матрицы обращение не производится до тех
пор, пока не будет вычисляться соответствующая часть L. По-
Последовательность вычислений изображена на рисунке.
Вычисленная часть
матрацы; доступ
к ней открыт
К этой часта
обращение /гака
не /граазбодалось
Доступ открыт;
происходит
перестройка
Последняя схема вычисления коэффициентов L — это алго-
алгоритм в форме скалярных произведений. Его можно описать так.
Для / = 1, 2, ..., N вычислить „
I
Для i = / + 1, / + 2, ..., N вычислить
Эта формулы можно вывести непосредственно, приравнивая эле-
элементы А соответствующим элементам произведения LU.
Как и в варианте с внешними произведениями, вычисляются
один за другим столбцы L, но к той части матрицы, которая на
§ 2.1. Алгоритм разложения 29
данном шаге еще не разложена, обращения не происходит. По-
Последовательность вычислений и характер обращений к элемен-
элементам А указаны на рисунке.
Обращения
не происходит
Эта часть вы числена \
доступ к не^
открыт
Доступ открыт;
происходит
перестройка
Две последние формулировки можно изложить на языке
одних скалярных произведений. Это можно использовать для
уменьшения погрешности численного разложения, накапливая
с двойной точностью скалярные произведения. На некоторых
вычислительных машинах такое накопление требует лишь не-
небольших дополнительных затрат.
2.1.3. Разложение разреженных матриц
Как было показано в главе 1, при разложении разреженной
матрицы она обычно претерпевает некоторое заполнение, т. е.
нижний треугольный множитель L имеет ненулевые элементы
в тех позициях, где в исходной матрице стояли нули. Вспомним
разложение матрицы
4 I
2 X 2
1^-000
2 0 3 0 0
2 0 0 0 16
из § 1.1. Ее треугольный множитель L выглядит так:
2
0.5
1
0.25
I
0
0.5
-1
-0.25
0
0
1
-0.5
-2
0
0
0
0.5
-3
0
0
0
0
1
30 Гл 2 Вводные сведения
следовательно, матрица А заполнилась в позициях C,2), D,2),
D,3), E,2), E,3) и E,4). Это явление заполнения, которое
обычно игнорируют при решении плотных систем, играет крити-
критическую роль в разреженном исключении.
Причину появления ненулевых элементов можно понять
лучше, если использовать формулировку процесса факториза-
факторизации, связанную с внешними произведениями. На t-м шаге под-
подматрица Н, модифицируется посредством матрицы vivTi/dt и
получается Я,. В результате подматрица Н, может иметь нену-
ненулевые элементы в позициях, которые были нулями в Н,. В при-
приведенном выше примере
Я,=
J.
У
0
0
0
3
0
0
0
_5_
8
0
0
0
О 0 0 16
Модификация на 1-м шаге дает (с точностью до трех значащих
цифр)
О м О
.25
-.5
-.125
-.5
— S
2
-.25
-1
-.125
-.25
.563
-.25
-.5
-1
- 25
15
Если при решении разреженной системы используется нали-
наличие нулей, то от заполнения зависят и требования к памяти, и
количество вычислительной работы. Напомним, что л(П) обозна-
обозначает число ненулевых элементов в П, где П может быть векто-
вектором или матрицей. Из B.1.2) и B.1.3) видно, что число ненуле-
ненулевых элементов в L выражается форм\лой
? B.1.6)
В нижеследующей теореме, а затем на протяжении всей
книги мы измеряем количество арифметической работы числом
мультипликативных операций (умножений и делений), назы-
называемых в дальнейшем просто «операциями». Большая часть
арифметики, выполняемой в матричных расчетах, образует по-
последовательность пар «умножить — сложить», поэтому число
§ 2.1. Алгоритм разложения 31
аддитивных операций приблизительно равно числу мультипли-
мультипликативных.
Теорема 2.1.2.
Число операций, необходимых для вычисления треугольного
множителя L матрицы А, равно
? Ч W fo (* <) + 3] = у ? h (LJ - 1 ] h (JLW) + 2]. B.1.7)
Доказательство. Три формулировки разложения различаются
лишь порядком выполнения операций. Для подсчета числа опе-
операций воспользуемся алгоритмом в форме внешних произведе-
произведений B.1.2). На /-м шаге требуется r\(vt) операций для вычисле-
вычисления vj^jdi и -g- Л (ft) [T|(»f) + 1] операций для формирования
симметричной матрицы
/ V
Результат получается суммированием по всем шагам.
Для плотного случая число ненулевых элементов в L есть
±N(N+1), B.1.8)
а арифметическая работа —
JV-1
/(/ + 3)=|/V3+i/V2-|-iV. B.1.9)
Рассмотрим еще в качестве примера разреженной матрицы
разложение Холесского для симметричной положительно опре-
определенной трехдиагональной матрицы. Можно показать (см.
главу 5), что если L — множитель такой матрицы, то T](L»,) = 2
для i = 1, ..., N— 1. В этом случае число ненулевых элементов
в L есть
ti(L) = 2,V-1,
а арифметическая работа при вычислении L —
Ы-1
Сравнивая эти результаты с подсчетами для плотного слу-
случая, видим огромное различие в требованиях к памяти и вычис-
вычислительной работе.
Стоимость решения эквивалентных разреженных систем с
разными упорядочениями также может быть весьма различной
32 Га. 2. Вводные сведения
Как показано в § 1.1, матрицу А, приведенную в начале этого
раздела, можно упорядочить так, что она вообще не испытывает
заполнения! Нужная для этого матрица перестановки есть
0 0 0 0 1
0 0 0 10
0 0 10 0
0 10 0 0
.10 0 0 0,
При применении к А она обращает ее упорядочение. В резуль-
результате получается матрица
РАР1
16
0
0
0
2
0
8
0
0
0
0
3
0
2
0
0
0
1
2
1
2
7
2
1
4
Этот простой пример демонстрирует, что разумный выбор Р
может повести к громадному сокращению заполнения и ариф-
арифметической работы. Поэтому при решении линейной системы
Ах=*Ь
общий подход состоит в том, чтобы сначала найти перестановку,
или упорядочение Р данной задачи. Затем система записы-
записывается в виде
(РАРТ) (Рх) = РЬ,
и метод Холесского применяется к симметричной положительно
определенной матрице РАРТ, что приводит к треугольному раз-
разложению LLT. Решая эквивалентную переупорядоченную си-
систему, часто можно достичь уменьшения запросов к машинной
памяти и времени исполнения
Упражнения
2.1.1 Поьазать, что разложение Чолесского симметричной положительно
определенной матрицы единственно
2.1.2 Пусть А — симметричная положительно определенная матрица по-
порядка N. Показать, что:
а) всякая главная подматрица А положительно определена;
б) А невырождена и А~' также положительно определена;
в)
max
max
§22 Решение треугольных систем 33
2.1.3 Пусть А— симметричная положительно определенная матрица. По-
Показать, что
а) ВГАВ положительно определена тогда и только тогда, когда В невы-
невырождена,
б) окаймленная матрица
положительно определена тогда и только тогда, когда s > u7A~lu.
2.1.4. Записать равенства, аналогичные равенствам B 1.2), B 1.3), кото-
которые давали бы разложение LDU, где L теперь — нижняя треугольная мат-
матрица с единицами на диагонали, a D — диагональная матрица с положитель-
положительными диагональными элементами
2.1.5. Пусть Е и F — нижние треугольные матрицы порядка /V, которые
при некотором k (I ^ к ^ /V) удовлетворяют условиям: е,/ = 1 для / > к;
ец = О для i > / и / > к; fn = 1 для / =s k; ftl = 0 для « > /' и / ^ к. Слу-
Случай W = 6, k = 3 изображен на рисунке.
*
*
*
•
•
*
*
*
•
•
*
*
*
•
•
1
0
0
0
1
0 1
F =
1
0
0
0
0
0
1
0
0
0
0
1
0
0
0
*
•
*
0
*
• •
Показать, что EF = Е + F — /, и тем самым установить справедливость
B.1.3).
2.1.6 Привести пример симметричной матрицы, которая бы не имела тре-
треугольного разложения LLT, и такой, которая бы дойускала более, чем одно
разложение.
§ 2.2. Решение треугольных систем
2.2.1. Вычисление решения
После того как вычислено разложение, нужно решить тре-
треугольные системы Ly = Ъ и Ux = у. В этом параграфе будет
рассмотрено численное решение треугольных систем.
Пусть мы имеем линейную систему
Тх = Ь
порядка N, где Т — невырожденная треугольная матрица. Без
потери общности можно предположить, что Т — нижняя тре-
треугольная. Существуют два распространенных способа решения
такой системы, отличающиеся лишь порядком выполнения опе-
операций.
В первом способе используются лишь скалярные произведе-
произведения. Определяющие уравнения таковы:
34 Гл. 2. Вводные сведения
ДЛЯ i= 1, 2 N
Последовательность вычислений изображена на рисунке
1
B.2.1)
I
I
Дальнейших обращении
нетребуется
F771 Это часть вычислена;
У//А доступ к ней открыт
Ш Вычисляемая
часть
? Обращений
пока не происходи/го
Во втором способе подматрицы из Т используются таким же
образом, как в варианте внешних произведений алгоритма раз-
разложения. Определяющие уравнения выглядят так:
для i= 1, 2, .... N
х,- - bi/th
B.2.2)
bN
—
•
- x,
*
Заметим, что эта схема позволяет использовать разреженность
решения х. Если в начале /-го шага ft/ оказывается нулем, то и
Xi — нуль, и весь шаг может быть опущен. Порядок обращения
к коэффициентам системы показан на рисунке.
вяа Дальнейших обращений
БеЭ не требуется
ртя Эта часть Вычислена;
ч61 доступ к ней открыт
U
Вычисляемая
часть
Обращении
пока не происходи/1 о
§ 2.2. Решение треугольных систем 35
В первом методе решения обращение к элементам нижней
треугольной матрицы происходит строка за строкой, поэтому
здесь применимы строчные схемы хранения. Если матрица хра-
хранится по столбцам, то более уместен второй метод. Интересно
отметить, что этот метод, с его ориентацией на столбцы, часто
используется для решения верхней треугольной системы
где L — нижняя треугольная матрица, хранимая посредством
строчной схемы.
2.2.2. Число операций
Установим теперь некоторые простые результаты, касаю-
касающиеся решения треугольных систем. Они будут нужны позже
при подсчете числа операций.
Рассмотрим решение системы
Г* = &
с невырожденной нижней треугольной матрицей Т.
Лемма 2.2.1.
Число операций при вычислении х равно
i
Доказательство. Из B.2.2) следует, что если Xi Ф 0, то г-й
шаг требует х\ (Т*,) операций.
Следствие 2.2.2.
Если разреженность решения х не используется (т. е. х счи-
считается плотным вектором), то число операций при вычислении х
равно г\(Т).
Таким образом, при решении системы Тх = Ь, где Тих
плотные, число операций есть
jN(N + l). B.2.3)
Приводимые ниже результаты указывают некоторые- связи
между структурой правой части Ь и структурой решения х ниж-
нижней треугольной системы. Лемма 2.2.3 и следствие 2.2.5 опи-
опираются на предположение о неуничтожении, т. е. если для двух
ненулевых величин выполняется сложение или вычитание, то
результат не равен нулю. Это значит, что в анализе мы игно-
игнорируем любые нули, которые могли появиться вследствие точ-
точного взаимного уничтожения. Такое уничтожение происходит
редко, и, чтобы его предсказать, нужно знать числовые значе-
значения Тиб. Но и в этом случае подобное предсказание, вообще
говоря, затруднительно, особенно в машинной арифметике, под-
подверженной ошибкам округлений.
36 Гл 2. Вводные сведения
Лемма 2.2.3.
В предположении о неуничтожении из bi ф О следует х, Ф О.
Доказательство. Поскольку Т невырожденна, tu Ф 0 для
1 ^ i ^ N. Теперь нужный результат следует из предположения
о неуничтожении и определяющего уравнения B.2.1) для Xi.
Лемма 2.2.4.
Пусть х — решение системы Тх = Ь. Если bt = О для l^ii^ik,
то я, = О для 1 ^ i '^С k.
Следствие 2.2.5.
При предположении о неуничтожении справедливо неравен-
неравенство х\{Ь) ^ ц{х).
Упражнения
2.2.1. Используя лемму 2.2.1, показать, что разложение по схеме окайм-
окаймления требует
4" Ц A №*(> - ») (Л №**) + 2)
операций.
2.2.2. Показать, что обратная к невырожденной нижней треугольной мат-
матрице также нижняя треугольная (использовать лемму 2.2.4).
2.2.3. Пусть Т — невырожденная нижняя треугольная матрица со свой-
свойством распространения, т. е. t,, ;_i ф 0 для 2 ^ i ^ N.
а) Показать, что при решении системы Тх = b из bi ф 0 следует х/ Ф О
для ( ^ / ^ N.
б) Показать, что Т~1 — заполненная нижняя треугольная матрица.
2.2.4. Зависит ли лемма 2.2.1 от предположения о неуничтожении? Объ-
Объяснить. Ответить на тот же вопрос в отношении теоремы 2.1.2 и леммы 2.2.4.
2.2.5. Доказать результат, аналогичный лемме 2 2.4, для верхних тре-
треугольных матриц.
2.2.6. Предположим, что нужно решить большое число нижних треуголь-
треугольных систем вида Ly = Ь порядка N, причем и L, и векторы b разрежены.
Известно, что для этих систем разрежены и решения у. Имеется выбор из
двух схем хранения L, иллюстрируемый ниже примером порядка 5; одна из
этих схем ориентирована на хранение по столбцам; другая — на хранение по
строкам. Какую из них вы выбрали бы и почему? Если бы вы написали фор-
транную программу для решения таких систем с выбранной структурой хране-
хранения, то было ли бы время исполнения пропорционально числу выполняемых
операций? Объяснить. (Считайте, что число выполняемых операций равно по
меньшей мере O(N).)
3 О
О 2
2 0 4
0 3 9 5
0 0 7 0 7
§ 2.2. Решение треугольных систем 37
1
1
2 4
2 3
3 9
ТТТ~1 , .
1 2 3 5 8 10
Схема 1
3 5
1
з~Т
2 4
3 4 5
4 $ 7
10
Индексы столбцов
Числовые значения
Индексный вектор
" Индексы строк
' Числовые значений
Индексный вектор
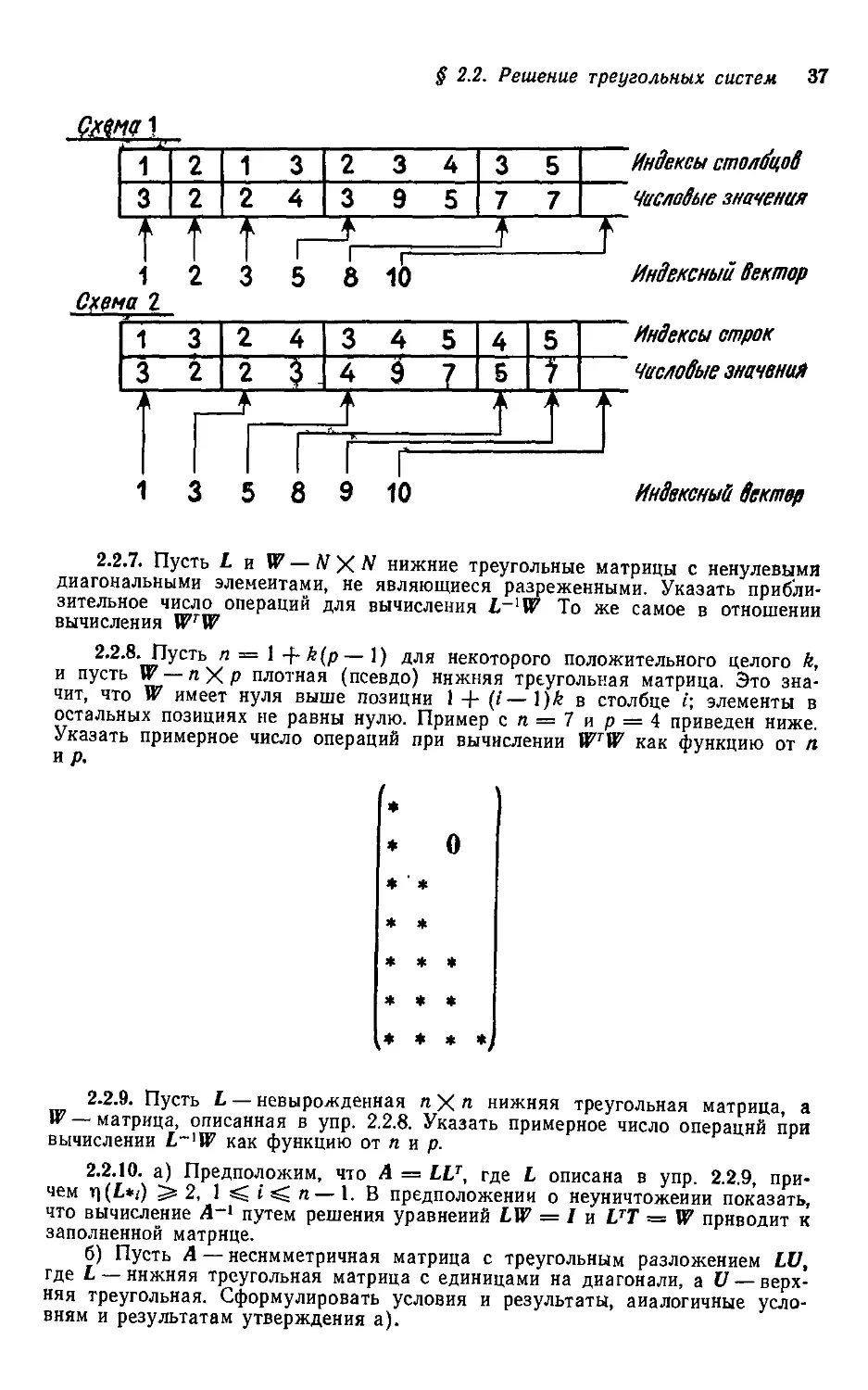
2.2.7. Пусть L и W —NXN нижние треугольные матрицы с ненулевыми
диагональными элементами, не являющиеся разреженными. Указать прибли-
приблизительное число операций для вычисления L~XW To же самое в отношении
вычисления WW
2.2.8. Пусть п = 1 -hk(p—1) для некоторого положительного целого k,
и пусть W — п X р плотная (псевдо) нижняя треугольная матрица. Это зна-
значит, что W имеет нуля выше позиции 1 + (/—\)k в столбце i; элементы в
остальных позициях не равны нулю. Пример сп = 7ир = 4 приведен ниже.
Указать примерное число операций при вычислении WTW как функцию от я
и р.
* о
* ' *
* *
* * *
* * *
* * * *
2.2.9. Пусть L — невырожденная яХл нижняя треугольная матрица, а
W—матрица, описанная в упр. 2.2.8. Указать примерное число операций при
вычислении L-'W как функцию от п и р.
2.2.10. а) Предположим, что А = LU, где L описана в упр. 2.2.9, при-
причем i\(L*t) 5s 2, 1 ^ i ^ п—1. В предположении о неуничтожеиии показать,
что вычисление А~1 путем решения уравнений LW = / и UT = W приводит к
заполненной матрице.
б) Пусть А — несимметричная матрица с треугольным разложением LV,
где L — нижняя треугольная матрица с единицами на диагонали, а V — верх-
верхняя треугольная. Сформулировать условия и результаты, аналогичные усло-
условиям и результатам утверждения а).
88 Гл 2. Вводные сведения
§ 2.3. Некоторые практические замечания
Целью изучения разреженной матричной технологии решения
линейных систем является снижение стоимости использования
разреженности данной системы. Сравнивая в разделе 2.1.3 ре-
решение плотной и трехдиагональной системы, мы видели, что
можно достигнуть огромных сокращений в запросах к памяти
и вычислительной работе.
Имеются различные схемы хранения разреженных матриц,
отличающиеся способом использования нулей. В некоторых слу-
случаях допускается хранение части нулей в обмен на упрощение
схемы хранения; в других — используются все нули системы,
В главах 4—8 мы обсудим наиболее распространенные разре-
разреженные схемы решения линейных систем.
Выбор метода хранения, естественно, влияет на запросы
к памяти и на использование стратегии упорядочения (выбор
матрицы перестановки Р). Кроме того, он оказывает сущест-
существенное воздействие на реализацию разложения и решения, а
следовательно, на сложность программ и время исполнения.
Однако, независимо от того какая схема разреженного хра-
хранения используется, в вычислительном процессе в целом могут
быть выделены четыре фазы.
Шаг 1 (упорядочение). Найти «хорошее» упорядочение (пе-
(перестановку Р) для данной матрицы А с учетом выбранного
метода хранения.
Шаг 2 (распределение памяти). Определить необходимую
информацию о множителе Холесского L матрицы РАРТ с тем,
чтобы сформировать подходящую схему хранения.
Шаг 3 (разложение). Разложить переупорядоченную матри-
матрицу РАРТ в произведение LU.
Шаг 4 (решение треугольных систем). Решить системы Ly =
¦в Ь и Uz = у. После этого положить х = Ртг.
Даже при заданном методе хранения имеется много способов
для выбора упорядочения, определения подходящей структуры
хранения и выполнения реальных вычислений. Схему разрежен-
разреженного хранения вместе с соответствующей комбинацией упоря-
упорядочения/распределения памяти/разложения/решения мы будем
в дальнейшем называть методом решения.
Чаще всего называемыми задачами при выборе метода ре-
решения являются: а) уменьшить запросы к памяти; б) уменьшить
время исполнения; в) уменьшить некоторую комбинацию памяти
и времени исполнения; эта комбинация отражает относительную
цену ресурсов в стоимости использования машинной системы.
Хотя есть и другие критерии, иногда управляющие выбором ме-
метода, названные являются главными. Они иллюстрируют труд-
трудности, связанные с оценкой стратегии.
§ 2.3. Некоторые практические замечания 39
Чтобы можно было заявить, что один метод лучше другого
в смысле одной из указанных выше мер, нужно иметь возмож-
возможность точно оценить эту меру для каждого метода, а такая
оценка значительно сложнее, чем кажется. Рассмотрим вначале
критерий машинной памяти.
2.3.1. Запросы к памяти
Память, используемая для хранения разреженных матриц,
обычно состоит из двух частей: основной памяти, содержащей
числовые значения, и накладной памяти, где хранятся указа-
указатели, индексы и другая информация, нужная для запоминания
Основная
память
Номадная
память
Основная
память
Накладная
память
Рис. 2.3.1. Основная и накладная память для двух различных методов.
структуры матрицы и облегчения доступа к числовым значе-
значениям. Поскольку за машинную память приходится платить не-
независимо от того, как она используется, всякая оценка запросов
к памяти для данного метода решения должна включать описа-
описание способа, которым будут храниться матрица или матрицы,
так чтобы в этой оценке накладная память могла быть учтена
наряду с основной.
Сравнение двух различных стратегий с точки зрения крите-
критерия памяти может сводиться к сравнению существенно различ-
различных структур данных, имеющих весьма различающуюся на-
накладную память. Поэтому метод, предпочтительный в смысле
величины основной памяти, может уступать конкуренту, если
в сравнении учитывается и накладная память. Эту ситуацию
иллюстрирует рис. 2.3.1.
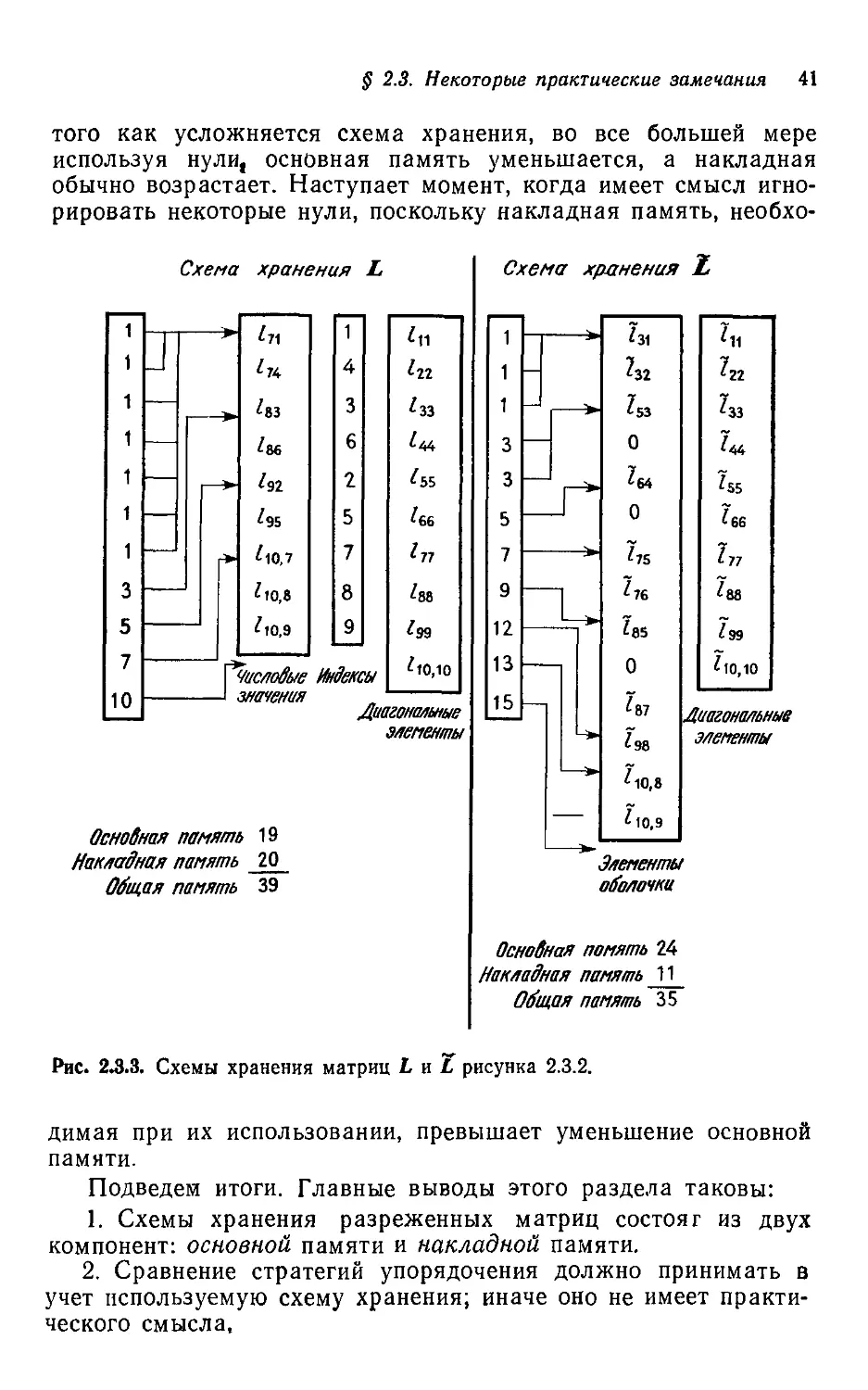
В качестве простого примера рассмотрим два упорядочения
матрицы на рис. 2.3.2 и соответствующие множители L и L. Эле-
Элементы нижнего треугольника L (исключая диагональ) хранятся
построчно в едином массиве; параллельный массив содержит
их столбцовые индексы. Третий массив указывает положение
каждой строки, а четвертый хранит диагональные элементы L
40 Гл 2 Вводные сведения
Для хранения матрицы L использована так называемая про-
профильная схема, описываемая в главе 4. Ненулевые элементы А
обозначаются символом *, а элементы заполнения в L или L —
звездочкой в кружочке.
* *
* *
* * * *
* * * *
* * *
* *
*#
* *
*г Пг Т^
*
Ч» -Г* Уг
*
Рис. 2.3.2. Два различных упорядочения разреженной матрицы А и erpjKTypa
ненулевых элементов соответствующих треугольных множителей L и L
Примеры на рисунках 2,3.2 и 2.3.3 иллюстрируют некоторые
важные моменты, связанные с упорядочениями и схемами хра-
хранения На поверхностный взгляд упорядочение 1, соответствую-
соответствующее А, кажется лучше, чем упорядочение 2, поскольку оно
вообще не приводит к заполнению, в то время как при втором
упорядочении заполнение состоит из двух элементов. Кроме
того, и схема хранения, выбранная для L, кажется хуже той,
что использована для L, поскольку первая игнорирует наличие
некоторых нулей, а в L разреженность эксплуатируется на сто
процентов. Однако из-за различий в накладной памяти комби-
комбинация упорядочения и хранения во втором случае приводит к
меньшим общим запросам к памяти. Конечно, различия здесь
тривиальны, но сам вывод полностью сохраняет силу. По мере
§ 2.3. Некоторые практические замечания 41
того как усложняется схема хранения, во все большей мере
используя нули, основная память уменьшается, а накладная
обычно возрастает. Наступает момент, когда имеет смысл игно-
игнорировать некоторые нули, поскольку накладная память, необхо-
Схема хранения L
'8з
'ее
Is2
'95
'iO,7
'ю,8
'iO,9
Числовые Индексы
значения
'и
1гг
'зз
'55
'бб
'77
'88
'10,10
элементы
ОсноЙная память 19
Накладная память 20
Общая память 39
Схема хранения ?
1
1
1
3
3
5
7
9
12
13
15
г—~^
—
г*
i
I
L
—I
->
¦-
'31
?32
у
0
?64
0
'75
'76
?85
0
'87
'~98
^10,8
h
7а
У
с
'S5
'бб
In
'88
'99
'10,10
Липронпльныв
гЩл tic* t/f/tlffl/ffGru
элементы
Элементы
оболочки
Основная помять 24
//окладная память 11
память 35
Рис. 2.3.3. Схемы хранения матриц L пТ рисунка 2.3.2.
димая при их использовании, превышает уменьшение основной
памяти.
Подведем итоги. Главные выводы этого раздела таковы:
1. Схемы хранения разреженных матриц состоят из двух
компонент: основной памяти и накладной памяти.
2. Сравнение стратегий упорядочения должно принимать в
учет используемую схему хранения; иначе оно не имеет практи-
практического смысла.
42 Гл. 2. Вводные сведения
2.3.2. Время исполнения
Перейдем теперь к критерию времени исполнения. При об-
обсуждении полезно выделить четыре этапа всего вычислитель-
вычислительного процесса: упорядочение, распределение памяти, разложе-
разложение и решение.
Как мы увидим в главе 9, время исполнения, необходимое
для различных упорядочений, может меняться в очень широких
пределах. Но даже если упорядочение найдено, остается сделать
еще многое, прежде чем можно будет начать реальные вычис-
вычисления. Нужно сформировать подходящую схему хранения для L,
а чтобы сделать это, нужно определить структуру L. Этот этап
распределения памяти также различен по стоимости в зависи-
зависимости от того, какие упорядочение и схема хранения применены.
Наконец, как демонстрируют многочисленные эксперименты,
представленные в главе 9, различия в схеме хранения могут
повести к существенным различиям в числе арифметических
операций, выполняемых в секунду, на этапах разложения и ре-
решения треугольных систем.
Обычно время исполнения разреженной матричной програм-
программы примерно пропорционально' (или должно быть пропорцио-
пропорционально) количеству производимой арифметики. Однако различия
в упорядочении и структуре данных могут привести к боль-
большим различиям в константе пропорциональности. Таким обра-
образом, число арифметических операций может быть не очень на-
надежной основой сравнения различных методов решения; по
крайней мере им следует пользоваться осмотрительно. Не кон-
константу пропорциональности влияет не только примененная струк-
структура данных, но также архитектура машины, транслятор и опе-
операционная система.
В дополнение к вариации относительных стоимостей испол-
HejHfl каждого из рассмотренных выше этапов сравнение раз-
различных стратегий часто зависит от конкретных обстоятельств
решаемой задачи. Если данную матричную задачу нужно ре-
решать лишь однажды, то сравнение стратегий, конечно, должно
включать время, необходимое для определения упорядочения и
формирования схемы хранения.
Напротив, если предстоит решать много различных задач
с одинаковой структурой, то при сравнении методов может ока-
оказаться оправданным игнорирование стоимости этого начального
этапа, поскольку львиную долю машинного времени забирают
разложение и решение треугольных систем. При других обстоя-
обстоятельствах нужно решать ряд систем, различающихся лишь пра-
правыми частями. В такой ситуации, может быть, разумно сравни-
сравнивать различные стратегии на основании времени, которого они
требуют при решении треугольных систем.
§23 Некоторые практические замечания 48
Подведем итоги. Главные выводы этого раздела таковы:
1. Весь процесс решения системы Ах = Ь состоит из четырех
основных этапов. Доля общего машинного времени, приходя-
приходящаяся на каждый из них, в общем случае существенно меняется
в зависимости от упорядочения и схемы хранения.
2. В соответствии с обстоятельствами конкретной задачи
время исполнения некоторых из упомянутых этапов может быть
практически несущественным при сравнении различных методов.
Упражнения
2.3.1. Предположим, что вы имеете выбор из двух методов решения раз-
разреженной системы уравнений Ах = Ь — метода 1 и метода 2, критерием вы-
выбора метода является время исполнения ^тапы упорядочения и распределе-
распределения памяти для метода 1 требуют совместно 20 секунд; соответствующее
время для метода 2 — всего лишь 2 секунды. Время разложения в методе
1 равно 6 секундам, а решения треугольной системы—0,5 секунды; для метода
2 соответствующие показатели равны 10 секундам и 1,5 секунды
а) Какой метод вы выбрали бы, если систему нужно решить лишь од-
однажды'
б) Какой метод вы выбрали бы, если нужно решить двенадцать систем
Ах = Ь с одинаковой структурой разреженности, но разными числовыми зна-
значениями А и 6?
в) Как бы вы ответили на вопрос б), если бы у систем различались лишь
числовые значения правых частей 6?
2.3.2. Предположим, что для данного класса разреженных положительно
определенных матричных задач имеется выбор из двух упорядочений, условно
называемых «черепаха» и «заяц» Ваш друг Пнтер показал, что упорядочение
«черепахой» дает треугольные множители, каждый из которых имеет ненуле-
ненулевых элементов щ(Ы)&Ы^2+ N—^fR; здесь N — порядок задачи. Он показал
также, что соответствующая функция для упорядочения «зайцем»_есть
¦ПЛ (TV) « 7.757Vlog2 (V# + l)-24W+ 11.5 -\/N\og2 (У# + l) + Пл/N +
+0.75 log2(V^ + 0-Еще один ваш приятель Гарольд написал программы ре-
решения линейных систем, использующие схемы хранения, подогнанные к соот-
соответствующему упорядочению. Гарольд обнаружил, что при реализации упоря-
упорядочения «зайцем» ему требуются по одному целому числу (индексу) для каж-
каждого ненулевого элемента L и, кроме того, еще три массива указателей; каж-
каждый массив — длины N. При реализации упорядочения «черепахой> накладная
память состоит лишь из N указателей.
а) Предположим, что ваш выбор метода основан исключительно на об-
общем объеме памяти, необходимом для хранения L, и что целые числа, как и
числа с плавающей точкой, хранятся полным машинным словом. Для каких
значений N вы использовали бы упорядочение «зайцем»1
б) Что бы вы ответили на вопрос а), если бы Гарольд переделал свои
программы так, чтобы целые числа были упакованы в машинном слове по
три?
3. Некоторые сведения из теории графов
и ее применение к исследованию
разреженных симметричных матриц
§ 3.0. Введение
В этой главе будут введены некоторые основные понятия
теории графов и установлено их соответствие с матричными
понятиями. Хотя лишь немногие результаты теории графов
нашли прямое приложение в анализе разреженных матричных
вычислений, ее обозначения и понятия удобны и полезны в опи-
описании алгоритмов, а также в опознании и характеризации струк-
структуры матрицы. Однако при использовании теории графов в та-
такого рода анализе легко перейти разумную грань; результат
ч"асто будет тот, что терминологическая элегантность затемняет
смысл некоторых по существу простых идей. Поэтому, принося,
возможно, в жертву единообразие изложения, мы всюду, где
это уместно и на пользу делу, даем определения и результаты
в терминах как теории графов, так и теории матриц. По тем же
причинам мы предпочитаем вводить большую часть терминов
теории графов там, где в этом возникает потребность, вместо
того чтобы ввести их все в этой главе, а затем отсылать к ней
в последующем тексте.
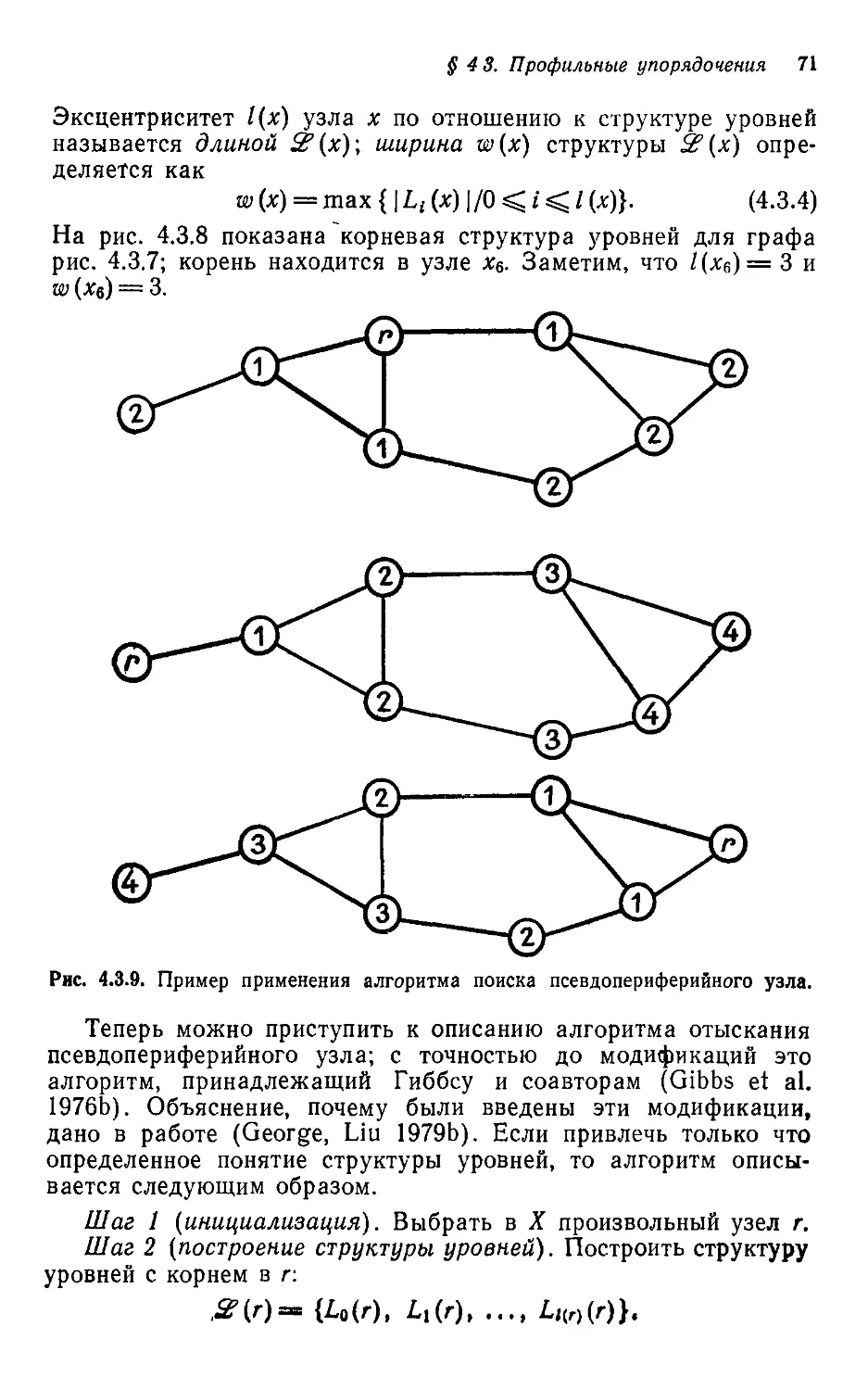
§ 3.1. Основная терминология и некоторые определения
Для наших целей граф G = (X, Е) можно представлять себе
состоящим из конечного множества узлов, или вершин, вместе
с множеством Е ребер, которые суть неупорядоченные пары вер-
шнн. Упорядочение {помечивание) а графа G = (X, Е) есть
попросту отображение множества {1, 2, ..., N} на X; здесь
N — число узлов G. Если специально не оговорено противопо-
противоположное, граф считается неупорядоченным. Граф G, помеченный
посредством а, будет обозначаться через Ga — (Ха, Е).
Вводя графы, мы намереваемся облегчить изучение разре-
разреженных матриц; поэтому сейчас мы установим связи между гра-
графами и матрицами. Пусть А— симметричная матрица порядка
N. Упорядоченный (помеченный) граф матрицы А, обозначае-
обозначаемый GA =(ХА, ЕА), — это граф, для которого N вершин GA про-
пронумерованы числами от 1 до /V и {*,-, х,} е ЕА тогда и только
§ 3.1. Терминология и некоторые определения 45
*
CD*
* © * *
* © *
* ©
* © *
* * ©
Матрица Л
Рис. 3.1.1. Матрица и ее помеченный граф. Символ * обозначает ненулевой
элемент А.
© *
* © * *
* (D *
* 0 *
*© *
* *
© * *
© *
* *©
*
Рис. 3.1.2. Граф рисунка 3 1.1 гтри различных помечивапиях и структуры со-
соответствующих матриц. Здесь Р и Q обозначают матрицы перестановок.
46 Гл. 8, Некоторые сведения из теории графов
тогда, когда a,j = а,, ФО, 1ф ']. Здесь х, — узел ХА с меткой /.
Рис. 3.1 Л иллюстрирует структуру матрицы и ее помеченного
графа. Чтобы подчеркнуть соответствие г'-го диагонального эле-
элемента матрицы с узлом i ее графа, мы указываем этот элемент
как i в кружочке. Внедиагональные ненулевые элементы обозна-
обозначены символом *.
Если Рф1 — произвольная (Л^Х Щ -матрица перестановки,
то непомеченные графы матриц А и РАРТ совпадают, а соот-
соответствующие помечивания различны. Таким образом, непоме-
непомеченный граф А представляет структуру А без упоминания о
каком-либо конкретном упорядочении. Он изображает класс
эквивалентности матриц РАРТ, где Р — любая (NX W)-матрица
перестановки. Отыскание «хорошей» перестановки для А можно
рассматривать как отыскание хорошего помечивания для ее
графа. Рис. 3.1.2 иллюстрирует сказанное.
Некоторые определения теории графов связаны с непомечен-
непомеченными графами. Чтобы интерпретировать такие определения в
матричных терминах, нужно ввести соответствующую матрицу,
что немедленно приводит к упорядочению графа. Хотя это и не
должно вызвать недор'азумсний, читателю все же не следует
приписывать какого-либо значения конкретному упорядочению,
выбираемому в наших матричных примерах и интерпретациях.
Когда мы говорим о «матрице, соответствующей графу G», мы
либо оговариваем некоторое упорядочение а для G, либо под-
подразумеваем, что упорядочение может быть произвольным.
Два узла х и у из G называются смежными, если {х, у} & Е.
Если У cr X'), то смежное множество для У есть
Adj (У) = {х <= X — У | {х, y}<sE для некоторого у <= У). C.1.1)
Словами: Adj (У) есть множество узлов G, не принадлежащих
У, но смежных хотя бы с одним узлом из У. Рис. 3.1.3 иллюстри-
иллюстрирует матричную интерпретацию множества Adj (У). Для удоб-
удобства узлы множества У были помечены последовательными це-
целыми числами. Если У имеет единственную вершину у, будем
писать Adj (у) вместо формально правильного Adj ({«/}).
Для УаХ степень У, обозначаемая через Deg(K), есть число
|Adj(K)|, где |5| — обозначение числа элементов множества 5.
Опять-таки, если У имеет единственную вершину у, будем писать
Deg(«/), а не Deg({«/}). Например, на рис. 3.1.3 Deg(Ar2)=3.
Частью G' = (X', Е ) графа G называется граф, для которого
Х'аХ и Е'сЕ. Если УаХ, то подграф G(y) — это часть
(У, Е(У)) графа G, такая, что
Я (К)-={{*, y}<sE\x<=Y, уввУ}. C.1.2)
') Здесь и всюду в книге обозначение У с: X допускает, что Y может
совпадать с X. Если важно, чтобы У было собственным подмножеством X,
это будет явно оговариваться.
§ S.I. Терминология и некоторые определения 47
На матричном языке подграф G(Y)— это граф матрицы, полу-
полученной из матрицы графа G вычеркиванием всех строк и столб-
столбцов, кроме тех, которые соответствуют У. Это иллюстрируется
рисунком 3.1.4.
Y =
Adj(Y) =.
Рис. 3.1.3. Иллюстрация к понятию смежного множества для множества
УаХ.
Подграф называется кликой, если все его узлы попарно
смежны. В матричной терминологии клике соответствует запол-
заполненная подматрица. Например, G({x2, xj) является кликой.
© *
* C)
Матрица
подграфа G(y)
GQO
Рис. 3.1.4. Пример подграфа G(Y) и соответствующей подматрицы. Исходный
граф G изображен на рис. 3.1.1.
Пример на рис. 3.1.4 иллюстрирует понятие, которое мы сей-
сейчас исследуем, а именно связность графа. Если х и у — различ-
различные узлы G, то путем из х в у длины / ^ 1 называется упорядо-
упорядоченное множество из /+1 различных узлов (vu v2, ..., иг+i)»
48 Гл. 3. Некоторые сведения из теории графов
такое, что vl+1 e Adj(i><), i«l,2 /, причем v, — х, vt+i =
= f/. Граф называется связным, если каждая пара различных
узлов соединена хотя бы одним путем. В противном случае G
несвязен и состоит из двух или более связных компонент. Если
говорить о матричных аналогиях, то должно быть ясно, что для
П
уть:
Рис 3.1. 5.Путь в графе и соответствующая матричная интерпретация.
несвязного графа О, состоящего из k связных компонент, при
последовательном помечивании этих компонент соответствую-
соответствующая матрица будет блочно-диагональной и каждый диагональ-
диагональный блок ассоциирован со связной компонентой. Граф G{Y) на
рис. 3.1.4 упорядочен именно так, и соответствующая ему ма-
матрица— блочно-диагональная. Рис. 3.1.5 показывает некоторый
путь в графе и его матричную интерпретацию.
Наконец, множество Y cz X называется разделителем связ-
связного графа G, если подграф G(X—У) несвязен. Так, например,
К== {л:3, xit Хь)—разделитель графа на рис. 3.1.5, потому что
граф G(X — Y) состоит из трех компонент с узловыми множест-
множествами {xi}, {xi} и {хб, хт) соответственно.
§ 3.2. Машинное представление графов 49
Упражнения
3.1.1. Симметричная матрица А называется разложимой, если найдется
матрица перестановки Р, такая, что
0 Ап
В противном случае Л называется неразложимой. Показать, что симметричная
матрица А неразложима тогда и только тогда, когда ассоциированный с ней
граф fr4 связен.
3.1.2. Пусть А—симметричная матрица. Показать, что матрица А обла-
обладает свойством распространения (см. упр. 2.2.3) тогда н только тогда, когда в
ассоциированном с ней графе ОЛ существует путь (хи х2 xN).
3.1.3. Охарактеризовать графы, ассоциированные со следующими матри-
матрицами:
** *
* * *
# * *
# * *
Ь)
'** *¦
#*#
***
*#*
#**
***
***
***
* ##
с)
* *
* *
* *
* *
* *
* #
* *
*#
§ 3.2. Машинное представление графов
Характеристики машинных алгоритмов, оперирующих с гра-
графами, обычно весьма чувствительны к способу их представле-
представления. В наших задачах. основной операцией с графами будет
ADJNCY
XADJ |
1
! 6 | 1
4 /
*
3
I
4
г
6
2 5 | 2
T
з
ч
9
6
1
11
5
I,
4
«I
номер Vina 1 2 3 4 5 6
Рис. 3.2.1. Пример структуры смежности.
выявление отношений смежности между узлами. Поэтому мы
нуждаемся в способе представления, позволяющем легко уста-
установить свойства смежности в графе и притом экономичном в
смысле памяти.
50 Гл. 3 Некоторые сведения из теории графов
Пусть G = (X, Е) — граф с N узлами. Списком смежности
для j;e! называется список, содержащий все узлы из Adj(jt).
Структура смежности графа G — это просто множество списков
смежности для всех j;el Такую структуру можно реализовать
очень просто и экономично, храня списки смежности последова-
последовательно в одномерном массиве ADJNCY; дополнительный индекс-
индексный массив XADJ длины N -\-1 содержит указатели начала каж-
каждого списка смежности в массиве ADJNCY. Пример показан на
Узел
1
2
3
4
5
6
2
1
2
2
3
1
Соседи
6
3
5
_
6
5
4
—
—
Рис. 3.2.2. Таблица связей графа на рис. 3.2.1. Неиспользуемые позиции таб-
таблицы указаны прочерками.
рис. 3.2.1. Из программистских соображений часто бывает удоб-
удобно иметь в XADJ дополнительную компоненту, так чтобы пере-
переменная XADJ(N-|- 1) указывала адрес первой свободной ячейки
в массиве ADJNCY (см. рис. 3.2.1). Ясно, что общая длина
массивов при такой схеме хранения равна |Х|-т-2|?|+ 1.
Для доступа к соседям данного узла можно воспользоваться
следующим программным сегментом:
NBRBEG - XADJ(NODE)
NBREND - XADJ(NODE + 1) - 1
IF (NBREND .LT. NBRBEG) GO TO 200
DO 100 I - NBRBEG, NBREND
NABOR - ADJNCY(I)
100 CONTINUE
200 •
Хотя во всех наших программах, оперирующих с графами,
используется описанная выше схема хранения., часто приме-
применяют и другие. Распространенной схемой хранения является
простая таблица связей, имеющая N строк и m столбцов, где
m = max{Deg(x)\x^X}. Список смежности t-ro узла хранится
в <-й строке. Эта Схема хранения может быть очень неэффектив-
неэффективной, если многие узлы имеют степень меньшую, чем т. В ка-
качестве примера на рис. 3.2.2 приведена таблица связей для
графа рисунка 3.2.1.
§ 3.2. Машинное представление графов 51
Описанные до сих пор две схемы имеют очевидный недоста-
недостаток. Если степени узлов неизвестны a priori, то трудно построить
схему хранения графа, заданного списком ребер, поскольку не-
неизвестны форматы отдельных списков смежности. Эту трудность
можно преодолеть, вводя поле связей. На рис. 3.2.3 изображен
NBRS LINK
1
г
3
4
5
6
MEAD
lo"
6
1
12
8
5
10
11
12
Рис. 3.2.3 Связные списки смежности для графа рис. 3.2.1.
\
6
2
3
1
1
4
3
5
6
5
2
11
-5
-1
7
9
4
г
-6
3
-4
пример такой схемы для графа рисунка 3.2.1. Значением ука-
указателя HEAD(t) является начало списка смежности t-ro узла;
при этом в массиве NBRS находим соседа узла i, а в массиве
LINK — указатель расположения следующего соседа этого узла.
Пусть, например, нужно отыскать соседей узла 5. Значение
HEADE) равно 8. Обращаемся к NBRS (8) и получаем 3. Это —
один из соседей узла 5. Переходим к LINK (8) и находим там 2.
Это значит, что следующего соседа узла 5 нужно искать в
NBRSB), где хранится 6. Наконец, находим LINKB)=— 5,
что указывает окончание списка смежности для узла 5. (Вообще
отрицательная связь —i указывает окончание списка смежности
52 Гл. 3. Некоторые сведения из теории графов
для узла i.) Общая длина массивов при таком способе пред-
представления графа равна \Х\ \-A\E\, что существенно больше, чем
в схеме хранения, используемой в наших ьрограммах.
Если в массивах NBRS и LINK достаточно места, то легко
можно добавлять новые ребра. Например, чтобы добавить к
структуре смежности ребро {3, 6}, изменим список смежности
узла 3, полагая LINKA3)=1, NBRSA3)=6, HEADC)=13.
Аналогичным образом изменим список смежности узла 6, пола-
полагая LINKA4)= 5, NBRSA4)= 3, HEADF)= 14.
§ 3.3. Некоторые общие сведения о подпрограммах,
оперирующих с графами
В последующих главах будут описаны многочисленные под-
подпрограммы, оперирующие с графами. Во всех этих подпрограм-
подпрограммах г.раф G = (X, Е) хранится посредством пары целых масси-
массивов (XADJ, ADJNCY), как разъяснено в § 3.2. Помимо этого,
у многих подпрограмм есть и другие общие параметры. Чтобы
избежать многократного описания таких параметров в дальней-
дальнейшем, обсудим их роль здесь, а затем, в сл>чае необходимости,
будем отсылать читателя к данному разделу.
Должно быть ясно, что сам факт хранения графа посред-
посредством пары массивов (XADJ, ADJNCY) предполагает конкрет-
конкретное помечивание этого графа. Такое упорядочение будем назы-
называть исходной нумерацией, и если мы говорим об «узле /», то
имеем в виду именно эту нумерацию. Когда подпрограмма на-
находит новое упорядочение, информация о нем хранится в
массиве PERM; при этом PERM(/) = & означает, что узел с
номером k в исходной нумерации имеет номер i при новом
упорядочении. Часто будет использоваться и родственный вектор
перестановки INVP (обратная перестановка); он имеет длину N
я INVP(PERM(i))=/. Таким образом, INVP(&) указывает по-
положение в массиве PERM узла, который в исходной нумерации
имел номер k.
Во многих наших алгоритмах необходимо оперировать лишь
: некоторыми подграфами графа G. Чтобы реализовать эти
операции, ряд наших подпрограмм использует для задания под-
подграфа целый массив MASK длины N. Подпрограммы принимают
в учет только те узлы i, для которых MASK (i) =7^=0. На рис. 3.3.1
представлен пример, иллюстрирующий роль целого массива
'MASK.
Наконец, некоторые наши подпрограммы имеют параметр,
обычно называемый ROOT, указывающий номер узла, для ко-
которого MASK (ROOT) =5^0. Эти подпрограммы, как правило,
оперируют с той связной компонентой подграфа, заданного мас-
массивом MASK, которая содержит узел ROOT. Таким образом,
§ 3.3. Подпрограммы, оперирующие с графами 53
комбинация ROOT и MASK определяет тот связный подграф в
G, который нужно обработать. Для ссылки на этот связный
подграф мы часто будем пользоваться словосочетанием «компо-
«компонента, задаваемая посредством ROOT и MASK». Например,
[раф G, помеченный
а соответствии со схемой
хранения на рис. 3.2.1
1
1
2
3
4
5
6
MASK(t)
1
1
0
1
1
0
Подграф графа Q,
задаваемый
массивом MASK
Рис. 3.3.1. Пример, показывающий использование массива MASK для задания
подграфа в графе G.
комбинация ROOT = 2 с массивом MASK и графом G на
рис. 3.3.1 задает граф
Резюмируя, перечислим некоторые часто используемые пара-
параметры наших подпрограмм вместе с их описанием:
(XADJ, ADJNCY) Пара массивов, хранящая граф при исход-
исходном упорядочении. Исходные метки узлов, смежных с уз-
узлом /, находятся в позициях ADJNCY (k), где XADJ(i) <: k <
<XADJ(i+ 1); XADJ(yV+ 1) = 2|?|+ 1.
PERM Целый массив длины N, содержащий новое упоря-
упорядочение.
INVP Целый массив длины N, содержащий обратную пе-
перестановку.
MASK Целый массив длины yV, используемый для задания
подграфа в графе G. Подпрограмма игнорирует те узлы, для
которых MASK (i) == 0.
ROOT Номер узла, для которого MAS К (ROOT) =^0. Под-
Подпрограмма обычно оперирует с той компонентой подграфа, за-
заданного массивом MASK, которая содержит узел ROOT.
B4 Гл. 3. Некоторые сведения из теории графов
Упражнения
3.3.1. Предположим, что для представления графа G = (X, Е) использо-
использована нижняя структура смежности. Это значит, что вместо хранения для каж-
каждого узла х полного смежного множества Adj (x) мы храним только те узлы
нз Adj(i), метки которых больше, чем у х. Например, граф рисунка 3.2.1
можно представить с помощью пары массивов LADJ н XLADJ, как показано
ниже.
Номер узла 1
LADJ
XLADJ
|2 6 | 3
0
:
J !
к
5
4 I 5
t
I I
1 1
6 6
1 6
t '
7
Л
6
Составьте подпрограмму, которая преобразует нижнюю структуру смеж-
смежности в полную. Считайте, что вы располагаете массивом LADJ длины 2|?|,
содержащим в первых \Е\ позициях нижнюю структуру смежности, и масси-
массивом XLADJ. Кроме тою, имеется рабочий массив длины \Х\. Когда программа
заканчивает работу, массивы XLADJ и LADJ должны содержать элементы
массивов XADJ и ADJNCY, как это описано в § 3.2.
3.3.2. Предположим, что несвязный граф G = (X, Е) хранится парой
массивов XADJ и ADJNCY в соответствии с описанием § 3.2. Напншнте под-
подпрограмму, для которой узел х е X является входным параметром и которая
выдает узлы связной компоненты G, содержащей х. Убедитесь, что вы опи-
описали все параметры подпрограммы и все виды необходимой вспомогательной
памяти.
3.3.3. Предположим, что (возможно, несвязный) граф G = (X, Е) хра-
хранится парой массивов XADJ и ADJNCY в соответствии с описанием § 3.2.
Пусть подмножество Y а X задано целым массивом MASK длины N, как это
разъяснено в § 3.3. Составьте программу, для которой входными параметра-
параметрами были бы число N и массивы XADJ, ADJNCY н MASK и которая выдава-
выдавала бы число связных компонент подграфа G(Y). Чтобы ваша программа была
проще и удобнее для чтения, может потребоваться рабочий массив дли-
длины N.
3.3.4. Предположим, что граф матрицы А хранится парой массивов
(XADJ, ADJNCY) в соответствии с описанием § 3.2, и пусть массивы PERM
и INVP соответствуют матрицам перестановок Р и Рт (см § 3 3). Напишите
подпрограмму, выдающую столбцовый индекс первого ненулевого элемента
каждой строки матрицы РАРТ. Ваша программа должна также печатать число
ненулевых элементов слева от диагонали в каждой строке РАРТ.
3.3.5. Составьте программу, которая отличалась бы от программы
упр. 3 3.4 только той дополнительной особенностью, что она оперирует с под-
подматрицей матрицы РАРТ, задаваемой массивом MASK
3.3.6. Предположим, что входной граф задан последовательностью ребер
(пар номеров узлов) и длины списков смежности заранее не известны. На-
Напишите программу под названием INSERT, с помощью которой можно было
бы построить связные списки смежности, пример которых показан на рис. 3.2.3.
Убедитесь, что вы ничего не упустили в списке параметров, и обдумайте, как
следует присвоить начальные значения массивам Вы не должны предпола-
предполагать, что числа \Х\ и |?| известны заранее. Предусмотрите нестандартные си-
ситуации, например, массивы не вмещают все ребра, илн некоторое ребро вве-
введено повторно, и т. д.
§ 3.3. Подпрограммы, оперирующие с графами 55
3.3.7. Предположим, что граф матрицы А хранится парой массивов
(XADJ, ADJNCY) в соответствии с описанием § 3.2. Составьте программу, для
которой входом были бы эти два массива вместе с двумя номерами узлов i и
/ и которая бы определяла, имеется ли в графе соединяющий их путь. Если
да, программа выдает длину такого кратчайшего пути; в противном случае
оиа выдает нуль. Описать все рабочие массивы, которые вам понадобятся.
3.3.8. Составьте программу, которая отличалась бы от программы упр. 3.3.7
только той дополнительной особенностью, что она оперирует с подграфом, за>
даваемым массивом MASK.
4. Ленточные и профильные ° методы
§ 4.0. Введение
В этой главе мы рассмотрим один из простейших подходов
к решению разреженных систем, а именно ленточные схемы и
тесно связанные с ними оболочечные, или профильные, методы.
Говоря приблизительно, цель здесь состоит в таком упорядо-
упорядочении матрицы, чтобы ненулевые элементы РАРТ группирова-
группировались «возле» главной диагонали. Поскольку это свойство со-
сохраняется соответствующим множителем Холесского L, такие
упорядочения привлекательны с точки зрения сокращения
заполнения и широко используются в практике (Cuthill 1972,
Felippa 1975, Melosh, Bamford 1969).
Хотя эти упорядочения зачастую далеки от оптимальных в
смысле критерия наименьшей арифметики или наименьшего за-
заполнения, они являются практически выгодным компромиссом.
Как правило, программы и структуры данных, нужные для
эксплуатации создаваемой ими разреженности, относительно
просты; тем самым издержки в памяти и вычислительной ра-
работе для них малы в сравнении с более сложными упорядоче-
упорядочениями (вспомните замечания в § 2.3). Само получение упоря-
упорядочений обычно значительно дешевле, чем для (теоретически)
более эффективных методов. Для малых задач и даже задач
среднего размера, которые нужно решать лишь в небольшом ко-
количестве, возможность применения методов, описываемых в этой
главе, должна рассматриваться всерьез.
§ 4.1. Ленточный метод
Пусть А —симметричная положительно определенная ма-
матрица порядка N с элементами atj. Для i-ii строки A, i — 1, 2,...
,.., Nr положим
/(Л) {|^0}
= i-ft( A).
1 В оригинале — envelope methods Мы предпочли буквальному переводу
«оболочечные методы» термин «профильные методы», — Прим, перев.
§ 4.1. Ленточный метод 57
Число fi(A) — это столбцовый индекс первого ненулевого эле-
элемента i-й строки А. Так как диагональные элементы аи положи-
положительны, имеем
Вслед за Катхиллом и Макки определим ширину ленты А
как')
Р (Л) = max {р, (Л) 11 < i < N)
= max{| i — /|| ацфО}.
Число Pi (А) называется i-й шириной ленты А. Ленту опреде-
определяем таким образом:
Band (A) = {{/, /}|0</-/<Р(А)}, D.1.1)
т. е. как область матрицы, удаленную от главной диагонали не
более чем на Р(Л) позиций. Поскольку А симметрична, в D.1.1)
;
1
2
3
4
5
в
7
/И)
1
1
3
1
3
3
5
АИ)
0
1
0
3
2
3
2
Рис. 4.1.1. Пример, показывающий fi(A) и р,(Л).
используются неупорядоченные пары {i, /}. Матрица на
рис. 4.1.1 имеет ширину ленты, равную трем. Матрицы с шириной
ленты, равной единице, называются трехдиагональными.
Применение ленточного метода подразумевает, что нули вне
Band (А) игнорируются; нули же внутри ленты обычно хра-
хранятся, хотя их присутствие часто используется на этапе числен-
численного решения. Использование разреженности основано на соот-
соотношении
Band (A) = Band (L + LT),
которое будет доказано в § 4.2, где рассматривается профиль-
профильный метод.
') Некоторые авторы называют шириной леиты А число 2E(Л) + 1.
68 Гл. 4. Ленточные и профильные методы
Обычным методом хранения симметричной ленточной матри-
матрицы А является так называемая диагональная схема хранения
(Martin 1971). Поддиагонали нижнего треугольника А, состав-
составляющие Band(Л), вместе с главной диагональю хранятся по
столбцам в прямоугольном массиве с размерами /VX(P(^)+ 1).
«II
\ "гг Симметрично
О 0 ап
041 О О О44
О flsj ^54 055
043 О О а66
О а75 076 077,
Матрица А
Рис. 4.1.2. Диагональная схема хранения.
- - «п
- ^21 022
О 0 ап
041 О О О44
О О53 О54 055
бз О О а66
О 07S O76 077,
Массив хранения
Это показано на рис. 4.1.2. Такая схема хранения очень проста
и вполне эффективна, если $i(A) не слишком меняется с изме-
изменением L
Теорема 4.1.1. Число операций, необходимых для разложения
матрицы А с шириной ленты р, в предположении, что лента
Band (JL+ 17) заполнена, равно
Доказательство. Утверждение следует из теоремы 2.1.2 и
формул
JP + 1, если 1</<#-Р,
ч( •*' \N-i-\-\, если N-$<i<N.
Теорема 4.1.2. Пусть А та же, что и в теореме 4.1.1. Число
операций, необходимых для решения системы Ах = Ъ при из-
известном множителе Холесского L матрицы А, равно
Доказательство. Утверждение следует из теоремы 2.1.2 и
формул для T\(L*i), приведенных в доказательстве теоре-
теоремы 4.1.1.
Как отмечалось выше, достоинство этого подхода — в его
простоте. Однако у него есть и некоторые потенциально серьез-
серьезные слабости. Прежде всего, если $i(A) сильно меняется при
изменении (, то диагональная схема хранения, показанная на
рис. 4.1.2, будет неэффективна. Кроме того, мы увидим позднее,
§ 4.2. Профильный метод 69
что имеются некоторые очень разреженные задачи, которые мо-
могут быть решены весьма эффективно; однако их нельзя упоря-
упорядочить так, чтобы они имели малую ширину ленты (см.
рис. 4.2.3). Таким образом, существуют задачи, для которых
ленточные методы просто непригодны. Возможно, самая убеди-
убедительная причина, почему не стоит быть энтузиастом ленточных
схем, та, что профильные методы, обсуждаемые в следующем
параграфе, имеют те же достоинства простоты, что и ленточные,
и лишь немногие из их недостатков.
Упражнения
4.1.1. Пусть А — симметричная положительно определенная NXN мат-
матрица с шириной ленты р. У вас имеются два набора подпрограмм для ре-
решения системы Ах = Ь. В обоих случаях в процессе разложения L записы-
записывается на место А. В первом случае А хранится как заполненная нижняя тре-
треугольная матрица; при этом строки нижней треугольной части хранятся одна
за другой в одномерном массиве в последовательности ац, 021, a22, язь ...
..., а„,„-1, а„п. Во втором случае А хранится по диагональной схеме, опи-
описанной в этом параграфе. Если р и N заданы, то какую схему вы выбрали бы,
пытаясь минимизировать запросы к памяти?
4.1.2. Рассмотрите звездный граф с N узлами, показанный на рис. 4.2.3а.
Докажите, что при любом упорядочении этого графа ширина ленты соответ-
соответствующей матрицы не будет меньше, чем f (N— 1 )/21 .
§ 4.2. Профильный метод
4.2.1.Матричная формулировка
Несколько более сложной схемой использования разрежен-
разреженности является так называемый оболочечный, или профильный,
метод, в котором удается извлечь выгоду из изменения р((А)
как функции от L Оболочка А, обозначаемая через Env (А),
определяется как
Env (А) = {{*, Л 10 < i - i < р, (А)}.
То же самое можно записать посредством столбцовых индексов
Env (А) =-{{/, /}|/, (Л) </<*}•
Величина |Env(A)| называется профилем или размером обо-
оболочки А. Справедлива формула
I Env (А) | = g( Э/ (А).
Лемма 4.2.1.
Env (A)
') Читатель должен помнить, что там, где это им удобно, авторы считают
пары {/, /} в определении Еа\(А} неупорядоченными; тогда оболочка «удваи-
«удваивается». — Прим. перев.
вО Гл 4. Ленточные и профильные методы
Доказательство. Докажем лемму индукцией по размерности
N. Предположим, что утверждение справедливо для матриц по-
порядка N—1. Пусть А — Л'ХЛ/ симметричная матрица, пред-
представленная в виде
(М и\
где s —скаляр, и —вектор длины /V — 1, а М — невырожденная
матрица порядка N—1, разложенная в произведение LML^
Env(A)
Рис 4.2.1. Иллюстрация к определению оболочки А. Элементы заполнении в
L обведены кружками.
По предположению индукции, Env(M) = Env(LjM + L^). Если
LU — симметричное разложение А, то треугольный множитель
L можно записать как
\wT t Г
где t — скаляр, а и> — вектор длины N—1. Теперь достаточно
показать, что /w (A) = fN (L + LT).
Согласно B.1.5), векторы и и w связаны соотношением
Lmxv = и.
Но и, = 0 для 1 ^ i < !n{A), а элемент Щы(а> не равен нулю.
Как следует из лемм 2 2.3 и 2.2.4, ш, = 0 для 1 < / < fN{A) и
? 0. Поэтому In (A) = In (L + LT), откуда
Теорема 4.2.2.
Env(A)<=Band(A).
Доказательство. Это следует из определений множеств Band
и Env.
1
1
2
3
4
5
6
7
«.И)
2
1
3
2
2
1
0
Л D)
0
1
0
3
2
3
2
§4 2. Профильный метод 61
На результате леммы 4 2.1 основана возможность использо-
использования нулей вне области, занятой оболочкой или лентой. Пред-
Предполагая, что используются лишь нули, лежащие вне Еп\(Л),
определим арифметическую работу при численном решении си-
системы. Для подсчета числа операций полезно понятие ширины
* *
* о * *
А - # <¦? 0 * * о
* * * ® *
* * *
Рис. 4.2.2. Иллюстрация к определениям ширины леиты и ширины фронта.
фронта, которое мы сейчас введем. Для матрицы А i-я ширина
фронта определяется как
юг (А) = | {k | k > i и akt ФО для некоторого /</} |.
Заметим, что со, (Л) есть число «активных» строк на j-м шаге
разложения, т. е. число строк оболочки А, которые пересекают
i-u столбец. Величину
а(А) = max {щ (Л) 11 < /< N}
обычно называют шириной фронта, или волновым фронтом А
(Irons 1970, Melosh 1969). Рис. 4.2.2 иллюстрирует эти опреде-
определения.
Полезность понятия ширины фронта в анализе профильного
метода демонстрирует следующее утверждение.
Лемма 4.2.3.
|Епу(Л)|=1 со, (Л).
Теорема 4.2.4.
Если используются лишь пули, находящиеся вне оболочки,
то число операций, необходимых при разложении А в произве-
произведение LU, выражается формулой
62 Гл. 4. Ленточные и профильные методы
а число операций, необходимых для решения системы Ах = Ь
при известном разложении А = LU, равно
1-Х
Доказательство. Если считать оболочку А заполненной, то
число ненулевых элементов в L»,- равно со,(А)+ 1. Теперь нуж-
нужное утверждение вытекает из теоремы 2.1.2 и леммы 2.2.1.
Рис. 4.2.3а. Звездный граф с N узлами.
" *
*
*
* *
* *
* *
* *
* *
* *
********
* *
* *
* *
тС С
*****
*
*
*
*
* *. * *
*
*
*
*
Упор/гЭочвнив, 0 ко/порам
центральный узел помечен
последним
Упорядочение с минимальной
шириной ленты
Рис. 4.2.36. Упорядочение с минимальным профилем и упорядочение с мини-
минимальной шириной ленты для звездного графа с JV узлами при N = 9.
Хотя переход от ленточных схем к профильным связан лишь
с очень небольшим усложнением, он может подчас дать весьма
впечатляющий выигрыш. Чтобы убедиться в этом, рассмотрим
пример на рис. 4.2.3, где показаны два упорядочения одной
матрицы.
Нетрудно проверить, что число операций, необходимых при
разложении матрицы, упорядоченной так, чтобы профиль был
минимален, и число ненулевых элементов в соответствующем
треугольном множителе суть величины порядка O(N). Такой же
порядок имеет ширина ленты. В то же время упорядочение с
минимальной шириной ленты требует O(N3) операций, a L имеет
O(N2\ ненулевых элементов.
§ 4.2. Профильный метод 63
Хотя этот пример сконструирован искусственно, есть много
практических задач, где профильные схемы много эффективней
ленточных. Некоторые примеры приведены в работе (Liu, Sher-
Sherman 1975).
4.2.2. Интерпретация на языке графов
Пусть симметричной NX.N матрице А сопоставлен неориен-
неориентированный граф
GA = (XA, EA),
узлы которого помечены в соответствии с нумерацией строк А:
ХА = {хи ..., xN).
Чтобы лучше понять комбинаторную природу профильного
метода, полезно дать интерпретацию в терминах теории графов
тех матричных понятий, которые введены в предыдущем раз-
разделе.
Теорема 4.2.5.
Если i < /, то включения {/, i} еЕпу(Л) и Xj e Adj({*i, ...
..., х,}) равносильны.
Доказательство. Если xt e Adj({*i, ..., *<}), то atk Ф 0 для
некоторого k, k ^ i, так что f/(A) ^ 4 и {/, i} e Епу(Л).
Обратно, если f/(A)^i</, это означает, что Xj^Ad](xf (Л)),
откуда х/ е Adj ({хи ..., д;,}).
Следствие 4.2.6.
Для i— I, ..., N справедливы равенства
Доказательство. Согласно определению ©г(А), имеем
©<(Л)-|{/>/|{/, *}<=Env(A)}|.
Теперь нужное утверждение вытекает из теоремы 4.2.5.
Рассмотрим матрицу и соответствующий ей помеченный граф
на рис. 4.2.4. Смежными множествами здесь будут:
Adj({Xl.x2}) =
2.Xl}) _ {лг4.лг5.лг6}
i. . . . ,Xl}) ш 0 ,
64 Гл. 4 Ленточные и профильные цетоды
Сравните их со строчными индексами элементов оболочки в
каждом столбце.
Рис. 4.2 4. Матрица и соответствующий ей помеченный граф
Множество Adj({A;I) ..., хг}) будет именоваться i-м фронтом
помеченного графа, а число элементов этого множества (как
и раньше)— i-й шириной фронта.
Упражнения
4.2.1. Доказать, что
N N
АЛЛ. Говорят, что симметричная матрица А имеет монотонный профиль,
если ft (А) </,(Д) при / < i. Показать, что для матрицы А с монотонным
профи чем
N N
4.2.3. Доказать эквивалентность следующих условий:
а) для 1 ^ ( ^ Л/ подграфы G({xu .., xi)) связны;
б) для 2 ^ ( ^ Л/ справедливо fi{A) < i.
4.2.4. {заполненная оболочка) Доказать, что матрица L -\- U имеет за-
заполненную оболочку, если f, (A) < i для 2 ^ ( ^ N Показать, что L + LT
имеет заполненную оболочку, если А — матрица с монотонным профилем.
4.2.5 Пусть L — N X N нижняя треугольная матрица с шириной ленты
Р < Л/, и пусть V — № у Р (псевдо) нижняя треугольная матрица, определен-
определенная в упр. 2 2 8 Указать приблизительное число операций, необходимых для
вычисления I-'V.
4.2.6. Пусть {*i, ..., Хк)—узлы графа GA, ассоциированного с симмет-
симметричной матрицей А. Показать, что следующие условия эквивалентны:
а) оболочка Env(<4) заполнена;
б) Adj({*,, ...,*,}) с Adjto) для 1< ( < JV;
в) G(Adj({tfi, .... */}) U{xi)) для 1 < 1 < Л^ является кликой
4.2.7. Доказать, что для связного графа GA справедливо азЛА) ф 0 для
1 <JV1
$ 4.3. Профильные упорядочения 65
§ 4.3. Профильные упорядочения
4.3.1. Обратный алгоритм Катхилла — Макки
Вероятно, наиболее широко используемым алгоритмом уши
рядочения, имеющим целью уменьшение профиля, является опи-
описываемый ниже вариант метода Катхилла — Макки. Опублико-
Опубликованный этими авторами в 1969 г. (Cuthill 1969) алгоритм пер-
первоначально предназначался для уменьшения ширины ленты
разреженной симметричной матрицы.
В основе метода — следующее замечание. Пусть у — поме-
помеченный узел, а г — непомеченный сосед у. Понятно, что, для торо
Рис. 4.3.1. Влияние на ширину ленты относительной нумерации смежных уа-
лов z и у.
чтобы уменьшить ширину ленты в строке, соответствующей г,
нужно присвоить г номер, как можно менее отличающийся от
номера у. Рис. 4.3.1 поясняет это замечание.
Схему Катхилла — Макки можно рассматривать как метод
уменьшения ширины ленты матрицы посредством локальной
минимизации чисел |3г. Это приводит к предположению, что
схему можно использовать и для уменьшения профиля 20* ма-
матрицы. Исследуя профильные методы, Джордж обнаружил
(George 1971), что упорядочение, получаемое обращением упо-
упорядочения Катхилла — Макки, часто гораздо сильнее уменьшает
профиль, чем первоначальное упорядочение, хотя ширина ленты
остается неизменной. Это упорядочение было названо обратным
упорядочением Катхилла — Макки (RCMI). Позднее было до-
доказано, что обратная схема всегда не хуже прямой в отношении
хранения и обработки оболочки (Liu 1975).
') От английского словосочетания — Reverse Cuthill—McKee. — Прим.
перев.
66 Гл 4. Ленточные и профильные методы
Для связного графа алгоритм RCM можно описать следую-
следующим образом. (Вопрос о выборе начального узла на шаге 1 раз-
разбирается в следующем разделе.)
Шаг 1. Определить начальный узел г и выполнить присваива-
присваивание Х\ -*~ Г.
Шаг 2 (основной цикл). Для /= 1 N найти всех нену-
ненумерованных соседей узла xt и занумеровать их в порядке возра-
е*ания степеней.
Шаг 3 (обратное упорядочение). Обратное упорядочение
Квтхилла —Макки есть г/ь г/2, .... JJn, где yi = xN-i+i для г =
1, .... N.
В случае если граф GA несвязен, описанный выше алгоритм
можно применять к каждой связной компоненте графа по оче-
очереди. Если начальный узел задан, алгоритм относительно прост.
Рис. 4.8.2. Граф, к которому применяется алгоритм RCM.
1
2
3
4
1
6
7
8
9
10
Уэел х,
g
h
е
Ъ
f
е
J
а
d
1
Ненумвробанныв
dbaeqit
о порядке возрастания
степеней
h.e,b,f
_
«
j
a.d
_
-
—
f
Рис. 4.8.3. Таблица, показывающая нумерацию иа шаге 2 алгоритма RCM.
Рассмотрим его применение к примеру, изображенному на
рис. 4.3.2.
Предположим, что в качестве начального взят узел «g»,
т. «. х\ ¦¦ g. На рис-4.8,3 показано, как нумеруются узлы на
§ 4.3. Профильные упорядочения 67
шаге 2 алгоритма. Обратное упорядочение Катхилла — Макки
приведено на рис. 4.3.4; размер оболочки равен 22.
Эффективность алгоритма упорядочения критическим обра-
образом зависит от выбора начального узла. Если в нашем примере
Симметрично
Рис. 4.3.4. Окончательное упорядочение и структура соответствующей мат-
матрицы.
Рис 4.8.5. RCM-упорядочение для графа на рнс. 4.3.2 прн другом начальном
узле.
в качестве начального взять узел «а», то получим меньший про-
профиль, равный 18. В разделе 4.3.2 будет описан алгоритм, кото-
который, как показала практика, дает хорошие начальные узлы для
алгоритма Катхилла — Макки.
Установим теперь грубую оценку сложности (времени испол-
исполнения) алгоритма RCM, считая, что начальный узел задан,
68 Гл. 4. Ленточные и профильные методы
В основе будет предположение, что время исполнения исполь-
используемого алгоритма сортировки пропорционально числу опера-
операций. Под операцией понимается сравнение либо выборка эле-
элемента информации из структуры смежности, применяемой для
хранения графа.
Рис. 4.3.6. Диаграмма, показывающая эффект обращения упорядочения по
сравнению с рис. 4.3.1.
Теорема 4.3.1.
Если для сортировки используется метод пузырька1), то
временная сложность алгоритма RCM ограничена величиной
О(пг\Е\), где m — максимальная степень узла.
Доказательство. Основной вклад в стоимость вносит, оче-
очевидно, шаг 2 алгоритма, поскольку шаг 3 может быть выполнен
за время O(N). Сортировка t элементов посредством метода
пузырька требует ct2 операций, где с — некоторая константа
(Aho 1974). Таким образом, общее время, затрачиваемое на сор-
сортировку, меньше, чем
cZ I Deg (x) |2<cm? I Deg(*) | = 2cm |Е\.
х<=Х Х€=Х
Для каждого индекса i мы должны обследовать на шаге 2
соседей узла i, выделить среди них ненумерованных и сортиро-
сортировать их по возрастанию степеней. Проход по структуре смежности
требует 2\Е\ операций. Вычисление степеней узлов требует еще
2\Е\ операций. Итак, алгоритм RCM требует не более чем
4\E\-r-2cm\E\ + N
операций, где последний член отображает время, необходимое
для обращения упорядочения.
') В оригинале — linear insertion.—Прим. перев,
§ 4.3. Профильные упорядочения 69
4.3.2. Определение начального узла
Обратимся теперь к задаче отыскания начального узла для
алгоритма RCM. Мы выделяем эту задачу, поскольку ее реше-
решение используется еще в нескольких алгоритмах, описываемых
в книге. Во всех случаях цель состоит в том, чтобы найти пару
узлов, удаленных друг от друга на максимальное или почти
максимальное «расстояние» (определяемое ниже). Значитель-
Значительный практический опыт свидетельствует, что такие узлы хороши
в качестве начальных для нескольких алгоритмов упорядочв'
ния, в том числе для алгоритма RCM.
Рис. 4.3.7. Граф О с 8 узлами, для которого 6(G) = 5.
Напомним (см. § 3.1), что путем длины k из узла Хо в узел
Xk называется упорядоченное множество различных вершин
(хо, х\, ..., хк), где xi e Adj(xi+i) для 0 ^ / ^ k — 1. Расстоя-
Расстояние d(x, у) между двумя узлами х и у связного графа G =
= (X, Е) есть просто длина кратчайшего пути, соединяющего
эти узлы. Следуя Бержу (Berge 1962), определим эксцентриси-
эксцентриситет узла х как величину
l(x) = max{d(x, y)\ye=X). D.3.1)
Теперь можно ввести понятие диаметра графа G:
или эквивалентно
6(G) = max{u?(x, y)\x, уе=Х}.
Узел «е! называется периферийным, если его эксцентри-
эксцентриситет равен диаметру графа, т. е. если l(x) = 6(G). На
рис. 4.3.7 показан граф с восемью узлами, диаметр которого
равен 5. При этом узлы х2, Хь и x^ периферийные.
Теперь, когда терминология установлена, можно сформули-
сформулировать цель данного раздела. Она состоит в описании эффек-
эффективного эвристического алгоритма для определения узлов с
большим эксцентриситетом. Подчеркнем, что алгоритм не дает
гарантии, что будет найден периферийный узел или хотя бы узел,
близкий к периферийному. Тем не менее получаемые узлы, как
правило, имеют большой эксцентриситет и являются хорошими
яачальными значениями для использующих их алгоритмов.
70 Гл. 4. Ленточные и профильные методы
Кроме того, исключая некоторые весьма тривиальные ситуа-
ситуации, нет оснований думать, что периферийные узлы сколько-
нибудь лучше в качестве начальных, чем те, которые опреде-
определяют данный алгоритм. Наконец, во многих случаях отыскание
периферийных узлов, даже если оно желательно, представляет
собой дорогостоящее предприятие, так как наилучший извест-
известный алгоритм для этой задачи имеет в качестве оценки времен-
временной сложности величину O(|Z||?|). В большинстве разрежен-
разреженных матричных приложений оценку можно заменить на O(|Z|2)
U(*e) = {xs,x7}
Рис. 4.3.8. Структура уровней с корнем в xt, для графа рис. 4.3.7.
В последующем изложении узлы, определяемые данным алго-
алгоритмом, будут называться псевдопериферийными.
Введем теперь некоторые обозначения и терминологию, нуж-
нужные для описания алгоритма. Читателю, возможно, будет по-
полезно вспомнить определения смежного множества, степени,
подграфа и связной компоненты (см. § 3.1). Основной конструк-
конструкцией алгоритма является корневая структура уровней') (Агапу
1972J). При заданном узле х структура уровней с корнем в х
есть разбиение & (х) множества X:
), ..., Lt(x)(x)},
такое, что
L0(x) =
/ = 2, 3, ...,
D.3.2)
D.3.3)
') В оригинале — the rooted level structure. — Прим. перев
2) Общая структура уровней есть разбиение 9? = Lo, Lh ..., Ц), где
Adj(Lo) c.Ii. Adj(L,) cri,-, и AdJ(L;) с 1,_, (J !<+!, i = 2, 3, .'.., /—1.
§4 3. Профильные упорядочения 71
Эксцентриситет 1(х) узла х по отношению к структуре уровней
называется длиной S'(x); ширина w(x) структуры %(х) опре-
определяется как
да (х) = max {| Lt (х) |/0 < / < / (*)}. D.3.4)
На рис. 4.3.8 показана корневая структура уровней для графа
рис. 4.3.7; корень находится в узле х6. Заметим, что /(л;6)= 3 и
да (дев) = 3.
Рис. 4.3.9. Пример применения алгоритма поиска псевдопериферийного узла.
Теперь можно приступить к описанию алгоритма отыскания
псевдопериферийного узла; с точностью до модификаций это
алгоритм, принадлежащий Гиббсу и соавторам (Gibbs et al.
1976b). Объяснение, почему были введены эти модификации,
дано в работе (George, Liu 1979b). Если привлечь только что
определенное понятие структуры уровней, то алгоритм описы-
описывается следующим образом.
Шаг 1 (инициализация). Выбрать в X произвольный узел г.
Шаг 2 (построение структуры уровней). Построить структуру
уровней с корнем в г:
72 Гл. 4. Ленточные и профильные методы
Шаг 3 (стягивание последнего уровня). Выбрать в S't^lrf
узел х с минимальной степенью.
Шаг 4 (построение структуры уровней).
а) Построить структуру уровней с корнем в х:
2?(x)={U(x), U(x) Цх)(х)}.
б) Если /(х)>/(г), положить г+-х и перейти к шагу 3.
Шаг 5 (финиш). Узел х является псевдопериферийным.
В следующем разделе описаны и обсуждаются подпрограммы
FNROOT и ROOTLS, реализующие этот алгоритм. На рис. 4.3.9
приведен пример, демонстрирующий работу алгоритма. Узлы
уровня i всех структур уровней помечены числом /.
4.3.3. Подпрограммы поиска начального узла
В этом разделе описаны и обсуждаются две подпрограммы,
реализующие алгоритм предыдущего раздела. В этих подпро-
подпрограммах и подпрограммах разделов 4.3.4 и 4.4.2 имеется не-
несколько общих входных параметров, которые были описаны
в § 3.3. Прежде чем продолжить чтение, читателю, возможно,
будет полезно вспомнить содержание этого параграфа.
ROOTLS (ROOTed Level Structure)
Назначение этой подпрограммы — генерировать структуру
уровней связной компоненты, задаваемой входными параметра-
параметрами ROOT, MASK, XADJ и ADJNCY, как описано в § 3.3 На вы-
выходе из подпрограммы будет получена структура уровней с
корнем в узле ROOT; она задается парой массивов (XLS, LS),
причем узлы уровня k суть значения переменных LS(/), где
XLS(&) ^ / < XLS(& + 1). Число уровней указывает перемен-
переменная NLVL. Отметим, что, так как в Фортране не допускаются
нулевые индексы, у нас не может быть «нулевого уровня»; по-
поэтому здесь k соответствует Lk-\ в структуре уровней раздела
4.3.2. По той же причине NLVL на единицу больше, чем эксцен-
эксцентриситет узла ROOT.
Подпрограмма определяет уровень за уровнем; новый уро-
уровень получается в результате каждого выполнения цикла DO
400 .... После определения каждого очередного узла (в резуль-
результате выполнения цикла DO 300 ...) его номер помещается в
массив LS, а соответствующее ему значение в массиве MASK
заменяется на нуль, чтобы этот узел не попал в LS вторично.
После того как структура уровней построена, значения массива
MASK, соответствующие узлам структуры, переопределяются
на 1 (что выполняется циклом DO 500 ...).
FNROOT (FiNd ROOT)
Эта подпрограмма определяет псевдопериферийный узел
связной компоненты данного графа при помощи алгоритма,
§ 4.3. Профильные упорядочения 73
с...................................................
с...................................................
С..*.***. ROOTLS ... КОРНЕВАЯ СТРУКТУРА УРОВНЕЙ
с*******
с
С ROOTLS ГЕНЕРИРУЕТ СТРУКТУРУ УРОВНЕЙ С КОРНЕМ В УЗЛЕ,
С ЗАДАВАЕМОМ ВХОДНЫМ ПАРАМЕТРОМ ROOT. УЧИТЫВАЮТСЯ
С ЛИШЬ УЗЛЫ, КОТОРЫМ СООТВЕТСТВУЮТ НЕНУЛЕВЫЕ
С ЗНАЧЕНИЯ MASK.
С ВХОДНЫЕ ПАРАМЕТРЫ
С ROOT - ЗАДАННЫЙ КОРЕНЬ СТРУКТУРЫ УРОВНЕЙ.
С
С (XADJ, ADJNCY) " ПАРА МАССИВОВ, ХРАНЯЩАЯ
С СТРУКТУРУ СМЕЖНОСТИ ЗАДАННРГО ГРАФА.
С MASK - НУЖЕН ДЛЯ ЗАДАНИЯ ПОДГРАФА. УЗЛЫ, ДЛЯ
С КОТОРЫХ MASK(I) = O, ИГНОРИРУЮТСЯ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ „
С NLVL - ЧИСЛО УРОВНЕЙ В СТРУКТУРЕ УРОВНЕЙ.
С (XLS, LS) - МАССИВЫ ДЛЯ СТРУКТУРЫ УРОВНЕЙ.
С
О...»..•••«««•>*.•*««.«.«..»...«..»...,«»«......«..««.....,«,
С
SUBROUTINE ROOTLS ( ROOT, XADJ, ADJNCY, MASK, NLVL, XLS, LS
С
INTEGER ADJNCY(l), LSA), MASK(l), XLS(l)
INTEGER XADJA), I, J, JSTOP, JSTRT, LBEGIN
1 CCSIZE, LVLEND, LVSIZE, NBR, NLVL,
1 NODE, ROOT
С
С
С ПРИСВОЕНИЕ НАЧАЛЬНЫХ ЗНАЧЕНИИ . . .
с
MASK(ROOT) - О
LSA) - ROOT
NLVL - О
LVLEND - О
CCSIZE - 1
С
С LBEGIN - УКАЗАТЕЛЬ НАЧАЛА ТЕКУЩЕГО УРОВНЯ.
С LVLEND УКАЗЫВАЕТ КОНЕЦ ЭТОГО УРОВНЯ .
с
200 LBEGIN - LVLEND + 1
LVLEND • CCSIZE
NLVL - NLVL + 1
XLS(NLVL) - LBEGIN
С
С ПОСТРОИТЬ СЛЕДУЮЩИЙ УРОВЕНЬ, НАХОДЯ ВСЕХ
С МАРКИРОВАННЫХ СОСЕДЕЙ1* УЗЛОВ ТЕКУЩЕГО УРОВНЯ
с -
DO 400 I - LBEGIN, LVLEND
NODE - LS(I)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE + 1) - 1
IF ( JSTOP .LT. JSTRT ) GO TO 400
74 Гл. 4. Ленточные и профильные методы
DO 300 J - JSTRT, JSTOP
NBR - ADJNCY(J)
IF (MASK(NBR) EQ 0) GO TO 300
CCSIZE - CCSIZE + 1
LS(CCSIZE) - NBR
MASK(NBR) - 0
gOO CONTINUE
CALL ORDRAl(S)
IF (IERR.EQ.O) GO TO 100
CALL SAVEC, S)
STOP
100 CONTINUE
400 CONTINUE
С
С ВЫЧИСЛИТЬ ШИРИНУ ТЕКУЩЕГО УРОВНЯ. ЕСЛИ ОНА НЕ РАВНА
С НУЛЮ, ПОСТРОИТЬ СЛЕДУЮЩИЙ УРОВЕНЬ.
С ..
LVSIZE - CCSIZE - LVLEND
IF (LVSIZE .GT. О ) GO TO 200
С __ _
В MASK ВОССТАНОВИТЬ 1 ДЛЯ УЗЛОВ СТРУКТУРЫ УРОВНЕЙ.
XLS(NLVL+1) - LVLEND + 1
DO 500 I - 1, CCSIZE
NODE - LS(I)
MASK(NODE) ' 1
500 CONTINUE
RETURN
END
1) Т.е. узлы, которым соответствуют ненулевые значения в массиве MASK.
в оригинале - Masked. - Прим. перед.
описанного в разделе 4.3.2. Подпрограмма оперирует со связ-
связной компонентой, задаваемой входными параметрами ROOT,
MASK, XADJ и ADJNCY, как описано в § 3.3.
о» •*».*..•**.•.*..•*•••«*•**•«..** .....,,.,....,
С....... FNROOT ПОИСК ПСЕВДОПЕРИФЕРИЙНОГО УЗЛА *•••••¦
с........... .............................................
с.............................................................
с
С FNROOT РЕАЛИЗУЕТ МОДИФИЦИРОВАННЫЙ ВАРИАНТ СХЕМЫ ГИББСА,
С ПУЛА И СТОКМЕЙЕРА ОТЫСКАНИЯ ПСЕВДОПЕРИФЕРИЙНЫХ УЗЛОВ.
С ОНА ОПРЕДЕЛЯЕТ ТАКОЙ УЗЕЛ ДЛЯ ПОДГРАФА ,
С ЗАДАВАЕМОГО MASK И ROOT.
С
t ВХОДНЫЕ ПАРАМЕТРЫ-
С (XADJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ ГРА«РА
С MASK - ЗАДАЕТ ПОДГРАФ. УЗЛЫ , ДЛЯ КОТОРЫХ
С MASK(I) = O, ИГНОРИРУЮТСЯ.
с
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР-
С ROOT - НА ВХОДЕ ( ВМЕСТЕ О MASK) ОПРЕДЕЛЯЕТ
§ 4.3. Профильные упорядочения 75
С КОМПОНЕНТУ, ДЛЯ КОТОРОЙ ИЩЕТСЯ
С ПСЕВДОПЕРИФЕРИЙНЫЙ УЗЕЛ .
С НА ВЫХОДЕ - ЭТО НАЙДЕННЫЙ УЗЕЛ .
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С NLVL - ЧИСЛО УРОВНЕЙ В СТРУКТУРЕ УРОВНЕЙ С КОРНЕМ
С В УЗЛЕ ROOT.
С (XLS.LS) - ПАРА МАССИВОВ ДЛЯ ХРАНЕНИЯ НАЙДЕННОЙ
С СТРУКТУРЫ УРОВНЕЙ .
с
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С ROOTLS.
С
с****** «
с
SUBROUTINE FNROOT ( ROOT, XADJ, ADJNCY, MASK, NLVL, XLS, LS )
С
с». » •
с
INTEGER ADJNCY(l), LSA), MASK(l), XLS(l)
INTEGER XADJ(l), CCSIZE, J, JSTRT, K, KSTOP, KSTRT,
1 MINDEG, NABOR, NDEG, NLVL, NODE, NUNLVL,
1 ROOT
С
с *•••• *
с
с -- —
С ОПРЕДЕЛИТЬ СТРУКТУРУ УРОВНЕЙ С КОРНЕМ В ROOT.
с
CALL ROOTLS ( ROOT, XADJ, ADJNCY, MASK, NLVL, XLS, LS )
CCSIZE - XLS(NLVL+1) - 1
IF ( NLVL .«Q. 1 .OR. NLVL .EQ. CCSIZE ) RETURN
С -=. -
С ВЫБРАТЬ В ПОСЛЕДНЕМ УРОВНЕ УЗЕЛ С МИНИМ. СТЕПЕНЬЮ .
С —-. -.
100 JSTRT ¦ XLS(NLVL)
MINDEG - CCSIZE
ROOT - LS(JSTRT)
IF ( CCSIZE .EQ. JSTRT ) GO TO 400
DO 300 J - JSTRT, CCSIZE
NODE - LS(J)
NDEG - 0
KSTRT • XADJ(NODE)
KSTOP - XADJ(NODE-tl) - 1
DO 200 К - KSTRT, KSTOP
NABOR - ADJNCY(K)
IF ( MASK(NABOR) .GT. 0 ) NDEG - NDEG + 1
200 CONTINUE
IF ( NDEG Gt. MINDEG ) GO TO 300
ROOT - NODE
MINDEG - NDEG
300 CONTINUE
С - --г
С И ПОСТРОИТЬ СТРУКТУРУ УРОВНЕЙ С КОРНЕМ В ЭТОМ УЗЛЕ.
400 CALL. ROOTLS ( ROOT, XADJ, ADJNCY, MASK, NUNLVL, XLS, Lg)
IF (NUNLVL .LE. NLVIO RETURN
NLVL - NUNLVL
IF ( NLVL .LT. CCSIZE ) GO TO 100
RETURN
END
7в Гл. 4. Ленточные и профильные методы
Первое обращение к подпрограмме ROOTLS соответствует
шагу 2 алгоритма. Если компонента состоит из единственного
узла или является цепью, для которой ROOT — одна из конце-
концевых точек, то ROOT — периферийный узел, a LS содержит
соответствующую корневую структуру уровней; поэтому работа
программы прекращается. В противном случае в последнем
уровне разыскивается узел с минимальной степенью (шаг 3 ал-
алгоритма; в подпрограмме этому соответствует цикл DO 300...).
Строится новая структура уровней с корнем в этом узле (обра-
(обращение с меткой 400 к подпрограмме ROOTLS), после чего
выполняется тест на окончание работы (шаг 46) алгоритма.
Если тест не проходит, управление передается оператору с мет-
меткой 100, и процедура повторяется. На выходе ROOT хранит
номер псевдопериферийного узла, а пара массивов (XLS, LS) —
соответствующую корневую структуру уровней.
4.3.4. Подпрограммы обратного алгоритма Катхилла — Макки
Здесь будут описаны три подпрограммы — DEGREE, RCM
и GENRCM, составляющие вместе с подпрограммами предыду-
предыдущего раздела полную реализацию описанного в разд. 4.3.1 ал-
алгоритма RCM. Роль входных параметров ROOT, MASK, XADJ,
ADJNCY и PERM та же, что и в § 3.3. Отношения управления
между подпрограммами указаны на рисунке.
GENRCM
FNROOT
RCM
ROOTLS
DEGREE
DEGREE
Эта подпрограмма вычисляет степени узлов связной -ком-
-компоненты графа. Подпрограмма оперирует с той связной ком-
компонентой, которая задана посредством входных параметров
ROOT, MASK, XADJ и ADJNCY.
Начиная с первого уровня (состоящего из единственного
узла ROOT), вычисляются степени узлов; для каждого уровня
определение степеней осуществляет цикл DO 400 I = ... . При
обследовании соседей для узлов данного уровня (цикл DO 200
J = . .) те из них, которые еще не были записаны в массив LS,
теперь помещаются туда, тем самым генерируется новый уро-
о................................
С •« DEGREE ... СТЕПЕНИ В МАРКИРОВАННОЙ*> КОМПОНЕНТЕ ••••¦•
С...........
с.................... ..*.
с
С ПОДПРОГРАММА ВЫЧИСЛЯЕТ СТЕПЕНИ УЗЛОВ В СВЯЗНОЙ
С КОМПОНЕНТЕ, ЗАДАВАЕМОЙ MASK И ROOT. УЗЛЫ,
С ДЛЯ КОТОРЫХ MASk(l)=O, ИГНОРИРУЮТСЯ.
с
С ВХОДНЫЕ ПАРАМЕТРЫ -
С ROOT - УЗЕЛ, ОПРЕДЕЛЯЮЩИЙ КОМПОНЕНТУ.
С (XADJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ.
С MASK - ЗАДАЕТ ПОДГРАФ г
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С DEO - МАССИВ, СОДЕРЖАЩИЙ СТЕПЕНИ УЗЛОВ
С В КОМПОНЕНТЕ. ч
С CCSIZE- ЧИСЛО УЗЛОВ КОМПОНЕНТЫ, ЗАДАННОЙ
С MASK И ROOT .
С РАБОЧИЙ ПАРАМЕТР-
С LS - ВЕКТОР ДЛЯ ХРАНЕНИЯ УЗЛОВ КОМПОНЕНТЫ,
. С УРОВЕНЬ ЗА УРОВНЕМ .
С
с.......................,......*.,....,,..,
с
SUBROUTINE DEGREE ( FOOT, XADJ, ADJNCY, MASK,
1 DEC, CCSIZE, LS )
С
С. «.««•.••..««.«««..••«<..*.....***««.«•»..*«*...•«*«>•*«.*•.•
С
INTEGER ADJNCY(l), DEO(l), LS(J). MASK(l)
INTEGER XADJU). CCSIZE, I, IDEG, J, JSTOP, JSTRT,
1 LBEGIN, LVLEND, LVSIZE, NBR, NODE, ROOT
С
с • ¦¦ •••
с
С ПРИСВОЕНИЕ НАЧАЛЬНЫХ ЗНАЧЕНИЙ ...
С МАССИВ XADJ ИСПОЛЬЗУЕТСЯ ДЛЯ УКАЗАНИЯ , КАКИЕ
С УЗЛЫ ОБРАБОТАНЫ НА ДАННЫЙ МОМЕНТ.
с ,
LSA) - ROOT
XADJ(ROOT) . -XADJ(ROOT)
LVLEND - О
CCSIZE - 1
С -
С LBEGIN - УКАЗАТЕЛЬ НАЧАЛА ТЕКУЩЕГО УРОВНЯ .
С LVLEND УКАЗЫВАЕТ КОНЕЦ, ЭТОГО УРОВНЯ .
С -• -- -
100 LBEGIN - LVLEND + I
LVLEND - CCSIZE
С ,.
С НАЙТИ СТЕПЕНИ УЗЛОВ ТЕКУЩЕГО УРОВНЯ
С И ПОСТРОИТЬ СЛЕДУЮЩИЙ УРОВЕНЬ.
с „
DO 400 I . LBEGIN, LVLEND
NODE - LS(I)
JSTRT - -XADJ(NODE)
JSTOP - IABS(XADJ(NODE + i)) - 1
IDEG - 0
IF ( JSTOP .LT JSTRT ) GO TO 300
DO 200 J - JSTRT, JSTOP
NBR - ADJNCY(J)
IF ( MASK(NBR) EQ 0 ) GO TO 200
IDEG - IDEG + 1
IF ( XADJ(NBR) .LT 0 ) GO TO 200
78 Гл. 4. Ленточные и профильные методы
XADJ(NBR) • -XADJ(NBR)
CCSI2E - CCSIZE + 1
LS(CCSIZE) ч NBR
200 CONTINUE
800 DEG(NObE) - IDEC
400 CONTINUE
С л --,•_
С ВЫЧИСЛИТЬ ШИРИНУ ТЕКУЩЕГО УРОВНЯ . ЕСЛИ ОНА
С НЕНУЛЕВАЯ , ПОСТРОИТЬ СЛЕДУЮЩИЙ УРОВЕНЬ .
LV8IZE - CCSIZE - LVLEND
IF ( LVSIZE .GT. 0 ) GO TO 100
с
t ВОССТАНОВИТЬ ПРАВИЛЬНЫЕ ЗНАКИ В XADJ . ВОЗВРАТ.
DO 500 I - I, COSIZE
N6DE - LS(I)
XADJ(NODE) = -XADJ(NODE)
800 gONTlNUE
BfETURN
END
' w~"—¦ : ~—: : •""-
8 оригина/ге - MASKED . - Прим. ntpsd.
вень. Когда узел заносится в LS, изменяется знак у соответ-
соответствующего значения в массиве XADJ, чтобы этот узел не запо-
запоминался в LS вторично. (Аналогичную функцию в подпро-
подпрограмме ROOTLS выполнял массив MASK; здесь, однако, MASK
должен сохранять свое входное содержимое, чтобы правильно
были определены степени узлов.) Переменная CCSIZE имеет
смысл числа узлов, находящихся в LS в данный момент. После
того как найдены все узлы и вычислены их степени, узлы, за-
записанные в LS, используются для восстановления первоначаль-
первоначальных знаков элементов XADJ (цикл DO 500 I = ...)•
RCM (Reverse Cuthill — McKee)
Эта подпрограмма применяет описанный в разделе 4.3.1
алгоритм RCM к связной компоненте подграфа. Она оперирует
с той связной компонентой, которая задана входными парамет-
параметрами ROOT, MASK, XADJ и ADJNCY. Начальным узлом яв-
является значение переменной ROOT.
Так как алгоритму необходимы степени узлов данной ком-
компоненты, то первым шагом будет вычисление этих степеней
посредством обращения к подпрограмме DEGREE-. Узлы опре-
определяются и упорядочиваются уровень за уровнем; каждый но-
новый уровень нумеруется в результате очередного выполнения
цикла DO 600 I = ... . Цикл DO 200 I = ... находит ненуме-
ненумерованных соседей данного узла; в остальной части цикла
DO 600 производится сортировка методом пузырька для упоря-
с* «•••••••••¦«••••••¦••••¦•¦•••¦••••¦••••••••••••••¦¦¦••••••••
Q*************************************************************
t******** RCM ... ОБРАТНОЕ УПОРЯДОЧЕНИЙ КАТХИЛЛА - МАККИ ¦¦¦
с*************************************************************
с*************************************************************
с
С RCM НУМЕРУЕТ СВЯЗНУЮ КОМПОНЕНТУ , ЗАДАННУЮ MASK И ROOT t
С ИСПОЛЬЗУЯ АЛГОРИТМ RCM .
С ПРОЦЕСС НУМЕРАЦИИ ДОЛЖЕН НАЧИНАТЬСЯ С УЗЛА ROOT .
С
С ВХОДНЫЕ. ПАРАМЕТРЫ -
С ROOT - УЗЕЛ , ОПРЕДЕЛЯЮЩИЙ СВЯЗНУЮ КОМПОНЕНТУ ;
С НАЧАЛЬНЫЙ ДЛЯ RCM - УПОРЯДОЧЕНИЯ .
с
С (XAbJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ
С ГРАЧ=А.
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР "
С MASK -РАССМАТРИВАЮТСЯ ЛИШЬ УЗЛЫ , КОТОРЫМ
С СООТВЕТСТВУЮТ НЕНУЛЕВЫЕ ВХОДНЫЕ ЗНАЧЕНИЯ
С В MASK . ДЛЯ УЗЛОВ , ПРОНУМЕРОВАННЫХ RCM ,
С В MASK ЗАДАЕТСЯ О .
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С PERM - СОДЕРЖИТ RCM - УПОРЯДОЧЕНИЕ .
С CCSIZE - ЧИСЛО УЗЛОВ СВЯЗНОЙ КОМПОНЕНТЫ ,
с пронумерованной подпрограммой rcm ,
с „
с рабочий параметр-
С DEG - ПАССИВ ДЛЯ ХРАНЕНИЯ СТЕПЕНЕЙ УЗЛОВ ПОДГРАФА ,
С ЗАДАННОГО ПОСРЕДСТВОМ MASK И ROOT.
С
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ
С DEGREE.
С
с*************************************************************
G
SUBROUTINE RCM ( ROOT, XADJ, ADJNCY, MASK,
1 PERM, CCSIZE, DEO )
С
с*************************************************************
с
INTEGER ADJNCY(l), DEO(l), MASK(l), PERM(l)
INTEGER XADJ(l), CCSIZE, FNBR. I, J, JSTOP,
1 JSTRT, K, L, LBEGIN, LNBR, LPERM,
1 LVLEND, NBR, NODE, ROOT
С
С*••••••••••••••••••••••¦•••••••••••••••••••••••••¦•••••••••••
С
С -.------.----.---»---_-_-_-_._-.-.-.-¦-.«¦¦¦
С НАЙТИ СТЕПЕНИ УЗЛОВ В КОМПОНЕНТЕ .
С ЗАДАННОЙ MASK И ROOT .
CALL DEGREE ( ROOT, XADJ, ADJNCY, MASK, DEG.
I CCSIZE, PERM )
MASK(ROOT) > О
IF-( CCSIZE .LE. 1 ) RETURN
LVLEND > О
LNBR - I
С LBEGIN И LVLEND УКАЗЫВАЮТ НАЧАЛО И КдНЕЦ
С ТЕКУЩЕГО УРОВНЯ .
t •»•• — — — •- — — — — — — — — — — ~—• — — •-—. — — •. — —— e«»eieieiee»ee«™e«»e
100 LBEGIN ¦ LVLEND + 1
LVLEND . LNBR
DO 600 I . LBEGIN, LVLEND
80 Гл. 4. Ленточные и профильные методы
С ДЛЯ КАЖДОГО УЗЛА В ТЕКУЩЕМ УРОВНЕ . . .
с -
NODE - PERM(I)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
С НАЙТИ НЕНУМЕРОВАННЫХ СОСЕДЕЙ .
С FNBR И LNBR УКАЗЫВАЮТ ПЕРВОГО И ПОСЛЕДНЕГО
С ИЗ НЕНУМЕРОВАННЫХ СОСЕДЕЙ
С ТЕКУЩЕГО УЗЛА ИЗ PERM .
С
FNBR - LNBR + 1
DO 200 J - JSTRT, JSTOP
NBR - AOJNCY(J)
IF ( MASK(NBR) EQ. 0 ) GO TO 200
LNBR • LNBR + 1
MASK(NBR) - О
PERM(LNBR) - NBR
200 CONTINUE
IF ( FNBR .GE. LNBR ) GO TO 600
С --
С УПОРЯДОЧИТЬ СОСЕДЕЙ ДАННОГО УЗЛА ПО ВОЗРАСТАНИЮ
С СТЕПЕНЕЙ . СОРТИРОВКА МЕТОДОМ ПУЗЫРЬКА .
с - ----
Q
С
С
Q
300
400
500
BOO
700
К '
L ¦
CONTINUE
IF (LNBR
ПОЛУЧЕНО
НИЖЕ ОНО
» FNBR
• К
К - К + 1
NBR - PERM(K)
IF ( L .LTC FNBR ) GO TO 500
LPERM - PERM(L)
IF ( DEG(LPERM) .UE. DEG(NBR) ) GO TO 500
PERM(L+1) - LPERM
L - L - 1
GO TO 400
PERM(L+1) - NBR
IF ( К LT. LNBR ) GO TO 300
.CT. LVLEND) GO TO 100
УПОРЯДОЧЕНИЕ КАТХИЛЛА - МАККИ .
БУДЕТ ОБРАЩЕНО.
К - CCSIZE/2
L - CCSIZE
DO 900 I
LPERM
- 1. К
ч PERM(L)
PERM(L) » PERM(I)
PERM(I) - LPERM
L - L
CONTINUE
RETURN
END
- 1
дочения этих соседей по возрастанию степеней. Новое упорядо-
упорядочение записывается в массив PERM, как объяснено в § 3.3.
Финальный цикл (DO 700 I =...) обращает упорядочение; в
результате будет получено не стандартное, а обратное упоря-
упорядочение Катхилла — Макки.
§ 4.3. Профильные упорядочения 81
Отметим, что, так же как и в подпрограмме ROOTLS, пере-
переменной MASK@ при записи узла i присваивается нулевое значе-
значение. Однако в отличие от ROOTLS подпрограмма RCM не вос-
восстанавливает исходное состояние массива MASK. Элементы
MASK, соответствующие узлам пронумерованной связной ком-
компоненты, остаются равными нулю на выходе из подпрограммы.
GENRCM(GENeral RCM)
Эта подпрограмма находит RCM — упорядочение произволь-
произвольного несвязного графа. Она просматривает граф и обращается
к подпрограмме RCM, чтобы пронумеровать каждую связную
компоненту. Входными данными подпрограммы являются число
узлов (или уравнений) NEQNS и граф, заданный парой масси-
массивов (XADJ, ADJNCY). GENRCM обращается к подпрограммам
с» ««*..« ,»,,.»,».,,,...,,,,,»,»,....,,.».»....».,,.„.
с............*............
О«» GENRCM... ОБРАТНОЕ УПОРЯДОЧЕНИЕ КАТХИЛЛА- МАККИ ......
С............. ПРОИЗВОЛЬНОГО ГРАФА ¦¦.......«........*......
с............ .,.,.,»,,.,.,,,»
с
С GENRCM НАХОДИТ ОБРАТНОЕ УПОРЯДОЧЕНИЕ КАТХИЛЛА - МАККИ
С ПРОИЗВОЛЬНОГО ГРАФА. ДЛЯ КАЖДОЙ СВЯЗНОЙ
С КОМПОНЕНТЫ ГРАФА УПОРЯДОЧЕНИЕ ДОСТИГАЕТСЯ
С ВЫЗОВОМ RCM .
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С (XADJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ
? ГРАФА МАТРИЦЫ .
С ВЫХОДНОЙ ПАРАМЕТР -
С PERM - ВЕКТОР, СОДЕРЖАЩИЙ RCM - УПОРЯДОЧЕНИЕ.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С MASK - ВЕКТОР ДЛЯ МАРКИРОВКИ ПЕРЕМЕННЫХ ,
С ПРОНУМЕРОВАННЫХ В ПРОЦЕССЕ УПОРЯДОЧЕНИЯ.
С НАЧАЛЬНЫЕ ЗНАЧЕНИЯ КОМПОНЕНТ РАВНЫ 1 ; ОНИ
С ЗАМЕНЯЮТСЯ НА О ПРИ НУМЕРАЦИИ УЗЛОВ.
Q XLS - ИНДЕКСНЫЙ ВЕКТОР ДЛЯ СТРУКТУРЫ УРОВНЕЙ ,
С ХРАНЯЩЕЙСЯ В НЕИСПОЛЬЗУЕМЫХ НА ДАННЫЙ МОМЕНТ
С ПОЗИЦИЯХ ВЕКТОРА ПЕРЕСТАНОВКИ PERM.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ
С FNROOT RCM
С
с............................».»................*....»...*....
с
SUBROUTINE GENRCM ( NEQNS, XADJ, ADJNCY, PERM, MASK, XLS )
С '
с *
с
INTEGER ADJNCY(l), MASK(I), PERM(l). XLS(l)
INTEGER XADJ(l), CCSIZE, I, NEQNS. NLVL.
NUM. ROOT
82 Гл. 4. Ленточные и профильные методы
с
DO 100 1-1, NEONS
MASK(I) - 1
100 CONTINUF
NUM - 1
DO 200 I - 1, NEQNS
С --____.
С ДЛЯ КАЖДОЙ МАРКИРОВАННОЙ СВЯЗНОЙ КОМПОНЕНТЫ.
с _
IF (MASK(I) .EQ. 0) GO TO 200
ROOT - I
с
С ВНАЧАЛЕ НАЙТИ ПСЕВДОПЕРИФЕРИЙНЫЙ УЗЕЛ ROOT.
С СТРУКТУРА УРОВНЕЙ, НАЙДЕННАЯ FNROOT,
С ХРАНИТСЯ , НАЧИНАЯ С PERMCNUM) . ЗАТЕМ
С ПРОИСХОДИТ ОБРАЩЕНИЕ К RCM . ROOT - НАЧАЛЬНЫЙ
С УЗЕЛ ПРИ УПОРЯДОЧЕНИИ КОМПОНЕНТ.
С — ._ — _
CALL FNROOT ( ROOT, XADJ, ADJNCY, MASK,
1 NLVL, XLS, PERM(NUM) )
CALL RCM ( ROOT, XADJ, ADJNCY, MASK,
1 PERM(NUM), CCSIZE, XLS )
NUM - NUM + CCSIZE
IF (NUM .GT. NEQNS) RETURN
200 CONTINUE
RETURN
END
FNROOT и RCM, которые используют массивы MASK и XLS
как рабочие.
Подпрограмма начинает работу с того, что присваивает зна-
значение 1 всем компонентам массива MASK (цикл DO 100
I = ...). Затем выполняется цикл, в котором MASK просмат-
просматривается до тех пор, пока не будет найдено i, для которого
MASK@ = !• Узел i вместе с MASK, XADJ и ADJNCY опреде-
определяет связный подграф исходного графа Q. Далее происходит
обращение к подпрограммам FNROOT и RCM для упорядоче-
упорядочения узлов этого подграфа. (Вспомним, что RCM устанавливает
нулевые значения в MASK для пронумерованных узлов.)
Отметив, что переменная NUM указывает первую свобод-
свободную позицию массива PERM; ее значение изменяется после
каждого обращения к RCM. Формальному параметру PERM
в RCM соответствует фактический параметр PERM(NUM)
в QENRCM, тем самым массиву PERM в RCM соответствуют
последние NEQNS — NUM + 1 элементов массива PERM
в QENRCM Отметим еще, что те же элементы PERM исполь-
используются в подпрограмме FNROOT для хранения структуры
уровней. Они соответствуют массиву LS в списке формальных
параметров этой подпрограммы.
После того как очередная компонента упорядочена, возоб-
возобновляется поиск следующего значения i, для которого
§ 4.3. Профильные упорядочения 83
MASK(O=5tO- Работа программы заканчивается, когда таких
значений i больше нет либо оказалось, что пронумерованы
NEQNS узлов.
Упражнения
4.3.1. Пусть граф, соответствующий заданной матрице, является
сеточным графом. На рисунке показан случай п = 5.
а) Показать, что если работа обратного алгоритма Катхилла—Макки
2
начинается с углового узла, то профиль равен — я3+ О(п2).
б) Каков будет профиль, если алгоритм начинает работу с центрального
узла?
4.3.2. Привести пример, в котором узел, найденный алгоритмом раз-
раздела 4.3.2, не будет периферийным. Найти пример большого порядка, для ко-
которого ответ х, полученный алгоритмом, будет особенно плох, например экс-
эксцентриситет х будет меньше диаметра G на значительную долю \Х\. Авторам
не известен нн один большой пример, где время работы алгоритма было бы
больше, чем О(|?1). Сможете ли вы найти такой пример?
4.3.3. Первоначальный алгоритм Гиббса и соавторов' (Gibbs et al. 1976b)
для отыскания псевдопериферийного узла не имел «стягивающего шага». Ша-
Шаги 3 и 4 были таковы:
Шаг 3 (сортировка последнего уровня). Упорядочить узлы в L^n(r) по
возрастанию степеней.
Шаг 4 (тест на окончание работы). Для хеЬцп(г) в порядке возраста-
возрастания степеней построить структуры
S(x) = {L0(x), L,(x) Ll(
Если /(*) > I (r), положить r<-jn перейти к шагу 3.
Привести пример, показывающий, что время работы этого алгоритма мо-
может быть больше, чем О(|?|). Ответьте на первые два вопроса упр. 4.32 по
отношению к этому алгоритму.
4.3.4. Предположим, что в алгоритме раздела 4.3.1 опущен шаг 3. Упо-
Упорядочение Х\, хг, ..., хм называется упорядочением Катхилла — Макки Пусть
Ас — матрица, упорядоченная этим алгоритмом Показать, что:
а) матрица Ас имеет монотонный профиль (см. упр. 4.2.2);
б) в графе G с для 1 < I ^ N
Adj ({лгх xN}) <= {xf
4.3.5. Показать, что Env(i4r) = Env(i4c) тогда и только тогда, когда мат-
матрица А, имеет монотонный профиль. Здесь А, — матрица, упорядоченная ал-
алгоритмом раздела 4.3 1, а Ас описана в упр 4 3 4
4.3.6. Что вынуждает окончание работы алгоритма поиска псевдоперифе-
псевдопериферийного узла из раздела 4.3.2?
84 Гл. 4. Ленточные и профильные методы
4.3.7. Рассмотрим симметричную положительно определенную систему
уравнений Ах = Ь порядка Л', полученную из конечиоэлементной сетки л X п
следующим образом. Сетка состоит из (и—IJ малых квадратов, как пока-
показано на рис. 4.3.10 для п = 5. Узлы расположены в вершинах и на серединах
сторон квадратов; с каждым узлом связана переменная xi Если каким-либо
образом пометить N = Зл2 — Чп узлов графа, то соответствующая матрица А
имеет такое свойство: ац Ф 0 тогда и только тогда, когда ассоциированные
переменные xt и х, отвечают одному и тому же квадрату сетки.
Пусть имеется выбор из двух упорядочений ai и аг, показанных иа
рис. 4 3.10. Упорядочения схожи в том отношении, что в обоих лннни сетки
нумеруются последовательно, одна за другой. Различие состоит в том, что в
случае ai нумеруются одновременно узлы каждой горизонтальной линии и
45
43
It
15
1
4т7
50
44 i
41
30
V
32
16
17
18
2
4
52
55
49
53
33
35
19
21
5
1
57
60
54
56
SI
36
22
Ч
24
8
а
62
' 65
59
61
63
3.
19
1 41
26
и
27
11
12
64
42
28
Т4"
ю 13
St
а
3
54
56
W
*f
38
Ц
28
24
t
2
\
57
99
55
4,1
45
41
29
31
27
10
13
7
6,0
62
58
4,6
48
44
32
' 14
30
15
18
12
1*
V
65
61
49
51
47
35
* 37
П
20
23
17
19
64
50
39
га
Рис. 4.3.10. Два упорядочения aj и
II 16 21
«1
конечноэлементной сетки 5X5
узлы вертикальных линий, лежащие как раз над данной горизонталью. При
упорядочении а2 нумеруются одновременно узлы горизонтальной линии и
лежащие прямо под ней узлы вертикальных линий Это указано на диаграм-
диаграммах прерывистыми линиями.
а) Какова ширина ленты А для упорядочений ai и а2?
б) Предположим, что для решения системы Ах = Ь при упорядочениях
oti и аг соответственно используется профильный метод. Пусть 9i и 9г — число
арифметических операций в том и другом случае, г|, и г|г — соответственные
запросы к памяти. Показать, что для больших п
9, = 6/г4 + О (и3),
92 = 13.5л4 + О (/г3),
Ц2 = 9п3 + О (/г2).
Упорядочения ai и а2 сходны с упорядочениями, которые порождают соот-
соответственно алгоритм RCM и стандартный алгоритм Катхилла — Макки. При-
Приведенные результаты иллюстрируют существенное различие в памяти и числе
операций, которое может наблюдаться для этих двух алгоритмов. Детали см.
в работе (Liu 1975).
4.3.8. (Упорядочение Кинга) Кингом предложен (King 1970) алгоритм
уменьшения профиля симметричной матрицы, который в случае связного гра-
графа можно описать следующим образом.
§ 4.4. Реализация профильного метода 88
Шаг 1 {инициализация). Определить псевдопериферийный узел г и поло-
положить Х\ ¦*- Г.
Шаг 2 (основной цикл). Для i = 1 N — 1 найти узел у е Adj({*i, ...
..., xii), для которого величина
| Adj ({ж, xlt y})\
минимальна.
Пометить узел у как xi+i.
Шаг 3 (выход). Упорядочение Книга есть х\, х2, ¦ ¦., Хк.
Этот алгоритм уменьшает профиль путем локальной минимизации ши-
ширины фронта. Реализуйте этот алгоритм для случая произвольного несвязного
графа. Проверьте свою программу на матрицах тестового множества #1 из
главы 9. Сравните результаты этого алгоритма с результатами алгоритма
RCM.
§ 4.4. Реализация профильного метода
4.4.1. Профильная схема хранения
Наиболее употребительной схемой хранения в профильном
методе является схема Дженнингса (Jennings 1966). В каждой
строке матрицы хранятся все элементы от первого ненулевого до
О\\
«22
Симметрично
«33
«55
DIAG
ENV
XENV
| 1
«22
«33
044
«55
<»43
«53
«62
1
1
10 |
Рис. 4.4.1. Пример профильной схемы хранения.
диагонального. Эти отрезки строк размещены в последователь-
последовательных позициях одномерного массива. Однако мы будем поль-
пользоваться модификацией этой схемы, в которой диагональные
элементы хранятся отдельным вектором. Преимущество такого
варианта в том, что он легко приспосабливается к случаю не-
несимметричной матрицы А; это соображение развивается
в упражнении, приведенном в конце главы.
86 Гл. 4. Ленточные и профильные методы
В схеме имеется основной массив ENV, содержащий эле-
элементы оболочки из всех строк матрицы. Для указания начала
отрезка каждой строки используется вспомогательный индекс-
индексный вектор XENV длины N -\- 1. Чтобы добиться единообразия
при индексировании, полагаем XENV(iV+l) равным
jEnv(A)J-f 1. Индексный вектор XENV дает возможность
удобного доступа к любому ненулевому элементу. Отображе-
Отображение Епу(Л) на множество {1, 2 |Епу(Л)|} задается та-
таким образом:
{I, }} -+ XENV (i+1) -(<-/)•
Другими словами, значение элемента а.ц, принадлежащего про-
профильной области А, находится в ENV (XENV(t + l)— (i — /)).
Рис. 4.4.1 иллюстрирует эту схему хранения. Пусть, например,
нужно найти значение элемента а64- Имеем
XENV G) - F - 4) = 8,
поэтому а64 хранится в 8-м элементе вектора ENV.
Чаще всего используемой операцией являемся выделение
профильного отрезка какой-либо строки. Это удобно делать,
пользуясь следующим фрагментом:
JSTRT - XENV(IROW)
JSTOP - XENV(IROW+1) - i
IF (JSTOP LT.JSTRT) GO TO 200
DO 100 J - JSTRT. JSTOP
ELEMNT - ENV(J)
100 CONTINUE
200
Основная память в данной схеме равна \Env(A)\+ N
а накладная — N+1. Структура данных для схемы хранения
может быть сформирована за время О(\Е\). Эту функцию
выполняет подпрограмма FNENV, обсуждаемая в следующем
разделе.
4.4.2. Подпрограмма распределения памяти FNENV
(FiNd — ENVelope)
В этом разделе мы описываем подпрограмму FNENV. Вход-
Входными данными этой подпрограммы являются граф матрицы А,
хранимый парой массивов (XADJ, ADJNCY), вектор переста-
перестановки PERM и вектор обратной перестановки INVP (см. § 3.3).
Назначение подпрограммы — вычислить компоненты введенного
в разделе 4.4.1 массива XENV, который используется при хра-
хранении множителя L матрицы РАРТ. Выдается также значение
ENVSZE, представляющее собой размер оболочки L и равное
С*'
FNENV
ОПРЕДЕЛЕНИЕ ОБОЛОЧКИ
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с*
с
FNENV НАХОДИТ СТРУКТУРУ ОБОЛОЧКИ ПЕРЕУПОРЯДОЧЕННОЙ
МАТРИЦЫ .
ВХОДНЫЕ ПАРАМЕТРЫ -
NEQNS - ЧИСЛО УРАВНЕНИЙ.
(XADJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ
ГРАФА МАТРИЦЫ.
PERM.INVP - МАССИВЫ С ИНФОРМАЦИЕЙ О ПЕРЕСТАНОВКЕ
ДЛЯ ПЕРЕУПОРЯДОЧЕНИЯ МАТРИЦЫ.
ВЫХОДНЫЕ ПАРАМЕТРЫ -
XENV - ИНДЕКСНЫЙ ВЕКТОР СТРУКТУРЫ ДЛЯ ХРАНЕНИЯ
НИЖНЕЙ СИЛИ ВЕРХНЕЙ) ОБОЛОЧКИ
ПЕРЕУПОРЯДОЧЕННОЙ МАТРИЦЫ .
ENVSZE - РАВЕН XENV(NEQNS+1) - 1 .
BANDW - ШИРИНА ЛЕНТЫ ПЕРЕУПОРЯДОЧЕННОЙ МАТРИЦЫ.
SUBROUTINE FNENV ( NEQNS, XADJ, ADJNCY, PERM, INVP,
1 XENV, ENVSZE, BANDW )
с
с*
с-
INTEGER ADJNCY(l), INVP(l), PERM(l)
INTEGER XADJ(l), XENV(l), BANDW, I, IBAND,
1 IFIRST, IPERM, J, JSTOP, JSTRT, ENVSZE,
1 NABOR, NEQNS
с
с
с
100
20
BANDW - О
ENVSZE - 1
DO 200 I -
XENV(I)
IPERM -
JSTRT -
JSTOP -
1, NEQNS
- ENVSZE
PERM(I)
XADJ(IPERM)
XADJ(IPERM +
1)
- 1
GO TO 200
IF ( JSTOP .LT. JSTRT )
НАЙТИ ПЕРВЫЙ НЕНУЛЕВОЙ ЭЛЕМЕНТ СТРОКИ I.
IFIRST - I
DO 100 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
NABOR - INVP(NABOR)
IF ( NABOR .LT. IFIRST ) IFIRST - NABOR
CONTINUE
IBAND -I - IFIRST
ENVSZE - ENVSZE + IBAND
IF ( BANDW .LT. IBAND ) BANDW - IBAND
CONTINUE
XENV(NEQNS+1) - ENVSZE
ENVSZE » ENVSZE - 1
RETURN
END
88 Гл. 4. Ленточные и профильные методы
XENV (NEQNS+ 1) — 1. Здесь, как и раньше, NEQNS —
число уравнений или узлов.
Подпрограмма проста и почти не нуждается в пояснениях,.
Цикл DO 200 I = ... обрабатывает каждую строку; индекс
первого ненулевого элемента /-й строки (IFIRST) матрицы
РАРТ определяется циклом DO 100 J = ... . В конце каждого
исполнения этого цикла соответствующим образом изменяется
значение переменной ENVSZE. Использование PERM и INVP
связано с тем, что пара массивов (XADJ, ADJNCY) хранит
структуру А, а структура L, которую нужно найти, соответ-
соответствует матрице РАРТ.
§ 4.5. Подпрограммы численного решения ESFCT, ELSLV
и EUSLV
В этом разделе мы опишем подпрограммы, осуществляющие
численное разложение и решение треугольных систем. Они
используют профильную схему хранения, о которой говорилось
в разделе 4.4.1. Подпрограммы для решения треугольных си-
систем—ELSLV (Envelope-Lower-SoLVe) и EUSLV (Envelope-
Upper-SoLVe)—будут описаны до подпрограммы разложения
ESFCJ_ (Envelope-Symmetric-FaCTorization), поскольку послед-
последняя "использует подпрограмму ELSLV.
4.5.1. Подпрограммы для решения треугольных систем ELSLV
иEUSLV
Эти подпрограммы выполняют численное решение нижней
и верхней треугольных систем
соответственно, где L — нижняя треугольная матрица, храни-
хранимая в соответствии с описанием в разделе 4.4.1.
В подпрограмме ELSLV имеются несколько важных осо-
особенностей, которые заслуживают разъяснения. Прежде всего
определяется номер (IFIRST) первого ненулевого элемента
в правой части (RHS). Затем программа выполняет цикл
(DO 500 I = ...) по строкам L с номерами IFIRST, IFIRST +
-|- 1 NEQNS; при этом используется схема скалярных про-
произведений (см. раздел 2.2.1). Однако программа пытается
использовать последовательности нулевых компонент решения.
Переменная LAST хранит индекс последней (на данный мо-
момент) вычисленной ненулевой компоненты решения. (Компо-
§ 4.5. Подпрограммы ESFCT, ELSLV и EUSLV 89
ненты решения записываются на места соответствующих ком-
компонент правой части в массив RHS.)
Настоятельно рекомендуем читателю смоделировать работу
подпрограммы для примера, изображенного иа рис. 4.5.1. Про-
Проверьте, что ELSLV реально использует лишь ненулевые эле-
элементы, обозначенные звездочкой в квадрате.
(XENV, ENV)
*
*
*
*
*
*
*
*
*
*
*
Решение Правой
часть
(RHS)
(RHS)
Рис. 4.5.1. Элементы L, реально используемые подпрограммой ELSLV, обозна-
обозначены звездочкой в квадрате.
Заметим, что LAST позволяет опустить операции с некото-
некоторыми строками; мы все же выполняем умножения с нулевыми
операндами внутри цикла DO 300 К =... по той причине, что
для большинства машин проверка, помогающая избежать та-
такого умножения, стоит дороже, чем его выполнение.
Проверка и подгонка переменной IBAND, предшествующие
циклу DO 300'..., также требуют некоторых объяснений.
В некоторых обстоятельствах ELSLV используется для реше-
решения нижней треугольной системы, матрица коэффициентов ко-
которой является лишь подматрицей матрицы L, переданной под-
подпрограмме парой массивов (XENV, ENV). Ситуация изобра-
изображена на рисунке. Некоторые строки оболочки ¦ простираются
вовне используемой подматрицы, и IBAND подгоняется так,
90 Гл. 4. Ленточные и профильные методы
чтобы учесть это обстоятельство. В примере на рисунке L
имеет порядок 16. Если нужно решить систему с указанной
Используемая
часть матрицы
коэффициентов
j**
¦щ *
* * *;
_|* *
# * * * *
* * *
¦A/ _t/ I-V _t/ I
o^ 4* f^* *^*
*
Решение
1
Правая
часть
подматрицей порядка 11 и правой частью RHS, следует произ-
произвести вызов
CALL ELSLVA1, XENVE), ENV, DIAGE), RHS).
В подпрограмме XENVE) интерпретируется как XENV(l),
XENVF) становится XENVB) и т. д. Этот «трюк» исполь-
используется в подпрограмме ESFCT, обращающейся к ELSLV.
Перейдем теперь к описанию подпрограммы EUSLV, ре-
решающей задачу Ux = у, причем L хранится по той же схеме,
что и в ELSLV. Это значит, что мы имеем удобный доступ
к столбцам U и разреженность можно использовать полностью,
применяя схему внешних произведений (см. раздел 2.2.1).
Столбец с номером / матрицы U использ'уется в вычислениях
только в том случае, если t-я компонента решения не равна
нулю.
Как и ELSLV, подпрограмму EUSLV можно использовать
для решения верхних треугольных систем, матрицы которых
являются подматрицами для L, заданной парей массивов
(XENV, ENV). Техника здесь аналогична описанной выше. Зна-
Значение переменной IBAND подгоняется соответствующим обра-
образом для тех столбцов U, которые простираются вовне реально
используемой части L.
Все подпрограммы, выполняющие численное решение, со-
содержат помеченный общий блок SPKOPS, состоящий из един-
единственной переменной OPS. Каждая- подпрограмма подсчиты-
подсчитывает число проделанных ею операций (умножений и делений)
§ 4.5 Подпрограммы ESFCT, ELSLV и EUSLV 91
с. ..........
С •••« ELSLV ... РЕШЕНИЕ НИЖНЕЙ ТРЕУГОЛЬНОЙ СИСТЕМЫ'
С... ..¦*..«**« ПРОФИЛЬНЫМ МЕТОДОМ .«.»»¦..»¦»..•*.
с........ ......I
с
С ПОДПРОГРАММА РЕШАЕТ НИЖНЮЮ ТРЕУГОЛЬНУЮ СИСТЕМУ
С LX * RHS. МНОЖИТЕЛЬ L ХРАНИТСЯ В ПРОФИЛЬНОМ
С ФОРМАТЕ .
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С (XENV, ENV) - МАССИВЫ ДЛЯ ОБОЛОЧКИ L.
С DIAO - ПАССИВ ДЛЯ ДИАГОНАЛИ L.
С
f ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С RHS - НА ВХОДЕ СОДЕРЖИТ ВЕКТОР ПРАВЫХ ЧАСТЕЙ .
С НА ВЫХОДЕ - ВЕКТОР РЕШЕНИЯ .
С OPS - ПЕРЕМЕННАЯ С ДВОЙНОЙ ТОЧНОСТЬЮ, СОДЕРЖАЩАЯСЯ
С В ОБЩЕМ БЛОКЕ SPKOPS . ЕЕ ЗНАЧЕНИЕ
С БУДЕТ УВЕЛИЧЕНО НА ЧИСЛО ОПЕРАЦИЙ,
С ВЫПОЛНЯЕМЫХ ЭТОЙ ПОДПРОГРАММОЙ.
с
SUBROUTINE ELSLV ( NEQNS, XENV, ENV, DIAG, RHS )
С
с
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), ENVA), RHS(l), S
INTEGER XENV(l), I, IBAND, IFIRST, K, KSTOP,
1 KSTRT, L, LAST, NEQNS
С
с
с
С -
С НАЙТИ НОМЕР ПЕРВОГО НЕНУЛЕВОГО ЭЛЕМЕНТА В RHS
С И ПОМЕСТИТЬ ЕГО В IFIRST.
с
IFIRST - О
100 IFIRST . IFIRST + 1
IF ( RHS(IFIRST) .NE. O.OEO ) GO TO 200
IF ( IFIRST .LT. NEQNS ) GO TO 100
RETURN
200 LAST - 0
С
С LAST СОДЕРЖИТ НОМЕР ПОСЛЕДНЕЙ ВЫЧИСЛЕННОЙ
С НЕНУЛЕВОЙ КОМПОНЕНТЫ РЕШЕНИЯ .
с
DO 500 I - IFIRST, NEQNS
IBAND - XENV(I+1) - XENV(I)
IF ( IBAND .GE. I ) IBAND - I - 1
S - RHS(I)
L - I - IBAND
RHS(I) - O.OEO
С СТРОКА ОБОЛОЧКИ ПУСТА ИЛИ ВСЕ СООТВЕТСТВУЮЩИВ
С КОМПОНЕНТЫ РЕШЕНИЯ - НУЛИ ,
92 Гл. 4. Ленточные и профильные методы
If ( IBAND EQ. О .OR LAST LT L ) GO TO 409
KSTRT - XENV(I+1) - IBAND
KSTOP - XENVUtl) - 1
DO 3UO К - KSTRT, KSTOP
S « S - ENV(K)«Rflg(L)
L - L + 1
300 CONTINUE
COUNT - IBAND
OPS - OPS + COUNT
400 IF ( S .KQ. 0.0E0 ) 00 TO 800
RHS(I) - S/DJA0(I)
OPS - OPS + i.ODO
laSt - i
500 CONTINUE
RETURN
END
и соответственным образом увеличивает значение OPS. По-
Поэтому если пользователь желает контролировать число выпол-
выполняемых операций, он может описать такой же общий блок
в своей вызывающей программе и следить за значением OPS.
Переменная OPS была описана как переменная с двойной
точностью, чтобы избежать ошибок округления при подсчете
числа операций. Наши подпрограммы могут использоваться
для решения очень больших систем, так что OPS вполне может
принимать значения, достигающие 108 или 109, хотя отдельная
подпрограмма может увеличивать OPS на сравнительно не-
небольшую величину. На многих машинах прн использовании
обычной точности сложение в арифметике с плавающей точкой
малого числа (скажем, меньшего чем 10) с числом 108 снова
дает 108. (Проверьте это, моделируя шестизначную арифметику
с плавающей точкой!) Использование двойной точности для
OPS делает ошибку округления при подсчете числа операций
чрезвычайно маловероятной.
4.5.2. Подпрограмма разложения ESFCT
В этом разделе мы обсудим некоторые детали подпрограммы
численного разложения ESFCT. Подпрограмма вычисляет раз-
разложение Холесского LU данной матрицы А, хранимой по про-
профильной схеме (см. раздел 4.4.1). Используется вариант ме-
метода Холесского, называемый методом окаймления (см. раз-
раздел 2.1.2).
Напомним, что если представить А в виде
\ит sj'
§4 5. Подпрограммы ESFCT, ELSLV и EUSLV 93
с...........
С.......... EUSLV РЕШЕНИЕ ВЕРХНЕЙ ТРЕУГОЛЬНОЙ
С« СИСТЕМЫ ПРОФИЛЬНЫМ МЕТОДОМ ........
С
С ПОДПРОГРАММА РЕШАЕТ ВЕРХНЮЮ ТРЕУГОЛЬНУЮ СИСТЕМУ
С UX = RHS. МНОЖИТЕЛЬ U ХРАНИТСЯ В ПРОФИЛЬНОМ
С <РОРМАТЕ.
С
С ВВОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С (XENV, ENV) - МАССИВЫ ДЛЯ ОБОЛОЧКИ D.
С DIAG - МАССИВ ДЛЯ ДИАГОНАЛИ U.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С RHS - НА ВХОДЕ СОДЕРЖИТ ВЕКТОР ПРАВЫХ ЧАСТЕЙ.
С НА ВЫХОДЕ - ВЕКТОР Р|ШЕНИЯ .
С OPS - ПЕРЕПЕННАЯ С ДВОЙНОЙ ТОЧНОСТЬЮ,
С СОДЕРЖАЩАЯСЯ В ОБЩЕМ БЛОКЕ SPKOPS.
С ЕЕ ЗНАЧЕНИЕ БУДЕТ УВЕЛИЧЕНО НА ЧИСЛО ОПЕРАЦИЙ,
С ВЫПОЛНЯЕМЫХ ЭТОЙ ПОДПРОГРАММОЙ.
С
с......
с
SUBROUTINE EUSLV ( NEQNS, XENV, ENV, DIAG, RHS )
С
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAGA), ENV(l), RHS(l), S
INTEGER XENV(l), I, IBAND, K, KSTOP, KSTRT,
NEQNS
I - NEQNS + 1
100 I - I - 1
IF ( I EQ 0 ) RETURN
IF ( RHS(I) EQ О 0Е0 ) GO TO 100
S - RHS(I)/DIAG(I)
RHS(I) - S
OPS - OPS + 1 0D0
IBAND - XENV(I+1) - XENV(I)
IF ( IBAND GE^ I ) IBAND - I - 1
IF ( IBAND EQ 0 ) GO TO 100
KSTRT - I - IBAND
KSTOP - I - 1
L - XENV(I+1) - IBAND
DO 200 К - KSTRT, KSTOP
RHS(K) - RHS(K) - S'ENV(L)
L - L + 1
200 CONTINUE
COUNT - IBAND
OPS - OPS + COUNT
GO TO 100
END
94 Гл. 4. Ленточные и профильные методы
с • « •¦».« .........................
с ..........к..
С...... ESFCT ... СИММЕТРИЧНОЕ РАЗЛОЖЕНИЕ ПРОФИЛЬНЫМ »«»•
С.......... МЕТОДОМ
С...
С ПОДПРОГРАММА ВЫЧИСЛЯЕТ РАЗЛОЖЕНИЕ L*L (ТРАНСПОНИРОВАННАЯ)
С ДЛЯ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ МАТРИЦЫ А,
С ХРАНЯЩЕЙСЯ В ПРОФИЛЬНОМ ФОРМАТЕ. ИСПОЛЬЗУЕТС*»
С СТАНДАРТНЫЙ МЕТОД ОКАЙМЛЕНИЯ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С XENV - ИНДЕКСНЫЙ ВЕКТОР ОбОЛОЧКИ.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С ENV - ОБОЛОЧКА L - НА МЕСТО ОБОЛОЧКИ А .
С DIAG - ДИАГОНАЛЬ t - НА МЕСТО ДИАГОНАЛИ А.
С IFLAG - ИНДИКАТОР ОШИБКИ. ЕМУ ПРИСВАИВАЕТСЯ 1,
С ЕСЛИ ПРИ РАЗЛОЖЕНИИ ОБНАРУЖЕН О
С ИЛИ КОРЕНЬ ИЗ ОТРИЦАТЕЛЬНОГО ЧИСЛА .
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С ELSLV.
С
о*..*
с
SUBROUTINE ESFCT ( NEQNS, XENV, ENV, DIAG, IFLAG )
С
с......... ....*.......*.......
с
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), ENV(l), S, TEMP
INTEGER XENV(l), I, IBAND, IFIRST, IFLAG, IXENV,
J, JSTOP, NEONS
С
Q •
с
IF ( DIAG(l) .LE. O.OEO ) GO TO 400
DIAG(t) - SQRT(DIAGA))
IF ( NEQNS .EQ. 1 ) RETURN
С —
С ЦИКЛ ПО СТРОКАМ 2,3,..., NEQNS ...
с
DO 300 I - 2, NEQNS
IXENV - XENV(I)
IBAND - XENV(I+1) - IXENV
TEMP - DIAG(I)
IF ( IBAND .EQ. 0 ) GO TO 200
IFIRST - I - IBAND
с
С ВЫЧИСЛИТЬ СТРОКУ I ТРЕУГОЛЬНОГО МНОЖИТЕЛЯ.
с
CALL ELSLV ( IBAND, XENV(IFIRST), ENV,
1 DIAG(IFIRST), ENV(IXENV) )
JSTOP - XENV(I+1) - 1
DO 100 J - IXENV, JSTOP
S - ENV(J)
§4 5. Подпрограммы ESFCT, ELSLV и EUSLV
100
too
300
TEMP - TEMP -
CONTINUE
IF ( TEMP .LE. O.OEO
DIAG(I) - SQRT(TEMP)
COUNT - IBAND
OPS - OPS + COUNT
CONTINUE
RETURN
S«S
) GO TO 400
С
с
§
400
УСТАНОВИТЬ 1 ДЛЯ IFLAO: МАТРИЦА - HE ПОЛОЖИТЕЛЬНО
ОПРЕДЕЛЕННАЯ.
IFLAG - 1
RETURN
END
где М — ведущая главная подматрица А с разложением Холес-
ского LmLm, to множитель L матрицы А можно записать как
'Lm О'
где LMw = и и t = (s — wTw)U2. Тем самым множитель Холес-
ского можно вычислять строка за строкой, начиная с матрицы
аи порядка 1 и переходя к матрицам М все большего порядка.
Рис 4.5.2. Иллюстрация к способу использования разреженности в подпро-
подпрограмме ESFCT; в вычислении w по и участвует лишь L.
Самое интересное в ESFCT — это использование того обстоя-
обстоятельства, что векторы и — «короткие», так как мы работаем
с профильной матрицей.
Обращаясь к рис. 4.5.2, предположим, что закончены первые
i— 1 шагов разложения, так что разложена ведущая главная
подматрица А порядка i—1. (Тем самым выполнены опера-
операторы, предшествующие циклу DO 300 1 = 2, ...; сам цикл был
выполнен i — 2 раза.) Чтобы вычислить /-ю строку L, нужно
решить систему уравнений LMw = и.
96 Гл. 4. Ленточные и профильные методы
Однако из рисунка (а также из лемм 2.2.1 и 2.2.4) видно,
что в вычислениях участвует лишь часть LM; именно та часть,
что обозначена L. Поэтому при обращении к ELSLV размер
треугольной системы, т. е. порядок и и L, задает переменная
IBAND; при этом IFIRST есть индекс в L первой строки L.
Упражнения
4.5.1. Пусть А имеет симметричную структуру, но А Ф Ат\ и пусть гаус-
гауссово исключение, примеиеииое к А, численно устойчиво без выбора главных
элементов. Уравнения метода окаймления для разложения А, аналогичные ура-
уравнениям, использовавшимся в разделе 4.5.2 для подпрограммы ESFCT, будут
таковы:
\uT s
~p, Ulw
' и,
V
¦ s —wTg
Здесь L — нижняя треугольная матрица с единицами на дяагонали и, разу-
разумеется, L ф V7.
а) Приняв в качестве основы ELSLV, составить фортран-подпрограмму
EL1SLV, решающую нижние треугольные системы с единичными диагональ-
диагональными элементами с использованием профильной схемы хранения.
б) Используя ESFCT как основу, составить фортран-подпрограмму EFCT,
которая бы раскладывала А в произведение LV, где L и VT хранятся по про-
профильной схеме.
в) Какие подпрограммы понадобятся вам для решения системы Ах = Ь,
где А — матрица описанного выше типа. Указания:
1) В подпрограммах ELSLV и ESFCT нужны лишь очень небольшие из-
изменения.
2) Ваша реализация EFCT должна использовать EL1SLV и ELSLV.
4.5.2. Пусть Lab имеют структуру, изображенную на рисунке, причем
L хранится массивами XENV, ENV и DIAG, как описано в разд. 4.4.1.
Сколько арифметических операций проделает подпрограмма ELSLV при реше-
решении системы Lx = Ь? Сколько операций выполнит EUSLV при решении си-
системы Ux = Ь?
* *
§ 4.6. Дополнительные замечания
То, что мы не проявляем энтузиазма в отношении ленточ-
ленточных упорядочений, отчасти связано с тем обстоятельством, что
§46 Дополнительные замечания 97
в нашей книге рассматриваются методы, не использующие
внешнюю память. Если же приходится прибегать к внешней
памяти, то ленточные упорядочения становятся привлекатель-
привлекательными, поскольку очень легко составить подпрограммы разло-
разложения и решения, использующие внешнюю память и примерно
Р(Р + 1)/2 слов оперативной памяти (Felippa 1970). В работе
(Wilson et al. 1974) описана ленточная схема, обходящаяся
еще меньшим объемом оперативной памяти; программа авто-
авторов может работать даже тогда, когда памяти хватает лишь на
хранение двух столбцов из ленты L.
Другая ситуация, в которой важны ленточные упорядоче-
упорядочения,— это применение так называемых ленточных методов
с минимальной памятью (Sherman 1975). Основная вычисли-
вычислительная схема та же, что и для методов с внешней памятью,
однако здесь столбцы L вычисляются, используются и затем
- «отбрасываются», вместо того чтобы быть записанными во
внешнюю память. Части L, которые понадобятся в дальней-
дальнейшем, перевычисляются.
Было предложено несколько алгоритмов упорядочения для
получения малого профиля, отличающихся от приведенных
в этой главе. В работе (Levy 1971) описан алгоритм, нумерую-
нумерующий узлы по принципу наименьшего приращения в размере
оболочки. Кинг (King 1970) предложил аналогичную схему
с тем отличием, что круг кандидатов на помечивание ограничен
такими узлами, у которых есть по крайней мере один нумеро-
нумерованный сосед; следовательно, здесь требуется выбор началь-
начального узла. В последние годы были предложены некоторые алго-
алгоритмы, более близкие к описанному нами (Gibbs et al. 1976b,
Gibbs 1976c).
Некоторые авторы (Melosh 1969, Irons 1970) описали
«фронтальные» методы (методы «волнового фронта»), исполь-
использующие вариации в ширине ленты и рассчитанные на привле-
привлечение внешней памяти. В этих схемах требуется приблизи-
приблизительно ю((о+1)/2 слов оперативной памяти вместо P(fJ + l)/2
слов в случае ленточных схем, хотя программы, как правило,
оказываются значительно более сложными. Идея фронтальных
методов была высказана в контексте решения конечноэлемент-
ных систем уравнений, и еще одной новой чертой этих методов
является то, что в них уравнения генерируются параллельно
с процессом решения системы.
Было доказано (Chan 1979), что при заданном начальном
узле алгоритм'RCM можно реализовать так, чтобы он выпол-
выполнялся за время О(|?|). Поскольку .каждое ребро графа должно
быть исследовано хотя бы раз, этот метод, очевидно, является
оптимальным.
Набор подпрограмм, аналогичных подпрограммам ELSLV,
EUSLV и ESFCT, содержится в работе (Eisenstat i974).
5. Универсальные разреженные методы
§ 5.0. Введение
В этой главе будут рассмотрены методы, которые в отличие
от методов главы 4 стараются использовать все нулевые эле-
элементы треугольного множителя L матрицы А Метод упорядо-
упорядочения, изучаемый в данной главе, называется алгоритмом ми-
минимальной степени (Rose 1972a). Это эвристический алгоритм
для отыскания такого упорядочения матрицы А, при котором
она в процессе разложения претерпевает лишь небольшое за-
заполнение. Алгоритм широко используется в прикладных рас-
расчетах и имеет хорошую репутацию. Машинные реализации под-
подпрограмм распределения памяти и численного решения суть
адаптации соответствующих подпрограмм Йельского пакета
для разреженных матриц (Eisenstat 1981).
§ 5.1. Симметричное разложение
Пусть А — симметричная разреженная матрица. Структура
ненулевых элементов А определяется как
Nonz (А) = {{г, /} | а{, ф 0 и / Ф /}.
Предположим, что посредством алгоритма Холесского матрица
разложена в произведение LLT,s Матрица заполнения F(A) для
А есть матричная сумма L-\-LT. Когда из контекста ясно, о ка-
какой матрице речь, будем писать F вместо F{A). Соответствую-
Соответствующая ей структура ненулевых элементов —
Nonz(F) = {{i, })\}{1ФО и 1Ф]).
Напомним, что во всей книге мы придерживаемся соглашения
о том, что точное числовое взаимное уничтожение не имеет
места; поэтому при заданной структуре Nonz (А) соответствую-
соответствующее множество Nonz (F) полностью определено. Тем самым
Nonz(F) не зависит от числовых значений элементов А
Из предположения о неуничтожении немедленно следует, что
Nonz(A)c= Nonz(F).
Заполнение матрицы А можно теперь определить как
Fill (Л) = Nonz (F) - Nonz (Л).
§ 5.1. Симметричное разложение 99
Рассмотрим, например, матрицу на рис. 5.1.1, где элементы
заполнения указаны звездочкой в кружочке. Соответствующие
множества здесь таковы:
Nonz(A) = {{l, 5}, {1, 8}, {2, 4}, {2, 5}, {3, 8},
{4, 7}, {5, 6}, {6, 8}, {8, 9}}.
Fill (А) = {{4, 5}, {5, 7}, {5, 8}, {6, 7}, {7, 8}}.
В следующем разделе мы рассмотрим методы получения
Fill (А) из Nonz(A).
ф * *
ф * *
не * ® * ® ® *
Рис 5.1.1. Пример множеств Nonz и Fill.
5.1.1. Модель графов исключения
Установим теперь связь между применением к А симмет-
симметричного гауссова исключения и соответствующими изменениями
в ее графе. Напомним (см. главу 2), что первый шаг алгоритма
в форме внешних произведений, примененного к iVXiV сим-
симметричной положительно определенной матрице А = Aq, можно
описать уравнением:
А = An = Нп
/*-l
1 0
О Я,
F.1.1)
Мв Гл. 5. Универсальные разреженные методы
где
Hi — Н\ — v\vf/di. C.1.2)
Основной шаг затем рекурсивно применяется к Ни Н2 и т. д.
При обычном предположении, что точное взаимное уничтоже-
уничтожение не имеет места, из уравнения E.1.2) следует, что элемент
(/, k) матрицы Н\ не равен нулю, если соответствующий эле-
элемент в Hi уже отличен от нуля или если одновременно
J
к
*
*
У
*
к
*
(*)
Рис. 6.1.2. Графическая иллюстрация заполнения в варианте внешних произ-
произведений
и (t>i)fc#0. Конечно, может выполняться и то и другое; од-
однако, если справедливо лишь последнее, происходит заполне-
заполнение. Ситуацию наглядно изображает рис. 5.1.2. После заверше-
завершения первого шага разложения предстоит разложить мат-
матрицу Ни
Вслед за Партером (Parter 1961) и Роузом (Rose 1972a)
установим соответствие между преобразованием Яо в Н\ и со-
соответствующими изменениями в ассоциированных с ними гра-
графах. Как обычно, графы Но{= А) и Hi обозначаем через
тт тт
G ° и G ' соответственно; для удобства узел a(i), где а — по-
мечивание GA, индуцированное матрицей А, записываем как х,-.
Теперь, как показывает пример на рис. 5.1.3, граф матрицы Hi
получается из графа матрицы Но:
1) удалением узла х\ и инцидентных ему ребер;
2) добавлением к графу ребер с таким расчетом, чтобы
узлы из Adj (jci) были в 0н' попарно смежными.
Этот рецепт принадлежит Партеру (Parter 1961).
Таким образом (как отмечено Роузом), симметричное гаус-
гауссово исключение можно интерпретировать как построение по-
последовательности графов исключения
G? = GH< = (XlE?), i=l,2 N-l,
где G? получается из Gf-\ в соответствии с описанной выше
процедурой. Когда а известно из контекста, мы будем писать
G, вместо G?. Пример иа рис. 5.1.3 иллюстрирует эту операцию
§ 5.1. Симметричное разложение 101
исключения вершины. Жирные линии изображают ребра, до-
добавленные цри разложении. Например, исключение узла х2
##1 =
=
##3 =
=
Gs © Нъ =
Рис. 5.1.3. Последовательность графов всключения.
в графе G\ порождает в G2 три ребра заполнения {х3,
{xi, хв} и {х3, х6}, так как смежное множество ха в G\
\Хц, Х\, Xs}.
есть
102 Гл. 5. Универсальные разреженные методы
Пусть L — треугольный множитель матрицы А. Определим
граф заполнения для GA как симметричный граф Gh =(XF, EF),
где F = L-\-U. Здесь множество ребер Ег состоит из всех
ребер ЕА плюс ребра, добавленные при разложении. Очевидно*,
XF = ХА. Связь между множествами ребер EF и ЕА устанав-
устанавливается следующей леммой, принадлежащей Партеру (Раг-
ter 1961). Ее доказательство предоставляется читателю в ка-
качестве упражнения.
Лемма 5.1.1.
Неупорядоченная пара {xi, x,} e Ef тогда и только тогда,
когда {х,, х,} е ЕА либо для некоторого k {xh хк) е Ег и
{хк, Xj} e EF, причем k < min {i, /}.
* ©@® *
F= L+lT OF
Рис. 5.1.4. Граф заполнения и матрица заполнения для примера на рис. 5.1.3.
Понятие графа исключения позволяет интерпретировать
шаги процесса исключения как последовательность преобразо-
преобразований графа. Кроме того, множество ребер, добавленных к
графам исключения, соответствует множеству элементов запол-
заполнения. Так, для примера на рис. 5.1.3 структура соответствую-
соответствующей матрицы F = L -f- U и графа заполнения GF показана на
рис. 5.1.4.
Итак, мы видим, что граф заполнения GF легко построить
по последовательности графов исключения. Построение GF важ-
важно, поскольку им определяется структура L. Мы должны знать
этот граф, если намерены применить схему хранения, исполь-
использующую все нули L.
5.1.2. Моделирование исключения посредством
достижимых множеств
В разделе
исключения
5.1.1 определена последовательность графов
§ 5.1. Симметричное разложение 103
и данб рекурсивное описание множества ребер EF. Часто бы-
бывает полезно как в теоретическом, так и вычислительном плане
иметь описание G, и Ер непосредственно через исходный граф
GA. Наша цель в этом разделе — дать такое описание с по-
помощью понятия о достижимых множествах.
Прежде всего установим причину, почему в примере на
рис. 5.1.3 было образовано ребро заполнения {х4,х6}. В Gi
имеется путь
XхА> Х2, Х6},
поэтому, когда исключается х2, возникает ребро {х*, Хб}. Од-
Однако в исходном графе нет ребра {х2, х6}; оно образовалось
из пути
(Х2, Х\, Х6)
при исключении х\ из Go. Объединяя эти два замечания, ви-
видим, что за ребро заполнения {хц, х6} в действительности от-
ответствен путь (х4, х2, Х\, х6) в исходном графе. Это мотивирует
Рис. 5.1.5. Пример, иллюстрирующий понятие достижимого множества.
использование достижимых множеств, которые сейчас будут
определены (George 1980).
Пусть S — подмножество множества узлов, и пусть х ф S.
Говорят, что узел х достижим из узла у через S, если сущест-
существует путь (у, v\, ..., Vk, x) из у в х такой, что c,eS для
1 ^ i ' ^ k. Заметим, что k может быть нулем, так что каждый
смежный с у узел, не принадлежащий S, достижим из у че-
через S.
Теперь можно определить достижимое множество у через S;
будем обозначать его
Reach (у, S) = {* ф S \х достижимо из у через 5}. E.1.3)
Чтобы проиллюстрировать понятие достижимого множества,
рассмотрим пример на рис. 5.1.5. Если S ={si, S2, S3, 54}, то
Reach {у, S) = {а, Ь, с],
104 Гл. 5. Универсальные разреженные методы
поскольку имеются следующие пути через Si
(У, s2, s4, a),
(У, Ь),
{У, su с).
Следующая теорема характеризует граф заполнения по-
посредством достижимых множеств.
Теорема 5.1.2.
Reach (xt, {хи x2, ..., *,_,})}.
Доказательство. Пусть х/ е Reach(x,, {xx *;-i}). По
определению в GA имеется путь (xh уи ..., yt, x/), такой, что
Рис. 5.1.6. Помечивание графа, изображенного на рис. 5.1.6.
Ук е {х\, .. , х,-\} для 1 ^ k ^ /. Если t = 0 или t = 1, нуж-
нужный результат немедленно следует из леммы 5.1.1. Если t > 1,
простая индукция по / с использованием леммы 5.1.1 показы-
показывает, что {Xi, х,} е EF.
Обратно, предположим {xt, x,} e EF и i ^ /. Доказатель-
Доказательство проводится индукцией по i. Утверждение верно при i = 1,
так как из {х,, х,} е EF следует {xt, x,} e ЕА. Пусть утвержде-
утверждение верно для значений индекса, меньших чем L Если {х,, х,} е
е ЕЛ, то доказывать нечего. В противном случае по лем-
лемме 5.1.1 найдется k, ?<min{t, /}, такое, что {x,,Xk}^EF и
{х,, xk) e Еь. По индуктивному предположению в подграфе
GA{{x\, ..., Хц} U {х,, х,}) можно найти путь из х, в х,, прохо-
проходящий через Хц. Отсюда и следует, что
Xf e Reach (xh {xu ..., jc^J).
На матричном языке множество Reach(х,,{х\, ..., xt-i})
«сть попросту множество строчных индексов, отвечающих не-
ненулевым компонентам столбца L»,. Пусть, например, граф на
рис. 5.1.5 помечен так, как указано на рис. 5.1.6. Если
§51. Симметричное разложение 105
положить S, ~{xi х,}, то из определения достижимого мно-
множества легко следует:
Reach (x^.S^)
Reach (x}.S2) = {xs}
Reach (x^St) = {xs,x-j}
Reach (x$.St) = {х6,дс7.дс8}
Reach (jc^Sj) = {дс7,х8}
Reach (x7>S6) = {xs}
Reach (xg,S7) = {x9}
Reach (x9.S») = 0
Согласно теореме 5.1.2, структура соответствующей матрицы L
такова, как изображено на рис. 5.1.7. Таким образом, мы
описали структуру L непосредственно через структуру А. Еще
Рис. 5.1 7.
более важно, что имеется удобный способ для описания (вве
денных в разделе 5.1.1) графов исключения посредством до-
достижимых множеств. Пусть Go, Gu ..., Gn-\ — последователь-
последовательность графов исключения, определяемая узлами Х\, х2, ..., х».
Рассмотрим граф G, = (Xt, E,). Имеем
106 Гл. 5. Универсальные разреженные методы
Теорема 5.1.3.
Пусть у — узел в графе исключения G, = (Xi, Et). Множе-
Множество узлов, смежных с у в Git есть
Reach (у, {хи ..., xt}),
где оператор Reach применяется к исходному графу Go.
Доказательство. Доказательство можно провести индукцией
по L
Обратимся снова к примеру на рис. 5.1.3. Рассмотрим графы
Go и G2.
Пусть S2 = {х\, х2). Ясно, что
Reach (x3, S2) = {xit х5, х6},
Reach (x4, S2) = {x3, x6),
Reach (лг6, S2) = {x3, x6}
Reach (x6, S2) — {x3, xit x5},
поскольку в графе 'Go имеются пути
и
{х3, х2, Xi, л:6)
н
(Х^ Х2, Х\, Х^.
Эти достижимые множества суть в точности смежные множе-
множества графа G2.
Теорема 5.1.3 объясняет важность той роли, какую дости-
достижимые множества играют в разреженном исключении. При за-
заданном графе G= (X, Е) и заданной последовательности узлов
хи х2, .. •, xn весь процесс исключения можно описать неявно
с помощью этой последовательности и оператора Reach. Такое
описание можно рассматривать как неявную модель исключе-
исключения в противоположность явной модели, основанной на графах
исключения (раздел 5.1.1).
§ 5.2. Машинное представление графов исключения 107
Упражнения
5.1.1. Пусть Nonz(A) — произвольная заданная структура ненулевых эле-
элементов. Всегда ли можно найти матрицу А*1), такую, что соответствующая
матрица заполнения F* имеет идентичные логическую и численную структуры
ненулевых элементов? Объясните свой ответ.
5.1.2. Рассмотрим звездный граф с 7 узлами (рис. 4.2.3). Предполагая,
что центральный узел нумеруется первым, определите последовательность гра-
графов исключения.
5.1.3. Для данного помеченного графа GA = (ХА, ЕА) показать, что
Reach (х{, {*,, х2, .... *,_,}) сг Adj ({*,, х2 х{}).
Вывести отсюда, что Fill (Л) сг Епу(Д).
5.1.4. Показать, что подграф
GA (Reach (xt, {*, *,_,}) U {*<})
является кликой в графе заполнения GF
5.1.5. (Rose 1972a) Граф называется триангулированным, если для каж-
каждого цикла (х\, Х2, .... xi, Jti) длины / > 3 найдется ребро, соединяющее
две несоседние вершины цикла. (Такое ребро называется хордой цикла.) По-
Покажите, что следующие условия эквивалентны:
а) граф GA триангулирован;
б) существует матрица перестановки Р, такая, что
РШ(РАРГ)=0.
5.1.6. Показать, что граф GF(A) триангулирован. Указать перестановку Р
такую, что Fil\(PF(A)PT) = 0. Вывести отсюда (или доказать каким-либо
иным способом), что
Nonz (F {А)) = Nonz (P (F (А))).
5.1.7. Пусть 5 сг Т и у ф. Т Показать, что
Reach (у. S) cz Reach (у, Т) [) Т.
5.1.8. Пусть у ф 5. Определим окрестность у в S как множество
Nbrhd {у, S) =
|s s 5 | s достижимо из у через подмножество множества J).
Пусть хфБ. Показать, что если
Adj (x) a Reach (у, S) U Nbrhd (у, S) U {у},
то
а) Nbrhd (х, 5) <= Nbrhd (у, 5),
б) Reach (x, S) cz Reach {у, S) U {у).
5.1.9. Доказать теорему 5.1.3
§ 5.2. Машинное прелставление графов исключения
Как уже говорилось в §5.1, гауссово исключение для раз-
разреженной симметричной линейной системы можно моделиро-
моделировать последовательностью графов исключения. В этом разделе
') Со структурой Nonz (Л). — Прим. перев.
108 Га 5. Универсальные разреженные методы
мы изучим способы машинного представления и преобразова-
преобразования графов исключения. Эти вопросы важны для реализации
универсальных разреженных методов.
5.2.1. Явные и неявные представления
Графы исключения являются в конечном счете симметрич-
симметричными графами, поэтому они могут быть представлены посред-
посредством одной из описанных в § 3.2 схем Однако нам важно,
чтобы представление было подогнано под исключение, так что-
чтобы в последовательности графов исключения можно было легко
выполнять переход от любого члена к следующему.
Исследуем шаги преобразования. Пусть G, — граф исклю-
исключения, полученный из Gt-\ исключением узла х,. Структуру
смежности G, можно найти следующим образом
Шаг 1. Определить смежное множество AdjO/_, (х{) в гра-
графе G,_b
Шаг 2. Удалить узел х, и его список смежности из струк-
структуры смежности.
Шаг 3. Для каждого узла у е А6]0{1 (xt) новый список
смежности у в G, получается объединением подмножеств
Это — алгоритмическая формулировка рецепта Партера
(раздел 5.1.1) для выполнения преобразования Нужно отме-
отметить два момента, связанные с реализацией. Во-первых, место,
занимаемое в структуре смежности множеством AdjOf_] (x{),
можно после шага 2 использовать для других целей Во-вто-
Во-вторых, явная структура смежности для G, может потребовать
значительно большей памяти, чем структура G«_i. Например,
если в звездном графе с N узлами (рис. 4.2.3) центральный
узел нумерован первым и Go = (Хо, Ео), G\ = (X1,El)—соот-
(X1,El)—соответствующие графы исключения, то легко показать (см
упр. 5.1.2), что
|?1 О(Л0
Эти замечания показывают, что явная реализация, позво
ляющая динамическое изменение структуры 1рафов исключе-
исключения, должна использовать очень гибкую структуру данных
Подходящей кандидатурой являются описанные в § 3.2 связные
списки смежности.
Всякое явное машинное представление имеет два недо-
недостатка. Во-первых, за гибкость структуры данных приходится
расплачиваться значительными издержками в памяти и време-
§5 2. Машинное представление графов исключения 109
ни исполнения. Во-вторых, максимум необходимой памяти не-
непредсказуем. Памяти должно хватать для наибольшего ') из
получающихся графов исключения G,. Это может значительно
превысить память, требуемую для хранения исходного графа Go.
Максимум этого превышения неизвестен до самого конца про-
процесса исключения
Теорема 5 1 3 дает другой способ представления графов
исключения Они могут храниться неявно посредством исход-
исходного графа G и исключенного подмножества S,. Множество уз-
узлов, смежных с у в G,, можно получить, генерируя по исход-
исходному 1рафу достижимое множество Reach (у, St). Это неявное
представление не имеет недостатков, свойственных явному ме-
методу. Запросы к памяти здесь скромны н предсказуемы, и
структура смежности заданного графа сохраняется.
Однако работа, необходимая для построения достижимых
множеств, может оказаться чересчур большой, особенно на
поздних этапах исключения, когда велико число |S,|. В следую-
следующем разделе мы рассмотрим другую модель, более приспособ-
приспособленную для машинной реализации и сохраняющую многие из
достоинств техники достижимых множеств.
5.2.2. Модель фактор-графов
Рассмотрим вначале процесс исключения для графа, изо-
изображенного на рис. 5.1.6. После исключения узлов Х\, х2, Хз, х±,
Рис. 5.2.1. Пример графа и соответсгвуюшего графа исключения
х5 получается граф исключения, приведенный на рис. 5 2.1.
Заштрихованы на нем исключенные узлы
Пусть S = {х\, х2, Хз, Xt, Хъ). Чтобы, пользуясь неявной мо-
моделью, установить, что v6 <= Reach(jc7> S), нужно найти путь
') Здесь слово «наибольший» относится к числу ребер, а ие к числу ys-
лов.
110 Гл. 5. Универсальные разреженные методы
Аналогично xs e Reach (x7, S), поскольку существует путь
(Х7, Хц, Х2, X*,, #ь Х^).
Отметим, что длины этих путей равны 4 и 5 соответственно.
Сделаем следующие два замечания:
а) работу по генерированию достижимых множеств можно
было бы сократить, если бы были уменьшены длины путей
к неисключенным узлам;
б) если эти пути укоротить до предела, мы получим явные
графы исключения с теми нежелательными их свойствами, ка-
какие были отмечены в предыдущем разделе.
Поищем компромиссное решение. Отождествляя связанные
исключенные узлы, мы получим новую графовую структуру,
Рис. 5.2.2. Граф, полученный отождествлением связанных исключенных узлов.
полезную для наших целей. Например, на рис. 5.2.1 в графе
G(S) имеются две связные компоненты; соответствующие мно-
множества узлов суть {хи х% х4, х5} и {хз}. Образуя два «супер-
«суперузла», придем к графу, изображенному на рис. 5.2.2.
Удобно обозначать эти связные компоненты 5 через х,ь =
= {хиХ2,х4,х5} и хз = {*3}. Замечаем, что в новом графе пути
(х7, х5, х6) и (х7, х5, х8)
имеют длину два и ведут от узла х7 к Хв и xs соответственно.
В общем случае, если мы принимаем эту стратегию, длины
всех таких путей не превосходят 2. Это очевидное преимуще-
преимущество по сравнению с генерированием достижимых множеств на
исходном графе, где пути могут быть произвольной длины
(меньшей чем N).
А каковы преимущества по отношению к явным графам
исключения? В следующем разделе мы покажем, что данный
метод можно реализовать на месте; т. е. не требуется допол-
дополнительной памяти по сравнению с исходной графовой структу-
структурой. Короче, новая структура графов позволяет весьма эффек-
эффективно генерировать достижимые" множества (или смежные мно-
§ 5.2. Машинное представление графов исключения 111
жества в графе исключения) и при этом использует фиксиро-
фиксированное место в памяти.
Чтобы формализовать эту модель исключения, введем по-
понятие фактор-графа. Пусть G = (X, Е) — заданный граф, ф —
разбиение его множества узлов X:
$ = {У„ Y2, .... Yp).
р
Это значит, что (J Yk — X и Yt [\ Y, = 0 для i ф}. Определим
фактор-граф графа G относительно ф как граф (% &), для ко-
которого {Yt, Y,} е & тогда и только тогда, когда M'i(Y,)f\Yi
ф 0. Этот граф в дальнейшем часто обозначается через ОД$,
Например, граф на рис. 5.2.2 есть фактор-граф для графа
на рис. 5.2.1 относительно разбиения
{хи х2, х4, д:5}, {дг3}, {дг6}, {х7}, {х8} {дг9}.
Понятие фактор-графа более подробно будет исследовано в
главе 6, где рассматриваются блочные матрицы. Здесь мы изу-
изучим роль этих графов в моделировании исключения. Новая мо-
модель изображает процесс исключения как последовательность
фактор-графов.
Пусть G = (X, Е) — заданный граф. Рассмотрим этап
исключения, соответствующий множеству S исключенных узлов.
Сопоставим ему фактор-граф относительно множества S, как
это подсказывает пример на рис. 5.2.2. Определим множество
/(S)= E.2.1)
{CcS|G(C) — связная компонента в подграфе
и разбиение множества X:
E.2,2)
Они однозначно определяют фактор-граф
0/7 (S);
можно считать, что этот граф получен отождествлением свя-
связанных узлов в S. Граф рис. 5.2.2 есть фактор-граф относи-
относительно множества S = {х\, х2, х3, х.\, х^}.
Изучим теперь связь фактор-графов с исключением. Пусть
хи х2, ..., Xn — порядок исключения узлов в заданном графе О.
Как и прежде, положим
S, = {xi, x2, ..., xt),
Для каждого i подмножество S,- индуцирует разбиение / (Si)
и соответствующий фактор-граф
7 F.2.3)
112 Г л, 5. Универсальные разреженные методы
Таким образом, по заданной последовательности исключения
узлов определяется последовательность фактор-графов
Рис. 5.2.3 показывает такую последовательность для_графа на
рис. 5.2.1. Из соображений удобства «суперузлы» в S(St) обоз-
обозначаются как у, а не {у}.
Рис. 5.2.3. Последовательность фактор-графов
Следующая теорема показывает, что фактор-графы вида
E.2.3) действительно являются представлениями 1рафов
исключения.
§ 5.2. Машинное представление графов исключения ИЗ
Теорема 5.2.1.
Для y<=X — Si
ReachG(*/, S?) = Reachy.(*/, /(S,)).
Доказательство. Пусть и е Reacho (у, Si). Если узлы у и и
смежны в G, то это же верно для тех же узлов в Si. В против-
противном случае в G найдется путь
У, Si st, и,
где {si st} с=5г. Пусть G(C)—связная компонента в
G(Si), содержащая s\. Тогда в Si имеется путь
у, С, и;
поэтому и е Reach^ (у, t Eг)).
Пусть, обратно, и е Reach^? (у, (Eг)). Найдется в $, путь
у, С\, ¦ ¦., Ct, и,
такой, что {С\, ..., Ct} cz/E,). Если t = 0, то у и и смежны
в исходном графе G. Если же t ~j> 0, то, по определению связ-
связных компонент, t не может быть больше единицы; следова-
следовательно, путь должен иметь вид
у, С, и,
так что в графе G есть путь из у в и через С. Поэтому
Me=ReachG(#, 5().
Построение достижимых множеств по фактор-графу St
весьма просто. Следующий алгоритм вычисляет множество
Reach.?. (г/, / (St)j по заданному узлу у ф t (Si).
Шаг 1 {инициализация). R~<-0.
Шаг 2 (найти достижимые узлы).
Для xeAdj^ (г/)
Если х е t (St)
то /?<- /?(J Adj^ (л:)
иначе /?<-/? U {х}.
Шаг 3 (выход) R есть искомое достижимое множество.
Связь между графами исключения и фактор-графами E.2.3)
вполне очевидна. В самом деле, структуру графа исключения
Gt можно получить из структуры 'St следующим простым алго-
алгоритмом.
Шаг I. Удалить суперузлы и инцидентные им ребра из
фактор-графа.
Шаг 2. Для каждого Се/E,) добавить к фактор-графу
ребра так, чтобы все узлы, смежные с С, были попарно смеж-
смежны в графе исключения.
114 Гл. 5. Универсальные разреженные методы
С целью иллюстрации рассмотрим преобразование ^4 в G4
для примера на рис. 5.2.3. Граф исключения G4 показан на
рис. 5.2.4.
Рис. 5.2.4. От фактор-графа к графу исключения.
Как средство представления процесса исключения и по сте-
степени неявности модель фактор-графов лежит между методом
достижимых множеств и моделью графов исключения.
Достижимые множества
по исходному —>. Фактор- —>¦ Граф
графу граф исключения
Соответствие между тремя моделями суммировано в табли-
таблице 5.2.1.
Таблица 5.2.1.
Представление
Смежность
Неявная модель
S,
•
•
SAT-.
Reach (у, S{)
Фактор-модель
9Х
щ
Reach » (о, / (Sf))
Явная модель
о,
о»
Adj Qi (у)
5.2.3 Реализация фактор-модели
Рассмотрим фактор-граф $?=G/f(S), отвечающий исклю-
исключенному множеству S. Если s e S, то удобно пользоваться
обозначением s для той связной компоненты подграфа G(S),
§ 6.2. Машинное представление графов исключения 115
которая содержит узел s. Например, для фактор-графа на
рис. 5.2.2
Х5 = Х\ = Х2 — Х4 = \ХЬ Х2, Хц, Х5}.
С другой стороны, для заданного Се /(S) можно выбрать
произвольный узел х из С и использовать х как представитель
С, это означает, что х = С. Прежде чем обсуждать способ вы-
выбора представителя в реализации, установим некоторые ре-
результаты, которые будут использованы для демонстрации, что
модель можно осуществить на месте, т. е. на сегменте памяти,
отведенном для структуры смежности исходного графа.
Лемма 5.2.2. Пусть G= (X, Е), и пусть С а X таково, что
G(C) есть связный подграф. Тогда
X |Adj(*)|>|Adj
Доказательство. Так как G(C) связен, в нем имеется по
крайней мере \С\ — 1 ребер. В сумме X IAdj(jc)| эти ребра
С
засчитываются дважды, откуда и следует утверждение.
Пусть х\, х2, ..., xn — последовательность узлов и Si
о= {Х\, ..., Xi), 1 ^ i г?Г N. ПОЛОЖИМ
= G(St), 8д.
Лемма 5.2.3.
Пусть у е X — Si. Тогда
Доказательство. Это следует из неравенства
где у е X — Sl+l. Проверка этого неравенства предоставляется
читателю в качестве упражнения.
Теорема 5.2.4.
max \8t\K\E\.
Доказательство. Рассмотрим фактор-графы $,• и S^+i. Если
в подграфе G(S,+i) узел xt+\ изолирован, то ясно, что |<!T/+i| =
= \<?,\. В противном случае x,+i присоединяется к некоторым
компонентам в S,; в результате получается новая компонента
в Si+j. Применяя результаты лемм 5.2.2 и 5.2.3, получим
\8l+l\ <\8t\.
Следовательно, во всех случаях
\8M\<,\8i\,.
откуда вытекает нужное утверждение.
116 Гл. 5. Универсальные разреженные методы
Теорема 5.2.4 показывает, что последовательность фактор-
графов, порождаемая исключением, требует памяти не больше,
чем структура исходного графа. При объединении узлов связ-
связного множества С в суперузел лемма 5.2.2 гарантирует, что
места, отведенного для множеств Adj(x), х e С, достаточно
для хранения Adj(C). Более того, при |С|> 1 имеется избыток
в 2(|С|—1) слов, который можно использовать для связей
или указателей.
Рис. 5.2.5 иллюстрирует структуру данных, используемую
для представления множества Adj^C) в фактор-графе &, при-
причем С= {а,Ь,с}. Нуль указывает конец данного списка в $.
I I
Исходная структура Фактор-структура
Рис. 5.2.5. Структура данных для фактор-графа.
Заметим, что в этом примере в качестве представителя мно-
множества С = {а, Ь, с) выбран узел «а». При машинной реали-
реализации важно, чтобы каждому Се/E) соответствовал един-
единственный представитель: тогда любую ссылку на С можно за-
заменить ссылкой на представителя.
Пусть х\, х2, . . . , xn — последовательность узлов, и пусть
Се/E). В качестве представителя С будем выбирать узел
jt,eC такой, что
r = max{j\x,<=C}. E.2.4)
Таким образом, хг — узел из С, исключенный последним.
До сих пор говорилось о структуре данных для фактор-гра-
фактор-графов и о том, как представлять суперузлы. Другим важным
аспектом в реализации факторной модели исключения является
преобразование фактор-графа, отвечающее исключению узла.
Рассмотрим поэтому, как можно получить структуру смежно-
смежности 'Si из структуры смежности &,-i при исключении узла xi.
Это преобразование выполняет следующий алгоритм.
Шаг 1 (подготовка). Определить множества
Я —Reach^fo, /(S,_,)).
§ 5.2. Машинное представление графов исключения 117
Шаг 2 {формирование нового суперузла и разбиения). Об-
Образовать
*i = {xt) U Т,
f{Sl) = (/(Sl_l)-T)[} {х,}.
Шаг 3 (изменение списков смежности). Adj^. (х() = /?.
Для у е= R
(У) = Ш U
1 I 5 I 8
2 I 4 I 5 I
4 I 2 I 7 I
5 Г 1 I 2 I 6 I
6 Г ТТЛ
' Ш
8 Г 1 I 3 I 6 I 9 I
•СП
Рис. 5.2.6. Представление структуры смежности.
Применим этот алгоритм к преобразованию Э\. в ^ь в при-
примере на рис. 5.2.3. В ^4
§ / О \ __ S v v V \
ъ l*-^4/ ^~~ I 1j * 4j*
Выполняя для узла дг5 шаг 1, получим
и
/? = {лг6, л:7, xs).
Следовательно, новым «суперузлом» будет
Х§ l^/ U X\ (J Л4 \X\) Xfy X4t X§jt
а новым разбиением —
»/с\ г? ? •)
Наконец, на шаге 3 модифицируются смежные множества:
\ If Y \
5, x6,
118 Гл. 5. Универсальные разреженные методы
* ©
©
1 ГбТП
2?
3
4
5
б ГШП
8 HI3I6I9I
9
8 Г.51 3 I 6 I 9 I
9 Ш
3 [Щ
J
8
|»| Игнорируется ^\ Коней, списка ^ЦМодифицируется
Рис 5.2.7. Преобразование фактор-графа на месте.
§ 5.3. Алгоритм минимальной степени 119
5(*5) = /? = {x6) x7, х8}.
Воздействие трансформации фактор-графа на структуру
данных можно иллюстрировать примером. Будем считать, что
для графа на рис. 5.2.3 структура смежности представлена так,
как показано на рис. 5.2.6.
Рис. 5.2.7 демонстрирует некоторые важные этапы построе-
построения фактор-графов для этого примера. При формировании
фактор-графов S\, W2 и ^3 структура смежности остается не-
неизменной. При преобразовании &3 в ^4 узлы х2 и *4 отождеств-
отождествляются, так что в ^4 смежное множество для узла л:4 содержит
смежное множество для {х2, х4} в исходном графе. Этим смеж-
смежным множеством будет {х5<х7}. Последняя ячейка в списке
смежности для х4 используется для связи. Заметим еще, что
в списке смежности узла х5 сосед х2 был заменен в W4 на лг4,
поскольку узел х4 стал представителем компоненты {х2,х4}.
Представления по этой схеме для *§?, и 3?в также приведены
на рис. 5.2.7. Такой способ представления фактор-графов ис-
исключения будет использован в реализации алгоритма мини-
минимальной степени, обсуждаемого в § 5.4.
Упражнения
5.2.1. а) Составьте подпрограмму под названием REACH, которую можно
было бы использовать для вычисления достижимого множества данного узла
ROOT через подмножество S Подмножество задается с помощью массива
SFLAG. узел ( принадлежит S, если переменная SFLAG(i') не равна нулю.
Опишите параметры подпрограммы и дополнительную память, которая вам
потребуется
б) Пусть граф хранится парой массивов (XADJ, ADJNCY). Используйте
подпрограмму REACH для вывода на печать структур смежности графов
исключения для любого заданного порядка исключения.
5.2.2. Для множеств ( (S,), определенных в E 2.2), показать, что
5.2.3. Доказать неравенство, используемое при выводе леммы 5.2.3.
5.2.4. Пусть X = {С/С е t (S,) для некоторого г}. Показать, что \Х\ = N.
5.2.5. Пусть C^f(Sl) и х, = С, где
г = max {/| Xj^ С).
Доказать, что:
а) Adjc(C) = Reacho(x,, S,);
б) Reacho(xr, S,) = Reacho(*,, Sr_,).
5.2.6 Начертить последовательность {Si} фактор-графов для звездного
графа с семью узлами. Центральный узел занумерован первым.
§ 5.3. Алгоритм минимальной степени
Пусть А — заданная симметричная матрица, а Р- матрица
перестановки. Хотя структуры ненулевых элементов А и РАР
различны, их размеры одинаковы: |Nonz(А) \ = |Nonz(PAPr) |
120 Гл. 5. Универсальные разреженные методы
Однако, и это обстоятельство огромной важности, между
|Nonz(F(.4)) | и | Nonz {F (РАРТ)) | для некоторой переста-
перестановки Р различие может быть очень велико. Иллюстрация
этого факта — пример на рис. 4.2.3.
В идеале мы хотели бы найти перестановку Р*, которая бы
минимизировала размер структуры ненулевых элементов мат-
матрицы заполнения:
| Nonz О (Р'АР'Т)) | = min | Nonz (F (РАРт)) |
До сих пор нет эффективного алгоритма для отыскания такой
оптимальной Р* в случае произвольной симметричной матрицы.
>v УПОРЯДОЧЕНО
у\
п
О
р
я
д
о
ч
Е
н
О
W
\\
у]
;;
*.*
• *i
\
\
Рис. 5.3.1. Мотивировка алгоритма минимальной степени.
Аналогичная задача для случая несимметричной А, как было
показано, очень трудна и принадлежит классу так называемых
NP-полных задач (Rose 1975). Поэтому приходится прибегать
к эвристическим алгоритмам, которые бы давали упорядочение
с приемлемо малой, хотя и не обязательно минимальной вели-
величиной \Nonz (F(PAPT))\.
Бесспорно, самой популярной схемой уменьшения заполне-
заполнения среди используемых является алгоритм минимальной сте-
степени (Tinney 1969), которому в случае несимметричных матриц
соответствует схема Марковица (Markowitz 1957). В основе
алгоритма — следующее наблюдение, иллюстрируемое рис. 5.3.1.
Пусть помечены узлы {хи .... х,-,}. Число ненулевых эле-
элементов в этих столбцах графа заполнения в дальнейшем не
меняется. Ясно, что для уменьшения числа ненулевых элемен-
элементов i-ro столбца1) в еще не факторизованной подматрице на
место i-ro столбца нужно перевести столбец с наименьшим
•) В графе заполнения. — Прим. пврев.
§ 6.3. Алгоритм минимальной степени 121
числом ненулевых элементов. Другими словами, схему можно
рассматривать как метод уменьшения заполненности путем
локальной минимизации чисел т] (/,*<) для разлагаемой матрицы.
5.3.1. Основной алгоритм
Легче всего алгоритм минимальной степени описать в тер-
терминах упорядочения симметричного графа. Пусть Go=(^, Е)—
непомеченный граф. Используя модель графов исключения,
можно изложить основной алгоритм следующим образом.
Рис. 5.3.2. Упорядочение графа алгоритмом минимальной степени.
Шаг 1 {инициализация). i-*-\.
Шаг 2 (выбор минимальной степени). В графе исключения
Gi-\ = (X,-\, ?i-i) выбрать узел Xi, имеющий в G,_i минималь-
минимальную степень.
Шаг 3 (преобразование графа). Построить .новый граф ис-
исключения G, = (Xi, Ei), исключая из G,_i узел xt.
Шаг 4 (цикл или остановка). i-*-i-\-\. Если ?>|Х| —
остановка. В противном случае перейти к шагу 2.
В качестве иллюстрации алгоритма рассмотрим граф на
рис. 5.3.2.
Рис. 5.3.3 показывает шаг за шагом работу алгоритма ми-
минимальной степени. Отметим, что на отдельных шагах может
быть несколько узлов с минимальной степенью. В этом при-
примере мы выбираем произвольный нз таких узлов. Однако раз-
различные стратегии выбора в подобной ситуации неоднозначно-
неоднозначности дают разные варианты алгоритма минимальной степени.
5.3.2. Описание алгоритма минимальной степени
посредством достижимых множеств
Использование графов исключения в алгоритме минималь-
минимальной степени дает механизм, с помощью которого мы выбираем
для нумерации следующий узел. Каждый шаг связан с преоб-
преобразованием графа, что является с точки зрения реализации
122 Гл. 5. Универсальные разреженные методы
I \Гра<р исключения
Выбранный
узел
Минимальная
степень
f
8
1
О
Рис. 5.3.3. Нумерация в алгоритме минимальной степеии.
§ 5.3. Алгоритм минимальной степени 123
наиболее дорогостоящей частью алгоритма. Этих преобразо-
преобразований можно было бы избежать, если бы мы располагали дру-
другим способом вычисления степеней узлов а графе исключения.
Теорема 5.1.3 дает средство для этого, состоящее в исполь-
использовании достижимых множеств. С их помощью алгоритм мини-
минимальной степени можно переформулировать следующим об-
образом.
Шаг 1 (инициализация). S-«-0. Для х^Х положить
Deg(xLAdj(x)|.
Шаг 2 (выбор минимальной степени). Выбрать узел г/е
e^-S, такой, что Deg (у) = min Deg (х). Присвоить узлу у
*<=x-s
следующий номер и положить 7-«-SU {у}
Шаг 3 (пересчет степеней). Для и^Х— Т положить
Deg(M)+-|Reach(«, т)\-
Шаг 4 (цикл или остановка). Если Т — Х — остановка.
В противном случае положить S+-T и перейти к шагу 2.
При таком подходе на протяжении всего процесса исполь-
используется структура исходного графа. Действительно, алгоритм
можно реализовать, используя лишь структуру смежности
G0 = (X,E).
Здесь уместно указать, что на шаге 3 алгоритма (пересчет
степеней) нет необходимости перевычислять размеры достижи-
достижимых множеств для каждого узла из X — Т, так как для боль-
большинства из них эти множества не меняются. Это замечание
формализуется в следующей лемме, чье доказательство выте-
вытекает из определения достижимых множеств и предоставляется
читателю.
Лемма 5.3.1.
Пусть y<?S и T = S\J {у}. Тогда
(Reach (x, S) для х ф Reach (у, S),
Reach (x, T) = \ Reach (x, S) U Reach (у, S)-{x, г/}1'
[ в противном случае.
В примере на рис. 5.3.3 рассмотрим этап, соответствующий
исключению узла d.
,. ') Здесь {х, у] — обозначение множества, состоящего из двух узлов х я
у, а не ребра, инцидентного им. — Прим. перее
124 Га. 5. Универсальные разреженные методы
Имеем S={a,c}, так что Reach(d, 5)= {b, g}. Следова-
Следовательно, исключение d воздействует лишь на степени узлов Ь
и g. Учитывая это замечание, шаг 3 алгоритма можно перефор-
переформулировать так:
Шаг 3 (пересчет степеней). Для и е Reach (г/, 5) положить
Deg(M) ¦— | Reach (и, Т)\.
Следствие 5.3.2.
Пусть у, S, Т — те же, что и в лемме 5.3.1. Для х&Х— Т
I Reach (*, Г) | > | Reach (x, S) \ — 1.
Доказательство. Утверждение вытекает непосредственно из
леммы 5.3.1.
5.5.3. Ускорение алгоритма
Согласно приведенной формулировке алгоритма, при каж-
каждом выполнении цикла нумеруется ровно один узел. Однако
йри определении на шаге 2 узла у с минимальной степенью
чисто бывает возможно обнаружить такое подмножество узлов,
которым следует присвоить дальнейшие номера автоматически
без дополнительного поиска минимальной степени.
Начнем исследование этого вопроса с введения некоторого
отношения эквивалентности. Рассмотрим этап процесса исклю-
исключения, соответствующий множеству 5 исключенных узлов. Го-
Говорят, что два узла х, jeX — 5 неразличимы по отношению
к исключению'), если
Reach (x, S) U {х} = Reach (у, S) [} {у}. (б.3.1)
Рассмотрим граф на рис. 5.3.4. Множество 5 состоит из
36 заштрихованных узлов. (Это реальная ситуация, имеющая
место при применении к такому графу алгоритма минимальной
степени.) Замечаем, что узлы а, Ь и с неразличимы по отноше-
отношению к исключению, так как все множества Reach (a,S)\J {a},
Reach F, 5) U {&}, Reach (с, S) [) {с} совпадают с
{а, Ъ, с, d, e, f, g, h, j, k}.
Есть еще две группы неразличимых узлов. Это {/, k} и {/, g}.
Изучим теперь следствия этого отношения эквивалентности
и его роль в алгоритме минимальной степени. Как будет пока-
показано ниже, оно может быть использовано для ускорения ра-
работы алгоритма минимальной степени.
') В последующем тексте предполагается, что узлы, названные «нераз-
«неразличимыми», неразличимы по отношению к исключению.
§ 5.3. Алгоритм минимальной степени 125
Теорема 5.3.3.
Пусть х, у е X — S. Если
Reach (х, 5) U {*} = Reach (у, S) [) {у},
то для любого Т такого, что X — {х, у} гэ Т гз 5,
Reach (x, T) U {х} = Reach (у, Т) [} {у}.
Доказательство. Очевидно, что лге Reach (у, S)cz
cz Reach (у, Т) U Т (см. упр. 5.1.7), так что х е Reach (у, Т).
Рис. 5.3.4. Пример к определению неразличимых узлов.
Теперь мы хотим показать, что Reach(x, T)a Reach(j/, T)[){y}.
Пусть ге Reach(x, T). Тогда существует путь
(X, S], . . ., Sf, Z),
где {si, ..., St} с Т. Если все s« e S, то доказывать нечего.
В противном случае пусть st — первый узел из множества
{si, ..., st}, не принадлежащий S, т. е.
s{ s Reach (x, S) П {Т}.
Отсюда следует s, e Reach (у, S), а потому г s Reach (у, Т).
В совокупности имеем
Reach (x, T) (J {х} <= Reach (у, Т) U {у}.
Обратное включение следует из симметрии ролей х и у\ это
и дает нужный результат.
186 Гл. 5. Универсальные разреженные методы
Следствие 5.3.4.
Пусть х и у неразличимы по отношению к подмножеству S.
Тогда для Т zi S
I Reach (х, Т) |=| Reach (у, Т)\.
Другими словами, если два узла становятся неразличимыми
на какой-то стадии исключения, то они остаются неразличимы,
пока один из них не будет исключен. Более того, как показы-
показывает нижеследующая теорема, они могут быть исключены
в алгоритме минимальной степени один за другим.
Теорема 5.3.5.
Если на каком-то этапе алгоритма минимальной степени
два узла становятся неразличимы, то они могут быть исклю-
исключены один за другим.
Доказательство. Пусть х и у неразличимы после исключе-
исключения подмножества 5. Предположим, что х становится узлом
с наименьшей степенью после того, как исключено множество
Т Т id iS ¦ т е
| Reach(Jt, T) |<| Reach(z, T)\
для всех z^X — Т. Тогда, по следствию 5.3.4,
| Reach (i/, Щ {*}) I = I Reach (у, Г)-{*}| =
= | Reach (у, Т) | - 1 = | Reach (x, Т)\-1.
Поэтому для всех zeI — (Т[) {х})
| Reach (у, Т [} {х}) | < | Reach (z, Т) \ - 1 < | Reach (z, T U {х}) |.
Здесь использовано следствие 5.3.2. Другими словами, после
исключения узла х узел у становится узлом с наименьшей сте-
степенью.
Эти замечания можно использовать при реализации алго-
алгоритма минимальной степени. Как только поиск минимальной
степени определил, что следующим должен быть исключен узел
у^Х — S, сразу вслед за у можно пронумеровать узлы, не-
неразличимые с ним. Вдобавок при пересчете степеней можно
сократить работу, пользуясь следствием 5.3.4: неразличимые
узлы имеют одинаковую степень в графах исключения. С того
момента, когда узлы квалифицированы как неразличимые, они
могут быть «склеены» и рассматриваться впоследствии как
единый суперузел
Например, рис. 5.3.5 демонстрирует два этапа исключения,
где из Неразличимых узлов формируются суперузлы. Для про-
простоты не указаны исключенные узлы. После исключения нераз-
неразличимого множества {а, Ь, с) все узлы имеют одно и то же
§ 5.3 Алгоритм минимальной степени 127
достижимое множество, так что их можно слить в один супер-
суперузел.
В общем случае опознание неразличимых узлов, если исхо-
исходить из их определения E.3.1), требует большой работы. По-
Поскольку наш прием не требует слияния всех неразличимых уз-
узлов, то поищем какое-нибудь простое, легко реализуемое усло-
условие. Ниже будет представлено условие, которое, как показала
практика, является очень эффективным. В большинстве случаев
с его помощью опознаются все неразличимые узлы.
Рис. 5.3.5. Неразличимые узлы на двух этапах исключения для графа на
рис. 5.3.4.
Пусть G = {X, Е), a S — множество исключенных узлов.
Пусть G(C\) и G{C2)— связные компоненты подграфа G(S),
т. е. Си C2€=/(S).
Лемма 5.3.6.
Пусть R\ = Adj(Cj), tf2 = Adj(C2). Если ye=Ri(]R2 и
Adj (у) с= tf, U R2 U С, U С2,
Доказательство. Пусть x^Ri\JR2. Предположим,, что 16
e#i = Adj(Ci). Поскольку G(C\)—связная компонента G(S),
то можно найти путь из у в х через C\CzS. Следовательно,
*<= Reach Q/,S)U{</}.
С другой стороны, у ^ RiU R2 по определению. Если же
х е Reach {у, S), то существует путь из у в х через S:
У,
s2
st, x.
Если t = 0, то хё Adj (г/) — ScrftiUfo- В противном случае
если t > 0, то sj e Adj (у) (] S c= Cj U С2. Это значит, что {su ...
.... st) есть подмножество либо С\, либо С2, так что хеRi\JR2-
Следовательно,
Reach {у, S) U M<=*iU*2.
128 Гл. 5. Универсальные разреженные методы
Теорема 5.3.7.
Пусть Си Сг и Ru R2— те же, что и в лемме 5.3.6. Тогда
узлы множества
Y = {у е Rx П R21 Adj (у) a Rx [} R2 U С, U C2} E.3.2)
неразличимы по отношению к исключенному подмножеству S.
Доказательство. Утверждение следует из леммы 5.3.6.
Следствие 5.3.8.
Для у е Y
IReach((/, S)|= |tf, U/?2| -1.
Теорему 5.3.7 можно использовать для слияния неразличи-
неразличимых узлов из пересечения двух достижимых множеств Ri
и R21)- Проверка на неразличимость проста и выполняется
инспекцией смежных множеств для узлов, принадлежащих пе-
пересечению Ri П #2.
Представление о неразличимых узлах можно применить
к алгоритму минимальной степени. Модифицированный алго-
алгоритм формулируется следующим образом.
Шаг 1 {инициализация). S<-0. Для jcel положить
Шаг 2 {выбор). Выбрать узел jel — S такой, что
= min Deg (x).
S
Шаг 3 {исключение). Присвоить узлам множества
Y = {x^X— S\x неразличимо с у}
номера, следующие за номером у.
') Почему смежные множества Ri и Ri можно трактовать как достижи-
достижимые, разъясняется в упр. 5.2.5. — Прим. черев.
§ 5.3. Алгоритм минимальной степени 129
Шаг 4 (пересчет степеней). Для и е Reach (у, S)—У поло-
положить
Deg(«) = | Reach (и, S[}Y)\
и найти неразличимые узлы в множестве Reach (у, S)—Y.
Шаг 5 (цикл или остановка). Положить S-^-SU^- Если
S = X— остановка. В противном случае перейти к шагу 2.
5.3.4. Реализация алгоритма минимальной степени
Реализация алгоритма минимальной степени, которая будет
здесь представлена, включает в себя использование неразличи-
неразличимых узлов, как это описано в предыдущем разделе. Узлы, ква-
квалифицированные как неразличимые, сливаются, образуя супер-
суперузел. В остальной части алгоритма они будут обрабатываться,
по существу, как один узел. Они имеют одно и то же смежное
множество, одинаковую степень и могут быть исключены в ал-
алгоритме один за другим. Ссылка на такой суперузел в реали-
реализации производится через его представителя.
Алгоритм требует определения достижимых множеств при
пересчете степеней. С этой целью и для повышения общей эф-
эффективности алгоритма используется модель фактор-графов
(раздел 5.2.2). Связанные исключенные узлы сливаются,
и применяется машинное представление последовательности
фактор-графов (раздел 5.2.3).
Нужно подчеркнуть, что идея факторизации (или слияния
узлов в суперузлы) используется здесь в двух различных кон-
контекстах:
а) для связанных исключенных узлов, чтобы облегчить опре-
определение достижимых множеств;
б) для неисключенных неразличимых узлов, чтобы ускорить
исключение.
Это иллюстрируется рис. 5.3.6. Он поясняет, как в нашей
реализации посредством двух видов факторизации хранится
граф рис. 5.3.4. Заштрихованные дважды окаймленные узлы
соответствуют исключенным суперузлам; незаштрихованные
дважды окаймленные суперузлы сформированы из неразличи-
неразличимых узлов.
В этом разделе будет представлен набор подпрограмм, реа-
реализующий алгоритм минимальной степени в том варианте, ка-
какой описан в -предыдущих разделах. Некоторые из используе-
используемых параметров те же, что обсуждались в главе 3. Мы кратко
напомним их здесь, а за деталями отошлем читателя в пара-
параграф 3.3.
Граф G = (X, Е) хранится посредством пары целых масси-
массивов (XADJ, ADJNCY); число узлов в X задается переменной
130 Гл. 5 Универсальные разреженные методы
NEQNS. Полученное подпрограммой упорядочение по мини-
минимальной степени хранится вектором PERM, а обратное упоря-
упорядочение—вектором INVP.
Данный набор подпрограмм требует несколько рабочих век-
векторов для реализации модели фактор-графов и техники нераз-
неразличимых узлов. Текущие степени узлов в (неявном) графе ис-
исключения хранятся в массиве DEG. Для узлов, которые уже
исключены, в DEG устанавливается значение —1.
Рис. 5.3.6. Фактор-граф, образованный двумя типами суперузлов.
В представлении последовательности фактор-графов связан-
связанные исключенные узлы сливаются, образуя суперузел. Как от-
отмечено в разделе 5.2.3, для ссылок достаточно выбрать в су-
суперузле представителя. Если G(C) — такая связная компонента,
то мы всегда выбираем для представления С последний ис-
исключенный узел ieC. Это означает, что остальные узлы С
можно игнорировать в последующих фактор-графах.
То же замечание относится к неразличимым группам неис-
ключенных узлов. Для каждой группы в данной фактор-струк-
фактор-структуре будет рассматриваться только представитель.
Для маркировки тех узлов, которые можно игнорировать
в структуре смежности, используется рабочий вектор MARKER.
Для таких узлов в MARKER записываются значения, равные
—1. Тот же вектор используется, чтобы облегчить генерирова-
генерирование достижимых множеств.
§ 5.3. Алгоритм минимальной степени 131
Еще два массива QSIZE и QLINK используются для пол-
полного описания неразличимых суперузлов. Если представителем
QLINK
8
QSIZE
О
MARKER
Рис 5.3.7. Иллюстрация роли рабочих массивов QLINK, QSIZE и MARKER.
суперузла является узел i, то число узлов этого суперузла за-
задается переменной QSIZE (г), а сами узлы суть
i, QLINK (О, QLINK (QLINK (*))
Рис. 5.3.7 иллюстрирует использование векторов QSIZE,
QLINK и MARKER. Узлы {2, 5, 8} образуют неразличимый
QMDRCH
GENQMD
QMDUPD
QMDQT
/ \
QMDMRG
QMDRCH
Рис. 5.3.8. Отношеяия управления между подпрограммами в алгоритме мини-
минимальной степени
суперузел, представляемый узл01М 2. Поэтому в массиве
MARKER значения для узлов 5 и 8 равны —1. С другой стороны,
{3, 6, 9} есть исключенный суперузел. Его представитель —
узел 9, так что MARKER C) и MARKER F) равны —1.
В данном наборе пять подпрограмм, а именно: GENQMD,
QMDRCH, QMDQT, QMDUPD и QMDMRG. Отношения управ-
управления между ними показаны на рис. 5.3.8. Ниже эти подпро-
подпрограммы описываются подробно.
с»
с»
с»
с»
с»
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
О'
с
с
с
с»
с
GENQMD ... УПОРЯДОЧЕНИЕ МИНИМАЛЬНОЙ
СТЕПЕНИ С ИСПОЛЬЗОВАНИЕМ ФАКТОРИЗАЦИИ
ПОДПРОГРАММА РЕАЛИЗУЕТ АЛГОРИТМ МИНИМАЛЬНОЙ СТЕПЕНИ .
ИСПОЛЬЗУЮТСЯ НЕЯВНОЕ ПРЕДСТАВЛЕНИЕ ГРАФОВ ИСКЛЮЧЕНИЯ
ПОСРЕДСТВОМ ФАКТОР-ГРАФОВ И ТЕХНИКА
НЕРАЗЛИЧИМЫХ УЗЛОВ. ПРЕДУПРЕЖДЕНИЕ - СОДЕРЖИМОЕ
ВЕКТОРА СМЕЖНОСТИ ADJNCY НЕ СОХРАНЯЕТСЯ.
ВХОДНЫЕ ПАРАМЕТРЫ -
NEQNS - ЧИСЛО УРАВНЕНИЙ.
(XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
ВЫХОДНЫЕ ПАРАМЕТРЫ -
PERM - УПОРЯДОЧЕНИЕ МИНИМАЛЬНОЙ СТЕПЕНИ.
INVP - ОБРАТНОЕ К PERM ,
МБОЧИЕ ПАРАМЕТРЫ -
DEG - ВЕКТОР СТЕПЕНЕЙ. ОТРИЦАТЕЛЬНОЕ DEG(I)
УКАЗЫВАЕТ, ЧТО УЗЕЛ I НУМЕРОВАН.
MARKER - ВЕКТОР МАРКИРОВКИ. ОТРИЦАТЕЛЬНОЕ MARKER(I)
УКАЗЫВАЕТ, ЧТО УЗЕЛ I СЛИТ С ДРУГИМ УЗЛОМ
И ЕГО МОЖНО ИГНОРИРОВАТЬ.
rchset - вектор для достижимого множества.
NBRHD - ВЕКТОР ДЛЯ ОКРЕСТНОСТИ .
QSIZE - ВЕКТОР ДЛЯ ХРАНЕНИЯ РАЗМЕРОВ НЕРАЗЛИЧИМЫХ
СУПЕРУЗЛОВ.
QLINK - 8ЕКГОР, ХРАНЯЩИЙ НЕРАЗЛИЧИМЫЕ УЗЛЫ.
I, QLINK(t), QLINK(QLINKU)) ... - ЭЛЕМЕНТЫ
СУПЕРУЗЛА , ПРЕДСТАВЛЯЕМОГО УЗЛОМ I.
ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ •
QMDRCH, QMDQT, QMDUPD.
SUBROUTINE GENQMD ( NEQNS, XADJ, ADJNCY, PERM, INVP, DEG,
1 MARKER, RCHSET, NBRHD, QSIZE, QLINK,
1 NOFSUB )
INTEGER ADJNCY(l), PERM(l), INVP(l), DEG(l), MARKER(l),
1 RCHSET(l), NBRHD(l), QSIZE(l), QLINKA)
INTEGER XADJ(l), INODE, IP, IRCH, J, MINDEG, NDEG,
1 NEQNS, NHDSZE, NODE, NOFSUB, NP, NUM. NUMP1,
1 NXNODE, RCHSZE. SEARCH, THRESH
С
С
с
С ИНИЦИАЛИЗИРОВАТЬ DEGREE И ДРУГИЕ РАБОЧИЕ ПЕРЕМЕННЫЕ .
MINDEG - NEQNS
NOFSUB - О
DO 100 NODE - 1, NEQNS
PERM(NODE) - NODE
INVP(NODE) - NODE
MARKER(NODE) - 0
QSIZE(NODE) - 1
QLINK(NODE) - 0
NDEG - XADJ(NODE*1) - XADJ(NODE)
DEG(NODE) - NDEG
IF ( NDEG . LT. MINDEG ) MINDEG • NDEO
100 CONTINUE
NUM ¦ 0
С
С БАРЬЕРНЫЙ ПОИСК УЗЛА С МИНИМАЛЬНОЙ СТЕПЕНЬЮ.
С SEARCH УКАЗЫВАЕТ, ОТКУДА НАЧИНАТЬ ПОИСК.
С -. _
200 SEARCH - 1
THRESH - MINDEG
MINDEG - NEQNS
300 NUMP1 - NUM + 1
IF ( NUMP1 .GT. SEARCH ) SEARCH - NUMP1
DO 400 J - SEARCH, NEQNS
NODE - PERM(J)
IF ( MARKER(NODE) .LT. 0 ) GOTO 400
NDEG - DEG(NODE)
IF ( NDEG .LE. THRESH ) GO TO 300
IF ( NDEG .LT. MINDEG ) MINDEG - NDEff
400 CONTINUE
GO TO 200
С
С МИНИМАЛЬНУЮ СТЕПЕНЬ ИМЕЕТ NODE. ОПРЕДЕЛИТЬ ЕГО
С ДОСТИЖИМОЕ МНОЖЕСТВО, ОБРАЩАЯСЬ К QMORCH.
с
300 SEARCH - J
NOFSUB - NOFSUB + DEG(NODE)
MARKER(NODE) - 1
CALL QMDRCH (NODE, XADJ, ADJNCY, DLG, MARKER,
RCHSZE, RCHSET, NHDSZE, NBRHD )
С -
С ИСКЛЮЧИТЬ ВСЕ УЗЛЫ , НЕРАЗЛИЧИМЫЕ С NODE . «ГО
С БУДУТ NODE , Q(.INK(NODE?, .. .
с ....
NXNODE - NODE
600 NUM - NUM + 1
NP - INVP(NXNODE)
IP - PERM(NUM)
PERM(NP) - IP
INVP(IP) - NP
PERM(NUM) . NXNODE
INVP(NXNODE) - NUM
DEG(NXNODE) - - 1
NXNODE - QLINK(NXNODE)
IF (NXNODE .GT. 0) GOTO 600
С
IF ( RCHSZE .LE. 0 ) GO TO 800
С
С ПЕРЕСЧИТАТЬ СТЕПЕНИ УЗЛОВ В ДОСТИЖИМОМ
С МНОЖЕСТВЕ И ОПРЕДЕЛИТЬ НЕРАЗЛИЧИМЫЕ УЗЛЫ .
с - -
CALL QMDUPD ( XADJ, ADJNCY, RCHSZE, RCHSET,
1 QSIZE, QLINK, MARKER,
1 RCHSET(RCHSZE+1), NBRHD(NHDSZE+1)
С
С ИЗМЕНИТЬ В MARKER ЗНАЧЕНИЯ, СООТВ. УЗЛАМ
С ДОСТИЖИМОГО МНОЖЕСТВА. ИЗМЕНИТЬ БАРЬЕРНОЕ
С ЗНАЧЕНИЕ ДЛЯ ЦИКЛИЧЕСКОГО ПОИСКА. ВЫЗВАТЬ QMOQT.
с .
MARKER(NODE) . 0
DO 700 IRCH - 1, RCHSZE
INODE - RCHSET(IRCH)
IF ( MARKER(INODE) .LT. 0 ) GOTO 700
MARKER(INODE) • б
NDEG - DEG(INODE)
IF ( NDEG .LT. MINDEG ) MINDEG • NDE4
IF ( NDEG .GT. THRESH ) GOTO 700
MINDEG - THRESH
184 Гл 5. Универсальные разреженном методы
THRESH - NDEG
SEARCH . INVP(INODE)
700 CONTINUE
IF ( NHDSZE .GT. 0 ) CALL QMDQT ( NODE, XADJ,
1 ADJNCY, MARKER, RCHSZE, RCHSET. NBRHD )
800 IF ( NUM LT NEQNS ) GO TO 300
RETURN
END
GENQMD (GENeral Quotient Minimum Degree algorithm)
Назначение этой подпрограммы — определение упорядоче-
упорядочения по минимальной степени для произвольного несвязного
графа. Она оперирует с входным графом, задаваемым посред-
посредством NEQNS' и пары (XADJ, ADJNCY); полученное упорядо-
упорядочение хранится векторами PERM и INVP. Подпрограмма не
сохраняет исходную структуру смежности, поскольку послед-
последняя используется для хранения последовательности фактор-
графов.
Работа подпрограммы начинается с присвоения начальных
значений рабочим массивам QSIZE, QLINK, MARKER и век-
вектору DEG. Затем происходит подготовка к основному циклу
алгоритма. В этом цикле подпрограмма прежде всего опреде-
определяет узел с минимальной степенью посредством техники барь-
барьерного поиска1). Используются две переменные: THRESH
и MINDEG. Всякий узел, текущая степень которого равна зна-
значению THRESH, является узлом минимальной степени в графе
исключения. Переменная MINDEG хранит значение степени,
следующее по величине за барьерным значением THRESH; она
используется для модификации значения THRESH.
После того как найден узел NODE с минимальной степенью,
GENQMD определяет достижимое множество NODE через ис-
исключенные суперузлы; для этого она обращается к подпро-
подпрограмме QMDRCH. Достижимое множество помещается в век-
вектор RCHSET, а его размер—в RCHSZE. Потом с помощью
вектора QLINK разыскиваются и нумеруются (исключаются)
узлы, не различимые с NODE.
Далее пересчитываются степени узлов достижимого множе-
множества и в то же время определяются новые неразличимые узлы.
В программе это достигается вызовом подпрограммы QMDUPD.
Затем значение барьера также изменяется.
Прежде чем программа вернется на начало цикла—поиск
очередного узла минимальной степени, выполняется (посред-
(посредством подпрограммы QMDQT) преобразование фактор-графа.
Программа заканчивает работу, когда пронумерованы все узлы
графа.
') В оригинале — threshold searching. — Прим. перев.
§ 5.3. Алгоритм минимальной степени 135
QMDRCH (Quotient MD ReaCHable set)
Эта подпрограмма определяет достижимое множество дан-
данного узла ROOT через множество исключенных узлов. Пред-
Предполагается, что структура смежности хранится в формате фак-
фактор-графа, как это описано в разделе 5.2.3. На выходе най-
найденное достижимое множество помещается в вектор RCHSET,
а его размер будет значением переменной RCHSZE. В качестве
побочного продукта определяется множество исключенных су-
суперузлов, смежных с ROOT; оно помещается в вектор NBRHD;
значением NHDSZE будет размер этого множества. Для узлов
указанных двух множеств будут установлены ненулевые зна-
значения в массиве MARKER.
Подпрограмма является точной реализацией алгоритма из
раздела 5.2.2. После присвоения начальных значений в цикле
DO 600 ... исследуется каждый сосед узла ROOT. Если этот
сосед — представитель исключенного суперузла, то циклом
DO 500 ... в достижимое множество включается смежное мно-
множество суперузла в фактор-графе. В противном случае в дости-
достижимое множество включается сам сосед.
с • • •¦
с............... ....,.»»,
С......... QMDRCH . ВЫЧИСЛЕНИЕ ДОСТИЖИМОГО МНОЖЕСТВА •••
С......... В АЛГОРИТМЕ МИНИМАЛЬНОЙ СТЕПЕНИ .»«.......,
с............
с
С ПОДПРОГРАММА ОПРЕДЕЛЯЕТ ДОСТИЖИМОЕ МНОЖЕСТВО УЗЛА ЧЕРЕЗ
С ДАННОЕ ПОДМНОЖЕСТВО. ПРЕДПОЛАГАЕМ, ЧТО СТРУКТУРА
С СМЕЖНОСТИ ХРАНИТСЯ В ФОРМАТЕ ФАКТОР - ГРАФА.
С
С ВХОДНЫЕ ПАРАМЕТРЫ, -
С ROOT - ЗАДАННЫЙ УЗЕЛ ВНЕ ЗАДАННОГО ПОДМНОЖЕСТВА.
С (XADJ, ADJNCY) - МАССИВЫ ДЛЯ СТРУКТУРЫ СМЕЖНОСТИ.
С DEG - ВЕКТОР СТЕПЕНЕЙ. DEG(l).LT.O ОЗНАЧАЕТ,
С ЧТО УЗЕЛ I - В ДАННОМ ПОДМНОЖЕСТВЕ ,
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (RCHSZE, RCHSET) - ДОСТИЖИМОЕ МНОЖЕСТВО.
С (NHDSZE, NBRHD) - ОКРЕСТНОСТЬ.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С MARKER - ВЕКТОР МАРКИРОВКИ ДЛЯ ДОСТИЖИМОГО
С МНОЖЕСТВА И ОКРЕСТНОСТИ. ПОЛОЖИТЕЛЬНОЕ
С ЗНАЧЕНИЕ КОМПОНЕНТЫ УКАЗЫВАЕТ, ЧТО УЗЕЛ-
С В ДОСТИЖИМОМ МНОЖЕСТВЕ , ОТРИЦАТЕЛЬНОЕ - БЫЛ СЛИТ
С С ДРУГИМИ ИЛИ ПРИНАДЛЕЖИТ ОКРЕСТНОСТИ.
с...........
с
SUBROUTINE QMDRCH ( ROOT, XADJ, ADJNGft DEC, MARKER,
1 RCHSZE, RCHSET, NHDSZE, NBRHD )
С
С.............................. ..........,.,...,,,л
K56 Гл. 5. Универсальные разреженные методы
INTEGER ADJNCY(l), DEG(l), MARKER(l),
1 RCHSET(l), NBRHD(l)
INTEGER XADJ(l), I, ISTRT, ISTOP, J, JSTRT, JSTOP,
1 NABOR, NHDSZE, NODE, RCHSZE, ROOT
С ЦИКЛ ПО СОСЕДЯМ УЗЛА ROOT
С В ФАКТОР - ГРАФЕ .
с —
NHDSZE - О
RCHSZE - О
ISTRT - XADJ(ROOT)
ISTQP - XADJ(ROOT+1) - 1
IF ( ISTOP .LT. ISTRT ) RETURN
DO 600 I - ISTRT, ISTOP
NABOR - ADJNCY(I)
IF ( NABOR .EQ. 0 ) RETURN
IF ( MARKER(NABOR) .NE. 0 ) GO TO 600
TF ( DEG(NABOR) .LT. 0 ) GO TO 200
C
С ВКЛЮЧИТЬ NABOR В ДОСТИЖИМОЕ МНОЖЕСТВО.
с —
RCHSZE - RCHSZE + 1
RCHSET(RCHSZE) - NABOR
MARKER(NABOR) - 1
GO TO 600
¦C
С
NABOR - ИСКЛЮЧЕННЫЙ УЗЕЛ. НАЙТИ УЗЛЫ,
ДОСТИЖИМЫЕ ИЗ НЕГО.
200 MARKER(NABOR) - -1
NHDSZE - NHDSZE + 1
NBRHD(NHDSZE) - NABOR
300 JSTRT - XADJ(NABOR)
JSTOP - XADJ(NABOR+1) - 1
DO 500 J - JSTRT, JSTOP
NODE - ADJNCY(J)
NABOR - - NODE
IF (NODE) 300, 600, 400
400 IF ( MARKER(NODE) .NE. 0 ) GO TO 500
RCHSZE - RCHSZE + 1
RCHSET(RCHSZE) - NODE
MARKER(NODE) • 1
300 CONTINUE
600 CONTINUE
RETURN
END
QMDQT (Quotient MD Quotient graph Transformation)
Эта подпрограмма выполняет преобразование фактор-графа
на структуре смежности (XADJ, ADJNCY). Новый исключен-
исключенный суперузел содержит узел ROOT и узлы из массива
NBRHD; ROOT будет его представителем в новой структуре.
Его смежное множество в новом фактор-графе описывается
парой (RCHSZE, RCHSET).
§ 5.3. Алгоритм минимальной степени 137
с ¦
с •
С....... QMDQT ... ПРЕОБРАЗОВАНИЕ ФАКТОР - ГРАФА
С....... В АЛГОРИТМЕ МИНИМАЛЬНОЙ СТЕПЕНИ *•¦
С
С ПОДПРОГРАММА ПРЕОБРАЗУЕТ ФАКТОР - ГРАФ ПОСЛЕ
С ИСКЛЮЧЕНИЯ ОЧЕРЕДНОГО УЗЛА.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С ROOT - ТОЛЬКО ЧТО ИСКЛЮЧЕННЫЙ УЗЕЛ. ОН СТАНОВИТСЯ
С ПРЕДСТАВИТЕЛЕМ НОВОГО СУПЕРУЗЛА.
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ .
С (RCHSZE, RCHSET) - ДОСТИЖИМОЕ МНОЖЕСТВО УЗЛА ROOT
С В СТАРОМ ФАКТОР - ГРАФЕ .
С NBRHD - ОКРЕСТНОСТЬ ROOT, БУДЕТ СЛИТА С НИМ
С ПРИ ФОРМИРОВАНИИ НОВОГО СУПЕРУЗЛА.
С MARKER - ВЕКТОР МАРКИРОВКИ.
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР "
С ADJNCY - ПЕРЕХОДИТ В ADJNCY ДЛЯ ФАКТОР - ГРАФА .
С
С.
С
SUBROUTINE QMDQT ( ROOT, XADJ, ADJNCY, MARKER,
1 RCHSZE, RCHSET, NBRHD )
С
INTEGER ADJNCY(l), MARKER(l), RCHSETA), NBRHDA)
INTEGER XADJ(l), INHD, IRCH, J, JSTRT, JSTOP, LINK,
1 NABOR, NODE, RCHSZE, ROOT
С
С •
с
IRCH - О
INHD - О
NODE - ROOT
100 JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 2
IF ( JSTOP .LT. JSTRT ) GO TO 300
с
С ПОМЕСТИТЬ ДОСТИЖИМЫЕ УЗЛЫ В СПИСОК СМЕЖНОСТИ NODE.
С j
DO 200 J - JSTRT, JSTOP
IRCH - IRCH + 1
ADJNCY(J) - RCHSET(IRCH)
IF ( IRCH .GE. RCHSZE ) GOTO 400
200 CONTINUE
С
С ПЕРЕХОД НА ДРУГОЙ СЕГМЕНТ ПАМЯТИ, ЗАНИМАЕМЫЙ NBRHD.
300 LINK - ADJNCY(JSTOP+1)
NODE - - LINK
I.F ( LINK .LT. 0 ) GOTO 100
INHD - INHD + 1
NODE - NBRHD(INHD)
ADJNCY(JSTOP+1) - - NODE
GO TO 100
С ---
С
J38 Гл. 5 Универсальные разреженные методы
С ВСЕ ДОСТИЖИМЫЕ УЗЛЫ РАЗМЕЩЕНЫ . ЗАКОНЧИТЬ СПИСОК
С СМЕЖНОСТИ. ДОБАВИТЬ ROOT К СПИСКУ СОСЕДЕЙ КАЖДОГО
С УЗЛА ИЗ ДОСТИЖИМОГО МНОЖЕСТВА.
С
400 ADJNCY(J+1) - О
DO 600 IRCH . 1, RCHSZE
NODE - RCHSET(IRCH)
IF ( MARKER(NODE) . LT. 0 ) GOTO 600
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
DO 500 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
IF ( MARKER(NABOR) .GE. 0 ) GO TO 500
ADJNCY(J) - ROOT
GOTO 600
500 CONTINUE
600 CONTINUE
RETURN
END
После присвоения начальных значений новое смежное мно-
множество из (RCHSZE, RCHSET) будет помещено в список
смежности узла ROOT в структуре (цикл DO 200 ...). Если
места не хватает, то программа использует память, отведенную
для узлов массива NBRHD. Согласно разделу 5.2.3, этой до-
дополнительной памяти уже всегда достаточно.
Прежде чем закончить работу, программа добавляет узел-
представитель ROOT в список соседей каждого узла из
RCHSET. Это делается циклом DO 600 .. .
QMDUPD (Quotient MD UPDate)
Эта подпрограмма выполняет пересчет степеней в алгоритме
минимальной степени. Узлы, чьи новые степени нужно опре-
определить, задаются парой (NLIST, LIST). Подпрограмма также
сливает неразличимые узлы этого подмножества, пользуясь
теоремой 5.3.7.
Первый цикл DO 200 ... и обращение к подпрограмме
QMDMRG определяют группы неразличимых узлов в заданном
множестве. Они сливаются, и их степени пересчитываются.
Для узлов, которые не подвергаются слиянию, новые сте-
степени определяются в цикле DO 600 ... посредством обращения
к подпрограмме QMDRCH. Векторы RCHSET и NBRHD ис-
используются как рабочие массивы.
QMDMRG (Quotient MD MeRGe)
Эта подпрограмма осуществляет проверку условия E.3.2)
для того, чтобы определить неразличимые узлы. Пусть С\, Сг,
§ 5.3. Алгоритм минимальной степени 139
С............ *.
с »..•
<>•• QMDUPD .... ПЕРЕСЧЕТ СТЕПЕНЕЙ В АЛГОРИТМЕ *•
С ..........».*...¦« МИНИМАЛЬНОЙ СТЕПЕНИ ......*...
с«........
с
С ПОДПРОГРДММА ВЫПОЛНЯЕТ ПЕРЕСЧЕТ СТЕПЕНЕЙ ДЛЯ ЗАДАННОГО
С МНОЖЕСТВА УЗЛОВ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С (NLIST, LIST) - СПИСОК УЗЛОВ, ЧЬИ СТЕПЕНИ НУЖНО
С ПЕРЕВЫЧИСЛИТЬ.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С DEG - ВЕКТОР СТЕПЕНЕЙ.
С QSIZE - РАЗМЕРЫ НЕРАЗЛИЧИМЫХ СУПЕРУЗЛОВ.
С QLINK - СВЯЗНЫЙ СПИСОК ДЛЯ НЕРАЗЛИЧИМЫХ УЗЛОВ.
С MARKER - ИСПОЛЬЗУЕТСЯ ДЛЯ МАРКИРОВКИ УЗЛОВ.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С RCHSET - ДОСТИЖИМОЕ МНОЖЕСТВО.
С NBRHD - ОКРЕСТНОСТЬ.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
Q QMDMRG, QMDRCH.
С
SUBROUTINE QMDUPD ( XADJ, ADJNCY, NLIST, LIST, DEG,
1 QSIZE, QLINK, MARKER, RCHSET, NBRHD )
С
С...
С
INTEGER ADJNCY(l), LIST(l), DEG(l), MARKER(l),
1 RCHSET(l), NBRHD(l), QSIZE(l), QLINK(l)
INTEGER XADJ(l), DEGO, DEG1, IL, INHD, INODE, IRCH,
1 J, JSTRT, JSTOP, MARK, NABOR, NHDSZE, NLIST,
1 NODE, RCHSZE, ROOT
С
с
с Найти все исключенные суперузлы , смежные
С С УЗЛАМИ ДАННОГО СПИСКА LIST.
С ПОМЕСТИТЬ HXB(NHDSZE, NBRHD).
С DEGO - ЧИСЛО УЗЛОВ В СПИСКЕ .
IF ( NLIST .LE. 0 ) RETURN
DEGO - О
NHDSZE - О
DO 200 IL - 1, NLIST
NODE - LIST(IL)
DEGO - DEGO + QSIZE(NODE)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
DO 100 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
IF ( MARKER(NABOR) .NE. 0 .OR.
1 DEG(NABOR) GE. 0 ) GO TO 100
MARKER(NABOR) - - 1
140 Г л S. Универсальные разреженные методы
NHDSZE - NHDSZE + 1
NBRHD(NHDSZE) - NABOR
100 CONTINUE
200 CONTINUE
С
С СЛИТЬ НЕРАЗЛИЧИМЫЕ УЗЛЫ В ЗАДАННОМ СПИСКЕ,
С ВЫЗВАВ QMDMRG.
С
IF ( NHDSZE .GT. 0 )
1 CALL QMDMRG ( XADJ, ADJNCY, DEC. QSIZE, QLINK,
1 MARKER, DEGO, NHDSZE, NBRHD, RCHSET,
1 NBRHD(NHDSZE+1) )
С НАЙТИ НОВЫЕ СТЕПЕНИ УЗЛОВ, КОТОРЫЕ НЕ БЫЛИ
С СЛИТЫ.
DO 600 IL . 1, NLIST
NODE - LIST(IL)
MARK - MARKER(NODE)
TF ( MARK .GT. 1 .OR. MARK .LT. 0 ) GO TO 600
MARKER(NODE) - 2
CALL QMDRCH ( NODE, XADJ ,¦ ADJNCY, DEC, MARKER,
1 RCHSZE, RCHSET, NHDSZE, NBRHD )
DEG1 - DEGO
IF ( RCHSZE .LE. 0 ) GO TO 400
DO 300 IRCH - 1, RCHSZE
INODE • RCHSET(IRCH)
DEG1 - DEG1 + QSIZE( INODE)
MARKER(INODE) - 0
300 CONTINUE
400 DEC(NODE) - DEG1 - 1
IF ( NHDSZE .LE. 0 ) GO TO ciOO
DO 500 INHD - 1, NHDSZE
INODE - NBRHD(INHD)
MARKER(INODE) - 0
500 CONTINUE
600 C0NT1NUF
RETURN
END
ru r2 и у _те же, что и в лемме 5.3.6. Подпрограмма предпо-
предполагает, что С\ и R\ были найдены ранее. Для узлов нз R\ зна-
значения в массиве MARKER равны 1.
Подпрограмма QMDMRG может иметь на входе несколько
компонент С2. Они содержатся в паре (NHDSZE, NBRHD),
где каждая переменная NBRHD(i) указывает исключенный
суперузел (т. е. связную компоненту).
Цикл DO 1400 ... применяет условие к каждой заданной
связной компоненте. Вначале в цикле DO 600 ... определяется
множество /?2—Ru хранимое посредством (RCHSZE, RCHSET),
и пересечение ЯгЛЯь описываемое парой (NOVRLP, OVRLP).
Для каждого узла нз пересечения в цикле DO 1100 ... прове-
проверяется условие E.3.2). Если условие удовлетворено, то узел
§ 5.3. Алгоритм минимальной степени 141
включается в сливаемый суперузел, что достигается помеще-
помещением его в вектор QLINK. Вычисляется также размер нового
суперузла.
Упражнения
5.3.1. Пусть л;; —узел, выбранный из G;_, в алгоритме минимальной сте-
степени. Пусть г/eAdjg (л:г) и
Показать, что у будет узлом минимальной степени в Gt.
5.3.2. Пусть xt и Gi-i— те же, что в упр. 5.3.1, и «/eAdj0. (д.^. До-
Доказать, что если
AdJo,_,<0>c:AdJoJ_1(*i)U{*l},
то у будет узлом минимальной степени в Gi
с • »¦¦• •
С.......... QMDMRG ... . СЛИЯНИЕ 8 АЛГОРИТМЕ МИНИМАЛЬНОЙ
С....................... СТЕПЕНИ ...¦»....»..«.*.»»•*.,
С
С ПОДПРОГРАММА СЛИВАЕТ НЕРАЗЛИЧИМЫЕ УЗЛЫ В АЛГОРИТМЕ
С МИНИМАЛЬНОЙ СТЕПЕНИ И ВЫЧИСЛЯЕТ
с новые степени новых суперузлов.
с
с
С 8ХЭДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С DEGO - ЧИСЛО УЗЛОВ В ЗАДАННОМ МНОЖЕСТВЕ .
С (NHDSZE, NBRHD) - МНОЖЕСТВО ИСКЛЮЧЕННЫХ СУПЕРУЗЛОВ»
С СМЕЖНЫХ С УЗЛАМИ ЗАДАННОГО МНОЖЕСТВА,
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С DEG - ВЕКТОР СТЕПЕНЕЙ .
С QSIZE - РАЗМЕРЫ НЕРАЗЛИЧИМЫХ СУПЕРУЗЛОВ.
С QLINK - СВЯЗНЫЙ СПИСОК ДЛЯ НЕРАЗЛИЧИМЫХ УЗЛОВ.
С MARKER - В ЗАДАННОЕ МНОЖЕСТВО ВХОДЯТ УЗЛЫ,
С КОТОРЫМ В MARKER C00T8. ЗНАЧЕНИЕ 1.
С ДЛЯ УЗЛОВ, СТЕПЕНЬ КОТОРЫХ ИЗМЕНЕНА,
С БУДЕТ УСТАНОВЛЕНО ЗНАЧЕНИЕ 2. '
С РАБОЧИЕ ПАРАМЕТРЫ -
С RCHSET - ДОСТИЖИМОЕ МНОЖЕСТВО.
С OVRLP - ВЕКТОР, ХРАНЯЩИЙ ПЕРЕСЕЧЕНИЯ ДВУХ
С ДОСТИЖИМЫХ МНОЖЕСТВ .
С
SUBROUTINE QMDMRG ( XADJ, ADJNCY. DEG, QSIZE, QLINK
1 MARKER, DEGO, NHDSZE, NBRHD RCHSET
Д OVRLP )
С
с» ««•••«««•««•«•«««•«••*«««»««••««««•««*•«¦«•«¦¦«¦«««««¦«*«*¦•
с
INTEGER ADJNCY(l), DEG(l), QSIZE(l), QLINK(l),
1 MARKER(l), RCHSET(l), NBRHDA), OVRLP(l)
INTEGER XADJ(l), DEGO, DEG1, HEAD, INHD, IOV, IRCH,
1 J, JSTRT, JSTOP, LINK, LNODE, MARK, MRGSZE,
1 NABOR, NHDSZE, NODE, NOVRLP, RCHSZE, ROOT
С
c***«»«*
с
с -
С ПРИСВОЕНИЕ НАЧАЛЬНЫХ ЗНАЧЕНИЙ . . .
с --
IF ( NHDSZE .LE. 0 ) RETURN
DO 100 INHD - 1, NHDSZE
ROOT - NBRHD(INHD)
MARKER(ROOT) - 0
100 CONTINUE
С - - —
С ЦИКЛ ПО ИСКЛЮЧЕННЫМ СУПЕРУЗЛАМ ПАРЫ
С (NHDSZE, NBRHD).
С
DO 1400 INHD - 1, NHDSZE
ROOT - NBRHD(INHD)
MARKER(ROOT) - - 1
RCHSZE - 0
NOVRLP - 0
DEG1 - 0
200 JSTRT - XADJ(ROOT)
JSTOP - XADJ(ROOT+1) - 1
с
С ОПРЕДЕЛИТЬ ДОСТИЖИМОЕ МНОЖЕСТВО И
С ЕГО ПЕРЕСЕЧЕНИЕ С ВХОДНЫМ ДОСТИЖИМЫМ МНОЖЕСТВОМ.
с
DO 600 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
ROOT - - NABOR
IF (NABOR) 200, 700, 300
300 MARK - MARKER(NABOR)
IF ( MARK ) 600, 400, 500
400 RCHSZE - RCHSZE + 1
RCHSET(RCHSZE) - NABOR
DEG1 - DEG1 + QSIZE(NABOR)
MARKER(NABOR) - 1
GOTO 600
500 IF ( MARK .GT. 1 ) GOTO 600
NOVRLP - NOVRLP + 1
OVRLP(NOVRLP) - NABOR
MARKER(NABOR) - 2
600 CONTINUE
С
С НАЙТИ В ПЕРЕСЕЧЕНИИ УЗЛЫ , КОТОРЫЕ МОГУТ
БЫТЬ СЛИТЫ .
700 HEAD - О
MRGSZE • О
DO 1100 IOV - 1, NOVRLP
NODE - OVRLP(IOV)
JSTRT - XADJ(NOF*E)
JSTOP - XADJ(NODE+1) - 1
DO 800 J - JSTF.T, JSTOP
NABOR - ADJNCY(J)
IF ( MARKES(NABOR) .NE. 0 ) GOTO 800
MARKER,NODE) - 1
GOTO WOO
800 CONTINUE
§ 5.4. Схемы хранения разреженных матриц 143
С
с
с
с
УЗЕЛ ПРИНАДЛЕЖИТ НОВОМУ СЛИТОНУ СУПЕРУЗЛУ.
МОДИФИЦИРОВАТЬ QLINK И QSIZE .
MRGSZE - MRGSZE + QSIZE (NODE ^
MARKER(NODE) - - 1
LNODE - NODE
900 LINK - QLINK(LNODE)
IF ( LINK LE 0 ) GOTO iOOO
LNODE - LINK
GOTO 900
1000 QLINK(LNODE) - HEAD
HEAD - NODE
1100 CONTINUE
IF ( HEAD .LE. 0 ) GOTO 1200
QSIZE(HEAD) - MRGSZE
DEG(HEAD) - DEGO -> DEG1 . 1
MARKER(HEAD) • 2
МОДИФИЦИРОВАТЬ ЗНАЧЕНИЯ В МАССИВЕ MARKER*.
1201 ЧООТ - NBRHD(INHD)
lARKER(ROOT) - О
F ( RCHSZE LE 0 1 GOTO 1400
DO 1300 IRCH - 1 RCHSZE
NODE - RCHSET(IRCH)
MARKER(NODE) - 0
1300 CONTINUE
1400 CONTINUE
RETURN
END
С
С
с
§ 5.4. Схемы хранения разреженных матриц
5.4.1. Обычная схема1)
Структура данных для универсальных разреженных мето-
методов должна предусматривать хранение только (логически) не-
ненулевых элементов факторизуемой матрицы. Обсуждаемая
здесь схема ориентирована на алгоритм разложения в форме
скалярных произведений (см. раздел 2.1.2); ее можно найти,
например, в работах (Gustavson 1972) и (Sherman 1975).
В схеме имеется основной массив LNZ, содержащий все не-
ненулевые элементы нижнего треугольного множителя. Отво-
Отводится ячейка для хранения каждого логически ненулевого эле-
элемента в множителе. При этом ненулевые элементы L, исклю-
исключая диагональные, хранятся в LNZ столбец за столбцом. Пре-
Предусмотрен сопровождающий вектор NZSUB, дающий^ строчные
индексы ненулевых элементов Кроме того, для указания на-
начала ненулевых элементов каждого столбца в массиве LNZ
(нлн, что все равно, в массиве NZSUB) используется индекс-
') В оригинале — the uncompressed scheme. — Прим. перев.
144 Г л 5. Универсальные разреженные методы
Симметрично
агг
"S3 «54 S
6
, L =
/.I
Рис. 5.4.1. 7 X 7-матрица А и ее множитель L.
DIAO
NZSUB 2 4 4
6 5 6 7
LNZ
XLNZ
bx <?4i|0
i
1 :
>
1
; 7
*54
0 ^75
t '
1 г
9 10
Разложение
DIAG
^22 ^33 ^44 ^55 ^66
nzsub \г 4
Б 6
5 6 7 7
LNZ
XLNZ
|fcf Ui| ^42
1 :
^53 hi
1 t
1 r~
1 1
t- 6 7
9
10
'»., I
I i
Рис. 5.4.2. Обычная схема хранения для матрицы и треуюльного множителя
иа рис. 5.4.1.
§ 5.4. Схемы хранения разреженных матриц 145
ный вектор XLNZ. Диагональные элементы хранятся отдельно
в векторе DIAG.
Если нужен доступ к ненулевому элементу ач или (ч, то
нет никакого прямого метода для вычисления соответствую-
соответствующего индекса в массиве LNZ. Приходится выполнять проверку
индексов в NZSUB. С этой целью можно использовать приводи-
приводимый ниже фрагмент программы. Заметим, что всякий элемент,
не представленный в структуре данных, равен нулю.
K3TRI - XLNZ(J)
KSTOP - XLNZ(J+l) - 1
AIJ - 0.0
IF (KSTOP LT KSTRT) GO TO 300
DO 100 К . KSTRT, KSTOP
IF (NZSUB(K).EQ.I) GO TO 200
100 CONTINUE
GO TO 300
200 AIJ - LNZ(K)
ЭОГ •
Хотя эта схема не слишком хорошо приспособлена для
случайного доступа к ненулевым элементам, она вполне при-
пригодна при разреженной факторизации и решении. Основная
память в этой схеме, т. е. векторы LNZ и DIAG, составляет
|Nonz(F) | -f- N ячеек; такова же накладная память (NZSUB
nXLNZ)-\Nonz(F)\ + N.
5.4.2 Компактная схема ')
Эта схема, являющаяся модификацией обычной, принадле-
принадлежит Шерману (Sherman 1975). Мотивировку схемы можно дать,
рассматривая упорядочение по минимальной степени в той
форме, как оно описано в разделе 5.3.3. Мы видели, что можно
одновременно пронумеровать или исключить целое множество
узлов У. Узлы из У удовлетворяют условию неразличимости
Reach (х, i)U {*} = Reach (у, S)[){y}
для всех х, j/еУ. С точки зрения матричного множителя L
это означает, что все строчные индексы ниже диагонального
блока, соответствующего У, одинаковы во всех столбцах. Ил-
Иллюстрацией является рис. 5.4.3.
Если бы для хранения использовалась обычная схема, то
в этом блоке строчные индексы любого столбца, кроме первого,
составляли финальную подпоследовательность строчных индек-
индексов предыдущего столбца. Естественно, вектор индексов
NZSUB можно сжать, устраняя избыточную информацию. Это
достигается удалением строчных индексов любого столбца, для
') В оригинале — compressed scheme. — Прим. перев.
146 Гл. 5. Универсальные разреженные методы
которого они образуют финальную подпоследовательность ин-
индексов предыдущего.
У
и
ххххххххх
ххххххххх
ххххххххх
ххххххххх
\
Рис. 5.4.3. Мотивировка экономичной схемы хранения,
DIAG
<*77
LNZ
XLNZ
NZSUB
1
:
0
t
<
GS3 °63
1
^ (
* —
'54
/
С
0 <?75
, )
) 10
i
lO
XNZSUB И
8
Рис 5.4.4. Компактная схема хранения для матрицы на рис 5.4 I.
Взамен на получаемое сжатие приходится вводить дополни-
дополнительный индексный вектор XNZSUB, указывающий для каж-
каждого столбца начало его строчных индексов ч массиве NZSUB.
§ 5 4. Схемы хранения разреженных матриц 147
Компактная схема для примера с рис. 5.4.1 показана на
рис. 5.4.4.
Теперь доступ к ненулевому элементу, стоящему в позиции
(/,/), осуществляется следующим образом.
KSTRT - XLNZ(J)
KSTOP - XLNZ(J+1) - 1
AIJ - 0.0
IF (KSTOP.LT.KSTRT) GO TO 300
KSUB - XNZSUB(J)
DO 100 К • KSTRT, KSTOP
IF(NZSUB(KSUB).EQ.I) GO TO 200
KSUB - KSUB + 1
100 CONTINUE
GO TO 300
200 AIJ - LNZ(K)
300 •
В экономичной схеме основная память остается прежней,
но накладная память изменяется; она всегда не превосходит
| Nonz (F) j -f- 2yV ячеек. Рассмотренный нами пример слишком
мал, чтобы выявить достоинства экономичной схемы. В таб-
таблице 5.4.1 приведены данные, полученные для девяти больших
Таблица 5.4.1
Сравнение обычной и компактной схем хранения.
Для обычной схемы основная память равна накладной
u,.r/ln Накладная память Накладная память
Wonz{A)\ \JVbnz(F)\ Зля обычной д/гя компактной
схемы схемы
936 2664 13870 14806 6903
1009
1089
1440
1180
1377
1138
1141
1349
2928
3136
4032
3285
3808
3156
3162
3876
19081
18626
19047
14685
16793
15592
15696
23726
20090
19715
20487
15865
18170
16730
16837
25075
8085
8574
10536
8436
9790
8326
8435
10666
задач, которые составляют один из обсуждаемых в главе 9
тестовых наборов. Упорядочение, использовавшееся при полу-
получении этих результатов, было найдено алгоритмом минималь-
минимальной степени, аналогичным описанному в предыдущем пара-
параграфе. В типичном случае для задач такого и большего по-
порядка накладная память сокращается по меньшей мере на 50%
в сравнении с обычной схемой.
148 Г л 5 Универсальные разреженные методы
5.4.3. О символическом разложении
Как указывает название, символическое разложение есть
процесс моделирования численного разложения данной мат-
матрицы, позволяющий получить структуру нулевых и ненулевых
элементов ее множителя L Поскольку в этом вопросе числовые
значения элементов матрицы не играют роли, задачу удобно
изучать, пользуясь методами теории графов.
Пусть Ga = (Ха, Е)— упорядоченный граф, где \Ха\= N.
Для удобства положим a(i)=xt. Согласно теореме 5.1.2, сим-
символическое разложение можно рассматривать как вычисление
множеств
Reach (я,, {*, **_i}), /= I, ... , N.
Положим S, = {хи ..., xt}.
Докажем следующий результат относительно достижимых
множеств.
Лемма 5.4.1.
Reach(*„ St..,)-» Adj (*,)U
( у {Reach (xk, Sk_t) \x, e Reach (xk, S».,)}) - S,
Доказательство. Пусть / > i. Тогда по лемме 5.1.1 и тео-
теореме 5.1.2 условие */ е Reach(xt, S,-i) эквивалентно условию
{xt, x,} e EF, а оно в свою очередь — условию {х,, х,} ^ЕА либо
\xt,Xk)^EF и {xh Xk} e EF для некоторого k < min {i, /}. По-
Последнее же означает, что xt e Adj (x,) либо Xi, X/ e
е Reach(хн, Sk-i) для некоторого k. Отсюда и следует утвер-
утверждение леммы.
Лемма 5.4.1 подсказывает алгоритм вычисления достижи-
достижимых множеств (и, следовательно, структуры множителя L). Он
может быть описан следующим образом.
Шаг 1 (инициализация). Для k = 1, ..., N
Reach (xk, Sk_{) «— Adj (xfe) — Sk_{.
Шаг 2 (символическое разложение). Для k— 1, ..., N если
xt e Reach (л:*, Sk~\), то
Reach (xh S,_,) ¦—Reach (*,, S,_,) U Reach (xk, Sk_i) — St.
Иллюстрация этой схемы показана на рис. 5.4.5. Алгоритм
едва ли удовлетворителен, так как он по существу моделирует
полный процесс разложения, и его стоимость будет пропорцио-
пропорциональна числу операций, указанному в теореме 2.1.2. Поищем
способ повысить эффективность алгоритма.
§ 5.4. Схемы хранения разреженных матриц 149
Рассмотрим этап, соответствующий исключенному множе-
множеству S,-\ = {х\, ..., Xi-\). Для целей этого обсуждения доста-
достаточно рассмотреть случай, когда х, имеет две смежные с ним
Рчс. 5.4.5. Слияние достижимых множеств для вычисления Reach(*,, 5(_i).
связные компоненты в G(S,_i). Пусть их множества узлов бу-
будут d и С2.
Как легко видеть, в этом случае
Reach (х„ S,_,) = Adj (л;,) U Adj (С,) U Adj (C2) - S,.
Однако в С\ и Сг можно выбрать представителей кт и хг соот-
соответственно так, чтобы
= Reach(xri, S,,.,)
Adj (C2) = Reach {xft, Sr%_x)
150 Гл. 5 Универсальные разреженные методы
(см. упр. 5.2.5). Правило выбора представителя указано фор-
формулой E.2.4): это — узел из компоненты, исключенный послед-
последним. Теперь достижимое множество можно записать в виде
Reach (*„ S,_,) = A dj(je,)U Reach (jcv S,,-.i)U
Reach (xft, Srj_,) —S,.
Таким образом, вместо того чтобы сливать большое количе-
количество достижимых множеств, что предлагает лемма 5.4.1, мы
Рис. 5.4.6 Экономия при слиянии достижимых множеств для построения
Reach(xt, St-i).
можем выбирать представителей. Описываемые ниже идеи мо-
мотивируются этим замечанием.
Для k = 1, ..., N положим
mft = min{/U, «= Reach (xk, Sfe_,)}. E.4.1)
На матричном языке m* есть индекс первого ненулевого эле-
элемента, исключая диагональный, в столбце L^
Лемма 5.4.2.
Reach (хь Sk_{) с: Reach (дгп^ S^^) U {xmk}.
Доказательство. Пусть х, е Reach (л:*, Sft_i); тогда k <
< mk ^ i. Если i — mk, то доказывать нечего1). В противном
') То есть xt — xm , очевидно, принадлежит правому множеству. — Прим.
иерее.
§ 5.4 Схемы хранения разреженных матриц 151
случае по лемме 5.1.1 и теореме 5.1.2
xt е= Reach (xmk, Smk_l),
Из леммы 5.4.2 вытекает следующий важный вывод. Если
xi ^ Reach(xk,Sk-i) и i>mk, то при построении множества
Reach(xt, S,_i) в алгоритме излишне рассматривать
Reach (xk, Sk-i), потому что все узлы, достижимые через хк,
могут быть найдены в множестве Reach (xmk, Smft_,).Таким об-
образом, достаточно сливать достижимые множества некоторых
к
1
2
3
4
тк
5
4
8
5
Reach(xk<Sk-,)
XsSe
Ж4,Х5
Рис. 5.4.7. Иллюстрация к определению чисел от*.
представительных узлов. Рис. 5.4.6 демонстрирует получаемую
при этом экономию для примера с рис. 5.4.5. Лемму 5.4.1 можно
усилить следующим образом:
Теорема 5.4.3.
Reach (*„ S,_1) = Adj (*,)U
( у {Reach (xk, Sk_,) I mk = /}) - St.
Доказательство. Рассмотрим произвольный узел xk такой,
что х, е Reach{xk, Sk-i). Полагая m{k)=mk, получим возрас-
возрастающую последовательность индексов, ограниченную сверху
числом I:
k < m(k) <m(m (k)) <m3{k)< ... < i.
Найдется такое натуральное р, что mp+l(k)=i. Из леммы 5.4.2
следует
Reach(xk, Sk_l) — St a Reach(^,4,, Sm(k)-i) — St
a
cReach(*mP(Jk), Sm" (A)_, __ )sr
Отсюда и вытекает утверждение теоремы.
Рассмотрим построение множества Reach (x5, SO Для графа
на рис. 5.4.7. Если бы использовалась лемма 5.4.1, то при-
пришлось бы сливать с Adj(x5) множества Reach(x\, So),
152 Гл. 5 Универсальные разреженные методы
Reach (x2) Si) и Reach (хц, S3). С другой стороны, согласно тео-
теореме 5.4.3, достаточно рассмотреть множества Reach (*i,S0)
и Reach (x4, S3). Заметим, что ш2 = 4 и
Reach (x2, S,) = {х4, х5} cr Reach (x4, S3) U {х4}.
Алгоритм символического разложения можно теперь усо-
усовершенствовать таким образом.
Шаг 1 (инициализация). Для k = \, ..., N
Reach (**, 5fe_,) = Adj(xfe) —Sft.
Шаг 2 (символическое разложение). Для k = 1 N если
Reach(xfe,Sk-i)?= 0, то выполнить
m = min{/U/<= Reach (xk, Sfe_,)}
Reach (xm, Sm_,) <— Reach (xm, Sm_{) U Reach (xk, Sk_t) — {xm}.
Теорема 5.4.4.
Символическое разложение можно выполнить за O(\EF\)
операций.
Доказательство. Для каждого столбца k значение tnk един-
единственно. Это значит, что обращение к Reach (xk, Sk-i) происхо-
происходит лишь тогда, когда вычисляется Reach(xmk, Smk-\). Таким
образом, множество Reach(xk,Sk-\) исследуется только один
раз на протяжении всего процесса. Кроме того, объединение
двух множеств можно выполнить за время, пропорциональное
сумме их размеров (см. упр. 5.4.3). Следовательно, символиче-
символическое разложение требует О( \EF\) операций, где
| е"\ = ?1 Reach (х„, S*_,)|.
5.4.4. Распределение памяти для компактной схемы
и подпрограмма SMBFCT
Здесь мы представим подпрограмму, выполняющую симво-
символическое разложение, как оно описано в предыдущем разделе.
Результатом процесса является структура данных .для ком-
компактной схемы из раздела 5.4 2.
Подпрограмма составлена коллективом авторов (Eisenstat
1981) и включена в Йельский пакет для разреженных матриц.
По существу, она реализует усовершенствованный алгоритм из
предыдущего раздела с перестановкой порядка при слиянии
достижимых множеств.
Шаг 1 (инициализация). Для i=\ N положить
Rt = 0.
Шаг 2 (символическое разложение).
§ 5.4. Схемы хранения разреженных матриц 153
Для 1= 1 N
Reach (х„ S,_,)=Adj(x,) —S,.
Для й е #, выполнить
Reach (л:,, S,_,) «— Reach (*,, S,_,) U Reach (xk, Sk_i) — Sl
m = min{/|*/e Reach (*;, Si_1)}
К — «mu«.
В этом алгоритме используется множество /?,, аккумули-
аккумулирующее тех представителей, чьи достижимые множества воз-
воздействуют на достижимое множество xi. Имеется одно оче-
очевидное следствие теоремы 5.4.3, которое можно применить для
ускорения алгоритма. Кроме того, оно полезно при формиро-
формировании компактной схемы хранения.
Следствие 5.4.5.
Если для данного i имеется лишь одно тк такое, что nik=i,
и при этом
Adj (Xi) — St с: Reach (xk, Sk_i),
то
Reach (*,, S(_,) = Reach {xk, S*_,)— {*,}.
Входными данными подпрограммы SMBFCT являются граф
матрицы, хранимый парой массивов (XADJ, ADJNCY), а также
вектор перестановки PERM и вектор обратной перестановки
INVP. Назначение подпрограммы — сформировать структуру
данных для компактной разреженной схемы, т. е. вычислить
компактный вектор индексов NZSUB и индексные векторы
XLNZ и XNZSUB. Присваиваются также значения переменным
MAXLNZ и MAXSUB, равные соответственно числу внедиаго-
нальных ненулевых элементов треугольного множителя и числу
индексов в компактной схеме.
Подпрограмма SMBFCT использует три рабочих вектора
RCHLNK, MRGLNK и MARKER. Вектор RCHLNK облегчает
операцию слияния достижимых множеств, в то время как век-
вектор MRGLNK осуществляет слежение за представительными
множествами {Ri}, введенными выше. Вектор MARKER ис-
используется для проверки условия, указанного в следствии 5.4.5.
Работа подпрограммы начинается с присвоения начальных
значений рабочим векторам MRGLN-K и MARKER. Затем вы-
выполняется основной цикл, в котором вычисляется достижимое
множество для каждого узла. Вначале определяется множество
Adj(**;) — Sk, помещаемое в вектор RCHLNK. В то же время
проверяется условие следствия 5.4.5. Если оно удовлетворяется,
то слияние достижимых множеств можно опустить. В против-
противном случае на основе информации из MRGLNK в RCHLNK осу-
о..........
о»*»* • •
С........ SMBFCT ... СИМВОЛИЧЕСКОЕ РАЗЛОЖЕНИЕ ........
с...................
с....
с
С ПОДПРОГРАММА ОСУЩЕСТВЛЯЕТ СИМВОЛИЧЕСКОЕ РАЗЛОЖЕНИЕ .
С ПЕРЕУПОРЯДОЧЕННОЙ ЛИНЕЙНОЙ СИСТЕМЫ И ФОРМИРУЕТ
С КОМПАКТНУЮ СТРУКТУРУ ДАННЫХ ДЛЯ НЕЕ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С (XADJ, ADJNCY) - СТРУКТУРА СНЕЖНОСТИ.
С (PERM, INVP) - ВЕКТОРЫ ПЕРЕСТАНОВКИ И ОБРАТНОЙ
С ПЕРЕСТАНОВКИ.
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР-
С MAXSUB - РАЗМЕР МАССИВА NZSUB. НА ВЫХОДЕ РАВЕН ЧИСЛУ
С ИСПОЛЬЗОВАННЫХ ИНДЕКСОВ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С XLNZ - ИНДЕКСЫ ДЛЯ ВЕКТОРА НЕНУЛЕВЫХ ЭЛЕМЕНТОВ LNZ.
С (XNZSUB, NZSUB) - ИНДЕКСНЫЕ ВЕКТОРЫ КОМПАКТНОЙ СХЕМЫ .
С MAXLNZ - ЧИСЛО НАЙДЕННЫХ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ.
С FLAG - ИНДИКАТОР ОШИБКИ . ПОЛОЖИТЕЛЬНОЕ ЗНАЧЕНИЕ
С УКАЗЫВАЕТ, ЧТО РАЗМЕР NZSUB НЕДОСТАТОЧЕН.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С MRGLNK - ВЕКТОР ДЛИНЫ NEQNS. НА К - ОМ ШАГЕ СПИСОК
С MRGLNK(K), MRGLNKCMRGLNK(K-)) ,
С СОДЕРЖИТ НОМЕРА ВСЕХ СТОЛБЦОВ L(*,J), ДЛЯ
С КОТОРЫХ J< К И ПЕРВЫЙ НЕНУЛЕВОЙ
С ВНЕДИАГОНАЛЬНЫИ ЭЛЕМЕНТ- L(.K,J) . Т.О.,
С СТРУКТУРУ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ СТОЛБЦА L(*, К)
С МОЖНО ОПРЕДЕЛИТЬ СЛИЯНИЕМ СТРУКТУР ТАКИХ
С СТОЛБЦОВ LC*,J) с° СТРУКТУРОЙ А(«, К).
С RCHLNK - ВЕКТОР ДЛИНЫ NEQNS. ИСПОЛЬЗУЕТСЯ ДЛЯ
С НАКАПЛИВАНИЯ СТРУКТУРЫ ОЧЕРЕДНОГО СТОЛБЦА
С L(*, К). В КОНЦЕ К-ГО ШАГА СПИСОК RCHLNK(K),
С RCHLNK(RCHLNKCK)) ,
С СОДЕРЖИТ ПОЗИЦИИ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ
С К" ОГО СТОЛБЦА МНОЖИТЕЛЯ L.
С MARKER - ЦЕЛЫЙ ВЕКТОР ДЛИНЫ NEQNS ДЛЯ ПРОВЕРКИ
С ВОЗМОЖНОСТИ ГРУППОВОГО СИМВОЛИЧЕСКОГО
С ИСКЛЮЧЕНИЯ . Т. Е. , С ЕГО ПОМОЩЬЮ ПРОВЕРЯЕТСЯ,
С БУДЕТ ЛИ СТРУКТУРА ОБРАБАТЫВАЕМОГО В ДАННЫЙ
С МОМЕНТ К-ОГО СТОЛБЦА ПОЛНОСТЬЮ ОПРЕДЕЛЕНА
С ЕДИНСТВЕННЫМ СТОЛБЦОМ С НОМЕРОМ MRGLNK(K).
С
С
с
SUBROUTINE SMBFCT ( NEQNS, XADJ, ADJNCY, PERM, INVP,
1 XLNZ, MAXLNZ, XNZSUB, NZSUB, MAXSUB,
1 RCHLNK, MRGLNK, MARKER, FLAG )
С
С....
С
INTEGER ADJNCYA), INVPA), MRGLNKA), NZSUBA),
1 PERM(l), RCHLNK(l), MARKERA)
INTEGER XADJ(l), XLNZA), XNZSUBA),
1 FLAG, I, INZ, J, JSTOP, JSTRT, K. KNZ,
1 KXSUB, MRGK, LMAX, M, MAXLNZ, MAXSUB,
1 NABOR, NEQNS, NODE, NP1, NZBEG, NZEND.
1 RCHM, MRKFLG
с
Q
9 ИНИЦИАЛИЗАЦИЯ...
NZBEG - 1
NZEND - О
XLNZ(l) - 1
DO 100 К - 1, NEQNS
MRGLNK(K) - 0
MARKER(K) - 0
100 CONTINUE
c j.
С ДЛЯ КАЖДОГО СТОЛБЦА... . KNZ ПОДСЧИТЫВАЕТ ЧИСЛО НЕНУЛЕВЫХ
С ЭЛЕМЕНТОВ К-ОГО СТОЛБЦА, НАКАПЛИВАЕМОГО В RCHLNK.
Г* _ —
NP1 - NEQNS + 1
DO 1500 К - 1, NEQNS
KNZ - О
MRGK - MRGLNK(K)
MRKFLG - О
MARKER(K) - К
IF (MRGK NE 0 ) MARKER(K) - MARKFR(MRGK)
XNZSUB(K) - NZEND
NODE - PERM(K)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
IF (JSTRT.GT.JSTOP) GO TO 1500
С
С ИСПОЛЬЗУЯ RCHLNK , СОСТАВИТЬ СПИСОК НЕНУЛЕВЫХ
С ПОДДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ СТОЛБЦА А(* ,К) .
с
RCHLNK(К) - NP1
DO 300 J ' JSTRT, JSTOP
NABOR - ADJNCY(J)
NABOR - INVP(NABOR)
IF ( NABOR .LE. К ) GO TO 300
RCHM - К
200 M • RCHM
RCHM - RCHLNK(M)
IF ( RCHM .LE. NABOR ) GO TO 200
KNZ - KNZ+1
RCHLNK(M) - NABOR
RCHLNK(NABOR) - RCHM
IF ( MARKER(NABOR) .NE. MARKER(K) ) MRKFLG -
300 CONTINUE
¦C
С ВОЗМОЖНО ЛИ ГРУППОВОЕ СИМВОЛИЧЕСКОЕ ИСКЛЮЧЕНИЕ . . .
с
LMAX - О
IF ( MRKFLG NE. О OR. MRGK ,EQ. 0 ) GO TO 350
IF ( MRGLNK(MRGK) NE 0 ) GO TO 350
XNZSUB(K) - XNZSUB(MRGK) + 1
KNZ - XLNZ(MRGK+1) - (XLNZ(MRGK) + 1)
GO TO 1400
С
С ДЛЯ КАЖДОГО СТОЛБЦА I, ВОЗДЕЙСТВУЮЩЕГО НА Ц»,К),
350 I • К
400 I - MRGLNK(I)
IF (I.EQ.O) GO TO 800
INZ - XLNZ(I+1) - (XLNZ(I)+1)
JSTRT - XNZSUB(I) + 1
JSTOP - XNZSUB(I) + INZ
IF (INZ.LE.LMAX) GO TO 500
LMAX - INZ
XNZSUB(K) • JSTRT
с
С ПРИСОЕДИНИТЬ К RCHLNK СТРУКТУРУ L(*,I) ИЗ NZSUB .
С
500 RCHM - К
DO 700 J - JSTRT. JSTOP
eon
700
С
с
с
с
с
с
800
900
1000
1100
н
1200
С
с
С
С
1300
с
с
с
с
с
1400
1500
NABOR » NZSUB(J)
М - RCHM
RCHM . RCHLNK(M)
IF (RCHM.LT.NABOR) GO TO 600
IF (RCHM.EQ.NABOR) GO TO 700
KNZ - KNZ+1
RCHLNK(M) - NABOR
RCHLNK(NABOR) - RCHM
RCHM - NABOR
CONTINUE
GO TO 400
ДУБЛИРУЮТ ЛИ ИНДЕКСЫ ИНДЕКСЫ ДРУГОГО СТОЛБЦА
IF (KNZ.EQ.LMAX) GO TO 1400
СООТВ. ЛИ КОНЕЦ (К-О-ОГО СТОЛБЦА НАЧАЛУ К-ОГО.-
с
с
с
1600
IF (NZBEG.GT.NZEND) GO TO 1200
I - RCHLNK(K)
DO 900 JSTRT-NZBEG.NZEND
IF (NZSUB(JSTRT)-I) 900, 1000, 1200
CONTINUE
GO TO 1200
XNZSUB(K) - JSTRT
DO 1100 J.JSTRT,NZEND
IF (NZSUB(J).NE.I) GO TO 1200
I - RCHLNK(I)
IF (I.GT.NEQNS) GO TO 1400
CONTINUE
NZEND - JSTRT - 1
ПЕРЕНЕСТИ СТРУКТУРУ Ц*. К) ИЗ RCHLNK
В СТРУКТУРУ ДАННЫХ (XNZSUB, NZSUB).
NZBEG - NZEND + 1
NZEND - NZEND + KNZ
IF (NZEND.GT.MAXSUB) GO TO 1600
I - К
DO 1300 J-NZBEG,NZFND
I . RCHLNK(I)
NZSUB(J) - I
MARKER(I) - К
CONTINUE
XNZSUB(K) - NZBEG
MARKER(K) - К
МОДИФИЦИРОВАТЬ MRGLNK. НАЙДЕННЫЙ L(*, К) ПОТРЕБУЕТСЯ
ПРИ ОПРЕДЕЛЕНИИ СТОЛБЦА L(*,J), ГДЕ L(J, К) -ПЕРВЫЙ
НЕНУЛЕВОЙ ПОДДИАГОНАЛЬНЫЙ ЭЛЕМЕНТ В 1Д*, К) .
IF (KNZ.LE.l) GO TO 1500
KXSUB - XNZSUB(K)
I - NZSUB(KXSUB)
MRGLNK(K) - MRGLNK(I)
MRGLNK(I) - К
XLNZ(K+1) - XLNZ(K) + KNZ
MAXLNZ - XLNZ(NEQNS) - 1
MAXSUB - XNZSUB(NEQNS)
XNZSUB(NEQNS+1) - XNZSUB(NEQNS)
FLAG - 0
RETURN
ОШИБКА- МАЛО ПАМЯТИ ДЛЯ ИНДЕКСОВ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ.
_.____ — — —¦ — — — — — — — — — — —.— —— — — — — — — — — — — — — — — — — — ______«__„«..»_———_ — —,
FLAG - 1
RETURN
END
§ 5.5. Подпрограммы численного разложения и решения 157
ществляется слияние с предыдущими достижимыми множе-
множествами. Когда новое достижимое множество полностью сфор-
сформировано в RCHLNK, подпрограмма проверяет возможность
сжатия индексов и с учетом ситуации устанавливает соответ-
соответствующую часть структуры данных Наконец, соответственно из-
изменению множеств {Ri} перестраивается вектор MRGLNK,
Благодаря слиянию лишь тщательно отобранных достижи-
достижимых множеств подпрограмма SMBFCT способна очень эффек-
эффективно находить новое достижимое множество. Поскольку число
индексов, нужных в компактной схеме, заранее не известно,
длина вектора NZSUB может оказаться недостаточной для
хранения всех индексов. В этом случае выполнение программы
прекращается и устанавливается значение 1 для индикатора
ошибки FLAG.
Упражнения
5.4.1. Пусть А—матрица, удовлетворяющая условию fi(A) <l для 2<
sg i sg N. Показать, что тк = k + 1 для всех k, k < N. Вывести отсюда (или
показать каким-либо иным способом), что для 1 < i < N
Reach (х,, 5,_,) = (АA](х,) U Reach (*,_,, S,_2))-S,.
5.4.2. Пусть Л—ленточная матрица с шириной леиты р. Предположим,
что лента А заполнена.
а) Сравнить для А обычную и компактную схемы хранения.
б) Сравнить два алгоритма символического разложения, содержащиеся
в лемме 5.4.1 и теореме 5.4 3 соответственно
5.4.3. Пусть Ri a Ri — два заданных множества целых чисел, значения ко-
которых не превосходят N. Предположим, что имеется рабочий массив длины
N, компонентам которого присвоены нулевые значения. Показать, что объеди-
объединение R\ U R2 можно определить за время, пропорциональное \Rt\ + \Rt\.
§ 5.5. Подпрограммы численного разложения и решения
В этом параграфе будут описаны подпрограммы, выполняю-
выполняющие численное разложение и решение линейных систем, храни-
хранимых компактной схемой. Подпрограмма разложения GSFCT
(от слов general sparse symmetric factorization') использует
алгоритм разложения в форме скалярных произведений. Так
как ненулевые элементы нижнего треугольника А (или множи-
множителя L) хранятся по столбцам, то вариант со скалярными
произведениями должен быть адаптирован к этому способу
хранения. Подпрограмма GSFCT получена незначительной мо-
модификацией подпрограммы из Йельского пакета для разрежен*
ных матриц.
') Симметричное разложение произвольных разреженных матриц.—Прим,
пьрев.
168
Гл 5. Универсальные разреженные методы
5.5.1. Подпрограмма GSFCT (General sparse Symmetric
FaCTorization)
Входными данными подпрограммы GSFCT являются струк-
структура компактной схемы (XLNZ, XNZSUB, NZSUB) и векторы
основной памяти DIAG и LNZ. На входе массивы DIAG и LNZ
содержат ненулевые элементы матрицы А1). На выходе на
места элементов матрицы А будут записаны ненулевые эле-
элементы множителя L. Подпрограмма использует три рабочих
вектора LINK, FIRST и TEMP, все длины N.
FIRST-
LINK
Пусть нужно вычислить столбец L4l множителя. Участвуют
в формировании этого столбца в точности те столбцы L»/, для
которых /,; ф 0. Перестройку г-го столбца можно провести по
шагам, так что на каждом шаге добавляется лишь один стол-
столбец. Именно:
Для ?.#; таких, что /,, ф 0, выполнить:
•
*-
L
In,
.4
') В позициях массива LNZ, соотвекпвующих заполнению, в А стоят
нули. — Прим. перев.
с •• • ...,
с ..,
С...... GSFCT „СИММЕТРИЧНОЕ РАЗЛОЖЕНИЕ
о«.... произвольной разреженной матрицы ¦>
с
С ПОДПРОГРАММА ВЫПОЛНЯЕТ СИММЕТРИЧНОЕ РАЗЛОЖЕНИЕ
С ДЛЯ ПРОИЗВОЛЬНОЙ РАЗРЕЖЕННОЙ СИСТЕМЫ, ХРАНИМОЙ
С В ФОРМАТЕ КОМПАКТНОГО ИНДЕКСИРОВАНИЯ.
С
С ЗХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ .
С XLNZ - ИНДЕКСНЫЙ ВЕКТОР ДЛЯ LNZ. XLNZ(l) УКАЗЫВАЕТ
С НАЧАЛО НЕНУЛЕВЫХ ЭЛЕМЕНТОВ СТОЛБЦА I МНОЖ"ЛЯ L.
С (XNZSUB, NZSUB) - СТРУКТУРА КОМПАКТНОГО ИНДЕКСИРОВАНИЯ
С ДЛЯ L.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С LNZ - НА ВХОДЕ СОДЕРЖИТ НЕНУЛЕВЫЕ ЭЛЕМЕНТЫ А,
С НА ВЫХОДЕ - НЕНУЛЕВЫЕ ЭЛЕМЕНТЫ L.
С DIAG - ДИАГОНАЛЬ L - НА МЕСТО ДИАГОНАЛИ А.
С IFLAG - ИНДИКАТОР ОШИБКИ . РАВЕН 1 , ЕСЛИ ПРИ
С РАЗЛОЖЕНИИ ВСТРЕТИТСЯ О ИЛИ КОРЕНЬ ИЗ ОТРИЦ.
С ЧИСЛА.
С OPS - ОБЩАЯ ПЕРЕМЕННАЯ ДВОЙНОЙ ТОЧНОСТИ.
С ЕЕ ЗНАЧЕНИЕ БУДЕТ УВЕЛИЧЕНО НА ЧИСЛО
С ВЫПОЛНЕННЫХ ОПЕРАЦИЙ.
С
С ТкБОЧИЕ ПАРАМЕТРЫ -
С LINK - НА ШАГЕ J СПИСОК
с linkCj), unkClinkCj)),
С СОДЕРЖИТ НОМЕРА СТОЛБЦОВ, УЧАСТВУЮЩИХ
С В МОДИФИКАЦИИ L(*,J).
С FIRST - РАБОЧИЙ ВЕКТОР, УКАЗЫВАЮЩИЙ ПОЗИЦИЮ
С В LNZ 1-ГО НЕНУЛЕВОГО ЭЛЕМЕНТА КАЖДОГО
С СТОЛБЦА, УЧАСТВУЮЩЕГО В МОДИФИКАЦИИ.
С TEMP - РАБОЧИЙ ВЕКТОР ДЛЯ НАКАПЛИВАНИЯ ПОПРАВОК.
С
с.......
с
SUBROUTINE GSFCT ( NEQNS, XLNZ, LNZ, XNZSUB, NZSUB, DIAG,
1 LINK, FIRST, TEMP, IFLAG )
С
c««««»«
с
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), LNZA), TEMPA), DIAGJ, LJK
INTEGER LINK(l), NZSUB(l)
INTEGER FIRST(l), XLNZ(l), XNZSUB(l),
1 I, IFLAG, II, ISTOP, ISTRT, ISUB, J
1 K, KFIRST, NEQNS, NEWK
С
с
с
С ИНИЦИАЛИЗИРОВАТЬ РАБОЧИЕ ВЕКТОРЫ . . .
DO 100 I - 1, NEQNS
LINK(I) - О
TEMP(I) - О.ОЕО
100 CONTINUE
с
t ВЫЧИСЛИТЬ L(*,J) ДЛЯ J= 1, NEQNS.
JDO 600 J - 1, NEQNS
С ДЛЯ КАЖДОГО L(*, К") , ВОЗДЕЙСТВУЮЩЕГО НА Ц*, J).
с
DIAGJ - O.OEO
NEWK • LINK(J)
200 К • NEWK
IF ( К .EQ. О ) GO TO 400
NEWK - LINK(K)
с
С МОДИФИКАЦИЯ L(*,J) ПОСРЕДСТВОМ U(*, К) НАЧИН.
С С ПОЗИЦИИ FIRST(K) 1-ГО НЕНУЛЕВОГО ЭЛЕМЕНТА Ц*,К").
KFIRST - FIRST(K)
LJK - LNZ(KFIRST)
DIAGJ - DIAGJ + LJK«LJK
OPS - OPS + 1.ODO
ISTRT - KFIRST + 1
ISTOP - XLNZ(K+1) - 1
IF ( ISTOP .LT. ISTRT ) GO TO 200
с
С ДО ВЫПОЛНЕНИЯ ПОПРАВКИ ИЗМЕНИТЬ FIRST И LINK
С ДЛЯ ПОСЛЕДУЮЩИХ ШАГОВ МОДИФИКАЦИИ.
С -
FIRST(K) - ISTRT
I - XNZSUB(K) + (KFIRST-XLNZ(K)) + 1
ISUB - NZSUB(I)
LINK(K) - LINK(ISUB>
LINK(ISUB) - К
ПОПРАВКИ НАКАПЛИВАЮТСЯ В TEMP.
с --
DO 300 II - ISTRT, ISTOP
ISUB - NZSUB(I)
TEMP(ISUB) . TEMP(ISUB) + LNZ(II)*LJK
I - I + 1
300 CONTINUE
COUNT - ISTOP - ISTRT + 1
OPS - OPS + COUNT
GO TO 200
с
С ПРИБАВИТЬ ПОПРАВКИ, НАКОПЛЕННЫЕ В TEMP,
С К СТОЛБЦУ Ц*, J).
с
400 DIAGJ - DIAG(J) - DIAGJ
IF ( DIAGJ .LE. O.OEO ) GO TO 700
DIAGJ - SQRT(DIAGJ)
DIAG(J) - DIAGJ
ISTRT - XLNZ(J)
ISTOP - XLNZ(J+1) - 1
IF ( ISTOP .LT. ISTRT ) GO TO 600
FIRST(J) - ISTRT
I - XNZSUB(J)
ISUB ¦ NZSUB(I)
LINK(J) - LINK(ISUB)
LINK(ISUB) - J
DO 500 II - ISTRT, ISTOP
ISUB - NZSUB(I)
LNZ(II) - ( LNZ(II)-TEMP(ISUB) ) / DIAGJ
TEMP(ISUB) - O.OEO
I - I + 1
BOO CONTINUE
COUNT - ISTOP - ISTRT +1
OPS - OPS + COUNT
600 CONTINUE
RETURN
§55 Подпрограммы численного разложения и решения 161
С ОШИБКА - НУЛЬ ИЛИ КОРЕНЬ ИЗ ОТРИЦ. ЧИСЛА .
с
700 IFLAG - 1
RETURN
END
На /-м шаге номера тех столбцов, которые воздействуют на
L»,, задаются списком
LINK(i), LINK (LINK (i)),....
Чтобы сократить поиск индексов, используется вектор FIRST.
Для / = LINK(t). LINK(LINK(t)), •¦¦ переменная FIRST(/)
указывает позицию в векторе LNZ ненулевого элемента /,/.
Тем самым модификация L», посредством L*, может начинаться
с позиции FIRST(/) в LNZ. Третий рабочий вектор TEMP слу-
служит для накапливания поправок к столбцу L*,
Работа подпрограммы GSFCT начинается с присвоения на-
начальных значений рабочим векторам LINK и TEMP. Циклом
DO 600 J... обрабатывается каждый столбец. Переменная
с. » ..,.,.....««,
с» **
С GSSLV РЕШЕНИЕ ПРОИЗВОЛЬНОЙ РАЗРЕЖЕННОЙ •••••»*•
С. ....*«¦¦•*¦**. СИММЕТРИЧНОЙ СИСТЕМЫ **«.«»....*..«*»••
с •¦¦
с
С ВЫЧИСЛЯЕТ РЕШЕНИЕ ФАКТОРИЗОВАННОИ СИСТЕМЫ , МАТРИЦА
С КОТОРОЙ ХРАНИТСЯ В ФОРМАТЕ КОМПАКТНОГО
С ИНДЕКСИРОВАНИЯ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ.
С (XLNZ, LNZ) - СТРУКТУРА НЕНУЛЕВЫХ ЭЛЕМЕНТОВ L.
С (XNZSUB. NZSUB) - СТРУКТУРА КОМПАКТНОГО ИНДЕКСИРОВАНИЯ.
С DIAG - ДИАГОНАЛЬНЫЕ ЭЛЕМЕНТЫ L.
С
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР -
С RHS - НА ВХОДЕ - ЭТО ВЕКТОР ПРАВЫХ ЧАСТЕК
С НА ВЫХОДЕ - ВЕКТОР РЕШЕНИЯ.
С
с« ......*•.......»..*..**»»».......«».*»..»....»......«.....*»¦*•
с
SUBROUTINE GSSLV ( NEQNS, XLNZ, LNZ, XNZSUB, NZSUBr
1 DIAG, RHS )
С
с...•*...........................................................
с
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), LNZ(l), RHS(l), RHSJ, S
INTEGER NZSUB(l)
INTEGER XLNZ(l), XNZSUB(l), I, II, ISTOP.
ISTRT, ISUB, J, JJ, NEQNS
162 Гл 5 Универсальные разреженные методы
С
с
С ПРЯМОЙ ХОД . . .
с
DO 200 J - 1, NEQNS
RHSJ - RHS(J) / DIAG(J)
RHS(J) - RHSJ
ISTRT - XLNZ(J) -
ISTOP - XLNZ(J+1) - 1
IF ( ISTOP .LT. ISTRT ) GO TO 200
I - XNZSUB(J)
DO 100 II - ISTRT, ISTOP
ISUB > NZSUB(I)
RHS(ISUB) - RHS(ISUB) - LNZ(II)«RHSJ
I - I + 1
100 CONTINUE
200 CONTINUE
COUNT - 2*(NEQNS + ISTOP)
OPS - OPS + COUNT
с
С ОБРАТНАЯ ПОДСТАНОВКА . . .
с
J - NEQNS
DO 500 JJ - 1, NEQNS
S - RHS(J)
ISTRT - XLNZ(J)
ISTOP - XLNZ(J+1) - 1
IF ( ISTOP .LT. ISTRT ) GO TO 400
I - XNZSUB(J)
DO 300 II - ISTRT, ISTOP
ISUB - NZSUB(I)
S - S - LNZ(II)»RHS(ISUB)
I - I + 1
30U CONTINUE
400 RHS(J) - S / DIAG(J)
J - J - 1
500 CONTINUE
RETURN
END
DIAGJ и вектор TEMP накапливают поправки к текущему
столбцу. В то же время модифицируются рабочие векторы
FIRST и LINK. Наконец, поправка добавляется к элементам
текущего столбца.
5.5.2. Подпрограмма GSSLV (General sparse Symmetric SoLVe)
Подпрограмма GSSLV предназначена для численного реше-
решения факторизованной системы, матрица которой хранится
в формате компактного индексирования (см. раздел 5.4.2).
Входными данными являются число уравнений NEQNS, а так-
также структура данных и числовые значения элементов матрич-
матричного множителя. Сюда относятся структура компактного индек-
индексирования (XNZSUB, NZSUB), диагональные элементы (мае-
§ 5.6 Дополнительные замечания 163
сив DIAG) множителя и его ненулевые внедиагональные эле-
элементы, хранимые парой массивов (XLNZ, LNZ).
Поскольку ненулевые элементы нижнего треугольного мно-
множителя хранятся по столбцам, метод решения должен быть
адаптирован так, чтобы и доступ к элементам осуществлялся
столбец за столбцом. Прямой ход использует форму «внешних
произведений»; в обратной подстановке компоненты решения
вычисляются посредством «скалярных произведений». Оба спо-
способа были рассмотрены в разделе 2.2.1 главы 2.
§ 5.6. Дополнительные замечания
При исследовании исключения используется также элемент-
элементная модель (George 1973, Eisenstat 1976). Здесь процесс раз-
разложения моделируется посредством структуры клик графов
исключения. Этот подход мотивирован приложениями метода
конечных элементов, где структура клик матричного графа по-
появляется естественным образом. Элементная модель тесно свя-
связана с изучавшейся в § 5.2 моделью фактор-графов.
Реализацию алгоритма минимальной степени, основанную
на элементной модели, можно найти в работе (George, Mclntyre
1978). В статье (George 1980) алгоритм минимальной степени
реализован посредством неявной модели: вычисление достижи-
достижимых множеств по исходному графу. В реализацию внесены мо-
модификации, ускоряющие работу алгоритма.
Есть и другие алгоритмы упорядочения, имеющие целью со-
сократить заполнение. В алгоритме минимального дефицита
(Rose 1972a) следующий номер присваивается тому узлу, чье
исключение приводит к наименьшему заполнению. Здесь
требуется существенно больше работы, чем в алгоритме мини-
минимальной степени. В то же время практика показала, что полу-
получаемое упорядочение лишь в редких случаях значительно пре-
превосходит упорядочение по минимальной степени.
В работе (George 1977) для универсальных разреженных
методов предложена другая схема хранения. В ней используется
ситуация, когда ненулевые внедиагональные элементы образуют
заполненные блоки. Для хранения каждого ненулевого блока
нужно лишь несколько слов дополнительной информации, а при
оперировании с блоками могут использоваться стандартные
методы для заполненных матриц.
6. Методы фактор-деревьев
для конечноэлементных
и конечноразностных задач
§ 6.0. Введение
В этой и двух последующих главах будут исследованы алго-
алгоритмы, предназначенные главным образом для систем, возни-
возникающих в приложениях метода конечных элементов и конечно-
разностных методов к решению различных задач строительной
механики, гидро- и термодинамики, теории упругости и приле-
прилегающих областей (Zienkiewicz 1977). Те задачи, которые мы
имеем в виду, мржно описать следующим образом.
Конечноэлементная сетка № Конечноэлементный граф,
с восемью узлами ассоциированный с Л
Рис. 6.0.1. Конечноэлементная сетка с восемью узлами и ассоциированный с
ней конечноэлемеитный граф.
Пусть Ж — плоская сетка, представляющая собой объеди-
объединение треугольников и/или четырехугольников, называемых
элементами, причем соседние элементы имеют общую сторону
или общую вершину. В каждую вершину сетки Ж помещен
узел; узлы могут быть расположены также и на сторонах эле-
элементов (см. рис. 6.0.1), и внутри их. Каждому узлу сопостав-
сопоставляется переменная л:,-. При выбранном помечивании узлов и пе-
переменных числами от 1 до JV мы определяем конечноэлемент-
ную систему Ах = Ь, ассоциированную с Ж, как систему с сим-
симметричной и положительно определенной матрицей А, для ко-
которой ац ф 0 означает, что переменные Xi и х\ связаны с
узлами одного и того же элемента. Граф, соответствующий мат-
матрице А, будем называть конечноэлементным графом, ассоции-
ассоциированным с Ж (рис. 6.0.1),
§ 6.1. Решение блочных систем уравнений 165
Для многих практических ситуаций это определение «конеч-
ноэлементной системы» недостаточно широко, так как часто
некоторым или даже всем узлам сопоставляется более чем одна
переменная. Однако наше определение схватывает существен-
существенные черты таких задач и упрощает изложение идей. Кроме
того, способ распространения основных идей на более общий
случай очевиден, а поскольку наши алгоритмы и программы
оперируют с ассоциированными графами, они будут работать
и в общем случае.
Конечноэлементные матричные задачи часто решают, ис-
используя описанные в главе 4 ленточные или профильные ме-
методы. Для относительно малых задач эти методы часто оказыва-
оказываются наиболее эффективными, особенно для одноразовых задач,
где сравнительно высокая стоимость вычисления упорядо-
упорядочений с малым заполнением перевешивает приносимый ими вы-
выигрыш в арифметике и памяти. Для задач достаточно большого
порядка и/или в ситуации, когда нужно решить ряд систем
с одинаковой структурой, становятся привлекательными более
сложные упорядочения, пытающиеся минимизировать заполне-
заполнение, такие, как алгоритм минимальной степени из главы 5 или
алгоритм вложенных сечений главы 8.
Методы глав 4 и 5 в известном смысле представляют собой
концы «спектра усложнения»: профильные методы слабо ис-
используют структуру А и L, в то время как методы главы 5 пы-
пытаются выжать из нее все возможное. В данной главе будут
рассмотрены методы, лежащие где-то посреди между этими
двумя концами. Для некоторых размеров и типов конечноэле-
ментных задач они оказываются более эффективными, чем каж-
каждая из двух других стратегий. Время упорядочения и число
операций обычно сравнимы с профильными методами, но за-
запросы к памяти, как правило, значительно ниже.
§ 6.1. Решение блочных систем уравнений
Методы, рассматриваемые в этой главе, существенно опи-
опираются на использование блочных матриц и на некоторые
приемы эксплуатации разреженности таких матриц. Все при-
применяемые упорядочения будут симметричны в том смысле, что
строки и столбцы подвергаются одинаковым перестановкам.
6.1.1. Разложение матрицы блочного порядка два
Чтобы проиллюстрировать наиболее важные идеи, исполь-
используемые при вычислениях с разреженными блочными матри-
матрицами, рассмотрим блочную линейную систему Ах = Ь блочного
порядка два:
a s)o(?>
166 Гл. 6. Методы фактор-деревьев
где В и С — подматрицы порядков г и s соответственно, г -j
Множитель Холесского L для А, разбитый на блоки соот-
соответствующим образом, выглядит так:
la/
Lc
Здеоь LB a Lc — множители Холесского соответственно для мат-
матриц В и С= С—¦ VTB~lV, a W = LB~lV. «Матричную поправку»,
вычитаемую из С при получении С, можно представить в виде
Вычисление множителя L можно организовать по приводи-
приводимой ниже схеме. По причинам, которые выясняются чуть позже,
она будет называться симметричной схемой блочного разло-
разложения.
Шаг 1. Разложить матрицу В в произведение LBL^
Шаг 2. Решить треугольные системы
Шаг 3. Модифицировать еще не факторизованную подмат-
подматрицу
c=c-wTw.
Шаг 4. Разложить матрицу С в произведение Lcllc- После-
Последовательность вычислений изображена на рис. 6.1.1.
Будет ли эта блочно-ориентированная схема иметь какое-
либо преимущество с точки зрения числа операций по сравне-
сравнению с обычным пошаговым разложением? Процитируем из ра-
работы (George 1974) следующий результат.
Теорема 6.1.1.
Число операций при вычислении множителя L матрицы А
будет одним и тем же как в пошаговой схеме исключения, так
и в симметричной схеме блочного разложения.
Интуитивно это утверждение очевидно, поскольку в обоих
случаях выполняются одни и те же численные операции, хотя
и в различном порядке. Есть, однако, другой способ реализации
блочного разложения, где число арифметических операций мо-
может уменьшиться или возрасти. Альтернативный способ осно-
основан на том наблюдении, что матричную поправку VTB~lV
можно вычислять двумя существенно различающимися путями,
а именно: как обычное произведение
{VtLbT) (LElV) = lPrW F.1.3)
§ 6.1. Решение блочных систем уравнений 167
Разложение В в произведение LBlIB
\
Решение системы LeW=V
И
вычисление матрицы C = C-
Разложение С S произведение
Ж
Только
считываются
Не считываются
и нв изменяются
вчитываются
и изменяются
Рис. 6.1.1. Диаграмма, показывающая последовательность вычислений в сим-
симметричной схеме блочного разложения и характер обработки данных.
168 Гл 6 Методы фактор-деревьев
или как
vT (Lbt fts1 v)) = v
T (Lf
= vTw.
F.1.4)
Этот последний метод организации вычислений мы будем «азы-
вать асимметричной схемой блочного разложения.
Степень расхождения двух указанных способов определяется
стоимостью вычисления WTW в сравнении со стоимостью реше-
решения матричного уравнения LbW = W и последующего вы-
вычисления VTW. В качестве примера, иллюстрирующего различия
* *
* * *
* * *
* * *
** *
* **
***
***
**
*
*
*
*
*Т* *Т* *Р *Т*
*
*i
*l
и
**
**
**
№№№№№/!
Рис. 6.1.2. Структура матрицы А блочного порядка два и ее множителя Хо-
лесского 1
в арифметической работе, рассмотрим блочную матрицу А,
изображенную на рис. 6.1.2.
Поскольку матрица W заполнена (см. упр. 2.2.3), то по
следствию 2.2.2 стоимость решения уравнения LTBW~W
равна 4X19 = 76 операций. Стоимость вычисления VTW—10
операций, а общая стоимость асимметричной схемы — 86 опера-
операций. С другой стороны, стоимость вычисления WTW равна
Ю X Ю= 100 операций.
В дополнение к потенциальной возможности сократить число
арифметических операций асимметричная схема может позво-
позволить значительно уменьшить запросы к памяти по сравнению
со стандартной схемой. Главный момент состоит в том, что при
вычислении х можно обойтись без W, если только сохранена V.
Всякий раз, когда нужно вычислить произведение WTz или Wz,
мы можем вычислять VT{ЬвТг) или Lb (Vz), т. е. решить тре-
§ 6.1. Решение блочных систем уравнений 169
угольную систему и умножить на разреженную матрицу. Если
V значительно более разрежена, чем W, как часто и бывает, то
мы сэкономим одновременно и память, и арифметическую ра-
работу.
С точки зрения вычисления разложения важно отметить
следующее: если мы не планируем сохранить W, то вычисление
С в асимметричной схеме F.1.4) позволяет вообще избавиться
от хранения W. Произведение VTW можно вычислять столбец
Ж,
Cmo/rtfeu, за
Строка за строкой
Рис. 6.1.3. Диаграмма, показывающая характер доступа к столбцам W или
V при вычислении нижнего треугольника матрицы VTB~lV столбец за столб-
столбцом либо строка за строкой
за столбцом, стирая вычисленный столбец, как только он был
использован для модификации С. Требуется лишь один рабо-
рабочий вектор длины г. Напротив, если вычислять VTB-[V как
WTW, то, по-видимому, нельзя избежать хранения на каком-то
этапе всей матрицы W, хотя бы она и не была нужна в даль-
дальнейшем.
Асимметричный вариант алгоритма разложения можно опи-
описать следующим образом.
Шаг I. Разложить матрицу В в произведение LBLTB.
Шаг 2. Для каждого столбца v = V«, матрицы V:
2.1) Решить систему LBw = v.
2.2) Решить систему LbW =w.
2.3) Положить С„ = С»,- — VTw.
Шаг 3. Разложить матрицу С в произведение LcLc.
Разумеется, при формировании С,« на шаге 2.3 используется
симметрия С. Каким бы из указанных двух способов мы ни
вычисляли произведение VTB-IV, все еще остается некоторая
170 Гл 6 Методы фактор-деревьев
свобода в выборе порядка вычисления элементов. Считая, что
определяется нижний треугольник, мы можем вычислять эле-
элементы строка за строкой либо столбец за столбцом
(см. рис. 6.1.3); при этом нужен различный порядок доступа
к столбцам W или V.
6.1.2. Решение треугольной системы блочного порядка два
Если вычислен множитель Холесского блочной матрицы, то
решение линейной системы выполняется очевидным образом.
Прямой ход
Решить систему LBy\ = Ь\.
Вычислить Ь2 = Ь2 — WTyh
Решить систему ЪсУг = $2-
Обратный ход
Решить систему LqX2 = Уг •
Вычислить у\ = ух — Wx2.
Решить систему LTBX\ = ух.
Этот метод решения мы будем именовать стандартной схе-
схемой. Однако, как было отмечено в разделе 6.1.1, может ока-
оказаться выгодным не строить матрицу W, сохраняя V; при этом
всякий раз, когда нужно оперировать с W, используется опре-
определение W = Lb'V. Идя таким путем, мы получим следующий
алгоритм, называемый в дальнейшем неявной схемой. В нашем
описании t\ — это рабочий вектор.
Прямой ход
Решить систему LBy\ = Ь\.
Решить систему LTBt\ =У\.
Вычислить &2 = Ь2 — VTtu
Решить систему Ьсуг = Ь2.
Обратный ход
Решить систему LTcX2 = y2-
Решить систему LBt\ = Vx2.
Вычислить «л = #1 — h-
Решить систему
В неявной схеме нужны лишь подматрицы {LB, Lc, V}, а в
стандартной — подматрицы {LB, Lc, W}. Согласно следст-
следствию 2.2.5,
)
и для разреженных матриц V может иметь значительно мень-
меньшее число ненулевых элементов, чем W. Для матрицы на
§ 6.1. Решение блочных систем уравнений 171
рис. 6.1.2
в то время как
Таким образом, с точки зрения величины основной памяти при-
применение неявной схемы может оказаться очень привлекательным.
Что касается числа операций, то относительные достоинства
двух схем зависят от разреженности матриц LB, V и W. Так
как стоимость вычисления Wz равна 4(W), а стоимость вы-
вычисления Lb1 (Vz) равна ц (V) + Ч (is), то получаем следую-
следующий результат (разреженность вектора z здесь не исполь-
используется).
Лемма 6.1.2.
Стоимость вычислений по неявной схеме не превосходит
стоимости стандартной схемы в том и только том случае, когда
В следующем параграфе мы распространим эти идеи на ли-
линейные системы блочного порядка р, где р > 2. Для разре-
разреженных блочных систем типично, что асимметричный вариант
блочного разложения и неявная схема решения предпочтитель-
предпочтительнее с точки зрения вычислительной работы и памяти. Поэтому
в остальной части главы мы рассматриваем только этот вариант.
Упражнения
6.1.1. Пусть А— симметричная положительно определенная блочная мат-
матрица вида
( В V
А-
( В V\
= W с)'
где обе матрицы В и С — трехдиагональные порядка т, а V — диагональная.
В своих ответах на приводимые ниже вопросы считайте, что т велико, и пре-
пренебрегайте младшими членами при подсчете числа операций,
а) Представим треугольный множитель матрицы А в виде
О
L
Опишите структуру ненулевых элементов LB, Lr и W.
б) Определив число операций (умножений и делений), необходимых для
вычисления L посредством описанных в разделе 6.1.1 алгоритмов симметрич-
hofo и асимметричного разложения.
в) Сравните стоимость явной и неявной схем из раздела 6.1.2 для этой
задачи. Можно считать заполненной правую часть Ь системы Ах_ = Ь.
г) Ответьте на вопросы а), б) и в) для случая, когда В и С заполнены,
а V — диагональная
д) Ответьте на вопросы а), б) и в) для случая, когда В и С заполнены,
а V — нулевая, за исключением заполненной первой строки.
172 Г л 6 Методы фактор-деревьев
6.1.2. Асимметричную схему разложения можно рассматривать как метод
вычисления следующей факторизации матрицы А
LBLTB о \П w\
VT LCLTC)\O l)'
где W = B~1V и предполагается, что хранятся множители матриц В и С, а
не сами эти матрицы Опишите для такой факторизации явную и неявную
процедуры, аналогичные тем, что приведены в разделе 6 12 Будет ли полу-
получено какое-нибудь сокращение числа операций по сравнению с разделом 6 1 2'
Что можно сказать о запросах к памяти, если в каждом случае хранить вне-
диагоиальные блоки сомножителей?
6.1.3, Доказать теорему 6.1.1.
§ 6.2. Фактор-графы, деревья и древовидные разбиения
Читателю, по-видимому, ясно, что успех неявной схемы,
рассмотренной в разделе 6.1.2, был связан с очень простой
формой внедиагонального блока W. В случае произвольной
блочной матрицы блочного порядка р внедиагональные блоки
множителя не будут иметь столь простой формы; хранить вме-
вместо них исходные блоки А и затем по существу перевычислять
их при необходимости было бы слишком дорого с точки зрения
вычислительной работы. Это сейчас же приводит к вопросу:
какие характеристики должна иметь блочная матрица, чтобы
внедиагональные блоки ее множителя имели нужную простую
форму? В данном параграфе мы ответим на этот вопрос и за-
заложим основы алгоритма, определяющего подходящие раз-
разбиения.
6.2.1. Блочные матрицы и фактор-графы
Мы уже установили связь между симметричными матрицами
и графами. В этом параграфе приводятся дополнительные све-
сведения из теории графов, которые позволят нам оперировать
с блочными матрицами.
Пусть А разбита на р2 подматриц Ач, 1 ^ I, j ^ р. Будем
рассматривать каждый блок как единственный элемент, равный
нулю, если блок нулевой, и отличный от нуля в противополож-
противоположном случае. Тогда мы можем связать с матрицей А блочного
порядка р граф с р узлами, соединяя любые два узла ребром,
если соответствующий внедиагональный блок ненулевой.
Рис. 6.2.1 иллюстрирует эту конструкцию. Заметим, что, как
и в скалярном случае, упорядочение этого нового графа опре-
определяется матрицей, которой он отвечает. Как и прежде, мы
должны находить разбиения и упорядочения непомеченных
графов. Это мотивирует определение фактор-графов, введенное
нами в главе 5.
§ 6.2. Фактор-графы, деревья и древовидные разбиения 173
Пусть G = (X, Е) — заданный непомеченный граф, и пусть
Щ — разбиение его множества узлов X:
$ = {У„ Y2, .... Yp}.
Напомним (глава 5), что фактор-граф графа G относительно $
есть граф ($, <S) такой, что {К,, Уу}е^Г, если и только если
АсУ(У,)П Y, ф 0. Этот граф будем обозначать через G/$.
Отметим, что наше определение фактор-графа относится
к непомеченному графу. Говорят, что упорядочение а графа G
**
*
*
*
*
*
*
*
*
* * *
* *
*
*
Рис. 6.2.1. Блочная матрица А, индуцированное ею разбиение множества узлов
ее графа и граф ее блочной структуры
совместимо с его разбиением $, если а нумерует узлы каждого
множества Y, из ^ последовательными целыми числами. Ясно,
что упорядочения и разбиения графов, отвечающих блочным
матрицам, должны иметь это свойство. Упорядочение а, сов-
совместимое с $, индуцирует или подразумевает упорядочение на
G/S|3; обратно, упорядочение <хр на G/% индуцирует класс упо-
упорядочений G, совместимых с $. Рис. 6.2.2 иллюстрирует сказан-
сказанное. Если явно не оговорено противоположное, то всякий раз,
когда мы упоминаем об упорядочении блочного графа, мы под-
подразумеваем, что упорядочение совместимо с разбиением — ведь
интерес для нас представляет упорядочение блочных матриц.
В общем случае при выполнении для блочной матрицы
(блочного) гауссова исключения нулевые блоки могут стать
ненулевыми. Таким образом, может происходить «блочное за-
заполнение» точно так же, как заполнение происходит в скаляр-
скалярном случае. Например, в блочной матрице на рис. 6 2.1 имеются
174 Га 6 Методы фактор-деревьев
два нулевых внедиагональных блока, которые после разложе-
разложения станут ненулевыми. Структура треугольного множителя
показана на рис. 6.2.3.
(а)
Рис. 6.2.2. Пример индуцированных упорядочений для графа на рис 6 2!.
(а) Упорядочение ОД!, индуцированное исходным упорядочением графа
на рис. 6 2.1.
(б) Другое упорядочение, совместимое с ф.
Однако при заданном разбиении симметричной матрицы ха-
характер появления блочного заполнения не обязательно в точ-
точности соответствует скалярной ситуации. Другими словами, мы
*
* *
*
* *
Рис. 6.2.3. Структура треугольного множителя для матрицы на рис. 6 2.1.
не можем просто выполнить символическое исключение на фак-
фактор-графе и получить тем самым блочную структуру множи-
множителя L Таким путем мы найдем лишь наихудшее возможное
заполнение, которое, конечно, никогда нельзя исключить, так
§ 6.2 Фактор-графы, деревья и древовидные разбиения 175
как любой ненулевой блок может быть заполнен. Иллюстрация
сказанного приведена на рис. 6.2.4.
Итак, символическое разложение фактор-графа блочной
матрицы может указать большую величину блочного заполне-
заполнения, чем имеет место в действительности. Интуитивно причина
этого ясна: модель исключения предполагает, что произведение
* *
* *
*
*
*
*
*
*
* *
* *
*
*
* *
* *
*
*
* * *
* * *
*
*
*
*®
*®
*
*
* *
*®
*
* *
*
* *
* * *
Граф заполнения Я/тя
GA/
Рис. 6.2.4. Пример, показывающий, что символическое исключение на фактор-
графе G/ф может переоценить величину блочного заполнения
двух ненулевых величин всегда будет ненулевым, что верно для
чисел. Однако две ненулевые матрицы вполне могут иметь
произведение, логически ') равное нулю.
6.2.2 Деревья, фактор-деревья и древовидные разбиения
Деревом Т = (X, Е) называется связный граф без циклов.
Легко проверить, что для дерева Т выполняется соотношение
|Х| = |?|+1 и что каждая пара различных узлов связана
ровно одним путем. Корневое дерево есть упорядоченная пара
') То есть независимо от числовых значений ненулевых элементов пере-
перемножаемых матриц —Прим перев.
176 Гл 6 Методы фактор-деревьев
{г,Т), где г — выделенный узел Т, называемый корнем Так
как каждая пара узлов Т связана только одним путем, то путь
от г к произвольному узлу j:eI единствен. Если этот путь
проходит через у, то х называется потомком у, а у — предком к.
Если к тому же {*, у} е Е, то х — сын у, а у — отец х Если Y
состоит из узла у и всех потомков этого узла, то подграф Т(Y)
называется поддеревом дерева Т. Заметим, что отношение пре-
предок-потомок определено только для корневых деревьев.
Рис. 6.2.5 иллюстрирует введенные определения.
Корень
Отец d
Сын Ь
Дерево Т
Рис. 6.2.5. Корневое дерево и его поддерево.
Поддерево
дерева Т
Упорядочение а корневого дерева (г, Т) называется моно-
монотонным упорядочением, если каждый узел нумеруется раньше
своего отца. Ясно, что корень должен быть помечен последним.
Если дерево Т не имеет корня, то упорядочение а будет мо-
монотонным, если оно монотонно для корневого дерева
{а{\Х\),Т). Важность монотонно упорядоченных деревьев объ-
объясняется тем, что соответствующие им матрицы не испытывают
заполнения при разложении Следующая лемма принадлежит
Партеру (Parter 1961).
Лемма 6.2.1.
Пусть А — симметричная матрица порядка N, помеченный
граф которой является монотонно упорядоченным деревом.
Если A = LLT, еде L — множитель Холесского матрицы А, то
из а,, = 0 следует 1Ч = 0, i > /.
Доказательство предоставляется читателю в качестве
упражнения.
Лемма 6.2.2.
Пусть А и L — те же, что и в лемме 6 2 1 Тогда
U, = ач/1„, i > j.
§62 Фактор-графы, деревья и древовидные разбиения 177
Доказательство Напомним (см. раздел 2.1.2), что компо-
компоненты L выражаются формулами
/ /-I \ /
= [at, - Z( /«//*)i 1ц, i > h
Утверждение леммы будет установлено, если мы покажем, что
/-¦
У /tft/,ft=0. Предположим, напротив, что l,mlim ф О для не-
k-\
которого m такого, что 1 ^/л ^ /—1. Согласно лемме 6.2.1,
*
o^r *f. yr
**
1,2}, {3,4,5}, {6,7}, {8,9,10}}
Рис. 6.2.6. Пример блочной матрицы, ее графа и ее фактор-графа, являюще-
являющегося деревом
это означает, что a,mam Ф 0 и, следовательно, узлы i и / свя-
связаны с узлом m в ассоциированном дереве, причем i>m
и ] > m Но тогда дерево не будет монотонно упорядо-
упорядоченным
Леммы 6.2.1 и 6.2 2 сами по себе не так важны, как может
показаться на первый взгляд. Дело в том, что графы матриц,
возникающих в приложениях, редко бывают деревьями. Важ-
Важность этих лемм связана г тем, что они непосредственно пере-
переносятся на блочные матрицы.
178 Гл 6. Методы фактор-деревьев
Предположим, что А, как и прежде, разбита на р2 подмат-
подматриц Л,/, 1 ^ i, j ^ р, и пусть L,; — соответствующие подмат-
подматрицы ее множителя Холесского L. Предположим далее, что по-
помеченный фактор-граф блочной матрицы А является монотонно
упорядоченным деревом (иллюстрация приведена на рис. 6.2.6).
Тогда без труда проверяется аналог леммы 6.2.2 для такой
блочной матрицы, именно
Ltl = Ai,Ljl = (ц}Ац)т
для каждой ненулевой подматрицы А,/ нижнего треугольника
А. Если разбиение $ графа G таково, что G/$ есть дерево, то
мы называем $ древовидным разбиением G.
Мы достигли теперь той цели, какую намечали, а именно:
определить, какие характеристики должна иметь блочная мат-
матрица, чтобы к ней были применимы идеи раздела 6.1. Ответ
таков: мы хотим, чтобы ее помеченный фактор-граф был мо-
монотонно упорядоченным деревом. Если это свойство имеется,
то мы можем отказаться от хранения внедиагональных бло-
блоков L, храня лишь ее диагональные блоки и внедиагональные
блоки нижнего треугольника А.
6.2.3. Асимметричное блочное разложение и неявное
блочное решение систем с древовидным разбиением
Пусть А — матрица блочного порядка р с блоками Atj,
1 ^ i, / ^ Р. и пусть L,, (i > /) — соответствующие блоки L.
Если фактор-граф А является монотонно упорядоченным дере-
деревом, то под каждым диагональным блоком А и L (кроме по-
последнего) будет расположен ровно один ненулевой блок (по-
(почему?); пусть этим блоком будет A^k *, 1 ^С ? ^С р—1. Алго-
Алгоритм асимметричного блочного разложения для таких задач
формулируется следующим образом.
Шаг 1. Для k = \, 2, ..., р— 1 выполнить следующее:
1.1) Разложить Akk.
1.2) Для каждого столбца и блока А*,цА решшь
систему Akkv = u, вычислить векгор w = A*, ^v и вычесть его
из соответствующего столбца блока ЛцА, цА.
Шаг 2. Разложить Арр.
Процесс модификации блока A\ik,\>.k показан на рис. 6.2.7.
Заметим, что вся дополнительная память, какая нужна в алго-
алгоритме,—это место для хранения векторов и и w, длина кото-
которых равна порядку наибольшего блока. (Вектор v можно запи-
записать на место вектора и.) Конечно, можно использовать сим-
симметрию диагональных блоков.
Неявная схема решения для таких блочных систем тоже
вполне очевидна. В нашем описании t и t—промежуточные
векторы, которым можно отвести одно и то же место в памяти.
§ 6.2 Фактор-графы, деревья и древовидные разбиения 179
Прямой ход неявной блочной схемы (Ly = Ь):
Шаг I. Для k = 1, ..., р — 1 выполнить следующее:
1.1) Решить систему LkkHk = &*•
1.2) Решить систему Lkkt = уk-
П
)
1.3) Положить
Ьн — A*. Ht.
Ьн
Шаг 2. Решить систему Lppyp = Ьо.
*. Ht
Рис. 6.2.7. Иллюстрация к процессу асимметричного блочного разложения.
Обратный ход неявной блочной схемы (LTx — у):
Шаг I. Решить систему Lppxp = ур.
Шаг 2. Для k = p—1, р — 2, ..., 1 выполнить следующее:
2.1) Вычислить / = Ak ukX\ik-
2.2) Решить систему Lkki = t.
2.3) ПоложитьУк-^-Ук — t.
2.4) Решить систему L\kxk = yk.
Рис. 6.2.8 показывает этапы прямого хода блочного реше-
решения для системы блочного порядка 4.
Упражнения
6.2.1. Доказать лемму 6 2 1
6.2.2. Пусть С7/? = (ф, SF) — фактор-граф отнорительно разбиения
% для графа заполнения, полученного из G, и пусть (<j/!pjf = (!p, SF) —граф
180 Гл 6 Методы фактор-деревьев
V////A
к = 4
\ууу\ считывание
ШШ модификация
Рис. 6.2.8. Прямой ход неявной блочной схемы для системы блочного по-
рядкл 4
§62 Фактор-графы, деревья и древовидные разбиения 181
заполнения для G/5R Пример на рис 6 2 4 показывает, что число элементов
SF может быть меньше, чем у 8F Другими словами, блочная структура мно-
множителя L блочной матрицы А может быть более разреженной, чем показы-
показывает граф заполнения для фактор-графа G/ф Показать, что если диагональ-
диагональные блоки L имеют свойство распространения (см упр 2 2 3), то граф за-
заполнения для G/SP правильно отражает блочную структуру L То есть пока-
показать, что в этом случае <$F = SF
6.2.3. Пусть SF и <?F —те же, что и в упр 6 2 2, причем граф G поме-
помечен, а <Р = {У,, У2, , Yp)
а) Доказать, что если подграфы О(Уг), i = 1,2, , р, связны, то
SF = iF
б) Привести пример, показывающий, что обратное утверждение может
быть неверным
в) Доказать, что если подграфы О I I) Y i I, / = 1, 2, ..., р — 1,
\t-\ /
связны,
TO Sf — 0'
6.2.4. Древовидное разбиение ф ¦= {Yu У2, .., Ур} графа G = (X, Е) на-
называется максимальным, если не существует древовидного разбиения Q =
= {Zu Z2, , Zt) такого, что р < t и для каждого i справедливо Z, d Yk при
некотором fc, I ^ k ^ p Другими словами, разбиение !Р максимально, если
мы не можем разбить какие-нибудь из множеств У, на части и все еще сохра-
сохранить структуру фактор-дерева
Предположим, что для каждой пары х, у различных узлов любого У, су-
существуют два различных пути от х к у
X* Х\, ^2» • • •» Xs, У
И
х, 2/i, У2> ¦¦¦ . У и У<
причем множества
S = U {Z
T=
xt
Z, 1 < i < s),
не пересекаются Показать, что разбиение ф максимально
6.2.5. Пусть А — блочно-трехдиагональная матрица
А =
VI Ап V,
V] А»
182 Гл 6 Методы фактор-деревьев
где каждая Ati — заполненная квадратная матрица порядка т, а каждая
Vj — диагональная матрица
а) Какова будет арифметическая работа при выполнении асимметричного
блочного разложения? Сравнить ее с работой для симметричного варианта.
б) Что, если каждая подматрица V; имеет такую форму разреженности:
Го">
Считайте, что m велико, и игнорируйте при подсчете числа операций
младшие члены
§ 6.3. Алгоритм вычисления древовидного разбиения
6.3.1. Эвристический алгоритм
Результаты § 6.2 подсказывают, что было бы желательно
найти разбиение $={Уь Уг, ••, Ур}, содержащее по возмож-
возможности больше членов и согласованное с требованием, чтобы
G/SP было деревом. В этом разделе мы представим алгоритм,
определяющий древовидное разбиение графа.
Предлагаемый алгоритм тесно связан с понятием структуры
уровней (см. § 4.3). Поэтому мы начнем с описания соотноше-
соотношения между структурой уровней графа и разбиением, которое
она индуцирует на соответствующей матрице. Пусть GA — не-
непомеченный граф, ассоциированный с А, и пусть 2? =
= {Lo, L], ..., Li) —структура уровней на GA. Из определения
структуры уровней легко следует, что фактор-граф G/S яв-
является цепью; поэтому если мы пронумеруем узлы каждого
уровня L, последовательными целыми числами, начиная с Lo
и кончая Ц, то уровни 2? индуцируют блочно-трехдиагональ-
ную структуру на соответствующим образом упорядоченной
матрице. Пример показан на рис. 6.3.1.
Алгоритм, который будет описан в конце этого раздела, на-
начинает работу с корневой структуры уровней и пытается затем
получить более мелкое разбиение, исследуя уровни исходной
структуры. Пусть 3? = {Lq, L\, ..., Li) — корневая структура
уровней, и пусть $ = {У\, Y2, ..., Yp} — разбиение, получаемое
подразделением каждого L/ следующим образом. Обозначим
через В, подграф, определяемый формулой
F-зл)
тогда L/ разбивается на подмножества Y такие, что
K = L,nC, F.3.2)
где G(C) —связная компонента В/. Рис. 6.3.2 иллюстрирует на
примере простого графа эту процедуру подразбиения.
§ 6.3. Алгоритм вычисления древовидного разбиения 183
Рассмотрим разбиение уровня Li = {d, ё). Заметим, что
B2 = G({d, e, I, g, f, h}),
и В2 состоит из двух связных компонент с множествами узлор
{d, i, g} и {е, f, h) соответственно. Согласно F.3.2), уровень L2
можно разбить на {d} и {ё}.
*
***
*
Рис. 6.3.1. Блочно-трехдиагональное разбиение, индуцированное структурой
уровней.
{а)
Рис. 6.3.2. Пример вычисления более мелкого разбиения
ней 2.
структуре уров»
Теперь можно перейти к описанию алгоритма, находящего
древовидное разбиение. В нашем описании используется опре-
определение множества SPAN (У), где У — подмножество X:
SPAN(y)= {x^X\ существует путь от у к х для некото-
некоторого у е= У.} F з.з)
Если У состоит из единственного узла у, то SPAN (У) — это
просто связная компонента, содержащая у.
184 Гл. 6. Методы фактор-деревьев
В алгоритме используется стек; тем самым устраняется не-
необходимость в явном вычислении связных компонент подграфа
Крестообразный граф Корневая структура уровней jCОУ
Рис. 6.3.3. Граф, корневая структура уровней и вычисленное фактор-дерево.
В/, которые входят в описание F.3.2) процедуры подразбиения
уровней. Мы считаем, что корень г для исходной корневой
структуры задан. Выбор г мы обсудим в этом же разделе не-
несколько позже.
§ 6.3. Алгоритм вычисления древовидного разбиения 18^
Шаг 0 (инициализация). Очистить стек. Построить структу-
структуру уровней 3?(г) = {Lo, L\, L2, .... Li(r)} с корнем в л и вы-
выбрать произвольный узел t/eZ-/(r>- Положить l = l(r) и 5 =
= {</}¦
Шаг 1 (продвинуть стек). Если множество узлов Т на вер-
вершине стека принадлежит Lt, то вытолкнуть Т и положить
s ч- s и г.
Шаг 2 (сформировать возможный член разбиения). Опреде-
Определить множество У = SPAN(S) в подграфе G(L,). Если / < 1(г)
и некоторый узел из Ad'}(Y)f\Li+i еще не принадлежит ника-
никакому члену разбиения, то перейти к шагу 5.
Шаг 3 (новый член разбиения). Поместить Y в $р.
Шаг 4 (новый уровень). Определить множество S =
= Adj (Y) П Lt-i и положить /¦*-/—1. Если / Г> 0, перейти к
шагу 1, в противном случае — останов.
Шаг 5 (частично сформированный член разбиения). Поме-
Поместить S в стек. Выбрать yi+\ <= Adj (Y) f| U+\ и найти путь yi+i,
yi+2, .... yi+t такой, что yi+t e Ц+t и Adj (yt+t) П Li+t+i = 0. По-
Положить S = {yi+t} и l-*-l-\-t, затем перейти к шагу 2.
Пример на рис. 6.3.3, 6.3.4, взятый из работы (George, Liu
1978с), показывает работу алгоритма. Первоначальная струк-
структура уровней с корнем в узле 1 превращена в фактор-дерево
с десятью узлами. При этом У] = {20}, У2 = {18, 19}, Ys =
= {16}, У4={10, 15}, Y5={9, 14, 17} и У6 = {5, 11}; Ц =
= Y5 U Y6, L5=Y2[)YinLe = Y,\] Y3.
Чтобы закончить описание алгоритма, вычисляющего древо-
древовидное разбиение, нужно указать способ выбора корневого узла
г для структуры уровней. Мы находим г и 3'(г) посредством
подпрограммы FNROOT, обсуждавшейся в разделе 4.3.3. Так
как мы заинтересованы в получении разбиения с возможно
большим числом членов, то, по-видимому, выбор этого способа
разумен, поскольку обычно приводит к структуре, имеющей от-
относительно умного уровней.
6.3 2. Подпрограммы для вычисления древовидного разбиения
В этом разделе обсуждается набор подпрограмм, реализую-
реализующих алгоритм вычисления фактор-дерева. Параметры NEQNS,
XADJ и ADJNCY, как и прежде, используются для задания
структуры смежности графа. Вектор PERM на выходе содер-
содержит вычисленное древовидное упорядочение. Кроме упорядоче-
упорядочения нужна' еще информация о разбиении; ее дают переменная
NBLK.S и вектор XBLK. При этом NBLKS указывает число
блоков разбиения; номера узлов конкретного блока, скажем
k-то, указывают компоненты
{PERM (/) | XBLK (k) < / < XBLK (k + 1)}.
186 Г л 6 Методы фактор-деревьев
Разбиение
Ук
B0)
08,19}
{16}
{10,15}
{9,14,17}
{5,11}
{8,13,12,6}
Уровень
6
5
6
5
4
4
3
Смежное
множество
Стек
© ©
{18,19}
{14,17}
{10,15}
{9,14}
{8,13}
{14,17}
{14,17}
0
{6,12}
{8,13}
0
Рис. 6.3.4. Нумерация в алгоритме вычисления фактор дерева.
§63 Алгоритм вычисления древовидного разбиения 187
Разбиение
УроВень
Смежное
множество
Отек
и т.д.
и т.д.
{4,7}
{2,3}
{1}
{2,3}
{1}
0
0
0
Рис. 6.3.4.
188 Г л 6 Методы фактор-деревьев
Рис. 6.3.5 демонстрирует представление древовидного упорядо-
упорядочения для примера на рис. 6.3.3.
Как видно из этого примера, вектор XBLK имеет длину
NBLKS + 1. Последний, дополнительный указатель включен в
PERM: |2O|18 19|16|1O 1S|9 14 17|t1 5 | 8 13 12 6 | 4 7 | Z 3
i t
, ¦ i >
XBLK: | 1 2 4 5 7 10 12 16 18 20 2i] —
NBLKS:10
Рис. 6.З.5. Пример структуры данных для разбиения.
вектор для того, чтобы блоки можно было обрабатывать еди-
единообразно. Для нашего примера, чтобы получить пятый блок,
замечаем, что XBLKE)=7, XBLKF) = 10. Следовательно,
Рис. 6.3.6. Отношения управления между подпрограммами в алгоритме вы-
вычисления фактор-дерева.
узлы этого блока задаются переменными PERMG), PERM(8)
и PERM (9).
В нашем наборе семь подпрограмм, две из которых были
подробно рассмотрены в главе 4. Остановимся вначале на от-
отношениях управления между ними, показанных на рис. 6.3.6.
Подпрограммы FNROOT и ROOTLS используются для опре-
определения псевдопериферийного узла связной компоненты задан-
заданного графа. За деталями этих двух подпрограмм мы отсылаем
читателя к разделу 4.4.3. Подпрограмма COPYSI — служебная,
она попросту переносит содержимое одного целого массива в
§ Ь.З. Алгоритм вычисления древовидного разбиения 18Ь
другой. (Листинг этой подпрограммы приводится вслед за ли-
листингом RQTREE.) Теперь мы подробно опишем остальные под-
подпрограммы этой группы.
GENRQT (GENeral Refined1 Quotient Tree)
Эта подпрограмма — управляющая при определении древо-
древовидного упорядочения для произвольного несвязного графа.
Она исследует граф и вызывает подпрограмму RQTREE для
нумерации узлов каждой его связной компоненты. Требуются
три рабочих массива XLS, LS и NODLVL. Пара массивов
(XLS, LS) используется подпрограммой FNLVLS, чтобы получить
с»
с.............................................................
с...... GENRQT .... ВЫЧИСЛЕНИЕ РАФИНИРОВАННОГО *•¦¦
С»».»». ФАКТОР - ДЕРЕВА ДЛЯ ПРОИЗВОЛЬНОГО ГРАФА ¦¦•¦
с.............................................................
с
С УПРАВЛЯЮЩАЯ ПОДПРОГРАММА ПРИ ОПРЕДЕЛЕНИИ БЛОЧНОГО
С УПОРЯДОЧЕНИЯ ДЛЯ ПРОИЗВОЛЬНОГО, БЫТЬ МОЖЕТ,
С НЕСВЯЗНОГО ГРАФА.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО ПЕРЕМЕННЫХ.
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (NBLKS, XBLK1 - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С PERM - ВЕКТОР ПЕРЕСТАНОВКИ.
С
С РАБОЧИЕ ПАРАМЕТРЫ-
с <xls. ls) - пассивы для структуры уровней;
С ИХ ИСПОЛЬЗУЕТ FNROOT.
С NODLVL - РАБОЧИЙ ВЕКТОР ДЛЯ НОМЕРОВ УРОВНЕЙ,
С СООТВЕТСТВУЮЩИХ УЗЛАМ.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С FNLVLS, RQTREE.
С
с.............................................................
с
SUBROUTINE GENRQT ( NEQNS, XADJ, ADJNCY, NBLKS, XBLK,
1 PERM, XLS, LS, NODLVL )
С
с....................................
с
INTEGER ADJNCY(l), LSA), NODLVL(l), PERM(l),
1 XBLK(l), XLS(l)
INTEGER XADJ(l), I, IXLS, LEAF, NBLKS, NEQNS, NLVL,
1 ROOT
С
с •
с
') Определение refined в названии алгоритма указывает на то, что он
получает, вообще говоря, более мелкое разбиение, чем цепь, соответствующая
структуре уровней Название алгоритма мы в дальнейшем переводим как
«алгоритм вычисления рафинированного фактор-дерева». — Прим. перев.
190 Гл 6 Методы фактор-деревьев
С
С ИНИЦИАЛИЗАЦИЯ...
С
DO 100 I - 1 , NEQNS
NODLVL(I) - 1
100 CONTINUE
NBLKS - 0
XBLKA) - 1
С
С ДЛЯ КАЖДОЙ СВЯЗНОЙ КОМПОНЕНТЫ ОПРЕДЕЛИТЬ КОРНЕВУЮ
С СТРУКТУРУ УРОВНЕЙ И ВЫЗВАТЬ RQTREE ДЛЯ БЛОЧН. УПОРЯДОЧ.
С
DO 200 I - 1 , NEQNS
IF (NODLVL(I) LE 0) GO TO 200
ROOT - I
CALL FNLVLS ( ROOT, XADJ, ADJNCY, NODLVL,
1 NLVL, XLS, LS )
IXLS - XLS(NLVL)
LEAF - LS(IXLS)
CALL RQTREE ( LEAF, XADJ, ADJNCY, PERM,
1 NBLKS, XBLK, NODLVL, XLS, LS )
200 CONTINUE
RETURN
END
структуру уровней с корнем в псевдопериферийном узле,
а вектор NODLVL хранит для каждого узла соответствующий
ему номер уровня в структуре уровней.
Работа подпрограммы начинается с присвоения начальных
значений вектору NODLVL и переменной NBLKS. Затем она
исследует граф, пока не найдет еще не пронумерованный узел.
Отметим, что для нумерованных узлов в векторе NODLVL
устанавливаются нулевые значения. Найденный узел i вместе
с массивом NODLVL определяет связный подграф исходного
графа. Далее происходит обращение к подпрограммам
FNLVLS й RQTREE, которые упорядочивают узлы этого под-
подграфа. Подпрограмма заканчивает работу, когда все компо-
компоненты графа обработаны.
FNLVLS (FiNd LeVeL Structure)
Подпрограмма FNLVLS строит корневую структуру уровней
для компоненты, заданной посредством NODLVL; в качестве
корня берется псевдопериферийный узел. Кроме того, запоми-
запоминаются номера уровней, соответствующие узлам в структуре
уровней.
Связная компонента задается входными параметрами ROOT,
XADJ, ADJNCY и NODLVL. FNLVLS прежде всего обращается
к подпрограмме FNROOT, которая вычисляет требуемую кор-
корневую структуру уровней, помещая ее в (NLVL, XLS, LS). За-
Затем циклом по структуре уровней (DO 200 LVL = .. ) опреде-
определяются номера уровней, соответствующие узлам; они записы-
записываются в NODLVL.
§6 3. Алгоритм вычисления древовидного разбиения 191
о»
с*
С....... F-NLVLS . . ПОСТРОЕНИЕ СТРУКТУРЫ УРОВНЕЙ ••
с«»»«.•• ••
<>•••• ..,..,....,,.,.,,,,..,,........
с
С СТРОИТ КОРНЕВУЮ СТРУКТУРУ УРОВНЕЙ ДЛЯ МАРКИРОВАННОГО
с связного подграфа; корень структуры берется
С В ПСЕВДОПЕРИФЕРИЙНОМ УЗЛЕ. ЗАПОМИНАЮТСЯ НОМЕРА
с уровней.
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С NLVL - ЧИСЛО УРОВНЕЙ В ПОСТРОЕННОЙ СТРУКТУРЕ.
С (XLS, IS) -ПОСТРОЕННАЯ СТРУКТУРА УРОВНЕЙ.
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С ROOT - НА ВХОДЕ ВМЕСТЕ С NODLVL ЗАДАЕТ КОМПОНЕНТУ,
С ЧЕЙ ПСЕВДОПЕРИФЕРИЙНЫЙ УЗЕЛ НУЖНО НАЙТИ.
С НА ВЫХОДЕ " ЭТО НАЙДЕННОЙ УЗЕЛ.
С NODLVL - НА ВХОДЕ ЗАДАЕТ ПОДГРАФ. НА ВЫХОДЕ
С СОДЕРЖИТ НОМЕРА УРОВНЕЙ, СООТВЕТСТВУЮЩИЕ
С УЗЛАМ.
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С FNROOT.
С
SUBROUTINE FNLVLS ( ROOT, XADJ, ADJNCY, NODLVL,
1 NLVL, XLS, LS )
INTEGER ADJNCY(l), LS(I), NODLVL(l), XLS(l)
INTEGER XADJ(l), J, LBEGIN, LVL, LVLEND, NLVL,
1 NODE, ROOT
CALL FNROOT ( ROOT, XADJ, ADJNCY, NODLVL,
1 NLVL, XLS, LS )
DO 200 LVL - 1, NLVL
LBEGIN - XLS(LVL)
LVLEND - XLS(LVL + 1) - 1
DO 100 J - LBEGIN, LVLEND
NODE - LS(J)
NODLVL(NODE) - LVL
100 CONTINUF
200 CONTINUE
RETURN
END
RQTREE (Refined Quotient TREE)
Это та самая подпрограмма, которая реализует описанный
в разделе 6.3.1 алгоритм вычисления фактор-дерева. Для хра-
хранения подмножеств узлов используется стек; его организацию
192 Гл 6 Методы фактор-деревьев
мы и рассмотрим прежде, чем входить в детали подпро-
подпрограммы.
Для каждого подмножества, помещенного в стек, нужно за-
запомнить число узлов в нем и соответствующий ему номер уров-
уровня. В массиве под названием STACK мы храним в последова-
последовательных позициях узлы подмножества; в двух следующих пози-
позициях хранятся число узлов и номер уровня. Используется еще
переменная TOPSTK, указывающая число занятых на данный
0
0
//
Vjopstk
Начальное состояние вектора STACK
Номер уродня —^ Номер уровня -ч.
0
0
Подмножество
узлов
\
т
Z/Подмно-
f/жество
^ Число ,.
узлов Число
J узлов
)
X
^TOPSTK
STACK
Рис. 6.3.7. Организация стека в подпрограмме RQTREE.
момент позиций стека. Рис. 6.3.7 иллюстрирует организацию
вектора STACK.
Чтобы поместить подмножество 5 уровня i в стек, мы про-
просто переписываем узлы 5 в вектор STACK, начиная с позиции
TOPSTK -f- 1. Затем мы записываем число |5| и номер уровня г
и, наконец, изменяем значение переменной TOPSTK. С другой
стороны, чтобы вытолкнуть подмножество узлов из магазина,
мы вначале определяем по значению переменной STACK
(TOPSTK—1) число узлов этого подмножества, после чего
можно выбрать из STACK само подмножество, начиная с по-
позиции TOPSTK— |S| — 1. Наконец, снова изменяется значение
TOPSTK, чтобы отразить новый статус стека.
Теперь мы рассмотрим детали подпрограммы RQTREE. Она
оперирует со связным подграфом, заданным посредством
LEAF, XADJ, ADJNCY и NODLVL. Неявно предполагается, что
для этого подграфа сформирована структура уровней, причем
массив NODLVL содержит номера уровней его узлов, а пере-
переменная LEAF задает листовой узел структуры уровней. Гово-
Говорят, что узел х является листом структуры уровней 2? =
= {/.о, /-I,.-., М> если х s U и Adj (х) Г) i.i+i = 0.
§ 6.3 Алгоритм вычисления древовидного разбиения 193
с.......*.....*.*..*..........*
С......... RQTREE . . . РАФИНИРОВАННОЕ ФАКТОР - ДЕРЕВО • •
С........................
С... ,
С
С НАХОДИТ ДРЕВОВИДНОЕ УПОРЯДОЧЕНИЕ ДЛЯ КОМПОНЕНТЫ,
С ЗАДАННОЙ ЧЕРЕЗ LEAF И NODLVL.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ. ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С LEAF - ВХОДНОЙ УЗЕЛ, ОПРЕДЕЛЯЮЩИЙ СВЯЗНУЮ
С КОМПОНЕНТУ. ЭТО ЛИСТОВОЙ УЗЕЛ КОРНЕВОЙ
С СТРУКТУРЫ УРОВНЕЙ, ПЕРЕДАВАЕМОЙ ПОДПРОГРАММЕ
С RQTREE, Т.Е. НЕ ИМЕЕТ СОСЕДЕЙ В СЛЕДУЮЩЕМ
С УРОВНЕ.
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С PERM - ВЕКТОР ПЕРЕСТАНОВКИ, СОДЕРЖАЩИЙ УПОРЯДОЧЕНИЕ.
С (NBLKS, XBLK) - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР -
С NODLVL - ВЕКТОР, СОДЕРЖАЩИЙ НОМЕРА УРОВНЕЙ ДЛЯ УЗЛОВ,
С ПРОНУМЕРОВАННЫМ УЗЛАМ СООТВЕТСТВУЮТ НУЛЕВЫЕ
С ЗНАЧЕНИЯ В NODLVL.
С
С РАБОЧИЕ ПАРАМЕТРЫ
С ADJS - РАБОЧИЙ ВЕКТОР, ХРАНЯЩИЙ ПЕРЕСЕЧЕНИЕ
С СМЕЖНОГО МНОЖЕСТВА С УРОВНЕМ.
С STACK - РАБОЧИЙ ВЕКТОР ДЛЯ ОРГАНИЗАЦИИ СТЕКА.
С ХРАНЕНИЕ ПРЕДУСМОТРЕНО ТАК -
С С ПОДМНОЖЕСТВО УЗЛОВ, ЧИСЛО УЗЛОВ, НОМЕР
С У_РОВНЯ)>
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ-
С FNSPAN, COPYSI.
С
с....................... ......«••
с
с
с*
с
SUBROUTINE RQTREE ( LEAF, XADJ, ADJNCY, PERM,
1 NBLKS, XBLK, NODLVL, ADJS, STACK )
INTEGER ADJNCY(l), ADJS(l), NODLVL(l), PERMA),
i STACK(l), XBLK(l)
INTEGER XADJ(l), BLKSZE, IP, J, JP, LEAF, LEVEL,
1 NADJS, NBLKS, NODE, NPOP, NULEAF,
1 NUM, TOPLVL, TOPSTK
С
с................ ,
с
с
С ИНИЦИАЛИЗИРОВАТЬ STACK И ЕГО УКАЗАТЕЛИ.
С
STACK(l) - О
STACKB) - О
TOPSTK - 2
TOPLVL - О
NUM - XBLK(NBLKS+1) - 1
С
С СОЗДАТЬ ЛИСТОВОЙ БЛОК, Т.Е. БЛОК, НЕ ИМЕЮЩИЙ
С СОСЕДЕЙ НА БЛИЖАЙШЕМ ВЕРХНЕМ УРОВНЕ.
194 Гл. 6. Методы фактор-деревьев
с -
100 ILVEL - NODLVL(LEAF)
NODLVL(I EAF) - 0
PERM(NUM+1) - LEAF
B1KSZE - I
CALL FNSPAN ( XADJ. ADJNCY. NODLVL, BLKSZE. PERM(NUM+1),
1 LEVEL. NADJS. ADJS, NULEAF »
IF ( NULEAF .LE. 0 ) GO TO 300
JP - NUM
DO 200 J - 1. BLKSZE
JP - JP + 1
NODE - PERM(JP)
NODLVL(NODE) - LEVFL
200 CONTINUE
LEAF - NULEAF
GO TO 100
С
С НАЙДЕН НОВЫЙ БЛОК . . .
300 NBLKS - NBLKS + 1
XBLK(NBLKS) - NUM + 1
NUM - NUM + BLKSZE
С НАЙТИ СЛЕДУЮЩИЙ ВОЗМОЖНЫЙ БЛОК, ИСПОЛЬЗУЯ ПЕРЕСЕЧЕНИЕ
С СМЕЖН. МНОЖЕСТВА С НИЖНИМ УРОВНЕМ И ВЕРХИ. ПОДМНОЖЕСТВО
С УЗЛОВ СТЕКА (ЕСЛИ НОМЕР УРОВНЯ СОВПАДАЕТ ) .
с -- - -- —
LEVEL - LEVEL - 1
IF ( 1EVFL LE О ) GO TO 500
CALL COPYSI ( NADJS, ADJS, PERM(NUM+1) )
BLKSZE - NADJS
IF ( LEVEL NE. TOPLVL ) GO TO 400
с — --
С УРОВЕНЬ ВЕРХНЕГО ПОДМНОЖЕСТВА УЗЛОВ СТЕКА
ТОТ ЖЕ ЧТО У СМЕЖНОГО МНОЖЕСТВА .
ВЗЯТЬ ЕГО ИЗ ОТЕКА .
NPOP - STACK(T0PSTK-1)
TOPSTK - TOPSTK - NPOP - 2
IP - NUM + BLKSZE + 1
CALL COPYSI ( NPOP, STACK(TOPSTK+1), PERM(IP) )
BLKSZE - BLKSZE + NPOP
TOPLVL • STACK(TOPSTK)
400 CALL FNSPAN ( XADJ, ADJNCY. NODLVL, BLKSZE,
1 PERM(NUM+l), LEVEL, NADJS, ADJS, NULEAF )
IF ( NULEAF .LE 0 ) GO TO 300
С -
С ПОМЕСТИТЬ ТЕКУЩЕЕ МНОЖЕСТВО УЗЛОВ В СТЕК.
С - ~-
CALL COPYSI ( BLKSZE, PERM(NUM+1), STACK(TOPSTK+1) )
TOPSTK - TOPSTK + BLKSZE + 2
STACK(TOPSTK-1) - BLKSZE
STACK(TOPSTK) - LEVEL
TOPLVL - LEVEL
LEAF - NULEAF
GO TO 100
С
С ПЕРЕД ВЫХОДОМ . ..
с
800 XBLK(NBLKS+1) - NUM +7 I
RETURN
END
§ 6.3 Алгоритм вычисления древовидного разбиения 195
С COPYSI КОПИЯ ЦЕЛОГО ВЕКТОРА «¦¦¦¦¦
с»
с ¦....
с
С ПЕРЕПИСЫВАЕТ N ЦЕЛЫХ ЧИСЕЛ ИЗ ВЕКТОРА А В ВЕКТОР В
С ( МАССИВЫ КОРОТКИХ ЦЕЛЫХ ЧИСЕЛ) .
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С N - ДЛИНА ВЕКТОРА .
С А - ЦЕЛЫЙ ВЕКТОР.
С
С ВЫХОДНОЙ ПАРАМЕТР.
С В - ВЫХОДНОЙ ЦЕЛЫЙ ВЕКТОР,
С
с..«. .................,*
с
SUBROUTINE COPYSI ( N, А, В )
С
с» .».».,,
с
INTEGER A(l), ВA)
INTEGER I, N
С
С..
С
IF ( N LE. О ) RETURN
DO 100 I . 1, N
100 CONTINUE
RETURN
END
Помимо STACK подпрограмма использует еще один рабо-
рабочий вектор ADJS. В нем хранится пересечение смежного мно-
множества текущего блока с нижним уровнем, которое является
потенциальным подмножеством следующего блока.
Работа подпрограммы начинается с присвоения начальных
значений вектору STACK, указателю TOPSTK и переменной
TOPLVL. Локальная переменная TOPLVL хранит номер уров-
уровня верхнего подмножества магазина. Затем определяется ли-
листовой блок: это делается посредством вызова подпрограммы
FNSPAN, которой передается узел LEAF. (Листовой блок —
это подмножество Y такое, что Ус L, и Adj (F) П ^-i+i = 0 ) Най-
Найденный блок нумеруется как следующий блок фактор-дерева
(оператор с меткой 300).
Мы спускаемся теперь на следующий уровень (LEVEL =
= LEVEL — 1 и последующие операторы). Построение очеред-1
ного потенциального блока начинается с пересечения нового
уровня и смежного множества предыдущего блока. Если под-
подмножество узлов, находящееся на вершине стека, принадлежит
тому же уровню, оно выталкивается из магазина и включается
в потенциальный блок. Затем происходит обращение к подпро-
196 Гл 6 Методы фактор-деревьев
грамме FNSPAN (оператор с меткой 400), которая находит
оболочку') этого объединения. Если оболочка не имеет не-
ненумерованных соседей на верхнем уровне, то она становится
очередным нумерованным блоком. В противном случае она
кладется на стек и определяется листовой блок, который и бу-
будет следующим нумерованным блоком.
Подпрограмма проходит все уровни, пока не дойдет до пер-
первого. К этому времени должны быть пронумерованы все узлы
компоненты, и работа подпрограммы заканчивается.
FNSPAN (FiNd SPAN)
Эта подпрограмма используется подпрограммой RQTREE
и имеет несколько функций, одна из которых состоит в вычис-
вычислении оболочки множества. Пусть 3? = {Lo, Li, ..., L(} — задан-
заданная структура уровней, a S — подмножество уровня i. Подпро-
Подпрограмма определяет оболочку S в подграфе G(L,) и находит
пересечение смежного множества для S с уровнем L,_i. Если
же оболочка S имеет ненумерованных соседей в уровне L,+\,
то программа находит ненумерованный листовой узел; в этом
случае оболочка 5 может остаться лишь частично сформиро-
сформирований.
Входной информацией для подпрограммы являются: струк-
структура графа, хранимая парой массивов (XADJ, ADJNCY), струк-
структура уровней, неявно хранимая вектором NODLVL, и подмно-
подмножество (NSPAN, SET) уровня LEVEL в структуре уровней. На
выходе содержимое вектора SET расширится, включив в себя
оболочку заданного множества. Значение переменной NSPAN
будет увеличено до числа элементов оболочки.
После присвоения начальных значений подпрограмма про-
проходит циклом по узлам частичной оболочки. Переменная
SETPTR указывает текущий узел рассматриваемой оболочки.
Затем выполняется цикл DO 500 J = ..., в котором инспекти-
инспектируются номера уровней соседей. В зависимости от номера уров-
уровня сосед либо игнорируется, либо включается в оболочку, либо
включается в смежное множество. Наконец, есть еще одна возт
можность: сосед принадлежит более высокому уровню. В этом
случае прослеживается путь по ненумерованным узлам вверх по
структуре уровней, пока не будет найден листовой узел. После
восстановления первоначальных значений в массиве NODLVL
для узлов частично сформированного смежного множества
(цикл DO 900 I = ...) происходит выход из подпрограммы.
При нормальном же выходе из FNSPAN полностью сформи-
сформированные оболочка и смежное множество будут находиться со-
соответственно в (NSPAN, SET) и (NADJS, ADJS). Переменная
LEAF при этом имеет нулевое значение.
') То есть множество У = SPAN E), а точнее Y П iievei. — Прим. перев.
§68 Алгоритм вычисления древовидного разбиения 197
с
с • • •••
С FNSPAN ПОСТРОЕНИЕ ОБОЛОЧКИ
с »••
с
С ИСПОЛЬЗУЕТСЯ ЛИШЬ ПОДПРОГРАММОЙ RQTREE. ОСНОВНАЯ
С ЗАДАЧА - НАЙТИ ОБОЛОЧКУ ДАННОГО ПОДМНОЖЕСТВА
С В ПОДГРАФЕ ЗАДАННОГО УРОВНЯ. ОПРЕДЕЛЯЕТСЯ ТАКЖЕ
С ПЕРЕСЕЧЕНИЕ СМЕЖНОГО МНОЖЕСТВА ОБОЛОЧКИ
С С НИЖНИМ УРОВНЕМ . ЕСЛИ ОБОЛОЧКА ИМЕЕТ
С НЕНУМЕРОВАННОГО СОСЕДА В ВЕРХНЕМ УРОВНЕ ,
С ТО БУДЕТ НАЙДЕН НЕНУМЕРОВАННЫЙ ЛИСТОВОЙ УЗЕЛ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С LEVEL - НОМЕР УРОВНЯ ТЕКУЩЕГО МНОЖЕСТВА .
С
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С (NSPAN, SET) - ВХОДНОЕ МНОЖЕСТВО. НА ВЫХОДЕ
С СОДЕРЖИТ ПОЛУЧЕННУЮ ОБОЛОЧКУ.
С NODLVL - ВЕКТОР НОМЕРОВ УРОВНЕЙ. ДЛЯ ИССЛЕД-ЫХ УЗЛОВ
С В NODLVL ЗАНОСИТСЯ 0.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (NADJS, ADJS) - ПЕРЕСЕЧЕНИЕ СМЕЖНОГО МНОЖЕСТВА
С ОБОЛОЧКИ С НИЖНИМ УРОВНЕМ.
С LEAF - ЕСЛИ ОБОЛОЧКА ИМЕЕТ НЕНУМЕРОВАННОГО
С СОСЕДА В ВЕРХНЕМ УРОВНЕ , ТО LEAF -
С НЕНУМЕРОВАННЫЙ ЛИСТОВОЙ УЗЕЛ ;
С ИНАЧЕ, LEAF = О .
С
с
с
SUBROUTINE FNSPAN ( XADJ, ADJNCY, NODLVL, NSPAN, SET,
i LEVEL, NADJS, ADJS, LEAF )
С
с......... ....»
с
INTEGER ADJNCYA), ADJS(l), NODLVL(l), SET(l)
INTEGER XADJ(l), I, J, JSTOP, JSTRT, LEAF, LEVEL,
1 LVL, LVLM1, NADJS, NBR, NBRLVL, NODE,
1 NSPAN, SETPTR
С
с»
с
с
С ИНИЦИАЛИЗАЦИЯ...
с
LEAF - О
NADJS - О
SETPTR - О
iOO SETPTR - SETPTR + 1
IF i SETPTR GT NSPAN ) RETURN
С ДЛЯ КАЖДОГО УЗЛА ЧАСТИЧНОЙ ОБОЛОЧКИ
NODE - SET(SETPTR)
JSTR1 - XADJ(NODE>
198 Гл 6 Методы фактор-деревьев
JSTOP - XADJ(NODE + 1) - 1
IF ( JSTOP .LT. JSTRT ) GO TO 100
С
С ДЛЯ КАЖДОГО СОСЕДА ПРОВЕРИТЬ ЗНАЧЕНИЕ В NODLVL.
С —.
DO 500 J . JSTRT, JSTOP
NBR - ADJNCY(J)
NBRLVL - NODLVL(NBR)
IF (NBRLVL LE 0) GO TO 500
IF (NBRLVL - LEVEL) 200, 300, 600
С
С СОСЕД В УРОВНЕ LEVEL-1, ЗАНЕСТИ ЕГО В ADJS.
200 NADJS - NADJS -I- 1
ADJS(NADJS) - NBR
GO TO 400
Q , ,
С СОСЕД В ДАННОМ УРОВНЕ, ДОБАВИТЬ ЕГО К ОБОЛОЧКЕ.
Q .. . ы
300 NSPAN - NSPAN + 1
SET(NSPAN) - NBR
400 NODLVL(NBR) - О
500 CONTINUE
GO TO 100
Q
с сосед в уровне level +1. найти ненумерованный
С ЛИСТОВОЙ УЗЕЛ, ПОДНИМАЯСЬ ПО СТРУКТУРЕ УРОВНЕЙ, И ДЛЯ
С УЗЛОВ ИЗ ADJS ВОССТАНОВИТЬ ИСХОДНЫЕ ЗНАЧЕНИЯ В NODLVL.
с ,.—
600 LEAF > NBR
LVL - LEVEL + 1
700 JSTRT - XADJ(LEAF)
JSTOP . XADJ(LEAF+1) - 1
DO 800 J - JSTRT, JSTOP
NBR - ADJNCY(J)
IF ( NODLVL(NBR) LE. LVL ) GO TO 800
LEAF - NBR
LVL - LVL + 1
GO TO 700
800 CONTINUE
IF (NADJS LE. 0) RETURN
LVLM1 - LEVEL - 1
DO 900 I - 1. NADJS
NODE - ADJS(I)
NODLVL(NODE) - LVLM1
900 CONTINUE
RETURN
END
Упражнение
6.3.1. Пусть Р = {Yi, Yz, ..., YB) — разбиение графа О, полученное алго-
алгоритмом из раздела 6 3.1.
а) Показать, что G/ф — фактор-дерево
б) Доказать, что это фактор дерево максимально в смысле упр. 6 2 4
[Указание, пусть Уеф и Ya.L,(r); L,(r) определено в разделе 6.3 1. Пока-
Показать, что для любых двух узлов х и у из Y существуют два соединяющих их
пути —один в О I (J Li (г) I, другой в G j \J Lt (г) }. После этого исполь-
\i-o / (-ж, '
зовать результат упр. 6.2.4.) '
§64 Схема хранения и процедура распределения памяти 199
§ 6.4. Схема хранения и процедура распределения памяти
В этом параграфе мы опишем схему хранения, специально
предназначенную для блочных матричных задач, чьи фактор-
графы являются монотонно упорядоченными деревьями. Вместо
внедиагональных блоков треугольного множителя L хранятся
блоки исходной матрицы А. Другими словами, используется не-
неявная схема, описанная в конце раздела 6 2 3
6.4.1. Схема хранения
Снова будем считать, что А разбита на рг подматриц Ац,
1 ^ t, / =?5 Р, и пусть L4 — соответствующие подматрицы L, где
А = LLT. Так как заранее не известно, будет ли А иметь одну
из указанных ниже форм
или
(отвечающих весьма различным фактор-деревьям) или что-то
среднее между ними, то наша схема хранения должна быть
очень гибкой. Определим матрицы
~\к
, 2<к<р
F.4.1)
Тогда А можно представить в следующем виде, где р взято
равным 5.
200 Гл. 6. Методы фактор-деревьев
Аи
Ah
А\А
у*
л21
AL
Ab
У}
An
А„
лй
у,
А»
Наша вычислительная схема требует хранения диагональ-
диагональных блоков Lkk, I ^ k ^ р, и ненулевых внедиагональных бло-
блоков А. Схему хранения иллюстрирует рис. 6.4.1. Диагональные
блоки L считаются образующими блочно-диагональную матри-
матрицу, которая хранится по профильной схеме, уже описанной в
разделе 4.4.1. Это значит, что диагональ хранится в массиве
DIAG, а строки нижней оболочки — посредством пары масси-
массивов (XENV, ENV). Кроме того, для запоминания разбиения
$ используется массив XBLK длины р+1; при этом XBLK F)
указывает номер первой строки &-го диагонального блока. Для
удобства мы полагаем XBLK(p+l) = N + 1-
Ненулевые элементы матриц Vu, I < k ^ р, хранятся по
столбцам в едином одномерном массиве NONZ, начиная с эле-
элементов V2. Для хранения строчных индексов элементов из
NONZ используется параллельный целый массив NZSUBS, а
вектор XNONZ длины N-\-\ указывает начало каждого столб-
столбца в NONZ. Для удобства программирования полагаем
XNONZ(iV+l)==T)+l, где т) обозначает число элементов в
NONZ. Заметим, что равенство XNONZ(i+l) = XNONZ(i)
означает, что соответствующий столбец V'и нулевой.
Предположим, что XBLK (k) ^j<XBLK(^+ 1), и мы хотим
вывести на печать столбец с номером i — XBLK(&)-f I блока
Ajk, где / < k. Следующий фрагмент программы показывает,
как это можно сделать. Предполагается, что элементы Каждого
столбца хранятся в NONZ в порядке возрастания строчных ин-
индексов.
3000
100
200
MSTRT - XNONZ(I)
MSTOP - XNONZ(I+1)-1
IF (MSTOP LT.MSTRT) GO TO 200
DO 100 M - MSTRT, MSTOP
ROW - NZSUBS(M)
IF(ROW.LT XBLK(J)) GO TO 100
IF(ROW GT XBLK(J+1)) GO TO 200
VALUE - NONZ(M)
WRITE F,3000) ROW. VALUE
FORMAT AX.15H ROW SUBSCRIPT-,13,7H VALUE->F12.e)
CONTINUE
CONTINUE
§6 4. Схема хранения и процедура распределения памяти 201
Память, требуемая для векторов XENV, XBLK, XNONZ и
NZSUBS, должна рассматриваться как накладная (вспомните
А =
ENV
XBLK
1 | 2
A A
L_
МММ—
з
1
1—|
0
3
0
1
0
1
*l
1
51
/f
1 -1 1
XENV H 1 I 2 2 3 | 3 3 3 I 5 8 8 | 9 9 I 10 I
—i * * t
10
12 1Г
NZSUBS
NONZ
1
6
2
7
2I
ool
3
9
8 Б
10 | 11
6
12
10
13
«I
14|
XNONZ
hr-m I
11113
444446 89 10
Рис. 6.4.1. Пример, показывающий массивы, используемые в схеме хранения
фактор-дерева.
наши замечания в разделе 2.3.1), так как она используется не
для хранения числовых значений коэффициентов. Кроме того,
для реализации процедур разложения и решения нужны неко-
некоторые рабочие массивы. Этот аспект обсуждается в § 6.5, где
202 Гл 6 Методы фактор-деревьев
рассматриваются подпрограммы численных процедур TSFCT
(Tree Symmetric FaCTorization) и TSSLV (Tree Symmetric
SoLVe).
6.4.2. Внутреннее переупорядочение блоков
Описанный в § 6 3 алгоритм упорядочения определяет дре-
древовидное разбиение связного графа. До сих пор мы предпо-
¦К-
Упорядочение «хт Упорядочение а2
Рис. 6.4.2. Пример, показывающий эффект внутриблочного переупорядочения.
лагали, что узлы внутри блока (или члена разбиения) помече-
помечены произвольным образом. Это, разумеется, не влияет на чис-
число ненулевых элементов исходной матрицы, расположенных
вне диагональных блоков.
Однако поскольку в нашей схеме хранения используется
профильная структура диагональных блоков, то от способа
6 4 Схема хранения и процедура распределения памяти 203
упорядочения узлов внутри блока может зависеть основная
память для диагональной оболочки. Наша цель в этом разде-
разделе— обсудить стратегию внутреннего упорядочения и описать
ее реализацию.
Эта стратегия должна использовать в каждом блоке не-
некоторую схему уменьшения оболочки/профиля. Простой и очень
эффективный обратный алгоритм Катхнлла — Макки (см. раз-
раздел 4.3.1) кажется подходящим выбором. Пусть *$ = {У\,
Y2 Ур}— заданное разбиение, определяющее монотонно
упорядоченное фактор-дерево. Метод описывается следующим
образом.
Для каждого блока Yk из ф выполнить:
Шаг 1. Определить подмножество
U = iy<= Yk\Ad) (у) П (К, U ••• U Yk_{) = 0}.
Шаг 2. Переупорядочить узлы G(U) посредством обратного
алгоритма Катхилла — Макки.
Шаг 3. Произвольным образом присвоить узлам Yk — U
номера, следующие за номерами U
Пример на рис. 6.4.2 демонстрирует эффект этого переупо-
переупорядочивающего шага Оболочка диагональных блоков для упо-
упорядочения ai состоит из 24 элементов, в то время как для сс2 —
только из 11 элементов. Таким образом, переупорядочение дей-
действительно может дать существенное сокращение необходимой
памяти.
Реализация этой внутриблочной схемы переупорядочения
вполне очевидна. Ее выполняют две новые подпрограммы
BSHUFL и SUBRCM вместе с тремя другими, уже рассмотрен-
рассмотренными в предыдущих главах.
Новые подпрограммы ниже обсуждаются подробно.
BSHUFL
SUBRCM
FNROOT
RCM
ROOTLS
204 Гл 6 Методы фактор-деревьев
с»
С» •••• BSHUFL ....ВНУТРИБЛОЧНОЕ ПЕРЕУПОРЯДОЧЕНИЕ •¦
с» *.
о«
с-
С ПЕРЕУПОРЯДОЧИТЬ УЗЛЫ КАЖДОГО БЛОКА, ЧТОБЫ УМЕНЬШИТЬ
С ЕГО ОБОЛОЧКУ. УЗЛЫ БЛОКА, У КОТОРЫХ НЕТ СОСЕДЕЙ
С В ПРЕДЫДУЩИХ БЛОКАХ, НУМЕРУЮТСЯ ПОДПРОГРАММОЙ
С SUBRCM РАНЬШЕ ОСТАЛЬНЫХ УЗЛОВ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С (NBLKS, XBLK ) - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР-
С PERM - ВЕКТОР ПЕРЕСТАНОВКИ. НА ВЫХОДЕ СОДЕРЖИТ
С НОВУЮ ПЕРЕСТАНОВКУ.
С
С РАБОЧИЕ ВЕКТОРЫ-
С BNUM - ХРАНИТ БЛОЧНЫЙ НОМЕР КАЖДОЙ ПЕРЕМЕННОЙ.
С MASK - ВЕКТОР ДЛЯ МАРКИРОВКИ ПОДГРАФА.
С SUBG - ВЕКТОР ДЛЯ НАКОПЛЕНИЯ ПОДГРАФА.
С XLS - ИНДЕКСНЫЙ ВЕКТОР ДЛЯ СТРУКТУРЫ УРОВНЕЙ.
С
С ИСПОЛЬЗУЕМАЯ ПОДПРОГРАММА -
С SUBRCM.
С
с ¦••• «••• •
с
SUBROUTINE BSHUFL ( XADJ, ADJNCY, PERM, NBLKS, XBLK,
1 BNUM, MASK, SUBG, XLS )
С
с «.
с
INTEGER ADJNCYA), BNUMA), MASKA), PERMA),
1 SUBG(l), XBLK(l), XLS(l)
INTEGER XADJ(l), I, IP, ISTOP, ISTRT, J,
1 JSTRT, JSTOP, K, NABOR, NBLKS, NBRBLK,
1 NODE, NSUBG
С
с • • •• .........,*
с
IF ( NBLKS .LE. О ) RETURN
С ИНИЦИАЛИЗАЦИЯ НАЙТИ БЛОЧНЫЙ НОМЕР КАЖДОЙ
С ПЕРЕМЕННОЙ И ИНИЦИАЛИЗИРОВАТЬ MASK.
DO 200 К - 1, NBLKS
ISTRT - XBLK(K)
ISTOP - XBLK(K+1) - 1
DO 100 I - ISTRT,ISTOP
NODE - PERM(I)
BNUM(NODE) - К
MASK(NODE) - 0
100 CONTINUE
200 CONTINUE
С ДЛЯ КАЖДОГО БЛОКА НАЙТИ УЗЛЫ , НЕ ИМЕЮЩИЕ СОСЕДЕЙ
С В ПРЕДЫДУЩИХ БЛОКАХ, И ЗАНЕСТИ В SUBG. ИХ НОМЕРА
С ПРЕДШЕСТВУЮТ НОМЕРАМ ОСТАЛЬНЫХ УЗЛОВ БЛОКА.
с - -- -
§64 Схема хранения и процедура распределения памяти 205
DO 500 К • 1,NBLKS
ISTRT - XBLK(K)
ISTOP - XBLK(K+1) - 1
NSUBG - О
DO 400 I - ISTRT, ISTOP
NODE - PERM(I)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
IF (JSTOP LT. JSTRT) GO TO 400
DO 300 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
NBRBLK • BNUM(NABOR)
IF (NBRBLK LT К) GO TO 400
300 CONTINUE
NSUBG - NSUBG + 1
SUBG(NSUBG) - NODE
IP - ISTRT + NSUBG - 1
PERM(I) - PERM(IP)
400 CONTINUE
С
С ВЫЗВАТЬ SUBRCM ДЛЯ ПЕРЕУПОРЯДОЧЕНИЯ ПОДГРАФА,
С ХРАНИМОГО В (NSUBG, SUBG).
с
IF ( NSUBG GT 0 )
1 CALL SUBRCM ( XADJ , ADJNCY, MASK, NSUBG,
1 SUBG, PERM (ISTRT), XLS)
500 CONTINUE
RETURN
END
BSHUFL (Block SHUFfLe)
Входной информацией для этой подпрограммы являются:
структура графа, хранимая парой массивов (XADJ, ADJNCY),
древовидное разбиение, задаваемое посредством (NBLKS,
XBLK), и вектор PERM. Подпрограмма переставит компоненты
вектора PERM в соответствии со схемой, описанной ранее в
этом разделе. Требуются четыре рабочих вектора. BNUM хра-
хранит блочный номер каждого узла; SUBG накапливает узлы
подграфа; MASK и XLS нужны подпрограмме SUBRCM.
Работа подпрограммы начинается с присвоения начальных
значений рабочим векторам BNUM и MASK (цикл DO 200
К = ...). Циклом DO 500 К = • •. обходится каждый блок раз-
разбиения. Для каждого блока в векторе SUBG накапливаются
узлы, не имеющие соседей в предыдущих блоках (цикл DO
400...). Переменная NSUBG указывает число узлов подграфа.
Затем вызывается подпрограмма SUBRCM, которая переупо-
переупорядочивает этот подграф, используя алгоритм RCM. Выход
из программы происходит после того, как все блоки будут
обработаны.
206 Гл 6 Методы фактор-деревьев
SUBRCM (SUBgraph RCM)
Эта подпрограмма аналогична подпрограмме GENRCM,
за исключением того, что она оперирует с подграфом. Под-
Подграф, который может быть и несвязен, задается парой (NSUBG,
SUBG). Массивы MASK и XLS — это рабочие векторы, ис-
используемые подпрограммами FNROOT и RCM (см. разделы
4.3.3 и 4.3.4).
С SUBRCM ... ОБРАТНОЕ УПОРЯДОЧЕНИЕ КАТХИЛЛА - МАККИ
С»»................. НА ПОДГРАФЕ
С»
С
С НАХОДИТ RCM - УПОРЯДОЧЕНИЕ ДЛЯ ЗАДАННОГО ПОДГРАФА
С (ВОЗМОЖНО, НЕСВЯЗНОГО).
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С (NSUBG. SUBG) - ЗАДАННЫЙ ПОДГРАФ. NSUBG - ЧИСЛО
С УЗЛОВ ПОДГРАФА , SUBG СОДЕРЖИТ ЕГО УЗЛЫ .
с
С ВЫХОДНОЙ ПАРАМЕТР-
С PERM - ВЕКТОР ПЕРЕСТАНОВКИ . ИСПОЛЬЗУЕТСЯ
С ВРЕМЕННО ДЛЯ ХРАНЕНИЯ СТРУКТУРЫ УРОВНЕЙ.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С MASK - ВЕКТОР МАРКИРОВКИ С НУЛЕВЫМИ КОМПОНЕНТАМИ.
С ИСПОЛЬЗУЕТСЯ ДЛЯ УКАЗАНИЯ УЗЛОВ ПОДГРАФА.
С XLS - ИНДЕКСНЫЙ ВЕКТОР ДЛЯ СТРУКТУРЫ УРОВНЕЙ,
С ХРАНИМОЙ В ЧАСТИ ВЕКТОРА PERM.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С FNROOT, RCM.
С
SUBROUTINE SUBRCM ( XADJ, ADJNCY, MASK, NSUBG, SUBG,
1 PERM, XLS )
INTEGER ADJNCY(l), MASK(l), PERM(l), SUBG(l),
XLS(l)
INTEGER XADJ(l), CCSIZE, I, NLVL, NODE, NSUBG, NbM
DO 100 I - 1, NSUBG
NODE • SUBG(I)
MASK(NODE) • 1
100 CONTINUE
NUM - 0
DO 200 I - 1, NSUBG
NODE - SUBG(I)
IF ( MASK(NODE) .LE. 0 > GO TO 200
С
С КАЖДУЮ СВЯЗНУЮ КОМПОНЕНТУ ПОДГРАФА
§64 Схема хранения и процедура распределения памяти 207
УПОРЯДОЧИТЬ , ВЫЗЫВАЯ FNROOT И RCM .
CALL FNROOT ( NODE, XADJ, ADJNCY, MASK,
1 NLVL, XLS, PERM(NUM+1) )
CALL RCM ( NODE, XADJ, ADJNCY, MASK,
1 PERM(NUM+1), CCSIZE, XLS )
NUM - NUM + CCSIZE
IF ( NUM .GE NSUBO ) RETURN
800 CONTINUE
RETURN
END
6.4.3. Распределение памяти и подпрограммы FNTENV,
FNOFNZ «FNTADJ
Теперь мы опишем две подпрограммы FNTENV (FiNd Tree
ENVelope) и FNOFNZ (FiNd OFf-diagonal NonZeros), предна-
предназначенные для того, чтобы по графу G, упорядочению а и
разбиению $ сформировать структуру данных, описанную в
разделе 6.4.1. Кроме того, чтобы получить эффективную реали-
реализацию процедуры численного разложения, необходимо построить
вектор, содержащий структуру смежности ассоциированного
фактор-дерева G/$. Это является функцией третьей подпрограм-
подпрограммы FNTADJ (FiNd Tree ADJacency), которую мы также описы-
описываем в данном разделе.
FNTENV (FiNd Tree ENVelope)
Эта подпрограмма определяет структуру оболочки диаго-
диагональных блоков блочной матрицы. Входной информацией яв-
являются: структура смежности (XADJ, ADJNCY), упорядочение
(PERM, INVP) и древовидное разбиение (NBLKS, XBLK).
Структура, полученная подпрограммой и помещенная в XENV,
может не совпадать в точности со структурой оболочки диа-
диагональных блоков, хотя она всегда содержит в себе реальную
оболочку. Для достижения большей простоты и эффективности
при построении структуры оболочки используется следующее
замечание.
Пусть ?р ={Уь .... Yp}— заданное древовидное разбиение и
xi, х, е У*. Если
то подпрограмма включает {xt, xi) в структуру оболочки диа-
диагональных блоков.
Хотя этот алгоритм может приводить к чрезмерно большой
оболочке диагонального блока (приведите пример почему),
для упорядочений, генерируемых алгоритмом RQT, он обычно
дает результат, очень близкий к точной оболочке. Так как
208 Гл 6 Методы фактор>деревьев
с»
О»* FNTENV ... ПОСТРОЕНИЕ ОБОЛОЧКИ ДИАГОНАЛЬНЫХ ¦*
с........ БЛОКОВ ДРЕВОВИДНО УПОРЯДОЧЕННОЙ МАТРИЦЫ ••••
С.............................................................
с
С ОПРЕДЕЛЯЕТ ИНДЕКСНЫЙ ВЕКТОР ДЛЯ ОБОЛОЧКИ
С ДИАГОНАЛЬНЫХ БЛОКОВ ДРЕВОВИДНО УПОРЯДОЧЕННОЙ
С МАТРИЦЫ.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С (PERM, INVP) - ВЕКТОРЫ ПЕРЕСТАНОВОК.
С (NBLKS, XBLK) - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С XENV - ИНДЕКСНЫЙ ВЕКТОР ОБОЛОЧКИ.
С ENVSZE - ЧИСЛО ЭЛЕМЕНТОВ НАЙДЕННОЙ ОБОЛОЧКИ.
С
SUBROUTINE FNTENV ( XADJ, ADJNCY, PERM, INVP,
1 NBLKS, XBLK, XENV, ENVSZE )
С
с
с
INTEGER ADJNCY(l), INVP(l), PERMA), XBLKA)
INTEGER XADJ(l), XENV(l), BLKBEG, BLKEND,
1 I, IFIRST, J, JSTOP, JSTRT, K, KFIRST,
1 ENVSZE, NBLKS, NBR, NODE
С
с. *.............
с
ENVSZE - 1
С
С ЦИКЛ ПО БЛОКАМ РАЗБИЕНИЯ
с
DO 400 К - 1 NBLKS
BLKBEG - XBLK(K)
BLKEND - XBLK(K+1) - 1
С
С KFIRST УКАЗЫВАЕТ ПЕРВЫЙ УЗЕЛ КТО БЛОКА,
С ИМЕЮЩИЙ СОСЕДЕЙ В ПРЕДЫДУЩИХ БЛОКАХ.
с
KFIRST - BLKEND
DO 300 I - BLKBEG, BLKEND
XENV(I) - ENVSZE
NODE - PERM(I)
JSTRT « XADJ(NODE)
JSTOP - XADJ(NODE+1) - 1
IF ( JSTOP .LT. JSTRT ) GO TO 300
с
С IFIRST УКАЗЫВАЕТ ИНДЕКС ПЕРВОГО НЕНУЛЕВОГО
С ЭЛЕМЕНТА 1-Й СТРОКИ ВНУТРИ К - ГО БЛОКА .
С
IFIRST - I
DO 200 J - JSTRT, JSTOP
NBR - ADJNCY(J)
NBR - INVP(NBR)
§ 6.4. Схема хранения и процедура распределения памяти 209
IF ( NBR .LT. BLKBEG ) GO TO 100
IF ( NBR .LT. IFIRST ) IFIRST - NBR
GO TO 200
100 IF ( KFIRST .LT. IFIRST ) IFIRST ¦ KFIRST
IF ( J .LT. KFIRST ) KFIRST - I
200 CONTINUE
ENVSZE - ENVSZE + I - IFIRST
300 CONTINUE
400 CONTINUE
XENV(BLKEND+1) - ENVSZE
ENVSZE - ENVSZE - 1
RETURN
END
он работает очень хорошо, мы пользуемся им, а не более
сложной (и более дорогой) схемой, которая бы определяла
точную оболочку. Для других алгоритмов древовидного упоря-
упорядочения, например для описываемого в главе 7 алгоритма па-
параллельных сечений, требуются более сложные схемы.
FNOFNZ (FiNd OFf-diagonal Non Zeros)
Подпрограмма FNOFNZ используется для определения
структуры ненулевых элементов заданной блочной матрицы,
расположенных вне блочной диагонали. В терминах схемы
хранения из раздела 6.4.1 эта подпрограмма находит индекс-
индексный вектор NZSUBS и индексный вектор XNONZ. Выходным
значением переменной MAXNZ является число ненулевых эле-
элементов матрицы, находящихся вне диагональных блоков.
Входная информация подпрограммы: структура смежности
графа (XADJ, ADJNCY), древовидное упорядочение (PERM
INVP), древовидное разбиение (NBLKS, XBLK) и длина мас-
массива NZSUBS, задаваемая переменной MAXNZ. Подпрограмма
проходит циклом блоки разбиения. Для каждого блока вы-
выполняется цикл DO 200 J = ..., в котором исследуется каж-
каждый узел блока. Всякий сосед, принадлежащий одному из
предыдущих блоков, соответствует ненулевому элементу, рас-
расположенному вне блочной диагонали; этот элемент добавляет-
добавляется к структуре данных. Когда определены все индексы дан-
данной строки1), они упорядочиваются по возрастанию посред-
посредством подпрограммы S0RTS1; последняя очень проста и не
нуждается в объяснениях. Ее листинг следует за листингом
FNOFNZ.
Заметим, «то если длина заданного пользователем индекс-
индексного вектора 2) недостаточна, то подпрограмма обнаружит это
') В отличие от описания, приведенного в разделе 6.4.1, подпрограмма
FNOFNZ определяет столбцовые индексы элементов нижнего треугольника
матрицы. — Прим. перев.
г) NZSUBS. — Прим перев.
с.................................
С.... FN0FN7. .. ОПРЕДЕЛЕНИЕ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ, ••
С........... РАСПОЛОЖЕННЫХ ВНЕ БЛОЧНОЙ ДИАГОНАЛИ ••••
с.............................
с
С НАХОДИТ СТОЛБЦОВЫЕ ИНДЕКСЫ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ
С НИЖНЕГО ТРЕУГОЛЬНИКА БЛОЧНОЙ МАТРИЦЫ,
С РАСПОЛОЖЕННЫХ ВНЕ БЛОЧНОЙ ДИАГОНАЛИ .
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С (PFRM, INVP) - ВЕКТОРЫ ПЕРЕСТАНОВОК.
С (NBLKS XBLK) - БЛОЧНОЕ РАЗБИЕНИЕ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (XNONZ. NZSUBS) - СТОЛБЦОВЫЕ ИНДЕКСЫ НЕНУЛЕВЫХ
С ЭЛЕМЕНТОВ А, РАСПОЛОЖЕННЫХ ЛЕВЕЕ
С ДИАГОНАЛЬНЫХ БЛОКОВ, ХРАНЯТСЯ ПОСТРОЧНО
С 8 ПОСЛЕДОВАТЕЛЬНЫХ ПОЗИЦИЯХ NZSUBS.
С XNONZ - ИНДЕКСНЫЙ ВЕКТОР ДЛЯ NZSUBS.
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР -
С MAXNZ - НА ВХОДЕ УКАЗЫВАЕТ ДЛИНУ NZSUBS,
С НА ВЫХОДЕ - ЧИСЛО НАЙДЕННЫХ НЕНУЛЕВЫХ
С ЭЛЕМЕНТОВ.
С
с...........................
с
SUBROUTINE FNOFNZ ( XADJ, ADJNCY, PERM, INVP.
1 NBIKS, XBLK, XNONZ, NZSUBS, MAXNZ )
С
с»**»»*** •
с
INTEGER ADJNCYO ), INVP( 1 ) , NZSUBS(l). PERMA),
1 XBLK(l)
INTEGER XADJ(l), XNONZ(l), BLKBEG, BLKEND, I, J,
1 JPERM, JXNONZ, K, KS"OP, KSTRT, MAXNZ,
1 NABOR, NBLKS. NZCNT
€
Q • • * *•••
С
NZCNT - 1
IF ( NBLKS LE 0 ) GO TO 400
С
С ЦИКЛ ПО БЛОКАМ
с
DO 300 I • 1, NBLKS
BLKBEG = XBLK(I)
BLKEND - XBLK(I+1) - 1
с
С ЦИКЛ ПО СТРОКАМ 1-ГО БЛОКА
t
DO 200 J - BLKBEG, BLKFND
XNONZ(J) - NZCNT
JPERM - PERM(J)
KSTRT - XADJ(JPERM)
KSTOP - XADJ(JPERM+1) - 1
IF ( KSTRT .GT. KSTOP ) GO TO 200
ЦИКЛ ПО НЕНУЛЕВЫМ ЭЛЕМЕНТАМ J - Й СТРОКИ . . .
DO 100 К - KSTRT, KSTOP
NABOR - ADJNCY(K)
NABOR - INVP(NABOR)
НАХОДИТСЯ ЛИ ЭЛЕМЕНТ СЛЕВА ОТ 1-ГО
ДИАГОНАЛЬНОГО КЛОКА.
§ 6.4. Схема хранения и процедура распределения памяти 211
С
С
С
IF ( NABOR .GE. BLKBEG ) GO TO 100
IF ( NZCNT .LE. MAXNZ ) NZSUBS(NZCNT) - NABOR
NZCNT - NZCNT + 1
100 CONTINUE
УПОРЯДОЧИТЬ ИНДЕКСЫ J - Й СТРОКИ .
JXNONZ - XNONZ(J)
IF ( NZCNT - 1 .LE. MAXNZ )
1 CALL S0RTS1 (NZCNT - JXNONZ, NZSUBS(JXNONZ))
200 CONTINUE
300 CONTINUE
XNONZ(BLKEND+1) - NZCNT
400 MAXNZ - NZCNT - 1
RETURN
END
О ••••••••¦•
c«« • •• •• ••
С S0RTS1 ... СОРТИРОВКА МЕТОДОМ ПУЗЫРЬКА ••
с..............
с...........
с
С УПОРЯДОЧИВАЕТ ЗАДАННЫЙ МАССИВ КОРОТКИХ ЦЕЛЫХ
С ЧИСЕЛ ПО ВОЗРАСТАНИЮ МЕТОДОМ ПУЗЫРЬКА.
С
С ВХОДНОЙ ПАРАМЕТР -
С NA - ДЛИНА ЦЕЛОГО МАССИВА.
С
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР -
С ARRAY - ЦЕЛЫЙ ВЕКТОР, ЕГО КОМПОНЕНТЫ НА ВЫХОДЕ
С УПОРЯДОЧЕНЫ ПО ВОЗРАСТАНИЮ.
С
о» » «
с
SUBROUTINE SORTS 1 ( NA, ARRAY )
С
с.....
с
INTEGER ARRAY(l)
INTEGER K. L, NA, NODE
С
с
с
IF (NA .LE. 1) RETURN
DO 300 К - 2, NA
NODE - ARRAY(K)
L - К - 1
100 IF (L .LT. 1) GO TO 200
IF ( ARRAY(L) .LE. NODE ) GO TO 200
ARRAY(L+1) - ARRAY(L)
L - L - 1
GO TO IOC
200 ARRAY(L+1) - NODE
300 CONTINUE
RETURN
END
212 Г л 6 Методы фактор-деревьев
по значению входного параметра MAXNZ. Она будет продол-
продолжать считать ненулевые элементы, но перестанет хранить их
столбцовые индексы. Перед выходом из подпрограммы пере-
переменной MAXNZ присваивается значение, равное числу най-
найденных ненулевых элементов. Поэтому пользователь должен
проверить, не было ли значение MAXNZ увеличено подпрограм-
подпрограммой. Увеличение свидетельствует, что заданная длина массива
NZSUBS недостаточна.
FNTADJ (FiNd Tree ADJacency)
Назначение этой подпрограммы — определять структуру
смежности заданного монотонно упорядоченного фактор-дере-
фактор-дерева. Напомним (раздел 6.2.2), что структура монотонно упо-
упорядоченного корневого дерева полностью характеризуется
father |2J5|4|5l7l7l8|9|i0|0
Рис. 6.4.3. Пример вектора FATHER.
функцией Father, для узла х соотношение Father (x) =у озна-
означает, что г/eAdj (х) и (единственный) путь от корня к х про-
проходит через у. Наше представление структуры фактор-дерева
является вектором (называемым FATHER) длины р, где р —
число блоков. На рис. 6.4.3 показан вектор FATHER для фак-
фактор-дерева рисунка 6.3.3. Заметим, что FATHER (p) всегда по-
полагается равным нулю.
Входными данными подпрограммы FNTADJ являются: струк-
структура смежности графа (XADJ, ADJNCY), древовидное упоря-
упорядочение (PERM, INVP) и древовидное разбиение (NBLKS,
XBLK). Для хранения номеров блоков, соответствующих уз-
узлам при заданном разбиении, используется рабочий вектор
BNUM длины N.
С FNTADJ ОПРЕДЕЛЕНИЕ СТРУКТУРЫ СМЕЖНОСТИ ¦
С •¦¦•¦ ФАКТОР - ДЕРЕВА
С
С ОПРЕДЕЛЯЕТ СТРУКТУРУ СМЕЖНОСТИ ФАКТОР - ДЕРЕВА
С ДЛЯ ЗАДАННОГО ГРАФА. СТРУКТУРА ПРЕДСТАВЛЯЕТСЯ
С ВЕКТОРОМ FATHER .
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С (PERM, INVP) - ВЕКТОРЫ ПЕРЕСТАНОВОК.
С (NBLKS, XBLK) - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С
С ВЫХОДНОЙ ПАРАМЕТР -
С FATHER - ВЕКТОР ОТЦОВСТВА ДЛЯ ФАКТОР-ДЕРЕВА.
С
с рабочий параметр -
С BNUM - РАБОЧИЙ ВЕКТОР, ХРАНЯЩИЙ НОМЕР БЛОКА
С ДЛЯ КАЖДОЙ ПЕРЕМЕННОЙ.
с
с •••• ••
с
SUBROUTINE FNTADJ ( XADJ, ADJNCY, PERM, INVP,
I NBLKS, XBLK, FATHER, BNUM )
С
INTEGER ADJNCY(l), BNUMA), FATHER(l), INVP(l),
1 PERM(l), XBLK(l)
INTEGER XADJ(l), I, ISTOP, ISTRT, J, JSTOP, JSTRT,
1 K, NABOR, NBLKS, NBM1, NBRBLK, NODE
С
С
С ЗАПОЛНИТЬ ВЕКТОР ДЛЯ НОМЕРОВ БЛОКОВ.
с
DO 200 К - I, NBLKS
ISTRT - XBLK(K)
ISTOP - XBLK(K+1) - 1
DO 100 I - ISTRT, ISTOP
NODE - PERM(I)
BNUM(NODE) - К
100 CONTINUE
200 CONTINUE
С
С ДЛЯ КАЖДОГО БЛОКА.
с
FATHER(NBLKS) - 0
NBM1 - NBLKS - 1
IF ( NBM1 .LE. 0 ) RFTURN
DO 600 К • 1, NBM1
ISTRT - XBLK(K)
ISTOP - XBLK(K+1) - 1
с .
С НАЙТИ ОТЦОВСКИЙ БЛОК В СТРУКТУРЕ ДЕРЕВА
С
DO 400 I - ISTRT, ISTOP
NODE - PERM(I)
JSTRT - XADJ(NODE)
JSTOP - XADJ(NODE+1) -1
IF / JSTOP .LT. JSTRT ) GO TO 400
DO 300 J - JSTRT, JSTOP
NABOR - ADJNCY(J)
NBRBLK - BNUM (NABOR)
2l4 Гл 6. Методы фактор-деревьев
IF ( NBRBLK .GT. К ) GO TO 500
300 CONTINUE
400 CONTINUE
FATHER(K) . 0
GO TO 600
50f FATHER(K) - NBRBLK
600 CONTINUE
RETURN
END
Работа подпрограммы начинается с заполнения вектора
BNUM (цикл DO 200 К =...). Затем она проходит циклом
(DO 600 К—...) по блокам разбиения, устанавливая для
каждого номер отцовского блока. Если такого блока нет, то со-
соответствующее значение в массиве FATHER полагается равным
нулю.
§ 6.5. Подпрограммы численных этапов TSFCT (Tree Symmetric
FaCTorisation) и TSSLV (Tree Symmetric SoLVe)
В этом разделе мы опишем подпрограммы, реализующие
численное разложение и решение блочных линейных систем,
ассоциированных с фактор-деревьями и хранимых по разре-
разреженной схеме, введенной в разделе 6.4.1. Подпрограмма
TSFCT выполняет асимметричный вариант разложения, поэто-
поэтому мы напомним процедуру асимметричного блочного разло-
разложения из раздела 6.1.1 и исследуем возможности ее усовер-
усовершенствования.
6.5.1 Вычисление матричной поправки
Пусть матрица А, как и в разделе 6.1.1, представлена в
блочном виде
(*
W с
Напомним, что в схеме разложения матричная поправка
VTB~1V, используемая для формирования матрицы С = С —
— VTB~lV, вычисляется следующим образом.
Vt(t ztw\ VTW
Заметим еще, что матричная поправка VTW симметрична и
Nonz (V)cr Nonz(W) Поищем теперь эффективный способ вы-
вычисления произведения VW.
Пусть G — разреженная (rXs)-матрица, Н—(sX^)-матри-
Н—(sX^)-матрица. Для 1-й строки G положим
§6 5. Подпрограммы TSFCT и TSSLV 215
Таким образом, ft(G) —это столбцовый индекс первого нену-
ненулевого элемента /-й строки G. Предположим, что матричное
произведение GH симметрично. Ниже мы покажем, что для
вычисления этого произведения нужна лишь часть матрицы
Н. На рис. 6.5.1 показан пример для г = 4 и s = 8. Если про-
произведение GH симметрично, то при его вычислении можно
игнорировать заштрихованную часть И, как это вытекает из
следующей леммы.
* *
*
0_ можно
игнорировать
Рис. 6.5.1. Разреженное симметричное матричное произведение
Лемма 6.5.1.
Если матричное произведение GH симметрично, то оно пол-
полностью определяется матрицей G и следующим подмножеством
элементов матрицы Н:
Доказательство. Достаточно показать, что каждый элемент
матричного произведения можно вычислить по G и указанному
подмножеству элементов матрицы Н. Так как произведение
симметрично, то его элементы в позициях (г, k) и (k, i) можно
определить по любой из двух формул:
ИЛИ
Для определенности положим f'k(G)^. f,(G). Тогда элемент
(i, k) можно вычислять, пользуясь первой формулой, для чего
нужны элементы G и те h,k, для которых fk(G) ^ fi(G) ^ / ^ s.
Они принадлежат заданному подмножеству элементов. С другой
стороны, если fk(G) > /,(G), то можно использовать вторую
формулу, которая опять-таки требует только элементов задан-
заданного подмножества. Это доказывает лемму.
216 Гл. 6 Методы фактор-деревьев
* *
*.
##
*
Рис. 6.5.2. Иллюстрация к вычислению произведения GH.
$ 6.5. Подпрограммы TSFCT и TSSLV 217
Порядок, в котором вычисляются элементы произведения,
зависит от структуры матрицы (или, точнее, от столбцовых
индексов fi(G), l^i^r). Например, при формировании GH
для матриц рисунка 6 5.1 порядок вычислений тот, что указан
на рис. 6.5.2.
С учетом сказанного можно исследовать преобразование
подматрицы С ъ C = C — VtB-]V=C-Vt(LbT(Lb1V)). Как
отмечено в разделе 6.1.1, поправку можно вычислять по столб-
столбцам следующим образом:
1) Распаковать столбец v = Vtl матрицы V.
2) Решить систему Bw = v путем решения треугольных
систем LbW = v и Lbw = w.
3) Вычислить вектор г = VTw и положить С», = С* —г.
Так как матрица VTW симметрична, то к этому процессу
модификации приложима лемма 6.5.1, и потому нет необходи-
необходимости вычислять на шаге 2 по о полный вектор w При реше-
решении системы Lb{Lbv) = v можно не вычислять компоненты
w,' находящиеся выше первого ненулевого элемента v Таким
образом, в действительности достаточно решить меньшую си-
систему. Это может значительно сократить вычислительную ра-
работу в процессе разложения. Пример приведен в упр. 6 5.1.
Не вычисляются
Первый
ненулевой
элемент
и> w
6.5.2 Подпрограмма TSFCT (Tree Symmetric FaCTorization)
Подпрограмма TSFCT выполняет асимметричное блочное
разложение ') для системы со структурой фактор-дерева. Спо-
Способ вычисления матричной поправки — тот, что описан в пре-
предыдущем разделе.
Входными данными подпрограммы являются: информация о
древовидном разбиении, хранимая парой (NBLKS, XBLK) и век-
вектором FATHER; структура данных, состоящая из XENV, XNONZ
') Оборот «симметричное разложение» относится к тому обстоятельству,
что матрица, как и всегда в методе Холесского, представляется произведе-
произведением взаимно транспонированных множителей, а оборот «асимметричное блоч-
блочное разложение» — к тому, что при этом используется асимметричная схема
из раздела 6.1.1.—Ярил, перев.
218 Гл. 6 Методы фактор-деревьев
и NZSUBS, и векторы основной памяти DIAG, ENV и NONZ.
При входе векторы DIAG и ENV содержат ненулевые элементы
блочной диагонали матрицы А. На выходе ненулевые элемен-
элементы блочной диагонали L будут записаны на место одноименных
элементов А. Поскольку используется неявная схема, то нену-
ненулевые элементы Л, расположенные вне диагональных блоков,
хранятся в NONZ без изменения.
Используются два рабочих вектора длины N. Вещественный
вектор TEMP используется для распаковки столбцов внедиаго-
нальных блоков, и в нем выполняются операции над распако-
распакованными столбцами, предусмотренные численной процедурой.
COLBEG--. s— COLEND
ROWBEG К 1 Г! Г1 \\
ROWEND
Внедиагона/гьныЗ
-FNZ
COLSZE
Рис. 8.5.3. Иллюстрация роли некоторых важных локальных переменных, ис-
используемых подпрограммой TSFCT.
Второй рабочий вектор FIRST — это целый массив, облегчаю-
облегчающий индексирование вектора NZSUBS. (См. замечания отно-
относительно FIRST, приводимые ниже.)
Подпрограмма TSFCT начинает с присвоения начальных зна-
значений рабочим векторам TEMP и FIRST (цикл DO 100 I = ...).
Затем для каждого блока разбиения выполняется основной
цикл DO 1600 К = ... .В основном цикле прежде всего вызыва-
вызывается подпрограмма ESFCT, факторизующая k-н диагональный
блок. Следующий шаг—выяснить, где расположен внедиагональ-
ный блок; его указывает компонента FATHER (k). Далее выпол-
выполняются циклы DO 200.... и DO 400..., определяющие соответст-
соответственно первый и последний ненулевые столбцы внедиагональ-
ного блока, так что поправку можно выполнять лишь в пре-
пределах, обозначенных этими столбцами. Рис. 6.5.3 показывает
роль некоторых важных локальных переменных в подпро-
подпрограмме.
Цикл DO 1300 COL = ... осуществляет модификацию диа-
диагонального блока с номером FATHER (k). Каждый столбец
TSFCT ... СИММЕТРИЧНОЕ РАЗЛОЖЕНИЕ
ДРЕВОВИДНО УПОРЯДОЧЕННОЙ МАТРИЦЫ
с
С ВЫПОЛНЯЕТ СИММЕТРИЧНОЕ РАЗЛОЖЕНИЕ ДЛЯ СИСТЕМЫ
С СО СТРУКТУРОЙ ФАКТОР - ДЕРЕВА.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (NBLKS, XBLK, FATHER) - ДРЕВОВИДНОЕ РАЗБИЕНИЕ.
С XENV - ИНДЕКСНЫЙ ВЕКТОР ОБОЛОЧКИ.
С (XNONZ. NONZ, NZSUBS) - НЕНУЛЕВЫЕ ЭЛЕМЕНТЫ
С ИСХОДНОЙ МАТРИЦЫ ВНЕ БЛОЧНОЙ
С ДИАГОНАЛИ .
С ИЗМЕНЯЕМЫЕ ПАРАМЕТРЫ -
С (DIAG, ENV) - ОСНОВНАЯ ПАМЯТЬ ДЛЯ ОБОЛОЧКИ
С ДИАГОНАЛЬНЫХ БЛОКОВ МАТРИЦЫ. НА ВЫХОДЕ
С СОДЕРЖИТ ДИАГОНАЛЬНЫЕ БЛОКИ МНОЖИТЕЛЯ.
С IFLAG - ИНДИКАТОР ОШИБКИ. РАВЕН 1 , ЕСЛИ В ХОДЕ
С РАЗЛОЖЕНИЯ ВСТРЕТИТСЯ О ИЛИ КОРЕНЬ
С ИЗ ОТРИЦ. ЧИСЛА.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С TEMP - РАБОЧИЙ ВЕКТОР ДЛЯ РЕАЛИЗАЦИИ
1 АСИММЕТРИЧНОГО РАЗЛОЖЕНИЯ.
С FIRST - РАБОЧИЙ ВЕКТОР, УПРОЩАЮЩИЙ
С ИНДЕКСИРОВАНИЕ ВЕКТОРА NONZ
С (ИЛИ NZSUBS) ПРИ ОПЕРАЦИЯХ С НЕНУЛЕВЫМИ
С СТОЛБЦАМИ ВНЕДИАГОНАЛЬНЫХ БЛОКОВ.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С ESFCT, ELSLV, EUSLV.
С
с....................
с
SUBROUTINE TSFCT ( NBLKS, XBLK, FATHER, DIAG, XENV, ENV,
1 XNONZ, NONZ, NZSUBS, TEMP, FIRST, IFLAG )
С
DOUBLE PRECISION OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), ENV(l), NONZA), TEMPA), S
INTEGER FATHER(l), NZSUBS(l), XBLKA)
INTEGER FIRST(l), XENVA), XNONZA),
1 BLKSZE, COL, COL1, COLBEG, COLEND,
1 COLSZE, FNZ, FNZ1, I, IFLAG, ISTRT, ISTOP,
I ISUB, J, JSTOP, JSTRT, K, KENV, KENVO, KFATHR,
1 NBLKS, NEQNS, ROW, ROWBEG, ROWEND
С
с ...*,
с
с
С ИНИЦИАЛИЗАЦИЯ . . .
с
NEQNS - XBLK(NBLKS+1) - 1
DO 100 I - 1, NEQNS
TEMP(I) - 0.0E0
FIRST(I) - XNONZ(I)
100 CONTINUE
С
С ЦИКЛ ПО БЛОКАМ
с ,
DO 1600 К - 1, NBLKS
ROWBEG - XBLK(K)
ROWEND • XBLK(Kfl) - 1
BLKSZE - ROWEND - ROWBEG + 1
CALL ESFCT ( BLKSZE. XENV(ROWBEG), ENV,
1 DIAG(ROWBFG), IFLAG )
IF ( IFLAG .GT. 0 ) RETURN
С МОДИФИЦИРОВАТЬ ОТЦОВСКИЙ ДИАГОНАЛЬНЫЙ БЛОК "
С A(FATHER(K), FATHER(K)) ПОСРеДСТВОМ
С ВНЕДИАГОНАЛЬНОГО А(К, FATHER(K)).
с
KFATHR - FATHER(К)
IF ( KFATHR .LE. 0 ) GO TO 1600
COLBEG - XBLK(KFATHR)
COLEND - XBLK(KFATHR+1) - 1
С НАЙТИ ПЕРВЫЙ И ПОСЛЕДНИЙ НЕНУЛЕВЫЕ СТОЛБЦЫ
С ВНЕДИАГ. БЛОКА. ИЗМЕНИТЬ COLBEG, COLEND.
С
DO 200 COL - COLBEG, COLEND
JSTRT - FIRST(COL)
JSTOP - XNONZ(COL+1) - 1
IF ( JSTOP .GE. JSTRT .AND
1 NZSUBS(JSTRT) .LE. ROWEND ) GO TO 300
200 CONTINUE
300 COLBEG - COL
COL - COLEND
DO 400 C0L1 - COLBEG, COLEND
JSTRT - FIRST(COL)
JSTOP - XNONZ(COL+1) - 1
IF ( JSTOP .GE. JSTRT .AND.
1 NZSUBS(JSTRT) .LE. ROWEND ) GO TO 500
COL - COL - 1
400 CONTINUE
500 COLEND - COL
DO 1300 COL - COLBEG, COLEND
JSTRT - FIRST(COL)
JSTOP - XNONZ(COL+1) - 1
с
С НЕ БУДЕТ ЛИ СТОЛБЕЦ НУЛЕВЫМ. FNZ УКАЗЫ В.
С ИНДЕКС ПЕРВОГО НЕНУЛЕВОГО ЭЛЕМЕНТА.
с ,
IF ( JSTOP .LT. JSTRT ) GO TO 1300
FNZ - NZSUBS(JSTRT)
IF ( FNZ .GT. ROWEND ) GO TO 1300
С
С РАСПАКОВАТЬ СТОЛБЕЦ ВНЕДИАГ. БЛОКА И РЕШИТЬ
С ДЛЯ РАСПАКОВАННОГО СТОЛБЦА НИЖНЮЮ
С И ВЕРХНЮЮ ТРЕУГОЛЬНЫЕ СИСТЕМЫ.
с ,
DO 600 J - JSTRT, JSTOP
ROW - NZSUBS(J)
IF ( ROW .GT. ROWEND ) GO TO 700
TEMP(ROW) - NONZ(J)
600 CONTINUE
700 COLSZE - ROWEND - FNZ + 1
CALL ELSLV ( COLSZE, XENV(FNZ), ENV,
1 DIAG(FNZ), TEMP(FNZ) )
CALL EUSLV ( COLSZE, XENV(FNZ), ENV,
1 DIAG(FNZ), TEMP(FNZ) )
С -
С ВЫПОЛНИТЬ МОДИФИКАЦИЮ, ОБХОДЯ СТОЛБЦЫ
С И ВЫЧИСЛЯЯ СКАЛЯРНЫЕ ПРОИЗВЕДЕНИЯ.
с .
KENV0 - XENV(COL+1) - COL
DO 1100 C0L1- COLBEG, COLEND
ISTRT - FIRST(COLl)
ISTOP - XNONZ(COL1+1) - 1
НЕ БУДЕТ ЛИ СТОЛБЕЦ НУЛЕВЫМ.
с
с
с
6.5 Подпрограммы TSFCT и TSSL\ 221
FNZ1 - NZSUBS(ISTRT)
IF ( ISTOP .LT. ISTRT .OR.
FNZ1 .GT. ROWEND ) GO TO 1100
ВЫЧИСЛЯТЬ ЛИ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ,
LT. FNZ ) GO TO 1100
EQ. FNZ .AND.
LT. COL ) GO TO 1100
800
IF ( FNZ1
IF ( FNZ1
C0L1
S - 0.0E0
DO 800 I - ISTRT, ISTOP
ISUB - NZSUBS(I)
IF ( ISUB .GT. ROWEND )
S - S + TEMP(ISUB) •
OPS - OPS + 1.0D0
CONTINUE
GO TO 900
NONZ(I)
С
с
с
900
1000
1100
С
с
с
МОДИФ. ОБОЛОЧКУ ИЛИ ДИАГ. ЭЛЕМЕНТ.
IF ( C0L1 .EQ. COL ) GO TO 1000
KENV - KENVO + C0L1
IF ( C0L1 .GT. COL )
KENV . XENV(COL1+1) - C0L1 + COL
ENV(KENV) - ENV(KENV) - S
GO TO 1100
DIAG(COLl) - DIAG(COLl) - S
CONTINUE
УСТАНОВИТЬ О ДЛЯ ЧАСТИ TEMP.
1200
1300
DO 1200 ROW .
TEMP(ROW)
CONTINUE
CONTINUE
FNZ, ROWEND
. 0.0E0
С
С
с
с
с
с
1400
1500
1600
МОДИФИЦИРОВАТЬ FIRST В ПОЗИЦИЯХ,
ОТВЕЧАЮЩИХ СТОЛБЦАМ БЛОКА FATHER(K).
ОНИ БУДУТ УКАЗЫВАТЬ НАЧАЛО СТОЛБЦОВ
СЛЕДУЮЩЕГО ВНЕДИАГОНАЛЬНОГО БЛОКА.
DO 1500 COL - COLBEG, COLEND
JSTRT - FIRST(COL)
JSTOP - XNONZ(COL+1) - 1
IF ( JSTOP .LT. JSTRT ) GO TO 1500
DO 1400 J - JSTRT, JSTOF
ROW - NZSUBS(J)
IF ( ROW .LE. ROWEND ) GO TO 1400
FIRST(COL) - J
GO TO 1500
CONTINUE
FIRST(COL) - JSTOP + 1
CONTINUE
CONTINUE
RETURN
END
внедиагонального блока распаковывается в векторе TEMP (цикл
DO 600 J = ...), после чего происходит обращение к профиль-
профильным подпрограммам решения треугольных систем ELSLV и
222 Гл 6 Методы фактор-деревьев
EUSLV Наконец, внутренний цикл DO 1100 COL1 = ... вы-
выполняет модификацию так, как это описано в разделе 6.5.1.
Прежде чем подпрограмма перейдет к рассмотрению следу-
следующего блока, она модифицирует рабочий вектор FIRST в тех
позициях, которые соответствуют столбцам блока FATHER (k).
Эти компоненты FIRST будут теперь указывать на следующие
элементы, которые нужно обработать в этих столбцах (цикл
DO 1500 COL = ...).
Когда все диагональные блоки обработаны, происходит вы-
выход из подпрограммы.
6.5.3. Подпрограмма TSSLV (Tree Symmetric SOLVe)
Реализация процедуры решения линейной системы со струк-
структурой фактор-дерева не следует той последовательности вы-
вычислений, что указана в разделе 6.2.3. Вместо этого исполь-
используется альтернативное разложение, которое, согласно упр. 6.1.2,
приводит к асимметричной схеме:
/В V\ /В о \ // w\
А = ( ) = ( II V F.5.2)
\vT с) KvT сДо i) '
Здесь W = B-[V, причем W не вычисляется в явном виде, а
При записи А в этой форме решение системы
сводится к решению систем
В 0
гТ л
С
и
/ W
(
о
Предполагается, что подматрицы В а С были разложены в
произведения LbLb и LcLc соответственно. Схему можно
записать следующим образом.
Прямой ход
Решить LB (LbZi) = Ь\.
Вычислить Ь2 = Ь2— VTzx.
Решить Lc {LcZz) = 6а.
§65 Подпрограммы TSFCT и TSSLV 228
Обратная подстановка
Положить х2 = г2.
Вычислить tx = Vx2.
Решить Lb (Ltb t\)—t\.
ВЫЧИСЛИТЬ ДС] = Z] — #,.
Эта схема является простым переупорядочением указанной
в разделе 6.1.2 последовательности операций. Единственное
различие состоит в том, что в прямом ходе не требуется ра-
рабочего вектора. (Что, впрочем, не дает реального выигрыша!
Почему?) Мы выбрали эту схему по той причине, что она упро-
упрощает организацию программы для случая древовидно упоря-
упорядоченной системы произвольного блочного порядка р
Рассмотрим теперь обобщение описанной асимметричной
схемы. Пусть А — древовидно упорядоченная матрица блоч-
блочного порядка р с блоками Ath I ^ I, j ^ р. Пусть Lt, — соот-
соответствующие подматрицы треугольного множителя L.
Напомним (см. раздел 6.2.2), что для матрицы А с древо-
древовидным разбиением внедиагональные блоки L,, (i > /) за-
задаются формулами
Ltt = AlSLJiT. F.5.3)
Мы хотим определить асимметричное блочное разложение
A = IV, F.5.4)
аналогичное разложению F.5.2). Вид множителя L очевиден;
его элементы выражаются формулами
fiiLn, если i = /,
Uj, если i > j,
О в противном случае.
Выпишем явное выражение для L для случая р = 41)*
An
An
Ам
0
Ап
АА2
0
0
*зз^
^43
0
0
0
^44^44;
') На приводимой картинке по крайней мере три виедиагоиальных б юка
At, должны быть нулевыми (см. начало раздела 6 2.3) — Прим перев
224 Гл. 6. Методы фактор-деревьев
Лемма 6.5.2.
L=L
Доказательство. Утверждение леммы является прямым след-
следствием формулы F.5.3), связывающей внедиагональные блоки
древовидно упорядоченной матрицы Л и ее множителя L.
С помощью леммы мы можем представить верхний тре-
треугольный множитель U из F.5.4) в виде
U
О
V
22
LT
Отсюда выводим
V,,
I вали i ™ к
Lj~TLl воли I < к
О иначе
При i < k выражению для Uik можно придать другую форму,
учитывая F.5.3):
Ul
lk
Теперь для случая р = 4 мы можем выписать явно оба со-
сомножителя асимметричного разложения F.5.4)'):
') См примечание на сгр. 223
§ 6.5. Подпрограммы TSFCT и TSSLV 225
2i
0
L22L{2
A32
0
0
^33^-33
0
0
0
V
Чтобы перейти к процессу реального решения, мы должны
связать асимметричное разложение с блочной схемой хранения,
описанной в разделе 6.4.1. Как и прежде, положим
А1к
А2к
2<к?р
t 1Д
Метод решения должен быть подогнан под нашу схему хране-
хранения, в которой ненулевые элементы, расположенные вне блоч-
блочной диагонали, храня.тся столбец за столбцом, причем сохра-
сохраняется естественный порядок матриц
В принятом нами методе используется то обстоятельство, что
-1
О
-\
U4-J
- itit - \Lk _ 1/A _ |
i-i
226 Гл 6 Методы фактор-деревьев
Прямой ход Lz = Ь
Шаг 1. Решить систему (LuLT\\)z\ =5i.
Шаг 2. Для k = 2, ..., р выполнить следующее:
2.1) Вычислить
** -
2.2) Решить систему (jLftfejLfe *) *fe ™ **•
Обратная подстановка Ux = z
Шаг 1. Присвоить рабочему вектору z значение 0.
Шаг 2. Положить хр = гр.
Шаг 3. Для k = p— I, p — 2, ..., 1 выполнить следующее:
ЗЛ)
3.2) Решить систему {LkklXk) Хн
3.3) Вычислить xk = zk — xk.
**•
Отметим, что рабочий вектор z используется в обратной
подстановке для накопления произведений. Как именно это
происходит, показано на рис. 6.5.4.
Подпрограмма TSSLV реализует эту схему решения. В от-
отличие от TSFCT она не требует при задании древовидного
разбиения вектора FATHER, хотя и зависит от него неявно.
Входной информацией для TSSLV являются: древовидное раз-
разбиение (NBLKS, XBLK), диагональ DIAG, оболочка диаго-
диагональных блоков (XENV, ENV) и ненулевые элементы внедиа-
гональных блоков, хранимые посредством (XNONZ, NONZ,
NZSUBS).
В подпрограмме TSSLV — два основных цикла; один выпол-
выполняет прямой ход, другой — обратную подстановку. В прямом
ходе до обращения к подпрограммам ELSLV и EUSLV моди-
модифицируется (циклом DO 200 ROW =i..) вектор правых ча-
§ 6.5. Подпрограммы TSFCT и TSSLV 227
\
\
\
<1
N
\
Рис. 6.5.4. Обратный ход в асимметричной схеме.
.С TSSLV ... РЕШЕНИЕ ТРЕУГОЛЬНЫХ СИСТЕМ НЕЯВНОЙ
С СХЕМЫ ••
О««» • «••• ••¦• ••
С
С РЕШАЕТ ФАКТОРИЗОВАННУЮ СИСТЕМУ СО СТРУКТУРОЙ
С ФАКТОР " ДЕРЕВА МЕТОДОМ НЕЯВНОЙ ОБРАТНОЙ
С ПОДСТАНОВКИ.
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (NBLKS, XBLK) - РАЗБИЕНИЕ.
С (XENV, ENV) - ОБОЛОЧКА ДИАГОНАЛЬНЫХ БЛОКОВ.
С (XNONZ. NONZ, NZSUBS) - СТРУКТУРА ДАННЫХ
С ДЛЯ НЕНУЛЕВЫХ ЭЛЕМЕНТОВ ВНЕДИАГ. БЛОКОВ.
с
с изменяемый параметр -
С RHS - НА ВХОДЕ - ВЕКТОР ПРАВЫХ ЧАСТЕЙ.
С НА ВЫХОДЕ - ВЕКТОР РЕШЕНИЯ .
С РАБОЧИЙ ВЕКТОР -
С TEMP - ИСПОЛЬЗУЕТСЯ В ОБРАТНОЙ ПОДСТАНОВКЕ.
С
С ПОДПРОГРАММЫ -
С ELSLV, EUSLV.
?•••.*«.«•••*««•.««•••.«»••.......«••.«•...•.««•.....«.«.•«.•«
С
SUBROUTINE TSSLV ( NBLKS, XBLK, DIAG, XENV, ENV,
1 XNONZ, NONZ, NZSUBS, RHS, TEMP )
С
DOUBLE PRECISION COUNT, OPS
COMMON /SPKOPS/ OPS
REAL DIAG(l), ENV(l), NONZ(l), RHS(l), TEMPA), S
INTEGER NZSUBS(l), XBLK(l)
INTEGER XENV(l), XNONZA), COL, COL1, COL2, I, J,
1 JSTOP, JSTRT, LAST, NBLKS, NCOL, NROW, ROW,
1 ROW1, ROW2
С
с» ..............,............*.....
с
с
С ПРЯМОЙ ХОД
DO 400 I - 1. NBLKS
ROW1 • XBLK(I)
R0W2 . XBLK(I+1) - 1
LAST - XNONZ(ROW2+1)
IF ( I .EQ. 1 .OR. LAST .EQ. XNONZ(ROWl) ) GO TO 300
С -
С ВЫЧЕСТЬ ИЗ RHS ПРОИЗВЕДЕНИЕ ВНЕДИАГОНАЛЬНОГО
С БЛОКА НА СООТВЕТСТВУЮЩУЮ ЧАСТЬ ЭТОГО ВЕКТОРА.
С
DO 200 ROW - ROW1, R0W2
JSTRT - XNONZ(ROW)
IF ( JSTRT .EQ. LAST ) GO TO 300
JSTOP - XNONZ(ROW+1) - 1
IF ( JSTOP .LT. JSTRT ) GO TO 200
S - O.OEO
COUNT - JSTOP - JSTRT + 1
OPS - OPS + COUNT
DO 100 J - JSTRT, JSTOP
COL - NZSUBS(J)
S - S + RHS(COL).NONZ(J)
100 CONTINUE
RHS(ROW) - RHS(ROW) - 5
§ 6.5. Подпрограммы TSFCT и TSSLV 229
200 CONTINUE
300 NROW • ROW2 - ROW1 + 1
CALL ELSLV ( NROW, XENV(ROWl). ENV. DIAG(ROWl),
1 RHS(ROWl) )
CALL EUSLV ( NROW, XENV(ROWl), ENV, DIAG(ROWl).
1 RHS(ROWl) )
400 CONTINUE
С
С ОБРАТНАЯ ПОДСТАНОВКА...
С
IF ( NBLKS .EQ. 1 ) RETURN
LAST - XBLK(NBLKS) - 1
DO 500 I - 1, LAST
TEMP(I) - 0.0E0
300 CONTINUE
I - NBLKS
oOLl - XBLK(I)
COL2 - XBLK(I+1) - 1
600 IF ( I .EQ. 1 ) RETURN
LAST - XNONZ(COL2 + 1)
IF ( LAST .EQ. XNONZ(COLl) ) GO TO 900
С - - - —
С УМНОЖИТЬ ВНЕДИАГ. БЛОК НА СООТВ. ЧАСТЬ
С РЕШЕНИЯ. ПРИБАВИТЬ РЕЗУЛЬТАТ К TEMP.
с
DO 800 COL - C0L1, C0L2
S - RHS(COL)
IF ( S .EQ. 0.0E0 ) GO TO 800
JSTRT - XNONZ(COL)
IF ( JSTRT .EQ. LAST ) GO TO 900
JSTOP - XNONZ(COL+1) - 1
IF ( JSTOP .LT.'JSTRT ) GO TO 800
COUNT - JSTOP - JSTRT + 1
OPS - OPS + COUNT
DO 700 J - JSTRT, JSTOP
ROW - NZSUBS(J)
TEMP(ROW) - TEMP(ROW) + S*NONZ(J)
700 CONTINUE
800 CONTINUE
900 I - I - 1
COL1 - XBLK(I)
C0L2 - XBLK(I+1) - 1
NCOL - C0L2 - C0L1 + 1
CALL ELSLV ( NCOL, XENV(COLl), ENV,
1 DIAG(COLl), TEMP(COLl) )
CALL EUSLV ( NCOL, XENV(COLl), ENV, DlAG(COLl),
1 TEMP(COLl) )
DO 1000 J - C0L1, C0L2
RHS(J) - RHS(J) - TEMP(J)
1000 CONTINUE
GO TO 600
END
стей'-). При обратной подстановке подготовка к вызову
ELSLV и EUSLV предусматривает накапливание в веществен-
вещественном рабочем векторе TEMP произведений внедиагональных
блоков и частей решения. По окончании работы подпрограммы
в массиве RHS будет находиться вектор решения.
') Это не относится к I = \. — Прим. перев.
230 Гл. 6. Методы фактор-деревьев
Упражнение
6.5.1. Пусть L и V — матрицы, описанные в упр. 4.2.5, причем V имеет
только три ненулевых элемента в каждом столбце. Сравните число операций
при вычислении произведения VTL-TL~'V как Vr(L-T(L~lV)) и как
(VTL-T)(L^V). Считайте пир большими числами, так что младшие члены
можно игнорировать
§ 6.6. Дополнительные замечания
Идея «отбрасывания» внедиагональных блоков множителя
L матрицы А, обсуждавшаяея в данной главе, может приме-
применяться рекурсивно (George 1978c). Чтобы пояснить эту стра-
стратегию, предположим, что А — матрица блочного порядка р,
а векторы х и Ь разбиты на части соответственно А. Через А(«
обозначим ведущую главную подматрицу блочного порядка k,
через хщ и Ьщ — соответствующие части х и Ь, Наконец, опре-
определим подматрицы в А так же, как в F.4.1); аналогичным обра-
образом разобьем L. Это разбиение показано на рисунке для р = 5.
Угт
Уг
Лгг
Уз
Уа
Мл\
-22
m
Ць
В этих обозначениях систему Ах = 6 можно записать как
D)
п
*55
а разложение матрицы А — в виде
0\// А-^Л
Abs)\O I J
где Аъь = Ая —
А
Формально систему Ах = Ь можно решать следующим обра-
образом:
а) Разложение: вычислить матрицу А55 и разложить ее
в произведение Lss^ss. (Заметим, что поправку V54D)^5 можно
вычислять по столбцам, затирая каждый столбец после того,
как он использован!)
§ в. Дополнительные замечания 281
б) Решение:
6.1) Решить систему
6.2) Решить систему
6.3) Решить систему
6.4) ВЫЧИСЛИТЬ ДСD) = УD) — *D)-
Отметим, что мы всего лишь использовали идеи § 6.1 и
упр. 6.1.2, позволяющие избежать хранения W5; требуется толь-
только V5. Главное здесь заключается в следующем: все, что нужно
для решения системы блочного порядка 5 без хранения W5,—
это возможность решать системы блочного порядка 4. Очевид-
Очевидно, что той же стратегией можно воспользоваться для решения
систем блочного порядка 4 без хранения W4 и т. д.
Таким образом, мы получили метод, который, по видимости,
решает систему блочного порядка р, требуя хранения лишь
диагональных блоков L и внедиагональных блоков V, исходной
матрицы. Заметим, однако, что каждый уровень рекурсии тре-
требует рабочего вектора хи) (на шаге б.3); поэтому наступит
момент, когда более мелкое разбиение уже не даст уменьше-
уменьшения в запросах к памяти. С этой процедурой связано много
интересных и неисследованных вопросов. Изучение степени при-
применимости идей разбиения и отбрасывания является, по-види-
по-видимому, плодотворной областью исследований.
Блочные методы успешно применялись и в варианте с ис-
использованием внешней памяти (Von Fuchs 1972). Значение р
выбирается таким образом, чтобы наличный объем оператив-
оперативной памяти выражался каким-либо подходящим кратным числа
(N/pJ. Так как А разрежена, то некоторые из блоков будут
нулевыми. В оперативной памяти хранится массив указателей;
каждая его компонента либо указывает текущий адрес соот-
соответствующего блока, если в нем есть ненулевые элементы,
либо равна нулю. Если (р X р) -матрица указателей слишком
велика для того, чтобы храниться в оперативной памяти, то
эту матрицу также можно разбить на клетки и рекурсивно ис-
использовать ту же идею. Эта схема управления памятью, оче-
очевидно, связана с определенными издержками. Практика пока-
показывает тем не менее, что она является жизнеспособной альтер-
альтернативой другим схемам, использующим внешнюю память, на-
например ленточным или фронтальным методам. Одно из до-
достоинств этой схемы в том, что для реальных матричных опе-
операций используются простые структуры данных, а именно
только квадратные и прямоугольные массивы.
В работе (Shier 1976) рассмотрено применение древовид-
древовидных разбиений к задаче явного обращения матрицы и предло-
предложен алгоритм вычисления древовидного разбиения графа, от-
отличающийся от нашего.
7. Методы параллельных сечений
для конечноэлементных задач
§ 7.0. Введение
В этой главе мы рассмотрим стратегию упорядочения, пред-
предназначенную главным образом для задач, возникающих в при-
приложениях метода конечных элементов. Эта стратегия сходна
с методом главы 6 в том отношении, что отыскивается древо-
древовидное разбиение и используются вычислительные идеи неяв-
неявного решения и асимметричного разложения. Основное преиму-
преимущество описываемого в этой главе алгоритма параллельных
сечений — гораздо меньшие, как правило, запросы к памяти,
чем в ленточных или древовидных схемах, обсуждавшихся в
предыдущих главах. Для ко.нечноэлементных задач, за исклю-
исключением систем сверхвысокого порядка, методы данной главы
с точки зрения требуемой памяти часто оказываются наилуч-
наилучшими среди всех методов, рассматриваемых в этой книге. Вре-
Время решения также будет очень мало, хотя время разложения
может быть больше, чем у некоторых других методов.
Так как упорядочения, изучаемые в этой главе, являются
древовидными, то применимы методы хранения и вычисления
из главы 6; по этой причине названные вопросы не будут здесь
рассматриваться. Однако схема параллельных сечений требует
несколько более сложной процедуры распределения памяти,
чем та, что описана в разделе 6.4.3. Эта более общая процедура
распределения будет предметом § 7.3.
§ 7.1. Пример — задача на (тХ'
7.1.1. Упорядочение посредством параллельных сечений
В этом разделе мы обсудим задачу на (т X/) -сетке, кото-
которая мотивирует алгоритм из § 7.2. Рассмотрим (тХ^-сетку,
показанную на рис. 7.1.1; она имеет N = ml узлов и m s^ I,
Ассоциированная конечноэлементная матричная задача Ах~Ь,
которую мы будем изучать, имеет следующее свойство: при не-
некотором упорядочении уравнений (узлов) от I до iV неравен-
неравенство ач ф 0 означает, что узел i и узел / принадлежат одному
и тому же малому квадрату.
§ 7.1. Пример — задача на (т ХО -сетке
238
Пусть теперь а — целое число, такое, что 1 < а < i. Выбе-
Выберем а вертикальных линий (называемых в дальнейшем разде-
разделителями) , которые рассекут сетку на о -J- 1 независимых бло-
блоков приблизительно одинакового размера. Это показано на
Рис. 7.1.1. (пг X /)-сетка для m = 6 и I = 11.
рис. 7.1.2 для а = 4. Пронумеруем вначале о-\- 1 независимых
блоков (построчно), а затем разделители, как указано стрел-
стрелками на рис. 7.1.2. Матричная структура, которую такое упо-
m
I I I
Рис. 7.1.2. Упорядочение (тХ1)-сетки посредством параллельных сечений
указано стрелками Здесь а = 4, что приводит к разбиению с 2а + 1 = 9 чле-
членами, пронумерованными взятыми в кружок числами.
рядочение индуцирует на треугольном множителе L, показана
на рис. 7.1.3, где заштрихованы внедиагональные блоки, под-
подвергшиеся заполнению. Положим
Смысл этой величины — расстояние между секущими.
284 Гл. 7. Методы параллельных сечений
Рассматривая А и L как блочные матрицы, разбитые на q1
подматриц (<7 = 2а4-1), отметим прежде всего размерности
различных клеток:
1) Akk — mb X тб, если 1^^<а + Ь
2)Akj — my<_m6, если k > а + 1 и /<а + 1, G.1.1)
3) Akj — mXm, если />а+1 и k> a + 1-
Разумеется, реально а должно быть целым числом, и если б
не является целым, то ведущие а + 1 диагональных блоков не
Рис. 7.1.3. Структура матрицы L, индуцированная посредством параллельных
сечений сетки рис 7 1 2 Заштрихованные области указыва-ют позиции внедиа-
гональных блоков, подвергшиеся заполнению
будут в точности одинаковой величины. Однако мы увидим
позднее, что эти аберрации не имеют большого практического
значения. Во всяком случае, наша цель в этом разделе — из-
изложить некоторые основные идеи, а не исследовать во всех под-
подробностях данную сеточную задачу. Нам будет удобно считать
а и б целыми числами, a m и I — настолько большими, что
m < m2 и / < I2
§ 71 Пример — задача на (т X 0 -сетке 285
Как мы уже отметили, полезность этого упорядочения за-
зависит от использования развитой в главе 6 техники блочных
матриц. В самом деле, если не привлекать эту технику, то не-
нетрудно проверить, что наше упорядочение не лучше и даже
хуже, чем стандартное ленточное упорядочение (см. упр. 7.1.2
и 7.1.3).
Наиболее важное соображение, позволяющее нам приме-
применить описанную в главе 6 методику фактор-деревьев, состоит
в следующем: если считать, что а блоков, соответствующих
разделителям, образуют единый член разбиения, то результи-
результирующее разбиение, теперь уже с р = а + 2 членами, имеет
Рис. 7.1.4. Фактор-дерево, соответствующее упорядочению посредством па-
параллельных сеченнй н объединению разделителей в одни член разбиения.
структуру монотонно упорядоченного фактор-дерева. Рис. 7.1.4
иллюстрирует ситуацию для примера на рис. 7.1.2.
Таким образом, можно использовать схему хранения, об-
обсуждавшуюся в § 6.4, и хранить лишь диагональные блоки L
и внедиагональные блоки А При обсуждении удобно продол-
продолжать рассматривать А я L как матрицы блочного порядка q,
где q = 2a-\-\. Однако читатель должен понимать, что при
вычислении последние а членов разбиения объединяются, так
что в действительности остается р = а -+- 2 членов.
7.1.2. Требования к памяти
Обозначим через Llf подматрицы L, соответствующие под-
подматрицам Ач, l^i, /^2а+1. Мы получим сейчас оценку
для памяти, необходимой в алгоритме параллельных сечений,
при условии, что используется неявная схема хранения из раз-
раздела 6.4.1. Основная память подсчитывается таким образом:
1) Lkk, l^&^a+l. Ширина ленты у этих ленточных
матриц равна (/+1)/(а+1). В целом для всех Lkk требуется
ячеек
m (l-o)V + l) ,, „I2
(o+l) ~"
236 Гл. 7. Методы параллельных сечений
2) Lki, а+ 1 < /, k ^ 2<т -f 1, / < k Всего здесь 0—1 за-
заполненных блоков и а нижних треугольных блоков; все имеют
порядок т. В целом требуется ячеек
, «\ о i от(т+1) За/л2
(а-1)т2 + K-^L-L^-1--
3) А*/, &s^a-f-l, />а-|-1. Каждый узел разделителя
связан с шестью узлами ведущих a -f- 1 блоков; исключение со-
составляют только граничные узлы. Таким образом, основная па-
память для этих матриц равна приблизительно бот ячеек.
Накладная память для матриц из 1) и 2) равна lm -f- a -f- 3
(для массивов XENV и XBLK) и примерно бот -}- 1т для
XNONZ и NZSUBS. Тем самым если пренебречь младшими
членами, то общие запросы к памяти для нашего упорядоче-
упорядочения (при использовании неявной схемы хранения из разде-
раздела 6.4.1) выражаются такой приближенной формулой:
G.1.2)
Если наша цель состоит в минимизации памяти, то а нужно
выбрать так, чтобы минимизировать функцию S(а). Диффе-
Дифференцируя по а, получим
dS _ ml2 . 3m2
da * a2 + 2
Отсюда заключаем, что S приближенно минимизируется вы-
выбором а = а*, где
что дает _
S (а*) = V6 тЩ + О (ml). G.1.4)
Отметим, что соответствующее оптимальное значение б* равно
Интересно сравнить полученный результат с памятью, не-
необходимой при использовании стандартной ленточной или про-
профильной схемы. Так как т ^ /, то мы нумеровали бы узлы
сетки столбец за столбцом, что приводит к матрице с шириной
ленты т -\- 1. При больших т и I память, необходимая для L,
была бы равна m2l-\-O(ml). Таким образом, асимптотически
схема параллельных сечений сокращает запросы к памяти по
сравнению со стандартными схемами главы 4. Коэффициент
сокращения равен
ндартн
¦у/б/т.
§ 7.1. Пример—задача на (т X 0 -сетке 237
7.13. Число операций при разложении
Теперь оценим вычислительную работу в алгоритме парал-
'лельных сечений. По существу, нам нужно просто сосчитать
число операций в алгоритмах разложения и решения из § 6.2.
Однако внедиагональные блоки Ak! для й^а+1 и-/ > а + 1
имеют довольно специальную «псевдотрехдиагональную струк-
структуру», которая используется подпрограммами TSFCT и TSSLV.
Поэтому получение достоверной приближенной оценки числа
операций далеко не тривиально. В данном разделе мы рас-
рассмотрим разложение. Подсчет приближенного числа операций
при решении приведен в разделе 7.1.4.
При выводе оценки полезно разбить все операции на три
указанные ниже категории и игнорировать в суммах младшие
члены.
1. Разложение а + 1 ведущих диагональных блоков.
(В нашем примере на рис. 7.1.1—7.1.3, где а = 4, это вычис-
вычисление матриц Lkk, I ^ k =g; 5.) Замечая, что ширина ленты у
этих матриц равна (I -\- 1)/(а+ 1), й используя теорему 4.1.1,
заключаем, что число операций этой категории — приблизи-
приблизительно
ml3
2а2'
2. Вычисление Lk! для k ^ / и / > о -f 1-
Это соответствует разложению матрицы порядка та, имею-
имеющей блочную трехдиагональную структуру с блоками поряд-
порядка т. Используя результаты § 2.1 и 2.2, находим, что число
операций равно приблизительно
3. Поправки к A,i, A/+i, / и А/+1,/+1 для / > о -f- 1 посред-
посредством внедиагональных блоков Ащ и вычисленных матриц Lkk,
&=s;a + l. Рис. 7.1.5 показывает, как вычисляются такие по-
поправки.
Ниже приводится подсчет числа операций третьей катего-
категории.
При вычислении матричной поправки по асимметричной
схеме мы должны вычислять произведения
Lit {LkUk,) <7.1.5)
для / > a + 1 и k^.a-\- 1. Результаты § 6.5 показывают, что
в каждом столбце матрицы Lkk (LUkAkj) нет необходимости
вычислять ту часть, которая находится выше первого ненуле-
ненулевого элемента соответствующего столбца матрицы Ak\. Поэтому
238 Гл. 7. Методы параллельных сечений
при вычислении W = LkkAkj мы используем верхние нули в
столбцах Akj, а при вычислении W = Lkk W останавливаем
счет, как только получен последний требуемый элемент W.
Рис. 7.1.6 иллюстрирует сказанное.
Рис. 7.1.5. Матрицы, которые взаимодействуют с Lkk, А*; и А*, ж и модифи-
модифицируются ими; k = 3, / = 7.
}п/п
Рис. 7.1.6. Структура Akj и той части W, которую нужно вычислять.
Несложно проверить, что число операций для вычисления
указанной части W приближенно выражается формулой
„(Р+1)(г-1), G.1.6)
где Aki—(п X г) -матрица, a Lkk + Lkk — ленточная матрица
порядка п с шириной ленты Р <С « (см. упр. 7.1.5). Здесь п яа
« т//а, р да //о и г ~ гп; поэтому выражение G.1.6) превра-
превращается в
02
§ 7.1. Пример —задача на (тХ1) -сетке 289
Заметим, что всего имеется 2а таких внедиагональных блоков;
тем самым работа по вычислению всех произведений
равна приблизительно
«... 2.2
G.1.7)
2т2/2
операций.
Оценим теперь стоимость вычисления поправок к матрицам
Akj, k>o-\-l, / > а + 1. Замечаем, что если произведения
G.1.5). вычислены, то модификация каждого элемента диаго-
диагональных блоков Айа, k > о -f- 1, может быть получена за шесть
операций, а модификация элемента внедиагонального блока
Ай, k-\ требует трех операций. Следовательно, стоимость всего
процесса модификации есть О (am2).
Итак, оценка полного числа операций, нужных для разло-
разложения в схеме параллельных сечений, дается формулой
Если в алгоритме параллельных сечений мы ставим целью
минимизировать число операций при разложении, то нужно
выбрать Of, которое бы минимизировало Qf(o). Можно пока-
показать, что при больших /пи/ выбор
OF = i
приближенно минимизирует G.1.8), давая значение (см.
упр. 7.1.6)
Qf (of) = {Щ-)''тЩ + О (тЧ). G.1.9)
Соответствующее 6> равно
Снова интересно сравнить полученный результат с числом
операций, необходимых в стандартной ленточной или профиль-
профильной схеме (глава 4). Для данной сеточной задачи число опе-
операций в разложении было бы » -j тЧ. Таким образом, асимп-
асимптотически схема параллельных сечений сокращает число опе-
операций в разложении; коэффициент равен приблизительно
240 Гл. 7. Методы параллельных сечений
7.1.4. Число операций при решении
Выведем теперь оценку числа операций, необходимых для
решения .системы Ах = Ь. Предполагается, что «разложение»,
описанное в предыдущем разделе, уже вычислено.
Заметим прежде всего, что каждый из а + 1 ведущих диа-
диагональных блоков Lkk, l^fe^a+1, используется четыреж-
четырежды: два раза при решении нижней треугольной системы и еще
два — при решении верхней. Это требует приблизительно
4ml2
операций. Все ненулевые блоки Lku k > a -\- 1, / > а+ 1, ис-
используются дважды при общей оценке числа операций Зат2 -|-
4-0(ат). Дважды используется и каждая из матриц Ащ,
k>a-\-l, /^а+1, что обходится примерно в 12ат опера-
операций. Таким образом, в качестве оценки числа операций при
решении системы посредством алгоритма параллельных сече-
сечений можно принять
es (а) = -^ + Зат2. G.1.10)
о
Если мы желаем минимизировать 0s, то соответствующее при-
приближенное значение а равно
21
откуда
И опять интересно сопоставить G.1.11) с соответствующей
оценкой числа операций, равной примерно 2т2/, при исполь-
использовании стандартной ленточной или профильной схемы. Видим,
что асимптотически упорядочение посредством параллельных
сечений сокращает число операций при решении системы;
коэффициент равен приблизительно 2 <\Щт.
Разумеется, мы не можем посредством одного значения а
минимизировать сразу и память, и работу при разложении, и
работу при решении. Так как низкие запросы к памяти являют-
являются наиболее привлекательной чертой описанного метода, то
в алгоритме следующего параграфа а выбирается из условия
минимизации памяти.
Упражнения
7.1.1. Каковы будут коэффициенты прн старших членах в G.1.8) и
G.1.11), если для а взято значение а* из формулы G.1.3)?
7.1.2. Предположим, что применено упорядочение посредством параллель-
параллельных сечении, для а взято значение О {if л/т), но не используется техника не-
неявного хранения, т. е. вычисляются н хранятся внедиагональные блоки Li/,
§ 7.1. Пример — задача на (тУ,1)-сетке 241
О о + 1, у <; а + 1. Каковы теперь будут требования к памяти? Каково бу-
будет число операций 0s, если использовать эти блоки в схеме решения?
7.1.3. Предположим, что применено >[поридочение посредством параллель-
параллельных сечений, для а взято значение // упг, но вместо асимметричного исполь-
используется симметричный вариант схемы разложения (см. раздел 6.1.1). Пока-
Покажите, что теперь число операций при разложении будет О (от3/), а ие О(т5/2/).
Какая рабочая память потребуется для проведения вычислений?
7.1.4. На протяжении всего § 7.1 мы предполагали, что m ^ /, хотя ни-
нигде явно этот факт не использовался. Применимы ли наши результаты и при
пг > /? Зачем мы сделали предположение пг ^ /?
7.1.5. Пусть М — п~Х.п симметричная положительно определенная лен-
ленточная матрица с шириной ленты р<л и разложением Холесского LU.
Пусть V — п X г (/•<«) «псевдотрехдиагональная» матрица, у которой веду-
ведущий ненулевой элемент столбца i стоит в позиции
и пусть № = L-r(L-'V). Покажите, что число операций при вычислениий//,
1 ^ i ^ r, \it ^ /' ^ п, равно приблизительно я(Р + 0 (г — 1)- (Заметим, что
эти элементы приближенно составлиют псевдонижний треугольник W, описан-
описанный в упр. 2.2.8.)
7.1.6. Пусть Of минимизирует функцию dt(a) из формулы G.1.8). Пока-
Покажите, что нижнюю границу для Of дает число
причем
7.1.7. В описании упорядочения (тХ')-кти посредством параллельных
сечений, которое было дано в этом параграфе, разделительные блоки нумеро-
нумеровались монотонно Оказывается, что порядок нумерации этих разделительных
блоков важен. Например, блоки рнс. 7.1.2 могли бы быть пронумерованы, как
указано на диаграмме.
а) На рисунке, аналогичном рис. 7.1.3, покажите структуру L, соответ-
соответствующую этому упорядочению. Возрастет или уменьшится число блоков за-
заполнения по сравнению с рис. 7.1.2?
б) Для упорядочении (пг X 0 -сетки посредством параллельных сечений,
показанного на рис. 7.1.2, число блоков заполнения равно а—1. Покажите,
что для некоторых нумераций разделителей число блоков заполнения может
достигать 2а — 3.
242 Гл. 7. Методы параллельных сечений
§ 7.2. Алгоритм построения параллельных сечений
для задач на нерегулярных сетках
7.2.1. Алгоритм
Описание и анализ предыдущего параграфа подсказывают,
что и в общем случае нам следовало бы искать набор «парал-
«параллельных» разделителей, состоящих из относительно немногих
узлов. Эти разделители должны разбивать граф или сетку на
компоненты, которые можно было бы переупорядочить к форме
с малой оболочкой. По существу, это и пытается делать изла-
излагаемый ниже эвристический алгоритм.
Алгоритм оперирует с заданным графом G = (X,E), который,
мы будем считать связным. Обобщение на несвязные графы
очевидно. Напомним (глава 3), что множество Ус! называется
разделителем связного графа G, если подграф G(X—У) несвя-
несвязен.
Приведем теперь пошаговое описание алгоритма, вслед за
которым даны пояснения к важным его шагам. В этом описании
N=\X\, a m и I примерно соответствуют числам пг и I—1 из
§ 7.1. Значение а в алгоритме выбирается из условия прибли-
приближенной минимизации памяти, но несложная модификация позво-
позволяет минимизировать число операций при разложении или ре-
решении.
Шаг 1 (построить структуру уровней). Найти псевдоперифе-
псевдопериферийный узел х посредством алгоритма раздела 4.3.2 и построить
структуру уровней с корнем в х:
Шаг 2 (оценить б). Вычислить m = N/(l-\-l) и положить
ш + 13
Шаг 3 (предельный случай). Если б < 1/2 и \Х\ > 50, пе-
перейти к шагу 4. В противном случае положить р=\, YP = X и
перейти к шагу 6.
Шаг 4 (найти разделитель). Положить i =1, } = L^ + 0.5 J и
7 = 0.
До тех пор пока / < /, выполнять следующее:
4.1) Выбрать 7\= {xe=L/|Adj(x)fU/+i=^0}-
4.2) Положить T<-*T[)Tt.
4.3) Положить i-e-u + 1 и / = Цб + 0.5 J .
Шаг 5 (определить блоки). Взять в качестве Yk, k = \, ...,
р—1. связные компоненты подграфа G(X — Т); положить
§ 7.2. Алгоритм параллельных сечений на нерегулярных сетках 243
Шаг 6 (внутреннее переупорядочение). Последовательно про-
пронумеровать узлы каждого множества Yk, k = 1, s.., р, пользуясь
методом раздела 6.4.2.
Шаг 1 алгоритма порождает (можно надеяться) длинную и
узкую структуру уровней. Структура с такими свойствами же-
желательна, поскольку разделители выбираются как подмножества
некоторых уровней L/.
Вычисление чисел m и / на шаге 2 непосредственно мотиви-
мотивировано анализом (т X /) -сетки из § 7.1. Так как m — среднее
число узлов на уровне, оно служит мерой ширины структуры
уровней. Формула G.1.3) для <т* была получена путем весьма
грубых выкладок — нашей целью в § 7.1 было просто изложить
основные идеи. Более тщательный анализ и некоторый экспери-
экспериментальный опыт подсказывают, что значение
Зет+ 13
лучше подходит для а*. Соответствующее значение б* дает фор-
формула, используемая на шаге 2.
Назначение шага 3 — опознавать аномальные ситуации,
когда т <С / или N попросту слишком мало для того, чтобы ис-
использование метода параллельных сечений имело смысл. Экспе-
Эксперименты показывают, что для малых конечноэлементных задач
и/или задач типа «long slender»1' методы главы 4 более эффек-
эффективны независимо от того, что берется за основу для сравнения
В таких случаях весь граф обрабатывается как один блок (р =
= 1). Тем самым получается обычное профильное упорядочение
графа, обсуждавшееся в главе 4.
Действительный выбор разделителей происходит на шаге 4.
Это делается по существу так же, как если бы граф соответст-
соответствовал (тХ/)-сетке (см. §7 1). Как уже отмечалось, каждый
уровень L, из 9? является разделителем G. На шаге 4 из 9? вы-
выбираются приблизительно равноудаленные уровни, а затем на-
находятся подмножества этих уровней (Г,), которые все еще будут
разделителями.
Наконец, на шаге 6 узлы р(^а+1) независимых блоков,
полученных удалением разделителей из графа, нумеруются по-
посредством (описанной в разделе 6.4.2) схемы внутреннего пере-
переупорядочения.
Хотя значение для а и метод выбора разделителей могут по-
показаться довольно грубыми, мы обнаружили, что переход к бо-
более сложным решениям часто не дает сколько-нибудь существен-
существенного выигрыша (исключая некоторые нереалистические, специ-
специально сконструированные примеры). Как и в случае регулярной
') То есть длинных и тонких. — Прим перев.
244 Г i. 7. Методы параллельных сечений
прямоугольной сетки, характер функции запросов к памяти в ок-
окрестности точки минимума мало отличается от константы. Даже
сравнительно большие возмущения в значении о и выборе разде-
разделителей обычно ведут к довольно малым изменениям в количе-
количестве памяти.
Рис. 7.2.1. Диаграмма нерегулярной сетки, показывающая разделители, вы-
выбранные алгоритмом
На рис. 7.2.1 приведен пример задачи на нерегулярной сетке
вместе с некоторыми указаниями шагов, выполняемых алгорит-
алгоритмом. (Для этой иллюстрации мы будем считать, что из алгорит-
алгоритма удален тест |Х|>50 на шаге 3.) Рис. 72.1 (а) показывает
номера уровней в исходной структуре уровней, а рис. 7.2.1 (б) —
узлы, выбранные для разделителей. Здесь m = N/A -f- 1I =
= 25/11 « 2.27, б =V9.91 « 3.12. Поэтому разделители выби-
выбираются из уровней с номерами 4 и 8.
7.2.2. Подпрограммы для вычисления разбиения методом
параллельных сечений
Набор подпрограмм, реализующих алгоритм параллельных
сечений, показан на диаграмме управления рис. 7.2.2. Подпро
§ 7.2. Алгоритм параллельных сечений на нерегулярных сетках 245
граммы FNROOT и ROOTLS вместе определяют псевдоперифе-
псевдопериферийный узел связной компоненты заданного графа. Они были
детально разобраны в разделе 4.3.3. REVRSE — это служебная
Рис. 7.2.2. Отношения управления между подпрограммам*, в алгоритме парал-
параллельных сечений.
подпрограмма, используемая для обращения порядка в. целом
массиве. Выполнение оператора вызова
CALL REVRSE (NV, V)
приведет к следующей перестановке компонент целого вектора V
длины NV:
V(/)**V(NV —/+1), 1</<LNV/2J.
Остальные две подпрограммы GEN1WD и FN1WD ниже опи-
описаны подробно.
GEN1VVD (GENeral 1-Way Dissection)
Это главная подпрограмма при применении к произвольному
несвязному графу метода параллельных сечений. Входные и вы-
выходные параметры в GEN1WD следуют тем же обозначениям,
что и в реализациях других алгоритмов упорядочения. Пара-
Параметры NEQNS, XADJ и ADJNCY описывают структуру смеж-
смежности заданного графа. Выходными данными подпрограммы яв-
являются упорядочение посредством параллельных сечений, содер-
содержащееся в векторе PERM, и информация о разбиении в (NBLKS,
246 Гл. 7. Методы параллельных сечений
XBLK). Подпрограмма GEN1WD использует три рабочих
вектора: MASK., XLS и LS. Пара массивов (XLS, LS) нужна
подпрограмме FN1WD для хранения структуры уровней с кор-
корнем в псевдопериферийном узле, а вектор MASK используется
для маркировки уже пронумерованных узлов.
Работа подпрограммы начинается с установления исходного
состояния для массива MASK, при котором все узлы считаются
ненумерованными. Затем просматривается граф, пока не будет
найден еще не нумерованный узел i. Этот узел определяет неупо-
неупорядоченную связную компоненту графа, параллельные сечения
которой вычисляет вызываемая подпрограмма FN1WD. Множе-
Множество узлов сечений образует блок разбиения. Каждая компонента
в остатке рассеченного подграфа также составляет блок; эти
компоненты определяются вызовом подпрограммы ROOTLS.
После того как все связные компоненты графа обработаны,
подпрограмма обращает порядок в векторе перестановки PERM
и векторе блочного разбиения XBLK. Причина та, что хотя узлы
параллельных сечений определяются раньше прочих узлов ком-
компоненты, они должны иметь большие номера.
с.................. .....................................
с.
С........ GEN1WD ... МЕТОД ПАРАЛЛЕЛЬНЫХ СЕЧЕНИЙ ДЛЯ *•
О»»* ••••• ПРОИЗВОЛЬНОГО ГРАФА
с.........................
с
С ОПРЕДЕЛЯЕТ РАЗБИЕНИЕ ПРОИЗВОЛЬНОГО ГРАФА МЕТОДОМ
С ПАРАЛЛЕЛЬНЫХ СЕЧЕНИЙ. ДЛЯ УПОРЯДОЧЕНИЯ КАЖДОЙ
С СВЯЗНОЙ КОМПОНЕНТЫ ИСПОЛЬЗУЕТСЯ FN1V/D.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ.
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (NBLKS, XBLK) - НАЙДЕННОЕ РАЗБИЕНИЕ.
С PERM - УПОРЯДОЧЕНИЕ ПОСРЕДСТВОМ ПАРАЛЛЕЛЬНЫХ
С СЕЧЕНИЙ.
С РАБОЧИЕ ВЕКТОРЫ -
С MASK - ИСПОЛЬЗУЕТСЯ ДЛЯ МАРКИРОВКИ ПЕРЕМЕННЫХ,
С УЖЕ ПРОНУМЕРОВАННЫХ ПРИ УПОРЯДОЧЕНИИ.
С (XLS, LS) - СТРУКТУРА УРОВНЕЙ, ИСПОЛЬЗУЕМАЯ ROOTLS.
С
С ИСПОЛЬЗУЕМЫЕ ПОДПРОГРАММЫ -
С FN1WD, REVRSE, ROOTLS.
С
FN1WD (FiNd 1-Way Dissection ordering)
Эта подпрограмма применяет алгоритм параллельных сече-
сечений из раздела 7.2.1 к связной компоненте графа. Она оперирует
со связной компонентой, заданной входными параметрами ROOT,
SUBROUTINE
1
GEN1WD ( NEONS
NBLKS
XADJ
XBLK
ADJNCY MASK,
PERM. XLS LS )
С
с»
с
INTEGER ADJNCY(l), LSA) MASKA) PERMA)
1 XBLK(l). XLS(l) /
INTEGER XADJ(l), CCSIZE, I J, Й, LNUM
1 NBLKS, NEQNS, NLVL NODE NSEP
1 NUM, ROOT
С
С
С
DO 100 I - 1 NEQNS
MASK(I) . 1
100 CONTINUE
NBLKS - 0
NUM - 0
DO 400 I - 1, NEQNS
IF ( MASK(I) EQ
0 ) GO TO 400
ПАРАЛЛЕЛЬН. СЕЧЕНИЯ ДЛЯ КАЖДОЙ КОМПОНЕНТЫ.
С
С
С
С
С
ROOT - I
CALL FN1WD ( ROOT
NSEP
NUM - NUM + NSEP
NBLKS - NBLKS + 1
XBLK(NBLKS) - NEQNS
CCSIZE - XLS(NLVL+1)
XADJ, ADJNCY MASK
PERM(NUM+1) NLVL XLS
LS
NUM
1
+ 1
ПРОНУМЕРОВАТЬ ОСТАЛЬНЫЕ УЗЛЫ КОМПОНЕНТЫ.
КАЖДАЯ КОМПОНЕНТА ОСТАВШЕГОСЯ ПОДГРАФА
ОБРАЗУЕТ НОВЫЙ БЛОК РАЗБИЕНИЯ.
200
300
400
С
с
с
с
с
DO 300 J - 1 CCSIZE
NODE - LS(J)
IF ( MASK(NODE) ?Q 0
CALL ROOTLS ( NODE
NLV1
LNUM - NUM + 1
NUM - NUM + XLS(NLVL+1)
NBLKS - NBLKS + 1
XBLK(NBLKS) - NEQNS
DO 200 К - LNUM, NUM
NODE - PERM(K)
MASK(NODE) - 0
CONTINUE
IF ( NUM GT NEQNS )
CONTINUE
CONTINUE
ХОТЯ УЗЛЫ СЕЧЕНИЙ ОПРЕДЕЛЯЮТСЯ РАНЬШЕ ПРОЧИХ
УЗЛОВ, ИМ НУЖНО ПРИСВОИТЬ БОЛЬШИЕ НОМЕРА. ВЫЗОВ
REVRSE, ОБРАЩАЮЩЕЙ ПОРЯДОК В PERM И XBLK.
) GO TO 300
XADJ ADJNCY MASK.
XLS PERM(NUM+1) )
1
NUM + 1
GO TO 500
500
CALL REVRSE ( NEQNS PERM )
CALL REVRSE ( NBLKS XBLK I
XBLK(NBLKS+1) - NEQNS ¦ 1
RETURN
END
848 Гл. 7. Методы параллельных сечений
MASK, XADJ и ADJNCY. Выходная информация подпрограм-
подпрограммы— набор узлов сечений, описываемый парой (NSEP, SEP).
Первым шагом подпрограммы является построение структуры
уровней с корнем в псевдопериферийном узле, что достигается
обращением к подпрограмме FNROOT. В зависимости от харак-
характеристик структуры уровней (числа уровней NLVL и средней
ширины WIDTH) подпрограмма определяет нужное приращение
номера уровня DELTA. Если число уровней NLVL или размер
компоненты слишком малы, то вся компонента передается на вы-
выход в качестве «сечения».
Когда DELTA найдено, подпрограмма обходит структуру
уровней, выбирая те уровни, подмножества которых образуют
набор параллельных сечений.
с.......................................
с..............................................
С.*.*... FNIWD .. ПОСТРОЕНИЕ ПАРАЛЛЕЛЬНЫХ СЕЧЕНИИ •*•
с................................ •
с........................... ..,.........,...,..,»..,,....¦
с
С НАХОДИТ ПАРАЛЛЕЛЬНЫЕ СЕЧЕНИЯ ДЛЯ СВЯЗНОЙ КОМПОНЕНТЫ,
С ЗАДАННОЙ MASK И ROOT.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С ROOT - УЗЕЛ, ЗАДАЮЩИЙ (ВМЕСТЕ С MASK)
? КОМПОНЕНТУ ДЛЯ ОБРАБОТКИ.
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ-
С NSEP - ЧИСЛО УЗЛОВ В ПАРАЛЛЕЛЬНЫХ СЕЧЕНИЯХ.
С SEP - ВЕКТОР, СОДЕРЖАЩИЙ УЗЛЫ СЕЧЕНИИ.
с
с изменяемый параметр -
С MASK - ДЛЯ УЗЛОВ СЕЧЕНИИ В MASK УСТАНАВЛИВАЕТСЯ
С ЗНАЧЕНИЕ 0.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С (XLS, IS) - СТРУКТУРА УРОВНЕЙ, ИСПОЛЬЗУЕМАЯ FNROOT.
С
С ПОДПРОГРАММЫ -
С FNROOT.
С
С • •
с
SUBROUTINE FNIWD ( ROOT, XADJ, ADJNCY, MASK,
NSEP, SEP, NLVL, XLS, LS )
С
с.......................
t
INTEGER ADJNCY(l), LSA), MASK(l), SEP(l), XLS(l)
INTEGER XADJ(l), I, J, K, KSTOP, KSTRT, LP1BEG, LP1END,
1 LVL, LVLBEG, LVLEND, NBR, NLVL, NODE,
1 NSEP, ROOT
REAL DELTP1, FNLVL, WIDTH
§72 Алгоритм параллельных сечений на нерегулярных сетках 249
CALL FNROOT ( ROOT, XADJ. ADJNCY. MASK.
1 NLVL. XLS, LS )
FNLVL - FLOAT(NLVL)
NSEP - XLS(NLVL + 1) - 1
WIDTH - FLOAT(NSEP) / FNLVL
DELTP1 -10+ SQRT(C 0«WIDTH+13.0)/2.0)
IF (NSEP .GE. 50 .AND DELTP1 .LE. 0.5«FNLVL) GO TO 300
С - -- ---- - - -
С КОМ-НТА СЛИШКОМ МАЛА, ЛИБО СТР-РА УР-НЕИ ОЧЕНЬ
С ДЛИННАЯ И УЗКАЯ. ПЕРЕДАТЬ НА ВЫХОД ВСЮ КОМ-НТУ.
DO 200 I - 1. NSEP
NODE • LS(I)
SEP(I) - NODE
MASK(NODE) • 0
200 CONTINUE
RETURN
С НАЙТИ ПАРАЛЛЕЛЬНЫЕ СЕЧЕНИЯ.
с - ---
300 NSEP • О
1-0
400 I - I + 1
LVL - IFIX (FLOAT(I)»DELTP1 + 0.8)
IF ( LVL .GE. NLVL ) RETURN
LVLBEG - XLS(LVL)
LP1BEG - XLS(LVL + 1)
LVLEND - LP1BEG - 1
LP1END - XLS(LVL + 2) - 1
DO 500 J - LP1BEG, LP1END
NODE - LS(J)
XADJ(NODE) - - XADJ(NODE)
500 CONTINUE
С - •--
С ДЛЯ СЕЧЕНИЯ БЕРЕМ УЗЛЫ УРОВНЯ LVL. В РАЗД-ЛЬ
С ВКЛЮЧАЕМ ТОЛЬКО УЗЛЫ, ИМЕЮЩИЕ СОСЕДЕЙ В УРОВНЕ
С LVL+1. XAOJ ИСПОЛЬЗУЕМ ДЛЯ МАРККИ УЗЛОВ УРОВНЯ LVL+1.
с - - -
DO 700 J - LVLBEG, LVLEND
NODE • LS(J)
KSTRT - XADJ(NODE)
KSTOP - IABS(XADJ(NODE+1)) - 1
DO 600 К - KSTRT. KSTOP
NBR • ADJNCY(K)
IF ( XADJ(NBR) .GT. 0 ) GO TO 600
NSEP - NSEP + 1
SEP(NSEP) - NODE
MASK(NODE) . 0
CO TO 700
«00 CONTINUE
700 CONTINUE
DO 800 J - LP1BEG. LP1END
NODE - LS(J)
XADJ(NODE) . - XADJ(NODE)
800 CONTINUE
GO TO 400
END
260 Гл. 7. Методы параллельных сечений
§ 7.3. Об определении структуры оболочки диагональных блоков
В главе 4 изучалась структура оболочки симметричной мат-
матрицы Л. Было показано, что эта структура сохраняется при сим-
симметричном разложении. Другими словами, если F — матрица
заполнения для Л, то
В этом параграфе мы исследуем структуру оболочки для диа-
диагональных блоков матрицы заполнения при заданном разбиение
Это важно при формировании структуры данных для схем хра-
хранения из раздела 6.4.1.
7.3.1 Постановка задачи
Пусть разреженная симметричная матрица Л разбита на
блоки:
in •¦• A,
*зг ' " ' Ai
G.3.1)
Все Akk — квадратные подматрицы. Блочной диагональю мат-
матрицы А при заданном разбиении называется матрица
о
«32
Bdiag(A) =
G.3.2)
0
§ 7.3. Об определении структуры оболочки диагональных блоков 251
Пусть треугольный множитель L матрицы А разбит на блоки
таким же образом: \
п о4
Тогда блочной диагональю соответствующей матрицы заполне-
заполнения F будет матрица
О
Bdiag(F)
1
где Fkk = Lkk + Lkk, 1 ^ k ^ p.
Наша цель — определить структуру оболочки матрицы
Bdiag (F). Хотя Env (A) = Env (F), это равенство, вообще го-
говоря, не переносится на матрицы Bdiag (А) и Bdiag (f) вслед-
вследствие того, что при разложении вне множества Env (Bdiag (А))
могли появиться ненулевые элементы.
7.3.2. Характеризация оболочки блочной диагонали
посредством достижимых множеств
Напомним (глава 4), что структура оболочки матрицы А оп-
определяется столбцовыми индексами
ft (А) = min {/1 ац
1 < I < N.
С точки зрения ассоциированного графа GA = (ХА,ЕА), где
ХА = {xi хц}, эти числа описываются формулами
/, (А) = min{s\xge Adj (xt) U {*,}}.
G.3.3)
252 Гл. 7. Методы параллельных сечений
В этом разделе мы исследуем структуру оболочки матрицы
Bdiag(F), для чего установим связь столбцового индекса пер-
первого ненулевого элемента •> со структурой соответствующего
графа.
Пусть GA=(X*,EA) и GF=(XF,EF)—ненаправленные
графы, ассоциированные с симметричными матрицами А и F
соответственно. Пусть $ = {Yu Y2, ... Yp) — разбиение множе-
множества ХА, отвечающее блочному разбиению А. Полезно отметить,
что
и
^.Bdiag (/О _ /„A pBdiag {F)\
В нижеследующем тексте мы пишем /, вместо f, (Bdiag(F)).
Пусть строка i принадлежит k-uy блоку разбиения. Другими
словами, пусть xt ^ У*. С точки зрения графа заполнения числб//
выражается формулой
ft = min {s \s = i или {xs, xt) s EF
Свяжем теперь это число с исходным графом GA, используя
введенные в разделе 5.1.2 достижимые множества. Согласно
теореме 5.1.2, которая характеризует заполнение в терминах до"-
стижимых множеств, имеем
fl=min{s\xs^Yk, xt<=. Reach ({*s, {*i ^s-i})U {¦*«}}• G.3.4)
В теореме 7.3.2 мы установим более сильный результат.
Лемма 7.3.1.
Пусть х, е Yk, и пусть
S = Yl[J...[JYk_1.
Таким образом, S содержит все узлы первых k — 1 блоков..
Тогда
xt<= Reach (xfl, S)[){xu}.
Доказательство. Из определения/, следует, что {х(, Xf J е Е ,
поэтому, по теореме 5.1.2, х( е Reach fxf , {aCj xf _;}V Тогда
можно найти путь хг, хг , ..., xr, xf, где \хг , ..., х } с:
(}
-*) Уже в Bdiag(F), — Прим, перев.
§ 7.3 Об определении структуры оболочки диагональных блоков 263
Теперь мы покажем, что х, можно достигнуть из х, также и
через S, являющееся подмножеством множества {хи ..., xf _,}.
Если t = 0, то ясно, что xt e Reach (xf , S\. С другой стороны,
* *
*
* *
*
*
*
**
**
*
*
* *
*
*
***
*
*
*
* *
**
*
**
Рис. 7.3.1. БЛочная матрица А порядка 11.
если / ф 0, то пусть хг будет узлом с наибольшим номером
среди хг, ..., хт. Тогда х{, хг хг , хг есть путь от
xi к xr через {д:,, х2 хг _,), так что
Но rs < /,, поэтому, согласно определению /,, хг ф Yk или, дру-
S
гими словами, хт е S. Из выбора rs следует
{хг>, .... xrjcS,
и потому xt e Reach(xf , S\
Теорема 7.3.2.
Пусть xt e= Yk и S = У, U ... U Y*_i. Тогда
fi = min {s\ xs e Yk, xt e Reach (xs, S) (J {acs}}.
Доказательство. Если принять во внимание лемму 7.3.1, то
остается показать, что xt ф Reach (xr, S) для ^еУц и г < fi.
264 Гл. 7. Методы параллельных сечений
Предположим, напротив, что можно найти хг S Yk, для которого
г < fi и Xi e Reach (Яг, S). Так как
то x;S Reach (JCr, {xi, ..., Xr-i}). Поэтому {*,, Jcr} ^EF(Yk), что
противоречит определению /<•.
Следствие 7.3.3.
Пусть Xi и S — те же, что и в теореме 7.3.2. Тогда
fi — min {s | xs e Reach (xu S) [) {^}}.
Доказательство. Это утверждение вытекает из теоремы 7.3.2
и симметрии оператора «Reach».
Интересно сравнить полученный результат с тем, что дает
G.3.4). Для иллюстрации рассмотрим блочную матрицу на
рис. 7.3.1.
Возьмем У2= {Х5, Xs, Хт, х&}. Соответствующее множество S
есть {хи х2, х3, х^}. Имеем
Reach {хъ, S) = {xl0, xn},
Reach {х6, S) = {x7, xs, х<,, х10},
Reach {x7, S) = {^6, ^8},
Reaches, S) = {x6, x7, Xi0, xn).
Согласно следствию 7.3.3,
f8(Bdiag(P)) = 5,
U (Bdiag (F)) = f7 (Bdiag (F)) = fs (Bdiag (F)) = 6.
7.3.3. Алгоритм и подпрограммы вычисления оболочки
диагональных блоков
Из следствия 7.3.3 несложно получить метод вычисления чи-
чисел /, (Bdiag (F)), которые определяют структуру оболочки мат-
матрицы Bdiag (F). Однако при фактической реализации проще
применять лемму 7.3.1. Соответствующий алгоритм можно опи-
описать так.
Пусть §={Y\, ..., Yp}—заданное разбиение. Для каждого
блока Yk из разбиения выполнить следующее:
Шаг 1 (инициализация). S = Yi [) ... [] Yk-U T = S\]Yk.
Шаг 2 {основной цикл). Для каждого узла хт из Yk вы-
выполнить:
2.1. Определить множество Reach (xr,S) в подгра-
подграфе G(T).
2.2. Для каждого узла xi e Reach (Xr,S) положить
f
f
2,3. Переопределить Т: T*-i1 — {Reach(*,,S)U
§ 7.3. Об определении структуры оболочки диагональных блоков 255
Этот алгоритм реализован двумя подпрограммами, обсуж-
обсуждаемыми ниже.
FNBENV
REACH
REACH (find REACHable sets)
В графе заданы множество 5 и узел хф-S. Для изучения
достижимого множества Reach(x, S) полезно ввести родствен-
родственное понятие окрестности. Формально окрестность узла х в мно-
множестве 5 определяется так:
Nbrhd (х, S) =
{seS|s достижи.мо из х через подмножество множества 5}.
Достижимые множества и окрестности связаны следующей
леммой.
Лемма 7.3.4.
Reach (x, S) = Adj (Nbrhd (xy S) (J {*}).
Подпрограмма REACH использует это простое соотношение
для вычисления достижимого множества в заданном подграфе.
Подграф задается входными параметрами XADJ, ADJNCY и
MARKER. Узел принадлежит подграфу, если в массиве MARKER
ему соответствует нулевое значение. Подмножество 5 задается
вектором маски SMASK: узел принадлежит 5, если соответст-
соответствующее ему значение в массиве SMASK не равно нулю. Пере-
Переменная ROOT — это входной узел, чье достижимое множество
нужно определить.
Вычисленное достижимое множество содержится в (RCHSZE,
RCHSET). В качестве побочного продукта вычисляется также и
окрестность, помещаемая в (NHDSZE, NBRHD). Для узлов до-
достижимого множества и окрестности в массиве MARKER уста-
устанавливается значение, равное ROOT,
После присвоения начальных значений подпрограмма циклом
обходит соседей заданного узла ROOT. Соседи, не принадлежа-
принадлежащие подмножеству 5, включаются в достижимое множество, а
соседи из подмножества 5 — в окрестность. Далее исследуется
каждый сосед в подмножестве 5, в результате чего находятся
новые достижимые узлы. Этот процесс повторяется до тех пор,
пока не будут исчерпаны все соседи из S.
c>
с...............
С««........... REACH ДОСТИЖИМОЕ МНОЖЕСТВО *¦•*
С» ч.« •
с......... .....*. ••.....
С
С ИСПОЛЬЗУЕТСЯ ДЛЯ ОПРЕДЕЛЕНИЯ ДОСТИЖИМОГО МНОЖЕСТВА
С УЗЛА Y ЧЕРЕЗ ПОДМНОЖЕСТВО S(T,E. MH-BA REACH(Y,S))
С В ЗАДАННОМ ПОДГРАФЕ. ТАКЖЕ ВЫЧИСЛЯЕТ ОКРЕСТНОСТЬ
С Y В S, Т.Е. NBRHD(Y,8), MH-BO УЗЛОВ ИЗ S, КОТОРЫЕ
С МОГУТ БЫТЬ ДОСТИГНУТЫ ИЗ Y ЧЕРЕЗ ПОДМН-ВО
С MH-BA S.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С *ООТ - ЗАДАННЫЙ УЗЕЛ, НЕ ПРИНАДЛЕЖАЩИЙ S,
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С SMASK - ВЕКТОР МАСКИ ДЛЯ S. КОМПОНЕНТА
С - О, ЕСЛИ УЗЕЛ НЕ ПРИНАДЛЕЖИТ S,
С > О, ЕСЛИ УЗЕЛ ПРИНАДЛЕЖИТ S.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С (NHDSZE, NBRHD) - ОКРЕСТНОСТЬ.
С (RCHSZE, RCHSET) - ДОСТИЖИМОЕ МНОЖЕСТВО,
С ИаМЕНЯЕМЫЙ ПАРАМЕТР-
С MARKER - ИСПОЛЬЗУЕТСЯ ДЛЯ ЗАДАНИЯ ПОДГРАФА. УЗЛАМ
С ПОДГРАФА СООТВЕТСТВУЕТ О. ДО ВЫХОДА ЗНАЧЕНИЯ
С КОМПОНЕНТ ДЛЯ УЗЛОВ ДОСТИЖИМОГО МНОЖЕСТВА
С И ОКРЕСТНОСТИ ПЕРЕОПРЕДЕЛЯЮТСЯ НА ROOT.
С
с*
с
SUBROUTINE REACH ( ROOT. XADJ, ADJNCY, SMASK, MARKERr
I RCHSZE, RCHSET. NHDSZE, NBRHD )
С
INTEGER ADJNCYA), MARKER(l), NBRHD(l), RCHSET(l).
1 SMASK(l)
INTEGER XADJ(l), I, ISTOP, ISTRT, J, JSTOP, JSTRT,
1 NABOR, NBR, NHDBEG, NHDPTR, NHDSZE, NODE,
1 RCHSZE, ROOT
С
<:•»*••• ^......,........ ,
с
с
<г ИНИЦИАЛИЗАЦИЯ . . .
NHDSZE - О
RCHSZE - О
IF ( MARKER(ROOT) .GT. О ) GO TO 100
RCHSZE • 1
RCHSET(l) - ROOT
MARKER(ROOT) - ROOT
100 ISTRT - XADJ(ROOT)
ISTOP - XADJ(ROOT+1) - 1
IF ( ISTOP .LT. ISTRT ) RETURN
С
С ЦИКЛ ПО СОСЕДЯМ УЗЛА ROOT
С
DO 600 I - ISTRT, ISTOP
NABOR - ADJNCY(I)
IF ( MARKER(NABOR) .NE, 0 ) GO TO 600
IF ( SMASK(NABOR) .GT. 0 ) GO TO 200
С NABOR HE ВХОДИТ В S. ВКЛЮЧИТЬ В ДОСТ-МОЕ ПН-ВО.
6 I
§ 7.3. Об определении структуры оболочки диагональных блоков 237
RCH3ZE - RCHSZE + 1
RCHSET(RCHSZE) - NABOR
MARKER(NABOR) - ROOT
GO TO 600
С
С NABOR ВХОДИТ В S И ПРЕЖДЕ НЕ РАССМАТРИВАЛСЯ.
С ВКЛЮЧИТЬ В ОКРЕСТНОСТЬ. НАЙТИ УЗЛЫ,
С ДОСТИЖИМЫЕ ИЗ ROOT ЧЕРЕЗ NABOR.
С .
200 NHDSZE - NHDSZE + 1
NBRhD(NHDSZE) - NABOR
MARKER(NABOR) • ROOT
300
NHDBEG ¦
NHDPTR ¦
NODE
JSTRT .
JSTOP ¦
¦ NHDSZE
¦ NHDSZE
¦ NBRHD(NHDPTR)
¦ XADJ(NODE)
¦ XADJ(NODE+1) - 1
DO 500 J • JSTRT, JSTOP
NBR •
. ADJNCY(J)
IF ( MARKER(NBR) .NE. 0 ) GO TO 500
IF ( SMASK(NBR) .EQ. 0 ) GO TO 400
NHDSZE - NHDSZE + 1
NBRHD(NHDSZE) - NBR
MARKER(NBR) - ROOT
GO TO 500
400 RCHSZE - RCHSZE + 1
RCHSET(RCHSZE) - NBR
MARKER(NBR) - ROOT
500 CONTINUE
NHDPTR - NHDPTR + 1 <
IF ( NHDPTR LE. NHDSZE ) OO TO 300
600 CQNTINUE
RETURN
END
FNBENV (FiNd diagonal Block ENVelope)
Эта подпрограмма имеет то же назначение, что и FNTENV
из раздела 6.4.3. Обе используются для определения структуры
оболочки диагональных блоков факторизованной матрицы. В от-
отличие от FNTENV подпрограмма FNBENV находит точную
структуру оболочки. Хотя она работает для произвольных блоч-
блочных матриц, ее использование обходится дороже, чем FNTENV;
в то же время для упорядочений, производимых алгоритмом
RQT, структура, которую определяет FNTENV, вполне удовлет-
удовлетворительна. Однако для алгоритма параллельных сечений при-
применение более сложной подпрограммы FNBENV является весь-
весьма важным.
Входные данные FNBENV: структура смежности (XADJ,
ADJNCY), упорядочение (PERM, INVP) и разбиение (NBLKS,
XBLK). Информацию о структуре оболочки подпрограмма
помещает в индексный вектор XENV; переменная MAXENV ука-
указывает размер оболочки.
Требуются три рабочих вектора. Вектор SMASK используется
для задания узлов подмножества 5 (см. описание предыдущей
258 Гл 7 Методы параллельных сечений
подпрограммы). С другой стороны, узлам множества Г отве-
отвечают нулевые значения в массиве MARKER Последний ис-
используется также для временного хранения первого соседа
каждой строки обрабатываемого блока. Третий рабочий вектор
RCHSET содержит достижимое множество и окрестность. Так
как эти два множества не пересекаются, то вектору RCHSET
можно придать организацию, указанную на рисунке.
NHDSZE RCHSZE
RCHSET
Окрестность
Достижимое
множество
BLKBEG
с....... • • ••
с •••• • ••••• •
С....... FNBENV ... ПОСТРОЕНИЕ ОБОЛОЧКИ ДИАГ. БЛОКОВ ••
<:••• •• •• •
<:••••• • •
с
С НАХОДИТ ТОЧНУЮ СТРУКТУРУ ОБОЛОЧКИ ДИАГОНАЛЬНЫХ БЛОКОВ
С МНОЖИТЕЛЯ ХОЛЕССКОГО ДЛЯ ПЕРЕУПОРЯДОЧЕННОЙ БЛОЧНОЙ
С ПАТРИЦЫ.
с
С ВХОДНЫЕ ПАРАМЕТРЫ-
<Р (XADJ. ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С (PERM. INVP) - ВЕКТОРЫ ПЕРЕСТ-КИ И ОБРАТНОЙ ЛСРЕСТ-КИ,
С (NBLKS, XBLK) - РАЗБИЕНИЕ.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ_-
С XENV - ИНДЕКСНЫЙ ВЕКТОР ОБОЛОЧКИ.
С ENVSZE -W3MEP ОБОЛОЧКИ.
С
С РАБОЧИЕ ПАРАМЕТРЫ -
С SMASK - МАРКИРУЕТ РАССМОТРЕННЫЕ УЗЛЫ.
С MARKER - ИСПОЛЬЗУЕТСЯ В REACH.
С RCHSET - ИСПОЛЬЗУЕТСЯ В REACH. ХРАНИТ ДОСТИЖИМЫ!
С МНОЖЕСТВА И ОКРЕСТНОСТИ.
С
с
с
См«
с
с
о
с
с
с*
ПОДПРОГРАММЫ -
REACH.
SUBROUTINE FNBENV ( XADJ. ADJNCY. PERM. INVP. NBLKS. XBLK.
1 XENV. ENVSZE, SMASK. MARKER. RCHSET )
INTEGER ADJNCYA). INVP(l), MARKER(l). PERM(l),
1 RCHSETA). SMASKA). XBLKA)
INTEGER XADJ(l). XENVA). BLKBEG. BLKEND. I,
1 IFIRST. INHD. K. ENVSZE, NBLKS. NEONS.
1 NEWNHD. NHDSZE. NODE. RCHSZE
ф 7,3 Об определении структуры оболочки диагональных блоков 259
С
с
С ИНИЦИАЛИЗАЦИЯ.. .
с
NEQNS - XBLK(NBLKS+1) - 1
ENVSZE - 1
DO 100 I - 1, NEQNS
SMASK(I) - 0
MARKER(I) - 1
100 CONTINUE
С
С ЦИКЛ ПО БЛОКАМ
с
DO 700 К - 1, NBLKS
NHDSZE • О
BLKBEG - XBLK(K)
BLKEND - XBLK(K+1) - 1
DO 200'I - BLKBEG, BLKEND
NODE - PERM(I)
MARKER(NODE) - 0
200 CONTINUE
С - -
С ЦИКЛ ПО УЗЛАМ ТЕКУЩЕГО БЛОКА
С
DO 300 I - BLKBEG, BLKEND
NODE - PERM(I)
CALL REACH ( NODE, XADJ, ADJNCY, SMASK,
1 MARKER, RCHSZE, RCHSET(BLKBEG),
1 NEWNHD, RCHSET(NHDSZE+1) )
NHDSZE - NHDSZE + NEWNHD
IFIRST - MARKER(NODE)
IFIRST - INVP(IFIRST)
XENV(I) - ENVSZE
ENVSZE - ENVSZE + I - IFIRST
300 CONTINUE
С -
С ДЛЯ УЗЛОВ ИЗ ОК.Р-СТИ ИЗМЕНИТЬ MARKER.
t r-
IF ( NHDSZE .LE 0 ) GO TO 500
DO 400 INHD - 1, NHDSZE
NODE - RCHSET(INHD)
MARKER(NODE) • 0
400 CONTINUE
С - -
С ДЛЯ УЗЛОВ ТЕКУЩЕГО БЛОКА ИЗМЕНИТЬ
С ЗНАЧЕНИЯ В MARKER И SMASK.
с
500 DO 600 I - BLKBEG, BLKEND
NODE - PERM(I)
MARKER(NODE) - 0
SMASK(NODE) - 1
600 CONTINUE Л
700 CONTINUE
XENV(NEQNS+1) . ENVSZE
ENVSZE - ENVSZE - 1
RETURN
END
260 Гл. 7. Методы параллельных сечений
Работа подпрограммы начинается с установления исходных
состояний для рабочих векторов SMASK и MARKER. В основ-
основном цикле последовательно обрабатываются все блоки. Узлы
очередного блока добавляются к подграфу путем присвоения
нулевых значений соответствующим компонентам массива
MARKER. Для каждого узла i данного блока вызывается под-
подпрограмма REACH; узлы найденного достижимого множества
будут иметь узел i своим первым соседом. Прежде чем перейти
к обработке следующего блока, восстанавливаются прежние
значения в массиве MARKER и узлы текущего блока добавляют-
добавляются к подмножеству S.
7.3.4. Анализ временной сложности алгоритма
Для произвольных блочных матриц сложность алгоритма
вычисления оболочки диагональных блоков зависит от блочного
порядка р, разреженности матрицы и характера связей между
блоками. Однако для разбиений, полученных посредством парал-
параллельных сечений, имеется следующий результат.
Теорема 7.3.5.
Пусть G=(X,E), и пусть $={У\, ..., Ур}—разбиение,
полученное посредством параллельных сечений. Сложность ал-
алгоритма FNBENV есть О(\Е\).
Доказательство. Для узла xt из первых р—1 блоков под-
подпрограмма REACH при вызове всего лишь просматривает список
смежности этого узла. С другой стороны, при обработке узлов
последнего блока Ур просматриваются не более чем по разу
списки смежности всех узлов графа. Следовательно, в алгоритме
в целом структура смежности проходится не более чем два
раза.
Упражнения
7.3.1. Постройте пример блочной матрицы А с фактор-структурой дерева,
для которой' посредством подпрограммы FNTENV не удается определить точ-
точную структуру оболочки блочно-диагональной матрицы Bdiag(F), где F —
матрица заполнения для А.
7.3.2. Приведите пример, доказывающий, что теорема 7.3.5 справедлива
не для любого древовидного разбиения ф.
7.3.3. Это упражнение предполагает решение нескольких конечноэлемент-
ных матричных задач Ах = Ь порядка ml и типа, рассмотренного в § 7.1.
При этом m последовательно принимает значения 5, 10, 15, 20, а / = 2т. По-
Положите диагональные элементы А равными 8, внедиагоиальные') равными
—1 н выберите правую часть Ь таким образом, чтобы все компоненты реше-
решения были равны единице. С помощью программ главы 4 решите указанные сн-
') Имеются в виду внедиагональные элементы, принадлежащие опнсан-
ВРЙ в § 7,1 структуре ненулевых элементов Nonz(/4).—Прим. перев.
§ 7.4. Дополнительные замечания 261
стемы, записывая количество необходимой памяти и время исполнения каж-
каждой фазы решения каждой системы. Проделайте то же самое, используя при-
приведенные в этой главе подпрограммы метода параллельных сечений вместе
с соответствующими подпрограммами из главы. 6. Сравните оба метода ре-
решения этих коиечноэлемеитных задач с точки зрения критериев, обсуждавших-
обсуждавшихся в § 3 главы. 2.
§ 7.4. Дополнительные замечания
Интересно было бы испытать более сложные способы выбора
параллельных сечений. Например, вместо фиксированного б
можно было бы использовать последовательность б,, i = 1,2
где б, определяется на основе локальной информации о той части
Рис. 7.4.1. Двухуровневое упорядочение посредством параллельных сечеиий.
Здесь ctj = 2 сечений 1-го уровня, Ог = 3 сечеиий 2-го уровня н (о\ + 1) (аг +
+ 1) = 12 независимых блоков. Узлы каждого нз них нумеруются в соответ-
соответствии с их расположением на сетке, столбец за столбцом.
структуры уровней, которую остается обработать после выбора
первых i— 1 сечений. Исследования такого рода, нацеленные на
получение робастного эвристического алгоритма, являются хо-
хорошей темой для курсовых и дипломных работ.
Основная идея, придающая эффективность методу параллель-
параллельный сечений,—-это использование приема «отбрасывания»
(см. § 6.2). Этот прием можно применять рекурсивно, как опи-
описано в разделе дополнительных замечаний главы 6. Отсюда сле-
следует, что и схему параллельных сечений данной главы можно
обобщить аналогичным образом. В простейшей форме идея
состоит в том, чтобы использовать технику параллельных сече-
сечений и для а+1 независимых блоков вместо того, чтобы упоря-
упорядочивать их посредством алгоритма RCM. Рис. 7.4.1 иллюстри.
рует суть этой двухуровневой схемы.
262 Гл. 7. Методы параллельных сечений
Разумеется, эту идею можно обобщить на случай большего
числа уровней. Однако на практике использование более чем
двух уровней, по-видимому, не дает существенного выигрыша.
Можно показать, что для сеточной п X п задачи (т = / = п)
при оптимальном выборе Oi и о2 память и число операций для
двухуровневого упорядочения будут величинами порядка О(п7/3)
и О(п10/5) соответственно. Аналогичные цифры для обсуждав-
обсуждавшейся в этой главе обычной (одноуровневой) схемы параллель»
ных сечений — О(п5/2) и О(п7'2) (Ng 1979).
8. Методы вложенных сечений
§ 8.0 Введение
В главе 7 мы познакомились с так называемым методом па-
параллельных сечений. Мы видели, что этот метод легко приспо-
приспосабливается к неявной схеме древовидного разбиения из главы 6.
В этой главе мы рассмотрим другой метод сечений, который,
так же как и алгоритм минимальной степени из главы 5, пы-
пытается минимизировать заполнение.
" Метод вложенных сечений этой главы предназначен главным
образом для матричных задач, возникающих в конечноразност-
ных и конечноэлементных приложениях. Главные преимущества
алгоритма из § 8.2 в сравнении с алгоритмом минимальной сте-
степени — это его скорость и его скромные и заранее предсказуе-
предсказуемые требования к памяти. Получаемые упорядочения по харак-
характеру схожи с теми, какие дает алгоритм минимальной степени.
По этой причине в данной главе мы не касаемся вопросов схемы
хранения, процедуры распределения памяти или организации
численных подпрограмм. Для метода вложенных сечений го-
годятся соответствующие решения из главы 5
Разделители, введенные нами в § 3.1, играют центральную
роль при исследовании разреженной матричной факторизации.
Пусть А — симметричная матрица, GA — ассоциированный с ней
неориентированный граф Рассмотрим разделитель S, удаление
которого разбивает граф GA на две части, множества узлов кото-
которых суть Ci и С2.
Если узлы S нумеровать после нумерации узлов С\ и С2, то
это индуцирует разбиение соответствующим образом упорядо-
упорядоченной матрицы, форма которого, показана на рис. 8.0.1 Сделаем
теперь ключевое замечание: нулевой блок матрицы остается
нулевым и после разложения Поскольку одной из главных целей
при исследовании разреженных матричных вычислений является
сохранение по возможности большего числа нулевых элементов,
то использование разделителей указанным способом приобретает
важное значение. При подходящем их выборе можно надеяться
на получение большой подматрицы, которая гарантированно
остается нулевой. Ту же идею можно применять рекурсивно,
сохраняя аналогичным образом нули в подматрицах.
264 Гл 8 Методы вложенных сечений
Рекурсивное применение этой основной идеи приводит к ме-
методу, за которым закрепилось название метода вложенных се-
сечений1). В 1973 г. Джордж использовал эту технику для разре-
разреженных систем, ассоциированных с регулярными (л X я)-сетка-
At 0 У,
О А% У%
' 1 % ™S
Рис. 8.0.1. Использование разделителя для разбиения матрицы.
ми, состоящими из (п— IJ малых элементов. В следующем па-
параграфе мы проведем подробный анализ метода для этого спе-
специального случая.
§ 8.1. Вложенные сечения регулярной сетки
8.1.1. Упорядочение
Пусть X— множество вершин регулярной (п X п) -сетки.
Через So обозначим множество узлов сеточной линии, которая
делит X на две по возможности равные части R1 и R2. Рис. 8.1.1
показывает случай п = 10. Если вначале пронумеровать строка
за строкой узлы компонент R1 и R2, а затем узлы 50, то получим
матричную структуру, изображенную на рис. 8.1.2. Такое упоря-
упорядочение будем называть одноуровневым упорядочением посред-
посредством сечений.
Чтобы получить упорядочение, соответствующее методу вло-
вложенных сечений, перейдем к сечению двух оставшихся компо-
компонент. Выберем множества вершин
S'czR1, j = l, 2,
состоящие из узлов сеточных линий, которые делят R1 (по
возможности) на равные части. Если переменные, ассоцииро-
ассоциированные с вершинами из R' — S', пронумеровать прежде, чем
переменные, ассоциированные с вершинами S1, то мы индуци-
индуцируем на двух ведущих главных подматрицах в точности ту
же структуру, что и на всей матрице.
') В оригинале — the nested dissection method. — Прим. перев.
§81. Вложенные сечения регулярной сетки 265
86
81
76
71
66
61
56
51
46
41
87
82
77
12
67
62
57
52.
47
42
88
83
78
73
68
63
58
53
48
43
89
84
79
74
69
64
59
54
49
44
90
85
80
75
70
65
60
55
50
45
100
99
98
97
96
95
94
93
92
91
40
36
32
28
24
20
16
12
8
4
39
35
31
27
23
19
15
11
7
3
38
34
30
26
22
18
14
10
6
2
37
33
29
25
21
17
13
9
5
1
Рис. 8.1.1. Одноуровневое упорядочение посредством сечений сетки 10 X
• *•• •
и. *.
. ;:. •.
• •• •
•¦ ••• •
\>. \
•:Х\
. "И. *.
V».'-.
-."•« \
• •• •
• ••• •
' • • . .
• • .
•
•
•
•
•
•
•
•
•
•
*
•
•
•
•
•
•
Ч.
Рис. 8.1.2. Структура матрицы, соотвегетвующая одноуровневому упорядоче-
упорядочению посредством сечений.
266 Гл 8 Методы вложенных сечений
Процесс можно продолжать, пока не останутся уже неде-
неделимые компоненты. Это и дает упорядочение посредством вло-
вложенных сечений. Рис. 8.1.3 показывает такое упорядочение для
78
76
80
74
72
77
75
79
73
71
85
84
S3
82
81
68 67
66 65
70
64 63
62 61
90 «9 88 87 86
54
52
56
50
53
51
55|
49
60
59
58
57
46 45
44 43
48 47 |
42 41
100
99
98
97
96
95
94
93
92
91
29 28
27 26
31 30
25 24
23 22
36
¦*<;
34
33
32
20
19
21
18
17
40 39 38 37
10
12
16
15
14
13
3
2
4
1
Рис. 8.1.3. Упорядочение сетки 10 X Ю посредством вложенных сечений.
сеточной задачи 10X10, а рис. 8.1.4— структуру соответственно
упорядоченной матрицы. Отметьте повторение в этой структуре
основного шаблона.
8.1.2. Требования к памяти
Метод вложенных сечений использует стратегию, обычно
называемую «разделяй и властвуй». Эта стратегия разделяет
задачу на меньшие подзадачи; их индивидуальные решения
можно скомбинировать и получить решение исходной задачи.
Кроме того, подзадачи имеют и структуру, аналогичную перво-
первоначальной; поэтому процесс можно повторять рекурсивно, пода
решения подзадач не станут тривиальны.
При исследовании таких стратегий обычно приходится ре-
решать те или иные разностные уравнения. Мы сформулируем
сейчас некоторые результаты, которые понадобятся при ана->
лизе требований к памяти для метода вложенных сечений. Их
доказательство оставляется читателю.
Лемма 8.1.1.
Пусть f(n) = 4f(n/2)+kn2+O(n). Тогда
§81 Вложенные сечения регулярной сетки 267
Лемма 8.1.2.
Пусть g(n)=g(n/2)+kn2log2n+O(n2). Тогда
g()
Лемма 8.1.3.
Пусть h(n)=2h(n/2)+kn4og2n+O (л2). Тогда
h(n) = 2kn2log2n-\-O(n2).
Чтобы провести анализ метода вложенных сечений, мы вве-
введем окаймленные («Х«)-сетки. Окаймленная (пХп) -сетка —
П?ТЛЧ-.
В! .'!
ГУ* •
"I i .. .
•••
г..
[•'..:;i!.;::;t
I:
.5};
Рис. 8.1.4. Структура матрицы, соответствующая упорядочению посредством
вложенных сечений
это обычная (лХя) -сетка плюс окаймление одной или несколь-
нескольких сторон границы посредством дополнительных сеточных
линий. На рис. 8.1.5 приведены некоторые примеры окаймлен-
окаймленных CX3)-сеток.
268 Г л 8 Методы вложенных сечений
Теперь мы можем приступить к подсчету объема памяти,
необходимого для метода вложенных сечений. Пусть S(n,i)
«0
1"ис. 8.1.5. Примеры окаймленных сеток 3X3.
обозначает число ненулевых элементов треугольного множи-
множителя для матрицы, ассоциированной с («Хп)-сеткой, окай-
окаймленной вдоль / сторон. Предполагается, что сетка упорядо-
Рис. 8.1.6. Сечение сеткн п X п..
чена по методу вложенных сечений. Ясно, что нужная нам ве-
величина— это S(n, 0). Впредь в случае i=2 мы всегда имеем.
в виду сетку, показанную на рис. 8.1.5 (в), а не такую сетку:
§81. Вложенные сечения регулярной сетки 269
В последующем тексте мы установим соотношения между
величинами S(n,i), О ^ i ^ 4. Рассмотрим вначале S(n, 0).
На рис. 8.1.6 сетка «Х« разделена на 4 меньшие подсетки по-
посредством крестообразного разделителя. Переменные из обла-
областей 1, 2, 3 и 4 должны быть пронумерованы прежде, чем
переменные из области 5. Тогда будет индуцирована матрич-
матричная структура, показанная на рис. 8.1.7
Ая
Агг
А*
Аъг
4н
45л
4k
АЬ
Аьь
1-51 I 1-52
Рис. 8.1.7. Структура матрицы для сочения^ показанного на рис. 8.1.6.
Ненулевые элементы треугольного множителя сосредоточе-
сосредоточены в блоках Llt, I ^ i ^ 4, и L5t, I ^ i ^ 5. Поскольку та же
стратегия применяется к меньшим подсеткам, имеем
т) (Lit) + т] {Ьы) « S (л/2, 2), I < / < 4.
Так как L55 соответствует узлам крестообразного разделителя,
то число ненулевых элементов можно определить, пользуясь
теоремой 5.1.2. Оно равно
= 2 Z l + /2 + О («) = 7п2/4 + О (п).
1-п
Тем самым получено первое разностное уравнение-
S(n, 0) = 4S(?,
(8.1.1)
270 Гл. 8. Методы вложенных сечений
Остальные уравнения могут быть установлены таким же
образом. Все они выражают равенство: S{n,i) — стоимость
хранения четырех окаймленных подсеток п/2 X п/2 -\- стои-
стоимость хранения крестообразного разделителя. Предоставляем
читателю проверку следующих результатов:
5 (л, 2) = S (п/2, 2) + 2S (п/2, 3) + S (п/2, 4) + 19п2/4 +
+ О(п), (8.1.2)
S(n, 3) = 2S(n/2, 3) + 2S(n/2, 4) + 25«2/4 + О (п), (8.1.3)
S (п, 4) = 4S (п/2, 4) + 31п2/4 + О (п). (8.1.4)
Теорема 8.1.4.
Число ненулевых элементов треугольного множителя L
матрицы, ассоциированной с регулярной (n~X.fi)-сеткой, кото-
которая упорядочена посредством вложенных сечений, выражается
формулой
Доказательство. Нужный результат следует из разностных
уравнений (8.1.1) — (8.1.4). Применяя лемму 8.1.1 к уравнению
(8.1.4), получаем
После подстановки в (8.1.3) имеем
S (п, 3) = 2S (п/2, 3) + 31 (n2log2n)/8 + О(п2).
Согласно лемме 8.1.3, решением этого уравнения будет
S(n, 3) = 31 (n2log2n)/4 + О (п2).
Подставляя выражения для S(n, 3) и S(n, 4) в уравнение
(8.1.2), получим
S(n, 2)=S(n/2, 2) + 93(ra2log2rt)/16 + O(«2).
Решение этого уравнения —
S(n, 2) = 31 (n2log2ra)/4 + О (я2),
а тогда
ц (L) = S (п, 0) = 31 (n2log2n)/4 + О (п2).
В доказательстве теоремы 8.1.4 интересно отметить тот
факт, что асимптотические оценки для всех S(n,i), i=0, 2, 3,
4, совпадают и равны 31 (n2log2 п)/4 (а при i= 1?)
8.1.3. Число операций
Пусть А—матрица, ассоциированная с (п X п) -сеткой, упо-
упорядоченной методом вложенных сечений. При оценке числа
операций в разложении А мы можем следовать тем же путем,
§81. Вложенные сечения регулярной сетки 271
что и в предыдущем разделе. Вначале сформулируем некоторые
дополнительные результаты о разностных уравнениях
Лемма 8.1.5.
Пусть f{n)=f{n/2) + kn* + O(n2log2n). Тогда
Лемма 8.1.6.
Пусть g{n) = 2g(n/2)+kn3 + O{n2\og2n). Тогда
Лемма 8.1.7.
Пусть h{n) = 4/i(л/2) + kn3 + О(п2). Тогда
h(n) = 2kn3+O(n2log2n).
По аналогии с S(n,i) введем число Q{n,i) операций, не-
необходимых при разложении матрицы, ассоциированной с (дХ
Хя)-сеткой, которая окаймлена вдоль / сторон. Предполагает-
Предполагается, что сетка упорядочена методом вложенных сечений. Для
вычисления 9(л,0) снова рассмотрим рис. 8 1.6. Ясно, что
9 (л, 0) есть стоимость исключения в четырех окаймленных
(я/2Хя/2)-подсетках плюс стоимость исключения узлов в
крестообразном сечении. Применяя теорему 2.1.2, имеем
Зп/2 п
в (я, 0)«49(д/2, 2) + ?V + 4j>
= 49 (л/2, 2) + 19д3/24 + п3/6 + О (п2)
= 4в(я/2, 2) + 23л3/24 + О (п2). (8.1.6)
Предоставляем читателю проверку следующих равенств:
в (я, 2)=в (я/2, 2) + 26 (л/2, 3) + в(я/2, 4) + 35л3/6 + О (га2), (8.1.6)
в (я, 3) = 26 (я/2, 3) + 29 (л/2, 4) + 239л3/24 + О (л2), (8.1.7)
9 (л, 4) = 49(л/2, 4) + 371д3/24 + О(л2). (8.1.8)
Теорема 8.1.8.
Число операций, необходимых для разложения матрицы,
ассоциированной с (п~Х,п)-сеткой, в методе вложенных сечений
равно
829д3/84 + О (n2log2n)
Доказательство. Нужно определить число 9(д, 0). Применяя
лемму 8.1.7 к уравнению (8.1.8) получаем
9 (я,4) = 371л3/12 + О {n2log2n).
Теперь уравнение (8.1.7) можно переписать в виде
в (л, 3) = 29 (га/2, 3) + 849д3/48 + О (n2log2n).
8T2 Гл 8 Методы вложенных сечений
Согласно лемме 8.1.6,
6 (га, 3) = 283га3/12 + О rra2log2ra).
Подставляя выражения для &(га, 3) и б(га,4) в (8.1.6), получим
6 (га, 2) = 6 (га/2, 2) + 1497га3/96 + О (ra2log2ra),
откуда по лемме 8.1.5
6 (га, 2) = 499га3/28 + О (ra2log2ra).
Наконец, из уравнения (8.1.5) следует
8 (га, 0) = 829га3/84 + О (ra2log2ra).
8.1.4. Оптимальность упорядочения
В этом разделе мы установим нижние оценки для числа
ненулевых элементов треугольного множителя (т. е. объема
основной памяти) и числа операций при выполнении симметрич-
симметричного разложения для произвольного упорядочения матрицы,
ассоциированной с регулярной (га X «) -сеткой. Мы покажем,
что для разложения требуется не менее О(п3) операций, а со-
соответствующий нижний треугольный множитель должен иметь
по меньшей мере O(ra2log2«) ненулевых элементов. Метод вло-
вложенных сечений из раздела 8.1.1 достигает этих нижних гра-
границ и, следовательно, может рассматриваться как оптималь-
оптимальный по порядку.
Выведем вначале нижнюю оценку для числа операций.
Лемма 8.1.9.
Пусть G = (X, E)— граф, ассоциированный с (гаХ«) -сет-
-сеткой. Пусть х\,щХ2, ¦¦¦, xn — произвольное упорядочение G. Тогда
найдется узел xt такой, что
| Reach (л;,, {*,, ..., ж^}) |>га~ 1.
Доказательство. Пусть xt — первый узел, исключение кото-
которого завершает исключение какой-либо строки или столбца се-
сетки. Пусть для определенности это будет столбец (строка). На
этом этапе еще остаются по крайней мере га—1 сеточных строк
(столбцов), не все узлы которых исключены. В каждой из этих
строк (столбцов) имеется хотя бы один узел, которого можно
достигнуть из xi через подмножество {х\, ..., xt~\}. Это дока-
доказывает лемму.
Теорема 8.1.10.
Разложение матрицы, ассоциированной с (га X я) -сеткой,
требует не менее О (га3) операций.
§81 Вложенные сечения регулярной сетки 273
Доказательство. Согласно лемме 8.1.9, найдется узел х, та-
такой, что подграф, определяемый множеством
Reach (xh {xt **-i})U{*J>
является кликой в графе заполнения С^ (см. упр. 5.1.4) и
при этом имеет по меньшей мере п узлов. Он соответствует за-
заполненной («Х«) -подматрице в матрице заполнения F, по-
поэтому симметричное разложение требует не менее п3/6 + О(п2)
операций.
Вывод нижней оценки для основной памяти следует иной
линии. Для произвольной (&Х k) -подсетки в нижеследующей
лемме указывается специальное ребро в результирующем гра-
графе заполнения.
Лемма 8.1.11.
Рассмотрим произвольную (& X k)-подсетку заданной сет-
сетки п X п. В графе С найдется ребро, соединяющее пару па-
параллельных граничных линий подсетки.
Доказательство. В (k X &)-подсетке— четыре граничные се-
сеточные линии. Пусть xt — первый граничный узел подсетки,
после исключения которого будет полностью исключена какая-
либо граничная линия (в которую не включаются угловые вер-
вершины). Всегда найдутся два узла в остающихся параллельных
граничных линиях, которые связаны через множество
(См. узлы, указанные на рисунке.) Другими словами, в OF
имеется соединяющее их ребро.
Граница,
исключенная
пврВой
О
Еще не исключенные
узлы
Исключенные
узлы
Теорема 8.1.12.
Треугольный множитель матрицы, ассоциированной с («X
X «) -сеткой, имеет не менее O(«2log2«) ненулевых элементов.
274 Гл. 8. Методы вложенных сечений
Доказательство. Рассмотрим произвольную подсетку раз-
размера k. Из леммы 8.1.11 следует, что в С имеется ребро, со-
соединяющее пару граничных линий подсетей. Такое ребро мо-
может отвечать, самое большее, k различным подсеткам размера
k. Число всех подсеток размера k равно (п — k -f lJ. Поэтому
число различных ребер указанного типа ограничено снизу ве-
величиной
(n-k + iy
Кроме того, для подсеток разных размеров соответствующие
ребра должны быть различны. Отсюда следует, что
(п-* + 1)»
Упражнения
8.1.1. Пусть А — матрица, ассоциированная с (л X л)-сеткой, которая упо-
упорядочена по одноуровневой схеме сечений. Показать, что:
а) число операций при выполнении симметричного разложения равно
A3/24)л4 + О(л3);
б) число непулевых элементов множителя L равно п3-\-О(п2).
8.1.2. Доказать формулы для решений разностных уравнений из лемм
8.1.1-8.1.3 и 8.1.5—8.1.7.
8.1.3. При выводе уравнения (8.1.6) для 9(«, 2) мы предполагали^ что
крестообразный разделитель упорядочен в соответствии с рисунком (а). Обо-
Обозначим через 9'(л, 2) аналогичное число при использовании упорядочения (б).
лТ&
h
Показать, что
9' (п, 2) = 9' (я/2, 2) + 29 (п/2, 3) + 9 (п/2, 4) + 125п3/24 + О (п!).
Сравнить числа 8 (л, 2) и 9'(л, 2).
8.1.4. Доказать утверждения, аналогичные теоремам 8.1.4 и 8.1.8, для про-
произвольной (пг X /) -сетки, где m велико я/п<1.
8.1.5. Доказать, что любому упорядочению сетки л X л отвечает матрица,
ширина ленты которой не меньше л — 1.
8.1.6. Рассмотрим сетку л X п. Известно, что ассоциированный граф О =
= (X, Е) удовлетворяет изопараметрическому неравенству: для произволь-
произвольного подмножества 5 такого, что |5| ^ п2/2, справедливо
Доказать, что при любом упорядочении G профиль не будет меньше, чем
О(л3).
§ 8.2. Вложенные сечения для произвольных задач
275
8.1.7. Предположим, что для сеточной (яХя)-задачи выполняется «не-
«неполный алгоритм вложенных сечений» (George et al. 1978c). Это значит, что
производятся лишь сечения / уровней, где / < Iog2 n, а остающиеся незави-
независимые сеточные массивы упорядочиваются построчно. Показать, что при
/ ^ Iog2 у п. число операций для такого упорядочения остается величиной
О(пъ). Показать, что число ненулевых элементов соответствующего множителя
L равно О (п2 V"")-
8.1.8. Используя метод, принадлежащий Штрассену (Strassen 1969) и об-
обобщенный Банчем и Хопкрофтом (Bunch, Hopcroft 1974), можно решать за-
заполненные системы линейных уравнений и перемножать две заполненные мат-
матрицы порядка т за О (ff!log3 7) операций. На основе этого результата и моди-
модифицируя леммы 8.1.5—8.1.7, показать, что сеточные (пХя)-задачи можно
решать, пользуясь методом вложенных сечений, за О (nlog '7) операций (Rose
1976b)
§ 8.2. Вложенные сечения для произвольных задач
8.2.1. Эвристический алгоритм
Оптимальность метода вложенных сечений для сеточной
(п X я)-задачи была установлена в предыдущем разделе. Оче-
Очевидна важность основной идеи: деления сетки на две части
приблизительно одинакового размера посредством малого раз-
разделителя. В этом разделе мы опишем эвристический алгоритм,
который применяет эту стратегию к упорядочению произволь-
произвольного графа.
Как найти малый разделитель, который разбивал бы за-
заданный граф на компоненты примерно одинакового размера?
Наш метод состоит в построении для графа длинной структу-
структуры уровней и выборе малого разделителя из «среднего» уров-
уровня. Пусть G=(X,E)—заданный граф. Алгоритм упорядоче-
упорядочения посредством сечений можно описать так.
Шаг 1 (инициализация). Положить R = X, N=\X\.
Шаг 2 (построить структуру уровней). Найти в G(R) связ-
связную компоненту G(C) и построить для нее структуру уровней
с корнем в псевдопериферийном узле г:
<?(r) = {Z.o, Lu ..., L,}.
Шаг 3 (найти разделитель). Если / =?[ 2, положить S = С и
перейти к шагу 4. В противном случае положить / = |_ (I +
+ 1)/2 J и определить множество S с: Lj такое, что
Шаг 4 (упорядочение разделителя и цикл). Пронумеровать
узлы разделителя S числами от N— \S\ -\- 1 до N. Положить
R+-R — S и N^-N — \S\. Если R Ф 0, перейти к шагу 2.
На шаге 3 алгоритма разделитель S можно получить про-
простым отбрасыванием тех узлов из Z./, которые не смежны ни с
276 Гл 8 Методы вложенных сечений
одним узлом из L,+i. Во многих случаях это уменьшает размер
разделителя '>.
8.2.2. Машинная реализация
Набор подпрограмм, реализующих алгоритм упорядочения
посредством вложенных сечений, показан на рисунке.
GENND
FNDSEP
REVRSE
FNROOT
ROOTLS
Подпрограммы FNROOT и ROOTLS описаны в разделе 4.3.3,
а служебная подпрограмма REVRSE — в разделе 7.2.2. Осталь-
Остальные две подпрограммы описываются ниже.
GENND (GENeral Nested Dissection ordering)
Это — ведущая подпрограмма набора. Она используется для
упорядочения произвольного несвязного графа методом вло-
вложенных сечений. Входной граф задается посредством NEQNS
и (XADJ, ADJNCY); выходное упорядочение хранится векто-
вектором PERM. Рабочий вектор MASK используется для марки-
маркировки узлов, которые уже пронумерованы в процессе упорядо-
упорядочения. Нужны еще два рабочих вектора (XLS, LS); они ис-
используются вызываемой подпрограммой FNDSEP.
Работа подпрограммы начинается с установления началь-
начального состояния для вектора MASK. Затем обходится граф, пока
не будет найден еще не нумерованный узел L Этот узел i оп-
определяет компоненту в неупорядоченной части графа. Далее
происходит обращение к подпрограмме FNDSEP, которая на-
находит разделитель для компоненты. Заметим, что разделитель
помещается в вектор PERM, начиная с позиции NUM-|-1. По-
Поэтому после нумерации всех узлов для получения окончатель-
окончательного упорядочения необходимо обратить порядок компонент в
векторе PERM.
М По сравнению с \Lj\. — Прим перев.
О««*...« GENND ... АЛГОРИТМ ВЛОЖЕННЫХ СЕЧЕНИЙ ДЛЯ *¦
с* •• ••• произвольного графа .«.«...........••
с •
с
С НАХОДИТ УПОРЯДОЧЕНИЕ ПРОИЗВОЛЬНОГО ГРАФА МЕТОДОМ
С ВЛОЖЕННЫХ СЕЧЕНИЙ.
С
с
С ВХОДНЫЕ ПАРАМЕТРЫ -
С NEQNS - ЧИСЛО УРАВНЕНИЙ.
С (ХАШ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ- „
С PERM - УПОРЯДОЧЕНИЕ ПОСРЕДСТВОМ ВЛОЖЕННЫХ СЕЧЕНИЙ.
С
С (ИБОЧИЕ ПАРАМЕТРЫ-
С MASK - ИСПОЛЬЗУЕТСЯ ДЛЯ МАРКИРОВКИ ПЕРЕМЕННЫХ»
С ПРОНУМЕРОВАННЫХ ПРИ УПОРЯДОЧЕНИИ.
С (XLS, LS) - ЭТА ПАРА^ИСПОЛЬЗУЕТСЯ В FNROOT ДЛЯ
С ВРЕМЕННОГО ХРАНЕНИЯ СТРУКТУРЫ УРОВНЕЙ.
С
С ПОДПРОГРАММЫ -
С FNDSEP REVRSE
С
SUBROUTINE GENND ( NEQNS, XADJ, ADJNCY, MASK,
1 PERM, XLS, LS )
INTEGER ADJNCY(l), MASKA), LSA), PERMA),
XLS(l)
INTEGER XADJ(l), I, NEQNS, NSEP, NUM, ROOT
DO 100 I - 1, NEQNS
MASK(I) - 1
100 CONTINUE
NUM - 0
DO 300 I - 1, NEQNS
С ДЛЯ КАЖДОЙ МАРКИРОВАННОЙ КОМПОНЕНТЫ...
с
200 IF ( MASK(I) .EQ. О ) GO TO 300
ROOT - I
С
С НАЙТИ РАЗД-ЛЬ. ПРИСВ. УЗЛАМ ОЧЕРЕДНЫЕ НОМЕРА.
с
CALL FNDSEP ( ROOT, XADJ, ADJNCY, MASK,
1 NSEP, PERM(NUM+1), XLS, LS )
NUM - NUM + NSEP
IF ( NUM .GE. NEQNS ) GO TO 400
GO TO .200
300 CONTINUE
с ___.
С Т.К. ПОРЯДОК, В К-РОМ ОПРЕДЕЛЯЮТСЯ РАЗДЕЛИТЕЛИ,
С ОБРАТЕН ИХ ПОРЯДКУ В ИСКОМОЙ СТР-РЕ, ТО ВЫЗЫВАЕТСЯ
С REVRSE, ОБРАЩАЮЩАЯ УПОРЯДОЧЕНИЕ PERM.
С
400 CALL REVRSE ( NEQNS, PERM )
RETURN
END
278 Га 8 Методы вложенных сечений
FNDSEP (FiND SEParator)
Эта подпрограмма используется в GENND для поиска раз-
разделителя в связном подграфе. Связная компонента задается
входными параметрами ROOT, XADJ, ADJNCY и MASK. Най-
Найденный разделитель хранится парой (NSEP, SEP). Пара мас-
массивов (XLS, LS) используется для хранения структуры уровней
компоненты.
Сначала подпрограмма генерирует структуру уровней с кор-
корнем в псевдопериферийном узле. Для этого вызывается подпро-
подпрограмма FNROOT. Если число уровней меньше, чем 3, го вся.
компонента в качестве «разделителя» передается на выход.
В противном случае определяется средний уровень с номером
с.................
с
С............ FNDSEP НАЙТИ РАЗДЕЛИТЕЛЬ •¦.*.»•
с..........
с............
с
С ИСПОЛЬЗУЕТСЯ ДЛЯ ОПРЕДЕЛЕНИЯ МАЛОГО РАЗДЕЛИТЕЛЯ
С В СВЯЗНОЙ КОМПОНЕНТЕ ЗАДАННОГО ГРАФА,
С УКАЗЫВАЕМОЙ ПОСРЕДСТВОМ MASK.
С
С ВХОДНЫЕ ПАРАМЕТРЫ -
С ROOT - УЗЕЛ, ОПРЕДЕЛЯЮЩИЙ МАРКИРОВАННУЮ
С КОМПОНЕНТУ.
С (XADJ, ADJNCY) - СТРУКТУРА СМЕЖНОСТИ ГРАФА.
С
С ВЫХОДНЫЕ ПАРАМЕТРЫ -
С NSEP - ЧИСЛО ПЕРЕМЕННЫХ В РАЗДЕЛИТЕЛЕ.
С SEP - ВЕКТОР, СОДЕРЖАЩИЙ УЗЛЫ РАЗДЕЛИТЕЛЯ.
С
С ИЗМЕНЯЕМЫЙ ПАРАМЕТР-
С MASK - ДЛЯ УЗЛОВ РАЗДЕЛИТЕЛЯ В MASK
С УСТАНАВЛИВАЕТСЯ О.
С
С РАБОЧИЕ ПАРАМЕТРЫ-
С (XLS, LS) - ПАРА ДЛЯ ХРАНЕНИЯ СТРУКТУРЫ УРОВНЕЙ,
С НАЙДЕННОЙ FNROOT.
С
С ПОДПРОГРАММЫ -
С FNROOT
С
с..............................
с
SUBROUTINE FNDSEP ( ROOT, XADJ, ADJNCY, MASK,
1 NSEP, SEP, XLS , LS )
О
с**««.......................................
с
INTEGER ADJNCY(l), LSA), MASKA), SEPA), XLS(l)
INTEGER XADJ(l), I, J, JSTOP, JSTRT, MIDBEG,
1 MIDEND, MIDLVL. MP1BEG, MP1END,
1 NBR, NLVL, NODE, NSEP. ROOT
С
с.............................................................
§82. Вложенные сечения для произвольных задач 279
CALL FNROOT ( ROOT, XADJ, ADJNCY, MASK,
1 NLVL, XLS, LS )
С
С ЕСЛИ УРОВНЕЙ МЕНЬШЕ 3, ПЕРЕДАТЬ ВСЮ
С КОМПОНЕНТУ КАК РАЗДЕЛИТЕЛЬ НА ВЫХОД.
с
IF ( NLVL GE 3 ) GO TO 200
NSEP - XLS(NLVL+1) - 1
DO 100 I - 1. NSEP
NODE - LS(I)
SEP(I) • NODE
MASK(NODE) - 0
100 CONTINUE
RETURN
С НАЙТИ СРЕДНИЙ УРОВЕНЬ КОРНЕВОЙ СТР-РЫ УРОВНЕЙ.
С
200 MIDLVL
MIDBEG
MP1BEG
MIDEND
MP1END
(NLVL + 2)/2
XLS(MIDCVL)
XLS(MIDLVL + 1)
MP1BEG - 1
XLS(MIDLVL+2) - 1
с
С В РАЗДЕЛИТЕЛЬ ВКЛЮЧАЮТСЯ ТОЛЬКО УЗЛЫ СРЕДНЕГО
С УРОВНЯ, ИМЕЮЩИЕ СОСЕДЕЙ В СЛЕДУЮЩЕМ УРОВНЕ.
С XAOJ ИСПОЛЬЗУЕТСЯ ДЛЯ ВРЕМЕННОЙ МАРКИРОВКИ
С УЗЛОВ УРОВНЯ MIDLVL+1.
с
DO 300 I - MP1BEG, MP1END
NODE - LS(I)
XADJ (NODE) - - XADJ (NODE)
300 CONTINUE
NSEP - 0
DO 500 I - MIDBEG, MIDEND
NODE - LS(I)
JSTRT - XADJ(NODE)
JSTOP - IABS(XADJ(NODE+1)) - 1
DO 400 J - JSTRT, JSTOP
NBR - ADJNCY(J)
IF ( XADJ(NBR) .GT 0 ) GO TO 400
NSEP - NSEP + 1
SEP(NSEP) - NODE
MASK(NODE) • 0
GO TO 500
400 CONTINUE
500 CONTINUE
С
С ВОССТАНОВИТЬ ЗНАКИ КОМПОНЕНТ В XADJ.
с
DO 600 I - MP1BEG, MP1END
NODE - LS(I)
XADJ (NODE) - - XADJ (NODE)
600 CONTINUE
RETURN
END
MIDLVL. В цикле DO 500 I =... обходятся узлы этого сред-
среднего уровня Узел включается в разделитель, если у него есть
сосед в следующем уровне. Разделитель помещается в (NSEP,
SEP).
280 Гл. 8. Методы вложенных сечений
Упражнения
8.2.1. Эта задача предполагает модификацию подпрограмм CENND и
FNDSEP, с тем чтобы реализовать некоторый вариант «неполного алгоритма
вложенных сечений». Введите в обе подпрограммы параметр MINSZE н моди-
модифицируйте FNDSEP таким образом, чтобы она выполняла сечение передан-
переданной ей компоненты лишь в том случае, если число узлов компоненты превы-
превышает MINSZE. В противном случае компонента упорядочивается посредством
подпрограммы RCM нз главы 4. Проведите эксперимент с целью проверки,
будет ли тот результат, который требовалось доказать в упр. 8.1.7, сохранять
силу для эвристических упорядочений, получаемых алгоритмом данного пара-
параграфа. Одним из способов такой проверки является решение последователь-
последовательности задач возрастающего порядка, например задач тестового набора # из
главы 9, причем MINSZE следует положить равным -\/N. (Заметьте, что для
сеточной (п X п) -задачи условие /^log2(V^) означает, что независимые
блоки последнего уровня имеют О (я) = O(yN) узлов, где N = п?). Зафик-
Зафиксируйте число операций для каждой задачи и сравните эти числа с соответ-
соответствующими значениями для исходного (полного) алгоритма вложенных се-
сечений. Аналогичным образом вы можете сравнить требования к памяти, с тем
чтобы проверить, будут ли они расти в вашем неполном алгоритме со ско-
скоростью
8.2.2. Покажите, что в алгоритме из раздела 8.2.1 число элементов запол-
заполнения и число операций при разложении не зависят от порядка нумерации
узлов разделителя.
§ 8.3. Дополнительные замечания
В работе (Lipton, Tarjan, Rose 1979) достигнут значительный
прогресс в направлении созданий автоматических алгоритмов
вложенных сечений. Авторы предложили алгоритм, основанный
на следующем фундаментальном результате (Lipton, Tarjan
1977).
Пусть G — произвольный плоский граф с N узлами. Узлы
графа G можно разбить на три множества А, В и С таким об-
образом, 4ToAdj(/l)nfi = 0 |С|=О(д/Л/),а щ и |?| ограниче-
ограничены числом 2Л73. При этом существует алгоритм, который на-
находит Л, б и С за время 0{N).
Липтон и соавторы построили для двумерных конечноэле-
ментных задач алгоритм упорядочения с гарантированными
оценками 0{N3h) для числа операций и O(N\og2N) для памя-
памяти. Сам алгоритм упорядочения имеет временную сложность
O{N\og2N). Недостатком алгоритма является значительно
большая сложность по сравнению с простым эвристическим ме-
методом данной главы. Возможно, что практичным решением бы-
была бы комбинация обоих методов; при этом более сложная
схема использовалась бы лишь тогда, когда простой алгоритм,
описанный нами, дает «плохой» разделитель.
Использование идеи вложенных сечений оказалось эффек-
эффективным и для задач, связанных с трехмерными структурами
§ 8.3. Дополнительные замечания 281
(George 1973, Duff, Reid 1976; Rose, Whitten 1976; Eisenstat
1976). Поэтому исследования, имеющие целью разработку ав-
автоматических алгоритмов вложенных сечений для этих непло-
неплоских задач, представляются потенциально плодотворной об-
областью.
Рядом авторов (Calahan 1975, 1976, George et al. 1978g,
Lambiotte 1975) рассматривалась организация методов сечений
на параллельных и векторных машинах. Векторные машины
наиболее эффективны, если они могут оперировать с «длинны-
«длинными» векторами; использование же техники сечений обычно по-
порождает короткие векторы, если только не применяются какие-
то нестандартные способы организации данных. Поэтому глав-
главной задачей в этой области является балансировка нескольких
конфликтующих критериев с целью получить наименьшее вре-
время решения. Часто такая балансировка ие соответствует мини-
минимизации выполняемой арифметики.
9. Численные эксперименты
§ 9.0. Введение
В главе 1 мы сделали такое утверждение- успешность алго-
алгоритмов для разреженных матричных вычислений решающим
образом зависит от качества их машинной реализации Вот
почему мы включили в книгу программы, реализующие описан-
описанные в ней алгоритмы, и дали детальный разбор того, как ра-
работают эти программы В этой главе мы приведем результаты
численных экспериментов, в которых наши программы исполь-
использовались для решения некоторых тестовых задач.
Наша главная цель здесь — подкрепить конкретными при-
примерами основные положения § 2.3, где обсуждались «практи-
«практические замечания» и где было отмечено, как трудно сравнивать
различные методы. Структуры данных различны по сложности,
а время решения задачи состоит из нескольких компонент, от-
относительная важность которых зависит от стратегии упорядоче-
упорядочения и типа задачи. Численные результаты, приведенные в этой
главе, дадут пользователю информацию, позволяющую оценить
значение высказанных положений.
Кроме того, полезными для читателя будут сведения о вре-
времени и памяти, требуемых для разреженных матричных вычис-
вычислений довольно представительного класса на типовой вычис-
вычислительной машине.
Тестовые задачи имеют общий характер, типичный для ко-
нечноэлементных приложений. Причина такого самоограниче-
самоограничения та, что мы хотим лишь проиллюстрировать основные по-
положения. Попытку собрать информацию об относительных до-
достоинствах различных методов для большого числа разных
классов задач мы сочли для себя слишком амбициозной. Бо-
Более или менее самоочевидно, что для некоторых классов задач
один из методов может равномерно превосходить все остальные
или что относительные достоинства методов из нашей книги
могут быть совершенно разными для разных классов задач.
Ограничивая свое внимание задачами одного класса, мы про-
просто устраняем одну из переменных и без того в сложном ис-
исследовании.
И все же наши тестовые задачи представляют большую и
важную область приложений разреженной матричной технологии.
§90 Введение 283
(а) Квадрат
{6) Градуированное L
{в) Крестообразная область (г) И-образная область
1
\
\1>ч1^\1\
s
1
NISN
\N\
\
ч
(8) Квадрат с дырой (малая дыра) (е) Квадрат с дырай
(большая выра-)
(ж) Область с тремя дыр/сами (?) Область с шестью
дырками
(и) Область с граничным прокопан
Рис. 9.1 1. Сеточные задачи при s = 1.
284 Гл. 9. Численные эксперименты
У них есть то дополнительное преимущество, что они связаны
с физическими объектами (сетками), которые дают картину
(граф) матричной задачи.
Остальная часть данной главы устроена следующим обра-
образом. В § 9.1 мы описываем тестовые задачи. В § 9.2 мы объяс-
объясняем, какая информация содержится в таблицах, и причины,
почему она приведена. Сами таблицы с «сырым» эксперимен-
экспериментальным материалом находятся в конце § 9.2. В § 9.3 мы даем
обзор основных критериев, использующихся при сравнении ме-
методов, а затем переходим к сравнению в соответствии с этими
критериями наших пяти методов в применении к тестовым за-
задачам. Наконец, в § 9.4 исследуется зависимость между схемой
хранения, с одной стороны, и памятью и эффективностью под-
подпрограмм численных этапов — с другой.
§ 9.1. Описание тестовых задач
Два наших набора тестовых задач — это положительно оп-
определенные системы, типичные для тех, что возникают в струк-
структурном анализе или исследовании теплопроводности (Zienkie-
wicz 1977). (Отличным введением в предмет может служить
Рис. 9.1.2. Область с граничным проколом. Коэффициент разбиения s ра-
равен 3.
глава 6 книги (Strang 1973).) На рис. 9.1.1 показаны сетки,
составленные йЗ треугольных элементов. 3fa сетки и порож-
порождают наши задачи следующим образом. Основная сетка (из
тех, что показаны на рисунке) подразделяется очевидным обра-
§ 9.1. Описание тестовых задач 285
зом с коэффициентом разбиения s. В результате получится
сетка, имеющая треугольников в s2 раз больше, чем исходная.
Рис. 9.1.2 иллюстрирует этот процесс разбиения для области с
граничным проколом; здесь s = 3. Задание основной сетки и
коэффициента разбиения определяет новую сетку с N узлами.
Таблица 9.1.1
Данные о тестовых задачах набора #1
Приведены коэффициент разбиения, использованный при построении задачи,
число полученных уравнений и число ребер в соответствующем графе
Задача Коэффициент разбиения
Квадрат
Градуироданное L
Крестообразная область
И-образная область
Ma/raft дыра
Большая дыра
3 дыры
6 дыр
Граничный прокоп
32
8
9
8
12
9
б
б
19
N
1089
1009
1180
1377
936
1440
1138
1141
1349
\Е\
3136
2928
3285
3808
2665
4032
3156
3162
3876
Таблица 9.13
Даииые о тестовых задачах набора #2
Эти задачи получены из основной сетки — градуированное L — при значениях
коэффициеита разбиения s, равных соответственно 4, 5, ..., 12
Коэффициент
раэоивния
4
5
6
7
8
9
!0
11
12
N
265
406
577
778
1009
1270
1561
1882
2233
744
1155
1656
2247
2928
3699
4560
5511
6552
Далее, при фиксированном помечивании этих N узлов мы
строим симметричную положительно определенную систему
Ах = Ь порядка W, в которой ач Ф 0 тогда и только тогда, когда
узлы сетки i и / соединены ребром. Таким образом, построен-
построенные сетки можно рассматривать как графы соответствующих
матричных задач,
286 Гл. 9. Численные эксперименты
Из этих сеток конструируются два набора тестовых задач.
В тестовый набор ф1 входят девять основных сеточных задач,
взятых с такими коэффициентами разбиения, чтобы получаю-
получающиеся из них системы имели примерно от 1000 до 1500 уравне-
уравнений (см. таблицу 9.1.1). Второй набор — это последовательность
из девяти задач, полученных разбиением основной сетки (градуи-
(градуированное L на рис. 9.1.1) с коэффициентами s = 4, 5, ..., 12.
Данные об этих задачах см. в таблице 9.1.2.
§ 9.2. Что означают приведенные числа
В главах 4—8 были описаны пять методов, для которых
здесь будет использоваться следующая мнемоника: RCM —об-
—обратный алгоритм Катхилла — Макки, RQT — алгоритм рафи-
рафинированного древовидного разбиения, 1WD — алгоритм парал-
параллельных сечений, QMD — алгоритм минимальной степени с
использованием факторизации и ND — алгоритм вложенных се-
чеиий. В то же время мы описали лишь три основные структу-
структуры данных и соответствующие подпрограммы численных эта-
этапов. Дело в том, что алгоритмы 1WD и RQT могут использовать
одни и те же структуры данных, и это же относится к алгорит-
алгоритмам QMD и ND.
В таблицах, приводимых в конце этого параграфа, слово
«операции» означает мультипликативные операции (умноже-
(умножения и деления). По причинам, уже обсуждавшимся в главе 2,
мы рассматриваем число таких операций как разумную меру
количества выполненной арифметики: ведь в матричных вы-
вычислениях арифметические операции обычно образуют после-
последовательность пар «умножить — сложить». Время исполнения
измеряется в секундах и сообщается для машины IBM 3031.
Эта машина имеет весьма современную архитектуру и исполь-
использует сверхоперативную память. Типовые операции на ней тре-
требуют от 0.4 микросекунды для операций с фиксированной точкой
над регистровыми операндами до примерно 7 микросекунд для
деления с плавающей точкой. Как обычно, в вычислительной
среде с многопрограммной обработкой трудно получить точ-
точное время работы программы; поэтому приводимые нами ре-,
зультаты могут содержать ошибки в пределах 10%. Мы пыта-
пытались несколько уменьшить эти ошибки, прибегая к неоднократ-
неоднократному повторению счета или выходу на машину в такое время,
когда она слабо загружена. Программы компилировались в
оптимизирующем режиме транслятора, что обычно дает очень
эффективные машинные программы.
Напомним один из выводов параграфа 2.3: при сравнении
различных стратегий упорядочения может оказаться разумным
игнорирование одного или нескольких из четырех основных
§ 9.2. Что означают приведенные числа 287
шагов общей процедуры решения. По этой причине в числен-
численных экспериментах мы регистрировали время исполнения каж-
каждого из четырех шагов: упорядочения, распределения памяти,
разложения и решения треугольных систем.
В таблицах приводятся четыре вида статистики, связанной
с памятью: память на этапе упорядочения, память на этапе рас-
распределения, общая память (память на численных этапах) и на-
накладная память. Все наши эксперименты проводились с помощью
пакета для разреженных матриц, называемого SPARSPAK
(George, 1978 a, 1979 а). В нем все необходимые для работы
массивы распределяются из одного большого одномерного мас-
массива. Сообщаемые нами данные о памяти на этапах упорядоче-
упорядочения, распределения и численного решения относятся как раз
к количеству памяти, использованной в рамках этого большого
массива. Мы полагаем, следовательно, что эти числа отражают
Таблица 92.1
Массивы, учитываемые в статистике памяти для каждой фазы каждого
из пяти методов. Память, необходимая для подчеркнутых массивов
в столбце «численные этапы», регистрируется как «накладная память»
¦Упорядочение
Распределение
памяти
Численные
этапы
RCM
XADJ.ADJNCY,
PERM.XLS,
MASK
XADJ.ADJNCY,
PERM.INVP.XENV
PERM.INVP.RHS
XENV.ENV.DIAQ
XADJ.ADJNCY,
PERM.BNUM,
1WD LS(SUBG),XBLK,
MASK.XLS
XADJ.ADJNCY.
PERM.INVP.XBLK,
MASK,MARKER,
FATHER,XENV,
PERM.INVP,RHS,
XENV.ENV.DIAO,
XNONZ,NZSUBS,NGNZ,
TEMPV,FIRST
NZSUBS,RCHSET(XNONZ)
XADJ.ADJNCY,
PERM,XBLK,MASK,
RQT NODLVL(BNUM) ,
XLS.LS(SUBG)
XADJ.ADJNCY,
PERM.INVP.XBLK,
MASK.FATHER,
XENV,XNONZ,
NZSUBS
то же , что и выше
ND
XADJ.ADJNCY,
PERM.LS,
XLS,MASK
XADJ.ADJNCY,
PERM.INVP.XLNZ,
XNZSUB.NZSUB,
MRGLNK.RCHLNK,
MARKER
PERM.INVP.RHS.
XNZSUB.NZSUB,XLNZ,
LNZ,DIAG,LINK.FIRST.
TEMPV
QMD
XADJ, 2КОПии
ADJNCY.PERM,
MARKER,DEG,
RCHSET,NBRHD,
QSIZE.QLINK
то же, что и выше то же, что и выше
288 Гл 9. Численные эксперименты
Таблица 9.2.2
Результаты алгоритма RCM для тестовых задач набора 4И
(число операций и память масштабированы умножением на 10~4)
Задача Упорядочение
Распределение
памяти
Численные этапы
Врепя Попять Время Память Время Число операции Память
936
1009
1089
1440
1180
1377
1138
1141
1349
0.21 (
0.27 (
0.24
0.32
0.32
0.30
0.30
0.25
0.36
3.91
3.99
1.06
.38
1.13
.31
.09
.09
.31
0.04
0.04
0.05
0.06
0.06
0.06
0.06
0.05
0.06
0.91
0.99
1.06
1.38
1.13
1.31
1.09
1.09
1.31
Реа/ю- решение Разло-
Разложение и жение
2.85
3.43
3.25
4.74
2.86
1.99
2.81
4.40
5.74
0.40
0.46
0.45
0.62
0.44
0.40
0.45
0.52
0.69
30.18
37.49
34.46
53.77
31.87
18.64
28.88
54.08
64.95
°euiCHUt
4.55
5.25
5.11
7.23
5.17
4.34
4.92
6.75
7.95
2.65
3.03
2.99
4.19
3.06
2.72
2.92
3.83
4.52
,ИеклеЗ-
' ноя
0.28
0.30
0.33
0.43
0.35
0.41
0.34
0.34
0.40
Таблица 9.2.3
Результаты алгоритма 1WD для тестовых задач набора #1
(число операций и память масштабированы умножением на 10~~4)
Задача Упорядочение
Распределение
памяти
Численные этапы
Время Память Время Память Время Чиспо операции Память
936
1009
1089
1440
1180
1377
1138
1141
1349
0.38
0.47
0.45
0.60
0.55
0.57
0.52
0.46
0.61
.19
.29
1.39
.81
.48
.73
.43
.43
.72
0.25
0.28
0.30
0.39
0.33
0.37
0.30
0.31
0.36
.24
.35
.46
.89
.56
.82
.49
.49
.79
Резло- р
жение
3.39
5.47
5.23
4.43
3.35
3.25
3.17
5.10
7.03
antSuiif.
0.36
0.40
0.42
0.52
0.42
0.49
0.41
0.44
0.56
, Разло-
Разложение
26.60
44.90
41.48
33.04
24.50
21.41
23.56
41.08
58.38
rnU/Snt
3.06
3.66
3.62
4.32
3.48
3.57
3.48
3.77
4.79
„Humot
rttift
1.72
1.94
2.03
2.51
2.03
2.21
1.98
2.07
2.57
0.61
0.66
0.72
0.94
0.78
0.92
0.75
0.74
0.88
скорее количества памяти, нужной при работе подпрограмм
в практических ситуациях, а не тот неприводимый минимум,
который требуется для каждой из них в отдельности. Проиллю-
Проиллюстрируем сказанное примером. Подпрограмма упорядочения
QMD при работе портит входной граф. При пользовании этой
подпрограммой самой по себе нет необходимости сохранять граф
исходной матрицы, однако в большинстве случаев он все же бу-
будет сохранен, так как нужен для следующего шага — символи-
символического разложения. Цифра, приводимая для QMD в столбце
§ 9.2. Что означают приведенные числа 289
Таблица 9.2.4
Результаты алгоритма RQT для тестовых задач набора #1
(число операций и память масштабированы умножением на 10-4)
Задача Упорядочение Pacnrc,%fjffiuef"/e Численные этапы '
Время Память Время Помять время Число операций Ламять
ё Решете™ые. Решение Общая н^"а'
936 0Л8 U9 0.15 U9 4.17 0.53 32.84 4.83 2.14 0.75
1009 0.26 1.29 0.16 1.30 4.88 0.59 39.32 5.49 2.38 0 81
1089 0.22 1.39 0.17 1.40 4.68 0.61 37.04 5.43 2.45 0.88
1440
1180
1377
1138
1141
1349
0.29
0.31
0.28
0.30
0.23
0.36
1.81
1.48
1.73-
1.43
1.43
1.72
0 22
0 19
0.21
0.17
0.17
0.21
1.81
1.49
1.74
1.43
1.42
1.72
6.75
2.39
2.30
4.32
7.18
7.79
0.82
0.54-
0.58
0.60
0.72
0.86
>.\46
13.52
11.69
31.98
63.98
67.68
7.44
3 41
3.53
5.13
6.92
8.30
3
2
2
2
2
3
.29
.04
.27
.41
.86
42
1.15
0.95
1.12
0.91
0.91
1.08
Таблица 9.2Л
Результаты алгоритма ND для тестовых задач набора #1
(число операций и память масштабированы умножением на 10~4)
Задача
936
1009
1089
1440
1180
1377
1138
1141
1349
Упорядочений
Распределение
памяти
Численные этапы
Время Память Время Память Время
0.77
0.95
0.92
1.35
1.10
1.30
1.15
1.14
1.39
1.00
1.09
1.17
1.53
1.25
1.45
1.20
1.20
1.45
0.24
0.25
0.27
0.34
0.28
0.32
0.27
0.27
0.33
1.78
1.97
2.10
2.68
2.17
2.51
2.11
2.13
2.60
Раэао-1
жение '
2.19
3.77
3.40
2.69
2.05
2.34
2.32
2.35
4.41
'эдем
0.29
0.37
0.37
0.41
0.31
0.36
0.32
0.32
0.48
Число операций
тРазло-1
16.25
31.11
26.82
19.05
14.22
15.71
16.89
17.23
35.48
Решение
2.96
4.00
3.91
4.06
3.15
3.59
3.32
3.34
4.98
Память.
Odtutu
2.73
3.38
3.43
3.90
3.09
3.54
3.14
3.16
4.31
.Нвхлес
* ней
1.15
1.29
1.36
1.72
1.40
1,61
1.37
1.38
1.69
«память на этапе упорядочения», включает в себя память, необ-
необходимую для хранения исходного графа.
Еще один пример. Очевидно, что нет нужды сохранять мас-
массивы PERM и INVP после того, как завершено распределение
памяти, поскольку подпрограммы разложения и решения тре-
треугольных систем не используют эти массивы. Однако, как пра-
правило, их сохраняют, чтобы правильно разместить числовые зна-
значения коэффициентов А и Ь в структуре данных и чтобы восста-
восстановить исходный порядок компонент вектора х после того, как
будет вычислено (переупорядоченное) решение. В таблице 9.2.1
290 Гл. 9. Численные эксперименты
Таблица 9.2.6
Результаты алгоритма QMD для тестовых задач набора #1
(число операций и память масштабированы умножением на К)-4)
Задача Упорядочение Ра%'^я%/!^'"" Численные этапы
Время Память Время Память Время Число операций Память
936
1009
1089
1440
1180
1377
1138
1141
1349
1.47
1.57
1.78
2.33
1.89
2.09
1.97
2.07
2.07
1.91
2.08
2.23
2.91
2.38
2.76
2.29
2.29
2.76
0.21
0.24
0.26
0.34
0.27
0.30
0.27
0.27
0.32
1.80
1.97
2.12
2.74
2.19
2.52
2.15
2.17
2.62
%a!2i
2.27
3.37
3.00
2 70
1.44
1.50
1.82
2.03
3.70
РешениеМ^'РешенаеМщоя"^
0.30
0.37
0.36
0.42
0.27
0.30
0.29
031
0.46
19.34
30.91
26.31
21.62
9.86
10.00
13.80
16.24
32.41
3.11
3.95
3.85
4.21
2.72
2.99
3.04
3.20
4.82
2.83
3.36
3.42
4.04
2.90
3.25
3.04
3.14
4.26
1.18
1.29
1.38
1.79
1.42
1.62
1.41
1.43
1.71
Результаты алгоритма RCM для тестовых задач набора #2
(чнсло операций и память масштабированы умножением на 10~4)
Таблица 9.2.7
Задача
265
406
577
778
1009
1270
1561
1882
2233
Упорядочение
7е0в/гем
чята
ие
<
Время Память время Пенять Время
0.07
0.12
0.16
0.22
0.27
0.34
0.42
0.51
0.62
0.25
0.39
0.56
0.76
0.99
1.25
1.54
1.86
2..20
0.01
0.02
0.03
0.03
0.05
0.06
0.07
0.09
0.10
0.25
0.39
0.56
0.76
0.99
1.25
1.54
1.86
2.20
РОЗ/70 "
/кенве ¦
0.33
0.71
1.30
2.15
3.43
5.19
7.50
10.62
14.44
'¦/ис/генные этапы
Число операции Папять
Решение ?$jfif/Peur*HBe0<te(t
0.07
0.13
0.21
0.32
0.46
0.62
0.83
1.11
1.40
2,97
6.62
12.88
22.78
37.49
58.37
86.95
124.90
174.10
0.75
1.39
2.32
3.59
5.25
7.36
9.97
13.14
16.91
0.48
0.86
1.39
2.10
3.03
4.19
5.61
7.32
9.35
кНак/1,
0.08
0.12
0.17
0.23
0.30
0.38
0.47
0.56
0.67
перечислены массивы, учитываемые в нашей статистике памяти,
для различных фаз вычислительного процесса (упорядочение,
распределение памяти, разложение, решение) и для каждого из
пяти методов. Обозначение А (В) в этой таблице имеет следую-
следующий смысл: массивы А и В один вслед за другим используют
одно и то же место в памяти.
Строго говоря, следовало бы различать память на этапе раз-
разложения и память на этапе решения треугольных систем, так
как несколько массивов, используемых подпрограммами TSFCT
и GSFCT, не нужны соответствующим подпрограммам для
треугольных систеь^ Однако эти массивы обычно малы в срав-
§ 9.2. Что означают приведенные числа 291
нении с общей памятью, необходимой при решении треугольных
систем. Поэтому в наших таблицах приводится только «память
на численных этапах».
До сих пор мы говорили лишь о первых трех категориях па-
памяти: на этапах упорядочения, распределения и численного ре-
решения. Четвертая категория — это «накладная память». Мы вклю-
включили ее, чтобы показать, какая часть всей памяти, используемой
на этапах разложения и решения, занята информацией, не яв-
являющейся значениями ненулевых элементов матрицы L и правой
части Ъ (на место которой записывается х). Если ячейка памяти
Таблица 9.2.8
Результаты алгоритма 1WD для тестовых задач набора #2
(число операций и память масштабированы умножением на Ю-4)
ЗаЗача
265
406
577
778
1009
1270
1561
1882
2233
Упорядочение
Pacnpei/епение
памяти
Численные
Время Память Время Память Время
0.12
0.18
0.27
0.35
0.48
0.60
0.70
0.91
1.05
0.33
0.52
0.74
0.99
1.29
1.63
2.00
2.42
2.87
0.07
0.11
0.17
0.20
0.28
0.35
0.43
0.51
0.62
0.35
0.54
0.77
1.04
1.35
1.70
2.09
2.51
2.98
РОЭ/ТС
0.65
1.29
2.39
3.69
5.46
7.76
11.09
14.73
19.64
'Peuiet,
0.09
0.15
0.22
0.32
0.41
0.54
0.68
0.85
1.04
этапы
число епераций
4.38
9.25
18.11
29.22
44.90
66.00
97.14
Г31.13
177.17
Решет
0.69
1.18
1.87
2.68
3.66
4.87
6.36
7.90
9.91
Память
еМиь
0.42
0.69
1.04
1.45
1.94
2.53
3.25
4.00
4.89
т НвЯ
0.18
0.27
0.38
0.51
0.66
0.83
1.02
1.22
1.45
Таблица 9.2.9
Результаты алгоритма RQT для тестовых задач набора #2
(число операций и память масштабированы умножением на 10~4)
Задача
265
406
577
778
1009
1270
1561
1882
2?33
Упорядочение
Время Память
0.07
0.10
0.16
0.20
0.26
0.33
0.40
0.48
0.56
0.33
0.52
0.74
0.99
1.29
1.63
2.00
2.42
2.87
Рас/юеШение
памяти
Время
0.04
0.07
0.09
0.12
0.16
0.20
0.25
0.30
0.35
/Лгмят,
0.34
0.52
0.74
1.00
1.30
1.63
2.01
2.43
Ш
Численные этапы
ь Врамя
разло-.
жение
0.57
1.12
1.94
3.15
4.86
7.15
10.14
14.06
19,20
0.12
0.20
0.29
0.43
0.60
0.78
1.04
1.31
1.67
Число операций Память
.„Разм-
'"жение
3.24
7.11
13.70
24.03
39.32
60.94
90.43
129.48
179.99
0.81
1.49
2.46
3.78
5.49
7.67
10.35
13.59
17.44
0.47
0.78
1.19
1.72
2.38
3.19
4.15
5.28
6.60
„ШЛ1
0.21
0.33
0.46
0.63
0.81
1.02
1.25
1.51
1.79
292 Гл. 9. Численные эксперименты
Таблица 92.10
Результаты алгоритма ND для тестовых задач набора ф2
(число операций и память масштабированы умножением на 10~4)
Задача Упорядочение Pttcn%e?Sfae
Численные этапы
Время Память Время Память время Число операции /Томять
265
406
577
778
1009
1270
1561
1882
2233
0.20
.0.33
0.49
0.68
0.95
1.22
1.56
1.93
2.35
0.28
0.43
0 62
0 84
1.09
1.38
1.69
2.04
2.43
0.06
0.10
0.14
0.20
0.26
0.32
0.39
0.50
0.58
0.49
0.77
1.10
1.51
1.97
2.49
3.08
3.74
4.45
рвало-ввш/ч/ия P°3M-i
женив нешвн11В жение '
0.46
0.93
1.62
2.58
3.80
5.30
7.34
9.73
12.79
0.07
0.12
0.19
0.29
0.37
0.49
О!63
0.78
0.94
3.25
6.93
12.56
20.10
31.11
44.45
62.57
83.85
111.18
Ъшент
0.72
1.27
1.99
2.88
4.00
5.27
6.82
8.54
10.57
0.70
1.17
1.77
2.50
3.38
4.39
5.58
6.90
8.42
,Намад-
'нея
0.32
0.50
0.72
0.99
1.29
1.63
2.01
2.44
2.92
Таблица 9.2.П
Результаты алгоритма QMD для тестовых задач набора #2
(число операций и память масштабированы умножением на К)-4)
ЗаЗача Упорядочение Pac%gejJ,%%me
Численные этапы
Время Память Время Память Время Число операций Память
1
265
'406
577
778
1009
1270
1561
1882
2233
0.39
0.72
1.01
1.39
1.55
2.48
2.56
3.32
3.53
0.54
0.83
1.18
1.60
2.08
2.62
3.23
3.90
4.63
0.06
0.09
0.13
0.19
0.24
0.34
0.39
0.48
0.55
0.49
0.78
1.12
1.52
1.97
2.53
3.09
3.76
4.43
0.36
0.78
1.26
2.22
3.43
4.59
5.90
8.36
12.06
'ешени,
0.07
0.11
0.18
0.26
0.38
0.48
0.60
0.76
0.98
рРезло-f.
2.65
6.35
10.35
19.65
30.91
42.56
55.43
80.10
119.13
'ешение
0.65
1.19
1.83
2.80
3.95
5.15
6.53
8.49
10.71
Odiuan
0.67
1.14
1.70
2.48
3.36
4.37
5.45
6.91
8.47
Наши-
0.32
0 50
0.73
1.00
1.29
1.66
2.03
2.47
2.89
he предназначена для хранения элемента L либо 6, то мы отно-
относим ее к накладной памяти. Массивы, составляющие накладную
память, подчеркнуты в таблице 9.2.1. Заметим, что разряд «па-
«память на численных этапах» включает в себя накладную память.
Есть еще одна причина для того, чтобы выделить накладную
память в отдельную рубрику. На машинах с длинным словом
может оказаться разумной упаковка нескольких целых чисел
в одном слове. Некоторые производители ЭВМ даже включают
возможность работать с короткими целыми числами в свои вер-
версии Фортрана. Например, IBM Fortran допускает описание це-
§ 9.3. Сравнение методов 293
лых чисел как INTEGER*2 или как INTEGER*4. В первом
случае для представления числа используется 16, а во втором —
32 бита. Так как большую часть накладной памяти составляет
целочисленная информация, то читатель сможет оценить потен-
потенциальную экономию памяти в том случае, если доступный ему
транслятор с Фортрана позволяет использование коротких целых
чисел. Заметим, однако, что все наши эксперименты были вы-
выполнены на IBM 3031 с обыкновенной точностью и как целые
числа, так и числа с плавающей точкой представлялись посред-
посредством 32 битов.
§ 9.3. Сравнение методов
9.3.1. Критерии сравнения методов
В этом параграфе мы не пытаемся в общем виде разрешить
вопрос, какой метод следует использовать. Типы разреженности
весьма разнообразны, а наши тестовые задачи принадлежат
лишь одному специальному классу. Наша цель здесь — проил-
проиллюстрировать, опираясь на данные § 9.2, факторы, которые
нужно учитывать при выборе метода для конкретной задачи или
конкретного класса задач. Эти факторы уже обсуждались или
по крайней мере упоминались в § 2.3.
Главными критериями были: а) запросы к памяти; б) время
исполнения и в) стоимость. В одних случаях наибольшее значе-
значение имеет уменьшение запросов к памяти, в других — малое
время исполнения. Но чаще всего, по-видимому, интерес пред-
представляет выбор метода, для которого стоимость машинных ре-
ресурсов минимальна. Эта стоимость обычно является довольно
сложной функцией от количества E) используемой памяти, вре-
времени исполнения G), количества вводимой и выводимой инфор-
информации и других параметров. Для нашего класса задач и мето-
методов, которые мы рассматриваем, стоимость очень хорошо аппро-
аппроксимируется функцией вида
COST(S, T) = TXP(S),
где p(S)—многочлен степени d; обычно d— 1 (однако иногда
d = 0, а в некоторых случаях, когда большие запросы к памяти
нежелательны, d = 2). Для наших иллюстративных целей
вполне достаточно взять p(S)= S.
В § 2.3 было отмечено, что относительная важность этапов
упорядочения, распределения памяти, разложения и решения
зависит от контекста, связанного с разреженной матричной за-
задачей. В некоторых ситуациях нужно решить лишь одну задачу
данной структуры, поэтому любое сравнение методов, конечно,
должно учитывать стоимость упорядочения и распределения па-
памяти. В других случаях приходится решать большое число задач
294 Гл. 9. Численные эксперименты
с одинаковой структурой. Здесь может быть разумно игнориро-
игнорировать затраты на упорядочение и распределение. Наконец, неред-
нередки обстоятельства, когда нужно решать ряд систем, отличаю-
отличающихся только правыми частями. Тогда вполне уместно рассмат-
рассматривать лишь время и/или память, необходимые для решения
треугольных систем при вычисленном разложении.
В некоторых таблицах, приводимых ниже, мы сообщаем «ми-
«минимальную» и «максимальную» общую стоимость. Различие
между ними состоит в следующем. Максимальная стоимость вы-
вычисляется в предположении, что каждый из четырех этапов
(упорядочение, распределение памяти, разложение, решение) tfc-
пользует одно и то же количество памяти, равное максималь-
максимальному из тех запросов, которые выдвигает каждый этап в отдель-
отдельности (обычно этот максимум достигается на этапе разложения).
Минимальная стоимость вычисляется исходя из того, что память
дня каждого этапа равна тому минимуму, который необходим
именно этому этапу (см. таблицу 9.2.1). Мы приводим оба вида
стоимости, чтобы показать, что для некоторых методов и задач
они могут очень заметно различаться. В таких случаях имеет
смысл сегментирование общего вычислительного процесса на
отдельные этапы и использование для каждого этапа только
обязательной для него памяти.
9.8.2. Сравнение методов для тестовых задач набора ф/
Рассмотрим теперь таблицу 9.3.1, полученную усреднением
результатов таблиц из § 9.2, относящихся к тестовому набору
ф 1, и последующим вычислением различных стоимостей. Один
Таблица 9JU
Средние значения различных критериев для задач набора #1
(число операций и память масштабированы умножением на 10~4)
MemoS
1WD
RQT
ND
QMD
Шш,ая
СШс.)
14.60
•12.22
15 60
15.63
16.66
Стоимость
Память
Общая Разложение Решение
{мин) +Решение
13.86
11 72
15.11
12 92
14.52
13.47
10 45
14 44
10 89
9.30
1.64
0.95
1.68
1.22
1.15
3.32
2.12
2.58
3.41
3.36
Время исполнения
Общее,
+
4 39
5 77
6.04
4.59
4.96
Разлажен,
Решет
4 06
4.94
5.59
3.19
2.77
ю Реше-
Решение
0 49
0.45
0.65
0.36
0.34
из наиболее важных выводов, которые из нее следуют, — это то,
что для девяти задач данного тестового набора выбор метода
сильно зависит от критерия, который желательно оптимизиро-
оптимизировать. Например, если основой сравнения является общее время
§ 9.3. Сравнение методов 295
работы, то следует выбрать алгоритм RCM. Если наибольшее
значение имеют время решения, или суммарное время разложе-
разложения и решения, или суммарная стоимость разложения и решения,
то нужно выбрать алгоритм QMD. Наконец, если наиболее важ-
важны критерии памяти, стоимости решения или общей стоимости,
то предпочтительным оказывается алгоритм 1WD.
Заслуживают внимания еще некоторые аспекты таблицы 9.3.1.
Очевидно, что QMD дает несколько лучшее упорядочение, чем
ND, что отражается^ меньших времени и стоимости на этапах
разложениями решения и в меньших запросах к памяти. Однако
упорядочение для ND вычисляется значительно быстрее, чем для
QMD, что в итоге приводит к меньшим значениям для общей
стоимости и общего времени для ND по сравнению с QMD.
Еще одно интересное обстоятельство, связанное с общей
стоимостью ND и QMD, — это существенное различие между
максимальной и минимальной стоимостями. Напомним (см. раз-
раздел 9.3.1), что максимальная стоимость вычисляется в предполо-
предположении, что память, используемая на любом этапе (упорядочение,
распределение памяти, разложение, решение), равна максимуму
из тех запросов, которые выдвигает каждый этап в отдельности;
минимальная же стоимость вычисляется исходя из того, что
каждый этап использует только необходимый минимум, ука-
указанный таблицей 9.2.1. Наши данные свидетельствуют, что даже
для «одноразовых» задач вполне оправдано сегментирование об-
общего вычислительного процесса на естественные составные части
и использование для каждого этапа лишь необходимой ему па-
памяти.
Изучив таблицу 9.3.1, читатель может задаться вопросом,
имеют ли какой-нибудь практический смысл такие методы, как
RQT или ND, которые ни по одному из рассматриваемых крите-
критериев не превосходили три других метода. Однако усреднение
имеет тенденцию сглаживать различия между задачами. Чтобы
показать, что для каждого метода есть место, мы приводим
Таблица 9.3.2
Для тестового набора #1 и различных критериев приведено число задач,
для которых тот или иной метод оказывался лучше других
Метод Стайность Напять Время исполнения
1WD
RQT
ND
QMD
Общая
(Макс)
3
4
1
1
0
Общая Разложение Решение
(Мин) +Решение
3
4
1
1
0
1
2
0
1
5
0
7
0
0
2
0
9
0
0
0
Odtnee P
+
4
0
1
3
1
Ъэложенй
Решение
0
0
0
2
7
'вРвт
0
0
О
3
*
296 Гл. 9. Численные эксперименты
таблицу 9.3.2. В ней для тестового набора #1 и различных крите-
критериев указано число задач, для которых тот или иной метод ока-
оказывался лучше других. Заметим, что в этой таблице нет нулевых
строк. Это свидетельствует, что даже внутри фиксированного
класса задач и при фиксированном критерии (скажем, времени
или памяти) выбор метода существенно зависит от задачи. Нуж-
Нужно также иметь в виду, что почти для любой задачи каждый ме-
метод может при подходящей комбинации критериев считаться
лучшим.
В таблице 9.3.2 бросаются в глаза превосходные характери-
характеристики метода 1WD в категориях стоимости и памяти.
9.3.3. Сравнение методов для тестовых задач набора ф2
Для иллюстрации некоторых дополнительных соображений
мы приводим в данном разделе таблицы 9.3.3 и 9.3.4. Эти таб-
таблицы получены из таблиц 9.2.7—9.2.11 параграфа 9.2; послед-
последние содержат экспериментальный материал для тестовых задач
набора ф2. Таблица 9.3.3 дает ту же информацию, что и таб-
таблица 9.3.1, для задачи «Градуированное L» с s = 4 (при этом
N = 265). Такова же таблица 9.3.4, только коэффициент раз-
разбиения s равен 12, a N = 2233.
Таблица 9.3.3
Значения различных критериев для задачи «Градуированное L» при s = 4,
N — 265 (стоимость и память масштабированы умножением на 10~4)
Метод
RCM
1WD
RQT
ND
QMD
О0ш,ая
{.макс)
0.23
0.39
0 38
0.56
0.59
Стоимость
Память
Время исполнения
О0щая Разложение Решение 01?щее Разложение Реше-
(мин) -^Решение
0.21
0.37
0.36
0.46
0.53
0.19
0.31
0.32
0.37
0.29
0.04
0.04
0.06
0.05
0.04
0.48
0.42
0.47
0.70
0.67
^Решение
0.48
0.93
0.81
0.79
0.88
0.40
0.73
0.69
0.53
0.43
' ние
0.07
0.09
0.12
0.07
0.07
Отметим прежде всего, что для N = 265 метод RCM обнару-
обнаруживает значительное преимущество в большинстве характери-
характеристик, а в остальных он вполне конкурентоспособен. Однако для
N = 2233 он теряет преимущество во всех разрядах, кроме об-
общего времени исполнения. (Некоторые другие эксперименты по-
показывают, что и в этой характеристике он уступает методу ND
Д7Я несколько большей задачи того же класса.) Один из глав-
главных выводов, которые мы хотим здесь сделать, таков: даже для
таких по существу одинаковых задач, как эти, порядок задачи
§ 9.4. Зависимость от структуры данных 297
Таблица 9.3.4
Значения различных критериев для задачи «Градуированное L» при s = 12,
N = 2233 (стоимость и память масштабированы умножением на 10~4)
Метод
RCM
1WD
RQT
ND
QMD
Стоимость Память Время исполнения
Общая Общая Разложение Решение Общее Разложение Реше-
(накс') (нин) +Решение i-Решение ние
154.83
109.41
143.69
140.45
145.07
149.69
106.10
140.30
124.03
129.28
148.10
101.25
137.67
115 74
110.49
13.09
5.11
10.99
7 95
8.33
9.35
4.89
6.60
8.42
8.47
16.56
22.35
21.78
16.67
17.13
15.84
20.69
20.87
13.74
13.04
1.40
1.04
1.67
0.94
0.98
может повлиять на выбор метода. Грубо говоря, для «малых
задач» нет смысла применять сложные методы.
Снова обращает на себя внимание эффективность метода
1WD в смысле памяти и стоимости.
Отметим еще, что вес этапов упорядочения и распределения
памяти в,общей стоимости снижается с ростом N для всех пяти
методов. Для методов RCM, 1WD и RQT эти два этапа стано-
становятся относительно маловажными в общих стоимости и времени
уже при М, близких к 2000. Однако для методов ND и QMD
этапы упорядочения и распределения при N = 2233 требуют все
еще значительной доли общего времени. Так как эти этапы в об-
общем используют меньшую память, чем последующее численное
решение, то различие между максимальной и минимальной стои-
стоимостями остается существенным даже для N = 2233.
§ 9.4. Зависимость от структуры данных
В нескольких местах этой книги мы подчеркивали роль струк-
структур данных (схем хранения) в вопросах, связанных с разрежен-
разреженными матрицами. В § 2.3 мы провели грань между основной и
накладной памятью и проиллюстрировали простым примером,
что программы нельзя сравнивать между соб.ой, исходя лишь из
потребляемой ими основной памяти, так как накладная память
этих программ может быть весьма различной. Там же было от-
отмечено, что разные структуры данных могут вести к существенно
различающимся значениям показателя «число арифметические
операций в секунду» для соответствующих подпрограмм числен-
численного решения. Основная задача данного параграфа — предста-
представить некоторые экспериментальные свидетельства в поддержку
этих заключений и показать возможную величину упомянутых
различий.
298 Гл. 9. Численные эксперименты
9.4.1. Запросы к памяти
В таблице 9.4.1 для каждого из пяти методов, в применении
к тестовым задачам набора Ф 2 указана основная и общая па-
память. Напомним, что основчая память — это то, что используется
для хранения числовых значений коэффициентов L и Ъ, а на-
накладная память — это «все остальное», и состоит она главным
образом из целочисленной информации — указателей, необходи-
необходимых для компактного представления L.
Таблица 9.4.1
Основная н общая память для каждого метода в применении к тестовым
задачам набора #2 (числа масштабированы умножением на 10~4)
Основная память
Метод
RCM
1WD
RQT
ND
QMD
Метоа
RCM
1WD
RQT
ND
QMD
265
0.40
0.24
0.26
0.39
0.35
265
0.48
0.42
0.47
0.70
0.67
406
0.74
0.42
0.45
0.67
0.64
406
0.86
0.69
0.78
1.17
1.14
577
1.22
0.66
0.73
1.05
0.97
577
1.39
1.04
1.19
1.77
1.70
Число уравнений
778
1 87
0.94
1.10
1.52
1.48
1009
2.73
1.28
1.57
2.10
2.08
1270
3.81
1.70
2.17
2.76
2.70
Общая память
Число уравнений
778
2.10
1.45
1.72
2.50
2.48
1009
3.03
1.94
2.38
3.3*
3.36
1270,
4.19
2.53
3.19
4.39
4.37
1561
5.14
2.23
2.90
3.57
3.42
1561
5.61
3.25
4.15
5.58
5.45
1882
6.76
2.78
3.77
4.46
4.43
1882
7.32
4.00
5.28
6.90
6.91
2233
8.68
3.45
4.80
5.51
5.58
2233
9.35
4.89
6.60
8.42
8.47
Данные таблицы 9.4.1 иллюстрируют следующие практически
важные моменты:
1. Для некоторых методов накладная компонента памяти
очень значительна, даже для больших задач, где ее относитель-
относительная важность несколько уменьшается. Так, для метода QMD
отношэние (накладная память)/(общая память) изменяется п-ри-
мерно от 0.48 до 0.34 при росте N от 265 до 2233. Следовательно,
хотя это отношение убывает, оно еще весьма внушительно даже
для очень больших задач.
Для сравнения укажем, что в методе RCM, использующем
очень простую структуру данных, отношение (накладная па-
память) I (общая память) изменяется для тех же задач от пример-
примерно 0.17 до 0.07.
§ 9.4. Зависимость от структуры, данных 299
2. Другой момент (по существу являющийся следствием
пункта 1) —это то, что основная память является очень нена-
ненадежным показателем общих запросов программы к памяти. На-
Например, если бы мы сравнивали методы RCM и QMD, исходя
только из объема основной памяти, то при всех N следовало бы
выбрать QMD. Между тем реально потребляемая память у ме-
метода RCM меньше вплоть до N « 1500!
Это сравнение демонстрирует также потенциал, заключенный
в возможности хранить целые числа более компактно, чем числа
с плавающей точкой. Во многих случаях число двоичных разря-
разрядов в представлении числа с плавающей точкой по крайней мере
вдвое превосходит то, что необходимо для представления целых
чисел достаточной величины. Если возможно использовать это
обстоятельство, то роль накладной компоненты, очевидно, станет
менее заметной. Так, если бы для целых чисел требовалось ровно
в два раза меньше разрядов, чем для чисел с плавающей точкой,
то память, потребляемая методами RCM и QMD, выравнивалась
бы уже при N « 600, а не при N & 1500, как указано выше.
3. Вообще говоря, информация из таблицы 9.4.1 показывает,
что, хотя сложные алгоритмы упорядочения существенно сокра-
сокращают основную память по сравнению со своими более простыми
конкурентами, чистый выигрыш в общей памяти не так значите-
значителен как можно бы предположить, исходя из различия в основной
памяти. Причина состоит в использовании более сложных схем
хранения. Например, показатель основной памяти для 1WD при
N > 778 составляет менее 50% от аналогичного показателя для
RCM, и это преимущество увеличивается с ростом N. Если же
рассматривать общую память, то, хотя и здесь превосходство
1WD над RCM растет с увеличением N, момент, когда память
для 1WD вдвое меньше памяти для RCM, не достигнут и при
N = 2233.
9.4.2. Время исполнения
В таблице 9.4.2 представлены значения показателя «число
операций в секунду» для подпрограмм разложения и решения
каждого из пяти методов в применении к тестовым задачам на-
набора ф 2. Эта информация подсказывает такие выводы.
1. Вообще говоря, эффективность (т. е. число операций в се-
секунду) подпрограмм увеличивается с ростом N. Этого и следо-
следовало ожидать, так как циклы, будучи инициированы, выпол-
выполняются все большее число раз. Тем самым при возрастании N
относительно уменьшаются издержки, связанные с инициирова-
инициированием циклов.
Отметим в этой связи, что повышение эффективности на от-
отрезке от Л' = 265 до Л" = 2233 существенно разное для рассмат-
рассматриваемых нами шести подпрограмм и пяти упорядочений
300 Гл. 9. Численные эксперименты
Таблица 9.4.2
Показатель «число операций в секунду» для каждого метода
в применении к тестовым задачам набора #2
(число операций масштабировано умножением на 10~4)
Метод
RCM
1WD
RQT
ND
QMD
Метод
RCMf
1WD
RQT
ND
QMD
265
9.01
6.78
5.68
7.07
7.30
265
10.21
7.96
6.79
10.25
9.77
406
9.37
7.19
6.33
7.42
8.10
406
10.69
8.05
7.45
10.28
10.52
577
9.91
7.57
7.07
7.75
8.19
577
10.87
8.50
8.38
10.49
9.98
Разложение
Число уравнений
778
10.58
7.93
7.63
7 78
8.87
1009
10.92
8.22
8.10
8.20
9.01
Решение
1270
П.24
8.51
8.53
8.38
9.27
Число уравнений
778
11.21
8.27
8.78
9.81
10.65
1009
11.50
9.00
9.16
10.71
10.50
1270
11.81
9.01
9.83
10.83
10.65
1561
Л 59
8.76
8.92
8.52
9.39
1561
11.97
9.31
9.95
10.89
10.89
1882
11.76
8.90
9.21
8 62
9 59
1882
11 87
9.30
10.35
11.00
11.12
2233
12.06
9.02
9.37
8 69
9.88
2233
12.08
9.50
10 47
11.20
10.89
(Вспомните, что методы 1WD и RQT используют одни и те же
подпрограммы численного решения, и это же верно для методов
ND и QMD.) Например, для подпрограммы GSSLV метода ND
эффективность повышается незначительно — от 9.44 X 104 до
10.15 X Ю4 на полном отрезке изменения N. В то же время эф-
эффективность подпрограммы TSSLV метода RQT возрастает
с 6.07 X 104 до 9.50 X 104. Эти различия, по-видимому, объяс-
объясняются разным количеством вспомогательных додпрограмм.
Например, TSFCT использует подпрограл\шы ELSLV, EUSLV и
ESFCT (которая в свою очередь обращается к ELSLV),
а у GSFCT вспомогательных подпрограмм вообще нет. Вызовы
подпрограмм при малых порядках задач существенно изменяют
время исполнения.
Различия в эффективности подпрограмм численного решения
показывают, насколько нереалистично делать выводы практиче-
практического характера только на основании числа операций. Так, если
бы мы сравнивали методы RCM и QMD по числу операций при
разложении, то для задач тестового набора ф 2 мы выбрали бы
во всех случаях QMD. Однако по времени работы QMD уступает
RCM до тех пор, пока не будет N я: 1600.
2. Мы уже отметили, что эффективность различна для раз-
разных подпрограмм и разных Л'. Интересно и то, что при фиксиро-
§ 9.4. Зависимость от структуры данных 301
ванной задаче и подпрограмме эффективность зависит от приме-
примененного упорядочения. В качестве примера рассмотрим показа-
показатели разложения для методов 1WD и RQT при N=2233. (Вспом-
(Вспомните, что оба метода используют подпрограмму TSFCT). Разли-
Различие в эффективности методов можно объяснить таким образом.
В отличие от подпрограмм ESFCT и GSFCT, где большая часть
арифметической работы выделена в один цикл, вычисления, про-
проводимые TSFCT, распределены между тремя вспомогательными
подпрограммами (с различной эффективностью) и основным вы-
вычислительным циклом внутри ее самой. Поэтому для одного упо-
упорядочения TSFCT может оказаться эффективней, чем для дру-
другого, просто по той причине, что большая доля вычислений вы-
выполняется самым эффективным из четырех вычислителей: трех
вспомогательных подпрограмм и цикла из TSFCT.
Дополнительное усложнение в это сравнительное исследова-
исследование показателей разложения для 1WD и RQT вносит то обстоя-
обстоятельство, что доля вычислений, выполняемых различными вы-
вычислительными циклами подпрограммы TSFCT, по-видимому,
меняется вместе с N, и зависимость от N различна для упорядо-
упорядочений 1WD и RQT. Для малых задач TSFCT эффективнее рабо-
работает при упорядочении 1WD, но с ростом N ситуация обращается,
причем показатели обоих методов сравниваются при N « 1700.
Мы должны предостеречь читателя от того, чтобы делать
слишком глубокие заключения на основании частного примера.
На другой машине с другим транслятором и набором команд от-
относительные эффективности вспомогательных подпрограмм и
вычислительного цикла в TSFCT могут быть совершенно иными.
Однако этот пример все же показывает, что эффективность яв-
является функцией не только используемой структуры данных, но
и может зависеть довольно неочевидным образом от упорядоче-
упорядочения и порядка задачи:
Приложение А. Некоторые указания
к использованию подпрограмм
§ А.1. Примеры скелетных ведущих программ
В главах 4—8 были описаны различные методы решения раз-
разреженных линейных систем. Они различаются схемами хранения,
с
С СФОРМИРОВАТЬ ДЛЯ СИСТЕМЫ АХ ¦ В
С МАССИВЫ XAOJ И ADJN6Y.
с
CALL GENRCM(N,XADJ,ADJNCY,PERM,MASK,XLS)
CALL INVRSE(N,PERM,INVP)
CALL FNENV(N,XADJ,ADJNCY,PERM,INVP,XENV,ENVSZE,BANDW)
С
с
С ВВЕСТИ ЧИСЛОВЫЕ ЗНАЧЕНИЯ В DIAG, ENV И RHS.
С -
CALL ESFCT(N,XENV,ENV,DIAG,IERR)
CALL ELSLV(N,XENV,ENV,DIAG,RHS,IERR>
CALL EUSLV(N,XENV,ENV,DIAG,RHS,IERR)
С
С ---
С СЕЙЧАС В RHS - ПЕРЕУПОРЯДОЧЕННОЕ РЕШЕНИЕ.
С ВОССТАНОВИТЬ ИСХОДНЫЙ ПОРЯДОК НЕИЗВЕСТНЫХ.
? ._
С
CALL PERMRV(N,RHS,PERM)
Рис. АЛЛ. Скелетная ведущая программа для профильного метода.
стратегиями упорядочения, структурами данных и/или числен-
численными подпрограммами. Однако общая процедура при использо-
использовании этих методов одна и та же. В ней можно выделить четыре
фазы:
Шаг 1. Упорядочение.
Шаг 2. Формирование структуры данных.
§ A.I. Примеры скелетных ведущих программ 303
Шаг 3. Разложение
Шаг 4. Решение треугольных систем.
В главы 4—8 включены подпрограммы, реализующие эти
шаги для каждого метода. На рис. А.1.1—А.1.3 приведены
тексты трех скелетных программ; они обслуживают соответст-
с
С СФОРМИРОВАТЬ ДЛЯ СИСТЕМЫ АХ
С МАССИВЫ XADJ И ADJNCY.
с
CALL GENRQT(N,XADJ,ADJNCY,NBLKS,XBLK,PERM,XLS,LS,NODLVL)
CALL BSHUFL(XADJ,ADJNCY,PERM,NBLKS,XBLK,BNUM.MASK,SUBG,XLS)
CALL INVRSE(N,PERM,INVP)
CALL FNTADJ(XADJ,ADJ NCY,PERM,INVP,NBLKS,XBLK,FATHER,MASK)
CALL FNTENV(XADJ,ADJNCY,PERM,INVP,NBLKS,XBLK,XENV,ENVSZE)
CALL FNOFNZ(XADJ,ADJNCY,PERM,INVP,NBLKS,XBLK,XNONZ,
NZSUBS.NOFNZ)
С
c т Г
С ВВЕСТИ ЧИСЛОВЫЕ ЗНАЧЕНИЯ В NONZ, DIAO, ENV И RHS.
с
CALL TSFCT(NBLKS,XBLK,FATHER,DIAG,XENV,ENV,XNONZ,NONZ,
NZSUBS.TEMPV,FIRST,IERR)
CALL TSSLV(NBLKS,XBLK,DIAG,XENV,ENV,XNONZ,NONZ,NZSUBS,
RHS,TEMPV)
С
с
С СЕЙЧАС В RHS НАХОДИТСЯ ПЕРЕУПОРЯДОЧЕННОЕ РЕШЕНИЕ.
С ВОССТАНОВИТЬ ИСХОДНЫЙ ПОРЯДОК НЕИЗВЕСТНЫХ.
Q .
С
CALL PERMRV(N,RHS,PERM)
Рис. А. 1.2. Скелетная ведущая программа для метода древовидного разбие-
разбиения.
венно профильный метод (глава 4), метод древовидного разбие-
разбиения (глава 6) и метод вложенных сечений (глава 8). Эти про-
программы указывают, каждая для своей схемы, порядок, в котором
должны вызываться подпрограммы при решении данной разре-
разреженной системы. Заметьте, что это всего лишь скелетные про-
программы; предполагается, что нужные массивы были описаны со-
соответствующим образом и не выполняется никакой проверки
возможных ошибок.
При вызове подпрограммы упорядочения считается, что рас-
расположение ненулевых элементов разреженной матрицы А задано
304 Приложение А. Указания к использованию подпрограмм
посредством структуры смежности, хранимой парой массивов
(XADJ, ADJNCY). Маловероятно, чтобы у пользователя были
под рукой удобные средства для заготовки такого представле-
представления. Поэтому он должен самостоятельно сформировать требуе-
требуемую структуру до выполнения упорядочивающего шага.
с
С СФОРМИРОВАТЬ ДЛЯ СИСТЕМЫ АХ = В
С МАССИВЫ X.ADJ И ADJNCY.
С
CALL GENND(N,XADJ,ADJNCY,MASK,PERM,XLS,LS)
CALL INVRSE(N,PERM,INVP)
CALL SMBFCT(N,XADJ.ADJNCY,PERM,INVP,XLNZ,NOFNZ,XNZSUB,
NZSUB,NOFSUB,RCHLNK,MRGLNK,MASK,FLAG)
С
с
С ВВЕСТИ ЧИСЛОВЫЕ ЗНАЧЕНИЯ В LN2,DIAG И RHS.
с
CALL GSFCT(N,XLNZ,LNZ,XNZSUB,NZSUB,DIAG,LINK,FIRST.
TEMPV.IERR)
CALL GSSLV(N,XLNZ,LNZ,XNZSUB,NZSUB,DIAG,RHS)
С
с
С СЕЙЧАС В RHS НАХОДИТСЯ ПЕРЕУПОРЯДОЧЕННОЕ РЕШЕНИЕ.
С ВОССТАНОВИТЬ ИСХОДНЫЙ ПОРЯДОК НЕИЗВЕСТНЫХ.
с
с
CALL PERMRV(N,RHS,PERM)
Рис. А. 1.3. Скелетная ведущая программа для метода вложенных сечений.
Формирование структуры смежности не является тривиаль-
тривиальной задачей, особенно в тех случаях, когда пары (i, /), для кото-
которых ctij?=O, задаются в произвольном порядке. Мы не будем
здесь обсуждать эту задачу. Упражнения 3.3.1 и 3.3 6 главы 3
указывают способ частичного ее решения. Описываемый в При-
Приложении В пакет SPARSPAK. дает средства для генерирования
структуры смежности в формате пары массивов (XADJ,
ADJNCY).
В текстах скелетных программ встречаются две подпрограм-
подпрограммы, которые не упоминались прежде. Подпрограмма INVRSE,
вызываемая после того, как было определено упорядочение
PERM, используется для вычисления обратного упорядочения
(или перестановки) INVP. Вектор INVP нужен при формирова-
формировании структуры данных для разложения и при занесении в нее
числовых значений.
$ A 2 Пример подпрограммы ввода числовых значений 305
Когда проработают численные подпрограммы разложения и
решения треугольных систем, будет получено решение х переупо-
переупорядоченной системы
(РАР7) х = РЬ.
Подпрограмма PERMRV используется для обратного переупо-
переупорядочения вектора х к исходному порядку неизвестных.
После того как формирование структуры данных для треу-
треугольного множителя успешно завершено, пользователь должен
задать реальные числовые значения коэффициентов матрицы А
и правой части Ь. Чтобы правильно разместить эти числа
в структуре данных, пользователю требуется детальное знание
схемы хранения. В следующем параграфе мы опишем одну из
подпрограмм, осуществляющих ввод матрицы. Понятно, что для
разных методов хранения такие подпрограммы ввода должны
быть различны. Разобрав пример из § А.2, читатель сможет
самостоятельно написать аналогичные подпрограммы для других
методов. Нужно подчеркнуть, что в пакете SPARSPAK. (см. При-
Приложение В) имеются все необходимые подпрограммы ввода
§ А.2. Пример подпрограммы ввода числовых значений
Прежде чем обратиться к численным подпрограммам разре-
разреженного метода, необходимо ввести в структуру данных число
вые значения коэффициентов. Здесь мы разберем подпрограмму
которая в рамках метода древовидного разбиения вводит число
вое значение элемента ац в соответствующую структуру данных.
Напомним (глава 6), что в этой схеме хранения предусмот-
предусмотрены три вектора для числовых значений. Вектор DIAG
содержит диагональные элементы матрицы. Элементы, принад-
принадлежащие оболочке диагональных блоков, хранятся массивом
ENV. Наконец, в векторе NONZ находятся ненулевые элементы,
расположенные вне блочной диагонали. Для заданного ненуле-
ненулевого элемента а,, подпрограмма ADAIJ модифицирует один из
трех векторов хранения DIAG, ENV или NONZ, в зависимости
от местонахождения этого элемента в матрице.
Оператор вызова подпрограммы ввода матричного элемента
выглядит так:
CALL ADAIJ (I, J, VALUE, INVP, DIAG, XENV,
ENV, XNONZ, NZSUBS, IERR).
Здесь I и J — индексы элемента в исходной (т. е. еще не пере-
переупорядоченной) матрице A, a VALUE — его числовое значение.
Подпрограмма прибавляет VALUE к значению at,, находяще-
находящемуся в данный момент в памяти. Сложение вместо присваива-
присваивания используется для того, чтобы приспособиться к ситуациям,
с
с........ •». «...,,.......,..¦•¦..
С........ ADAIJ ПРИБАВИТЬ ЧИСЛО К ЭЛЕМЕНТУ МАТРИЦЫ
<:«•• • •••
<>••• •
с
С ПРИбАВЛЯеТ ЗАДАННОЕ ЧИСЛО К ЭЛЕМЕНТУ Ql,J) МАТРИЦЫ,
С ХРАНИМОЙ ПОСРЕДСТВОМ НЕЯВНОЙ БЛОЧНОЙ
С СХЕМЫ.
с
С ВХОДНЫЕ ПАРАМЕТРЫ -
С (ISUB,JSUB) - ИНДЕКСЫ ИЗМЕНЯЕМОГО ЭЛЕМЕНТА.
С ПРЕДПОЛАГАЕТСЯ, ЧТО ISUB . GE . JSUB.
С DIAG - МАССИВ ДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ ПАТРИЦЫ
С КОЭФФИЦИЕНТОВ.
С VAIUE - ЗНАЧЕНИЕ ПРИБАВЛЯЕМОГО ЧИСЛА.
С INVP - INVP(I) - НОВЫЙ НОМЕР ПЕРЕМЕННОЙ,
С ИСХОДНЫЙ НОМЕР КОТОРОЙ РАВЕН I.
С (XENV, ENVM - ПАРА, СОДЕРЖАЩАЯ СТРУКТУРУ
С ОБОЛОЧКИ ДИАГОНАЛЬНЫХ БЛОКОВ.
С (XNONZ, NONZ, NZSUBS) - МАССИВЫ ДЛЯ ЧАСТЕЙ
С СТРОК НИЖНЕГО ТРЕУГОЛЬНИКА ИСХОДНОЙ
С МАТРИЦЫ, РАСПОЛОЖЕННЫХ ВНЕ БЛОЧНОЙ
С ДИАГОНАЛИ.
С ВЫХОДНОЙ ПАРАМЕТР -
С IERR - ИНДИКАТОР ОШИБКИ .
С О - ОШИБОК НЕ ОБНАРУЖЕНО.
С 5 - В СТРУКТУРЕ ДАННЫХ НЕТ МЕСТА
С ДЛЯ ЭЛЕМЕНТА С ИНДЕКСАМИ
С(I,J)
С
SUBROUTINE ADAIJ ( ISUB, JSUB, VALUF, INVP, DIAG,
1 XENV, ENV, XNONZ NONZ, NZSUBS,
4 IERR )
С
REAL DIAG(l), ENVA), NONZ(l), VALUE
INTEGER INVP(l), NZSUBS(l)
INTEGER XENV(l), XNONZ(l), KSTOP, KSTRT,
1 I. IERR, ISUB, ITEMP, J, JSUB, К
С
C«*t *«•**................
I - INVP(ISUB)
J - INVP(JSUB)
IF ( I EQ J ) GO TO 400
IF ( I GT J ) GO TO 100
ITEMP - I
I - J
J - ITFMP
? ЭЛЕМЕНТ ПРИНАДЛЕЖИТ ОБОЛОЧКЕ ДИАГ. БЛОКОВ.
? __ _
ЮС К - Xf-NV(I + l ) - I + J
IF ( К IT XENV(I) ) GO TO 200
ENV(K) = ENV(K) + VALUE
RETURN
С -
С ЭЛЕМЕНТ РАСПОЛОЖЕН ВНЕ ДИАГОНАЛЬНЫХ БЛОКОВ.
С —
200 KSTRT =¦ XNONZ(I)
KSTOP • XNONZ(I+1) - 1
IF ( КЬТОР LT KSFRT ) GO TO 500
С
DO 300 К - KSTRT, KSTOP
IF ( NZSUBS(K) ,NE J ) GO TO 300
jji A.3 Совмещение па пяти в Фортране 307
NONZ(K) - NONZ(K) + VALUE
RETURN
300 CONTINUE
GO TO 500
С
С ЭЛЕМЕНТ НАХОДИТСЯ НА ДИАГОНАЛИ МАТРИЦЫ.
с ..
400 DIAG(I) - DIAG(I) + VALUE
RETURN
С
С УСТАНОВИТЬ ИНДИКАТОР ОШИБКИ.
с тЩ
500 IERR - 5
RETURN
С
END
когда значения элементов матрицы получаются путем накопления
(так обстоит дело в некоторых конечноэлементных приложе-
приложениях).
Подпрограмма проверяет, будет ли заданный ненулевой эле-
элемент принадлежать диагонали или оболочке диагональных бло-
блоков. Если да, то его значение прибавляется к соответствующей
компоненте векторов DIAG или ENV. В противном случае про-
производится поиск в структуре индексов (XNONZ, NZSUBS), со-
соответствующей ненулевым элементам, расположенным вне блоч-
блочной диагонали; после этого VALUE прибавляется к соответст-
соответствующей компоненте вектора NONZ.
Именно по той причине, что в подпрограмме ADAIJ присваи-
присваивание заменено сложением, до ввода числовых значений элемен-
элементов А нужно установить нулевое начальное состояние на прост-
пространстве, отведенном для хранения L Поэтому ввод матрицы Л
в методе древовидного разбиения должен осуществляться таю
• Установить нулевое начальное состояние для векторов
DIAG, ENV и NONZ.
• {Повторные обращения к подпрограмме ADAIJ}.
Ввод числовых значений для вектора правых частей Ь можно
выполнить аналогичным образом.
§ 'A3. Совмещение памяти в Фортране
Рассмотрим скелетную ведущую программу профильного ме-
метода (рис. А.1.1). Подпрограмма GENRCM генерирует упорядо-
упорядочение PERM, исходя из структуры смежности (XADJ, ADJNCY)
Она использует также два рабочих вектора MASK и XLS
После ввода числовых значений в структуру данных для обо
лочки рабочие векторы MASK и XLS уже больше не нужны.
308 Приложение А Указания к использованию подпрограмм
Более того, даже структура смежности (XADJ, ADJNCY) в даль-
дальнейшем не понадобится. При необходимости экономии память,
отведенная для указанных векторов, может быть переструкту-
переструктурирована и использована подпрограммами численного решения
для других целей. Аналогичные замечания применимы и к ос-
остальным разреженным методам.
В этом разделе мы покажем, как можно осуществить совме-
совмещение памяти в Фортране. Общий прием состоит в том, что
в ведущей программе описывается большой массив, из которого
распределяется память для всех массивов, необходимых подпроч-
граммам. Ведущая программа управляет памятью с помощью
указателей, регистрирующих положение массивов из подпро-
подпрограмм в основном векторе хранения.
В качестве иллюстрации предположим, что имеются две под-
подпрограммы SUB1 и SUB2:
SUBROUTINE SUB1 (X, Y, Z), SUBROUTINE SUB 2
(X, Y, U,V).
Для подпрограммы SUB1 нужны два целых массива X и Y дли-
длиной соответственно 100 и 500 и еще рабочий целый массив Z
длины 400. Подпрограмме SUB2 требуются четыре массива: X и
Y — векторы на выходе SUB1 —и еще два массива U и V длины
40 и 200 соответственно.
Т Т f
IX IY IZ
т т t t
IX IY IU IV
Нижеследующая иллюстративная ведущая программа ис-
использует основной вектор хранения SA000) и последовательно
вызывает подпрограммы SUB1 и SUB2. Она управляет памятью
с помощью указателей, «перемещаемых» в массиве S,
INTEGER S(iOOO)
IX - 1
IY - IX + 100
it - I* + 500
CALL SUB1 (8(IX).S(IY),S(IZ))
IU г 1У + 800
IV - IU + 46
CALL SUB2 <S(IX),S(IY),S(IU),S(IV))
§ A3. Совмещение памяти в Фортране 309
Таким образом, память, использовавшаяся рабочим вектором Z,
может быть распределена для векторов U и V.
Ту же технику совмещения памяти можно использовать при
работе с последовательностью подпрограмм, реализующих метод
решения разреженных систем. Пакет SPARSPAK (Приложе-
(Приложение В) по существу опирается на эту самую технику в системе
подпрограмм интерфейса, которая избавляет пользователя от
всех задач управления памятью при использовании подпрограмм
этой книги.
Приложение В. SPARS PA К. Пакет
для разреженных матриц
§ В.1. Мотивировка
Скелетные программы Приложения А иллюстрируют некото-
некоторые важные характеристики разреженных матричных программ
и подпрограмм. Во-первых, нестандартные структуры данных,
используемые для хранения разреженных матриц, приводят
к тому, что подпрограммы имеют чересчур длинные списки па-
параметров. Смысл большей части этих параметров мало или вовсе
ие знаком пользователю, если только он (или она) не понимает
и помнит все детали прим-еняемой структуры данных.
Во-вторых, процесс вычислений состоит из нескольких раз-
различных фаз с многочисленными возможностями совмещения.па-
совмещения.памяти. Чтобы повысить эффективность подпрограмм, пользова-
пользователь должен определить, какие массивы, эксплуатируемые в од-
одном модуле, понадобятся в качестве входных для другого, а
какие больше не потребуются, и, следовательно, память, зани-
занимаемая ими, может быть использована для других целей.
В-третьих, во всех случаях количество памяти, необходимой
для этапов численного решения, неизвестно до тех пор, пока не
будет завершен хотя бы один из предыдущих этапов. Обычно
»то количество становится известно лишь по выполнении под-
подпрограммы распределения памяти (например, FNENV). В неко-
некоторых случаях нельзя заранее предсказать даже, какой объем
памяти нужен для успешного выполнения самой подпрограммы
распределения (так обстоит дело, например, с SMBFCT). Поэ-
Поэтому нередко вычисления приходится прерывать на полпути из-
за недостатка памяти, и пользователь, если он желает избежать
повторения законченных фрагментов процесса, должен каким-то
способом сохранить информацию, необходимую для возобновле-
возобновления вычислений.
Указанные обстоятельства, а также наша собственная прак-
практика в использовании «разреженного» матобеспечения побудили
нас сконструировать для пользователя удобный интерфейс с опи-
описанными в этой книге подпрограммами. Такой интерфейс пред-
представляет собой попросту слой подпрограмм между пользова-
пользователем, у которого предположительно имеется необходимость в
решении разреженной Системы уравнений, и подпрограммами,'
§ B.2. Базисная структура пакета SPARSPAK 311
реализующими методы данной книги (см. рис. В.1.1). Этот ин-
интерфейс вместе с подпрограммами, которые он обслуживает,
составляет пакет, которому мы дали название SPARSPAK
(George 1979a). Помимо подпрограмм из глав 4—8 и подпро-
подпрограмм интерфейса, SPARSPAK содержит также ряд служебных
подпрограмм для печатания сообщений об ошибках, изображений
структуры разреженных матриц и т. д.
Интерфейс выполняет ряд функций. Прежде всего он осво-
освобождает пользователя от всякой заботы о распределении памяти
(Пользователь^
\\
Подпрограммы
интерфейса
// / / г
Подпрограммы
из этой книги
Служебные
подпрограммы
Рис. В.1.1. Схематическое изображение компонент пакета SPARSPAK.
для массивов. Вся память распределяется интерфейсом в грани-
границах задаваемого пользователем одномерного массива; при этом
применяется техника, сходная с той, что описана в § А.З. Уста-
Устанавливается также контроль правильности порядка при вызове
подпрограмм интерфейса. Кроме того, пользователю предостав-
предоставляются удобные средства приостановки и последующего возоб-
возобновления вычислений. Наконец, имеется развернутая диагности-
диагностика ошибок.
Назначение последующих параграфов — дать краткий обзор
различных возможностей SPARSPAK; они отнюдь не являются
инструкцией для пользователя. Подробная инструкция для поль-
пользователя и указания по «наладке» пакета поставляются вместе
с ним. Необходимую информацию читатель может получить у
авторов.
§ В.2. Базисная структура пакета SPARSPAK
Для любого из методов, описанных в главах 4—8, взаимо-
взаимодействие пользователя и SPARSPAK при решении системы
Ах = Ь охватывается следующей схемой:
.il2 Приложение В. SPARSPAK: Пакет для разреженных матриц
Шаг 1 (Ввод структуры). Пользователь задает пакету струк-
структуру ненулевых элементов матрицы А, обращаясь к соответству-
соответствующим подпрограммам интерфейса.
Шаг 2 (Упорядочение и распределение памяти). Выполнение
в программе пользователя оператора вызова специальной под-
sprspk \ Инициирование
Ввод структуры
{Шаг 1)
HBEGN
INIJ(I, J, S)
INROW(I, NR, IR, S)
INIJIJ(NIR,-II, JJ, S)
INCLQ(NCLQ, CLQ, S)
IJEND(S)
•» Упорядочение и распределение
ordrx i (s) \ памяти {Шаг 2. Смысл
J символов х и i разъясняет
рис. В.3.1)
Ввод матрицы
Ввод правых частей
5)
INAIJl(I. J, VALUE, S)
INROWi(I, NIR, IR, VALUES, S)
INMATi(NIJ, II, JJ, VALUES, S)
INBI(I, VALUE, S)
INBIBI(NI, II, VALUES, S)
INRHS(RHS, S)
«„,,«, сч \ Разложение а решение
solvei(s) S Шаги 4.a 6)
Рис. B.2.I. Названия некоторых подпрограмм интерфейса из пакета SPARS-
SPARSPAK.
программы служит для пакета указанием на необходимость вы-
вычисления упорядочения и формирования структуры данных
для L.
Шаг 3 (Ввод матрицы). Пользователь задает числовые зна-
значения элементов А, обращаясь к соответствующим подпрограм-
подпрограммам интерфейса.
Шаг 4 (Разложение А). Вызов специальной подпрограммы
служит для пакета указанием на необходимость разложения А
в произведение LLJ.
Шаг 5 (Ввод правых частей). Пользователь задает числовые
значения компонент Ь, обращаясь к соответствующим подпро-
подпрограммам интерфейса. (Этот шаг может быть выполнен до шага 4
и объединен с шагом 3.)
Шаг 6 (Решение). Вызов специальной подпрограммы служит
для пакета указанием на необходимость вычисления х, исходя
из полученной на шаге 4 матрицы L и вектора Ъ, введенного на
шаге 5.
§ В.З. Головная программа пользователя 313
Названия некоторых подпрограмм интерфейса вместе со спис-
списками аргументов и общими функциями приведены на рис. В.2.1.
Детали можно найти в последующих разделах.
§ В.З. Головная программа пользователя — пример
SPARSPAK распределяет всю память в границах единого
одномерного вещественного массива, который нам удобно будет
обозначать через S. Помимо этого массива пользователь должен
задать и его длину MAXS, которая передается пакету через об-
общий блок j SPKUSR |, содержащий четыре переменных:
COMMON /SPKUSR/ MSGLVL, IERR, MAXS, NEQNS
Здесь MSGLVL — указатель уровня печати, используемый для
управления количеством информации, которая печатается паке-
пакетом. Вторая переменная IERR — индикатор ошибки, посредством
которого программе пользователя сообщается об ошибках, най-
найденных пакетом. Переменная NEQNS — это число уравнений,
устанавливаемое пакетом.
Приводимая ниже программа показывает, как используя
SPARSPAK, решить систему уравнений Ах — Ь профильным
методом главы 4. Рассматриваемая система имеет порядок 10
и симметричную трехдиагональную матрицу А. Все диагональ-
диагональные элементы А равны 4, наддиагональные и поддиагональные
элементы равны (—1), все компоненты вектора Ь равны 1.
Цифра i и буква х в именах некоторых подпрограмм интер-
интерфейса указывают, каким методом должна решаться задача.
Здесь мы должны отметить, что SPARSPAK позволяет решать
как симметричные, так и несимметричные системы. В последнем
случае предполагается, что структура матрицы А симметрична
и что не нужен выбор главного элемента для обеспечения устой-
устойчивости (см. упр. 4.5.1). На рис. В.3.1 указаны методы, входящие
в состав пакета.
С ПРОГРАММА, ИЛЛЮСТРИРУЮЩАЯ ИСПОЛЬЗОВАНИЕ SPARSPAK.
с -- -
с
COMMON /SPKUSR/ MSGLVL, IERR, MAXS, NEQNS
REAL' SBS0)
CALL SPRSPK
MAXS - 250
С
С ВВССТИ СТРУКТУРУ МАТРИЦЫ. ДИАГОНАЛЬ ВСЕГДА ПРЕДПОЛАГАЕТСЯ
С НЕНУЛЕВОЙ. Т.К. МАТРИЦА СИММЕТРИЧНА, ВВОДИМ ТОЛЬКО
С ПОЗИЦИИ ПОДДИАГОНАЛЬНЫХ ЭЛЕМЕНТОВ.
CALL IJBEGN
DO 100 1-2, 10
ЗН Приложение В. SPARSPAK: Пакет для разреженных матриц
CALL INIJ( I, 1-1, S )
100 CONTINUE
CALL IJEND( S )
НАЙТИ УПОРЯДОЧЕНИЕ И РАСПРЕДЕЛИТЬ ПАМЯТЬ
CALL ORDRA1( S )
ВВЕСТИ ЧИСЛОВЫЕ ЗНАЧЕНИЯ. (НИЖНИЙ ТРЕУГОЛЬНИК).
DO 200 I - 1, 10
IF ( I .GT.l ) CALL INAIJK I, 1-1, -1.0, S )
CALL INAIJ1( I, I. 4.0, S )
CALL INBIA,1.0, S )
200 CONTINUE
РЕШИТЬ СИСТЕМУ. Т.К. МАТРИЦА И ПРАВАЯ ЧАСТЬ
СИСТЕМЫ УЖЕ ВВЕДЕНЫ, ТО ПОДРЯД ВЫПОЛНЯЮТСЯ
РАЗЛОЖЕНИЕ И РЕШЕНИЕ ТРЕУГОЛЬНЫХ .СИСТЕМ.
CALL SOLVE1( S )
ВЫВЕСТИ НА ПЕЧАТЬ РЕШЕНИЕ, НАХОДЯЩЕЕСЯ В ПЕРВЫХ
10 ПОЗИЦИЯХ РАБОЧЕГО МАССИВА S.
KRITEF, 11) (S(I), I - 1, 10)
11 FORMAT*,/ 10H SOLUTION ,/, EF10.6))
ВЫВЕСТИ НА ПЕЧАТЬ СТАТИСТИКУ, СОБРАННУЮ ПАКЕТОМ.
CALL PSTATS
STOP
END
ORDRx/
x 1
A
A
A
A
В
В
A
A
В
В
1
2
3
4
3
4
5
6
5
6
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Упорядочение
Описание
RCM; симметричная
RCM, несимметричная
1WD симметричная
1WD несимметричная
RQT симметричная
RQT несимметричная
ND симметричная
ND несимметричная
QMD, симметричная
QMD, несимметричная
А
А
А
А
А
А
А
А
А
А
Ссылка
' Гл. 4
Гл. 4
Гл. 7
Гл. 7
Гл. 6
Гл. 6
Гл. 8
Гл. 8
Гл. 5
Гл. 5
Рис. В.3.1. Методы, входящие в состав пакета SPARSPAK
Подпрограмма SPRSPK. должна вызываться до обращения
к какой-либо части пакета. Ее роль состоит в инициировании
некоторых системных параметров (например, логического номера
печатающего устройства), присвоении значений тем переменным
§ B.4 Краткое описание основных подпрограмм интерфейса 315
(например, указателю уровня печати), которые не определены
пользователем, и выполнении некоторых машинно-зависимых
функций (например, запуск программы измерения времени).
В программе пользователя SPRSPK следует вызывать только
один раз. Заметим, что единственная переменная в общем блоке
|SPKUSR1, которой пользователь должен присвоить значение,—
это MAXS.
В пакете имеется подпрограмма интерфейса, именуемая
PSTATS, к которой пользователь может обратиться за информа-
информацией о памяти, времени, числе операций и т. д. при решении
системы.
Предполагается, что подпрограммы, составляющие
SPARSPAK, оттранслированы и помещены в библиотеку и что
пользователь может обратиться к ним из фортранной програм-
программы, как обращаются к стандартным библиотечным подпрограм-
подпрограммам Фортрана SIN, COS и т. д. Обычно пользователю нужна
лишь небольшая часть подпрограмм SPARSPAK.
§ В.4. Краткое описание основных подпрограмм интерфейса
ВАЛ. Модули для ввода структуры матрицы
SPARSPAK должен знать структуру матрицы, прежде чем
он сможет определить подходящее упорядочение для системы.
В SPARSPAK имеется группа подпрограмм, которые предостав-
предоставляют пользователю разнообразные способы информирования па-
пакета о расположении ненулевых элементов, т. е. передачи ему
пар индексов (i, j) таких, что ацФО. До вызова любой из этих
подпрограмм ввода пользователь должен обратиться к подпро-
подпрограмме инициирования, называемой IJBEGN, которая сообщает
пакету, что предстоит решить систему с новой структурой.
а) Ввод ненулевого элемента.
Чтобы сообщить SPARSPAK, что матричный элемент a,j не
равен нулю, пользователь просто выполняет оператор
CALL INIJ (I, J, S),
где I и J — индексы ненулевого элемента, a S — рабочий массив,
описанный пользователем и эксплуатируемый пакетом.
б) Ввод структуры строки или части строки.
Когда известна структура строки или части строки, то может
оказаться более удобной подпрограмма INROW. Соответствую-
Соответствующий оператор —
CALL INROW (I, NIR, IR, S),
где I обозначает номер рассматриваемой строки, IR — массив,
содержащий столбцовые индексы всех или части ненулевых эле-
элементов 1-й строки, NIR — число индексов в IR, a S — описанный
816 Приложение В. SPARSPAK' Пакет для разреженных матриц
пользователем рабочий массив. Индексы могут быть расположе-
расположены в массиве IR в произвольном порядке, и строки также можно
вводить в любом порядке.
в) Ввод структуры подматрицы.
SPARSPAK позволяет пользователю вводить структуру под-
подматрицы Оператор вызова имеет вид:
CALL INIJIJ (NIJ, II.JJ, S),
где NIJ — число вводимых пар индексов, а II и JJ — массивы,
содержащие эти индексы.
г) Ввод заполненной подматрицы.
Структура матрицы будет вполне известна, если заданы все
ее заполненные подматрицы. В тех случаях, когда такие под-
подматрицы легко определить, полезна подпрограмма INCLQ. Она
вызывается оператором
CALL INCLQ (NCLQ, CLQ, S),
где NCLQ — поцядок подматрицы, a CLQ — массив, содержащий
индексы подматрицы.
Так, чтобы сообщить пакету, что подматрица, соответствую-
соответствующая индексам 1, 3, 5 и 6, заполнена, достаточно следующего
текста:
CLQ(l) - 1
CLQB) - 3
CLQC) - 5
CLQD) - 6
CALL TNCLQD, CLQ, S)
Какую именно подпрограмму ввода применить, зависит от
обстоятельств, в которых пользователь получает* структуру мат-
матрицы. Во всяком случае, всегда можно выбрать подпрограмму,
наиболее подходящую для данной ситуации. Пакет позволяет
смешанное использование подпрограмм при вводе структуры
матрицы. SPARSPAK автоматически устраняет дублирование,
так что пользователю не нужно беспокоиться по поводу возмож-
возможного повторного ввода пар индексов
Когда все пары введены посредством одной подпрограммы
либо комбинации нескольких, пользователь должен явно указать
это пакету, вызвав посредством оператора
CALL IJEND (S)
подпрограмму IJEND. Назначение подпрограммы — преобразо-
преобразовать данные из формата, использовавшегося в фазе записи,
в стандартный формат (XADJ, ADJNCY), используемый всеми
подпрограммами этой книги. Пользователь никак не связан
с этим входным представлением или процессом преобразования.
§ В 1 Краткое описание основных подпрограмм интерфейса 317
8.4.2. Модули для упорядочения и распределения памяти
Когда внутреннее представление структуры ненулевых эле-
элементов матрицы получено, SPARSPAK готов к переупорядоче-
переупорядочению задачи. Пользователь инициирует этот процесс, вызвав под-
подпрограмму упорядочения, название которой имеет вид ORDRjct.
Здесь i — цифра от 1 до 6, указывающая метод хранения; х —
буква, обозначающая стратегию, упорядочения (см. рис. В.3.1).
Подпрограмма ORDRxi определяет упорядочение, а затем фор-
формирует структуру данных для переупорядоченной задачи. Теперь
пакет готов к вводу числовых значений.
8.4.3. Модули для ввода числовых значений
Модули этой группы аналогичны модулям для ввода струк-
структуры матрицы. Они дают средства для передачи пакету реаль-
реальных числовых значений коэффициентов системы. Так как струк-
структуры данных для разных методов хранения различны, то пакет
должен иметь свою подпрограмму ввода матрицы для каждого
метода. Названия этих подпрограмм различаются лишь послед-
последним символом — цифрой, определяющей метод; списки парамет-
параметров для всех методов одинаковы.
Имеются три способа передачи числовых значений пакету.
Во всех трех индексы вводимых элементов соответствуют исход-
исходной задаче. Пользователю не нужно беспокоиться о перестанов-
перестановках, которые могли произойти на этапе упорядочения.
а) Ввод ненулевого элемента.
Для этой цели служит подпрограмма INAIJ i, вызываемая
оператором
CALL INAIJ i (I, J, VALUE, S),
где I и J — индексы элемента, VALUE — его числовое значение.
Вместо присваивания подпрограмма INAIJ/ прибавляет VALUE
к текущему значению элемента аИ, находящемуся в памяти. Та-
Такой образ действий учитывает ситуации (встречающиеся, напри-
например, в конечноэлементных приложениях), когда числовые значе-
значения коэффициентов получаются в результате накопления. Напри-
Например, в результате выполнения операторов
INAIJ 2 C,4,9.5, S)
INAIJ 2 C, 4, —4.0, S)
значением элемента ац будет число 5.5.
б) Ввод ненулевых элементов строки.
Для ввода числовых значений элементов строки или части
строки можно воспользоваться подпрограммой INROWt. Олера-
818 Приложение В SPARSPAK Пакет для разреженных матриц
тор вызова этой подпрограммы аналогичен оператору вызова
подпрограммы INROW (см. раздел В.4.1):
CALL INROW/ (I, NIR, IR, VALUES, S).
Дополнительная переменная VALUES—это идентификатор мас-
массива, содержащего числовые значения ненулевых элементов
строки. И здесь числовые значения добавляются к тем, что в дан-
данный момент находятся в памяти.
в) Ввод подматрицы
Подпрограмма ввода подматрицы называется INMATi. One-4
ратор вызова для нее соответствует оператору вызова подпро-
подпрограммы INIJIJ, за исключением дополнительного параметра
VALUES — идентификатора массива, хранящего числовые зна-
значения ненулевых элементов:
CALL INMATi (NIJ, II, JJ, VALUES, S).
И снова числа из VALUES прибавляются к текущим значениям,
хранимым пакетом.
Разрешается смешанное использование подпрограмм INAIJ/,
INROWt и INMATi. Пользователь может выбирать наиболее
удобные для него подпрограммы.
Те же удобства предоставляются и при вводе правых частей
системы. В пакете имеется подпрограмма INBI, которая вводит
одну компоненту вектора 6. Оператор вызова —
CALL INBI (I, VALUE, S).
Здесь I — индекс компоненты, VALUE — ее числовое значение.
Для ввода подвектора можно воспользоваться подпрограм-
подпрограммой INBIBI, оператор вызова которой —
CALL INBIBI (NI, II, VALUES, S),
где II и VALUES — векторы, содержащие соответственно ин-
индексы и числовые значения. В обеих подпрограммах 1) значения
»лементов вычисляются путем накопления.
В тех случаях, когда вектор 6 известен полностью, пользова-
пользователь может обратиться к подпрограмме INRHS, которая пере-
передает пакету весь этот вектор. Оператор вызова —
CALL INRHS (RHS, S),
где RHS — вектор, содержащий числовые значения.
Во всех трех подпрограммах задаваемые числа прибавляются
к тем, что в данный момент хранятся пакетом; использование
подпрограмм может быть смешанным. При первом обращении
') INBI и INBIBI. — Прим перев.
§ В 5. Средства для запоминания и возобновления 319
к какой-либо из них пакетом устанавливается нулевое начальное
состояние массива, отведенного для хранения Ь.
В.4.4 Модули для разложения и решения
Вычисление решения системы инициируется оператором
CALL SOLVE/ (S), где S — рабочий массив, используемый па-
пакетом. Последний символ — цифра i — снова используется для
различения подпрограмм, относящихся к различным методам
хранения.
Подпрограмма SOLVEr включает в себя и этап разложения,
и этап решения треугольных систем. Если разложение было про-
произведено при предыдущем вызове SOLVEr, то пакет автомати-
автоматически опускает этап разложения и прямо переходит к решению
треугольных систем. Вычисленный вектор решения размещается
в первых NEQNS позициях вектора S. Если обращение
к SOLVEr происходит еще до ввода правых частей, то выпол-
выполняется только разложение. В качестве решения выдается нуле-
нулевой вектор.
§ В.5. Средства для запоминания и возобновления
SPARSPAK. содержит две подпрограммы, называемые SAVE
и RESTRT, которые позволяют пользователю прервать вычисле-
вычисления в желаемом месте, запомнить результаты (в виде последо-
последовательного файла) на внешнем накопителе, а потом, некоторое
время спустя, возобновить счет с места прерывания. Для запо-
запоминания результатов, вычисленных до момента прерывания,
пользователь выполняет оператор
CALL SAVE (К, S)
где К — логический номер накопителя, куда нужно записать ре-
результаты вместе с другой информацией, необходимой для во-
возобновления вычислений. Если вычисления затем прекращаются,
то в дальнейшем состояние процесса можно восстановить с по-
помощью оператора
CALL RESTRT(K, S).
Если обнаружена ошибка, препятствующая продолжению вы-
вычислений, то переменной IERR присваивается положительное
значение. Чтобы убедиться в правильности выполнения модуля,
пользователю достаточно проверить значение IERR. Индика-
Индикатор ошибки совместно со средствами запоминания/возобновле-
запоминания/возобновления можно использовать для сохранения результатов успешно
820 Приложение В. SPARSPAK: Пакет для разреженных матриц
завершенных этапов процесса. Это иллюстрируется следующим
фрагментом программы:
100
CALL ORDRAl(S)
IF (IERR.EQ.O) GO TO 100
CALL SAVEC S)
STOP
CONTINUE
Другой возможный вариант использования модулей SAVE и
RESTRT — это возврат пользователю управления рабочим мас-
массивом S еще до окончания разреженных матричных вычислений.
После выполнения подпрограммы SAVE массив S можно ис-
использовать для других целей.
§ В.6. Решение многих систем с одинаковой структурой
или одинаковой матрицей коэффициентов
В некогорых приложениях приходится решать большое число
систем с одинаковой структурой разреженности, но разными зна-
SPRSPK
Ввести структуру
CALL ORDRxi
Ввести числовые
значения для А и Ь
i
CALL SOLVEi
Рис. В.в.1, Блок-схема, иллюстрирующая использование SPARSPAK при ре-
решении многих систем с одинаковой структурой.
чениямн коэффициентов. Пакет очень легко приспосабливается
к этой ситуации. Нужная управляющая последовательность
§ B.6. Решение многих систем с одинаковой структурой 321
изображена блок-схемой рис. В.6.1. Когда после выполнения
подпрограммы SOLVE/ в первый раз происходит обращение
к подпрограммам ввода числовых значений (INAIJ i, INBI и
т. д.), пакет замечает это и устанавливает нулевое начальное
SPRSPK
SPRSPK
Ввести структуру
4
ВВести структуру
4
CALL ORDRxi
CALL ORDRxi
Ввести числовые
значения для Л
ВВести числовые
значения для А
CALL
>
SOLVE!
Ввести числовые
значения для b
CALL S0LVE1
«"I
Ввести числовые
значения для Ь
CALL SOLVEi
A)
B)
Рис. В.6.2. Блок-схемы, иллюстрирующие использование SPARSPAK при ре-
решении многих систем с одинаковой матрицей коэффициентов, но разными пра-
правыми частями.
состояние на пространстве памяти, отведенном для ^ранения А
и Ь.
Отметим, что если такую совокупность систем приходится
решать в течение продолжительного периода времени (т. е.
в разных выходах на машину), то пользователь может после вы-
выполнения ORDRxi обратиться к SAVE, что позволяет избежать
ввода структуры А и вызова ORDRxi при решении последую-
последующих систем.
В других приложениях встречается необходимость решения
ряда систем, различающихся лишь правыми частями. В таких
322 Приложение В SPARSPAK: Пакет для разреженных матриц
случаях достаточно один раз разложить матрицу А, после чего
ее множители используются для вычисления вектора х для каж-
каждого очередного Ь. И к этой ситуации пакет приспосабливается
очевидным образом, как показывают блок-схемы рисунка В.6.2.
Когда SPARSPAK используется в соответствии с блок-схе-
блок-схемой A) на рис. В.6.2, он обнаруживает при первом выполнении
подпрограммы SOLVEi, что правые части не были заданы, и,
выполняет только разложение. При последующих обращениях
к SOLVEi пакет замечает, что разложение уже получено, и эта
часть модуля SOLVEi обходится. В блок-схеме B) рис. В.6.2
при первом вызове SOLVE i производятся и разложение, и ре-
решение треугольных систем, а при последующих вызовах — только
решение.
Заметим, что если пользователь хочет сохранить разложение
для будущих расчетов, то после вызова SOLVEi он может об-
обратиться к подпрограмме SAVE.
§ В.7. Вывод на печать
Как уже говорилось, пользователь задает одномерный веще-
вещественный массив S, в границах которого распределяется память
для всех массивов пакета. В частности, интерфейс отводит для
решения системы первые NEQNS позиций S. После того как
для ааннстго метода успешно проработали все модули интер-
интерфейса, пользователь может вывести решение на печать из этих
позиций S.
Кроме решения х пакет может выдавать на печать и другую
информацию о процессе вычислений, определяемую такими фак-
факторами, как значение переменной MSGLVL, были ли обнаруже*
ны ошибки, вызывался ли модуль PSTATS.
Литературах)
* [Aho 1974] А. V. Aho, J. E. Hopcroft, and J. D. Ullman,
The Design and Analysis of Computer Algorithms, Addlson-
Wesley, Reading, Mass. A974).
[Arany 1972] I. Arany, W. F. Smyfh, and L. Szoda,
"An improved method for reducing the bandwidth of sparse
symmetric matrices," Information Process'ng 71: Proc. of IFIP
Congress, North-Holland, Amsterdam A972).
[Baty 1967] J. P. Baty, and K. L. Stewart,
"Dissection of Structures," J. Struct. Div. ASCE 5 A967),
pp. 217-232.
*[Berge 1962] С Berge,
The Theory of Graphs and Its Applications, John Wiley & Son!
Inc., New York A962).
[Birkhoff 1973] G. Birkboff, and Alan George,
"Elimination by nested dissection," in Complexity of Sequential
and Parallel Numerical Algorithms, edited by J. F. Traub,
Academic Press A973).
[Bunch 1974] J.p. Bunch, and J. E. Hopcroft,
"Triangular factorization and inversion by fast matrix multiplica-
multiplication," Math. Сотр. 28 A974), pp. 231-236.
[Bunch 1976] J. R. Bunch, and D. J. Rose, ed.,
Sparse Matrix Computations, Academic Press A976).
[Calahan 1975] D. A. Calahan,
"Complexity of vectorized solution of two dimensional finite ele-
element grids," Tech. Rept. 91, Systems Engrg. Lab., University of
Michigan A975).
[Calahan 1976] D. A. Calahan, W. N. Joy, and D. A. Orhits,
"Preliminary report on results of matrix benchmarks on a vector
processor," Tech. Rept. 94, Systems Engrg. Lab., University <pf
Michigan A976).
[Chan 1979] W. M. Chan, and Alan George,
"A linear time implementation of the Reverse Cuthill McKee algo-
algorithm," B.I.T 20 A980), pp. 8-14.
[Chang 1969] A. Chang,
"Application of sparse matrix methods in electrical power system
') Работы, переведенные на русский язык, отмечены звездочкой — СМ,
стр. 329.
324 Литература
analysis," in Sparse Matrix Proceedings, edited by R. A.
Willoughby, IBM Research Rept. RA 1.211707, Yorktown
Heights, N. Y. A969).
[Crane 1976] H. L. Crane Jr., N. E. Gibbs, W.G. Poole Jr., and P.
K. Stockmeyer, "Algorithm 508: Matrix bandwidth and profile
reduction," ACM Trans on Math Software 2 A976),
pp 375-377.
[Cuthill 1969] E. Cuthill, and J. McKee,
"Reducing the bandwidth of sparse symmetric matrices," Proc.
24th Nat Conf. Assoc Comput. Mach., ACM Publ. A969),
pp. 157-172.
[Cuthill 1972] Elizabeth Cuthill,
"Several strategies for reducing the bandwidth of matrices" in
Sparse Matrices and their Applications, edited by D. J. Rose and
R. A. Willoughby, Plenum Press, New York A972), pp. 157-166.
[Duff 1974] I. S. Duff, and J. K. Reid,
"A comparison of sparsity orderings for obtaining a pivotal se-
sequence in Gaussian elimination," J. Inst Math Applies. 14
A974), pp. 281-291.
[Duff 1976a] I. S. Duff, A. M. Erisman, and J. K. Reid,
"On George's nested dissection method," S1AM J Numer Anal.
/5A976), pp. 686-695.
[Duff 1976b] I. S. Duff, and J. K. Reid,
"A comparison of some methods for the solution of sparse
overdetermined systems of linear equations," J. Inst. Math. Appl-
Applies. /7A976), pp. 267-280.
[Duff 1977] I. S. Duff,
"A survey of sparse matrix research," Proc. IEEE 65 A977),
pp. 500-535.
[Duff 1979] I. S. Duff, and G. W. Stewart, ed.,
Sparse Matrix Proceedings 1978, SIAM Publications, Philadelphia
A979).
[Eisenstat 1974] S. C. Eisenstat, and A. H. Sherman,
"Subroutines for envelope solution of sparse linear systems,"
Research Rept. 35, Dept. of Computer Science, Yale University
A974).
[Eisenstat 1976] S. f. Eisenstat, M. H. Schultz, and A. H. Sherman,
"Applications of an e'ement model for Gaussian elimination," in
Sparse Matrix Computations, edited by J. R. Bunch and D. J.
Rose, Academic Press, New York A976), pp 85-96.
[Eisenstat 1981] S. С Eisenstat, M. С Gursky, M. H. Schultz, and
A. H. Sherman, "Yale Sparse Matrix Package I. The Symmetric
Codes," ACM Trans, on Math. Software (to appear)
[Erisman 1972] A. M. Erisman, and G. E. Spies,
"Exploiting problem characteristics in the sparse matrix approach
Литература 325
to frequency domain analysis," IEEE Trans, on Circuit Theory,
CT-19A972), pp. 260-269.
[Felippa 1970] С Felippa, and R. W. Clough,
"The finite element method in solid mechanics," in Numerical
Solution of Field Problems in Continuum Mechanics, edited by G.
Birkhoff and R. S. Varga, SIAM-AMS Proc., Amer. Math. Soc.
A970), pp. 210-252.
[Felippa 1975] С A. Felippa,
"Solution of linear equations with skyline-stored symmetric
matrix," Computers and Structures 5 A975), pp. 13-29.
*[Forsythe 1967] George E. Forsythe, and Cleve B. Moler,
Computer Solution of Linear Algebraic Systems, Prentlce-HaH
Inc., Englewood Cliffs, N. J. A967).
[George 1971] Alan George, ,
"Computer implementation of the finite element method,"' Tech.
Rept. STAN-CS-208, Stanford University A971).
[George 1973] Alan George,
"Nested dissection of a regular finite element mesh," SIAM J.
Numer Anal. 10 A973), pp. 345-363.
[George 1974] Alan George,
"On block elimination for sparse linear systems," SI A M J. Numer,
Anal. 11 A974), pp. 585-603.
[George 1975] Alan George, and Joseph W-H Uu,
"A note on fill for sparse matrices," SI AM J. Numer. Anal. 12
A975), pp. 452-455.
[George 1977] Alan George,
"Numerical experiments using dissection methods to solve n by я
grid problems," S1AM J. Numer. Anal. 14 A977), pp. 161-17».
[George 1978a] Alan George, and Joseph W-H Uu,
"User guide for SPARSPAK: Waterloo Sparse Linear Equations
Package," Rept CS-78-30, Dept. of Computer Science, University
of Waterloo A978).
[George 1978b] Alan George,
"An automatic one-way dissection algorithm for irregular finite
element problems," Proc. 1977 Dundee Conf. on Numerical
Analysis, Lecture Notes No. 630, Springer Verlag A978),
pp. 76-89.
[George 1978c] Alan George, and Joseph W-H Liu,
"Algorithms for matrix partitioning and the numerical solution of
finite element systems," SIAM J. Numer. Anal. 15 A978).
pp. 297-327.
[George 1978d] Alan George, and Joseph W-H Liu,
"An automatic nested dissection algorithm for irregular finite ele-
element problems," SIAM J. Numer. Anal. 15 A978),
pp. 1053-1069.
326 Литература
[George 1978e] Alan George, W. G. Poole'Jr., and Robert G. tolgf,
"Incomplete nested dissection for solving n by n grid problems,"
SIAMJ. Numer. Anal 15 A978), pp. 662-673.
[George 19 7 8 f] Alan George, and David R. Mclntyre,
"On the application of the minimum degree algorithm to finite ele-
element systems," S1AM J Numer Anal. 15 A978), pp. 90-112.
[George 1978g] Alan George, W. G. Poole Jr., and R. G. Voigt,
"Analysis of dissection algorithms for vector computers," J Сотр.
and Maths, with Applies 4 A978), pp. 287-304.
[George t979a] Alan George, and Joseph W-H Liu,
"The design of a user interface for a sparse matrix package,"
ACM Trans, on Math. Software 5 A979), pp. 139-162.
[George 1979b] Alan George, and Joseph W-H Liu,
"An implementation of a pseudo-peripheral node finder," AC\i
Trans, on Math Software 5 A979), pp. 286-295.
[George 1980] Alan George, and Joseph W-H Liu,
"A minimal storage implementation of the minimum degree algo-
algorithm," SIAMJ Numer Anal. 17 A980), pp. 282-299.
[Gibbs 1976a] N. E. Gibbs, W. G. Poole Jr., and P. K. Stockmeyer,
"A comparison of several bandwidth and profile reduction algo-
algorithms," ACM Trans, on Math Software 2 A976), pp. 322-330.
[Gibbs 1976b] N. E. Gibbs, W. G. Poole Jr., and P. K. Stockmeyer,
"An algorithm for reducing the bandwidth and profile of a sparse.
matrix," SIAMJ. Numer. Anal. 13 A976), pp. 236-250.
[Gibbs 1976c] N. E. Gibbs,
"Algorithm 509: A hybrid profile reduction algorithm," ACM
Trans, on Math. Software 2 A976), pp. 378-387.
[Gustavson 1972] F. G. Gustavson,
¦'Some basic techniques for solving sparse systems of equations," ia
Sparse Matrices and their Applications, edited by D. J. Rose and
R. A. Willoughby, Plenum Press, New York A972), pp. 41-52.
[Hachtel 1972] G. D. Hachtel,
"Vector and matrix variability type in sparse matrix algorithms,"
in Sparse Matrices and their Applications, edited by D. J. Rose
and R. A. Willoughby, Plenum Press, New York A972),
pp. 53-66.
[Hahsen 1978] Richard J. Hansen, and John A. Wisniewski,
''A single set of software that implements various storage methods
for sparse matrices," Rept. SAND78-O785, Sandia Laboratories,
Albuquerque, N. M. A978).
JHoffman 1973] A. J. Hoffman, M. S. Martin, and D. J. Rose,
'"Complexity bounds for regular finite difference and finite element
grids," SIAMJ. Numer. Anal. 10 A973), pp. 364-369
[Irons 1970] Bruce M. Irons,
"A frontal solution program for finite element analysis," Internal.
Литература 327
J. Numer. Meth. in Engrg. 2 A970), pp. 5-32.
[Jennings 1966] A. Jennings
"A compact storage scheme for the solution of symmetric linear
simultaneous equations," Comput. J. 9 {1966), pp. 281—285.
[King 1970] I. P. King,
"An automatic reordering scheme for simultaneous equations
derived from network problems," Internet J. Numer. Meth.
Engrg. 2A970), pp. 523-533.
[Lambiotte 1975] J. J. Lambiotte,
"The solution of linear systems of equations on a vector
computer," Ph. D. Diss., Dept. Appl. Math, and Сотр. Sci., Unfft.
of Virginia A975).
[Levy 1971] R. Levy,
"Resequencing of the structural stiffness matrix to improve compu-
computational efficiency," JPL Quart. Tech. Rev. 1 A971), pp. 61-70.
[Lipton 1977] Richard J. Lipton, and Robert E. Tarjan,
"A separator theorem for planar graphs," Proc. Conf. on
Theoretical Computer Science, Univ. of Waterloo (Aug. 15-17,
1977), pp. 1-10.
[Lipton 1979] R. J. Lipton, D. J. Rose, and R. E. Tarjan,
"Generalized nested dissection," SIAM J. Numer. Anal. 16
A979), pp. 346-358.
[Liu 1975] Joseph W-H Liu, and Andrew H. Sherman,
"Comparative analysis of the Cuthill-McKee and the reverse
Cuthill-McKee ordering algorithms for sparse matrices," SIAM J.
Numer. Anal. 13 A975), pp. 198-213.
[Liu 1976] Joseph W-H Liu,
"On reducing the profile of sparse symmetric matrices," Rept.
CS-76-07, Dept. of Computer Science,-Univ. of Waterloo (Feb.
1976).
[Martin 1971] R. S. Martin, and J. H. Wilkinson,
"Symmetric decomposition of positive definite band matrices," in
Handbook for Automatic Computation Vol. II, edited by J. H.
Wilkinson and С Reinsch, Springer Verlag A971).
[Markowitz 1957] H. M. Markowitz,
"The elimination form of the inverse and its application to linear
programming," Management Science 3 A957), pp. 255-269..
[Melosh 1969] R. J. Melosh, and R. M. Bamford,
"Efficient solution of load deflection equations," /. Struct. Div,'
ASCE, Proc. Paper No. 6510 A969), pp. 661-676.
[Meyer 1973] С Meyer,
"Solution of linear equations — State-of-the-art," J. Strut t Div,
ASCE, Proc. Paper No. 9861 A973), pp. 1507-1526.
[Ng 1979] Esmond Ng, "A two-level one-way dissection scheme for
finite element problems," Proc. Ninth Manitoba Conference on
328 Литература
Numerical Math, and Computing, Sept. 26-29, 1979.
[Parter 1961] S. V. Parter,
"The use of linear graphs in Gauss elimination," SIAM Rev 3
A961), pp. 119-130.
[Pooch 1973] U. W. Pooch, and A Neider,
"A survey of indexing techniques for sparse matrices," ACM
Computing Surveys 5 A973), pp. 109-133.
[Rose 1972a] D. J. Rose,
"A graph-theoretic study of the numerical solution of sparse
positive definite systems of linear equations," in Graph Theory and
Computing, edited by R. C. Read, Academic Press, New York
A972).
[Rose 1972b] D. J. Rose, and R. A. Willoughby, ed.,
Sparse Matrices and their Applications, Plenum Press A972).
[Rose 1974] D. J. Rose, and G. F. Whitten,
"Automatic nested dissection," Proc. ACM Nat. Conf. A974),
pp. 82-88.
[Rose 1975] D. J. Rose, and R. E. Tarjan,
"Algorithmic aspects of vertex elimination," Proc 7th Annual
Symposium on the Theory of Computing A975), pp. 243-254.
[Rose 1976a] D. J. Rose, R. E. Tarjan, and G. S. Lneker,
"Algorithmic aspects of vertex elimination on graphs," SIAM J.
on Computing 5 A976), pp. 266-283.
[Rose 1976b] D. J. Rose, and G. F. Whitten,
"A recursive analysis of dissection strategies," in Sparse Matrix
Computation, edited by J. R. Bunch and D. J. Rose, Academic
Press A976), pp. 59-84.
(Ryder 1974] B. G. Ryder,
"The PFORT Verifier," Software Practice and Experience 4
A974), pp. 359-377. >
[Sherman 1975] A. H. Sherman,
"On the efficient solution of sparse systems of linear and non-
nonlinear equations," Rept. No. 46, Dept. of Computer Science, Yale
University A975).
[Shier 1976] D. R. Shier,
"Inverting sparse matrices by tree partitioning," J. Rei of the
Nat. Bur. fif Standards, V80b, No 2 A976).
[Smyth 1974] W. F. Smyth, and W. M. L. B«nzi,
"An algorithm for finding the diameter of a graph," IFIP
Congress 74,- North-Holland Publ. Co. A974), pp. 500-503.
[Stewart 1973] G. W. Stewart,
Introduction to Matrix Computations, Academic Press, New York
A973).
[Strang 1973] Gilbert W. Strang, and George J. Fix,
An Analysis of the Finite Element Method, Prentice-Hall Inc.,
Литература
Englewood Cliffs, N. J A973).
fStrassen 1969] V. Strassen,
"Gaussian elimination is not optimal," Numer. Math. 13 A969),
pp 354-356
[Tinney 1969] W. F. Tinney,
"Comments on using sparsity techniques for power system
problems," in Sparse Matrix Proceedings, IBM Research Rept.
RAI 3-12-69 A969)
[Varga 1962] R. S. Varga,
Matrix Iterative Analysis, Prentice-Hall, Englewood Cliffs. N J.
A962)
[Von Fuchs 1972] G. von Fuchs, J. R. Roy, and E. Schrem.
"Hypermatrix solution of large sets of symmetric positive definite
linear equations," Comp Meth in Appl Mech and Engrg I
A972), pp. 197-216
[Wilkinson 1961] J. H. Wilkinson,
"Error analysis of direct methods of matrix inversion," J Assoc
Contput Mach «A961), pp. 281-330
[Wilson 1974] E. L. Wilson, K. L. Bathe, and W. P. Doherty,
"Direct solution of large systems of linear equations," Computers
and Structures 4 A974), pp 363-372
[Young 1971] D. M. Young,
Iterative Solution of Large Linear Systems, Academic Press, New
York A971).
[Zienkiewicz 1977] О. С Zienkiewicz, The Finite Element Method,
McGraw Hill, London A977).
Работы, переведенные на русский язык
Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ
вычислительных алгоритмов.—М.: Мир, 1979.
Берж К. Теория графов и ее применения.—М.: ИЛ, 1962.
Форсайт Дж. Е., Молер К. Численное решение систем линей-
линейных алгебраических уравнений. — М.: Мир, 1969.
Мартин Р. С, Уилкинсон Дж. — в сб. Уилкинсон Дж., Райнш.
Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра.—
М.: Машиностроение, 1976.
Стренг Г., Фикс Дж. Теория метода конечных элемен-
элементов.— М.: Мир, 1977.
Оглавление
От переводчика •> 5
Предисловие ?
Глава t. Введение 9
§ 1.0. Об этой книге 9
§ 1.1. Метод Холесского и проблема упорядочения Ю
§ 1.2. Положительно определенные и неопределенные матричные задачи 17
§ 1.3. Итерационные и прямые методы 18
Глава 2. Вводные сведения 21
§ 2.0. Введение 21
2.0.1. Обозначения 21
Упражнения 23
§ 2.1. Алгоритм разложения 23
2.1.1 Существование и единственность разложения 23
2.1.2. Вычисление разложения 25
2.1.3 Разложение разреженных матриц . . . '. 29
Упражнения 32
§ 2.2. Решение треугольных систем 33
2.2.1 Вычисление решения 33
2.2.2. Число операций 35
Упражнения 36
§ 2.3. Некоторые практические замечания . . • 38
2.3.1. Запросы к памяти . 39
2.3.2 Время исполнения 42
Упражнения 43
Глава 3. Некоторые сведения из теории графов и ее применение к ис-
исследованию разреженных симметричных матриц 44
§ 3.0. Введение 44
§ 3.1. Основная терминология и некоторые определения 44
Упражнения 49
§ 3.2. Машинное представление графов 49
§ 3.3. Некоторые общие сведения о подпрограммах, оперирующих с
графами 52
Упражнения 54
Глава 4. Ленточные и профильные методы 56
§ 4.0. Введение 56
§ 4.1. Ленточный метод ^
Упражнения . . 69
§ 4.2. Профильный метод 59
4.2.1 Матричная формулировка 54
4.2.2 Интерпретация на языке графов 63
Упражнения 64
§ *.3. Профильные упорядочения 65
4.3 1 Обратный алгоритм Катхилла — Макки 65
4.3.2 Определение начальною узла 69
Оглавление 331
4.3.3. Подпрограммы поиска начального узла 72
4.3.4. Подпрограммы обратного алгоритма Катхилла — Макки . 76
Упражнения 83
§ 4.4. Реализация профильного метода 85
4.4.1. Профильная схема хранения < 85
4.4.2. Подпрограмма распределения памяти FNENV (FiNd-EN-
Velope) 86
§ 4.5. Подпрограммы численного решения ESFCT, ELSLV и EUSLV 88
4.5.1. Подпрограммы для решения треугольных систем ELSLV и
EUSLV 88
4.5.2 Подпрограмма разложения ESFCT 92
Упражнения 96
§ 4.6. Дополнительные замечания 96
Глава 5. Универсальные разреженные методы 98
§ 5.0. Введение - 98
§ 5.1. Симметричное разложение , . . . 98
5.1.1. Модель графов исключения 99
5.1.2. Моделирование исключения посредством достижимых мно-
множеств 102
Упражнения 107
§ 5.2. Машинное представление графов исключения 107
5.2.1. Явные и неявные представления 108
5.2.2. Модель фактор-графов 109
5.2.3. Реализация фактор-модели 114
Упражнения 119
§ 5.3. Алгоритм минимальной степени 119
5.3.1. Основной алгоритм 121
5.3.2 Описание алгоритма минимальной степени посредством до-
достижимых множеств 121
5.3.3. Ускорение алгоритма 124
5.3.4. Реализация алгоритма минимальной степени 129
Упражнения 141
§ 5.4. Схемы хранения разреженных матриц 143
5.4.1. Обычная схема 143
5.4.2. Компактная схема 145
5.4.3. О символическом разложении 148
5.4.4. Распределение памяти для компактной схемы и подпро-
подпрограмма SMBFCT 152
Упражнения 157
§ 5.5. Подпрограммы численного разложения и решения 157
5.5.1. Подпрограмма GSFCT (General sparse Symmetric FaCTo-
rization) 158
5.5.2. Подпрограмма GSSLV (General sparse Symmetric SoLVe) 162
§ 5.6. Дополнительные замечания 163
Глава 6. Методы фактор-деревьев для конечноэлементных и конечно-
разностных задач 164
§ 6.0. Введение 164
§ 6.1. Решение блочных систем уравнений 166
6.1.1. Разложение матрицы блочного порядка два 165
6.1.2. Решение треугольной системы блочного порядка два . .170
Упражнения 171
§ 6,2. Фактор-графы, деревья и древовидные разбиения 172
6.2.1. Блочные матрицы и фактор-графы 172
6.2.2. Деревья, фактор-деревья и древовидные разбиения ... 175
6.2.3. Асимметричное блочное разложение и неявное блочное ре-
решение систем с древовидным разбиением 178
Упражнения ,,,.,,, f ,,,,,,. 179
332 Оглавление
§ 6.3. Алгоритм вычисления древовидного разбиений ....... 182
6.3.1. Эвристический алгоритм 182
6.3.2. Подпрограммы для вычисления древовидного разбиения . 185
Упражнение ... . . .... - 198
§ 6.4. Сх-_>ма хранения и процедура распределения памяти .... 199
6.4.1. Схема хранения 199
6.4.2. Внутреннее переупорядочение блоков 202
6.4.3. Распределение памяти и подпрограммы FNTENV, FNOFNZ
и FNTADJ . . 207
§ 6.5. Подпрограммы численных этапов TSFCT (Tree Symmetric FaC-
Torization) и TSSLV (Tree Symmetric SoLVe) 214
6.5.1. Вычисление матричной поправки 214
6.5.2. Подпрограмма TSFCT (Tree Symmetric FaCTorization) . . 217
6.5.3 Подпрограмма TSSLV (Tree Symmetric SoLVe) 222
Упражнение . . . 230
§ 6.6. Дополнительные замечания 230
Глава 7. Методы параллельных сечений для конвчноэлементных задач 232
§ 7.0. Введение 232
§ 7.1. Пример — задача на (тХ/)-сетке 232
7.1.1. Упорядочение посредством параллельных сечений .... 232
7"!l.2. Требования к памяти у 235
7.1.3. Число операций при разложении 237
7.1.4. Число операций при решении 240
Упражнения 240
§ 7.2. Алгоритм построения параллельных сечеиий для задач на нере-
нерегулярных сетках . . 242
7.2.1. Алгоритм 242
7.2.2. Подпрограммы для вычисления разбиения методом парал-
параллельных сечений . . ....">. 244
§ 7.3. Об определении структуры оболочки диагональных блоков . . 260
7 3.1. Постановка задачи 250
7.3.2. Характеризация оболочки блочной диагонали посредством
достижимых множестз 261
7.3.3. Алгоритм и подпрограммы вычисления оболочки диаго-
диагональных блоков ... . . 254
7.3.4. Анализ временной сложности алгоритма 260
Упражнения ". 260
§ 7.4. Дополнительные замечания 261
Глава 8. Методы вложенных сечений 263
§ 8.0. Введение 263
§ 8.1. Вложенные сечения регулярной сетки 263
8.1.1. Упорядочение . 263
8.1.2. Требования к памяти 266
8.1.3. Число операций 270
8.1.4. Оптимальность упорядочения . . .' 272
Упражнения 274
f 8.2. Вложенные сечеиия для произвольных задач Ж)
8.2.1. Эвристический алгоритм 275
8.2.2. Машинная реализация 276
Упражнения 280
§ 8.3. Дополнительные замечания 280
Глава 9. Численные эксперименты , . . . . 282
§ 9.0. Введение 282
§ 9.1. Описание тестовых задач . • 284
§ 9.2. Что означают приведенные числа 286
§ 9.3. Сравнение методов . 293
9.3.1. Критерии сравнения методов 293
Оглавление 333
9.3.2. Сравнение методов для тестовых задач набора #1 . . . 294
9.3.3. Сравнение методов для тестовых задач набора #2 . . . 296
§ 9.4. Зависимость от структуры данных 297
9.4.1. Запросы к памяти 298
9.4.2 Время исполнения 299
Приложение А. Некоторые указания к использованию подпрограмм . . 302
§ АЛ. Примеры скелетных ведущих программ 302
§ А.2. Пример подпрограммы ввода числовых значений ....... 305
§ А.З. Совмещение памяти в Фортране 307
Приложение В. SPARSPAK: Пакет din разреженных матриц 310
§ В.1. Мотивировка 310
§ В.2. Базисная структура пакета SPARSPAK 311
§ В.З. Головная программа пользователя — пример 313
§ В.4. Краткое описание основных подпрограмм интерфейса .... 315
8.4.1. Модули для ввода структуры матрицы 315
8.4.2. Модули для упорядочения и распределения памяти . . .317
8.4.3. Модули для ввода числовых значений А и Ь 317
8.4.4. Модули для разложения и решения 319
§ В.5. Средства для запоминания н возобновления 319
§ В.6. Решение многих систем с одинаковой структурой или одинако-
одинаковой матрицей коэффициентов 320
§ В.7. Вывод на печать 322
Литература 323
Алан Джордж, Джозеф Лю
ЧИСЛЕННОЕ РЕШЕНИЕ БОЛЬШИХ
РАЗРЕЖЕННЫХ СИСТЕМ УРАВНЕНИЙ
Научн. ред К Г. Батаев
Мл. научн ред Р И Пяткнна
Художник А Б Проценко
Художественный редактор В. И. Шаповалов
Технический редактор Т. А Максимова
Корректор Н Н Яковлева
ИБ № 3623
Сдано в набор 13.05.83 Подписано к печати 23.11.83 Фор-
Формат 60X90'/ia Бумага типографская № 2 Гарнитура литератур-
литературная. Печать высокая. Усл. кр.-отт 21 Объем 10,50 бум. л.
Усл. печ. л. 21 Уч.-нзд. л. 18,67 Изд № 1/2464 Тираж
9.700 экз Зак 2470 Цена 1 р. 60 к
ИЗДАТЕЛЬСТВО «МИР»
129820, Москва, И-110, ГСП, 1-й Рижский пер., 2.
Отпечатано с матриц Ленинградской типографии № 2 голов-
головного предприятия ордена Трудового Красного Знамени Ле-
Ленинградского объединения «Техническая книга» им Евгении
Соколовой Союзполиграфпрома при Государственном коми-
комитете СССР по делам издательств, полиграфии и книжной
торговли 198052. г Ленинград, Л-52, Измайловский про
спект, 29 в Ленинградской типографии № 4 ордена Трудо-
Трудового Красного Знамени Ленинградского объединения «Тех
ннческая книга» им Евгении Соколовой Союзполиграф-
Союзполиграфпрома при Государственном комитете СССР по делам из-
издательств, полиграфии и книжной торговли 191126, Ленин-
Ленинград Социалистическая ул , 14