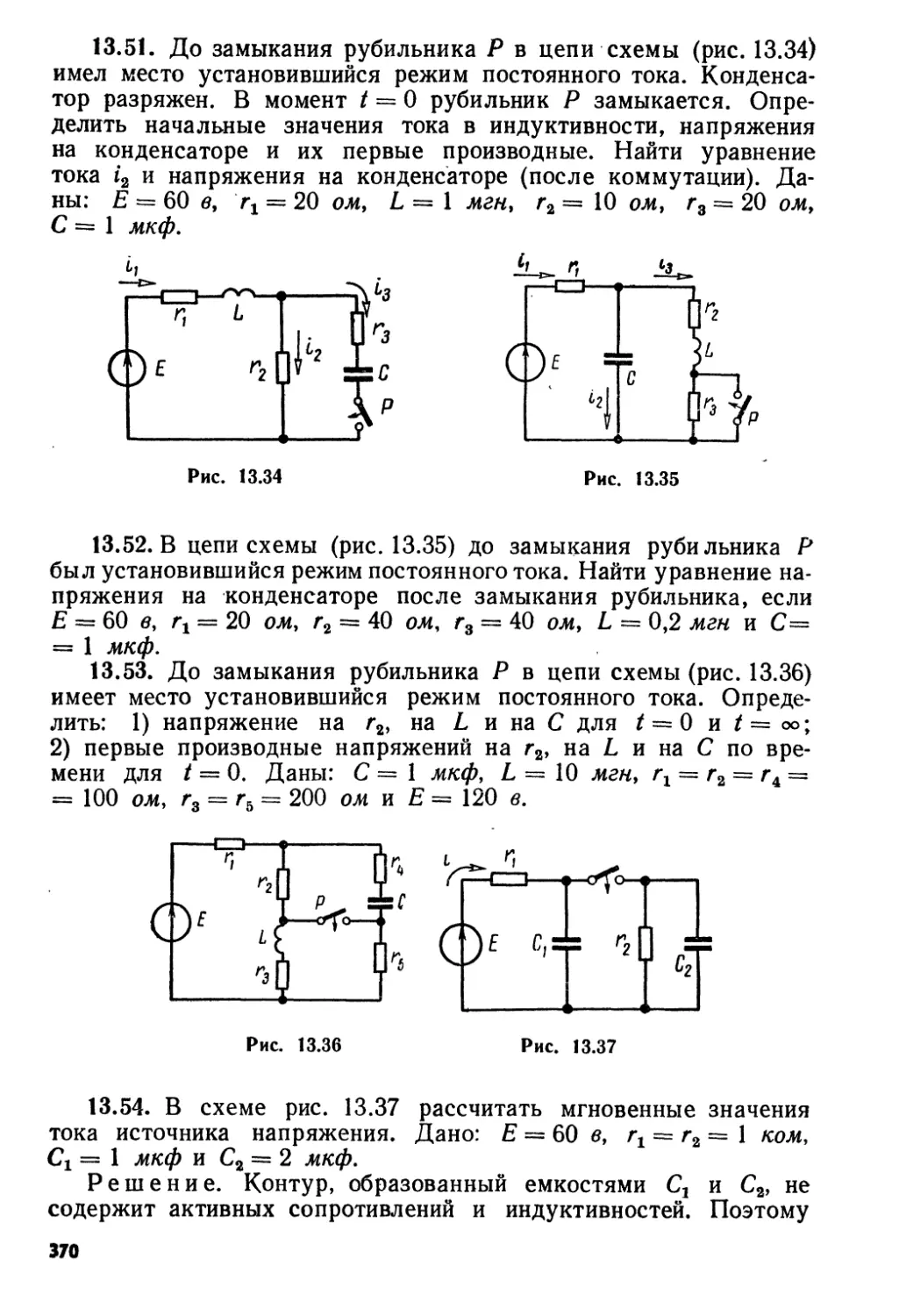
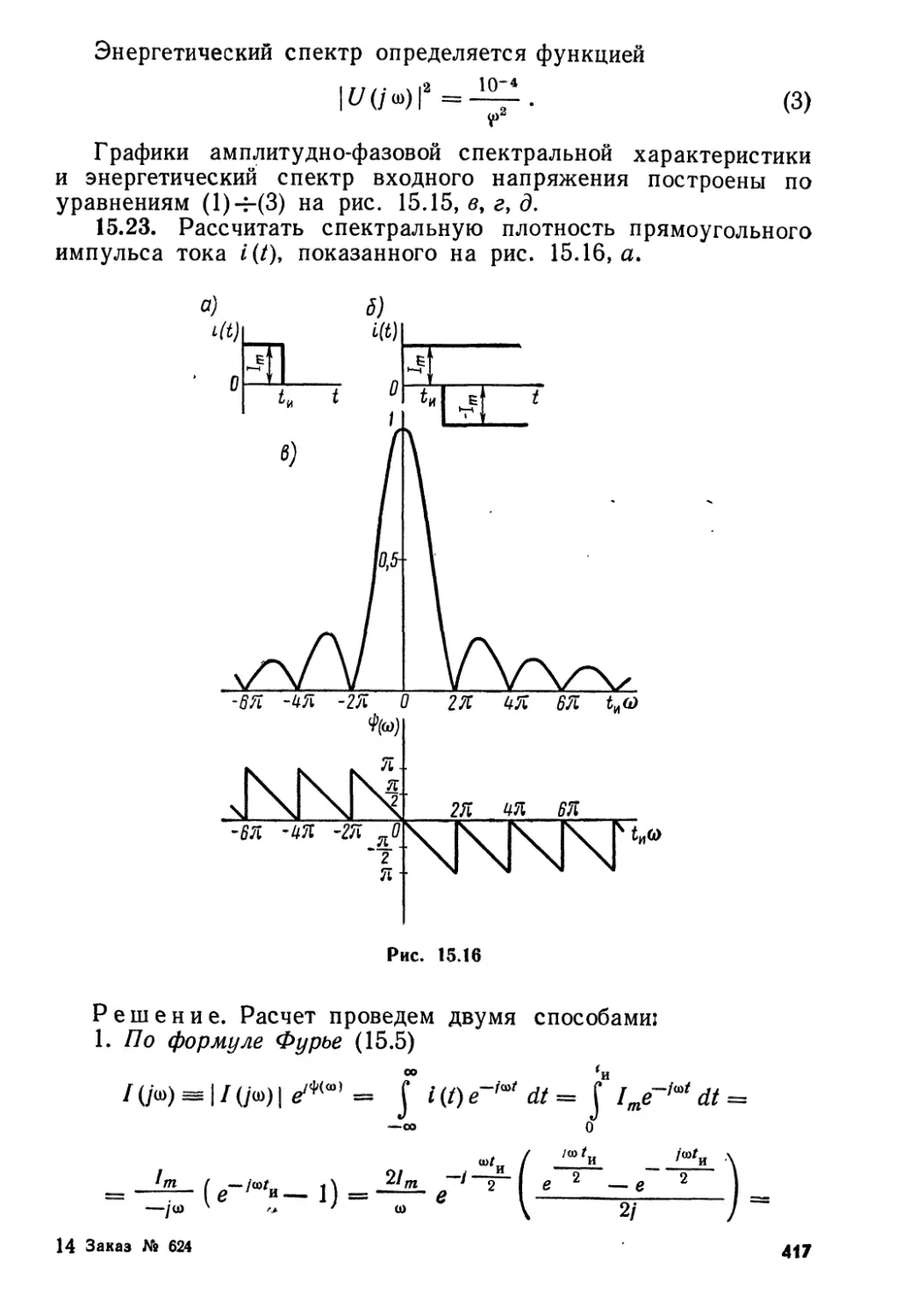
Текст
М. Р. ШЕБЕС
ТЕОРИЯ
ЛИНЕЙНЫХ
ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ
В УПРАЖНЕНИЯХ
И ЗАДАЧАХ
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов электротехнических
и радиотехнических специальностей
вузов
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
Москва — 1967
УДК 621.372
Ш—302
В книге даются краткий теоретический материал и расчет-
ные формулы, типовые задачи с подробными решениями и по-
яснениями, задачи для самостоятельного решения.
На большом числе примеров показано применение основных
методов расчета электрических цепей как в установившемся,
так и в переходном режимах.
Для значительного числа решенных задач даны векторные
диаграммы. Указаны приемы их построения.
Учебное пособие предназначено для студентов электротех-
нических и радиотехнических вузов и факультетов.
Рецензенты:
кафедра теоретических основ
электротехники Московского
энергетического института
кафедра теории линейных
цепей Московского элек-
тротехнического института
связи
3—3—8
146—66
ПРЕДИСЛОВИЕ
Теория линейных электрических цепей — основная теоретико-
базовая дисциплина в подготовке инженеров по радиотехнике,
радиосвязи, радиовещанию и телевидению, автоматической и мно-
гоканальной электрической связи и другим аналогичным специ-
альностям. Программа по курсу «Теория линейных электрических
цепей» обширна и разнообразна. Усвоение материала курса
невозможно без приобретения практических навыков, получаемых
в процессе решения задач.
Цель учебного пособия — оказать помощь студентам в их
самостоятельной работе. Поэтому большое количество задач
дано с подробными решениями и пояснениями, к некоторой части
задач даны методические указания, ко всем остальным задачам —
ответы.
В начале каждой главы приводятся основные положения
теории и важнейшие формулы, которые могут быть использованы
при решении задач. Все формулы и расчеты даны в Междуна-
родной системе единиц (СИ).
На значительном числе примеров показывается применение
основных методов расчета электрических цепей как в установив-
шемся, так и в переходном режимах. При рассмотрении вопросов
расчета цепей постоянного и переменного тока уделено большое
внимание таким цепям, в которых действуют и источники напря-
жения и источники тока. Подробно разобраны резонансные яв-
ления в одиночном и индуктивно связанных контурах, имеющих
исключительно важное практическое значение во всех специаль-
ных курсах. Приводится достаточное количество упражнений и
задач по теории двухполюсников, четырехполюсников, электри-
ческих фильтров и цепям с распределенными параметрами.
В главах о переходных процессах рассмотрены задачи и упра-
жнения, решаемые классическим, операторным и спектральным
методами и методом наложения. Введена глава по синтезу цепей.
!♦
3
Как известно, при изучении теории переменных токов большое
значение имеют векторные диаграммы. Они являются не только
хорошей иллюстрацией соотношений между отдельными величи-
нами в цепях переменного тока, но и значительно облегчают
решение многих задач. Поэтому к большому числу задач даны
векторные диаграммы и указаны приемы их построения.
Книга предназначена в качестве учебного пособия для сту-
дентов электротехнических институтов связи, радиотехнических
вузов и факультетов. Приведенный в ней большой методический
материал делает ее особенно полезной и нужной студентам-
вечерникам и заочникам, имеющим недостаточное количество ча-
сов на упражнения.
Автор выражает свою признательность канд. техн, наук
М. Г. Виткову за помощь, оказанную им в редактировании и
подготовке рукописи к печати. Им же совместно с автором на-
писаны главы 11 и 15.
Замечания рецензентов кафедры теоретических основ электро-
техники МЭИ А. А. Мухина, Б. Я. Жуховицкого и Г. П. Андреева
и кафедры линейных цепей МЭИС, возглавляемой докт. техн,
наук проф. Л. А. Жекулиным, и рецензента С. Д. Купаляна спо-
собствовали улучшению рукописи, за что автор приносит им
свою благодарность.
Замечания по книге просьба направлять в издательство «Выс-
шая школа» (.Москва, К-51, Неглинная ул., д. 29/14).
Автор.
ГЛАВА ПЕРВАЯ
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Пассивный линейный элемент — электрическое со-
противление (рис. 1.1). Ток I и напряжение U электрическо-
го сопротивления связаны законом Ома: ---оа
ab
где г — сопротивление.
Величина, обратная сопротивлению,
(1.1)
(1.2)
Рис. 1.1
— электрическая проводимость.
Активные линейные элементы — источники электрической
энергии.
06
Источник напряжения (идеальный).
Напряжение UаЬ источника напряжения не за-
висит от величины его тока I и характеризуется
его электродвижущей силой (э. д. с.) Е (обоз-
начения положительных направлений показаны
на рис. 1.2):
ab
Рис. 1.2 Внутреннее сопротивление ис-
точника напряжения равно ну-
лю.
Источник тока (идеальный). Ток / ис-
точника тока (рис. 1.3) не зависит от вели-
чины приложенного к нему напряжения
(внутренняя проводимость утечки источника
тока равна нулю, сопротивление источника
тока — бесконечно велико).
5
Источник э. д. с. (с внутренним сопротивлением), или ге-
нератор (рис. 1.4, а), можно изобразить двояко: 1) в виде ге-
нератора напряжения — последовательной схемы, содер-
жащей внутреннее (или входное) сопротивление генератора гг,
и источник напряжения с э. д. с. генератора £г, численно равной
напряжению генератора Uab в режиме холостого хода (рис. 1.4,6);
Рис. 1.4
2) в виде генератора тока — параллельной схемы, содержа-
щей сопротивление генератора гг и источник тока /г генератора,
численно равный току короткого замыкания генератора (рис. 1.4, в).
Переход от схемы генератора напряжения к схеме генератора
тока и обратно осуществляется по формулам
/г = -у-; Ет = гт1т. (1.4)
1 г
2. Закон Ома применяется для ветви или для одноконтурной
замкнутой цепи (не имеющей разветвлений).
При написании закона Ома следует прежде всего выбрать
произвольно некоторое положительное направление тока.
е
Рис. 1.5
Для ветви, состоящей
только из сопротивлений и
не содержащей э.д.с. (на-
пример, для ветви тп рис.
1.5), при положительном на-
правлении тока от точки т
к точке п
Фт Фп Vтп.
г ' г 9
' тп г тп
(1-5)
где и — потенциалы
точек т и п;
итп — разность потенциалов или напряжение между точ-
ками т и п\
Гтп = + rfi — полное сопротивление ветви между точками тип.
Для ветви, содержащей э. д. с. и сопротивления (например,
для ветви acb рис. 1.5),
где UаЬ = фд — Ф* — напряжение на кон-
цах ветви acby от-
считываемое по вы-
бранному положи-
тельному направле-
нию тока;
— алгебраическая сумма э. д. с., находящихся
в этой ветви;
^гаъ — арифметическая сумма ее сопротивлений.
В ветви acb (см. рис. 1.5) '£1Е = Е1 — £2; Игаь ==Г1 + Г2+Л>-
Формулу (1.6) называют обобщенным законом Ома.
Примеры в задачах 1.6 и 1.8.
Для замкнутой одноконтурной цепи
(1.7)
где — арифметическая сумма всех внешних и внутренних
сопротивлений цепи;
^Е— алгебраическая сумма ее электродвижущих сил.
Со знаком «плюс» берут те э. д. с., направления которых
совпадают с выбранным положительным направлением тока, и со
знаком «минус» — э. д. с. с противоположными направлениями.
3. Законы Кирхгофа. Для написания законов Кирхгофа необ-
ходимо задаться положительными направлениями токов каждой
ветви.
Первый закон Кирхгофа
24 = 0.
(1.8)
Алгебраическая сумма всех токов, сходящихся в любом уз-
ле, равна нулю. Токи, направленные к узлу, условно принима-
ются положительными, а направленные от него — отрицательны-
ми (или наоборот).
Второй закон Кирхгофа
п
' k1 k
*=1
(1.9)
Алгебраическая сумма э. д. с. замкнутого контура равна
алгебраической сумме падений напряжений в нем.
Направление обхода контура выбирается произвольно; при
записи левой части равенства э. д. с., направления которых
совпадают с выбранным направлением обхода (независимо от на-
правления тока, протекающего через них), принимаются положи-
тельными, а э. д. с., направленные против выбранного направ1
ления обхода, — отрицательными. При записи правой части
равенства со знаком «плюс» берутся падения напряжения в тех
ветвях, в которых выбранное положительное направление тока
совпадает с направлением обхода (независимо от направления
э. д. с. в этих ветвях), и со знаком «минус» — падения напря-
жения в тех ветвях, в которых положительное направление тока
противоположно направлению обхода.
Пример в задаче 1.21.
Распределение напряжений при последовательном соединении
двух сопротивлений
_ 2L.
^2 Г2 *
^ = £/-ГТТ-
Г1 "Г Г2
(1-10)
где U — общее напряжение, действующее на участке цепи, содер-
жащем два сопротивления t\ и г2 (см. рис. 1*5).
Распределение токов в двух параллельных ветвях
где — ток в неразветвленной части цепи (см. рис. 1.6).
4. Методы расчета сложных цепей постоянного тока (цепь
состоит из NB ветвей, имеет Ny узлов и NT источников тока).
Приводимые ниже формулы пригодны для расчета цепей, содер-
жащих и источники напряжения, и источники тока. Они справед-
ливы и для тех частных случаев, когда в цепи имеются только
источники напряжения, либо только источники тока.
Применение законов К и рхгоф а. Устанавливается чи-
сло неизвестных токов, которое равно NB— Nt. Для каждой
ветви задаются положительным направлением тока.
Число взаимонезависимых уравнений, составляемых по перво-
му закону Кирхгофа, равно числу узлов без единицы (iVy— 1).
Число К взаимонезависимых уравнений, составляемых по второму
закону Кирхгофа, равно
К = NB — А/у+ 1 — Л/т.
(1.12)
При составлении уравнений по второму закону Кирхгофа
следует выбирать независимые контуры, не содержащие источ-
ников тока. Общее число уравнений, составляемых по первому
и второму законам Кирхгофа, равно числу (NB — NT) неизвестных
токов.
Примеры в задачах 1.21 и 1.34.
Метод контурных токов (Максвелла) позволяет
уменьшить количество уравнений системы до числа К, опреде-
ляемого формулой (1.12). Метод основывается на том свойстве,
что ток в любой ветви цепи может быть представлен в виде
алгебраической суммы независимых контурных токов, протекаю-
щих по этой ветви. При пользовании методом вначале выбирают
и обозначают независимые контурные токи (по любой ветви цепи
должен проходить хотя бы один выбранный контурный ток). Из
теории известно, что общее число независимых контурных токов
равно (2VB — Ny + 1). Рекомендуется выбирать /VT независимых кон-
турных токов так, чтобы каждый из них проходил через один ис-
точник тока (эти контурные токи можно считать совпадающими
с соответствующими токами источников тока: /г1, /г2, .. . , /гл/т »
и они обычно являются заданными условиями задачи), а остав-
шиеся К = NB — Ny + 1 — Л^т-контурных токов— выбирать про-
ходящими по ветвям, не содержащим источников тока. Для оп-
ределения последних контурных токов составляют по второму
закону Кирхгофа для этих контуров К уравнений в виде:
Г11Л + Г12^2 + • • • + rvJk + Г1г1 41 + • rjVT47VT = ^11»
rkiJi + г^4 + • • • + rkk h + r*ri 4i + • • • + rk Г2ут 4.vT = Ekk,
где rnn — собственное сопротивление контура n (сумма сопротив-
лений всех ветвей, входящих в контур п);
— общее сопротивление контуров п и /, причем rnl = rln,
если направления контурных токов в ветви, общей для
контуров п и Z, совпадают, то гп1 положительно (гп1 >
> 0), в противном случае гп1 отрицательно (гп1 < 0);
Епп— алгебраическая сумма э. д. с„ включенных в ветви,
образующие контур п;
rnri — общее сопротивление n-го контура с контуром, содер-
жащим источник тока /гГ.
Примеры в задачах 1.36, 1.38 и 1.40.
9
Метод узловых потенциалов позволяет уменьшить
количество уравнений системы до числа У, равного количеству
узлов схемы без одного:
У = 2Vy—1. (1.14)
Сущность метода заключается в том, что вначале определя-
ются потенциалы всех узлов схемы, а токи ветвей, соединя-
ющих узлы, определяются с помощью закона Ома по форму-
ле (1.6).
При составлении уравнений по методу узловых потенциалов
вначале полагают равным нулю потенциал какого-либо узла;
для оставшихся (Ny— 1) узлов составляют уравнения по первому
закону Кирхгофа, формулируя его: алгебраическая сумма токов,
выходящих из рассматриваемого узла по всем сходящимся в этом
узле ветвям, равна нулю. При этом в ветвях с источниками тока
токи считаются, очевидно, отрицательными, если они направлены
к рассматриваемому узлу, а не выходят из него; токи остальных
ветвей записываются выраженными через разность потенциалов
узлов, которые они соединяют, по формуле (1.6).
Примеры в задачах 1.41 и 1.44.
Если в цепи некоторые узлы соединяются ветвями, не имею-
щими сопротивлений (они могут содержать источники напряже-
ния, так как сопротивления последних равны нулю), то число У
уравнений, составляемых по методу узловых потенциалов, умень-
шается:
У = 2Vy —2VH—1, (1.15)
где Nn—число ветвей с нулевыми сопротивлениями.
Примеры в задачах 1.42 и 1.47.
Метод двух узлов. Для схем, имеющих два узла (для
определенности узлы а и Ь). узловое напряжение Uab опреде-
ляется формулой (при отсутствии источников тока)
S Епёп
[1 — 2L________
8т
т
(1Л6)
где %Engn—алгебраическая сумма произведений э. д. с. ветвей
(э. д. с. считаются положительными, если они на-
правлены к узлу а, и отрицательными, если от
узла а к узлу Ь) на проводимости этих ветвей;
—сумма проводимостей всех ветвей, соединяющих
т
узлы а и Ь.
Пример в задаче 1.66.
ю
Метод наложения. Если в электрической цепи задан-
ными величинами являются э. д. с. источников напряжения и
токи источников тока, то расчет токов по методу наложения со-
стоит в следующем. Ток в любой ветви может быть рассчитан
как алгебраическая сумма токов, вызываемых в ней э. д. с. каж-
дого источника напряжения в отдельности и током, проходящим
по этой же ветви от действия каждого источника тока. При этом
надо иметь в виду, что когда ведется расчет токов, вызванных
каким-либо одним генератором, то остальные источники напря-
жения в схеме заменяются короткозамкнутыми участками (внут-
реннее сопротивление источников напряжения равно нулю), а вет-
ви с источниками тока остальных генераторов отключаются
(внутреннее сопротивление источников тока бесконечно). В то же
время сопротивления всех генераторов схемы сохраняются.
Примеры в задачах 1.48, 1.50 и 1.51.
Методы преобразования. Во всех случаях преобра-
зования замена одних схем другими, им эквивалентными, не дол-
жна привести к изменению токов или напряжений на участках цепи,
не подвергшихся преобразованию.
Замена последовательных сопротивлений одним эквивалент-
ным. Сопротивления последовательны, если они обтекаются
одним и тем же током (например, сопротивления г2 и г9 соеди-
нены последовательно (см. рис. 1.5); также последовательны сопро-
тивления г7 и г8).
Эквивалентное сопротивление цепи, состоящей из п последова-
тельно соединенных сопротивлений, равно сумме этих сопротив-
лений.
Замена параллельных сопротивлений одним эквивалентным.
Сопротивления параллельны, если все они присоединены к од-
ной паре узлов (например, сопротивления г45 = г4 + гь и г10,
рис. 1.5).
Эквивалентное сопротивление цепи, состоящей из п парал-
лельно соединенных сопротивлений, определяется из формулы
п
-Г = 2тг- (1-17)
гэ rk
В частном случае параллельного соединения двух сопротив-
лений гг и г2 эквивалентное сопротивление
= (1-18)
Замена смешанного соединения сопротивлений одним эквива-
лентным, Смешанное соединение — это сочетание последователь-
ного и параллельного соединения сопротивлений. Например,
и
сопротивления rx, г2 и r3 (см. рис. 1.6) находятся в смешанном
соединении. Их эквивалентное сопротивление
Гэ = '1 +
г 2 Г3
Г2~Ь гз
(1-19)
При смешанном соединении сопротивлений токи определяют-
ся по формулам
(1.20)
Формулы преобразования треугольника сопротивлений
(рис. 1.7, а) в эквивалентную звезду сопротивлений (рис. 1.7,6)
и наоборот имеют вид
Г23Г 31
(1-21)
Г31Г23
gl ё2
3
g3 gl
где g—проводимость соответствующей ветви.
12
Формулы (1.22) можно записать через сопротивления:
(1.23)
Пример в задаче 1.53.
Метод эквивалентного генератора (или метод
активного двухполюсника). Для нахождения тока / в произволь-
ной ветви ab электрической цепи (рис. 1.8, а) по методу экви-
Рис. 1.8
валентного генератора рассматривают часть цепи, подключенную
к этой ветви, в виде некоторого эквивалентного генератора
с э. д. с. Ег и сопротивлением гг (рис. 1.8, б). Ток в искомой
ветви схемы (рис. 1.8, б), имеющей сопротивление r = rI+r2
и э. д. с. и Е2, определяется по закону Ома (1.7):
Для нахождения э. д. с. эквивалентного генератора Ег до-
статочно рассмотреть режим схемы с отключенной ветвью ab
(режим холостого хода). При этом, как видно из схемы
(рис. 1.8, в), э. д. с. совпадает с напряжением холостого хода:
* Ег == Uabx.x (фд Фь)х.х • (1.25)
Расчет схемы в режиме холостого хода (рис. 1.8, г) для оп-
ределения э. д. с. Ет проводится любым известным методом.
Сопротивление гг эквивалентного генератора равно сопротивле-
нию относительно зажимов а и b исходной схемы, из которой
исключены все источники (источники напряжения заменены ко-
роткозамкнутыми участками, а ветви с источниками тока отклю-
чены рис. 1.8, д). На рис. 1.8, д знак П указывает на пассивный
характер полученной цепи, из которой исключены источники,
а знак А на схемах рис. 1.8 указывает на то, что часть схемы,
обозначаемая прямоугольником, может иметь источники, т. е.
быть активной.
13
Сопротивление генератора определяется сворачиванием этой
пассивной схемы к зажимам а и Ь.
Возможен и другой метод определения сопротивления экви-
валентного генератора. Он заключается в расчете любым спо-
собом тока короткого замыкания /г. к. з схемы эквивалентного
генератора (рис. 1.8, е). Из ее схемы замещения (рис. 1.8, ж)
видно, что если рассчитан ток короткого замыкания генератора,
то его сопротивление гг можно определить по формуле
Гг = h. . (1.26)
'г. К. 3
Так как э. д. с. эквивалентного генератора определяется в ре-
жиме холостого хода, то последняя модификация метода эквива-
лентного генератора иногда называется методом холостого
хода и короткого замыкания.
Примеры на метод эквивалентного генератора в задачах
1.56, 1.57, 1.62 и 1.63.
Метод замены нескольких параллельных ге-
нераторов напряжения одним эквивалентным.
Если имеется несколько генераторов напряжения с э. д. с. Ev
Е2, . . . , Еп и внутренними сопротивлениями rv г2, . . . , гп , ра-
ботающих параллельно на общее сопротивление нагрузки г
(рис. 1.9, а), то они могут быть заменены одним эквивалентным
генератором напряжения, э. д. с. которого Е3, а внутреннее
сопротивление гз (рис. 1.9, б), при этом
(1.27)
Ток в сопротивлении т
(1.28)
14
Ток в каждой из ветвей
= (1.29)
где U = Uab = 1г.
Пример в задаче 1.66.
Метод замены параллельно соединенных
генераторов тока одним эквивалентным. Если не-
сколько генераторов тока с токами Zr, Z2..Zn и внутрен-
ними проводимостями gt, g2, , gn соединены параллельно
(рис. 1.10, а), то они могут быть заменены одним эквивалент-
ным генератором тока (рис. 1.10, б), ток которого Z равен ал-
Рис. 1.10
гебраической сумме токов, а его внутренняя проводимость равна
сумме внутренних проводимостей отдельных генераторов:
п
I = —z3 +... + = 2 I* > (1.зо)
fe=i
п
8 = Si + 82 + S3 + • • • + ~ 2 8ь (1-31)
6=1
5. Принцип компенсации. Любое сопротивление в электри-
ческой цепи может без изменения распределения токов в ее вет-
вях быть заменено э. д. с., численно равной падению напряжения
в заменяемом сопротивлении и направленной ’навстречу току.
6. Входное сопротивление цепи относительно ветви k опре-
деляется как отношение э. д. с. Ek, действующей в этой ветви,
к току в этой же ветви при э. д. с., в остальных ветвях
равных нулю,
Входная проводимость ветви k — величина, обратная входно-
му сопротивлению этой ветви:
8ьь ? •
л rkh
(1.33)
15
Входная проводимость может быть рассчитана по приращению
тока входной ветви А/вызванному приращением э. д. с. ДЕЛ
этой ветви:
(1-34)
Рис. 1.11
Пример. Для схемы рис. 1.11 вход-
ные сопротивления цепи относитель-
но ветвей 1, 2 и 3 соответственно
равны
^22 —
33 “
где D = гхг2 + r2r3 + г3гг
Взаимная проводимость ветвей k и I — отношение тока Л в
ветви с номером k к вызывающей его э. д. с. Ez в ветви I (при
отсутствии других источников энергии):
s«=4f- <L35)
Если ток Ik создается единичной э. д. с. Et = 1 в, то вза-
имная проводимость gkl численно равна току h -
В случае, когда э. д. с. некоторых ветвей цепи не равны
нулю, взаимная проводимость ветвей k и I может быть рассчи-
тана по изменению А/* тока ветви k, вызванному изменением
AEZ э. д. с. ветви /, по формуле
= —. (1.36)
Пример в задаче 1.70.
Взаимное сопротивление ветвей k и I—отношение напряже-
ния Uk на ветви k к величине создающего его тока It (предпола-
гается, что в ветви I включен источник тока Zz, а все другие
источники энергии в схеме отсутствуют):
(1.37)
7. Принцип взаимности. В линейной электрической цепи,
составленной из сопротивлений, источников напряжения и источ-
ников тока, соответственные взаимные проводимости glk = gkl—
равны. Из принципа взаимности следует: если э. д. с. Е, нахо-
дящаяся в ветви ab сколь угодно сложной цепи, вызывает ток /
16
в другой ветви cd этой же цепи, то при переносе этой э. д. с.
в ветвь cd она вызовет в ветви ab такой же ток /.
8. Линейные соотношения. При изменении одного из элемен-
тов линейной электрической цепи (одного сопротивления, или
одной э. д. с., или тока одного из источников тока) связь между
любыми двумя токами /z и /*, между двумя напряжениями Ui и Ut,
между любым током /k и произвольным напряжением Ui являет-
ся линейной с постоянными коэффициентами <at, blt .
Например,
►
/ь = аь + и т. д. ,
(1.38)
Пример в задаче 1.72.
9. Баланс мощности. Для любой замкнутой электрической
цепи сумма мощностей Ри, развиваемых источниками электриче-
ской энергии, равна сумме мощностей Р, расходуемых в прием-
никах энергии.
При составлении баланса мощности должны быть учтены
внешние сопротивления и сопротивления источников энергии.
Пример в задаче 1.21.
УПРАЖНЕНИЯ И ЗАДАЧИ
1.1. Для цепи (рис. 1.12) найти эквивалентные сопротивле-
ния между зажимами а и Ь,
си d, d и /, если i\ = 6 ом,
г2 = 5 ом, г3 = 15 ом, г4 = 30 ом
и г5 = 6 ом.
Решение. Расчет сопро-
тивления гаЬ. Эквивалентное
сопротивление соединенных
параллельно сопротивлений
г4 и г5 найдем по формуле
<1.18):
30-6 с
30 + 6 — 5 ом>
Рис. 1.12
оно соединено последовательно с г2; их общее сопротивление
г' = г2 + — 5 + 5 = 10 ом.
Сопротивление цепи состоит из сопротивления rv последо-
вательно с которым соединены два параллельных сопротивления
и г3:
. г'гз с . 10-15
rab — Г1 + г' + га — 6 + !о + 15 — 12 0Л1,
17
Расчет сопротивления rcd. Сопротивления г4 и гъ теперь со-
единены параллельно друг другу; сопротивление г3 к ним вклю-
чено последовательно:
г" = гя 4 = 15 -н 5 = 20 ом.
8 г4 + Гв
Сопротивление rcd состоит из двух параллельно соединенных
сопротивлений г2 и г" и равно
5-20
5 4-20
4 ом.
Расчет сопротивления rdf. Эквивалентное сопротивление це-
пи между точками d и f состоит из трех параллельно соединен-
ных сопротивлений г5, г4 и г2 + гя и может быть определено из
формулы (1.17):
rdf Г, + с, 4 Гз 6 30 20 4 ’
откуда rdf = 4 ом.
1.2. Определить эквивалентное сопротивление цепи между
точками а п b при разомкнутом и замкнутом ключе К (рис.
1.13,а). Даны: t\ = г2 — г3 = г4 = гъ = гв = г1 — 10 ом.
Рис. 1.13
Решение. При разомкнутом ключе заданная схема может
быть изображена согласно рис. 1.13,6.
Искомое сопротивление
25-10
35
= 12,1
ом.
При замкнутом ключе заданная схема имеет вид, изображен-
ный на рис. 1.13,в.
18
Сопротивление цепи равно сумме двух сопротивлений;
10» 10
= ------- = О ОМ,
20
«и г", определяемого из формулы
откуда г" = 3,33 ом.
Таким образом,
fab = г' + г" « 5 + 3,33 =
8,33 ом.
1.3. Определить сопро-
тивление каждой из цепей
(рис. 1.14,а, б, в, г) между
зажимами 1 — Г при холос-
том ходе (точки 2 и 2' ра-
зомкнуты) и при коротком
замыкании (точки 2 и 2' зако-
рочены). Сопротивления в
омах даны на схеме.
1.4. Найти сопротивление между зажимами
Рис. 1.14
г
а и Ь для схемы
рис. 1.15fa. Значения сопротивлений в омах даны на схеме.
Рис. 1.15
Решение. От данной схемы можно перейти к более простым
схемам, изображенным на рис. 1.16,6 и в.
Искомое сопротивление
240 180 +
?ab
300»450 \
750 /
240 4- 180 +
300-450
750
== 144 ом.
19
1.5. Источник с э. д. с. Е = 100 в, внутренним сопротивлением
г0 = 1 ом замкнут на внешнее сопротивление г, которое меняется
от нуля до бесконечности (рис. 1.16,а). Определить в функции
этого сопротивления: ток /; напряжение на зажимах источника
U; мощность, отдаваемую источником во внешнюю цепь Р„„о,„„:
опсШп"
°)
б)
Рис. 1.16
мощность, затрачиваемую в самом источнике Рвнутр; общую мощ-
ность Робщ; коэффициент полезного действия т]. При каком внеш-
нем сопротивлении Рвнешн будет максимальным? Чему оно равно?
Построить кривые 1 = F\ (г), U = Р2 (г), Рвнешн = F8 (г), Р =
= F4(r), Робщ = Р8(г), -4 = Ft(r); УР
20
Написать уравнения и построить кривые зависимостей Ur
^внеппр ^внутр> ^обш И 7] В фуНКЦИИ ТОКИ /.
Решение.
внешн
Р общ
Определим г, при котором Рвнешн будет максимально. Для
этого вычислим производную от Рвнешн по г и приравняем ее
нулю:
dP внешн = £» (г 4~ го)2 (г 4- г0) г __ q
dr (г 4- г0)2
Взяв вторую производную, можем убедиться, что она отри-
цательна. Это соответствует условию максимума.
Отсюда найдем, что г = г0, т. е. при внешнем сопротивлении,
равном внутреннему сопротивлению, мощность, поступающая*
во внешнюю цепь, максимальна. При этом по уравнению для
к. п. д. равен 0,5. Величина максимальной мощности, поступаю-
щей во внешнюю цепь при г = г0,
£2
внеш, max ~ 2500 вт.
4г6
По написанным выше уравнениям на рис. 1.16,6 построены
кривые. *
Искомые уравнения зависимостей в функции тока /
U = Е— 1г$,
^внешн
внутр
= EI - /%;
— 12г •
обш = Е1-, 7]= 1--^
По этим уравнениям на рис. 1.16,в построены кривые.
1.6. В схеме рис. 1.17 э. д. с. Е1= 120 в, Е2 — 40 в, а сопро-
тивления г, = 12 ом, г2 = 8 ом. Определить напряжение между
точками а и Ь.
Решение. Задавшись положительным направлением тока
по часовой стрелке, на основании закона Ома (1.7), имеем
♦ Рис. 1.17
откуда
Так как результат оказался положи-
тельным, то фактическое направление тока
совпадает с выбранным. Напряжение меж-
ду точками а и Ь можно найти по закону
Ома (1.6), примененному к участку атЬ*.
/ . ab
?2
UаЪ ~ Е% + г2/ = 40 4- 4 • 8 = 72 в.
Такой же результат можно получить, если применить ту же
формулу к участку Ьпа:
/ = ~ь-а-+ El , или иЬа == г,/ — £1 = 4-12— 120 = — 72 в,
Г1
а следовательно, UаЪ = 72 в.
Замечание. Следует усвоить, что если на участке цепи, содержа-
щем э. д. с. и сопротивление, ток и э. д. с. совпадают по направлению, то
напряжение на зажимах участка меньше э. д. с. на величину падения напря-
жения в сопротивлении участка, а если направление тока противоположно
направлению э. д. с., то напряжение на зажимах участка больше э. д. с. на
величину падения напряжения в рассматриваемом участке.
1.7. Определить показание вольтметра
(рис. 1.18), сопротивление которого весьма
велико по сравнению с гх и г2.
1.8. Построить график изменения по-
тенциала вдоль цепи, изображенной на
рис. 1.19,а, при замкнутом и при разомк-
нутом ключе, предполагая в обоих слу-
чаях, что точка а заземлена(срй « 0). В схе-
ме найти точку, равнопотенциальную точке а.
Рис. 1.18
Определить, потенциал какой точки следует принять равным
нулю, чтобы потенциалы всех остальных точек были положи-
тельны (при замкнутом ключе).
Электродвижущие силы равны Et = 25 в, £2 = 5 в, Е3 = 20 в,
£4 == 35 в. Внешние сопротивления гг == 8 ом, г2 в 24 ом, г3 ==
== 40 ом и г4 == 4 ом. Внутренние сопротивления источников
электрической энергии г10 = 2 ом, г2о =6 ом, г30=2 ом и г40=4 ом.
22
Решение. Ключ замкнут. Задавшись положительным на-
правлением тока по часовой стрелке, на основании закона Ома
(1.7), найдем
/ в+ £2 — = о,5а.
,’1+/’1о4‘,'2~1"/’2в"1",з4" Г30 4" ^4 + ГМ 90
Пользуясь (1.5) и (1.6),
вычислим потенциалы всех
точек, обходя контур тока
по часовой стрелке:
Фо == 0;
Ф* = Фо — rj = -0,5-8 =
= — 4 в;
Ф<- = ф» + £1— rwl =
= — 4 4-25-г-0,5-2 = 20 в;
Ф^ = Фс — rJ = 20 —
— 0,5-24 = 8 в;
Ф/= Фо + £2 — rwl =
= 84-5 — 0,5-6 = 10 в;
Ф^ = Ф/—Г3/ = 10 —
—0,5-40 = — 10 в;
Фл= Фг—£3—гзо/ =
= -10 — 20 — 0,5-2 = 31 в;
Рис. 1.19
Фл — Фл — rJ = — 31 —0,5-4 = —33 в;
Фа — ф^ + £4 — г -----33 4-35 — 0,5 -4 = 0.
На рис. 1.19,6 начерчен потенциальный график. По оси абс-
цисс отложены величины сопротивлений отдельных участков
цепи, а по оси ординат — значения потенциалов в отдельных
точках цепи.
Найдем точку, равнопотенциальную точке а. Из графика
видно, что искомая точка т находится на участке сопротивле-
ния fg, так как в этой точке прямая падения потенциалов пе-
ресекает ось абсцисс, потенциал которой равен фо = 0. Обозна-
чая участок сопротивления между точками / и т через г,т и
применяя к участку abcdfm формулу закона Ома (1.6) и учиты-
вая, что фа = фт, найдем
Уо — 4-£1 4-£2
,14-г1о4-г24-Гго4"/7т
или 0,5 =----------,
40 4- г fm
23
откуда rfm = 20 ом, т. e. точка tn находится на середине сопро-
тивления г3.
Для нахождения точки, потенциал которой следует принять
равным нулю при условии, чтобы потенциалы всех остальных
точек были положительны, следует обратиться к потенциаль-
ному графику, из которого видно, что такой точкой является
точка А.
Ключ разомкнут. Тока в цепи нет, поэтому точки а и b рав-
аопотенциальны, т. е. = ф^ = 0. Потенциал точки с превы-
шает потенциал точки Ь на величину э. д. с. Ег и qc = Е± =
= 25 в\ рассуждая аналогично, найдем
Фй = Фс = 25 Ф/ = Фй + = 30 в; q>g = <pz = 30 в;
Фй = Ф^ — Е3 = 10 в; q>ft = <рл = 10 в; <р; = <pft -f- = 10 + 35 =
= 45 в.
На основе полученных результатов на рис. 1.19,6 начерчен
график изменения потенциала при разомкнутом ключе.
1.9. Для схемы (рис. 1.20) построить потенциальные графики
Cabcdfghkl при разомкнутом и замкнутом ключе.
Рис. 1.21
Рис. 1.20
1.10. Определить токи в ветвях цепи (рис. 1.21,а) и показа-
ние вольтметра, включенного между точками с и d, считая, что
его сопротивление во много раз превышает сопротивление каж-
дого из элементов цепи.
Чему равно показание амперметра, включенного между точ-
ками end, сопротивление которого считать равным нулю.
Сопротивления элементов цепи гх = 10 ом, г2 = г3 — гь = 25 ом
и г4 = 50 ом, а приложенное к ней напряжение U = 120 в.
Решение. Расчет показания вольтметра. Из условия выте-
кает, что его включение не оказывает влияния на распределе-
14
нне токов в цепи. Для расчета токов сначала определяем экви-
валентное сопротивление всей цепи (рис. 1.21,а):
Г = /\ + = 10 + = 40 ом.
В неразветвленной части цепи протекает ток
Токи, протекающие через сопротивления га + г4 игз + г5*
можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно про-
порционально их сопротивлениям (1.11):
2. Найдем напряжение на зажимах параллельных ветвейг
Токи в ветвях с сопротивлениями г2 Д-и гз+г5 равны
Напряжение на зажимах параллельных ветвей может быть
найдено как разность между приложенным напряжением и паде-
нием напряжения на сопротивлении rx: Uab = U —
Найдем показания вольтметра, равное напряжению между
точками cud:
Uy ~исд = — — 1,2*25 1,8*25— 15 в.
Наконец, вычислим ток, проходящий через амперметр, он?
равен току короткого замыкания ICd (рис. 1.21,6). Для его на-
хождения вычислим токи:
Искомый ток, проходящий через амперметр,
/ = fa = 1'2-1’4=2L = о,51 а.
А 47
2>
1.11. Для измерения тока применены амперметры, пределы
измерений которых равны 5 и 2,5 а, и шунт, сопротивление
которого неизвестно. Первый амперметр, включенный с шунтом
в некоторую цепь, показал 3,6 а, второй — с тем же шунтом
показал в той же цепи ток 2 а. Сопротивления амперметров
0,002 ом и г2 = 0,004 ом. Чему равен ток в цепи?
1.12. Для цепей рис. 1.22,а,б
определить отношение напряже-
ния на выходе f/2 (выходные зажи-
мы цепи разомкнуты) к напряжению
на входе цепи Uv Сопротивления
отдельных ветвей цепи в омах ука-
заны на схеме.
1.13. В схеме рис. 1.22,а каким
сопротивлением надо нагрузить вы-
ходные зажимы (зашунтировать
сопротивление 30 ом), чтобы полу-
чить отношение U2: = 1 : 24.
1.14. В схеме рис. 1.23 найти
сопротивление гх, если = 2,6 а,
/3 = 0,6 а, г\ — 0,5 ом, г2 = 1,4 ом,
Рис. 1.22
г3 = 3 ом, г4 = 2,5 ом. Найти э. д. с.
Рис. 1.23
Применяя закон Ома
и сопротивления и
батареи Е, если ее внутреннее соп-
ротивление г0 = 0,1 ом.
Решение. На основании первого
закона Кирхгофа
/2 = /1 — /3 = 2,6 — 0,6 = 2а.
По закону Ома, примененному к
участку цепи, содержащему сопротив-
ление г2,
(/^ = г2/2 = 2,1,4 = 2,8 в.‘
Е
к участку цепи ab, содержащему э. д. с.
г0, найдем искомую э. д. с.:
£ = Uab + (G + го) Л = 2>8 + 0,6-2,6 == 4,36 в.
Теперь найдем напряжение на параллельных ветвях с со-
противлениями г4 и гх и токи в них:
и ас = и аЬ — г3/3 = 2,8 - 0,6.3 = 1 в;
1Х = 13 — /4 = 0,6 —0,4 = 0,2 а.
Искомое сопротивление
г = ==__
* 1Х 0,2
1.15. В схеме мостика (рис. 1.24) известны сопротивления
800 ом, г3 = 400 ом. Сопротивление гальвано-
Через сопротивление протекает ток /х =
приложено напряжение U = 2,5 в. Найта
= 5 ом.
rt = 1300 ом, г2 =
метра гг « 600 ом.
= 1 ма. К мостику
сопротивление г4.
напряжение U == 2,5 в. Найта
-0[/0—
Рис. 1.24
1.16. В цепи (рис. 1.25)
= г2 = 1 ком, г3 = 4 ком, r4 — ~
показывает 4 ма, а Л4 — 3 ма\ полярности приборов показаны
на схеме, а их сопротивлениями можно пренебречь.
1.17. Однопроводная линия с
сопротивлением г0 на единицу
длины, питаемая батареей с
э. д. с., равной Е, закорочена на
приемном конце (рис. 1.26). На
каком месте линия должна иметь
утечку с сопротивлением г,
чтобы ток 1 на приемном конце
был минимальным?
1.18. Для определения места повреждения изоляции линии
применяется схема, изображенная
найти Ег и гх, если Е2 = 3 в,
= 2 ком, гъ = 1 ком. Амперметр At
Рис. 1.26
рис. 1.27,а; гг и г?— мага-
на
Рис. 1.27
27
зины сопротивлений. Правый зажим гальванометра заземлен.
Свободные концы тип линии соединены между собой нако-
ротко. Подбором сопротивлений гх и г2 добиваются отсутствия
тока в гальванометре. Показать, что если сечения обоих прово-
дов одинаковы, то расстояние от места повреждения изоляции
2/г2
до начала линии равно----------.
Указание. Заданная схема может быть заменена схемой рис. 1.27,6.
1.19. При проверке постоянной С счетчика оказалось, что
при силе тока 10 а и напряжении 120 в якорь его в продолже-
ние 30 сек сделал 37 оборотов. Определить ошибку в показа-
ниях счетчика, если на счетчике указано, что 1 гвт-ч соответ-
ствует 400 оборотам счетчика.
Примечание. Постоянной счетчика называется число ватт-
часов, приходящихся на один оборот счетчика.
Рис. 1.28
1.20. Каково должно быть сечение медных проводов линии
для передачи потребителю мощности Р = 16 кет при условии,
что потеря мощности не превысит р = 5%, если длина линии
I = 180 ж и напряжение в конце линии равно (72 = 220 в?
1.21. Для схемы (рис. 1.28),
пользуясь законами Кирхгофа,
найти токи и проверить баланс
мощностей, если э. д. с. генера-
торов напряжения Ех = 15 в,
Е2 = 70 в, Е3 = 5 в, их внутрен-
ние сопротивления гхо = г20 =»
= 1 ом, г30 = 2 ом, сопротивле-
ния элементов в цепи гх = 5 ом,
г2 = 4 ом, г3 = 8 ом, г4 = 2>5 ом,
= 15 ом.
Решение. Всего в схеме
пять ветвей (7VB = 5 : bfa, adc, ba,
be, ca), число узлов Уу = 3(а, fr и с), генераторов тока нет (2УТ =
= 0), число неизвестных токов равно 2VB — = 5. Число неза-
висимых уравнений, составляемых по первому закону Кирхгофа,
равно числу узлов минус единица, т. е. двум (/Vy— 1 = 3— 1 =
= 2). Число уравнений, составляемых по второму закону Кирх-
гофа, согласно (1.12) равно трем (К = NB — + 1— NT = 5—
— 3 + 1 — 0 = 3). Таким образом, общее число независимых
уравнений, составляемых по первому и второму законам Кирх-
гофа, равно числу неизвестных токов в пяти ветвях схемы.
Выберем положительные направления токов и обозначим их
стрелками. Выберем и обозначим стрелками направление обхода
28
трех независимых контуров: I, II и III. Составим систему урав-
нений Кирхгофа
для узла а
/х — /2 -[- /3 —р /5 = 0; (1)
для узла Ь
-Л-/з-Л = 0; (2)
для контура I
Ei + Е3 = (гх 4~ /*ю) (г3 + г3о) I3f (3)
для контура II
Е3 = -- (/*3 + Гзо) 3 + Г4^4 + r (^)
для контура III
Е<% = (^2 Н~ '’го) ^2 “Н ^*5^5* (5)
Уравнения (1) — (5) после подстановки в них числовых зна-
чений будут иметь следующий вид:
/х — /2 + /з + /5==0; Л + 1з + 4== 0;
6/х — IO/3 = 20; — IO/3 -f- 2,5/4 ~Ь 15/5 = 5; 5/2 4~ 15/5 = 70.
Решая эту систему уравнений, получим
1г = 5 а; /2 = 8 а; /3 = 1 а; /4 = —6 а; /5 = 2 а.
Отрицательный знак для тока /4 означает, что истинное
направление тока в сопротивлении г4 противоположно принято-
му. Истинное направление тока в сопротивлении г4 обозначе-
но Л и показано на схеме пунктирной стрелкой. При проверке *
баланса мощностей надо иметь в виду, что в тех ветвях цепи,
где истинное направление тока совпадает с направлением э. д. с.,
соответствующая э. д. с. является источником энергии, а в тех
участках, где направления э. д. с. и тока противоположны,
э. д. с. — потребитель энергии. Все сопротивления, как внешние,
так и генераторов энергии, независимо от направления проте-
кающего через них тока будут являться потребителями энергии.
Баланс мощностей для рассматриваемой схемы
+ Е212 — £3/3 = l\ (гх 4- г10) 4~ /2 (г2 4- г20) 4- /3 (гз + гзо) + 4~
+ 5»
или
15.5 4- 70.8 — 5.1 == 52-6 + 82-5 4- I2-10 4~ 62-2,5 4- 22-15,
получено тождество 630 = 630.
29
1.22. В схеме (рис. 1.29) найти все токи.
Лг-20в
Г}0 - 0,2ом s 70М
rt £5ом
г2(гО,4ом
г?-5 ом
Рис. 1.30
Рис. 1.29
1.23. Для цепи, изображенной на рис. 1.30, рассчитать токи
и определить показание вольтметра, если Е± — 40 в, Е2 == 5 в,
Е3 — 25 в, гх = 5 ом, г2 = г3= 10 ом. Током, протекающим через
вольтметр, можно пренебречь.
1.24. Аккумуляторная батарея из 20 последовательно соеди-
ненных элементов работает параллельно с генератором на сеть,
имеющую нагрузку 30 а. Каждый аккумулятор имеет э. д. с.
1,82 в и сопротивление 0,001 ом. Э. д. с. генератора 36,4 в и его
сопротивление 0,04 ом. Определить нагрузку генератора и бата-
реи (т. е. отдаваемые ими токи) и напряжение на их зажимах.
Какую э. д. с. должен развивать генератор, чтобы нагрузка
распределилась поровну между генератором и батареей?
1.25. По трехпроводной линии длиной 0,5 км (рис. 1.31) от
двух генераторов 1 и 2 питаются две группы ламп 50 em, 110 в.
В первой группе Л/х == 200 ламп, а во второй — N2 — 600 ламп.
Сечение крайних проводов q == 35 мм2, а сечение среднего (ну-
левого) провода q=l6MM2. Каждый генератор имеет внутрен-
нее сопротивление 0,01 ом и развивает э. д. с. 120 в. Определить
токи во всех проводах линии и напряжение на зажимах каждой
группы ламп, сопротивления которых считать постоянным. Ма-
териал проводов линии — медь.
Рис. 1.31
30
1.26. Напряжения, измеренные электростатическим вольтмет-
ром, между узловыми точками схемы и землей равны £/10 =
_ J_ 15 в, U20 = 52 в, t/30 == 64 в (рис. 1.32). Определить токи в
ветвях и отходящих проводах при Ех = 80 в, Е3 = 70 в, rt = 5 ом,
г3 == 10 ом, г3 = 12 ом. N
Решение. Вычислим напряжения между точками 1 и 2, 2
и 3, 3 и /:
Ulo - U*> = U12 = - 15 - 52 = - 67 в-
UW — UM = Ui3 = 52 — 64 = — 12 в;
(7го — = U31 = 64 — (—15) = 79 в.
Произвольно выберем положительные направления токов
ветвей и укажем их стрелками.
Применяя к ветвям закон Ома, определим
Л
_ -67 + 80 _ 9 fi
5
/2 = JL=l,2a;
г2 10
/ = = ..79~79. = 0,75 а.
8 г3 12
Токи в ответвлениях от узловых точек находим по первому
закону Кирхгофа:
/4 = /3 — /1 = — 1,85а; /5 = /3 4- /2 = 3,8 a; /в =— 12 —
= — 1,95 а.
Токи и /в получились со знаком «минус». Это указывает
на то, что через узлы 1 и 3 в схему протекают «истинные» поло-
жительные токи Л и /6, обозначенные на схеме пунктирными
стрелками.
1.27. В цепи (рис. 1.33) известны э. д. с. = 120 в, Е2 =
= 40 в, Е3=70в и сопротивления = 20 г2 = 10 ом. г3 =
= 40 ом. Потенциалы точек а. b и с относительно земли соот
ветственно равны (определены посредством вольтметра) (7fl0 =
31
= 160 e, Ub0 = 180 в, U.q = 50 в. Определить токи в ветвях ab,
Ьс, са и в проводах аа, Ы/ и сс', подходящих к точкам а, b и с.
Рис. 1.34
1.28. В цепи, изображенной на рис. 1.34, найти токи и пока-
зания вольтметров, если известно, что Ег = 32 в, Е2 = 64 в, Е3 ==
= 72 в, = 9 ом, r10 == 1 ом, г2 = 5 ом, г20 = 1 ом, г3 ~ 2 ом,
r3Q = 1 ом, г4 = 2 ом, r5 « 1 ом. Сопротивления вольтметров весь-
ма велики по сравнению с сопротивлениями элементов цепи.
1.29. Для схемы (рис. 1.35,а) найти токи и проверить баланс
мощностей, если Uab = 12 в, Ucd = 5,6 в, гг = 4 ом, г2 = 5 ом,
г3 = 3 ом.
Рис. 1.35
Указание. Данная схема может быть заменена эквивалентной,
торой между точками а и
в ко-
д. с.,
значение которых Ех == иаъ
1.35,6). Обращаем
включении
с э.
Ь, с и d
включены источники напряжения
численное :
и E2 = Ucd (рис.
внимание на то, что при
э. д. с. следует соблюдать заданные по-
лярности напряжений.
1.30. В цепи (рис. 1.36) найти
токи и проверить баланс мощ-
ностей.
32
1.31. Чему равно показание вольтметра на рис. 1.37, если
током вольтметра можно пренебречь по сравнению с токами
в нагрузках?
Определить показания ваттметров и убедиться в том, что их
сумма равна сумме мощностей, расходуемых в сопротивлениях
г2 и г3. Потерями в катушках ваттметров пренебречь.
Рис. 1.37
Рис. 1.38
1.32. Определить ток, проходящий через сопротивление г ==
= 5 ом, подключенное к генератору тока (рис. 1.38), парамет-
ры которого: ток /г = 6 ма и внутренняя проводимость gr =
= 0,04 ом"1.
Решение. Внутреннее сопротивление генератора тока
гг = — = —!—=25 ом
ёг 0,04
Ток /г распределяется по двум параллельным ветвям г и гг
обратно пропорционально их сопротивлениям.
Поэтому искомый ток
1.33. Источник тока /г = 30 ма (рис. 1.39). Чему равны токи
в ветвях, сопротивления которых гг=\&ком, г2 = 3ком, г3 =
= 1,5 ком, г4 = 2 ком?
2 Заказ Xs 624
33
Рис. 1.39
1.34. Цепь (рис. 1.40) содержит генератор тока, имеющий
внутреннюю проводимость gQ = 5-10-5 ом'1 и источник тока /г=
= 80 ма, и генератор напряжения с э. д. с. Ег = 230 в; сопро-
тивления гх = 1 ком, г2 = 2 ком. Определить все токи.
Решение. Выберем положительные направления токов, как
это указано на рис. 1.40, и составим уравнения по законам
Кирхгофа. Цепь содержит четыре ветви (7VB = 4), два узла А и
В (М = 2), один генератор тока (NT = 1). Число уравнений,
составляемых по первому закону Кирхгофа, равно Ny—1 = 1,
а по второму закону Кирхгофа (1.12)
K = — 2VT = 4 — 2 + 1 — 1=2.
Выберем два независимые контура, не содержащих источника
тока, и обозначим их стрелками I и II.
Уравнение для узла А
/г—10 — /2 + = 0;
для контура I
/•J1 +Гг1г = Ер
для контура II
г2/2 - — 70 = 0.
g©
Подставляя цифровые значения в эти уравнения и решив их,
получим
/ = ЮО ма\ /х = 30 ма\ 10 = 10 ма.
1.35. Два источника тока /Г1 = 100 ма и /г2 = 50 ма (рис.
1.41) включены в схему, содержащую сопротивления ^ = 200^,
г2 = 50 ом, г3 = 30 ом.
Вычислить все токи.
Рис. 1.41
1.36. Методом контурных токов найти токи в цепи, схема
которой изображена на рис. 1.42. Даны: = 100 в, Е2 = 30в,
Е3 = 10 в, Е4 = 6 в, i\ = 10 ом, г2 = 10 ом, г4 = 6 ом, = 5 ом,
= 15 ом, г40 = 1 ом.
34
Решение. Выберем направления контурных токов, кото-
рые обозначим через /р /п, /1П.
Составим систему уравнений для контуров:
£*! Е2 Е3 = (гj г2) Ц г21ц;
^2 ^4 = (Г2 + Г5 + r40 + r4)Al Н^(Г40 + ГIШ Г2 Л 1
Е3 Е4 = (гв 4- Г40 + г4) /щ + (г4о 4~ Г4) /п .
После подстановки числовых значений имеем
60 = 20/, — 10/н;
24 == — 10/j + 22/п + 7/П1;
—16 = 7/п + 2271П .
Решив эту систему уравнений, найдем контурные токи:
/г = 5 а\ 1и = 4 а\ /1П = —2 а,
а затем найдем истинные токи во всех ветвях.
В ветви, где действует э. д. с. Е19 истинный ток имеет
направление контурного тока /, и равен Ц = Ц = 5 а.
В ветви с сопротивлением г5 истинный ток /5 имеет направ-
ление контурного тока /п и равен /5 = /п = 4 а.
В ветви с сопротивлением ге истинный ток /в имеет направ-
ление, «противоположное контурному току /П1, и равен /в =
= Ли —
В ветви с сопротивлением г2 истинный ток /2 получится от
наложения контурных токов 1Х и 1и и будет иметь направле-
ние большего контурного тока Ц :
Л h ~
В ветви с сопротивлением г4 истинный ток 14 получится от
наложения контурньТх токов /п и /ш и будет иметь нап-
равление контурного тока /п:
/4 = 1и + /ш = 4 + (—2) == 2а.
В ветви, где действует э. д. с. Е3, истинный ток /3 полу-
чится от наложения контурных токов /т и /ш и будет иметь
направление тока /г:
Л == Л + ш = $ + (—2) = За.
В целях упражнения покажем, как эта же задача может
быть решена путем использования определителей. Для этого
уравнения контурных токов следует записать в форме (1.13):
^иЛ 4“ r\Jп 4" г1зЛп = ^и»
Г21Л 4“ г2%1 н 4“ Г2зЛп “ ^22*>
Г31Л 4- Г32^П + '’ззЛп ^33’
2*
35
где
ru = r\ + ft = 20 ом; ri2 = r21 = — r2 = —10 ом:
ris — Г31
= 0; rM = r2 + r5 + r40 + rt = 22 ом.
гзз = гзз = rto + r4 = 7 ом; r33 = re 4- r40 + r4 = 22 ом;
22
= E2 — £4 = 24 e;
£33 — £3 £4 — 16 e.
Составим
определитель Д и вычислим его значение:
Г11 Г12 Г13
г2] Г22 Г23
Г31 Г32 Г33
20 —10 0
—10 22 7
0 7 22
= 20-22-22 + (—10)-7-0 + 0- (—Ю)-7—0-22-0—20-7-7 —
— (—10) • 22 = 9680—980—2200 == 6500.
Вычислим значения алгебраических дополнений определи-
теля, рассчитав его миноры и умножив каждый из них на
(—1)*+/, где k — номер вычеркиваемой строки, а I — номер вы-
черкиваемого столбца;
Дп — это алгебраическое дополнение, получающееся из основ-
ного определителя Д путем вычеркивания первой строки и
первого столбца, умноженное на (—1)1+1:
—1)2 =22.22—7-7 = 435;
Д12 — алгебраическое дополнение, получающееся из основ-
ного определителя Д при вычеркивании первой строки и вто-
рого столбца, умноженное на (—1),+2:
Q 22 (-1)3 —(-10-22-7-0) = 220 = Д21;
аналогично
— 10
? (— 1)4 = —10-7—22-0 = — 70 = Д31;
Д22 —
20
0
0
22
(—1)4 = 20-22—0-0 = 440;
0
36
23 —
20
0
— 10
33 —
20
— 10
— 10
— I)6 ==2(l-22—10-10=340.
Искомые контурные токи
ТТГ — д
"11
21
31
11
11
31
11
21
11
-*22
22
32
12
'22
32
33
23
33
+-24-
13
33
33
12 ' 13
22 Г23
7 р
"22 *"33
-Н^+£зз^=б0.
^.„16.1=70)
6500 6500
Л 21
11 Д
(-140)
4 ДО
6500 —16‘ 6500
А31
и ~Т~
А 32
зз
435
6500
220
6500
^83 __ gQ . ( 70)
д
6500
' “ Д
Д
+£зз^ =60-
= -2а.
6500 6500
образом,
получили, правда,
а
Рис. 1.43
Таким
затратив больше времени, те же резуль-
таты, что и ранее.
1.37. Найти все токи и определить
потенциалы точек а, b и с относительно
земли (рис. 1.43). Задачу решить мето-
дом контурных токов. Ег = 85 в, Е2 =
— 84 в, Е3 = 5 в, Е4 =12 в, t\ = 8 ом,
га=10 ом, г3=10ом, г4=10 ом, 10 ом,
г6=4 ом.
1.38. Для схемы (рис.
лить токи. Даны
1.44) вычис-
токи и внутренние
проводимости генераторов тока соответ-
ственно первого и второго: /Г1 = 50ла, g, — 10-4 ом~1, = бОма,
g2= 0,5- 10-яол-1, э. д. с. генератора напряжения Ё3=270 в;
сопротивления r3 = 1 ком, rt=2 ком, г&=7,5 ком, г6=3 ком.
Решение. Рассматриваемая цепь содержит восемь ветвей
(#в=8), четыре узла (ЛГу=4), два генератора тока (Л\=2). По
37
формуле (1.12) находим, что число уравнений, составляемых
по методу контурных токов, равно трем (K~NB—Ny + 1—Nr**
= 8—4-1-1—2=3). На рис. 1.44 показаны выбранные направ-
ления трех искомых контурных токов , /п, /ш, протекаю-
Рис. 1.44
щих по трем независимым контурам, не содержащим источни-
ки тока. Там же нанесены известные контурные токи /Г1 и /г2.
Составим уравнения по методу контурных токов:
П —гбЛ + (г4 + г5 + гб) Лг г<Лп —О*
Подставляем сюда цифровые значения:
I' 6- 103/х —3-103/11—2.103/П1 =390;
IF —З-Ю3/, + 12,5-103/п—2-103/ш =0;
III' — 2’Ю3/,— 2- 103/п +14-103/1П = 380.
Решив эти уравнения, найдем контурные токи:
/, =95 ма, 1и = 30 ма, /ш =45 ма.
Вычислим токи в каждой из ветвей. По сопротивлению
проходит ток Л ==Л1—Ли =50—45=5 ма. По сопротивлению^
проходит ток Л = ^2+Ли —Л =60+45—95=10 ма. Через
сопротивление г3 течет ток /3 = Ц =95 ма, в ветви с сопро-
тивлением г4 проходит ток /4 = /ш — /п=45—30=15 ма, че-
рез сопротивление г5 — ток /5 =/п = 30 ма, в ветви с сопро-
тивлением г6— ток /6 = Л — /и = 95 — 30 = 65 ма.
38
1.39. Вешить задачу 1.34 методом контурных токов.
1.40. Цепь (рис. 1.45) содержит источник тока I = 50 ма,
генератор напряжения с э. д. с. Е = 60 в и сопротивления
г * = 5 ком, г2 = 4 ком, г3 = 16 ком, г4 = 2 ком, г5= 8 ком.
Вычислить все токи методом
контурных токов. Проверить баланс
мощностей.
Решение. Схема содержит
шесть ветвей (NB = 6), четыре узла
(Ny= 4), один генератор тока (AfT=l).
Число независимых уравнений, со-
ставляемых по методу контурных то-
ков, равно двум (К~6—4 + 1—1=2).
Зададимся направлениями контур-
ных токов , /п, как показано
на рис. 1.45. Там же нанесен из-
вестный контурный ток I . Соста-
вим систему уравнений для первого
Рис. 1.45
и второго контуров:
Подставляя цифровые значения и решая эти уравнения,
найдем контурные токи:
= — 30 ма и /и = 40 ма.
Искомые токи
{Г = 10 ма;
= 10 ма.
Баланс мощностей
Подставляя числовые значения
. 1 ,2 вт.
о)
получим тождество: 11,2 вт ==
Рис. 1.46
1.41. Для схемы (рис. 1.46, а), пользуясь методом узловых
потенциалов, определить все токи. Дано: £1=30 в, Е2— 10 в,
Е3 — 200 в, Et = 56 в, гг — 20 ом, г2 = 30 ом, г3 = 6 ом, г2 =
= 8 ом, г6 = 15 ом, гй = 40 ом и г7 = 10 ом.
39
Решение. Примем потенциал точки 3 ф3 = 0. Составляем
уравнения по методу узловых потенциалов. Сумма токов, вы-
текающих из узла 1 (с учетом выражения токов по (1.6)], рав-
на нулю:
?1~?2~| — ?2
Г1 4“ Г 7 ГЪ
аналогично для узла 2
?2 — 4- । У2—| ^2 — ^2
Г1 4- Г-1 ГЬ Г2
+ ъ + £а =о
г3
Подставляя числовые значения в эти уравнения, после пе-
регруппировки членов (собирая числовые коэффициенты при
неизвестных <рх и ф2 и перенося известные значения в правые
части) получим
0,25 ф, —0,1 ф2=30 —-56 — = — 6;
—"—О,1 ф1 4~ 0,Зф2 == — 30---------4~ Ю
----200—^—34.
30 6
Решив последние два уравнения, найдем потенциалы то-
чек / и 2:
Ф! = — 80 в; ф2 = — 140 в.
Наконец, применяя закон Ома для отдельных ветвей, оп-
ределим искомые токи:
/ = — —804-140—30 __
1 Г1 30
I __ <Рз-<р2 4“ ^2 _ 1404-10 _
30
I *р2—?з 4-^з —1404-200
/3— •
6
. <рз——£4 80—56
8
_ -804-140
'з
<Р1 — ?2
= 10 а;
в—
''в
Направления
(рис. 1.46, б)*.
Рекомендуем
нуль потенциал
15
80 9 „
— = z а.
40
найденных токов указаны на
читателю решить ту же задачу,
узловой точки 1.
графе цепи
приняв за
* Графом цепи называется такое изображение схемы электрической
цепи, в котором все ветви заменены линиями, источники напряжения зако-
рочены, а источники тока разомкнуты. В графе сохраняются все ветви и
все узлы данной схемы.
40
1.42. Методом узловых потенциалов определить токи во
всех ветвях схемы, изображенной на рис. 1.47, а. Заданы Er~
=20 в, Е2 = 30 в, Е3 = 2 в, Е4 = 1,2 в, £*5 = 5,6 в, г2 = 50 ом,
г3 = 10 ом, г* = 20 ом, г5 = 10 ом, гв = 100 ом, г1 = 50 ом,
гл = 20 ом.
о
Решение. В цепи имеется ветвь с источником напряже-
ния, не содержащая сопротивления. Целесообразно принять рав-
ным нулю потенциал одной из узловых точек, к которой под-
ходит указанная ветвь, например потенциал узла 3 (ф3=0).
Тогда потенциал точки 1 имеет значение, равное Et т. е. =
= 20 в. Общее число уравнений, согласно формуле (1.15), рав-
но двум (Ny = 4, NH = 1, У = Ny — NH — 1 = 2). Таким обра-
зом, в данной задаче достаточно составить по методу узловых
потенциалов всего два уравнения для узлов 2 и 4. .
Для узла 2
?2 —?2 — । ф2—
г7 г3 г4
Для узла 4
?4~ ?1 _|_ ?4~?2 —^4 । ^5
^8 Г4 Ъ
Подставляя в эти уравнения числовые значения сопротивле-
ний, э. д. с., а также значение фх=20 в, получим после пере-
группировки членов для двух неизвестных потенциалов ф2 и ф4
систему уравнений:
/ 1 , 1 , 1 \ 1 2
Ф О. I ' * """'* “4"* .... " I ~ ———— I ——- ф * — । ।
\ 50 10 20 / 20 10
1 , 1 1 \ М
1 1 '« "! ' —ntyw** “1 ' 1 " 1 - —
20 20 10 / 20
фл ’
2 20
ИЛИ
1,2 20 .
20 + 50 ’
5,6 20
10 20 ’
0,17ф2—0,05ф4 = 0,54;
—0,05ф2 + 0,2ф4 = 1,62.
41
Решая эту систему уравнений, найдем
<р2=6 в; ф4=9,6 в.
Наконец, применяя к отдельным ветвям формулы закона
Ома, получим значения всех токов, которые нанесены на ске-
летной схеме (рис. 1.47, б):
/2=0,2 а; /3=0,4 а; /4=0,12 а; /5=0,4 а;
/6 = 0,2 а; /7 = 0,28 а; /8=0,52 а.
Обращаем особое внимание на то, что в ветви без сопро-
тивления ток Д не определяется законом Ома и вычисляется
на основании первого закона Кирхгофа:
Л = —/2~0,8 а.
1.43. Методом узловых потенциалов рассчитать токи в цепи
(рис. 1.48).
Указание. Для решения задачи
согласно (1.15) достаточно составить всего
одно уравнение.
1.44. По данным задачи 1.38
(см. рис. 1.44) найти токи методом
узловых потенциалов.
Решение. Потенциал узла
4 примем равным нулю (ф4 =
=0). Составим систему уравне-
ний по методу узловых потен-
циалов для узлов /, 2, 3.
Сумма люков, вытекающих из узла, с учетом формулы (1.6),
для узла 1
yi — Q । <Р1 — Уз
г6
У1 — ?2
г2 —0.
Здесь перед током /г2 источника тока стоит знак «минус»,
так как этот ток не вытекает от узла /, а направлен к нему
(см. основные положения, стр. 10).
Аналогично
для узла 2
Ъ-Ъ + JP22Z0 + ; + / = 0;
г2 Г3 Г1
для узла 3
Уз—У1 । Уз—УгЧ-^з । Уз—У4 _ q
г, г3 гь
Подставляя числовые значения в уравнения и решая их,
найдем потенциалы узловых точек фх=—30 в, ф2=—50 в и
Ф3— — 225 в.
42
Наконец, определяем по закону Ома токи в каждой из
ветвей
I, = (Ф*—ф2)^1 — (0—(—50)] 10"< = 5- 10-s а = 5 ма;
/а= (Ф1 — Фг)^ — (—30—(—50)] 0,5 • 10~3 == 10-10~s а = 10 ма;
I ?»-*+£». = -225- (-50) + 270 =95. jq-з а = 95 жа;
8 г3 1-10»
/ — ZrzSl. —15. io*3 а = 15 ма;
г 4
/ = =30. IO"3 а = 30 ма;
Г5
/6— = 65 • 10~3 а = 65 ма.
1.45. Решить задачу 1.35 методом узловых
1.46. Рассчитать токи в це-
пи рис. 1.49. Дано: /Г1 = 10 ма
gx = 1 • 10“3 ом~1, /г2 = 45 ма,
g2=2,5-10~3 ом~\ /г3=160 ма,
g3 = 4 • 10~3 ом'1, = 55 в,
г4 = 300 ом, Гь = 500 ом,
г6 — 200 ом.
Задачу решить методами
контурных токов и узловых
потенциалов.
1.47. Цепь (рис. 1.50) со-
держит генератор тока
(7Г1=80 ма, г\ == 2 ком), источ-
ник тока /г2=50 ма и источ-
ник напряжения с э. д. с.
Е3=50я. Сопротивления г4=г5=
= 100 ом.
Найти все токи методами
узловых потенциалов и кон-
турных токов.
Решение. В соответствии
с формулой (1.15) надо сос-
тавить всего лишь одно урав-
потенциалов.
<3
Рис. 1.50
нение (Ny=3, Na=l, V=Ny—
— NH—1=3—1—1 = 1). Примем потенциал узла 3 равным нулю
(ф3=0), тогда потенциал узла 2 <р2 — + Е3 =50 в. Чтобы оп-
ределить потенциал узла 1 необходимо составить для этого
узла уравнение по методу узловых потенциалов
43
Подставляя числовые значения и решая это уравнение, по-
лучим <pj ^60 в.
Применяя к ветвям г4 и г5 закон Ома, найдем
/4=0,5 а\ /5=0,1 а.
Наконец, применяя первый закон Кирхгофа к узлу /, оп-
ределим
Л = 1п + /г2 — Л = 80-10-3 + 50. КГ3 — 0,1 = 0,03 а.
Решение задачи методом контурных токов рекомендуем чи-
тателю проделать самостоятельно.
1.48. Методом наложения рассчитать токи в схеме (рис.
1.51, а), если ^ = 10 в, Е2=40 в, Е3=5 в, г10=5 ом, г20=г30=э
=2 ом, г, = 30 ом, г2 = 3 ом, г3 = 8 ом.
Рис. 1.51
Решение. Обозначим положительные направления токов
исходной схемы на рис. 1.51, а. Предположим, что действует
только э. д. с. Ev а э. д. с. Е2 и Е3—недействующие (рис.
1.51, 6).
Тогда
г' ________________________
Z1 г ’
где
Г г I г I (Г2 + Г2о) (г3 4- Г30) _or . 5-10 115
г1э = Г1 + г1оН--:---;---:---— □□+ — — — ом.
Ток
/; - 10 :
115
3
6
23
а.
44
Токи в параллельных ветвях определяются по (1.11):
Проведем расчет, предполагая, что действует э. д. с. £а,
а э. д. с. Ej и Е3 не действуют (рис. 1.51, в):
де
72 16 56
------------== ------а.
23 23 23
Аналогично рассчитаем величины токов при
ко одной э. д. с. Е3 (рис. 1.51, г):
'’зэ — гъ 4- ^зо 4-
Г1 + Г10 + г2 4" г20
(Г 14"rio) (Г2 "h г 2о)
действии толь
ом\
Истинное значение тока в каждой ветви найдется как ал-
гебраическая сумма токов, определяемых каждой э. д. с. в от-
дельности.
Ток в первой ветви
72____7
23 ~23
Ток во второй ветви
Ток в третьей ветви
56______8
23 23
45
1.49. Найти токи в ветвях цепи, изображенной на рис. 1.52.
Задачу решить методами наложения и контурных токов.
1.50. В схеме (рис.
1.53, а) методом нало-
жения найти все токи.
Даны: Е\=96 в, Е2=75 в,
г3=3 ом, г4=15 ом,
г5=10 ом, гв=6 ом.
Решение. Положим,
что действует только
э. д. с. Ev а э. д. с. £2 не
действует. В этом слу-
чае схема примет вид,
изображенный на рис.
1.53, б. Так как внут-
реннее сопротивление
источника напряжения
Е2 равно нулю, то на
его месте между точками
Рис. 1.53
Ь и d показано короткое замыкание.
Для большей наглядности схему рис. 1.53, б можно начертить
в виде схемы рис. 1.53, в.
Полное сопротивление этой схемы
___ Г3Г6
1э .
3-6 . 15-10 Q
-------------= 8 ом.
9 25
Определим все токи:
I' = А- = J*L = 12 а;
1 Пэ 8
/з=Г-7тЬ = 12 •-|- = 8 а; а>
’ Ч " I * 6
- Л777 = I2'= 4'8 ''-- = Г' - "13
~ 4 I г5
Г2 — /' — /<= 8—4,8=3,2 а или /' = Г&— Г6 =3,2 а.
46
Допустим, что действует только э. д. с. Ег, а э. д. с. Е,
не действует (рис. 1.53, г).
Схему (рис. 1.53, г) для большей наглядности можно пред-
ставить в виде схемы рис. 1.53, д.
Ее полное сопротивление
г2э = = — + — = 6,25 ом.
гз+г* г6+гв 18 16
Вычислим
Г = = 2L = 12 а;
2 ггэ 6,25
Г = Г = 12 • — = 10 а; Г. = П—1\ =2 а;
3 2 Г3+г, 18 4 2 3
/; = /; — Гв =10—7,5=2,5 а.
Складывая алгебраически токи, полученные от действия
каждой э. д. с. в отдельности (см. рис. 1.53, б и 1.53, г), нак
дем токи в каждой ветви исходной схемы (рис. 1.53, а):
= ]' + Г = 124-2,5= 14,5 а; /2 = Е 4- Г = 3,2 4- 12 = 15,2 а;
•11 £» £
/3 = /;+ /; =8+10=18 а\ — =4,8-2 = 2,8 а;
/5 =/; + /; =7,2+4,5=11,7 а; 1е = - /6 =7,5-4=3,5 а.
1.51. Решить задачу 1.34 (см. рис. 1.40) методом наложения.
Решение. Предположим, что
действует только генератор напря-
жения с э. д. с. Ег; в этом случае
генератор тока следует считать не-
действующим, и в схеме надо ос-
тавить лишь его внутреннюю про-
водимость g0 (рис. 1.54, а). Для
этой схемы рассчитаем токи. Сна-
чала найдем полное сопротивление
гэ, которое является суммой сопро-
тивления г± и параллельных сопро-
1
тивлении г2 и —;
go
Рис. 1.54
31 . Z4U
= -jp • 103 ом.
47
Находим
2300
31
10-3 а-
Г = Г—Г9 = • 10-3 а.
0 1 9 31
Теперь допустим, что в цепи действует только генератор
тока, при этом генератор напряжения следует считать недей-
ствующим (Ey = 0), и в схеме надо оставить лишь его внутрен-
нее сопротивление гг (рис. 1.54, б). Имея в виду, что в парал-
лельных ветвях токи распределяются прямо пропорционально
их проводимостям, найдем
/'. = / ---21----=80-10-3---------------------------= ^222.10-3 а;
gi+g2+go ЮО-10"5+50-10-“4-5-10"6 31
г = 1Т.------= 800 .10_3 а.
§1 Т g% 4" go 31
go = 80
gi Т- g2 go 31
10-3 a.
Искомые токи в каждой ветви найдем в результате наложе-
ния токов (с учетом их направлений), проходящих в каждой
из ветвей, созданных генератором напряжения и генератором
тока:
[А = = 30 жа; /2= Г2 + Г2 = 100 ма;
Q =10 ма
1.52. Методом наложения решить задачу 1.35 (см. рис. 1.41),
1.53. Найти эквивалентное соп-
Рис. 1.55
ротивление цепи (рис. 1.55, а) и все
токи, если £/=114 в, гА = 30 ом,
ом> г4^26 ом, гъ = 11 ом,
г8 = 10 ом, г1 ~ 40 ом, г8 = 50 ом.
Задачу решить методом преобразо-
вания треугольника сопротивлений
в эквивалентную звезду.
Решение. Заменим треуголь-
ники сопротивлений аЬс й dfg экви-
валентными звездами (рис. 1.55, б).
В преобразованной схеме появились
новые узлы е и т. Обратим внима-
ние на то, что в преобразованной
схеме сохраняются значения токов
/, /4, Л в участках цепи, которые
не подверглись преобразованию.
Подсчитаем сопротивления лучей звезды г10, г20 и г30, экви-
валентной треугольнику abc сопротивлений i\, г2, г3 (1.21)
48
rio=----— =6 ом; rw==--------------J .8 ,= 6 ом;
ri4"ra + f3 G •Hj + 's.
r .=---r-£^--- =2 0Jt.
® n+r8 + r,
Сопротивления лучей звезды г40, г50, гв0 эквивалентной треуголь
нику dfg сопротивлений гв> г7, г8 равны
г40==—---------=4 ом; Г5О=—-------------= 5 ом;
Га -4- г, 4- Го га 4- Г, 4- Га
------------- = 20 ом.
rG + Г7 + Г8
Эквивалентное сопротивление всей схемы
где
= г2о 4- Г4 + rw = 36 ом; гп = г30 + гь + г60 = 18 ом.
Ток в неразветвленной части цепи
11*
/ = — = — = 3 а.
гэ 38
Токи в параллельных ветвях
/5 = / — /4 = 2 а.
Теперь найдем токи в сопротивлениях заданной цепи. Для
этого предварительно из схемы (рис. 1.55, б) определим напря-
жения между точками а и Ь, а и с, с и b, d и g, f и g, f и d:
Uab “ Г1(/ + r20^4 = * 3-4-6 • 1 =24 e\
4-r30/5 = 6’3-4-2*2=22 e\
Ucb = Uab ~Uac = (<Pa “ Фб) ~ (<Pa ~ ФС) = <PC ~ <Pft =24 — 22= 2 в;
Udg ~ 40^4 "b eo^ = 4 • 1 4“ 20 3 = 64 e;
U= r5 -|-гв0/ = 5- 2-|-20-3=70 в;
Ufd = Ufg— Uag = (<P/— <Pg) — (<Pd~<Pg) = <pz — q>d=70—64 = 6 в.
49
Искомые токи
/1= -Маь_ = 2L = 0,8 а; /2= = — = 2,2 а;
п 30 Г2 10
7 JA_ = А = 0,2 а; /4 = 1 а;
г3 10
/5 = 2 а; /в = = _А = о,6 а;
ге 10
/,= = 1,6 а; / = _А«_ = = 1,4 а.
г, 40 8 гй 50
1.54. В схеме (рис. 1.56) найти токи, применив преобразо-
вание треугольника в звезду. Определить эквивалентное сопро-
тивление между точками а и &.
Определить показание ваттметра и убедиться в трм, что
оно равно сумме мощностей, расходуемых во всех сопротив-
лениях.
Рис. 1.57
1.55. Вычислить токи, приходящие во всех ветвях схемы
(рис. 1.57), если Е = 213 в, Ег = 90 в, гх=6 ом, г2=40 ом,
г3 = 10 ом, г4 = 100 ом, г5=60 ом.
Задачу решить преобразованием треугольника в эквивалент-
ную звезду.
Определить входное сопротивление относительно ветви rv
'ч 1.56. Для схемы (рис. 1.58, а) методом эквивалентного ге-
нератора тока найти ток в ветви с сопротивлением если Е^
= 18 в, Е2=21 в, г10=1 ом, гг=2 ом, г20=2 ом, г2=1 ом, г3=
=6 ом.
Решение. Обозначим положительное направление искомо-
го тока It на исходной схеме (рис. 1.58, а). Рассмотрим часть
схемы, подключенную к исследуемой первой ветви и обведен-
ную штриховой линией в качестве эквивалентного генератора
с э. д. с. Ег и сопротивлением гг. Нарисуем эквивалентную
электрическую схему с эквивалентным генератором (рис. 1.58, б).
50
На схеме произвольно выбрано положительное направление
э. д. с. эквивалентного генератора Ег к точке р. Это позволя-
ет записать для режима холостого хода эквивалентного гене-
ратора с отключенной ветвью (рис. 1.58, в)
Е? = Е)рцх.к = (фр Фр)х.х •
Рис. 1.58
Индекс «х.х» указывает на то, что величины соответствуют
режиму холостого хода. Развернутая схема эквивалентного ге-
нератора в режиме холостого хода показана на рис. 1.58, г.
Ток холостого хода Л.х во внутренних ветвях генератора
Напряжение холостого хода определяет э. д. с. генератора:
Цэ^х.х =^з/х.х =б • 1,4=8,4 в = Ег.
Найдем сопротивление гг эквивалентного генератора.
Для подсчета сопротивления генератора преобразуем его
схему (рис. 1.58, г), заменив источник напряжения Е2 коротко-
замкнутым участком, как показано на схеме (рис. 1.58, 3).
Входное сопротивление последней схемы является сопротивле-
нием эквивалентного генератора:
Возвращаясь к схеме (рис. 1.58, б), находим искомый ток
по закону Ома:
/ = __ 8,44-18
гг 4- гю 4- ri 3,64-14-2
( 1.57. ^Методом эквивалентного генератора найти ток /б
(рис. 1.59, а), проходящий через сопротивление г6, если Е=
= 120 в, гх=60 ом, г2 = 15 ом, г3=90 ом, г4=60 ом, г6=12 ом.
Тем же методом определить ток в сопротивлении г4.
Решение. Обозначим на схеме (рис. 1.59, а) произвольное
положительное направление искомого тока 7б. Часть схемы
51
(внешнюю к исследуемой ветви г5) рассмотрим в виде некоторо-
го генератора напряжения Ег, гт. Стрелку э. д. с. £г произ-
вольно направим к точке с (рис. 1.59, б). Таким образом, э.д. с.
генератора определится напряжением холостого хода:
Ег—Ucdx.* — (фс Фа)х.х •
На развернутой схеме генератора в режиме холостого хода
(рис. 1.59, в) обозначим токи в ветвях /ох, /1х и /зх.
Рис. 1.59
По закону
Ома
1х —
Зх —
75
120 л п
— == О,о U.
150
в:
тс/х.х — ^асх.х — ' Vlx
((ра ф^)х.х = Uadx.x == '"з^Зх = = 72 в.
Таким образом, э.д. с.эквивалентного генератора
Ег = (фс—<Prf)x.x = (фс — Фа 4- Фа — ф4)х.х = (фа—Фа)х.х —
— (Фа-Фс)х.х “ 72 — 96 г= — 24 в.
Найдем сопротивление эквивалентного генератора двумя
способами.
1. Путем непосредственного расчета по схеме.
Для этого в схеме (рис. 1.59, в) источник напряжения заме-
ним короткозамкнутым участком. После этого схему рис.
1.59, в нарисуем в виде рис. 1.59, а.
52
Сопротивление генератора гг равно сопротивлению цепи меж-
ду точками end:
'3'4
60-15 90-60 = 48
75 150 ~
ом.
2. То же сопротивление можно найти и другим путем. Для
этого надо в схеме рис. 1.59, в замкнуть точки с и d накоротко,
вычислить ток /г.к.з, протекающий через короткозамкнутый уча-
сток (рис. 1.59, д), и найти сопротивление короткого замыкания
по (1.26). Источник напряжения Е в короткозамкнутой схеме
(рис. 1.59, д) нагружен на эквивалентное сопротивление.
Ток источника
напряжения
Ок
Гэ
Токи в ветвях
1К
0к
2к
Ок
Гз
60-90 15-60
+ 75
= 48 ом.
120
90
Во
60
75
а.
э
Отсюда
1г. к. з 11к 2к = 0,5 а,.
Сопротивление генератора
г.к.з
— 24
— 0,5
= 48 ом.
Оба способа привели к одинаковому значению сопротивления
генератора.
Возвращаясь к схеме (рис. 1.59, б), находим искомый ток /5
по закону Ома:
24
12 + 48 = ~ °,4 а '
Таким образом, ток в гб течет от точки d к точке с и равен
0,4 а.
Расчет тока в сопротивлении г4 методом эквивалентного гене
ратора проводится аналогично. Заменяем часть схемы, подклю-
ченную к точкам d и b ветви г4, эквивалентным генератором
Ег, гг (рис. 1.59, е). Э. д. с. генератора совпадает с напряже-
нием в режиме холостого хода:
£ = Udb^x .
53
Для определения этого напряжения рассчитываем вначале то-
ки /3 и /0 в развернутой схеме генератора в режиме холостого
хода (рис. 1.59, ж):
/о , П(^з + г5) ~~ 95 а; 'з Z0 г1+г3+г5 19 й*
Г2 + П + г3 ч- г5
Отсюда находим э. д. с. генератора
о' тт' г’ , г' 840
db х.х + г2 /0 19 '
Для определения сопротивления генератора рассмотрим соот-
ветствующую пассивную схему (в схеме генератора источник
напряжения заменен короткозамкнутым отрезком), показанную на
рис. 1.59, з. Для ясности последняя схема перерисована еще по-
иному (рис. 1.59, и).
Сопротивление генератора, равное входному сопротивлению
последней схемы относительно зажимов d и
Наконец, находим искомый ток /4 по
схеме эквивалентного
генератора (рис. 1.59, е)
1.58. Для схемы (рис. 1.60) мето-
дом эквивалентного генератора найти
ток в ветви с сопротивлением 5 ом.
1.59. Считая зажимы а и b
входными клеммами схем (рис. 1.61, а,
Рис. 1.60 б, в, а), определить параметры соот-
Рис. 1.61
54
ветствующих эквивалентных генераторов
(рис. 1.61, д).
1.60. Для экспериментального иссле-
дования двухполюсников собрана схема
рис. 1.62. Требуется найти э. д. с. и
сопротивление генераторов, эквивалент-
ных исследовавшимся двухполюсникам,
по данным двух опытов (для каждого
двухполюсника):
Ег и гг со схемой
3)
в /, а
20 2
30 3
1/, в 1, а
20 12
30 14
(/, в /, а
20 3
30 5
1.61. Определить ток /3 в ветви г3 = 12 ом (рис. 1.63, а).
Э. д. с. генераторов напряжения = 120 в, Е3 = 100 в, их
внутренние сопротивления гг — 6 ом, г2 = 4 ом.
Рис. 1.63
Решение: Задачу решаем двумя способами: 1) методом
эквивалентного генератора тока и 2) методом преобразования.
1. Часть схемы, подключенную к зажимам т и п ветви г3.
обведенную на рис. 1.63, а штриховой линией, можно рассматри-
вать в виде эквивалентного генератора тока /г, гг, обведенного
штриховой линией на рис. 1.63, б. Ток генератора /г определя-
ется по опыту короткого замыкания (рис. 1.63, в).
На развернутой схеме генератора (рис. 1.63, г)
1г = -у- + = 45 а,
Г1 г2
55
а внутреннее сопротивление генератора тока равно сопротивлению
пассивной цепи между зажимами тип при разомкнутой ветви г8
(рис. 1.63, д):
г. = —— = 2,4 ом.
г П + г»
По схеме эквивалентного генератора тока, представленной на
рис. 1.63, б, находим искомый ток
1а 1г ГГ + г3 45 2,4 4- 12 ~ 7,5 а-
2. При решении методом преобразования, заменяем генераторы
напряжения схемы (рис. 1.63, а) эквивалентными генераторами
тока (рис. 1.63, е). Токи генераторов
/а = —= 25 а
2 г2 4
Преобразуем полученную схему, заменив параллельные сопро-
тивления и г2 эквивалентным сопротивлением:
Г1 г* 6-4 п л
г _ —L—2— = _ = 2,4 ом
''i + 6 4- 4
и параллельные источники тока 1г и /2 — одним эквивалентном
источником тока /г, снова приходим к схеме (рис. 1.63, б),
причем,
/=/+/= 20 + 25 = 45 а.
1 Д’® ’
Ток /г последней схемы разветвляется по сопротивлениям гг и г8:
1з = 1г -Нтт- = 45 тттбг = 7>б а-
1.62. Два генератора тока соединены в цепь, показанную на
рис. 1.64, а. Ток первого генератора /х = 3 ма, его внутренняя про-
водимость ^=0,05 ом'1, второго генератора /2=2 ма, g2=0,01 ом'1.
Рис. 1.64
56
Сопротивления r3 = 5 ом, = 30 ом. Определить ток, проходя-
щий через сопротивление г4.
Решение. Способ 1. Преобразуем генераторы тока в экви-
валентные генераторы напряжения (рис. 1.64, б). Э. д. с. и внут-
ренние сопротивления генераторов напряжения находим по (1.4):
~ 77 ~ 0,05 = мв'< Г' = 17 = 0,05 = 20 011 ’
'• - А- = 100 ом.
Далее, любым способом находим искомый ток. Выберем ме-
1 ' 1
тод узловых потенциалов. Обозначив g} = —, находим
^1 S\ "к
g| Н" #2 + S4
60‘ 20 + 5 + 200 • ЮО
Uab = 52,8
Гл 30
= 1,76 ма.
= 52,8 мв.
Способ 2. Решим задачу методом эквивалентного генератора
тока. Для этого заменим всю цепь, за исключением ветви с г4,
эквивалентным генератором тока (рис. 1,64, в). Для определения
его параметров /э и g3 сначала исключим ветвь с г4, а точки
а и b закоротим (рис. 1.64, г). Найдем ток короткого замыкания,
равный /э. Для этого предварительно определим токи 13 и /2
(рис. 1.64, б):
/3 = ~-------= 2,4 ма;
/2 == 2 ма
Следовательно, ток эквивалентного генератора тока
Л ==7д4-72 = 2,4-|“2 = 4,4 ма.
Определим внутреннюю проводимость эквивалентного генера-
тора тока g3 между точками а и Ь. Для этого исключим генера-
торы тока и оставим лишь их внутренние проводимости (рис. 1.64, е)
ёэ = gab = ------+ ё2 = 54Г26 + 0,01 °’05 0М^-
В искомой ветви (рис. 1.64, в) ток
1
/4 — /э
20
20 + 30
= 1,76 ма.
1.63. Вычислить ток в ветви г6 задачи 1.40 (рис. 1.45), поль-
зуясь преобразованием схем с источниками тока в эквивалентные
схемы с источниками напряжения, и наоборот.
е) *)
Рис. 1.65
Решение. Способ 1. Для ясности перерисуем схему
(рис. 1.45) в виде рис. 1.65, а. Эквивалентность исходной и но-
вой схем очевидна: к соответствующим узлам обеих схем подхо-
дят одинаковые токи. В частности, результирующий ток, подво-
димый к узлу а, равен нулю. Преобразуем генераторы тока I
последней схемы в генераторы с э. д. с. Ег и Е3 (рис. 1.65, б):
Ег = It\ = 50-10-3-5.103 = 250 в.
Е3 = 1г3 == 50-IO"3-16-103 = 800 в.
Складывая последовательные элементы ветвей, приводим схе-
му рис. 1.65, б к виду (рис. 1.65, в), для которой
£6 = Е - Е. = 60 —250 = — 190 в;
г6 = гх 4- га = 9 ком\ г7 = г3 4- г4 = 18 ком.
Преобразуем схему (рис. 1.65, в) в схему с источниками тока
(рис. 1.65, г):
т __ Eq ____ __ _ __ 91 1 МП. / __ ^7 __.
/л — □ —‘ 7 — ——
Гв * »7
800
18
= 44,4 ма.
$8
Перерисуем схему рис. 1.65, г в виде рис. 1.65, д, сложив
параллельные элементы:
/з = 17, — 21,1 "I- 44>4 = 23,3 ма.
В ветвь г5 ответвляется часть тока 19 , равная
/5 = /э —— = 23,3 • -4- = 10 ма.
гэ+'5 14
Способ 2 (метод эквивалентного генератора тока). Определим
ток /э эквивалентного генератора тока, который равен току
/к.з при замыкании накоротко сопротивления г5 (рис. 1.65, е).
Ток /к.3 можно вычислить различными способами, например ме-
тодом контурных токов:
(^3 + r<) — Л3 /к.з = 0 .
Подставляя числовые значения и решая эти уравнения,
найдем
Г = 21,1 ма\ Г'= 44,4 ма\ 13 = /к<3 = Г— Г== 23,3 ма.
Затем рассчитаем внутреннюю проводимость g3 генератора
тока. Она равна проводимости пассивной цепи между зажимами
а и Ь при разомкнутой ветви гь (рис. 1.65, ж)\ ветвь, содержащая
генератор тока, показана разомкнутой, так как внутреннее сопро-
тивление идеального генератора тока бесконечно велико:
ёэ
На рис. 1.65, д приведена схема эквивалентного генератора
тока относительно зажимов а и Ь. Из нее находим искомый ток:
/5 = 1э—£2— = 23,3-10-3= 10 -10*3 а = 10 ма.
1.64. Для цепи (см. рис. 1.49) по данным задачи 1.46 найти
ток в г4, пользуясь преобразованиями генераторов тока в генера-
торы напряжения и наоборот.
1.65. Цепь (рис. 1.66), содержащая два генератора тока
(Л = 30 ма, gt = 1 • 10-3 ом~1, /2 = 20 ма, g2 = 1,5-10~3 ом~1)
и генератор напряжения (Е3 = 45 в, г3 = 100 ом), включена
59
на нагрузочное сопротивление гн = 20 ом.
ток /н.
Определить
Рис. 1.66
Рис. 1.67
1.66. Три генератора напряжений, э. д. с. которых Et= 48 в,
Е2 = 45 в, Е3 = 45 в, а внутренние сопротивления == 1,2 ом,
r2 = 1 ом, г3 = 1,5 ом, работают параллельно на общую нагруз-
ку, сопротивление которой г = 4,2 ом (рис. 1.67). Произвести
замену заданных генераторов напряжений одним эквивалентным,
определив его э. д. с. и внутреннее сопротивление. Чему равны
токи, протекающие через каждый генератор и нагрузку?
Решение. Значения э. д. с. и внутреннего сопротивления
эквивалентного генератора напряжения могут быть определены
по формулам (1.27):
+ — = 2,5 ом~х, гэ == 0,4 ом.
гз
Ток в нагрузке
46
4,2 4-0,4
= 10 а.
Напряжение в нагрузке
U - 1г = 10-4,2 = 42 в.
Таково же напряжение на каждой из параллельных ветвей.
Ток в каждой из ветвей найдем по уравнению (1.29):
сумме то-
Проверка показывает, что ток в нагрузке / равен
ков Ц, /2 и Лг
60
1. 67. Воспользовавшись принципом взаимности, найти пока-
зания амперметров А4 и Л5 (рис. 1.68). Даны: Е == 30 в,
= 6 ком, г2 = 4 ком, г3 = 8 ком, г4 = г3 = 2 ком.
Рис. 1.69
1. 68. В схеме рис. 1.69 простейшим способом вычислить то-
ки. Даны: Ех = 100 в, Е2 = 80 в, Е3 = 40 в, = г2 = 10 ом,
г3 = 20 ом, г4 = 15 ом.
1.69. По данным задачи 1.49 (см. рис. 1.52) методом эквива-
лентного генератора определить ток в сопротивлении г4.
L70. Для схемы, изображен-
ной на рис. 1.70, рассчитать
входные и взаимные проводимос-
ти ветвей, необходимые для вы-
числения токов 1±, /3. /4, если t\ =
= 24 ом, 8 ом, г3 = rQ= 10 ом,
Гь — 30 ом, rh = 9 ом, Ех =180 в,
Е3 = 100 в, Е^ = 90 в. Исполь-
зуя найденные значения проводи-
мостей, вычислить указанные то-
ки.
Решение. Для определения
входной проводимости gn и
взаимных проводимостей gin
между первой и остальными вет-
вями исключим все заданные
э. д. с. и положим, что в ветвь гх
включена э. д. с., равная 1 в. Затем любым способом (напри-
мер, по методу контурных токов) вычислим токи, вызванные
ею в каждой из ветвей. Их числовые значения равны соответ-
ствующим проводимостям. В результате расчета получим, что
1 1 .
ток в первой ветви равен а, поэтому gu ом, ток во
1 1
второй ветви а, поэтому gn == ом' и аналогично да-
лее £1з = ом-\ gu =-^ ом~1, g15 = ом-', gle = ом~'.
61
Расчет входной проводимости g22 и взаимных проводимостей
между второй и остальными ветвями g2n не производим, так
как в ветви г2 нет э. д. с. и поэтому при расчете токов соот-
ветствующие проводимости не используются. По тем же сооб-
ражениям не вычисляем g55, g5fv g3Q и g3n.
Вычисляем входную проводимость g33 и взаимные проводи-
мости между третьей и остальными ветвями. Для этого анало-
гично предыдущему, исключая все э. д. с. в ветвь г3, вводим
э. д. с. 1 в и вычисляем токи, созданные ею в каждой из вет-
вей. В результате получим
^зз ~ 250 * ^31 = 50 = ^13* ^32 ~ *50” *
£84 = пЬ- ом~': = °; ёзв = -Д- ом-1.
Подобным путем находим входную и взаимные проводимо-
сти для четвертой ветви:
107 -1 7 -1 1 -1.
811 4500 * ^41 900 ^14 ’ 300 ’
2-1 1-1 19 1
813 = Т25" 0М = $31> 813 = -9Q- ОМ g46 = ОМ \
Отметим, что входная проводимость каждой ветви является
суммой входных проводимостей между рассматриваемой ветвью
и каждой из остальных ветвей, присоединенных к одному из
двух узлов, к которому присоединена эта ветвь. Например,
ветвь гг присоединена к узлам а и Ь, ее проводимость gn рав-
няется сумме проводимостей g13 и g14 или сумме g12 и g15.
Действительно,
. 11.7 . 1
811 81з “г Si4> 50 ’ 900 * или gn g12 г Si5> зб
__L r_L
60 + 90
т. е. получены тождества.
Наконец, находим токи в ветвях, применив принцип нало-
жения:
/з — £31 El “Ь 8зз ^3 Н~ £34 ^4
= 8,64 а;
/4 = — £41 Ei + £43 Ea + £44 £4 = 2,34 а.
Направления найденных токов^ нанесены на схеме рис. 1.70.
62
1.71. В схеме рис. 1.71 известны: г. = 10 ом, г, = 16 ом,
га — 60 ом, — г6 = 40 ом,
Е. = 80 в.
О
Рассчитать все входные и
взаимные проводимости и все
токи.
1.72. В цепи (рис. 1.72, а)
сопротивление г является пере-
менной величиной. Даны: Ег =
= 100 в, Е2 = 120 в, = 10 ом,
г2 = 20 ом, г3 = г4 = 10 ом.
Найти зависимости: 1) напря-
жения U на сопротивлении г от
тока I, протекающего через это
сопротивление; 2) тока /3, про-
ходящего через г3 от напряже-
ния U на зажимах сопротивле-
ния г.
Решение. 1. Воспользуемся
линейным соотношением (см. п. 8
основных положений)
U = А + BI. (1)
= 120 в, Е3 = 150 в,
Для определения двух пос-
тоянных А и В достаточно най-
ти значения Un I для каких-
либо двух режимов работы цепи.
Проще всего это сделать для
холостого хода и короткого замы-
кания.
В режиме холостого хода
(т. е. при г = оо) ток I ~ 0, а
напряжение U = (7Х. х можно опре
способом в схеме цепи рис. 1.72,
Рис. 1.72
ч
делить, рассчитав токи любым
б. Например, по методу кон-
турных токов имеем
£"1 Е2 — I (^i + r2) G >
Z?2 = I" (г2 + г3 + г4) — Г г,
Подставляя цифровые значения и решив эти уравнения, най-
дем Г = 4 a; U == С7Х. х = г4 Г = 40 в. Подставляя в уравне-
ние (1) значения напряжения и тока при холостом ходе (U =
= 40 в, / = 0), получим, что А = 40 в.
В режиме короткого замыкания, т. е. при г = 0, напряжение
U = Uк. з = 0, а ток ZK. з (рис. 1.72, в) может быть найден различ-
ными способами. Определим его по методу узловых потенциалов,
63
для чего найдем напряжение
Eigi + £2g2 _ 100-0,1 + 120-0,05
gi+ga + gs- 0,1+0,05 + 0,1
16
0,25
= 64 в
и ток
Подставляя в уравнение (1) величины напряжения и тока
при коротком замыкании (U ~ UK 3 = 0; / = /к а = 6,4 а),
получим
0 = А + 6,4 В,
откуда
В = — =------Д- = — 6,25 ом.
6,4 6,4
Искомая зависимость на основании уравнения (1) имеет вид
U == 40 — 6,25 /.
2. Воспользуемся линейным соотношением
/8 = а + bU.
(2)
Для определения постоянных а и b воспользуемся значения-
ми напряжений в ветви г и токов в ветви г3 при холостом ходе
и коротком замыкании ветви г.
При коротком замыкании (рис. 1. 72, в) напряжение 4/ =
= UK з = 0, а ток в г3 равен /3 = /к. 3 = 6,4 а. Подставляя
U = Uк. з = 0 и /3 = /к . == 6,4 а в уравнение (2), найдем
а ~ 6,4 а.
При холостом ходе (рис. 1.72, б), как было найдено выше,
напряжение 4/ = 4/х. х = 40 в, а ток в ветви г3 — Г = 4 а. Под-
ставляя U = Uх. х = 40 в и / = /" = 4 а в уравнение (2), полу-
чим 4 = 6,4 + 40 Ь, отсюда b = — 0,06.
Искомое уравнение примет вид
/_ = 6,4 — 0,06 а.
о 7 9
1,73. На рис. 1.73 изображена схема с сопротивлением г,
изменяющимся от нуля до бесконечности.
Найти зависимость напряжения U на сопротивлении г от
тока /, протекающего через это же сопротивление, если Ег =
= 45 в, Е2 = 54 в, ^ == г4 = 5 ом, г2 = г8 = 20 ом. Задачу
64
решить методом эквивалентного генератора и методом линейно-
сти исследуемого соотношения между током и напряжением.
Рис. 1.73
Рис. 1.74
1.74. Источник тока /0 = 10 ма включен в цепь, сопротив-
ления элементов которой равны rx = 1 ком, га= 5 ком, г3 ~
= 4 ком и сопротивление г изменяется от нуля до бесконечно-
сти (рис. 1.74).
Найти зависимости каждого из токов от напряжения Uab на
переменном сопротивлении г.
3 Заказ № 624
ГЛАВА ВТОРАЯ
ПРОСТЕЙШИЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Мгновенное значение величины, синусоидально
щейся с течением времени,
а = Ат sin (ш/ + ф) = Ат sin
изменяю*
(2.1)
где Ат — максимальное значение, или амплитуда;
ш t + ф — фаза (фазовый угол);
ф — начальная фаза (начальный фазовый угол);
----начальный фазовый сдвиг;
о) — угловая частота.
Период Т, угловая частота w и частота f связаны соотноше-
нием
ш = 2к/ = -^-; /=4-- (2.2)
По уравнению (2.1) на рис. 2.1 изображена синусоида и со-
м
ответствующая векторная диаграмма (вектор Ат вращается с
постоянной угловой скоростью <в против часовой стрелки).
2. При сложении двух синусоид ах — Alm sin (ш t 4- фх) и
оа = А2т sin (ш t + ф8) одинаковой частоты получается синусо-
ида а той же частоты (рис. 2.2)
Рис. 2.2
а = а, + а2 = Alm sin (ш/ + <|>х) + А2т sin (at 4- ф2) =
= Ат sin (at + ф). (2.3)
Амплитуда Ат и начальная фаза ф синусоиды а равны
"I- ^1т “Ь ^2m COS (Ф1 W»
|g Ф _ Alm sin ф, + Aim sin
g Aim cos + A2m cos ф2
В частном случае, когда ах ~ Alm sin <о t (фх = 0),
= А2п cos at (ф2= Л-), получим (рис. 2.3)
(2.4)
=
3*
67
Alm
3. Действующие значения синусоидально изменяющихся тока,
э. д. с. и напряжения равны
/ = —— = 0,707 Im; Е = ; U = (2.6)
У~2 УТ УТ
4. Средние значения синусоидально изменяющихся тока,
э. д. с. и напряжения за положительную полуволну равны
/ср = V 1т = 0,637 /т; Еср = -J- Ет-, UCf> = Um. (2.7)
с
Рис. 2.4
Среднее значение синусоидально изме-
няющейся величины а = Ат sin (со t + ф)
за целый период равно нулю.
5. Уравнение второго закона Кирх-
гофа для мгновенных значений напряже-
ний и тока, проходящего в одноконтур-
ной цепи, состоящей из последовательно
соединенных активного сопротивления г,
индуктивности L и емкости С (рис. 2.4):
fZ z== и *
(2.8)
где иа = ir — падение напряжения на активном сопротивлении,
г di
uL = L —тт — падение напряжения на индуктивности, причем
U’l'
и, — — е. где э. д. с. самоиндукции
t
I = -р J uL dt + i (0);
о
ис — падение напряжения на емкости, причем
t
ис ~ ] idt + ис № -
о
6. Если цепь, состоящая и? последовательно соединенных г,
L и С, включена на синусоидально изменяющееся напряжение
u = Um sin (ш/ 4- ф),
то по ней проходит ток
i = lm sin (ш t + ф — ф) ,
68
где
Соотношение (2.9а) является уравнением закона Ома для
амплитудных значений напряжения и тока. Закон Ома для дей-
ствующих значений напряжения и тока имеет вид
где
xL = со L — индуктивное сопро-
тивление;
1
хс s ~~^с----емкостное сопротив-
ление;
т 1
х = xL — хс = со L-----— реактивное сопротив-
ление;
]/г2+х2 — полное
сопротивле-
ние.
Обращаем внимание на то, что х и х—положительные величины, а
£* О е
реактивное сопротивление х может быть как положительным (при индуктивном
характере ветви, когда х > х ), так и отрицательным (при емкостном ха-
рактере ветви, т. е. х < х ). Например, для ветви (см. рис. 2.4) при
L* О
х — Xi = 5 ом, х — — *2 = 7 ом реактивное сопротивление х = х —
л* (a L
— хг — xi + хч = 5 — 7 — — 2 ом.
W
7. Треугольник напряжений. Приложенное к цепи напряже-
ние U может быть разложено на составляющие (рис. 2.5): 4/а=
= 1г -— активную, совпадающую по фазе с током, и (7р — ре-
активную; вектор £7р опережает вектор тока I на четверть пери-
ода, если в цепи преобладает индуктивное сопротивление х =
= xL — хс > 0 (рис. 2.5, a); £7р отстает от I на четверть перио-
69
да, если в цепи преобладает емкостное сопротивление х =
= xL — хс< 0 (рис. 2.5, б):
Uа = Ir = U cos <р;
Up = lx = U sin <р;
(2.10)
(2.П)
(2-12)
8. Из треугольника сопротивлений (рис. 2.6) следуют соотно-
шения
cos ср = sin <р =; tg(p = ~-. (2.13)
9. Треугольник токов. Ток /, проходящий в цепи, может быть
разложен на две составляющие (рис. 2.7): /а — активную, сов-
Рис. 2.7
падающую по фазе с приложенным напряжением, и /р — реактив-
ную; 7р отстает от напряжения U на четверть периода, когда
70
в цепи преобладает индуктивное сопротивление х = х. — х„ > о
(рис. 2.7, а), и опережает U на четверть периода при преобла-
дании емкостного сопротивления х = xL — хс < 0 (рис. 2.7, б):
/а -= I cos <р = U g;
/р = / sin <р = lb;
' = /T+TT=иу-
(2.14)
(2.15)
(2.16)
Цепь, состоящая из последовательно соединенных активно-
го г и реактивного сопротивлений х = xL — хс (см. рис. 2.4),
может быть заменена эквивалентной схемой, состоящей из па-
раллельно соединенных активной проводимости g и реактивной
проводимости b (рис. 2.8, а).
Рис. 2.8
Реактивная проводимость может быть положительной вели-
чиной (Ь >0), если цепь имеет индуктивный характер b = bL =
= —J— (рис. 2.8,6), и может быть отрицательной величиной
(6< 0), если цепь имеет емкостный характер 6= — Ьс ==—юСп
(рис. 2.8,в).
10. Треугольник проводимостей (рис. 2.9) подобен треуголь-
нику токов (см. рис. 2.7).
cosq>=-^-; sin<p=4-; tgcp=-^-. (2.17)
У У ё
11. При переходе от последовательной схемы (см. рис. 2.4)
к эквивалентной параллельной (см. рис. 2.8) можно воспользо-
ваться формулами
71
г
г
у = V g* + ь- =
(2.18)
При переходе от параллельной схемы (см. рис. 2.8) к экви-
валентной последовательной (см. рис. 2.4) ее параметры опре*
деляются
(2.19)
12. Активная, реактивная и полная мощности
Р = /V = UI cos <р; (2.20)
Q = Рх = UI sin ср; (2.21)
S = ]/Pf+ Q2 ^Ul = Pz == U2y. (2.22)
Для всякой электрической цепи справедливы следующие
балансы мощностей:
источников
2Qисточников
13. При
(рис. 2.10)
последовательном соединении
сопротивлении
п п
Uа = ~ ^k*
k=l k=\
(2.24)
// n \2 / П \2
24 + 24
\^i / j v=i 7-
Сдвиг фаз между общим напряжением U и током I
п
2-,
(2.25)
п
Рис. 2.10
1
Рис. 2.11
14. При параллельном соединении сопротивлений (рис. 2.11)
п. п
fe=1 fc=1
п п
Сдвиг фаз между напряжением U и током /, проходящим в
неразветвленной части цепи,
п
4=1
(2.27)
в; i = 5 sin 11571--------) а.
\ о /
и = 100 sin (1571 +
УПРАЖНЕНИЯ И ЗАДАЧИ
2.1. Построить кривые изменения напряжения и тока во вре-
мени и начертить векторы, изображающие заданные синусои-
дальные функции:
То
Чему равен сдвиг фаз между напряжением и током? Опре-
делить период, частоту, моменты начала положительных полу-
волн напряжения и тока. Какой вид примут уравнения для за-
данных напряжения и тока, если за начальную фазу, т. е. фа-
зу, равную нулю, принять фазу для тока? Для этого случая
построить синусоиды напряжения и тока и векторную диаграмму.
Решение. Синусоиды и и i и векторы Uт и 1т изображены
на рис. 2.12,а.
73
Период и частота
Ток по фазе отстает от напряжения на угол
Ф = (40°30').
Моменты начала положительной полуволны напряжения и
тока
тс
е =-------— = — JL • — = — ~ = — 0,002 сек = — 2 мсек-,
со 20 20
гс
t" — = ~iV •- = -£• = 0,0025 се/4 = 2,5 мсек.
со 10 со 1b /
При начальной фазе тока, равной нулю, уравнения для нап-
ряжения и тока примут вид
и' = 100 sin (157/ +
i' — 5 sin (157 t)a.
74
Кривые и', ir и соответствующие векторы О'т и изображены на
рис. 2.12,6.
2.2. Напряжения и токи изменяются во времени по следую-
щим законам:
a) Ul = 300sin (mt + -^-р; = 10sin / со/ 4- <*> == 314 сек'1;
б) i2 = 5sin Iи/ + -у) ма;
/3 = 3sin (со/ —
ма;
<о = 6,28-105 сек'1;
в) и2 ~ 300 cos (оз/ — 2) в; и3 == 200 cos (mt — 0,43) в;
m = 105 сек~1.
Построить векторные диаграммы и графики изменения нап-
ряжений и токов. Для каждого из случаев найти сдвиг фаз
между соответствующей парой синусоидальных функций.
Принимая фазу для (в случае а), г3 (в случае б) и и2
(в случае в) за начальную, написать уравнения и построить
графики напряжений и токов. Для указанного случая постро-
ить векторы, изображающие соответствующие синусоиды. Най-
ти период, частоту и моменты начала положительных полуволн
напряжения и тока.
2.3. Найти аналитически и при помощи векторной диаграммы
сумму и разность двух синусоидальных токов:
/х = 100 sin (mt 4-30°) ма;
i2 = 120 sin (mt — 45°) ма.
Решение. Найдем сумму токов:
ir = ix /2 = 100 sin (mt 4- 30°) 4- 120 sin (mt — 45°)= I sin(a>/4-$z).
/ZZ
Значения I и <J>' определяем по формулам (2.4), в которых
полагаем
Л1Я> =/lm = 100; А2,„ = = 120; ф, = 30’; ф2 = -45°;
/ = 1Л1003 + 1202 + 2• 100-120 cos 75° = 175 ма;
m '
tg<p' =
100 sin 30° + 120 sin (— 45°)
100 cos 30° + 120 cos (— 45°)
= —0,179;
(]»' = — 10’10'.
75
На рис. 2.13 начерчена
(по масштабу) могут быть
Рис. 2.13
векторная диаграмма, из которой
получены те же значения.
Разность токов
i" = — /2 == ЮО sin (<oZ 4- 30°) —
—120 sin (oj/ — 45°).
Воспользовавшись тригономет-
рической формулой
— sin a = sin (a 4- 180°),
перепишем выражение для тока:
Г = 100 sin (o)Z + 30°) + 120sin(W +
+ 135°) = /^sin(o)Z 4- yz),
где
1'т=У ЮО2 + 1202 + 2-100-120cos(— 105°) = 135 мег,
f Л" _ 100 sin 30° + 120 sin 1350
100 cos 30° 4- 120 cos 135°
" = 87°.
2.4. Найти сумму двух синусоидальных напряжений путем
непосредственных вычислений и при помощи векторной диаг-
раммы для двух случаев:
1) = 100 sin ojZ 4-
u2 = 150 sin ио/ 4- -^-1 в\
2) и3 = 310 cos 3141 в\ == 180 sin (314/ + в.
2.5. Катушка с активным сопротивлением г = 10 ом и ин-
дуктивностью L = 0,05 гн подключена к источнику синусоидаль-
ного напряжения, действующее значение которого U = 120 в, а
частота f = 50 гц.
Определить полное сопротивление катушки, ток и сдвиг
фаз между напряжением и током. Чему равны активная, реак-
тивная и полная мощности?
Вычислить активную и реактивнукгхсоставляющие напряже-
ния на зажимах катушки. Чему равна электродвижущая сила
самоиндукции, наводимая в катушке? Построить векторную
диаграмму напряжений и тока.
Считая, что ток изменяется синусоидально (i =/wsin о>/), на-
писать уравнения для мгновенных значений активной и реак-
тивной uL составляющих и всего приложенного напряжения и,
активной ра, реактивной pL и полной мощности р и энергии
76
магнитного поля. Начертить кривые зависимостей этих величин
в функции времени.
Решение, х. = oL = 2^-50-0,05 = 15,7 ом\
л*
г = К г2 + (шЛ)2 = /10® + 15,72 = 18,6 ом;
tg<p = ^ = l,57-, ср = 57°30';
т и 120 ~ лс-
/ _ г _ (8,б — 6,45 а,
Р = Рг = 6,452- 10 = 416 вт;
Q = Px = б,452-15,7 = 653 вар;
8 = 1*2 = 6,452• 18,6 = 773 ва;
(/а = /г = 6,45-10 = 64,5 в;
U, = 1х, =6,45-15,7= 103 в; Е. = — U,= — 103 в.
L L L. L*
Векторная диаграмма приведена на рис. 2.14,а.
100 200 3006
10 20 30а
200 0-00 6006т,вар,ва
0,25 0,50 0,75 dn<
Рис. 2.14
i -- lm sin со/ = 6,45 У2 sin о/ = 9,1 sin о/ а;
ya = ir = Imr sin о/ = 91 sin о/ e\ uL = Im &L cos w/ =
= 146 cos co/ e;
77
и = 120У2 sin (ю/ + ср) = 170 sin (ю/ + 57°30') в\
Ра~ ш% = I2 г sinW = Fr (1—cos 2<о/) = 416 (1—cos2o>/) вт\
tflr
п = iu. = si п со// оз А со <d/ = /2o)Lsin 2o>/ ==
= 653 sin 2w/ eap\
p = iu = Im sin (о/ Um sin (o>Z + ф) = U1 Jcos ф — cos (2<о/ + ф)] =
= 416 — 773 cos (2ш/ + 57°30') ea\
Li2 LI2 L!2
'}м~~Т = ~T sin2o>/ = — (1 —cos2w/)= 1,04(1 —cos2o>/) дж.
По этим уравнениям на рис. 2.14 6 построены кривые.
2.6. Для данных предыдущей задачи за начальную фазу
принять фазу приложенного напряжения, т. е. полагать, что
и ~ Um sin со/. Написать уравнения для /, ua, uL, ра, pL , р и
построить кривые зависимостей этих величин от времени.
Рис. 2.15
2.7. Для определения активного соп-
ротивления г и индуктивности L катушки
в цепь переменного тока с частотою f =
= 50 гц были присоединены вольтметр,
амперметр и ваттметр (рис. 2.15). Прибо-
ры дали следующие показания: U = 65 в,
I = 5 а, Р = 125 вт. Определить актив-
ное сопротивление и индуктивность катуш-
ки.
еш ени е.
Р 125 г
р 52 5 ОМ,
_ 65 __
/ ~ 5 ~
13 оХ;
х, = v — = 1/132 — 52 = 12 ом;
Xj 1Z
L = — = -75—ртг = 0,0382 гн — 38,2 мгн.
о» 2тс • 50
2.8. При включении индуктивной катушкн в цепь постоян-
ного тока амперметр показал 2,5 а, а вольтметр — 30 в. Затем
ту же катушку включили в цепь переменного тока частотой
^ = 50 гц. При этом вольтметр показал 120 о, а амперметр —
6 а. Чему равны активное сопротивление г и индуктивность L
катушки?
2.9. К последовательно соединенным реостату с сопротивле-
нием г = 120 ом и конденсатору емкостью С = 30 мкф подве-
дено напряжение и = 311 sin314/ в (рис. 2.16,а).
78
Вычислить полное сопротивление цепи, действующие значе-
ния напряжения и тока, мощность, расходуемую в цепи, реак-
тивную мощность и разность фаз напряжения и тока. Постро-
ить векторную диаграмму напряжений и тока. Построить кри-
вые мгновенных значений приложенного к цепи напряжения и,
тока /, активной составляющей напряжения аа, реактивной
ис , активной мощности ра, реактивной рс и полной мощности р,
энергии электрического поля .
100 200 300 8т. бар. ба
0.05 0.1 0.15 дж
Рис. 2.16
Решение.
хс = ~ 314-30-1о~6 = ом
t
г = у г2 + = У 1202 + 1 Об2 = 160 ом;
U = -21L- = 220 в;
У2
I — — 1 37 а-
1 г 160 ~ 1,6 а'
Р = Fr = 1,372 • 120 = 226 вт;
Q = — Рхс = - 1,372 • 106 = — 210 вар;
. Хс 106
tg<p =----=—0,885; <р = —41°30'.
Векторная диаграмма приведена на рис. 2.16 6. ,
79
Составим уравнения мгновенных значений величин:
i = lm sin (wt — <р) = 1,37 /2 sin (3141 + 41°30') =
= 1,94 sin (314/ + 41°30')а;
иа = lm г sin (ш/ — <р) = 233 sin (3141 + 41°30') в;
и„ — Imxrsin (u>t — ф — 90°) = 206 sin (3141 — 48°30') в;
ра = 1гг = I2 г sin2 (ш/ — ф) = 226 [1 — cos (6281 + 83°)] вт\
рс = ис i = 210sin (628/ + 83°) вар;
(I
р = ui = 311 sin 3141-1,94 sin (314 / + 41°30') =
= 226 — 302 cos (628 / + 41 °30') ва;
Рис. 2.17
Cu2c 30-10-«-2062 sin2 (3141 — 48°30')
tjy9 = __ — _ e
= 0,319[1—cos(628/ — 97°)] дж.
Соответствующие кривые даны на рис. 2.16, в.
2.10. Если в предыдущей задаче принять равной нулю на-
чальную фазу для тока Z = 7msin<o/, то как в этом случае из
менятся уравнения мгновенных значений и, иа, ис, р, wa ? На-
чертить векторную диаграмму напряжений и тока.1
2.11. При ПОМОЩИ
осциллографа были сняты
кривые напряжения и и
тока i на входе пассивно-
го двухполюсника (рис.
2.17). Чему равна частота
переменного тока, если
масштаб времени Mt =
= 2,5 мсек! см. Опреде-
лить, из каких эквива-
лентных элементов сос-
тоит двухполюсник и че-
му равны’ его эквивалент-
ные параметры. Масшта-
бы для напряжения и
тока соответственно равны
= 5 а!см.
Решение. Период переменного тока
Т = Ме±см = 2,5-10“3-4 = IO"2 сек,
а его частота
1 f = + = T(F = 100 гц‘
МТ,= 100 в!см
80
Из рис. 2.17 паходим амплитудные значения напряжения и
тока:
Um = М„-2 см = 100-2 = 200 в;
llv yj
/_ = М. • 1 см = 5 • 1 = 5 а.
HL i
Полное сопротивление схемы
7__ U т _ 200 _ , <
Z = 7— == = 4AJ ОМ.
* т 5
Так как напряжение опережает ток, то параметрами эквива-
лентной схемы являются активное сопротивление и индуктив-
ность. По рис. 2.17 находим угол сдвига фаз <р = -Ц- . Таким
образом,
г9 = z cos ср = 40 cos -g- = 34,6 ом\
хэ = z sin ср = 40 sin -у = 20 ом\
= = аГТбб = °-0318 гн = 31 >8 *гн-
2.12. На рис. 2.18 изображены кривые напряжения и тока
на входных зажимах пассивного двухполюсника. Масштабы вре-
мени, напряжения и тока соответственно равны
Mt = 0,5 мсек/см-, Му — 50 мв/см; М, = 10 ма/см.
Определить частоту переменного тока и эквивалентные па-
раметры двухполюсника.
Рис. 2.18 Рис. 2.19
2.13. Последовательно с реостатом, имеющим только актив-
ное сопротивление гх = 20 ом, включена катушка, параметры
81
которой г = 6,7 ом и L = 42,7 мгн (рис. 2,19,а). Определить
ток, проходящий в цепи, разность фаз между напряжением и
током, напряжения на реостате и катушке, а также сдвиг фаз
между напряжением источника и напряжением на катушке, ес-
ли (7 = 220 в. Частота переменного тока / = 50 гц. Вычислить
активную, реактивную и полную мощности катушки. Построить
векторную диаграмму.
Решение.
«>L = 2ir-50-42,7-10"3 = 13,4 ом;
zKaT = = V 6,72 + 13,42 = 15 ом;
z3 = V(/-! + г)2 + (wL)2 =У26,72 + 13,42 = 29,9 ом.
В цепи проходит ток
, U 220 _ ос
/ = = 2Тэ = 7’35 а‘
Разность фаз между напряжением и током определяется из
соотношения „
с
tg <р9 = = °-5; <Рэ = 26°30'-
Напряжения на реостате и катушке
= 1^ = 7,35-20= 147 в;
t7KaT = ^кат = 7,35-15 =110 в.
Сдвиг фаз между напряжением источника и напряжением
на катушке <р найдется как разность фазовых углов <ркат и <рэ
(см. векторную диаграмму рис. 2.19,6):
tg <ркат = = 2; <ркат = 63°30';
<Р = Фиат — Фэ = 63°30' — 26°30' = 37°.
Активная, реактивная и полная мощности катушки
Ркат = /V = 7,352.6,7 = 362 от;
QKaT = РшЬ = 7,352-13,4 = 724 etip;
____л____. SKaT = UK„I = 110-7,35 = 808 ва.
I Л<11 Л <11 '
''П (л)
। т у 2.14. По показаниям трех вольтметров,
Cv гП 1 включенных в цепь (рис. 2.20), определить
I Т (з) мощность, расходуемую в индуктивной ка-
? L 3 । тушке r,L, если г, = 20 ом, а показания при-
•—•-----*—। боров равны U — 120 в, = 80 в, U2 =
Рис. 2.20 = 60 в.
82
Указание. Задачу проще всего решить, если вначале построить век-
торную диаграмму.
2.15. К цепи, состоящей из последовательно соединенных ак-
тивного сопротивления г — 3 ом, индуктивности L = 8 мгн и
емкости С == 15 мкф, подключено напряжение U = 20 в с часто-
той f = 500 гц. Найти ток, напряжение на каждом элементе це-
пи и мощность, расходуемую в ней. Построить векторную диаг-
рамму.
Решение. Сопротивления элементов цепи
г, — = 2^-500-8-10“3 = 25,2 ом;
хс~ = 2я-500-15-10~° = ’2 ом'>
г = + (Xt — хс )2 = ]/32 + (25,2 — 21,2)2 = 5 ом.
В цепи проходит ток
/= "
Z
20
5
который по фазе отстает от напряжения на угол <р, определяе-
мый из соотношения
tg ф = Xl ~Хс- = 4- = 1,333; ф = 53°10'.
г о
Вычислим напряжения на активном сопротивлении, индук-
тивности и емкости:
(/а = /г = 4-3= 12 в,
U. = 1х, = 4-25,2 « 101 в;
Ur — /х„ = 4-21,2 ® 85 в.
С* Crf
В цепи расходуется мощность
Р = U1 cos ср = 20-4cos53°10' = 48 вт.
На рис. 2.21 приведена векторная диаграм-
ма.
2.16. Через реостат = 40 ом и катушку
индуктивности г£=12 ом, <oL = 18 ом, соеди-
ненные последовательно, проходит ток 1 = 2,2 а.
Чему равно приложенное к цепи напряжение?
Подсчитать активные, реактивные и полные
мощности всей цепи и ее отдельных элементов.
Каков сдвиг фаз между приложенным напряже-
нием и напряжением на катушке?
Указание. Решение начать с построения векторной диаграммы.
83
Рис. 2.22
2.17. К двум последовательно соединенным
реактивным катушкам (рис. 2.22), параметры ко-
торых г\ = 5,2 ом, Lx = 30 мкгн, г2 = 4,2 ом,
L2= 10 мкгн, подведено напряжение U = 120 в.
Частота f = 50 кгц. Определить ток, напряже-
ние на зажимах каждой из катушек их и t/2,
активные и реактивные мощности в каждой
катушке и во всей цепи. Построить векторную
диаграмму напряжений и тока.
2.18. Последовательно с реактивной катушкой
г, L включено активное сопротивление гх; с
помощью вольтметров измерены напряжения: на зажимах це-
пи U = 120 в, на активном сопротивлении i\ == 60 в и на
катушке — U2 = 80 в. Амперметр показал ток I = 2 а.
Найти активное сопротивление г и индуктивность L катуш-
ки.
Частота переменного тока f = 50 гц.
2.19. Реактивная катушка, параметры
которой гх = 10,5 ом, L — 382 мкгн, и кон-
денсатор (с потерями), эквивалентные пара-
метры которого г2 == 3,5 ом, С == 0,533 мкф,
соединены последовательно (рис. 2.23). Ка-
кое напряжение U приложено к цепи,
если амперметр показал ток / = 2,4 а?
Частота переменного тока f = 5 кгц. Оп-
ределить напряжение на катушке £7Кати
конденсаторе с потерями UK0WV а также
мощность, расходуемую в каждом из этих
Ukqt
Рис. 2.23
элементов. Постро-
ить векторную диаграмму напряжений и тока.
Чему равны добротность катушки и добротность конденса-
тора? Определить угол потерь конденсатора.
Замечание. Напомним, что добротностью к а т у ш к и называет-
<о£
ся отношение QL , а добротностью конденсатора — отно-
1
шение Qc = .
Г2
тс
Углом потерь называют угол S — |ср|, где ср — разность фаз
тока и напряжения на конденсаторе с потерями.
2.20. Для определения параметров эквивалентной схемы пас-
сивного двухполюсника АВ (рис. 2.24, а) были измерены напря-
жение иг = 26 в, ток /х = 4 а и мощность Рх=40 вт. С целью опре-
деления характера эквивалентного реактивного сопротивления
этого двухполюсника последовательно с ним включили конденса-
тор (рис. 2.24, б); в этом случае, при том же приложенном нап-
84
ряжении приборы показали 1г = 5,53 а и Р2 ~ 76,5 вт. Частота
переменного тока f = 50 гц.
Определить параметры эквивалентной схемы двухполюсника.
Рис. 2.24
Решение. Параметры эквивалентной схемы двухполюсника:
Р 40 о с
.2 42 2,5 ОМ,
ч
20 ~ г,
гэ = = — == 6,5 ом,
|хэ| = == ]/б,52 —2,52 = 6 ом.
Из данных второго опыта найдем
171 26 , 7
z = -х = -R-RQ- = 4,7 ом.;
#2 5,53
|Х|= /г2-Га = 1^4,3^ — 2,52 = 4 ом.
При неизменном напряжении, подключенном к цепи, и пос-
тоянном активном сопротивлении ток /2 оказался больше тока /1#
Введенное дополнительное емкостное сопротивление уменьшает
общее реактивное сопротивление цепи. Это значит, что х3 имеет
индуктивный характер. Величина Аэ=-~- ==g~=19,l мгн.
Неизвестную величину дополнительно введенного емкостного
сопротивления хс можно определить следующим путем. Рань,
ше установили, что х3 = ±6 ом, и так как характер полного
реактивного сопротивления х заранее неизвестен, то х = +4 ом,
либо х = —4 ом. Из данных второго опыта следует, что —хс +хэ==
= х, отсюда получаем, что хс = 2 ом или хс = 10 ом.
Укажем, что для определения характера эквивалентного ре-
активного сопротивления двухполюсника х3 неизвестная величи-
85
на дополнительно вводимого емкостного сопротивления хс дол-
жна быть меньше 2хэ. Это можно видеть из рис. 2.24, в, г, на
котором начерчена векторная диаграмма сопротивлений, соответ-
ствующая второму опыту. В случае хэ>0 и при | хс | < 12хэ 11 Ф11 <
<|фэ| (рис. 2.24, в), а при х9<0 | cp21 > I Фэ I (рис. 2.24, г). Ес-
ли взять | хс | > 12хэ |, то каждый из углов | <рх | и |<р2| будет
больше |ф9|.
Если величина дополнительно вводимого сопротивления хс
заранее известна, то она может быть взята и более 2хэ.
2.21. Решить предыдущую задачу по данным опытов в двух
случаях:
1) первый опыт: Ul = 120 в, /т = 4,3 а, Pt = 370 вт;
второй опыт: t/2 = 120 в, /2 = 1,31 а, Р2 = 34,4 вт;
2) первый опыт: = 120 в, = 4,3 а, Рк — 370 вт;
второй опыт:
U2 = 120 в, /2 = 2,21 а, Р2 = 97,8 вт.
При проведении вторых опытов каж-
дый раз вводилось емкостное сопротив-
ление, равное 70 ом.
2.22. Приборы, подключенные к пас-
сивному двухполюснику АВ (на рис. 2.25
ключ К разомкнут), показали t/x = 100 в,
^—2 а, Рг = 160 вт. Для определения
характера реактивного сопротивления
двухполюсника параллельно ему был
подключен конденсатор (ключ /С замкнут), емкостное сопротив-
ление которого = 100 ом, при этом приборы показали:
U2 = ЮО в, /2=2,73 а, Р2=160в/п. Определить эквивалент-
ные параметры двухполюсника.
Решение. Параметры двухполюсника (рис. 2.25):
г= = 40 ом; z = — = 50 ом; | х |=]/502 — 402 = 30 ом,
S 4Q2 । зо2 0,016 ом 1,
I Ь I = 4024Г302- = °>012 ом~\
Проводимость конденсатора
Ь = а) С = 0,010 ом~1.
О
Параметры эквивалентной схемы:
_ 160
G — 2>732
= 21,6 ом; z9 =
100
2,73
= 36,7 ом;
86
|лэ I = J/36.72 -21,62 = 29,7 ом; g3 —21,6*+ 29,72 = °>016™'';
I | = 21,62 + 2Э.72 = 0M *•
Так как | b31 = | b\ + bc, то, следовательно, реактивное соп-
ротивление исследуемого двухполюсника имеет емкостный ха-
рактер. Тот же результат вытекает и из следующих соображе-
ний. Так как при том же напряжении U ток после подключе-
ния конденсатора стал больше, чем до подключения, то общая
проводимость цепи увеличилась. Это может быть в том случае,
когда реактивная проводимость подключаемой ветви Ьс имеет
тот же характер, что и заданная реактив-
ная проводимость двухполюсника Ь, при о— ------------
условии, что |6С| < |26|. л Х/] п
2.23. Линия передачи электрической $
энергии (рис. 2.26) обладает активным соп- о— ----------J
ротивлением гл = 15 ом и индуктивностью 22б
£л= 0,191 гн. В конце этой линии присо-
единен приемник энергии, потребляющий
мощность Р2 = 84 кет при напряжении 472= 5,1 кв и coscp2 =
= 0,8 (ф2 > 0). Частота тока f = 50 гц. Определить напряже-
ние источника U19 подключенного к началу линии, а также
падение напряжения и потерю напряжения в линии.
Чему равен к. п. д. линии передачи электрической энергии?
2.24. Генератор, питающий линию передачи электрической
энергии, отдает мощность Рг = 27 кет. Напряжение генератора
иг = 3 кв. Параметры линии передачи гл= 20 ом, хл=60 ом.
Мощность, потребляемая приемником, подключенным в конце
линии, Р2 = 22,5 кет. Определить параметры приемника.
2.25. Линия передачи имеет активное сопротивление гл = 2 ом,
индуктивное хл = 4,8 ом. Напряжение в начале линии =1,1 кв.
Определить при каком сопротивлении приемника, для кото-
рого отношение—= 3, в нем будет расходоваться максималь-
г пр
ная мощность и вычислить ее величину.
К той же линии приключен приемник с постоянным актив-
ным сопротивлением гпр = 20 ом и изменяющимся реактивным
сопротивлением хпр. При какой величине хпр приемник поглотит
максимальную мощность и какова ее величина?
Определить наибольшую мощность, которую вообще можно
получить при передаче по заданной линии, т. е. полагать, что
могут изменяться и гпр и хпр.
Указания. Если <рпр = const, то мощность максимальна, если гпр —
= г при этом
Л
87
cos <pnp
Pnp.max = 2гл [1 H-COS (<рл—<pnp)l ’
При изменении только реактивного сопротивления приемника в нем выде-
ляется максимальная мощность при условии хпр ==—хл, а ее величина
U2 г
_ гпр
прлпах ('л + Гпр)2
Наибольшая мощность, которую вообще можно получить в приемнике, бу-
дет при условии, если сопротивление приемника сопряжено с сопротивлением
линии (т. е. гпр = гл и хпр ==—хл). Величина этой мощности
* пр.max
л
Укажем, что те же условия сохраняются при передаче мощности во внеш-
нюю цепь генератора с постоянной э. д. с. и постоянным внутренним сопро-
тивлением гвнуТр.
2.26. По показаниям приборов, включенных в цепь (рис.
2.27, а), определить ток, проходящий в неразветвленном участ-
ке цепи, сопротивление каждой ветви и полное сопротивление
цепи. Заменить данную цепь эквивалентной последовательной
цепью гэ хэ . Построить векторную диаграмму.
Рис. 2.27
Даны: U= 120в, /х = 3а, /2 = 6а, /3 = 2а.
Решение. Сопротивления и проводимости отдельных вет-
вей и всей цепи:
и Г~7Г~ 120 11. : 3 = 40 ом; g= г = ом~1;
и Xl — г = -g- = 20 ом; bL = х = 20 ом1; L
и *3 120 сл , ! 1 т = 60 ом; Ьс = —^ы ом ' и
g9 = g = io ом~1;
88
Ьэ — bL bc — 20 60 — 30 ом 1
(индуктивный);
Уз = V g2s + bl = 40 ) ( 30 ) 24 0M 1#
1 пл
z, = — = 24 ом.
3 Уз
Заданная схема цепи может быть заменена другой, ей экви-
валентной и состоящей из последовательно соединенных элемен-
тов, параметры которой по (2.19) равны
= = 40
у1
-j-r- = 14,4 ом-,
24 )
1
Ь 30
хэ = = /--1 -г-2- = 19,2 ом.
Проверка.
z3 = ]/ 14,42 + 19,22 = 24 ом.
Векторная диаграмма построена на рис. 2.27,6.
2.27. Для определения параметров конденсатора с потерями
его подключили к источнику синусоидального напряжения U =
= 19,5 в (f = 50 кгц). При этом амперметр показал ток / = 0,3 а,
а ваттметр — мощность Р = 153 мет. Определить гх, Сх иг2, С2
двух схем (рис. 2.28, а, 6), эквивалентных конденсатору с по-
терями. Чему равны тангенс угла потерь указанного конденса-
тора и его добротность?
Рис. 2.28
Решение. Определим сдвиг фаз между напряжением U и
током /:
“s f = <Г7 ~ = °-Щ62'’ Ф “ 88°30'-
89
Из схемы рис. 2.28, а видно, что P=U1 cos <р = С//а, откуда
найдем активную составляющую тока:
= = 7,85- 10-3а = 7,85 ма.
Так как
la = Ug = = 7,85 •10"’ а,
ТО
G = 2,48- Ю3 ом = 2,48 ком.
I > оЭ
Реактивный ток
/р = / sin <р = 0,3-0,99966 « 0,3 а,
но так как
/р = Ubc = t/wCi = 0,3 а,
то емкость
^1 = 19,5.6,28.50.10s = 49- Ю 9Ф = 49 нф.
Для схемы рис. 2.28, б
_ Р _ 15,3-10-» _ . 7
'2 ^2 q ' ОМ,
U 19,5 сс
г = Т = "оХ = 65 ом'
| х21 = ]/г2-^г| = 652 — 1,72 ~ 65 ом.
Отсюда
'Xt । ~ = 65 ом- Ct — 65-2ТС.50-108 = 49-10 9 = 49 нф.
\
Угол потерь 8 и его тангенс соответственно равны
8 = 90° — | <р | = 90° — 88°30' = 1 °30';
‘8 5 = -.иГГ- = ,О30' = °>0262-
Для схем рис. 2.28 а и б даны соответствующие векторные
диаграммы на рис. 2.28 виг.
Добротность конденсатора
Qc = —— = ~Р7 = [ИЛИ Qc = I.
' 2 1 » 1 \ 5 '
90
2.28. По показаниям трех амперметров, включенных в цепь
(рис. 2.29), определить мощность, расходуемую
ящей из последовательно соединенных гх и
Показания приборов: А — 6,5 а, Лх— 3,5 а,
А2— 4 а. Активное сопротивление г2 = 30 ом.
Указание. Задачу проще всего решить, если
сначала построить векторную диаграмму.
2.29. Две параллельные ветви, сопротив-
ления которых rt= 8 ом, xL = 6ол1,г2 = VZom.
хс = 5 ом, присоединены к источнику напря-
жения U = 130 в (рис. 2.30, а). Определить
токи /х, /2> I и эквивалентные параметры схе-
мы, состоящей из последовательно соединен-
в ветви, состо-
Рис. 2.29
ных активного и реактивного сопротивле-
ний. Построить топографическую векторную диаграмму. Вычис-
лить активные и реактивные мощности каждой ветви и всей
цепи. Найти напряжение между точками а и Ь.
а)
&
У I.
11
2 'г
0 Масштабы
20 W 606
I I 1 I
О 2 Ч 6а
Рис. 2.30
^2 /Р U
&
и
Решение. Проводимости отдельных ветвей и всей цепи
вычислим по формулам (2.18):
Si = g2 _|_ ga = 0,08 ом \
Ь1 = 8^Тб2 = 0,06 °М'1’
£2 = । о2 | 52 0,071 ом \
^2
—5
0,0296 ом'1;
ёз = gi + £2 = 0,151 ом'1;
Ьэ = + Ь2 == 0,0304 ом'1 (индуктивный);
у3 = ]/0,1512 + 0,03042 = 0,154 ом'1.
9f
Токи в ветвях и в неразветвленной части цепи
' = (WF - 13 “• *8 = Т - °-75; Т" = 36’50';
' = ” 10 а- *8 ’‘“-ТГ- “ -°’4167’
Ф2 = arctg(—0,4167) = —22°40';
1 = Uy3 = 130-0,154 = 20 a; tg <р9 = - = 0,201;
U, lu 1
<рэ = 11°20'.
На рис. 2.30, б построена топографическая векторная диаг-
рамма; отложен вектор U, от него под углом фх в сторону от-
ставания отложен вектор тока /х и в фазе с ним вектор 1^ =
= Uca (его конец — точка с), затем от вектора U в сторону опе-
режения на угол <р2 отложен вектор тока /2 и в противофазе с
ним от точки с вектор — /2г2 = Ubc (его конец—точка Ь).
Параметры схемы, эквивалентной заданной и состоящей из
последовательно соединенных сопротивлений (рис. 2.30, в), по
2.19) равны
9 0,1Ь4а
0,0304 1 по /
гэ = —•б"154~-~ ~ 1>28 ом (индуктивный).
Активные и реактивные мощности каждой ветви и во всей цепи
Pr = /?q = 132-8 = 1352 вт;
Р2 — — 1200 вт;
Q, = 12{Х1 = 132-6 = 1014 вар,
Qt = /гха = —500 вар;
Р — {//coscp9 = 130-20-cos 11°20' = 2552 вт;
Q = t7/sin ф9 = 130-20-sin 11°20' = 514 вар.
Проверка показывает, что Р = Рх + Р2 и Q = Qt + Qa.
Наконец, найдем напряжение между точками а и Ь. Оно (в
принятом масштабе) определяется отрезком ab (рис, 2.30, б);
Uab = WiH)8 + (Лл)2 — 2(/1r1)(/ara) cos (<рх — <р2) =112 в.
Тот же результат может быть получен непосредственным из-
мерением отрезка ab в масштабе, принятом для напряжения.
2.30. Какое напряжение приложено к цепи (рш*. 2.31, а), если
напряжение на конденсаторе Uc = 192 в, а сопротивления эле-
ментов цепи равны гг = 28 ом. г2 = 50 ом и хс ~ 96 ом?
п
Вычислить все токи и параметры эквивалентной схемы, со-
стоящей из последовательно соединенных элементов. Написать
уравнения мгновенных значений iv i2, i и и, еслиы(,= 192)/ 2х
XsintuZ в.
Рис. 2.31
Решение. Ток, проходящий в левой ветви,
/1 =исч>С= gg- = 2 а.
Напряжение, приложенное к цепи,
U = /X ri + хс = 2^282 + 96* = 200 в.
Ток правой ветви
щ 200
г2 ~~ 50
= 4а.
Ток в неразветвленной части цепи найдем из уравнений:
/1а = ugi = 200 -28^9^ = 0,56 а;
/аа = Ug9 = 200— = 4 а.
'а 1 la “Г 12a u,
____ / — _____POP 96 __1 Q9
P Ip
a\
I = К II +/p = V4,56* + 1,922 = 5 a.
Параметры эквивалентной схемы:
ёэ = + & = 0,0228 олг1; 6Э = ^ = —0,0096 олг1;
Уз = КЯэ + Ь1 = 0,0247 олг1; г9 = = 40,4 ом;
14 а
г __ ёз ___ 0 > 0228 __ л-т о
9 „2 0.02472 ом^
i/э
Y __ ^з ___ —Q > 0096 __ 1 г —
9 0,02472 ~ 10,Z 0Mt
93
Наконец, запишем уравнения мгновенных значений всех то-
ков и приложенного к цепи напряжения, полагая, что угол на-
чальной фазы напряжения на конденсаторе равен нулю:
ис = 192]/2 sin <о/ в.
Ток опережает напряжение на конденсаторе ис на 90° >
поэтому __
i*i = Ilm sin(<o/ + 90°) = 2]/2cosW а.
Приложенное к цепи напряжение и отстает от тока на
угол <рх, определяемый из соотношения
'8 = ТГ = -3'43; - -73'45';
и = 200)/Jsin И + 90° — 73°45') =200]/2 sin(«/ + 16°15') в.
Ток i2 совпадает по фазе с приложенным напряжением, по-
этому
z2 = 4]/2 sin («о/ + 16° 15') а.
Ток в неразветвленной части цепи
i = i± + г2 = 2]/2 sin(<o/ +90°) +4/2sin(a)/+ 16°15') =
= 5/2 sin («)/ + 39°5') а.
На рис. 2.31, б начерчена векторная диаграмма, в которой
по горизонтальной оси отложен вектор напряжения на конден-
саторе Uc, имеющий заданную начальную фазу, равную нулю.
2.31. Мгновенное значение напряжения на конденсаторе Сг
изменяется по закону ис\ == 351^2 sin (о/ в. Написать уравнения
мгновенных значений токов iv i2 и i, приложенного к цепи на-
пряжения 1/(рис. 2.32) и построить векторную диаграмму. Па-
раметры схемы: rt = 48 ом, = —14 ом, г2 = 15 ом, х2 ==-
= —20 ом.
С/ sbP?
I
Рис. 2.32
Рис. 2.33
2.32. Цепь, изображенная на рис. 2.33, подключена к источ-
нику синусоидального напряжения U = 96 в. Сопротивления це-
пи г = 4 ом, Xl — 5 ом, хс — 6 ом. Определить все токи, ак-
тивную, реактивную и полную мощности. Подсчитать эквива-
лентные сопротивления схемы замещения, стоящей из после-
94
довательно соединенных активного и реактивного сопротивлений,
и начертить ее. Построить векторную диаграмму.
2.33. По реактивной катушке, сопротивления которой равны
гх = 12 ом и xL = 16 ом, проходит ток /х = 6 а (рис. 2.34). Па-
раллельно к ней- присоединена ветвь, состоящая из последова-
тельно соединенных активного сопротивле-
ния г2 = 24 ом и емкостного Хс = 7 ом.
Найти ток в неразветвленной части цепи и
приложенное к ней напряжение. Подсчитать
параметры эквивалентной схемы, состоящей
из последовательно соединенных активного
и реактивного сопротивлений, и начертить ее.
2.34. Приемник энергии потребляет мощ-
ность Р = 2 кет при напряжении U == 220 в
и cos <р == 0,65 (индуктивный). Частота пе-
ременного тока / = 50 гц. Найти емкость и
реактивную мощность батареи конденсато-
ров, которые устанавливаются для того,
чтобы повысить коэффициент мощности до
0,9 (индуктивный) (рис. 2.35, а).
Решение. В приемнике энергии прохо-
Рис. 2.34
<*)
ДИТ ток
/ _ р — 2-1000 _ 14
~ f/costp 220-0,65 14 а*
После улучшения коэффициента мощ-
ности cos фо = 0,90 в неразветвленном участ-
ке цепи проходит ток /0, который может
быть найден из соотношения (см. вектор-
ную диаграмму рис. 2.35, б)
/0 cos фо = I cos ф,
откуда
/ / cosф .. 0,65 «л .
/о = 1---— = 14 • .....- = 10,1 а.
0 cos ф0 0,90 ’
Рис. 2.35
По известным cos <р = 0,65 и cos <р0 — 0,9 определим ф =
= 49°30'; ф0 = 25°50'; sin ф = 0,760; sin ф0 = 0,436.
Через конденсатор проходит ток /с, величина которого мо-
жет быть найдена как разность проекций векторов токов / и /0
на вертикальную ось (рис. 2.35, б):
1с = / sin ф — /0siп фо = 14-0,760 — 10,1-0,436 = 6,2 а.
Искомые емкость и реактивная мощность батареи конденсаторов
М ~ 314-220 ~ 90 МК$’
Qc= /CU = 6,2-220 » 1360 вар.
2.35. Для приемника энергии предыдущей задачи найти ем-
кость и реактивную мощность батареи конденсаторов, необходи-
мую для повышения коэффициента мощности до единицы.
9S
ГЛАВА ТРЕТЬЯ
МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
(СИМВОЛИЧЕСКИЙ)
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
I. Комплексные числа. Комплексное число, соответствующее
точке, в которой лежит конец вектора А (рис. 3.1), может быть
написано в
Рис. 3.1
формах.
Здесь
«1
алгебраической
А = аг + ja2,
тригонометрической
А == a(cos а + /sin а),
показательной
А = a eJa а е х p(ja),
полярной (угловой)
А — а^а
== a cos а = Re [Л]*
—вещественная часть комплексного числа А;
а2 = a sin а = Im [А]*
— мнимая часть комплексного числа;
-Я
/ = ]/—1 = е
(3.1а)
(3.16)
(3.1в)
(3.1г)
(3.2а)
(3.26)
(3.2в)
— мнимая единица или оператор поворота на угол-£- = 90° (умно-
* Re и Im — сокращенные записи английских терминов real (реальный,
действительный) и imaginary (мнимый) или соответствующих французских тер-
минов reel (reelle) и imaginaire, а также немецких — real и imaginar.
96
жение на / сводится к повороту вектора против часовой стрел-
ки на угол -у, а умножение на —j — e 2— к повороту век-
тора на прямой угол по часовой стрелке);
а = \А1 = У а2 + а2 = -51- (3.2г)
’ 1 r sin a cos а ' }
*»
— модуль комплексного числа А (всегда положителен);
а = arctg — (3.2д)
01
— угол (или аргумент) комплексного числа.
Формула Эйлера
cos а ± / sin а = е\ (3.3)
* -—/а
Комплексное число А = а±— / а2 = ае называется ком-
л . гг
плексно-сопряженным числу Л = + = • Произ-
ведение комплексно-сопряженных чисел — число действительное,
равное квадрату их модуля:
* /а —/а
АА = ае ае = а2,
/у
е —оператор поворота на угол ср.
Умножение комплексного числа А на число е* сводится к
повороту вектора А в комплексной плоскости на угол <р : Ае* =
/а /<р Да-Н)
= ае е = ае
2. Действия над комплексными числами. Сложение и вычи-
тание комплексных чисел.
А 4~ В = (#i + №) ± (^i + /^2) = (^1 — ^1) + j ± ^2)* (3.4)
Умножение.
АВ = (^ + /а2) (/>! + /Ь2) = (а1Ь1 — o2i>2) + j (a2b1 + а^) =
= ае be = abe . (3.5)
Деление.
*
Л___АВ ______ аг + __ <hbi -}- а2Ьъ , . a2bi — _
в вв *1 + ibt
= -т^Г = -т- eJ'^' • Р-о/
Ье^ о
Возведение в степень.
Ап = (ае^а )п = аПе>ап = a" (cos п а + j sin п а). (3.7)
Ь b b -j- -
12 1*1
а
4 Заказ № 624
97
Рис. 3.2
Символ мнимой
Извлечение корня.
t a-f-2£rc
П ,-П г — п,----------- -Z
Д = |/ ае1л = а е , (3.8)
где k — целое число.
При п целом и положительном корень имеет п различных
значений, соответствующих числам k = 0, 1,2, . . ., п — 1 (мно-
гозначность извлечения корня).
3. Проекция вращающегося против часовой стрелки с посто-
янной угловой скоростью о) вектора Vm на мнимую ось числовой
плоскости дает мгновенное значение синусоидальной величины v
(рис. 3.2). Этот вращающийся вектор за-
писывается в виде Vmef^^K Угол а показы-
вает положение вектора Vm в начальный
момент t = 0(Vт = Vте!'а). Числовая величи-
на мнимой части выражения дает
мгновенное значение синусоидально изменя-
ющейся величины v ~Vm sin (о>/ + a) ==
=Im[vy(<e<+*,] = Im(VTOeM).
части Im иногда опускают и последнее вы-
ражение записывают в форме v Ф Vт е** , где Ф — знак соответ-
ствия. Комплексное число Ит==1/т^/а называется комплекс-
ной амплитудой.
Комплексное действующее значение — комплексное число
V == Ve , сопоставляемое переменной синусоидальной величине
v. Модуль комплексного действующего значения V совпадает с
действующим значением соответствующей синусоидальной вели-
чины, а аргумент совпадает с начальной фазой этой величины.
Комплексные амплитуда и действующее значение связаны равен-
ством
V = ф . (3.9)
/2
4. Источник напряжения (рис. 3.3, а) с э. д. с. е = Emsin (о^ + е)
(амплитуда э. д. с. Ет и начальная фаза е) можно полностью
охарактеризовать, задав комплексную амплитуду э. д. с. Ет =
= Ете^ или комплексное действующее значение э. д. с. Е =
= Ее е (Е = фД .
\ /2/
Источник тока (рис. 3.3, б) I = /msin (ад/ + ф) полностью оп-
О ° п I 1
ределяется комплексной амплитудой тока = 1те или его
комплексным действующим значением I = le , где / =
98
5. Пассивный элемент электрической цепи (рис. 3.3, в) опре-
деляется своим комплексным сопротивлением Z = ze19 — комплек-
сным числом, равным отношению комплексного напряжения на
зажимах данного элемента к комплексному току этого элемента:
Z = — = г + jx = ze* , (3.10) .
i
где U и / — комплексные действующие значения напряжения и
тока;
г — вещественная часть комплексного сопротивления
Z, равная активному сопротивлению цепи;
х — мнимая часть Z, равная реактивному сопротивлению
цепи;
z — модуль комплексного сопротивления цепи, равный
полному сопротивлению цепи;
— аргумент Z, равный углу сдвига фаз между током
и напряжением.
Рис. з.з
Отношение комплексного тока в данной цепи к комплексному
напряжению на ее зажимах называется комплексной про-
водимостью электрической цепи:
Y = — = g — jb = уё~* , (3.11)
и
где g— вещественная часть Y, равная активной проводимости
цепи;
b— мнимая часть У, равная реактивной проводимости цепи;
у — модуль комплексной проводимости цепи, равный полной
проводимости цепи; <р — аргумент У, равный углу сдви-
га фаз между напряжением и током, взятому с обратным
знаком.
Комплексная проводимость обратна комплексному сопротив-
лению цепи:
^ = 7-- (3-12)
6. Закон Ома для не содержащего э. д. с. участка цепи,
сопротивление которого Z (рис. 3.3, в), принимая положительное
W
направление напряжения, совпадающее с положительным направ-
лением тока, имеет вид
U = Uab ~ Uba ~ ^a — ^b~iz, (3.13)
7. Законы Кирхгофа. Для записи уравнений на основании за-
конов Кирхгофа надо выбрать положительные направления для
всех токов и обозначить их на схеме.
Первый закон Кирхгофа в применении к узлу электрической
цепи
п
2 /4=о. (3.14}
4} з=|
При записи этого уравнения токи, направленные к узлу, еле
дует записать со знаком «плюс», а направленные от узла — со
знаком «минус» (или наоборот).
Второй закон Кирхгофа применяется к любому замкнутому
контуру цепи и имеет вид
Л . Л .
2Eft = 2/»z*. (3.15)
*=»! k=\
где У Ек — алгебраическая сумма комплексных э. д. с. источ-
fe==’ ников напряжения. Со знаком «плюс» записываются
те из них, положительные направления которых
совпадают с выбранным направлением обхода кон-
тура; э. д. с., имеющие направления, противопо-
ложные обходу контура, записываются со знаком
«минус»;
п .
y/feZfc — падения напряжений на комплексных сопротивлени-
ях Zk отдельных участков. Со знаком «плюс» бе-
рутся те, для которых направление тока совпадает
с направлением обхода, а со знаком «минус» — те,
для которых направление тока противоположно на-
правлению обхода контура.
8. При последовательном соединении участков цепи комплекс-
ное эквивалентное сопротивление равно сумме комплексных соп-
ротивлений отдельных участков:
п
г = ^гк. (3.16)
&=з|
При параллельном соединении ветвей цепи комплексная эк-
вивалентная проводимость равна сумме комплексных проводи-
мостей ветвей:
п
(3.17)
100
В частном случае двух параллельно соединенных сопротив-
лений и Z8 эквивалентное комплексное сопротивление
2 =
Zj + Z,
(3.18)
Комплексные токи, проходящие в каждой из двух параллель-
ных ветвей, могут быть рассчитаны через комплексный ток
/, проходящий в неразветвленной части цепи, и комплексные со-
противления ветвей по формулам
/ = / —h— ; / = / —h------------, (3.19)
Zj -f- Zj Z, + Z,
9. Комплексная мощность
S == U I = UI cos <p + jUl sin ср = P + jQ = Sev , (3.20)
где S == Ul — полная мощность;
P = Re [S] = Re [U I] = UI cos <p — активная мощность,
Q = Im [U I] = UI sin <p — реактивная мощность;
I — комплексный ток, сопряжен-
ный с / .
10. Как и для цепей постоянного тока, источник электриче-
ской энергии переменного тока (с потерями) может быть изобра-
жен либо в виде генератора напряжения (рис. 3.3, г), параметры
которого Ег и Zr, либо в виде генератора тока (рис. 3.3, д) с
параметрами /г и Zr (см. основные положения и соотношения,
гл. 1, п. 1).
Переход от генератора напряжения к эквивалентному генера-
тору тока и обратно осуществляется по формуле
/г=-у-; Er = IrZr, (3.21)
11- При расчете цепей переменного тока посредством ком-
плексных чисел остаются справедливыми все методы расчета,
применяемые для расчета цепей постоянного тока (см. основные
положения и соотношения, гл. 1, п. 4).
УПРАЖНЕНИЯ И ЗАДАЧИ
3.1. Записать в показательной, тригонометрической, алгебраиче-
ской и полярной формах выражения комплексных действующих
значений тока и напряжения, мгновенные значения которых равны
и = 100 У 2 sin (со t + 15°) в,
i = 5l/~2" sin (со t —20°) а.
101
3.2. Пользуясь счетной линейкой, представить в показательной
форме следующие комплексные числа:
1) 3,2 ± / 1,25; 2) 1,25 ± /3,2; 3) —3,2 ± / 1,25; 4) —1,25 ±
±/3,2; 5)3,2 + j 12,5; 6)3,2-/0,125; 7)0,125 4-/3,2; 8)—0,1254-
4-/3,2; 9) 0,32-/1,25; 10) 23 4-/0,06; 11) —2,8—/64.
3.3. Пользуясь счетной линейкой, записать в алгебраической
форме следующие комплексные числа:
1) 32е±/1в°; 2) 32е±/71’; 3) 32?'161°; 4) -32е±/2°35’; 5)32е±/87°25';
6) 32/°°43’; 7) 32е-/0°12'; 8) 32е/92°35' ; 9) 32е-/177°35'; 10) 7,3<Г86°40' ;
11) 150е/191°; 12) 28е /97°3°'; 13) е'; 14) 10е ‘°'5.
|—|» 3.4. Приборы, подключенные к цепи (рис.
„ _ *1 /ТА 3.4), дали следующие показания: U = 65 в,
Т уП / = 5 а, Р = 300 вт.
(у) гПг Вычислить комплексные сопротивления Z
j т и комплексные проводимости Y цепи для слу-
0-*—(X) ’ чаев: а) <р > 0; б) <р < 0.
Рис 3 4 Решение. Модуль сопротивления и его
аргумент определяются по формулам
и 65 1О
г = — — — = 13 ом;
I 5
COS <Р = — = = 0,923; ф = ± 22° 40'.
U1 65 • 5
Искомые комплексные сопротивления и проводимости цепи:
а) <р >0
Z = ге* = 13е 22040 = 13cos22°40' 4- j 13sin22°40' = 13 • 0,923 4-
4-/13 • 0,385 = (12 4- /5) ом;
У = = 140, = 0,077 Г-40' =(7,1 - /2,96) 10- олг»;
2 13е'
б) ф < 0
—722°40'
Z = 13е =(12 — /5) о л;
У = (7,1 4- /2,96)- 10- ом'1.
3.5. Комплексные напряжение и ток пассивного двухполюс-
ника имеют
(7 = (804-/60) в и / = (24 —/7) а.
Вычислить комплексные сопротивление Z, проводимость У
и указать, каковы эквивалентные параметры двухполюсника.
Чему равен сдвиг фаз между напряжением и током? Определить
102
активную и реактивную составляющие напряжения и тока, ак-
тивную, реактивную и полную мощности. Построить вектор-
ную диаграмму напряжений и токов.
Решение. Запишем комплексные напряжение и ток в по-
казательной форме и изобразим их на
(рис. 3.5):
, . 60
Г--„----X- /агс*2'яп'
и = /80г+602 е 80 =
/36°50'
= 100 е в (Ф(/ =36° 50');
/=/242 + 72е 24 =
= 25е /16°15' а (Ф/ = — 16°15').
Комплексное сопротивление опреде-
ляем по формуле (3.10):
векторной диаграмме
Рис. 3.5
1ОО?36050' _а/53»5'
—/16°15' “ 4е
25 е
Следовательно, эквивалентными параметрами цепи являются
активное сопротивление г = 2,4 ом и индуктивное сопротивле-
ние х = 3,2 ом, соединенные последовательно.
Комплексная проводимость цепи по (3.12)
— (0,15 — / 0,2) ом"1.
Эквивалентные параметры цепи: активная g = 0,15 ом~1 и
реактивная (индуктивная) b = 0,2 ом~1 проводимости, соединен-
ные параллельно.
Угол сдвига фаз между напряжением и током (он же аргу-
мент Z)
Ф = Фо — Ф/ = 36° 50' — (— 16° 15') = 53° 05'.
Активные и реактивные составляющие напряжения и тока
Ua — U cos <р = 100 cos 53° 5' ~ 60 в;
Up = U sin ф = 100 sin 53° 5' = 80 в-
/а = I cos ф = 25 cos 53° 5' ~ 15 а;
/р = I sin ф — 25 sin 53° 5' » 20 а. —
Необходимо обратить внимание на то, что вещественные и
мнимые составляющие комплексных напряжения и тока в общем
случае отличаются от их активных и реактивных составляющих.
103
Активная, реактивная и полная мощности
Р = рг = 252 • 2,4 = 1500 вт = 1,5 кет-,
Q = Р х = 252 • 3,2 — 2000 вар — 2 квар;
S = UI = 100 • 25 = 2500 ва = 2,5 ква.
Те же мощности можно определить по формуле (3.20):
S = Р + jQ = U I = (80 + /60) (24 + /7) = 1500 + /2000.
3.6. Дать ответы на вопросы предыдущей задачи при
a) U = (—40 + /40) е; / = (2 + /4) а;
—/ —
б) U = — ЮОе 6 в;
/ = (7+ /24) а;
. те те
в) и = 120е'Т в; / = бе Т а.
Рис. 3.6
3.7. Последовательно с катушкой,
параметры которой г = 3 ом, L = 25л<гн,
включен реостат сопротивлением г =
= 10 ом (рис. 3.6, а). Определить на-
пряжение на катушке {7кат, его сдвиг
фазы по отношению к приложенному на-
пряжению, а также мощность, расходуе-
мую в катушке. К цепи подведено на-
пряжение U = 120 в, частота f = 50 гц.
Построить векторную диаграмму напря-
жений и тока.
Решение. Комплексное сопротивле-
ние всей цепи
Z = г -j- q + /(oL == 13 + /7,85 =
Направим вектор
= U= 120 в.
Комплексный ток
1ПП '31°5'
= 15,2 е ом.
U по оси вещественных чисел, т. е. U=
Напряжение на катушке
• • —/31°5/ —/31°5'
(7кат = / 2кат = 7,9 е (3 + j 7,85) = 7,9 е х
—/31°5'
х 8,4 е
/69°5'
/38°
66,4 е
в.
104
Оно сдвинуто по фазе по отношению к приложенному на-
пряжению на угол <р = 38°. Векторная диаграмма приведена на
рис. 3.6, б.
Мощность, расходуемая в катушке,
П О Г Л И Г> ГСС Л /38’ <7 П /31°5' 1
Ркат = Re [t/KaT л = Re [66,4 е • 7,9 е ] =
= Re [525 е/69°5' ] = 525 cos 69° 5' = 187 вт.
Та же мощность может быть подсчитана и другим путем:
Ркат = Рг = 7,92 • 3 = 187 вт.
3.8. Катушка, параметры которой гг = 4 ом и Lr = 20 мгн,
соединена последовательно с другой катушкой, имеющей актив-
ное сопротивление г2 = 5 ом и индуктивность L2 = 2,8 мгн. Ка-
тушки включены на синусоидальное напряжение U = 120 в, ча-
стотою f = 500 гц. Вычислить напряжения на каждой катушке,
сдвиг фаз между ними, а также относительно приложенного
напряжения, мощности, расходуемые в каждой из них.
3.9. Последовательно с реостатом, сопротивление которого
г} = 40 ом, соединена реактивная катушка с активным сопро-
тивлением г2 = 20 ом. Через катушку проходит ток I = 2 а, а
общее напряжение, приложенное к цепи, U = 122 в. Частота
тока f = 50 гц. Определить индуктивность катушки.
3.10. Электрическая цепь (рис. 3.7) состоит из активного со-
противления rt — 7 ом и пассивного двухполюсника АВ, содер-
жащего последовательно соединенные активное сопротивление
г = 8 ом и конденсатор емкостью С — 125 мкф. Напряжение,
приложенное к цепи, U — 120 в. Угловая частота <» = 1000 сек'1.
Чему равен ток, проходящий в цепи, и какова мощность, рас-
ходуемая в двухполюснике?
Рис. 3.7 Рис. 3.8
3.11 Какое напряжение приложено к цепи (рис. 3.8), если
амперметр показывает ток / = 0,8 а, а сопротивления ее эле-
ментов равны
= 12 ом, —= 5 ом, г2 = 132 ом, —!— = 12 ом.
w С1 а> С %
105
3.12. В цепи схемы (рис. 3.8) напряжение на участке
rv С\ равно 24 в. Сопротивления и емкости равны гг = 30 ом.
г2 = 40 ом, Cj = 5 мкф, С2 = 1 мкф. Угловая частота <о =
= 5000 сект* 1 *. Чему равно напряжение, приложенное к цепи?
Решение. Реактивные сопротивления и комплексные со-
противления первого участка и всей цепи
с\~~
------------= 40 ом;
5000-5-10-’
хг^ =----= 200 ом;
co С2
_____________/54° Ю'
—/ХС1 =30 —/40 = 50е ом;
/(V +х_) = 70—/240=250е ом.
Примем аргумент комплексного напряжения на первом участ-
• /о°
ке равным нулю: U1 — U1e = 24 в. Тогда комплексный ток в
цепи
/ = "1 =______*-----= O,48Z3°10'
Ь 50е—/53°10'
Приложенное напряжение
• • ' Л /53° 10'
окл -/73°45' 1ОП -/20°35'
• 250 е = 120 е
3.13. Напряжение U2 на участке г2, С2 равно 40 в (рис. 3.8).
Чему равны приложенное к цепи напряжение и расходуемая
в ней мощность?
Даны: t\ = 10 ом
г2 = 7 ом
в.
= 120 ом
и --------= 24 ом.
(О с2
U
V
xct
Рис. 3.9
3.14. К напряжению U — 127 в подключены
последовательно соединенные катушка индук-
тивности (гх = 10 ом, xL = 50 ом) и конден-
сатор с потерями (r2 = 1 ом, хс = 30 ом).
Определить комплексные напряжения на ка-
тушке U, и конденсаторе U2 и сдвиг фаз
между ними (рис. 3.9).
3.15. Схема цепи (рис. 3.10, а) питается
источником переменного тока 1 = 5 а. По-
строить топографическую векторную диаграмму
и определить по ней напряжение между точками
также напряжение источника тока. Даны: =
i»L2=18 ом, г2 = 10 ом, г3 = 14 ом,
1 о
—= 8 ом.
а и а.оие, си[, а
= 10 ом, (dLj — 6 ом,
—= 7 ом, гл = 6 ом,
со с3
106
Те же напряжения вычислить аналитически.
Решение. Топографическая диаграмма является векторной
диаграммой потенциалов ср всех точек цепи, отложенных от об-
щего начала координат — точки нулевого потенциала (в рас-
сматриваемом примере от точки /, так как на схеме точка f за-
землена естественно принять ее потенциал ф/ = 0).
Построение диаграммы показано на рис. 3.10, б. Примем
начальную фазу тока равной нулю и в некотором масштабе от-
ложим по горизонтальной оси вектор тока, полагая I = /.
Начало координат отметим точкой /(ф7 = 0). Комплексный
потенциал точки е определяется законом Ома:
<ре = ф/+ == ф/+/ Г—/—-—) .
\ "С3 /
Численное значение второго слагаемого Uef правой части на-
писанного равенства Uef — / —-— = 5 • 7 = 35 в откладываем в
(О (7g
выбранном масштабе напряжений (рис. 3.10, б) от точки f в на-
правлении— //, т. е. в направлении, определяемом поворотом
вектора тока / на прямой угол по часовой стрелке. Конец по-
строенного вектора IJef определяет точку е топографической ди-
аграммы. Точно также, потенциал точки d
Ф</ = Че + Ude = фв + 1 Г3.
Численное значение второго слагаемого (Ude) равно Ude =
= I г3 = 70 в и откладывается в направлении I от точки е к
искомой точке d. Аналогично строятся потенциалы точек с, Ь,
a, h.
Для построения точки g определяем потенциал
Фг = Ф/ + Ugf = Ф/ - Ufg= Ф, - / г4.
107
Вычислив значение 7г4 = 30 в, откладываем его в направле-
нии, противоположном направлению тока I, до точки g (рис.
3.10, 6).
Потенциал точки I
ulg = <pg- ugl = <vg-i (-/ = <i>, + / / -7- •'
\ <0 / u> U4
Значение 1 = 40 в откладываем в направлении //, т. е.
в направлении, повернутом против часовой стрелки на угол
у, что и определяет искомую точку / диаграммы. Для нахож-
дения напряжения между какой-либо парой точек в цепи следу-
ет соединить между собою соответствующие точки на диаграм-
ме; длина полученного отрезка в выбранном масштабе даст
искомое напряжение. Так, Uad = 130 в; Ube = 150 в; (7^=125 в.
напряжение источника тока UM = 205 в.
Те же результаты могут быть получены аналитическим путем:
Uad = 1 |Г2 + /<*7-2 + I = / V г2 + (°^2 + °^1)2 = 130
be = 1 I Г2 + Г3 + /Ш^2 I = 150 Ъ
= 125 в;
^hl = Г1 + foLy 4- г2 + /со^2 + Г3 --------------/
(0C3
+Г 4 — /
1
<оС4
= 205 в.
3.16. Параметры цепи, изображенной на рис. 3.11, а, имеют
следующие значения: = 8 ом, = 6 ом, г2 = 12 ом, хС2 =
= 0,5 ом.
Рис. З.П
108
Вычислить комплексные токи 1, llt /2 и мощность, потреб-
ляемую цепью, если U = 130 в. Найти напряжение между точ-
ками а и Ь. Построить топографическую векторную диаграмму.
Решение. Примем U — U = 130 в, тогда
; и 130 1Л . .-о ,n -/36W
/1 g j )6 Ю,4 /7,8 13# а,
i й 130 о no I -о «л in
/а = = 12—15 = 9,23 "* J 3,84 ~ а'
• • • —I 1 ]°20'
/ = /, 4- /2 = 19,6 — /3,96 = 20е а.
Мощность, потребляемая цепью,
Р = Re [til ]=Re [130 • 20е IIO2°'] = 130 • 20cos ll°20' = 2550 etn.
Проверка.
P = />, + = 13® • 8 4- 10® • 12 = 1352 4- 1200 s* 2550 em.
Найдем напряжение между точками а и Ь:
id~(f,a = Uda = ift
Фй~ Фй = Л(~/№).
Вычитая первое выражение из второго, найдем
йаЬ= (фа~ Ф») — (ф<* — Фа) = А(— jxC2)—=
= —/5(9,23 4-/3,84) — 8(10,4 —/7,8) = —64 4-/ 16,2=
/ 165’50'
= ЬЬе в.
Для построения топографической векторной диаграммы пос-
тупаем так: на основании проведенного расчета откладываем
векторы токов /х, /2 и /; векторы составляющих напряжения
на отдельных участках цепи отложены на диаграмме в том же
порядке, в каком на схеме следуют соответствующие элементы
цепи (рис. 3.11, б).
3.17. Определить токи во всех ветвях цепи, показанной на
рис. 3.12, при U = 100 в, гх = 12 ом, х1 = — 16 ом, rt = 7 ом,
хг — —24 ом. Построить топографическую векторную диаграмму.
а) Определить показание вольтметра при условии, что током,
проходящим через вольтметр, можно пренебречь в сравнении с
юч
токами ветвей. Чему будет равно показание амперметра, вклю-
ченного вместо вольтметра между точками а и Ь.
б) Что покажет вольтметр, если сопротивления г2 и х2 поме-
нять местами?
Рис. 3.12
Рис. 3.13
Рис. 3.14
3.18. При каком напряжении U, приложенном к цепи (рис.
3.13), вольтметр V покажет напряжение, равное 50 в? Частота
/ = 50 гц. Параметры цепи: гх — 5 ом, г —4 ом, г2 = 10 ом,
L — 20 мгн, С = 150 мкф. Током вольтметра пренебречь в срав-
нении с токами цепи.
3.19. Найти токи в ветвях и неразветвленной части цепи
(рис. 3.14), если приложенное напряжение U = 220 в, а сопро-
тивления = 55 ом, г3 — 7 ом, х2 = 24 ом, х3 =—44 ом. По-
строить векторную диаграмму.
3.20. В цепи (рис. 3.15, а) даны: U = 120 в, Z = r1-[-jx1 —
= (10 + /6) ом, Z2 = r2 + jxt = (24 — /7) ом, Z3 = г3 + jx3 =
= (15-j-/20) ом. Определить токи Ilt /2, 13, активные и реактив-
ные мощности всей цепи и отдельных ветвей. Построить век-
торную диаграмму.
Рис. 3.15
Решение. Полное сопротивление цепи
Z = Zr + /Д- = 10 + /6 + (24 ~ jj5 + >20) =
Z2 ~Г ^3 оУ Т / *«
/ 23°55'
= 24,4 +/ 10,8 = 26,7е ом.
по
В неразветвленной части цепи проходит ток
/ _ = 120 _ 4 23'55’
11 ~ Z 26,7^ 23°55' ~ '
Токи в параллельных ветвях могут быть выражены через ток
в неразветвленной части цепи по (3.19):
/ _ i z-3 _ 4 «с,-/23’55' # 15 + i 20 2 74 /10045'
/а— 11 Z2 + Z3 ~ %0£? 39+ /13 — 2,/б а'
i,= I. = 2,74г-'5"6' а.
° . Zg ~г Zg ОУ ~г / 1О
Токи 72 и ?з можно было бы найти и другим путем:
11 —17 — i Z*Zs — &. 4z>~ > 23°55' (24 —/7) (15 + /20) _
'Jab 'lLab ll Z2 + Z3 4,0е 39 + /13
= 68,4е-/5°30' в;
i — Uab _ 68,4е____________ g -. / ю’45' „
/2— Za — 24 — i7 Z,l^e а’
i — Uab _ 68,4g- /53° _ „ 7. -158’35'
'3 ~ ~zT - 15 + / 20 ~’ а‘
Найдем активные мощности всей цепи и отдельных ее ветвей:
• *
Р = Re VIt
= Re 120 • 4,5е/23°55' = 120-4,5cos23°55' = 494 вт;
Рг = = 4,52 - 10 = 202 вт; Р3 = 12г3 = 180 вт;
Р3 = llr3 =112 вт.
Проверка показывает, что Р = Рг + Р2 + Р3.
Наконец, определим реактивные мощности всей цепи и от*
дельных ее ветвей:
Q= lm [UI ] = Im[120 • 4,5e/23°55' ] = 120 • 4,5sin23°55'=218eap;
Q, = 72Xj = 4,52 • 6 = 122 вар; = 7|x2 = — 52,5 вар;
Qs = 13X3 — 150 вар.
Учитывая, что Q, и Q3 положительны (энергия реактивных
катушек), a Q2 — отрицательно (энергия конденсатора), получим
Q= 122 — 52,5 + 150 =218 вар.
На рис. 3.15, б приведена векторная диаграмма. Порядок ее
построения таков: по результатам расчетов отложены векторы
токов llt 72 и 13; затем по направлению отложен вектор Ц г\
"in
и перпендикулярно к нему в сторону опережения — вектор jxtl,.
Их сумма дает вектор Далее в фазе с /8 построен вектор
/2г2 и перпендикулярно к нему в сторону отставания (так как х2
отрицательно)—вектор/х8/8, а их сумма дает вектор напряже-
ния на параллельном участке Uat). Тот же вектор может быть
получен, если в фазе с /8 отложить /8г8 и к нему прибавить
вектор /х8/8, опережающий /8 на Сумма векторов и Uab
дает вектор приложенного напряжения.
3.21. Определить токи во всех частях цепи, показанной на
рис. 3.15, а, при U = 100 мв, Z, = (НО + j 160) ом, Z2 = (50 —
—/ 150) ом, Z3 — (200 + j 150) ом.
3.22. Чему равно напряжение U, подключенное к цепи
(рис. 3.16), если известно, что через сопротивление Z8 проходит
ток /8 = 2а? Чему равен сдвиг фаз между приложенным напря-
жением и напряжением между точками а и Ь. Сопротивления
г, = 27 ом, х, = —25 ом, г2 = 30 ом, х2 = —18 ом, г3 — 20 ом,
х3 = 30 ом. Вычислить активную и реактивную мощности. По-
строить векторную диаграмму.
Указание. Решение удобно начинать с вычисления напряжения между
точками а и b (йаЬ ~ I3Z3 = I3Z3), а затем токов /2 и и напряжения U •
Рис. 3.16
Рис. 3.17
3.23. В неразветвленной части цепи (рис. 3.17) проходит ток,
изменяющийся по закону it = 12 У 2 sin(o>/)a. Сопротивления
элементов цепи
<в£2 =100 ом,
== 22,5 ом,
г2 = 40 ом,
—tv- = 20 ом.
Вычислить действующие значения всех токов и приложен-
ного к цепи напряжения; написать для них уравнения мгновен-
ных значений. Построить векторную диаграмму напряжений и
токов.
112
' 3.24. Параметры цепи (рис. 3.18) равны: г2 = 40 ом, хг =
= 100 ом, хл = — 20 ом. Определить величину и характер реак-
тивного сопротивления Z,, если известно, что через него про-
ходит ток = 12 а, а напряжение, прило-
женное к цепи, U = 30 в.
Решение. Сопротивление разветвленной
части цепи
= (Ю + I 100) . <- , 20) _ 2 _ 24 ом
аЬ 40 + j 80
Общее сопротивление цепи
и зо
Z = — = —
Z,
Рис. 3.18
= 2,5 ом.
12
Оно может быть выражено и так:
z = У 22 + (хх — 24)2 = 2,5 ом;
отсюда (хх— 24)2 = 2,25, или xt—24 = ±1,5.
Возможны два решения задачи:, искомое сопротивление име-
ет индуктивный характер и равно либо х\ = 25,5 ом, либо
х[ = 22,5 ом.
3.25. Амперметр, включенный в неразветвленную часть цепи
(рис. 3.19), показал ток I = 2,4 а, а вольтметр — напряжение
U = 120 в. Известно, что сопротивление Zx представляет собой
реактивную катушку с активным сопротивлением гх = 7 ом.
Определить величину индуктивного сопротивления этой катуш-
ки, если известны г2 = 20 ом, = 30 ом, г3 = 10 ом,
-4г- = 20 ом.
шСз
3.26. Цепь (рис. 3.19) имеет параметры: Zx = (6 + /8) ом,
Z2 = (20 — j 8) ом, Z3 = (10 + j 8) ом. Через сопротивление Zx
проходит ток /х = 6 а. Вычислить остальные токи и напряже-
ние, приложенное к цепи.
ложенное
Указание. Вычислить полное сопротивление всей цепи Z, затем при-
к ней напряжение U = ItZ и, наконец, по (3.19) — токи /в и /8.
Рис. 3.19
Рис. 3.20
3.27 Вычислить все токи в цепи (рис. 3.20) и построить
векторную диаграмму, если известно, что напряжение (/=120 в,
= 12 ом, —4“ = 20 ом, ZH = 40 ом.
113
3.28. Через сопротивление нагрузки ZH = (25 4- /60) ом про-
ходит ток /н — 0,4 а (рис. 3.20). Определить все токи и прило-
женное к цепи напряжение U. Сопротивления элементов цепи
1 ГТ
равны: = 40 ом, «>Л — 10 ом. Построить векторную диаг-
рамму токов и напряжений.
3.29. Каким активным сопротивлением г2 следует зашунти-
ровать сопротивление Zr ~ rt -4 j*v чтобы ток, проходящий че-
рез Zv отставал от приложенного напряжения U на 90°
(рис. 3.21). Сопротивления г = 5 ом, х = 11 ом, rt = 10 ом,
Xj = 25 ом.
Построить векторную диаграмму.
Рис. 3.21
Решение. Обозначим
Z = г 4- jx; Z, = + jxi, Z2 = r2.
Ток в неразветвленной части цепи
/ = и = и .
^вх -f- + ^^2
Через сопротивление Zj проходит ток
j ______________ J ^2 _____U______
1 ~ Z1 + Z2 7 , 7 , •
1 + zi + IT
Для того чтобы ток 1Х отставал по фазе от напряжения U
на 90°, знаменатель последнего выражения должен быть чисто
мнимой (по знаку положительной) величиной.
Выпишем этот знаменатель и выделим в нем вещественную
и мнимую составляющие:
Z 4- Zj 4=Л — г 4- /• 4. / (х 4- Xj) 4-
^2
(г + jx) (П + jXj)
114
Вещественную часть полученного выражения приравняем
нулю:
отсюда
25.11-5-10 1С
---_ , ---= 15 ом.
Векторная диаграмма представлена на рис. 3.21,6.
3.30. К напряжению U — 40 в подключены два последова-
тельно соединенных комплексных сопротивления Z1=(3-f-/ 13) ом
и Zg = (10+/40) ом. Определить, каким чисто емкостным со-
противлением следует шунтировать сопротивление Zt для того,
чтобы ток в неразветвленной части цепи (т. е. в Сопротивле-
нии Zj) совпал по фазе с приложенным напряжением. Вычис-
лить при этом все токи и построить векторную диаграмму.
Указание. Комплекс полного сопротивления цепи должен быть вещест-
венной величиной, иными словами, мнимую составляющую комплекса полного
сопротивления необходимо приравнять нулю.
3.31. В цепи (рис. 3.21, а) известны: г = 3 ом, х = 9 ом,
rt = 20 ом, хх = 10 ом. Найти, при каком сопротивлении г2 ток
в неразветвленной части цепи будет сдвинут по отношению к
приложенному напряжению на угол, равный 45°.
Указание. Следует вычислить комплекс полного сопротивления схемы
2Э = гэ 4- jx3, в котором надо принять отношение
L =1 (т. е. tg ®э = tg 45° = .
г3 V г3 1
3.32. Показать, что при угловой частоте о> = —— ток I в
J/2LC
неразветвленной части цепи рис. 3.22 при любых значениях ак-
тивного сопротивления г является величиной постоянной и рав-
няется -Д-, а фаза тока (при изменении г от 0 до со) изменяет-
ся в пределах от + до-----------.
Какую емкость С следует включить в цепь для регулирова-
ния фазы при f = 50 гц, если индуктивность цепи равна 5 гм?
Начертить кривую изменения фазы в зависимости от г при его
изменении от 0 до 1000 ом.
3.33. Из теории известно, что мостик (рис. 3.23) будет урав-
новешен, если ZXZ4 = Z.2Z3. Пользуясь этим условием, опреде-
лить величину емкости С4, при которой ток в гальванометре
отсутствует. Известно, что Zx = 200 ом, Z2~ 100 ом и Z3=;
= — /120 ом. Частота переменного тока f = 50 гц.
3.34. Для определения индуктивности катушки Lx приме-
няется мостик, схема которого изображена на рис. 3.24. Вели-
чины г19 г2, г3 и L3 известны.
Показать, что при равновесии мостика одновременно должно
быть удовлетворено равенство трех отношений
Z1 ==
Г2 ГХ
Замечания. 1. Катушка индуктивности Lx всегда обладает активным
сопротивлением, величина которого при небольших частотах может быть опре-
делена путем измерения на постоянном токе., При высоких частотах, когда
резко выражен поверхностный эффект, активное сопротивление г проводника
круглого сечения при переменном токе может быть определено по формуле
а 1/ W
г “ го 2 F 2 ’
где г0— сопротивление, проводимое при постоянном токе;
а — радиус проводника;
со — угловая частота тока;
— абсолютная магнитная проницаемость;
о — удельная электрическая проводимость проводника.
2. Сначала уравновешивают мостик на постоянном токе, добиваясь pa-
ri гз
венства — = —, а затем его уравновешивают при переменном токе (при
'2 ГХ
этом сопротивления гг и г3 не меняют, а г2 и гх изменяют одновременно так,
чтобы сохранялась пропорция — == — )•
*2 'X 1
Обычно на практике для возможности регулировки мостика последователь-
но с катушкой (Lx, гх) включают дополнительное регулируемое активное со-
противление, и потому под гх надо понимать сумму сопротивлений катушки и
этого дополнительного сопротивления.
Рис. 3.25
3.35. С целью определения емкости и по-
терь мощности в диэлектрике конденсатора
(Сг, G) при высоком напряжении используется
схема мостика, изображенного на рис. 3.25.
Величины гх, г3, С3 и С4 известны.
Показать, что
П (1 + г?)
* \ 1 О О) •
Замечания. l.Ha практике величина w2C| r^< 1,
поэтому
2. Обычно падение напряжения на сопротивлении г\ и в параллельных
ветвях г3, С3 мало по сравнению с падением напряжения в плече Сх, гх и на
116
С4, поэтому напряжение на обкладках испытуемого конденсатора Сх можно
принять равным (/; в этом случае потери в диэлектрике конденсатора Сх равны
(J2 U2(H2C3C^
И
3.36. Для определения параметров эквивалентной схемы кон-
денсатора с потерями (С2 и г2) собран мост По схеме рис. 3.26,
который уравновешен (ZXZ4 = Z2Z8). Чему равны С2 и г2, если
известно, что = 2500 ом, г3 = 10 ом, L3 = 1 гн, г4 = 800 ом?
-о «ан-
Рис. 3.26
Рис. 3.27
3.37. На рис. 3.27 изображена схема мостика, используемого
для измерения частоты. Показать, что при равновесии мостика
1
О) = ---------_ .
j/" Г <2? 4С2С4
3.38. Параметры цепи (рис. 3.28, а)
равны
Zr = t\ + jx± = (10 4- /80) ом,
Z = г + jx = (50 + / 60) ом,
Z2 = г2 = 40 ом.
При каком активном сопротивлении г3,
включенном в диагональ моста, ток про-
ходящий через каждое из сопротивлений Zx,
будет сдвинут по отношению к вектору
приложенного напряжения £7=154 в на
угол ср = 90°? Для этого случая найти все
токи * и построить векторную диаграмму
напряжений.
Указание. Надо составить систему уравне-
ний Кирхгофа, решив которую найти комплексный
ток /х. При решении учесть, что токи в противопо-
ложных ветвях (ad и Ьс, а также ab и de) равны друг
Другу. Чтобы было сдвинуто по фазе по отноше-
нию к U на 90°, надо приравнять нулю вещест-
венную составляющую в выражении для тока /j.
Рис. 3.28
117
В результате решения должно быть получено
На основе
диаграмма.
3.39. Для
xxL — гг2 — rrt — 2r ^2
Гэ~ 2r + и + г» “ 0 ом‘
вычисленных значений на рис. 3.28 6 построена векторная
цепи (рис. 3.29) вычислить комплексный коэффи-
циент передачи — отношение напряжения U2 на ее выходе к на-
пряжению Ui на входе цепи. Даны: г, = 50 ом, г2 = 150 ом
хС1 = 80 ом, хС2 => 100 ом. Зажимы 2—2' разомкнуты.
.Каким будет коэффициент передачи, если к зажимам 2—2'
подключить активное сопротивление: а) 125 ом; б) 1250 ом?
Рис. 3.29
Рис. 3.30
3.40. Вычислить величину активного сопротивления г2, к°-
торое надо подключить к зажимам цепи 2—2' (рис. 3.30), чтобы
отношение напряжения на нем С/2 к напряжению на входе цепи
равнялось k. Числовой расчет проделать при гх = 100 ом,
хс = 50 ом, k = С/2: и1 = 0,2.
Решение. Входное сопротивление всей цепи
где
Вычислим напряжение (/2, для чего сначала найдем токи
_______^1^3_________
ZiZ2 + Z2Zj + Z3Z1
у %3
2^3
(/1Z2
118
Отсюда находим отношение комплексных напряжений:
а отношение модулей напряжений:
Подставляя числовые значения, после простых преобразова-
ний, получим квадратное уравнение относительно г2:
г2—10г2 —500 = 0.
Решение этого уравнения дает величину искомого сопротив-
ления г2 = 28 ом.
3.41. В схеме рис. 3.31 даны: г4 = 25 ом, г3 = 5 ом и
хс = 15 ом. При какой величине активного сопротивления г2
отношение модулей напряжений U2: Ui = k = 0,4?
Рис. 3.31
Рис. 3.32
3.42. Сопротивления цепи (рис. 3.32)
Zj = 18 ом, Z2 = 12 ом, Z3 = (35 4- /15) ом,
Z4 = (10 + /15) ом и Z8 = (20 —/30) ом.
Чему равно отношение напряжения Ucd
тивлении Z = 25 ом к напряжению Uab,
3.43. Два генератора (рис. 3.33),
соединенных параллельно, питают при-
емник, сопротивление которого Z =
= (2,4 4- /3,2) ом. Э. д. с. генераторов
= 400 в, Ё2 = 400е / Ь в, а их внут-
ренние сопротивления Zx= Z2= (0,04 4-
4-j 0,2) ом.
Определить все токи и мощность,
на нагрузочном сопро-
подведенному к цепи?
Рис. 3.33
119
отдаваемую каждым генератором. Задачу решить следующими
способами: 1) при помощи уравнений Кирхгофа; 2) методом кон-
турных токов; 3) путем замены, двух заданных источников э. д. с.
одним эквивалентным; 4) методом наложения; 5) найти ток в
приемнике методом эквивалентного генератора напряжения;
6) то же методом эквивалентного генератора тока.
Решение. Система уравнений, составленных на основании
первого и второго законов Кирхгофа, при указанных на рис. 3.33
положительных направлениях токов в ветвях будет:
для узла b I = /х + /а;
для контура I Е1 — Е2 = /XZX — /2Z2;
• • •
для контура II Е2 = /2Z2 + IZ.
Решая эти уравнения относительно /, /х, /2> найдем
£i (z2 + Z) - Ёгг ,
ZjZ2 + ZjZ + zz2 ’
j = + г) - £iZ
2 ZjZ2 + ZiZ + zz2 ’
Подставляя числовые значения для э. д. с. и сопротивлений
и учитывая, что Ё2= 400е 7 =(386 — /104) в, получим
А = (280 — /26) а; /2 = (— 234 — j 59) а
и из уравнения первого закона Кирхгофа
I = /х -|- /2 = (46 — / 85) а.
Мощность, отдаваемая каждым генератором,
Plr = Re [ДД = Re [400 (280 + /26)] = 400 • 280 = 112 кет;
Р2г = Re Ё2 /2 = Re [(386 — j 104) (— 234 + / 59)1 =
= 386 (—- 234) + 104 • 59 = —84,3 кет
Отсюда следует, что второй генератор не доставляет энергию,
а является потребителем. Это результат нарушения синхрони-
зации генераторов. Работа мощных генераторов в подобном ре
жиме недопустима.
Мощность, расходуемая в приемнике энергии, и потери
мощности в каждом из генераторов
Рпр = рг = (J/462 4- 852 ) 2 - 2,4 » 22,4 кет;
Pi внут = /fri = (К 2802 + 262 ) 2 - 0,04 » 3,1 кет;
Р2 внут = 122гг = (К 2342 4- 592 )2- 0,04 « 2,2 кет.
120
Нетрудно видеть, что соблюдается баланс мощностей
₽1г ~Ь ^2 г = ^пр ~Ь ‘1 внут ^2 внут
ИЛИ
112 — 84,3 = 22,4 4-3,1 + 2,2.
Решение задачи другими методами рекомендуется проделать
самостоятельно.
3.44. В схеме предыдущей задачи известны = £2 = 400 в,
т. е. генераторы синхронизированы, а внутренние сопротивле-
ния генераторов равны Z1=(0,04 + /0,2) ом, Z2=(0,06+/0,3) ом.
Определить все токи методами, указанными в предыдущей
задаче.
3.45. Воспользовавшись преобразованием треугольника в
звезду, найти все токи в неуравновешенном мостике (рис. 3.34).
Приложенное к цепи напряжение U = 130 в. Сопротивления
элементов цепи Zt = 10 ом, Z2 = /5 ом, Z3 — j 10 ом, Zt = 5 ом
и Z6 — — /10 ом. Вычислить мощность, расходуемую в цепи.
3.46. Решить задачу 3.45 методами контурных токов и узло-
вых потенциалов, методом эквивалентного генератора напряже-
ния найти ток, проходящий через конденсатор, и ток в сопро-
тивлении Z4; в тех же ветвях найти ток методом эквивалентного
генератора тока.
Указание, Разобрать из гл. 1 решение задачи 1.57.
Рис. 3.34
Рис. 3.35
Рис. 3.36
3.47. Методом эквивалентного генератора напряжения опре-
делить показание амперметра, включенного в цепь рис. 3.35.
Даны: £ = 40 в, гх = 200 ом, г2= 160 ом, г3 = 120 ом, г4=80 ом
и хс = 60 ом.
3.48. В цепи схемы (рис. 3.36) комплексные сопротивления
Zx = (19 — / 2) ом, Z2 = 40 ом, Z8 = (6 + j 8) ом, Z4=(5 — / 15) ом,
Z5 = (5 — j 20) ом и Ze = (5 + / 15) ом.
Напряжение U = 100 в. Вычислить все токи путем преобра-
зования треугольника в звезду, методами контурных токов и
узловых потенциалов, методами эквивалентного генератора на-
пряжения и тока определить ток, проходящий через сопротивле-
ние Z6.
121
3.49. В схеме рис. 3.37 включен источник синусоидального
тока, действующее значение которого I = 10 ма. Даны: Zt —
— 2 ком, Z2 = 3 ком, Z3 — —j 10 ком, Zi = (2-\- j 10) ком и
Zs = 5 ком.
Найти все токи методами контурных токов и узловых потен-
циалов. Определить показание ваттметра и убедиться в том, что
оно равно сумме мощностей, расходуемых во всех активных со-
противлениях цепи.
Методами эквивалентного генератора напряжения и эквива-
лентного генератора тока определить ток в ветви" Z4; то же в
ветви Z5.
Указание: Из гл. 1 разобрать решение задач 1.40, 1.57, и 1.63.
Рис. 3.37
3
Рис. 3.38
3.50. В цепь (рис. 3.38) включены два генератора сину-
соидального тока: iri=50/2 sin и/ ма, ir2 = 20^2 sin <ot ма.
Даны: = 10 ком, г2 = 25 ком, г3 = 20 ком и хс — 34 ком.
Определить все токи. Задачу решить методами узловых потен-
циалов, контурных токов и наложения.
3.51. Цепь, состоящая из последовательно соединенных ак-
тивного сопротивления г и реактивного х, подключена к источ-
нику синусоидального напряжения, действующее значение кото-
рого U = 120 в.
Построить круговую диаграмму токов для двух случаев:
1) г = 30 ом, х изменяется от —оо до +°°; 2) х — 50 ом, г из-
меняется от нуля до бесконечности. Пользуясь диаграммой, най-
ти ток: 1) х = 26 ом, 2) г — 20 ом.
3.52. Электрическая цепь состоит из двух параллельных вет-
вей: первая содержит последовательно соединенные активной
сопротивление гх = 10 ом и изменяющееся от нуля до бесконеч-
ности индуктивное сопротивление xlt вторая — последовательно
соединенные активное сопротивление г2 = 7,7 ом и емкостное
сопротивление ха = —18,6 ом. Напряжение на зажимах цепи
переменного тока U — 75 в.
Построить круговую диаграмму неразветвленного тока /.
Пользуясь ею, определить, при каком значении переменной вели-
122
чины хх наступит резонанс токов и чему при этом равны токи
I и /х.
3.53. Цепь состоит из двух параллельных ветвей: в первой
последовательно соединенные гх = 10 ом и хх = 16 ом; во вто-
рой — х2 = — 6,25 ом и изменяющееся от нуля до бесконечности
активное сопротивление г2.
Построить круговую диаграмму и при ее помощи найти вели-
чину сопротивления г2, при котором в цепи будет резонанс то-
ков. Чему в этом случае равен ток 7? При каких значениях г2
ток 1 в неразветвленной части цепи имеет максимум и минимум?
Определить их. Напряжение U — 120 в.
ГЛАВА ЧЕТВЕРТАЯ
РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Если в электрической цепи или участке цепи, содержащем
реактивные элементы, напряжение и ток совпадают по фазе, то
имеет место явление резонанса. Эквивалентное реактивное
сопротивление или реактивная проводимость цепи или участка
цепи, где имеется резонанс, равны нулю.
2. Резонанс при последовательном соединении г, L и С. Ре-
Рис. 4.1
зонанс напряжений возможен в
цепи или участке цепи, содержащем по
следовательно соединенные индуктивность
и емкость. Цепь схемы (рис. 4.1) назы-
вают последовательным колеба-
тельным контуром.
Входное комплексное сопротивление
последовательного контура
Z == г + j(^L---------= г + jx = ze^ . (4.1)
где х = oL------~ — реактивное сопротивление контура;
(оС
— полное сопротивление контура;
0)L----7;
Ф = arctg -
Условие
— сдвиг фаз между напряжением и током,
резонанса напряжений:
к = 0 или <uL = .
(4.2)
Угловая
резонансная частота
«>о = 2к/0 =
(4.3)
124
При резонансе напряжений применяются следующие соотно-
шение и формулы:
характеристическое сопротивление контура — сопротивление
каждого из реактивных элементов при резонансе
f = "•' = -ir = // <4Л>
добротность контура
« = -?-, (4-5)
затухание контура
d = ~ . (4.6)
При резонансе напряжений ток в контуре
/о = у- . (4.7)
а напряжение на индуктивности равно напряжению на емкости
Ul. = UCi = /ор = UQ = £ . (4.8)
Абсолютная расстройка
До = о — о>о или Д/ = f — fQ.
Относительная расстройка
Д<о _______________________ А/
(4-9)
(4.Ю)
Обобщенная расстройка
е = — = —--------------= q(— - =tg?. (4.П)
Зависимость' комплексного тока в контуре от обобщенной
расстройки
I « ... й-_ = 6 . = (4 12)
Z(/o.) г (14-/5) г/14-е2 г ’
где
Z (/<») — г 4- jx = г + fir — комплексное полное со-
противление;
z = г 1 4- — модуль полного сопротив-
ления;
<р = arctg 5 — сдвиг фаз между напряже-
нием и током.
(4.13)
12S
Уравнение резонансной кривой по току — отношение модуля
тока при любой частоте к току при резонансной частоте (при
неизменных значениях напряжения и параметров цепи):
(4.14)
Уравнение фазовой характеристики
ф = arctg $ = arctg«= arctg Q -----. (4.11a)
Комплексные коэффициенты передачи по напряжению
(4.15)
При небольших расстройках формулы (4.11)-j-(4.15) имеют
вид
В = — «2Q— ; х=2р—; (4.116)
г х <Л0 ’ Г<й0 '
(4.156)
При использовании приближенного равенства (4.116) расчеты
по (4.126)-=-(4.156) дают относительную ошибку, которая может
быть определена по формуле
й____________________________________Д«>
2«>о ’
(4.16)
126
Полоса пропускания определяется из условия, что
ток на частотах Д и /а, соответствующих границе полосы про-
пускания, уменьшается в У 2 раз.
’ Абсолютное и относительное значения
определяются по формулам
SA=/8-/i = -^;
„ «А 1
So ~ 7Г ~ V *
полосы пропускания
(4.17)
3. Резонанс токов может быть
в цепи, содержащей параллельно соеди-
ненные индуктивности и емкости.
Резонанс токов для цепи с потерями
энергии в обеих ветвях. Цепь схемы
(рис. 4.2) называют простым параллель-
ным колебательным контуром.
Условие резонанса:
bt = — bt или
Угловая резонансная
toL
частота
(4.19)
где характеристическое сопротивление
(4.20)
Сопротивление параллельного контура при резонансе
г>=г" = • (4-21>
Добротность контура
е=• <4-22*
Ток в неразветвленной части цепи при резонансе
7р = ^-- (4.23)
Частные случаи резонанса токов для цепи рис. 4.2.
Цепь не имеет потерь (га = г2 = 0).
Условие резонанса:
(4.18а)
12>
Угловая резонансная частота
шр = <оо
(4.19а)
Сопротивление контура при резонансе
Zn = оо.
(4.21а)
Рис. 4.3
Для добротного контура 1 (рис. 4.2 и
4.3), т. е. при малых потерях можно считать,
что
<»р
(4.196)
Сопротивление этого контура при резонансе
= = <421б>
где
' = G + Г2-
Токи в каждой из ветвей при резонансе примерно одинаковы
Лр =» hp, и каждый из них больше тока в неразветвленной час-
ти цепи /р в Q раз:
(4.24)
Мощность, выделяемая в параллельном контуре при резо-
нансе.
Лр _ ^4р _
Рр ^рГР Лр Г1 "Ь Лр Г*‘
(4.25)
При небольшой расстройке контура (Дш = <о — шр), т. е. когда
I Д<» I < а =
Zu
(4.26)
комплексное сопротивление можно определять по приближенной
формуле
где
Z (/ш) — ! | ^2 / 1 _р_ £2 £ ГЭ 4“ /Хэ —
(4.27)
u)L — —
Фэ = — arctg 5 = —+ -
128
Включение простого параллельного контура к генератору на-
пряжения с э.д.с. Е и внутренним сопротивлением Rt показано
на (рис. 4.4).
Ток в неразветвленной части
цепи и напряжение на параллель-
ном контуре U при любой частоте
определяются по формулам
(4.28)
а при резонансе Рис. 4.4
Отношение этих напряжений
и 1 1 —/<рэ
—- =----------------—--------------------- е э
(4.30)
где эквивалентная (приведенная) добротность
Q* =-----^-=------. (4.31)
1 + ^Г- 1 + -^7
а угол сдвига фаз напряжения на контуре при любой частоте к
тому же напряжению при резонансе
<рэ = arctg Q9 (4.32)
Полоса пропускания определяется из условия, что ~~ =
С/р
1
~~ /2“
Абсолютная и относительная полоса пропускания
5ао = /2-а = -^-; (4.зз)
5о1/=-^= ’ . (4.34)
/р Чэ
5 Заказ Xs 624
129
Комплексный коэффициент передачи по напряжению — отно-
шение комплексного напряжения на параллельном контуре к
э.д.с. генератора при любой частоте
п Р
(4.35)
Кс/(/«>)= 4
(О) 0>о
(л)0 О)
При резонансе
А-
Ki
(4.36)
Их отношение
Ку
(4.37)
Г = Гг + г2;
4. Резонанс токов в сложном парал-
лельном контуре (рис. 4.5). Для добротных
КОНТУРОВ, у КОТОрЫХ Гу <
“L2 о>С2
полное сопротивление определяется по
приближенной формуле
rXjX2
ХХХХ2
Хэ —
(4.38)
где
Гз
rxtx2
г2 4- х2 *
ХХуХ2
г2 х2
Условие резонанса токов (приближенное):
х, « —х2 или ---------------tv— ~ ----
1 г Р 1 tOpCj о)рС2 ₽
(4.39)
отсюда угловая резонансная частота
1
(4.40)
где L = Ly + L2 — полная индуктивность контура;
„ СХС2
С = .... % — полная емкость контура.
г С2
Добротность контура
СОпД. (ОгчЬ 1
Q — Р — —Р — ___________
Г1 + Г ШрСг ’
(4.41)
где г = г, + г2.
130
Полное сопротивление контура при резонансе определяется
реактивным сопротивлением каждой из ветвей:
(4.42)
где г = гх + г2.
Если обозначить niL = -р- , тс то полное сопро-
тивление контура при резонансе
гр = Q2/' — тс )2. (4.43)
Эта формула показывает возможность изменения величины
/р в широких пределах при данных L и С путем их перерас-
пределения по ветвям, при неизменной частоте резонанса токов.
Для контура схемы (рис. 4.5) в случае малых потерь спра-
ведливы формулы (4.24), (4.25) и (4.27), приведенные выше для
схемы рис. 4.2.
УПРАЖНЕНИЯ И ЗАДАЧИ
4.1. Определить емкость С, которую надо включить после-
довательно с катушкой, имеющей активное сопротивление г =
= 16 ом и индуктивность L = 158 мкгн, для того чтобы цепь
была настроена на резонанс при частоте /0 = 1 Мгц. Найти ток,
мощность, выделяемую в цепи, напряжений на конденсаторе и
катушке при резонансе, если приложенное к цепи напряжение
U = 0,8 в.
4.2. Последовательный колебательный контур (г, L, С) под-
ключен к генератору синусоидальной э.д.с. Е = 1,6 в с внутрен-
ним сопротивлением /?г = 16 ом. При какой величине сопротив-
ления контура г в нем выделится максимальная мощность при
резонансе и чему она будет равна?
4.3. Цепь состоит из индуктивной катушки г, L, соединенной
последовательно с конденсатором без потерь. Приложенное ко
всей цепи напряжение U = 35 в. Определить напряжение на ка-
тушке при резонансе, если при этом напряжение на конденса-
торе равно 120 в.
4.4. Цепь схемы (рис. 4.1), Настроенная на резонанс при
угловой частоте 5000 сек-1, потребляет мощность 0,1 вт при
токе 0,1 а. Напряжение на конденсаторе 200 в. Найти парамет-
ры цепи г, L, С и приложенное к ней напряжение.
4.5. Какому условию должны удовлетворять частоты Д и /2,
при которых цепь, составленная из последовательно соединен-
ных г, L и С, обладает одинаковыми по абсолютной величине,
но противоположными по знаку реактивными сопротивлениями?
5*
131
. 4.6. Найти параметры катушки (г, L), емкость С и сопротив-
ление реостата г19 включенного в цепь, схемы, изображенной
на рис. 4.6, если при резонансе приборы
z-x показали U = 220 в, (710 = 204 в, £72о ==
Т (ДгЧ—I = 180 в, /0 = 4 а. Частота переменно-
fiS Yfn г0 тока/==50гч.
I I 4.7. Реостат с активным сопротивле-
I I ц^| f I нием г = 100 ом, катушка с индуктив-
0 II ностью L== 5,05 мгн и конденсатор ем-
Рис. 4.6 костью С=0,05 мкф соединены последо-
вательно. Вычислить резонансную
частоту напряжения Ulq и Uco при этой частоте. При каких ча-
стотах напряжения на конденсаторе Ucmax и катушке Ubmax
достигнут максимума? Чему они будут равны, если действую-
щее значение напряжения переменной частоты, приложенного
к цепи, U = 10 в?
Решение.
1_________________1___________
/ЕС ~~ У5,05.10-3-0,05.10~6
= 6,28-104 сект1',
. __ ш0 ____ 6,28-104 ___
0 ~ ~ 2-3,14
(/10=(/С0=р = 1/_Ь д 1/5,р5-10:з =
V С V 0,05-10-6
1 Г 100 А 01 Л
d — — = -jig- — 0,314.
Частоты, при которых напряжения на индуктивности и ем-
кости максимальны, и значения этих максимальных напряжений
определятся по формулам, известным из теории:
«Ч = У= 6,28-10* У2-_02314з = 6,45-10* сек-1;
“с = шо У ” 2 = 6,13-10* сек-1;
/д = -Й- = Ю250 гц; fc=~r =9750 гц-
Г 7 _ J 1 _ 2(7 _ 2’10 QQ Q
6/дтах - UС max - d ~ 0,314/4-0,314* ~ 32,2
4.8. Катушка с индуктивностью L = 5,05 мгн и конденсатор
с емкостью С = 0,05 мкф соединены последовательно с реоста-
том, сопротивление которого г. Ответить на вопросы задачи
4.7 для двух значений сопротивления: 1) г = 318 ом и 2) г =450 ом.
132
4.9. Электрическая цепь состоит из последовательно соеди-
ненных активного сопротивления г = 10 ом, катушки индуктив-
ностью L — 100 мкгн, и конденсатора емкостью С = 100 пф.
Определить резонансную частоту ш0, характеристическое сопро-
тивление р, затухание d и добротность Q. Чему равны ток /0,
расходуемая в цепи мощность Ро, напряжения на индуктивности
Ulo и емкости Uco при резонансе, если контур включен на на-
пряжение U = 1 в? Вычислить абсолютное значение полосы
пропускания контура.
Решение. По (4.3) -г (4.8) находим
ю0 — —~= — -====J========- = 10’ сект1,
V LC yi00-10-»-10010-«
А, = ~ 1>6-10’ = 1>6 Мг«-
~\f L -\Г 100-10~6 1АЛП А Т Ю ЛЛ1
? ~ V ~с ~ г юо-1 о-12 ~ ЮОО ом' d — ~— looo — 0,01;
Q = = ЮО; /0 = -^- = -А- = 0,1 а = 100 лад;
Ро = = 0.12, Ю = 0,1 вт — 100 мет;
Ulo = Uco = ZoP = 0,1 • 1000 = 100 в;
Полосу пропускания определяем по (4.17):
с f0 1,6-10’ 1ЙАЛП .
Sa — q — 100 — 16 000 гц.
4.10. К контуру, данные которого приведены в задаче 4.9,
подведено напряжение U = 1 в с угловой частотой ш = 1,002 X
X 10’ сек-1 .Чему при этом равны реактивное и полное сопротив-
ления цепи, ток, мощность, напряжение на конденсаторе, сдвиг
фаз <р между приложенным напряжением и током, сдвиг фаз <р'
между приложенным напряжением и напряжением на конденса-
торе, коэффициенты передачи по току и по напряжению?
Решение. Прежде всего вычислим абсолютную, относи-
тельную и обобщенную расстройки по (4.9), (4.10) и (4.116):
Дю = ш — <1>0 = 0,002 • 10’ сек-1; — = 0,002;
<»о
e = 2Q— = 2-100-0,002 = 0,4.
(О0
Реактивное и полное сопротивления находим из (4.116) и
(4.136):
к = Кг = 0,4-10 = 4 ом;
г = г ]/1 -Н2 = 10 /1 + 0,42 = 10,77 ом.
133
Ток и расходуемая в контуре мощность
/ == — = = 0,093 а = 93 ла;
г \v.Tl
Р = Рг = 0.0932 • 10 = 0,0865 вт = 86,5 мет.
Напряжение на конденсаторе находим из (4.156):
UQ 1-100
~ /1+52 ~У 1+0,42 =93 в.
Сдвиг фаз между напряжением и током вычисляем из (4.136):
tg ф = = 4 = °-4; <р = 21°50'-
Найдем сдвиг фаз ф' между U и Uc* Так как расстройка по-
ложительна, то «о L > —— и ток I отстает от напряжения на
угол ф; вектор напряжения на конденсаторе Uc отстает от век-
тора тока I на 90° (рис. 4.7), поэтому Uc отстает от U на угол
ф'= Ф + 90° = 111о50'.
ф а При заданной расстройке коэффици-
г • енты передачи по току (4.146) и по
ggy l напряжению (4.156) равны
k. = = ...-4-----= 0,93;
***^ 1 /1 +$2 У 1 +о,42
. . Q _ ЮО Q„
J> W k k, .-------------------------т-- 93.
1 Uc с L /1+62 / 1-4-0,4а
Рис> 4,7 4.11. Для контура и данных, рассмот-
ренных в задачах 4.9 и 4.10, построить ам-
плитудные и фазовые характеристики тока и напряжения на кон-
денсаторе в зависимости от отношения от отношения рас-
стройки частоты питающего генератора Д/ к резонансной часто-
те /0 (построение сделать для частот, отличающихся от резонанс-
ной на ± 10%) и от обобщенной расстройки В (в пределах ±4).
Решение. Построение амплитудной и фазочастотной характе-
f
ристик тока и напряжения на конденсаторе в зависимости от —*—
/о
г
и -г- проводится на основании уравнений, получаемых из (4.14)-*
и (4°. 146), (4.11а) и (4.116), (4.15):
134
На практике обычно приходится иметь дело с небольшими
расстройками Д о> = о> — <оо. В этом случае, учитывая, что
<>» щ2 — “о
(О (Од (О
(0
О)0
написанные
Д он
<ов ’
формулы для /, <р, ис и <р' примут вид
Д (О
<о0
О) о (О
д-^-; ф = arctg 2Q
(Од /
UQ
; ф' = arctg 2Q —
<0q
те
Для удобства расчеты сведены в табл. 4.1. При этом сле-
дует иметь в виду, что =£ ~ — и — = —.
То шо Го w о
Таблица 4.1
Задаваемые величины Величины, рассчи- тываемые при про- межуточных вычис- лениях по приб- лиженным формулам Искомые величины, рассчитанные по приближенным формулам
Д / —— или /0 f fo Д со 2 со0 2C ) А у Л ма • в V'
—0,10 0,90 —0,20 -20 5,0 —87° 10' 5,0 2°50'
—0,08 0,92 —0,16 -16 6,2 —86°25' 6,2 3°35'
—0,06 0,94 —0,12 -12 8,3 —85°15' • 8,3 4°45'
—0,04 0,96 —0,08 - 8 12,4 —82°50х 12,4 7° 10'
*—0,02 0,98 —0,04 - 4 24,3 —76° 24,3 14°
0 +0,02 1,00 1,02 0 +0,04 0 h 4 100 24,3 0 +76° 100 24,3 90° +166°
-{-0,04 1,04 +0,08 h 8 12,4 +82°50' 12,4 +172°50'
+0,06 1,06 +0,12 Н12 8,3 +85° 15' 8,3 +175°15'
+о 1,08 +0,16 hl6 6,2 +86°25' 6,2 +176° 25'
+0,10 1,10 +0,20 1-20 5,0 +87° 10' 5,0 +177° 10'
По данным табл. 4.1 на рис.
вые в зависимости от и .
io Го
4.8 начерчены требуемые кри-
Ш
Кривые зависимостей от обобщенной расстройки надо строить
по уравнениям (4.12), (4.13) и (4.15):
ryr+F; ф = агс1б^:
ис= 7=^- ’ ф' = arctg?+~г •
Результаты расчетов сведены в табл. 4.2, а соответствующие
кривые даны на рис. 4.8.
1/с,в
О Рис. 4.8
£ 7, ма 9 С/с,- в
Т аблица 4.2
—4 24,3 —82°50' 24,3 7° 10'
—3 31,6 —71°35' 31,6 18°25'
—2 44,7 —63° 30' 44,7 26°30'
—1 70,7 —45° 70,7 45°
0 100 0 100 90°
+ 1 70,7 45° 70,7 135°
—2 44,7 63°30' 44,7 153°30'
—3 31,6 71°35' 31,6 161°35'
-4 24,3 82°50' 24,3 172°50'
Наконец А/ f „ выясним, каким значениям -т- и -т— соответствует
136
фиксированная величина 5. Пусть 6 = ± 1. Тогда из выражения
$ = 20 — = ± 1 находим, что
шо
= ± ЙГ = ± -2100-= ± °’005’
(Oq Г q 1UU
ИЛИ
отсюда
= /- — 1 = ± 0,005;
Го Го
4- = 1 ± 0,005.
Таким
образом, значению В = ± 1 соответствуют -у- =
= ±0,005, у-= 1,005, или 0,995, т. е. частота генератора напря-
жения отклоняется от резонансной на ± 0,5%. Аналогично
найдем, что £ = 2 соответствует = ±0,01; при $ = 3 =
= ± 0,015; при 5 = 4 = ± 0,02.
4.12. Резонансный контур состоит из последовательно вклю-
ченных L = 100 мкгн, С = 100 пф и активного сопротивления г.
Построить амплитудные и фазовые характеристики для коэф-
фициентов передачи по току k, и по напряжению на емкости kc
в зависимости от 4^ и /-для трех значений активного сопротив-
Го Го
ления г = 5 ом; г = 10 ом и г = 20 ом.
Указание. Искомые величины рассчитать по (4.11а), (4.14) и (4.15),
ZOOM
Амплитудно - частот-
ные характеристики
20ом
Юом
5ом
20
5ом
Юом
20 ом
j
20ом
Юом
5ом
0.2
' 1,005 1,01 1,015 1,02
0,005 0,01 0,15
Рис. 4.9
Юом
5ом
-0,02-0.015-0.0! -0.005
0,98 0,985 0,99 0,995
Фаза - частотные
характеристики
V
?о
f0
137
Предварительно вычисляем добротности, которые соответст-
венно равны Qx = 200; Q2 = 100; Q3 = 50.
На рис. 4.9 изображены требуемые кривые.
4.13. В последовательном колебательном контуре, имеющем
добротность Q = 150 и настроенном на резонансную частоту
/о = 2 Мгц при некотором напряжении U, проходит ток /0 =
= 60 ма. Определить ток в контуре, сдвиг фаз между напряже-
л. 1. иС
нием и током, коэффициент передачи kc — при его подклю-
чении к генератору такого же по величине напряжения U, но с
частотой / = 2,02 Мгц.
Указание. Вычислив обобщенную расстройку по (4.116), воспользо-
ваться (4.126), (4.136) и (4.156).
4.14. Последовательный контур настроен на частоту /0 =
= 1 Мгц. При какой добротности этот контур пропустит поло-
су частот: 1) 3А =2,5 кгц и 2) SA = 10 кгц?
4.15. Для контура и по данным задачи 4.9 найти частоты,
соответствующие границе полосы пропускания.
4.16. Через последовательный контур (С = 100 пф, rL = 8ол0,
настроенный на резонанс при частоте /0 = 400 кгц, надо пропус-
тить полосу частот SA = 104 гц так, чтобы отношение тока на
максимальной частоте /0 + —2— к Т0КУ ПРИ резонансной час-
тоте было равно m = 0,8. Определить добротность цепи и вели-
чину добавочного сопротивления, которое надо включить в кон-
тур для выполнения заданных условий.
Решение. Используя формулу (4.146) согласно условию,
имеем
откуда
или, так как A f =
Подставляя числовые значения, найдем Q = 30.
Активное сопротивление цепи определим из (4.4) и (4.5):
__ Р ___ 1 __ 1 ___ J Q Q
Г ~ ~Q ~ <о0 CQ ~ 2 тг-400- 10э-100-10~12-30 ~~ 1'3’° 0М’
Таким образом, добавочное сопротивление
Гдоб — г — rL~ 13,3 — 8 = 5,3 ом.
138
4.17. Последовательный контур, содержащий постоянные г
и L и регулируемую емкость С, подключен к источнику сину-
соидального напряжения неизменной частоты. В результате
Измерений установлено, что наибольший ток получается при
Ср = 250 пф, а ток, в У~2 раз меньший, — при емкостях С± =
= 245 пф и Са = 255 пф. Чему равна добротность этого конту-
ра?
4.18. В последовательном колебательном контуре емкость С
шунтируется активным сопротивлением гш (рис. 4.10, а).
Рис. 4.10
Как при этом изменится добротность эквивалентного последова-
тельного контура? Дать числовой расчет, если известны г=20 ом,
L = 400 мкгн, С — 625 пф и гт — 80 ком.
Решение. Вычислим эквивалентные параметры гэ и С,
(рис. 4.10,6). Для этого определим комплексное сопротивление
При гш —с в знаменателях можно пренебречь вторыми сла-
гаемыми по сравнению с первыми, тогда последняя формула
будет
где
Отсюда видно, что шунтирование емкостного сопротивления
большим активным сопротивлением не меняет емкость и вносит
в цепь добавочное активное сопротивление гл .
139
Проделаем числовой расчет:
<1>0 == г1_ =2-10® сек'1- р = —Ur- = 800 ом,
° / LC “ос
т. е. выполняется условие гш = 80-103 с = 800.
В этом случае добавочное сопротивление
( 1 \8
Ld 8оо2 о
Гз “ гш ~ 80-Ю3 ~8ом-
Эквивалентная добротность (рис. 4.10, б)
Qa = 7ТГ = = 28Д
До шунтирования добротность контура составляла
О = JL = 40
г 20
конденсаторе до и после
Рис. 4.11
4.19. По данным задачи 4.18 вычислить ток и напряжение на
шунтирования конденсатора при рас-
стройке частоты генератора на 0,5%,
если к контуру приложено напряже-
ние U == 1 в.
4.20. Цепь, состоящая из трех
параллельных ветвей (рис. 4.11), пара-
метры которых г = 16 ом. L = 1,6 мгн,
С = 25 мкф, подключена к генератору
синусоидального напряжения, дей-
ствующее значение которого U ~ 10 в.
Найти резонансную частоту /р и токи 1 , IL, Iс при резонансе.
Построить кривые токов I = FL (/), /£ = F2(f), Ic = F3 (/) и угла
сдвига фаз между U. величина которого поддерживается постоян-
ной, и / в зависимости от частоты [<р = F± (/)]. Частоту из-
менять в пределах от 0 до 4 /0-
4.21. Генератор, напряжение которого U = 10 в. а частота
0 = 5000 сек"1, подключен к цепи, изображенной на рис. 4.11.
Чему равна индуктивность L, при которой цепь настроена в ре-
зонанс, если г == 16 ом. С = 25 мкф?
Полагая, что приложенное к цепи напряжение изменяется по
закону и = U V 2 sin построить в зависимости от времени
кривые i. iL. ic. pL. pc. p и кривые энергии wM и w9. запасае-
мой в магнитном и электрическом полях цепи.
4.22. Вычислить частоту, при которой в цепи (см. рис. 4.2)
наступит резонанс токов. Параметры цепи гг = 32 ом. L = 40 мгн.
г2 = 24 ом и С = 25 мкф. При каком значении сопротивления
г2 резонанс в цепи вообще невозможен? 'При каких значениях
140
сопротивлений rt и га резонанс в данной цепи будет иметь место
при любой частоте?
4.23. Напряжение U = 20 мв, частота которого / = 50 кгц,
подключено к цепи, изображенной на рис. 4.2. Определить ем-
кость С, при которой наступит резонанс, если гх = 4 ом, =
= 3,2 ом, L = 9,56 мкгн. Найти токи при резонансе и построить
векторную диаграмму.
Для каждого из найденных значений емкости С определить
сдвиг фаз между приложенным к цепи напряжением и током,
проходящим через конденсатор. В какой связи находятся найден-
ные углы?
Решение. Сначала вычислим при резонансе сопротивление
xL =(dL=2tc-50- 103-9,56-10~6 = 3 ом и, сопоставив его величину
со значениями активных сопротивлений цепи, увидим, что задан-
ный контур не является высокодобротным. Поэтому задачу ре-
шим не по упрощенным формулам, а непосредственно. Запишем
комплексное сопротивление всей цепи и умножим числитель и
знаменатель на комплекс, сопряженный знаменателю:
+ / [О'! + Га) (r2xL —rrxc)— (XL —ХС) (rt r2 + XL xc )]
(И + 'г)2 + (XL — xc )2
При резонансе полное сопротивление цепи должно быть ве-
щественной величиной, поэтому мнимую составляющую послед-
него выражения приравняем нулю:
Подставив сюда числовые значения и после упрощений, по-
лучим квадратное уравнение
3x2 _ 25хг + 30,72 == 0.
Решая его, найдем
Хс = 6,83 ом; С' = —V- = 0,466 мкф;
(Л хс
п 1
Хс = 1,5 ом; С" =--------*— = 2,12 мкф.
со Xq
141
Сопротивления правой ветви при найденных значениях ем-
костного сопротивления соответственно равны
Z2 = V rl + х,2с = V 3,22 4-6,832 = 7,5 ом; .
г;= |/ г22 + х?= И 3,22 + 1,52 = 3,53 ом.
Вещественная часть Z при найденных хси х"с равна
г'3 = 4,6 ом; г’ = 2,4 ом.
Ток в левой ветви
, U 20 .
I, = ----= —— — - = 4 ма
]/ г* + (»ЬГ ]/>+32
Токи в правой ветви и в неразветвленной части цепи и сдвиг
фаз между этим током и приложенным напряжением при Хс =
= 6,83 ом
7’ = Д = Д = 2,68 ма; Г = Д = Д = 4,34 ма;
г2 7,5 гэ 4,6
Г
tg ф' =~ = = 2-135; Ч' = 64°55':
при Хс = 1,5 ом
Рис. 4.12
U 20 о ол
= -у = 2 4 = 8,34 ма;
0,468; ф" = 25°05'.
Обращаем внимание на
то, что сумма углов <р' 4~
+ ф" = 90°. Это имеет мес-
то всегда, когда в цепи (см.
рис. 4.2) ищется резонанс-
ное значение L или С, а ос-
тальные величины являют-
ся заданными. Векторная
диаграмма построена на
рис. 4.12.
4.24. В цепи (см. рис. 4.2)
даны = 40 ом, о> L = 30 ом,
= 15 ом. Чему равно г2 при резонансе токов и каково при
этом полное сопротивление цепи?
4.25. К катушке индуктивности, параметры которой г—11,2 ом,
L = 4 мгн, подключен конденсатор емкостью С — 2,5 мкф (см.
рис. 4.3). При какой частоте наступит резонанс токов? Для най-
142
Рис. 4.13
денной частоты определить полное сопротивление цепи. По-
строить векторную диаграмму при резонансе, если U — 10в.
4.26. Для цепи (см. рис. 4.3) найти значение индуктивности
L, при которой наступит резонанс на угловой частоте ш =
= 5000 сект1. Параметры цепи; г — 14 ом, С~2 мкф.
Для каждого из найденных значений L вычислить сдвиг фаз
между приложенным напряжением и током, проходящим по ка-
тушке. В какой связи находятся найден-
ные углы?
4.27. При перемещении ползунка соп-
ротивление г распределяется между вет-
вями параллельного контура (рис. 4.13).
Определить пределы изменения резо-
нансной частоты контура в зависимости
от параметра k (0 <IZ?<1)- Даны:
L = 2 мгн, С = 500 пф, г = 1 ком.
4.28. Найти резонансную частоту
и полное сопротивление параллельного
контура (см. рис. 4.2), параметры которого равны: = 9 ом,
гг = 1 ом, L — 100 мкгн, С = 100 пф. Рассчитать то-
ки, проходящие в каждой из ветвей при резонансе, и выделяе-
мую в контуре мощность, если приложенное напряжение U =
= 200 в.
Решение. В данном случае потери малы (Q1). Действи-
тельно,
100-Ю-6
ffl-10'12 = 100
10
Поэтому резонансную частоту можно определить по прибли-
женной формуле (4.19,6):
<ап — шп = --------- = 10’ сек'1;
р /100-10-М00-10-12
/р = 1,6 Мгц.
Вычислим сопротивление контура при резонансе по (4.216):
L loo-io-6 1пь ,ПЛ
Гр ~ ('i+''г) С ~ 10-100-10-1“ ~ 1° 0М~ Ю0 К0М"
Токи в каждой из ветвей
, U 200 п „
/ , — у-. —.
|/ Г| + (“Р L)2 1/ 92 +Ю002
143
J и 200 o n o
/о = — = —гтгг- = 2-10 3 a = 2 ма.
p Гр 105
Расходуемая в цепи мощность
Рр = /2 Гр = (2-10~3)2-105 = 0,4 вт.
Та же мощность может быть подсчитана и так:
Рр = /f гг + ^2 — 0,22 • 10 = 0,4 вт.
4.29. Для контура и данных задачи 4.28 определить, че-
му будут равны эквивалентные активное, реактивное и полное
сопротивления контура, если вследствие расстройки частота ста-
нет на 0,2% больше резонансной. Для этого случая вычислить
все токи и мощность, выделяемую в контуре, полагая, что ве-
личина приложенного к цепи напряжения осталась^ прежней
(U = 200 в).
Решение. Произведем расчеты при <о = 1,002шр. Найдем
абсолютную и обобщенную расстройки и искомые сопротивления
по (4.9), (4.116) и (4.27):
Д со = (о — о)р = 0,002 (Dp = 0,002 -107 = 2 -104 сек"1;
l = 2Q — =2-100 Q’002^ = 0,4;
wp wp
Гр 100 оЛ
'э j । £2 | । о 86» 2 ком,
хэ = —1гэ — — 0,4-86,2 = — 34,4 ком,
хэ имеет емкостный характер, так как $ положительно (см. 4.27).
э
гр
100 по о
—...— = 93,3 ком;
= *э __ 64,4 _
э г9 86,2
э = — 21°50'.
Так как <рэ отрицателен, то ток опережает напряжение:
200
92+ (1,002-107-100-10~6)2
~ 0,2а;
----- j - ~ 0,2а;
V 1 + I 1,002-107-100-10-12 )
I = -L= «2,15-Ю-3 а = 2,15 ма-,
<70 У О • 11/
P = U1 cos<рэ = 200-2,15-10~3 cos 21° 50'= 0,4 вт.
144
или
Р=1\ г = 0,22-10 = 0,4 вт.
Заметим, что даже при небольшой расстройке (0,2%) в пол-
ном сопротивлении контура появилась значительная реактивная
составляющая хэ , вследствие которой и оказался сдвиг фаз <рэ
между током / и напряжением U. Ввиду небольшого изменения
частоты реактивные сопротивления каждой из параллельных вет-
вей и токи в них почти не изменились и ненамного изменился
ток в неразветвленной части цепи.
4.30. Для контура и по данным задачи 4.28 построить резо-
нансную кривую неразветвленного тока в зависимости: а) от от-
ношения расстройки частоты питающего генератора А/ к ре-
зонансной частоте /0 (построение сделать для области частот,
отличающихся от резонансной на ± 10%); б) от отношения
f
4- и в) от обобщенной расстройки 5.
/о
Построить те же кривые, если рассмотренный контур имеет
«активное сопротивление: 1) гх = 4,5 ом и г2 = 0,5 ом; 2) гг =
= 18 ом и г2 = 2 ом.
4.31. Параметры параллельного контура (см. рис. 4.2) имеют
«следующие значения: ^=15 ом, £ = 338 мкгн, r2 = 1 ом,
С = 300 пф. Чему равны резонансная частота и сопротивление
контура при резонансе? Вычислить эквивалентные активное,
реактивное и полное сопротивления контура при частоте
/ = 496 кгц. Определить все токи и мощность, выделяемую в
контуре, если к нему подведено напряжение U == 150 в.
4.32. Определить эквивалентные величины активной, реактив-
ной составляющих и полного сопротивления параллельного кон-
тура (см. рис. 4.3) при частоте f по следующим данным: 1) С =
= 300 пф; г = 16,3 ом\ Q = 65; f = 505 кгц; 2) £ = 93,5 мкгн;
/р=1,5 Мгц; Q = 40; /= 1490 кгц; 3) £ = 600 мкгн; Q = 66;
гр = 100 ком; [ = 400 кгц.
4.33. Параллельный контур с малыми потерями (т. е. Q^>1)
включен к генератору с э. д. с. Е = 200 в и внутренним сопро-
тивлением = 69 ком (см. рис. 4.4). Определить параметры
контура г и £, если известны резонансная частота/р = 500 кгц,
емкость С = 300 пф и что сопротивление контура при резонансе
гр равно внутреннему сопротивлению генератора 7?z. Вычислить
токи генератора, каждой из ветвей, мощность, доставляемую ге-
нератором и выделяемую в нем и в параллельном контуре при
резонансе.
Решение. Находим индуктивность из (4.196):
1
шр2С
= 338 мкгн.
145
Имея в виду, что по условию rp = Rt из (4.216), находим ак-
тивное сопротивление:
L _ 338-10"’ _ifiq
Г 7~С~ ~ 69- 10s-300-10"12 ~ lo.dOJK.
Ток генератора и напряжение на параллельном контуре при
резонансе
_j_ Гр — 2-69-10s = 1 «45-10 8 а — 1,45 ма.
Ц, = /р гр= 1,45-10~3-69-10s = 100 в.
Токи в каждой из ветвей контура
I и 100 пл о
/1о = . : ....--------------------= 94,2 Мй\
Р V г2 + (<ор1.)2 у 16,32 + 10602
/ар = С =100-2 к 500- 103-300-1(У12 = 94,2- 1СГ3 а = 94,2 ма.
Мощность, доставляемая генератором (Ргр), расходуемая в нем
(РВНут) и выделяемая в контуре (Рр),
Ргр = Е1р = 200-1,45-10"3 = 0,29 вт,
Рвнут = /р = (1,45-10-3)2-69-103 = 0,145 вт-,
Рр = /р гр = (1,45-10-3)2-69-103 = 0,145 вт.
4.34. Для задачи 4.33 определить абсолютное значение и от-
носительную величину полосы пропускания контура по напря-
жению.
Решение. Предварительно вычислим характеристическое
сопротивление и добротность контура:
р = 1/А = Ю60 ом, Q = -Ь = 65.
Искомые значения абсолютной и относительной величины по-
лосы пропускания контура по напряжению равны [см. формулы
(4.33) и (4.31)]
гр \ 500-103 /, . 69 \ 1Слпп
Rij = “65— + 69 ) = 15400
^ОО ~
15400 ____. п
500-103 ~0,031,
4.35. По данным задачи 4.33 вычислить указанные там вели-
чины, если э. д. с. генератора напряжения останется той же
(Е = 200 в), а вследствие расстройки его частота увеличится на
0,5%.
Указание. Разобрать решение задачи 4.29.
146
гене-
час-
час-
п ре-
4.36. Для контура и по данным задачи 4.33 (£ = 338 мкгн,
С = 300 пф, г =16,3 ом) построить частотные характеристики
для коэффициента передачи (к^ =£/:£) для трех значений ак-
тивного сопротивления, равных 0,5 г; г; 2г. Построение дать в
зависимости от отношения расстройки частоты питающего
ратора к резонансной частоте (построение сделать для
тот, отличающихся от резонансной на ± 10%); отношения
f
Тот (в пределах 0,9 4- 1,1); обобщенной расстройки ? (в
IV
делах ±4).
Построить также резонансную кривую неразветвленного
\ 7Р /
4.37. Найти резонансную частоту и неизвестный параметр
параллельного контура (см. рис. 4.4), выделяемую в нем мощ-
ность при резонансе по данным:
тока
1) Е = 150 в, 4- г2 = 22 ом, С ~ 300 пф,
Q = 60, = 35 ком;
2) £=100 в, L = 10,3 мкгн, С = 68 пф, Q = Ill, /?z =30 ком.
Для каждого из случаев вычислить абсолютное значение по-
лосы пропускания и относительную величину полосы пропуска-
ния по напряжению.
4.38. Определить резонансную частоту и эквивалентное со-
противление контура при резонансе нагруженного на сопротив-
ление г (рис. 4.14), исходя из того, что
Каковы резонансная частота и сопро-
тивление цепи при резонансе, если г гх?
Решение. Обозначим
Рис. 4.14
1
Комплексное сопротивление цепи, состоящей из параллельно
соединенных сопротивлений Zr и Z2,
1
Zt Z, _____________________г шр С (‘“р L ~ /г»)_________________
L / 1 1 \
Г1г + 7Г—/ шрС ~ '"р^ + п Шрс j
<47
Так как то в скобках числителя последнего вы-
ражения можно пренебречь вторым слагаемым по сравнению с
первым, тогда комплексное сопротивление примет вид
При резонансе комплексное сопротивление должно быть чис-
то вещественной величиной, поэтому мнимую компоненту знаме-
нателя следует приравнять нулю. Решая это уравнение относи-
тельно резонансной частоты, найдем
Написанное выражение для Z при резонансе равно
2р — Гр—
р2
, Р2 ’
ri + г
где
При г гх полученное выражение для сор примет вид
1
р 0 V LC
Заметим, что при г -> оо выражение для сопротивления при
к р2 .
резонансе обратится в гр = — , т. е. перейдет в формулу для
простого параллельного контура.
4.39. Параллельный контур, параметры которого/т, — 16,3 омг
L — 338 мкгн, С — 300 пф, подключен к генератору напряжения^
имеющему э. д. с. Е = 200 в и внутреннее сопротивление =
= 69 ком.
1. Вычислить эквивалентную добротность контура и полосу
его пропускания. Найти все токи и расходуемую в контуре мощ-
ность при резонансе.
2. Чему будут равны эквивалентная добротность контура и
полоса его пропускания, если его нагрузить на активное сопро-
тивление г = 138 ком (рис. 4.15, а)? Определить для данного
148
случая все токи, мощность, доставляемую генератором, расходу-
емую в контуре и в нагрузочном сопротивлении г при резонансе.
Решение. 1. Для заданного конту-
ра вычисляем
fo —
= 3,14 10е секг1\
^~= 500 кгц.
Р = = 1060 ом-, Q = =
1060
16,3
ro = Q2r, = 69 ком.
Эквивалентную добротность заданно-
го контура с учетом внутреннего сопро-
тивления генератора напряжения и поло-
су его пропускания определяем по фор-
мулам (4.31) и (4.33):
= 15 400 гц. ----~^а
Так как данные контура, э. д. с. fyH гП
генератора и его внутреннего сопротив- т т
ления те же, что и в задаче 4.33, то __________
в решении были уже вычислены требуе-
мые по условию /р, /1р, /2р, Рг.р, Рр.
2. Решение задачи в случае нагрузки ис’
контура на сопротивление г проще всего
может быть получено, если осуществить замену относительно
зажимов ab заданного генератора напряжения с Е и и
подключенным к нему параллельно сопротивлением г
(рис. 4.15,6) эквивалентным’ генератором напряжения с
э. д. с. Еэ и внутренним сопротивлением гэ (рис. 4.15, в). Для
определения Еэ отключим параллельный контур (рис. 4.15, б и в)
и вычислим напряжение холостого хода Uab, равное Е3 :
р _ _ 200» 138 _ । on
Гэ 69+138 100 в'
Сопротивление короткого замыкания, равное внутреннему
14*
сопротивлению эквивалентного генератора (рис. 4.15, а),
rRt 69-138 .с
Гз ~~ r+Ri ~~ 69+138 — 46 К0М-
Для схемы 4.15, в согласно формулам. (4.31) и (4.33) экви-
валентные добротность и полоса пропускания равны
Q' =-----5— = 26; S' = А. = 19200 гц.
3 1 + _гр_ Аи
г э
Следует отметить, что подключение к контуру сопротивления
г приводит к уменьшению эквивалентной добротности и увели-
чению полосы пропускания.
Рассчитаем ток в неразветвленной части заданной цепи, на-
пряжение на контуре, токи в ветвях контура и нагрузочном со-
противлении г, мощность, доставляемую генератором, ^выделяе-
мую в контуре и в сопротивлении г:
200
138-69
69 + 138+69
= 1,74 ма;
U'p = E—IpRi = 200—1,74-10s-69-103 = 80 в;
и'Р = 80
г? + («чД42 У 16.3а+1060»
= 75,5 ма;
= 75,5 ма;
<оС
ио
ZH.p = —р = О-58 ма;
р'г.Р = Е1Р = о-348 в«;
Р'= I'*R, = 0,209 вт;
внут р I 7 ’
Рк.р = = 0-093 вт;
рн.р = /н2₽'-= 0,046 вт.
Проверка показывает, что
Р' ___ р' I р' I Р'
гг.р гвнут * гк.р ' н.р’
4.40. Решить задачу 4.39, если принять, что нагрузочное со-
противление
а) г = и б) г = . Остальные данные те же, что и в за-
даче 4.39.
150
4.41. Параметры параллельного контура (рис. 4.16) имеют
следующие значения: гг = 1 ом, = 25 мкгн, Сг = 1600 пф,
г2 — 4 ом, Lz— 150 мкгн.
Найти частоты резонанса токов, напря-
жений и сопротивления цепи при этих час-
тотах. Чему равна добротность контура и
эквивалентная добротность при его под-
ключении к генератору с внутренним соп-
ротивлением Rt = 20 ком? Какова при этом
полоса пропускания контура? Определить
область частот, при которых модуль соп-
ротивления параллельного контура больше
10 ком. Определить эквивалентные ак-
тивное и реактивное сопротивления кон-
тура на границах этой области. При каком
ление контура при резонансе токов будет иметь максимально
возможное значение?
Решение. Частота резонанса токов (4.40)
Рис. 4.16
условии сопротив-
<о1 = --=========
V(L1 + L2)C
= 189-10® сек-1;
Д = = 3 • 10s гц = 300 кгц.
Сопротивление контура при этой частоте [формула (4.42)]
х2 (<OiL2)2
г — ---------- = --- = 16 КОМ.
Частота резонанса напряжений
= 5 • 10е сект1}
t 5-10е
/2 = — = <95 кгц.
ли
Сопротивление каждой из ветвей и всего параллельного кон-
тура при этой частоте
— ri +7 I w2 М = гх = 1 ом;
Z2 = rt + = (4 4- /750) ом;
Zx22
1 (4+/750)
5+/750
» 1 ОМ.
1S1
Добротность контура по формуле (4.41) и эквивалентная доб-
ротность по (4.31)
Q = (L1 + = 1.89-10i,-175-10-6 = 6бд
Q =-----------= 66,,fi = 36,8.
э е_ 1 , 16
Ri 20
Полосу пропускания найдем по (4.33):
q /р 300 О 1 Е
~ Qs 36JT ~ 8’ 5 кгц'
Для определения области частот, при которых модуль соп-
ротивления параллельного контура больше 10 ком, используем
формулу (4.27) для модуля полного сопротивления:
гэ (ш)= 10000
16 000
отсюда найдем обобщенную расстройку, Е= ± 1,25 и из (4.27)
с учетом величины 6 из (4.26) — соответствующую ей абсолют-
ную расстройку
л SOi+'a) 1,25-5 17nnn _!
Ла) 2(L14-L2) 2-175-10~в — 17900 cefc i
А „ 17 900
Д/ — — = 2850 гц.
£ Iw
Искомая область частот, при которой z3 (<о) > 10 ком опре-
деляется из неравенства
(Д — Д/) < f < (/i + Л/), или 297 150 гц < 302 850 гц.
Эквивалентные активное и реактивное сопротивления при
? = 1,25 найдем по (4.27):
^2- == 6,25 ком,
хэ =------1 ?2- £ = — 7,81 ком.
Наконец, вычислим максимально возможное сопротивление
параллельного контура при резонансе токов. Оно имеет место
тогда, когда вся индуктивность будет сосредоточена в одной из
ветвей, а емкость — в другой. В этом случае согласно формуле
(4.216)
L 175*10~6
гр = Тс = 5-1600-ю’12 = 21,8‘103 ом 21,8 к'0Мл
4.42. Для контура, изображенного на рис. 4.5, найти резо-
нансные частоты и вычислить его активное, реактивное и пол-
ное сопротивления при этих частотах. Даны: гх = 9,4 ом, Lt =
= 256 мкгн, Ci = 270 пф, га=12 ом, £2=660 мкгн, С2=430 пф.
152
4.43. Как надо перераспределить индуктивности L, и А2 меж-
ду отдельными ветвями контура задачи 4.41, чтобы при той же
частоте резонанса токов полное сопротивление параллельного
контура равнялось 12 ком?
Решение. Пусть при требуемых условиях («^ остается той
же) полная индуктивность контура L = L1 + Li = 175 мкгн рас-
пределится так, чтобы в левой ветви была индуктивность L', а
в правой — L" = L — L'. При этом полное сопротивление кон-
тура (4.42) при частоте резонанса токов
(<01 L")2
rp = 12 000 = • ^+f"- • |---------1
Отсюда ® Пи
.—--------- Ц ^2
_ V ГрОч + 'г) _ по и1С?н. 3 I ==
<°1 0 ?
L' = L — L" = 175 — 130 = 45 мкгн. Т .
4.44. Дан колебательный контур (рис. Рис 417
4.17) . Найти емкости Сг и С2 , если из-
вестно, что /1 = 5 ом, L± = 150 мкгн, сопро-
тивление контура при резонансе г = 20 ком и полная емкость кон-
/ сгс2 \
тура С = 500 пф ^ак надо включить элементы
этой схемы, чтобы сопротивление контура было максимально и
чему оно при этом равно?
4.45. Контур имеет в каждой ветви индуктивность, емкость
и активное сопротивление (см. рис. 4.5). Определить активную
и реактивную составляющие эквивалентного сопротивления кон-
тура для частоты, которая на 0,5 % отличается от частоты ре-
зонанса токов. Значения параметров контуров взять из задачи
4.42.
Указание. Решение задачи 4.45 начать с разбора задачи 4.29.
4.46. Определить значение сопротивления г2, при котором в
цепи (рис. 4.18, а) имеется резонанс напряжений на настоте
/=500 гц. Вычислить все токи. Построить векторную диаграмму.
Даны: гг = 2,7 ом, L = 286 мкгн, С = 318 мкф, U = 30 в.
Решение.
(dL = 2k • 500-286-10"6 = 0,9 ом;
1 1
О)С — 2п . 500 • 318 - 10“6 ~
л
•1 г2 —
Z3 = 2,7 + / 0,9 + =2,7 + /0,9 + 22 ''
г»—/* г24- 1
153
При резонансе реактивная составляющая сопротивления долж-
^.2
на быть равна нулю, т. е. 0,9 — 2 = 0, откуда г2 = 3 ом.
Г2+1
Рис. 4.18
При найденном значении г2 пол-
ное сопротивление цепи имеет толь-
ко вещественную составляющую:
I 3 о
« 32 _|-1
Ток в неразветвленной части
цепи
; U 30 1Л
/ = — = —- = Ю а,
1 Г3 3
Токи в параллельных ветвях
= 1— /3=3,16 е^1’35' а;
г2—/хс
3 п | П К _/18°25' „
= 10-^—т = 9-F/3 = 9,5 е а,
о 11
На рис. 4.18, б начерчена векторная диаграмма. На основе
расчета отложены векторы токов /2, /3 и /,» далее построены
векторы /2г2 == —и и = Itrt +
Наконец, построен вектор U, являющийся суммой векторов на-
пряжений на неразветвленном /1Z1 и на параллельном /2Z2 уча-
стках.
4.47. К зажимам цепи схемы рис. 4.18, а подведено напря-
жение U частотою /. Параметры цепи r19 L и С известны. Оп-
ределить, каким минимальным активным сопротивлением га
можно шунтировать конденсатор С, при котором еще может
иметь место резонанс. Чему в этом случае равен ток в нераз-
ветвленной части цепи?
4.48. Определить, при каком значении и характере сопро-
тивления Zi в цепи (рис. 4.19) показание ваттметра наиболь-
154
шее, если известно, что г2 = 8 ом, XL2 = 6 ом, г3 = 12 ом,
Хс = 5 ом, U = НО в. Чему равно показание ваттметра при
этом режиме? Построить векторную диаграмму.
Указание. Требуемое условие будет выполнено при резонансе напря-
жений .
Рис. 4.19 Рис. 4.20 Рис. 4.21
4.49. При каком реактивном сопротивлении Z3 (рис. 4.20)
приложенное напряжение U и ток /х совпадут по фазе? Даны:
Zx = (12 + /14) ом, Z2 = (10 + /15) ом. Для найденного значения
Z3 вычислить все токи и построить векторную диаграмму
при U — 120 в.
4.50. Для цепи схемы (рис. 4.21) найти емкостное сопротив-
ление хс, при котором имеется резонанс напряжений. Даны:
= 12 ом, г2 = 12 ом, хс = 16 ом, г3 = 20 ом. Вычислить для
этого режима токи и построить векторную диаграмму, если
£7 = 220 в/
4.51. При каком индуктивном сопротивлении xlb цепи (рис.
4.21) наступит резонанс напряжений? Вычислить токи и постро-
ить векторную диаграмму, если г\ = 1,5 ом, хс = 1,25 ом,
г2 = 3 ом, г3 ~ 5 ом, U = 120 в.
4.52. В неразветвленной части цепи (см. рис. 4.3) при ре-
зонансе проходит ток I = 8 а при напряжении U = 100 в. Соп-
ротивление конденсатора хс = 25 ом. Определить активное и
индуктивное сопротивления катушки.
4.53. В цепи (см. рис. 4.21) имеет место резонанс. В этом
режиме в ее неразветвленной части проходит ток / = 2,5 а при
U == ПО в. Известны rt = 24 ом, xl = 32 ом, г3 = 40 ом. Вы-
числить активное сопротивление г2 и емкостное сопротивление
Хс. Найти все токи.
4.54. К цепи схемы рис. 4.22 подведено напряжение £7=30 в.
Сопротивления элементов цепи: = 1 ом, хг = —3 ом, г2=4ом,
х2 = 8 ом, г3 = 4 ом, г4 = 3 ом. Найти величину и характер
реактивного сопротивления х4, чтобы в цепи был резонанс то-
ков при указанной частоте. В этом случае найти все токи и
построить векторную диаграмму.
155
У к а з а н и е. Мнимую часть комплекса полной проводимости надо при-
равнять нулю.
Рис. 4.22
Рис. 4.23
4.55. Определить частоты резонансов напряжений и токов в
цепи (см. рис. 4.20), если известны гг = 12 ом, = 6,31 мгн,
г2 = 3 ом, L2 = 0,29 мгн, С = 11,6 мкф.
4.56. Выяснить, при каком значении и характере реактив-
ного сопротивления х4 напряжение U и ток /, проходящий в
неразветвленной части цепи (рис. 4.23), совпадут по фазе. Со-
противления элементов: Zt = 12 ом, Z2 = (20 + /4) ом, Z3 =
= (6+/6)ол<, г4 = 8 ом, Z5 = — /6 ом.
Указание. Треугольник сопротивлений Zlt Z3t Zb преобразовать в эк-
вивалентную звезду и затем мнимую часть полного сопротивления цепи при-
равнять нулю.
ГЛАВА ПЯТАЯ
ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Приступая к расчету электрической цепи с взаимной ин-
дуктивностью, следует на схеме отметить стрелками произволь-
но выбираемые положительные направления токов в ветвях (и
контурных токов в случае применения метода контурных то-
ков). Кроме того, одинаковыми условными значками (буквами,
звездочками и т. п.) обозначить одноименные зажимы каждой
пары индуктивно связанных элементов цепи (катушек).
Одноименными считаются такие зажимы, при втекании
через которые выбранных положительных токов магнитные по-
токи самоиндукции и взаимной индукции складываются.
Заметим, что при наличии трех (или более) индуктивно свя-
занных катушек зажимы второй и третьей катушек, являющи-
еся одноименными по отношению к какому-либо зажиму пер-
вой катушки, могут в общем случае оказаться разноименными
относительно друг друга (пример в задаче 5.38). В таком слу-
чае каждая пара одноименных зажимов отмечается особыми
значками.
При составлении уравнений второго закона Кирхгофа с помо-
щью комплексных чисел jвеличины э. д. с. взаимной
индукции Eks=—j&MksIs обычно из части уравнения, содер-
жащей э. д. с., переносятся с переменной знака в другую часть,
содержащую падения напряжения, в виде членов типа ±.Uks ==
* “Ё s == i zks is.
Верхние (положительные) знаки принимаются тогда, когда
при обходе контура, содержащего ветвь k, направление обхо-
да этой ветви и направление положительного тока s относи-
тельно одноименных зажимов одинаково; в противном случае
принимаются отрицательные знаки.
Здесь Eks — комплексная э. д. с. взаимной индукции в Л-й
катушке, определяемая током в s-й катушке;
157
Mks — взаимная индуктивность этих катушек;
со — угловая частота;
Zks == i®Mks — сопротивление взаимной индукции.
Указанное правило разметки зажимов и выбора знаков спра-
ведливо, если М считать всегда положительным.
2. При последовательном соединении двух индуктивно свя-
занных катушек эквивалентное комплексное сопротивление и
эквивалентная индуктивность определяются по формулам
L = Lx 4~ £2 ± 2Л112,
где Z12 — /(оЛ412.
Знак «плюс» соответствует согласному включению катушек,
а знак «минус» — встречному.
Примеры в задачах 5.1, 5.2 и 5.8.
3. При параллельном соединении двух индуктивно связан-
ных катушек эквивалентное комплексное сопротивление
- zf2
Z14~^2 -F2Z12 ’
а эквивалентная индуктивность (при условии, что активные со-
противления катушек равны нулю).
т _ ЬгЬ2 - М2
Li+L2=p2M ‘
(5-4)
Знак «минус» в знаменателе уравнений (5.3) и (5.4) ставит-
ся при согласном включении, а знак «плюс» — при встречном.
Примеры в задачах 5.10, 5.11.
Рис. 5.1
4. Уравнения второго закона Кирхго-
фа для двух индуктивно связанных
контуров (рис. 5.1) имеют вид
/ц/i Z12/2 — 6/х;
*
^22^2 ^21Л
где Zxx = Zx + >LX = Zx + /хх = лхх +
+ jx'ii + № = ''и + />iiJ
Z22 = z2 -|- >L2 2h = Z2 + jx2 + ZH = Г22 + j%22 + jx2 4~
+ '’h + /Xi ~ r22 + jX22>
ZX2 = Z21 = /(oTU = /xX2.
158
Схема рис. 5.1. может быть заменена эквивалентной (рис.
5.2), содержащей вносимые в первый контур активное и ре-
активное сопротивления, соответственно равные
5. Развязка индуктивных связей. Цепи схем рис. 5.3, а и б,
соответственно эквивалентны цепям рис. 5.3, в, г и д, не со-
держащим индуктивные связи. Поэтому, например, при анали-
зе схемы рис. 5.1 достаточно исследовать схему рис. 5.3, в.
Примеры в задачах 5.18,5.19,5.33 и 5.34.
6. Индуктивно связанные ре-
зонансные контуры (рис. 5.4).
Собственное комплексное соп-
ротивление первого контура
Zi = Г1 + /хр где Xj == cdLj —
1
----------реактивное сопротив-
ление первого контура. Собствен-
Рис 54 ное комплексное сопротивление
ис’ ’ второго контура Z2 = г2 + /х2 с
j реактивным сопротивлением
x2=(dL2---Комплексное сопротивление связи Z12= /о>Л1=/х12.
15»
Действующие значения токов в связанных контурах
(5.10)
(5.9)
^12
где гвн1 = —— г2 — вносимое активное сопротивление в первый
22 контур;
х2
х12
хвн1 =------— х2 — вносимое реактивное сопротивление в пер-
г2 вый контур;
х2
гвн2 = —ri — вносимое активное сопротивление во второй
*1 контур;
*12
хвн2 ==-----—Xi — вносимое реактивное сопротивление во вто-
рой контур.
7. Резонансы в связанных контурах (см. рис. 5.4):
а) Первый частный резонанс достигается при изме-
нении параметров первого контура при неизменных параметрах
второго контура и постоянном коэффициенте связи #. Условие
этого резонанса:
х2
Х-£э == Х1 *^вн1 == Х1 2 *^2 (5. Н)
г2
при этом вторичный ток достигает максимального значения:
I __
* 21 max — Т7Т ГТ"
(5.12)
б) Второй частный резонанс получается подбором
параметров второго контура при неизменных параметрах пер-
вого контура и постоянном А. Этот резонанс имеет место при
х2
Х2э := х% ~Ь' ^вн2 == Х2 2 *^1 (5.13)
г1
В этом случае ток во вторичном контуре достигает макси-
мума, равного
^211 max = / Л г • (5.14)
21(^2 + гвнг) 7
в) Сложный резонанс достигается одновременным из-
менением параметров одного из контуров и подбором оптималь-
ного коэффициента связи k.
160
При настройке изменением элементов первого контура [дол-
жно соблюдаться условие (5.11)] оптимальное значение сопро-
тивления связи:
^12 опт == ^2 1/ 7 • (5.15)
г <2
При настройке вариацией параметров второго контура [дол-
жно соблюдаться условие (5.13)] оптимальному коэффициенту
связи соответствует сопротивление связи:
Х^опт = Z, . (5.16)
В обоих случаях — (5.15) и (5.16) — ток во вторичном кон-
туре достигает максимального возможного значения («максимум—
максиморум»), равного
'““та- (5Л7)
г) полный резонанс имеет место при резонансной на-
стройке порознь каждого из контуров:
(5.18)
и при подборе оптимальной связи между контурами &опт=-уг=- ,
У QiQz
которой соответствует сопротивление связи:
-^12опт = ^1^*2* (5.19)
При полном резонансе вторичный ток имеет такое же значе-
ние, как и при сложном резонансе (см. ф-лу 5.17).
8. Резонансные характеристики связанных контуров. Вход-
ное сопротивление системы связанных контуров (рис. 5.4) опре-
деляется формулой
х\2
х2
х\2
'2
2
В случае, когда оба контура—первый и второй—порознь на-
строены в резонанс на близкие частоты, соответственно ш01 и
<оО2, при небольших расстройках До^ = ш — <o0i Шо1 и Дш2 ~
= ш — %2 шо2 входное сопротивление системы связанных кон-
туров равно
Z (/(о) = г1э 4- /х1э « гх
где
(5.21)
— обобщенная расстройка первого кон-
тура;
6 Заказ № 624
161
L = — ss 20» — обобщенная расстройка второго кон-
Г2 (О02
тура;
А = — фактор связи.
У г1гг
Действующее значение вторичного тока и модуль коэффи-
циента передачи (амплитудно-частотная характеристика) при
одинаковых резонансных частотах контуров определяются вы-
ражениями
______________EjA_______________
/(^ + i-e1£2)2 + (£i + w2 ’
(5.22)
k„ = =--------------- A . (5.23)
«c2 ]/7Г^ /(Л2 + 1-$i£2)2+ (5i +$2)2
В случае, когда каждый из контуров настроен порознь на
частоту о>0, т. е. ——•— = <оО1 = соо = соО2 = —» то разли-
У LiCx УТ^Съ
чают случаи связи больше и ниже критической. Критической
связи соответствует значение
* = *кр = |Z . (5-24)
, 1 , 1
где d, = 75— и d2 = 75----затухания первого и второго контуров.
41 42
При слабой связи k < &кр резонансная кривая тока /2 имеет
один максимум. При сильной связи, большей критической
(£ > &кр), резонансная кривая тока /2 имеет два максимума,
наступающих при частотах связи ш, и ши (ш, < ш0 < шп ):
При небольших расстройках (Дю = ш — ш0 <оо) системы оди-
наковых связанных контуров = Е2 = В действующее значение
вторичного тока и модуль коэффициента передачи
(5.22а)
k
___________Е1А____
г у (А2 + 1 — 52)2 + 45s
(5.23а)
162
Полоса пропускания двух идентичных («*01 = а>02 = <»#,
d = d2 = d) индуктивно связанных контуров на уровне—
У 2
«0,707 зависит не только от затухания контуров d, но и от
коэффициента связи k.
При связи ниже критической (k < d) и при идентичных кон-
турах относительная полоса пропускания
При связи, равной критической (k = d), и при идентичных
контурах относительная полоса пропускания
S0=K2"d. (5.27)
При связи выше критической и при идентичных контурах отно-
сительная полоса пропускания.
s° — d d j 1 +2( d У*
Максимальная полоса
пропускания имеет место при
связи, обеспечивающей в
точке нулевой расстройки ток,
равный 0,707 /мм(рис. 5.5).
При этом k — 2,41 d, а
Somax = 3,ld. (5.29)
9. Энергетические соот-
ношения в индуктивно свя-
занных контурах.
Мощности, выделяемые
в каждом из двух связан-
ных контуров, равны
Рис. 5.5
К. п. д. системы двух связанных контуров находится как
отношение мощности второго контура Ра ко всей затраченной
мощности Р = Рх Р2, т. е.
(5.31)
6’
163
К. п. д. вычисляется по формуле
*1 = Т^7—• (5.32)
При настроенных первичном и вторичном контурах (хг = О,
х2 = 0), но при любом коэффициенте связи k к. п. д. опреде-
ляется по формуле
’I - <5'33»
При полном резонансе мощность во вторичном контуре дос-
тигает максимального значения, равного
Р2мм = Лмм = • (5.34)
При этом к. п. д. составляет 50%.
УПРАЖНЕНИЯ И ЗАДАЧИ
5.1. Определить
цепи (рис. 5.6,а),
эквивалентное комплексное сопротивление
ток и напряжения между точками а и 6,
end, если известны U= 130 в,
i\ = 2 ом, г2 =3 ом, =
= 3 ом, o)L2 = 7 ом, о)7И = 1 ом.
Построить векторную диаграмму.
Решение. Проследив по рис.
5.6, а прохождение тока по вит-
кам обеих катушек, видим, что в
каждой из них потоки самоиндук-
ции и взаимной индукции дей-
ствуют попутно. Таким образом,
Рис. 5.6
катушки включены согласно.
Заданная цепь может быть пред-
ставлена схемой, показанной на
рис. 5.6,6. Составим для нее урав-
нение второго закона Кирхгофа:
(7 — Zi 7 + z12i -j- z2 7 + zj,
где
= G + /о>£1 = (2 + /3) ом\
Z2 = r2 + /o)L2 = (3 + /7) ом\
Z12 = Z21 = /о)Л4 = /1 ом.
Эквивалентное комплексное сопротивление цепи
Z = Zj + Z2 + 2Z12 = 5 + /12 = 13е/67 20 ом.
Искомый комплексный ток
130
= ю е-/67°20'
Комплексные напряжения между точками а и Ь, с и d рав-
ны.
• • —/3°50'
Uab = I{ZX + Z12) = 44,7 е в;
• • / 2°5'
Ucd ~I(Z2+ Z21) = 85,5 е в.
На рис. 5.6, в представлена векторная диаграмма. По ве-
щественной оси отложен вектор напряжения, от него в сторо-
ну отставания на 67°20' направлен вектор тока, затем отложе-
ны векторы падения напряжения в каждой из катушек.
5.2. Для цепи, изображенной на рис. 5.7, а, найти ток и
напряжение между точками а и &, с и d. Даны:
1\ = 2 <ж, г2 = 4 ож, = 6 ом, = 4 ом, <пЛ1 = 1 ом.
К цепи приложено напряжение U = 100 в. Построить вектор-
ную диаграмму.
Рис. 5.7
Решение. Соединение катушек встречное. Для эквива-
лентной схемы (рис. 5.7,6) запишем уравнение второго закона
Кирхгофа:
165
Искомый ток и напряжения
, „ —/53°10'
10 е
. • / 15°5'
U ab = (^1 ^12) 53,9 в в\
— / 16°20'
(/^ = (Z2-Z12)Z = 50e в.
На рис. 5.7, в начерчена векторная диаграмма.
5.3. К цепи (см. рис. 5.7,а) приложено напряжение U =
= 100 в. Найти ток и напряжения LLb и Ucd, а также построить
векторную диаграмму. Даны: ^ = 30 ом, г2 — 50 ом,
= 120 ом, wL2 = 30 ом. Коэффициент связи k = 0,75.
Замечание. По результатам решения обратить внимание на то, что
напряжение на одной из катушек отстает по фазе от тока.
Рис. 5.8
5.4. Вычислить ток и напряжение между
точками а и Ь, если гх = 5 ом, г2 = 3 ом,
(oL. = 4 ом, o)L2 = 2 ом, о)Л1 = 2 ом, -U = 4 ом,
*
а приложенное к цепи (рис. 5.8) напряжение
U = 100 в. Построить векторную диаграмму.
5.5. Чему равно напряжение на конден-
саторе емкостью С = 43 мкф, включенном
между двумя индуктивно связанными ка-
тушками, параметры которых гг = 10,5 ом, L1 = 22 мгн, г2=
= 9,2 ом, L2~ 18 мгн, М = 6,5 мгн? К цепи приложено нап-
ряжение U = 100 в (рис. 5.9). Частота переменного тока f =
= 200 гц. Построить векторную диаграмму.
Рис. 5.9
Рис. 5.10
5.6. Вольтметр и амперметр, включенные в цепь (рис. 5.10),
показали U = 88 мв, I = 2,2 ма. Чему равна емкость С, если
гг = 9,5 ом, u)L1 = 14,6 ом, г2= 11,6 ом, ш£2 = 17 ом, =
= 3,2 ом? Частота тока f = 50 кгц.
Решение. Из уравнения закона Ома
166
Модуль полного сопротивления определим из показаний при-
- и 88.10-» лп с
боров как отношение -г- = 2 2.io-s = 40 ом. Его можно так-
же найти из выражения
г =
Подставляя числовые значения, будем иметь
(г1 -4- г^)2 -f-1 -J- 2wM —
Решая это уравнение, получим
-тг ~ 4 ом или Дг = 72 ом,
о)С cog
и, наконец, С — 0,796 мкф или С = 0,0442 мкф.
5.7. Для цепи предыдущей задачи вычислить коэффициент
связи k, если U = 85 мв, I =1,7 ма, гг = 16 ом, u>L1 =26 ом,
г2 = 14 ом, wL2 = 28 ом, 4у = 20 ом.
5.8. Для определения взаимной индуктивности двух кату-
шек их соединили последовательно и подключили к генерато-
ру; были измерены напряжение, ток и мощность в двух слу-
чаях: в первом — зажим 2 первой катушки был соединен с за-
жимом <3 второй катушки (рис. 5.11,а), во втором — зажим 2
Рис. 5.11
первой катушки был соединен с зажимом 4 второй катушки
(рис. 5.11,6). Показания приборов при первом опыте: £71=120в,
4 = 12 а, Рг = 864 вт-, при втором — U2 = 120 в, 12 = 10 а,
Р2 = 600 вт.
Чему равна взаимная индуктивность катушек, если частота
переменного тока f = 50 гц? Выяснить в какой из двух схем
соединение катушек соответствует согласному включению.
Решение. По данным первого опыта найдем полное соп-
ротивление схемы zr , ее активное г, и реактивное сопротивле-
ния х, :
zr = = 10 ом; rf = — = 6 ом; z\ —г, = 8 ом
1 ч
167
Аналогично из данных второго опыта
гп = = 12 ом\ гп = = 6 ом\ хп = ]/" Zjj— Tjj = 10,4 ом.
2 ^2
Равенство полученных значений активного сопротивления
rj == гп свидетельствует об отсутствии ошибок измерения. Ре-
активное же сопротивление во втором опыте оказалось больше,
чем в первом (хп > ). Это указывает на то, что вторая схе-
ма соответствует согласному включению, а первая — встреч-
ному.
Искомая взаимная индуктивность найдется из уравнений:
wLj + + 2шД4 = хп и oLj + — 2«)Л1 = xz .
Вычитая одно уравнение из другого, получим
х1Х — х. 10,4 — 8
М = -А—- = -л о = 1.91 мгн.
4а) 4-2гс50
5.9. При включении одной первой катушки (рис. 5.12,а) при-
боры показали Ur = 52 в, 1г = 4 а, Р1 = 80 вт, а при включе-
нии только одной второй катушки (рис. 5.12,6) U2 = 52 в, /2 =
= 4,16 а, Р2 = 60,5 вт. При включении же катушек по схеме
рис. 5.12, в приборы показали U = 76 в, I = 4 а.
Рис. 5.12
Выяснить, включены катушки согласно или встречно и под-
считать взаимную индуктивность М, если частота переменного
тока f = 50 гц.
5.10. Даны две параллельно соединенные катушки (рис.
5.13,а), параметры которых i\ = 20 ом, mL1= 10 ом, г2 — 20 ом,
wL2 = 20 ом и сопротивление взаимной индукции соЛ4 = 10 ом.
К цепи подведено напряжение U = 150 в. Определить все токи
и построить векторную диаграмму. Определить показание каж-
дого ваттметра и мощности тепловых потерь в каждой из вет-
вей.
Решение. Из рис. 5.13, а видно, что катушки соединены
согласно, так как каждую из них магнитные потоки само- и
взаимной индукции про-низывают в одном и том же направле-
нии. На рис. 5.13,6 начерчена схема заданной цепи.
168
Введем обозначения:
Z-^ = гj “I- /о)/^ == (20 /10) ол^:
Z2 = r2 + /0)L2 = (20 + /20) ом-, ZM = j<»M = /10 ом.
По законам Кирхгофа
U = I1Zl +I2ZM; (1)
u = i2z2+i1zM-, (2)
i = 4 + z2. (3)
Решив совместно уравнения (1) и (2), приняв U = U =
= 150 в, получим
j у Z2~^2. =4-/3=5е-/36050, а;
1 z.z^-zh
i.=u Z1-Z^ = 2-i4^ 4,47 а-'63’30' а;
ZtZ2-Z2M
— I 49’25'
/=/^4=6-/7 = 9,22 6 а.
169
На рис. 5.13, в по уравнениям (1)-г-(3) построена векторная
диаграмма. По вещественной оси отложен вектор U . На осно-
ве расчетов построены векторы /2 и I. Затем на основании
уравнения (1) построены векторы /х rv 7Х/ш£1,/2/<оЛ1; их сумма
дает вектор U. Аналогично построены векторы по уравнению (2).
Определяем показания каждого из ваттметров:
Р, = Re [С/ 7J = Re [150(4 + /3)] = 150-4 = 600
вт;
Р2 —' Re
= Re[150(2 + /4)] = 150-2 = 300 вт;
Р = Re \ui = Re [150(6 + /7)] = 150-6 = 900 вт.
Тепловые потери в первой и второй ветвях соответственно
равны
APi = = 52-20 = 500 вт;
&Р2 = = 4,472-20 = 400 вт,
2
а их сумма ЛРг + ЛР2 равна мощности Р, поступающей во всю
рассматриваемую цепь (900 вт).
Активная мощность Р± = 600 вт, потребляемая первой вет-
вью от источника энергии, частично расходуется на тепловые
потери в этой ветви (ДРХ = 500 вт) и остальная часть (600 —
— 500= 100 вт) поступает в магнитное поле, откуда вследст-
вие взаимной индукции передается во вторую катушку. Пока-
жем это.
Напряжение взаимной индукции на первой катушке
4 = /10 (2 - /4) = (40 + /20) в,
а мощность, передаваемая полем из первой катушки во вторую.
Рш = Р.м А ] = К40 + /20)(4 + /3)1 = 40-4-20-3= 100 вт.
Аналогично
= Zm А = /1° (4 - /3) = (30 + /40) в;
• *
V2М
?2М ~~
= Re [(30 + /40)-(2 + /4)] = 30-2 — 40-4=
= — 100 вт.
5.11. Вычислить токи и построить векторную диаграмму для
цепи схемы (рис. 5.14,а), параметры которой равны = (20 4-
+ /10) ом, Z2 = (20 + /20) ом, ZM = /10 ом. Напряжение U =
= 150 в.
170
Указание. Катушки цепи, изображенной на рис. 5.14,6, соединены
встречно. При указанных на схеме положительных направлениях токов система
уравнений Кирхгофа будет
u^z,- i,z^, i = i, +/a.
По результатам расчетов на рис. 5.14,в построена векторная
диаграмма.
а)
Рис. 5.14
5.12. Вычислить токи и
цепи схемы (рис. 5.14, а),
U = 120 в. Zx=(5+/10) ом,
построить векторную диаграмму для
к которой подведено напряжение
Z2—(100+/20) ом, Zm=/10 ом.
Замечание. Получив результат решения задачи обратить внимание на
то, что ток в одной из ветвей опережает приложенное напряжение.
5.13. Подобрать емкость С так, чтобы
в цепи схемы (рис. 5.15) при угловой ча- .---|L-____
стоте <п = 5-105 сект1 был резонанс напря- I ।—X— .
жений. Параметры цепи: гг = 100 ом, Lt= I* г
= 0,1 мгн, г2 « 100 ом, L2 = 0,2 мгн, М = и 'П ц2
= 0,1 мгн. При найденной емкости опре- рг
делить токи и построить векторную диаграм- ? •
му, если U = 75 мв. I-----------
5.14. Решить предыдущую задачу в слу- Рис- 5Л5
чае встречного включения катушек.
5.15. При какой емкости С, включенной в цепь (рис. 5.16,а)
будет резонанс токов на частоте / » 104 гц> Параметры цепи:
= 318 мкгн, L2= 159 мкгн, М= 124 мкгн. Вычислить токи
и построить векторную диаграмму при U = 40 мв.
171
Решение. Обозначим
По законам Кирхгофа
а)
Совместное решение этих
уравнений даст
Zx Z2 - z|2 ’
(1)
(3)
”4
Рис. 5.16
ния комплексных сопротивлений
приравнивая его нулю, найдем
Так как цепь содержит
только реактивные элемен-
ты, то условие резонанса то-
ков сводится к тому, что
ток / в неразветвленной час-
ти цепи должен равняться
нулю. Подставляя значе-
в числитель формулы (3) и
+ L2 — 2M) (2^.104)2(318+ 159 —2-124). IQ-6 1,1 МК$'
При этом необходимо проверить, что знаменатель не обращает-
ся в нуль. В данном случае это условие удовлетворено.
Расчет токов осуществляется по уравнениям (1) и (2):
/1== / 17,6-10-3 а = /17,6 ма; /а = — / 17,6-10’3 а = — /17,6 ма.
На рис. 5.16,6 приведена векторная диаграмма токов и на-
пряжений.
5.16. Решить предыдущую задачу при встречном включении
катушек.
172
5.17. К первичной обмотке трансформатора без стального
сердечника подведено напряжение Ur = 120 в (рис. 5.17, а). Оп-
ределить напряжение (72 на
Zx= гх4- /о)£1= (10 + j 42) ом,
Z2~ (1^ + /70) ом,
' z = г — = (5—/ 10)<ш,
ZM = jwM = j 20 ом.
Построить векторную ди-
аграмму.
Решение. Система
уравнений второго закона
Кирхгофа для этого случая
будет
Л z,-i,zu=Ui, (1)
Z2(Z2+Z)-/1ZA1 = 0. (2)
Решая эти два уравне-
ния, получим
7* 1 ’О О ~/71°35'
/х = 1 — ] 3 = 3,16 е а\
. __ / txo°in'
/2 = 0,6 —/0,8 = 1е а.
Напряжение на сопроти-
влении Z
i/2 = /2Z = —5 — j 10 =
Векторная диаграмма при-
ведена на рис. 5.17,6. По-
рядок ее построения таков:
на основе расчетов отложе-
ны векторы токов Iv 12, да-д
лее, в соответствии с урав-
нением (1), векторы 11г1,
Л — К j®M, их сумма
дает вектор U, Аналогично
нагрузочном сопротивлении Z при
а)
г' м гг
---1 М |--Г"^-—у
Рис. 5.17
Рис. 5.18
построены векторы по урав-
нению (2).
5.18. Во вторичной обмотке трансформатора без стального
сердечника проходит ток /2 = 0,5 а (рис. 5.18, а). Коэффициент
173
связи между первой и второй обмотками k = 0,5. Вторичная
обмотка трансформатора замкнута на конденсатор емкостью С.
Сопротивления элементов цепи = 60 ом, wLj = 80 ом, г2 = 90 ом,
<о£« = 45 ом и -L- = 210 ом,
А (ОС
Определить ток в первичной обмотке и приложенное к
ней напряжение U,. Построить векторную диаграмму.
j-ч t~\ f h/i. t>
Решение. Зная, что k = —== —----------------_— , найдем
У «Li O)L2
шУИ « k У <»£., u>Lt = 0,5 j/80-45 == 30 ом.
Из уравнения второго закона Кирхгофа для вторичного
контура
2 d)C
/2 —/о>Л1 /х = О
определим ток в первичной обмотке:
1 — х2
Л __ ... о , л — / 151°30'
=— 2,75 — /1,5= 3,14 е
/о>М
Приложенное к цепи напряжение найдем из уравнения вто-
рого закона Кирхгофа, составленного для первичного контура:
. г . ; . Г ЛИГ .ПАГГ “ /97°50*
м
&
0
&
0
с
Рис. 5.19
0'1= V1 + ‘г = — 40 — 1 = о2ое в.
У-
Та же задача может быть решена и путем замены задан-
ной схемы другой, ей эквивалентной (рис. 5.18, б), в соответ-
ствии с рис. 5.3. Векторная диаграмма построена на рис. 5.18, в.
5.19. Вблизи колебательного кон-
тура без потерь 1 расположена корот-
козамкнутая цепь 2 (рис. 5.19, а). Чему
равна резонансная частота, если Лх =
= 9 мгн, Л2 = 4 мгн, М = 2 мгн,
С = 0,2 мкф?
Решение. На рис. 5.19,6 пред-
ставлена схема, эквивалентная задан-
ной (см. рис. 5.3).
Резонанс токов наступит, когда
реактивная проводимость равна нулю.
Вычисляем ее, начиная с определе-
ния эквивалентного комплексного со-
противления двух параллельных вет-
к точкам b и с:
— /шоМ foo (L2 М) t
be
подключенных
вей,
2
be
joi0M (L2 — М)
174
_ /«>„ (Li La - Л12).
~ L2
^9 = Yad + Yac = /4^ + ju>0 (Li ц _ = °>
ИЛИ
Ш0 C = Шо(£1 ц_М2) •
отсюда
ш0 = л/~______£*_____. = 2,5-10* сект1.
° V C(L,Lt- м2)
5.20. Какое сопротивление Z„ следу- _____ м t
ет подключить ко вторичной обмотке 0 1х"Ч.£* |
трансформатора без стального сердеч- . б П НГг п
ника (рис. 5.20), чтобы ток на входе пер- X X "и
вичной катушки был равен 15 а и сов- |
падал по фазе с первичным напряжением 0 ~
иг = 120 в? Даны: гх = 2 ом, = 8 ом, ис‘ ’
г2 = 3 ом, o)L2 = 15 ом, ч>М = 10 ом.
5.21. К цепи, изображенной на рис. 5.21, а, подключено на-
пряжение U = НО в. Параметры цепи: гх = 20 ом, г2 — 15 ом,
г3 = 10 ом, = 0,4 гн, L3 — 0,3 гн, М = 0,2 гн. Частота тока
f = 50 гц. Найти все токи.
Рис. 5.21
Решение. Выбрав положительные направления токов, как
это указано на рис. 5.21, а, изобразим заданную цепь схемой,
показанной на рис. 5.21,6.
175
Для решения задачи воспользуемся методом контурных то-
ков. В соответствии с выбранными направлениями контур-
ных токов и /п по законам Кирхгофа
== ZnZj £37ц Z12 Zjj; (1)
О = Z22 Zn Z3 7j . (2)
Здесь
Zn = fj -f- r3 + /a)£1 = (30 + j 126) om\
Z22 == + гз + = (25 + j94,2) ом;
Z3 = r3= 10 ом; Z12 = j^M = /62,8 ом.
Решая совместно уравнение (1) и (2), получим
• i 75° 10'
;__________UZtt __ 110-97,5/ , 9 , - i 71’40' _
1 — (Z3+Zi2)a __8630e~ ^38
= (0,39-/1,18) a-,
: _ U (Z3 + ZI2) _ 110(10 + ? 62,8) __
II - Zu Z22 - (Z3 + Z12)a _ 8630 e- i 33’10' -
________ j 65°50r
= 0,81 e =(0,33 —/0,74) a.
Искомые токи в отдельных ветвях
; ; . -/71’40' ; ; Л -/65’50'
/,=/,= 1,24 е а\ /п = 0,81 е а;
. . . _ f82°90'
/3 = _ 1и = 0,06 — / 0,44 = 0,444 е а.
На рис. 5.21, в построена векторная диаграмма.
5.22. Вычислить токи, про-
ходящие в цепи, изображенной
на рис. 5.22. Числовые значе-
ния активных и реактивных
сопротивлений и приложенного
напряжения те же, что и в пре-
дыдущей задаче.
Рис. 5.23
176
5.23. Найти емкостное сопротивление хс, при котором в
цепи (рис. 5.23, а) наступит резонанс напряжений, если извест-
ны = 30 ом, c»Li = 20 ом, г2 = 50 ом, &L2 = 10 ом, ==
= 10 ом, г3 = 50 ом. При найденном хс определить все токи и
построить векторную диаграмму, если U = 120 в.
Решение. Обозначим Zx = (гх 4- j^L^) = (30 + / 20) ом;
Z2 = (г2 + >^2) = (50 + j Ю) ом; Z3 = гз — jxc = (50 — jxc);
Z12 = /шЛ4 = /10 ом.
Наметим ход решения задачи. Для того чтобы в цепи имел-
ся резонанс напряжений, надо, чтобы приложенное напряжение
U и ток 1Г в ее неразветвленной части совпадали по фазе. По-
; й
этому найдем lt и вычислим отношение —, которое должно
Л
быть вещественной величиной.
Для определения токов составим уравнения по законам Кирх-
гофа:
[7 = Z^ 4~ Z3I3 — Z12/2; (1)
0 = Z12/1 4~ Z3/3 Z2I2, \ (2)
4 = А+ 4 (3)
Решая их, находим
/____________________________^(Z2 + Z3)_______. (лх
11 ” (Z, + Z3)(Z2 + Z3) - (Z3 + Z12)2 ’
__ __________U(Z2 - Z12)__________
~ (Zj + Z3)(Z2 + Z3) - (Z3 + z12)2 *
(5)
Из уравнения (4) определим отношение — (входное соп-
11
ротивление цепи ZBX):
U у ______ZiZ3 4~ ZXZ2 4“ Z2Z3 2Z12Z3 — Z|2
• == ZBX == 717 •
Ц ^-2
Подставив числовые значения всех сопротивлений, выделим
вещественную и мнимую составляющие:
7 (30 4- /20)(50 - jxc) + (30 + /20)(50 + /10) f
Zbx 100 4- /(10 — хс) +
(50 4- /10) (50 — jxc) — /20(50 — jxc) 4-100
J 100+ /(10 —xc) ~
(80ж£ — 1600xc + 558 000) + /(10x^ — 2700xc + 126 000)
10 000+ (10 —xc)8 • (7)
177
В полученном выражении коэффициент при мнимой части
приравняем нулю:
10 х2с — 2700 хс + 126 000 = 0.
Решая это квадратное уравнение, получим
ха =210 ом', Хс2 = 60 ом.
Определим токи.
При Xci =210 ом вещественная часть входного сопротивле-
ния по (7)
Zbx 1о 000 ч- (10 — 210)2 ~ '° ом>
а ток
По формуле (5) ток
/2 = (1,44 —/0,32)а,
и, наконец, комплексный ток
/8 = Л — /2 = 1,6 —(1,44 —/0,32) == (0,16 + /0,32)а.
При Хс2 = 60 ом вещественная часть входного сопротивления
равна 60 ом, а токи /х == 2 а\ /2 = (1,2 — /0,4)а; /3 — (0,8 + /0,4)а.
На рис. 5.23, б дана векторная диаграмма напряжений и то-
ков, построенная для хсч = 60 ом на основании уравнений (1)-?(3).
5.24. Решить задачу 5.23 при условии: проводники, подхо-
дящие к зажимам второй катушки (г2, Л2), поменять местами, т. е.
считать, что звездочка на схеме рис. 5.23 а стоит не справа, а
слева. Параметры цепи: гх = г2 = 10 ом, (оЦ = = 8 ом, <»№=
= 2 ом, г3 = 0, U = 100 в.
5.25. Для цепи рис. 5.24, а определить емкостное сопротив-
ление Хс, при котором наступит резонанс токов. Сопротивле-
ния элементов цепи Zx =>= (20 + /34) ом, Z2 = (12 X /10) ом, ZX2=
= /6 ом, Z3 = —jxc.
При найденном значении емкостного сопротивления найти
все токи и построить векторную диаграмму, если приложенное
к цепи напряжение U = 200 в. /
Указание. Следует сначала определить все токи, а затем напряжение
(jab на участке ab. Резонанс токов будет при условии совпадения по фазе на-
пряжения Uab и тока /х.
По результатам вычислений должно быть получено следующее выражение
отношения:
Мнимую часть этого отношения приравниваем нулю, откуда находим два
значения емкостного сопротивления хс — 19 ом и хс = 0. Второе значение
178
хс == 0 (короткое замыкание) отбрасываем, как не удовлетворяющее требова-
ниям задачи.
По результатам расчетов для = 19 ом на рис. 5.24, б построена век-
торная диаграмма.
Рис. 5.24
5.26. В цепи схемы (рис. 5.24,а) поменять местами провод-
ники, подходящие к зажимам второй катушки Z2, т. е. считать,
что у нее звездочка на схеме стоит не слева, а справа. Определить
Хс, при котором будет резонанс токов, если
Zj = (8 + /6) ом, Z2 == (4 4~ /6) ом, Z12 == —/2 ом.
Вычислить все токи при U = 120 в.
5.27. При каком коэффициенте связи k в цепи (рис. 5.24,а)
будет резонанс токов? Даны: гг = 4 ом, == 6 ом, г2 = 4 ом,
х2 = 6 ом и хс = 8 ом. Для указанного случая вычислить токи
и построить векторную диаграмму, если U= 115 в.
5.28. К цепи схемы (рис. 5.25, а) приложено напряжение f/=
== 250 мв. Найти токи и определить напряжение между точка-
ми а и Ь схемы. Сопротивления л = 50 ом, шЛ = 20 ом, ш£2=
1
« 20 ом, o>L3 = 20 ом = 50 ом, шМ12 = 10 ом, шМ23 = 10 ом.
Построить векторную диаграмму напряжений и токов. Задачу
решить методом контурных токов.
179
Решение. Обозначим
Zj = f\ + /(oLx = (50 + /20) ом; Z2 == /ш£2 = /20 ом;
Рис. 5.25
Пользуясь введенными обозначениями, составим уравнения
контурных токов:
Совместное решение этих уравнений дает
h = (1 + /2) ма; /ц= (—4 —/8) ма.
Комплексные токи, проходящие в каждой ветви,
Л = Л = (1 + j2} ма; 1г = Л + /ц = (—3 —/6), ла; /3 = —/п =
= (4 + /8) ма.
Напряжение между точками а и b
UаЬ— ^2^23 — (180 /90) мв.
г
Тот же результат можно получить и из уравнений
== U A^i2> аЪ ^3^23*
Векторная диаграмма построена на рис. 5.25,6.
180
5.29. Параметры цепи, изображенной на рис. 5.26, при неко-
торой частоте имеют
Zx = г, = 13 ом;
Z2 = г2 + /<оЛ2 = (8 + /12) ом;
Z3 = гз + Мз = (6 + /8) ом;
Z4 = г4 + /<оЛ4 = (10 + /15) ом;
Zi------
= —/20 ом;
Z23 = >M23= /6 ом; Z34 = >М34 = /10 ом.
Через конденсатор С4, являющийся нагрузкой, проходит ток
/4 = 2 а. Вычислить все токи и напряжение Uv подведенное
к цепи. Определить отношение напряжения на нагрузке к на-
пряжению и1.
5.30. В цепи схемы (см. рис. 5.25,а) поменять местами про-
водники, подходящие к зажимам катушки L3. Найти токи и нап-
ряжение Uab, если U — 120 в, а сопротивления цепи
Z1 = (120 -j- /30) ом; Z2 = /20 ом; Z3 = —/20 ом;
Z12 = /10 ом; Z23 = /10 ом.
5.31. Определить все токи, если сопротивления элементов
цепи (рис. 5.27,а) i\ = 8 ом, = 56 ом, г3 = 10 сш, «)А2 = 20 ом,
г3 = 15 ом, mL3 = 20 ом, г4 = 5 ом, и>М12 = 10 ом, ыМ13 = 10 ом.
Напряжение, приложенное к цепи, U = 100 в. Построить век-
торную диаграмму. Составить баланс мощностей.
Решение. = (8 + /56) ом; Z2 = (10 4- /20) ом; Z3 = (15 4-
+ /20) ом; Z4==5 ом; Z12 = /10 ом; Z13 == /10 ом.
181
Задавшись положительными направлениями токов, обозначен-
ными на схеме, составим систему уравнений Кирхгофа:
' ^1г) + а(^2 ^12) 8^13
/Л —4212 —/Л = 0;
Л.^*18 =
л = 4 + Л-
Решив их, найдем
4 = 0,56 — /1,92 = 2 е-/73°45 а;
4 = 0,4— /0,8 = 0,894 в-'630'0 а;
/8 = 0,64-/0,48 = 0,8 е_/36°50 а;
♦ —/82°
/4 = 0,16 — /1,12= 1,13 е а.
На основе полученных данных построим векторную диаграм-
му (рис. 5.27,6).
Проверим баланс мощностей
иЦ cos ср, = Reff/Zj =/1Г1+4г2 + 4r3 + 4r4,
или
Ref 100(0,56 + /1,92)] = 2s .8-4-0,8942-10 + 0,82.15+ l,132-5;
или
100-0,56 = 32 + 8 + 9,6 + 6,4,
получилось тождество
56 = 56.
5.32. В цепи схемы (рис. 5.27, а), поменять местами провод-
ники, подходящие к зажимам второй катушки (г2, Д2), т. е. счи-
тать, что звездочка поставлена вверху. Сопротивления элемен-
тов цепи: Z4=(17 + /44)ол»; Z2 = (25 + /50) ом; Z3 — (37,5 + /50)ол<;
Z4 = 7,5 ом; Z12 = /25 ом; Zlg = /25 ом. Напряжение U = 120 в.
Вычислить все токи и построить векторную диаграмму. За-
дачу решить, пользуясь законами Кирхгофа и методом контур-
ных токов.
5.33. В схеме рис. 5.28,а определить г4 и М, при которых
мост уравновешен. Даны: = 10 ом, гй = 20 ом, rs = 25 ом,
Lx = 4 мгн, L2=6 мгн. Найти входное сопротивление цепи, если
о> = 104 сек'1.
182
Решение. Воспользовавшись развязкой индуктивных свя-
зей (см. п. 5 основных положений), преобразуем исходную схе-
му рис.5 28,а в эквивалентную, не содержащую взаимных индук-
тивностей (рис. 5.28,6); при этом следует обратить внимание на
появление новой узловой точки. Для последней схемы записы-
ваем условие равновесия моста:
[rx + XLj — М)]г4 = [г2 + /<о(Л2 — М)]г3
Приравняем соответственно вещественные и мнимые состав-
ляющие:
= г2г3; ш(£1 — МУ 4 = u>(L2 — M)r3.
Решая эти уравнения, найдем
г4 = 50 ом; М = 2 мгн.
Определяем входное сопротивление цепи:
7 _ rskt + MLt-M)] Г4Ь + М^-^)1 _ Д1 к?33’40'
т ~ Г3 +n + /«.(Lj-TW) + rt + г2 +/ш(£2-Л4) - 41 ’йе
5.34. Вычислить входное сопротивление цепи (рис. 5.29,а), если
х4 = 25 ом, х2 = 40 ом, х3 = 65 ом, х12 = 20 ом, х23 = 10 ом,
х31 = 25 ом, Хс — 12,5 ом.
Рис. 5.29
При каком сопротивлении хс в цепи будет резонанс напря-
жений?
183
Указание. Заданная схема может быть заменена эквивалентной, пред-
ставленной на рис. 5.29, б, в которой появились новые узловые точки Л, В, С
(см. решение задачи 5.33). В ней следует треугольник сопротивлений АВС
заменить эквивалентной звездой.
Рис. 5.30
5.35. Определить емкостное сопротивление хс, при котором
в цепи (рис. 5.30) наступит: а) резонанс токов; б) резонанс на-
пряжений. Для каждого из случаев
определить показания амперметров.
Даны: U = 24 в, гг = 20 ом, хг = 4 ом,
х2 = 14 ом, х3= 18 ом, х23 = 2 ом.
5.36. Сопротивление первичной об-
мотки трансформатора (рис. 5.31, а)
= (5 4- /20) ом, а сопротивления
двух частей его вторичной обмотки
^2а — (4 4~ /32) ом\ Z2b = (34- /22) ом.
Комплексное сопротивление взаимной
индуктивности между первичной об-
моткой и верхней частью вторичной Zla == /5 ом, а между пер-
вичной и нижней частью вторичной Zlb = /3 ом. Комплексное
сопротивление взаимной индуктивности между отдельными ча-
стями вторичной Zab = /4 ом. Определить все токи, если части
вторичной обмотки трансформатора нагружены на сопротивления,
равные Z2a = (6 — /7) ом, Z2b = 5 ом, а напряжение источника,
подведенного к первичной обмотке трансформатора, = 120 в.
hb
Рис. 5.31
Решение. Начертим схему, эквивалентную заданной цепи
(рис. 5.31, б), и наметим положительные направления токов. Для
разметки зажимов катушек трансформатора примем зажим Нг
за начало первичной катушки. Тогда, проследив по схеме за
направлениями намотки катушек, убедимся в том, что одноимен-
ным ему является зажим Н2а верхней части вторичной обмотки;
зажим Н2Ь нижней части вторичной обмотки также одноименен
зажиму Hi, вместе с тем зажимы Н2а и Н2Ь являются одноимен-
ными. Поэтому все три одноименных зажима Hv Н2а и Н2Ь име-
ют одинаковое обозначение — звездочку.
184
Обозначим
Z%a = ^2а 4" ^2а = (10 4“ /25) ОМ; ^2Ь~ ^-2Ъ 4" %2Ь = (8 4“ /22) ОМ.
По второму закону Кирхгофа
4Z1 Ka^la ^ЧЬ^ХЬ == (О
K^la ~\~ha^4a 4" Ца^аЬ == 0> (2)
ЛЛ, ~V^4a^ab 4“ ^ЧЬ^ЧЬ == О’ (®)
Подставив числовые значения и решив эти уравнения, най-
дем искомые токи:
„ _ —/74°10' • , —/53°35' ; Л —/60°
/1=6,13е а; 12а = 1,05е а; 12Ь = 0,62е а.
5.37. В цепи схемы (рис. 5.32) каждая из трех катушек ин-
дуктивно связана с двумя другими. Вычислить все токи, если
Z1=r1+ /а)Лх = (7 + /20) ом; Z2 = r2 + juL2 = (6 + /16) ом; Z3 =
== /(14 — 22) = — /8 ом; Z12
ом;
Z31 = j6 ом.
Напряжение U = 100 в. Звез-
дочкой отмечены одноименные за-
жимы каждой из катушек относи-
тельно двух других.
Решение. Составим уравне-
ния по методу контурных токов:
*
= /4 ом; Z23 = /5
Рис. 5.32
Решая их, найдем контурные токи, а затем и токи в ветвях:
i г п па /40°45' } i a Q -/120°50'
Ц = h = 7,76е а; /2 = /ц = 5,Зе а;
; ; ; . ~ ~ /48° кг
/3 = Л — 7ц = 12,9е и.
5.38. В цепи схемы рис. 5.33, а каждая из трех катушек
индуктивно связана с двумя другими. Сопротивление первой ка-
тушки Z1 = r1-\- /(оЛх = (5 4- /15) ом, сопротивление второй ка-
тушки Z2 = г2 + ^ч = (2 + /17) ом, а сопротивление третьей ка-
тушки и последовательно включенного с ней конденсатора С3
равно
2з = гз 4- /ш^з ^”й>с3 = 3 4-/Ю — /35 = (3 —/25) ом.
185
Комплексные сопротивления между первой и второй катуш-
ками Z12 = /7 ом, между второй и третьей Z23 = j4 ом и между
третьей и первой ZS1 — /5 ом. Вычислить все токи, если к цепи
приложено напряжение U = 120 в.
Рис. 5.33
Решение. Пометим одноименные зажимы каждой пары ин-
дуктивно связанных цепей: звездочкой — одноименные зажимы
катушек, 1 и 2, квадратиками — одноименные зажимы 2 и 3 и тре-
угольником — 1 и 3. Следует проследить за направлением намотки
катушек, убедиться в правильности разметки одноименных за-
жимов. Далее начертить схему цепи (рис. 5.33, б) и выбрать
положительные направления токов.
По закону Кирхгофа
контур I
контур II
узел с
4“ ^3^3 + Л^12 "Ь V13 4~ Л231 ^2^32 — U\
2^2 4~ Л^21 ^3^23 'з4 Л^31 4~ ^2^32 — Ф
Л = 4 + Л-
Совместное решение этой системы уравнений дает следую-
щие значения токов:
• „ —/13°50' • л —/96°25' -г л Л /71°20'
Zi = 1,04е а\ /а = 4,82е а; /3 == 4,8е а.
5.39. Даны два индуктивно связанных колебательных конту-
ра (рис.5.4), имеющих параметры: = 15 ом, L* == 250 мкгн?
г% = 100 ом, L2 = 300 мкгн, С2= 1150 пф, коэффициент связи
k = 16,5%.
При какой емкости С± будет выполнено условие первого
частного резонанса, если частота генератора f = 600 . кгц?
Чему при этом равны токи первичного и вторичного конту-
ров, первичная и вторичная мощности и к. п. д., если Et == 50 же?
186
Решение. Вычислим
wL, = 942 ом; u>L2 =1130 ом;
х2 = <о£2 —
-х- == 230 съи;
coCg
-4— = 900 ом; z2 = У 1002 + 9002 = 905 ом;
coCg
х12 = (»Л1 = k\/ ~ 170 ом.
Из условия первого частного резонанса (5.11)
_ _ *12 _ 1702-900 _ о, о
Xj — хвн1 9 Xg 9052 01,0 ОМ*
так как
то
—^—= ш£
(oCj
= 292 пф.
Далее
1 — х1 = 942 31,8 » 910 ом; Сг = 2^-600-103-sub
170М00 Q-Q
905 ~ 0М‘
- ъ г
ГВН1 « Г2 =
По формулам (5.9) и (6.12) находим
ности:
токи, а по (5.30) — мощ-
max
50
= 2,7 ма;
1
== 0,507 ма;
. __ EiXl2 ___________ 50-170
/2lffla3t ~ г2(п + гвн1) 905-18,5
Piimax = /iimax/'i = (2,7- IO’3)2-15 = 110 мквт;
₽21max = /ilmax^ = (0,507 • 10-3)2 • 100 = 25,8 МКвГЩ
^21тах 25,8 л 1 n
*4 р । р 135 8 0,19.
*11тах • *21 max 100’°
5.40. В схеме (рис. 5.4), параметры которой г, = 15 ом, =
= 250 мкгн, г2 = 100 ом, L* = 300 мкгн, С2 = 1150 пф, путем
настройки первого контура и изменением коэффициента связи
k требуется обеспечить режим сложного резонанса при частоте
генератора f = 600 кгц. Чему при этом равны М, первич-
ный и вторичный токи, мощности каждого из контуров и к. п. д.,
если Et = 50 мв.
Решение. По данным задачи вычисляем
ш£. = 942 ом-, wL2 =1130 ом; —1— = 230 ом; х2 = <dLz-— =
= 900 ом; z2 = V И? +*2 = 905 ом.
187
По формуле (5.15) находим оптимальное сопротивление связи:
хЬопт = 905 = 350 ом; = 93 мкгн.
Далее из (5.11) определяем
%I ?2опт 3502 Qnn 1Qr-
= —2— х2 = 905— • 900 = 135 ом;
Z2
и так как хА == cdLj--------------,
= о)£х — хг = 807 ом;
Сг = 330 пф.
Наконец, по (5.9), (5.17) и (5.30) определяем токи и мощно-
сти:
г 50 1
llMM~ г, + rBW — 15+15 ~ 1,67 ма’
I2MM = —/-1 —~ = —?° = = 0,645 ма;
2/v2 2^15-100
Pimm = (1,67-10~3)2-15 = 42 мквт.
Ргмм = (0,645-10“3)2-100 = 42 мквт; V] = -79-7-79- = 0,5.
5.41. Для индуктивно связанных контуров, параметры кото-
рых = 15 ом, Lt = 250 мкгн, г2 = 100 ом и Ь2 = 300 мкгн,
требуется осуществить режим полного резонанса настройкой пер-
вого и второго контуров и подбором оптимальной связи при ча-
стоте / = 600 кгц. Определить С1У С2, х12опт. Чему равны токи
/шм» I1MM И мощности Pimm. Р‘2мм и к. п. д., если Ег = 50 мв.
Решение. При полном резонансе реактивное сопротивление
каждого из контуров равно нулю (5.18), отсюда
ci= = 281 пф’ Сг = 234 пф-
ID Z-zJ ID £>2
Оптимальное сопротивление связи по (5.19)
-^12опт == = V15-100 = 38,7 ом.
Искомые токи и мощности
11ММ= - I1 — = 1,67 ма-, 12ММ== -~^====г == 0,645 ма;
zri 2у ггг2
Ршм — 11ммг1 = 42 мквт; Р2мм= iImm^z — 42 мквт;
Р\ММ п г
Ч = ~р—Хр--------= °’5-
*2ММ
5.42. Задана система из двух индуктивно связанных конту-
ров (рис. 5.4) с параметрами: q == 12 ом, = 400 мкгн, Сг =
= 333 пф, г2 = 16 ом, Ь2 = 500 мкгн и М = 60 мкгн.
Рассчитать емкость С2 второго контура так, чтобы при о> =
=3-106 рад/сек было выполнено условие второго частного резо-
нанса. Чему При ЭТОМ равны Pillmax, Climax и 7], если Ex= 20 в?
188
5.43. Для двух индуктивно связанных контуров, параметры
которых даны в задаче 5.42, определить С2 и Л40ПТ, соответству-
ющие режиму сложного резонанса. Вычислить при этом режиме
Р\мм, Pimm и -г;, если Et = 20 в, и = 3-10® рад!сек.
5.44. Параметры двух индуктивно связанных контуров t\ =
= 12 ом, Lx — 400 мкгн, г2 = 16 ом и = 500 мкгн. Рассчитать
и С2 и Мопт, ПРИ которых будет режим полного резонанса.
Определить Pimm, Р?мм и kj, если Ег = 20 в, о» = 3-10® рад!сек.
5.45. Антенный контур I (рис. 5.34) индуктивно связан с вход-
ным контуром II усилителя. Оба контура настроены в резо-
нанс на частоту принимаемого сигнала <о = 2,5-10* рад!сек. В ан-
тенном контуре наводится э. д. с. Elt равная 100 мкв. Даны: гг =
= 10 ом, Ц = 200 мкгн, г2 = 20 ом, L2 = 400 мкгн, коэффици-
ент связи k = 0,03.
Рис. 5.34
Считая входное сопротивление усилителя бесконечным, опре-
делить: емкости С\ и С2; добротности Qi и Q2 каждого контура;
взаимную индуктивность Му ток во втором контуре /2 и напря-
жение на сетке входной лампы при частоте о)0; частоты связи
и о)ц ток /2 и напряжение на сетке лампы при этих часто-
тах; полосу пропускания индуктивно связанных контуров и срав-
нить ее с полосой пропускания каждого контура в отдельности.
Решение. По условию имеем
= = “о = 2,5-10* сек~1,
V M’Vl Г ^2^2
отсюда
Сг = 800 пф\ С2 = 400 пф\
= 50,
Qi — ~ — 50; Q2-----
т. е. добротности контуров одинаковы.
Взаимная индуктивность
М = k ут^ьг = 0,03 / 200 • 10-® • 400 • 10-* « 8,5 мкгн.
При ш = о>01 = о>о2 расстройка S = 0, тогда из (5.22а) и (5.23 а)
189
учитывая, что фактор связи А = - -х™ < = °* =1,5 найдем
V
12 = -----= 3,27 мка;
Vv, У(А»+1Г
U2 — Exkr = 3,27 мв.
Частоты связи находим по формуле (5.25), учитывая, что
d — -L- = 0,02 (в расчетах использовано приближенное соотно-
1 _ а
шение при а 1 : -- = 1 + -у):
2,5-10е 2,5-10’ с 1Пв оо ,_.х ,
<В] = — =——г----------= (2,5 • 10® —2,8 • 104) сект1;
У1 + ]/0,032—0,022 КИ-2,24-10~2
Да», = —2,8 • 104 сект1.
<оп =-----------------= (2,5 • 10® 4- 2,8 • 104) сек-1;
У1 — (Л),032—0.022
До)п = 2,8 • 104 сект1.
Обобщенная расстройка 6 контуров при этих частотах
en = -er==2Q^ = 2.5o.^i=i,i2.
По (5.22а) и (5.23а) ток и напряжение при частотах связи
/2 == ——------------—--....— - = 3,54 мка;
У'S2 У (^+1-^)2+4«?)
и.г = Е^гс (шп) = 3,54 мв.
Относительная полоса пропускания So для связи, большей
критической (k > d), вычисляется по (5.28):
So = 0,02 1/ (2ig)2-1 + 2 = 4,12 . 10~2.
Она значительно превосходит относительную полосу пропуска-
ния So одиночного контура:
s; = d = 2 • io-a.
5.46. Решить предыдущую задачу, если коэффициент связи
уменьшен до критического значения kKp.
5.47. Два одинаковых индуктивно связанных контура, пара-
метры которых: = L2 = 250 мкгн, =^2 = 10 ом, настроены
порознь на одну и ту же частоту /0 — 5 • 10® гц.
190
Определить: 1) полосу пропускания каждого контура; 2) по-
лосу пропускания индуктивно связанных контуров при критичес-
кой связи; 3) максимальную полосу пропускания двух связанных
контуров; 4) при каких коэффициентах связи полоса пропуска-
ния двух связанных контуров будет: а) в У 2 раз меньше, б) в
1,2 раза больше и в) в 2 раза больше по сравнению с полосой
пропускания одиночного контура.
Решение. Относительная полоса пропускания одиночного
контура определяется затуханием контура [см. формулу (4.17)]:
тогда абсолютная полоса пропускания каждого контура
SA = f0So = 5 • 105 • 12,7 • IO’3 = 6350 гц.
Относительная полоса пропускания двух индуктивно свя-
занных контуров при критической связи рассчитывается по
(5.27): _
So кр = У 2 d = 1,41 • 0,0127 = 0,018.
При этом абсолютная полоса пропускания
5а. кр = /о50. кр = 5 • 103 • 18 • 10- = 9000 гц.
Максимальная полоса пропускания двух индуктивно связан-
ных контуров по (5.29)
5О max = 3,м = 3,1 • 0,0127 = 0,0394;
S. = 5 • Ю5 • 39,4 • 10- = 19 700 гц.
A max ' и о max ’
Для ответа на вопросы п. 4а и 46, условия которых соот-
ветствуют полосе пропускания при связи ниже критической,
для которой So = 1,4Id, нужно воспользоваться формулой
(5.26): ________________________
a) So=d|/ (А)’- 1 + /2 [1 + (А)*]' =-Ай,
ИЛИ
(4)’-1 + /2 [‘ + (4)‘1=°'5-
Решая последнее уравнение относительно k, найдем k —
= 3,6 • ю-
б) So = d (А)2 - 1 -ь У2 [1 + (А)4] = l,2d
ИЛИ
(4У -1 + /2['+(4Г] =
Решая это уравнение относительно k, найдем k = 10,6 - 10—.
191
в) Для ответа на вопрос пункта 4в нужно воспользоваться
формулой (5.28), пригодной для случая связи выше критической:
s»=d V (4Г-1 +2 4 = и
ИЛИ
Решая последнее уравнение, найдем k = 18,4 • 10~3.
5.48. Полосовой фильтр состоит из двух одинаковых конту-
ров, связанных индуктивно (см. рис. 5.4).
Параметры контуров: == L2 = 400 мкгн, = С2 = 100 пф,
^ = ^=10 ом. Определить наибольшую полосу пропускания
фильтра и коэффициент связи, при котором эта полоса обеспе-
чивается. Найти взаимную индуктивность фильтра.
5.49. Система из двух одинаковых индуктивно связанных
контуров, настроенных в отдельности на частоту == 106 сек~\
имеет абсолютную полосу пропускания SA = 5,38 • 103 гц и вза-
имную индуктивность М = 340 мкгн (см. рис. 5.4). Определить,
какова связь между контурами: ниже, выше или равна крити-
ческой — при d = 0,024 и d = 0,03. Найти коэффициент связи,
индуктивность и активное сопротивление контуров для этих
двух значений d.
Решение. Относительная полоса пропускания
So = 4^- = 5а — = —-38 'in°8' 2п = 33-8 • 10-3-
0 /о % 106
Для того чтобы определить, какова связь между контурами,
сравним So и d*.
0,0338 ini о 1Л1л
~d~ о 024 1 >41» или So 1,41 d,
что согласно (5.27) соответствует случаю критической связи.
При этом k = d = 0,024.
Вычислим индуктивности контуров при Ьг = L2 == L.
т, . М М
Из выражения k = —-------= -у- находим
l
340 • 10’6 . . п 1П_Ч . . о
----------= 14,2 • 10 3 гн = 14,2 мгн.
0,024
Активные сопротивления контуров
г = d(D0L = 0,024 • 106 • 14,2 • 10"3 = 340 ом.
Для случая d = 0,05 соотношение
__ 0,0388 _ < 19R
0,03 ~ ’ ’
т. е. So = 1,128d, что соответствует связи ниже критической.
192
Для определения k воспользуемся формулой (5.26), откуда
= 0,78:
k = 0,78d = 0,78 • 0,03 = 23,4 • IO’3.
Рассчитаем индуктивности контуров. Из выражения k =
находим
м
k
мгн.
Активные сопротивления контуров
г = d^L = 0,03 • 10е . 14,5 . 10‘3 = 435 ом.
5.50. Параметры двух одинаковых индуктивно связанных
контуров: = L2 = L — 0,8 мгн, С\ — С2 = С = 750 пф, =
= г2 = г = 20 ом, М = 50 мкгн. Построить резонансную кривую
тока во втором контуре при изменении угловой частоты от
1,2 - 106 сек~' w 1,5 • 106 сек"1. Определить частоты связи и
полосу пропускания.
Решение. Определим, какова связь между контурами. Для
этого вычислим о)о, d и k и последние величины сравним между
собой:
О>0 = —и =1,29- 10е сек-1-,
у LC
k = — = 6,25 • 10-2;
L
d = = 1,935 • IO-2.
w0L
Отсюда видно, что k > d, следовательно, связь выше крити-
ческой.
Для построения кривой задаемся различными значениями со,
находим соответствующие им величины А и 5, входящие в фор-
мулу (5.22а). Результаты расчетов для удобства следует свести
в таблицу, которую надо составить самостоятельно. При вы-
боре точек кривой обязательно включить резонансную частоту
<о0 и частоты связи шт и о)п, которые определяются по (5.25) и
при k > d имеет вид:
<°0
0), ---—
1,29 • 106 1 ОС 1 Aft 1
— ’ ----------= 1,25- 106 се/г1;
/1+ 6,25* 10~2
<о0 1,29.10е
а)п —-и- - = ——?-------------
yT—k V 1 —6,25 . 10-2
= 1,33 • 106 сект1.
По данным расчетов строим кривую (рис. 5.35).
Для определения полосы пропускания проводим на графике
7 Заказ № 624
193
прямую - = —— ~ 0,707, которая определит границы поло-
'2 ММ У 2
сы пропускания. Как видно из рис. 5.35, полоса пропускания
разбивается на две части:
от «j = 1,238 • 10е сект1 др <в2 = 1,268 • 10е сек~} и
от ш3 = 1,312 • 10е сект1 до = 1,344 • 10е сек'1.
^2!
Рис. 5.35
5.51. Два индуктивно связанных контура имеют параметры:
L, = 400 мкгн, Сг — 500 пф, = 20 ом, = 360 мгн,
Са — 580 пф, г2 = 15 ом, М. = 40 мкгн.
Амплитуда э. д. с. генератора Е1т = 100 в, его угловая
частота а> = 2 • 106 сект1. Определить мощности Р, и Ра, расхо-
дуемые в первом и втором контурах, найти к. п. д. при задан-
ной связи.
Определить оптимальную связь, токи в первом и втором
контурах, а также значение максимально возможной мощности
и к. п. д. во втором контуре при полном резонансе.
Решение. Реактивные сопротивления каждого контура
xt — wLt----!— = — 200 ом, Хъ = члЬъ---------— = — 140 ом.
(&С 2
Эквивалентные активное и реактивное сопротивления соот-
ветственно равны
, . (°< - on I (2- 10e-40-10-6)2-15 о
г13 = + ^вн а = G +-—r-fa = 20 + *-------------т--=24,8 ом;
19 1 * вн 1 1 * о а । 15а 4- 1402
194
•^1э — "т -^вн1
(2-10°-40-10~6)2 • 140
152 + 1402
Мощность, расходуемая в первом контуре,
Л = — I* г, = — = — 0,6362 • 20 = 4,05 вт,
1 2 ,т 1 2 \ г13 ) 1 2
где
г19 = | Z131 — | г19 + j*is I = 124,8 — / 1551 = 157 ом\
= = 0,636 а.
г1Э
Мощность, расходуемая во втором контуре,
=4 4^=4 4^1=4 °-6362 •4)8=°-973 вт’
£ & £
где
(<оЛ4)2 . о
Гвн1 = *-Г- г2 = 4’8 0М'
Коэффициент полезного действия
Vi = —— = 0,194 = 19,4%.
Pi + Pt
Оптимальную связь определим по (5.19)!
Л40пт = il2™!. = ±21^. = V2? • 15 = 8 65 . 10_6 = 8 65 мкгн^
СО (О лй * 1 к/
При оптимальной связи х19 = 0, тогда
Токи в контурах
(о2Л12
-----221 = 2rr = 40 ом.
г* 1
1
т
2 ММт гg
1ЛГЛ1„
т
= 2,16 а.
Значение максимально возможной мощности определится из
(5.34):
t/2
^2мм = ^imm ~ 8<1 ~ вт< = 0>8 = 50%.
5.52. Пользуясь данными задачи 5.51, определить Р2 и
к. п. д., если взаимная индуктивность М = 10 мкгн, при усло-
вии, что оба контура в отдельности настроены в резонанс с
частотой генератора.
7*
195
5.53. В схеме рис. 5.4 известны параметры: = 350 мкгн,
Сх = 250 пф, гг = 10 ом, = 365 мкгн, г2 = 8 ом. Амплитуда
э. д. с. генератора равна 200 в. Оба контура в отдельности
настроены в резонанс на одну и ту же частоту /0.
При каком значении коэффициента связи к. п. д. схемы ра-
вен 75%? Чему при этом равна мощность второго контура Р2?
На сколько эта мощность меньше максимальной?
Решение. Резонансная частота и затухание каждого из
контуров
<оо = —-— = 3,4 • 10е се/г1;
Уис,
d, = -4- = 0.0084; dt = —= 0,00645.
1 <o0Li * (D0b2
Из формулы (5.33) найдем k при = 75%:
k = = У °’75 ' Y-0 75 106 = °-0128-
М = k УцЦ = 0,0128 у 350 • 10-6 • 365 • Ю’6 = 4,58 мкгн.
Эквивалентное сопротивление
7 I (<“Л4)а in , 3,42 • 1012 • 4,582 • 10“ia .п
zi3 = г1э = Ч + Нт2- =Ю-|- —--------------------------= 40 ом
Г 2 °
JL / 200 У2
2 \ 40 /
• 10 == 125 вт.
Из формулы (5.31)
п -цР. 0,75 • 125 О7г-
р == —~ _2------------= 375 вт
1— Y] 1—0,75
Значение Pzmm определим по (5.34):
> __ 1т
2ММ
2002
8 • 10
= 500 вт.
ГЛАВА ШЕСТАЯ
ТРЕХФАЗНЫЕ ЦЕПИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Мгновенные значения и комплексы трехфазной симметрич-
ной системы напряжений имеют вид
ил = Um sin v>t\
Uq U m sin
(4тс
--5-
(6.1)
2. В симметричной трехфазной цепи комплексные сопротив-
ления составляющих ее фаз одинаковы.
Для симметричной трехфазной системы при соединении звез-
дой существуют следующие зависимости между линейными и
фазными напряжениями и токами:
ия = /3~ иф-, /л = /ф. (6.2)
Для симметричной трехфазной системы при соединении
треугольником, линейные и фазные напряжения и токи связаны
соотношениями:
ия = иФ; /л=/з"/ф. (6.3)
Мощность в симметричной трехфазной системе
Р = и 3 иЯ1Я cos Фф = 3(/ф/ф cos <Рф. (6.4)
3. Расчеты несимметричных трехфазных цепей могут быть
проведены с помощью законов Кирхгофа или любого метода
расчета электрических цепей. <
Если к трехфазному генератору, соединенному звездой,
приключен приемник энергии, также соединенный звездой,
197
то смещение нейтрали — напряжение Un между нейтральными
(нулевыми) точками приемника и генератора определяется по
формуле
Ua Ya+Ub Yb+Uc Yc
(6.5)
где U А, UB, Uc — фазные напряжения генератора;
Ya , Yв, Yc, Yn — проводимости отдельных фаз и нейтраль-
ного (нулевого) провода.
Токи в фазах и нейтральном проводе
Если нагрузка соединена звездой без нейтрального (нуле-
вого) провода и известны линейные напряжения UAB, Uвс, UCA,
то фазные напряжения UA Uв,
ся по формулам
Uc (рис. 6.1) нагрузки находят-
Рис. 6.1
_ Uав^в
А~~ V . -к
__ ^ВС^С
В~ V . 4-
UcAY А
вс1 в
где YA, Yв и Yc — проводимо-
фаз.
линей-
сти
Для любой трехфазной системы сумма комплексных
ных напряжений равна нулю:
ВС + Уса = °-
УПРАЖНЕНИЯ И ЗАДАЧИ
6.1. К симметричному трехфазному генератору с фазной
э. д. с. Е = 127 в и внутренним сопротивлением Zo — (0,3 +
+ /0,9) ом через линию, сопротивление каждого провода кото-
рой Znp = (0,5 + /1) ом, подключена симметричная нагрузка
Z = (10 + /6) ом, соединенная звездой (рис. 6.2, а). Определить
ток в каждой фазе, фазное и линейное напряжения генератора,
СА1 С ,
ав1 a .
198
ток, фазное и линейное напряжения нагрузки, мощность, дос-
тавляемую генератором и расходуемую в нагрузке. Построить
векторную диаграмму.
Рис. 6.2
Решение. Ввиду полной симметрии системы напряжение
между нулевыми точками генератора и нагрузки равно нулю.
Каждую фазу можно рассматривать независимо от других фаз.
Так, например, ток в фазе А находится на основании закона
Ома (полагаем ЕА — Е = 127 в):
127
10,8+ /7,9
„ _ — /36’10'
= 9,5 е а.
Фазные напряжения на зажимах генератора и нагрузки
• • • 7 осо 1ft'
UA0= еа- 127-9,5а' • (0,3 +/0,9) =
— / 2’30'
119,7а
в;
и == 9,5а '36°10'.(10 + /6)= 111а /5°10'в.
Такие же напряжения в других фазах сдвинуты соответст-
венно на 120° и 240°:
— / 122°30' • — / 242°30'
иво= 119,7е в\ (7С0=119,7в в;
/, ш —/125*10' • -/ 245°10'
Ц>01=111е uc0l =1116 в-
Линейные напряжения на зажимах генератора и нагрузки
UAB-UA0~UB0= 119,7е -119,7а'
= 208а в;
^ab = ^aOt ~lJbOt = Ш0 — Шв =192б в.
«К
Мощность, доставляемая генератором,
Рг = 3 • 127 • 9,5 cos 36° 10''= 2920 вт.
Мощность в нагрузке Рн = 3 • 9,5а • 10 == 2710 вт.
Векторная диаграмма построена на рис. 6.2, б.
6.2. В трехфазную симметричную сеть, линейное напряже-
ние которой U — 220 в, включены звездой три одинаковых со-
противления ZA = ZB = lc = 7ф=(10 + j 10) ом. Определить токи
в каждой фазе нагрузки, фазные напряжения и мощность, рас-
ходуемую в трехфазной нагрузке.
6.3. Приемник энергии, сопротивления фаз которого одина-
ковы, потребляет мощность 5,46 кет при созфф ~ 0,8(фф> 0).
Линейное напряжение на нагрузке равно 370 в. Чему равна
фазная э. д. с. генератора, соединенного звездой, внутреннее
сопротивление каждой фазы которого Zo = (0,3 + /0,9) ом, а
сопротивление каждого провода линии Znp = (0,4 +/0,8) ом?
6.4. Сопротивления отдельных фаз симметричной нагрузки,
соединенной звездой, равны Za = Zb = Zc = (20 + j 15) ом.
К симметричному генератору с фазной э. д. с. Еф = 4500 в
и внутренним сопротивлением каждой фазы 2ф = (0,5 +/2) ом
через линию, сопротивление каждого провода которой Znp =
== (0,5 + /1) ом, подключена указанная нагрузка.
Определить токи каждой фазы генератора и нагрузки, фаз-
ные напряжения генератора и нагрузки, мощность, отдаваемую
генератором. Построить векторную диаграмму напряжений и
токов.
Замечание. Показать, что мощность, отдаваемая генератором, равна
сумме мощностей, расходуемых в нагрузке, линии и генераторе.
6.5. К трехфазной линии с симметричными линейными на-
пряжениями 1/л = 220 в подключен треугольником приемник, со-
противление каждой фазы которого Z = (10 + j 10) ом (рис. 6.3, а).
Найти токи в каждой фазе нагрузки и линии и показания каж-
дого ваттметра. Найти те же величины в случае обрыва в точ-
ке аг.
Решение. Решим задачу, пользуясь символическим мето-
дом. Примем, что комплекс напряжения UAB вещественней.
Тогда комплексы линейных напряжений будут
• • • • — / 120°
Uab = Uat> = 220 в; t/BC= Ubc= 220е в;
а
• • — / 240е
исА= Uca=220e в.
200
Определим комплексы фазных и линейных токов:
/в6= = 15,6е“ /45° = (11 — /11) а;
ab Z 10 4-/10
/ = = .-gfe = 15,6е~'165 = (— 15 — /4,03) а;
Ьс Z 10 4-/Ю
I = '.°- = 15,6'75° = (4,03 + /15) а;
са Z 10 4- / Ю 7
iA = iab - iea = 6,97 - j 26 = 26,9e-' 75° a;
I в = ibc - iab = -26 + /6,97 = 26,9? I66° a;
/с = ica~ ibc = 19 + / 19 = 26,9? 45° a.
Рис. 6.3
Найдем показания ваттметров:
220 • 26,9 ?75°
= 220-26,9cos 75°= 1530 вт\
Р2 = Re [<7св /с] = Re [ —220е~' 120° • 26,9е-' 45°
~ Re [220? 60° • 26,9е~'45°] = 220-26,9 cos 15° = 5730 вт.
201
Активная мощность цепи
Р = Pj + Р2 = 1530 + 5730 = 7260 вт.
Проверка. Р = 31$г = 3-15,56а•10 = 7260 вт.
На рис. 6.3, б построена векторная диаграмма напряжений и
токов.
Обрыв в точке ах (рис. 6.3, в). Токи в фазах нагрузки
220е~^12О°
10+ /10
= (-15-/4,03) а;
220е~/12°6
2 (10 + j 10)
= (7,5 + / 2,02) а.
Вычислим линейные
токи:
1а = 0;
ic = —iB = ica —ibc = 22,5 + /6,05 = 23,3ez 15° a.
Определим показания ваттметров
Л = 0;
Р2 = Re рсв /с] = Re [220 е' 60° • 23,3е~' 15° =
= 220 • 23,3 cos 45° = 3630 вт.
6.6. Решить задачу 6.5 при одинаковых сопротивлениях всех
фаз и равных Z = (10 — /10) ом.
В дополнение к случаю обрыва в точке а± рассмотреть также
случаи обрывов в точках Ь± и Ь2 (см. рис. 6.3, а).
6.7. К зажимам симметричной трехфазной сети, линейное
напряжение которой равно £/л, подключены три одинаковых сопро-
тивления Z, соединенные треугольником. Условные знаки А и X
соответственно обозначают «начало» и «конец» фазы А; В и Y—
фазы В; С и Z— фазы С.
Определить, во сколько раз уменьшится ток в подводящих
проводах и потребляемая мощность, если те же сопротивления
при помощи переключателя 77 соединить звездой (рис. 6.4)
Замечание. Результаты данной задачи сравнить с результатами, по-
лученными в задачах 6.2 и 6.5е
202
6.8. К концу линии, сопротивление каждого провода которой
Znp = (0,5 + j 1,5) ом, подключен соединенный треугольником
приемник энергии. Сопротивление каждой фазы его Zab — Zbc —
= Zca~ Z = (8,4 + /6,6) ом. Линейные напряжения в начале ли-
нии U ab = Uвс = U с а = 230 в (рис. 6.5). Рассчитать линейные
и фазные токи, а также напряжения на фазах нагрузки, соеди-
ненной треугольником. Определить потерю напряжения в линии.
Построить векторную диаграмму.
Указание. Задачу проще решить при помощи преобразования треу-
гольника сопротивлений нагрузки в эквивалентную звезду.
6.9. Дан симметричный генератор, соединенный треугольни-
ком (рис. 6.6). Фазные э. д. с. генератора £ф = 230 в, а внут-
реннее сопротивление каждой его фазы 2ф = (0,3 + /0,9) ом.
Через линию, сопротивление каждого провода которой Znp =
= (0,15 +/0,12) ом, генератор соединен с приемником энергии,
соединенным звездой. Сопротивление каждой фазы его Z = (2 +
+ /1,5) ом. Определить напряжения у зажимов генератора и
приемника энергии и токи в фазах генератора и приемника
энергии.
6.10. Вычислить все токи и напряжения на фазах симмет-
ричной нагрузки, соединенной треугольником, если трехфазный
генератор симметричен, его фазная э. д. с. Еф = 230 в, сопро-
тивление каждой фазы генератора Z* = (0,3 + /0,9) ом, сопро-
тивление каждого провода Znp — (0,15 + /0,12) ом, сопротивление
каждой фазы нагрузки Z = (2 + j 1,5) ом (рис. 6.7).
Рис. 6.7
203
6.11. Для измерения активной мощности трехфазной равно-
мерной нагрузки, имеющей индуктивный характер, соединенной
звездой и подключенной к симметричной трехфазной сети, ли*
нейное напряжение которой ил = 220 в, были включены два
ваттметра (рис. 6.8), показания которых Р± = 1080 вт и Р2 =
Рис. 6.8
= 1920 вт. Определить фазное напряжение, ток и сдвиг фаз
между ними. Чему равна общая мощность, расходуемая в на-
грузке? Построить векторную диаграмму напряжений и токов.
6.12. Решить задачу 6.11, если (7Л = 380 в, Рх = 0 и Р2 =
= 2,5 кет.
6.13. Для цепи схемы рис. 6.3, а вычислить токи в нагрузке
и в линии, сопротивление каждой фазы нагрузки, общую мощ-
ность, если нагрузка и линейные напряжения симметричны и
равны ил = 220 в, а показания ваттметров РА = 1,65 кет, Р2~
= 5,81 кет.
6.14. Чему равно показание ваттметра, включенного в цепь
рис. 6.9, и какую мощность он учитывает? Нагрузка фаз сим-
метрична: гА = гв = гс = 12 ом, хА= хв== хс = 9 ом. Система
линейных напряжений тоже симметрична UR «= 380 е.
6.15. В цепи (рис. 6.10) гАВ = гвс = гСА = 12 ом, хАВ =
= хвс ~ хСА = 9 ом. Система линейных напряжений симметрична
ил = 380 е. Чему равно показание ваттметра и какую мощность
он учитывает?
204
6.16. На расстояние / = 60 км нужно передать мощность
Р = 3000 кет при линейном напряжении у потребителей (7Л =
= 35 000 & и созфф = 0,8 так, чтобы потеря мощности не пре-
вышала 5% от полезной. Определить необходимое для этого
количество меди (в тоннах) при: а) трехфазной и б) однофазной
системах передачи энергии.
6.17. Симметричный трехфазный трансформатор питает сим-
метричную нагрузку, общая мощность которой Р == 600 кет.
а созфф = 0,8 (фф> 0). Линейное напряжение на нагрузке
ил = 6 кв. От трансформатора до потребителя проложена воз
душная линия, сечение каждого провода которой S = 35 мм2,
а длина / = 2,3 км. Материал проводов линии — медь (удельное
сопротивление р = 0,0175 ом • мм21м). Индуктивное сопротивление
каждого километра провода равно 0,4 ом.
Вычислить ток и линейное напряжение в начале линии и
построить векторную диаграмму.
6.18. Решить -задачу 6.17, полагая, что вместо воздушной
линии проложен кабель с тем же сечением медных проводов,
индуктивностью которых можно пренебречь. Остальные данные
те же, что и в задаче 6.17.
6.19. Дана двухфазная система э. д. с. (рис. 6.11, а}\ Ex =
= Е2 = 220 в, (Ev Е2) = 90°. Сопротивление каждой фазы гене-
ратора Zq = (0,5 + / 1,5) ом. Сопротив-
ление каждой фазы нагрузки Zr = Z2 =
= Z = (5,5 + /8) ом. Сопротивление
провода, общего для двух фаз, при-
нять равным нулю. Найти 1оки в про-
водах, фазные и линейные напряжения
нагрузки. Построить векторную диаг-
рамму.
Решение. Выразим э. д. с. гене-
ратора через комплексы. Примем, что
= Ег = 220 в. тогда Ё2 = Еге~~^ 90° =
= —/220 е. Применяя закон Ома к
каждой фазе, получим
= 10,4 — /16,5 = 19,6е~'/57°47' а;
I - - ~/220
4- Zo 6 4- j 9,5
= _ 16,5 — j 10,4 = 19,бе-' 1470 47' а.
Рис. 6.11
205
Ток в провода, общем для двух фаз,
iN = /1 ± /2 = - 6,1 - / 26,9 = 27,бе4 1020 35' а.
Фазные напряжения
U, = Дг, = (10,4 — / 16,5) - (5,54-/8) = 190-/7,5 = 190е“/2°16' в;
йг = /Л = (— 16,5 — / 10,4) • (5,5 + /8) = — (7,5 + j 190) =
= 190е-/92°16 в.
Комплекс линейного напряжения
Ult = U,—Ut = 197,5 + / 182,5 = 269е/42’43' в.
На рис. 6.11, б построена
векторная диаграмма.
6.20. К симметричному трех-
фазному генератору с фазной
э. д. с. Е = 230 вис внутрен-
ним сопротивлением Zo= (0,3 +
+ /0,9) ом подключена несим-
метричная нагрузка, соединен-
ная в звезду с нулевым про-
водом (рис. 6.12, а). Сопротив-
ления фаз нагрузки Za=^= (2+/4)
ом, Zb == (4 — / 8) ом, Zc= 5 ом.
Сопротивление каждого прово-
да линии Znp =» (0,4 + /0,3) ом,
а сопротивление нейтрального
провода ZN = 0,5 ом. Опреде-
лить токи и напряжения на
каждой фазе нагрузки и гене-
раторе при наличии нейтраль-
ного провода и при его обры-
ве. Для каждого случая по-
строить векторную диаграмму.
Решение. Запишем фаз-
ные э. д. с. генератора в ком-
плексном виде:
£*.==£.== 230 в\ Ё =
A A D
= 23О<?~/120’ = —115(1+/1,73)в;
Ёс = 230<?~/24°° =
= —115(1-/1,73) в.
246
Комплексные проводимости фаз
= (0,0788-/0,152) ом-1;
A ““
0 । ^пр
1
В ~~
L-----= (0,0688 + /0,0995) ом'1;
пр
= (0,168-/0,0354) ом-1;
пр
У =------=-------= 2 ом-1.
N ZN 0,5
При наличии нейтрального провода.
По формуле (6.5) найдем напряжение между точками Ог и О.
Л 230(0,0788 —/0,152)— 115(1 + / 1,73) (0,0688+/0,0995)
jn~
2,32-/0,088
115(1 -/ 1,73)(0,168 — /0,0354) = 8,03 —j9,38= 12,4е-/49°25' в,
2,32— /0,088
а по (6.6) все токи
1А = (Ёл —UN) УД = 18,9 — / 33 = 37,9<?-/60°'°' а;
1в= (Ёв —Un) Yb = 10,4-/25,2 = 27,4е~/67‘40' а;
1С = (Ёс — UN) Yc = — 13,3 + j 39,4 = 41,6? 1в8°35' a;
IN = uN Yn= 16 — /18,8 = 24,8e-/ 49°25' a.
Проверка показывает, что
• • • •
7л+ I в + Ic — In — 0.
Напряжения на фазах нагрузки
Uaot = iAZa = 170 ?3°15 в; UbOt = IBZb = 23O«-/134’20' в;
Uc о, = Ic Zc= 208? 108°35' в.
Напряжения на каждой фазе генератора
Uao = EA-iAZ0=\95e~l2°5' в; Uво = Ёв-1BZ0 = 243e~il2&° в;
^со = Ёс—1сг0 = 213?110°45' в.
На рис. 6.12, б построена векторная диаграмма.
207
При обрыве нейтрального провода (YN = 0)
• • •
у = Еа Ya +EbYb + Ес Ус = _ 51 = 87 /36’ 15’ в
N ya + yb+ yc
Токи
Л = (ЁА - U'N) Y. = 20,4 - / 20,1 = 28,6 е~/44°40’ а;
4 = (Ёв - С/;) У в = 1,9 — / 28,6 = 28,6 е~'86°1S' а;
I' = (Ёг — U' ) Y„ = — 22,3 + /48,7 = 53,6?114’40' а.
О у vrf /V /С/ *
Напряжения на фазах нагрузки
= iAZa = 128^,вМ5' * = 4^ = 256е-/149°40 в-
ё;01 = /с^ = 268е/1М°35’ в-
Напряжения на фазах генератора
йА0 = EA-iAZ0 = 206 - / 12,3 = 206 ё~1 3°25' в;
UB0 = ЁВ — IBZ0 = - 141 - /192 = 239еч 125°20’ в;
U' = Ёг — i'Zn = — 64,5 + /205 = 215^I07°ffi' в.
На рис. 6.12, в построена векторная диаграмма в случае
обрыва нейтрального провода.
6.21. Решить задачу 6.20, если Zo=* 0,2 ом.
6.22. В четырех проводную линию трехфазной симметричной
сети с фазным напряжением иАО~иво~исо = иф=120 в
с линейным напряжением
включены три группы одинаковых
ламп (рис. 6.13): I — 30 ламп,
II — 25 ламп и III — 20 ламп. Со-
противление каждой лампы счи-
тать неизменным и равным 300 ом.
Определить ток в нейтральном
проводе. Под каким напряжением
окажется каждая группа ламп при
обрыве нейтрального провода в
точке /и?
6.23. К зажимам трехфазного
симметричного источника энергии
== 380 в приключена соединен-
ная звездой несимметричная нагрузка (рис. 6.14, а), сопротивления
фаз которой ZA = (6 + / 8) ом, ZB = (24 + j 7) ом и Zc = 20 ом.
208
Определить токи и напряжения на каждой фазе, показания
каждого ваттметра, общую мощность, расходуемую в нагрузке.
Построить векторную диаграмму токов и напряжений.
Рис. 6.14
Решение. Способ 1. Заданная схема может быть заменена
новой (рис. 6.14, б), для которой фазные напряжения
t/ф = = 220 в,
/3 /3
а внутренние сопротивления источников равны нулю. (
Проводимости фаз нагрузки
= -j- = —L- = (0,06 - /0,08) = 0,le-'5S’10' ом~1-,
ZA 6 + / 8
YB = —— =-------!---= (0,0384 — /0,0112) = 0,04е-/16°16' ом~\
в ZB 24 +/7
У_ = —— = — = 0,05 ом-1.
с Zc 20
Принимая IJA — UA — 220 в, а следовательно, йв = 220е /120 в
и Uc — 220 е'120 в, по формуле (6.5) найдем напряжение между
нулевыми точками нагрузки и генератора:
_ 1,364-/14,13
N 0,1484-/0,0912
= 49,0 — j 64,9 = 81,2 е~/52“57
в.
Напряжения на фазах нагрузки
UAOt = UA-UN = 171 + /64,9 = 183е/2°О46' а;
f)B0, =UB — UN = — 159 — /126 = 203е~/141°42' а;
209
Ucn = Uc — UN = — 159 + /255 = 30\е~‘ 121°53' в,
wvj la /V
а токи в фазах
7Л = iJAOi ya = 18,Зе-732°24’ = (15,46-/9,72) а;
4 = иво, У в = 8>12е-/ 1S7°58' = (— 7>51 — / 3.04) а;
Л = Urn • Yr = 15,05?121°53' = (— 7,95 + /12,76) а.
la laL/j (a \ /
В правильности решения можно убедиться проверкой:
/л + 1В + 1С = 15,46 — /9,72 — 7,51 — /3,04 — 7,95 + j 12,76 = 0.
Способ 2. Напряжения на фазах нагрузки могут быть найде-
ны по формулам (6.7). Для этого предварительно вычислим ком-
плексы линейных напряжений. Так как раньше было принято
U. = 220 в, то
А
VАВ = У А — йв = 220 — 220 еч 120° = 380? 30° в;
UBC = йв —йс= 220<?_/120“ — 220?120° = 380е~19°° в;
йГА = UиА = 220?120° — 220 = 380? 150° в.
1а/1 (а А
Искомые напряжения находим по формулам (6.7):
у = 380? 30° •0,04е-/|6°|6' -380? 150° -0,05 = j gg^20» 45'
А0' 0,1484-/0,0912
j, _ 380е~у 90°• 0,05 — 380?30° • 0,1 е~<53°|0' _ 9nq -/ ui»4
В0‘ 0,1484-/0,0912 е ’
= 380?150° • 0,1е-/53° 10, -ЗбОе-'900 0,04е-'16°16’
со* ~ 0,1484-/0,0912
= 301? 12,0 50' 8.
Определим показания каждого ваттметра:
Р, = Re 7л] = Re [з80?3°°
18,Зе-/32°24'] = 3230 вт-,
15,05е-; 121°53’] = 4870 вт.
Сумма показаний ваттметров дает мощность, расходуемую
в нагрузке,
р = р р = 8100 вт.
Л 1 л
210
Действительно,
р = I2Ar. + 1в г R + Ic rr = 18.32 -6 + 8,12а • 24 + 15,052 • 20 =
= 2000 4- 1580 + 4520 = 8100 вт.
На рис. 6.14, в, дана векторная диаграмма напряжений и
токов.
6.24. Для цепи схемы рис. 6.8 определить токи и показания
ваттметров, если: а) в фазе А произошел обрыв в точке я;
б) в фазе В произошел обрыв в точке Ь\ в) в фазе В — в точ-
ке г) фаза А оказалась закороченной; д)4сороткое замыкание
произошло в фазе В. Для решения задачи воспользоваться
данными задачи 6.23.
6.25. Фазы нагрузки, соединенные звездой, имеют чисто ак-
тивные сопротивления гА = 9 ом, rB = 11 ом и гс ~ 14 ом. Через
линию, активное сопротивление каждого провода которой гпр =
= 1 ом (индуктивностью проводов линии
пренебречь), указанная нагрузка подклю- ад
чается к зажимам симметричного источ- Т
ника трехфазного тока с линейным напря- •*-
жением Un — 380 в. Определить токи и Т
напряжения на фазах нагрузки. ю/тО
6.26. Для определения порядка чере-
дования фаз применяется схема (рис. 6.15),
состоящая из трех равных по модулю
сопротивлений, соединенных звездой, из ко- Рис- 615
торых одно емкостное, а два других — актив-
ные (лампы накаливания). Система линей-
ных напряжений ил симметрична. Определить фазные напряже-
ния и построить векторную диаграмму.
Замечание. При расчете принять, что к фазе А подключается нагруз-
ка, содержащая конденсатор. Тс рда получится, что лампочка, включенная
в фазу В, будет находиться под напряжением, в 3,71 раза большим, чем та,
которая в фазе С.
6.27. К симметричной системе линейных напряжений Un под-
ключены соединенные звездой три сопротивления, равные по
численной величине, из которых одно индуктивное х£, а два
других Гх и г2 — активные сопротивления (лампочки накалива-
ния). Показать, что если фазу, соединенную с индуктивностью,
считать за первую, то лампочка, включенная во вторую фазу,
будет находиться под напряжением, в 3,71 раза меньшим, чем
лампочка, включенная в третью фазу, т. е. —— = 3,71.
U в
6.28. Для цепи рис. 6.3, а, определить фазные и линейные
токи, общую мощность приемника, показание каждого ваттмет-
211
ра и построить векторную диаграмму, если трехфазный источник
симметричен UAB = UBC = UCA = 220 в, а сопротивления отдель-
ных фаз нагрузки, соединенных треугольником, равны
Zab= 10 ом, Zbc = (Q+j8)0M и Zca = —j 10 ом.
6.29. К симметричной трехфазной системе с линейным на-
пряжением ил = 220 в подключена нагрузка, соединенная тре-
угольником (см. рис. 6.5). Сопротивления фаз нагрузок Zab =
= (12 + j 16) ом, Zbc = 20 ом и Zea = (16 — /12) ом. Сопротивле-
ние каждого провода Znp = (1 + /3) ом. Вычислить фазные и
линейные токи, напряжение на фазах нагрузки, мощность, рас-
ходуемую в нагрузке.
6.30. В трехфазную симметричную сеть без нулевого провода
с линейным напряжением ил = 220 в включены три группы
одинаковых ламп (рис. 6.16). В первой группе имеется пг = 17
ламп, во второй—м2 = 23 лампы и в третьей — я3=19 ламп.
Сопротивление каждой лампы считать неизменным и равным
590 ом.
а) Определить линейные и фазные токи; б) вычислить все
токи и напряжения на зажимах каждой группы ламп при
перегорании предохранителя на вводе фазы С.
6.31. В трехпроводную систему трех-
фазного тока, линейные напряжения ко-
торой симметричны и равны ил = 127 в,
включены две лампы, потребляющие
мощности Р^ЪЪвт и Р2~200вт (рис.
6.17). Рассчитать токи, проходящие через
каждую лампу и в каждом из проводов
линии, и построить векторную диаграм-
му напряжений и токов. Определить
показания ваттметров.
Вен
£е>
Ъ Каделъ
Рис. 6.16
Рис. 6.17
6.32. Вольтметры, подключенные к линейным зажимам трех-
фазной системы, показали UAB~ 210 в, UBC = 220 в и UCA =
= 225 в. К указанной системе подключен приемник энергии,
соединенный звездой, сопротивления фаз которого ZA = 25 ом,
ZB = (24 + /7) ом и Zc = (16 — /12) ом (см. рис. 6.8).
Найти токи и фазные напряжения. Каковы показания ватт-
метров?
Указание. По заданным значениям линейных напряжений следует по-
строить треугольник напряжений АВС (рис. 6.18). Углы векторов UCA и Uвс
определяются решением этого треугольника. Например, угол
/ ^вс
Рис. 6.18
cos Фвс =
772 I 772 772
UAB > UBC UCA
АВ ^ВС
6.33. К трехфазной сети, ли-
нейные напряжения которой
(7.п = 210 в, (7^ = 220 в и
Ad .oG
UCA == 225 в, подключена симмет-
ричная нагрузка, соединенная
звездой, сопротивления каждой
из фаз которой равны ZA = ZB =
= Zc = (20 + j 15) ом. Найти на-
пряжения и токи в каждой фазе.
Указание. Так, как нагрузки
всех фаз одинаковы, то задача, может
быть решена графически: строится в
масштабе треугольник линейных напряже-
ний и находится точка пересечения его медиан. Соединяя ее с вершинами
• • •
треугольника, получим векторы фазных напряжений UA, UB, Uc. Векторы
токов отстают по фазе от соответствующих фазных напряжений на один и тот
же угол фф = arctg —- = 36° 50'.
6.34. В цепи схемы рис. 6.19 даны: Znp = (l 4-/2) ом, ZA =
= (8-|-/10) ом, ZB = 14 ом, Zc = (10 — /6) ом. Измерения ли-
нейных напряжений трехфаз- z™
ной сети дали следующие ве- Ло—с=5------------------j
личины: UлП = 120 в, U = гПр
= ПО в и UrA == 125 в. Най- 0 ~ 7 ?
ти токи и напряжения на фа- cq—г—ь—jCX
зах нагрузки. _______’_______j
6.35. Линейные напряжения
трехфазной сети UAB = 120 в, ----------
(7ЯГ = ПО в и UeA = 125 в. К Рис 6,9
С/ Л
этой сети приключена нагрузка,
соединенная треугольником, сопротивления фаз которой ZAB~
= 25 ом, Z„r * *= 20 ом и ZrA = (16 4- /8) ом. Найти линейные и
x>G G71 ' J '
фазные токи. '
6.36. Линейные напряжения трехфазной системы (7ЛВ = 220 в,
UBC = 215 в и UCA ~ 225 в. Определить линейные и фазные токи,
21)
если Znp = (1 +/3) ом, а сопротивления фаз нагрузки, соеди-
ненной треугольником (см. рис. 6.5) Zab = 20 ом, Zbe = (15 +
+ / 5) ом и Zca — (16 — /8) ом.
Рис. 6.20
6.37. Система линейных напряжений симметрична Un= 220в.
Сопротивления фаз нагрузки (рис. 6.20) ZA = ZB = 20 ом, Zc =
= (24 — /7) ом, ZAB = ZBC = (20 + / 15) ом и ZCA = 20 ом. Вы-
числить все токи.
Рис. 0.21
6.38. В цепи схемы (рис. 6.21) определить все токи. Даны:
ZA = ZB = Zc — (16 /' 12) ом, ZAB = ZBC = ZCA = r = 30 ом и
Znp = (1 +/3) ом. Рассчитать напряжения на фазах нагрузки и
все токи, если U = URr = 220 в и U„. — 210 в.
Ad dG GA
У Казани е. Треугольник сопротивлений преобразовать в эквивалентную звез-
ду. В дальнейшем схема легко сворачивается, если учесть, что в случае сим-
метричных нагрузок смещения нейтралей равны нулю.
214
ГЛАВА СЕДЬМАЯ
ЦЕПИ ПЕРИОДИЧЕСКОГО
НЕСИНУСОИДАЛЬНОГО ТОКА
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Всякая периодическая функция f(t) с периодом Т, удов-
летворяющая условиям Дирихле (т. е. ограниченная функция,
имеющая за период конечное число разрывов первого рода и
конечное число максимумов и минимумов), может быть разложе-
на в тригонометрический ряд.
Разложение периодической функции в тригонометрический
ряд может быть записано в двух формах:
со
/(О = ~~ + S («„cosnw^ + Z>„ Sinn (Bi/); (7.1)
n==l
00
f (О = + S c* sin (« M + Ф»)- (7.2)
Коэффициенты ряда (7.1) равны
т т
-у- = J f(№ ап = -^- f (t) cos nwjdt'
° 0 (7.3)
т
bn = \ f (/) sin noij/ dt.
о
Переход от первой формы ряда (7.1) ко второй (7.2) осу-
ществляется с помощью формул
Сп= + Htg<|>„ = -g-, (7.4)
215
а обратный переход
6n = сп cos фп; an = c„sin <|>B. (7.5)
Обращаем внимание на то, что при определении угла по
формулам (7.4) надо по знакам коэффициентов ап и Ьп устано-
вить, в какой четверти этот угол находится. Так, если Ьп по-
ложительно, а ап отрицательно, то угол лежит в четвертой
четверти, если Ьп < 0 и ап < 0, то — в третьей четверти,
если 6Л<0, а а„>0, то — во второй. Проверкой этого
служат формулы (7.5).
При пользовании первой формой разложения в тригономет-
рический ряд (7.1) коэффициенты ап и Ьп зависят от выбора
начала отсчета, а при пользовании второй формой разложения
(7.2) амплитуды гармоник сп не зависят от выбора начала от-
счета и определяются только видом кривой; аргументы фЛ за-
висят от начала отсчета. При сдвиге начала отсчета вдоль оси
времени t на ±/с амплитуды сп сохраняются, а фазы полу-
чают приращение ±^ntc (теорема сдвига).
Ряду (7.1) можно придать более компактный вид, если ус-
ловно ввести отрицательные частоты и перейти к суммированию
по п от — оо до + о* (в этом случае каждая гармоника, кроме
нулевой, входит под знак суммы дважды):
00
f (0 = — У (Яп cos п <0, t 4- ьп sin п ш^). (7.6)
П——ОО
Тригонометрическая форма ряда Фурье может быть преобра-
зована в комплексную:
оо
/(0 = (7.7)
П=в—00
где комплексный коэффициент
К &п fair
2. Если периодическая кривая обладает тем или иным видом
симметрии, то при ее разложении в ряд Фурье отсутствуют не-
которые составляющие. В табл. 7.1 дается соответствующая
сводка.
3. В тех случаях, когда периодическая кривая в пределах
периода имеет не одно аналитическое выражение, а разным
частям периода соответствуют различные аналитические выра-
жения, как, например, для рис. 7.2, при расчете коэффициентов
ряда интегрирование производится по отдельным частям перио-
да, соответствующим различным аналитическим выражениям
(примеры в задачах 7.1 и 7.2).
216
№ Кривая симметрична
п.п. относительно
Рисунок
оси ординат (чет-
ная функция)
2
начала координат
(нечетная функ-
ция)
3
оси абсцисс при
совмещении двух
полупериодов
Таблица 7.1
Математическое условие симметрии Особенности разложения
f (t)=f (,-t) Отсутствуют синусоидальные
гармоники (bk = 0)
Отсутствуют постоянная со- ставляющая и косинусои-
• дальние гармоники (а^ = = afe = 0)
\ / Отсутствуют постоянная со- ставляющая и четные си- нусоидальные и косинусои- дальные гармоники (а® = =а2л — ^2Л ~С2П — 0)
Кривая симметрична
относительно
оси ординат и
оси абсцисс при
совмещении по-
лупериодов
начала координат
и оси абсцисс
при совмещении
двух полупери-
одов
Продолжение табл. 7.1
Математическое условие симметрии Особенности разложения
t
Отсутствуют постоянная со-
ставляющая и все синусои-
дальные гармоники, а так-
же четные косинусоидаль-
ные гармоники (а0 — Ь^=
= = ^2П = С%П = 0)
Отсутствуют постоянная '’со-
ставляющая и все косину-
соидальные гармоники, а
также четные синусо-
идальные гармоники (а0 =
—ak = а%п ~ ^2л — С2д=0)
4. Действующее значение периодической величины f(t)
(7.8)
Действующие значения периодичес-
ких величин, например э. д. с. (или на-
пряжений, токов) не зависят от на-
чальных фаз гармоник и определяются по
действующим значениям их гармоничес-
ких составляющих:
Рис. 7.2
5. Если периодическое несинусоидальное напряжение подклю-
чено к какой угодно разветвленной или неразветвленной линейной
цепи, то расчет токов производится для каждой из гармоник в
отдельности по методам расчета цепей переменного тока; при
этом индуктивные и емкостные сопротивления для /г-й гармоники
равны соответственно k^L и—-—. Расчет постоянной состав-
k (Oj С
ляющей тока производится по методам расчета цепей постоян-
ного тока. После этого могут быть подсчитаны действующие
значения токов, проходящих в отдельных ветвях, и действую-
щие значения напряжения на отдельных участках цепи по (7.9).
В простейшем случае неразветвленной г, Л, С-цепи, с сопро-
тивлением для &-й гармоники Zk = zk^k = г + / (k^L-------!—),
\ ko^C ]
к которой подключено периодическое напряжение
со
«=(/0 + S Ukms\n(k^ t + фА),
k^\
в цепи устанавливается периодический ток
I = Ц + S 1 km sin + Ф* — Фл).
Л=1
В цепи будет постоянная составляющая тока /0, если нет
емкости.
Комплексные амплитуды гармоник тока и напряжения свя-
заны соотношением
= (7-Ю)
Лк
219
6. Активная Р, реактивная Q и полная S мощности вычис-
ляются по формулам
р = f Uklk cos фА; (7.11а)
4=0
(7.116)
k=]
S = UI=y f ul£ Il . (7.11b)
r 4=0 4=0
Мощность искажения
T == ]/S2 —P2 —Q2 . (7.1 Ir)
7. Характеристики формы периодических несинусоидальных
кривых.
Коэффициент формы кривой /(/) — отношение дейст-
вующего значения F к среднему по модулю значению за пе-
риод Fcp:
/"* т
1/ у J (/(0N*
*Ф = у- = —----------г---------’ <7Л2>
ср 1 Г с
у J \M\dt
о
Коэффициент амплитуды — отношение максимального
к действующему значению функции f(t):
=------- fmax . (7.13)
т
1/ у f l/(0N*
Г о
Коэффициент искажения — отношение действующего
значения основной гармоники к действующему значению всей
функции:
К = у =---------1- ... . (7.14)
г / т
1/ у У l/(0N*
Г о
220
Коэффициент гармоник— отношение действующего
значения высших гармоник к действующему значению основной
гармоники:
(7.15)
УПРАЖНЕНИЯ И ЗАДАЧИ
7.1. Разложить в тригонометрический ряд периодическую
функцию напряжения, выражаемую кривой, симметричной отно-
сительно точки перехода через нуль (рис. 7.3,а). Расчеты про-
т т
делать для: 1) /, = — ; 2) — 0; 3) tv = — . Для каждого
4 2
случая на основе разложения в
ряд построить линейчатый
спектр частот.
Рис. 7.3
Решение. У равнения кривой для различных интервалов
периода: при изменении t от 0 до
и
<*• I
при изменении t от tx до —
щ*
По условию симметрии (табл. 7.1, п. 2) в разложении кривой
содержатся только синусоиды. Для определения коэффициентов
ряда Ьп по (7.3) разбиваем область интегрирования на два участ-
т
ка от 0 до tx и от /х до — (см. п. 3 основных положений) и
так как интегрирование производится не за целый период, а за
половину периода, то перед интегралом появляется множитель 2:
т_
2 1
Um , •
—/Sin П о)
.0
221
Взяв интегралы, получим выражение коэффициентов иско-
мого ряда:
, 4 Г ит { 1 . . . 1 . ATS'»
bn =— ——-----------------/cos и 0)1/4-------sin mo)j/) —
Т L /1 \ П 1Г /Р /J/s0
Т
U /e V 21/ / 1 \
—[cos nt»!/] =z---------------1-------------sin ntDi/i — cos птг I. (1)
П nit \ fl (Oj ?! /
T
1) Значение /i = -j- (кривая рис. 7.3,а). Формула для bn
примет вид
. 2Um / 2 . nit \
bn =-----/------sin---------cos П7Г| .
nit \ nit 2 J
Придавая п значения, равные 1,2,3,
., получим
Наконец, запишем искомый ряд:
и =
2Um
7С
2) Значение /1=0 (кривая примет вид рис. 7.3,6). При =0
Первое слагаемое в полученном ранее выражении (1) для Ьп об-
ращается в неопределенность, раскрывая которую найдем (путем
деления производной числителя на производную знаменателя и
переходя к пределу при стремлении к нулю), что
/ sin п (Oj ti \ _ ।
\ П й>! ti
Таким образом,
bn = —т - (1 — cos пл) = -4—- sin2
nit ' ' nit
222
Придавая п значения, равные 1, 2, 3, .... получим
е = = = ь‘ = °-
А _ 1 4(7т
Р5 - -g —.......
Искомый ряд
и — ( sin (ог/ 4- — зшЗю^ +—- sin5<o1/+.. .)в.
тс \ 3 5 /
Т
3) Значение tt = — (кривая примет вид рис. 7.3,в). Ранее
полученная для Ьп формула (1) примет вид
. 2t/m / 1 . \ 2Um
bn = —— ------sin пк — cos п к) =-----— cos ПК.
пТС \ ПТС ) лтс
При п = 1, 2, 3, ... коэффициенты ряда будут равны:.
= Ь, = —L. (, > .-St;
*1 л 2 2 к 3 1С
. _ 1
Искомый ряд
u = 2t/m- fsin (Dj t-----------------— sin 2<u! t 4- —- sin 3<ox t —
тс \ 2 3
1 • л / f \
-----sin 4g), t 4- ... e.
4 /
На рис. 7.4 изображены спектры пе-
риодических сигналов соответствующие
кривым рис. 7.3,а,б и в. Графическое изоб-
ражение спектра амплитудной характе-
ристики таково: на оси абсцисс отклады-
вается номер гармоники, а на оси ординат —
вертикальные отрезки, имеющие длины,
пропорциональные амплитудам гармо-
ник.
7.2. Разложить в тригонометрический
ряд функцию, выражаемую кривой пери-
одических импульсов напряжения постоян-
ной амплитуды Um, длительностью t„ (рис.
7.5,а). Даны: Um = 10 в, ta = 0,2 мсек, Т =
= 1 мсек.
Полученную функцию представить так-
же в виде комплексного ряда Фурье. Пост-
роить линейчатый спектр частот в зависн-
ет
Для кривой а)
- 11 I i ... .
0l23456T89i,
°кт
Для кривой 5)
-Li if,
О < 23456189 к
Для кривой в)
Рис. 7.4
223
мости от: а) номера гармоники пи б) угловой часто-
ты ш.
Такие же спектры построить, если Т = 2 мсек, остальные
данные те же.
Решение. Уравнения заданной кривой:
в интервале от t — 0 до /и
в интервале от t = 1И до t = Т
h (О = 0.
Рис. 7.5
Z
д)
7‘2мсек> tn* 0,2 мсек
11 I I. I Li 11 I I 1 » . » i.i 11 .i « -
2 3U56789U) 10 4
С помощью (7.3), разбивая область интегрирования на два
участка (см. п. 3 основных положений), находим коэффициенты
ряда и начальные фазы гармоник:
= 1Q.
2 ’ 1
(1)
224
и
о
cos n^tdt
f2 (t) cos n wxt dt
Um cos n tdt = 2^-— sinnw^j, = sinziwj /и;
п<лхТ im
(2)
tl
fH л
f ft (t) sin nw2tdt + J f2 (0 sin n iDft dt
*И
О
f Ums\nn^tdt =-----[созп®Ди
J
0
on
—— [1 —cosno)1/H];
тем
(3)
Unm = V a2n + b* = к sin2n®!/„ + [1—cos (мео,/и)]2 =
n n Itn
МШЖЖКМ*- 0 I | -Щ"""
кл 2
sin n О)! /и _ ct псо^и
1—COSnw^H 2
О
И
/I toj
Вычисляем коэффициенты ряда и начальные фазы гармоник.
При этом имеем в виду, что
<0, = 2^- = _5L_=2k. 108 се«-', 0)Ли=2к- 10s• 0,2• 10-3=0,4z рад.
1 Т МО-’
Для удобства расчеты сведены в табл. 7.2.
Искомый ряд
и = [2 *4“ 3,74 sin -4~ 0,3^0 3,03 siп (2(0^ -|” 0,1 тс) -|-
4- 2,02 sin (Зшг/ — 0,1тг) -|- 0,935 sin (4а)!/ — 0,Зтг) — 0,624 sin (бо^ t —
—0,7к) — 0,866 sin (7о)х/ — 0,9тс) — 0,757sin (8о)^ — 1,1те) —
— 0,416 sin (Эш^ — 1,3тс) 4- ...] в,
8 Заказ № 624
225
п 0 1 2 3
<лп = 72<X>J 0 103 103 6к 103
й) и/u п и /ч 1Л-4 0 0,2г. 0,4к 0,6т:
2 п
fl G)j /jj sin 2 0 0,588 0,951 0,951
U пап. е 9 3,74 3,03 2,02
<р„, рад 0,3~ 0,1г. —0. lit
Таблица 7.2
4 5 о 7 8 6 ю
8т: 103 10я 108 12я 10s 14л 103 16л 10s 18л 10s 20л 10s
0.8~ Я 1,2л 1,4л 1,6л 1,8л 2л
0,588 0 —0,588 —0,951 —0,951 —0,588 0
0,935 0 —0,624 —0,866 —0,757 —0,416 0
—0,3 л —0,7 л —0,9 л — 1, 1л — 1,3л
или, учитывая что — sin(n^t — фп) = sin(n^t — ± я), полу-
чим окончательно
и ~{2 + 3,74sin -|- 3,03sin (2<цх/-|- 0,lir)4-2,02sin (Зш^—
— 0,1я) + 0,935 sin (4о)х/ — 0,Зя) + 0,624 sin 4- 0,Зя) +
+ 0,866 sin (7u>j/ + 0,1я) 4- 0,757sin (всо^ — 0,1я) +
+ 0,416 sin (Эо)^ — 0,Зя) + ...] в.
Для определения ряда Фурье в комплексной форме (7.7)
находим комплексные амплитуды:
Fn =а„ — jbn = [sin я —/(1 —cosnioj^)] =
_ п ПоМи р 7
•— . 01 jj с
лл 2
Таким образом, комплексная форма
Ла>1>и
ряда Фурье
„:п
0111 —
пп 2
е v
п=—со
На основе полученных результатов на рис. 7.5,6 изображен
линейчатый спектр напряжения в зависимости от номера гармо-
ники (расчеты для п от 1 до 10 даны в табл. 7.2; аналогичные рас-
четы для п = 11 -~30 рекомендуется проделать самостоятельно).
По данным этой таблицы на рис. 7.5,в построен линейчатый
спектр в зависимости от о>л . Для построения графика выбраны мас-
штабы: по оси абсцисс одному делению соответствует 1 • 10~4 сек"1;
по оси ординат в одном делении 100- 10’в в-сек (при построе-
нии последнего графика спектральные амплитуды приведены к
нормированному масштабу путем деления на (ох == .
Для случая, когда Т = 2 мсек на рис. 7.5,г построен линей-
чатый спектр в зависимости от п, а на рис. 7.5,3 спектр изображен
в нормированном масштабе в зависимости от (расчеты реко-
мендуется читателю проделать самостоятельно).
Из рис. 7.5,в и д видно, что спектральные характеристики
импульсов одной и той же длительности /и зависят от периода Т
следования импульсов, и чем он больше, тем гуще располагают-
ся спектральные линии, а амплитуды соседних гармоник близки
по величине.
8*
227
7.3. Кривая напряжения содержит четыре гармоники:
и = (80cos <ох/ 4- 60cos 2шх/ — 15cos Зюх/ — 12cos 4<о1/ 4- lOOsin wxZ —
— 20sin 2<i>1/ 4- 30sin 3<ох/ — 8sin 4<ux/) в.
Записать этот ряд в форме (7.1), содержащей только сину-
соиды с начальными фазами и в комплексной форме (7.7). На-
чертить линейчатый спектр частот (амплитуд и фаз) в зависи-
мости от номера гармоники.
7.4. Разложить в тригонометрический ряд функцию тока,
график которой выражает телеграфные сигналы в случае перио-
дической передачи точек (рис. 7.6).
Рис. 7.6
Рис. 7.7
7.5. Разложить в тригонометрический ряд функцию напряже-
ния, выражаемую кривой пилообразного напряжения (рис. 7.7).
Сравнить полученный результат с разложением в ряд функции
задачи 7.1 п.З. По найденному выражению построить
кривую, составленную только из постоянной составляющей и
первой гармоники разложения функции, и выяснить графически,
насколько пилообразная кривая отличается от синтезируемой
кривой. То же—в случае добавления к постоянной составляю-
щей первой и второй гармоник. То же—в случае добавления
к предыдущему и третьей гармоники.
7.6. Напряжение на сетке лампы имеет вид периодически
ломаной линии, изображенной на рис. 7.8. Разложить в триго-
нометрический ряд функцию на-
пряжения, выражаемую указанной
кривой.
Указание У равнение кривой в ин-
тервале от 0 до
__ .
и1 — , •
а в интервале от до 2тс;
и
; 2л
Рис. 7.8
«2 = - о ~.- № — М)«
228
Из общего выражения следует получить частные случаи: 1) = 2гс
(сравнить полученные выражения с результатами задачи 7.5); 2)
3) “1/1= — Л.
7.7. Ограничившись тремя гармониками, разложить в ряд
Фурье кривую тока i, изображенную на рис. 7.9. По результа-
там разложения построить линейчатый спектр (амплитуд и фаз)
кривой тока.
а)
Рис. 7.9
Решение. Одним из графоаналитических методов разло-
жения периодической кривой в тригонометрический ряд являет-
ся следующий: период кривой f (w^) = f (х) разбивают на т рав-
2к
ных частей, каждая из которых А (ш^) = Дх =------, и при под-
ал
счете коэффициентов ряда по формулам (7.3) вместо интеграла
от произведений ординат кривой на ординаты соответствующей
синусоиды или косинусоиды берут суммы следующего вида:
229
2те т т
7- = f f{x)dx -А- £ Д(х)Дх= — 2 AW;
2 2к J 2к *-* т
О 6=1 6=1
ап =
2те т
— I f (х) cos (пх) dx ~ 2----У fk (х) cos. (пх) Дх
kJ 2л
о Ь=\
т
= — У /* (X) cosft пх;
т
6=1
т
bn = — y.fk (X) sinA пх,
т
6=1 '
(1)
где k — переменный индекс, принимающий значения от 1 до /и;
/л(х), cosAnx, sinAnx—значения /(х), cosnx, sin их при х =
= ЛДх.
Точность разложения тем больше, чем больше число частей т.
Если разлагаемая в ряд кривая обладает симметрией того
или иного вида, то заранее известно, какие гармоники содер-
жатся в ее разложении (см. п. 2 основных положений и соотно-
шений), и только эти гармоники следует подсчитывать. В этом
случае, в зависимости от вида симметрии подсчет средних зна-
чений произведений Д(х)созА/гх и fk(x)sinknx необходимо брать
не за целый период, а соответственно за половину или четверть
периода, а результат суммирования умножать соответственно на
2 или на 4.
Разделим период кривой на т = 24 части. Значения ординат
кривой в точках деления, равные занесены в табл. 7.3.
Там же приводятся значения cos^nw^ и их произведе-
ния на fk (о)/) для трех гармоник (и = 1, 2, 3). В той же табли-
це приведены вычисления сумм по отдельным столбцам, которые
используются при расчетах коэффициентов ряда по форму-
лам (1):
6=24
/о = v = — S 1079=45;
2 т 24
6=1
24
Cj = — У fk (0)10 cosft t = -^—(—442,6) = — 36,9;
т 24
6=1
bi = • 654 = 54,5;
6=1
230
№ k 3 п=1
<6 Q & 3 9 •ее с се 9 •ее сп О о /’от ^soo (;’<») 2(01/, град. 9 сч •ее с <л
1 52 15 1-0,259 НО,966 Н13,5 Н50,1 30 -0,500
2 84 30 -0,500 НО,866 Н42,0 Н72,7 60 -0,866
3 87 45 -0,707 НО,707 Н61,3 Н61,3 90 -1,0
4 86 60 1-0,866 НО,500 Н74,3 Н43,0 120 НО,866
5 82 75 но,966 (-0,259 Н79,0 (-21,3 150 1-0,500
6 80 90 (-1,0 0 , (-80,0 0 180 0
7 85 105 но,966 -0,259 1-82,0 -22,0 220 -0,500
8 94 120 НО,866 -0,500 (-81,2 -47,0 240 -0,866
9 98 135 1-0,707 -0,707 (-69,2 -69,2 270 -1,0
10 98 150 НО,500 -0,866 Н9,0 -84,8 300 -0,866
и 95 165 0,259 -0,966 Н24,6 -91,8 330 -0,500
12 88 180 0 -1,0 0 -88,0 360 0
13 78 195 -0,259 -0,966 -20,2 -75,2 390 (-0,500
14 64 210 -0,500 -0,866 -32,0 -55,3 420 НО,866
15 43 225 -0,707 -0,707 -30,4 -30,4 450 (-1,0
16 25 240 -0,866 -0,500 -21,6 -12,5 480 НО, 866
17 8 255 -0,966 -0,259 -7,7 -2,1 510 НО,500
18 —6 270 -1,0 0 4-6,0 0 540 0
19 —20 285 -0,966 1-0,259 Н19,3 -5,2 570 -0,500
20 —32 300 -0,866 [-0,500 Н27,7 -16,0 600 -0,866
21 —41 315 -0,707 -0,707 Н29,0 -29,0 630 -1,0
22 —41 330 -0,500 -0,866 Н20,5 -35,5 660 -0,866
23 —28 345 -0,259 но,966 +7,3 -27,0 690 -0,500
24 , 0 360 0 -1,0 0 0 720 0
2 сумма 1+Ю79|
| +654|—442,б| |
Табл ица 7.3
п=2 п=3
3 сч •ее сп О о •К» ' 3 см •ее с ОТ •и 3 •се 4ч. г* 3 сч •ее СП О U «4 3 я 3 со 3 СО •се с от ’К» 3 со •се от О о /’от£ ^UlS (/’от) 3 со •ее от О Q чМ 3 ^ле
+0,866 -26,0 +45,0 45 +0,707 +0,707 +36,7 +36,7
+0,500 Н72,6 +42,0 90 +1,0 0 -84,0 0
0 г 87,0 0 135 +0,707 —0,707 +61,4 —61,4
—0,500 Н74,4 —43,0 180 0 —1,0 0 —86
—0,866 +41,0 —71,0 225 —0,707 —57,8 —57,8 —57,8
—1,0 0 —80,0 270 -1,0 0 —80,0 0
—0,866 -42,5 —73,5 315 —0,707 +0,707 —60,0 +60,0
—0,500 -81,4 —47,0 360 0 +1,0 0 —94,0
0 -98,0 0 405 +0,707 +0,707 +69,2 —69,2
+0,500 -84,8 +49,0 450 + 1,0 0 -98 0
+0,866 -47,5 +82,3 495 +0,707 —0,707 —67,1 —67,1
+1,0 0 +88,3 540 0 -1,0 0 —88
+0,866 +39,0 +67,5 585 —0,707 —0,707 —55,1 —55,1
+0,500 Н55,4 +32,0 630 —1,0 0 —64,0 0
0 1-43,0 0 675 —0,707 +0,707 —30,4 -30,4
—0,500 1-21,7 —12,5 720 0 +1,0 0 -25,0
—0,866 +4,0 —6,9 765 +0,707 +0,707 +5,7 +5,7
—1,0 0 +6,0 810 +1,0 0 —6,0 0
—0,866 hlO.O +17,3 855 +0,707 —0,707 -14,1 +14,1
—0,500 h27,7 +16,0 900 0 —1,0 0 -32,0 '
0 1-41,0 0 945 —0,707 —0,707 +29,9 +29,9
+0,500 1-35,5 —20,5 990 -1,0 0 -41,0 0
+0,866 1-14,0 —24,2 1035 —0,707 +0,707 -19,8 —19,8
+1,0 0 0 1080 0 +1,0 0 0
1+238,11+66,8 1+145,4 —38,2
/I)B = q= Г <*?+*? =65,6; tg(|»1 = -^ = —g^- =
bi o4, о
= -0,677; ф1 = — 34° 10';
a2 = --— 66,8 = 5,6; b2 = —-238,1 = 19,8;
24 24
= c2 = V a*+ b* = 20,6; tg фа = = 0,283;
(/2 1*7,0
|2 = 15°50';
й3 =—-(—38,2) = —3,2; da= —- 145,4= 12,1;
24 24
-c, = VW+W- 12.5; >еф.“=
= —0,264; ф3 = — 14° 50'.
Следовательно, заданная кривая выражается уравнением
i == [45 + 65,6 sin (ш^ — 34°10') + 20,6 sin (2^/ + 15° 50') +
4-12,5 sin (Эф^ — 14° 5O')J ма.
На рис. 7.9,а построены постоянная составляющая /0 и от-
дельные гармоники ilt i2 и i3 кривой тока i. При графическом
построении отдельных гармоник необходимо помнить, что масш-
таб по оси абсцисс для разных гармоник неодинаков, так для
третьей гармоники масштаб абсцисс в три раза мельче, чем для
основной гармоники и т. д.
построена на рис. 7.9,6.
7.8. К зажимам цепи (рис..
7.10), параметры которой г =
= 30ол<, Лг = 60 мгн, = 18 ом,.
приложено напряжение и =
= [120 4- 200 sino)^ +
4- 50sin(3«)1/ 4- 30°)] в. Частота
основной гармоники /=50 гц.
Написать выражения мгновен-
ных значений тока I, напря-
жения иаЬ на участке ab. Определить показания приборов,,
если Аг и Vr — приборы магнитоэлектрической системы — пока-
зывают среднее значение, Л2 и V2 — приборы индукционной си-
стемы— показывают действующее значение переменной состав-
ляющей, А3 и V3 — приборы тепловой системы — показывают
действующее значение тока и напряжения. Вычислить активную
мощность, расходуемую в цепи.
Примечание. Рубильники Pi9 Р2 и Р3 служат для включения в цепь
того или иного амперметра.
Спектральная характеристика
Рис. 7.10
232
Решение. Постоянные составляющие тока и
на участке ab
напряжения
‘т
^ab (0) ~ г11(0) — 45 в.
Расчет для первой гармоники
Г m (1) 200 000 /21°25' _
* т (1) — у “• _ । _ । • г 3,88 б С1,
2(1) г + г, 4- /
Напряжение на участке ab
ab т (1) т (1) ^ab (1) — (1) (Г1 + / ~ 3,88 в X
х 26,1 е7 46020 = 101 е'24°55'в.
Расчет для третьей гармоники
U 50 е13°°
I = == . .. = о,674 e~'^w а-,
т<3> Z г 4-гх 4- |3 wxL,
^ab т (3)= (3) %ab (3) = т (3) (Г1 + / 3 0>х Lx) = 40 в.
Уравнения для i и иаЬ
I = [2,5 + 3,88 sin — 21°25') + 0,674 sin (3 wx t — 19° 40')] a;
uab = [45 + 101 sin (<ox t + 24° 55') + 40 sin (3a>x t + 52° 40')] e.
Наконец, найдем показания приборов:
амперметр Дх — /0 — 2,5 а;
вольтметр Vt — Uо = 120 в;
л г 1 / 3,88а , 0,674а о _о
амперметр А.г — /г — I/ -----1---— = 2,78 а;
w £ £
« I/ г, 1/ 2б№ ; 50*“
вольтметру^—t/2= I/ —s------1---к— = 146 в;
амперметр А3— /8= 1Л 2,5а 4- 4- = 3,74 а.
вольтметр V3 — U3 = 1/ 120а Н—= 189 в.
Г 4W 4W
233
Мощность, расходуемая в цепи, по (7.11а)
Р = ^(0)^(0)+ ^(i)Ло cos^(i) + ^<з) Лз> C0S<P(3) ~ 120-2,5 +
_2М_ . 2-8± cos 21° 55' + cos49°40' = 670 вт.
У 2 V 2 V 2 V 2
7.9. Цепь, состоящая из последовательно соединенных ак-
тивного сопротивления г = 8 ом и индуктивности L == 15 мгн,
подключена к периодическому напряжению с действующим зна-
чением 220 в, в разложении которого отсутствуют четные гар-
моники. Действующие значения гармоник связаны соотношени-
ями U3 = 0,4 U19 = 0,2 U\ и U7 = 0,05 иг. Гармониками
порядка выше седьмого можно пренебречь. Найти действующее
значение тока и коэффициент мощности цепи. Частота первой
гармоники f — 50 гц.
7.10. К цепи из последовательно соединенных активного
сопротивления и индуктивности подключено напряжение и ~
= (30 + 60 sin (ох /) в. Найти действующее значение тока и
мощность, расходуемую в цепи, если г = 3 ом и <ох L = 4 ом.
Написать выражения мгновенных значений тока и напряжения
на индуктивности. Построить кривые i, и, uL.
7.11. Цепь, составленная из последовательно соединенных
активного сопротивления и конденсатора, находится под дейст-
вием напряжения:
и = 100 + 200sin (Dj t 4- 30 sin /3wx t-~Y1 e.
Параметры цепи г = 5 ом, —— = 3 ом. Выразить ток i
и напряжение на зажимах конденсатора ис как функции време-
ни. Вычислить действующие значения напряжения, тока и мощ-
ность, расходуемую в цепи. Определить показание вольтметра,
подключенного к конденсатору, если это прибор: а) магнито-
электрической и б) электродинамической систем.
7.12.
при
На рис. 7.11 изображена схема цепи, параметры кото-
основной
частоте имеют
рои
Рис. 7.11
= 30 ом,
а активные сопротивления гх = 6 ом,
г2 = 5 ом и г3 = 20 ом. Приложенное к
цепи напряжение и = UQ + Um (i) sin <ox t-f-
+i/m(3) sin (3 (ox t + фз), где t/(0) = 30 в,
Um(\) = 100 в, Um(3) “40 в и ф(3) =20°. За-
писать уравнение мгновенного значения то-
ка неразветвленного участка цепи. Опре-
делить действующее значение каждого
тока. Вычислить мощность, расходуемую
в цепи.
234
Решение. Расчет постоянной составляющей.
Эквивалентное сопротивление цепи и величины постоянного
тока в неразветвленной части цепи и в ветвях с сопротивле-
ниями г2 и г3
—= 10 ом;
U on
(0) 30 о
1 (0) |Q о ач
э (0)
^2(0) Л (0) г । г 2,4 а, /? (0) Ц ^2(0) 0,6 а,
if * %>
4 (0) 0.
Расчет для первой гармоники. Определим комплексное со-
противление трех параллельных ветвей:
ab(D
2 (D
‘ Z
з (1)
4 (1)
1
20
— /30
= (79.6 — /37.7) 10"' ОЛТ1,
отсюда
(79,6-/37,7) 10"8
;25°20' =(10,254-/4,83) ом.
Комплексное сопротивление всей цепи
э (I)
ab(l)
716°30 ом.
Комплексные (максимальные) токи в неразветвленной части
цепи, напряжение на параллельных ветвях и токи в них
т (I)
100 = 5,88 e-/16°30' a;
17 ? 16°30'
ab т (1)
2т(1)
ab т (1)
Z2(I)
67 е> 8° 5"'
= 5,15
- / 58° 30
Зт (I)
Uab tn (I) __
Z3(l>
20
U ab т (1)
Z4 (1)
67 е'8”50'
е! 98°50'
— /30 ;
4m (1)
235
Расчет для третьей гармоники производится аналогично
1 (3) — 0М’ ^2 (3)
е / 82° 10'
= 36,5 eJ ом;
3 (3) = 0М> ^4 (3) = 1 3(0, С
30= — /10 ом;
ab (3)
^0 + .= (53’77 + '72’8)-10~3 0М
-1
abm = 6,56 - /8,9 = 11,05 е~/53°35' ом-
(ли \О) *
= Z + Z и = 12,56 — /8,9 = 15,35 е~/35°5' ом;
3 (3) 1 (3) ab (3) ' ’
40 е* 200
15,35 е“/35о5'
1т (3)
= 2,6е'ет
. т = 2,6 е/55°5 -11,05 е~т'
ао т (3) ’ ’
28,7
/ 1’30’
2т (3)
Зт (3)
4т (3)
U ab т (3)
%2 (3)
Ugb т (3)
%3 (3)
U ab т (3)
Z4 (3)
0,79 е-'"
2,87 ? 91°30'
а;
Уравнение тока в неразветвленной части цепи
= [3 + 5,88 sin (^t— 16°30') + 2,6 sin (З^ t + 55°5')] а.
Действующее значение каждого тока по (7.9)
Л = )/ 3’ + + 2’6* = 5,45 а
!, = /2,4. + + —4,4 ai
1, - /0,6- + -3'У.+-1--4.У = 2,64 о;
/. _ / = 2,57 а
236
Мощность, расходуемая в цепи, по (7.11 а)
Р = 30-3 + 4- ЮО-5,88 cos 16°30' +
£
+ 4- 40-2,6.cos 35°5' = 415 вт.
£
Проверка.
Р = l\ Г1 + Il г2 + Il r3 = 5,452-6 + 4,42»5 + 2,642-20 = 178 +
+ 97 + 140 = 415 вт.
7.13. В схеме, изображенной на рис. 7.12, ток, проходящий
по ветви, содержащей индуктивность, имеет постоянную состав-
ляющую 12(0) = 1 о, основную гармонику 7г(1> = 0,8 а и третью
гармонику /2(з> = 0,3 а. Найти действующее значение прило-
женного к цепи напряжения и мощность, расходуемую в ней,
если гг = 100 ом, г2 = 80 ом, L2 = 0,02 гн и С3 = 1 мкф. Ча-
стота основной гармоники / = 800 гц.
d
Рис. 7.12
Рис. 7.13
7.14. Найти токи, проходящие в отдельных ветвях (рис. 7.13),
если к цепи приложено напряжение и = (150 + 100 sin o>x t -j-
+50sin 3 (O] t) в. Даны: rx=500 ом, а>1 = 1000 ом, г2= 1000 ом,
«j L2 — 500 ом, г3 = 600 ом и —^-4— = 400 ом. Чему равна
мощность, расходуемая в цепи?
7.15. Для питания нагрузочного сопротивления г2 = 600 ом
от источника двухполупериодного выпрямленного синусоидаль-
ного напряжения (рис. 7.14, а) применен фильтр, сопротивления
элементов которого при частоте равны t\ = 100 ом, =
= 3000 ом, —4* =20 ом.
Определить отношение постоянной составляющей тока, про-
ходящего через сопротивление г2, к действующему значению
всего тока, проходящего через то же сопротивление при под-
237
ключении нагрузочного сопротивления через фильтр (рис. 7.14, б)
и сравнить с отношением тех же величин при непосредственном
а) ,-----------------
П/2 Я ЗЛ/2 2Л
Рис. 7.14
подключении г2 к источнику однофазного двухполупериодного
выпрямленного напряжения. Разложение в ряд заданной кривой
имеет вид
4t/m /11 1
и = -------s- 4—г-5- cos 2 ш, t — cos 4 w. t 4-
it \ z 1 • .4 л • n
COS 6 <»1 t —
7.16. Подобрать емкости Ct и C2 так, чтобы цепь (рис. 7.15)
была настроена в резонанс напряжений для основной гармоники
и не пропускала ток третьей гармоники. Угловая частота тока
основной гармоники <«i = 5000 сек’1. Параметры цепи: гх=50 ом
и L = 2 мгн. Написать выражения мгновенных значений токов
и напряжения на параллельном участке цепи, если к цепи
приложено напряжение и = (20 sin + 10 sin Зо^/) в. Под-
считать действующие значения токов, напряжения на параллель-
ном участке и мощность, расходуемую в цепи.
Рис. 7.15
Рис. 7.16
7.17. К цепи, состоящей из последовательно соединенных
г = 100 ом, L = 63,7 мгн и С = 17,7 мкф (рис. 7.16), подведе-
но напряжение
и — (10 sin «j t 4- 5 sin 3 o>i t 4-2 sin 9 o>1 t) в.
238
Частота основной гармоники Д = 50 гц. Чему равна мощность
искажения?
7.18. К цепи рис. 7.17 подведено напряжение и = (50 sin о>х t 4-
+ 22 sin 2 Wj t) в. Сопротивления элементов цепи (для основной
гармоники) равны = 12 ом,
Определить сопротивление г3 и действующее значение
каждой ветви, если известно,
находится в режиме резонанса.
-= 10 ом, r2= 12 ом, ом.
тока в
что на второй гармонике цепь
Рис. 7.17
Рис. 7.18
7.19. Напряжение, приложенное к двум индуктивно связан-
ным контурам (рис. 7.18), изменяется по закону и = (100 4-
4- 70,7 sin ^t) в. Параметры контуров: гг = 40 ом, г2~ 60 ом,
<n1L1 = 30 ом, (Oj L2 = 60 ом, Л4 =20 ом. Найти выражения
мгновенных токов в каждом из контуров.
Решение. Все токи по величине и фазе определяются для
каждой гармоники в отдельности.
Постоянная составляющая тока, проходящая в первом кон-
туре, во вторичном контуре э. д. с. не наводит.
Уравнения для двух контуров (для основной гармоники)
4~ Л°1М) / Ш1 М /2;
Д (f2 + + /А М Л = 0»
или
(40 + /30) I, + j 20 /2 = :
Г 2
(60 + /60) /а + / 20 4 = о.
Решая эти уравнения, получим
Д = 0,984 е~~! 31°30' а; /2 = 0,232 ё"1166°30 а.
Постоянная составляющая тока в первом контуре
1 — — 2 5 а
7° ~~ г, 40 ~~ а'
239
Выражение мгновенного тока в первом контуре
= [2,5 4- 0,984 V~2 sin (<М — 31°30')[ а,
и соответственно, во втором
i2 = 0,232 j/~2~ sin t — 166°30') а.
7.20. Найти действующие значения токов для контуров в
цепи (рис. 7.19), если и = (20 sin + 5 sin 3 Oj t) в. Парамет-
ры цепи: = 2 ом, L2 = 4 ом, г2 ~ 3 ом, —— =
= 6 ОМ И Wj М = 1 ом.
7.21. Определить показание теплового
амперметра, включенного в диагональ моста
(рис. 7.20), если приложенное напряже-
ние и = (30 + 60 sin Wj/ + 15 sin 3 в,
а сопротивления элементов цепи для ос-
0 и 0
Рис. 7.20
Рис. 7.19
новной частоты имеют: i\ = 30 ом, а)х = 50 ом, г2 == 30 ом,
=30 ом, r3 == 40ojh, (Dj L3 = 10 ом, r4 = 30 ом и г5 = 60 ом.
7.22. К четырехполюснику (рис. 7.21) подводится напряже-
ние и = (20 sin Wj t + 10 sin 3 Wj t) в. Сопротивления элементов
четырехполюсника для основной частоты гх = 5 ом, Lr =
= 10 ом, Wj L2 == 10 ом, —* = 15 ом, а сопротивление на-
(01 Gg
грузки —7^— = 24 ом. Вычислить отношение действующего
сн
значения напряжения на нагрузке к действующему значению
приложенного напряжения.
Рис. 7.22
Рис. 7.21
240
7.23. В схеме (рис. 7.22) известны гх = 12 ом, ~с =
= 18 ом, г8 = 14 ом и L = 8 ом. Определить показания
вольтметра электродинамической системы, если
и = [50 + 80 cos ш11 — 30 sin (2 шх t + 60°)] в.
Считать, что сопротивление
вольтметра во много раз превы-
шает сопротивление каждого из
элементов схемы.
7.24. В цепи (рис. 7.23) на
частоте <ох = 9600 сек'1 имеет
место резонанс токов, а на треть-
ей гармонике наступает резо- 0-----------------------------
нанс напряжений. Определить ин-
дуктивность катушек Lx и L2, если ис' ’
гх = Ю ом, г2 = 5ом и С = 2,5лисф.
7.25. Вычислить коэффициенты формы, амплитуды и искаже-
ния кривой напряжения, уравнение которой
« = Ulm sin а>х / + U2m sin 2 <ох/ (Ulm = 100 в и Uim — 30 в).
Решение. Сначала вычислим действующее значение напря-
жения по (7.9):
., -1 / 1002 , 302 „„ о
и = у —2-----------Ь ~2~ ~ 73>8 в
Рис. 7.24
Затем найдем среднее по мо-
дулю значение напряжения. Вви-
ду симметрии кривой и и положи-
тельности ее значений за полови-
ну периода (рис. 7.24) для его оп-
ределения достаточно ограни-
читься половиною периода:
i/cp ==
те
=—J (^lm ^П <ОХ t +
о
+ U2m sin 2 u>x t) du\t =
t/Xm cos u>x t +
63,7 в.
241
Теперь определим максимальную ординату кривой и:
du
lm cos «>! t + 2 Utm cos 2 o>i t = 0,
или, так как cos 2 I = 2 cos2 w11 — 1, то
4 U2m cos2 («j t + Ulm cos Wj t — 2 = 0;
120 cos2 4- 100 cos — 2=0,
откуда, решая квадратное уравнение, получим
cos шЛ = 0,404; w, t = 66° 10'
(знак «минус» перед корнем не годится, так как в этом случае
косинус окажется больше единицы), а
67max ~ 1100 sin (Oj t +30 sin 2 (Oj t =s 66o JO’ = 116,7 в.
Наконец, по формулам (7.12) -+(7.14) вычислим искомые коэф-
фициенты:
। __ 73,8 __ .
63,7 — 1,10;
116,7
73,8
a
100
и
73,8 ’
7.26. Найти коэффициенты формы, амплитуды и искажения
кривой напряжения:
а = Ulm sin 1 — U3tn sin 3 t = 100 в\ U3m = 30 в).
ГЛАВА ВОСЬМАЯ
КАТУШКИ И ТРАНСФОРМАТОРЫ
С ФЕРРОМАГНИТНЫМИ СЕРДЕЧНИКАМИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. В цепях с ферромагнитными сердечниками (в цепях «со
сталью») магнитный поток полностью или частично заключен в
одном или нескольких сердечниках.
Особенности цепей с ферромагнитными сердечниками:
а) нет прямой пропорциональности между магнитным потоком Ф
и током i\ это приводит к искажению форм кривых тока и
э. д. с.; индуктивность не является постоянной величиной и за-
висит от силы тока.
Уравнение и = ir 4- L , справедливое для катушек без
ферромагнитного сердечника, должно быть заменено уравнением
dW
dt
(8.1)
б) замыкание потока через сердечник связано при перемен-
ном токе с затратой энергии, превращаемой в тепло.
2. Потери в сердечнике. Потери мощности на магнитный
гистерезис определяются по эмпирической формуле
(3.2)
Для индукций в пределах от 1 до 1,6 тл (от 10000 до
16 000 гс) вместо предыдущей формулы можно воспользоваться
(8.3).
Потери на вихревые токи выражаются
(8.4)
243
где -q--удельные потери, отнесенные к 1 кг веса сердеч-
ника, вт\
f — частота, гц\
Вт—амплитуда магнитной индукции, тл\
а, р, аг, ав— коэффициенты, зависящие от марки материала, фор-
мы и размеров сердечников. Их значения для листо-
вых сердечников двух распространенных марок маг-
нитных сталей приведены в табл. 8.1.
Таблица 8.1
Сорт стали Толщина листов, мм а р аг % Удельные потери при В = 1 тл (вт/кг) If it
ЭИ 1,0 0,9 3,5 4,4 22,4 7,8
0,5 0,9 3,5 4,4 5,6 3,6
0,35 0,9 3,8 4,7 3,2 3,15
Э42 0,5 0,4 2,6 3,0 1,2 1,8
0,35 0,3 2,1 2,4 0,6 1,35
3. В катушке с ферромагнитным сердечником — дросселем
(рис. 8.1) различают: Фо — основной магнитный поток, линии
магнитной индукции которого замыкаются через стальной сер-
дечник; Ф$,—поток рассеяния, линии которого замыкаются че-
рез воздух. С основным магнитным потоком связывают основ-
ную индуктивную проводимость Ьо параллельной схемы заме-
щения катушки с ферромагнитным сердечником (рис. 8.2, а) или
основное индуктивное сопротивление xQ последовательной схемы
замещения катушки (рис. 8,2, б).
Рис. 8.2
Рис. 8.1
С магнитным потоком рассеяния связывают индуктивность
рассеяния Ls и соответствующее индуктивное сопротивление
рассеяния xs. Потери в сердечнике учитываются активной про-
водимостью g0 параллельной схемы замещения или активным
сопротивлением г0 последовательной схемы замещения; потери
в обмотке катушки (сопротивление провода обмотки) определя-
ются сопротивлением гоб.
244
Напряжение, приложенное к катушке с ферромагнитным
сердечником, определяется формулой*
й = iro6 + j^Lsi + йф. (8.5)
Здесь напряжение 7/ф связано с изменением основного маг-
нитного потока катушки:
йф = /4,44 fw Фи = / 4,44 fwSBm. (8.6)
Реактивная составляющая тока /р и активная составляющая
тока /а схемы замещения (рис. 8.2, а) выражаются
/₽ = иф Ьо", 1Л = ифёо. (8.7)
На рис. 8.3 вычерчена векторная
диаграмма катушки со стальным сер-
дечником.
Потери в сердечнике Рф и в обмот-
ке Роб
4. В трансформаторе с ферромаг- , £
нитным сердечником (рис. 8.4, а) разли-
чают основной магнитный поток Фо, Рис 83
замыкающийся по сердечнику и сцеплен-
ный как с первой wv так и со
второй обмотками трансформатора, и замыкающиеся по воз-
духу магнитные потоки Ф15 и Ф21 рассеяния первой и второй
обмоток.
Рис. 8.4
* Расчет п.п. 3 и 4 проводится в приближении замены несинусоидальных
токов, напряжений, индукций, потоков и т. д. эквивалентными синусоидаль-
ными функциями.
245
Схема замещения трансформатора с ферромагнитным сердеч-
ником, приведенная к первичной обмотке, показана на рис. 8.4, б.
Здесь fjo6 и г2об — сопротивления провода соответственно пер-
вой и второй обмоток трансформатора; Lls и Lis— индуктивности
рассеяния обмоток; Ьо — основная индуктивная проводимость
катушки; g0 — активная проводимость, учитывающая потери в
сердечнике. Последовательный вариант схемы замещения транс-
форматора с основным индуктивным сопротивлением х0 и со-
противлением потерь в сердечнике г0 показан на рис. 8,4 в.
Штрихами помечены на схемах замещения величины, изменен-
ные в соответствии с правилами приведения к первичной обмот-
ке:
' _ /7 . г' i 7' — ( Wi V 7 .
2 ~ Щ,1’ ‘ 7 = U>i Z®’ ^2 — \ Wi ) Л2,
е / 0^1 \2 , ( \2
Гг = НН r* Xi = НН х%- (8-9)
Отношение-^1- называют коэффициентом трансфор-
м а ц и и .
При синусоидальном напряжении уравнения Кирхгофа в сим-
BOJ и веской форме для первичной и вторичной обмоток трансфор-
матора имеют вид
— гюб Л + h + ^ф;
Оф = /*2 об 2 + ] ш L‘2S I 2 + U2 »
(8.10)
(8.Н)
УПРАЖНЕНИЯ И ЗАДАЧИ
8.1 Катушка со стальным сердечником (см. рис. 8.1), пред-
назначенная для работы при номинальном напряжении U= 100 в
переменного тока промышленной частоты f = 50 гц, имеет об-
мотку с числом витков w = 1003 и активным сопротивлением
гоб = ЮО ом. Сердечник катушки весом G = 1,8 кг набран из
пластин стали Э42 толщиной 0,5 мм, кривые удельных потерь
которой заданы графиками рис. 8.5. Общее сечение стали сер-
дечника 3,2 см2, Пренебрегая магнитным рассеянием, опреде-
лить параметры параллельной схемы замещения катушки (см.
рис. 8.2, а).
Решение. По условию задачи пренебрегаем магнитным
рассеянием xs = 0.
По схеме замещения (см. рис. 8.2, а) напряжение катушки
0 — i гоб + •
146
В первом приближении полагаем = U — 100 в. По (8.6)
максимальное значение магнитной индукции (в первом прибли-
жении)
Рис. 8.5
По кривым удельных потерь (рис. 8.5) определяем соот-
ветствующие значения удельных активной и реактивной
мощностей, связанных с перемагничиванием сердечника,
которые в первом приближении составляют —= 3 вт!кг и
Q(0
—= 26 ва!кг. Умножая на вес сердечника, определяем &
рассматриваемом приближении
Р(|) = 3-1,8 = 5,4 вт; Q(1) = 26-1,8 = 46,8 ва.
Вычисляем активную /а и реактивную 1р составляющие тока
схемы (см. рис. 8.2, а).
В первом приближении
Р(1> 5,4
~ ~100
'ж*
= 0,054 а; =
В рассматриваемом приближении ток катушки
/0) = + =(0,054-/0,468) а,
247
а напряжение
(7(1) =(0,054 — /0,468)-100 + 100 = 115 e-'23’55' в
на 15% превосходит по модулю точное значение U ~ 100 в.
Для уточнения во втором приближении зададим меньшие
значения
1 о г/2) л лл t od(2) no
== 1,3 тл и t/ф = 4,44 fwSBm = 93 в.
Повторяя аналогично расчет во втором приближении, опре-
делим
р(2) л(2) .£ >2)
= 2,5 вт/кг\ == 16 ва/кг\ Р = 4,5 вт\ Q = 28,8 аа;
(j и
я»
р(2) О(2)
/(? = М2) = 0,0484 а-, /<2> = ^(2j = 0,31 а;
иф u ф
?2> = (0,0484 — /0,31) а.
U(2) = (0,0484-/0,31)-100 + 93 = 97,8 — / 31 = 102,5е-/17°35' в.
Напряжение всего на 2,5% отличается от точного значе-
ния U = 100 в.
В последнем приближении параметры схемы замещения
{рис. 8.2,а) катушки в номинальном режиме:
а __ __ 0,0484 _ гn 1 л-з а __ _ 0,31 ___
~~ Z7<2) ~~ 93 10 0М ’ °° ~~ гг(2) ~~
Ф Ф
= 3,33-10~3 ом"1.
8.2. Известно, что при Д = 50 гц потери в стали Р1ст»
= 1,5 вт/кг, а при /2 == 100 гц Р2СТ = 4 вт/кг. Разделить потери
в стали на потери от вихревых токов и от магнитного гистерезиса,
считая, что магнитная индукция остается неизменной.
Решение. Потери в стали на магнитный гистерезис при
Вт == const прямо пропорциональны частоте f формулы (8.2) и
(8.3), а потери на вихревые токи пропорциональны квадрату
частоты (8.4), поэтому
Р1СТ = afi + б/, = 50 а + 2500 b = 1,5 впг/кг\
Р2СТ = af2 + bfl = 100 а + 10 000 Ь = iem/кг,
где а и b—постоянные коэффициенты, зависящие от сорта ста-
ли и величины магнитной индукции.
I
I
248
Решая эти два уравнения, найдем
а — 0,02 дж/кг\ 6 = 2-10~4 дж-сек!кг.
Искомые величины:
при Д = 50 гц
Plr — afy = 0,02 • 50 = 1 вт/кг\ Р1В = bf\ = 2 • 10~4 • 2500 =
= 0,5 вт!кг\
при Д = 100 гц
Р2Г = аД = 2 ет/кг-, Р2в = bfl — 2 вт/кг.
8.3. Потери в стали трансформатора при некоторой частоте
составляют 600 вт. При удвоенной частоте и неизменной ампли-
туде магнитной индукции потери в стали увеличиваются втрое.
Произвести разделение потерь на вихревые токи и на гистерезис.
8.4. При номинальном первичном напряжении потери в стали
трансформатора составляют Рст = 1 кет. Определить потери в
стали трансформатора при повышении и понижении напряжения
на 10%. Частота и форма кривой э.д. с. остаются неизменными.
Потери на гистерезис определять по (8.3).
8.5. Катушка со стальным сердечником включена на напря-
жение Ux = 100 в и по ней проходит ток = 5 а, отстающий
по фазе от напряжения на угол <рр причем cos= 0,7. Этаже
катушка при том же напряжении, но без стального сердечника
потребляет ток /2 = 10 а, отстающий от напряжения на угол
<р2, причем cos <р2 = 0,9. Определить потери в стали и меди и
построить векторную диаграмму при наличии сталь-
ного сердечника. С помощью векторной диаграммы определить
г0 и х0 в схеме замещения катушки со стальным сердечником.
Решение. При отсутствии сердечника катушка имеет толь-
ко потери в меди:
122г = UJ2C0S ф2.
Отсюда активное сопротивление обмотки катушки
Ui cos п
г = — -. т - == 9 ом.
<2
При наличии стального сердечника в катушке расходуется
мощность
Рх = UJi cos фх = 350 вт.
Часть этой мощности
Роб = /2Г = 225 вт
идет на покрытие потерь в меди, а другая часть—на потери в
стали
Рст = pi — роб = 125 вт.
249
Эквивалентная последовательная схема катушки со сталью,
не имеющей рассеяния, дана на рис. 8.6,а.
На рис. 8.6,6 начерчена векторная диаграмма катушки со
стальным сердечником.
Ё^-йф
Рис. 8.6
Из векторной диаграм-
мы следует, что активная
составляющая приложен-
ного напряжения
их cos <рх = Л (г + г0),
откуда
г __ и 1 cos <?!
г0 - - г
Из диаграммы видно,
что
{4 sin <рх = /хх0
и, следовательно,
х0 =
Ui sin
100-0,715
5
= 14,3 ОМ.
Величина э.д.с., наводимой в катушке,
Е ~ / V Го + Хо = 75,6 в .
8.6. Сердечник однофазного трансформатора набран из стали
Э11 толщиной d = 0,35 мм, имеет прямоугольное сечение 150 х
X 100 мм2 и длину средней линии магнитной индукции 120 см.
Изоляция между листами занимает 10% сечения. Первичная об-
мотка его состоит из шх = 1500 витков и включена на напря-
жение (7Х == 6000 в. Определить потери в стали. Частота пере-
менного тока f = 50 гц.
Указание. Воспользовавшись формулой (8.6), определить магнитный
поток Фт. Зная активное сечение сердечника S = 0,9-15-10-10-4 м*, найти
магнитную индукцию Вт. Потери в стали найти по (8.3) и (8.4).
8.7. Первичное и вторичное напряжения трансформатора
равны иг = 3300 в, U2 = 220 в. Сердечник его имеет сечение
S = ЮО см2 и вес G = 350 кг и набран из листов электротехни-
ческой стали ЭН толщиной d ~ 0,35 мм. Максимальная магнит-
ная индукция в сердечнике Вт = 0,8 тл (8000 гс). Определить
необходимое число витков первичной и вторичной обмоток, ток
холостого хода и коэффициент мощности трансформатора при
холостом ходе.
250
Частота переменного тока f = 50 гц.
Решение. Пренебрегая в опыте холостого хода падением
напряжения на сопротивлениях обмоток и индуктивностях рас-
сеяния, из формулы (8.6) найдем, что
У* -г = 1860 витков и
~ = 124 витка.
Средняя длина магнитопровода, равная длине средней линии:
магнитной индукции, найдется из формулы G = Sid, где плот-
ность стали d = 7,6 г/см3. Отсюда I = 4,6 м.
По кривой намагничивания для стали ЭН (см. приложение 1>
найдем, что при В& = 0,8 тл Н = 318 а-м.
Намагничивающая сила (амплитудное значение)
^aw = HI = 318*4,6 = 1460 а,
и так как
У aw = wxl\m ~ 1460 а,
то ток намагничивания
1460
=0,555 а.
Потери в стали определяем по (8.2) и (8.4):
Рст = (0,9 * 0,5 * 0,8 + 3,8 * 0,5 * 0,64 + 3,2 • 0,25 * 0,64) * 350 =
= 2,09*350 = 730 вт-
Так как Рст = то
__ 730
а ~ 3300
/а 0,22 Л
C0S Фо ~~ /j 0,555 “ °’397 *
На рис. 8.7 приведена
трансформатора.
векторная диаграмма холостого
хода
Рис. 8.8
25?
8.8. В катушке со стальным сердечником расходуется мощ-
ность Р = 0,2 кет при напряжении U = 100 в и токе I = 10 а.
Активное сопротивление обмотки гоб — 0,5 ом и реактивное со-
противление рассеяния xs = 1 ом. Частота тока f — 50 гц.
Определить из векторной диаграммы ток /р параллельной
схемы замещения (см. рис. 8.2,а), сопротивления г0 и х0 после-
довательной схемы замещения (рис. 8.2,6) и составляющую при-
ложенного напряжения t/ф , уравновешивающую э.д.с., которая
индуктируется в обмотке катушки основным магнитным пото-
ком, пронизывающим сердечник. При построении диаграммы
предполагать, что ток изменяется по гармоническому закону.
Решение. Построение векторной диаграммы показано на
рис. 8.8.
Из соотношения P = (7/cos<p найдем, что cos <р = 0,2.
Отрезок Ob — I (г + г0) = U cos q>,
отсюда
U COS 9 , с
г0 =---т—1---г = 1,5 ом.
Отрезок Ьс == С/sin <р = 97,9, с другой стороны, be = ае 4-
+ ef = 1х0 + Ixs, отсюда х0 = 8,79 ом.
Теперь найдем
иф = V (Оа)* + (ае)2 = / У го + *о = 88,5 в.
Реактивный ток
Л= /cosa=10-4H- =9,94 а.
8.9. Однофазный трансформатор с коэффициентом трансфор-
мации k = : w2 == 2 с разомкнутой вторичной обмоткой при-
ключен к сети с напряжением U = 220 в. Полагая, что транс-
форматор изготовлен из стали марки Э11 (удельный вес 7,8г/сл*3),
толщина листов которой d = 0,5 мм, определить потери в стали,
величину тока в обмотке и построить векторную диаграмму.
Потоком рассеяния пренебречь. Число витков первичной обмот-
ки = 74, активное сечение сердечника S = 100 см2, средняя
длина сердечника /ср = 150 см. Частота / == 50 гц.
Указание. При определении магнитной индукции в стали трансформа-
тора в первом приближении можно считать напряжение на зажимах равным
э.д.с. обмотки трансформатора. Для определения намагничивающего тока /j
необходимо при расчете магнитной цепи воспользоваться кривой намагничива-
ния для листовой стали ЭН, приведенной в приложении 1.
8.10. Однофазный трансформатор = 6600/220 в с номи-
нальной мощностью Р = 50 ква имеет потери /холостого хода
рх х = 380 вт и к.п.д. при полной нагрузке ?] = 96,15% с
cos ф2 = 0,8. Определить активное сопротивление первичной и
252
вторичной обмоток, считая, что первичные и вторичные потери
в меди одинаковы.
Решение. Известно, что ток холостого хода имеет незна-
чительную величину по сравнению с номинальным током. Поэ-
тому при холостом ходе можно пренебречь потерями в обмотке
(потерями в меди) и считать, что потери холостого хода при-
близительно равны потерям в стали Рх.х Рст ~ 380 вт.
Общие потери мощности при нагрузке трансформатора
Ле + Лт = 11—= 1540 вт.
Отсюда
Роб = 1540 — 380= 1160 вт-
Лоб = Лоб = = 580 вт.
Номинальный ток в первичной цепи при нагрузке
= = 7,6 tz;
активное сопротивление первичной обмотки
г1об = -^г- = Ю>1 ом.
11
Так как по условию активное сопротивление первичной об-
мотки равно приведенному сопротивлению вторичной:
г
г юб = 2об == 2об^2»
где
Ъ — — 6600 — QO
R w* 220
то
г20б = -^4- = 0,011 ом.
8.11. Опыты холостого хода и короткого замыкания однофаз-
ного трансформатора дали следующие результаты: холостой
ход—t/ix.x = 400 в, /1х.х = 0,4 a, Pix.x = 20 вт, короткое замы-
кание— С/1К.з =32 в, /1К З = 5 в, Pik.s =80 вт.
Данный трансформатор — повышающий и имеет коэффициент
трансформации k = = -1=- .
ID
Предполагая, что активное и реактивное сопротивления рас-
сеяния первичной обмотки равны соответственным приведенным
сопротивлениям вторичной обмотки (г10б = г2об, xls = x2s == х2),
определить их величины.
253
При холостом ходе можно пренебречь падением напряжения
в первичной обмотке. При коротком замыкании можно пренеб-
речь намагничивающей составляющей первичного тока.
Решение. На рис. 8.4, в изображена эквивалентная схема
трансформатора.
Из опыта холостого хода, пренебрегая падением напряжения
в первичной обмотке, имеем
1Л- X
гх.х = ' = 1000 ом;
11х.х
cos <рх х = —. Р‘х.х------ = 0,125;
и\х.х 11х.х
%х.х ^х.х sin фх.х = 992 ом;
Рис. 8.9
^1к,3 £ л
zK ,з = -т----- = 6,4 ом;
' 1к.з
Гх.х — ^х.х COS фх.х — 125 ОМ.
Если пренебречь составляющей
тока /0, эквивалентная схема транс-
форматора при коротком замыкании
примет вид, изображенный на рис.
8.9, и тогда
Р
cos<p1K,3 = т.—^4------= 0,5;
^Чк.З '1К.З
Так как
то
Г10б + г2об = гк.з COS Ф1К.З = 3,2 ОМ;
Xls + X2s = -3 Sin Ф1К.З = 5,54 ом.
гЮб = Г2об*’ ^15 = X2s>
г1об = I»6 ом* г2об = -5" = 360
= 2,77 ом;
X2s =
2s
k2
== 623 ом.
8.12. Ко вторичным зажимам трансформатора предыдущей
задачи приключен приемник энергии, имеющий cos ф2 = 0,92
(ф2 > 0), при этом напряжение на вторичных зажимах U2 =•
== 6000 в, сила тока во вторичной цепи /2 = 0,25 а. Найти на-
пряжение на первичных зажимах — силу тока в первичной
обмотке к.п.д. т] и коэффициент мощности соэфр Найти по-
тери в стали и меди при. нагрузке трансформатора.
Решение. Задачу проще всего решить, если применить
символический метод к эквивалентной схеме трансформатора
(см. рис. 8.4,в).
254
Приведенные величины вторичного напряжения, тока и со-
противлений
U' = Utk = 400 в; 1'=-Ь- = 3,75 а;
* * FV
(/,
г2н = -р- = 106,6 ом; г2н = z2H cos <р2 = 98 ом;
'2
Х2н = 22н Sin ^2 = 41 ’6 0М-
Напряжение t/ф на параллельных ветвях
г2н + г2/ + / ( *2н + %2s ) == (374 4" /167) в,
‘ t
где /г направлено по вещественной оси, и, следовательно,
Г2 = /2 = 3,75 а;
'о = 4== °-4k""50’ = <°-21 -'-о’з5> а’
I. = L + /0 = 3,96 — /0.35 = 3,96e a.
Приложенное напряжение
f/j = +йф = 383,5 4- /175 = 420e-/24°15 в.
Сдвиг фаз между напряжением на входе трансформатора и
первичным током
Ф! = 24° 15' — (— 5°5') = 29°20'.
Мощность, подводимая к трансформатору,
Р, = UlIl cos cpj = 1450 в tn.
Мощность, расходуемая в приемнике энергии,
Р2 =z t/2/2cos ф2 == 1380 вт.
К.п.д. трансформатора
V = = 0,95.
Потери в стали при нагрузке трансформатора
Рст = ^ого = 21 вт-
Потери в меди при нагрузке трансформатора
^06 = Р1 — Р2 — Р„ = 49 вт.
2SS
8.13. К трансформатору задачи 8.12 приложено напряжение
U1 = 420 в. Найти величину напряжения U2 на вторичных за-
жимах при холостом ходе, пренебрегая при этом падением на-
пряжения в первичной обмотке. Показать возможность такого
пренебрежения.
Решение. При холостом ходе можно положить ~ U$ =
= 420 в. Тогда
Ut = = 6300 в.
л к
Пренебречь падением напряжения в первичной обмотке мож-
но, так как - = °’ton’2 ~ 0,003 = 0,3%, т. е. падение
с/1
напряжения в первичной обмотке составляет всего 0,3% от при-
ложенного напряжения.
ГЛАВА ДЕВЯТАЯ
ДВУХПОЛЮСНИКИ
6
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Комплексное сопротивление Z пассивного двухполюсника,
содержащего активные и реактивные элементы, определяется
выражением
7 _ апРп + an-i Рп~* + . . . 4- akpk + . . . + ахр 4- а0 /о i \
(р) “ ЬпгРт + Ь^р™-' + . . . 4- bkp* + . ..+blP + b0 ’
где р =/ш, a ak и bk—коэффициенты, зависящие от элементов
схемы двухполюсника. Для любых двухполюсников коэффици-
енты п и т не могут разниться более чем на 1, поэтому воз-
можны случаи п = т либо п — т= ± 1; кроме того, а0 либо bQ
могут равняться нулю.
2. Эквивалентные двухполюсники — двухполюсни-
ки различной структуры, если их сопротивления взаимно равны
на любой частоте. В табл. 9.1 приведены некоторые схемы и
условия их эквивалентности.
Таблица 9.1
Схемы некоторых эквивалентных
двухполюсников
Условия эквивалентности
Ь = а (1 4- а)
с = (1 4- а)2
d = 1 4- я
9 Заказ Ks 624
257
Схемы эквивалентных двухполюсников, содержащие наимень-
шее возможное число элементов в виде сосредоточенных сопротив-
лений, емкостей и индуктивностей, называются каноническими.
3. Обратные двухполюсники — двухполюсники с со-
противлениями Z и Z', произведение которых является действи-
тельным положительным числом /?2, не зависящим от частоты
(постоянно):
ZZ' = /?2. (9.2)
D2
Сопротивление Z' = называется обратным сопротивлению
Z в отношении /?2.
Пример в задаче 9.7.
4. Реактивные двухполюсники — двухполюсники,
состоящие только из реактивных элементов. Их сопротивления
реактивны:
z (/(о) = jx ((D). (9.3)
В канонических схемах реактивных двухполюсников (рис.
9.1,а и б и 9.2,а и б) число индуктивностей или равно числу емко-
стей или отличается от него на единицу. Для канонических
258
схем общее число резонансных частот на единицу меньше об-
щего числа элементов. Частоты резонансов напряжений и токов
реактивных двухполюсников чередуются; между любыми двумя
резонансами напряжений имеется один резонанс токов и между
любыми двумя резонансами токов имеется один резонанс напря-
жений (рис. 9.1,в и г; 9.2, в и г). При возрастании частоты ре-
активное сопротивление двухполюсника х(ш) в точках непрерывно-
сти возрастает (с учетом знака реактивного сопротивления). Если
в схеме двухполюсника имеется путь для постоянного тока, то
первым будет резонанс токов, а если такого пути нет, то пер-
вым станет резонанс напряжений.
В зависимости от характера сопротивления при частотах
ш —> 0 и со -> оо (вблизи нуля и бесконечности) двухполюсники
делят на 4 класса (см. табл. 9.2).
Таблица 9.2
Класс двухполюсника Нули и полюсы при Характер сопротивления при частоте
со = 0 со = со со -* 0 со со
I 0 X индуктивный индуктивный
II X 0 емкостный емкостный
III 0 0 индуктивный емкостный
IV X X емкостный индуктивный
Две основные формы канонических схем двухполюсников
класса IV показаны на рис. 9.1,а и б.
Сопротивление четырехполюсника класса IV
( ш2п—1 — °*2)
7/- X #
Z (]&) = —
М ' /О)
(Oq --- (О2)
- /
~~ °*2)
/2 о\
(9.4)
где Юр ю3, ... — частоты резонансов напряжений;
<о2, w4’ • • • — частоты резонансов токов; при этом <
< < . . . < О)2п~2 < ш2п~1 .
От канонической схемы (рис. 9.1, а) для двухполюсников
класса IV можно перейти к соответствующим каноническим
схемам двухполюсников класса I, исключив из схемы емкость
С2л, класса II — индуктивность £2л и класса III — ветвь L2rt, С2л.
Например, для двухполюсника класса I на рис. 9.2,а, бив по-
казаны схема, расположение нулей и полюсов и ; изменение
реактивного сопротивления соответственно.
Соответствующее выражение сопротивления двухполюсника
класса I
(2 9\( 2 2
(0о — (О45 (О л — (О“
1О) = 1°>н ~гЧ—J
t (о । — 40 11 w3 — &
( w2n—2 0)2 )
(2 2\ ’
( a)2/i-3“ )
(9.5)
9*
259
где Фр w3,... — частоты резонансов токов;
ф2, ш4> • • • — частоты резонансов напряжений.
Постоянные Я, входящие в выражение сопротивлений реак-
тивных двухполюсников, имеют размерность индуктивности для
двухполюсников классов I и IV и размерность, обратную емко-
сти,— классов II и III. Для нахождения постоянной Н можно
определить характер сопротивления двухполюсника (индуктив-
ный или емкостный) при частоте, превышающей наибольшую
резонансную. Если оно имеет емкостный характер, из схемы
следует исключить все ветви, содержащие индуктивности, и оп-
ределить эквивалентную емкость С3 полученной схемы, а за-
тем приравнять Н этой обратной эквивалентной емкости
(н =^—\. В случае индуктивного характера все емкости схемы
следует заменить короткозамкнутыми участками, подсчитать
эквивалентную индуктивность L3 оставшейся схемы и ее при-
равнять Н (Н = L3 ).
Пример в задаче 9.10.
УПРАЖНЕНИЯ И ЗАДАЧИ
9.1, В схемах (табл. 9.3) известны сопротивления и х2 ре-
активных двухполюсников при двух частотах Д и /2.
Для каждого варианта найти резонансную частоту и значе-
ние индуктивности и емкости.
Таблица 9.3
Схема
Номер
варианта
Значение частоты и соответствующего реактивного
сопротивления
ft, кгц
10,6
2,65
5,3
h, кгц
15,9
10,6
21,2
х2, ом
-1-160
— 90
4-225
X,, ом
7,95
2,65
21,2
—72
4-40
—16
9.2. Для схем реактивных двухполюсников (рис. 9.3.) начер
тить (в масштабе) кривые изменения реактивных сопротивлений и
проводимостей в функции угловой частоты и определить резо-
нансные частоты.
260
9.3. Найти схемы и параметры элементов двухполюсников,
обеспечивающих их эквивалентность двухполюсникам (рис. 9.4).
Указание. Использовать табл. 9.1.
Рис. 9.4
9.4. Найти схемы и параметры элементов двухполюсников,
эквивалентных двухполюсникам, изображенным на рис. 9.5.
Указание. Использовать табл. 9.1.
а) 120ом 80 мгн
Рис. 9.5
9.5. Вычислить входное сопротивление Z двухполюсников
(рис. 9.6), если t\ = г2 = г = = 500 ом.
9.6. Найти коэффициенты и написать
уравнение сопротивления двухполюсника
(рис. 9.7).
9.7. Составить схему двухполюсника,
обратную в отношении R2 = 100 схеме
рис. 9.8, а, и определить значения ее
элементов, если Lt = 2 мгн, L2 = 5 мгн,
С3 = 100 мкф, L^ — 5 мгн, гь = 10 ом,
CQ = 25 мкф, г1 = 20 ом.
Решение. Найдем сопротивление ZJ,
обратноесопротивлению Z1~j со Lv по(9.2):
261
Z' =— = Ri = 1 = 1
1 zi 1<° Li . [ Li\ jaC.
1 Ц) I - I ' 1
\R2
2-10~8
100
= 2 • 10~5ф == 20 мкф — емкость, определя-
ющая элемент, обратный элементу Zv
Рис. 9.7
Рис. 9.8
Аналогично рассчитываем элементы, обратные индуктивности
£2, емкости С3, индуктивности Л4, сопротивлению г5, емкости Св
и сопротивлению г7 в отношении R2 = 100. Это будут соответ-
ственно емкость С' = — = — = 5 • 10“б ф = 50 мкф' ин-
дуктивность L'3 = C3R2 = 100 • 10~e • 100 = 10‘2 гн = 10 мгн\ ем-
кость С'4 = ~ — == 5 • 10“б ф = 50 мкф; сопротивление
10 ом, индуктивность Lg=C67?2=25‘ 10~6-100=
= 25 • 10~4 гн = 2,5 мгн. Сопротивление г' = — = = 5 ом.
Последовательно включенным элементам исходной схемы со-
ответствуют параллельно включенные обратные элементы об-
ратной схемы. Поэтому искомая обратная схема имеет структу-
ру, показанную на рис. 9.8, б.
9.8. Найти схему и элементы двухполюсника, обратного в
отношении /?2 = 106, изображенному на схеме (рис. 9.9).
10 мгн 0,25 мкф
0.05 мкф Оком
Рис. 9.9
50ом 2 мгн 100ом
Рис. 9.10
200ом
262
9.9. Найти элементы двухполюсника и составить схему двух-
полюсника, обратную в отношении /?2 = 104 схеме рис. 9.10.
Указание. Искомая схема, так же как и заданная, имеет цепочечный
вид, при этом каждый последовательный элемент заданной схемы в обратной
схеме станет параллельным, и наоборот.
9.10. Найти класс двухполюсника
(рис. 9.11, а), его каноническую схему
и параметры и составить уравнение его
сопротивления. Даны : С± = С2 = 0,2 мкф,
С3 = 0,4 мкф, С4 = 1 мкф, L =^0 мгн.
Решение. Определим класс двух-
полюсника. Для этого выясним характер
сопротивления и его величину при
о = 0 и о) = оо. Из заданной схемы
видно, что постоянный ток через двух-
полюсник проходить не может, следо-
вательно, при (в = 0 его сопротивление
бесконечно велико, т. е. оно имеет ем-
костный характер; при (о = оо сопро-
тивление двухполюсника стремится к
нулю, т. е. оно также имеет емкостный
характер. Сопоставляя эти результаты с
табл. 9.2, устанавливаем, что двухпо-
люсник относится к классу II.
Для определения канонической
схемы двухполюсника выберем не-
Рис. 9.11
зависимые контуры согласно схеме рис. 9.11, а, составим
уравнения по методу контурных токов и решим их совместно,
установив связь между U и Ц !
263
Подставляя числовые значения и умножая все члены урав-
нений на /о) IO"6, получим:
I U j <о. 10-6 = 11 + 10/п + 6/1П ;
II 0= 10/j -}» 12,5/jj -j- 5/1П ;
III 0 = 6/’ + 5/n + (6 —4o)2 10-«)/in .
Исключая из последней системы уравнений токи 1п и 7Ш ,
находим
З.'О.-
/ О) (108 — <О2)
Таким образом, комплексное сопротивление имеет две
резонансные частоты =
= 8170 сек~х и 104 сек~'
и принадлежит трехэлементному двухполюснику класса II. Гра-
фик реактивного сопротивления в функции частоты и канониче-
ская схема двухполюсника показаны на рис. 9.11, бив.
Для определения Н и параметров канонической схемы
(рис. 9.11, б) выразим сопротивление двухполюсника при часто-
тах о) со через параметры заданной схемы, отбросив в ней
ветвь с индуктивностью L (см. п. 4 основных положений):
а также выразим через параметры двухполюсника (рис. 9.11, б)
резонансные частоты:
(о1 = —----1..-..— = 8170 сек’1; (2)
У (С5 + С6)
о2 = -• 1-----= Ю4 сек’1. (3)
Решая систему уравнений (1)~(3), находим параметры эле-
ментов канонической схемы: С6 = Ce = 1 мкф, Lx = 10 мгн.
264
Указание. Задача может быть решена и другим способом — путем
преобразования треугольника емкостей Сь С2» Сз в эквивалентную звезду.
9.11. При какой емкости С в цепи (рис. 9.12) имеет место
резонанс токов на частоте 5 Мгц. Известны: = 0,4 мгн и
L2 = 0,5 мгн. Определить класс двухполюсника и составить
уравнение его сопротивления.
Рис. 9.12
Рис. 9.13
9.12. Определить элементы двухполюсника (рис. 9.13), если
известны его резонансные частоты о)г = 4080 сект1, о)2 = 7070 сек"1,
а при заданной частоте «)3 = 3200 сек''1 модуль его сопротивле-
ния равен 510 ом.
ГЛАВА ДЕСЯТАЯ
ЧЕТЫРЕХПОЛЮСНИКИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Связь между входными и выходными напряжениями и то-
ками UY и I19 U2 и /2 линейного пассивного четырехполюсника
(рис. 10.1, а) может быть выражена одной из шести групп ос-
новных уравнений. Из них ниже приводятся три группы.
Л21
Рис. 10.1
Уравнения в форме [Л]
U. = AU2 + В/2;
А = Cf72 + D/2.
(10.1а)
Вместо коэффициентов Л, В, С и D часто пишут Ли,
и Л22.
Уравнения в форме [Z]
Л12,
(10.16)
266
Уравнения в форме [У]
Л — + ^12^2;
А = + У ^2 . .
(10.1в)
Коэффициенты Л, В, С и D или (Aik), Zik—параметры хо-
лостого хода, Ylk — параметры короткого замыкания (где f, k ==
= 1, 2, любой из групп уравнений) полностью характеризуют
произвольный режим четырехполюсника. Связь коэффициентов
различных групп уравнений показана в матричной форме
табл. 10.1 (при выборе положительных направлений напряжений
и токов в соответствии с рис. 10.1, а и записи основных урав-
нений четырехполюсника в виде 10.1 а, б, в).
Таблица 10.1
(10.2а)
(10.26)
(10.2в)
Здесь |Z| — ZjjZ22 ^i2^2i> |У| — УцУ22 — У12У21 — определите-
ли, составленные из коэффициентов соответствующих матриц.
Определители из коэффициентов Zik и из Yik взаимно обрат-
ны
|2| = -J- . (10.3)
Коэффициенты каждой группы в свою очередь связаны меж-
ду собой:
|Л| = AD — ВС = 1;
7----------7 •
*-12 — *-21>
Г 12 = К21.
(10.4а)
(10.46)
(10.4в)
267
Таким образом, несимметричный, четырехполюсник характе-
ризуется тремя независимыми параметрами.
2. Помимо параметров, указанных в п. 1, широко при-
меняются характеристические параметры четырех-
полюсника: характеристические сопротивления Zlc и Z2c и ха-
рактеристическая (или собственная) постоянная передачи g, ко-
торые также полностью характеризуют четырехполюсник.
Здесь
g = a + jb, (10.5)
где а — характеристическое (или собственное) затухание, неп
или дб\
b — характеристический (или собственный) коэффициент
фазы, рад или град.
Характеристические параметры определяются через парамет-
ры Л, В, С и D:
- • z -1/^ •
1<т ~ Г CD ’ 2с ~ Т СА ’
(10.6)
g=ln(VAD +VBC). (10.7)
Коэффициенты Д, В, С и D могут быть выражены через ха-
рактеристические параметры:
Л = ch g; В = к Zlc Z2c sh g;
c = - Sh g; D= 1 f chg. (10.8)
V 21cz2c V Ztc
3. В расчетах используются также параметры холостого
хода Zlxx и Z2x x и короткого замыкания Z1K3 и Z2k з ,
измеренные соответственно со стороны первичных и вторичных
зажимов, которые связаны между собой соотношением
7 7
1х.х ___ 1к.з
7 7
^2х.х ^2к.з
(10.9)
Характеристические параметры выражаются через параметры
холостого хода и короткого замыкания:
(10.10)
(10.11)
268
Сопротивления холостого хода и короткого замыкания опре-
деляются через характеристические параметры или коэффициен-
ты Л, В, С и D:
, = ги с th s _ А; th s _ А;
С/
г2х.х = Z2C Cth g = А; Z2K з = Z2c th g = A .
О Z1
(10.12)
Коэффициенты четырехполюсника
по сопротивлениям холостого хода и
Л, В, С и D вычисляются
короткого замыкания:
4. В частном случае симметричного четырехполюсника все
написанные выше формулы упрощаются, если учесть, что при
этом имеются равенства:
Л = D; Zlc= Z2c~ Zc‘, Zlx.x = Z2x.x = Zx.x;
7 =7 = 7
^1к.з ^2к.з K.3 •
(10.14)
5. В табл. 10.2 приводятся формулы коэффициентов Л, В,
С и D для некоторых простейших четырехполюсников.
6. Входное сопротивление четырехполюсника (рис. 10.1, б)
со стороны зажимов 1—Г (прямая передача) может быть опре-
делено либо через его коэффициенты [Л], либо через параметры
холостого хода и короткого замыкания, либо через характери-
стические параметры:
__ AZ„ +В __ z
~ CZn^D~ 1хх
2>L-T^- = Zlc th & + n), (10.16a)
2x.x "r Zh
где
n == — In -Zu + Zh ,
2 72c Zh
(10.166)
ZH — сопротивление нагрузки.
Если сопротивление генератора Zr не равно характеристиче-
скому сопротивлению четырехполюсника Zc со стороны входных
зажимов 1—Г, то имеет место несогласованность сопротивлений
на входе, и если сопротивление нагрузки ZH=^= Z2c, то несогла-
сованность на выходе. Относительная величина несогласованно-
269
w
м
о
Таблица 10.2
Схема и наименование Параметры — коэффициенты Номер формулы '
А В с D
1 г г 0 CZ3 0 1 Z 0 1 (10.15а)
0,— <3 / 2 Одноэлементный последовательный 1 2 0 -у „ ..0 |]z 1 0 1 1 (10.156)
1' ~ 2' Одноэлементный параллельный 1 2 0—0” у- -0 z,r fiz 0. —1—0 /' 2 Г~ образный ~ сч N N Zjr Z 1 22Г Z 1 (10.15в)
Продолжение
Схема и наименование Параметры — коэффициенты Номер формулы
А В С D
fl-образный
Продолжение
Параметры — коэффициенты
Схема
и наименование
Номер
формулы
2Z1Z2 Z2 Zi N Ю 1 10 N N N t9 H* 1 + N tsj t— ri (10,15ж)
Zi (Zi 2Z2) 2Zj 4~ Z3 Zз । (10.15з)
P P P
гд< г p = Zj +2ZjZ2 -f~ Z22 Г‘3
сти определяется коэффициентами отражения (несогласованности)
на входе рг и на выходе рн:
2Г Zie .
Zr + 21с
(10.17)
Погрешность входного сопротивления — относи-
тельная величина отклонения Z1BK от Zlc, определяемая по формуле
= Ри е~ге-
Отсюда
_ 7 \+рие-^
1B,t lc {_pue-.g
(10.18а)
(10.186)
7. Коэффициенты передачи (передаточные функции)
по напряжению и току для схемы рис. 10.1, а соответственно
равны
Ки ; К, = . (10.19)
1/1 Л
8. Рабочей постоянной передачи при включении
четырехполюсника' между сопротивлением нагрузки Ztt и гене-
ратором с э. д. с. Ег, и сопротивлением Zr (рис. 10.1, б) назы-
вается величина, равная
+ In (10.20)
F /Sp
Здесь U' и /' относятся к схеме (рис. 10.1,г), в которой со-
противление нагрузки берется равным сопротивлению генератора
Zr и подключается непосредственно к генератору. Напряжение
U2 и ток /2 относятся к схеме (рис. 10.1, б), в которой нагрузка
ZH подключается к генератору через четырехполюсник.
Рабочая постоянная передачи может быть вычислена по
формуле
gp = g +1 n+1 n +
P S 2/ ZrZlc 2/ ZHZ2C
+ In (1 — pr pa erzs) = flp + /ftp,
где ap—рабочее затухание;
bt — рабочая фазовая постоянная.
(10.21)
273
Рабочее затухание может быть определено по одной
из формул
ар = In
Ет
2Ut
Zr
(10.22а)
ор = а + In
+ In
+ In |1 — рграе-2е\, (10.226)
где а—собственное затухание четырехполюсника;
рг и ря—коэффициенты отражения (несогласованности) на входе
и выходе.
Вносимая постоянная передачи
£вн = In 1/ и. = авн + jbH, (10.23)
где U" и Г —напряжение и ток на нагрузке при непосредствен-
ном подключении ее к генератору (рис. 10.1, д);
U2 и /2—напряжение и ток в той же нагрузке при подклю-
чении ее к генератору через четырехполюсник
(рис. 10.1, б);
ввн —* вносимое затухание;
Ьв„ — вносимая фазовая постоянная.
Вносимое затухание
(10.24)
Вносимое и рабочее затухания могут быть отрицательными
даже для пассивной цепи, что характеризует изменение условий
согласования генератора с нагрузкой при включении между ними
четырехполюсника.
Примеры в задачах 10.39 и 10.40.
9. Для корректирования возникающих в цепях ампли-
тудно-частотных искажений часто используются Т-образная мос-
товая и Г-образные четырехполюсники (рис. 10.2) с постоянным,
не зависящим от частоты входным сопротивлением R, равным
активному сопротивлению нагрузки R. Такое сопротивление на-
274
зывается повторным. Это имеет место, если комплексные
сопротивления Z1 продольных и Z2 поперечных плеч взаимно
обратны, т. е.
ZtZ2 = R\ (10.25)
Как правило, каждый из пассивных двухполюсников Zt и
Z2 содержит один активный и реактивные элементы.
Рис. 10.2
При нагрузке четырехполюсников рис. 10.2 на сопротивление
R рабочая постоянная корректора gK равняется собственной по-
стоянной передачи четырехполюсника и вычисляется по формуле
£раб = ёк = 1П (1 + 4-V
\ к /
(10.26)
Важными в практике являются схемы корректоров, у кото-
рых Zx состоит из параллельно соединенных активного сопротив-
ления гг и реактивного /хх (на рис. 10.3 приведена схема, соот-
ветствующая корректору рис. 10.2, б). В этом случае рабочее
затухание
(10.27)
где хг— алгебраическая величина, которая в зависимости от
частоты плавно изменяется и может принимать как положительные,
так и отрицательные значения, т. е. она может иметь емкостный
или индуктивный характер.
На рис. 10.4 приведены кривые зависимостей затухания ак
в функции частоты f для корректоров рис. 10.2. Кривая 1 со-
ответствует случаю, когда элемент хх содержит только емкость
кривая 2 — только индуктивность Lv 3—параллельно сое-
диненные Lt и Сг, 4~ последовательно соединенные Lt и Сх,
5 — последовательно соединенные £х и шунтированные кон-
денсатором, емкостью Ci , 6 — последовательно соединенные
£х и Cv шунтированные индуктивностью Ц .
275
В целях использования четырехполюсников (см. рис. 10.2) в
качестве амплитудных корректоров крутизну кривой затухания
в нужном интервале частот можно изменять путем регулирования
сопротивления гг и резонансных частот реактивного сопротивле-
ния х± (рис. 10.3).
УПРАЖНЕНИЯ И ЗАДАЧИ
10.1. Определить коэффициенты [Л] и [Z] Т-образного четы-
рехполюсника (рис. 10.5), если i\ ~ 30 ом, хг = 40 ом, г2 = 10 ом,
х2 = — 30 ом, г3 = 40 ом, х3 = 60 ом.
Решение. Расчет коэффициентов [Л]
проведем по формулам (10.15д), в которых
= (30 /40) ом, ^2т =
= (10 — /30) ом; Z3T = (40 + /60) ом;
1T
С2Т
/85°36'
10 — /30
771°34'
В = 107е ом; С = 0,0316е ом~\
/102°32'
Результаты вычислений проверяются по
(10.4а):
AD — ВС= 1,30/5°36' • 1,84е102°32' - 1О7/14°10' • 0»0316е/71°34'
Коэффициенты [Z] вычисляем по (10.26):
1,ЗОе/85 36' .. п /М°2’
-----= 41,3 е ом;
°34'
0,031б£?
А
11 = "Z
276
1 Q1 я7108°26' 7
12 =-------= 31, бе ом = — Z21;
22 —
—/149°2'
ОМ.
10.2. Найти коэффициенты [Л] и [У]
люсника (рис. 10.6), у которого г\ = 30
= — 20 ом.
Т-образного четырехпо-
ом, х2 = 10 ом и х3 =
10.3. Вычислить коэффициенты [Л], [Z] и [У] П-образного
четырехполюсника (рис. 10.7), у которого гг = 1000 ом, г2 =
= 1000 ом, х2 — 2000 ом и х3 = — 2500 ом.
У казание. Вначале по формулам (10.15е) вычислить коэффициенты [Л],
а затем использовать (10.26 и в).
10.4. Определить коэффициенты [Л], [Z],
[У] Г-образного четырехполюсника (рис. 10.8),
если Zir = (20 + /30) ом, Z2r = (5 + /15) ом.
10.5. Найти комплексные сопротивления Т-и
П-образных схем, эквивалентных четырехпо-
люснику, коэффициенты которого
Рис. 10.8
л = 0,6 4- /о,1; В = (17 4- /72) ом и D = 0,5 4- /0,2.
Решение. Пользуясь формулой (10.4а), вычислим коэффи-
циент
(0,6+ /0,1) . (0,5 +/0,2)-1
= /0,01 ом~\
17 + /72
Сопротивления Т-образного четырехполюсника находим по
формулам, которые легко получить из (10.15д):
7 Л ----- 1 0,6 + /0,1 — 1 /1 А I *л п\
Z “ — - -------------------= <10 + '40> »'"•
Z2T = ~ = —/100 ом\ Z3T = -—- = (20 + /50) ом.
с с
277
Сопротивления П-образного четырехполюсника найдем по фор-
мулам, полученным из (10.15е):
Zln = В = (17 + /72) ом; Z2n = -^-y = (20,3-/136) ом;
Z3n = —— = (0,235-/17,9) ом.
А ~ 1
10.6. Найти сопротивления Zv и Z2 мостового четырехполюс-
ника [рис. к формуле (10.15ж)], эквивалентного симметричному
Т-образному четырехполюснику [рис. к формуле (10.15д)], эле-
менты которого Z1T = Z3T, Z2T известны.
10.7. Параметры трансформатора без стального сердечника
(рис. 10.9, а): гх = 2 оле, = 0,5 мгн, г2 = 3 ом и Ь2 = 0,72 мгн.
Коэффициент связи между обмотками
м трансформатора ^ = 0,5. Чему равны
0 коэффициенты Л, В, С и D четырехпо-
U /пн люсника, эквивалентного указанному
1 | трансформатору, при частоте f = 10 кгц?
0---_г т—Решение. Прежде всего определим
rt l ~м L -м г 2 взаимную индуктивность М между обмот-
' ' 22 ками трансформатора:
М = k УЦЦ = 0,3 • 10-3 гн.
Введем обозначения
Zj = гх + jwLj = (2 + /31,4) ом\
Z2 = r2 +j^L2 = (3 +]45,2) ом-,
Z12 = jd)M = /18,9 ом.
Решим задачу двумя способами.
Способ 1. Составим уравнения по второму закону Кирхгофа
для первого и второго контуров:
/1Z1 —^1» (1)
Из уравнения (2) имеем
<3>
После подстановки этого значения в уравнение (1) и
простых алгебраических преобразований получим
(4)
278
Сопоставляя уравнение (4) с первой формулой (10.1 а) и
уравнение (3) со второй формулой (10.1а), получим
Л12 "12 ^12 "12
Способ 2. Заданная схема может быть заменена эквивалент-
ной согласно рис. 10.9, б (см. п. 5 основных положений гл. 5).
Для нее
Zu = G + > (Lr — Л4>= zi — zi^ Z2T = j®M = Z12;
Z3T = r2 + /a) (L2 — Л4) = Z2 — Z12.
Полученный Т-образный четырехполюсник имеет коэффици-
енты, которые определяются по (10.15д):
Результаты те же, что были получены по способу 1. Под-
ставляя числовые значения, найдем
Л = 2-+у = 1,66-/0,106;
В = (2 + = (9,76 + /56) ом\
/1о,У
С = TiU = - /°>о53 0Л-1; D = 3U45o’2 = 2,39-/0,159.
/10,9 /10,9
10.8. Определить комплексные сопротивления Т- и П-образ-
ных четырехполюсников, эквивалентных трансформатору пре-
дыдущей задачи.
10.9. Вычислить комплексные сопротивления при частоте
f = 10 кгц для Т-образной схемы, эквивалентной автотрансфор-
матору без стального сердечника (рис. 10.10), параметры кото-
рого гг = 2 ом, = 0,35 мгн, г2 = 3 ом, £2 = 0,5 мгн и
М = 0,25 мгн.
Указание. Составить уравнения Кирхгофа, затем совместно их решить
так, чтобы первичные напряжения и ток были выражены через вторичные на-
пряжение и ток. Сравнив коэффициенты полученных уравнений с (10.1а), по-
279
лучить выражения параметров-коэффициентов [Л]» Зная их, по (10.15д) найти
искомые сопротивления.
Рис. 10.10
о 2
<г>2'
Рис. 10.11
10.10. В месте соединения воздушных и кабельных линий
связи используются автотрансформаторы с конденсаторами
(рис. 10.11). Вычислить коэффициенты Д, В, С, D четырехпо-
люсника, если Zi = Z2 = (5 + /20) ом> Z12 = /10 ом,
Z3 ~ — jxc ~ — /30 ом.
10.11. Даны два четырехполюсника, коэффициенты которых
соответственно равны: первого — Alf Bv и второго — А2,
Рис. 10.12
= Ajj’2 + В/2,
и для второго
U\ = A2U2-\- В212>
В2, С2, D2. Чему равны коэф-
фициенты Д, В, С, D четы-
рехполюсника, составленного
из данных путем их каскад-
ного (цепочечного) соединения
(рис. 10.12).
Решение. Пользуясь вве-
денными обозначениями (рис.
10.12), получим для первого
четырехполюсника
= Сгй2 + 0^1% (1)
71 = C2(72-|-Z)272. (2)
Для определения коэффициентов Д, В, С, D искомого четы-
рехполюсника нужно найти зависимость между Uv и (72, /2.
Выходные напряжение и ток первого четырехполюсника равны
соответствующим величинам на входе второго четырехполюсни-
ка: О) = их, /2 = 7ь
Подставляя эти значения из уравнения (2) в (1), получим
= (ла + в,с2) й2 + (л2в2 + b,d2) /а; (3)
280
На основании уравнения (10.1а) видно, что
А = -J- Bfi^ В ~ АХВ2 4“
С = С\Л2 4" ^1^*2» В ~ ^1^2 4” ^1^2* .
Покажем более простое решение задачи при помощи мат-
ричной алгебры. В соответствии с обозначениями на рис. 10.12
основные уравнения каждого из четырехполюсников в Л-пара-
метрах в матричной форме имеют вид
здесь [А'] и [Л"]— матрицы первого и второго четырехполюс-
ников.
Учитывая, что при каскадном соединении (72 = U\ и /2== Л, и
подставляя (7) в (6), получим
2
2
Это совпадает с полученными соотношениями (5).
Следовательно, при каскадном соединении четырехполюсни-
ков Л-матрица результирующего четырехполюсника равна про-
изведению Л-матриц отдельных четырехполюсников. Обращаем
внимание на то, что матрицы, подлежащие перемножению, за-
писываются в том же порядке, в каком отдельные четырехпо-
люсники находятся в схеме соединения сложного четырехпо-
люсника, так как умножение матриц не подчиняется переме-
стительному закону.
281
Рис. 10.13
10.12. Определить коэффициенты Л, В, С, D четырехполюс-
ника, эквивалентного двум другим четырехполюсникам, пара-
метры которых [Д] и [Л2] заданы соеди-
ненным параллельно (рис. 10.13).
Решение. При параллельном соедине-
нии четырехполюсников наиболее удобной
формой являются уравнения передачи,
записанные в форме [У], так как при
этом виде соединения складываются вход-
ные и соответственно выходные токи каж-
дого из четырехполюсников, а входные и
выходные напряжения каждого четырех-
полюсника остаются одинаковыми. [КЗ-
параметры каждого четырехполюсника найдем по формулам
табл. 10.1.
Для каждого из четырехполюсников запишем уравнения в
форме (10.1в):
для первого
/1 == + K12 U<2\ (1а)
i 2 = К21 й\ + ^22^2 5 (16)
для второго
Складывая уравнения (1а) и (2а), а также (16) и (26) и учи-
тывая, что й\ == й\ = (7Х, U2 = U2 = (72, /1 + /1 = /г,
I 2 -|- i 2 = /2, получим
Л == I + i 1 == (Уп + Кп) c/i+ (К12 + К12) t/2 =
= Y11U1 + Yjj* (За)
где [К] — параметры эквивалентного четырехполюсника, равные
Yи = Y\\ + ^11 ; К12 = Y12 + К12» Г21 = К21 + ^21*» Y22= У22 + ^22- (4)
Отметим, что последний результат может быть получен и
записан более компактно в матричной форме. Используя систе-
му У-параметров, запишем уравнения заданных четырехполюс-
ников:
282
• ft
1 2 _
У11 У12
If It
Y 21 Y22^
• It
u,
• n
Ui
• If
Vi
• ff
U2
(6)
где [У'1 и [У"]— матрицы первого и второго четырехполюсни-
ков.
В рассматриваемой схеме U{ = = {7Р U2 == U2 = О2.
Ток 4 на входе результирующего четырехполюсника равен сум-
ме токов /1 и / 2» протекающих через входные зажимы каж-
дого из четырехполюсников, и аналогично на выходе /2 = /2+ /2.
Учитывая это и складывая (5) и (6), получим
Это совпадает с полученными соотношениями (4).
Итак, при параллельном соединении четырехполюсников
У-матрица эквивалентной схемы равна сумме У-матриц исход-
ных четырехполюсников.
Требуемые параметры [Л] могут быть вычислены через
[У]-параметры по (10.2а). В результате расчетов получим
(Лл — Л2) • (Di — Р2)
2
Г) __ ^1^2 + £>1^2
В1 + В2 •
10.13. Определить коэффициенты Л,
В, С, D четырехполюсника, составлен-
ного из двух других, соединенных
последовательно, коэффициенты которых
Л1? Bv Op В} и Л2, В2, С2, £>2(рис. 10.14).
Указание. Наиболее простое решение по-
лучается при использовании уравнений передачи в
форме [Z] формулы (10.16). Запись наиболее
компактна в матричной форме.
10.14. Дан четырехполюсник, пара-
метры которого Л, В, С, D извест-
Рис. 10.14
283
ны. Определить параметры [Л] результирующего че-
тырехполюсника, обведенного пунктиром на рис. 10.15, а, б,
виг.
10.15. По данным задачи 10.1 определить характеристические
параметры четырехполюсника (см. рис. 10.5).
Рис. 10.15
Решение. Используя
найденные в задаче 10.1, па-
раметры-коэффициенты [Л],
по формулам (10.6) най-
дем характеристические со-
противления:
1 ,ЗОе/85°36' . 107е /114°10'
0,0316^71О34'.1,84^102°32^
= 49 ?,2°50' ом;
о /29°46'
= 69,3г ом.
Характеристическую постоянную передачу находим по (10.7).
Для этого предварительно вычислим величину подлогарифмен-
ного выражения:
VAD -ь / ВС = /1,30 ?85°36' • 1,84 е/,02°32' +
+ J/107 e/,14°10'-0,0316?71°34' = 1,55е'94°4' + 1,84 ?92°52’ =
= _ о, 11 + /1,55 — 0,092 + /1,84 = — 0,202 + /3,39 = 3,39 е/93°24'.
Таким образом,
g = а + jb = In 3,39е/93°24' = 1,22 + /93°24'.
Зная, что 1 рад — 57,3°, получим
93°24' = 93,4° = = 1.63 рад.
Следовательно,
ea+ib = eael'b = /.63
т. е. а = 1,22 неп, b = 1,63 рад, g = 1,22 + j 1,63.
284
Рис. 10.16
10.16. Определить характеристическое сопротивление и ко-
эффициент передачи четырехполюсника (рис.
ления которого Zx = — /1000 ом и Zo =
= 1000 ом.
10.17. По данным задачи 10.4 вычис-
лить характеристические параметры Г-об-
разного четырехполюсника (см. рис. 10.8).
10.18. Определить коэффициенты Д, В,
С, D симметричного четырехполюсника,
если Zr = 680e/3°26 ом и g= 18,35 е/86°15 .
10.19. Симметричный Т-образный четы-
рехполюсник (рис. 10.17) имеет параметры
L = 10 мгн и С = 8 мкф. Вычислить коэф-
фициенты Л, В, С, D, характеристическое
сопротивление Zc и характеристическую по-
стоянную передачи g при частотах, равных
0,5 о»; 2о), если о) = 5000 сект1.
10.20. Вычислить комплексные сопротивления элементов
П-образной схемы, эквивалентной симметричному четырехпо-
люснику Т-образного мостового типа (рис. к формуле 10.15, з),
если Zx = 1000 ом, Z2 = / 1000 ом и Z3 = — / 1000 ом.
Решение. Наметим общий ход решения. Сначала непо-
средственно по схеме вычислим сопротивления холостого хода
Zx.x и короткого замыкания ZK3 , затем по (10.13) определим
коэффициенты четырехполюсника A—D и В и, наконец, по фор-
мулам, полученным из (10.15 е), найдем Zin, Z?n = 2зп:
10.16), сопротив-
Рис. 10.17
Zx.x = + Z2 = (600 + /80°) 0М<
= (600—/800) ом;
А
. Г600+ /800
У /1600
0,79е-/18°25'
в = лгк,3 = 0,79 е~/18°25 (600—/800) = 790 е~'71°35' ом,
Zm = 790 е-/71°35' ом;
7 __ 7 5 790е Ш 35 /63°25'
— 4ш— 0 /|8о25'_1 3160 е ом.
10.21. Вычислить сопротивления холостого хода и коротко-
го замыкания со стороны первичных и вторичных зажимов че-
285
тырехполюсника, коэффициенты которого А = 0,2 — /0,4, S =
= (—16—/28) ом, D = —0,6 — /0,8.
Решение. Из формулы (10.4а) определим коэффициент
С = = (0,02-/0,04) ом'1.
При холостом ходе (/2 = 0) формулы (10.1а) примут вид
t/lx.x - Л(?2х.Х»
lx.x
— С^Лх.х •
Отсюда сопротивление холостого хода со стороны первичных
зажимов
^1х.х --
&1хх
lx.x
А 0,2—/0,4
С ~~ 0,02-/0,04 — 10 0М
При коротком замыкании вторичных зажимов ((7а == О) по-
лучим
• • • ________ •
СЛк.з = BI 2к.з 1 I 1к.з = DI 2к.з
И
7 U\K.3 В ---------- 16- /28 /QQ ..v
-Z1K.3 — - ~ ~D" — —0,6—/0,8 — (32 + Я) ом-
< 1к.з
Сопротивления холостого хода и короткого замыкания, из-
меренные со стороны вторичных зажимов четырехполюсника,
определяются по тем же формулам, в которых коэффициенты А
и D меняются местами:
^2х.х — с — о,02 —/0,04 /20) ом;
„ В —16—/28
Z2k з = ~л~ ~ “7Го-7ГТ“ = (40—/60)041.
/к.з д 0,2 —/0,4 ' 1 '
10.22. Коэффициенты симметричного четырехполюсника
А = 1 + /2 и В = (—80 4- /240) ом. Определить сопротивления
холостого хода и короткого замыкания.
10.23. Для схемы (рис. 10,7) и по данным задачи 10.3 вычи-
слить входные сопротивления при холостом ходе и коротком
замыкании двумя способами: непосредственным вычислением
указанных сопротивлений; с помощью коэффициентов четырех-
полюсника Л, В, С, D.
10.24. У несимметричного четырехполюсника со стороны
первичных зажимов были измерены напряжения, токи и мощ-
ности при холостом ходе и коротком замыкании, а также со
286
стороны вторичных зажимов—напряжение, ток и мощность при
холостом ходе. Определить коэффициенты А, В, С, D четырех-
полюсника, если измерения показали
£Лх.х — Ю Iix.x — 316 ма, Р|х.х — 3 etn (ф1Х.х > 0);
t/iK.s = 5 в, Лк.з = 139 ма, PiK.3 = 0,576 вт (<piK.3 > 0);
t^2x.x — 6 в, 1гх..х — 600 ма, Р2х.х ~ 0 (фгх.х <0).
Решение.
21х.х — “7
' 1Х.Х
Ю л *1х
= о> = 31’6 ом' cos(plx* = -777;-х-71х;
3
_____________= о 949
100,316______’ ’
Ф1х.х= 18°25'; Zlx.x = г11ДА’ = 31,бе718’25' = (З04-/Ю)_ол;
^Лк.З 5 АЛ
21к’3 ~ о71зэ ~ 36 ом’
*1к.з 0,576 л QQe
cos Ф1К.З — и f — 5>0 139 — 0.83,
A Ik • о 1 Ik • О
ф1к.3 = 33°50'; Z1KS = Z1K.3 е/1>1к-3 = З6е/33°50' = (30-J-/20) ом-,
^2х.х 6 .«
2х х ~ ~ 0^ ~ °
Так как Р2х.х = 0, то Z2x.x имеет чисто реактивный (ем-
костный) характер, т. е. Фгх.х = — 90°, поэтому
Z2x.x = Z2X.X = 10е-79°° = —/10 ом.
Коэффициенты четырехполюсника по (10.13)
д ____________304-j 10_________ । .g.
V—/10[(30 + /10) — (304-/20)] 7 ’
С = = зо-ь/10 = —/0,1 ом *;
£>=CZ2x.x = —/ 0,1(—/10) = - 1;
В = DZ1K,3 = — 1 (304-/20) = (— 30 — /20) ом.
10.25. Для симметричного четырехполюсника опыты холо-
стого хода и короткого замыкания дали результаты: t/ix.x =
= 10 в, /ix.x = 1^, Pix.x = Ю вт-, UiK.a ~ Ю в; Ак.з = 0,8 а,
PiK.s = 8 вт. Вычислить коэффициенты А, В, С и D этого четы-
рехполюсника и начертить Т-образную схему замещения.
10.26. Коэффициенты четырехполюсника Л =1,2 4-/0,2,
В = (16 4- /6) ом, С = 0,05 ом"1.
287
Определить, какое чисто реактивное сопротивление надо
включить к его выходным зажимам, чтобы первичные напря-
жение и ток были друг с другом в фазе.
10.27. Коэффициенты четырехполюсника А— 1,3+/0,2, С —
=0,05 ом'1, D = 1 — /0,5. При каком чисто активном сопротив-
лении нагрузки напряжение Z7, и ток совпадают по фазе?
10.28. При каком сопротивлении нагрузки ZH, подключенной
ко вторичным зажимам симметричного четырехполюсника, вход-
ное сопротивление ZiBX равно Z„? Коэффициенты четырехпо-
люсника Л = 0=2,17 е/12 30 и С = 0,0542 е~'40 40 ом'1. Каковы
при этом токи и /2, если U1 = 90 в?
Указание. Искомое сопротивление ZH = Zc.
10 29. Коэффициенты симметричного четырехполюсника
А = 1,46 е/46°50 и С = 0,0267 ом~1. Определить нагрузочное со-
противление, при котором входное сопротивление четырехпо-
люсника равно сопротивлению этой же нагрузки. Вычислить при
этой нагрузке токи на входе и выходе четырехполюсника, если
приложенное напряжение U± = 70 в. Определить сопротивления
Т-образной схемы, эквивалентной данному четырехполюснику.
10.30. Опыты холостого хода и короткого замыкания для
симметричного четырехполюсника дали результаты: (7Х.Х = 10 в,
/х.х = 0,447 tz, Рх.х 2 вт (фх.х 0), L/к.з = Ю в, /к.з = 0,5 tz,
рк з=3 вт (фк.з > 0). Определить характеристическое сопро-
тивление и характеристическую постоянную передачи четырехпо-
люсника.
Решение.
гх.х = = 22,4 ом\ соБфх.х = 7Т~~7— = 0,447;
ZX.X их.х zx.x
фх,х = 63°30'; Zxx = 22,4 ?63°30' ом;
и Р
гк.3 *= Д— = 20 ом; cos <рк.3 = Г)—Д— = 0,6;
‘к.з ик.з ‘к.з
Фк.з = 53° 10'; ZK,3 = 20 в'53’10’ ом.
Характеристическое сопротивление и характеристическую по-
стоянную передачи определим по (10.10) и (10.11):
Zc = J/ZX XZK.3 = V 22,4е'63°30' 20е>53°10'= 21,2 e/58°20' ом;
thg = \f = 1/" 2°e//63.-3o7 - = ~\[0,895 e-'10°20' =
V zx.x V 22,4e'63 30 v
= 0,945e-'5°10'=0,94-/0,085.
288
Чтобы по известному значению thg найти g, поступим так:
es—e-s
= ez+e-s
eg e^g— 1
отсюда
2g _ 14-th^f _ 1,94—/0,085 __ 1,94e~/2°30’ _ .q - -/57°20>
e 1—thg 0,064-/0,085 ~ O,lO4e/54050' ’
Пользуясь таблицами показательных функций, найдем, что
18,7 = е2’92. Далее, переходя, к радианной мере, имеем 57°20's
as 1 рад.
Таким образом,
e2g = е2,92-/1 ,
отсюда
1 2а 4- /2d = 2,92 — /1,
или
а= 1,46 неп, Ь = — 0,5 рад', g = 1,46 — /0,5.
10.31. Вычислить характеристическое сопротивление и харак-
теристическую постоянную передачи симметричного четырехпо-
люсника по следующим данным, полученным из опытов холос-
того хода и короткого замыкания: (7ix.x = 10 в, Iix^ = 1 а,
Р\х.х = Ю вт, UiK,3 = 10 в, /1к.з = 0,8 а, Р\к,3 = 8 вт.
10.32. Определить коэффициенты А, В, С, D, характеристи-
ческие сопротивления Zlc, и характеристическую постоянную
Рис. 10.18
передачи g сложного четырехполюсника (рис. 10.18), образован-
ного каскадным согласованным соединением (Z?, = Zc) Г- и сим-
метричного Т-образного четырехполюсника. Характеристические
параметры Г-образного четырехполюсника равны
Z\c = 1,34 • 10»е'3,°45’ ом, Z2c = 1,5 - lO3^15’ ом,
gr = 0,53 + /0,45, Т-образного—Z„. = 1,5-Ю3?58’15 ом,
gT = 1,06 + /0,9.
10.33. Г-образный четырехполюсник [рис. в табл. 10.2 к фор-
муле (10.15 в)], параметры которого Zir = (100-Т-/500) ом,
289
10 Заказ Xs 624
2гг = — / ЮОО ом, включен между генератором, имеющим со-
противление Zr = Гг = 600 ом и нагрузкой ZH = 1500 е~'ю°
(рис. 10.1,6).
Определить входное сопротивление четырехполюсника ZiBX
и его отклонение (по модулю и фазе в процентах) от характе-
ристического сопротивления Zic- Найти коэффициенты отраже-
ния на входе рг и выходе рн четырехполюсника. Вычислить
рабочее и вносимое затухания. Подсчитать коэффициенты пере-
дачи по напряжению Ки и току Кг
Решение. Коэффициенты [4] четырехполюсника, необхо-
димые для дальнейших расчетов определяются по (10,15в):
Д = 0,51 е'11’20'; В=51Ое/78°40' ом; С = /10"3 омг\ 0=1,
характеристические сопротивления по (10.6) и постоянная пере-
дачи по (10.7):
7 l/o,51e^1020' .5 1 0 ?78°40' ,1П
= V ~CD~ = V -----------По=М--------= 510 0М’
- /т!-=-1000 °*
g = In (V~AD + = In (Ко,51 е/"’20' • 1 +
4- ]/510е'78°40' • /10~3) = In (0,714 е'5’40' + 0,714 е''84°20') =
= In (0,7805 + /0,7805) = In (1,1036 =
= ln(e3,1 е/45°) = 0,1 + /45° = 0,1 + /0,785.
По первой из формул (10.16 а)
Z1BX
АХц В
czH 4- Б
O.51?1*020' • 1500е—/40° +510 e^w
/10-3 -1500е—/40° + 1
782е'9°50’
- з.гве'30020'
= 343е~/20°30’ ом.
I
Отклонение входного сопротивления от характеристического
по модулю и фазе в процентах:
JZ1Bx|-|Zid . 100% = 343 510 . 100о/о = _ 330/
I X . 1 ГЧ I I 1 *
У1ВХ - Ф1С . 100о/о = 2=±^зоо . 1ООо/о = _ 100 О/
<f>ir —20 30
290
Коэффициенты рг и p№ (no 10.17)
pr = = 0,081;
_ ZH — Z2C _ 1500е—/40° — 1ОООе~-'"°20'
P«~ZH + Z2c~ 1500е-'40°
785е-/77°30'
= /28’40' = °>324 е-/48°50'.
2420е~;28 40
Рабочее и вносимое затухания находим по (10.226) и (10.24),
Для этого предварительно вычисляем значения отдельных сла-
гаемых, входящих в эти
In
= In
In
= In
выражения:
= In - . Ч0-; = 0,013;
2-/600 • 500
1500е~,4°° + 1ОООе~;|1°20'
2- l/1500e-^o°.1000e-'11020'
= In 10,9878 e~'3° | = In 0,9878 = — 0,012,
.-/Н°20'
r^ic
2С
?2С
2420г~/28°40'
2450е"~/25°40
ргрн е-2г = 0,081 • 0,324 e-'48”50' • е-о,2е-/оо’ = о,0215 е-Лза’БО-
= — 0,016 —/0,014;
In 11—prpHe-2s| =1п 11,016 + /0,0141 » In 11,016 е/45'| =
= 1п 1,016 = 0,016.
In
= In
=ln
у -^н
2000 е-'28°50'
1897 e~i2t)Q
600 + 1500 е~/40°
2 - И 600 • 1500 е_/40°
= In 11,054 e-'8’50' I = 0,053.
н
Итак,
ар = 0,1 +0,013 — 0,012+0,016 = 0,117 неп-,
aBH = Qp — In
H
= 0,117—0,053 = 0,064 неп.
Коэффициенты передачи по напряжению и току по (10.19):
К — гв _ 1500е~/4°°
ЛУ AZH+B 0,51?11O20'.1500e-/40O+510^8°40' ~~
= 1500е~/4°°
~ 78Ое/9°50'
= 1,92 e~/49°S0';
= ---------:---—— =-----------i____ — о 44-/30’20'
/10-M500e-'4° +l 1,964+71,15 ’
10*
291
10.34. Определить входное сопротивление четырехполюсни-
ка предыдущей задачи со стороны зажимов 2—2' (т. е. при пе-
редаче энергии в обратном направлении) при нагрузке зажимов
1—Г на прежнее сопротивление ZH (см. рис. 10.1, в),
10.35. Г-образный четырехполюсник (см. рис. 10.8) включен
между генератором, имеющим сопротивление Zr = 1000 ом и
нагрузкой ZH = 600 ом. Даны: Zlr = —j 1000 ом, Z2r = /2000 ом.
Вычислить Z1BX, рг, рн, gBH, Ко и Ki .
10.36. По данным задачи 10.33 определить величину вход-
ного сопротивления четырехполюсника, использовав формулу
погрешности (10.186).
10.37. Два симметричных четырехполюсника, параметры ко-
торых Av Bv Cv и A2. B2, C2, D2, соединейы в цепочку.
К входным зажимам первого четырехполюсника подведен источ-
ник напряжения с внутренним сопротивлением Zr, а к выход-
ным зажимам второго присоединена нагрузка сопротивлением ZH.
Определить входное сопротивление со стороны генератора,
коэффициенты передачи по напряжению и току, если характе-
ристические сопротивления четырехполюсников друг другу рав-
ны (Zlc = Z2c) и выполняются условия согласования на входе в
выходе (Zr = Zlc = ZH = Z2c = Zc).
10.38. Вычислить рабочее и вносимое затухания четырехпо-
люсника (рис. 10.1, а), если Е = 3 в, Zr = 600 ом, t/a = 0,l в и
ZH = 400 ом.
10.39. Определить рабочее и вносимое затухания четырех-
полюсника (рис. 10,1, б), если /х = 1 ма, Zr = Zlc = 103 ом, I2==
=0,08 ма, ZH = Z2c = 105 ом.
10.40. Для создания условий выделения максимальной мощно-
Рис. 10.19
сти в нагрузке генератора, имеющего сопротивление Zr=(9,6 + /98)
ом, с Harpy3KoftZH=(10+/100) ом применен
простейший четырехполюсник с емкостным
сопротивлением Хс = 50 ом (рис. 10.19).
Рассчитать рабочее и вносимое зату-
хания и убедиться, что они в рассматрива-
емом примере отрицательны.
10.41. Показать, что при нагрузке
четырехполюсников (рис. 10.2) со сторо-
ны зажимов 2—2' на сопротивление /?,
их входные сопротивления со стороны зажимов /—/'равнытому
же сопротивлению /?, а рабочая постоянная передачи равна соб-
ственной постоянной передачи при условии, что ZXZ2 = /?2.
10.42. Определить элементы и начертить схему Г-образного
корректирующего четырехполюсника (рис. 10.20, а), имеющего
постоянное входное (повторное) сопротивление ZBX = /? = 600 ом
и элементы г' = 480 ом, Сх = 60 нф. Рассчитать и построить
кривую рабочего затухания корректирующего контура в диапа-
зоне 0,3—8 кгц.
292
Решение. Из сравнения рис. 10.20, а с рис. 10.2 6 (см.
п. 9 основных положений) видно, что заданный корректор дол-
жен иметь в продольной ветви параллельно соединенные актив-
ное сопротивление R. и комплексное сопротивление Z1, сос-
тоящее из параллельных t\ и
Су (рис. 10.20, б). Из эквива-
лентности схем рис. 10.20, а)
а и б следует, что г' долж-
но равняться параллельно со-
единенным Гу и /?, откуда и
^находим неизвестное Гу.
Рис. 10.20
*
480-600 п.пп
— 600—480 ~~_2400 ом-
Элементы комплексного сопротивления Z2 поперечной ветви
должны быть обратны сопротивлению Zt (10.25). Определим их,
как это указано в гл. 9:
6002 1Г-а г D2
— ~~г — о.ллп — 150 ojt, L2 — С\ R —
= 60-10”9-6002 = 21,6-10~3 гн.
Кривую рабочего затухания рассчитываем по (10.27). Резуль-
таты расчетов сведены в табл. 10.3.
Таблица 10.3
О.з 8860 0,271 0,074 25,074 1,074 24,8 3,21 1,605
1.0 2650 0,906 0,81 25,81 1,81 14,23 2,655 1,327
4.0 662 3,62 13,1 38,1 14,1 2,7 0,99 0,495
8.0 331 7,25 52,5 77,5 53,5 1,44 0,367 0,184
L,
Рис. 10.21
По данным этой таблицы на рис. 10.4
(кривая/)построен график ак в функции /.
10.43. Рассчитать элементы и начертить
схему Г-образного корректора (рис. 10.21),
входное сопротивление которого постоян-
но и равно ZBX = /?= 1400 ом. Даны:
г' = 420 ом» 50 мгн. Построить кри-
293
вую рабочего затухания корректора в диапазоне 0,3 —
4 кгц.
10.44. Определить элементы и начертить схему Г-образного
корректора (рис. 10.22, а)
с постоянным входным сопротивле-
нием ZBX == R = 600 ом, элементы ко-
торого г' = 480 ом, Lv = 4 мгн,
Сг == 1 мкф. Определить частоту,
при которой затухание передачи
максимально, и величину актах
этого затухания. Построить кривую
рабочего затухания корректора в
полосе частот от 0 до 4 кгц.
Решение. Схема корректора
приведена на рис. 10.22Д. Вычи-
слим ее элементы:
г' R
г, = 75—т- = 2400 ом; г„ =
= ~т ~ 150 ом; = 0,36 гн;
С2== ^- = 0,111 мкф.
Рис. 10.22
Из формулы (10.27) следует, что
затухание передачи максимально,
когда реактивное сопротивление
продольного плеча хг равно бес-
конечности. Сопротивление парал-
лельно соединенных Lt и Сг рав-
но
«о Lx
X1 = 1 — 0>г Li С, •
Отсюда видно, х, = оо при = —т=—- = 15 800 селг1,
У L\ С]
j\ = 2520 гц. По (10.27) находим, что при xL = оо величина мак-
симального затухания передачи
к max
2400 I I R 1 £1
-gQQ-l=ln 5= 1,61 неп.
Кривая рабочего затухания, рассчитанная по (10.27), приве-
дена на рис. 10.22, б.
10.45. Найти элементы и начертить схему Г-образного кор-
ректора (рис. 10.23, а), имеющего постоянное входное сопротив-
294
ление /? = 600 ом и элементы г' » 525 ом, Сг == 0,04 мкф, Lx =
= 16 мгн, Ci = 0,2 мкф. Определить частоту, при которой за-
тухание передачи ак будет максимально, и чему эта величина
(актах) равна.
Решение. Схема корректора
и значения величин элементов
даны на рис. 10.23, б. Они рас-
считаны аналогично предыдущей
задаче. Определим эквивалентное
сопротивление реактивных эле-
ментов:
Затухание передачи макси-
мально при | хг | = оо, что име-
ет место, когда знаменатель выра-
жения обратится в бесконеч-
ность. Как видно из полученного
для хг выражения, это будет при
о) = 0 (т. е. f = 0) и при частоте
Рис. 10.23
£ 1 Л /~ С1+С1
-69
Величину максимального
хг = оо) находим по (10.27)
затухания (учтя, что при этом
aKmax=lnl 1 + -gQQ-) = 2,08 неп.
ГЛАВА ОДИННАДЦАТАЯ
ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Электрические фильтры — четырехполюсники, об-
ладающие избирательными свойствами; они пропускают токи в
определенной полосе частот с небольшим затуханием (полоса
пропускания, или прозрачности), а токи с частотами, лежащими
вне этой полосы, с большим затуханием (область задерживания,
или затухания).
Рис. 11.1
2. На рис. 11.1 изображены?-, П-и Г-образные схемы фильт-
ров. Звенья Т- и П-образные могут быть образованы цепочеч-
ным соединением соответствующих полузвеньев Г-образной фор-
мы так, что при этом выполняются условия согласования по характе-
ристическим сопротивлениям. Это связано с тем, что для всех
схем рис. 11.1 характеристические сопротивления со стороны, со-
ответственно Т- и П- входов определяются по одинаковым формулам:
(11.1)
Характеристическое сопротивление фильтра в полосе пропус-
кания— активное, а в полосе задерживания—реактивное.
296
Характеристическая (собственная) постоянная передачи для Т
и П-образных схем (рис. 11.1, а и б) имеет одну и ту же величину
g = а + jb = gT= gn
(П.2)
и вычисляется по одной из формул
(П.З)
а характеристическая постоянная передачи для Г-образного звена
(рис. 11.1, б) равняется половине характеристической постоянной
передачи Т- и П-образных звеньев, т. е.
«г=т = т = т = 1+'4- <11Л>
Здесь а и b соответственно характеристическое (или собствен-
ное) затухание и коэффициент фазы фильтра типа Т или П.
3. В табл. 11.1 приведены формулы характеристик Т-, П- и
Г-образных реактивных фильтров (рис. 11.1, а, б и в), у кото-
рых Z1 = /x1, Z2 == jx2. Выражение этих характеристик в различ-
ных областях частот определяется величиной и знаком отноше-
Zt
ния
Таблица 11.1
Полоса
пропускания
А.
4Z2
Полоса зату-
хания
4. Фильтрами типай называют схемы Т-, П- и Г-вида,
у которых сопротивления Zr последовательных и Z2 параллельных
плеч взаимно обратны, т. е.
Zx Z2 = /?2.
Параметр /? = j/Zi 22 называется номинальным харак-
теристическим сопротивлением и для данного фильт-
ра является величиной постоянной.
В табл. 11.2 приведены схемы полузвена и формулы парамет-
ров реактивных фильтров типа k: нижних частот (ФНЧ), верх-
них частот (ФВЧ), полосовых (ПФ) и заграждающих (ЗФ).
297
Таблица 11.2
Частоты среза
Полоса про-
пускания
b
sin ~2
при а=0
Формулы для расче-
та элементов фильт
Ра
Примечание.
« (/2 - fl)
Я(/2-Л)
fi
^(/2~Л)Я
fl h '
f fm
’1~ '
Я (7 2 - fl)
2- 4Я(/2-Д)
2 =
5. Фильтры типа tn являются производными фильтров типа k
(рис. 11.2 и 11.3). Изменение плеч полузвена типа k по схеме
рис. 11.2 приводит к последовательно-производному
полузвену типа т, характеристическое сопротивление Zt которого
совпадает с сопротивлением Zt исходного звена типа k—прототи-
па производного фильтра. Изменение плеч полузвена типа k по схе-
ме рис. 11.3 приводит к параллельно-производному
полу звену типа т, у которого характеристическое сопротивление
Zn совпадает с соответствующим сопротивлением прототипа —
исходного звена типа k.
Рис. 11.2
Рис. 11.3
Характеристические сопротивления Znm последовательно-про-
изводного и Zym параллельно-производного фильтров выражают-
ся формулами
2nm = Zn
Ztw = Zt
1 +
1\
1 + (1 — m2)
*14-2
(11-5)
Собственное
из выражения
{ch} / а \=___
затухание в полосе задерживания
определяется
4Z2
f
где 0 = 4— для ФНЧ;
/с
0 = -у- для ФВЧ;
т
2
»
т 0
300
при fm== V f2 для ПФ и
® = тт Для ЗФ.
hl
В выражение 11.6 входит функция ch при 1>(1 — /и2) @2 и
функция sh при 1<(1 — /и2) 02.
В полосе задерживания фильтра типа т частоты , при ко-
торых выполняется равенство
* = 1 — т2,
(И.7)
соответствуют бесконечному затуханию. Фильтры типа т с ве-
личиной т в пределах 0,506—0,62 имеют значительно более ста-
бильное значение характеристических сопротивлений Zym и Znm
в значительной части области пропускания (табл. 11.3). При
т = 1 фильтр типа т переходит в фильтр типа k.
Таблица 11.3
Значения параметра т фильтров, обеспечивающих заданную стабильность
характеристических сопротивлений ZT/ra и Znm в наибольшей рабочей
полосе частот в зоне пропускания
Наибольшее отклонение Z„ и Z„ от значения Тт Пт R, % Значение т Значение параметра 0 на границах рабочей полосы частот
± 5 0,6 0,88
±10 0,542 0,94
±15 0,506 0,96
±20 0,473 0,97
6. На рис. 11.4, а, б и в показаны три эквивалентные фор-
мы (последняя—условная) изображения симметричных мости-
ковых фильтров. Здесь Z1 и Z2— сопротивления мостика. Харак-
Рис. 11.4
301
теристическое сопротивление ZM мостиковой схемы и ее характе-
ристическая постоянная передачи g определяются формулами
Характеристическое сопротивление мостикового фильтра мо-
жет быть сделано постоянным и равным R в любом диапазоне
частот, если сопротивления Zr и Z2 выбрать взаимно обратными
в отношении R2 (т. е. Z2 = /?2). Собственное затухание мос-
тикового фильтра бесконечно при выполнении условия = Z2.
Это позволяет проектировать балансные схемы, имеющие бес-
конечное затухание при всех частотах.
Мостиковый фильтр имеет наиболее общие характеристики
и к его схеме может быть приведен симметричный фильтр произ-
вольной схемы. В частности, симметричные Т- и П-образные
фильтры (рис. 11.5, а и б) эквивалентны друг другу и мостико-
вому фильтру (рис. 11.5, в) при условии
Z1T 2Zin Z9n Z1T
Zim = . Z2M =2Z2T + -4b =2Z2n . (11.9)
Рис. 11.5
Мостиковые фильтры имеют сравнительно много элементов,
поэтому их обычно реализуют эквивалентными Т-, П-фильтра-
ми, а также в виде эквивалентных дифференциально-мостиковых
Рис. 11.6
схем, с применением идеальных
трансформаторов (ИТ), как по-
казано на рис. 11.6.
Свойства реактивных мости-
ковых фильтров, имеющих реак-
тивные сопротивления плеч Zt =
= jxv Z2 = jx2, приведены в
табл. 11.4.
В полосе пропускания знаки
b и хг совпадают, а в полосе
302
Таблица 11.4
Полоса про- пускания — оо < 7 <0 ^2 а = 0 (ГО ' to O’ II ZM = У |Z, Z2|
-О
Полоса за- 0 < ф- < 1 IO О 1 w И* ь = о = == dz / У | Zi Z<z\
тухания
непропускания знак Ь определяется из непрерывности функции
b == b (о>), которая изменяется скачком на ± к только в точках
бесконечного собственного затухания, т. е. при Zx = Z2.
Знак ZM в полосе непропускания совпадает со знаком х±.
УПРАЖНЕНИЯ И ЗАДАЧИ
11.1 Определить элементы Т-образного ФНЧ типа k, пред-
назначенного для работы при сопротивлении нагрузки /? ==
= 2000 ом и обладающего частотой среза /с = 1000 гц. Рассчи-
тать и построить кривые зависимостей характеристического со-
противления ZT , затухания а и коэффициента фазы b от час-
тоты.
Решение. По формулам, приведенным в табл. 11.2, опре-
деляем индуктивность и емкость элементов фильтра:
2000
2-3,14-1000
» 0,32 гн\
тс/с# 3,14-1000-2000 ~ 0,16 МКФ*
а также частотные характеристики Zt , а и Ь\ результаты под-
счетов сведены в табл. 11.5.
303
По данным табл. 11.5 на рис. 11.7 построены кривые.
11.2. Найти элементы П-образного ФНЧ
типа k при сопротивлении нагрузки
R — 2000 ом и частоте среза /с = 1000 гц.
11.3. Определить частоту среза Т-образ-
ного ФНЧ типа k, предназначенного для
целей телеграфирования, у которого ин-
дуктивность каждого плеча равняется 3 гн,
а емкость—5,3 мкф.
11.4. Требуется рассчитать Т-образный
ФВЧ типа k, предназначенный для рабо-
ты на нагрузку, сопротивление которой
R — 5000 ом. Частота среза /с = 500 гц.
Построить частотные характеристики Zt ,
Рис. 11.7 а и Ь.
Таблица 11.5
Полоса f, гц 1 >с (N , ом и а ch - а ~2 ’ неп 3! |СЧ С ••м В. CU • -е> Ь, град 1
Пропус- 0 0 1 1 2000 1 - -I 0 0 0 0 0
кания 200 0,2 0,96 0,98 1960 мм» 0 0 0,2 11,5 23
400 0,4 0,84 0,917 1834 —— 0 0 0,4 23,5 47
600 0,6 0,64 0,8 1600 «мм» 0 0 0,6 37 74
800 0,8 0,36 0,6 1200 —мм 0 0 0,8 53 106
1000 1,0 с 0 0 1 0 0 1 90 180
Задержи- 1500 1,5 — 1,25 / 1,12 / 2240 1,5 0,962 1,924 — 90 180
вания 2000 2 г / 1.74 /• 3480 2 1,32 2,64 «МММ 90 180
3000 3 —t 1 / 2,83 i 5660 3 1,765 3,53 •ммм 90 180
4000 4 —1 5 / 3,87 / 7740 4 2,065 4,13 МММ 90 180
5000 5 —24 /4,9 / 9800 5 2,29 4,58 —- 90 180
11.5. Определить частоту среза П-образного ФВЧ типа k, у
которого 2L2 = ОД гн, Сх = 0,7 мкф, и найти затухание при
f = 0,5 /с.
11.6. Определить индуктивность и емкость ФВЧ типа k, ес-
ли частота среза /с = 500 гц и номинальное характеристическое
сопротивление R = 1000 ом. Чему равен коэффициент затуха-
ния этого фильтра при частоте f = 250 гц?
11.7. ФВЧ типа k, состоящий из двух звеньев с номиналь-
ным характеристическим сопротивлением R == 5000 ом, должен
иметь затухание, равное 8 неп при частоте f = 250 гц. Опреде-
лить частоту среза, индуктивность и емкость одного звена
фильтра. При расчете использовать формулы табл. 11.2.
304
Решение. Каждое звено фильтра должно иметь затухание
а = 4 неп. при f = 250 гц.
Частоту среза определяем из формулы (см. табл. 11.2)
ch = ch -£- = ch2=-^- = ggg,
отсюда
/с = 250 ch — = 250 ch 2 = 250-3,76 = 940 гц.
Индуктивность и емкость (по табл. 11.2)
£ = -l ______о 494 гн-
й 4к/с 4-3,14-940 —
= 4тс/с/? = 4.3J4-940.5000 = 0,017
11.8. Частоты среза П-образного ПФ типа k Д = 200 гц,
f2 = 2400 гц. Найти параметры элементов этого фильтра, пред-
назначенного для работы на активную нагрузку R ~ 2000 ом,
и определить его затухание на частотах 150 и 3000 гц.
Решение. Расчет элементов звена полосового фильтра про-
водим по формулам табл. 11.2:
£ == == 0,29 гн\
1 (Ла — А)
£2 = = 0,73 гн.
2 4 к fi ft
С. — -~л^т~Г7>— ~ 0.1825 мкф; С2= —Г.—--т-. = 0,0725 мкф.
Таким образом, в продольном плече фильтра должны быть
последовательно соединенные индуктивность Lt = 0,29 гн и ем-
кость Сх = 0,1825 мкф, а каждое из поперечных плеч состоит
из параллельного соединения индуктивности 2L2 = 1,46 гн и
емкости ~ = 0,03625 мкф.
Для определения затухания фильтра при указанных часто-
тах предварительно находим
fm = /7Г77 = / 200-2400 = 693 гц
л значения || при /'==150 и /"=3000 гц
150 __ 693
693 150
2400 __ 693
693 2400
3000 _ 693
__ „ _ 693 3000
— ~ 2400 __ 693
693 2400
= 1,285.
305
Наконец, находим (см. табл. 11.2)
ch ~ | = 1,38; а' — 1,69 неп;
ch = |т)" | =1,285; а" = 1,47 неп.
11.9. Рассчитать элементы звена ЗФ типа k, не пропускаю-
щего полосу частот от Д = 20 кгц до /2 = 23 кгц при нагру-
зочном сопротивлении R = 600 ом и определить собственное за-
тухание фильтра на частоте 21 кгц.
11.10. ФНЧ типа т с частотой среза /с = 2800 гц предна-
значен для работы на нагрузку в виде активного сопротивле-
ния 7? = 600 ом. Определить его элементы, если отклонение
характеристического сопротивления от его номинального значе-
ния для рабочей полосы должно быть не более ± 10%. Рас-
считать также собственное затухание фильтра в полосе частот
2800 4- 5600 гц.
Решение. По табл. 11.3 находим величину параметра т—
== 0,542, обеспечивающую требуемую степень постоянства ве-
личины характеристического сопротивления ± 10% в пределах
рабочей полосы частот 0 4- 0,94 /с = 2630 гц.
Для расчета элементов производного фильтра типа т опре-
делим по формулам табл. 11.2 элементы прототипа — ФНЧ ти-
па постоянной k\
г R 600 по о
~~ nfc ~ 3,14-2800 68,2 МгН}
3,14-2800-600 0,189 МК$*
Выбираем П-образное последовательно-производное звено, со-
ставленное из двух Г-образных полузвеньев рис. 11.2 в виде
скелетной схемы рис. 11.8, а. Подробная схема производного
фильтра, в соответствии с характером полузвена ФНЧ типа по-
стоянной k, показана на рис. 11.8, б и в. Элементы фильтра
рассчитываем в соответствии с рис. 11.8, бив по формулам
= 0,542-68,2 = 37 мгн\ 2L2m =
1 — т2 г __
2т 1
0,705 со о алл
2-0 542 ,68'2=:44»4 мгн-
2 0,542-0,189 nnt-1Q .
— — -------_2----= 0,0513 мкф.
306
По (11.7) определяем частоту fM бесконечного затухания:
Рис. 11.8
Расчет собственного затухания по (11.6) сведем в табл. 11.6
Таблица 11.6
f 'С 02 т 0 (т 0)2 х = ] 1 — 82-{- 4- (т 0)21 / X (ch) / а X 1 *2*) {s4 k ' _ т 8 "Г X а, неп
2800 \ 1 1 0,542 0,294 0,294 0,542 1 0
3000 1,07 1,15 0,58 0,338 0,188 0,433 1,34 1,61
3200 1,14 1,31 0,619 0,383 0,073 0,27 2,29 2,94
3500 1,25 1,56 0,678 0,460 0,10 0,316 2,15 3,01
4000 1,43 2,05 0,775 0,603 0,447 0,666 1,16 1,98
5600 2 4 1,084 1,17 1,83 1,35 0,8 1,47
График собственного затухания рассчитанного фильтра ти-
па т построен на рис. 11.8, г.
11.11. Определить параметр т и элементы оптимального
Г-образного последовательно-производного ФВЧ типа т, харак-
теристическое сопротивление Znm которого отклоняется от зна-
307
чения R = 600 ом не более чем на 5% в рабочей области час-
тот от 5600 гц и выше. Чему равна частота среза фильтра?
11.12. Вычертить схему и рассчитать элементы Т-образного
параллельно-производного ПФ типа т (т = 0,6, R = 1 ком) с
полосой частот от Д = 2,0 Мгц до /2 == 2,2 Мгц. Вычислить его
собственное затухание при частоте 1 Мгц.
11.13. Определить частоты бесконечного затухания и вели-
чину собственного затухания при /= 15 кгц П-образного ЗФ
типа т (т = 0,6, R = 200 ком) с полосой непропускания от 10 до
20 кгц.
11.14. Определить элементы мостикового и дифференциаль-
но-мостикового фильтров, эквивалентных П-образному последо-
вательно-производному ФВЧ типа постоянной т с элементами
С1т = 03 мкф, 2L2m = 50 мгн, = 0,12 мкф (рис. 11.9, а) .
Рис. 11.9
Решение. По формулам (11.9) сопротивление одного плеча
мостикового фильтра совпадает с сопротивлением поперечного
плеча П-фильтра (рис. 11. 5, б):
~~ 2^2п — 2 / a) L2m 4- . w ,
а сопротивление другого плеча _
_ 2Zin Z2n _ 4 Zin- z2n
^1M 7 I 47 i
zin + 4Z2n J_Zin+2Z2n
2 in 1 2 zn
составлено из двух параллельных ветвей с сопротивлениями
22„п и Z.n, причем последнее сопротивление равно
л*л А у, 111
1 7 — 1 1
2 Zin ~ 2 ’ ’
308
Соответствующая схема искомого мостикового фильтра изоб-
ражена на рис. 11. 9, б. Ее элементы: емкость 2С1т = 0,2 мкф,
Q
емкость—^— = 0,12 мкф, индуктивность 2L2m = 50 мгн.
В соответствии со схемой рис. 11.6 сопротивления плеч диф-
ференциально-мостикового фильтра
2Z2m = 4Z2n= + “ПТг—
__ 21П * 4^2П
IM" Zin+4Z2n-
Причем последнее сопротивление составлено из параллель-
но включенных:
422П — 222М И 21П — / О) с1т •
Схема дифференциально-мостикового фильтра показана на
рис. 11.9, в. Ее элементы: С1/п = 0,1 мкф, 4L2m = 100 мгн,
Of- = 0,06 мкф.
11.15. Вычертить схему и определить элементы мостикового
фильтра, эквивалентного Т-образному последовательно-производ-
ному ФНЧ типа постоянной т с параметрами т = 1,27, R =
= 1 ком, fc= 10 кгц.
11.16. Вычертить схему и определить элементы мостикового
фильтра, эквивалентного П-образному параллельно-производно-
му ФНЧ типа постоянной т с параметрами т = 1,27, R = 1 ком,
/с = 10 кгц.
ГЛАВА ДВЕНАДЦАТАЯ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Параметры (первичные) однородной линии на единицу ее
длины: г0 — активное сопротивление, ом\ LQ — индуктивность, гн\
CQ — емкость, ф- g()—проводимость изоляции между провода-
ми (утечка), ом~1.
Характеристики (вторичные параметры) однородной линии
ZB и у. Волновое (характеристическое) сопротивление — отно-
шение комплексов напряжения и тока в бегущей (например,
прямой) волне:
___ ^пр — 1/" Г° +
В г Г + /ш^0
/пр
(12.1)
Коэффициент распространения
1 /(г о + Но) (go + /(иСо) = 1т1«'г = а +- /р. (12.2)
где | у | — модуль коэффициента распространения 7;
i— аргумент 7;
а = | 7 | cos 8 — коэффициент затухания;
р = | у | sin В — коэффициент фазы.
Коэффициент распространения определяет основные пара-
метры бегущих волн (длину волны к, фазовую скорость уф):
\ __ к. __ tO / 1 Г) О \
Т р' * (12.3)
Для воздушных линий из медных, бронзовых и алюминиевых
проводов имеют место неравенства (особенно при высоких ча-
310
стотах) ®L0 г0 и шС0 g0; в этом случае справедливы приб-
лиженные выражения
а— 2 (гв +£<>2 * * * *в);
р = (о ]/L0 Со ;
(12.4)
Уф 3-108 м!сек.
Для неискажающей линии должно выполняться условие
При этом
(12.5)
(12.6)
В линии без потерь rQ — go = O. Линия без потерь — неиска-
жающая; для нее
(12.7)
2. Выражения для определе-
ния комплексов напряжения и
тока в любой точке М линии
(рис. 12.1) в виде наложения пря-
мой и обратной бегущих волн.
Начало Конец
линии линии
Рис. 12.1
При отсчете расстояния х
от начала линии до точки М
При отсчете расстояния у=
= I — х от конца линии до
точки М
е^х
+ ^обр2 е = ^пр (#) +
+ <>обр (у); (12.86)
4“ ^o6pi е Uпр (^) +
+ £>обР(*); , (12.8 а)
311
Ui
zB -т*
----е
U 2 •
7 —
ZB -w \ .
2 ^пр (У)
ех =/пр (х) -
— Л>бр (*), (12.9 а)
где Ui и 1Г— комплексы напря-
жения и тока в
начале линии;
£7пр1, ^обр1 — соответствующие
комплексы напря-
жения прямой и
обратной волн в
начале линии.
-Л>брО/). (12.9 6)
где U2 и /2 — комплексы напря-
жения и тока в
конце линии;
(/Пр2» ^обр2 — комплексы напря-
жения прямой и
обратной волн в
конце линии.
t/np и Лтр — прямые (падающие) волны;
£/Обр и 4бр—обратные (отраженные) волны. Отношения комплек-
сов токов или напряжений обратной и прямой волн называют-
ся коэффициентом отражения р.
В случае однородной линии с волновым сопротивлением
ZB, нагруженной на сопротивление ZH, коэффициент отражения
в конце линии определяется формулой.
(12.10)
В случае, когда нагрузка длинной линии ZH = ZB (согла-
сованная нагрузка), то коэффициент отражения равен
нулю, а напряжение (или ток) совпадают с напряжением (или
током) прямой волны. Уравнения напряжения и тока в линии
упрощаются, например, для напряжения
(7(х) =4пр(х) =1/, е (12.11а) U{у) =Uap(y) е"'. (12.11,6)
3. Уравнения длинной линии в гиперболических функциях
U = Ui ch 7 к —
—/jZgSh'fx; (12.12 а)
/ = /ich-(X — -^-sh^x. (12.13а)
U = Utch'[y +
-f-/2ZBsh-[z/. (12.126)
/= 4 ch +^-shiy. (12.136)
ZB
312
Входное сопротивление линии представляет отношение ком-
плексных напряжений к току в точках приключения генера-
тора:
Z _ А (12 14)
j в zb chTZ + ZHshT/ ’ '
Однородная линия при заданной частоте источника питания
может быть заменена симметричным четырехполюсником, коэф-
фициенты которого связаны с характеристиками линии соотно-
шениями
Л = D = ch-iZ; B = ZBsh-[/, С=^-. (12.15)
4. В линии без потерь гиперболические функции заменяют-
ся круговыми: ch 7 Z = ch / р Z = cos pZ; sh 71 = sh j p I = /sin pZ.
Уравнения длинной линии без потерь:
при отсчете расстояний х
от начала линии
U (х) = cos Рх —
—/7iZBsinPx; (12.16а)
1 (х) = /j COS Рх —
— j^-sin^x; (12.17а)
ZB
при отсчете расстояний у
от ее конца
U(y) +
+ /72 ZB sin py. (12.166)
i (у) = 4 cos py +
+ №sin py. (12.176)
XB
Входное сопротивление линии без потерь
. __ 7 + /2В tg ,3/
1 - ZB zB + /Zh tg у *
(12.18)
УПРАЖНЕНИЯ И ЗАДАЧИ
12.1. Первичные параметры воздушной медной линии, диа-
метр проводов которой равен 3 мм при частоте / = 800 гц, име-
ют г0 = 2,52 ом/км, Lo = 2 мгн/км, Со == 6 • 10-9 ф/км, g0 —
= 1 • 10-* ом"1/км, длина линии Z = 100 км.
Определить! модуль zB и фазу <рв волнового сопротивления;
коэффициент затухания линии, коэффициенты фазы и распрост-
ранения (а, р и 7); фазовую скорость распространения электро-
магнитной волны вдоль линии Оф и длину волны X; отношение
из
^2Пр / 2Пр
77— = -г— при нагрузке линии на сопротивление, равное вол-
новому, где /2пр и (72пр— амплитуды тока и напряжения пря-
мой (падающей) волны в конце линии,/1пр и £/1пр — то же в на-
чале линии.
Решение. Волновое сопротивление по (12.1) .
1/"2,52 +/2л.800-2. Ю’3 _1/* 2,52 + /10 •
Г 10~6+ /2л-800-6-10""® ~ V 10-6(1+/30)
10,375055'
10-6 30 е188°5'
== 585 е 16°5 ом.
Коэффициент распространения по (12.2)
1 = /10.3е',Е,Б5'.10-30е'“’5' = 17.6.10- е'“' ы
отсюда коэффициенты затухания и фазы
а = 17,6 • 10“3 cos 82° = 2,44 • 10”3 неп/км\
р = 17,6- КГ3 sin 82°= 17,4- КГ3 рад/км.
Фазовая скорость и длина волны в линии по (12.3)
> 2л 2-3,14
К р 17,4-10~3 6Ь0 КМ,
= -у- = 289 000 км/сек.
Отношения амплитуд напряжений и тока для прямой волны
в конце и начале линии по (12.11а)
^2ПР _ /2ПР _______1 _ п 7ое
<Лпр~Лпр “ е2,44.10-3.100
12.2 Для линий, данные которых приведены в табл. 12.1,
определить ZR, 7, а, р, уф, к и вычислить отношение при
нагрузке линии на волновое сопротивление.
12.3 Фидер с расстоянием между проводами D = 5 см, ра-
диус проводов которого а = 2 мм, имеет параметры: г0 =
== 0,03 ом/м, gQ = 1 • 10"9 ом~1/м при к = 30 м. Найти ZB , а, р.
Решение. При высокой частоте, соответствующей длине
волны 30 м, можно считать, что уф = с = 3.108 м/сек.
Таким образом,
о с ЗЛО3 1П7
/ =-Г = ~зб~ = 10 гЧ-
314
Таблица 12.1
Название линии « Го, ом/км ^о> гн/км Со, ф/км go, ом-1/км Длина линии, км f, гц
Воздушная стальная линия диаметром 3 мм. . . . 29,2 9-Ю-3 6-10-’ 10"® 100 800
Воздушная бронзовая линия диаметром 3 мм. . . . 5,4 2-IO'3 6-10-» 10-® 100 800
Телефонный двухпроводный кабель диаметром 2 мм Н.4 0,6-10-® 38-10"’ 0,8.10"° 100 800
Морской телеграфный коак- сиальный кабель. * а , 7 0,3-10-® 0,2-10-’ 0,5.10"® 200 800
Индуктивность и емкость единицы длины (1 jw) двухпровод-
ной линии
Lo = In — = 4тс'10"7'1 In Л = 12,9- IO'7 гн,
"па п 0,2
1____
Со = 3б71--15°9— = 0,863-10"11 ф.
In -- In
а 0,2
Так как
о£0 = 2тс. 107.12,9-10~7 = 81 > г0 = 0,03
и
<оСо = 2к. 107.0,863 • 10-11 = 5,4 - IO"4 > g0 = 10“9,
то по (12.4)
7 l/L0 1/" 12,9-Ю"7 00'7 Л
2В У с0 V 0,863-10"11 ~ 387 ОЛ.
В случае, когда >5 и ^^>-5, а и 8 могут быть под-
го ёо
считаны по (12.4):
“ = 4“ (г° Ут; + Vlj-) = 39 •10-6 неп,м'
р = о) YLqCq = 0,21 рад/м,
этот же результат можно получить и по (12.3):
315
12.4. Даны параметры цепей: а) воздушной линии из медных
проводов при / = 800 гц г0 = 2,87 ом!км, Lo= 1,94-10*3 гн/км,
Со = 6,35-10~9 ф/км и g0 = 0,14-10*® ом~Чкм\ б) воздушной ли-
нии из медных проводов при частоте / = 20000 гц, г0 =
= 6,76 ом/км, Lo= 1,89-10~3 гн/км, Со = 6,3-10*9 ф/км и g0 =
= 5,7-10*® омтЧкм. Определить ZB, у, а и >3 и сравнить со зна-
чениями, полученными для соответствующих величин по упро-
щенным формулам (12.4).
12.5. Даны параметры кабельной цепи при / = 800 гц'. г0 =
= 22,6 ом/км, Le = 0,6-10*3 гн/км, Со = 35,5-10*9 ф/км и g0=
= 0,7• 10~® омтЧкм.
Определить ZB, 7, а и р и сравнить их со значениями соот-
ветствующих величин, полученными по упрощенным формулам
для кабеля при умеренных частотах (800 гц и меньше), когда
г0 wL0 и go и» “Со, что приводит к приближенным равенствам
It
12.6. Двухпроводная цепь из медных проводов диаметром
d = 4 мм при частоте f = 800 гц имеет параметры: г0 =
= 2,87 ом/км, £0 == 1,94 мгн/км, Со = 6«10-9 ф/км, gQ =
= 0,14 мком^/км.
Полагая, что при изменении частоты в пределах от 200 до
2400 гц параметры линии остаются неизменными и равными
тем, которые указаны выше, построить частотные зависимости
коэффициента затухания и коэффициента фазы (т. е. кривые
зависимости а и р от частоты) при изменении f от 200 до
2400 гц. При построении брать точки для частот, разнящихся
друг от друга на 200 гц.
12.7. Экспериментально установлено, что мощность телефон-
ного аппарата как передатчика на зажимах телефонной цепи
составляет 1 мет, а мощность телефонного аппарата как при-
емника должна быть порядка 1 мквт, т. е. может быть допу-
щено уменьшение мощности в 1000 раз. Имея это в виду, для
трех воздушных линий и телефонного кабеля, параметры кото-
рых приведены в задачах 12.1 и 12.2 (полагая, что в каждом
из случаев сопротивления телефонного аппарата согласовано е
соответствующей линией или кабелем), определить: а) макси-
мально допустимое затухание; б) допустимую дальность связи,
считая, что все потери энергии сосредоточены в линии (пере-
дающий и приемный аппараты присоединены непосредственно к
линии); в) отношение модулей напряжения и тока в начале ли-
нии к соответствующим величинам в конце линии.
316
Решение. Максимально допустимое затухание в неперах
b = -4- In In 1000 = 3,45 неп,
4 г 2 Z
так как 1 неп = 8,69 дб или 1 дб = 0,115 неп, то
6 = 8,69-3,45 = 30 дб;
отсюда для воздушной медной линии дальность передачи
/6 3,45 « • ол
I == — = о л’л.in-? == 1420 КМ.
а 2,44» 10 3
Отношение модулей напряжений и токов равно
12.8. Вторичные параметры однородной двухпроводной цепи
из медных проводов диаметром 4 мм при частоте f = 104 гц
имеют
— / 1°10'
ZB =548е ом; а = 4,7 мне'п/км, р = 0,219 рад/км.
Длина линии I = 100 км. Напряжение в конце разомкнутой
линии изменяется по уравнению и2 == C^sin со/ (6/2 = 10 в и
/ = 10* гц).
Вычислить комплексные значения напряжения и тока в на-
чале линии и в точке, отстоящей от конца линии на 20 км.
Для тех же точек линии написать уравнения мгновенных зна-
чений напряжения и тока.
Решение. Вычислим \у для начала линии (у — Г);
ll = (а + /\3)I = (4,7-IO-’ + /0,219).-100 = (0,47 + /21,9) рад.
-*1 — •у/
Определим е , е , sh %l, ch-f Z, th у/. При расчете этих ве-
личин нам придется вычислить значения тригонометрических
функций, аргументом которых является р/ = 21,9 рад. Приве-
дем его к значению, меньшему 2тс, для этого из р/ вычтем 2тс,
взятое целое число раз. В данном случае вычтем бтс = 18,85;
получим 21,9—18,85 = 3,05 рад. Так как 1 рад = 57,3°', то
3,05.57,3° = 174°45'. Поэтому sin21,9 = sin3,05 = sin 174°45' =
= 0,091; cos 21,9 = cos 174°45' = — 0,996.
317
Итак,
/=e°‘47 е/21’9 = е0,47 (cos 21,9 4- /sin 21,9) = 1,60( — 0,996 4-
+ /0,091) = — 1,593 + /0,146;
-TZ -0,47 —/21,9 -0,47
е = е е = е
(cos 21,9 — /sin 21,9) =
= 0,625 (— 0,996 — j 0,091) = — 0,623 — j0,057;
sh-// = 0,5 (e7'—e~7') = — 0,485 4- /0,102 = 0,495 e 168°10':
rl —ч1 i 177°40'
ch 7/ = 0,5(e7 +e 7) = — 1,108 + /0,045 = l,108e
Заметим, что значения гиперболических синуса и косинуса
могут быть также вычислены по формулам (4) и (5) приложе-
ния 4:
sh 7/ = sh (0,47 + /21,9) = sh (0,47 4- /3,05)=
где
S = /0,5 (ch 0,94 —cos 6,1) = /0,5 (1,475 — 0,973) = 0,50;
rn tg3,05 0,092 __П91- m ____
= 'th 0,47- = “МЗв- = “ °’21’ = 168 10 *
Следовательно,
, , Л / 168° 10'
sh 7/ = 0,50 e
Аналогично
ch 7/ = ch (0,47 4- /21,9) = ch (0,47 4- /3,05)=Ce/?c;
где
C = 1/0,5 (ch 0,94 4-cos 6,1) = /0,5(1,475 4-0,973) = 1,107;
tg <pc = th 0,47- tg 3,05 = 0,438 (— 0,092) = — 0,0403;
<p,= 177°40'.
Следовательно,
ch у/ = 1,107 e
/ 177°40'
Результаты вычислений shy/ и ch у/ двумя способами почти
совпадают. Заметим, что при вычислениях вторым способом
углы <р5 и срс по значениям tgq\ и tg взяты во второй чет-
верти, что вытекает иЗ свойств гиперболических синуса и коси-
318
нуса от комплексного аргумента (см. приложение 3). Углы ф^,
и <рс находятся в той же четверти, в какой лежит угол р/ (в
данном случае во второй), при этом выполняется неравенство,
справедливое для четных четвертей:
= 168°10' < р/ = 174°45/ < ф, = 177°40'.
Действующее значение напряжения в конце линии выразим
в символической форме U2 = U = 10 в.
Действующие значения напряжения и тока в начале линии
при холостом ходе (/2 = 0) по формулам (12.126) и (12.136)
/ 177°40' / 177°40'
t/lx x = (72‘chTf/= 10-1,107 е = 11,07е в;
Лх х = гл» -/ibfd^,0>5g = 9,1е ма.
1х-х 548 е м 10
Амплитудные значения напряжения и тока при холостом
ходе в начале линии
t/.xxm = 11,07/Г= 15,5 в; /1ххот =9,1 /2’= 12,9 ма.
Мгновенные значения напряжения и тока в начале линии
при холостом ходе
и = 15,5 sin(<D^+ 177°40') в; i. Y = 12,9sin(<о/+ 169°20') ма.
В режиме холостого хода ток Zlx х отстает от напряжения
м1хх на 8°20\ Для точки, удаленной от конца линии на у =
= 20 км, расчет проводится аналогично. В этом случае
^ = (0,095+/4,38); shTy = О.Эбе7258010'; chTz/ = 0,34ez 195°20';
/, п и -./195’20' • и, , , /259’20'
(7= [/2сп w=3,4e в\ / = --?-sh = 17,4 £ ма\
ZB
и = 4,8 sin (о)/ + 195°20') в\ i = 24,6 sin (со/ + 259°20') ма,
В этой точке линии ток опережает напряжение на 64°.
12.9. Линия, параметры которой даны в предыдущей задаче,
замкнута накоротко. При этом ток в конце линии Z = /2/wsinu)Z
(/2 = Ю ма, f = 104 гц). Вычислить комплексные значения на-
пряжения и тока в начале линии и написать уравнения их
мгновенных значений. Определить входные сопротивления ли-
нии при холостом ходе и коротком замыкании.
319
Решение. По формулам (12.126) и (12.136) в режиме
короткого замыкания (С/а == О и приняв /а = /а = 10 ма)
• * —/ 168°10'
(71к з =Z2ZB sh 7/= Ю.10~3-548е -0,5е =
О 7 Л 7 ,67°
= 2,74е в\
• • / 177°40' / 177°40'
Г =/achT/= 10-10-». 1,107е = 11,07 <? ма\
1К.0 * ’ '
u.Ka = 3,88sin(w/ 4- 167°) в; i. , = 15,6 sin (ш/ + 177°40') ма.
В режиме короткого замыкания ток f1K 3 опережает напря-
жение и1к 3 на 10°40'. Для определения входных сопротивлений
линии вычислим значение th 7/:
_shT/ О,5О/,68°10'
"chT/ = 1,107/|77°40'
0,452 е“,9°30.
Этот же результат можно получить и по формуле (6) прило-
жения 4.
Искомые входные сопротивления линии находим по (12.14),
полагая соответственно Z„ v v = °° и Z„ „ = 0:
н« х. х н»к«з
— в
Х.х 1 л
548 е 71 1О1П / 8°20'
-----------== 1210 е’ ом\
0,452 е~19 °0 ’
Z„ = Zoth-rZ =548е П°'°
К.З о •
0,452е
—/ 9°30'
= 248е
— / 10°40'
ОМ.
12.10. Линия, параметры которой даны в задаче 12.8, наг-
ружена на сопротивление ZH = 500 10° ом. Вычислить комп-
лексные значения напряжения и тока в начале линии и напи-
сать уравнения мгновенных значений этих величин, если нап-
ряжение в конце линии u2 = U2m sin ю/ (t/2 = 10 в, f = 104 гц).
Определить комплексные значения прямой и обратной волн на-
пряжения в начале линии. Написать уравнения для мгновенных
значений прямой и обратной волн напряжения в начале и кон-
це линии.
Решение. Напряжение и ток в начале линии при нагруз-
ке по (12.126) и (12.136)
10. 1,107/ 177°4С' +-1° .548е-/,в,0'.0,5/16«''40' =
. 1 500 е~' 10
==.16,64-/0,73= 16,6/2О30’ в;
Э20
_________10
1 ~~ 500 е~ ' 10°
1,107е
/ 177’40'
10 Л С р/ 168°10'
548в"' ‘°40' ’
= 31 + /2,6 = 31 4°50' ма;
Uln = 16,6 /2 = 23,4 в; 11п= 31/2'= 43,7 ма;
Ui = 23,4 sin (wt + 2°30') в; = 43,7 sin (ш/ + 4°50') ма.
Комплексные значения прямой и обратной волн в начале
линии определим по (12.8а):
<>1+AZB 16,бе/2’30'+31 -IO-з е'4’50'. 548e-'1”10'
npi =-----2---- = -------------------2------------------
. = 16,8е'315 в = Unpl g-^npi ;
+р, - = М ‘ е‘ *
Мгновенное значение прямой волны напряжения в начале
линии
।
unpi = /2 t/npjSin(<oZ + фпр1) = /Т • 16,8 sin (ш/ +3°15') =
= 23,8 sin (ш/ + 3°15') в.
Мгновенное значение прямой волны напряжения в конце ли-
нии [в задаче 12.8 было вычислено а/= 0,47, р/ = 21,9 рад =
= (бтс + 3,05) рад = 360°-3 + 174О45/, или, отбрасывая целое
. число окружностей, $1 = 174°45']
«ирг = V~2 Unple al (sin wt + <1>пр1 — $1 )=
= /Г- 16,8e~0'47sin(w/.+3o15/— 174°45')= 14,9sin(ш/—171°30') в.
Мгновенное значение обратной волны напряжения в начале
линии
«обР1 = /2-f/oopi sin(<0/ + <{>обр1) = /2 -0,6 sin (О)/ —
— 132°20') = 0,85 sin (<ot — 132°20') в.
Мгновенное значение обратной волны напряжения в конце
линии
«обР2 = sin (wt — 132°20' + 174°45') =
= /2 • 0,6e°’47sin(o>/ — 132°20' + 174°45') = 1,36 sin (о>/ +
+ 42°25') в.
11 Заказ № 624
321
12.11. Линия, параметры которой даны в задаче 12.8, замк-
нута на сопротивление, равное волновому. Напряжение на ее
приемном конце u2 = V2m sin wt (t/2 = 10 в, f = 10 4 гц).
Чему равно затухание в линии? Написать уравнения, по-
строить кривые распределения действующих значений напря-
жения и тока вдоль линии. Определить комплексные действую-
щие значения напряжения и тока в начале и в конце линии.
Записать уравнения мгновенных значений напряжения и тока в
начале линии. Вычислить мощность, расходуемую в нагрузке и
подводимую к линии. Начертить кривые распределения мгно-
венных значений напряжения вдоль линии для двух моментов
времени: t = 0 и t ~ 10 мксек.
Решение. Затухание в линии
а/ = 4,7-IO"3-100 = 0,47 неп, или а/ = 0,869-0,47 = 4,1 дб.
При нагрузке линии на волновое сопротивление й2= /2 Zb
будут только прямые волны напряжения и тока. Их комплекс-
ные значения (действующие) в функции расстояния у по (12.86)
и (12.96), считая С/2 = £/а •= 10 в, равны
U(у) = 4- 44 + 4 ZB ) е<"= V» U2е(л + ^у =
Юе4’7'10”^70*219^;
ш=4-(4+-^4 «т</=^^=
z \ гв / LB
10е(а+/(,)г/
548е-'|О1°'
10е<ж + ^>» „ 4,7.10-’» / (0,219»+ 2,03-10-’)
548 е-/2,03.10-’
(1)
(2)
Полагая в этих уравнениях у = I и у = 0, получим комп-
лексные выражения для действующих значений напряжения и
тока в начале и соответственно в конце линии:
йг= 1Ое0’47 е721’9 = 16 е721,9в; 4= 18,2е0’47 е7(21’9 + 2-03-10”> =
= 29,1 е> 175°55' ма-,
U2 = 10 в; 4 = 18,2 е71’10' ма.
Мгновенные значения напряжения и тока в начале линии
Z
U1 = 16 yTsin(o>f + 174°45') = 22,6 sin (о>/ + 174°45') в;
G = 29,1 pTsin^/ + 174°45' + 1°10') = 41 sin(o>/ +
+ 175°55') ма.
322
Кривые действующих значений напряжения и тока вдоль
линии (рис. 12.2,а) строят по уравнениям7
U (у) = 10е4,7’*°~’®в;
1(у)=> 18,2 е4,7,10”® ма.
Рис. 12.2
На основании уравнения (1) построена спиральная диаграм-
ма изменения величины и фазы действующих значений напря-
жений (рис. 12.2,6). .
Мощность, расходуемая в нагрузке и подводимая к линии,
Ra = Re[(7a/a ] = Re [10-18,2-10-3 е“/2,°3-10”] » 0,182 вт,
Р1 = Re 4 ] = Re [ 16 е121>9-29,1 • 10'3е~1 (21’9 + 2,03‘ 10"а) ]«
я» 0,465 вт.
Мгновенные значения падающих вдоль линии прямых волн
напряжения и тока по (1) и (2):
и = j/T U2eau sin (о/ + Ру) J/2 • 10e4'7,10-a®sin (ш/ + 0,219 у) в;
i = j/2” /а e“®sin (wt + Ру + фс) = К2" • 18,2 e4'7,10”*®sin (ш/ +
+ 0,219 у 4-2,03-Ю-3) ма.
11*
323
Кривые распределения мгновенных значений напряжения
вдоль линии для двух моментов времени (рис. 12.2 в) построены:
при t = О
«= 14,1 е0’47,10-**'sift 0,219 у в;
при t — 10 мксек
и = 14,1е°л7-10-‘р Sin(<o. Ю-5 + 0,219у) =
= 14,1 е0-47'10-» sin ( 0,219t/+ в.
12.12. Линия из медных проводов, параметры которой даны
в задаче 12.8, нагружена на сопротивление Zh = 2Zb. Частота
f = 104 гц. Написать выражения для мгновенных значений нап-
ряжения и1 и тока в начале линии, если напряжение на наг-
рузке = t/2zrasin о)/ ([72 = 10 в). Определить входное сопротив-
ление нагруженной линии.
12.13. Решить предыдущую задачу, если ZH =-^~ Zb . Пара-
метры линии, напряжение и частота тока те же, что и в зада-
че 12.12.
12.14. Вторичные параметры двухпроводной воздушной цепи
из стальных проводов диаметром 4 мм при частоте f = 800 гц
имеют
ZB = 1350е“/24° ом, а = 17,5 мнеп!км, р = 0,039 рад!км.
Длина линии 20 км. Концы линии разомкнуты. В начале ли-
нии действует напряжение = Ulm sin а)/([7х = 10 в, / = 800 гц).
Определить действующие значения напряжения в конце ли-
нии и тока в начале линии в режиме холостого хода и написать
уравнения их мгновенных значений.
12.15. К короткозамкнутой линии, параметры которой при-
ведены в предыдущей задаче, подведено напряжение =
= [7lmsino>/ (f7i = 10 в, / = 800 гц). Найти действующие значе-
ния токов в конце и начале линии и написать уравнения мгно-
венных значений этих токов.
12.16. Линия, параметры которой приведены в задаче 12.14,
замкнута на активное сопротивление г = 1000 ом. К началу
линии подведено напряжение = 10 в, f = 800 гц).
Вычислить комплексные значения напряжений [/2 и тока /2 в
конце линии, тока в начале линии и написать уравнения их
мгновенных значений. Подсчитать комплексные значения прямой
и обратной волн напряжения и тока в начале и конце линии.
12.17. К линии, параметры которой указаны в задаче 12.14,
подключено напряжение = Ulm sin о)Ц{/х =10 в, f = 800 гц).
Линия нагружена на сопротивление, равное волновому. Чему
равны комплексные напряжение и ток в конце линии? Вычис-
324
лить мощность, расходуемую в нагрузке и подводимую к линии.
Построить кривые распределения действующих значений напря-
жения и тока вдоль линии. Построить кривые распределения
мгновенных значений напряжения вдоль линии для двух момен-
Т
тов времени: t = 0 и t =• .
12.18. Найти напряжение и ток в конце линии из стальных
проводов, параметры которой приведены в задаче 12.14, если
она нагружена на сопротивление ZH. Задачу решить в двух слу-
чаях: 1) ZH = 2ZB , 2) ZH = -i- Zb .
12.19. Вычислить сопротивления Т-образной схемы замеще-
ния воздушной двухпроводной цепи из медных проводов диамет-
ром 3 мм, длиною / = 100 км при f = 800 гц. Параметры ли-
нии взять из данных задачи 12.1.
12.20. Определить сопротивления П-образной схемы замеще-
ния однородной воздушной бронзовой цепи диаметром 3 мм, дли-
ною 1= 100 км при / = 800 гц. Данные цепи взять из условия
задачи 12.2.
12.21. Воздушная медная линия при / = 800 гц имеет пер-
вичные параметры, указанные в задаче 12.1. Как следует изме-
нить индуктивность этой линии (это достигается путем введения
в линию через определенные расстояния индуктивных катушек),
чтобы она удовлетворяла условию неискаженной передачи? Чему
в этом случае равны Zb , а, р?
Эта неискажающая линия длиною / = 250 км нагружена на
активное сопротивление, равное волновому при
нагрузке (72 = 10 в.
Подсчитать напряжение, ток и мощность на
также /2 и Р2 на нагрузке.
Указание. Для определения вторичных параметров
мулы (12.5) и (12.6).
напряжении на
входе линии, а
использовать фор-
12.22. Энергия передается на высокой частоте от генератора
к излучающей системе при помощи фидера (линии) индуктивно-
стью Lq = 1,57 мкгн!м и емкостью С0 = 7,1 пф!м. Потерями в
фидере можно пренебречь (r0 = gQ = 0). Частота переменного тока
/= 108 гц.
Определить входное сопротивление отрезка этого фидера
1
длиною в -g- длины волны при холостом ходе и коротком замы-
кании.
1 3
Расчет повторить для отрезков фидера длиною в -g- и
1 гг
-ят длины волны. Для каждого из рассчитанных случаев начер-
тить эквивалентную схему фидера.
325
Начертить кривые изменения входных сопротивлений Zx.x
(при холостом ходе) и ZK,3 (при коротком замыкании) в функ-
ции длины фидера.
Решение. Вычислим Zb. р по (12.7) и К по (12.3):
„ -1/1,57-10-« ._А
ZB = гв = |/ 7д-.-до~12— = 470 ом;
р = 2«108/1,57- 10-в-7,1 • 10-12 = 2,10 рад/м;
> _ 2тс 2к _____ q
Л Г ~ 2J0 — й м-
Из формулы (12.3) рх = 2к, а для фидера длиною I = X
Входное сопротивление определим по (12.18). При холостом
ходе ZH = оо выражение (12.18) обращается в неопределенность;
ее раскрываем путем деления числителя и знаменателя на ZH:
= —/ZB = —/470 ом.
При коротком замыкании ZH = 0
ZK.3 = ZB = /Zb tg р/ = /ZB tg-J- = /470 ом.
Эквивалентная схема двухполюсника при холостом ходе —
емкость с сопротивлением 470 ом, при коротком замыкании —
индуктивность с сопротивлением 470 ом.
Расчет для других длин фидера рекомендуем проделать са-
мостоятельно:
При / — 4 X Zx.x — 0, ZK,3 — ooj
при I = X Zx.x = /470 ом, ZK.S = —/470 ом;
при I =”2~ X Zx x = °°» Zk.s = 0.
Кривые изменения входного сопротивления в функции длины
фидера I (могут быть рассчитаны по уравнению (12.18):
при холостом ходе ZH= оо, Zx.x =—/Zectgp/;
при коротком замыкании ZH = 0, ZK.3 = /ZBtgPL
Во всех рассмотренных случаях входное сопротивление линии
является чисто реактивным: Z = /х, Zx.x = /хх.х, ZK,3 = /хк,3 .
326
Кривая хх.х = ft(l) имеет вид котангенсоиды, а кривая хк,3 =
— f2(l)— тангенсоиды (рис. 12.3, а, и б).
ё) При коротком замыкании
Рис. 12.3
12.23. Фидер, параметры которого приведены в предыдущей
задаче, имеет длину I — 5 м и находится в режиме холостого
хода. Подсчитать действующие значения напряжения в конце и
тока в начале линии, если к фидеру подключено напряжение
= (7lmsino>/ (U1== 10 в, /= 108 гц). Начертить кривые распре-
деления действующих значений напряжения и тока вдоль фиде-
ра. Написать уравнения мгновенных значений напряжения и тока
в начале фидера. Начертить кривые распределения мгновенных
значений напряжения и тока вдоль фидера для двух моментов
Т
времени: t = 0 и t = -g-. Определить коэффициенты отраже-
ния и бегущей волны.
Решение. Подсчитаем величины, которые потребуются в
дальнейших расчетах, а именно:
р/ = 2,1 • 5 = 10,5 рад = (4,22 + 2тс) рад;
cos р/ = cos(4,22 + 2тс) = —0,472;
sin р/ = sin(4,22 -f- 2тс) == —0,881.
Примем U1 — U1 = 10 в. Из формулы (12.166) для режима
холостого хода /2 == 0 определим действующее значение напря-
жения в конце линии у = I:
^=-Аг = п\°79- = — 21.2 в.
* cos^Z —0,472
Действующее значение тока в начале линии вычислим по
(12.176):
А = / -y^-sin pZ = j (—0,881) = 39,7 ма.
327
Рис. 12.4
На рис. 12.4 построены кривые распределения вдоль линии
действующих значений напряжений и токов по уравнениям, запи-
санным на основании (12.166) и (12.176):
U{y) =(/acos $у =
= —21,2 cos 2,1 у в\
1(У) sin $у =
ZB
—21,2 . п ,
sin 2,1 у
= —45 sin 2,1г/ лш.
Мгновенные значения напря-
жений и токов при режиме холо-
стого хода (/2 = 0) в общем виде
и = U2m cos $у sino)/;
i ~ sjn Зу cos O)t
ZB
Для момента t = 0
и = 0; i = —^-sin $y sin 2,\y = —63,6 sin 2,\y ма\
т' I v
T
для момента Z = —
о
и = U2mcos fly sin io-у = —21,2]/2 cos pr/sin =
= — 21,2 cos 2,1 у e\
: о T
~7~ sin 3y COS W-g- =
ZB ™ 8
—21,2]<2
470
cos-5-sin pz/ = —45sin2,lz/jza.
На рис. 12.4 нанесены кривые напряжения и тока для мо-
ментов t = 0 и / = — .
Коэффициент отражения у нагрузки по (12.10)
_______________________ <
ps~ Z„ + ZB - к
za **“
Коэффициент бегущей волны
к.б.в. =-<~ !Рв! = 0.
1 + |Рн|
328
12.24. Фидер без потерь, параметры которого LQ = 1,57 мкгн/м,
Cq — ТЛ пф/м, имеет длину / = 35 м и нагружен на сопротив-
ление, равное волновому. Напряжение на приемном конце фидера
и2 — ^sin о)/ = 10 мв, f = 108 гц).
Написать выражения для мгновенных значений напряжения
и тока ii в начале фидера. Построить кривую распределения
действующих значений напряжения U и тока / вдоль линии.
Определить коэффициенты отражения и бегущей волны. Начер-
тить кривые распределения мгновенных значений тока и напря-
жения в функции расстояния для трех моментов времени:
12.25. Решить задачу 12.24 при нагрузке фидера на сопро-
тивление ZH = 2Zb .
12.26. Линия без потерь имеет длину I = 200 м и парамет-
ры Lq = 2-10’6 гн/м и Со = 5,55-10"6 мкф/м. Длина волны в
линии к = 60 м. В конце линии включена индуктивность L =
= 0,01 мгн.
Найти характеристики (вторичные параметры) линии. Дока-
зать, что в линии будут стоячие волны тока и напряжения.
Найти, на каком расстоянии от конца линии будут ближай-
шие пучности напряжения и тока.
Найти отношение амплитуд, напряжения и тока в пучности
и в конце линии.
Найти отношение амплитуд, напряжения и тока в пучности
и в начале линии.
Решение. Волновое сопротивление линии
ZB = j/bt- = 600 ом.
Коэффициент фазы
р = -^- = = 0,1047 рад/м.
Пользуясь уравнениями (12.126) и (12.136) и имея в виду,
что ZB = zB, 7 = /Р и /2 = ^, где jx = jwL = ZH = /2k/L =
/Л
= /2« -0,01 • IO'3 = /314 ом,
получим
(7(1/) = {/2(cos pz/+ -j5- sin p у} = cos (Pz/ — 3);
/(z/) = Z2(cos — -J- sin $y) = — sin (pz/ — 8),
Olli 'J
329
где
& = arctg = arctg = 62°30' = 1,09 pad.
Переходя к мгновенным значениям и считая, что напряжение
— •
имеет начальную фазу, равную нулю (т. е. Uz — U2, тогда
• • /90°
/2 = — /72, — /2 = /72 = /2 е ), получим
cos Ь
cos (₽#— 8) sin <о/
i = sin (8z/— 3) cos W
sin b 7
= U2m cos — 8) sin to/;
= I2m sin $y — 8) cos a)/.
Эти уравнения показывают,
что в линии имеют место
стоячие волны (рис. 12.5).
Ближайшая от конца линии
пучность напряжения опреде-
лится из уравнения cos —
— 8) = 1, т. е.
— в = о, ух = А- =
и ~
Ближайшая от конца
У г = У1 +
линии пучность тока на расстоянии
4- = Ю,5 + -4 = 25,5 м.
4 4
Отношение амплитуды напряжения в пучности к амплитуде
напряжения в конце линии равно
^2 . т J 1 _ 1 __ О 1 К
cos & * 2 cos b cos 62°30' ’ ’
а для тока такое отношение будет
^2 . J 1
sin Ь ‘ 2 sin &
1,13.
Отношение амплитуды напряжения в пучности к амплитуде
напряжения в начале линии равно
- У* _ • _cos (8/___8^=__________!________=______1___—
cosS • cosb cos(0,1047-200—1,09) cos 19,85
= 1 = 1 - 1 __ I M
cos(19,85 — 6k) cos 1 cos57,3° ’ *
330
а для тока такое отношение равно
sin (?/ — 8) = . J, „0 = 1,19.
sinb sin Ь vr ' sin 57,3
12.27. Линия без потерь, имеющая волновое сопротивление
ZB = 500 ом, питается напряжением частотой / = 108 гц. Опре-
делить амплитуду тока при холостом ходе в точке, находящей-
ся от конца линии на расстоянии у = 0,5 м, если напряжение
на конце линии U2m = 100 мв.
12.28. Измерения сопротивления холостого хода Zlx.x и ко-
роткого замыкания ZiK,3 воздушной двухпроводной телефонной
линии длиной 200 км при угловой частоте ш = 5000 сек"1 дали
результаты: Zix.x = 747 е~/26°30' ом, ZiK,3 == 516 е^°3°г ом. Опре-
делить характеристики (вторичные параметры) линии Zb , а, ?
и первичные параметры линии г0, Со. •
Решение. Входные сопротивления линии при холостом хо-
де и коротком замыкании [соответственно, ZH = °° и ZH = 0 опре-
деляются из формулы (12.14)]
2ix.x = = W-
Перемножая эти выражения, найдем
ZB = ]/Zix.xZiK3 = 620 е->13°== (587-/139,5) ом,
а поделив, получим
th т/ = 1/= 0,83е'13°30' = 0,806 + /0,193,
г £1х.х
НО
е1‘_ е-V е1‘ е^-1
thT/~ e^ + e-f1 ' el‘ ~ е^‘ + 1 ’
откуда
1 + th у1 1,806+ /0,193 а /(514-2™)
е* =-r^tht/ = 0,1^4-/0,193 = 6>72в
где п— целое число.
Так как е2ч‘ = е2га е{2&1, то ем — модуль комплексного числа,
а 2р/ — его аргумент:
e2al = 6,72 и а = In 6,72 = 47,5-10”4 неп/км;
2р/ = 51° + 2nit = (0,89 + 2пте) рад.
Для определения величины п, которая должна быть взята в
в последней формуле целым положительным числом, необходи-
мо приблизительно знать величины Lo и Со измеряемой линии,
331
а следовательно, знать приблизительно число окружностей, ко
торое содержится в выражении 2₽/.
Так как для медных цепей
р « <«]/'LqCq и 2pZ ~ 2Z<o‘J/ L0C0,
то приблизительное число окружностей
п =
L/C'
где U и С' — приблизительные величины, известные из преды-
дущих измерений или вычисленные по теоретиче-
ским формулам.
Этой формулой можно пользоваться и для стальных цепей.
В данном случае примем величины, известные из предыдущих
задач, для L' 2-10~3 гн!км и С' »6-10"9 ф!км и тогда
200-5 000/2-10—6-10- . 1С
П — ----------------------= 1,15,
п
хотя здесь и получается дробное число, но п должно быть взя-
то ближайшим целым числом п=1.
Таким образом,
2₽/= 0,89+ 2* = 7,17;
Р = J’2qq = 180-10- рад! км-,
у = а + /р = (47,5 + /180)-10- = 186- 10-е'75° км~г.
Определим первичные параметры линии. Для этого восполь-
зуемся выражениями (12.1) и (12.2)
I = К/о + foLoKgo + /шСо) =186- Ю-е'75” пг1;
Zb = = 620е-'|3° ом.
У go + 1“>Со
Их произведение
tZb = Л) + Мо = (6,4 + /10,2) ом/км,
откуда
г0 = 5,4 ом/км-,
L°==2,04 10-3 гн/км-
Из отношения
4- = ^0 + /«Со = (0,96-10- + /30-10-) олтЧкм
ZB
найдем, что
go = 0,96* 10“® ом"1/км,
Со = “-Елпй-= 6-10 ф/Ol.
332
ом.
х.х
12.29. Сопротивления воздушной бронзовой линии длиною
/ = 250 км были измерены при частоте f = 800 гц, холостом хо-
де и коротком замыкании и оказались равными
= 525е~'17° ом, ZK,3 = 720е~/9°40'
Определить Zb и 7, а также первичные параметры линии г0,
^о> Со, g0.
12.30. Рассчитать входное сопротивление сверхвысокочастот-
ной длинной линии без потерь, которая нагружена на последо-
вательно включенные сопротивление Z и короткозамкнутый
шлейф (короткозамкнутый отрезок длинной линии без потерь),
как показано на рис. 12.6. Даны волновые сопротивления длинной
линии и шлейфа ZB = ZBtJU = 600 ом, сопротивление Z = 500 ом,
длины линии Z = 190 см и шлейфа 1Ш = 10 см. Длина волны в
линии и шлейфе одинакова К = лш = 120 см.
Решение. Входное сопротивление короткозамкнутого шлей-
фа по (12.18)
= гв.ш jtg (Мш) = 2в.ш /tg (-^ /ш) =
СЛП ч /360°. 10 \ .о,с
— 600 /tg (—120—) = / 346 ом.
Сопротивление нагрузки длинной линии складывается из вход-
ного сопротивления короткозамкнутого шлейфа и сопротивле-
ния Z:
z„ =• zm + Z = /346 + 500 = 610е/34°40' ом.
Входное сопротивление длинной линии
333
12.31. Клистронный СВЧ генератор создает на входе длинной
линии без потерь напряжение 10 в (рис. 12.7). Линия с волно-
вым сопротивлением Zb = 100 ом нагружена на согласованное со-
противление ZH = 100 ом. В средней части линии включен корот-
козамкнутый шлейф (линия без потерь) с тем же волновым со-
противлением ZB.m = ЮО ом и длиной /ш где X — длина вол-
ны, одинаковая в линии и шлейфе. Длина линии / = Рассчитать
входное сопротивление линии и ток клистронного генератора.
I
Рис. 12.8
12.32. На входе высокочастотной линии связи длиною I =
= 1,5 км создается сигнал напряжением = 0,5 в и частотой
f = 300 кгц. Линия, состоящая из двух участков — медной двух-
проводной линии длиной /j = 0,7 км с параметрами ZB1 = 586 ом,
Pi = 6,46 рад/км и кабельной линии длиной /2 = 0,8 км с пара-
метрами ZB2 = 76 ом, р2 = 6,7 рад!км, нагружена на сопротив-
ление приемника Z„ = 600 ом (рис. 12.8). Рассчитать напряже-
ние на приемнике. Потерями в линии связи пренебречь.
ГЛАВА ТРИНАДЦАТАЯ
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА
ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
Классический метод решения задач на переходные процес-
сы в разветвленных цепях с постоянными параметрами, в ко-
торых осуществляется коммутация (включение, выключение,
переключение, изменение параметров цепи и т. п.), сводится к
следующему.
1. Для каждой ветви схемы, получающейся после коммута-
ции, следует задаться положительным направлением тока и на
основании законов Кирхгофа составить систему уравнений для
мгновенных значений напряжений и токов переходного режима.
Так как
t
eL = ~dl И ис ~ J
о
то в общем случае это будет система неоднородных линейных
дифференциальных уравнений с постоянными коэффициентами
^от интегралов можно освободиться, продифференцировав все
i \
члены ПО /, получив - -v;-— = .
2. Эта система уравнений может быть решена относительно
одного из токов или напряжения на обкладках одного из кон-
денсаторов. В результате получим неоднородное линейное диф-
ференциальное уравнение с постоянными коэффициентами п-го
порядка, где п равно или меньше количества индуктивных ка-
тушек и конденсаторов в схеме. В соответствии с порядком
дифференциального уравнения, составленного для схемы после
коммутации, говорят о том, что схема после коммутации имеет
порядок п.
335
3. Общее решение полученного неоднородного линейного
дифференциального уравнения представляет собой сумму двух
величин: частного решения неоднородного уравнения, выражаю-
щего принужденный режим, задаваемый источниками, и
решения однородного дифференциального уравнения, выра-
жающего свободный режим. В соответствии с этим для тока
(или напряжения на конденсаторе) в некоторой ветви получим
i = ‘пр + ‘св (или ис = «Спр + иссв). Здесь tnp (или испр) — со-
ставляющая тока (или напряжения на конденсаторе) принужден-
ного режима (или, более кратко, принужденный ток или принуж-
денное напряжение) [в случае постоянного или синусоидального
напряжения могут быть найдены обычными методами расчета ус-
тановившегося процесса в цепи после коммутации]; ZCB (или uCcQ)
составляющая тока (или напряжения) свободного режима (или,
более кратко, свободный ток или напряжение).
Вид функции fnp = Fi (0 [или uCnp==F1 (/)] зависит как от
формы действующих в цепи источников напряжения и тока, так
и от характера самой цепи. Вид функции fCB == /%(/) [или
иссв = (01 зависит только от характера самой цепи.
4. Свободный ток zCB = F2 (0 схемы порядка п имеет п ли-
йейно независимых составляющих (собственных функций)
п
Ч (0 : гсв = S ik (0- Вид собственных функций определяется
Z?==l
видом корней pk (k = 1,2,... п) характеристического уравнения
схемы. Каждому корню соответствует собственная функция (в
рассматриваемой записи — собственный ток) вида (t)=Afc ePk* *
Если корни характеристического уравнения pt = р1+1 =
= д/+2 ==,,.== pUJn-i равны между собой (т. е. корень pz имеет
кратность т), то соответствующие им собственные функции име-
ют вид:
4(f)—Ate 1 , f/+i(/) = ePi > • • • > 4+m-i (f) t Ai+m-i ePl •
Пример в задаче 13.44 (2).
Если имеется пара комплексно-сопряженных корней р& =
= — ak ± / (flk — собственное затухание, — собственная
частота), то соответствующая ей собственная функция (с двумя
постоянными интегрирования А^ и ф^) может быть найдена в
форме
ik (0 + ik+i (0 = Ak e~akt sin W + Ф*)»
где ф&, A & Лр ... — постоянные интегрирования, число кото-
рых равно порядку п дифференциального
уравнения, их значения определяются из
начальных условий.
Примеры в задачах 13.44 (3) и 13.45.
336
5. В качестве независимых начальных условий используются
величины токов t’L(0_), проходящих через каждую индуктив-
ную катушку, и напряжений пс(О-) между обкладками конден-
саторов к моменту коммутации. Если коммутация происходит
мгновенно в момент t = 0 и если мощность обмена энергией
между отдельными элементами цепи остается конечной, то имеет
место непрерывное изменение всех тех величин, значения ко-
торых определяют энергию, содержащуюся в элементах цепи. В
этом случае выполняются следующие законы коммутации:
токи катушек индуктивности и напряжения между обкладками
конденсаторов в момент начала коммутации не изменяются
скачками (внезапно), т. е. они являются непрерывными функ-
циями времени. После коммутации iLk (0) = iLk (0_), uCk (0) —
= «« (0-)*-
Начальные значения токов в других ветвях, не содержащих
индуктивностей, или напряжений на элементах, не являющихся
емкостями, могут в момент коммутации изменяться скачком.
Эти начальные значения токов и напряжений (зависимые началь-
ные значения) определяются по законам Кирхгофа с примене-
нием законов коммутации.
Примеры в задачах 13.19, 13.26, 13.44 и 13.45.
6. При составлении характеристического уравнения в соответ-
ствующей однородной системе уравнений для схемы символы диф-
ференцирования заменяют сомножителем р,
рования — сомножителем
и приравнивают
а символы интегри-
нулю соответст-
Р
вующий (характеристический) определитель системы.
Пример в задаче 13.38.
7. При составлении характеристического уравнения часто
бывает легче составить характеристическое входное сопротивле-
ние схемы, при составлении которого индуктивностям L припи-
сывают сопротивления pL, а емкостям С — сопротивления—
и приравнять характеристическое входное сопротивление нулю.
Примеры в задачах 13.44 и 13.45.
УПРАЖНЕНИЯ И ЗАДАЧИ
13.1. Катушка, индуктивность которой 0,12 гн и сопротивле-
ние 1 ом, включается на постоянное напряжение 30 в. Чему
равна постоянная времени этой катушки? G какой скоростью
нарастает ток в начальный момент? Чему равно установившееся
значение тока?
* Случаи, когда токи в индуктивностях и напряжения на емкостях изме-
няются скачком, рассмотрены в задачах 13.54 4- 13.57.
337
13.2. Цепь, содержащая последовательно соединенные актив-
ное сопротивление г и индуктивность L, включается на постоян-
ное напряжение 47 = 120 в. Определить, через какой промежу-
ток времени ток станет равным 99% тока установившегося
режима, если г == 100 ом и L == 0,2 гн. Найти закон изменения
э. д. с. самоиндукции, наводимой при включении, и вычислить,
через какой промежуток вре-
мени после включения ско-
рость запасания энергии (т. е.
мощность р) в магнитном поле
будет максимальна.
Замечание. На рис. 13.1
изображены кривые, построенные на
основе полученных решений.
13.3. Сопротивление катуш-
ки равно 1,2 ом, индуктив-
ность 9 гн. В момент, когда
через катушку проходит ток
50 а, она замыкается накорот-
ко. С какой скоростью начнет
убывать ток в катушке? Чему
равна скорость убывания тока
в момент, когда величина тока
равна 25 а?
13.4. Катушка, параметры которой г = 50 ом, L == 125 мгн,
находится под постоянным напряжением U = 150 в. После прак-
тически полного установления тока катушка посредством клю-
ча с переходным контактом быстро отключается от источника
электрической энергии и замыкается на сопротивление гг ==
= 12,5 ом. Найти закон изменения тока в катушке (рис. 13.2).
Показать, что энергия, выделившаяся в цепи после переключе-
ния в форме тепла, равна первоначальному запасу энергии маг-
нитного поля.
Рис. 13.2
Рис. 13.3
13.5. Цепь с весьма большой индуктивностью (обмотка воз-
буждения генератора постоянного тока) отключается от источ-
ника постоянного тока с напряжением U = 120 в (рис. 13.3).
Определить, во сколько раз повысится напряжение на зажимах
вольтметра, а также найти энергию, которая выделится в вольт-
338
метре после размыкания, если г = 40 ом, L = 100 гн. Сопротив-
ление вольтметра равно 5000 ом. Его индуктивностью можно
пренебречь.
13.6. Определить законы изменения тока и напряжения в
каждой из двух последовательно соединенных индуктивно свя-
занных реактивных катушек, параметры которых г1 = 40 ом,
Li = 0,2 гн, г2= 10 ом, L2 = 0,l гн, а взаимная индуктивность
М = 0,1 гн, при включении их на постоянное напряжение U =
= 100 в (рис. 13.4, а).
Рис. 13.4
Задачу решить для согласного и встречного соединений ка-
тушек.
Указание. Составить уравнение второго закона Кирхгофа
(bj + -±: 2ЛТ) + (Г1 И- r2) I = U.
Знак «плюс» соответствует согласному включению катушек, а знак «ми-
нус»— встречному.
Характеристическое уравнение, согласно п.6 основных положений и со-
отношений, равно
(Li + L2 ± 2М) р + (Г! + г2) = 0;
р = — ' Pl = ~ 100 сек~1' Р2 = —500 сек~1’
В результате решения должно быть получено:
для согласного включения
i = 2(l — e-ioo') а;
И1 = (80 — 20 e-i°0/) в; и2 = (20 4- 20 в”100*) в;
для встречного включения
i = 2 (1— е-б00<) сс,
щ = (80 -ь 20 е-800*) в; и, = (20 — 20 е"800') в.
339
На рис. 13.4, б даны кривые тока и напряжений для согласного включе-
ния.
13.7. При замыкании рубильника Рх и при разомкнутом ру-
бильнике Р2 к источнику постоянного напряжения включается
реактивная катушка г, L, последовательно с которой соединен
реостат сопротивлением (рис. 13.5, а). Через сек после за-
мыкания рубильника Рх замыкается рубильник Р2, который ос-
тается в таком состоянии на продолжительное время.
Рис. 13.5
Построить кривую изменения тока в катушке с момента
включения рубильника PY до момента практически полного за-
тухания тока в катушке (например, до 1% от максимального
значения тока).
Решение. При замыкании рубильника Рх и разомкнутом
рубильнике Р2 переходной ток в катушке
п —t
l'= Т^Т (1 - е L )• (1)
К моменту включения рубильника Р2 ток в катушке достиг-
нет величины
п -Li±L t
d ~е L ) = Л <2)
Второй закон Кирхгофа для контура катушки, замкнутой
рубильником Р2 (при t > /J, будет
L >+•'. '"О-
Решение этого уравнения дает
- f-
ii = Ае . (3)
Постоянная интегрирования А найдется из начального усло-
вия, согласно которому для момента t = /, i ~ iv Ток по (3)
и /1
»i =----г~ (1 — е L ) е L
1 Г, + г ' '
Э40
На рис. 13.5, б начерчены кривые изменения тока.
13.8. Цепь постоянного тока состоит из индуктивности L ==
= 0,1 гн и двух сопротивлений г= 10 ом и гх=30 ом (рис. 13.6).
Приложенное напряжение U = 120 в.
Сопротивление внезапно замыкается накоротко. Найти
уравнение тока в катушке после замыкания ключа; начертить
график изменения тока по времени.
13.9. В цепи (рис. 13.6) ключ замкнут. Найти закон измене-
ния тока после внезапного размыкания ключа, вводящего в
цепь добавочное сопротивление гх. Цифровые данные те же,
что и в задаче 13.8.
Рис. 13.6
Рис. 13.7
13.10. В цепи постоянного тока (рис. 13.7) реактивная ка-
тушка L2, г2 замыкается накоротко рубильником Р.
Определить законы изменения токов в обеих катушках и
в рубильнике спустя 0,05 сек после его замыкания, если =
= 6 ом, Lr = 0,3 гн, 4 ом, Л2 = 0,8 гн, U = 120 в.
.13.11. Телеграфная цепь состоит из батареи, э. д. с. кото-
рой 10 в и внутреннее сопротивление 2 ом, линии, имеющей
чисто активное сопротивление 51,6 ом, и реле, активное сопро-
тивление которого 21,4 ом и индуктивность 1,25 гн. Если якорь
реле не притягивается до тех пор, пока ток не станет равным
0,05 а, то сколько времени пройдет после замыкания цепи до
начала работы реле?
13.12. Цепь, изображенная на рис. 13.8, включается под
действие постоянного напряжения U = 120 в. Найти выражения
для токов iv (2 и i3 и изобразить их графически; гх = 20 ом,
г2 = 30 ом, L = 0,3 гн.
Рис. 13.8
Рис. 13.9
341
13.13. Для замедления скорости нарастания тока в электро-
магните г, L применяют шунтирование его активным сопротив-
лением гш (рис. 13.9, а). Найти ток i в электромагните и срав-
нить скорость его нарастания со скоростью нарастания тока
электромагнита в случае отсутствия шунта. Для упрощения
положить г = гш.
Решение. У равнения Кирхгофа
Е ^*1 “Ь (1)
rm = lr + L (2)
G — (3)
Подставив из (3) значение ir в (1), получим
Подставляя это значение в (2), найдем
Полагаем
= ^пр ^св» (5)
где /пр — ток принужденного режима в катушке, который мо-
жет быть подсчитан по обычным формулам для цепей постоян-
ного тока (в этом случае индуктивность никакой роли не иг-
рает). Так как при установившемся режиме = 0 (в этом
случае i = inp = const), то
^пр
Е гш
Г ГХ 4- г гш ч- G 'щ
Свободный ток найдется из решения уравнения (4) без пра-
вой части
(7)
где для сокращения положено
Е (^1 4~ Гщ)
"ч 4-"Чп 4-п
(8)
Таким образом, подставляя (6) и (7) в (5), получим
t
i = Ае
Е г щ
ГГ14- "ш 4- п гш •
i
ГСв = А& 9
342
Постоянная А
торому при t = 0
найдется
i = 0, т. е.
из начального условия, согласно ко-
-0,
или
ш
Окончательно
ток
В частном случае при гш = г ток
t
где
(9)
(Ю)
(П)
Если же шунт снять, то, полагая гш = оо в уравнении (9),
где
t
—
(12)
(13)
Сравнивая выражения (11) и (13), устанавливаем, что т1>т2,
т. е. постоянная времени при наличии шунта больше, чем в
его отсутствие.
Вычислим скорость нарастания тока. При наличии шунта из
формулы (10) имеем
di
dt
(14)
в отсутствие шунта из (12) получим
di __________ Е
~dt t*=o ~ ч (г 4- rj)
(15)
Сравнивая выражения (14) и (15), легко устанавливаем, что
при наличии шунта скорость нарастания тока меньше, чем при
его отсутствии.
По уравнениям (10) и (12) на рис. 13.9, б начерчены кривые
токов.
343
13.14. Электрическая цепь состоит из активного сопротивле-
ния гх = 120 ом, последовательно с которым соединено элект-
ромагнитное реле rk = 50 ом, Lk = 0,75 гн, шунтированное со-
противлением гш = 200 ом (рис. 13.10). Составить выражение
тока, проходящего через реле при его вне-
г’ запном отключении от источника напряже-
нием U = 80 в. Определить также время
fiTj* 1 срабатывания реле, приняв, что ток его сра-
0 St ^0 батывания равен половине тока, проходящего
г 5*1 через реле при установившемся режиме.
о________J 13.15. В цепи (рис. 13.11, а) даны: на-
пряжение U = 30 в, сопротивления г = 10 ом,
Рис. 13.10 гх = 5 ом, г2 = 30 ом и индуктивность Lr = 2 гн.
Найти законы изменения по времени всех
токов и напряжения на параллельном участке
цепи после замыкания рубильника (до коммутации в цепи
был установившийся режим). Построить кривые изменения
этих величин.
Решение. На основании законов Кирхгофа
t — Ч Ч»
U = ir + Ч G + ;
• ( г di,
Ч G М — Ч г&
(1)
(2)
(3)
Эту систему уравнений решим совместно относительно од-
ного из токов. Обычно предпочтительнее выбирать тот ток, для
которого наиболее очевидны начальные условия; в данном слу-
чае этот ток в ветви с индуктивностью.
Подставим в уравнение (2) значение i из (1) и значение i2 =
= — Ч + — • из уравнения (3) и после простых преобразо-
Г<2 Г 2 ЯГ
ваний получим
dii______. rri + rr2 + ri r2 . _ U гг
dt "* Li (г + г2) 1 Lx (г + г2) ’
(4)
или после подстановки числовых значений
-^- + 6,25^=11,25. (4а)
Общее решение этого уравнения
G Чпр Чсв>
(5)
344
где {inp — установившийся ток, который может быть определен
из уравнения (4), учитывая, что при установившемся
режиме = 0:
11,25 , о
1 ~ 6,25 ~ 1,8 а'
(6)
Свободный ток i1CB найдется как интеграл уравнения (4а),
когда в его правой части будет нуль:
-^>- + 6,25 <1СВ = О,
Нсв -- Ав »
где
----= 0,16 сек\ — = 6,25 сек”1.
Подставляя ilnp и /1св в (5), получим
—6,25/
= 1,8 Ае
Постоянная А найдется из начального условия
= —= 2 а, или (1,8 + Ае~6’™ } =2,
г + 4 * 7 t=o
отсюда
А = 0,2.
Окончательно
^ = (1,84-0,2 Г6'25') а. (9)
Подставляя это значение it в уравнение (3), найдем ток
= iх 4- А = (0,3 — О.Обе-6,25' 1 а. (10)
2 г2 1 ‘ r2 dt \ ’ / v 7
Подставляя найденные в (9) и (10) значения токов ц и i2 в
уравнение (1), получим
t= (2,1 4- 0,15 е”6’25' ) а. (11)
Отметим, что по окончании переходного процесса (t = со)
токи i, ix и i2, как это следует из выражений (9), (10) и (11),
обратятся соответственно в 2,1, 1,8 и 0,3 а. Нетрудно прове-
рить, что те же значения получатся, если произвести расчет
токов данной цепи любым методом расчета установившихся
процессов в цепях постоянного тока.
345
Что же касается начала переходного процесса (/ = 0), то в
этот момент времени ток остается таким же (2а), каким он
был до момента замыкания ключа; это объясняется наличием
индуктивности. Токи i и ia при замыкании ключа изменяются
скачкообразно, сразу принимая значения i = 2,25 а и i2 =
= 0,25 а.
Ветви, по которым проходят эти токи, содержат только ак-
тивные сопротивления; скачкообразное изменение тока в этих
ветвях не связано с внезапным изменением запаса электромаг-
нитной энергии и становится поэтому физически осуществи-
мым.
На рис. 13.11, б начерчены кривые токов.
а)
Рис. 13.11
№-$'=0,в35ИГ6се*
।----1
t
Рис. 13.12
Г
13.16. Цепь (рис. 13.12, а), параметры которой гг = 5 ом,
г2 == 10 ом, г3 = 5 ом, = 15 ом, С = 1 мкф, при разомкнутом
рубильнике Р находится в установившемся режиме под воз-
действием постоянной э. д. с. Е = 15 в.
Требуется после включения рубильника определить: 1) на-
чальные значения переходных (полных) токов и напряжения на
конденсаторе, а также начальные значения их принужденных и
свободных составляющих и производную свободной составляю-
щей напряжения на конденсаторе в момент начала переходно-
го процесса; 2) законы изменения во времени всех токов и на-
пряжения на конденсаторе.
346
Решение 1. Расчет режима до коммутации (рубильник
разомкнут). Токи в ветвях и напряжение на конденсаторе равны
t‘i (0_) = i2 (0.) = , f , . = 0,5 a; i3 (0_) = 0;
* 1 I ^2 I * 4
ис (0_) = (га +г4) ц (0.) == 25-0,5 = 12,5 в.
Расчет принужденного режима после коммутации (рубиль-
ник замкнут). Токи и напряжение на конденсаторе
Чпр Чпр = ~ 1^» Цпр =
UC пр = Г2*2пр == Ю -1 = 10 в.
Расчет переходных токов и напряжения на конденсаторе
для момента t = 0. По законам Кирхгофа составляем уравне-
ния для схемы после коммутации:
ч — ч ~ь ч» 0)
4l4 ”F ис = E*t (2)
ЧЛ = r3i3 + ис . (3)
• По закону коммутации напряжение на конденсаторе не мо
жет измениться скачком, поэтому
M0) = uc(0_) = 12,5 в.
Используя уравнения (1)4-(3) для момента t = 0, с учетом
того, что ис (0) == 12,5 в, имеем
Ч (0) = Ч (0) + /3 (0);
G4 (0> +r3i9 (0) + 12,5 = 15;
>44 (0) = r3i3 (0) + 12,5.
Решая их, вычислим
Ч (0) = 0,8 а; Ч (0) = 1,1 а; i3 (0) = — 0,3 а.
Рассчитаем начальные значения свободных составляющих
токов и напряжения на конденсаторе. Для этого каждый пе-
реходной ток и напряжение на конденсаторе представим в ви-
де суммы принужденной (после коммутационной) и свободной
составляющих, например, для первого тока
ч (0) = /1Пр (0) + Чсв (0),
347
отсюда
Чсв (0) = h (0) - 4пр (0) = 0,8 -1 = - 0,2 a.
Аналогично для других токов и напряжений
i2cB (0) = 4 (0)- »2пр (0) = 1,1 — 1 = 0,1 а;
Ьсв (0) = i3 (0) - /ЗПр (0) = — 0,3 — 0 = — 0,3 а;
^Ссв (0) = ис (0) — ис пр (0) = 12,5 — 10 = 2,5 в.
2. Определение законов изменения во времени искомых ве-
личин. Для этого составляем характеристическое уравнение в
виде характеристического входного сопротивления послекомму-
тационной схемы (см. основные положения и соотношения,
п. 7), которое приравнено нулю:
/ 1 \
г2 I Го + —7^ I
7 /пч г , \ рс/ рс (Г! Г2 + Г! г3+г2 Г3)+Г1 + г2 п
Z (р)__г1 + ———— - (г2 + г3ГП -°’
Г2 + Гз+ рС
его единственный корень
р = р =------—-------Zk+f*.......-— = — 12• 104 сек"1.
к ™ С (Г1 r2 + п г3 ч- г2 г3)
Так как характеристическое уравнение имеет только один
корень, то свободную составляющую каждой искомой величи-
ны ищем в виде Аер^. Итак, переходные токи и напряжение на
конденсаторе
Ч ~ ^inp + Чсв Н е == 1 0,2 е а\
Е „ -12-104 t
^*2 = ^2пр + *2св == —Ь ^2 ePxt = 1 + 0,1 е а;
= ^зпр 4” ^зсв = 0 4~ rig ер^ = 0,3 е а\
Uc пр св ^пр ВеРх Ю + 2,5 е в.
Графики найденных величин изображены на рис. (13.12, б).
13.17. В схеме рис. 13.13 до коммутации (рубильник замк-
нут) был установившийся режим. Даны: = 50 ом, г2 = 30 ом,
г3 = 20 ом, С = 10 мкф, U = 80 в. Определить после выключе-
348
ния рубильника: 1). начальные значения переходных токов и на-
пряжения на конденсаторе и их принужденных и свободных
составляющих; 2) законы изменения во времени всех токов и
напряжения на конденсаторе.
Рис. 13.13
Рис. 13.14
13.18. В схеме рис. 13.14 до замыкания рубильника был
установившийся режим. Даны: гг = 8 ом, г\ = 10 ом, гг — IOojh,
L = 25 мгн, г3 = 30 ом, Е = 60 в.
Требуется: найти свободные составляющие i1CB (0), 1%.в (0),
Л Л du, rR
i3CB (0)» wLcB (Q)>~' ~~ 1,__0 ; определить законы изменения всех
токов в цепи после замыкания рубильника.
13.19. Цепь, изображенная на рис. 13.15, а, включается под
действие постоянного напряжения U = 48 в. Найти законы из-
менения токов ilt i2 и i3 во времени и изобразить их графиче-
ски, если = 160 ом, Lr = 100 мгн, г3 = 90 ом, = 36 мгн.
3)
Рис. 13.15
Решение. Способ 1. Уравнения Кирхгофа
dit
~dF
(О
V — /"j
(2)
(3)
+ ^з»
dZ2
г Ж — 1з гз-
349
Полученную систему уравнений решим относительно одного
из токов.
Подставив значение ц = — • —из уравнения (3 ) в
г3 аг
уравнения (1) и (2), получим
(4)
U = <г G + + Д.-£- . (5)
Наконец, подставив из (4) в (5), получим дифференциаль-
ное уравнение относительно тока г2:
^2 ^2пр + ^2св* (7)
Для нахождения г2пр воспользуемся тем, что при установив-
шемся режиме г2пр = const, а = 0, тогда из (6)
»2пр = • (8)
Этот результат можно было получить непосредственно из
схемы (рис. 13.15, а), в которой параллельный участок закоро-
чен катушкой индуктивности, не имеющей активного сопротив-
ления.
Теперь найдем выражение для свободного тока i2CB. Оно мо-
жет быть получено из уравнения (6), в правой части которого
стоит нуль. Это решение имеет вид
‘зев == А + Аа еР^ (9)
где At и А2 — постоянные интегрирования;
рг и р2 — корни характеристического уравнения:
‘-’ + fe+4j+ = о»)
или
р2 4- 5000 р + 4- 10е = О,
откуда
р, = — 1000 сект1, р% = — 4000 сект1.
Подставляя (8) и (9) в (7), получим
ia = Аг ер^ + Д2 еРг‘ .
(И)
350
Для определения At и Л2 воспользуемся начальными усло-
виями
h (0) = h (0.) = 0 (I) и i2 (0) = i2 (0_) = 0, (II)
а следовательно, согласно (1) i8 = 0.
Из выражения (11)
(0) = 4- А2 + -ур = 0;
(12)
из уравнения (3)
i (0) = _Ь_ . ^A1P1ep,t + А^ ),=0 =
Г3 а1 /=о Г8
= АР1 4" А%Рз — 0» (13)
Решая (12) и (13), рассчитаем
д _ UP% . д _ uPi
1 ^(pi— р2) ’ 2 Г1(Р» — Pl) '
(14)
Подставляя их в (11), найдем i2, а затем из (3) ток ts и из
(1) — ток /х.
Таким образом, окончательные выражения токов
(15)
Так как произведение корней квадратного уравнения равно
свободному члену, т. е. р,р2 = -tty— > то
3 —
--------( ePit____________е
4 = h + h •
Подставляя в (15) и (17) числовые значения, получим
i Q ЛИ ✓»—1000/ j л * —4000/ \
t2 = — и,4е + и,1е )а;
(16)
(17)
»з = 0,16(е-,000'-г-4000/)а;
= (0,3 — 0,24<?~1000/ — 0,06 е~4000/) а.
На рис. 13.15,6 приведены кривые токов.
Способу 2. Решим задачу, не выписывая дифференциальных
уравнений системы, приравнивая нулю характеристическое
3S1
входное сопротивление цепи (см. основные положения
ношения п.7)
И
COOT-
2 (р) = fl + Р^ +
Р^Л
pL2 Г3
p2LiLa 4~ (г 1^2 + гзМ 4~ гз^г) Р ~Ь г1гэ
pU + r3
= 0.
Подставляя сюда числовые значения, находим два корня р
Pi = — 103 сект1; р2 = — 4 • 103 сект1. (1)
Так как характеристическое уравнение имеет два корня, то
свободную составляющую каждого из токов ищем в виде
/св = 4- Л2е₽2/ , а его производная = р^е^ 4- p2A2ePit ,
Входящие в эти уравнения постоянные интегрирования Д и
А2 найдем по начальным значениям каждого переходного тока
и его производной.
Запишем, например, выражения переходного тока и его
первой производной:
Ч Чпр + ^1св ~ Чпр + А2е? ; (2)
4- = Т + р№' + . (3)
Для начального момента времени после коммутации t = 0
h (0) = Чпр (0) + А + А2\
(4)
dii
~dt
rfZinp
/=о dt
+ pM, + P2A = - lOM, - 4 • 103Д.
(5)
До коммутации все токи равны нулю.
Рассчитаем принужденный режим после коммутации. Ин-
дуктивности Lt и L2 не оказывают сопротивления прохождению
постоянного тока, поэтому для этого режима сопротивление г3
шунтировано накоротко, токи в ветвях
inp Asnp 0,3 а, ^*зпр 0
Определим начальные значения токов для момента t = 0.
Ддя этого составляем уравнения по законам Кирхгофа:
dit
dT
I — I
3^3 — ь2 dt
(7 = г ^4 4" А
+ ^3^3 »
4 — ^2 4 •
(6)
(7)
(8)
352
По закону коммутации .токи i, и t2 не могут измениться
скачком, т. е. (0_) = (0) = 0, i2 (0_) = i2 (0) = 0. Подставляя
эти значения в систему уравнений (6) 4- (8), находим зависимые
начальные значения L (0) = 0, — 0;
t=o
di, _£
/=0
= 480 а/сек. Подставляя найденные значения i
di’inp
1пр —
= 480 а/сек в уравнения
(4) и (5), вычислим постоянные интегрирования Лх = —0,24;
Л2 = — 0,06. Следовательно, согласно (2), «ток i± = (0,3 —
— 0,24 е-10”' — 0,06 ё~4’10’') а.
Аналогично для тока i2 и его производной имеем
Ч == Чпр + *2св = 0,3 + Вхе₽1/ + В?рР** ;
которые при t = 0, с учетом найденных принужденного и на-
чального значений тока /2:
4 (0) = 0 = 0,3 + Вх 4- В2;
X
-%- ==0 = —1000 В, —4000 Ва.
/=0 12
Совместное решение этих уравнений дает Вх = — 0,4 а,
В2 = 0,1 а.
Уравнение тока
/2 = (0,3 — 0,4е + 0,1е )а.
Ток i3 находим из уравнения (8):
. . • п 1000/ 4000/ х
— t'l i2 — Ю (е " е ) а •
13.20. При полном разряде конденсатора емкостью С =
== 200 мкф на активном сопротивлении выделяется в виде теп-
ловой энергии 1 дж. Спустя 0,06 сек После начала разряда на-
пряжение на обкладках конденсатора равнялось 5 в, а) До ка-
кого напряжения был заряжен конденсатор и какова величина
сопротивления, через которое он разряжается? б) Через какой
промежуток времени после начала разряда напряжение конден-
сатора упадет до 0,001% своего первоначального значения?
13.21. Конденсатор емкостью 45 мкф заряжается через со-
противление 10 ком от источника энергии с напряжением 500 в.
Чему равен заряд конденсатора, когда ток составляет половину
12 Заказ № 624
353
своей начальной величины? С какой скоростью нарастает заряд
в этот момент? Чему равна ошибка в процентах, если принять,
что конденсатор зарядится полностью в конце десятой секунды?
13,22. Между точками а и b включены последовательно со-
единенные активное сопротивление 1000 ом и конденсатор ем-
костью 50 мкф, а между точками b и с включены последова-
тельно соединенные конденсатор емкостью 25 мкф и активное
сопротивление 500 ом. Чему равны начальные и конечные на-
пряжения между а и b, Ь и с после того, как к зажимам а и с
будет подведено постоянное напряжение 120 в?
13.23. К цепи, состоящей из активного сопротивления 1000 ом,
соединенного последовательно с двумя параллельными ветвями,
причем в первой ветви включено активное сопротивление
1000 ом, а во второй—последовательно соединенные активное
сопротивление 5000 ом и конденсатор емкостью 50 мкф, подве-
дено постоянное напряжение 120 в. Чему равны начальные и
конечные значения токов в параллельных ветвях?
13.24. Последовательно с активным сопротивлением =
= 30 ом включены две параллельные ветви: одна из них содер-
жит последовательно соединенные активное сопротивление г2 ==
= 50 ом и конденсатор С = 2 мкф, вторая — последовательно
соединенные активное сопротивление г3 = 70 ом и катушку ин-
дуктивностью L = 0,4 гн. Указанная цепь подключается к ис-
точнику постоянного напряжения U = 120 в. Определить началь-
ные и конечные токи и напряжения на сопротивлении t\ и на
параллельном участке.
13.25. Конденсатор емкостью С, предварительно заряженный
до напряжения Uo, подключается через сопротивление к источ-
нику постоянного напряжения U (рис. 13.16). Найти законы из-
менения напряжения на обкладках конденсатора и тока, прохо-
дящего в цепи при замыкании рубильника.
13.26. Конденсатор = 10 мкф, заряженный до напряжения
= 100 в, замыкается на цепь, состоящую из последователь-
но соединенных активного сопротивления г = 125 ом и заряжен-
Рис. 13.16
Рис. 13.17
ного до напряжения [72 = 20 в конденсатора С2 = 40 мкф (рис.
13.17). Найти как функцию времени ток в цепи и напряжение
на обкладках каждого конденсатора, а также построить графи-
ки найденных функций. Найти величину энергии электрического
354
поля до замыкания рубильника и по окончании переходного
процесса.
13.27. Решить задачу 13.26 при условии, что полярность за-
ряда конденсатора Са противоположна той, которая изображена
на рис. 13.17. Цифровые данные те же, что в предыдущей за-
даче.
13.28. Конденсатор Сг = 20 мкф, заряженный до напряжения
Uo = 25 в, замыкается на цепь, состоящую из последовательно
соединенных активного сопротивления г — 125 ом и незаряжен-
ного конденсатора Са = 5 мкф. Найти как функцию времени
ток в цепи и напряжения на обкладках каждого конденсатора,
а также построить графики найденных функций.
,13.29. Цепь, изображенная на рис. 13.18, включается на по-
стоянное напряжение. Найти уравнения токов и начертить кри-
вые изменения их во времени. Данные цепи: U = 10 в, г1~
=40 ом, га = 10 ом, С = 25 пф.
Рис. 13.18
Рис. 13.19
13.30. Цепь, изображенная на рис. 13.19, включается на по-
стоянное напряжение U = 100 в. Найти выражение для напря-
жения на конденсаторе Са, если Сг = 100 мкф, Са = 20 мкф,
= 10 ОМ, г% = 100 ом.
13.31. Конденсатор с утечкой, параметры которого С = 2 мкф
и г = 50 ком, отключается от источника постоянного тока с на-
пряжением U = 120 в (рис. 13.20). Определить напряжение на
конденсаторе через t = 0,1 сек после отключения.
Рис. 13.20
Рис. 13.21
13.32. Определить законы изменения напряжения на конден-
саторе и всех токов при замыкании рубильником Р (рис. 13.21)
и построить их кривые: Е = 24 в, г = 20 ом, t\ = 50 ом, га =
= 100 ом, С = 3 мкф.
12*
355
13.33. Реактивная катушка с активным сопротивлением г =
= 10 ом и индуктивностью L —- 364 мгн включается в момент
t = 0 под действие синусоидального напряжения
и = 160 sin ш! -|-
7U
3
в.
Определить значение тока через два периода после момента
включения. Частота переменного тока / = 50 гц.
13.34. К переменному напряжению, действующее значение
которого U = 220 в, присоединена цепь (рис. 13.22,а), состоя-
щая из двух последовательно соединенных приемников энергии
с параметрами, равными rt = 2 ом, = 40 мгн и г2 == 6 ом,
Ь2 = 9,8 мгн.
Включением рубильника Р приемник (rt, Lx) закорачивается
в момент, когда мгновенное значение приложенного напряже-
ния равно действующему значению и > 0. Найти выраже-
ние тока, проходящего через вторую катушку (г2, L2) и пост-
роить его график. Частота переменного тока f = 50 гц.
Решение. Пусть приложенное к цепи напряжение и =
= Um sin (ад/ + Ф). где ф — угол включения, определяемый из ус-
ловия задачи, при t = 0
и = Um sin ф = ,
3S6
т. е.
sin ф =
и одно из возможных значений угла ф = 45°.
До включения рубильника в цепи проходил ток
i = Im sin(<»/+ ф —<р),
где
j __ Um _____ 2201<2 j??
_____________________— ------------ 17,7 а
V (Г1 + Г2)а + (<oLi + coL2)2 /82 4- 15,72
И
tg ф = = 1,962; ф = 63°.
Г1 “Г г2 О
После включения рубильника
и = i2r2 + l2 -%. .
Принужденный (установившийся) ток
»2пр = hrn sin (ш/ + Ф — ф2);
причем
22° /2 .Л
= . г — = 46 а
У62+3,О62
<р2 = arctg - = arctg0,51 = 27°.
Свободный ток
—Г-М
1*» = Ае La
и общий ток
4 = Ifim sin (otf + ф — ф2) + Ае
Начальным условием является непрерывность тока, прохо-
дящего в катушке (г2, L2) в момент включения, т. е. при t = 0,
i — i2, или
sin (ф — ф2) + А = Im sin (ф — ф),
отсюда
л = Im sin (ф — ф) — I2m sin (Ф — ф2).
Таким образом,
i2 = I2m sin (ш/ -j- ф — ф2) + [lm sin (ф — ф) —
— /2т8Ш(ф— Фа)]е ц = [46sin(wZ 4-18°)—19,7е-мзПа.
3S7
На рис. 13.226 изображен график тока.
13.35. К зажимам цепи (рис. 13.23) приложено синусоидаль-
ное напряжение и = Lfmsin(o)/ + ф), Um = 10 в, = 5000 сект1.
Параметры цепи: — 3 ом, г2 = 4 ом, Lr = 0,8 мгн и L2 =
= 4 мгн. В момент прохождения тока через положительный
максимум включается рубильник Р. Найти уравнения токов 4
и i2 и построить их кривые.
Рис. 13.24
13.36. Цепь, изображенная на рис. 13.24, включается на си-
нусоидальное напряжение. Построить кривую тока для случая,
когда включение производится в момент прохождения тока ус-
тановившегося режима через нулевое значение при > 0
г — 20 ом, С = 400 мкф, f = 50 гц и. Um = 141 в.
13.37. К синусоидальному напряжению, действующее значе-
ние которого равно U, присоединена цепь рис. 13.24. Чему дол-
жно быть равно мгновенное значение напряжения и в момент
включения, чтобы не было свободного тока и каково при этом
начальное значение установившегося тока?
13.38. В схеме рис. 13.25, а до замыкания рубильника был
установившийся режим. Даны: г\ = г\ = 20 ом, г2 = 16 ом, С =
= 11,1 мкф, а) = 5000 сек'1, e(/) = 25sin (ш/ — 30°) в. Найти за-
коны изменения тока в неразветвленной части цепи и напряже-
ния на конденсаторе после замыкания рубильника Р.
Решение. Расчет режима до коммутации. Сначала най-
дем комплексные значения тока и напряжения на конден-
саторе Uc:
25 -/зо°
---—-- е
/2 д-.я = 0,356 е-720045'а;
1О» 1о
4°—/ 16 —/18
• • > • —/62°5'
Uc = Е —(г, 4- /-J/j = 4,26 в в.
358
Соответствующие мгновенные значения
ix = 0,504 sin (ш/ — 20°45') а;
ис = 6,02 sin (ф/ — 62°5') в.
К моменту начала коммутации ток и напряжение имели
значения
ix (0_) = — 0,504 sin 20°45' = — 0,175 а;
ис (0_) = — 6,02 sin 62°5' = — 5,32 в.
Рис. 13.25
Расчет тока и напряжения на конденсаторе в принужден-
ном, режиме после коммутации.
0,59е
;15°20'
ri b i с ПК /55°40'
испР = £ — ri ЛпР = 6,95<? в;
11пр = 0,84 sin (ф/ 4- 15°20') а;
ысп₽ ~ 9,8 s^n № — 55°40') в.
359
Расчет переходных токов и напряжения на конденсаторе.
Выбрав для послекоммутационной схемы контурные токи, как
показано на рис. 13.25,а, составим уравнения свободных кон-
турных токов:
(Г1 + гг) г1св r2fHcB = Ф
— 4- ~ f i„^dt = 0.
« 1СВ 1 " Пев 1 1 Пев
Подставляя числа и заменяя символ интегрирования сомно-
жителем (см. основные положения и соотношения п. 6), по-
лучаем характеристическую систему
36*1св 1б1цсв = 0;
16*1св+^6+ 11,1-10-вр ) *Псв °-
Составим характеристический определитель этой системы и
приравняем его нулю, это и будет характеристическое урав-
нение:
Д (р) =
36
— 16
— 16
11,ыо-6р
его единственный корень р =
р± = — 1,01 • 104 се/г1.
Свободный ток и напряжение на конденсаторе
/1СВ = А^ = АГ1’01’104' ;
иСгв = BePi‘ = Be-1’01-104'
Сев
Переходный ток и напряжение на конденсаторе
G = hnp + »кв = 0,84 sin (ш/ + 15°20z) 4- Ле-1’01’10*' а;
иг = иГпп + иг„п = 9,8 sin (ю/ — 55°40') 4- Ве~1,0Ь1°4' в.
Для определения постоянных интегрирования надо исполь-
зовать начальное условие. Независимое начальное условие со-
стоит в том, что напряжение на конденсаторе не может изме-
ниться скачком, т. е.
ис (0) = ис (0_), или [9,8 sin И — 55°40z) 4- Ве~''01'10'‘ ]/=0=
= - 5,32,
360
отсюда
В — 2,8 в.
Для нахождения постоянной интегрирования А необходимо
знать начальный ток 1\(0). Он может быть рассчитан по урав-
нению Кирхгофа:
(0 = Gh + ис (0,
из которого при t == 0 получим
4(0) =
«1 (0) — ис (0)
—25 sin 30° — 5,32
20
= —0,891 а.
Из написанного выше выражения для переходного тока 4
для момента t = 0 находим А:
(0) = 0,84 sin 15°20' + А = — 0,891,
отсюда
Л = —1,11 а.
Наконец, запишем искомые величины.
4 = 0,84 sin (5000/ + 15°20') —1,11 е-1,01,10"' а;
ис = 9,8 sin (5000/ — 55°40') + 2,8 е-1,01,104' в.
На рис. 13.25, б изображены кривые: 1 — э.д.с. е(/); 2 — ток
1хдо коммутации; 3 — ток f1CB; 4 — ток г1пр; 5 — переходной ток ц.
13.39. К цепи рис. 13.26 подключа-
ется синусоидальное напряжение
u = Um sin (о)/ + <р).
Рис. 13.26
Включение происходит в момент, ког-
да приложенное напряжение имеет поло-
жительный максимум. Найти закон изме-
нения напряжения между обкладками
U = 65 мв, i\ = 12 ом, 3 =1 ом и о) = 2 • 105 сек'1.
если
13.40. Конденсатор С = 50 мкф, заряженный предварительно
до напряжения U = 500 в, разряжается через цепь, активное
сопротивление которой г — 100 ом и индуктивность L = 10 мгн.
Определить, через какой промежуток времени, считая от на-
чального момента разряда, ток в цепи достигнет максимального
значения и какова величина последнего. Вычислить, в какой
момент времени в индуктивной катушке наведется максималь-
ная э.д.с., и найти ее величину.
361
13.41. Ответить на вопросы предыдущей задачи, если
г = 2 (L = 10 мгн и С = 50 мкф), U = 500 в.
t__| 13.42. Подсчитать частоту собственных
г*I незатухающих колебаний и частоту <оо затуха-
ssC М ющих колебаний контура, изображенного на
г рис. 13.27, если L = 25 мгн, С = 2500 пф и
I г = 4000 ом.
Рис 13 27 13.43. Сколько потребуется полных коле-
ис’ * баний, чтобы в контуре, имеющем логарифми-
ческий декремент затухания & = 0,02, ампли-
туда тока уменьшилась до 1% от своей первоначальной
величины?
13.44. Цепь схемы рис. 13.28,а включается на постоянное
напряжение U = 125 в.
Рис. 13.28
362
Найти выражение мгновенного значения напряжения на кон-
денсаторе ис для трех случаев: 1) г = 250 ом, L=667 мгн,
С = 2 мкф; 2) г = 100 ом, L = 40 мгн, С = 1 мкф; 3) г ~ 100 ом,
L = 40 мгн, С = 5 мкф.
Решение. Наметим план решения задачи. Напряжение на
конденсаторе будем находить в виде суммы принужденного и
свободного значений:
UC ~ UCnp "Ь UCcb ’ 0)
Принужденное значение напряжения на конденсаторе равно
нулю (цс = 0), так как установившееся значение тока i2np не-
изменно, и, следовательно, оно не создает падения напряжения
на индуктивности uLnp = иСпр — L—= 0 (при установив-
шемся режиме конденсатор шунтирован индуктивностью катуш-
ки накоротко).
Для нахождения вида решения свободной составляющей со-
ставим характеристическое входное сопротивление цепи и при-
равняем его нулю (см. основные положения и соотношения п. 7):
Pb- -t-
рС
Z(p)^r+--------ip. (2)
pL + -±
рС
В полученном характеристическом уравнении освободимся
от знаменателя, приведя его к виду
rLCp2 + Lp + г = 0. (3)
Это уравнение второго порядка и, следовательно, оно имеет
два корня:
pi,2 ~ 2гС ~ Г 4г2С2 LC * W
Для каждого из трех заданных случаев по уравнению (4)
определим вид корней (действительные разные, действительные
кратные и комплексно-сопряженные) и "в соответствии с ним
ищем свободное решение «Ссв по одной из формул, указанных
в п. 4 основных положений. Заметим, что свободная составля-
ющая напряжения на конденсаторе содержит две постоянные
интегрирования.
Для определения постоянных интегрирования поступим так.
Составим уравнения по законам Кирхгофа:
*
Й = I _
C/ = r1i1+«„ J W
Л Л
363
Запишем независимые начальные условия:
ис (0.) = ис (0) = 0 (I); г2 (0_) = (0) = О (II)
Подставляем их в (5) для начального момента времени (пос-
ле коммутации) и получим
h (0) == *2 (0) + (0); 1
и = rix(0) + ис (0). I (6)
Решив их, находим /3(0). Затем, используя зависимость i3 =
duc
3 — для момента t = 0, получим
(7)
Наконец, определим две неизвестные постоянные интегриро-
вания из следующих двух уравнений: из (1), в которое подстав-
ляются найденные иСп и цСсв, и из (7).
Конкретное применение указанной методики расчета рассмот-
рим для каждого из трех заданных случаев.
1. Подставим в (4) числовые значения первого случая
— 1 4- 1 /7 1 V 1
^1,2 ~~ 2-250-2-10-6 ± у 2-250-2-10”6 ) 667-10~3-2-10~6
= (— 1000 ± 500) сект1,
т. е.
рг = — 500 сект1; р2 = — 1500 сект1.
Получены корни действительные и различные, следовательно,
свободная составляющая напряжения на конденсаторе имеет вид
£/Ссв = Ле-500/ + А2е-1500'.
(8)
Далее из уравнений (6) с учетом начальных условий (I) и
(II) получим
й (0) = ч (0) + 1з (0) = 0 + i3 (0) = i3 (0),
и = rix (0) + Uc (0) = 250ix (0) + 0 = 125.
Решая эту систему уравнений, находим i3 (0) = 0,5 а.
Подставим в (1) и в выражение тока i3 уравнение (8):
ис = ыспр + “сев = 0 + Ае-800' + Л2е-1500/; '
i3 = с = 2 • 10-6 (— 500А^*00' — 1500е-1500/).
364
Перепишем эти уравнения для момента 1 = 0 и затем, под-
ставляя в них ис(0) = 0 и /3(0) = 0,5 а, получим
О = + А2 ;
0,5 = — 10-% — 3-10-М2.
Отсюда Д = —А2 = 250 в. Таким образом, искомое напряже-
ние согласно (1) и (8)
ис (0 = исев (0 = (250е-500' — 250е‘1500/) в.
График отдельных составляющих решения и суммарного зна-
чения напряжения на конденсаторе построен на рис. 13.28,6.
Кривые : / — 250 е"500'; 2 — 250e-1500Z; 3 — uc(t) = uCcB(t).
В целях упражнения вычислим также все токи и построим
их графики:
ia = с = 2 • I0-6 (250е-500' — 250е-1500') =
= (0,75е-1500/ — 0,25е-500') а;
U — ur 125 —(250е-500/— 250е*1500/)
i =-----=------------5---- -----------1 = (о,5 - а.
Г МО
i2 = i. — i3 = (0,5 — 0,75е-500' + 0,25e~15W) а.
Графики токов даны на рис. 13.28,в.
2. Подставим в формулу (4) численные значения второго
случая:
- 1 ч-i /7 * у * -
2-100-Ь10"в ± 2-100-1-10"6 ) 40-IO"3* 1 • 10”6
= 5 -103 сект1 = Pi==
Корень—двухкратный, следовательно, решение ищем в форме
(см. п. 4 основных положений)
иСсъ = В1ем +B2te^w. (9)
Далее, как и в первом случае, из уравнений (6) с учетом
начальных условий (I) и (II) найдем *3(0)= 1,25 а.
* Подставим в (1) и в выражение i3 уравнение ^9):
ис = «Спр + «сев = 6 + в1е'5000' + s2 /е-6000';
i3 = С = 10-® (В2 — SOOOBj — 5000В2/) е’5000'.
365
Переписывая эти уравнения для момента t = 0 и затем под-
ставляя в них ис(0) = 0 и i3(0)= 1,25 а, получим
0 = Вх;
1,25 = 10-6(В2 —5000BJ.
Следовательно, Вг = О, В2 = 1,25- 10е e/сек. Таким образом
искомое напряжение согласно (1) и (9)
uc(t) = ^ссв(0 = 1,25- 10V5000/ в.
График построен на рис. 13.28, г.
3. Наконец, рассмотрим третий случай численных значений
параметров схемы рис. 13.28, а.
Подставляя эти значения в (4), находим
— 1 4- 1 / / 1 \2 1 _
^1,2— 2-100-5-10-6 ~ \ 2-100-5U0-6 j 40-10~3-5-10“6
= (— 1000 ± /2000) сект1.
Корни характеристического уравнения образуют комплексно-
сопряженную пару чисел (рЬ2 = — а ± j®), следовательно, сво-
бодную составляющую напряжения на конденсаторе следует ис-
кать в виде (см. п. 4 основных положений)
иссв ^e~at s*n + ф) == Л^“1000/ sin (2000/ 4- ф)- (10)
По аналогии с предыдущими случаями из уравнений (6) с
учетом (I) и (II) получим f3(0) = 1,25 а.
Подставим в (1) и в выражение i3 уравнение (10)
ис = испр + иСсв = 0 + Аг*000' sin (2000/ + ф);
/3 = С = 5 • 10-в А [2000 cos (2000/ + ф) —
— 1000 sin (2000/ + <[»)] er1000'.
Переписывая эти уравнения для момента / = 0 и затем под-
ставляя в них ис(0) = 0 и i3(0) = 1,25 а, будем иметь
0 = 5- 10~в A sin ф;
1,25 = 5 • 10-« (2000Л cos ф — 1000Л sin ф).
Решая их, находим ф = 0, Л = 125 в. Таким образом, иско-
мое напряжение согласно (1) и (10)
ис (/) = 125е-1000/ sin 2000/ в.
График построен на рис. 13.28,5.
366
13.45. Цепь, изображенная на рис. 13.28,а, включается на
постоянное напряжение U = 100 в. Параметры элементов цепи:
г = 100 ом, L = 40 мгн, С = 5 мкф. Определить ток /2 в индук-
тивности.
Решение. Ищем решение в виде суммы принужденного и
свободного значений:
(1)
Рассчитав установившийся режим схемы (после коммутации),
найдем принужденное значение:
___ п. . _ . _ U __ 100
Зпр 12пр Чпр г 100
(2)
Для определения свободной составляющей тока составим ха-
рактеристическое входное сопротивление цепи и приравняем его
нулю:
Z(p) = r +----P~ = Q.
PL4—L-
После упрощения оно примет вид
p2LCr + pL 4- г = 0.
Корни характеристического уравнения
^1.2 2Сг 1/ ( 2Cr ) LC ± /2000) сек 1
образуют комплексно-сопряженную пару (р{ 2 = — а ± /ш).
Поэтому свободная составляющая решения имеет вид
12св = (<о/ + ф) = Xe~l000/sin (2000/ 4- ф).
(3)
Для определения постоянных интегрирования Лиф запишем
для начального момента времени (после коммутации) выражение
тока i2 по (1)
h (0) = *гпр (0) + Чсв (0) = 1 + Л sin ф
и его производную (с учетом (3))
rft*2 ^2ПР d^2CB л «ллл л
dt 1=0
/=о dt
(4)
= 0 — 1000Л sin ф 4- 2000Л cos ф.
(5)
367
Начальные значения определим с помощью независимых на-
чальных условии:
ис (0) = ис (0_) = 0 и t2 (0) = t2 (0_) = 0.
По закону Кирхгофа для рассматриваемой схемы (рис. 13.28, а)
u(0) = L-^- = ис(0) = 0,
ь dt /—о
и, следовательно, отсюда производная тока в начальный момент
dl<%
dt
= 0.
1
Подставляем найденные начальные значения в (4):
0 = 1 + A sin ф,
или
— 1 = A sin ф, (6)
и в формулу (5)
0 = — 1000 A sin ф + 2000 A cos ф. (7)
Для решения системы уравнений (6) и (7) разделим порознь
левую и правую части уравнения (7) на соответственно левую
и правую части уравнения (6):
о = — 1000 + 2000 ^4- = — 1000 + 2000 сtg ф.
1 sin ф ' & т
Отсюда ctg ф = -i-; ф=63°30';
sin ф =0,895 и из уравнения (6)
А =-------Д-г- = — 1,12 а.
Sin ф
Окончательно искомый ток
после коммутации по (1)
f2 =
= 1—1,12e~ loowsin(2OOO4-63°3O').(8)
График тока г2 построен на
рис. 13.29.
13.46. Цепь, изображенная на рис. 13.30, включается на по-
стоянное напряжение U = 30 в. Найти законы изменения во
времени всех токов и напряжения между обкладками конденса-
тора, если С = 16 мкф, г = 100 ом, L = 1 гн. Начертить кривые
токов и напряжения на конденсаторе. Выяснить предельное
368
значение сопротивления, при котором процесс сохраняет еще
колебательный характер»
Рис. 13.30
Рис. 13.31
13.47. Цепь схемы (рис. 13.31) включается на постоянное
напряжение U = 120 в. Сопротивления ветвей t\ = г2 = г = ЬЪом,
индуктивность L = 0,08 гя. Показать, что если емкость С = ,
то ток i в неразветвленной части цепи в любой момент времени
и
имеет постоянное значение, равное —.
Замечание. При заданном выборе параметров данная цепь имеет резо-
нанс токов при любой частоте.
13.48. Схема (рис. 13.31) подключается под действие синусо-
идальной э. д. с. е = Ет sin (W -ф- ф). Полагая, что гх = г2 = г =
= 40 ом, L = 0,08 гн, С == -^, = 120 У2 в, о> = 314 сек~' и
ф = , определить законы изменения токов , t2 и I во времени.
13.49. Цепь, состоящая из последовательно соединенных г,
L и С, конденсатор которой закорочен, включена на постоянное
напряжение U = 120 в. При установившемся режиме внезапным
размыканием рубильника Р конденсатор вводится в цепь
(рис. 13.32). Найти напряжение на обкладках конденсатора и ток,
проходящий в цепи, в двух случаях: 1) г — 100 ом, L = 40 мгн,
С = 25 мкф', 2) г = 80 ом, L = 40 мгн, С = 20 мкф. Начертить
кривые ис и i.
13.50. Найти токи в цепи схемы (рис. 13.33) после включения
рубильника Р, если известны == 20 ом, L = 0,4 мгн, г2 = 10
г3 == 20 ом, С = 1 мкф, £ = 60 в.
369
13.51. До замыкания рубильника Р в цепи схемы (рис. 13.34)
имел место установившийся режим постоянного тока. Конденса-
тор разряжен. В момент t = 0 рубильник Р замыкается. Опре-
делить начальные значения тока в индуктивности, напряжения
на конденсаторе и их первые производные. Найти уравнение
тока i2 и напряжения на конденсаторе (после коммутации). Да-
ны: Е = 60 в, rt = 20 ом, L = 1 мгн, гг = 10 ом, г3 = 20 ом,
С = 1 мкф.
Рис. 13.34
Рис. 13.35
13.52. В цепи схемы (рис. 13.35) до замыкания рубильника Р
был установившийся режим постоянного тока. Найти уравнение на-
пряжения на конденсаторе после замыкания рубильника, если
Е = 60 в, гх = 20 ом, г3 = 40 ом, г3 = 40 ом, L = 0,2 мгн и С=
= 1 мкф.
13.53. До замыкания рубильника Р в цепи схемы (рис. 13.36)
имеет место установившийся режим постоянного тока. Опреде-
лить: 1) напряжение на г2, на L и на С для t~0 и t — оо;
2) первые производные напряжений на г2, на L и на С по вре-
мени для t — 0. Даны: С — 1 мкф, L = 10 мгн, = rz = г4 ==
= 100 ом, г~ = г. = 200 ом и Е — 120 в.
9 О м
Рис. 13.36 Рис. 13.37
13.54. В схеме рис. 13.37 рассчитать мгновенные значения
тока источника напряжения. Дано: Е = 60 в, r4 = r2 = 1 ком,
= 1 мкф и С2 = 2 мкф.
Решение. Контур, образованный емкостями С4 и С2, не
содержит активных сопротивлений и индуктивностей. Поэтому
370
напряжение конденсаторов может изменяться скачком за счет
мгновенного переброса заряда в этом контуре. До коммутации
заряжен только конденсатор С, до напряжения иС1 (0_) = Е =
= 60 в. Заряд его (0_) = CjUcl (0_) = 6 • 10“6 к в начальный
момент после коммутации перераспределится между емкостями
так, что будет выполняться второй закон Кирхгофа:
uCI(0) = «C2(0). (1)
При этом суммарный заряд емкостей в начальный момент не
изменится:
^i«ci (°) + Сгисг(0) = 6-10-» к. (2)
Подставляя численные значения и решая систему уравнений
(1)4-(2), находим начальные значения напряжений на емкостях:
«С 1 (°) = “С2 (°) = 20 (3)
Ток источника напряжения ищем в виде наложения принуж-
денной и свободной составляющих тока:
4 = 4пр -|~ 4СВ. (4)
Принужденное значение тока в схеме после коммутации
inp = —— = -б°- = 3.10-г а. (5)
Для нахождения свободной составляющей тока составим ха-
рактеристическое уравнение, приравнивая нулю характеристиче-
ское входное сопротивление схемы:
Z (р) = Г, Ч-------------— = о.
pCi + рС% ----
?2
Характеристическое уравнение преобразуем к виду
Р + С2) + f ——h —1 = 0.
\ Г2 Г1 /
Единственный корень характеристического уравнения
Следовательно,
2-108
ЮМ-10-°
= —6,67-10* сек-1.
Для вычисления
начального момента
/св= Ле-6’67-,02/- (6)
постоянной интегрирования запишем для
времени
I (0) = iH₽ (0) + fCB (0) = 3 -10“* + А.
(7)
371
Начальное значение тока находим по второму закону Кирх-
гофа
Е = i (0) г 4- иС1 (0) = i (0) 103 + 20 = 60, (8)
откуда
i (0) = JOrJ-L = 4.10-2 а (9)
Подставляя найденное начальное значение в (7), определяем
значение А = 10“2, и, следовательно, искомое значение тока (4)
источника напряжения после коммутации:
i = (3-10~2 + ю-2е~е,е7,102') а. (10)
“с
Рис. 13.38
Рис. 13.39
13.55. Вычислить начальные значения напряжения на кон-
денсаторе до и после коммутации в схеме рис. 13.38. Даны:
Ех =. 120 в, Е2 = 100 в, = 20 ом и г2 = 80 ом.
13.56. Определить начальное значение тока во вторичной об-
мотке трансформатора (рис. 13.39) после мгновенного выключе-
ния цепи первичной обмотки. Даны: Е= 100 в, i\ = 10 ом>
г2 = 2 ом, Lr = L2 == 0,02 гн и М ~ 0,01 гн.
Решение. Схема содержит идеальный выключатель, на за-
жимах которого в процессе выключения может наводиться про-
извольно большое напряжение. Следовательно, возможны скачки
тока в индуктивностях.
До коммутации токи цепи
h = = 10 а\ i2 = 0.
После коммутации
Ч (0) = 0,
т. е. скачок тока в первичной обмотке
(0) = — 10 а.
Для нахождения начального значения тока t2(0) после ком-
мутации используем уравнение второго закона Кирхгофа для
контура вторичной обмотки «в момент» коммутации (ограничиваемся
372
бесконечными слагаемыми и пренебрежем конечной величи
ной i2r2):
— М-^- +L-^- = 0,
dt dt
и проинтегрируем его по «времени начального скачка»:
— М f -^dt
J dt
t=0-
— M Ar*! + L = 0.
т. e.
Из последнего уравнения определим искомое начальное зна-
чение тока во вторичной обмотке трансформатора:
• /А\ А • г"
г2(0)=kt2=—= — 5 а.
La
13.57; Рассчитать ток источника напряжения схемы (рис. 13.40)
до переключения рубильника Р и в начальный момент после
мгновенного переключения его из положения 1 в положение 2.
Даны: Е = 100 в, Lr = 1 мгн, L2 = L3~ 3 мгн н г2 = г3= 10 ом.
Рис. 13.40
13.58. В цепи схемы (рис. 13.41) действует импульсный ис-
точник тока (/) = 0 при /<0, G(/) = /i при />>0. Рассчитать
переходной ток индуктивности.
Решение. Ищем ток индуктивности в виде наложения
принужденного и свободного токов:
^пр ~Ь ^св*
В установившемся режиме uab пр = 0, £пр == /х. Форма сво-
бодного тока определяется видом корней характеристического
уравнения, которое составляем, приравнивая нулю входное со-
противление относительно ветви с индуктивностью:
pL + г2 = 0,
373
причем учтено, что входное сопротивление источника тока ра-
вно бесконечности. Единственному корню характеристического
уравнения р = —соответствует свободный ток /св = Ае L
с постоянной интегрирования А == — При этом удовлетво-
ряется начальное значение тока индуктивности i (0) = i (0_) =^= 0.
Окончательно, ток индуктивности
Л - при > 0
) L (t) — ^1 (1 )•
13.59. В цепи схемы (рис. 13.42)
действуют источник постоянного
напряжения Е = 20 в и источник им-
пульсного тока i(/)=0 при /<0,
/(/)== 0,1 а при Параметры
L = 1 мгн. С2 = 0,02 мкф. Рассчитать
переходное напряжение на емкости.
Рис. 13.42
л = 0.5 ком
ГЛАВА ЧЕТЫРНАДЦАТАЯ
ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА
ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. В- основу операторного метода положено следующее:
функция /(/) [обычно ток i(t) или напряжение «(/)] веществен-
ного переменного t (времени), называемая оригиналом, за-
меняется соответствующей ей функцией F (р) комплексного
переменного р, называемой изображением.
Указанные функции связаны соотношением
F(p) = lf{t)e-P(dt, (14.1)
О
называемым прямым преобразованием Лапласа.
Эта связь сокращенно записывается в виде
F(P) = m
В таблице (14.1) приводятся оригиналы простейших функций
и их изображения, полученные на основе формулы (14.1) и ис-
пользуемые при решении задач на переходные процессы.
2. Операторные сопротивления цепей записываются так
же, как и сопротивления для тех же цепей в комплексной фор-
ме, в которых /о) заменено на р. Так, для цепи, состоящей из
последовательно соединенных элементов г, L и С> операторное
сопротивление имеет вид
Z(p) = r + pL + -^~. (14.2)
рС
3. Закон Ома для ветви в операторной форме (с учетом не-
нулевых начальных условий). На рис. 14.1 изображена ветвь ab,
содержащая последовательно соединенные элементы г, L, С и
375
Таблица 14.1
c в £ Оригинал Изображение № п.п I Оригинал Изображение
1
2
3
4
5
6
7
8
9
10
11
12
1
t
tn
n — целое поло-
жительное число
e+a1
— aerat
ei {^ot 4- Ф)
te~at
(1 — at) e~at
a(l —e~at)
----—e~at)
a—b
ae~at — be~bi
a — b
1 Р 13 COS <о0£ p
P2 + ®0
1 14 sin (о0/ (D0
Р2 P2 + “o
и! 15 sin(<o0/ + ф) psin^ + о)0созф
рп+1 P2 + «0
1 16 sin <о0/ <o0
р ± а (P + a)2 + “o
Р 17 cos <о0/ p + a
р + а (p + a)2 + m2
1 18 sh at a
Р ± j wo p2 — a2
19 20 ch at 1 1 / e~bt P
р — м 1 p2 —a2 1
(р + а)2 ab b—a \ b e~at \ а / P(P + a) (p+ 6)
р 21 t2 o—at 1
(р + а)2 2 (P + a)3
1 22 / a \ t 1 1 —— t) e~at \ 2 / p
р (р + а) (p + a)3
1 23 1 1
(Р + а) (Р+ Ь) jA тЛ VT
р 24 HI ** СЧ 1
(р + а) (р + Ь) p/F
376
источники э. д. с. er(f) и е2(/), являющаяся частью сложной
цепи.
Изображение тока I (р) в ветви ab связано с изображением
напряжения Uab(p), приложенного к зажимам а и b ветви, за-
коном Ома в операторной форме:
на рис. 14.1,
а).
иг (0_)
Uab (Р) + (Р) + Li (0-) - С - - Et (р)
/ (р) =------------------ ---------Р-----------, (14.3)
2 (р)
где £*i(p) и Е2(р) — изображения э. д. с. e1(t) и е2(/);
. i (0_) и ис (0_) — значения тока в индуктивности и напряжения
на конденсаторе в начальный момент времени
(положительное направление напряжения на
конденсаторе ис = uef = — ufe следует при-
нимать совпадающим с выбранным поло-
жительным направлением тоКа, как пока-
зано
4. Операторная схема
замещения. Уравнения для
изображений тока и на-
пряжения произвольной
цепи могут быть получе-
ны по обычным законам
электрических цепей (за-
конам Ома и Кирхгофа),
записанным для оператор-
ных схем замещения. Опе-
раторная схема замеще-
ния произвольной ветви
(рис. 14.1, а) показана на
рис. 14.1, б. При ее со-
ставлении, во-первых, все
переменные величины за-
меняются их оператор-
ными изображениями [/(/)
на /(р), u(t) и г(/) соот-
ветственно на U (р) и
Е(р)]; во-вторых, индуктив-
ности L заменяются после-
довательными схемами,
состоящими из операторного
ника напряжения с э. д. с. Li (0_), где t(0_)— начальное значение
тока в индуктивности; в-третьих, емкости С заменяются после-
довательными схемами, состоящими из операторного сопротив-
ления —— и источника напряжения с э. д. с. Uc , где
рС - • р
ис(0.) — начальное значение напряжения на емкости.
сопротивления pL и источ-
377
На рис. 14.2, а и б показаны некоторый участок электриче-
ской цепи и соответствующая ему операторная схема замещения.
Замечание. Обращаем внимание на то, что указанные на рис. 14.1,6
иг(0_)
и 14.2, б направления э. д. с. П(0_), Ы3(0_), -г- соответствуют направ-
Р
лениям положительных токов и напряжений на конденсаторах, данным на
рис. 14.1, а и 14.2, а.
5. Законы Кирхгофа в
Рис. 14.2
операторной форме.
Первый закон.
2^(р) = 0. (14.4)
Для схемы (рис. 14.1, а и б)
первый закон Кирхгофа имеет вид
4 (Р) + 4 (р) — / (Р) = О, или
4(Р) + 4(Р) = Цр)-
Второй закон. В общем слу-
чае при ненулевых начальных ус-
ловиях для какого-либо контура,
содержащего NB ветвей,
4=1 L
"в
^h(P)Zk(p), (14.5а)
4=1
где ik (0_) и иС1г (0_) — начальные значения тока, проходящего
через катушку индуктивности и напря-
жения на конденсаторе в ветви k;
Zk(p) = rft+ pLk-\—J-операторное сопротивление ветви k.
Пример. Для контура рис. 14.2, а и б второй закон Кирхгофа в опера-
торной форме имеет вид
Е (р) + Ы3 (0_) + = pLla (р) 4- г/! (р) - 1 4 (/>)•
р pk
В случае нулевых начальных условий формула (14.5а) при-
мет вид
"в "в
Z^W^Z^P^tP). (14.56)
4=1 4=1
378
4. Теорема разложения. Если изображение искомого тока или
напряжения имеет вид рациональной дроби:
fi(p) _ атрт + ат-1 Р"1'1 + + Q1P + Др
Fz (Р)
ЬпРп + bn-i Рп~' + • • • + bip +&о
атРт + “m-iP"1-1 + • • + diP + «о
ЬП(Р — Р1) (Р —Р^ ••• (Р — Рп)
(14.6)
причем многочлены (относительно р) F1(p) и F2(p) удовлетво-
ряют следующим условиям: степень /^(р) ниже степени F2 (р),
ak и bk — вещественные числа, а корни pv р2, ... , рп уравне-
ния Р2(р) = 0 различны, то оригинал определяется выражением
Fj (Р) у Л (Pfe) ePkt
Лг(р) ’ F'2(Pk)
&=1
(14.7)
В случае, если, знаменатель последнего выражения имеет
один корейь, равный нулю, т. е. F2(p) — pF3(p), то оригинал
находится по формуле
Л(Р) = Л(Р) Fi (0) , у Ft (pft) epkt
Ft(.p) pF3(p) ’ f3(0) PkF3(Pk)
4=1
Примеры в задачах 14.1, 14.4 и 14.16.
Замечание. Если среди корней уравнения F2 (р) = 0 имеются комплек-
сно-сопряженные корни pk и pk, то при вычислении соответствующих им сла-
гаемых, стоящих в правой части суммы уравнений (14.7) и (14.8), достаточно
определить слагаемое для одного из этих корней, например pkt а для сопря-
женного корня pk следует взять сопряженное значение. Сумма, соответствую-
щая этим двум слагаемым, равна удвоенному значению действительной части,
найденной для одного из корней.
Примеры в задачах 14.4 (3), 14.9 и 14.17.
Если в уравнении (14.8) Г2(р) имеет п различных корней
(рх, р2> • • • > Ря) и из них корень рх кратностью mv корень р2
кратностью /п2, . . . , корень рп кратностью тп, то по изобра-
жению
Мр)
орипйал вычисляется по формуле
Л (Р)
F2(p)
(mk — 1) I
Здесь выражение, стоящее в знаменателе квадратной скобки,
надо сначала сократить на (р — Pft)m* и лишь после этого диф-
ференцировать.
379
Если уравнение Р2(р) содержит одновременно и простые и
кратные корни, то для определения слагаемых соответствующих
простым корням используется формула (14.7) [или (14.8), если
имеется простой корень р=0] и для кратных — формула (14.9).
6. Методика решения задач операторным методом сводится к:
а) составлению уравнений Кирхгофа (или соответствующих
им уравнений по тому или иному методу расчета) в оператор-
ной форме с учетом независимых условий;
б) решению их относительно изображения искомой величины;
в) нахождению оригинала (при помощи теоремы разложения,
таблиц, связывающих оригиналы и их изображения, или другими
методами) по найденному изображению тем или иным способом.
УПРАЖНЕНИЯ И ЗАДАЧИ
14.1. Для схемы, изображенной на рис. 14.3, операторным
методом найти выражения мгновенных значений тока в нераз-
ветвленной части цепи и напряжения на
обкладках конденсатора при замыкании
рубильника Р. Даны: U == 200 в, t\ =
= 100 ом, г2 = 400 ом и С =5 мкф.
Решение. Находим изображение
тока в неразветвленной части цепи по
закону Ома:
Л (Р) =
У(р)
Z(P) ’
где изображение постоянного
напряжения (по табл. 14.1, п. 1)
а операторное сопротивление
Итак,
1
Z(p) = r1 +--------
г2 4“ тг
рс
0,4р + 200
р(0,2р + 500)
0,2р + 500
2«10~3р + 1
Л (р) =
(1)
Оригинал этого тока определим двумя способами.
Способ /. Используем табл. 14.1, связывающую оригинал и
его изображение. Для этого преобразуем /х(р) так, чтобы полу-
чить изображения, имеющиеся в ней.
380
табл. 14.1:
Zi (р) представим в виде суммы двух функций, которые после
преобразования примут вид формул пп. 4 и 10
ад _ °-4 +-------_ ','4
0,2р 4-500 р(0,2р 4-500) 0,2
500
200
0,2
500
0,2 0,2
500 \ ’ 500
2500
= 2<г2500' 4- 0,4 (1 — е'2500/) == (0,4 4- 1,6е-2б00/) а = i, (/).
Способ 2. Решим задачу при помощи теоремы разложения
(14.8).
В данном случае
(Р) = °>4р + 200; F3 (р) = 0,2р + 500.
Вычисляем корень:
F3 (р) == 0,2р + 500 = 0; рг = — 2500 сетг1.
Определяем
Л (0) = (0,4р + 2ОО)р==о = 200; F3 (0) = (0,2р + 5ОО)р=о = 500;
Fr (Р1) = (0,4р + 200) = 0,4 (— 2500) + 200 = — 800;
Л* /'I
f;(p) = o,2.
Подставляя найденные значения в формулу (14.8), получим
Л(Р) =
fi (Р)
PF з (р)
0,4р 4-200
р(0,2р + 500)
fl (0) , fl (Pl) еР'‘
F3(0) Pifs(Pi)
200
500
— 800e~2500*
-—2500*0,2
= (0,4 + l,6e~2500Z)a
Проверка. При t = 0 ix(0) = 0,4 1,6 = 2 а. Действительно,
в момент начала переходного процесса напряжение на конден-
саторе равно нулю. Это соответствует тому, что конденсатор
ведет себя так, будто он закорочен, и тем самым шунтирует
сопротивление г2, и поэтому ток 4(0) определяется только
величиной сопротивления
Определим напряжение на конденсаторе в операторной форме:
^с(р) = t/(P) --утт = U{P) f1----------) =
Z (р) \ Г1Г«Ср 4- G 4- г2 /
_ г2 U (р) = Цгг_8-10«
ГуГ^рр -|- г14- г2 Р Оу2Ср 4" *14” ^г) Р(0,2р 4-500)
381
Применяя один из указанных выше способов, найдем
мс(/) = 160(1 — е'2500') в.
Рис. 14.4
Проверка. При t = 0 ис (0) = 0, что
соответствует начальному условию.
14.2. Определить напряжение на
разомкнутых зажимах 2—2' цепи схе-
мы рис. 14.4 при ее включении на
постоянное напряжение 100 в.
Даны: t\ = г2 =*= 250 ом, Сг = 20 мкф,
С2 = 4 мкф.
14.3. Решить задачу 13.12 опера-
торным методом.
14.4. Решить задачу 13.44 операторным методом.
Решение. Прежде всего найдем операторное сопротивле-
ние цепи
Z (р) = Г +
rLCp2 + Lp-\-r
p2LC+ 1
Далее определим изображение тока l^p) через изображение
входного напряжения и (р) == —:
р
I („) = = U (LCP2 + 1)
1 Z(p) p(r LOp* Lpr)‘
Изображение напряжения на емкости получим умножением
изображения тока на операторное сопротивление параллельных
ветвей L, С:
VCU>} = IM-----—— -------------т--------(*>
rC/p.+_L„+_q
Р 'LC \ rC Р LC )
где числитель
Л(Р) = -^> (2)
г о
а знаменатель
^2(Р) = Р2 + +-777 = (Р —Р1)(Р —Рг). (3)
причем корни знаменателя
3S2
1. Решим задачу для первого варианта численных значений
по формуле разложения (14.7). По (2) 4-(4)
р / \___ 125
1 W ~ 250-2-10е
250-2-10-’
= p2 +2000p 4- 0,75-10«.
667 - 10~3 - 2 • IO'»
Найдем корни:
/?2(р)=р24т2000р4-0,75- 10е =0; pt= —500 сек~х\ р2~ — 1500ce/c-1.
Вычисляем производную F2 (р) и ее значения при р = Pl и
Р = Рг-
t
F2 (Pl) = 2 (— 500) + 2000 = 1000;
F2 (p2) = 2 (— 1500) + 2000 = — 1000.
По (1)
и (о) = =___________°’25-10
с Рг(р) р2 4- 2000р + 0,75-10’
По формуле разложения (14.7)
Pit
0,25-Ю8 е 500/
1000
и {р} = Zi
с р2 ы
О 94. 106 р-1500^
4- ’ -1000-------= 250 (е — е ) в==ис (0-
Те же результаты могут быть получены по п. 11 табл. 14.1,
если знаменатель изображения напряжения на конденсаторе
представить в виде F2 (р) = (р + 500)(р 4* 1500).
2. Решим задачу, подставляя численные значения второго
варианта. По (2) 4- (4)
= -..iob-bio- = 1>25-1°6; f2+ 5000)а;
рх = = — 5000 сект1.
Изображение напряжения (1) на емкости
П (Р) __ 1,25-100
‘ ^(Р)^ (р + 5000)2*
В связи с тем что имеются кратные корни (порядок крат-
ности тх == 2), оригинал находим по (14.9), в которой
тк = т, = 2; (mk - 1) I = (2 - 1)! = 1; - F* (р) =
(Р-Pi) *
(p + 5000)2
383
Таким образом,
= [1,25- 10«/е*"1 =D = 1,25-10“/e~souoz e = uc(t).
Можно было также определить оригинал по формуле
п. 8 табл. 14.1.
3. Рассмотрим третий вариант цифровых значений.
По (2) (4)
Л = -100-5?10-<»' = °’25’ 10*: = pi + 2000р + 5‘ 10*;
р. „ = — 1000 ±/2000 сек'1.
Производная от F* (р) и ее значения при р = и р = р2
равны
F2 (р) = 2р 4- 2000;
F'2 (рх) = 2 (— 1000 + /2000) + 2000 = /4000;
F2 (p2) = 2(— 1000 — /2000) + 2000 = — /4000.
Искомый оригинал (с учетом замечания на стр. 379)
по (14.7)
0,25-10“
0,25-10“
— /4000
F^) ~
. 0,25- 10е /— Ю00 + / 2000) i
•106 ~ /4000 е
1000 — / 2000) t _
tz
= 2 Re
= 2Re
/ 2000 7
3,25 • 106 е-1000'---------
4000 е
0,25• 106 е~~ 10001 (2ооо t — 90°)
4000
— 90°) = 125 е'1000' sin 2000/ в.
получить по п. 16 табл. 14.1,
2-0,25-10“ ioooz /0000,
=-----Зооб-- е1 cos (2000/
Те же результаты можно
если знаменатель F2 (р) представить в виде:
F2 (Р) = (Р — Pi) (Р — Pi) = IP — (— Ю00 + /2000)] (р —
_ (_ Ю00 — /2000)] = (р + 1000)2 + 2000®.
14.5. Решить задачу 13.46 операторным методом.
14.6. Операторным способом найти выражение для тока в
первой катушке при включении рубильника Р (рис. 14.5).
Даны: Ьг = Ь2= 10 мгн, М = 5 мгн, r1 = r2== 1 ком и U == 100 в.
Э84
Указание. Дифференциальные уравнения для первого и второго кон-
туров будут:
. I I di* । лл II
r* к + ~S~ + M ~di~ = U'
Соответствующие им операторные уравнения
/1 (Р) + P^i /1 (р) + р М /2 (р) = U (р)\
г* I* (Р) + Р^2 к (Р) + Р М h (р) = 0.
Из последних уравнений надо найти изображение тока 1\ (р), а затем,
пользуясь теоремой разложения или табл. 14.1, определить оригинал.
Рис. 14.5
14.7. Найти мгновенное значение тока, проходящего по ка-
тушке при включении цепи схемы (рис. 14.6). Э. д. с. источни-
ка энергии Е, параметры катушки (г, L), сопротивления гг и г2
и емкость С известны. Задачу решить -операторным методом.
14.8. Определить ток, проходящий по катушке при включении
цепи, изображенной на рис. 14.7. Е = 40 в, г0 = ЮО ом, гш ==
== 2000 ом, г = ПО ом, L = 3 гн и С = 1 мкф.
Рис. 14.8
14.9. К цепи схемы (рис. 14.8) подключается синусоидальное
напряжение и = Um sin ((о0 t + ф). Пользуясь операторным ме-
тодом, найти выражение для мгновенных м значений напряжения
между обкладками конденсатора.
3JB5
13 Заказ № 624
Решение. Найдем операторное выражение напряжения на
конденсаторе:
А (р) = ----------
г 4-
* 1
+ ~vC
U(p) (ra Ср + 1)
ri r2 Ср + п 4- г2
ис (р) = и (р)- Г, Up) =-----------...... .
г 1 ср +1 + -
г<2
; > « "
По п. 16 табл. 14.1 находим изображение входного на-
пряжения и = Um sin (а>0 / 4- ф) в виде U (р) = Um --in ц>0^08 .
Р2 + <»0
Следовательно,
U с (Р> =
где
Fx (Р) = Um (Р sin Ф + % cos ф); (р) = (р2 + 4) (qCp 4-14-—
корни знаменателя (F2 (рк) = 0] plt2 = ± /а>0,
Сделаем расчет по формуле разложения (14.7). Для этого
находим
Fi (Pi) = Um (i «>о sin ф + о>0 cos ф);
Fi (р2) = Um (— j а>0 sin ф 4- а>0 cos ф);
где
Л (Рз) = (-----sin Ф + <оо qos ф) =
= Um |/( 0,(2 Sin (Ф ~ Н
<р = arctg
Fi (р) = Г, С (р2 + 4 ) + 2р (fl Ср 4- 1 4- ;
\ Г2 /
386
Подставляя найденные значения в (14.7) и используя заме-
чание на стр. 379, относящееся к комплексно-сопряженным
корням Pi и р2, получим оригинал напряжения на конденса-
торе:
п — I1SP1 • , Л (Р2) (/) ।
Uc{p} F2(p)~ F2(p1} + F'2(p2)
13*
38?
Um Sin (u>^t + ф — ср)
t/m sin (<j> — ф) e
14.10. К цепи схемы, изображенной на рис. 14.9, подключа-
ется гармоническое напряжение и = Um sin (u)01 4- ф). Найти
закон изменения во времени тока, проходящего в неразветвлен-
ной части цепи. Даны: t\ = 100 ом, г2 = 250 ом, L = 1 гн,
Um = 170 в и f = 50 гц.
14.11. Найти законы изменения по времени тока в неразвет-
вленной части цепи и напряжения ис при включении цепи
(рис. 14.10) на синусоидальное напряжение и = Um sin а>01.
Даны:. Um = 500 в, г — 50 ом, L = 0,3 гн, С = 100 мкф и
= 314 сек'1.
Рис. 14.9 Рис. 14.10 Рис. 14.11
14.12. Решить задачу 13.15 операторным методом.
Решение. Это пример задачи с ненулевым начальным ус-
ловием для тока i19 проходящего через индуктивность. Опера-
торная схема замещения изображена на рис. 14.11. Составляем
для нее уравнения Кирхгофа:
1 (Р) = Л (Р) + 1г (р); (1)
и (р) = г! (р) + /8 (р); (2)
U (р) + Li li (0_)= П (р) 4- (/-j + pLt) (р). (3)
В этих уравнениях ix (0_) = . — начальное значение то-
ка, проходящего через индуктивную катушку; U (р) = —
изображение постоянного напряжения.
Уравнения (1) 4- (3) решим совместно относительно то-
ка Ц (р): i
m
А (Р) =
/ Z-i (г + г«) ггг + Г1Г2
у Г “I- Г1 & Г ~|~ Tj
Р frrt + ГГ1 + nr2 + £1 (г + г2)р]
_ 2р + 11,25
~ Р (Р + 6,25) ‘
8р + 45
р (4р + 25)
По формуле разложения (14.8) оригинал функции
(/) = (1,8 + 0,2 е“6’25') а.
В целях упражнения эту же задачу решим сведением к ну-
левым начальным условиям. Для этого вычислим напряжение
на разомкнутом рубильнике Р (см. рис. 13.11, а):
«руб (0_) = иаЬ (0.) = г, I, (0_) =
Добавим в ветвь рубильника два встречно включенных ис-
U ri
точника напряжения с э. д. с. ех= е2= ируб = утртр как пока*
зано на рис. 14.12, а.
Расчет схемы после коммутации проведем по методу нало-
жения. Составляющая тока ii (от системы э. д. с. ей совпа
дает со своим значением (0_) до коммутации, так как под-
ключение э. д. с. е± = ируб (0.) (рис. 14.12, б), не вызовет каких-
либо изменений в исходной схеме с выключенным рубильни-
ком Р.
Таким образом,
i'i = ii (0-) = ~ ^Г1 =2 а.
Вызываемая действием э. д. с. ег, подключаемой к обесто-
ченной схеме (рис. 14.12, в), составляющая тока и может быть
записана в операторной форме в виде
Р (г -I- n) [rr, + rrt + rt rt 4- (rt + r) p ’
389
Подставляя численные значения и переходя к оригиналу
i\ (/) по (14.8) для искомого тока, получим
Ч = h + h = (1,8 0,2 с * ) и.
14.13. Решить задачу Д3.8 операторным методом.
14.14. Решить задачу 13.9 операторным методом.
14.15. Решить задачу 13.32 операторным методом.
Рис. 14.13
Решение. Эта задача имеет
ненулевое начальное условие для
напряжения на конденсаторе ис .
Операторная схема замещения изоб-
ражена на рис. 14.13. По законам
Кирхгофа для этой схемы
-у = Г, Л (Р) + /2 (Р); (1)
"г (0_) i 1 \
—Р--------= ('-!-------jc~) 1 — г2 у2 (Р>; (2)
/1 (Р) = (Р) + I (Р)- . (3)
Решая эти уравнения относительно / (р) и учитывая, что
нс(О-) = £, найдем
Подставив числовые значения, получим
J / ч __ __ 3,6*10 8 __ __ Q « г
/ (р) ОЛ. 1П-8п I 10,15
На основании (14.7) определим оригинал:
i (/) = — 0,15 г"6250' а.
Аналогично из уравнений (1)-~(3) можно найти два других
тока и напряжение на обкладках конденсатора.
14.16. При установившемся режиме в схеме рис. 14.14, а
замыкается рубильник Р, включающий конденсатор С, предва-
рительно заряженный до напряжения (70. Найти выражения то-
ков при переходном процессе. Даны: Е == 60 в\ гл == 400 ом,
г2 = 800 ом, L = 0,2 гн, С = 2,5 мкф и Uo = 20 в.
Решение. Найдем начальное значение тока, проходящего
через индуктивную катушку
L (0_) = i2 (0_) = --= 0.05 а.
1 ' ' 1 ' ’ rt -|- г, 1200
390
Выберем положительные направ-
ления токов, как указано на исходной
схеме (рис. 14.14, а) и на операторной
схеме замещения (рис. 14.14,6). Сос-
тавим уравнения Кирхгофа в опера-
торной форме:
G к (р) + (<•» + PL> h (Р) =
=Е(Р)+ Ь-а(0_); (1)
G^(P) +
Г u
р . . “с (°-)
=£(р)---------—;
Г
Ii(P) = li(P) 4- Мр)-
(2)
(3)
Отсюда, учитывая, что Е (р) =
— и ис (0_) = Uo, решая уравне-
ния (1)ч-(3), для тока Д (р) получим
Рис. 14.14
, ,n, Lc (Е ~ Р2 + [гв C(g - Uo)+ Щ (О-)] Р+ Е Ft (р)
1 ' р \riLCp2 4- (Г1Г2С + L) р + И -Ь 'г! = Р2(р)’ ' '
где
Рг(р) = 0,2-2-5-IO”6-40р2 + (800-2,5-1 О’®-40 4- 0,2-0,05)p-f-60=
= 2-10’8p2 + 0,09р + 60; (5)
F2 (р) = ррз (р) = р [400-0,2-2,5-10-® р2 + (400-800-2,5 х
х 10-® + 0,2) р + 1200[ = р (2-10-* р2+р+1200). (6)
Находим корни уравнения Fa (р) = 0:
р, = — 2000 сек~х\ Р2 — — 3000 сект1. (7)
Далее вычисляем
Ft (0) = 60; Р8 (0) = 1200; (8)
Ft (p^ = 2-10-» (— 2000)2 + 0,09 (— 2000) 4- 60 = — 40; (9)
Fa (р2) = 2-10-® (— 3000)2 4- 0,09 (— 3000) 4- 60 = — 30; (10)
Fs(p) = 4-10-®р 4- 1;
Рз (Pi) = 4-10-* (— 2000) 4- 1 = 0,2; (11)
Рз(Р8) = 4-10-Ч— 3000) 4- 1 =- 0,2. (12)
391
Подставляя (7)4-(12) в формулу разложения (14.8), получим
.• /А _ 60 , —40 е"2000' — 30 е"3000/ _ А АС
1200 + —2000-0,2 + —3000-(—0,2) — и>ио +
4- 0,1 e'2U00z — 0,05e-«00W а.
Затем находим мгновенное значение напряжения на парал-
лельных ветвях и остальные токи:
uab = Е — цг, = 60 — (0,05 4- 0,1 e-200w — 0,05 e'3UW) 400 =
== (40 — 40 *r200W + 20 e-»«ooz) в;
i9 = C = (0,2 e-2wat— 0,15 e-8000/) a;
UI
ia = _ ia = (0,05 — 0,1 e-2000' 4- 0,1 е-8000/) a.
Проверим правильность полученных результатов для началь-
ного момента. При t = 0 i2(0) = 0,05 а; иаЬ (0) = 20 в, т. е.
результат правильный.
14.17. В схеме рис. 14.15, а при разомкнутом рубильнике
имеется установившийся процесс. В момент t = 0 рубильник
lt(p) Lbt(O.)
b
Рис. 14.15
замыкается и накоротко шунтирует
сопротивление г4. Найти выражения для
токов и напряжение на конденсаторе
при переходном процессе. Даны: U =
= 125 в, гг == 50 ом, Г2 = 200 ом,
г4 = 250 ом, L = 0,01 гн и С == 5 мкф.
Задачу решить при помощи теоремы
разложения.
Решение. Это пример задачи с
ненулевыми начальными условиями.
Определим их. Через индуктивную ка-
тушку до замыкания рубильника прохо-
дит постоянный ток:
и
h (0.) = f2 (0.) =
500 “ 0’25 а*
Напряжение на конденсаторе до коммутации
ис (0.) = г2 /2 (0_) = 0,25-200 == 50 в.
Для схемы, образующейся после коммутации, начертим опе-
раторную схему замещения (рис. 14.15, б) и для нее составим
уравнения Кирхгофа в операторной форме:
1 «г (0-)
(г, 4- pL) /8(р) = и (р) + 1Л, (0) - с 4 (1)
392
(G + pL) Ц (p) + га /2 (p) = U (p) + Lix (0_); (2)
4 (P) = 4 (P) + /3 (P) • (3)
Ищем ток Д (p). Из совместного решения уравнений
и
(I) 4-(3) и учитывая, что U (р) = —, найдем
р
CL r3 it (0.) р2 4- [(7С r2 + Lh (0_) - ис (0_) Cr2| р + U _
1 Р [г2 р2 + (Оч r2 + L) р +/j + r2j ~
Подставляя числовые значения, имеем
F1(p) = 5-IO'8• 0,01-0,25-200 р24- (125• 5- 10~в-200 4- 0,01 X
X 0,25 —50-5 -10-®.200) р 4- 125 = 2,5- 10"в р2 4- 0,0775 р4-125; (5)
F2 (р) = pf3 (р) = р [0,01-5- 10-в-200р2 4- (5- 10~в • 50 • 200 4-
4-0,01)р 4-250] =р(10-5р2 4- 0,06 р 4-250). (6)
По изображению (4) найдем оригинал тока iv (/) при помощи
теоремы разложения (14.8). Для этого определим значения фун-
кций Fx(p) и F3(p) при р = 0:
Fr (0) = 125; F3 (0) = 250. (7)
Затем находим корни уравнения
F3 (р) = IO’5 р2 4- 0,06 р 4- 250 = 0;
_ -0,06 4- V 0,0036 —4-10-5-250~ _
р1.2 — 2-10'5 ~
= ~°’v1;fe^’08' = (— 3000 ± j4000) сект1;
Pi = (— 3000 4- / 4000) сек~1; р2 = (—3000 — /4000) сект1. (8)
Далее вычислим производную и ее значения при р — рх
и р = р2:
Fs' (р) = 2-10-»р4- 0,06;
F3' (pi) = 2- IO'5 (— 3000 4- /4000) 4- 0,06 = /0,08; (9)
Fs' (р2) = 2 • IO’5 (— 3000 — j 4000) 4- 0,06 = — /0,08. (10)
Определим Fx (p) при p — pt и p = pa:
Pi (Pi) = 2,5- IO'6 (— 3000 + j 4000)2 + 0,0775 (— 3000 + /4000) +
+ 125 = — 125 + /250;
(И)
Pi (Pi) = 2,5- 10“* (— 3000 — /4000)2 4- 0,0775 (—3000— /4000) +
4- 125 = — 125—/250.
(12)
Наконец, подставим полученные в (7) 4-(12) значения в (14.8)
и, учитывая замечание на стр. 379, получим
125
Ь ~ 250 = Re
(_ 125+ /250) е(-зоо<)+/4ООО)г
(—3000 + /4000)-/0,08
281 е/|1в°30' е/4Ш‘
. 5000 е'126°50'. 0)08 е/90»
£-3000Г
= 0,5 4- Re [1,4 е1(i000t ~ 100°20'>] е-3000' = 05 + 1>4 е-зооо/ х
х cos (4000/— 100°20') а = 0,5 + 1,4 г?-3000' sin (4000/— 10°20') а.
Проверка. При t = 0 (0) = 0,25 а, что удовлетворяет
начальному условию.
Остальные два тока могут быть найдены аналогичным пу-
тем. Однако их можно определить и следующим образом: если
из U вычесть падение напряжения на г\ L-ветви, то будет най-
дено мгновенное значение напряжения на параллельных ветвях:
иаЬ == U rih
Затем определяем токи
; __ иаЬ . ; __ г* duat)
Ц - ь dt •
14.18. Решить задачу 13.48 операторным методом.
14.19. Решить задачу 13.49 операторным методом.
14.20. Операторным методом решить задачу 13.50.
14.21. Решить задачу 13.51 операторным методом.
14.22. Решить задачу 13.35 операторным методом.
Решение. До замыкания рубильника в цепи проходит
ток
/"Ги • / / , , ч
* = ---- sin (а)0/-|_ ф _
<С>
где ______________________________
z = V (гу + га)2 4- (% Li + % Li)2, = 2,5 ом;
= arctg 3,43 = 73°44'.
394
По условию задачи в момент включения этот ток максима-
лен, т. е.
Z(0_) - i (0) =
sin (w01 4- ф — <p)
Отсюда может быть рассчитан угол включения ф:
sin (ф — ф) = 1; ф — ф = 90°; ф - 90° + ф = 163°44'
Так как изображение синусоидальной функции определяется
сравнительно сложной формулой, в данной задаче операторным
методом вычислим, только свободную составляющую тока i1CB, а
принужденную составляющую тока цпр найдем, рассчитав схему
задачи (см. рис. 13.23) после коммутации символическим мето-
дом:
= =
Р Г1 + / ш0 ^"1 *"1 + / “о ^>1
10е'163°44'
— 3 + / 5-103-0,8-10~3
ilnp = 2 sin (w0Z + 110°34') а\ ilnp
= ге7110034' а;
(0) = 2 sin 110°34' = 1,87 а
= 0,4 — 1,87 = — 1,47 а.
Начальное значение свободного тока
йсв (0) = i (0-) - hnp (0)
I
Операторная схема заме-
щения для расчета свободной
составляющей переходного про-
цесса, с учетом ненулевых
начальных значений свободных
токов, вычерчена на рис. 14.16.
По второму закону Кирхго-
фа для первого контура имеем
Рис. 14.16
Li йсв (0) = Лев (р) (G + pLi),
и, подставляя численные значения и вычисляя изображение сво-
бодного тока, находим
Т („\ _ МЬсв(0) _ 0,8.10-3.1,47 1,47
1св w Г1 + р L1 3 + р 0,8.10-3 — р _|_ 3J5.103 ’
По формуле разложения
Чсв= — 1,47 е~3’75-103' а.
Суммирование принужденного и свободного токов определяет
искомый ток:
it = [2sin («»of + 110°34z) — l,47e~3175,103' ] a.
395
Аналогично вычисляем второй ток. Некоторое отличие здесь
будет в связи с равенством нулю принужденного тока:
Поэтому
^2прт
^2пр — 0.
^2СВ (0) = *2 (0) - i (0.) = 0,4 а.
По второму закону Кирхгофа для второго контура (рис. 14.16)
(Р) = /2СВ (Р) =
^2 ^2СВ (0)
4.10-8.0,4
4 4- 4.10-8 р
0,4
р + Ю3 •
+ р L2
По формуле разложения
1*2 — ^2св — 0,4 е и.
14.23. До включения рубильника Р
по цепи проходит синусоидальный ток,
вызванный действием синусоидальной
э. д, с. е = 180 sin (3141 4- 30°) в.
В момент t = 0 включается рубиль-
ник Р (рис. 14.17). Найти выражения
переходных токов, если i\ = 30 ом,
г2 = 60 ом, г3 = 50 ом и С = 80 мкф.
Решение. Вычислим ток и на-
Рис. 14.17
пряжение на конденсаторе при установившемся режиме до
замыкания ключа:
180 е/30°
lm '2m 90 — /314-80-Ю"»
180 е'30“
90 — / 39,8
180е/3°°
98,3 /23°50'
1,83е'33°50'
а;
иСт= -jxciim = -/39,8-1,83е'53’50' =72,8 e”736’10' в\
ис =72,8 sin (3141 — 36°10') в.
Напряжение на конденсаторе при t = 0
ис (0.) = 72,8 sin (— 36°10') = — 43 в.
Составим уравнения по методу контурных токов в оператор-
ной форме:
<!\ + гз) h (Р) — гз (Р) = Е (Р)>
— гз Л (Р) +(^з + r2 Н----рС~) р---’
396
Определим ток /2 (р). Для этого решим последние уравнения
относительно /2 (р):
Up) =
Е (р) с r3 р — ис (0) (fj 4- r3) С
гъ 4- П г3 + г2 г3) Ср + ri + г3
Перепишем его в комплексной форме. Так как в рассматри-
ваемом случае действует синусоидальная э. д. с. е (t), то рас-
чет значительно упрощается, если оперировать с мгновенной
комплексной э. д. с. е (/) == Ете/(Шо/+ф), изображение которой
значительно проще и имеет вид
А . . 180е'30°
p—j314
Для учета ненулевых условий второе слагаемое умножим
на /. Итак, подставив числовые значения, получим
^2т(Р)
-----------во. io-6-50р --
р - /314
(—43)-80-80-10"6
(30 • 60+30 • 50+60 • 50) • 80 • 10- вр + 80
О,72е/зо°Р
(р—/314) • (0,504р+80)
0,276
"* 1 0,504р+80 '
Найдем комплексный оригинал тока. Его можно отыскать
разными путями: при помощи пп. 12 и 4 табл. 14. 1 или при
помощи теоремы разложения. Изберем первый путь:
0,72е/3°° . 0,276
0,504 (р —/314) (р+159) 0,504 (р + 159) ~
= 1,43е/зо°
—/314е'314' — 159<Г1Ж
. —/314—159
1 43в'3°и / .об»
+ /0,548е~159/ = ——----------- е~' • 314е/314/ —159е-159*
—З52е/63°10’
+ /0,548е'159'= [ l,27e'(3l4/+56°50') + 0,646e-18We-/33°10'
+ /0,548е~159'] а = t2 (/).
Искомый ток определится как мнимая часть последнего вы-
ражения:
/2 (0 = Im [/2 (/)] = 1,27 sin (314/ + 56°50') +
+ 0,646 sin (—33°10') е'1Ш+0,548 е-^ =
= П,27 sin (314/ + 56°50') + 0,196 r15W] а.
397
Рис. 14.18
Выражения двух других токов и напряжения на конденса-
торе рекомендуется рассчитать самостоятельно.
При этом для отыскания комплексного оригинала использо-
вать теорему разложения.
14.24. Найти переходные токи в
цепи и напряжение на индуктивности
при замыкании рубильника Р в мо-
мент /=0 (рис. 14.18). Даны:
е «= 100 sin (314/ -|- 60°) в, t\ ~ 25 ом,
г^Шом,г3 = 30 ом и Л=0,1 гн. Задачу
решить операторным методом (при по-
мощи законов Кирхгофа и методом
эквивалентного генератора).
14.25. Цепь схемы, состоящая из
последовательно соединенных ак-
г == 5 ом и индуктивности L =
= 2,5 гн, включается под действие напряжения, изменяющегося
по закону показательной функции и= UQe~at (Uo= 10 в, а =
= 4 сект1).
Определить закон изменения тока в цепи и построить кри-
вую тока.
Решение. Классический способ решения. По второму за-
кону Кирхгофа составляем дифференциальное уравнение для
цепи
L "77 +ri = Uoe~at. (1)
at
ТИВНОГО
Решение его
/ = /пр fCB,
(2)
где /св = Ае
— общий интеграл уравнения (1) без правой
части;
fnp—частное решение уравнения (1).
Найдем /п . Как известно из курса математики, частное ре-
шение рассматриваемого линейного дифференциального уравне-
ния ищется в форме показательной функции:
*пр e Be~at.
(3)
Подставляя это значение в (1), получим
— BLae~at 4- Bre~at = UQe~att
откуда
Up
г—La ’
398
и подставляя в (3), получим
и<>. erat.
г—La
(4)
Переходный ток
Г
i = Ае L ' Ч---------— e~at.
г—La
(5)
Для определения постоянной интегрирования А используем
начальное условие i (0.) == 0:
г—La
отсюда
Таким образом,
i= —Д—( е-“‘ — е L ' =2(е-« — (6)
г—La \ / (
Кривая тока изображена на рис. 14.19.
Ток имеет максимум. Найдем его:
— = 2 (—2е~2' + 4е~4/
dt
Приравнивая эту производную нулю,
получим момент времени t == tm, при ко-
тором величина тока максимальна:
^“2/ 2£~4^,
отсюда
t = — = =0,347 сек
2 2
Подставив это значение в (6), имеем
/ О ( °’693 „—1,386 \ А г
'max = 2 (е —е ) = 0,5 а.
Рекомендуется решить задачу операторным методом: а) при
помощи табл. 14.1; б) теоремы разложения.
14.26. Напряжение, изменяющееся по показательному закону и =
=^U^e~at 10в, а= 2 сект1), включается в цепь схемы, состоящую
из последовательно соединенных активного сопротивления г=2 ом
399
и индуктивности L = 1 гн. Определить максимальное значение
тока, которого он достигнет после включения.
1 14.27. Цепь схемы, состоящая из последовательно соединенных
активного сопротивления г — 2000 ом, емкости С=50 мкф, вклю-
чается под действие напряжения «=100 е“6/ в. Найти законы
изменения тока i и напряжения на обкладках конденсатора ис.
14.28. Цепь схемы, состоящая из последовательно соединен-
ных г= 10 ом и L = 4 гн, включается под действие напряже-
ния «=120 (1—erif) в. Найти выражения для тока и напряже-
ния на индуктивности.
14.29. Цепь схемы, состоящая из последовательно соединенных
активного сопротивления г=104 ом и конденсатора С=50 мкф,
включается под действие напряжения «=120 (1—е-4/) в. Найти
выражения для тока и напряжения на конденсаторе.
ГЛАВА ПЯТНАДЦАТАЯ
РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ МЕТОДОМ
ИНТЕГРАЛА ДЮАМЕЛЯ И СПЕКТРАЛЬНЫМ МЕТОДОМ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. При включении цепи в начальный момент t=О к источнику
единичного напряжения или тока реакция цепи (напряжение нд
Любом ее участке или ток в любой ее ветви как функция вре-
мени) называется переходной функцией k(t) (напряжения
или тока соответственно). При включении цепи к источнику
напряжения переходная функция тока называется переход-
ной проводимостью y(t)\ при включении цепи к источ-
нику тока переходная функция напряжения называется пере-
ходи ычм сопротивлением и обозначается z (t) (см.
табл. 15. 1).
Таблица 15.1
Воздействие Реакция
Ток Напряжение
Единичное напряжение y(t) k(t)
Единичный ток . k(t) z(t)
При включении в момент т источника постоянного воздей-
ствия Fr (например, напряжения с э. д. с. ЕГ = Fr или источ-
ника тока /г = Fr) реакция цепи /(/) [и (/) или i (/)] равна
/(0 = Fr^-x). (15.1)
Переходные функции не зависят от формы и амплитуды
действующих в схеме источников э. д. с. и тока и определяются
самой схемой и параметрами ее элементов.
Примеры:
а) При включении на постоянное напряжение U цепи, со-
стоящей из последовательно соединенных г и L, ток, напря-
401
жение на индуктивности и напряжение на активном сопротивле-
нии равны
/ ______
~—I 1—е т ); uL = Ue х ;
£
где т ==-----постоянная времени цепи.
г
Деля на величину U, найдем, что переходная проводимость
/ * \
1 ( - — I
уЦ) = —\ 1 —с К а переходные функции для напряжения
г
на индуктивности и на активном сопротивлении соответственно
___________________t t
равны k. (t) = е т ; Лг(/) = 1—е 1 .
б) При включении на постоянное напряжение U цепи, состоя-
щей из последовательно соединенных г и С, ток и напряжения
на конденсаторе и на активном сопротивлении определяются по
формулам
t
иг = Ue ,
где ъ — гС—постоянная времени цепи.
Принимая в этих формулах U— 1, получим
Рис. 15.1
__ /
Г u
t _t_
— I — е. х \ kr (/)— е х в
2. Если генератор оказывает в це-
пи воздействие /г(/), зависящее от
времени, имеющее вид ступенчатой
функции (рис. 15. 1, а), то реакция це-
пи может быть рассчитана методом
наложения. При этом ступенчатая фун-
кция представляется в виде наложения
постоянных воздействий FVF2, ...,
начинающихся в моменты времени
соответственно /х, /2, ..как показано
на рис. 15. 1, б.
402
В этом случае реакция цепи для различных моментов вре-
мени определится формулами
f(t) = 0 при t < (15. 2,а)
/(/) = Fiktt—tt) при /j </ < (2; (15. 2,6)
f(f) = Fi k(t — tt) 4- F2 k(t —t2) при t2 < t < t3. (15. 2,b)
/(0 = Fik(t — Q + F2k(t — /2) — F3k(t —t3) при t>t3. (15.2,r)
Пример в задаче 15.9.
3. Если в момент t = 0 включается воздействие ft (/), яв-
ляющееся непрерывной функцией времени (рис. 15.2), то реак-
ция цепи f (0 определяется интегралом Дюамеля по формуле
t
fit) == fv (Q)k(t) + j Л № V — (15.3)
6
где /г (0) — начальное значение воздействия;
[Г (т) = -Г.—обозначение производной воздействия;
dt (=1
k(t—т) — переходная функция, в которой t заменено
на t — т.
В случае, если функция воздействия /г(/) имеет различные
выражения на разных интервалах времени (/г(О=Л.(О ПРИ
0 /г(0=/2(0 ПРИ т0 интервал интегрирования
разбивается на отдельные участки.
t
f (t) = /г (0) k(t) + [ /; (т) k(t—Т) dx при Q<t<tv
L t
f(t)=fr (0) k (t) 4- \ f\ (r)k(t-x) dx 4- J f2^)k(t-x) dz
0 fi
при
Пример в задаче 15.11.
4. Функция воздействия
Д/г (рис. 15.3, а). В этом случае реакцию цепи можно рассчи-
тывать по методу наложения, разложив воздействие на непре-
рывную составляющую /Г1 (ломаная линия 1 рис. 15.3,6.) и
постоянное воздействие Д/г, включаемое в момент скачка
(линия 2 рис. 15. 3, б).
403
< Для примера рис. 15.3
/(/) = 0 при t < О;
/ (О = /г (0) k (f) + i /г W k (t— x)d т при О < t <
о
t
Kt) = fr (0) k а) + f /г t (x) ktt- x)dx + д fr k (t -/j
b
при t > tv
Пример в задаче 15.18.
5. Сущность спектрального представления состоит
заданной функции времени суммой синусоидальных
(15.3а)
в замене
функций
различных частот.
Абсолютно интегрируемая функция времени может быть вы-
числена в виде наложения своих гармонических составляющих
с помощью интеграла Фуръе:
со
f(t) = —F (/“) dw; (15.4)
— с»
Здесь интенсивность спектральных составляющих определя-
ется спектральной плотностью F (ую), которая может
быть вычислена по формуле Фурье:
со
F (/«>) = [ f(t)e~fat dt. (15.5)
Рис. 15.4
Выражения (15.4) и (15.5) называются соответственно обрат-
ным и прямым преобразованиями Фурье.
6. Теорема сдвига (запаздывания). Если известна спект-
соответствующая заданной вре-
менной функции /(/) (кривая 1
рис. 15.4), то для сдвинутой
вдоль оси времени на время
запаздывания т временной
функции /(/ — т) (кривая 2)
спектральная плотность отли-
чается фазовым множителем
и имеет вид e~Ja)XF(ju).
Примеры в задачах 15.22,
15.27 и 15.31.
7. Сравнение формулы Фурье (15.5) с формулой (14.1) пока-
зывает, что для временных функций f (/), отличных от нуля
лишь при А>0, спектральная плотность совпадает с соответ-
ствующим изображением Лапласа, в котором параметр р заме-
нен комплексной частотой /ш. Отмеченное свойство делает воз-
можным применение таблицы преобразования Лапласа для вы-
числения функций спектральной плотности и позволяет для за-
404
ведомо равных нулю при t < 0 временных функций f (t) вычис-
лять их мгновенные значения, пользуясь изложенной в гл. 14
методикой нахождения оригиналов [в том числе и в тех случа-
ях, когда функция спектральной плотности F (/<о) имеет полю-
сы на оси действительных частот ш, и формула (15.4) теряет
смысл].
Примеры в задачах 15.5, 15.22, 15.23 и 15.31.
8. Спектральная плотность F (Jti) реакции цепи [например,
спектральная плотность напряжения U (р) или тока / (/w) про-
извольного элемента цепи] вычисляется по спектральной плот-
ности воздействия Fr (fo) генератора и соответствующей комп-
лексной функции передачи цепи К (J®)
F (/<•>) = К (/<«) FT
(15.6)
Частные случаи комплексной функции цепи: со-
противление передачи Z проводимость переда-
чи У (/<*>)•
Примеры в задачах 15.4 и 15.5.
9. Энергия импульса f (/) пропорциональна интегралу энер-
гии
А = J/2
(15.7)
Интеграл энергии импульса может быть вычислен по фор-
муле Релея, если задана его спектральная плотность F (fo):
Д = u_L | | Р( /(о)|2
тс j
о
(15.8)
Функция квадрата модуля |F (/«>)|2, определяющая плотность
распределения энергии импульса по спектру, называется
энергетическим спектром данного импульса.
Пример в задаче 15.22.
УПРАЖНЕНИЯ И ЗАДАЧИ
15.1. Рассчитать: переходную проводимость у (/) схемы
(рис. 15.5) и переходную функцию k (/) передачи по напряже-
нию. Параметры элементов схе-
мы: гг=2 ком, г2 = 4 ком и _||£_.
С = 1 мкф. 0_, 1—------
Решение. 1) Проводим клас-
сическим или операторным ме- ,, rt Av
то дом расчет тока /,(/) схемы при " ' Ц г'
подключении к зажимам 1 — 1'
в начальный момент t = 0 посто- 01
янного воздействия в виде напряже- 1'
ния U: Рис. 15.5
405
4
— t
Url e V.C =y 1Q-3 /1 ,1 c-750f
rg(''i4-'«) \6 12
Разделив на амплитуду воздействия U, найдем значение пе-
реходной проводимости:
у (^)= Ю-* (1,67 + 0,83 е-750') om~l.
2) Выходное напряжение по закону Ома
ы2 (0 = i2 (0 = U (0,667+0,333 е~750+
Разделив на амплитуду U, получим переходную функцию
передачи по напряжению:
k (t) = 0,667 +0,333 е~79+
15.2. Рассчитать в буквенном виде: переходную проводимость
схемы (рис. 15.6) и переходную функцию передачи по напря-
жению.
Рис. 15.6 Рис. 15.7
15.3. В схеме (рис. 15.7) гх «= г2 «= 5 ком и Сх = С2 = 10 мкф.
Определить переходную функцию передачи по напряжению
и переходную проводимость схемы.
15.4. В цепи, показанной на рис. 15.8, а, действует источник
напряжения с э. д. с. е (/). Вычислить: переходную функцию
k (/) и комплексную функцию передачи К для расчета на-
пряжения на емкости; переходную проводимость у (t) и комп-
лексную проводимость передачи Y для расчета тока
а) д) в)
Рис. 15.8
406
Решение. Переходная функция k (/) численно совпадает с иско-
мой функцией напряжения иСб (0> создаваемого при включении
в начальный момент /=0 единичного напряжения еб = Еб = 1 в
(рис. 15.8, б). Для расчета этого напряжения применим класси-
ческий метод:
Следовательно, переходная функция по напряжению
(О ЧС6 (/) «Сб.пр ЫСб.св ~ г, + г. \ 1 е
1 • ® \
Комплексная функция передачи по напряжению при сину-
соидальном воздействии е = V~2~Ев sin <d t представляет собой
отношение действующих значений комплексного напряжения на
зажимах конденсатора к приложенному, которое может быть
рассчитано символическим методом (рис. 15.8, в):
и так как
то
1
Переходная проводимость y(t) численно совпадает с током
f16, создаваемым в рассматриваемой схеме при включении еди-
ничной э. д. с. еб = £*6 = 1 6 (рис. 15. 8, б):
_ri r2 j _G 4~ г2 ;
4/(0 = 116 (I) = ——е г'ГгС =--------------?---е г'ГгС .
Комплексная проводимость передачи (взаимная проводимость
ветви источника и первой ветви цепи) численно совпадает с
407
комплексом тока /1в при синусоидальной единичной э.д.с. ев =
== ]/*2 Ев sin (о/, Ё9 = 1в:
Рис. 15.9
15.5. В цепи, показанной на
рис. 15.9, а, действует источ-
ник тока i(f). Вычислить: пере-
ходную функцию k(f) и комплек-
сную функцию передачи (/w) для
расчета тока /2; переходное со-
противление z(t) и комплексное
сопротивление передачи Z(/w) для
расчета выходного напряжения
п2.
Решение. Переходная
функция k (/) совпадает численно
со значением переходного тока
i2 *2б в рассматриваемой цепи
при воздействии единичной фун-
кции тока i = i6 = О при t < О
и i = i6 = /б = la при / > О (рис.
15.9,6). Операторная схема за-
мещения для расчета соответствующего тока показана на рис.
15.9,в. Изображение переходной функции
;б (р) j
к (р) = /2б (р) = j = р(г2 Ср+ 1) •
Г2 + "Ср
Переходя к оригиналу, находим
*(0 = »2б(0=
Комплексную функцию передачи получаем, заменив в изобра-
жении переходной функции /< (р) параметр р комплексной частотой
jo) (см. п. 2 основных положений и соотношений гл. 14):
= /<> (/ф Сгг + 1) •
Это же значение можно получить, рассчитав символическим
методом цепь схемы рис. 15.9,а при синусоидальном единичном
408
воздействии (i = iB — /Bsin ш/; IB = la), с учетом, что соот-
ветствующее значение комплекса тока /2 = /2в численно совпа-
дает с комплексной функцией передачи.
Переходное сопротивление z(t) численно совпадает с выходным
напряжением a2 (t) — и2& (/), возникающим в схеме под действием
единичного тока /б = 1а, показанного на рис. 15.9,6. Оператор-
ная схема замещения показана на рис. 15.9,в. Оператор пере-
ходного сопротивления Z(p) численно совпадает с оператором
выходного напряжения U^lp) этой схемы:
г —
Z (р) = t/26 (р) — 16 (р) j = р ^Ср j) .
г*+~сТ
Переходя к оригиналу, с помощью табл. 14.1 найдем пере-
ходное сопротивление:
Подставляя комплексную частоту /ш вместо параметра р в
выражение операторного переходного сопротивления, определим
комплексное сопротивление передачи:
Z = /<»(/о>Сг2+ 1) •
Последнее значение можно получить, рассчитав символиче-
ским методом напряжение цепи (рис. 15.9,a) t/2 = t/2B при еди-
ничном синусоидальном источнике тока i = iB = ]/~2 /в sin vt>t,
IB=la, с учетом численного равенства Z (/ш) = t/2B (/ш).
15.6. Для схемы рис. 15.8,а определить переходную прово-
димость и комплексную проводимость для расчета тока генера-
тора.
15.7 В цепи схемы рис. 15.8,а гх = 1 ком, га = 200 ом и
С = 40 мкф. Определить, при какой частоте модуль комплекс-
ной проводимости, определяющей ток t3, проходящий через кон-
денсатор (взаимной комплексной проводимости ветвей источни-
ка и конденсатора), в раза меньше своего максимального
значения. Рассчитать переходную проводимость для тока 13.
15.8. Рассчитать переходную функцию для тока емкости це-
пи (рис. 15.9,а). При какой частоте модуль соответствующей
комплексной функции передачи в )/2 раз менее своего макси-
мального значения?
15.9. Цепь, состоящая из последовательно соединенных г и
L, включается на прямоугольный импульс напряжения U, дей-
469
ствующий в течение времени t„ (рис. 15.10,а). Найти уравнение
тока i и напряжения на индуктивности uL в зависимости от вре-
мени. Построить кривые I и uL.
Рис. 15.10
Решение. Классический способ. Для интервала времени от
t = 0 до t — tn ток определяется так же, как и в случае вклю-
чения той же цепи на постоянное напряжение U:
(1)
Напряжение на индуктивности
г rfi г, с
U, = L - =s> ив
(2)
Для t > /и напряжение на зажимах цепи равно нулю, поэто-
му по ней пройдет только свободный ток, являющийся одновре-
менно переходным. Протекание его определяется запасом энер-
гии, накопленной в магнитном поле за время от 0 до /и. Итак,
для t > /и, когда и = 0, уравнение второго закона Кирхгофа
п -|- L =* 0.
’ dt
Его решение
Постоянную интегрирования А определим из того, что в момент
/ = tu ток в цепи, содержащей индуктивность, не может изме-
ниться скачкообразно:
отсюда
410
Подставляя это значение А в уравнение; (3), получим урав-
нение тока при
и ( ~Г | ~~~т1
г — - у в 1 у е , (3)
Уравнение для напряжения на индуктивности при £H<J < оо
По уравнениям (1)4- (4) на рис. 15.10,6 построены графики.
Отметим, что в момент t = 0 напряжение на индуктивности из-
меняется скачком на величину, равную U. Скачок напряжения
на индуктивности имеет место и при t ==? /и.
Решение при помощи метода наложения. Прямоугольный
импульс может быть рассмотрен как результат действия двух
постоянных напряжений: напряжения (/, включаемого в момент
/ == 0 и действующего неограниченно долго, и отрицательного
напряжения, равного — U, вступающего в действие в момент
t = /и и также действующего неограниченно долго (рис. 15.10,в).
Итак, для 0< /и ток определяется, как и прежде, по (2).
Для f и оо ток
15.10. Импульс напряжения прямоугольной формы
(рис. 15.10,а) подводится к цепи, содержащей последовательно
соединенные г и С. Найти уравнение тока в функции времени.
15.11. Импульс в форме полуволны синусоиды (рис. 15.11,а)
включается на цепь, содержащую последовательно соединенные
г = 10 ом и L = 0,1 гн,
Т
Уравнение напряжения в интервале времени от 0 до tw =
^(Z) == Um sin w0/ {Um = 10 мв, То = 0,02 сек).
Решение. Задачу решим при помощи интеграла Дюамеля.
В интервале времени имеем
щ (/) = Ums\n о)0/; и\ (т) = (я0итсо$ wot; u1(0) = 0. (1)
y(t) =
У (t — т) =
411
i(t) = и
Ток в этом интервале находим по формуле интеграла Дюа-
меля (15.3):
Рис. 15.11
/
J (O0t/W cos
о
— sin сол-с
_ О)0
-т< (Т'
— е 1 е
COS О)0т б/т*
sin
. L ‘
со о Le
I
<оо£ sin (oo/)g
(3)
— е
о
о
и
1
du =
г
о
t
где г = У>г 4- (<о0 ^)2: tg? = .
* Этот интеграл является табличным, при его взятии используется формула
С a cos bx -I- о sin bx Л
I е°х cos bx dx =---^4-"^-----е
412
• Ток в интервале времени определяем с помощью
интеграла Дюамеля, разбивая интервал интегрирования 0 4-/ на
два участка: первый участок (0 4- /х), где выполняются выраже-
ния (1), и второй участок (/и 4-7), на котором и2(/)= 0 и и'2(ъ) =
= 0:
i(t)=u (O)y(t) + f и\ (y)y(t — С у (t — x) dz ==
г - 1 (
= 0 + I о)о Um cos ш0 т — \1 — е j d'z + 0 =
6
т
— sin<oo/H — e
^0
--- COS <oeT 4” otySin (o0T
L___________•_______e
(—Y, 2
I t J "I* “0
*и
JO
I - Ь
^-1 sin o>oZ„ — ------
r ° ” 4- (ШаП
z/и
si П 0J0/„--
/ . . r , . L и
(r cos <*VH4-(o0L sin <ооги)е
T
Имея ввиду, что (о0/и = <о0—— = к и поэтому sin<oo/H = О,
ш 2
cos <i>q ta = —1 последнее выражение после некоторых упроще-
ний примет вид
ЧО =
Um Sin <Р
г
(4)
Из Выражения (3), полученного для первого интервала вре-
мени для момента t = ток
sin? (l-f-e L и )
Z
То же значение имеет ток, полученный из выражения (2).
Это проверка правильности полученного решения.
По уравнениям (3) и (4) на рис. 15.11, б начерчена (в масш-
табе) кривая тока.
15.12. Импульс напряжения в форме полуволны синусоиды
(рис. 15.11,а) включается в цепь, содержащую последовательно
соединенные г и С. Найти уравнение тока. Даны и = Um sin <о0/,
{/w = 10 мв, То = 0,002 сек, г = 10 ом и С = 50 мкф.
413
15,13. Решить задачу 14.25 при помощи интеграла Дюамеля.
15.14. Решить задачу 14.27 при помощи интеграла Дюамеля.
15,15, Решить задачу 14.28 при помощи интеграла Дюамеля.
15.16. Решить задачу 14.29 при помощи интеграла Дюамеля,
15.17. Цепь, содержащая последовательно соединенные г и
Рис. 15.12
С, включается на напряжение, растущее
по линейному закону и (/) = U <о0/. Найти
уравнения тока и напряжения на кон-
денсаторе.
15.18. Цепь из последовательно со-
единенных г === 100 ом и С = 25 мкф вклю-
чается на импульс напряжения, линейно
нарастающий до момента /и = 2 мсек (рис.
15.12,а). Дано Um = 10 в. Найти урав-
нение напряжения на конденсаторе.
Решение. Переходная функция k (/)
численно совпадает с функцией иско-
мого напряжения на емкости при
включении rC-цепи на единичное напря-
жение и = 1 в (см. стр. 402 пример б п.1
основных положений):
k(t)=\ — e гС = 1—е“400/;
k {t - Т) = 1 - е-400 = 1 - е-400/ e40<h
Для времени и и(0==-^-/ === 5« 103/;
= 5- Ю8.
! !Л du
и' (/) = ---- =
dt
0
По формуле интеграла Дюамеля для интервала времени
>t<tu
t i
Uc (0 = и (0) k (t) + J u' (t) k (t — t) d't = 0 + f 5 • 108 [1 —
<r о
—e~400t e400xl dt = f5 • 103t — 5 • 108 e“40w -^-1 =
L 4UU Jt=o
= (5-108/ — 12,5 + 12,5e-400/) в.
В дальнейшем расчете следует учесть скачок входного на-
пряжения в момент времени /и (спад напряжения от Um до 0).
Для этого представим входное напряжение в виде суммы не-
прерывного напряжения u^t) (ломанная линия 1 рис. 15, 12,6) и
включаемого в момент t„ постоянного напряжения (—Um) (ли-
ния 2). Напряжение
Ы1 (/) = «(/)=/ при 0</</„; u1(t) = Um при t>t„;
414
= -У-У- ,== 5-10® в!сек. при 0 <; t < ta;
dt 1И
«',(0 = ~dt~= 0 при 1 >tu-
По принципу наложения и с помощью интеграла Дюамеля
(15.3,а) находим для
t
uc(t) = ur (0) k (t) + J u\ (x) k(t — v)dx — Umk(t — tK) =
b
*
=0+ f 5• 10s 11 - e~400' a400'1] dz 4- J 0 dz - Um [1 - a-400] =
0 '
Г* 400т Iх
= 5-Ю3т — 5-10se_400'4m- — Ю [1 — е~400(<~'и1 ] =
4UU Jx=s0
= 5 • 103/н — 12,бе-4004- 12,бе-400' — 10 4- Юе-400 I'-'») =
= [5 • 103/и — 10 — 2,5a-400 4- 12,5e~40“ ] e.
Подставляя значение /и = 2- IO"3 сек, находим (для
uc(t) = (_2,5г400-2’10'8 + 12,5)^400/ = 6,94г~400' в,
15.19. Импульс напряжения, приведенный в предыдущей
задаче: Um = 10 в, /и = 2 мсек, подается на цепь из последова-
тельно соединенных г = 100 о и L = 0,2 гн. Найти уравнение
тока.
15.20. На вход дифференцирующей цепи (рис. 15.13,а) по-
дается напряжение u^t), имеющее форму, показанную на рис.
15.13,6. Найти уравнение напряжения uAt) на выходе четырех-
полюсника, если г = 1 ком, С — 1 мкф, и = 100 в и = 4 мсек.
Рис. 15.13
Рис. 15.14
15.21. Найти уравнение выходного напряжения u2(t) (рис.
15.14), если на вход подается линейно растущее напряжение
(/)=== а
415
15.22. Рассчитать спектральную плотность входного напря-
жения и (/), график которого показан на рис. 15.15,а. Вычислить
энергетический спектр входного напряжения.
а)
Рис. 15.15
Решение. Вход-
ное напряжение име-
ет вид ступенчатой
функции, сохраняющей
постоянное значение
при t -> оо. Поэтому
интеграл Фурье (15.5)
для этой функции рас-
ходится и вычисление
спектральной плотно-
сти будет проведено
заменой на комплекс-
ную частоту параметра
р в соответствующем
изображении Лапласа
ступенчатой функции
показанной на
рис. 15.15,6, и последу-
ющим сдвигом к исход-
ной ступенчатой функ-
ции.
Изображение функ-
ции по Лапласу (рис.
15.15,6)
соответствующая ,спек-
тральная плотность
Спектральная плотность входного найряжения «(/), сдвину»
того по времени на —5 мксек относительно напряжения их (I),
определяется по теореме сдвига:
и Цш) = I и = t/i (» I0”) e '2
(0
где = (1); Ф(®)-----v +5‘10-ey>. (2)
|ш| 2
416
Энергетический спектр определяется функцией
|£/(/“)|2 =-^- (3)
V1
Графики амплитудно-фазовой спектральной характеристики
и энергетический спектр входного напряжения построены по
уравнениям (1)4-(3) на рис. 15.15, в, г, д.
15.23. Рассчитать спектральную плотность прямоугольного
импульса тока «(/), показанного на рис. 15.16, а.
Решение. Расчет проведем двумя способами!
1. По формуле Фурье (15.5)
со (и
I (у») 1I (/ф) | = j I (0 dt = J Ime~la>t dt =
—со О
14 Заказ № 624
417
со/
I \ / и
— S1 n ( ш*и \ e ? .
- О 1 1 1 l Л I v ,
CD \ Z /
2. На рис. 15.16, б показано разложение импульса тока на
две ступенчатые составляющие тока с амплитудами 1т и —1т.
Изображение по Лапласу первой составляющей и соответствую-
щая спектральная плотность, соответственно равны
Л(Р)=-^; Л •
р
Спектральная
ремы сдвига
Спектральная
плотность второй составляющей с учетом тео-
/2 (/«>) = —
1т “'“'и
/(D
плотность импульса суммарного тока
АО) + АО) = А (1 - е~/ш'и) =
/<о
-/“'и
2/\
=—— sin—— \е
ID \ 2 /
На рис. 15.16, в и г построены графики амплитудно-фазовой
спектральной характеристики суммарного тока На рис. 15.16, в
1 77- X
по оси ординат отложено -г-~.— /(/со) .
15.24. Рассчитать спектральную плотность входного напря-
жения и (/)=0 при t < 5 мксек, и (/) = 100 sin [о>0 (/ — 5 • 10“6)] в при
t^b мксек, = рад/сек (рис. 15.17). Построить графики
амплитудно-фазовой спектральной характеристики входного на-
пряжения.
Рис. 15.17
Рис. 15.18
15.25. Рассчитать спектральную плотность напряжения теле-
графной посылки «(() = 50 sin «>0/ при и u(t) — 0
при <оо/ *< 0 и >> 4тс (рис. 15.18), о)0 = 2- 10s рад/сек Построить
графики амплитудно-фазовой спектральной характеристики.
418
Указание. При решении удобно рассматривать заданный импульс в
виде синусоидального напряжения, начинающегося в момент t = 0, и наклады-
вающегося на него такого же отрицательного синусоидального напряжения, но
4п
начинающегося в момент, равный ------, для чего использовать теорему сдвига.
ш0
15.26. Рассчитать спектральные
плотности двух импульсов u^t) и
w2 (/), составленных из отрезков си-
нусоиды и показанных на рис. 15.19,
а и б.
15.27. Вычислить комплексный
коэффициент передачи K(j<*>) иде-
альной линии задержки, обеспечи-
вающей сдвиг входного импульса
на время задержки т = 0,5 мксек.
Амплитуда входного импульса
уменьшается при прохождении ли-
нии задержки в 100 раз (на 40 дб).
Решение. Обозначим функ-
цию входного импульса Д (/). По
условию задачи функция выходно-
го импульса /2(Д удовлетворяет
уравнению
/г (О =
100
А (/
a)
Рис. 15.19
Если (j (d) — спектральная плотность
входного импульса, то спектральная плот-
ность выходного импульса F2(ju)
р2 а «о = e~lun л а ч
Таким образом, комплексный коэффициент
передачи исследуемой линии задержки
—/(ОТ — /0,5-10~всо
О Q
= юо = Гбо •
Модуль и фазовый угол коэффициента
передачи построены на графиках рис. 15.20.
15.28. Определить комплексный коэффициент передачи иде-
14*
419
ального дифференцирующего фильтра, осуществляющего опера-
цию
«2(0 = 0,1-^-,
2 ' dt
где ur(t) — функция входного напряжения;
(0— функция выходного напряжения.
Указание. Дифференцированию оригинала соответствует умножение
изображения на параметр р = / ю.
15.29. Вычислить комплексный коэффициент передачи опера-
ционного фильтра, осуществляющего преобразование входного
напряжения их(0, по формуле
t
(0 = aut (0 + b —1 — + с f ur (0 dt.
dt J
—00
Указание. Интегрированию оригинала соответствует деление изображе-
ния на параметр р = j ю.
15.30. При воздействии на схему ступенчатого напряжения
«! = 0 при t <0 и «х = 100 в при />-0 выходное напряжение
изменяется по закону ы2(/) = 50(1—е~500/)в. Вычислить комп-
лексный коэффициент передачи.
15.31. На вход rC-цепи подается импульс напряжения в
виде равнобедренного треугольника (рис. 15.21, а) продолжитель-
ностью имеющий амплитуду U. Найти спектральную фун-
Рис. 15.21
420
кцию выходного напряжения U2 (j и) на емкости. Построить гра-
фик модуля спектральной функции | U2 (j <о) |, если U = 20 в,
г = 100 ом, С = 1 мкф, /и = 1 мсек.
Решение. Спектральная функция выходного напряжения —
реакции цепи (см. п. 8 основных положений и соотношений)
{/.</<"> = = ТТт' - (1)
где U1(j о>) — спектральная функция заданного напряжения (воз-
действия); Z(/ o>) = г Н-----------!----сопротивление цепи
j О) С
в спектральной форме.
В целях упражнения (/<*>) найдем двумя способами.
Способ 1. Заданное напряжение может быть представлено
в виде наложения трех прямых (рис. 15.21, а): 1 — начинающей-
ся в момент t = 0 и действующий неограниченно долго; 2 —
имеющей отрицательный наклон, а крутизну, в два раза боль-
шую, чем прямая /, но начинающуюся в момент и 3 — име-
ющей такой же наклон, как и прямая /, но начинающейся в
момент /и; прямые 2 и 3 также действуют неограниченно долго.
Уравнение прямой
Соответствующие
14.1) и спектральная
1 напряжения
/А <
*и
ему изображение по Лапласу (п. 3 табл,
плотность
гч 2U тга х 2U
U(P) = Т~Т’ и^=гг~^
*иР ta (/со)
Спектральные плотности прямых 2
сдвига запишутся аналогично.
Спектральная плотность суммарного
пряжения
2С/
/иша
и 3 с учетом теоремы
импульса входного
на-
-/с^и
4U -----—
----е
ri \
Г дСО СО
Г ~/Ю'и
2 —(1+СО8ш(и — /sino)fH)
2U
2<
г>. 2
СО^р» СО£м
—~ COS--------
2 2
4U
cos
-/ю<и
(О I тя \ 9
— е
\ /<о/и
Д-1е~
(2)
2(7 —/
-------Q У И =5
/и СО2
421
Способ 2. Найдем спектральную функцию входного напряже-
ния путем использования формулы Фурье (15.5). Для этого за-
пишем уравнение импульса:
u(t) —------1 при <——,
•и 2
«(/) =-----— t 4- 2U при
ги 2
Подставляя u(t) в (15.5) и учитывая, что функция входного
напряжения в пределах от —°° до 0 и от/й до +<» равняется
нулю, будем иметь
4-00 2 'и
^1(7“) = J u(t)e~lwtdt = J -у te~latdt + f “у z +
0 Jn
2
+ 2U) e~ia>l dt.
Проинтегрировав, получим то же выражение (2).
Подставляя (2) в (1), найдем
где
tg ф (о)) = о)Сг, ф ((d) = arctg со Сг.
По этому уравнению на рис. 15.21,6 построен график модуля
спектральной функции. В точке (d = 0 модуль равен 10e-cezc.
Модуль равняется нулю в точках = (k — целое поло-
жительное число). Первый нуль (k == 1) будет в точке (d=— =
= 4к«103 сек~1, это соответствует частоте f = —— = 2000 гц =
= 2 кгц.
15.32. Определить спектральную функцию U2(j<s>) выходного
напряжения, если на вход LC-цепи (см. рис. 15.14) подается
линейно растущее напряжение и, (/) = U^t.
ГЛАВА ШЕСТНАДЦАТАЯ
ОСНОВЫ СИНТЕЗА
ЛИНЕЙНЫХ ЦЕПЕЙ
ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ
1. Задача синтеза—нахождение схем электрических цепей й
величин входящих в них элементов по известным частотным или
временным свойствам цепей.
В данной главе рассматриваются вопросы построения элект-
рической цепи двухполюсника по заданному уравнению F (р),
выражающему его частотные свойства. '
Функция F (р) комплексного переменного (комплексной часто-
ты) р = о +/о> может быть комплексным коэффициентом пере-
дачи К(р), комплексным сопротивлением Z(p) или комплексной
проводимостью Y (р) некоторой пассивной электрической цепи
с сосредоточенными параметрами.
Функция F (р) может быть реализована в виде электрической
цепи с сосредоточенными параметрами при условии, что она
является дробно-рациональной функцией:
Р (и) = Л М = апРП + ап~1РП"1 + - - • + flip + Др
W В (р) ЬтРт + Ьт~1Рт-1 + . . . + Ь1Р 4- Ьо
= н ^Р PQ*) ’ * ’ (р Р°п^ (16 1)
(Р~ Ppi) • • • (Р — Ррт)
у которой коэффициенты ak и bk — положительные и действи-
тельные числа, причем все полюсы pk = apk 4- j(ppk лежат в ле-
вой части комплексной полуплоскости (т. е. apk 0), в том числе
могут быть простые (не кратные) полюсы, лежащие на мнимой
оси (т. е. ppkz=ja)pk). Для функции передачи К(р) нули могут
лежать и в правой полуплоскости.
Функция цепи, не имеющая нулей в правой полуплоскости
комплексного переменного р, называется функцией мини-
мальной фазы.
423
2. Положительной действительной функцией
(п. д. ф.) называется такая функция F (р), которая удовлетворяет
двум условиям: 1) ее действительная часть положительна при
положительных значениях действительной части р (условие по-
ложительности); 2) она действительная при действительных (не
комплексных) значениях р (условие действительности).
Входная функция F (р) пассивной электрической цепи —
входное сопротивление Z (р) или входная проводимость Y (р)
есть п. д. ф.
Необходимое и достаточное условие возможности реализации
рациональной функции F (р) (16.1) в виде входной функции не-
которой пассивной цепи заключается в одновременном выполне-
нии следующих требований:
а) все коэффициенты ak и bk полиномов Л(р) и В(р) должны
быть положительными;
б) наибольшие степени р в Л(р) и В(р) не могут отличаться
более чем на единицу; то же и в отношении минимальных сте-
пеней р;
в) в правой полуплоскости F (р) нет полюсов, т. е. все
полюсы лежат в левой полуплоскости, в том числе могут быть
полюсы на мнимой оси; если на мнимой оси имеются полюсы,
то они могут быть только простыми (не кратными) с действитель-
ными положительными вычетами.
Замечание. Напомним, что вычет функции F (р) = в простом
полюсе pi вычисляется по формуле
[Res F (р)]^ = [(р - Pl) F (р)]р=/>1 = = , (16.2)
р Pl
где В' (р) — производная от В (р) по р;
г) нули уравнения Л(р) = 0 лежат в левой полуплоскости,
а если имеются нули, расположенные на мнимой оси, то они
могут быть только простыми (не кратными);
д) действительная часть функции F (р) на мнимой оси (при
р = /ш) неотрицательна.
Пример в задаче 16.1.
3. Синтез реактивных двухполюсников (т. е. двухполюсников,
состоящих только из индуктивностей и емкостей). Функции со-
противления ZLC (р) и проводимости Ylc (р) таких двухполюс-
ников называются реактивными функциями. Нули и
полюсы реактивной функции простые и лежат на мнимой оси
/ф, взаимно чередуясь. Значения реактивной функции F (/<в) на
мнимой оси /ш являются чисто мнимыми и возрастают в точках
dF (j<a) . n
непрерывности с ростом частоты ~ > °*
424
Простым признаком реактивной рациональной функции явля-
ется то, что либо полином числителя четный (а0 + а2р2 +
+ а4р4 +...), а полином знаменателя нечетный (&хр + Ь3р3 +
+ ^бР5 + • • •)> либо наоборот.
Функция реактивного сопротивления может быть разложена
на простые дроби в виде
п
z^ip) = k„p + + X , (16.3)
р “Г
/=1
где Аоо — вычет функции ZLC(p) в полюсе р= оо;
kQ — вычет в полюсе р = 0;
Л/ — вычет в полюсе pz = /«>z .
Схема реализации функции ZLC (р) имеет вид первой формы
Фостера (рис-. 16.1, а)—последовательное соединение параллельных
LC-контуров. Ее элементы находятся по формулам
Это следует из того, что в операторной форме индуктивное
т к 1
сопротивление записывается в виде pL=k<x>pt емкостное-----=
рС
kn
= —, сопротивление параллельного контура, состоящего из
р
Lt и Ch равно
(1646)
Функция реактивной проводимости может быть разложена на
простые дроби в виде
Ylc (Р) = k'«> Р +
2k\ р
(16.5)
где ka> и ko—вычеты функции Y(р) соответственно в полюсах
р = оо и р=0;
k\— вычет в полюсе pz
Схема реализации имеет вид второй формы Фостера (рис.
16.1,6)—параллельное соединение последовательных £С-ветвей.
Ее элементы находятся по формулам
_ 1 . г _ h'. , _ 1 . п _ 2fe,'
(16.6а)
425
Это вытекает из того, что в операторной форме индуктивная
1 *0
проводимость имеет вид------=-----, емкостная проводимость
, Ph р
pCt = k„p, а проводимость последовательно соединенных эле-
ментов Lt и Ct равна
Рис. te.l
Рис. 16.2
Две другие формы реализации могут быть получены путем
разложения заданной функции сопротивления (или проводимости)
в непрерывную дробь, начиная деление с высших (или с низших)
степеней р. Соответствующие схемы реализации имеют вид цеп-
ных (лестничных) схем, соответствующих первой (рис. 16.2, а) и
второй (рис. 16.2, б) формам Кауэра.
Пример в задаче 16.5.
4. Синтез двухполюсников, состоящих из активных сопротив-
лений и емкостей.
Особенности функции ZrC(p):
а) высшая степень полинома числителя меньше или равна
высшей степени полинома знаменателя;
б) все полюсы и нули расположены на отрицательной веще-
ственной полуоси и взаимно чередуются, причем ближайшим к
началу координат является полюс (он может, в частности, на-
ходиться и в начале координат).
Особенности функции Yrc (рУ
а) высшая степень полинома числителя больше или равна
высшей степени полинома знаменателя;
426
б) полюсы и нули расположены на отрицательной вещест-
венной полуоси, причем первым является нуль.
Функция сопротивления Zrc (р) может быть разложена на сле-
дующие простые дроби:
Zrc (р) = к» +
п
/=1
(16.7)
где kM, k0 и kt — вычеты функции Zrc(p) в бесконечно удален-
ной точке (в полюсе р = <»), в начале коор-
динат (в полюсе р = 0) и в полюсах — az.
Схема реализации функции Zrc (р) по (16.7) имеет вид первой
формы Фостера (рис. 16.3, а) — последовательное соединение
параллельных г С-контуров. Ее элементы вычисляются по формулам
(16.8а)
Рис. 16.3
Это вытекает из того, что в операторной форме активное
сопротивление выражается действительным числом гт = Л», ем-
1 k0
костное сопротивление ----= ——, а сопротивление параллель-
рС0 р
ного контура, состоящего из г, и С, , равно
Р + °i
(16.8 б)
Аналогично функция проводимости YrC (р) может быть раз-
ложена на простые дроби
уrc (Р) = *« Р + *0 + S 7^7- > (16.9)
/=1
где k'a, k'o и ^ — вычеты функции — Угс(р) в полюсах р= «>,
р = 0 и р = —aj .
427
Схема реализации функции YrC (р) по (16.9) имеет вид второй
формы Фостера, показанной на рис. 16.3,6 — параллельное сое-
динение последовательных rC-ветвей. Ее элементы определя-
ются по формулам
1 1 k-
rt = ±;C„ = ka-, G =(16.10а)
Это следует из того, что в операторной форме активная прово-
димость — = k' есть действительное число, емкостная прово-
г0
димость записывается в виде рС«> — pkm, а проводимость ветви,
состоящей из последовательно соединенных элементов г, и Ct,
равна
1 Г, Р
yt(p) =------Ц— = —=...................., • (16.106)
Г/ +---- Р +---------- Р +
1 pCi Г fit
По аналогии с LC-цепью можно получить две другие формы
реализации путем разложения заданной функции сопротивления
ZrC (р) [или проводимости Yrc (р)] в непрерывную дробь, начиная
деление с высших или низших степеней р. Схемы реализации
имеют вид цепных (лестничных) схем, соответствующих первой
(рис. 16.4, а) и второй (рис. 16.4, б) формам Кауэра.
Пример в задаче 16.7.
Рис. 16.4
5. Синтез двухполюсников, состоящих из активных сопро-
тивлений и индуктивностей.
Особенности функции ZrL (р):
а) высшая степень полинома числителя больше или равна
высшей степени полинома знаменателя;
б) полюсы и нули расположены на отрицательной вещест-
венной полуоси и чередуются, при этом первым к началу ко-
ординат расположен нуль; в начале координат может распола-
гаться только нуль, в бесконечности может быть только полюс.
Свойства функции YrL (р), очевидно, обратны свойствам функ-
ции ZrL (р).
Функции ZrL (р) и YrL (р) могут быть разложены на простые
дроби:
428
ZrL (P) = k№p + k0+ 2
YrL (P) = k„ +
(16.11)
(16.12)
где km, k0 и kt — вычеты функции, — Ztl (p\,
k'n, k'o и — вычеты функции YrL (p) в точках
= 0 и p = — а, либо р — — Ct.
р— со, Р =
Схемы реализации по формулам (16.11)
и (16.12) имеют вид соответственно пер-
вой ,и второй форм Фостера и показаны
на рис. 16.5, а и б. Их элементы вычис-
ляются по формулам
г, = /г4;
_ ki
°1
(16.13а)
(16.14а)
Рис. 16.5
Это следует из того, что сопротивление ветви, состоящей
из параллельно соединенных элементов rt и Lif равно ’
kip
р + ъ
(16.136)
Проводимость ветви, состоящей из
ненных элементов rt и Lz, равна
последовательно соеди-
1
(16.146)
^0
P
Следует заметить, что функция сопротивления двухполюс-
ника из элементов r-L аналогична функции проводимости
двухполюсника из элементов r-С, а функция проводимости
двухполюсника из элементов r-L аналогична функции сопроти-
вления из элементов г-С.
429
Разлагая функцию сопротивления ZrL (р) (проводимости УГ£ (р)
в непрерывную дробь, начиная деление с высших или низших
степеней р, можно получить схемы Кауэра (рис. 16.6).
Пример в задаче 16.9.
6. Синтез двухполюсников, состоящих из активных сопро-
тивлений, индуктивностей и емкостей. Реализация двухполюсни-
ков общего вида возможна одним из следующих методов:
1. Выделение из Z(p) чисто мнимых полюсов (если они име-
ются) и реализация их в виде последовательного соединения эле-
ментов цепей без потерь, т. е.
К
П
z (р) = р + -^- + У -^ Р + Zl (р). (16.15)
р “ р2 4-
1~1
Первые два слагаемых и S реализуются в виде реактивных
элементов, показанных на рис. 16.7, а. Далее, если функция
Zx(p) имеет нули на мнимой
Рис. 16.7 Этот этап реализации по-
казан на рис. 16.7, б.
Если Z2 (р) имеет полюсы
на мнимой оси, то они вновь выделяются по аналогии с
предыдущим (см. ф-му 16.15). Наконец, в результате будет полу-
чена функция, не имеющая полюсов и нулей на мнимой оси. Такая
функция называется функцией минимального реактив-
ного сопротивления (или минимальной реактив-
ной проводимости). Если нули и полюсы этой функции
лежат на отрицательной вещественной полуоси, то они реали-
зуются в виде элементов r-L и (или) г-С.
Пример в задаче 16.11.
оси, то их выделяют из функ-
ции проводимости Ух (р) в виде
1___
Z2(P) '
2Л, р
(16.16)
430
2. Реализация путем разложения заданной функции в непре-
рывную дробь.
Примеры в задачах 16.13 и 16.14.
Существуют и другие способы реализации, рассматриваемые
в специальной литературе по синтезу электрических цепей (на-
пример: Н. Балабанян. Синтез электрических цепей. Гос-
энергоиздат, 1961).
УПРАЖНЕНИЯ И ЗАДАЧИ
16.1. Проверить положительность и действительность функ-
ции
F(p) =
ра + р + 1
Р2 + Р + 4
Решение. Заданная функция рациональна. Она будет по-
ложительной и действительной, если выполнятся пять требова-
ний, указанных в п. 2 основных положений и соотношений.
Проверим это. Условие а) выполняется, так как все коэффици-
енты ak и bk положительны. Пункт б) также выполняется, так
как наибольшие и соответственно наименьшие степени р в чис-
лителе и знаменателе одинаковы.
Для проверки условия в) выясним расположение полюсов
F (р). Сначала найдем их, приравнивая знаменатель F (р) нулю:
Р2 4~ Р + 4 = О,
отсюда
р12 = — 0,5± /0,5/15 ,
т. е. полюсы лежат в левой полуплоскости, что соответствует
выполнению условия.
Проверим выполнимость условия г). Для этого найдем кор-
ни числителя р2 + р 4- 1 = 0:
Pi.2 = -0,5 ±/ГО.75,
т. е. нули F (р) лежат в левой полуплоскости, что соответст-
вует выполнению условия.
Наконец, проверим выполнимость условия д). Для этого
найдем выражение F (р) на мнимой оси (т. е. при р == /о>) и оп-
ределим его действительную часть
[F (р)]Р=/«, = F(/<o) =
Р2+р+1 ”| —ю2+/о> -|- 1
Р24-р+4 Jp=/o) —а)24-/(0 4" 4
__ (1 (О2 4~ /о>)(4 — <о2 /О)) (со2 — 2)2 4“ /3<О
(4 — со2 4~ /со) (4 — (О2 — /со) (4 — со2)2 (О2
Отсюда видно, что действительная часть этого выражения
при любых со положительна, т.е. условие д) тоже выполняется.
431
Итак, выполняются все пять условий, следовательно, заданная
функция F(p) является п. д. ф.
16.2. Проверить положительность и действительность функ-
ций
22р2+46р+45
* = 44р2+48р+54
Р(п\ — 2Р8+8Р
Г I О'/
2
16.3. Показать, что функции a) F (р) = и б) F (Р) =
Зр
__ . пе являются положительными действительными
Р "Г *Р ~г 1
функциями.
16.4. Показать на комплексной плоскости полюсно-нулевое
изображение функций
а)/(р)= р(р2 ^tp +1) ’ б) 7?(р) = (р+1) (р+2) (р+З) ’
в) F(P) = (р4-1)(р^+р4-1) и г) = Р4 + 5р2 + 4
и указать, какие из них являются п. д. ф., а какие таковыми
не являются.
16.5. Осуществить реализацию функции сопротивления
7(гл 8р4+40р2+32
{Р) 20р3 + 45р
разложением на простейшие дроби и разложением в непрерыв-
ную дробь.
Решение. Заданная функция представляет собой отноше-
ние четного полинома к нечетному, поэтому она является ре-
активной функцией (см. п. 3 основных положений и соотноше-
ний).
Решим задачу разложением на простейшие дроби (16.3). Для
этого найдем корни знаменателя:
20р3 + 45р = 5р(4р2 + 9) = О,
отсюда
Pi = 0; р2,з = ± •
Так как высшая степень полинома числителя больше выс-
шей степени полинома знаменателя, то путем деления числите-
ля на знаменатель, начиная с высших степеней р, выделим
слагаемое kwp\
8 р4 + 40 р2 + 32 20 р3 + 45 р
8р4 + 18р2 2
22 р2 + 32 5 р
432
Таким образом,
через
22р2+32
20р34-45р ‘
полученном выражении второе слагаемое, обозначаемое
Zx(p), разложим на простые дроби:
7 , ЗОр2 +32 __ k0 , 2^р
2
1
Z(p) =
5
(1)
20ps+45p p
Р
2kip
45
20
(2)
2_ 45 9
0)1 20 “ 4 *
Определим k0 — вычет функции Zx(p)
мечание в п. 2 основных положений):
Г 22р2+32 ’
где
в точке pj = 0 (см. за-
k0 = Res [Z^^o =
32
_ . 3
Вычислим — вычет Z1 (р) при р — р2 = / ----корень зна-
менателя последнего слагаемого в выражении Zx(p):
= [Res Zx(p)] з
p=iT
! з \2
22 / -s-!
/ 3 \2
60 / -тг-
36 •
. з
р=/т
Той же величине равен вычет Zt(p) при сопряженном
. 3
значении корня р = р3 — — j .
Учитывая найденные значения kQ и k19 окончательно из (1)
и (2) получим разложение выражения заданного сопротивления
в виде суммы простых
32
45
Р
Z(p) = -5
дробей:
36
18
5 н 1 45
32 р
(3)
собой индуктивное сопро-
2
тивление, индуктивность которого равна ,
ное сопротивление, емкость которого равна
Первое слагаемое представляет
второе — емкост-
45
32 ’
81
параллельное соединение индуктивности -jj- и
а третье —
18
емкости —
433
[см. (16.4,а)]. На рис. 16.8,а приведена схема, составленная
на основе формулы (3)—первая форма Фостера. Все величины
L и С в гн и ф (в ряде случаев расчеты ведутся в нормали-
67
, 2 45
О) i 32 Г^1 5)
Рис. 16.8
зованных величинах, тог-
да L и С величины без-
размерные).
Осуществим разложе-
ние на простейшие дроби
функции проводимости:
_ 20р34-45р
— 8р<+40р2+32 ’
Найдем корни знаменателя этого выражения:
8р4 + 40р2 + 32 = 8(р2 + 1) (р2 + 4) = О,
отсюда
Р1.2 = ± /, Рз.4 = ±/2.
Так как наибольшая степень показателя числителя при р в
выражении У(р) меньше наибольшей степени показателя р в
знаменателе, то при разложении по (16.5) нет слагаемого k„ pi
й0
нет и слагаемого —- , так как знаменатель У(р) не содер-
жит множителя р; в разложении будут только слагаемые вида
2k't(p)
р2 4- ш2
Итак,
V - 2°Ра+45Р 2k'iP и- ш
w 8р*+40р2+32 р2+1 "*"р2-|-4' w
/
Найдем k\ — вычет У(р) при р = рх = j (он такой же и при
Р2 = — /):
k\ = [Resy(p)]p=/ =
20р3 + 45р
32р3 4- 80р
_ 20(—/)34-45/ _ 25
„=/ ~ 32(-/)34-80/ ~ 48 •
Аналогично вычислим — вычет
вычет и при р = — /2):
У (р) при р = /2 (такой же
k2 = [Res У (р)1Р=/2 =
’ 20р3 4- 45р _ 20(-j2)34-45-/2 _ 35
. 32р’4-80р ]р=/2 — 32(—/2)34-80-/2 “ IS- ’
Г 9
Подставляя найденные значения k\ и k% в (4), получим
25 35
24 р 24 р
р24-1 р2 + 4 *
(«)
434
По (16.6 а) находим элементы первой параллельной ветви,
состоящей из последовательно соединенных
о 25
, _ 1 _ 1 _ 24 р _ 2ft| __ 48 25
1 ~ 2fe: ~ 25 1 «>? ~ 1 ~‘2Г’
z’ 48
и второй параллельной ветви, состоящей из последовательно
соединенных
9 35
r _ 1 1 _ 24 р _ 2*2 _ 2 48 35
а~ 2*2 “ 9 35 35 ~ 4 = 96 *
z ’ 48
На основе полученных результатов на рис. 16.8, б дана
схема, соответствующая уравнению (5)—второй форме Фостера.
Осуществим реализацию заданной функции Z(p) разложе-
нием ее в непрерывную дробь. Здесь можно идти двумя путями.
1) Осуществим деление, начиная с высших степеней р. Для
этого поступим так: делим числитель на знаменатель, получим
первое слагаемое, остановимся. При этом высшая степень р ос-
татка числителя станет на два ниже, чем была, и на единицу
меньше, чем высшая степень знаменателя. Далее делим дели-
тель на этот остаток и т. д., пока процесс деления не закон-
чится без остатка. Результат каждого деления обведен рамкой:
8р4 +40р2+32
8р4 + 18 р2
20 р3 4- 45р
20р3 + 45 р
20р3 + Р
22р2+32^ р
175
тг~р
175
ТГ Р
_____32
175
352 р
242
175 Р
Таким образом, непрерывная дробь имеет вид
Z(p) = -g- р 4 jg I
11 Р + 242 1
175 Р+ 175
352 р
(6)
43S
2
где ------индуктивность;
О
10
----емкость;
242
175
— индуктивность;
----емкость, что видно из конструкции выражения Z(p).
Формуле (6) соответствует схема рис. 16.9, а—первая форма
Кауэра. Все величины L и С соответственно в гн и ф.
Рис. 16.9
2) Осуществим разложение Z(p) в непрерывную дробь,
начиная деление с низших степеней р (результат каждого де-
ления обводим рамкой):
32 -|- 40p2-j-8p4
45р+20р3
45р
45р + 20р3
ЛЕ I 405 О
4бр + -29Р3
232 2 , о 4
-д-р2+8р4
232 2,04
—р2+8р4
175 о
29 Р
6728
1575 р
175
232 р
О
Следовательно, получена следующая непрерывная дробь:
2 (Р) “ 45 р + 405 1 ’
232 р + 6728 , 1
1575 р’ 175
232р
436
индуктивность;
45
где —--------емкость;
232
405
1575
-6728---емкость;
232
—175----индуктивность.
Формуле (7) соответствует схема (рис. 16.9, б)—вторая фор-
ма Кауэра.
16.6. Осуществить реализацию реактивных функций:
а) ад - ,
б) Z (р) = —,
' р(р +4)
в)
71п\ _ (р2+1)-(рЧ-9)
(Р) ~ р (р2+4)
(р2+1)(р2+9)
Р (р2+4)
разложением на элементарные дроби и в непрерывную дробь.
16.7. Найти схемы по формам Фостера и Кауэра, реализу-
ющие функцию входного сопротивления Z(p) = (р-РЗ) ’
Решение. Из выражения данной функции видно, что она
определяет цепь, состоящую только из элементов г и С, так
как все ее полюсы и нули чередуются и лежат на отрицатель-
ной вещественной полуоси, при этом функция сопротивления
первым имеет полюс, а не нуль (см. п. 4 основных положений
и соотношений).
Решим задачу методом разложения Z(p) на элементарные
дроби (см. ф-лу 16.7). Вначале из Z(p) выделим постоянную вели-
чину kco, не зависящую от р и равную:
kco — 1 i 1П Z (ftyp.+ao —
p2+6p+8\
p2+4p-|-3/
Затем, вычтя ее из Z(p), получим
Zt(p) = Z(p)—l =
p2+6p+8 1 2p+5
p4+4p + 3 1 ~ p* + 4p+3 ' *
В рассматриваемой задаче в формуле (16.7) kQ = 0, так как
функция Z (р) не имеет полюса при р — 0.
Итак, согласно (16.7)
kl kn
Z(p) = k„+ yp- +
(la)
437
Найдем — вычет функции Zt(p) при р — — 1:
/ 2p-j—5 \ 3
kx = [Res Z1(p)]p==_1 = р_^_з ур=_! == •
Аналогично вычислим k2—вычет функции Zt(p) при р=—3:
/ 2р+5 \ 1
^2 ~ [Res ^1(р)]р=—3 “ p_|_f 3 ~2~ *
Итак, искомое сопротивление
3 1
2(Р) 1 + р+1 + р+з •
(16)
Первое слагаемое — активное сопротивление, равное 1; вто-
рое слагаемое представляет собой параллельно соединенные
активное сопротивление и емкость, вычисляемые по (16.8а):
з
2
Аналогично определяем элементы третьего слагаемого:
3 — 6 I ^2—
= 2.
Таким образом, уравнение (1 б) представляет собой три по-
следовательно соединенные цепочки, первая из которых — ак-
тивное сопротивление, а каждая из двух остальных—параллель-
ное соединение г и С. Схема реализации изображена на
рис. 16.10, а (первая форма Фостера). Все величины г и С со-
ответственно в ом и ф (если расчеты ведутся в нормализован-
ных величинах, то г и С безразмерные).
3
2
Ф I
Z(p>
2
3
Рис. 16.10
>438
Вторую форму Фостера получим путем разложения по (16.9>
на простые дроби выражения проводимости У(р), умноженной
на —
Р wm - (р+Шр+З) = р2 + 4р + з .
р w р(р+2)(р+4) р8+6р2+8р
1 Л. Aq
= + + (2Л
Выражение (2а) в соответствии с (16.9) не содержит слагае-
мого km, так как Y(p) не имеет, полюса при р= оо.
Вычислим коэффициенты ko, k\ и k%.
ko = Res — Y(p) ₽=o = ( 3^ i2p + 8 l=o = T ’
o 1 \7/ J / P2 + 4p + 3 \ 1
Res V y(P^Jp=_ 2 — 3p2 + 12p + 8 Jp=-2 “ 4 ’
Подставляя найденные значения ko, ki и k% в (2a) и умно-
жая обе части равенства на р, получим выражение проводи-
мости Y (р) в виде суммы простых дробей:
Первое слагаемое представляет собой активное сопротивле-
8
ние, равное -у-; второе и третье слагаемые—последовательно
О
соединенные цепочки, составленные из г и С. Их элементы,
рассчитаем по (16.10а):
Таким образом, схема реализации по (26) имеет вид, пока-
занный на рис. 16.10, б (см. также рис. 16.3, б).
Осуществим реализацию путем разложения Z(p) в непре-
рывную дробь. Начнем деление с высших степеней р, поступая
аналогично тому, как это было сделано при решении задачи 16.5:
439*
-|-6р +8
р2+4р+3
р2+4р+3
Т
1
1
о
J3
Г
з
Итак, получена следующая непрерывная дробь
Z(p) — 1 -j---------j----
Т 1 I
3 + 3 1
“Гр+ 1
3
(3)
где 1 — активное сопротивление;
1
-----х---емкость;
4
- 5--активное сопротивление;
3
- и--емкость;
£
1
----активное сопротивление.
Схема, соответствующая (3), представлена на рис. 16.11, а
(см. также рис. 16.4, а) — первая форма Кауэра.
Осуществим разложение в непрерывную дробь, начиная де-
ление с низших степеней р, предварительно инвертируя дробь,
переписав ее в виде
Z 3-|-4р+р2 ’
8+6р+ра
440
Заметим, что непосредственное, до инвертирования, деление*
числителя на знаменатель, начиная с низших степеней р, привело
бы к отрицательному остатку, что не имеет смысла, так как он
не может быть реализован положительными элементами г и С:
Рис. 16.11
2
968
21 р
8 4~ 6р р2
Т
8
44 р
44 р
О
Р2
“3
44
Таким образом, получена следующая непрерывная дробь:
2 W = j----------л-----------
8 +32 1
7р+ 49 1
88 + 968 1
21р + 3
44
(4)
441
где ------активная проводимость, соответствующая активному
8
сопротивлению -х- ;
О
32
j- — емкостное сопротивление, соответствующее емкости
32’ И Т‘Д’
Схема реализации по (4) приведена на рис. 16.11, б (см. так-
же рис. 16.4,6) — вторая форма Кауэра.
16.8. Требуется построить канонические схемы двухполюсни-
ков, состоящих из элементов г и С, по заданным входным функ-
циям путем разложения на простейшие дроби и в непрерывные
дроби:
a) Z(p) = ; б) Y (р) =
' р(р+2) z ' “ *
16.9. По функции входного сопротивления Z(p) = yi|- осу-
тгР“Г~О
ществить реализацию двухполюсника.
Решение. Найдем полюсы и нули функции. Полюс равен
----4*» а нуль-----g-. Так как оба они лежат на отрицатель-
ной действительной полуоси и ближайшим к началу координат
является нуль (-=- < -у) , то заданная функция может быть
реализована простейшим образом из элементов г и L (см. п. 5
основных положений и соотношений).
1. Определим схему, получающуюся в результате разложе-
ния Z(p) на простые дроби по (16.11). Вычислим входящие в
нее коэффициенты km ,k0 и kt. Коэффициент km = 0, так как выс-
шие степени относительно р числителя и знаменателя одинако-
вы, и это означает, что Z (р) не имеет полюса в бесконечности.
Коэффициенты k0 и — вычеты функции — Z(p) соответствен-
р
но при р = О и р = — cjj = —д— :
11 5р4-2 1
k0 = Res — Zip) = Res ...............,-лГ =
I P Jp=o L p (4p+3) Jp=o
’ 5p+21 2
_ 8p+ 3_ p=^Q 3 ’
г 1 о 1 Г5р+21
k. = Res — Z(p) . = = T *
4 4
442
Итак, заданная функция в соответствии с (16.11) может быть
представлена в виде
Здесь первое слагаемое по (16.13,а) — активное сопротивление
2
г0 = — . Второе слагаемое выражает параллельно соединенные
гх и Lv вычисляемые по (16.13,а):
7
_ _ 12 7
Гх — — 12 ; — 3 — 9 .
4
Согласно (1) схема состоит из последовательно со-
единенных активного сопротивления г0 и параллельной
г1А1-цепочки (рис. 16.12, а)
— первая форма Фостера.
Ос уществим реализацию
по второй форме Фостера.
Для этого разложим функ-
цию проводимости Y(p) =
= на простые дроби
по (16.12). Найдем коэффи-
циенты kw, ko и k\:
7
Рис. 16.12
^оо — [Res Y (р)]р=оо
4p-f-3
_ 5Р4“2 _ £=00
4
5“ ‘
Коэффициент &о = 0, так как функция Y(p) не имеет полю-
са в точке р = 0.
Наконец, определим k\ — вычет функции Y{p) при р=3{ =
2
5 2
k\ = [ Res У (р)]₽=_2 +
_ 7
n=—1 — 25 •
Итак, на основании (16.12) функция входной проводимости
5
Соответствующая этому выражению схема рис. 16.12, б со-
стоит из двух параллельных ветвей: в первой активная прово-
4 ( 1 5 \
димость -ё- (или сопротивление г» = тг = ~г > а вторая—по-
0 \ 4 /
443
следовательно соединенные активное сопротивление гк и индукти
вность Lv определяемые по (16.14а):
2. Найдем цепные схемы, получающиеся в результате раз-
ложения заданной функции Z(p) на непрерывные дроби. Если
начать деление непосредственно с высших степеней р, то по-
лучится отрицательный остаток, который будет указывать на не-
возможность реализации цепи положительными элементами.
Деление с низших степеней р приводит к возможной реали-
зации. Действительно,
2 4- 5р 3 4- 4р
о
Итак,
Z(p) =
(3)
2
где -я----активное сопротивление;
О
9
— индуктивная проводимость, имеющая индуктивность
7
9 *
7
— активное сопротивление.
Схема, соответствующая уравнению (3), та же, что и на
рис. 16.12, а (схема Кауэра).
Наконец, получим еще одну форму Кауэра, представив
входное сопротивление в виде
7(d) 5р + 4 _______
W 4р + 3 4р + 3
5р + 2
444
и разложив знаменатель в непрерывную дробь, начиная деле-
ние с высших степеней р:
7
5
7
5
О
7
10
Следовательно,
(4)
Этому уравнению соответствует схема рис. 16.12,6. В рас-
сматриваемой задаче были получены всего две (вместо четырех)
канонические схемы. Это произошло оттого, что заданная
функция имела простой вид. Заметим, что получение всех че-
тырех канонических схем не всегда возможно.
3. Найденные схемы (рис. 16.12 а и б) являются канониче-
скими (простейшими) и каждая содержит лишь по три элемента.
Можно найти еще и другие схемы, содержащие большее число
элементов. Например, если сопротивление представить в виде
суммы двух таких дробей:
то первое слагаемое — параллельный контур, состоящий из
и Lx, сопротивление которого по (16.136)
отсюда
445
Второе слагаемое — также параллельный контур, состоящий
из г2 и С2, сопротивление которого по (16.86) равно
Отсюда
Рис. 16.13
Следовательно, формуле (5) соот-
ветствует схема рис. 16.13,а.
Можно найти еще одну схему,
если записать выражение для прово-
димости в виде двух слагаемых:
(6)
Первое выражает проводимость
последовательно соединенных и
Сх, а второе — проводимость после-
довательно соединенных г2 и £а. Схема, соответствующая урав-
нению (6), дана на рис. 16.13,6.
16.10. Найти канонические схемы двухполюсников, состоя-
щих из г и L, по заданным входным функциям:
a) Z(p) =
б) Y (р) =
(р + 2) (р + 4)
(р + 1) (р + 3)
путем разложения на простейшие дроби и в непрерывные дроби.
16.11. Найти схему и элементы двухполюсника, входное со-
противление которого
р (4р3 + Юр2 + 44р + 10)
(р2 + 3) (2р2 + 8р + 1)
Решение. Схему реализации будем искать путем посте-
пенного выделения мнимых полюсов и нулей функции сопро-
тивления (см. п. 6 основных положений и соотношений).
Из выражения Z(p) видно, что имеется пара мнимых полю-
сов при р — + j j/T. Выделим их. Это рассчитывается так же,
как и при синтезе чисто реактивных двухполюсников (см. п. 3
446
основных положений). Для этого находим вычет от Z (р) при
р== + /]/3~ [см. формулу (16.2)]:
ki = [Res Z (р)]р=//т
J p=i V 3
To же значение имеет вычет и при р = —
Таким образом, из Z(p) может быть выделена функция
- представляющая собой параллельный контур
(16.46), элементы которого определяются по (16.4а):
_ 2Л, _ 2 • 2 _ 4 r 1 _ 1 _ 1
1 ~ со* ~ 3 “ 3 ’ 1 ~ 2Л, “ 2 • 2 - 4 •
Поэтому Z(p) может быть представлено схемой рис. 16.14,а,
для которой Z (р) = + zi (/>)•
Отсюда
z, (р) = z (р)__4-Р- = 4р4 + 10р3 ±-10-р- -
1 р2 + 3 + 3) (2р2 + 8р + 1)
_ 4Р _ 2р (Р + D
р2 + 3 2р2 + 8р + 1
Функция сопротивления Zx(p) имеет нуль при р==0, или
функция проводимости
и (р) = —L- = . 2р2 + 8р + 1
Z^p) 2р(2р + 1)
имеет полюс при р = 0. Аналогично предыдущему выделим его:
[Res У1 (р)]р=0 =
Jp=O
Следовательно, проводимость Yr (р) имеет
равную 2, проводимость которой —— =—, т.
индуктивность,
е.
отсюда
^(Р) = гг(р)--Ь =
2р2 4- 8р 4- 1 1 р 4- 3
2р(2р4- 1) 2? ~ 2р 4- 1 ’
Инвертируя эту проводимость, получим сопротивление
Z2 (р) —
2р4- 1
р 4* 3
447
Поэтому рис. 16.14, а можно представить в виде рис. 16.14,6.
Функция Z2(p)— функция минимального реактивного сопро-
тивления, состоящая только из элементов г и L, так как она
содержит нуль в точке р==-----лежащий ближе к началу
координат, чем полюс в точке р = — 3 (см. п. 5 основных по-
ложений). Функцию Z2(p) можно разложить на простые дроби
(см. п. 5 основных положений и решение задачи 16.9):
4
Рис. 16.14
которым соответствуют две схемы
рис. 16.15, а и б. Если Z2(p) предста-
вить в виде непрерывных дробей:
^2 (Р) —
^2 (Р) —з F
9
5р +__5_
3
то будут получены те же схемы.
Окончательно для Z(p) получим схемы в виде рис. 16.16, а
или 16.16,6.
Рис. 16.16
Рис. 16.15
448
16.12. Используя выделение мнимых полюсов и нулей, най-
ти схемы двухполюсников по их входным сопротивлениям.
Даны:
а\ Z(p) = 8Р3 + 4р2 + 6р + 2 . Z(n}— 35р* 14р3 66р2+24р + 8
7(2р3 + р2 + Зр+1) ’ ’ W Р(Р2 + 4) (5р2+2р + 1) *
16.13. Дана функция входного сопротивления двухполюсника
_ 24р4 + 58р3 4- 120р2 + 115р + 20
~ 12р3 + 26р2 + 54р + 45
Реализовать ее, используя метод разложения в непрерывную
дробь.
Решение. Осуществим разложение в цепную дробь, на-
чиная деление с высших степеней р полиномов:
1
24р4 4- 58р3 + 120р2 + 115р 4- 20
24р2 4- 52р3 4- Ю8р2 4- 90р
12р3 4- 26р2 4- 54р 4- 45
2р|
6р3 4- 12р2 4- 25р 4- 20
12р3 4- 26р2 4- 54р 4- 45 6р3 4- 12р2 4- 25р 4- 20
2
12рз 4- 24р2 4- 50р 4- 40
2
3
2р2 + 4р 4- 5
6р3 4- 12р3 4- 25р4- 20
6р3 4- 12ра 4- 15р
2р2 4~ 4р 4~ 5
|3р|
Юр 4-20
4
5
2р2 4- 4р 4- 5
2р2 4- 4р
Г
Юр 4- 20
Юр 4- 20
~~о o’
Юр 4-20
1
5^
5
2р 4- 4
Таким образом, получена следующая непрерывная дробь:
Z (р) = 2р 4----------i-------.
2 + ~. 1 ~
3Р4- j j
5 Р + ~2р + 4
Ей соответствует схема рис. 16.17.
449
15 Заказ № 624
16.14. Требуется реализовать функцию входного сопротив-
ления:
2(р) =
используя разложение в непрерывную дробь.
Решение. Так как степень числителя выше степени зна-
менателя, то имеется полюс в бесконечности, который выделим,
а остальную часть разложим в непрерывную дробь, при этом
перейдем на деление с низших степеней полиномов (при делении
с высших степеней получится отрицательный остаток, который
не может быть реализован положительными элементами):
16р3 + 16р2 + 8р + 3
16р3 + Юр2 + 6р
2р
Следовательно,
7 ( ч . 6р2 + 2р -и 3 о ,
Z (р) = 2р + - й\ Т / = 2р+
8р2 + 5р + 3
Знаменатель последнего выражения
ную дробь:
1
3 + 5р + 8р2 *
3 + 2р + 6р2
разложим в непрерыв-
0
450
Рис. 16.18
Итак,
Z(p) = 2р +------------------Ц----------
1+ Х 1
р -* 1 1
2р + Т
Этому выражению соответствует схема рис. 16.18.
16.15. Используя метод разложения в непрерывную дробь,
найти схему двухполюсника, соответствующую входному со-
противлению:
Z(p) =
6р3 + 7р2 + 20р + 10
р (2р2 + 7р + 5)
15*
ОТВЕТЫ
Глава 1. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1-3. а) Г1х.х = 120 0М’ Г1к.з = 72 °М‘> ® Г1х.х = 20 0М’ Г1к.з =
= 18 ом; в) г1х х = 838 ом, г1к 3 = 200 ом; г) г1х х = 40 ом,
^к.з = 30 ом. i.7. 15 в. 1.11. 18 а; гш ~ 0,0005 ом. 1.12. а) 0,15;
б) 0,05. 1.13. 6 ом. 1.15. 750 ом. 1.16. 12 в; 2 ом. 1.17. На се-
редине линии. 1.19. 7,5%. 1.20. Точное значение 41,8 мм2, по
ГОСТу надо взять 50 мм2. 1.22. Ц =2,5 а; /2 = 1,5 а; 13=1а.
1.23. ^ = 5 а; /2 = 1 а; /8 — 4 a; Uba — 30 в. 1.24. 20 а, 10 а,
36 в; 36,7 в. 1.25. /х = 98 а; 13 = 144 а; 10 = 46 a; Ux = 102 в;
U2 = 71 в. 1.27. /х = 5 а; /2 = 9 а; /8 = 1 а. 1.28. /х = 8 а; /2=
= 2 а; /3 = 6 а; <рх = 78 в; <р2 = 20 в. 1.30. /х = 1,2 а; /2 =
= 0,3 а; I = 1,5 а. 1.31. 25 в; Рх = 9 вт; Р2 — 15,6 вт. 1.33. /х=
= 10 ма; /2 = 4 ма; 13 = 20 ма; /4 = 6 ма. 1.35. /х = 105 ма;
/2 = 45 ма; /8 = 5 ма. 1.37. /х = 2 а; /2 = 2,7 а; 13 = 0,7 а;
Ц = 2,2 а; /5 — 4,7 а; 1в = 2,5 а; <ра = — 22 в; (рй — 47 в; tpc —
= — 10 в. 1.41. q>x = 0; ф2 — — 60 в, <р8 = 80 в. 1.43. /х = 2,25 ма;
/2 = 1,4 ма; /3 = 0,85 ма; /4 = 0,75 ма; 1Ъ = 0,1 ма; /6 = 1,5 ма.
1.45. См. ответ к задаче 1.35. 1.46. /х = 5 ма; /2 = 20 ма; 13 —
= 140 ма; Ц = 40 ма; — ма; /в = 65 ма. 1.49. /х = 0,8 а;
/2 = 0,75 а; 13 — 2 а; 74 = 1,55 а; / = 2,75 а. 1.52. См. ответы
к задаче 1.35. 1.54. 0,3 а; 0,2 а; 0,15 а, 0,1 а, 0,15 а, 0,005 а;
гаЬ = 100 ом; Р = 9 вт. 1.55. / = 3,8 а; /х = 0,5 а; 12 = 1,5 а;
13 = 3,3 а; Ц = 1,8 а; /5 = 2 а; гп = 33 ом 1.58. 0,6 а.
1.59. a)Er = kE, rT = k(l — k) г; 6)Er — kE — Ег, rr=rx-j-
rr = -~r It Vlr r ' L6°- 1) ^ = 0, re= 10 ом;
rl Г2~ГГ1 '3“ГГ1 '4T Г2 ГЗТгЗ '4
2) E = 40 et r0 == 5 om\ 3) E =» 5 e, rQ =5 ом. <
4S2
1.64. 40 ма. 1.65. 0,4 а. 1.67. /4 = 3,8 ма; I3 = 1 ма. 1.68. 4 =
= 3,6 а; 12 = 1,6 а; /3 = 5,2 а; Ц = 0. 1.69. См. ответ к
задаче 1.49. 1.71. gn = ом'1; g22 = ом'1; g33 = омг1;
£«4 = "48 ~ 4оо ОМ S12 = Sli = go ом Х! S13 ~
1 1 1-1 1 -1 „ 1 _1
— J50 ОМ i gis — ЮО ’ ^23 120 240
1 1 1-1 1-1 1 -1 г
— "go" ’ ^34 000 ’ ^®5 200 400
= 2,2 а;12 — 0,25 а; 13 — 0,8а; /4=2,45 а;/6 =0,55 а. 1.73. U—
= 40,5 — 3,757. 1.74. I = 8-10"2 3 — 4- 10~*t7; 4=8-10-® —
— 2-10-4 U; 4 = 2-10-* U; 13 = 2-10~3 4-2-10-4 U.
Глава 2. простейшие электрические цепи синусоидального тока
2.2. а) Ф = -п? ; М1 = 300 sin®/ в; = 10 sin (wt— a;
T = 0,02 сек; f = 50 гц; 6) <p= -5- ; i2=5 sin I
О
= 3 sin о)/ ма; T = 10 мксек; f= 105 гц;
в) ф = 1,57
= 90°; u2=300 sinto/ в; u3 = 200 sin (<d/+
T = 0,06 сек, /=16 4- гц. 2.4. 1) 232
О
= 200 cos wt
sin(<oi + 32°45')
в;
в;
2) 475 sin (<o t + 79°05') в. 2.6. 1) 7 = 9,1 sin(w/ — 57°30') a;
ua =91 sin (wt — 57°30') в; uL = 146 cos (wt — 57°30') в; pa —
= 416 [1 — cos (2 wt—115°)] em; pL =653 sin (2 wt—115°) ;
p = 416 — 773 cos (2 wt — 57°30'); w= 1,04 [1—cos (2 wt —
— 115°)] дж. 2.8. 12 ом; 51 мгн. 2.10. и = 311 sin (wt — 41°30') в;
ua = 233 sin wt в; uc — — 206 cos wt в; p — 226—302 cos (2wt—
— 41°30') ea; даэ = 0,319 (l+cos2<o/) дж. 2.12. / = 400 гц;
гэ— 16,2 ом; хэ = 11,8 ом (индуктивное). 2.14. ПО вт. 2.16. U—
= 121 в; Рсх = 252 вт; QCx = 37,l вар; Scx = 266 ва; Рреост =
= 193,6 вт; Рк„ = 58,4 вт; QKaT = 87,1 вар. <р — <ркат = 37°30'.
2.17. I = 7,68 a; U1 = 82,5 в; Рг = 307 вт; Qy = 557 вар; U2 =
= 40 в; Р2 = 248 вт; Q2 = 186 вар, Рсх — 555 вт; Qa = 743 вар.
2.18. г= 18,3 ом; £=113 мгн. 2.19. U = 120 в; 7/кат = 38,2 в;
Ркат == 60,6 вт, ^7конд == 144 в, Т^конд == 20,2 вт, = 1,14, =
= 17,2. 2.21. 1) 19,5 ом (емкостный), 2) 19,5 ом (индуктивный).
2.23. 74 = 6,3 кв; Uaai=l,27 кв; &U =1,2 кв; vj = 93%.
2.24. 1) г2 = 100 ом; х3 = 100 ом; 2) г2 = 100 ом; х3 = — 220 ом.
2-25- Рпр max ~ 18-3 ют; ^ргпах = 50 Ют И Рпр 151 КвГП.
2.28. 210 вт. 2.31. ix = 2,5 У" 2 cos wt a; i3 = 5 2 sin («> t +
4- 126°55') a; i = 7,2/2sin(wt + 114°45') a; и = 125 KiTsin (<o/4-
+ 73°45') в. 2.32. 4= 15 a; Z2= 16 a; I = 10,3 a; P = 900em;
453
Q = 415 вар', S = 990 ва; r3 = 8,5 ом; х = — 3,9 ом. 2.33. 1 =
= 8,9 a; U = 120 в; гэ=12,4 ом; хэ=5,23 ом. 2.35. С=155мкф;
Qc = 2330 вар.
Глава 3. метод комплексных амплитуд (символический)
3.1. и = ЮОе' 15°= lOOcos 15° 4- /100sin 15° = 96,6 + /25,9 =
= 100 15° в; / = 5е~'20° = 5cos20° — /5 sin 20° = 4,7 — /1,71 =
= 5^ — 20° а. 3.2. 1) 3,44е±/'21О20';2)3,44е±/е8О40';3)3,44е±/158040';
4) З,44е±/И|020'; 5) 12,9е'75°4°'; 6) 3,2е~/2°14'; 7) 3,2е/87°46';
8) 3,2./92°14'; 9) 1,29^ 75°4°'; 10) 23е'°°9'; 11) ЫГ19™'; 3.3. 1)
30,2 ±/10,4; 2) 10,4 ±/30,2; 3) —30,2 ±/10,4; 4) —32т/1,44;
5) 1,44 ±/32; 6) 324-/0,4; 7)32-/0,112; 8) — 1,44 + /32;
9)—32 —/1,44; 10)0,425-/7,3; 11) — 147 —/28,6; 12)—3,66—
— /27,8; 13) 0,54 4-/0,841; 14) 8,78-/4,79.3.6. a) Z = (4 4-
4- / 12) ом; Y — (0,025 — /0,075) олг1; гэ = 4 ом; х3 = 12 ом (ин-
дуктивный); ср = 71°35'; (/а = 17,9 в; Up = 53,6 в; /а = 1,41 а;
/р = 4,24 а; Р = 80 вт; Q = 240 вар; S = 253 ва; б) Z=(0,9524-
4-/3,888) ом; Y = (0,0595 — /0,243) ом~р г3 = 0,952 ом; х3 =
= 3,888 ом (индуктивный); ф = 76° 15'; U3 = 23,8 в; (7р = 97 в;
1Л = 5,95 а; /р = 24,25 а; Р = 595 вт; Q=2425 вар; 5=2500 ва;
в): Z = / 20 ом, Y =—/0,05 ом-1; г3 = 0; х3 = 20 ом (индуктив-
ный); ф = 90°; Ua = 0; Up = 120 в, 13 = 0; /р = 6а; Р3 = 0; Q =
= 720 вар; S = 720 ва. 3.8. Ut = 51,1 в; (/2 = 69,5 в, а = 2°44';
Ф1== —1°31'; ф2=Г13/; Р1=188вт; Р = 238вт.8.9. L =
= 35 мгн. 3.10. /«7 а; Р « 400 вт. 3.11. (7= 116 в. 3.13. (/=
• / 17°30' • _714Q°15'
=232 в; Р = 43,5 вт. 3.14. Uj = 284е в; U2 = 167е в;
• Z"4 • • / 53°10г • / 73°45'
(/х,//2 = 166°45'. 3.17. /х=5е а; /2 = 4е а; / =
= 8,85е/62°20' а; a) Uv = 35,2 в; 1А « 1,2 а; б) 93,5 в. 3.18. (/ =
—/ 74°
= 50,8 в. 3.19. Zj = 4 а; Z2 = 8,8е а; /3 = /5 а; Z =
= 7,3е~'28°а. 3.21. /, = (0,384— /0,112) ма; /2 = (0,3744 4-
4-/0,1408) ма; /3 = (0,0096 — /0,2528) ма. 3.22. /2= 2,0ве,&7°2°' а;
/х = 2,94е/44 25 a; U = 161/23 в; угол между U и (7ai,a=33°20';
Р = 440 вт; Q= 173 вар (емкостный). 3.23. /х = 12 а; /2=2,68а;
/3= 14,45 a; U = 30 в; и = 42,4 sin (ш/ — 36°50') в; i2 =
= 3,8sin(o>/—153°25') а; z3 = 20,4sin(ш/ + 4°45') а; 3.25. ш£х =
= 51 ом. 3.26. /2 = 2,5б/ 38 4° а; /3 = 4,Зе /2150; (/ ==
= 109е' 35°45' в; 3.27. / = (8,1 — /11,35) а; Д = (3,25 — /10,5) а;
72=(4,85 — /0,85)а; /3=(6,8 — /7,1) а; /н = (— 3,55 — /3,4) а.
454
3.28. (У = (3,125+/14,5) в; / = (—0,75+/0,4375) а; 4= (—0,2+
+ /0,25) а; /2 = (— 0,55 + /0,1875) а; /3 = (— 0,6 + /0,25) а.
3.30. хс — 10 ом; /, = 10 а. 3.31. г2=10 ом. 3.32. С = 1,012 мкф.
3.33. С = 53 мкф. 3.36. г2 = 2 • 105 ом; С = 0,5 мкф. 3.38.
4 = — j 0,5 а; /2 = (0,8 — / 0,2) а; /3 = (— 0,8 — / 0,3) а; /=(0,8-
-/0,7) а. 3.39. (/,:(/,= 0,38^91°2°'; a) 0,265f/64°10';
б) 0,38е/86°50’. 3.41. 50 ом. 3.42. 0,18. 3.44. / = 97е'54°а; 4 =
= 58,2 7 54 а; /2=38,8е 154 а. 3.45. / = (6— /22)а; 1г = (4 —
— /6) а; /2 = (12 — /18) а; /3 = (2 —/16)а; /4 = (— 6— /4) а;
/5 = (— 8 + / 12) а; Р = 780 вт. 3.46. См. ответ к задаче 3.45.
3.47. 56 ма. 3.48. 4= 1>82е/2° 10 а;
= 2,37# а; Ц~ 1,59е а
/ 122° 20' • /58°10'
= 1,83е а. 3.49. Л=13,и
/70° 40' —/84°20'
/3 = 23,бе ма; 14 = 22,2е ма;
= 23,6 вт. 3.50.
г. /2°50'
/2 = 0,56е а;
Т ОГК 183035'
/б = 2,55е а;
11 е 74°20'
. = 11,5е
.. . /85°25'
11,1е
—i 8° 30’
/2= 17,8е
Фз = °;
2) 2,23 а. 3.52.
=дое ма.
п / 47°
= 3,6е ма;
<р2 = 445е /83° в. 3.51. 1) 2,85 а;
6,6 ом; I = 3,7 а или 6,7 а (соответственно); 1г =
6,3 а. 3.53. При резонансе г2 = 10 ом; I = 12 а; I
при г2 = оо; /тах = 15 а при /*2 = 2,2 ом.
6 —
ма;
ма; Р=
ма; 1
<Pi = 350е
15,2 ом
в;
или
или
min ==: 6»35 а
з —
з
Глава 4. резонанс в электрических цепях
4.1. 160 пф; 50 ма; 40 мет; 49,6 в. 4.2. 16 ом; 40 мет
4.3. 125 в. 4.4. 10 ом; 0,4 гн; 0,1 мкф; 1 в. 4.5. /0 =---------?-----=
2л У LC
= Кftf2. 4.6. 24 ом; 0,143 гн; 70,8 мкф; ^ = 31 ом. 4.8. 1) о>о=
= 62,8 • 103 шг1; <*>L = 88,6 • 103 сек’1; о>с = 44,4 • 103 сек’1;
UL max — UC max = 11 '6 в> 2) <°0 == 62,8 * 103 СвК’1; “>L = 00 J <*>с =
= 0; 10 в. 4.13. 19 ма; 71°30'; 47,5. 4.14. 1) 400; 2) 100.
4.15. 0,995 • 107 сек’1; 1,005 • 107 сек’1. 4.17. 50. 4.19. До шун.
тирования: 46,4 ма; 37 в; после шунтирования: 34 ма; 27 в.
4.20. <0р = 500 се/г1; /0 == /а = 0,625 a; Ifn = I = 1,25 а
. п, , с . . V~2 U . , . U
4.21. 1,6 мгн; i = t, = ------sin wt; i, = — -—— cos <»/; i„ =
Г r r L iiiL <*
= VT Uu>C cos a>t; pL =--------sin 2 wt; pc = U2<»C sin 2wt; pr =
fl2 fl2
= -y- (1 — cos 2Ы); wM (1 + cos2u>(); w9 = U2C (1 — cos 2W).
455
4.22. 1000 сект1; резонанс невозможен при г2 > 40 ом-, резонанс
будет при любой частоте, если гх = г2 = 40 ом. 4.24. г2 = 32 ом,
гр = 24 ом. 4.25. 9600 сект1; 143 ом. 4.26. L' = 19,6 мгн; L" =
= 0,4 мгн-, у'=81° 52'; ф" = 8°08'; <р'+ ф" = -у • 4.27. /ш!п =
— 138 кгц; f mayL == 1S4: кгц. 4.31. 500 кгц; гр = 70,2 ком; 32,9 ком;
34,9 ком; 48 ком; 3,12 ма; 141 ма; 320 мет. 4.32. 1) 25,6 ком;
33,4 ком; 42 ком; 2) 27,4 ком; 14,6 ком; 31 ком; 3) 50,7 ком;
50 ком; 71,2 ком. 4.35. /=1,64е/15° ма; U = 95е~'18° в;
11=90е~'|07° °5' ма; /2=90е'72° ма; Рт— 317 мет; Рвнут=186 мет;
Р= 131 мет. 4.37.1)400 кгг/; 525 мкгн; \35мвт; 21,8 код So=0,0545.
4.40. a) Qg = 21,7; <$л = 23 кгц; 1р=\,$3ма; Up=67 в; РнагР. Р =
= 64 мет; б) Q’3= 16,25; = 30,8 кгц; 7р = 2,18 ма; 77р= 50 в;
Рнагр. р = 72,25 мет. 4.42. Резонанс напряжений: а) 605 кгц;
9,4 ом; б) 298 кгц, 12 ом; резонанс токов при 408 кгц, гр =
= 28,8 ком. 4.44. Сх = 1180 пф; С2 = 865 пф; ^ртах = 60 ком.
4.45. гэ = 13 ком; х3 = ± 14,3 ком; zB= 19,3 ком. 4.47. r2min =
= 2 <uL;/ = - V + '2 ) 4.48. Z, = /1,28 ом; Ртах = 1,9 кет.
'•i + + Г1^<о2Са 1 1 • тах
4.49. a) Z8=—/10 ом; /х= 6 а; 12= (—2,4 — /4,8) а; /3=(8,4+
+ /4,8) а; б) Z3 = —/15,7 ом; 4 = 3,28 а; 4 = (0,36— /5,12) а;
/8= (2,92+ /5,12) а. 4.50. хс = 5 ом; 4=10 a; Ц=5,6е-/ж°№' а.
/8= 5,бе'26’ 35' а. 4.51. 1) o>L'= 4 ом; 4=30 а; 4=(15—/7,5)а;
/' = (15 + /7,5) а; 2) «>L"= 16 ом; = 20,4 а; Г2 =(2,55—/5,1) а;
7” = (17,85 + /5,1) а. 4.52. г = 10 ом; шЬ = 5ом; 4.53. г2=24 ом,
хс=10ом; /2= 1,4е_/26°30' а; /8= 1,4е'26°30' а. 4.54. 1) х'4 =
= шЛ; = 1 ом; 1=15 а, = (6 + /3) а; Г2 = (2,25 — /0,75) а;
Г3 = (3,75 + /3,75) а; Г4 = (9 — /3) а; 2) х’4 = «>L'4 = 9 ом; /"=7 а;
4 = (6 + /3) а; Г2 = (2,25 - /0,75) а; Г3 = (3,75 + /3,75) а; ГА =
=(1—/3)а. 4.55. /-=2200 гц; /н=2800 гц. 4.56. х'.=—4-=88 ом;
<»с4
х" = —г =8 ом.
4 <оС4
Глава 5. цепи с взаимной индуктивностью
5.3. /=(0,8-/0,6) a; Uab = (59 + /42) в; Ucd = (31- / 42) в.
5.4. 7 = Юг/36’50' a; Uab = 18eii3°w' в. 5.5. йс = 74е~/128° в.
5.7. А = 0,111. 5.9. Включение встречное. Л4 = 11,1 мгн.
4S«
5.11. /1=(8 —/1) а; /2 = (6 —/2)‘а; /=(14 — /3) а. 5.12. 4 =
= (6,4 —/8,6) а; /2 = (2,1 + /0,22) а; / = (8,5 —/8,38) а.
5.13. С = 0,0324 мкф; /=1,42 ма; ^ = (0,75 +/0,17) jwa;
/2 = (0,67 — /0,17) ма. 5.14. С = 0,182л/сф; / = 1,46 ма; 1Г =
= (0,82 + /0,07) ма; I, = (0,64-/0,007) ма. 5.16. С = 0,35 мкф;
4 = /2,25 ма; Ц = —/2,25 ма. 5.20. ZH = (3 — /7) ом.
5.22. it = 1 ,05е_/59° а; /2 = 0,685е'1440 а; /3 = 1,7е~/ 50°30' а.
5.24. хс=8 ом; 4 = 5 а; /2 =— /5 а; /3 = (54-/5) а.
5.25. 4 = (2,4 — j 1,8) а; Ц = а; /3 = (2,4 4-/3,2) а.
5.26. хс = 10 ом; I, = (7,06 — /1,76) а; I, — (5,3 — /8,82) а;
/3 = (1,76 4-/7,06) а. 5.27. fe =-у-; 4 = 4,55е~' 18°20' а; /,=
= 10,2е-'81°50'а; 4= 9,1е'71°40’ а; 5.29. 4 = (3,2 4-/4,6) а;
4 = (2,2+/2,6) а; /3 = (1 + /2) а; 4 = 2 a; в;
= 0,35. 5.30. 4 = (0.64 — j 0,48) а; /2 = (1 «28 — j 0,96) а;
4 = (-0,64 +/0,48) a; Uab = (19,2 + /25,6) в. 5.32. 4=(1,85 —
— /1,42) а; /2 = (—1,0 —/0,22) а; /3 = (0,93 — /0,01) а; Ц =
= (2,85 -/1,20) а. 5.34. ZBX = — /19 ом; хс= 10,24 ом.
5.35. а) хс = 28 ом; Д- 0; Л2 = Л3 = 2 а; б) хс = 20 ом;
Лх = 1,2 а; Л2 = 0,6 а; Л3 = 1,8 а. 5.42. С2 = 250 пф; Р{мп =
= 4,85 вт; Р2Л1П = 7,85 вт; 7] = 0,617. 5.43. Л4ОПТ = 77 мкгн;
С2=270 пф; Р1ММ = ^глш^8’33 '*1 = 0,5. 5.44. 278 пф,
^2:== 222 пф, ^опт= 4,6 мкгн, Р^мм = Рчмм == 3,33 вт, т] = 0,5.
5.46. С\= 800 пф; С2 = 400 пф; Qj = 50; Q2= 50; М = 5,66 мкгн;
/2= 3,54 мка; (/2 = 3,54 мв; 50= 2,82-10"2. 5.48. 1250 гц; 0,011;
4.4 мкгн. 5.52. 61,5 вт; 57%.
Глава 6. трехфазные цепи
6.2. IA = 1В = 1С =* /ф =» 8,97 a; £/ф = 127 в, Р = 3,43 кет.
6.3. Еф = 230 в. 6.4. /ф г = /ф. н = 163 а; (/ф г = 4230 в; иф н =
= 4070 в; РГ = 1670 кет. 6.6. /ф = 15,6 а; /л= 27 а; Р1=5730 вт;
Р2=1530 вт. Обрыв в точке 1Ьс= 15,5 a; Iba== Iac = 7J5 а;
IА = 0; Iв = 1с~ 23,3 а; Рг= 0; Р2= 3630 вт. Обрыв в точке bt:
1са= 15,5 a; Icb= 1Ьа= 7,75 а; Рг~ Р2=* 1815 вт. Обрыв в точке
Ь%. фазные и линейные токи те же, что и при обрыве в точке Ь±;
Pi=4950 вт; Р2 = 1330 вт. 6.7. Линейные токи и общая мощ-
457
ность уменьшатся в три раза. 6.8. /л = 26,8 а; /ф = 15,5 а;
(/ф н= 165 в; Д(7 = 65 в. 6.9. (7Г= 209 в; /г= 26 а; (7пр= 112,5 в;
/пр = 45 а. 6.10. /г = 59 а; /л =102 а; (7Н = 148 в; /н = 59 а.
6.11. (7Ф = 127 в; I = 8,75 а; срф = 25°50'; Р = 3 кет, 6.12. [Уф =
= 220 в; I = 7,6 а; срф = 30 , Р = 2,5 кет, 6.13. /н = 11 а;
/л = 19,05 а; 2ф = (16 + j 12) ом, 6.14. 3,34 квар, 6.15. 10,02 квар,
6.16. При удельном сопротивлении р= 1,75-10"6 ом-см и удель-
ном весе d = 8,9 г/см3: a) 129 m, 6)172 т, 6.17.6,3 кв. 6.18.6,1 кв,
6.21. При наличии нейтрального провода/л = 38,76 7 61 30 а;
Iв — 27,65 е а; Ic = 4U,3 е а; IN = 26,9 е а.
Напряжения на фазах генератора: UA0 = 194 e~J155 в; UB0 =
= 246 е~/125° в; йсо = 213,3 е/ш°5 в. Напряжение на фазах
нагрузки: UaOt = 173,5 е1 ’’ ®' в; (7^ = 247 е-'129’20' в- =
= 202 е/|08°20'в.6.22.1N = 3,46 а; Щ = 108 в; Un = 121 в; Ц*, =
= 132 в. 6.24. а) /л=0; 1В = 1С = 8,54 а; Рх = 0; Р2 =
= 3200 вт; б) /А = 1С= 14 а; 1В =0; Рх = 1170 вт; Р2 =
= 5080 вт; в) 1А = 1С = 14 а; Iв =0; Рх = 1190 вт; Р2 =
= 3890 вт; г)/л= 31,8 а; 1В = 15,2 а; 1С= 19а;Рх=9160 вт;
Р2 = 3600 вт; д) 1А = 38 а; 1В = 35,2 а; 1С = 19 а; Рг =
= 8660 вт; Р2 = 7220 вт. 6.25. 1А = 19,8 а; 1В = 18,4 а; 1С =
= 16,1 a; UA = 178в; U в —202 в; Uc = 225 в. 6.28. Если принять
UAB = илв = 220 б> то = 22 а; 1Ьс = 22 е-/,73°10' а; fca =
= 22 е“/150° а; /л = (41 + /11) а; I в = - (43,8 + /2,6) а;
/ = (2,8 — /8,4) а; Р± = 9040 вт; Р2— — 1296 вт. 62.9. Ли-
нейные токи: 1А = 17,3 а; Iв = 10 а; 1С = 14,3 а. Фазные токи:
= 8,1 а; 1Ьс=Ш a; Ica = 9,34 а; Р = 4220 вт. 6.30.
а) Линейные токи: IА = 11,6 а; Iв = 12,9 а; 1С = 13,6 а. Фаз-
ные токи: IАВ = 6,34 а; Iвс — 8,55 а; IСА = 7,07 а; б) Ли-
нейные токи: 1А = 1В = 10,22 а; 1с-= 0. Фазные токи: 1АВ =
= 6,34 а; 1ВС = 1СА = 3,88 а. 6.31. 1А = Л = 0,433 а; 1В =
= 1,83 а; 1С= 12 = 1,57 а; Рх = 28 вт; Р2 = 227 вт,
6.32. 1А = 6,54 е-/29°35' о; 1В = 4,2 а- 1С=5,Э8 е1'^20' а;
UA =(142-/80,8) в; UB = (— 68 —/80,8) в; йс = (31,8 +
+ /115) в; Рх = 1,19 кет; Р2 = 870 вт. 6.33. UA = 125,3 в;
UB = 122,2 в; t/c=131 в; 1Д = 5,01 а; 1В = 4,88 а; 1С =
= 5,24 а. 6.34. I. = 6,43 а; /„ = 2,19 а; 1Г = 7,03 a; U. =
4Г1 ЛЭ <1
458
= 82,2 в; Uв = 30,7 в\ {/с = 81,8 в. 6.35. 1АВ = 4,8 а; =
= 5,5 а; 1СА = 6,98 а; 1А — 9,15 а; 1В — 8,68 а; 1С = 11,9 а.
6.36. Л = 19,1 а; 1В = 17,2 а; /с = 14 а; = 8,5 а; 1ВГ =
= 10,7 а; lCA = 11,1 а. 6.37. При UAB = UAB = 220 в для звез-
ды ГА = (6,06 — /2,68) а; Гв = (— 4,95 — /2,69) а;
1с=(—1,11 +/5,37) а; для треугольника: I ав = (7,04 — /5,28) а;
/вс = (—8,1—/3,46)а. 1са = (—5,5 + /9,5) а, на входе линии
1А =(18,60 — /17,46) а, /в = (— 20,1 —/0,87) а, !с = (1,5 +
+ /18,33) а. 6.38. На фазах звезды Uа = Uc — 93,2 в; UB =
= 97,6 в; на фазах треугольника Uab = Ubc = 146 в, Uca —
= 139 в.
Глава 7. цепи периодического несинусоидального тока
7.3 и = 128 sin (^ t + 38°40') + 63,3 sin (2 Wj / + 108°25') +
+ 33,6 sin (3 <»! t — 26°30') + 14,4 sin (4 t — 123°40') в\ u(t) =
n=4
= 4 S Un где U. =и.г = 128 е-'61°20' в, Ut= U.2 =
it
п — — 4
= 63,3 е'18°20' в, U3 = Z/_8= 33,6 е-'116’30' в, U. = U., =
= 14,4 Z46°2°' «•
459
ит ит / 1 1 \
1) и = —5 sin о», t + =- sin2 e>! / + —у sin 3 /+•.. 1; Z ТС \ Z о / ит Шт 1 1 1 _ \
2) и = 2 ^2 1 cos t -f- -£2-cos3 (Oj t 52 cos 5 (DjZ-p* • •
3) и = SUm / 1 . „ 1 . r . \ —5 ISin “1 — -jp SIH 3 tojt + -gy sin 5 0>! t—. . .)—
2 1
COS 0)-^ t —J- COS 2 t ~q2 COS 3 t +
«Л»
3it2
+ -7F cos 4 (Oj t + .. .1. 7.9. 7 = 22,4 a; cos <p = 0,82. 7.10. I—
T“^ J
= 13,1 a; P = 5\6em; i = [10 + 12 sin (141 — 53°)] a; uL =
= 48 cos (©j t — 53°) в. 7.11. i = [34,3 sin («ij t + 31°) +
4-5,9 sin — 78°40')] a; «с = [100 + 103 sin — 59°) +
4-5,9 sin — 168°40') e; U = 174 в; I = 24,6 a; P = 3040 em;
a) 100 e; 6) 127 в. 7.13. 280 e; 388 em. 7.14. =[0,1 +-
4-0,0744 sin ((o1/ — 42°25/) 4- 0,0157 sin (3<ox/ — 71°20')la; i2 =
= [0,1 + 0,0336 sin № — 79°40/) + 0,00458 sin (Зш^ — 124°20')J a;
i3 = [0,052 sin(<0^— 19°25') + 0,0134 sin (3<»^ — 55°30')]a; P =
= 17,9 em. 7.15. При подключении через фильтр /г<о) •* Л ~ 1, без
фильтра /г(0) ' h — 0,905. 7.16. Сг = 17,8мкф; С3= 2,22 мкф\ =
= 0,4 sin a; i2 = (— 0,05 sin a>xf + 0,333 cos 3o>x t) a; i3 =
= (0,45 sin ш,/ — 0,333 cos uab = (4,5008(0!/+ 10 sin 3o>j/)e;
Ir = 0,283 a; /2 = 0,238 a; I3 = 0,4 a. Uab = 7,75 в; P = 4 em.
7.17. P = 0,271 em; Q = 0,215 eap; 5 = 0,418 ea; 7 = 0,235 ea.
7.18. r3 — 20 ом; 7x = 1,8 a; I3 = 1,06 a; I3 = 0,81 a. 7.20. 1г =
= 4,26 a; /2= 1,18 a. 7.21. 76 = 0,0263 a. 7.22. 77c:7/=l,95.
7.23. 78 в. 7.24. L3 = 4,29 мгн (большее значение); кг = 0,545 мгн.
7.26. Лф = 1,28; kA = 1,76; feu = 0,96.
Глава 8. катушки и трансформаторы с ферромагнитными
СЕРДЕЧНИКАМИ
8.3. При частоте f Р1г = Р1В = 300 вт, при частоте 2/ Р2г =
s= 600 вт, Р2й = 1200 вт. 8.4. При повышении напряжения на
10% потери равны 1,21 кет, а при понижении напряжения на
10%—0,81 кет. 8.6. 710 вт. 8.9. Рст = 757 вт; /0 = 26,6 а.
Глава 9. двухполюсники
9.1. Для всех вариантов L = 1,8 мгн; С — 0,5 мкф. 9.2. а)о>р=
= 5-103 сек"1; б) а)р = 5*103 сек"1; в) «)р1 = 3,54-103 сек"1; —
460
— 7,05-103 сект1; г) ®р1 = 2,5-104 сект1; шра = 5-104 сект1.
9.3.
9.5. а) 500 ом; б) 500 ом. 9.6. Z(p) =
__Р3СЦ L2 4- P2C^L2r1 4- L^) 4~ P(rir2^ 4~ M Ьз) 4~ (fi + <*2) _ CL L ’
p3C 4" pCr2 4“ 1 si
tig = 0(Z.a/* 1 "b 2)1 flj = ry2^ Ч- "b ^-2» ^0 ~ ^*1 ^*2» ^2 OZ-2,
bi = Cr 2; bo = 1.
9.8. 9.9.
9.11. C = 1,13 пф; класс 1.
£(/<>) =/0)222-10-6 • 9-12- Ct =0,3 мкф; Ca =
= 0,15 мкф; L = 133 мгн.
Глава 10. четырехполюсники
10.2. Л=1 — /3; В = (—30 —/20) ом; С = —/0,1 ом'1; D =
= — 1; У„ = У1а = —У21 = (2,31 — /1,54)- IO"3 ом-1; У22 = (—2,31—
— /8,45)• 10-2 ом-1. 10.3. А = 1 4-/0,4; В = 1000 ом; С = (36 4-
4-/8)-10'5 ом-1; D = 1,2 —/0,4; Zn = 2,92^9’15' ком, Zia = —Zai=
= 2,71е'167°30' ком, Z22 = 3,42е/149°5' ком, Уц = 1,26- Ю-^-'18”25' омт1,
У12 = —У21 = 10-3 ом-1, У22 = 1,08- 1О-3е-/158°10' омт1. 10.4. А =
= 3,2 —/0,6; В = (20 4- /30) ом; С = (2 — /6)-10-2 ом-1; D = 1;
Zn= 51,5^61° ом; Z12 = — Z21 = Z22 = 15,8е-/*08°25' ом; Уи =
= 2,77- 1О-2е-/5е°20' омт1; У12 = — Yn = 2,77- К)-2^’28’40' ом’1; У2а =
= 9,05- 10~2е/113°5' олг1. 10.6. = Z1T; Z2 = Z1T + 2Z2T. Ю.8. Z1T=
= (2 4” /12,5) ом; Z%t = /18,9 ом; Z^t = (3 4~ /26,3) ом; Zm =
461
= (9,76 + /56) ом; Z2n ~ (2,4 /40,5) ом; Zm — (1,17 4~ /85,3) ом.
1#9. Zu = 37,6е/86°55' ом; Z2T = 47,1 е'86°22' ом; Z3T = 15,7 е'82°40' ом.
10.10. А = 2 4-/6; В = (65 4- /Ю) ом; С = 0,2 ом'1; D = 1 — j2.
10 14 Л______^1^2 4- А&1. о___ М1С2 4- Л2С1) • (DiC^ — D^Ci) — (Ci4-C2)2 .
С( + С2 '°- CiC2(C,4-C2)
С = pC1f* ; D = P1^traC1 • 10.14. а)Ла = Л; Ba = В;
Ч тЧ Ь1 -f- Gg
Bq — В; С б —
= С 4- 4-» D6 = D. в) Ав = А + ZC; Вв = В 4- ZD; Св = С; DB=D.
г) АГ = А; Br = B + Z.A; Сг = C;Dr = D + ZC. 10 16. Zc =
= 1500 e-/58’i5' ол; 1,06-/0,905. 10.17. ZCT = 43,1 е'58°38' ом;
Zcn = 13,3е/69°15' ом; gr = 1,2 — /0,113. 10.18. A = D =
= 1,74e-/26’20' . в = !,09- 103е-/32° ом; С = 2,35- 10-3е~/38°50’ ом'1.
10.19. При ш A~D = — 1, В = 0; С = /0,04 ом'1; Zc = 0, а =
= 0, b = ± к. При 0,5 <» А = D = 0,5, В — /37,5 ом, С =/0,02 ом'1;
Zc = 25]/3 ом, a = 0, b = ~^- рад, при 2а> A = D = —7, В =
= — /600 ом, С = /0,08 ом, Zc =/50 КЗ ом, а = 2,64 неп, Ь —
= ± it рад. 10.22. Zix.x Z2x.x = (80 4- /60) ом; Z[K 3 = Z2k 3 =
= (80 4- /80) ом. 10.23. Zix.x = (2880 4- /450) ом; ZlK 3 = (750 4-
4- /250) ом; Z2x.x = (2940 — /1765) ом; Z2k 3 = (862 — /344) ом.
10.25. А = /2; В = /25 ом; С = /0,2 ом'1. 10.26. х = —10 ом или
— 90 ом. 10.27. 10 ом. 10.28. = 2,5 е-/56’20' a; L =
= 0,61е-/'70°20' а. 10.29. Z2 = (30 + /50) ом; Л = 1,20 е~'59° а;
4 = 0,4 е-/”2’10' a; Z1T = Z3T = /40 ом; Z2T = 37,5 ом. 10.31. Zc=
= 11,18 ом; g = 1,44 4-/-J-. 10.32. А = 2,23е''63°5’; В =
= 3,61 e/123’20' ком; С = 1,79 ^33°20' ком'1; D = 2,5 е'89’35' ; Zlc =
= 1,34 ^31°45' ком; Zic = 1,5^/58’15' ком. g = 1,59 + /1,35.
10.34. Z2BX = 693 в-/60’58, ом. ю.35. Z1BX= 1000б-/56<М0' ом; рг =
= 0; Рн — —0,54; ар = 0,174 wen; b„ =—0,785 рад; ави = 0,14 wen,
6ВЯ = —0,785 рад; Ко = 0,575 е'73°20' ; Ki = 0,96 е'16<>45' .
10.36. Z1BX = 346 е~/20°40' ом. 10.37. Z1BX = 5
г С1 г С* о
К задаче 10.43
10.38. яр = 2,5 неп; явн = 2,48 неп.
10.39. Яр = 0,223 неп\ явн = — 1,396 неп.
10.40. яр»явн — —2,3 неп. 10.43. гг =
= 600 ом; С = 25,5 нф; г2 — 3267 ом;
затухание при 0,3 и 4 кгц a3QQ = 0,012
яея; я4000= 0,306 неп.
462
Глава 11. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
11.2. Lx = 0,638 гн; = 0,08 мкф. 11.3. «57 гц.
11.4. L2 « 0,8 гн; 2С± = 0,064 мкф. 11.5. 212 гц; 2,64 неп.
11.6. L2 = 0,159 гн; Сх = 0,159 мкф. 11.9. = 0,62 мгн; 2Сг =
= 88,6 нф; L2 = 15,9 мгн; С2 = 3,45 нф; 3,45 неп. 11.11. т =
= 0,6; С1т = 90 нф; С2т = 50,3 нф; L2m = 32,3 мгн; /с = 4930 гц.
11.12. Lx = 0,Д77 мгн; Сх = 12 пф; L2 = 6,76 мкгн; С2 = 1590 пф;
L3 = 6 мкгн; С3 = 1900 пф; а= 1,38 неп. 11.13. /100 =10,7 кгц;
/2оо = 18,6 кгц; а = 4,88 неп. 11.15. Li =20,2 мгн; L2 = 12,5 мгн;
С2 = 0,0202 мкф. 11.16. Lx=20,2 мгн; Сх = 0,0125 мкф; С2 =
= 0,0202 мкф.
К задаче 11.12
К задаче 11.15.
К задаче 11.16
Г лава 12. электрические цепи с распределенными
ПАРАМЕТРАМИ
12.2.
ZC- ом у, км—' а, неп/км 3, рад/км у, км/сек к, км
1340 ё -/15°40' 40-10-3 /2°25' 12,2-Ю-з 38,4-10-» 130 000 163 0,297
615 е —/13°20' 18,5-Ю-з е/74°45’ 4,9-10~3 18,Ь 10-3 277 000 346 0,62
250 ё -/37°25' 47,3-Ю-з Z2°15' 29,2.10-3 37,6.10-3 133 000 167 0,053
84,6 —/39° е 8,46-Ю-з е;5'° 5,36-IO"2 6,62-10~2 75 600 95 0,000025
12.4. а) По полным формулам (12.1) 4-(12.2), Zb =
= 564 е—/8°15' ом; а = 2,37 мнеп/км; р= 18,1 мрад/км; по приб-
лиженным формулам (12.4) Zb = 554 ом; а = 2,64 мнеп/км; р =
= \1,§мрад/км. б) По формулам (12.1)4-(12.2) ZB = 550 е“/0°40' ом;
а= 7,6 мнеп/км; р = 435 мрад/км; по приближенным формулам
463
(12.4) Zb =546 ом; a = 8,2 мнеп/км; p = 435 мрад/км. 12.5. По
полным формулам (12.1) 4-(12.2), Zb = 357 е~/41°05' ом; 7 =
= 0,0634 е/'48’40' км'1; а = 0,042 неп/км; р = 0,048 рад/км; по
приближенным формулам Zb = 358 е~/45° ом; у = 0,0634 е'45° км'1;
а = 0,045 неп/км; р = 0,045 рад/км. 12.6. При f = 200 гц а =
= 2,29 мнеп/км, р = 4,82 мрад/км; при f = 1200 гц, а =
= 2,49 мнеп/км, р = 25,85 мрад/км; при f = 2400 гц, а =
= 2,28 мнеп/км, р = 51,60 мрад/км. 12.7. 1) 283 км; 2) 705 км;
3) 118 км; 4) 650 км. 12.12. иг = 19,1 sin(«>/ + 175°55') в; i,=
= 27,2 sin(W + 173°10') ма; ZBX = 705 е'2’45' ом. 12.13. и, =
= 29,7sin°(<»/ + 173° 10') в; i2 = 69,5sin (W + 177°05') ма; Zn =
= 427е-/3 55 ом. 12.14. UiX.K= 12,6 в; Zix.x=7,35 ма; M2x.x = 17,8sinx
18°20')e; ilx.x = 10,4sin(a>/ + 76°50')ла. 12.15. Z1K.3= 7,5 ма;
Z2k,3 = 9,4 ма; iK,3 = 10,6sin (а>/ — 28°50') ма; = 13,2 sin (а>/ —
— 47°10')л<а. 12.16. f72=5,55e-/34°50'в; /2 =5,55е-/34°50'л1а; /г =
= б^бе715’ ма; «2 = 7,83sin (о>/ — 34°50') в, t2 = 7,83sin (<о/—
— 34°50')>иа; 8,55sin («tf-f-lS0) ма; Ulnp =9,04е~/4°в; (710тр =
= 1,15 ?33’20' в; Ц = 6,65 е/1Г20' ма; /10тр = 0,85е/58° ма; t/2np =
=6,45е~/48°40' в. t/2OTp=l,63Z8°e; Z2np = 4,5е4^20' ма; /20тр =
= \,2eim°w ма. 12.17. U. = 7,05е~{^ю'в; Ц=5,2е^40' ма; Р.2 =
=33,Зквт;Р1=67мвт;[)(у)=7,О5е°'от!/е/0'У39г/в; Z(p)=5,O2e°’o,w х
Хе'0-039* ма. 12.18. 1) £/г=9,3<?_/35°20' в; /2 =3,44е~‘“°20' ма; 2)(/2 =
= 4,65 е-/54° в; Ц = 6,9 е“/30’ ма. 12.19. Z1T = Z3T =69Ое/69°50' ом;
Z2T = 576 е-'98°25' ом. 12.20. Zin = 676 е/82°35' ом; Z2n = Z3n =
= 502в“/7б°55' ом. 12.21. Индуктивность следует увеличить на
13,12 мгн/км; ZB = 1590 ом; а = 1,59 мнеп/км; р = 48 мрад/км;
12 = 6,3ма; Р2^63мвт, = 14,9е-/32°25*в; Л = 9,4е-/32°25' ма;
Pt = 140 мет. 12.24. иг = 10 sin (оз/ — 108°45') мв; =
= 21,3 sin (оз/—108°45') мка. При = 0 и = lOsin 2,\у мв, i~
= 21,3sin2,ly мка; при /2
мв
= 21,3 sin 2,1# Н-----мка; при t8 = — и = 10cos2,l# мв; i =
\ 4 / 4
= 21,3cos2,lz/ мка; ря — 0, КБВ = 1. 12.25. ur = 5,72sin +
+ 235°50') мв; I = 20,4sin + 260°20') мка; рн = — , КБВ=0,5.
3
12.27. 0,173 ма. 12.29. ZB = 615е-/12 13°20' ом; у = (4,9 + /18,1) X
X 10’3 км'1; г0 = 5,4 ом/км; Lo = 2 мгн/км; С0 = 6.10‘9 ф/км;
g0 = 1 • 10“® ом'1 /км. 12.31. ZBX = 141 е~'45° ом; /вх = 71 ма.
12.32. 0,081 в.
464
Глава 13. классический метод расчета
ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
13.1. 4 = 0,12 сек; 250 а!сек; /пр = 30а. 13.2. 9,2 мсек; i =
= 1,2(1 —е~500') а; = — 120е-500' в; а>м=0,144(1 — е-^дж;
рм = 144 (е-5°°' — g-ioow) вт- j д МСек. 13.3. 6,67 а!сек; 3,34 а/сек.
13.4. I = Зе-500’' а; % = Г, = 0,5625 дж. 13.5. В 125 раз; 450 дж.
13.8. I = (12 — 9е~100')а. 13.9. i = (3 + Эе’400') а. 13.10. t\ =
= (20 —8е~20') a; i2 = 12е'8' а; 7,7 а. 13.11. 7,8 мсек. 13.12. i2 =
= 2,4е~40' а; г3 = 6(1 — e~Mt) а; - i2 + i3. 13.14. = 0,4е х ,
где т = 3 мсек, 4раб — 2,07 мсек. 13.17. 1) ч(0) = 1 a; i2(0) =
= 0,6 a, i3 (0) = 0,4 а, и^,(0) == 30 в, i^n^ — ^2пр — 0,8 а, ^Зпр === О,
"спр ~ 'ice (0) = 0,2 a, i2cB (0) — 0,2 а, 1*3св=0,4 а, ^+св (0)=
= — 10 в; 2) it = (0,8 + 0,2е-4104') a; i2 = (0,8 — 0,2 а;
i3 = 0,4e-410<'a; ис = (40—10е-41°4') в. 13.18. tlcB(0) = — 0,9 а;
Чсв (0) = - 1,14 а; 'Зсв (0) = 0,24 a; uLcB(0) = 18,6 в; (±£l) =
\ dt /t=*o
= — 12,2-103 в! сек; == (3,87 — 0,9е-в53') а; i2 -(2,905 —
— 1,14е“в539 а; 13 = (0,965 + 0,24е~в53/) а. 13.20. 100 в; 0,23 сед:.
13.21. 11,25-10'3 к; 25 ма. 13.22. При t - 0 Uab - 80 в; Ubc^
= 40 в; при t — оо Uab — 40 в, Ubc — 80 в. 13.23. При t — О
It — 54,6 ма; /2 — 10,9 ма; при t = оо = 60 ма, /2 — 0.
13.24. При t - О Д - /2 - 1,5 а, 13 - 0, [/, - 45 в, (У2 - 75 в,
при t — о© /г — /3 — 1,2 а, Ur — 36 в, £/2 = 84 в, /2 — 0.
___t ___i_ t
13.25. ис = U + (Uo — U) е rC ; t = У~и° е гС .13.26.1 =
= 0,64 в*1000' а; иС1 = (64е-1000' + 36) в; иС2 = (—16 в-*000' + 36) в;
И7нач = 58 мдж; W30H = 32,4 мдж; 1Гтепл = 25,6 мдж. 13.27. i =
= 0,96 е'1000' а; иС{ = (4 + 96 е"1000') в; иС2 = (—4 + 24е-1000') в.
13.28. i = 0,2 е’2000' а; иС1 = 5 (4 + е’2000') в; иС2 = 20 (1 — е’2000') в.
13.29. <1=(0,2+0,05е-510’')а; t2=(0,2-0,2e-5 '0,')a; i3=0,25e-5-10"а.
13.30. иС2 = 81,3 (е"178' — е~в325') в. 13.31. ас= 120е'10‘ в; при
t = 0,1 сек ис = 44,2 в. 13.32. ис = (16 + 8 е-6-2510*') в;
it = (0,16 — 0,1 e-e.25io><) а. i2 =(0,16 +0,05 в-6-2510*') а;
I = — 0,15 е-6.2510»/ а. 13.33. _ 0 39 а 13.35. =
= [2 cos И + 20°35')— 1,47 е-3750'] a; i2 = 0,4 е*1000' а.
у / J_\ ____________
13.36. I — —^-(^sin wt—tg<p ex j , где z = у r2 + ; ^=rC;
1 7U
tg <P -----. 13.37. и = Um sin <|», где ф = -j- + <p; tg <p =
(0 Cr
13.39. ur = 5
О
—t
sin(W + 22°40') — 0,385 e1^
M8.
465
13.40. /max = 4,68 а при tm = 405 мксек; El max =86,5 в при
t = 2tm. 13.41. /max = 13,1 а при tm =0,707 мсек; £ьтах=68,5в
при tm = 1,414 мсек, 13.42. <oo = 98-103 ce/cl; <o0 = 126,4-103 сект1.
13.43. 230 колебаний. 13.46. = 0,02 X (16 e“500/— е"125/)л; i2 =
- 0,1 (4 e-500/ —e’125z) a; i3 = 0,08 (<r125' — e"500 ') a; uc = (30 -
— 40 e~50(U 4- 10 е“12б/) в. При г > имеет место колеба-
t п
тельный заряд. 13.48.^ = — sin (<о/ + ф —(pj—sin(*p—<рх) е
sin (<п/4-ф—<р2) 4- —^-sin (ф—<рх) е
а Z1
о
sin (w/4-ф)
где
tg <Р1 =
; z2
2
— Ы г
tg<b = -^c-= ctgcpp
13.49.
U
° \2L rC! Sh at
2aL sh atJ’ где
а=
2
= 750 сект1; b ~ jfr- = 1250 сек-1; 2) и
о>0 \2L
sin (о0 t
U
r \
75—r sin (oo t , где (o0=
ZO)q £> J
2
= 5000 сект1;
b = = 1000 сек-1. 13.50. = (2—2 e-5’104' + 5- 104/e-5,04/) a;
i2 = (2—2 r8-10*') a; is = 5-104/ e-s-104'. 13.51. i\ (0) = 2a;
uc(0) = 0; -“Fl-о = 6’67' '03 alceK', iz_0 — 6,67-105 в!сек;
i2 = 2 +0,94 e~3',04/ sin(104/— 45°) a; uc = 2Q+2\,2 e-3104'sinX
X(104/—71°35')e. 13.52. uc = (40 + 24 t?-105' — 16 ) в.
13.53. Для / = 0 z/2 = 64,3 в, uL =—42,9 в, uc = 90 в,
= — 2,32-108 в/сек, =1,3-106 в!сек, =—2,58 x
X 10s в!сек; для t — <x> u2 = 40 в, uL = 0, uc — 40 в.
13.55. t/c(0_) = 80 в; uc(0) = — 20 в. 13.57. i\ (CL) = 10 a;
1^(0) = 2,5 a. 13.59. ис = 20впри/<0;ис = (70 + 8,5е-3'621()4/ —
— 58,5 г-1 •з8’106') в.
466
Глава 14. операторный метод расчета
ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
14.2. = (83,3 — 33,3 е“600/) в. 14.3. См. ответы к задаче
13.12.14.5. См. ответы к задаче 13.46.14.6. ^=0,1—0,05е~6’67 104г—
— 0,05 е~2,1°6/ а. 14 .7. При вещественных корнях
sh р/; при комплексных
при равных корнях 1 =
Ег^е~а1
корнях i—
где а =
i+гг)
sin wZ;
i - Р = i” =
= V 1>2—4 ас, а = LC + r2); b=C (rtr2 + гг2 + п\), c=r+rt.
14.8. i =
где а =
14.10.
sin (ty—а) е z
Ь)Ь(Г1-\-Гъ) t
¥2 ’
— а4~Р) —
где
tga =
tg 8 = —• т = _L(ri+r*>
14.11. / = [(7,22 sin (314 / + 43°50') + 8,3 r1"01 sin (153 t —
— 37°20')[ a\ uc =346 sin(314/ —46° 10') —412<r100' -sin(153/ —
— 37°20') в. 14.24. /2 = [1,18 sin (314/+ 16°40') + 0,43 e’336' a.
14.26. 1,85 a. 14.27. / = (0,1 e-10‘ — 0,05 e~5t) a-, uc = 200 (e~i( —
— e~iu‘) в. 14.28. / = (12 + 20 e~u — 32 e"2«6/) а; = 320(е'2-5'—
— е-4') в. 14.29. / = 0,024 (е‘2< — е-«) а; ис = (120 + 120 ег“ —
— 240 е-2/) в.
Глава 15. расчет линейных электрических цепей
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ МЕТОДОМ
ИНТЕГРАЛА ДЮАМЕЛЯ И СПЕКТРАЛЬНЫМ МЕТОДОМ
15.2. у (/) =-L -
G г2 z
!г,+'2’ . 15.3. у(/) = (5,5 е‘7’6'
+ 14,5 е 52’4/).1О-5 ол-i; k(t) = (1 — 0,72 <Г7>6 ' — 0,28+52-4 ') в.
467
15.6. y(t) =
r^aC
r2 (ri + гг)
;У (/«>) =
. 15.7.
to = 150 рад!сек; у (t) — 5-10-3 e~150/ ом-1.
____t
I5.8.fe(t) = e r‘
(0 =
1
и ~~тс*
— e
r
; при t
— (1 - e rc 1
15.12. При
(1
I =
г
sin (со/— <p) + sin <p e
; при
— I sin («)/ — q>)e
z
t
+ sin<pe
. где
co
j / —L
—. 15.17. iff) = t7(ooC 1—e rC
mrC 4
t \
rC). 15.19. При 0 < t <2-IO-3 сек
15.20. При 0<7 < «2=25 (1—e~10'z) в; при t > u2 = 1340e-10’' =
= 24,5e~10’ в. 15.21. и2 = U <оо/ — yTC ш0 sin
«гол 11,- X 2-10’ -/«5-10-» 2-10’
15.24. U (/ ш) =-----------------e . 15.25. U (/ <o) =-------------------------
v ’ 4 • 1010 — «>2 4 • 1010 — <®2
—Д { 10“6<o------ 4ir T
\ 2Л 15.26. t/j(jШ) = j , sin шТ0;
— a)*5 T
0
8л To : 2
----x—— sin2
0)2 Го» _ 4K2
. 11
7 ~2~
250
/ <*> “f- 500
15.32.
U «>0
468
Глава 16. основы синтеза линейных
ЦЕЛЕЙ
16.3. а) Не п. д. ф., так как наибольшие степени р числи-
теля и знаменателя отличаются более, чем на единицу (см. п.
2,6 основных положений); б) не п. д. ф., так как на мнимой
оси имеются кратные полюсы (см. п. 2, в основных положений).
в
469
16.10.
а) г£=Ъ
/
0-----
6)jj"
8
0------
/
з.
в
3
32
ш- з & йз
3. 49 6
8 88 88
шш
2
0-
3. 49 6
8 88 88
0-
0-4 Г ~—г 0 * - *---------1 0
16.12.
ц.
16.15.
33' 330
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Данные основной кривой намагничивания, afto.
Слабо- и среднелегированная листовая электротехническая сталь (Э11)
В 0/0 0.01/100 0.02/200 0,03/300 0,04/400 0,05/500 0,06/600 0,07/700 0,08'800 0,09/900
тл гс
0,4 4 000 140 143 146 149 152 155 158 161 164 167
0,5 5 000 171 175 179 183 187 191 195 199 203 207
0,6 6 000 211 216 221 226 231 236 241 246 251 256
0,7 7 000 261 266 271 276 281 287 293 299 306 312
0,8 8 000 318 324 330 337 344 352 360 369 378 387
0,9 9 000 397 407 417 427 437 447 458 469 480 491
1,0 10 000 502 514 527 541 555 570 585 600 615 631
1,1 11 000 647 664 682 701 720 739 759 779 800 821
1,2 12 000 843 866 891 918 946 976 1010 1040 1070 1100
1,3 13 000 1140 1180 1220 1260 1300 1340 1380 1430 1480 1530
1,4 14 000 1580 1640 1710 1780 1860 1950 2050 2150 2260 2380
1,5 15 000 2500 2640 2790 2950 3110 3280 3460 3660 3880 4120
1,6 16 000 4370 4630 4910 5220 5530 5880 6230 6600 6980 7370
1,7 17 000 7780 8200 8630 9070 9630 10 100 10 600 11 100 11 600 12 200
1,8 18 000 12 800 13 400 14 000 14 600 15 200 15 900 16 600 17 300 18 000 18 800
1,9 19 000 19 700 20 600 21 600 22 600 23 600 24 600 25 600 26 800 28 200 29 600
2,0 20 000 31 100 32 500 34 300 36 500 39 000 42 000 45 500 49 500 54 500 59 500
Примеры пользования таблицей:
при В = 0,8 тл = 8000 $с Н = 318 —*,
2) при В = 1,13 тл = 11 300 ?с Н = 701 — .
м
О
ПРИЛОЖЕНИЕ 2
Переход от алгебраической формы комплексного числа к показательной
и обратный — при помощи логарифмической линейки
Если комплексное число С задано в алгебраической форме
С —a + jb.
то его аргумент а и модуль г определяются по формулам
tga = 4’’ 0)
г = -4— = , (2)
ЗШ a cos а * v '
тогда
а + jb = ге1*. (3)
Проще всего находить а и г при помощи логарифмической
линейки. При этом надо иметь ввиду, что на шкале тангенсов
нанесены углы только до 45°. Поэтому надо различать следую-
щие случаи:
1. а>0, 6 > 0 и 1. В этом случае угол а прямо нахо-
дится на шкале тангенсов.
2. а>0, 6>0 и >1. В этом случае на шкале тан-
генсов находится угол (90° — а), так как tg(90° — а) = 1-
3. Одно из чисел а и b (или оба) отрицательно. Предвари-
тельно определяем, в какой четверти лежит а. Затем, найдя на
линейке острый угол, тангенс которого равен -у—-, по извест-
ным из тригонометрии формулам приведения определяем
угол а.
Для выполнения указанных операций нужно движок линей-
ки перевернуть так, чтобы шкалы синусов и тангенсов оказа-
лись снаружи.
Рассмотрим несколько типичных случаев.
Пример 1.
Сг = 26 + / 11.
Устанавливаем волосок над меньшим числом 11 на основной
нижней шкале и делим его на 26, для чего движок передви-
гаем до тех пор, пока его конец не станет под числом 26.
Тогда на шкале тангенсов под волоском найдем
а = 22°55'.
Для определения модуля по формулам (2) передвигаем дви-
жок до тех пор, пока под волосок не попадает угол в 22°55',
472
нанесенный на шкале синусов. Тогда под концом движка на
основной шкале найдем г = 28,3:
26+ /11=28,2е'22 55 .
Пример 2.
Са = 4 -j- j 7.
Деля, как и в первом примере, меньшее число 4 на большее
7, найдем на шкале тангенсов угол 29°45'. Так как />>а, то
а = 90° — 29°45'= 60°15'.
Передвигаем движок и устанавливаем под волоском угол в
29°45' со шкалы синусов. На основной шкале найдем г = 8,06:
4 + /7 = 8,Обе760016' .
Пример 3.
С3 = 382 + / 28.
Так как <0,1, то угол меньше 5°45' (tg 5°45' я»
я» sin5°45'я» 0,1) и находится на средней шкале (где обозначе-
но S и Т). Деля меньшее число 28 на 382, на этой шкале
найдем
а = 4° 12'.
Так как для углов, меньших 5°45', tga«sina, то модуль
равен 382:
382 +/28 = 382ем°12'.
Пример 4.
С4 = ПО —/90.
Угол а лежит в четвертой четверти, так как |6|< |а|, то
по абсолютной величине он меньше 45°. Деля меньшее число
90 на ПО, найдем угол 39°20'. Следовательно, а =— 39°20'.
Модуль находится, как в предыдущих примерах:
110-/90= 142е_'39°20'.
Пример 5.
13
Угол а лежит во второй четверти. Так как -§->1, то а<
< 135° (tg 135° = — 1). Следовательно, a = 90° + угол, найден-
ный на линейке.
Деля меньшее число 8 на 13, найдем угол 31°35':
a = 90° + 31°35' = 121°35';
- 8 + j 13 = 15,3?,21035'.
473
Рассмотрим,, как выполнить обратный переход от показа-
тельной формы к алгебраической.
Пример 6.
С6= 74е/28° = 74 cos 28° + / 74 sin 28°.
Устанавливаем волосок над числом 74 на нижней основной
шкале и совмещаем с этим числом конец движка. Умножая 74
на cos 28° = sin 62° (для чего устанавливаем волосок на 62°
шкалы синусов), получим
74 cos 28° = 74 sin 62° = 65,3.
Умножая 74 на sin 28°, для чего нужно только передвинуть
бегунок так, чтобы под волоском оказалось 28° шкалы синусов,
получим 74 sin 28° = 34,7.
Следовательно, 74^/28 = 65,3 4-/34,7.
ПРИЛОЖЕНИЕ 3
О расчете гиперболических функций от комплексного аргумента
При решении задач на четырехполюсники, фильтры, длин-
ные линии приходится определять значения гиперболических
синуса, косинуса и тангенса от комплексного аргумента Г =
= а + jb. Для вычисления указанных функций рекомендуется
пользоваться формулами (4) -4- (6) приложения 4. В курсе выс-
шей математики показывается, что при вычислении sh (а-(-/&)
и ch (а + jb) углы и находятся в тех же четвертях окруж-
ности, что и угол Ь, причем для нечетных четвертей окружнос-
ти Ь^> <рг, а угол Ф, > 0; для четных четвертей окружнос-
ти Ф5<6<Ф,, а угол ф,<0.
Пример 1. Найти sh(0,65 + j 1,334); ch (0,65 + j 1,334);
th (0,65 + /1,334).
Решение. Здесь a = 0,65, b = 1,334 рад, но так как 1 рад=
= 57,3°, то b = 1,334 • 57,3° = 76,5° = 76°30', т. е. b лежит в
первой четверти.
По таблицам функций действительного аргумента находим
ch 2 а = ch 1,30 = 1,971; cos 2 6= cos 2,668 = — 0,891.
По формулам (4)ч-(6) приложения 4 находим
5 = /0,5(1,971 + 0,891) = 1,196; tg <p,= = 7,27.
Ф5 == 82° 12', следовательно, sh(0,65 + j 1,334) = 1,196ez 82 12.
474
с = V 0,5 (1,971 — 0,891) = 0,735; tg <рс = 4,165 • 0,572 = 2,385;
<pf = 67° 12', поэтому ch(0,65 + j 1,334) = 0,735? 67°12'.
Наконец,
т = -£- = 1,628; <p, = <p5 —<pc = 82°12' —67°12'= 15°.
U , / oD
th (0,65 + /1,334) = 1,628? 15°.
Согласно отмеченному раньше, так как угол b лежит в пер-
вой (нечетной) четверти, фу = 82° 12' > b = 76°30' > <pf = 67° 12'.
Пример 2. Найти sh (1,15 +/2,825), ch(1,15 + /2,825) и
th (1,15 + /2,825).
Решение. а= 1,15, b = 2,825 рад = 162°, т. е. b лежит
во второй четверти.
По таблицам находим
ch2а = ch 2,3 = 5,037; cos2b = cos5,65 = 0,809;
S = 1,454; tg ~ °’397; = 158°2°/;
sh (1,15 + /2,825) = 1,454? 158°20';
C= 1,710; tg<pr = —0,325 • 0,818 =—0,266; <pf = 165°07';
ch(l,15 + /2,825) = 1,710? I65°07';
T = ГЖ = °’850; = 158°20' — 165°07z = — 6°47';
th (1,15 + /2,825) = 0,850e-/6°47'.
Так как угол b лежит во второй (четной) четверти, то ф5 =
= 158°20' < b = 162° < Ф, = 165°07'.
Пример 3. Найти sh (1,15 +/5,965), ch (1,15 + /5,965)„
th (1,15 +/5,965). В случаях когда угол b > кщ где k — целое
число, величины S, С и Т останутся неизменными, если из b
вычесть kn. В нашем случае b = 5,965 = 342°, т. е. больше и
лежит в четвертой четверти. Если из b вычесть к, то получим
Ь' — Ь—к = 5,965 — 3,14 = 2,825, т. е. то же числовое значение,
которое было во втором примере. Поэтому sh(1,15 + /5,965) =
= 1,454?(,58°20' + ,80°)= 1,454? 338°20'; ch (1,15 + /5,965) =
= 1,710?(165°07'+180°)=1,710?345°07'; th(1,15 + /5,965)=0,850е-/6°47';
*
47S
ПРИЛОЖЕНИЕ 4
Соотношения между круговыми и гиперболическими функциями
1. sh jx — jsinx.
2. ch jx = cos x.
3. th jx = j tg x.
4. sh (x + jy) — sh x cos у + j ch x sin у = Sefvs,
где _______________________________
S = yr-^-(ch2x — cos2y), =
5. ch (x + jy) = ch x cos у 4- j sh x sin у = Ce,
где ___________________
С = у(ch 2x + cos 2 y), tg <pc = th x tg y.
6. th (x + jy) ==
где
т=У 4- соф. t
F ch2x-j-cos2# ь т/ sh2x
ПРИЛОЖЕНИЕ 5
Таблица значений показательных и гиперболических функций
от действительного аргумента
х, рад ех е~х sh х ch х th х X, 0
0,0 1,0000 1,0000 0,0000 1,0000 0,0000 0,00
0,1 1,1052 0,9048 0,1002 1,0050 0,0997 5,73
0,2 1,2214 0,8187 0,2013 1,0201 0,1974 11,46
0,3 1,3499 0,7408 0,3045 1,0453 0,2913 17,19
0,4 1,4918 0,6703 0,4108 1,0811 0,3800 22,92
0,5, 1,6487- 0,6065 0,5211 1,1276 0,4621 28,65
0,6 1,8221 0,5488 0,6367 1,1855 0,5371 34,38
0,7 2,0138 0,4965 0,7586 1,2552 0,6044 40,11
0,8 2,2255 0,4493 0,8881 1,3374 0,6640 45,84
0,9 2,4596 0,4066 1,0265 1,4331 0,7163 51,57
1,0 2,7183 0,3679 1,1755 1,5431 0,7616 57,30
1,1 3,0042 0,3329 1,3357 1,6685 0,8005 63,03
1,2 3,3201 0,3012 1,5095 1,8107 0,8337 68,75
1,3 3,6693 0,2725 1,6984 1,9709 0,8617 74,48
1.4 4,0552 0,2466 1,9043 2,1509 0,8854 80,21
1,5 4,4817 0,2231 2,1293 2,3524 0,9052 85,94
1,6 4,9530 0,2019 2,3756 2,5775 0,9217 91,67
476
Продолжение
х, рад ех е~х sh х ch х th х «, °
1,7 5,4740 0,1827 2,6456 2,8283 0,9354 97,40
1,8 6,0497 0,1653 2,9422 3,1075 0,9468 103,13
1,9 6,6859 0,1496 3,2682 3,4177 0,9562 108,86
2,0 7,3891 0,1353 3,6569 3,7622 0,9440 114,59
2,1 8,1662 0,1225 4,0219 4,1443 0,9705 120,32
2,2 9,0250 0,1108 4,4571 4,5679 0,9757 126,05
2,3 9,9742 0,1003 4,9370 5,0372 0,9801 131,78
2,4 11,0232 0,0907 5,4662 5,5570 0,9837 137,51
2,5 12,1825 0,0821 6,0502 6,1323 0,9866 143,24
2,6 13,4637 0,0743 6,6947 6,7690 0,9890 148,97
2,7 14,8797 0,0672 7,4062 7,4737 0,9910 154,70
2,8 16,4447 0,0608 8,1919 8,2527 0,9926 160,43
2,9 18,1742 0,0550 9,0596 9,1146 0,9940 166,16
3,0 20,0855 0,0498 10,0179 10,0677 0,9955 171,89
3,1 22,1980 0,0451 11,0765 11,1215 0,9960 177,62
3,2 24,5325 0,0408 12,2459 12,2867 0,9967 183,35
3,3 27,1126 0,0369 13,5379 13,5748 0,9973 189,08
3,4 29,9641 0,0334 14,9654 14,9987 0,0978 194,81
3,5 33,1155 0,0302 16,5426 16,5728 0,9982 200,54
3,6 36,5982 0,0273 18,2855 18,3128 0,9985 206,26
3,7 40,4473 0,0247 20,2113 20,2360 0,9980 211,99
3,8 44,7012 0,0224 22,3394 22,3618 0,9990 217,72
3,9 49,4025 0,0202 24,6911 24,7114 0,9992 223,45
4,0 54,5982 0,0183 27,2899 27,3082 0,9993 229,15
4,1 60,3403 0,0166 30,1619 30,1784 0,9995 234,91
4,2 66,6863 0,0150 33,3357 33,3507 0,9996 240,64
4,3 73,6998 0,0136 36,8431 36,8567 0,9996 246,37
4,4 81,4509 0,0123 40,7193 40,7316 0,9997 252,10
4,5 90,0171 0,0111 45,0030 45,0141 0,9998 257,83
4,6 99,4843 0,0101 49,7371 49,7472 0,9998 263,56
4,7 109,9472 0,0091 54,9690 54,9781 0,9998 269,29
4,8 121,5104 0,0082 60,7511 60,7593 0,9999 273,02
4,9 134,2898 0,0075 67,1412 67,1486 0,9999 280,75
5,0 148,4132 0,0067 74,2032 74,2100 0,9999 286,48
5.1 164,0219 , 0,0061 82,0079 82,0140 0,9999 292,21
5,2 181,2722 0,0055 90,6334 90,6389 0,9999 297,94
5,3 200,3368 0,0050 100,1659 100,1709 1,0000 303,67
5,4 221,4064 0,0045 110,7008 110,7055 1,0000 309,40
5,5 244,6919 0,0041 122,3439 122,3480 1,0000 315,13
5,6 270,4264 0,0037 135,2114 135,2150 1,0000 320,86
5.7 298,8674 0,0034 149,4320 149,4354 1,0000 326,59
5,8 330,2996 0,0030 165,1483 165,1513 1,0000 332,32
5,9 365,0375 0,0027 182,5174 182,5201 1,0000 338,05
6,0 403,4288 0,0025 201,7132 201,7156 1,0000 343,77
6,3 544,5719 0,0018 272,2850 272,2869 1,0000 360,96
ЛИТЕРАТУРА
Основная
Атабеков Г. И. Теоретические основы электротехники. Линейные элек-
трические цепи, ч. I. Энергия, 1966.
Бессонов Л. А. Теоретические основы электротехники в трех частях.
Изд. 5-е. «Высшая школа», 1965.
Гоноровский И. С. Радиотехнические цепи и сигналы. «Советское
радио», 1964.
Зевеке Г. В., Ионкин П. А. и др. Основы теории цепей. «Энер-
гия», 1965.
Ионкин П. А., Мельников Н. А., Даревский А. И., Ку-
харкин Е. С. Теоретические основы электротехники, ч.1. «Высшая шко-
ла», 1965.
Каплянский А. Е., Лысенко А. П. и др. Теоретические осно-
вы электротехники. Госэнергоиздат, 1961.
Кощеев И. А. Основы теории электрической связи. Связьиздат, 1954.
Кульбацкий Е. Е., Аносович Б. Ф. Лекции по курсу «Теория
электрической связи». ВЗЭИС, 1964.
Нейман Л. Р., Калантаров П. Л. Теоретические основы элект-
ротехники, ч. I и II. Госэнергоиздат, 1959.
Нейман Л. Р., Демирчян К. С. Теоретические основы электро-
техники. Т. 1. Энергия, 1966.
Поливанов К. М. Теоретические основы электротехники, ч. I. Энер-
гия, 1965.
Жуховицкий Б. Я., Негневицкий И. Б. Теоретические основы
электротехники, ч. 2. Энергия, 1965.
Харкевич А. А. Основы радиотехники. Связьиздат, 1962.
Дополнительная
Гарднер М. Ф., Бернс Д. А. Переходные процессы в линейных
системах. Физматгиз, 1961.
Конторович М. И. Операционное исчисление и нестационарные яв-
ления в электрических цепях. Госиздат технико-теоретической литературы,
1949
Круг К. А. Переходные и установившиеся процессы в линейных элек-
трических цепях. Госэнергоиздат, 1948.
Куп ф мюллер К. Основы теоретической электротехники. Госэнерго-
издат, 1952.
Максимович Н. Г, Линейные электрические цепи и их преобразова-
ния. Госэнергоиздат, 1961.
Реза Ф. и Сили С. Современный анализ электрических цепей. Энер-
гия, 1964.
Сету С., Балабанян Н. Анализ линейных цепей. Госэнерго-
издат, 1963.
Зернов Н. В. и Карпов В. Г. Теория радиотехнических цепей.
Энергия, 1965.
478
Задачники
Гольдин О. Е. Задачник по курсу теоретических основ электротехни-
ки. Госэнергоиздат, 1960.
Заездный А. М. Основы расчетов радиотехнических цепей. Связь,
1966.
Зайцев И. А., Лурье А. Г. Задачник по теоретическим основам
электротехники. Госэнергоиздат, 1961.
Задачник по теоретическим основам электротехники (теория цепей) под ред.
Поливанова К. М. Госэнергоиздат, 1962.
Садовский А. С. Задачник по теории электрической связи. Связьиз-
дат, 1963.
Шебес М. Р. Сборник упражнений и задач по теоретическим основам
электротехники. «Высшая школа», 1962.
ОГЛАВЛЕНИЕ
П редисловие .................................................. 3
Глава 1. Линейные электрические цепи постоянного тока .... 5
Глава 2. Простейшие электрические цепи синусоидального тока 66
Глава 3. Метод комплексных амплитуд (символический) ..... 96
Глава 4. Резонанс в электрических цепях.......................124
Глава 5. Цепи с взаимной индуктивностью.......................157
Глава 6. Трехфазные цепи..................................... 197
Глава 7. Цепи периодического несинусоидального тока..........215
Глава 8. Катушки и трансформаторы с ферромагнитными сердеч-
никами .......................................................243
Глава 9. Двухполюсники.......................*................257
Глава 10. Четырехполюсники....................................266
Глава 11. Электрические фильтры...............................296
Глава 12. Электрические цепи с распределенными параметрами . . 310
Глава 13. Классический метод расчета переходных процессов в эле к-
трических цепях с сосредоточенными параметрами . . . 335
Глава 14. Операторный метод расчета переходных процессов в элек-
трических цепях с сосредоточенными параметрами ... 375
Глава 15. Расчет линейных электрических цепей с сосредоточенны-
ми параметрами методом интеграла Дюамеля и спектраль-
ным методом . ................................................401
Глава 16. Основы синтеза линейных цепей.......................423
Ответы . . . * *..............................................452
Приложения ................................................• 471
Литература .................................................. 478
Шебес Михаил Романович
ТЕОРИЯ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
В УПРАЖНЕНИЯХ И ЗАДАЧАХ
Редактор Е. В. Басавина. Переплет художника Л. М. Чернышева. Художе-
ственный редактор Т. М. Скворцова. Техн, редакторы В. А. Зорина
и Н. Н. Баранова. Корректор Р. А. Уварова
Т—02871. Сдано в набор 10/VI—66 г. Подл, к печати 22/111—67 г, Формат
60х901/1в. Объем 30 печ. л. Уч.-изд. 22,49 л. Индекс ЭР—12/64. Тираж 40.000
экз.Цена 89 кош Изд-во «Высшая школа», Москва, К-51, Неглинная ул., 29/14.
Тематический план издательства «Высшая школа» (вузы и техникумы) на 1966 р.
___________________________Позиция № 146___________________________
Ярославский полиграфкомбинат Главполиграфпрома Комитета по печати при
Совете Министров СССР. Ярославль, ул. Свободы, 97. Зак» 624.