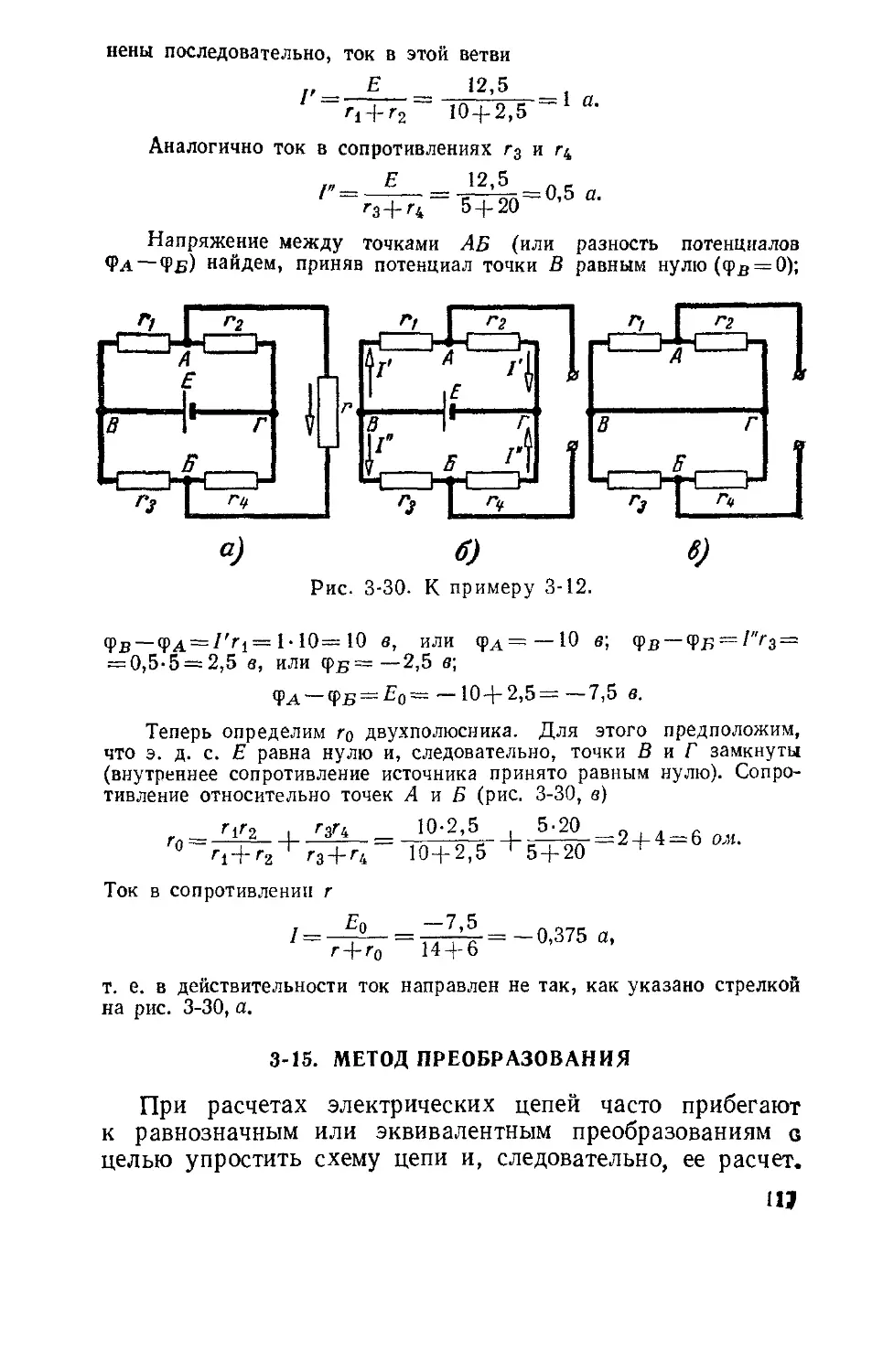
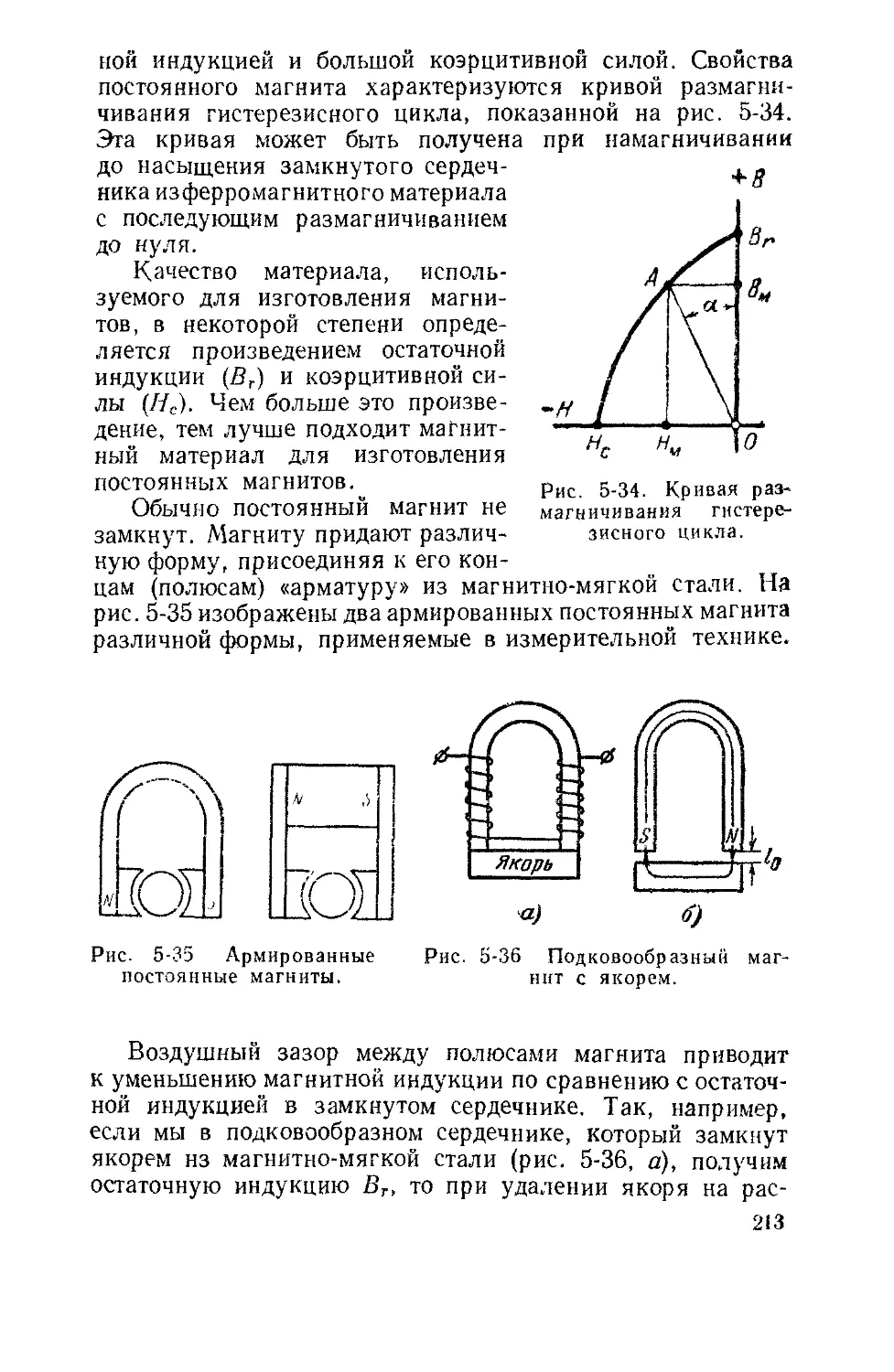
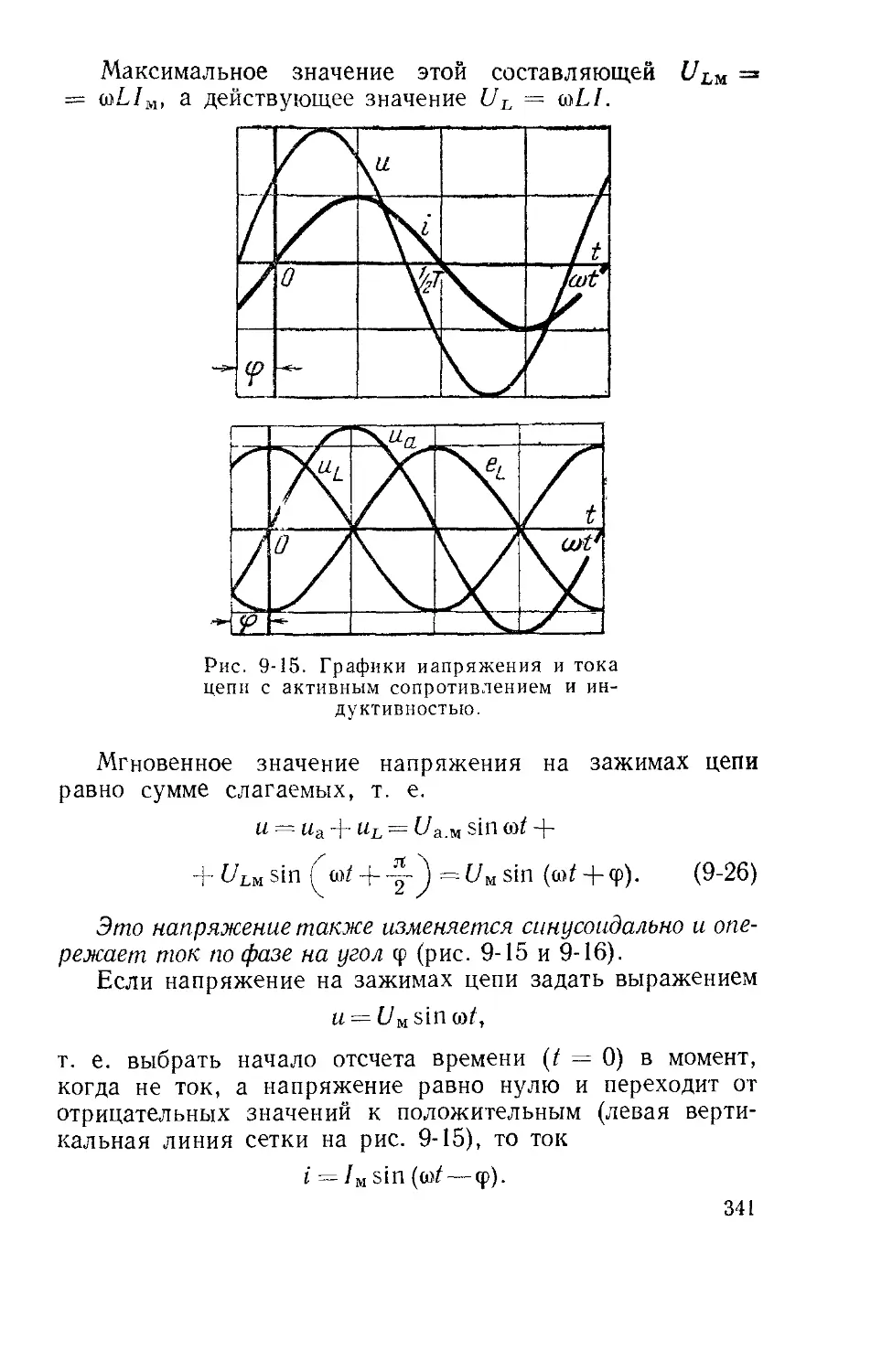
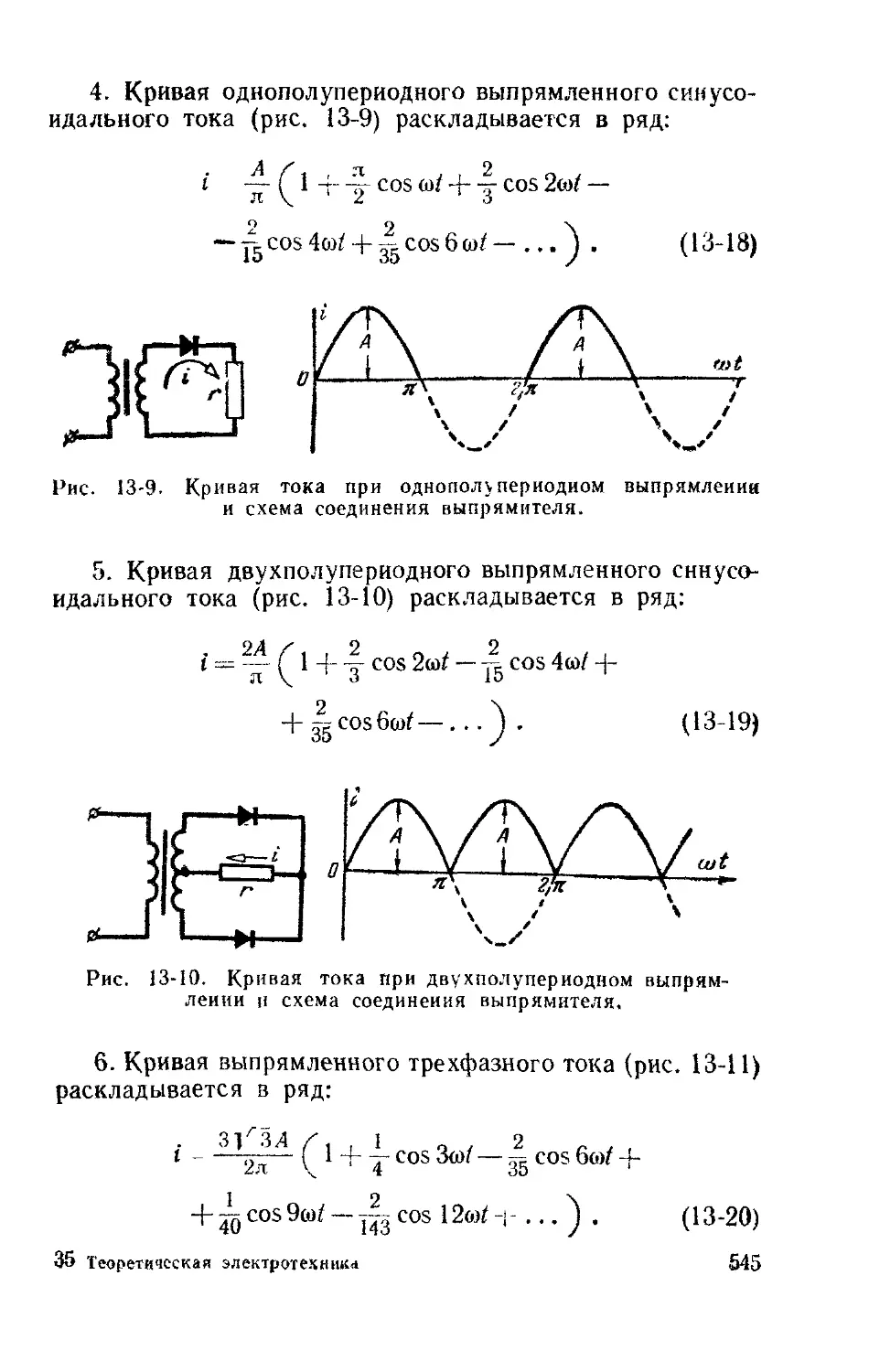
Текст
Н. Н. МАНСУРОВ и В. С. ПОПОВ
ТЕОРЕТИЧЕСКАЯ
ЭЛЕКТРОТЕХНИКА
ИЗДАНИЕ ДЕВЯТОЕ, ИСПРАВЛЕННОЕ
SS
ИЗДАТЕЛЬСТВОМ Н Е Р Г И Я»
МОСКВА 1966 ЛЕНИНГРАД
УДК 621.3.01(02)
М 23
В книге рассматриваются физические процес-
сы, происходящие в электрическом и магнитном
полях, в электрических линейных и нелинейных
цепях постоянного и переменного тока. Излага-
ются основные методы расчета, принятые в элек-
тротехнике. Даны описания лабораторных работ.
Изложение поясняется большим количеством при-
меров с решениями.
Книга предназначается для лиц, изучающих
основы электротехники в объеме курса технику-
мов различных электротехнических специально-
стей, и может быть полезна при самообразовании.
Мансуров Николай Николаевич и Попов Виктор Степанович
Теоретическая электротехника, изд. 9-е, исправленное, М.— Л., издательство
«Энергия», 196'6, 624 с. с черт.
Бланк заказа № 35, 1965 г,, п. 16
Редактор Г. Н. Сапков
Техн, редактор Н. А. Будьдяев
Сдано в набор 22/VI 1965 г. Подписано к печати 1/Х 1965 г. Т-13250
Бумага 84Х1081/з2 Печ. л. 32,76. Уч.-изд. л. 32,57. Тираж 310 000 экз.
(2-й завод 150000 экз.) Цена 1 р. 22 к.
Московская типография № 16 Главполиграфпрома Государственного комитета
Совета Министров СССР по печати. Москва, Трехпрудный пер., д. 9.
Отпечатано во Владимирской типографии Главполиграфпрома
Государственного комитета Совета Министров СССР
по печати
Гор. Владимир, ул Победы, д. 18-6. Зак. 2515,
ПРЕДИСЛОВИЕ
С каждым годом в нашей стране увеличивается размах
энергостроительства, возрастает производство электроэнер-
гии и применение ее в различных областях промышленно-
сти, транспорта и сельского хозяйства. Таким образом
во все возрастающих масштабах воплощается в жизнь завет
великого Ленина об электрификации страны. Непрерывно
возрастает потребность в кадрах электротехников. Для
того чтобы овладеть электротехникой, необходимо изу-
чить основы наук и, в частности, основы электротехники.
С 1944 г. данная книга являлась учебником по теорети-
ческой электротехнике для техникумов энергетических
и электротехнических специальностей и на протяжении
восьми изданий неоднократно подвергалась переработке.
Настоящее, девятое издание отличается от предыдущего
издания только тем, что в нем нашли отражение
ГОСТ 9867-61 на Международную систему единиц СИ
и ГОСТ 7624-62 на условные графические обозначения для
электрических схем.
В связи с изменениями в учебных планах и программах,
вызванными сокращением срока обучения в техникумах,
настоящая книга выпускается без грифа учебника. Однако
она может быть использована при изучении теоретической
электротехники как учащимися техникумов, так и электри-
ками-производственниками, повышающими свою квали-
фикацию.
R, С, Попов
СОДЕРЖАНИЕ
Предисловие .............................................. 3
Введение................................................. 13
Глава первая. Электрическое поле
1-1. Основные понятия............................... 17
1-2. Напряженность электрического поля.............. 18
1-3. Электрическое поле точечного заряда............ 21
1-4. Диэлектрическая проницаемость ................. 22
1-5. Закон Кулона .................................. 23
1-6. Электрическое поле нескольких точечных зарядов 25
1-7. Электрический диполь .......................... 26
1-8. Поток вектора напряженности.................... 27
1-9. Теорема Остроградского и Гаусса................ 27
1-10. Потенциал электрического поля.................. 28
1-11. Электрическое напряжение ...................... 30
1-12. Однородное электрическое поле.................. 31
1-13. Равнопотенциальные поверхности................. 34
1-14. Электропроводность вещества.................... 36
1-15. Проводники .................................... 37
1-16. Диэлектрики.................................... 39
1-17. Поляризация диэлектрика......................... 39
1-18. Пробивная напряженность диэлектрика............ 40
1-19. Электрическое смещение ........................ 41
1-20. Полупроводники................................. 44
Глава вторая. Электрическая цепь постоянного тока
2-1. Электрическая цепь ............................ 44
2-2. Электрический ток ............................. 47
2-3. Электродвижущая сила .......................... 49
2-4. Источники э. д. с.............................. 51
А. Первичные элементы............................. 51
Б. Аккумуляторы.................................... 53
В. Термогенератор (термопара)..................... 56
2-5. Электрический ток и плотность тока в проводнике 59
2-6. Закон Ома...................................... 61
2-7. Сопротивление ................................. 62
2-8. Зависимость сопротивления от температуры ... 68
2-9. Электрическая работа и мощность.................70
2-10. Единицы измерения работы и мощности............ 72
2-11. Закон Ома для электрической цепи............... 73
2-12. Преобразование электрической энергии в тепловую 73
2-13. Нагревание проводов током..................... 74
4
2-14. Короткое замыкание. Предохранители ............. 76
2-15. Электрическая цепь с несколькими э. д с......... 77
2-16. Потенциальная диаграмма ........................ 79
Глава третья. Расчет электрических цепей
постоянного тока
3-1. Правила Кирхгофа.......................... 83
3 3- Последовательное соединение сопротивлений ... 85
3-3. Параллельное соединение сопротивлений .... 87
3-4. Смешанное соединение сопротивлений........ 89
3-5. Последовательное, параллельное и групповое соеди-
нения первичных элементов и аккумуляторов . . 91
3-6. Неразветвленная цепь с переменным сопротивлением 93
3-7. Потеря напряжения в проводах................... 96
3-8. Измерение тока и напряжения.................. 100
3-9. Измерение сопротивлений....................... 103
3-10. Расчет сложных цепей методом узловых и контур-
ных уравнений ................................. 104
3-11. Метод узлового напряжения...................... 108
3-12. Параллельное соединение генераторов............. НО
3-13. Принцип наложения (суперпозиции)............... 112
3-14. Метод холостого хода и короткого замыкания
(метод эквивалентного генератора) ............. 113
3-15. Метод преобразования .......................... 117
3-16. Четырехполюсник................................ 121
3-17. Постоянные четырехполюсника................... 125
3-18. Определение постоянных четырехполюсника . . . 126
3-19. Испытание четырехполюсника..................... 127
3-20. Лабораторная работа. Исследование электрического
поля в проводящей среде........................ 129
3-21. Лабораторная работа. Измерение удельного сопро-
тивления проводов (§ 2-7) 130
3-22. Лабораторная работа. Измерение потенциалов точек
электрической цепи (§ 2-16) ................... 130
3-23. Лабораторная работа. Исследование процесса нагре-
вания катушки электрическим током (§ 2-4, 2-8 и 2-13) 132
3-24. Лабораторная работа. Последовательное и парал-
лельное соединения сопротивлений (§ 3-2 и 3-3) . . 134
3-25. Лабораторная работа. Исследование неразветвлен-
ной электрической цепи при одном переменном
сопротивлении (§ 3-6) ......................... 135
3-26. Лабораторная работа. Измерение потери напряжения
в проводах (§ 3-7)............................. 136
3-27. Лабораторная работа. Расширение пределов изме-
рения тока и напряжения (§ 3-8)................ 138
3-28. Лабораторная работа. Измерение э. д. с. компенса-
ционным методом ............................... 140
3-29. Лабораторная работа. Измерение сопротивлений
измерительным мостом (§ 3-9) ........... 141
3-30. Лабораторная работа. Опытная проверка принципа
наложения (§ 3-13) ............................ 142
3-31. Лабораторная работа. Испытание четырехполюсника
(§ 3-16-3-19) ............................... 143
5
Глава четвертая. Нелинейные электрические цепи
постоянного тока
4-1. Основные понятия............................. 144
4-2. Двухэлектродная электронная лампа............. 145
4-3. Трехэлектродная электронная лампа............. 148
4-4. Параметры трехэлектродной лампы............... 150
4-5. Ламповый усилитель............................ 151
4-6. Электрический ток в газах..................... 153
4-7. Самостоятельный разряд в газе................. 155
4-8. Темный и тлеющий разряды...................... 156
4-9. Искровой разряд............................... 156
4-10. Дуговой разряд ............................. 157
4-11. Проводимость полупроводников ................. 159
4-12. Влияние примесей на проводимость полупровод-
ников ........................................ 161
4-13. Электронно-дырочный переход .................. 162
4-14. Полупроводниковый вентиль .................... 163
4-15. Полупроводниковый усилитель .................. 164
4-16. Меднозакисные и селеновые вентили............. 165
4-17. Расчет нелинейных цепей....................... 167
4-18. Балластное сопротивление ..................... 170
4-19. Стабилизаторы тока и напряжения............... 172
4-20. Лабораторная работа. Снятие характеристик двух-
электродной и трехэлектродной ламп (§ 4-2—4-4) 173
4-21. Лабораторная работа. Снятие вольт-амперной харак-
теристики полупроводникового вентиля (§ 4-14, 4-16) 174
4-22. Лабораторная работа. Исследование нелинейной
цепи при последовательном н параллельном соеди-
нении (§ 4-17)................................ 176
Глава пятая. Электромагнетизм
5-1. Магнитное поле электрического тока............ 178
5-2. Магнитная индукция............................ 178
5-3. Магнитная индукция в центре кольцевого провод-
ника с током.................................. 180
5-4. Магнитная проницаемость ..................... 181
5-5. Единицы измерения магнитной индукции .... 182
5-6. Линии магнитной индукции...................... 183
5-7. Магнитный поток .............................. 184
5-8. Трубка магнитной индукции..................... 185
5-9. Напряженность магнитного поля................. 186
5-10. Магнитное напряжение.......................... 187
5-11. Закон полного тока............................ 188
5-12. Магнитное поле прямолинейного провода с током 190
5-13. Магнитное поле коаксиального кабеля........... 194
5-14. Магнитное поле кольцевой катушки.............. 194
5-15. Магнитный момент. Намагниченность............. 196
5-16. Намагничивание ферромагнитных материалов . . . 198
5-17. Циклическое перемагничивание ................. 201
5-18. Магнитное поле на границе раздела двух сред
с различной магнитной проницаемостью.......... 204
5-19. Магнитная цепь................................ 206
5-20. Магнитные цепи электрических машин............ 207
6
5-21. Расчет магнитной цепи ....................... 298
5-22. Постоянные магниты........................... 212
5-23. Электромагнитная сила........................ 216
5-24. Электромагнитные силы, действующие на парал-
лельные провода с токами ..................... 218
5-25. Работа электромагнитных сил.................. 220
5-26. Работа электромагнитных сил при перемещении
контура с током .............................. 222
5-27. Магнитоэлектрический измерительный механизм 224
Глава шестая. Электромагнитная индукция
6-1. Сила, действующая на электрон, движущийся в маг-
нитном поле ..................................... 225
6-2. Электродвижущая сила электромагнитной индукции 226
6-3. Преобразование механической энергии в электри-
ческую ....................................... 229
6-4. Электрические генераторы ..................... 330
6-5. Преобразование электрической энергии в механи-
ческую ....................................... . . 233
6-6. Электрические двигатели ...................... 234
6-7. Электродвижущая сила электромагнитной индукции
в контуре ................................... ..... 236
6-8. Потокосцепление............................... 240
6-9. Вихревые токи................................. 241
6-10. Баллистический гальванометр................... 243
6-11. Возбуждение электрического заряда изменяющимся
магнитным потоком ............................. 244
6-12. Измерение магнитного потока и магнитной индукции 245
6-13. Измерение магнитного напряжения 246
6-14. Индуктивность................................. 247
6-15. Индуктивность катушки......................... 248
6-16. Индуктивность двухпроводной линии............ 249
6-17. Электродвижущая сила самоиндукции............. 251
6-18. Переходный процесс при подключении цепи, обла-
дающей сопротивлением и индуктивностью, к источ-
нику питания с постоянной э. д. с.............. 251
6-19. Переходный процесс в короткозамкнутом контуре 255
6-20. Электродвижущая сила самоиндукции при выклю-
чении цепи .................................... 256
6-21. Энергия магнитного поля....................... 257
6-22. Плотность энергии магнитного поля............. 258
6-23. Электромагниты ............................... 259
6-24. Взаимная индуктивность .................. 262
6-25. Энергия магнитного поля индуктивно связанных кон-
туров .......................................... 264
6-26. Электродвижущая сила взаимной индукции .... 264
6-27. Магнитная связь контуров .................. 265
6-28. Лабораторная работа. Измерение магнитной индук-
ции (§ 5-14—6-12) 267
6-29. Лабораторная работа. Измерение магнитного напря-
жения (магнитный пояс) (§ 6-13)........... 268
6-30. Лабораторная работа. Исследование гистерезиса
(§ 5-16, 5-17) 270
7
Глава седьмая. Электрическая емкость
7-1. Емкость конденсаторов ......................... 272
7-2. Параллельное соединение конденсаторов .... 275
7-3. Последовательное соединение конденсаторов . . . 276
7-4. Плоский конденсатор ........................... 277
7-5. Плоский конденсатор с двухслойным диэлектриком 278
7-6. Цилиндрический конденсатор .................... 280
7-7. Емкость двухпроводной линии............... 282
7-8. Зарядный ток конденсатора....................... 284
7-9. Электрический ток смещения................ 287
7-10. Энергия электрического поля............... 288
7-11. Плотность энергии электрического поля..... 289
7-12. Разрядка конденсатора на сопротивление .... 290
7-13. Саморазрядка конденсатора ..................... 291
7-14. Разрядка конденсатора через катушку (колеба-
тельный контур) ............................... 292
7-15. Закон изменения тока и напряжения в колебатель-
ном контуре ................................... 294
7-16. Период и частота собственных колебаний .... 295
7-17. Затухающие колебания .......................... 296
7-18. Лабораторная работа. Исследование зарядки и раз-
рядки конденсатора (§ 7-8, 7-12)............... 298
7-19. Лабораторная работа. Генератор пилообразных
напряжений .................................... 299
Глава восьмая. Основные понятия и определения,
относящиеся к переменным токам
8-1. Период и частота переменного тока.............. 301
8-2. Зависимость частоты переменного тока от числа пар
полюсов и скорости вращения генератора .... 303
8-3. Фаза. Сдвиг фаз................................ 306
8-4. Графическое изображение синусоидальных величин 309
8-5. Сложение и вычитание синусоидальных величин 312
8-6. Средние значения тока и напряжения............. 317
8-7. Среднее значение тока при однополупериодном и
двухполупериодном выпрямлении ................. 319
8-8. Среднее значение наведенной э, д. с............ 320
8-9. Действующие значения тока, напряжения и э. д. с. 321
8-10. Коэффициент формы и коэффициент амплитуды . . 324
Глава девятая. Неразветвлениые цепи переменного тока
9-1. Общие замечания ............................... 325
9-2. Цепь с сопротивлением.......................... 326
а) Ток и напряжение цепи......................... 326
б) Мгновенная мощность........................... 327
в) Активная мощность ............................ 328
9-3. Цепь с индуктивностью.......................... 329
а) Ток и напряжение. Индуктивное сопротивление . 329
б) Мгновенная мощность .......................... 331
в) Реактивная мощность .......................... 332
9-4. Поверхностный эффект и эффект близости .... 332
8
9-5. Цепь с емкостью ................................ 335
а) Ток и напряжение. Емкостное сопротивление . . . 335
б) Мгновенная мощность ............................ 338
в) Реактивная мощность ............................ 339
9-6. Цепь с сопротивлением и индуктивностью .... 339
а) Ток и напряжения................................ 339
б) Треугольник напряжений ..........................342
в) Полное сопротивление. Треугольник сопротивлений 343
г) Мгновенная мощность. Активная и реактивная
мощности ......................................... 344
д) Полная мощность. Треугольник мощностей . . . 347
9-7. Цепь с сопротивлением и емкостью................ 349
а) Ток и напряжение ............................... 349
б) Треугольник сопротивлений ...................... 351
в) Мгновенная мощность. Активная, реактивная и
полная мощности .................................. 352
9-8 Цепь с сопротивлением, индуктивностью и емко-
стью ......................................... ..... 353
а) Ток и напряжение ............................... 353
б) Реактивное сопротивление. Треугольник сопротивле-
ний ............................................ 356
в) Знак угла.................................. 356
г) Соотношение между напряжениями на зажимах и на
отдельных участках цепи........................ 358
д) Мгновенная мощность ............................ 359
9-9. Общий случай последовательного соединения . . . 362
9-10. Резонанс напряжений ............................. 365
9-11. Резонансные кривые .............................. 368
9-12. Круговые диаграммы неразветвленных цепей . . . 371
а) Основные понятия н определения............. 371
б) Круговая диаграмма неразветвленной цепи с
постоянным активным и переменным реактивным
сопротивлениями................................... 372
в) Круговая диаграмма неразветвленной цепи с
постоянным реактивным и переменным активным
сопротивлениями................................... 375
г) Круговая диаграмма неразветвленной цепи, состоя-
щей из катушки и переменного активного сопро-
тивления ......................................... 377
9-13. Переходные процессы при включении цепи с сопро-
тивлением и индуктивностью под синусоидальное
напряжение ..................................... 381
9-14. Переходные процессы при включении цепи с сопротив-
лением и емкостью под синусоидальное напряжение 386
Глава десятая. Разветвленные цепи переменного тока
10-1. Расчет разветвленной цепи с двумя ветвями . . . 392
10-2. Метод проводимостей.............................. 394
10-3. Общий случай параллельного соединения .... 398
10-4. Цепи со смешанным соединением сопротивлений . 401
10-5. Конденсатор с потерями........................... 405
10-6. Резонанс токов .................................. 408
10-7. Резонанс токов в контуре без потерь.............. 415
9
10-8. Коэффициент мощности и его значение............ 471
10-9. Активная и реактивная энергия.................. 421
10-10. Круговые диаграммы разветвленных цепей .... 422
а) Круговая диаграмма разветвленной цепи с изме-
няемым активным сопротивлением................. 422
б) Круговая диаграмма разветвленной цепи с изме-
няемым индуктивным сопротивлением................ 424
10-11. Измерение тока и напряжения.................. 426
10-12. Измерение частоты ............................ 426
10-13. Измерение мощности............................ 427
10-14. Измерение сдвига фаз.......................... 429
10-15. Лабораторная работа. Сложение синусоидальных
напряжений (§ 8-5)............................. 431
10-16. Лабораторная работа. Снятие кривых мгновенных
значений переменного тока и напряжения .... 433
10-17. Лабораторная работа. Исследование неразветвлен-
иой цепи переменного тока (§ 9-8)............. 436
10-18, Лабораторная работа. Резонанс напряжений (§9-10,
9-11).......................................... 438
10-19, Лабораторная работа. Построение круговой диа-
граммы нераззетвленной цепи переменного тока
(§9-12).............................................. 439
10-20, Лабораторная работа. Исследование разветвленной
цепи переменного тока (§ 10-1, 10-2 и 10-3) .... 440
10-21, Лабораторная работа. Резонанс токов (§ 10-6) . . 441
10-22. Лабораторная работа. Построение круговой диа-
граммы разветвленной цепи переменного тока
(§ 10-10,а) ......................................... 443
10-23. Лабораторная работа. Измерение коэффициента
мощности, повышение коэффициента мощности
(§ 10-10, б)......................................... 444
Глава одиннадцатая. Расчет электрических цепей
символическим методом
11-1. Основные понятия .............................. 445
11-2. Сложение н вычитание комплексных чисел .... 449
11-3. Умножение и деление комплексных чисел .... 451
11-4. Токи, напряжения и сопротивления в символиче-
ской форме .................................... 455
11-5. Мощность ...................................... 460
11-6, Правила Кирхгофа............................... 461
11-7. Цепи с последовательно и параллельно соединен-
ными сопротивлениями .......................... 463
11-8. Цепи со смешанным соединением сопротивлений
Сложные цепи................................... 465
11-9. Получение угла сдвига фаз между напряжением
и током, равного 90°........................... 468
11-10. Индуктивно связанные цепи................... 469
а) Воздушный трансформатор....................... 470
б) Индуктивно связанные катушки, соединенные парал-
лельно .......................................... 472
в) Индуктивно связанные катушки, соединенные после-
довательно .............................. 475
10
11-11. Измерение взаимной индуктивности............. 476
11-12. Лабораторная работа. Получение сдвига фаз 90°
между напряжением и током (§11-9)............. 477
11-13. Лабораторная работа. Измерение индуктивности
и взаимной индуктивности (§11-10).................... 479
Глава двенадцатая. Трехфазный ток
12-1. Трехфазные системы ........................... 481
12-2. Соединение обмоток трехфазного генератора звездой 483
12-3. Соединение обмоток трехфазного генератора тре-
угольником .................................... 486
12-4. Соединение приемников энергии звездой ..... 488
12-5. Роль смещения нейтрали. Нейтральный провод . 491
12-6. Соединение приемников звездой при равномерной
нагрузке фаз................................... 494
12-7. Топографическая диаграмма .................... 495
12-8. Соединение приемников энергии треугольником . 498
12-9. Соединение приемников энергии треугольником при
равномерной нагрузке фаз................ 501
12-10. Включение электрических ламп н электродвигателей
в цепь трехфазного тока........................ 502
12-11. Свойства сумм линейных токов и линейных напря-
жений трехфазной цепи.......................... 503
12-12. Преобразование треугольника сопротивлений в звезду 505
12-13. Мощность трехфазного тока. Уравновешенная трех-
фазная система ................................ 508
12-14. Измерение мощности в цепи трехфазного тока . . 510
12-15. Вращающийся магнитный поток при трехфазном токе 514
12-16. Уравнение вращающегося магнитного потока . . 516
12-17. Разложение пульсирующего магнитного потока на
два вращающихся в разные стороны............... 519
12-18. Принцип действия асинхронных электродвигателей 519
12-19. Вращающийся магнитный поток при двухфазном токе 520
12-20. Последовательность фаз н способы ее нахождения 521
12-21. Симметричные составляющие несимметричной трех-
фазной системы ................................ 524
12-22. Лабораторная работа. Исследование четырехпровод-
ной н трехпроводной цепей трехфазного тока при
соединении приемника энергии звездой (§ 12-4—12-7) 528
12-23. Лабораторная работа. Исследование цепи трехфаз-
ного тока при соединении приемника энергии тре-
угольником (§ 12-8 и 12-9)........................... 530
12-24. Лабораторная работа. Исследование цепи трехфаз-
ного тока при неоднородной нагрузке фаз. Построе-
ние топографической диаграммы (§12-4, 12-5,12-7 и
12-20)........................................ 531
12-25. Лабораторная работа. Исследование вращающегося
магнитного потока ................................... 533
Глава тринадцатая. Несинусоидальные токи
13-1. Основные понятия ............................. 535
13-2. Виды периодических кривых.................... 539
13-3. Разложение периодических кривых на гармоники 543
И
13-4. Несинусондальные токи и напряжения в электриче-
ских цепях .................................... 546
13-5. Действующие значения несинусоидального тока
и напряжения .................................. 552
13-6. Мощность при несинусоидальном токе............... 555
13-7. Фильтры........................................... 557
13-8. Высшие гармоники в цепи трехфазного тока . . . 559
Глава четырнадцатая. Цепи переменного тока со сталью
14-1. Ток, напряжение и магнитный поток в цепи со сталью 565
14-2. Построение кривой намагничивающего тока . . , 567
14-3. Мощность................................... 569
14-4. Расчет намагничивающего тока............... 569
14-5. Влияние гистерезиса на формуй величину намагни-
чивающего тока ................................ 571
14-6. Магнитный поток при синусоидальном намагни-
чивающем токе.................................. 572
14-7. Вольт-амперная характеристика катушки со сталью 573
14-8. Потери энергии от гистерезиса..................... 575
14-9. Потери энергии от вихревых токов.................. 577
14-10. Потери в стали .................................. 577
14-11. Угол потерь....................................... 578
14-12. Векторная диаграмма катушки со стальным сер-
дечником ............................................ 579
а) Влияние активного сопротивления.................... 579
б) Влияние магнитного рассеяния...................... 582
14-13. Схема замещения катушки со стальным сердечником 583
14-14. Переходный процесс при включении катушки со
стальным сердечником под переменное напряжение 584
14-15. Последовательное соединение конденсатора и катуш-
ки со стальным сердечником........................... 589
14-16. Устройство и принцип работы трансформатора . . . 592
14-17. Автотрансформатор ............................... 595
14-18. Утроитель частоты................................. 596
14-19. Лабораторная работа. Измерение потерь в стали
(§ 14-8, 14-9 и 14-10)............................... 596
Глава пятнадцатая. Длинные линии (электрические
цепн с распределенными параметрами)
15-1. Общие замечания .................................. 598
15-2. Уравнения однородной линии........................ 600
15-3. Падающие и отраженные волны напряжения и тока
в однородной линии ............................ 604
15-4. Вторичные параметры однородной линии .... 607
15-5. Однородная линия постоянного тока................ 609
15-6. Линия переменного тока без потерь................. 610
15-7. Коэффициент отражения ............................ 611
15-8. Однородная линия с потерями, замкнутая на согла-
сованную нагрузку.............................. 613
15-9. Приближенные уравнения ........................... 616
15-10. Стоячие волны..................................... 617
Приложения................................................. 620
12
ВВЕДЕНИЕ
Со второй половины XIX в. начался период бурного
расцвета и практического применения нового вида энер-
гии—электричества. Электрическая энергия обладает
очень ценными свойствами: она просто преобразуется
из других видов энергии (механической, химической
и др.), передается с малыми потерями на большие рас-
стояния (сотни километров) в города, на заводы и фаб-
рики. В пункте потребления электрическая энергия просто
дробится и преобразуется в нужный вид энергии: механи-
ческую, тепловую, химическую и др. Таким образом,
электричество позволяет использовать и транспортировать
дешевую энергию, накопленную в природе (энергия падаю-
щей воды), или удешевляет ее использование (торф, низко-
сортный уголь).
Замечательные свойства электрической энергии на-
ходят еще большее применение при использовании но-
вой — ядерной — энергии.
После Великой Октябрьской социалистической рево-
люции под руководством Коммунистической партии вы-
росла передовая индустриально-колхозная держава —
Союз Советских Социалистических Республик.
В СССР электрификация проводится в грандиозных
все возрастающих масштабах. Замечательный призыв
В. И. Ленина, сформулированный им в 1920 г.: «Комму-
низм — это есть Советская власть плюс электрификация
всей страны» успешно воплощается в жизнь.
В трудных условиях гражданской войны Советское
правительство и Коммунистическая партия неустанно
заботились о строительстве новых электростанций,
прежде всего на базе использования местных энергети-
ческих ресурсов. В 1918 г. началось строительство Вол-
ховской гидроэлектростанции. В 1919 г. развернулась
13
стройка Каширской электростанции, работающей на
подмосковном угле. В 1920 г. в Шатуре была пущена элек-
тростанция на торфе.
В. И. Ленин отчетливо представлял себе, что без элек-
трификации страны, без развития ее энергетической базы
не может быть индустриализации России. Поэтому непо-
средственно после захвата власти пролетариатом он
поставил вопрос о разработке плана электрификации.
Такой план был составлен Государственной комиссией
по электрификации России — план ГОЭЛРО и утверж-
ден VIII съездом Советов в 1920 г.
По плану ГОЭЛРО было намечено в течение 10—15 лет
ввести в действие 30 новых районных электростанций
общей мощностью 1,5 млн. кет и расширить действующие
электростанции, увеличив их мощность на 250 тыс. кет.
Как известно, первый план электрификации был
не только выполнен, но и перевыполнен. В 1934 г., т. е.
спустя 14 лет после утверждения плана, мощность элек-
тростанций СССР достигла 3 666 тыс. кет, превысив задание
плана ГОЭЛРО более чем в 2 раза.
С 1929 г. электрификация страны проводилась по ве-
ликим планам пятилеток. История не знала таких гран-
диозных масштабов и таких высоких темпов строитель-
ства, какими осуществлялось в нашей стране создание
электростанций в годы пятилеток. В период первых пяти-
леток зажглись огни крупнейшей в Европе Днепровской
гидроэлектростанции, были пущены Челябинская, Зуев-
ская, Кузнецкая и многие другие тепловые электростан-
ции.
Рост энергетической базы явился важным фактором
для подготовки нашей страны к активной обороне. На-
кануне Великой Отечественной войны в 1940 г. электро-
станции СССР произвели около 50 млрд, квт-ч электро-
энергии: в 25 раз больше, чем электростанции России
в 1913 г.
За годы пятилеток в СССР почти заново создана элек-
тротехническая промышленность. Было освоено производ-
ство мощных турбин и генераторов, сверхмощных высоко-
вольтных трансформаторов, нормальных и специальных
электродвигателей, освоено изготовление разнообразных
проводов и кабелей, точных электроизмерительных при-
боров и аппаратов. Старые электромашиностроительные
заводы — «Динамо», «Электросила» и др. были реконструи-
14
рованы и превратились по существу в совершенно новые
предприятия.
Несмотря на большие разрушения, произведенные
во время Великой Отечественной войны, энергетика на-
шей страны стала после войны более мощной, чем до
войны.
В результате успешного восстановления и развития
народного хозяйства уже в 1950 г. выработка энергии
составила 92 млрд, квт-ч, на 87% превзойдя выработку
в 1940 г., а мощность электростанций в том же 1950 г.
достигла 19,6 млн. кет вместо 11 млн. кет в 1940 г. Вы-
работка электроэнергии в 1960 г. увеличилась до
292 млрд, квт-ч, а установленная мощность электро-
станций — до 66,7 млн. кет.
Дальнейшее развитие энергетики Советского Союза
характеризуется все увеличивающимся ростом выработки
электроэнергии и установленной мощности электростан-
ций. В 1965 г. выработка электроэнергии достигнет 500—
520 млрд, квт-ч, а мощность электростанций 113 млн. кет.
Придавая важнейшее значение электрификации страны
и изобилию дешевой электроэнергии как основному усло-
вию развития ее производительных сил, Программа Ком-
мунистической партии Советского Союза, принятая на
XXII съезде, дает величественные перспективы развития
советской энергетики. Производство электроэнергии в 1970 г.
должно достигнуть 900—1 000 млрд, квт-ч в год при мощ-
ности электростанций 190—220 млн. кет, а в 1980 г. —
2 700—3 000 млрд, квт-ч при мощности электростанций
540—600 млн. кет. За 20 лет намечено строительство
около 200 тепловых электростанций мощностью до 3 млн. кет
каждая и примерно 180 мощных гидроэлектростанций.
Велики наши успехи и достижения в науке и технике;
об этом свидетельствуют такие выдающиеся события по-
следнего периода, какими являются пуск первой в мире
атомной электростанции, пуск величайших по мощности
Братской гидроэлектростанции на Ангаре, Волжских —
имени В. И. Ленина и имени XXII съезда КПСС, пуск
крупнейшего в мире синхрофазотрона для изучения атом-
ного ядра, запуск искусственных спутников земли, лунни-
ков, космических ракет и кораблей и, наконец, полеты
человека в космическое пространство. Но нам нельзя
успокаиваться на том, что уже сделано. Электротехника
развивается так стремительно, что сегодняшний высокий
15
уровень ее развития завтра может оказаться недоста-
точным
Электротехника — увлекательная и интересная наука.
Но изучение электротехники требует настойчивости, воли
и большой энергии. Учащиеся советских учебных заведе-
ний должны помнить о больших задачах, стоящих перед
ними как строителями коммунистического общества, и о
большой ответственности за свою работу перед советским
народом.
ГЛАВА ПЕРВАЯ
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
1-1. ОСНОВНЫЕ понятия
Опытным путем установлено, что во всяком теле содер-
жится большое количество электрически заряженных ча-
стиц вещества Эти частицы или входят в состав молекул,
или являются «свободными» (не входят в состав молекул).
В обычных условиях в достаточно большом элементе объема
тела находится в среднем равное количество положительно
и отрицательно заряженных частиц или, как короче гово-
рят, положительных и отрицательных электриче-
ских зарядов, и тело является электриче-
ски нейтральным. Выражение «в среднем» озна-
чает, что мы не считаемся с малыми и быстрыми измене-
ниями числа зарядов в данном объеме, происходящими
в результате теплового движения молекул и «свободных»
частиц В электрически заряженном теле
(или части тела) преобладают положительные или отрица-
тельные заряды.
Если вблизи заряженного тела (частицы) находится
другое заряженное тело (частица), то между ними возни-
кают силы электрического взаимодействия.
Разноименные заряженные частицы притягиваются друг
к другу, одноименною отталкиваются.
Взаимодействие заряженных частиц объясняется тем,
что каждая из них неразрывно связана с окружающим
ее электрическим полем. Электрически заря-
женные частицы вещества и электрическое поле являются
видами материи. Электрическое поле обладает энергией,
которую называют электрической энергией.
Электрическое поле неподвижных зарядов называют элек-
тростатическим. Если в электрическое поле,
2 Теоретическая электротехника 17
которое окружает электрически заряженную частицу ве-
щества, внести другую заряженную частицу, то последняя
будет испытывать действие силы поля, в свою очередь элек-
трическое поле второй частицы будет действовать на первую
частицу.
По силе взаимодействия можно определить величины
электрических зарядов и установить для них единицу
измерения. Электрический заряд обозначается буквой Q
(или q) и измеряется в электротехнике в кулонах (сокра-
щенно к). Электрический заряд мельчайшей частицы ве-
щества-электрона составляет 1,60-10-1’ к, т. е. суммар-
ный электрический заряд 6,3-1018 электронов составляет
один кулон.
1-2. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Каждая точка электрического поля характеризуется
напряженностью электрического по-
л я (обозначается g). Опытом установлено, что чем больше
заряд Q, тем больше величина напряженности его элек-
трического поля g.
Для измерения напряженности внесем в поле неподвиж-
ного заряда Q другой очень маленький (по сравнению
с Q) «пробный» заряд q. Силу поля, действующего на заряд q,
обозначим буквой F. Сила поля F будет прямо пропорцио-
нальна заряду q, но и при неизменной величине проб-
ного заряда сила поля может иметь разную величину
в отдельных точках одного и того же электрического поля.
Таким образом, сила поля зависит не только от величины
пробного заряда, но и от свойств поля в той точке, где
расположен пробный заряд. Величина, характеризующая
электрическое поле в каждой его точке, и называется на-
пряженностью электрического поля. Чем больше напряжен-
ность поля, тем больше и сила F, действующая на заряд q.
Итак, сила поля F пропорциональна величине пробного
заряда q и напряженности электрического поля g, т. е.
F=£q. (1-1)
Пользуясь зависимостью (1-1), найдем напряженность
электрического поля:
g = ^. (1-2)
18
Выше мы указали, что сила F прямо пропорциональна
пробному заряду q. Если q уменьшить (или увеличить)
в п раз, то во столько же раз уменьшится (или увеличится) F,
а их отношение останется неизменным. Таким образом,
напряженность электрического поля не зависит от вели-
чины пробного заряда и является характеристикой самого
электрического поля. Заметим, что при q, равном единице,
g численно равна F, т. е. напряженность в данной точке
поля численно равна силе поля, которая действует на еди-
ничный пробный заряд.
Формула (1-2) дает возможность установить единицу
измерения напряженности электрического поля. С 1963 г.
в СССР применяется Международная система единиц,
обозначаемая СИ или SI (см. приложение 2). Основные
единицы этой системы: метр, килограмм, секунда, ампер,
градус Кельвина и свеча. В системе СИ сила измеряется
в ньютонах (н), электрический заряд в кулонах (к), длина
в метрах (л), масса в килограммах (кг), время в секундах
(сек). Сила 1 н сообщает массе 1 кг ускорение, равное 1 м/сек
за секунду, т. е. 1 н = 1 кг-1 м/сек2. Сила в 1 н на пути
длиной 1 м совершает работу в 1 джоуль: 1 дж — 1 н-1 м
и, следовательно, 1 н — 1 дж/\ м.
Выражая силу через работу и путь, можно определить
единицу напряженности электрического поля:
_ Г F *1 "н _ дж
® L <7 J к м-к
Ниже мы познакомимся с электрическим потенциалом
и напряжением, единицей измерения которых служит
вольт (в), причем 1 в = 1 дж : 1 к. Поэтому, короче, еди-
ница измерения напряженности электрического поля
^ = 1 •
Это, однако, не значит, что в расчетах напряженность
поля следует всегда выражать в в/м. Длину и вообще любые
линейные размеры тел и устройств часто удобнее измерять
в сантиметрах (см) или миллиметрах (мм). Аналогично
и напряженность поля определяют в в/см или в/мм, при-
чем 1 в/м = 10~2 в/см = 10~3 в/мм.
Напряженность электрического поля рассматривают
как векторную величину. За направление вектора напря-
женности принимают направление силы, с которой поле
2* 19
действует на положительный пробный заряд, помещенный
в данную точку поля.
Электрическое поле, во всех точках которого векторы
напряженности одинаковы, называется однородным.
Для изображения электрического поля пользуются
линиями напряженности электричес-
кого поля (электрическими
линиями).
Каждая линия напряженности
электрического поля проводится
так, чтобы направление вектора
напряженности электрического
поля в любой ее точке совпадало
Рис. 1-1. Элек-
трическое поле
между двумя
разноименно за-
ряженными пло-
скими парал-
лельными пла-
стинами.
Рис 1-2 Электриче-
ское поле заряженно-
го шара
с направлением касательной в
этой точке. Электрические ли-
нии поля неподвижных зарядов
не замкнуты; они начинаются на
телах, обладающих положительным зарядом, и окан-
чиваются на телах, обладающих отрицательным зарядом.
Линии напряженности проводят так, чтобы по их густоте
можно было судить о величине напряженности электри-
ческого поля. Для этого через каждую единичную площадку,
построенную перпендикулярно вектору напряженности по-
ля, проводят не произвольное число линий напряженности
поля, а такое число линий, которое равно или пропорцио-
нально величине напряженности поля в этой области поля.
Единичная площадка (1 см2, 1 мм2 и др.) должна быть
достаточно малой, чтобы во всех ее точках g было оди-
наковым. На рис. 1-1 показаны электрические линии между
двумя разноименно заряженными плоскими параллель-
20
ними пластинами. В средней части в любых точках поля
векторы напряженности одинаковы (на рисунке показаны
векторы g в двух точках), т. е. в центральной части поле
однородное. У краев пластин векторы напряженности не
равны по величине и не параллельны, значит, поле неод-
нородно. Направления векторов g всюду совпадают с на-
правлениями касательных.
На рис. 1-2 изображены линии напряженности элек-
трического поля вокруг уединенного положительно заря-
женного шара (в этом случае их надо считать оканчиваю-
щимися в бесконечности). По мере удаления от шара число
линий, приходящихся на единичную площадку, стано-
вится все меньше. Значит, чем дальше находится точка
поля от шара, тем напряженность меньше.
1-3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ТОЧЕЧНОГО ЗАРЯДА
Вначале рассмотрим электрическое поле точечного заря-
женного тела (точечного заряда). Точечным называется
заряженное тело, линейные размеры которого весьма малы
по сравнению с расстоянием R
от тела до точек, в которых оп-
ределяется поле.
Опыты Кулона показали, что
электрическое поле точечного за-
ряда Qi (рис. 1-3) действует на
помещенный в точке А точечный
заряд Qz с силой Fit прямо про-
порциональной величине обоих
зарядов, обратно пропорциональ-
Рис 1-3 Электрическое по-
ле точечного заряда
ной квадрату расстояния R меж-
ду ними и зависящей, кроме того, от среды, в которой
расположены оба заряда. Поэтому напряженность поля
заряда Qt в точке А может быть выражена формулой
81 =
<?2 ~
Qi
4лД2еа
(1-3)
где еа — величина, учитывающая влияние среды и называе-
мая ее абсолютной диэлектрической
проницаемостью.
В знаменателе вместо квадрата расстояния R от дан-
ной точки до точечного заряда Qi введена пропорциональ-
ная R2 величина шаровой поверхности 4лК2, проходящей
21
через точку А и имеющей центр в точке расположения
заряда Qi. Направление вектора напряженности поля
в точке А совпадает с направлением прямой, проходящей
через точечный заряд Qi и точку А.
Очевидно, что во всех точках, удаленных от точечного
заряда Qt на одно и то же расстояние R, т. е. расположен-
ных на шаровой поверхности радиуса R, величина (но не
направление) напряженности поля одинакова, а линии
напряженности электрического поля точечного заряда Qi
направлены радиально (рис. 1-3).
1-4. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
Преобразуя выражение для напряженности поля, най-
дем единицу измерения абсолютной диэлектрической про-
ницаемости:
Г₽ 1 — Г Q ~| — К'М - К —
1 а L 4л7?2^ J м2-в в-м м ‘
Единицу к/в называют фарада (фарада — единица емко-
сти, с которой мы познакомимся в § 7-1) и сокращенно
обозначают ф.
Различные вещества имеют разную абсолютную ди-
электрическую проницаемость. Опытным путем установлено,
что абсолютная диэлектрическая проницаемость пустоты
(вакуума)
е = А = 8,85-10“12 — . (1-4)
и 36л м м ' '
Абсолютную диэлектрическую проницаемость вакуума
е0 называют еще электрической постоян-
ной. Абсолютные диэлектрические проницаемости дру-
гих веществ удобно выражать через электрическую по-
стоянную.
Отношение абсолютной диэлектрической проницаемости
еа данного вещества к электрической постоянной е0
называют диэлектрической проницаемо-
стью вещества (обозначается е), так что
е = —, а еа = еое = 8,85-10~12е ф!м.
ео
Диэлектрическая проницаемость е — отвлеченная вели-
чина. В табл. 1-1 приведены значения е для некоторых
22
веществ. Для воздуха можно практически считать е = 1,
т. е.
еа = е0 = 8,85-10'12 ф!м.
Вводя диэлектрическую проницаемость в формулу дли
напряженности поля точечного заряда и опуская индекс 1,
получим;
« _ Q _ Q (1 _5\
4лее07?2 4яеа7?2 ' ' '
Таблица 1-1
Материал
е
Бумага парафинирован-
ная ..................
Вода дистиллированная
Масло минеральное . . .
Мрамор...............
Миканнт .............
Резина ..............
Слюда ...............
Стекло ..............
Фарфор...............
Шифер ...............
4,3
80
2,2
8,3
5,2
2,7
6-7,5
5,5-8
5,8
6,7
Для упрощения расчетов в формулу (1-5) подставим
еще величину е0, тогда
_ 9(?-109
® . IO-» е7?2
4яе — R-
ЗЬя
[в/м].
Здесь следует подставлять в метрах и Q в кулонах.
1-5. ЗАКОН КУЛОНА
Выразив из формулы (1-3) силу
F1 = Qog1 = Q2—^<— (1-6)
1 х-24леео^2 v '
и переписав последнее выражение в несколько иной форме
р _ л @2
1 '*1 4ЯВ80/?2 ’
23
мы вправе заключить, что заряд Q2 создает поле, напря-
женность которого
да ___Q2__
с'2 4лее0/<2 ’
где R — расстояние от заряда Q2. Это поле действует на
заряд (?! с силой
т. е. с такой же, с которой поле заряда Qj действует на
заряд Q2:
F^F.^F
или
_9Q1Q2-10»
[Н]-
Под влиянием сил взаимодействия разноименные заряды
(положительный и отрицательный) притягиваются друг
к другу (рис. 1-4), а одноименные (оба положительные или
оба отрицательные) отталкиваются (рис. 1-5).
Рис. 1-4. Взаимо-
действие разно-
именных электри-
ческих зарядов.
Рис. 1-5. Взаимодействие
одноименных электриче-
ских зарядов.
Соотношение (1-6) носит название закона Ку-
лона. Оно было получено Кулоном на основании ряда
опытов.
Силы взаимодействия неподвижных электрических
зарядов называют электростатическими.
Пример 1-1. На точечный заряд <? = 2-10~7 к действует сила
F2=0,1 н. Определить расстояние, на котором находится заряд
Q2 = 4,5-10-7 к от Qt. Оба заряда находятся в воздухе (рис. 1-5).
Преобразуя формулу закона Кулона, находим:
г ./W»
Г еР2 ’
где е = 1.
Подставляя численные значения, находим:
fi= = = „=9
24
1-6. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ НЕСКОЛЬКИХ ТОЧЕЧНЫХ
ЗАРЯДОВ
Если электрическое поле создается не одним, а несколь-
кими точечными зарядами, то, как показывает опыт, имеет
место принцип наложения. Это значит, что
сила, с которой два заряда Qi и Q2 действуют на третий
заряд q, равна геометрической сумме двух сил: во-пер-
вых, силы, с которой Qi действует на q в отсутствие Q2
и, во-вторых, силы, с которой Q2 действует на q в отсут-
ствие Qi. Таким образом, к заряду q приложена сила,
равная геометрической сумме сил:
р _ Qi? и Г $2?
1 4лее0Р^ 2 4лее0Р| ’
где Ri—расстояние от Qi до q и R2-—расстояние от Q2
до q-
Вектор напряженности поля зарядов Qi и Q2 также
равен геометрической сумме двух векторов напряжен-
ности:
§ = ^ + §2, (1-7)
где и g2—векторы напряженности поля каждого из
зарядов;
со _ Tj _ Q1 , СС> __ Т2 _ Q2_
61 — q — 4лее0/?5 ’ ₽2 <1 ~ 4лее0/?1 ’
а направление каждого из векторов определяется, как
указывалось выше.
Пример 1-2. В воздухе на расстоянии 10 см друг от друга
находятся два точечных заряда Q1 = 4-10~n к и Q2=6-10-11 к.
Определить напряженность поля в точке Г, если перпендикуляр Г В,
опущенный на прямую АБ (рис. 1-6), делит ее пополам и равен ее
половине, т. е. АВ = ВБ =ГВ.
Определим расстояние до точки Г от точечного заряда Qp
(АВ)2 + О)2 = /52 + 52 = /2-5 cm = V2'0,05 м.
Расстояние до точки Г от точечного заряда Q2
R2 = Ri-
Напряженность электрического поля в точке Г от первого точечного
заряда
„ 9Q..10» 9'4- 10-и. Ю9
=----* ...= -----rv = /2 8 м-
RI (1/2-0,05)2
25
Так как (22=1,5(2! и Rz = Rlt то напряженность поля в точке Г от
второго точечного заряда
^2=1,5^!= 1,5-72 = 108 в/м.
Результирующая напряженность электрического поля в точке Г
в общем случае
^=<fi+ %2.
В нашем случае векторы н <f2 направлены под углом 90е
друг к другу (рис. 1-6), поэтому
(if О2+(^ = /722+1082^ 130 в/м.
1-7. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ
Часто приходится определять электрическое поле двух
точечных зарядов, равных по величине и противополож-
ных по знаку q и —q. Если нужно опре-
делить поле на расстоянии R от зарядов,
много большем, чем расстояние между за-
рядами I, то пару зарядов рассматривают
как единое целое — электрический
г, , , _ диполь. Векторная величина, равная
трический дн- произведению абсолютного значения одного
поль. из данных зарядов и расстояния между
ними и направленная от отрицательного
заряда к положительному, называется электриче-
ским моментом диполя (рис. 1-7): р = ql.
26
1-8. ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ
Произведение напряженности электрического поля
и небольшой площадки, в пределах которой напряженность
поля одинакова и которая перпендикулярна к направлению
Г ж»
Рис. 1-8. Нормаль-
ная составляющая
вектора напря-
женности электри-
ческого поля.
электрических линий, называется потоком векто-
ра напряженности поля (обозначение N)
сквозь эту площадку. Для однородного электрического
поля размеры площадки S не имеют
значения
W = gS. (1-8)
В более общем случае, когда век-
тор g не перпендикулярен площадке S
(рис. 1-8), необходимо определить нор-
мальную (перпендикулярную площадке)
составляющую вектора напряженности
поля gH и
N=g„S. (1-9)
Единица измерения потока вектора
напряженности
[?V] = [gHS] ~~-м2 — в-м.
В неоднородном электрическом поле поток через пло-
щадку S можно вычислить, разбив эту площадку на малые
элементы dS. Вследствие малости dS вектор напряжен-
ности поля одинаков во всех точках этой площадки, т. е.
элементарный поток
dN = $BdS.
Поток через любую площадку S можно найти, суммируя
элементарные потоки,
= J gHdS.
s
(МО)
1-9. ТЕОРЕМА ОСТРОГРАДСКОГО И ГАУССА
Теорема ОстроградскогоиГаусса уста-
навливает зависимость между потоком вектора напряжен-
ности поля сквозь произвольную замкнутую поверхность
и величиной заряда внутри этой поверхности.
27
Рассмотрим в качестве простейшего примера поле
точечного заряда. Поместим в центре шаровой поверх-
ности радиуса У? точечный зряд Q (рис. 1-9).
1 Напряженность поля на шаровой поверхности согласно
® ‘ 4лее01?2 ’
т. е. имеет одинаковое значение для всех точек шаровой
поверхности.
Так как электрические линии перпендикулярны ша-
ровой поверхности (рис. 1-2 и 1-9), то Йн = и поток
вектора напряженности поля (1-Ю)
сквозь шаровую поверхность
8 8
где §dS = 4nR2—площадь шаровой
8
поверхности радиуса R. Подставляя
значение находим поток:
У = -г-Ц-.-4л/?2 = -^-. (1-11)
4лее0/<г еео
Рис. 1-9. Заряжен-
ная частица внут-
ри шаровой по-
верхности.
Заметим, что полученное выражение потока не зависит
ни от формы поверхности, ни от места расположения заря-
дов внутри нее, так что выведенное для шаровой поверхно-
сти уравнение (1-11) справедливо для замкнутой поверх-
ности любой формы и произвольно расположенных внутри
нее электрических зарядов.
1-10. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Если в электрическом поле положительного точечного
заряда Q в точке М находится другой точечный пробный
положительный электрический заряд q, то на заряд q
действует сила
где —напряженность поля заряда Q в точке М;
RM — расстояние от точки М до заряда Q.
28
Допустим, что заряд q под действием этой силы уда-
ляется за пределы поля (на бесконечно большое расстояние).
При этом силами поля производится работа за счет энер-
гии совместного поля точечных зарядов (обо-
значение W), которая, таким образом, убывает.
Уменьшение энергии
Й=оо Н==со со
R~ RM R—RM RM
Отношение WM к величине заряда q является одной
нз характеристик электрического поля в данной точке (Л4).
Величина, измеряемая этим отношением, называется
потенциалом (обозначение ср) данной точки элект-
рического поля заряда Q и не зависит от величины
пробного заряда q. По определению потенциал точки М
поля точечного заряда Q
СО
q J члееолм
Единица измерения потенциала [ф] = [ё-/?] = = в.
Аналогично потенциал другой точки Н
СО
ф=Лд= Г g^ =g #
т q J 4лее0/?н " "
н j,.
м
и вообще для произвольной точки электрического поля
точечного заряда Q
Q 9Q-10» .
<р—4лее07?— eR 2)
При R =оо получаем фоо = 0, т. е. потенциал беско-
нечно удаленной точки поля равен нулю.
Если электрическое поле создается не одним, а не-
сколькими точечными зарядами, то потенциал произволь-
ной точки равен алгебраической сумме потенциалов:
Ф = Ф1 + ф2-{- ... (1-13)
Пример 1-3. Определить потенциал точки Г примера 1-2.
Потенциал точки Г от заряда
ф1= £^=72 /2-0,05 = 5,1 в.
29
Так как Q2= 1,5с?! и Rz — Rl, то потенциал точки Г от заряда Q2
ф2= 1,5<Р1= 1,5-5,1 =7,6 в.
Потенциал точки Г
ф == Ф1 + Ф2 — 5,1 + 7,6= 12,7 в.
1-11. ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ
При перемещении силами поля заряда q из точки М
не в бесконечность, а в точку Н, независимо от формы
пути совершается работа А, равная уменьшению запаса
энергии совместного поля:
так как WM = qtpM, a WH = qq>H, то
Л = д(фм—Фн). (1-14)
Таким образом, работа пропорциональна разности
потенциалов (фм—фн) обеих точек (М и Н).
Разность потенциалов двух точек электростати-
ческого поля называется электрическим напряжением
(обозначение U) между этими точками, т. е.
^ = Фм~Фн = J $dR— ^$dR = J gdR. (1-15)
RM RH RM
Формулы (1-14) и (1-15) сохраняют силу, если к потен-
циалам всех точек поля прибавить какую-нибудь одина-
ковую величину ф0, например
Л == <7 [(Фл/+ Фо) — (фн + Фо)1 = 9 (Фм —Фн)-
Это значит, что можно принять потенциал равным нулю
не только бесконечно удаленной, но и другой произволь-
ной точки поля. Тогда потенциал любой точки поля мож-
но определить как отношение уменьшения энергии поля
(или произведенной силами поля работы) при перемеще-
нии пробного заряда в эту новую произвольно выбранную
точку к величине заряда. В технических расчетах удобнее
всего нулевой потенциал выбрать на поверхности земли.
Заменив в формуле (1-14) разность потенциалов напря-
жением, получим:
A = qU,
(1-16)
30
откуда
t7 = y, (1-17)
т. е. электрическое напряжение между двумя точками
поля равно отношению работы, совершенной силами поля
при перемещении пробного заряда q из одной точки поля
в другую, к величине переносимого заряда.
В Международной системе единиц СИ, как уже указы-
валось, работа, а следовательно, и энергия измеряются
в джоулях (дж). Поэтому единицей измерения напряже-
ния служит дж!к или вольт (в).
Таким образом,
Более крупной единицей напряжения является кило-
вольт (кв)
1 кв = 103 в,
а более мелкими—милливольт (мв)
1 мв= 10~3 в
и микровольт (мкв)
1 мкв= 10-6 в.
Электрическое напряжение является одной из важней-
ших электротехнических величин. При помощи напряже-
ния определяют напряженность электрического поля,
работу и мощность, развиваемую при перемещении элек-
трических зарядов в электрическом поле.
Пример 1-4. В электрическом поле при перемещении заряда
д = 2-10-4к совершена работа 4=0,4 дж. Определить напряжение
между начальной и конечной точками пути.
Напряжение
U = — = =2 000 в = 2 кв.
q 2-Ю-4
1-12. ОДНОРОДНОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
В практической электротехнике часто приходится встре-
чаться с однородным электрическим полем, у которого
векторы напряженности во всех точках равны и электри-
ческие линии параллельны друг другу.
31
Из условий симметрии следует, что однородное элек-
трическое поле возникает, например, вокруг бесконечной
плоской металлической пластины, заряженной с равно-
мерной плотностью положительным или отрицательным
зарядом (если пластина имеет не бесконечные размеры, то
поле у краев искажается).
На рис. 1-10 показаны электрические линии поля по-
ложительно заряженной плоской пластины, перпендику-
лярные к ее поверхности. Если предположить, что элек-
Рис. 1-11. Определение направ-
ления вектора напряженности
к равнопотенциальиой поверх-
ности.
Рис. 1-10. Элек-
трическое поле
плоской заряжен-
ной пластины.
трические линии поля и, следовательно, векторы напря-
женности направлены не перпендикулярно к заряженной
металлической поверхности, то в отдельных точках на
заряженной поверхности векторы напряженности могут
быть разложены на две составляющие: нормальные
(перпендикулярные к поверхности) и касательные,
или тангенциальные (направленные вдоль поверх-
ности).
Так, на рис. 1-11 вектор § в точке А на поверхности S,
не перпендикулярный этой поверхности, разложен на
нормальную составляющую gH и тангенциальную §г.
Под действием касательных составляющих заряды (сво-
бодные) должны двигаться по поверхности. В данной же
главе мы рассматриваем поле только неподвижных зарядов
(электростатическое). Поэтому касательных составляющих
вектора напряженности не может быть и электрические
линии направлены перпендикулярно заряженной метал-
лической поверхности.
Однородное электрическое поле двух плоских парал-
лельных разноименно заряженных пластин получается
32
наложением полей положительной и отрицательной пла-
стин. Между пластинами электрические линии обеих пла-
стин направлены одинаково. Вне пластин линии направ-
лены встречно и при одинаковой плотности зарядов на-
пряженность поля равна нулю. Электрическое поле наблю-
дается только между пластинами. Такие две
пластины образуют
денсатор.
Напряженность
между пластинами
пропорциональна
плотности ;
(обозначение о).
Выделим на одной из пластин плоского
конденсатора площадку S (рис. 1-12).
Заряд этой площадки
Q = oS.
Проведем вокруг заряда Q замкнутую
поверхность (на рис. 1-12 показана пун-
ктиром). По теореме Остроградского — Гаусса (1-11) поток
вектора напряженности через замкнутую поверхность
ее0
Имея в виду, что в однородном поле между пластинами
конденсатора
ll л о с к и и
К 0 Ji-
> электрического поля
: плоского конденсатора
поверхностной
электрического заряда
s
Рис 1-12. При-
менение теоре-
мы Остроград-
ского и Гаусса
к полю плоского
конденсатора.
N = $S,
а вне конденсатора электрическое поле отсутствует,
получим:
откуда напряженность поля между пластинами плоского
конденсатора
(1-18)
При конечных размерах пластин практически одно-
родное поле получится при условии, если расстояние между
пластинами мало по сравнению с их линейными размерами.
У краев пластин поле всегда получается неоднородным.
Электрическое поле плоского конденсатора изображено
на рис. 1-12.
3 Теоретическая электротехника 33
Для однородного поля можно установить простую
связь между напряжением и напряженностью поля.
Работа, выполняемая при перемещении заряда q в на-
правлении сил поля (в направл нии электрической линии)
_____________________. на расстоянии I (рис. 1-13),
A — Fl=^ql,
Ч ф f ф 3 с другой стороны, согласно(1-16)
A — qU.
Рис. 1-13. Перемещение за-
ряда q в однородном поле.
Сравнивая эти выражения, на-
ходим, что U — а
(МФ
т. е. напряженность электрического поля равна отно-
шению напряжения между двумя точками электрической
линии к соответствующей ее длине.
В общем случае для неоднородного поля величина
напряженности электрического поля
(1-20)
где dl—бесконечно малый отрезок электрической линии,
в пределах которого поле можно считать одно-
родным;
dU—напряжение между концами этого отрезка.
1-13. РАВНОПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
Поверхность, проведенная в электрическом поле так,
что все ее точки имеют одинаковый потенциал, называется
равнопотенциальной (эквипотенциальной).
Вектор напряженности поля и, следовательно, электри-
ческие линии всегда перпендикулярны к равнопотенциаль-
ной поверхности. Чтобы прийти к этому выводу, предпо-
ложим, что вектор напряженности поля g направлен под
углом а к равнопотенциальной поверхности S (рис. 1-11).
Тангенциальная (касательная) слагающая вектора напря-
женности поля
= g cos а.
Произведение и совпадающего с ней по направле-
нию расстояния А/ между двумя точками А и Б поверх-
34
ности S равно по формуле (1-20) напряжению между
этими точками
Л£7 = gzAZ.
Но так как поверхность S имеет во всех точках одина-
ковый потенциал, то
фд = фв и ДС/ = фА —фв = 0;
следовательно,
g; = g cos а = 0,
откуда а = 90°, и вектор напряженности поля нормален
к равнопотенциальной поверхности, В частности, элек»
Рис. 1-14. Равнопотенци-
альные поверхности заря-
женного шара.
Рис. 1-15. Рав-
нопотенциаль-
ные поверхно-
сти плоского
конденсатора.
трнческие линии перпендикулярны к любой металличе-
ской поверхности (например, на рис. 1-10, 1-12), т. е.
всякая металлическая поверхность в электрическом по-
ле — равнопотенциальна.
На рис. 1-14 изображено электрическое поле заряжен-
ного шара (поле вне заряженного шара такое же, как
у заряда, сосредоточенного в центре шара), причем кон-
центрические шаровые равнопотенциальные поверхности
проведены так, что напряжения между любыми смежными
поверхностями одинаковы. По мере увеличения расстоя-
ния от центра шара и уменьшения напряженности поля
густота электрических линий уменьшается обратно про-
порционально квадрату расстояния (g уменьшается обрат-
3* 35
но пропорционально R2). Вместе с тем растут расстояния
между соседними равнопотенциальными поверхностями,
так как в более слабом поле требуется большее расстояние
для изменения потенциала на одну и ту же величину.
Равнопотенциальные поверхности однородного поля
внутри плоского конденсатора (рис. 1-15) параллельны
пластинам, причем соседние поверхности при одинаковом
напряжении между ними находятся на одинаковом рас-
стоянии друг от друга.
Пример 1-5. Напряженность электрического поля на сфериче-
ской равиопотенциальной поверхности, в центре которой помещен
точечный заряд Q, составляет 9 000 в/м. Радиус сферы 1 см. Опре-
делить, каким радиусом нужно провести равиопотеициальные сфе-
рические поверхности с тем, чтобы напряжение между смежными
поверхностями составляло 10 в.
Сопоставляя формулы потенциала (1-12) и напряженности то-
чечного заряда (1-5)
Ф = ^— • (g- Q
4 4лее0/? ’ 4яее07?а ’
заключаем, что произведения <tR и равны одной и той же по-
стоянной величине
Потенциал первой поверхности
<Pi=iSi#i = 9 000-0,01 =90 в,
и, следовательно, £ = 0,9 в-м. Потенциал следующей поверхности
равен 80 в, откуда
Ь n q
/?2=—- = -^--0,0112 м= 1,12 см
z ф2 80
и т. д.
1-14. ЭЛЕКТРОПРОВОДНОСТЬ ВЕЩЕСТВА
Окружающие нас вещества (тела) состоят из атомов
и молекул, которые имеют положительно заряженные ядра
и отрицательно заряженные электроны. Атомы и моле-
кулы электрически нейтральны, так как заряд ядра равен
суммарному заряду электронов, окружающих ядро. При
некоторых условиях, например при увеличении темпера-
туры, атом или молекула теряют электрон. Такой атом
(молекула) превращается в положительный ион.
36
Оторвавшийся электрон может присоединиться к другому
атому (молекуле), так что образуется отрицатель-
ный ион, или остаться свободным. Процесс
образования ионов называют ионизацией. Коли-
чество свободных электронов или ионов в единице объема
вещества (тела) называется концентрацией элек-
трически заряженных частиц и обозначается буквой п.
В веществе, помещенном в электрическое поле, под
действием сил поля возникает процесс движения сво-
бодных электронов или ионов в направлении сил поля,
получивший название электрического тока.
Свойство вещества проводить электрический ток под дей-
ствием электрического поля называется электропро-
водностью вещества. Электропроводность веще-
ства (тела) зависит от концентрации свободных электрически
заряженных частиц. При высокой концентрации электро-
проводность вещества больше, чем при малой. Все веще-
ства в зависимости от электропроводности делятся на про-
водники, диэлектрики (электроизоляционные материалы)
и полупроводники.
1-15. ПРОВОДНИКИ
Проводники обладают очень высокой электро-
проводностью. Проводники делятся на два класса. К про-
водникам первого класса, в которых возможно перемещение
только электронов, относятся металлы и их сплавы. В ме-
таллах электроны, расположенные на внешних орбитах,
сравнительно слабо связаны с ядрами атомов, отчего часть
электронов перемещается между атомами, переходя из
сферы действия одного ядра в сферу действия другого
и заполняя пространство между ними наподобие газа,
который иногда называют «электронный газ».
Эти свободные электроны принято называть элек-
тронами проводимости.
Представление о свободных электронах подтверждается
тем, что раскаленные металлы испускают электроны в окру-
жающую среду. Свободные электроны отличаются большой
подвижностью и находятся в состоянии беспорядочного
(теплового) движения в отличие от положительно заряжен-
ных ионов металла, составляющих остов проводника, обла-
дающих весьма малой подвижностью и совершающих лишь
небольшие колебания около своего среднего положения.
37
В проводниках второго класса (водные растворы кислот,
солей и пр.) под действием растворителя молекулы вещества
распадаются на отрицательные и положительные ионы,
которые подобно электронам в металлах могут перемещаться
по всему объему проводника.
Внутри проводника невозможно существование электро-
статического поля. Так, например, если зарядить метал-
лический шар, то под действием сил взаимодействия все
свободные заряды расположатся на поверхности шара.
Движение зарядов прекращается только тогда, когда
Рис. 1-16. Проводник в элек-
трическом поле.
напряженность электрического поля всюду внутри прово-
дящего шара станет равной нулю.
Если проводник (металлическую пластину) поместить
в электрическое поле (рис. 1-16), то под действием сил
поля свободные электроны металлической пластины нач-
нут перемещаться в направлении, противоположном на-
правлению электрических линий, отчего на одной поверх-
ности пластины возникнет избыточный отрицательный за-
ряд, на другой — избыточный положительный и в прово-
дящей пластине создается добавочное электрическое поле,
направленное навстречу основному полю. Результирую-
щее поле в пластине ослабнет, т. е. уменьшится сила,
действующая на свободные электроны и вызывающая их
перераспределение. Разделение зарядов в пластине прекра-
тится, когда напряженность результирующего поля внутри
пластины окажется равной нулю.
Явление разделения электрических зарядов на прово-
дящем теле под действием внешнего электростатического
38
поля называется электростатической индук-
цией.
Если в электрическое поле поместить не сплошную
металлическую пластинку (рис. 1-16), а металлическую
замкнутую оболочку, то в результате электростатической
индукции электрическое поле отсутствует не только в обо-
лочке, но и внутри нее (рис. 1-17).
Такая металлическая оболочка может служить экра-
ном, защищающим приборы и устройства, помещенные
внутри оболочки, от действия внешних электростатических
полей. В технике для экранирования вместо сплошных
металлических оболочек обычно применяют более легкие
металлические сетки.
1-16. ДИЭЛЕКТРИКИ
Вещества (тела) с ничтожной электропроводностью назы-
ваются диэлектриками или изоляторами;
к ним относятся газы, часть жидкостей (минеральные
масла, лаки) и почти все твердые материалы, за исключе-
нием металлов и угля.
Однако при некоторых условиях в диэлектриках про-
исходит расщепление молекул на ионы (например, под
действием высокой температуры или в сильном поле);
в этом случае диэлектрики теряют свои изолирующие свой-
ства и становятся проводниками.
Диэлектрики обладают свойством поляризоваться,
и в них возможно длительное существование электроста-
тического поля.
1-17. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКА
Если электрическое поле создается в вакууме, то вели-
чина и направление вектора напряженности поля в дан-
ной точке зависят только от величины и места располо-
жения зарядов, создающих поле. Если же поле создается
в каком-либо диэлектрике, то в молекулах последнего
происходят физические процессы, оказывающие влияние
на электрическое поле.
Под действием сил электрического поля электроны на
орбитах смещаются в направлении, противоположном полю.
В результате ранее нейтральные молекулы становятся дипо-
лями (рис. 1-7) с равными зарядами ядра и электронов
на орбитах. Это явление называется поляризацией
39
диэлектрика. При исчезновении поля исчезает и смеще-
ние. Молекулы опять становятся электрически нейтраль-
ными .
Поляризованные молекулы — диполи создают свое элек-
трическое поле, направление которого противоположно
направлению основного (внешнего) поля; поэтому добавоч-
ное поле, складываясь с основным, ослабляет его. Чем
сильнее поляризуется диэлектрик, тем слабее получается
результирующее поле, тем меньше становится его напря-
женность в каждой точке при тех же зарядах, создающих
основное поле, а следовательно, согласно (1-5) диэлектри-
ческая проницаемость е такого диэлектрика больше.
Если диэлектрик находится в переменном электриче-
ском поле, то смещение электронов становится также пере-
менным. Этот процесс приводит к усилению движения
частиц и, следовательно, к нагреванию диэлектрика. Чем
чаще изменяется электрическое поле, тем сильнее
нагревается диэлектрик. На практике это явление исполь-
зуется для нагрева влажных материалов с целью их сушки
или получения химических реакций, происходящих при
повышенной температуре.
1-18. ПРОБИВНАЯ НАПРЯЖЕННОСТЬ ДИЭЛЕКТРИКА
При нормальных условиях диэлектрик обладает незна-
чительной электропроводностью. Это свойство сохраняется,
пока напряженность электрического поля не увеличится до
некоторого предельного для каждого диэлектрика значения.
В сильном электрическом поле, как указывалось, проис-
ходит расщепление молекул диэлектрика на ионы и тело,
которое в слабом поле было диэлектриком, становится про-
водником. Напряженность электрического поля, при кото-
рой начинается ионизация молекул диэлектрика, называется
пробивной напряженностью (электриче-
ской прочностью) диэлектрика. Величина напряженно-
сти электрического поля, которая допускается в диэлек-
трике при его использовании в электрических установках,
называется допустимой напряженностью.
Допустимая напряженность обычно в несколько раз мень-
ше пробивной. Отношение пробивной напряженности к до-
пустимой определяет запас прочности.
Лучшими непроводниками (диэлектриками) являются
вакуум и газы, особенно при высоком давлении. Например,
40
для увеличения допустимого напряжения между пластинами
плоского конденсатора или
его помещают в стеклянный
вают воздух. Такой кон-
денсатор называют ваку-
умным.
Следует указать, что
у газов и жидких диэлек-
триков изолирующие свой-
ства восстанавливаются
при понижении напряжен-
ности поля до величины,
меныпей пробивной напря-
женности .
В табл. 1-2 приведены
значения пробивной напря-
женности (при нормальных
условиях и в однородном
постоянном поле) некоторых
конденсатора другой формы
баллон, из которого откачи-
Таблица 1-2
Материал Пробивная напряжен- ность, Кв/ММ
Бумага, пропитанная
парафином . . . 10,0-25,0
Воздух 3,0
Масло минеральное 5,0-15,0
Мрамор 3,0—4,0
Микаиит 15,0—20,0
Электрокартон . . 9,0—14,0
Слюда 80,0—200,0
Стекло 10,0—40,0
Фарфор 6,0-7,5
Шифер 1,5-3,0
наиболее распространенных
диэлектриков.
Пример 1-6. Пространство между плоскопараллельными метал-
лическими пластинами заполнено парафинированной бумагой. Опре-
делить допустимое и пробивное напряжение между пластинами при
условии, что допустимое напряжение должно быть меньше пробив-
ного в 2,5 раза. Расстояние между пластинами <2 = 0,1 мм.
Пробивное напряжение
(7пр = '^пр 104-0,1 = 1 000 в.
Допустимое напряжение
УПР
1/=_Д£. = 400 в.
1-19. ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
В электрическом поле могут находиться материалы
с различными диэлектрическими проницаемостями в. В этом
случае расчет напряженности поля часто упрощается, если
ввести вспомогательную величину, которую называют
электрическим смещением (обозначение D).
Электрическое смещение связано с напряженностью элек-
трического поля простым соотношением
£> = ea^ = eeog, (1-21)
41
откуда нетрудно определить единицу измерения электри-
ческого смещения:
Таким образом, единица измерения электрического сме-
щения та же, что и у поверхностной плотности заряда,
Электрическое смещение и поверхностная плотность
заряда не только имеют одну и ту же единицу измерения,
но и совпадают по величине на поверхностях всех проводя-
щих тел, помещенных в электрическое поле. Например,
у внутренней поверхности пластины плоского конденсатора
(рис. 1-12) напряженность электрического поля, как
и в любой другой точке поля, равна (1-18):
у . Q
® ee0S '
Электрическое смещение в любой точке поля, в том
числе у металлической поверхности
D = Б60§ = = <т,
о
т. е. совпадает по величине с поверхностной плотностью
заряда на пластине.
Рассмотрим теперь еще раз электрическое поле заря-
женного металлического шара (рис. 1-14). Так как внутри
проводника электрического поля нет, то весь заряд Q
распределен на поверхности шара. Поверхностная плот-
ность заряда
Q
где Яш — радиус шара.
Поле вне заряженного шара, как уже указывалось,
совпадает с полем точечного заряда, сосредоточенного
в центре шара, т. е.
8 = 45^’ (1-22)
где Я—расстояние от центра шара.
42
В частности, у поверхности шара напряженность поля
_____Q
~ 4nee0R^ ’
а электрическое смещение
D = eeog = ^r- = <r.
Этот результат сразу может быть получен при помощи
теоремы Остроградского и Гаусса для электрического
смещения. В § 1-9 было найдено, что поток вектора
напряженности электрического поля через шаровую
поверхность
^ = ^dS = g-4n/?2.
s
Подставим в последнее выражение величину D. Тогда
= = 4л/?2,
tJ 88q 88q
S
где N—поток вектора напряженности поля.
Для электрического смещения целесообразно ввести
поток вектора электрического смещения
ND = §DdS, (1-23)
в
который больше потока /V в ее0 раз:
Nd = бе0М = D 4л/?2 = бе0$5 • 4 л/?2.
Подставляя значение g (1-22), получим:
/VD = Q, (1-24)
т. е. поток вектора электрического смещения через шаро-
вую поверхность равен заряду, находящемуся внутри
поверхности. Заметим, что выражение (1-24) справедливо
для замкнутой поверхности любой формы.
По формуле (1-24) найдем теперь сразу электрическое
смещение у поверхности шара. Так как поток через шаро-
43
вую поверхность радиуса /?ш
Wd = D.4«/?L
то
D — —-—
4л^т ’
что совпадает с ранее полученным результатом.
1-20. ПОЛУПРОВОДНИКИ
Вещества (тела), электропроводность которых зани-
мает промежуточное положение между электропроводно-
стью проводников и диэлектриков, называются полу-
проводниками. К полупроводникам относятся: крем-
ний, германий, селен, закись меди и др.
Электропроводность любого вещества не является по-
стоянной величиной; например, на электропроводность
проводников и диэлектриков влияет изменение температуры.
Для полупроводников характерно более резкое изменение
электропроводности под действием температуры; кроме
того, электропроводность полупроводников резко изме-
няется при введении в их состав даже незначительного
количества примесей.
ГЛАВА ВТОРАЯ
ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА
2-1. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
Свободные электроны в металлическом проводнике или
ионы в электролите находятся в состоянии беспорядочного
движения. Количество электричества или заряд, который
переносится при этом через любое поперечное сечение
проводника, в среднем равен нулю.
Если же на свободные заряженные частицы действуют
в определенном направлении силы (например, силы элек-
трического поля), то к скоростям их беспорядочного дви-
жения прибавляется слагающая скорости в направлении
действующей силы. В этом случае через любое поперечное
сечение проводника проходит определенный заряд, т. е.
в проводнике возникает электрический ток.
44
Для того чтобы получить электрический ток в провод-
никах, нужно создать электрическую цепь.
Электрическая цепь образуется из источников
электрической энергии, в которых возбуж-
дается электродвижущая сила (сокращенно
э. д. с.), и потребителей электрической энергии или, короче,
потребителей. При наличии тока в источниках
энергии происходит непрерывное преобразование различ-
ных видов энергии в электромагнитную или, как говорят
короче, в электрическую; в потребителях, наоборот, элек-
трическая энергия преобразуется в другие виды энергии.
Источники энергии и потребители (или приемники энергии)
соединяются обычно медными проводами.
При направленном движении заряженных частиц по про-
водникам электрической цепи кинетическая энергия заря-
женных частиц в результате их столкновения с ионами
и молекулами вещества частично преобразуется в энергию
беспорядочного движения. Эта энергия выделяется и рас-
сеивается в виде тепла в источниках энергии, потребителях
и соединительных проводах. Поэтому источники энергии,
потребители и соединительные провода, т. е. все элементы
электрической цепи, обладают сопротивлением (направ-
ленному движению частиц).
В современной технике в качестве источников энергии
применяют главным образом электрические ге-
нераторы, в которых механическая энергия преобра-
зуется в электрическую, и первичные элементы и аккуму-
ляторы, в которых происходит преобразование химической
энергии в электрическую.
Потребители электрической энергии очень многообраз-
ны. К ним, например, относятся: электродвигатели, в кото-
рых электрическая энергия преобразуется в механическую;
электрические печи, лампы накаливания, различные нагре-
вательные приборы, в которых электрическая энергия пре-
образуется в тепловую; электролитические ванны, в кото-
рых происходит преобразование электрической энергии
в химическую.
Потребители, в которых электрическая энергия пре-
образуется в тепловую, естественно, характеризуются,
как указывалось выше, сопротивлением, ограничивающим
ток в электрической цепи. Но во многих потребителях
электрическая энергия преобразуется в другие виды энер-
гии. Однако с точки зрения расчета электрической цепи,
45
например определения величины тока, и этих потребителей
принято характеризовать некоторым сопротивлением.
Величина этого сопротивления должна быть выбрана
такой, чтобы в нем выделялась тепловая энергия, численно
равная механической энергии электродвигателя или хими-
ческой энергии электролитической ванны, и т. д.
В качестве вспомогательного оборудования в электри-
ческую цепь входят аппараты для включения и отключения
Рис. 2-1. Про-
стейшая элект-
рическая цепь.
(например, рубильники), приборы для из-
мерения электрических величин (например,
амперметры и вольтметры), аппараты за-
щиты (например, предохранители).
Графическое изображение электриче-
ской цепи, показывающее последователь-
ность соединения ее участков и отобра-
жающее свойства электрической цепи, на-
зывается схемой электрической
цепи. Источники энергии, потребители
электрической энергии и вспомогательная
аппаратура на электрических схемах условно обозначаются
знаками, приведенными в табл. 2-1.
89
Таблица 2-1
Наименование
Условный
знак
Наименование
Условный знак
Электрический ге-
нератор постоян-
ного тока
Первичный эле-
мент или акку-
мулятор
Электрический
двигатель посто-
янного тока
Электрическая
лампа
Соединитель-
ный провод
Однополюсный
рубильник
Предохрани-
тель
Амперметр
Вольтметр
На рис. 2-1 показана простейшая электрическая цепь.
Источник энергии (Я) рассматривается как в н у т р е н-
46
ний участок электрической цепи, потребитель энер-
гии (П) и соединительные провода составляют внеш-
ний участок электрической цепи.
2-2. ЭЛЕКТРИЧЕСКИЙ ТОК
Мерой электрического тока служит величина тока
(или просто ток), измеряемая количеством электричества
(зарядом), которое проходит через поперечное сечение
проводника в 1 сек. Если величина тока не изменяется
с течением времени, то такой ток называется постоян-
ным (обозначается прописной буквой /). По определению
/ = •£, (2-1)
где Q—заряд, проходящий через поперечное сечение
проводника за время t.
Изменяющийся ток в отличие от постоянного обозна-
чают строчной буквой i. За бесконечно малый промежуток
времени dt изменение заряда также мало, и можно пользо-
ваться для определения тока формулой, аналогичной (2-1):
где dQ—бесконечно малый заряд, проходящий через
поперечное сечение проводника за время dt.
Единица тока называется ампер (а). Ток в про-
воднике равен 1 а, если через поперечное сечение провод-
ника за 1 сек проходит электрический заряд, равный 1 к.
За направление тока принимается направление, в котором
перемещаются положительно заряженные частицы, т. е.
направление, противоположное перемещению электронов.
Направление тока в цепи указывают стрелкой (рис. 2-1).
Более мелкими единицами тока являются милли-
ампер (ма)
1 ма — 10"3 а
и микроампер (мка)
1 Ai/ca=10-6 а.
Более крупной единицей тока служит килоам-
пер (ка)
1 ка = 103 а.
47
Величина, равная отношению тока к площади попе-
речного сечения проводника 3, называется плотно-
стью тока (обозначение 6); таким образом,
& = (2-3)
Рис. 2-2. Электрический ток и
плотность тока в различных
сечениях неразветвленной
электрической цепи.
При этом предполагается, что ток равномерно распределен
по сечению проводника. Плотность тока в проводах обычно
измеряется в а/мм2.
Плотность тока — векторная величина. Вектор плот-
ности тока в проводах, соединяющих источники энергии
и потребителей, направлен
нормально к площади попереч-
ного сечения провода.
В неразветвленной элект-
рической цепи ток в различ-
ных сечениях проводников
имеет одинаковое значение.
Если допустить, что величина
постоянного тока в сечениях
Sj и 32 неодинакова (рис. 2-2),
то заряды, которые проходят
за единицу времени через сечения St и S2, были бы раз-
личными. В результате в объеме проводника между этими
сечениями накапливался бы положительный или отрицатель-
ный заряд. При постоянном токе происходило бы бесконеч-
ное накопление зарядов, что невозможно при неизменяю-
щемся токе. Плотность тока при различных площадях
поперечного сечения проводника St и 32 не одинакова:
62 = , 62 = ц^-. При Si>S2 получим < 62.
Электрический ток в металлах образуется перемеще-
нием только свободных электронов, прохождение же тока
в электролитах связано с перемещением положительных
и отрицательных ионов, различных для разных электроли-
тов. Ионы электролита при прохождении тока осаждаются
на электродах, опущенных в электролит.
Процесс выделения вещества из электролита электри-
ческим током называется электролизом. Он широ-
ко применяется для добычи цветных металлов из раство-
ров их соединений (медь, алюминий). Количество выде-
48
ленного из электролита вещества пропорционально коли-
честву прошедшего через электролит электричества:
G = cQ = clt,
где с—коэффициент пропорциональности, называемый
электрохимическим эквивалентом.
Для различных веществ электрохимический эквива-
лент имеет различные значения, например для серебра —
1,118 мг!к, для цинка — 0,338 мг!к, для меди — 0,329 мг/к,
для никеля — 0,304 лг/к.
Электролиз применяется и для покрытия металлов
защитным слоем другого металла (например, хромирование).
Этот процесс называется гальваностегией.
В гальванопластике, основы которой были разработаны
в 1840 г. акад. Б. С. Якоби, при помощи электролиза
получают металлические рельефные отпечатки для изго-
товления клише и печатания рисунков.
2-3. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
Наиболее распространенный электрический генератор
в принципе представляет собой прямолинейный провод А Б,
который перемещается в магнитном поле.
Рис. 2-3. Действие сторонних
сил на электроны.
Рис. 2-4. Накопление электри-
ческих зарядов на концах про-
вода под действием сторонних
сил.
При этом на каждый элементарный отрицательный
и положительный заряд провода АБ (рис. 2-3) действует
неэлектростатическая (сторонняя) сила FCT (более подроб-
но о возникновении сторонних сил см. в § 6-1).
Отношение сторонней силы, действующей на отдельную
заряженную частицу, к ее заряду q равно напряженности
стороннего поля
= (2-4)
ч
4 Теоретическая электротехника 49
Если сторонние силы, действующие на заряды, имеют
одинаковое значение и параллельны друг другу, то сторон-
нее поле однородно. Произведение напряженности одно-
родного стороннего поля и длины провода АБ, в пре-
делах которого действуют сторонние силы (сторонние силы
направлены по оси провода), дает значение э. д. с., кото-
рая возникает при движении провода. Электродвижущая
сила обозначается буквой Е. Таким образом,
Е — (2-5)
Так как напряженность поля численно равна силе,
с которой поле действует на единичный заряд, то э. д. с.
численно равна работе, которая совершается сторонними
силами при переносе единицы заряда на участке АБ.
В проводе А Б под действием сторонних сил электроны
переместятся на конец Б (рис. 2-4), образуя избыточный
отрицательный заряд —Q. Этот зажим генератора обозна-
чается знаком «—». На другом конце провода А возникает
избыточный положительный заряд +Q. Соответственно
зажим обозначается знаком «+». Внутри провода обра-
зуется электрическое поле зарядов +Q и —Q и на каждый
электрон, кроме сторонней силы, действует еще электро-
статическая сила электрического поля F, направленная
противоположно FCT.
Перемещение электронов в проводе прекратится, когда
силы электрического поля уравновесят сторонние. В этом
случае F = FCT и g = gCT. Электрическое напряжение
на концах (зажимах) незамкнутого провода (генератора)
и вообще любого источника питания
Еаб — ^а— фв = ШаБ~ gCT^AB — F, (2-6)
т. е. напряжение (разность потенциалов) на зажимах
незамкнутого источника питания равна его э. д. с.
Электродвижущая сила измеряется в тех же единицах,
что и электрическое напряжение, т. е. в вольтах.
Устройство, в котором возникает э. д. с., в общем слу-
чае будем называть источником э. д. с. или, ко-
роче, источником.
Электродвижущая сила Е направлена в источнике
э. д. с., как и сила FCT, действующая на положительный
заряд, т. е. обратно силе FCT, действующей на электрон
(рис. 2-3, 2-4), от отрицательного к положительному за-
жиму.
50
Электродвижущие силы могут быть как постоянными,
так и переменными. В настоящей главе рассматриваются
цепи, в которых действуют э. д. с., не изменяющиеся во
времени.
Ниже мы увидим, что источники э. д. с. могут рабо-
тать не только в режиме источников питания, но и в режиме
потребителей.
2-4. ИСТОЧНИКИ Э. Д. С.
Кроме электрических генераторов, к источникам
э. д. с. относятся первичные элементы, акку-
муляторы и термогенераторы (термо-
пар ы).
А. Первичные элементы
ЦиХк Медь
Водный раствор
Рис. 2-5. Гальваниче-
ский
Одним из простейших источников питания является
гальванический элемент Вольта (рис. 2-5).
Элемент Вольта состоит из двух
пластин (электродов) — цинковой, на-
зываемой катодом, и медной,
называемой анодом, опущенных
в водный раствор серной кислоты
(электролит).
В растворе часть молекул серной
кислоты распадается на положитель-
ные (2Н) и отрицательные (SO4) ионы.
Катод, опущенный в электролит, под
действием химических сил частично
растворяется в электролите. Положи-
тельные ионы цинка переходят в раст-
вор и соединяются с отрицательными
остатка (SO4), образуя нейтральные молекулы цинкового
купороса (ZnSO4). Оставшиеся от молекул цинка свободные
электроны создают избыточный отрицательный заряд на
катоде, а в электролите, наоборот, образуется избыточный
положительный заряд ввиду нейтрализации части отрица-
тельных ионов.
В результате этого процесса в пограничном слое со-
прикосновения катода и электролита возникает электри-
ческое поле, направленное от электролита к катоду, и появ-
ляется разность потенциалов между цинковым электродом
4+ 51
элемент.
ионами
кислотного
и электролитом. Силы электрического поля противодейст-
вуют переходу положительных ионов цинка в электролит.
Растворение катода прекращается, когда силы электри-
ческого поля уравновесят химические сторонние силы, под
действием которых ионы цинка переходят в раствор.
Анод, опущенный в электролит, практически не рас-
творяется. Между электролитом и анодом не возникает
разности потенциалов. Таким образом он заряжается
положительно, его потенциал равен потенциалу электроли-
Рис. 2-6 Сухой элемент.
та. Разность потенциалов между анодом и катодом, когда
цепь не замкнута, т. е. э. д. с. элемента Вольта, состав-
ляет около 1,1 в.
При соединении электродов элемента проводником
в цепи возникает ток, свободные электроны переходят
на медную пластину, электрическое поле между цинковым
электродом и электролитом ослабляется. В результате
нарушается равновесие электрических и сторонних сил,
и под влиянием последних ионы цинка снова переходят
в раствор, а положительные ионы водорода приближаются
к медной пластине, взаимодействуют с ее свободными
электронами и превращаются в нейтральные молекулы
водорода. Медный электрод оказывается отделенным
от электролита непроводящим слоем водорода. Это явление
называется поляризацией элемента.
Чтобы избежать поляризации, в состав элемента вводят
вещества (деполяризаторы), легко отдающие кислород,
52
например перекись марганца (МпО2). Превращая водород
в воду, деполяризаторы освобождают электрод от непрово-
дящего слоя водорода.
В настоящее время промышленностью выпускаются пер-
вичные элементы, называемые «сухими элементами». Внеш-
ний вид и устройство сухого элемента показаны на рис. 2-6.
В цинковой коробке Ц, являющейся катодом, помещается
электролит Э, состоящий из раствора нашатыря, сгущен-
ного пшеничной или картофельной мукой. В середине
помещен угольный стержень У, являющийся анодом. Вокруг
угольного электрода расположен деполяризатор Д, состоя-
щий из мелких частиц перекиси марганца, графита и сажи,
смоченных раствором нашатыря. Между электродами воз-
никает э. д. с. около 1,5 в.
Наибольший ток, который можно допустить в элементе,
называется допускаемым разрядным то-
ком, а количество электричества, которое можно полу-
чить от элемента за все время работы, называется его е м-
костью.
Процесс, происходящий в некоторых типах элементов,
обратим. Если через элемент пропускать ток в обратном
направлении, то в нем накапливается
химическая энергия, которую можно
превратить в электрическую при ис-
пользовании элемента снова в каче-
стве источника питания.
Б. Аккумуляторы
Элементы, которые способны на-
капливать энергию (заряжаться),
а затем отдавать ее (разряжаться),
называются аккумулятор а-
м и.
Чаще всего применяются два вида
аккумуляторов — свинцовые, или
кислотные, и кадмиево-ни-
к е л с в ы е, или щелочные.
Свинцовый аккумулятор. Этот аккумулятор состоит из
двух блоков свинцовых пластин, опущенных в сосуд
с раствором серной кислоты (рис. 2-7). Положительные
пластины, соединенные между собой при помощи свинцовой
полосы, располагаются между отрицательными пластинами,
53
Рис. 2-7. Свинцовый
аккумулятор.
также соединенными между собой. Каждая пластина со-
стоит из свинцового каркаса, в который впрессована «актив-
ная масса». Пластины после изготовления подвергаются спе-
циальной электролитической обработке — формиро-
ванию.
У готового заряженного аккумулятора активная масса
положительной пластины состоит из перекиси свинца
(РЬО2), а отрицательной — из губчатого свинца (РЬ).
Электролитом служит 25—34%-ный водный раствор хими-
чески чистой сеоной кислоты (H2SO4).
Рис. 2-8. Изменение напряжения на
зажимах кислотного аккумулятора
при зарядке и при разрядке.
Электродвижущая сила заряженного аккумулятора со-
ставляет около 2,2 в.
Аккумулятор, замкнутый на приемник, является источ-
ником электрической энергии. Такой режим работы акку-
мулятора называется разрядкой.
При разрядке в аккумуляторе происходит химическая
реакция, выражающаяся уравнением
РЬО2 + 2H2SO4 + Pb -» PbSO4 + 2Н2О ф- PbSO4,
на пластинах аккумулятора накапливается сернокислый
свинец (PbSO4) и снижается плотность электролита.
Напряжение при разрядке быстро падает с 2,2 до 2 в,
а затем медленно до 1,8 в (рис. 2-8). При дальнейшем
54
падении напряжения разрядку следует прекратить, так
как иначе аккумулятор можно повредить.
При зарядке через аккумулятор пропускается ток
от другого источника энергии, обычно от сети переменного
тока после его выпрямления, причем положительный
электрод аккумулятора присоединяется к
а отрицательный — к минусу.
В этом режиме работы в аккумуля-
торе совершается обратная химическая
реакция и на его электродах восста-
навливаются РЬО2 и РЬ, а плотность
электролита повышается.
При зарядке напряжение быстро
поднимается до 2,2 в, а затем медленно
до 2,3 в. Когда процесс восстановления
свинца на отрицательной пластине за-
кончится, начинается выделение водо-
рода, который в виде пузырьков подни-
мается на поверхность раствора (кипе-
ние акумулятора). В это время напря-
жение повышается до 2,6—2,7 в и за-
рядку следует прекратить.
Аккумулятор характеризуется наи-
большим количеством электричества,
плюсу источника,
Рис. 2-9. Щелочной
аккумулятор.
которое можно получить, не причиняя
ему вреда. Это количество электричества называется емко-
стью аккумулятора и обычно измеряется в амперчасах
(а-чу
1 а-ч — 1 а-3600 сек = 3600 а-сек = 3600 к.
Емкость аккумулятора зависит от размеров поверхности
пластин; чем больше поверхность, тем больше емкость.
Емкость увеличивается с ростом температуры электролита.
Наконец, емкость зависит от разрядного тока; чем меньше
ток, тем больше емкость аккумулятора.
Следует заметить, что аккумуляторы нужно периодиче-
ски заряжать даже в том случае, если они не работали
источниками питания, так как всегда наблюдается само-
разрядка из-за несовершенства изоляции между электро-
дами; саморазрядке содействуют кислород воздуха и мест-
ные токи в электролите.
Главное повреждение аккумулятора — это сульфата-
ция пластин, т. е. образование на пластинах нераствори-
55
мых крупнокристаллических соединений свинца. Это по-
вреждение вызывается неправильным включением аккуму-
лятора при зарядке, систематической недозарядкой аккуму-
лятора, длительным хранением незаряженного аккумуля-
тора, большой плотностью электролита (свыше 1,32),
высокой температурой (свыше 30° С), снижением уровня
электролита.
Свинцовый аккумулятор, понятно, не возвращает всей
энергии, которая затрачивается на его зарядку, так как
часть энергии тратится на нагрев и необратимые химические
процессы. Коэффициент полезного действия свинцового
аккумулятора равен 75—84%.
Кадмиево-никелевый аккумулятор (рис. 2-9). Электроды
этого аккумулятора выполнены в виде железных решеток
с карманами, заполненными активной массой. Активная
масса у положительной пластины состоит из гидрата окиси
никеля Ni(OH)3, а у отрицательной — из губчатого кад-
мия Cd. Электролитом служит 21%-ный водный раствор
едкого кали (КОН).
При разрядке в аккумуляторе происходит химическая
реакция по уравнению
2Ni(OH)3 + 2КОН + Cd -> 2Ni(OH)2 + 2КОН + Cd(OH)2.
При зарядке происходит восстановление активной массы
электродов. При зарядке, как и при разрядке, концентра-
ция электролита не изменяется.
Электродвижущая сила заряженного щелочного акку-
мулятора составляет около 1,45 в. Разрядку нужно прекра-
тить при понижении напряжения до 1,15 в. Щелочные
аккумуляторы менее требовательны к уходу, легко пере-
носят перегрузку и не портятся от несвоевременной зарядки.
Щелочные аккумуляторы не выделяют вредных испарений,
обладают большой механической прочностью и сравни-
тельно малым весом, что делает их незаменимыми, напри-
мер, в помещении, где работают люди. Однако к. п. д. ще-
лочных аккумуляторов невелик (около 54%).
В. Термогенератор (термопара)
При соприкосновении разнородных металлов между
ними возникает контактная э. д. с., не завися-
щая ни от формы, ни от размеров соприкасающихся метал-
лов и определяемая лишь тем, какие металлы сопри-
56
касаются друг с другом и какова температура в месте их
соприкосновения.
Возникновение контактной э. д. с. объясняется сле-
дующим образом.
При неодинаковой концентрации свободных электро-
нов в различных металлах наблюдается диффузия элек-
тронов. Часть свободных электронов из металла с большей
концентрацией переходит в другой металл, где концен-
трация меньше (действие сторонней си- _________
лы). В результате один из металлов,
имевший меньшую концентрацию свобод- /у 2
ных электронов, получает отрицательный II Н
заряд, а другой — положительный; ме- ff
жду металлами возникает электрическое
поле и устанавливается электрическое
напряжение или, как говорят, контакт-
ная э д с Рис. Термо-
Переход электронов и рост напря- пара,
жения прекратятся, когда электрические
силы уравновесят сторонние силы, вызывающие диффузию
свободных электронов.
Контактная э. д. с. (в вольтах) выражается уравнением
(вывод которого не рассматриваем)
£аб = 2,87-1О-701п-^,
пБ
(2-7)
где 0—абсолютная температура стыка металлов;
и Пб — число электронов в единице объема соответ-
ствующих металлов.
Соединим две полосы из различных металлов (А и Б)
так, чтобы они образовали замкнутую цепь (рис. 2-10),
и определим сумму контактных э. д. с. во всей цепи при
условии, что места стыков имеют одинаковую температуру
01 = 02 — 0:
1Е = Еаб + Еба = 2,87 • IO"’© f In + In =
V пБ пА У
--2,87 • 107© In 1 =0.
Сумма контактных э. д. с. равна нулю, следовательно,
в таком замкнутом контуре тока нет, несмотря на наличие
контактных э. д. с. в каждом стыке.
57
Другое дело, если температура ("Ц одного из стыков
(например, первого) будет больше температуры второго
стыка (рис. 2-10).
В этом случае
ЕЕ = 2,87-10-76,]п --А-~ 2,87-1О-7021п —=
пВ пА
= 2,87-lO"7(01-02)ln-^-.
ПВ
Результирующая э. д. с. (ЕЕ) называется термо-
э. д. с. и обозначается Ет.
Обозначая еще
2,87-10"7 In-”—= Е0,
пв
получим:
Ет = Ео(01—02), (2-8)
т. е. термо-э. д. с. пропорциональна разности температур
стыков металлов. Коэффициент пропорциональности Ео
называется удельной термо-э. д. с. Значения Ео
приведены в табл. 2-2.
Таблица 2-2
Термопары Fo, мкв/град
Медь — константан ..... 53
Серебро — платина 12
Никель — платина 11
Платина — платинородий (5%) 6,4
Термогенератор (термопара) в простейшем виде выпол-
няется из двух сваренных в одном месте разнородных
проволок или пластин (например, медной и константано-
вой). При нагревании места соединения на зажимах термо-
пары появляется разность потенциалов.
Применяемые в настоящее время термопары имеют
ничтожную мощность и низкий к. п. д. и используются
главным образом для измерения температуры. Однако
уже разрабатываются более мощные термогенераторы
(с к. п. д. до 5—7%) из полупроводников, в которых воз-
можно преобразование большого количества тепловой
58
энергии, например выделяющейся при ядерных преобра-
зованиях, непосредственно в электрическую энергию. Полу-
проводниковые термогенераторы, в которых преобразуется
энергия домашних отопительных и осветительных прибо-
ров, устанавливаются, например, для питания радиоаппа-
ратуры. Срок действия таких источников питания в отли-
чие от аккумуляторов и первичных элементов практически
не ограничен.
2-5. ЭЛЕКТРИЧЕСКИЙ ТОК И ПЛОТНОСТЬ ТОКА
В ПРОВОДНИКЕ
Величина тока на отдельных участках электрической
цепи зависит от напряжения на концах этих участков цепи.
Присоединим к зажимам генератора проводник, имею-
щий по всей длине одно и то же поперечное сечение. В про-
воднике возникнет однородное электрическое поле, линии
которого направлены па-
раллельно оси провода, а
равнопотенциальные по-
верхности совпадают с по-
перечными сечениями про-
водника.
Проведем в проводнике
две равнопотенциальные по-
Рис. 2-11. Линейный проводник.
верхности на расстоянии I
друг от друга (рис. 2-11). Потенциал первой поверхности
обозначим <рл, второй фБ.—Напряжение между поверхно-
стями
U = U аб = Фа — фБ-
Напряженность электрического поля в проводни-
ке (1-19)
»=т-
Свободные электроны, заполняющие пространство между
молекулами проводника, в отсутствие поля находятся
в состоянии беспорядочного теплового движения. При нали-
чии поля на беспорядочное движение электронов накла-
дывается их равномерно ускоренное движение навстречу
направлению поля. Движение электрона продолжается
до столкновения его с другим электроном или молекулой
59
Под действием силы поля F=tgq электрон приобре-
тает ускорение
где g— напряженность поля;
q—абсолютное значение заряда электрона;
т0—масса электрона.
В момент столкновения скорость направленного дви-
жения электрона равна ат, а после столкновения она падает
до нуля. Здесь т — время свободного пробега электрона
между двумя последовательными столкновениями.
Средняя скорость движения электрона вдоль линий поля
при равномерно ускоренном движении
аг __ '£qx
V ~~ 2 “ m02 ’
т. е. пропорциональна напряженности электрического по-
ля в проводнике.
Величина
£ 2т0
называется подвижностью электрона. Она чис-
ленно равна средней скорости движения электрона в элек-
трическом поле, напряженность которого равна единице.
Электрический заряд, заключенный в участке провод-
ника длиной I и сечением 3,
Q = nqSl,
где п—концентрация свободных электронов в проводнике.
Отношение этого заряда к тому времени, в течение
которого он покидает участок, проходя через концевое
сечение проводника, определяет величину тока. Таким
образом, ток
I -j- = nqS~ = nqSv, (2-9)
а плотность тока
л I
0 = -^- = nqv.
о
Подставив выражение средней скорости в формулу
плотности тока и обозначив у = nqb, получим:
b = nqb'§ ~ yg.
60
Плотность тока в проводнике зависит от концентрации
свободных заряженных частиц, их подвижности и напря-
женности электрического поля. Концентрация и подвиж-
ность в свою очередь зависят от температуры. С ростом
температуры подвижность обычно уменьшается, так как
сокращается время свободного пробега т.
Понятие о подвижности электронов, строго говоря, от-
носится только к проводникам второго рода — электро-
литам.
2-6. ЗАКОН ОМА
Установим теперь зависимость между током в проводе
и напряжением на концах этого провода.
При неизменяющейся температуре для каждого про-
вода плотность тока пропорциональна напряженности
ПОЛЯ'.
6 = yg, (2-Ю)
где коэффициент пропорциональности у называется
удельной проводимостью данного вещества
(материала провода). При неизменной температуре
удельная проводимость постоянна; она характеризует
электропроводность вещества.
Так как в однородном поле <£ = UH, то
Умножая обе части последнего уравнения на площадь
vS
поперечного сечения провода, получим 65 = -^-17 или
I = ^U = gU, (2-11)
уЗ
где g = ~t-величина, зависящая от материала провода,
его длины и поперечного сечения и назы-
ваемая проводимостью; при неизменной
температуре проводимость данного провода
постоянна.
Выражение (2-11), найденное опытным путем в пер-
вой половине XIX в.,— это один из основных законов
электротехники — закон Ома для участка электрической
цепи. Согласно закону Ома ток в проводе прямо пропорцио-
нален напряжению между его концами.
61
2-7. СОПРОТИВЛЕНИЕ
Как мы уже упоминали, во всех элементах электри-
ческой цепи происходит преобразование энергии, т. е.
элементы цепи обладают сопротивлением направленному
движению свободных зарядов. С количественной стороны
это явление характеризует величина, обратная проводи-
мости, которая так и называется — сопротивлением и обо-
значается буквой г.
Таким образом,
и
7 = ^ = 4- (2-13)
или
V = Ir. (2-14)
Закон Ома устанавливает линейную зависимость между
напряжением и током. Коэффициентом пропорциональности
между напряжением на концах провода и протекающим
по нему током является сопротивление провода. Величина
сопротивления определяется удельной проводимостью мате-
риала и геометрическими размерами провода.
Записав закон Ома в форме г = UU, установим единицу
измерения сопротивления
[г] = = в/а.
Единица сопротивления в!а называется о м (обозна-
чение ojw). Сопротивлением в 1 ом обладает проводник,
в котором устанавливается ток 1 а при напряжении 1 в.
Более крупными единицами сопротивления являются
килоом (ком)
1 ком = 103 ом
и мегом (Мо.и)
1 Мом = 10е ом.
Единица измерения проводимости обратна ому, т. е.
[g] = —5— = сименс /сим/.
62
Величина, обратная удельной проводимости, называет-
ся удельным сопротивлением (обозначение р):
e = J- = -b (2-15)
* у qnb ' '
Так как г — 1/yS, то, заменив у» получим:
г = е4~, (2-16)
О
откуда
Пользуясь последней формулой, установим единицу
измерения удельного сопротивления.
В Международной системе единиц СИ длина измеряет-
ся в метрах, а площадь в квадратных метрах. Поэтому
г , г rS д ом-м2
Однако удельное сопротивление, измеренное в ом • м,
для металлов выражается очень малыми числами; кроме
того, при практических расчетах удобнее поперечное
сечение провода выражать не в квадратных метрах, а в квад-
ратных миллиметрах. Поэтому под удельным сопротивле-
нием понимают часто величину, численно равную сопротив-
лению провода длиной 1 м при поперечном сечении 1 мм*
и температуре 20° G.
В этом случае удельное сопротивление измеряется
в ом-мм*/м, а удельная проводимость — в м/ом-мм*,
1 1 лй ОМ • ММ2
причем 1 ом • м = 10“ —-—.
Значения удельных сопротивлений для некоторых про-
водников указаны в табл. 2—3.
Сравнительно малым удельным сопротивлением обла-
дают проводники (из них наименьшим — серебро, медь,
золото, алюминий). Сопротивление диэлектриков огромно
по сравнению с сопротивлением проводников. Удельное
сопротивление диэлектриков обычно измеряют в ом см,
причем 1 ом • м = 100 ом • см.
Провода из металлов с наименьшим удельным сопротив-
лением (медь, алюминий) широко применяются для соедине-
ния потребителей электрической энергии с генераторами;
из этих материалов выполняются линии передачи и рас-
63
89
Таблица 2-3
Ма гериал 1 Плотность, г/см^ Предел прочно- сти на разрыв, кГ/мм? Температура плавления, °C Удельное сопро- тивление, ом мм2/м Среднее значе- ние температур- ного коэффици- ента (0° С до 100° С), 1/град
Алюминий . . 2,7 14-22 657 0,029 0,004
Бронза .... 8,8—8,9 50-60 900 0,021—0,4 0,004
Вольфрам . . . 18,7 415 3 370 0,056 0,00464
Железо .... 7,7 — 1 520 0,13—0,3 0,006
Константан . . 8,8 40 1 200 0,4—0,51 0,000005
Латунь .... 8,1 40 900 0,07—0,08 0,002
Манганин . . 8,1 55 960 0,42 0,000006
Медь 8,9 25—40 1 083 0,0175 0,004
Нихром .... 8,2 70 1 360 1,1 0,00015
Сталь .... 7,8 80-150 1 400 0,13—0,25 0,006
Фехраль . . . 7,6 — 1 450 1,4 0,00028
Хромаль . . . 7,1 80 1 500 1,3 0,00004
кабели,
обмотки элек-
сети,
Рис. 2-12. Обозначе-
ние сопротивления.
пределительные электрические
трических машин и трансформаторов и т. д.
Для изготовления обмоток нагревательных приборов
и реостатов применяются сплавы с большим удельным
г сопротивлением (нихром, фехраль
।— ------1 и др.). Из формулы (2-16) следует,
I--------* что при заданном сопротивлении дли-
на провода I == rS/Q, поэтому нуж-
ный для обмотки провод с сопротив-
лением г получается тем короче, чем
больше Q. Более короткий провод проще разместить в на-
гревательном приборе.
Условное обозначение сопротивления на электротехни-
ческих схемах показано на рис. 2-12.
Следует подчеркнуть, что термину «сопротивление»
соответствуют два понятия:
1. Как только что было показано, под сопротивлением
понимают определенное свойство материала, провода или
прибора. В этом смысле, например, говорят: лампа накали-
вания обладает сопротивлением 400 ом или провод имеет
сопротивление 0,5 ом.
2. Сопротивлением называют устройство, предназначен-
ное для включения в электрическую цепь с целью регули-
64
рования, уменьшения или ограничения тока цепи. К таким
устройствам относится, например, реостат, предназначен-
ный для включения в электрическую цепь с целью регули-
рования тока путем изменения величины сопротивления.
Проволочные реостаты выполняются с плавной или
ступенчатой регулировкой сопротивления. В первом случае
реостат состоит из трубки, изготовленной из какого-либо
изолирующего материала, на которую наложена проволоч-
Рис. 2-13. Реостат.
ная спираль (рис. 2-13). К виткам этой спирали прижи-
мается подвижный контакт. Один зажим реостата 1 соеди-
няется с подвижным контактом, другой зажим 2— с одним
из концов спирали. Перемещая подвижный контакт, можно
изменять длину проволоки, расположенной между зажи-
мами реостата 1 и 2, и тем самым изменять величину сопро-
тивления, включенного в цепь. Спираль имеет еще один
зажим 3, который необходим для включения реостата
в цепь как делителя напряжения (см. далее, например,
рис. 3-38, 3-43 и др.).
В схемах автоматики и радиотехники реостаты такого
типа не применяются по двум причинам. Во-первых, эти
реостаты, рассчитанные на значительные токи (до десяти
ампер), слишком велики — длина их 30—40 см, во-вторых
при работе в цепях изменяющегося тока таких реостатов
надо считаться с индуктивностью спирали (понятие об ин-
дуктивности будет дано в гл. 6). Часто применяются пере-
менные сопротивления непроволочного типа (рис. 2-14).
5 Теоретическая электротехника 65
К цилиндрическому корпусу 1 из пластмассы прикреплена
дужка 2 из гетинакса, на поверхности которой нанесен
тонкий проводящий слой. Этот слой состоит из частиц
сажи (углерода), скрепленных лаком. Концы слоя соедине-
ны через заклепки 3 с крайними выводами 4 и 5. Металли-
ческая втулка 6 с гайкой служит для крепления сопротив-
ления. В отверстие втулки вставлена ось 7 с гетинаксовой
пластинкой 8 на конце, на которой укреплена пружинящая
щетка 9 из проволочек. Щетка соединена со средним выво-
дом 10. Поворот оси ограничен упором 11. При повороте
оси сопротивление между вы-
водами 10 и 4 (или 10 и 5)
изменяется. Наибольшее вы-
держиваемое напряжение от-
носительно корпуса состав-
ляет 400—600 в, сопротивление
Рис 2-14. Непроволочное переменное сопротивление.
между выводами 4 и 5 от сотен ом до нескольких мегом.
Диаметр корпуса 10—30, высота 10—20 мм.
Кроме переменных сопротивлений, в электрические
цепи аппаратуры включаются и постоянные сопротивления
проволочные и непроволочные.
Проволочные сопротивления представляют собой кера-
мическую трубку с намотанной на ней проволокой, которая
сбычно покрыта предохранительным слоем эмали. У концов
трубки укреплены выводы.
Непроволочные сопротивления выпускаются различных
типов, например ВС (рис. 2-15). Сно состоит из керами-
ческого цилиндра, на поверхности которого нанесен слой
полупроводника. На концы цилиндра насажены латунные
хомутики с выводами. Проводящий слой покрыт сверху
влагостойкой эмалью. Сопротивления типа ВС рассчитаны
на рабочее напряжение до 1500 в и имеют сопротивление
66
от десятков ом до 10 Мом, диаметр от 5,4 до 27, длина от 17,5
до 120 мм. Для малогабаритной аппаратуры изготовляются
специальные постоянные непроволочные сопротивления
типа МЛТ и УЛМ. Длина сопротивлений типа УЛМ-0,12
всего 6 мм, диаметр 2 мм.
Пример 2-1. Для изготовления обмотки нагревательного прибора
при напряжении 220 в и токе 2 а применяется нихромовая лента.
Вычислить длину ленты, приняв допустимую плотность тока
10 а/мм2.
Сечение провода
I 2
S=4- = —Д- = 0,2 мм2,
О 10
Сопротивление обмотки
Искомая длина
Удельная проводимость электролитов зависит от числа
ионов в 1 см3 электролита, которое в свою очередь опре-
деляется концентрацией
электролита (концентраци-
ей электролита называется ~
масса вещества в 1 см3
раствора). Чем меньше кон- °,
центрация электролита, тем |
сильнее действие раство- |
Рис 2-15. Непроволочнсе по-
стоянное сопротивление.
Рис. 2-16 Зависимость проводи-
мости водного раствора серной ки-
слоты от концентрации.
рителя (увеличивается степень электролитической дис-
социации) и тем относительно большая часть молекул
электролита распадается на ионы. Но, с другой стороны,
снижение концентрации приводит к уменьшению числа
5* 67
молекул в 1 см3 вещества. Поэтому с увеличением концен-
трации удельная проводимость вначале растет, достигая
при некотором значении концентрации максимума, а при
дальнейшем увеличении концентрации уменьшается. В каче-
стве примера на рис. 2-16 изображена зависимость удель-
ной проводимости водного раствора H2SO4 от концентрации
при неизменной температуре.
Сопротивление электролита, как и сопротивление метал-
лического провода, определяется по формуле (2-16).
2-8. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ
С повышением температуры провода подвижность сво-
бодных электронов b уменьшается, так как столкновения
частиц следуют чаще и при одной и той же напряженности
поля средняя скорость их движения уменьшается. Умень-
шение подвижности электрона приводит, как следует
из формулы (2-15), к увеличению удельного сопротив-
ления.
Действительно, при нагревании металлов наблюдается
рост удельного сопротивления и сопротивления всего
провода. При нагревании электролитов и угля, кроме
уменьшения подвижности Ь, увеличивается концентрация
электронов п. В результате, несмотря на уменьшение Ь,
удельное сопротивление этих проводников при нагревании
не растет, а уменьшается.
С достаточной точностью в пределах от 0 до 100° С отно-
сительное приращение сопротивления Аг металлических
проводов можно считать пропорциональным приращению
температуры А© — (02—®i), т. е.
— = аА0
н
или
^1 = а(02-01),
откуда
'2 = п + па(02—®i)» (2-17)
где г2—сопротивление при температуре 02;
— сопротивление при температуре 04;
а — температурный коэффициент сопротивления, чис-
ленно равный относительному приращению сопро-
тивления при нагревании проводника на 1°С.
68
Температурный коэффициент сопротивления химически
чистых металлов близок к 0,004 Пград, поэтому, например,
сопротивление меди увеличивается примерно на 4% при
нагревании па 10° С.
Наконец, следует сказать, что изменение температуры
почти не влияет на сопротивление некоторых сплавов
металлов (например, константан, манганин). Сплавы обла-
дают большим удельным сопротивлением, чем составляющие
их металлы. Это объясняется неправильной структурой
сплавов и малым средним временем свободного пробега
электронов. Изменение температуры сплава незначительно
влияет на изменение Ь, поэтому удельное сопротивление
некоторых сплавов почти не зависит от температуры.
Температурный коэффициент сопротивления таких сплавов
очень мал. Поэтому они используются для изготовления
образцовых сопротивлений и магазинов сопротивления,
применяются для изготовления шунтов и добавочных
сопротивлений к измерительным приборам и т. д.
Уголь и электролиты имеют отрицательный температур-
ный коэффициент сопротивления. Температурный коэффи-
циент для большинства электролитов равен примерно —
0,02 Пград.
Пример 2-2. Вычислить сопротивление медного провода линии
передачи сечением Х = 95.и.и2, длиной /=120 им при температурах
0 и 20° С.
Сопротивление провода
I
r^~S'
так как Q задано как раз для температуры 20° С, то, подставляя
значения / и 3, находим:
Сопротивление провода при 0° С
Г2=Г1 + па Д0 = 21,74-21,7-0,004( —20) = 20 ом.
Пример 2-3. Определить, иа сколько процентов изменяется
сопротивление медной обмотки при нагревании ее иа 40° С.
Приращение сопротивления, выраженное в процентах,
Дг
-у-. 100% = аА0-1ОО% =0,004-40-1ОО?'о = 16%.
Пример 2-4. Определить, на сколько процентов изменяется
сопротивление цепи, составленной из медной обмотки сопротивле-
69
нием 10 ом и манганиновой обмотки сопротивлением 90 ом, при
нагревании на 40° С.
Сопротивление меди увеличится на 16% (пример 2-3), прираще-
ние сопротивления
ДГ1==Г1 100= ,6 0М'
Приращение сопротивления манганиновой обмотки
Дг2 = г2а2Л0 = 90• 0,000006-40 я» 0,02 ом.
Таким образом, сопротивление цепи увеличится на
Аг = 1,6 + 0,02= 1,62 ом.
В процентах
2-9. ЭЛЕКТРИЧЕСКАЯ РАБОТА И МОЩНОСТЬ
В источнике э. д. с. под действием химических сил
(в первичных элементах и аккумуляторах) или электро-
магнитных в электрических генераторах происходит раз-
деление зарядов. Работа, которая совершается сторонними
силами в источнике при перемещении заряда Q или, как
принято говорить, «выработанная» в источнике электри-
ческая энергия, находится по формуле (1-16), полагая
U = Е:
A = QE. (2-18)
Если источник замкнут на внешнюю цепь, то в нем
непрерывно происходит разделение зарядов, причем сторон-
ние силы по-прежнему совершают работу А = QE, или,
имея в виду, что Q = It,
A = EIt. (2-19)
По закону сохранения энергии электрическая энергия,
выработанная в источнике э. д. с., за то же время «расходует-
ся» (т. е. преобразуется) в другие виды энергии в участках
электрической цепи.
Часть энергии затрачивается во внешнем участке:
Л1 = ^ = П//, (2-20)
где U — напряжение на зажимах источника, которое при
замкнутой внешней цепи уже не равно э. д. с.
Другая часть энергии «теряется» (преобразуется в тепло)
внутри источника:
A2 = A-A1 = (E-U)It = U0It. (2-21)
70
В последней формуле Uo — это разность э. д. с. и напря-
жения на зажимах источника, которая называется внут-
ренним падением напряжения. Таким
образом,
U0 = E — U, (2-22)
откуда
E = U + U0, (2-23)
т. е. э. д. с. источника равна сумме напряжения на зажимах
и внутреннего падения напряжения.
Величина, характеризующая скорость, с которой про-
исходит преобразование энергии, или скорость, с которой
совершается работа, называется мощностью (обозна-
чение Р):
Р=~ (2-24)
или
если работа совершается неравномерно.
Величина, характеризующая скорость, с которой меха-
ническая или другая энергия преобразуется в источнике
в электрическую, называется мощностью генера-
тора:
рг = А = _ф- = £/. (2-25)
Величина, характеризующая скорость, с которой про-
исходит преобразование электрической энергии во внешних
участках цепи в другие виды энергии, называется мощ-
ностью потребителя:
Р1 = А.= ^£=(//, (2-26)
Мощность, характеризующая непроизводительный расход
электрической энергии, например на тепловые потери
внутри генератора, называется мощностью потерь:
P0^-^=^- = ^L = U0I. (2-27)
По закону сохранения энергии мощность генератора равна
сумме мощностей потребителей и потерь:
Р< — ^1 + Ро-
71
2-10. ЕДИНИЦЫ ИЗМЕРЕНИЯ РАБОТЫ И МОЩНОСТИ
Единица измерения мощности находится из форму-
лы (2-24):
[Р] = -ру- = дж/сек.
Единица измерения мощности дж/сек называется ватт
(обозначение вт), т. е.
1 вт = 1 дж/сек.
С другой стороны, по (2-18) 1 дж—\ к-1 в, откуда
, 1 в-1 к , , ,
1 вт = —-----=1 s • 1 а = 1 в-а,
1 сек
т. е. ватт есть мощность электрического тока в 1 а при
напряжении 1 в. Более крупными единицами мощности
являются гектоватт
1 гвт — 100 вт
и киловатт
1 кет — 103 вт.
Электрическая энергия подсчитывается обыкновенно
в ватт-часах (вт-ч) или кратных единицах: гектоватт-
часах (гвт-ч) и киловатт-часах (квт-ч).
Кроме Международной системы единиц СИ, в технике
довольно часто пользуются и иными единицами измерения
работы и мощности. Приведем соотношения между некото-
рыми единицами мощности и работы в различных систе-
мах единиц:
1 лошадиная сила (л. с.) = 75 кГ • м/сек = 736 вт =
- 0,736 квт\
1 квт— -п *„,. л. с. = 1,36 л. с.;
и, /оо
1 кГ-м/сек = ^вт = 9,81 вт-.
75
1 кГ-м = 9,81 вт-сек = 9,81 дж",
1 дж = п * кГ • м — 0,102 кГ • м.
У 5 о 1
Так как 1 калория (кал) составляет 0,427 кГ -м, то
1 0,102 _ п.
1 дж = Q- 42? кал = 0,24 кал.
72
Пример 2-5. Электрическая лампа включена в сеть 120 в и по-
требляет ток 0,8 а. Определить мощность лампы и стоимость энер-
гии, расходуемой ею в течение 10 ч, считая, что киловатт-час
стоит 4 коп:
Р — UI ~ 120 0,8 = 96 вт;
Л = Р/ = 96-10=960 вт-ч = 0.96 квт-ч.
Стоимость энергии = 4 —— • 0,96 квт-ч = 3,8 коп.
кет • ч
2-11. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Для электрической цепи, составленной из источника
питания с э. д. с. Е и сопротивлением г0 (внутреннее сопро-
тивление), который замкнут на внешнюю цепь с сопротив-
лением г (рис. 2-1), справедливо уравнение (2-23)
E = U0 + U.
В такой простой цепи ток на всех участках одинаков,
поэтому, выразив напряжения Uo и U по закону Ома:
U0 = Ir0 и U = 1г, и подставив их в предыдущую формулу,
получим:
E^Ir0 + Ir,
откуда ток в цепи
Формулу (2-28) называют законом Ома для
электрической цепи.
2-12. ПРЕОБРАЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
В ТЕПЛОВУЮ
При прохождении по проводу электрического тока
происходит преобразование электрической энергии в теп-
ловую.
Скорость процесса преобразования электрической энер-
гии в тепловую характеризуется мощностью
P = UI.
- Подставив выражение U = 1г в предыдущую формулу,
получим, что тепловая мощность
Р = Рг или Р = -^-. (2-29)
Количество электрической энергии W, преобразован-
ной в тепловую за время t,
73
W' = Pt = I2rt. (2-30)
Имея в виду, что 1 дж~ 0,24 кал, найдем выражен-
ное в калориях количество тепла (обозначение Q), выде-
ленного током в проводнике:
Q = 0,24 Ш; (2-31)
эта зависимость была открыта опытным путем в 1844 г.
русским ученым, членом Петербургской академии наук
Э. X. Ленцем и называется законом Джоуля
и Ленца (одновременно с Э. X. Ленцем этот закон
сформулировал английский ученый Джоуль): Количество
тепла, выделяемого током в проводнике, пропорционально
квадрату тока, сопротивлению проводника и времени
прохождения тока.
2-13. НАГРЕВАНИЕ ПРОВОДОВ ТОКОМ
Преобразование электрической энергии в тепловую
имеет большое практическое значение для создания ламп
накаливания, нагревательных приборов и печей. Однако
выделение тепла в проводах и обмотках электрических
машин, трансформаторов, измерительных и других при-
боров — не только бесполезная трата электрической энер-
гии, но и процесс, который может привести к недопустимо
высокому повышению температуры и к порче изоляции
проводов и даже самих устройств.
Количество тепла, выделяющегося в проводе, пропор-
ционально объему провода и приращению температуры,
а скорость отдачи тепла в окружающее пространство
пропорциональна разности температур провода и окру-
жающей среды.
В первое время после включения цепи разность темпе-
ратур провода и окружающей среды мала. Только неболь-
шая часть тепла, выделяемого током, рассеивается в окру-
жающую среду, а большая часть тепла остается в проводе
и идет на его нагревание. Этим объясняется быстрый рост
температуры провода в начальной стадии нагрева. По мере
увеличения температуры провода растет разность темпе-
ратур провода и окружающей среды и увеличивается
количество тепла, отдаваемое проводом. В связи с этим
рост температуры провода все более замедляется. Наконец,
при некоторой температуре устанавливается тепловое рав-
74
новесие: за одинаковое время количество выделяющегося
в проводе тепла становится равным рассеивающемуся
во внешнюю среду.
При дальнейшем прохождении неизменяющегося тока
температура провода не изменяется и называется уста-
новившейся температурой. Время нагре-
вания до установившейся температуры неодинаково для
различных проводников:
вается за доли секун-
ды, электрическая маши-
на — за несколько ча-
сов (как показывает
анализ, теоретически
время нагревания беско-
нечно велико; мы под
временем нагревания бу-
дем понимать время, в
течение которого про-
вод нагревается до тем-
пературы, отличающейся
от установившейся не
более чем на 1%).
На рис. 2-17 показа-
нить лампы накаливания нагре-
Рис. 2-17. Зависимость температуры
проводника от времени нагревания.
но изменение температуры провода в зависимости от вре-
мени прохождения тока.
Нагрев изолированных проводов нельзя допустить выше
определенного предела, так как изоляция при сильном
перегреве может обуглиться или даже загореться; перегрев
голых проводов ведет к изменению механических свойств
(натяжения проводов). Для изолированных проводов нор-
мами установлена предельная температура нагрева 55—
100° С в зависимости от свойств изоляции и условий мон-
тажа. Ток, при котором установившаяся температура
соответствует нормам, называется предельно допу-
стимым или номинальным током провода
(/ = /пом на рис. 2-17). Значение номинальных токов
для различных сечений проводов приводится в специальных
таблицах (например, для медных проводов с резиновой
изоляцией в табл. 2-4).
Мощность, развиваемая током в проводе, при которой
наступает тепловое равновесие и устанавливается допусти-
мая температура, называется допустимой мощностью рас-
сеивания.
75
Таблица 2-4
f Поперечное сечение, мм.2 Наибольший допустимый ток, а Поперечное сечеиие, мм2 Наибольший допустимый ток, а Поперечное сечение, мм2 Наибольший допустимый ток, а Поперечное сечеиие, мм2 Наибольший допустимый | ток, а
0,50 10 4,0 36 35 150 150 390
0,75 13 6,0 46 50 190 185 450
1,0 15 10 68 70 240 240 535
1,5 20 16 90 95 290 300 615
2,5 27 25 120 120 340 400 735
Если по проводу проходит ток больше номинального
(/>/ном на рис. 2-17), то провод оказывается «перегру-
женным». Однако, поскольку установившаяся температура
достигается не сразу, кратковременно (в течение времени
f, рис. 2-17) можно допустить в цепи ток больше номи-
нального (до момента, пока температура провода не достиг-
нет предельного значения). Слишком большая температура
провода, как правило, получается при коротком
замыкании.
Пример 2-6. В сеть 120 в включено 15 одинаковых ламп по
15Э вт. Определить необходимое сечение медного провода.
Полная мощность
Р = 150-15 = 2 250 вт.
Ток в проводе
, Р 2 250
/=77=Т2^ = 18,75 “•
По табл. 2-4 выбираем сечение провода:
5=1,5 мм2.
2-14. КОРОТКОЕ ЗАМЫКАНИЕ. ПРЕДОХРАНИТЕЛИ
Короткое замыкание возникает при соединении двух
проводов цепи, присоединенных к разным зажимам (+ и —)
источника через очень малое сопротивление, которое срав-
нимо с сопротивлением самих проводов. Ток при коротком
замыкании может превысить номинальный ток цепи во мно-
го раз. В таких случаях цепь должна быть разорвана
раньше, чем температура проводов достигнет опасных
значений.
76
Для защиты проводов от перегрева и предупреждения
воспламенения окружающих предметов в цепь включается
плавкий предохранитель.
Предохранитель выполняется из проволоки меньшего
сечения, чем провода защищаемой цепи. Сечение проволоки
предохранителя выбирается так,
чтобы она плавилась, когда ток
в цепи превысит номинальный.
Схематическое устройство одного
из типов предохранителей изо-
бражено на рис. 2-18.
2-15. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
С НЕСКОЛЬКИМИ Э. Д. С.
Рис. 2-18. Плавкий двух-
полюсный предохранитель.
Рассмотрим более сложную
электрическую цепь, чем на
рис. 2-1, составленную, напри-
мер, из приемника с сопротив-
лением г и двух источников с внутренними сопротивле-
ниями г01 и г02, э. д. с. которых Et и Е2 направлены на-
встречу друг другу (рис. 2-19). Сопротивлением соедини-
тельных проводов здесь и всюду в дальнейшем, когда не
сделано специальной оговорки, мы будем пренебрегать.
Ток в такой цепи можно определить по принципу
наложения. Согласно этому принципу ток в цепи
равен алгебраической сумме токов, создаваемых в ней источ-
никами э. д. с., действующими отдельно друг от друга,
при неизменных сопротивлениях всех участков цепи.
Предположим, что в цепи действует только э. д. с. £р
В этом случае ток
I _ Ei
1 r0i + r02 + r
и совпадает по направлению с э. д. с. £Р Напомним, что
э. д. с. источника направлена от отрицательного зажима
к положительному. Затем выразим ток, который проходит
при действии в цепи только э. д. с. £2; в этом случае
/ =—Е2 .
2 г01 + г02 + г ’
Этот ток совпадает по направлению с э. д. с. £2.
Если бы э. д. с. Ei и £2 имели одинаковое направление,
то ток в цепи был бы равен сумме токов Е и /2. В нашем
77
случае э. д. с. Et и Е2 направлены встречно. Общий ток
равен разности токов Ц и /2, т. е.
J J ____ I __ ^2
1 2 г01+г02 + г
(2-32)
В
Рис. 2-19. Электрическая цепь
с двумя источниками э д. с.
Очевидно, что электрический ток возникает только
при условии Ei =# Е2. Его направление совпадает с направ-
лением большей э. д. с. Пусть Е{ > Е2; в таком случае
ток в цепи протекает по направлению движения часовой
стрелки (рис. 2-19), т. е.
совпадает по направлению
с Et, и направлен навстре-
чу Е2. Электродвижущая
сила (Е2), направленная
противоположно току, на-
зывается встречной,
или п р о т и в о - э. д. с.
Рассматр иваемую эле кт-
рическую цепь можно раз-
делить на три участка: А Б,
Б В и АВ. Участок А Б
обладает сопротивлением, в котором электрическая энер-
гия преобразуется в тепловую; развиваемая при этом
мощность
Раб = 12г,
напряжение между точками А и Б
АБ
Раб
I
1г
(2-33)
(напряжение на концах сопротивления называется также
падением напряжения).
Участок БВ обладает сопротивлением г02, и в этом
участке действует встречная э. д. с. Е2. В участке Б В,
кроме тепловой мощности /2г0г, развивается дополнительно
электрическая мощность Ег1, так как электрическими
силами совершается работа по преодолению сторонних сил.
Поэтому, помимо преобразования электрической энергии
в тепловую, в этом участке наблюдается преобразование
электрической энергии в механическую или химическую
энергию в зависимости от происхождения сторонних сил.
Источник с противо-э. д. с. работает в режиме потребителя.
78
Развиваемая в участке БВ мощность
РБВ ~ Н~ РГ02’
а напряжение между точками Б и В
иБВ = ^р = Е2 + 1г02, (2-34)
т. е. напряжение между положительным и отрицательным
зажимами источника э. д. с., работающего в режиме по-
требителя, равно сумме э. д. с. и внутреннего падения на-
пряжения.
Участок АВ обладает сопротивлением foil на этом
участке действует э. д. с. Ei, направленная так же, как
и ток 1. Источник э. д. с. Ei работает в режиме источника
энергии. Электродвижущая сила источника энергии равна
сумме напряжения на зажимах и внутреннего падения
напряжения (2-23):
Ei — UabA-Uq — + /гОц
откуда напряжение между точками А и В
Uab = Ei — Ifoi- (2-35)
Таким образом, напряжение на зажимах источника
энергии (генератора) равно разности э. д. с. и внут-
реннего падения напряжения.
Развиваемая им мощность [см. (2-25)]
Е^Е^ + и^и^ + Ег^.
Обобщив формулы (2-34) и (2-35), можно прийти
к выводу, что в общем случае напряжение на зажимах
источника э. д. с. (между положительным и отрицатель-
ным зажимами)
U = <р+ — ф_ = Е ± If о- (2-36)
При разомкнутой внешней цепи (/ = 0) напряжение
на зажимах источника равно его э. д. с. Наконец, в режиме
короткого замыкания, когда напряжение на зажимах
источника равно нулю, внутреннее падение напряжения
оказывается равным э. д. с. источника.
2-16. ПОТЕНЦИАЛЬНАЯ ДИАГРАММА
Исследования электрических цепей, изучение режимов
их работы значительно упрощаются, если для цепи ввести
вспомогательное понятие о потенциале. При вычислении
79
потенциалов отдельных точек электрической цепи потен-
циал точки, соединенной с землей, принимается равным
нулю, а потенциалы других точек определяются по уравне-
ниям (2-33) и (2-36). Таким образом, под потенциалом
точки электрической цепи понимают напряжение между
этой точкой и землей.
Пусть, например, нужно определить потенциалы точек
Б, В, Г и Д электрической цепи, представленной на
рис. 2-20. Направления э. д. с. Ei и Е2 и направление
Рис. 2-20. Схема электрической цепи.
тока известны, из чего следует, что источник с э. д. с. Е2
работает в режиме генератора, а источник с э. д. с. Е4
в режиме потребителя. Вначале определим потенциал
точки Д.
Между точками Д и А включено сопротивление г3.
Потенциал Д больше потенциала А, так как ток направлен
из точки Д в точку Л. Ток в сопротивлении возникает
под действием электрических сил и всегда направлен от точки
с более высоким потенциалом к точке с меньшим потенциа-
лом. Разность потенциалов срд — фд выражает напряже-
ние между точками Д и А; поэтому фд — <рд = иДА =
=/г3. Точка А заземлена. Таким образом, фд = 0,
а фЛ == 1г3.
Потенциал срд точки Д является также потенциалом
положительного зажима источника э. д. с, Е2, а потенци-
ал фр точки Г — потенциалом отрицательного зажима
того же источника. Имея в виду, что напряжение на зажи-
мах источника можно выразить как разность потенциалов
и что источник с э. д. с. Е2 работает в режиме генератора,
составим уравнение
Ф+ — ф_ = Фд — Фг = fa —
откуда потенциал фг = фд—Ег + 1г02.
80
Потенциал фВ больше <рг на величину 1г2, т. е.
Фд-~ Фг 4-7г2-
Источник с э. д. с. Ei является потребителем энергии,
a Ei — встречной э. д. с. Разность потенциалов между
положительным и отрицательным зажимами этого источника
Фб— фв = Ej Iroi‘
Из этого уравнения определяется потенциал точки Б.
Рис. 2-21. Электрическая цепь с одним
источником и ее потенциальная диаграмма.
Графическое изображение распределения потенциалов
в электрической цепи в зависимости от сопротивлений
участков цепи называется потенциальной диа-
граммой. При построении диаграммы по оси абсцисс
откладывают в масштабе сопротивления участков в том
порядке, в котором участки следуют друг за другом в цепи
(иногда вместо сопротивлений по оси абсцисс откладывают
длины участков, из которых составлена цепь), а по оси
ординат — значения потенциала в выбранном масштабе.
На рис. 2-21 построена потенциальная диаграмма для
участка АГ цепи, изображенной на том же рисунке. По оси
абсцисс отложены rit г2 и г3\ таким образом, получились
точки а, б, в и г, соответствующие точкам А, Б, В и Г цепи.
6 Теоретическая электротехника 81
В полученных точках отложены ординаты, выражающие
потенциалы ф^, Фб, фл и фг. Концы ординат соедине-
ны прямыми отрезками. В данном случае потенциальная
диаграмма имеет вид прямой линии, так как по всем сопро-
тивлениям проходит одинаковый ток, отчего между изме-
нением потенциала и сопротивлением цепи получается
линейная (прямая) зависимость.
Рис. 2-22. Потенциальная диаграмма
к примеру 2-7.
Пример 2-7. Построить потенциальную диаграмму для цепи, изо-
браженной на рис. 2-20, по следующим данным:
Н = 4 ом; г2~=2 ом; г3 = 6 ом; rol = rO2 = ''o~i ом!
E<i= 18 в; Е2 = 46 в.
Предварительно вычислим ток:
/ = £2-^1 = 46 — 18 =
гг+ гз+roi+г02 4-)-2-)-6-)-14-1
После этого найдем потенциалы всех точек.
Потенциал точки А, соединенной с землей, примем равным нулю:
<рА = 0.
Из уравнения Фа —Фб = ^г1 найдем:
Фб = Фа—’ ^4 = — 2-4 = — 8 в.
Между точками Б и В в цепи включен источник, работающий
в режиме потребителя. Разность потенциалов на его зажимах
ФБ —Фв = £1 + /го,
откуда
Фв = Фб — £1 — ^о=—8—18 — 2=—28 в.
Потенциал точки Г найдем из уравнения <рв — Фп = /г2, откуда
Фг = Фв~ 1г2= —28 — 2-2= —32 в.
82
Положительный зажим источника с э. д. с. Е2, работающего
в режиме источника питания, присоединен к точке Д, а отрица-
тельный—к точке Г, поэтому
Фд~Ч>г = ^2—Не-
откуда
Фд = Фд+£*2——32+46 — 2=12 в.
Наконец, из уравнения <рд—фл = ^гз убеждаемся, что
<Ра = Ч>д—Нз=12—2-6 = 0.
На рис. 2-22 представлена потенциальная диаграмма, построен-
ная по полученным результатам.
ГЛАВА ТРЕТЬЯ
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
ПОСТОЯННОГО ТОКА
3-1. ПРАВИЛА КИРХГОФА
Во всех участках неразветвленной цепи (образующей
один замкнутый контур) постоянный ток имеет одинаковое
значение. Если же цепь разветвлена, то токи в отдельных
ветвях могут иметь различные значения, причем сум-
марный заряд, притекающий кточке разветвле-
ния (узлу), всегда равен суммарному заряду, утекаю-
щему от этой точки за то же время. В этом и заключается
первое правило Кирхгофа, которое обычно
формулируется следующим образом: сумма токов, направ-
ленных к точке разветвления, равна сумме токов, направ-
ленных от нее.
Так, например, для узла, изображенного на рис. 3-1,
Л + ^з+Л = 4+Л- (3-1)
Преобразуя это соотношение, получим:
Л + (—!г) + ^з + (— Л) + h = 0
или в общем виде:
2/ = 0, (3-2)
т. е. алгебраическая сумма токов в точке разветвления
равна нулю. При этом токи, направленные к узлу, счита-
ются положительными, а токи, направленные от узла,—
отрицательными (или наоборот).
6‘ 83
В сложных электрических цепях имеем уже не один,
а ряд замкнутых контуров, питаемых несколькими источ-
никами. На рис. 3-2 представлен один контур сложной
цепи. Направления э. д. с. источников и направления
токов в отдельных участках контура известны. Обходя
контур в произвольно выбранном направлении (например, по
направлению движения часовой стрелки), проследим измене-
ние потенциала от ис-
ходной точки А, потен-
циал которой равен <рд.
Рис. 3-1. Узловая Рис. 3-2. Контур разветвленной
точка электриче- цепи.
ской цепи.
На участке цепи между точками А и Б происходит
повышение потенциала на величину Iirlt так как ток в со-
противлении проходит от точки Б с более высоким потен-
циалом к точке А с меньшим потенциалом. Таким образом,
Фб~фл = Лн, откуда
Фб = Фл4~Лг1- (3-3)
На участке БВ включен источник с э. д. с. Е1Г рабо-
тающий в режиме источника энергии. Разность потенциалов
на его зажимах <рв — ц>в — Е!—Преобразуя это урав-
нение, находим:
Фв = Фб—+ (3'4)
Аналогично (3-3) определяем потенциал точки Г\
фГ — фв + Izr2- (3-5)
Потенциал точки Д найдем из уравнения Фд —фг =
= £,2 + 4',02, откуда
фд — Ф-Г + ЕъА- ^2Г02 (3-6)
и, наконец,
фх —фд —hr3. (3-7)
84
Сложив почленно уравнения (3-3) —(3-7), получим
в обеих частях одинаковые суммы фд + фв + фв + фг + фд.
которые, таким образом, взаимно уничтожаются. Оконча-
тельно сумма уравнений для замкнутого контура АБВГДА
примет вид:
0= —Ei + £2 + Л (П -г Пн) + /2 (г2 + гоз) hrs
или
— £1 + £2 = — Л (с 4" С») — ^2 (г2 4- f02) 4- hrз- (3-8)
В общем виде для любого замкнутого контура
2£ = 2(/г). (3-9)
Это уравнение выражает второе правило Кирх-
гофа: в замкнутом контуре электрической цепи алге-
браическая сумма э. д. с. равна алгебраической сумме падений
напряжения в отдельных сопротивлениях. При этом поло-
жительными надо считать э. д. с., направления которых
совпадают с произвольно выбранным направлением обхода
по контуру (т. е. э. д. с. положительна, если при обходе
мы сначала попадаем на отрицательный зажим источника,
а потом на положительный). Падение напряжения на сопро-
тивлении положительно там, где направление тока совпа-
дает с направлением обхода.
В частном случае, когда контур не содержит источников,
2(/г) = 0.
3-2. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
СОПРОТИВЛЕНИЙ
Если сопротивления включены таким образом, что
образуют неразветвленную цепь или участок цепи — ветвь
и по ним проходит один и тот же ток, то соединение сопро-
тивлений называется последовательным; пример
последовательного соединения показан на рис. 3-3.
По закону Ома напряжения между концами отдельных
участков цепи составляют:
U1 = Zr1; h2 = Ir2, U3 = Ir3.
Следовательно,
Ui: U2: U3 = / j: г2 ’ О, (3-10)
т. е. падения напряжения в отдельных сопротивлениях
пропорциональны величинам сопротивлений.
85
С другой стороны,
1А —Фа— Фб! (Л = Фб — фв> ^з = фв— фг«
Складывая правые части уравнений, получим:
фА —фв + фБ —фв + фв —фГ==фА —фг-
а так как полное напряжение, приложенное к цепи,
^ = Фа—фг,
то приходим к выводу, что сумма падений, напряжения
в отдельных сопротивлениях равна приложенному к цепи
напряжению:
Ui + U2 + V3 = U. (3-11)
Рис. 3-3. Последовательное соедине-
ние сопротивлений.
Иногда для расчетов
удобно заменить не-
сколько последователь-
но соединенных сопро-
тивлений одним равно-
значным (общим) со-
противлением г. Вели-
чина этого сопротивле-
ния должна быть такой,
чтобы при том же токе
I напряжение U между
концами сопротивления
г равнялось напряжению данной цепи, т. е. Ir = U. Сле-
довательно,
г— — ^i + ^г+^з г > । /о [п\
г— ।--------j----бт^тг3' (3-12)
Итак, общее сопротивление при последовательном
соединении равно сумме отдельных сопротивлений.
Из выражения общего сопротивления следует, что
/2г = 7^-№ + /%,
т. е. мощность всей цепи равна сумме мощностей отдель-
ных участков, а также
Рг.Р2: Рз = П :г2:г3,
т. е. развиваемая в отдельных участках мощность про-
порциональна сопротивлениям участков.
Пример 3-1. Первичный элемент, у которого Е— 1,5 в и г0 = 0,2 ом,
замкнут на сопротивление г=14,8о.и.
86
1. Вычислить, чему равна ошибка в определении тока, если пре-
небречь величиной внутреннего сопротивления элемента.
Действительная величина тока
Е _ 1,5
0,24-14,8 ’ а’
а его приближенное значение
F 1 'i
/' = — = ,-4’- = 0,1013 а.
г 14,8
Погрешность
y=-^ioo% = ^^ioo%=^ = i,3%.
2. Определить то же, если г=0,3 о.ч:
, Е 1,5
Го-К 0,24-0,3 ’
Погрешность
У = ~—7— 100% 100% =66,7%.
1 о
3-3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ СОПРОТИВЛЕНИЙ
Если два или большее число сопротивлений включено
между одними и теми же двумя узлами А и Б так, что
напряжение U на них одинаково (рис. 3-4), то соединение
сопротивлений называется параллельным. При
параллельном соединении цепь получается разветвленной,
а параллельно включенные сопротивления служат ее вет-
вями.
По закону Ома токи в отдельных ветвях определяются
соотношениями
Л=~ = ^; /2=~ = ^2; /3 = -^- = ^3,
следовательно,
: /2 ' 1з~ gi ' g2: gs = — :— ’ — > (3-13)
т. е. распределение тока между отдельными ветвями
прямо пропорционально проводимостям ветвей или обратно
пропорционально их сопротивлениям.
87
Несколько параллельно соединенных сопротивлений
можно заменить одним общим сопротивлением г. Это сопро-
тивление должно быть выбрано так, чтобы при токе в сопро-
тивлении I, равном сумме токов в отдельных ветвях, напря-
жение U между концами сопротив-
ления равнялось приложенному
напряжению, т. е. чтобы
или
J_ __ Л 4" /з __ __I_1_I_
г ~ U rt' >-2 ' г3'
Заменяя сопротивления про-
водимостями, находим:
ё = gi + ёг + ёз, (3-14)
т. е. общая проводимость цепи
равна сумме проводимостей от-
дельных ветвей (таким образом,
общее сопротивление будет мень-
ше, чем самое малое из сопротивлений). Из выражения
общей проводимости следует, что
^4
Рис. 3-4. Параллельное
соединение сопротивле-
ний.
а так как
U2g= I2r2g= I2r — Р,
то
р — Pj + Р2 + р3,
т. е. мощность всей цепи равна сумме мощностей отдель-
ных ветвей.
При параллельном соединении двух сопротивлений
(рис. 3-5) у=7- + 7- = ^, (3-15) Г Г] Г2 Г У 2
откуда г_ ГХГ2 4+ Г2’
т. е. общее сопротивление равно произведению обоих со-
противлений, деленному на их сумму.
88
Рассмотрим, как в этом случае выражаются токи в от-
дельных ветвях через ток неразветвленной части цепи.
Очевидно,
1г = и 1г = /2г2,
откуда
г2
Подставляя вместо г найденное значение, получаем:
I = I Гг = I 81 • )
Г1 + Г2 ’ < (3-16)
= = /—-g— I
rl+r2 + '
При параллельном соединении п равных сопротивле-
ний г0 общее сопротивление
г = -£. (3-17)
Рис. 3-5. Параллельное соединение
двух сопротивлений.
При параллельном включении приемников режим рабо-
ты одного из них не влияет на режим работы другого.
Совершенно противопо-
ложное наблюдается при
последовательном соеди-
нении приемников, где
выключение одного из
них приводит к разрыву
цепи, т. е. к отключению
всех приемников энер-
гии.
Потребители электр и-
ческой энергии—лампы,
электродвигатели и др.—
обычно соединяются параллельно друг другу.
Последовательное соединение применяют там, где напря-
жение источника превышает номинальное напряжение
потребителей. Например, в трамвае электрические лампочки
соединяют последовательно.
3-4. СМЕШАННОЕ СОЕДИНЕНИЕ СОПРОТИВЛЕНИЙ
Когда электрическая цепь может быть разделена на уча-
стки, которые соединены последовательно, причем некоторые
из них образованы параллельно включенными сопротив-
89
лениями или, наоборот, участки параллельно соединены,
но состоят из последовательно включенных сопротивлений,
Рис. 3-6. Схема к примеру
3-2.
то мы имеем дело со с м е ш а н-
ным соединением со-
противлений. Способов
смешанного соединения может
быть очень много.
Рассмотрим цепь, представ-
ленную на рис. 3-6, и покажем
на примере, как рпределяются
токи при смешанном соединении
сопротивлений.
Пример 3-2. Определить токи и
напряжения в цепи, избраженной иа
рис. 3-6, при следующих данных:
Е — 2 в; го = 0,5 ом; г1 = 3,5 ом;
г2 = 5 ом; г3=100 ом; г4 = 25 ом.
Находим проводимость параллельно соединенных ветвей:
й'ЛБ = й'2 + й'з + й'4 = у + уо0 + 25 = О,25 сим,
откуда следует, что сопротивление этого участка
'•аб=ЛГ-=4 ом’
8аб
общее сопротивление всей цепи
г = го-|-Г1 + г^в = 0,5-|-3,5-|-4 = 8 ом.
Ток в неразветвленной части цепи
F 2
/.=—=4 = 0,25 а.
г 8
Напряжение между точками АБ
ПАБ =//АБ = 0,25-4 = 1 в.
Ток в отдельных ветвях
1 Par
/.,= —^—=4 = 0,2 а; /3=—^- = 0,01 а;
2 г2 5 г3
Раб
/,=-^® =0,04 а.
а
Различные последовательные и параллельные соедине-
ния потребителей и их сочетание (смешанное соединение)
90
при одном источнике питания образуют цепи, которые будем
называть простыми цепями постоянного тока.
В простой цепи токи и напряжения отдельных участков
можно определить, если известны э. д. с. генератора и сопро-
тивления участков цепи. Основным расчетным уравнением
является закон Ома.
Однако когда мы сталкиваемся с разветвленной сложной
цепью, в которой в произвольном порядке размещены
сопротивления и источники, закона Ома для ее расчета
недостаточно. В этом случае расчетные уравнения состав-
ляются по первому и второму правилам Кирхгофа (§3-1).
в развивают мощность
f
Рис. 3-7.
а—последовательное и б—параллельное со-
единения аккумуляторов.
3-5. ПОСЛЕДОВАТЕЛЬНОЕ, ПАРАЛЛЕЛЬНОЕ И
ГРУППОВОЕ СОЕДИНЕНИЯ ПЕРВИЧНЫХ ЭЛЕМЕНТОВ
И АККУМУЛЯТОРОВ
Первичные элементы развивают обычно мощность, рав-
ную долям ватта, при напряжении 1—1,5 в. Аккумуля-
торы при напряжении
до нескольких десятков
ватт. Поэтому мощность
потребителя часто пре-
вышает мощность отдель-
ного элемента. В этом
случае элементы соеди-
няются для совместной
работы в батарею.
Соединение допуска-
ется только для одно-
родных элементов, имею-
щих одинаковые э. д. с.
и внутренние сопротив-
ления.
Применяются три способа соединения элементов в бата-
рею: последовательное, параллельное
и групповое.
Последовательное соединение (рис. 3-7, а) применяется
в том случае, когда ток потребителя не превышает номи-
нального (предельно допускаемого) тока элемента, а напря-
жение потребителя U больше э. д. с. Ео одного элемента.
В этом случае число элементов п, соединяемых последо-
вательно, берется не меньше отношения ~. У всех п элс-
91
ментов э. д. с. должны иметь одинаковые направления,
для чего отрицательный зажим первого элемента соеди-
няется с положительным зажимом второго и т. д. Емкость
батареи из последовательно включенных элементов равна
емкости одного элемента, э. д. с. батареи
Е = пЕ0, (3-18)
внутреннее сопротивление батареи
г = пг0. (3-19)
Параллельное соединение элементов применяется при
напряжении потребителя, равном э. д. с. одного элемента,
но при нормальном (рабочем) токе потребителя I, большем,
чем разрядный ток /р элемента. В этом случае число эле-
ментов т, соединенных параллельно, должно быть не
меньше отношения ~.
При параллельном соединении положительные зажимы
всех источников соединяются в один узел, а отрицатель-
ные — в другой (рис. 3-7, б).
Электродвижущая сила батареи из параллельно вклю-
ченных элементов равна э. д. с. элемента
Е = Е0; (3-20)
внутреннее сопротивление батареи
(3-21)
Емкость батареи равна сумме емкостей параллельно
соединенных элементов. Групповое соединение представ-
ляет собой комбинацию последовательного и параллель-
ного соединений элементов. Оно применяется, когда номи-
нальные напряжение и ток потребителя больше э. д. с.
и разрядного тока одного элемента.
Пример 3-3. Определить число аккумуляторов (Eq = 2 в; !р — 8 а)
и выбрать способ их соединения для питания электроэнергией аварий-
ного освещения. Мощность всех ламп 2,2 кет, напряжение НО в.
Определим ток потребителя:
, Р 2 200
/ = ТГ = 'ПУ=20 “•
Так как напряжение и ток потребителя больше, чем Ео и
одного элемента, то следует применить групповое соединение.
92
Число параллельных групп
/
т>
20
8
= 2,5;
выбираем т = 3. В каждой группе нужно соединить последовательно
п элементов:
и НО «
П=^=-Т=55
(пренебрегая внутренними падениями напряжения в аккумуляторах).
Таким образом, общее число аккумуляторов
N = nm = 55-3= 165.
3-6. НЕРАЗВЕТВЛЕННАЯ ЦЕПЬ С ПЕРЕМЕННЫМ
СОПРОТИВЛЕНИЕМ
Рассмотрим режим электрической цепи, содержащей
два последовательно включенных сопротивления и г2 при
Рис. 3-8. Последовательное соединение при одном
переменном сопротивлении.
изменении одного из них (например, г2) от бесконечности
до нуля и при неизменном напряжении U = Е на зажимах
цепи (рис. 3-8, а).
Ток в такой цепи
1 = —^— (3-22)
Г1 + Г2
г и п
и принимает при г2 = со нулевое значение /х = —=0,
а при г2 = 0—наибольшее значение /к = — .
Режим цепи при г2 = 00 называется режимом холо-
стого хода, а режим при г2 = 0 — режимом корот-
кого замыкания.
Проследим за изменением напряжений и Ui на зажи-
мах сопротивлений и г2 в зависимости от тока цепи.
93
Напряжение на зажимах первого постоянного сопро-
тивления Ui = lrl. Это напряжение пропорционально току;
оно изменяется от нуля (при I = /х= 0) до наибольшего зна-
чения U, равного напряжению на зажимах цепи (при/=/к).
Напряжение на зажимах второго переменного сопро-
тивления U2 = U — Ui = U — Irt. Это напряжение также
линейно зависит от тока и изменяется от наибольшего зна-
чения U (при I = /х = 0) до
нуля (при / = /к).
При Г1 = Гг или при
т U /к ,,
1 напряжения СД
и U2 равны друг другу.
На рис. 3-9 представлены
графики, показывающие изме-
нение напряжений 7Д и (72
в зависимости от тока I.
Рис. 3-9. Графики изменения
напряжений в зависимости от
тока.
Полная мощность цепи
Р — UI изменяется пропор-
ционально току от наимень-
шего значения Рх = 0 (при
I = 1Х = 0) до наибольшего Р,- = UIK. Мощность в по-
стоянном сопротивлении Л = UJ = Pt\, т. е. изменяется
пропорционально квадрату тока. При изменении тока
мощность Р( принимает различные значения от наимень-
шего Р1Х = 0 (при / = 1Х = 0) до наибольшего Р1к = Рк
(при I — 1К). Мощность в переменном сопротивлении г2
определяется как разность Р и Р4, т. е. Р2 = Р — Pi =
= UI — Pri. Мощность Р2 равна нулю при I = /х = 0
и при I = /к.
Для определения наибольшего значения мощности Р2
найдем первую производную функции Р2(/) = UI — Pt\
и приравняем ее нулю. Так как Р'2(1) = U — 2Irt = 0, то
наибольшая мощность получается при токе I = Ш2г(.
Но при любом значении сопротивления г2 (в любом режи-
ме) ток определяется по формуле (3-22). Сравнивая эти
выражения, находим, что мощность Р2 достигает наиболь-
шего значения при г2 = G. Ток в этом режиме
1 __ м _______ Jir
2rt ~ 2
и максимальная мощность
П ,2 U2 UlK
Р2 макс — 7'2 — Гц — —4— .
94
Графики зависимостей Р, Pi и Р2 от тока даны на
рис. 3-10.
Неразветвленную электрическую цепь с постоянным
и переменным сопротивлениями можно рассматривать как
схему замещения электрической цепи из источника питания
(с постоянным внутренним сопротивлением и сопротивле-
нием подводящих проводов
г4) и приемника с перемен-
ным сопротивлением г2
(рис. 3-8,6).
Выясним целесообраз-
ные режимы работы источ-
ника энергии. Этот во-
прос можно рассматривать
с двух точек зрения.
Во-первых, следует выяс-
нить, при каких условиях
источник развивает макси-
мальную полезную мощ-
ность, и, во-вторых, при
каком режиме будет самый
высокий к. п. д. Полезной
Рис. 3-10. Графики изменения
мощностей в зависимости от тока.
мощностью в цепи является мощность в переменном со-
противлении Р2. Мощность в постоянных сопротивлениях Pi
следует рассматривать как мощность потерь.
Как уже известно, режим, при котором развивается
наибольшая полезная мощность, имеет место при г2 = гй
в этом случае 1 = н полезная мощность равна мощ-
ности потерь, т. е.
= л =
мощность, развиваемая источником,
P = Pl + P2 = ±^-
Коэффициент полезного действия
т] = -^- = -^-, или 50%.
95
Наибольший к. п. д. получается при г2=со, т. е.
в режиме холостого хода, действительно,
„ р2 U2I ^E-U^E-lr
ц ' Р ~ El Е Е ’
откуда при 7 = 0 имеем т] = 1, или 100%.
Таким образом, передача с высоким к. п. д. должна
выполняться при режимах, близких к холостому ходу.
Пример 3-4. В электрическую сеть с напряжением 120 в вклю-
чена плитка мощностью 720 вт. В штепсельной розетке с течением
времени образовался плохой контакт. Определить наибольшую мощ-
ность, которая может быть выделена в штепсельной розетке.
Сопротивление плитки
t/2 14 400
fl“' Р “ 720 -2° °М'
Наибольшая мощность в розетке будет при сопротивлении кон-
такта г2=г1 = 20 ом.
Ток в цепи прн таком сопротивлении контакта
, U 120 _
rj + f! 20+20
Мощность в контакте
/’2=/2г2= 9-20= 180 вт.
3-7. ПОТЕРЯ НАПРЯЖЕНИЯ В ПРОВОДАХ
Передача электрической энергии от генератора к прием-
никам обычно происходит по проводам, которые образуют
электрическую сеть. В
Рис. 3-11. Электрическая
сеть с приемником на конце.
простейшем случае энергия пере-
дается по двум проводам (каж-
дый длиной /). Провода и прием-
ник энергии образуют неразвет-
вленную цепь (рис. 3-11).
Сопротивление обоих прово-
дов определяется по известной
формуле (2-16):
г-=2=- (3-23)
При передаче энергии в результате падения напряже-
ния в проводах напряжение в конце 7+ меньше напряже-
ния в начале Ui. Разность между напряжениями Ui и U2
называется потерей напряжения (обозначение
96
&U). Таким образом,
\U = Ui—U2. (3-24)
Та же величина по закону Ома
At7 = 7r = 2Z—V- (3-25)
Потеря напряжения обычно допускается небольшой
по сравнению с напряжением Uit во-первых, с целью эко-
номии энергии и, во-вторых, для обеспечения незначитель-
ного колебания напряжения у приемника при изменении
сопротивления, а значит, и тока приемника.
Ток потребителя или, как говорят, «нагрузка»
при различных сопротивлениях приемника изменяется
от нуля до некоторого максимального значения. Потеря
напряжения в сети при этом также колеблется от нуля
до своего максимального значения. При постоянном напря-
жении Ui в начале сети напряжение в конце изменяется
от U2 = Ui при I = 0 и АС/ = 0 до (7' = (74 — АС/. Поэто-
му допускаемая потеря напряжения в сети равна допу-
скаемому колебанию напряжения на зажимах приемника
U2 — U'2 = Ui — U'2= ьи.
Так, для электрических ламп допустимо изменение
начцяжения 1—2%, для электродвигателей 2—5% номи-
нального значения напряжения.
Очень часто при расчете потерей напряжения задаются
и определяют необходимое сечение провода.
Согласно (3-25) сечение
s = 2'w- (3-26>
Выразив потерю напряжения в процентах напряжения
у потребителя
е = 4^-100% (3-27)
^2
и подставив значение АС/ в (3-26), получим:
„ 211-100
yU2e
Умножая числитель и знаменатель правой части (3-28) на
U2, найдем, что
5 = = .100%. (3-29)
yU2e U2 уЩе ' 7
7 Теоретическая электротехника 97
Выбранное по условию потери напряжения сечение
провода обязательно проверяется на нагрев.
Из выражения (3-29) следует, что относительно малое
сечение провода при передаче больших мощностей на дале-
кие расстояния получится, если применить высокое напря-
жение.
При передаче энергии некоторая ее часть «теряется»
в проводах. Мощность потерь
ДР = /2f = 2/a-V или ДР = /ДП.
yS
Коэффициент полезного действия электрической сети
Pj-ЬР _UjI-&U! Uj-W , U2
1 Pi ~ Uii ~ Ui ~ Ui '
Обычно передача энергии происходит при к. п. д.;
равном 0,98—0,95, и напряжение на зажимах потреби-
теля отличается от напряжения в начале сети на 2—5%.
Рис. 3-12. Электрическая сеть с не-
сколькими приемниками.
В том случае, когда участок сети имеет несколько при-
емников, присоединенных в различных местах линии
(рис. 3-12), потерю напряжения во всей сети можно пред-
ставить как сумму потерь напряжения на отдельных участ-
ках:
Д(7 = &Ui + АН, + АП3.
Но так как потери напряжения на отдельных участках
i = (/i + /2 + /3) Н» А//2 = (/2 +/3) г2;
Л//з — /з^З!
то
~ (/} /2 4“ /3) Н 4“ (У2 ^з) ^*2 “Ь /з^*3*
98
Раскрывая скобки, находим, что
А(7 = ZjTj + 12Ti + I зг i + 4rz Ч~ ЛаЧ- /згз
и вынося за скобки одинаковые токи, получим:
AJ7 = Л/д Ч* 4 (А Ч- А) Ч- 4 (ri Ч~ АЧ- гз).
Если цепь выполнена проводом одинакового сечения
по всей длине, то
AZ7 = Л -А. 1Х +12(Ц + /2) Ч- /з 4“
Выражения, стоящие в скобках, представляют собой
расстояния от генератора до соответствующего приемника.
Обозначая
li — Lt', = L2, 4 Ч-4 Ч-4 = 4з,
находим потерю напряжения:
= (ЦЦ + I2L2 + 13L3), (3-31)
г-5
‘откуда при заданной потере напряжения можно опреде-
лить требуемое сечение проводов:
*5 = уД1/ (4^1 Ч" 4^2 Ч~ 4Ез) (3-32)
Пример 3-5. Помещение освещается группой ламп общей мощ-
ностью 2 квпг. Напряжение на зажимах генератора (/(=125 в. Рас-
стояние от генератора до помещения, где установлены лампы, 80 м.
Определить сечение медных проводов, при котором напряжение
на лампах будет не менее 120 в.
Допустимая потеря напряжения
MJ = Ui-U2= 125- 120 = 5 в
или в процентах
е— • 10°% = -А- • 100% = 4,16%.
IJ 2 * Хи
Принимая во внимание, что проводка будет выполнена медными
проводами (у = 58 м/ом-мм2), находим необходимое сечение:
с_ W 1ПП(>, 2-2 000.80
yeUl •)00'/°- 58-4,16-1202’ !00~ 9 мм
(ближайшее стандартное сечение S = 10 мм2).
7*
99
Проверяем выбранное сечение на нагрев. Изолированный медный
провод сечением 10 мм2 допускает ток 68 а, а в нашем примере
1
Р2
и2
2 000
120
= 16,7 а,
т. е. значительно меньше допустимого.
3-8. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ
Прибор, который служит для измерения тока, называется а м-
перметром.
Если измеряемый ток меньше ампера, прибор называется мил-
лиамперметром; при измерении токов меньше 10-8 а —мик-
оамперметром или г а л ь -
Рис. 3-13. Тепловой амперметр.
ванометром.
Главной частью амперметра
является измерительный механизм.
Ток, проходя по измерительному
механизму, благодаря тепловым
или электромагнитным действиям
вызывает поворот стрелки изме-
Рис. 3-14. Включение шунта.
рительного механизма. Это позволяет на шкале прибора нанести
значения тока, соответствующие разным углам поворота стрелки, и,
таким образом, проградуировать прибор для измерения тока.
Для создания измерительного механизма можно, например, вос-
пользоваться тепловым действием тока. Главной частью теплового
механизма является платино-серебряная или платино-иридиевая
нить КК (рис. 3-13), которая удлиняется от нагревания при про-
хождении по ней тока. Удлинение нити преобразуется системой
оттяжек во вращательное движение соединенного со стрелкой блока,
который охватывается одной из этих оттяжек О. Поэтому каждому
значению измеряемого тока соответствует определенный угол пово-
рота стрелки прибора. По нити может проходить ток не свыше 0,5 а.
Jijwi измерения больших токов (/ > 0,5 а) механизм И шунтиру-
ется, т. е. параллельно нити присоединяется сопротивление посто-
янной величины (шунт), по которому и проходит большая часть
измеряемого тока (рис. 3-14). Другая часть тока /и проходит по
иити; эта часть тока ие должна превышать 0,5 а. Отношение
р=4- (3-33)
7И
100
называется шунтирующим множителем. Это число показы-
вает, во сколько раз расширится предел измерения тока, если при-
менить шунт.
Так как в соответствии с (3-16)
то, разделив обе части уравнения на I, находим:
1д __ 1_______гш
I ~~ Р ~ Гш + Ги ’
откуда
p = Zni±ri?_=i+_pl_. (3-34)
'Ш гш
Из этого уравнения определим сопротивление шунта в зависи-
мости от необходимого значения р. Из формулы (3-34)
откуда
гш — р । • (3-35)
Шунт обычно выполняется из проводников с малым температур-
ным коэффициентом сопротивления (манганин).
Амперметр включается в цепь последовательно с приемником
(рис. 3-15). Как правило, сопротивление амперметра должно быть
малым (доли ома) с тем, чтобы уменьшить падение напряжения
в амперметре и его мощность.
Прибор, служащий для измерения напряжения, называется
вольтметром. Измерительный механизм вольтметра такой же,
как у амперметра.
Для измерения напряжения между двумя точками цепи зажимы
вольтметра присоединяют непосредственно к этим точкам, так что
вольтметр оказывается включенным параллельно некоторой части
цепи (рис. 3-16).
В вольтметре (с целью экономии энергии) не допускаются зна-
чительные токи (более 0,1 а). Поэтому последовательно с механиз-
мом включают добавочное сопротивление гд. В этом
случае измеряемое напряжение распределяется между добавочным
сопротивлением и сопротивлением измерительного механизма га
(рис. 3-17). Отношение измеряемого напряжения U к напряжению
на измерительном механизме Uu называется множителем до-
бавочного сопротивления р. Таким образом,
U
P^U~. (3-36)
101
Так как через вольтметр и добавочное сопротивление проходит один
и тот же ток, то
JL = п = 2и_+гД = 1
Un ги га ’
откуда
Гд = гп(Р— !)• (3-37)
Иногда вольтметр имеет несколько добавочных сопротивлений,
так что получается многопредельный прибор на несколько номи-
нальных значений измеряемого напряжения, например 50 и 150 в.
Рис. 3-17. Включение
добавочного сопротив-
ления.
Рис. 3-15. Схема
включения ампер-
метра.
Рис. 3-16. Схе-
ма включения
вольтметра.
Необходимо заметить, что на практике для измерения постоян-
ных напряжений и токов применяют почти исключительно наиболее
точные приборы магнитоэлектрической системы. В этих приборах
поворот стрелки получается в результате действия магнитного поля
постоянного магнита на рамку с измеряемым током (см. § 5-27).
Пример 3-6, К измерительному механизму сопротивлением
ги = 0,27 ojk нужно присоединить шунт, чтобы увеличить предел
измерения в 10 раз. Определить сопротивление шунта.
Сопротивление шунта
г„ 0,27
гш р_____j jQ_____j 0,03 ом.
Пример 3-7. К измерительному механизму на 45 мв сопротив-
лением ги = 9 ом нужно присоединить добавочное сопротивление гд,
чтобы повысить предел измерения напряжения до 90 в. Опреде-
лить Гд.
Множитель добавочного сопротивления
р~ 0,045 ~ 2000,
Сопротивление
гд = ги (р — 1) = 9 (2 000—1)= 17 991 ом.
102
3-9. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ
Рассмотрим несколько способов измерения сопротивлений. Самый
простой способ —способ амперметра и вольтметра, показанный на
рис. 3-18. Искомое сопротивление определяется расчетом по формуле
Рис. 3-18. Измерение со-
противления методом
амперметра н вольт-
метра.
Рис. 3-19. Измерение со-
противления методом
амперметра и вольт-
метра.
г =-р , где U и I — показания приборов. Подсчитанная в этом
случае величина сопротивления не точно равна искомому, так как
вольтметр измеряет не только напряжение на концах сопротивления,
но и падение напряжения в ампер-
метре:
U^Ir + Ir^
откуда
U
г = — — га. 38)
При относительно малом со-
противлении амперметра (по срав-
нению с г) его величиной можно
пренебречь и полученный резуль-
тат считать искомым сопротивле-
нием
Неизвестное сопротивление
можно также измерять по схеме,
изображенной на рнс. 3-19.
U
В этом случае также г ~ -j- ,
Рис. 3-2U. Мост для измере-
ния сопротивлений.
но подсчитанная величина не точ-
но равна искомому сопротивлению, так как амперметр измеряет
не только ток, проходящий по сопротивлению, но и ток вольтметра /в;
поэтому точнее
U
г =
(3-39)
Если сопротивление вольтметра велико по сравнению с искомым,
то током, проходящим по вольтметру, можно пренебречь и полу-
ченный результат считать искомым сопротивлением.
103
Сопротивления часто измеряются при помощи моста (рис. 3-20).
Три известных сопротивления rt, г2, г и одно неизвестное гх
образуют замкнутый контур АБВГА. К точкам А и В присоеди-
няется первичный элемент или аккумулятор, а к точкам Б и Г—
гальванометр. При замкнутых кнопках и К2 в сопротивлениях
г2, гх и г проходят токи, которые соответственно обозначены
Л> ^21 Л и Л-
Изменением сопротивлений г, г1 и г2 добиваются равенства по-
тенциалов точек Б и Г: <Рб = <Рг. При этом ток в гальванометре
равен нулю, и Ц = = кроме того, при равенстве потенциалов
<Рв и (р^ равны и разности потенциалов —<рБ и — <рг, а также
Фб~<Рв и Фг— Фв или соответственно напряжения на сопротив-
лениях гх и гр а также г и г2;
1згх = Цг1, Iir = l2r2.
Разделив почленно последние уравнения и учитывая равенства
токов, получим:
гх _ Н
Г г2 ’
откуда
= (3-40)
3-10. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ МЕТОДОМ УЗЛОВЫХ
И КОНТУРНЫХ УРАВНЕНИЙ
Для расчета разветвленной сложной цепи, в которой
произвольно размещены сопротивления и источники пита-
ния, недостаточно применить закон Ома. В этом случае
расчетные уравнения, как указывалось выше, составляются
по первому (узловые уравнения) и второму (контурные
уравнения) правилам Кирхгофа.
Если заданы величины всех э. д. с. и сопротивлений,
то для вычисления всех токов по правилам Кирхгофа
нужно составить столько уравнений, сколько имеется
в цепи неизвестных токов. Однако число уравнений, кото-
рые можно составить по правилам Кирхгофа, всегда больше
числа неизвестных токов, т. е. часть этих уравнений являет-
ся следствием остальных. Для того чтобы расчетные урав-
нения были независимыми, нужно при их составлении
выполнить два условия:
1. Число узловых уравнений должно быть на единицу
меньше числа узловых точек электрической цепи. Напри-
мер, если цепь имеэт п узлов, то по первому правилу Кирх-
гофа нужно составить лишь (п — 1) уравнений, так как
104
уравнение для последнего n-го узла является следствием
уже составленных (п — 1) уравнений.
2. Недостающие уравнения составляются по второму
правилу Кирхгофа; при этом нужно выбирать наиболее
простые контуры (с меньшим числом источников э. д. с.
и сопротивлений) в таком порядке, чтобы в каждом но-
вом контуре содержалась по меньшей мере одна ветвь,
не входившая в контуры, для ко-
торых уже составлены уравнения.
На рис. 3-21 изображена раз-
ветвленная цепь с двумя источни-
ками. Требуется определить токи
в отдельных участках цепи. Вели-
чины и направления э. д. с. и со-
противления цепи заданы.
Прежде всего надо установить
направления токов, так как иначе
нельзя составить уравнения ни по
первому, ни (по второму правилам
Кирхгофа. Но у нас нет никаких
данных, позволяющих сделать ЭТОТ Рис 3.21 Разветвленная
выбор. Например, чтобы правиль- цепь.
но выбрать направление тока /5
(рис. 3-21), надо знать, какая из точек (Л или Б) обладает
более высоким потенциалом; ответить же на этот вопрос
можно лишь только после того, как найдено токораспре-
деление, т. е. все токи в цепи.
Эти затруднения отпадают, если считать ток алгебраи-
ческой величиной, которая может принимать как поло-
жительные, так и отрицательные значения, и выбрать
предварительно для каждого тока произвольное направле-
ние, которое называют положительным. Поло-
жительные направления указаны на рис. 3-21 стрелками.
Приписав току /5 положительное направление от Б кА,
мы еще ничего не утверждаем относительно того, какой
из двух потенциалов больше. Если в результате расчета
получим /5>0, то очевидно, что <рА<<рБ, но если полу-
чится /5<0, то <Рв<<Ра-
Приступая к расчету, мы вправе приписать токам любые
положительные направления. Если при расчете получится
отрицательное значение для какого-либо тока, то этот
ток в действительности протекает в направлении, противо-
положном выбранному и указанному на схеме стрелкой.
105
В рассматриваемой цепи три узловые точки (п = 3),
поэтому составим два узловых уравнения:
для узла А
—Л—Л + /s — О,'
для узла Б
— Г—1з—/5 — О-
Так как для расчета цепи нужно иметь пять неза-
висимых уравнений (пять неизвестных токов), то три
недостающих уравнения составляем, применяя второе
правило Кирхгофа.
Для контура АДГ А (порядок чередования букв опре-
деляет направление обхода контура, в данном случае—•
против направления движения часовой стрелки):
£”1 = Л (г01 + г1) hf4-
Для контура АГБА;
О = /4Г 4-/згз + 5*
Для контура БГВБ;
— Е%= /2 (гог + гг)
Мы могли бы написать еще несколько уравнений, напри-
мер для контуров АДГ ВБ А, АДГ Б А и АГ ВБ А. Эти урав-
нения уже не независимые, каждое из них легко получить
из ранее составленных уравнений (путем суммирования),
в чем и предлагаем убедиться читателю.
Иногда известны токи в отдельных ветвях, а неизвестны
некоторые э. д. с. Тогда для составления уравнений по пра-
вилам Кирхгофа нужно выбрать произвольно положи-
тельные направления этих э. д. с. Их действительные
направления выясняются в результате расчета.
Пример 3-8. Определить ток н мощность в каждом участке цепи,
изображенной на рис. 3-22, прн следующих данных: £'1=130 в;
Е%= 117 в; r01 = 1 ом; го2 = О>6 ом; г3=24 ом.
Задавшись положительными направлениями токов, составляем
три необходимых уравнения:
по первому правилу Кирхгофа для узла Б
Л +Д-Нз=°;
ио второму правилу Кирхгофа для контура АБГА
Ei—E2=1^01 — 1^02
106
и для контура БВГБ
^2— ^2r02— hr3-
Подставляя в последние уравнения численные значения изве-
стных величин, получаем:
130—117=1/!—0,6/2; 117 = 0,6/2 - 24/3.
Так как
^з= —Л—^2,
то
13 = 17j—0,672; И7=0,6/2+24/1 + 24/2
или
13= 1/j — 0,6/2; 117 = 2471+24,6/2,
Рис. 3-22. Схема к примеру 3-8.
откуда после исключения Ц получаем:
195= - 39/2
или
т. е ток /2 в действительности направлен обратно направлению
стрелки на схеме
Ток /4 определяем из уравнения /4— 0,6/2 = 13:
/4=13 + 0,6/2=13 — 3=10 а
и, наконец, ток
/3 = •— / j — /2 = — 10 + 5 = — 5
т. е. ток /3 в действительности направлен от точки Б к точке В
и <Рб> ТВ-
Мощность, развиваемая генератором,
Pt = ElIl= 130• 10-= 1 300 вт.
Мощность отдельных сопротивлений цепи
Р01 = /|г01= 100-1 = 100 вт; Ро2 = ^2/'о2=25-О,6= 15 вт;
Р3 = /|г3 = 25.24 = 600 вт.
107
Мощность, развиваемая вторым источником,
Р2 = £у2 = П7( —5)=—585 вт.
Этот источник э. д. с. является потребителем электрической
энергии, так как направления /2 и Т?2 противоположны.
Проверяем правильность решения задачи, составляя баланс мощ-
ностей, который является следствием закона сохранения энергии;
SPr = SP потр
или
Pi + Pi = Poi + Рог + Рз<
1 300-H—585)= 100+ 15 + 600.
Полученный баланс, однако, не отражает физической стороны про-
исходящего процесса, так как второй источник не отнесен к потре-
бителям электрической энергии. Поэтому перепишем уравнение
баланса так:
Pi = Poi + Р()2 + Рз + I Р2 I
или
1 300 em= 100+ 15+600 + 585= 1 300 вт.
3-11. МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ
В сложной цепи, имеющей всего два узла, токи можно
определить более простым методом, чем решением системы
А
Рис. 3-23. Сложная цепь
с двумя узлами.
Б
уравнений, составленных по пра-
вилам Кирхгофа.
На рис. 3-23 представлена
сложная цепь с двумя узлами.
Примем за положительное
направление токов во всех вет-
вях направление от узла Б к уз-
лу Л, т. е. предположим, что все
источники э. д. с. работают
в режиме генераторов.
Напряжение между узлами
А и Б (узловое напряжение)
обозначим U. Оно равно раз-
ности потенциалов этих двух
точек:
U = <Pa—фв-
По закону Ома ток в
первом участке [формула (2-35)]
^ = ^ = (^-[7)^.
(3-41)
В этом выражении г4—общее сопротивление первого
участка, включая внутреннее сопротивление генератора.
108
Аналогично для остальных участков цепи:
^2 ~ (^-2-Sz\ 1з = (Ез U) 8з'г
h~(0—U)gi=—Ugi.
По первому правилу Кирхгофа для узла А
Л + ^г + ^з+^4 — 0.
Подставив в это уравнение найденные выражения
токов, получим:
—И) gi + (Ег—U) §2 + (£з—U)gs + (—U) gt = 0.
Раскрыв скобки, найдем узловое напряжение:
у _ Ezg2-]-Езвз
£1Н~£2+£з + £4
или в общем виде
Н = (3-42)
Рис. 3-24. К приме-
ру 3-9.
т. е. «.узловое напряжение-» равно отношению алгебраической
суммы произведений э. д. с. на проводимости соответствую-
щих ветвей к сумме проводимостей всех ветвей, причем
если какая-либо э. д. с. направлена
от узла А к узлу Б, то в формулы
(3-41) и (3-42) она подставляется со
знаком минус.
Выражение (3-42) позволяет опре-
делить напряжение между узлами по
заданным значениям э. д. с. отдель-
ных генераторов и проводимостей
(пли сопротивлений) отдельных участ-
ков цепи (ветвей).
Подставив найденное узловое напряжение в уравнения
вида (3-41), легко определить токи в отдельных участках
цепи.
Пример 3-9. На рис. 3-24 представлена разветвленная цепь
с двумя узлами, причем £'1=113 в; Е2 = 112,5 в; г01 = 0,5 ом",
г02 = 0,5 ом', г =10 ом. Найти токи.
Вычисляем узловое напряжение:
11 — _ 113-2 + 112,5-2 __
gt + £г + +ч 2 + 24-0,1
10»
Токи в ветвях цепи:
/1 = (£'1-{/)£1 = (113-110)2 = 6 а’,
Л = (£2-О)й = (Н2,5-110)2 = 5 а;
/3=—t/g3= —110-0,1= —11 а.
Производим проверку решения:
Л 4~ ^2 + =~ ® + 5— 11 = 0.
3-12. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ГЕНЕРАТОРОВ
Пользуясь методом узлового напряжения, выясним
условия параллельной работы нескольких генераторов.
Потребители электрической энергии (освещение, сило-
вая нагрузка) в различное время суток имеют неодина-
ковую мощность. Ночью эта мощность минимальна, утром
постепенно увеличивается, достигая вечером наибольшего
значения. На электрической станции целесообразно иметь
несколько генераторов. При малой мощности работает
один генератор, с ростом мощности увеличивается число
работающих генераторов.
При параллельном соединении генераторов получается
цепь с двумя узлами, к которым присоединяются приемники
электрической энергии (рис. 3-23, где г — общее сопро-
тивление всех приемников). Применяя метод узлового
напряжения, определим ток в цепи каждого генератора:
Л = (£"1 U)St’ h — h — (E3 U) g3.
Одинаковые мощности и токи в цепи генераторов будут
при Ег = Е2 = Е3 = Е и gt = g2 = g3.
Обычно узловое напряжение U по величине очень
близко к значениям отдельных э. д. с., поэтому разность
Е — U составляет лишь несколько процентов от Е.
При таких условиях самое небольшое повышение какой-
либо из э. д. с. параллельно работающих генераторов (при
gi = gz = ga) приведет к тому, что ток этого генератора
окажется в несколько раз больше, чем у остальных. Напри-
мер, при э. д. с. генератора 122 в и узловом напряжении
120 в их разность Е — U = 2 в; если э. д. с. увеличится
на 1 в (меньше чем на 1%), т. е. достигнет значения 123 в,
то разность Е — U = 3 в возрастет на 50%. Ток генератора
также возрастает на 50%. Этим обстоятельством поль-
зуются, когда хотят «перевести нагрузку» с одного гене-
ратора на другой,
ПО
Генераторы окажутся также неодинаково загружен-
ными при равных э. д. с., но при различных внутренних
сопротивлениях. Более загруженным окажется генератор
с большей проводимостью, т. е. меньшим внутренним сопро-
тивлением.
При снижении э. д. с. генератора до величины узлового
напряжения (Е = U) ток в цепи генератора равен нулю:
I — (Е— U) g = 0, а следовательно, и мощность генератора
Р = EI = 0.
Генератор, находящийся в таком режиме, называется
уравновешенным (скомпенсированным). Если э. д. с. станет
меньше узлового напряжения, то ток изменит направле-
ние — он будет направлен навстречу э. д. с. В этом случае
генератор начнет работать в режиме потребителя энергии
(электродвигателем).
Пример 3-10. Два генератора Е1 = Е2=122 в; г01 = г02~0,5 ом
присоединены к сети параллельно. Сопротивление приемника энер-
гии г = 5,85 ом.
1. Определить мощность, развиваемую каждым генератором.
Проводимости участков цепи;
pt = —= 2сим; g2 = ^— — 2 сим; g = — = 0,171 сим.
+1 г02 г
Узловое напряжение
Ij__£1Е1_+_^2£2 _ 2' 122-2 _
Е1 + Е2+Е 2-|-24-0,171
Токи генераторов:
= — U)gi=10 a; J2 = (E2 — U) g2=l0 а.
Мощности, развиваемые генераторами:
Р1 = Е1/1= 1 220 вт; Р2 — Е212=\ЧЧЗвт.
2. Определить мощность, развиваемую каждым генератором,
если э. д. с. первого генератора увеличить до 126 в.
Узловое напряжение
,, 126-2+122-2
и= ~+Г71—=119 е’
Токи генераторов:
J^l^Ei — U) gi= 14 a; I2=(E2 — U)g2 = 6a.
Мощности генераторов:
Р1 = Е1/1=1764 вт; P2 = E2J2 = 732 вт.
3. Определить, до какой величины нужно повысить э. д. с.
первого генератора, чтобы второй генератор оказался совершенно
разгруженным, т, е. чтобы /2= (E2—U) 8z~ 0-
111
Очевидно, это возможно, если £2—U = 0, т. е. E2=U; следо-
вательно,
Eigi + E2g2
gt+gz+g 2’
откуда
g)==£l(gL±g>=!22.<2 + Q^0 = 132,5 о.
1 gi 2
3-13. ПРИНЦИП НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)
Возможность расчета электрических цепей по прин-
ципу наложения вытекает из того, что ток в любом участке
цепи равен алгебраической сумме частичных токов, созда-
ваемых в этом участке от всех э. д. с. цепи, действующих
отдельно друг от друга.
Вначале полагаем, что в цепи действует только одна
какая-либо э. д. с., причем все сопротивления цепи остаются
неизменными (включая внутренние сопротивления источ-
ников, даже и тех, гдеэ. д. с. приравниваются нулю). Для
такой схемы находим токораспределение. Затем повторяем
расчет, полагая, что действует вторая э. д. с., а все осталь-
ные не действуют. Аналогичные расчеты производим пооче-
редно для всех э. д. с.
Пусть ток в каком-нибудь участке равен I. По принципу
наложения
/ = (3-43)
где Г — ток, созданный в рассматриваемом участке дей-
ствием первой э. д. с. в предположении, что остальные
э. д. с. равны нулю. Аналогичное значение имеют состав-
ляющие I" и Г’" и т. д. Суммирование составляющих тока
производится с учетом их направления.
Заметим, что ток в любой ветви может быть представлен
не обязательно суммой частичных токов от всех э. д. с.,
действующих по очереди. По принципу наложения ток
можно представить и как сумму частичных токов, каждый
из которых создается группой э. д.. с. Например, можно
разбить все э. д. с. цепи на две группы, тогда I = Г I”,
причем Г — ток от первой группы э. д. с., а I “ — от второй
группы э. д. с.
Пример 3-11. Определить токи в отдельных участках цепи,
изображенной на рис. 3-25, а, если El—126 в; Е2~124 в; rt==l ом;
r2 — 1 ом; г3~ 12 ом.
112
Полагая
находим:
э. д. с. второго генератора недействующей (рис. 3-25, б),
= 65,52.-11- = 6°,48 а-,
г2~г r3 1 +
/'=/; = 65,52
'з+'з
ЕП2 =5’04 -
Полагая э. д. с. первого генератора недействующей (рИС< 3-25, в),
находим:
124
4тг2_=64-48
1 + 12
Л = /2-^-=64,48-т^Тп=59,52 а;
г1 + г3 1+12
^2
У 2---------------
г flf3
=64,48•
4,96 а.
Производим наложение токов:
/i==/i—z;==65,52 — 59,52 = 6 а\
— — а',
/3=—5,04—4,96=—10 а.
3-14. МЕТОД ХОЛОСТОГО ХОДА И КОРОТКОГО
ЗАМЫКАНИЯ (МЕТОД ЭКВИВАЛЕНТНОГО
ГЕНЕРАТОРА)
Вычисление тока в одном произвольно выбранном участ-
ке сложной электрической цепи можно выполнить методом
холостого хода и короткого замыкания. Этот метод часто
8 Теоретическая электротехника 113
сокращает громоздкие вычисления, например решение
системы уравнений со многими неизвестными.
Пусть дана произвольная электрическая цепь, содержа-
щая любое количество ветвей, соединенных каким угодно
образом. Определим ток I в одном из участков цепи, сопро-
тивление которого обозначим г. Для этого прежде всего
разобьем цепь на две части: на сопротивление г и на часть
цепи, остающуюся после отключения от нее сопротивле-
ния г. Эту вторую часть изобразим прямоугольником
с двумя зажимами (рис. 3-26) и назовем
двухполюсником. Ясно, что внут-
ри двухполюсника находится по меньшей
мере один источник э. д. с. Такой двухпо-
люсник называется активным.
Если последовательно к сопротивле-
нию г добавить еще два источника э. д. с.,
+
Лбут-
полюс-
ник
Рис 3-26 Двух-
полюсник и вы-
деленный уча-
сток цепи с со-
противлением г.
присоединив их так, как показано на
рис. 3-27, то величина тока в сопротив-
лении г не изменится: добавочные э. д. с.
равны по величине и направлены навстре-
чу друг другу, внутренние сопротивления
источников равны нулю.
В соответствии с принципом наложения, ток в сопро-
тивлении
7 = 7 —7О4~7О,
где суммируются три тока: I — ток в сопротивлении под
действием источников, находящихся в двухполюснике,
—70 — ток в сопротивлении под действием только э. д. с.,
обозначенной на схеме — Ео (этот ток имеет знак минус,
так как э. д. с.— Ео направлена навстречу току 7), и 10 —
ток в сопротивлении при действии одной э. д. с. +Е0.
Электродвижущую силу Ео, а следовательно, и вызы-
ваемый ею ток /0 можно выбрать различной величины.
Выберем ее так, чтобы выполнялось условие
1 — 7о = О или 1 = 10. (3-44)
Токораспределение в цепи рассмотрим как результат нало-
жения двух режимов: во-первых, режима, обусловленного
всеми э. д. с., кроме обозначенной на схеме +Е0> и, во-вто-
рых, режима, создаваемого э. д. с. +Е0, т. е. примем I —
= Г +1", где Г = I -Io; I" = 10.
114
(3-45)
Первому режиму соответствует ток в сопротивлении,
равный нулю [формула (3-44)]. Второму режиму (рис. 3-28,а)
при действии только э. д. с. +Е0 соответствует ток
} _ Е0
0 г + г0 ’
поэтому на основании (3-44) и
г + го
здесь г0—общее сопротивление двухполюсника, величина
которого нам неизвестна.
Неизвестной является также и величина Ео.
Выражения вида (3-45) нам встречались неоднократно.
Это, например, выражение тока в неразветвленной цепи,
Рис. 3-27. Вклю-
чение двух до-
полнительных
источников.
а) <0
Рис. 3-28 Схема при действии
одного источника э д с., равно-
значная схеме на рис. 3-26.
содержащей источник питания с э. д. с. Ео и внутренним
сопротивлением г0 и сопротивление приемника г. Таким
образом, мы приходим к весьма важному выводу, что
всякий активный двухполюсник может быть заменен источ-
ником с э. д. с. Ео и сопротивлением г0 (рис. 3-28, б). Схемы
рис. 3-26 и 3-28 эквивалентны, так как в интересующем нас
участке цепи с сопротивлением г протекает в обоих слу-
чаях ток I.
Для вычисления тока в отдельном сопротивлении цепи
г необходимо знать э. д. с. и внутреннее сопротивление
двухполюсника.
Величины Ео и г0 проще всего определяются опытным
путем. Если под действием э. д. с. двухполюсника и допол-
нительной э. д. с. —Ео ток в сопротивлении г равен нулю,
8* 115
то это равносильно разрыву внешней цепи двухполюсника.
Тогда отсутствует внутреннее падение напряжения и напря-
жение на зажимах двухполюсника равно э. д. с. Ео. Опыт-
ным путем эту э. д. с., т. е. напряжение на зажимах при
отключении внешней цепи, можно измерить вольтметром
на зажимах двухполюсника при отключении от него сопро-
тивления г, т. е. при холостом ходе (рис. 3-29, а).
Что касается сопротивления г0, то, как следует из фор-
мулы (3-45), оно может быть найдено путем измерения
двух-
полюс-
ник
двух-
полюс-
ник
Рис. 3-29. Опыты холостого хода и ко-
роткого замыкания.
тока короткого замыкания двухполюсника /к= —. Если
го
зажимы двухполюсника замкнуть через амперметр с ничтож-
ным сопротивлением по сравнению с г0> то амперметр
покажет ток Е01г0, откуда и найдется искомое сопротивле-
ние (рис. 3-29, б).
Электродвижущая сила двухполюсника Ео (напряже-
ние холостого хода) и сопротивление г0 могут быть найдены
также расчетом. Для определения Ео нужно принять
г = со и найти напряжение между точками, к которым
присоединено сопротивление г (зажимы «+» и «—» на
рис. 3-28, б). Для определения г0 нужно предположить,
что все э. д. с. в цепи двухполюсника равны нулю, и при
отключенном сопротивлении г определить общее сопро-
тивление относительно зажимов двухполюсника (зажимов
«+» и «—» на рис. 3-28, б).
Пример 3-12. Определить ток в сопротивлении г=14 ом
(рис. 3-30, а), если г±= 10 ом; г2 = 2,5 ом; г3=5 ом; г4 = 20 ом и
£=12,5 в.
Вначале определим напряжение между точками АБ при отклю-
ченном г (рис. 3-30, б). В этом случае сопротивления г4 и г2 соеди-
116
йены последовательно, ток в этой ветви
Е __ 12,5
-П + г2~ 10+2,5 -1 а'
Аналогично ток в сопротивлениях г3 и
„ Е 12,5 п_
Г3+Г4 5 + 20
Напряжение между точками АБ (или разность потенциалов
Фа~Фв) найдем, приняв потенциал точки В равным нулю(<рв = 0);
Рис. 3-30. К примеру 3-12.
Фв — Фд=/'Г1= !• 10= 10 в, или Фа ——Ю в; <рв — Фт5 = /'Т3 =
= 0,5-5 = 2,5 в, или q>jg=—2,5 в;
Фа — фв = £о——10+2,5=—7,5 в.
Теперь определим го двухполюсника. Для этого предположим,
что э. д. с. Е равна нулю и, следовательно, точки В и Г замкнуты
(внутреннее сопротивление источника принято равным нулю). Сопро-
тивление относительно точек А и Б (рис. 3-30, в)
. 'Т'г . г3г4 10-2,5 5-20 ._6
+ W2T + 5 + 20 -2 + 4-6
Ток в сопротивлении г
1 =
Е0
г + г0
— 7,5
14 + 6
-0,375
а,
т. е. в действительности ток направлен не так, как указано стрелкой
на рис. 3-30, а.
3-15. МЕТОД ПРЕОБРАЗОВАНИЯ
При расчетах электрических цепей часто прибегают
к равнозначным или эквивалентным преобразованиям g
целью упростить схему цепи и, следовательно, ее расчет.
UJ
Мы встречались с подобными преобразованиями при после-
довательных, параллельных и смешанных соединениях
сопротивлений. В электрических цепях нередко встречают-
ся соединения, получившие названия соединение тре-
угольником и соединение звездой.
Контур, состоящий из трех сопротивлений и имеющий
три узловые точки А, Б и В, образует схему, кото-
Рис. 3-31. Соединение со-
противлений треугольником.
Рис. 3-32. Соединение со-
противлений звездой.
рую принято называть треугольником сопротивлений
(рис. 3-31).
В некоторых случаях расчет цепи значительно упро-
щается, если треугольник сопротивлений заменить схемой
из трех сопротивлений, сходящихся в одной точке (име-
ющих один общий узел), т. е. соединенных звездой
(рис. 3-32).
В других цепях расчет упрощается, если сопротивле-
ния, соединенные звездой, заменить сопротивлениями,
соединенными треугольником. И в том и в другом случаях
замена должна производиться так, чтобы при неизменных
напряжениях между вершинами А, Б и В треугольника
и звезды токи IА, 1Б, Iв в проводах, соединяющих эти
вершины с остальной частью схемы, остались без изменения.
Треугольник и звезда, которые удовлетворяют этому
условию, называются равнозначными (эквивалентными).
Для вывода формул, связывающих сопротивления тре-
угольника гАБ, гБВ и гВА с сопротивлениями гА, гБ и гв
равнозначной звезды, воспользуемся уже известным нам
118
принципом наложения, но применим его не к э. д. с.,
а к токам.
Приравняв нулю ток 1А,найдем сопротивления между
точками Б и В обеих схем; в этом случае сопротивления
гАБ и г ва соединены последовательно, а сопротивление
гбв — параллельно суммарному сопротивлению гАБ -)-
+ г ва', последовательно соединены и сопротивления гБ
и г в. Поэтому
гп + гв= ;БВ^Б+,?-Ак- (3-46)
гав + гбв + гва
Приравняв нулю ток /Б, а затем и ток 1В, получаем
аналогичные соотношения:
г в+rA = ; <3’47>
Г АБ~Г ГБВ~Г ГВА
r | г г АБ (f ВА~У гБв) /Q
Пусть нам требуется преобразовать треугольник в
звезду, т. е. сопротивления гЛВ, гбв и гва заданы, а
сопротивления гА, гБ и гв нужно определить. Составим
полусумму левых и правых частей уравнений (3-47)
и (3-48):
] г АБГ ВА~\~ ~2~ г Б В (Габ + Гва)
Га + -о- (Гб + Г в) —--------—---у.----------
ГАБ^~ГБВ+ГВА
и из полученного результата вычтем уменьшенные левую и правую части уравнения (3-46). Это дает: вдвое (3-49)
Га = ГАБГВА
габ + гбв+ г ва ’
после чего уже легко получить:
Гб = гбвГаб (3-50)
габ + гбв + г ва
ГВАГБВ (3-51)
' в габ + гбв + г ва
Если же искомыми являются сопротивления треуголь-
ника (звезда преобразуется в треугольник), то из тех же
формул (3-46)—(3-48) следует, что
габ=га+гб + -^-; (3-52)
г в
119
=05-Ив+
гвгв
га
(3-53)
г ba —г вА~г а~\—. (3-54)
В правильности этого результата читатель может убе-
диться сам.
Пример 3-13. Вычислить токи в отдельных участках схемы мос-
та для измерения сопротивлений, представленного на рис. 3-33,
Рис. 3-33. Схема к приме-
ру 3-13.
Для этого находим:
_ rtr2 _______________________ 10-30
ГА~ о + 'в+'з ~ 100
при следующих данных: £ = 2,2 в;
0=10 ом; г2=30 ом; г3 = 60 сии;
0 = 4 ом и г5 = 22 ом.
В этой схеме мы можем заменить
одни из треугольников АБГ или ВБГ
звездой. Такая замена значительно
упростит схему. Заменим, например,
треугольник АБГ, стороны которого
образуются сопротивлениями о, г2 и
гз, звездой, сопротивления лучей
которой обозначим гд, гв и гг
(рис. 3-34).
Вместо сложной цепи, для рас-
чета которой нужно было бы со-
ставить шесть уравнений по прави-
лам Кирхгофа, мы получили схему
с простым смешанным соединением
сопротивлений. В новой цепи легко
определяются токи I, /4 и Z5.
ом;
гг =
Уз
Г1А-г2А-гз
60-10 _
100 ~
30-60
100
ом;
= 18 ом.
Б
_ r3ri
В ч + гг+гз
Общее сопротивление всей цепи
г = г , (гв + г^гг+гд __, , (6 + 4) (18+22) _
А г б + ^ 4 + г г + г5 6+4+18 + 22
сии.
Ток в неразветвленной части
£ _ 2,2
~ г ~ 11
= 0,2 а.
Токи в параллельных ветвях:
/4 = /-Г5 +--------= 0,2- fi 99 =0’16 а’
гб + г^ + гг+гь 6+4+18 + 22
/ = / ГД + Г* -----= 0,2- -. 6+* = 0,04 а.
rs + ri,+ rr+r6 6 + 4+18+22
120
Для вычисления остальных токов необходимо предварительно найти
одно из напряжений между вершинами полученной звезды. Так как
^бв = Фб — срв = Л^ = °>16'4 = °’64 е‘-
Uгв = Фр - Фв = Л/5 = °>04-22 = °’88 в>
то, принимая потенциал точки В равным нулю (срв = О), получим:
^бв = Фб1 ^гв = Ч)Г'
и напряжение между вершинами Г и Б:
^ББ = Фр — Фб — г в — Uвв~ ^>88 — 0,64 = 0,24 в.
Рис. 3-34. Преобразованная схема к при-
меру 3-13.
Теперь, возвращаясь к первоначальной схеме (рис. 3-33), вычис-
лим токи в оставшихся участках:
/з = "7~ = -^§—-=0,004 а; /2=/3 + Д = 0,044 а;
/1 = /4 — /3 = 0,156 а.
3-16. ЧЕТЫРЕХПОЛЮСНИК
Часть электрической цепи, имеющая две пары зажимов
(рис. 3-35), называется четырехполюсником.
К одной паре зажимов—входных (/'-—/") при-
соединяется источник питания, а к другой паре — в ы-
ходных (2*—2") присоединяется потребитель.
Если внутри четырехполюсника нет источников, то
его принято называть пассивным. Простейшими пас-
сивными четырехполюсниками являются двухпроводная
линия рис. 3-36, где г — сопротивление одного провода,
121
и рис. 3-37, где учтено сопротивление изоляции гиз между
проводами, трехконтактный реостат, используемый в ка-
честве делителя напряжения (рис. 3-38), и т. д.
В электротехнике с четырехполюсником особенно часто
приходится встречаться в цепях переменного тока. К четы-
Рис. 3-36. Схема соеди-
нения генератора с по-
требителем энергии.
Рис. 3-35. Четырехполюсник.
рехполюсникам относятся трансформаторы для преобра-
зования тока одного напряжения в ток другого напряже-
ния, фильтры для пропускания токов одних частот и за-
держивания токов других частот, кабели, соединяющие
Рис. 3-37. Схема соединения ге-
нератора с потребителем энергии.
Рис. 3-38. Схема соединения
генератора с потребителем
энергии.
аппаратуру, например телевизионные антенны с телеви-
зорами, и многие другие приборы. Все эти устройства
будут подробно рассмотрены в следующих главах.
Напряжение, создаваемое источником энергии между
входными зажимами четырехполюсника (/'—/"), назы-
вается входным напряжением и обозначается
Ui. Ток, который проходит от источника через входные
зажимы четырехполюсника, называется входным то-
коми обозначается Ц. Отношением входного напряже-
122
ния к входному току определяется входное сопро-
тивление четырехполюсника
Напряжение между выходными зажимами четырехпо-
люсника (2'—2") называется выходным напряже-
ние м и обозначается U2. Ток, который проходит через
выходные зажимы к потребителю, присоединенному к этим
Рис. 3-39. Т-образная схема за-
мещения четырехполюсника.
Рис. 3-40. П-образная схема
замещения четырехполюс-
ника.
зажимам, называется выходным током и обозна-
чается /2. Сопротивление потребителя
Между входным напряжением Ut, входным током
и выходным напряжением Uz и выходным током /2 четы-
рехполюсника получаются линейные зависимости, выра-
жаемые уравнениями четырехполюсни-
к а.
Любой пассивный четырехполюсник, сопротивления ко-
торого постоянны, можно при помощи эквивалентных
преобразований привести к трем сопротивлениям, соеди-
ненным звездой (Т-образная схема замещения, рис. 3-39)
или треугольником (П-образная схема замещения,
рис. 3-40).
Для вывода уравнений четырехполюсника восполь-
зуемся одной из схем замещения.
При Т-образной схеме, в которой три сопротивления
соединены звездой (рис. 3-39), входной ток
Л = /2+ = ^ + (^2 + hri)y~~ + Л ("1 + ;
'0 го \ 'о /
123
входное напряжение
^1 = ^/1 + hrz + ^2~ Е 5^ + (j гоО ^2-5 Г1^~
+ Лг2 + ^2= (^ 1 + уА^) ^2 + (Г1 Ч-^гН—^2‘
Обозначив для сокращения записи
Л=1+ —; В = Г1 + г2 + ^-; С = — ]
го 12' гй ' г0
и > (3-55)
О=1+^, ]
'О >
получим искомые уравнения четырехполюс-
ника:
U1 = AU2+BI2-> 1
Il — CU2~\~ D12,- J
(3-56)
При П-образной схеме с тремя сопротивлениями, со-
единенными треугольником (рис. 3-40),
S- — г 0 ^2 + + ^2—(^1 ~1~ уг') ^2 Г»/2 — Л^2 + ^2»
ji=^ + ^ + } < ±+± + 2Л_Л[/ +
1 Н '2 2 4'1'2 'Л) 2
+ ^1 4~т0 = CU2
и обозначив
А = 1+^; В=г0;
г2
С
± + ± + _Г»_
'1 г2 Г1Г2
D=
получим опять уравнения (3-56).
Поскольку четырехполюсник, состоящий из произ-
вольного числа сопротивлений, можно заменить эквива-
лентной Т- или П-образной схемой, то найденные зависи-
мости между UiJi, U 2 и /2 наиболее общие, т. е. справедли-
вы для любого пассивного четырехполюсника.
124
3-17. ПОСТОЯННЫЕ ЧЕТЫРЕХПОЛЮСНИКА
Величины А, В, С и D называются постоянными
четырехполюсника. Постоянные четырехполюс-
ника А и D — отвлеченные числа, В имеет размерность со-
противления, а С — проводимости. Постоянные четырех-
полюсника взаимосвязаны уравнением
AD—ВС=\. (3-57)
Получим это уравнение для Т-образной схемы. Про-
изведение
AD= (1 + ^\+^^г1+ГоГ2±г^ + г^==
] I г0г2 + г0г1Ч- г1г2
'О ’
а произведение
QQ = JL Лнго + ',2',о+н',2> _ +
Го Ч г0 у г§ ’
откуда
AD—ВС = 1.
Поменяем местами источник питания и потребитель,
т. е. подведем напряжение U2 к зажимам 2"—2", которые
станут входными, а к зажимам Г—1" присоединим то же
самое сопротивление г. Тогда, как можно показать, урав-
нения четырехполюсника примут вид (при обратных направ-
лениях токов):
V^DU^ ВЦ-
Ц = C(jt АЦ.
(3-58)
Сравнивая последние уравнения с уравнениями (3-56),
можно заметить, что постоянные А и D поменялись местами.
Четырехполюсник называется симметричным,
если при перемене мест источника питания и потребителя
входные и выходные напряжения и токи не изменяются.
Для этого у симметричного четырехполюсника должна
существовать дополнительная связь между постоянными.
A = D,
так как при А = D уравнения четырехполюсника одина-
ковы при взаимной замене источника питания и потре-
бителя.
125
3-18. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ
ЧЕТЫРЕХПОЛЮСНИКА
Обозначим напряжение между зажимами /'—1" при
холостом ходе, т. е. разомкнутых выходных зажимах,
Uix, а входной ток /1х (рис. 3-41). Уравнения четырех-
Рис. 3-41. Схема опыта холостого
хода четырехполюсника при пита-
нии со стороны зажимов 1'—1".
Рис. 3-42. Короткое замыкание че-
тырехполюсника при питании со
стороны зажимов /'—Г'.
Поменяв местами источник
во внимание, что постоянные А
полюсника при холостом
ходе (/2 = 0):
Uix = AU2 + BI2 = AU2,
iix = cu2a-di2=cu2.
При коротком замы-
кании (зажимы 2'—2"
замкнуты накоротко,
рис. 3-42) уравнения
четырехполюсника при-
нимают вид (t/2 = 0):
U tn = AU2 BI2 — Bl2,
/1к = CU2-|- D I2 = DI2.
Эти два опыта при
питании со стороны за-
жимов Г—/"дают воз-
можность записать, что
__ А , Цц; _ В_
Лх С ’ Iц; D
(3-59)
и потребитель и приняв
и D меняются местами,
получим два дополнительных соотношения из уравне-
ний (3-58):
Uzx _ D . Угк _
Лх С 12к А
(3-60)
Выбирая любые три из составленных зависимостей (чет-
вертое является следствием трех других) и учитывая из-
вестное соотношение AD—ВС=1, можно опытным путем
или расчетом определить постоянные четырехполюсника А,
В, С и D.
Например,
^1х 1 и ^2х ( ^1х UIX \ 1
Лх Лк CD /2х \ Лх Лк / С2
126
о ткуда
С = 1 . (3-61)
. / ^2х Л Ujx Л
’ 1?х \ Лх Лк /
После того как найдена постоянная С, легко находятся:
Я = С-^; D = C~-; B = D~- . (3-62)
‘ix ‘2х '1к
По полученным значениям А, В, С и D определяются,
например [при помощи формул (3-55)], параметры Т-образ-
ной схемы замещения:
го= с-;/•1=—с~;/'2=—с—• (3-63)
3-19. ИСПЫТАНИЕ ЧЕТЫРЕХПОЛЮСНИКА
При проведении испытаний четырехполюсников, напри-
мер определении напряжения и тока на входе четырех-
полюсника и Ц при заданном режиме работы приемника,
Рис. 3-43. Схема опыта холостого хода
при испытании четырехполюсника.
т. е. при заданных U2 и /2, может потребоваться очень
мощный источник питания (при большой мощности на вы-
ходе Р2 = UZ/2).
Затруднения отпадают, если испытание проводится
в режимах холостого хода и короткого
замыкания. В этих режимах мощность на выходе
практически равна нулю (равна только мощности измери-
тельных приборов), а мощность источника определяется
потерями в четырехполюснике.
В режиме холостого хода (рис. 3-43) напряжение между
зажимами 2'—2" должно иметь заданную величину U2,
что устанавливается по вольтметру V2. Для этого регу-
127
лирующими устройствами во входной цепи подбирается
напряжение на входе f7lx.
В режиме короткого замыкания напряжение на входе
Um должно иметь такую величину, чтобы ток в выходном
Рис. 3-44. Схема опыта короткого замы-
кания при испытании четырехполюсника.
контуре имел заданную величину /2 (рис. 3-44), что уста-
навливается регулирующими устройствами по амперметру
А2.
Напряжение на входе в режиме холостого хода (/2 =
= 0)
t/ix = /lt/2. (3-64)
Ток во входном контуре
Jtx = CU2. (3-65)
Напряжение на входе в режиме короткого замыкания
([/2 = 0)
UiK = B/2. (3-66)
Ток во входном контуре
/iK = D/2. (3-67)
Таким образом, из опытов холостого хода и короткого
замыкания
Ul = AU2 + BI2 = Ulx + UiK; (3-68)
Л = С^2 + Д/2 = /1х + /1к, (3-69)
т. е. и при заданном режиме работы приемника
(напряжении U2 и токе /2 и тем самым заданном сопро-
тивлении приемника г = П2//2) определяются путем нало-
жения режимов работы при холостом ходе и коротком
замыкании четырехполюсника.
128
Пример 3-14. Определить напряжение иа входе 0\ и ток во вход-
ном контуре /( четырехполюсника, если при заданных величинах
Uz^ 120 в и /2 = 2 а при холостом ходе П1Х = 375 в, /(х 10 а,
а при коротком замыкании tZiK = 25 в, /1к=190 а.
Сравнить мощность источника в этих режимах с мощностью,
которио должен развивать источник при испытании четырехполюс-
ника в рабочем режиме.
Напряжение н ток на входе
i71 = t/lx4-£71K = 3754-25 = 400 в;
fi = /|x-l-/iK=104 190 = 200 а.
Мощность, которую развивает источник, питающий схему, при
опыте холостого хода
7’Х = (/1Х/1Х 375-10 = 3750 вт =3,75 кет;
при опыте короткого замыкания
Рк ~^1кЛк — 25-190 = 4750 вщ = 4,75 кет.
Мощность, которую должен развить источник, если бы четырех-
полюсник испытывался при рабочем режиме,
= £/!/! = 400-200 =80-103 em-80 кет.
3-20. ЛАБОРАТОРНАЯ РАБОТА. ИССЛЕДОВАНИЕ
ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ПРОВОДЯЩЕЙ СРЕДЕ
1. Ознакомиться с приборами, необходимыми для выполнения
работы. Записать основные технические данные источника питания,
реостатов и измерительных
приборов.
2. Собрать схему
(рис. 3-45) и показать ее ру-
ководителю.
3. Включив рубильник,
реостатом установить в цепи
ток 15 — 20 а. Пользуясь
щупом, нанести мелом на
поверхности исследуемого
листа линии равного потен-
циала.
Для нанесения линий
равного потенциала одни
зажим гальванометра Г при-
соединяется к какой-либо
точке листа, а другой зажим
соединяется с латунным щу-
пом Щ. Острие щупа пере-
мещается по поверхности
листа и отмечаются точки, в
которых показания гальвано-
метра остаются неизменными.
9 Теоретическая электротехника
129
Убедиться в том, что линии равного потенциала направлены
перпендикулярно к краям листа. Между соседними линиями равного
потенциала выбрать одинаковые напряжения.
4. Перерисовать нанесенные линии равного потенциала на мил-
лиметровку, выбрав удобный масштаб.
5. Построить на бумаге линии тока. Линии тока должны пере-
секать линии равного потенциала под прямыми углами. В результа-
те нанесения линий равного потенциала и линий тока образуется
сетка. Линии тока надо проводить так часто, чтобы все ячейки
этой сетки имели одинаковое отношение средней длины в направле-
нии линий тока к средней ширине в направлении линий равного
потенциала. Целесообразно получить ячейки со средней длиной,
равной средней ширине.
Примерный вид линий тока и линий равного потенциала для
одной четвертой части листа показан на рис. 3-45.
6. Аналогичные измерения и построения выполнить для сталь-
ных листов разной формы.
3-21. ЛАБОРАТОРНАЯ РАБОТА. ИЗМЕРЕНИЕ
УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДОВ (§ 2-7)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, записать основные технические данные источника питания,
Рис. 3-46. Схема для измере-
ния удельного сопротивления
проводов.
реостата и измерительных приборов.
2. Собрать схему (рис. 3-46) и
показать ее руководителю.
3. Измерив ток и напряжение
на участке провода длиной /, оп-
ределить сопротивление провода
4. Повторить опыт при том же
токе для двух-трех участков дру-
гой длины. В каждом случае из-
мерить длину I и диаметр D про-
вода.
5. Повторить опыты для двух
других проводов.
130
6. По полученным данным определить удельное сопротивление
каждого провода. Показания приборов и результаты расчетов запи-
сать в табл. 3-1. По удельному сопротивлению определить материалы
проводов.
3-22. ЛАБОРАТОРНАЯ РАБОТА. ИЗМЕРЕНИЕ
ПОТЕНЦИАЛОВ ТОЧЕК ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
(§ 2-16)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать основные технические данные источников пита-
ния, магазинов сопротивления и измерительных приборов.
2. Измерить вольтметром э. д. с. каждого источника питания.
Рис. 3-47. Схема к работе
3-22.
Рис. 3-48. Схема к работе
3-22.
Рис. 3-49. Схема к рабо-
те 3-22.
3. Собрать схему (рис. 3-47) и после проверки ее руководите-
лем Измерить вольтметром потенциалы точек А, Б, В и Г и напря-
жение 0Бв (при замкнутом рубиль-
нике).
4. Собрать схему (рис. 3-48) и после
проверки ее руководителем измерить по-
тенциалы течек А, Б, В и Г и напря-
жение иБв (при замкнутом рубильнике).
5. Собрать схему (рис. 3-49) и после
проверки ее руководителем измерить по-
тенциалы точек А, Б, В и Г и напря-
жение иБв (при замкнутом рубиль-
нике).
6. Имея в виду, что >4 = 30 ом.
г2=60 ом и г3 = 90 ом, и зная э. д. с.
Ei и Е2, определить расчетом для каж-
дого случая <рА, фв, фВ, и UBB.
7. Показания приборов и результаты
расчетов записать в табл. 3-2.
8. Для каждого случая построить в масштабе по опытным дан-
ным потенциальную диаграмму контура АБВГДА.
9* 131
Таблица 3-2
Продолжение табл 3-2
3-23. ЛАБОРАТОРНАЯ РАБОТА. ИССЛЕДОВАНИЕ
ПРОЦЕССА НАГРЕВАНИЯ КАТУШКИ ЭЛЕКТРИЧЕСКИМ
ТОКОМ (§ 2-4, 2-8 и 2-13)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать технические данные измерительных приборов
и вспомогательной аппаратуры
Рис. 3-50. Схема для градуирования
термопары
2 Собрать схему для градуирования термопары с гальваномет-
ром и показать ее руководителю (рис. 3-50).
3. При различных значениях температуры записать в табл. 3-3
показания термометра и гальванометра.
132
Таблица 3-3
п,
делений
0.
град
4 По полученным данным построить градуировочную кривую
" 7(0),
где п — число делений по шкале гальванометра;
0 — температура.
5. Для исследования процесса нагревания катушки собрать
схему (рис. 3-51) и показать ее руководителю.
6. Замкнув рубильник, записывать показания приборов через
каждые 5 мин в течение 45 мин. Первое показание записать сразу
Рис 3-51 Схема к работе 3-23.
после замыкания рубильника. По полученным данным определить
температуру' катушки 0 в различные моменты времени. Температуру
определить двумя способами—по показанию гальванометра и по
формуле
0 10.,.
аг0
где 0П — температура катушки сразу после замыкания рубильника;
г0 —сопротивление катушки при температуре 0О;
г — сопротивление катушки при температуре 0;
а—температурный коэффициент сопротивления (меди).
Показания приборов и результаты расчета записать в табл. 3-4.
7. По полученным данным построить график зависимости темпе-
ратуры от времени:
0(0.
8. Выяснить, больше или меньше номинального тока тот
ток Л который проходит по катушке (предельная температура на-
грева катушки составляет 80' С).
133
Таблица 3-4
1 uju w 1 /, а U, в Г, ом t, мин П, деле- ний в, град Примеча- ние
1-й способ 2-й способ
9. Если I > /н, то определить, в течение какого времени можно
допустить прохождение этого тока по катушке?
3-24. ЛАБОРАТОРНАЯ РАБОТА. ПОСЛЕДОВАТЕЛЬНОЕ
И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ СОПРОТИВЛЕНИЙ
(§ 3-2 и 3-3)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать основные
Рис. 3-52. Последователь-
ное соединение сопротив-
лений.
технические данные источника, реоста-
тов и измерительных приборов.
2. Собрать схему (рис. 3-52) и по-
казать ее руководителю.
3. Присоединяя провода вольтмет-
ра к зажимам реостатов, измерить
падение напряжения в каждом ре-
остате и во всей цепи. Записать ве-
личину тока.
4. По полученным данным опре-
делить мощность каждого участка
и всей цепи, сопротивление каждого
реостата и сопротивление всей цепи.
Показания приборов и результаты ра-
счета записать в табл. 3-5.
134
5. Убед :гься что
U^U^U2 | U3; r^ri+r2+r3-, Р = Р1 + Р2+?д.
6. Собрать схему (рис. 3-53) и показать ее руководителю.
7. Измерить напряжения и токи в каждой ветви параллельного
соединения. Измерить ток до разветвления.
Рис 3-53 Паратлельное соединение со-
противлений
8 По полученным данным определить сопротивление, проводи-
мость и мощность каждой ветви и всей цепи. Показания приборов
9. Убедиться, что 1= /(+ /24 h', р = pi +рг +рз g = gi +
+ g2^g)-
3-25. ЛАБОРАТОРНАЯ РАБОТА. ИССЛЕДОВАНИЕ
НЕРАЗВЕТВЛЕННОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПРИ ОДНОМ ПЕРЕМЕННОМ СОПРОТИВЛЕНИИ
(§ 3-6)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать основные технические данные реостатов и изме-
рительных приборов.
2. Собрать схему (рис. 3-8, а) и показать ее руководителю.
3. Изменяя сопротивление г2 от нуля (короткое замыкание) до
бесконечности (разрыв цепи), для нескольких значений этого сопро-
тивления произвести измерения: /, t/t, U2 и U.
135
4. По полученным данным подсчитать: Pt, Р2, Р, rt, г2 и г.
5. Показания приборов и результаты расчетов записать в
табл. 3-7.
Таблица 3-7
21 U ГП 1 3) РР (/) 1 8 общей системе
Ut (/) | в общей системе координат. Р2(/) J коорДИ))ат-
u2U) I
3-26. ЛАБОРАТОРНАЯ РАБОТА. ИЗМЕРЕНИЕ ПОТЕРИ
НАПРЯЖЕНИЯ В ПРОВОДАХ (§ 3-7)
План работы
]. Записать основные технические данные измерительных при-
боров.
2. Собрать схему исследования линии с медными проводами
(рис. 3-54) и показать ее руководителю.
Рис. 3-54. Схема к работе 3-26.
3. Изменяя нагрузку, при трех-четырех различных ее значениях
записать показания вольтметров и амперметра.
4. Определить потерю напряжения в линии
&U' = Ut-U2.
J36
5. Измерив длину линии и диаметр провода, определить ту же
потерю напряжения другим методом:
ли" -21 -Л- .
уо
6. В том же порядке повторить измерения для линии со сталь-
ными проводами.
Рис 3-55. Схема к работе 3-26.
7. Подсчитать для всех случаев мощность потерь
АР-
и к. п. д. передачи
8. Результаты наблюдений и расчетов записать в табл. 3-8.
личных ее значениях записать показания вольтметров и ампермет ров.
J37
11. Определить потерю напряжения в линии
2
A£/' = t/1—1/3 и At/"= —- (/(Lj-I-Mc)-
ул
12. Результаты наблюдений и расчетов записать в табл. 3-9.
ИЗМЕРЕНИЯ ТОКА И НАПРЯЖЕНИЯ (§ 3-8)
Рис. 3-56 Схема для
определения постоянной
гальванометра.
ванометра по току
План работы
1 Ознакомиться с приборами, необходимыми для выполнения
работы, и записать технические данные источника, приборов и вспо-
могательной аппаратуры.
2. Собрать схему (рис. 3-56) и пока-
зать ее руководителю.
3 При трех различных значениях
сопротивления записать показания вольт-
метра и гальванометра По полученным
данным определить /г, Са, Св.
Примечание. При прохождении
тока по обмотке гальванометра его под-
вижная часть поворачивается на угол,
пропорциональный току. Отношение тока,
проходящего по гальванометру, к со-
ответствующему числу делений шкалы
называется постоянной г а л ь-
(обозначение Са):
Ток, при котором стрелка прибора устанавливается на последней
отметке шкалы, называется номинальным током гальванометра /н.
Номинальный ток является верхним пределом измерения прибора.
138
Напряжение, измеряемое гальванометром, равно произведению
тока на сопротивление гальванометра. Отношение напряжения, из-
меряемого гальванометром, к соответствующему числу делений шка-
лы называется постоянной гальванометра по напря-
жению (обозначение Св):
Наибольшее напряжение, которое можно измерить гальваноме-
тром, определяется произведением номинального тока на сопротив-
Рис. 3-58. Расширение пре-
дела измерения напряжения.
Рнс. 3-57. Расширение предела
измерения тока.
ление гальванометра и называется номинальным напряже-
нием.
Показания приборов и результаты расчета записать в табл. 3-10.
гальванометра.
5. Определить сопротивление шунта, который необходимо при-
соединить параллельно гальванометру для расширения предела из-
мерения тока в р раз (число р задается руководителем).
6. Собрать схему (рис. 3-57) и показать ее руководителю.
7. При различных значениях тока по миллиамперметру прове-
рить правильность расчета шунта. Показания приборов и результаты
расчета записать в табл. 3-11.
8. Определить добавочное сопротивление, которое необходимо
соединить последовательно с гальванометром, чтобы расширить
139
Таблица 3-1!
№
п'п
п, del I/n, a/det
С„ р, Прнмеча-
а/дел инс
предел измерения напряжения в р раз (число р задается руково-
дителем)
9 Собрать схему (рис 3-58) и показать ее руководителю
10 При различных значениях напряжения проверить по вольт-
метру правичьиость расчета добавочного сопротивления. Показания
приборов и результаты расчета записать в табл 3-12
Таблица 3-12
С'/п, Ср, Примечд
в/де' в/де i ине
3-28. ЛАБОРАТОРНАЯ РАБОТА. ИЗМЕРЕНИЕ Э. Д. С.
КОМПЕНСАЦИОННЫМ МЕТОДОМ
План работы
1 Ознакомиться с приборами, необходимыми для выполнения
работы, и записать их основные технические данные.
2 Собрать схему (рис 3-59) и показать ее руководителю
Рис 3-59 Схема к работе 3-28
140
3. Изменяя сопротивление г2, уравновесить искомою э д с.
(4 = 0)
4 По полученным данным определить Ех' а) сухого элемента;
б) двух сухих элементов, соединенных последовательно; в) то же—
параллельно; г) кислотного аккумулятора, д) щелочного аккумуля-
тора; е) термопары
Показания приборов и результаты расчетов записать в табт 3-13.
Таблица 3 13
Искомая э д. с
п/л
1
о
3
4
5
6
7
При-
меча-
ние
Первый сухой элемент
Второй сухой элемент
Последовательное соединение
двух элементов
Параллельное соединение двух
элементов
Кислотный аккумулятор
Щелочной аккумулятор
Термопара
3-29. ЛАБОРАТОРНАЯ РАБОТА. ИЗМЕРЕНИЕ
СОПРОТИВЛЕНИЙ ИЗМЕРИТЕЛЬНЫМ МОСТОМ
(§ 3-9)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать основные технические данные источника, мага-
зинов сопротивлений и приборов
Таблица 3-14
№
п/п
Измеряемое сопро-
тивление
г, ом
ом
'2,
ом
ом
°
РУ вт
2
3
4
5
Металлическая
лампа
Угольная лампа
Магнитоэлектри-
ческий вольт-
метр
Электромагнит-
ный вольтметр
Электродинами-
ческий вольт-
метр
)4)
2. Собрать схему (рис. 3-20) и показать ее руководителю.
3. Измерить в холодном состоянии сопротивление нитей метал-
лической н угольной ламп накаливания.
4. Измерить сопротивления вольтметров различных систем. По
полученным данным определить мощность каждого вольтметра при
поминальном напряжении.
5. Результаты измерений н расчета записать в табл. 3-14.
3-30. ЛАБОРАТОРНАЯ РАБОТА. ОПЫТНАЯ
ПРОВЕРКА ПРИНЦИПА НАЛОЖЕНИЯ
(§ 3-13)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать основные технические данные источников, рео-
_____ статов н измерительных приборов.
2. Измерить вольтметром
э. д. с. каждого источника питания.
3. Собрать схему (рис. 3-60)
и показать ее руководителю.
4. Определить сопротивление
каждого реостата, для чего изме-
рить ток и напряжение на зажи-
мах каждого реостата. Показания
приборов и результаты расчета за-
писать в табл. 3-15.
5. При переключателях и
/С2 в положении б измерить токи
12 И 7у.
6. При переключателях К, в
положении б, а Л'2 в положении а
Рис. 3-60. Схема к работе 3-30.
измерить токи /j, Гг и Г3.
7. При переключателях К\ в положении а, а в положении б
измерить токи Г[, Г3 и Г3.
Примечание. При выполнении пп. 5, 6 и 7 убедиться
в справедливости первого правила Кирхгофа.
Таблица 3-15
X» реостата
7, а г, ом
Реостат № 1
» № 2
» № 3
8. Определить токи [t, /2 и 13 методом наложения (измеренных
токов):
/[-71 = 7,; _/Н-71=7г; 13+13 = 13.
142
9. Зиая величины Е2, rit г2 и г3, определить расчетом 12,
13. /J, Г3, /2 и Ъ (сопротивлениями источников пита-
ния пренебречь). Сравнить результаты измерений с результатами
расчета.
10. Показания приборов и результаты расчета записать
в табл. 3-16.
Таблица 3-16
3-31. ЛАБОРАТОРНАЯ РАБОТА. ИСПЫТАНИЕ
ЧЕТЫРЕХПОЛЮСНИКА (§ 3-16-3-19)
1. Ознакомиться с приборами, необходимыми для выполнения
работы. Записать основные технические данные приборов и реостатов.
2. Определить постоянные четырехполюсника экспериментальным
путем, произведя опыт холостого хода и короткого замыкания, сна-
чала при питании со стороны зажимов Г — 1", а затем — со стороны
зажимов 2'—2". Схема опыта холостого хода показана иа рис. 3-41,
схема опыта короткого замыкания — на рис. 3-42 (перед включением
схемы необходимо показать преподавателю).
По полученным данным определить параметры А, В, С и D,
имея в виду, что AD — ВС—1, и выбирая из соотношений (3-59)
и (3-60) любые три.
3. По полученным данным подсчитать сопротивление Т-образной
схемы замещения [см. (3-63)].
Измерить сопротивление реостатов, которые образуют схему
замещения, и сравнить их с данными, полученными расчетом.
4. Для заданного режима работы приемника (U2 = 60в; /2 = 0,5а)
по результатам опытов холостого хода и короткого замыкания опре-
делить значения Ut и lt. Для этого произвести опыты холостого
хода и короткого замыкания (рис. 3-43 и 3-44).
При выполнении опытов холостого хода и короткого замыкания
движок реостата, регулирующего напряжение на входе, нужно вна-
чале поставить в такое положение, чтобы было равно нулю.
Затем постепенно увеличивать Ult пока U2 в первом опыте и /2 во
втором не достигнут заданных значений.
По полученным данным определить Ui и lt в рабочем режиме
(см. формулы (3-68) п (3-69)].
5. Сравнить мощность источника питания для опыта холостого
хода (^^/и), для опыта короткого замыкания и мощность
для испытания при полной нагрузке (L^/j).
143
ГЛАВА ЧЕТВЕРТАЯ
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
4-1. ОСНОВНЫЕ ПОНЯТИЯ
До сих пор мы рассматривали электрические цепи,
сопротивления участков которых считались не изменяю-
щимися при прохождении тока различной величины или
при изменении приложенного напряжения. Такие элек-
трические цепи называются линейными. Но, строго
говоря, линейных
Рие 4-1. Вольт-ам-
перные характери-
стики
электрических цепей не существует.
Например, в металлических прово-
дах различным токам соответствуют
разные температуры, а так как со-
противление провода зависит от тем-
пературы, то оно зависит и от тока,
который по нему проходит. Однако
часто эти изменения сопротивления
столь незначительны, что можно счи-
тать сопротивление постоянным,
а цепь линейной.
В других случаях, когда при про-
хождении тока температура изменяет-
ся в пределах нескольких сотен гра-
дусов или при прохождении тока
среде, через полупроводники сопро-
в вакууме, в газовой
тивление цепи не остается постоянным, зависимость тока
от напряжения резко отличается от линейной.
Электрические цепи, в которых сопротивления участков
являются функциями тока или напряжения, называются
нелинейными. Для расчета нелинейной цепи должны
быть заданы для всех сопротивлений зависимости г(/)
или косвенные характеристики I(U), по которым могутбыти
уже построены зависимости г(/).
График, выражающий зависимость тока от напряжения
1(U), называется вольт-амперной характе-
ристикой.
Для линейных участков цепи, сопротивление которых
не зависит от тока и напряжения, этот график имеет вид
прямой (а на рис. 4-1), проходящей через начало системы
координат. Для участков цепи, сопротивление которых
зависит от тока или напряжения, —нелинейных элементов
144
этот график выражается кривой линией. Например, вольт-
амперная характеристика электрической лампы с металли-
ческой нитью накаливания отличается от прямой, откло-
няясь вниз (б), а у лампы с угольной нитью, наоборот,
вверх (в). Резко отличаются от прямой вольт-амперные
характеристики электронных ламп, газоразрядных прибо-
ров, электрической дуги, полупроводниковых вентилей и др.
4-2. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА
Рис 4-2 Устройство и условное
обозначение двухэлектродной
электронной лампы.
К числу нелинейных элементов электрической цепи
относится двухэлектродная электронная
лампа или диод.
Двухэлектродная электронная лампа имеет стеклянный
(керамический, металлический) баллон, из которого откачан
воздух, так что внутри бал-
лона получается состояние
наивысшего разрежения
(вакуум). В баллоне нахо-
дятся два электрода: анод
и катод (рис. 4-2). Анод
выполняется в виде метал-
лической пластинки или
цилиндрической поверх-
ности, а катод — в виде
проволочной нити.
Сам по себе вакуум яв-
ляется непроводником, так
как в нем отсутствуют ча-
стицы газа и, следователь-
но, невозможна ионизация,
т е расщепление частиц
газа на ионы и свободные
этектроны, обусловлива-
ющие электропроводность.
Необходимые для электропроводности лампы заряженные
частицы — электроны, выбрасываются нагретым катодом.
Чтобы покинуть проводник, ид которого выполнен
катод, электроны должны преодолеть противодействующие
силы в поверхностном слое, т. е. совершить работу
выхода. Эта работа равна произведению заряда электро-
на q и величины <р, называемой потенциалом в ы-
х о д а (несколько вольт).
Ю Teopei ическая алектротсхьика 145
При нормальной температуре выхода электронов из ка-
тода почти не наблюдается, так как число электронов,
у которых запас кинетической энергии достаточен для
совершения работы выхода, очень мало. При нагревании
катода скорость свободных электронов увеличивается и чис-
ло свободных электронов, покидающих катод, возрастает.
Особенно активно выбрасываются свободные электроны
из раскаленного катода.
Явление выхода электронов из нагретого металла полу-
чило название термоэлектронной эмиссии.
Катод накаляете^ током от вспомогательной батареи накала
или трансформатора.
Обычно электронные лампы имеют вольфрамовую нить
накала Значительная эмиссия вольфрамовой нити может
быть получена, если нить нагрета до температуры 2 200° С.
Для уменьшения мощности, расходуемой на нагрев нити
накала, а также для увеличения срока ее службы воль-
фрамовую нить покрывают тонкой пленкой вещества, у ко-
торого работа выхода электрона меньше, чем у вольфрама,
и значительная эмиссия наблюдается при меньших тем-
пературах. К таким веществам относятся окиси щелочно-
земельных металлов — кальция, стронция и бария.
Если катод присоединить к отрицательному зажиму,
а анод к положительному зажиму источника питания,
т. е. подвести к лампе напряжение (анодное напря-
жение (7а), то электроны под действием сил электри-
ческого поля между электродами устремятся от катода
к аноду, образуя поток электронов, обратный по направ-
лению току /а, который принято называть анодным
током.
Электроны, покидающие катод, обладают вначале незна-
чительной скоростью, по мере движения к аноду скорости
электронов возрастают. Чем больше электронов покинуло
катод, тем сильнее тормозятся последующие электроны,
вылетающие из катода, так как они испытывают противо-
действие со стороны электронов, перемещающихся впереди
них. Поэтому электроны группируются вблизи катода
в виде «объемного отрицательного заряда». Объемный отри-
цательный заряд частично рассасывается иод действием
сил электрического поля между анодом и катодом, но одно-
временно пополняется электронами, покидающими катод.
Объемный заряд противодействует вылету электронов из
катода и перемещению электронов внутри лампы.
146
Постепенно увеличивая анодное напряжение, можно
установить, что ток в цепи возрастает пропорционально
иа/г. При некотором значении анодного напряжения U'a
ток достигает предельной величины, равной току эмис-
сии /э, и при дальнейшем повышении анодного напряже-
ния не увеличивается. В этом случае все выбрасываемые
катодом свободные электроны составляют анодный юк.
На место ушедших свободных электронов в каждую еди-
ницу времени появляется равное число новых, так что
Рис 4-3 Вольт-амперная
характеристика диода
Рис. 4-4 Односторонняя
проводимость электронной
лампы
заряд, проходящий в единицу времени по цепи, остается
одним и тем же.
Ток эмиссии может увеличиться, если возрастет интен-
сивность выхода свободных электронов, для чего нужно
повысить температуру катода.
График, выражающий зависимость анодного тока от на-
пряжения между электродами Ia(Ua), называется вольт-
амперной характеристикой диода (рис. 4-3).
Через двухэлектродную электронную лампу ток может
проходить лишь в одном направлении. Действительно,
если катод электронной лампы окажется присоединенным
к положительному зажиму, а анод — к отрицательному,
то электроны, покинувшие катод, под действием сил поля
возвратятся обратно к катоду (рис. 4-4). Ток в цепи при
обратном напряжении отсутствует. Таким образом, элек-
тронная лампа обладает проводимостью только в том слу-
чае, если катод присоединен к отрицательному зажиму,
а анод — к положительному.
10* 147
Это свойство электронной лампы широко используется
для выпрямления переменных токов. Электронная лампа,
применяемая для выпрямления переменного тока промыш-
ленной сети, называется кенотроном. Главный недо-
статок кенотрона — это значительное падение напряжения
между электродами даже при относительно большом анод-
ном токе.
Обратное напряжение между электродами не должно
превышать некоторого предельного значения. При слиш-
ком высоком обратном напряжении происходит вырывание
силами поля свободных электронов из анода (явление
автоэмиссии) и возникает обратный ток, вызывающий
порчу лампы.
4-3. ТРЕХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА
Трехэлектродная лампа, или триод (рис. 4-5),
отличается от двухэлектродной лампы наличием третьего
электрода сетки. Сетка выполняется в виде спиральной
Рис. 4-5. Устройство н услов-
ное обозначение трехэлектрод-
ной лампы.
нити, окружающей катод лам-
пы. Сетка необходима в лам-
пе, чтобы управлять анодным
током лампы. Она располо-
жена близко к катоду, и
незначительное изменение ее
потенциала оказывает резкое
влияние на анодный ток.
Увеличивая потенциал сетки
(по отношению к катоду),
мы содействуем «рассасыва-
нию» объемного заряда; при
этом анодный ток увеличи-
вается. Наоборот, уменьшая
потенциал сетки, мы еще в
большей степени затрудняем
перемещение электронов от
катода к аноду; анодный ток
уменьшается.
График, выражающий за-
висимость Ia(Ua), называет-
ся анодной характеристикой триода
(рис. 4-6). При различных потенциалах сетки анодные харак-
теристики не совпадают друг с другом. Чем больше отри-
148
нательный потенциал сетки, тем больше должно быть анод-
Рис 4-6 Анодные характеристики трех-
электродпой лампы
На рис. 4-7 представлены графики, выражающие зави-
симость анодного тока от потенциала сетки при различных
постоянных анодных напря-
жениях. При определенном
потенциале сетки все элек-
троны, выходящие из катода,
задерживаются противодей-
ствующими силами поля меж-
ду сеткой и катодом и лампа
оказывается «запертой». Гра-
фики, представленные на
рис. 4-7, называются сеточ-
н ы м и х а р а к т е р и с т и-
ка м и трехэлектродной лам-
пы. На рис. 4-8 приведена
Рис 4-7 Сеточные характери-
стики трехэлектроднон лампы.
схема для снятия анодных
и сеточных характеристик.
Катод лампы накаляется то-
ком от батареи накала £н.
Ток накала, т. е. темпера-
тура нити, регулируется ре-
остатом. При помощи батареи £е и делителя напря-
жения со средней точкой можно установить выбранное
положительное или отрицательное значение потенциала
149
сетки относительно катода. Вольтметры измеряют потен-
циал сетки и анодное напряжение, которое может регу-
лироваться. Миллиамперметр измеряет анодный ток, ампер-
метр — ток накала.
Рис 4-8 Схема для снятия характеристик трехэлектродной
лампы.
4-4. ПАРАМЕТРЫ ТРЕХЭЛЕКТРОДНОЙ ЛАМПЫ
Трехэлектродная лампа имеет три параметра:
1) крутизна характеристики
__
~ А47с
(4-1)
крутизна характеристики равна отношению приращения
анодного тока к соответствующему приращению сеточного
напряжения при постоянном анодном напряжении;
2) внутреннее сопротивление
At/a .
Д/а ’
(4-2)
внутреннее сопротивление равно отношению приращения
анодного напряжения к соответствующему приращению
тока в цепи анода при постоянном сеточном напряжении;
3) коэффициент усиления
Д(7а
A<VC
(4-3)
коэффициент усиления равен отношению приращения анод-
ного напряжения к такому обратному по знаку прираще-
150
нию сеточного напряжения, при котором анодный ток
останется без изменения.
Параметры лампы связаны соотношением
р. Srt, (4-4)
которое вытекает из формул (4-1)—(4-3).
Параметры лампы могут быть определены из характе-
ристического треугольника АБВ (рис. 4-7).
Пример 4-1. Определить параметры трехэлектродной лампы по
характеристическому треугольнику, построенному на рис 4-7
Из треугольника следует, что Д/а = 8 ма, ДС/с - 2,2 в, Д(7а =
= 50 в
Находим крутизну характеристики:
S = W = 2A2-=3’6 М/в-
Приращению сеточного напряжения Л(./(.-2,2я соответствует
обратное по знаку приращение анодного напряжения АС/а = 50 в.
Таким Образом, коэффициент усиления
„50
\ис ~2,2~
и, наконец, внутреннее сопротивление
р 23-1 000 с.п.
1^ = -—= — уу— = 6 300 о ч
4-5. ЛАМПОВЫЙ УСИЛИТЕЛЬ
Трехэлектродная лампа широко применяется в раз-
усилителях напряжения и уси-
личных областях техники в
лителях мощности (следует
заметить, что усиление на-
пряжения и мощности произ-
водится не лампой, а при по-
мощи лампы за счет источни-
Рис 4-9 Ламповый усилитель.
ков энергии, питающих анод-
ную цепь и нить накала).
Сущность процесса усиле-
ния (рис. 4-9) заключается
в том, что сравнительно сла-
бое изменение сеточного на-
пряжения (на зажимах гс) вы-
зывает подобное по форме, но более сильное изменение
напряжения на зажимах сопротивления га, включенного
151
в анодную цепь лампы. Это значит, что электрический
сигнал слабой мощности, поданный на сетку лампы (в со-
противлении гс), воспроизводится значительно более мощ-
ным в сопротивлении гл анодной цепи.
Увеличение сеточного напряжения Д(7С (на зажимах
гг) вызывает приращение анодного тока на величину Д/а,
несколько меньшую, чем ЛГп ~ S&UC. Действительно, при-
ращение анодного тока приводит к увеличению напряже-
ния на сопротивлении гя на величину
и уменьшению на такую же величину Д{7а — Л(7 анод-
ного напряжения лампы (при постоянном напряжении
питания U), что и приводит к уменьшению анодного
тока на величину
Д/" = Л'А .
гг
Таким образом, в рабочем режиме лампы приращение
анодного тока Д/а зависит от совместного изменения
потенциала сетки и анодного напряжения и меньше Д/а
на величину Д/а:
Д/„ ДД-ДД -5Д/7С—. (4-5)
r I
Имея в виду, что S =— и Д/а - = , цронз-
г у ra r a
ведем преобразование в уравнении (4-5). Получим:
ли лис ли
— — и.---------
Щ r h rt
ИЛИ
Д(/ +J> = \и .
Ч 'a rt ) с гг
Отношение Д6У/ДТ7с ру называют коэффициен-
том усиления усилителя. Из последнего уравне-
ния найдем:
(W)
Коэффициент усиления усилителя всегда несколько
меньше коэффициента усиления лампы, так как —r < 1;
152
при сопротивлении нагрузки, значительно большем сопро-
тивления лампы, р.у приближается к р.
Для того чтобы при усилении сигнала не происходило
искажения его формы, нужно выполнить два условия:
1) изменения сеточного напряжения должны лежать
в пределах прямолинейных участков сеточных характе-
ристик лампы,
2) при изменении сеточного напряжения потенциал
сетки не должен превышать потенциал катода, иначе
в цепи сетки возникнет ток, искажающий сигнал.
Для выполнения второго условия потенциал сетки
искусственно понижается на постоянную величину, назы-
ваемую «напряжением смещения», например путем вклю-
чения в цепь сетки источника э. д. с. Ес. Таким образом,
при Uc -- 0 потенциал сетки ниже потенциала катода
на величину Е( (рис. 4-9).
4-6. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
В обычных физических условиях свободных электронов
и ионов в составе газа почти нет. Поэтому газы не проводят
электрический ток. Та незначительная проводимость, кото-
рой обладают газы, объясняется постоянной их ионизацией
лучами радиоактивных веществ, содержащихся в земной
коре и атмосфере, и космическими лучами. Ионизация газа
возникает также под действием рентгеновских и ультра-
фиолетовых лучен, высокой температуры и, наконец, под
действием сильного электрического поля.
Процесс ионизации (разрушения нейтральных молекул)
происходит за счет энергии ионизатора (например, столк-
новением с быстро несущимися частицами материи); в ре-
зультате от атома или молекулы газа отщепляется элек-
трон и она превращается в положительный ион; отщеп-
ленный электрон в свою очередь может присоединиться
к какой-нибудь нейтральной молекуле, образуя отрица-
тельный ион.
При непрерывном действии какого-либо ионизирующего
фактора в 1 си® газа в единицу времени образуется опреде-
ленное число ионов, что, однако, не приводит к непрерыв-
ному нарастанию их числа, так как одновременно проис-
ходит процесс воссоединения ионов в нейтральные моле-
кулы, называемый рекомбинацией. Таким образом, при
непрерывном действии ионизатора через некоторое время
J53
число ионов в единице объема газа оказывается посто-
янным.
Представим себе, что между электродами, к которым
приложено напряжение (рис. 4-10), находится газ, иони-
зируемый с неизменной интенсивностью, например, косми-
ческими лучами. Под действием сил электрического поля
положительные ионы перемещаются в направлении поля,
электроны и отрицательные ионы — в обратном, образуя
ток.
Допустим, что- приложенное к электродам напряжение
мы можем изменять в самых широких пределах и в цепь
Рис. 4-10. Элек-
трический ток
в газе.
Рис 4-И Вольт-амперная ха-
рактеристика разряда в газе
включены приборы, измеряющие приложенное напряже-
ние и ток в цепи. Увеличивая напряжение от нуля, уста-
новим, что с ростом напряжения в цепи возникает ток,
пропорциональный напряжению. Вольт-амперная характе-
ристика, выражающая зависимость тока от напряжения
(рис. 4-11), имеет вид прямой. Однако при дальнейшем
повышении напряжения рост тока замедляется и, наконец,
несмотря на дальнейший рост напряжения, ток перестает
увеличиваться. В этом случае все ионы, образованные
внешним ионизатором, переносятся от одного электрода
к другому, не успевая нейтрализоваться. Такой ток назы-
вают током насыщения, ему соответствует участок
вольт-амперной характеристики, параллельный оси абсцисс.
Проводимость газа, возникающая при воздействии на газ
постороннего ионизатора, называется несамостоя-
тельной проводимостью. Она исчезнет, если
прекратится действие ионизатора.
154
4-7. САМОСТОЯТЕЛЬНЫЙ РАЗРЯД В ГАЗЕ
Сильное электрическое поле, созданное в газовой сре-
де, может вызвать самостоятельный разряд.
Будем увеличивать напряжение между' электродами
(рис. 4-10). При некотором значении напряжения, назы-
ваемом напряжением зажигания, ток в газе
резко увеличится и газ начнет светиться.
Сильное электрическое поле, созданное в газовой среде,
вызовет ионизацию газа толчком (ударом). Электрические
заряды, которые всегда в небольшом количестве содержатся
в газе, ускоряются и накапливают кинетическую энергию
ти2„аиС/2, достаточную для ионизации нейтральной моле-
кулы (отщепления свободного электрона). Вновь полу-
ченные электрические заряды в свою очередь ионизируют
нейтральные молекулы газа; процесс образования ионов
развивается лавинообразно. Пространство между элек-
тродами оказывается заполненным ионизированным газом,
который содержит нейтральные молекулы и одинаковое
количество положительно и отрицательно заряженных
частиц вещества, т. е. между электродами образуется газо-
разрядная плазма. Вещество, находящееся в со-
стоянии плазмы, обладает очень хорошей электропровод-
ностью, которая сильно возрастает при повышении тем-
пературы. Величина тока в этом случае ограничивается
сопротивлением гб (рис. 4-10), включенным последова-
тельно с газовым промежутком.
Работа ионизации молекулы газа
A-Uuq,
где Ua — ионизационное напряжение, т. е. разность потен-
циалов между конечными точками пути свободного пробега
заряда q в электрическом поле. Ниже приведены значения
ия для некоторых газов и паров металлов:
Цезий........... 3,9 в
Калий ...............4,3 в
Ртуть................10,4 в
Кислород..........13,5 в
Азот .............14,5 в
Неон..............21,5 в
Очевидно, что одно и то же напряжение зажигания
в газе с низким давлением можно получить при меньшей
напряженности поля, чем при высоком давлении, так как
в последнем случае уменьшается средняя длина свободного
пробега.
155
Для возникновения самостоятельного разряда необхо-
димо, чтобы
Одновременно с ионизацией происходит процесс воз-
буждения нейтральных атомов газа. У части электронов
накопленной энергии недостаточно для ионизации молекул
или атомов газа; при столкновении такого электрона и атома
газа ионизация не происходит, но энергия атома увеличи-
вается. Атом, получивший порцию энергии, возбуждает-
ся — один из электронов оболочки переходит на новую,
более удаленную орбиту (на другой энергетический уро-
вень). Через очень короткое время (10*7—10*8 сек) электрон
снова возвращается на прежнюю орбиту, выделяя при этом
избыточную энергию в виде светового излучения. Таким
образом, возникает свечение газа.
При нормальном и пониженном давлениях в газах наблю-
дается несколько различных стадий самостоятельного раз-
ряда; темный, тлеющий, искровой и дуговой.
4-8. ТЕМНЫЙ И ТЛЕЮЩИЙ РАЗРЯДЫ
Темный разряд может возникнуть при неодно-
родном электрическом поле в тех местах, где напряженность
поля достигает критического значения. Если заряженные
проводники имеют выступающие «заостренные» части,
то вблизи них напряженность поля имеет наибольшее значе-
ние; в этих местах начинается разряд, сопровождаемый
свечением — короной.
Темный разряд в газах с низким давлением иногда пере-
ходит в тлеющий. Тлеющий разряд в газах при
низких давлениях сопровождается свечением газа у анода —
«анодным свечением». В длинных трубках при сравни-
тельно невысокой степени разрежения анодное свечение
занимает значительную часть длины трубки. Такого рода
стеклянные трубки, наполненные неоном (красный свет)
и аргоном (голубой свет), применяются для рекламного
и декоративного освещения.
4-9. ИСКРОВОЙ РАЗРЯД
При распространении ионизации газа на всю длину
участка между электродами темный разряд переходит
в искровой. Ионизация в этом случае происходит
156
не по всему объему, а по отдельным ярко светящимся
каналам, форма которых зависит от «наиболее легкого
пути» ионизации. Лавина электронов, перемещающихся
в искровом канале, вызывает резкое повышение темпера-
туры и давления, отчего искровой разряд сопровождается
характерным треском.
Если мощность источника питания невелика, то воз-
никновение искры приводит к мгновенному снижению
напряжения между электродами почти до нуля, что объяс-
няется большой величиной тока при наличии искры. После
прекращения искрового разряда напряжение между элек-
тродами плавно нарастает до образования нового искрового
разряда.
Напряжение, достаточное для искрового разряда между
электродами, при прочих равных условиях зависит от длины
искры и давления газа. На этом принципе основано устрой-
ство шаровых разрядников, применяемых для измерения
высоких напряжений. По расстоянию между шарами, при
котором происходит искровой разряд, можно судить о на-
пряжении между ними.
Наибольших масштабов достигает искровой разряд
в случае молнии.
4-10. ДУГОВОЙ РАЗРЯД
При большой мощности источника искровой разряд
переходит в форму дугового разряда. Электри-
ческая дуга получается, например, между двумя уголь-
ными электродами, присоединенными через сопротивле-
ние к зажимам генератора.
Электрическая дуга была открыта в 1802 г. профессо-
ром физики Петербургской медицинской академии В. В. Пет-
ровым.
При электрической дуге происходит сильная иониза-
ция газа главным образом электронами, вылетающими из на-
каленного катода. Чтобы избежать всех предварительных
стадий разряда и сразу зажечь дугу, угли сближают так,
что в цепи появляется ток, нагревающий угли до высокой
температуры. Раздвигая электроды, получают между ними
дугу, излучающую ослепительный свет. Накален главным
образом анод, у которого из-за бомбардировки электронами
образуется кратер; температура кратера достигает 4 000° С.
Газоразрядная плазма между электродами имеет темпера-
157
Рис. 4-12. Вольт-ам-
перная характери-
стика электрической
дуги.
туру около 4 800° С и обладает очень высокой проводи-
мостью. Поэтому при электрической дуге возникает зна-
чительный ток, напряжение между электродами небольшое
(20—40 в).
Электрическое поле действует с одинаковой силой на
каждый свободный электрон и положительный ион (атом,
потерявший один электрон), но так как масса электрона
в несколько тысяч раз меньше массы положительного
иона, то подвижности электронов и ионов резко отличаются.
Электроны перемещаются значитель-
но быстрее ионов, поэтому ток при
дуговом разряде образуется главным
образом свободными электронами.
При увеличении тока температура
плазмы возрастает, увеличивается ее
проводимость, вследствие чего напря-
жение на участке дугового разряда
уменьшается. Таким образом, элек-
трическая дуга имеет «падающую ха-
рактеристику» (рис. 4-12).
Электрическая дуга применяется
для освещения (прожектор, проекци-
онные фонари) и нагревания (электро-
печи, электросварка). Впервые электрическая дуга была при-
менена для освещения в 1876 г. П. Н. Яблочковым, который,
расположив параллельно угольные электроды, подвел к ним
переменное напряжение. Дуга получилась устойчивой,
электроды изнашивались равномерно. Электрическая све-
ча Яблочкова — «русский свет» — применялась во мно-
гих странах мира до изобретения и усовершенствования
А. Н. Лодыгиным электрической лампы с накаливаемой
нитью.
Электрическая дуга служит для сварки металлов.
Электрическая сварка — один из прогрессивных техниче-
ских методов соединения металлов; она широко приме-
няется и все более совершенствуется и автоматизируется.
По сравнению с другими способами соединения метал-
лических частей сварка обладает рядом преимуществ:
экономия металла, времени, рабочей силы, высокая проч-
ность места соединения (шва). Электрическая сварка при-
меняется во многих областях промышленности как основ-
ной технологический процесс (сварка строительных кон-
струкций, труб, корпусов кораблей и т. д.).
158
Все большее применение находят экономичные лампы
дневного света. В длинной трубке (рис. 4-13) располагаются
два электрода в виде тонких спиралей, покрытых вещест-
вами, увеличивающими термоэлектронную эмиссию. Стенки
трубки покрываются особым составом — люминофором,
Рис. 4-13. Лампа дневного света.
Внутри трубки находятся пары ртути при низком давле-
нии. При разряде возникает мощное ультрафиолетовое
излучение. Люминофор светится под действием невидимых
ультрафиолетовых лучей.
4-11. ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ
Полупроводниками называются тела, зани-
мающие промежуточное положение среди проводников и изо-
ляторов. К наиболее распространенным полупроводни-
кам относятся: кремний, германий,
селен и закись меди. В отличие
от проводников полупроводники
имеют не только электронную, но
и «д ы р о ч н у ю» проводимость.
Рассмотрим возникновение элек-
тронной и дырочной проводимостей
на примере германия. Известно, что
химическая связь, возникающая между двумя атомами прц
образовании общей пары электронов — по одному от каж-
дого атома, называется ковалентной или двух-
электронной связью. Такая связь возникает, на-
пример, при сближении на очень малое расстояние двух
атомов водорода (рис. 4-14). Условно двухэлектронную
связь изображают двумя линиями, соединяющими атомы.
Полупроводник германий принадлежит к элементам
четвертой группы периодической системы элементов. Эти
элементы имеют на внешней орбите по четыре электрона
(валентные электроны). В кристалле германия каждый
159
Рис. 4-14. Ковалентная
связь атомов.
атом образует двухэлектронные связи с четырьмя другими
атомами, которые аналогично связываются с четырьмя
соседними атомами, как схематически представлено на
рис. 4-15. В идеальной кристаллической решетке германия
все четыре валентных электрона каждого атома образуют
ковалентные связи с валентными электронами других
атомов; свободных электронов нет, и такой кристалл гер-
мания не обладает проводимостью.
Если какой-либо валентный электрон получит допол-
нительную энергию, например при нагревании или облу-
Рис 4-15 Схема ко-
валентных связей в
кристаллической ре-
шетке германия
движения электрон
чении, то силы связи могут быть пре-
одолены и электрон станет свободным
Свободный электрон под действием
внешнего электрического поля может
перемещаться между кристаллами,
обусловливая электронную проводи-
мость. Образование свободного элек-
трона приводит к нарушению двух-
электронной связи и появлению сво-
бодного места, -которое может быть
снова занято электроном. Такое сво-
бодное место в нарушенной двухэлек-
тронной связи называется «дыркой».
Под действием, например, теплового
соседней связи может перейти в неза-
полненную связь, т. е. занять дырку. Одна двухэлектронная
связь восстанавливается, но разрушается другая, возникает
новая «дырка». Этот процесс можно рассматривать как
движение дырок. Под действием сил электрического поля
происходит направленное перемещение дырок в направле-
нии сил поля, т. е. в направлении, обратном перемещению
электронов. Такое явление следует рассматривать как
дырочную проводимость. Перемещение дырок эквивалент-
но току, который возникает при движении положительных
зарядов, по величине равных зарядам электронов.
При нарушении двухэлектронных связей в кристалле
одновременно возникают свободные электроны и дырки
и число электронов равно числу дырок. Вследствие тепло-
вого движения происходит не только образование пар
электрон — дырка, но и их воссоединение Таким образом,
при данной температуре в единице объема кристалла число
пар в среднем остается постоянным. Например, при тем-
пературе 20° С в 1 слг германия имеется около 2,5- 101! элек-
160
тронов и дырок при общем числе атомов ~4,2-10гз. Кон-
центрация электрически заряженных частиц в германии
(п = 2,5-1013) значительно меньше концентрации в метал-
лических проводниках, у которых п -- 1023—10аз (при-
мерно один свободный электрон на один атом).
Как видно из сопоставления концентраций, проводи-
мость германия при нормальной температуре значитель-
но ниже проводимости металлов. При повышении тем-
пературы число свободных электронов и дырок очень
сильно возрастает и хотя их подвижность несколько пони-
жается, проводимость германия значительно увеличивается.
Германий, как и другие полупроводники, имеет отрица-
тельный температурный коэффициент сопротивления, кото-
рый по абсолютной величине в 10—20 раз больше, чем
у металлов. Как известно (§ 2-8), при нагревании металла
на 1° С его сопротивление увеличивается приблизительно
на 0,4%. Сопротивление полупроводников при нагре-
вании на 1° С уменьшается на 4—8?6. Это свойство исполь-
зуется для различных технических целей, например для
создания термосопротивлений, величина которых резко
изменяется даже при небольших изменениях температуры.
4-12. ВЛИЯНИЕ ПРИМЕСЕЙ НА ПРОВОДИМОСТЬ
ПОЛУПРОВОДНИКОВ
Вводя в кристалл германия атомы других элементов,
можно, подбирая различные примеси, получить в кри-
сталле преобладание дырок над свободными электронами
или, наоборот, преобладание электронов над дырками.
При этом проводимость полупроводника сильно повы-
шается.
Полупроводники с преобладающей дырочной проводи-
мостью называют полупроводниками типа р
(от слова позитив — положительный), а полупроводники
с преобладанием электронной проводимости — типа п
(от слова негатив — отрицательный). Примеси, которые
вызывают преобладание дырочной проводимости, назы-
ваются акцепторными, а электронной — донор-
ными.
Для германиевых полупроводников акцепторной при-
месью является, например, индий. У атома индия всего
три валентных электрона. При замещении в решетке атома
германия атомом индия три связи атома индия с атомами
11 Теоретическая электротехника 161
германия окажутся заполненными, а одна связь с четвертым
атомом германия незаполненной, т. е. в решетке образуется
дырка. Эта дырка может быть заполнена электроном при
разрыве какой-либо соседней связи, т. е. в результате обра-
зования дырки в другом месте.
Донорной примесью для германия является, например,
мышьяк. Атом мышьяка имеет пять валентных электро-
нов. При замещении в кристаллической решетке атома
германия атомом мышьяка четыре валентных электрона
мышьяка образуют заполненные связи с соседними атома-
ми германия, а пятый электрон окажется слабо связанным
с атомом мышьяка и под действием теплового движения или
электрических сил может перемещаться между атомами
германия.
Рассмотрим, как влияют примеси на проводимость.
Пусть на один миллион атомов германия приходится
всего один атом мышьяка. Тогда в 1 см3 германия появится
дополнительно 1016 свободных электронов (число дырок
не изменится). В таком полупроводнике преобладает элек-
тронная проводимость.
4-13. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
Представим себе, что имеется полупроводник, одна
часть которого содержит акцепторные примеси и обладает
дырочной проводимостью (p-область), а другая — донор-
Рис. 4-16. Полупроводниковый выпрямитель
(вентиль).
ные примеси и обладает электронной проводимостью
(п-область).
В этом полупроводнике (рис. 4-16) свободные электроны
переходят (диффундируют) из «-области с электронной
162
проводимостью в p-область с дырочной проводимостью,
так как концентрация электронов в «области больше, чем
в p-области. Движение дырок происходит в обратном на-
правлении.
Вследствие диффузии части электронов и дырок погра-
ничный слой обедняется основными носителями зарядов
и его проводимость резко уменьшается. Тонкий непрово-
дящий промежуточный слой между полупроводниками
типа п и типа р получил название запирающего
слоя или электронно-дырочного перехода
(перехода Э — Д или р — п). С одной стороны перехода
Э — Д, прилегающей к « области, накапливаются поло-
жительные заряды, а с другой, прилегающей к р-области,—
отрицательные. Таким образом, в переходе Э — Д возни-
кают разность потенциалов (потенциальный барьер) и элек-
трическое поле, противодействующее дальнейшему перехо-
ду электронов из «-области в p-область и дырок в обратном
направлении. Диффузия электронов и дырок прекращается,
когда силы электрического поля в переходе Э — Д уравни-
вают силы, вызывающие эту диффузию.
4-14. ПОЛУПРОВОДНИКОВЫЙ ВЕНТИЛЬ
Полупроводниковый прибор, имеющий переход Э — Д,
обладает односторонней проводимостью (вентиль) и мо-
жет быть применен в выпрямителе, т. е. устройстве, через
которое ток проходит практи-
чески только в одном направле-
нии. Включив такой прибор
в цепь (рис. 4-16), создадим в по-
лупроводнике внешнее электри-
ческое поле. Если внешнее элек-
Рис 4-17. Германиевый вы-
прямитель (вентиль)
/—кристалл германия; 2—воль-
фрамовая проволока.
слой облегчится и про-
трическое поле направлено
встречно электрическому полю
в переходе Э — Д (рис. 4-16,а),
то движение свободных электро-
нов и дырок через пограничный
водимость кристалла сильно увеличится.
Наоборот, если внешнее поле направлено одинаково
с полем в переходе Э — Д (рис. 4-16, б), то движение элек-
тронов и дырок через границу еще более затруднится,
ширина непроводящего запирающего слоя как бы увели-
чится и проводимость кристалла будет очень мала.
163
Отношение тока при прямом напряжении (рис. 4-16, а)
к току вентиля при таком же обратном напряжении
(рис. 4-16,6) называется коэффициентом вы-
прямления:
На рис. 4-17 изображено устройство германиевого вен-
тиля.
4-15. ПОЛУПРОВОДНИКОВЫЙ УСИЛИТЕЛЬ
Рассмотрим теперь, как полупроводники используются
в усилителях. Полупроводниковый триод имеет пластинку,
в которой между двумя областями с однотипной проводи-
Рис. 4-18. Схема полупроводнико-
вого усилителя.
мостью (например, р) создана сравнительно тонкая область
с противоположной проводимостью (и).
Каждая область от другой отделена электронно-дыроч-
ными переходами (рис. 4-18). Отдельные части полупро-
водникового триода, от которых сделаны отводы, полу-
чили название: эмиттер, коллектор н осно-
вание или база. На переход Э — Д между эмиттером
и базой подаются прямое напряжение (источник питания
с э. д. с. £\) и сигнал, подлежащий усилению (ДС^). Кон-
центрация дырок в эмиттере должна быть в десятки раз
больше концентрации электронов в базе.
164
Под влиянием сил первого внешнего поля дырки пере-
ходят из эмиттера в базу, часть дырок рекомбинируется со
свободными электронами базы, а большая часть диффун-
дирует ко второму переходу Э — Ди под действием сил
второго внешнего поля переходит в коллектор, образуя ток
в сопротивлении нагрузки га. При этом незначительное
изменение напряжения на входных зажимах вызывает
на зажимах достаточно большого нагрузочного сопротивле-
ния гп значительное изменение напряжения ДС'2.
4-16. МЕДНОЗАКИСНЫЕ И СЕЛЕНОВЫЕ ВЕНТИЛИ
Рпс. 4-19. Элемент медно-
закисного выпрямителя,
/—болт; 2 — гайка; 3—шайба;
4— изолирующая шайба;
5—радиатор; 6— медь (катод};
7—слой закиси меди (анод);
8—свинцовая шайба; 0—дистан-
ционная шайба; 10—изолирую-
щая трубка,
В практической электротехнике в измерительных при-
борах и в устройствах преобразования переменного тока
промышленной сети в постоянный часто применяются еще
два типа полупроводниковых
вентилей: меднозакисные (куп-
роксные) и селеновые.
Элемент меднозакисного вы-
прямителя состоит из медного
диска толщиной 1—1,5 мм, по-
крытого с одной стороны слоем
закиси меди (Си2О), которая
является полупроводником с ды-
рочной проводимостью. Медь
и закись меди разделены тонким
запирающим слоем. Для лучше-
го контакта к слою закиси меди
прижимается свинцовый диск.
Отдельные элементы соединяют-
ся последовательно (на изоли-
рованной шпильке), образуя
«столбик» выпрямителя. Для
отвода тепла между отдельными
элементами располагаются ди-
станционные шайбы и радиатор-
ные пластины. Эскиз медноза-
кисного вентиля приведен на
рис. 4-19. С целью защиты от
влаги элемент покрывается водостойким лаком, так как
вода, попадая на поверхность закиси меди, восстанавли-
вает медь и элемент теряет вентильные свойства. Допусти-
мая плотность тока вентиля зависит от способа охлаж-
165
дения (нагревание допускается до температуры 50е С);
при естественном охлаждении допустима плотность тока
до 50 ма!см?. Предельное значение обратного напряжения
меднозакисных вентилей 20—30 в, а наибольшее допусти-
мое 8—10 в на один элемент.
Элемент селенового выпрямителя состоит из алюми-
ниевого диска, покрытого с одной стороны слоем селена
Рис 4-20. Элемент
селенового выпрями-
теля.
Рис. 4-21. График 6 (<7) для се-
ленового выпрямителя.
1 — болт: 2 — гайка;
3—шайба; 4—изолирую-
щая шайба, 5 — контакт-
ная шина; 6 — алюминие-
вый электрод; 7—слой
селена (анод): 8~катод-
ный слой: 9 —контактная
шайба; )0~изолирующая
трубка.
толщиной 0,05—0,1 мм. Селен —
полупроводник с дырочной про-
водимостью. Запирающий слой
в отличие от меднозакисного вен-
тиля образуется не между диском
и селеном, а между поверх-
ностью селена и покрывающим его
сплавом из олова, кадмия и висмута, который служит
вторым электродом. К поверхности сплава прижимается
пружинная контактная шайба из латуни. На рис. 4-20
представлен эскиз селенового вентиля, а на рис. 4-21 —
зависимость плотности тока д от напряжения U на элементе.
Наибольшая допустимая плотность тока для селеновых
вентилей, работающих в условиях естественного охлаж-
дения, составляет 30—40 ма]см\ а предельное значение
обратного напряжения на один элемент 50—80 в. Наи-
большее допустимое напряжение 20—45 в. Применяя после
166
довательно-параллельное соединение отдельных элементов,
можно собрать выпрямители на десятки и сотни ампер
и сотни и тысячи вольт.
4-17. РАСЧЕТ НЕЛИНЕЙНЫХ ЦЕПЕЙ
Аналитический расчет нелинейных цепей сложен, по-
этому нелинейные цепи часто рассчитывают графическими
методами.
Рассмотрим, как определяются токи и напряжения
в отдельных участках электрической цепи при последо-
вательном соединении
двух нелинейных эле-
ментов (рис. 4-22).
Рис. 4-23. Построение общей
вольт-амперной характери-
стики.
Рис 4-22. После-
довательное соеди-
нение нелинейных
элементов.
Выбрав одинаковый масштаб, построим в общей системе
координат вольт-амперные характеристики каждого элемен-
та цепи (рис. 4-23), причем Ц (U) — вольт-амперная
характеристика первого нелинейного элемента (Н.ЭЭ
и /2(Д) — вольт-амперная характеристика второго нели-
нейного элемента (Н.Э2).
По вольт-амперным характеристикам It(U) и Iz(U)
построим общую вольт-амперную характеристику /(//).
Для этого, выбрав произвольное значение тока Г, найдем
точки А' и А" на вольт-амперных характеристиках /1(4/)
и /2(Д), ординаты которых выражают ток Г, и сложим
абсциссы этих точек, поскольку при последовательном
соединении напряжения на отдельных элементах склады-
ваются; таким образом, мы получим точку А.
167
Задаваясь другими значениями тока /", найдем
точки Б, В, Г и т. д. .через которые проходит общая вольт-
Рис. 4-24. После-
довательное соеди-
нение линейного
н нелинейного со-
противлений.
жения на первом
образом,
амперная характеристика.
Пусть нам задано напряжение на
зажимах цепи Uс и требуется опреде-
лить ток. Чтобы найти ток, отложим
по оси абсцисс отрезок 00", выража-
ющий в выбранном масштабе приложен-
ное к цепи напряжение Uc, и восставим
перпендикуляр из точки О". Обозна-
чим точку пересечения перпендикуляра
с вольт-амперной характеристикой l(U)
буквой К. Ордината этой точки (КО")
выражает искомый общий ток /0, а отрез-
ки ДМ и ДН — соответственно напря-
и втором элементах и U2. Таким
/0-лга(КО"); U^-мДДМу, и2 = мв(ДН),
где Л1а и Л1в — масштабы тока и напряжения.
Если, наоборот, задан ток, то, отложив по оси ординат
отрезок, пропорциональный току, аналогично определим
общее напряжение и напряже-
ния на отдельных участках цепи.
При последовательном соеди-
нении нелинейного элемента
с линейным сопротивлением г
(рис. 4-24) определение тока по
заданному напряжению Uc мож-
но выполнить следующим об-
разом.
Напряжение на зажимах не-
линейного элемента
Рис. 4-25. График для оп-
ределения тока и напряже-
ния на отдельных участках
неразветвленной цепи.
U„.^Uc-UT = Uc~Ir, (4-8)
откуда
j __ Од — Он э Од Он. э
г г г
По этому линейному уравнению можно построить
график, выражающий зависимость тока I от напряжения
на нелинейном сопротивлении £/н.впри заданном напряже-
нии сети Uc. График имеет вид прямой линии (рис. 4-25),
168
проведенной через две точки А а Б. Точка А соответствует
7/„ э = 7/с и 7 = О, точка Б получается при Un э — 0 и I —
= Uc!r.
Построив в тех же осях вольт-амперную характеристику
l(U„ э) для нелинейного элемента, мы получим точку пере-
сечения В, которая и характеризует единственно возмож-
ный при данном напряжении Uc режим цепи, удовлетво-
ряющий как вольт-амперной характеристике нелинейного
элемента, так и линейному уравнению. Ордината точки
В (ВГ) выражает искомый ток /0, абсцисса (ОГ) — напря-
жение на нелинейном элементе (7П.Э, отрезок (ГА) — напря-
жение на сопротивлении Ur.
Пример 4-2. Последовательно с лампой накаливания включен
реостат с сопротивлением г = 80 ом. Определить ток и напряжения
на каждом участке цепи, если напряжение сети 120 в, а вольт-ам-
перная характеристика лампы может быть построена по следующим
данным:
ия, В 0 20 40 60 80 100 120
7Л, а 0 0,1 0,25 0,45 0,7 1 1,25
По приведенным данным построим вольт-амперную характери-
стику лампы (рис. 4-26).
По уравнению (7Л = (7С— 1г строим график, выражающий эту
зависимость. При 7 = 0 напряжение U^ = UC, т. е. (7л=120 в. Отло-
жив по оси абсцисс отрезок ОА,
соответствующий напряжению
120 е, получаем точку А. При
(7л = 0 ток /=---п-=1,5 а. От-
оО
дожив отрезок ОБ, соответст-
вующий току 1,5 а, находим
точку Б. Соединив точки А и Б
прямой, получим этот график.
Точка пересечения В опре-
деляет единственно возможный
режим цепи. Ордината точки В
выражает ток, который полу-
чился равным 0,6 а; отрезок ОГ
выражает напряжение на лам-
Рис. 4-26. К примеру 4-2.
пе, которое получилось равным
72 в; разность общего напряжения и напряжения на лампе, т. е.
напряжение на реостате, получается равным 48 в.
При параллельном соединении двух нелинейных эле-
ментов (рис, 4-27) ток в каждом элементе при заданном
169
напряжении на зажимах сети Uc можно найти по вольт-
амперным характеристикам элементов. На рис. 4-28
показаны те же вольт-амперные характеристики нелиней-
ных элементов /i(t/) и /2(t/), что и на рис. 4-23. Так как
напряжение на каждом элементе равно напряжению Uc,
то, откладывая отрезок 00", изображающий в масштабе
находим токи Ц и /2. Ток О
мв напряжение Ос, сразу
изображается в масштабе
ма отрезком О"М, а ток
/2—отрезком О"Н. Ток
источника I = /( + /2.
Рис. 4-27. Параллельное
соединение нелинейных
элементов
Рис. 4-28. Графический рас-
чет токов цепи по рис 4-27
Если задано не напряжение Uc, а ток источника I, то
предварительно следует построить общую вольт-амперную
характеристику 1(0'), суммируя ординаты (токи 0 и /2)
вольт-амперных характеристик нелинейных элементов.
Аналогично рассчитывается цепь с любым числом
параллельно включенных нелинейных и линейных эле-
ментов.
При смешанном (параллельно-последовательном) сое-
динении нелинейных элементов следует поочередно строить
для последовательно и параллельно включенных элементов
общие вольт-амперные характеристики. Затем режим цепи
(токи и напряжения) рассчитывается тем же методом, что
и для цепей рис. 4-22 и 4-27.
4-18. БАЛЛАСТНОЕ СОПРОТИВЛЕНИЕ
Рабочий режим некоторых устройств (газоразрядной
лампы, дуговой лампы и др.) с нелинейными характеристи-
ками не может быть устойчивым, если последовательно
170
Рис. 4-29. График для определе-
ния тока при последовательном
соединении электрической дуги
и сопротивления.
с ними не будет включено так называемое «баллас т-
ное сопротивление». Большое практическое зна-
чение имеет расчет величины балластного сопротивления,
в часгности значительный интерес представляет выбор
балластного сопротивления г для устойчивого горения дуги.
Воспользуемся для вычисления величины г методом
расчета нелинейных цепей, рассмотренным в § 4-17.
Как известно, электрическая дуга имеет специфическую
«падающую» характеристику — с возрастанием тока напря-
жение на дуге уменьшает-
ся. Поэтому после йострое-
ния прямой, как на
рис. 4-25, получим две
точки (Б и В) пересечения
прямой с вольт-амперной
характеристикой дуги
(рис. 4-29). Сумма падений
напряжения на сопротив-
лении и на дуге равна
приложенному напряже-
нию при двух значениях
тока /1 и /г- Однако устой-
чивое горение дуги будет
только при токе /2. При
токе /1 устойчивое горе-
ние невозможно. Действительно, случайное увеличе-
ние тока Л приведет к состоянию, при котором сумма
падений напряжения на участках цепи будет меньше при-
ложенного напряжения. Как показывает анализ режима
цепи при изменяющемся токе (переходный процесс) с учетом
возникающей э. д. с. самоиндукции, ток в цепи будет
продолжать увеличиваться до значения /2. Ордината точки
Г (ГО) выражает ток, равный отношению напряжения
на зажимах цепи Uc к балластному сопротивлению г,
откуда искомое сопротивление
ис
(ОГ) ма
Если последовательно с дугой включено сопротивле-
ние, большее чем
(ОД)ма ’
171
где ОД — отрезок на оси ординат, отсекаемый касательной,
проведенной к характеристике дуги из точки А, то точка
пересечения вольт-амперной характеристики дуги и линей-
ного графика отсутствует; устойчивое горение дуги при
данном сопротивлении г' вообще невозможно, и ток про-
ходить не будет.
4-19. СТАБИЛИЗАТОРЫ ТОКА И НАПРЯЖЕНИЯ
Среди различных нелинейных элементов есть такие,
у которых вольт-амперные характеристики имеют участки,
параллельные оси абсцисс или оси ординат (рис. 4-30
Рис. 4-30 Вольт-амперная харак-
теристика стабилизатора тока.
напряжения.
Рис. 4-31. Вольт-амперная ха-
рактеристика стабилизатора
и 4-31). Такие нелинейные элементы применяются в элек-
трических цепях в качестве стабилизаторов тока и стабили-
заторов напряжения.
К числу стабилизаторов тока относится, например,
бареттер (стальная нить в атмосфере водорода). На участке
А Б (рис. 4-30) характеристика бареттера почти парал-
лельна оси абсцисс. Если бареттер включить последователь-
но с сопротивлением г, то, как это видно из приведенных
на рис. 4-30 графиков, при изменении приложенного
напряжения от Uc' до Uc" ток в цепи почти не изменится
(Л' «Л")-
Конечно, диапазон изменения напряжения, при котором
ток в цепи не изменяется, зависит от величины сопротивле-
172
ния, включенного последовательно с бареттером, т. е. от
наклона прямых к оси абсцисс.
На рис. 4-31 показано, что при последовательном
соединении стабилизатора напряжения с изменяющимся
сопротивлением (г' > г") напряжение на стабилизаторе
Ut’ и Ui" не зависит от величины сопротивления (конечно,
при изменении его в некоторых пределах).
4-20. ЛАБОРАТОРНАЯ РАБОТА. СНЯТИЕ
ХАРАКТЕРИСТИК ДВУХЭЛЕКТРОДНОЙ
И ТРЕХЭЛЕКТРОДНОЙ ЛАМП (§ 4-2-4-4)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать их основные технические данные.
2. Собрать схему (рис. 4-32) и показать ее руководителю.
3. Установив номинальное напряжение иакала, снять зависи-
мость /а (t/a).
Примечание. Наибольшее значение анодного тока
как в этом, так и в последующих опытах ие должно пре-
вышать номинального анодного тока данной лампы.
Показания приборов записать в табл. 4-1.
По полученным данным построить график /а (17а).
4. Изменить полярность анодного напряжения. Убедиться в од-
носторонней проводимости двухэлектродиой лампы.
5. Собрать схему (рис. 4-8) и показать ее руководителю.
6. При значении анодного напряжения U’a и номинальном токе
накала, изменяя сеточное напряжение, отметить изменения анодного
тока.
Таблица 4-1
V , в 1 ма
а <1
Рис. 4-32. Схема к работе 4-19.
7. При анодном напряжении t/a<l/a и номинальном токе
иакала, изменяя сеточное напряжение, отметить изменения анодного
тока /а.
173
Показания приборов записать в табл. 4-2.
8. По полученным данным построить сеточные характеристики
трехэлектродной лампы /а (Пс).
Таблица 4-2
9. Определить параметры трехэлектродной лампы.
10. Установив (7с=0 и изменяя анодное напряжение, отметить
изменения анодного тока. Показания приборов записать в табл. 4-3.
(^а)-
4-21. ЛАБОРАТОРНАЯ РАБОТА. СНЯТИЕ
ВОЛЬТ-АМПЕРНОЙ ХАРАКТЕРИСТИКИ
ПОЛУПРОВОДНИКОВОГО ВЕНТИЛЯ (§ 4-14—4-16)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать их основные технические данные. Определить
номинальный ток и номинальное обратное напряжение вентиля.
2. Собрать схему (рис. 4-33) и показать ее руководителю.
174
3. Изменяя подведенное к вентилю напряжение U, снять харак-
теристику 6 —/(С70), где Uo — напряжение на одном элементе;
б —плотность тока, а/см2.
Примечание. Ток в цепи не должен превышать
номинального тока вентиля.
Рис. 4-33. Схема для снятия характери-
стики полупроводникового выпрямителя
при прямом напряжении.
4. Собрать схему (рис. 4-34) и показать ее руководителю.
5. Изменяя подведенное напряжение, снять характеристику при
обратном напряжении.
Примечание. Обратное напряжение на один эле-
мент не должно превышать номинального напряжения
элемента.
Рис. 4-34. Схема для снятия характеристики
полупроводникового выпрямителя при обрат-
ном напряжении.
6. Показания приборов записать в табл. 4-4 и 4-5. В таблицах
п—число последовательно соединенных элементов; S — площадь
элемента.
7. По полученным данным построить характеристику d (t/c).
Таблица 4-4
№ п/п. Прямое напряжение
и, в п Uo, в /, а S, см2 б, а/см2
175
Таблица 4-5
НЕЛИНЕЙНОЙ ЦЕПИ ПРИ ПОСЛЕДОВАТЕЛЬНОМ
И ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ (§ 4-17)
План работы
1. Ознакомиться с приборами, необходимыми для выполнения
работы, и записать технические данные приборов.
Рис. 4-35. Схема для снятия вольт-ампер-
ной характеристики лампы накаливания.
2. Собрать схему для снятия вольт-амперной характеристики
лампы с металлической нитью (рис. 4-35) После проверки схемы руко-
водителем измерить ток при напряжениях 20, 40, 60, 80, 100 и 120 в.
3. Аналогично снять вольт-амперную характеристику для лампы
с угольной нитью.
Таблица 4-6
Металлическая лампа Угольная лампа
№ п/п. U, в /, а № п/п. и, в 1, а
176
4. Показания приборов записать в табл. 4-6. По полученным
данным построить в общей системе координат в одинаковом мас-
штабе для каждой лампы график I (U).
5. Определить графически ток и напряжение на зажимах каж-
дой лампы при последовательном соединении ламп и напряжениях
питания 90 и НО в.
6. Собрать схему (рис. 4-36) и после проверки ее руководите-
лем установить напряжение питания 90 в. Измерить ток и напряже-
Рнс. 4-36. Последовательное соеди-
нение двух ламп накаливания.
ние на зажимах каждой лампы. Аналогичные измерения выполнить
при напряжении питания ПО в.
Сопоставить результаты, полученные из опыта, с результатами,
полученными графически.
7. Показания приборов и результаты расчета записать
в табл. 4-7.
Таблица 4-7
ную характеристику.
9. Построить в общей системе координат вольт-амперные ха-
рактеристики параллельного соединения ламп по опытным данным
п 8. и по вольт-амперным характеристикам отдельных ламп.
12 Теоретическая электротехника
177
ГЛАВА ПЯТАЯ
ЭЛЕКТРОМАГНЕТИЗМ
5-1. МАГНИТНОЕ ПОЛЕ ЭЛЕКТРИЧЕСКОГО ТОКА
Магнитное поле, как и электрическое поле,
является одним из видов материи. Оно возникает, например,
при движении электрически заряженных частиц вещества
и вокруг проводников с током. Магнитное поле обладает
энергией, которая называется энергией магнит-
ного поля. Поэтому если в магнитное поле, окружаю-
щее провод с электрическим током, внести другой провод
с током, то последний испытывает действие силы магнитного
поля. В свою очередь магнитное поле второго провода
с током действует на первый. Под действием сил поля
провод с током может перемещаться; в этом случае произ-
водится работа за счет энергии магнитного поля. Электри-
ческий ток в проводе и магнитное поле вокруг него — нераз-
рывно связанные явления.
5-2. МАГНИТНАЯ ИНДУКЦИЯ
Интенсивность магнитного поля в каждой его точке
характеризуется магнитной индукцией (обо-
значается буквой В). Магнитная индукция в какой-либо
точке поля вокруг провода с электрическим током зависит
ог величины тока, формы провода, расстояния точки от
провода и, наконец, от свойств среды, в которой создается
магнитное поле. На основании опытного закона Био и Сава-
ра — Лапласа всякий элемент провода длиной dl с током
1 (рис. 5-1) создает в точке А на расстоянии гот элемента
магнитное поле, индукция которого
= (5-1)
4л л2 ' ’
Таким образом, индукция dB прямо пропорциональна
длине элемента dl, величине тока 7, синусу угла а между
направлением тока и радиусом-вектором, соединяющим
данный элементе точкой поля, и обратно пропорциональна
квадрату длины радиуса-вектора.
Множитель ца, входящий в уравнение (5-1), называется
абсолютной магнитной проницаемо-
178
стью среды. Он учитывает влияние окружающей среды
на величину магнитной индукции.
Магнитная индукция, как и напряженность электриче-
ского поля,— векторная величина. Вектор dB направлен
перпендикулярно плоскости S, в которой расположены
радиус-вектор г и элемент dl. Направление вектора dB
определяется по правилу буравчика: если буравчик дви-
жется вдоль элемента провода по направлению тока, то один
Рис 5-1. К закону Био и Савара—Лапласа.
конец его рукоятки проходит сквозь плоскость S в том
же направлении, в котором ее пронизывает вектор dB; при
этом точка, в которой этот конец рукоятки проходит сквозь
плоскость S, должна лежать по ту же сторону элемента
dl или его продолжения (по прямой), что и точка А. Если
изменить направление тока в проводе, то изменится на про-
тивоположное направление вектора магнитной индукции.
В действительности ток проходит не по отдельным изоли-
рованным элементам провода dl, а по проводам различной
формы. Поэтому вектор магнитной индукции в любой точке
поля равен геометрической сумме элементарных векторов
магнитной индукции dB, созданных в этой точке током,
проходящим по элементарным участкам провода, т. е.
В= j dB.
(5-2)
По формулам (5-1) и (5-2) можно найти магнитную
индукцию для проводов с током различной формы.
12
179
Магнитное поле, в различных точках которого индукция
имеет различные значения, называется неоднород-
ным, и наоборот, магнитное поле называется однород-
н ы м, если во всех точках поля векторы магнитной индук-
ции имеют одинаковую величину и параллельны друг другу.
5-3. МАГНИТНАЯ ИНДУКЦИЯ В ЦЕНТРЕ
КОЛЬЦЕВОГО ПРОВОДНИКА С ТОКОМ
С помощью закона Био и Савара — Лапласа определим
магнитную индукцию в центре проводника, имеющего
Рис. 5-2 Магнит-
ная индукция в
центре кругового
тока
(рис. 5-2). В этом случае радиус-вектор
г равен радиусу кольца R и для всех
элементов кольца лежит в одной пло-
скости с кольцом; следовательно, все
элементарные составляющие вектора
индукции в центре кольца имеют оди-
наковое направление.
Кроме того, и sina=l.
По закону Био и Савара — Лапласа
(5-1) составляющая магнитной индукции
jr_______________ Ра ! dl
4л ' 7?2 ’
Суммируя значения dB от каждого элемента провод-
ника по всей длине проводника, т. е. по длине окруж-
ности радиуса R, находим значение магнитной индукции
в центре:
В = Г =
J 4л 7?2 j
(5-3)
Знак £ указывает, что происходит суммирование по замк-
нутому контуру.
Так как в данном случае сумма элементов длины
^dl = 2nR,
то магнитная индукция
р__ _ ИЛ
2R D ’
(5-4)
где D— диаметр кольца.
180
5-4. МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
Магнитная индукция поля зависит, как уже указыва-
лось, от свойств среды, в которой создается магнитное поле.
Для того чтобы получить представление о магнитных
свойствах среды, нужно сравнить магнитное поле вокруг
провода с током в данной среде с магнитным полем вокруг
того же провода, но находящегося в вакууме. Таким образом,
можно установить, что в одних случаях поле получается
более интенсивным, чем в вакууме, в других — менее
интенсивным. Это объясняется различными магнитными
свойствами сред и материалов, окружающих провод с током.
Материалы или среды, в которых поле получается сильнее,
чем в вакууме, называются парамагнитными,
а материалы или среды, в которых поле становится слабее,—
диамагнитными. Магнитные свойства среды харак-
теризует абсолютная магнитная проницаемость ра, имею-
щая различную величину для разных веществ.
Абсолютная магнитная проницаемость вакуума назы-
вается магнитной постоянной (обозначение р0).
Еще в XIX в. теоретически и экспериментально было
найдено, что электрическая постоянная е0 и магнитная
постоянная связаны уравнением
е»Ио = . (5-5)
где с = 3-103 м/сек—скорость света в вакууме.
В Международной системе единиц СИ магнитная
постоянная выбрана равной
ц0~ 4л-10“’ ом-сек/м. (5-6)
Поэтому в той же системе единиц электрическая постоян-
ная
1 _ 1 _ 1 ,,
9 ЮМ.4л 10-7 — 36л-10»
так как
1 _ сек сек-а _ к ф
(м2/сек2)(ом-сек/м)~~ м-ом м-ом-а м-в м '
Это значение е0 и было указано в § 1-4.
Единицу ом-сек называют генри (генри единица
индуктивности, с которой мы познакомимся в § 6-14)
и сокращенно обозначают гн.
181
Введя новое обозначение, получим:
цо=4л-1О“7 гн/м. « 125-10~8 гн/м.. (5-7)
Абсолютные магнитные проницаемости других веществ
удобно сравнивать с магнитной постоянной.
Отношение абсолютной магнитной проницаемости како-
го-либо вещества к магнитной постоянной называется
магнитной проницаемостью вещества (обозначение р),
так что
ц = (5-8)
Ио
Магнитная проницаемость вещества — отвлеченное
число.
Для диамагнитных веществ р < 1, для парамагнитных
р > 1. К диамагнитным веществам относится, например,
медь, у которой р = 0,999995, к парамагнитным — боль-
шинство веществ, в том числе и воздух, у которого
р = 1,0000031. Для технических расчетов магнитная про-
ницаемость диамагнитных и парамагнитных тел прини-
мается равной единице.
Особую группу составляют так называемые ферро-
магнитные материалы, играющие громадную роль
в электротехнике; магнитная проницаемость этих материа-
лов может достигать десятков тысяч. Вместе с тем опа
не постоянна и изменяется при изменении магнитной
индукции и температуры.
5-5. ЕДИНИЦЫ ИЗМЕРЕНИЯ МАГНИТНОЙ ИНДУКЦИИ
Для определения единицы измерения магнитной индук-
ции используем зависимость (5-4)
, п, Г МД 1 гн а ом-с’к-а в-сек вб
BJ = Ц- =--------=--------— — =—^ — тл.
L D J мм м-м м2 м2
В Международной системе единиц СИ магнитная индук-
ция измеряется в веберах на квадратный метр или теслах.
Вольт-секунда носит название вебер (вб), а вольт-
секунда на квадратный метр — тесла (тл).
Тесла — крупная единица, поэтому при расчетах иногда
пользуются более мелкой единицей, не принадлежащей
к системе СИ.— гаусс (гс):
1 гс ~ 10“4 тл= 10“4 вб!м?.
182
5-6. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
Рис 5-3 Магнитное поле
прямолинейного проводни-
ка с током.
вокруг провода с током
Линии магнитной индукции или, короче,
магнитные линии применяются для изображения магнит-
ного поля. Линии магнитной
индукции проводят так, чтобы
вектор магнитной индукции
в каждой точке был направлен
по касательной к линии в этой
точке. Линии магнитной индук-
ции всегда замкнуты. На рис. 5-3
показаны замкнутые линии маг-
нитной индукции вокруг прямо-
линейного провода с током.
В этом случае каждая линия
имеет форму окружности, центр
которой лежит на оси провода
Направление линий магнитной
индукции определяется направ-
лением вектора магнитной ин-
дукции, поэтому оно зависит от
направления тока в проводе.
Эта зависимость устанавливается
правилом буравчика: направле-
ние линий магнитной индукции
совпадает с направлением вращения рукоятки буравчика,
если поступательное движение буравчика совпадает с на-
правлением тока в проводе.
Рис. 5-4 Магнитное поле витка с током.
На рис. 5-4 изображено магнитное поле витка с током,
а на рис. 5-5— катушки с током. В случае витка или катуш-
ки с током правилом буравчика удобнее пользоваться
в несколько измененном виде: если совместить направление
вращения рукоятки с направлением тока в контуре, то
183
поступательное движение буравчика укажет направление
магнитных линий, пронизывающих поверхность, ограничен-
ную контуром тока. Само со-
бой разумеется, что при задан-
ном направлении линий маг-
нитной индукции правилом
буравчика можно пользовать-
ся для определения направ-
ления тока.
Густотой линий магнитной
индукции можно характери-
зовать величину магнитной
индукции. Для этого через
каждую единичную площадку
(1 м2, 1 см2 или 1 лии2), пер-
Рис 5-5 Магнитное поле к а- пендикулярную к направле-
тушки с током. нию линий магнитной индук-
ции, проводится такое число
линий, которое равно или пропорционально величине
магнитной индукции в этой области поля.
5-7. МАГНИТНЫЙ ПОТОК
Поток вектора магнитной индукции или просто маг-
нитный поток (обозначение Ф) через площадку,
перпендикулярную вектору магнитной индукции, в одно-
родном поле равен произведению магнитной индукции
и величины площадки:
Ф-BS. (5-9)
В Международной системе единиц СИ магнитный поток
измеряется в вольт-секундах (в-сек) или веберах (еб):
|Ф] = [BS] = в'^к •м2 — в‘ сек = вб.
Более мелкой единицей измерения магнитного потока
является максвелл (мкс):
1 мкс = 10*8 вб.
Если площадка S не перпендикулярна направлению
поля, т. е. вектор магнитной индукции образует с нормалью
к площадке угол 0 (рис. 5-6), то для определения потока
184
необходимо найти составляющую вектора магнитной индук-
ции Вн, нормальную к поверхности площадки:
Вн = В cos р.
Магнитным потоком в этом случае на-
зывается произведение нормальной состав-
ляющей вектора магнитной индукции и ве-
личины площадки:
Ф-В„£. (5-10)
В неоднородном магнитном поле сле-
дует брать произведение нормальной состав-
ляющей вектора магнитной индукции и эле-
ментарной площадки dS, что дает элемен-
тарный магнитный поток:
dO = B„dS,
а поток через площадку S конечных размеров
Ф-Дв„Ф5. (5-11)
1
Рис 5-6 К оп-
ределению маг-
нитного потока.
5-8. ТРУБКА МАГНИТНОЙ ИНДУКЦИИ
В § 5-6 было указано, что при помощи магнитных линий
можно наглядно изобразить магнитное поле и величину
магнитной индукции в различных его точках. Покажем
Рис. 5-7. Магнитная трубка.
теперь, что при помощи магнитных линий можно также
наглядно изображать и величину магнитного потока.
С этой целью разобьем магнитное поле на части, проведя
в нем ряд непрерывных поверхностей, имеющих форму
185
трубок, расположенных вдоль магнитных линий, т. е, не
пересекающих их (рис. 5-7). В таком случае магнитный
поток сквозь любое поперечное сечение данной трубки
имеет одну и ту же величину. Его можно изобразить,
проведя внутри каждой трубки такое количество магнит-
ных линий, которое было бы равно или пропорционально
магнитному потоку трубки. Это дает возможность рассмат-
ривать магнитный поток сквозь любую площадку, взятую
в магнитном поле, как совокупность магнитных линий,
пронизывающих эту площадку.
Суммарный магнитный поток через замкнутую поверх-
ность равен нулю, так как магнитные линии замкнутые:
всякая магнитная линия, входящая в замкнутую поверх-
ность, должна из нее выйти. Следовательно, магнитный
поток, входящий в замкнутую поверхность, равен потоку,
выходящему из нее.
5-9. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ
При расчетах магнитного поля часто пользуются вели-
чиной, называемой напряженностью магнит-
ного поля (обозначение Н). Напряженность магнит-
ного поля в однородной среде не зависит от магнитных
свойств вещества, в котором создается поле, но учитывает
влияние величины тока и формы проводников на интенсив-
ность магнитного поля в данной точке. Магнитная индукция
и напряженность поля связаны между собой следующим
соотношением:
В — раН = (5-12)
Напряженность магнитного поля в Международной
системе единиц СИ измеряется в а/м:
[Я1л11=4£^Е=в/л.
1 1 L Ца J мг-ом-сек.
Иногда пользуются другой единицей напряженности
поля, не принадлежащей к системе СИ — эрстедом (э):
1 э = 79,6 а/м ~ 80 а/м. — 0,8 а/см.
Напряженность магнитного поля, как и магнитная
индукция,— векторная величина. Направление вектора
напряженности магнитного поля в средах с одинаковыми
магнитными свойствами во всех направлениях (изотропных
186
средах) совпадает с направлением магнитного поля в дан-
ной точке.
Напряженность поля необходимо знать при расчете
магнитных цепей электрических машин, различных элек-
тромагнитных аппаратов и всюду, где линии магнитной
индукции проходят в материалах с различными магнитны-
ми проницаемостями; таким образом, напряженность поля
является важной расчетной величиной. В тех случаях,
когда напряженность поля известна, нетрудно найти маг-
нитную индукцию (5-12).
Разделив на ца обе части уравнения (5-1), получим
закон Био и Савара — Лапласа для напряженности маг-
нитного поля:
,,, 1 dl sin а
аН = —j—s—
5-10. МАГНИТНОЕ НАПРЯЖЕНИЕ
Аналогично электрическому напряжению для электри-
ческих полей при расчете магнитного поля применяется
понятие магнитного напряжения (обозначе-
ние 5-8. Магнитное напряжение.
ние i/M). Если напряженность магнитного поля одинакова
во всех точках данной магнитной линии, как, например,
вдоль магнитной линии прямолинейного провода с током
(рис. 5-3) или в однородном магнитном поле (рис. 5-8,е),
то магнитное напряжение между двумя точками этой
магнитной линии равно произведению напряженности маг-
нитного поля и участка длины магнитной линии:
U„ = Hl. (5-13)
В более общем случае, например при определении
магнитного напряжения между двумя точками однород-
ного поля, находящимися на расстоянии / друг от друга,
187
но расположенными не на одной и той же магнитной
линии (рис. 5-8,5),
U^Hd,
где Hi — проекция вектора напряженности на отрезок I.
В общем случае, когда в различных точках пути I
напряженность магнитного поля не одинакова.
Uu^Hidl, (5-14)
i
причем в отличие от электростатического поля величина
зависит от выбранного пути между начальной и конеч-
ной точками.
Из последних формул следует, что магнитное напряже-
ние измеряется в амперах:
Ш - [Н1\ = • м-- а.
Часто в расчетах приходится определять магнитное
напряжение по произвольно проведенному в магнитном
поле замкнутому контуру. Магнитное напряжение, вычис-
ленное по замкнутому контуру, называется намагни-
чивающей силой (сокращенно н. с.) или магни-
тодвижущей силой (м. д. с.) и обозначается
буквой F. Таким образом,
F = ^Htdl. (5-15)
5-И. ЗАКОН ПОЛНОГО ТОКА
В некоторых случаях зависимость между напряжен-
ностью магнитного поля и током можно установить значи-
тельно проще, применяя вместо закона Био и Савара —
Лапласа закон полного тока.
Полным током называется алгебраическая сумма токов,
пронизывающих поверхность, ограниченную замкнутым кон-
туром, или, как говорят, сцепленных с контуром.
Рассмотрим контур, проведенный в магнитном поле,
поверхность которого пронизывается двумя токами F и /2
(рис. 5-9). Произвольно выберем положительное направпе-
ние обхода контура, например по направлению движения
часовой стрелки. В соответствии с выбранным направлением
188
будем считать ток, пронизывающий контур, положитель-
ным, если его направление совпадает с поступательным
движением буравчика, рукоятка которого вращается в по-
ложительном направлении обхода контура, и отрицатель-
ным, если не совпадает. Так, на рис. 5-9 ток Ц— положи-
тельный, а ток /2— отрицательный. Полный ток 2 / = Ц—/2.
Напряженность поля в точках, расположенных на кон-
туре, имеет в общем случае различное значение. Пред-
положим, что в точке Л (рис. 5-9)
вектор напряженности поля об- Напра£м- П
разует с элементом длины конту-
pa dl угол а. Тогда
Hi = H cos а
— касательная к контуру (тан-
генциальная) составляющая век-
нГ" »
тора напряженности магнитного у
поля. Произведение Ht dl равно
магнитному напряжению на эле- Рис. 5-9 К закону полного
ментарном участке контура dl. тока-
Магнитное напряжение Ht dl по-
ложительно, если направление вектора Hi совпадает с на-
правлением обхода контура, и отрицательно, если направ-
ление вектора Hi противоположно направлению обхода
контура. Эти соображения следует иметь в виду при вы-
числении намагничивающей силы вдоль замкнутого кон-
тура.
Опытным путем установлено, что намагничивающая
сила вдоль контура равна полному току (алгебраической
сумме токов), проходящему сквозь поверхность, ограничен-
ную этим контуром. Эта зависимость и получила название
закона полного тока.
Таким образом,
F = 21 или §Hidl=21.
(5-16)
В некоторых случаях целесообразно контур (который
мы вправе проводить в магнитном поле произвольно)
совместить с магнитной линией, в таком случае вектор
напряженности поля будет направлен по касательной
к контуру, т. е. Hi = Н и^ Н dl = 2/.
Если, кроме того, напряженность поля во всех точках
контура одинакова, то напряженность поля Н в формуле,
189
выражающей закон полного тока, можно вынести за знак
интеграла:
H§dl- 27.
И так как §dl -I, где I — длина замкнутого контура,
то
Hl = ZI. (5-17)
По этой формуле в некоторых случаях весьма просто
определяется напряженность магнитного поля.
5-12. МАГНИТНОЕ ПОЛЕ ПРЯМОЛИНЕЙНОГО ПРОВОДА
С ТОКОМ
Воспользуемся законом полного тока для определения
напряженности магнитного поля вокруг прямолинейного
Рис 5-10 К расчету маг-
нитного поля прямолиней-
ного провода с током
провода с током в произволь-
ной точке А, отстоящей от оси
щовода на расстояние г :> а (а —
{ адиус провода). Проведем ра-
диусом г замкнутый контур во-
круг провода в плоскости, пер-
пендикулярной оси провода.
Во всех точках, удаленных от
оси провода на одинаковое рас-
стояние, напряженность поля
в силу симметрии одинакова по
величине (рис. 5-10).
Так как контур совпадает
с магнитной линией, то вектор
напряженности и его касательная составляющая равны
между собой: Н = Ht.
Полный ток в этом случае равен току в проводе, т. е.
2/ = /, а так как / = 2лг, то
I
2яг
Н
(5-18)
Умножив значение напряженности поля на абсолют-
ную магнитную проницаемость, найдем магнитную индук-
цию:
В = цр0Н = рр0~ = 125р 10 8 [/пл]. (5-19)
190
Имея в виду, что -^- = 2-10 7 ся/л и 1 тл — 104 гс,
можно получить более удобную формулу для В в гауссах:
9/
где /—в амперах, г—в метрах.
Если проводник находится в диамагнитной или пара-
магнитной среде, то с достаточной точностью можно
считать р — 1 и
I 9 1
В = 125 2^'10 8 [тл] ИЛИ В==Тоз -7
Строго говоря, эта формула справедлива для любого
значения г лишь в том случае, если провод имеет бесконеч-
ную длину, однако ею можно воспользо-
ваться и для определения магнитной ин-
дукции, когда длина провода значи-
тельно больше расстояния г.
Пользуясь законом полного тока,
можно определить напряженность поля
и внутри цилиндрического
проведав точке, удаленной от его
оси на расстояние г < а (рис. 5-11).
Плотность тока
Л I 1 Рис 5-11 Магвит-
® ~ ное поле внутри
прямолинейного
одинакова ко всему поперечному сече- провода с током,
нию провода. Выбрав в качестве замкну-
того контура окружность, радиуса г с центром на оси
провода, можно на основании закона полного тока на-
писать уравнение
I 2лг
где 5г = лг2—площадь, ограниченная контуром;
6Sr— полный ток, пронизывающий площадь Sr.
Подставив значение полного тока, получим;
,,__ /яг2 _ /
яа22лг 2л<з2 Г
(5-20)
т. е. напряженность поля в произвольной точке внутри
провода пропорциональна расстоянию г этой точки от
191
оси провода. Следовательно, в центре (при г = 0) Н = 0
и В О.
Напряженность поля на поверхности провода (г —а)
„ I____________/_
м ~ 2лиа а 2ла
наибольшая для данного магнитного поля.
Рис 5-12 График изменения напря-
женности магнитного поля.
Магнитная индукция внутри провода
В= 125р10~8 [тл|.
На рис. 5-12 дан график изменения напряженности
поля внутри и вне провода.
Пример 5-1. Определить напряженность магнитного поля и маг-
нитную индукцию в точках, расположенных на расстояниях 0,2; 0,4
и 1 см от оси прямолинейного провода. Радиус провода а = 0,4 см;
ток в проводе / = 50 а и р = 1.
Точка, лежащая на расстоянии 0,2 см от осн провода, находит-
ся внутри провода:
/г, 50-0.002 .
Hi~ 2лО2 “ 2-3,14-0,0042 °°° а!м’
В1 = р0Н1= 125-1 000-10-8= 125-10-5 12,5 гс.
Точка, лежащая на расстоянии 0,4 см от осн провода, находится
на его поверхности:
/ 40
-тогда-2 000 а!*
Вг = (10Н2= 125-2 000-10-8 = 250-10-5 тл = 25 гс.
192
Наконец, точка, лежащая на расстоянии 1 см от оси провода, на-
ходится за пределами провода:
В.з ^Цо/'Лз125-8ОО-IO'8 -100-10-5 тл - 10 гс.
Индукцию в любой точке магнитного поля токов, про-
ходящих по двум проводам, можно определить, складывая
геометрически векторы магнитной индукции в данной точке:
B Bj в2.
Магнитное поле токов, проходящих по двум проводам,
можно представить как результат наложения магнитных
с токами
полей токов в первом и втором проводах. Поле, окружаю-
щее два параллельных провода с равными токами одного
направления, показано на рис. 5-13, а, поле противополож-
но направленных токов — на рис. 5-13, б.
На том же рисунке построены графики напряженности
поля в точках, лежащих на прямой, соединяющей оси
двух параллельных проводов при одинаковом и при встреч-
ном направлениях токов.
13 Теоретическая электротехника 193
5-13. МАГНИТНОЕ ПОЛЕ КОАКСИАЛЬНОГО КАБЕЛЯ
В некоторых областях электротехники применяются
коаксиальные кабели, состоящие из сплошного провода
1 и трубчатого 2, имеющих общую ось (рис. 5-14). Такую
конструкцию имеют, например, кабели, соединяющие
антенны с телевизорами. По проводам 1 и 2 проходят рав-
Рис. 5-14. Коак-
сиальный кабель.
ные токи противоположного направления.
Рассчитаем магнитное поле кабеля.
Обозначим радиус сплошного провода /?1,
внутренний радиус трубчатого прово-
да и внешний /?3- Применив закон
полного тока, найдем напряженность
магнитного поля в точках, удаленных
от оси кабеля на различные расстоя-
ния г.
1. При г -< по закону полного
тока 1см. (5-20)]
/7 ____L— г
п 2nRf г'
2. При /?)<г<7?2 [см. (5-18)]
3. При /?2 < Г <" R3
Rl-Rl J '
4. При r2>R- полный ток равен нулю и
/7 = 0.
Таким образом, вне коаксиального кабеля магнитное
поле отсутствует.
5-14. МАГНИТНОЕ ПОЛЕ КОЛЬЦЕВОЙ КАТУШКИ
Воспользуемся законом полного тока для определения
напряженности поля в катушке с w витками, намотанной
с равномерной плотностью на кольцевой сердечник
(рис. 5-15).
Благодаря симметрии напряженность магнитного поля
И во всех точках, удаленных от оси кольца на расстояние
г, будет одинакова; поэтому, проведя замкнутый контур,
194
совпадающий с магнитной линией (окружностью радиуса г),
напишем по закону полного тока (5-17):
Hl = Iw, (5-21)
Рис. 5-15. Кольцевая
катушка.
где I = 2лг; Iw — S/, так как поверхность, ограниченную
рассматриваемым контуром, пронизывает w проводников
с током одинакового направления.
Из (5-21) определим напряжен-
ность поля:
Н - . (5-22)
Очевидно, что напряженность
поля имеет отличное от нуля зна-
чение лишь при г>Д, (/?д—внут-
ренний радиус сердечника) и
г < Rz (R2— внешний радиус сер-
дечника). Алгебраическая сумма
токов, проходящих через поверх-
ность, ограниченную контуром,
радиус которого меньше Rt и боль-
ше R2, равна нулю.
Магнитная индукция внутри
катушки (в точке А)
B = ppof/ = HHo-^=125p~-lO-s [тл]. (5-23)
Напряженность поля и магнитная индукция внутри
катушки имеют большее или меньшее значение в зави-
симости от расстояния точки А от центра кольца 0. Мак-
n Iw
симальное значение омакс — ЦЦо магнитная индукция
имеет на внутренней поверхности кольца, а минимальное
йМип М-М.о^^—на внешней. Чем меньше разница меж-
ду Rt и R2, тем ближе по величине Вмакс и Вмин. Маг-
нитная индукция на средней линии кольца
Вс Wo = 125р-^--108, (5-24)
1С ‘С
где /с = 2лДс, a Rc—средний радиус сердечника.
Для сердечника из неферромагнитного материала в фор-
мулах (5-23) и (5-24) можно принять р = 1.
Напряженность магнитного поля внутри кольцевой
катушки (формула (5-22)] численно равна н. с., прихо-
13* 195
дящейся на единицу длины катушки, поэтому напряжен-
ность магнитного поля в какой-нибудь точке А можно
выразить как отношение н. с. на части дуги (Iw') к длине
этой дуги /' (рис. 5-16, а):
,, Iw Iw'
Цилиндрическую катушку (рис. 5-16, б) можно рассма-
тривать как кольцевую бесконечно большого радиуса,
у которой обмотка расположена только на части сердеч-
Рис 5-16. Цилиндрическая катушка.
ника длиной I. Напряженность поля на осевой линии
такой катушки можно определить по той же формуле
Я = —, (5-25)
где Iw—н. с. катушки; I-—ее длина.
Последняя формула является лишь приближенной,
так как в этом случае витки располагаются не по всей
длине катушки; ошибка будет тем меньше, чем длиннее
катушка. Особенно большую ошибку мы получим, если
по этой формуле определим напряженность поля или
магнитную индукцию у краев катушки. Более точно маг-
нитная индукция в точке А на оси катушки конечной
длины (рис. 5-16,6) определяется по формуле
(cospi4-cosp2)- (5-26)
Формулами (5-25) и (5-26) можно пользоваться только
для катушек без сердечника или с сердечником из нефер-
ромагнитного материала.
5-15. МАГНИТНЫЙ МОМЕНТ. НАМАГНИЧЕННОСТЬ
Замкнутый электрический ток в элементарном контуре,
т. е. в контуре весьма малых размеров по сравнению с рас-
196
стояниями до точек, в которых определяется магнитное поле,
называется элементарным электрическим
током или магнитным диполем.
Векторная величина, равная произведению тока i и эле-
ментарной площадки S, ограниченной элементарным кон-
туром с током, и направленная перпендикулярно к этой
площадке согласно правилу буравчика, называется магнит-
ным моментом элементарного электр ическогб тока (рис. 5-17).
Рис. 5-17 Маг-
нитный момент
элементарного
тока.
Рис 5-18. Магнитный
момент тела
Магнитный момент обозначается буквой т и измеряется
в а м2, а • см'1 или а • мм2 в зависимости от выбранной
единицы измерения площади,
т = iS. (5-27)
Геометрическая сумма магнитных моментов всех элемен-
тарных электрических токов (рис. 5-18), например молеку-
лярных токов в веществе (теле), дает магнитный момент
тела (обозначается М), т. е.
М — т, 4- т2 + т3 +
(5-28)
Величина, измеряемая отношением магнитного момента
тела к его объему (V), называется намагниченно-
стью тела (обозначается J),
м
J
(5-29)
Намагниченность тел измеряется в а!м (а • м2,’м3 =
= а/м) или а/см, т. е. в тех же единицах, что и напряжен-
ность магнитного поля.
197
5-16. НАМАГНИЧИВАНИЕ ФЕРРОМАГНИТНЫХ
МАТЕРИАЛОВ
Тела, магнитная проницаемость которых велика (ц > 1),
получили название ферромагнитных. К ферро-
магнитным материалам относятся: железо, сталь, чугун,
кобальт, никель и ряд сплавов (алюминий с никелем и др.).
В практической электротехнике ферромагнитные мате-
риалы (ферромагнетики) имеют очень важное значение.
Стальные сердечники имеют промышленные электрические
машины (генераторы и двигатели), электромагниты, транс-
форматоры, реле, многие измерительные приборы и другие
устройства. Такие сердечники применяются во всех слу-
чаях, когда необходимо при относительно небольших токах
получить сильное магнитное поле.
Сравним, например, индукцию магнитного поля в двух
одинаковых по числу витков и геометрическим размерам
кольцевых катушках с равными токами, одна из которых
имеет деревянный сердечник, а др5гая стальной. Магнит-
ная проницаемость деревянного сердечника р = 1, а сталь-
ного в зависимости от сорта стали и величины тока в катуш-
ке достигает нескольких сотен (у ферромагнитных материа-
лов, как будет показано далее, магнитная проницаемость
непостоянна). Следовательно, в стальном сердечнике мож-
но получить магнитный поток, в сотни раз больший, чем
в деревянном.
Итак, если в магнитное поле внести ферромагнитный
материал, то магнитная индукция поля значительно возрас-
тет. В этом смысле принято говорить, что ферромагнитные
материалы имеют свойство «намагничиваться».
Сущность процесса намагничивания заключается в сле-
дующем.
Ферромагнитное тело делится на очень малые самопро-
извольно (спонтанно) намагниченные области (объем каж-
дой из этих областей около 10” с.и3). Магнитный момент
области обусловливается молекулярными элементарными
электрическими токами. При отсутствии внешнего магнит-
ного поля в ферромагнитном теле элементарные магнитные
моменты направлены самым различным образом и ком-
пенсируют друг друга; суммарный магнитный момент тела
оказывается равным нулю.
Под действием внешнего магнитного поля, создавае-
мого, например, током в катушке, намотанной на стальной
198
сердечник, изменяются направления элементарных магнит-
ных моментов и при усилении внешнего поля увеличивается
магнитный момент тела, т. е. сумма элементарных магнит-
ных моментов, совпадающих с направлением магнитного
поля намагничивающей катушки. Таким образом, появляет-
ся добавочное магнитное поле,
которое складывается с внеш-
ним и усиливает его.
При заданной напряжен-
ности И внешнего магнитно-
го поля в неферромагнитной
среде (р = 1) магнитная ин-
дукция
В0 = ро#- (5-30)
Рис. 5-19. Кривая намагничи-
вания.
В ферромагнитной среде
к этой индукции прибавляет-
ся индукция добавочного магнитного поля р0/, где J—
намагниченность ферромагнетика.
Результирующая магнитная индукция в ферромаг-
нитном материале
В ро (// Н/).
(5-31)
С другой стороны, магнитная индукция связана с на-
пряженностью магнитного поля соотношением
В =-- = .
Отсюда следует, что
Ра -- Ро 1 + •
Намагниченность J ферромагнитного материала не мо-
жет возрастать безгранично. Если направление полей само-
произвольного намагничивания во всех областях окажется
совпадающим с направлением внешнего магнитного поля,
намагниченность среды достигнет своего предельного зна-
чения /нас, называемого намагниченностью на-
сыщения. Характер зависимости J от И Представлен
пунктирной линией на рис. 5-19. Здесь же показано пря-
молинейное возрастание индукции Во по мере увеличения
Н в соответствии с (5-30). Складывая ординаты кривой
р0/ и прямой Во, получим новую кривую зависимости
В (//) — кривую намагничивания. Эта кри-
199
вая может быть разбита на три участка: участок Оа, на
котором магнитная индукция возрастает почти пропорцио-
нально напряженности поля, участок аб, на котором рост
магнитной индукции замедляется и который часто называют
коленом кривой намагничивания, и уча-
сток за точкой б, где зависимость В от И становится почти
Рис 5-20 Кривые наматичивания дтя ста-
ли и чугуна
прямолинейной, но уже с небольшим углом наклона к оси
абсцисс.
Каждый ферромагнитный материал имеет характерную
кривую намагничивания. На рис. 5-20 приведены кривые
намагничивания для различных сортов стали и чугуна.
Впервые ход кривой намагничивания был установлен
в 1872 г. профессором Московского университета А. Г. Сто-
летовым. Работа А. Г. Столетова имеет громадное практи-
ческое значение для расчета магнитных цепей электри-
ческих аппаратов и машин.
Непрямолинейный характер изменения J в зависимости
от И, представленный на рис. 5-19, показывает, что отноше-
200
ние ЛИ не является постоянной величиной. С увеличением
Н это отношение вначале весьма быстро возрастает (начало
участка Оа'), затем его рост замедляется, в небольшом
интервале Н оно остается практически постоянным и, нако-
нец (за точкой б'), начинает падать, асимптотически прибли-
жаясь к нулю. Подобный же характер зависимости от Н
имеет абсолютная магнитная
проницаемость
Ра ~ Цо ,
которая при И->со асимпто-
тически стремится к р0. Деля
обе части последнего соотно-
шения на р(, получим выра-
жение магнитной проницае-
мости:
р 1+4 • <5-32)
2500
гиоо
1500
1000
500
° 5 Ю 15 20 25а/см
Рис 5-21 Магнитная прони-
цаемость стали.
Примерный график зави-
симости ц от Н представлен
на рис. 5-21. Как видно из этого графика, магнитная про-
ницаемость ферромагнитного материала изменяется при
изменении напряженности поля (например, в результате
изменения тока в намагничивающей катушке) в весьма
широких пределах. Поэтому эта величина во многих слу-
чаях малопригодна для практических расчетов магнитного
поля в ферромагнетике.
5-17. ЦИКЛИЧЕСКОЕ ПЕРЕМАГНИЧИВАНИЕ
Магнитное состояние ферромагнетика, подвергающего-
ся переменному намагничиванию, характеризуется гисте-
резисным циклом. Допустим, что кольцевой сердечник
(рис. 5-15) до включения тока не был намагничен
(В = 0, точка О на рис. 5-22). Затем мы постепенно уве-
1 т
личиваем ток, пока напряженность поля Н ~ при
максимальном токе 1а не достигнет значения На, которой
соответствует значение магнитной индукции Ва (рис. 5-22).
Доведя намагничивание до некоторого значения индукции
Ва, будем уменьшать ток и напряженность магнитного
поля. Кривая, изображающая изменение магнитной индук-
201
ции в этом случае, не совпадет с кривой первона-
чального намагничивания Оа, а пойдет не-
сколько выше, и для одного и того же значения Н величины
В при намагничивании и размагничивании будут различ-
ными.
Когда ток и напряженность поля будут равны нулю,
магнитная индукция сохранит некоторое значение, назы-
ваемое остаточной индукцией (Об на рис. 5-22).
Таким образом, величина магнитной индукции зависит
не только от напряженности поля, но и от предварительного
Рис. 5-22. Гистерезисный цикл.
состояния намагничивания, в котором находился материал.
Это явление называют магнитным гистерези-
сом.
Чтобы довести магнитную индукцию до нуля, нужно
изменить направление тока в обмотке и создать поле с напря-
женностью Нв, которая называется коэрцитивной
силой. При дальнейшем росте напряженности поля сер-
дечник намагничивается в противоположном направлении,
и при напряженности поля Нг = — На магнитная индук-
ция Вг ~—Ва. Если теперь довести напряженность поля
снова до нуля, то магнитная индукция достигнет значения
Bg=—В6. При вторичном изменении направления тока
и увеличении напряженности поля до прежней величины
На индукция увеличивается почти до прежнего значения Ва-
В результате повторного циклического перемагничи-
вания магнитная индукция изменяется в зависимости от
202
напряженности поля по замкнутой кривой абвгдеа, которая
называется гистерезисным циклом (петля ги-
стерезиса). Следует заметить, что свою окончательную фор-
му кривая получает после нескольких циклов перемагни-
чивания при одном и том же значении На.
При различных максимальных значениях напряженно
сти магнитного поля гистерезисные циклы оказывают^
Рис. 5-23. Основная кривая намагничи-
вания.
как бы вложенными друг в друга (рис. 5-23). Геометри-
ческое место их вершин дает кривую, которая называется
основной кривой намагничивания и при-
мерно совпадает с кривой первоначального намагничи-
вания.
Ферромагнитные материалы разделяются на магни-
тно-мягкие и магнитн о-ж е с т к и е. У маг-
нитно-мягких материалов восходящая (гдеа) и нисходя-
щая (абвг) ветви петли гистерезиса почти сливаются с основ-
ной кривой намагничивания, у магнитно-жестких, наоборот,
резко расходятся; на рис. 5-20 даны основные кривые
намагничивания.
Циклическим перемагничиванием можно воспользо-
ватьсядляразмагничиваниясердечника (у размагниченного
сердечника В = 0). Для этого на образец воздействуют
переменным по направлению и постепенно уменьшающимся
по величине магнитным полем.
Перемагничивание ферромагнитного сердечника связа-
но с затратой энергии (потери от гистерезисе). Можно
доказать, что потери энергии в ферромагнитном материале
203
за полный цикл перемагничивания выражаются (в опре-
деленном, конечно, масштабе) полной площадью петли гисте-
резиса. Если учесть, что при циклическом перемагничива-
нии ферромагнитные сердечники нагреваются, то становится
очевидным, что затрачиваемая при этом энергия превра-
щается в тепло. Это тепло обычно никак не используется.
Поэтому энергию, затрачиваемую на перемагничивание,
называют потерями энергии от гистере-
зиса.
5-18. МАГНИТНОЕ ПОЛЕ НА ГРАНИЦЕ РАЗДЕЛА
ДВУХ СРЕД С РАЗЛИЧНОЙ МАГНИТНОЙ
ПРОНИЦАЕМОСТЬЮ
Магнитный поток, переходя из одной среды в другую,
не изменяется по величине (линии магнитной индукции
непрерывны). Однако если магнитная проницаемость одной
среды отличается от магнитной проницаемости другой,
то значения магнитной индукции
в той и другой средах окажутся
в общем случае различными.
Пусть 3 (рис. 5-24) — не-
большая плоская площадка на
поверхности раздела двух сред
с магнитными проницаемостями
Рис. 5-24 Изменение ин-
дукции магнитного поля
на границе раздела двух
сред.
Pi и р2.
Магнитный поток Ф направ-
лен из первой среды во вторую.
В силу непрерывности магнит-
ного потока
или
В. cos «13-= B2 cos а23,
где Bai и ВН2 — нормальные составляющие векторов маг-
нитной индукции в первой и во второй
средах.
Произведя сокращение, получаем Bt cos at — В2 cos a2,
т. e. Btll — B„2 или
Pf/71 cosat — р2Д2 cosas. (5-33)
Напряженность поля в каждой среде можно характери-
зовать вектором, совпадающим по направлению с вектором
магнитной индукции. Докажем, что составляющая вектора
204
напряженности поля, параллельная плоскости раздела
(касательная составляющая Hi), имеет по обе стороны
площадки (рис. 5-25) одинаковые значения.
Напишем уравнение по закону полного тока для замкну-
того контура небольшой длины 2/, обозначенного пунктир-
ной линией, близко прилегающего к нашей площадке.
Контур будем обходить по направлению движения часовой
стрелки. Так как при таком обходе сцепления с током нет
Рис. 5-25. Изменение напряжен-
ности магнитного поля на грани-
це раздела двух сред.
Рис. 5-26. К примеру 5-2.
(внутри контура отсутствуют токи), то Нц1 — Н121 ~ О,
откуда Нц = Hi2 или
//j sin cq — Н2 sin а2. (5-34)
Теперь можно установить зависимость между углами
а, и а2, образованными векторами магнитной индукции
или векторами напряженности поля и нормалью к поверх-
ности раздела S.
Разделив почленно уравнение (5-34) на уравнение (5-33),
получим:
Hi sin а, _ Н2 sin <х2
Pj/fjCOSCtj — p2/f2cos<X2 ’
откуда
При переходе потока из ферромагнитной среды (щ)
в другую неферромагнитную (р2) или наоборот магнитная
индукция в иеферромагнцтной среде у поверхности раз-
дела направлена практически перпендикулярно к поверх-
ности раздела. Действительно, из (5-35) tga2 ——-tga(,
а так как р( > Рг> т« tg а2 «О и а2л? 0.
205
Пример 5-2. Магнитная проницаемость стали при заданной на-
пряженности поля р, = 1 500. Вектор магнитной индукции в стали
составляет с нормалью к поверхности раздела угол а, = 88° или
угол с поверхностью раздела р( = 90—88° = 2°. Определить угол,
который образует вектор магнитной индукции в воздухе с нормалью
к поверхности раздела (рис 5-26):
tg «2 = tga^ Т5оо" 88° - та- °’019;
а2=Р06', а р2~=90° — а2 88'54'.
5-19. МАГНИТНАЯ ЦЕПЬ
Рис 5-27. Неразветв-
ленная магнитная цепь.
Магнитной цепью называется устройство, в котором
замыкается магнитный поток. Простейшей магнитной цепью
является сердечник кольцевой катушки (рис. 5-15). У элек-
трических машин, трансформато-
ров, электроизмерительных прибо-
ров магнитная цепь имеет более
сложнуюформу. Отдельные участки
магнитной цепи выполняются из
различных материалов (главным
образом из ферромагнитных) и в об-
щем случае имеют разную длину
и различное сечение.
Так же как и электрические
цепи, магнитные цепи бывают н е-
разветвленные (рис. 5-15
и 5-27), которые можно рассматри-
вать как одну трубку магнитной индукции, и развет-
вленные (рис. 5-28 и 5-29). В неразветвленной магнитной
цепи магнитный поток во всех сечениях имеет одно и то же
значение.
Разобьем магнитную цепь на ряд однородных участков,
каждый из которых имеет одинаковое поперечное сечение
и выполнен целиком из одного материала. За длины участ-
ков /j и /2 и т. д. примем соответствующие длины средней
магнитной линии.
Практически в любой точке данного сечения реальной
магнитной цепи напряженность магнитного поля, а значит,
и индукцию можно считать одинаковыми и равными значе-
ниям И и В в этом же сечении на средней линии (однород-
ное поле). Для однородного поля Ф = BS и так как Ф1 —
Ф2 и т. д., то BjSj — B2S2 и т. д.
20о
Магнитное напряжение на любом из участков магнитной
цепи
или
(7И=Ф'/?М. (5-36)
Величина /?м ——Ц- называется магнитным со пр о-
уивлением участка магнитной цепи.
Зависимость (5-36) сходна с законом Ома и обычно
непосредственно для расчета магнитной цепи почти непри-
менима, так как магнитная проницаемость ферромагнитных
материалов непостоянна.
При расчетах магнитных цепей обычно пользуются пер-
вым правилом Кирхгофа для магнитной цепи, которое выте-
кает из свойств непрерывности магнитного потока и маг-
нитных линий: алгебраическая сумма магнитных потоков
в точке разветвления равна нулю:
2Ф - 0. (5-37)
На основании закона полного тока можно сформулиро-
вать второе правило Кирхгофа для магнитной цепи: алгебраи-
ческая сумма магнитных напряжений на отдельных участ-
ках цепи равна алгебраической сумме намагничивающих сил:
ZUM = ZF = XIw. (5-38)
Для создания относительно большого потока при задан-
ной н. с. нужно магнитную цепь выполнить с возможно
меньшим магнитным сопротивлением. Наименьшим магнит-
ным сопротивлением обладают ферромагнитные материалы,
так как у них относительно велика магнитная проницае-
мость; поэтому во всех электрических машинах и аппаратах
магнитная цепь выполняется таким образом, чтобы поток
замыкался главным образом по стали, а воздушные зазоры
выполняются достаточно малыми.
5-20. МАГНИТНЫЕ ЦЕПИ ЭЛЕКТРИЧЕСКИХ МАШИН
На рис. 5-28 схематически показана магнитная цепь
двухполюсной электрической машины.
Линия 00' делит магнитную цепь на две одинаковые
части, каждая из которых является магнитной трубкой
207
с потоком Ф/2. Намагничивающая сила определяется током,
проходящим по обмотке возбуждения (О. В.). Магнитный
поток Ф.'2 замыкается через станину (С), полюсы (7Z),
полюсные наконечники (77. Н.), воздушные зазоры и якорь
(Я). Полюс, из которого выходят магнитные линии, назы-
вается северным (Л'), а в который входят,— южным (S).
Многие электрические машины имеют магнитную цепь
в виде двух стальных цилиндров, имеющих общую ось
(рис. 5-29) и отделенных друг от друга небольшим воздуш-
Рис 5-28. Магнитная Рис. 5-29. Магнитная цепь
цепь электрической ма- электрической машины,
шииы.
ным зазором. Обмотка возбуждения располагается на вну-
треннем вращающемся цилиндре, обычно называемом рото-
ром (Р). Наружный неподвижный цилиндр носит назва-
ние статор а (С). При наличии тока в обмотке возбужде-
ния в магнитной цепи возникает магнитный поток, замы-
кающийся по ротору, воздушному зазору и статору. Места
выхода линий магнитной индукции из ротора является север-
ным полюсом, а место входа — южным.
5-21. РАСЧЕТ МАГНИТНОЙ ЦЕПИ
Расчет неразветвленной магнитной цепи (рис. 5-27) часто
заключается в определении и. с. по заданному магнитному
потоку (или магнитной индукции) и размерам цепи. Для
определения н. с. нужно вначале, разбив магнитную цепь
на участки, вычислить для каждого участка значения маг-
нитной индукции (Вь В2, В3 и т. д.), после чего по кривым
208
намагничивания найти значения напряженности магнит-
ного поля для этих участков цепи.
Для участков из неферромагнитного материала (воз-
душных зазоров) напряженность поля в а'м определяется
не по кривым намагничивания, а по формуле —,
Но
причем Яо = ’ если 8° задан0 8 тл’ или
Н0 = 80В0, если Во задано в гауссах, и, наконец,
До (а/си] — О,8Во [гс]. (5-39)
Намагничивающая сила находится по закону полного
тока. Сумма магнитных напряжений для отдельных уча-
стков
/Д/,//2/2-г Яо4 + • • • -
На рис. 5-30 представлена разветвленная магнитная
цепы магнитный поток Фа делится здесь на два магнитных
потока: Фв и Фв. Если
участки Б и В совершенно
одинаковы, то Фв = Ф д;
в таком случае магнитная
цепь называется с и мм ет- ф
р и ч н о й. 2
Для расчета разветвлен-
ной симметричной магнит-
ной цепи применяется сле-
дующий прием: цепь делят
по оси симметрии (00' на
рис. 5-30) на отдельные Рис. 5-30 Разветвленная снм-
части (в нашем примере - метричная магнитная цепь,
на две части). Каждая из
полученных частей магнитной цепи рассматривается как
магнитная трубка, во всех сечениях которой поток оди-
наков. Применяя закон полного тока, легко определить
н. с. аналогично тому, как это было сделано при расчете
неразветвленной магнитной цепи.
Пример 5-3. Определить н. с. катушки, расположенной на сред-
нем стержне (рис. 5-31), с тем, чтобы в нем получить магнитную
индукцию Bj — 14 000 гс. Размеры (мм) указаны на чертеже. В ме-
стах стыка воздушный зазор 0,1 мм. Материал сердечника — электро-
техническая сталь.
Разделив сердечник по оси АБ на две симметричные части,
проведем в одной нз них среднюю магнитную линию. По рисунку
14 Теоретическая электротехника 209
определим длину линии в каждом участке магнитной цепи. Так как
магнитный поток во всех участках имеет одинаковое значение, опре-
делим магнитную индукцию в каждом участке по формуле
где, например, Si=—<7—=-45 см2—половина площади попереч-
ного сечения среднего стержня.
Рис. 5-31. Магнитная цепь к примеру 5-3.
Заданные величины и результаты расчета записываем в табл. 5-1.
Таблица 5-1
№ участ- ков Материал В, гс 1, см ajcM а
I Электротехническая 14 000 25 20 500
сталь
11 и 111 То же 11 200 66,5 6 399
IV Воздух (зазор а) 14 000 0,01 И 200 112
V Воздух (зазор б) 11 200 0,01 8 960 90
Таким образом, искомая н С.
= — \ 101 а.
Обратная задача расчета магнитной цепи, а именно —
определение- магнитного потока в данном сердечнике при
заданной н. с. — решается несколько сложнее.
Рассмотрим порядок этого расчета на примере.
210
Пример 5-4. На замкнутом сердечнике из листовой электротех-
нической стали, размеры которого даны на рис. 5-32, расположена
обмотка, имеющая 1 000 витков, по которой проходит ток 4 а. Опре-
делить магнитный поток при условии, что в месте каждого стыка
воздушный зазор составляет 0,25 мм.
Эту цепь можно рассматривать как цепь, составленную из двух
частей: воздушного зазора, в котором между Ф и (/Ом существует
Рис. 5-32. Магнитная цепь к примеру 5-4.
линейная зависимость, и стального сердечника, в котором зависи-
мость между Ф и нелинейна.
Пользуясь кривой намагничивания стали (рис. 5-20), построим
для нелинейного элемента цепи «магнитную характеристику», т. е.
зависимость Ф((/м). Для этого определим по чертежу (рис. 5-32)
длину средней магнитной линии по стали Z = 480 ai,h = 48 см и пло-
щадь поперечного сечения сердечника S = 16 см2, затем умножим
значения И, отложенные по оси абсцисс графика В (Н), на 48 см,
а значения В — на 16 см2 и по полученным данным (табл^ 5-2)
построим магнитную характеристику для стали Ф (UM) (рис. 5-33).
Таблица 5-2
С/ = HI, а м 960 1 440 1 920 2 440 2 840 3 320
Ф = В5, мкс 224 000 240 000 253 000 259 000 262 000 264 000
С другой стороны, U „ для стали аналогично (4-8): t/M= Iw—Ф/?ом, (5-40)
где —магнитное сопротивление воздушных зазоров. В нашем
примере
р 10 _ Ю~3__________ 10* 1
°* p0S 4л-10~7-16-10-4 64л гн ’
Уравнение (5-40) линейное и графически представляется прямой
линией. Для построения этой прямой зададимся Ф =0, при этом U„ —
=/а» = 4000 а. Отложив по оси абсцисс отрезок, пропорциональный
[4* 211
Iw--- 4000 а, получим точку А. При l/M~0 получим магнитный
поток
Фо = = - Д4°д° = 0,008 йб.-^ 800 000 л<лг=8()0 к мкс.
Rom 108/64л
Отложив по осн ординат отрезок, пропорциональный Фо, отме-
тим точку 5. Соединив точки А и Б прямой, получим график урав-
нения (5-40). Прямая АБ пересекается с магнитной характеристи-
кой в точке Г (рис. 5-33). Ордината точки Г определяет искомый
магнитный поток, который в нашем случае составляет 270 000 мкс.
Этому значению потока соответствует магнитная индукция
п 270 000 _ о „ „о
В =----—— = 16 800 гс = 1,68 тл.
I b
Для расчета обратной задачи в случае разветвленной
магнитной цепи, как правило, требуется выполнить гра-
фические построения.
5-22. ПОСТОЯННЫЕ МАГНИТЫ
Для создания магнитного поля в электроизмеритель-
ных приборах и аппаратах часто применяются посто-
янные магниты.
Постоянные магниты выполняются из магнитно-жестких
ферромагнитных материалов, обладающих высокой остаточ-
212
ной индукцией и большой коэрцитивной силой. Свойства
постоянного магнита характеризуются кривой размагни-
чивания гистерезисного цикла, показанной на рис. 5-34.
Эта кривая может быть получена при намагничивании
до насыщения замкнутого сердеч-
ника изферромагнитного материала
с последующим размагничиванием
до нуля.
Качество материала, исполь-
зуемого для изготовления магни-
тов, в некоторой степени опреде-
ляется произведением остаточной
индукции (Вг) и коэрцитивной си-
лы (//с). Чем больше это произве-
дение, тем лучше подходит магнит-
ный материал для изготовления
Рис. 5-34. Кривая раз-
магничивания гистере-
зисного цикла.
постоянных магнитов.
Обычно постоянный магнит не
замкнут. Магниту придают различ-
ную форму, присоединяя к его кон-
цам (полюсам) «арматуру» из магнитно-мягкой стали. На
рис. 5-35 изображены два армированных постоянных магнита
различной формы, применяемые в измерительной технике.
Рис. 5-35 Армированные
постоянные магниты.
Рис. 5-36 Подковообразный маг-
нит с якорем.
Воздушный зазор между полюсами магнита приводит
к уменьшению магнитной индукции по сравнению с остаточ-
ной индукцией в замкнутом сердечнике. Так, например,
если мы в подковообразном сердечнике, который замкнут
якорем нз магнитно-мягкой стали (рис. 5-36, а), получим
остаточную индукцию Вт, то при удалении якоря на рас-
213
стояние /0 (рис. 5-36, б) индукция в сердечнике уменьшится
до значения В№. Уменьшение магнитной индукции можно
объяснить следующим образом.
Совместим замкнутый контур со средней магнитной ли-
нией, проходящей через сердечник и якорь, и напишем
для контура уравнение по закону полного тока:
H^Jm Ч- 2/7о/о -4- НЯ1Я — 0, (5-41)
Рис. 5-37. Индукция и
напряженность магнит-
ного поля постоянного
магнита.
где Нм — напряженность поля в сердечнике магнита;
Но—напряженность поля в воздушном зазоре;
Ня— напряженность поля в якоре;
1м, /0 и /я —соответствующие длины участков.
Если якорь выполнен из стали с высокой магнитной
проницаемостью, то магнитным напряжением НЯ1Я по срав-
нению с 27УО/О в уравнении (5-41)
можно пренебречь.
В таком случае
Н м^м = О,
откуда
Н^-Н^. (5-42)
В воздушном зазоре Во = р0 Но
и векторы индукции и напряжен-
ности имеют одинаковое направле-
ние. Магнитные линии непрерывны,
и направление вектора индукции
в сердечнике совпадает с направле-
нием вектора индукции в зазоре
(рис. 5-37). Как показывает выра-
жение (5-42), направление вектора
напряженности в сердечнике об-
ратно направлению вектора напря-
женности в зазоре, т. е. обратно вектору магнитной ин-
дукции в сердечнике. Это равноценно размагничивающему
действию тока, который нужно было бы пропустить в об-
ратном направлении по обмотке магнита, замкнутого яко-
рем (рис. 5-36,а). Таким образом, воздушный зазор ока-
зывает размагничивающее действие на постоянный магнит.
Соединив точку А на петле гистерезиса (рис. 5-34), коор-
динаты которой Ни и Вм, с началом координат, мы получим
214
угол а между этой прямой и осью ординат, тангенс которо-
го назовем коэффициентом размагничива-
ния (N). Таким образом,
2V=tga-=bjMl
°м
Зная коэффициент размагничивания и гистерезисную
кривую для материала, из которого изготовлен магнит,
можно найти индукцию в магните. Рассмотрим приближен-
ное определение N для нашего примера. Примем индукцию
в зазоре Во равной индукции в сердечнике Вм (считая сече-
ние зазора равным сечению сердечника); тогда
1М
Вм
Ко
2£о
откуда
дг — I I =_____L.
Вщ Ио
(5-43)
Таким образом, коэффициент N тем больше, чем короче
магнит, и зависит от величины воздушного зазора.
Для изготовления постоянных магнитов применяются
вольфрамовые, хромистые и кобальтовые стали, а также
сплавы железа с алюминием, никелем, медью и кобальтом.
В табл. 5-3 приведены материалы, применяемые для
изготовления магнитов, и значения Вг и Нс.
Таблица 5-3
Материал
Состав, % (остальное железо)
Вольфрамовая сталь
Хромистая сталь . .
Кобальтовая сталь . .
Альни .............
Альииси ...........
Альнико ...........
Магнико............
14
14
10
8
— —. 4 800 1
3 — — — —. 4 800 0,9
5 5 — — — 7 200 0,9
— .— 25 5 — 44 000 0,44
— — 34 — 1,0 64 000 0,4
12 17 6 —. 40 000 0,7
— 24 13 3 — 44 000 1,25
215
5-23. ЭЛЕКТРОМАГНИТНАЯ СИЛА
Поместим в магнитное поле прямолинейный провод
(рис. 5-38) длиной I и пропустим по нему ток /, подведя
его при помощи гибких проводников (подводящие провода
на рис. 5-38 не показаны). Из этого опыта легко убедиться
Рис 5-38 Действие магнитного поля на
прямолинейный провод с током
в том, что на провод с током действует сила, получившая
название электромагнитная сила (обозначение F).
Направление этой силы перпендикулярно как направлению
линий магнитной индукции, так и направлению тока, а вели-
чина пропорциональна величине тока / и длине провода I.
Однако даже при одинаковом токе и одинаковой длине
провода на провод действует не одинаковая электромагнит-
ная сила в различных магнитных полях или в отдель-
ных местах одного и того же магнитного поля; это указы-
вает на зависимость силы от магнитной индукции по-
ля В.
Сила, действующая на отрезок провода с током, имеет
наибольшее значение, если направления тока и вектора
магнитной индукции В взаимно перпендикулярны
(рис. 5-38). В этом (и только в этом) случае справедливо
соотношение
F — IIB.
(5-44)
216
Зависимость (5-44) используется для измерения магнит-
ной индукции. Выразив магнитную индукцию
F
П
В —
получим, что магнитная индукция измеряется силой, кото-
рая действует на провод единичной длины, по которому
проходит ток, также равный единице.
Если расположенный в однородном магнитном поле про-
водник поворачивать так, чтобы
зованный направлением тока и
Рис 5-39. Правило левой
руки.
изменялся угол а, обра-
направлением магнитных
линий, то при неизмен-
ных В, I и I сила, дей-
ствующая на провод,
изменяется пропорцио-
нально sin а. Когда про-
Рис. 5-40 Криволиней-
ный провод с током в
магнитном поле.
вод расположен параллельно вектору магнитной индук-
ции (а = 0), сила равна нулю.
Следовательно, в общем случае
F = llBsma. (5-45)
Для определения направления силы, с которой поле
действует на провод с током, очень удобно «правило левой
руки». Если ладонь левой руки повернуть так, чтобы вектор
магнитной индукции входил в нее, а четыре вытянутых
пальца совпадали с направлением тока в проводе, то отогну-
тый большой палец укажет направление силы, действую-
щей на провод (рис. 5-39).
Рассмотрим определение’ силы F в общем случае.
Силу, действующую на провод произвольной формы,
расположенный в неоднородном магнитном поле, можно
217
определить как геометрическую сумму элементарных сил
dF, действующих на отдельные элементы длины провода dl.
Провод бесконечно малой длины dl можно считать пря-
молинейным, а магнитное поле, в котором он располагает-
ся,— однородным (рис. 5-40), поэтому
dF — 1 dl В sin а,
а сила, действующая на участок провода длиной I,
F = j dF. (5-46)
i
магнитном поле находится прямоли-
расположенный перпендикулярно на-
правлению поля; ток в прово-
де 100 а, индукция В — бОООгс.
Определить силу, действующую
на провод.
Сила
F = IlB sin а =
= 100-0,5-^-1=30 н.
м,
Пример 5-5. В однородном
нейный провод длиной 0,5
параллельных проводов с токами.
5-24. ЭЛЕКТРОМАГНИТНЫЕ
СИЛЫ, ДЕЙСТВУЮЩИЕ НА
ПАРАЛЛЕЛЬНЫЕ ПРОВОДА
С ТОКАМИ
Определим силы взаи-
модействия двух проводов
с токами, учитывая, что
провод с током /2 нахо-
дится в магнитном поле
тока Iiи, наоборот, провод
с током Ii—- в магнитном
поле тока /2 (рис. 5-41).
Если расстояние I, на котором провода идут параллель-
но друг другу, значительно больше расстояния между
проводами а, то по формуле (5-19) индукция магнитного
поля тока /1 в тех точках, где расположен второй провод,
В, = ИИотД- •
1 2ла
Направление вектора Bt перпендикулярно плоскости,
в которой расположены провода, и определяется по пра-
вилу буравчика.
218
На второй провод действует сила
F2 = B,lh = W^l. (5-47)
В свою очередь первый провод находится в магнитном
поле тока /2, причем В2 = ри0 , а сила, действующая
на первый провод,
по величине равна силе F2 даже при В} В2, т. е. Ц 12.
Направления сил Fi и F2 определяются по правилу
левой руки. При этом оказывается, что провода с токами
одинакового направления притягиваются друг к другу,
а провода с токами противоположного направления оттал-
киваются друг от друга.
Для практических расчетов удобнее подсчитывать силу,
действующую на единицу длины проводов:
Fo = у = ННо • (5-48)
Подставляя в эту формулу значение магнитной постоян-
ной |ло 4л-1О-7 гн!м для воздуха (считая р=1), полу-
чаем силу в ньютонах на метр:
p (5-49)
и 2л а а ’ ' '
где 11 и 1г—в амперах, а—в метрах.
Преобразуя формулу (5-48), при /4==/2 находим:
/2 F^ia . (5 50)
Сила взаимодействия между проводами достигает осо-
бенно больших значений при коротких замыканиях в элек-
трической цепи.
Пример 5-6. Чему равны одинаковые токи в двух параллельных
проводах, которые расположены на расстоянии 20 см, если на каждый
метр провода действует сила 100 н/мЭ
Подставляя в (5-50)
р.о = 4л-1О_7 гн/м,
получим:
219
5-25. РАБОТА ЭЛЕКТРОМАГНИТНЫХ СИЛ
Выше было установлено, что на прямолинейный провод
с током, внесенный в однородное магнитное поле, действует
сила
F - ВИ sin а
или 192
F ВИ,
Пусть под
в направлении
этой
Работа элек-
Рис. 5-42.
тромагнитных сил.
если провод расположен перпендикулярно направлению
магнитных линий.
гм силы F провод перемещается
ы на расстояние Ь (рис. 5-42). При
перемещении провода производится
работа
Д. Fb-BIlb. (5-51)
Произведение lb равно площад-
ке S, описанной проводом при его
движении перпендикулярно на-
правлению поля, а произведение
BS — магнитному потоку Ф сквозь
площадку S. Таким образом,
А = BIS - 7Ф, (5-52)
т. е. механическая работа, совер-
шаемая при перемещении провода
с неизменяющимся током в магнитном поле, равна произ-
ведению тока и пересеченного проводом магнитного по-
тока. Под выражением «пересеченный магнитный поток»,
мы понимаем произведение магнитной индукции на пло-
щадь, очерченную проводом при его движении.
Пример 5-7. В однородном магнитном поле (5= 10 000 гс) пер-
пендикулярно его направлению расположены на расстоянии ( = 0,5 л
Рис. 5-43. К примеру 5-7.
два параллельных рельса длиной b — 3,6 м (рис. 5-43) По рельсам
может перемещаться провод, на котором укреплен снаряд с массой
220
кг. Какой ток нужно пропустить по цепи, чтобы
покидая рельсы, развивал скорость о = 60 м!сек>
Кинетическая энергия, приобретенная снарядом к
вылета,
снаряд»
моменту
w. /по2 1 • 602 , ол_ ,
W = —~ — —-—= 1 800 дж.
2 2
Эта энергия приобретается за счет работы перемещения в магнит-
ном поле несущего снаряд провода с
током. Таким образом,
—=./ф,
2
откуда
Рис. 5-44. Перемещение
криволинейного провод-
ника в магнитном поле.
Формулу (5-52) можно приме-
нять для расчетов и в более общем
случае. Пусть в неоднородном маг-
нитном поле перемещается провод
произвольной формы с неизменяю-
щимся током (рис. 5-44). Работа,
производимая при перемещении
элемента длины провода dl в направлении действующей
силы,
dA = dF db == Bl dl sin a db,
но так как
dldb—dS,
a
3T n
j — a = ₽.
где p—угол между вектором В и прямой, перпендику-
лярной элементу dl и силе dF (пунктирная прямая), т. е.
перпендикулярной площадке dS, то
sin a cos р.
Проекция вектора В на эту прямую, т. е. нормаль к dS,
Вп = В cos р = В sin а,
а произведение BHdS есть поток пересечений элементом
при перемещении на расстояние db, т. е.
= Вп dS = В dS sin а.
Таким образом, работа
dA = /В„dS - 1d(D.
221
Мы пришли бы к такому же выражению элементарной
работы, если бы рассматривали перемещение элемента про-
водника под некоторым углом к направлению силы. В этом
случае удобно перемещение db разложить на два взаимно
перпендикулярных перемещения: одно — в направлении
силы, другое — в перпендикулярном направлении. Работа
производится лишь при первом перемещении, которое мы
и рассматривали. Полная работа, совершенная при пере-
мещении в магнитном поле проводника длиной /,
ф
А = I d& = /Ф,
о
что совпадает с (5-52). В последнем выражении, как и рань-
ше, Ф означает поток через ту площадь, которую зачерчи-
вает провод при движении, т. е. поток, который пересечет
провод при движении.
5-26. РАБОТА ЭЛЕКТРОМАГНИТНЫХ СИЛ
ПРИ ПЕРЕМЕЩЕНИИ КОНТУРА С ТОКОМ
Любой проводник может обтекаться током лишь при
условии, что он входит составной частью в замкнутый
контур.
Как следует из уравнения (5-52), при перемещении кон-
тура с током силами поля совершается работа лишь при
условии изменения потока
сквозь контур. Рассмотрим,
например, прямоугольную
рамку с током I в неоднород-
ном магнитном поле (рис. 5-45),
где направления сил получены
в соответствии с правилом ле-
вой руки, а источник питания
рамки не указан. Магнитные
линии, пронизывающиерамку,
направлены от наблюдателя.
Пусть магнитная индукция
слева направо, т. е. Fz = F4
Рис. 5-45. Контур с током в
магнитном поле.
возрастает в направлении
и F3 > Ft. Нижняя и верхняя стороны рамки в этом случае
находятся в одинаковых условиях, и результирующая сила
совпадает по направлению с F3. Условимся считать ток кон-
тура положительным, а магнитный поток сквозь контур
222
положительным или отрицательным, смотря по. тому, соот-
ветствуют ли направления I и Ф правилу буравчика или
нет. В нашем случае поток положителен, а его абсолютная
величина при перемещении контура вправо возрастает.
Так как работа, совершаемая при движении сторон
бв и аг, равна нулю (угол между направлениями силы
и перемещения равен 90°), то
А - ~ Ааб + Авг,
причем сумма эта алгебраическая,
так как составляющая Даб отрица-
тельна (перемещение совершается
против силы Ft).
Таким образом,
Л = — 1Ф’ + 1Ф" =--- /АФ, (5-53)
где АФ—разность магнитных пото-
ков Ф" и Ф', пересеченных сторо-
Рис. 5-46. Положе-
ние контура с током,
при котором поток по-
ложительный и мак-
симальный.
нами контура вг и аб, или разность значений потоков
сквозь контур в конце и в начале движения
АФ = Ф2—Ф
(5-54)
где Ф2—поток, пронизывающий контур в конечном его
положении;
Ф! — начальное значение потока, пронизывающего кон-
тур.
Если работа производится силами поля, то контур
переместится вправо (Г3>В}) и приращение АФ положи-
тельно (Ф.,>Ф,).
При движении контура под действием сил поля магнит-
ный поток сквозь контур всегда имеет положительное при-
ращение. Рассмотренное явление позволяет сделать весьма
важный практический вывод. Всякий контур с током,
помещенный в магнитное поле, под влиянием сил взаимо-
действия поля с током стремится занять положение, при
котором поток, пронизывающий контур, оказался бы поло-
жительным и максимальным. Так, например, на виток с то-
ком в однородном магнитном поле действует вращающий
момент. Под действием этого момента виток стремится
занять такое положение, при котором плоскость витка
перпендикулярна направлению внешнего магнитного поля.
По достижении устойчивого положения силы, действую-
щие на контур, стремятся только растягивать его так,
223
чтобы проходящий через контур магнитный поток еще
увеличился (рис. 5-46).
Если виток с током находится в неоднородном магнит-
ном поле, то, кроме вращательного движения, возникает
и поступательное — в направлении к участкам поля с наи-
большей индукцией (конечно, если виток под действием
сил поля может вращаться и перемещаться).
При отрицательном приращении магнитного потока
сквозь контур совершаемая механическая работа отрица-
тельна, т. е. происходит не под действием сил поля, а под
действием направленных противоположно внешних сил.
5-27. МАГНИТОЭЛЕКТРИЧЕСКИЙ ИЗМЕРИТЕЛЬНЫЙ
МЕХАНИЗМ
Для измерения тока, напряжения, сопротивления, магнитного
потока, магнитной индукции и магнитного напряжения применяются
приборы, основной частью
Рис. 5-47. Магнитоэлек-
трический измеритель-
ный механизм.
которых является магнитоэлектрический
измерительный механизм. Магнитная цепь
измерительного механизма (рис. 5-47)
состоит из постоянного магнита A'S,
к концам которого прикреплены стальные
пластины и полюсные наконечники (баш-
маки) N'S'. Между полюсными наконеч-
никами расположен стальной цилиндр
для уменьшения воздушного зазора,
а следовательно, и магнитного сопротив-
ления цепи. В воздушном зазоре А маг-
нитной цепи создается радиально направ-
ленное магнитное поле. В этом зазоре
находится прямоугольная катушка (рам-
ка) В. Оиа укреплена иа двух полуосях,
иа одной из которых закреплена указа-
тельная стрелка прибора. Под свободным
концом стрелки расположена шкала при-
бора. Ток к подвижной катушке подво-
дится через две спиральные пружины.
Проходящий по катушке ток взаимо-
действует с магнитным полем, так что
возникает пара сил, образующих враща-
ющий момент. Под действием этого мо-
мента катушка В поворачивается на угол
а, при котором вращающий момент урав-
новешивается противодействующим моментом, создаваемым пружи-
нами прибора. Так как противодействующий момент пропорционален
углу закручивания пружин, то чем больше ток в катушке прибора,
тем больше вращающий момент и тем больше угол поворота подвиж-
ной части. По этому углу определяют величину тока или другую
измеряемую величину, которую нужно предварительно преобразо-
вать в ток.
224
ГЛАВА ШЕСТАЯ
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
6-1. СИЛА, ДЕЙСТВУЮЩАЯ НА ЭЛЕКТРОН.
ДВИЖУЩИЙСЯ В МАГНИТНОМ ПОЛЕ
Силу F = ВИ, действующую на провод с током, когда
провод расположен перпендикулярно магнитным линиям,
можно представить как сумму сил, которые действуют на
свободные электроны, направлен-
ное движение которых образует ток
в проводе.
Силы, действующие на движу-
щиеся в магнитном поле заряды,
называются электромагнит-
ными.
Как известно, ток в проводе
(§ 2-5)
i = ^.fL = nqSv,
где п— концентрация свободных
Рис 6-1 Направление
силы, действующей на
движущийся электрон.
электронов;
<7—абсолютная величина заряда электрона;
S — площадь поперечного сечения провода;
v—средняя скорость направленного движения элек-
тронов.
Число свободных электронов, заключенных в объеме
провода сечением S и длиной I, при концентрации заря-
женных частиц п составляет nSl. Поэтому электромагнит-
ная сила, действующая на отдельный свободный электрон,
F°=^r=BlrSr=Bc^
(6-1)
т. е. сила прямо пропорциональна магнитной индукции
и скорости v, с которой электрон движется перпендику-
лярно направлению линий магнитной индукции. Направ-
ление этой силы определяется по правилу левой руки
(§ 5-23), причем четыре вытянутых пальца руки должны
быть направлены в сторону, противоположную направле-
нию движения электрона (рис. 6-1).
15 Теоретическая электротехника 225
6-2. ЭЛЕКТРОДВИЖУЩАЯ СИЛА ЭЛЕКТРОМАГНИТНОЙ
ИНДУКЦИИ
В проводе, который, двигаясь в магнитном поле, пере-
секает магнитные линии, возбуждается э. д. с. Это физи-
ческое явление было открыто в 1831 г. М. Фарадеем и полу-
чило название электромагнитной индукции.
Рассмотрим возникновение э. д. с. электромагнитной
индукции в прямолинейном проводе, который перемещает-
ся с постоянной скоростью в однородном магнитном поле
перпендикулярно векто-
ру магнитной индукции
(рис. 6-2). При движении
провода со скоростью v с той
же скоростью перемещают-
ся элементарные заряжен-
ные частицы (свободные
электроны и положитель-
ные ионы). Так как движе-
ние провода происходит
в магнитном поле, то на
каждую заряженную эле-
ментарную частицу дей-
ствует электромагнитная
сила Fo. Направление силы
Рис. 6-2. Перемещение электро-
нов в проводнике под действием
электромагнитных сил.
определяется по правилу
левой руки. Под действием электромагнитных сил сво-
бодные электроны перемещаются на один конец провода,
создавая на этом конце избыточный отрицательный заряд.
На другом конце провода ввиду недостатка электронов
возникает избыточный положительный заряд. Таким обра-
зом, на концах провода создаются равные и противополож-
ные по знаку электрические заряды. По мере накопления
зарядов усиливается напряженность электрического поля
этих зарядов в проводе и на каждую заряженную частицу
внутри провода, кроме электромагнитной силы, действует
сила электрического поля F, направленная противополож-
но электромагнитной силе (см. также § 2-3).
По достижении равновесия этих сил перемещение элек-
тронов и, следовательно, разделение зарядов прекращает-
ся. Электромагнитная сила, действующая на каждый элек-
трон,
F0 — Bqv.
226
Отношение силы к величине заряда подобно (2-4) выра-
жает напряженность электрического поля индукции:
%wC=~ = Bv. (6-2)
Сила электрического поля накопившихся зарядов
Равновесие сил, действующих на электроны, наступает
при F0 = F, т. е. ёипд = ё, откуда напряженность элек-
трического поля в проводе
s = ёинд=Bv.
Разделение зарядов, возникающее под действием элек-
тромагнитной силы, можно рассматривать как результат
действия э. д. с., которую называют э. д. с. электро-
магнитной индукции. При разомкнутом прово-
де величина э. д. с. равна напряжению между концами
провода. Так как при равновесии сил в проводе устанавли-
вается однородное электрическое поле зарядов, накопив-
шихся на концах провода, то напряжение
и = $1=Ы,
где I — длина провода и э. д. с.
E = $uinl = Bvl. (6-3)
Наведенная в прямолинейном проводе, пересекающем ли-
нии магнитной индукции, э. д. с. электромагнитной индук-
ции пропорциональна магнитной индукции поля, длине
провода и скорости его движения.
Направление э. д. с. совпадает с направлением элек-
тромагнитной силы, действующей на положительный заряд,
и противоположно направлению электромагнитной силы,
действующей на электрон (рис. 6-2). Обычно направление
э. д. с. определяется «правилом правой руки». Ладонь пра-
вой руки располагается так, чтобы магнитные линии вхо-
дили в нее', отставленный большой палец направляется вдоль
вектора скорости, тогда остальные четыре пальца покажут
направление индуктированной э. д. с. (рис. 6-3).
Предположим теперь, что провод движется в магнитном
поле таким образом, что угол между векторами В и v равен
не 90°, а некоторой произвольной величине а (рис. 6-4).
227
Такое движение может быть разложено на два: во-первых,
на движение вдоль вектора В со скоростью ут — v cos а
и, во-вторых, в направлении, перпендикулярном В, со
скоростью vn = ysina.
При совпадении направлений скорости и магнитной
индукции сила, действующая на переносимые при таком
движении заряды, оказывается равной нулю. Этот ре-
зультат вытекает непосредственно из формулы (5-45), пра-
вая часть которой имеет множителем синус угла между
Рис 6-3 Правило правой
руки.
Рис. 6-4. К опреде-
лению нормальной
составляющей ско-
рости.
направлением В и направлением того тока, на который
действует магнитное поле (направлением /).
Итак, при расчете напряженности электрического поля
в проводе следует принимать во внимание лишь проекцию
скорости v на направление, перпендикулярное вектору В.
В связи с этим формула (6-2) перепишется в виде
^чпд = Bv sin a = Bv sin / (v, В). (6-4)
Соответственно видоизменяется и формула (6-3):
Е = Blv sin a = Blv sin / (v, В), (6-5)
т. e. в более общем случае э. д. с. электромагнитной индук-
ции зависит от синуса угла между вектором магнитной
индукции и вектором скорости.
Если концы провода, перемещающегося в магнитном
поле, замкнуты другим проводом, расположенным вне маг-
нитного поля, то в этой электрической цепи под действием
228
э. д. с. электромагнитной индукции возникнет непрерывное
перемещение электронов, т. е. электрический ток.
Величина тока определяется по закону Ома:
где Sr — суммарное сопротивление цепи.
Направление тока совпадает с направлением э. д. с.,
и его можно определить по правилу правой руки.
6-3. ПРЕОБРАЗОВАНИЕ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
В ЭЛЕКТРИЧЕСКУЮ
Поместим в однородное магнитное поле с индукцией
В прямолинейный провод длиной I. Предположим, что
провод расположен перпендикулярно вектору В и пере-
мещается со скоростью v, как
показано на рис. 6-5. Провод
замкнут на внешнее сопро-
тивление г. В проводе возни-
кает э. д. с., а в замкнутой
цепи — ток I.
Электромагнитная сила,
действующая на провод с то-
ком,
F—BU.
Направление силы опреде-
ляется по правилу левой руки.
Построив вектор этой силы,
Рис 6-5 Движение проводни-
ка в магнитном поле и возник-
новение тормозной силы.
мы убедимся, что сила F яв-
ляется тормозной силой, направленной противоположно
вектору скорости v (рис. 6-5). Таким образом, движение про-
вода возникает при действии внешней силы, равной и про-
тивоположно направленной тормозной силе. Первичный
двигатель, создающий внешнюю силу, должен развить меха-
ническую мощность
Р мех — F V-
Подставив в последнее уравнение выражение силы F,
получим, что
PKex = BlIv = lE, (6-6)
229
т. е. развиваемая двигателем мощность равна мощности
электрического тока в замкнутой цепи. Таким образом,
при движении замкнутого проводника в магнитном поле
под действием внешних сил происходит преобразование ме-
ханической энергии в электрическую.
6-4. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
Электрические машины, в которых происходит преобра-
зование механической энергии в электрическую, называют-
ся генераторами. Схематическое устройство электри-
ческого генератора было показано на рис. 5-28. Следует
лишь добавить, что на якоре машины располагаются прово-
да (обмотка), в которых при вращении якоря наводятся
э. д. с. Вращательное движение проводов получить про-
ще, чем поступательное, но наводимые э. д. с. в этом слу-
чае не постоянны как по величине, так и по направлению.
При помощи дополнительных устройств (коллектора) мож-
но получить от такого генератора ток постоянного напра-
вления.
Переменные токи и напряжения в технике стремятся
получить изменяющимися по простейшему периодическому
закону — синусоидальному закону (ниже в § 8-1 поясняет-
ся, почему стремятся получить синусоидальные перемен-
ные токи).
На рис. 6-6 приведена схема устройства простейшего
генератора переменного тока. Между полюсами N и S
электромагнита расположен якорь — стальной цилиндр А,
на поверхности которого укреплен виток проволоки. Кон-
цы витка присоединены к двум медным изолированным
кольцам, на которые наложены щетки, соединенные с внеш-
ней цепью.
Предположим, что магнитная индукция на поверхности
якоря (рис. 6-7) нормальна к ней (напомним, что магнит-
ные линии выходят и входят в ферромагнитные тела под
почти прямым углом) и изменяется вдоль окружности яко-
ря по синусоидальному закону. На рис. 6-8 приведена
диаграмма радиально-синусоидального магнитного поля.
Направление вектора индукции в отдельных точках поля
на поверхности якоря совпадает с направлениями радиусов
(указано стрелками). Величины индукции изображены от-
резками, расположенными между окружностью якоря и оги-
бающей кривой. Такое распределение индукции в воздуш-
230
ном зазоре можно, например, получить, придавая полюсам
такую форму, при которой воздушный зазор увеличивается
от центра полюса к его краям.
Рис. 6-6. Устройство простейшего генератора пере-
менного тока.
Обозначим буквами В — магнитную индукцию в какой-
нибудь точке на поверхности якоря, Ва — максимальную
Рис. 6-7. Устройство генератора
переменного тока.
Рис. 6-8. Диаграмма ин-
дукции магнитного поля
в воздушном зазоре ге-
нераторов, изображен-
ных на рис. 6-6 и 6-7,
индукцию под серединой полюса, а — угол, образованный
нейтральной плоскостью 00' и плоскостью,
проходящей через ось якоря и произвольно выбранную
231
точку на его поверхности. Тогда
В = Вм sin а
(плоскость, проходящая через точки поверхности якоря,
в которых В —О, называется нейтральной плоскостью
генератора).
При равномерном вращении якоря в таком магнит-
ном поле в проводниках а'б' и а"б" (рис. 6-6) наводятся
одинаковые э. д. с.:
е' = Blv = B№lv sin а.
Так как проводники соединены последовательно, то
суммарная э. д. с.
е — 2е' = 2BKlv sin а = Е№ sin а, (6-7)
где максимальное значение э. д. с.
£м= 2B№lv.
Если вместо одного витка на цилиндре поместить ка-
тушку, имеющую w витков, то максимальная э. д. с.»
индуктированная в катушке, будет в w раз больше:
EM — 2B№lvw. (6-8)
При вращении якоря в магнитном поле с постоянной
угловой скоростью со за один оборот, т. е. при изменении
угла а на 2л, завершается цикл изменения э. д. с.
Время, в течение которого совершается один цикл,
называется периодом и обозначается буквой Т. Период
измеряется в секундах (сек). Величина, обратная периоду,
называется частотой. Частота обозначается буквой f.
Согласно определению f = ~; частота измеряется в 1 сек.
.Эту единицу называют герц (гц).
Угловая скорость вращения якоря
Угол поворота якоря в зависимости от времени
а = at = t = 2nft,
а э. д. с., наведенная в обмотке якоря,
е = Ем sin а = Ем sin at = Ем sin 2л//. (6-10)
232
Пример 6-1. В магнитном поле, индукция которого изменяется
по синусоидальному закону, вращается якорь с прямоугольной ка-
тушкой шириной (диаметр яко-
ря) d = 0,2 м и длиной
( = 0,4 м. Катушка имеет 20 вит-
ков. Скорость вращения якоря
3 000 об/мин. Максимальное зна-
чение магнитной индукции
Вм— 1 тл.
Определить f, Т и Ем.
Так как одному обороту
якоря соответствует один цикл
э. д. с., то число циклов в се-
кунду (частота) равно числу
оборотов якоря в секунду, т. е.
, п 3 000 1 -п
' 60 60 сек
Рис. 6-9. Устройство генератора
переменного тока с обмоткой воз-
буждения на роторе.
Период
Т=4- = Л = 0,02 сек.
f 50
Максимальная э. д. с.
_ „„ , „„ , ndn . 3,14-0,2-3000 оп
ЕМ = 2ВМ(Щ4>= 2ВМ/ —t4> = 2-0,4---------=--------20=502 в.
” 60 60
Генераторы переменного тока большой мощности, рас-
считанные на напряжения 3—15 кв, выполняются с непо-
движной обмоткой на статоре машины и вращающимся
электромагнитом — ротором (рис. 5-29). При такой конструк-
ции легче надежно изолировать провода неподвижной об-
мотки и проще отвести ток во внешнюю цепь. Схематическое
устройство генератора с вращающимся электромагнитом
приведено на рис. 6-9.
6-5. ПРЕОБРАЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
В МЕХАНИЧЕСКУЮ
В результате действия магнитного поля на провод с то-
ком происходит преобразование электрической энергии
в механическую.
Пусть по прямолинейному проводу, расположенному
в однородном магнитном поле и включенному в цепь с э. д. с.
Е, проходит неизменяющийся ток (рис. 6-10).
Магнитное поле действует на провод с током с силой
F — B11,
233
и провод движется под действием силы со скоростью и
(направление силы и скорости определяется по правилу
левой руки).
При движении провода в нем возникает э. д. с. элек-
тромагнитной индукции, направленная навстречу току,
Евстр Blv.
По второму правилу Кирхгофа для контура
Е — Евстр ~ Е,
где г — сопротивление прямолинейного провода;
г0—сопротивление остальной части цепи.
Обозначив
Е — 1г0 Uab,
найдем, что напряжение на
зажимах провода
Еаб = 1Г + Евстр- (6-11)
Умножив почленно выра-
жение (6-11) на ток I, опре-
делим электрическую мощ-
ность на зажимах провода:
U ав! = Ег 4* Евстр/.
Имея в виду, что Евстр~-= Blv, получим:
иАБ1 = Er + BlvI = Er + Fv.
(6-12)
В правой части уравнения (6-12) первое слагаемое выра-
жает мощность тепловых потерь в проводе, второе — меха-
ническую мощность. Таким образом, при движении провод-
ника с током в магнитном поле под действием сил поля
происходит преобразование электрической энергии в тепло-
вую и механическую.
6-6. ЭЛЕКТРИЧЕСКИЕ ДВИГАТЕЛИ
Первый электродвигатель, имевший практическое зна-
чение, был изобретен в 1834 г. русским академиком
Б. G Якоби, который в 1838 г. применил его для движе-
ния лодки, а затем — и тележки.
234
Рис. 6-11. Схема иклю-
чения электродвигателя.
другую — обмотка воз-
Еще в § 3-12 отмечалось, что каждый генератор посто-
янного тока переходит в режим электродвигателя, если
его э. д. с. окажется меньше напряжения на зажимах.
Указанный принцип обратимости электриче-
ских машин был открыт в 1833 г.
Э. X. Ленцем и затем сформули-
рован Б. G. Якоби«
Таким образом, те же машины,
которые служат генераторами, мо-
гут работать электродвигателями.
На рис. 6-11 приведена схема вклю-
чения электродвигателя. Некото-
рые электродвигатели имеют две
параллельные ветви. В одну вклю-
чены пусковой реостат и якорь, в
буждения (на рис. 6-11 не показана). Пусковой реостат
ограничивает пусковой ток якоря. В начальный момент
пусковой ток
(6-13)
' 1 'я
где г — сопротивление реостата;
га — сопротивление якоря.
Без сопротивления реостата г пусковой ток имел бы
значение, во много раз превышающее номинальный ток
электродвигателя (см. пример 6-2).
При вращении якоря в нем возникнет встречная э. д. с.
Поэтому ток уменьшается и необходимость в пусковом
реостате отпадает, сопротивление реостата постепенно умень-
шают до нуля.
Пример 6-2. К зажимам электродвигателя подведено напряже-
ние 120 в. Встречная э. д. с. при номинальном режиме составляет
116 в. Сопротивление обмотки якоря 0,4 ом.
Определить: 1) номинальный ток двигателя; 2) сопротивление
пускового реостата, с тем чтобы пусковой ток не превышал 2/н;
3) пусковой ток в цепи, если двигатель включить без пускового
реостата.
Номинальный ток двигателя
, U-E 120-116
/”==^Г"==-оз —10 а-
Сопротивление пускового реостата можно найти из формулы
(6-13):
U U 120 „ , с г
r=~i-----r» ol----Гя =9~Тп~0,4 = 5’6 °М’
'пуск Z'H z-iu
235
Пусковой ток при включении без реостата
, U 120
^пуск - 0>4 ~30J а.
6-7. ЭЛЕКТРОДВИЖУЩАЯ СИЛА ЭЛЕКТРОМАГНИТНОЙ
ИНДУКЦИИ В КОНТУРЕ
Пусть прямолинейный провод, который движется в одно-
родном магнитном поле перпендикулярно направлению век-
тора магнитной индукции, за время dt перемещается на
расстояние db. Скорость движения провода, которая в об-
щем случае может быть и непостоянной,
Наводимая в проводе в любой момент времени э. д. с.
(мгновенное значение э. д. с.) согласно (6-3)
е Blv-Bl —
dt
(э. д. с. обозначена строчной буквой е, чтобы подчеркнуть,
что величина ее в общем случае непостоянна).
Произведение длины провода и пути (Idb) выражает
площадку (dS), описанную проводом при его движении
перпендикулярно направлению вектора В. Произведение
магнитной индукции В и площадки dS равно магнитному
потоку d<D, пересеченному проводом при его движении,
BdS-dO),
а наведенная в проводе э. д. с.
или
По формуле (6-14) определяется э. д. с. в прямолиней-
ном проводе, который движется в однородном поле перпен-
дикулярно его направлению. Но эта формула позволяет
определить э. д. с. и в более общем случае. Например, при
движении провода под некоторым углом а =0= 90° к напра-
влению вектора магнитной индукции поток, пересеченный
236
проводом, будет не BdS, a B^dS, где Вя — Bsin а выра-
жает нормальную составляющую вектора магнитной индук-
ции к площадке dS. Этот поток обозначим по-прежнему
дф. Тогда и в этом случае э. д. с. может быть найдена по
формуле (6-14). При движении провода произвольной фор-
мы (рис. 5-44) в неравномерном магнитном поле его можно
рассматривать состоящим из большого числа небольших
прямолинейных элементов,
а суммарную э. д. с. в нем
определить опять-таки по фор-
муле (6-14).
В практических условиях
часто возникает необходи-
мость определить величину и
направление э. д. с. не в от-
дельном проводе, а в замкну-
том контуре, например витке
или катушке. Замкнутый кон-
тур из провода, расположен-
ный в неоднородном магнит-
ном поле, показан на рис. 6-12.
Магнитные линии, пронизы-
Рис. 6-12. Электродвижущая
сила в контуре.
вающие поверхность, ограниченную контуром, направлены
от наблюдателя. Пусть контур (рис. 6-12) перемещается
справа налево. При перемещении контура за время dt на
бесконечно малое расстояние одна его часть (левая) пере-
сечет магнитный поток dd>i, который теперь будет прони-
зывать контур, и в этой части контура наводится э. д. с.
Cj = d<£>t/dt. Другая часть контура (правая) пересекает
магнитный поток с(Ф2, который, наоборот, не будет уже
пронизывать контур; э. д. с., наведенная в этой части кон-
тура, е2 = б/Фг/с!/. Результирующее приращение магнит-
ного потока в контуре
dФ ^=dФi — dФ2.
Определив по правилу правой руки направление э. д. с.
Pi и е2, установим, что они действуют в контуре навстречу
ДРУГ другу.
Положительное направление наводимой в контуре э. д. с.
связывают с положительным направлением магнитного по-
тока правилом буравчика. Так как линии магнитной индук-
ции, пронизывающие поверхность, ограниченную конту-
ром, направлены от наблюдателя, то в соответствии с пра-
237
видом буравчика положительное направление э. д. с. в кон-
туре совпадает с направлением движения часовой стрелки
и, следовательно, с направлением э. д. с. е2 и противополож-
но направлению t?i. Поэтому результирующая э. д. с., наво-
димая в контуре,
d®2 —d®j d®! — d®, d®
= —---------------<6-15>
Из формулы (6-15) следует, что непременным условием
возникновения э. д. с. электромагнитной индукции в замк-
нутом контуре является изменение величины магнит-
ного потока, пронизывающего контур. Это условие
является не только необходимым, но и достаточным. По-
этому э. д. с. возникает не только в движущемся в неод-
нородном поле контуре, но и в неподвижном контуре,
который пронизывает изменяющийся магнитный поток.
По величине э. д. с., наведенная в контуре, равна скоро-
сти изменения потока внутри контура.
Направление (знак) наведенной э. д. с. зависит от знака
приращения магнитного потока. Если поток сквозь контур
d<I’ Л е.
возрастает, т. е. > 0, то знак э. д. с. будет отрица-
тельным, если поток убывает, т. е. -^-<0, го знак э. д. с.
будет положительным.
Следует еще раз подчеркнуть, что эти знаки э. д. с.
соответствуют положительному направлению э. д. с., вы-
бранному по правилу буравчика.
На рис. 6-13, а показан возрастающий магнитный поток
сквозь неподвижный контур. Так как линии магнитной
индукции направлены сверху вниз, то ручка буравчика,
указывающая положительное направление э. д. с., будет
поворачиваться по направлению движения стрелки часов
(если смотреть по направлению магнитного поля). Однако
поскольку э- Д- с. получится с отрицательным
знаком, т. е. будет направлена в сторону, противополож-
ную направлению движения стрелки часов, и вызовет ток
такого же направления (рис. 6-13). Если магнитный поток
убывает, т. е. -^-<0. то э. д. с. получается с положи-
тельным знаком. Убывающему магнитному потоку соот-
ветствует рис. 6-13, б. Электродвижущая сила в этом
238
случае положительна, и ее направление также находится
непосредственным применением правила буравчика,
Э. X, Ленцем был сформулирован общий закон, уста-
навливающий направление наведенного тока: ток, возни-
кающий в контуре под действием наведенной э. д. с., всегда
направлен таким образом, что противодействует измене-
нию магнитного потока сквозь контур (закон Ленца). При-
меняя его к замкнутому контуру рис, 6-13, можно сразу
наметить направление тока в контуре.
Рис. 6-13. Направление наведенного тока
в контуре при возрастающем (а) и убывающем
(6) магнитных потоках.
Итак, э. д. с., возникающая в замкнутом контуре про-
извольной формы вследствие изменения магнитного потока,
пронизывающего контур или, как еще говорят, сцепляю-
щегося с контуром,
С другой стороны, э. д. с. можно представить по фор-
муле (6-3) как сумму произведений <gun}ldl в пределах
всего замкнутого контура, т. е.
е — £ипд dl.
Таким образом,
$ $инд dl = — . (6-16)
Это уравнение показывает, что э. д. с. контура не зави-
сит от материала, из которого он выполнен. Уравнение
распространяется и на контуры, которые можно выделить
239
в проводящей среде или диэлектрике. В любом замкну-
том контуре, ограничивающем поверхность, которую про-
низывает переменный магнитный поток, возникает э. д. с.
электромагнитной индукции. В проводящей среде э. д. с.
вызывает ток проводимости, в диэлектрике переменная
э. д. с. вызывает ток, называемый током смещения. Под
током смещения понимают изменение электрического поля
во времени. Таким образом, при изменении магнитного
потока в любой среде одновременно наблюдается и электри-
ческое поле.
6-8. ПОТОКОСЦЕПЛЕНИЕ
На рис. 6-14 показана неподвижная катушка, вдоль
оси которой передвигается постоянный магнит. При пере-
мещении магнита изменяется поток, сцепленный с витками
катушки, и в катушке наводится э. д. с.
Рис. 6-14. Электродвижущая сила в ка-
тушке.
В этом случае э. д. с. возникает в каждом витке катуш-
ки и суммарная э. д. с.
е = + е2 + -. • + ek = —(</Ф1 + dO2 + • • • + d®k) =
~ ~ dT + • • • + Фа)-
Алгебраическая сумма потоков, сцепленных с отдель-
ными витками цепи, называется потокосцеплением
и обозначается буквой Т, т. е.
Y — Ф14- Ф2 + ... + Фд.
Таким образом, суммарная э. д. с.
240
Если каждый виток катушки сцеплен с одинаковым
магнитным потоком (Ф1 = Ф2 = Фз= ••• =Ф), то э. д. с.
в катушке в w раз больше, чем в одном витке,
(6-18)
где w—число витков катушки.
В этом случае потокосцепление равно произведению
числа витков и сцепленного с любым витком магнитного
потока:
¥ = шФ. (6-19)
6-9. ВИХРЕВЫЕ ТОКИ
В § 6-7 было установлено, что при изменении магнит-
ного потока наблюдается электрическое поле. Электри-
ческие линии этого поля расположены в плоскости, перпен-
дикулярной направлению магнитного потока, и в отличие
от линий электростатического поля замкнуты (вихревое
поле). Если в изменяющемся магнитном поле находятся
массивные проводящие тела (сталь, медь, латунь и др.),
то под действием э. д. с. электромагнитной индукции в этих
проводниках возникают вихревые токи, которые
являются частным случаем наведенных токов.
Если, например, в обмотке катушки с массивным сталь-
ным сердечником проходит переменный ток, то в сердеч-
нике наводятся вихревые токи, которые замыкаются в пло-
скости, перпендикулярной вектору магнитной индукции.
Эти токи вызывают нагрев стали и тем самым снижают
коэффициент полезного действия (к. п. д.) электромагнит-
ных механизмов. Для уменьшения вихревых токов при-
меняются сердечники, выполненные из отдельных изоли-
рованных друг от друга листов стали (рис. 6-15). В этом
случае увеличивается сопротивление сердечника для вихре-
вых токов и сами токи уменьшаются.
Вихревые токи возникают при вращении в магнитном
поле якоря электрической машины. На рис. 6-16, а пока-
зана половина якоря электрической машины, выполнен-
ного из сплошной стали. При вращении якоря в магнит-
ном поле в нем возникают вихревые токи, показанные на
рис. 6-16, а пунктирными линиями. Применяя якорь, на-
бранный из листов стали (рис. 6-16,6), можно вихревые
токи в значительной степени уменьшить. В этих машинах
16 Теоретическая электротехника 241
и многих аппаратах и механизмах вихревые токи необхо-
димо подавлять. В ряде других устройств и механизмов
вихревые токи могут быть целесообразно использованы
Рис. 6-15. Вихревые
токи в сердечнике из
листовой стали.
Рис. 6-16. Вихревые токи в якоре.
для приведения механизмов в действие или для обеспече-
ния необходимого режима работы.
На рис. 6-17 показан диск измерительного прибора.
При вращении диска между полюсами постоянного магнита
t)
Рис. 6-17. Вихревые токи в диске при движе-
нии его в магнитном поле постоянного магнита.
в нем возникают вихревые токи. Сила взаимодействия этих
токов с полем постоянного магнита тормозит диск, что
необходимо для работы прибора.
Все больше вихревые токи используются для нагрева
металлов при поверхностной закалке стальных деталей,
242
особенно шестерен и коленчатых валов, для плавки спе-
циальных сортов стали и цветных металлов, для нагрева
жидкостей и газов, находящихся в металлических сосу-
дах, и т. д. Во всех этих устройствах нагреваемую деталь,
материал или сосуд помещают в переменное магнитное
поле, которое возбуждается током в катушке-индукторе.
6-10. БАЛЛИСТИЧЕСКИЙ ГАЛЬВАНОМЕТР
Для измерения магнитного потока и магнитной индукция су-
ществует много методов.
Рассмотрим баллистический способ измерения, разра-
ботанный А. Г. Столетовым.
Для баллистических измерений применяется магнитоэлектриче-
ский гальванометр (§ 5-27). .Как указывалось, в результате действия
магнитного поля на рамку с постоянным током рамка поворачивает-
ся так, что по углу поворота можно судить о величине постоянного
тока.
Сложнее процесс в том случае, когда по обмотке проходит ток
кратковременный — толчок (импульс) тока. Под действием импульса
тока стрелка отбрасывается направо или налево по шкале. Затем
под действием связанных с осью рамки спиральных пружинок стрел-
ка возвращается с ускорением в положение равновесия, проходит
через него, отклоняется в противоположную сторону и т. д. Посте-
пенно колебания стрелки затухают. Таким образом, в этом случае
подвижная часть гальванометра подобна маятнику, колебания кото-
рого возбуждены коротким ударом.
Если длительность импульса тока мала по сравнению с перио-
дом колебания подвижной части гальванометра, то максимальное
отклонение стрелки прямо пропорционально величине заряда,, про-
шедшего через обмотку (для увеличения периода собственных коле-
баний подвижная часть гальванометра снабжается специальными
грузиками).
В самом деле, сила, вызывающая отклонение стрелки, пропор-
циональна току, проходящему через обмотку [формула (5-44)].
С другой стороны, по основному закону механики сила пропорцио-
нальна ускорению, т. е. изменению скорости. Следовательно, ток
в рамке гальванометра /г пропорционален величине v/r, где т — ма-
лый интервал времени, в течение которого по обмотке проходит ток.
Итак, скорость и, с которой стрелка выходит из положения равнове-
сия, пропорциональна произведению /гт, т. е. электрическому заря-
ду Q, прошедшему через обмотку гальванометра. Но по закону
движения маятника амплитуда его колебаний пропорциональна ско-
рости v в положении равновесия, откуда
Q.-Ca, (6-20)
где а —наибольший угол отклонения стрелки. В электроизмеритель-
ных приборах угол поворота стрелки обычно измеряется числом
делений шкалы или длиной шкалы. В баллистических гальваноме-
трах угол поворота измеряется в миллиметрах длины шкалы
243
Коэффициент пропорциональности С в формуле (6-20) назы-
вается баллистической постоянной. Величина этого коэффициента
зависит от конструкции и параметров прибора. Баллистическая по-
стоянная
обычно измеряется в мкк/мм. Величина, обратная постоянной, назы-
вается чувствительностью гальванометра. Чувствительность гальва-
нометра измеряется в мм/мкк.
6-11. ВОЗБУЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
ИЗМЕНЯЮЩИМСЯ МАГНИТНЫМ ПОТОКОМ
На рис. 6-18 показан кольцевой сердечник, на поверхности кото-
рого равномерно уложена обмотка, состоящая нз витков. Концы
обмотки через реостат и рубильник присоединены к источнику с по-
стоянной э. д. с. Е. На первую обмотку
наложена вторая, имеющая w2 витков.
К зажимам этой обмоткн присоединен
баллистический гальванометр БГ.
После замыкания рубильника в пер-
вой обмотке установится ток Iit величи-
на которого определяется э. д. с. Е источ-
ника и сопротивлением первичной цепи,
равным сумме сопротивлений первой об-
мотки и реостата. Прн этом значении
тока магнитная индукция в сердечнике
(см. (5-23)]
В=рр0~7—.
(6-21)
где / — длина средней магнитной линии.
Начальное значение магнитного по-
тока в сердечнике (до замыкания рубиль-
ника) равно нулю, конечное значение
потока Ф — BS, где S —сечение сердеч-
ника. Прн нзмененнн магнитного потока
г.о вторичной обмотке возбуждается
э. д. с.
Рнс. 6-18. К измерению
магнитного потока
</ф
e2=_tt,2__.
Под действием э. д. с. е2 во вторичной цепи возникает ток
i - е*
z2— -Г-,
г2
(6-22)
где т2—сопротивление вторичной цепи, состоящее нз сопротивлений
гальванометра и обмоткн.
244
Подставив выражение е2 в формулу (6-22), получим
йФ
'2 " TTdt '
откуда
(2 d/ = — —-</Ф
г2
Произведение г2 di выражает электрический заряд, который воз-
буждается во вторичной цепи при изменении магнитного потока за
врем? di на величину </Ф. Электрический заряд, который проходит
по вторичной цепи, а следовательно, и через обмотку баллистиче-
ского гальванометра, при нарастании магнитного потока за время г
от 0 до конечного значения Ф
t Ф
Q = \ (2 di = —j ДФ (6-23)
О о
или
При размыкании рубильника магнитный поток за время г изме-
нится от Ф до О В этом случае
Q — (6-24)
6-12. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА
И МАГНИТНОЙ ИНДУКЦИИ
Преобразуя формулу (6-24), найдем, что
Ф = С’ (6 25>
т. е. магнитный поток пропорционален заряду, прошедшему через
гальванометр, а следовательно, и углу отклонения его стрелки:
Ф = а (6-26)
и’о
Тем же методом может быть измерена магнитная индукция
Ф Го
В=-гг = С—Va, (6-27)
S w2S ' '
а при известной величине тока It найдена из (6-21) магнитная прони-
цаемость сердечника
В1
—г— . (6-28)
245
6-13. ИЗМЕРЕНИЕ МАГНИТНОГО НАПРЯЖЕНИЯ
Для измерения магнитного напряжения применяется магнит-
ный пояс. Магнитный пояс — это длинная (1=1— 1,5 л) гибкая
катушка с неферромагнитным сердечником (р= 1), обмотка которой
состоит нз четного числа слоев (например, двух), намотанных в одну
сторону с равномерной плотностью w0 = w/l. Концы обмотки выведены
к зажимам, укрепленным на середине
пояса. К этим зажимам, скрученным
шнуром, присоединяется гальвано-
метр для баллистических измерений
(рис. 6-19).
Если нужно, например, измерить
намагничивающую силу катушки, то
магнитным поясом охватывают витки
катушки (пояс продевают в катушку,
его концы А и Б прижимают друг
к другу) и производят выключение
Рис. 6-19. Магнитный пояс.
(или включение) тока в катушке.
При выключении тока в сердечнике в поясе кратковременно из-
меняется магнитный поток и по цепи пояс — гальванометр проходит
заряд Q, измеряемый гальванометром.
Согласно (6-26)
Са =
где ЧС— ц.'Ф — потокосцепление с магнитным поясом;
г — сопротивление цепи пояс—гальванометр.
Отдельные элементы пояса имеют различные потокосцепления:
’Fj = Ф^Л/,; 4^2= Ф2Щ)Л/2,
где А/ — длина участка пояса, в пределах которого поле можно счи-
тать однородным.
Сумма потокосцеплений Ч^, 4f2 и т. д. составляет потокосцепле-
ние всего пояса, т. е.
V = Чг 1 + ¥2 + ...= Ф^'уА/,-j-Ф2а>оЛ/2 + ...
Магнитный поток, пронизывающий произвольно взятый виток пояса,
имеющий сечеиие S,
Ф = ВН$,
где Ва — проекция вектора индукции на нормаль к витку (нормаль-
ная составляющая).
Магнитное напряжение
(7М= J Htdl.
Выберем в качестве пути / путь вдоль пояса. Если пояс разбит иа
участки А/, то UM = XH[А1, где /// — составляющая вектора напря-
женности, совпадающая по направлению с А/. Отрезки пути вдоль
пояса А/ перпендикулярны виткам пояса на всех участках, т. е.
совпадают с нормалью к виткам участка. Поэтому и Hi совпадает
246
по направлению с нормалью, т. е. с нормальной составляющей
индукции:
йн=|1о^(
и
Ф = |10//(5.
Подставив значение соответствующих Ф в формулу потокосцепления,
получим, что
Ч' = ц'оЦо-S {Hn&li Л/у/Л • • •) = k'op.O'S^A,,
откуда ш Сг UM - —= ——с- а - Спа, (6-29) U'oPoS
где С„ =-------„—постоянная цепи пояс — гальванометр.
to0(i0S
6-14. ИНДУКТИВНОСТЬ
Замкнутый контур электрической цепи всегда прони-
зывается магнитным потоком, созданным проходящим по
этой цепи током. Величина магнитного потока пропорцио-
нальна току (при неизменной магнитной проницаемости
среды, т. е. при отсутствии ферромагнитных сердечников).
При прохождении тока по катушке каждый ее виток про-
низывается магнитным потоком.
Алгебраическая сумма пронизывающих витки магнит-
ных потоков, которые обусловлены электрическим током
в этой цепи, составляет потокосцепление самоиндукции
(обозначение W/,). Если один и тот же ток проходит по
катушкам различных размеров и с разным числом витков
или по разным контурам, то и потоки, пронизывающие
отдельные витки или контур, и сумма потоков, т. е. пото-
косцепление, будут различными. Таким образом, для раз-
ных катушек и контуров коэффициент пропорциональности
между потокосцеплением и током неодинаков. Но отноше-
ние потокосцепления к току у катушки или контура, харак-
теризующее связь потокосцепления самоиндукции с током
в данной электрической цепи, является постоянной величи-
ной, называемой индуктивностью (обозначение L):
L = ^. (6-30)
Индуктивность характеризует свойства самой катушки или
самого контура. Индуктивность необходимо знать, чтобы
247
при заданном токе в катушке найти потокосцепление само-
индукции или магнитный поток.
Единица измерения индуктивности
_ , Г Yr "I в-сек
\L[ — [~г |-—ом-сек.
Для ом-секунды, как указывалось, существует спе-
циальное название — генри (гн). Часто индуктивность
не достигает значения одного генри и измеряется тысяч-
ными или миллионными до-
лями генри.
L L’г Одна тысячная часть генри
—1~— называется миллигенри
10~3 гн—1 мгн,
Рис 6 20 Условное обозна-
чение индуктивности.
а миллионная — м и к ро-
ге н р и
10-е гн = 1 мкгн.
На электротехнических схемах индуктивность L изо-
бражается, как показано на рис. 6-20, а, а катушка с индук-
тивностью L и сопротивлением г — как на рис. 6-20, б.
6-15. индуктивность катушки
Вычислить индуктивность можно довольно просто лишь
в некоторых случаях. Определим, например, индуктив-
ность кольцевой катушки (рис. 5-15). Если средний радиус
сердечника катушки -^i-51 значительно больше радиуса ее
витков, то в любом сечении сердечника можно считать
индукцию В одинаковой в каждой точке, т. е. вести расчет
по длине средней магнитной линии; магнитный поток катуш-
ки с достаточной точностью определяется по формуле
O = BS = pp0^S=125|i~S-10-8 [вб].
I I
Так
тушки,
как магнитный поток пронизывает все витки ка-
то потокосцепление самоиндукции
= S,
248
откуда
L = 2^ = fX}10^= 125^-^ 10~8 [гн], (6-31)
где I — в метрах;
S — в квадратных метрах.
Аналогично определяется индуктивность цилиндриче-
ской катушки. Прямую цилиндрическую катушку, если
ее длина велика по сравнению с диаметром, можно рас-
сматривать как часть кольцевой катушки, у которой радиус
равен бесконечности; поэтому ее индуктивность вычисляет-
ся по формуле (6-31), причем I — длина катушки.
6-16. ИНДУКТИВНОСТЬ ДВУХПРОВОДНОЙ линии
Практически важно найти индуктивность двухпровод-
ной линии (рис. 6-21).
Определим магнитный поток между проводами, находя-
щимися на расстоянии а друг от друга. Магнитный поток
Рис. 6-21. Двухпроводная линия.
сквозь элементарную площадку dS = Idr {I — длина про-
вода линии), создаваемый током 1 первого провода,
dOj = Bi dS = Bd dr = pp0 I dr.
Полный поток, создаваемый этим током между прово-
дами с радиусами г0,
r=a—t'o a—
Ф,= J 5 Л (6-32)
г=га ГО
249
Поток, создаваемый током второго провода, также ра-
вен Фь так как токи в проводах одинаковы.
Векторы магнитной индукции В1 и В2 параллельны
друг другу (так как токи имеют противоположное напра-
вление), поэтому поток между проводами
Ф = 2Ф, = 2up0 In Il In .
* 2л г0 л
Так как обычно расстояние между проводами а значи-
тельно больше радиуса проводов г0, то вместо разности
а — г0 можно подставить а и формула примет вид:
ф= W^/Лп —.
л га
Индуктивность двухпроводной ЛИНИИ (йУ=1)
Для воздушной линии р = 1, и так как
ро = 4л-1О~7 [гн!м\,
то индуктивность в генри
L = 4-10-71 In . (6-33)
где / — длина линии в метрах.
Ввиду значительной длины линии удобно определить
индуктивность на 1 км ее длины (£0); так как 1 км= 103 м,
то
£о^4-1О“41п— [гн/км].
го
В наших рассуждениях мы не учитывали магнитного
потока внутри самих проводов; с учетом этого потока
индуктивность двухпроводной линии определяется по
формуле
Lo— ^4 In 4- р^ • 10~4 {гн!км}, (6-34)
где р — магнитная проницаемость провода, которая для
всех проводов, кроме стальных, может быть принята рав-
ной единице.
250
6-17. ЭЛЕКТРОДВИЖУЩАЯ СИЛА САМОИНДУКЦИИ
Изменение тока в цепи вызывает изменение потокосце-
пления самоиндукции, и при нарастании или уменьше-
нии потокосцепления возникает э. д. с.
Это своеобразное явление, когда э. д. с. возбуждается
в контуре в результате изменения тока в этом же контуре,
называют самоиндукцией.
Электродвижущая сила самоиндук-
ции определяется, как и всякая наведенная э. д. с., по
формуле (6-17)
или, учитывая выражение Ть = Ы (6-30), по формуле
(6-35)
откуда следует, что э. д. с. самоиндукции пропорциональна
индуктивности и скорости изменения тока в контуре.
Направление э. д. с. самоиндукции определяется по
закону Ленца. Например, при увеличении тока (Q
э. д. с. самоиндукции отрицательна, т. е. направлена
навстречу току в контуре (противо-э. д. с.). Наоборот,
при уменьшении тока ^-^--<0^) э- Д- с. самоиндукции
положительна и направлена одинаково с током в контуре.
6-18. ПЕРЕХОДНЫЙ ПРОЦЕСС ПРИ ПОДКЛЮЧЕНИИ
ЦЕПИ, ОБЛАДАЮЩЕЙ СОПРОТИВЛЕНИЕМ
И ИНДУКТИВНОСТЬЮ, К ИСТОЧНИКУ ПИТАНИЯ
с постоянной э. д. с.
Присоединим катушку с сопротивлением гк и индуктив-
ностью L к источнику, э. д. с. которого Е и внутреннее
сопротивление г0 (рис. 6-22). При замыкании рубильника
Е
ток не сразу достигнет значения ~ _^_г , так как в этом кон-
туре, помимо э. д. с. Е, действует э. д. с. самоиндукции
eL, препятствующая изменению, т. е. нарастанию, тока.
По второму правилу Кирхгофа
E-Eez = ri,
где г = г04-г„.
251
Так как cL = —L, то предыдущее уравнение можно
Рис. 6-22. Включе-
ние катушки к ис-
точнику постоянной
э. д. с.
Следовательно,
записать в виде
• г di
Е — tr — L -77-
аг
или, разделив обе части последнего уравнения на г,
•_ А. А
г 1 г dt ‘
Отношение для данной цепи постоянно, посколь-
ку L и г не изменяются, и называется постоянной
времени (обозначение т). Постоян-
ная времени измеряется в секундах
(гн/ом = сек).
Таким образом,
т = (6-36)
£
Обозначим через I — -- уста-
новившееся значение тока,
т. е. ток в цепи, когда э. д. с. са-
моиндукции перестанет действовать,
уравнение цепи (рис. 6-22)
т. е. закон изменения тока в цепи задается дифферен-
циальным уравнением.
Запишем это уравнение, разделив переменные,
di dt ..
— - (6-
Продифференцируем разность токов ([—<)
d. (1—i) — — di
и подставим —di в (6-37); тогда получим:
d(l-i) _ _dt_
l — i ~ т
Интегрируя каждую часть последнего уравнения,
находим:
In (I — г) — ~ 4 + const.
252
Постоянную интегрирования для удобства записи решения
представим как логарифм некоторой новой постоянной К:
1п(/— 0= ~ у+1пК или 1п ~ 4 ’
откуда, потенцируя, получим:
или
I — i = Ke х.
(6-38)
Постоянная К определяется из условия, что в момент
включения (t = 0) ток в цепи равен нулю. В самом деле,
если бы в момент вклю-
чения ток отличался от
нуля, то это означало бы
скачок тока, так. как
в разомкнутой цепи ток,
конечно, равен нулю.
Но скачкообразному из-
менению тока сопутство-
вало бы такое же изме-
нение магнитного пото-
ка, и э. д. с. самоиндук-
ции (как производная
потока) была бы беско-
нечно велика, что физи-
чески, очевидно, невоз-
можно.
Возвращаясь к урав-
нению (6-38), мы видим,
Рис. 6-23. График изменения тока
при включении катушки под по-
стоянное напряжение.
что условию
г = 0 при / = 0(е г--=е°=^1)
соответствует K — I, и, следовательно,
t = Z(l—— е Ч.
(6-39)
На рис. 6-23 построен график изменения тока в зависи
мости от времени. Процесс изменения тока в цепи после ее
включения (или отключения) называют переходным
процессом.
t
253
В момент включения ток возрастает от нуля с наиболь-
шей скоростью. Согласно (6-37) при t — 0, когда i — О,
эта скорость
\ dt у макс т Г г L '
По мере увеличения тока скорость его роста умень-
шается; в произвольный момент времени из (6-37) на-
ходим
t t
di I — t 1 x E t
=--------= — e = -j- e
at т т L
и, наконец, при t = co, когда ток достигнет установивше-
, Е .
гося значения I == —:
г
e~f=0 и 4 = 0.
at
Теоретически ток достигнет установившегося значения
через бесконечно большое время. Однако в практических
условиях, часто спустя доли секунды, ток достигает зна-
чения, почти равного установившемуся, и можно считать
процесс изменения тока закончившимся за очень малое
время. О практической продолжительности переходного
процесса судят по постоянной времени; действительно, если
t == т, то ток
= / (1 — е'1) = 7 (^1 —0 ъ 0,63/,
т. е. за время, равное т, ток возрастает от нуля до 63%
от 1. При I = Зт
= /(1-е-3) = /(1-1) = 0,95/,
т. е. через время, равное Зт после включения, ток отличает-
ся от установившегося всего на 5%. Часто считают пере-
ходный процесс закончившимся, когда ток в цепи отли-
чается от установившегося всего на 1%, т. е. i = 0,99/.
В этом случае t « 4,6т.
Очевидно, если цепь обладает очень малой индуктив-
ностью (т = L/r мало), то ток в цепи достигает устано-
254
вившегося значения почти мгновенно.
Электродвижущая сила самоиндукции, возникающая
при переходном процессе,
_£ _t_
eL=-L^- = — Lе т = — Ire х = — Ее х. (6-40)
Электродвижущая сила самоиндукции в момент включения
максимальна ^макс = — Е и по мере роста тока спадает
до нулевого значения.
6-19. ПЕРЕХОДНЫЙ ПРОЦЕСС В КОРОТКОЗАМКНУТОМ
КОНТУРЕ
Если участок цепи, обладающий индуктивностью L
и сопротивлением г, по которому проходит ток /, замкнуть
накоротко (рис. 6-24), то в результате действия э. д. с.
самоиндукции ток в этом участке исчезает не сразу. Тон
определяется дифференциальным уравнением
• _ сц _ Е
г г ’ dt •
Разделив переменные
di _ dt
i — т ’
решим полученное дифференциальное уравнение:
1п/= — у-}-1пК,
откуда
t
i = Ke~*.
В начальный момент при t — О ток не изменяется скач-
ком, т. е.
j(O) = /=K.
Таким образом,
t
i = Ie т, (6-41)
где I—ток в цепи до короткого замыкания;
т—постоянная времени короткозамкнутого контура.
255
Рассмотрим еще цепь, изображенную на рис. 6-25. Для
измерения сопротивления катушки со стальным сердечни-
ком, обладающей большой индуктивностью, включены ам-
перметр и милливольтметр. При размыкании рубильника
в контуре катушка — милливольтметр в первый момент
времени (I = 0) пройдет ток, величина которого (6-41)
равна току /, проходившему в катушке при измерении
сопротивления.В результате обмотка милливольтметра,
Рис. 6-24. Короткое замы-
кание участка цепи, обла-
дающего сопротивлением
и индуктивностью.
Рис. 6-25. К вопросу о раз-
мыкании цепи
номинальный ток которой мал, будет сожжена. Во избежа-
ние повреждения прибора перед размыканием рубильника
милливольтметр следует отсоединить от катушки.
6-20. ЭЛЕКТРОДВИЖУЩАЯ СИЛА САМОИНДУКЦИИ
ПРИ ВЫКЛЮЧЕНИИ ЦЕПИ
Переходный процесс при выключении цепи с индуктив-
ностью протекает сложнее, чем при включении. На рис. 6-26
приведена схема, на которой показан источник питания,
катушка, обладающая сопротивлением и индуктивностью,
и включающее устройство, например однополюсный рубиль-
ник. При выключении цепи контакты рубильника расходят-
ся и в цепь последовательно включается сопротивление
воздушного промежутка между удаляющимися друг от дру-
га контактами рубильника. Если предположить, что прово-
димость воздуха ничтожно мала, то ток в такой цепи дол-
жен мгновенно уменьшиться до нуля и в цепи возникнет
бесконечно большая э. д. с. самоиндукции. Практически
возникает не бесконечно большая, но все же очень большая
э. д. с. самоиндукции. Эта э. д. с. может вызвать между
расходящимися контактами рубильника сильное электри-
ческое поле, так что произойдет ионизация воздуха, воз-
256
можно даже вырывание с поверхности контактов рубиль-
ника свободных электронов (явление автоэмиссии), тогда
в воздушном промежутке возникнет искровой или даже
дуговой разряд.
Таким образом, газовый промежуток между расходя-
щимися контактами рубильника при выключении цепи обла-
дает проводимостью и ток в цепи при
выключении уменьшается до нуля не
мгновенно. Сопротивление газового
промежутка между контактами выклю-
чающего устройства нелинейно, по-
этому математический анализ переход-
ного процесса при выключении очень
сложен. Следует помнить, что выклю-
чение цепей, по которым проходят зна-
чительные токи (сотни, тысячи ампер
и более), протекает очень тяжело для
выключающей аппаратуры. Для раз-
Рис. 6-26. Электро-
движущая сила само-
индукции при выклю-
чении цепи.
рыва таких цепей применяются -специальные выключаю-
щие устройства, не разрушающиеся от дугового разряда,
обеспечивающие быстрое его гашение и разрыв цепи тока.
6-21. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
При подключении к источнику с постоянной э. д. с-
цепи, обладающей сопротивлением и индуктивностью, ток,
как показано в § 6-18, плавно возрастает от нуля, стремясь
к установившемуся значению. С возрастанием тока в окру-
жающей цепь среде создается магнитное поле, в котором
запасается часть энергии, израсходованной питающим цепь
источником. Наличие эн'ергии в магнитном поле можно
обнаружить, например, при выключении тока. Действи-
тельно, при закорачивании катушки (рис. 6-24) энергия
в катушку из цепи не поступает, а ток в катушке не исче-
зает мгновенно, а постепенно спадает. Энергия, переходя-
щая во время этого процесса в тепло (в сопротивлении
катушки г), преобразуется из энергии магнитного поля
катушки.
Найдем энергию магнитного поля катушки при под-
ключении ее к источнику с постоянной э. д. с. Вернемся
к схеме рис. 6-22 и запишем уравнение по второму правилу
Кирхгофа в виде
Е==1Г 1 Lw
17 Теоретическая электротехника
257
Умножив обе части уравнения на i dt, получим
в левой части выражение энергии, выработанной источ-
ником за время dt,
Ei dt = i2r dt + Li di, (6-42)
или, подставляя L di — d (Li) = dY,
Ei dt ~ Er dt-\-i d4. (6-43)
В правой части уравнений (6-42) и (6-43) первое сла-
гаемое выражает энергию, переходящую за время dt
в тепло; наличие второго члена указывает, что источник
отдал, а цепь приняла еще некоторое добавочное коли-
чество энергии 28
dW = Lidi = idW,
связанное с увеличением потокосцепления цепи, т. е.
с изменением магнитного поля. Отсюда можно заключить,
что второе слагаемое выражает прирост энергии магнит-
ного поля при возрастании тока на величину di.
Полная энергия, запасенная в магнитном поле при
возрастании тока от 0 до 1,
№ = J Lidi^~^~ . (6-44)
о
6-22. ПЛОТНОСТЬ ЭНЕРГИИ МАГНИТНОГО ПОЛЯ
Допустим, что магнитное поле создается внутри коль-
цевой катушки (рис. 5-15), имеющей такие размеры, что
индукцию В можно считать одинаковой в любой точке
сердечника; в этом случае
Т = <bw = BSw.
С другой стороны
откуда
j_ HI
w
258
Подставляя в выражение энергии магнитного поля
(6-44) найденные значения Т и /, получим:
1Г/ V/ BSwHl _ ВИ
W~ 2 “ 2ш “ 2
Произведение S/ = V—это объем сердечника катушки;
поэтому
W = -^-V = #-V. (6-45)
2 2uu0
Магнитная энергия в единице объема, или плотность
энергии (обозначение №0),
w вн В2 ...
= -2fS-' (б-46»
Найденное выражение плотности магнитной энергии
справедливо как для однородного, так и для неоднород-
ного поля.
Пример 6-3. По кольцевой катушке с деревянным сердечником
(ц=1) проходит ток 25 а; сечение сердечника 25 см2, средняя длина
300 см, число витков катушки 2 100. Определить энергию магнит-
ного поля.
Напряженность магнитного поля
Iw 25-2100
W - у- = - зоо...= 175 а/см.
Магнитная индукция
В = ц07/ = 4л• 10~9-175 = 22-10~7 тл.
Объем сердечника И = SI = 25-300 = 7 500 см2.
НВ 175-22-IO-’
Энергия магнитного поля W = —я— V =-------и-----7 500 =
= 1,44 дж.
Пример 6-4. По контуру проходит
ние контура Чг = 5-10~2 вб. Определить
Энергия магнитного поля
V/ 5-IO—2-12
ток /=12 а. Потокосцепле-
энергню магнитного поля.
0,3 дж.
2
6-23. ЭЛЕКТРОМАГНИТЫ
Если около катушки, по которой проходит ток, распо-
ложить стальной сердечник (рис. 6-27), то он намагничи-
вается и втягивается в катушку. Сердечник стремится
17* 259
занять положение в середине катушки так, чтобы проходя-
щий через него магнитный поток имел максимальное зна-
чение. Работа, производимая при перемещении сердечни-
ка, и увеличение энергии маг-
нитного поля происходят за
счет энергии источника пита-
ния катушки. Обычно сталь-
ной сердечник 1 располагает-
Рнс. 6-28. Электромаг-
нит.
Рнс. 6-27. Взаимодействие
катушки с током и стально-
го сердечника
ся неподвижно внутри катушки 2, а к нему притяги-
вается стальной якорь 3. Такое устройствопринято назы-
вать электромаг-
нитом (рис. 6-28).
Электромагниты ча-
сто применяются в из-
мерительных приборах,
реле, автоматах. Элек-
тромагниты устанавли-
ваются на подъемных
кранах, например для
погрузки лома черных
металлов.
Силу, которую надо
приложить к якорю,
чтобы оторвать его от
сердечника, называют
Рис. 6-29. К расче