А. Н. ТИХОНОВ, А. А. САМАРСКИЙ
УРАВНЕНИЯ
МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
6-Е ИЗДАНИЕ,
ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО МОСКОВСКОГО
УНИВЕРСИТЕТА
1999

УДК 517.95
Т4б
ББК 22.161.6
Тихонов А. Н., Самарский А. А.
Т46 Уравнения математической физики: Учеб. пособие. — 6-е
изд., испр. и доп. — М.: Изд-во МГУ, 1999.
ISBN 5-211-04138-0.
В книге (5-е изд. — 1977 г.) рассматриваются задачи
математической физики, приводящие к уравнениям с частными производными.
Расположение материала соответствует основным типам уравнений.
Изучение каждого типа уравнений начинается с простейпЕих
физических задач, приводящих к уравнениям рассматриваемого типа.
Особое внимание уделяется математической постановке задач,
строгому изложению репЕСния простейпЕих задач и физической
интерпретации результатов. В каждой главе помещены задачи и примеры.
В 6-е издание добавлено Дополнение III, посвященное
обобщенным репЕСниям краевых задач. Кроме того, распЕирено Приложение III
к гл. III; а также добавлен § 5 в Дополнение I, посвященный
итерационным методам репЕСния линейных уравнений.
Для студентов технических специальностей вузов.
УДК 517.95
ББК 22.161.6
ISBN 5-211-04138-0 © А. Н. Тихонов, А. А. Самарский, 1999.

ОГЛАВЛЕНИЕ
Предисловие к шестому изданию 11
Из предисловия к первому изданию 14
ГЛАВА I
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
§ 1. Классификация уравнений с частными производными 2-го
порядка 15
1. Дифференциальные уравнения с двумя независимыми
переменными (15). 2. Классификация уравнений 2-го порядка со многими
независимыми переменными (22). 3. Канонические формы линейных
уравнений с постоянными коэффициентами (24).
Задачи к главе I 26
ГЛАВА II
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
1. ПростейпЕие задачи, приводящие к уравнениям
гиперболического типа. Постановка краевых задач 27
1. Уравнение малых поперечных колебаний струны (27). 2. Уравнение
продольных колебаний стержней и струн (31). 3. Энергия колебаний
струны (32). 4. Вывод уравнения электрических колебаний в
проводах (34). 5. Поперечные колебания мембраны (35). 6. Уравнения
гидродинамики и акустики (38). 7. Граничные и начальные
условия (43). 8. Редукция общей задачи (48). 9. Постановка краевых
задач для случая многих переменных (49). 10. Теорема
единственности (50). Задачи (53).
2. Метод распространяющихся волн 54
1. Формула Даламбера (54). 2. Физическая интерпретация (57).
3. Примеры (59). 4. Неоднородное уравнение (62). 5. Устойчивость ре-
пгений (64). 6. Полуограниченная прямая и метод продолжений (68).
7. Задачи для ограниченного отрезка (74). 8. Дисперсия волн (78).
9. Интегральное уравнение колебаний (79). 10. Распространение
разрывов вдоль характеристик (83). Задачи (85).

ОГЛАВЛЕНИЕ
§ 3. Метод разделения переменных 87
1. Уравнение свободных колебаний струны (87). 2. Интерпретация
репгения (93). 3. Представление произвольных колебаний в виде су-
перпозипии стоячих волн (96). 4. Неоднородные уравнения (101).
5. Общая первая краевая задача (108). 6. Краевые задачи со ста-
пионарными неоднородностями (109). 7. Задачи без начальных
условий (111). 8. Сосредоточенная сила (116). 9. Общая схема метода
разделения переменных (119). Задачи (126).
§ 4. Задача с данными на характеристиках 128
1. Постановка задачи (128). 2. Метод последовательных приближений
для задачи Гурса (129). Задачи (135).
§ 5. Решение общих линейных уравнений гиперболического типа . 135
1. Сопряженные дифференпиальные операторы (135). 2.
Интегральная форма репгения (136). 3. Физическая интерпретапия функпии Ри-
мана (139). 4. Уравнения с постоянными коэффипиентами (143).
Задачи к главе Н 147
НриложениякглавеН 148
1. О колебании струн музыкальных инструментов 148
Н. О колебании стержней 151
HI. Колебания нагруженной струны 155
1. Постановка задачи (155). 2. Собственные колебания нагруженной
струны (156). 3. Струна с грузом на конпе (161). 4. Поправки для
собственных значений (161).
IV. Уравнения газодинамики и теория ударных волн 162
1. Уравнения газодинамики. Закон сохранения энергии (162). 2.
Ударные волны. Условия динамической совместности (165). 3. Слабые
разрывы (170).
V. Динамика сорбции газов 174
1. Уравнения, описывающие пропесс сорбпии газа (174). 2.
Асимптотическое репгение (178).
VI. Физические аналогии 185
ГЛАВА III
УРАВНЕНИЯ НАРАБОЛИЧЕСКОГО ТИНА
§ 1. Простейшие задачи, приводящие к уравнениям параболического
типа. Постановка краевых задач 189
1. Линейная задача о распространении тепла (189). 2. Уравнение
диффузии (193). 3. Распространение тепла в пространстве (194). 4.
Постановка краевых задач (196). 5. Принпип максимального значения (202).
6. Теорема единственности (205). 7. Теорема единственности для
бесконечной прямой (208).
§ 2. Метод разделения переменных 209
1. Однородная краевая задача (209). 2. Функпия источника (213).
3. Краевые задачи с разрывными начальными условиями (215). 4.
Неоднородное уравнение теплопроводности (222). 5. Общая первая
краевая задача (225). Задачи (227).

ОГЛАВЛЕНИЕ
§ 3. Задачи на бесконечной прямой 228
1. Распространение тепла на бесконечной прямой. Функпия источника
для неограниченной области (228). 2. Краевые задачи для
полуограниченной прямой (242).
§ 4. Задачи без начальных условий 250
Задачи к главе III 254
Приложения к главе III 256
1. Температурные волны 256
П. Влияние радиоактивного распада на температуру земной коры . 259
III. Метод подобия в теории теплопроводности 264
1. Функция источника для бесконечной прямой (264). 2. Краевые
задачи для квазилинейного уравнения теплопроводности (267). 3. Режимы
с обострением. Эффект локализапии тепла (274).
IV. Задача о фазовом переходе 277
V. Уравнение ЭйнпЕтейна — Колмогорова 282
VL ^-Функция 286
1. Определение (5-функпии (286). 2. Разложение (5-функпии в ряд
Фурье (289). 3. Применение (5-функпии к построению функпии
источника (291).
ГЛАВА IV
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
1. Задачи, приводящие к уравнению Лапласа 295
1. Стапионарное тепловое поле. Постановка краевых задач (295).
2. Потенпиальное течение жидкости. Потенпиал стапионарного
тока и электростатического поля (296). 3. Уравнение Лапласа в
криволинейной системе координат (298). 4. Некоторые частные репгения
уравнения Лапласа (301). 5. Гармонические функпии и аналитические
функпии комплексного переменного (303). 6. Преобразование
обратных радиусов-векторов (305).
2. Общие свойства гармонических функций 307
1. Формулы Грина. Интегральное представление решения Г307). 2.
Некоторые основные свойства гармонических функпии (313). 3.
Единственность и устойчивость репгения первой внутренней краевой
задачи (317). 4. Задачи с разрывными граничными условиями (318).
5. Изолированные особые точки (319). 6. Регулярность гармонической
функпии трех переменных в бесконечности (321). 7. Внепгние
краевые задачи. Единственность репгения двух- и трехмерных задач (322).
8. Вторая краевая задача. Теорема единственности (325).
3. Решение краевых задач для простейших областей методом
разделения переменных 328
1. Первая краевая задача для круга (328). 2. Интеграл Пуассона (333).
3. Случай разрывных граничных значений (336).

ОГЛАВЛЕНИЕ
§ 4. Функция источника 338
1. Функция источника для уравнения Aw = О и ее основные
свойства (338). 2. Метод электростатических изображений и функция
источника для сферы (343). 3. Функция источника для круга (346).
4. Функция источника для полупространства (347).
§ 5. Теория потенциала 348
1. Объемный потенциал (348). 2. Плоская задача. Логарифмический
потенциал (351). 3. Несобственные интегралы (353). 4. Первые
производные объемного потенциала (360). 5. Вторые производные
объемного потенциала (363). 6. Поверхностные потенциалы (367).
7. Поверхности и кривые Ляпунова (371). 8. Разрыв потенциала
двойного слоя (374). 9. Свойства потенциала простого слоя (377).
10. Применение поверхностных потенциалов к реп1ению краевых
задач (380). 11. Интегральные уравнения, соответствующие краевым
задачам (386).
Задачи к главе IV 391
Нриложениякглаве1У 393
1. Асимптотическое выражение объемного потенциала 393
Н. Задачи электростатики 396
HI. Основная задача электроразведки 401
IV. Определение векторных полей 408
V. Нрименение метода конформного преобразования в электростатике 412
VI. Нрименение метода конформного преобразования в
гидродинамике 416
VII. Бигармоническое уравнение 422
1. Единственность реп1ения (423). 2. Представление бигармонических
функций через гармонические функции (424). 3. Penienne бигармони-
ческого уравнения для круга (425).
ГЛАВА V
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
1. Задача с начальными условиями 427
1. Уравнение колебаний в пространстве (427). 2. Метод
усреднения (429). 3. Формула Пуассона (430). 4. Метод спуска (433). 5.
Физическая интерпретация (434). 6. Метод отражения (436).
2. Интегральная формула 437
1. Вывод интегральной формулы (437). 2. Следствия из интегральной
формулы (441).
3. Колебания ограниченных объемов 444
1. Общая схема метода разделения переменных. Стоячие волны (444).
2. Колебания прямоугольной мембраны (450). 3. Колебания круглой
мембраны (454).

ОГЛАВЛЕНИЕ
Задачи к главе V 460
Приложения к главе V 461
1. Приведение уравнений теории упругости к уравнениям колебаний 461
П. Уравнения электромагнитного поля 464
1. Уравнения электромагнитного поля и граничные условия (464).
2. Потенциалы электромагнитного поля (468). 3. Электромагнитное
поле осциллятора (470).
ГЛАВА VI
РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ
§ 1. Распространение тепла в неограниченном пространстве .... 477
1. Функция температурного влияния (477). 2. Распространение тепла
в неограниченном пространстве (481).
§ 2. Распространение тепла в ограниченных телах 486
1. Схема метода разделения переменных (486). 2. Остывание круглого
цилиндра (489). 3. Определение критических размеров (491).
§ 3. Краевые задачи для областей с подвижными границами .... 493
1. Формула Грина для уравнения теплопроводности и функция
источника (493). 2. Репгение краевой задачи (498). 3. Функция источника
для отрезка (500).
§ 4. Тепловые потенциалы 502
1. Свойства тепловых потенциалов простого и двойного слоя (502).
2. Репгение краевых задач (505). 3. Условия локализации граничных
режимов с обострением (507).
Задачи к главе VI 510
Приложения к главе VI 511
I. Диффузия облака 511
П. О размагничивании цилиндра с обмоткой 514
ГЛАВА VII
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
(продоллсение)
§ 1. Основные задачи, приводящие к уравнению Аг; -\- cv = О .... 519
1. Установивп1иеся колебания (519). 2. Диффузия газа при наличии
распада и при цепных реакциях (520). 3. Диффузия в движущейся
среде (520). 4. Постановка внутренних краевых задач для уравнения
Av + cv = 0 (521).
§ 2. Функции влияния точечных источников 522
1. Функции влияния точечных источников (522). 2. Интегральное
представление репгения (525). 3. Потенциалы (528).

ОГЛАВЛЕНИЕ
§ 3. Задачи для неограниченной области. Принцип излучения ... 531
1. Уравнение Av + cv = —/ в неограниченном пространстве (531).
2. Принпип предельного поглощения (532). 3. Принпип предельной
амплитуды (534). 4. Условия излучения (535).
§ 4. Задачи математической теории дифракции 541
1. Постановка задачи (541). 2. Единственность репгения задачи
дифракции (542). 3. Дифракция на сфере (545).
Задачи к главе VH 552
Приложения к главе VH 554
I. Волны в цилиндрических трубах 554
П. Электромагнитные колебания в полых резонаторах 565
1. Собственные колебания цилиндрического эндовибратора (565).
2. Электромагнитная энергия собственных колебаний (569). 3.
Возбуждение колебаний в эндовибраторе (572).
П1. Скин-эффект 574
IV. Распространение радиоволн над поверхностью земли 579
ДОПОЛПЕПИЕI
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
§ 1. Основные понятия 585
1. Сетки и сеточные функции (586). 2. Аппроксимация простейпгих
дифференциальных операторов (587). 3. Разностная задача (593).
4. Устойчивость (594).
§ 2. Разностные схемы для уравнения теплопроводности 597
1. Схемы для уравнения с постоянными коэффициентами (597). 2. По-
rpeniHOCTb аппроксимации (599). 3. Энергетическое тождество (601).
4. Устойчивость (605). 5. Сходимость и точность (608). 6. Разностные
схемы для уравнений с переменными коэффициентами (609). 7.
Метод баланса. Консервативные схемы (610). 8. Двухслойные схемы для
уравнения теплопроводности с переменными коэффициентами (614).
9. Трехслойные схемы (620). 10. Репгение систем разностных
уравнений. Метод прогонки (622). 11. Разностные методы репгения
квазилинейных уравнений (624).
§ 3. Метод конечных разностей для репЕСния задачи Дирихле . . . 628
1. Разностная аппроксимация оператора Лапласа (628). 2. Принцип
максимума (632). 3. Оценка репгения неоднородного уравнения (635).
4. Сходимость решения разностной задачи Дирихле (636).
§ 4. Разностные методы решения задач с несколькими
пространственными переменными 638
1. Многомерные схемы (638). 2. Экономичные схемы (640).
§ 5. Итерационные методы решения сеточных уравнений 649
1. Модельная задача (649). 2. Итерационные методы линейной
алгебры (651). 3. Выбор итерационных параметров (652). 4.
Итерационные методы вариационного типа (654). 5. Диагональный оператор
В (656). 6. Попеременно-треугольный итерационный метод (657).

ОГЛАВЛЕНИЕ
ДОПОЛНЕНИЕ Н
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
1. Введение (660). 2. Общее уравнение теории специальных
функций (662). 3. Поведение решений в окрестности ж = а, если к{а) =
= О (663). 4. Постановка краевых задач (665).
Часть 1. Цилиндрические функции 668
§ 1. Цилиндрические функции 668
1. Степенные ряды (669). 2. Рекуррентные формулы (673). 3. Функции
полуцелого порядка (674). 4. Асимптотический порядок
цилиндрических функций (675).
§ 2. Краевые задачи для уравнения Бесселя 678
§ 3. Различные типы цилиндрических функций 682
1. Функции Ханкеля (682). 2. Функции Ханкеля и Пеймана (684).
3. Функции мнимого аргумента (686). 4. Функция Kq(x) (688).
§ 4. Представление цилиндрических функций в виде контурных
интегралов 693
1. Контурные интегралы (693). 2. Функции Ханкеля (695). 3.
Некоторые свойства гамма-функции (696). 4. Интегральное представление
функции Бесселя (698). 5. Интегральное представление Kiy{x) (699).
6. Асимптотические формулы для цилиндрических функций (701).
§ 5. Интеграл Фурье — Бесселя и некоторые интегралы,
содержащие функции Бесселя 703
1. Интеграл Фурье — Бесселя (703). 2. Некоторые интегралы,
содержащие функции Бесселя (705).
Часть П. Сферические функции 709
§ 1. Полиномы Лежандра 709
1. Производящая функция и полиномы Лежандра (709). 2.
Рекуррентные формулы (711). 3. Уравнение Лежандра (712). 4.
Ортогональность полиномов Лежандра (713). 5. Норма полиномов
Лежандра (714). 6. Нули полиномов Лежандра (715). 7. Ограниченность
полиномов Лежандра (715).
§ 2. Присоединенные функции Лежандра 716
1. Присоединенные функции (716). 2. Норма присоединенных
функций (717). 3. Полнота системы присоединенных функций (718).
§ 3. Гармонические полиномы и сферические функции 720
1. Гармонические полиномы (720). 2. Сферические функции (721).
3. Ортогональность системы сферических функций (724). 4.
Замкнутость системы сферических функций (727). 5. Разложение по
сферическим функциям (728).
§ 4. Некоторые примеры применения сферических функций .... 732
1. Задача Дирихле для сферы (733). 2. Проводящая сфера в поле
точечного заряда (733). 3. Поляризация шара в однородном поле (734).
4. Собственные колебания сферы (737). 5. Внеп1няя краевая задача
для сферы (740).

10 ОГЛАВЛЕНИЕ
Часть III. Полиномы Чебышёва — Эрмита и Чебышёва —
Лагерра 742
§ 1. Полиномы Чебышёва — Эрмита 742
1. Дифференциальная формула (742). 2. Рекуррентные
формулы (743). 3. Уравнение Чебышёва — Эрмита (743). 4. Норма
полиномов Нп{х) (744). 5. Функции Чебышёва — Эрмита (745).
§ 2. Полиномы Чебышёва — Лагерра 745
1. Дифференциальная формула (745). 2. Рекуррентные
формулы (746). 3. Уравнение Чебышёва — Лагерра (746). 4.
Ортогональность и норма полиномов Чебып1ёва — Лагерра (747). 5. Обобпденные
полиномы Чебышёва — Лагерра (747).
§ 3. Простейшие задачи для уравнения Шрёдингера 749
1. Уравнение Шрёдингера (749). 2. Гармонический осциллятор (750).
3. Ротатор (752). 4. Движение электрона в кулоновом поле (753).
Часть IV. Формулы, таблицы и графики 758
1. Основные свойства специальных функций 758
П. Таблицы 764
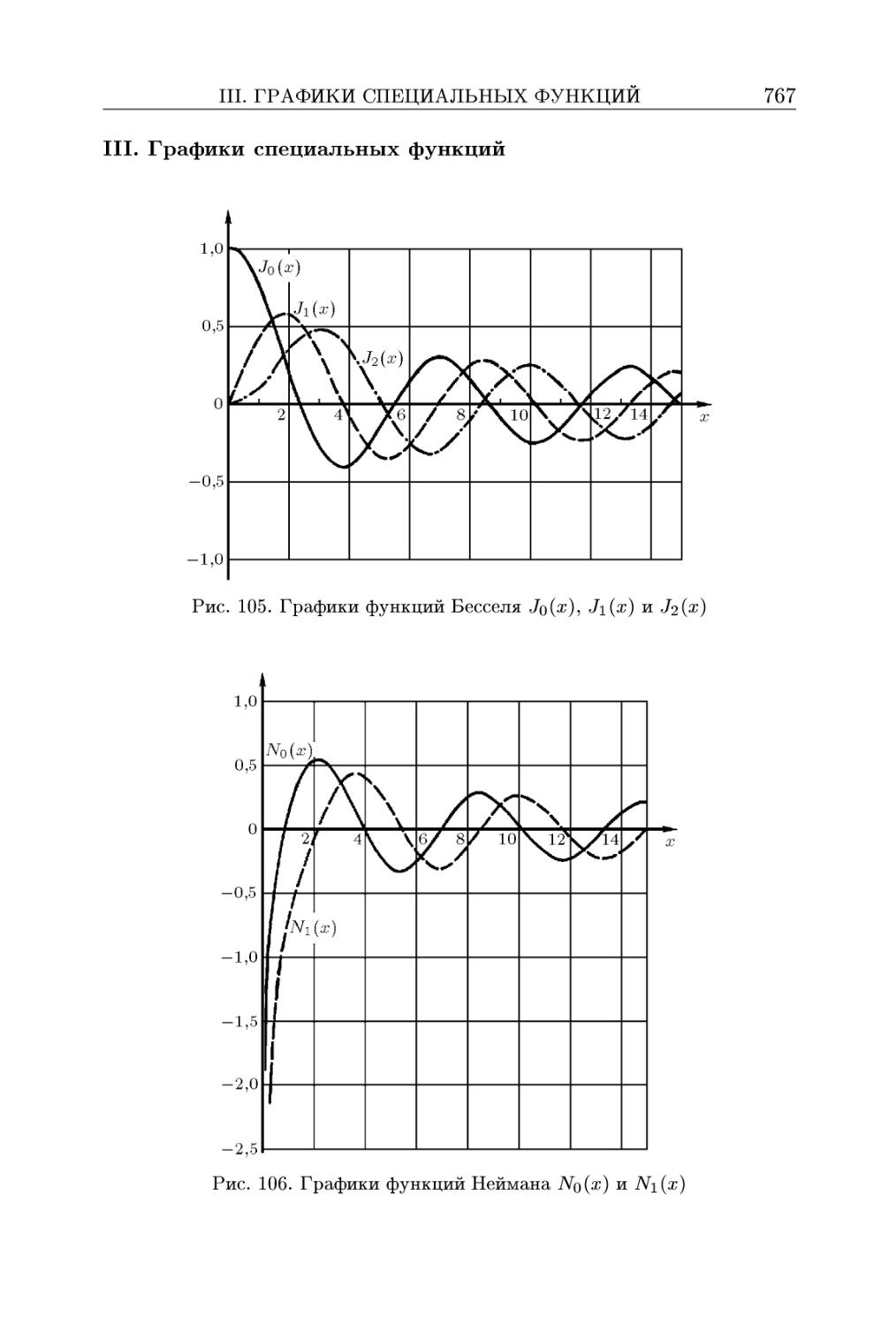
HI. Графики специальных функций 767
IV. Различные ортогональные системы координат 769
ДОПОЛНЕНИЕ III
ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
§ 1. Некоторые понятия функционального анализа 777
1. Вспомогательные сведения об интеграле Лебега, обобщенной
частной производной и некоторых функциональных пространствах (777).
2. Функциональные пространства (781).
§ 2. Обобщенное решение задачи Дирихле для уравнения Пуассона 782
1. Определение обобщенного решения задачи Дирихле (782). 2. Два
основных неравенства (785). 3. Единственность и существование
обобщенного решения задачи Дирихле (787).
Дополнительная литература 791
Предметный указатель 792

ПРЕДИСЛОВИЕ К ШЕСТОМУ ИЗДАНИЮ
Прошло почти 50 лет после выхода в свет 1-го издания этой книги
и более 20 лет после выхода 5-го. Книга прошла испытания во многих
высших учебных заведениях в нашей стране и за рубежом, была
переведена на 11 иностранных языков, сыграла большую роль в подготовке
специалистов по прикладной математике.
За последние 50 лет в науке произошли большие изменения в связи
с необходимостью решения таких крупных научно-технических
проблем, как:
1) овладение ядерной и термоядерной энергией;
2) создание высокоскоростных летательных аппаратов
(самолетов, ракет);
3) изучение физики плазмы в связи с проблемой управляемого
термоядерного синтеза;
4) проблемы риска и безопасности в связи с изучением
окружающей среды, созданием новых технологий, безопасных для окружающей
среды («экологически чистых»), и др.
Важнейшей задачей науки стала задача анализа сложных физико-
химических процессов и технических систем и управление ими на
основе знания.
Создание вычислительной техники колоссально расширило и
углубило научные исследования, привело к развитию
вычислительных методов, появлению методологии математического моделирования
и вычислительного эксперимента как новой, более высокой ступени
теоретического изучения явлений.
Математическое моделирование опирается на триаду
«математическая модель — вычислительный алгоритм — программа для
компьютера».
Математические модели — замкнутая система уравнений
(алгебраических, дифференциальных, интегральных и др.) для
характерных функций изучаемой задачи. Они описывают, как правило,
некоторые законы природы (например, законы сохранения энергии, массы,
импульса и т. д.) и включают информацию о свойствах среды
(например, в виде коэффициентов уравнений).
Процессы физики и техники характеризуются большими
диапазонами изменения основных термодинамических величин —
температуры, скорости, плотности и т. д. Для их описания используются
линейные и нелинейные модели, точнее, иерархия моделей разной сложности

12 ПРЕДИСЛОВИЕ
(полноты). Нелинейные модели включают в себя нелинейные
дифференциальные уравнения. Такие модели исследуются всеми доступными
средствами, как аналитическими, так и численными.
Понятие «реп1ить задачу» расп1ирилось: требуется не только дать
правильную математическую постановку задачи и исследовать ее
аналитическими методами (в той мере, в какой это возможно) — доказать
существование и единственность реп1ения задачи, найти ее частные и
общие реп1ения, но и дать численное penienne в нужной области
изменения входных данных (начальных и краевых данных, коэффициентов
уравнений, правых частей уравнений), т. е. провести
вычислительный эксперимент. Для практики — найти оптимальное (в некотором
смысле) penienne, что требует изучения класса задач с различными
входными данными.
Математическая физика — наука о математических моделях
физики. Она носит междисциплинарный характер. Одни и те же
модели (дифференциальные уравнения) могут описывать процессы разной
природы. Так, например, уравнение параболического типа может
описывать процессы теплопроводности, диффузии, фильтрации,
намагничивания и др. Поэтому можно говорить о базовых задачах
математической физики. Уравнения параболического, гиперболического и
эллиптического типов являются примерами базовых задач.
Сложные физические процессы описываются моделями,
являющимися, как правило, объединением нескольких базовых задач. Типичные
базовые задачи и рассматриваются в данной книге.
Материал этой книги — классический, устоявшийся, совершенно
необходимый для специалиста любого ранга при изучении задач
различной сложности. Многолетние испытания в педагогической
практике показали, что он «не стареет» и является совершенно необходимой
основой современного образования по специальностям
«Математическая физика» и «Математическое моделирование».
Линейные модели, которые детально изучаются в книге, по-
прежнему играют важную роль при решении задач любой сложности.
Их изучение (математическая постановка задачи, проблема
существования и единственности решения, типичные аналитические методы
исследования, отыскание частных решений задач) нужно для
понимания физических процессов, а сами частные решения используются в
качестве тестов для вычислительных алгоритмов.
В качестве Дополнения I в 3-е издание книги (1966 г.) был введен
раздел «Метод конечных разностей», в котором даны в простейшей
форме сведения о методе конечных разностей для решения типичных
уравнений математической физики и введены основные понятия
теории разностных схем. Более подробные сведения по теории разностных
схем и ее применениям изложены в цикле книг:
Самарский А. А. Теория разностных схем. М.: Паука, 1989.
Самарский А. А. Введение в численные методы. М.: Паука,
1987.
Самарский А. А., Гулин А. В. Устойчивость разностных

ПРЕДИСЛОВИЕ 13
уравнений. М.: Наука, 1973.
Самарский А. А., Гулин А. В. Численные методы. М.: Наука,
1989.
Самарский А. А., Андреев В. Б. Разностные методы
решения эллиптических уравнений. М.: Наука, 1978.
Самарский А. А., Попов Ю. П. Разностные схемы газовой
динамики. М.: Наука, 1990.
Самарский А. А., Николаев Е. С. Методы реп1ения
сеточных уравнений. М.: Наука, 1978.
Следует отметить, что эти книги по стилю и методологии
примыкают к настоящему изданию.
В ряде учебных пособий, написанных на ту же тему в последние
годы, изложение с самого начала основано на формализме обобщенных
решений. В данной же книге обобщенные решения вынесены в
Дополнение III «Обобщенные решения краевых задач», и это не архаизм:
книга предназначена для прикладников (физиков, инженеров),
которые должны не только уметь доказывать теоремы существования, но
и, в первую очередь, овладеть техникой решения задач с доведением
до ответа в виде формулы или вычислительного алгоритма и числа.
В б-е издание книги внесены редакционные исправления и
некоторые дополнения, из которых отметим разделы, посвященные краевым
задачам для квазилинейного уравнения теплопроводности, режимам с
обострением и эффектом локализации тепла, обнаруженным авторами
с сотрудниками.
Теоретический материал книги «Уравнения математической
физики» иллюстрируется прикладными задачами в приложениях к
каждой из глав. Кроме того, имеется «Сборник задач по математической
физике» (авторы — Б. М. Будак, А. А. Самарский, А. П. Тихонов), 4-е
издание которого находится в печати, где содержится большое число
задач на вывод уравнений и граничных условий, а также на
применение различных методов решения основных краевых задач
математической физики.
В заключение выражаю глубокую благодарность В. А. Ильину и
Е. И. Моисееву за неоценимую помощь при написании Дополнения III.
В подготовке б-го издания книги принимали участие П. П. Ваби-
щевич, В. А. Галактионов, П. П. Калиткин, Ю. Л. Левитан, А. С. Бол-
дарев, П. Г. Сиротенко, Е. В. Шильников, И. В. Абалакин, и особенно
большой вклад принадлежит СВ. Полякову.
При подготовке к печати предшествующих изданий книги оказали
большую помощь А. Г. Свешников, В. Л. Арсенин, В. В. Кравцов,
А. Ф. Никифоров, И. С. Гущин.
Всем им выражаю глубокую благодарность.
1999 г. А. А. Самарский

14 ПРЕДИСЛОВИЕ
ИЗ ПРЕДИСЛОВИЯ к ПЕРВОМУ ИЗДАНИЮ
Круг вопросов математической физики тесно связан с
изучением различных физических процессов. Сюда относятся явления,
изучаемые в гидродинамике, теории упругости, электродинамике и т. д.
Возникающие при этом математические задачи содержат много общих
элементов и составляют предмет математической физики.
Метод исследования, характеризующий эту отрасль науки,
является математическим по своему существу. Однако постановка задач
математической физики, будучи тесно связанной с изучением
физических проблем, имеет специфические черты.
Круг вопросов, относящихся к математической физике,
чрезвычайно широк. В предлагаемой книге рассматриваются задачи
математической физики, приводящие к уравнениям с частными
производными.
Мы стремились подчинить выбор и изложение материала
характеристике типичных физических процессов, в связи с чем расположение
материала соответствует основным типам уравнений.
Изучение каждого типа уравнений начинается с простейших
физических задач, приводящих к уравнениям рассматриваемого типа.
Особое внимание уделяется математической постановке задач, строгому
изложению решения простейших задач и физической интерпретации
получаемых результатов. В каждой главе помещены задачи,
преследующие в основном цель развития технических навыков. Некоторые
задачи сами по себе представляют физический интерес. В конце
каждой главы помещены приложения, в которых даются примеры
применения изложенных в основном тексте методов к решению различных
задач физики и техники, а также приводится ряд примеров,
выходящих за рамки задач, рассматриваемых в основном тексте. Выбор таких
примеров, несомненно, можно сильно варьировать.
Книга содержит лишь часть материала, входящего в курс
методов математической физики. В книгу не входят теория интегральных
уравнений и вариационные методы. Приближенные методы изложены
недостаточно полно.
В основу книги были положены лекции, читавшиеся свыше десяти
лет А. Н. Тихоновым на физическом факультете МГУ. Частично
содержание этих лекций было отражено в конспектах, изданных в 1948 —
1949 гг. В предлагаемой книге материал конспектов был расширен и
подвергнут коренной переработке.
Мы рады возможности выразить благодарность нашим ученикам
и товарищам по работе А. Б. Васильевой, В. Б. Гласко, В. А. Ильину,
А. В. Лукьянову, О. И. Панычу, Б. Л. Рождественскому, А. Г.
Свешникову и Д. Н. Четаеву, без помощи которых мы вряд ли смогли бы
подготовить к печати книгу в короткий срок, а также Ю. Л.
Рабиновичу, прочитавшему рукопись и сделавшему ряд ценных замечаний.
1951 г. А. Н. Тихонов, А. А. Самарский

ГЛАВА I
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Многие задачи математической физики приводят к
дифференциальным уравнениям с частными производными. Наиболее часто
встречаются дифференциальные уравнения 2-го порядка. В настоящей главе
мы рассмотрим классификацию этих уравнений.
§ 1. Классификация уравнений
с частными производными 2-го порядка
1. Дифференциальные уравнения с двумя независимыми
переменными. Дадим необходимые определения.
Уравнением с частными производными 2-го порядка с двумя
независимыми переменными ж, у называется соотношение между
неизвестной функцией и{х, у) и ее частными производными до 2-го
порядка включительно"*^^:
-^ \'^1 У-) ^1 '^xi '^yi '^xxi '^xyi '^yy) — '^•
Аналогично записывается уравнение и для большего числа
независимых переменных.
Уравнение называется линейным относительно
старших производных, если оно имеет вид
dllUxx + ^'Cil2Uxy + Ci22Uyy + Fi (ж, у, U, U^, Uy) = 0, (1)
где ац, ai2, «22 являются функциями х vl у.
Если коэффициенты ац, ai2, «22 не только зависят от ж и ^, а
являются, подобно Fi, функциями ж, ^, U, Ux^ Uy, то такое уравнение
называется квазилинейным.
^ Мы пользуемся следующими обозначениями для производных:
_ ди _ ди _ д^и _ д^и _ д^и

16 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
Уравнение называется линейным, если оно линейно как
относительно старших производных и^ж, Uxy, Uyy, так и относительно
функции и и ее первых производных и^, Uy:
dllUxx + ^'Cil2Uxy + Ci22Uyy + hUx + &2% + CU + / = 0, (2)
где ац, ai2, «22, ^1, ^2, с, / — функции только хну. Если
коэффициенты уравнения (2) не зависят от ж и ^, то оно представляет
собой линейное уравнение с постоянными коэффициентами. Уравнение
называется однородным, если /(ж, у) =0.
С помощью преобразования переменных
^ = (f{x, у), г] = ф{х, у),
допускающего обратное преобразование, мы получаем новое
уравнение, эквивалентное исходному. Естественно поставить вопрос: как
выбрать ^ и ?7, чтобы уравнение в этих переменных имело наиболее
простую форму?
В этом пункте мы дадим ответ на поставленный вопрос для
уравнений, линейных относительно старших производных вида (1) с двумя
независимыми переменными х и у:
dllUxx + ^'Cil2Uxy + Ci22Uyy + F (ж, у, U, U^, Uy) = 0.
Преобразуя производные к новым переменным, получаем
Ux = щ£,х -^Щ'Пх,
% = Ч^у +Ur^Vy,
Uxx = Щ^ il + 2u^^ ^хГ]х + Ur^T) Vl + Щ ixx + Ur^ Vxx, } (3)
Uxy ^ ^^^ ^x^y ~r '^^?7 y^xVy ~r ^yVx) ~r '^?7?7 VxVy ~r ^C ^^У "•" ^V Vxy^
Uyy = Щ^ ^l + 2Щг] ^уГ]у + Ur^r] rfy + Щ ^yy + U^ r]yy.
Подставляя значения производных из (3) в уравнение (1), будем иметь
^11 и^^ + 2ai2 и^г] + ^22 Ur^r] + ^ = о, (4)
где
«11 = ац Ц + 2ai2 СжСу + «22 С^,
^12 = «11 ^ж^ж + «12 (Сж% + 'Пх\у) + «22 Су%,
«22 = «11 ril + 2ai2 Г]х'Пу + «22 ^^,
а функция F не зависит от вторых производных. Заметим, что если
исходное уравнение линейно, т. е.
F (ж, у, и, Ux, Uy) = biUx + b2Uy -\- cu-\- f,
TO F имеет вид
F (^, ту, u, u^, u^) = Piu^ + /32'^/ry + 7^^ + (5,

§ 1] КЛАССИФИКАЦИЯ УРАВНЕНИЙ 2-ГО ПОРЯДКА 17
т. е. уравнение остается линейным-"^л
Выберем переменные ^ и г] так, чтобы коэффициент ац был
равен нулю. Рассмотрим уравнение с частными производными 1-го
порядка
ац zl + 2ai2 z^Zy + а22 z^ = 0. (5)
Пусть z = (р{х, у)—какое-нибудь частное penienne этого уравнения.
Если положить ^ = (р [х, у), то коэффициент ац, очевидно, будет
равен нулю. Таким образом, упомянутая выше задача о выборе новых
независимых переменных связана с решением уравнения (5).
Докажем следующие леммы.
1. Если Z = (р{х, у) является частным решением уравнения
ац zl + 2ai2 z^Zy + а22 Zy = О,
то соотношение (р (ж, у) = С представляет собой общий интеграл
обыкновенного дифференциального уравнения
ац dy^ — 2ai2 dx dy + a22 dx^ = 0. (6)
2. Если (f (ж, у) = С представляет собой обилий интеграл
обыкновенного дифференциального уравнения
ац dy^ — 2ai2 dx dy + a22 dx^ = 0,
mo функция z = (f{x, y) удовлетворяет уравнению (5).
Докажем первую лемму. Поскольку функция z = ip{x^ у)
удовлетворяет уравнению (5), то равенство
anf^) _ 2ai2 f-^) + а22 = О (7)
является тождеством: оно удовлетворяется для всех х, у в той
области, где задано решение. Соотношение (р (ж, у) = С является общим
интегралом уравнения (6), если функция у, определенная из неявного
соотношения (р{х, у) = С, удовлетворяет уравнению (6). Пусть
есть эта функция; тогда
dy_
dx
^х (ж, у)
^у (ж, у)
(8)
y=fix,C)
где квадратные скобки и индекс у = f {х, С) указывают, что в
правой части равенства (8) переменная у не является независимой
переменной, а имеет значение, равное /(ж. С). Отсюда следует, что
^ Отметим, что если преобразование переменных линейно, то F = F^ так
как вторые производные от ^ и т/ в формулах (3) равны нулю и F не
получает дополнительных слагаемых от преобразования вторых производных.
2 А. Н. Тихонов, А. А. Самарский

18 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
у = f {х, С) удовлетворяет уравнению (6), так как
ац
dy
2^12 -у- + а22
ах
ац 1- —) -2ai2 (-— ) +а22
О,
поскольку выражение в квадратных скобках равно нулю при всех
значениях ж, у^ а не только при у = / (ж, С).
Докажем вторую лемму. Пусть (/? (ж, у) = С — общий интеграл
уравнения (6). Докажем, что
ац (fl + 2ai2 (fx^y + «22 ^l
О
(Г)
для любой точки (ж, ^). Пусть (жо, ^о)—какая-нибудь заданная
точка. Если мы докажем, что в ней удовлетворяется равенство (7'), то
отсюда в силу произвольности (жо, ^о) будет следовать, что равенство
(7') есть тождество и функция ^ (ж, у) является реп1ением уравнения
(7'). Проведем через точку (жо, ^о) интегральную кривую уравнения
(6), полагая (р (жо, ^о) = Со и рассматривая кривую у = f {х, Со).
Очевидно, что Уо = f (^0 5 Со). Для всех точек этой кривой имеем
^dyY dy
- 2ai2 h «22 =
an
dx
dx
«11 -
^x
- 2ai2 -
^x
+ «22
0.
Jy=f(x,Co)
Полагая в последнем равенстве ж = жо, получаем
ац (fl (жо, ^о) + 2ai2 (fx (^о, Уо) ^у (^о, Уо) + «22 (fl (жо, Уо) = О,
что и требовалось доказать-"^л
Уравнение (6) называется характеристическим для
уравнения (1), а его интегралы — характеристиками.
Полагая ^ = (р{х,у), где ^{х, у) = const есть общий интеграл
уравнения (6), мы обращаем в нуль коэффициент при и^^. Если
ф{х, у) = const является другим общим интегралом уравнения (6),
независимым от (р (ж, у), то, полагая г] = ф {х, у), мы обратим в нуль
также и коэффициент при и^^.
^ Установленная связь уравнений (5) и (6) эквивалентна известной связи
между линейным уравнением с частными производными 1-го порядка и
системой обыкновенных дифференциальных уравнений (см.: Степанов В. В.
Курс дифференциальных уравнений. М., 1959. С. 314; Смирнов В. И.
Курс выспЕСЙ математики. Т. П. М., 1974. С. 67.). В этом можно убедиться,
разлагая левую часть уравнения (5) в произведение двух линейных
дифференциальных выражений.

dy
dx
dy _
_ CL12 + л/а^2 - CLiia22
ail
0^12 — V ^12 ~ ^11^22
КЛАССИФИКАЦИЯ УРАВНЕНИЙ 2-ГО ПОРЯДКА 19
Уравнение (6) распадается на два уравнения:
(9)
ах ац
Знак подкоренного выражения определяет тип уравнения (1)
0^11'^жж + '^CLl2Uxy + CL22Uyy + F = 0.
Это уравнение мы будем называть в точке М уравнением
гиперболического типа, если в точке М а^з — 0^110^22 > О,
параболического типа, если в точке М а^2 ~ ^11^22 = О,
эллиптического типа, если в точке М af2 ~ ^11^22 < 0^\
Нетрудно убедиться в правильности соотношения
ai2 - aiia22 = («12 - aiia22) D'^ , D ^^^Щ-'Пх iy,
из которого следует инвариантность типа уравнения при
преобразовании переменных, так как функциональный определитель (якобиан)
D преобразования переменных отличен от нуля. В различных
точках области определения уравнение может принадлежать различным
типам.
Рассмотрим область G, во всех точках которой уравнение
имеет один и тот же тип. Через каждую точку области G проходят две
характеристики, причем для уравнений гиперболического типа
характеристики действительны и различны, для уравнений эллиптического
типа — комплексны и различны, а для уравнений параболического
типа обе характеристики действительны и совпадают между собой.
Разберем каждый из этих случаев в отдельности.
1. Для уравнения гиперболического типа а^2 ~ ^11^22 > О и
правые части уравнений (9) и (10) действительны и различны. Общие
интегралы их (р {х, у) = С и ф {х, у) = С определяют
действительные семейства характеристик. Полагая
^ = (f{x,y), г] = ф{х,у), (11)
приводим уравнение (4) после деления на коэффициент при и^г] к виду
F
4v = Ф (^' V, и, щ, Urj), где Ф
2ai2'
^ Эта терминология заимствована из теории кривых 2-го порядка.
2*

20 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
Это — так называемая каноническая форма уравнений
гиперболического типа"'^^ Часто пользуются второй канонической формой.
Положим
^ = а-\- Р, Г] = а - Р,
т. е.
где а и /3 — новые переменные. Тогда
В результате уравнение (4) примет вид
Uaa -ирр = Ф1 (Ф1 =4Ф).
2. Для уравнений параболического типа а^2 ~ ^11^22 = О
уравнения (9) и (10) совпадают и мы получаем один общий интеграл
уравнения (6): (р (ж, у) = const. Положим в этом случае
^ = ip{x,y) и г] = г]{х,у),
где г]{х, у)—любая функция, независимая от (р. При таком выборе
переменных коэффициент
ац = an ^1 + 2ai2 ^х^у + «22 С^ = (лМГ^ж + л/^^?/)^ = 0^
^ Для того чтобы было возможно введение новых переменных ^ и т/
через функции ср -и. ф, надо убедиться в независимости этих функций,
достаточным условием чего является отличие от нуля соответствующего
функционального определителя. Пусть функциональный определитель
^х фх
ify фу
В некоторой точке М обращается в нуль. Тогда должна иметь место
пропорциональность строк, т. е.
что, однако.
^х
^У
^х _ фх
ify фу'
невозможно, так как
«12 + у«?2 -«11^22 ф^
ац '^ фу
(ai2 -aiia22 >
0)
«12 -
V«?2-
«11
-aiia22
(при этом мы считаем ац /О, что не является ограничением общности).
Тем самым независимость функций ср -и. ф установлена.

§ 1] КЛАССИФИКАЦИЯ УРАВНЕНИЙ 2-ГО ПОРЯДКА 21
так как ai2 = ^/ац ^/«22; отсюда следует, что
^12 = ац ^хГ]х + ai2 (Сж% + ^уГ]х) + а22 Су% =
После деления уравнения (4) на коэффициент при и^^ получим
каноническую форму для уравнения параболического типа
^гугу = Ф (С, ^, и,Щ,иг^) ( Ф = - ^ 1 .
V 0^22/
Если в правую часть не входит и^, то это уравнение будет
обыкновенным дифференциальным уравнением, зависящим от ^ как от
параметра.
3. Для уравнения эллиптического типа а^2 ~ ^11^22 < О и правые
части уравнений (9) и (10) комплексны. Пусть
(р{х, у) = С
— комплексный интеграл уравнения (9). Тогда
(/?* (ж, у) = с,
где (/?* —сопряженная к (f функция, будет представлять собой общий
интеграл сопряженного уравнения (10). Перейдем к комплексным
переменным, полагая
^ = (/?(ж, у), ту = (^*(ж, у).
При этом уравнение эллиптического типа приводится к такому же
виду, что и гиперболическое.
Чтобы не иметь дела с комплексными переменными, введем новые
переменные а и /3, равные
а = —-—, р —
2 ' ' 2г '
так что
^ = а + ip, Г] = а — ip.
В этом случае
ац ^1 + 2ai2 ^х^у + «22 ^1 =
= (ац al + 2ai2 а^ау + а22 «^) - (ац /3^ + 2ai2 РхРу + «22 /?^) +
+ 2г (ац а^/Зж + «12 {о^хРу + %/^ж) + «22 о^уРу) = О,
т. е.
«11 = «22 и ai2 = 0.

22 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
Уравнение (4) после деления на коэффициент при и^а принимает
вид ■'■^
/ F
Uaa -\-Upp = Ф {а, (3, и, Ua, Up) Ф = - ^
V ^22
Таким образом, в зависимости от знака выражения а^2 ~ ^11^22
имеют место следующие канонические формы уравнения (1):
0^12 ~ ^11^22 > О (гиперболический тип) Uxx — Uyy = Ф или Uxy = Ф,
0^12 ~ ^11^22 < о (эллиптический тип) Uxx + Uyy = Ф,
0^12 ~ ^11^22 = о (параболический тип) — Uxx = Ф-
2. Классификация уравнений 2-го порядка со многими
независимыми переменными. Рассмотрим линейное уравнение с
действительными коэффициентами
п п п
^ ^ aijUx-xj + ^ biUx- +CU + f = 0 {aij = aji), (12)
j=l i=l i=l
где a, b, c, / являются функциями xi, Ж2, ..., Xn- Введем новые
независимые переменные ^k, полагая
6 = 6 (^Ь Ж2, ..., Жп) {к=1, ..., п).
Тогда
-Л k=l
к=1 к=1 1=1
где
dxi
Подставляя выражения для производных в исходное уравнение,
получим
п п п
Y1 Y1 ^^i4kii + Ц ^кЩ^ + CU + / = о,
^ Подобное преобразование законно только в том случае, если
коэффициенты уравнения (1) — аналитические функции. Действительно, если ai2 —
— aiia22 < О, то правые части уравнений (9) и (10) комплексны, а
следовательно, функция у должна иметь комплексные значения. О репЕСнии
этих уравнений можно говорить липеь в том случае, когда коэффициенты
^ik (^7 у) определены для комплексных значений у. При приведении
уравнения эллиптического типа к канонической форме мы ограничимся случаем
аналитических коэффициентов.

§ 1] КЛАССИФИКАЦИЯ УРАВНЕНИЙ 2-ГО ПОРЯДКА 23
где
п п п п п
i=l j=l i=l i=l j=l
Рассмотрим квадратическую форму
п п
^^CLbViVj^ (13)
i=l j=l
коэффициенты которой равны коэффициентам aij исходного
уравнения в некоторой точке Mq (ж^, ..., ж^). Произведя над переменными
у линейное преобразование
п
k=l
получим для квадратической формы новое выражение
п п п п
^ ^ О'ы т т, где o,li=Y^Y^ а% Щк aji.
к=1 1=1 i=l j=l
Таким образом, коэффициенты главной части уравнения
изменяются аналогично коэффициентам квадратической формы при линейном
преобразовании.
Как известно, выбором соответствующего линейного
преобразования можно привести матрицу (а^) квадратической формы к
диагональному виду, в котором
141 = 1 либо 141=0;
4j- =0 {i^j, г, j = 1, 2, ..., n).
Согласно закону инерции число положительных, отрицательных
и равных нулю коэффициентов а!-- в каноническом виде квадратичной
формы инвариантно относительно линейного преобразования.
Назовем уравнение (12) в точке Mq уравнением
эллиптического типа, если все п коэффициентов of-- одного знака;
гиперболического типа (или нормального гиперболического типа),
если п — 1 коэффициентов а!-- имеют одинаковый знак, а один
коэффициент противоположен им по знаку; ультрагиперболического
типа, если среди of-- имеется т коэффициентов одного знака и п — т
коэффициентов противоположного знака (ттг, п — т > 1);
параболического типа, если хотя бы один из коэффициентов 4 Рс1вен нулю.
Выбирая новые независимые переменные ^i так, чтобы в точке
Мо
_ ОЬ _ ,.0
''" dXi ~ '''
где a^f^—коэффициенты преобразования, приводящего квадратиче-

24 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
скую форму (13) к каноническому виду (например, полагая ^k =
= ^Oi^Xi), получаем, что в точке Mq уравнение в зависимости от
типа приводится к одной из следующих канонических форм:
Uxixi + Ux2X2 + ... + Ux^x^ + Ф = О (эллиптический тип),
п
'^Ж1Ж1 = Z^'^^i^i ~^ ^ (гиперболический тип).
^^XiXi= ^ UxiXi+^ (Ш>1,П-Ш>1)
i=l i=m-\-l
п — т
2^ i^UxiXi) + Ф = О (ш > 0) (параболический тип).

(ультрагиперболический тип),
i=l
Мы не останавливаемся при этом на более подробном делении
уравнений параболического типа на уравнения
эллиптически-параболические, гиперболически-параболические и т. д.
Таким образом, если уравнение (12) в некоторой точке М
принадлежит к определенному типу, то его можно привести к
соответствующей канонической форме в этой точке.
Рассмотрим подробнее вопрос о том, можно ли привести
уравнение к канонической форме в некоторой окрестности точки М, если во
всех точках этой окрестности уравнение принадлежит к одному и тому
же типу.
Для приведения уравнения в некоторой области к каноническому
виду нам пришлось бы функции ^i {xi, Ж2, ..., ж^) (г = 1, 2, ..., п)
подчинить дифференциальным соотношениям uki = О для к ф I.
Число этих условий, равное п{п — 1)/2, превосходит п — число
определяемых функций ^ при п > 3. Для п = 3 недиагональные элементы
матрицы {cLik)^ вообще говоря, можно было бы обратить в нуль, но
при этом диагональные элементы могут оказаться различными.
Следовательно, при п ^ 3 уравнение нельзя привести к
каноническому виду в окрестности точки М. При п = 2 можно обратить в нуль
единственный недиагональный коэффициент и удовлетворить условию
равенства двух диагональных коэффициентов, что и было сделано в
п. 1.
Если коэффициенты уравнения (12) постоянны, то, приведя (12) к
канонической форме в одной точке М, мы получим уравнение,
приведенное к канонической форме во всей области определения уравнения.
3. Канонические формы линейных уравнений с
постоянными коэффициентами. В случае двух независимых переменных
линейное уравнение 2-го порядка с постоянными коэффициентами
имеет вид
ацПхх + '2.ai2Uxy + a22Uyy + biu^ + &2% + cu + / (ж, у) = 0. (14)

§ 1] КЛАССИФИКАЦИЯ УРАВНЕНИЙ 2-ГО ПОРЯДКА 25
Ему соответствует характеристическое уравнение с постоянными
коэффициентами. Поэтому характеристики будут прямыми линиями:
«12 + у^а^2 - CLiia22 , ^ CL12 - y^aj^ - CLllCi22 , ^
у= ^-^^ ж + Ci, у= ^-^^ х-\-С2-
С помощью соответствующего преобразования переменных уравнение
(14) приводится к одной из простейп1их форм:
и^^ + Ur^r] + biu^ + b2Ur^ -\- си -\- f = о (эллиптический тип), (15)
и^г] + biu^ + b2Ur^ -\- CU + f = о I
или > (гиперболический тип), (16)
и^^ — Ur^r] + biU^ + b2Ur^ -\- CU + f = 0\
и^^ + biu^ + b2Ur^ + си + f = о (параболический тип). (17)
Для дальнейшего упрощения введем вместо и новую функцию v:
и = е^^+^^ . V,
где Л и fi — не определенные пока постоянные. Тогда
u^=e^C+^^(^^+Ai;),
u^=e^^+M^(^^+^^),
Ur^r]=e^^^^'^ [vr^T] + 2/^^ry + A^^^).
Подставляя выражения для производных в уравнение (15) и сокращая
затем на е^^+^^, получаем
v^^ + Vr^r] + (^1 + 2Л) v^ + (62 + 2/i) Vr^ +
+ (Л^ + /i^ + biX + b2iii + c)v + fi= 0.
Параметры Л и /i выбираем так, чтобы два коэффициента, например
при первых производных, обратились в нуль (Л = — 6i/2; /j, = —62/2).
В результате получим
где 7 — постоянная, выражающаяся через с, 6i и ^2, /i = Je-(^^+^^).
Производя аналогичные операции и для случаев (16) и (17), приходим
к следующим каноническим формам для уравнений с постоянными ко-

26 КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. I
эффициентами:
v^^ + Vrjr] + 7'^ + /i =0 (эллиптический тип),
или > (гиперболический тип),
v^^ + b2Vrj + /i = 0 (параболический тип).
Как было отмечено в п. 2, уравнение с постоянными коэффициентами
в случае нескольких независимых переменных
п п п
i=l j=l i=l
при помощи линейного преобразования переменных приводится к
каноническому виду одновременно для всех точек области его определения.
Вводя вместо и новую функцию v:
и выбирая нужным способом Л^, мы можем дальше упростить
уравнение, что приводит нас к каноническим формам, сходным со случаем
п = 2.
ЗАДАЧИ К ГЛАВЕ I
1. Найти области гиперболичности, эллиптичности и параболичности
уравнения Uxx + yuyy = О и привести его к каноническому виду в области
гиперболичности.
2. Привести к каноническому виду уравнения:
а) Uxx + xyuyy = 0;
б) yuxx - xuyy + Ux + yuy = 0;
в) e^^'uxx + 2e^+^ Uxy + е^У Uyy = 0;
r) Uxx + (1 + y)^ Uyy = 0;
Д) XUxx + 2 y/xyuxy + yuyy — Ux = 0]
е) (ж - у) Uxx -\- {xy - y'^ - X -\- у) Uxy = 0;
ж) у Uxx — e ^ Uyy -\- ux = 0]
з) sin^ yuxx - e^^ Uyy + 3ux - 5n = 0;
и) Uxx + 2uxy + 4:Uyy + 2ux + 3% = 0.
3. Привести к каноническому виду и максимально упростить уравнение
auxx + '^CLUxy + CLUyy + bux + c% + n = 0; a, 6, с — постоянные.
4. Введя функцию выбирая соответствующим образом
параметры Л и /х, упростить следующие уравнения с постоянными
коэффициентами:
а) Uxx + Uyy + aux + /5% + 7'^ = 0; б) Uxx = ^ % + an + /3n^;
в) Uxx 2 '^^^ ^ ^'^^ + ^'^^ + '^'^' ^) '^^^ ^ ^'^^ + l^'^y-

ГЛАВА II
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
Уравнения с частными производными 2-го порядка
гиперболического типа наиболее часто встречаются в физических задачах,
связанных с процессами колебаний. Простейшее уравнение гиперболического
типа
^УУ
о
обычно называют уравнением колебаний струны. В
настоящей главе, как и в последующих, мы ограничимся рассмотрением
класса линейных уравнений.
§ 1. Простейшие задачи, приводящие к уравнениям
гиперболического типа. Постановка краевых задач
1. Уравнение малых поперечных колебаний струны.
Каждую точку струны длины / можно охарактеризовать значением
ее абсциссы х. Описание процесса колебания струны может быть
проведено при помощи задания положения точек струны в
различные моменты времени. Для определения положения струны в
момент времени t достаточно задать компоненты вектора смещения
{ щ (ж, t), U2 (ж, t), Us (ж, t) } точки X в момент t.
Мы рассмотрим наиболее простую задачу о колебаниях струны.
Будем предполагать, что смещения струны лежат в одной плоскости
X, и и что вектор смещения и
перпендикулярен в любой момент
к оси х; тогда процесс
колебания можно описать одной
функцией u{x,t), характеризующей
вертикальное перемещение
струны. Будем рассматривать струну
как гибкую упругую нить.
Математическое выражение понятия Рис. 1
гибкости заключается в том, что напряжения, возникающие в струне,
всегда направлены по касательным к ее мгновенному профилю (рис. 1).
Это условие выражает собой то, что струна не сопротивляется изгибу.
371372

28 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Величина натяжения, возникающего в струне вследствие
упругости, может быть вычислена по закону Гука-'^^ Будем рассматривать
малые колебания струны и пренебрегать квадратом Ux по сравнению
с единицей.
Пользуясь этим условием, подсчитаем удлинение, испытываемое
участком струны (xi, Х2). Длина дуги этого участка равна
Х2
' = / Y^l + {uxY dx ^X2-xi= S.
s
Таким образом, в пределах принятой нами точности удлинения
участков струны в процессе колебания не происходит; отсюда в силу закона
Гука следует, что величина натяжения Т в каждой точке не меняется
со временем. Покажем также, что натяжение не зависит и от ж, т. е.
Т {х) = Го = const.
Найдем проекции натяжения на оси х ж и (обозначим их Т^ и Ти)'.
Т
Тх(х) = Г (ж) cos а = , =Т(х),
Ти (х) = Т (х) sin а ^ Г (ж) tga = T (х) и^,
где а — угол касательной к кривой u{x,t) с осью х. На участок
(ж1, Х2) действуют силы натяжения, внешние силы и силы инерции.
Сумма проекций всех сил на ось х должна быть равна нулю (мы
рассматриваем только поперечные колебания). Так как силы инерции и
внешние силы, по предположению, направлены вдоль оси и, то
Tx{x2)-Tx{xi)=0, или T{xi)=T{x2). (1)
Отсюда в силу произвольности xi и Х2 следует, что натяжение не
зависит от ж, т. е. для всех значений х и t
Т(х)=То. (2)
После сделанных предварительных замечаний перейдем к выводу
уравнения поперечных колебаний струны. Воспользуемся вторым
законом Ньютона. Составляющая количества движения участка струны
(ж1, Х2) по оси и равна
Х2
XI
^^ Стрелков С. П. Механика. М., 1975.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 29
где р — линейная плотность струны. Приравняем изменение
количества движения за промежуток времени А^ = ^2 — ^i
h
Х2
XI
импульсу действующих сил, складывающихся из натяжения
-J-0'^x\x=X2 -J-0'^x\x=xi
В точках Ж2 и Ж1 и внеп1ней силы, которую будем считать
непрерывно распределенной с плотностью (нагрузкой) F (ж, t), рассчитанной
на единицу длины. В результате получим уравнение поперечных
колебаний элемента струны в интегральной форме
Х2
XI
t2 Х2 t2
= f То[и^ {Х2, т) - и^ {хг, T)]dT + f f F(^, T)d^dT. (3)
tl Xl tl
Для перехода к дифференциальному уравнению предположим
существование и непрерывность вторых производных от и{х, t)^\
Тогда формула (3) после двукратного применения теоремы о среднем
примет вид
u„iC,npin^tAx = {To[u,Ar,tn] + F{r\t*n}^tAx,
где
Г, Г, г* е (xi, Х2), а f, t*\ t*** G (h, h).
Сократив на A^ Ax и перейдя к пределу при Ж2 —>■ ^i, ^2 —>■ ^i,
получим дифференциальное уравнение поперечных колебаний струны
Го^жж = putt -F{x, t). (4)
В случае постоянной плотности р = const этому уравнению обычно
придают вид
utt = а Uxx + f {x,t) I а = ^/ — I , (5)
^ Делая предположение о двукратной дифференцируемости функций, мы
фактически условливаемся о том, что будем рассматривать липеь функции,
обладающие этим свойством. Таким образом, подобного типа
предположение связано с ограничением круга изучаемых физических явлений и не
содержит в себе утверждения, что не существует функций, удовлетворяющих
интегральному уравнению колебаний и не имеющих вторых производных.
Такие функции существуют и представляют значительный практический
интерес. Подробнее см. об этом § 2, п. 9.

30
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
где
f{x,t) = -F{x,t)
Р
(6)
есть плотность силы, отнесенная к единице массы. При отсутствии
внешней силы получим однородное уравнение
utt = a^Uxx
или
Uxx -Uyy = 0 {у = at),
описывающее свободные колебания струны. Это уравнение является
простейп1им примером уравнения гиперболического типа.
Если в точке xq {xi < xq < Х2) приложена сосредоточенная сила
/о (t) (рис. 2), то уравнение (3) запип1ется так:
Х2 Х2 t2
I'piO к (^, t2) - Щ (^, h)\ d^- I I f{^, т) didr =
Xl Xl ti
1^2 1^2
= To [u^ (ж2, r) - u^ {xi, t)] dT-\- fo (r) dr.
ti ti
Поскольку скорости точек струны ограничены, то при xi ^ xq и Ж2 —>■
—>- хо интегралы в левой части этого равенства стремятся к нулю и
равенство (3) принимает вид
t2 t2
I Го [и, (жо + о, г) - и, (жо - О, г)] dT = - [ fo (г) dr. (7)
ti ti
Пользуясь теоремой о среднем, сокращая обе части равенства на А^ и
переходя к пределу при ^2 -^ ti,
получаем
'^к
|/oW
Ux (ж, t)
жо+0 -j
О Хо
Рис. 2
этой точке должны выполняться два условия сопряжения:
и {хо -\-0, t) = и {хо - О, t),
Отсюда видно, что в точке приложения
сосредоточенной силы первые
производные претерпевают разрыв и
дифференциальное уравнение теряет смысл. В
Ux {хо + о, ^) - Ux {хо - о, ^) = - — /о (t),
-1-0
(8)

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 31
первое из которых выражает непрерывность струны, второе
определяет величину излома струны в точке жо, зависящую от /о (t) и
натяжения Tq.
2. Уравнение продольных колебаний стерлсней и струн.
Уравнения продольных колебаний для струны, стержня и пружины
записываются одинаково. Рассмотрим стержень, расположенный на
отрезке (О, /) оси х. Процесс продольных колебаний может быть
описан одной функцией и{х, t), представляющей в момент t смещение
точки, имевп1ей в положении равновесия абсциссу Х'^К При
продольных колебаниях это смещение происходит вдоль стержня. При выводе
уравнения будем предполагать, что натяжения, возникающие в
процессе колебания, следуют закону Рука.
Подсчитаем относительное удлинение элемента (ж, ж + Ах) в
момент t. Координаты концов этого элемента в момент t имеют
значения
X -\- и{х, t), X -\- Ах -\- и{х -\- Ах, t),
а относительное удлинение равно
[Ах -\-и{х-\- Ах, t) -и (ж, t)] - Ах
Ах
и^ (ж + 19 Аж, t) (0^6> ^ 1).
Перейдя к пределу при Аж —>- О, получим, что относительное
удлинение в точке ж определяется функцией Ux {х, t). В силу
закона Рука натяжение Т (ж, t) равно
T{x,t) = k{x)ux{x,t), (9)
где к (ж) — модуль Юнга в точке ж {к (ж) > 0).
^ Выбранная здесь геометрическая переменная х называется переменной
Лагранжа. В переменных Лагранжа каждая физическая точка стержня в
течение всего процесса характеризуется одной и той же геометрической
координатой X. Физическая точка, занимавпЕая в начальный момент (в
состоянии равновесия) положение ж, в любой последующий момент t находится
в точке с координатой X = х -\- и{х, t). Если мы фиксируем некоторую
геометрическую точку А с координатой X, то в различные моменты времени
в этой точке будут находиться различные физические точки (с разными ла-
гранжевыми координатами х). Часто пользуются также переменными
Эйлера X, t, где X — геометрическая координата. Если U {X, t) — смещение
точки с эйлеровой координатой X, то лагранжева координата
х = Х-и{Х, t).
Пример использования координат Эйлера приведен в п. 6.

32 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Пользуясь теоремой об изменении количества движения, получаем
интегральное уравнение колебаний
XI
t2 Х2 t2
= [k{x2)ux{x2, г) -k{xi)ux{xi, T)]dT+ / / F (^, T)d^dT, (10)
tl Xl ti
где F (ж, t) —плотность внешней силы, рассчитанная на единицу
длины.
Предположим существование и непрерывность вторых
производных функции и{х, t). Применяя теорему о среднем и совершая
предельный переход ^^ при Аж = Ж2 — Ж1 —>- О и А^ = ^2 — ^i —>■ О, приходим
к дифференциальному уравнению продольных колебаний стержня '^^
[к {х) u^]^ = putt - F (ж, t). (11)
Если стержень однороден {к (ж) = const, р = const), то это уравнение
записывают следующим образом:
Utt = a^Uxx +f{x,t) la = W-j, (12)
где
f{x,t) = ^^^^ (13)
Р
есть плотность силы, отнесенная к единице массы.
3. Энергия колебаний струны. Пайдем выражение для
энергии поперечных колебаний струны Е = К -\-U, где К — кинетическая
и и — потенциальная энергия. Элемент струны dx, движущийся со
скоростью V = щ, обладает кинетической энергией
- mv'^ = - р (х) dx (щ)^ {m = pdx).
^ В дальнейшем мы будем опускать подробности, связанные с
предельными переходами, которые были разобраны при выводе уравнения поперечных
колебаний струны.
^ Условие малости колебаний в данном случае связано только с границей
применимости закона Гука. В общем случае Т = А; (ж, Ux) Ux, и мы приходим
к квазилинейному уравнению
[к (ж, Ux) Ux]x = putt - F (ж, t).

ПРОСТЕЙШИЕ ЗАДАЧИ
33
Кинетическая энергия всей струны равна
^ = 2 Р(^) ['^t (ж, t)]'^ dx.
(14)
Потенциальная энергия поперечных колебаний струны, имеющей
при t = to форму и (ж, ^о) = '^0 (ж), равна работе, которую надо
совершить, чтобы струна перешла из положения равновесия в положение
щ (х). Пусть функция и (ж, t) дает профиль струны в момент t,
причем
и (ж, 0) = О, и (ж, ^о) = '^0 (х).
Элемент dx под действием равнодействующей сил натяжения
, ди
дх
x-\-dx
, ди
дх
— -Z. ^J^XX ^Ж
за время dt проходит путь щ (ж, t) dt. Работа, производимая всей
струной за время dt, равна
.0
^dx } dt
- TqUxU
' i
I
Id f rn / \2 7 m
~ 2di '^'^^^ "^ '^^ '^^
dt.
Интегрируя no ^ от 0 до ^o, получаем
^0
^JToiu^fdxl +Jtou,
Щ
dt
I to
- - / To [u^ (ж, ^o)]^ dx-\- To u^ щ
dt.
Нетрудно выяснить смысл последнего слагаемого правой части
этого равенства. Действительно, ToUx\x=^ есть величина натяжения
на конце струны ж = 0; ut{0,t) dt — перемещение этого конца, а
интеграл
^0
[Тои,
Ut\x=odt
(15)
представляет работу, которую надо затратить на перемещение конца
ж = 0. Аналогичный смысл имеет слагаемое, соответствующее ж = L
3 А. Н. Тихонов, А. А. Самарский

34 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Если концы струны закреплены, то работа на них будет равна нулю
(при этом и (О, t) = О, щ (О, t) =0). Следовательно, при перемещении
закрепленной на концах струны из положения равновесия и = О в
положение щ (х) работа не зависит от способа перевода струны в это
положение и равна
-\ j ToK{x)f dx, (16)
О
потенциальной энергии струны в момент t = to с обратным знаком.
Таким образом, полная энергия струны равна
Е=1 J[To Ю^ + р (х) {utf] dx. (17)
о
Совершенно аналогично может быть получено выражение для
потенциальной энергии продольных колебаний стержня. Впрочем, его можно
получить также, исходя из формулы для потенциальной энергии
упругого стержня
где /о — начальная длина стержня, / — конечная длина. Отсюда
непосредственно следует
и = ^ I k(ux)^ dx.
о
4. Вывод уравнения электрических колебаний в проводах.
Прохождение электрического тока по проводу с распределенными
параметрами характеризуется силой тока i и напряжением v, которые
являются функциями положения точки X и времени t. Применяя закон
Ома к участку длиной dx, можно написать, что падение напряжения
на элементе провода dx равняется сумме электродвижущих сил:
— Vx dx = iRdx-\-itLdx, (18)
где R и L — сопротивление и коэффициент самоиндукции,
рассчитанные на единицу длины.
Количество электричества, притекающее на элемент провода dx
за время dt,
[i (ж, t) — i{x -\- dx, t)] dt = —ix dx dt (19)
равно сумме количества электричества, необходимого для зарядки
элемента dx, и количества, теряющегося вследствие несовершенства
изоляции:
С [v (ж, t-\-dt) -V (ж, t)] dx-\-Gdx-vdt = {Cvt + Gv) dx dt, (20)

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 35
где С и G — коэффициенты емкости и утечки, рассчитанные на
единицу длины, причем величину потерь мы считаем пропорциональной
напряжению в рассматриваемой точке провода.
Из формул (18) — (20) получаем систему
г'ж + Lit + i^i = 0,j
называемую системой телеграфных уравнений^^.
Чтобы получить одно уравнение, определяющее функцию г,
продифференцируем первое равенство (21) по ж, второе — по ^, умножив
его на С. Произведя вычитание в предположении постоянства
коэффициентов, найдем
ixx -\-Gvx - CL itt - CR ц = 0.
Заменяя Vx его значением из второго уравнения (21), получаем
уравнение для силы тока
i^^ = СЫи + {CR + GL) it + GRi. (22)
Аналогично выглядит уравнение для напряжения:
Vxx = CL vtt + {CR + GL) vt + GRv. (23)
Уравнение (22) (или (23)) называется телеграфным уравнением.
Если можно пренебречь потерями через изоляцию и если
сопротивление очень мало [G = R = 0), то мы приходим к известному уравнению
колебаний
Vtt = Ci^Vxx ( ^ ^ V LT 1 ' ^^^^
5. Поперечные колебания мембраны. Мембраной называется
плоская пленка, не сопротивляющаяся изгибу и сдвигу. Рассмотрим
мембрану, натянутую на плоский контур С. Будем изучать
поперечные колебания мембраны, в которых смещение перпендикулярно
к плоскости мембраны.
Пусть ds — элемент дуги некоторого контура, взятого на
поверхности мембраны и проходящего через точку М (ж, у). Па этот
элемент действует натяжение, равное Tds. Вектор Т вследствие
отсутствия сопротивления изгибу и сдвигу лежит в касательной плоскости к
мгновенной поверхности мембраны и перпендикулярен к элементу ds.
Можно показать, что отсутствие сопротивления сдвигу приводит к
тому, что величина натяжения не зависит от направления элемента ds,
так что вектор натяжения Т = Т (ж, ^, 2;) является функцией ж, ^ и
^ Эти уравнения являются приближенными в рамках теории
электромагнитного поля, поскольку они не учитывают электромагнитных колебаний в
среде, окружающей провод.

36
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
D
У2[
t. Эти свойства вектора Т служат математическим выражением
отсутствия сопротивления изгибу и
сдвигу.
Будем изучать малые
колебания мембраны, пренебрегая
квадратами первых производных
Ux И Uy^ где функция и (ж, ^, t)
определяет форму мембраны в
момент времени t. Из этого
предположения сразу же следует, что
Th{x,y,t) — проекция натяжения
на плоскость (ж, у) —равна
абсолютной величине натяжения. В самом деле, при любой ориентации
дуги ds угол j' между вектором Т и плоскостью (ж, у) не
превосходит угла 75 образуемого нормалью к поверхности мембраны в точке
(ж, у) с осью Z. Поэтому
у = У1
X = XI
X = Х2
Рис. 3
COS У ^ COS 7 =
/
= 1,
1 + ul + ul
т. е. COS 7' — 1, и
П {х, у, z,t)=T cosy = Т {х, у, Z, t). (25)
Вертикальная составляющая натяжения, очевидно, равна
ди
Т
дп'
Выделим на поверхности мембраны элемент площади, проекция
которого на плоскость (ж, у) является прямоугольником ABCD со
сторонами, параллельными осям координат (рис. 3). Па этот элемент
действует сила натяжения, равная
Т* = * Tds.
ABCD
(26)
В силу отсутствия перемещения вдоль осей х ж у проекции Т* на
эти оси равны нулю:
с D
Т: = JT{x2,y,t)dy- JT{xuy.t)dy =
в А
У2
= l{T(x2,y,t)-T(xuy,t)}dy = 0.

ПРОСТЕЙШИЕ ЗАДАЧИ 37
Аналогично
Х2
Т; = J{T{x, у2, t)-T{x, уи t)}dx = 0.
XI
Пользуясь теоремой о среднем и учитывая произвол в выборе площади
ABCD, получаем
Г (ж, у1, t) =Т(ж, у2, t),\ .^7)
T{xuy.t)=T{x2,y,t),\
т. е. натяжение Т не меняется при изменении ж и ^ и может зависеть
лип1ь от t.
Площадь какого-либо элемента мембраны в момент времени t
равна в нашем приближении
11^ = II ^1+^4+^ dx dy - II dx dy. (28)
Следовательно, в процессе колебаний не происходит растяжения,
откуда в силу закона Гука вытекает независимость натяжений от
времени. Таким образом, мы установили, что натяжение не зависит от
переменных ж, у и t:
Г (ж, у, t) = const = Го. (29)
Перейдем к выводу уравнения колебаний мембраны.
Воспользуемся теоремой о приращении количества движения. Пусть Si —проекция
на плоскость (ж, у) некоторого участка мембраны, а Ci—граница Si.
Приравнивая изменение количества движения импульсу вертикальных
составляющих сил натяжения и внешних действующих сил с
плотностью i^ (ж, ^, ^), получаем уравнение колебаний мембраны в
интегральной форме
/ / [щ (ж, у, t2) - щ (ж, у, ti)] р (ж, у) dx dy =
s
t2 t2
= / To-^dsdt-\- Fdxdydt, (30)
ti Ci ti 5i
где p{x,y)—поверхностная плотность мембраны, a F{x,y,t) —
плотность внешней силы (на единицу площади).

38 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Для перехода к дифференциальному уравнению предположим, что
функция и{х, у, t) имеет непрерывные вторые производные. С
помощью теоремы Остроградского — Гаусса ""^^ контурный интеграл
преобразуется в поверхностный:
--ds= {и^х + Uyy) dx dy,
вследствие чего интегральное уравнение колебаний приводится к виду
Г I
{putt - То {uxx + Uyy) - F (ж, у, t)] dx dy dt = 0.
C2
Пользуясь теоремой о среднем, произвольностью выбора Si и
промежутка времени (^i, ^2), делаем заключение о тождественном
равенстве нулю выражения в фигурных скобках. Таким образом, приходим
к дифференциальному уравнению колебаний мембраны
putt = То {и^х + Uyy) + F (ж, у, t). (31)
Для однородной мембраны уравнение колебаний можно записать в виде
utt = а^ {uxx + Uyy) -\- f{x, y,t) la^ = —\ (32)
где / (ж, у, t) —плотность силы, рассчитанная на единицу массы
мембраны.
6. Уравнения гидродинамики и акустики. Для
характеристики движения жидкости пользуются функциями vi (ж, у, Z, t),
V2 {х, у, Z, t), vs {х, у, Z, t), представляющими компоненты вектора
скорости V в точке (ж, у, z) в момент t (эйлеровы переменные).
Величинами, характеризующими движение жидкости, являются также
плотность р (ж, у, Z, t), давление р{х, у, z,t) и плотность внешних
действующих сил F (ж, у, z, t) (если они имеются), рассчитанная на
единицу массы.
Рассмотрим некоторый объем жидкости Т и подсчитаем
действующие на него силы. Пренебрегая силами трения, обусловленными
вязкостью, т. е. рассматривая идеальную жидкость, получим для
результирующей сил давления выражение в виде поверхностного интеграла
-//'
pndS, (33)
S
где S — поверхность объема Т, п — единичный вектор внешней нор-
^^ См.: Смирнов В. И. Курс высшей математики. Т. П. М., 1974. С. 207;
Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 39
мали. Формула Остроградского — Гаусса ""^-^ дает
- [ [pndS = - fffgTd^dpdT. (34)
5 Т
При вычислении ускорения какой-либо точки жидкости
необходимо учесть перемещение самой точки. Пусть х = х (t), у = у (t), z —
— z (t)—уравнение траектории этой точки. Вычислим производную
скорости по времени:
dv длг длг , длг , длг ,
dt dt дх ду dz
где
^ . д . д В
ох Оу OZ
Такая производная по времени, учитывающая движение частицы
среды (субстанции), называется субстанциональной или
материальной. Уравнение движения жидкости выражает обычную связь
между ускорением частиц и действующими на них силами
P^dT = - JIJgva.dpdT + IIIpFdT, (35)
т т т
где последний интеграл представляет собой равнодействующую
внешних сил, приложенных к объему Т. Отсюда в силу произвольности
объема Т получаем уравнение движения идеальной жидкости в
форме Эйлера:
vt + (vV) V = - - gradp + F. (36)
P
Перейдем к выводу уравнения непрерывности. Если внутри Т нет
никаких источников или стоков, то изменение в единицу времени
количества жидкости, заключенной внутри Т, равно потоку через
границу S
^ В самом деле, рп = pcos (п, ж) i + pcos (n, y)i -\- pcos (n, z) k, где
i, j, к — единичные векторы в системе координат (ж, у, z),
II
S
pcos {rij х) dx = III ^— dr и т. д.

40 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Преобразование поверхностного интеграла в объемный дает
'др
III
^ + divpv б?г = 0.
ot
т
Так как это равенство справедливо для сколь угодно малых объемов,
то отсюда следует уравнение непрерывности
1^ + div(pv) = о,
ИЛИ
—- + vgradp + pdivv = 0. (38)
К уравнениям (36) и (38) следует присоединить термодинамическое
уравнение состояния, которое мы здесь возьмем в виде
p = f{p)-
Следовательно, мы получаем систему пяти уравнений с пятью
неизвестными функциями Vx^ Vy, Vz^ Р и р. Если бы уравнение
состояния содержало температуру, то нужно было бы добавить еще
уравнение теплопереноса (см. Приложение IV). Таким образом, система
уравнений
dv 1
— + (vV) V = F - - gradp,
^+div(pv)=0, ^
P = f{p)
представляет замкнутую систему уравнений гидродинамики.
Применим уравнения гидродинамики к процессу распространения
звука в газе. Сделаем следующие допущения: 1) внешние силы
отсутствуют; 2) процесс распространения звука является адиабатическим,
поэтому уравнением состояния служит адиабата Пуассона
Ро \PoJ V с^
где ро и ро—начальная плотность и начальное давление, Ср и Су —
теплоемкости при постоянном давлении и постоянном объеме; 3)
колебания газа малы, можно пренебрегать высшими степенями скоростей,
градиентов скоростей и изменения плотности.
Назовем конденсацией газа величину s{x,y,z,t), равную
относительному изменению плотности:
s{x,y,z,t) = ^^^^, (40)
Ро

(42)
§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 41
откуда
p = Po{l + s). (41)
Уравнения гидродинамики при сделанных предположениях
принимают вид
vt = gradp,
Ро
pt -\- podivv = О,
p = Po(l + 5)^=Po(l + 7^)J
так как
- gradp = — (1 — S + ...) gradp = — gradp + ...,
Р Ро Ро
div pv = V grad р -\- р div v = ро div v + ...,
где точками обозначены члены второго и высшего порядков малости.
Введя обозначение а^ = "уро/Ро, перепишем систему (42) в следующем
виде:
vt = -a^gmdsA
St + div V = 0. J
Применяя к первому уравнению (42') оператор дивергенции и меняя
порядок дифференцирования, будем иметь
div -— = -— div V = — а^ div (grad s) = — а^ \/^s = — а^ As,
dt dt \ь )
где
V.2 л д^ д^ д^
V = А = \ \
дх'^ ду^ dz^
— оператор Лапласа. Используя второе уравнение (42'),
получаем уравнение колебаний
As=\su, (43)
или
Отсюда и из (40) получаем уравнение для плотности
а'^ {рхх + Руу + Pzz) = Ри- (43')
Уравнения (43) и (43') являются уравнениями колебаний. Введем
теперь потенциал скоростей и покажем, что он удовлетворяет
тому же уравнению колебаний (43), что и конденсация.

42
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
Из уравнения
vt = — а^ grad s
следует
V (ж, у, Z, t) = V (ж, у, Z, 0) — а^ grad \ sdt
(44)
где V (ж, у, Z, 0) — начальное распределение скоростей. Если поле
скоростей в начальный момент потенциально:
v|t=o = -grad/(ж, у, z), (45)
то имеет место соотноп1ение
t
V = — grad
/(ж, у, z) + a'^ sdt
= - grad и,
(46)
которое означает, что существует потенциал скоростей [/(ж, у, z, t).
Знания потенциала скоростей достаточно для описания всего процесса
движения ■'■^:
V = — grad [/, ^
Подставив эти значения в уравнение непрерывности
St + div V = О,
получим уравнение колебаний для потенциала
а^ {и^сх + Uyy + и,,) = Utt,
или
Utt = а' АС/.
(47)
(48)
Для давления р и скорости v также можно получить уравнение
колебаний вида (48), называемое часто уравнением акустики.
^ Из формулы (46) видно, что потенциал U определен с точностью до
слагаемого, являющегося произвольной функцией t. Из уравнения v^ =
= — а grad S и соотнопесния (46) следует grad Is ^ Ut] = О, т. е. s =
= —^ Ut при соответствующей нормировке потенциала U.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 43
При решении задач для двумерного и одномерного случаев надо в
уравнении (48) оператор Лапласа заменить оператором —-^ + —-^ и
|1 со«„е.с™„»о. Посеянная
дх'^ ду
7Ро
Ро
имеет размерность скорости и, как будет показано в § 2, является
скоростью распространения звука.
Вычислим скорость звука в воздухе при нормальном
атмосферном давлении. В этом случае j = 7/5, ро = 0,001293 г/см^, ро =
= 1,033 кг/см^; следовательно.
ПРО оо« /
а = А = 335 м/с.
V Ро
В случае колебаний газа в ограниченной области на ее границе
должны быть заданы определенные граничные условия. Если граница
представляет собой твердую непроницаемую стенку, то нормальная
составляющая скорости равна нулю, что приводит к условиям
ди
дп
и или ——
on
0. (49)
7. Граничные и начальные условия. При математическом
описании физического процесса надо прежде всего поставить задачу,
т. е. сформулировать условия, достаточные для однозначного
определения процесса.
Дифференциальные уравнения с обыкновенными и, тем более, с
частными производными имеют, вообще говоря, бесчисленное
множество решений. Поэтому в том случае, когда физическая задача
приводится к уравнению с частными производными, для однозначной
характеристики процесса необходимо к уравнению присоединить некоторые
дополнительные условия.
В случае обыкновенного дифференциального уравнения 2-го
порядка решение может быть определено начальными условиями, т. е.
заданием значений функции и ее первой производной при «начальном»
значении аргумента (задача Коши). Встречаются и другие формы
дополнительных условий, когда, например, задаются значения функции
в двух точках (задача о цепной линии). Для уравнения с частными
производными возможны также различные формы дополнительных
условий.
Рассмотрим сначала простейшую задачу о поперечных
колебаниях струны, закрепленной на концах. В этой задаче и{х, t) дает
отклонение струны от оси X. Если концы струны О ^ ж ^ / закреплены, то

44 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
должны выполняться «граничные условия»
u{0,t) = 0, u{l,t) = 0. (50)
Так как процесс колебаний струны зависит от ее начальной формы и
распределения скоростей, то следует задать «начальные условия»:
и{х, to) = (f{x)A
щ{х, to) = ^{x).j
Таким образом, дополнительные условия состоят из граничных и
начальных условий, где (р (х) и ф (х)—заданные функции точки. В
дальнейшем мы покажем, что эти условия вполне определяют решение
уравнения колебаний струны
utt = a^Uxx- (52)
Если концы струны движутся по заданному закону, то граничные
условия (50) принимают другой вид:
и(0, t) =/ii(^),l
и {I, t) =/i2(^),J
где /iii (t) и /i2 (^)—заданные функции времени t. Аналогично
ставится задача для продольных колебаний струны или пружины.
Возможны и другие типы граничных условий. Рассмотрим,
например, задачу о продольных колебаниях пружины, один конец
которой закреплен (точка подвеса), а другой свободен. Закон движения
свободного конца не задан и зачастую является искомой функцией.
В точке подвеса ж = О отклонение
и {О, t) =0;
на свободном конце х = / натяжение пружины
ди I
Tii,t) = k^^
(53)
равно нулю (нет внешних сил), так что математическая формулировка
условия свободного конца имеет вид
Ux (/, t) = 0.
Если конец ж = О движется по определенному закону /i (^), а при х = /
задана сила I'it), то
и (О, t)=fi (t), и, (/, t) = iy (t) (ly {t) = ^fy (t)
Типичным является также условие упругого закрепления, скажем, для
X = I:
kux {I, t) = — аи (/, t),

ПРОСТЕЙШИЕ ЗАДАЧИ 45
и^ {I, t) = -hu (/, t) {h=^y (54)
при котором конец х = / может перемещаться, но упругая сила
закрепления вызывает на этом конце натяжение, стремящееся вернуть
сместивп1ийся конец в прежнее положение. Эта сила, согласно
закону Гука, пропорциональна смещению и{1, t); коэффициент
пропорциональности а называется коэффициентом жесткости закрепления.
Если точка (система), относительно которой имеет место упругое
закрепление, перемещается и ее отклонение от начального положения
дается функцией в (t), то граничное условие принимает вид
и^ (/, t) = -h[u (/, t)-e (t)], h=^>0. (55)
/с
Условие упругого закрепления на левом конце х = О имеет вид
и^ (О, t) = h[u (О, t)-0 {t)l h>0
(формально можно считать, что (55) имеет место и при ж = О, но
/г < 0). Следует отметить, что в случае жесткого закрепления {а
велико), когда даже небольшие сдвиги конца вызывают большие
натяжения, граничное условие (55) переходит в условие и{1, t) = ii{t)
{а = оо) при II {t) = e[t). В случае мягкого закрепления {а мало),
при котором большие сдвиги конца вызывают слабые натяжения,
граничное условие переходит в условие свободного конца
u^{l,t)=0 (а = 0).
В дальнейшем мы будем говорить о трех основных типах
граничных условий:
граничное условие 1-го рода и {О, t) = /а (t) —заданный режим,
граничное условие 2-го рода Ux {О, t) = и (t) —заданная сила,
граничное условие 3-го рода Ux (О, t) = h[u (О, t) — О (t)] —упругое
закрепление.
Аналогично задаются граничные условия и на втором конце х =
= I. Если функции, задаваемые в правой части {/а (t), v (t) или О (t)),
равны нулю, то граничные условия называются однородными.
Комбинируя различные перечисленные типы граничных условий,
мы получим шесть типов простейших краевых задач.
Более сложное граничное условие имеет место, например, при
упругом закреплении, не подчиняющемся закону Гука, когда
натяжение на конце является нелинейной функцией смещения и{1, t), так что
u,{l,t) = ^F[u{l,t)]. (56)

46 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Это граничное условие в отличие от рассмотренных выше является
нелинейным. Возможны, далее, соотношения между смещениями и
натяжениями на разных концах системы. Например, в задачах о колебании
кольца, когда ж = О и х = I представляют одну и ту же физическую
точку, граничные условия принимают вид
и (/, t)=u (О, t); и^ (О, t) = и^ (/, t), (57)
т. е. сводятся к требованиям непрерывности и и Ux- Производные
по t могут также входить в граничные условия. Если конец
пружины испытывает сопротивление среды, пропорциональное скорости его
движения (к концу пружины прикреплена пластинка, плоскость
которой перпендикулярна оси пружины), то граничное условие принимает
вид
кUx {Ij t) = — ащ (/, t). (58)
Если к концу X = / пружины прикреплен груз массы ттг, то при х = /
должно выполняться условие
mutt {I, t) = — к Ux {I, t) + mg. (59)
Для поперечных колебаний струны все граничные условия
записываются в той же форме с заменой к на Тд.
В дальнейшем мы ограничимся рассмотрением трех простейших
типов граничных условий, проводя основное изложение на примере
первого типа граничного условия и отмечая лишь попутно
особенности, связанные со вторым и третьим условиями.
Сформулируем первую краевую задачу для уравнения (5).
Найти функцию и (ж, ^), определенную в области О ^ ж ^ /,
t ^ О, удовлетворяющую уравнению
Utt = CL^Uxx + / {х, t) для о < X < I, t > о,
граничным
u{0,t)=fii{t),
и{1, t) = 112 (t)
и начальным условиям
и (ж, 0) = (f (ж),
щ (ж, 0) = -0 (ж)
{t > 0) 1) (600
(0<ж<0. (бО'О
Аналогично ставится задача для уравнения (11).
Если на обоих концах берутся граничные условия 2-го или 3-го
рода, то соответствующие задачи называют второй или третьей
краевыми задачами. Если граничные условия при ж = О и х = I
^ Мы не останавливаемся на случае, когда граничные условия заданы на
отрезке О ^ ^ ^ ^о-

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 47
имеют различные типы, то такие краевые задачи называют
смешанными, не проводя более подробной их классификации.
Обратимся теперь к рассмотрению предельных случаев
поставленной задачи. Влияние граничных условий в точке Mq, достаточно
удаленной от границы, на которой они заданы, сказывается через
достаточно большой промежуток времени.
Если нас интересует явление в течение малого промежутка
времени, когда влияние границ еще несущественно, то вместо полной
задачи можно рассматривать предельную задачу с начальными
условиями для неограниченной области.
Найти решение уравнения
utt = a^Uxx + / (ж, t) для — (Х)<ж<(Х), ^>0
с начальными условиями
и (ж, 0) =
щ (ж, 0) =
при — 00 < ж < 00. (61)
Эту задачу часто называют задачей Коши.
Если же мы изучаем явление вблизи одной границы и влияние
граничного режима на второй границе не имеет существенного
значения на протяжении интересующего нас промежутка времени, то мы
приходим к постановке задачи на полуограниченой прямой О ^ ж < оо,
когда помимо уравнения даны дополнительные условия
и(0, ^) =/i(^), ^^0
и (ж, 0) = (/? (ж),
щ{х, 0) = '^(ж).
О ^ ж < 00.
(62)
Характер явления для моментов времени, достаточно удаленных
от начального момента ^ = О, вполне определяется граничными
значениями, так как влияние начальных условий благодаря трению,
присущему всякой реальной системе, с течением времени ослабевает-"^^
Задачи этого типа встречаются особенно часто в случаях, когда
система возбуждается периодическим граничным режимом,
действующим длительное время. Такие задачи «без начальных условий» (на
установившийся режим) формулируются следующим образом.
Найти решение изучаемого уравнения для О ^ х ^ I и t > — оо
при граничных условиях
и(1, t) = 112 it)-
(63)
^ Уравнение колебаний с учетом трения, пропорционального скорости,
имеет вид
Utt = а Uxx - OLUt {а > 0).
Подробнее о постановке задач без начальных условий при а = О см. § 3, п. 7.

48
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
Аналогично ставится задача без начальных условий для
полуограниченной прямой.
В дальнейшем мы будем рассматривать помимо основных краевых
задач также предельные задачи:
1) задачи в бесконечной области, когда одна или обе границы
находятся в бесконечности;
2) задачи без начальных условий (на установившийся режим),
когда рассматривается решение, определенное в течение бесконечного
промежутка времени.
8. Редукция общей задачи. При решении сложной задачи
естественно стремиться свести ее решение к решению более простых задач.
С этой целью представим решение общей краевой задачи в виде суммы
решений ряда частных краевых задач.
Пусть Ui{x, t) (г = 1, 2, ..., n) — функции, удовлетворяющие
уравнениям
a^^^ + r{x,t) (64)
(65)
при о < X < I, t > О и дополнительным условиям
щ{1, t) = ii\{t)]
щ{х, 0) = (f' (х),
(УН •
Очевидно, что имеет место суперпозиция решений, т. е. функция
п
и(о)(ж, t) = "^щ{х, t) (66)
г=1
удовлетворяет аналогичному уравнению с правой частью
п
/(о)(ж, ^) = ^Г(ж, i) (67)
г=1
И дополнительным условиям, правые части которых суть функции
п >
^^Tii) = T.^^kii) (^ = 1,2),
г=1
п
<^(о)(ж) = ^^'(а;), \ (68)
п

(69)
§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 49
Указанный принцип суперпозиции относится, очевидно, не
только к данной задаче, но и к любому линейному уравнению с линейными
дополнительными условиями. Этим свойством мы в дальнейп1ем
неоднократно будем пользоваться.
Penienne общей краевой задачи
utt = a^Uxx + / (ж, t)
(0<ж </, ^>0);
и{1, t) = /i2 W;
и (ж, 0) = (/? (ж),
щ (ж, 0) = -0 (ж)
может быть представлено в виде суммы
и (ж, t) = ui (ж, t) + U2 (ж, ^) + ^3 (ж, ^) + U4 (ж, t), (70)
где ui, ^2, и^^ U4:—реп1ения следующих частных краевых задач:
(О <ж < /, ^>0),
Mi(0,i)=0, U2{0,t) = init), г*з(0,*)=0, W4(0,i)=0;
Wi(/,i)=0, W2(^,i) = 0, U3{l,t) = fi2{t), U4{l,t) =0,
■«i(a;,0) = (/9(ж), U2(x,0) = 0, ■«з(а;,0)=0, «4(2;,0) =0,
uit(x,0) =ф(х), U2tix,0) = 0, U3t(x,0)=0, Uitix,0) = 0.^
(71)
Мы ограничимся здесь этой формальной редукцией для того, чтобы
характеризовать частные краевые задачи, составляющие основные
этапы при решении общей задачи. Аналогичная редукция может быть
произведена и для предельных случаев общей краевой задачи.
9. Постановка краевых задач для случая многих
переменных. Мы подробно рассмотрели постановку краевых задач для случая
одной независимой геометрической переменной ж (и времени t). Если
число геометрических переменных п > 1 (например, п = 3), то первая
краевая задача ставится совершенно сходным образом.
Требуется найти функцию и (М, t) = и (ж, у, z, t), определенную
при t ^ О внутри заданной области Т с границей Е,
удовлетворяющую при t > О внутри Т уравнению
Utt = а' An + / (М, t) (М (ж, y,z)eT, t>0), (72)
граничному условию на Е
и\^ = II (Р, t) {Р (ж, y,z)e^, t^ 0), (73)
4 А. Н. Тихонов, А. А. Самарский

50 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
где /i (ж, ^, z^ t) — функция, заданная на Е, и начальным условиям
щ (М, 0) =ф (М) J
Разложение общей краевой задачи на ряд более простых происходит
аналогично предшествующему. Отметим, что возможна также
постановка предельных краевых задач для неограниченной области,
полупространства и т. д.
10. Теорема единственности. При решении краевых задач
надо убедиться в том, что:
1) дополнительные условия достаточны для выделения
однозначного решения; это достигается доказательством теоремы
единственности;
2) дополнительные условия не переопределяют задачу, т. е.
среди них нет несовместных условий; это достигается доказательством
теоремы существования; доказательство существования
решения обычно тесно связано с методом нахождения решения.
В настоящем пункте нами будет доказана следующая теорема
единственности.
Возмоэюно существование только одной функции и{х, t),
определенной в области О^ж^/, t ^ О и удовлетворяющей уравнению
о < ж < /, ^ > О,
начальным и граничным условиям
u{x,0) = (f{x), щ{х,0) =^{x)A
если выполнены условия:
1) функция u{x,t) и производные, входящие в уравнение (75),
а такэюе производная Uxt непрерывны на отрезке О ^ х ^ I при t ^
^0;
2) коэффициенты р{х) и к {х) непрерывны на отрезке О ^ х ^1.
Допустим, что существует два решения рассматриваемой задачи:
Ui{x,t), U2{x,t),
И рассмотрим разность v (ж, t) = ui (ж, t) — U2 (ж, t).
Функция v{x, t), очевидно, удовлетворяет однородному
уравнению
d'^v д (,dv\
'W^TxV'Tx) ^''^

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 51
и однородным дополнительным условиям
у{х,0)=0, v{0,t)=0,]
vt{x,0)=0; v{l,t)=0,j ^ '
а также условию 1 теоремы.
Докажем, что функция v {х, t) тождественно равна нулю.
Рассмотрим функцию
E{t) = \ j[k{v,f+p{vtf]dx (79)
О
и покажем, что она не зависит от t. Физический смысл функции Е (t)
очевиден: это полная энергия струны в момент времени t.
Продифференцируем Е (t) по t, выполняя при этом дифференцирование под
знаком интеграла ""^^i
dE{t)
dt
о
Интегрируя по частям первое слагаемое правой части, будем иметь
/-—/ ".
о о
Подстановка обращается в нуль в силу граничных условий (из
V (О, ^) = О следует vt (О, ^) = О и аналогично для х = I). Отсюда
dE{t)
= j\pv,vu - Щ [kv.U dx = j\, [pvu - (Ь.).] dx = о,
dt
о о
т. е. Е (t) = const. Учитывая начальные условия, получаем
Е (t) = const = ^ (0) = ^ [[к (v^)^ + р {vt)%=o dx = О, (81)
о
так как
V (ж, 0) = О, Vt (ж, 0) = 0.
^ Для дифференцирования под знаком интеграла достаточно, чтобы
получаемое при этом подынтегральное выражение было непрерывно на
отрезке О ^ ж ^ / при t ^ 0. Это требование в наптем случае выполнено, так
как функция v{x,t) удовлетворяет условию 1 теоремы, а р{х) и к (х) —
условию 2.

52 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Пользуясь формулой (81) и положительностью к и р, заключаем, что
Vx (ж, t) = О, vt (ж, t) = о,
откуда и следует тождество
v{x, t) = const = Co. (82)
Исходя из начального условия, находим
V (ж, 0) = Со = 0;
тем самым доказано, что
V (ж, t) = 0. (83)
Следовательно, если существует две функции: ui (ж, t) и U2 (ж, ^),
удовлетворяющие всем условиям теоремы, то ui (ж, t) = U2 (ж, ^).
Для второй краевой задачи функция v = ui — U2 удовлетворяет
граничным условиям
V, (О, t) = О, V, (/, t) = О, (84)
и подстановка в формуле (80) также обращается в нуль. Дальнейшая
часть доказательства теоремы остается без изменений.
Для третьей краевой задачи доказательство требует некоторого
видоизменения. Рассматривая по-прежнему два решения: ui и ^2,
получаем для их разности v (ж, t) = щ — U2 уравнение (77) и граничные
условия
v,{0,t)-hiv{0,t) = 0 {hi^O)A
v^{l,t) + h2v{l,t) = 0 {h2 ^0).J
Представим подстановку в (80) в виде
Интегрируя —— в пределах от нуля до t, получаем
at
(85)
t I
:dt
о о
_к
~ 2
откуда в силу уравнения и начальных условий следует
к
L i
E{t)-E{Q) = j j Vt [pvtt - {kv^)^] dx,
{h2 [v' (/, t) - v^ (/, 0)] + /ii [v^ (0, t) - v' (0, 0)]} ,
E{t) = -'-^ [h2 v^ {I, t) + hi v'^ (0, t)] ^ 0. (86)

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 53
Так как ввиду неотрицательности подынтегральной функции значения
Е (t) ^ О, то
E{t)=0, (87)
а следовательно, и
V (ж, t) = 0. (88)
Изложенный здесь метод доказательства теоремы
единственности, основанный на использовании выражения полной энергии, широко
применяется при доказательстве теорем единственности в различных
областях математической физики, например в теории
электромагнитных полей, теории упругости и гидродинамике.
Доказательство единственности других краевых задач (задачи
Коши и задачи без начальных условий) будет дано в дальнейшем в
соответствующем месте.
Зад ачи
1. Доказать, что уравнение малых крутильных колебаний стержня
имеет вид
где В есть угол поворота сечения стержня с абсциссой ж, G — модуль
сдвига, J — полярный момент инерции поперечного сечения, а к — момент
инерции единицы длины стержня. Дать физическую интерпретацию граничных
условий 1, 2 и 3-го рода для этого уравнения.
2. Абсолютно гибкая однородная нить закреплена на одном из концов и
под действием своего веса находится в вертикальном положении равновесия.
Вывести уравнение малых колебаний нити.
Ответ. -^—^ = а
dt'^ дх I дх\
где п (ж, t) — смещение точки, / — длина нити, д — ускорение силы тяжести.
3. Тяжелая однородная нить длины /, прикрепленная верхним концом
(ж = 0) к вертикальной оси, вращается вокруг этой оси с постоянной
угловой скоростью UJ. Вывести уравнение малых колебаний нити около своего
вертикального положения равновесия.
^2^
д и 2 д
Ответ, -—тг = а -^г-
ot^ дх
ди
2 2
+ о; п, где а
4. Вывести уравнение поперечных колебаний струны в среде,
сопротивление которой пропорционально первой степени скорости.
2 2 2
Ответ, vtt = cl Vxx — h vtj a -
5. Вывести граничные условия для уравнения продольных колебаний
упругого стержня (пружины) в случае, когда верхний конец стержня
закреплен жестко, а к нижнему подвепЕСн груз Р, если:

54 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
а) за положение равновесия принимается напряженное состояние
стержня под действием неподвижного груза Р, подвепЕСнного к нижнему концу
(статическое растяжение);
б) за положение равновесия принимается ненапряженное состояние
стержня (например, в начальный момент из-под груза убирается
подставка и груз начинает растягивать стержень).
6. Написать уравнение и условия, определяющие процесс крутильных
колебаний стержня, к обоим концам которого прикреплены пекивы.
Ответ. При ж = О, х = I должны выполняться граничные условия
вида
ви (О, t) = а\ е., (О, 1), ^и (/, 1) = -al в., (/, t).
7. В некоторой точке х = xq струны (О ^ ж ^ /) подвепЕСн груз массы
М. Вывести условия сопряжения в точке х = xq.
8. К концу X = I упругого стержня, упруго закрепленного в точке ж = О,
подвепЕСн груз массы М. Написать уравнение и условия, определяющие
продольные колебания стержня, предполагая, что на него, кроме того, действует
внепЕняя сила. Рассмотреть два случая:
а) сила распределена по стержню с плотностью F (ж, t)]
б) сила сосредоточена в точке ж = жо и равна Fq (t).
9. Рассмотреть процесс малых колебаний идеального газа в
цилиндрической трубке. Вывести сначала основные уравнения гидродинамики, а
затем, предполагая процесс адиабатическим, дифференциальное уравнение:
1) для плотности /9, 2) давления р, 3) потенциала U скорости частиц
газа, 4) скорости Vj 5) смещения и частиц. Привести примеры реализации
граничных условий 1, 2 и 3-го типов для этих уравнений.
10. Установить соотнопесния подобия между процессами механических,
акустических и электрических колебаний (см. Приложение VI к гл. П).
11. Привести примеры граничных условий 1, 2 и 3-го рода для
телеграфных уравнений.
12. Рассмотреть задачу о продольных колебаниях неоднородного
стержня {к = ki при ж < жо, к = к2 при ж > жо) и вывести условия
сопряжения в точке стыка однородных частей стержня (при ж = жо).
13. Дать физическую интерпретацию граничного условия
aux (О, t) + put (О, t) = 0.
14. Привести пример механической модели, для которой реализовалось
бы уравнение
utt = а Uxx + Ьщ + си.
§ 2. Метод распространяющихся волн
1. Формула Даламбера. Изучение методов построения решений
краевых задач для уравнений гиперболического типа мы начинаем с
задачи с начальными условиями для неограниченной струны:
Utt - a^Uxx = О, (1)
и(ж, 0) = (/?(ж),1
щ{х, 0) =^{x). \

§ 2] МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 55
Преобразуем это уравнение к каноническому виду, содержащему
смешанную производную (см. гл. I). Уравнение характеристик
dx^ - а^ dt^ = О
распадается на два уравнения:
dx — adt = О, dx -\- adt = О,
интегралами которых являются прямые
X — at = Cij X -\- at = €2-
Введя, как обычно, новые переменные
^ = X-\-at, Г] = X — at,
уравнение колебаний струны преобразуем к виду
Щг] = 0. (3)
Найдем общий интеграл последнего уравнения. Очевидно, для
всякого решения уравнения (3)
где /* (?7)—некоторая непрерывная функция только переменного г].
Интегрируя это равенство по г] при фиксированном ^, получаем
и it V) = Jr iv) dv + /1 (0 = /1 iO + /2 (ri), (4)
где /i и /2 являются функциями только переменных ^ и г].
Обратно, каковы бы ни были дважды дифференцируемые функции Д и /2,
функция и{^,г]), определяемая формулой (4), представляет собой
решение уравнения (3). Так как всякое решение уравнения (3) может
быть представлено в виде (4) при соответствующем выборе Д и /2,
то формула (4) является общим интегралом этого уравнения.
Следовательно, функция
и (ж, t) = /1 (ж + at) + /2 (ж - at) (5)
является общим интегралом уравнения (1).
Допустим, что решение рассматриваемой задачи существует,
тогда оно дается формулой (5). Определим функции Д и Д таким
образом, чтобы удовлетворялись начальные условия:
u{x,0) = h{x) + f2{x)=^{x), (6)
utix,0)=af[{x)-af^ix)=^ix). (7)
Интегрируя второе равенство, получаем
X
fi{x)-f2{x) = - f^{a)da + C,
а J
XQ

56
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
где хо и С — постоянные. Из равенств
Л (х) +/2 (ж) =^{х),
X
h{x) - h{x) = -^ j ф{а)йа + С
находим
X
1 If
+
С
XQ
h (ж) = 2 ^ (^)
X
da
С
2 '
жо
(8)
Таким образом, мы определили функции Д и /2 через заданные
функции (риф, причем равенства (8) должны иметь место для любого
значения аргумента ""^^ Подставив в (5) найденные значения Д и Д,
получим
и (ж, t)
(f{x + at) + (f{x — at)
x-\-at
+ -— < / ф (a) da — / Ф (a) da
XQ
XQ
и (ж, t)
(f{x + at)+(f{x — at)
x-\-at
+
i I -*("'
da.
(9)
Формулу (9), называемую формулой Даламбера, мы получили,
предполагая существование решения поставленной задачи. Эта
формула доказывает единственность решения. В самом деле, если бы
существовало второе решение задачи (1) — (2), то оно бы представлялось
формулой (9) и совпадало с первым решением.
Нетрудно убедиться, что формула (9) удовлетворяет (в
предположении двукратной дифференцируемости функции (f и однократной
дифференцируемости функции ф) уравнению и начальным условиям.
Таким образом, изложенный метод доказывает как единственность,
так и существование решения поставленной задачи.
^ В формуле (5) функции Д и Д определены неоднозначно. Если от Д
отнять, а к Д прибавить некоторую постоянную (7i, то и не изменится. В
формуле (8) постоянная С не определяется через ср -и. ф, однако мы можем
ее отбросить, не меняя значения и. При сложении Д и Д слагаемые (7/2
и — (7/2 взаимно уничтожаются.

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
57
2. Физическая интерпретация. Функция u{x,t),
определяемая формулой (9), представляет процесс распространения начального
отклонения и начальной скорости. Если фиксировать t = to, то
функция и{х, to) дает профиль струны в
момент ^о; фиксируя ж = Жо, получим
функцию u{xo,t), дающую процесс движения
точки X = хо (рис. 4). Предположим, что
наблюдатель, находивп1ийся в точке х = О
в момент ^ = О, движется со скоростью а в
положительном направлении. Введем
систему координат, связанную с наблюдателем,
полагая х' = х — at, t' = t. В этой
подвижной системе координат функция и{х, t) =
= / (ж — at) будет определяться формулой
и = f {х') и наблюдатель все время будет
видеть тот же профиль, что и в начальный
момент. Следовательно, функция и (ж, t) = рис. 4
= / (ж — at) представляет неизменный
профиль / (ж), перемещающийся вправо (в положительном направлении
оси ж) со скоростью а (распространяющуюся или бегущую волну).
Функция / (ж + at) представляет, очевидно, волну,
распространяющуюся влево (в отрицательном направлении оси ж) со скоростью а.
Таким образом, общее решение (9) задачи Коши для бесконечной
струны есть суперпозиция двух волн Д (ж + at) + /2 (ж — at), одна из
которых распространяется вправо со скоростью а, а вторая — влево с той
же скоростью. При этом
/i {х -\-at) = -(р{х -\- at) + Ф (ж + at),
где
/2 {х — at) = -(f{x — at) — Ф (ж — а^).
Ф(ж)
X
2а I
ф (а) da.
Для выяснения характера решения (9) удобно пользоваться
плоскостью состояний (ж, t), или фазовой плоскостью. Прямые ж —
— at = const и X -\- at = const являются характеристиками уравнения
(1). Функция и = f {х — at) вдоль характеристики х — at = const
сохраняет постоянное значение, функция и = f (х -\- at) постоянна вдоль
характеристики х -\- at = const.
Предположим, что / (ж) отлична от нуля только в интервале
(ж1, Ж2) и равна нулю вне этого интервала. Проведем характеристики
ж — а^ = Ж1 и ж — а^ = Ж2 через точки (ж1, 0) и (ж2, 0); они разбивают

58
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
полуплоскость (ж, ^ > 0) на три области: I, П, и П1 (рис. 5, а). Функция
и = f {х — at) отлична от нуля только в области П, где xi < х — at < Х2
и характеристики х — at = xi и х — at = Х2 представляют передний
и задний фронты распространяющейся вправо волны.
о Р{хо - ato,0) Q{xo + ato,0)
Рис. 5
l5
к
Рассмотрим теперь некоторую фиксированную точку (жо, ^о)
и проведем из нее обе характеристики х — at = xq — ato и ж +
-\- at = xq -\- ato, которые пересекут
ось X в точках Ж1 = жо — ato, t =
= 0 и Х2 = хо + atoj t = 0.
Значение функции U = /i (ж — at) +
+ /2 (ж + at) в точке (жо, ^о)
равно и (жо, ^о) = Л (^i) + /2 (Ж2), т. е.
определяется значениями функций
/i (ж) и /2 (ж) в точках {xi, 0)
и (ж2, 0), являющихся верп1инами
треугольника MPQ (рис. 5, ^,
образованного двумя
характеристиками и осью ж. Этот
треугольник называется
характеристическим треугольником
точки (жо, ^о)- Из формулы (9)
видно, что отклонение и (жо, ^о) точки
струны в момент ^о зависит
только от значений начального
отклонения в вершинах Р (жо — ato, 0) и
Q (жо + ato, 0)
характеристического треугольника MPQ и от значе-
Р^с- ^ НИИ начальной скорости на стороне
PQ. Это становится особенно ясным, если формулу (9) записать в
виде
Ь
^^^
^
XI
At = tj^i — t^
Х2
Х2 — XI
и{М)
^{P) + ^{Q)
+
PQ
(10)

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
59
Начальные данные, заданные вне PQ^ не оказывают влияния на
значения и{х, t) в точке М (жо, ^о)- Если начальные условия заданы
не на всей бесконечной прямой, а на отрезке PiQi, то они однозначно
определяют penienne внутри характеристического треугольника,
основанием которого является отрезок PiQi-
3. Примеры. Решение (9) можно представить в виде суммы и =
= ui (ж, t) + U2 (ж, t), где
щ (ж, t) = -[(р {х — at) -\- (р {х -\- at)],
(И)
x-\-at
U2 (ж, t)
4f (x + at) -4f {х - at) = —- / ф (a) da.
Za J
(12)
x — at
Если начальная скорость равна нулю ('^(ж) =0), то отклонение и =
= ui{x, t) есть сумма левой и правой бегущих волн, причем начальная
форма каждой волны определяется функцией 0,5 (р (ж), равной
половине начального отклонения. Если же (/? (ж) = О, то и = U2 {х, t)
представляет возмущение струны, создаваемое начальной скоростью.
Пример 1. Рассмотрим распространение начального
отклонения, заданного в виде равнобедренного треугольника. Такой
начальный профиль можно получить, если оттянуть струну в
середине отрезка [ж1, Ж2]. На рис. 6
даны последовательные положения
струны через промежутки
времени А^ = (ж2 — xi)/{Sa).
Наглядное представление о характере
процесса распространения можно
получить с помощью фазовой
плоскости (ж, t). Проведем
характеристики через точки Р (xi, 0) и
Q (ж2, 0); они разобьют
полуплоскость (— 00 < ж < 00, t ^ 0) на
шесть областей (рис. 7).
Отклонение щ {х, t) в любой точке (ж, t)
дается формулой (11). Поэтому в областях I, III, V отклонение равно
нулю, так как характеристический треугольник любой точки из этих
областей не имеет общих точек с отрезком [ж1, Ж2], на котором
заданы начальные условия. В области II решением является правая волна
и = 0,5(/?(ж — at), в области IV — левая волна и = 0,5(/?(ж -\- at), а в
области VI решение есть сумма левой и правой волн.
Пример 2. Пусть начальное отклонение (f (х) =0, а начальная
скорость отлична от нуля только на отрезке [xi, Ж2], где она
принимает постоянное значение фо- Ф (х) = фо при xi ^ ж ^ Ж2, ф (х) = О при
ж > Ж2 и ж < Ж1. В этом случае решением является функция U2 (ж, t).
Рис. 7

60
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
Вычислим функцию Ф (ж), выбрав при этом xq = О (рис. 8):
ф (ж) = — ф (а) da
о
О при X < xi,
{х — xi) V^o/^a при xi ^ X ^ X2j (13)
[(ж2 - Х1)фо/2а при X > Х2.
Penienne U2 (ж, t) есть разность правой и левой волн с профилем
Ф (х). Последовательные положения этих волн через промежутки
времени А^ = {х2 — xi)/{Sa) изображены
'^(^)А на рис. 9. Профиль струны для t ^
^ AAt имеет форму трапеции, рас-
П1иряющейся равномерно с
течением времени. Если ф (х) отлично от
постоянной на [xi, Х2], то изменится
^^ лишь профиль Ф(ж).
Для выяснения характера penie-
ния воспользуемся фазовой
плоскостью (ж, t) (см. рис. 7). Папип1ем
выражения для и{х, t) в различных областях фазовой плоскости.
В области I {х — at > Х2)
XI
Х2
Рис. 8
Ф (ж + а^) = Ф (ж — at) = const, и (ж, t) =
В области V (ж + а^ < Ж1)
Ф (ж - а^) = Ф (ж + at) =0, и (ж, t) = 0.
В области П1 {х — at < xi, х -\- at > Х2)
-г / ч Ж2 — Ж1 ,
Ф (ж + at) = const = — гро,
Аа
0.
Ф (ж — at) = 0, и (ж, ^) = — ipQ.
Аа
В области П {xi < X — at < Х2^ X -\- at > Х2)
Ф(ж + а^)= '^^ ^ фо.
Ф (ж - at) =
ж — а^ — Ж1
-00, u{x,t) =
Ж2 — (ж — а^)
2а "^' ' ' ' 2а
В области IV (ж1 < ж + а^ < Ж2, ж — а^ < Ж1)
-г , . ж + а^ - Ж1 .
Ф (ж + а^) = — фо,
т / \ гл / \ Ж + а^ — Ж1 .
Ф (ж — at) = 0, U (ж, t) = фо.
Аа
Фо-

2]
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
61
В области VI {х — at > xi, X -\- at < Х2)
^ , . X + at - xi ^
Ф (ж + at) = — V^o,
Ф (ж - at) = фо, и (ж, t) = tipo-
t = о
А^ = ti^i — t^ =
Х2 — Xi
Рис. 9
Пример 3. Рассмотрим задачу о колебаниях струны под
действием сосредоточенного импульса. Сообщая в начальный момент
точкам струны (ж, ж + Аж) постоянную скорость -00 (например, ударяя
струну молоточком), мы прикладываем к этому участку импульс /,
равный изменению количества движения при ^ = О, так что / =
= рАхфо, где р — линейная плотность струны. Таким образом, мы
должны решить задачу о колебаниях струны с нулевым начальным от-

62
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
клонением и начальной скоростью ф = Iq/р = фо на интервале (ж, ж +
+ Ах), ф = О вне этого интервала; здесь /о = 1/Ах — плотность
импульса. Анализ реп1ения этой задачи был дан вып1е при peniennn
примера 2. Отклонение, вызываемое импульсом, распределенным на
интервале (ж, X + Аж), представляет собой при t > Ах/{2а) трапецию с
нижним основанием 2at + Аж и верхним — 2at — Ах. Соверп1ая
предельный переход при Аж —>- О, / = const,
видим, что отклонения будут равны
нулю вне (ж — at, X -\- at) и 1/{2ар)
внутри этого интервала. Можно условно
говорить, что эти отклонения вызываются
точечным импульсом /.
Рассмотрим фазовую плоскость
(ж,^) и проведем через точку (жо, ^о) обе
характеристики:
ж — а^ = Жо — ato, х -\- at = xq -\- ato
(рис. 10). Они определяют два угла ai и «2, называемые
соответственно верхним и нижним характеристическими
углами для точки (жо, ^о)-
Действие точечного импульса в точке (жо, ^о) вызывает отклоне-
1 /
ние, равное внутри верхнего характеристического угла и нулю
2а р
вне его.
4. Неоднородное уравнение. Рассмотрим задачу Коши для
неоднородного уравнения колебаний
1
Рис. 10
■utt
Uxx +/(^5^)5 — 00 < ж < 00, ^ > О,
00 < ж < 00.
и (ж, 0) = (f (ж),
щ{х,0) =ф{х),^
Пусть Wf (ж, t; т)—решение вспомогательной задачи Коши
1
(14)
{Wf)tt = (Wf)^
• 00 < ж < 00, t > т,
(15)
Wf (ж, г; г) = О,
dwf
dt
(ж, г; г) = /(ж, г).
— 00 < ж < 00.
Формула Даламбера (9) дает
Wf (ж, t; т) =Wf{x,t-T;0) = — / / (^, г) d^.
ж+а (t — r)
х — а (t — r)
(16)
(17)

§ 2] МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 63
Перепишем формулу Даламбера (9) в виде
и (ж, ^) = ^ (ж, ^; 0) + w^ (ж, ^; 0), (18)
где
x-\-at x-\-at
w^ (ж, ^; 0) = — / ф (^) d^, w^ (ж, ^; 0) = — / (р (^) б?^
x — at x — at
ЯВЛЯЮТСЯ решениями задачи (15) — (16) при г = О и / = ф{х), / =
= (р{х) соответственно, так как непосредственное дифференцирование
показывает, что
x-\-at
dw^p ^ 4 п\ ^ ^ f /t\^t ^ {х-\-at)-\-(f {х — at)
^'''■''^ = ltl h^^^'^
dt
x — at
Докажем, что справедлива следующая лемма.
Решение неоднородного уравнения (14) с нулевыми начальными
данными щ (ж, 0) = О, и (ж, 0) = О имеет вид
t
и (ж, t) = а^ / Wf (ж, t; т) dr. (19)
о
Дифференцируя функцию (19) и учитывая условия (16) для
Wf (ж, t; г), находим
t
щ (ж, t) = а^ Wf (ж, t] t) -\- а^ 1 (ж, t] т) dr =
о
= аМ -^ (ж, ^; г) dr,
t
utt {х, t) = a^^ (ж, t; t)+a^ f ^^ (ж, t; r) dr = (20)
0
dt
b
2^ / -^ (ж, ^; r) dT-\-a^ f (ж, ^),
0
t t
/ Ч if д "Wf , . _ Г д Wf , . _
^жж (ж, t) =a -—- (ж, ^; T)dT = / -—- (ж, ^; r) dr.
0 0
Отсюда видно, что функция (19) удовлетворяет уравнению (14). Из

64 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
формул (19) и (20) сразу следует, что решение задачи (14) в силу (18)
и (19) можно представить в виде
t
и (ж, t) = -—^ (ж, t] 0) + w^ (ж, t] 0) + а^ / Wf (ж, t] т) dr. (21)
о
Пользуясь выражением (17) для Wf^ получаем
x-\-at
и (ж, t) = ^ ^-^ ^ + — J ^{Od^ +
x — at
t x+a {t — т)
+ 1/ / f{^,r)d^dT. (22)
0 x-a{t-T)
Прямая подстановка (22) в (14) показывает, что функция (22) в
самом деле является реп1ением задачи (14), если существуют
производные ip"{x)^ ф'{х) и df/dx.
Из формулы (17) следует, что функция Wf удовлетворяет
уравнению при t = т, если / дифференцируема по ж, т. е. представление
(21) возможно при тех же условиях, при которых penienne задачи Konin
существует.
Формула (21) показывает, что penienne общей задачи (14) может
быть сразу написано, если имеется penienne вспомогательной задачи
(15) — (16). Аналогичная формула имеет место и для решения задачи
Коши в неограниченном пространстве (см. гл. V).
5. Устойчивость решений. Решение уравнения (1)
однозначно определено начальными условиями (2). Докажем, что это решение
меняется непрерывно при непрерывном изменении начальных условий.
Каков бы ни был промеэюуток времени [О, ^о] и какова бы ни
была степень точности г, найдется такое (5(г, ^о), '^^^ всякие два
решения уравнения (1) ui{x, t) и и2(ж, t) в течение промеэюутка
времени to будут различаться меньше чем на е:
\ui (ж, t) - U2 (ж, ^)| < г {О ^t ^ to),
если только начальные значения
ui (ж, 0) = (fi (ж),
^ (^, 0) = ф, (ж)
U2{X, 0) = (f2 (ж),
^{Х,0)=ф2{х)
отличаются друг от друга меньше чем на S:
\(fi (ж, t) - (f2 (ж, t)\ <S; \ф1 (ж, t) - ф2 (ж, t)\ <S.
Доказательство этой теоремы чрезвычайно просто. Функции ui (ж, t)
и ^2 (ж, t) связаны со своими начальными значениями формулой (9),

_2\ МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 65
так что
I / ,ч / ,м / \(pi (х-\-at) - (р2 (х-\-at)\
\ui (ж, t) - U2 (ж, ^)| ^ ^-^-^ \ +
x-\-at
\(pi {х — at) — (р2 {х — at)\ 1
2а
x — at
/ \^i (а) -^2 {a)\da,
откуда получаем
л л 1
\щ {x,t)-U2{x,t)\^- + - + —S-2at^S{l + to),
что и доказывает наше утверждение, если положить
1 + to
Всякий физически определенный процесс, развивающийся во
времени, должен характеризоваться функциями, непрерывно зависящими
от начальных данных. Если бы не было этой непрерывной
зависимости, то два существенно различных процесса могли бы
соответствовать практически одинаковым системам начальных условий
(различие которых лежит в пределах точности измерений). Процессы такого
типа нельзя считать определенными (физически) начальными
условиями. Из предыдущей теоремы следует, что процесс колебаний струны
не только математически, но и физически определен начальными
условиями.
Если решение математической задачи непрерывно зависит от
дополнительных условий (от начальных, граничных данных и от правой
части уравнения — от исходных данных задачи), то говорят, что
задача устойчива.
В связи с изучением физически детерминированных явлений
вводится понятие корректности. Говорят, что математическая
задача поставлена корректно, если: 1) решение задачи
существует, 2) задача имеет единственное решение, 3) решение задачи
непрерывно зависит от исходных данных (устойчиво).
Отметим, что некорректно поставленные задачи часто
встречаются в приложениях и к их числу относятся многие хорошо известные
математические задачи.
Приведем пример некорректно поставленной задачи, решение
которой неустойчиво.
Функция и{х,у), являющаяся решением уравнения Лапласа
Uxx + Uyy = О, однозначно определяется своими начальными
условиями и (ж, 0) = (/? (ж), Uy (ж, 0) = ф (х) ■^\ Рассмотрим функции
и^"*"^ (ж, ^) = О и и^^^ (ж, ^) = т- sin Лж • ch Л^,
Л
^ Эти условия математически однозначно определяют penienne
уравнения Лапласа. В самом деле, задание Uy (ж, 0) эквивалентно Vx (ж, 0), где
5 А. Н. Тихонов, А. А. Самарский

66 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
удовлетворяющие уравнению Лапласа. Функция и^'^^ (ж, у) зависит от
Л как от параметра. Начальные значения
u(i) (ж, 0) = О, и(2) (ж, 0) = (/? (ж) = - sin Лж,
Л
4^) (ж, 0) = О, и^у^ (ж, 0) = V^ (ж) = О
различаются сколь угодно мало при достаточно больп1их Л. Однако
при этом penienne u^^^ (ж, у) может стать сколь угодно большим,
каково бы ни было фиксированное значение у. Следовательно, задача с
начальными условиями для уравнения Лапласа является некорректно
поставленной.
Естественно возникает вопрос: могут ли некорректно поставленные
задачи вообще соответствовать каким-либо задачам математической физики?
А также, какую научную ценность может представлять приближенное penie-
ние некорректно поставленных задач, поскольку малым опЕибкам в условиях
задач могут соответствовать больпЕие опЕибки рептения?
Подобные сомнения возникают в связи с тем, что в сказанном выпес
подразумевается, что в качестве приближенного репЕСния задачи берется
точное репЕСние задачи, соответствующее приближенным условиям.
Приведем пример некорректно поставленной задачи, имеющей важное
практическое значение.
Рассмотрим задачу о нахождении производной z (ж) = df /dx по
равномерным приближенным значениям для /(ж). Пусть мера точности при
задании / (ж) и определении z {х) задана как
max I/(ж) — / (ж)| и max |5 (ж) — ^ (ж)|.
Очевидно, что эта задача с точки зрения приведенной выпес терминологии
неустойчива (некорректно поставлена). В самом деле, если /(ж) = /(ж) +
+ dcosujx^ где ^ > О мало, то max |/ (ж) — / (ж)| = 6 тоже мал. Однако если
мы в качестве приближенного значения z {х) выбрали бы точную
производную для функции / (ж), то
Z (ж) = / {х) — 6UJ sin.UJX и max |5 (ж) — ^ (ж)| = ^ct;;
5uj при фиксированном 5 и больпюм о; может быть как угодно больпЕим
числом. Однако хоропю известно, что в качестве приближенного значения
f (х -\-h) — /(ж)
производной берется разностное отнопЕСние ; , которое пред-
h
ставляет исходную производную с как угодно малой погрепЕностью, если
только h и 6/h достаточно малы. Понятно при этом, что для получения
xoponiero приближения для df /dx по приближенному значению для / (ж)
погрепЕность 5 должна быть достаточно мала.
Итак, в приведенном примере, несмотря на неустойчивость задачи,
можно указать метод получения сколь угодно точных приближений для
искомого репЕСния по достаточно точным приближенным условиям задачи.
г; (ж, у) — функция, гармонически сопряженная для и{х^ у). Этим с
точностью до постоянной однозначно определяется аналитическая функция,
действительной частью которой является функция п (ж, у) (см. гл. IV, § 1, п. 5).

А.
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
67
Подобное положение типично для многих некорректно поставленных
задач "'"^.
Некорректно поставленные задачи часто встречаются в физике при
изучении объектов, недоступных непосредственному исследованию
(измерению). В этих случаях приходится делать заключения о характеристиках
«^» таких объектов по их косвенным (физически детерминированным)
проявлениям «п», доступным для экспериментальных измерений и связанным
с «^» функциональной зависимостью вида Az = и. В результате мы
приходим к задаче обработки наблюдений, которая является обратной задачей
и состоит в определении характеристик «^» объектов по данным «п»
эксперимента. Многие из этих задач являются некорректно поставленными. В
частности, приведенная выпес задача Копей для уравнения Лапласа имеет
непосредственное отнопЕСние к обратной задаче гравиметрии (об определении
формы тела по создаваемой им аномалии силы тяжести). Приведенный вы-
Hie пример о вычислении производной по приближенным значениям функции
типичен для многих экспериментов, где измерения проводятся по принципу
накопления.
Отметим теперь следующее обстоятельство. Очевидно, что
функция U (ж, ^), определяемая формулой (9), может быть реп1ением
уравнения (1) только в том случае, если функция ф {х) дифференцируема,
а функция ip {х) дифференцируема дважды. Из сказанного ясно, что
функции, изображенные на рис. 11 и 12, не могут являться
решением уравнения (1), так как они не всюду дважды дифференцируемы.
^
XI Х2
Рис. 11
ui
XI
Х2
Рис. 12
Более того, можно утверждать, что решения уравнения колебаний,
удовлетворяющего условиям (2), не существует, если функции ip {х) и
ф (ж) не имеют нужных производных. Действительно, повторяя
рассуждения, приведшие нас к формуле (9), мы можем утверждать, что
если существует решение уравнения колебаний, то оно должно
представляться формулой (9). Если же функции (/^ (ж), ф {х) не
дифференцируемы достаточное число раз, то формула (9) определяет функцию,
не удовлетворяющую уравнению (1), т. е. не существует решения этой
задачи.
^ Лаврентьев М. М. О некоторых некорректных задачах
математической физики. Новосибирск, 1962; Тихонов А. П. О репЕСнии некорректно
поставленных задач и методе регуляризации // ДАП СССР. 1963. Т. 151,
№ 3. С. 501—504; Тихонов А. П. О регуляризации некорректно
поставленных задач // Там же. Т. 153, № 1. С. 49—52; Тихонов А. П. О нелинейных
уравнениях первого рода // Там же. 1965. Т. 161, № 5. С. 1023—1026.

68 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Однако если немного изменить начальные условия, заменив их
дифференцируемыми функциями (р (х) и ф (х), то этим начальным
функциям уже будет соответствовать решение уравнения (1). Кроме
того, заметим, что при доказательстве теоремы настоящего пункта
мы фактически доказали, что функции, определяемые формулой (9),
непрерывно зависят от начальных функций (f (х) и ф (х) (независимо
от того, дифференцируемы эти функции или нет). Таким образом, если
некоторым функциям (f (х), ф (х) не соответствует решение
уравнения колебаний, удовлетворяющее условиям (2), то функция,
определяемая формулой (9), является пределом решений уравнения колебаний
с немного сглаженными начальными условиями.
Полученные таким предельным переходом функции
называются обобщенными решениями. Понятие обобщенных решений,
играющее большую роль в физике, было введено С. Л. Соболевым-"^л
6. Полуограниченная прямая и метод продоллсений.
Рассмотрим задачу о распространении волн на полуограниченной прямой
X ^ 0. Эта задача имеет особенно важное значение при изучении
процессов отражения волн от конца и ставится следующим образом.
Найти решение уравнения колебаний
O'^Uxx = Utt при О < ж < 00, ^ > О,
удовлетворяющее граничному условию
и (О, t) = fi (t) {или Ux (О, t) = 1У (^)), ^ ^ О,
и начальным условиям
и (ж, 0) = (f (ж),
щ (ж, 0) = ф (х)
(О ^ ж < оо).
Рассмотрим сначала случай однородного граничного условия
и {О, t) =0 (или Ux{0, t) =0),
т. е. задачу о распространении начального возмущения на струне с
закрепленным концом х = О (или свободным концом).
Отметим следующие две леммы о свойствах решений уравнения
колебаний, определенных на бесконечной прямой.
1. Если начальные данные в задаче о распространении колебаний
на неограниченной прямой {задача (1)—(2)) являются нечетными
функциями относительно некоторой точки жо, то
соответствующее решение в этой точке xq равно нулю.
2. Если начальные данные в задаче о распространении
колебаний на неограниченной прямой {задача (1) —(2)) являются четными
^ См. подробнее: Соболев С. Л. Уравнения математической физики.
М., 1992; Петровский И. Г. Лекции об уравнениях с частными
производными. М., 1961. См. также Дополнение III.

§ 2] МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 69
функциями относительно некоторой точки жо, то производная по
X соответствующего решения в этой точке равна нулю.
Докажем лемму 1. Примем жо за начало координат, жо = 0. В
этом случае условия нечетности начальных данных запишутся в виде
(/? (ж) = - (/? (-ж), ^{x) = -ф (-ж).
функция U (ж, ^), определяемая формулой (9), при ж = О и ^ > О равна
at
и (О, t) = "^^ ^ ^^ L + — у ф{а)(1а = {),
— at
так как первое слагаемое равно нулю в силу нечетности ^ (ж), а
второе равно нулю, поскольку интеграл от нечетной функции в пределах,
симметричных относительно начала координат, всегда равен нулю.
Аналогично доказывается лемма 2. Условия четности начальных
данных имеют вид
(/? (ж) = (/? (-ж), V^ (ж) = V^ (-ж).
Заметим, что производная четной функции является функцией
нечетной:
if'{x) = -if' {-х).
Из формулы (9) следует
и, (О, t) = ^P'^<^t)+^'i-<^t) + ^ [^ («^) _ ^ (_«^)] =0, i > О,
так как первое слагаемое равно нулю в силу нечетности ^' (ж), а
второе— в силу четности ф (ж) ^\
Приведенное выше доказательство фактически опирается на
формулу Даламбера и не связано с двукратной дифференцируемостью
функции U (ж, t). Тем самым доказано, что лемма 1 верна для
любых функций, представимых формулой Даламбера, а лемма 2 — для
функций того же вида с дифференцируемой функцией ip (ж), т. е. для
обобщенных решений задачи (1) — (2).
При помощи этих двух лемм можно решить следующую задачу.
Требуется найти решение уравнения (1), удовлетворяюш^ее
начальным условиям
щ[х, 0) = ф[х),
^ Эти две леммы являются следствием того, что если начальные
условия четны (или нечетны), то и при ^ > О функция ^(ж, ^), определяемая
формулой Даламбера, обладает тем же свойством (предоставляем читателю
доказать это). Геометрически очевидно, что нечетная непрерывная функция
и производная четной дифференцируемой функции равны нулю при ж = 0.

70
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
и граничному условию
и(0, ^) = 0, ^>0
(первая краевая задача).
Рассмотрим функции Ф (ж) и Ф(ж), являющиеся нечетным
продолжением (f (х) и ф{х), входящих в условие (2'):
Ф{х)
(f (х) для ж > о,
- (f {—х) для X < 0;
Ф(ж)
ф (х) для ж > о,
--^ (—ж) для ж < 0.
Функция
U (ж, ^) =
Ф (ж + а^) + Ф (ж - а^) 1
x-\-at
+
2а
/ ФН
б?а
определена для всех ж и ^ > 0. В силу леммы 1
и {О, t) =0.
Кроме того, эта функция удовлетворяет при ^ = О и ж > О следующим
начальным условиям:
и{х, 0) = Ф (ж) = (/?(ж),
щ{х, 0) = Ф(ж) =ф{х),
ж >0.
Таким образом, рассматривая полученную функцию и (ж, t) только
для ж ^ О, ^ ^ О, мы получим функцию, удовлетворяющую всем
условиям поставленной задачи.
Возвращаясь к прежним функциям, можно написать
if {х -\- at) -\- if {х — at)
и (ж, ^) = <
2
x-\-at
If ж
+-— / ф (а) da для t < —,
2(2 / а
x — at
(р {х -\- at) — (р {at — ж)
2 '
x-\-at
If ж
Н / ф (а) da для t>—,
2а J а
ж > 0
ж > 0
(23)
at — x

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
71
В области t < х/а влияние граничных условий не сказывается, и
выражение для и (ж, t) совпадает с решением (9) для бесконечной прямой.
Аналогично, если при х = О мы имеем свободный конец:
и^ (О, t) = О,
ТО, взяв четное продолжение функций (f (х) и ф (х)
(f (х) для ж > о.
Ф{х) =
(f {—х) для ж < 0;
Ф(ж)
ф (ж) для ж > о,
ф (—ж) для ж < о,
получим решение уравнения колебаний
Ф (ж + а^) + Ф (ж - at)
и (ж, t) =
x-\-at
+ 11 4>{a)da,
и (ж, t) = I
if {х -\- at) -\- if {х — at) 1
2 ^2а
x-\-at
I Ф{о^
)da для t <
ip {х -\- at) — ip {at — x)
+
x-\-at
at — x
+ -— < I Ф [a] da -\- Ф (a) da > для t > —,
удовлетворяющее в области ж ^ О начальным условиям (2) и
граничному условию Ux {О, t) =0.
В дальнейшем при решении различных задач нам часто придется
пользоваться методом продолжения на бесконечную область
начальных данных, определенных на некоторой части этой области.
Поэтому мы еще раз сформулируем полученные результаты в виде
следующих двух правил.
Для решения задачи на полу ограниченной прямой с граничным
условием и (О, ^) = О начальные данные надо продолэюитъ на всю
прямую нечетно.
Для решения задачи на полуограниченной прямой с граничным
условием Ux (О, ^) = О начальные данные надо продолэюитъ на всю
прямую четно.
Рассмотрим два примера. Пусть начальные данные на
полуограниченной прямой, закрепленной при ж = О, отличны от нуля только в

72
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
интервале {а, Ь), О < а < Ь, в котором начальное отклонение,
даваемое функцией ^{х), изображается равнобедренным треугольником,
а ф (х) = 0. Решение этой задачи будет получено, если начальные
данные нечетно продолжить на бесконечную прямую. Процесс
распространения волн изо-
^^ _ Х2 - XI бражен на рис. 13.
Вначале процесс происходит
так же, как и на
неограниченной прямой.
Заданное отклонение
разбивается на две волны,
движущиеся в разные стороны
с постоянной скоростью,
причем это
продолжается до тех пор, пока волна,
идущая налево, не дойдет
до точки ж = О (рис. 13).
В этот момент с левой
стороны (ж ^ 0), на
которой происходили
аналогичные процессы, к
точке ж = О подходит волна
с «обратной фазой». В
последующие моменты
происходит отражение волны
от закрепленного конца.
Это изображено в
деталях на рис. 13. Профиль отражающейся волны укорачивается,
отклонения исчезают, затем отклонения появляются с обратным знаком, и,
наконец, отраженная волна пойдет вправо за ушедшей туда волной с
той же скоростью. Таким образом, при отражении волны от
закрепленного конца струны ее отклонение меняет знак.
Рассмотрим второй пример. Пусть на полуограниченной прямой
ж ^ О, закрепленной при ж = О, начальное отклонение всюду равно
нулю, а начальная скорость ф (ж) отлична от нуля только в интервале
(ж1, Ж2) (О < Ж1 < Ж2), причем здесь ф (ж) = const. Продолжим
нечетно начальные данные. От каждого интервала (ж1, Ж2) и (—Ж2, —xi)
распространяются отклонения, подобные отклонениям, изображенным
на рис. 14. Как видно из рисунка, в начальной стадии в области ж > О
процесс идет так же, как и на бесконечной прямой. Затем происходит
отражение от закрепленного конца, и, наконец, волна с профилем в
виде равнобедренной трапеции с постоянной скоростью движется
вправо.
Изучение отражения от свободного конца проводится аналогично,
только начальные данные нужно продолжать четно, так что
отражение волны от свободного конца будет происходить не с измененной, а
с той же фазой.
Рис. 13

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
73
Мы рассмотрели задачи с однородными граничными условиями
и (О, t)= fi{t) = 0
«)
/
\
У^
\
У
V
^
\
\
^^
N^
у
у
1
У
у
у
^
у
у
Х2 — Х\
8а
Ч,
V ,
V ,
у \
^
/
"^^
у
г
^v
> '-
у V
0
и^ (О, i)^v (t) = 0.
В общем случае
неоднородных граничных условий
решение представляется в
виде суммы, каждое слагаемое
которой удовлетворяет
только одному из поставленных
условий (либо граничному,
либо начальному).
Обратимся теперь к
решению уравнения при
нулевых начальных и заданном
граничном условиях:
й{х, 0) = 0, щ{х, 0) = 0,
u{0,t)= fi{t), t>0.
Очевидно, что гра-
ничныи режим вызовет вол- ^^^- ^^
ну, распространяющуюся вдоль струны направо со скоростью а, что
Рис. 15
подсказывает нам аналитическую форму решения
й (x^t) = f {х — at).
Определим функцию / из граничного условия
U(0,t) = f{-at)=fi{t),
откуда
/M = .(-i)

74
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
так что
и{х, t) = fi [ —
X — at
а
/^
0-D-
Однако эта функция определена лишь в области х — at ^ О, так как
/J (t) определена для t ^ 0. На рис. 15 эта область изображается за-
п1трихованной частью фазовой плоскости.
Чтобы найти й{х, t) для всех значений аргументов, продолжим
функцию II (t) на отрицательные значения t, полагая /j{t) =0 для
^ < 0. Тогда функция
и{х, t) = fi (t — — j
будет определена для всех значений аргументов и будет удовлетворять
нулевым начальным условиям.
Сумма этой функции и функции (23), определенной в начале
настоящего пункта, представляет решение первой краевой задачи для
однородного уравнения колебаний. Для полуограниченной струны
и (ж, ^) = <
(f {х -\- at) -\- (f {х — at)
+
x-\-at
+
i I '^^^
)da для t <
(24)
('-D
ip {x -\- at) — ip {at ■
+
x-\-at
+
2a J
ф (a) da для t > —.
at — x
Аналогично может быть построено решение второй краевой
задачи. О третьей краевой задаче см. п. 9, с. 83.
Мы ограничимся здесь решением краевой задачи для однородного
уравнения колебаний.
Решение неоднородного уравнения см. в п. 9.
7. Задачи для ограниченного отрезка. Рассмотрим краевые
задачи для ограниченного отрезка (О, /). Будем искать решение
уравнения
utt = a'^Uxxj
удовлетворяющее граничным условиям
u{0,t)=/i,{t),
U{0,t)=fi2{t),
t^O,

А.
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
75
и начальным условиям
щ{х, 0) = V^(x),j
Рассмотрим предварительно случай однородных граничных усло-
и(0, t) =и{1, t) =0.
Будем искать решение задачи в этом случае методом продолжения,
предполагая возможность следующего представления:
и (ж, t) =
Ф (ж + а^) + Ф (ж - at) 1
2 ^2а
x-\-at
I Па) da,
где Ф и Ф — функции, подлежащие определению. Начальные условия
и{х,0) = Ф(х)=<р{х),] Q^^^i
ut{x,0) = ^{x)=i>{x),j ^ ^ '
определяют значения Ф и Ф в интервале (О, /).
Чтобы удовлетворить нулевым граничным условиям, наложим на
функции Ф (ж) и Ф (ж) требования нечетности относительно точек
ж = О, ж = /:
ф (ж) = - Ф (-ж), Ф (ж) = - Ф {21 - ж),
ф (ж) = - Ф (-ж), Ф (ж) = - Ф {21 - ж).

76 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Сопоставляя эти равенства, получаем
Ф {х') = Ф{х' + 21) [х' = -х)
и аналогично для Ф(ж), т. е. Ф и Ф являются периодическими
функциями с периодом 21.
Нетрудно видеть, что условия нечетности относительно начала
координат и условия периодичности определяют продолжение Ф (х) и
Ф (ж) на всей прямой — оо < ж < оо. Подставляя их в формулу (9),
получаем penienne задачи.
На рис. 16 совмещены фазовая плоскость (ж, t) и плоскость (ж, и),
в которой дано начальное отклонение и его продолжение. На фазовой
плоскости штриховкой выделены полосы, внутри которых отклонение
отлично от нуля (см. рис. 7). Знаки «плюс» и «минус», стоящие в
этих полосах, указывают на знак (фазу) отклонения (в виде
равнобедренного треугольника). Пользуясь рис. 16, легко представить себе
профиль отклонения в любой момент t. Так, в момент t = 21/а мы
получим отклонения, совпадающие с начальными. Таким образом,
функция и{х, t) будет периодической функцией t с периодом Т = 21/а (см.
с. 96).
Рассмотрим теперь задачу о распространении граничного
режима. Будем искать решение уравнения
utt = a^Uxx
с нулевыми начальными условиями
и (ж, 0) = (f (ж) = О,
щ (ж, 0) = V^ (ж) = о
и граничными условиями
и {I, t)=0, j
Из результатов п. 6 вытекает, что при t < 1/а решением служит
функция
и (ж, t) = fiU j , где fi{t) = <
0, ^ < 0.
Однако эта функция не удовлетворяет граничному условию
и (/, ^) = О при t > 1/а.
Рассмотрим «отраженную» волну, идущую налево и имеющую
при ж = / отклонение, равное fl{t — 1/а). Ее аналитическое выражение
дается формулой
[ I 1-х\ f 21 X
P[t =j2[t-- + -
\ а а J \ а а

(25)
§ 2] МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 77
Легко убедиться, что разность двух волн
/ х\ ( 21 х\
Ди-- -ft[t-- + -]
\ а/ \ а а J
есть решение уравнения при t < 21/а.
Продолжая этот процесс далее, получим penienne в виде ряда
v^ f 2n/ х\ v^ f 2n/ x\
n=0 ^ ^ n=l ^ ^
содержащего (для каждого фиксированного i) только конечное число
отличных от нуля членов, ибо с каждым новым отражением аргумент
уменьшается на 2//а, а функция p,[t) = О для ^ < 0. Выполнение
граничных условий проверяется непосредственно. В самом деле, положим
ж = О и выделим из первой суммы отдельно первое слагаемое при п =
= О, равное /i(^). Остальные слагаемые первой и второй сумм,
соответствующие одинаковым значениям п, взаимно уничтожаются; это
показывает, что и (О, t) = /а (t).
Заменяя п на п — 1 и изменяя в связи с этим пределы
суммирования, преобразуем первую сумму к виду
^ / 2п1 21-х\
п=1 ^ ^
Полагая теперь ж = /, непосредственно убеждаемся в том, что
слагаемые первой и второй сумм взаимно уничтожаются-"^л
Формула (25) имеет простой физический смысл. Функция
/^
i'-i)
представляет собой волну, возбуждаемую граничным режимом при
ж = О, независимо от влияния конца ж = /, как если бы струна
была бесконечна (О < ж < оо). Следующие слагаемые представляют
собой последовательные отражения от закрепленного края ж = / (вторая
сумма) и от края ж = О (первая сумма).
Аналогично функция
^^f^ {2п + 1)1 ^ х\ ^^f, {2п + 1)1 X
u{x,t) = )^lii[t +
^ п=1 ^
^-^ \ а а J ^—' V а а
дает решение однородного уравнения с нулевыми начальными
условиями
и (ж, 0) = О, щ (ж, 0) = О
^ Начальные условия также проверяются непосредственно, так как
аргументы всех функций отрицательны при ^ = О и выражение (25) при ^ = О
равно нулю.

78 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
и граничными условиями
и {О, t) =0, и{1, t) = fi{t).
На доказательстве единственности решения рассмотренной задачи и
непрерывной зависимости решения от начальных и граничных условий
мы не останавливаемся.
8. Дисперсия волн. Уравнение колебаний струны uu = cl^Uxx
допускает решение в виде бегущей волны и = f {х ^ at)
произвольной формы. Общее уравнение гиперболического типа с постоянными
коэффициентами
йи - а^йхх + Ъхщ + Ъ2йх + ей = О (26)
с помощью указанной в гл. I подстановки й = ие^^+^^, где Л =
= 0,562/а^, /i = —0,5^1, сводится к уравнению
Uu - a^Uxx + cu = О, (27)
где с = с— (6i/2)^ + (62/2а)^. Покажем, что уравнение (27) не
допускает решений в виде произвольной бегущей волны при с т^ 0. В самом
деле, подставляя и = f {х — at) в (27), находим a^f" — a^f" + с/ = О,
откуда в силу произвольности / следует с = 0.
Импульс или сигнал произвольной формы может быть
разложением в интеграл Фурье представлен в виде суперпозиции гармонических
волн вида
и(ж, ^) = е^(^^-^^\
где со — частота, к = 27г/Л — волновое число (Л — длина волны).
Скорость, с которой фаза волны а = cot — кх перемещается в
пространстве, называется фазовой скоростью волны и равна, очевидно,
V = со/к. Если фазовая скорость гармонической волны зависит от
частоты, то говорят о дисперсии волн. В этом случае гармонические
составляющие сигнала смещаются друг относительно друга, в
результате чего профиль сигнала искажается.
Очевидно, что если уравнение не допускает решений в виде волн
произвольной формы, то фазовая скорость гармонической волны
зависит от частоты, т. е. имеет место дисперсия.
Покажем, что для уравнения (27) имеет место дисперсия при с^О.
Подставляя в (27) и = e^i'^t-kx)^ получаем уравнение, связывающее со
и к:
и? - а^к^ + с = 0.
Отсюда следует, что фазовая скорость
V — — — , а
к у/и^^с
зависит от частоты. При условии с = О, т. е. для уравнения
колебаний струны Uu — a^Uxxi V = а яе зависит от частоты и дисперсия

§ 2] МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН 79
отсутствует. Условие с = О называют также условием отсутствия
искажения.
В качестве примера рассмотрим телеграфное уравнение (см. § 1,
п. 4)
i^^ = CLitt + {CR + LG) it-\-GRi.
Полагая i = ue~^^ где fi = 0,5 {CR + LG)/{CL), получаем для и
уравнение
Uxx = CLutt + CU,
где с = — {CR — LG)^/{4:CL). Отсюда видно, что при CR ф LG
сигнал по кабелю распространяется с искажением, так как имеет место
дисперсия волн. Условие
CR — LG, или — = — ,
Li с
называется условием отсутствия искажения в линии. В этом случае
телеграфное уравнение допускает решение в виде затухающей волны:
i{x,t) = е~^^ f{x-at), j=- = —, а = -=,
где / — произвольная функция.
Отсутствие искажения волн при их распространении по кабелю
имеет особо важное значение для телефонной и телеграфной связи на
больших расстояниях.
9. Интегральное уравнение колебаний. При выводе
дифференциального уравнения колебаний (5) в § 1 мы исходили из закона сохранения
количества движения, который привел нас к уравнению колебаний в
интегральной форме (3). Для того чтобы от интегрального уравнения перейти к
дифференциальному, мы предположили, что функция п (ж, t) имеет вторые
производные. Всякое предположение об ограничении класса
рассматриваемых функций некоторым свойством означает отказ от изучения функций,
не обладающих предполагаемым свойством. Таким образом, переходя от
интегрального уравнения колебаний к дифференциальному, мы
исключаем из рассмотрения процессы колебаний, не удовлетворяющих требованию
двукратной дифференцируемости.
Покажем, что всю теорию можно развить в классе непрерывных
кусочно-дифференцируемых функций, исходя из интегрального уравнения
колебаний
Х2
t2
/[(sl-(aj'*=/[('£L-('aj*-//-*-
Xl tl Xl ti
(28)
Этому уравнению можно придать следующую форму. Рассмотрим в
плоскости (ж, t) область G, ограниченную кусочно-гладкой кривой С, и покажем.

80
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
что для этой области имеет место интегральное соотнонгение
Н
р ^^ dx -\- к ^^ dt
dt
дх
)Ч1
Fdxdt = 0.
(29)
Для однородной среды эта формула принимает вид
ди 2 ди
-—- dx -\- а -7^ dt
dt ox
hll
fdxdt = 0 /
(29')
^n\
ж
с G
Если кривая С является контуром прямоугольника со сторонами,
параллельными осям координат, то формула (29) совпадает с формулой (28).
Если кривая С состоит из кусков, параллельных осям, то область G
можно представить как сумму
прямоугольников. Суммируя контурные интегралы,
соответствующие отдельным слагаемым,
мы получим, что слагаемые, относящиеся
к внутренним границам, взаимно
уничтожаются, так как интегрирование
производится в противоположных направлени-
I 1_| L^*"| I I Д I I I I I I ^^7 ^ остающиеся слагаемые дадут фор-
I ]^К^^ I I I I I I I I I I ^У-^У (29)- Пусть, далее, кривая С со-
''^' '''''''''''' ' ^ ^ держит дуги (7, не параллельные осям
и не являющиеся линиями разрыва
подынтегральной функции. Возьмем сетку
со сторонами, параллельными осям
координат, и рассмотрим ячейки сетки, пересекающиеся с областью G.
Обозначим через G* совокупность этих ячеек и через С*—границу области G*.
Формула (29) применима к G*. Переходя к пределу при уменьпЕающихся
размерах сетки, нетрудно убедиться в справедливости формулы (29) для
предельной кривой С.
В самом деле, первое слагаемое формулы (29), примененной к области
G*, состоит из слагаемых типа
Рис. 17
/■
Ф (ж, t) dx или / Ф (ж, t) dtj
Сп Сп
где Ф (ж, ^)—непрерывная функция и Сп — дуга контура С*,
аппроксимирующая дугу С (рис. 17).
Пусть t = tn (х)—уравнение ломаной Сп vi t = t (ж)—уравнение
кривой С. Очевидно, что tn (ж) равномерно сходится к t (ж) и
lim
п—>-сю
/ Ф [ж, tn (ж)] dx =
tn{x)]dx= / Ф[x,t{x)]dx,
что и доказывает законность предельного перехода ^.
^ Поскольку dx = О на вертикальных звеньях ломаной Сп, то в этой
формуле t = tn (х) есть уравнение горизонтальных звеньев кривой Сп-

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
81
Если кривая С содержит дуги, являющиеся линиями разрыва
подынтегральной функции, то формула (29) сохраняет силу, если брать в качестве
значений подынтегральной функции ее предельные значения с внутренней
стороны области G. Таким образом, справедливость интегральной формулы
(29) доказана.
Рассмотрим следующую задачу.
Найти функцию u{xjt)j определенную и кусочно-гладкую в области
— оо<ж<оо, t ^ Oj удовлетворяющую уравнению
/(
ди 2 ди
-^ ах -\- а т^ at
ot ox
hll
f{x,t)dxdt = 0
(29')
и начальным условиям
и (ж, 0) = (р (ж),
щ (ж, 0) = ipix),
где (р{х) —кусочно-гладкая функция, а функции ф{х) и f{x,t) кусочно-
непрерывны. Здесь С — произвольный кусочно-гладкий контур, лежащий
н
M(x,t)
в
X — at X -\- at
Рис. 18
Рис. 19
в области t ^ 0. Покажем, что эта задача имеет единственное рептение,
определяемое формулой Даламбера.
Допустим, что функция и{х, t) представляет репЕСние наптей задачи.
Рассмотрим треугольник АВМ (рис. 18), примыкающий к оси ^ = О, с вер-
П1ИН0Й в точке М (x^t), со сторонами, являющимися отрезками
характеристик X — at = const и X -\- at = const, и применим к нему формулу (29 ).
Вдоль отрезка AM имеет место равенство dx/dt = а, так что
ди 2 ди
-^dx -\- а ^^ dt
dt дх
--{
ди ,. ди ,
J = а du.
Вдоль отрезка МБ имеет место равенство
ди ^ 2 ди ,, f ди
dx
~di
ди
-а, так что
ди . 2 ди J, [ ди .^ ди . \ .
-;— dx -\- а -;— dt = — а -^г- dt + -^г— dx ] = — а du.
dt дх \dt дх J
Следовательно, подынтегральное выражение вдоль характеристик является
полным дифференциалом. Производя интегрирование вдоль отрезков ВМ
6 А. Н. Тихонов, А. А. Самарский

82 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
и MAj получаем
м
n^dx + a^^dt) =-а[и{М)-и{В)],
м
-dx^a'^^dt] =а [и (А) - и (М)],
так что формула (29 ) принимает вид
В
и (М) = ^—^ ^-^ Н I ^-dx^ / / fdxdt,
^ ^ 2 2а J dt 2а J J ^
А ABM
или
. . _ if {х -\- at) -\- if {х — at)
и (ж, t) — - h
x+at t x+a{t-T)
+ ^7'^^^''^^ + ^/'^^ / f^^^^)'^^- (30)
x-at 0 x-a{t-T)
Таким образом, если penienne поставленной задачи существует, то оно
однозначно определяется своими начальными значениями. В случае однородного
уравнения (/ = 0) эта формула совпадает с формулой Даламбера. Отсюда
следует теорема единственности для рассматриваемой задачи.
С помощью непосредственной подстановки нетрудно убедиться, что
функция типа
t х+а (t — r)
и (ж, t) = /i (ж + at) + /2 (ж - at) + j dr I /з (С, т) d^,
о x-a(t-T)
где /i и /2—кусочно-гладкие функции, а /з—кусочно-непрерывная
функция, удовлетворяет уравнению (28), а тем самым и уравнению (29 ). Это
доказывает теорему существования. Рептения задач, рассмотренных в п. 3 в
качестве примеров, являются кусочно-гладкими функциями и охватываются
изложенной теорией.
Обратимся теперь к первой краевой задаче на полуограниченной
прямой. Будем искать репЕСние уравнения (29) в некоторой точке М (ж, t) для
t > х/а (рис. 19). Так как в области t < х/а (под характеристикой х =
= at) влияние граничного режима не сказывается, то рептение определяется
формулой (30). Применим формулу (29 ) к четырехугольнику МАА В, в
котором МЛ, MB и АА —отрезки характеристик. Выполняя
интегрирование вдоль характеристик МЛ, АА и ВМ, получаем
В
2аи (М) = 2аи {А) + аи (В) - аи {А') + I ^ dx + II fdxdt.
А' МАА'В

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
83
Подставив сюда координаты точек М, Л, 5 и Л , будем иметь
. . (^ х\ и(х-\-at, 0) — u(at — X, 0)
и(х, t) = и ' '^ ^ 11^
{«■'-1)
x-\-at
+ ^ [ ^
2а J dt
at — x
[ЛИ
dx +
t x+a (t — r)
0 |a;-a(t-r)|
(31)
x-\-at t x+a{t-T)
at-x 0 \x-a{t-T)\
Из (31) непосредственно следует единственность ренгения рассматриваемой
задачи.
При / = О эта формула, как нетрудно заметить, совпадает с формулой
(24) § 2, п. 6. Аналогичным способом изучается и вторая краевая задача, а
также задачи для ограниченного отрезка.
При изучении первой краевой задачи мы видели, что задания двух
начальных условий
и (ж, 0) = (р (ж), щ (ж, 0) = гр (ж)
и одного граничного условия
достаточно для полного определения рептения. Отсюда следует, что должно
существовать соотноптение, связывающее функции (р, гр, /j, т v, где v (t) =
= Ux {О, t). Дифференцируя формулу (31) по ж и полагая ж = О, получаем
1у{г) = -{ф{аг)-[^1'{г)-а^'{ат,
(32)
где для простоты положено / = 0. Пользуясь формулой (32), можно,
например, третью краевую задачу свести к первой краевой задаче.
10. Распространение разрывов вдоль характеристик.
Обратимся к рассмотрению разрывов производных рептений уравнения (29).
Покажем, что линиями разрыва производных
функций и{х, t), удовлетворяющих уравнению (29),
могут быть только линии семейств
характеристик
X — at = const, X -\- at = const.
В самом деле, пусть некоторая
дифференцируемая кривая, определяемая уравнением
ж = ж (^),
является линией разрыва производных непре- ^^'
рывной, кусочно-дифференцируемой функции u{x,t). Предположим для
*| А
[ Е
D с
U-

84
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
определенности, что х (t) — возрастающая функция. Применим формулу
(29') к прямоугольнику ABCD (рис. 20):
BA+AD DC+CB
a также к криволинейным треугольникам Ai = BAD и A2 = BDC:
BA-\-AD
DB
''.+CB DB
DC+CB
где скобки ( )i^2 показывают, что надо брать предельные значения изнутри
треугольников Ai или А2. Вычитая из суммы последних двух равенств
предпЕССтвующее, получим
f { (ди , 2ди\ (ди , 2ди\ \
DB
ИЛИ, в силу произвольной малости дуги DBj
ди
'di
X -\- а
ди
дх
О,
(33)
где, как обычно, скобками обозначается величина разрыва функции:
[/] = /2-/l-
Возьмем производную по t от значения функции п (ж, t) вдоль линии
разрыва производных:
причем в качестве значения производных можно брать предельные значения
как из Ai, так и из А2. Разность правых частей при г = 1 и г = 2 дает
ди
+ ж
ди
дх
= 0.
Сопоставляя это равенство с равенством (33) и предполагая, что по
крайней мере один из разрывов
ди
Ш
ди
дх
отличен от нуля, видим, что эти
равенства возможны одновременно, если детерминант этой системы равен
нулю:
X а
1 х'
(ж ) —а = О,
ж = d=a^ + const.

А
МЕТОД РАСПРОСТРАНЯЮЩИХСЯ ВОЛН
85
Таким образом, линии разрыва производных ренгения уравнения колебаний
являются характеристиками.
Зад ачи
1. Начертить профиль струны для различных моментов времени в
следующих случаях.
I. Неограниченная струна (—оо<ж<оо):
а) начальная скорость равна нулю {ф (х) = 0), а начальный профиль
струны задан в виде рис. 21;
б) начальное отклонение равно нулю, а начальная скорость имеет
постоянное значение щ (ж, 0) = фо на участке струны (ж1, Ж2) и равна нулю
вне этого участка;
в) начальные условия имеют вид
(р{х) = О,
ф{х) = <
О при ж < с,
—7г X (2с — х) при с < ж < 2с,
2с^
О при X > 2с.
II. Нолуограниченная струна (О ^ ж < оо):
г) начальная скорость равна нулю {ф (х) = 0), а начальное
отклонение задано в виде треугольника, изображенного на рис. 21. Конец струны
закреплен;
д) та же задача для струны со свободным концом ж = 0;
е) начальные условия имеют вид
(^(ж) = 0, ф{х)
О при О < ж < с,
фо = const при с < ж < 2с,
, О при ж > 2с,
конец струны ж = О закреплен;
ж) аналогичная задача для струны со свободным концом ж = 0.
Профиль струны для всех задач 1а — ж следует начертить для
моментов времени
^0 = О, tf.
■к (А; = 1,2,
ср{х)
о ХА
Отметить для задач 1а — ж на фазовой плоскости
(ж, t) зоны, соответствующие различным стадиям
процесса.
2. Найти репЕСние задачи 1а для всех значений Рис. 21
переменных ж и ^ (формулы, выражающие функцию и{х, t), различны для
разных зон фазовой плоскости).
3. Определить отклонение в некоторой точке жо, to, пользуясь фазовой
плоскостью (ж, ^) и плоскостью (ж, п), в которой (рис. 21) заданы
начальные отклонения (-0 = 0), как для случая неограниченной струны, так и для
случая полу ограниченной струны с закрепленным (или свободным) концом.

86
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
4. В начале длинной цилиндрической трубки, заполненной газом,
находится HopniCHb, движущийся по произвольному закону X = f (t) со
скоростью V = f' (t) < а. Начальное смещение и скорость частиц газа равны
нулю. Найти смещение газа в сечении
с абсциссой X. Рассмотреть случай
движения порпЕня с постоянной
скоростью с < а. Что можно сказать о
репЕСнии задачи, если начиная с
некоторого момента скорость порпЕня
V > al (см. Приложение IV к гл. П).
5. Пусть по неограниченной
струне бежит волна u{x,t) =
= f{x — at). Состояние струны в
момент ^ = О принять за начальное
и репЕить уравнение колебаний при соответствующих начальных условиях.
Сравнить с задачей 1а.
6. Неограниченный упругий стержень получен соединением в точке х =
= О двух стержней с характеристиками
Рис. 22
ki, Р1, CL1 = y/ki/pi при ж < О,
^2, Р2, «2 = \/к2/р2 при ж > 0.
а) Пусть из области ж < О бежит волна
и (ж, t)
>{^-l)^
где / — заданная функция. Найти коэффициенты отражения и преломления
волны при прохождении через точку стыка (ж = 0). Установить, при каких
условиях отраженная волна отсутствует.
б) РепЕить аналогичную задачу, если задано локальное начальное
отклонение
О при ж < Ж1,
п (ж, 0) = "^ (^ (ж) при Ж1 < ж < Ж2 < О,
О при ж > Ж2,
жо подвепЕСн груз массы М и
а начальная скорость равна нулю.
7. Пусть в некоторой точке струны ж
из области ж < О бежит волна
и (ж, t)
'('-!)■
Найти выражения для преломленной и отраженной волн.
8. Полуограниченная трубка (ж > 0), заполненная идеальным газом,
имеет на одном конце, ж = О, свободно перемещающийся пор песнь массы
М. В момент времени ^ = О пор пеню при помощи удара сообщают
начальную скорость г^о- Исследовать процесс распространения волны в газе, если
известно, что начальные отклонения и начальная скорость частиц газа
равны нулю.
Указание. Рассмотреть penienne уравнения колебаний в области ж > 0.
Использовать граничное условие
Mutt{0,t) = SjpoUa^{0,t)

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 87
{pq — начальное давление газа, S — площадь поперечного сечения трубки,
7 = Cp/cv) и начальные условия на границе и (О, 0) = О, щ (О, 0) = г^о-
9. Бесконечная струна, имеющая в точке ж = О сосредоточенную массу
М, находится в положении равновесия. В начальный момент времени ^ = О
ударом молоточка массе М сообщается начальная скорость г^о- Доказать,
что в момент времени ^ > О возмущенная струна имеет вид, указанный на
рис. 22, где ui {х, t) и U2 (ж, t) определяются формулами
ui (ж, ^) = <
о при X — at > 0]
при X — at < О
(прямая волна)
U2 (ж, ^) = <
( Mavo Г, / 2Т , .\
О при X — at > 0.
при X — at < О
(обратная волна).
Указание. Воспользоваться условием
10. РепЕить задачу о распространении электрических колебаний в
бесконечном проводе при условии
G_R
С ~ L
и при произвольных начальных условиях.
11. Найти репЕСние интегрального уравнения колебаний для
полуограниченной струны при граничных условиях 3-го рода (см. п. 9).
12. На конце ж = О полу ограниченного стержня укреплена мембрана,
оказывающая сопротивление продольным колебаниям стержня,
пропорциональное скорости щ (О, t). Исследовать процесс колебания, если заданы
начальные смещения и щ (ж, 0) = ф (ж) = 0.
§ 3. Метод разделения переменных
1. Уравнение свободных колебаний струны. Метод
разделения переменных, или метод Фурье, является одним из
наиболее распространенных методов реп1ения уравнений с частными
производными. Изложение этого метода мы проведем для задачи о
колебаниях струны, закрепленной на концах. Penienne указанной задачи
мы рассмотрим с исчерпывающей подробностью и при дальнейп1ем
изложении курса будем ссылаться на этот параграф, опуская повторения
доказательств.
Итак, будем искать решение уравнения
Uu = a^Uxx, (1)
удовлетворяющее однородным граничным условиям
и(0, ^)=0, u{l,t) = 0 (2)

88 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
и начальным условиям
щ{х, 0) = '0(ж).|
Уравнение (1) линейно и однородно, поэтому сумма частных решений
также является решением этого уравнения. Имея достаточно большое
число частных решений, можно попытаться при помощи
суммирования их с некоторыми коэффициентами найти искомое penienne.
Поставим основную вспомогательную задачу.
Найти решение уравнения
utt = a^Uxx,
не равное тоэюдественно нулю, удовлетворяющее однородным
граничным условиям
и представимое в виде произведения
и{х, t) =X{x)T{t), (5)
где X (х) —функция только переменного ж, Т (t) —функция только
переменного t.
Подставляя предполагаемую форму решения (5) в уравнение (1),
получим
Х"Т = ^ Т"X,
или, после деления на XT,
X" {х) _ 1 T"{t)
Х{х) ~ ^ T{t)'
(6)
Чтобы функция (5) была решением уравнения (1), равенство (6)
должно удовлетворяться тождественно, т. е. для всех значений
независимых переменных О < ж < /, ^ > 0. Правая часть равенства (6)
является функцией только переменного ^, а левая — только х.
Фиксируя, например, некоторое значение х и меняя t (или наоборот),
получим, что правая и левая части равенства (6) при изменении своих
аргументов сохраняют постоянное значение
Х{х) а2 T{t) ' ^ '
где Л — постоянная, которую для удобства последующих выкладок
берем со знаком «минус», ничего не предполагая при этом о ее знаке.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 89
Из соотношения (7) получаем обыкновенные дифференциальные
уравнения для определения функций X (х) и Т (t):
X'' (ж) + Л X (х) =0, X (х) ^ О, (8)
Т" (t) + а^Л Г (^) = О, Т (t) ^ 0. (9)
Граничные условия (4) дают
и (О, t)=X (0) Т (t) = О,
u{l,t) = X{l)T{t) =0.
Отсюда следует, что функция X (х) должна удовлетворять
дополнительным условиям
Х(0) =Х{1) =0, (10)
так как иначе мы имели бы
Г (^) = О и и (ж, t) = О,
в то время как задача состоит в нахождении нетривиального penie-
ния. Для функции Т (t) в основной вспомогательной задаче никаких
дополнительных условий нет.
Таким образом, в связи с нахождением функции X (х) мы
приходим к простейшей задаче о собственных значениях.
Найти те значения параметра Л, при которых существуют
нетривиальные решения задачи
Х"{х)+ХХ{х)=0,\
X(0)=X{l)=0,j ^ '
а такэюе найти эти решения.
Такие значения параметра Л называются собственными
значениями, а соответствующие им нетривиальные решения —
собственными функциями задачи (11). Сформулированную
таким образом задачу часто называют задачей Штурма —
Л иуви л ля.
Рассмотрим отдельно случаи, когда параметр Л отрицателен,
равен нулю или положителен.
1. При Л < О задача не имеет нетривиальных решений.
Действительно, общее решение уравнения (8) имеет вид
X (х) = Cie^^^ + Сзе- ^^^
Граничные условия дают
X (0) = Ci + (72 = О,
X (О = Cie^ + Сзе-^ = 0 {а = /л/^),

90 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
т. е.
Ci = - С2 и Ci (е^ - е-^) = 0.
Но в рассматриваемом случае а действительно и положительно, так
что е^ — е~^ ф 0. Поэтому
Ci = О, С2 = О
и, следовательно,
X (ж) = 0.
2. При Л = О также не существует нетривиальных решений.
Действительно, в этом случае общее решение уравнения (8) имеет вид
Х[х) = Cix + C2.
Граничные условия дают
X(0) = [CiX + C2].=0 = C2=0,
т. е. (7i=0 и (72 =0 и, следовательно,
X (ж) = 0.
3. При Л > О общее решение уравнения может быть записано в
виде
X (ж) = Di cos vXx + D2 sinл/Лж.
Граничные условия дают
X (0) = i^i = О,
Х{1) =D2smVxi = 0.
Если X (ж) не равно тождественно нулю, то D2 ф О, поэтому
sin л/л/= О, (12)
или
где п — любое целое число. Следовательно, нетривиальные реп1ения
задачи (11) возможны лишь при значениях
Л = Л„=(::;^)'.
vT
Этим собственным значениям соответствуют собственные функции
Хп \х) = Dn 8Ш -— ж.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 91
где Dji — произвольная постоянная.
Итак, только при значениях Л, равных
К={^)\ (13)
существуют нетривиальные реп1ения задачи (11)
7ГТ1
Хп (х) = sin -— ж, (14)
определяемые с точностью до произвольного множителя, который мы
положили равным единице. Этим же значениям Л^ соответствуют
решения уравнения (9)
7ГТ1 7ГТ1
Тп (t) = An cos —- at + Вп sin —- at, (15)
где An и Bji — произвольные постоянные.
Возвращаясь к задаче (1) — (3), заключаем, что функции
/ 7ГТ1 7ГТ1 \ 7ГТ1
Un (ж, t) = Хп {х) Тп (t) = (An COS —- at + Вп sin —- at j sin —- x (16)
являются частными решениями уравнения (1), удовлетворяющими
граничным условиям (4) и представимыми в виде произведения (5)
двух функций, одна из которых зависит только от ж, другая — от t.
Эти решения могут удовлетворить начальным условиям (3) нашей
исходной задачи только для частных случаев начальных функций (р (х)
и ф (х).
Обратимся к решению задачи (1) — (3) в общем случае. В силу
линейности и однородности уравнения (1) сумма частных решений
сю сю
/ ч V^ / ч V^ /л '7ГП _, . 7ГП \ . 7ГП _ ^.
и (ж, t) = > Un (ж, t) = > ( An COS —- at + Вп sm —- at 1 sm —— x (17)
n=l n=l
также удовлетворяет данному уравнению и граничным условиям (2).
На этом вопросе мы подробнее остановимся несколько позже (см. п. 3
этого параграфа). Начальные условия позволяют определить Л.п и
Вп- Потребуем, чтобы функция (17) удовлетворяла условиям (3):
и (ж, 0) =(f (ж) = ^Un (ж, 0) = ^Ап sin -— ж,
п=1 п=1
сю r-w сю
щ{х, 0) =^{x) = 2_^-д^{х, 0) = ^^—аВп^т — х.
п=1 п=1
(18)

92 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Из теории рядов Фурье известно, что произвольная
кусочно-непрерывная и кусочно-дифференцируемая функция / (ж), заданная в
промежутке О ^ ж ^ /, разлагается в ряд Фурье ^^
7ГП
п=1
/И = X^^nSin —Ж, (19)
где
Ьп = ] jf{i)^m'^idi. (20)
о
Если функции ^{х) и ф {х) удовлетворяют условиям разложения в
ряд Фурье, то
сю о /»
/ ч V^ . 7ГП 1 I ,.. , -КП . _ , ,
(^) = 2^ V^n sm — Ж, ip^ = - I if (^) sm — ^ б?^, (21)
п=1
^(^) = ^ ^п sin ^ ж, ф^ = J ф (^) sin ^ЫС (22)
П=1 Q
Сравнение этих рядов с формулами (18) показывает, что для
выполнения начальных условий надо положить
An = (fnj Вп = V^n, (23)
^ Обычно рассматриваются периодические функции с периодом 21
сю
7^ / \ ^0 V^ / ТГП , . 7ГП \
^ (^) = "^ + ^ ( an COS -— Ж + 6п sm -— Ж 1 ,
п=1
+1 +1
1
^1 ^1
Если функция F (ж) нечетна, то an = О, так что
»=1 -/ 0
Если функция F (x) задана только в промежутке (О, /), то мы можем
продолжить ее нечетно и вести разложение в промежутке от — / до +/, что и
приводит нас к формулам (19) и (20). (См.: Будак Б. М., Фомин С. В.
Кратные интегралы и ряды. М., 1967.)

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 93
чем полностью определяется функция (17), дающая penienne
исследуемой задачи.
Мы определили penienne в виде бесконечного ряда (17). Если ряд
(17) расходится или функция, определяемая этим рядом, не является
дифференцируемой, то он, конечно, не может представлять penienne
нашего дифференциального уравнения.
В настоящем пункте мы ограничимся формальным построением
решения. Выяснение условий, при которых ряд (17) сходится и
представляет решение, будет проведено в п. 3.
2. Интерпретация решения. Обратимся теперь к
интерпретации полученного решения. Функцию Un (ж, t) можно представить в
виде
/ \ /'л '7ГП _, . 7ГП \ . 7ГП
(ж, t) = ( An cos —- at + Вп sm —- at J sm —- x =
7ГП . _ . . 7ГП , ^.
an COS —- a{t -\- On) sm —- ж, (24)
где
an = л/А1-\-В1, —-aSn = - arctg -^. (25)
I Лп
Каждая точка струны xq совершает гармонические колебания
7ГТ1 7ГТ1
Un (жо, t) = an cos —-a{t-\- Sn) sin -— xq
с амплитудой
. 7ГП
«nSin-—Жо.
Движение струны такого типа называется стоячей волной. Точки
X = т— (ш = 1, 2, ...,п — 1), в которых sm —- ж = О, в течение все-
п I
го процесса остаются неподвижными и называются узлами стоячей
волны Un (ж, t). Точки ж = — / (ттг = О, 1, ..., п — 1), в которых
sin —- ж = =Ы, совершают колебания с максимальной амплитудой an
и называются пучностями стоячей волны.
Профиль стоячей волны в любой момент времени представляет
синусоиду
7ГП
Un (ж, t) = Сп (t) sm -- ж.
где
Сп (t) = an cos ujn {t + Sn) (ujn = ~r ^) •

94
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
В моменты времени t, при которых cosa;^ {t -\- Sn) = =Ы, отклонения
достигают максимальных значений, а скорость движения равна нулю.
В моменты времени t, при которых cosa;^ (^ + (5п) = О? отклонения
равны нулю, а скорость движения максимальна. Частоты колебаний
всех точек струны одинаковы и равны
7ГП , ^.
uJn = -j-ci. (26)
Частоты LJn называются собственными частотами колебаний
струны. Для поперечных колебаний струны а^ = Т/р и,
следовательно,
7ГП
UJn =
(27)
Энергия п-й стоячей волны (п-й гармоники) для случая
поперечных колебаний струны равна
Еп
о ■-
dun
dt
+ Т
dun
дх
dx
f/
7ГП
pcj^ sin LJn {t + Sn) sin —- X +
+ T ( —- 1 cos^ a;n {t + (5n) cos^ —- x
dx =
2 2
/ 7Г7Т/ \ ^
po;^ sin^ (jJn{t + Sn) + T I—-] cos^ a;^ (^ + Sn)
так как
(28)
/ sin^ —- xdx =
cos
^ - xdx =
Пользуясь выражением для an, ojn, ^ также равенством Т = о?p^
получаем
En —
P^Wn I ^ ,^2 j^^ ^l^ Bl
(29)
где M = /p — масса струны.
Колебания струны воспринимаются нами обычно по звуку,
издаваемому струной. Не останавливаясь на процессе распространения
колебаний в воздухе и восприятия звуковых колебаний нашим ухом,
можно сказать, что звук струны является наложением «простых тонов».

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 95
соответствующих стоячим волнам, на которые разлагается колебание.
Это разложение звука на простые тоны не является операцией только
математического характера. Выделение простых тонов можно
произвести экспериментально при помощи резонаторов.
Высота тона зависит от частоты колебаний, соответствующих
этому тону. Сила тона определяется его энергией и, следовательно,
его амплитудой. Самый низкий тон, который может издавать
струна, определяется самой низкой собственной частотой uji = 7т/1 уТ~[р и
называется основным тоном струны. Остальные тоны,
соответствующие частотам, кратным a;i, называются обертонами. Тембр
звука зависит от присутствия наряду с основным тоном обертонов и
от распределения энергии по гармоникам.
Низший тон струны и ее тембр зависят от способа возбуждения
колебаний. Действительно, способ возбуждения колебаний определяет
начальные условия (3)
и (ж, 0) = (/? (ж); щ (ж, 0) = -0 (ж),
через которые выражаются коэффициенты А^ и В п. Если Ai = Bi =
= 0, то низшим тоном будет тон, соответствующий частоте а;^, где
п — наименьшее число, для которого А^ и В^ отличны от нуля.
Обычно струна издает один и тот же тон. В самом деле,
приведем струну в колебание, оттягивая ее в одну сторону и отпуская без
начальной скорости. В этом случае
щ (ж, 0) = О, и (ж, 0) = (f{x) > О
A, = j l^{O^inj^^>0,
о
так как
sin у ^ > 0.
Следующие коэффициенты, вообще говоря, значительно меньше
. 7ГП г. -г»
Ai, так как функция 8ш —— ^ знакопеременна при п ^ 2. В
частности, если (р (х) симметрична относительно середины отрезка, то
^2 = 0. Таким образом, если привести струну в колебание, оттягивая
ее в одну сторону {(р (х) > 0), то низшим тоном будет основной тон
струны, энергия которого больше энергии других гармоник.
Привести струну в колебание можно и другими способами.
Например, если начальная функция нечетна относительно середины струны,
то
Ai=0

96 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
и низший тон соответствует частоте
Если звучащую струну взять точно за середину, то звук ее резко
меняется и она звучит в октаву к своему тону. Этот прием изменения тона
часто применяется при игре на скрипке, гитаре и других струнных
инструментах и носит название флажолета. С точки зрения теории
колебания струн это явление совершенно ясно. В момент
прикосновения к середине струны мы гасим стоячие волны, имеющие в этой точке
пучности, и сохраняем лишь гармоники, имеющие в этой точке узлы.
Таким образом, остаются только четные гармоники и самой низкой
частотой будет
Если прикоснуться к струне на расстоянии 1/3 ее длины от края,
то высота основного тона повышается втрое, так как при этом
сохраняются лишь гармоники, имеющие узлы в точке х = //3.
Формулы
a;i = -W- и Г1 = —=2Ц/^, (30)
определяющие соответственно частоту и период основного колебания,
объясняют следующие законы колебания струн, открытые впервые
экспериментально (законы Мерсена).
1. Для струн одинаковой плотности и одинакового натяжения
период колебания струны пропорционален ее длине.
2. При заданной длине струны период меняется обратно
пропорционально корню квадратному из натяжения.
3. При заданной длине и натяжении период меняется
пропорционально корню квадратному из линейной плотности струны.
Эти правила легко демонстрируются на монохорде.
В настоящем пункте мы рассмотрели стоячие волны,
возникающие при колебании струны с закрепленными концами. Вопрос о
существовании решения вида
и (ж, t)=X {х) Т (t)
эквивалентен вопросу о существовании стоячих волн, так как профили
этого решения для различных моментов времени пропорциональны.
3. Представление произвольных колебаний в виде
суперпозиции стоячих волн, в п. 1 мы рассмотрели задачу о свободных
колебаниях струны, закрепленной на концах, и доказали
существование частных решений в виде стоячих волн. Там же была дана
формальная схема представления произвольного колебания в виде беско-

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 97
нечной суммы стоячих волн. В настоящем пункте дается обоснование
возможности представления произвольного реп1ения в виде
суперпозиции стоячих волн. В первую очередь рассмотрим обобщение хороню
известного для конечных сумм принципа суперпозиции на случай
бесконечных рядов.
Пусть L (и) — линейный дифференциальный оператор, так что
L (и) равен сумме некоторых производных функции (обыкновенных
или частных) с коэффициентами, являющимися функциями
независимых переменных.
Докажем лемму (обобщенный принцип суперпозиции).
Если функции Ui (г = 1, 2, ..., п,...) являются частными
решениями линейного и однородного дифференциального уравнения L (и) =
= О {обыкновенного или с частными производными), то ряд и =
= J^^i Ci Ui является такэюе решением этого уравнения, если
вычисление производных от и, фигурирующих в уравнении L (и) = О,
моэюно совершить при помош^и почленного дифференцирования ряда.
В самом деле, если производные и, фигурирующие в уравнении
L (и) = О, вычисляются почленным дифференцированием ряда, то в
силу линейности уравнения
(сю \ сю
Y^CiuA =Y,CiL{ui)=0,
г=1 ) i=l
так как сходящиеся ряды можно складывать почленно. Тем самым
доказано, что функция и удовлетворяет уравнению. В качестве
достаточного условия для возможности почленного дифференцирования
ряда мы постоянно будем пользоваться условием равномерной
сходимости ряда
X^Cib(u,), (31)
i=l
получаемого после дифференцирования ^"^.
Вернемся теперь к нашей краевой задаче. Мы должны прежде
всего убедиться в непрерывности функции
сю сю
/ \ V^ / \ V^ / /I '7ГП _, . 7ГП \ . 7ГП
и (ж, t) = >. Un (ж, t) = >. ( ^n COS —- at + Bn sm —- at J sm —- ж,
n=l n=l
(32)
ИЗ чего будет следовать, что и{х, t) непрерывно примыкает к своим
начальным и граничным значениям. Для этого достаточно доказать
^^ См.: Смирнов В. И. Курс высшей математики. Т. П. М., 1974;
Будак Б. М.,, Фомин С. В. Кратные интегралы и ряды. М., 1967.
7 А. Н. Тихонов, А. А. Самарский

98 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
равномерную сходимость ряда для и{х, t), так как общий член
этого ряда — непрерывная функция, а равномерно сходящийся ряд
непрерывных функций определяет непрерывную функцию. Пользуясь
неравенством
\un{x,t)\ ^ \Ап\ + \Вп1
заключаем, что ряд
сю
Y.{\An\ + \Bn\) (33)
п=1
является мажорантным для ряда (32). Если мажорантный ряд (33)
сходится, то ряд (32) сходится равномерно, т. е. функция и (ж, t)
непрерывна.
Чтобы убедиться в том, что щ (ж, t) непрерывно примыкает к
своим начальным значениям, надо доказать непрерывность этой функции,
для чего достаточно доказать равномерную сходимость ряда
сю гл СЮ
/ ч V^ ^'^п \-^ 7ГП / . . 7ГП _, 7ГП \ . 7ГП
щ (ж, t) ~ > --— = > а —— ( — An sm —- at + Вп cos -— at 1 sm —- x
(34)
ИЛИ сходимость мажорантного ряда
сю
^^п(К| + |Б„|). (35)
Наконец, чтобы убедиться в том, что функция и (ж, t) удовлетворяет
уравнению, т. е. применим обобщенный принцип суперпозиции,
достаточно доказать возможность двукратного почленного
дифференцирования ряда для U (ж, ^), для чего, в свою очередь, достаточно доказать
равномерную сходимость рядов
д'
сю г\0 о СЮ
ЕО Un f'^\ \~^ l( А '7ГП _, . 7ГП \ . 7ГП
-^ = - (^уJ 2^ п \Ап COS —-at-\-Bn sm — atj sm — ж,
n=l n=l
СЮ r-wO о СЮ
EOUn /TraX^v-^ 2/л ^^ ^ . 7ГП \ . 7ГП
-—- = - \^--j 2^ n [An COS -—at-\-Bn sm — atj sm — ж,
n=l n=l
которым С ТОЧНОСТЬЮ до множителей пропорциональности
соответствует общий мажорантный ряд
сю
J2n4\An\ + \Bn\). (36)
п=1
Так как
/
An — ^т Вп — "Фт
тгпа

А.
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
99
где
/ (f (х) sin —- xdx,
/ ф (х) sin —- xdx,
^п = J I ^[х) sm -— X их, фп
о о
то наша задача сводится к доказательству сходимости рядов
^п^|<^„| (fc = 0, 1, 2),
^п*^ \ф„
п=1
(fc = -1,0,1)
(37)
С этой целью мы используем известные ^^ свойства рядов Фурье.
Если периодическая с периодом 21 функция F (ж) имеет к
непрерывных производных, д, {к -\- 1)-я производная ее кусочно-непрерывна,
то числовой ряд
^п^{\ап\^\Ьп\
(38)
где an и Ьп — коэффициенты Фурье, сходится. Если речь идет о
разложении в ряд по sin —- X функции / (ж), заданной только в промежутке
(О, /), то надо, чтобы предшествующие требования были выполнены
для функции F (ж), получающейся при нечетном продолжении / (ж).
В частности, для непрерывности F (ж) необходимо, чтобы / (0) =0,
так как в противном случае при нечетном продолжении получится
разрыв в точке ж = 0; аналогично этому в точке ж = / должно быть
/ (/) = О, так как продолженная функция непрерывна и периодична
с периодом 21. Непрерывность первой производной при ж = О, ж =
= / получается автоматически при нечетном продолжении. Вообще
для непрерывности четных производных продолженной функции
надо потребовать, чтобы
/W(0) = /«(0 = 0 (fc = 0,2,4, ...,2п).
(39)
Непрерывность нечетных производных имеет место без
дополнительных требований.
Итак, для сходимости рядов
Y,n''\^Pn\ (fc = 0, 1, 2)
^ См., например: Смирнов В. И. Курс выснхей математики. Т. Н. М.,
1974; Будак Б. М., Фомин С. В. Кратные интегралы и ряды. М., 1967.

100 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
достаточно потребовать, чтобы начальное отклонение ^ (ж)
удовлетворяло следующим требованиям.
1°. Производные функции ^{х) до 2-го порядка включительно
непрерывны, третья производная кусочно-непрерывна и, кроме того,
^(0) = ^(0 = 0; <^" (0) = <^" (О = 0. (40)
Для сходимости рядов
сю
^n'^IVnl (fc = -1,0,1)
п=1
на начальную скорость ф (ж) необходимо наложить следующие
требования.
2°. Функция ф {х) непрерывно-дифференцируема, имеет кусочно-
непрерывную вторую производную и, кроме того,
V'(o) = V(0=o. (41)
Таким образом, нами доказано, что любое колебание и (ж, t) при
начальных функциях ^ (ж) и ф (ж), удовлетворяющих требованиям
1° и 2°, представляется в виде суперпозиции стоячих волн. Условия
1° и 2° являются достаточными условиями, связанными с
примененными здесь способами доказательства.
Аналогичная задача была нами peniena в § 2, п. 5 методом
распространяющихся волн. Ее ренЕСние имеет вид
x-\-at
, . Ф (ж - а^) + Ф(ж+ а^) 1 /" -г / ч 7 /.оч
п(ж, ^) = —^ —^ ^ -^Ya / *(^)^^' (^2)
x — at
где Ф и Ф являются нечетными относительно О и / продолжениями
начальных функций (^ (ж) и i\){x)^ заданных на отрезке (О, /). Функции Ф
и Ф, как было показано, периодичны с периодом 2/ и поэтому могут быть
представлены рядами
сю сю
Ф (ж) = ^ ^п sm — ж, Ф (ж) = ^ V'n sm —- ж,
где (^п и фп—коэффициенты Фурье функций (^ (ж) и ф{х). Подставляя
эти ряды в формулу (42) и пользуясь теоремой о синусе и косинусе суммы
и разности, получаем выражение
оо
/ .4 V^ f 7ГП , / , . 7ГП \ . 7ГП . .^.
п (ж, г) = > Шп COS —- аг Н фп sm —— аг sm —— ж, (43)
^^^ V / ппа I J I
п=1
совпадающее с представлением, даваемым методом разделения переменных.
Следовательно, формула (43) имеет место при тех же предположениях,
что и формула (42) (см. § 3, п. 1), которая была получена при условии, что
функция Ф (ж) непрерывно-дифференцируема дважды, а функция Ф (ж) —
один раз.

А.
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
101
Переходя к функциям (р (х) и ^p{x)j мы помимо условий дифференци-
руемости должны потребовать выполнения условий
^(0) = ¥'(0=0, ф{0) = ф{1) = 0, <р" (0) = <р" (I) = 0. (44)
Таким образом, условия 1° и 2°, являющиеся достаточными для
обоснования метода разделения переменных, зависят от метода доказательства
и содержат дополнительные условия по сравнению с условиями,
обеспечивающими существование рептения.
При обосновании возможности представления репЕСния как
результата суперпозиции стоячих волн мы привели первый метод доказательства
сходимости рядов, поскольку он не связан со специальной формулой (42),
применимой только к простейптему уравнению колебаний, и без труда может
быть перенесен на ряд других задач, хотя этот метод предъявляет несколько
повыпЕСнные требования к начальным функциям.
4. Неоднородные уравнения. Рассмотрим неоднородное
уравнение колебаний
utt = a^Uxx + / (ж, t), а^ = -, О < ж < /,
(45)
с начальными условиями
и{х, 0) =(р{х)А
щ{х, 0) = V^(x),J
и однородными граничными условиями
и(0, t) = 0,1
О ^ж ^/,
t> 0.
(46)
(47)
и(1, t) = 0,^
Будем искать решение задачи в виде разложения в ряд Фурье по х
\~^ . тгп
и (ж, t) = >. ^п \Ч sm —j- X,
n=l
I
(48)
рассматривая при этом t как параметр. Для нахождения и{х, t) надо
определить функцию Un{t). Представим функцию f {х, t) и
начальные условия в виде рядов Фурье:
/ {х, t)
N fn{t)^m--x, fn{t)
n=l
//(C,^)sin^C^C;
^
[x) = 2_^(fn sm — Ж,
^
n=l
ф{х)
= E
n=l
V^nSin
7ГП
■Ж,
n = у / (/:?(C)sin™^6?^;
0
(49)
sm -p$a4.

102 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Подставляя предполагаемую форму реп1ения (48) в исходное
уравнение (45):
7Г?7 1 / 7Г?7 \ 1
2^ sin — Ж <^ -а^ \-у) Un (t) - йп (t) + /n (t) > = О,
n=l ^ ^
видим, что оно будет удовлетворено, если все коэффициенты
разложения равны нулю, т. е.
un{t)+[—) a\n{t)=fn{t). (50)
Для определения Un (t) мы получили обыкновенное дифференциальное
уравнение с постоянными коэффициентами. Начальные условия дают
и (ж, 0) = (р [х) = 2_.^п (0) sm —- X = /.^п sm —- ж,
1 ^ 1 ^
п=1 п=1
сю сю
щ (ж, 0) = -0 (ж) = 2_^Un (0) sm -— ж = /^V^n sm -— ж.
7ГП ^-^ . 7ГП
-^ = L
n=l n=l
сю сю
7ГП ^-^ , . 7ГП
-^ = L
n=l n=l
откуда следует
(51)
Эти дополнительные условия полностью определяют penienne
уравнения (50). Функцию Un (t) можно представить в виде
где
t
«L'' {t) = — I sin '^a{t-T)-fn (r) dr (52)
тгпа J I
0
— решение неоднородного уравнения с нулевыми начальными условия-
/ттч . . 7ГП / , . 7ГП .^^.
^п \Ч — ^п COS —- at -\ грп sm —- at (53)
^ В этом можно убедиться непосредственно. Формула (52) может быть
получена методом вариации постоянных. См. также текст, набранный мелким
пЕрифтом в конце настоящего пункта.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 103
— решение однородного уравнения с заданными начальными
условиями. Таким образом, искомое решение запишется в виде
и {х
сю J ^
\ \~^ ^ / . '^^ / . . 7ГП г / \ 1
, ^) = > / sm--a{t- т) 8ш -- ж • fn (г) йт +
п=1 п
сю /
Е/ 7ГП
( (рп COS -— at -\-
п=1 ^ ^
/ , . 7ГП \ . 7ГП .^^.
грп 8ш —- at 8ш —- X. (54)
тгпа / / /
//■
Вторая сумма представляет penienne задачи о свободных
колебаниях струны при заданных начальных условиях и была нами
исследована ранее достаточно подробно. Обратимся к изучению первой
суммы, представляющей вынужденные колебания струны под действием
внешней силы при нулевых начальных условиях. Пользуясь
выражением (49) для fn (t), находим
и^^^ (ж, t) =
Я1 2 ^^ / . 7ГП . . . 7ГП . '7ГП . 1 . . . ч , . ,
t I
^ G{x,i,t-T)f{i,T)didT, (55)
о о
где
^г ^ . ч 2 ^ 1 . 7ГП . , . 7ГП . 7ГП ^ ,^^,
G (ж, ^, ^ — г) = — > — 8ш —- a\t — т) 8ш —- ж 8ш —- ^. (56)
TTCt lii L L
n=l
Выясним физический смысл полученного решения. Пусть
функция / (^, г) отлична от нуля в достаточно малой окрестности точки
Мо(Со,го):
Со ^ С ^ Со + А^, Го ^ г ^ Го + Аг.
Функция р f (С, т) представляет плотность действующей силы; сила,
приложенная к участку (Со, Со + АС), равна
Со+АС
F{r)=p I f{^,r)d^,
Со
причем
го+Аг го+Аг Со+АС
/= I F{T)dT = p I I f{^.T)d^dT
^0 ^0 Со

104 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
есть импульс этой силы за время Аг. Если применить теорему о
среднем значении к выражению
t I
u{x,t) = I Jg {х, ^,t-T)f (С, г) d^dr =
о о
ro+Ar Со+АС
= 11 G{xA,t-T)f{i,T)didT,
^0 Со
будем иметь
го+Аг Со+АС
u{x,t)=G{x,lt-f) I I f{^,T)d^dT, (57)
^0 Со
где
Со ^ f ^ Со + А^, Го ^ f ^ Го + Аг.
Переходя в формуле (57) к пределу при А^ —>■ О и Аг —>- О, получим
функцию
и (ж, t) =G (ж, Со, t - Го) -, (58)
Р
которую можно трактовать как влияние мгновенного сосредоточенного
импульса мощности /.
Если известна функция I/р • G {х, С, t ~ ^)^ представляющая
действие единичного сосредоточенного импульса, то непосредственно
ясно, что действие непрерывно распределенной силы / (ж, t) должно
представляться формулой
1 /
2а р
t I
u{x,t) = I Jg {х, ^,t-T)f (С, г) d^dr,
о о
(59)
совпадающей с формулой (55), полученной вы-
Hie.
t, - а[ - т) ^-\- a{t - т) Функция ВЛИЯНИЯ СОСрСДОТОЧеННОГО ИМ-
Pjj(. 23 пульса для бесконечной прямой была
рассмотрена в предыдущем параграфе. Напомним,
1 /
что она является кусочно-постоянной функцией, равной внутри
2а р
верхнего характеристического угла для точки {^, т) и нулю вне этого
угла. Функция влияния сосредоточенного импульса для закрепленной
струны (О, /) может быть получена из функции влияния для
бесконечной струны путем нечетного продолжения относительно точек х = О
VL X = I.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 105
Рассмотрим момент времени t, достаточно близкий к г, когда
влияние отражения от концов ж = О и х = I еще не сказывается. Для
этого момента функция влияния изображается графиком, приведенным
на рис. 23. Разложим эту функцию (полагая I = р) в ряд Фурье по
. 7ГП ^ ^
sm —- х; коэффициенты Фурье будут равны
^+a(t-T)
л 2 /^ ^ , . . . 7ГП _ 1 f . 7ГП _
^п = т I ^ [OL^ t,^ t — т) sm —- ada = — / sm —- a da
I J I al J I
0 ^-a{t-T)
1 f 7ГП r^ , ,, 7ГП r^ , ,Л
= COS — К - a (^ - r)] - cos ^ К + a (^ - r)]
2 . 7ГП . . 7ГП . .
= sm —- t, sm —- ait — T).
атгп I I
Отсюда получаем формулу
„ . . . 2 ^-^ 1 . 7ГП , . . 7ГП . 7ГП . , ^.
G (ж, ^, ^ — r) = — > — sm —- a{t — T) sm —- ж • sm —- ^, (60)
/I Ci ft i Li
n=l
которая совпадает с формулой (56), найденной методом разделения
переменных.
Для значений t, при которых начинает сказываться влияние
закрепленных краев, построение функции влияния при помощи
характеристик громоздко; представление же в форме ряда Фурье сохраняет
силу и в этом случае.
Мы ограничимся приведенной здесь формальной схемой решения,
не выясняя условий применимости полученной формулы.
Рассмотрим неоднородное линейное уравнение с постоянными
коэффициентами
L (и) = п(") + рщ^"-^) + ... + pn-iu^^^ +PnU = f (t) (1*)
dt'
и начальными условиями
n(^)(0) = 0 (г = 0, 1, ..., n-1). (2*
Его penienne дается формулой
t
u{t)= fu{t-T)f{T)dT, (3*
0
где и (t) — penienne однородного уравнения
L{U) = 0

106
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
с начальными условиями
и^') (0) = О (г = О, 1, ..., п - 2), и^""-'^ (0) = 1.
(п-1)
(4*
В самом деле, вычисляя производные и (t) дифференцированием
правых частей по ^, находим
г
О
t
{t-T)f{T)dT + U{0)f{t)
.(2)^
г(2).
tWi
и^-') (t) = / т^> (t - т) fir) dr + т'> (0) fit)
о
(f/(0) = 0),
((7«(0) = 0),
t
«(»-!)(i) = f г/^"-^){t - t) fir) dr + [/("-2'(0) fit) iu^"-^^(0) = 0),
0
t
-- f ?/("'it - t) fir) dr + г/^"-^)(0) fit) (f/("-i)(0) = 1).
} (5*)
«(")(<)
Подставляя эти производные в уравнение (1*), получаем
t
L{u) = j L[U{t-r)]f{r)dr + f{t) = f{t),
о
т. е. уравнение удовлетворяется. Очевидно, что начальные условия (2*)
также выполнены.
Нетрудно дать наглядную физическую интерпретацию функции U (t)
и формулы (3*). Обычно функция u{t) представляет смещение некоторой
системы, а f {t)—силу, действующую на эту систему. Пусть для ^ < О
Hania система находилась в состоянии покоя и ее смещение создается
функцией fs (t) (^ 0), отличной от нуля только в промежутке времени О < ^ < s.
Импульс этой силы обозначим
1= I fs{T)dT.
О
Обозначим Ue (t) функцию, соответствующую fe (t), считая е параметром
и полагая 1 = 1. Нетрудно убедиться, что при е ^ О существует lim Us {t)j
не зависящий от способа выбора fe (t), и что этот предел равен функции
и (t)^ определенной Bbinie:
U{t) = lim us{t),

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 107
если положить U (t) = О для ^ < 0. Таким образом, функцию U (t)
естественно назвать функцией влияния мгновенного импульса.
В самом деле, рассматривая формулу (3*) и применяя теорему среднего
значения, получаем
S
Us (t) = U{t- Ts) / fs (r) dT = U{t- Ts) {O^Ts <e< t).
0
Переходя к пределу при s ^ О, видим, что существует предел
lim ue (t) = lim U {t - r^) = U (t),
ЧТО и доказывает nanie утверждение.
Перейдем к представлению рептения неоднородного уравнения через
и (t) — функцию влияния мгновенного импульса. Разбив промежуток (О, t)
точками Ti на равные части
t
Ar=-,
т
представим функцию / (t) в виде
т
i=l
где
Тогда
п /^\ ^ / О при t <TiVLt^ Ti+l,
I /(^) при Ti^t < Ti+i.
u{t) = ^ni(^).
i=l
где Ui (t) суть репЕСния уравнения L (ui) = fi с нулевыми начальными
данными.
Если т достаточно велико, то функцию щ (t) можно рассматривать
как функцию влияния мгновенного импульса интенсивности
I = fi{Ti)AT = f{Ti)AT,
u{t) = y^U{t-Ti)f{Ti)AT у / U{t-T)f{T)dT,
1=1 Q
т. е. мы приходим к формуле
t
u{t)= fu{t-T)f{T)dT,
о

108 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
показывающей, что влияние непрерывно действующей силы можно
представлять суперпозицией влияний мгновенных импульсов.
В рассмотренном выпес случае щ^ ^ удовлетворяет уравнению (50) и
условиям Un (0) = йп (0) =0. Для функции влияния и (t) имеем
^"^(т) ^^^ = 0' t/(0)=0, L^(0) = 1,
так что
ТТ{+\ ^ . 7ГП
и it) = sm —— at.
тгпа I
Отсюда и из (3*) получаем формулу (52):
t t
u^^\t)= fu{t-T)fn{T)dT=— fsm^a{t-T)fn{T)dT.
J тгпа J I
0 0
Полученное выпес интегральное представление (3*) рептения
обыкновенного дифференциального уравнения (1*) имеет, как мы убедились, тот
же физический смысл, что и формула (59), дающая интегральное
представление репЕСния неоднородного уравнения колебаний.
5. Общая первая краевая задача. Рассмотрим общую
первую краевую задачу для уравнения колебаний.
Найти решение уравнения
utt = a'^u^x + f{x,t), 0<х<1, t>0, (45)
с дополнительными условиями
и (ж, 0) = (f (ж),
щ{х, 0) ='0(ж),
О^х ^1; (46)
t ^ 0. (47)
u{0,t)=fii{t),
и{1, t) =/i2 W,^
Введем новую неизвестную функцию v {х^ t), полагая
и (ж, t) = и (ж, t) -\- V (ж, t),
так что V {х, t) представляет отклонение функции и (ж, t) от
некоторой известной функции [/ (ж, t).
Эта функция г» (ж, t) будет определяться как penienne уравнения
vtt = a^v^^ + /(ж, t), /(ж, t) = /(ж, t) - [Utt -a^U:,:,]
с дополнительными условиями
V (ж, 0) = (^ (ж), ф{х) = (f (ж) — и (ж, 0),
vt (ж, 0) =ф (ж), ф{х) =ф (ж) - Ut (ж, 0);
v{0,t)=fii{t),fii{t)=iJi{t)-U{0,t),
V {I, t) = fl2 (t), Ц2 (t) = fi2 (t) - и {I, t).

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 109
Выберем вспомогательную функцию [/ (ж, t) таким образом, чтобы
Д1 (i) = о и Дз {t) = 0;
для этого достаточно положить
Uix,t)=l^i{t) + j[H2it)-l^i{t)].
Тем самым общая краевая задача для функции и{х, t) сведена к
краевой задаче для функции v {х^ t) при нулевых граничных условиях.
Метод решения этой задачи изложен выше (см. п. 4).
6. Краевые задачи со стационарными неоднородностями.
Весьма важным классом задач являются краевые задачи со
стационарными неоднородностями, когда граничные условия и правая часть
уравнения не зависят от времени:
utt = a^Uxx + /о(ж), (45')
и{х, 0) = ^{х)Л
щ{х, 0) =ф{х),1
и (о, t) = ui, ui = const,
и (/, t) = U2, U2 = const.
(46')
(47')
в этом случае решение естественно искать в виде суммы
и (ж, t) = й{х) -\- V (ж, t),
где й (х) — стационарное состояние (статический прогиб) струны,
определяемое условиями
аЧ" (х) + /о (х) = О,
й(0) = Ui, й{1) = U2,
а V (х, t) —отклонение от стационарного состояния. Нетрудно видеть,
что функция й {х) равна
и (ж) =Ui-\-{u2-Ui)j-\- J / d^i / —^ d^2 ~ / ^^1 / д2 ^^2.
0 0 0 0
в частности, если /о = const, то
й (ж) = Ui + {U2 -Ui) - + —^ {IX - Ж^).
Функция V {х, t), очевидно, удовлетворяет однородному уравнению
vtt = a'^Vxx

110 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
с однородными граничными условиями
V (О, t) = О,
v{l, t) =0
и начальными условиями
V (ж, 0) = ф{х), ф (х) = (f{x) — й (ж),
vt{x, 0) =ф{х).
Таким образом, v является решением простейшей краевой задачи,
рассмотренной нами в п. 1 настоящего параграфа.
При выводе уравнения колебаний струны и в ряде других случаев
мы не принимали во внимание действие силы тяжести. Из сказанного
выше следует, что вместо явного учета силы тяжести (и вообще сил,
не зависящих от времени) достаточно сформулировать задачу для
отклонения от стационарного состояния.
Решим простейшую задачу подобного типа при нулевых начальных
условиях:
ии = а Uxx + /о (ж), (45^0
п(ж, 0) = 0, щ{х,0) = 0, {46")
u{0,t) = ui, u{l,t) = U2. (47'0
В этом случае для функции г; (ж, t) получаем задачу
2
vtt = а Vxx,
V (ж, 0) = (р (ж) = —й (ж), vt (ж, 0) = О,
'^(0, t) = 0, v{l, t) = 0.
Нетрудно убедиться, что для решения этой задачи нет необходимости
пользоваться точным аналитическим выражением для й(ж).
Выражение для г; (ж, t) согласно формуле (17) имеет вид
сю
V (ж, t) = У^ {An COS а л/Xnt -\- Bnsina л/Xnt) Хп (ж).
п=1
где
Хп {х) = sin л/Хп X 1л/Хп = —-]
есть собственная функция следующей краевой задачи:
Х"-\-ХХ = 0, (8)
Х(0) = 0, Х(/) = 0. (10)
Из начальных условий следует, что

А.
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
111
- и{х)Хп (ж) dx.
о
Для вычисления этого интеграла весьма удобным является следующий
метод. Пользуясь уравнением (8), находим
Хп (ж) = - ^ Х'^ (х).
An
Подставим это выражение в формулу для An и выполним двукратное
интегрирование по частям:
А-п
IX,
(ж) Хг^{х) dx ■■
IXr,
uX'nix)
■и Хп{х)
I ^
о J
(ж) Хп{х) dx
Отсюда, учитывая уравнение и граничные условия для и (ж), находим
Аг.
2
/Л77
U2 Х'п (/) - «1 х; (0) - f ^^^ Хп (ж) dx
An
(-1) U2-UI- / 2— ^^
(ж) dx
В частности, для однородного уравнения (/о (ж) = 0) имеем
An = Г(-1)^ U2 - щ] .
7ГП ■- -■
Этим методом удобно вычислять коэффициенты Фурье для граничных
условий второго и третьего рода, а также в случае краевой задачи для
неоднородной струны
^[M.)f]+Ap(x)X = 0,
dx
если известны собственные функции и собственные значения.
7. Задачи без начальных условий. Как было показано выше,
задача о колебании струны при заданном граничном режиме может
быть сведена к реп1ению неоднородного уравнения с нулевыми
граничными условиями.
Однако этот прием зачастую усложняет решение задачи, которое
может быть найдено непосредственно.

112
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
При изучении влияния граничного режима важно найти какое-
нибудь частное решение (однородного уравнения), удовлетворяющее
заданным граничным условиям, так как вычисление поправки на
начальные данные сводится к решению того же уравнения с нулевыми
граничными условиями.
Весьма важным классом задач о распространении граничного
режима являются «задачи без начальных условий».
Если граничный режим действует достаточно долго, то
вследствие трения, присущего всякой реальной физической системе, влияние
начальных данных с течением времени ослабевает. Таким образом мы
естественно приходим к задаче без начальных условий (I).
(1а)
Найти решение уравнения
Utt = CL^Uxx — OLUt (а > 0), о < ж < /, ^ >
при заданных граничных условиях
и{1, t) = /i2 {t)'
■ 00
(61)
Эту задачу назовем (Iq,).
Слагаемое ащ в правой части уравнения соответствует трению,
пропорциональному скорости.
Рассмотрим сначала задачу о распространении периодического
граничного режима:
u{l^t)=Aco^ujt (или u{l^t)=B^m.ujt)^ (62)
и (О, t) = 0. (63)
Для дальнейшего нам удобнее записать граничное условие в
комплексной форме
u{l,t) = Лe^^^ (64)
Если
и (ж, t) = u^^^ (ж, t) + г и^^^ (ж, t)
удовлетворяет уравнению (61) с граничными условиями (63) и (64),
то и^"*"^ (ж, t) и и^^^ (ж, t)—его действительная и мнимая части — в
отдельности удовлетворяют тому же уравнению (в силу его
линейности), условию (63) и граничным условиям при ж = /
и(^) (/, t) = А cos cut,
/.(2)
(/, t) = ^sino;^.
Итак, найдем решение задачи
Utt
и {О, t) =0,
и{1, t) = Ле^'
Utt = o?Uxx
ащ,
(65)

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 113
Полагая
и (ж, t)=X (ж) е^^^
и подставляя это выражение в уравнение, получаем для функции X {х)
следующую задачу:
о;^ . ио
X" ^к^Х = ^ U^ = — - ш — , (66)
Х(0) = 0,
X (0 = А.
Из уравнения (66) и граничного условия (67) находим
X {х) = С^шкх.
Условие при X = / дает
sin Ы'
так что
Х{х) = А^Щ^ = Хг{х)+гХ2{х),
(67)
(68)
(69)
(70)
где Xi {х) и Х2 {х) —действительная и мнимая части X {х).
Искомое решение можно представить в виде
и (ж, t) = [Xi (х) + i Х2 (х)] е^^^ = и^^) (ж, t) + г и^^^ (ж, ^),
где
и^^^ (ж, ^) = Xi (ж) coso;^ — Х2 (х) sino;^,
и^'^^ (ж, t) = Xi (ж) sino;^ + Х2 (ж) coso;^.
Переходя к пределу при а —>- О, находим, что
к=\[тк=- (71)
а^О а
и, соответственно,
m / ч ,. m / ч . sin(a;/a • ж)
й'^^) (ж, ^) = lim u^^^ (ж, ^) = Л —V^ -f coso;^,
ск^о sm(a;/a • /)
(72)
r9W ч ■,. r9W ч , sin (о;/a • ж) . ,^.
й^^^ (ж, ^) = lim и^^^ (ж, ^) = Л . ; \ -^ sino;^. (73)
а^о sin(a;/a • /)
8 А. Н. Тихонов, А. А. Самарский

114 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Рассмотрим следующую задачу:
(1о)
utt = a'^Uxx, О < X <l, t>
и (О, t) = /ii (t), t > - oo;
[u{l, t) =/i2 W,
которую будем называть задачей (Iq). Очевидно, что и'^^^ (ж, t) и
й^^^ (ж, t) являются решениями задачи (Iq) при граничных условиях
й(1) (О, t) = О, й(^) (/, t) = А COS cut,
й(2) (О, t) = О, й(2) (/, t) = ^sino;^.
Решение задачи при а = О существует не всегда. Если
частота вынужденных колебаний со совпадает с собственной частотой соп
колебаний струны с закрепленными концами:
7ГП
UJ = uj^ = —-а,
то знаменатель в формулах для й^^^ (ж, t) и й^^^ (ж, t) обращается в
нуль и решения задачи без начальных условий не существует.
Этот факт имеет простой физический смысл: при со = сОп
наступает резонанс, т. е. не существует установившегося режима. Амплитуда,
начиная с некоторого момента t = to, неограниченно нарастает.
При наличии трения (а ф 0) установившийся режим возможен
при любом значении о;, так как svukl ф О при комплексном к.
Пусть \1\ (t) =0, а /i2 (t)—периодическая функция, представимая
в виде ряда
А "^
1Л2 (^) = —- + \^(Лп cosa;n^ + В^ sinujnt), (74)
п=1
где ио — наименьшая частота, А^ и В^ — коэффициенты Фурье. Тогда
решение задачи для случая а = О принимает вид
-/ ч ^0 v^/л 7-. . . 8ш(а;п/а • ж)
и{хЛ) = -— X -\- > [An cos cunt + Вп smujnt) ^-- — ,
2/ ^-^ smicun а-1)
п — 1 ^ ' ^
если только ни одна из частот ип не совпадает с собственными
частотами закрепленной струны.
Если же /i2 {t)—непериодическая функция, то, разлагая ее в
интеграл Фурье, аналогичным методом можно получить решение в
интегральной форме.
Отметим, что решение задачи без начальных условий при а =
= О определено неоднозначно, если только не накладывать каких-либо

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 115
дополнительных условий. В самом деле, прибавляя к какому-либо ре-
П1ению этой задачи любую комбинацию стоячих волн
Е/ . 7ГП _, . 7ГП \ . 7ГП
( An COS —- at + Вп sm —- at J sm —- x,
где An и Bn — произвольные постоянные, видим, что эта сумма будет
удовлетворять тому же уравнению и тем же граничным условиям.
Чтобы получить единственное решение задачи (Iq,) при а = О,
введем дополнительное условие «исчезающего трения».
Решение задачи (Iq) мы называем удовлетворяющим условию
«исчезающего трения:^, если оно является решением задачи (Iq,) при а —>-
Аналогично решается задача, если конец х = / закреплен, а при
ж = О задан граничный режим.
Решение общей задачи без начальных условий
U{0,t)=fii{t), U{l,t)=fi2{t)
определяется в виде суммы двух слагаемых, для каждого из которых
неоднородно лишь одно из граничных условий.
Докажем единственность ограниченного ренгения задачи без начальных
условий для уравнения (61). Нри этом мы будем предполагать
непрерывность репЕСния вместе с его производными до второго порядка включительно
в области О^ж^/, —оо<^<^0 7 если граничные значения
U{0,t)=fli{t), U{l,t)=fl2{t)
определены в области — оо < ^ < ^о •
Пусть ui {х, t) и U2 (ж, t)—два ограниченных репЕСния
рассматриваемой задачи (I),
\ui\<M, \U2\<M,
где М > О — некоторое число.
Разность этих функций
V (ж, t) = Ui (ж, t) — U2 (ж, t)
ограничена (It^l < 2М), удовлетворяет уравнению (61) и однородным
граничным условиям
'^(0, t) = 0, v{l, t) = 0.
Коэффициенты Фурье для функции v
I
Vn (t) = -г V (ж, t) sin —- ж dx,
о
очевидно, удовлетворяют уравнению
Vn + CXVn + UJnVn = О [uJn = ~r ^ ) ' (*)
так как вторые производные функции г; (ж, t) непрерывны для О ^ ж ^ /.

116 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Общее решение уравнения (*) имеет вид
Vn{t) = Ane^^ * + Бпе^^ % (**)
(1) (2)
где Qn yi- Qn — корни характеристического уравнения, равные
Так как а > О, то Reg^^ ' "^ < 0. Следовательно penienne (**) уравнения
(*) будет ограниченным при ^ ^ — оо линеь для An = О и Вп = 0, т. е.
Vn (t) = О для любого п.
Таким образом,
г; (ж, ^) = О и ui (ж, t) = U2 (ж, t).
8. Сосредоточенная сила. Рассмотрим задачу о колебаниях
струны под действием сосредоточенной силы, приложенной в точке
X = xq. Если сила распределена на некотором участке {xq — г, xq +
+ г), то penienne находится по формуле (55). Соверп1ая предельный
переход при г —>- О, можно получить penienne поставленной задачи.
С другой стороны, при выводе уравнения колебаний мы видели
(см. (8) из § 1, п. 1), что в точке xq, к которой приложена
сосредоточенная сила, происходит разрыв первой производной, а сама функция
остается непрерывной. Penienne задачи и{х, t) о колебаниях струны
под действием силы, сосредоточенной в точке жо, можно представить
двумя различными функциями:
и (ж, t) = Ui (ж, t) при О ^ ж ^ Жо,
и (ж, t) = U2 (ж, t) при жо ^ ж ^ L
(75)
Эти функции должны удовлетворять уравнению
Utt = a^Uxx при жт^жо, (76)
граничным и начальным условиям
Щ (О, ^) = О, и (ж, 0) = (/? (ж),
U2 (/, t) = О, щ (ж, 0) = -0 (ж)
(77)
и условиям сопряжения в точке ж = жо (см. (8) из § 1), состоящим из
условия непрерывности функции и{х, t):
щ (жо, t) = U2 (жо, t) (78)
и условия, связывающего величину разрыва производной с силой / (^),
сосредоточенной в точке жо:
ди
дх
""°-'"^.о,0-?^(.о,^) = -4^. (79)
^0-0 ^^ ^2;

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 117
Заботиться о соблюдении начальных условий нет необходимости. Если
мы найдем частное решение уравнения (76), удовлетворяющее
граничным условиям из (77), а также (78) и (79), то, прибавляя к нему
решение однородного уравнения колебаний, мы всегда сможем
удовлетворить заданным начальным условиям.
Рассмотрим частный случай
f (t) = А cos Lot, — оо < t < -\-оо,
и найдем решение, удовлетворяющее лишь граничным условиям,
предполагая, что сила действует все время, начиная от ^ = — оо
(установившийся режим), т. е. решим задачу без начальных данных. Будем
искать решение в виде
щ (ж, t) = Xi (х) cos Lot при о ^ ж ^ Жо,
U2 (ж, t) = Х2 (х) COS cut при Хо ^ X ^ I.
Из уравнения (76) следует
Х{' + (-) Xi = О при О ^ ж ^ жо,
Х^ + (-) ^2 = О при жо ^ ж ^ 1.
(80)
Функции Xi и ^2, кроме того, должны удовлетворять граничным
условиям
Xi (0) = о, Х2 (/) = о, (81)
вытекающим из (77), и условиям сопряжения
Хг{хо)=Х2{хо), Х[{хо)-Х^{хо) = ^, (82)
вытекающим из (78) и (79).
Из уравнений (80) и условий (81) находим
Xi (х) = С sin — ж, Х2 (х) = D sin — {I — х);
условия сопряжения (82) дают
с sin — xq — D sin — (I — xq) = 0,
a a
С — cos — xq ^ D — cos — (/ — жо) = —.
a a a a к

118
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
Определяя отсюда коэффициенты С и D, получаем
и (ж, ^) = <
Ui =
U2
sin — X cos cut при О ^ ж ^ жо,
а
^^sin-(/-xo)
kuj .00
sm — /
a
. sm — жо
^CL a . 00 ,^ . .
sm — (I — x) cosLot при Xq ^ X ^ l.
kuo . oj a
sm — /
a
Аналогично записывается решение при / {t) = Л sino;^.
Итак, получено решение для случая f {t) = ^coso;^ или f {t)
= ^sina;^. Если f {t)—периодическая функция, равная
сю
/ (^) = -— + 2_\ (^п COS uont + I3n sin uont)
n=l
{uo — наименьшая частота), то, очевидно.
u{x,t) = <
LOn
Ui
4{1^('-t)-i:
^ n=l
oo a sin — (/ — xq)
— a . oonx
sm X
uon
uon sm -
a
U2
X (an cos Lont + Pn sin cont) >, 0 ^ ж ^ жо;
. Lon
-, ^ oo asm Xq /y Ч
1Гаож/ ж\ ^ a "^ .^ a;n (/- ж)
^ I
oo a sm — жо
— a
. ci;n .
=1 Lon sm — /
a
sm ■
{an cos a;n^ + Pn sin a;n^) >, жо ^ ж ^ L
(83) 1)
Если функция / (t) непериодическая, то, представляя ее в виде инте-
^ Первые слагаемые этих сумм соответствуют стационарному прогибу,
определяемому по величине силы / (t) = ао/2 = const, как нетрудно видеть,
функциями
и= <
/ .4 / ч 1 О^О
щ (ж, t) =ui{x) = -—X
/ .4 / ч 1 Q^O
П2 (ж, ^) = П2 (ж) = - — жо
( 1 — —- 1 при о ^ ж ^ Жо,
(1 — — ) при Жо ^ ж ^ /.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 119
грала Фурье, аналогичным методом можно получить решение в
интегральной форме.
Если знаменатель у этих функций (83) равен нулю:
sm = О,
а
7тт
ujn = —— а = о;-
гт
Т. е. если спектр частот возбуждающей силы содержит одну из
частот собственных колебаний (резонанс), то установившегося решения
не существует.
Если точка приложения силы жо является одним из узлов стоячей
волны, соответствующей свободному колебанию с частотой о;^, то
8Ш Жо = О,
а
8Ш (/ — Жо) = 0.
а
При этом числители соответствующих слагаемых для и обращаются
в нуль и явление резонанса не имеет места. Если же точка приложения
силы, действующей с частотой о;^, является пучностью
соответствующей стоячей волны с частотой о;^, то
8Ш Жо = 1
а
и явление резонанса будет выражено наиболее резко.
Отсюда следует правило, что для возбуждения резонанса струны
при действии на нее сосредоточенной силой надо, чтобы частота ее и
была равна одной из собственных частот струны, а точка приложения
силы совпадала с одной из пучностей стоячей волны.
9. Общая схема метода разделения переменных. Метод
разделения переменных применим не только для уравнения колебаний
однородной струны, но и для уравнения колебаний неоднородной струны.
Рассмотрим следующую задачу.
Найти решение уравнения
^i"i=s
*w|
q{x)u = р{х)--^, 0<ж</, ^>0, (84)
удовлетворяющее условиям
u{0,t) = 0, u{l,t)=0, t^O, (85)
и (ж, 0) = (f (ж), щ (ж, 0) = ф (ж), О ^ ж ^ L (86)

120 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Здесь к, q и р — непрерывные на отрезке О ^ х ^ I положительные
функции {к > О, р > О, q ^ 0)^\ Проведем penienne этой задачи
методом разделения переменных. Для отыскания частных реп1ений
обратимся, как и paHbHie, к вспомогательной задаче о существовании
стоячих волн.
Найти нетривиальное решение уравнения (84), удовлетворяющее
граничным условиям
и {О, t) =0, и{1, ^) = 0
и представимое в виде произведения
и{х, t) =X{x)T{t).
Подставляя предполагаемую форму решения в уравнение и пользуясь
граничными условиями, после разделения переменных получаем
_d_
dx
^^<^)f
qX + \pX = 0,
T" + ЛГ = 0.
Для определения функции X (x) мы получим следующую
краевую задачу на собственные значения^л
Найти те значения параметра Л, при которых существуют
нетривиальные решения задачи
L [X] + ХрХ = О, (87)
X (0) = 0, X (О = О, (88)
а такэюе найти эти решения.
Такие значения параметра Л называются собственными
значениями, а соответствующие им нетривиальные решения —
собственными функциями задачи (87) — (88).
Сформулируем основные свойства собственных функций и
собственных значений краевой задачи (87) и (88), необходимые для
дальнейшего изложения.
1. Существует счетное множество собственных значений Ai <
< Л2 < ... < An ..., которым соответствуют нетривиальные решения
задачи — собственные функции Xi (ж), Х2 (х), ... , Хп (ж), ...
^ Тот случай, когда к (ж) в некоторых точках обращается в нуль,
рассматривается отдельно (см. Дополнение П).
^ При р = pQ = const, к = ко = const мы получаем краевую задачу о
собственных колебаниях струны с закрепленными концами:
Х(0) = 0, Х(/) = 0,
исследованную в § 2.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 121
2. При q ^ О все собственные знс1чения Xji положительны.
3. Собственные функции Хт (х) и Хп (х) при т ф п
ортогональны между собой с весом р {х) на отрезке О ^ ж ^ /:
I
Хт (ж) Хп (ж) р (ж) б^ж = О {тфп). (89)
4. Теорема разложимости В.А. Стеклова. Произвольная
функция F {х), дважды непрерывно дифференцируемая и
удовлетворяющая граничным условиям F (0) = F (/) = О, разлагается в
равномерно и абсолютно сходящийся ряд по собственным функциям Х^ (ж):
F{x) = Y. ^гг Хп (ж), Fn = ^^^ / F (х) Хп (х) р (х) dx, (90)
п=1 11^^11 {
\\Xr,f = jxl{x)p{x)dx.
Доказательство утверждений 1 и 4 основывается обычно на
теории интегральных уравнений, и мы не будем здесь его приводить. В
настоящем пункте мы остановимся на доказательствах свойств 2 и 3.
Прежде чем перейти к доказательству этих свойств, выведем
так называемую формулу Грина. Пусть и{х) vl v {х) — произвольные
функции, дважды дифференцируемые на интервале а < х < b и
имеющие непрерывную первую производную на отрезке а ^ х ^ Ь.
Рассмотрим выражение
uL[v]-vL[u] = u {kv'y - V {ки'У = [к {uv' - W)]'.
Интегрируя это равенство по ж от а до 6, получаем формулу
Грина
о
/
{uL[v] — V L [и]) dx = к {uv' — vu')
b
(91)
Докажем свойство 3. Пусть Х^ (ж) и Хп{х)—две собственные
функции, соответствующие собственным значениям Л^ и Л^.
Полагая в формуле (91) и = Хщ (ж), v = Хп (ж) и учитывая граничные

122 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
условия (88), будем иметь """-^
J{XmL[Xn]-XnL[Xm]}dx = 0 (а = 0, Ь = 1),
о
откуда, пользуясь уравнением (87), получаем
(Лп - Л^) / Хт (х) Хгг (х) р {х) dx = 0.
о
Таким образом, если Л^ ф А^, то имеет место условие
/
Хт {Х) Хгг {Х) р {Х) dx = О, (92)
выражающее ортогональность с весом р (х) собственных функций
Хт{х) И Хп{х).
Докажем теперь, что каждому собственному значению
соответствует с точностью до постоянного множителя только одна
собственная функция ^^). В самом деле, всякая собственная функция
определяется однозначно как решение дифференциального уравнения 2-го
порядка по значению самой функции и ее первой производной при ж = 0.
Допустив существование двух функций X и X, отвечающих одному
и тому же значению Л и обращающихся в нуль при ж = О, и взяв
^ Производные Х^ и Х^ непрерывны всюду на отрезке О ^ ж ^ /,
включая точки ж = О и ж = /, так как уравнение (87) дает
хо
к (ж) Х'т (ж) = (q- Хшр) Хш dx + С.
X
Отсюда и следует существование производной Х^ при ж = О и ж = /.
^ Доказываемое свойство первой краевой задачи основано на том, что
два линейно независимых рептения дифференциального уравнения 2-го
порядка не могут обращаться в нуль в одной и той же точке. Это
утверждение относится к краевой задаче с нулевыми граничными условиями. При
других граничных условиях (например, X (0) = X (/), X (0) = X (/))
могут существовать две различные собственные функции, соответствующие
одному и тому же собственному значению ( Х^ ^ (ж) = cos —-— ж, Х^ ^ (ж) =
. 27ГП ^ /27гп\2
= sm —— ж при Лп = ( —j— ] , п = О, 1, 2, .

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 123
функцию
ХЧх) = £^1(ж),
Х'{0)
видим, что эта функция удовлетворяет тому же уравнению 2-го
порядка (87) и тем же начальным условиям, что и функция X (х):
^(0) = ilMl'(o) = x'(0).
dx ' ' Х'(0)
Тем самым доказано, что X* (ж) = X (х) и что
X' (0) \
Х{х) =АХ{х) А
Х'(0)
Отметим, что в процессе доказательства мы учитывали
требование X' (0) 7^ О, которое безусловно выполняется, так как penienne
линейного уравнения (87), определяемое начальными условиями
X (0) = О, Т (0) = о,
тождественно равно нулю и тем самым не может быть собственной
функцией (см. с. 120).
В силу линейности и однородности уравнения и краевых
условий очевидно, что если Х^ (х) является собственной функцией при
собственном значении Л^, то функция Л^Х^ (ж) {A^ — произвольная
постоянная) также является собственной функцией для того же
значения Л^. Выше было доказано, что этим вполне исчерпывается класс
собственных функций. Собственные функции, отличающиеся
множителем, мы, разумеется, не считаем существенно различными. Чтобы
исключить неопределенность в выборе множителя, можно подчинить
собственные функции требованию нормировки
I
inf = jxl
Xnf= / Xl{x)p{x)dx = l.
Если некоторая функция Х^ {х) не удовлетворяет этому требованию,
то ее можно «нормировать», умножая на коэффициент А^.
Хп\

124 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Если подчинить собственные функции задачи (87) — (88) условию
нормировки (||Х^|| = 1), то они образуют ортогональную и
нормированную систему
/ Хт (х) Хгг (х) p{x)dx = <
О, т ф п^
т = п.
Обратимся к доказательству свойства 2. Докажем, что Л > О при
q ^ 0. Пусть Хп (х)—нормированная собственная функция,
соответствующая собственному значению Ал, так что
L[Xn\ = -\пр{х)Хп{х).
Умножая обе части этого равенства на Х^ {х) и интегрируя по х от
О до /, получаем
о
f Xl (ж) p{x)dx = - f Хп (х) L [Х„] dx,
An = - j ^n-v- U (^) —f^ \ dx -\- q{x) xl (x) dx,
0 0
так как функция Хп (х) предполагается нормированной. Интегрируя
по частям и пользуясь граничными условиями (88), получаем
An — — ХпкХ^
+ [ к{х) [Х; (х)]^ dx+ [ q (х) Xl [х) dx =
° о о
= j к{х) [Х; {x)f dx+ [ q (х) Xl (х) dx, (93)
о о
откуда и следует, что
An >0,
так как по условию к (х) > О и q{x) ^ 0.
Оставляя доказательство теоремы разложимости в стороне,
кратко остановимся на вычислении коэффициентов разложения.
Нетрудно видеть, что
Fn = т^^ ( p{x)F {х) Хп {х) dx. (94)
ll^nll J

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 125
В самом деле, умножая обе части равенства
сю
F{x) = Y,FnXn{x)
п=1
на р (х) Хп (х), интегрируя по ж от О до / и учитывая
ортогональность собственных функций, получаем написанное выше выражение
для коэффициентов Fn (коэффициентов Фурье) ""^^
Вернемся теперь к уравнению с частными производными. Для
функции Т (t) мы имеем уравнение
Т" + ЛпТ = О (95)
без каких-либо дополнительных условий. В силу доказанной
положительности Хп его решение имеет вид
Тп (t) = An cos л/Kt + Вп sin л/Kt,
где An и Вп — неопределенные коэффициенты. Таким образом,
вспомогательная задача имеет бесчисленное множество решений вида
Un (ж, t) = Тп (t) Хп (х) = {An COS ^УXnt + Вп sin л/Xnt) Хп (х).
Обратимся к решению задачи с заданными начальными
условиями. Будем искать решение в виде
сю
и (ж, t) = ^{Ап COS л/Kt + Вп sin л/Kt) Хп (х). (96)
п=1
Формальная схема удовлетворения начальным условиям (86)
основывается на теореме разложимости 4 и проводится совершенно так же,
как и для однородной струны. Из равенств
сю
и (ж, 0) =(f (ж) = ^АпХп (ж).
щ (ж, 0) =ф (ж) = ^Вп \/КХп (ж)
п=1
находим, что
An = (fn, Вп = —7^, (97)
где (fn и фп — коэффициенты Фурье функций (f (х) и ф (ж) при
разложении по ортогональной с весом р (ж) системе функций { Хп (ж) }.
^ Возможность почленного интегрирования ряда следует из теоремы Сте-
клова о равномерной сходимости ряда (90).

126 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Ограничиваясь общей схемой метода разделения переменных, мы
не приводим условий применимости этого метода как в отношении
коэффициентов уравнения, так и в отношении начальных функций.
Основополагающие работы по обоснованию этого метода
принадлежат В. А. С тек лову ■'■^
Зад ачи
1. Найти функцию и{х, t), определяющую процесс колебания струны
(О, /), закрепленной на концах и возбуждаемой (рис. 24) оттягиванием ее в
точке ж = с на величину /г, т. е. и (с, 0) = /г (см. Приложение I). Начальная
скорость равна нулю.
2. Закрепленная на концах струна в точке х = с оттянута силой Fq.
Найти колебания струны, если в начальный момент сила перестает
действовать, а начальная скорость равна нулю.
3. Найти функцию и{х, t), определяющую процесс колебания струны
(О, /), закрепленной на концах и возбуждаемой импульсом К,
распределенным на отрезке (с — 6, с-\- S): а) равномерно, б) по закону г'о cos ——^- тг (см.
2d
Приложение I), если начальное отклонение равно нулю.
4. Найти функцию и{х, t), определяющую процесс колебания струны
(О, /), закрепленной на концах и возбуждаемой импульсом К, приложенным
в точке X = с (см. Приложение I).
^—'Тч Начальное отклонение равно нулю.
^^^^"^^ I \. 5. Доказать аддитивность
^^^^^^^ I \. энергии отдельных гармоник для
_f^ -1- ^_ процесса колебаний при граничных
~ ~ ~ условиях и = О, Ux = 0. Рассмотреть
Рис. 24 также случай граничного условия
3-го рода Ux -\- hu = О (все ряды
предполагать равномерно сходящимися). Вычислить энергию отдельных
гармоник в задачах 1 — 4.
6. Пружина, закрепленная одним концом в точке ж = О, растянута
грузом массы М, подвепЕСнным в точке х = I. Найти колебания пружины, если
в момент ^ = О груз падает и в дальнейптем на конец ж = / не действуют
никакие силы.
7. Один конец стержня закреплен, а на второй действует сила Fq.
Найти колебания стержня, если в начальный момент сила перестает
действовать.
8. Исследовать процесс колебания пружины, один конец которой
закреплен, а ко второму концу в начальный момент подвепЕивается груз массы М.
Начальные условия нулевые.
9. К однородной струне с закрепленными концами ж = О и х = I в
точке х = с прикреплена масса М. Найти отклонение струны и{х, t), если:
^ Стеклов В. А. Задача об охлаждении неоднородного твердого
стержня // Сообщ. Харьк. мат. о-ва. Сер. 2. 1896. Т. 5, № 1, 2;
Стеклов В. А. Основные задачи математической физики. Т. I. Петроград,
1922; Ильин В. А. О разрепЕимости сменханных задач для гиперболических
и параболических уравнений // УМН. 1960. Т. 15, вып. 2. С. 97—154.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 127
а) в начальный момент в точке х = с струна оттянута на величину h от
положения равновесия и отпущена без начальной скорости; б) начальное
отклонение и начальная скорость равны нулю (см. Приложение HI).
10. Исследовать процесс колебания пружины со свободными концами
при равномерном начальном растяжении (представить модель этой задачи).
11. Исследовать процесс колебания пружины с упруго закрепленными
концами при одинаковых коэффициентах жесткости, если начальные
условия произвольны.
РепЕСние исследовать при малых h («мягкое» закрепление) и при боль-
П1ИХ h («жесткое» закрепление) и вычислить соответствующие поправки к
собственным значениям для струны со свободными и закрепленными
концами.
12. Найти отклонение п (ж, t) струны с жестко закрепленными
концами, если колебания происходят в среде, сопротивление которой
пропорционально скорости, а начальные условия произвольны.
13. Изолированный электрический провод длины / с
характеристиками L, Я, С и G = О заряжен до некоторого потенциала г^о- В начальный
момент один конец провода заземляется, а второй остается все время
изолированным. Найти распределение напряжения в проводе.
14. Струна с закрепленными концами колеблется под действием
гармонической силы, распределенной с плотностью /(ж, t) = Ф (х) sin ujt. Найти
отклонение п (ж, t) струны при произвольных начальных условиях.
Исследовать возможность резонанса и найти penienne в случае резонанса.
15. РепЕить задачу 14, предполагая, что колебания происходят в среде,
сопротивление в которой пропорционально скорости. Найти установивпЕиеся
колебания, составляющие главную часть рептения при ^ ^ оо.
16. Упругий стержень длины / расположен вертикально и жестко
прикреплен верхним концом к свободно падающему лифту, который, достигнув
скорости vqj мгновенно останавливается. Найти колебания стержня,
предполагая его нижний конец свободным.
17. РепЕить уравнение
utt = а Uxx — b и-\- А
при нулевых начальных условиях и граничных условиях
п(0, t) = 0, и{1, t) = Б,
где 6, Л и В — постоянные.
18. РепЕить дифференциальное уравнение
Utt = а Uxx + Ashx
при нулевых начальных условиях и граничных условиях
п(0, t) = Б, и{1, t) = С,
где А^ В ж С — постоянные.
19. К однородной струне с закрепленными концами ж = О и ж = / в
точке ж = с (О < с < /) приложена гармоническая сила
F{t) = Ро sin ujt,
действующая начиная с момента ^ = 0. Найти отклонение струны и{х, t),
предполагая начальные условия нулевыми.

128 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
20. Решить задачу о колебаниях неоднородного стержня длины / с
жестко закрепленными концами, составленного из двух однородных
стержней, соединенных в точке ж = с (О < с < /), если начальное отклонение имеет
вид
и (ж, 0)
X при О ^ ж ^ с.
с
h
{I — х) при с ^ ж ^ /,
а начальные скорости равны нулю.
21. Найти установивпЕиеся колебания пружины, один конец которой
закреплен, а на второй действует сила
F (t) = А sin ujit -\- В sin uj2t.
22. Найти установивпЕиеся колебания неоднородного стержня,
составленного из двух однородных стержней, соединенных в точке ж = с, если
один конец стержня закреплен, а второй движется по закону
и (/, t) = Asinuot.
§ 4. Задача с данными на характеристиках
1. Постановка задачи. Рассмотрим ряд задач, являющихся
развитием первой краевой задачи для уравнения колебаний струны. Для
простоты будем изучать явления вблизи одного края, считая другой
край удаленным в бесконечность, т. е. в качестве исходной задачи
возьмем задачу для полу бесконечной прямой.
Уравнение колебаний струны Щ!^! = o?Uxx симметрично
относительно переменных ж и ^, если положить а^ = 1, т. е. изменить
масштаб времени, введя переменную t = at'. Однако
дополнительные условия вносят асимметрию в математическое толкование х и
t: в начальных условиях (при ^ = 0) задаются две функции и (ж, 0) и
Ut (ж, 0), в то время как в граничных условиях (при ж = 0) задается
только одна функция и (О, t).
Как было отмечено в § 2, п. 9, между функциями и их
нормальными производными при ^ = О и ж = О существует соотношение
щ (О, z) + Ux (О, z) = щ {z, 0) + Ux {z, 0) (a^ = 1)
при произвольном значении z. Отсюда следует, что при ж = О и ^ = О
нельзя независимым образом задать все эти функции; произвольными
являются только три условия, что и указывает на невозможность
симметричной постановки дополнительных условий.
Дополнительные условия могут задаваться либо на прямых
линиях ж = О, ^ = О (с задачами подобного рода мы имели дело до сих
пор), либо на некоторых кривых в фазовой плоскости. Например,
граничные значения можно задавать на некоторой кривой Ci (ж = fi{t)),

А
ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ
129
Рис. 25
однако для разрешимости такой задачи кривая Ci должна быть
достаточно гладкой и удовлетворять еще некоторым дополнительным
условиям.
Рассмотрим процесс колебаний газа в трубе с подвижной
границей (подвижным поршнем). Ясно, что скорость
перемещения границы, движущейся по
закону ж = /i (t), нельзя
считать произвольной: она не
должна превосходить скорость звука
а {f[ (t) < а). Геометрическим
следствием этого является то,
что кривая Ci {х = fi{t))
должна быть отделена
характеристикой от линии ^ = О, несущей
начальные значения (рис. 25).
Если хотя бы в одной точке
линия Ci лежала ниже
характеристики X = at, то значение
функции и{х, t) вполне
определялось бы начальными условиями
и не могло бы задаваться
произвольно. Физический смысл этого связан с тем, что при движении газа
со скоростями, превосходящими скорость звука, уравнение акустики
теряет силу и надо пользоваться нелинейными уравнениями газовой
динамики ■'■^
Начальные условия можно задавать не только на оси ^ = О, но
и на некоторой линии С2 {t = /2(ж)), которая должна удовлетворять
требованию I/2 {х)\ < 1/а (при этом С2 лежит в области влияния
начальных данных). Задачи подобного типа легко решаются с помощью
интегрального уравнения колебаний (см. § 2, п. 7).
Не ставя своей целью дать полный перечень всех возможных
краевых задач, рассмотрим более подробно задачу определения решения
по данным на характеристиках. Эту краевую задачу часто называют
задачей Гурса. Задача с данными на характеристиках
представляет большой интерес с точки зрения физических приложений. Она
встречается, например, при изучении процессов сорбции и десорбции
газов (см. Приложение V), процессов сушки (см. задачу 1 в конце
параграфа) и многих других задач.
2. Метод последовательных приблилсений для задачи
Гурса. Рассмотрим простейшую задачу с данными на характеристиках
Uxy = /(ж, у),
и{х, 0) = (fi (ж),
и {О, у) = ^2{у)-
(1)
^^ См. Приложение IV, с. 163.
9 А. Н. Тихонов, А. А. Самарский

130 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Дополнительные условия даны на прямых х = О и ^ = О, являющихся
характеристиками уравнения (1). Будем предполагать, что функции
(fi (х) и (р2 (у) дифференцируемы и удовлетворяют условию
сопряжения (pi (0) = (р2 (0). Интегрируя последовательно по ж и ^ уравнение
(1), получим
X
1у (ж, у) = Uy (О, у)+ f (^, у)
d^,
У X
и {х, у)=и {х, 0)+и (О, у)-и{0,0) + Jdr]J f (С, Г]) d^,
о о
или
у X
и {х, у) = ip, (х) + ip2 (у) - ^1 (0) + 11 / (С, Г]) d^ dr]. (2)
о о
Таким образом, для простейшего уравнения, не содержащего первых
производных Ux, Uy и искомой функции, решение представляется в
явной аналитической форме (2). Из формулы (2) непосредственно
следует единственность и существование решения поставленной задачи.
Перейдем к решению линейного уравнения гиперболического типа
Uxy = а (ж, y)ux + b (ж, y)uy + c (ж, у) и + f (ж, у) (3)
при дополнительных условиях на характеристиках ж = О, ^ = О
и{х, 0) =^i{x),
и {О, у) =(f2{y),
где (fi (ж) и (р2 (у) удовлетворяют требованиям дифференцируемости
и сопряжения. Коэффициенты а, b и с будем предполагать
непрерывными функциями X VL у.
Формула (3) показывает, что функция и (ж, у) удовлетворяет ин-
тегродифференциальному уравнению
у X
и{х,у) = / [а (^, г])щ + Ь (^, r])ur^ + c (^, ту) и] d^ dr] +
о о
у X
+ 'Р1 (х) + <^2 {у) -'Pi{0) + l I f (е, V) d^ dv. (4)
О о
Для его решения воспользуемся методом последовательных приближе-

4]
ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ 131
НИИ. Выберем в качестве нулевого приближения функцию
щ (ж, у) = 0.
Тогда (4) дает для последовательных приближений следующие
выражения:
у X
ui (ж, у) = ifi {х) + (/?2 {у) - V^i (0) + / / / (С, Г]) d^dr],
о о
у X
in (ж, у) = ui (ж, У) +
о о
dun-1
а (С, Г]) ^^^ +
dun-i
дг]
+ С(^, r])Un-l
d^dr].
> (5)
Отметим попутно, что
у
dun _ дщ f
дх дх J
о
X
dun _ dui f
ду ду J
а (ж, Г]) ^ + b (ж, Г]) ^ + с (ж, Г]) Un-i
dr],
di.
Докажем равномерную сходимость последовательностей
(6)
{Un{x, у)], \ "^(^' у)
Для этого рассмотрим разности
Zn (ж, у) = Un+1 (ж, ^) - Un (ж, ^) =
}' {^*"'^'}-
У X
II
О о
а (С, ^) —^7^ + ^ (^' ^) g + с (^, ту) 2;п-1 (С, v)
d^dr],

132
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
dzn (ж, у) _ dun+i (ж, у) dun (ж, у)
дх
дх
дх
у
I
а (ж, Г]) —^ + Ь (ж, Г]) ^ + с (ж, Г]) Zn-i (ж, ту)
б^ту,
а^^п (ж, у) dun+1 (ж, ^) а^п (ж, ^)
а^
а^
а^
X
-I
а (^, 2/) " ^ + Ь (^, 2/) g" + с (^, у) Zn-i (^, у)
de
Пусть М — верхняя граница абсолютных величин коэффициентов
а (ж, у), Ь{х, у), с (ж, у) и Н — верхняя граница абсолютных величин
zo = Щ {х, у) и ее производных
ко|<я,
dzo
дх
<Я,
92;о
а^
<Н
при изменении х и у внутри некоторого квадрата (О ^ ж ^ L, О ^
^ у ^ L). Построим мажорантные оценки для функций Zn, dzn/dx,
dzn/ду. Очевидно, что
1^11 <ЗНМху <ЗНМ
dzi
{x + yf
дх
dzi
2! '
< ZHMy <SHM{x + y),
ду
< ЗНМх <ЗНМ{х + у).
Предположим, что имеют место рекуррентные оценки
\zn\ < ЗНМ'^К"
dz„
дх
dzn
ду
< ЗНМ"К'-
< ЗНМ"К'-
(п + 1)! '
_,{х + уГ
_,{х + уГ

§ 4] ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ 133
где К > О — некоторое постоянное число, значение которого уточним
ниже. Пользуясь этими оценками и формулой для (п + 1)-го
приближения, после ряда упрощений, усиливающих неравенство, получаем
.„,.|<ЗЯМ-..-(^±|Г^(^.2)<
<6tiM к ^^^2)! < кт (п + 2)! '
dzn+i
дх
dzn+i
ду
(n + 1)! к (n + 1)!
(n + 1)! к (n + 1)!
где К = L + 2.
В правых частях этих неравенств с точностью до множителей
пропорциональности стоят общие члены разложения е^кьм д^^^ оценки
показывают, что последовательности функций
дх дх дх дх ^
dun _ дщ dz^ dzn-i
ду ду ду ду
сходятся равномерно к предельным функциям, которые мы обозначим
и{х, у) = lim Unix, у),
п—>-сю
v{x, у) = lim -w^{x, у),
п-^оо ох
w{x, у) = lim ^(ж, у).
п-^оо оу
Переходя к пределу под знаком интеграла в формулах (5) и (6), будем

134
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
иметь
у X
и{х, у) = ui (ж, У)+ Н^^ ^) ^ + К^^ г])т-\- с(^, ту) и] d^ dr],
о о
у
v{x, у) = —^ (ж, у)+ 1 [а{х, rj)v + b{x, ту) w + с{х, rf) и] dr],
(7)
w{x, у) = -^ (ж, у)-\- [а(^, y)v-\- b{^, y)w-\- с(^, у) и] d^.
о
Вытекающие отсюда равенства
V = Ux, W = Uy
позволяют установить, что функция и (ж, у) удовлетворяет интегро-
дифференциальному уравнению
и (ж, у) = (fi (х) + (f2 (у) - (fi (0) +
у X
+
J J [а (С, г])щ + Ь (С, г])и^ + с (С, ту) U + / (С, ту)] d^ dr], (4)
о о
а также исходному дифференциальному уравнению (3), что
проверяется непосредственно дифференцированием (4) по х и у. Функция
й = и{х, у), как нетрудно убедиться, удовлетворяет и
дополнительным условиям.
Перейдем к доказательству единственности реп1ения
рассматриваемой задачи (3) — (3'). Допуская существование двух реп1ений:
щ (ж, у) и U2 (ж, у), сразу же получаем для их разности
и (ж, у) = ui (ж, у) - U2 (ж, у)
однородное интегродифференциальное уравнение
у X
и{х, у)= [ f{aUx + bUy + cU)d^dr].
о о
Обозначая далее через Hi верхнюю грань абсолютных величин
\и {х, у)\ < Яь \и, {х, у)\ < Яь \Uy {х, у)\ < Н,
ДЛЯ О^ж^Ь, О ^у ^ L и повторяя оценки, проведенные для функций
Zn (ж, у), убеждаемся в справедливости неравенства
\и\<^Н^^ К (^ + 2)! <Кт (п + 2)!

§ 5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 135
при любом значении п. Отсюда следует
и (ж, у) = О, или т (ж, у) = U2 (ж, у),
что и доказывает единственность решения задачи с данными на
характеристиках.
Если коэффициенты а, b и с постоянны, то уравнение (3) с
помощью подстановки
приводится к виду
v.y + CiV = /. (8)
При Ci = О мы получаем задачу для простейп1его уравнения (1), ре-
Hienne которой дается формулой (2).
Если Ci 7^ О, то penienne задачи для уравнения (8) также может
быть получено в явной аналитической форме методом, изложенным в
§5.
Зад ачи
1. Через трубу (ж > 0), заполненную веществом, содержащим влагу,
продувается воздух (со скоростью v). Пусть v (х, t) — концентрация влаги в
поглощаемом веществе, и{х^ t) — концентрация свободных паров. Вывести
уравнение для функций u{x,t) и v{x,t), описывающих процесс супЕки,
если: 1) процесс изотермический и 2) изотерма супЕки имеет вид и = jVj
где 7 — постоянная изотермы (см. также Приложение V).
2. По трубе (ж > 0) пропускается со скоростью v горячая вода.
Пусть и — температура воды в трубе, v — температура стенок трубы, uq —
температура окружающей среды. Вывести уравнения для и ж v,
пренебрегая распределением температуры по сечению трубы и стенок и считая, что
на границах вода — стенка и стенка — среда существует перепад
температур и происходит теплообмен по закону Ньютона (см. гл. HI, § 1).
§ 5. Решение общих линейных уравнений
гиперболического типа
1. Сопрялсенные дифференциальные операторы.
Установим некоторые вспомогательные формулы, нужные нам для
представления реп1ений краевых задач в интегральной форме. Пусть
С [и] = Uxx -Uyy-\-a (ж, y)ux-\-b (ж, y)uy-\-c (ж, у) и (1)
(а (ж, у), 6 (ж, у), с (ж, у)—дифференцируемые функции)
— линейный дифференциальный оператор, соответствующий
линейному уравнению гиперболического типа. Умножая С [и] на некоторую
функцию V, запишем отдельные слагаемые в виде
VUxx = {vUx)x - {VxU)x + UVxx, vbUy = {bvu)y - U {bv)y,
VUyy = {vUy)y — {VyU)y + UVyy^ vcu = ucv.
vaux = {avu)x — и {av)x,

136 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Суммируя отдельные слагаемые, получаем
^ г 1 . > г 1 дН дК
vC[u\=uM[v\ + — + —, (2)
где
М [v] = Vxx - Vyy - {civ)x - {bv)y + cv, (3)
H = vux — VxU + avu = {vu)x — (2г'ж — av) и = (4)
= -{vu)x + {2ux + au) V, (4')
К = —г^и^ + VyU + бг^и = —{vu)y + (2г'^ + бг») u = (5)
= {uv)y — {2uy — bu) V. {b')
Два дифференциальных оператора называются сопряженны-
м и, если разность
г» £ [и] — иМ [v]
является суммой частных производных по ж и ^ от некоторых
выражений Н VL К.
Рассматриваемые нами операторы £ и Л^, очевидно, являются
сопряженными.
Если С[и\ = ЛЛ [и], то оператор С [и] называется
самосопряженным.
Двойной интеграл от разности v С[и\—и ЛЛ [v] по некоторой
области G, ограниченной кусочно-гладким контуром С, равен
[ f{vC[u]-uM[v])d^dr]= f{Hdr]-KdO, (6)
G С
где и и V — произвольные дважды дифференцируемые функции
(двумерная формула Грина)""^^
2. Интегральная форма решения. Воспользуемся формулой
(6) для решения следующей задачи.
Найти решение линейного уравнения гиперболического типа
С [и] = Uxx -Uyy + a (ж, y)ux + b (ж, y)uy + c (ж, у)и = -f (ж, у), (7)
удовлетворяющее начальным условиям на кривой С
Un\c =Ф (х)
^ Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.

§ 5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 137
{un — производная по направлению нормали к кривой С), и найти ту
область, в которой решение
определяется условиями {7').
Кривая С задана при этом
уравнением
У = fix),
где /(ж) — дифференцируемая
функция. Наложим на кривую С
условие, чтобы всякая
характеристика семейств у — х = const и ^ +
+ ж = const пересекала кривую С
не более одного раза (для чего
необходимо, чтобы |/'(^)| < !)• Формула (6) для криволинейного
треугольника MPQ, ограниченного дугой PQ кривой С и отрезками
характеристик MP и MQ (рис. 26), дает
А
X Ц<
/ V
/ ^f •
/у - X
(mi
\^
^
^1
*■
-X
Рис. 26
//
MPQ
{v С[и\ — и М [v]) d^ drj =
м
= f{Hdr]-KdO+ f{Hdr]-KdO+ f{Hdr]-KdO-
Q M P
Преобразуем первые два интеграла, взятые вдоль характеристик MQ
и MP. Принимая во внимание, что
ds
d^ = -dr] = -—= на QM,
л/2
ds
d^ = -\-dr] = -—^ на MP
л/2
> {ds — элемент дуги вдоль QM и MP)
и пользуясь формулами (4) и (5), получаем
м
f{Hdr]-KdO = - [ d{uv)+ I (2^-^^v\uds =
Q
Q
ds 72
M
{uv)m + {uv
)„+/
dv a + b .
2 — ■=- V ] uds
ds л/2

138
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИНА
[ГЛ. Н
и, аналогично,
р
р м
{Hdrj- KdO = - {uv)m + {uv)p + / ( 2 o^ j^ vjuds.
M p
Отсюда и из формулы (6) следует
{uv)p + {uv)q
[UV)m = 7. \-
+
+
M M
[ fdv b-a \ , r fdv a + b \ ,
P Q
Q
i j{Hdi^ - KdO -\ jj («-CM -uM[v])didri.
(8)
P MPQ
Эта формула является тождеством, верным для любых достаточно
гладких функций и vi v.
Пусть и — решение поставленной выше задачи с начальными
условиями, а функция v зависит от точки М как от параметра и
удовлетворяет следующим требованиям:
^г)г) — (^'^)с ~ (^'^)гу + сг» = о внутри Л MPQ (9)
М [v] = v^^
dv
Ъ~8
b — а
2л/2
6 + а
I 2л/2
V на характеристике MP,
V на характеристике MQ,
i;(M) = 1.
Из условий на характеристиках (9') и условия (9'') находим
ехр
ехр
ГЬ-а
J 27f
^ fb + a
J 2л/2
6?s на MP,
6?s на MQ,
(9')
(9")
где So — значение s в точке М. Как мы видели в § 4, уравнение (9) и
значения функции v на характеристиках MP и MQ полностью
определяют ее в области MPQ. Функцию v часто называют функцией
Римана.

§ 5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 139
Таким образом, формула (8) для функции и, удовлетворяющей
уравнению (7), принимает следующий окончательный вид:
+ 2
- / [г» {и^ dr] + щ d^) — и {v^ dr] + Vj^ d^) -\- uv {adr] — b d^)] +
p
MPQ
Эта формула решает поставленную задачу, так как выражения,
стоящие под знаком интеграла вдоль PQ, содержат функции, известные
на дуге С. В самом деле, функция v была определена выше, а функции
и\с = (f{x),
Ux \с = Us С08(ж, s) + Un С08(ж, п) =
Uy \с = Us cos{y, s) + Un cos{y, n) =
вычисляются при помощи начальных данных.
Формула (10) показывает, что если начальные данные известны
на дуге PQ, то они полностью определяют функцию в
характеристическом APMQ, если функция /(ж, у) известна в этой области-"^^
Формула (10), полученная в предположении существования
решения, определяет его через начальные данные и правую часть уравнения
(7) и тем самым, по существу, доказывает единственность решения
(ср. с формулой Даламбера, гл. II, § 2, с. 56).
Можно показать, что функция и, определяемая формулой (10),
удовлетворяет условиям задачи (7) — (7'). Однако мы на этом
доказательстве не останавливаемся.
3. Физическая интерпретация функции Римана. Выясним
физический смысл функции v (М, М'). Для этого найдем решение
неоднородного уравнения
£[и] = -2Л (/ = 2/i)
^ Если характеристика пересекает кривую С в двух точках Р и Mi (см.
рис. 26), то значение и (Mi) не может задаваться произвольно, а
определяется по формуле (10) с начальными данными на дуге PQi и значениями
f(x,y) в APMiQi.

140 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
с нулевыми начальными условиями на кривой С. Обращаясь к
формуле (10), видим, что искомое решение имеет вид
и (М) = J J ^ {М, М') Л {М') dGM'. (И)
MPQ
Предположим, что Д (М)—локальная функция точки Mi,
равная нулю всюду, кроме малой окрестности S^ точки Mi, и
удовлетворяющая условию нормировки
II h{M')daM^=l. (12)
Se
Формула (11) в этом случае принимает вид
щ (М) = Цу {М, М') л {М') dGM'. (13)
Se
Пользуясь теоремой о среднем значении, можно написать
Uc
(М) = V (М, Ml) Л h {М') daw = V (М, МП,
где М^ — некоторая точка области S^.
Стягивая г-окрестность S^ в точку Mi (г —>- 0), находим
и (М) = lim щ (М) = V (М, Ml). (14)
Функция /i, как мы видели на ряде примеров, обычно является
плотностью силы, а переменная у —
yk временем. Выражение
и л (М') dciM' = II /i (^, V) d^ drj
Se Se
(15)
^^^ представляет собой импульс силы.
Q Отсюда ввиду формулы (11) заклю-
р 27 чаем, что v (М, Mi) является
функцией влияния единичного импульса,
приложенного в точке Mi. Функция v{M, Mi) = v{x, у; ^, 77) была
определена как функция параметров М (ж, у), удовлетворяющая по
координатам ^, г] точки Mi уравнению
А^(«,,)М=0 (16)
С дополнительными условиями (9').

§ 5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 141
Рассмотрим функцию
и = и{М, Ml),
являющуюся функцией параметров Mi (^,77) ^ удовлетворяющую по
координатам ж, у точки М уравнению
С дополнительными условиями (рис. 27)
b — а
ди
= <
2л/2
Ь + а
12л/2
U на характеристике MiQi,
и на характеристике Mi Pi,
u(Mi, Ml) = 1.
(17)
(18)
Из этих условий находим
и{М, Ml) = <
ехр
ехр
f S
/ 2~7f ' ^^ ^^ ^iQb
f s
fb + a
J 2л/2
ds на Ml Pi,
(19)
Vo
u(Mi, Ml) = 1.
Уравнение (17) и условия (18) полностью определяют функцию и
в четырехугольнике MPiMiQi, ограниченном отрезками
характеристик MPi, MQi и Ml Pi, MiQi.
Применяя формулу (6) к четырехугольнику MPiMiQi, получаем
Рг м Qi Ml
II {vC[u]-uM[v])didr]= l{Hdr]-KdO+ /+ /+ / =0
MPiMiQi
M
Qi Ml Pi
{R{^, rf)—переменная точка интегрирования в MPiMiQi). Пользуясь
формулами (4) и (5) для К и Н и условиями (9') на характеристиках
для функции V, нетрудно вычислить первые два интеграла правой

142 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
^1
/<
1V1
части:
Pi
{Н dr] - К d^) = - {uv)m + {uv)pi,
м
м
{Hdr]- к d^) = - {uv)m + {uy)Qi,
41
подобно тому, как это было сделано при выводе формулы (10).
Аналогично, пользуясь равенствами (4'), (5') и условиями (19) для
функции и (М, Ml) на характеристиках, находим
Ml
f{Hdr]-KdO =
Pi
Ml Ml
= j[- (vu), d, - iuv), diHJv [(2., d, + 2n, di) + iau d, - bu d^] =
Pi Pi
Ml Ml
= d(uv) + / 2 f —— uj vds = {uv)mi — {uy)pi
h^
Pi
d^ =
fdu
— drj -
a-\-b
2л/2
ds\
''T2)
Qi
/ {Hdr] -Kdi) = {uv)mi - {uv)qi id^ = dr]=-^j.
Ml
Суммируя все эти четыре равенства, получаем
2{uv)m = 2{uv)mi,
или
u(M, Ml) =v{M, Ml), (20)
так как
{u)mi = {v)m = 1.
Таким образом, мы видим, что v (М, Mi) —функцию влияния
единичного импульса, сосредоточенного в точке Mi — можно определить как
решение уравнения
£(,,У)Ь(М, Mi)] = 0, М = М{х,у), Ml = Ml (^,7,),
С дополнительными условиями (18).

5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 143
4. Уравнения с постоянными коэффициентами. В качестве
первого примера применения формулы (10) рассмотрим задачу с
начальными данными для уравнения колебаний струны:
^УУ
Uxx + /i (ж, t) [у = at, /i = ^
и (ж, 0) = (f (ж),
Uy (ж, 0) = фг (х) [ ф
Ф
В формуле (10) дуга PQ является отрезком оси ^ = 0.
Оператор
L^J — ^хх ^УУ
является самосопряженным, поскольку
М[и\ = С [и] = и^
^УУ
Так как а = 0 и 6 = 0, то функция v на характеристиках MP и
MQ равна единице. Отсюда следует, что
V (М, М') = 1
для любой точки М' внутри треугольника PMQ.
Р{х-у,0) Q(x+y,0)
Рис. 28
Учитывая затем, что в нашем случае
dr] = О на PQ,
получаем
Q
и{М)
и{Р)+и (Q) 1
+
J^vd^+l If f{^,v)d^dr].
PMQ
Замечая, что Р = Р (ж — ^, 0), Q = Q (ж + ^, 0), где х и у —
координаты точки М = М {х, у) (рис. 28), и пользуясь начальными

144 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
условиями, будем иметь
х+у у х+{у-г))
х-у о х-(у-г])
Возвращаясь к переменным х и t, получаем формулу Даламбера
(f{x — at) + (f{x + at)
и (ж, t) = - h
x-\-at t x+a{t-T)
x-at 0 x-a{t-T)
С которой МЫ уже встречались в § 2, п. 9 (формула (30)).
В качестве второго примера рассмотрим задачу с начальными
условиями для уравнения с постоянными коэффициентами
Uxx — Uyy + aux + buy + cu = 0, —(Х)<ж<(Х), у > О (21)
(а, b, с — постоянные числа),
u\y=o = (f{x), (22)
Uy\y=o = 'ф{х). (23)
Подстановка
и = ие^''^^У (24)
позволяет привести уравнение (21) к более простому виду:
1
4
Uxx — Uyy + cif/ = о, ci = - (4с — а^ + 6^), — 00 < ж < 00, ^ > О,
(25)
с дополнительными условиями
U\y=o = ^p{x)e'^''/^ =(pi{x), -оо<ж<оо, (22')
Uy\y=o=U{x)-^'p{x)]e^''/^=iji{x), -оо<ж<оо, (23')
если только выбрать параметры Л и /i соответствующим образом,
полагая
О' b , ^,
А=2, М=-2- (26)

§ 5] РЕШЕНИЕ ЛИНЕЙНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ 145
Определение функции [/ (ж, у) по начальным данным и
уравнению (25) сводится к построению функции Римана v (ж, у; ^, 77).
Функция V должна удовлетворять условиям
Vxx - Vyy + CiV = О, (27)
ГТ^Р М Р 1
(28)
г» = 1 на характеристике MP,
г» = 1 на характеристике MQ (см. рис. 28).
Будем искать v в виде
v = v{z), (29)
где
^ = л/(^ - С)' - (2/ - ^)' или ^2 = (ж - С)2 - (^ - ту)^ (30)
На характеристиках MP и MQ переменная z обращается в
нуль, так что v (0) = 1. Далее левая часть уравнения (27)
преобразуется следующим образом:
Vxx - Vyy + CiV = V" (z) {zl - Zy) + V' (z) {z^x " Zyy) + CiV = 0.
Дифференцируя выражение для z'^ дважды, по ж и ^, получим
^^х ^ X ^,
^% = -{y-v),
^^уу + ^у
Отсюда и из формулы (30) находим
^^уу -\- Zy — i.
2_2_i _ _^
^х ^у ~ ^^ ^хх Zyy — .
Уравнение для v принимает вид
v" + -i;' + cii; = О
z
при условии V ifi) = 1. PenienneM этого уравнения является функция
Бесселя нулевого порядка (см. Дополнение П, ч. I, § 1)
v{z) = 7о(л/сГ^),
или
V {х, у; е, V) = Jo {Vci [{х - О' -{у- vy] ) • (31)
10 А. Н. Тихонов, А. А. Самарский

146 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА [ГЛ. П
Воспользуемся теперь для нахождения U (ж, у) формулой (10),
которая в naniCM случае принимает вид
Q
ищ)^^[1^ЦЕШ^^ l^yU,d^-Uv,dO {dri = 0), (32)
р
Вычислим предварительно интеграл по отрезку PQ (ту = 0):
Q х-\-у
j{v U,-Uv^)d^= П Jo {Vci[{x-0'-y']) и, (е, 0) -
х-у
и it 0) v^y 4 [v^ ч/(^ - О' - у")
^С1[(х-а2-Й
Пользуясь начальными условиями (22'), (23'), находим
Ж + 2/
}
di. (33)
х-у
^ J V (ж - iY - у^
х-у
откуда в силу (24), (22') и (23') получаем формулу
/ ч ^{x-y)e-^^У+ if{x + y)e^^У
^ (ж, у) = ^
х-у
V (ж - ^)2 - г J
+ \ е^У'^ I Jo [V^Vi^-O'-y') е-«/2-(-«) ф (О d^, (35)
Х-у
дающую penienne поставленной задачи.

ЗАДАЧИ К ГЛАВЕ II 147
Рассмотрим частный случай а = О, b = О (тогда ci = с), т. е.
уравнение
Из формулы (35) сразу получаем
х+у
и{х,у)
(р{х - у)-\-(р{х-\-у) 1
+ 11 Jo{VcV{^-0'-y')^{Od^ +
х-у
+ 9^М /, ,,2 ^^^(Odt (36)
^ J V (ж - о - у
х-у
Полагая здесь с = О и у = at, приходим к формуле Даламбера
x-\-at
, . (f (х - at)-\-(f (х-\-at) 1 [ 7 гу,. ,. /о^тч
U (ж, t) = ^ ^-^ ^ + — J ф{0 d^, (37)
x — at
дающей решение уравнения колебаний струны
Uxx ^Utt =0
при начальных условиях
и (ж, 0) = (f (ж),
щ{х, 0) = ф{х),
ф (ж) = а?/^ (х) = аи^ (^, 0).
ЗАДАЧИ К ГЛАВЕ II
1. Решить задачу 1 из § 4, предполагая, что в начальный момент
концентрация влаги постоянна вдоль всей трубы и на вход подается поток сухого
воздуха.
2. РепЕить задачу 2 из § 4, считая, что начальная температура системы
равна По, а температура на конце трубы все время поддерживается равной
V0 > Uq.
3. РепЕить систему телеграфных уравнений (см. § 1, (21))
ix -\-Cvt-\-Gv = 0,
Vx -\- Lit -\- Ri = О
для бесконечной линии при начальных условиях
i (ж, 0) = (р (ж), V (ж, 0) = гр (ж).
10*

148
ПРИЛОЖЕНИЯ К ГЛАВЕ П
i^^ = CL itt + {CR + GL) it + GR
с начальными условиями i (ж, 0) = ср (ж),
di
dt
/1 R .\
t=0 ^ ^
Указание. Свести систему уравнений (§ 1 (21)) к уравнению 2-го
порядка для одной из функций г (ж, t) или v {х, t), например
'■(р{х) = гро (ж)
и воспользоваться затем формулой (35).
4. Исследовать penienne телеграфного уравнения, полученное (формула
(35)) для случая малых G ж R. Рассмотреть предельный случай G ^ О,
Я ^ О и получить из формулы (35) формулу Даламбера для рептения
уравнения колебаний струны.
прилож:ения к главе и
I. о колебании струн музыкальных инструментов
Колеблющаяся струна возбуждает колебания воздуха,
воспринимаемые ухом человека как звук, издаваемый струной. Сила звука
характеризуется энергией или амплитудой колебаний, тон — периодом
колебаний, а тембр — соотноп1ением энергий основного тона и
обертонов-"^^ Не останавливаясь на физиологических процессах
восприятия звука и на процессе передачи
звука по воздуху, мы будем
характеризовать звук струны ее энергией,
периодом и распределением энергии
по обертонам.
В музыкальных инструментах
Рис. 29 обычно возбуждаются поперечные
колебания струн. Различают три
типа струнных инструментов: щипковые, ударные и смычковые. В
ударных инструментах (например, рояль) колебание возбуждается ударом,
придающим струне начальную скорость без начального отклонения.
В щипковых инструментах (например, арфа, гитара) колебания
возбуждаются приданием струне некоторого начального отклонения без
начальной скорости.
Свободные колебания струны, возбуждаемой произвольным
способом, могут быть представлены в виде (см. гл. II, § 3)
сю
/ \ V^/ 7 . . . 7ГП / 7ГП \
и (ж, t) = >. (^п COS ujnt + On sm ujnt) sm —- x I ci;^ = —г~ a J .
Рэлей Дж. В. С. Теория звука. М., 1955. Т. I, гл. VI.

I. о КОЛЕБАНИИ СТРУН МУЗЫКАЛЬНЫХ ИНСТРУМЕНТОВ 149
В качестве упражнения к § 3 была предложена задача 1, лежащая
в основе простейп1ей теории возбуждения струн щипковых
инструментов. Penienne этой задачи показывает, что если начальное отклонение
струны представлено в виде треугольника с высотой h в точке ж = с
(рис. 29), то
2hP
. '7ГПС 7 гл /-,4
sm—-, bn = 0. (1)
7Г^П^с(/ — с) /
Энергия п-й гармоники равна
1 Jo 7Г71С
En = -plu;lal = Mh^-^^^^^j—-^sm'— {М = pi) (2)
И убывает обратно пропорционально in?.
В задаче 4 к § 3 рассматривается простейшая теория ударного
возбуждения струны при помощи сосредоточенного в точке с удара с
импульсом К. Решение этой задачи представляется в виде
. . 2К ^-^ 1 . 7ГПС . 7ГПЖ . / 7ГП \ , .
и (ж, t) = > — 8ш —;— 8ш —— ^m.ujn't оОп = -;- а] ^ (3)
-кар ^-^ п I I \ I J
п=1
^ К^ . 2 7ГПС ,^,
En = j^s^n^—. (4)
Таким образом, при возбуждении струны ударом,
сосредоточенным на небольшом интервале длины S, энергии различных гармоник
(для которых 5 мало по сравнению с расстоянием между узлами)
будут мало различаться между собой и тон, издаваемый так
возбужденной струной, насыщен обертонами. Это заключение легко проверяется
экспериментально. Если натянутую струну (на монохорде) ударить
лезвием ножа, то струна зазвенит: звук будет насыщен обертонами. В
рояле струна возбуждается ударом молоточка, обтянутого кожей.
Такое возбуждение струны можно представить при помощи следующих
схем.
1. Струна возбуждается заданием постоянной начальной скорости
г'о на интервале {с — S, c-\-S). Этот случай будет соответствовать
плоскому жесткому молоточку, имеющему ширину 25 и ударяющему
в точке с. Процесс колебаний описывается функцией (см. задачу 3 из
§3)
, . 4:Vol v~^ 1 . ТГПС . 7ГП6 . 7ГПХ .
и (ж, t) = -^z— у -^ 8Ш —;— 8Ш —— 8Ш —;— бШа;^^,
тг^а ^-^ п"^ I I I
п=1
и энергии отдельных гармоник равны
Еп = ^г-^ 8Ш^ —- ' 8Ш^ —-.

150
ПРИЛОЖЕНИЯ К ГЛАВЕ П
2. Струна возбуждается начальной скоростью
^^ ( п\
X — с 7Г
г'о cos —-— • — при |ж — с| < (5,
О
при |ж — с| > S.
Этот случай соответствует жесткому выпуклому молоточку П1ирины
26. Такой молоточек в центре интервала 26 возбуждает наибольп1ую
начальную скорость, что схематически может быть описано
приведенной BbiHie функцией. Возбужденное таким образом колебание имеет
вид (см. задачу 3 из § 3)
и (ж, t)
сю -,
Е-
7ТП6 . 7ТПС
COS —— sm ——
Svo6
^^ ^i"" 1_№у
. 7ТПХ .
sm —— sma;^^,
и энергии гармоник равны
16vl6^p
En
7ТП6
7ТПС
/7Г2
{26n/l)'^V
cos
■ sm
3. Молоточек, возбуждающий колебания струны, не является
идеально жестким. В этом случае колебания определяются уже не
начальной скоростью, а силой, меняющейся со временем. Таким образом, мы
приходим к неоднородному уравнению с правой частью
F(x,t)
X — с 7Г 7rt
Fq cos —-— • — sin —, если \x — c\ < 6, 0 ^ ^ ^ r,
0 2 T
0, если \x — c\ > 6, t > T.
Решение этого уравнения для t > т представляется в виде
и (ж, t)
16Fot6
тт^ра ^—' п
' п=1
сю ^
Е-
7ГП6 UJri'T '7ГПС
COS —— COS —-— sm ——
-m'
(=f)'
. 7ГПЖ . / r\
X sm —— sma;n (^ ~ 9 ) •
Рассмотренные примеры показывают, что ширина интервала, по
которому производится удар, и продолжительность времени удара
имеют весьма существенное влияние на величину энергии высоких

п. о КОЛЕБАНИИ СТЕРЖНЕЙ
151
обертонов. Отметим, кроме того, что присутствие множителя sin ——
показывает, что если центр удара молоточка приходится на узел п-й
гармоники, то энергия соответствующей гармоники равна нулю.
Наличие высоких обертонов (начиная с 7-го) нарушает
гармоничность звука и вызывает ощущение диссонанса ""^^ Наличие низких
обертонов, наоборот, вызывает ощущение полноты звука. В рояле
место удара молоточка выбирают близко от точки закрепления струны
между узлами 7-го и 8-го обертонов, чтобы уменьшить их энергию.
Регулируя ширину молоточка и его жесткость, стремятся увеличить
относительную энергию низких (3-го и 4-го) обертонов. В старых
конструкциях рояля, обладавших более резким, даже до некоторой
степени звенящим тоном, пользовались узкими и жесткими молоточками.
II. О колебании стерлсней
В курсах методов математической физики основное место
отводится уравнениям 2-го порядка. Однако большое число задач о колебаниях
стержней, пластин и т. д. приводит к уравнениям более высокого
порядка.
В качестве примера уравнения 4-го порядка рассмотрим задачу
о собственных колебаниях камертона, эквивалентную задаче о коле-
ШШ^
л
\У ^ X
Рис. 30
баниях тонкого прямоугольного стержня, зажатого одним концом в
массивные тиски. Определение формы и частоты колебаний камерто-
^ Например, если основная частота (первая гармоника) в 440 колебаний в
секунду соответствует ноте «ля» первой октавы, то в семь раз ббльптая
частота соответствует ноте «соль» четвертой октавы. Интервал «ля — соль»,
так называемая малая септима, имеет неприятный для слуха,
диссонирующий характер.

152
ПРИЛОЖЕНИЯ К ГЛАВЕ П
на сводится к решению «уравнения поперечных колебаний стержня»
(1)
к этому уравнению приходят во многих
задачах о колебаниях стержней, при
расчете устойчивости вращающихся валов,
а также при изучении вибрации
кораблей ^^.
Приведем элементарный вывод
уравнения (1). Рассмотрим прямоугольный
стержень длиной / (О ^ ж ^ /), высотой h и шириной b (рис. 30).
Выделим элемент длины dx. После изгиба торцевые сечения
выделенного элемента стержня, предполагаемые плоскими, образуют угол d(p.
Если деформации малы, а длина оси стержня при изгибе не меняется
{dl = dx), то
Рис. 31
dip =
ду_
дх
ду_
дх
x-\-dx
дх^
dx.
Слой материала, отстоящий от оси стержня ^ = О на расстояние г],
изменяет свою длину на величину г] d(f (рис. 31). По закону Гука сила
натяжения, действующая вдоль слоя, равна
dN = E-bdr]-r]
d(f
dx
-E
где E — модуль упругости материала стержня. Полный изгибающий
момент сил, действующих в сечении ж, равен
М
дх^
h/2
/ r]^dr]
-h/2
дх^
(2)
где
h/2
drj =
12
-h/2
— момент инерции прямоугольного сечения относительно своей
горизонтальной оси. Обозначим через М (ж) момент, действующий на
правую часть стержня в каждом сечении. В сечении х -\- dx, очевидно,
действует момент сил, равный — (М + dM).
^ См., например: Крылов А. Н. Вибрация судов. СПб., 1907; Собрание
трудов академика А. П. Крылова. Т. X. М.; Л., 1948.

п. о КОЛЕБАНИИ СТЕРЖНЕЙ
153
Избыточный момент —dM уравновешивается моментом
тангенциальных сил
dM = Fdx.
Отсюда в силу равенства (2) получаем величину тангенциальной силы
Приравняв действующую на элемент результирующую силу
(3)
дР
ох
Ej'^^dx
произведению массы элемента на ускорение
где р — плотность стержня, S — площадь поперечного сечения (при
этом мы пренебрегаем вращательным движением при изгибе),
получаем уравнение поперечных колебаний стержня
а2 =
EJ
~pS
(1)
Граничными условиями для заделанного конца ж = О являются
неподвижность стержня и горизонтальность касательной:
У
= 0,
х=0
ду_
дх
= 0.
(4)
х=0
На свободном конце должны равняться нулю изгибающий момент (2)
и тангенциальная сила (3), откуда следует, что
дх"^
О,
0.
(5)
Для того чтобы полностью определить движение стержня, нужно
еще задать начальные условия — начальное отклонение и начальную
скорость
t=o
./ ч ду
= (f{x) (O^x^l).
(6)
t=0
Таким образом, задача сводится к решению уравнения (1) с
граничными условиями (4), (5) и с начальными условиями (6).
Будем решать задачу методом разделения переменных, полагая
y = Y{x)T{t).
(7)

154
ПРИЛОЖЕНИЯ К ГЛАВЕ П
Y
ж=0
dY
dx
= 0,
ж=0
= 0,
х=1
= 0.
(8)
(9)
X = l
Подставляя предлагаемую форму решения в (1), имеем
Т" (t) _ У(^) (х) _
а2 T{t)~ У (х) ~ '
Для функции Y (х) получаем задачу о собственных значениях
у(4) _ лу = о,
d^Y
dx^
Общее penienne уравнения (8) представляется в виде
Y (х) = А ch л/л X -\- B^h л/Л х -\- С cos л/Л х -\- D^in у\х.
Из условий Y (0) = О, Y' (0) = О находим С = - Л, D = -В. Отсюда
следует, что
Y{x)=A (ch VX X — cos v^a;) + В (sh v^ X — sm
Условия Y" (0 = 0 и У''' (О = О дают
А (ch VXI + cos v^/) + В (sh v^/ + sin Vxi) = 0,
Л (sh VXI - sin v^A + В (ch v^/ + cos Vxi) = 0.
Эта однородная система имеет нетривиальные реп1ения А и В, если
определитель системы равен нулю. Приравнивая этот определитель
нулю, получаем трансцендентное уравнение для вычисления
собственных значений:
sh^ VXI - sin^ VXI = ch^ Vxi + 2ch v^/cos VXI + cos^ VXL
Так как ch ж — sh ж = 1, то это уравнение можно записать в виде
chjj, • cos/i = — 1 (/^ = Va/J .
(10)
чески
Корни уравнения (10) без труда вычисляются, например, графи-
1).
/ii ^ 1,875,
/i2 « 4,694,
/i3 « 7,854,
/^n
(2n — 1) при n > 3.
^ О вычислении корней уравнения (10) см.: Рэлей Дж. В. С. Теория
звука. М., 1955. Т. I, гл. VHI.

III. КОЛЕБАНИЯ нагруженной СТРУНЫ 155
Последняя формула дает значение /i^ с точностью до трех десятичных
знаков, начиная с п = 3, и с точностью до шестого знака для п ^ 7.
Рассмотрим теперь частоты колебаний камертона. Уравнению
Т" + а^ХггТ = О
удовлетворяют тригонометрические функции
Тп (t) = an cos 2'KVnt + Ьп sin 2'KVnt
с частотой
2^
Частоты Vn собственных колебаний относятся как квадраты /i^.
Так как
4 « 6,267, 4 « 17,548,
то второй собственный тон выше основного тона более чем на две с
половиной октавы, т. е. выше шестой гармоники струны при
равном основном тоне, третье же собственное колебание выше
основного тона более чем на четыре октавы. Например, если камертон имеет
основную частоту в 440 колебаний в секунду (принятый стандарт для
а' — ноты «ля» первой октавы), то следующая собственная частота
камертона будет равна 2757,5 колебания в секунду (между с"" = 2637,3
и f"" = 2794,0— между нотами «ми» и «фа» четвертой октавы
равномерно темперированной гаммы), третья же собственная частота в
7721,1 колебания в секунду уже выходит за пределы шкалы
собственно музыкальных звуков.
При возбуждении колебаний камертона ударом присутствует не
только первая, но и высшие гармоники, чем и объясняется
металлический звук в начальный момент. Однако с течением времени высшие
гармоники быстро затухают и камертон издает чистый звук основного
тона.
III. Колебания нагрулсенной струны
1. Постановка задачи. Рассмотрим задачу о колебаниях
закрепленной на концах струны (О, /), в нескольких точках которой
X = Xi (г = 1, 2, ..., п) помещены сосредоточенные массы Mi.
Условия в точке Xi можно получить двумя способами. Если в
точке Xi (г = 1, 2, ..., п) приложена сосредоточенная сила Fi (t), то
должны выполняться соотношения
и {xi -0,t)=u {xi + О, t), (1)
\Xi-\-0
kuj =-Fi. (2)
\xi-0

156
ПРИЛОЖЕНИЯ К ГЛАВЕ П
В данном случае под Fi следует понимать силу инерции. Подставляя
в формулу (2)
Fi = -MiUtt{xi, t),
получим
MiUtt {Xi, t) = kU:,
Xi-\-0
Xi-0
(3)
Возможен и другой вывод условия (3). Распределим массу Mi на
участке (xi — г, ж^ + г) с постоянной плотностью 5i и воспользуемся
уравнением колебаний для неоднородной струны
(/> + <50-« = ^(fc|^),
е < X < Xi -\- е,
(4)
где р — плотность струны. Пусть и^ (ж, t)—решение этого уравнения.
Интегрируя уравнение (4) по ж в пределах от Xi — е до Xi -\- е
и совершая предельный переход при г —>- О, получим условие (3) для
функции и{х, t) = lim и^ (ж, t). Па обосновании предельного перехода
МЫ не останавливаемся.
Сформулируем полностью нашу задачу.
Найти решение уравнения колебаний
д'^и д / ди
удовлетворяющее граничным условиям
условиям сопряэюения в точках х = Xi
и {xi — 0^ t) = и {xi + 0, ^),
(5)
(6)
MiUtt {xi, t) = ки^
и начальным условиям
Xi-0
{i
1,2,
п)
(7)
и (ж, 0) = (/? (ж),
щ{х, 0) = ^^(ж),
(8)
где (f{x) и ф (х) —заданные функции.
2. Собственные колебания нагрулсенной струны.
Остановимся прежде всего на исследовании собственных частот и профилей

III. КОЛЕБАНИЯ нагруженной СТРУНЫ 157
стоячих волн для нагруженной струны. Для этого мы должны найти
решение поставленной задачи, представимое в виде произведения
u{x,t) =X{x)T{t). (9)
Подставляя это выражение в уравнение (5) и пользуясь граничными
условиями, получим после разделения переменных
Т" + ЛГ = О (10)
и
^ (^ S) ^ АрХ = {кХ'У + ХрХ = О,
X (0) =0, X (О = 0.
Условия сопряжения дают
X{xi-0) = X(xi + 0),
\Xi-\-0
MiX{xi)r' = кХ'\ Т.
\xi-0
Принимая во внимание уравнение (10), перепишем последнее
соотношение в виде
кХ'
Xi-\-0
= -XMiX{xi).
Xi-O
Таким образом, для функции X (х) мы получаем следующую задачу
на собственные значения:
-^{кХ') + ХрХ = 0, к{х)>0, р{х)>0, (11)
ах
Х(0) = 0, Х(0 = 0, (12)
X{xi-0)=X{xi + 0) (г = 1, 2, ...,АГ),
кХ' {xi + 0) - кХ' {xi - 0) + XMi X (xi) = 0.
(13)
Отличительной особенностью рассматриваемой краевой задачи
является то, что параметр Л входит не только в уравнение, но и в
дополнительные условия.
Мы не будем здесь останавливаться на доказательствах
существования бесчисленного множества собственных значений и собственных
функций, положительности собственных значений, теоремы
разложимости. Эта краевая задача, так же как и задачи обычного типа,
рассмотренные нами в гл. II, § 3, сводится к некоторому интегральному

158 ПРИЛОЖЕНИЯ К ГЛАВЕ II
уравнению, которое в данном случае является нагруженным
интегральным уравнением и эквивалентно интегральному уравнению в
интегралах Стилтьеса.
Остановимся более подробно на выводе условия ортогональности
собственных функций
Х,{х), Х2{Х), ...,
которое в данном случае отлично от условия (92) из § 3 и называется
условием ортогональности с нагрузкой.
Как было показано в гл. II, § 3, собственные функции для краевой
задачи
X (0) =0, X (О = о
ортогональны с весом р на интервале (О, /):
[ X^{x)Xn{x)p{x)dx = 0 (т^п). (14)
о
Распределяя каждую массу Mi с постоянной плотностью 5i на
некотором интервале Xi — е < х < Xi -\- е, где е > О — малое число,
мы придем к задаче о собственных колебаниях неоднородной струны
с плотностью ps (х). Пусть Х^п и Х^п (х) — собственные значения и
собственные функции этой задачи, для которых должны выполняться
условия ортогональности
/ Х^гп (х) Xsn (х) ре (х) dx = 0 {тфп). (15)
о
Выделяя в равенстве (15) интегралы по участкам (ж^ — г, ж^ + г)
и совершая предельный переход при г —>- О, мы получим соотношение
I
N
Хт {х) Хгг {х) р {х) dx + S^Mi Х^ (Xi) Х^ (Xi) =0 (ш 7^ п), (16)
i=l
называемое условием ортогональности с нагрузкой-"^ л
Мы снова оставляем в стороне вопрос о возможности такого
перехода.
^ Курант Р., Гильберт Д. Методы математической физики. М.; Л.,
1951. Т. I, гл. VI.

III. КОЛЕБАНИЯ нагруженной СТРУНЫ 159
Условие ортогональности (16) может быть получено и чисто
формальным путем из уравнения и условий (11) — (13). Пусть Хт (х) и
Хп{х)—собственные функции задачи (11) — (13), соответствующие
собственным значениям Xfji и Л^^, удовлетворяющие уравнениям
Т' ( ^ ~Г^ ] + ^шрХт = О,
ах \ ах J
d (, dXn\
Умножим первое уравнение на Х^ (ж), второе — на Х^ (х) и вычтем
из первого результата второй. Интегрируя полученнное равенство
последовательно по участкам (О, xi); {xi, Ж2); ...; (ждг, /) и складывая,
будем иметь
(Л^ - Хп) / Хт (х) Хгг (ж) р (ж) dx
о
Xi+1
TV ^^-^
-Е у -^[X^kX'^-XnkXl]dx = {), (17)
причем мы полагаем жо = О, xn+i = 1- Выполняя интегрирование в
каждом из слагаемых суммы и объединяя члены, соответствующие
подстановкам ж = ж^ — О и ж = ж^ + 0, получаем сумму слагаемых вида
^г = {ХткХ^ — ХпкХ^ )x=Xi-0 — {ХщкХ^ — ХпкХ^ )х=х.-^о.
При этом подстановки при х = О и х = I в силу граничных условий
обращаются в нуль.
Для вычисления Ai воспользуемся условиями сопряжения
Xj{x,-0)=Xj(x, + 0), I .- ^ . (13')
kX'j {xi + 0) - kX'j {xi - 0) = - MiXj Xj {xi) j '■■' ^ >■ У I
Переписывая Ai в виде
Ai = X^ {xi) [kX'„ {xi - 0) - kX'„ {xi + 0)] -
- X„ {xi) [kX'^ {xi - 0) - kX'^ {xi + 0)]
И пользуясь формулой (13'), находим
Ai = Хт (Xi) MiXn Хп (Xi) - Хп (Xi) MiXm Хт (Xi) =
= Mi Xm (Xi) Xn (Xi) (An - Xm)'
Теперь равенство (17) можно записать в виде
[Хт — X
п)1 Хт (х) Хп (х) р (х) dx + Y^Mi Хт (Xi) Xn{Xi) > = 0.

160 ПРИЛОЖЕНИЯ К ГЛАВЕ II
Если Л^ ф ^п-, то отсюда сразу же следует условие ортогональности
с нагрузкой (16).
Норма собственных функций Х^ (ж) определяется по формуле
^ N
\\Xnf= fxl(x)p(x)dx + J2MiXl(xi). (18)
о «=1
Очевидно, что при разложении некоторой функции / (ж) в ряд:
оо
f{x) = Y,fnXn{x)
п=1
коэффициенты разложения будут определяться по формуле
N
I
/ {х) Хп {х) р {х) dx + Y^Mi f (xi) Xn {xi)
/n = rr^rW^ • (19'
ll^nll
Задача с начальными условиями, поставленная в п. 1, решается
по обычной схеме метода разделения переменных. Аналогично
рассматривается задача о колебании стержня (или балки) при наличии
сосредоточенных масс.
Задача о колебаниях струны, нагруженной сосредоточенными
массами, находит широкое применение в физике и технике. Еще Нуассон
решал задачу о продольном движении груза, подвешенного к упругой
нити. А. Н. Крылов показал "'^^, что к этой задаче сводится теория
индикатора паровой машины, крутильных колебаний вала с маховиком
на конце, разного рода «дрожащих» клапанов и т. д. Для теории
многих измерительных приборов важно изучение крутильных колебаний
нити, к концу которой подвешена масса (например, зеркальце).
Особую актуальность задача подобного типа приобрела в связи
с изучением устойчивости вибраций крыльев самолета. Для решения
этой задачи необходимо вычисление собственных частот крыла (балки
переменного сечения), нагруженного массами (моторы). Кроме того,
рассматриваемая задача встречается при расчете собственных
колебаний антенн, нагруженных сосредоточенными емкостями и
самоиндукциями (в связи с этим см. Приложение VI, посвященное аналогии
между механическими и электромагнитными колебаниями).
Мы не останавливаемся здесь на приближенных методах
нахождения собственных значений и функций задачи, аналогичных
приближенным методам нахождения соответствующих величин для
неоднородной струны.
^ Крылов А. Н. О некоторых дифференциальных уравнениях
математической физики. Л., 1933. Гл. VII.

III. КОЛЕБАНИЯ нагруженной СТРУНЫ 161
3. Струна с грузом на конце. Значительный практический
интерес представляет задача о колебаниях однородной струны, один
конец которой {х = 0) закреплен, а ко второму концу [х = I) подвеп1ен
груз массы М.
В этом случае условие при х = / принимает вид
Mutt = -kux (/, t)
и для амплитуды стоячих волн получается уравнение
с граничными условиями
х„(о) = о, х;(о = —л„х„(о.
Отсюда находим
sinvXTx
sm V An I
где Хп определяется из уравнения
/— М /—
ctg у/Хп1 = — л/Лп. (20)
Р
Условие ортогональности функций { Хп (х) } принимает вид
Хп (Х) Хт (Х) pdx + MXn (О Хт (О = 0.
/
О
Вычислим квадрат нормы
Nn= I Xl{x)pdx^MXl{l).
о
Используя уравнение (20), получаем
1р М М\ ^
^п=^^^^^Хп1.
Задача с начальными данными решается обычным методом.
4. Поправки для собственных значений. Вычислим
поправки для собственных частот в случае больших и малых нагрузок М.
Для простоты рассмотрим тот случай, когда груз подвешен к концу
струны. Возможны два предельных случая.
1. М = 0. Конец X = / свободен. Собственные значения
определяются из формулы
/ТоУ _ 2п + 1 7г
11 А. Н. Тихонов, А. А. Самарский

162 ПРИЛОЖЕНИЯ К ГЛАВЕ II
2. М = 00. Конец х = / жестко закреплен: и (/, t) = 0.
Собственные значения определяются из формулы
^(2) _
7ГП
Нас будет интересовать случай малых М {М —>- 0) и больп1их
М {М ^ оо).
1° М —>- 0. Найдем поправку к собственному значению Л^^ ^,
полагая
л/К = \/^ + еМ, (21)
где е — некоторое число. Подставляя (21) в уравнение (20) и
пренебрегая М^ и более высокими степенями М, получаем
2М\
т. е. собственные частоты нагруженной струны при М —>- О
возрастают, приближаясь к собственным частотам струны со свободным
концом.
2° М —>- 00. Выбирая 1/М в качестве параметра малости,
положим
VAn-V^n +е—.
Уравнение (20) дает
Р
е =
An = AW (l - ^ ) , (22)
An I
При этом мы пренебрегаем членами, содержащими 1/М^ и более
высокие степени 1/М.
Таким образом,
ГУ- _ ,/й^У I 1 Р л _ л(2) , 2Р /^оч
' (2) , М М/
An '
т. е. при увеличении нагрузки собственные частоты убывают,
равномерно приближаясь к собственным частотам струны с закрепленными
концами.
IV. Уравнения газодинамики и теория ударных волн
1. Уравнения газодинамики. Закон сохранения энергии.
Уравнения акустики (см. § 1) были получены в предположении
малости скоростей движения газа и малых изменений давления, что
позволило линеаризовать уравнения гидродинамики.

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 163
В задачах, возникающих при изучении полета ракет и скоростных
самолетов, в теории баллистики, взрывных волн и т. п., приходится
иметь дело с гидродинамическими процессами,
характеризующимися больп1ими скоростями и градиентами давлений. В этом случае
линейное приближение акустики непригодно и необходимо пользоваться
нелинейными уравнениями гидродинамики. Поскольку с такого рода
движениями на практике приходится встречаться для газов, то
принято о гидродинамике больших скоростей говорить как о газовой
динамике, или газодинамике.
Уравнения газодинамики в случае одномерного движения газа (в
направлении оси х) имеют вид
—- + —-(pv) = о (уравнение непрерывности), (1)
ot ох
dv dv dp . . .^.
р ——\- pv -^— = — -^— (уравнение движения), (2)
ot ох ох
р = f{pj Т) (уравнение состояния). (3)
Таким образом, уравнения газодинамики представляют собой
уравнения движения идеальной сжимаемой жидкости при отсутствии
внешних сил.
Перейдем теперь к выводу закона сохранения энергии. Энергия
единицы объема равна
^+.., (4)
где первый член есть кинетическая энергия, второй — внутренняя
энергия. Здесь г, очевидно, обозначает внутреннюю энергию
единицы массы.
Для идеального газа е = СуТ, где Су — теплоемкость при
постоянном объеме, Т — температура. Вычислим изменение энергии в единицу
времени:
Производя дифференцирование в первом слагаемом и пользуясь
уравнениями (1) и (2), получаем
д fpv'^\ v'^ dp dv v'^ д , . д fv'^\ dp ,^,
Для преобразования производной д {pe)/dt обратимся к первому
началу термодинамики, выражающему закон сохранения энергии:
dQ = de-\-pdT, (7)
11*

164
ПРИЛОЖЕНИЯ К ГЛАВЕ П
где dQ — количество тепла, получаемое (или отдаваемое) системой
извне, pdr — работа, затрачиваемая при изменении объема на величину
dr (г = 1/р — удельный объем).
Если процесс адиабатический (теплообмена со средой нет), то
de = — pd - = -^ dp.
р р2
Пользуясь этим равенством, будем иметь
Р
d (ре) = е dp -\- р de = е dp -\— dp = w dp,
Р
д dp
где
W = е -\-
(8)
(9)
(10)
(И)
— тепловая функция, или теплосодержание единицы массы.
Производная dw/dx в силу соотношений (9) и (11) удовлетворяет
уравнению
dw
dp
дх дх
(12)
Учитывая равенства (2), (5), (6), (10), (12), получаем закон
сохранения энергии в дифференциальной форме:
д [ pv
-\- ре
д_
дх
pv\—+w
(13)
Для выяснения физического смысла этого равенства проинтегрируем
его по некоторому объему (xi, Ж2):
д_
di
Х2
/(
pv^
-\- ре] dx
■pv [^+^
XI
Х2
XI
Слева стоит изменение энергии в единицу времени на интервале
(ж1, Ж2), справа — поток энергии, вытекающей в единицу времени из
рассматриваемого объема.
Если эффектом теплопроводности нельзя пренебречь, то
уравнение сохранения энергии принимает вид
д f pv
di
-\- ре
д_
дх
V- \ дТ
pv\ —+^) - к —
(14)
где X — коэффициент теплопроводности.

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 165
2. Ударные волны. Условия динамической совместности.
В случае больших скоростей возможны такие движения, при которых
на некоторых поверхностях, перемещающихся в пространстве,
возникают разрывы непрерывности в распределении гидродинамических
величин (давления, скорости, плотности и др.). Эти разрывы принято
называть ударными волнами.
На поверхности разрыва (фронте ударной волны) должны
выполняться условия непрерывности потока вещества, энергии и
количества движения (условия Гюгонио). Перейдем к выводу этих
условий.
Преобразуем уравнение (2) к более удобному для наших целей
виду. Умножая (1) на v и складывая с (2), получаем
|(Н = -|:(Р + .^^). (2')
Перепишем теперь уравнения непрерывности, движения и
сохранения энергии в виде
(2')
d{pv)
dt
^ fJ,^..,2^
д
дх
(13)
Рассмотрим на плоскости (ж, t) линию ж = а(^), являющуюся
«следом» поверхности разрыва на плоскости (ж, t). Пусть АС — некоторая
дуга линии разрыва ж = а (^), где А и С — точки с координатами Ж1,
ti и Ж2 = Ж1 + Аж, ^2 = ^1 + А^ соответственно. Построим
прямоугольник ABCD со сторонами, параллельными координатным осям.
Запишем закон сохранения вещества в интегральной форме:
/ [{p)t2 - {р)ч] dx = - [{pv):,^ - (pv):,^] dt, (15)
XI ti
где слева стоит изменение массы на интервале (ж1, Ж2) за
промежуток времени (^i, ^2), а справа — количество вещества, вытекающего
из интервала (ж1, Ж2) за время (^i, ^2)- Если функции р и pv
непрерывны и дифференцируемы всюду внутри ABCD, то уравнение (15)
эквивалентно уравнению (1'). В рассматриваемом случае это не имеет
места.
Воспользуемся теоремой среднего значения для каждого
слагаемого в отдельности:
[Р\ t=t2^ - Р\ t=ti^^ ] Д7 = ~ [{Р1^)\^ = ^2 - {Р'^)\^ = ^1^ ]
ж=ж* ж=ж** ^' t—t t—t

166 ПРИЛОЖЕНИЯ К ГЛАВЕ II
(здесь ж*, ж**, Г, Г*— средние значения аргументов х и t).
Переходя к пределу при Ах —>- О {х2 -^ xi) и А^ —>- О (^2 —>■ ^i) и
обозначая индексом 2 значения функций вып1е кривой х = а (t) (сзади
фронта ударной волны), а индексом 1 — значения функций ниже этой
кривой (перед фронтом), получаем
(p2-pi)f/ = -(Hl + (H2, (16)
где
da ,. Ах
(7 = —- = lim -—
dt At^o At
— скорость ударной волны.
В системе координат, движущейся вместе с ударной волной,
Ui = и — Vi, U2 = и — V2
обозначают соответственно скорости частиц перед фронтом и сзади
фронта ударной волны. Полученное выше соотношение (16) можно
переписать в виде
piui = P2U2. {!&)
Это равенство выражает непрерывность потока вещества через фронт
ударной волны.
Записывая в интегральной форме закон сохранения количества
движения, имеем
/ [ipv)t2 - ipv)ti] dx = - [{p + pv'^):,^ - (p + py'^)xi] dt,
XI ti
где справа стоит сумма импульса действующих сил (давления) и
потока количества движения. Переходя к пределу при Ах —>- О и А^ —>- О,
получаем закон сохранения потока количества движения на фронте
и [{pv)2 - {pv)l] = - (Р + pv'^)l + (Р + py^)2j
или
Pi + piuj =Р2+ p2ul. (17)
Аналогично получается уравнение сохранения энергии на фронте:
которое после несложных преобразований принимает вид
PlUi I ^1 + Y I = P'2U2 \У02 + —

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 167
или, в силу условия (16),
ul и\
Wi + ^=W2 + f. (18)
Таким образом, на фронте ударной волны должны выполняться
уравнения (условия динамической совместности, или
условия Гюгонио)
piui = P2U2, {!&)
Pl + piuj = Р2 + P2UI, (17)
Wi + ^=W2 + f. (18)
Из уравнений (16') и (17) выразим щ и U2 через р и р:
2 Р2 Р1-Р2 2 Р1 Pl - Р2
pl pl - P2 P2 pl- P2
откуда
^1 - ^2 = (Pl - P2).
P1P2
Подставляя затем это выражение в уравнение (18), находим
соотношение между значениями энергии по обе стороны фронта:
wi-W2 = {pl + Р2) (Pi - Р2)
^Pip2
и
^1-^2 = ^ {pl - P2){P1 +P2).
^Plp2
Рассмотрим идеальный газ, для которого
р = pRT] е = с^Г; w = СрТ = ^— RT =
Ср- Су 7-1 Р'
т. е.
^ = ^.^. (19)
7-1 Р
Пользуясь формулой (19), после несложных преобразований приходим
к так называемому уравнению адиабаты Гюгонио
Pl ^ (7 + 1)Р2 + (7-1)Р1 /20)
Р1 (7- 1)Р2 + (7 + l)Pi'

168 ПРИЛОЖЕНИЯ К ГЛАВЕ П
Р2 ^ (т + 1) Р2 - (т - 1) Р1 /21)
Pi (Т + 1) Pi - (Т - 1) Р2 '
По этой формуле можно определить одну из величин pi, pi, р2, Р2,
если известны три остальные величины.
Ударная волна всегда движется относительно газа от областей
с большим давлением к областям с меньшим давлением: р2 > Pi
(теорема Цемплена). Отсюда следует, что плотность газа за
фронтом больше плотности перед фронтом.
Формула (20) выражает зависимость между р2 и р2 при
заданных pi и р1. Функция р2 = р2 (Р2) при заданных pi и р1 является
монотонно возрастающей функцией, стремящейся к конечному пределу
при Р2/Р1 —>■ 00 (ударная волна большой амплитуды):
Р1 = 1±1, (22)
Р1 7-1
Эта формула показывает максимальный скачок плотности
(уплотнение), который может существовать на фронте ударной волны. Для
двухатомного газа j = 7/Ь и максимальное уплотнение равно 6:
Р1
Пользуясь равенствами (16'), (17) и (20) и полагая pi = О, находим
""' >' " ' - "2(7 + 1) pi'
Если ударная волна движется по покоящемуся газу (vi =0), то
скорость распространения ударной волны равна
JJ /7+1 Р2
т.е. она растет пропорционально квадратному корню из р2.
Рассмотрим простейшую задачу теории ударных волн,
допускающую аналитическое решение. В цилиндрической трубе ж > О, не
ограниченной с одной стороны и закрытой поршнем с другой (х =
= 0), находится покоящийся газ с постоянной плотностью pi и при
постоянном давлении pi. В начальный момент ^ = О поршень
начинает двигаться с постоянной скоростью V в положительном направлении
оси X. Перед поршнем возникает ударная волна, которая в начальный
момент совпадает с поршнем, а затем удаляется от него со скоростью
и > V. Между поршнем и фронтом ударной волны возникает область 2,
в которой газ движется со скоростью поршня. Перед фронтом (область
1) газ находится в невозмущенном состоянии: р = р^, р = р^ (г^ = 0).

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 169
Пользуясь условиями на фронте (16), (17) и (18), нетрудно
определить скорость фронта, а также величину скачка плотности и давления.
Введем безразмерные величины
0; = —; и = —; v = —; р= ^, (23)
Р2 CLl CLl Pldi
где ai = yTPifpi—скорость звука перед фронтом (в невозмущенной
области 1). Тогда уравнения сохранения запишутся в виде
ujU = U-v, или [/=—^, (24)
1 — (jj
р = 1 -\- jUv, или р = I-\-J , (25)
1 — (jj
pa; = 1 + (7 - 1) (uv - ^ ^Ч • (26)
Исключая отсюда р и U, получаем квадратное уравнение для
определения со:
2а;2 - о; [4 + (7 + 1) v'^] + [2 + (7 - 1) v'^] = 0. (27)
Так как по смыслу о; < 1 {р2 > pi), то выбираем меньший корень:
i02 = l + ^v'-v^l + ^^^^^v^. (28)
Из уравнений (24), (25) и (28) находим
^ = ^^ + Vl + Ц^^^ (29)
т(т + 1).2^...Л.(1±1)!.2
р = 1 + -^^—- г +jvdl+ " ' v^. (30)
Возвращаясь к прежним величинам, получаем
^ 7 + 1 ^^ ^ /-, (7 + 1)^ о
4 al ' ai У ' 16af
P2 = Pi 77—rm ' (31)
1 +
2af
7 + 1 „. , „ /, , (7 + 1)^
IQal
U=l^v + a,,ll+'-I^^v^ (32)
--i-^^^^v^-^-• (33)

170 ПРИЛОЖЕНИЯ К ГЛАВЕ II
Так как скорость ударной волны постоянна, то для положения фронта
в момент t будем иметь
x = ait) = \^v + a^Jl + ^^^^^vAt. (34)
В предельном случае v/ai ^ 1 (ударная волна больпюй
интенсивности) из формул (31) — (33) находим предельные соотноп1ения
7 + 1 гт 7 + 1 7(7 + 1) ^^
полученные нами ранее.
Если v/ai <^ 1 (волна малой интенсивности), то можно
пренебречь членами v'^/а\'.
Л ^
Р2 = Pi Ц
V «1
тт ^7 + 1
и = ai-\ — V,
Р2 = Pi IH
V «1
3. Слабые разрывы. Bbinie было рассмотрено движение
ударной волны, на фронте которой величины р, р, v и др. испытывают
скачки. Такого рода разрывы называются сильными.
Возможны и такие движения, при которых на некоторой
поверхности испытывают скачок первые производные величин р, р, v и др.,
в то время как сами эти величины остаются непрерывными. Такие
разрывы называются слабыми.
В § 2, п. 10 рассмотрено движение разрывов такого рода и
установлено, что эти разрывы распространяются вдоль характеристик. При
этом мы исходили из уравнения акустики. Однако и для нелинейных
задач газодинамики справедлив аналогичный результат.
Нетрудно убедиться в том, что поверхность слабого разрыва
распространяется относительно газа со скоростью, равной локальной
скорости звука. В самом деле, выделим малую окрестность поверхности
слабого разрыва и возьмем средние значения гидродинамических
величин в этой окрестности. Слабый разрыв, очевидно, можно
рассматривать на фоне средних значений как малое возмущение, которое
удовлетворяет уравнению акустики и должно распространяться с локальной
скоростью звука.
В качестве примера рассмотрим истечение газа в вакуум (волна
разрежения). Пусть в начальный момент ^ = О газ, заполняющий
полупространство ж > О, покоится и имеет постоянные значения плотности
ро и давления ро во всей области ж > 0. При ^ = О внешнее давление.

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 171
приложенное к плоскости ж = О, снимается и газ начинает двигаться;
при этом возникает слабый разрыв (волна разрежения),
распространяющийся со скоростью звука ао в положительном направлении
оси X. На переднем фронте газа х = xi (t) при ^ = О мы имеем
разрыв плотности и давления. Однако этот разрыв сразу же после начала
движения исчезает.
В самом деле, из условий непрерывности потоков вещества и
количества движения при х = Xi (t):
О = рГ (^1 - ^Г) = Pi (^1 - '^i)^
Pi + pi (^1 - ^г)^=pt+pi (^1 - ^]^)^
где p^, p^, v^—значения слева в точке xi (t), p^, p^, v^—значения
справа в точке xi (t), получаем
p+ = 0 и p+ = 0,
так как
Pi =Pl = ^Г = О-
Для адиабатического процесса уравнение состояния идеального газа
имеет вид
р=„(^); (35,
Решение задачи будем искать в форме
Р = р{0'^ Р = Р{0'^ ^ = ^(С), где ^ = x/t.
Вычисляя производные
dt t^dC дх t dC
где f = р, V или р, и подставляя результаты в уравнения (1) и (2),
получаем
dp dv
(36)
Умножим первое уравнение на {v — ^) и сложим со вторым:
^2 dp ^ dp
d^ d^
ИЛИ

172
ПРИЛОЖЕНИЯ К ГЛАВЕ П
Отсюда имеем
где а — скорость звука при адиабатическом процессе.
Поскольку мы рассматриваем движение слабого разрыва в
положительном направлении оси ж, надо выбрать в предыдущей формуле
знак «минус», т. е.
V — ^ = —а.
Подставляя это решение в уравнения (36), получаем
dv а
dp р '
или, что одно и то же,
dv _ 1
dp pa'
Пользуясь уравнением состояния (35), находим
2 Р
а = 7 ~
(37)
(38)
И после интегрирования уравнения (38) получаем
7-1
V =
7-1
do
Из последней формулы можно выразить р через v:
2
7 — 1 'Ь'
Р = Ро 1 +
2 ао
Здесь
^0 = VlPo/po
(39)
(40)
обозначает скорость звука при г» = О (в покоящемся газе). Формулу
(39) можно также переписать в виде
7-1
(а- ао).
(41)
Подставляя выражение (40) для р в уравнение состояния (35),
находим
Р = Ро 1 +
7 — 1 V
ао
27
(42)

IV. УРАВНЕНИЯ ГАЗОДИНАМИКИ И ТЕОРИЯ УДАРНЫХ ВОЛН 173
Из уравнений (41) и (37) получаем формулу
2
V =
^(f-ao), (43)
7 +
определяющую зависимость v от х и t. Подставляя затем
выражение (43) для V в формулы (40) и (42), получим зависимость р и
р от ж и ^ в явной форме. Все величины оказываются
зависящими от x/t. Если измерять расстояния в единицах,
пропорциональных ^, то картина движения не меняется. Такое движение называется
автомодельным.
Найдем скорость движения переднего фронта vi (t). Полагая в
равенстве (42) р = О, будем иметь
2
VI = 7^0- (44)
7-1
Отсюда следует, что скорость истечения газа в пустоту конечна. Для
двухатомных газов 7 = 7/5 и
vi = — 5ао.
Выражение (44) для скорости левого фронта х = xi (t) можно
получить также из уравнения баланса вещества
pdx = Р0Х2 = podot. (45)
XI
Х2
Введя переменную
получим
i = x/t,
ар
pd^ = Poao.
VI
Подставляя затем выражение для р из (40) и полагая
"О
будем иметь
1 + ^^^ = Л,
7 + 1 «о
А2
где
7 + 1 «о

174 ПРИЛОЖЕНИЯ К ГЛАВЕ П
После вычисления интеграла (46) получим
т. е.
откуда и следует
7+1 7+1
Ai=0,
2ао
7- -L
Задача об истечении газа в вакуум решена.
Мы ограничились выше рассмотрением лишь наиболее простых
задач газодинамики. Для более подробного ознакомления с
затронутыми здесь вопросами отсылаем читателя к специальной литературе ""^л
V. Динамика сорбции газов
1. Уравнения, описывающие процесс сорбции газа.
Рассмотрим задачу о поглощении (сорбции) газа ^^. Пусть через трубку
(ось которой мы выберем за координатную ось х), заполненную
поглощающим веществом (сорбентом), пропускается газовоздушная смесь.
Обозначим через а (ж, t) количество газа, поглощенного единицей
объема сорбента, а через и{х, t)—концентрацию газа, находящегося в
порах сорбента в слое х.
Папишем уравнение баланса вещества, предполагая, что скорость
газа v достаточно велика и процесс диффузии не играет существенной
роли в переносе газа. Рассмотрим слой сорбента от xi до Х2 в течение
промежутка времени от ti до ^2- Очевидно, для него можно написать
уравнение баланса вещества
[vu\^^ - vu\^^]SM = [{а + u)\t^ - (а + u)\t,]SAx, (1)
которое после сокращения на Ах At и перехода к пределу при Ах —>- О,
А^ —>- О принимает вид
ди д ,
^ См.: К о чин П. е., Кибель И. А., Розе П. В. Теоретическая
гидромеханика. М., 1963. Ч. П, гл. I; Ландау Л. Д., ЛифнЕиц Е. М. Механика
СПЛ0П1НЫХ сред. М., 1953. Гл. VH; Зельдович Я. Б. Теория ударных волн
и введение в газодинамику. М.; Л., 1946; Седов Л. И. Распространение
сильных взрывных волн // Прикладная математика и механика. 1946. Т. 10,
вып. 2. С. 241—260.
^^ Тихонов А. П., Жуховицкий А. А., Забежинский Я. Л.
Поглощение газа из тока воздуха слоем зернистого материала. П // ЖФХ.
1946. Т. 20, вып. 10. С. 1113—1126.

V. ДИНАМИКА СОРБЦИИ ГАЗОВ 175
Левая часть этого уравнения представляет количество газа,
накопляющегося за счет переноса, рассчитанное на единицу длины и времени,
правая часть — количество газа, израсходованного на повышение
концентрации сорбированного газа и газа, находящегося в порах. К этому
уравнению баланса следует присоединить уравнение кинетики сорбции
^=а{и-у), (3)
где /3 — так называемый кинетический коэффициент, у—
концентрация газа, находящегося в равновесии с сорбированным количеством
газа.
Величины а VL у связаны друг с другом уравнением
a = f{y), (4)
ЯВЛЯЮЩИМСЯ характеристикой сорбента.
Кривая а = f (у) называется изотермой сорбции. Если
7 (^0 + РУ)
то изотерма называется изотермой Ленгмюра. Наиболее
простой вид функции / соответствует так называемой изотерме
Генри, справедливой в области малых концентраций:
а=-у, (5)
7
где 1/7 — коэффициент Генри.
В этом случае мы приходим к следующей задаче.
Найти функции и (ж, t) и а (ж, t) из уравнений
ди ди да , .
|^=/3(и-7а) (6)
при дополнительных условиях
а (ж, 0) = 0,1
и(ж, 0) = 0,( ^ ^
^(0, ^)=uo, (8)
где щ — концентрация газа на входе.
Пренебрегая производной du/dt, представляющей расход газа на
повышение свободной концентрации в порах сорбента, в отличие от

176 ПРИЛОЖЕНИЯ К ГЛАВЕ II
производной da/dt, представляющей расход газа на увеличение
сорбированного количества газа, получаем ^"^
ди да , ,,
0(2
-— =p(u-ja), (6)
а (ж, 0) = 0,
и (О, t) = Uq.
Исключим функцию а (ж, t), дифференцируя первое уравнение по ^ и
используя второе уравнение:
- uuxt = /Зщ - Pjat = /Зщ + Pi^jUx,
или
Uxt -\- -щ-\- Pjux = 0.
Определим начальное условие для и, полагая в первом уравнении t =
= 0:
— uux (ж, 0) = Ри (ж, 0), и (о, 0) = По,
откуда находим
и(ж, O)=uoe-^/^-^
Задача нахождения функции и{х, t) свелась к интегрированию
уравнения
Uxt ^ -щ^ /3jUx = о (9)
при дополнительных условиях
и(ж, 0)=uoe-^/"•^ (10)
u{0,t)=uo. (8)
Характеристиками этого уравнения являются линии
X = const, t = const.
Дополнительные условия в этой задаче представляют значения
искомой функции и{х, t) на характеристиках. Аналогично ставится зада-
^ Для системы уравнений (2^) и (6) достаточно одного начального
условия, так как ось ^ = О в этом случае становится характеристикой. Подробнее
об этом см. примечание на с. 177.

V. ДИНАМИКА СОРБЦИИ ГАЗОВ
177
ча для функции а (ж, t):
dxt -\- -at-\- Pjax = О,
а (ж, 0) =0,
7
(И)
(7)
(12)
Следует заметить, что подобная задача встречается при
рассмотрении ряда других вопросов (например, процесс суп1ки воздуп1ным
потоком, прогревание трубы потоком воды и т. д.)"*^-^).
^ Переходя к уравнению (2^), мы пренебрегаем членом щ. Однако
нетрудно показать, что мы придем к тому же уравнению, если введем переменные
t--
V
r.U i
i
(рис. 32), в которых время в точке х отсчитывается от ^о = ^/^ — момента
прихода в эту точку потока газовоздупЕной смеси. В самом деле,
ди _ ди 1 ди д _ д
дх д^ 1У дт^ dt дт
и уравнение (2) принимает вид
ди да
да
д^
д^ дт'
■ P{u--fa).
Начальные условия (7) и уравнения (2) и (6) дают
и{х, 0) = 0,
щ (ж, 0) = О
;}
(2")
(6)
(7')
В области между прямой ^ = О и осью ^ мы получаем задачу определения
функции и по начальным условиям (7 )
(задача Копей). Очевидно, что в этой
области функция и{х, t) = О (а также
а = 0). Из уравнений (2^) и (6) видно,
что при г = О функция п (ж, t)
претерпевает разрыв, в то время как функция
а (ж, t) остается непрерывной. Таким
образом, при г = О функция п, как
было показано выпес, определяется из
уравнения (2 ) при а (ж, 0) = 0.
Определяя, как это было сделано выпес (см.
формулы (10) и (12)), значения и (ж, 0) и а (О, ^), мы получаем для функций
и{х, t) и а{х, t) задачи с данными на характеристиках.
Рис. 32
12 А. Н. Тихонов, А. А. Самарский

178 ПРИЛОЖЕНИЯ К ГЛАВЕ II
Решение уравнения (9) может быть получено в явном виде
методом, изложенным в § 5, и дается формулой
и (ж1, ^i) = ще
XI
е-*1
XlLl
/о {2^ДJ;) + — / е-^/^1 /о (2л/7) dr
Xl J
о
(13)
где Xl = Px/jy, ti = pt/j — безразмерные переменные, /q — функция
Бесселя первого рода нулевого порядка от мнимого аргумента.
Пользуясь асимптотическими формулами для функции /о,
нетрудно получить асимптотическое представление решения при
больших значениях аргументов.
2. Асимптотическое penienne. Выше мы изучали процесс
сорбции газа, подчиняющегося изотерме сорбции Генри, связывающей
количество поглощенного вещества а с равновесной концентрацией у
линейной зависимостью
1
а= -у.
7
Рассмотрим изотерму сорбции общего вида
a = fiy).
Если ввести безразмерные переменные
х/3 t/3 _ и у а
г/ ' 7 ' '^0' '^0' uol'
то система (2'), (6), (7), (8) примет вид
дй dv
dxi dti'
dv
(14)
v = h{z) = —f{zu^) (15)
uo7
при дополнительных условиях
^(0, ^i) = l, (16)
i;(xi,0) = 0. (17)
Пас будет интересовать асимптотическое поведение функций,
представляющих решение системы (14).
Относительно функции Д {z) мы будем предполагать следующее.
1- Л (^) — возрастающая функция, и Д (0) = 0.

V. ДИНАМИКА СОРБЦИИ ГАЗОВ
179
2. /i (z) имеет непрерывную производную для всех значений z,
O^z^l.
3. Луч, идущий из начала координат в точку (1, Д (1)), лежит
ниже кривой /i (z) в промежутке О ^ 2; ^ 1 (рис. 33), что, в частности,
имеет место для выпуклой изотермы.
Введя обозначение для обратной
функции
будем искать асимптотическое penienne
поставленной задачи в виде
распространяющейся волны ■'^^:
V = (f{0,
^ = X — at,
(18)
fiO)
Рис. 33
где а — скорость распространения волны,
подлежащая определению.
Это означает, что на больп1их расстояниях (при х —>- оо) или
через больпюй промежуток времени (^ —>- оо)
V {х, t) = V = (f{x — at),
й{х, t) = й = ф {х — at).
Концентрации й и v должны при ж = оо или t = оо удовлетворять
условию равновесия
'^^ = Л (й), или й = F (у).
Из условия (16) тогда следует
й\х=о ='0(-оо) = 1, (р {-оо) = v\х=0 =/i(l). (19)
t=(yo t=(yo
Из условия (17) вытекает, что
v\ ж=оо = (^ (+ оо) = О, ф{+оо) = й\ ж=оо = F (0) = 0. (20)
Условия (19) означают, что при ^ —>- оо (^ —>- — оо) должно
установиться всюду насыщение.
Подставляя предполагаемую форму решения в уравнения (14),
получим
ф' - a(f' = О, (21)
— a(f' = ф — F {(f).
Из (21) и (20) заключаем, что
' Для упрощения записи вместо xi, ti будем писать х, t.
12*
(22)
(23)

180 ПРИЛОЖЕНИЯ К ГЛАВЕ II
Из уравнений (19) тогда следует, что
_ф{0\
9(0
или, в размерных величинах.
^=— сю
/l(l)'
(24)
а = 7-, ао = /(«о). (24')
do
Из (22) и (23) находим
_^ %—=d^. (25)
После интегрирования будем иметь
ш{^)=^-^о, (26)
где со {(р) —какой-либо интеграл левой части, а ^о —постоянная
интегрирования. Отсюда искомая функция (f (^) определится с точностью
до неизвестной постоянной ^о-
^р = со-' (е - ^о), (27)
ф = аи;-'{^-^о). (28)
Выясним, может ли быть определена функция uj~'^ и будут ли
функции (риф удовлетворять поставленным условиям при ^ —>- + оо
и ^ —>- — 00. Покажем, что производная
dip сг(р- fi {(р)
т. е.
— МОНОТОННО убывающая функция (р. В самом деле, знаменатель в (29)
равен
(^^ - /Г^ {^) = т-цу ^ - /Г^ (^)-
Первое слагаемое есть принадлежащая ординате (р абсцисса точки,
лежащей на луче, идущем из начала координат в точку (1, Д (1))
(рис. 33). Так как мы условились, что кривая (р = fi (z) лежит
выше этого луча, то
и, следовательно,
(^V - /Г^ i'P) > 0.

V. ДИНАМИКА СОРБЦИИ ГАЗОВ
181
Кроме того,
^^ - /г' {^P) = О
при (/? = о и при (f = fi (1).
Отсюда следует, что
^ - ^Q = UJ {(f) = -\-оо при (/? = о,
^-^o=uj{(f) = -oo при (/? = л (1).
Для обратной функции получаем
(р = UJ-^ (^ - ^о) = Д (1) при ^ = - 00,
(/? = о;"^ (^ - ^о) = о при ^ = +00.
Далее в силу равенства (29) имеем
1
ф = a(f
/i(i)
ф = а(р =
/i(i)
(/? = 1 при ^ = — 00,
(/? = о при ^ = + 00.
Итак, все условия (19) и (20) удовлетворены и тем самым доказано,
что система уравнений имеет penienne в виде распространяющейся
волны, содержащей неопределенную постоянную ^о-
Для определения ^о интегрируем первое уравнение по ^ в
пределах от О до ^0 и по ж в пределах от О до xq:
'to to
й{хо, т) dr — й (О, г) dr
XQ XQ
/ V (ж, ^о) dx — V (ж, 0)
+ / V (х, to) dx — V (х, 0) dx\ = 0.
Lo
(30)
Полученное равенство выражает закон сохранения вещества. Переходя
к пределу при жо —>■ оо и пользуясь начальными условиями для й и v,
находим
^0
/ V (ж, ^о) dx = и (О, г) dr = to.
о о
Допустим, что для больших значений t решение нашей задачи
приближается к функциям й и v, найденным выше в виде
распространяющихся волн.
Если мы определим ^о из условия
сю
/
V (ж, ^о) dx — to ^ О {to —>■ оо).
(31)

182
ПРИЛОЖЕНИЯ К ГЛАВЕ П
это и будет то значение ^о? которое соответствует функциям й (ж, t)
и V (ж, t).
Преобразуем наш интеграл:
сю сю сю
/ V (ж, ^о) dx = (f{x — ato) dx = uj~^ {x — ato — ^o
) dx
0
СЮ
СЮ СЮ /
- crto - Co,
■ crto - Co J
Обозначим через (f* значение o;"-^ {() при С = О-
Нетрудно видеть, что если (р = uj~^ {()—обратная функция для (
= со ((/?), то (рис. 34)
сю и сю
I со-' (С) dC = I СО-' (С) dC + l СО-' (С)
dC
Cl
Cl
c^"MCi)
1^ 4Ci)+ / uj {(f) d(f + uj {(f)
d(p
(f*
(32)
Отсюда следует, что вместо предельного равенства (31) можно
написать
сю
/ .-МО
dC-to =
-crto-^0
(fi(-(Tto-^o)
{(Tto-\-^o)(f{-ato-^o)-\- / uj{(f)
d(p
} -to^
^0 (^o^oo). (32')

V. ДИНАМИКА СОРБЦИИ ГАЗОВ 183
Перейдем к пределу при to ^ оо. Тогда
aif i-ato - Ь) ^ aif (- оо) = аД (1) = 1. (32")
Чтобы вычислить предел выражения
ato(f {—crto — Со) - ^0,
воспользуемся уравнением (25). Разлагая Д~ {(f) = F {(f) в ряд вблизи
точки (ро = /i (1), получаем
а(р - F {(р) = а {(р - (ро) -\- 1 - F {(р) =
= a{(p-(fo)- [F {(f) - F {(fo)] = [a-F' {(fo)] {(f - (fo) + .. •,
откуда
[a-F'{(po)]{(p-(po) + --- ^ ^
где точками обозначены члены более высокого порядка относительно
Из требования 3 для функции Д следует, что
/i(l)'
Из уравнения (33) находим порядок роста (р при ^ —>- — оо:
(р = Ае^^+(ро, (34)
где А и к > О — некоторые постоянные.
Из (34) следует, что
lim to[a(p{-ato-^o)-l]= Ит ^о^^е"^ ^^^о+^о^ = 0. (32''')
Совершив в формуле (32') предельный переход при to ^ оо и принимая
во внимание (32") и (32'"), получаем
/i(i)
Со = - YJ]) / ^ (^) d^' (35)
о
Тем самым профили волны {й, v} определены полностью.
Особый интерес представляет случай изотермы Ленгмюра.
Найдем асимптотическое решение для процесса сорбции газа,
подчиняющегося изотерме Ленгмюра.
Уравнение (25) примет вид
- '"' =dt (36)
(Т(р —
1-р(р

184
ПРИЛОЖЕНИЯ К ГЛАВЕ П
где а = l//i(l) = 1 -\-р — скорость волны. Из (36) находим
где
{l-p(p)d(p
(jj
м = ^/
(f-a(f{l -p(f)
+ Л:
а-1
1
1п(сг — 1 — pa(f) — In (/?
+ А
Очевидно, что когда (f меняется от О до Д (1), то со {(f) меняется от
1,0
0,8
0,6
0,4
0,2
0,0
4 8 12 16 20 24
Рис. 35
+ 00 до —00. Выберем А так, чтобы
i\\
1\\
^
ш\
Щ
\\
\\
iV
Л>
?v?Y
\s
\\
\
\\
\ '
^^Ч
>^
\
V А
А
Кп
\lp
\is\
is\i
4\15
\16\
1 -
2-
- t =
- t =
0
0.4
3— t = 0,8
4 — t = 1,2
5 — t = 1,6
6—t = 2
7— t = 2,8
8—t = 3,6
9 — t = 4,4
10 —t = 5,2
11 — t = 6
12—t = 6,8
13 —i = 7,6
14 — t = 8,4
15 — t = 9,2
16—t = 10
28
T. e. чтобы
^* = 2/i(l)'
uj{(p*)=0 при (^* = -/i(l) = -—-.
При этом условии
A =
а-1
а \2^J \2l+p

VI. ФИЗИЧЕСКИЕ АНАЛОГИИ 185
Uj{(f) =
- In 2 (1 - a(p) - In 2 (1 + p) (/?
(7
a-1
Значение ^o определяется формулой
/i(i)
Co = - YJi) / ^{^)d(f = \n2-l
0
и не зависит от p = щ/у, т. е. от подаваемой концентрации.
Искомое асимптотическое penienne имеет вид
V (ж, t) = uj-^{x -at- ^о), .^^ч
й (ж, ^) = аио~^{х — at — ^о),
где о;""*" (^)—обратная для оо {<^) функция.
На рис. 35 приведены результаты численного интегрирования
уравнений (14) для изотермы Ленгмюра методом конечных разностей.
Эти графики даны для значений О < ^ ^ ^i = 10. Нри t = ti
результаты численного интегрирования совпадают с асимптотическим
решением с точностью до 1%. Для значений t > ti можно пользоваться
асимптотическими формулами.
VI. Физические аналогии
Нри рассмотрении явлений в различных областях физики мы
часто обнаруживаем общие черты в этих явлениях. Это приводит к тому,
что при математической формулировке задачи мы получаем одни и те
же уравнения, описывающие различные физические явления.
Простейшим примером может служить уравнение
описывающее различные колебательные процессы простейших систем:
математический маятник, колебание груза под действием силы
упругости пружины, электрические колебания в простом контуре с
индуктивностью и емкостью и т. д. Общность уравнений для различных
физических процессов позволяет на основании изучения свойств
одного явления делать заключение о свойствах другого, менее
изученного явления. Так, изучение различных акустических явлений может
быть значительно облегчено предварительным рассмотрением
подобных электрических схем.
Распространение электрических колебаний в системах с
распределенными постоянными описывается, как известно, телеграфными

186
ПРИЛОЖЕНИЯ К ГЛАВЕ П
уравнениями
(1)
где С, G, L, R — распределенные емкость, утечка, индуктивность
и сопротивление системы. Если можно пренебречь сопротивлением и
утечкой тока, то для V ш I получаются обычные волновые уравнения
дх"^
LC
W
a уравнения (1) принимают вид
_dl
дх
_dV
дх
С
dV_
Ж'
а/
(2)
др
дх
dv
дх
dv
1 dp
При решении задачи о распространении звука в одном направлении,
например при изучении движения воздуха в трубах, мы приходим к
уравнениям
(3)
где V — скорость колеблющихся частиц, р — плотность, р — давление,
а г = ро7 — коэффициент упругости воздуха.
Подобие уравнений (2) и (3) позволяет установить соответствие
между акустическими и электрическими величинами. Разности
потенциалов соответствует давление, току — скорость смещения частиц.
Индуктивности электрической цепи соответствует плотность,
определяющая инерционные свойства газа, а емкости электрической цепи
соответствует 1/г, т. е. обратная величина коэффициента упругости.
Это же соответствие можно установить и из выражений кинетической
и потенциальной энергий для электрической и акустической систем.
Возвращаясь к уравнениям (1), мы можем ввести акустические
аналоги сопротивления и утечки. Величину акустического
сопротивления приходится учитывать в тех случаях, когда при рассмотрении

VI. ФИЗИЧЕСКИЕ АНАЛОГИИ
187
движения газа оказывается существенным трение газа о стенки
сосуда. По аналогии с электрическим сопротивлением, которое
определяется как отношение напряжения к току, можно ввести и акустическое
сопротивление, определяемое отношением давления к току в среде,
который пропорционален скорости смещения частиц газа, Ra = p/uv. В
тех случаях, когда рассматривается движение газа в пористой среде,
приходится вводить величину, аналогичную утечке в электрических
цепях. Эта величина, обозначаемая через Р, называется пористостью
и определяется частью объема материала, которая оказывается
заполненной воздухом.
Механическим аналогом телеграфного уравнения является
уравнение продольных колебаний стержня, которое подобно уравнениям (2)
может быть записано в виде
dv _1 дТ дТ _ dv
дх к dt ^ дх dt'
где Т — натяжение стержня, v — скорость колеблющихся точек, р —
плотность и к — коэффициент упругости стержня.
Сравнивая это уравнение с уравнением (2), мы можем установить
подобие между механическими и электрическими величинами. Так,
установив соответствие между электрическим напряжением и
натяжением струны, током и скоростью движения частиц, мы получим,
что обратная величина коэффициента упругости соответствует
емкости, а плотность — индуктивности.
Таким образом, рассмотрение подобных динамических задач
приводит к установлению соответствия между рядом электрических,
акустических и механических величин. Это соответствие можно
иллюстрировать следующей таблицей ■'^'^:
а;
а;
3
а
н
Электрическая система
Напряжение
Ток
Заряд
Индуктивность
Емкость
Сопротивление
V
I
е
L
С
R
Акустическая система
Давление р
Скорость частиц v
Смещение и
Инертность
(плотность) ^
Акустическая ^ _ ^
емкость г
Акустическое „
сопротивление
Механическая система
Натяжение (сила) Т
Скорость смещения х
Смещение х
Плотность массы рт
Мягкость См = —
к
Механическое „
сопротивление ^
См., например: Ольсон Г. Динамические аналогии. М., 1947.

188 ПРИЛОЖЕНИЯ К ГЛАВЕ II
Развитые выше соображения позволяют в ряде акустических
задач получить некоторые сведения о характере явлений до реп1ения
задачи.
Так, задача о движении воздуха в порах для простых
гармонических волн приводит к уравнениям ^"^
— iujpmU + ТО = — gradp,
Ар + i —- (г - iujpm) Р = О,
где и — объемная скорость воздуха через поры, р — давление, р —
плотность, рт — эффсктивная плотность воздуха в порах, которая
может быть больше р, так как в порах вместе с воздухом могут
колебаться и частицы вещества, Р — пористость, а и со — скорость и частота
звука, г — сопротивление потоку, которое характеризует падение
давления в материале. Положив г = Ra, рт = La, ^Р/{ро?) = С а, мы
получим наши уравнения в виде
La-^ + Rau = - gradp.
Эти уравнения вполне подобны уравнениям распространения
электрических колебаний в линии. Поэтому мы по аналогии с волновым
сопротивлением линии
R + iujL
G + iujC
можем сразу написать выражение для сопротивления, называемого
характеристическим импедансом пористого материала:
Z = a^\l — ,
считая при этом G = 0. Выражение характеристического импеданса
указывает на затухание волн, распространяющихся в пористом
материале.
Установленная аналогия между электрическими и
акустическими явлениями позволяет заменить изучение ряда акустических задач
рассмотрением эквивалентных электрических схем.
Метод подобия в последнее время нашел большое применение в
моделирующих счетно-решающих устройствах, в которых для
решения уравнения, соответствующего какому-либо физическому процессу,
строится эквивалентная электрическая схема.
^^ См.: Фурдуев В. В. Электроакустика. М.; Л., 1948.

ГЛАВА III
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
Уравнения с частными производными 2-го порядка
параболического типа наиболее часто встречаются при изучении процессов
теплопроводности и диффузии. Простейшее уравнение параболического
типа
О
{у = аН)
обычно называют уравнением теплопроводности.
§ 1. Простейшие задачи, приводящие к уравнениям
параболического типа. Постановка краевых задач
1. Линейная задача о распространении тепла. Рассмотрим
однородный стержень длины /, теплоизолированный с боков и
достаточно тонкий, чтобы в любой момент времени температуру во всех
точках поперечного сечения можно было считать одинаковой. Если концы
стержня поддерживать при
постоянных температурах ui и ^2, то,
как хорошо известно, вдоль
стержня устанавливается линейное
распределение температуры (рис. 36)
и {х) = Ui +
U2 - Ui
I
(1)
При этом от более нагретого к
менее нагретому концу стержня бу- р^^^. зб
дет перетекать тепло. Количество
тепла, протекающее через сечение стержня площади S за единицу
времени, дается экспериментальной формулой
Q = -k
U2
ox
(2)
где к — коэффициент теплопроводности, зависящий от материала
стержня.

190 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Величина теплового потока считается положительной, если тепло
течет в сторону возрастания х.
Рассмотрим процесс распространения тепла в стержне. Этот
процесс может быть описан функцией и{х, t), представляющей
температуру в сечении х в момент времени t. Найдем уравнение, которому
должна удовлетворять функция и{х, t). Для этого сформулируем
физические закономерности, определяющие процессы, связанные с
распространением тепла.
1. Закон Фурье. Если температура тела неравномерна, то в нем
возникают тепловые потоки, направленные из мест с более высокой
температурой в места с более низкой температурой.
Количество тепла, протекающее через сечение х за промежуток
времени (^, t -\- dt), равно
dQ = qSdt, (3)
где
.= -М^)| (4)
— ПЛОТНОСТЬ теплового потока, равная количеству тепла, проходящего
за единицу времени через площадь в 1 см^. Этот закон
представляет обобщение формулы (2). Ему можно также придать интегральную
форму:
Q = -S f k^{x,t)dt, (5)
где Q — количество тепла, протекающее за промежуток времени
(^1, ^2) через сечение х. Если стержень неоднороден, то к
является функцией X.
2. Количество тепла, которое необходимо сообщить однородному
телу, чтобы повысить его температуру на Аи, равно
Q = cm Аи = cpV Аи, (6)
где с — удельная теплоемкость, т — масса тела, р — его плотность,
V — объем.
Если изменение температуры имеет различную величину на
разных участках стержня или если стержень неоднороден, то
Х2
Q= [ cpSAu{x)dx. (7)
XI
3. Внутри стержня может возникать или поглощаться тепло
(например, при прохождении тока, вследствие химических реакций и
т. д.). Выделение тепла может быть охарактеризовано объемной плот-

iL
ПРОСТЕЙШИЕ ЗАДАЧИ
191
ностью тепловых источников F{x, t) в точке х в момент t'^K В
результате действия этих источников на участке стержня (ж, ж + dx) за
промежуток времени {t, t -\- dt) выделится количество тепла
dQ = SF{x,t)dxdt, (8)
или, в интегральной форме,
Q = S [ [F{t,x)dxdt, (9)
где Q — количество тепла, выделяющегося на участке стержня {xi, Х2)
за промежуток времени (^1,^2)-
Уравнение теплопроводности получается при подсчете баланса
тепла на некотором отрезке (xi, Х2) за некоторый промежуток времени
(^1, ^2)- Применяя закон сохранения энергии и пользуясь формулами
(5), (7) и (9), можно написать равенство
t2
I
к^(х,г)
х=Х2
-к^(х,г)
X = Xl
Х2
XI
Х2 t2
dT-\-
ll''('^^
d£,dT
cp[u{^, t2) -u{^, ti)]d^,
(10)
которое и представляет уравнение теплопроводности в интегральной
форме.
Чтобы получить уравнение теплопроводности в
дифференциальной форме, предположим, что функция и{х, t) имеет непрерывные
производные Uxx и щ'^К
Пользуясь теоремой о среднем, получаем равенство
к ^ (X, г)
х=Х2
-fc|^(^,-)
X = Xl
At-\-F{x4, и) Ах At
[cp[u{i,t2)-u{i,h)]\
Аж,
(И)
i=X2,
^ Если, например, тепло выделяется в результате прохождения
электрического тока силы / по стержню, сопротивление которого на единицу длины
равно
^ Требуя дифференцируемости функции и{х^ t), мы, вообще говоря,
можем потерять ряд возможных репЕСний, удовлетворяющих интегральному
уравнению, но не удовлетворяющих дифференциальному уравнению. Однако
в случае уравнений теплопроводности, требуя дифференцируемости penie-
ния, мы фактически не теряем возможных репЕСний, так как можно доказать,
что если функция удовлетворяет уравнению (10), то она обязательно должна
быть дифференцируемой.

192
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
[ГЛ. HI
д
дх
. ди
k-{x,t)
Х = Х^
t=ts
которое при помощи теоремы о конечных приращениях можно
преобразовать к виду
Ах At -\- F{x4,t4) Ах At = \cp^{x,t)\ Ах At,
Ot х=х^
(12)
где ^3, ^4, Н и жз, Ж4, Ж5—промежуточные точки интервалов (^i, ^2)
и (Ж1, Ж2).
Отсюда после сокращения на произведение Ах At находим
д
дх
( ди\
I's)
+ F(x, t)
х=х^
t=ts
х=Х4
t=t4
ди
= ^^ж
t=4
х=Х2,
(13)
Все эти рассуждения относятся к произвольным промежуткам {xi, Х2)
и (^1, t2). Переходя к пределу при xi, Ж2 —>■ ж и ^i, t2 ^ t, получим
уравнение
д_
дх
.g)+F,.,,)
ср
ди
di'
(14)
называемое уравнением теплопроводности.
Рассмотрим некоторые частные случаи.
1. Если стержень однороден, то к, с, р можно считать
постоянными и уравнение (14) обычно записывают в виде
щ = а^и^х + /(ж, t),
к_
ср
f{x,t)
F{x,t)
ср
где а —постоянная, называемая коэффициентом
температуропроводности. Если источники отсутствуют, т. е. F {х, t) = О,
то уравнение теплопроводности принимает простой вид
Ut = a^Uxx' (14')
2. Плотность тепловых источников может зависеть от
температуры. В случае теплообмена с окружающей средой, подчиняющегося
закону Ньютона, количество тепла, теряемого стержнем-"^^
рассчитанное на единицу длины и времени, равно
F^ = h{u-e),
где в{х, t) — температура окружающей среды, h — коэффициент
теплообмена. Таким образом, плотность тепловых источников в
точке X в момент t равна
F = Fi{x, t) -h{u-0),
^ Поскольку в нашем приближении не учитывается распределение
температуры по сечению, то действие поверхностных источников эквивалентно
действию объемных источников тепла.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 193
где Fi (ж, t)—плотность других источников тепла.
Если стержень однороден, то уравнение теплопроводности с
боковым теплообменом имеет следующий вид:
щ = a^Uxx - аи-\- f (ж, t), (15)
h . . . _ . . Fi (х, t)
где а = —; j [х, t) = аО [х, t) -\ известная функция.
ср ср
3. Коэффициенты кис, как правило, являются медленно
меняющимися функциями температуры. Поэтому сделанное выше
предположение о постоянстве этих коэффициентов возможно лишь при условии
рассмотрения небольших интервалов изменения температуры.
Изучение температурных процессов в большом интервале изменения
температур приводит к квазилинейному уравнению теплопроводности,
которое для неоднородной среды запишется в виде
о^ I ^ (^, ж) — 1 + F (ж, ^) = С [и, X) р [и, X) -—
(см. Приложение III).
2. Уравнение диффузии. Если среда неравномерно заполнена
газом, то имеет место диффузия его из мест с более высокой
концентрацией в места с меньшей концентрацией. Это же явление имеет место
и в растворах, если концентрация растворенного вещества в объеме
непостоянна.
Рассмотрим процесс диффузии в полой трубке или в трубке,
заполненной пористой средой, предполагая, что во всякий момент времени
концентрация газа (раствора) по сечению трубки одинакова. Тогда
процесс диффузии может быть описан функцией и{х, t),
представляющей концентрацию в сечении х в момент времени t.
Согласно закону Пернста масса газа, протекающая через
сечение X за промежуток времени {t, t + А^), равна
dQ = -D — (ж, t)Sdt = WSdt,
ox
W = -Dp^, (16)
где D — коэффициент диффузии, S — площадь сечения трубки,
W {х, t) — плотность диффузионного потока, равная массе газа,
протекающего за единицу времени через единицу площади.
По определению концентрации, количество газа в объеме V равно
отсюда получаем, что изменение массы газа на участке трубки
(ж1, Х2) при изменении концентрации на Аи равно
Х2
I
AQ = c{x)Au-Sdx,
XI
13 А. Н. Тихонов, А. А. Самарский

194 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
где с{х)—коэффициент пористости-"^л
Составим уравнение баланса массы газа на участке (xi, Х2) за
промежуток времени (^1,^2):
t2
S
tl
1^2
i
D (Ж2) ^ (ж2, т) - D (xi) — (ж1, г)
dr
X2
= slc{0[u{^,t2)-u{^,h)]d^.
Отсюда (ср. с п. 1) получим уравнение
д f^du\ ди ,^^,
являющееся уравнением диффузии. Оно вполне аналогично
уравнению теплопроводности. При выводе этого уравнения мы
считали, что в трубке нет источников вещества и диффузия через стенки
трубки отсутствует. Учет этих явлений приводит к уравнениям,
сходным с уравнениями (14) и (15) (см. гл. VI, § 2, п. 3).
Если коэффициент диффузии постоянен, то уравнение диффузии
принимает вид
щ = a^Uxx,
где а^ = D/c.
Если коэффициент пористости с = 1, а коэффициент диффузии
постоянен, то уравнение диффузии имеет вид
Щ = DUxx.
3. Распространение тепла в пространстве. Процесс
распространения тепла в пространстве может быть охарактеризован
температурой и{х, у, Z, t), являющейся функцией х, у, z и t.
Если температура непостоянна, то возникают тепловые потоки,
направленные от мест с более высокой температурой к местам с более
низкой температурой.
Пусть da — некоторая площадка в точке Р(^, г], Q с нормалью п.
Количество тепла, протекающее через da в единицу времени,
согласно закону Фурье равно
ди
Wn da = (W n)da = -к -^— da,
on
^ Коэффициентом пористости называется отнонхение объема пор к
полному объему Vb, равному в наптем случае S dx.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 195
, ди
где к — коэффициент теплопроводности, — производная по напра-
оп
влению нормали п к da, равная
ди ди , . ди , . ди , . , ^ .
— = — cos(n, х)+ Q- cos(n, У)+ Q- cos(n, z) = (gradu, n).
Закон Фурье часто записывают в форме
W = —kgTdidu,
где W — вектор плотности теплового потока.
Если среда изотропная, то к есть скаляр. В случае
анизотропной среды к есть тензор, а вектор теплового потока W представляет
собой произведение тензора к на вектор — gradu. Мы будем
рассматривать только изотропные среды.
Перейдем к выводу уравнения теплопроводности в пространстве.
Рассмотрим некоторый объем V, ограниченный поверхностью S.
Уравнение баланса тепла для объема V за время At = t2 — ti имеет
вид
^ Cp[u{P,t2)-u{P,h)]dVp =
V
= - f dtffWnda+ f dt [jjj F{P,t)dVp\ , (18)
ti s ti \ V /
где P = P{^, Г], 0—точка интегрирования, dVp = d^dr]d( — элемент
объема, cp — теплоемкость единицы объема, Wn — нормальная
составляющая плотности теплового потока. Это уравнение выражает закон
сохранения тепла в объеме V за время А^: изменение количества
тепла в объеме V за время At = t2 — ti (левая часть в (18))
обусловлено потоком тепла через граничную поверхность S (первое слагаемое
в правой части равенства (18)), а также количеством тепла,
выделившимся в объеме V за время А^ в результате действия тепловых
источников.
Чтобы перейти от интегрального уравнения баланса к
дифференциальному уравнению, предположим, что функция и (М, t) =
= U (ж, у, Z, t) дважды дифференцируема по ж, у, z и один раз по
t и что эти производные непрерывны в рассматриваемой области.
Тогда можно воспользоваться формулой Остроградского — Гаусса
f fWnda= fffdivWdV
S V
13*

196 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
и преобразовать уравнение баланса к виду
Cp[u{P,t2)-u{P,h)]dVp =
///■
= - / fffdivWdVpdt+ I IIIF{P, t)dVpdt.
ti V ti V
(Будем предполагать F (P, t) непрерывной функцией своих
аргументов.)
Применяя теорему о среднем и теорему о конечных приращениях
для функций многих переменных, получаем
ди
M-V = -divW
P=Pl
At'V + F
P=P2
At'V,
Р=Рз
где ts, ^4, ^5—промежуточные точки на интервале А^, а Pi, Р2, Рз —
точки в объеме V. Фиксируем некоторую точку М (ж, у, z) внутри
V и будем стягивать V в эту точку, а А^ устремлять к нулю. После
сокращения на А^ 1/ и указанного предельного перехода получим
ди
ср-—{х, у, Z, t) = -divW(x, у, Z, t) + F (ж, у, z, t).
Заменяя W по формуле W = —/ijgradu, получим дифференциальное
уравнение теплопроводности
срщ = div(/i;gradu) + F,
си = — (k—]+—(k—]+—(k—]+F
дх \ дх) ду \ ду) dz \ dz)
Если среда однородна, то это уравнение обычно записывают в виде
F
щ = а^ {uxx + Uyy + Uzz) Н ,
ср
где о? = к/ср — коэффициент температуропроводности, или
Ut = a^Au^f (f=-
V ср
л д^ д^ д^
где А = -—^ + -—^ + —^ —оператор Лапласа.
аж^ оу^ oz"^
4. Постановка краевых задач. Для выделения единственного
решения уравнения теплопроводности необходимо к уравнению
присоединить начальные и граничные условия.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 197
Начальное условие в отличие от уравнения гиперболического
типа состоит лишь в задании значений функции и{х, t) в начальный
момент
Пограничные условия могут быть различны в зависимости от
температурного режима на границах. Рассматривают три основных типа
граничных условий.
1. На конце стержня ж = О задана температура
где iJ,{t)—функция, заданная в некотором промежутке to ^t ^Т,
{Т — момент времени, до которого изучается процесс).
2. На конце х = / задано значение производной
ди ,^ .
К этому условию мы приходим, если задана величина теплового потока
Q {I, t), протекающего через торцевое сечение стержня,
Q{l,t) = -k^{l,t),
откуда 7^ (/, t) = 1У (t), где г/ (t) —известная функция, выражающаяся
ох
через заданный поток Q {I, t) формулой
к
3. На конце х = / задано линейное соотношение между
производной и функцией
— {l,t) = -X[u{l,t)-e{t)].
Это граничное условие соответствует теплообмену по закону
Ньютона на поверхности тела с окружающей средой, температура которой в
известна. Пользуясь двумя выражениями для теплового потока,
вытекающего через сечение х = I:
Q = h{u-e)
ox
получаем математическую формулировку третьего граничного
условия в виде
— {l,t) = -X[u{l,t)-e{t)],

198 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
где Л = h/k — коэффициент теплообмена, в {t)—некоторая заданная
функция. Для конца ж = О стержня (О, /) третье граничное условие
имеет вид
Fill
^{Q,t) = \[u{Q,t)-9{i)].
Граничные условия при ж = О и х = 1 могут быть разных типов,
так что число различных задач велико.
Первая краевая задача для ограниченного стержня
состоит в следующем.
Найти решение и = и{х, t) уравнения теплопроводности
щ = a^Uxx при 0<ж</, 0<^^Т,
удовлетворяющее условиям
и (ж, 0) = (f (ж), О ^ ж ^ /,
и (О, t) = 111 (t), и (/, t) = 112 W, О ^ ^ ^ Г,
где (/?(ж). 111 (t) и /i2 (t) —заданные функции.
Аналогично ставятся и другие краевые задачи с различными
комбинациями краевых условий при ж = О и х = I. Возможны краевые
условия более сложного типа, чем те, которые были рассмотрены
выше.
Пусть на конце ж = О стержня помещена сосредоточенная
теплоемкость Ci (например, тело с большой теплопроводностью,
вследствие чего температуру по всему объему этого тела можно считать
постоянной) и происходит теплообмен со внешней средой по закону
Ньютона. Тогда краевое условие при ж = О (выражающее уравнение
теплового баланса) будет иметь вид
uu uu
где uq — температура внешней среды. Это условие содержит
производную du/dt (или д'^и/дх'^^ если учесть уравнение щ = o?Uxx)-
Если среда неоднородна и коэффициенты уравнения являются
разрывными функциями, то промежуток (О, /), в котором ищется
решение задачи, разбивается точками разрыва коэффициентов на
несколько частей, внутри которых функция и удовлетворяет уравнению
теплопроводности, а на границах — условиям сопряжения.
В простейшем случае эти условия заключаются в непрерывности
температуры и непрерывности теплового потока:
u{xi - о, ^) = u{xi + О, t),
uu uu
к {xi - 0) — {xi -0,t) = k {xi + 0) — {xi + 0, t),
ox ox

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 199
где Xi — точки разрыва коэффициентов.
Кроме названных здесь задач часто встречаются их
предельные случаи. Рассмотрим процесс теплопроводности в очень длинном
стержне. В течение небольпюго промежутка времени влияние
температурного режима, заданного на границе, в центральной части стержня
сказывается весьма слабо, и температура на этом участке
определяется в основном лишь начальным распределением температуры. В этом
случае точный учет длины стержня не имеет значения, так как
изменение длины стержня не окажет существенного влияния на
температуру интересующего нас участка; в задачах подобного типа обычно
считают, что стержень имеет бесконечную длину. Таким образом,
ставится задача с начальными условиями (задача Кош и) о
распределении температуры на бесконечной прямой.
Найти решение уравнения теплопроводности в области — оо <
<ж<(Х) и t ^ to, удовлетворяющее условию
и (ж, to) = (f{x) (— 00 < ж < + оо),
где (f (х) — заданная функция.
Аналогично, если участок стержня, температура которого нас
интересует, находится вблизи одного конца и далеко от другого, то в
этом случае температура практически определяется температурным
режимом близкого конца и начальными условиями. В задачах
подобного типа обычно считают, что стержень полубесконечен и координата,
отсчитываемая от конца, меняется в пределах О ^ ж ^ оо. Приведем
в качестве примера формулировку первой краевой задачи для
полу бесконечного стержня.
Найти решение уравнения теплопроводности в области О < х <
< 00 и t ^ to, удовлетворяюш^ее условиям
и (ж, ^о) = ^{х) (О < ж < оо),
u{0,t)=fi{t) (t^to),
где (f{x) и fi{t)—заданные функции.
Приведенные выше задачи представляют собой предельный
случай (вырождение) основных краевых задач. Возможны предельные
случаи основной задачи и другого типа, когда пренебрегают точным
учетом начальных условий. Влияние начальных условий при
распространении тепла по стержню ослабевает с течением времени. Если
интересующий нас момент достаточно удален от начального, то
температура стержня практически определяется граничными условиями,
так как изменение начальных условий не изменило бы
температурного состояния стержня в пределах точности наблюдения. В этом случае
практически можно считать, что опыт продолжается бесконечно, и
начальные условия тем самым отпадают.
Таким образом, мы приходим к краевым задачам без
начальных условий.

200 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Найти решение уравнения теплопроводности для О ^ х ^ I и
— оо < t, удовлетворяющее условиям
и{1, t) = fi2 (t).
В зависимости от характера граничного режима возможны и
другие виды задач без начальных условий.
Весьма важной является задача без начальных условий для
полубесконечного стержня (/ = оо), когда требуется найти решение
уравнения теплопроводности для 0<ж<(Х), ^>—оо, удовлетворяющее
условию
где /i (t) —заданная функция.
Наиболее часто встречаются задачи без начальных условий при
периодическом граничном режиме
jj, (t) = А cos LOt
(см. Приложение I к гл. П1).
Естественно считать, что по прошествии большого промежутка
времени температура стержня практически также меняется по
периодическому закону с той же частотой. Однако если мы захотим точно
учитывать начальные условия, то формально никогда не получим
периодического решения, так как влияние начальных условий хотя и
будет ослабевать с течением времени, но в нуль не обратится;
учитывать это влияние ввиду ошибок наблюдения нет никакого смысла.
Рассматривая периодическое решение, мы пренебрегаем влиянием
начальных данных.
Постановка краевых задач, изложенная выше, относится, конечно,
не только к уравнению с постоянными коэффициентами. Под словами
«уравнение теплопроводности» мы могли бы понимать любое из
уравнений предыдущих пунктов.
Помимо перечисленных выше линейных краевых задач ставятся
также задачи с нелинейными граничными условиями, например вида
Это граничное условие соответствует излучению по закону
Стефана — Больцмана с торца ж = О в среду с температурой в (t).
Остановимся более подробно на постановке краевых задач.
Рассмотрим первую краевую задачу для ограниченной области.
Решением первой краевой задачи будем называть
функцию и{х, t), обладающую следующими свойствами:
1) и{х, t) определена и непрерывна в замкнутой области
О ^ ж ^ /, to^t^T;

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 201
2) и{х, t) удовлетворяет уравнению теплопроводности в
открытой области
О < ж < /, to <t <Т;
3) и{х, t) удовлетворяет начальному и граничным условиям, т.е.
и (ж, ^о) = Ч^ (ж), и (О, t) = 111 (t), и (/, t) = /i2 (t),
где (/^(ж), /ii (^), /^2 (^)—непрерывные функции, удовлетворяющие
условиям сопряжения
(f (0) = fil (to) [=u{0,to)] и (f (l) = fi2 (to) [=u{l,to)],
необходимым для непрерывности u{x, t) в замкнутой области.
Рассмотрим плоскость фазовых состояний (ж, t) (рис. 37). В
нашей задаче ищется функция u{x,t), определенная внутри
прямоугольника ABCD. Эта область определяется самой постановкой
задачи, так как изучается процесс распространения тепла в
стержне О ^ ж ^ / за промежуток времени to ^ t ^ Т, в течение
которого нам известен тепловой режим на краях. Пусть ^о = 0; мы
предполагаем, что и{х, t)
удовлетворяет уравнению только при О <
< X < I, о < t ^ Т, но не при t = ^
= О (сторона АВ) и не при ж = О,
X = / (стороны AD и ВС), где
начальными и граничными условиями
непосредственно задаются значения
этой функции. Если бы мы
потребовали, чтобы уравнение
удовлетворялось, например, при ^ = О, то этим р^^^ 37
мы потребовали бы, чтобы
существовала производная (р'' = Uxx {х, 0), входящая в уравнение. Этим
требованием мы ограничили бы область изучаемых физических явлений,
исключив из рассмотрения те функции, для которых это требование
не выполняется. Условие 3 без предположения непрерывности и{х, t)
в области О^ж^/, О^^^Т (т. е. в замкнутом прямоугольнике
ABCD) или какого-либо другого условия, заменяющего это
предположение, теряет смысл ""^^
Действительно, рассмотрим функцию г» (ж, ^), определенную
следующим образом:
v{x,t) = C (0<ж</, 0<^^Г),
v{x, 0) =(/?(ж) (О^ж ^0,
v{^,t)=iii{t),
V{l,t) =fi2{t)
(O^t^T),
^ Пиже будут рассмотрены краевые задачи с разрывными граничными
и начальными условиями. Для этих задач будет уточнено, в каком смысле
понимается выполнение граничных условий.

202 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
где С — произвольная постоянная. Функция г» (ж, ^), очевидно,
удовлетворяет условию 2, а также граничным условиям. Однако эта
функция не представляет процесса распространения тепла в стержне при
начальной температуре ip{x) ф С и граничных температурах /ii {t) ф
Ф С и /J2 (t) ф С, так как она разрывна при ^ = О, ж = О, х = I.
Непрерывность функции и (ж, t) при 0<ж</, О < t ^Т
следует из того, что эта функция удовлетворяет уравнению. Таким
образом, требование непрерывности и (ж, t) при О^ж^/, О^^^Т, по
существу, относится только к тем точкам, где задаются граничные
и начальные значения. В дальнейшем мы под выражением «решение
уравнения, удовлетворяющее граничным условиям», будем
подразумевать функцию, удовлетворяющую требованиям 1, 2, 3, не оговаривая
эти условия каждый раз, если в этом нет особой необходимости.
Аналогично ставятся и другие краевые задачи, в том числе задачи
на бесконечном стержне и задачи без начальных условий.
Для задач с несколькими независимыми геометрическими
переменными все сказанное выше сохраняет силу. В этих задачах
при t = to задается начальная температура, на поверхности тела —
граничные условия. Можно рассматривать также и задачи для
бесконечной области.
В отношении каждой из поставленных задач возникают
следующие вопросы (ср. с гл. П, § 2.):
1) единственность решения поставленной задачи,
2) существование решения,
3) непрерывная зависимость решения от дополнительных условий.
Если поставленная задача имеет несколько решений, то слова
«решение задачи» не имеют определенного смысла. Поэтому, прежде чем
говорить о решении задачи, необходимо доказать его единственность.
Для практики наиболее существенным является вопрос 2, так как при
доказательстве существования решения обычно дается способ
вычисления решения.
Как было отмеченно ранее (см. гл. П, § 2, п. 5), процесс
называется физически определенным, если при малом изменении начальных
и граничных условий задачи ее решение меняется мало. В
дальнейшем будет доказано, что процесс распространения тепла физически
определяется своими начальными и граничными условиями, т. е.
небольшое изменение начального и граничных условий мало изменяет
само решение.
5. Принцип максимального значения. В дальнейшем мы
будем рассматривать уравнение с постоянными коэффициентами
vt = a^Vxx -\- /3vx -\-jv.
Как мы видели, это уравнение подстановкой
^^^^x+xt,^ при /^ = -^, ^ = ^"4^

приводится к виду
ПРОСТЕЙШИЕ ЗАДАЧИ 203
щ = a^Uxx-
Докажем следующее свойство решений этого уравнения, которое
мы будем называть принципом максимального значения.
Если функция U (ж, ^), определенная и непрерывная в замкнутой
области О ^t ^Т и О ^ х ^ I, удовлетворяет уравнению
теплопроводности
щ = a^Uxx (19)
6 точках области О < х < I, О < t ^Т, то максимальное и
минимальное значения функции и (ж, t) достигаются или в начальный момент,
или в точке границы х = О либо х = I.
Функция и{х, t) = const, очевидно, удовлетворяет уравнению
теплопроводности и достигает своего максимального (минимального)
значения в любой точке. Однако это не противоречит теореме, так
как из ее условия следует, что если максимальное (минимальное)
значение достигается внутри области, то оно также (а не только) должно
достигаться или при ^ = О, или при ж = О, или при х = I.
Физический смысл этой теоремы очевиден: если температура на
границе и в начальный момент не превосходит некоторого значения
М, то при отсутствии источников внутри тела не может создаваться
температура, большая М. Остановимся сначала на доказательстве
теоремы для максимального значения.
Доказательство теоремы ведется от противного. Обозначим
через М максимальное значение и{х, t) при ^ = О (О ^ ж ^ /), или при
ж = О, или при ж = / (О^^^Т)-'^^и допустим, что в некоторой
точке (жо, ^о) (О < жо < /, О < ^0 ^ ^) функция U (ж, t) достигает своего
максимального значения, равного
и(жо, ^о) = М + г.
^ Если не предполагать непрерывность и{х, t) в замкнутой области О ^
^ ж ^ /, О ^ ^ ^ Т, то функция и (ж, t) могла бы не достигать своего
максимума ни в одной точке и дальнейпЕие рассуждения были бы неприменимы.
В силу теоремы о том, что всякая непрерывная функция достигает своего
максимального значения в замкнутой области, мы можем быть уверены, что:
1) функция и (ж, t) достигает максимального значения на нижней или
боковых сторонах прямоугольника, которое мы обозначили через М; 2) если
u{xj t) хотя бы в одной точке больпте М, то существует точка (жд, ^о)? в
которой и (ж, t) достригает, максимального значения, превосходящего М:
п(жо, 1о) = М + е {е> 0),
причем
О < жо < /, О < ^0 ^ Т.

204 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Сравним знаки левой и правой частей уравнения (19) в точке
(жо, ^о)- Так как в точке (жо, ^о) функция достигает своего
максимального значения, то необходимо, чтобы
СУи (j 11
— {xo,to)=0 и —{xo,to)^0^\ (20)
Далее, так как и {хо, to) достигает максимального значения при t = to,
то 2)
^(^o,io)^0. (21)
Сравнивая знаки правой и левой части уравнения (19), мы видим, что
они различны. Однако это рассуждение еще не доказывает теоремы,
так как правая и левая части могут быть равны нулю, что не
влечет за собой противоречий. Мы привели это рассуждение, чтобы яснее
выделить основную идею доказательства. Для полного доказательства
найдем точку [xi, ti), в которой —-^ ^ О и —- > 0. Для этого
расах"^ at
смотрим вспомогательную функцию
V (ж, t) =и (ж, t) + k {to - t), (22)
где к — некоторое постоянное число. Очевидно, что
V (жо, ^о) = и (жо, to) = М -\-е
и
к {to -t) ^ кТ.
Выберем к > О так, чтобы кТ было меньше г/2, т. е. к < е/2Т] тогда
максимальное значение г» (ж, t) при ^ = О или при ж = О, ж = / не будет
превосходить М + г/2, т. е.
V {х, t) ^ М -\- - (при ^ = О, или ж = О, или ж = /), (23)
так как для этих аргументов первое слагаемое формулы (22) не
превосходит М, а второе не больше г/2.
^ Действительно, как известно из анализа, достаточными условиями для
того, чтобы функция /(ж) в точке жо, лежащей внутри интервала (О, /),
/
имела локальный минимум, являются следующие условия:
ах
= 0,
> 0. Таким образом, если / (ж) в точке хо имеет максималь-
\X = Xq
ное значение, то: 1) / (жо) = 0 и 2) не может быть, чтобы / (жо) > О, т. е.
/" (хо) < 0.
^ При этом ясно, что если ^о < Т, то ^- = 0; если же ^о = Т, то ^- ^ 0.

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 205
В силу непрерывности функции v (х, t) в замкнутой области она
должна в некоторой точке (xi, ^i) достигать своего максимального
значения. Очевидно, что
v{xi, h) ^ v{xo, to) = М -\-е.
Поэтому ^1 > О и О < Ж1 < /, так как при ^ = О или ж = О, х = I
имеет место неравенство (23). В точке {xi, ti), по аналогии с (20)
и (21), должно быть Vxx (^1, ^i) ^ О, vt (ж1, ^i) ^0. Учитывая (22),
находим
Uxx (Ж1, ^i) = Vxx (Ж1, ^i) ^ О,
щ (ж1, ^i) =Vt{xi,ti)-\-k^k> 0.
Отсюда следует, что
щ (ж1, ^i) - a^Uxx (ж1, h) ^ к > О,
т. е. уравнение (19) во внутренней точке (xi, ^i) не удовлетворяется.
Тем самым доказано, что решение и (ж, t) уравнения
теплопроводности (19) внутри области не может принимать значений,
превосходящих наибольшее значение и (ж, t) на границе (т. е. при ^ = О, ж = О,
х = 1).
Аналогично может быть доказана и вторая часть теоремы — о
минимальном значении. Впрочем, это не требует отдельного
доказательства, так как функция ui = —и имеет максимальное значение там,
где и — минимальное.
Обратимся теперь к установлению ряда следствий из принципа
максимального значения. Прежде всего докажем теорему
единственности для первой краевой задачи.
6. Теорема единственности. Если две функции щ (ж, t) и
U2 (ж, ^), определенные и непрерывные в области О^ж^/, 0^^^
^ Т, удовлетворяют уравнению теплопроводности
щ = a^Uxx + / (ж, t) (для О < ж < /, ^ > 0), (24)
одинаковым начальным и граничным условиям
ui (ж, 0) = U2 (ж, 0) = (/? (ж),
Ui(0, ^) = U2(0, ^) =/il(^),
Ui (/, t) = U2 (/, t) = 112 (t),
mo ui (ж, t) = U2 (ж, t) ■^\
Для доказательства этой теоремы рассмотрим функцию
V (ж, t) = U2 (ж, t) — ui (ж, t).
^ В § 2, п. 3 эта теорема будет усилена и требование непрерывности при
^ = О снято.

206 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Поскольку функции щ {х, t) и U2 (ж, t) непрерывны при
то и функция V {х, t), равная их разности, непрерывна в этой же
области. Как разность двух реп1ений уравнения теплопроводности в
области О < X < I, t > О, функция V {х, t) является реп1ением однородного
уравнения теплопроводности в этой области. Таким образом, принцип
максимального значения применим к этой функции, т. е. она
достигает своего максимального и минимального значений или при ^ = О, или
при ж = О, или при X = I. Однако по условию мы имеем
v{x,0) = 0, v{0,t) = 0, v{l,t)=0.
Поэтому
V (ж, t) = о,
т. е.
Ui (ж, t) = U2 (ж, t).
Отсюда следует, что решение первой краевой задачи единственно.
Докажем еще ряд прямых следствий из принципа максимального
значения. При этом в дальнейшем мы будем говорить просто «решение
уравнения теплопроводности» вместо более подробного перечисления
свойств функций, удовлетворяющих, кроме того, начальным и
граничным условиям.
1. Если два решения уравнения теплопроводности щ (ж, t) и
U2 (ж, t) удовлетворяют условиям
ui (ж, 0) ^ U2 (ж, 0),
Ui (О, t) ^ U2 (О, t), Ui (/, t) ^ U2 (/, t),
то
Ui (ж, t) ^ U2 (ж, t)
для всех значений О^ж^/, О ^t ^Т.
Действительно, разность v (ж, t) = U2 (ж, t) — щ (ж, t)
удовлетворяет условиям, при которых установлен принцип максимального
значения, и, кроме того,
i; (ж, 0)^0, v{0,t)^0, v{l,t)^0.
Поэтому
v{x,t)^0 для О < ж < /, О < ^ ^ Г,
так как иначе функция v {х, t) имела бы отрицательное минимальное
значение в области
0<ж</, 0<^^Г.
2. Если три решения уравнения теплопроводности
u{x,t), u{x,t) и u{x,t)

§ 1] ПРОСТЕЙШИЕ ЗАДАЧИ 207
удовлетворяют условиям
и (ж, t) ^ и (ж, t) ^ й (ж, t) при t = О, ж = 0 и X = I,
то эти эюе неравенства выполняются тоэюдественно, т. е. для всех
ж, t из области О^ж^/, О ^ t ^Т.
Это утверждение доказывается применением следствия 1 к
функциям
u{x,t), u{x^t) и u{x,t), u{x^t).
3. Если для двух решений уравнения теплопроводности щ (ж, t)
и U2 (ж, t) имеет место неравенство
\ui (ж, t) — U2 (ж, ^)| ^ г для ^ = О, ж = О, ж = /,
то оно тоэюдественно, т. е. имеет место для всех ж, t из области
О^ж^/, О^^^Г.
Это утверждение вытекает из следствия 2, если его применить к
реп1ениям уравнения теплопроводности
и(ж, t) = —г,
и (ж, t) = Щ (ж, ^) — и2(ж, t),
й (ж, ^) = е.
Следствие 3 позволяет установить непрерывную зависимость ре-
П1ения первой краевой задачи от начального и граничных значений.
Рассмотрим в области О^ж^/, О ^ t ^ Т решение и (ж, t)
уравнения теплопроводности, соответствующее начальному и граничным
условиям
и (ж, 0) = (f (ж), и (О, t) = /ii (^), U (/, t) = /i2 W-
Пусть u* (ж, ^)—решение того же уравнения, соответствующее
начальному и граничным условиям, определяемым функциями (р* (ж),
/^1 (^)5 /^2 (^)- Если в рассматриваемой области эти функции близки к
функциям (f{x), fii{t), fi2{t):
\^ (ж) - (/.* (ж)| ^ г, l/ii (^) - /it Ш ^ е, |/i2 W - /i^ Wl ^ е,
то и* (ж, ^) отличается от и{х, t) в пределах той же точности е:
\и (ж, t) — и*(ж, ^)| ^ е.
В этом и заключается принцип физической определенности задачи.
Мы подробно провели изучение вопроса о единственности и
физической определенности задачи на примере первой краевой задачи для
ограниченного отрезка. Теорема единственности первой краевой
задачи для ограниченной области в пространстве двух или трех
измерений может быть доказана буквальным повторением приведенных выше
рассуждений.

208 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Подобные же вопросы возникают при изучении других задач,
целый ряд которых был поставлен нами в предп1ествующих пунктах.
Эти задачи требуют некоторого видоизменения метода
доказательства.
Единственность решения задачи для неограниченной области (см.
п. 7) или задачи без начальных условий имеет место лишь при
наложении некоторых дополнительных условий на изучаемые функции.
7. Теорема единственности для бесконечной прямой. При
решении задачи на бесконечной прямой существенным является
требование ограниченности искомой функции во всей области, т. е.
существование такого М, что |и (ж, ^)| < М для всех —(Х)<ж<+(Х) и
Если ui{x^t) и U2{x^t)—непрерывные^ ограниченные во всей
области изменения переменных (ж, t) функции^ удовлетворяющие
уравнению теплопроводности
щ = a^Uxx (— 00 < ж < + 00, ^ ^ 0) (19)
и условию
то
ui (ж, 0) = U2 (ж, 0) (— 00 < ж < оо).
ui (ж, t) = U2 {х, t) (— 00 < ж < 00, t ^ 0).
Рассмотрим, как обычно, функцию
V (ж, t) = Ui (ж, t) — U2 (ж, t).
функция V (х, t) непрерывна, удовлетворяет уравнению
теплопроводности, ограничена во всей области:
1^; (ж, ^)| ^ 1^1 (ж, ^)| + \u2 (ж, t)\<2M (- 00 < ж < 00, ^ ^ 0)
и удовлетворяет условию
v{x, 0) = 0.
Принцип максимального значения, которым мы пользовались при
доказательстве единственности задачи для отрезка, здесь неприменим,
так как в неограниченной области функция г» (ж, t) может нигде не
достигать максимальных значений. Чтобы воспользоваться этим
принципом, рассмотрим область
|ж| ^L,
где L — вспомогательное число, которое затем будем неограниченно
увеличивать, и функцию
V{x,t) = ^-^(^+aHy (25)

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 209
Функция V {х, t) непрерывна, удовлетворяет уравнению
теплопроводности, в чем нетрудно убедиться с помощью дифференцирования, и,
кроме того, обладает следующими свойствами:
У(х,0)^|.;(х, 0)1=0,
V{±L,t)^2M^\v{±L,t)\. ^ ^
Для ограниченной области |x|^L, О^^^Т справедлив принцип
максимального значения. Применяя следствие 2 из предыдущего
пункта для функций и = —V {х, t), и = V {х, t) и й = V (ж, t) и учитывая
(26), получаем
~1X\Y^ ) ^ ^ (^' ^) ^ 7^ (^У + ^^
Фиксируем некоторые значения {х, t) и, воспользовавшись
произволом выбора L, будем его неограниченно увеличивать. Переходя к
пределу при L —>- оо, получаем
V (ж, t) = О,
что и доказывает теорему.
§ 2. Метод разделения переменных
1. Однородная краевая задача. Перейдем к решению первой
краевой задачи для уравнения теплопроводности на отрезке:
щ = а^и^х + f{x,t) {0<х <1, t>0) (1)
с начальным условием
u{x,0) = (f{x) (O^x^l) (2)
и граничными условиями
и{1, t) = Il2{t) J
Изучение общей первой краевой задачи начнем с решения
следующей простейшей задачи I.
Найти непрерывное в замкнутой областей {О ^ х ^ I, О ^t ^Т)
решение однородного уравнения
ut = a^Uxx, О < X <1, О <t ^Т, (4)
удовлетворяющее начальному условию (2)
и (ж, 0) = (f (ж), О ^ ж ^ /,
и однородным граничным условиям
u{0,t) = 0, u{l,t) = 0, O^t^T. (5)
14 А. Н. Тихонов, А. А. Самарский

210 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Для решения этой задачи рассмотрим сначала, как принято в
методе разделения переменных, основную вспомогательную задачу.
Найти решение уравнения
щ = a^Uxx,
не равное тоэюдественно нулю, удовлетворяющее однородным
граничным условиям
u{0,t) = 0, u{l,t) = 0 (5)
и представимое в виде
и{х, t) =X{x)T{t), (6)
где X (х) —функция только переменного ж, Т (t) —функция только
переменного t.
Подставляя предполагаемую форму решения (6) в уравнение (4) и
производя деление обеих частей равенства на а^ XT, получаем
^т' _Х" _
где Л = const, так как левая часть равенства зависит только от ^, а
правая — только от х.
Отсюда следует, что
X" + ЛХ = О, (8)
Г+ а^ЛГ = 0. (80
Граничные условия (5) дают
X (0) =0, X (О = 0. (9)
Таким образом, для определения функции X (х) мы получили задачу
о собственных значениях (задачу Штурма — Лиувилля)
X'' + ЛХ = О, X (0) =0, X (О = О, (10)
исследованную при решении уравнения колебаний в гл. П, § 3, п. 1. При
этом было показано, что только для значений параметра Л, равных
А„=(^)' (п = 1,2,3,...), (11)
существуют нетривиальные решения уравнения (8), равные
Хп{х) =sin™x. (12)
Этим значениям Л^ соответствуют решения уравнения (8')
T„(i) = C„e-'^'^"*, (13)
где Сп — не определенные пока коэффициенты.

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 211
Возвращаясь к основной вспомогательной задаче, видим, что
функции
Un (ж, t) = Хгг {Х) Тгг (t) = Сп e'^^^^' sin ^ X (14)
ЯВЛЯЮТСЯ частными решениями уравнения (4), удовлетворяющими
нулевым граничным условиям.
Обратимся теперь к решению задачи (I). Составим формально
ряд
ОО о
и (ж, t) = 2Z^^ ^~ ^ ^ sin — X. (15)
Функция U (ж, t) удовлетворяет граничным условиям, так как им
удовлетворяют все члены ряда. Требуя выполнения начальных условий,
получаем
сю
ip[x) = и (ж, 0) = 2_\ С'п sin —- ж, (16)
т. е. Сп являются коэффициентами Фурье функции (р (ж) при
разложении ее в ряд по синусам на интервале (О, /):
Сп — ^п
■ J^iOsin'^^dC (17)
Рассмотрим теперь ряд (15) с коэффициентами Сп,
определяемыми по формуле (17), и покажем, что этот ряд удовлетворяет всем
условиям задачи (I). Для этого надо доказать, что функция и{х, t),
определяемая рядом (15), дифференцируема, удовлетворяет уравнению
в области 0<ж</, ^>0 и непрерывна в точках границы этой области
(при ^ = О, ж = О, X = I).
Так как уравнение (4) линейно, то в силу принципа суперпозиции
ряд, составленный из частных решений, также будет решением, если
он сходится и его можно дифференцировать почленно дважды по ж и
один раз по t (см. лемму в гл. II, § 3, п. 3). Покажем, что при t ^ i > О
(i— любое вспомогательное число) ряды производных
сю r-w СЮ r-wO
EOUn v^ O^Un
dt ^ dx^
СХОДЯТСЯ равномерно. В самом деле,
ди
dt
С.(^) aVв-(V)^^^Чin^ж < |С.|(^) .aVe-(V)^^^^
В дальнейшем будут сформулированы дополнительные
требования, которым должна удовлетворять функция ^{х). Предположим
14*

212
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
[ГЛ. HI
сначала, что ^{х) ограничена: |(/^(ж)| <М. Тогда
\Сп\ = I
1 Ч^ {О sin ™
idi
<2М,
откуда следует, что
I ди
dt
и аналогично
дЧп
дх^
< 2М (j) о?п^ е" (т^) ''^* для tr^t
<2м(^)'п2е-(^)'<''* для t^t.
Вообще
<2М
(у)
"'^'.п-^^^.а-^.е-'-^''"'-'
\^fa4
для f^ 1.
I di^ дх^ I
Исследуем сходимость мажорантного ряда Yl^=i ^п, где
По признаку Даламбера этот ряд сходится, так как
- (х)^а^ (n^+2n+l)f
(15')
lim
n—>-CXD
«n+1
= lim
n—>-CXD
(n + 1)^ e"
n^
= lim ( 1 +
ix^
(f) a2(2n+l)f ^Q^
Отсюда вытекает возможность почленного дифференцирования ряда
(15) любое число раз в области t ^ i > 0. Далее, пользуясь принципом
суперпозиции, заключаем, что функция, определенная этим рядом,
удовлетворяет уравнению (4). В силу произвольности i это имеет место
для всех ^ > 0. Тем самым доказано, что при ^ > О ряд (15)
представляет функцию, дифференцируемую нужное число раз и
удовлетворяющую уравнению (4) '^К
Если функция (f (х) непрерывна, имеет кусочно-непрерывную
производную и удовлетворяет условиям (/? (0) = О и (р (1) = О, то ряд
(15)
^ 2 2,
\-^ ^ (T^riY^^. . 7ГП
n=l
^ При доказательстве того, что ряд (15) удовлетворяет уравнению щ =
а Пхх при ^ > О, была использована только ограниченность коэффициентов
Фурье (7п, которая, в частности, будет иметь место для любой ограниченной
функции (^(ж).

А
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
213
определяет непрерывную функцию при t ^ 0.
Действительно, из неравенства
\un (ж, ^)| < \Сп\ (при ^ ^ о, о ^ ж ^ о
сразу же следует равномерная сходимость ряда (15) при t ^ О, О ^ ж ^
^ /, что и доказывает справедливость сделанного выше утверждения,
если учесть, что для непрерывной и кусочно-гладкой функции (f (х)
ряд из модулей коэффициентов Фурье сходится, когда ^ (0) = (р (1) = 0
(см. гл. II, § 3, п. 3).
Итак, задача нахождения решения первой краевой задачи для
однородного уравнения с нулевыми граничными условиями и
непрерывным, кусочно-гладким начальным условием решена полностью.
2. Функция источника. Преобразуем полученное решение (15),
заменяя Сп их значениями:
п=1
\-^ ^ {^п\^^2. . 7ГП
, (ж, t) = 22^n е~ У~) ^ Чш — ж =
^ I
L о
е W J ^ * 8ш
7ГП
п L П=1
2.2^ . 7ГП . 7ГП .
8Ш —;- X • 8Ш —- £,
viOdt
Изменение порядков суммирования и интегрирования всегда законно
при ^ > О в силу того, что ряд в скобках сходится равномерно по ^
при ^ > 0^).
Обозначим
о 9
П=1
2^2^ . 7ГП . 7ГП .
8Ш —- Ж • 8Ш —- ^.
(18)
Пользуясь функцией G (ж, ^, ^), можно представить функцию и (ж, ^)
в виде
u{x,t) = jG{x,^,t)ip{Od^-
о
(19)
Функция G (ж, ^, ^) называется функцией мгновенного
точечного источника или, более подробно, функцией температурного
влияния мгновенного точечного источника тепла.
^ Ряд ^ап, где an определяется формулой (15^), при q = О является
мажорантным для ряда, стоящего в скобках.

214 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Покажем, что функция источника G {х, ^, t), рассматриваемая
как функция ж, представляет распределение температуры в стержне
О ^ X ^ I в момент времени t, если температура в начальный момент
^ = О равна нулю и в этот момент в точке ж = ^ мгновенно выделяется
некоторое количество тепла (величину которого мы определим позже),
а на краях стержня все время поддерживается нулевая температура.
Выражение «количество тепла Q, выделяющееся в точке ^»
означает, как обычно, что мы имеем дело с теплом, выделившимся на
«небольшом» интервале около изучаемой точки ^. Изменение
температуры (ре (^), вызываемое появлением тепла около точки, будет, очевидно,
равно нулю вне интервала {£,—£,£,+£), на котором выделяется
тепло, а внутри этого интервала (р^ (^) можно считать положительной,
непрерывной и дифференцируемой функцией, для которой
ср I ^,{ade = Q, (20)
так как левая часть этого уравнения и представляет количество
тепла, вызвавшее изменение температуры на величину (р^ (О- Процесс
распространения тепла в этом случае определяется формулой (19):
щ{х,1) = j G{x,^,t)^,{Od^. (21)
о
Совершим теперь предельный переход при г —>- 0. Принимая во
внимание непрерывность G при ^ > О и равенство (20) и применяя
теорему среднего значения при фиксированных значениях ж, ^, будем
иметь
= G{x,e,t) [^uade = G{x,e,t)^, (210
J cp
где ^* —некоторая средняя точка интервала {^ — s^ ^-\- s)- В силу
непрерывности функции G (ж, ^, t) по ^ при ^ > О получаем
т / ^Ч Q ^/ /^ ^Ч Q 2^ _firn\2 2 . 7ГП . 7ГП .
hm Ue (ж, t) = — G{x, ^^ t) = — • - у e w J ^ ^ 8ш -- ж • 8ш -- ^.
£^0 Cp Cp I ^-^ I I
(22)
Отсюда следует, что G (ж, ^, t) представляет температуру в точке ж
в момент ^, вызванную действием мгновенного точечного источника

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 215
мощности Q = ср, помещенного в момент времени ^ = О в точке ^
промежутка (О, /).
Отметим следующее свойство функции G{x,^,t): функция
G{x, ^,t) ^0 при любых ж, ^ и ^ > 0. Действительно, рассмотрим
начальную функцию (ps (ж), обладающую перечисленными свойствами,
и соответствующее ей penienne (21'). Из неотрицательности
начального и граничных условий в силу принципа максимального значения
следует, что
Us (ж, t) ^ О
для всех О ^ X ^1 и ^>0. Отсюда, воспользовавшись формулой (21'),
имеем
Us{x,t) =С(ж, Г,^)— ^0 (при ^>0). (2Г')
ср
Переходя к пределу при г —>- О, из (21') получаем неравенство
G (ж, ^, ^) ^ О при О ^ ж, ^ ^ / и ^ > О,
которое и надо было доказать. Этот результат имеет простой
физический смысл. Однако установить его непосредственно из формулы (19)
было бы затруднительно, поскольку G {х, ^, t) представляется
знакопеременным рядом.
3. Краевые задачи с разрывными начальными условиями.
Изложенная выше теория относится к решениям уравнения
теплопроводности, непрерывным в замкнутой области О^ж^/, О ^t ^Т. Эти
условия непрерывности являются весьма ограничительными. В самом
деле, рассмотрим простейшую задачу об остывании равномерно
нагретого стержня при нулевой температуре на краях. Дополнительные
условия имеют вид
и (ж, 0) = uqj и (О, t) = и (/, t) = 0.
Если uo 7^ О, то решение этой задачи должно быть разрывным в
точках (О, 0) и (/, 0). Этот пример показывает, что поставленные выше
условия непрерывности начального значения и условия сопряжения его
с граничными условиями исключают из рассмотрения практически
важные случаи. Однако формула (19) дает решение краевой задачи
и в этом случае.
В приложениях часто пользуются формулами, выходящими за
границы условий их применимости, зачастую вообще не ставя вопрос
об условии применимости формул. Последовательное обоснование всех
формул было бы весьма громоздким и отвлекало бы внимание
исследователя от количественных и качественых сторон явления,
характерных для физической сущности процесса.
Однако мы считаем нужным, по крайней мере на простейших
примерах, дать обоснование математического аппарата, достаточное для
решения основных задач.

216 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Рассмотрим краевые задачи с кусочно-непрерывными
начальными функциями, не предполагая, что начальная функция сопряжена с
граничными условиями. Этот класс дополнительных условий является
достаточно общим для потребностей практики и достаточно простым
для изложения теории. Наша цель — доказать, что та же формула
(19) дает решение поставленной задачи. Проведем ее исследование в
несколько этапов. Сначала докажем следующую теорему:
Решение уравнения теплопроводности
щ = а^и^х {0<х<1, t>0), (4)
непрерывное в замкнутой области (О ^ ж ^ /, О ^ t ^ Т) и
удовлетворяющее условиям
u{0,t) =u{l,t) = 0, t^O, (5)
u{x,0) = (f{x), O^x^l, (2)
где ip {x) —произвольная непрерывная функция^ обращающаяся в нуль
при ж = О, ж = /, определено однозначно и представляется формулой
и (ж, t)
lG{x,^,t)<p{OdC (19)
Эта теорема была доказана выше в предположении дополнительного
условия о кусочно-непрерывной дифференцируемости функции (f (х).
Освободимся от этого условия. Рассмотрим последовательность
непрерывных кусочно-дифференцируемых функций (рп (х) {(рп (0) =
= V^n (О — 0)? равномерно сходящуюся к ^{х). (В качестве (рп{х)
можно выбрать, например, функции, представимые ломаными
линиями, совпадающими с (р (х) в точках 1к/п, /;; = О, 1, 2, ..., п.)
Функции Un (ж, t), определяемые формулой (19) через (рп (ж),
удовлетворяют всем условиям теоремы, так как (рп (ж) удовлетворяют условию
кусочной дифференцируемости. Эти функции равномерно сходятся и
определяют в пределе непрерывную функцию u{x,t). В самом деле,
для любого е можно указать такое п (е), что
\^П1 (х) - (Рп2 {х)\ < е (О ^ ж ^ /), если ni, П2 ^ п (г),
так как эти функции по условию сходятся равномерно. Отсюда в силу
принципа максимальных значений следует также, что
\uni{x,t) — Un2{x,t)\ < е (о ^ ж ^/, о ^ ^ ^ Т), если П1,П2^п(г),
что и доказывает равномерную сходимость последовательности
функций Un {х, t) К некоторой непрерывной функции и{х, t).
Если мы, фиксировав точку (ж, ^), перейдем к пределу под знаком
интеграла, то получим, что функция
u{x,t) = lim Un{x,t) = lim / G{x,^,t) (pn{0 d^ = / G{x,^,t) ^{^) d^
n—>-CXD n—>-CXD J J

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 217
непрерывна в замкнутой области О^ж^/, О ^ t ^ Т и
удовлетворяет начальному условию (2). В силу примечания на с. 212 нетрудно
убедиться, что она также удовлетворяет уравнению (4) при ^ > 0.
Доказательство теоремы закончено.
Формула (19) дает единственное непрерывное penienne
рассматриваемой задачи.
Обратимся к доказательству теоремы единственности для
случая кусочно-непрерывной начальной функции «^(ж), не
предполагая, что эта функция сопряжена с граничными условиями.
Функция, непрерывная в области ^ > О, удовлетворяющая уравнению
теплопроводности
щ = а Uxx (4)
в области О < ж < /, ^ > О, нулевым граничным условиям
и {О, t) =u{l,t) = 0 (5)
и начальному условию
и{х,0) = >р{х), (2)
определена однозначно, если:
1) она непрерывна в точках непрерывности функции ^ (х)]
2) ограничена в замкнутой области О^ж^/, О ^ t ^ to, где to —
произвольное положительное число.
Предположим, что такая функция существует. Очевидно, что в силу
предпЕССтвующей теоремы она может быть представлена в области t > i
формулой
u{x,t)= G (ж, ^,t-i) if^ (С) d^ {t>t> 0) (190
0
при любом ij где i—вспомогательное значение,
0<^^^, (рт (х) = u{xjt).
СоверпЕим предельный переход в этой формуле при ^ ^ О, сохраняя ж
и t неизменными. Покажем ^, что возможен переход под знаком интеграла
^ Доказываемая ниже теорема является частным случаем теоремы
Лебега о возможности перехода к пределу под знаком интеграла, если
последовательность функций Fn (ж) почти всюду сходится к предельной
суммируемой функции i^ (ж) и если эта последовательность ограничена суммируемой
функцией. Это доказательство приводится, чтобы избежать пользования
теоретико-множественными понятиями. Если воспользоваться теоретико-
множественными понятиями, то соверпЕСнно аналогично можно доказать
теорему о том, что penienne уравнения теплопроводности и{х, t)j
удовлетворяющее нулевым граничным условиям, однозначно определено:
1) если и{х, t) ^ F{x), где F (ж) — некоторая суммируемая функция, и
2) если почти всюду
lim и (ж, t) = ш (ж),
где (^ (ж) — заданная начальная суммируемая функция.

218
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
[ГЛ. HI
и, следовательно, функция и{х, t) представима в виде интеграла:
u{x,t) = Jg (ж, с, t) ^ (О d^ [^ (О = и (С, 0)],
о
(19)
однозначно ее определяющего.
Пусть Ж1, Ж2, ..., Хп — точки разрыва функции ^{х). Полагая жо =
= О и Жп+1 = I (рис. 38) и беря замкнутые отрезки Ij. = {х : xj. -\- 6 ^ х ^
^ xj^j^i — ^ } (А; = О, 1, ..., п), где 6 — некоторое фиксированное достаточно
малое число, нетрудно убедиться, что подынтегральная функция из (19 )
i
Хк — ^ Xk + S
2;о=0
Xk^i-8 Xk^i+6 Xn-\-i-S
^
^k-i
Xk
Рис. 38
^k-\-i
Xn^l= I
равномерно сходится к подынтегральной функции из (19) на всяком отрезке
/j^ (А; = О, 1, 2, ..., п). На отрезках Ij. = {х : Х}. — 6 ^ х ^ Х}. -\- 6} {к =
= 1, 2, 3, ..., п), Iq = {х : хо ^ X ^ хо -\- 6} и /п+1 = { ж : Xn-\-i — S ^ х ^
^ Хп-\-1 } подынтегральные выражения в (19) и (19 ) ограничены некоторым
числом N при любом t {О ^ t ^ to) в силу предположенной
ограниченности функции и{х, t) ив силу непрерывности G (ж, ^, t) при О ^ ^ ^ /, ^ > 0.
Представим разность интегралов (19) и (19 ) в виде суммы 2п + 3
интегралов, взятых по /j^ (А; = О, 1, ..., п) и /j^ (А; = О, 1, ..., п + 1). Возьмем
^^
1
2п + 3 4iV'
Тогда
1 [G{x, С, t-t)^^ (О -G{x, С, t)^{0] d^
^
2п + 3
Можно выбрать t настолько малым, что
\G{x,^,t-i)^^{0-G{x,^,t)^{0\ <
^Т'о—Г^ ^^^ *^* "^ ^к (А; = О, 1, ..., п).
I [G{x, С, t-i)^^ (О -G{x, С, t)^{0] d^ <
2n + 3
для t ^t (A; = о, 1, ..., n).

А
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
219
Отсюда следует неравенство
1 [G {х, ^,t-i) cpj (С) - G {х, С, t) ^ (О] di
< е для t ^ tj
доказывающее законность перехода к пределу при ^ ^ О под знаком
интеграла. Таким образом, если существует функция и{х, t), удовлетворяющая
условиям теоремы, то она представима в виде (19), что и доказывает
единственность такой функции.
Докажем теперь, что формула (19) представляет
ограниченное решение уравнения (4),
удовлетворяющее условиям (2) для лю- ^|
бой кусочно-непрерывной функции
(/?(ж), непрерывное во всех точках
непрерывности (f{x).
Эту теорему мы докажем в два
приема. Докажем, что она верна,
если (р (х) — линейная функция:
^{х)
сх.
{2')
Рис. 39
Рассмотрим последовательность вспомогательных непрерывных
функций (рис. 39)
^п (х) = <
СХ для о ^ X ^ I
а{1 — х) для М 1 —
1-1
п
<x<L
а
(п - 1) с.
Функции Un (ж, t), определенные при помощи формулы (19) для
(Рп (ж), ЯВЛЯЮТСЯ непрерывными реп1ениями уравнения
теплопроводности с нулевыми граничными условиями и начальными условиями
Unix, 0) = (fn{x).
Так как
^п (х) ^ (fn+1 (х) {О ^Х ^1),
то в силу принципа максимальных значений
Unix, t) ^ Un+1 (ж, t).
Функция Uq (ж) = сх является непрерывным решением уравнения
теплопроводности. В силу принципа максимального значения
Un{x, t) ^ ^/о(ж),
так как это неравенство имеет место при ж = 0, х = I и ^ = 0. Таким
образом, Un (ж, t) есть монотонно не убывающая последовательность.

220 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
ограниченная сверху функцией Uq (ж), откуда следует, что эта
последовательность сходится. Нетрудно видеть, что
и {х
, t) = lim Un (ж, t) = lim I G (ж, ^, t) (fn (0 d^ =
n—>-CXD n—>-CXD J
0
так как переход к пределу под знаком интеграла законен. В силу
примечания на с. 212 эта функция удовлетворяет уравнению и нулевым
граничным условиям при ^ > 0. Докажем, что эта функция
непрерывна при ^ = О для О ^ ж ^ L Пусть х^ < I. Выберем п так, чтобы
жо < / (1 — 1/п). В этом случае (рп (^о) = f^o (^о)- Принимая во
внимание, что
Un (ж, t) ^ и (ж, t) ^ Uo (х)
lim Un (ж, t) = lim Uq (x) = (p (xq),
заключаем, что существует предел
lim и (ж, t) = (f (жо),
ж—>-жо
не зависящий от способа стремления ж —>- жо и ^ —>- 0. Отсюда и
следует непрерывность и (ж, t) в точке (жо, 0). Эта функция ограничена,
так как она не превосходит Uq (ж). Итак, для (р (ж) = сх теорема
доказана.
Заменив ж на / — ж, убеждаемся в том, что теорема верна для
(fix) = b{l-x). (Г)
Отсюда следует, что она верна для любой функции типа
(р{х) = В -\- Ах,
так как подобная функция может быть получена суммированием (2')
и (2''). Далее, отсюда следует также, что теорема верна для любой
непрерывной функции без предположения о том, что (/? (0) = (/?(/)= 0.
В самом деле, любую функцию (f (ж) такого типа можно представить
в виде
<^(x) = [<^(o) + y(^(0-<^(o))]+v(x),
где слагаемое в квадратных скобках — линейная функция, а ф (х) —
непрерывная функция, обращающаяся в нуль на концах отрезка:

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 221
ф (0) = ф (1) =0. Так как мы убедились уже в том, что для
каждого слагаемого теорема применима, то отсюда следует, что теорема
верна и для (р (х).
Обратимся теперь к доказательству теоремы для произвольной
кусочно-непрерывной функции ^{х). Формула (19) и в этом случае
определяет решение, удовлетворяющее уравнению и нулевым
граничным условиям.
Пусть точка xq — какая-либо точка непрерывности функции
^{х). Докажем, что для любого е можно найти S{e), такое, что
\и (ж, t) — (р {хо)\ < г, если \х — хо\ < S (е) и t < S (е). В силу
непрерывности функции (f (х) в точке xq существует r]{s), такое, что
\(f (х) - (f {хо)\ ^ - для \Х -Хо\ <Г]{€),
откуда
^Ы) - ^^^{х) ^(f{xo) + - для \х -хо\ <г]{е). (23)
Построим вспомогательные непрерывные функции (f (х) и (f (х):
(а)
Тр{х) = (/?(жо) + - для \х - жо| < ту (г).
2
^(ж) ^ ^{х) для \х - жо| > ту (г).
^(ж) = (/?(жо) - - для |ж-жо| < ту (г),
(/? (ж) ^ (/? (ж) для |ж - жо| > ту (г).
(б)
Па интервале |ж —жо|>7у(е) функции (/? (ж) и (/? (ж)
удовлетворяют только условиям (а) и (б), а в остальном произвольны. В силу
неравенств (23)
^(ж) ^ (/?(ж) ^^(ж). (24)
Рассмотрим функции
о

222 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Ввиду непрерывности функций ^(ж) и (f (х) функции u{x,t) и
и{х, t) непрерывны в точке жо, т. е. найдется такое 5{е)^ что
|й(ж, t) -Тр{х)\ ^ -,
^ для \х-х^\<5{е), t<5{e),
\и{х, t) -^{х)\ ^ -
откуда
U (ж, ^) ^ (/? (ж) + - = (/? (жо) + г,
М (ж, ^) ^ ^ (ж) - - = (/? (жо) - е
для |ж - жо| < (5(e), ^<(5(г).
В силу неотрицательности функции G (ж, ^, ^) из формулы (24)
следует, что
и (ж, t) ^ и (ж, t) ^ й (ж, ^). (25)
Отсюда получаем неравенства
(р (жо) - г ^ U (ж, ^) ^ (/? (жо) + е для |ж - жо| < (5 (е), t < S (е)
или
|и (ж, t) - (р (жо)| < е для |ж - жо| < (5 (е), t < S (е),
что и требовалось доказать. Ограниченность функции \и{х, t)\
следует из (25) и из ограниченности функций й (ж, ^) и и (ж, ^). Этим
теорема доказана.
4. Неоднородное уравнение теплопроводности. Рассмотрим
неоднородное уравнение теплопроводности
щ = а^и^х + / (ж, ^) (1)
с начальным условием
и (ж, 0) = О (26)
и граничными условиями
и(0, ^)=0,
и(/, ^)=0. ^ ^
Будем искать решение этой задачи и{х, t) в виде ряда Фурье по соб-
/-1-14 . 7ГП
ственным функциям задачи (11), т. е. по функциям sm —- ж:
7ГП
iLn [t) sin
п=1
\ (ж, ^) = ^ Un (^) sin — ж, (27)

А
МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
223
считая при этом t параметром. Для нахождения функции и{х, t) надо
определить функции Un (t). Представим функцию f {х, t) в виде ряда
сю
/ (^. t) = ^fn (t) sin — ж,
n=l
где
fn{t) = ] j f{i,t)^\n'^idi.
(28)
Подставив предполагаемую форму решения в исходное уравнение (1),
будем иметь
сю г
Е, 7ГП I /7ГП\
п=1 ^
a'un it) + йп (t) - fn it) } = 0.
}-
Это уравнение будет удовлетворено, если все коэффициенты
разложения равны нулю, т. е.
/ 7Г77, \ ^
unit) = -a^[—j Unit) + fn(t). (29)
Пользуясь начальным условием для и (ж, t)
сю
и (ж, 0) = > Un (0) sm —- ж = О,
п=1 ^
получаем начальное условие для Un (t):
Un (0) = 0. (30)
Решая обыкновенное дифференциальное уравнение (29) с нулевым
начальным условием (30) ^\ находим
t
u„{t) = le-i^f-'^'-^^U{T)dT. (31)
О
Подставляя выражение (31) для Un{t) в формулу (27), получаем ре-
Hienne исходной задачи в виде
и (ж, t) = Y^
п=1
г
|е-(^)'<'^ (*-)/„ (г) dr
. 7ГП
8Ш —- Ж.
(32)
^ См. текст, набранный мелким нхрифтом в конце п. 4 § 3 гл. П.

224 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Воспользуемся выражением (28) для /^ (г) и преобразуем
найденное penienne (32):
t I
= I l'G{x,^,t-T)f{^,T)d^dT, (33)
0 0
где
G (ж, ^, ^ - r) = - 2]] e- y—) ^ ^^-^) sin — ж • sin — ^ (34)
n=l
совпадает с функцией источника, определяемой формулой (18).
Выясним физический смысл полученного решения (33)
t I
u{x,t) = I Jg {х, ^,t-T)f (С, г) d^dr.
о о
Предположим, что функция / (^, г) отлична от нуля лип1ь в
достаточно малой окрестности точки Mq {^q, tq)
Со ^ С ^ Со + А^, То ^ г ^ Го + Аг.
Функция F (С, т) = ср f {^, т) представляет плотность тепловых
источников. Общее количество тепла, выделяющееся на отрезке (О, /)
за все время действия источника (т. е. за Аг), равно
го+Аг Со+АС
Q= I j cpf{i,T)didT. (35)
^0 Со
Применим теорему о среднем к выражению
t I
u{x,t) = I Jg {х, ^,t-T)f (С, г) d^dr =
о о
ro+Ar Со+АС
= 11 G{x,i,t-T)f{i,T)didT = G{x,lt-f)^=u{x,t),
^0 Со
где
Со < С < Со + АС, Го < f < Го + Аг.

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 225
Перейдя к пределу при А^ —>- О и Аг —>- О, получим функцию
и (ж, t) = lim й{х, t) = — G (ж, ^о, ^ — '^о), (36)
АС^о ср
которую можно интерпретировать как функцию влияния мгновенного
источника тепла, сосредоточенного в точке ^о в момент tq .
Если известна функция Q/{cp) • G {х, ^, t — т),
представляющая действие единичного мгновенного сосредоточенного источника,
то действие источников, непрерывно распределенных с плотностью
F (ж, t) = cpf{x, t), должно выражаться формулой (33), как это
непосредственно следует из физического смысла функции G (ж, ^, t — т).
Итак, температурное влияние тепловых источников, действующих
в области (^0 5 Со + Д^) X ('^"о, т^ + Аг), дается выражением
С(х,^,*-г)/(^,г)ДеДг (^^=/(е,г)А^Аг
Если источники распределены непрерывно, то, суммируя тепловые
влияния источников, действующих во всей области 0^^^/, О^г^^,
после предельного перехода при А^ —>- О и Аг —>- О получим
t I
u{x,t) = I Jo (ж, С, ^ - г) / (С, г) d^dr.
о о
Таким образом, исходя из физического смысла функции источника
G (ж, С, t), можно было бы сразу написать выражение (33) для
функции, дающей решение неоднородного уравнения.
Имея форму, в которой должно представляться решение задачи,
можно исследовать условия применимости этой формулы в отношении
функции / (С, г). Мы не будем проводить этого исследования.
Мы рассматривали здесь неоднородное уравнение с нулевыми
начальными условиями. Если начальное условие отлично от нуля, то к
этому решению следует прибавить решение однородного уравнения с
заданным начальным условием и (ж, 0) = (f (ж), найденное в п. 1.
5. Общая первая краевая задача. Рассмотрим общую первую
краевую задачу для уравнения теплопроводности.
Найти решение уравнения
щ = a^Uxx + / (ж, t) (1)
с дополнительными условиями
и(ж, 0) = (/.(ж), (2)
u(0,^)=/ii(^),l
15 А. Н. Тихонов, А. А. Самарский

226 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Введем новую неизвестную функцию v (х, t):
и{х, t) = U{x, t)+v{x, t), (37)
представляющую отклонение от некоторой известной функции U{x,t).
Эта функция V {х, t) будет определяться как penienne уравнения
f{x,t) = f{x,t)-[Ut-a^U,,],
с дополнительными условиями
V (х, 0) = ф (ж), (р{х) = ip (ж) — и (х, 0);
г; (О, t) = Ml (t), Ml (t) = Ml (t) - U (0, t);
V {I, t) = M2 (t), M2 (t) = M2 (t) - и {I, t).
Выберем вспомогательную функцию [/ (ж, t) так, чтобы
Mi(i)=0 и M2(i)=0,
для чего достаточно положить (см. гл. II, § 3, п. 5)
[/(ж, i)=MiW + y[/*2(i)-MiW]-
Таким образом, нахождение функции и (ж, ^), дающей penienne общей
краевой задачи, сведено к нахождению функции v{x^ t), дающей
penienne краевой задачи с пулевыми грапичпыми условиями. Метод
нахождения функции V (х, t) дан в п. 4.
Изложенная вьппе формальная схема ре1пения задач при наличии
неоднородностей в уравнении и граничных условиях не всегда удобна
для представления искомой функции и (ж, t). Трудности,
возникающие при нахождении вспомогательной функции v{x^ t), зависят от
функции и {х, t), от которой ищется отклонение.
В частности, для задач со стационарными неодпородностями
удобнее выделять стационарное решение и искать отклонение от этого
решения (см. гл. II, § 3, п. 6).
Рассмотрим, например, задачу для ограниченного стержня (О, /),
концы которого поддерживаются при постоянных температурах щ и
ui:
Щ = 0?
и (ж, 0) =
и (0, t)
и{1, t) --
'^XXl
:(/?(ж).
= -^0,
= U1.
Решение будем искать в виде суммы
и (ж, t) = й{х) -\- V (ж, ^),

§ 2] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 227
где й (х) —стационарная температура, а v {х, t) —отклонение от
стационарной температуры.
Для функций й (ж) и V (х, t) будем иметь условия
й''= О, vt = a'^Vxx;
й (0) = По, V (ж, 0) = (f{x) — й (х) = (fi (ж);
й{1) =ui, v{0, t) =v{l, t) =0.
Отсюда находим
X
й{х) = щ -\- - {ui - щ).
функцию V (х, t), определяемую начальным условием и
однородными граничными условиями, без труда находим методом разделения
переменных.
Зад ачи
1. Вывести уравнение для процесса нагревания однородной тонкой
проволоки постоянным электрическим током, если на ее поверхности
происходит теплообмен с окружающей средой.
2. Вывести уравнение диффузии в среде, равномерно движущейся в
направлении оси X со скоростью W. Рассмотреть случай одной независимой
переменной.
3. Исходя из уравнений Максвелла, предполагая Ех = Ez = О, Hz = О
и пренебрегая токами смещения, показать, что в однородной проводящей
среде составляющая электромагнитного поля Еу удовлетворяет уравнению
д'^Еу _ 47га дЕу
где а — проводимость среды, с — скорость света. Вывести уравнения для
Нх.
4. Дать физическое истолкование следующих граничных условий в
задачах теплопроводности и диффузии:
а) u{0,t) = 0, б) ux{0,t) = 0,
в) ux{0,t)-hu{0,t) = 0,
ux{l,t)-hhu{l,t) = 0 ^ ^'
5. РепЕить задачу об остывании равномерно нагретого однородного
стержня при нулевой температуре на концах, предполагая отсутствие
теплообмена на боковой поверхности.
6. Начальная температура стержня п (ж, 0) = по = const при О < ж < /.
Температура концов поддерживается постоянной: и (О, t) = ui^ и (/, t) = U2
при О < ^ < оо. Найти температуру стержня, если теплообмен на боковой
поверхности отсутствует. Найти стационарную температуру.
7. РепЕить задачу 6 при следующих граничных условиях: на одном
конце поддерживается постоянная температура, другой конец теплоизолирован.
15*

228 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
8. Решить задачу о нагревании тонкой однородной проволоки
постоянным электрическим током, если начальная температура, граничная
температура, а также температура окружающей среды равны нулю.
9. Цилиндр длины /, заполненный воздухом при давлении и
температуре окружающей среды, открывают с одного конца в начальный момент
времени, и из окружающей атмосферы, где концентрация некоторого газа
равна По, начинается диффузия газа в цилиндр. Найти количество газа,
диффундировавпЕСго за время t, если начальная концентрация газа в
цилиндре равна нулю.
10. РепЕить задачу 9 в предположении, что левый конец цилиндра
закрыт полупроницаемой перегородкой.
11. РепЕить задачу об остывании однородного стержня с
теплоизолированной боковой поверхностью, если его начальная температура п (ж, 0) =
= ср (ж), а на концах происходит теплообмен со средой нулевой температуры.
Рассмотреть частный случай ср (ж) = uq.
12. РепЕить задачу 11, предполагая, что температура окружающей
среды равна Uq.
13. РепЕить задачу 11, считая, что на боковой поверхности происходит
теплообмен со средой, температура которой:
а) равна нулю;
б) постоянна и равна ui.
14. Найти установивпЕуюся температуру стержня, пренебрегая
теплообменом на боковой поверхности и считая, что один конец стержня
теплоизолирован, а ко второму концу подводится поток тепла, гармонически
меняющийся во времени.
15. РепЕить задачу 14, считая, что один конец стержня имеет
нулевую температуру, а температура второго конца гармонически меняется во
времени.
16. Стержень (О, /) составлен из двух однородных кусков одинакового
поперечного сечения, соприкасающихся в точке ж = жд и обладающих
характеристиками ai, ki и а2, к2 соответственно. Найти установивпЕуюся
температуру в таком стержне (тепловые волны), если один конец стержня
(ж = 0) поддерживается при нулевой температуре, а температура второго
меняется синусоидально во времени.
17. Левый конец составного стержня из задачи 16 поддерживается при
температуре, равной нулю, а правый — при температуре п (/, t) = ni,
начальная же температура стержня равна нулю. Найти температуру п (ж, t)
стержня в регулярном режиме (первый член разложения).
18. Найти температуру п (ж, t) стержня, начальная температура
которого равна нулю, а граничные условия имеют вид
п(0, t) = Лe~'^^ и{1, t) = Б,
где А^ В ж OL > О — постоянные.
§ 3. Задачи на бесконечной прямой
1. Распространение тепла на бесконечной прямой.
Функция источника для неограниченной области. Рассмотрим на
бесконечной прямой задачу с начальными данными (задачу Коши).

§ 3] ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 229
Найти ограниченную функцию и (ж, ^), определенную в области
— (Х)<ж<(Х), t ^ О, удовлетворяющую уравнению
теплопроводности
Щ = 0,'^Uxx, — ОО < X < оо, t > О, (1)
и начальному условию
и (ж, 0) = (/? (ж), — 00 < ж < 00. (2)
Если (f (х)—непрерывная функция, то выполнение начального
условия будем понимать в том смысле, что функция и{х, t) непрерывна
при ^ = О, т. е.
lim и (ж, t) = (р (жо).
Как мы видели в § 1, п. 7, penienne уравнения теплопроводности
однозначно определяется своими начальными условиями, если оно
ограничено. Поэтому в формулировку теорем вводится условие
ограниченности.
Дадим сначала формальную схему решения поставленной задачи,
основанную на разделении переменных.
Будем искать ограниченное нетривиальное решение уравнения
(1), представимое в виде произведения
u{x,t) =X{x)T{t). (3)
Подставляя выражение (3) в (1), получаем
X" _Г _ 2
X - г - "-^ '
где Л^—параметр разделения. Отсюда следует
Т' + а^Л^Г = О, (4)
X" + Х^Х = 0. (5)
Решая уравнения (4) и (5), найдем частные решения уравнения (1)
вида
ил(ж, ^) = Л(Л)e-^'^'^±^^^ (6)
удовлетворяющие условию ограниченности. Здесь Л — любое
вещественное число: — 00 < Л < оо; поэтому в (6) возьмем знак «плюс»
и образуем функцию
и (ж
сю
, i) = I А{Х) 6-»'^'*+»^=^ dX. (7)

230 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Если производные, входящие в уравнение (1), можно вычислять путем
дифференцирования под знаком интеграла (7), то функция (7),
очевидно, будет удовлетворять уравнению (1) как суперпозиция частных
реп1ений этого уравнения.
Требуя выполнения начального условия при ^ = О, будем иметь
сю
f А (Л) е*^^ dX. (8)
(^ (ж) = / А (Л) е'^^ dX.
— СЮ
Воспользуемся теперь формулой обратного преобразования интеграла
Фурье
сю
^(А) = ^ l\{Oe-'^idC (9)
— СЮ
Подставляя (9) в (7) и меняя порядок интегрирования, получим
сю / сю \
u{x,t) = ^ f I f <р{0 e-'^^ di I e-«'^'*+»^=^ dX =
— СЮ \— СЮ /
СЮ / СЮ \
= ^ / / e-'^'^'^+^'^^-^'^A ^piOd^. (10)
— СЮ \— СЮ /
Внутренний интеграл в (10) равен-"^^
1 7 2,2,^.w .4 1 (^-O^
_L ^-a М+гХ(.-О^Х=^^=е~^^^. (11)
27T J 2л/^^
— сю
Подставляя (11) в (10), приходим к интегральному представлению
искомого решения
сю
и (ж, t) =
G{xA.t)^{Odi. (12)
где
1 {x-iY
G{x,^,t) = -^=e 4а2, . (13)
Функцию G{x, ^, t), определяемую формулой (13), часто называют
фундаментальным решением уравнения
теплопроводности.
^ Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.

А.
ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
231
Непосредственной проверкой можно убедиться в том, что функция
G (х, t t-to) =
Q
ср2 у^тга^ (^ — ^о)
g 4а2 {t-tQ)
(13')
представляет температуру в точке х в момент времени ^, если в
начальный момент времени ^ = ^о в точке ^ выделяется количество
тепла Q = ср.
Функция G (ж, ^, t — to) удовлетворяет уравнению
теплопроводности по переменным (ж, t)'^\ что можно проверить непосредственным
дифференцированием.
Количество тепла, находящееся на оси х в момент t > to, равно
ср
сю сю
/ G{x, ^,t- to) dx = —= I
g 4a2 {t-tQ)
dx
2 y^o? {t - to)
_Q
СЮ
7Г J
da = Q = cp,
так как
сю
/
e '^ da = \pK
x-i
da
dx
\ 2 Va2 (t - to)' 2 ^a^(t-to)) '
Таким образом, количество тепла на нап1ей прямой не меняется с
течением времени. Функция G (ж, ^, t — to) зависит от времени только
через аргумент в = а^ {t — to), так что эту функцию можно записать
^ В самом деле,
Gx
х-^
{x-iY
2л/^ 2[а2(^-^о)]^/2
^хх —
Gt
2^
1
+
{--о'
2 [a^{t-to)fl^ A[a^{t-to)P
а" а" {х-О'' ■
2[а2(^-^о)]'/2 A[aHt-to)P^\
{x-iY
g 4a^(t-tQ)^
Gt — а Gxx-

232
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
[ГЛ. HI
в виде
G =
40
(13^0
2л/^ л/^
На рис. 40 изображен график функции G в зависимости от х для
различных значений в. Почти вся площадь, ограниченная этой кривой,
находится над промежутком
где е — сколь угодно малое число, если только в = а^ {t — to) —
достаточно малое число. Величина этой площади, умноженная на ср.
i
3,0
2,о/
Ко
iG
1^1 = 0
■--ч|У2 =
01
= 0,05
N^3 = 0,1-
^4 = 0,5
х-С
-2,0 -1,5 -1,0 -0,6 -0,2 О 0,2 0,6 1,0 1,5
Рис. 40
2,0
равна количеству тепла, подведенному в начальный момент. Таким
образом, для малых значений ^ — ^о > О почти все тепло
сосредоточено в малой окрестности точки ^. Из сказанного выше следует, что в
момент ^0 все количество тепла помещается в точке ^.
Рассматривая изменение температуры в фиксированной точке х =
= ^ + /г с течением времени при /г = О, т. е. при ж = ^, получим
Таким образом, температура в этой точке, где выделяется тепло, для
малых в неограниченно велика.

А.
ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
233
Если X ^ ^, т.е. h ^ О, то функция G представляется в виде
произведения двух множителей
1 1
Gx^^ -
4в
[2у^ v^J
Второй сомножитель меньп1е единицы: при больп1их в он
приблизительно равен 1, при малых в он близок к 0. Отсюда следует, что
Охф^ ^ Gx=^ для больп1их в, Gx^^ ^ Gx=^ для малых в. Чем мень-
Hie /г, т. е. чем ближе ж к ^, тем больп1е второй множитель. Графики
функций Gx=^ и Gx^^ при /^2 < hi приведены на рис. 41.
Нетрудно видеть, что
lim Схфр = 0.
Раскрывая неопределенность, находим
lim
-м
-—— lim
2д/7Г 6*^0
%
4i92
6 4^
0.
^^0 2 0F v^
Формула (13') показывает, что во всякой точке х температура,
создаваемая мгновенным точечным источником,
действующим в начальный момент ^ = О,
отлична от нуля для сколь угодно малых моментов
времени. Подобный факт можно было бы
интерпретировать как результат бесконечно
быстрого распространения тепла (бесконечная
скорость) . Однако это противоречит молекулярно-
кинетическим представлениям о природе тепла.
Такое противоречие получается в связи с тем,
что выше при выводе уравнения
теплопроводности мы пользовались феноменологическими Рис. 41
представлениями о растекании тепла, не учитывающими
инерционность процесса движения молекул.
Теперь выясним условия применимости формулы (12).
Докажем, что формула
и (ж, t)
{^-iY
.е 4a2t ^{^)di^
(120
называемая интегралом Пуассона, для любой ограниченной
функции |(/^(^)| < М представляет при ^ > О ограниченное решение
уравнения теплопроводности, непрерывно примыкающее при ^ = О к
(/? (ж) во всех точках непрерывности этой функции.
Докажем предварительно лемму (обобщенный принцип
суперпозиции).
Пусть функция U (ж, ^, а) по переменным (ж, t) удовлетворяет
линейному дифференциальному уравнению
L{U)=0

234 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
при любом фиксированном значении параметра а. Тогда интеграл
такэюе является решением того эюе уравнения L (и) = О, если
производные, входящие в линейный дифференциальный оператор L{U),
моэюно вычислять при помощи дифференцирования под знаком
интеграла.
Доказательство леммы крайне просто. Линейный
дифференциальный оператор L {U) представляет сумму производных функции U с
некоторыми коэффициентами, зависящими от ж и ^.
Дифференцирование функции U, по предположению, можно производить под знаком
интеграла. Коэффициенты также можно внести под знак интеграла.
Отсюда следует, что
L (и) = L (и (ж, t, а)) (р (а) da = О,
т. е. что функция и (ж, t) удовлетворяет уравнению L (и) = 0.
Напомним достаточные условия дифференцируемости под знаком
интеграла, зависящего от параметра.
Функция
b
F (ж) = / / (ж, а) da
а
при конечных пределах а и b дифференцируема под знаком интеграла,
если —— (ж, а) является непрерывной функцией переменных ж и а в
ох
области их изменения ^^.
Нетрудно видеть также, что функция
b
Fi (х) = f (ж, а) (f (а) da
при конечных пределах а ж Ь дифференцируема под знаком
интеграла при тех же условиях относительно функции f (х, а) и
произвольной, ограниченной (и даже абсолютно интегрируемой) функции (р (а).
Если пределы интегрирования бесконечны, то в этом случае требуется
равномерная сходимость интеграла, полученного в результате
дифференцирования подынтегральной функции по параметру '^^.
Эти же замечания относятся к кратным интегралам, зависящим
от параметров.
^ См. Будак Б. М., Фомин С. В. Кратные интегралы и ряды. М.,
1967.
^ См. там же.

§ 3] ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 235
Для линейных уравнений L (и) = О имеет место принцип
суперпозиции, заключающийся в том, что функция
п
и{х, t) = ^^СгЩ (ж, t),
представленная в виде суммы конечного числа частных реп1ений,
является также реп1ением уравнения. Если мы имеем penienne и (ж, ^,а),
зависящее от параметра, то интегральная сумма
^u{x,t,an)Cn {Сп = (f (an) Аа) (14)
также является решением уравнения L (и) = 0. Доказанная лемма, как
и лемма на с. 97, устанавливает условия, при которых предел суммы
(14), в нашем случае равный
ui.,t) = lui.,t,a)^ia)da,
также является решением уравнения L (и) = 0. С этой точки
зрения доказанную лемму, как и лемму на с. 97, естественно называть
обобщенным принципом суперпозиции.
Обратимся к изучению интеграла (12'). Докажем, во-первых, что
если функция (f (х) ограничена, |(/?(ж)| < М, то интеграл (12')
сходится и представляет ограниченную функцию. В самом деле.
1 Г 1 (^-О^
\u{x,t)\<M-^ / -у=е 4аЧ d^
OG
e-^^da = M (a= ^ ^
2VaH
так как
сю
/ e~^ da = д/тг-
Докажем далее, что интеграл (12') удовлетворяет уравнению
теплопроводности при ^ > 0. Для этого достаточно доказать, что
производные этого интеграла при ^ > О можно вычислять при помощи
дифференцирования под знаком интеграла.
В случае конечных пределов интегрирования это законно, так как
все производные функции
1 (х-О^
4a2t
2л/7гаЙ
при ^ > о непрерывны. Для возможности дифференцирования под зна-

236 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
ком интеграла при бесконечных пределах достаточно убедиться в
равномерной сходимости интеграла, полученного после
дифференцирования под знаком интеграла. Проведем это исследование на примере
первой производной по X.
Итак, для доказательства дифференцируемости функции (12) по
ж, а также равенства
t))9{0d^
достаточно убедиться в равномерной сходимости интеграла,
стоящего справа; при этом для установления дифференцируемости в точке
(жо, ^о) достаточно доказать равномерную сходимость интеграла в
некоторой области значений переменных, содержащей исследуемые
значения (жо, ^о), например в области
^1 ^ ^0 ^ ^2, \х\ ^ X.
Достаточным условием равномерной сходимости интеграла
(аналогичным признаку равномерной сходимости ряда) является
существование положительной функции F (^), не зависящей от параметров
(ж, t), которая мажорирует подынтегральную функцию:
^G{x,^,t)^p{0\^F{0, ^>х, ^<-х, (15)
и интеграл от которой сходится:
сю —XI
JFiOd^Koo, 1 FiOd^<<x>. (15')
XI — оо
Величина xi обозначает некоторое число, начиная с которого
выполняется неравенство (15).
Найдем оценку сверху для абсолютной величины
подынтегрального выражения в формуле для ди/дх:
1 \£-х\ (^-^)^
М \^\+х
при любых |ж|^ж и ti ^ t ^ t2' Нетрудно убедиться в сходимости
интегралов (15') от функции F{^). Интеграл
XI XI XI—X
(6 = 1^ - х)

§ 3] ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 237
сходится, так как под знаком интеграла стоит множитель типа (а^ +
-\-Ь)е ^^ . Отсюда заключаем, что
сю
ди
дх
I ^{x,^,t)<f{Od^.
Аналогично доказывается возможность вычисления всех
остальных производных под знаком интеграла. Тем самым доказано, что
функция (12') удовлетворяет уравнению теплопроводности.
Обратимся теперь к выяснению основного свойства интеграла
(12'), а именно докажем, что
и{х, t) ^ (р (хо) при ^ —>-о и ж —>- Жо
во всех точках непрерывности функции (р (х).
Итак, пусть (р (х) непрерывна в некоторой точке xq. Мы должны
доказать, что
lim и (ж, t) = (р (жо),
Т. е. каково бы ни было г > О, можно указать такое 5 (г), что
|и(ж, t) -(f{xo)\ < е,
коль скоро
|ж-Жо| <S{€) и 1^1 < S{€).
в силу предполагаемой непрерывности функции (р (ж) в точке жо
существует такое Г] (е), что
\(р (х) - (f {хо)\ < |, (17)
если только
|ж - Жо| < Г].
Разбивая промежуток интегрирования на части, представим
и{х, t) в виде суммы трех слагаемых:
XI Х2
— OO Xl
CXD
+ у-/= / ... d^ = ui{x,t) -\- U2 (ж, t) + Us (ж, t),
X2
где
Xl = xo - Г] и Ж2 = Жо + ту. (18)

238 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Главное слагаемое этой суммы U2 можно представить в виде
XI
Х2
XI
Интеграл Д вычисляется непосредственно:
Х2-Х
Х2 (х-е)'^ 2л/^
Ж1
7Г У Va^^ л/тг У
где
a = ;—, da = ;—. (19)
2л/^ 2л/^
При |ж — жо| < ?7 верхний предел положителен, а нижний —
отрицателен, и при ^ —>- О верхний предел стремится к + оо, а нижний к — оо.
Отсюда следует, что
lim /i = (f{xo).
X^-Xq
Таким образом, можно указать такое Si, что
|/1-<^(жо)|<|, (20)
если только
\х - хо\ < Si и 1^1 < Si.
Покажем, что остальные интегралы: /2, щ и щ — малы. Оценим
прежде всего интеграл /2:
1 Г 1 (^-о
V^ J \/o?t
2л/^
XI
Из равенств (18) видно, что при
Ж1 < ^ < Ж2
имеет место неравенство
|^-Жо| <Г].

А.
ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
239
Пользуясь неравенством (17), а также тем, что
1 Г _ 2 1 f _ 2
-= е "^ da < —= / е "^ da = 1
гк J л/тг У
при любых х' и х", получаем
i/.u;-
6 20F
ж 2
- /-
(^-ir
г ia^t df=--
Н ^62
^ / «-"'^«<|,(21)
Ж1
где новая переменная а определяется формулой (19). Оценим ^з (ж, ^):
1^3 (ж, ^)|
2л/^
сю
(д^-0^
:е 4a2t if {^) d£,
Х2
<
<
^ / -'
б?а ^ О при ж^жо, ^^0, (22)
Х2-Х
2VaJt
И аналогично щ (ж, ^):
1 I
1^1 (ж, ^)| =
2л/^
J л/^
(а^-0^
е ^аЧ (f{^)d^
<
<
da ^ ^ при ж —>- жо, ^ —>■ 0. (23)
Справедливость (22), (23) вытекает из того, что если ж —>- жо, то Ж2 —
— ж>0 и Ж1—ж<0, и если ^ —>- О, то в последних членах (22) и (23)
нижний и, соответственно, верхний пределы стремятся к + оо и — оо.
Следовательно, можно указать такое (^2, что
1^3 (ж, ^)1 < 3 ^ 1^1 (^' ^)1 < 3'
(24)
если только
|Ж - Жо| < (^2 И 1^1 < 52.
Пользуясь установленными выше оценками (20), (21) и (24), получаем
\и (ж, t)-^ (жо)| ^ 1^1 + [/i - (/? (Жо)] + /2 + -^^з! ^
^ |и1| + |/1-(/р(жо)| + |/2| + |пз| <| + | + | + |=г, (25)

240 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
если только
\х - хо\ < S и 1^1 < S,
где 5 равно наименьшему из чисел 5i и (^2.
Таким образом, мы доказали, что функция
1 г 1 (^-о
u{x,t) = -^ / -у=е ^a^^iOd^ (120
— сю
ограничена, удовлетворяет уравнению теплопроводности и
начальному условию.
Если начальное значение задается не при ^ = О, а при t = to, то
выражение для и{х, t) приобретает вид
u{x,t) = -^ f } е~ ^^^i^^ ^ (О dC (12")
— СЮ
Единственность полученного решения для непрерывной функции
(р (х) следует из теоремы, доказанной в § 2, п. 3. Если начальная
функция (f (х) имеет конечное число точек разрыва, то интеграл (12'')
представляет ограниченное решение уравнения (1), непрерывное всюду,
кроме точек разрыва функции (р {х)^\
Рассмотрим в качестве примера следующую задачу.
Найти решение уравнения теплопроводности, если начальная
температура {при t = to = 0) имеет постоянные, но различные
значения для X > О и X < О, а именно:
Пользуясь формулой (12'), получаем решение задачи в виде
1 г 1 (^-о
U{x,t) = -^ / -у=е 4аЧ ^{^)d^
- сю
о . оо
di , Ti [ _(^ di
= ^ / ^ ^" * —T^ "^—^ / <
л/^ J 2л/^ л/^ J
2Va2l
- oo 0
СЮ
= —= I e ^ da -\ -= / e ^ da =
л/тг У л/тг У
— по ^
^ Пользуясь методом, изложенным в § 2, п. 3, можно убедиться, что
функция и{х, t) перечисленными условиями определяется однозначно.

_3^ ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 241
2 уЛ
Г1+Г2 Г1-Г2 Г _,2
О
так как
-^ е '^ da = —= е ^ da ^ / е ^ б?а = ^ 1 е ^ da
/^ J уД J уД J 2 V^y
— сю
и
сю О 2
^ /e-"'da = ^ + ^ /e-«'da = ^ + ^ [е-"'da (z = -^] .
лАУ 2 дАУ 2 дАУ V 2л/^У
-2 -2 О
в частности,если
Т2 =0, Ti = 1,
то
Профиль температуры в заданный момент t дается кривой
Z
О
где Z представляет абсциссу точки, в которой определяется
температура, если за единицу длины, в зависимости от ^, принимается
значение 2 уаН. Построение этой кривой не представляет труда, так как
интеграл
w = ;^/'
Ф{г) = ^ I е-^' da,
о
называемый обычно интегралом ошибок, часто встречается в
теории вероятностей и для него существуют подробные таблицы-"^л
Формула (26) при произвольных Ti и Т2 может быть записана в
виде
и (ж, t) = \ Ф
2л/а21
^^ См., например, «Исчисление вероятностей» А. А. Маркова (М., 1924),
где даны таблицы этого интеграла с пхестью десятичными знаками. См.
также табл. 1 в Дополнении П, ч. IV.
16 А. Н. Тихонов, А. А. Самарский

242 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Отсюда видно, что в точке х = О температура все время постоянна и
равна полусумме начальных значений справа и слева, так как Ф (0) =
= 0.
Penienne неоднородного уравнения
щ = ci^Uxx -^ f {х, t) {— ОО < X < оо, t > 0)
с нулевым начальным условием
и{х, 0) =0,
очевидно, должно представляться формулой
t сю
uix,t) = I I G{х, i,t-T)f [i, т) d^dT, (27)
О - оо
как то следует из смысла функции G (ж, ^, г) (см. § 2, п. 4). Мы не
будем подробнее заниматься изучением этой формулы и условий
применимости, которые надо наложить на функцию / (ж, t).
2. Краевые задачи для полуограниченной прямой. Как мы
уже отмечали в § 1, п. 4, в тех случаях, когда интересуются
распределением температуры вблизи одного из концов стержня, а влияние
второго конца несущественно, принимают, что второй конец
находится в бесконечности. Это приводит к задаче об определении решения
уравнения теплопроводности
щ = a^Uxx, ж > О, ^ > О,
на полу бесконечной прямой х > О для значений ^ > О,
удовлетворяющего начальному условию
и (ж, 0) = (f (х) {х > 0)
и граничному условию, которое в зависимости от заданного характера
граничного режима берется в одном из следующих видов:
и (О, t) = /J (t) (первая краевая задача),
-^ {О, t) = 1У (t) (вторая краевая задача)
-^ (О, t) = \[и (О, t) — в {t)] (третья краевая задача).
В дальнейшем мы ограничимся подробным исследованием только
первой краевой задачи, заключающейся в отыскании решения
уравнения теплопроводности при дополнительных условиях
и(ж, 0) = (/?(ж), и(0, ^) =/i(^). (28)

§ 3] ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 243
Для того чтобы условия задачи определяли единственное решение,
необходимо наложить некоторые условия в бесконечности. Потребуем
дополнительно, чтобы функция и{х, t) была всюду ограничена:
\u{x,t)\< М для 0<ж<(Х) и ^^0,
где М — некоторая постоянная. Отсюда следует, что начальная
функция ip {х) должна также удовлетворять условию ограниченности:
\^{х)\ < М.
Решение поставленной задачи можно записать в виде суммы
и (ж, t) = ui (ж, t) + U2 (ж, t),
где ui(ж, t) представляет влияние только начального условия, а
U2 (ж, t) — только граничного условия. Эти функции можно
определить как решения уравнения (1), удовлетворяющие условиям
ui (ж, 0) = (/? (ж), ui (О, ^) = О (280
U2{x, 0) = 0, П2(0, ^) =ii{t). (28^0
Очевидно, что сумма этих функций будет удовлетворять
условиям (28). Докажем предварительно две леммы относительно функции
U (ж, ^), определяемой интегралом Пуассона:
1 г 1 ^^-о
U{x,t) = -^ / ^=e 4a2, ^(^)^^. (29)
1. Если функция ф (x) является нечетнощ т. е.
ф{х) = -ф{-х),
то функция (29)
1 г 1 (^-^)
и (ж, t) = -^ / ^= е 4a2t V^ (^) б?^
— сю
обращается в нуль при ж = 0:
и(0, t) =0.
При этом, конечно, предполагается, что интеграл, определяющий
функцию u{x,t), сходится, что имеет место, если ф (х)
ограничена. Подынтегральная функция в интеграле
u{0,t) = -^ [ -1^^е-^Мф[^)с1^
2л/^ У \/o?t
— сю
16*

244 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
нечетна относительно ^, так как является произведением нечетной
функции на четную. Интеграл же от нечетной функции в пределах,
симметричных относительно начала координат, равняется нулю;
следовательно,
и(0, t) =0,
что и доказывает лемму 1.
2. Если функция ф (х) является четнощ т. е.
ф{х) =ф{-х),
то производная функции и (ж, t) из формулы (29) равна нулю при х =
для всех t > 0.
В самом деле.
ди
дх
х=0
1 с {х-£) (^-^^
= 0,
ж=0
так как при ж = О подынтегральная функция нечетная, если ф (^) —
четная.
Перейдем теперь к построению функции ui (ж, ^),
удовлетворяющей условиям (28').
Введем вспомогательную функцию [/ (ж, ^), определенную на
бесконечной прямой — 00 < ж < 00 и удовлетворяющую уравнению, а
также условиям
[/(О, ^) = 0,
и (ж, 0) = (/? (ж) для ж > 0.
Эту функцию, пользуясь леммой 1, можно определить при помощи
начальной функции Ф (ж), совпадающей с ^ (ж) для ж > О и являющейся
нечетным продолжением ip (ж) для ж < О, т. е.
ф(^)^ I ^Н для ж > О,
I —(/? (—ж) для ж < о.
так что
1 г 1 ^^-о
,^) = -— / в-^^ф(с)^е
[/(ж
Рассматривая значения функции [/ (ж, ^) только в интересующей нас
области ж ^ О, получим
ui (ж, t) = и (ж, ^) при ж ^ 0.

§ 3] ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 245
Пользуясь определением функции Ф (х), будем иметь
и (ж, t) =
о . оо
1 Г 1 (^-О 1 Г 1 (^-О^
— / -=е- 4.2, ф(^)^^+ / ^^^" ^^'* ФЮ^С =
2л/^
о
сю
о о
причем в первом интеграле сделана замена ^' = — ^ и использовано
равенство
ф(0 = -'^(-а = -¥'(Г)-
Соединяя оба интеграла вместе, получим искомую функцию
сю
uiix,t) = -^ ^=и *аЧ -е *аЧ \ip{£)di (30)
в виде, не содержащем вспомогательных функций. Заметим, что при
ж = О выражение в фигурных скобках обращается в нуль и ui (О, ^) = 0.
Пользуясь леммой 2, нетрудно убедиться, что решение уравнения
теплопроводности с однородным граничным условием второго рода
г\ —
-Z— (О, ^) = О и начальным условием ui (ж, 0) = (/? (х) представляется
ох
в виде
1 7 1 Г (^-^^ _(^±i)^l
U1(X, ^) = -^ / ^= е 4а2, +е 4а2, U (^) С^^ (30^
о
Применим полученную формулу к решению задачи об остывании
равномерно нагретого стержня, на границе которого поддерживается
постоянная температура, которую мы примем равной нулю. Задача
состоит в определении решения уравнения теплопроводности,
удовлетворяющего условиям
VI (ж, to) = Т, VI (О, t) = 0.
Учитывая, что начальное условие задается не при ^ = О, а при
t = to, вместо формулы (30) получим
т 7 ( - (^-^)^ _ (^+^)^ 1 н^
VI (ж, t) = —-^ и 4а2 (*-*0) - е 4а2 (*-*о) \ ^ ^^^ . (31)
л/а2 {t - to)'

246 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Разбивая интеграл на два слагаемых и вводя переменные
^-X С + ж
а = ^, ai —
получаем
где
2 ^а^ {t - to)' 2у/аЦг-гоУ
■"<^-«=^4v^^w^ ■ '"■'
Ф{г) = ^ [ е-""^ da
V ^ i
о
— интеграл ошибок.
Обратимся теперь к отысканию функции U2 (ж, t),
представляющей вторую часть решения первой краевой задачи.
Пусть
fi (t) = /io = const.
Функция
V (ж, t)= fio^ i , I (32)
\2y/aHt-to)J
является решением уравнения теплопроводности, удовлетворяющим
условиям
v{x, to) = /io, ^(0, t) = 0.
Отсюда следует, что функция
V (ж, t) = /Jo -V (ж, t) = /io
1-Ф
2у^Щ^^^
(33)
и является искомой, так как она удовлетворяет тому же уравнению и
условиям
v{x,to) = 0 (ж > 0) и v{0,t)=iJo {t>to).
Представим v {х, t) в виде
v{x, t) = /JoU {х, t -to),
где
[/(ж, ^-^o) = 1-Ф I , ^ I = ^ / е-^'^а (34)
2^/a2(t-to)

А.
ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
247
является решением той же задачи, что и v (ж, ^), при fiQ = 1.
По определению функция U {х, t — to) имеет смысл только при
t ^ to. Продолжим определение этой функции, полагая
и {х, t — to) = О для t < to.
Очевидно, что это определение согласуется со значением функции
и {х, t) при ^ = О и определенная таким образом функция будет
удовлетворять уравнению теплопроводности для всех t при х > 0.
Граничное значение этой функции (при ж = 0) является
ступенчатой функцией, равной нулю при ^ < ^о и равной единице при t > to-
Функция [/ (ж, t) весьма часто встречается в приложениях и является
вспомогательным звеном для нахождения функции U2 (ж, t).
Рассмотрим вторую вспомогательную задачу, заключающуюся в
нахождении решения уравнения теплопроводности со следующими
начальными и граничными условиями:
v{x,to) = ^, v{0,t)=/j{t) =
/Jo для to <t <ti,
0 для t > ti.
Непосредственной проверкой нетрудно убедиться, что
V (ж, t) = fio
U{x, t-to) -U{x, t-ti)
Вообще, если граничная функция /j, (t) задается в виде ступенчатой
функции:
/^W = <
/Jo для to <t ^ti,
/il для ti <t^t2j
[/in-1 ДЛЯ tn-1 < t ^tn,
TO, рассуждая совершенно аналогично, получим, что решение краевой
задачи с подобной функцией /i (t) может быть записано следующим
образом:
п-2
и (ж, t) = ^/ii
i=0
и {x,t - ti) -U {x,t- ti^i)
Пользуясь теоремой о конечном приращении, получаем
-\- /in-lU {Х, t-tn-l).
(35)
и (ж, t) = ^/г,
i=0
ди (ж, t - т)
di
Ат-\- /in-iU {х, t-tn-i)
(36)
для ti ^Ti ^ ti^i.

248
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИНА
[ГЛ. HI
Обратимся теперь к задаче о нахождениии решения и{х, t)
уравнения теплопроводности с нулевым начальным условием и граничным
условием
и(0, t) = ii{t) {t> 0),
где /j{t)—произвольная кусочно-непрерывная функция.
Приближенное решение этой задачи легко получить в виде (36), если функцию
/J (t) заменить кусочно-постоянной функцией. Переходя к пределу при
уменьшении интервалов постоянства вспомогательной функции,
получаем, что предел суммы (36) будет равен
I
— {x,t-T)fi (г) dr,
так как при х > О
Иш /1п-1 и {х, t- tn-i) = 0.
Очевидно, что искомое решение U2 (ж, t) второй задачи должно быть
равно
t
U2 (ж, t)= / —{x,t-T)/j (г) dr.
(37)
Мы не будем подробно останавливаться на правомерности
предельного перехода и выяснении условий применимости этой формулы
в отношении функции /j (г).
Нетрудно убедиться в том, что
ди , , д
I
сю
\
da
I
2 лА^ {aHfl-^
е 4:a^t
й=о
G
2л/^л/^
1 _ (--О'
Таким образом, искомое решение в случае произвольной функции
fi (t) может быть представлено в виде
U2 (ж, t)
t
— f
iV^ J
to
a2 (t - t)P
e 4a^ (*-r) ^j (^-r) dr,

_3^ ЗАДАЧИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ 249
/ВС
-—{x,0,t-T)fi{T)dT^\ (38)
Отметим, что в процессе получения формулы (38) мы не
пользовались никакими специальными свойствами уравнения
теплопроводности, кроме его линейности. Мы нигде не пользовались также
аналитической формой функции [/ (ж, ^), для нас было важно только то,
что она удовлетворяет граничным и начальным условиям
и (О, ^) = 1 для ^ > О,
и (ж, 0) = О для X > О
или
^ ^ |0 для ^ < 0.
Очевидно, что когда мы имеем дело с решением какого-либо
линейного дифференциального уравнения при граничном условии
и(0, t) = ii{t) {t> 0),
нулевых начальных условиях и нулевых дополнительных граничных
условиях, если такие имеют место (например, при ж = /), то решение
этой задачи может быть представлено в виде
Г ди
J ~dt
u{x,t) = — (ж, t-T)fi (г) dr, (39)
о
где и {х, t) —решение аналогичной краевой задачи при
[/(0,^) = 1.
Сформулированный здесь принцип, называемый принципом
Дюгамеля, показывает, что основную трудность при решении
краевых задач представляет постоянное граничное значение. Если краевая
задача с постоянным граничным значением решена, то решение
краевой задачи с переменным граничным условием выражается формулой
(39). Этим принципом часто пользуются при решении многих краевых
задач, приводя решение только для постоянного граничного условия,
не оговаривая, что решение краевой задачи с переменным fi (t) дается
формулой (39).
^ Это представление решения первой краевой задачи с нулевыми
начальными условиями дано здесь для удобства сравнения с репЕСнием той же
задачи, полученным в гл. VI, § 4 другим методом.

250 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
Сумма функций
Щ (ж, t) + U2 (ж, t)
дает решение первой краевой задачи для полубесконечной прямой для
однородного уравнения.
Пользуясь формулой (27) из § 3, п. 1 и принципом нечетного
продолжения, нетрудно убедиться в том, что решение неоднородного
уравнения
щ = a^Uxx + f {х, t) (О < ж < 00, ^ > 0)
при нулевом начальном и нулевом граничном условиях {и (О, ^) = 0)
дается формулой
щ (ж, t) =
t сю
е~^^Ч^-e~^^(t--) } f{^,T)d^dT. (40)
^/a-{t-т) I
о о
Сумма
t ОО г
~ йЩ! J Ja^ it-r)Y
Щ (ж, t) + U2 (ж, t) + Us (ж, t) = и (ж, t)
дает решение первой краевой задачи
щ = a'^Uxx + /(ж, t),
и (о, t) = fi (^), и (ж, 0) = (/? (ж).
§ 4. Задачи без начальных условий
Если изучается процесс теплопроводности в момент, достаточно
удаленный от начального, то влияние начальных условий
практически не сказывается на распределении температуры в момент
наблюдения. В этом случае ставится задача об отыскании решения уравнения
теплопроводности, удовлетворяющего граничным условиям одного из
трех типов, заданным для всех ^ > — оо. Если стержень ограничен, то
задаются граничные условия на обоих концах стержня. Для полу
бесконечного стержня задается лишь одно граничное условие.
Рассмотрим первую краевую задачу для полубесконечного
стержня.
Найти ограниченное решение уравнения теплопроводности в
области ж > О, удовлетворяющее условию
uiO,t)=fx(t), (1)
где /j{t) —заданная функция. Предполагается, что функции и{х, t)
и II (t) ограничены всюду, т. е.
|и(ж, t)\< М,
|/i(^)|<M.

А
ЗАДАЧИ БЕЗ НАЧАЛЬНЫХ УСЛОВИЙ
251
Как будет показано ниже (см. текст, набранный мелким шрифтом),
функция и{х, t) определяется однозначно. Возьмем наиболее часто
встречающийся случай граничного условия
II {t) = Aco^ujt. (2)
Эта задача изучалась еще Фурье и впервые была применена при
определении температурных колебаний почвы (см. Приложение I).
Запишем граничное условие в виде
^(^) = Лe^^^ {2')
Из линейности уравнения теплопроводности следует, что
действительная и мнимая части некоторого комплексного решения уравнения
теплопроводности, каждая в отдельности, удовлетворяют тому же
уравнению.
Если найдено решение уравнения теплопроводности,
удовлетворяющее условию (2'), то его действительная часть удовлетворяет
условию (2), а мнимая — условию
и (О, t) = 111 (t) = Asincut.
Итак, рассмотрим задачу
щ = а Uxx,
(3)
Ее решение будем искать в виде
(4)
где а и /3 — не определенные пока постоянные.
Подставляя выражение (4) в уравнение (3) и граничное условие,
находим
откуда
/9
V а^
Для и (ж, t) имеем
и (ж, t) = Л ехр
UJ (1 + г)
л/2
= ±
X +
Действительная часть этого решения
+ г
и (ж, t) = А ехр ( =Ь ^/ —^ X I cos | =Ь
X -\- ujt
X -\- LOt
(5)
(6)

252 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
удовлетворяет уравнению теплопроводности и граничному условию
(2). Формула (6) в зависимости от выбора знака определяет не
одну, а две функции. Однако только функция, соответствующая знаку
«минус», удовлетворяет требованию ограниченности. Таким образом,
решение поставленной задачи получаем в виде
и (ж, t) = Л ехр ( - \ у^ ж j cos ( - \ у^^ + ujt\ . (7)
Аналогично решается задача без начальных условий для
ограниченного отрезка
щ = a^Uxxj
и {О, t) = Aco^uot, ) (8)
и {I, t) =0.
Переписывая граничные условия в виде
и (О, t) = Лe-^^^ й{1, t) = 0,
будем искать решение в форме
U{x,t) =X(ж)e-^^^ (9)
Подставив это выражение в уравнение (8), получим для функции
X {х) уравнение
X'' + — X = О, или X" + 7^ = О,
V а"^ V 2а"^
(10)
и дополнительные условия
Х(0)=Л, Х(0=0. (11)
Отсюда для функции X (х) будем иметь
X{x)=A^-^^^^^=Xiix)+iX2{x), (12)
где Xi и Х2 — вещественная и мнимая части функции X (х). Для
функции й{х, t) получаем выражение
, sin 7 (^ — ж) • ,^ ,_^.
и (ж, t) = А / , e"*^^ (13)
sm7t
Выделяя вещественную часть функции й (ж, ^), находим решение
исходной задачи без начальных условий в виде
и (ж, t) = Xi (ж) coso;^ + Х2 (ж) sino;^. (14)

А
ЗАДАЧИ БЕЗ НАЧАЛЬНЫХ УСЛОВИЙ
253
Мы не даем здесь явного выражения для Xi и Х2, хотя это и нетрудно
сделать.
Если граничная функция представляет собой комбинацию
гармоник разных частот, то решение такой задачи может быть получено как
суперпозиция решений, соответствующих отдельным гармоникам.
Докажем единственность ренгения задачи без начальных условий для
полуограниченной прямой. Будем исходить из формулы
и (ж, t)
t
iV^ J [a2
X
2 aAF у [a'^it- r)]%
CXD
e 4a^(t-T) ^(0, T)dT-\-
(x-^r
(x+O^
= Il+l2 (15)
(t > to),
которая представляет любое ограниченное рептение уравнения
теплопроводности через его начальное значение и{х, to) и граничное п (О, t) = fi{t) в
области ж ^ О, t ^ to.
Покажем, что
lim /2 (ж, t) = О,
если только
\u{x,t)\ < М
при любом t. Действительно,
IhK
м
7^
сю
/
е~^1dai -
сю
/
е-^'з ^0,2
(^ 2^a2(t-to)
2^Уa'2(t-to)
> =
(16)
2^а2(*-*о)
/
е '^ da,
где
ai
С-ж
2У^2-(^^^
и «2
С + ж
2у^а2(^-^о)'
Отсюда и следует равенство (16), так как ж и ^ фиксированы, а ^о ^ ~ сю.
Если в формуле (15) фиксировать х ж t ж устремить to ^ — оо, то и{х, t)

254 УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА [ГЛ. HI
будет равно пределу только первого слагаемого и мы получим формулу
t .
и (ж, t) = -^ / ^ е~ ^аГ(ГГ) ц (^) ^^ (17)
— СЮ
доказывающую, что двух различных рептений наптей задачи быть не может.
Можно также доказать, что для любой ограниченной кусочно-непрерывной
функции /i {t) формула (17) представляет репЕСние поставленной задачи.
Аналогично может быть исследована задача без начальных условий для
ограниченного отрезка (О ^ ж ^ /). Эта задача без условия ограниченности
имеет многозначное penienne, так как функция
/ ,ч ^ - ( ^ ) a^t . 7ГП
Un [х, t) = С е \ I / sm —- х
при любом п представляет penienne этой задачи с нулевыми граничными
значениями. Однако рептения такого типа при ^ ^ — оо не ограничены и не
составляет труда доказать единственность ограниченного рептения
поставленной задачи.
ЗАДАЧИ К ГЛАВЕ HI
1. Найти функцию влияния мгновенного точечного источника тепла
для:
а) полуограниченного стержня при граничных условиях 1-го и 2-го рода
и при отсутствии теплообмена на боковой поверхности;
б) неограниченного стержня при наличии теплообмена на боковой
поверхности;
в) полуограниченного стержня при наличии теплообмена на боковой
поверхности и при граничных условиях первых двух типов.
2. Найти функцию влияния мгновенного точечного источника тепла для
полуограниченного стержня с теплоизолированной боковой поверхностью
Ои
для третьей краевой задачи (граничное условие вида -^ (О, t) — hu (О, t) =
= /(*))•
3. РепЕить уравнение теплопроводности для случаев, описанных в
задачах 1а — 1в, если:
1) в точке ж = ^0 действует источник тепла Q = Q{t), в частности
Q = Qo = const;
2) задано начальное распределение температуры и{х, 0) = «^(ж), в
частности
, . (uq при о < ж < /,
[^ о вне интервала (О, /);
3) тепловые источники распределены с плотностью / (ж, t) по всему
стержню, а начальная температура равна нулю; рассмотреть, в частности,
случай f = qq = const (стационарные источники).
4. Нолу ограниченный стержень с теплоизолированной боковой
поверхностью был равномерно нагрет до температуры
и (ж, 0) = uq = const (ж > 0).

ЗАДАЧИ К ГЛАВЕ III 255
Конец стержня, начиная с момента ^ = О, поддерживается при температуре,
равной нулю:
u{0,t) = 0 {t>0).
Найти температуру стержня п (ж, t) и, пользуясь таблицами интеграла
ОПЕИбОК
/тг J
9 Г 2
^ I —ГУ
О
построить графики по х на интервале О ^ ж ^ / функции п (ж, t) при t =
= /Vl6a^ t = /V2a^ t = I'^/a^.
Указание. Удобно ввести безразмерные переменные
X = ж//, 9 = а t/l J V = u/uq.
5. Конец полу ограниченного цилиндра в начальный момент времени
^ = О открывают в атмосфере, где концентрация некоторого газа равна uq.
Найти концентрацию газа в цилиндре п (ж, t) для ^ > О и ж > О, если
начальная концентрация п (ж, 0) = 0. Пользуясь таблицами интеграла опЕибок,
установить, через какое время в слое, отстоящем на расстояние / от конца
цилиндра, концентрация газа достигнет 95% внепЕней концентрации. Найти
закон движения фронта постоянной концентрации.
6. К концу полу ограниченного стержня, начальная температура
которого была равна нулю, подводится тепловой поток kux (О, t) = q (t). Найти
температуру и (ж, t) стержня, если:
а) стержень теплоизолирован с боков;
б) на боковой поверхности стержня происходит теплообмен (по закону
Ньютона) со средой нулевой температуры.
Рассмотреть частный случай q = qq = const.
7. Конец полуограниченного стержня поддерживается при постоянной
температуре uq ; на боковой поверхности стержня происходит теплообмен со
средой, постоянная температура которой равна ui. Начальная температура
стержня равна нулю. Найти и{х, t) — температуру стержня.
8. Решить задачи 6а, 66, считая, что гА(ж, 0) = по = const.
9. Найти установивпЕуюся температуру вдоль полу ограниченного
стержня с теплоизолированной боковой поверхностью, на конце которого
а) задана температура п (О, t) = Acosujt\
б) задан тепловой поток Q (t) = В sin ujt]
в) происходит теплообмен по закону Ньютона со средой, температура
которой меняется по закону v (t) = Csino;^.
10. Пользуясь методом отражения, построить функцию влияния
мгновенного точечного источника для ограниченного стержня с
теплоизолированной боковой поверхностью при граничных условиях 1-го и 2-го рода.
11. Неограниченный стержень составлен из двух однородных стержней,
соприкасающихся в точке ж = О и обладающих характеристиками ai, ki и
а2, к2 соответственно. Начальная температура
Найти температуру п (ж, t) стержня для случая, когда боковая поверхность
теплоизолирована.

256 ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
прилож:ения к главе ш
I. Температурные волны
Задача о распространении температурных волн в почве является
одним из первых примеров приложения математической теории
теплопроводности, развитой Фурье, к изучению явлений природы.
Температура на поверхности земли носит, как известно, ярко
выраженную суточную и годовую периодичность. Обратимся к задаче
о распространении периодических температурных колебаний в почве,
которую будем рассматривать как однородное полупространство О ^
^ ж ^ 00. Эта задача является характерной задачей без начальных
условий, так как при многократном повторении температурного хода
на поверхности влияние начальной температуры будет меньше
влияния других факторов, которыми мы пренебрегаем (например,
неоднородность почвы). Таким образом, приходим к следующей задаче""^л
Найти ограниченное решение уравнения теплопроводности
ди 9 д^"^
т^ д^ (0^ж<оо, -oo<i), (1)
удовлетворяющее условию
и(0, t) = Aco^ujt. (2)
Эта задача была рассмотрена в гл. 1П. Ее решение имеет вид (см.
гл. III, § 4, (7))
и{х, t) = Лехр f -\ у^х] cos ( \ у^^ -ujt\ . (3)
На основании полученного решения можно дать следующую
характеристику процесса распространения температурной волны в
почве. Если температура поверхности длительное время периодически
меняется, то в почве также устанавливаются колебания температуры с
тем же периодом, причем верны следующие утверждения.
1. Амплитуда колебаний экспоненциально убывает с глубиной:
Л (ж) = Л ехр
т.е. если глубины растут в арифметической прогрессии, то амплитуды
убывают в геометрической прогрессии (первый закон Фурье).
2. Температурные колебания в почве происходят со сдвигом фазы.
Время 5 отставания максимумов (минимумов) температуры в почве от
^^ Карслоу X. С. Теория теплопроводности. М.; Л., 1947. Гл. III.

I. ТЕМПЕРАТУРНЫЕ ВОЛНЫ 257
соответствующих моментов на поверхности пропорционально глубине:
2а;а2
(второй закон Фурье).
3. Глубина проникновения тепла в почву зависит от периода
колебаний температуры на поверхности. Относительное изменение
температурной амплитуды равно
А{х)
-Г = ^^р г
Эта формула показывает, что чем меньп1е период, тем меньп1е
глубина проникновения температуры. Для температурных колебаний
с периодами Ti и Т2 глубины xi и Ж2, на которых происходит
одинаковое относительное изменение температуры, связаны соотношением
Х2
(третий закон Фурье). Так, например, сравнение суточных и годовых
колебаний, для которых Т2 = 365 Ti, показывает, что
Х2 = л/3б5ж1 « 19,1 Ж1,
т. е. что глубина проникновения годовых колебаний при одинаковой
амплитуде на поверхности была бы в 19,1 раза больше глубины
проникновения суточных колебаний.
В качестве примера приведем результаты наблюдений над
годовыми температурными колебаниями на станции Гош в Приамурье ^^:
Глубина (м) 12 3 4
Амплитуды (° С) 11,5 6,8 4,2 2,6
Эти данные показывают, что амплитуда годовых колебаний на
глубине 4 м уменьшается до 13,3% своего значения на поверхности,
равного 19,5°. Па основании этих данных можно определить
коэффициент температуропроводности почвы. Используя формулы
А{х) _ / U. 2
In—-— = —W—— ж, а
А У2а^'^' ^ 21п'(Л(ж)/Л)'
находим, что коэффициент температуропроводности почвы равен
а^ ?^4.10"^ cmVc.
^^ Сумгин М. и., Качурин СП., Толстихин П. И., Тумель В. Ф.
Общее мерзлотоведение. М.; Л., 1940. Гл. V.
17 А. Н. Тихонов, А. А. Самарский

258 ПРИЛОЖЕНИЯ К ГЛАВЕ III
Время запаздывания максимальной температуры на глубине 4 м
достигает 4 месяцев.
Следует, однако, иметь в виду, что изложенная здесь теория
относится к распространению тепла в сухой почве или горных породах.
Наличие влаги усложняет температурные явления в почве, и при
замерзании происходит выделение скрытой теплоты, не учитываемое этой
теорией.
Температуропроводность является одной из характеристик тела,
важных для изучения его физических свойств, а также для различных
технических расчетов. На изучении распространения температурных
волн в стержнях основан один из лабораторных методов определения
температуропроводности ^^.
Пусть на конце достаточно длинного стержня поддерживается
периодическая температура /а (t). Представив эту функцию в виде
ряда Фурье
/ ч CLO \-^ ( 27ГП _ . 27ГП \
/i (^) = у + 2^ \ап cos -^- t + bn sm -j^ tj
n=l ^ ^
-^ + ^ An COS
^ n=l
'-^(t-sl)
rp 7
An = л/4 + ^n. ^n= W—- arctg -^,
zTrn an
где T — период, и рассмотрев температурные волны,
соответствующие каждому слагаемому, получим, что температура и (ж, t) для
любого X будет периодической функцией времени и ее п-я гармоника
равна
/ ч / ч 27ГП 7 / ч . 27ГП
Un (ж, t) = an [х) COS -—- t -\- bn [х) sm -—- t =
= Л^ехр ( -\/jr^x ] cos
7ГП 27ГП 27ГП Q
7Г" tiy t/ vy,v^
Ta^ T T ""
или
V-lM + bi^)^^^/f^^^^_^^.^
Эта формула показывает, что если произвести измерение
температуры в каких-нибудь двух точках xi и Ж2 за полный период,
то, находя коэффициенты а^ (^i), bn (xi), an (^2), bn (^2) при помощи
^ Специальный физический практикум. М.; Л., 1945. Т. I, задача 35.

IL ВЛИЯНИЕ РАДИОАКТИВНОГО РАСПАДА 259
гармонического анализа, можно определить коэффициент
температуропроводности стержня а^.
Периодические колебания температуры в стержне можно вызвать,
например, следующим образом. Поместим один из концов стержня в
электрическую печь и будем через одинаковые промежутки времени
включать и выключать ток. В результате такого периодического
нагревания в стержне через некоторое время установятся периодические
колебания температуры. Измеряя с помощью термопар температуры
и (ж1, t) VL и (ж2, t) в каких-либо двух точках xi и Х2 за полный
период изменения граничного режима и подвергая щ и U2 описанной выше
обработке, можно определить а^—коэффициент
температуропроводности материала, из которого сделан стержень. Естественно, что для
применимости изложенной выше теории стержень должен быть
теплоизолирован с боков, а также необходим контроль температуры на
другом конце стержня, чтобы иметь возможность пользоваться теорией
температурных волн в полу бесконечном стержне.
Для возможности использования теории температурных волн в
полубесконечном стержне надо убедиться в том, что температура на
свободном конце стержня постоянна. Это контролируется с помощью
дополнительной термопары.
II. Влияние радиоактивного распада
на температуру земной коры
Для суждения о внутреннем температурном состоянии Земли мы
имеем немногие данные, получаемые из наблюдений на ее
поверхности. Основные сведения о термическом поле земной коры заключаются
в следующем. Суточные и годовые колебания температуры происходят
в сравнительно тонком поверхностном слое (порядка 10-20 м для
годовых колебаний). Пиже этого слоя температура с течением времени
меняется очень медленно.
Наблюдения в шахтах и скважинах, относящиеся к верхним 2-3 км
земной коры, показывают, что температура с глубиной повышается в
среднем на 3° С на каждые 100 м.
Первые попытки дать теоретическое объяснение наблюдаемого
геотермического градиента, относящиеся к концу прошлого столетия,
встретили непреодолимые трудности-"^л Эти попытки исходили из
представления об охлаждении Земли, раскаленной в прошлом.
Начальная температура, характеризующая этот процесс остывания, должна
иметь порядок То = 1200° С (температура плавления горных пород),
а поверхностная температура имеет порядок 0° С и не могла
значительно (больше 100°) отклоняться от этой величины за весь период
существования жизни на Земле. Простейшая количественная теория
^^ Карслоу X. С. Теория теплопроводности. М.; Л., 1947. Гл. П1.
17*

260 ПРИЛОЖЕНИЯ К ГЛАВЕ III
остывания Земли приводит к решению уравнения теплопроводности
ди 2 ^^'^
в полупространстве О < 2; < оо при следующих начальных и
граничных условиях:
u{z, 0) =Го, и {О, t) =0.
Penienne этой задачи было рассмотрено в § 3 настоящей главы и
дается формулой
da.
о
Градиент этой функции при z = О равен
ди
dz
4a2t
=0
Подставляя сюда известные значения геотермического градиента
du/dz \z=o = J = S • 10~^ K/cM, To = 1200° C, a также значение a^ =
= 0,006 CM^/c, соответствующее среднему экспериментально
определяемому коэффициенту температуропроводности гранитов и
базальтов, получим для продолжительности процесса остывания значения
t « 0,85 • 10^^ с « 27000 000 лет. Такое представление о возрасте Земли
никак не согласовывалось с геологическими данными. Приближенный
характер рассматриваемой теории (пренебрежение кривизной
Земли, непостоянство коэффициента температуропроводности,
приближенность значения То) не может, конечно, изменить порядка
найденного значения для возраста Земли, который по современным данным
оценивается приблизительно в 2 • 10^ лет.
Физическая схема температурного режима Земли подверглась
существенному пересмотру после открытия явления
радиоактивного распада. Радиоактивные элементы, рассеянные в земной коре,
при распаде вызывают ее нагревание, так что уравнение
теплопроводности должно иметь вид
ди _ 2^ г f f - А
dt dz'^ \ ср
где А — объемная плотность тепловых источников. Па основании
многочисленных измерений радиоактивности горных пород и их
тепловыделения принято значение
А^ 1,3-10-^^ кал/(см^-с).
Это значение учитывает тепло, выделяемое ураном, торием и калием
вместе с их продуктами распада.

п. ВЛИЯНИЕ РАДИОАКТИВНОГО РАСПАДА
261
Предположим, что плотность радиоактивных источников внутри
земного Hiapa постоянна и равна значению А, определенному для
верхних слоев земной коры. В этом случае количество тепла,
выделяющегося во всем земном шаре за единицу времени, будет равно
4 о
Q = -ttR^A.
о
Сделаем второе предположение о том, что Земля радиоактивным
теплом не нагревается. В этом случае поток тепла через единицу
поверхности
ди
^
Q
АтгЕ^'
где к и du/dz\z=o суть коэффициент теплопроводности и
геотермический градиент у поверхности Земли.
Отсюда для du/dz при 2; = О находим значение
ди
dz
>
AR
~Sk
6,8 • 10-^ К/см,
где i^ = 6,3 • 10^ км — радиус Земли и к = 0,004 — среднее значение
коэффициента теплопроводности осадочных пород.
Таким образом, геотермический градиент, вычисленный в
предположении, что распределение радиоактивных элементов постоянно и
что Земля не нагревается благодаря радиоактивному распаду, на два
порядка превышает наблюдаемое значение геотермического
коэффициента
7 = 3- 10~^ К/см.
Откажемся от гипотезы постоянства распределения
радиоактивных элементов и предположим, что радиоактивные элементы
расположены в слое мощности Н у поверхности Земли. Пренебрегая
кривизной Земли, получим для определения стационарной температуры
уравнение
д'^и
д^
к
для о ^ Z ^ Н,
О для Z > Н
с условиями
и{0) = 0,
ди
dz
= 0.

262
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
Очевидно, что решение поставленной задачи равно
u{z) = ■{
^ Hz- —], O^z^H,
А IP
z>H,
так как эта функция непрерывна вместе с первой производной при
z = Н ш удовлетворяет условиям задачи.
Определяя значение градиента этой функции при z = Q, равное
ди
z=0
АН
"Г'
и сопоставляя его с наблюдаемым значением 7 = 3 • 10 ^ К/см,
находим, что
Я = ^ ^ 10^ см = 10 км.
А
Оценим влияние сделанного предположения о стационарности
температуры на получаемое значение геотермического градиента.
Рассмотрим для этого решение уравнения теплопроводности
dt dz^
f=<
cp
0, z> H,
с нулевыми начальными и граничными условиями
w{z, 0) = 0,
w{0, t) = 0.
Решение этой задачи представляется, как мы видели в § 3, интегралом
сю t
w{z,t) = 1 lGiz,C,t-T)f{OdTdC,
О о
где G — функция источника для полу бесконечной прямой, равная
G{z,Ct-T)
(z-cr
(z+cr
2 v^7ra2 {t - r)
g 4a^ (t-т) _ g 4a^ (t-т)

п. ВЛИЯНИЕ РАДИОАКТИВНОГО РАСПАДА
263
Вычислим значение градиента при z = О, принимая во внимание
значение функции /:
dw
dz
А
н t
7Г I I V[^4t-rW
О ср2уД J J ^[а^ (t - т)]
А
4а^ (t-r)
сруД J v^a2 {t - т)
Q V V
^ J уЩГ^т) J
t
^ J л/а-
e ^ dadr =
1 — e 4a2^
dO, где 0 = t — т.
Таким образом,
dw
где
А 1 2лД Н
.0 ^pV^
\2Vt_H Г _^2 dc
7г I а а"^ J а
da
2
Н
а =
2Va^0
Вычислим интеграл
ос 2
Г _^2 da _ е-^
его
Н
da с?
о-о
2л/^' ^^ Я д/^'
сю 2 сю
/2 Р~^0 /* 2
е-^ ^а = 2 / е-^
da.
о-о
его
откуда
(9w
2а лД
1-е
Отметим, что
Иг
dw
+ я
л/тг
сю
о-о
е"^ ^о-
. (1)
z=0
-."■
так как сра^ = /;;, предел первого слагаемого в фигурных скобках
равен нулю, а предел второго слагаемого равен Н.
Вычислим отклонение dw/dz от его предельного значения для
^ = 2 . 10^ лет ?^ б • 10^^ с.

264 ПРИЛОЖЕНИЯ К ГЛАВЕ III
Значение ctq мало:
^0 = -^ = , ^^' = Лт^ =0,025.
2л/^ 2 л/б-10-3. 6-1016 2-19
Разлагая функции, входящие в формулу (1), в ряды, получим
А
I
Л dw
к dz
0,014,
Q П. tVTTCTo ' ^/7г ) к
т. е. dw /dz \z=() отличается от своего предельного значения на 1,4%.
Нетрудно было бы вычислить функцию w {z^ t) для 2; > О и
убедиться, что при z^ Н она далеко еще не достигает своего предельного
значения для ^, равного возрасту Земли ^^ (хотя, как мы видим,
градиент у поверхности практически равен своему предельному значению).
Приведенные выше рассуждения носят, конечно, лишь оценочный
характер. Однако, принимая во внимание весьма большую
устойчивость скорости радиоактивного распада, не изменяющейся под
воздействием доступных нам температур и давлений, мы должны прийти к
заключению о том, что концентрация радиоактивных элементов
должна быстро убывать с глубиной, если основываться на значении А для
верхних слоев земной коры, установленном многочисленными
измерениями. Физическое объяснение, позволяющее установить закон
убывания концентрации радиоактивных элементов с глубиной, до сих пор
отсутствует.
III. Метод подобия в теории теплопроводности
Для решения ряда задач теплопроводности весьма полезен метод
подобия. В качестве примера рассмотрим две задачи.
1. Функция источника для бесконечной прямой.
Уравнение теплопроводности, как нетрудно видеть, остается неизменным при
преобразовании переменных
х' = кх, t' = k'^t, (1)
т. е. если масштабы длины меняются в к раз, то масштаб времени
следует изменить в к'^ раз.
Будем искать сначала решение уравнения теплопроводности
щ = a^Uxx (2)
с начальным условием
/ ПА J ^0 "Р^ ж > О,
I О при ж < 0.
^ Тихонов А. Н. О влиянии радиоактивного распада на температуру
земной коры // Изв. АН СССР. Отд. матем. и естеств. наук, сер. геогр. 1937.
№ 3. С. 431—459.

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ 265
При указанном выше изменении масштабов начальное условие (3)
остается также без изменения, поэтому для функции и (ж, t)
должно иметь место равенство
и (ж, t) =и {кх, k^t) (4)
при любых значениях ж, t и к.
Полагая
к=^, (5)
получаем
4x,*) = M^^>4J="°4w!j- ^'^
Таким образом, и зависит только от аргумента
(7)
2лД'
Вычисляя производные для и из формулы (6):
д'^и _ (Pf 1
ди X ■ щ df Z d f
подставляя в уравнение теплопроводности (2) и сокращая на
множитель uo/4:t, получаем
dz^ dz
«^^ = -2-^ (8)
при дополнительных условиях
/(-<х)) = 0, /(<х)) = 1, (9)
соответствующих начальному условию для функции и.
Интегрируя уравнение (8), будем иметь
a'^j = -2z, f = Ce-^'/-\
z z/a
f = cf e-«'/«' d^ = Ci f e"'^" dC.
— CXD — CXD
Здесь нижний предел выбран так, чтобы выполнялось первое условие
(9). Чтобы удовлетворить второму условию (9), следует положить

266
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
Таким образом,
и (ж, t)
Up
di
Uq
У
где
Ф(^)
Z
= 7^.1'
Ц-Ф
d^
2VaH
(10)
(интеграл ошибок). Если начальное значение имеет вид
Uq при ж > ж,
и (ж, 0) =
О при X < X,
то
и (ж, t) =
Uo
1 + ф
ж — ж
(И)
(12)
Обратимся теперь к решению второй вспомогательной задачи, где
начальные значения задаются в виде
и (ж, 0) = <
О при Ж2 < ж,
Uo при Ж1 < ж < Ж2,
о при ж < Ж1.
(13)
в этом случае
и (ж, t) =
Uo
Ф
ж — Ж1
ф
ж - Ж2
ЛЫаЧ) \2VaH.
Начальная температура uo соответствует количеству тепла
Q = ср{х2 - xi)uo.
Если
Q = ср,
то
U (ж, ^)
Ж2 — Ж1 2
ф
ж - Ж2
2л/^
ф
ж — Ж1
2л/^
(14)
Функция влияния источника, сосредоточенного в точке, очевидно,
представляет предел функции и (ж, t) при жг — Ж1 —> 0.
Предельный переход в формуле (14) дает
и (ж, t) =
д_
2 \2уШ
(15)
i=xi

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ 267
так как в правой части формулы (14) стоит разностное отношение,
пределом которого является производная в (15).
Производя дифференцирование, находим
^2
т. е. и (ж, t) = G (ж, Ж1, t)—функция мгновенного точечного
источника.
2. Краевые задачи для квазилинейного уравнения
теплопроводности. Рассмотрим квазилинейное уравнение
теплопроводности
9 Л , , ди\ ди ,^^,
С коэффициентом теплопроводности, зависящим от температуры.
Найдем решение этого уравнения, удовлетворяющее граничному
и начальному условиям
и(0, ^)=ui, и(ж, 0)=U2. (18)
В этом случае преобразование (1) также не меняет уравнения (17) и
дополнительных условий (18). Отсюда следует, что
Пользуясь этим выражением, получаем для / уравнение
d
•><
= -2cpz ^ (20)
dz
dz
с дополнительными условиями
/(0)=«1, fioo)=U2. (21)
функция /, в тех случаях когда ее не удается найти аналитически,
может быть найдена при помощи численного интегрирования.
Уравнение (20) при весьма общих предположениях
относительно функций к и ср имеет единственное решение, удовлетворяющее
условиям (21). Однако на доказательстве этого факта мы не будем
останавливаться.
Рассмотрим в качестве примера уравнение (17), где к (и) = ко -\-
+ ki и — линейная функция, а ср — постоянная величина. Изменяя
масштаб времени и шкалу значений и, получим для преобразованной
функции уравнение
(l + au)-
ди
д_
дх
с начальными и граничными условиями
и{х, 0) = 0, и(0, t) = 1.

268
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
Полагая
u{x,t) = f{z), z =
2лД'
получаем для / краевую задачу
dz
(1 + «/)
df
dz
-2z
dz '
/(0) = 1, /(oo)=0. (22)
Па рис. 42 приведены результаты численного решения задачи (22) для
различных значений а.
/Wj
1 0 -
J.,и
0 8-
0 6-
П 4 -
и,Ч: -
П 9 -
U,Z
0 0-
1
а = 0^^
а = 1,0
^^^а
= од^***.^
0,4
0,8
1,2 1,6
Рис. 42
2,0
2,4
Рассмотрим некоторые другие частные решения уравнения (17).
Одним из них является решение типа «бегущей волны» (ср. с гл. П,
§ 2). Оно имеет вид
и{х, t) = f{z),
x-Dt,
(23)
где D > {) — произвольная постоянная (скорость движения волны). В
каждый фиксированный момент времени пространственный профиль
решения (23), определяемый видом функции f {z)^ остается
неизменным, перемещаясь со временем в положительном направлении оси х со
скоростью D (тепловая волна неизменной пространственной
структуры «бежит» в указанном направлении с постоянной скоростью, отсюда
название «бегущая волна»). Если постоянная Z) < О, то волна будет
двигаться в противоположном направлении.

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ 269
Подставляя (23) в (17), получаем для f (z) обыкновенное
дифференциальное уравнение
Из (23) следует, что решение и{х, t) определено при всех ^ ^ О и ж ^ О
и удовлетворяет дополнительным условиям
U(o,i) = /(-Di), i^o,
\u{x,Q) = f{x), х^О. ^ '
Первое условие (25) показывает, что граничное условие при ж = О
определяется значениями функции / {z) при отрицательных z^ а для
задания начальной функции при ^ = О необходимо найти / {z) при
всех 2; ^ 0. Таким образом, для того чтобы определить решение
уравнения (17) в виде (23) в области t ^ О, ж ^ О, необходимо найти
функцию / (z), удовлетворяющую уравнению (24) на всей оси — оо < 2; <
< +00.
Уравнение (24) интегрируется в квадратурах. Исходя из
физических соображений, будем искать непрерывное решение этого
уравнения, обладающее непрерывным «тепловым потоком» —k{f{z)) х
X df{z)/dz, что обеспечивает непрерывность по ж и ^ реального
теплового потока
Wix,t) = -k{u{x,t))^^^^^ (26)
И является очень существенным (см. об этом ниже). Интегрируя один
раз уравнение (24), находим
k(f)^ = -Dcpf + Co, (27)
где Со — произвольная постоянная. Предположим для определенности,
что «бегущая волна» начала свое движение по невозмущенному
(нулевому) фону температуры, т. е. f (z) ^ О при z ^ -\- оо. Тогда в силу
априорной непрерывности «теплового потока» k{f{z)) • df/dz —>- О при
2; —>- + 00, т. е. Со = О, уравнение (27) принимает вид
и легко интегрируется.
Рассмотрим, например, случай, когда коэффициент к (и)
является степенной функцией температуры: к (и) = kou^, где ко и а —
фиксированные положительные постоянные. Такая зависимость от
температуры характерна, в частности, для коэффициента
электронной теплопроводности в полностью ионизованной плазме, при этом

270
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
а = 5/2. Подставляя в уравнение (28) к (f) = ко f^j после
интегрирования получаем для / (z) следующее выражение:
fiz)
aDcp
ко
i-z)
l/a
О
при Z ^0,
при 2; > О
(постоянную интегрирования мы здесь также положили равной нулю).
Решение (23) принимает вид
и (ж, t)
Uo
1/ / X \1/^
(29)
при X > Dt,
где введено обозначение щ =
aD^cp
ко
I/O
Рассмотрим решение (29) подробнее. Оно представляет собой
характерный и наглядный пример так называемого обобщенного
решения квазилинейного вырождающегося параболического уравнения. В
чем его основные особенности?
Во-первых, функция (29) является финитной ""^^ по ж в любой
конечный момент времени. Решения линейного уравнения
теплопроводности, как известно, таким свойством не обладают.
Во-вторых, решение (29), вообще говоря, не имеет всюду
непрерывных производных, входящих в уравнение (17), что также неверно
в случае линейного уравнения. Например, если сг = 1, то производные
du/dt и ди/дх имеют на прямой х = Dt разрывы 1-го рода; если же
сг = 2, то в точках «фронта» тепловой волны х = D t все производные:
du/dt, ди/дх и д'^и/дх'^ — претерпевают разрыв 2-го рода. В то же
время вне множества х = Dt решение (29) является достаточно
гладким. Отметим, что, несмотря на указанные разрывы производных,
тепловой поток (26) является непрерывной функцией. Действительно, из
(29) получаем
W (ж, t)
koUQ
0-+1
aD
;V. (]
J при 0 ^ X ^ Dt,
Dt
(30)
при X > Dt.
Отсюда W{Dt-0,t) = 0 = W{Dt-\-0,t) при любых t ^ 0.
^ Функция g (x) называется финитной (по ж), если существует
постоянная Л > О, такая, что д (ж) = О при всех х ^ А.

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ 271
Перечисленные особенности решения (29) в первую очередь
связаны с тем, что коэффициент теплопроводности к (и) = ко и^
обращается в нуль при и = 0. Параболические уравнения (17) с
коэффициентами к (и), удовлетворяющими условию к{0)=0, называются
вырождающимися.
Отличительной особенностью вырождающихся уравнений (17)
является то, что они могут описывать процессы с конечной скоростью
распространения возмущений. Другими словами, их решения могут
быть финитными функциями. Достаточное условие финитности по х
решения типа «бегущей волны» без труда выводится из уравнения
(28). Оно имеет вид
/
^^"^^ dr]<+ОС. (31)
Г]
Действительно, при выполнении условия (31) уравнение (28) можно
переписать в виде
d
dz
/-
/
0
Г]
drj =
dr] = —Dcp,
-Dcp {zo - X
откуда получаем
(32)
ч
о
где zq — постоянная интегрирования. Из (32) непосредственно следует,
что решение f (z) обращается в нуль в точке z = zq, т. е. функция
(23) финитна. Отметим, что при выполнении условия (31) финитным
по X является рассмотренное выше решение (19). Неравенство (31)
является необходимым и достаточным условием конечности скорости
распространения возмущений в процессах, описываемых уравнением
(17).
Итак, из условия (31) следует существование конечного
«фронта» тепловой волны, где может теряться необходимая гладкость
решения. Это, в свою очередь, требует определения решения в некотором
обобщенном смысле. Обобщенное решение вырождающегося
уравнения (17) удовлетворяет не самому дифференциальному уравнению, а
некоторым построенным на его основе интегральным соотношениям,
которые не содержат производных du/dt, ди/дх, д'^и/дх'^
(претерпевающих, быть может, разрывы). Существенно, однако, то, что эти
соотношения специальным образом учитывают непрерывность
теплового потока (26).
Перейдем теперь к исследованию других частных решений
уравнения (17). Предварительно заметим, что рассмотренные выше
решения (19) и (23) выбраны в первую очередь не случайно. Оказывается,

272 ПРИЛОЖЕНИЯ К ГЛАВЕ III
это единственные типы нетривиальных автомодельных решений,
которые допускает уравнение (17) при произвольных коэффициентах к (и).
Здесь автомодельными мы называем такие реп1ения нелинейного
уравнения в частных производных, конкретный вид которых
определяется путем интегрирования некоторых обыкновенных
дифференциальных уравнений (иногда под автомодельными подразумевают более
узкий класс таких решений). Наличие у рассматриваемой краевой
задачи автомодельного решения существенно упрощает ее исследование.
Новые типы автомодельных решений появляются только у
уравнений (17) специального вида. Рассмотрим уравнение со степенной
нелинейностью (здесь и далее для простоты полагаем ср = 1)
д ( ди\ ди
Пусть температура на границе х = О степенным образом зависит от
времени:
u{0,t) =ио^^, t^O; ш = const > 0. (34)
Пусть, кроме того,
и(ж, 0)=0, х^О. (35)
Краевая задача (33) — (35) допускает автомодельное решение
следующего вида:
u{x,t)=uot'-f{z), ,= ^,^-^1-——^ (36)
где функция / {z) определяется из обыкновенного дифференциального
уравнения, получающегося после подстановки выражения (36) в
уравнение (33):
d (,,dj\ , l + ma dj
В силу (34) и (35) функция / (z) должна также удовлетворять таким
краевым условиям:
/(0) = 1, /(+(Х))=0. (38)
Поскольку уравнение (33) является вырождающимся и допускает
конечную скорость распространения возмущений, необходимо
дополнительно потребовать, чтобы «тепловой поток» —/^ • df/dz был
непрерывной функцией.
При т ф1/а задачу (37) — (38) можно решить лишь численно
(в случае т = 1/а решение (36) в точности совпадает с «бегущей
волной» (29)). С помощью замены
C = lnz, ^piO=z-'/'fiz) (39)

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ 273
уравнение (37) сводится к автономному виду (проведите эти выкладки)
и допускает понижение порядка. Тем самым в новых переменных
становится возможным его анализ на фазовой плоскости. Это позволяет
доказать существование и единственность реп1ения задачи (37) — (38),
а также определить его основные свойства.
Например, при любых значениях параметра ттг > О функция / (z)
является финитной: существует такое zq = zq (ттг, а) > О, что / (z) =
= О для всех Z ^ zo и / (2;) > О при О ^ z ^ zq. Поэтому решение (36)
также финитно по ж и представляет собой тепловую волну,
движущуюся по невозмущенному фону температуры (последнее, в частности,
свидетельствует о том, что решение и (ж, t) удовлетворяет
уравнению (33) в обобщенном смысле). Из выражения (36) для переменной
Z следует, что положение точки «фронта» волны Хф (t),
характеризующееся равенством z = zq, определяется в каждый момент времени
по формуле
x^{t)=zokl/\^,/'t^'+"'^y'. (40)
Таким образом, в отличие от рассмотренных выше решений (19) и
(23) тепловая волна (36) ускоряет со временем свое движение и в
пределе при ^ —>- + 00 нагревает до бесконечно больших температур все
пространство ж ^ 0.
При незначительных нарушениях краевых условий (34) и (35)
основные закономерности процесса нагрева, которые дает
пространственно-временная структура автомодельного решения (36),
сохраняются. Например, вместо (35) можно взять произвольную ограниченную
финитную начальную функцию
и (ж, 0) = uo (ж) ^0, ж ^ О,
и тем не менее при достаточно больших t с высокой степенью
точности будет выполняться равенство (40). Иными словами,
автомодельное решение (36) является асимптотически устойчивым при ^ —>- + оо
относительно «малых» возмущений краевых данных (более того,
установлено, что оно асимптотически устойчиво по отношению к «малым»
отклонениям коэффициента теплопроводности к (и) от степенной
зависимости к = kou^). И хотя в реальных задачах физики и техники
бесконечных температур достигнуть нельзя, все это позволяет
говорить об автомодельном решении (36) как о промежуточной
асимптотике рассматриваемого процесса нагрева, которая всегда реализуется
при не слишком малых и не очень больших временах.
Уравнение со степенной нелинейностью имеет также
автомодельное решение другого вида:
u{x,t)=uoe^'f{z), z= ^ ^ (41)
где С — произвольная постоянная. Мы рассмотрим ниже случай С >
> 0. Функция / (z) определяется из краевой задачи для обыкновенного
18 А. Н. Тихонов, А. А. Самарский

274 ПРИЛОЖЕНИЯ К ГЛАВЕ III
дифференциального уравнения
dz \ dz) 2 dz ' ' /Д2А
/(0) = 1, /(+00) =0.
Краевые условия, порождающие данное автомодельное решение,
определяются видом функции f (z). Из (41) непосредственно следует, что
они таковы:
u{0,t) =иое'^\ t^O,
Решение задачи (42) существует и единственно, функция / {z)
финитна (следовательно, решение (41) является обобщенным). Точка
«фронта» тепловой волны движется со временем по закону
(здесь zq = zq {а) > О — длина носителя функции f (z)). При ^^+00
волна полностью «заполняет» пространство ж ^ 0. Все качественные
заключения, сделанные выше по отношению к автомодельному
решению (36), справедливы и в данном случае.
3. Релсимы с обострением. Эффект локализации тепла.
В этом пункте мы рассмотрим новый класс автомодельных реп1ений
уравнения (33), которые обладают целым рядом отличительных
особенностей.
Пусть температура на границе х = О изменяется в режиме с
обострением:
u{0,t) =ио{Т -г)"", 0^t<T; r = const>0. (44)
Предполагается, что постоянная п < О, поэтому и{0, t) —>- + оо при
t ^ Т~ = Т — 0. Режимом с обострением называется такой
закон изменения некоторой величины, который обеспечивает ее
неограниченное возрастание в течение конечного времени (в данном случае
равного Т < + оо). Режимы с обострением, аналогичные (44),
используются при описании многих существенно нестационарных физических
процессов. Оказывается, таким специфическим граничным условиям
отвечают решения с очень интересными и весьма необычными
свойствами.
Уравнение со степенной нелинейностью (33) имеет автомодельное
решение, удовлетворяющее граничному режиму (44):
u{x,t)=uo{T-trf{z), z= J (45)

III. МЕТОД ПОДОБИЯ В ТЕОРИИ ТЕПЛОПРОВОДНОСТИ
275
Подставляя (45) в (33), для функции f (z) получаем задачу
d
dz
f
dl
dz
1 + пег d f
2 ^~dz
nf = 0, z > 0,
(46)
/(0)
/(+<x))=0.
(47)
Существование и единственность решения задачи (46) — (47)
устанавливается путем сведения уравнения (46) с помощью указанной вы-
Hie замены (39) (см. рассуждения, относящиеся к задаче (37) — (38))
к уравнению первого порядка и последующего анализа поля его
интегральных кривых.
Из (45) вытекает, что это автомодельное решение удовлетворяет
краевой задаче с граничным режимом (44) и начальным условием
«(ж, 0)=иоГ"/
1/^ а/г, _^ l+ncr
(48)
^0 "-о
Свойства решения задачи (46) — (47) (как, впрочем, и самого
автомодельного решения (45)) существенно зависят от соотношения между
величинами п и ст. Так, если п < —1/сг, то функция f (z) имеет
конечный носитель длины zq = Zq {п, а) < + оо. Вблизи точки z = Zq (в
левой ее окрестности) справедливо разложение
/W
(1 + псг)
■azo
V.
{zo - zfl^ X
1 (1 - по)
2а^ (1 + пег) Zo (сг + 1)
{zo - z)-\-
(49)
В случае п > —1/а решение задачи (46) — (47) строго положительно
при любых конечных 2; > О и является бесконечно дифференцируемой
функцией (как следует из (49), при п < —1/а производные функции
f (z) могут иметь разрыв в точке z = Zq). При больших z
выполняется разложение
f{z) = Cz^^ +... , (50)
где С = С (п, а) > О — некоторая постоянная. Величина С, так же как
и значение zq = zq (n, а) в случае п < —1/сг, определяется в
результате численного решения задачи (46) — (47).
Наиболее простым является случай п = —1/сг. Здесь решение
задачи (46) — (47) выписывается в явном виде:
f{z) = {
1-^
2/а
при о ^ Z ^ Zo,
при Z > Zo,
(51)
18*

276
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
где zq—длина носителя финитной функции (51)
формуле
-вычисляется по
zo =
(а+ 2)
V2
Теперь мы перейдем к самому важному моменту — анализу
пространственно-временной структуры автомодельного решения (45) при
различных значениях п. Пусть сначала п = — 1/сг. Тогда, как следует
из (51), функция (45) представляет собой весьма необычную тепловую
волну с остановившимся фронтом ""^^i
и (ж, ^) = <
щ
(T-t) V- (1-
Хо
%
, о ^ ж ^ жо.
О, X > Хо =
2<^±^..<1''"
(52)
Здесь тепловые возмущения далее глубины х = xq вообще не
проникают, несмотря на неограниченный рост температуры на границе ж = О
и во всех внутренних точках отрезка [О, xq]. Решение (52) наглядно
проявляет свойство локализации («инерции») тепла, которое в данном
случае характеризуется тем, что в пространстве образуется область с
отличной от нуля температурой, не меняющая своих размеров в
течение конечного времени. Внутри области локализации О < ж < жо
температура и количество поступающей туда энергии неограниченно
возрастают при t —>- Т~. Величина жо называется глубиной
локализации.
В общем случае локализованным называют такое решение,
которое неограниченно возрастает в течение конечного времени в
ограниченной части пространства (это определение является наиболее
универсальным, оно, в частности, не содержит требования конечной
скорости распространения возмущений; см. об этом в гл. VI, § 1).
Граничный режим, отвечающий показателю п = — 1/сг в (44),
называется S-режимом. Он разделяет семейство степенных режимов с
обострением на два класса: в первом из них п > —1/сг (это так
называемые LS-режимы), во втором — п < — 1/сг (П8-режимы). При
п > —1/сг автомодельное решение растет до бесконечности только в
одной точке: ж = О, и при всех ж > О оно ограничено сверху равномерно
по ^. В соответствии с введенным выше определением такие решения
также называются локализованными. Укажем одну важную
особенность граничного LS-режима. Обозначим через Жэф (t) эффективную
^ Впервые это решение было построено в работе: Самарский А. А.,
Соболь И. М. Примеры численного расчета температурных волн // ЖВМ
и МФ. 1963. Т. 3, №4. С. 703—719.

IV. ЗАДАЧА О ФАЗОВОМ ПЕРЕХОДЕ 277
глубину (полуширину) проникновения тепловой волны, которая в
каждый фиксированный момент времени определяется из равенства
и{х,ф (t), t) = ^и{0, t) = ^{Т - tr.
Тогда, обозначив через z* единственный корень уравнения
1
fizl-,,
из (45) получим
Поскольку при п > — 1/сг показатель (1 + па)/2 положителен,
глубина проникновения волны, несмотря на бесконечный рост температуры
на границе, сокращается при t ^ Т~ вплоть до нуля. Тем самым
поступающая в среду энергия сосредоточивается во все сокращающейся
части пространства. Отметим, что никакие другие из ранее
рассматривавшихся автомодельных решений таким свойством не обладали.
В случае п < —1/сг тепловая волна является уже не
локализованной, а бегущей волной; как следует из (45), ее фронт движется
по нулевому фону температуры со все увеличивающейся скоростью
(1 + пег < 0) по закону
//2 .,72
Хф (t) = zo к^^ V {T-t)^, 0^t<T,
и к моменту обострения t = Т уходит на бесконечное расстояние. В
результате при t —>- Т~ температура неограниченно возрастает во всем
пространстве. В этом смысле решение (45) при п < —1/сг
принципиально не отличается от автомодельных решений (36) и (41). И там и
здесь температура всюду неограниченно растет, только в одном случае
за конечное, а в двух других — за бесконечные времена ""^л
IV. Задача о фазовом переходе
При изменениии температуры тела может происходить
изменение его физического состояния, в частности при переходе
температуры через точку плавления — переход из жидкой фазы в твердую
(или обратный переход). Па поверхности фазового перехода все
время сохраняется постоянная температура. При движении поверхности
^ Более подробную информацию о результатах исследования эффекта
локализации тепла в произвольных нелинейных средах см. в работе:
Галактионов В. А., Кур д ЮМОВ СП., Михайлов А. П., Самарский А. А.
Локализация тепла в нелинейных средах // Дифференциальные
уравнения. 1981. Т. 17, №10. С. 1826—1841. См. также приведенный там список
литературы.

278
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
фазового перехода происходит выделение скрытой теплоты
затвердевания (плавления). Сформулируем те дополнительные условия, которые
должны выполняться на поверхности затвердевания ""^ л
Рассмотрим плоскую задачу, когда поверхностью раздела
является плоскость X = ^ (t). С момента времени t до момента времени
t + А^ граница х = ^ переместится от точки ^ = xi до точки ^ =
= Ж2 = Ж1 + А^. При этом затвердевает масса рА^ (или
расплавляется, если А^ < 0) и выделяется соответствующее количество тепла
Для выполнения теплового баланса это количество тепла должно
равняться разности количеств тепла, прошедших через границы ^ =
= Ж1 и ^ = Ж2, т. е. должно выполняться условие
h
dui
дх
du2
дх
At = ЛрА^,
где ki и к2 —коэффициенты теплопроводности первой и второй фазы,
а Л — скрытая теплота плавления.
Переходя к пределу при А^ —>- О, мы и получим дополнительное
условие на границе раздела в следующем виде:
ki
dui
дх
du2
дх
Хр
dt'
Это условие имеет место как для процесса затвердевания (когда А^ >
> О и d^/dt > 0), так и для процесса плавления (когда А^ < О и
d^/dt < 0); направление процесса определяется знаком левой части.
Рассмотрим процесс замерзания воды, при котором температура
фазового перехода равна нулю. Будем рассматривать массу воды х ^
^ О, ограниченную с одной стороны плоскостью ж = 0. В начальный
момент ^ = О вода обладает постоянной температурой с > 0. Если на
поверхности ж = О все время поддерживается постоянная температура
ci < О, то граница промерзания х = ^ будет со временем проникать в
глубь жидкости.
Задача о распределении температуры при наличии фазового
перехода и о скорости движения границы раздела фаз (например, внутри
замерзающей воды) сводится к решению уравнений
дщ 2 ^^^1 п / / ^
dU2 о d^U2
dt ^
d'^U2
-—- для 4 < ж < ^
(1)
^ Франк Ф., Мизес Р. Дифференциальные и интегральные уравнения
математической физики. Л.; М., 1937. Гл. ХП1.

IV. ЗАДАЧА О ФАЗОВОМ ПЕРЕХОДЕ 279
с дополнительными условиями
ui = ci при ж = о,
U2 = с при ^ = О
(2)
и условиями на границе замерзания
Ml = «2 = О при X = ^, (3)
к —
дх
-к —
.=С ^*
Apf, (4)
где ki^ а\ и /;;2, а| — коэффициенты теплопроводности и
температуропроводности соответственно твердой и жидкой фаз. Задачу (1) — (4)
часто называют задачей Стефана, задачей о фазовом переходе,
или задачей о промерзании.
Penienne задачи будем искать в виде
Ui= Ai^Bi^i ^ ) , U2 = ^2 + ^2 Ф
2ai V V \2a2VV
где ^1, 5i, Л2 и В2—пока не определенные постоянные, а Ф-
интеграл ошибок
о
Удовлетворяя условиям (2) и (3), получим
-4l=Ci, А2+В2=С
из условия (2) и
Л1+Б1Ф(—^) =0,
Лз + Бз Ф ( —^ ) = О
ИЗ условия (3). Последние условия должны иметь место для любых
значений t. Это возможно лишь при выполнении соотношения
i = aVi, (5)
где а —некоторая постоянная. Соотношение (5) определяет закон
движения границы замерзания.

280
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
Для постоянных ^1, 5i, Л2 и В2 получаются выражения
Ai = ci,
Bi = -
Ф
2ai
Ao =
^'[й)
Ф
2a^
Bo =
Ф
2a2
(6)
Чтобы определить постоянную a, надо воспользоваться соотно-
HienneM (4):
ki ci e
ai Ф
2ai
+
koce
«2
1-Ф
2a^
Xpa
v^
(7)
Penienne этого трансцендентного уравнения и дает значение а.
Наличие хотя бы одного решения при ci < О, с > О следует уже из того"*^^,
что при изменении а от О до + оо левая часть уравнения изменяется
от —00 до +00, а правая — от О до — оо. В случае если с равно
температуре плавления (с = 0), выражения (6) и (7) для определения
коэффициентов принимают более простой вид:
^2 = ^2 = о,
Л1=С1, Bi =
Ф
Cl
2ai
{&)
ki Cl e
ai Ф
a
2a~i
= — Xpa
(7')
Положив aj2a\ — /3, можем переписать уравнение (7') в таком виде:
1 е-^' _
' Асимптотическое представление функции 1 — Ф (^) при
с. 758.
оо см. на

IV. ЗАДАЧА О ФАЗОВОМ ПЕРЕХОДЕ
281
где постоянная D определяется выражением
^ Лр а?
kici
Воспользовавп1ись графиком функции (р {/3) =
рис. 43, легко графически
определить значение а.
Решение задачи о промерзании
может быть также получено при
помощи метода подобия, приведенного
в Приложении П1 к этой главе.
Задача о промерзании является в
некотором смысле предельным
случаем нелинейных краевых задач,
рассмотренных в Приложении П1. В
самом деле, коэффициенты
теплопроводности и теплоемкости в задаче
о промерзании являются кусочно-
постоянными функциями, и, кроме
того, при и = О теплоемкость имеет
бесконечно большое значение. Этот
случай можно получить как
предельный при г —>- О, когда скрытая
теплота выделяется не мгновенно, а
лАФ(/3)'
данным на
2,5
2,0
1,5
1,0
0,5
0,0
111
^(р)'
[\
\\
\
\
\
\\
1
/5-
0,0
0,0
0,0
0,0
-Щг^
^\
0,04
0,03
0,02
0,01
р1 -^
1 С
о о
-1 j.,o ^,^
0,5
1,5
2,0
1,0
Рис. 43
на некотором промежутке (—е, +е), причем должно выполняться
условие
Е
I
С (и) du = Л.
Однако эту задачу можно решить и непосредственно, пользуясь
методом подобия. Нетрудно убедиться, что все условия задачи
останутся неизменными, если масштаб длины увеличить в к раз, а
масштаб времени — в к'^ раз. Это значит, что решение задачи зависит от
аргумента ж/лД, т. е. что
и (ж, t)= f
2лД
Отсюда, в частности, следует, что движение нулевой изотермы будет
описываться уравнением ^ = о. лД, где а — значение аргумента, при
котором / {а) = 0. Для определения функции / мы имеем следующие

282 ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
условия:
9^Vi dfi
ai ——г- = -2z —— для О < z < а,
dz"^ dz
dz^ dz
aj , ^ = —2z —;— для a < z < CO,
/i(0)=ci, /2(<x))=c, /i (a) =/2 (a) = 0,
fci/l(a)-fc2^(a) = A^,5.
Поэтому функция / (z) имеет вид
2
fi{z) = Ai-\- В1Ф (^] , если 0 < 2; < a,
/2 (2;) = Л2 + ^2 Ф f -— j , если a < z < oo.
Для определения постоянных Ai, Bi, Л2, B2 мы должны
использовать условия (2) и (3), из которых вытекают формулы (6). Для
определения а получается условие (7). Таким образом,
аналитическая часть реп1ения в обоих методах одинакова.
Изложенные здесь соображения показывают, что задачу о
промерзании можно peniaTb также и в тех случаях, когда скрытая теплота
выделяется не при фиксированной температуре, а на некотором
интервале температур. Подобным же методом можно реп1ить задачу, если
имеется не одна, а несколько критических температур, что
встречается при фазовых превращениях в процессе перехода от одной
кристаллической структуры к другой, например при перекристаллизации стали.
Наиболее эффективным методом численного решения задач о
фазовых переходах является метод конечных разностей, который применим
для случая двух и трех пространственных переменных при наличии
нескольких фазовых переходов (см. Дополнение I, § 4).
V. Уравнение Эйнштейна — Колмогорова
Микроскопические частицы, находящиеся в среде в свободном,
взвешенном состоянии, совершают беспорядочное движение,
называемое броуновским. Обозначим вероятность для частицы, вышедшей
из точки Мо в момент ^о, находиться в момент t в малой
окрестности А V точки М функцией
WiM,t;Mo,to)-AV. (1)
Вероятность здесь понимается в том смысле, что если в течение
некоторого малого промежутка А^ = ^ — ^о из точки Mq выходит

V. УРАВНЕНИЕ ЭЙНШТЕЙНА —КОЛМОГОРОВА 283
достаточно большое количество частиц N (причем взаимодействие
между ними пренебрежимо мало), то концентрация этих частиц при
А^ —>- О в точке М в момент t будет равна W (М, t; Mq, ^о)- При этом
за единицу массы частиц принимается вся масса выходящих из точки
Мо частиц.
С подобным же явлением мы встречаемся при диффузии газа,
происходящей в какой-либо (например, воздуп1ной) среде. Функция
W {М, t; Mq, ^о) представляет функцию точечного источника,
соответствующего единичной массе.
Очевидно, что
/
W {М, t- Мо, to) dVM = 1 (i > io) (2)
И что если начальная концентрация частиц в некоторый момент
времени ^0 равна (р{М), то концентрация и{М, t) этих частиц в момент
t > to будет равна
u{M,t)= fw (М, t; Р, ^о) ^ (Р) dVp, (3)
где интеграл берется по всему пространству.
Из последнего равенства следует уравнение ^^
W (М, t', Мо, to)= fw (М, t; Р, в) W (Р, в; Мо, ^о) dVp, (4)
имеющее место для любого значения to < в < t. Это последнее
уравнение называют уравнением Эйнштейна — Колмогорова.
Покажем, что при определенных условиях, наложенных на
функцию И^ (М, t; Мо, to), решение уравнения Эйнштейна — Колмогорова
удовлетворяет некоторому уравнению с частными производными
параболического типа. Рассмотрим случай, когда положение точки М
характеризуется одной координатой х. Предположим, что функция
W {х, t; хо, to) удовлетворяет следующим условиям.
1°.
Иш -—^ = Иш - [{х -OW{x,t + г; С, t)dx = A (^, t). (5)
г^О Г Т J
Если за время г частица переходит из положения ^ в положение ж,
то {х — ^)/т является средней скоростью частицы. Таким образом,
первое условие означает требование существования конечной скорости
упорядоченного движения частицы.
^^ Леонтович М. А. Статистическая физика. М.; Л., 1944. Гл. VI;
Колмогоров А. Н. Об аналитических методах в теории вероятностей //
УМН. 1938. Вып. 5. С. 5—41.

284 ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
2°.
lim ^—^ = lim - [{х - 0'^ W{x,t + г; ^, t) dx = 2В (^, t). (6)
Величина {х — ^)^ не зависит от направления смещения точки х
относительно точки ^. Среднее значение квадрата отклонения за время г
{х - С)2 = /(ж - 0^ W{x,t + г; С, ^) dx
обычно рассматривается как мера неупорядоченности движения за
этот промежуток времени. Требование 2° означает предположение
линейной зависимости среднего квадрата от времени при малых г.
3°.
lim ^-—^ = lim - [ \х- в^ W{x,t + г; ^, t) dx = 0.
r^O Г Т J
(7)
функция W {х, t -\- т; ^, ^), являющаяся функцией точечного
источника, для малых значений г должна быстро убывать, когда |ж — ^| —>- оо,
и возрастать, когда |ж — ^| мало.
Для получения дифференциального уравнения
Эйнштейна—Колмогорова умножим обе части уравнения (4) на произвольную функцию
ф (х), обращающуюся в нуль вместе со своей производной на границах
области интегрирования, и проинтегрируем по всей этой области:
/
W {х, t -\- г; жо, ^о) Ф (х) dx =
= fw{^,t;xo,to)d^ fw{x,t + т;^,t)ф{x)dx.
Разложив в правой части функцию ф (х) в ряд Тейлора по х — ^:
Ф(х) = ф (О + Ф' {О {^-0 + ^ (^ - о' + ^^^ (^ - О',
где ^*—среднее значение, заключенное между ж и ^, и разделив на
г, после простых преобразований будем иметь
/
W{x,t + г; жр, ^о) - W (ж, t; жр, ^р) ^^
/
W (^, t; хо, to) \ф' (О ^^ + Г (О К^ 1 d^ +
IT It л
Предполагая, что ф'" (ж) ограничена:
\ф"'{х)\<А,

V. УРАВНЕНИЕ ЭЙНШТЕЙНА —КОЛМОГОРОВА
285
и учитывая, что
мы получим
/
W{^,t;xo,to)d^
г // ^''' ^^*^ ^^ " ^^' ^ ^^' ^' ^'' ^'^ ^ (^' ^ + ^' ^' ^) ^^^^
<
А\х-^\^
^ - f\x-^\^W{x,t + г; С, ^) ^ж = ^^^
т J т
Из условия 3° вытекает, что это выражение при г —>- О стремится
к нулю. Поэтому, переходя к пределу при г —>- О и используя условия
1°, 2°, получаем
/
^^^^dW{x,t-,x„t,)^^
dt
/
W (е, i; хо, io) [ V-' (О ^ (e, i) + Ф" iO В (e, i) ] de
После интегрирования по частям правой части, принимая во внимание,
что функция ф обращается в нуль вместе со своей производной на
границе области интегрирования, получим
/
ф{х)
dW д {AW) д'^ {BW)
dt дх дх^
dx = 0.
Так как это соотношение должно иметь место для произвольной
функции ^Ij{x), то для функции вероятности W {х, t; Xq, to) мы
получаем дифференциальное уравнение Эйнштейна —
Колмогорова
dW д (AW) д'^ {BW)
dt дх дх^
(8)
Полученное уравнение является уравнением параболического типа,
подобным уравнению теплопроводности, и может быть записано в виде
где
dW_d_f^dW\ dW
dt дх \ дх J дх
а = -А-\- Вх, Р = -Ах + Вхх = о^х-
(9)
Из уравнения (9) видно, что величина В имеет физический смысл
коэффициента диффузии. Если рассматриваемый процесс однороден в
пространстве и времени, т. е. функция W зависит только от разности
^ = X — хо и в = t — to, то коэффициенты А и В яе зависят от х

286 ПРИЛОЖЕНИЯ К ГЛАВЕ III
и ^ и являются постоянными. Уравнение (8) в этом случае является
уравнением с постоянными коэффициентами
Если функция зависит только от |ж — ^|, т. е. вероятности смещения
направо и налево на одинаковые расстояния от точки ^ равны, то
очевидно, что А должно быть равно нулю. Аналитически это следует
из формулы (5) в силу того, что подынтегральная функция нечетна.
В этом случае уравнение (8) является простейшим уравнением
теплопроводности
VI. <S-Функция
1. Определение <^-фyнкции. Наряду с непрерывно
распределенными величинами (масса, заряд, тепловые источники, механический
импульс и т. п.) часто приходится иметь дело с сосредоточенными
величинами (точечная масса, точечный заряд, точечный источник
тепла, сосредоточенный импульс и т. д.). Не следует забывать, что эти
понятия являются «предельными образами» и могут быть
охарактеризованы при помощи понятия «обобщенных функций» ^К
Имея ввиду физический смысл задачи, рассмотрим потенциал в
точке М (см. гл. IV, § 5) единичной массы, сосредоточенной внутри
некоторого объема Т в окрестности точки Мд. Возьмем какую-либо
последовательность функций {рп} {рп ^ 0), каждая из которых равна
нулю вне шара S^^ радиуса Еп с центром в точке Mq, где г^ —^ О
при п —>- 00, и для которых, начиная с некоторого п,
Рп (Р) drp = III Рп (Р) drp = 1. (1)
т „Мо
Рассматривая последовательность функций
т
являющихся потенциалами масс, распределенных с плотностями р^,
и совершая предельный переход при п —>- оо, получаем
Иш Un = . (2)
^ Подробнее см.: Курант Р. Уравнения с частными производными. М.,
1964; Гельфанд И. М., Шилов Е. Г. Обобщенные функции и действия
над ними. М., 1959. (Обобщенные функции; Вып. 1).

VI. ^-ФУНКЦИЯ 287
Этот результат, очевидно не зависит от выбора последовательности
{рп}- Хотя последовательность {un} и сходится к 1/г, однако
последовательность {рп} не имеет предела в классе рассматриваемых
кусочно-дифференцируемых функций. «Предельный образ»,
соответствующий последовательности {рп}, называют функцией S{M, Mq).
Основным свойством, определяющим (5-функцию, является
следующее формальное операторное соотноп1ение:
///
S (м, мо) / (м) drM = {' 'Г'^ '*^™ f; 11: (3)
' ^^ если Мо ^ ^ ,
где / (М) —произвольная непрерывная функция точки М. Имея в
виду, что при п —>- 00 функции рп равномерно стремятся к нулю во
всякой области, не содержащей точки Mq, и неограниченно возрастают
в окрестности S^^ точки Мд, иногда определяют (5-функцию
формально при помощи соотношений
ММ,М.) = (»°''»"^"»' ,4)
I 00 при М = Мо
т ^
Равенство (5) является очевидным следствием формулы (3) при / = 1.
При рассмотрении последовательностей функций в различных
задачах приходится иметь дело с разными определениями сходимости.
Говорят, что последовательность функций
{ Un (ж) } = Ui (ж), U2 (ж), . . . , Un (ж), ... (6)
СХОДИТСЯ равномерно на интервале {а,Ь), если для любого е>
> О можно указать такое N, что при п, т > N для любого х из
(а, Ь) будет выполняться условие
1'^п (ж) — '^т {х)\ < е при п, т > N.
Говорят, что последовательность (6) сходится в среднем на
интервале (а, Ь), если для любого г > О можно указать такое N, что
при п, т > N
ъ
h -
а
\un (ж) -Um {х)\^ dx < е.
Говорят, что последовательность (6) сходится слабо на
интервале (а, 6), если для любой непрерывной функции / существует

288 ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
предел
о
lim / / (ж) Un (х) dx.
п—>-сю J
При рассмотрении сходящихся последовательностей обычно
вводят предельные элементы последовательностей. Рассмотрим
класс непрерывных функций на интервале (а, Ь). В случае
равномерной сходимости предельный элемент принадлежит тому же классу
функций, что не всегда имеет место для сходимости в среднем и
слабой сходимости. Если предельный элемент не принадлежит
рассматриваемому классу функций, то вводят предельные элементы, расп1иряя
исходный класс. При этом под расп1ирением понимается совокупность
исходных и предельных элементов. С понятием расп1ирения
встречаются в теории действительного числа, когда иррациональные числа
вводятся как предельные элементы, определяемые классом
эквивалентных последовательностей.
Рассматривая предельные элементы в смысле слабой сходимости,
мы будем говорить, что две последовательности, { Un } и { г^^ }, имеют
один и тот же предельный элемент, если они эквивалентны, т.е.
последовательность {un — Vn} слабо сходится к нулю:
ь
lim / / (ж) [un (х) - Vn (х)] dx = 0.
п—>-сю J
а
Будем называть последовательность неотрицательных функций
{(5^} нормированной локальной последовательностью
точки жо, если функция Sn равна нулю вне интервала {xq — Sn, xq -\-
+ Sn), где Sn ^ О при п —>- 00, и
b
/ Sn (х) dx = 1.
а
Очевидно, что последовательность {Sn} сходится слабо. Предельный
элемент последовательности {(5п } обычно называют (5-функцией
точки Xq.
В том случае, если предельный в смысле слабой сходимости
элемент и последовательности {un} выходит из класса функций Un, то
интеграл от произведения некоторой функции / на элемент и
определяется как предел
b b
lim / / (ж) Un (х) dx = f {х)и (ж) dx.
п^оо J J

VI. ^-ФУНКЦИЯ 289
Очевидно, что для (5-функции точки xq имеет место равенство
b
f {х)5{х, xo)dx = /(жо).
/.
Это соотношение часто принимают за определение (5-функции.
2. Разлолсение (У-функции в ряд Фурье. (5-Функцию можно
определить так же, как предельный образ других
последовательностей, эквивалентных в смысле слабой сходимости приведенной вып1е
последовательности Sn{x) локальных нормированных функций точки
Xq.
Рассмотрим последовательность функций
^ . .11 v^ / Ш7Г Ш7Г . Ш7Г . Ш7Г \
дп [х, хо) = — + J 2_^ { COS -— X • COS -— хо + sm —- х • sm -— xq 1
1 1 v-^ Ш7Г , , ,^.
= ^ + 7 2^ ^^^ ~r ^"^ ~ ^^^' ^^
m=l
ИЛИ, В комплексной форме,
1 ""
Sn{x,xo) = -Y,e'^f^---o\ (Г)
— п
определенных на интервале (—/, /).
Очевидно, что для любой функции д{х), разлагаемой в ряд
Фурье, имеет место следующее предельное равенство:
lim Sn{x, xo)g{x)dx = д{хо), (8)
n—>-CXD J
-I
которое показывает, что в классе функций {д{х)}, разлагаемых в
ряды Фурье, приведенная выше последовательность Sn (ж, xq)
эквивалентна в смысле слабой сходимости последовательности Sn{x, жо),
т. е. что
г / ч 1 1 V^ ^^ / ч /^ч
^ (ж, жо) = — + у 2^ COS — (ж - жо), (9)
т=1
если это равенство понимать с точки зрения слабой сходимости.
С этой же точки зрения имеет место равенство
сю
5 (ж, Хо) = ^ ^п (х) (fn (жо), (10)
п=1
19 А. Н. Тихонов, А. А. Самарский

290
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
где { (fri {х) } — полная ортогональная и нормированная система
функций, определенных на некотором интервале (а, 6), а также равенство
сю сю
5 (ж, х^) = ^ [ е'^ (^-^о) dk=- [ COS к {х- хо) dk. (11)
ZTT J 7Т J
- оо О
Покажем, что при вычислении интегралов, содержащих (5-функцию,
можно пользоваться рядом (9), производя почленное интегрирование
подынтегральной функции.
Рассмотрим некоторую функцию д (ж), разложимую в ряд Фурье,
и интеграл
I
д (х) S (ж, Хо) dx.
Подставляя сюда вместо функции (5 (ж, жо) ее выражение из формулы
(9), выполним почленное интегрирование ряда, стоящего под знаком
интеграла. В результате получим
5(х) = | +
т=1
I
ху
(1Г)
где
S^ = Т 9{xo)dxo,
1 ? ^^ л
9т = J g{xo)cos——xodxo,
1 f ттт
grn = j g{xo)sm—-xodxo.
(12)
Сопоставление формулы (11) с равенством
S (ж, жо) д (ж) dx = д (жо) (-/ < жо < О
/•
показывает, что выполненное выше почленное интегрирование ряда
для (5-функции приводит к правильному результату.
Таким образом, в классе функций, разложимых в ряд Фурье,
последовательность частичных сумм
к
9/ ^-^
21
п= — к

VI. ^-ФУНКЦИЯ 291
эквивалентна нормированной локальной последовательности {Sn}-
Другие формы представления (5-функции также основаны на
использовании некоторых функциональных последовательностей,
эквивалентных в смысле слабой сходимости последовательности {Sn}-
3. Применение <^-фyнкции к построению функции
источника. Рассмотрим следующую задачу:
Ut = a'^Uxx, (13)
и{х,0)=^{х), (14)
и(0, t) =u{l,t) =0. (15)
Заданной функции (р (х) соответствует единственное penienne задачи
и (ж, t) = C[(f (х)].
Допустим, что оператор С можно представить в виде
и (х, t)=C[^ (х)] = IG (х, С, t) ^ (О di, (16)
о
где G (ж, ^, t)—ядро оператора С.
Для того чтобы найти ядро G (ж, ^, ^), положим
^{х)=5{х-х^). (140
Заменяя в формуле (16) ^ (ж) (5-функцией, получим
и{х, t) = G{x, жо, t), (17)
т. е. G (ж, жо, t) является решением задачи (13) при начальном
условии (14').
Представим (5-функцию в виде ряда Фурье:
е- / ч V^ 2 , ПТГ . П7Г
о [х — хо) = > у sm —- X sm —- xq.
n=l
Ядро G, очевидно, надо искать в виде суммы
сю
G (ж, жо, t) = ^ An (t) sin — ж, (18)
n=l ^
каждое слагаемое которой должно удовлетворять уравнению
теплопроводности. Отсюда следует, что
Из начального условия сразу же получаем
7-. 2 . П7Г
Вп = J sm —жо.
19*

292 ПРИЛОЖЕНИЯ К ГЛАВЕ III
Таким образом, мы формально получили для ядра G выражение
г» сю / \ 2
„. ч 2 ^-^ _(njLYa^t . ^7Г . П7Г ,_^.
G (ж, жо, ^) = у > е V Z У sm —- ж sm —- жо, (19)
п=1
совпадающее с представлением для функции источника, которое было
исследовано в § 3. Penienne задачи (13) — (15) дается формулой (16),
где G (ж, жо, t)—функция, определяемая формулой (19).
Подобным же образом можно найти выражение для функции
источника на неограниченной прямой. Функция G в этом случае будет
определяться условиями
щ — a^Uxx =0 (— 00 < ж < оо), (20)
и (ж, 0) = (/? (ж) = (5 (ж — жо). (21)
Имея в виду разложение (5-функции в интеграл Фурье
сю
S {х — Жо) = — / COS л (ж — Жо) dX,
7Г J
о
будем искать G (ж, жо, ^) в виде
ею
G (ж, Жо, t) = - Ах (t) cos Л (ж - Жо) ^Л. (22)
о
Из уравнения (20) находим
Ах (t) = Af^ e-'^'^''. (23)
Полагая i = О и сравнивая формулы (23) и (21), получаем
ЛТ = 1-
Таким образом,
ею
1 /* _ 2\2f
С(ж, жо,^) = - / е "" ^ ЧosЛ(ж - жо)б?Л.
о
Вычисление этого интеграла дает
1 _ (ж-жо)^
G{x,xo,t)= е ^аЧ .
2 л/тга^^
Отсюда следует, что решение задачи о распространении тепла на
бесконечной прямой должно выражаться формулой
ею
u{x,t)= I G{x,^,t)<p{Odt (24)

VI. ^-ФУНКЦИЯ 293
Выяснение границы применимости формул, полученных методом
(5-функции, требует специального исследования.
В качестве примера рассмотрим теперь неоднородное уравнение
щ = а Uxx Н , (25)
ср
где F {х^ t)—плотность распределенных тепловых источноков. Если
в точке ж = ^ в момент t = to помещен мгновенный источник тепла
мощности Qo, то
F{x,t)=QoS{x-OS{t-h). (26)
Найдем решение неоднородного уравнения
щ = а^и,, + ^5{x-OHt-to) {to > 0) (27)
ср
при нулевом начальном условии
и{х, 0) =0.
Учитывая интегральное представление
сю
S {х — ^) = — / COS л (ж — ^) б?Л,
7Г J
о
будем искать функцию и{х, t) в виде
сю
и{х, t) = — / u\ (t) COS Л (ж — ^) dX.
7Г J
О
Подставляя эти выражения в уравнения (27), получаем уравнение для
^л(^):
ux{t)+a'X'ux{t) = ^S{t-to)
ср
с начальным условием
ил (0) = 0.
Как известно, решение неоднородного уравнения
й-\-а^и = f{t), и{0) = 0
имеет вид
t
u{t)= f е-^^ ^^-^^ f (т) dr. (28)

294
ПРИЛОЖЕНИЯ К ГЛАВЕ Ш
В нашем случае
t
ср J
их
при t < to,
I cp
\' (t-to)
при t > to.
Таким образом,
(29)
и {x.
сю
t) = 9l- fe--'^'^'-'^^co^X{x-OdX=^G{x,^,t-to),
cp 7T J cp
где
G{x,^,t-to)
2 v^vra^ {t - to)
g 4a2(t-to)
— функция влияния мгновенного точечного источника.
Подобный метод построения функции влияния часто используется
в теоретической физике ^^.
^ См. подробное изложение теории ^-функции и многочисленные примеры
ее применения в книге: Иваненко Д. Д., Соколов А. А. Классическая
теория поля. (Новые проблемы). М.; Л., 1951. Гл. I.

ГЛАВА IV
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
При исследовании стационарных процессов различной физической
природы (колебания, теплопроводность, диффузия и др.) обычно
приходят к уравнениям эллиптического типа. Наиболее
распространенным уравнением этого типа является уравнение Лапласа
Аи = 0.
Функция и называется гармонической в области Т, если
она непрерывна в этой области вместе со своими производными до
2-го порядка и удовлетворяет уравнению Лапласа.
При изучении свойств гармонических функций были разработаны
различные математические методы, оказавшиеся плодотворными и в
применении к уравнениям гиперболического и параболического типов.
§ 1. Задачи, приводящие к уравнению Лапласа
1. Стационарное тепловое поле. Постановка краевых
задач. Рассмотрим стационарное тепловое поле. В гл. III было показано,
что температура нестационарного теплового поля удовлетворяет
дифференциальному уравнению теплопроводности
щ = а /ли [ а = —
V ср
Если процесс стационарен, то устанавливается распределение
температуры и (ж, у, z), не меняющееся с течением времени и,
следовательно, удовлетворяющее уравнению Лапласа
Аи = 0. (1)
При наличии источников тепла получаем уравнение
А« = -/, / = р (2)
где F — плотность тепловых источников, а к — коэффициент
теплопроводности. Неоднородное уравнение Лапласа (2) часто называют
уравнением Пуассона.

296 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Рассмотрим некоторый объем Т, ограниченный поверхностью Е.
Задача о стационарном распределении температуры и (ж, у, z) внутри
тела Т формулируется следующим образом.
Найти функцию u{x,y,z), удовлетворяющую внутри Т
уравнению
Au = -f{x,y,z) (2)
и граничному условию, которое моэюет быть взято в одном из
следующих видов:
а) и = fi на Е (первая краевая задача),
ди
б) 7^ = /2 на Е (втораякраеваязадача),
on
ди
в) ——\- h{u — /з) =0 на Е (третья краевая задача),
^де /i, /2, /3, h—заданные функции, ди/дп—производная по
внешней нормали к поверхности Ti^\
Физический смысл этих граничных условий очевиден (см. гл. П1,
§ 1). Первую краевую задачу для уравнения Лапласа часто
называют задачей Дирихле, а вторую краевую задачу — задачей
Неймана.
Если ищется решение в области То, внутренней (или внешней) по
отношению к поверхности Е, то соответствующую задачу называют
внутренней (или внешней) краевой задачей.
2. Потенциальное течение лсидкости. Потенциал
стационарного тока и электростатического поля. В качестве второго
примера рассмотрим потенциальное течение жидкости без
источников. Пусть внутри некоторого объема Т с границей Е имеет место
стационарное течение несжимаемой жидкости (плотность р = const),
характеризуемое скоростью v (ж, у, z). Если течение жидкости не
вихревое, то скорость V является потенциальным вектором, т. е.
v = -grad(/?, (3)
где ip — скалярная функция, называемая потенциалом
скорости. Если отсутствуют источники, то
divv = 0. (4)
^ Очевидно, что стационарное распределение температуры может
установиться липЕь при условии равенства нулю суммарного потока тепла через
границу области. Отсюда следует, что функция /2 должна удовлетворять
дополнительному требованию
//■
/2 da = 0.
Е

§ 1] ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА 297
Подставляя сюда выражение (3) для v, получим
divgrad(/? = О,
или
A^p = О, (5)
т. е. потенциал скорости удовлетворяет уравнению Лапласа.
Пусть в однородной проводящей среде имеется стационарный ток
с объемной плотностью j (ж, ^, z). Если в среде нет объемных
источников тока, то
divj = 0. (6)
Электрическое поле Е определяется через плотность тока из
дифференциального закона Ома
E = i, ,7)
где Л — проводимость среды. Поскольку процесс стационарный, то
электрическое поле является безвихревым, или потенциальны м"*^^,
т. е. существует такая скалярная функция ip (ж, ^, z)^ для которой
E = -grad(/? (j =-Agrad(/?). (8)
Отсюда на основании формул (6) и (7) заключаем, что
A^p = О, (9)
т. е. потенциал электрического поля стационарного тока
удовлетворяет уравнению Лапласа.
Рассмотрим электрическое поле стационарных зарядов. Из
стационарности процесса следует, что
rotE = 0, (10)
т. е. поле является потенциальным и
E = -grad(/?. (80
Пусть р (ж, ^, z) — объемная плотность зарядов, имеющихся в
среде, характеризуемой диэлектрической постоянной г = 1. Исходя из
основного закона электродинамики
[ [ EndS = 47rY,ei = ^7r Ш pdr (11)
S т
(где Т — некоторый объем, S — поверхность, его ограничивающая,
^ ef — сумма всех зарядов внутри Т) и пользуясь теоремой
Остроградского — Гаусса
f f EndS= fff div E dr, (12)
S T
^ Из второго уравнения Максвелла — Н = — rot Е следует, что rot Е = 0.
с

298 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
получаем
div Е = 4:7гр.
Подставив сюда выражение (8) для Е, будем иметь
A(f = -47гр, (13)
т. е. электростатический потенциал (f удовлетворяет уравнению
Пуассона. Если объемных зарядов нет (р = 0), то потенциал (р должен
удовлетворять уравнению Лапласа
Основные краевые задачи для рассмотренных процессов
относятся к трем типам, приведенным вып1е. Мы не будем здесь
останавливаться на некоторых других
краевых задачах, характерных для
различных физических процессов. Некоторые
из этих задач будут приведены в
приложениях.
3. Уравнение Лапласа в
криволинейной системе координат.
Выведем выражение для оператора
Лапласа в ортогональной криволинейной
системе координат. Пусть в пространстве
вместо декартовых координат х, у, z введены криволинейные
координаты qi, q2, Qs с помощью соотношений
Qi= fi{x,y, z), q2 = f2{x,y, z), дз = fsix.y, z), (14)
разрешая которые относительно ж, у, z, можно написать
х = ^1 {qi, ^2, ^з), У = ^2 {qi, ^2, ^з), z = (рз fe, ^2, ^з). (15)
Полагая qi = Ci, ^2 = С'2, ^з = С'з, где Ci, С2, С3—постоянные,
получим три семейства координатных поверхностей:
fi{x,y, z) = Ci, f2{x,y, z) = C2, /з{х,у, z) = Сз. (16)
Рассмотрим элемент объема в новых координатах, ограниченный
тремя парами координатных поверхностей (рис. 44). Вдоль ребра АВ
q2 = const, q3 = const, вдоль AD qi = const, q2 = const, вдоль AC
qi = const, q3 = const. Направляющие косинусы касательной к ребрам
АВ, АС и AD пропорциональны соответственно
d(fi d(f2 d(f3. d(fi d(f2 d(f3 ^ d(fi d(f2 д(рз
о' о' о' о' о' о' о' о' о'
oqi oqi oqi oq2 oq2 oq2 oqs oqs oqs
Условие ортогональности ребер будет иметь вид
dqi dqu oqi dqu dqi dqu

ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА
299
Вычислим элемент длины в новых координатах:
ds^ = dx^ + dy^ + dz^ =
V dqi ^ dq2
dq2 + -^— dqs
oqs
+
+
d(p2 , 9(p2 , , d(p2 ,
^— d^i + -— dq2 + ^— dqs
oqi oq2 dqs
+
+
-^— dqi + -— dq2 + ^— й^з
oqi oq2 dqs
(18)
Раскрывая скобки и учитывая условия ортогональности (17), получаем
где
ds'^ = Hi dqi + Hi dqi + Hi dqi,
Hl =
(19)
dqi
Щ
я| =
dq2
dqs
+
+
+
d(f2
dqi
d(f3
dqi
d(f2
dq2
d(f2
dqs
+
d(f3
dq2
d(f3
dqs
(20)
Вдоль каждого из ребер элементарного объема меняется только
одна координата, поэтому для длины этих ребер согласно формуле (19)
будем иметь
dsi = Hi dqi, ds2 = H2 dq2, dss = H3 dqs, (21)
так что элемент объема равен
dv = dsi ds2 dss = Hi H2 Hs dqi dq2 dq^. (22)
Рассмотрим теперь некоторое векторное поле А (ж, у, z).
Вычислим divA, определяемую известной формулой векторного анализа
//
AndS
divA = lim
(23)
где S — поверхность, ограничивающая некоторый объем vm^
содержащий рассматриваемую точку М. Применим эту формулу к элементу
объема dv, изображенному на рис. 44.
Пользуясь теоремой о среднем, можно представить разность
потоков вектора А через противоположные грани, например через правую
и левую, в виде
Ql = Ai dS2 ds^\q^j^dqi " М dS2 ds^\q^ .

300
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Принимая во внимание формулы (21), получим
Qi =
Н2 Hz Ai \gj^+dqi — H2 Hz Ai Igj
dq2 dqz =
_d_
dqi
{H2HzAi)dqidq2dqz. (24)
Аналогично вычисляются две другие разности потоков через
противоположные грани:
Q2 = ^— (Яз Hi А2) dqi dq2 dqs,
oq2
(25)
Q3 = ^— (^1 H2 A3) dqi dq2 dq^.
dqs
(26)
Подставляя в формулу (23) значение J J An dS = Qi -\- Q2 -\- Qs и поль-
зуясь формулой (22), получаем выражение дивергенции в
криволинейных ортогональных координатах:
div А
Н1Н2Н3
г\ г\ л
-- {Н2ЩА1) + -- {ЩН1А2) + ^- (Я1Я2ЛЗ)
dqi dq2 dqs
Предположим, что поле А потенциальное, т. е.
А = gradu.
Тогда
(27)
(28)
Ai
ди
1 ди
dsi Hi dqi'
1 ди 1 ди
Н2 dq2' ^ Щ dqs'
Подставив в (27) выражения (29) для Ai, А2, As, получим выражение
для оператора Лапласа:
Аи = div grad и =
Hi Н2 Hs
д /Я2Я3 ди
dqi
Hi dqi
+
д fHsHi ди\ д fHiH2 ди
dq2 V Н2 dq2) dqs \ Щ dqs J \ '
(30)
Таким образом, уравнение Лапласа Аи = О в ортогональных
криволинейных координатах qi, q2 и дз записывается следующим образом:
д (HiHz ди
Я1Я2Я3 [dqi V Hi dqi
+
д /HzHi ди\ д (HiH2 ди
dq2 \ Яг 9^2/ dqz \ Hz dqz
= 0.
(31)

§ 1] ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА 301
Рассмотрим два частных случая.
1. Сферические координаты. В этом случае qi = г, q2 = О,
q-^ = (f VL формулы преобразования (15) принимают вид
ж = г sin^cos(/?, ^ = г sin^sin(/?, 2; = rcos^.
Вычислим ds^:
ds^ = (sin в cos (fdr + r cos 0 cos (fdO — rs'mO sin (f d(f)^ +
+ (sin в sin (f dr -\- r cos в sin (p dO -\- r sin в cos (p d(p)^ +
+ (cos в dr — r sin в dO)^;
после раскрытия скобок и упрощений находим
ds'^ = dr'^ + r^ dO'^ + r^ sin^ 6> ^(/:?^
T. e.
Я1 = 1, Я2=г, Яз =r sin i9.
Подставив значения Я1, Я2, Яз в формулу (31), получим уравнение
Лапласа в сферических координатах:
9 f о . л ди\ д { . ^ ди\ д { I ди
или окончательно
= 0,
(32)
2. Цилиндрические координаты. В этом случае qi = р,
Q2 = ^, qs = Z и
X = pcosip, у = psiuip, Z = Z,
так что
Щ = 1, Я2 = р, Яз = 1.
Уравнение Лапласа в цилиндрических координатах принимает вид
1д_[ди\ ^ а^ dhj.
р dp \ dp) р^ д^'^ dz^
^p,^,zU=-^Ap^J+-^^^ + ^^ = 0. (33)
Если искомая функция и не зависит от z, то уравнение (33)
упрощается:
^--'' = -рЭр['Тр)^7э^ = '- ^''^
4. Некоторые частные решения уравнения Лапласа. Боль-
П10Й интерес представляют реп1ения уравнения Лапласа, обладающие
сферической или цилиндрической симметрией, т. е. зависящие только
от одной переменной г или р.

302 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Решение уравнения Лапласа и = U (г), обладающее сферической
симметрией, будет определяться из обыкновенного дифференциального
уравнения
Интегрируя это уравнение, находим
г
где Ci и (72—произвольные постоянные. Полагая, например, Ci = 1,
(72 = О, получаем функцию
Uo = -, (35)
Г
которую часто называют фундаментальным решением
уравнения Лапласа в пространстве.
Аналогично, полагая
и = и{р)
И пользуясь уравнением (33) или (34), найдем решение, обладающее
цилиндрической или круговой симметрией (в случае двух независимых
переменных), в виде
U{p)=Ci\np + C2.
Выбирая (7i = — 1 и (72 = О, будем иметь
Uo=\n-. (36)
Р
Функцию Uo (р) часто называют фундаментальным
решением уравнения Лапласа на плоскости (для двух независимых
переменных).
Функция Uo = 1/г удовлетворяет уравнению Аи = О всюду,
кроме точки г = О, где она обращается в бесконечность. С точностью до
множителя пропорциональности она совпадает с полем точечного
заряда е, помещенного в начале координат; потенциал этого поля равен
е
Аналогично функция \п{1/р) удовлетворяет уравнению Лапласа
всюду, кроме точки р = О, где она обращается в (положительную)
бесконечность, и с точностью до множителя совпадает с полем заряженной
линии (см. подробнее § 5, п. 2), потенциал которого равен
и = 2ei In -,
Р

§ 1] ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА 303
где 61—плотность заряда, рассчитанная на единицу длины. Эти
функции имеют большое значение в теории гармонических функций.
5. Гармонические функции и аналитические функции
комплексного переменного. Весьма общим методом решения
двумерных задач для уравнения Лапласа является метод, использующий
функции комплексного переменного.
Пусть
W = f{z) =и (ж, у) + iv (ж, у)
— некоторая функция комплексного переменного z = х -\- iy, причем
и VL V являются вещественными функциями переменных х и у.
Наибольший интерес представляют так называемые аналитические
функции, для которых существует производная
dw ,. Aw ,. f(z + Az)-f(z)
dz Az^O Az Az^O Az
Приращение Az = Ax + i Ay, очевидно, может стремиться к нулю
многими способами. Для каждого из способов стремления Az к нулю,
вообще говоря, может получиться свое значение предела. Однако, если
функция W = f (z) аналитическая, то предел Иш Af/Az = f (z) не
зависит от выбора пути.
Необходимыми и достаточными условиями аналитичности
функции являются так называемые условия Коши — Римана
Ux=Vy, 1 ^^^^
Эти условия можно получить, например, следующим образом.
Пусть W = и -\- iv = f (z) — аналитическая функция. Вычисляя
производные
dw
dz '
. dw
dz
и требуя равенства значений dw /dz, определяемых из этих двух
соотношений, получаем
dw
Ux \ IVx — Vy lUy — — ,
откуда и следуют условия Коши — Римана. На доказательстве
достаточности этих условий мы не будем останавливаться.
В теории функций комплексного переменного доказывается, что
функция, аналитическая в некоторой области G плоскости z = х -\-
+ гу, имеет в этой области производные всех порядков и разлагается
^ж
Wy
= Пж + ivx =
= Uy -\- iVy -
dw (z)
dw {z)

304 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
в степенной ряд. В частности, для такой функции и (ж, у) и v (ж, у)
имеют непрерывные производные 2-го порядка по ж и ^.
Дифференцируя первое равенство формулы (37) по ж, а второе по
у, получаем
Uxx + Uyy = О, ИЛИ A2U = 0.
Подобным же образом, меняя порядок дифференцирования, находим
'^хх + '^уу = о, или A2'L' = 0.
Таким образом, действительная и мнимая части аналитической
функции удовлетворяют уравнению Лапласа. Обычно говорят, что и
и V, удовлетворяющие условию Коши — Римана, являются
сопряженными гармоническими функциями.
Рассмотрим преобразование
ж = ж(и, v), и = и{х, у)А
у = у{и, v), V = v{x, y),j
взаимно однозначно отображающее некоторую область G плоскости
(ж, у) на область G' плоскости {и, v), так что каждой точке области
G соответствует определенная точка области С и, обратно, каждой
точке области С соответствует определенная точка области G.
Пусть
и = и{х,у)
— некоторая вещественная дважды непрерывно дифференцируемая
функция, определенная внутри области G. Выясним, как
изменяется при преобразовании (38) оператор Лапласа функции
и = и {х (и, г»), у (и, v)) = и (и, v).
Вычислим производные функции U:
^х — ^^и'^х ~г ^v'^^x-i ^у — ^^и'^у ~г ^v'^^y-i
^^XX ^ ^^ии'^х "•" ^vv'^x "•" ^^uv'^x'^x ~г ^^и'^хх ~г ^^v'^xx^
УУ — ^ии^у ~г ^vv'^y ~г ^^uv'^y'^y ~г ^и'^уу ~г ^v'^yy'
Используя их при преобразовании оператора Лапласа, получаем
Uxx + Uyy = Uuu {ul + uD + tj^^ {vl + vD +
+ 2Uuv {UxVx + UyVy) + Uu {Uxx + Uyy) + Uy {^xx + Vyy)- (39)
Если и VL V являются сопряженными гармоническими функциями,
то преобразование (38) эквивалентно преобразованию,
осуществляемому аналитической функцией
W = f (z) = и -\- iv {z = X -\- iy). (40)

§ 1] ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА 305
В этом случае в силу условий Коши — Римана (37) для функций
и VL V должны выполняться соотношения
UxVx + UyVy = 0.
Следовательно, с учетом гармоничности и и v формула (39)
принимает вид
U.. + Uyy = iUuu + Uvv)\f{z)\\ (41)
или
1
Таким образом, в результате преобразования (40) гармоническая в
области G функция U (ж, у) переходит в функцию U = U {и, v),
гармоническую в области G'J если только \f'{z)\^ ^ 0.
6. Преобразование обратных радиусов-векторов. При
изучении гармонических функций часто пользуются преобразованием
обратных радиусов-векторов. Преобразованием обратных
радиусов-векторов в сфере радиуса а называется такое
преобразование, при котором всякой точке М ставится в соответствие точка
М', лежащая на том же луче из начала координат, что и точка М,
радиус-вектор которой г' связан с радиусом-вектором г точки М
соотношением
^-,-^=^7777^^-,^^- (410
г'г = а^, или г'= —. (42)
г
В дальнейшем будем считать а = 1, чего можно всегда добиться
изменением масштаба длины.
Покажем, что гармоническая функция двух независимых
переменных и {р, (р) преобразованием обратных радиусов-векторов
переводится в гармоническую функцию
v{p', (р) =и{р,(р), где р=—. (43)
В самом деле, функция и {р, (/?), а тем самым и функция v{l/р, (/?),
как функции переменных р и (р удовлетворяют уравнениям
2 л д [ ди\ дЧ ^
20 A. Н. Тихонов, A. A. Самарский

306
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Переходя к переменным р' и (f, получаем
dv dv dp'
, dv
^ dp ^ dp' dp ^ dp''
откуда и следует, что v {р', ip) удовлетворяет уравнению Ар^^^г» = О,
так как
Переходя к случаю трех независимых переменных, покажем, что
функция
V (г'. О, (f) = ги (г. О, (/?), где г
1
(44)
удовлетворяет уравнению Лапласа A^/^q^^v = О, если и {г, в, (р) —
гармоническая функция своих переменных: Аг^о,(р'^ = О-
Преобразование (44) часто называют преобразованием
Кельвина.
Легко убедиться непосредственным дифференцированием, что
первое слагаемое в операторе Лапласа (32) преобразуется к виду
1 а / 2 9и\ _d'^u 2 du _1 d'^ (ru)
J.2 Qrp \ Qrp J Qrp^ r dr r dr'^
(45)
так что
гАг
d'^ (ru) 1
sin i9 dO
д f . .du\ 1
sm ^ ^^ I +
2^,1
ИЛИ
d^V 1^
Qj.2 J.2
= 0,
sin0 дв V'"" дв) ^sin^e dip^l
= 0.
Замечая, что
dv dv dr' ,2 dv
dr dr' dr dr''
находим, что г; удовлетворяет уравнению Дг/^^,^г> = 0, так как
1 d { . „dv\ 1 d'^v
,2 d f ,2 dv \ ,2
dr' V dr'
d / . dv
sinede [^''' de) ^sin^^ dip^
= 0,
ИЛИ
r' A^i^o^^v = 0.

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 307
§ 2. Общие свойства гармонических функций
В настоящем параграфе дается интегральное представление
гармонических функций, являющееся основным аппаратом для изучения
их общих свойств. Одним из важнейших следствий интегральной
формулы является принцип максимального значения, многократно
используемый нами в дальнейшем как при доказательстве теоремы
единственности, так и при решении краевых задач. Здесь также дается
математическая постановка внутренних и внешних краевых задач для
уравнения Лапласа и доказывается единственность и устойчивость
решения этих задач.
1. Формулы Грина. Интегральное представление
решения. При изучении уравнений эллиптического типа мы часто будем
пользоваться формулами Грина, являющимися прямым следствием
формулы Остроградского — Гаусса.
Формула Остроградского — Гаусса в простейшем случае имеет
вид ^^
-^— dxdy dz = R cos 7 da,
(1)
где Т — некоторый объем, ограниченный достаточно гладкой
поверхностью Е, R{x, у, z)— произвольная функция, непрерывная в
области Т + Е и дифференцируемая внутри Т, 7 — угол между внешней
нормалью к Е и осью z. В справедливости этой формулы нетрудно
убедиться, выполняя интегрирование по z.
Формулу Остроградского — Гаусса обычно записывают в виде
/// (S ^ ^ ^ S) "^^ " // (^со^« + Qcos/^ + i^cos7) da, (2)
Т Е
где dr = dxdydz — элемент объема, а = (пж), /3 = {пу), 7 = (^^) —
углы внешней нормали п к поверхности Е с координатными осями,
Р, Q, R — произвольные дифференцируемые функции ^л
Если Р, Q, R рассматривать как компоненты некоторого вектора
А = Pi + Qj + i^k, то формулу Остроградского — Гаусса (2) можно
записать следующим образом:
divA^r= [ [ Anda, {2')
^ Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.
^ В дальнейнЕем мы будем предполагать, что к тем областям, с которыми
мы будем иметь дело, применима формула Остроградского — Гаусса.
Такими поверхностями являются, например, поверхности с кусочно-непрерывной
кривизной, а также поверхности Ляпунова (см. § 5).
20*

308 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
где
,. , дР dQ dR
divA = ^- + ^ + ^-
ох оу OZ
и
An = Р COS а + Q cos [3 -\- R cos 7
— составляющая вектора А вдоль внешней нормали.
Перейдем теперь к выводу формул Грина.
Пусть и = и{х, у, z) и V = V (ж, у, z)— функции, непрерывные
вместе со своими первыми производными внутри Т + Е и имеющие
непрерывные вторые производные внутри Т.
Полагая
^ dv ^ dv ^ dv
Р = и^-, Q = u^-, R = u^-
ох оу OZ
и пользуясь формулой Остроградского — Гаусса (2'), приходим к так
называемой первой формуле Грина:
fff л л f f ^^ ri f f f f ди dv du dv du dv\
JJJ J J On JJJ \dx dx дуду dz dz J
T 1: T
(3)
d^ d^ d^ ^ д д
где A = 77-^ + 77-^ + 77-77—оператор Лапласа, 7^ = cos а 7;; h
аж^ оу^ oz"^ on ox
о 9 д
+ cos р ——h COS 7 77 производная по направлению внешней норма-
оу OZ
ли.
Если учесть соотношение
^ ^ _ _ ди dv ди dv ди dv
gradugradi; = Vu-Vv = -- -- -\- -- -- -\- -- --,
ox ox оу оу OZ OZ
то формулу Грина можно представить в виде
/ / / uAvdT = - / / / VuVvdT-\- и w^ da. {3')
т т т.
Меняя местами функции и ж v^ будем иметь
vAudT = -\/v\/udT-\-v-^da. (4)
т т Е
Вычитая из равенства (3') равенство (4), получаем вторую
формулу Грина
{и Av — V Аи) dr = / / lu — V -^ I da. (5)
Т Е

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 309
Область Т может быть ограничена несколькими
поверхностями. Формулы Грина применимы и в этом случае, причем
поверхностные интегралы следует брать по всем поверхностям, ограничивающим
область Т.
Для функций и = и{х, у), V = V {х, у) двух переменных имеют
место аналогичные формулы Грина. Вторая формула Грина в области
S с границей С имеет вид
lliuA,v-vA,u)dS = l(u^-v^ys,
S С
где dS = dxdy, ds — элемент дуги вдоль С, А2'Ь' = Vxx + "^уу^ д/дп —
производная по направлению внешней к
контуру С нормали п.
Как мы видели (§ 1, п. 4), функция
где
f^o(M) = -, / [--Шу^. k
R = л/(ж - жо)2 + {у- уоУ + {z- zo^ Рис. 45
— расстояние между точками М (ж, у, z) и Mq (жо, ^о, ^о),
удовлетворяет уравнению Лапласа при М ф Mq.
Пусть и (М) — функция, непрерывная вместе с первыми
производными в области Т + Е и имеющая вторые производные в Т.
Рассмотрим функцию V = I/RmMq, где Mq—некоторая внутренняя точка
области Т. Поскольку эта функция имеет внутри Т разрыв
непрерывности в точке Mq (жо, Уо, zq), то непосредственно применить
вторую формулу Грина в области Т к функциям и и v нельзя. Однако
функция V = I/RmMq ограничена в области Т — К^ с границей Е +
+ Eg, где К^ — шар радиуса е с центром в точке Mq и поверхностью
Eg (рис. 45).
Применяя вторую формулу Грина (5) к функциям и и v = 1/R в
области Т — К^, получаем
л 1 1 л ^ у
и А -- — —- Аи ат =
R R )
Е Ее Ее
В правой части этого равенства только последние два интеграла
зависят от е. Вычисляя производную по внешней нормали к области
Т — К^ на Eg, найдем, что
dn\R
д_ /1_
dr\R

310
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
откуда
(7)
где и* — среднее значение функции и{М) на поверхности Е^.
Преобразуем третий интеграл:
IIh^'''' = -eII
ди
е J J дп
da
Лже'
дп)
(8)
Здесь {ди/дпУ—среднее значение нормальной производной ди/дп на
сфере Eg. Подставляя выражения (7) и (8) в формулу (6) и учитывая,
что А {1/R) = О в Т — К^, будем иметь
IIIHh4I
Т-Ке
д
dn\R
1 ди
da + 4:7ги* — 47гг
ди
дп
(9)
Устремим теперь радиус е к нулю. Тогда получим:
1) lim и* = и(Мо), так как и{М)—непрерывная функция, а
U*—ее среднее значение по сфере радиуса г с центром в точке Mq;
2) lim 47гг {ди/дпУ = О, так как из непрерывности первых произ-
ВОДНЫХ функции и (М) внутри Т сразу же вытекает ограниченность
нормальной производной
ди ди ди ^ ди
т;— = т;- cos а + 7^ cos р + 7^ cos 7
on ox оу oz
в окрестности точки Mq;
3) по определению несобственного интеграла
lim
R
Аи] dr =
R
Аи dr.
Т-Ке
В результате указанного предельного перехода г —>- О мы
приходим к основной интегральной формуле Грина
47ги (М(
"•-Я
"(^'1;
( 1 ^
KRmqp)
1 ди
RmqP дп
_ГГГА
dap -
и{М)
RmqM
dTM,
(10)
где Р = Р (^, г]^ С)—точка с координатами ^, ?7, С? лежащая на
поверхности Е.

А
ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ
311
Если точка Mq находится вне области Т, то v = I/RmMq
непрерывна и гармонична во всех точках области Т. Поэтому слева в
формуле (10) получим нуль.
Рассмотрим случай, когда Mq принадлежит поверхности Е.
Предположим, что Е имеет в Mq касательную плоскость с
непрерывными угловыми коэффициентами. Сфера Е^ радиуса е с центром
в Мо пересекает поверхность Е и делит ее на две части: Ei и Е2,
часть El лежит внутри шара К^. Формулу Грина (5) применим к и
J/L V = 1/R в области Т —Ti, где Ti—область, ограниченная Ei и
частью сферы Е^, лежащей внутри Т. Общая схема рассуждений,
приведших к (9), остается неизменной. При этом следует лишь учесть, что
интеграл по Ei + Е^ стремится к 27ги(Мо), и внести
соответствующие изменения в (7), (8) и (8'). В результате мы приходим к формуле,
получающейся из (10) при замене 47г на 27г.
Объединяя все случаи, запишем основную формулу Грина в виде
О • и (Мо)
//
ди
[RmqP дпр
{Р)-и{Р)
д
дпр
RmqP J \
Аи{М)
R
MqM
dap —
dru,
(10')
где О принимает следующие значения:
О
47Г, если точка Mq лежит внутри Т,
27Г, если точка Mq лежит на границе Е,
О, если точка Mq лежит вне Т.
Отметим, что если точка Mq является конической вершиной
поверхности Е, то О = а, где а — величина телесного угла, образуемого
касательными к Е в точке Мд.
Для гармонической функции Аи = О и формула (10) принимает
вид
и{Мо)
4^ J J
ди
RmqP дпр
{Р)-и{Р)
д
дпр \RmqPJ\
dap (11)
(здесь Мо — точка внутри Т).
Таким образом, значение гармонической функции в любой
внутренней точке области выражается через значение этой функции и ее
нормальной производной на поверхности области. При этом
предполагается непрерывность функции и и ее первых производных вплоть до
границы. Отметим сразу же, что каждый из интегралов
//
м(л
Rmp
dap
II
д
дпр \Rmp
iy{P)dap, (12)

312 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
где fi и и — непрерывные функции, является гармонической
функцией вне поверхности Е. В самом деле, поскольку подынтегральные
функции и все их производные непрерывны вне поверхности Е, то
производные функций (12) любого порядка можно вычислять при
помощи дифференцирования под знаком интеграла. Так как, кроме того,
функции 1/Rmp и
д f 1 \ д (1\ д (1\ ^ д (1\
= —: — COS OLp -\- —- [ — ] COS РР + тг: 7^ ^О^ iP
дпр \RmpJ д^ \RJ дг] \Rj "^ дС \R
удовлетворяют уравнению Лапласа по переменным М (ж, у, z), то в
силу обобщенного принципа суперпозиции (см. лемму на с. 233),
функции (12) также удовлетворяют уравнению Лапласа по переменным ж.
Отсюда вытекает важное следствие: всякая гармоническая
функция внутри области гармоничности дифференцируема бесчисленное
множество раз-'^л Отметим также, что гармоническая функция ана-
литична (разлагается в степенной ряд) во всякой точке Mq области
Т. В этом можно убедиться с помощью рассуждений, основанных на
том же интегральном представлении (11).
Аналогичные формулы имеют место и для гармонических
функций двух независимых переменных. Пусть S — некоторая область на
плоскости (ж, у), ограниченная контуром С, а п — направление
нормали к этому контуру, внешнее по отношению к области S.
Полагая во второй формуле Грина
V = ln(l/i^MoP),
где
RmqP = л/(ж - хоУ + {у
Уо)
— расстояние от фиксированной точки Mq (жо, ^о) ДО точки Р (ж, у),
и проводя рассуждения, подобные тем, которые были проведены для
трехмерного случая, получим основную формулу Грина на плоскости:
О • и (Мо)
/
RMqP ОПр ОПр \ RmqP
dsi
II
Аи{Р)\п- dsp,
RmqP
^ Если для функции и, гармонической внутри Т, не выполнено
условие непрерывности ее вместе с первой производной на поверхности Е, то
теорема все же сохраняет силу, в чем можно убедиться, окружая точку М
областью, лежащей вместе со своей границей внутри Т.

А
ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ
313
где
0= (
27Г, если точка Mq лежит внутри S,
7г, если точка Mq лежит на границе С,
О, если точка Mq лежит вне S.
Если и{М) — гармоническая внутри S функция и Mq лежит
внутри 5, то
С
In
R
MqP
'"(Р)-«(Р)'
дп
дп}
In
R
MqP
dsp.
2. Некоторые основные свойства гармонических
функций. Установим несколько важнейших свойств гармонических
функций.
1. Если V — функция, гармоническая в области Т, ограниченной
поверхностью Е, то
II
dv
дп
da = 0,
(13)
где S—любая замкнутая поверхность, целиком леэюащая в области
Т.
В самом деле, подставляя в первую формулу Грина (3') какую-
либо гармоническую функцию v {Av = 0) и функцию и = 1, сразу же
получаем формулу (13). Из формулы (13) следует, что вторая краевая
задача
Аи = 0 в Г,
ди
дп
/ на Е
может иметь решение только при условии
//
fda = 0.
Это свойство гармонических функций можно интерпретировать как
условие отсутствия источников внутри области Т.
2. Теорема о среднем значении. Если функция и (М)
гармонична в некоторой области Т, а Mq — какая-нибудь точка,
леэюащая внутри области Т, то имеет место формула
"(^°' = 4^//"^"'
(14)
где Еа —сфера радиуса а с центром в точке Mq, целиком леэюащая
в области Т.

314
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Эта теорема утверждает, что значение гармонической функции в
некоторой точке Mq равно среднему значению этой функции на любой
сфере Т>а с центром в Mq, если сфера Е^ не выходит из области
гармоничности функции и (М).
Применим формулу (11) к шару К а с центром в точке Mq и
поверхностью Е^:
4.. (Мо) = -//[. 1^(1
1 ди
пЖ1
da.
Принимая во внимание, что
1 1
R
на Е
•"//
^а
дп ^ дп \R
-i-
dR\R
(направление внешней нормали к Е^ совпадает с направлением
радиуса), сразу же получаем (14) ^\
Записывая (14) в виде
47гр'
^и(Мо)= j j и
(Р) dat
и интегрируя по р от О до а, получаем
и(Мо) = -- udTM,
Va
47Г
Ка
Т. е. и (Мо) есть среднее по объему шара Ка с границей Е^.
Для случая двух независимых переменных имеет место
аналогичная теорема о среднем значении:
<"»' = i/
uds.
(15)
^ При доказательстве этой теоремы мы пользовались равенством (13),
предполагающим существование производных на поверхности сферы. Если
функция n(M), непрерывная в замкнутой области Т + Е, удовлетворяет
уравнению An = О только для внутренних точек Т, то предпЕССтвующее
заключение для сферы Eag, касающейся Е, было бы необоснованным.
Однако теорема верна для любого а < ао, и, переходя к пределу при а ^ ао,
получаем
и(Мо)
4™^ II
и (М) da.

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 315
где С а — окружность радиуса а с центром в точке Mq , лежащая в
области гармоничности и.
3. Принцип максимального значения. Если функция
и{М), определенная и непрерывная в замкнутой области Т + Е,
удовлетворяет уравнению Аи = О внутри Т, то максимальное и
минимальное значения функции и (М) достигаются на поверхности Е.
Допустим, что функция и (М) достигает максимального значения
в некоторой внутренней точке Mq области Т, так что щ = и (Мд) ^
^ и (М), где М — любая точка области Т. Окружим точку Mq сферой
Ер радиуса р, целиком лежащей внутри области Т. Поскольку, по
предположению, и (Мо) есть наибольшее значение функции и (М) в Т + Е,
то u|e ^и (Мо). Пользуясь формулой среднего значения (14) и заменяя
под интегралом всюду и{М) значением и(Мо), получаем
и{Мо) = ^ f fu{M)daM^^ f fu{Mo)da = u{Mo). (16)
Если предположить, что хотя бы в одной точке М сферы Ер
и (М) < и (Мо), то очевидно, что вместо знака ^ будем иметь знак <,
а это приводит к противоречию. Таким образом, на всей поверхности
Ер имеет место и (М) = и (Мо).
Если р'о' — минимальное расстояние от Мо до поверхности Е, то
и{М) = U (Мо) для всех точек, лежащих внутри Ерт. Отсюда
следует, что в точках М*, принадлежащих общей части Ерт и Е, по
непрерывности и (М*) = и (Мо). Это и доказывает теорему,
поскольку мы убедились, что максимальное значение и (Мо) достигается в
точках границы М*.
Нетрудно убедиться, что если область Т связная и
максимальное значение достигается хотя бы в одной внутренней точке Мо,
то и (М) = и (Мо) во всей области. Пусть М^^^ —какая-либо другая
точка области Т. Соединим
точку м(о) с точкой Мо ломаной
линией L (рис. 46), длину которой
обозначим I. Пусть Mi есть
последняя точка выхода линии L из
Ерт. В этой точке и (Mi) = u{Mq).
Опишем из нее сферу Ерт радиуса
р^ ^ касающуюся Е, и пусть М2 —
последняя точка выхода L из Ерт;
в этой точке и (М2) = и (Мо).
Продолжая процесс дальше, получим,
что не более чем через р = I/р^^^ Рис. 46
шагов, где р^^^—минимальное
расстояние от L до Е, одна из этих сфер захватит точку М^^^ отку-

316 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
да следует, что и (MW) =и{Мо). В силу произвольности и
непрерывности и (М) в замкнутой области Т + Е заключаем, что
и (М) = и (Мо) всюду, включая точки границы. Таким образом, из
всех гармонических функций только постоянная может достигать
своего максимального значения во внутренних точках области.
Аналогичную теорему можно доказать и относительно
минимального значения.
Следствие 1. Если функции и и U непрерывны в области Т -\-
+ Е, гармоничны в Т и если
и ^и на Ti,
то
и ^ и всюду внутри Т.
В самом деле, функция U — и непрерывна в Т + Е, гармонична в
Т и
и -и^О на Е.
В силу принципа максимального значения
и — и ^ О всюду внутри Т,
откуда и следует наше утверждение.
Следствие 2. Если функции и и U непрерывны в области Т -\-
+ Е, гармоничны в Т и если
\и\ <и на Т.,
\и\ ^ и всюду внутри Т.
Из условий теоремы следует, что три гармонические функции:
— U, и VL и — удовлетворяют неравенствам
-и ^и^и на Е.
Применяя дважды следствие 1, получаем, что
— U^u^U всюду внутри Т,
или
|и| ^ [/ всюду внутри т.
Следствие 3. Для гармонической в Т и непрерывной в Т + Е
функции и (М) выполняется неравенство
\и\ ^ max \и\ |е
всюду 6 Т + Е.
Для доказательства следствия 3 достаточно положить U =
= max Ы| |е и воспользоваться следствием 2.

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 317
Хотя изложение проводилось для трех измерений, однако все
результаты переносятся на случай гармонических функций любого числа
переменных.
3. Единственность и устойчивость решения первой
внутренней краевой задачи. Пусть дана область Т, ограниченная
замкнутой поверхностью Е, на которой задана некоторая функция /. В
простейшем случае, когда граничная функция / непрерывна, первая
внутренняя краевая задача (внутренняя задача Дирихле) для
уравнения Лапласа обычно ставится следующим образом.
Требуется найти функцию и, которая:
а) определена и непрерывна в замкнутой области Т + Е, включая
границу;
б) удовлетворяет внутри области Т уравнению Аи = 0;
б) принимает на границе Е заданные значения /.
В условии «б» предполагается гармоничность функции внутри
области Т. Требование гармоничности на границе является
излишним, так как оно повлекло бы за собой дополнительные ограничения
для граничных значений.
Условие непрерывности и в замкнутой области (или какое-либо
другое условие, разъясняющее смысл того, что функция и принимает
на границе заданные значения) необходимо для единственности. Если
отказаться от этого условия, то любую функцию, равную постоянной
С внутри Т и заданной функции f на Т>, можно рассматривать как
решение задачи, поскольку она удовлетворяет условиям «б», «в».
Докажем теорему единственности.
Первая внутренняя краевая задача для уравнения Лапласа не мо-
эюет иметь двух различных решений.
Допустим, что существуют две различные функции ui и ^2,
являющиеся решениями задачи, т. е. функции, непрерывные в
замкнутой области Т + Е, удовлетворяющие внутри области уравнению
Лапласа и на поверхности Е принимающие одни и те же значения /.
Разность этих функций и = щ — U2 обладает следующими
свойствами:
1) Аи = О внутри области Т;
2) и непрерывна в замкнутой области Т + Е;
3) u|e = 0.
Функция и (М), таким образом, непрерывна и гармонична в
области Т и равна нулю на границе. Как известно, всякая непрерывная
функция в замкнутой области достигает своего максимального
значения. Убедимся в том, что и = 0. Если функция и ^ О и хотя бы в
одной точке U > О, то она должна достигать положительного
максимального значения внутри области, что невозможно. Совершенно так
же доказывается, что функция и не может принимать нигде внутри
Т отрицательных значений. Отсюда следует, что
и = 0.

318 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Перейдем к доказательству непрерывной зависимости решения
первой краевой задачи от граничных данных. Напомним, что задача
называется физически определенной, если малому изменению условий,
определяющих penienne задачи, в данном случае граничных условий,
соответствует малое изменение самого решения.
Пусть ui и U2—непрерывные в Т + Е и гармонические внутри
Т функции, для которых \ui — U2\ ^ е на Е. Тогда это же неравенство
выполняется внутри области Т.
Это утверждение непосредственно вытекает из следствия 2 (с. 316)
в силу того, что и = е является гармонической функцией.
Таким образом, мы доказали непрерывную зависимость решения
от граничных условий и единственность решения первой внутренней
краевой задачи.
4. Задачи с разрывными граничными условиями. Часто
встречается также первая краевая задача с разрывными
граничными условиями. Функция, непрерывная в замкнутой области, не может
быть решением этой задачи. Поэтому требуется уточнить постановку
первой краевой задачи применительно к рассматриваемому случаю.
Пусть на кривой С, ограничивающей область S на плоскости
(ж, у), задана кусочно-непрерывная функция f (Р). Требуется найти
функцию и{М): 1) гармоническую внутри области 5; 2)
непрерывно примыкающую к граничным значениям в точках непрерывности
последних; 3) ограниченную в замкнутой области S -\- С.
Заметим, что дополнительное требование ограниченности
фактически относится к окрестностям точек разрыва функции / (Р).
Докажем следующую теорему.
Решение первой краевой задачи с кусочно-непрерывными
граничными значениями единственно.
Пусть ui и U2—два решения поставленной задачи. Разность
V = щ — U2
1) является гармонической функцией внутри 5;
2) непрерывно примыкает к нулевым граничным значениям на
границе, за исключением точек разрыва / (Р), в которых она может
претерпевать разрыв;
3) ограничена в S -\- С: \v\ < А.
Построим гармоническую функцию
п ^
где е — произвольное положительное число, D—диаметр области,
Vi — расстояние от рассматриваемой точки М до г-й точки
разрыва Pi. Функция и (М) положительна, так как все слагаемые больше
нуля.

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 319
Построим в каждой точке разрыва Pi круг Ki радиуса S, выбрав
S так, чтобы каждое слагаемое
, D
ет —
на соответствующей окружности Ci превосходило А, т. е. чтобы
e\n{D/5) ^ А. Функция v непрерывна в замкнутой области S —
— ^^=1 Ki = S', и [г»! ^ [/ на границе этой области.
Поэтому в силу принципа максимума U является мажорантой
функции v:
\v{M)\ ^U{M).
Фиксировав произвольную точку М из области S и устремляя е к
нулю, получаем
lim и (М) = 0.
Следовательно,
v{M) = 0,
так как v не зависит от г, или
Ui = U2,
ЧТО и требовалось доказать.
5. Изолированные особые точки. Рассмотрим особые точки
гармонической функции. Пусть Р — изолированная особая точка,
лежащая внутри области гармоничности функции и. Представляются
возможными два случая:
1) гармоническая функция ограничена в окрестности точки Р;
2) гармоническая функция не ограничена в окрестности точки Р.
С особыми точками второго рода мы уже встречались (например,
точка О функции 1п(1/г)). Следующая теорема показывает, что
первого типа особых точек не существует.
Если ограниченная функция и (М) является гармонической
внутри области 5, за исключением точки Р, то моэюно так
определить значение и{Р), чтобы функция и{М) была гармонической
всюду внутри S.
Возьмем круг К^ радиуса а с центром в точке Р, целиком
лежащий внутри S, и рассмотрим внутри него гармоническую функцию
V, совпадающую с функцией и на окружности С а круга К(^^\
Составим разность w = и — v, которая:
1) гармонична всюду внутри К^, кроме точки Р, в которой w
не определена;
2) непрерывно примыкает к нулевым граничным условиям на Са]
^ Существование такой функции будет установлено в § 3, причем
построение ее не базируется на доказываемой теореме.

320 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
3) ограничена в замкнутой области К^ + Са {\w\ < А).
Так же, как и при доказательстве предыдущей теоремы (п. 4),
построим неотрицательную гармоническую функцию
и(М)=е\п-.
г
Здесь е — произвольное положительное число, а — радиус круга К^,
г — расстояние от рассматриваемой точки М до точки разрыва Р.
Построим круг Ks с центром в точке Р, выбрав его радиус S так,
чтобы на его окружности значение U превосходило Л, и рассмотрим
область К а — Ks. Функция w непрерывна в замкнутой области S ^
^ г ^ а, и на границе этой области имеет место неравенство lu^l ^ U.
В силу принципа максимального значения неотрицательная функция
и является мажорантой функции w:
\w\^U{M) для S^r^a.
Фиксируя произвольную точку М области К^, не совпадающую с Р,
и совершая предельный переход при г —>- О, получаем
lim и (М) = 0.
Следовательно, всюду, за исключением, быть может, точки Р,
W = 0.
Таким образом, функция и всюду в области S, за исключением точки
Р, совпадает с функцией v. Полагая и (Р) = v (Р), получим функцию
и = V, гармоническую всюду внутри области S. Тем самым теорема
доказана.
Аналогично проводится доказательство теоремы для случая трех
измерений, где в качестве мажорантной функции может быть взята
функция
и{М)=е(---
\г а
При доказательстве теоремы этого пункта мы предполагали, что
функция и ограничена в окрестности точки Р. Однако те же
рассуждения остаются в силе, если предположить, что функция и в
окрестности точки Р удовлетворяет неравенству
|u(M)|<6(r)log^, (17)
грм
где е (г)—произвольная функция, стремящаяся к нулю при г —>- О,
т. е. в окрестности точки Р функция и (М) растет медленнее, чем
log(l/rpM).
Итак, если функция и (М) является гармонической функцией
внутри области S за исключением точки Р в окрестности которой

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 321
она растет медленнее, чем log (1/гмр) при М ^ Р, то эта
функция является ограниченной в окрестности точки Р, и моэюно так
определить значение и{Р), что функция и будет гармонической во
всей областей S.
Аналогично в случае трех независимых переменных получим: если
гармоническая функция и{М) в окрестности изолированной особой
точки Р растает, медленнее, чем 1/г:
\и{М)\<е{г) (г(г)^О при г ^ 0), (18)
гмр
то она ограничена в окрестности этой точки и моэюно так
определить значение и{Р), чтобы функция и{М) была гармонична и в
самой точке Р.
6. Регулярность гармонической функции трех
переменных в бесконечности. Гармоническая функция трех переменных
и{х, у, z) называется регулярной в бесконечности, если
Н<7
(9?/
дх
А
< —
(9?/
ду
А
< —
(9?/
dz
А
< —
(19)
при достаточно большом г ^ го.
Докажем, что если функция и{х, у, z) гармонична вне некоторой
замкнутой поверхности Е и равномерно стремится к нулю на
бесконечности, то она регулярна на бесконечности.
Условие равномерного стремления к нулю на бесконечности
означает, что существует такая функция г* (г), что
\и (М)| < г* (г) (г* (г) ^0 при г ^ оо), (20)
где г — радиус-вектор точки М.
Совершив преобразование Кельвина
v{r', в, (р) =та(г, в, (/?),
где
г
получим, что функция V гармонична всюду внутри поверхности Е',
в которую переходит поверхность Е при преобразовании обратных
радиусов-векторов, за исключением начала координат, где она имеет
изолированную особую точку.
Из условия (20) следует, что в окрестности начала координат для
функции V имеет место неравенство
\v{r',e,<p)\^e*(^]^=eir') ^
где
г'
г (г') = е* ( 1 ) ^ О при г' ^ 0.
21 А. Н. Тихонов, А. А. Самарский

322 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
На основании последней теоремы п. 5 функция v (г', в, (f)
ограничена и гармонична при г' ^ г'^:
\v{r',e,^)\^A при г'^г'^, (21)
откуда и следует, что
и г, 0,^) = ' ^ ' '^^' ^ - при г ^ Го = -.
в силу гармоничности функции v при г' = О можно написать:
ди{х,у, z) д (I , , Л
/V» I I ^п\ y^rv*' У^П% У^П й' У^П% .rf^/v' I
(22)
где
ж 1
Ж = -Г ,
Г
Зг» 9ж' Зг» ду' dv dz'
дх' дх ду' дх dz' дх
, У , 1^1
г/=-г, Z — -г .
г г
Отсюда, вычисляя производные дх'/дх, ду'/дх, dz'/дх и принимая во
внимание ограниченность первых производных функции v в
окрестности точки г' = О, получаем
ди
дх
А
^ — при г —>- 00.
Аналогичные оценки имеют место для производных ди/ду и du/dz.
7. Внешние краевые задачи. Единственность решения
двух- и трехмерных задач. Внешние краевые задачи по-разному
ставятся для трех и двух независимых переменных.
Рассмотрим сначала случай трех переменных. Пусть Т —
область, внешняя к некоторой замкнутой поверхности Е.
Первая внешняя краевая задача (внешняя задача
Дирихле) состоит в следующем.
Требуется найти функцию и (ж, у, z), удовлетворяющую
условиям:
1) Аи = О в неограниченной области Т;
2) и всюду непрерывна, включая поверхность Е;
3) u\j: = / (ж, у, z), где f —функция, заданная на поверхности Е;
4) и (М) равномерно стремится к О на бесконечности: и (М) -^
—>- О при М —>- 00.
Последнее условие является существенным для единственности
решения, в чем легко убедиться на простом примере. Пусть
требуется решить внешнюю первую краевую задачу для сферы Sr радиуса
R с постоянным граничным условием
u\sji = const = /о.

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 323
Опуская условие 4, видим, что решениями задачи могут служить
функции щ = /о и ^2 = foR/r, а также любая функция
и = ащ-\-/3u2, где а-\-/3 = 1.
Докажем, что внешняя первая краевая задача для гармонических
функций с тремя независимыми переменными имеет единственное
решение.
Предполагая существование двух решений щ и ^2,
удовлетворяющих условиям 1 — 4, видим, что их разность и = ui — U2
представляет собой решение задачи с нулевыми граничными условиями.
Поскольку условие 4 выполнено также для
функции и, то для произвольного г > О можно указать
такое R*, что
\и{М)\ < е при г ^ R*.
Если точка М лежит внутри области Т' (рис. 47),
заключенной между поверхностью Е и сферой Sr
{г ^ R"")^ то и (М) < г, как то следует из
принципа максимального значения, примененного к об л а- р ^^
сти Т'. В силу произвольности £ заключаем, что
U = О в области Т', а также и во всей области Т, что и доказывает
единственность решения внешней первой краевой задачи в
пространстве.
Первая внешняя краевая задача на плоскости
ставится следующим образом.
Требуется найти функцию и, удовлетворяюш^ую условиям:
1) Аи = О 6 рассматриваемой бесконечной области Е,
ограниченной контуром С;
2) и всюду непрерывна, включая границу С;
3) и\с = f {х, у), где f —функция, заданная на С;
4) и (М) ограничена в бесконечности, т. е. суш^ествует такое
число N, что \и{М)\ ^ N.
Требование обращения решения в нуль
на бесконечности и здесь оказывается
достаточным, чтобы доказать, что двух
разных решений быть не может, но оно
является слишком сильным, так как при нем
задача может оказаться вообще
неразрешимой.
Докажем, что внешняя первая краевая
задача для функций двух переменных
имеет единственное решение.
Допуская существование двух различ- Рис. 48
ных решений ui и ^2 и рассматривая их разность и = ui — U2,
являющуюся решением первой краевой задачи с нулевыми граничными
условиями, в силу условия 4 будем иметь
\и\ ^N = Ni+N2,
21*

324 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
где А^1 и А^2 таковы, что \ui\ ^ A^i, \u2\ ^ N2. Обозначим через Ei
область, лежащую внутри С и являющуюся дополнением к области
Е, так что Е + El есть вся плоскость. Возьмем точку Mq внутри Ei
и окружность радиуса R с центром в точке Mq, лежащую внутри Ei
(рис.48). Гармоническая функция \п{1/Кммо) не имеет особенностей
в области Е; функция \п{Кмм^/R) положительна во всей области Е
включая С. Пусть Cr^—окружность радиуса Ri с центром в Mq,
содержащая целиком контур С, и Е' — область, ограниченная кривыми
С и Cr^ . Функция ur-^ , определяемая равенством
есть гармоническая функция, равная N на окружности радиуса Ri,
положительная на С. Из принципа максимального значения следует,
что ur^ является мажорантой для модуля функции и (М) в области
Е:
\u{M)\<UR,{M).
Фиксируем точку М и будем неограниченно увеличивать Ri.
Очевидно, что ur^ (М) —>- О при i^i —>- 00. Отсюда следует, что
и{М) =0.
Тем самым, в силу произвольности М, единственность решения
поставленной задачи доказана.
Единственность решения этой задачи можно также доказать,
пользуясь преобразованием обратных радиусов-векторов,
переводящим область, внешнюю к контуру С, в область, внутреннюю к
контуру С, в который переходит контур С. При этом бесконечно удаленная
точка перейдет в изолированную особую точку, в окрестности которой
функция V ограничена. Из теоремы п. 5 будет вытекать
гармоничность функции V в начале координат, а тем самым и единственность
решения.
Из приведенных рассуждений следует, что гармоническая
функция двух переменных и (М), ограниченная в бесконечности,
стремится к определенному пределу при М, стремящейся к бесконечности.
Различие в постановке первой внешней краевой задачи для двух и
трех переменных можно пояснить на следующем физическом примере.
Пусть дан шар радиуса R, на поверхности которого
поддерживается постоянная температура щ, и требуется определить стационарное
распределение температуры во внешнем пространстве. Функция и =
= щ (R/r) представляет решение этой задачи, обращающееся в нуль
на бесконечности.
Рассмотрим теперь двумерную задачу. Пусть на окружности
радиуса R задано постоянное граничное значение:
'^|е = /о = const.

А
ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ
325
В этом случае и = fo есть единственное ограниченное решение
задачи и никакого решения, обращающегося в нуль на бесконечности, не
существует. Мы уже встречались с принципиально различным
характером поведения гармонических функций в бесконечности для двух и
трех независимых переменных (например, поведение 1/г и In (1/г) на
бесконечности).
Для пространственной и плоской неограниченных областей имеет
место принцип максимального значения. В этом нетрудно убедиться с
помощью рассуждений, аналогичных тем, которые были использованы
при доказательстве теорем единственности. Отсюда, в свою очередь,
вытекает непрерывная зависимость решения от граничных условий.
8. Вторая краевая задача. Теорема единственности.
Решением второй краевой задачи будем называть гармоническую функцию
U, непрерывную в области Т + Е г/ удовлетворяющую на
поверхности Е условию
ди
дп
f{M).
Докажем, что решение второй внутренней краевой задачи
{внутренней задачи Неймана) определяется с точностью до произвольной
постоянной.
Доказательство проведем при дополнительном предположении,
что функция и имеет непрерывные первые производные в области
Г + Е^).
Пусть ui и U2—две непрерывно дифференцируемые в Т +
+ Е функции, удовлетворяющие уравнению Аи = О в Т и условию
ди/дп |е = / (^) на Е. Для функции и = ui — U2 будем иметь
ди
дп
= 0.
Полагая в первой формуле Грина (3)
Аи = О и ди/дп |е = О, получаем
и и учитывая соотношения
///
ди\ f ди
дх) \ду
+
диУ
д^)
dT = 0.
^ Предположение относительно непрерывности первых производных в
Т + Е сделано для упрощения доказательства. Доказательство
единственности при наиболее общих предположениях было дано М. В. КелдыпЕСм и
М. А. Лаврентьевым. (См.: Келдып! М. В., Лаврентьев М. А. О
единственности задачи Неймана // ДАН СССР. 1937. Т. 16, № 3. С. 151—152;
Смирнов в. И. Курс высшей математики. Т. IV. М., 1958.)

326
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Отсюда в силу непрерывности функции и и ее первых производных
следует
ди ди ди _
дх ду dz
т. е. и = const,
что и требовалось доказать.
Изложенный здесь метод доказательства применим и в случае
неограниченной области для функций, удовлетворяющих требованиям
регулярности на бесконечности.
Покажем, что в случае неограниченной области, внешней к
замкнутой поверхности, формула Грина (3) применима для функций,
регулярных на бесконечности.
Рассмотрим область Т, внешнюю к замкнутой поверхности.
Проведем сферу Ед столь большого радиуса, чтобы Е лежала внутри Ед.
Обозначим Tr область, ограниченную Е и Ед (рис. 49). Применив
в области Tr формулу Грина к двум функциям и и v, регулярным в
бесконечности, получим
', Av dr =
ди dv ди dv ди dv
\_дх дх ду ду dz dz
dT-\-
Рис. 49
-Щ
Оценим интеграл по Ед, используя при этом свойство регулярности
функций и Vi V'.
1И£
da
u{vx COS а -\- Vy cos Р + Vz cos 7) da
^
^
II
A ЗА
RB?
da
3^2 ^ „ 127ГЛ2
Отсюда видно, что
Я»
lim I I и—-
R^oo J J an
^R
da = 0.
Стоящий справа в (24) интеграл по Tr стремится к интегралу по
всей области Т при R ^ оо. Этот интеграл существует, так как
подынтегральное выражение в силу регулярности и и v убывает на

§ 2] ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ 327
бесконечности как 1/R^. Следовательно, существует предел
lim 11 1 ^ ^^ dr = 1^ ^^ ^^•
Tr Т
В результате мы приходим к формуле
fff л л _ fff Г^'^ ^'^ ^'^ ^'^ ^'^ ^'^1 л [ [ ^^ ^
JJJ JJJ [дх дх дуду dz dz\ J J дп
Т Т Е
(25)
Тем самым установлена применимость первой, а следовательно, и
второй формул Грина для неограниченных областей к функциям,
регулярным на бесконечности.
Покажем теперь, что вторая внешняя краевая задача {внешняя
задача Неймана) имеет единственное решение, регулярное на
бесконечностей.
Полагая в формуле (25) v = и = щ — U2 и учитывая, что Аи = О
и ди/дп\^ = О, получаем
[ul -\-Uy -\- ul) dr = 0.
т
Отсюда в силу непрерывности производных функции и следует, что
^ж = О, и^ = О, 1/^ = 0 и и = const.
Так как и = О на бесконечности, то
U = О, т. е. Ul = ^2,
что и требовалось доказать.
Естественно возникает вопрос: можно ли доказать этим же
методом единственность решения первой краевой задачи?
Пусть Ul и U2 —различные решения первой краевой задачи
(внутренней). Применим формулу (3) к функциям и = Ui — U2 и v = и в
области Т, ограниченной поверхностью Е:
{ul +ul + ul) dT + j j и-^ da.
и Au dr = ■
T T
Отсюда, принимая во внимание условия
Аи = О, u|e = О,
получаем
/// ^''' ^"' ^ '''^ "^^" °
т

328 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
и, следовательно,
Ux = Uy = Uz = О и и = const.
На поверхности Е функция и равна нулю, поэтому мы можем
утверждать, что
и = О и щ = U2.
Однако это доказательство некорректно, поскольку в процессе
доказательства мы предполагали существование производных искомой
функции на поверхности Е, что самой постановкой задачи не
предусматривается. Доказательство единственности, основанное на принципе
максимального значения, свободно от этого недостатка.
§ 3. Решение краевых задач для простейших
областей методом разделения переменных
Решение краевых задач для уравнения Лапласа может быть
найдено методом разделения переменных в случае некоторых
простейших областей (круг, прямоугольник, шар, цилиндр и др.).
Получающиеся при этом задачи на собственные значения (задачи
Штурма— Лиувилля) приводят к различным классам специальных
функций. В этом параграфе мы рассмотрим задачи Дирихле (внутреннюю
и внешнюю), при решении которых используются только
тригонометрические функции. Позже, при изучении специальных функций,
будут рассмотрены задачи Дирихле для сферы и цилиндра.
1. Первая краевая задача для круга. Решим первую краевую
задачу для круга.
Найти функцию и, удовлетворяющую уравнению
Аи = О внутри круга (1)
и граничному условию
и = f на границе круга, (2)
где f — заданная функция.
Предположим сначала, что функция / непрерывна и
дифференцируема и решение и (М) непрерывно в замкнутой области; в
дальнейшем мы освободимся от условия дифференцируемости и даже
непрерывности функции / (ср. с § 2, п. 4). Наряду с внутренней краевой
задачей будем рассматривать также внешнюю краевую задачу (см. § 2,
п. 7).
Введем полярную систему координат {р, ip) с началом в центре
круга. Уравнение (1) в полярных координатах имеет вид
1 д f ди\ 1 д^и ^

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 329
(см. формулу (34) § 1). Будем решать задачу методом разделения
переменных, т. е. будем искать частное решение уравнения (1) вида
Подставив предполагаемую форму решения в уравнение (3), получим
dpyl^J _ ф" _
R -"^-^'
Р
где Л = const. Отсюда получаем два уравнения:
Ф" + ЛФ = О, Ф ^ О, (4)
Первое из этих уравнений дает
Ф {(f) = А cos л/л (/? + Б sin л/л (f.
Заметим, что при изменении угла (f на величину 27г однозначная
функция и {р, (р) должна вернуться к исходному значению:
и{р, (р -\- 27г) = и {р, (р) (условие периодичности).
Отсюда следует, что Ф ((/? + 27г) = Ф ((/?), т. е. Ф {(f) является
периодической функцией угла (р с периодом 27г. Это возможно, только если
л/л = п, где п — целое число, и
Фп {^) = An COS п(р + Вп sin П(р.
функцию R {р) будем искать в виде R {р) = р^. Подставляя в
уравнение (5) и сокращая на р^, находим
п^ =/i^, или р = ±п (п > 0).
Следовательно,
R(p) = Cp^ + Dp-'^,
где С и D — постоянные.
Для решения внутренней задачи надо положить R = Ср^ (/i = п),
так как если D ^ О, то функция и = Е{р)Ф {(f) обращается в
бесконечность при р = О и не является гармонической функцией внутри
круга. Для решения внешней задачи, наоборот, надо брать R = Dp~^
{р = —п), поскольку решение внешней задачи должно быть ограничено
в бесконечности.

330 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Итак, частные решения нашей задачи найдены ""^^i
Un{pj (f) = р^ {An COS n(f + Bn^inn(f) для p ^ a,
Un (pj (f) = — (An cosTKf + Bn s'mn(f) для p ^ a.
p^
Суммы этих решений
сю
и (р, (f) = 2Z Р^ (^^ ^^^^^ "^ ^п ^^^^^) ^^^ внутренней задачи,
п=0
сю -J
U (р, (/?) = У^ — [An COS п^ + 5^ sin п(/?) для внешней задачи
^-^ р^
при достаточно хорошей сходимости также будут гармоническими
функциями.
Для определения коэффициентов An и Вп используем граничное
условие
сю
и (а, (/?) = 2_\ ^^ (^п cosTKf + Вп s'mn(f) = /. (6)
п=0
Считая, что / задана как функция угла (р, возьмем ее разложение в
ряд Фурье
сю
/ (v^) = Y "^ Х^ '^^^ ^^^ ^^ "^ ^^ ^^^ ^^)' ^'^^
^ Выражение оператора Лапласа в полярной системе координат (3) при
р = О теряет смысл. Докажем, что Aun = О также при р = 0. Для
доказательства этого факта мы уже не можем пользоваться полярной системой
координат.
Перейдем к декартовой системе координат. Частные рептения
р^ cos пер и р^ sin пер,
будучи действительной и мнимой частями функции
р"е^"^=(ре^'^)" = (ж + г2/Г,
являются многочленами по ж и |/. Очевидно, что многочлен,
удовлетворяющий уравнению Аи = О при /? > О, в силу непрерывности вторых
производных удовлетворяет также этому уравнению при р = 0.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 331
где
7Г
^0 = - ЦФ) d^,
— 7Г
7Г
ап = - Л'ф)со^п'ф(1'ф (п = 1, 2, ...),
7Г
-и
Рп = - М{ф)^тпф(1ф (п = 1, 2, ...).
Сравнивая ряды (6) и (7), получаем
^ Oio an ^ Рп
Ло = -—, An = —, г>п = — для внутренней задачи,
2 а^ а^
Ло = —, An = OLnCi^^ Вп = /?пО^^ для внешней задачи.
Таким образом, мы получили формальное penienne первой
внутренней задачи для круга в виде ряда
сю
/ ч «о .
и (
п=1
а penienne внеп1ней задачи в виде ряда
сю
, (р, (/?) = ^ + ^ (-] (anCosn(/? + /3nSinn(/?), (8)
сю / \ ^
Чтобы убедиться в том, что полученные функции действительно
являются искомыми реп1ениями, нужно убедиться в применимости
принципа суперпозиции, для чего надо доказать сходимость рядов,
возможность их почленного дифференцирования, а также непрерывность этих
функций на границе круга. Оба ряда можно представить одной
формулой:
сю
'^(^5 V^) = ^ + Х^^"" (anC0sn(/? + /3nSinn(/?),
^ п=1
где
t= <
(Р -i
- ^ 1 при р ^ а (внутренняя задача),
а
- ^ 1 при р ^ а (внешняя задача),
^Р

332 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
о^п, Рп — коэффициенты Фурье функции f {^).
Докажем, что ряды (8), (9) можно дифференцировать при ^ < 1
любое число раз. Пусть
Un = t^ (c^n COS п(р + /Зп sin П(р).
Вычислим к-ю производную функции Un по (р:
—-^ = Гп^ ^ап cos (^ткр -\-k-j-\-l3n sin (^ткр + ^ 2 )] '
Отсюда получаем оценку
д(р^
^ еп" 2М,
где через М обозначен максимум модуля коэффициентов Фурье а^ и
\ап\ ^ М, |/3„| ^ М. (10)
Фиксируем некоторые значения ро < а (для внутренней задачи) или
р1 = CL^/ро > CL (для внеп1ней задачи), при этом ^о = po/ct < 1-
Рассматривая ряд
сю сю
п=1 п=1
видим, ЧТО ОН СХОДИТСЯ равномерно при ^ ^ ^о < 1 Для любого к.
Поэтому ряды (8) и (9) можно дифференцировать ио (р в любой точке
внутри (вне) круга любое число раз. Аналогично доказывается, что по
переменной р также можно дифференцировать ряды (8) и (9) внутри
(вне) круга радиуса ро < а {pi > а) сколько угодно раз.
В силу произвольности ро заключаем, что ряды (8) и (9) почленно
дифференцируемы во всякой внутренней (внешней) точке круга. Из
возможности почленного дифференцирования следует применимость
принципа суперпозиции. Таким образом, доказано, что функции (8) и
(9) удовлетворяют уравнению Аи = О^К
При этом доказательстве мы пользовались только тем свойством
функции / ((/?), что ее коэффициенты Фурье ограничены (формула
(10)). Это имеет место для любой ограниченной функции (и даже
^ Это уравнение удовлетворяется также при у9 = 0; в самом деле, выражая
производные по декартовым координатам через производные по полярным
координатам, нетрудно убедиться, что функции (8) и (9) при t ^ to можно
дифференцировать по ж и |/ любое число раз. В силу примечания на с. 330
отсюда следует, что
Аи = О при /9 = 0.

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 333
для любой абсолютно интегрируемой функции). Таким образом, ряды
(8) и (9), соответствующие любой ограниченной функции, определяют
функции, удовлетворяющие уравнению
Аи = О для ^ < 1.
Этим замечанием мы воспользуемся позже при обобщении
результатов, полученных в настоящем пункте.
Обратимся теперь к доказательству непрерывности функции в
замкнутой области {t ^ 1). Очевидно, что без более детальных сведений
относительно свойств функции / {(f) этого сделать нельзя.
Из предположенной непрерывности и дифференцируемости
функции / ((/?) следует ее разложимость в ряд Фурье, а также сходимость
ряда
сю
п=1
С другой стороны, имеем
|ГапС08П(/?| ^ l^nl, |r/3nsinn(/?| ^ \/Зп\-
Поэтому ряды (8) и (9) сходятся равномерно при ^ ^ 1 и,
следовательно, представляемые ими функции непрерывны на границе круга.
Из формулы (11) видно, что функция (9), полученная для внешней
задачи, ограничена на бесконечности.
Таким образом, установлено, что ряды (8) и (9) удовлетворяют
всем условиям рассматриваемых задач.
2. Интеграл Пуассона. Преобразуем теперь формулы (8) и (9)
к более простому виду. Для определенности рассмотрим внутреннюю
задачу, а для внешней напишем результат по аналогии.
Подставляя выражения для коэффициентов Фурье в формулу (8)
и меняя порядок суммирования и интегрирования, будем иметь
^ } (^ °^ п ]
и{р, (f) = — /(?/;) < - + yZ ( ~ ) (^^^ ^'^ ^^^ ^^ "^ ^^^ ^'^ ^^^ ^^) ( (^Ф =
( п=1 )
— 7Г
= I I fi^)U + fl{^y^^^^iv-i')\d^. (12)
Произведем следующие тождественные преобразования:
- + ^ i" cos п ((/? - V) = 2 + 2 Z1 *" к" ^'^'"''^ + ^~'" '^"'''1 =
Y + ite-^^^-^Y] \ =

334
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
(-^')-
2 1-2^ cos ((/? - V^) + ^2
Подставляя полученные результаты в равенство (12), получаем
а'^-р^
4p,^) = ^//W;^2apcos(^-^)+a2
йф. (13)
Полученная формула, дающая penienne первой краевой задачи
внутри круга, называется интегралом Пуассона, а
подынтегральное выражение
К{р, (/?, а, ф) =
а'^-р^
р^ — 2ар cos ((/? — -0) + а^
— ядром Пуассона. Отметим, что К {р^ (/?, а, -0) > О при р < а,
так как 2ар < а^ -\- р^ ^ если р ф а.
Интеграл Пуассона выведен в предположении р < а] при р = а
представление (13) теряет смысл. Однако
lim и{р, (р) = f{ipQ),
так как ряд, из которого получен интеграл Пуассона, является
непрерывной функцией в замкнутой области.
Функция, определенная формулой
и {р, (/?) = <
7Г
'-Р'
COS {(f — ф) -\- а
2 dil; при р < а,
(13')
1/Ы
при р = а,
удовлетворяет уравнению Аи = О при р < а и непрерывна в
замкнутой области включая окружность р = а.
Решение внешней краевой задачи, очевидно, имеет вид
и {р, (/?) = <
7Г
2^ У
/W-
р2-а2
■ (1ф при р > а,
27Г ./ '' ^^^р2 — 2apcos((/? —-0) + а^ /-|.ч
/м
при р = а.
В самом начале мы предположили, что функция / {(f) непрерывна
и дифференцируема, и, пользуясь этим, доказали, что решение задачи

§ 3] МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 335
можно представить в виде бесконечного ряда. В дальнейшем с
помощью тождественных преобразований мы переп1ли от ряда к интегралу
Пуассона.
Докажем теперь, что интеграл Пуассона дает решение первой
краевой задачи и в том случае, когда функция f {(р) только
непрерывна.
Интеграл Пуассона представляет решение уравнения Лапласа при
р < а (^ < 1) для произвольной ограниченной функции / {(f). В самом
деле, при р < а (^ < 1) интеграл Пуассона тождественен ряду (8) и,
как было отмечено на с. 332, удовлетворяет уравнению Аи = О при
произвольной ограниченной функции / {(f).
Таким образом, нам остается доказать, что функция и в
нашем случае непрерывно примыкает к граничным значениям.
Выберем какую-либо последовательность непрерывных дифференцируемых
функций
ЛМ, /2М,..., лм,...,
равномерно сходящуюся к функции / {(р) ^^:
Иш fk{(p) =/М.
Последовательности граничных функций будет соответствовать
последовательность гармонических функций Uk{p,(f), определяемых по
формуле (13) или (8). Равномерная сходимость последовательности
{ fk {^) } означает, что для любого г > О можно указать такое ко {е) >
> О, что
\fk{^)-fk+i{^)\<£ при к>ко{е), I > 0.
Для функций Uk (г, (р), представляющих решения первой краевой
задачи, в силу принципа максимального значения будем иметь
\uk {р, (f) - Uk+i {р, ^)\ < е при р ^ а, к > ко (г), / > 0.
Таким образом, последовательность {uk} сходится равномерно к
некоторой функции и = Иш Uk. Предельная функция и{р, (р) непре-
рывна в замкнутой области, поскольку все функции Uk^
представляемые интегралами
7Г
/ Ч 1 /" С? - Р^ л / , Ч 7 ,
'^к (Р, ^) = 7Г ~2 ^ 1 1\ I 2 Л {Ф) d^,
27Г J р^ — 2ар cos {(f — гр) -\- а^
^ Мы не будем останавливаться на том, как это осуществить. Такую
последовательность можно выбрать многими способами.

336 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
непрерывны в замкнутой области. Очевидно, что
и {р, (f) = lim Uk {р, (f) =
^2 ^2
If a^ - p^ я / , Ч 7 ,
— / -^ 7 7T 5" / [ф) аф при p < a,
— 7Г
l/M прир = а,
так как последовательность {ft} сходится равномерно к /, и поэтому
предельный переход под знаком интеграла законен.
Таким образом, функция
7Г
— 7Г
при произвольной непрерывной функции / ((/?) является реп1ением
уравнения Лапласа, непрерывно примыкающим на границе круга к
заданным значениям.
3. Случай разрывных граничных значений. Докажем, что
формулы (13') и (14) дают решение краевой задачи для произвольной
кусочно-непрерывной функции / ((/?), т. е. что это решение ограничено
во всей области и непрерывно примыкает к граничным значениям в
точках непрерывности функции / ((/?), являясь, таким образом,
единственным решением, обладающим этим свойством (ср. с § 2, п. 4).
Пусть (/?о — какая-либо точка непрерывности функции / ((/?).
Надо доказать, что каково бы ни было г > О, найдется такое 5 (г), что
1^(Р, Ч^) -/(V^o)l <е,
если
\р-а\<5{£) и \ip-ipQ\<5{£).
В силу непрерывности функции / ((/?) существует такое 5^ {г),
что
I/(V^)-/(V^o)l < 2' ^с™ |(/?-(/?о| < ^о(е).
Рассмотрим вспомогательные непрерывные и дифференцируемые
функции / ((/?) и / ((/?), удовлетворяющие условиям
_ £
f{^) = f (Ы -\- - для \(f - (fo\ < So (г),
f{^)^f {^) для \(f-(fo\> So (г)

_3^ МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ 337
/М ^ /М для \(f-(fo\ > So{e),
а в остальном произвольные. Если при помощи формулы (13) мы
определим для / и / функции й{р, (р) и и{р, (р), то это будут
гармонические функции, непрерывно примыкающие к f {(р) и f {^).
В силу положительности ядра Пуассона имеем
и{р, (f) ^ и{р, (f) ^ й{р, (f),
так как
Из непрерывности функций й {р, (р) и и {р, (р) на границе при (р = (pQ
следует существование такого Si (г), что
\й{р, (f) - f{(fo)\^ 2 ^^^ |p-«l<^i(^)^ \(f - (fo\ < Si (е)
|м(р, V^)-/(V^o)l ^ 2 ^^^ \p-a\<Si{e), \(p - (po\ < Si (e).
Из этих неравенств находим
€
2
й {р, ^) ^ fi^o) + I = / (^о) +еЛ \p-a\<S (г),
> для
где S = min ((5о, (^i).
Сопоставляя полученные неравенства, заключаем, что
/ {(ро) - е ^ и{р, (р) ^ и {р, (р) ^ й {р, (р) ^ f {(ро) + е,
или
\и{р,^)-1Ы)\<^ для \p-a\<S{e), \(р - (ро\ < S (е),
что и доказывает непрерывность и {р, (р) в точке (а, (/?о).
Ограниченность и (р, (/?) следует из того, что в силу
положительности ядра Пуассона
27Г
If о? - р^
\и{р,^)\<М- / ^—^— ^ 6?V^ = м,
7г J а^ ^- р^ - 2ар cos ((/? - -0)
о
22 А. Н. Тихонов, А. А. Самарский

338 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
если I/ {(р)\ < М. Значение же интеграла
27Г
If
— ^1
р^ — 2apcos{(p — ф)
так как в силу ранее доказанного левая часть представляет
гармоническую функцию, непрерывно примыкающую к граничным значениям
/ = 1, а такая функция тождественно равна 1. Аналогично и {р, (р) >
> Ml, если / > Ml, что и доказывает ограниченность модуля
функции и{р, (f).
§ 4. Функция источника
Метод функции источника дает удобный аппарат для
аналитического представления решения краевых задач.
В настоящем параграфе будут даны определение и основные
свойства функции источника для уравнения Лапласа, а также будут
построены функции источника для ряда простейших областей (круг,
сфера, полупространство). Это построение проводится методом
электростатических изображений.
1. Функция источника для уравнения Аи = 0 и ее
основные свойства. Для всякой функции и, непрерывной вместе с
первыми производными в замкнутой области Т (ограниченной достаточно
гладкой поверхностью Е) и имеющей вторые производные внутри Т,
как было показано в § 2, п. 1, имеет место интегральное представление
MMo) = i^//
' '\Р)-и(Р)'
[ RpMo дп дп \ RpMo J J
-iflf
dap —
Au
R
MMq
dTM- (1)
Если функция и (М) гармоническая, то объемный интеграл равен
нулю; если же и (М) удовлетворяет уравнению Пуассона, то объемный
интеграл является известной функцией.
Пусть V (М) —некоторая гармоническая функция, непрерывная в
Т + Е вместе с первыми производными, не имеющая нигде
особенностей. Вторая формула Грина
(и /S.V — V Аи) dr = / / [и — V 7^— I da
J J \ an dnj
дает
»=//("l-l)--///— <^'

§ 4] ФУНКЦИЯ ИСТОЧНИКА 339
Складывая (2) и (1), получаем
Е Т
где
G(M,Mo) = -^ +^ (30
— функция двух точек Mq (ж, ^, 2;) и М (^, ту, С). Точка Mq
фиксирована, и поэтому ж, ^, Z играют роль параметров.
Формула (3) содержит и\^ и ди/дп\^. Между тем при peniennn
первой краевой задачи задается лип1ь и\^, а при peniennn второй
краевой задачи— значение ди/дп\^. Функция v выбирается таким
образом, чтобы G|e = О для первой краевой задачи и dG/дп |е = О для
второй краевой задачи. Определим функцию G (М, Р) при помощи
следующих условий.
1. G{M, Р) как функция точки Р (^, ?7, С) при фиксированной
точке М (ж, ^, z) удовлетворяет уравнению Лапласа
AG = G^^ + Gr^r, + Gcc = О, Рф М,
во всех точках Р области Т, кроме точки Р = М.
2. G (М, Р) при совпадении аргументов (М = Р)
обращается в бесконечность и представима в виде (3'), где v = v{M, Р) —
гармоническая всюду в Т функция.
3. G (М, Р) на границе обращается в нуль:
G(M, Р) = 0, если PgE.
Этому условию можно удовлетворить, потребовав, чтобы
Функцию G, определенную таким образом, будем называть
функцией точечного источника первой краевой задачи
для уравнения Лапласа. Функция источника позволяет дать
явное представление для решения первой краевой задачи для уравнения
Аи = 0. В самом деле, формула (3) дает
'^''^^ = -lh'^''=-lh'^'' ^^="1^^-
(4)
Следует иметь в виду, что формула (4) получена с помощью
формулы Грина, предполагающей выполнение определенных условий в
отношении функций и и G и поверхности Е. В формулу (4)
входит выражение dG/dn, существование которого на поверхности Е не
следует непосредственно из определения функции G.
22*

340 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
При получении формулы (4) мы исходим из того, что
существует гармоническая функция и, принимающая на поверхности Е
значение /. Тем самым даже для тех областей, для которых существует
функция источника, удовлетворяющая условиям применимости
формулы Грина, формула (4) дает явное представление лишь тех решений и
первой краевой задачи, которые удовлетворяют условиям
применимости формулы Грина (доказывая единственность этого класса решений
первой краевой задачи).
Подробное исследование формулы (4), проведенное А. М.
Ляпуновым, показало, что для широкого класса поверхностей, называемых
поверхностями Ляпунова (см. § 5), она представляет решение первой
краевой задачи при весьма общих условиях.
Остановимся еще раз на определении функции G. Функция G
определяется при помощи функции v, являющейся решением первой
краевой задачи для уравнения
Ai; = 0
с граничными значениями
I 1
^ Е = -
4:7TR
Может создаться впечатление, что имеет место порочный круг. Для
нахождения функции и — решения первой краевой задачи — надо
найти функцию V — решение той же задачи. Па самом деле порочного
круга нет, так как знание функции источника позволяет решить
первую краевую задачу с произвольными граничными значениями (u|e =
= /), в то время как для нахождения самой функции G
достаточно решить краевую задачу со специальными граничными значениями
('^^|е = ~l/(4'7ri^)), что, как мы увидим на ряде примеров, значительно
проще.
При электростатической интерпретации функция источника
G(M,Mo) = ^+.
представляет потенциал в точке М точечного заряда ""^^ помещенного
в точку Мо внутри заземленной проводящей поверхности Е. Первое
^ При термической интерпретации стационарная температура точечного
источника тепла интенсивности q определяется формулой
Атгкг
где к — коэффициент теплопроводности. Таким образом, функция 0{М, Mq)
является температурой в точке М, если температура поверхности тела
равна нулю, а в точке Mq помещен тепловой источник интенсивности q = к.
Если размерность длины выбрана так, что А; = 1, то функция G
соответствует источнику интенсивности, равной единице.

А
ФУНКЦИЯ ИСТОЧНИКА
341
слагаемое l/(47ri^) есть, очевидно, потенциал точечного заряда в
свободном пространстве, а второе слагаемое v обозначает потенциал поля
зарядов, индуцированных на проводящей
поверхности Е. Таким образом, построение функции
источника сводится к определению
индуцированного поля.
Остановимся на некоторых свойствах
функции источника. При этом мы будем
предполагать, что рассматриваемые области таковы, что
для них существуют функции источника,
обладающие нормальными производными на
поверхности Е и удовлетворяющие условиям
применимости формулы Грина.
1. Функция источника всюду положительна
внутри Т. В самом деле, функция G
обращается в нуль на границе области Е и положительна
на поверхности достаточно малой сферы,
описанной вокруг полюса. Отсюда следует, в силу принципа максимального
значения, ее положительность во всей области. Заметим также, что
Рис. 50
дп
^0,
что непосредственно вытекает из доказанной положительности и
условия G|e = 0.
2. Функция источника симметрична относительно своих
аргументов Mo{x,y,z) и М(^, ту. С):
G(M, Mo) = G(Mo, М).
Пусть Mq и Mq—некоторые фиксированные точки в области Т.
Проведем сферы El и Е2 радиуса е с центрами в точках Mq и Mq
(рис. 50). Полагая
u{M) = G (М, М(^), v{M) = G (М, МЦ)
и применяя формулу Грина
(и Av — V Аи) dr = / / [и — V 7^—
J J \ дп дп
da
(5)
Те Е1+Е2+Е
К области Tg, ограниченной поверхностями Е,
//
о ,м. Mj) ^Щ^МЙ _ о ,м. MS) ?" ("• "S'
//
G{M,Mi
дп
dG (м. Mi;)
дп
El и Е2, будем иметь
daM +
G{M,M'')
дп
dG (М, M'q
дп
daM = О,

342 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
так как левая часть уравнения (5) равна нулю, поскольку AG = О,
а интеграл по поверхности Е равен нулю в силу граничных условий.
Переходя затем к пределу при г —>- О и используя особенность функции
источника, получаем ^^
G{MiM'') = G{M'',M',),
ИЛИ
G(M, Mo) = G(Mo, М).
Доказанная симметрия функции источника является
математическим выражением принципа взаимности в физике: источник,
помещенный в точку Мо, производит в точке М такое же действие,
какое производит в точке Мд источник, помещенный в точку М.
Принцип взаимности носит весьма общий характер и относится к
различным физическим полям (электромагнитным, упругим и т. д.).
Отметим, в частности, что из свойства симметрии следует, что
при фиксированном М и (Mq) = G (М, Mq), как функция переменных
X, у, Z точки Мо, обладает тем же свойством, что и функция v (М) =
= G{M, Мо) переменных ^, г], ( точки М при фиксированном Мо,
т. е. AmqG = О при М ^ Мо, G = О при Мо G Е.
Функция источника G (М, Мо) для случая двух измерений,
очевидно, будет определяться следующими условиями.
1. AG = О всюду в рассматриваемой области S, кроме точки М =
= Мо.
2. В точке М = Мо функция G имеет особенность вида
' In '
27Г RmMq
3. G\c = О, где С — граница области S.
Функция источника в этом случае имеет вид
G{M, Мо) = :^ In -^ +i;(M, Мо),
где V — всюду непрерывная гармоническая функция,
удовлетворяющая на границе условию
I 1 1 1
ZTT UmMq
Решение первой краевой задачи для уравнения Лапласа при этом
дается формулой
/f)G
f^ds и = и\с).
с
^ Ляпуновым установлена эта теорема в применении к классу
поверхностей, называемых поверхностями Ляпунова.

§ 4] ФУНКЦИЯ ИСТОЧНИКА 343
2. Метод электростатических изобралсений и функция
источника для сферы. Наиболее распространенным методом
построения функции источника является метод электростатических
изображений. Идея его состоит в том, что при построении функции
источника
G(M,Mo) = -^ +V
47ГЯмМо
индуцированное поле v представляется как поле зарядов,
расположенных вне поверхности Е и
выбираемых таким образом, чтобы
выполнялось условие
Эти заряды называются
электростатическими
изображениями единичного заряда,
помещенного в точку Мо и создающего в
отсутствие поверхности Е потенциал
1/{4:7tR). Во многих случаях выбор Рис. 51
таких зарядов не составляет труда.
Ниже мы приведем примеры построения функции источника методом
электростатических изображений.
Из представления функций источника, полученных во всех этих
примерах, непосредственно видна непрерывность первых производных
функций G на поверхности Е.
В качестве первого примера рассмотрим функцию источника для
сферы.
Пусть дана сфера радиуса R с центром в точке О и требуется
найти для нее функцию источника.
Поместим в точку Mq единичный заряд и отложим на радиусе,
проходящем через точку Мд, такой отрезок OMi, что
PqPi=R^^ (6)
где ро = \ОМо\ и pi = \OMi\ (рис. 51).
Преобразование (6), ставящее в соответствие точке Mq
определенную точку Ml, является преобразованием обратных радиусов, а сама
точка Ml называется сопряженной с точкой Mq. Это
преобразование взаимно, и точку Mq можно рассматривать как сопряженную с
точкой Ml.
Докажем, что для всех точек Р, расположенных на сфере,
расстояния до Мо и Ml пропорциональны. Для этого рассмотрим
треугольники ОРМо и OPMi (рис. 51). Они подобны, так как угол при
вершине О общий, а прилежащие к нему стороны пропорциональны:
Ро _R |ОМо| _ R

344
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Из подобия треугольников следует
Г0_ _ Р0_ _ В^ /уч
п ~ R~ pi' ^ '
где Го = |Moi^|, ri = |Mi?|. Из пропорции (7) получаем
Ро
для всех точек сферы. Поэтому гармоническая функция v =
= —R/po • 1/ri на сфере принимает то же значение, что и
функция — 1/го. Она представляет, очевидно, потенциал заряда величины
—R/po, помещенного в точку Mi.
Таким образом, функция
С{Р,Мо) =
47Г V^o Ро П
(8)
И является искомой функцией источника для сферы, так как это —
гармоническая функция, имеющая в Mq особенность 1/(47гго) и
обращающаяся в нуль на сфере.
Решение первой краевой задачи дается формулой (4).
Вычислим производную
dG_J_
дп 47Г
д_ Г1\ _Rd_fl_
дп \roJ Ро дп \Г1
(9)
где п — внешняя нормаль, ri = (М, вообще говоря,
на сфере).
Производные от 1/го и 1/ri по направлению п равны
cos(r^7n),
не лежит
как
дп
А
дп
(а
(й
д
дго
д
дгх
\roJ
\rij
1 дго
' дп
1 дг1
' дп
cos(rT7h),
дго дп
—- =cos(ro, п), -— =cos(ri, п).
Нетрудно найти величины cos (гоГп) и cos (гГГп):
r^ + 4-pI
cos (rVn)
COS (гТГп)
2Rro
R^ +rf- pI
(10)
(11)
(11')
(11")

А
ФУНКЦИЯ ИСТОЧНИКА
345
Используя пропорцию (7), будем иметь
cos(rT7h)|E =
d2
р1
Pi _pl+rl-R^
'^Рого
так как pi = В? /р^ по определению точки Mi и ri = i^/po * ^о на
сфере Е. Пользуясь формулами (10), а также выражениями (9), (11')?
(11''), найдем
дС_
дп
1
47Г
1 Д^+rg-pg pg R pl^rl-R^
2Дго
й^^о /Оо 2jOoro
1 R^-pI
^-kR
Таким образом, функция и (Мо) в соответствии с формулой (4) равна
и{Мо)
Ы/
47гД
f{P)
R'-pI
dap.
(12)
Введем сферическую систему координат с началом в центре
сферы. Пусть (i^, ^, (f) — координаты точки Р, а (ро, ^о, V^o) —
координаты точки Мо; 7 — угол между радиусами-векторами О г и OMq.
Тогда формулу (12) можно переписать в виде
и{ро, во, (ро)
47Г
27Г 7Г
//^^^'
¥>)
R^-pI
о о
где
(i^2_2i^pocos7 + pg)'/2
COS 7 = COS в COS ^0 + sin в sin ^o cos ((/? — (/?o) ^^ •
sin OdOd(f,
(12')
(13)
Эта формула называется интегралом Пуассона для
сферы.
^ В самом деле, направляющие косинусы векторов ОР и OMq равны
соответственно (sin в cos ср, sin в sin ср, cos ^) и (sin ^о cos cpo^sin во sin cpo^cos во),
откуда
cos 7 = cos ^ cos ^0 + sin в sin ^o (cos cp cos (^o + sin cp sin (^o) =
= cos в cos ^0 + sin в sin ^o cos {cp — cpo).

346
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Тем же методом может быть построена функция источника для
области, внешней к сфере:
G(M, Ml)
1
47Г
pi Го
(14)
где г I = |MMi|—расстояние от фиксированной точки Mi, лежащей
вне сферы, го = |ММо|—расстояние от точки Мд, сопряженной с
точкой Ml, pi — расстояние от начала координат до точки Mi, а, R —
радиус сферы.
Учитывая различие направлений нормалей для внутренней и
внеп1ней задач, получим
27Г 7Г
,(pi,^i,(/.i) = —уу
р1
к^
о о
[i^2_2pii^COS7 + P?]^/2
/ (^, (/?) sinOdOd^p,
где cos 7 дается формулой (13) (индекс О надо заменить на 1).
3. Функция источника для круга. Функция источника для
круга может быть получена таким же способом, как и функция
источника для сферы. В этом случае ее следует искать в виде
^ 111
G = -—In - +V.
27Г г
(15)
Повторяя рассуждение предыдущего пункта от формулы (6) до
формулы (8), мы найдем функцию G в виде
G (Р, Мо)
1
27Г
, 1
In —
L ^0
. R 1
-In
Ро П
(16)
где Ро = |ОМо|, Го = |МоР|, п = \MiP\, R = |0Р|—радиус круга
(рис. 52). Нетрудно убедиться в том, что определенная таким образом
гармоническая функция обращается в нуль на границе:
G\
С
0.
Для решения первой краевой
задачи надо вычислить значения
dG/дп на окружности С.
Вычисления производятся аналогично
случаю сферы и дают
Рис. 52
дС
дп
1 r'-pI
27tR
Пусть (р, в)—полярные координаты точки Р, лежащей на
окружности, а {ро, во)—координаты точки Mq, тогда
rl=R^ +р1- 2Rpo cos {О - во).

А
ФУНКЦИЯ ИСТОЧНИКА
347
Подставляя в формулу
И'^'^^ч
- р1 ds_
R
это выражение для г о и принимая во внимание, что
и{Р)\с = !{в) и ds = RdO,
приходим для функции и (Мо) к выражению
27Г
и{ро, Оо)
1- [
р1 - 2Rpo cos {в-во)
f(0)de, (17)
называемому интегралом Пуассона для круга (см. с. 334,
формулу (13)). Эта же формула с точностью до знака дает решение
внешней задачи.
4. Функция источника для полупространства. Понятие
функции источника и формула (4) имеют место и для
неограниченного пространства, если рассматривать функции, регулярные на бес-
M{x,y,z)
Mo(xo,yo,zo)
У^
I /
■ [/
Mi{xo,yo, -zo)
Рис. 53
конечности (см. § 2, п. 6). Найдем функцию источника для
полупространства 2; > 0. Поместим в точку Mq (жо, уо, zq) единичный заряд,
который создает в неограниченном пространстве поле, потенциал
которого определяется функцией
-7- s , где RmqM = л/(ж - хоУ + {у - УоУ + {z - zq)^.
47Г HmqM
Нетрудно видеть, что «индуцированное поле» v является полем
отрицательного единичного заряда, помещенного в точку Mi (жо, ^о, — ^о),
являющуюся зеркальным изображением точки Мд в плоскости 2; = О
(рис. 53). Функция G, равная

348
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
[ГЛ. IV
где
R, = \Mji\ = y/{x-xo)^ + {y-yo)^ + {z + zo)^,
обращается в нуль при z = О и имеет нужную особенность в точке
Мо.
Вычислим dG/dn\z=o = —dG/dz\z=o. Очевидно, что
dG_J_
dz 47Г
z - Zo z -\- Zo
Щ
Rl
Полагая 2; = 0, находим
ас
дп
z=0
dG
dz
z=0
Zq
Решение первой краевой задачи дается формулой
^0
где Ео — плоскость z = О, f (Р) = u\z=o, или
сю сю
и{хо,уо, zo) = — / /
[{х-хоГ + (у-уоГ+г1]
213/^
/(ж, y)dxdy.
(18)
§ 5. Теория потенциала
Функция
1
представляющая
R ^[x-0'' + {y-n? + {z-C?
потенциал поля единичной массы (заряда), помещенной в точке
^0 (^5 ^5 С)? является решением уравнения Лапласа, зависящим от
параметров ^, ?7, С- Интегралы от этой функции по параметрам
называются потенциалами и имеют существенное значение с точки
зрения непосредственных приложений в физике, а также и с точки
зрения развития методов решения краевых задач.
1. Объемный потенциал. Пусть в некоторой точке Mq (^, ?7, С)
помещена масса т^. По закону всемирного тяготения на массу ттг,
помещенную в точке М (ж, ^, z)^ действует сила притяжения
ШШо
(1)

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 349
где г = H/R — единичный вектор в направлении MqM (R = MqM), а
7 — гравитационная постоянная. Выбирая систему единиц так, чтобы
7 = 1, и полагая ттг = 1, получим
F = г.
R^
Проекции этой силы на координатные оси будут равны
А = Fcosa = - —^ (ж - 4),
Y = Fcosf3=-'^iy-rj),\ (2)
Z = Fcosj = -^(z-0,
где а, /3 VL j — углы, образованные вектором F с координатными
осями.
Введем функцию и, называемую потенциалом силового
п о л я ""^^ и определяемую равенством
х =
F = gradu.
_ди у _ди ^ _
Шо
ди
dz
В нашем случае
Потенциал поля п материальных точек вследствие принципа
суперпозиции силовых полей будет выражаться формулой
Е^^ т
Rj
Перейдем к случаю непрерывного распределения массы. Пусть
дано тело Т с плотностью р (^, г], (). Определим потенциал этого тела
в точке М (ж, у, z). Для этого разобьем тело Т на достаточно мелкие
части Аг. Сделаем естественное предположение, что действие
элемента Аг эквивалентно действию его массы, сосредоточенной в некоторой
^ Не следует смешивать потенциал с потенциальной энергией силового
поля. Термин «потенциал» употребляется здесь в том же смысле, что и
силовая функция в механике.

350 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
«средней» точке ""^^ объема Аг; тогда для компоненты силы,
действующей на точку М, получим следующее выражение:
где
Интегрирование по всему объему Т дает компоненту полной силы
притяжения точки М телом Т:
X
-Ifh'-^'- (3)
Потенциал в точке М будет определяться формулой
и{М) = IIJp^dT. (4)
т
Если точка М лежит вне тела, то в этом можно убедиться
непосредственно дифференцированием под знаком интеграла ^л
Аналогично вычисляются и производные высших порядков. Очевидно, что
потенциал и (М) вне тела Т удовлетворяет уравнению Лапласа (см.
подробнее с. 361). В дальнейшем, не стремясь к построению теории в
наиболее общих условиях, мы будем пользоваться указанными выше
свойствами потенциалов и сформулируем ряд теорем при условии, что
р — ограниченная функция (подразумевая ее интегрируемость).
Если точка М лежит внутри области Т, нельзя утверждать, что
X = ди/дх, без дополнительного исследования, которое и будет дано
ниже.
^ Более точно, при этом предполагается, что действие некоторого тела
Т массы т на точку, лежащую вне выпуклого объема Т, содержащего это
тело, можно заменить действием некоторого эффективного центра той же
массы ?тг, лежащего внутри Т.
^ Для возможности дифференцирования определенного интеграла вида
-I
f{M)= / FiM,P)cp{P)dTp
ПО параметру под знаком интеграла достаточно непрерывности производной
функции F (М, Р) по параметру и абсолютной интегрируемости функции
(р{Р). Обычно эта теорема формулируется при (р (Р) = 1. Доказательство
ее для naniero случая ничем не отличается от обычного.

А
ТЕОРИЯ ПОТЕНЦИАЛА
351
2. Плоская задача. Логарифмический потенциал.
Рассмотрим распределение масс в пространстве, зависящее лип1ь от двух
координат (ж, у). В любой плоскости z =
= const потенциал, очевидно, принимает
одно и то же значение. Поэтому достаточно
исследовать потенциал точки (ж, у), лежащей
в плоскости Z = 0.
Определим потенциал однородной
бесконечной прямой L. Направим ось z вдоль
этой прямой. Пусть погонная плотность
(т. е. масса единицы длины) равна /i. ^
Сила притяжения элементом Az точки Р^^- ^^
Р (ж, 0) (рис. 54) и ее составляющая по оси х равны
соответственно
AF
fiAz
II Az
(Ж2 + ^2) '
АХ = AFcosa = -jiAz
VW^^
.2A3
Отсюда
X =
сю
/
lix
dz
(ж2+^2)3/2 ^^ ^.
7г/2
— / COS ada =
^. J X
2/i
-7г/2
(^ = *S")-
Если P (ж, у) —произвольная точка, то сила притяжения точки
линией L будет, очевидно, направлена вдоль О г и равна по величине
где
р = л/ж2~+~^.
Потенциал этой силы называется логарифмическим
потенциалом и равен
У = 2/i In
1
(5)
в чем легко убедиться непосредственным дифференцированием.

352 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Логарифмический потенциал является решением уравнения
Лапласа с двумя независимыми переменными, обладающим круговой
симметрией вокруг полюса в точке р =
= 0, в которой он обращается в
бесконечность.
Таким образом, потенциал
однородной прямой дает плоское поле и
выражается формулой (5). Представление
потенциала в виде интеграла было получено
нами лишь для ограниченных объемов ^^.
р^^ кк Отметим, что в отличие от объемного
потенциала логарифмический не
обращается в нуль на бесконечности, а имеет там логарифмическую
особенность.
Вычислим теперь компоненты силы притяжения точки Р (рис. 55):
X I X
X = F cos а = —2/i -^ cos а = —
Р^ \ Р
Y = Fs'ma = —2/i ^- ( sin а = -
Р^ \ Р
Если имеется несколько точек (бесконечных прямых с
распределенной вдоль них массой), то в силу принципа суперпозиции силовых
полей потенциалы точек (линий) будут складываться.
В случае области S с непрерывно распределенной плотностью
/i (^, Г]) ^^ (рис. 56) компоненты силы притяжения точки Р выразятся
^ При вычислении потенциала бесконечной прямой нельзя было
непосредственно интегрировать потенциалы отдельных элементов, так как в этом
случае получается расходящийся интеграл. В самом деле, потенциал
элемента Az равен
Аи = /1 ■
л/?
Формальное интегрирование дает расходящийся интеграл
dz
I
М
Vf
.2
^ Это соответствует в пространстве цилиндру с образующей,
параллельной оси Z, и сечением S в плоскости (ж, у), с объемной плотностью fi (^, ту),
не зависящей от С.

А
ТЕОРИЯ ПОТЕНЦИАЛА
353
двойными интегралами:
Х = -2||/*(^,г,)
Y = -2IIflit г^)
х-^
(х - О' + {у- Я?
d^dr],
d^drj
(6)
и потенциал будет равен
и{х,у) = 2 /J (^, ту) In
л/(^ - О' + {У- Г}?
d^dr],
(7)
Р{^,у)
что нетрудно проверить дифференцированием для точек, лежащих вне
S. Если же точка Р лежит в области S, то необходимо провести
дополнительное исследование.
3. Несобственные интегралы. Потенциалы и компоненты
силы притяжения представляются с помощью интегралов, у
которых подынтегральные функции
обращаются в бесконечность, если мы
рассматриваем их значения в точках, находящихся в
области, содержащей притягивающие
массы.
Как известно, если подынтегральная
функция обращается в некоторой точке
области интегрирования в бесконечность,
то интеграл нельзя определить как предел
интегральной суммы. Действительно, в этом случае интегральная
сумма не имеет предела, так как слагаемое, относящееся к
элементарному объему, содержащему особую точку, может как угодно сильно
менять величину суммы в зависимости от выбора промежуточной точки.
Интегралы от подобных функций определяются как интегралы
несобственные.
Пусть в области Т задана функция F (ж, у, z), обращающаяся в
бесконечность в некоторой точке Mq {xq, уо, zq). Рассмотрим
определенный интеграл по области Т — К^, где К^ — некоторая окрестность
точки Мо диаметра, не превосходящего г.
Если при произвольном стягивании области К^^ к точке Mq
последовательность интегралов
Рис. 56
/п =
Fdr (Sn^O)
Т-Ке
имеет предел, не зависящий от выбора областей К^^^ то этот
предел называется несобственным интегралом от функции
23 А. Н. Тихонов, А. А. Самарский

354 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
F (ж, у, z) по области Т и обозначается, как обычно,
/= [[[ Fdr.
Если существует хотя бы одна последовательность областей К^^
такая, что при г^ —>- О существует предел /, а для других
последовательностей К^^ этот предел имеет другие значения или даже вообще не
существует, то предел / называется условно сходящимся
несобственным интегралом. Ясно, что при рассмотрении условно сходящегося
несобственного интеграла / нужно указывать ту последовательность
областей К^^^ по которой определяется этот интеграл.
Мы ограничимся здесь рассмотрением того случая, когда
подынтегральная функция имеет особенность в изолированной точке.
Исследуем сходимость интегралов типа
С
■dTM, (8)
///
т
где С VL а > О — некоторые постоянные,
R = RmMo = л/(жо - 0^ + {Уо - г]У + (^0 - О'
(Мо — точка области Т). Не ограничивая общности, можно считать,
что Т есть шар радиуса R с центром в точке Mq. Возьмем в качестве
области К^^ шар радиуса £п с центром в точке Mq и будем искать
предел последовательности интегралов
27Г 7г я R
-^dT= [d(f f^mOdO [ -^dr = 27r'2C [ -^ =
Ла J "^ J J ^a-2 J ^a-2
T-Ken 0 0 en ^n
AttC
S — a .
, если a 7^ 3,
l47r(7[lnrl^ , если a = 3.
Переход к пределу при г^, стремящемся к нулю, показывает, что при
а < S предел существует, при а ^ 3 предела не существует.
Покажем, что если функция F (ж, у, z) неотрицательна и
существует предел интегралов
/п= /77 Fdr (гп^О),
где Ksn — шар радиуса Sn с центром в точке Mq , то существует
предел интегралов 1^ при любом выборе последовательности
областей i^£„, стягивающихся к точке М, и значение этого предела не

А
ТЕОРИЯ ПОТЕНЦИАЛА
355
зависит от формы области К^^. Действительно, любую область К^^
можно заключить между двумя сферами К^^ и К^ , радиусы
которых Ещ И еп2 стремятся к нулю вместе
с Sn (рис. 57). В силу положительности
подынтегральной функции
Т-Ке
Fdr^ /// Fdr^
Т-Кегг Т-К,
Fdr.
Отсюда видно, что
lim
п—>-сю
F dr = lim
n—>-CXD
FdT = I,
T-Ke
T-Ke
Рис. 57
так как пределы крайних интегралов
существуют и равны этому числу.
Таким образом, в случае трех независимых переменных
несобственный интеграл
^ dr (8)
существует^ если а < 3, и не существует^ если а ^ 3.
Для другого числа независимых переменных критическое
значение а, определяющее границы сходимости интегралов типа (8), равно
числу измерений; так, например, для двух независимых переменных
интеграл
С
//
р^
da
при а < 2 сходится, а при а ^ 2 расходится.
Остановимся на признаке сходимости несобственных интегралов.
Докажем, что для сходимости несобственного интеграла
F (ж, у, z) dxdy dz
(9)
достаточно, чтобы существовала такая функция F (ж, у, z), для
которой несобственный интеграл по области Т сходится, и чтобы
имело место неравенство
\F{x, у, z)\ <F{x, у, z).
(10)
Рассмотрим некоторую последовательность областей К^,
содержащих особую точку Мо._ В силу сходимости последовательности
интегралов In от функции F для всякого г > О существует такое N {г),
23*

356
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
что
\in.
1-П2 I
///
FdT
<e,
коль скоро Hi, П2 > N (e). Так как F является мажорантной функцией
для F {х, у, z), то можно написать
\1п.
'-П2 I
///
FdT
(10')
если П1, П2 > N (г). Выполнение условия (10') в силу признака
сходимости Коп1и является достаточным для сходимости
последовательности
'■■411
FdT
Т-Ке
К некоторому пределу
/ = lim /^
п—>-сю
■■-III
FdT.
Нетрудно видеть, что этот предел не будет зависеть от формы
областей К^^. Тем самым существование несобственного интеграла (9)
доказано.
Если же для некоторой функции F (ж, у^ z) можно указать такую
положительную функцию F (ж, ^, z)^ что F (ж, ^, z) > F, причем
несобственный интеграл от F по области Т расходится, то
несобственный интеграл (9) будет, очевидно, расходиться.
Следствие. Если для некоторой функции F {М, Р),
обращающейся в бесконечность при Р = М, имеет, место неравенство
|F(M, Р)|<
С
а = const < 3, С = const < оо.
то песо б ставенный интеграл по области Т, содерэюащей точку М,
F (М, Р) dTp
сходится.
Из теории собственных интегралов, зависящих от параметров,
известно, что непрерывность подынтегральной функции по параме-

А
ТЕОРИЯ ПОТЕНЦИАЛА
357
трам и независимым переменным является достаточным условием
непрерывности самого интеграла как функции параметров-"^^ Для
несобственных интегралов непрерывность подынтегральной функции не
имеет места, и поэтому указанный выше критерий неприменим.
Установим критерий непрерывности несобственных интегралов, зависящих
от параметра.
Будем рассматривать несобственные интегралы
V{M) = j F{P,M)f{P)dTp,
(И)
где F (Р, М)—функция, обращающаяся в бесконечность при
совпадении аргументов и непрерывная по М, а / (Р) —
ограниченная функция.
Интеграл (11) называется равномерно
сходящимся в тропке Мо, если для любого г > О моэюно
указать такое (5(e), что имеет место
неравенство
\Vsie){M)\
I
^S{e)
F{P,M)f{P)dTp
^е
Рис. 58
для любой точки М, расстояние которой от Mq
меньше (5(e), и для любой области Ts(^s)j содерэюащей точку Mq и
имеющей диаметр d ^ ^ (е).
Докажем, что интеграл
V{M) = j F{P,M)f{P)dTp,
равномерно сходящийся в точке Mq , есть непрерывная функция в этой
точке Mq. Мы должны доказать, что для любого е можно указать
такое 5 (г), что
\V{M^)-V{M)\<e
при
|ММо| <5{е).
Выберем внутри области Т некоторую область Ti, содержащую
точку Мо (рис. 58), и разобьем интеграл на два слагаемых:
^ Будак Б. М., Фомин С. В. Кратные интегралы и ряды. М., 1967.
С. 442.

358
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
где интеграл Vi берется по области Ti, а V2 — по области Т2 = Т —
— Ti. В дальнейшем мы более точно определим размеры области Ti.
Рассмотрим неравенство
\V (Mo) -V{M)\^ \V2 (Mo) - V2 (M)| + 1^1 (Mo)| + 1^1 (M)|
и покажем, что каждое из слагаемых, стоящих справа, можно сделать
меньше г/3 при достаточно малом |МоЛ1|. Выбирая область Ti
внутри сферы радиуса 6'{е/3), будем иметь
|У1(Мо)|^| и |У1(М)|^|, если |МоЛ1| ^ (5'(|) .
Существование такого S' вытекает из условия равномерной
сходимости интеграла (11) в точке Мо. Выбор области Ti определяет
область Т2.
Так как точка Мо лежит вне области Т2, то интеграл V2
является непрерывной функцией в этой точке. Отсюда следует существование
такого S"{e/3), что
|1^2(Мо)-У2(М)|^| при |МоЛ1| ^ (5''(I) .
Полагая
^и=™" к (!)• *"(!)]
получим
\V{M)-V{Mo)\^e при \MoM\^S,
что и означает непрерывность равномерно сходящегося интеграла.
Отметим, что полученные результаты справедливы не только для
интегралов по объему, но также и для интегралов по поверхностям и
линиям. Это обстоятельство будет использовано нами в дальнейшем.
Рассмотрим потенциал
V{M) =
Р{Р)
Rmp
drp
(12)
И компоненты силы притяжения
Х{М)
III
Р{Р)
{x-^)dTp,
'-^">=-III ж1^«-">'''•
т
Р{Р)
Z{M) =
{z - С) drp
(13)

А
ТЕОРИЯ ПОТЕНЦИАЛА
359
в точках, лежащих внутри притягивающего тела Т. Несобственные
интегралы (12) и (13) являются сходящимися, если плотность р (М)
ограничена: |р(М)| < С. Для потенциала V {М) это очевидно, так
как
-— < —— (а = 1 < 6).
Для компонент силы притяжения это следует из неравенства
так как |ж — ^| < R.
Для иллюстрации понятия равномерной сходимости
несобственных интегралов покажем, что интегралы (12) и (13) являются
непрерывными функциями.
Для этого надо доказать, что интегралы (12) и (13) равномерно
сходятся во всякой точке Mq.
Оценим модуль интеграла (12) по области Т§ ^^:
р{р)
Rmp
drp
Ts
^С
drp
Rmp
к
Mq
здесь К^ ° — шар радиуса 5 с центром в точке Mq , содержащий
область Т(5. Непосредственное вычисление мажорирующего интеграла
по области К^ ° с центром в точке Мд неудобно. Для его вычисления
целесообразно перейти к сферической системе координат с центром в
точке М. Очевидно, что
С
drp
Rmp
^С
drp
Rmp
= CS7rS'^,
к:
к''
где К^ — шар радиуса 25 с центром в точке М. Если нам задано
некоторое г > О, то выбрав
5{е) =
87гС"
мы убедимся в равномерной сходимости интеграла V.
Повторяя аналогичное рассуждение для интеграла
Х{М) =
X - ^
^МР
^ Отметим, что интеграл (12) получается из интеграла (11) при
F(M,P) = 1/Rmp, f{P)=p{P).

360 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
получаем
JJJ ^МР JJJ ^МР JJJ ^МР
^МР
MP JJJ "-^мр
если
е
5^5{е) =
SttC
Таким образом, потенциал V и компоненты силы притяжения X,
У, Z являются непрерывными функциями во всем пространстве"*^л
4. Первые производные объемного потенциала. Функции,
стоящие под знаками интегралов
Х{М) = - jjj p{P)'^dTp, Y{M), Z{M),
Т
ЯВЛЯЮТСЯ производными по соответствующим переменным от
функции, стоящей под знаком интеграла
(«)=///:
^МР
т
Если для функции V законно дифференцирование под знаком
интеграла, то
dV dV dV
дх^ ду ^ dz ^
т.е. V является потенциалом поля, компоненты которого равны X,
Y, Z.
Если точка М лежит вне области Т, то функция
х-^ -{х-о д 1
Rmp [{x-0^ + {y-vY + {z-O^P' дхКмр
непрерывна по обоим аргументам М (ж, ^, z) и Р (^, ?7, С)-
Следовательно, в этом случае дифференцирование под знаком интеграла V
законно.
Производные более высокого порядка можно также вычислять при
помощи дифференцирования под знаком интеграла всюду вне тела Т.
^ Равномерная сходимость интегралов V (М) и X (М) доказана в
предположении ограниченности плотности \р\ < С. Следовательно, эти
интегралы непрерывны также и в точках разрыва функции /?, например на границе
области, заполненной массами.

А
ТЕОРИЯ ПОТЕНЦИАЛА
361
Отсюда в силу леммы из гл. III, § 3 следует, что потенциал вне
притягивающих масс удовлетворяет уравнению Лапласа:
АУ = О вне тела Т.
Докажем, что вычисление производных потенциала V можно
осуществлять путем дифференцирования под знаком интеграла и в том
случае, когда точка М лежит внутри тела Т.
При доказательстве мы будем пользоваться только
ограниченностью функции р (ж, ^, z) (|р(ж, ^, z)\ < С), не предполагая ее
непрерывности, откуда будет следовать, что функция V (ж, у, z)
дифференцируема и в точках границы, которые можно рассматривать как точки
разрыва функции р (ж, ^, z)^ равной нулю вне тела.
Покажем, что для любого г можно найти такое 5 (г), что
1/(ж +Аж, у, z) -У (ж, у, z)
X
<г.
если
|Аж| <5{е).
Мо
Заключим точку Mq в достаточно малый шар К^, °, размеры
которого мы уточним в дальнейшем, и разобьем V на два слагаемых:
У = 1^1+^2,
где Vi и V2 соответствуют интегрированию по объему Ti = К^
дополнительному объему Т2 = Т — К^, °. Тогда
1/(ж +Аж, у, z) -У (ж, у, z) ^
Аж ~
Vi (ж + Аж, у, z) - Vi (ж, у, z) 1/2 (ж + Аж, у, z) - V2 (ж, у, z)
Аж
+
Аж
При любых фиксированных размерах области Ti
V2{x-\- Ax,y,z) -V2{x,y,z)
hm = X2 =
Аж^О Аж
так как точка Mq лежит вне области Т2.
Полагая X = Xi -\- Х2, оценим
^(^'^'^'ifi'^"'
Т2
X -
1/(ж +Аж, у, z) -У (ж, у, z)
Аж
<
<
Хо-
V2 (ж + Аж, у, z) - V2 (ж, у, z)
Аж
+ l^il +
Vi (ж + Аж, у, z) - Vi (ж, у, z)
Аж

362
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
и покажем, что каждое из слагаемых можно сделать меньше чем г/3.
В самом деле,
1^11
так как
dT
<С
S' 2ж ж
III
0 0 0
г^ sin 'dd'ddwdr , ^ ^, s
, = ^^С5' < -,
(15)
R
< 1 и \р\ < С. Рассмотрим последнее слагаемое
\s\ =
Vi {х + Аж, у, z) - Vi (ж, у, z)
Аж
R — Ri
RRi
dT
где
R, = ./[{x + Ax) - ^]2 + {y- пУ + {z- C)2,
Стороны треугольника MqMMi равны г, ri и |Аж|. Отсюда следует,
что
\R-Ri\ ^ \Ах\.
Поэтому
\s\^c
III
RRi^ 2
инчи
Д2 f '
так как для любых чисел а и Ь
ab^^(a^ + b^).
При этом
Д2
= 47Г(5' и
Ti
Ti
^
2S'
dT
Щ
= SttS',
где K^g} — шар радиуса 2S' с центром в точке Mi.
При соответствующем выборе S' можно обеспечить неравенство
|5| < ^127г6' = 6жС6' < |.
^ О
(16)

_5^ ТЕОРИЯ ПОТЕНЦИАЛА 363
Выбирая 5' из условия (16), мы удовлетворим обоим неравенствам
(15) и (16). Фиксируем область Ti = К.,^, а тем самым и область
T2 = T-Ti.
Равенство (14) в применении к выбранной области Т2 означает,
что для любого е можно указать такое 5", что
V2 {х + Аж, у, z) - V2 (ж, у, z)
А2
£
Аж
коль скоро |Аж| < 5". Выбирая, наконец, 5 = min [5'^ 5"]^ мы получаем
|1/(ж +Аж, у, z) -V {х, у, z)
X
< г, если |Аж| < S.
Ах
Тем самым доказано, что существует производная dV/dx, равная
dV
Формулы
а. = ^^ ("'
Оу OZ
не требуют специального доказательства.
Таким образом, доказано, что дифференцирование под знаком
интеграла законно и что компоненты силового поля X, У, Z являются
компонентами gradl/.
5. Вторые производные объемного потенциала.
Несобственный интеграл
т т
не сходится абсолютно для внутренних точек Р тела Т. В этом случае
мажоранта для подынтегральной функции имеет вид
с
-—- при а = 6.
Установим формулы, по которым вычисляются внутри Т вторые
производные потенциала У, в предположении непрерывности и
непрерывной дифференцируемости плотности р{х, у, z) в окрестности
исследуемых точек. В частности, исследование, проводимое ниже, не
будет применимо к граничным точкам, где, как правило, имеет место
разрыв плотности.
Представим потенциал V в виде суммы двух слагаемых:
У = 1^1+^2,

364
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
относящихся к областям Ti и Т2, где Ti = К^ ° — шар радиуса 5 с
центром в рассматриваемой точке Mq, внутри которого функция р
дифференцируема.
Вторую производную от V2 можно вычислять
дифференцированием под знаком интеграла, так как точка Mq лежит вне области
д_
дх
дх
д^
^ Ыт.
Т2
Первая производная Vi по х равна
dVi
дх
Ti
так как
д
'Тх
д_
дх
^ Ыг =
д_
д^
1
R
'Щ
^]dT,
(19)
Преобразуем интеграл (19), пользуясь формулой
Остроградского — Гаусса:
dVi
дх
Ti
д_
dr
-III
д_
1 dp
кЩ\
dr
--II
R
cos ada -\-
Ti
1^
dr,
^Mq
где E^ °—поверхность сферы, ограничивающая объем Ti, а — угол
между внешней нормалью к поверхности Е^ ° и осью х. Первое
слагаемое является дифференцируемой функцией в точке Мд, так как Мд
лежит вне Е^ °. Второе слагаемое в окрестности точки Мд является
также дифференцируемой функцией, поскольку функция р имеет
производную в Ti. Отсюда следует, что в точке Мд существует вторая
производная функции Vi. Перейдем к ее вычислению:
дх\дх ) J J ^ дх \R
cos ada -\- /// т^ —
д_
дх
^5
Ti
dp
Для второго слагаемого в точке Мд имеет место следующая оценка:
///
д_
дх
др
д^
dr
<С,
III
Д2
CiAttS,
(20)

А
ТЕОРИЯ ПОТЕНЦИАЛА
365
если
др_
<Ci.
Применив к поверхностному интегралу теорему о среднем, полу-
Здесь р*—значение плотности в некоторой точке Е^ °,
dx\R
R^
R^
cos a
И, кроме того,
f f cos^ a ^ 1 f f 1 , о On 247 4
Переход к пределу при (5 —>- О дает
lim
d^Vi
5^0 дх^
Равенство
lim
6^0
-//
^^U''°^"^"
-^р(Мо). (21)
а^У a^^i d^V2
+
9ж^ 9ж^ 9ж^
верно при всяком (5, и левая часть его не зависит от (5, поэтому
d^V
lim
дх^ 5^0 V 9ж^
a^^i d^V2
+
9ж^
Т2
в"
дх^ \R
dr.
(22)
Из существования второй производной д V/dx , доказанного выше,
следует существование
ыи
Т2
^а^и'^"
///
^£(i'^"
(23)
Последний интеграл получен при специальном способе
предельного перехода, когда стягиваемые к точке Mq области являются
шарами ""^^ что и отмечается чертой над интегралом в формуле (23).
Изменение формы этих областей, вообще говоря, может менять значение
^ Предел (23) обычно называют главным значением интеграла.

366 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
предела; интеграл (23) следует рассматривать как условно
сходящийся. Таким образом,
dW ._ . ГГГ д^ П\ ^ 47Г
,,.(Mo) = yyyp^^^j^r--,(Mo). (24)
т
Отсюда видно, что вычисление вторых производных потенциала при
помощи формального дифференцирования под знаком интеграла
привело бы нас к неверному результату.
Для производных d^V/dy^ и d^V/dz^ получаются аналогичные
выражения. Подставляя значения всех трех производных в выражение
для оператора Лапласа, находим
,,, d'^V d^V d^V
AV = --^ + --^ +
dx^ dy^ dz^
r
dx^ \r) ^ dy^ \r) ^ dz^ \R
dr - 4:7тр{Мо) =
:-4^p(Mo), (25)
так как 1/R — гармоническая функция-"^л
Таким образом, объемный потенциал удовлетворяет уравнению
Пуассона
AV = —4:7гр внутри тела
и уравнению Лапласа
AV = О вне тела.
Неоднородное уравнение
Аи = -/ (25')
при условии дифференцируемости / внутри некоторой области Т
имеет частное решение
fdr
Uo
4^ JJJ R
Отсюда следует, в частности, что решение краевой задачи для
неоднородного уравнения (25') можно свести к решению аналогичной
^ Формула (25) установлена в предположении дифференцируемости
функции /9, что является достаточным условием и может быть заменено менее
стеснительными условиями. Однако условия непрерывности функции р (М)
для справедливости (25) недостаточно, так как существуют примеры таких
непрерывных функций р{М), для которых объемный потенциал не имеет
вторых производных.

А
ТЕОРИЯ ПОТЕНЦИАЛА
367
краевой задачи для уравнения Лапласа Av = О, если искомую
функцию представить в виде суммы и = щ -\- v.
6. Поверхностные потенциалы. Как
формула Грина (см. § 2)
показывает основная
<"'=1^//
ди
д
Rmp дп дп \Rmp
dap,
M{x,y,z)
любая гармоническая функция может быть представлена с
помощью интегралов, являющихся
поверхностными потенциалами.
Рассмотрим поле, создаваемое
массами, распределенными на
поверхности "'^^, и определим
потенциал этого поля. Поверхностной
плотностью fi (Р) в точке Р
поверхности Е называют предел
отношения массы, находящейся на
некотором элементе da поверхности Е,
площади при стягивании da к точке Р
ставляется поверхностным интегралом
Рис. 59
содержащем точку Р, к его
Потенциал этих масс пред-
V{M)
//
Rmp
dai
(26)
называемым потенциалом простого слоя.
Другим типом поверхностного потенциала является потенциал
двойного слоя. Перейдем к его определению.
Рассмотрим диполь, образованный двумя массами: —т и +?7i,
расположенными в точках Pi и Р2 на расстоянии А1 (рис. 59).
Произведение т • А1 = N называется моментом диполя. Потенциал
диполя в некоторой точке М (ж, у, z) равен
Г2
т
— =771
Г1
1
Г2
т)--^^
1 1
Г2 Г1
Р2-
где Г1 и Г2 — расстояния точки М от точек Pi и
Если А1 мало по сравнению с расстоянием до точки М (Al/ri <^ 1),
то, пользуясь теоремой о конечных приращениях, можно написать
R=^{x- 0^ + {у- гу)2 + {z- с?
^ Если массы с объемной плотностью р расположены в некотором слое
толщины h около поверхности Е и поле изучается на расстояниях, больпЕих
по сравнению с h {h/R ^1), то учет толщины поверхности, вообще
говоря, не имеет смысла. Поэтому вместо объемного потенциала с плотностью
р целесообразно рассматривать поверхностный потенциал с поверхностной
плотностью р = ph.

368
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
где производная берется по направлению от отталкивающей массы к
притягивающей и R — расстояние от точки М (ж, у, z) до некоторой
средней точки Р (^, ту, С) отрезка AL
Вычислим производную по направлению 1:
где вектор г направлен от диполя к фиксированной точке М, а, (р
есть угол между вектором 1 и вектором г. Таким образом, потенциал
диполя равен
V{M)=N
COSip
(27)
где N — момент диполя.
Пусть на двух поверхностях Е и Е' (рис. 60), находящихся друг
от друга на малом расстоянии S, распределены массы таким образом,
что масса каждого элемента по-
^(x,y,z) верхности Е' равна по величине
и противоположна по знаку
массе соответствующего элемента
поверхности Е. Обозначим
через п общую нормаль к
поверхностям Е и Е', направленную
от отталкивающих масс к
притягивающим. Перейдя к
пределу при (5 —>- О, получим двойной
слой как совокупность двух простых слоев с взаимно
противоположными плотностями, находящихся друг от друга на малом расстоянии.
Если 1У — поверхностная плотность момента, то момент элемента
поверхности dap будет равен
dN = 1У dap.
Для потенциала элемента da в точке М (ж, у, z) будем иметь
Рис. 60
d
dnp \ Rmp
cos ifi
dap = v [P) —2 dap,
где (/?i—угол между векторами n и РМ.
Назовем потенциалом двойного слоя интеграл
W
(M)^-jj
d
dnp \ Rmp
jy{P)dap.
(28)
Это определение, очевидно, соответствует случаю, когда внешняя
сторона поверхности является отталкивающей, а внутренняя —
притягивающей.

А
ТЕОРИЯ ПОТЕНЦИАЛА
369
Очевидно, что
W
-II
COS(/?
iy{P)dap,
где (f — угол между внутренней нормалью и направлением из точки
поверхности Р на фиксированную точку М. Если поверхность
незамкнутая, то мы должны считать ее двусторонней, так как потенциал
двойного слоя определяется только для таких поверхностей.
Потенциалы простого и двойного слоев в случае двух независимых
переменных имеют вид
V = 1ц{Р)\п
Rmp
ds.
(29)
W
-/'<-) s^('°^)*^/£?'<-)*.
(30)
где С — некоторая кривая, /i — линейная плотность простого слоя,
V — плотность момента линейного двойного слоя, ip — угол между
внутренней нормалью к линии С и направлением на фиксированную
точку.
Если точка наблюдения М (ж, ^, z) находится вне поверхности
(вне притягивающих масс), то подынтегральные функции и их
производные по ж, ^, Z любого порядка в формулах
V{M)= ff^^{P)-^dap,
J J ^МР
E
'^(«' = -//''<''>5^Ш^'
E
непрерывны по переменным ж, у, z. Поэтому в точках, лежащих вне
поверхности Е, производные поверхностных потенциалов можно
вычислять при помощи дифференцирования под знаком интеграла.
Отсюда в силу принципа суперпозиции следует,
что поверхностные потенциалы
удовлетворяют уравнению Лапласа всюду вне
притягивающих масс. Функции (29) и (30),
очевидно, удовлетворяют уравнению Лапласа с
двумя независимыми переменными.
Поверхностные потенциалы в точках
поверхности Е представляются
несобственными интегралами. Покажем, что если по-
Р
Рис. 61
верхность имеет непрерывную кривизну, то потенциал двойного слоя
24 А. Н. Тихонов, А. А. Самарский

370
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
в точках этой поверхности существует. Проведем доказательство для
случая двух независимых переменных:
W
-I
С08(р
R
1У ds.
Рассмотрим кривую на плоскости (ж, ^) и выберем начало
координат в точке Р, ось X направим по касательной, а ось у — по нормали в
этой точке (рис. 61). Уравнение кривой в некоторой окрестности точки
Р запип1ется в виде
у = у{х).
Кривая имеет, по предположению, непрерывную кривизну, т. е. у (х)
имеет непрерывную вторую производную. Поэтому
у{х)=у (0) + ху' (0) + у у" {'9х) (О ^ t? ^ 1),
откуда вследствие выбора координатных осей
у{х) = -х-'у"{'&х)
Отсюда будем иметь
R = л/ж2 + ^2 = . L2 ^ ^4
f i'dx)
X \ 1 -\- х'^
С08(р :
ху'' {Щ
R
2Wl + x2
у"i^x)
j" i'dx)
COS(/?
R
Из выражения кривизны
следует
Поэтому
у"i^x)
2 О + ж2
у"i^x)
К
У"
lim
{1 + у"Р
у"{0)=К{Р).
1
COS(/?
|мр|^о R
К{Р),

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 371
что доказывает непрерывность (со^ (f)/R вдоль дуги, а тем самым
и существование потенциала двойного слоя в точках кривой С для
ограниченной функции и.
Потенциал двойного слоя в случае трех независимых переменных
также существует в точках поверхности, имеющей конечную кривизну,
потому что функция
COS(/?
имеет интегрируемую особенность порядка 1/R. Существование
потенциала простого слоя не вызывает сомнений.
7. Поверхности и кривые Ляпунова. Предположение о конечности
кривизны оказывается излиненим для существования поверхностных
потенциалов.
Потенциалы простого и двойного слоев в точках поверхности Е
являются несобственными интегралами. Покажем, что эти интегралы сходятся
для определенного класса поверхностей, называемых поверхностями
Ляпунова, если плотность потенциала ограничена: |i^(P)| < С, где С — некоторая
постоянная.
Поверхность называется поверхностью Ляпунова, если
выполняются следующие условия.
1. В каждой точке поверхности Е существует определенная нормаль
(касательная плоскость).
2. Существует такое число с? > О, что прямые, параллельные нормали
в какой-либо точке Р поверхности Е, пересекают не более одного раза часть
Ер поверхности Е, лежащую внутри сферы радиуса d с центром Р. Эти
участки поверхности Ер называются окрестностями Ляпунова.
3. Угол J {Pj Р') = (прТ^рО? образованный нормалями в точках Р и
Р , удовлетворяет следующему условию:
7(Р, P')<V, (31)
где г — расстояние между точками Р ж Р ^ А— некоторая постоянная и
0<^^ 1.
Пусть Ро—некоторая точка поверхности Е. Выберем прямоугольную
систему координат, помещая начало координат в точку Pq и направляя ось
Z вдоль внепЕней нормали. Плоскость (ж, у) при этом совпадает с
касательной плоскостью, в силу условия 2 существует такое /Oq, что уравнение
поверхности Е может быть представлено в виде
для
f{x,y)^^ (32)
= л/ж2+^2<^^. (33)
^ Отметим, что если функция / (ж, у) имеет непрерывные вторые
производные в окрестности точки Pq, то поверхность z = f {х, у) удовлетворяет
условиям Ляпунова. Таким образом, поверхности с непрерывной кривизной
являются поверхностями Ляпунова.
24*

372 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Обозначим через Ер окрестность точки Pq на поверхности Е,
определяемую условиями (32) и (33). Установим некоторые оценки для функции
f {х, у) и ее производных.
Из существования нормали в каждой точке поверхности (условие 1)
следует дифференцируемость функции f {х, у). Направляющие косинусы
нормали (внепЕней) выражаются формулами
cosp = — , C0S7-
Y^l + ^1 + 4 V 1 + ^i + 4 V 1 + ^1 + 4
В силу выбора напЕСЙ системы координат Zx (Pq) =0, Zy (Pq) = 0. Будем
считать, что поверхность Ер столь мала {ро столь мало), что
1 ^ C0S7 = . \ , > L (34)
VI + ^1 + ^2 2
Обозначим через Пр проекцию вектора пр на плоскость {х, у) и через а ,
Р — углы, образованные вектором Пр с осями х ж у. Очевидно, что
cos а = sin 7 cos а , cos /3 = sin 7 sin a .
Так как sin 7 < 7, то в силу условия 3
sin7 <ArppQ
и, следовательно.
|cosa| < Агрр^^ |cos/3| < Агрр^^ (35)
cos ol cos 3 1
а так как Zx = , Zy = , причем < 2, то
cos 7 cos 7 cos 7
|^^|<2Лг|.р^, |^^|<2Лг|.р^.
Пользуясь формулой Тейлора для функции z = f {х, у) в окрестности
точки Ро (О? 0)? будем иметь
^ (ж, у) = Z (о, 0) + ж^ж (ж, ^) + 2/% (ж, у),
где
О^ж^ж, О ^ у ^ у.
Отсюда следует, что
\z(x,y)\<AAr]+^^. (36)
Полученные оценки (34), (36) позволяют доказать, что в точках, лежащих
на поверхности Е, потенциал двойного слоя
W{M) = jj ^v{P)dap (28)
является сходящимся несобственным интегралом, если Е — поверхность
Ляпунова.

А
ТЕОРИЯ ПОТЕНЦИАЛА
373
Пусть М = Pq—точка поверхности Е. Выбирая систему координат,
как было указано вынес, представим уравнение поверхности Е в окрестности
точки Pq в виде
z = f{x, у).
функция /(ж, у) удовлетворяет условиям (34) и (36). Вычислим cos (^, где
ср — угол между направлением внутренней нормали в точке Р (^, т/, Q и
направлением PPq. Нетрудно видеть, что
I coscfl
— COS Oi -\- -^ COS Р -\- -^ COS 7
R R R
^ |cosa| + |cos/3| + Щ ^
R
^ AR%p^ + AR%p^ + 4ЛЯрр^ = QAR^
РРо
COS(p
R^
^6А
1
(0<^^ 1).
(37)
Я2-^
Представим W в виде суммы двух интегралов:
W = Wi-\-W2,
где Wi—интеграл по поверхности Ер , содержащей особую точку Pq, а
интеграл W2 берется по остальной части поверхности Е — Ер . Так как
подынтегральная функция в интеграле W2 нигде не обращается в
бесконечность, то для сходимости интеграла W достаточно убедиться в сходимости
интеграла Wi. Поскольку
d$,dr] р dp d9
da = = ,
cos 7 cos 7
где p = v^^ +^^7 ^ — полярные координаты на плоскости (ж, у), то
преобразование переменных в этом интеграле дает
Wi
II
^Ро
COS(p
R^
V (Р) dap
РО 27Г
//
О О
COS(p
R^
V{P)
COS 7
pdpdO.
Для подынтегральной функции в силу оценок (34), (36) и (37) имеем
HP)
COS(p 1
COS 7
^F =
12AC
так как р < R.
Такой вид мажорантной функции F обеспечивает сходимость
несобственного интеграла в случае двух независимых переменных (см. п. 3).
Нетрудно установить, что для поверхности Ляпунова потенциал
простого слоя
V{M)
J J Rmp
(P) dap
(26)
также сходится в точках поверхности. Следует отметить, что эта
сходимость имеет место и для поверхностей более пЕирокого класса.

374
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
В случае двух независимых переменных потенциалы простого и
двойного слоев сходятся в точках кривой (см. формулы (29) и (30)), если эти
потенциалы берутся для кривых Ляпунова, определяемых условиями,
аналогичными условиям 1 — 3 для поверхностей Ляпунова.
8. Разрыв потенциала двойного слоя. Покажем, что
потенциал двойного слоя в некоторой точке Pq •, лежащей на поверхности Е,
является разрывной функцией, для которой имеют место соотноп1ения
W3(Po) = W^(Po) + 27ri/(Po),
W^{Po) = W{Po)-2t:p{Po),
(38)
где И^в (Д)) —предельное значение потенциала двойного слоя при
подходе к точке Ро с внутренней стороны, а W^ (Pq) —предельное
значение с наружной стороны поверхности-"^ л
В случае двух независимых переменных соответствующие
формулы имеют вид
Жз(Ро) = И^(Д))+7гг/(Ро),
Жн(Ро) = И^(Ро)-7гг/(Ро)-
(39)
Потенциал двойного слоя для двух независимых переменных
выражается интегралом
W{M)
I
COS(/?
Rmp
v{P)dsp.
Рассмотрим некоторый элемент дуги ds^ концами которого
являются точки Р и Pi. Проведем через точку Р дугу окружности
радиуса MP с центром в точке М до
пересечения ее с отрезком MPi в точке Q. Тогда
с точностью до бесконечно малых высшего
порядка можно написать (рис. 62):
ds cos(/? = б?сг, —- = б?а;, (40)
R
где ds =PPi, da =PQj duo — угол, под
которым видна дуга ds из точки М. Знак duo
совпадает со знаком cos(/?, так что б?а; > О,
Рис. 62 если (/? (угол между внутренней нормалью
в точке Р и вектором РМ) меньше 7г/2, и б?а; < О, если ^ > 7г/2.
^ Если Е — незамкнутая поверхность, то внутренняя сторона может быть
условно определена соглапЕСнием о том, какая нормаль в точке Pq
называется «внутренней» и какая — «внепЕней». Следует иметь в виду, что в случае
незамкнутых поверхностей потенциал двойного слоя определяется только
для двусторонних поверхностей.

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 375
Если dcj > О, т. е. (f < 7г/2, то из точки М видна «внутренняя»
сторона кривой С; при duj < О {^ > '7г/2) из точки М видна «наружная»
сторона кривой. Отсюда следует, что угол видимости некоторой дуги
Р1Р2 равен углу Р1МР2, который описывает луч MP, когда точка
Р пробегает дугу Р1Р2.
Рассмотрим потенциал двойного слоя W^ на замкнутой кривой
С с постоянной плотностью и = i/Q = const. Луч MP описывает угол
I 27Г, если точка М лежит внутри кривой С,
О = < 7г, если точка М лежит на кривой С,
I О, если точка М лежит вне кривой С,
когда точка Р пробегает всю кривую С. Отсюда для потенциала W^
получаем
\27тщ, если точка М лежит внутри кривой С,
W = щО^ = < 7гг/0 5 если точка М лежит на кривой С,
I О, если точка М лежит вне кривой С.
Таким образом, потенциал с постоянной плотностью является
функцией кусочно-постоянной, причем
где И^з , Wq, W^ — значения потенциала внутри, на и вне кривой С.
Аналогично в случае трех независимых переменных будем иметь
da cos о? , , ^.
—^ = <^^ (42)
где duo — телесный угол, под которым виден элемент da поверхности
Е. Пусть da' — элемент сферической поверхности, получающийся при
пересечении сферы, описанной радиусом MP из точки М, с конусом,
имеющим вершину в точке М и опирающимся на элемент поверхности
da. Элемент поверхности da' = da cos (p. Отсюда и следует формула
(42). Замечание, сделанное выше относительно знака dco, остается в
силе, что приводит нас к формулам
(Аттщ, если точка М лежит внутри поверхности Е,
W = i/qCI = < 27ТЩ, если точка М лежит на поверхности Е,
I О, если точка М лежит снаружи поверхности Е,
характеризующим кусочное постоянство функции W^, а также к
формулам

376 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
где W^, W^ — значения потенциала W^ внутри и снаружи
поверхности Е, а W^—значение W^ на Е.
Рассмотрим теперь потенциал двойного слоя с переменной
плотностью и докажем, что в точках непрерывности плотности имеют место
формулы, аналогичные формулам (41) и (41').
Пусть Pq — точка поверхности Е, в которой функция ту (Р)
непрерывна. Введем потенциал двойного слоя W^ с постоянной плотностью
щ = 1У (Ро) и рассмотрим функцию
I{M) = W (М) - W"" (М) = [[[и (Р) - щ] ^ dap.
Е
Докажем, что функция / непрерывна в точке Pq. Для этого
достаточно доказать равномерную сходимость интеграла / (М) в точке Pq.
Зададимся некоторым числом г > 0. Из непрерывности функции и (Р)
в точке Ро следует, что для любого наперед заданного числа ?7 > О
можно найти El—окрестность точки Pq на поверхности Е, такую,
что
|г/(Р)-г/(Ро)|<г?,
если Р G El. Представим интеграл / в виде суммы
i = h + h,
где интеграл Д берется по поверхности Ei, а /2—по поверхности
Е2 = Е — El. Из определения Ei следует оценка
\h\<vBj:,
где Ре—постоянная, определяемая условием
I COS(/?'
//
р2
dap ^ Ре (43)
при всевозможных положениях точки М, не зависящая от выбора
поверхности El. Подробнее относительно этой постоянной будет сказано
ниже.
Выбирая Г] = s/Bj2, убеждаемся в том, что для любого г > О
можно найти такое Ei, содержащее Pq, что
|/i(M)|<e
при любом положении точки М. Отсюда и следует равномерная
сходимость интеграла I (М) в точке Pq, а также его непрерывность в
этой точке.
Если И^в (Ро) и И^н (Ро)—пределы потенциала W (М) при М -^
—>- Ро с внутренней и наружной сторон поверхности Е, то
Жз(Д)) = W^{Po) + /(Ро) = W%Po) + /(Ро) + 27ГЩ = W{Po) + 2ж1у{Ро)

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 377
и, аналогично,
W„{Po) = W{Po)-2wiy{Po).
Справедливость формулы (38) установлена.
Проведенное выше доказательство справедливо для поверхностей,
удовлетворяющих условию ограниченности (43). Для выпуклой
поверхности, которую всякий луч из точки М пересекает не более двух
раз, В^ ^ Зтг; для поверхностей, состоящих из конечного числа
выпуклых частей, Bj2 также ограничено. Таким образом, наше
доказательство относится к весьма широкому классу поверхностей.
Все приведенные выше рассуждения остаются в силе и для
функций двух независимых переменных. В этом случае формулы (41)
принимают вид (39)
WUPo)=W{Po)+7Tiy{Po),
W„{Po)=W{Po)-7ny{Po).
9. Свойства потенциала простого слоя. В отличие от
потенциала двойного слоя потенциал простого слоя (26)
V{M)= ffJ—t^(P)dap
J J ^МР
E
непрерывен в точках поверхности Е. Убедимся в этом для случая
гладкой поверхности Е. Для этого достаточно установить
равномерную сходимость интеграла V (М) в точках поверхности Е.
Действительно, пусть Pq — некоторая точка поверхности Е.
Представим потенциал V в виде суммы
V= [ [ ^l^{P)dap+ f f -^,j{P)dap = Vi+V2,
J J ^MP J J ^MP
El E2
где El —достаточно малая часть поверхности Е, содержащаяся в
сфере радиуса 5 с центром в точке Pq • Величину 5 мы более точно
определим в дальнейшем.
Рассмотрим систему координат с началом в точке Pq, ось z
которой направлена по внешней нормали в Pq. Пусть М (ж, ^, z) —
произвольная точка, отстоящая от Pq (О, О, 0) на расстояние MPq < ^•
Обозначим через Е'^^ проекцию Ei на плоскость (ж, ^), а через К^ —
круг радиуса 25 с центром в точке М' (ж, ^, 0), целиком содержащий
область Ti'-^. Предполагая ограниченность функции /i:
\li{P)\<A
И принимая во внимание, что
da' d^ dr]
da
cos 7 cos 7
R = ^{x-0' + {y-v? + {z-C? ^ Vi^ - 0' + {y- vf = P,

378
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
получаем
i'''<«'i<V/i^=V/
da'
^\
7л/(^-С)' + (2/-^)' + (^-С)'
<
cos
< 2А
//
d^dr]
.J{x-0^ + {y-vY
< 2А
II
d^dr]
к^
м'
Vi^-O' + iy-vr'
если S настолько мало, что cos 7 > 1/2.
Введем в плоскости (ж, у) полярную систему координат (р, (р) с
началом в точке М'. Тогда можно написать
\Vi{M)\<2aJJ
d^dr]
к^
м'
^{х - О' + (у- пУ
2А
2(5 27Г
//
pdpd(f
SAttS.
о о
Выбирая S = г/(87гЛ), будем иметь
\Уг{М)\<е,
если |МРо| < ^- Следовательно, V (М) равномерно сходится во всякой
точке Ро G Т, и является непрерывной функцией в этой точке.
Обратимся теперь к изучению поведения нормальных
производных потенциала простого слоя на поверхности. Покажем, что они
имеют на Е разрыв такого же типа, как
и потенциал двойного слоя.
Внешняя и внутренняя нормальные
производные функции V — dV/dn^ и
dV/dn^ — определяются следующим
образом. Пусть Ро—некоторая точка Е. Из
точки Д) проведем ось z^ которую можно
направить либо вдоль внешней, либо вдоль
внутренней нормали.
Рассмотрим производную dV/dz в
некоторой точке М оси Z. Обозначим через
(dV/dz)^ и {dV/dz)^ пределы производной
dV/dz при стремлении точки М к точке Pq с внутренней или
наружной стороны поверхности Е. Если ось z направлена по внешней
(внутренней) нормали, то эти значения называются внутренними и
внешними предельными значениями производной по внешней (внутренней)
нормали в точке Д) ""^ •
1) тт ^W
^ Предел разностного отнонхения
^(^^о)
|^р I при М ^ Ро равен
пределу извне для производной по внепЕней нормали или пределу изнутри
для производной по внутренней нормали, в зависимости от того, с какой
стороны точка М приближается к точке Pq.

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 379
Исследуем разрывы внутренней нормальной производной
потенциала простого слоя на Е. Производная dV/dz в точке М оси z^
направленной по внутренней нормали, равна
г<«>=//''<'''|^ш--//17''<'''-- <"'
Е Е
где "ф — угол между осью z и вектором Проведем из точки Р
(рис. 63) нормаль PQ и прямую PN^ параллельную оси z (нормали
в точке Ро), и обозначим через в угол NPQ, равный углу между
нормалями в точках Р и Ро ""^ • Выражение для потенциала двойного
слоя W (М) содержит множитель (cos(/?)/i^^, где ^ = /_MPQ. Так
как угол MPN равен тг — -0, то
cos(7r — ф) = cos (f cos в -\- siiKf sin в cos О = — cos -0,
где О — двугранный угол с ребром PQ^K Отсюда следует, что
9V , ^ ^, f f _ cos о? , f f . _ _ sin о? ^
—— (M) = — fi COS б' acr — / / fismU cos i 2 acr =
E E
= -И^1-/(М), (45)
где T^i (М)—потенциал двойного слоя с плотностью //i = fj, cos в,
имеющий разрыв на поверхности S. Очевидно, что интеграл / (М)
является функцией, непрерывной в точке Ро, так как I {М) сходится
равномерно в этой точке (см. примечание на с. 378).
Возвращаясь к формуле (45), видим, что
dv_
dz
dv
dz
= -WiiPo)-2TTfi,iPo)-I{Po),
= -WiiPo) + 2TTfi,iPo)-I{Po).
(46)
^ Очевидно, что О и sin^ стремятся к нулю, когда Р ^ Pq. Если
поверхность обладает конечной кривизной в окрестности точки Рд? т. е. ее
уравнение можно представить в виде
z = f{x, у),
где /(ж, у) имеет вторые производные, то sin^ будет дифференцируемой
функцией ж, 2/ и, следовательно,
sin О < Ar
(для поверхностей Ляпунова sin в < Аг ).
^ Если направление PQ принять за ось новой сферической системы, то
эта формула совпадает с формулой (13) на с. 345.

380
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Обозначим
^)__ = -И'.,Р,)-ДР„,
/А
COS (/?
COS в da
Ih
sm в cos \ I _^ da
R^
II
M=Po
cos-00
/^
7?2
6?cr,
где -00 — угол между осью z и вектором PqP.
Замечая, что /ii (Pq) = /^ (Д))? находим
9У
9Пв
(47)
так как по условию ось z направлена по внутренней нормали. Если
ось Z направить по внешней нормали, то знак cos?/^ изменится и мы
получим
дУ
дУ
Ш/^'^'™'
Ш.-^'^'™-
(48)
Для случая двух переменных имеют место аналогичные формулы
с заменой 27г на тг.
10. Применение поверхностных потенциалов к решению
краевых задач. Метод разделения переменных и метод функции
источника позволяют получить явное выражение для решения краевых
задач только в случае областей простейшего вида. Сведение краевых
задач для уравнения Лапласа (или Пуассона) при помощи
поверхностных потенциалов к интегральным уравнениям, с одной стороны,
удобно для теоретического исследования вопроса о разрешимости и
единственности краевых задач, с другой стороны, дает возможность
эффективного численного решения краевых задач для областей
сложной формы. Рассмотрим внутренние краевые задачи для некоторого
контура С.

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 381
Найти функцию и, гармоническую в области Т, ограниченной
контуром С, и удовлетворяющую на С граничным условиям
и\с = f (первая краевая задача)
или
ди
дп
= / (вторая краевая задача).
с
Аналогично ставятся внешние краевые задачи-"^л
Будем искать решение внутренней первой краевой задачи в виде
потенциала двойного слоя:
С С
При любом выборе v (Р) функция W (М) удовлетворяет уравнению
Лапласа внутри С. Функция W{M) разрывна на контуре С. Для
выполнения граничного условия, очевидно, надо, чтобы
Жз(Д)) = /(Д)).
Принимая во внимание формулы (39), получаем уравнение для
определения функции 1У (Р):
^г/ (Ро) + / ^ г/ (Р) dsp = / (Ро). (49)
С
Если обозначить через sq и s дуги контура С, соответствующие
точкам Ро и Р, то уравнение (49) можно переписать в виде
L
тгг^ (so) -\- К {so, s) iy{s) ds = /(sq), (50)
0
где L — длина контура С и
. . _ ^ Л 1 \ _ COS(/?
dnp \ Rppq J RpPq
^ При постановке второй краевой задачи, как внутренней, так и вненЕней,
в граничном условии нормаль будем считать внутренней.

382 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
— ядро этого интегрального уравнения, являющегося интегральным
уравнением типа Фредгольма 2-го рода-'^^ Для внешней задачи
получается аналогичное уравнение
L
-T^v (80) + / К (80, S) V {s) ds = f (so). (52)
о
Для второй краевой задачи получаются уравнения
L
—TTfi (sq) -\- Ki (so, s) fi{s) ds = f (sq) (внутренняя задача), (53)
о
L
TTjj, (sq) -\- Ki (so, s) /i(s) ds = f (sq) (внешняя задача), (54)
о
где
если ее решение искать в виде потенциала простого слоя
,(М)= f\n-^^{P)dsi
J ^МР
с
Вопросы, связанные с разрешимостью этих уравнений, будут
рассматриваться в п. 11 настоящего параграфа.
Рассмотрим краевые задачи для некоторых простейших областей,
для которых соответствующие интегральные уравнения легко
разрешимы.
^ Интегральные уравнения, содержащие интегралы с постоянными
пределами, называются уравнениями Фредгольма:
Ь
I К (ж, s) if (s) ds = f (ж) (1-го рода),
a
b
(f (x) -\- / К (ж, s) (f (s) ds = f (x) (2-ro рода).
a
^ Нетрудно видеть, что К {sq, s) = Ki (s, sq). Такие ядра называются
сопряженными, а соответствующие им уравнения называются
сопряженными интегральными уравнениями.

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 383
1. Первая краевая задача для круга. Если контур С
является окружностью радиуса R^ то внутренняя нормаль в точке Р
направлена по диаметру и
COS(/? 1
RpPo 2i^
так как ^ есть угол Р^РР' (рис. 64). Интегральное уравнение для
функции V принимает вид
^ («о) + - [ i^'^is)ds=-f (so). (56)
7Г J ZK 7Г
С
Нетрудно видеть, что его решением является функция
i^(s) = -f(s)+A, (57)
7Г
где А — некоторая постоянная, подлежащая определению. Подставляя
предполагаемую форму решения в уравнение (56), имеем
-/(5о)+Л+- f±(^f{s)+A)ds=-f{so),
7Г 7Г J ZK \7Г у 7Г
С
откуда находим для постоянной А выражение через заданную функ-
цию:
С
Таким образов
u(s)
С
является решением интегрального уравнения (56).
Соответствующий потенциал двойного слоя равен
с с
Преобразуем правую часть предыдущей формулы, предполагая, что

384
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
М лежит внутри С:
С \ с /с
с \ с /
и
С08(р
1
Rmp 2i^
/ (s) ds. (59)
Из Л ОРМ (рис. 65) видно, что
К
cos (/? 1 _ 2R cos (f - Rmp _ 2RRmp cos (f - Rj^p
Rmp 2i^
2RRmp
zHHj^p
R'-pI
2R [Д2 +pI- 2Rpo 008(6» - 6*0)]'
(60)
так как
Pq = R -\- Rj^p - 2RRmp cos (p.
Подставляя выражение (60) для К в формулу (59), получаем интеграл
Пуассона
27Г
О
{R'-Pl)f{0).
R^ +pl-2Rpo cos(i9-6>o)'
(61)
P{s)
дающий решение первой краевой задачи для круга.
Р
Po(so)
Рис. 64
Рис. 65
Проведенные в этом пункте рассуждения показывают, что при
любой непрерывной функции / формула (61) определяет гармоническую
функцию, непрерывно примыкающую к граничным значениям /.
Если функция / кусочно-непрерывна, то в силу свойства
потенциала двойного слоя функция W также непрерывна во всех точках

§ 5] ТЕОРИЯ ПОТЕНЦИАЛА 385
непрерывности /. Из ограниченности функции /
икс
следует ограниченность функции (61):
27Г
\W{po,Oo)\<C^ [ J,. , ^ ~^' .. .,de = C,
27Г У R^-\-р^ - 2Rpo со^{в - во)
о
так как
27Г
р2 _ ^2
^ /^0 лл _ 1 1) /^9^
i^2 + р2 _ 2Rp^ C0S(^ - ^о) ' ^ ^
О
2^ У
2. Первая краевая задача для полупространства.
Пайти гармоническую функцию, непрерывную всюду в области z ^
^ О, принимающую на границе z = О заданное значение / (ж, у).
Будем искать решение этой задачи в виде потенциала двойного
слоя:
+ сю
Wix,y,z)= и ^-^,,(^,r,)d^dr,, R^ = {x-0' + iy-V?+z'.
— СЮ
в данном случае
cos (р Z Z
и ядро интегрального уравнения
1 /COS(/?>
i /COS(/?\
2^ V К^ )z=o^
0.
Таким образом, плотность потенциала двойного слоя
и искомая функция равна
+ сю
и{х,у, z) = —- // ^f{^,r])d^dr].
- i [(^ - ^)' + (^ - ^)' + ^']
Нетрудно показать, что и(ж, у, z) равномерно стремится к нулю при
R = V ж^ + ^^ + 2;^ —>- 00, если этим свойством обладает функция /.
^ Равенство (62) следует из того, что левая часть представляет решение
первой краевой задачи при / = 1.
25 А. Н. Тихонов, А. А. Самарский

386 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
11. Интегральные уравнения, соответствующие краевым
задачам. При решении краевых задач для уравнения Лапласа с
помощью потенциалов простого и двойного слоев мы пришли к
интегральным уравнениям Фредгольма второго рода (50).
Условия разрешимости интегральных уравнений Фредгольма
второго рода с непрерывным ядром и ограниченной (интегрируемой)
правой частью сходны с условиями разрешимости систем линейных
алгебраических уравнений (к которым они сводятся, если интеграл
заменить интегральной суммой). Первая теорема Фредгольма заключается
в следующем.
Неоднородное интегральное уравнение второго рода имеет
решение, и притом единственное, если соответствующее однородное
уравнение имеет только нулевое решение^\
Докажем, опираясь на сформулированную теорему, что
интегральное уравнение (50) имеет единственное решение.
Ограничимся рассмотрением выпуклых контуров, не содержащих
прямолинейных участков границы. В этом случае ядро уравнения (50)
К (Ро, Р) неотрицательно, так как
К(Ро, P)dsp = duj,
где duj есть угол видимости дуги dSp из точки Pq.
^ Для кривых с ограниченной кривизной теория Фредгольма применима
непосредственно, так как ядро интегрального уравнения (50) непрерывно.
Теория Фредгольма применима также в том случае, когда непрерывно
одно из повторных ядер:
j^(n+i) ^р^^ р^^ ^ [[ ^^'^ ^^^' М)К(") (М, P2)daM,
Е
К^^^ (Р, М) = К{Р, М).
Докажем, что если Е — поверхность Ляпунова, то повторные ядра наптего
уравнения, начиная с некоторого номера, непрерывны. Как мы видели, для
поверхностей Ляпунова
COS(^
с
<
Повторные ядра могут быть представлены в виде
i^i,2 (Рь Р2) = 11 Ki (Pi, М)К2 (М, P2)daM.
Е
Покажем, что если
\Кг\ < S^ (П = РгМ; Qi > 0; г = 1, 2),

А
ТЕОРИЯ ПОТЕНЦИАЛА
387
Рассмотрим прежде всего первую краевую задачу для
внутренней области. Однородное уравнение, соответствующее уравнению (50),
имеет вид
1j
■(so)+ /if (so, s) I/(s) rfs = 0.
(63)
|ifl,2|<
С
',2 — ai—a2 '
если ai + «2 < 2, r = |PiP2|-
Очевидно, что эту оценку достаточно установить для случая,
когда точка Р2 лежит в окрестности
Ляпунова Ео точки Pi, причем вместо
интеграла по Ео можно рассматривать интеграл
по проекции So этой окрестности на
касательную плоскость в точке Pi в силу того,
что
р(Р,М)
(где р (Р, М) — расстояние между
проекциями точек Р и М на касательную
плоскость, В — некоторая постоянная), а также в си-
лу связи между элементом поверхности da и .тис.
его проекцией dS: da = dS/cos j, где согласно формуле (34) cos 7 >
> 1/2.
Для плоской области справедлива следующая лемма.
С
Если \Ki\ < ^_^ _ , то
II
So
Ki(Pi, M)K2{M,P2)dxdy
<
С
->2 — а-\ —ао
Обозначим через R диаметр области Sq. Разобьем интеграл / на два
интеграла: /i—взятый по кругу Gi радиуса 2г с центром в точке Pi, и
/2—распространенный на оставпЕуюся область G2 (рис. 66). Так как для
точек М, лежащих в G2,
П 2
2^-^х
Г2 3
Г1 ^ Г2 +Г ^ 2Г2,
Г2 ^ Г1 + Г ^ Г1 + у = —
25*

388
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
[ГЛ. IV
Как мы видели (см. п. 8), имеет место равенство
L
К (so, s) ds = 7г,
о
пользуясь которым, однородное уравнение (63) можно записать в виде
L
{у (so) + V (s)] к (so, s) ds = 0. (64)
о
1j
Пусть Pq* (^o) — точка контура С, в которой функция |i^(s)|
достигает своего максимального значения. Отсюда следует, что сумма
г/ (sq) + г^ {s) знакопостоянна. Тогда, полагая в (64) so = Sq и пользуясь
тем, что i^(so, s) ^ О, получаем равенство
z/(sS) + i/(s) = 0,
то для интеграла /2 получаем оценку
27Г R
1
Г1 dri d(p
I о 2r
|/2|<4CiC2
27Г и
J J ^^-
Сз
<
^2-ai-a2' «l+«2<2,
Производя в интеграле по Gi замену переменных х = гх , у = гу , полу-
\h\<
1 f f C1C2 , I , I
^2-ai-a2 J J ^/2-^1^,2-^2 ^ ^
^#1 2
В последнем интеграле, взятом по кругу Gi с радиусом, равным 2г, Г]^
есть расстояние от центра, г2 — от середины радиуса, вследствие чего этот
интеграл сходится, причем он не зависит от положения точки P2j т. е. от г.
Отсюда
|/ii<
Ci
-.2 —СК1 —ао
j,^ — ai—a2
Положив (7з + С4 = с, получим искомое неравенство:
С
\1\<
^(^^^1+^2-2^ ai+a2 >2.
Отсюда следует, что, начиная с некоторого номера, интегралы,
производящие повторные ядра, ограничены и равномерно сходятся, т. е. являются
непрерывными функциями своих аргументов.

_5^ ТЕОРИЯ ПОТЕНЦИАЛА 389
противоречащее непрерывности в точке Sq, если только ^^(^о) ^ 0.
Следовательно, однородное уравнение (63) имеет только нулевое
penienne, и тем самым неоднородное уравнение имеет единственное
penienne при любой функции f^\
Внеп1няя вторая краевая задача, как мы видели (см. п. 10),
сводится к интегральному уравнению (54)
L
TT/i (so) + Ki (so, s) II {s) ds = f (so),
0
ядро которого Ki (so, s) является сопряженным по отношению к ядру
К (so, s), т. е. Ki (so, s) = К (s, so).
Вторая теорема Фредгольма состоит в следующем.
Число линейно независимых решений некоторого однородного
интегрального уравнения равно числу линейно независимых решений со-
пряэюенного уравнения.
Из этой теоремы следует, что решение уравнения (54) определено
однозначно.
Внешней первой краевой задаче соответствует уравнение (52)
L
-7Т1У (so) -\- к (so, s) 1У (s) ds = f (so).
0
Однородное уравнение (/ = 0) согласно предыдущему может
быть приведено к виду
L
[v (so) - V (s)] к (so, s) ds = 0. (65)
0
Обозначив через Sq точку, в которой |г^ (s)| достигает
максимального значения, получим из (65)
Отсюда следует, что только
jy (s) = const = щ
является решением однородного уравнения. В силу второй теоремы
Фредгольма сопряженное однородное уравнение будет иметь
единственное решение.
1^
^ При наличии прямолинейных участков границы рассуждения несколько
усложняются, хотя доведение их до конца не вызывает затруднений.

390 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
Условие разрешимости неоднородного уравнения дает третья
теорема Фредгольма.
Пусть некоторое однородное интегральное уравнение
^
о
(ж) = К (ж, s) (f (s) ds
имеет к линейно независимых решений (pi{x) (г = 1, 2, ..., /;;). Тогда
сопряэюенное неоднородное уравнение
b
ф{х) = [к (s, х) ф (s) ds + f (х)
а
имеет решение, если
/ (х) (fi (х) dx = О, г = 1, 2, ..., к.
I
Применяя третью теорему Фредгольма к уравнению (53),
соответствующему внутренней второй краевой задаче, получаем условие
разрешимости этой задачи
I
f{s)ds = 0, (66)
С которым мы уже встречались в § 1.
Условие разрешимости внешней первой краевой задачи имеет вид
1^
/
/ (s) h (s) ds = О, (67)
где h{s)—решение однородного уравнения, соответствующего (53).
Нетрудно выяснить физический смысл этой функции.
Пусть цилиндрический проводник, имеющий в сечении форму S,
заряжен до некоторого потенциала Vq . В проводнике весь заряд
находится на поверхности. Обозначим через h (s) плотность
поверхностных зарядов. Потенциал, создаваемый этими поверхностными
зарядами, является потенциалом простого слоя с плотностью h (s) и
выражается формулой (29). Нормальные производные его изнутри равны
нулю, так как внутри проводника V = const. Поэтому функция h (s)
удовлетворяет однородному уравнению (53) и пропорциональна
функции h{s), определенной выше, что и определяет физический смысл
этой функции.

ЗАДАЧИ К ГЛАВЕ IV 391
Таким образом, интегральные уравнения, к которым сводятся
краевые задачи, разрешимы всегда для внутренней первой и внешней
второй краевых задач и разрешимы при условиях (66) и (67) для
внутренней второй и внешней первой краевых задач ^"^.
ЗАДАЧИ К ГЛАВЕ IV
1. Найти функцию и, гармоническую внутри круга радиуса а и
принимающую на окружности С значения:
а) и\с = Л coscf]
б) и\с = А-\- В sin ср.
2. РенЕить уравнение Лапласа Аи = О внутри прямоугольника О ^ ж ^
^ а, О ^ у ^Ь при следующих граничных условиях:
и\х=0 = fl{y), и\у=о = f2{x), и\х=а=0, и\у=ь = ^^
Доказать, что получающиеся при этом формулы дают репЕСние задачи для
произвольной кусочно-непрерывной функции, заданной на границе.
РепЕить задачу для частного случая
Л (у) = Ау{Ъ- у), /2 (ж) = Б cos — X.
3. РепЕить уравнение An = 1 для круга радиуса а при граничном
условии и\г=а = 0.
4. РепЕить уравнение An = Аху для круга радиуса а с центром в точке
(О, 0) при граничном условии и\г=а = 0.
5. РепЕить уравнение An = А-\- В {х — у ) в кольце а ^ р ^Ь, если
ди
др
= 0.
р=Ь
Начало координат находится в центре кольца.
6. Построить функцию источника для уравнения Лапласа (первая
краевая задача): а) для полукруга, б) для кольца, в) для слоя (О ^ ^ ^ /).
7. Найти гармоническую функцию внутри кольца а ^ р ^ Ь,
удовлетворяющую следующим граничным условиям:
и\р=а = h {^)-> и\р=ъ = /2 (<^).
8. Найти репЕСние уравнения Лапласа An = О в полуплоскости у ^ О
с граничным условием
Го при ж < О,
п(ж, 0) = <^
[по при X > 0.
9. Найти функцию п (/?, (^), гармоническую внутри кругового сектора
/9^а, О ^ (f ^ (fo при граничных условиях:
Si)u\^=0=qi, u\(p=(pQ=qi, u\p=a=q2, где qi и q2—постоянные;
б) и\^=о = u\^=^Q = о, и\р=а = f {(р).
^ См. подробнее: Петровский И. Г. Лекции об уравнениях с частными
производными. М., 1961. § 39.

392 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. IV
10. Методом конечных разностей ренЕить первую краевую задачу для
уравнения Аи = О внутри прямоугольника О^ж^а, О ^у ^Ь, подразделяя
каждую из его сторон на 8 равных частей, если граничные условия имеют
вид
у / у \ X 7V
и\х=о ^ I у-~ l) ' ^\у=Ь ^ а ^^^а ^' ^''^"'' ^ ^'^"° ^ ^'
Сравнить с аналитическим репЕСнием (см. Дополнение I, § 3).
11. Найти объемный потенциал сферы при постоянной плотности р =
= РО-
Указание. РепЕить уравнения Аи = О вне сферы и Аи = 47Г/9о внутри
сферы и репЕСния сопрягать на поверхности сферы.
12. Найти потенциал простого слоя, распределенного с постоянной
плотностью 1У = щ на сфере.
Указание. Искать penienne уравнения Аи = О вне и внутри сферы и
воспользоваться для сопряжения условиями разрыва производной
потенциала простого слоя.
13. РепЕить первую краевую задачу для ограниченного круглого
цилиндра (/9 ^ а, О ^ ^ ^ /):
а) на основаниях цилиндра заданы нулевые граничные условия
(первого или второго рода), а на боковой поверхности
и\р=а = /(^);
б) на боковой поверхности и на одном из оснований цилиндра заданы
нулевые граничные условия (первого и второго рода), а на втором основании
цилиндра
например / (р) = Ар (1 — р/а).
14. РепЕить неоднородное уравнение
Au=-f
В неограниченной цилиндрической области при нулевых граничных
условиях (первого или второго рода) и построить функцию источника.
15. Найти гармоническую внутри сферы функцию, равную ui на одной
половине сферы и U2 на второй половине сферы.
16. Написать разложение по сферическим функциям плотности
поверхностных зарядов, индуцированных на проводящей сфере точечным зарядом.
17. РепЕить задачу о поляризации диэлектрического niapa в поле
точечного заряда.
18. Вычислить гравитационный потенциал плоского диска. Сравнить с
асимптотическим представлением гравитационного потенциала на больпЕих
расстояниях.
19. Вычислить магнитный потенциал кругового тока.
20. РепЕить задачу о возмущении плоскопараллельного электрического
поля идеально проводящей сферой. РепЕить задачу для абсолютно
непроводящей сферы.

i. асимптотика объемного потенциала 393
прилож:ения к главе iv
I. Асимптотическое выралсение объемного потенциала
При изучении объемного потенциала
///
V{M)= III f^^Y^P, где d = RMP, (1)
на больших расстояниях от тела обычно принимают значения
потенциала равными m/R, где т — масса тела Т, R — расстояние от его
центра тяжести до точки наблюдения. Установим более точное
асимптотическое выражение для V '^К
Пусть Е — сфера с центром в начале координат, целиком
содержащая тело Т. Вне этой сферы потенциал будет гармонической
функцией.
Рис. 67
Расстояние от точки наблюдения М {х, у, z) до переменной точки
внутри тела Mi {xi, yi, zi) (рис. 67), по которой производится
интегрирование, равно
d = д/г^ + г? — 2гг1 cos^
V (2)
откуда
(г = |ОМ|, ri = |OMi|),
1 1
d г Vl + «'-2a/i'
а = —, /i = cos^
^^ Смирнов в. И. Курс высшей математики. М., 1981. Т. IV, ч. 2.

394 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Так как ri < г, то а < 1, и поэтому имеет место разложение (см.
Дополнение II, ч. II, § 1)
1 1 '^
где Рп (/i) — полином Лежандра п-го порядка. Подставляя это
выражение в формулу (1) и учитывая, что 1/г не зависит от переменных
интегрирования, получаем
У(М) = - fffpf^a^p^{,j)dT = Vi+V2 + V3 + ... =
^ ^ ^ ^
Pdr+^ III priPi (//) dT+^ III prlP2 {ii)dT + ... (5)
T T T
Первый член равен ттг/г, где т — масса всего тела, и дает нам первое
приближение для вычисления потенциала при больших г.
Перейдем к вычислению следующих членов разложения (5).
Подынтегральное выражение во втором члене равно
pFi im г I = piiri = pri cos в = .
r
Величины ж, ^, 2; и r не зависят от переменных интегрирования и
могут быть вынесены за знак интеграла. После этого второй член
разложения потенциала принимает вид
1 fff 1 М
pnPi (fi) dr = — {Mix + М2У + Msz) = —{ХХ + УУ + zz),
T
где
Mi= pxidT = Mx, M2= pyidT = My,
T T
M3 = / / / pzidT = Mz
T
— моменты 1-го порядка, ж, у, z — координаты центра тяжести.
Таким образом, второй член убывает как 1/г^. Если начало координат
поместить в центре тяжести (ж = 0, ^ = 0, ^ = 0), то 1^2 =0.
Рассмотрим третий член разложения. Преобразуем
подынтегральное выражение:
2 2 3/i^ - 1 2 3 {XXI + yyi + ZZi)^ - r\r^
РГ1Р2 (/i) = pri = pr^
2^2^2
2r2
^ v^[^ (^1^ + y^y + ^1^)^ ~ ^1^^] •

I. АСИМПТОТИКА ОБЪЕМНОГО ПОТЕНЦИАЛА 395
Вводя обозначения
III pXiXk dr {x = Xi, у = Ж2, z = Жз),
T
приходим к следующему выражению для Vs:
т
= ^ I ж' [ЗМц - (Mil + M22 + M33)] +
+ У^ [3M22 - (Mil + M22 + M33)] + z^ [ЗМ33 - (Mil + M22 + M33)] +
+ 2 . 3x^Mi2 + 2 . 3xzMi3 + 2 • З^^М2з |.
Полином, стоящий в фигурных скобках, является гармоническим
полиномом, так как он может быть записан в виде
1^3 = ^ I (^' - У^) [Мц - М22] - {z^ - х^) [Ми - Мзз] +
+ (^2 - 2;^) [М22 - Мзз] + б [x^Mi2 + xzMi^ + yzM2^] у
где каждое слагаемое удовлетворяет уравнению Лапласа.
Коэффициенты, стоящие в квадратных скобках, выражаются через моменты
инерции. Момент инерции тела Т относительно оси х, как известно,
равен
А = /// р {у1 + zl) dr = М22 + М33.
т
Аналогично моменты инерции относительно осей у ж z равны
В = Мзз + Мц, С = Мц + М22.
Отсюда следует, что
Мц -М22 = В -А, Мц - Мзз = С - Л, М22 -Мзз = С -В.
В результате мы приходим к асимптотическому выражению для
потенциала
+ {z^ -x^){A-C)+6{xyMi2+yzM23 + zxM3i)y (6)

396 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
справедливому с точностью до членов порядка 1/г^.
Выражение (6) упрощается, если поместить начало координат в
центре тяжести, а оси координат направить по главным осям инерции:
^ - 7 + 2^ {(^2 - у') (В-А) + {у' - z') {С-В) +
+ {z'-x-'){A-C)}. (7)
Полученное асимптотическое представление потенциала
позволяет ответить на ряд вопросов обратной задачи теории потенциала,
заключающейся в определении характеристик тела по его потенциалу
(или каким-либо его производным).
В самом деле, определяя коэффициенты разложения (6), можно
найти массу, координаты центра тяжести и моменты инерции тела.
II. Задачи электростатики
В задачах электростатики решение уравнений Максвелла
сводится к отысканию одной скалярной функции— потенциала (/?, связанного
с напряженностью поля соотношением
Е = — grad(/?.
Используя уравнение Максвелла
div Е = 47гр,
получаем
Д(^ = —47гр.
Таким образом, потенциал удовлетворяет уравнению Пуассона в тех
точках пространства, где находятся электрические заряды, и
уравнению Лапласа — в тех точках, где зарядов нет.
1. Основной задачей электростатики является
отыскание поля, создаваемого системой зарядов на заданных проводниках.
При этом возможны две различные постановки этой задачи.
а) Задаются потенциалы проводников и требуется определить
поле вне проводников и плотность зарядов на проводниках.
Математическая формулировка задачи состоит в следующем.
Требуется найти функцию (/?, удовлетворяющую уравнению
Лапласа
всюду вне заданной системы проводников, обращающуюся в нуль на
бесконечности и принимающую заданные значения ipi на
поверхностях проводников Sf.
(f\s- = (fi, (fi = const.

IL ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 397
Таким образом, в этом случае мы приходим к первой краевой задаче
для уравнения Лапласа. Единственность ее реп1ения следует из общей
теории.
б) Возможна и обратная постановка задачи. На проводниках
задаются полные заряды. Требуется определить потенциалы проводников,
распределение зарядов по их поверхностям и поле вне проводников.
Penienne этой задачи сводится к отысканию функции (р,
удовлетворяющей уравнению Лапласа
вне заданной системы проводников, обращающейся в нуль на
бесконечности, принимающей на поверхностях проводников некоторые
постоянные значения
^\si= const
и удовлетворяющей интегральному соотношению на поверхностях
проводников
^^ л л
-—da = -47rei,
on
где ei —полный заряд г-го проводника.
2. Единственность реп1ения второй задачи из общей теории не
следует, но может быть легко доказана.
Предположим, что существует два реп1ения ipi и ip2 задачи «б».
Тогда их разность
(/?'=(/?!- (/?2
будет удовлетворять уравнению
и условиям
-—6?cr = 0, (^'1^=0.
Si
Заключим все заданные проводники внутрь сферы Ед достаточно
большого радиуса R и применим к функции ip' первую формулу
Грина в области Тя, ограниченной сферой Ед и поверхностями
проводников Si'.

398 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
В силу условий на бесконечности ^> и на поверхностях, мы получим
^2 dr = О,
lim [{Vip')
Tr
откуда, вследствие положительности подынтегрального выражения,
следует
V^p' = О, или if' = const,
всюду в рассматриваемой области. Учитывая условие на
бесконечности (р'\оо = о, получаем
что И доказывает единственность поставленной задачи.
3. Из единственности решения краевой задачи для уравнения
Лапласа следует, что потенциал уединенного проводника прямо
пропорционален сообщенному ему заряду.
в самом деле, если на уединенный проводник поместить заряды е
и е' = ттге, то соответствующие потенциалы (р и (р' должны
удовлетворять уравнениям
A(f = О, A(f' = О
и граничным условиям
^' е'
откуда и следует, что (f — икр = 0, т. е. — = —.
(р е
На поверхности уединенного проводника получаем
е' е
— = — = С = const.
Эту постоянную с называют емкостью уединенного проводника.
Она не зависит от заряда проводника, а определяется формой и разме-
^ Из условия (р'\оо =0 следует регулярность функции ср' на
бесконечности (см. с. 321), в силу чего
/
ш ^г— da ^ О при R ■
on

IL ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 399
рами последнего. Таким образом, для уединенного проводника имеет
место соотношение
S
Емкость уединенного проводника численно равна заряду, при
сообщении которого проводник приобретает потенциал, равный 1. Если
проводник не уединен, то его потенциал существенно зависит от
формы и расположения других проводников. Для системы проводников
имеют место соотношения
61 = Cii^i + Ci2{^2 -^l) + . . . + Cin{^n - ^l),
62 = C2l{4^l - (f2) + C22(f2 + . . . + C2n{^n " ^2) j
en = Cnl{(fl - (fn) + Cn2{^2 - ^n) + . . . + Cnn^n,
где Ci VL (pi — заряд и потенциал г-го проводника. Величина Cik имеет
смысл взаимной емкости г-го проводника по отношению к к-му
проводнику. Она может быть определена как тот заряд, который должен
быть сообщен г-му проводнику для того, чтобы все проводники, кроме
к-го, имели нулевой потенциал, а к-й проводник — потенциал 1.
4. Легко показать, что матрица коэффициентов Cik является
симметричной, т. е. имеют место соотношения
^ik — ^ki-
Для определенности рассмотрим случай двух проводников, хотя и в
случае п проводников доказательство остается тем же.
Пусть заданы два проводника а и Ь. Тогда определение
коэффициентов Cab И Сьа сведется к определению функций и^"*"^ и и^^\
удовлетворяющих уравнениям
Аи^^) =0 и Аи^^) = О
и граничным условиям
«W|s<.=0; u«|s. = 1; w«|oo=0;
1 Idu^'^, (1) r<
Sa
u(^)|5.=l; u^'^\s,=0; u(^)|oo = 0;
1 /au(2) , (2)
47Г / dn
Sb
da = ey = Cba-

da = 0,
400 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Опишем сферу Ед достаточно большого радиуса R, заключаю-
ш:ую оба проводника а и 6, и применим формулу Грина к функциям
и^"*^^ и и^^^ в области между поверхностью Ед и поверхностями
проводников Sa И Sb'.
Интеграл в левой части этого равенства равен нулю. Используя
граничные условия и условия в бесконечности, получаем
J дп J дп
Si) Sa
ИЛИ
Cab = Сьа^
ЧТО и требовалось доказать.
5. Перейдем к конкретным примерам.
Рассмотрим задачу о поле заряженного шара. Пусть на
поверхности проводящего шара радиуса а задан потенциал (ро. Решая задачу
1, легко показать, что поле и плотность зарядов на поверхности шара
в этом случае будут определяться выражениями
(f = — а и а = -—.
г Атта
Если вместо потенциала на поверхности шара (fo задан полный заряд
ео, сообщенный шару, то
(/?о = —, (т=-—^, ^=— {г>а).
а 47га^ г
При этом емкость шара
С = а,
т. е. в абсолютных единицах емкость уединенного шара численно
равна его радиусу.
В качестве следующего примера рассмотрим задачу о
сферическом конденсаторе (система двух концентрических проводящих сфер).
Пусть внутренний шар радиуса ri имеет заданный потенциал
Vo, а внешний шар радиуса г2 заземлен. Тогда определение поля
внутри конденсатора сводится к отысканию функции (р,
удовлетворяющей уравнению
и условиям
^\г1 = Vb, (р\г2 = О-

III. ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОРАЗВЕДКИ 401
Легко показать, что в этом случае
Г1Г2 ^. (I 1
Г2 - ri \Г г2
а емкость сферического конденсатора равна
(7 = ^:1^.
Более сложной задачей является определение потенциала сферы
в присутствии другой сферы, не концентрической с данной. Эта
задача решается методом отражений. Аналитическое решение довольно
громоздко, и мы здесь приводить его не будем-"^^
6. Перейдем к двумерным задачам.
В качестве примера рассмотрим цилиндрический конденсатор,
образованный двумя бесконечно длинными коаксиальными
цилиндрами, на одном из которых равномерно распределен электрический заряд.
Очевидно, что решение задачи одинаково во всех плоскостях,
параллельных плоскости нормального сечения цилиндра. Поэтому задачу
можно рассматривать как плоскую и вместо полного заряда задавать
заряд на единицу длины х.
Если внешний цилиндр радиуса Г2 заземлен, а на внутреннем —
радиуса ri — задан заряд х, то потенциал поля в конденсаторе
определяется выражением
г
(р = 2х In —,
Г2
а емкость единицы длины цилиндрического конденсатора равна
с
21П(Г2/Г1)"
Рассмотренный пример позволяет решить более сложную задачу
определения емкости провода, расположенного над проводящей
плоскостью. Пусть над бесконечной плоскостью на расстоянии / от нее
находится бесконечно длинный провод радиуса р, на котором
распределен заряд с плотностью х (заряд на единицу длины). Ясно, что и
эта задача может решаться как двумерная.
III. Основная задача электроразведки
Для изучения неоднородности земной коры в целях разведки
полезных ископаемых широко применяются электрические методы.
Основная схема электроразведки постоянным током заключается в
следующем. При помощи заземленных электродов в землю пропускается ток
^ См.: Франк Ф., Мизес Р. Дифференциальные и интегральные
уравнения математической физики. Л.; М., 1937. Т. П. С. 713.
26 А. Н. Тихонов, А. А. Самарский

402
ПРИЛОЖЕНИЯ К ГЛАВЕ IV
от питающей батареи. На поверхности земли измеряются
напряжения созданного таким образом поля постоянного тока. Нри помощи
наблюдений на поверхности определяют подземную структуру.
Методы определения подземных структур (интерпретация наблюдений)
базируются на математическом решении соответствующих задач.
Потенциал поля постоянного тока в однородной среде
удовлетворяет уравнению Лапласа
АУ = О (^ > 0)
(1)
при дополнительном условии
dV
dz
(2)
которое означает, что вертикальная составляющая плотности тока
(см. с. 297) на («дневной») поверхности z = О равна нулю, так как
полупространство 2; < О (воздух) непроводящее.
Рассмотрим точечный электрод на границе полупространства в
точке А. Очевидно, что потенциал поля будет равен
V
1р
27tR'
(3)
где R — расстояние от источника А, р — удельное сопротивление
среды, а / — сила тока. Эта функция отличается от функции источника
в неограниченном пространстве коэффициентом 2 в силу условия (2).
Измеряя разность потенциалов в точках М и N, лежащих на
одной прямой с Л, при помощи измерительной цепи, получаем
dV
V{M)-V (N) = — Ar,
где Ar — расстояние между точками N и М.
Предполагая, что точки М и N достаточно близки между собой,
имеем
V{M)-V (N)
Ar
dV_
дг
Ip
27ГГ2'
где г — расстояние точки О (центра приемной цепи MN) от
питающего электрода. Сила тока / в питающей цепи известна, так как
регистрируется в течение хода работы. Отсюда для сопротивления
однородного полупространства получим
27гг2
1 — 1
дг
(4)

III. ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОРАЗВЕДКИ 403
Если среда неоднородна, то величину р, определяемую по формуле (4),
называют кажущимся сопротивлением и обозначают через pk] рк не
будет постоянной величиной.
Рассмотрим задачу о вертикальном электрическом зондировании,
когда слои земной коры залегают горизонтально и сопротивление их
зависит только от глубины:
р = p{z).
в этом случае кажущееся сопротивление будет функцией
расстояния г = \А0\. Задача интерпретации результатов вертикальных
электрических зондирований заключается в определении функции p{z)^
дающей «электрический разрез» среды по известным значениям р^ (г).
Рассмотрим подробнее задачу о двухслойной среде, когда
однородный слой мощности / и сопротивления ро лежит на однородной среде
с сопротивлением pi:
/ ч \ Ро при О ^ 2; < /,
Р{^) = < j^
\pi при / < Z.
Очевидно, что на небольших расстояниях г ^ / кажущееся
сопротивление pk равно ро, так как влияние подстилающей среды будет
сказываться мало. Для больших расстояний {г ^ I) pk будет равно
Р1'
Задача сводится, таким образом, к нахождению решения
уравнения Лапласа Vq в слое 0<z<IvlVib полупространстве z > I. При
Z = / должны выполняться условия непрерывности потенциала
VoU=i = ViU=i (5)
И непрерывности нормальных составляющих плотности тока
1^
Ро dz
1 dVi
z=i ~ pi dz
(6)
При z = О потенциал Vq должен удовлетворять условию (2), а в
точке Л, которую мы выберем за начало цилиндрических координат
(г, (p,z), потенциал Vq должен иметь особенность типа (3):
где г'о — ограниченная функция.
Функция Vi должна быть ограниченной на бесконечности.
Функции г'о и Vi удовлетворяют уравнению (1), которое в силу
цилиндрической симметрии задачи приобретает вид
д^У IdV д^У _
26*

404 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Метод разделения переменных дает для V два типа реп1ений,
ограниченных при г = 0:
e±^^Jo(Ar),
где Jo — функция Бесселя нулевого порядка (см. Дополнение II, ч. I,
§ 1), а Л — параметр разделения. Будем искать решение в виде
(Лг) dX,
сю
/<
У1 (г, z) = / (Л1 е--^^ + В, е^') Jo (Лг) ^Л,
о
где Ло, 5о, ^1, Bi—некоторые постоянные.
Условие (2) дает связь между Aq и Bq. Вычислим
сю
If -^^ + /(-АЛ е-- + ЛБо е-) Jo (Лг) dA.
О
Условие (2) принимает вид
дУр _ Pol
dz
f{Bo-Ao)Jo{Xr)XdX = 0
о
при произвольном г, откуда
Из условия ограниченности Vi при z ^ оо следует, что
Bi =0.
Таким образом.
сю
Xz
I
Vi (г, z)= Ai е-^' Jo (Лг) dX
СЮ
Уо (г, z) = /foe-^^ + Ао (е-^^ + е^^)] Jo (Лг) ^Л.
о
При этом мы воспользовались формулой
лЛ
сю
(8)

III. ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОРАЗВЕДКИ
405
(см. Дополнение II, ч. I, § 5) и обозначили —— = q.
Оставшиеся постоянные А^ и Ai определяются из условий (5) и
(6) для Z = I, которые сводятся к системе алгебраических уравнений
Ао {е-'^^ + 1) - ^1 е
-2X1
-qe
-2X1
1
Ло(е"
-2X1
■Ах е
-2X1
РО Р1
откуда находится коэффициент
Я_ -2X1
Ро
Ao = q
{р1 + Ро) - {р1 - Ро)е 2^^'
и penienne Vq для верхнего слоя дается формулой
Vo (г, Z)
1ро
27Г
сю
/
^-Xz I ^^ t^-Xz , ^Xz^
I _ 1.^-2X1
{e-^' + e^
Jo (Ar) dX, (9)
где положено
Pi - Po
pi + Po
k.
Преобразуем полученное выражение. Так как |/;;| < 1, то можно
записать
ке
-2X1
l_^g-2A/
п=1
• е
-2Х1п
сю
Vo {r,z) = ^J^f fc" е"^ (2n/+.) j^ (д^) ^д ^
п=Оо
сю
+ ^У [ к"е-^ (2п/-.) j^ (д^) ^д_ (д/^
27Г ^ У
Отсюда, воспользовавшись формулой (8), получим
1 ^ 1 \
Voir,z) = l^{Y^k-
+ Е^"
27Г \^;^^ v^r2 + (z + 2n/)2 ;^^ v^r2 + (z-2nOV '
(10)
Это выражение для решения (9) может быть сразу написано, если
решать задачу методом отражений.

406
ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Полагая z = О, получаем распределение потенциала на
поверхности земли:
Vo (г, 0) =
1ро
27Г
1 ^'Г- к""
-+2у —,
г ^^ v^r2 + (2п/)2
(И)
откуда
дг
1ро
27Г
^ сю
,р2 .Z_-/
A;"r
^^ [г2 + {2п1уГЬ
И для pk по формуле (4) имеем
Рк = Ро
1+2$:
п=1
+ (2п02]'/2
= Ро
1+2$:
fc" (^/2)3
[(^/2)2+п^
21^2
= /00/(6, (12)
где ^ = г//, /(^) обозначает выражение в квадратных скобках. При
г <^ I имеем
Рк = Ро-
Чтобы оценить поведение pk при больших г, устремим в формуле (12)
г —>- (X) (^ —>- (X)). Предел п-го члена суммы будет равен к^ ^ откуда
следует, что
lim pfe = ро 1 + 2 V А;^
г—>-сю \ ^—^
= РО 1 +
Ро
2А;
1-А;
1 + А;
Pi + Ро + (pi - Ро)
Ро ■ 7 г = Р\'
L- к Р1^ PQ- [Pl - РО)
Сравнивая экспериментальную кривую с кривой, задаваемой формулой
(12), мы можем определить ро по значениям pk при малых
значениях г и pi — по значениям pk при больших значениях г. Мощность
верхнего проводящего слоя / определяется подбором. Она равна тому
значению /, при котором эмпирическая кривая как функция р{^) =
= р{г/1) наиболее близко подходит к кривой, вычисляемой по формуле
(12). Па технике подбора, производимого с помощью билогарифмиче-
ских масштабов, мы не будем останавливаться-"^^
В случае многослойных разрезов кривые для pk вычисляются
аналогично. Характер электрического разреза среды определяется при
помощи подбора теоретической кривой, наиболее точно
аппроксимирующей эмпирическую кривую. При увеличении числа слоев техника
^См., например, прекрасную книгу А. И. Заборовского
«Электроразведка» (М.; Л., 1963.)

III. ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОРАЗВЕДКИ 407
интерпретации весьма осложняется, так как число вспомогательных
теоретических кривых сильно растет.
Отметим, что при различных электрических разрезах pi {z) ф
Ф р2 {z) соответствующие кажущиеся сопротивления также
различны:
следовательно, задача об определении электрического разреза по
кажущемуся сопротивлению с математической точки зрения имеет
единственное решение ^^.
Задачи, аналогичные рассмотренной задаче электроразведки,
встречаются в различных областях физики и техники.
С электростатическими задачами мы встречаемся при
конструировании различных электронных приборов, с тепловыми и
гидродинамическими— во многих областях техники (теплоотдача зданий,
фильтрация воды под плотиной и т. д.) ^л
Задачи определения магнитного поля в неоднородной среде
встречаются, например, в магнитной дефектоскопии. Для определения
дефекта в детали, например наличия пустот под поверхностью,
металлическую деталь помещают между полюсами магнита и измеряют
магнитное поле на поверхности детали. По возмущению магнитного
поля требуется определить наличие дефекта, а также, если возможно,
размеры дефекта, глубину его залегания и т. д.
Для решения задач используются методы моделирования,
основанные на подобии потенциальных полей различной физической
природы ^^.
В самом деле, рассмотрим потенциальные поля в неоднородных
средах различной физической природы (например, стационарное
поле температур, магнитное поле в неоднородной среде,
электростатическое поле, поле скоростей жидкости при фильтрации). Потенциальные
функции этих полей и{х, у, z) в каждой однородной области
удовлетворяют уравнению Лапласа Аи = 0. Па границе областей Gi и G2
с различными коэффициентами теплопроводности, магнитной
проницаемости и т. д. выполняется условие
h -^— = к2
дп дп
где ki и к2 — соответствующие физические постоянные.
^ Тихонов А. Н. О единственности ренгения задачи электроразведки //
ДАН. 1949. Т. 69, № 6. С. 797.
^ Павловский П. П. Теория движения грунтовых вод под
гидротехническими сооружениями и ее основные приложения. Пг., 1922. Гл. XIV.
^ Лукьянов А. В. Об электролитическом моделировании
пространственных задач // ДАН. 1950. Т. 75, № 5. С. 613—615.

408 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Пусть на границах равных геометрических областей заданы
численно равные значения потенциалов или их нормальных производных
различных физических полей. Предположим, что физические
неоднородности этих областей геометрически равны и одинаково
расположены; отношения физических постоянных (теплопроводностей,
магнитных проницаемостей и т. д.) любой пары соответственных неоднород-
ностей тоже равны. Тогда численные значения потенциалов этих
полей во внутренних соответственных точках также равны, поскольку
являются решением одной и той же математической задачи, имеющей
единственное решение.
IV. Определение векторных полей
Наряду со скалярными задачами во многих вопросах
электродинамики и гидродинамики часто встречаются задачи об определении
векторного поля по заданным ротору и дивергенции этого поля.
Докажем, что векторное поле А однозначно определено внутри
некоторой области G, ограниченной замкнутой поверхностью S, если
заданы ротор и дивергенция поля внутри G:
rotA = B, (1)
divA = C, (2)
а на границе S задана нормальная составляющая вектора А:
A„\s = f{M). (3)
Отметим, что функции В, С и / не могут быть заданы
произвольно. Должны выполняться соотношения
divB = 0, (4)
II f{M)dS = llJcdr, (5)
S G
Функцию / будем считать непрерывной на поверхности S, функции
В и С — непрерывными в G вместе со своими производными и
поверхность S — такой, что для нее разрешима вторая внутренняя краевая
задача при непрерывных граничных значениях.
Поставленную задачу будем решать в несколько этапов. Пайдем
вектор Ai, удовлетворяющий условиям
rotAi=0, (6)
divAi=a (7)
Из соотношения (6) следует, что
Ai=grad(/?. (8)

IV. ОПРЕДЕЛЕНИЕ ВЕКТОРНЫХ НОЛЕЙ 409
Взяв функцию (/? в виде
G
МЫ удовлетворим и уравнению (7).
Определим теперь вектор А2 так, чтобы
rotA2 = B, (10)
divA2 = 0. (11)
Полагая
А2 =т1ф, (12)
мы удовлетворим условию (11). Подставив (12) в (10), получим
graddiv^-AV^ = B. (13)
Потребуем, чтобы
divV^ = 0. (14)
Тогда уравнение (13) для вектора ф примет вид
AV^ = -B. (15)
Рассмотрим область Gi, целиком содержащую область G и
ограниченную поверхностью Si. Продолжим вектор В в область Gi — G,
потребовав выполнения условий:
1) нормальная составляющая В^ вектора В на границе S
непрерывна (сам вектор В, вообще говоря, разрывен): Bni = Впе]
2) 5n = 0Ha5i; (16)
3) divB = OBGi -G. (40
Укажем, как осуществить такое продолжение В на область Gi —
— G. Положим
В = gradx в Gi — G.
Условие div В = О дает
Ах = О в Gi-G. (17)
Граничные условия в силу 1 и 2 имеют вид
^=Bni на S, (17')
|| = 0 на 5i, (17")

410 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
где Bni — предельное значение Вп на внутренней стороне S. Для
функции X мь1 получим вторую краевую задачу (17) — (17'').
Необходимое условие разреп1имости этой задачи
//1''^=//^"^^=°
выполнено, так как
//
BndS = I divB^r = 0.
Положив
^^^^-глт-^
RpQ
мы, очевидно, удовлетворим уравнению (15).
Нетрудно убедиться в том, что условие (14) также выполнено. В
самом деле, вычислим производные
дфх дфу дф^
дх ^ ду ^ dz
Представляя интеграл по области Gi в виде суммы интегралов по G
и Gi — G и учитывая соотношение
после интегрирования по частям будем иметь
д_
дх
G G S
д f [ f Вх ,_ fffdBx 1 ,_ f f г, cosa ,^ f f r> cosai
G\—G G\—G S S\
где cos a = cos(n7x)|5, cosai = cos(n7x)|5^ (n — направление
внешней нормали к поверхности).
Для дфх/дх получим
дфх 1 fffOB,!^ , 1 ffB,e-B,i ,^
— ат-\--— cos ааЬ —
дх 47Г J J J д^ R 47Г 7 7 R
Gi S
4^ J J
4^ J J
Si
Bx '-^ dS.
R

IV. ОПРЕДЕЛЕНИЕ ВЕКТОРНЫХ ПОЛЕЙ 411
Аналогичные выражения имеют место для производных
ду dz
Отсюда следует, что
Gi Si S
В силу условий (4), (4') и (16), а также непрерывности нормальных
составляющих вектора В на 5 {Bni = Впе), вектор А2,
определяемый формулой (12), удовлетворяет уравнению (10), если вектор ф
удовлетворяет условиям (14) и (15).
Ясно, что вектор Ai + А2 удовлетворяет условиям
rot(Ai+A2) = B, (18)
div(Ai+A2)=a (19)
Чтобы найти вектор А, нам остается удовлетворить граничному
условию (3). Для этого найдем вектор Аз, удовлетворяющий условиям
внутри G
rot A3 = О, (20)
div A3 = О, (21)
и условиям на S
Лзп\з = f{M)- A,n\s - A2n\s = /* (М). (22)
Ясно, что функция /* (М) определена однозначно. Из уравнения (20)
следует, что
Аз = grad^.
Подставляя это значение Аз в уравнение (21), получим внутри G
АО = 0. (23)
Условие (22) дает
дО
дп
= Г{М), (24)
S
т.е. для определения функции в мы получим вторую краевую задачу.
Поэтому вектор Аз определится однозначно.
Таким образом, доказано, что задача (1) — (3) имеет единственное
решение
А = Ai + А2 +A3.

412 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
V. Применение метода конформного преобразования
в электростатике
1. Для решения двумерных электростатических задач часто
используется теория функций комплексного переменного. Рассмотрим,
например, следующую задачу электростатики.
Найти электрическое поле нескольких заряэюенных проводников^
потенциалы которых равны щ, U2, ...
Такая задача, как известно (см. Приложение П), приводит к
уравнению
Аи = 0 (1)
с граничными условиями
u\si=Ui, (2)
где через Si обозначена поверхность проводника с номером i.
Если поле можно считать плоским, не меняющимся, например,
вдоль оси Z, то уравнение (1) и граничные условия принимают вид
u\ci = Щ, (4)
где Ci — контур, ограничивающий область Si.
Будем искать потенциал и как мнимую часть некоторой
аналитической функции
f{z)=v{x,y)-\-iu{x,y) {z = x-\-iy), (5)
причем в силу условий Коши — Римана
Vx =Uy, Vy = -Ux (6)
И
VxVy -\-UxUy =0. (7)
Из граничного условия (4) следует, что функция / (z) имеет
постоянную мнимую часть на контурах Ci, ограничивающих наши
проводники.
Обращаясь к условию (6), замечаем, что уравнение
V (ж, у) = const (8)
представляет собой уравнение семейства силовых линий-"^^ в то время
как уравнение
и (ж, у) = const (9)
^ В самом деле, уравнение силовых линий имеет вид dx/ux = dy/uy.
Заменив Ux И Uy согласно условиям (6) на —Vy и Vxj получим
Vx dx -\- Vy dy = dv = О, или v (ж, у) = const.

V. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ В ЭЛЕКТРОСТАТИКЕ 413
в силу условия (7) определяет семейство эквипотенциальных линий.
Таким образом, для реп1ения поставленной задачи достаточно
найти конформное преобразование
W = f{z),
переводящее плоскость комплексного переменного
Z = X -\-гу
в плоскость
W = V -\- ги^
при котором границы проводников переходят в прямые
U = const, или Imu' = const.
Если известна такая функция w = f (z), то искомый потенциал
находится по формуле
и = и{х, у) =lmf{z).
Зная потенциал, можно вычислить электрическое поле:
ди ди
дх^ ^ ду
и плотность поверхностных зарядов на единицу длины по оси z:
^- = - ^' Еу = -—. (10)
которая в силу условий Коши — Римана равна
- = i\n^)\- (11)
2. Поле полу бесконечного плоского конденсатора.
Найдем поле конденсатора, образованного бесконечно тонкими
металлическими пластинами у = —d/2 и ^ = б?/2, простирающимися в
области ж < 0. Не останавливаясь на выводе конформного преобразования,
переводящего область, изображенную на рис. 68, в слой | Im u^l ^ тг, мы
применяем его непосредственно к решению указанной задачи-"^^
Преобразование
z=A(^ + e^) {w = if + i^) (12)
27Г
^ См.: Франк Ф., Мизес Р. Дифференциальные и интегральные
уравнения математической физики. Л.; М., 1937. Т. П, гл. XV, § 5.

414
ПРИЛОЖЕНИЯ К ГЛАВЕ IV
переводит плоскость z = x-\-iy с двумя разрезами (^ = =Ь б?/2, ж < 0) в
Рис. 68 Рис. 69
слой l?/^! ^ 7г плоскости W = ip -\- гф (рис. 69). В качестве комплексного
потенциала выберем функцию
По
2."'
(13)
где через и^ обозначена разность потенциалов между пластинами
конденсатора, так что потенциал электрического поля выражается
функцией
где ф связано с ж и ^ соотношениями
ж = т;— (v^ + е'^ cos?/^),
(14)
(15)
27Г
(V^ + e'^ sinV^).
На рис. 70 изображены эквипотенциальные и силовые линии
полубесконечного плоского конденсатора.
Рис. 70
Перейдем к исследованию поля конденсатора.
Из формул (15) видно, что при (/?—>-— 00
d
У
^ I
(16)

V. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ В ЭЛЕКТРОСТАТИКЕ 415
т. е. внутри конденсатора, далеко от краев, поле является плоским, а
при (/?—>-+ 00
р= л/ж2~+^?^ т^е'^, в = 8iTctg- ^ф, (17)
27Г X
т.е. вне конденсатора, на больп1их расстояниях от его краев,
эквипотенциальные линии являются кругами.
Если вместо w ввести комплексный потенциал
•^ 27Г '
так что
2^ „
Uo
то связь между z и f (z) задается уравнением
откуда следует
а при / = -—((/? ± 7гг) мы получаем
27Г
-- = —(1-е'^), или f{z) =
df ио' '' ' ' ' d{l-e^)'
Полагая uq = 1, мы получаем для плотности зарядов а согласно
формуле (11) следующее значение:
47Г 47r6?|l-e'^l' ^ ^
Отсюда следует, что при (/?—>-— оо
СГ « 1/47Г6?,
а при (/?—>-+ 00
о-?^ 1/47г^е'^,
т. е. в этом случае плотность зарядов убывает на внешней стороне
пластин как 1/р.
Из формулы (18) видно, что при (/? = О (на краю конденсатора)
СГ = 00. В самом деле, край плоской пластины имеет бесконечную
кривизну, и для того чтобы зарядить его до некоторого потенциала,
необходимо поместить на него бесконечный заряд.
Круг задач, решаемых методом конформного преобразования,
очень широк. С его помощью может быть успешно решен вопрос о

416 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
влиянии края толстой стенки плоского конденсатора, ряд задач,
относящихся к влиянию изгибов в конденсаторе и т. п. Конформное
преобразование может быть также применено к расчету динамических
задач. Недостатком изложенного метода является то, что конформное
преобразование применяется в основном лишь к плоским задачам,
сводящимся к двумерному уравнению /S.2U = 0.
VI. Применение метода конформного преобразования
в гидродинамике
1. Нри решении задач о движении твердого тела в
жидкости существенную роль играют граничные условия на
поверхности тела.
В случае идеальной жидкости граничное условие состоит в том,
что проекция Vn скорости жидкости на направление нормали к
поверхности тела должна равняться нормальной составляющей скорости
движения тела.
Если тело неподвижно, то граничное условие принимает простой
вид
^п = О
на поверхности тела.
Если рассматриваемое движение потенциально, т. е.
V = grad(/?,
то граничные условия принимают вид
дп
дп
= 0 в случае неподвижного тела,
S
= Un В случае тела, движущегося со скоростью и.
S
Как известно из гидродинамики, потенциал скоростей для
несжимаемой жидкости удовлетворяет уравнению
Таким образом, задача о потенциальном обтекании твердого тела
потоком несжимаемой идеальной жидкости сводится к решению
уравнения Лапласа
с дополнительным граничным условием на поверхности обтекаемого
тела
d(f
дп
S

VL КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ В ГИДРОДИНАМИКЕ 417
т. е. к решению второй краевой задачи для уравнения Лапласа.
Если рассматриваемое движение плоское, то penienne задачи
может быть получено при помощи теории функций комплексного
переменного.
В случае плоского движения несжимаемой жидкости уравнение
непрерывности дает
дщ ^ д{-Уу)
дх ду
Запишем уравнения линии тока
dx dy
Ух Уу
в виде
Vx dy — Vy dx = О (2)
и введем функцию ф при помощи соотношений
дф дф
Тогда из уравнения (1) следует, что левая часть выражения (2)
является полным дифференциалом функции ф:
Ух dy — Уу dx = dф.
Однопараметрическое семейство кривых
ф (ж, у) = С
представляет собой линии тока несжимаемой жидкости.
Если существует потенциал скоростей, то равенство rot v = О
равносильно уравнению
Из выражений для Vx и Vy следует
d(f дф d(f дф
дх ду' ду дх^
т. е. функции (риф удовлетворяют условиям Коши — Римана.
Следовательно, функция комплексного переменного
w{z) = (f{x, у) +гф{х, у)
является аналитической.
Итак, всякое потенциальное плоское движение жидкости
соответствует определенной аналитической функции комплексного
переменного, и обратно, всякая аналитическая функция связана с определенной
кинематической картиной движения жидкости (точнее, с двумя
картинами, так как функции (риф можно поменять ролями).
27 А. Н. Тихонов, А. А. Самарский

418 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Рассмотрим конкретные примеры применения теории
аналитических функций к реп1ению задач об обтекании тел плоским потоком
жидкости.
2. Обтекание кругового цилиндра. Пусть на круговой
цилиндр радиуса г = а набегает плоский поток жидкости, имеющей на
бесконечности постоянную скорость и. В случае стационарного
движения задачу можно обратить и рассматривать движение цилиндра с
постоянной скоростью и относительно жидкости.
Свяжем с цилиндром неподвижную систему координат и
направим ось Ох параллельно скорости движения цилиндра.
Па поверхности движущегося в жидкости тела, очевидно,
выполняется граничное условие
дф ду
ds ds'
где ds — элемент дуги на контуре, ограничивающем тело.
В случае поступательного движения со скоростью и это условие
может быть проинтегрировано на поверхности тела и мы получим
ф = иу + С
на поверхности тела.
Итак, наша задача свелась к решению уравнения
со следующими граничными условиями:
1) ф = иу -\- С на поверхности цилиндра,
2) дф/дх и дф/ду стремятся к нулю на бесконечности.
Последнее условие означает, что функция
dw дф . дф
dz ду ох
является вне круга С однозначной аналитической функцией,
обращающейся в нуль в бесконечно удаленной точке. Это позволяет
представить функцию W в виде
W = Ci mz — — — ^- + ...
Z Z"^
Положив
Ck = Ak -\- iBk,
мы определим постоянные А^ и В^ из граничного условия
ф = иа sin в -\- С,
перейдя к полярным координатам z = а е*^.

VI. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ В ГИДРОДИНАМИКЕ 419
Для постоянных получаются выражения
Ai=0,
Отсюда
^2='
Бз = 0, Аз = Вз = О,
^^ = -2-.-
W = In Z
2ш
(f = -— в — и COS в —,
27Г г
гр = — -— [пг + и 8тв —
27Г г
Первый член в выражении для w выражает циркуляцию
интенсивности Г вокруг цилиндра. В простейп1ем случае отсутствия циркуляции
мы получим
^2
Комплексный потенциал для потока, обтекающего неподвижный
цилиндр и имеющего на бесконечности скорость и, записывается в виде
иа^ Г ,
W = UZ -\ h -;—: m z.
z zm
3. Обтекание пластинки. Полученные результаты для
обтекания кругового цилиндра позволяют решать задачи об обтекании
произвольных контуров. При этом применяется метод конформного
преобразования. Рассмотрим его применение на конкретной задаче об
обтекании пластинки.
©
у
Рис. 71
Пусть на бесконечно длинную пластинку ширины 2а,
расположенную на оси Ох (рис. 71), набегает постоянный плоский поток,
имеющий на бесконечности скорость с компонентами и и v. При
помощи аналитической функции
. = |(<.1)=/(0
27*

420 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
можно установить взаимно однозначное соответствие между областью
вне пластинки на плоскости z и областью вне круга единичного
радиуса на плоскости (". При этом точке 2; = оо будет соответствовать
точка С = 00, а
dz а ^ .
_ = ->0 при С = оо.
Посмотрим, как изменится условие на бесконечности. Для
комплексного потенциала
-ш (2;) = (/? + г?/^
мы имеем
— сопряженное значение комплексной скорости.
Пайдем значение комплексной скорости фиктивного течения на
плоскости (:
Р 1 . dw dw dz
откуда
{Ж)с=''- (' = ^)-
Итак, фиктивное течение представляет собой обтекание цилиндра
единичного радиуса потоком, имеющим на бесконечности комплексную
скорость kVoQ. Для такого движения комплексный потенциал имеет
вид
Из соотношения z = f {() следует
с
Z + л/^^ — а^ 1 Z — л/^^ — а^
с
Используя эти соотношения, мы получим для комплексного
потенциала жидкости, обтекающей пластинку, выражение
г л ■ П 2^ Г {z^^f£^^^\
W (z) = UZ — iv V ^ — а^ + -—: ш .
zm \ а I
В случае отсутствия циркуляции это выражение принимает вид
W (z) = UZ — iv у z^ — а^.

VL КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ В ГИДРОДИНАМИКЕ 421
Из полученных соотношений видно, что скорость на концах
пластинки достигает бесконечно больп1их значений. В реальных условиях это,
конечно, не имеет места. Hanin результаты объясняются тем, что мы
считаем жидкость идеальной. Применяя теорему Бернулли, можно
найти выражение для силы, действующей на обтекаемое жидкостью
тело.
Изучением сил, с которыми воздух действует на движущееся в нем
крыло самолета, занимается аэродинамическая теория крыла. В
развитии этой теории исключительная роль принадлежит русским и
советским ученым, в первую очередь П. Е. Жуковскому и С. А. Чаплыгину.
В простейшем случае бесциркулярного обтекания цилиндра плоским
потоком жидкости мы получаем парадоксальный результат — поток
не оказывает на цилиндр никакого действия. В случае наложения на
поступательный поток циркуляции скорости вокруг цилиндра
возникает сила, действующая на цилиндр перпендикулярно к направлению
скорости потока в бесконечности.
Теория аналитических функций может быть использована лишь
в случае плоского движения. В трехмерном случае приходится
прибегать к другим методам решения задачи об обтекании жидкостью
твердого тела. В общем случае решение задачи представляет
большие трудности. Рассмотрим простейший случай движения шара в
безграничной покоящейся жидкости с постоянной скоростью. Задача
заключается в решении уравнения
= и cos в на поверхности шара
вне шара с граничным условием
дп
и
д^ д(р д(р
-^— = -^— = -^— = и в бесконечности.
ох Оу OZ
Решение ищем в виде
cos^
if = А-
Используя граничное условие, получаем
что и дает решение поставленной задачи.
Во всех рассмотренных случаях мы считали жидкость идеальной.
Для вязкой жидкости граничные условия изменяются. Па
поверхности тела должно выполняться условие прилипания, а именно: в
точках твердой границы скорость жидкости по величине и направлению
должна совпадать со скоростью соответствующей точки границы.

422 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Задачи обтекания тел вязкой жидкостью приводят к большим
математическим трудностям. В развитии этой области гидродинамики
большую роль сыграли теории пограничного слоя.
VII. Бигармоническое уравнение
В Приложении П к гл. П было получено уравнение поперечных
колебаний стержня
Задача о колебании тонкой пластинки, свободной от нагрузки и
закрепленной на краях, также приводит к аналогичному уравнению ^^
a^2+«4^ + ^ + 'a^;wj='' "™ ^ + «^АД. = 0, (2)
И граничным условиям
ди ^ /о\
U = О и —— = 0 на границе. (3)
on
Кроме того, функция и должна удовлетворять начальным условиям
uu
и (ж, ^, 0) = (/? (ж, у), — (ж, ^, 0) = V^ (ж, у). (4)
Если на пластинку действует внешняя сила, распределенная с
постоянной плотностью / (ж, ^), то статический прогиб закрепленной по
краям пластинки будет определяться из уравнения
ДА« = / (5)
при граничных условиях (3)
ди
и = 0 и — =0.
on
Уравнение
AAu = О (50
называется бигармоническим, а его решения, имеющие
производные до 4-го порядка включительно, называются бигармонически-
ми функциями.
Основная краевая задача для бигармонического уравнения
ставится следующим образом.
Найти функцию и{х,у), непрерывную вместе с первой
производной в замкнутой области S + С, имеющую производные до 4-го
^^ Смирнов в. И. Курс высшей математики. М., 1981. Т. IV, ч. 2.

VIL БИГАРМОНИЧЕСКОЕ УРАВНЕНИЕ 423
порядка в 5, удовлетворяющую уравнению (5) или {Ъ') внутри S и
граничным условиям на С
I ( \ ^^
h{s), (6)
где g{s) и h{s) —непрерывные функции дуги s.
При решении сформулированной выше задачи (2) — (4) с
начальными условиями методом разделения переменных полагают, как
обычно,
u{x,y,t)=v{x,y)T{t). (7)
Подставляя это выражение в уравнение (2) и разделяя переменные, мы
приходим к задаче об отыскании собственных значений уравнения
AAi; - Ai; = О (8)
при граничных условиях
i; = о, -^ = О на С. (9)
on
1. Единственность решения. Докажем, что бигармоническое
уравнение
AAu = 0
при граничных условиях
I ( \ ^'^
h{s) {3')
имеет единственное решение.
Пусть существует два решения ui и ^2- Рассмотрим их разность
V = щ — U2.
Функция V удовлетворяет бигармоническому уравнению (5') и
однородным граничным условиям
dv I
^1- = «' Эп
= 0.
с
Применяя формулу Грина
G С
К функциям (р = V, ф = Av, получаем
f f{Av)US = 0,
G

424 ПРИЛОЖЕНИЯ К ГЛАВЕ IV
откуда
Av = 0.
Принимая во внимание, что v\c = О, получаем
V = О и щ = U2.
Следовательно, бигармоническая функция однозначно определяется
граничными условиями (3').
2. Представление бигармонических функций через
гармонические функции. Докажем следующую теорему.
Если щ и U2—две гармонические в некоторой области G
функции^ то функция и = xui + U2 бигармонична в области G.
Для доказательства воспользуемся тождеством
Положив
(/? = ж, -0 = Ui,
найдем
Д(ж«1) = 2^. (11)
Применяя еще раз оператор А и учитывая, что AAu2 = О, получим
AA(xui +U2) = 0.
Если область G такова, что каждая прямая, параллельная оси
ж, пересекает ее границу не более чем в двух точках, то имеет место
обратная теорема.
Для каэюдой заданной в области G бигармонической функции и
найдутся такие гармонические функции щ и U2j что
и = хщ + U2.
Для доказательства этого утверждения, очевидно, достаточно
установить возможность выбора функции щ, удовлетворяющей двум
условиям:
Aui = О, (12)
A{u-xui) = 0. (13)
Из условия (13) и формулы (11) следует
Au = A{xui) =2^. (14)

VIL БИГАРМОНИЧЕСКОЕ УРАВНЕНИЕ 425
Уравнению (14) удовлетворяет функция
щ (ж, у) = -Аи (^, у) d^.
XQ
Так как
— Aui = А — U1 = - ААи = О,
то Ащ зависит только от у:
Aui =v{y).
Определим функцию щ (у) так, чтобы
л- ^'"1 г ^
И ПОЛОЖИМ ui = ui -\- ui. Эта функция, очевидно, будет удовлетворять
обоим условиям (12) и (13).
Рассмотрим другой вид представления бигармонических функций.
Допустим, что начало координат выбрано внутри области G и что
любой луч, выходящий из начала координат, пересекает границу области
G в одной точке. Тогда любая бигармоническая в G функция и мо-
эюет быть представлена с помощью двух гармонических функций щ
и U2 в виде
и = {г'^ - Го) Ui + U2. (15)
Здесь г^ = ж^ + ^^, а го—заданная постоянная.
Данное утверждение доказывается аналогично предыдущему с
помощью тождества (10) и соотношений
^ 9 . дщ дщ дх дщ ду
Аг^ = 4, —- = — \ —.
дг дх дг ду дг
3. Решение бигармонического уравнения для круга.
Рассмотрим круг радиуса го с центром в начале координат и будем искать
бигармоническую функцию, удовлетворяющую при г = го граничным
условиям (6). Как было указано выше, искомую функцию можно
представить в виде суммы (15)
и = (г^ -rl)ui +U2,
где ui и U2 — гармонические функции. Из граничных условий находим
u2\r=rQ = д- (16)
Отсюда видно, что U2 есть решение первой краевой задачи для
уравнения Лапласа, и оно может быть представлено с помощью интеграла

426
ПРИЛОЖЕНИЯ К ГЛАВЕ IV
Пуассона:
27Г
U2
2^ J '
{rl -r'^)gda
+ Го — 2гго cos {а — в)'
Из второго граничного условия получаем
du2 I
2roUi +
дг
h.
(17)
(18)
=ro
Нетрудно убедиться непосредственным дифференцированием, что
функция
г du2
2roUi +
Го дг
(19)
удовлетворяет уравнению Лапласа и поэтому может быть выражена
интегралом Пуассона:
27Г
г dU2 If
Го ar ZTT J 1
(го - r^) /гб?а
+ Гд — 2гго cos {а — в)'
(20)
Продифференцировав (17) по г и подставив значение du2/dr в
формулу (20), найдем щ. Заменив в формуле (15) щ и U2 их выражениями,
получим
2\2
27ГГ0
ir'-rl)
27Г
1 f —hda
2 J r^ + Го - 2гго cos {a - в)
+
27Г
/
д[го — г cos (а — ^)] da
[r^ + Го — 2гго cos {а — в)]'^

ГЛАВА V
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
В этой главе рассматривается задача с начальными данными
(задача Коши) для уравнения колебаний
1 д'^и
^^=^л;^-/' u = u{M,t), (1)
в неограниченном пространстве (М = М(ж, ^, z)) и на плоскости (М =
= М{х,у)).
§ 1. Задача с начальными условиями
1. Уравнение колебаний в пространстве. Простейшим
уравнением гиперболического типа является уравнение колебаний (1),
которое в физике часто называют уравнением Даламбера.
В гл. II было показано, что уравнение (1) описывает процесс
распространения звука в газе, процесс колебаний мембраны; в этом случае
(1) имеет вид
А2П = Uxx -\-Uyy = — Utt - /(ж, у, t).
к уравнению (1) приводят также задачи о распространении
электромагнитных полей в непроводящей среде и задачи теории упругости
(см. Приложение I к гл. V).
Для уравнения (1) рассматриваются задача с начальными
данными (задача Коши) в бесконечном пространстве и краевые задачи в
ограниченной области.
В этой главе мы будем рассматривать задачу Коши в
неограниченном пространстве.
Найти решение уравнения
Аи =^ии- f{M,t), М = M{x,y,z), (1)
при
t > О, —00 < x,y,z < 00,

428 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
удовлетворяющее начальным условиям
и{М, 0) = (f{M), щ{М, 0) = ф{М) при t = О, (2)
где /,(р,ф — заданные функции.
Решением уравнения (1) в некоторой области при ^ > О будем
называть функцию u{M,t), непрерывную вместе со своими
производными, входящими в уравнение (1) во всех точках рассматриваемой
области и для всех ^ > 0.
Рассмотрим частные реп1ения однородного уравнения
Au=—utt, (3)
обладающие центральной симметрией относительно некоторой точки
Мо, т. е. реп1ения вида
u{M,t) = u{r,t),
где г = гммо — расстояние между точками М и Mq. В этом
случае уравнение колебаний (3) сводится к одномерному уравнению для
функции V = ги:
о?
vtt- (4)
В самом деле, если и = u{r,t), то оператор Лапласа в сферической
системе координат с центром в точке Mq (см. гл. IV, § 1, п. 3) может
быть преобразован к виду
Аи=-—(г^—]=- — (ги)
г'^ дг \ дг) г дг^'
в чем можно убедиться дифференцированием. Поэтому уравнение (3)
принимает вид - irujrr = -rrUu- Вводя затем функцию v = ги, полу-
чаем для нее уравнение (4). Если функция и{г, t) ограничена при г = О,
то функция V = ги обращается в нуль при г = О, v{0,t) = 0. Поэтому
задача Коши для уравнения (3) с начальными данными
и{г, 0) = (f{r), щ{г, 0) = ^{г) (5)
сводится к задаче о колебаниях полуограниченной струны (О ^ г < оо)
с закрепленным концом г = 0:
Vrr = ^vtt, v{r,0) =r(f{r), vt{r,0) =гф{г), v{0,t)=0, (6)
рассмотренной в гл. П.
Общее решение уравнения (4) имеет вид

ЗАДАЧА С НАЧАЛЬНЫМИ УСЛОВИЯМИ 429
и, следовательно,
uir,t) = -h(t--)+-f2(t+-
Г \ ajr\ а
где /i(^) и /2(0 — произвольные дважды дифференцируемые
функции. Частные решения уравнения (3)
1 , / г\ 1 . /^ ^
ui = - fi\t и П2 = - /2 И + -
г \ а J г \ а
называются сферическими волнами; ui{r,t) есть расходящаяся
сферическая волна, U2 (г, t) — сходящаяся в точку г = О сферическая волна,
а — скорость распространения волн. В отличие от плоских волн /(^ =Ь
=Ь х/а) сферическая волна убывает обратно пропорционально
расстоянию от центра.
Таким образом, общее penienne уравнения (3) в случае
центральной симметрии представляется в виде суммы двух сферических волн.
Учитывая условие г'(0, t) = О, находим О = fi{t) + f2{t) или f2{t) =
= ~fi{t) = f{t) для всех значений t, т. е.
u{r,t) = -f(t+-)--f(t--) (7)
Г \ а/ г \ а/
и, в частности,
u{0,t) = -f{t). (Г)
а
2. Метод усреднения. Рассмотрим в неограниченном
пространстве задачу Konin
utt = а'^Аи = a'^{uxx+Uyy + Uzz), -00 < x,y,z < 00, ^ > 0;1
и
(M, 0) = (/.(M), ut{M, 0) = ф{М), M = M{x, y, z).
Предположим, что penienne этой задачи существует, и найдем для
него интегральное представление. Пусть Мо{хо,уо, zq) — фиксированная
точка. Введем сферическую систему координат (г, 0,(р) с началом в
точке Mq.
Рассмотрим функцию
r,t) =Мг[и] = -^ [ [ udS=^ [ [ udn {dS = r^dn), (9)
и{
являющуюся средним значением и на сфере Sr радиуса г с центром в
точке Мо, б?0 = sin OdO d(p.
Из (9) видно, что
u{Mo,to)=u{0,to). (10)

430
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
[ГЛ. V
Покажем, что функция ru{r,t) = v, обладающая сферической
симметрией относительно точки Mq, удовлетворяет уравнению (4).
Проинтегрируем уравнение (8) по объему шара К^, ограниченного сферой Sr'-
Audr =
utt dr.
Кг
Кг
Для преобразования левой части полученного равенства используем
первую формулу Грина (см. гл. IV) при v = 1, и = u{r,t) и учтем, что
нормаль к Sr направлена по радиусу {ди/дп = ди/дг):
Кг Sr
or or
Я"
L Sr
dVt
wg, (11)
r r
^ III"" "^^" ^ а^2 / ^'"^^ \l h'^^\ ^i I ""^^' *^ ^' '^^" ^"^^^
Kr 0 L Sr J 0
Дифференцируя (11) и (12) по г и полагая v = гй, получаем (4).
Из формулы (7') следует, что
«(Мо,*о)=й(0,*о) = -/'(^о)-
(13)
Выразим / через (риф. После дифференцирования й = 1/г • [/(^ +
+ г/а) — f{t — г/а)] по г и t найдем {гй)г + 1/а • {ru)t = 2/а • f'{t +
+ г /а) = 2/а • f (to) при ^ = О и г = ato. Отсюда и из (13) и (9) следует
u{Mo,to) = —
iJr '^V
d^
(14)
-■ r=atQ, t=0
3. Формула Пуассона. Пользуясь начальными условиями (8) и
опуская индекс О при Mq, ^о, получаем из (14) формулу Пуассона
u{M,t)
1
47Г
д_
di
. jj (p{p)d^p^t jj Ф{Р)
Sat Sat
dCtj
(15)
{dSp = {at)^dnp),
которую, учитывая (9), можно записать в виде
и{М, i) = — tMatM + tMat[lp],
(16)

ЗАДАЧА С НАЧАЛЬНЫМИ УСЛОВИЯМИ 431
где
M.M = lll^dn = ^ll^dS. (17)
аМ аМ
Здесь S^ = Sat — сфера радиуса at с центром в точке М.
Пусть и^ — решение задачи (8) при (/^ = О,
и^{М,1)=1Маг[Ф]- (18)
Из (16) видно, что решение задачи (8) можно записать в виде
д
u{M,t) = —и^+и^, (19)
где
U^=tMaM^^. (180
Из формулы Пуассона, полученной в предположении
существования решения задачи (8), следует единственность указанного решения.
В самом деле, предполагая, что задача Коши имеет два решения ui
и ^2, получим для их разности начальные условия (^ = О, -0 = 0.
Применяя к функции и = Ui — U2 предыдущие рассуждения, приходим к
формуле (15), в которой (^ = О, -0 = О и, следовательно, и = О, или ui =
Покажем, что функция u{M,t), определяемая формулой Пуассона,
в самом деле дает решение задачи Коши (8), если (p{x,y,z)
непрерывна вместе со своими производными до третьего порядка, di ф{х,у,г) —
до второго порядка включительно. Доказательство проведем,
предполагая сначала, что (р = О, т. е. и = и^. Введем новые переменные а, /3,
7, положив ^ = ж + ata, г] = у -\- at/3, ( = z -\- atj. Отсюда видно, что
а, /3, J — направляющие косинусы радиуса-вектора точки Р{^,г]Х)
сферы Sat (с^ = COS (г, ж) и т. д.). Тогда интеграл по Sat преобразуется
в интеграл по сфере Si (а^ -\- /3^ -\- j^ = 1) единичного радиуса, причем
dSi = 6?0i = dS/a^t'^, а под знаком интеграла (15) будет
ф{х + ata, у + atp, z + at^) — ф{^, ту, ().
Нетрудно заметить, что
^^ = ^ll^{^.vX)dSu (20)
Si
Au^ = (и^)жж + {uii^)yy + {uii^)zz = ^ / / (V^CC + 'Ф^ + V^CC) dSi =
^^ Cp. (19) с формулой Даламбера.

432 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
t
47Г
[[аФ(1П, (21)
так как фхх = Ф^^ и т. д. При дифференцировании по t под знаком
интеграла (20) получим
— = а [ф^а + фг^р + V^^7) = ^ "^ '
5,
at
Дифференцируя (22) по t, найдем {t{u^)t)t = ^('^v^)tt + ('^v^)t = ('^v^)t +
-^vt, т. е.
('^V^)tt = -Щ' (23)
Первая формула Грина дает
at
"=i//^ "*=i///^-^ *=i/"'*//'''*''*• <'-"
'S'at ^at О Sp
где Xat — шар радиуса at^ Sp — сфера радиуса р с центром в
точке M{x,y,z). Вычислим производную, пользуясь при этом равенством
(21):
аН^
Аф(13 = a^tAu^
Vt = —j— / / iXipdb = a ti\u^.
Отсюда и из (23) следует {и^)и = о? Аи^^ т. е. и^ удовлетворяет
уравнению (8). Нетрудно убедиться в том, что функция du^p/dt также
удовлетворяет уравнению (8), если имеет производные до третьего
порядка включительно.
Покажем, что и^, определяемая формулой (20), удовлетворяет
начальным условиям. Формулы (20), (22) дают и^(М, 0) = О, \imu^/t =
= ф{М), \imv/t = О, так как функция ф непрерывна и все интегралы
ограничены. Поэтому, согласно (22), {uф)t = l/t • Пф + 1/t • v -^ ф{М)
при ^ —>- О и, аналогично, и^^ —>- О при ^ —>- 0. Из формулы (18') для u^p
видно, что {u^p)tt = О при i^ = О и, следовательно, функция (16)
удовлетворяет условиям (8). Тем самым доказано, что формула Пуассона
(16) определяет решение задачи Коши (8).
Из формулы (16) непосредственно видна непрерывная зависимость
решения задачи Коши от начальных данных.

iL
ЗАДАЧА С НАЧАЛЬНЫМИ УСЛОВИЯМИ
433
4. Метод спуска. Полученная в предыдущем пункте формула
(19) дает penienne в пространстве {x,y,z) однородного уравнения
колебаний с начальными условиями, являющимися, вообще говоря,
произвольными функциями переменных х, у и z. Если начальные функции
(р VL ф яе зависят от z, то, очевидно, и функция и, даваемая формулой
(19), также не будет зависеть от переменного z. Следовательно, эта
функция будет удовлетворять уравнению
utt = о
и начальным условиям
и{х,у,0) = (р{х,у),
щ{х,у,0) =ф{х,у).
Таким образом, формула, дающая решение пространственной
задачи, позволяет также решить задачу для плоскости.
В формуле (15) интегрирование происходит по сфере S^. В силу
независимости начальных данных от z интегрирование по верхней
полусфере можно заменить
интегрированием по кругу Е^, получающемуся при
пересечении сферы S^ с плоскостью (ж, у)
(рис. 72). Элемент поверхности dS связан
с элементом плоскости da соотношением
pat
da = dS cos J,
где
cos 7
VW
at
(a; - 0^ -{y- я?
at
Рис. 72
To же относится к интегрированию по нижней полусфере;
следовательно, интеграл по кругу следует взять дважды.
В результате мы приходим к формуле
u{M^t) = u{x^y^t)
1
27га
д_
di
И
at
^{^,r])d^dr]
^{aty -{х- О' -{у- vy
+
+
//
^at
^{i,r])didr]
^{aty -{х- О' -{у- г]У
(25)
в которой интегрирование производится по внутренности круга
радиуса at с центром в точке {х,у).
28 А. Н. Тихонов, А. А. Самарский

434 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Аналогично, если начальные функции (риф зависят только от
одного переменного ж, то формула (19) позволяет найти функцию и{х, t),
являющуюся решением уравнения
Uxx ^Utt =0
с начальными данными
и(ж,0) = (f{x),
щ{х,0) = 'ф{х).
Для этого введем сферическую систему координат, направив полярную
ось по оси X. Элемент поверхности dS выразится следующим образом:
dS = г^ sin OdOd(f = —г d(f с?^,
так как
^ = ж + гсо8^, d^ = —rs'mOdO.
Интегрируя в формуле Пуассона (15) по углу (р, получим
x-\-at x-\-at
uix,t) = l
^ I 'P{Od^+ I i^iOd^
dt
L x — at x — at
Выполняя В первом интеграле дифференцирование по t, приходим к
известной из гл. II, § 2 формуле Даламбера
x-\-at
ш(х-\-at)-\-ш(х — at) 1 f ,,^. ,^ .^^ч
и{х, t) = ^ '-^ '- + - J Ш) dt (26)
X — at
Уравнения колебаний с тремя, двумя и одним пространственным
аргументом часто называют соответственно уравнениями
сферических, цилиндрических и плоских волн. Эта терминология вполне
соответствует примененному выше методу, называемому методом спуска,
поскольку при решении уравнения колебаний на плоскости и на
прямой мы исходили из пространственной задачи, как бы «спускаясь» к
меньшему числу переменных. Полученные решения для двух и одного
переменного носят характер цилиндрических и плоских волн.
Метод спуска применим не только к уравнению колебаний, но и
к другим типам уравнений и позволяет в ряде случаев из формулы,
определяющей решение уравнения для многих переменных, извлечь
решение задачи для уравнения с меньшим числом независимых
переменных.
5. Физическая интерпретация. Формулы (15) и (25) дают
возможность выяснить физическую картину распространения
сферических и цилиндрических волн. Начнем со случая трех переменных, для
которого физический характер процесса распространения существенно
отличается, как мы увидим из дальнейшего, от случая двух
пространственных переменных.

iL
ЗАДАЧА С НАЧАЛЬНЫМИ УСЛОВИЯМИ
435
Рис. 73
Ограничимся изучением распространения локального
возмущения, когда начальное состояние (функции (р > О vl ф > 0) отлично от
нуля только в некоторой ограниченной области Tq. Рассмотрим
сначала изменение состояния u{Mo,t) в точке Mq, лежащей вне области То
(рис. 73). Состояние и в точке Mq в
момент времени t определяется в силу (15)
начальным состоянием в точках,
лежащих на сфере 5^^° радиуса at с центром
в Mq. Функция u{Mo,t) отлична от
нуля только в том случае, если сфера 5^^°
пересекает область начальных значений
Tq. Пусть d и D — расстояния от
точки Мо до ближайшей и наиболее
удаленной точек области То (рис. 73).
Очевидно, если t достаточно мало (^ < ^i =
= d/a), то сфера 5^^° не пересекается с
областью То, поверхностные интегралы
в формуле (15) равны нулю: до точки Mq возмущение еще не дошло.
Начиная с момента ti = d/a до момента t2 = D/a сфера 5^° (^i < ^ <
< ^2) будет пересекать область То; поверхностные интегралы в
формуле (15), вообще говоря, отличны от
нуля: точка Mq находится в
возбужденном состоянии. При дальнейшем
увеличении t сфера S^f^ будет содержать
область То внутри себя,
поверхностные интегралы равны нулю:
возмущение прошло точку Mq. Таким образом,
при распространении локального
возмущения в трехмерном пространстве
явление последействия отсутствует.
Рассмотрим теперь мгновенную
пространственную картину
возмущения u{M,to) в некоторый момент
Лоточки М, находящиеся в
возбужденном состоянии, характеризуются тем.
Рис. 74
что сферы S^ пересекают область начальных возмущений То. Иными
словами, это означает, что геометрическое место точек W, в которых
возмущение отлично от нуля, состоит из точек М, находящихся на
сферах 5^Q радиуса ato с центрами в точках Р области То. Огибающие
семейства сфер 5^ будут границами области W. Внешняя огибающая
называется передним фронтом, внутренняя — задним фронтом
распространяющейся волны. На рис. 74 изображены передний и
задний фронты волны (1 и 2) для того случая, когда область То является
сферой радиуса Rq.
Таким образом, начальное возмущение, локализованное в
пространстве, вызывает в каждой точке Mq пространства действие, ло-
28*

436
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
[ГЛ. V
кализованное во времени; при этом имеет место распространение
волны с резко очерченными передним и задним фронтами (принцип
Гюйгенса).
Перейдем к случаю двух переменных. Пусть начальное
возмущение задано в области So на плоскости {х,у). Рассмотрим изменение
состояния u{Mo,t) в точке Мд, лежащей вне Sq. Состояние u{Mo,t) в
точке Мо в момент t определяется согласно (25) начальными
значениями в точках Р, принадлежащих кругу Е^^° радиуса ato с центром в Mq.
Для моментов времени t < ti = d/a (d — расстояние от Mq до
ближайшей точки области So) функция и{Мо, t) = 0: до точки Mq возмущение
еще не дошло. Если t > ti, то u{Mo,t) ф 0. Это значит, что, начиная
с момента t — 1\^ в точке Мд возникает возмущение, которое сначала,
вообще говоря, возрастает, а затем, начиная с некоторого момента,
постепенно убывает до нуля (при ^ —>- оо). В этом явлении последействия
и заключается отличие плоского случая от пространственного.
Влияние начальных возмущений, локализованных на плоскости, не
локализовано во времени и характеризуется длительно продолжающимся
последействием. Принцип Гюйгенса не имеет места.
Мгновенная картина возмущений на плоскости имеет резко
очерченный передний фронт, но не имеет заднего фронта. Задачу для двух
измерений можно рассматривать как пространственную задачу, когда
начальные возмущения заданы в бесконечном цилиндре и не зависят от
третьей координаты. Пользуясь этой схемой, легко себе представить
процесс последействия.
6. Метод отралсения. Задача с начальными условиями для
уравнения колебаний в случае областей, ограниченных плоскостями,
может быть решена методом отражений.
Рассмотрим задачу для полупространства 2; > 0.
Найти решение уравнения колебаний
1
Аи = -^utt,
удовлетворяющее начальным условиям
u{x,y,z,0)=(p{x,y,z),
щ{х,у,г,0)=ф{х,у,г) ^
и граничному условию
= 0
z=0
ди
(ОО)
= 0.
z=0
Решение этой задачи дается формулой (15), если начальные условия
продолжить на все пространство нечетно по z (при u\z=o = 0):
(f{x, у, z) = -(/?(ж, у, -z)] ф{х, у, z) = -^{х, у, -z)

§ 2] ИНТЕГРАЛЬНАЯ ФОРМУЛА 437
или четно (при du/dz \z=o = 0):
(р{х, у, z) = (/?(ж, у, -z); ф{х, у, z) = ^{х, у, -z).
Убедимся, что при нечетном по переменной z продолжении функций ^
и ф граничное условие i/l^^o = О выполняется автоматически. В самом
деле,
u{P,t) =u{x,y,0,t) = —
д ff^i^.vX),^ , ff^i^^^^O^^
ir-^-чр-
о,
dt J J at J J at
qP qP
так как поверхностные интегралы по сферам с центрами в точках
плоскости Z = О равны нулю при нечетных функциях (риф.
Аналогично может быть решена задача для плоского слоя О ^ z ^1
при граничных условиях первого и второго рода
и = О при Z = О и Z = I
или
ди ^ ^ ^
-^г- = О при Z = о и Z = I
OZ
и соответствующих начальных условиях.
Формула (15) сразу же дает решение задачи, если начальные
условия продолжить нечетно (или четно) относительно плоскостей 2; = О и
Z = I. Определяемые таким образом начальные функции (риф будут
периодическими по переменному z с периодом 21 (ср. гл. II, § 2, п. 7).
Если в слое О < 2; < / начальные функции риф являются
локальными, отличными от нуля в области То, то продолженные функции
будут отличны от нуля в ряде областей Т^, получающихся из То при
помощи зеркальных изображений. Функция u{M,t) для всякого М и t
представляется как сумма конечного числа слагаемых, определяемых
возмущениями в Т^ (ср. с гл. II, § 2, п. 7). Физический смысл этого
заключается в том, что за конечный промежуток времени происходит
конечное число отражений от стенок z = О и z = I. Аналогично может
быть решена задача для параллелепипеда.
§ 2. Интегральная формула
1. Вывод интегральной формулы. При решении уравнения
колебаний струны
1 ,
Uxx wUtt = -J
методом распространяющихся волн мы широко пользовались
понятием характеристического угла. Переходя к решению уравнения
колебаний на плоскости или в пространстве
Аи -uu = -f, (1)

438
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
[ГЛ. V
рассмотрим поверхность
-гммо = 1^ - ^о|,
называемую характеристическим конусом для точки Mq и
момента ^о- Совокупность точек «фазового» пространства (М, t), в ко-
Случай п = 2
Рис. 75
торые приходит сигнал, распространяющийся со скоростью а и
вышедший из точки Мо в момент ^о, определяется уравнением
1 , ,
- ^ммо — t — to [t > to)
и является верхней полостью характеристического конуса точки Mq.
Аналогично сигнал, вышедший из точки М в момент ^, приходит в
точку Мо в момент ^о, если
1 , ,
- ^ммо — to — t [t < to).
Геометрическое место таких точек (М, t) образует нижнюю полость
характеристического конуса (рис. 75).
Для определения в точке (Мо,^о) функции u{M,t),
представляющей решение уравнения (1), введем вместо времени t локальное время
^* точки Мо, полагая
t*=t-{to-'-^)
и оставляя при этом неизменными геометрические координаты.
Пользуясь сферической системой координат (г, 0,(р), связанной с точкой Мо,
мы приходим к новой системе переменных
= в, <p*=ip, t*=t- (to - ^)

§ 2] ИНТЕГРАЛЬНАЯ ФОРМУЛА 439
Установим уравнение, которому удовлетворяет функция
Оператор Лапласа в сферической системе координат имеет вид
д'^и 2 ди 1 д [ . ,ди\ 1 д'^и
Аи = —^ + - ^— + , . , — smr
Выразим производные функции и через производные функции U:
Ur = Ur* -\- - Ut* ,
а
2 1
Urr = Ur*r* Н— Ur*t* Н—к Ut*t*j
а а^
щ = [/б1*; U6I6I = Uo*e*,
"^(р — ^ ip* 1 "^(pip — ^ р* р* J
Уравнение (1) переходит в уравнение
Д^^ = - Л Л (^*^**) - Пг*,0*,^р*,П, (2)
где
Пусть точка Мо(жо, ^о, ^о) принадлежит некоторому телу Т,
ограниченному поверхностью 5. Рассматривая (2) как неоднородное
уравнение Лапласа, в котором ^* играет роль параметра, воспользуемся
основной формулой Грина (см. гл. IV). Применим ее к области Т,
полагая при этом ^* = 0"*^^:
47г[/(М(
"•»'=//
}_ди__ д_ f 1_
г* дп дп \г*
dS+
т т
Точка Mq является особой точкой сферической системы координат.
Поэтому объемные интегралы естественно рассматривать как пределы
при г —>- О соответствующих интегралов, взятых по объему Т — Т^, где
^ В силу принятого в гл. IV условия знаки в формуле соответствуют
вненЕней нормали.

440 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Т^ — шар радиуса е с центром в точке Mq. Преобразуем объемный
интеграл:
2 д f ^ ди\ ,
ат
аг*^ дг* \ dt
Т-Те
///:
///^^(•••f)-"^-'^"-^
Т-Те
Интегрируя по переменному г*, получим
5
так как
Is= 7^ cos(n, Г*) ^5 - / / -^г- dS,
J J аг* dt* ^ ' ^ J J ar* dt* '
dSn = dS cos(7^*) = r*^ sin i9* dO* d(f\
Второе слагаемое в /^ стремится к нулю при г —>- О, так как площадь
поверхности 5^ равна 47гг^. Таким образом, предел /^ при г —>- О равен
JJJ ar* or* \ at*J J J ar* ot* dn
T s
так как
cos(n,r*)
dn
что дает
5
ar* ot* dn J J J J T*
T
Вернемся к старым переменным и функции и:
и{М,t) = U{M,Г) (^t = r+to- "^^^^
так что
[/(Мо,0)=и(Мо,^о),
а также
ди _ди 1 ди dr
дп ди а dt* dn
^ При этом преобразовании мы пользуемся тем, что dr = (г*) dQdr,
интегрируем по г* и затем заменяем dfl = dS/{r*) .

А
ИНТЕГРАЛЬНАЯ ФОРМУЛА
441
В результате для функции u{Mo,to) получаем следующую
интегральную формулу:
""»•'»'-i/ZI?
ди
дп
^^ - + —
on \г аг
ди
dr
dn
dSM +
47Г
[/]
dru, (3)
часто называемую формулой Кирхгофа"'^^ Здесь квадратные скобки
показывают, что значение функций надо брать для ^* =0, т. е. при
t = to- гмом/а, так что [/] = f{M,t- гммо/а).
2. Следствия из интегральной формулы. Формула (3)
находит свое применение при peniennn целого ряда задач. В качестве
первого примера рассмотрим задачу с начальными данными.
Найти решение уравнения колебаний
Аи -utt = 0
в неограниченном пространстве^ если заданы начальные условия
^к=о = (f{x,y,z),
Ut\t=o =ф{х,у,г).
Нижняя полость характеристического «конуса» г = a{to — t) точки
(Мо,^о) пересекается с многообразием ^ = О по сфере 5^^° (г = ato)
радиуса ato с центром в точке Mq. Воспользуемся формулой (3),
полагая в ней S = S^^Q. Для любой функции v{M,t) значение [v] на сфере
5^^° имеет вид
[v] = V lM,to —j = г'(М, 0), так как гммо = cito-
^ Формула Кирхгофа была обобщена С. Л. Соболевым для уравнения
гиперболического типа с четным числом переменных. Нри помощи этой
формулы Кирхгофа — Соболева может быть построено penienne задачи с
начальными условиями для указанного уравнения (Соболев С. Л. Об одном
обобщении формулы Кирхгофа // ДАН СССР. 1933. Т. 1, № 6. С. 256-262.)

442
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
[ГЛ. V
Поэтому, если точка М лежит на сфере S^^q , то
[u]s = u{M,0) = ^{M),
ди
ди
ди
Далее
1
ди
дп
дп
дп
д^(М,0)=ф(М),
1 dip
г дг
if
д_ (\
дг
Подставляя это выражение в (3), находим
dS
^2 Qj,
{r(f).
1
47Г
d_
dr
f f r(fdn + - f f riljdn
J r=atQ
откуда, опуская индексы О при Mq и ^о, получаем формулу Пуассона
u{M,t)
1
47га
д_
di
sr^^^4i
Ф{Р)
ГМР
dS
qM
qM
{гмр = at) (4)
(см. (15) из § 1).
В качестве второго примера рассмотрим теперь penienne
неоднородного волнового уравнения с нулевыми начальными данными.
Выбирая по-прежнему S = S^^^, убеждаемся в том, что поверхностный
интеграл в (3) обращается в нуль, вследствие чего получаем
u{Mo,to)
[/]
1. fffll
47Г J J J r
dTM,
(5)
atQ
пМо
где Т^^^ — шар радиуса ato с центром в Mq . Исследуем подробнее тот
случай, когда правая часть является периодической функцией времени
f{M,t) = MM)e
loot

§ 2] ИНТЕГРАЛЬНАЯ ФОРМУЛА 443
где UJ — заданная частота колебаний. Из (5) находим
и{МоМ) = в'"'° ^ III ММ) ^ dTM (^ = ^ ' ^ = ^ммо) .
atQ
(6)
Пусть fo{M) — локальная функция, т. е. функция, отличная от
нуля только внутри некоторой области Т. Если Mq лежит вне области
Т и расстояние от Mq до ближайшей точки области Т равно d, то
интеграл по TatQ равен нулю для ^о < б?/а. Для таких значений возмущение
не успевает дойти до точки Mq. Если расстояние от Mq до
наиболее удаленной точки области Т равно D, то для моментов ^о > D/a
интеграл в правой части постоянен и сводится к интегралу,
распространенному по всей области Т. Таким образом, во всякой точке Mq,
начиная с момента ^о = D/a, имеют место периодические колебания с
амплитудой
у{Мо) = -г /// /о(М) dTM, (7)
т
так что
Прямая подстановка выражения (6) для и (при ^о > D/a) в
уравнение колебаний показывает, что функция v{M) должна удовлетворять
уравнению
А^ + k^v = -/о(М) {к > uj/a), (8)
которое мы будем в дальнейшем называть волновым
уравнением (см. гл. Vn). Оно часто также называется уравнением Гельмголь-
ца.
Рассмотрим формулу (3) для случая установившихся колебаний,
когда
u{M,t) =i;(M)e^^^
где v{M) — амплитуда колебаний, удовлетворяющая волновому
уравнению (8).
В этом случае имеем
[u]=u[M,t-'^)=v{M)e
ди
дп
(cot —кг)
. ^ у— у _ ,
dv
. gi {uot-kr)
дп
гЬ(М)е^(^^-^^),
[/] = /о(М)е^М-^^).
ди

444 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Подставляя эти выражения в формулу (3), приходим к интегральной
формуле для волнового уравнения (8):
,(«.) = 3^|/
е dv д
г дп дп
dSM+
которая часто также называется формулой Кирхгофа.
При к = О (о; = О — статический случай) формула (9) переходит
в основную формулу Грина (гл. IV, § 2) для неоднородного уравнения
Лапласа.
§ 3. Колебания ограниченных объемов
1. Общая схема метода разделения переменных. Стоячие
волны. Задача о колебании ограниченных объемов состоит в
следующем.
Найти решение уравнения
div{kgTdidu)-q{M)u = p{M)utt, к > О, q ^ О, (1)
где
1-/7 14 ^ Л 9и\ д Л ди\ д Л ди\
М = M{x,y,z), внутри некоторого объема Т, ограниченного
замкнутой поверхностью Е, удовлетворяющее дополнительным условиям
u{M,0) = (f{M), щ{М,0)=ф{М) в Г + Е, (2)
u|s =0 для t^O. (3)
В случае однородной среды {к = const, р = const) для q = О
уравнение (1) принимает вид
1 f 2 к
Аи= —utt [а = -
С задачами подобного типа мы встречаемся при изучении процесса
колебаний мембраны (случай двух независимых геометрических
переменных), акустических колебаний газа, электромагнитных процессов
в непроводящих средах. Особое значение имеют задачи, связанные с
генерацией электромагнитных колебаний в замкнутых полых
резонаторах (эндовибраторы, клистроны, магнетроны и т. д.).

§ 3] КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ 445
Заметим, что однородность граничного условия (3) не связана с
ограничением общности. В самом деле, случай
(где /J — произвольная функция точки Р поверхности Е и времени
t) легко сводится к случаю однородного граничного условия методом,
который изложен в гл. II, § 3 для одного переменного и заключается
в том, что рассматривается отклонение от заданной функции.
Аналогично ставятся вторая и третья краевые задачи.
Будем искать решение u{M,t) однородного уравнения (1) с
условиями (2) и (3) методом разделения переменных. В дальнейшем мы
ограничимся изложением формальной схемы решения. С этой целью
рассмотрим основную вспомогательную задачу (ср. гл. II, § 3).
Найти нетривиальное решение однородного уравнения
div{kgTdidu) - qu = putt в Т, ^>0 {к > О, р > О, q ^ 0), {!')
удовлетворяющее однородному граничному условию
иЬ = О, (3)
представимое в виде произведения
u{M,t) =v{M)T{t). (4)
Подставляя предполагаемую форму решения (4) в (1) и разделяя, как
обычно, переменные, приходим к следующим уравнениям для функций
v{M) mT{t):
diY{kgTa,dv) — qv -\- Xpv = 0, v ^ 0; ^
(5)
^|e=0;
T" + ЛГ = 0. (6)
Для v{M) получаем задачу на собственные значения (задачу
Штурма — Лиувилля).
Найти те значения параметра Л, при которых существуют
нетривиальные решения задачи
div(/i;gradг') — qv -\- Xpv = 0 {к > О, q ^ О, р > 0)А
} (5)
^|е=0, J
а такэюе найти эти решения. Такие значения параметра Л
называются собственными значениями, а соответствующие им
нетривиальные решения — собственными функциями задачи (5).
Остановимся подробнее на этой задаче, аналогичной основной
задаче из гл. II, § 3. В нашем случае уравнение для собственных функций
представляет собой уравнение с частными производными, вследствие

446 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
чего трудно рассчитывать на получение явного представления
собственных функций для произвольной области Т. В дальнейшем (пп. 2
и 3) будут рассмотрены примеры областей Т, для которых явное
представление возможно, хотя и требует введения нового класса
специальных функций. Здесь мы рассмотрим общие свойства собственных
функций и собственных значений и приведем формальную схему
метода разделения переменных. Перечислим эти свойства.
1. Существует счетное множество собственных значений Ai ^ Л2 ^
^ ... ^ An ^ ..., которым соответствуют собственные функции
VI (ж, у, Z), V2{X, y,z),..., Vn{x, y,z),...
Собственные значения A^^ с возрастанием номера ti неограниченно
возрастают; А^ ^ оо при п ^ оо.
2. При q ^ О все собственные значения А положительны:
Ап>0.
3. Собственные функции {vn} ортогональны между собой с весом
p{x,y,z) в области Т:
/■
, (М) Vn (М) р{М) dTM = 0 (т^п), (7)
М = M{x,y,z); dTM = dxdydz.
4. Теорема разложимости. Произвольная функция F{M),
дваэюды непрерывно дифференцируемая и удовлетворяющая
граничному условию
F = О на Е,
разлагается в равномерно и абсолютно сходящийся ряд по
собственным функциям {vn{M)}:
F{M) = Y,FnVn{M),
где Fn — коэффициенты разлоэюения.
Доказательство свойств 1 и 4 основывается обычно на теории
интегральных уравнений. Перейдем к доказательству свойств 2 и 3, не
требующему специального математического аппарата. Докажем
ортогональность собственных функций {vn} (свойство 3). Пусть Vn{M)
и Vm{M) — две собственные функции, соответствующие различным
собственным значениям А^ и А^:
^- к —— ] + ^- [к -^— ] + ^ [к -^— - qvm + ЛшрУш = О,
ох \ ох J Оу \ Оу J OZ \ OZ J
ох \ ох J оу \ оу J OZ \ OZ J

§ 3] КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ 447
причем Vjn = О и г'п = О на S. Умножая первое уравнение на Vn{M) и
вычитая из него второе уравнение, умноженное на г'^(М), находим
{vn div{k grad Vm) - Vm div{k grad Vn)} dr +
T
+ (Л^ - An) / / / VnVrnpdr = 0.
T
Отсюда после преобразований, аналогичных тем, которые
используются при выводе второй формулы Грина"*^^, получаем
Е Т
В силу граничных условий г^^^ = О и г'п = О на Е
(Л^ - An) / / / VmVnpdr = о,
т
откуда и следует, что при Л^^ 7^ А^
/ / / VmVnpdr = 0 (ш 7^ п),
т
т. е. собственные функции, соответствующие разным собственным
значениям, ортогональны между собой с весом р{М).
При изучении аналогичной краевой задачи для одного
независимого переменного
X" + ХрХ = О,
Х(0) = о,
Х{1) = о
было доказано, что каждому собственному значению соответствует
одна нормированная собственная функция. Для двух и трех
независимых переменных это обстоятельство не имеет места. Как видно из
примеров собственных функций прямоугольника и круга,
рассмотренных ниже (пп. 2 и 3), одному и тому же собственному значению
может соответствовать несколько собственных функций. Однако
каждому собственному значению, как это следует из теории интегральных
^ В эту формулу входят нормальные производные собственных функций
на поверхности Е. Обоснование этой формулы для поверхностей типа
Ляпунова см.: Смирнов В. И. Курс выспесй математики. Т. IV. М., 1981.

448 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
уравнений, может соответствовать лишь конечное число собственных
функций, линейно независимых между собой. Пусть некоторому значе-
л - л. " (1) (2)
нию Лп соответствует система линейно независимых функции Vn ,Vn ,
..., Vn • Очевидно, что любая линейная комбинация этих функций
^aiV.
(i)
также является собственной функцией для того же собственного
значения Хп. Пользуясь известным приемом ортогонализации"*^^,
можно построить функции Vn , ..., Vn , являющиеся линейными
комбинациями исходных функций и ортогональные между собой. Таким
образом, если собственные функции, соответствующие некоторому Л^, не
ортогональны между собой, то мы можем ортогонализировать их и
получить новую систему собственных функций, ортогональных между
собой и соответствующих тому же Л^.
Совокупность таких систем собственных функций для разных Л^
образует ортогональную систему собственных функций
рассматриваемой краевой задачи
diY{kgTa,dv) — qv -\- Xpv = О,
V = О на Е.
Число
Vnpdrl
III'
называется нормой собственной функции. Умножая каждую
функцию Vn на Х/Цг'пЦ, получим систему собственных функций,
нормированных к единице.
Для доказательства положительности собственных значений
(свойство 2) достаточно воспользоваться первой формулой Грина:
(*g,acl„„)^* = -///.,.cliv(*g,acl.„)* + //.„.^*,=
qv^dr + Xn I I I v^pdr.
T T
Отсюда видно, что при q ^ О собственные значения Л^^ положительны.
^ См., например: Смирнов В. И. Курс выснхей математики. Т. IV. М.,
1981.

§ 3] КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ 449
В дальнейшем мы будем пользоваться теоремой разложимости
(свойство 4), отсылая за доказательством к соответствующему
разделу интегральных уравнений. Пусть
сю
F{M) = Y.^rгVn{M).
п=1
Отсюда обычным способом, используя условие ортогональности (7),
находим коэффициенты разложения:
///
т
F{M)vn{M)pdT
Гп — г г г ' ^^
JJJ '^"^'^
т
Вернемся теперь к уравнению в частных производных. Решение
уравнения
^п + ^пТп = о
имеет вид
Tn{t) = An cos л/X^t + В
п sin л/Xfi tj
так что решением нашей основной вспомогательной задачи будет
произведение
Un{M,t) = Тп{t)vn{M) = {An cos л/Л^t + Вп sin y^t)vn{M).
Общее решение исходной задачи с начальными данными естественно
искать в виде суммы:
сю сю
и{М, t) = J2 ^п{М, t) = J2 (^п COS y^t + Вгг sin y^t) Vn{M). (9)
n=l n=l
Удовлетворяя начальным условиям (2)
сю
и{М,0) = ^{М) = Y,^nVn{M),
п=1
сю
щ{М, 0) = ф{М) = ^ ВпуО^Уп{М)
п=1
и пользуясь теоремой разложимости 4, находим
An = (fnj Вп V An = фги
где ipn ^ фп — коэффициенты Фурье функций ^{М) и ф{М) в их
разложении по ортогональной с весом р{М) системе функций Vn{M). Тем
самым формальное построение решения исходной задачи закончено.
29 А. Н. Тихонов, А. А. Самарский

450 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Физическая интерпретация полученного реп1ения вполне
аналогична случаю одного переменного. Частные решения
Un{M, t) = {An cos vAn t-\- Bn sin vA^ t) Vn{M)
представляют собой стоячие волны, которые могут существовать
внутри ограниченного объема Т.
«Профили» стоячих волн, определяемые функцией Vn{M), для
разных моментов времени отличаются лишь множителем
пропорциональности. Линии или поверхности (соответственно для двух или
трех переменных), вдоль которых Vn{M) =0, называются узловыми
линиями (поверхностями) стоячей волны Vn{M). Точки, в которых
Vn{M) достигает относительных максимумов или минимумов,
называются пучностями этой стоячей волны-'^л Общее решение
представляется в виде бесконечной суммы таких стоячих волн. Возможность
представления общего решения в виде суммы слагаемых подобного
типа и означает возможность представления произвольного колебания в
виде суперпозиции стоячих волн^^.
Таким образом, задача о колебании мембран или объемов
сводится, по существу, к нахождению соответствующих собственных
функций. В ПН. 2 и 3 мы рассмотрим колебания прямоугольной и круглой
мембран, обращая при этом главное внимание на построение
собственных функций. Как уже отмечалось выше, нахождение собственных
функций в явной аналитической форме сопряжено с большими
трудностями для областей более сложной формы. В случае произвольных
областей для построения собственных функций могут быть
использованы приближенные методы. Существуют различные приближенные
методы, основанные на использовании интегральных уравнений,
вариационных принципов, конечных разностей.
2. Колебания прямоугольной мембраны. Процесс колебаний
плоской однородной мембраны, как было показано в гл. П, § 1,
описывается уравнением колебаний
utt = а^ Аи. (10)
Пусть в плоскости (ж, у) расположена прямоугольная мембрана со
сторонами bi и ^2, закрепленная по краям и возбуждаемая с помощью
^ Если возбудить колебания мембраны, посыпанной песком, то песок из
пучностей будет сбрасываться к узловым линиям, образуя при этом так
называемые хладниевы фигуры, воспроизводящие узловые линии собственных
функций.
^ Обоснованию метода разделения для случая многих переменных
посвящены работы О.А.Ладыженской (О сходимости рядов Фурье,
определяющих репЕСние сменханной задачи для гиперболических уравнений // ДАП
СССР. 1952. Т. 85, № 3. С. 481-484) и В. А. Ильина (О разрешимости сме-
пЕанных задач для гиперболических и параболических уравнений // У МП.
1960. Т. 15, вып. 2. С. 97-154).

§ 3] КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ 451
начального отклонения и начальной скорости. Для нахождения
функции u{x,y,t), характеризующей отклонение мембраны от положения
равновесия, мы должны решить уравнение колебаний
при заданных начальных условиях
и{х,у,0) = (f{x,y)
ди ( (11)
— (ж,^,0) =ф{х,у)
и граничных условиях
u{0,y,t) = 0, u{buy,t) = 0, (12)
u{x,0,t) = 0, u{x,b2,t)=0. (13)
Мы ищем, как обычно, решение методом разделения переменных,
полагая
u{x,y,t)=v{x,y)T{t). (14)
Подставляя (14) в (10) и разделяя переменные, получаем для функции
T{t) уравнение
Т" + а^ЛГ = О, (15)
а для функции v{x,y) — следующую краевую задачу:
Vxx + Vyy + Лг' = 0;
v{0,y)=0, v{buy) = 0;\ (16)
v{x,0) =0, v{x,b2) = 0.^
Таким образом, сама задача для собственных значений состоит в
решении однородного уравнения в частных производных при однородных
граничных условиях. Будем и эту задачу решать методом разделения
переменных, полагая
v{x,y)=X{x)Y{y).
Проводя разделение переменных, получаем следующие
одномерные задачи на собственные значения:
Х(0)=0, X(bi)=0;J
^" + ^^^ = 4 (18)
У(0)=0, Y(h)=0,j
29*

452 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
где г/ и /i — постоянные разделения переменных, связанные coothohic-
нием /i + г/ = Л. При этом граничные условия для Х{х) и Y{y)
вытекают из соответствующих условий для функции V. Например, из
v{0,y)=X{0)Y{y)=0
следует Х{0) = О, так как Y{y) ^ О (мы ищем нетривиальные
решения).
С решением задач, подобных (17) и (18), мы уже встречались при
изучении колебаний струны. Решения уравнений (17) и (18) имеют вид
Хп[х) = 8Ш -— Ж, Ym[y) = 8Ш -— у]
01 02
\ 2 / \ 2
П7Г \ / ттгтг
Собственным значениям
/"пттЛ / ттгтг ^
таким образом, соответствуют собственные функции
. . П7Г . ттгтг
Уп,ш = Лп,ш 8Ш -— Ж 8Ш -— у,
01 02
где Л^^-^ — некоторый постоянный множитель. Выберем его так,
чтобы норма функции Vn,m с весом 1 была равна единице:
bi 62 bi 62
/ / ^l,rn dx dy = Л^^ / sin^ ^xdx j sin^ '^ydy = l.
00 0 0
Отсюда
A ■ ^
0102
Ортогональность функций {vn,m} очевидна и не нуждается в
доказательстве. Следовательно, функции
/ \ / 4 . тттг . ттгтг ,..
V Oi02 О1 О2
образуют ортонормированную систему собственных функций
прямоугольной мембраны.
Число собственных функций, принадлежащих Хп,т (кратность
Хп,т), зависит от количества целочисленных решений п и т
уравнения
ггтг\ / ттгтг \

А.
КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ
453
Найденная система собственных функций Vn,m такова, что любая
функция F{x,y), дважды непрерывно дифференцируемая и
удовлетворяющая граничному условию, может быть разложена в абсолютно и
равномерно сходящийся ряд по Vn,m- Это утверждение можно
обосновать, сославп1ись на теорию кратных рядов Фурье.
Покажем, что система (19) содержит все собственные функции на-
П1ей задачи о собственных значениях. Предположим, что существует
собственная функция uq, принадлежащая собственному значению Aq.
Так как функция щ ортогональна всем собственным функциям,
принадлежащим другим значениям Л, то в ее разложении по системе (19)
останется лишь конечное число членов, соответствующих
собственным функциям, принадлежащим собственному значению Хп,т = ^о-
Поэтому uq является линейной комбинацией лишь тех функций (19),
которые соответствуют Хп,т = Aq. Таким образом, все функции
прямоугольной мембраны даются формулой (19).
Щ,1
Щ,2 + г;2Д
Щ,2
г^з,з
N
ЩЛ +У4:Л
Возвращаясь к исходной задаче для уравнения (10), мы видим, что
частные решения
п,т (^t + Bji^YYi sin \/\ri,m ^^)
представляют собой стоячие волны, профиль которых определяется
собственными функциями г'п,т- Геометрические места точек внутри
прямоугольника, в которых собственные функции обращаются в нуль,
называются узловыми линиями. Рассмотрим для простоты
квадрат со стороной b {bi = Ь2). Узловые линии функции
2 . П7Г . ттт
ЯВЛЯЮТСЯ прямыми, параллельными осям координат (рис. 76, а).
При кратных собственных значениях линейная комбинация
собственных функций также будет собственной функцией. Ее узловые
линии могут иметь весьма сложную форму (рис. 76, 6).

454 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Искомое решение уравнения (10) при дополнительных условиях
(11) — (13) имеет вид
сю сю
u{x,y,t)= ^ ^{Вп,ш COS л/Хп,ш at + Вп,ш sin л/Х^ш at) Vn,m{x, у),
т=1 п=1
где Vn,m определяется формулой (19), а коэффициенты Вп,т и Вп,т
равны
bi 62
Вп,ш= / hp{x,y)vn,rn{x,y)dxdy =
о о
bi 62
-— / (р{х,у)8т-—х sin-—уdxdy,
1^2 J J bi b2
b^ .
0 0
. bi 62
= 1 ^ f f I / . . П7Т . ттт _ _
Bfi m = —> \ -z—— / / wix.y) sm -— X sm -— у dxdy.
J^^K^Sbib2 J J ^^ '^^ b, b2 ^ ^
0 0
3. Колебания круглой мембраны. При изучении колебаний
круглой мембраны полезно перейти к полярным координатам. Тогда
уравнение колебаний запишется в виде
Будем искать решение этого уравнения при заданных начальных
условиях
и{г,9,0) = h{r,9)A
щ{г,в,0) = f2{r,e) }
И граничном условии
u{ro,0,t) = 0 (22)
(закрепленная по краям мембрана радиуса го). Как и в случае
прямоугольной мембраны, мы прибегаем к разделению переменных.
Положив
uir,e,t)=vir,e)Tit),
МЫ получим уравнение для T{t):
Т" + а^ЛГ = О,
которое имеет решение
Г = Ci cos л/о^Л ^ + С2 sin л/о^Л ^,

§ 3] КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ 455
и следующую задачу на собственные значения для функции у{г,в):
|г'(0,^)| < 00 (условие ограниченности),
v{rojO) = О (граничное условие),
г>(г,0) = v{r,0 + 27г) (условие периодичности).
Функция V должна быть однозначной и дифференцируемой функцией
точки; поскольку же в является циклической координатой, то для
однозначности V мы должны потребовать, чтобы выполнялось условие
периодичности с периодом 27г, т. е. v{r,0 + 27г) = v{r,0).
Положим
Подставляя предполагаемую форму решения в наше уравнение и
производя деление на i^0, получаем
d ( dR^
dr \ dr J , e'' , , 2
+ -- + Xr^ =0.
R 0
Отсюда приходим к уравнениям
в{в) = в{в + 27Г), в'{в) = в'{в + 27Г),
1 _^ / dR\ / _ /i^
г dr \ dr I V г
-- (^—) + (A-^)i^ = 0,
i^(ro) = 0, |i^(0)| < 00.
Нетривиальные периодические решения для 0(^) существуют лишь
при \j? — V? [п — целое число) и имеют вид
0^(^) = В\п cos пд + D2n sin nQ.
Отметим, что собственному значению v? принадлежат две линейно
независимые собственные функции со^пв и sinn^.
Для определения функции R{r) мы имеем уравнение
d'^R 1 dR f ^^А o_Q
dr'^ г dr \ r^ /
с однородными граничными условиями
R{ro) = о,
I Д(0) I < 00.
(24)

456 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Таким образом, для определения функции R{r) мы должны решить
задачу о собственных значениях.
Второе условие, налагаемое на функцию R{r), представляющее
условие ограниченности при г = О, связано с тем, что г = О
является особой точкой уравнения; для особых же точек в качестве
граничного условия достаточно выставить требование ограниченности (см.
Дополнение П, ч. I).
Вводя новую переменную
X = л/Лг
и обозначая
К{г)=к(^^^ =у{х),
получаем для определения функции у{х) уравнение цилиндрических
функций п-го порядка (см. Дополнение П, ч. I)
(Ру 1 dy / п^\ _
dx'^ X dx \ ж^у
с дополнительными условиями
у{хо) = 0 (жо = л/Лго), ^ ^
(26)
\у{0)\<оо.
Общее решение уравнения цилиндрических функций имеет вид
у{х) = diJn{x) + d2Nn{x), (27)
где Jn{x) — функция Бесселя, А^-^ — функция Неймана п-го порядка
(см. Дополнение П, ч. I). Из второго условия следует, что б?2 = 0. Первое
условие дает
^п(л/Аго)=0, или Jn(/i)=0 (/^ = л/Лго). (28)
Если /irn — тп-й корень уравнения Jn{^) = О, то
А„,™ = Ш\ . (29)
Этому собственному значению принадлежит собственная функция
(30)
Rn,m = y{VXr) = J„ -^^ Г .
Отметим следующие свойства собственных функций (30) (см.
Дополнение П, ч. I, § 2).

А.
КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ
457
1. Собственные функции R{r), принадлежащие различным
собственным значениям Л, ортогональны с весом г:
го
/ rRnmi (г) Кпгп2 {г) dr = О {гПх ф Ш2)
о ^ ^
^ (п)
Го
Г \ dr = 0.
2. Квадрат нормы этих функций равен
го
/.J,;(^r)* = | [■'>&'>]'■
в частности, квадрат нормы функции Jq \ —^ г 1 равен
V ^0 /
(31)
(31')
ГО
Jo
/,,(0) М
'^Л
\'' )\
2
dr =
„ ?
io
2
Jlip't^)
(32)
3. Всякая непрерывная в интервале (0,го) функция /(г), имеющая
кусочно-непрерывные первую и вторую производные и
удовлетворяющая граничным условиям задачи, может быть разложена в абсолютно
и равномерно сходящийся ряд:
причем коэффициенты разложения определяются формулой
(33)
го
Jrf{r)Jn
рттг
^0
Г dr
Jm —
"^nKl^m )
(34)
Возвращаясь к задаче о собственных значениях для круглой
мембраны, получим для собственного значения
'^п,т — I I
\ ''о /

458
РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ
[ГЛ. V
две собственные функции
Vn,m = Jn -^^r COS)
\ ''0 /
Jn (^^r jsinn^. (35)
Составив их линейную комбинацию, получим
(Jrb) \
Vn,m {г, 0) = Jn\ -^^ Г {Ащт COS пв + В„^гп sin пв). (36)
V ГО ;
Вычислим норму собственной функции Vn^m] попутно получится
доказательство ортогональности собственных функций, вытекающее
также из общей теории. Для упрощения вычислений ограничимся
собственными функциями Vji^ra'.
27Г го
//
о о
"^ni ,?T2l'^П2 ,77^2 ^ ^^ ^"
го
j Jn,
l^m
(m)
Го
-r\ Jn
' ("2)
Pm2
^0
rdr
COS riiO COS П2О dO
(0 при Til 7^ П2,
0 при m = П2, Ш1 7^7712,
■^ -.2
Jnil^m )\ ^ при m = П2 = n 7^ 0 И Ш1 = Ш2 = Ш,
(37)
-/o(mL"))'
27Г при m = П2 = 0 и Ш1 = Ш2 = Ш.
Аналогичные условия имеют место для функции
/>) \
г'п.ш = Jn -^^ г sinnO.
\ Го /
//■
Выражение для квадрата нормы можно записать в виде
2 2
<mdcT =Y^en [j;(//^')] (da = rdrde), (38)
E
где
J 2 при n = 0,
I 1 при n 7^ 0.

А.
КОЛЕБАНИЯ ОГРАНИЧЕННЫХ ОБЪЕМОВ
459
Из общей теории следует утверждение.
Всякая непрерывная функция F{r, в) с непрерывными первыми и
вторыми производными, удовлетворяющая граничным условиям
задачи, моэюет быть разлоэюена в абсолютно и равномерно сходящийся
ряд
F{r, 0) =Y^ {An,rnVn,rn{'^, 0) + Bn,rn
(39)
no собственным функциям задачи о собственных значениях для круга.
Коэффициенты разложения вычисляются по формулам
А —
27Г го
//
о о
F{r,e)Jn j^^r j cosnOrdrde
7ГГ|
2 "
"^пУРт )
27Г Го
//f(..-.)
' (n)
Jji r sin пв r dr dO
\ ^0 /
0 0
Bri
Отметим, что функция
^e„[j;(ML"))]"
(40)
Vo,m(r,ff) = Jo I -^r
\ro )
не зависит от в.
Если заданная функция F зависит только от г, F = F(r), то ряд,
представляющий разложение F по собственным функциям, будет
содержать ЛИП1Ь функции V()^rn'.
(41)
где
го
J F{r)Jo
рттг
^0
Г \ Г dr
^0,m —
(42)
'О т2
Jlipt^)
Все остальные коэффициенты Ап^ш и Вп^ш равны нулю.

460 РАСПРОСТРАНЕНИЕ ВОЛН В ПРОСТРАНСТВЕ [ГЛ. V
Возвращаясь к исходной задаче колебания мембраны при
заданном начальном отклонении и начальной скорости, можем написать ее
penienne в виде
U{r,e,t)= Y1 ^п,ш{г,0) \ An,rnCOS ^^ + 5n,mSin ^П +
п,т=0 \ /
'^ _ ( аа^ш^ аа^ш^ \
+ У] Vn,rn{r,0) \Cn,rnCOS ^^t-\-Dn,rn^^^ ^n.
n,m=0 \ /
Коэффициенты An,m, Bn,m, Cn,m, Dn,m опрсдсляются ИЗ начальных
условий
сю
U(r,6>,0)= ^ {An,mVn,m + Cn,mVn,m) = fl{r,0),
п,т=0
сю (п)
Щ{г,в,0) = V {Bn,rnVn,rn +Dn,rnVn,rn) ^ = /2(г,6>)
п,т=0
ПО формулам
27Г го
/ / л(^,^) Jn Ы^п,тг] COSnl9ГdrdO
о о
4 —
2
27Г го
^^п [4(л/^п,тГо)]
Г' - Q Q
/ / f2{r,0)Jn (^y^Xn^mrj^mnOrdrdO
2 ^"
.2
Аналогичные формулы имеют место для а y/Xn,m Вп,т и,
соответственно, для а л/Х
п,т
ЗАДАЧИ К ГЛАВЕ V
1. Решить задачу с начальными данными для уравнения колебаний
2 л
utt = ci ^и в пространстве, предполагая, что начальная скорость всюду
равна нулю, а начальные отклонения г^!^—о = (f имеют вид
{;
внутри единичной сферы,
^ вне единичной сферы

I. ПРИВЕДЕНИЕ УРАВНЕНИИ ТЕОРИИ УПРУГОСТИ 461
, Л cos -— г внутри сферы радиуса го,
б) (р= { 2го
О вне сферы радиуса го-
2. РенЕить задачу о колебании полупространства ^ > О при однородном
граничном условии первого или второго рода, если заданы:
а) локальное возмущение, т. е. начальная скорость и начальное
отклонение в некоторой области Tq;
б) сосредоточенная сила, действующая по произвольному закону.
3. РепЕить задачу 2 для слоя —l^z^l.
4. РепЕить уравнение колебаний в области, представляющей собой клин,
угол раствора которого равен 7г/2 и вообще тг/п (п — целое число), если
заданы однородные граничные условия первого или второго рода, а также
начальная скорость и начальное отклонение.
5. Вывести аналог интегральной формулы (3) из § 2 для уравнения
utt = ci Аи + си, где с = const.
Рассмотреть случай с < О и найти penienne задачи с начальными данными
для неоднородного уравнения. Дать физическую интерпретацию
полученных результатов.
6. Найти функцию u{p,(p,t), характеризующую колебания мембраны
под действием импульса К, сосредоточенного
а) в центре круглой мембраны,
б) в произвольной точке круглой мембраны,
в) в произвольной точке прямоугольной мембраны.
7. Найти собственные частоты и собственные функции мембран,
имеющих форму:
а) полукруга,
б) кольца,
в) кругового сектора,
г) кольцевого сектора.
Рассмотреть первую и вторую краевые задачи.
8. Найти установивпЕиеся колебания круглой мембраны (мембраны
микрофона) под действием периодической силы, распределенной по мембране с
постоянной плотностью / = Asinujt. РепЕить ту же задачу, если / = А(1 —
— г^/(?) sinct;^, где с — радиус мембраны.
9. Вывести уравнение распространения звука в среде, движущейся с
постоянной скоростью. Преобразовать полученное уравнение, перейти к
системе координат, движущейся вместе со средой.
прилож:ения к главе v
I. Приведение уравнений теории упругости
к уравнениям колебаний
Теория упругости ставит своей целью изучение возникающих в
упругих телах деформаций и движений при помощи математических

462
ПРИЛОЖЕНИЯ К ГЛАВЕ V
методов. Возникающие под действием внешних сил деформации и
движения можно характеризовать с помощью вектора смещений и,
проекции которого на координатные оси ж, ^, z будем обозначать
u{x,y,z,t), v{x,y,z,t), w{x,y,z,t). Эти смещения возникают в
упругом теле под действием внутренних сил (напряжений), которые
образуют симметрический тензор напряжений
/ СГх
'ух
\
'ху
I zy
' XZ
^yz
CTz
где ах, Гх
У^
— составляющие силы (напряжения), действующей
на единицу площади поверхностного элемента, перпендикулярного к
оси ж; аналогично Тух, сгу, Ту^ и т^х, ^zy, (Jz — компоненты
напряжений, действующих на единицу площади поверхностных элементов,
перпендикулярных к осям у ж z. Компоненты Gx, сгу, Gz
называют нормальными напряжениями, а г^^, Txz и т. д. называют
скалывающими напряжениями. Рассматривая элемент объема
и составляя для него уравнение движения, получаем
д'^и _ дах , дтху , дтхг , ^
df^ дх
ду
dz
d'^v дт,
ух ^^У OTqj
d'^w Otzx
ox oy OZ
dt^
dx
Otzv daz ^
ay OZ
(1)
где p — объемная плотность в точке {x,y,z), X, Y, Z —
составляющие внешних объемных сил. Связь напряжений, возникающих при
деформации, с ее характеристиками дается законом Гука, который
записывается в следующем виде:
При этом величины
^ху — ^'Ухуч
^yz — ^Jyzj
^zx ^ ^Izx -
(2)
Sx =
ди
дх '
£у —
dv
ди dv
'"' ду
dv dw
£z =
dw
dw du
^"^ ~ dy^ dx' ^"^ ~ dz^ dy' ^^" ~ dx^ dz)
(3)

I. ПРИВЕДЕНИЕ УРАВНЕНИИ ТЕОРИИ УПРУГОСТИ
463
образуют симметрический тензор деформаций
/
^х
1уХ
Izx
Ixy
£у
Izy
Ix
ъ
Sz
\
в формулах (2) мы пользуемся следующими обозначениями: G —
модуль сдвига, т — коэффициент, характеризующий сжатие
тела в поперечном направлении при его удлинении в продольном на-
„ ,. ди dv dw
правлении, в = div и = -—\- -—h ^;—.
ох оу OZ
К уравнениям (1) и (2) следует еще присоединить граничные
условия (на границе заданы, например, смещения и, v, w либо
поверхностные силы и т. д.), на которых мы здесь не будем останавливаться.
Уравнения (1) и (2) образуют полную систему
дифференциальных уравнений в частных производных для напряжений и деформаций.
Подставляя выражения для напряжений из (2) в уравнения движения
(1) и учитывая соотношения (3), получаем систему уравнений для
смещений:
^ f л m дв] ^
-{
Aw-\-
771 — 2 dy j
m дв
}-J
(4)
Ш — 2 dz
Часто вводят вместо постоянных G vl т так называемые
постоянные Ламэ Ли/i, связанные с ними соотношениями
2
/i = G,
Л =
С.
ш-2
Это позволяет записать предыдущую систему уравнений в виде одного
векторного уравнения
р —-у = (Л + 2/i) grad div u — /i rot rot u + F,
(5)
где u — вектор смещения с составляющими u, г» и -ш, F — вектор
объемных сил с составляющими X, У, Z. Уравнение (5) обычно называют
уравнением Ламэ.
Покажем, что уравнения (5) могут быть сведены к волновым
уравнениям для соответствующим образом выбранных функций"*^^.
^ Соболев С. Л. Некоторые вопросы теории распространения
колебаний. М.; Л., 1930; Франк Ф., Мизес Р. Дифференциальные и
интегральные уравнения математической физики. М.; Л., 1937. Гл. ХП.

464 ПРИЛОЖЕНИЯ К ГЛАВЕ V
Произвольный вектор F всегда можно представить в виде суммы
F = gradf/ + rotL,
где и — скалярный, а L — векторный потенциал.
Положим
U = gradФ + rot А,
где
Нетрудно убедиться прямой подстановкой, что определенный таким
образом вектор и действительно удовлетворяет уравнениям упругости
(4).
Если объемные силы отсутствуют, то для потенциалов Ф и А мы
получаем однородные уравнения колебаний
д'^Ф д'^А
Уравнение колебаний для векторного потенциала А в некоторых
случаях (например, в декартовой системе координат) распадается на
три скалярных уравнения. Однако вопрос о приведении уравнений
упругости к отдельным скалярным уравнениям колебаний не может
быть рассмотрен до конца без привлечения граничных условий,
которые могут связывать разные компоненты, а в этом случае возникают
значительные трудности для полного расщепления уравнений.
II. Уравнения электромагнитного поля
1. Уравнения электромагнитного поля и граничные
условия. Электромагнитное поле характеризуется векторами Е и Н на-
пряженностей электрического и магнитного полей и векторами D и
В электрической и магнитной индукции. Полная система уравнений
Максвелла, связывающих эти величины, имеет вид
^^^ 1 дТ> 47Г . 47Г ..,^ ,^,
rotH=--- + —J + —j^^), 1
с at с с
divB = 0, (3)
div D = 47гр, (4)

IL УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 465
где j — объемная плотность токов проводимости, j^^^ — плотность
токов, происходящих от действия сторонних ЭДС, р — объемная
плотность зарядов, с — скорость света в пустоте. В дальнейп1ем мы часто
будем считать j^^-^ = 0.
К этим уравнениям следует присоединить так называемые
материальные уравнения поля
D = гЕ, (5)
В = /iH, (6)
J = ^Е, (7)
где £ — диэлектрическая постоянная, р — магнитная проницаемость,
а — проводимость среды. В дальнейшем мы будем предполагать среду
однородной и изотропной. В этом случае г = const, /i = const, а = const.
Мы часто будем рассматривать электромагнитные процессы в
пустоте, где 6 = /i = l, сг = 0, при условии отсутствия зарядов и токов. В
этом случае уравнения Максвелла упрощаются:
rotH=-^, divH = 0,
с at
1 3Y\
rotE = — , divE = 0.
с dt '
Уравнения (1) и (4) совместны, так как между р и j имеется
соотношение
|. divide,
выражающее закон сохранения электрического заряда.
Законы электромагнитного поля, выраженные в
дифференциальной форме уравнениями (1) — (4), могут быть выражены в
интегральной форме:
JHsds=^ jjinda, (1')
С Е
S
где
— полный ток (jcM = -. т: ток смещения). Интегрирование про-
47Г ot
изводится по контуру С и по поверхности Е, опирающейся на этот
контур; Ф = JJ Вп da — поток индукции, пронизывающий контур С.
Е
30 А. Н. Тихонов, А. А. Самарский

466 ПРИЛОЖЕНИЯ К ГЛАВЕ V
Обозначив через Т некоторый замкнутый объем, а через Е —
ограничивающую его поверхность, будем иметь вместо (3) и (4)
//
Bnda = 0, (3')
//
Dnda = 4:7T pdT = 47ге, (4')
где е — полный заряд внутри объема Т.
Уравнения (1') — (4') имеют простой физический смысл и
являются математическим выражением опытных фактов, послуживших
основанием для вывода уравнений Максвелла. Так, уравнение (1') является
обобщением известного закона Био и Савара, уравнение (2')
выражает закон электромагнитной индукции Фарадея, уравнение (4') может
быть непосредственно выведено из закона Кулона, уравнение (3')
является следствием замкнутости силовых линий магнитного поля.
Если среда неоднородна, то к уравнению Максвелла следует
присоединить условия сопряжения. На границе раздела двух разных сред
1 и 2 должны выполняться следующие условия:
£;w = £;p) (9)
(непрерывность тангенциальных составляющих вектора Е),
Hi'^=Hi'^ (10)
(непрерывность тангенциальных составляющих вектора Н), а также
В(1) = Б(2) (11)
(непрерывность нормальных составляющих вектора В),
i'iV - ^»2 = 4^^' и™ e,Ei'^ - e2Ei^^ = 4ж1У, (12)
где П1 и П2 — нормали к поверхности раздела двух сред, причем rii
направлена внутрь первой среды, а П2 — внутрь второй среды, и —
поверхностная плотность зарядов. Эти условия легко получаются из
уравнений (1') — (4').
Уравнения Максвелла вместе с граничными условиями позволяют
однозначно найти электромагнитное поле в пространстве по заданному
начальному состоянию поля. Нри этом для однозначного определения
поля достаточно использовать условия (9) и (10) непрерывности
тангенциальных составляющих поля.
Если электромагнитный процесс является статическим, т. е. не
меняется во времени, то уравнения Максвелла принимают вид
47Г 4:7Т г \
rotE = 0, rotH= — сгЕ+ —з^^\
с с
div еЕ = 47гр, div /iH = 0.

IL УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 467
Если, кроме того, среда не обладает проводимостью, т. е. сг = О, то
мы получаем две независимые системы уравнений для электрического
и магнитного полей:
rotE = 0,
div гЕ = 4:7гр
(уравнения электростатики).
^ } (уравнения магнитостатики),
div /iH=0
Уравнения электростатики были рассмотрены нами в гл. IV и в
приложениях к гл. IV.
В случае однородной среды нетрудно получить уравнения для
каждого из векторов Е и Н в отдельности. Предположим, что р = О,
jW = 0.
Применяя к уравнению (1) операцию rot, имеем
^^ е д ^ 47Г
rot rot Н = - -- rot Е Н а rot Е,
с at с
откуда в силу уравнения (2) и соотношения rot rot Н = grad div Н —
— АН получим
graddxvH-AH = -|^--/-
или
так как
divH = 0.
Аналогично выводится уравнение для Е
1 а^Е 47ra/i Ж
АЕ = \ — . (14)
В частности, компоненты Ех^ Еу, Е^ и Нх, Ну, Н^ векторов Е и Н,
удовлетворяющих уравнениям (13) и (14), будут удовлетворять
аналогичному уравнению
где и — одна из перечисленных компонент.
Характер процесса определяется свойствами среды. Если среда
непроводящая (сг = 0), то мы получаем обычное уравнение колебаний
30*

468 ПРИЛОЖЕНИЯ К ГЛАВЕ V
т. е. электромагнитные процессы распространяются в непроводящей
среде без затухания со скоростью а = с/д/гД, и в частности в пустоте
со скоростью света с.
Если среда обладает больпюй проводимостью и можно пренебречь
токами смещения по сравнению с токами проводимости, то будем
иметь уравнение параболического типа
. 47Гcr/i ди , ^,
В общем случае, когда токи проводимости и токи смещения одного
порядка, уравнение (15) является уравнением гиперболического типа,
описывающим процессы распространения с затуханием, вызываемым
диссипацией энергии вследствие проводимости.
Для установившихся процессов, например в задачах дифракции
мы приходим к уравнению эллиптического типа
Ai; + (A;^-i^^)i; = 0, (18)
где
о;^ 2 4:7та/ло
1=^^- (l^)
Статические поля, как было уже отмечено в гл. IV, описываются
уравнением Лапласа.
2. Потенциалы электромагнитного поля. Для определения
электромагнитного поля мы должны найти шесть величин,
являющихся составляющими векторов Е и Н. В ряде случаев, однако, можно
свести эту задачу к отысканию четырех, а иногда и меньшего числа
величин. С этой целью вводят потенциалы поля — векторный А,
скалярный (f — следующим образом. Рассмотрим уравнение Максвелла
в однородной среде, например в пустоте. Из уравнения (3)
div Н = О
следует, что вектор Н соленоидален и потому может быть представлен
с помощью другого вектора. А, в виде
H = rotA. (20)
Подставляя это выражение в уравнение (2)
1 дН
TotE = --—-,
с at
получаем
1 дА
rot
с at
= 0,

IL УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 469
т. ^ 9А
т. е. вектор Ь Н -— является потенциальным и потому может быть
с at
представлен в виде градиента некоторой скалярной функции (р:
1 дА
E+--- = -grad(/., (21)
с ot
откуда следует
. I дА
Е = -grad(/? —.
с ot
Введенные таким образом векторный потенциал А и скалярный
потенциал (р определены не однозначно. В самом деле, из формул (20)
и (21) видно, что мы получим одни и те же поля, если заменим А и (/?
потенциалами
1 дГ
А' = А + gradF, р' = р - -—-^
с ot
где F — произвольная функция. Чтобы устранить эту
неопределенность, налагают на потенциалы А и (/? дополнительное условие
divA+-5=0, (22)
с ot
называемое часто условием Лоренца. Покажем, что при
выполнении этого условия потенциалы А и (/? удовлетворяют уравнениям
А^ - 4 ё = -4^Л (23)
1 av _
С2 dt^ ~
1 д^А
-47гр,
47Г .
J
с
где р и j — плотности заданных зарядов и токов.
Подставляя выражения (20) и (21) в уравнение (1)
^^ 1 аЕ 47Г .
rotH= -^ + —J
с ot с
и пользуясь векторным тождеством
rot rot А = grad div А — ДА,
будем иметь
grad^d.vA+--j-AA = -- —+ -J,
откуда в силу условия (22) и следует уравнение (24). Подставляя затем
выражение (21) в четвертое уравнение Максвелла
div Е = 4:7гр

470 ПРИЛОЖЕНИЯ К ГЛАВЕ V
и учитывая условие (22), получаем уравнение (23) для (/?.
В случае однородной проводящей среды {а ф 0) потенциалы
вводятся с помощью соотноп1ений
1 дК
В = rot А, E = -grad(/? — . (25)
с di
divA+^^ + l^^ = 0 (26)
А и (/? связаны между собой соотноп1ением
г/i д^ 47Г/.
с Ы с
и удовлетворяют уравнениям
г^ а^А. _ 47r/io- ЗА _ _ 47ф .
к которым относится все сказанное вып1е по поводу уравнений (23) и
(24).
Если свободных зарядов нет (р = 0), то потенциал (/? = О и векторы
поля выражаются через один вектор-потенциал А, удовлетворяющий
дополнительному условию
divA = 0.
В ряде случаев электромагнитные поля можно описывать с
помощью векторного потенциала, у которого отлична от нуля лишь одна
компонента.
Некоторые из примеров будут рассмотрены в дальнейшем (см.
также Приложение I к гл. VH).
3. Электромагнитное поле осциллятора.
1. В теории излучения электромагнитных волн часто
пользуются понятием осциллятора или вибратора. Это понятие тесно связано
с представлением о линейных токах. Осциллятор представляет собой
линейный ток бесконечно малой длины.
Рассмотрим прямолинейный ток L, сила которого меняется во
времени. В простейшей модели предполагается, что сила тока неизменна
по длине проводника.
Ток, постоянный по длине проводника, связан с наличием на его
концах зарядов, меняющихся во времени. Но аналогии с
электростатическим диполем, представляющим совокупность двух зарядов +е и
—е, осциллятор можно характеризовать моментом
p(i)=e(i)l. (29)
Сила тока в осцилляторе, очевидно, равна
j{t) = e{t),

IL УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 471
так что
f = JWl. (30)
Произведение J{t)l = Jo(^) называют моментом тока.
2. Найдем электрическое поле, возбуждаемое осциллятором с
моментом
Р = Po/W (31)
В неограниченном пространстве, предполагая, что сг = 0,г = 1,/^ = 1
(вакуум).
Рассмотрим задачу о возбуждении электромагнитного поля
прямолинейным током L, предельным случаем которого является
осциллятор.
Вне тока L электромагнитное поле определяется из уравнений
Максвелла
rotH=-^, divH = 0,
с at
1 BJ-\
rotE = — , divE = 0.
с dt '
(32)
Ha линии тока L векторы поля Н и E должны иметь особенность,
характеризующуюся тем, что циркуляция по бесконечно малой
окружности К^, охватывающей линию тока L, имеет следующее значение:
/47Г
H,ds= — J, (33)
с
Ке
где J = J{t) — сила тока.
Из этого условия следует, что составляющая Hg на токе имеет
особенность типа
2 /
Я, « — , (34)
ср
где р = |МоР| (Мо — точка на линии L, Р — точка на К^ (при р = г)).
Для однозначного определения поля надо добавить начальные
условия, которые мы предполагаем нулевыми.
Для решения этой задачи целесообразно ввести потенциалы А и
(/?, через которые, как мы видели (см. с. 468), поля выражаются
следующим образом:
H = rotA, Л

472 ПРИЛОЖЕНИЯ К ГЛАВЕ V
причем
divA+-?^ =0. (36)
с ot
Векторный потенциал вне тока L удовлетворяет однородному
уравнению колебаний
1 г^^А
АА-^^ = 0. (37)
Введем декартову систему координат, направив ось z вдоль тока L.
Положим
где z^ — единичный вектор оси z.
Функция Л (ж, у, z), очевидно, удовлетворяет вне линии тока L
однородному уравнению колебаний
1 В'^ А
А^-^^=0. (38)
Чтобы выяснить особенность вектора А на токе, воспользуемся
условием (34). Из уравнения (35) следует, что
дА
др
Пользуясь далее условием (34), находим, что функция А{х, у, z) должна
в точках линии L иметь особенность вида
А^ — \пр. (39)
с
Будем искать потенциал А в виде
A{P,t) = 1 A,{P,M,t)dlM {P = P{x,y,z)), (40)
L
где Ao (P, M, t) = Ai (P, M, t) (им — вектор-потенциал элементарного
тока осциллятора, момент которого равен Jq = J dl.
Для того чтобы потенциал А имел нужную особенность, функция
Ао (Р, М, t) должна иметь особенность вида
Л(Р,М,*)«4^. (41)
в самом деле, предполагая, что Aq имеет указанную особенность, и
вычисляя по формуле (40) значение А вблизи тока L (О < 2; < /), полу-

п. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
473
чаем
~ J cRmp с J
dC
с У Vp' + iz- СУ
= -\n\z-C+ Vp2 + (^ _ ^)2
С L
(l-z)
l+^/p'' + {z- /)2
J
In
-1 + 1 +
2(/
+ ...
2J
z + Vp' + ^'
lnp+...,
где точками обозначены члены, не обращающиеся в бесконечность при
р = 0.
3. Таким образом, функция Ло(Р, М, ^) должна удовлетворять по
переменным P{x,y,z), t уравнению колебаний
АЛ-4^=0
(42)
с2 9*2
всюду, кроме точки М, а, в этой точке она должна иметь особенность
вида
А.
Mt)
(43)
cRmp
Начальные условия в силу сказанного вып1е — нулевые.
Penienne этой задачи, как мы видели в гл. V, представляется в
виде запаздывающего потенциала
Ao{M,P,t) =
Jo{t- Rmp/c)
cRmp
Как было отмечено выше, момент тока равен
Jo(i) = J{t)d\-
dp
"ей
Po/(i).
(44)
(45)
Таким образом, вектор-потенциал осциллятора можно также
представить в виде
Ро/(^ - г/с)
сг
(46)
Часто вместо вектора-потенциала пользуются поляризационным
потенциалом, или вектором Герца П, полагая
1 Ш
с~дГ
(47)

474
ПРИЛОЖЕНИЯ К ГЛАВЕ V
Вектор П также удовлетворяет уравнению
1 д^и
АП-^^=0 (48)
И связан со скалярным потенциалом соотношением
(/? = -divn. (49)
Векторы поля Е и Н выражаются через поляризационный потенциал
с помощью формул
1 д^и
Е = grad div П
Н
С2 dt^
= rot rot П, (50)
1 dU
с at
(51)
Учитывая cooTHOHienne (46), получаем
следующее выражение поляризационного потенциала
для осциллятора:
ро f{t - г/с) p{t - г/с)
11о = , или 11о = .
Рис. 77
(52)
4. Для вычисления полей Е и Н перейдем к сферической системе
координат (г,'i9,(/?), в начале координат которой поместим осциллятор
и направим ось z {'д = 0) вдоль вектора ро (рис. 77). Обозначим через
i^, i^, i^p единичные векторы сферической системы координат.
Вектор По, параллельный вектору р, может быть представлен в
виде
По = По co^'dir — По sin 7^1^,
По = |По|.
(53)
Подставляя выражение (53) в формулы (50) и (51), пользуясь
выражением дифференциального оператора rot F в сферической системе
координат
rotF
1
г sin^^
-(sm^F,)- —
Ir +
г [smr; о(р or
и учитывая, что По = По(г, ^), получаем
2cos?9 dUo
дг
Er —
Eo'i =
г
siwd д
г дг
дПо
дг
1^ +
Е^=0,
(54)

п. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
475
Нг = О, Нг^ = о,
с or at J
(55)
Из уравнений (54) и (55) следует, что электрическое и магнитное поля
осциллятора взаимно перпендикулярны.
5. Рассмотрим частный случай, когда момент диполя
периодически зависит от времени:
p(i)=poe--*.
В этом случае формулы (54) и (55) дают
Er = 2 cos 'д
Е^ = sin 'д
По,
ik
г
е)и„ (. = ^),
Н^ = ik sin'д [ik ) По,
(56)
где
По = Ро е
-iujt
(57)
Исходя из формул (56), легко установить особенности строения поля
осциллятора. На расстояниях, малых по сравнению с длиной волны Л =
= 27:/к {кг ^ 1), в формулах (56) можно ограничиться одним членом.
Получающиеся при этом формулы для напряженности электрического
поля соответствуют полю статического диполя, электрический момент
которого р равен мгновенному значению момента осциллятора p(t).
Для напряженности магнитного поля получается выражение,
соответствующее закону Био и Савара. Па больших расстояниях от диполя
R^ X {кг ^ 1) в формуле (56) можно пренебречь всеми членами более
высокого порядка чем 1/г. При этом получим
Ег = 0, Е^=Н^ = -к^ sin^^Ho, (58)
т. е. поле становится поперечным относительно направления
распространения. Такие удаленные области поля, где поле излучения
становится поперечным, называются волновой зоной осциллятора.
Чтобы подсчитать поток энергии через поверхность сферы радиуса
R с центром в осцилляторе, надо вычислить вектор Умова — Пойн-
тинга
[ЕН]|
5=- _
47Г ' ' ' ' 47Г
и проинтегрировать это выражение по сфере.
ЕН

476 ПРИЛОЖЕНИЯ К ГЛАВЕ V
Из формул (57) и (58) следует, что в волновой зоне вещественная
часть векторов H^^ и Е^ определяется выражением
Н^ = Е^ = ро cos о; U
С^г V с/
откуда
^=-л ^^ cos'a;U-- .
47Г г'^С'^ V с/
Поток энергии через сферу радиуса R за время одного полного периода
Т = 27t/uj будет определяться выражением
Т 7Г 27Г Т
^ = ^ f dt f f SR^ sin^Md^p = ^^ ^ f CDs'" со (t - ^] dt
0 0 0 0
Энергия, излучаемая гармоническим осциллятором, пропорциональна
четвертой степени частоты:
или
1
^-л-
где Л — длина волны.

ГЛАВА VI
РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ
§ 1. Распространение тепла
в неограниченном пространстве
1. Функция температурного влияния. В гл. III было
показано, что процесс распространения тепла в однородном изотропном
пространстве определяется уравнением теплопроводности
щ = а^ Аи (а^ = — ) , (1)
где и{М, t) — температура точки М(ж, ^, z) в момент t^ р — плотность,
с — коэффициент удельной теплоемкости, к = const и а^ = к/{ср) —
коэффициенты теплопроводности и температуропроводности. Уравнение
(1) допускает также диффузионное истолкование. В этом случае и —
концентрация диффундирующего вещества, о? = D — коэффициент
диффузии.
Рассмотрим в неограниченном пространстве следующую задачу.
Найти решение неоднородного уравнения теплопроводности
f ( ^\
щ — а^ Аи Н ( а^ = — ) , —оо < x,y,z < оо, t > О (2)
ср V cpJ
(/ — плотность тепловых источников) при начальном условии
u{x,y,z,0) = (p{x,y,z). (3)
Решение этой задачи может быть представлено в виде суммы
где щ — решение однородного уравнения (1) с неоднородными
начальными условиями, U2 — решение неоднородного уравнения (2) с
нулевыми начальными условиями. При изучении соответствующих
одномерных задач мы видели, что для их решения достаточно определить
функцию источника.
Построим функцию источника для уравнения теплопроводности в
неограниченном пространстве.

478 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Предварительно докажем следующую лемму, которая будет нами
использована в дальнейшем.
Если решение уравнения Аи — 1/а^ • щ = О зависит только от г
и t, то функция V = ги удовлетворяет уравнению
d'^v _ 1 dv
Qj.2 д2 Q-f-
(4)
В самом деле, записывая оператор Лапласа в сферической системе
координат, видим, что функция и = u{r,t) удовлетворяет уравнению
д^и 2 ди _ 1 ди _
Qj.2 J. Qj. д2 Q^
ИЛИ
1 д'^{ги) 1 ди
г дг^' а^ dt
0;
полагая затем ги = г», получаем для v уравнение (4) (ср. с гл. V, § 1,
п. 1).
Пусть в начале координат помещен непрерывно действующий
тепловой источник постоянной мощности д', а в остальном пространстве
начальная температура равна нулю:
u(r, 0) = О при г 7^ 0.
Очевидно, что в этом случае температура и является функцией только
г VL t.
Наличие теплового источника при г = О означает, что тепловой
поток в единицу времени через сферу S^ с центром в г = О и радиусом
£ при г ^ О равен q^ т. е.
lim
-II
к —— da
on
q-
Так как нормальная производная ди/дп = ди/дг в силу симметрии
постоянна на поверхности S^, то
1 9^ л 2
-к -^— • 47ГГ
or
—>- q при г —>- О,
что означает наличие у производной ди/дг при г = О особенности
вида —q/{4:7Tkr^). Следовательно, сама функция при г = О должна иметь
особенность вида
и ~
4:7ткг
так что произведение ги = v остается ограниченным при г = 0.

НЕОГРАНИЧЕННОЕ ПРОСТРАНСТВО
479
Функция г», определяемая условиями
d'^v 1 dv
выражается формулой
v{r,t) = Vo 1 - Ф
Qj.2 д2 Q-f-
i;(r,0) = 0,
2VaH
1 2
4:7гк у/уг
сю
da
(5)
(см. формулу (33) из гл. III, § 3). Следовательно, решение задачи о
распространении тепла при непрерывно действующем источнике
мощности q, помещенном в начале координат (г = 0), имеет вид
сю
u{r,t) = qU{r,t) = q-—---= / е-"" da,
Аттк г д/тг J
(6)
где U{r,t) — температура, соответствующая единичному источнику
Чтобы перейти к случаю мгновенного источника, рассмотрим
источник мощности q, помещенный в точку (^, 77? С) и непрерывно
действующий в течение промежутка времени г.
Такой источник эквивалентен двум источникам мощности: -\-q и
—q, первый из них включается при ^ = О, второй — при t = т.
Распределение температур при этом выражается формулой
Ur{r,t) = q[U{r,t) - U{r,t - т)].
За промежуток времени г выделяется количество тепла Q = qr,
поэтому
Ur{r,t) = ^[U{r,t)-U{r,t-T)].
т
Переходя к пределу при г —>- О и считая Q постоянным, находим
ди 0 2- г^ г
uo(r, t) = lim Ur(r, t) = Q -—- = -— ^ e 4a2t , a^.
uo{r,t) = —G{x,y,z,t;^,r]X),
cp

480 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
где
G{x, у, Z, t; С, ту, С) = -^^ е ^аЧ . (7)
Функция G{x,y,z,t;^,r]X) есть функция температурного
влияния мгновенного источника тепла. Она представляет собой
температуру в точке X, у, Z в момент времени t, вызываемую точечным
источником мощности Q = ср, помещенным в момент ^ = О в точку
(е,'?,С)-
Нетрудно убедиться в том, что
G{x,y,z,t;^,r]X)d^r]dC = l. (8)
В самом деле, тройной интеграл (8) можно представить в виде
произведения трех интегралов, каждый из которых равен единице:
сю сю
г 1 (^-О 1 /• 2 / £-а; \
/ , е 4a2t d^=^ е-" da = l ia= ^^ .
— СЮ —сю
Из формулы (7) видно, что функция влияния G обладает
свойством симметрии
G{x, у, Z, t; ^, ту. С) = G(^, ту. С, t; ж, у, z),
являющимся выражением принципа взаимности: действие в точке
{x,y,z) источника, находящегося в точке (^,ту,С), равно действию в
точке (^,ту,С) такого же источника, помещенного в точку {x,y,z).
Однако относительно переменной t такая симметрия не имеет места, что
является выражением необратимости тепловых процессов во времени.
Определим вид функции влияния G в случае двух измерений.
Пусть на прямой, параллельной оси z и проходящей через точку (^, ту),
расположен бесконечный линейный источник; обозначим через Q =
= const мощность источника, отнесенную к единице длины. Функция
влияния G2 такого источника не будет зависеть от 2; и вполне
характеризуется своими значениями в плоскости (х^у). Вычислим функцию
G2- Пусть на элементе d( выделяется количество тепла
dQ = QdC,
тогда распределение температуры в пространстве дается интегралом
сю _
= / G{x,y,z,t;^,r]X)-
J ср

§ 1] НЕОГРАНИЧЕННОЕ ПРОСТРАНСТВО 481
Вычисляя интеграл
сю
"'^а = 2лЛ^ (а- ^
Г i^-cr I [ 2
2^JoH
получаем
где
ср
2 ('^_t^2_l
Сопоставляя эту функцию с формулой (7), видим их сходство по
структуре.
Аналогичным способом можно получить выражение для функции
источника в одномерном случае. Рассматривая бесконечный плоский
источник с постоянной плотностью Q, получаем
сю сю = =
J J ср ср
— сю —сю
где
1 (х-О'^
Gi{x,t;0
2 Vira^t
— функция источника для одного измерения.
В гл. III были даны графики, характеризующие поведение
функции влияния G{x,t;^). Качественная характеристика функции
источника, данная там же, имеет место и для пространственного случая.
2. Распространение тепла в неограниченном
пространстве. Используем теперь функцию источника, полученную в
предыдущем пункте, для решения задачи о распространении начальной
температуры в неограниченном пространстве.
Пусть требуется найти решение уравнения
щ = а^ Аи, —oo<x,y,z<oo, t > О, (1)
удовлетворяющее начальному условию
u{x,y,z,0) = (p{x,y,z). (3)
Начальное температурное состояние, очевидно, можно
представить как результат суперпозиции действия мгновенных
источников, создающих начальную температуру. Рассмотрим элемент объема
d^dr]d(, содержащий точку {^,г]Х)- Для создания начальной
температуры ^{£,,г]Х) необходимо в объеме d^drjdC, поместить количество
тепла dQ = ср(р{^, vX) d^ dr] d(.
31 A. Н. Тихонов, A. A. Самарский

482 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Это сосредоточенное количество тепла создаст в точке {x,y,z) в
момент t температуру
— G{x, у, Z, t; ^, Г], С) = G{x, у, z, t; ^, ту, С) ^{^, V, С) d^ dr] dC,. (9)
ср
В силу принципа суперпозиции penienne нап1ей задачи может быть
получено интегрированием (9) по всему пространству:
сю
u{x,y,z,t) = /// G{x,y,z,t;^,r]X)H^,vX)d^dr]dC. (10)
Формула (10) получена нами в результате наводящих рассуждений, не
определяющих границы ее применимости и не имеющих доказательной
силы.
Докажем следующее утверждение.
Если функция (р кусочно-непрерывна и ограничена, \(р\ < А, то
функция и, определяемая выраэюением
u{x,y,z,i)^\-—==\ JJIe 4a2t ip{^,r]X)d^dr]dC,
— сю
(10')
1) ограничена во всем пространстве: \и\ < А;
2) является решением уравнения теплопроводности при t > 0;
3) при t = О непрерывна в точках непрерывности функции (f и
удовлетворяет условию u{x,y,z,0) = (p{x,y,z).
Для доказательства того, что (10') удовлетворяет уравнению (1),
воспользуемся известной леммой (см. гл. III, § 3).
Пусть U{x,y,z,t;^) при любом значении параметра ^ является
решением уравнения С{и) = О, где С{и) — линейный
дифференциальный оператор. Тогда функция
u{x,y,z,t) = / U{x,y,z,t;^)(f{^)d^
такэюе будет решением уравнения С{и) = О, если производные
функции U, входящие в оператор С{и), моэюно вычислять
дифференцированием под знаком интеграла.
В нашем случае U = G удовлетворяет уравнению
теплопроводности при любых ^, ?7, С и ^ > 0. Как известно, дифференцирование
по параметру под знаком несобственного интеграла возможно, если:
1) производная по параметру от подынтегральной функции
непрерывна и 2) интеграл, полученный после формального дифференцирования,
равномерно сходится.

§ 1] НЕОГРАНИЧЕННОЕ ПРОСТРАНСТВО 483
Произведя формальное дифференцирование интеграла (10') по ж,
получим
сю
"^ ^'е ^аЧ ^{^,r]X)d^r]dC (И)
2аН
Подынтегральная функция непрерывна при f > ^ > О, а наличие
множителя е 4а2* обеспечивает равномерную сходимость,
если (f ограничено: \(f\ < А. Аналогичные результаты мы получим при
повторном дифференцировании по ж и при дифференцировании по ^; то
же относится и к дифференцированию по ^ и 2;. Таким образом,
функция G удовлетворяет всем условиям леммы при ^ > 0. Следовательно,
функция и при ^ > о удовлетворяет уравнению теплопроводности.
Ограниченность функции и, определяемой формулой (10'),
которую мы перепишем в виде
u{M,t)
сю
|||G{M,M',t)^p{M')dтм',
M = M{x,y,z), M' = M\i,r^,0,
устанавливается непосредственно, если принять во внимание
равенство (8):
и\<А GdT = A. (12)
Перейдем к доказательству непрерывности u{x,y,z,t) при ^ = 0.
Рассмотрим точку Mo{xo,yo,zo), являющуюся точкой
непрерывности функции (/?, и докажем, что для любого г > О существует такое
S{e) > О, что
\u{M,t)-(f{Mo)\<e при \MMo\<S{e) и t<5{e). (13)
Построим вспомогательную область Ti, содержащую точку Мд;
ее размеры будут определены ниже; остальную часть пространства
обозначим через Т2. Принимая во внимание равенства
u{M,t) = fffG{M,M',t)^{M')dTM' + fffG{M,M',t)^{M')dTM4
Ti T2
^{Мо) = JJJ G{M,M',t)ip{Mo)dTM'+^{Mo)JJJ G{M,M',t)dTM4
Ti T2
31*

484 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
а также положительность функции G{M, М' ^t)^ будем иметь
|и(М,^)-(/.(Мо)|^ J1 + J2, (14)
где
J^ = JJJ G{M,M',t)\^{M')-^{Mo)\dTM4 (15)
J2 = 2А III G{M, M', t) dTM>. (16)
Из непрерывности функции ^ в фиксированной точке Mq следует:
каково бы ни было т] > {)^ найдется такое 5'{rf) > О, что
то
\ip{M') - ip{Mo)\ < Г], если \М'Мо\ < 6\г]).
Следовательно, если диаметр области Ti не превосходит S'{e/3),
сю
Ti -00
Остановимся теперь подробно на выборе области Ti. В качестве
Ti мы можем выбрать сферу с центром в точке M{x,y,z), что удобно
для оценки интеграла J2. Оценка (17) интеграла Ji сохраняет силу,
если радиус этой сферы выбрать равным
Ро 2
^'(1)
И если \ММо\ < Ро.
Переходя к сферической системе координат с центром в точке М,
получаем
3 7 2
[[[ Gdr = 47г(—^=) [е ^a^tr'^dr
JJJ \2лЛ^^У J
РО
= —= / а^е""" da > —= / а^е""^ б?а = 1
л/тг У ^^0 л/тгУ
о о
так как
оо сю
2VaH
f а^е""" rfa = - ^ ае""' +\ J ^~"
А
,2
4
о о

§ 1] НЕОГРАНИЧЕННОЕ ПРОСТРАНСТВО 485
Таким образом,
[[[Gdr = 1 - [[[Gdr ^0 при ^ ^ О,
т. е. для всякого г > О можно указать такое S"{e), что
Т2
И, следовательно,
J2 < I, (18)
если только t < S"{e).
Выбирая из чисел 1/2 • S'{e/3) и S"{e) наименьшее и обозначая его
через S{e), будем иметь неравенство
\u{M,t)-(f{Mo)\<e при \MMo\<S{e) и t<S{e), (13)
которое и доказывает непрерывность и{М, t) при ^ = О во всякой точке
Мо непрерывности функции ^{М).
Перейдем теперь к решению неоднородного уравнения
щ = а^ An Н , —00 < ж, ^, 2; < 00, ^ > О,
при нулевом начальном условии и(ж,^,2;,0) = 0. Рассмотрим точку
(^, ?7, С) в момент времени т < t. Количество тепла, выделяющегося
в элементе d^ dr] d( за время dr и равное
dQ = f d^ dr] d( dr,
обеспечивает в точке {x,y,z) в момент времени t температуру
— G{x, у, Z, t; ^, ту. С, г) /(^, ту. С, г) d^ dr] dC dr.
cp
Пользуясь принципом суперпозиции, мы можем написать решение
поставленной задачи в виде
t сю
u{x,y,z,t)= / /// —G{x,y,z,t;^,r]X,r)f{^,r]X,r)d^dr]dCdT.
о -оо
(19)
Па доказательстве справедливости этой формулы и выяснении
условий ее применимости мы не останавливаемся.
Задачи для полупространства с однородными граничными
условиями первого и второго рода решаются методом отражения.

486 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
§ 2. Распространение тепла в ограниченных телах
1. Схема метода разделения переменных. Ранее мы
рассматривали распространение тепла в неограниченном пространстве. При
изучении распространения тепла в ограниченном теле необходимо к
уравнению и начальному условию добавить условия на границе
тела, которые в простейших случаях являются граничными условиями
первого, второго или третьего рода.
Рассмотрим простейшую задачу с однородным граничным
условием первого рода.
Найти решение уравнения теплопроводности
щ = а^ Аи внутри Т при ^ > О (1)
с начальным условием
u{x,y,z,0) = (f{x,y,z)
и граничным условием
^|е=0,
где Е — граница области Т.
Решение этой задачи может быть получено обычным методом
разделения переменных, изложенным применительно к уравнению Uu =
= а^ Аи в гл. V, § 3; применяется этот метод к нашей задаче
совершенно аналогично.
Рассмотрим вспомогательную задачу.
Найти нетривиальное решение уравнения
щ-а'^ Аи = 0 в Т при ^ > О, (2)
удовлетворяющее однородному граничному условию
^|е = 0
и представимое в виде произведения
u{M,t) =v{M)T{t) ^0.
Разделяя переменные обычным способом, приходим к следующим
условиям, определяющим функции v{M) и T{t):
А^ + Ai; = О в Г, v{M) ^ О, 1
i; = О на Е J ^ ^
и
Г+ а^ЛГ = 0. (4)
Для функции V получаем задачу на отыскание собственных значений,
с которой мы встречались при рассмотрении колебаний ограниченных
обьемов (см. гл. V, § 3, п. 1).

§ 2] РАСПРОСТРАНЕНИЕ ТЕПЛА В ОГРАНИЧЕННЫХ ТЕЛАХ 487
Пусть Ai, Л2, ..., An, ... — собственные значения, а vi, V2, ...
... ,Vn, • • • — собственные функции задачи (3). Функции {vn} образуют
ортогональную систему.
Соответствующие функции Tn{t) имеют вид
Tn{t) = С„е-«'^"*,
И вспомогательная задача имеет нетривиальное решение
Un{M,t) = CnVn{M)e-^'^-'. (5)
Общее решение исходной задачи может быть представлено в виде
сю
u{M,t) = Y,Cne-''^-'vn{M), (6)
п=1
Удовлетворяя начальному условию
сю
и{М, 0) = ^{М) = ^ CnVn{M), (7)
п=1
находим коэффициенты
/
(f{M')vn{M')dTM'
On — —
WnW =
j<{M').
норма функции v^
Ьп\?
где
) dTMi —
.т J
Функция (6) и представляет решение задачи.
Уравнение
ut-a'Au = f{M,t) (/=^) (8)
при однородных граничном и начальном условиях может быть также
решено методом разделения переменных.
Полагая, как обычно,
сю
u{M,t) = J2Tn{t)vn{M) (9)
п=1
и разлагая функцию f{M,t) по собственным функциям Vn{M):
f{M,t) = y2U(t)Vn(M), fn{t) = ---r^ / f{M',t)Vn(M')dTM',
(10)

488 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
получаем для определения Tn{t) уравнение
T'^ + a''\nTn = fn{i) (11)
С начальным условием Т^(0) = О, если и(М, 0) = О, penienne которого
имеет вид
t
T„{t) = le-^'^"^*--^fniT)dT. (12)
О
Отсюда получаем
"(^' ^) = / / {£ '~'^^'" '~^' ^T^F^} ^^''' "^'""''"
(13)
Выражение в фигурных скобках, очевидно, соответствует функции
влияния мгновенного источника мощности Q = ср, помещенного в
точку М' в момент г:
сю
^1 IKIP
G(M,^,M',r) = V ^'"V-y -»^- ^ е-» ^" (*--). (14)
Решение первой краевой задачи й для уравнения
теплопроводности с неоднородными граничными условиями й\^ = /i легко
приводится к решению и неоднородного уравнения с однородными граничными
условиями U |е = О, если положить
й = и-\-Ф, (15)
где Ф — произвольная (достаточно гладкая) функция, принимающая
значения /i на Е (см. гл. П1, § 2). Весьма часто встречающийся случай
постоянных граничных значений, /ig = const, приводится к задаче с
однородными граничными условиями, если ввести функцию
й = и -\- /jQ (Ф = const = /io),
представляющую отклонение от стационарного решения.
Таким образом, основная трудность при решении задач о
распространении тепла в ограниченной области состоит в нахождении
собственных функций и собственных значений для данной области.
Форма решения (6), полученная методом разделения переменных,
удобна для исследования достаточно развитой стадии процесса при
больших t. В самом деле, собственные значения Л^ для любой
области быстро возрастают с номером п. Поэтому при ^ > О ряд быстро
сходится и, начиная с некоторого момента, первый отличный от нуля
член преобладает над суммой остальных членов:
и{М, t) ^ Civi (М) e-^'^l^ (16)

§ 2] РАСПРОСТРАНЕНИЕ ТЕПЛА В ОГРАНИЧЕННЫХ ТЕЛАХ 489
Это соответствует тому физическому факту, что независимо от
начального распределения, начиная с некоторого момента, в теле
устанавливается «регулярный» температурный режим, при котором
«профиль» температуры не меняется во времени и амплитуда убывает
по экспоненте с возрастанием времени. Этот факт положен в основу
нестационарных методов определения коэффициента
температуропроводности. В самом деле, измеряя температуру тела в произвольной
точке Мо, находим, что
In \u{Mo,t)\ ^ -a^Xit + In \CiVi{M)\. (17)
График этой функции изображается, начиная с некоторого
момента времени, прямой линией с угловым коэффициентом —o?\i. Зная
величину Ai, зависящую от формы области, можно найти
коэффициент температуропроводности.
2. Остывание круглого цилиндра. Рассмотрим задачу об
остывании бесконечно длинного цилиндра радиуса го, имеющего
некоторую начальную температуру, если на его поверхности
поддерживается температура, равная нулю. Предположим, что начальная
температура не зависит от z (ось z направлена вдоль оси цилиндра).
Тогда, очевидно, в дальнейшем температура также не зависит от 2; и
меняется только в поперечном сечении S цилиндра. Выбирая в этом
сечении полярную систему координат с полюсом, находящимся в
центре круга 5, мы приходим к задаче об определении функции u{r,(p,t),
удовлетворяющей уравнению
д'^и 1 ди 1 д'^и 1 ди
Qj.2 J. Qj, J.2 Qf^2 g2 Qf
начальному условию
и граничному условию
u{r,ip,0) = Ф{r,ip) (19)
u{ro,<p,t)=0. (20)
Как мы видели, решение задачи такого типа может быть
представлено в виде
сю
и = ^С„е-«'^"*г;„(М), (21)
П=1
где суммирование распространяется на все собственные функции
задачи:
d'^v 1 dv 1 d'^v , ^
аг^ г or г^ o(f'^
v{ro,(f) = 0.
(22)

490 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Эта задача на собственные значения была исследована нами при
изучении колебаний круглой мембраны (см. гл. V, § 3). Каждому
собственному значению
2
'^тп, —
^^
(п)'
Го
(23)
соответствуют две собственные функции
Упт = Jn -^^ Г COSTKf И Vnm = Jn ^^ Г sinn(/?, (24)
квадраты нормы которых равны
^nXi
т о
J:
п (/^т )
Хп)
где firn — ^^-и корень уравнения
Jn(/i)=0.
Пользуясь выражениями для г» и Л, получаем
(26)
и{г, V?, *) = X] XI (^"^ ^°^ '^'^ + ^""^ ^^^ '*'^) "^"
п=0 т=1
Го
-Г е
(п)
(27)
где коэффициенты Спт и Спт определяются начальной функцией
^0 27Г
/ / Ф{r,(f)Jn
Го
Г I COS п(/? г d(^ dr
^пт, —
О О
^ пт —
^0 27Г
/./ *•-
0 0
7ГГ2
2 "
,'p)Jn
[^;(/*L"')]'
/ (п) \
V ^0 J
\ /
^in TKfi
"- difdr
ТТГП
~ \2, п = 0.
'п (Mm )
(28)
Если начальная температура Ф зависит только от г, то двойной ряд
(27) заменяется однократным рядом
2
/.,(0) \ -«'( ^ М
,^r,t)=Y.^rnJo[^r\e V
.(0)
(29)

§ 2] РАСПРОСТРАНЕНИЕ ТЕПЛА В ОГРАНИЧЕННЫХ ТЕЛАХ 491
где
2 U{r)Jo('^r\rdr
Cm = -^ , ,^^,,2 (-^1 = --^о), (30)
а fim — ^^-й корень уравнения Jo(/i) = 0.
Остановимся подробнее на задаче об остывании равномерно
нагретого цилиндра при нулевой темературе на поверхности. Если
начальная температура
u(r,0) = Ф = uo,
то
2uo I Jo I —^ г \ rdr
\ ^° / 2и
О / Jo
так как aJo(a) = [aJi{a)]'. Таким образом, мы получаем
»(f,t) ^ ^ "о (А°У) _(,»))'
«о ir'w,.L°)j,(/.W)^ V" го' - г,
.2,
В таблицах цилиндрических функций (см. с. 766, табл. 3) даются
" (0) 7 Мо)А
численные значения как для корней /i^n , так и для Ji (/i^n I •
Например,
11^^^ ?^2,40, Ji (/i^^^) ?^0,52,
Ряд (31) сходится быстро, и при больших t можно ограничиться
первым членом этого ряда. В частности, на оси цилиндра
u{r,t)
Щ
^^0 2,40 . 0,52
2 e-(2,40)2^^^gQ^-5,76^ fe = ^y (32)
3. Определение критических размеров. Процесс диффузии
неустойчивого газа, скорость распада которого пропорциональна
концентрации, приводит к уравнению
щ = а^Аи + Ри (/3<0). (33)

492 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Большой интерес представляют процессы диффузии при наличии
цепных реакций. Цепные реакции характеризуются тем, что
частицы диффундирующего вещества, вступая в реакцию с окружающей
средой, «размножаются». Так, например, при столкновении нейтронов
с «активными» ядрами урана происходит реакция деления ядер,
сопровождающаяся появлением новых нейтронов, число которых больп1е
единицы. Эти нейтроны в свою очередь вступают в реакцию с
другими активными ядрами, вызывая их деление с выделением новых
нейтронов, и т. д. Таким образом происходит процесс размножения
нейтронов, носящий характер цепной реакции.
Рассматривая описанный процесс в «диффузионном
приближении», мы приходим к следующему уравнению:
щ = а'^Аи + ри (/3>0), (330
так как цепная реакция эквивалентна наличию источников
диффундирующего вещества (нейтронов), пропорциональных концентрации
(плотности нейтронов).
Рассмотрим следующую задачу.
Найти решение уравнения (33)
щ = а^ Аи + /Зи внутри Т,
удовлетворяющее начальному условию
и(М,0) =(f{M) (34)
и граничному условию
п|е=0. (35)
С помощью подстановки
u{M,t) =u{M,t)e^^ (36)
уравнение (33) переходит в уравнение (1); начальные и граничные
условия при этом остаются неизменными. Таким образом, искомая
функция и имеет вид
сю
и{М, t) = Y, С„е('5-'^'^") * Vn{M), (37)
П=1
где Сп определяются начальной функцией по формуле (10). В случае
/3 < О (диффузия с распадом) показатели ряда (37) меньше
соответствующих показателей ряда (6). Это означает, что при наличии
распада убывание концентрации происходит быстрее по сравнению со
случаем чистой диффузии (/3 = 0). В случае /3 > О (диффузия с
размножением), если хотя бы один из показателей /3 — о?\ > О, т. е. /3 > a^Ai,
то с течением времени будет происходить, вообще говоря (Ci ф 0),
нарастание концентрации по экспоненциальному закону (цепная
реакция). Величина [3 является характеристикой вещества (коэффициент

§ 3] ЗАДАЧИ ДЛЯ ОБЛАСТЕЙ С ПОДВИЖНЫМИ ГРАНИЦАМИ 493
размножения), а Ai существенно зависит от формы и размеров
области. Будем говорить, что некоторая область Ткр имеет при заданном [3
критические размеры, если Ai = [З/о?. Определим критические
размеры для бесконечного слоя, цилиндра и сферы.
1. Бесконечный слой О^ж^/. Считая задачу одномерной,
имеем (см. гл. II, § 3)
А.
/7ГП\2 7Г^
/,р = ^ « ^^ (/3 > 0). (38)
Критическая толщина слоя /кр, начиная с которой будет происходить
процесс лавинного нарастания концентрации и, определяется из
условия
атг 3,14 а
2. Бесконечный цилиндр. Считая задачу плоской, видим,
что наименьшее значение А соответствует собственной функции,
обладающей радиальной симметрией, и равно
/ (0) \ ^
Л(^)=^ (/.(^)« 2,4048).
Отсюда для критического диаметра получаем формулу
3. Сфера. Наименьшее значение А соответствует собственной
функции, обладающей сферической симметрией, и равно
откуда для критического диаметра £>кр получаем формулу
2-ка _ 6,28 а
Dkp = ^^ « ^^ . (40)
§ 3. Краевые задачи для областей
с подвилсными границами
1. Формула Грина для уравнения теплопроводности и
функция источника. Для уравнения теплопроводности можно ставить краевые
задачи для областей с границами, перемещающимися со временем.
Для простоты будем рассматривать эту задачу для уравнения с одной
геометрической переменной
С{и) = а Uxx - щ = 0j (1)

494 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
хотя все изложенное ниже может быть перенесено на случай многих
переменных.
^1 Рассмотрим область BAEF (рис. 78),
ограниченную характеристиками АВ и EF
{t = const) и кривыми, определяемыми урав-
Mi / нениями
М 1о x = xi{t) (для АЕ)
и
x = X2{t) (для BF).
Первая краевая задача для этой области со-
^^' стоит в определении рептения уравнения
теплопроводности (1), удовлетворяющего начальному и граничным условиям
и = (^(ж) на АВ^
..}
(2)
Из принципа максимального значения непосредственно следует, что эта
задача не может иметь более одного непрерывного репЕСния. Аналогично
могут быть поставлены и другие краевые задачи.
Установим формулу Грина для уравнения (1) и интегральное
представление репЕСний этой задачи.
Рассмотрим оператор
интегрируя выражение
'фС{(р) - (fMitp) = а (tpifx - (р'фх)х - {^^)t
по некоторой области PABQ (рис. 78), где ^{x^t) и ф{х,1) — произвольные,
достаточное число раз дифференцируемые функции, и пользуясь формулой
Грина, получаем
I 1[фС{^р)-^рМ{ф)](1х(И= j> \лрф(1х + а^ ('^||~'^|^)Н '
где правый интеграл берется по замкнутому контуру PABQ. Если С{^р) = О
и Л4{ф) = О, то, преобразуя правую часть, получаем
/ срф dx = срф dx -\- \ срф dx -\- а (ф — ср ^— ) dt
PQ АВ BQ
д(р дф\
— (П I ,
I
h-^-l^g-^S)-]^ ,4,
АР
Пусть (^(ж, t) = и{х^ t) — какое-либо penienne уравнения
теплопроводности С{и) = О, а -0 = Go{x,t,$,,T) — функция источника для этого уравнения
на неограниченной прямой, равная
Go{x,t,^,T)= AaHt-r)^ (5)
2 у^тга^ {t - т)

§ 3] ЗАДАЧИ ДЛЯ ОБЛАСТЕЙ С ПОДВИЖНЫМИ ГРАНИЦАМИ 495
часто называемая фундаментальным ренгением уравнения
теплопроводности. Функция Со(ж,^,^,г) удовлетворяет уравнению
C{Go) = О по переменным ж, ^ и сопряженному уравнению A4{Go) = О по
переменным ^, т.
Пусть M(xjt) — некоторая фиксированная точка внутри области
BAEFj в которой мы хотим определить значение функции u{xjt)j а Mi —
точка с координатами (ж,^ + /г), где h > 0. Проводя через точку М
характеристику PQj заменяя в формуле (4) ж на ^, ^ на г и применяя (4) затем к
области ABQP (рис. 78) и функциям
<^ = '^(С,^)
ф{^,г) = С^{х,1 + Н,^,г),
будем иметь
(6)
/
PQ
u{U)d^ =
-- [ \u{^,T)Go{x,t + h,^,T)d^ + a^ fGoЦ-u^^dт] . (7)
PABQ
Переходя к пределу при /г ^ О и учитывая непрерывность по h функции
Go{x,t + /г,^,г) и дОо/д^ на PABQ, а также равенство
е 4:a^h
lim / ,
^^0 J 2 Vna^h
PQ
lim /
h^o J
u{$,,t) d$, = u{x,t)
(8)
(cm. гл. hi, § 3.), если (x^t) лежит на отрезке PQ, получаем основную
интегральную формулу
u{x,t)
/ u{^jr)Go{x,t,^,T)d^-\- / а'^ lOo —-u-^j dr,
(9)
PABQ
BQ+PA
дающую представление произвольных peniennn уравнения
теплопроводности. НерепипЕСм ее еще раз более подробно:
u{x,t)
I
4а2 (t-r)
PABQ
2 у^тга^ {t - г)
u{^,r)d^ +
. /
BQ+PA
{x-iY
' (*--) ди
2 v^Tra^ (t - r) ^C
dr-
BQ+PA
и{^^г)щ
g 4a2 (t-т)
\
2 y'na^ (t - t]
dr.
(9')
Эта формула не дает репЕСний краевых задач, так как для вычисления
правой части надо знать значения не только п, но и ди/д^ вдоль дуг АЕ и
BF.

496
РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
При помощи преобразования, подобного тому, которое было выполнено
для уравнения Лапласа при введении функции источника, можно исключить
из этой формулы ди/д^.
Пусть V — какое-либо рептение сопряженного уравнения M{v) = О,
обращающееся в нуль на PQ, и п — penienne уравнения
теплопроводности С{и) = 0. Применив формулу (4) к функциям v vi и для области PABQ,
получим
О
/
u{^jr)v{^,T)d^-\-a
ди
dv
д^ ^^С
dr
PABQ
Вычитая из (9) равенство (10), будем иметь
u{x,t)
I
PABQ
и(^, г) G{x, t, (,, T)d(, + а
ди
где
G{x,t,i,T) = Со(ж,^,^,г) -V.
Если функцию V выбрать так, чтобы
G = 0 на РА и BQ,
то получим интегральное представление для u{xjt) в виде
(10)
(И)
(12)
u{x,t)
-- / u{^iT)G{x,t,^,T)d^-\-a^ / u-—dT-a' I и-—dr.
AB АР BQ
(13)
Формула (13) дает penienne краевой задачи (1) — (2), в условиях которой
задаются значения функции и на АР и BQ^ а также на прямой АВ.
Остановимся подробнее на рассмотрении функции G. Она определяется
при помощи представления (12), где функция г;(^,г) характеризуется
следующими условиями:
1) г;(^, г) определена в области PABQ и для т <t удовлетворяет
сопряженному уравнению M{v) = 0;
2) г» = О на PQ, т. е. при т = t]
3) v{^,t) = -Со(ж,^,^,г) на РА и QB.
В силу этих условий функция V зависит от параметров ж, ^, так что
V = г;(ж,^,^,г), и для ее определения надо репЕить краевую задачу для
уравнения A4{v) = О, которая эквивалентна рептению краевой задачи типа (2)
для уравнения С{и) = О, в чем легко убедиться изменением знака у т.
Таким образом, при представлении функции u{x,t) с помощью формулы (11),
дающей penienne краевой задачи (2), основная трудность заключается в
нахождении функции г;(ж,^,^,г).
Рассмотрим функцию ^(ж,^,^,г), определяемую условиями:
1) ^(ж,^,^,г) определена в области PABQ для ^ > г и как функция
переменных ж, t удовлетворяет уравнению теплопроводности C{v) = 0;
2) ^ = О на АВ, т. е. при t = т]
3) V = -Go на АР и BQ.
Докажем, что г;(ж,^,^,г) = 'г;(ж,^,^,г).

§ 3] ЗАДАЧИ ДЛЯ ОБЛАСТЕЙ С ПОДВИЖНЫМИ ГРАНИЦАМИ 497
Рассмотрим функцию G{x,t,^,T) = Go-\-v. Очевидно, что для любого
ренЕСния й уравнения Л4{и) = О имеет место формула, аналогичная (9):
й{^^г)= / uGodx-\-a'^ (й-^-Go—] dt, {9")
BQPA
а также формула, аналогичная (13):
^i^^'^) — / uG dx-\-а I й ^—dt — а / й——dt. (13')
PQ BQ АР
Эти формулы могут быть получены из формул (9) и (13) изменением знака
у г, так как при этом уравнение Л4 = О переходит в уравнение С = 0.
Применяя формулу (13) к области PQSR (рис. 79), где RS — отрезок
прямой, соответствующий ординате ^, (^ > ^ > г), и к непрерывному в этой
области репЕСнию u{x,t) = (5(ж,^,^,^) уравнения С{и) = О, получим
e,.,„.„ = /e,.'.,«,.,G,..,./,„^'.
RS
так как интегралы по RP и SQ в силу условия 3 равны нулю.
Применяя аналогично формулу (13 ) к области ARSB и непрерывному
в этой области рептению й(^, г) = С(ж,^, ^, г) уравнения М(и) = О, получаем
й,.,„.„ = /о,м,.'..)в(.',«,«,.)^'.
RS
так как интегралы но BS ж AR равны нулю. Сравнение этих формул
показывает, что
G{x,t,^,r) = G{x,t,^,r).
Q
Из этого равенства следует, что функция
G, рассматриваемая как функция ж, ^,
имеет при ^ = г и ж = ^ особенность,
характерную для функции источника, равна нулю
при t = т ж X ф ^^ удовлетворяет
уравнению Cx,t{G) = О внутри APQB и
обращается в нуль на АР и BQ. Такую функцию Рис. 79
естественно назвать функцией
влияния точечного источника для уравнения теплопроводности в области
APQB.
Итак, любое решение уравнения теплопроводности может быть
представлено формулой (13) при помощи функции источника.
Если задано неоднородное уравнение С{и) = f{xjt)j то в формуле (13)
к правой части следует прибавить слагаемое
//'
G{x,t,^,T)f{^,T)d^dT.
S
32 А. Н. Тихонов, А. А. Самарский

498
РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
2. Решение краевой задачи. Полученная Bbinie формула (13) дает
реп1ение краевой задачи для ограниченного отрезка с подвижными
концами. Если же концы отрезка АВ неподвижны, то дуги АЕ и BF заменяются
отрезками прямых, параллельных оси t. Область S в этом случае имеет
вид прямоугольника со сторонами, параллельными координатным осям. Из
общей формулы (11) можно предельным переходом получить формулу
Пуассона, дающую репЕСние уравнения теплопроводности с заданным начальным
условием на бесконечной прямой.
Предположим, что в части полосы,
ограниченной двумя характеристиками
^ = О и ^ = ^, проходящими через точки
А ж Е (рис. 80), функции и ж Ux
удовлетворяют неравенствам
^2
Е
Р
\
t
8 t = 6
t = 0 X = I
F
Q
X
Рис. 80
|n(x,^)| e
du
dx
-Kx^
<N
-Kx^
(A)
<N,
где i^>OHiV>0 — некоторые числа. Заменим дугу BQ отрезком прямой
ж = /, где / — положительное число, которое в дальнейптем будем
неограниченно увеличивать. При этом мы будем исходить из формулы (9), которую
перепипЕСм в виде
^2
и{х
..)= /
4а2 {t-r)
2 у^тга^ {t - т)
п(С, г) d^ + a^^^dr- п(С, г) ^^-^
dr
PABQ
Рассмотрим интеграл по отрезку BQ
I
BQ
4а2 (t-r)
2 у^тга^ {t - т)
и{1,г)
i=l
2{t-
dr-
f 2(ди
4a2 (t-r)
^=1 2 Y^Tra^ {t - t]
dr-
(x-iy
e 4a^ (t-r) (д. _ /) d^
4 y^na^ {t -r){t- r)
h + h
и покажем, что он стремится к нулю при / ^ оо.
Оценим интеграл /i при больпЕих значениях /:
\h\^
Na^
кг
16а
'"" I
dt
^/Г
( если X < - и {t — т) < 5
)■
Очевидно, что |/i| ^0 при / -^ оо, так как К — фиксированное число, а 6
может быть выбрано как угодно малым числом, например так, что
1
К <
16а2^

3] ЗАДАЧИ ДЛЯ ОБЛАСТЕЙ С ПОДВИЖНЫМИ ГРАНИЦАМИ 499
Аналогично доказывается, что |/2| ^0 при / ^ оо.
Если для функции u{x,t) и ее производной ди/дх неравенства (А)
выполняются также при отрицательных ж, то можно принять за кривую АЕ
отрезок прямой ж = — / и, повторяя изложенные выпес рассуждения,
убедиться в том, что при предельном переходе интеграл по РА в формуле (9)
стремится к нулю. В результате мы приходим к известной нам из гл. HI, § 3
формуле Нуассона ^
и{х
2^f^ J
+О0 (x-ir
Vi
■u{C,0)dC.
Рассматривая полубесконечную область и предполагая, что для
функции источника G{x^t^^^T) выполнены неравенства (А), с помощью
аналогичных рассуждений находим
u{x,t) = - / « mW -qF
PA
^=XA
ос
/
dT+ / ^{OG{x,t,^,^)d^,
(14)
XA
где
li{t) = u{xAjt) и (p{x) = u{XjO).
Как нетрудно убедиться, функция источника для полубесконечной
прямой ж ^ О может быть получена методом отражения и равна
С(ж,^,С,г) =
1
2 у/^;^2"(^^:7)
(х-О^
(х+О^
4а^ (t-r) _ g 4а^ (t-r)
так как она представима в виде (12), удовлетворяет уравнению
теплопроводности по переменным ж, ^ и обращается в нуль при ж = 0:
G{0,t,^,T) = 0.
Вычислим производную
^2
дС
и, подставив ее значение в (14), получим формулу
4а2 (t-r)
u{x,t)
СЮ
2уД
(х-0^
4a2t
(х+0^
4a2t
^(Od^-
+
1 f а'х
е 4a^(t-r) д^(^)^^^ (15)
^ Приведенные рассуждения нельзя рассматривать как вывод этой
формулы, так как мы основывались на ней при выводе формулы (9).
32*

500 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
которая определяет функцию u{x,t), удовлетворяющую уравнению
щ = а Uxx (О < ж < оо, ^ > 0)
и дополнительным условиям
uiO,t)=n(t)
3. функция источника для отрезка. Рептение уравнения
теплопроводности на ограниченном отрезке О < ж < / дается формулой (11), которая
после замены дуг РА и BQ отрезками прямых и сдвига начала координат
в точку А принимает вид
t t I
= a^ / — fii{T)dT-a^ — fi2{r) dr-\- / G{x,t,^,0) (p{^) d^,
0 '^-^
^=1
где
Mi(^) = u{0,t), ii2{t) = u{l,t), ip{x) = u{x,0).
функция источника G^x^t^^^r) для отрезка может быть построена методом
отражения. Помещая положительные источники в точках 2п1 + ^ и
отрицательные источники в точках 2п1 — ^, представим функцию источника с
помощью ряда
сю
u{x,t)= ^ [Go{x,t,2nl + i,T)-Go{x,t,2nl-i,T)], (16)
п= — оо
где
G^{x,t,i,T) = , , в ^-Н^-г)
2 ^J-Ka^ (t - т)
— функция источника для неограниченной прямой.
Сходимость ряда, а также выполнение граничных условий G \х=о = О и
G \х=1 = О устанавливается без труда.
В гл. HI, § 2 была получена иная форма представления функции
источника:
CXD 2 2 о
П=1
Докажем эквивалентность обоих представлений.
Формулу (17) можно рассматривать как разложение функции
G{x^t^^^T) в ряд Фурье по синусам на отрезке (О,/):
сю
7ГП
G(x,<,C,r) = ^G„(x,<,r)sm^e (18)
п=1

§ 3] ЗАДАЧИ ДЛЯ ОБЛАСТЕЙ С ПОДВИЖНЫМИ ГРАНИЦАМИ 501
Вычислим коэффициенты Фурье Gn функции G, определяемой рядом
(16):
/
2 f 7Г77
Gn = j G{x,t,^,T)sm — ^d^ =
о
Е {jGoix,
t, 2nl -\- ^Ijt) sin —- ^1 d^i -
- / Go{x,t,2nl-^2,r)sm^^2d^2 } •
Введя новые переменные интегрирования
C' = 2n/ + Ci и ^" = 2nl-^2^
получим
' (2n+l)/
с
^-j 12
/ Go (ж, t, ^', t) sin ™ i' di' +
/
2n/
2nl
I Go{x,t,i" ,т)^ш'^ i" di" ) ,
(2n-l)/
откуда следует, что
+ CXD
I
I
+ CXD
= 2 / I
^ J 2 л/тга^ (^ - r
e 4a^(t-T) sin ^c?^.
V^7ra2 (^ - r) ^
Введем переменную
Л =
^-x
2y^a^t-r)'
Тогда
dX
d^
, ; sm —- ^ = sm —- (ж + 2 y/a^ (t - r) Л)
a^ it — t) ^ ^
2 л/в2 (t - r)
7ГП 27ГП
7ГП . 27ГП
sm —- X COS —— Y a^ (^ — r) Л + cos —- ж sin —— у a^ (^ — r) Л;

502 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
+ CXD
„ 2 . 7ГП 1 f _\2 27ГП / о /. ^л 7л
l I Y 7Г J I
+ CXD
2 7ГП
1 /^ _\2 ^ 27ГП / о /. ^л 7л
+ - COS —- X —= / e sm —— у a^ (^ — r) Л ал.
/ / у 7Г J I
— сю
Второй интеграл равен нулю, так как под интегралом стоит нечетная
относительно начала координат функция.
Первый интеграл является частным случаем интеграла
+ CXD
1{а,13) = / e~'^^\ospXdX,
— сю
равного
V а
27ГП
В нап1ем случае а = 1, /3 = —-— у а^ (^ — г), так что
2 2 о
/ = утге 1"^
2 -ILn ^2(^_^^ ^ 7ГП
Gn = 76 ^ sm —- X.
Подставляя найденное выражение для коэффициентов Фурье Gn в формулу
(18), сразу же получаем второе представление (17) для функции
источника G. Тем самым эквивалентность двух разных представлений (16) и (17)
доказана.
§ 4. Тепловые потенциалы
1. Свойства тепловых потенциалов простого и двойного слоя.
Как мы видели, всякое рептение уравнения теплопроводности может быть
представлено в виде (см. рис. 79)
и{х, t) = Gqu d^- Gqu d^-\- Gqu d^-\-a^ / IGq-^-u -—^- j dr.
AB AP BQ BQ+PA
Займемся изучением отдельных слагаемых этой суммы и докажем в
первую очередь, что каждое из них в отдельности удовлетворяет уравнению
теплопроводности. Действительно, первое слагаемое является интегралом
Пуассона, для которого это уже было доказано.

§ 4] ТЕПЛОВЫЕ ПОТЕНЦИАЛЫ 503
Докажем, что для внутренних точек области PABQ уравнению
теплопроводности удовлетворяют интегралы
t 2
АР о ^
АР О
Функции у и VF называются тепловыми потенциалами (простого слоя и
двойного слоя соответственно).
Производные функций У и VF вычисляются при помощи
дифференцирования под знаком интеграла, так как подстановка, входящая при
дифференцировании по ^, равна нулю. Например,
GQ{x,t,xi{r),r)^i{r)
1 1
2л/^ у/а2 {t - т)
'(*--) /i(r)
в силу того, что X ф XI (^)- Таким образом, дифференцирование по
параметрам ж, t будет относиться к функции Go, которая является репЕСнием
уравнения теплопроводности. Изучение остальных слагаемых проходит
аналогично.
Рассмотрим теперь поведение функций У, W на кривой АР (ж = Xi(^))-
Очевидно, что интеграл V непрерывен при переходе точки (ж,^) через
кривую АР^ так как он сходится равномерно (см. гл. IV, § 5). Докажем, что W
претерпевает разрыв при переходе через кривую АР^ причем
^ U=Xl(^)+0 = ^ \x=Xl{t) + MW.
Это доказательство будет проведено в предположении дифференцируемости
функций XI (^) и м(^)-
Рассмотрим сначала W при постоянной плотности /х(^) = /xq:
лО/
1л/^ J
x-Xi{t-)
^ ^ 2aV^; (^-г)%
^0
и вспомогательный интеграл
J_ / 2x'i(r)
2a VTT J
to
являющийся, в силу сделанного выпес замечания, непрерывной функцией в
точках дуги АР.

504 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Разность W^ - V^ вычисляется непосредственно:
to
^ [x-xi(r)]^ -
x-Xi{r) 2x1 (г)
L {t - r)% Vt^^l
liodr =
где
Mo
7^ J
e ^ da
2у/аЦг-т)Г
+00, еся1^ X > xi{t)^
Q^o = "( 0, если X = Xi{t) = ^Oj
I—oo, еслиж<Х1(^)-
При ж ^ жо ± О мы получаем
[W°{xo ± 0,i) - W°{xo,t)] - [V{xo ±0,t)- V{xo,t)] =
zbcxD
MO
V^ J
e ^ da = -^^JLQ.
В силу непрерывности V имеем
V{xQ±Q,t)-V{xQ,t) = Q.
Таким образом,
W°(xo±0,<) = H^°(xo,t)±/io.
Если ^(t) не постоянна, то
где
W{x,t) = W^{x,t)-i;{x,t),
[x-Xl{r)Y
^{x,t)
^/sif^'" *"""-"'"«-"Mi^^-
в силу сделанных предположений о дифференцируемости функции ^{t)
этот интеграл имеет такую же особенность при т = t, как и V, сходится
равномерно и является непрерывной функцией на кривой АР. Таким образом,
предел W{x,t) при ж = жо ± О равен
W{xo±0,t) = w\xo,t)±fi,
что и требовалось доказать.

§ 4] ТЕПЛОВЫЕ ПОТЕНЦИАЛЫ 505
dV
Нетрудно убедиться, что производная —— (ж,^), подобно W{x^t)^
разрывна при X = XQ. Эта производная равна
t
dV _ 11 Г x-xi{r)
1 1 f x-Xi^
dx 2a0F 2 У (^ - r)%
0
и равна — VF(x,^) с плотностью
М*)= 2
Отсюда следует, что
^,«.«,,=f,«,<,±t^
где интеграл
^ж ^ ^' ^ 2а^ 2 J {t-rfh ^ ^
о
равен полусумме производных У в точке жд справа и слева:
1 Г^У ^F
_[_(,„+0,.) + _(.о-0,.)
Отметим, что функция V{x^t) в самой точке жо не имеет производной.
На этом мы заканчиваем исследование потенциалов вдоль АР. Свойства
потенциалов вдоль кривой BQ соверпЕСнно аналогичны.
2. Решение краевых задач. Тепловые потенциалы являются
удобным аналитическим аппаратом для рептения краевых задач.
Рассмотрим сначала первую краевую задачу для полуограниченной
области X ^ х(^)-
Найти решение уравнения
ut=auxx при x^xi{t)i t^to,
удовлетворяющее условиям
u{x,to) = (р{х), X ^ XI(^о);
u[xi{ty,t]=fi{t), t^to.
Без ограничения общности можно считать, что (р{х) = О, так как, взяв
разность между и{х, t) и произвольным рептением уравнения
теплопроводности v{x^t)^ удовлетворяющим тому же начальному условию, получим новую
функцию, для которой (^(ж) = о, а граничное значение по-прежнему будет
известно.
Предполагая, что приведение к нулевому начальному условию уже
сделано, представим рептение в виде
1 ^^^, ,, г dGo
to
^(*'*) = ^^(*'*) = / ^^(»^>*'Xl(T),-r)/i(r)dr :

506 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
4л/^У [аЦг-т)р^^
■е 4a2(t-r) p,{r)dT.
Эта функция удовлетворяет уравнению при х > Xil^)? ограничена в
бесконечности и имеет нулевое начальное значение при любом выборе fl{t). При
X = XI (t) она разрывна, и ее предельное значение при ж = xi (^) + О должно
быть равно fi{t):
t
т , 1 rxi{t)-xi{r)
2а2 4 0F7 [а2(^-г)]%
^0
'(*-^) fl{T)dT = fi{t).
Это cooTHOHienne является интегральным уравнением типа Вольтерра
второго рода для нахождения функции Д(г), определяющей искомое репЕСние
u{x,t). Существование репЕСния всегда имеет место в силу общей теории,
если кривая х = xi (t) определяется дифференцируемой функцией.
Это уравнение особенно просто, если граница наптей области
неподвижна: Xi{t) = xq. В этом случае интеграл обращается в нуль и
Pit) = 2aV(*),
так что искомое penienne имеет вид
о
С этой формулой мы уже встречались дважды (см. гл. HI, § 3 и гл. VI,
§ 3, п. 2), однако только здесь дано доказательство того, что эта функция
удовлетворяет уравнению и дополнительным условиям.
Вторая и третья краевые задачи рептаются аналогично при помощи
потенциала. Рассмотрим краевую задачу для ограниченной области, беря
дополнительные условия в виде
п(ж,0) = (^(ж), XI(0) <ж<Х2(0),
и[х1 (t) ;t]=fii (t), и[х2 (t) ;t]=fi2 (t) {t>0).
Считая, что начальное значение приведено к нулю: (^(ж) = О,
представим penienne в виде
u{x,t) = ^{Wi+W2) =
t t
= / -^ {x,t,xi{r),r) fli{T)dT -\- / —^(ж,^,Х2(г),г)Д2(г)сгг.
о о
Эта функция удовлетворяет уравнению и нулевому начальному условию при
любом выборе функций pi (t) и р2(t)• Она разрывна при х = xi{t) '^ х = Х2(t)•,
и ее предельные значения при x = xi(^) + 0 и ж = Х2(^) — О должны быть

§ 4] ТЕПЛОВЫЕ ПОТЕНЦИАЛЫ 507
равны fii{t) и fi2{t)^ что дает систему уравнений
^ fxi{t)-xi
А у [а2(*-г)
о
2а2 4^^/ [а2 (i _-г)]^/^
о
A2W , 1 /X2W-Xl(r)^-^
л/тгУ [а
о
2а2 4 0Fy [а2(^-г)]%
е 4а^(*-т) jj,i(T)dT-
X2{t)-X2{r)
о
Эта система является системой интегральных уравнений типа Вольтерра,
всегда имеющей penienne.
3. Условия локализации граничных релсимов с обострением К
В этом пункте тепловые потенциалы используются для исследования
довольно тонкого (и весьма необычного) свойства локализации рептений уравнения
теплопроводности
щ = а Uxx- (1)
Рассмотрим для (1) первую краевую задачу в области ж ^ О, О ^ ^ <
<Т (Т — фиксированная положительная постоянная) с заданным при ж = О
граничным режимом с обострением
n(0,^)=/i(^), 0^^<Т;
/i(^)^+oo при t^T~, Т~=Т-0. ^^
Без ограничения общности положим и{х,0) = 0.
Напомним (см. Приложение П1 к гл. П1), что репЕСние задачи
называется локализованным (или, другими словами, в задаче (1) — (2) существует
локализация тепла), если рептение неограниченно возрастает при t -^ Т~ в
конечной по своим размерам части пространства (например, при всех О ^
^ ж < жо < +00 и, быть может, в точке ж = жд), несмотря на бесконечный
рост репЕСния на границе. Часть пространства О < ж < жо, где u{x,t) -^ +оо
при t -^ Т~, будем тогда называть областью локализации, а величину
Жо < +00 — глубиной локализации.
Если же u{x,t) -^ +00 при t -^ Т~ во всем пространстве ж ^ О, то
локализация в задаче отсутствует.
^ См.: Самарский А. А. О новых методах исследования
асимптотических свойств параболических уравнений // Тр. Мат. ин-та им. В. А. Стек-
лова АП СССР. 1981. Т. 158. С. 153-162. Там же дан список литературы.

508 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
Естественно, наличие локализации тепла или ее отсутствие
определяется видом краевого условия (2) (подчеркнем, что свойство локализации
могут проявлять только граничные режимы с обострением). Для выяснения
условий локализации воспользуемся интегральным представлением penie-
ния задачи (1) — (2) в виде теплового потенциала двойного слоя. Он имеет
вид
u{x,t) = -^ [ \ e~^^^^(^)^{r)dr. (3)
0
Переходя в (3) к пределу при t -^ Т~, получим выражения для
«предельных» значений репЕСния в момент времени t = Т:
Т
2
о
Напомним, что, по предположению, ^(t) -^ +оо при t -^ Т~. Поэтому
интеграл в (4) является несобственным. В тех точках ж > О, где интеграл в
правой части (4) расходится, репЕСние неограниченно возрастает при t -^
-^ Т~. Напротив, во всех точках ж > О, где и{х,Т) < +оо, решение u{xjt)
ограничено сверху (например, величиной и{х,Т)) в течение всего времени.
Вид подынтегральной функции в (4) указывает на то, что наиболее
интересным является анализ семейства «экспоненциальных» граничных
режимов с обострением вида
/i(t) = Mo(r-<)''e''o(^-*)", 0^t<T. (5)
Здесь n<0,i^, no>0, 6о>0 — фиксированные постоянные. Подставив (5)
в (4), получим следующее выражение:
Т
ф, Т) = ^^ / ^-^ в" ^^^fc) . в^о (Т-гГ d (6)
^ ^ 2а,Д J (T-rfl^-^ ^ ^
о
которое подвергнем дальнейптему исследованию.
Покажем, что свойства рептения рассматриваемой задачи (1) — (2), (5)
существенно зависят от величины параметра п < 0. Именно, возможно три
случая.
а) Пусть п = — 1. Тогда (6) приводится к такому виду:
п(ж,Т) = -^ / '"-^. е4«2(т-г) ^^^ (7)
т
по [
2a^J (Т-
0
2 2
-rfh-v
где введено обозначение
жо = 2а v%. (8)
Из (7) непосредственно следует, что penienne задачи является
локализованным и величина жо в (8) определяет глубину локализации: при всех

§ 4] ТЕПЛОВЫЕ ПОТЕНЦИАЛЫ 509
О ^ ж < жо интеграл в (7) расходится (т. е. u{x^t) -^ +оо при t -^ Т~), а для
любых X > XQ решение ограничено сверху «предельным распределением»
2v
и(х,Т) —
22^а2
< X /
V2
+ CXD
/
-"г/'^-^г d,, < +00 (7')
2 _ 2
(выражение {7') получается из (7) заменой ^ —^-— = г] под знаком инте-
4а^ (Т — т)
грала).
Таким образом, сравнительно простой непосредственный анализ
теплового потенциала показывает, что рассматриваемый процесс диффузии
тепла проявляет необычное свойство тепловой «инерции»: накапливающееся в
конечной по своим размерам области О < х < xq неограниченно больпюе
количество энергии практически не растекается в окружающее пространство
к моменту времени t = Т.
С помощью теплового потенциала можно определить также другие,
более тонкие свойства репЕСния задачи, например характер нарастания penie-
ния в граничной точке области локализации х = xq. Оказывается, он
существенно зависит от величины параметра и в режиме с обострением (5).
Полагая в (7) ж = жо, получаем, что в случае и > 1/2 функция u{xo,t)
ограничена сверху величиной
— 7777 < +^-
7Г ^' — 1/Z
Если же f ^ 1/2, то и{хо,Т) = +оо, т. е. в этой точке penienne неограниченно
возрастает при t -^ Т~.
Вычислим производную Ux{xjT) в точке ж = Жд . Дифференцируя
выражение (7), получаем, что при и > 3/2 она конечна и определяется по формуле
"-<«»■'■'= -2^'-'"'*
2Ьо
1У-3/2 1У-1/2
(если 1У ^ 3/2, то Ux{xq,T) = —оо). Отметим, что при Т > 26о г-т^г
производная Ux{xqjT) положительна, т. е. «предельное распределение» и{х,Т)
в области ж > жо носит немонотонный характер. Это связано с
возникающей в этом случае немонотонностью граничного режима (5) (проверьте этот
факт).
Граничные режимы с обострением, порождающие локализованные ре-
пЕСния с глубиной локализации, отличной от нуля, называются S-ре
жимами (ср. Приложение П1 к гл. П1).
б) Пусть — 1 < п < 0. Тогда интеграл в (6) сходится при любых
значениях ж > О (докажите это), т. е. penienne растет до бесконечности только в
граничной точке ж = 0. Тем самым в задаче существует локализация теп-

510 РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРОСТРАНСТВЕ [ГЛ. VI
ла, причем по определению глубина локализации жд = 0. Такие граничные
режимы с обострением мы называем LS-режимами (отметим, что LS-
режимы с обострением степенного вида реализуются также в случае п = О,
1У<0).
в) Пусть теперь п < —1 в (5). Тогда, наоборот, интеграл в (6)
расходится при всех ж > О (докажите). Это означает, что рептение неограниченно
возрастает при t -^ Т~ во всем пространстве и локализация в задаче
отсутствует. Такие режимы с обострением называются HS-режимами.
ЗАДАЧИ К ГЛАВЕ VI
1. Сфера радиуса Rq в начальный момент заполнена газом
концентрации UQ] вне сферы концентрация равна нулю. Найти функцию и,
характеризующую процесс диффузии газа в неограниченном пространстве. РепЕить ту
же задачу для полупространства при наличии газонепроницаемой границы
z = 0.
2. РепЕить задачу о нагревании сферы радиуса Rq, если начальная
температура равна нулю, а на границе поддерживается постоянная
температура.
3. Найти температуру niapa, на поверхности которого происходит
теплообмен со средой нулевой температуры, если начальная температура
постоянна и равна uq.
4. Однородное твердое тело ограничено двумя концентрическими
сферами с радиусами а и 2а. Внутренняя поверхность тела теплоизолирована, а
на внепЕней поверхности происходит теплообмен со средой нулевой
температуры. Найти распределение температуры в теле в момент t, если начальная
температура тела равна uq.
5. Вывести уравнение диффузии в среде, движущейся с постоянной
скоростью. Написать выражение для функции точечного источника в
неограниченном пространстве.
6. Рассмотреть стационарную задачу диффузии в подвижной среде,
считая скорость движения постоянной и пренебрегая диффузией вдоль
направления движения среды (задача о газовой атаке). Написать функцию
источника для полупространства, считая, что плоскость z = О газонепроницаема.
7. Построить функцию теплового источника для слоя, ограниченного
плоскостями ^ = О и ^ = /, а также для клина с раствором тг/п (п — целое
число) при нулевых граничных условиях. Рептение исследовать.
8. Найти функцию влияния мгновенного источника тепла мощности Q,
равномерно распределенного на поверхности сферы радиуса а.
9. РепЕить задачу о нагревании бесконечного цилиндра, начальная
температура которого равна нулю, а на поверхности поддерживается
постоянная температура. Пользуясь таблицами функций Бесселя, найти профиль
температуры (взяв на радиусе десять точек) и среднюю температуру по
сечению для больпЕих моментов времени. Построить соответствующие
графики.
10. Рассмотреть задачу о намагничивании бесконечного цилиндра
постоянным магнитным полем, параллельным оси цилиндра. Пользуясь
таблицами бесселевых функций, подсчитать величину потока индукции через
поперечное сечение цилиндра.
11. Построить функцию мгновенного точечного источника тепла для
бесконечной цилиндрической области произвольного сечения при граничных

I. ДИФФУЗИЯ ОБЛАКА 511
условиях первого рода. Рассмотреть частный случай поперечного сечения
круглой формы.
Указание. Представить репЕСние в виде
сю
n=l
где грп{М) — собственная функция поперечного сечения цилиндра.
прилож:ения к главе vi
I. Диффузия облака
Рассмотрим процесс диффузии газового облака, образующегося
при разрыве снаряда.
При разрыве снаряда выделяется некоторое количество дыма Q,
который распространяется во все стороны, образуя облако. Облако
сначала растет, затем оно светлеет по краям, его темная непрозрачная
часть уменьшается, все облако светлеет, начинает «таять» и, наконец,
исчезает. Эта картина особенно отчетливо видна в ясный день на фоне
голубого неба.
Процесс распространения дымового облака можно трактовать как
процесс диффузии дыма от мгновенного точечного источника
мощности Q в неограниченном пространстве. Такой процесс диффузии носит
не молекулярный, а турбулентный характер; ему соответствует
некоторый эффективный коэффициент турбулентной диффузии D. Мы
не учитываем здесь начальный разброс дыма, а также практически
совершенно несущественное влияние земли. В этих предположениях
концентрация дыма дается формулой
1 ^^
u{x,y,z,t) = Ql—=lJ е ^Dt {D = a'),
если начало координат поместить в точку разрыва снаряда.
Остановимся на вопросе о видимости облака. Время, за которое
облако полностью «растает», зависит от поглощения света в
атмосфере и от порога чувствительности измерительного прибора (глаз,
фотопленка и т. д.).
Как известно, интенсивность света, проходящего через
однородные слои газа, приближенно равна
/ = /ое-"',
где /о — первоначальная интенсивность света, а = aou —
коэффициент поглощения, пропорциональный концентрации поглощающего газа
(«о = const, и — концентрация газа в слое), / — толщина слоя.

512 ПРИЛОЖЕНИЯ К ГЛАВЕ VI
Если имеется два слоя толщины li и I2 с разными концентрациями
газа щ и ^2, то
Отсюда ясно, что интенсивность света, проходящего через облако с
непрерывно меняющейся концентрацией дыма, будет определяться
формулой
/ = /о ехр -ао
) udlj .
Видимость облака определяется отношением ///о, зависящим от
величины Judl.
Пусть S — порог чувствительности инструмента наблюдения;
тогда при
^0 - ^ ^ л
—-— < 0, или
^0
облако становится невидимым; при
f > 1 - <5,
—-— > 1 - д, или — < 0,
^0 ^0
облако кажется совершенно непрозрачным. Если
5<^<1-
S,
ТО облако кажется наблюдателю частично прозрачным. Степень
прозрачности зависит от величины отношения
— = ехр I —ао udlj
/о
т. е. от величины интеграла J udl.
Направим теперь ось z по лучу зрения и будем считать, что
наблюдатель находится в бесконечности. При этом облако проектируется
на плоскость (ж, у). Для оценки видимости различных участков облака,
соответствующих точкам {х,у), вычислим интеграл
сю о сю
udl = / и{х, у, z,t) dz = Q I — ) / ^ ^^* dz =
-00
Q —^= е ^Dt
Если количество дыма по лучу зрения мало:
S
/■
<
ао

I. ДИФФУЗИЯ ОБЛАКА
513
то ///о > 1 — (5 и соответствующий участок полностью прозрачен.
Если количество дыма по лучу зрения велико:
А
/
udl >
ао
то ///о < е ^ = (5, т. е. при надлежащем выборе А = \n{l/S)
соответствующий участок облака соверп1енно непрозрачен. При
условие
S Г „ А
— ^ udl < —
ао J ао
10 и (
idl = S, или
aoQ
е "^Dt
{р'^х'^у\
определяет границу облака, за пределами которой оно становится не-
Рис. 81
видимым. Радиус облака, очевидно, равен (рис. 81)
р = 2^ -Dt\n
SAnDt
Qao
При малых значениях t радиус облака р мал и растет вместе с t; при
aoQ
t = to =
4:7reSD
р достигает максимума:
2^Dto
neS
при t > to радиус облака р уменьшается и при
_ Qao
^ ~ S47TD
обращается в нуль (облако исчезает).
33 А. Н. Тихонов, А. А. Самарский

514 ПРИЛОЖЕНИЯ К ГЛАВЕ VI
Наблюдая процесс расплывания облака, можно определить
коэффициент турбулентной диффузии D в свободной атмосфере (например,
из формулы для ti или для ^о)-
II. О размагничивании цилиндра с обмоткой
Рассмотрим задачу о размагничивании цилиндра с обмоткой.
Такая задача возникает в связи с теорией баллистического гальваномет-
paD.
Нри включении или выключении магнитного поля в обмотке
возникает индукционный ток. Нри точной постановке задачи нужно
учитывать обратное воздействие этого тока на поле внутри цилиндра.
Однако тормозящее действие обмотки обычно не учитывается и
задачу решают с упрощенными граничными условиями.
Познакомимся, прежде всего, с такой упрощенной постановкой
задачи. Рассмотрим бесконечный цилиндр радиуса R^ на поверхности
которого намотана проводящая обмотка. Цилиндр находится в
однородном магнитном поле Н^^ параллельном оси цилиндра Oz. В момент
^ = О поле выключается.
Внутри цилиндра, очевидно, будет удовлетворяться уравнение
1 riJ-f
АЯ=^- (Я = Я.), (1)
где
2 ^
а —
В силу осевой симметрии поля
H,=H{r,t)
И уравнение (1) может быть переписано в виде
д'^Н 1 дН 1 дН
\ = . (1 )
Если пренебречь влиянием индукционного тока в обмотке на
процесс размагничивания цилиндра, граничное условие на его
поверхности будет иметь вид
H{R,t)=0 {t>0). (2)
Нри t = О
Я(г,0) = Яо. (20
^ Введенский Б. А. Токи Фуко при апериодических процессах в
железе; поверхностный эффект // Журн. Рус. физ.-хим. о-ва. 1923. Т. 55, № 1-3.
С. 1-12.

IL О РАЗМАГНИЧИВАНИИ ЦИЛИНДРА С ОБМОТКОЙ 515
Решение уравнения (1') при граничном условии (2) без труда
получается методом разделения переменных (см. с. 490):
'f)^-
Ч.г^). (3)
H{r, t) - 1,60 ■ Ще '•'' h * Jo (2,4 ^) . (5)
Здесь Jo и Ji — функции Бесселя нулевого и первого порядка, ii\, —
k-vi корень уравнения
Jo(//) = 0. (4)
Так как о? весьма велико, то для достаточно больших t можно
ограничиться в формуле (3) первым членом (регулярный режим):
Отсюда для потока индукции получаем
R
Ф(^) =27г [ /jH{r,t)rdr^ 4фoe"^lS^^ (6)
о
где Фо — начальный поток (при ^ = 0), /ii = /i-[ .
Формулой (6) пользуются для практических расчетов при
измерениях с помощью баллистического гальванометра.
Чтобы определить область применимости этой формулы,
следует решить указанную выше задачу, учитывая тормозящее действие
обмотки-'-л
Электродвижущая сила индукции в контуре (витке) L, как
известно, равна
^инд = Ф Eidl.
L
Преобразуем контурный интеграл, используя для этой цели
теорему Стокса, второе уравнение Максвелла и уравнение (1):
^инд = IJTot.EdS =-^ll^dS =
47Гсг J J 47Гсг J dv
S L
S
^ Эта задача была решена В. Н. Никитиной.
33*

516 ПРИЛОЖЕНИЯ К ГЛАВЕ VI
Здесь 5 — поперечное сечение цилиндра, L — контур,
ограничивающий 5, I/ — нормаль к контуру L.
Граничные условия на поверхности цилиндра запип1утся в виде
условия скачка поля
H(R-0,t)-H(R + 0,t) = —nJ,
с
где J — индукционный ток в обмотке, п — число витков на единицу
длины цилиндра. Отсюда, учитывая, что H{R + 0,^) = О,
где р — линейное сопротивление обмотки, / — длина одного витка,
получаем
Н{Е, t) = H{R - О, ^) = — n ^ . (8)
с р1
Сопоставляя соотношения (7) и (8), окончательно приходим к
граничному условию
и
H(R,t) + —Hr(R,t) = 0.
pa
Таким образом, мы должны решить уравнение
Нгг Н— Нг = ^^ Ht (9)
при дополнительных условиях
Я(г,0) = Яо,
H{R,t)-\-aHr{R,t) = 0 (а= —
V р^
Решение будем искать методом разделения переменных, полагая
H{r,t)=Xir)Tit).
Для функций Х{г) и T{t) получим условия
X" + -Х' + Х'^Х = 0;
(10)
X{R) + aX'(R) = О (Х(0) < оо),
Т' + Х^а^Т = 0, (11)

IL О РАЗМАГНИЧИВАНИИ ЦИЛИНДРА С ОБМОТКОЙ 517
где Л^ — параметр разделения.
Из второго уравнения сразу же находим
T(t)
-а^\Н
Частными решениями уравнения (10) являются функции Jo(Ar) и
No{Xr) (см. Дополнение II, ч. I), однако условию ограниченности при
г = О удовлетворяет лишь Jo(Ar). Поэтому
X{r)=AJo{Xr).
Граничное условие при г = R дает уравнение для определения
собственных значений
Т/ЛГ.Ч dJo{XR) ^
Jo(Ai^)+a^^^=0,
или
Му)-РуМу) = о, (12)
где
р = a/R, у = XR.
Корни этого уравнения могут быть найдены либо графически,
либо разложением функций Бесселя в ряд по степеням у = XR.
Обозначим через yk корни уравнения (12), так что
Afe =yk/R-
Общее решение нашей задачи будет иметь вид
сю
Н{г, t) = J2 AkJo {vk ^) е-^Ук/^^' -'к (13)
к=1
Коэффициенты А^ находим из начального условия
R
1 Но Jo [г
] г dr
о 2HoJi{yk)
^ yklJiivk) + Jiivk
jjl{r^)rdr
О
(14)
Члены ряда (13) быстро убывают, так как о? = с^/An/ia велико
(~ 10"*^^ — 10"*^^). Поэтому с достаточной степенью точности можно
ограничиться первым членом
2НоМу,)Му,г/К)
„2
^2
H{r,t) ^ "^ТАТ'л "'"т2'/\7 е~'>'^^\ (15)
yi[Jl{yi) + JliVi)]

518
ПРИЛОЖЕНИЯ К ГЛАВЕ VI
что приводит к следующему выражению для потока:
Фад = Фо
4Jf(?/i
yl[Jl{yi)^Jl{yi)]
-yib'
(16)
где
Фо = NHqttR {N — полное число витков в обмотке).
Расчеты приводят к следующим формулам потока для различных
значений параметра /3:
Ф(^)
0,804 Фое-4'^^^ при /3 = 0,1,
0,872 Фoe-^'^^^ при /3 = 0,2,
0,912 Фоб
-3,35 6»
при /3 = 0,3,
R^
позволяющим проследить за тормозящим действием тока на спадание
поля в цилиндре. С увеличением /3, т. е. с увеличением тока в
обмотке, скорость убывания потока уменьп1ается. При /3 = 0 естественно
приходим к выражению (6) для потока, являющемуся, таким образом,
нулевым приближением.
В теории баллистического гальванометра важно знать время г
спадания потока от Фо до значений, определяемых
чувствительностью гальванометра, которое характеризует инерционность прибора.
Пусть 7 — относительная чувствительность гальванометра, т. е.
гальванометр может регистрировать лишь значения Ф ^ 7Фо- Величину г,
очевидно, можно найти, полагая Ф = 7Ф0 в момент t = т в формуле
Ф(^) =aФoe-^^
Из сравнения полного решения (16) с грубым решением (6) видно,
что коэффициент в формуле (6) завышен. Это означает завышенное
значение чувствительности прибора при одном и том же значении г.
Приведенная ниже таблица содержит значения г для различных
/3, в том числе и для /3 = 0, при 7 = 10~^.
Железо
/i = 500
а = 10^ (Ом-см)-^
Альсифер
fi = 2000
а = 1,3-10^ (Ом-см)-^
Я,
см
1
1
a^/R^
1,59
5,12
г {(3 = 0)
0,71
0,217
г{Р = ОД)
0,888
0,272
г{Р = 0,2)
1,15
0,330
г{Р = 0,3)
1,28
0,405

ГЛАВА VII
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИНА
(продоллсение)
§ 1. Основные задачи, приводящие
к уравнению Дг; + cv = О
1. Установившиеся колебания. Весьма широкий класс
вопросов, связанных с установившимися колебаниями
(механическими, акустическими, электромагнитными и т. д.), приводит к так
называемому волновому уравнению
Av + k^v = 0 {к^ = с>0). (1)
Рассмотрим в качестве примера мембрану S, закрепленную по
границе С и колеблющуюся под действием периодических во
времени сил. Соответствующее уравнение имеет вид
A2U = -izUtt- Fq(ж, у) cos ujt. (2)
При изучении периодических процессов удобно пользоваться
комплексными функциями, заменяя (2) уравнением
^2U=\utt-Fo{x,y)e'^K (3)
Функция й, очевидно, является вещественной частью функции и из (3).
Будем искать установившиеся колебания, имеющие вид
u^ve'^'K (4)
Для амплитуды установившихся колебаний v получаем
следующее уравнение:
к которому надо добавить граничное условие
«|с = 0. (6)

520 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Если контур мембраны С не закреплен, а совершает периодические
колебания с той же частотой о;,
и\с = ке'^\ (6')
ТО для функции V на контуре С имеет место неоднородное граничное
условие
v\c = h. (6")
Как было уже отмечено вып1е, задачи об установивп1ихся
колебаниях характерны также для акустики и теории
электромагнитного поля. Кроме того, часто встречаются задачи об установившихся
колебаниях в неоднородной среде, в частности в кусочно-однородной
среде (когда, например, в пространстве имеются отдельные области,
нарушающие однородность). К этому кругу вопросов относятся задачи
теории дифракции, на которых мы остановимся ниже.
2. Диффузия газа при наличии распада и при цепных
реакциях. При диффузии некоторых газов (например, эманации
радия) происходит реакция распада молекул диффундирующего газа.
Скорость реакции распада обычно принимают пропорциональной
концентрации газа. При написании уравнения диффузии это
эквивалентно наличию отрицательных источников газа. В случае стационарного
процесса диффузии мы приходим к уравнению
D/:^v^cv = ^ (с<0), (7)
где D — коэффициент диффузии. Как было указано в гл. VI, § 2, п. 3,
большой интерес представляет случай с > О, соответствующий
диффузии при наличии цепных реакций, ведущих к размножению
диффундирующих частиц. В стационарном случае мы получаем при этом
уравнение
A^ + ci; = 0 (о 0),
так как цепная реакция эквивалентна наличию источников
диффундирующего вещества, пропорциональных концентрации v{x,y,z).
3. Диффузия в двилсущейся среде. В гл. IV была рассмотрена
задача о диффузии газа в неподвижной среде. Рассмотрим задачу о
диффузии газа в заданном стационарном потоке, скорость которого
в точке M{x,y,z) имеет компоненты 'di{x,y,z), 7^2(^,^,2;), 'ds{x,y,z).
Количество газа, протекающего через элементарную площадку da в
точке M{x,y,z), равно
dQ = —Dn grad uda -\- w&n da,
где u{x,y,z) — концентрация газа в единице объема, п — единичный
вектор, нормальный к площадке da, D — коэффициент диффузии в
точке {x,y,z), '&{x,y,z) — вектор скорости потока.
Составляя уравнение сохранения вещества для некоторого объема
Т с границей Е, получаем
/
[—DngTdidu + w&n] da = 0.
Е

§ 1] ЗАДАЧИ, ПРИВОДЯЩИЕ К УРАВНЕНИЮ Av-\-су = О 521
Преобразуем поверхностный интеграл в объемный, пользуясь
формулой Остроградского — Гаусса:
/
[div(Dgradu) - div(ut?)] dr = 0.
т
Отсюда в силу произвольности объема Т вытекает уравнение
диффузии в заданном потоке
div(D grad и) - div(ut?) = О, (8)
или, в скалярной форме,
д / ди\ д / ди\ д f j^ ди
дх \ дх) ду \ ду) dz \ dz
-|:("'^^)-|м.)-|Мз) = о. (8')
К такому же уравнению приводит задача о распространении тепла
в движущейся среде.
Рассмотрим следующий пример. Пусть в полупространстве z ^ О
имеется воздушный поток с постоянной скоростью щ, направленной
по оси X. Считая коэффициент диффузии постоянным, получаем из (8)
уравнение
ди
DAu-uo--=0,
ох
являющееся простейшим вариантом уравнения газовой атаки.
Полагая
и выбирая затем
/J = uo/2D,
получим для функции v{x,y,z) уравнение
Av-\-cv = 0, где с= - -J- <0.
4. Постановка внутренних краевых задач для уравнения
Дг; + CV = 0. Как было показано в гл. I в связи с изучением
канонических форм уравнений с постоянными коэффициентами, всякое
уравнение эллиптического типа с постоянными коэффициентами может быть
приведено к виду
Av-\-cv = 0. (9)
Свойства решения уравнения (9) существенно зависят от знака
коэффициента с, что физически очевидно, если иметь в виду
диффузионную интерпретацию этого уравнения.

522 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Остановимся на вопросе единственности решения первой краевой
задачи для уравнения (9). Для уравнения Av -\- cv = О при с < О имеет
место принцип максимального значения в следующей форме.
Решение v{M) уравнения Av + сг» = О (с < 0), определенное
внутри некоторой областей Т с границей Е, не моэюет достигать во
внутренних точках области Т полоэюителъных максимальных {и
отрицательных минимальных) значений.
В самом деле, допустим, что в некоторой точке Мд, лежащей
внутри Т, функция v{M) достигает положительного максимального
значения {v{Mo) > 0)). Тогда в точке Mq
d'^v ^ d'^v ^ d'^v
-^ ^ О, ^^ ^ О, ^^ ^ О
аж^ оу^ oz"^
и, следовательно, Av ^ О, что находится в противоречии с
отрицательностью коэффициента с и положительностью v{Moy\
Из принципа максимального значения автоматически следует
единственность решения первой краевой задачи для уравнения (9).
Моэюет существовать только одно решение уравнения Av -\- cv =
= 0 (с ^ 0), определенное и непрерывное в замкнутой области Т + Е,
принимающее на границе Е заданные значения
Действительно, допуская существование двух различных решений
vi и г'2, рассматривая их разность г»! — г'2 и проводя рассуждения
способом, изложенным выше (см. гл. III и IV), мы приходим к противоречию
с принципом максимального значения.
Если с = О, то мы получаем первую краевую задачу для уравнения
Лапласа, единственность решения которой была доказана.
Если с > О, то единственность может не иметь места.
Рассматривая в гл. V задачу о собственных значениях краевой задачи
Av-\-Xv = 0, v\^ = О,
мы убедились на примерах в существовании нетривиальных решений
(собственных функций) при Л > 0. Очевидно, что вопрос о
множественности или единственности решения первой краевой задачи
эквивалентен вопросу о том, совпадает ли Л с одним из собственных значений
Хп в рассматриваемой области Т.
§ 2. Функции влияния точечных источников
1. Функции влияния точечных источников. Теория
потенциалов, развитая в гл. IV для уравнения Лапласа, может быть
распространена и на уравнение Av -\- cv = 0. Для построения функций влияния
^ Ср. с доказательством принципа максимального значения для
уравнения теплопроводности.

§ 2] ФУНКЦИИ ВЛИЯНИЯ ТОЧЕЧНЫХ источников 523
точечного источника рассмотрим решение г'о, зависящее только от г.
Оператор Лапласа для функции г'о (г) в сферической системе координат
имеет вид
г'^ dr \ dr J г dr'^
что приводит к обыкновенному дифференциальному уравнению
d'^w ^ , ,
—— -\- CW = О iw = vor).
dr"^
Вводя обозначение с = к^ для с>Оис=—х^ для с < О, получаем
^ + ew = 0 (с>0), (1)
^-^w = 0 (с<0). (1')
Из уравнения (1) находим
W = Cie'^"^ + 026-'^"^ (2)
и, соответственно,
^ikr p — ikr
vo = Ci + ^2 . (3)
г г
в случае вещественного к получаем два линейно независимых
решения е*^^/г и е~*^^/г, которым соответствуют вещественные линейно
независимые решения
cos кг sin кг
и .
г г
При с < О (с = —>^^), пользуясь уравнением (1'), получаем два
действительных линейно независимых решения
И — (х>0). (4)
г г
функции
(с>0) и ^^ (с<0)
^±ikr р±>г:г
при Г = О терпят разрыв непрерывности, обращаясь в бесконечность
как 1/г. Такой же характер особенности имела функция источника для
уравнения Лапласа (с = 0), пропорциональная 1/г.
Рассмотрим поведение этих функций на бесконечности. Случай
с < О соответствует процессу, сопровождающемуся поглощением (см.

524 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
уравнение диффузии (7) из § 1). Одно из решений е~^^/г
экспоненциально стремится к нулю на бесконечности, что в терминах задачи
диффузии означает убывание концентрации, вызываемое
поглощением. Это убывание происходит тем сильнее, чем больп1е коэффициент
\с\ = х^, характеризующий интенсивность поглощения. Второе
решение экспоненциально возрастает на бесконечности и физического
смысла для задачи в неограниченной области не имеет (его можно было
бы интерпретировать как наличие источника в бесконечности).
Случай с = /i;^ > О соответствует установившимся волновым
процессам (см. § 1, п. 1). Функция V представляет амплитуду функции
u{M,t) =i;(M)e^^^
удовлетворяющей уравнению колебаний (§ 1).
Одно из главных решений уравнения (1)
p — ikr
Щ{г) =
Г
соответствует процессу колебаний
А (cot —кг)
uo{r,t) = ,
г
который имеет характер сферической волны, расходящейся от
источника в точке г = 0. Второе решение
^ikr
Щ{г) =
Г
pi (ujt-\-kr)
соответствует процессу колебаний
uo{r,t) =
/•
имеющему характер сферической волны, приходящей из бесконечности
в точку г = О (сходящиеся волны). Очевидно, что это решение при
изучении процессов, возбуждаемых точечным источником в
неограниченном пространстве, прямого физического смысла не имеет.
Отметим, что функцию v{M) можно рассматривать как
амплитуду колебаний типа е*'^^ или е"*'^^. Мы брали временной фактор первого
типа. Во втором случае расходящаяся волна имеет вид
^-i(u;t-kr)
uo{r,t) = ,
г
т. е. ей соответствует второе решение
^ikr
г

А
ФУНКЦИИ влияния ТОЧЕЧНЫХ источников
525
Первое же решение
ikr
Vo{r) =
при этом физического смысла не имеет.
2. Интегральное представление решения. Для уравнения
(9) из § 1 при с 7^ О можно написать формулы, аналогичные
формулам Грина, которые были установлены для уравнения Лапласа. Вводя
обозначение
сразу же получаем формулу
Аи + си.
/ {uC{v) - vC{u)) dr = / Ы д^ ~ ^ g^j ^^'
(5)
(6)
являющуюся аналогом и прямым следствием второй формулы Грина
(см. гл. IV, § 2). Подставляя сюда вместо v одну из «функций точечного
источника», например e~^^/R, и повторяя дословно все рассуждения
гл. IV, § 2, приходим к аналогу основной формулы Грина
и(М(
«'-i^/
д_
-ycR
R
-ycR
ди
R ди
dau +
+
s/да'
-hR
R
■ dTM {R = RmMq), (7)
где u{M) — решение неоднородного уравнения C{u) = —f{M).
Для случая с = k^ имеет место аналогичная формула
и{Мо)
4^7
_д_
diy
-ikR
R
-ikR
ди
R dv
d(TM +
+
зЦл"'
-ikR
R
■dTM, (7')
которая была получена в гл. V как следствие формулы Кирхгофа.
Введем понятие функции источника уравнения С{и) = О для
заданной области Т с границей Е. Пусть v{M) — решение уравнения
C{v) =0, регулярное всюду в Т. Формула (6) дает
°=-/("1^-"£)^''+/^'^^^-
(8)

526 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Складывая (8) с равенством (7), получаем
и{Мо) = - \и— { -r:j;-+v] - { -7377+^1 —I daM +
^ J [^^
T
47rR J du
+ vj f{M) dTM {R = RmMo)- (9)
Эта формула справедлива для произвольного реп1ения v{M) уравнения
Av — K^v = О, регулярного в области Т. Пользуясь произволом выбора
функции V, получаем
и{Мо) = - 1 u{M)^^^^^^dc7M + 1 G{Mo,M) fiM)dTM, (Ю)
Е Т
где
G{Mo,M) = ^-^+v (11)
— функция источника, обладающая следующими свойствами:
1) G(M, Мо) обращается в бесконечность при М = Mq как
l/(47ri^), что следует из формулы (11);
2) G{M, Mq) удовлетворяет уравнению С{и) =0 всюду в Т, кроме
точки Мо;
3) G{P, Mq) = о в точках Р, лежащих на границе Е.
Вопрос о существовании функции источника связан с вопросом о
существовании функции v, удовлетворяющей уравнению
C{v) = О в Г
и граничному условию
е-^^
на
47rR
Очевидно, что функция 0{М, Mq) однозначно определена для любой
области, допускающей единственное решение первой краевой задачи.
В частности, при с = — х^ < О эта функция определена для любой
области. В простейших случаях функцию источника можно найти в явной
форме, пользуясь методом, аналогичным методу электростатических
изображений-'^^
Так, например, для полупространства 2; > О функция источника
имеет вид
^ — hR ^ — hRi
G(M,M.) = —-^^, (12)
^ Для сферы метод электростатических изображений неприменим при
с/0.

_2\ ФУНКЦИИ ВЛИЯНИЯ ТОЧЕЧНЫХ источников 527
R = RmMq = л/(ж - жо)^ + {у - УоУ + (^ - ZoY,
Ri = RmMi = л/(ж - хоУ -\-{у - УоУ + {z + 2;о)^,
где Mi(xo,^0 5 — ^о) — изображение точки Мо(жо,^0 5^о) относительно
плоскости 2; = 0.
Мы не останавливаемся здесь на вопросе о применимости
предыдущих формул для неограниченной области, что, впрочем, без труда
может быть установлено в случае с < 0. Задачи для
неограниченного пространства при с > О связаны с «принципом излучения» и будут
рассмотрены в следующем параграфе.
Для функции источника G(M, Mq), определенной для
произвольной области Т, имеет место принцип взаимности, выражаемый
равенством
G(M,Mo) = G(Mo,M).
Доказательство этого свойства является буквальным повторением
соответствующего доказательства для случая уравнения Лапласа
(гл. IV, § 4).
В случае двух независимых переменных уравнение для функции
г'о(г) имеет вид
- — г —— + /;; г'о = О, или -—г- -\ -— + /;; г'о = О,
г аг \ аг J аг"^ г аг
т. е. является уравнением Бесселя нулевого порядка,
общее решение которого может быть записано следующим образом (см.
Дополнение II):
где Hq '(кг) и Hq '(кг) — функции Ханкеля нулевого
порядка первого и второго рода.
Функции Н^^\кг) и Н^^\кг) при г = о имеют логарифмическую
особенность:
7Г
г(2)/ ^ 2г . 1
(Р = kr),
7Г р
где точками обозначены слагаемые, остающиеся конечными при р = 0.
На бесконечности (при р —>- оо) поведение функций Ханкеля
определяется асимптотическими формулами
V 'тгр
Я^(р) = ./Ае-(р-/4) + ...,
V '^Р

528 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
где точками обозначены члены более высокого порядка малости
относительно 1/ р.
Таким образом, уравнение А2г' + /г^^г» = О имеет два
фундаментальных решения:
, > fHi"(*r).
имеющих логарифмическую особенность и соответствующих
функциям е*^^/г и е~*^^/г для пространства.
Выбор той или иной фундаментальной функции зависит от вида
условий излучения на бесконечности (см. § 3, п. 4). Если временная
зависимость берется в виде е*'^^, то функция Щ '{кг) определяет
расходящуюся цилиндрическую волну. При временной зависимости е"*'^^
расходящуюся волну определяет функция Hq \кг).
При с = — х^ < О уравнение С{и) = О принимает вид
dr^ г dr
и его линейно независимыми решениями являются цилиндрические
функции мнимого аргумента
/о(хг) и К^{>1:г).
Первая из этих функций, 1о{>сг), ограничена при г = О и
экспоненциально возрастает при г —>- оо; функция Ко{>сг) имеет в точке г = О
логарифмическую особенность
Ко(р)=1п- + ...
р
и тем самым является искомым фундаментальным решением. Па
бесконечности она убывает по закону
Ко{р) =
Мы не останавливаемся подробно на формулах Грина и понятии
функции источника G в случае двух независимых переменных, так как
изложение этого было бы повторением предыдущего.
3. Потенциалы. В гл. IV были рассмотрены потенциалы для
уравнения Аи = 0. Такого же типа потенциалы могут быть построены
и для уравнения Аи — к^и — 0.
Будем называть объемным потенциалом (для уравнения
Аи — х^и = 0) интеграл
V{M) = J p{P)^drp, (13)
т

А
ФУНКЦИИ влияния ТОЧЕЧНЫХ источников
529
R = R
MP
л/i^
^)2 + (у _ ^)2 + (^ _ ^)2^ а^^ = а^ rf^ ^^^
где р{Р) — плотность потенциала.
Сформулируем кратко основные свойства объемного потенциала,
доказательство которых проводится аналогично тому, как это сделано
в гл. IV.
1. Вне области Т функция V{M) удовлетворяет уравнению
AV - к^У = 0.
2. Внутри области Т интеграл (13) сходится, сходятся также
интегралы, получающиеся при помощи формального дифференцирования
1/(М) под знаком интеграла:
I
Ж,^,С)
д_
дх
R
d^dr]d( и т. д.
3. Функция V{x,y,z) дифференцируема, и ее первые производные
можно вычислять дифференцированием под знаком интеграла:
-:kRi
—-— d^dijdC и т. д.
К
Дифференцируемость функции V{x,y,z) доказывается в
предположении только ограниченности функции р. Отсюда, в частности, следует
дифференцируемость 1/ и в точках поверхности Е, ограничивающей
область Т, где, как правило, имеет место разрыв плотности р{М).
4. Во внутренних точках области Т, в окрестности которых
плотность р дифференцируема, вторые производные объемного потенциала
V существуют и потенциал V удовлетворяет уравнению
AV -H^V = -47гр(М).
5. Первые производные объемного потенциала представляются
равномерно сходящимися интегралами в предположении равномерной
ограниченности р. Поэтому первые производные являются
непрерывными функциями во всем пространстве включая точки поверхности
Е.
Объемные потенциалы позволяют представить решение краевой
задачи для неоднородного уравнения Аи — х^и = — / в виде суммы
и{М) = y(M)+ui(M),
где V{M) — объемный потенциал с плотностью р = //47г, ui{M) —
решение краевой задачи для однородного уравнения Ащ — k^ui = 0.
Перейдем к обзору свойств потенциалов простого и двойного слоя.
Назовем потенциалом двойного слоя интеграл
^(^' = /''(^)а^
R
dap {R = Rmp),
(14)
34 А. Н. Тихонов, А. А. Самарский

530 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
где fi{P) — поверхностная плотность потенциала W.
Перечислим основные свойства потенциала двойного слоя,
отсылая за их доказательством к гл. IV, § 5.
1. Вне поверхности Е потенциал двойного слоя всюду
удовлетворяет однородному уравнению AW — y^W — 0.
2. Потенциал двойного слоя сходится в точках границы, если Е
принадлежит классу поверхностей Ляпунова.
3. Функция W разрывна в точках поверхности Е, и имеют место
соотношения
Vre(Mo)=Vr(Mo) + 2^/i(Mo),
VrH(Mo) = Vr(Mo)-2^/i(Mo).
Здесь W^{M{^^ — предельное значение функции W{M^ при стремлении
М к Мо изнутри области Т, W^[M^) — предельное значение W[M)
при стремлении М к Мд снаружи Т. Потенциал простого слоя,
определяемый поверхностным интегралом
V{M) = J p{P)^^dap {R = Rmp), (15)
E
обладает следующими свойствами.
1. Вне поверхности Е потенциал простого слоя всюду
удовлетворяет однородному уравнению AV — y^V — 0.
2. Интеграл равномерно сходится на Е и определяет функцию
1/(М), непрерывную во всем пространстве.
3. Нормальные производные потенциала простого слоя для
поверхностей класса Ляпунова удовлетворяют соотношениям (ср. с (48) из
гл. IV, § 5)
dV\
dv_
] =Uo + 2ttp{Mo),
Uo-2ttp{Mo),
dV\ {dV
где
— предельные значения для нормальной производной
соответственно изнутри и извне S в точке Мо на поверхности И (у — внешняя
нормаль),
UoiMo) = Iр{Р) ^
^->cR
R
dap {R = Rmop)-

§ 3] НЕОГРАНИЧЕННАЯ ОБЛАСТЬ. ПРИНЦИП ИЗЛУЧЕНИЯ 531
Поверхностные потенциалы позволяют для весьма п1ирокого
класса поверхностей (например, поверхностей класса Ляпунова) сводить
краевые задачи к интегральным уравнениям.
Рассмотрим первую внутреннюю краевую задачу для уравнения
при граничном значении и\^ = /. Предположим, что
искомую функцию можно представить в виде потенциала двойного слоя
u{M) = W{M) = 11л{Р)^
S
е->.л
R
dap, (14)
который, как было отмечено выше, удовлетворяет внутри Т
однородному уравнению Аи — я^и = 0. Требуя выполнения граничного условия
u|e = /, приходим к следующему интегральному уравнению для
определения функции /а:
27Г fi{M)+ f fi{P) ^
dvp
Е
R
dap = f{M),
которое является линейным интегральным уравнением Фредгольма
второго рода. Па вопросах существования и единственности решения
этого интегрального уравнения мы здесь не останавливаемся.
Для уравнения Аи — я^и = О, так же как и для уравнения Лапласа,
применим метод конечных разностей.
§ 3. Задачи для неограниченной области.
Принцип излучения
1. Уравнение Av + cv = —f в неограниченном
пространстве. Рассмотрим решение неоднородного уравнения
Av + cv = -f (1)
в неограниченном пространстве. Для простоты изложения будем
считать, что / отлична от нуля внутри некоторой ограниченной области
(локальная функция). Характер решения этого уравнения существенно
зависит от знака коэффициента с.
Остановимся сначала на случае с = — х^ < 0. Решение уравнения
Av — K^v = —f можно представить в форме объемных потенциалов
f(P)^^dTp и V2{M) = j f{P)^-^dTp {R = Rmp).
T T
Таким образом, решение уравнения (1) без дополнительных условий
в бесконечности определено неоднозначно. Будем искать по аналогии
с внешней задачей для уравнения Лапласа решение уравнения (1),
обращающееся в нуль на бесконечности. Этому условию
удовлетворяет функция vi{M) и не удовлетворяет функция V2{M).
34*

532 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Докажем следующую теорему единственности.
Уравнение
Av — K^v = —/
не моэюет иметь более одного решения, обращающегося в нуль на
бесконечности^^.
Допустим, что существует два различных решения поставленной
задачи v{M) и v{M), и рассмотрим их разность w = v — v. По
предположению, найдется такая точка Мд, что w{Mo) = А ^ 0. Для
определенности будем считать Л > 0. В силу того, что w{M) —>- О в
бесконечности, можно указать такое Rq, что при г > Rq функция w < А/2.
Отсюда следует, что точка Mq лежит внутри Tr^ — niapa радиуса
Rq — и что функция w{M) достигает своего максимального значения
внутри Trq. Таким образом, мы приходим к противоречию с
принципом максимального значения, имеющим место для нашего уравнения
(см. § 1, п. 4). Теорема единственности доказана.
Рассмотрим теперь случай с = к'^ > 0.
Функции
f(P)^^^dTp и v2iM) = Jf(P)^dTp (R = Rmp)
т т
по-прежнему являются решениями уравнения (1). Однако в этом
случае обе функции убывают на бесконечности. Отсюда вытекает
необходимость введения дополнительных условий на бесконечности,
однозначно определяющих решение уравнения (1). Эти условия будут
разобраны в пп. 2 — 4 настоящего параграфа.
2. Принцип предельного поглощения. Задача о
вынужденных колебаниях с затуханием приводит к уравнению
А^ = ^ utt + Рщ - F{M, t) (/3 > 0). (2)
Будем считать, что функция F{M, t) является периодической по
времени, т. е. F{M,t) = f{M) е*'^^. В этом случае уравнение (2) имеет
периодическое решение вида
u{M,t) =v{M)e'''K (3)
Функция v{M), очевидно, удовлетворяет уравнению
Av + q^v = -f{M), (4)
где q^ = к^ — i/3uj является комплексной величиной, к = со/а.
^ Под термином «функция, обращающаяся в нуль на бесконечности» мы
понимаем следующее: каково бы ни было s, найдется такое r(s), что для
любой точки M(r,'?^,(^), для которой г > г{е), верно |n(M)| < s, т. е. мы
предполагаем равномерное стремление к нулю при г ^ оо.

§ 3] НЕОГРАНИЧЕННАЯ ОБЛАСТЬ. ПРИНЦИП ИЗЛУЧЕНИЯ 533
Будем называть уравнение (4) с комплексным значением
коэффициента q^ уравнением с комплексным поглощением 1-го
(Img'^<0) или 2-го (Img'^ > 0) типа в зависимости от знака
мнимой части q^ ^ что соответствует временной зависимости е^'^^ (1-го
типа) или е"*'^^ (2-го типа).
Фундаментальные решения этого уравнения, зависящие только от
г, имеют вид
%{r) = И VQ{r) = ,
Г Г
где
о-"'
^ио
= =Ь < V 7^ ^ V 7^ > = ^0 - ^qi. (5)
Знаки корней выберем так, чтобы qi > 0. Следовательно,
е
-гдог piQQr
Щ{г) = e-«l^ Voir) = e^i"-.
Г г
Условию ограниченности на бесконечности удовлетворяет только
функция vo{r); функция vo{r) неограниченно возрастает при г —>- оо
и потому не имеет прямого физического смысла.
Объемный потенциал
/p-iqoR
f{P) -j^ e-«i« drp {R = Rmp) (6)
T
представляет единственное решение уравнения (4), обращающееся в
нуль на бесконечности. Предел v{M) при /3^0 равен
г -ikR
v{M) = Ит ^(М) = у f{P)^-^dTp {R = Rmp),
т
так как при /3 —>- О имеем qo ^ к и qi ^ 0. При выбранной нами
временной зависимости е*'^^ величина qo > О, так как знак qo связан со
знаком qi соотношением 2qoqi = /Зсо.
Если зависимость от времени взята в виде е"*'^^ {1т q"^ > 0), то
положительному значению qi соответствует qo < О vl предел qo при
Р ^ О равен —к.
Таким образом, дополнительным условием, позволяющим
выделить решение волнового уравнения
Av + k'^v = -/,

534 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
соответствующее расходящимся волнам, является требование, чтобы
функция v{M) была пределом ограниченного решения волнового
уравнения с комплексным поглощением первого рода при стремлении к
нулю коэффициента ног лощения-"^ л
3. Принцип предельной амплитуды. С волновым уравнением
А^ + k^v = -/ (7)
чаще всего приходится встречаться при изучении установившихся
колебаний, возбуждаемых периодическими силами (см. § 1, п. 1).
Рассмотрим уравнение колебаний с периодической правой частью
Au-\uu = -F (F = /e^-*). (8)
Для определенности решения к уравнению следует добавить некоторые
начальные условия, например нулевые:
и{М,0)=0,\
ut{M,0)=0.j ^ '
Функция и{М, t) в начальной стадии процесса не будет строго
периодической. Однако с течением времени в системе будут устанавливаться
периодические колебания с частотой вынуждающей силы, т. е.
решение u{M,t) примет вид
u{M,t) =i;(M)e^^^ (10)
где v{M) представляет предельную амплитуду колебаний, т. е. v{M) =
и удовлетворяет уравнению
А^ + k^v = -f (^к= -)
Требование, чтобы v{M) было предельной амплитудой колебаний с
нулевыми начальными данными, и представляет то дополнительное
условие, которое надо присоединить к волновому уравнению для
выделения единственного решения.
Таким образом, приходим к следующей задаче.
Найти решение волнового уравнения Av + k^v = —/, являющееся
предельной амплитудой для решения уравнения колебаний
Au-\uu = -f{M)e'-' (8')
С начальными условиями (9)
и(М,0) =0,
и,(М,0)=0.
^^ См.: Свешников А. Г. Принцип излучения//ДАН СССР. 1950. Т. 73,
№ 5. С. 917-920.

§ 3] НЕОГРАНИЧЕННАЯ ОБЛАСТЬ. ПРИНЦИП ИЗЛУЧЕНИЯ 535
Представим предельную амплитуду в явной форме. Для этого найдем
penienne уравнения колебаний (8') с нулевыми начальными данными,
пользуясь формулой
u{M,t) = — J -^^ ^ ^ drp {R = Rmp),
полученной в гл. V (§ 2, (6)). Здесь Т^ — шар радиуса at с центром
в точке М.
Пусть f{P) — локальная функция, отличная от нуля только
внутри некоторой ограниченной области Tq. Тогда для предельной
амплитуды v{M) получим выражение
v{M) = lim u{M,t)e-'''^ = lim — / —p^f{P)dTp =
t^-oo t^-oo 47Г J R
Tr
at
To
Таким образом, предельная амплитуда представляется объемным
потенциалом, определяемым главным решением e~*^^/i^, которое
соответствует расходящимся волнам е^^^^~^^^ /R.
Принцип предельной амплитуды приводит математически к
тому же результату, что и принцип предельного поглощения. Это и
естественно, так как оба эти принципа выделяют решение,
соответствующее расходящимся волнам.
4. Условия излучения. В предшествующих пунктах были
рассмотрены общие физические основания, позволяющие найти решение
волнового уравнения, соответствующее расходящимся волнам. Однако
такой путь требовал обращения к решениям вспомогательных задач.
Установим теперь аналитическое условие, характеризующее
расходящуюся волну и выраженное непосредственно в терминах изучаемого
решения волнового уравнения.
Плоские волны, распространяющиеся вдоль оси ж, имеют вид:
— прямая волна (идущая в
положительном направлении оси ж);
й = f it -\— J — обратная волна (идущая в
отрицательном направлении оси х).
Прямая волна характеризуется соотношением
дй 1 дй
дх а dt
/('-е

536 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
OD.
(-Э
(12)
обратная волна — соотношением
дй 1 дй
дх а dt
Для установившегося режима
эти соотношения принимают вид
dv
дх
dv
дх
Перейдем теперь к случаю сферических волн. Если сферическая
волна возбуждается источниками, расположенными в ограниченной
части пространства, то на больших расстояниях от источников
сферическая волна подобна плоской волне, амплитуда которой убывает
как 1/г. Отсюда естественно считать, что расходящаяся сферическая
волна должна удовлетворять соотношению^^
V
аналогично для сходящейся сферической волны:
+ ikv = О для прямой волны.
ikv = О для обратной волны.
ди 1 ди
дг а dt
(13)
ди
дг
1 ди
а dt
= о
(14)
Для амплитуды установившихся колебаний эти условия принимают
вид
dv
дг
dv
дг
+ ikv = о
ikv = о
для расходящихся сферических волн, (15)
для сходящихся сферических волн.
(16)
Соотношения (15) и (16) мы получили, предполагая, что на
больших расстояниях всякая расходящаяся волна подобна плоской волне,
амплитуда которой убывает как 1/г. Убедимся в правильности этого
утверждения.
^ Написанные соотнонесния представляют уравнения с частными
производными 1-го порядка, репЕСния которых имеют вид прямой и обратной
волны.
2
В дальнейпЕСм мы пользуемся двумя обозначениями: О(^) —
величина, убывающая, как ^ при ^ ^ О, о(^) — величина более высокого порядка
малости, чем ^ при ^ ^ 0.

§ 3] НЕОГРАНИЧЕННАЯ ОБЛАСТЬ. ПРИНЦИП ИЗЛУЧЕНИЯ 537
1. В случае точечного источника, находящегося в начале
координат, это утверждение совершенно очевидно, поскольку сама волна
имеет вид
u{r,t) = =voir)e'^\
Г
так что
-^— + гкУо = о( -
or \г
2. Пусть сферическая волна возбуждается точечным источником,
Мо R М
Рис. 82
находящимся в некоторой точке Мд. Амплитуда сферической волны
равна
^ — ikR
vo(M) =
R '
где R — расстояние между точками М и Мд, равное (рис. 82)
R = л/г^ + Ро ~ ^^/^0 cos 'д.
Вычислим производную:
В силу п. 1
дК г — ро cos'^ ^ -, п (^
дг R \г
Проверим справедливость формулы (15)
^{щ) = -тА + ^kvQ = о ( -
or \г
в самом деле,
дщ_ _ дщ dR _ дщ / . , ^
дг dR дг dR \ \г
(15')
dvo ^ /1

538 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
так как
Отсюда и из п. 1 следует
что и требовалось доказать.
3. Покажем, что объемный потенциал
/^ — ikR
fiP) -^^ drp {R = Rmp)
т
удовлетворяет условию (15). Очевидно, что
'^^ = I ^(^) ^ (S^) ^- = / ^(^) ^ (}) ^- = ЧJ) •
т т
Формула (11) представляет амплитуду расходящейся волны,
возбуждаемой источниками, произвольно распределенными внутри
ограниченной части пространства Т. Мы видели, что функция v{M)
удовлетворяет волновому уравнению
Av + k^v = -f{M)
и стремится к нулю как 1/г на бесконечности; кроме того, как было
показано, для нее на бесконечности выполняется соотношение
dv ., /1
-- + ikv = о [ -
or \r
являющееся необходимым дополнительным условием.
Покажем, что справедливо следующее утверждение.
Существует единственное решение волнового уравнения
Av + k^v = -f{M),
где f{M) — локальная функция, удовлетворяющее на бесконечности
условиям
'V
О
dv .^ /1
or \г
(а)
^ и. п. Веку а показано, что первое из приведенных здесь двух условий
является следствием второго; см.: В еку а И. П. О метагармонических
функциях // Тр. Тбил. Мат. ин-та. 1943. Т. 12. С. 105-174.

§ 3] НЕОГРАНИЧЕННАЯ ОБЛАСТЬ. ПРИНЦИП ИЗЛУЧЕНИЯ 539
Допуская существование двух различных решений vi и г'2,
получаем, что их разность
W = Vi — V2
удовлетворяет однородному уравнению и условиям (а). Пусть Ед —
сфера радиуса R, который мы в дальнейп1ем устремим в
бесконечность. Пользуясь основной формулой Грина для функций w{M) и
^ — ikR
vo{M)
4:7TR
будем иметь в точке Мд, лежащей внутри Е,
w{Mo) = J [^o^-w—j da.
Условия (a) для vo{r) и w{M) дают
^0
dw
dr
w
dvp
dr
Щ
-ikw + о
w
■ikvo + о
Поэтому
w{Mi
.)=/»(^)
= voo[-
wo \ -] = о( —
r J V r^
da ^ 0 при i^ —>- 00,
откуда и следует, в силу произвольности точки Mq, единственность
реп1ения нап1ей задачи.
Условия (а)
v = 0
dv
——h гку = о
or \r
часто называют условиями излучения или условиями Зоммер-
фельда.
Следует отметить, что для неограниченных областей, не
совпадающих со всем пространством, условия на бесконечности могут иметь
форму, отличную от условий Зоммерфельда.
Таким образом, соотношения (а) представляют аналитическую
форму условий излучения для неограниченного пространства и не
основаны на физическом принципе, который позволил бы
сформулировать эти условия для областей более сложной формы.
Условия излучения, получающиеся при введении в волновое
уравнение бесконечно малого комплексного поглощения, впервые были ис-

540 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
пользованы B.C. Игнатовским-'^л Принцип введения бесконечно малого
комплексного поглощения легко применим для неограниченных
областей различной формы и для более сложных задач.
Для задач на плоскости, связанных с уравнением
A2V-\-k^v = О,
условия излучения на бесконечности принимают вид
1
(17)
О
V^
dv
lim д/r ( ——h ikv
0.
(18)
Простейшими решениями этого уравнения являются функции Ханкеля
нулевого порядка Н^^\кг) и Н^^\кг) (см. Дополнение П, ч. I, § 3).
Из асимптотических формул
2
-ккг
Н1^\кг) = W^e^(^--W2-V4)
1 + 01 -
г
И рекуррентных соотношений
i {kr — TTv/2 — тт/А)
dH,
(1)
dx
-Н['\х),
dH,
(2)
dx
1 + 01 -
г
-яГ^Н
Г(2)
ВИДНО, что условиям излучения удовлетворяет лишь функция Н^ (кг).
Таким образом, функция щ \кг) удовлетворяет уравнению (17),
условиям излучения (18) и имеет логарифмическую особенность при
(2)
Г = 0. Поэтому функция Hq ^(кг), как уже отмечалось в § 2,
играет роль функции точечного источника для волнового уравнения (7) в
случае двух независимых переменных. Решение неоднородного
уравнения
A2V-\-k'^v = -/
выражается формулой
v{M) = -lJ 1 ^^о'' {кКмр) f{P) dap,
где S — область, в которой функция / отлична от нуля.
^^ Ignatowsky W. V. Reflexion elektromagnetischer WeUen an einen Draht
// Ann. Physik. 1905. Bd 18, H. 3. S. 495-522.

А
ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 541
§ 4. Задачи математической теории дифракции
1. Постановка задачи. Распространение волновых процессов
(электромагнитных, упругих, акустических и т. д.) сопровождается
целым рядом типичных явлений (дифракция, преломление, отражение
и т. д.). Решение задач, связанных с этими явлениями, проводится
непосредственно или имеет много общего с решением волнового
уравнения в неоднородной среде
д_
дх
Р
dv
дх
д
Р-
dv
+
д
ду \ ду J dz \ dz
Р-
dv
+ puj^v = -f {р>0), (1)
где р и р — параметры среды.
Наибольший интерес с точки зрения физических приложений
представляет случай кусочно-постоянных параметров р и р.
Соответствующая математическая задача состоит в следующем. В
неограниченном пространстве имеется ряд ограниченных областей Ti с
постоянными параметрами pi и pi; часть пространства То, внешняя по
отношению к областям Т^, также однородна (ро = const, ро = const).
Волновое уравнение внутри каждой области Ti принимает обычный
вид
где щ
Avi + eiVi = -fi в Ti (г = 0,1,
значение искомой функции и внутри Т^,
п).
(2)
PiUJ^
Pi
fi
I
Pi
в области Ti. На поверхностях Е^, ограничивающих области Т^-*^^,
дифференциальные уравнения заменяются условиями сопряжения
Vi = г'о
на Ef,
Pi
dvi
дп
Ро
dvp
дп
на
(г = 1, 2,
п).
(3)
На бесконечности функция г'о, являющаяся решением волнового
уравнения Av -\- k^v = —fo bTq, должна удовлетворять условиям излучения
vo{M)=0 -
dvo , .,
or
(4)
^ При этом мы рассматриваем для простоты тот случай, когда
неоднородности Ti имеют общую границу только с окружающей средой.

542 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Ниже будет показана достаточность условий сопряжения и
условий излучения для однозначного определения функции v во всем
пространстве. Поставленная вып1е задача является простейп1ей задачей
математической теории дифракции.
2. Единственность решения задачи дифракции. Докажем, что
задача математической теории дифракции, сформулированная в п. 1,
имеет единственное penienne. Для упрощения записи будем предполагать, что
однородность среды наруптается только одним телом Ti, ограниченным
замкнутой поверхностью Ei, вне которой расположена область Тд. При этом
мы не делаем предположения об односвязности области Ti.
Докажем следующую теорему.
Может существаватъ только одна функция, удовлетворяющая:
а) уравнениям
Co{vo) = AvQ -h kovo = -/о в
Ci{vi) = A-^i -h kivi = -/i в
6) условиям сопряэюения на поверхностей Ei
Vi = vo
dvi dvo
b) условиям излучения на бесконечностей (4)
(20
(3)
Vo
dvQ
дг
+
Допуская существование двух различных рептений
v = {vi,vo} и v = {vi,vo},
получаем, что их разность
W = {wi.wo},
где
Wi =Vi -VI, Wo =щ - Vo,
удовлетворяет однородным уравнениям и прежним дополнительным услови-
Co{wo) = 0 в То, C^{wi) = 0 в Ti, (2*)
dwi dwo ^ .^*.
wi=wo, Р^~я^^Р^~я^ "^ ^1' (^ ^
Wo = о 1-] J — h ikwo = ^ ( ~ ) при г ^ оо. (4*)

§ 4] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 543
Для функций Wqj Wij комплексно сопряженных к функциям wq и wij
очевидно, будут удовлетворяться однородные уравнения (2*), условия (3*) и
условия излучения
Пусть Ед — сфера достаточно больпюго радиуса Я, охватывающая
область Ti, и Тл — область, ограниченная поверхностями Ei и Ед.
Применяя формулу Грина к функциям wi, w^ в области Ti ж wq, Wq в
области Тд, получаем
/ [-^i/:! (-Ш!) - w^Ci (wi)] dr = Iwi -^ - wl -^ \ da = 0,
Ti El
/ [wqCo (wq) - WqCo (wo)] dr =
Tr
f f dwQ * ^-^0 \ . , f f dwl * ^-^0 \ , ^
E
R
где i/Q — нормаль, внепЕняя к области Тд, ui — нормаль, внепЕняя к области
Ti. Очевидно, д/дщ = —d/dvi на Ei.
Умножая первое равенство на pi, второе — на ро? складывая их и
пользуясь условиями сопряжения (3*), находим
/(■
^-^0 * dwQ \
^R
Выражая из условий излучения производные
дг
приходим к следующему равенству:
{ равенству:
2ik I woWoda-\- / \wo о (—j - wq о (—j da = 0.
^R ^R
Второй интеграл при R ^ oo стремится к нулю, поэтому
/ wqWq da = / l^tt'ol dfl ^ 0, R ^ oo {dfl = sin в dO dcp).
^R ^R
В Дополнении П, ч. П, § 4 показано, что функция
(5)

544 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
где
С^ш\р)
^H^Wp) (P = f'or),
и Yrn{0, (f) — сферическая функция ?тг-го порядка, удовлетворяет волновому
уравнению
Co{Vm) = AVm + ЩУш = О
И условию излучения
дУш
дг
-\-ikoVm = о(-] .
Применим формулу Грина в области Тд к функциям wq и Vm'-
0=1 [woCiVm) - VmCiwo)] dr =
Tr
dVm x^ 9 Wo
Of
Of
)d-+/(«'o^
.. ^™^)^^ = ^.+^я.
Второе слагаемое 1л в силу условий излучения стремится к нулю при R -^
-^ оо (см. теорему из § 3, п. 4). Так как первый интеграл /i не зависит от
Я, то отсюда вытекает, что /i = О и, следовательно, Ir = О при любом Я,
т. е.
dCm (крт
dr
I
^R
woYrn{0,(p)dQ - С
(2)
/
дг
Yrn{0,ip)dn = 0.
Если обозначить
/
woYrn{0, (р) dQ = arn{koR),
то можно написать
4^ (koR) arnikoR) - a'mikoR) Cm\koR) = О
откуда находим
(2)
am{koR) = атСт (koR),
где am — постоянный множитель.
Условие замкнутости сферических функций
и формула (5) дают
/сю
\Rwo\^dn= Y.R'^^mikoR)
^ т=0
Ram{koR) -^ о при Я ^ оо.
(6)

§ 4] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 545
Однако согласно асимптотической формуле
4^)(р)«1е-(''-^-),
Р
(2)
произведение гС,гп v^qv) остается по модулю больпте некоторого
положительного числа при больпЕих значениях г; следовательно, am = О, т. е. am{koR) =
= 0; отсюда в силу уравнения замкнутости (6) вытекает, что wq = О из,
сфере Его- Таким образом, если сфера Е^о некоторого радиуса го
охватывает область Ti, то вне этой сферы функция г^; = 0. Отсюда в силу
аналитичности ^ репЕСния уравнения С = О заключаем, что функция wq = О
всюду в области Tq. Далее из условий сопряжения следует, что на
поверхности El
«;,=0 и ^=0. (7)
Основная формула Грина, примененная в области Ti к функции wi,
показывает, что
/л^ч 1 f Ге-^^1^ dwi{P) ,„, д fe
R
da = 0 (8)
(где R = Rmp) в любой точке М области Ti.
Итак, мы убедились, что w{M) = О во всем пространстве; это и
доказывает теорему единственности.
3. Дифракция на сфере.
1. Практически важным классом рептений уравнения колебаний
An -utt = ^
являются плоские волны. Плоской волной, распространяющейся в каком-
нибудь заданном направлении, называется penienne, зависящее от времени
и от одной пространственной координаты, отсчитываемой в направлении
распространения. Например, плоская волна, распространяющаяся вдоль оси
ж, удовлетворяет уравнению с двумя независимыми переменными
Uxx T^Utt =^
и имеет вид
u{x,t) = f(t-'^y
в случае установивпЕСгося режима, когда зависимость от времени определя-
ется множителем е , плоская волна имеет вид
м(ж,*) = Ае'('"*-*='), (9)
где к = UJ/а — волновое число, \А\ — амплитуда.
^ Аналитичность функции w в области Ti следует из формулы (7) § 2
для комплексного значения >с = ik ж для поверхности Е, целиком лежащей
внутри Ti.
35 А. Н. Тихонов, А. А. Самарский

546 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Плоская волна, распространяющаяся в направлении 1, где 1 =
= {Ixilyilz) — единичный вектор, может быть записана следующим образом:
и(х, у, г, <) =у1е*И-Ц»^'-+г''!/+^'^)] =Ле* ["*-'=''•]. (10)
Функции
v{x) = Ае~^ ^^ v{x,y,z) = Ае~^ ^, (11)
являющиеся рептениями волнового уравнения
Av-\-k^v = 0, (12)
обычно также называются плоскими волнами.
В математической теории дифракции обычно изучаются возмущения
поля в однородной среде, создаваемые наличием включений Т^, наруптающих
однородность среды. Пусть v{M) — поле в однородной среде, создаваемое
заданными источниками, которые мы считаем расположенными вне
области Ti (г = 1, ..., п); в частности, это могут быть достаточно удаленные
источники, вызывающие появление плоских волн:
vix,y,z) = Ae-"'"'. (13)
Действительное поле г^о, имеющее место в области Tq при наличии неодно-
родностей, можно представить в виде суммы
vo{M) = wo{M) + ^о(^),
где ^о(^) — «падающая волна», wo{M) — дифрагированная, или
отраженная, волна, представляющая возмущение внепЕнего поля v неоднородностями
Тг.
Будем искать в области Tq дифрагированное поле wo{M), а внутри
Ti — «преломленное поле» Vi. Установим условия, определяющие искомые
функции wq -и. Vi {i = 1, 2, ..., п):
а) функции wq и Vi удовлетворяют уравнениям
А^о+А;о^о = 0 в То, (14)
Avi-\-kiVi = 0 в Ti (г = 1, 2, ..., п);
б) на границах раздела Е^ областей Ti и Tq выполняются следующие
условия сопряжения:
Vi = wq-\-щ на Ef, (15)
где ^0 — заданная функция,
Pi^=Po^^ + /i на Ei, (16)
где fi=po' дщ/ди — заданная функция;
в) отраженная волна wo{M) на бесконечности ведет себя, как
расходящаяся сферическая волна, т. е. удовлетворяет условию излучения
WO{M)=OQ;^
dwo ., /1\
-^ h ikwQ = о - .
or \r J

§ 4] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 547
2. Рассмотрим более подробно дифракцию плоской волны на сфере К
Пусть в направлении оси z из бесконечности падает плоская волна
щ = Ае-'''' (17)
на Hiap радиуса R с центром в начале координат. Ищем отраженное и
преломленное поля в виде разложения по сферическим функциям; щ -и. f = ро •
• дщ/дг, входящие в правые части условий сопряжения, разложим по
сферическим функциям.
Положим Z = rcos^; тогда можно воспользоваться следующим
разложением плоской волны по сферическим функциям:
ikr cos (
= Y, (2m + l)(-z)'^V'm(A;r)^m(cos^), (18)
где
m=0
■фт(кг) = \ 7П- Jm+^hi^'^)
2кг ''™+V2^
(JjyiA^i/^ikr) — функция Бесселя первого рода {т + 1/2)-го порядка),
Ргп{со8в) — полином Лежандра ?тг-го порядка. В самом деле, слева стоит
репЕСние волнового уравнения, зависящее только от z. Всякое рептение
волнового уравнения может быть представлено как сумма произведений
сферических функций на гргп{кг). Поскольку в наптем случае левая часть (18)
обладает зональной симметрией, то
сю
^-ikrcosO ^ ^ Сгпфш{кг)Рт{с08в), (19)
т=0
где Cm — неопределенные пока коэффициенты. Пользуясь
ортогональностью полиномов Лежандра и их нормой (см. Дополнение П, ч. П), получаем
1
Сшфш{р) = ^^^^ / е-''^Рт{0 d^ (20)
{р = кг, ^ = cos в).
Пайдем первый член асимптотического представления для интеграла,
стоящего в правой части; сравнение его с первым членом
асимптотического разложения функции фт{р) позволит нам определить коэффициент Cm-
Проинтегрируем т раз по частям, интегрируя каждый раз е~*^^ и
дифференцируя Рт{0- В результате получим разложение интеграла по степеням
^ Аналогичные методы часто используются в квантовой механике в
задачах о рассеянии частиц.
35*

548 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
1//9. Сохраняя только первый член разложения, будем иметь
+1
/
1
e-'''^Pm{OdC=^r- е-^''«Рш(0
+1
-^ {е-">Рш{1) - е">Рш{-1)) = ^ (е-*" - (-1)™ е*") =
I / —ip _ —imTT ip\
-ip \ J
sin(/9 — т7г/2)
-im7r/2
g-i(p-m7r/2) _^i(p-m7r/2)
n-i)"
С другой стороны, как известно (см. Дополнение II, ч. I, § 1),
/ / ч ^ sin(/9 - т7г/2)
фш{р) = .
Р
Сравнивая эти выражения, находим из (20)
Cш = i2m + l){-iГ,
ЧТО и доказывает формулу (18).
Из (17) следует
"^^0 I
=Я = ^ атРт{с08в),
т=0
агп = А {2т + 1) (-г)"^ фш{к^К)\ )
(21)
(22)
Ро
дщ_
дг
r=R
У^ bmPm{cOsO),
т=0
brn = Акоро (2т + 1) (-г)"^ Ф'ш{коЯ)- }
(23)
Отраженное и преломленное поля являются рептениями волнового
уравнения и, так же как и падающее поле, обладают зональной симметрией.
Поэтому функции VI и wq мы ищем в виде
VI = ^^ ат'фт{к1г) Рт{с08в),
т=0
сю
г^о = ^ f^mCmikor) Рт{с08в),
т=0
и(р) = У^я1^),/^(,).
(24)
(25)
(26)

§ 4] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 549
Перейдем теперь к определению коэффициентов разложения аш и firn-
Пользуясь условием сопряжения и сравнивая коэффициенты при Pm{cos9)j
получаем
агпфш{к1П) - pmCmikoR) = агп = А{2т-\-1) (-г)"^ фгп{коП),
pikiam^'m{kiR) - pokoPmCmikoR) = Ьщ = АкоРо (2т + 1) {-i)^ tp'rnikoR),
откуда
_ iU-Л^ ^°^° y^m{koR)C'm{koR)-Crn{koR)^l;'m{koR)]
(27)
о =л(2 I iw •.mPikiipm{koR)il;m{kiR)-pokoil;m{koR)il;m{kiR)
^" ^ "^ ^^ '^ p^k^^m{kiR)C'rn{k^R)-piki^'m{klR)Cm{k^R) '
(28)
3. Рассмотрим в качестве примера задачу о рассеянии звука твердым
сферическим препятствием. Пусть на абсолютно твердую и неподвижную
сферу радиуса R с центром в начале координат падает плоская звуковая
волна, распространяющаяся в направлении оси z. Звуковое давление р{х, у, z, t),
как было установлено в гл. П, § 1, удовлетворяет уравнению колебаний
д'^р 2 д 2 Ро
где а — скорость звука, 7 — показатель адиабаты, ро ж pQ — давление и
плотность среды в невозмущенном состоянии.
Давление в падающей волне дается функцией
Ро
^^^-ii.t-kz) {к=^У
где А — постоянная.
Рассматривая установивпЕийся процесс
p{x,y,z,t) =p{x,y,z)e~"^\
получаем для p{x,y,z) волновое уравнение
Ар + к^р = 0.
Па поверхности сферы Sji в силу ее абсолютной твердости должна
равняться нулю нормальная составляющая скорости и. Проекция скорости на
направление нормали п связана с давлением следующим уравнением:
dun _ 1 dp
dt р дп^
которое в стационарном случае дает
1 др
Un = ^- .
lujp on
Отсюда получаем граничное условие
f^l =0-
дп \зл

550 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
Полагая р = pQ -\- w, где w{x,y,z) — давление рассеянной волны,
получаем для определения w следующие условия:
а) функция w{x,y,z) удовлетворяет волновому уравнению
Aw -\- к W = 0]
б) на поверхности сферы Sji выполняется граничное условие
dw
дп
^ _ дро
Sr дп
Sr
в) рассеянная волна w ведет себя на бесконечности как расходящаяся
сферическая волна, т. е. удовлетворяет условию излучения при г ^ оо:
{М) = о(1),
dw
——h ikw
or
Нетрудно видеть, что эта задача является частным случаем
рассмотренной выпЕС задачи дифракции и соответствует значению параметра pi =
= 0.
Полагая в формуле (28) pi = О, из (28) и (25) получаем
/3™ = -Л(2т + 1)(-гГ^?^^5§ (29)
и
w = -л V (2т + 1) i-гГ тНМг Ст(^ог) Рш{со8в). (30)
т=0
Если длина волны велика по сравнению с размерами niapa, т. е. koR ^
<^ 1, то в формуле (29) можно воспользоваться разложениями функций
фгп{кК) и C,m{kR) в ряды, которые следуют из разложений функций
(2)
Jr^^i/AkR) и Н^ ^ -у. (кВ) по степеням малого аргумента kR (см.
Дополнение II, ч. I, § 1 и 3):
'^"(^^^ = Уш [^mi—rw^j' ^'^'''^^ = уш -Pi5jw'
лr^m~• n^mmZ^ лr^m~ ■ Г^ {kR/2)-'/^
Так как
r(l/2) = V^, Г(3/2) = ^, r(5/2) = |v^, Г(-1/2) = -2^^,
ТО получаем
Co(feB)--^, Ci{kR) =
kR' ^'^ ^ (feB)2 '

§ 4] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ 551
откуда следует
(kR)^ ' ^'' ' (kR)^ '
Подставляя в формулу (29) найденные выражения для гр^ и ("^,
находим
Нетрудно видеть, что следующие коэффициенты пропорциональны (kR) ,
поэтому при рассеянии длинных волн (kR <^ 1) возмущение w приближенно
представляется двумя первыми членами ряда (30):
W = Moikr) + f3iCi{kr) cos в ]
\ (31)
[Pq (cos 6>) = 1, Pi (cos в) = cos в]. J
На больпЕих расстояниях от возмущающей сферы (кг ^ 1) в так
называемой «дальней», или «волновой», зоне для функций Со{кг) и Ci(^^) имеем
асимптотические представления
<о(кг)^^^е-''^'-, Cl(И^-^e-*^^ (32)
которые вытекают из асимптотических представлений функций Ханкеля.
Подставив в формулу (31) выражения (32) для Со{кг) и Ci(^^) и заменив
/Зо и /^1 их приближенными значениями, получим
_ Ak^R^ /. 3
W = —
(l-^cos^) е-^^". (33)
Зг
Обратимся теперь к вычислению интенсивности рассеянной волны; эта
величина определяется как среднее значение потока энергии (вектора Умо-
ва), равного произведению избыточного звукового давления w на скорость п,
причем под ити следует понимать действительные части соответствующих
выражений. В наптем случае
W = wo cos{ujt -кг) Л
и = uq cos{ujt — kr)jj
где wq -и. uq — соответствующие амплитуды.
Вычислим интенсивность звука / в волновой зоне, сохраняя при этом
главные члены асимптотических разложений:
Т
I = период .
< UJ )
1^^ Uos\u,t-kr)dt =
0
3 уравнения движения
ди
UqWo
2
1 dw
р дг

552 УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА (продолжение) [ГЛ. VII
и формул (34) находим
ио
ар
Таким образом,
2ар 18а/9г2 V^ 2
Обозначая мощность, рассеянную сферой в конус dd, через
/ = тг^ = ^ 1 — 7: cos в
2ар 18а/9г2 \ 2 )
27ГГ Е((9) sinOde,
будем иметь
^.„. А"/е^Д" /3 „V
18а/9 V 2
Полярная диаграмма интенсивности рассеянного niapoM звука приведе-
Рис. 83
на на рис. 83 (маснЕтабы не соблюдены). Если
2
cos ^ = + - ,
то в направлении 9 = а рассеяние отсутствует.
ЗАДАЧИ К ГЛАВЕ VII
1. Найти функцию влияния стационарного точечного источника газа,
предполагая, что газ распадается в процессе диффузии. РепЕить задачу для
диффузии в пространстве и на плоскости.
2. РепЕить задачу 1 в полуплоскости у > О, считая, что при у = О
концентрация равна нулю.
3. а) РепЕить внутреннюю и внепЕнюю задачи для уравнения
Аи — >с п = О,

ЗАДАЧИ К ГЛАВЕ VII 553
если на сфере г = го задано граничное условие и \г=го = AcosO.
В случае вненЕней задачи сформулировать условия на бесконечности,
обеспечивающие единственность ренгения.
Рассмотреть аналогичные задачи, предполагая, что
и\г=го =Р{в).
б) РепЕить аналогичные задачи для уравнения с двумя независимыми
переменными, когда граничные условия заданы на окружности радиуса го
и имеют вид
и \r=rQ = Acos^p
и, соответственно,
u\r=rQ =F{(p).
4. РепЕить задачи За и б для уравнения
В случае внутренней задачи исследовать вопрос о том, при каких значениях
Го существует единственное рептение (к считать заданным).
Сформулировать условия, гарантирующие единственность рептения
как для двух, так и для трех независимых переменных.
5. На глубине h под поверхностью земли находится среда, в которой с
постоянной плотностью распределено радиоактивное вещество. Найти
концентрацию эманации, считая, что концентрация ее на поверхности равна
нулю.
6. Найти собственные частоты мембраны, имеющей форму кольца,
радиусы которого равны а и 6 (а < 6), считая, что v\r=a = О и г; |^—^ = 0.
Показать, что предел первого собственного значения при а ^ О равен
первому собственному значению круглой мембраны радиуса b с закрепленной
границей.
7. Найти собственные колебания и собственные частоты для эндови-
братора цилиндрической формы, считая его стенки идеально проводящими.
Рассмотреть ту же задачу в акустической интерпретации.
Указание. В случае электромагнитных колебаний ввести
поляризационный потенциал (см. Приложение I к гл. VII).
8. Определить электромагнитное поле точечного диполя в неограни-
iujt
ченном пространстве, считая, что величины поля пропорциональны е
Исследовать асимптотическое поведение рептения на больпЕих расстояниях
(в волновой зоне). РепЕить ту же задачу для диполя, находящегося над
идеально проводящей поверхностью (вертикальный диполь).
Указание. Ввести поляризационный потенциал.
9. Поставить задачу о распространении электромагнитных волн
внутри бесконечного цилиндрического радиоволновода произвольного сечения с
идеально проводящими стенками. Рассмотреть волну электрического типа,
распространяющуюся вдоль круглого цилиндрического волновода и
имеющую наибольпЕую длину. Найти поле, вычислить поток энергии через
сечение, перпендикулярное к основанию (см. Приложение I к гл. VII).
10. РепЕить неоднородное уравнение
Аи -\- к и = —/
в неограниченной цилиндрической области круглого сечения, на
поверхности которой имеют место однородные граничные условия 1-го или 2-го рода,
и построить функцию источника (см. Приложение II к гл. VII).

554 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
11. Построить функцию источника в случае первой краевой задачи для
уравнения
Аи-\-к'^и = О
а) в полупространстве ^ > 0;
б) на полуплоскости у > 0]
в) внутри слоя —l^z^l.
12. РепЕить задачу о дифракции плоской электромагнитной волны на
бесконечном идеально проводящем цилиндре. РепЕить эту же задачу в
акустической интерпретации.
13. Пайти собственные электромагнитные колебания сферического эн-
довибратора с идеально проводящими стенками. Рассмотреть случаи
колебаний типа ТЕ и ТМ (см. Приложение II к гл. VII).
14. Пайти собственные электромагнитные колебания эндовибратора,
представляющего собой область, заключенную между двумя коаксиальными
цилиндрическими поверхностями и двумя плоскостями,
перпендикулярными к оси цилиндров.
Указание. Для поляризационного потенциала Ип гп воспользоваться
формулой, аналогичной формуле (14) из Приложения II к гл. VII.
прилож:ения к главе vii
I. Волны в цилиндрических трубах
1. При конструировании различного рода радиоустановок
приходится решать важную задачу о передаче электромагнитной энергии от
передатчика к передающей антенне или, наоборот, от антенны к
приемнику. Вопросы трансляции электромагнитной энергии встречаются
также в ряде других практических задач современной радиотехники.
До последнего времени эта задача удовлетворительно решалась с
помощью двухпроводной линии, представляющей собой два
металлических провода, между которыми распространяется электромагнитная
волна. Но оказывается, что наряду с недостатками, свойственными
вообще передающим линиям, такая двухпроводная линия излучает
электромагнитную энергию, причем это излучение увеличивается с
повышением частоты радиоволн. Поэтому такой вид передающей линии
становится малоудобным в области ультракоротких радиоволн.
В последние годы в технике ультракоротких (сантиметровых и
дециметровых) радиоволн для передачи энергии применяются
совершенно другие передающие устройства — полые металлические трубы
(радиоволноводы), внутри которых происходит распространение
радиоволн. Такие передающие устройства, обладая малыми потерями,
являются очень удобными линиями передач-'^л
^^ Введенский Б. А., Аренберг А. Г. Радиоволноводы. М.; Л., 1946.
Ч. I.

I. волны в ЦИЛИНДРИЧЕСКИХ ТРУБАХ 555
Математическая теория распространения радиоволн по трубам
была заложена еще Рэлеем, изучавп1им распространение
акустических волн в трубах. Интенсивное развитие теория радиоволноводов
получила в последние годы, особенно в работах советских ученых. В
настоящее время свойства круглого, прямоугольного и других типов
волноводов изучены достаточно хорошо.
Рассмотрим сначала свойства радиоволноводов произвольного
поперечного сечения, а затем проиллюстрируем их рядом конкретных
примеров. Итак, рассмотрим цилиндрическую трубу, неограниченно
простирающуюся вдоль оси z. Будем предполагать стенки трубы
идеально проводящими. Обозначим Е — поверхность, S — поперечное
сечение трубы и С — контур, ограничивающий это сечение.
Предположим, что: 1) характеристики среды, заполняющей такой волновод, е
и \1 равны 1, сг = 0; 2) внутри волновода отсутствуют источники поля;
3) поля периодически меняются по закону е~^^^.
Уравнения Максвелла в этом случае принимают вид
rotH = -гШ^Л
rotE = ikYi,
divH = 0,
div Е = О
('-?)■ w
Поскольку стенки волновода являются идеально проводящими,
тангенциальная компонента Ei на стенке волновода равна нулю:
Et \ъ = 0. (2)
Покажем, что внутри волновода могут распространяться бегущие
электромагнитные волны. Будем искать решение уравнений (1) в виде
E = graddivn + Pn,^
(3)
11 = -ikvotU, )
где П — поляризационный потенциал. Рассмотрим случай, когда
вектор П имеет лишь одну компоненту, направленную вдоль оси z {Н^ =
= 0). В этом случае уравнения (1) после подстановки в них выражений
(3) дадут
АН + к^и = О, или АзП + —- + А;2П = О (4)
oz^
(п = т,).
Условие (2) будет выполнено, если потребовать, чтобы
П|е = 0. (5)

556 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Ищем решение в виде
n{M,z)=i;{M)f{z), (6)
где М — точка, лежащая в поперечном сечении S. Подставляя (6) в (4),
приходим к выводу, что ф{М) является собственной функцией задачи
о колебаниях мембраны, закрепленной по контуру, т. е.
А2'0 + AV^ = О внутри 5,1
Ф\с = 0, j ^'
Здесь А2 = 7г^ + тг^ — двумерный оператор Лапласа.
Обозначим через {Л^} и {фп} систему собственных значений и
собственных функций этой задачи. Частное penienne задачи (4) имеет
вид
ип{М,г)=фп{М)и{г),
где функция fn{z) определяется из уравнения
/;' + (fc2-A„)/„ = 0. (8)
Общее решение уравнения (8) дается формулой
Uz) = Апе'->"' + Впе-'->"' {jn = \/к^ - К) ■ (9)
Нетрудно видеть, что первый член в формуле (9) соответствует
волне, бегущей в положительном направлении оси z, второй же член —
волне, бегущей в обратном направлении.
Рассматривая лишь волну, бегущую в одном направлении,
положим
тогда получим решение в виде
П„(M,z) = A„Vn(M)e^'^"^ (10)
где An — постоянная, определяемая из условий возбуждения полей.
Подставляя выражение (Ю) в формулы (3) и восстанавливая
множитель е"*'^^, находим составляющие поля в виде
Fn{M)e'^^^'-''^\ (11)
где Fn — функция, выражающаяся через собственную функцию
мембраны фп{М) или ее производные.
Если к^ > Хп, то 7п вещественно и выражение (11)
представляет собой бегущую волну, распространяющуюся вдоль оси z с фазовой
скоростью
(jj с
'^ = / ^ = , = > с.

I. волны в ЦИЛИНДРИЧЕСКИХ ТРУБАХ 557
Групповая скорость волны, очевидно, равна
и = — = С л/1 — Хп/к^ < с,
V
т. е. в пустом волноводе имеет место дисперсия.
Если к^ < Хп, то 7п = '^^п {^п > 0) и вместо выражения (11)
получаем затухающую волну
Fn(M)e-^^^-^-^ (12)
распространяющуюся вдоль оси z в положительном направлении.
Так как собственные частоты Л^ мембраны неограниченно
возрастают с увеличением номера п, то, какова бы ни была частота со,
начиная с некоторого номера п = N будем иметь
к < Xji.
Следовательно, в волноводе может распространяться лишь конечное
число бегущих волн. Если к^ < Ai, то в волноводе не может
существовать ни одной бегущей волны.
Для того чтобы в волноводе заданной формы и размеров могла
распространяться хотя бы одна бегущая волна, должно, очевидно,
выполняться условие
7 2 л 2^
Ai < А; , или Л <
где Л — длина волны, распространяющейся в трубе.
Для волновода прямоугольного сечения со сторонами а и b имеем
И, следовательно, бегущая волна может существовать лишь при
условии
fc>.^^ + l, или Л<2/у^1 + 1. (14)
Решениями уравнений Максвелла могут быть также поля с равной
нулю ^^-составляющей электрического поля
Е, = 0. (15)
Вводя вектор П = Hi^ и полагая
E = ikT0tU, H = graddivn + A;^n (16)
(4=0),

558 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
убеждаемся, что функция П(М, 2;) должна определяться из уравнения
АП + к^и = О, или АзП + —- + А;2П = О, (17)
и граничного условия
дй
^ = О на Е. (18)
Повторяя приведенные выше рассуждения, найдем решения этой
задачи:
(19)
П„ = АпММ) е'^"' (% = \/а;2-Л„) ,
которым соответствуют решения уравнения Максвелла вида
F^(M)e^(^-^-^^).
Здесь фп{М) и Хп означают собственные функции и собственные
частоты мембраны S со свободной границей:
А2'0п + КФп = О В 5,
-Z— =0 на 6.
Таким образом, в волноводе могут существовать
электромагнитные поля двух типов: {Е,Н} и {Е,Н}, определяемые по формулам (3)
и (16). Принята следующая терминология: говорят об электрических
волнах (или волнах типа ТМ), если Н^ = О, или о магнитных
волнах (типа ТЕ), если Е^ = 0. Мы убедились, что в волноводе могут
существовать волны ТЕ и ТМ. Можно показать"*^^, что любое поле в
волноводе представимо в виде суммы полей ТЕ и ТМ. Отсюда следует,
что произвольное поле в волноводе можно определить, если известны
две скалярные функции: Il{M,z) и I[{M,z).
2. Пайдем величину энергии, уносимой бегущей волной, например,
типа ТМ.
Для этого вычислим величину потока вектора Умова — Пойнтин-
га через сечение S:
W, = ^ II [Ell*l dS, (20)
где Н* — вектор, комплексно сопряженный вектору Н, 5 —
перпендикулярное сечение волновода.
^ Тихонов А. П., Самарский А. А. К теории возбуждения
радиоволноводов // Вести. Моск. ун-та. 1948. № 7. С. 39-60.

I. волны в ЦИЛИНДРИЧЕСКИХ ТРУБАХ
559
Введем прямоугольную систему координат ж, ^, z. Тогда
Выразим составляющие поля через поляризационный потенциал П по
формулам
Ет.
а^п
Я! = %к
dxdz
Е,
а^п
ду
^ dydz'
и подставим их значения в равенство (21):
W, = ---ik
87Г
г г г д^и
J J [д^^
dz дх dydz ду '
Функция П и сопряженная ей функция П* согласно (10) представимы
в виде
П(M,z)=Л„Vn(M)e*^"^
U*iM,z) = AlMM)e-
■^'JnZ
где фгг — собственная функция закрепленной мембраны {фп \с = 0)-
Отсюда следует, что вместо (22) можно написать
TJ7 ^^
п\Лп\'11
дфпУ [дфг1^ ^
дх ) \ ду
dxdy =
Применяя первую формулу Грина
||(VV^n)' dS = - Цфп А2фп dS +l^n ^dS = Xn jj^l dS = Xn,
s s с s
получаем выражение для потока энергии бегущей волны номера п:
W, = ^\Ап\^7пХп-
07Г
(23)
Если одновременно распространяется несколько волн, то Wz будет
равно сумме слагаемых вида (23).

560 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Перейдем теперь к задаче о возбуждении электромагнитных полей
в волноводе заданными токами-'^^
3. Пусть в некотором объеме Vq внутри волновода Е заданы токи
j(M, z) е"*'^^, меняющиеся во времени по гармоническому закону.
Найдем поля, возбуждаемые этими токами. В силу принципа суперпозиции
полей достаточно, очевидно, решить задачу о возбуждении волновода
элементарным диполем произвольной ориентации.
Чтобы дать представление о методе решения поставленной выше
общей задачи, рассмотрим более простой случай возбуждения
волновода линейным током / = /0(2;) е"*'^^, заданным на отрезке L,
параллельном оси Z.
Для определения электромагнитных полей, возбужденных в
волноводе, надо использовать:
1) уравнения Максвелла (1);
2) граничные условия
^tang = 0 на Е;
3) условие излучения в виде требования отсутствия волн,
приходящих из бесконечности;
4) условие возбуждения, которое мы берем в виде (см. гл. V,
Приложение II, п. 3)
Hsds = — /о, или Hs « —- , (24)
с ср
Ке
где К^ — окружность радиуса е (г —>- 0), охватывающая линию L, р =
= |ММо|, где Мо — точка на токе, М — точка на окружности К^.
Иными словами, электромагнитное поле на токе должно иметь особенность
определенного типа.
Перейдем к потенциалу П, воспользовавшись для этого
формулами (3). Пусть (Мо, ^) — произвольная точка на токе. Введем
цилиндрическую систему координат р, (р, z с центром в точке (Мо, ^) и вычислим
Hs, пользуясь уравнением (3):
Hs = ik—-.
dp
Отсюда и из (24) следует, что в точке (Мо, ^) функция П должна иметь
логарифмическую особенность:
П « - ^ In 1. (25)
гкс р
^ Самарский А. А., Тихонов А. Н. О возбуждении
радиоволноводов. I // ЖТФ. 1947. Т. 17, № 11. С. 1283-1296; II // Там же. № 12. С. 1431-
1440.

I. волны в ЦИЛИНДРИЧЕСКИХ ТРУБАХ 561
Таким образом, функция П(М, 2;) должна удовлетворять волновому
уравнению (4), граничному условию П = О на Е, условию излучения
и условию возбуждения (25).
Будем искать решение этой задачи в виде
П = к|по(М,Мо;^,С)/о(С)^С, (26)
L
где По(М, Мо; 2;, С) — функция источника, определяемая как решение
уравнения
АПо + к^Щ = О
по переменным (М, z) и (Мд, С)? удовлетворяющее граничному условию
По = О на Е,
условию излучения и имеющее особенность типа при совпаде-
47Г г
НИИ аргументов, т. е. представимое в виде суммы
(r = y/p^ + {z-0\ р=\Мм'о\\
где V — регулярная функция, определяемая из волнового уравнения и
граничного условия:
^ikr
V = — -— на Е.
47ГГ
Нетрудно видеть, что функция П(М, z), определяемая по формуле
(26), будет иметь логарифмическую особенность и условие
возбуждения выполнится, если положить нормирующий множитель
к = -^.
ike
Отсюда следует, что
П(М,г) = -^у"по(М,Мо;г,С)/о(С)^С-
L
В частности, для элемента тока длины Д/
П{М,г) = -^1о-А1-По.
ЪгьС
Следовательно, Но имеет физический смысл поляризационного
потенциала, соответствующего возбуждению элементом тока,
помещенным в точке (Мо,С) параллельно оси волновода.
36 А. Н. Тихонов, А. А. Самарский

562 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Таким образом, задача определения поля в волноводе полностью
сведена к построению функции источника По первой краевой задачи
для уравнения Аи -\- к^и = О внутри бесконечного цилиндра.
Для построения функции источника может быть применен метод,
изложенный в гл. VI, § 2. Рассмотрим неоднородное уравнение
Au + k^u = -f{M,z), (27)
где f{M,z) — заданная функция, с граничным условием
п|е=0.
Будем искать функцию u{M,z) в виде ряда
сю
u{M,z) = Y,M^)MM), (28)
п=1
где фг1{М) — нормированные собственные функции мембраны 5,
А2фп + КФп = О, фп \с = 0. (7)
Разлагая f{M,z) в ряд
f{M,z) = f^U{z)MM), fn{z) = fff{M',z)i;n{M')daM',
n=l •'J
(29)
И подставляя выражения (28) и (29) в уравнение (27), получаем
^п(^) - Pl^niz) = -fn{z), Рп = VK -к'^- (30)
Решение этого уравнения, как нетрудно заметить, представляется
формулой
сю
/р-Рп \z-C\
^^^ fniOdC, (31)
— сю
которая в силу формулы (29) может быть записана в виде
сю
г г Г р-Рп \z-C\
''n{z) = JJ J -^^— 1{М'Х)Фп{М')с1ам' dC (ЗГ)
5 -оо
Подставляя это выражение в формулу (28) и меняя порядок
суммирования и интегрирования, будем иметь
u{M,z) = IIIUo{M,M',z - С) f{M',С)(1ам: dC, (32)
т

I. волны в ЦИЛИНДРИЧЕСКИХ ТРУБАХ
563
где
пo(м,м^z-c) = x^
п=1
-Рп \z-C\
(33)
Ряд ДЛЯ По(М, М', Z — о при Z ^ ( равномерно и абсолютно сходится
в силу оценок для собственных функций-*^^ и присутствия
экспоненциального множителя. Функция П(М, М', z — () в точке (М = М', z = ()
имеет особенность типа 1/г. На доказательстве последнего
утверждения мы не останавливаемся^^ Из сказанного вып1е следует, что
G(M, М', z-C) = По(М, М', Z - С),
т. е. функция источника По имеет вид
UoiM,M',z-0 = J2
п=1
фп{М)фп{М')
-Рп \z-C,\
Из формулы (33) вытекает, что поле в этом случае представится в
виде суперпозиции волн вида (11) и (12). Как было замечено на с. 557,
ряд (33) будет состоять из конечного числа слагаемых вида
Впфп{М) е'^^ 1^~^1 (бегущие волны) (jn = ^^^ - К^ Рп = -Пп)
^ Для собственных функций ^ri{M) имеет место равномерная оценка
\^n{M)\ ^ АЛп, где А — постоянная, не зависящая ни от точки М, ни от
индекса п. В самом деле, краевая задача (7) равносильна интегральному
уравнению ^n{M) = Хп JJ G{M, М') tpniM') daj^t, где G{M,M') — функ-
5
ция источника для уравнения Лапласа /S.2U = О при граничном условии
и\с = 0. Из этого интегрального уравнения в силу неравенства Копей —
Буняковского вытекает
\^n\ ^ \\п\
\
П G''{M,M')daM> П ^UM')daM> ^ А\\п\,
S S
Аналогичным методом получаются оценки для производных
дфп
дх
^ ВХг.
дгрп
ду
^ВХ'
^ См.: Самарский А. А., Тихонов А. Н. О возбуждении
радиоволноводов. I // ЖТФ. 1947. Т. 17, № 11. С. 1283-1296.
36*

564 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
и из бесконечного числа слагаемых вида
В'^фп{М) е~^'^ \^-^\ (затухающие волны),
где
Для определения полей надо воспользоваться формулами (26) и (3).
Задача о возбуждении волновода элементом магнитного тока,
параллельным оси Z (бесконечно малая петля с электрическим током в
плоскости Sz=q)^ приводит нас ко второй функции источника
удовлетворяющей граничному условию дйо/ди = 0 на Е. При этом
47Г
Hz = 0; П = ;— кАШо (кА1 — момент элемента магнитного тока).
ike
Аналогичным методом можно решить задачу о возбуждении
произвольно ориентированным диполем (элементом тока), найдя
особенности полей в этом случае. Соответствующие функции П будут
определяться по формуле, аналогичной формуле (33). В случае
поверхностных и объемных токов функции П даются поверхностными и
объемными интегралами (по аналогии с (26)). Дальнейшее вычисление полей
производится по формулам (3).
Тем самым задача о возбуждении любого цилиндрического
волновода произвольными заданными токами решается полностью. Чтобы
использовать общие формулы для волновода определенного сечения,
достаточно найти собственные колебания мембраны, имеющей форму
перпендикулярного сечения волновода.
Приведем выражения для ортонормированных собственных
функций прямоугольной мембраны со сторонами а и Ь:
фпуМ) =фпш{х,у) = \ -Г 8ш х^т—-у;
фп{М) =фпш{х,у) = \ -^^ cos xcos—-y {sj = 2, j 7^0; го = 1);
ab a b
2/'"' "'
^^~b^

IL ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В РЕЗОНАТОРАХ 565
Для круглой мембраны радиуса а имеем
/ /т\/г\ I / \ I ^п Jnyl^rnnf' (^) COS
7/71/г\ 7 / \ / ^п f^mn ^Jn\f^mn'^ / (^) COS
где fimn — корень уравнения Jn{l^) = 0; Л^^ = l4nn/^^^ Р^шп — корень
уравнения J'^{ij) = 0; \тп = f^mn/^^^-
II. Электромагнитные колебания в полых резонаторах
В последние годы в радиотехнике получили широкое
распространение объемные резонаторы, или эндовибраторы,
представляющие собой металлические полости, заполненные диэлектриком (в
частности, воздухом). В эндовибраторах могут существовать
стационарные электромагнитные поля (стоячие волны), называемые
собственными электромагнитными колебаниями.
В радиотехнике ультракоротких волн применяются
эндовибраторы весьма сложной формы. Общая проблема определения собственных
колебаний эндовибраторов произвольной формы чрезвычайно сложна,
однако для эндовибраторов простейшей формы решение получается в
явном виде. Так как стенки изготовляются из хорошо проводящего
металла, то при расчете собственных колебаний обычно предполагают
стенки идеально проводящими. Поправки на конечную проводимость
можно получить, используя граничные условия Леонтовича. В
дальнейшем мы будем предполагать, что стенки эндовибратора являются
идеально проводящими и все величины поля меняются во времени по
закону е"*'^^.
Не ставя своей целью дать исчерпывающее изложение теории
эндовибраторов, остановимся на некоторых общих вопросах теории этих
колебательных систем.
1. Собственные колебания цилиндрического
эндовибратора. Проблема определения собственных электромагнитных
колебаний состоит в нахождении нетривиальных решений уравнений
Максвелла"'^^ точнее, в определении собственных частот о;, при
которых система однородных уравнений Максвелла с однородными
краевыми условиями имеет нетривиальные решения, а также самих
нетривиальных решений.
Множитель е ^'^ всюду опускаем.

566
ПРИЛОЖЕНИЯ К ГЛАВЕ VU
Уравнения Максвелла в этом случае имеют вид
rotH = -ikE,
(-Э
rotE = -ikH,
divE = 0,
div H = 0
внутри полости Т, на поверхности которой Е выполняются условия
(1)
или
Et=0
dv
= 0;
(2)
(3)
оба эти условия, как нетрудно показать, эквивалентны.
Приведем расчет собственных колебаний для эндовибратора,
представляющего «отрезок» цилиндрического волновода
произвольного сечения, ограниченный двумя боковыми стенками z = ^1 (ось z
параллельна образующей цилиндра).
Так же как и в цилиндрическом волноводе, в рассматриваемом
эндовибраторе возможны колебания и электрического (Н^ = 0), и
магнитного {Ez = 0) типа.
Для волн электрического типа положим
E = graddivn + Pn,^
(4)
11 = -ikvotU, )
где П = ni^ (i^ — единичный вектор, направленный по оси z) —
поляризационный вектор-потенциал, у которого отлична от нуля лишь
составляющая по оси z. Из формул (4) сразу видно, что в этом случае
я, = 0.
функция П, как обычно, удовлетворяет волновому уравнению
АП + ГП = 0.
(5)
Выберем на поверхности Е локальную прямоугольную систему
координат (s, I/, i^), где и — единичный вектор, направленный по
нормали к поверхности, as — по касательной к контуру С,
ограничивающему перпендикулярное сечение S цилиндрического эндовибратора.
В силу граничных условий (2) имеем
Es\b =
Е,\^ =
dsdz
= 0,
Е
+ eu\
>
= 0.
Е )
(6)

п. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В РЕЗОНАТОРАХ 567
Оба эти равенства будут удовлетворены, если потребовать, чтобы
П|е = 0. (7)
При 2; = =Ь/ из (2) получаем условия
Е,
S \z = ±l =
Е,
z=±l
dsdz
dv dz
= 0,
z=±l
о,
\z=±l
для выполнения которых достаточно положить
ап I
^^ \z=±l
= 0.
Таким образом, мы приходим к следующей краевой задаче.
Найти нетривиальные решения волнового уравнения
с однородными граничными условиями (7), (8)
П|е=0,
(8)
(60
dz
= 0.
z=±l
Как и в случае цилиндрического волновода (см. с. 556), penienne
ищем в виде
ЩM,z)=ф{M)f{z).
(9)
Подставляя это выражение в уравнение (6') и используя условие (7),
получаем для функции ф{М) задачу о собственных колебаниях
закрепленной мембраны:
А2Ф + Хф = 0 в 5, (10)
ф = 0 на С. (11)
Для определения функции f{z) после разделения переменных
получаем уравнение
/" + (fc2-A)/ = 0 (12)
С граничным условием
/'(±/) = о, (13)
вытекающим из условия (8).

568 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Следует иметь в виду, что здесь, в отличие от задачи для
волноводов, к^ не является заданной величиной, а входит в уравнение в
качестве параметра. Мы должны найти те значения к^, при которых
задача (6) — (8) допускает нетривиальное penienne.
Реп1ая уравнение (12) с условиями (13), находим собственные
функции
fm{z) = Am COS ^ (^ " ^)^
соответствующие собственным значениям
/^ш = (^) (ш = 0, 1, ...),
где
Краевая задача (10) — (11) дает спектр собственных значений
{Лп} с соответствующей системой нормированных собственных
функций {'0^(М)}. Отсюда вытекает, что в эндовибраторе могут
существовать только такие колебания, собственные или резонансные частоты
которых равны
п т-
Этим частотам соответствует система собственных функций
— 7Г77Т/
Un,rn{M, Z) = Агг,гпФп{М) COS ^ (^ " ^). (14)
ИЛИ
где
Un,rn{M, Z) = Ап^т^п{М) fm{z), (W)
^-^")=\/¥'^'i^^^-") (^-={1:
шт^О;
ш = 0
— нормированные к единице функции. Решение определено с
точностью до амплитудного множителя Ап,т, который находится из условий
возбуждения колебаний данного типа.
Если собственные функции мембраны фп{М) известны, то по
формулам (14) и (4) можно вычислить компоненты поля.
Если поперечное сечение S эндовибратора представляет собой
прямоугольник со сторонами а и 6, то будем иметь
/ 4 7Тр 7TQ
фп{М) =фр^д{х,у) = d—8m—-x8m — y {p,q = 1, 2, 3, ...),
Хп = Х,,,=п (- + -
2егп . тгр . тгд тгш
—- sm — xsm — y cos —-
аЫ а о 21
Пп,т = Am,p,q \/ —^ SIH -—X SlU — у COS -7^ [l - Z).

II. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В РЕЗОНАТОРАХ 569
В этом случае наименьшей собственной частоте
W0,1,1 = с VAi,i = С7Г ^ — + -
соответствует максимально допустимая длина волны
в частности, при b = а наибольп1ая длина волны
Ло = ал/2
равна диагонали квадрата, получающегося в перпендикулярном
сечении. Следовательно, в таком эндовибраторе возможны лишь
собственные колебания с частотой
^ ^ ^0,1,1
или длиной волны
Л^Ло.
Совершенно аналогично находятся собственные колебания
магнитного типа (Ez = 0). В этом случае полагаем
Е = ikvottl,
H = graddivn + A;^n,
где
Для определения П(М, 2;) получаем уравнение (6') с граничными
условиями
n\z=±i=0, (Г)
о, (80
решая которые находим
/\ /\ /\ 7Г77Т/
Пп,т = An,rn^m{M) sin ^ (^ " ^)- {Щ
В этом случае под фп{М) следует понимать собственные функции
мембраны S при граничном условии дф/ди = О на С.
2. Электромагнитная энергия собственных колебаний.
Вычислим энергию электрического и магнитного полей в стоячей
волне в цилиндрическом эндовибраторе.

570
ПРИЛОЖЕНИЯ К ГЛАВЕ VU
Для простоты ограничимся случаем волны электрического типа.
Учитывая в формулах (4) зависимость Е и Н от времени по закону
-icot
И беря только действительную часть, получаем
Е:г,
Д
dzdx
am
^ ~ dzdy
cos Ujt,
COS U)t,
E, = I ^ + k^n ] cosujt;
(16)
Hx = —k —— smcot,
dy
Ну = к —— smuit,
ox
Я, =0.
(17)
Для вычисления энергии электрического и магнитного полей
воспользуемся известными формулами:
4л (i)
87Г
///
E^dr,
(18)
£м{1)
Втг
///
WdT,
(19)
где интегрирование производится по объему Т эндовибратора.
Подставляя в формулу (18) выражения (16) и пользуясь формулой
(14'), будем иметь"*-^
,.„,<). 1^ со,-.J//(g)% (1)1 ^/[ГИР..
+
IlijUaJir + k'ffdzl.
^ Индексы т, п мы временно опускаем.

IL ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В РЕЗОНАТОРАХ 571
Произведя несложные вычисления, получим
у[/'(z)]2 dz = ff t, - I ff" dz = {e -X) j fdz = k-'- Л, (19')
jU" + k''ffdz = X^ j fdz = \\
-I -I
так как в силу нормировки функций /
j fdz = l.
(20)
(21)
Для вычисления интегралов по S воспользуемся первой формулой
Грина, уравнением для функции -0^, граничными условиями и
условием нормировки:
//
дх) \ду
dxdy
= //(V,«=
da =
= - f f il;A2il;da+ f ф ^ ds = X f f ф^ da = X, (22)
s с s
где V2 — оператор «набла» в плоскости 5, А2 — двумерный оператор
Лапласа. В результате получаем выражение для энергии
электрического поля
^зл(^) = -—k^Xcos'^Lot. (23)
отг
Для энергии магнитного поля в силу формул (17), (19) и (14')
имеем
откуда, учитывая равенства (21) и (22), находим
£м{1)
87Г
л sin^ ojt.
(24)
Полная энергия электромагнитного поля, очевидно, не меняется во
времени:
£ = £sn{t) + £M{t) = ^^ X.
07Г
(25)

572 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Из формул (23) и (24) видно, что в стоячей волне происходит
взаимное превращение электрической энергии в магнитную и обратно,
причем средняя за период энергия электрического поля
4я = ^^^Л=-5 (26)
равна средней энергии магнитного поля
3. Возбулсдение колебаний в эндовибраторе. Для
возбуждения поля в эндовибраторе внешним источником надо ввести через щель
в его оболочке элемент связи. Таким элементом связи может быть
либо виток, либо стержень, действующий как маленькая антенна. Для
того чтобы элемент связи не возмущал поля в эндовибраторе,
необходимо, чтобы его размеры были много меньше длины волны. Возможны
и другие способы возбуждения эндовибратора, например пучком
электронов, пронизывающим полость эндовибратора (через отверстия в его
стенках).
Решение задачи о возбуждении эндовибратора антенной,
помещенной внутрь, или, в предельном случае, элементарным диполем требует
учета конечной проводимости стенок, иначе установившийся процесс
невозможен. Учет конечной проводимости стенок может быть
произведен с помощью условий Леонтовича.
Мы рассмотрим здесь задачу о возбуждении сферического
эндовибратора диполем, допускающую простое аналитическое решение"'^^
Пусть в центре сферы радиуса го помещен диполь, колеблющийся с
частотой UJ и амплитудой 1 и направленный вдоль оси z. Требуется
найти поле внутри сферы, учитывая конечную проводимость стенок.
В этом случае поля Е и Н можно выразить через функцию [/:
psmO дв \ дв
Остальные компоненты E^p^ Н^^ Hq равны нулю.
Так как диполь направлен по оси 2; (^ = 0), то поля, очевидно, не
должны зависеть от угла ip.
^ См.: Р ы т о в С. М. Возбуждение полого сферического резонатора
расположенным в его центре диполем // ДАН СССР. 1946. Т. 51, № 2. С. 107-110.

п. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В РЕЗОНАТОРАХ
573
Функция и удовлетворяет уравнению
?l(^=f)-?l^l(-^fi-^'=«' (^''
где р = кг, причем U имеет при р —>- О особенность вида
ikr -pgi
(30)
На поверхности сферы (р = ро) должно выполняться условие Леонто-
вича
Eq — аН^,
где
а = pkd
d
у/2щюъ:
(31)
(32)
— эффективная глубина скин-слоя.
Из соотношений (31) и (28) вытекает граничное условие для
функции \J\
д_
др
(pU) - ipoaU
= 0,
Р=РО
или
ро
+ (1 - ipoa) и
Р=РО
0.
(33)
Р=РО
Решением уравнения (29), имеющим особенность (30), очевидно,
является функция
и = -к' ,/f [Я«(/,) + СЛ/^{р)] Pi (cos 0),
где Pi (cos 0) — полином Лежандра 1-го порядка, Н^^^ — функция Хан-
келя 1-го рода, Js/ — функция Бесселя,
(1)
Pi (cos ^) = cos^.
«';>'=/5''"й-0' •'''»=v5(^7^-"^^
Постоянная С определяется из граничного условия (33):
1
С
э^РО
1- ^ +а [ —
Ро Ро \^Ро
С08 ро
Ро
+ 1
1 \ . . / sinpo
-^ ^т Ро — га cos ро
Ро) V ро

574 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
Полученное решение можно использовать для определения величины
потерь в стенках. Мощность, поглощаемая в стенках,
7Г
Q=^l\H^\'27, р1 sine de
О
вычисляется непосредственно и равна
/jLok^d 1
Q =
б |Б-ШЛ|2'
где
А = cospo, ^ = Ь 1 ^ smpo-
Ро Ро \ PoJ
Если диполь расположен не в центре сферы, то расчет полей сильно
усложняется, однако решение может быть получено в виде рядов.
III. Скин-эффект
Переменный ток в отличие от постоянного не распределяется
равномерно по сечению проводника, а имеет большую плотность у его
поверхности. Это явление называют скин-эффектом (от англ.
skin — кожа)"'"^
Рассмотрим для простоты бесконечный однородный
цилиндрический провод (fi = const, а = const), по которому течет переменный ток.
Будем предполагать, что полный ток / = /де*'^^, протекающий через
сечение провода, известен.
Пренебрегая токами смещения по сравнению с током
проводимости^^ и считая процесс установившимся, т. е. зависящим от времени по
закону е*'^^, получим после сокращения на множитель е*'^^ уравнения
Максвелла в виде
47ГСГ ^ , ,
rotH= Е, (1)
с
TotE =-ik/iili, (2)
divE = 0, (3)
divH = 0, (4)
^ Тамм И. E. Основы теории электричества. М., 1976.
^ Отметим, что внутри проводников, в частности внутри металлов,
плотность токов смещения ничтожно мала по сравнению с плотностью токов
проводимости: jcM ^ i = сгЕ. В напЕСм случае последнее условие эквивалентно
требованию еоо ^ а. Ввиду того что для твердых металлов проводимость
сг ^ 10 абс. ед., токами смещения можно пренебречь для всех частот,
употребляемых в технике.

III. СКИН-ЭФФЕКТ 575
где к = (j/c. Уравнения (3) и (4) в данном случае, очевидно, следуют
из уравнений (1) и (2).
Введем цилиндрическую систему координат {r,z,(f) так, чтобы
ось Z совпадала с осью провода. Тогда в силу осевой симметрии тока
все величины можно считать зависящими только от переменной г.
Так как в нашем случае вектор Е направлен вдоль оси z, то из
уравнений (1) и (2) будем иметь
Id 47ГСГ
- :г ^^'/^ = ~~
г аг с
(гЩ) = --Е,, {!')
d
dr
Исключая отсюда Н(р, найдем
Е, =ikijH^. {2')
-— (г —\ = г ^^^^^ Е (Ъ)
г dr \ dr ) с
Введем граничное условие на поверхности провода при г = R. Для
этого воспользуемся тем, что нам известен полный ток /д,
протекающий по цилиндру.
Запишем первое уравнение Максвелла (1) в интегральной форме:
47Г
Hsds = —/о,
с
где С — контур, охватывающий провод, Hs — тангенциальная
составляющая вектора Н на С Если в качестве такого контура взять
окружность г = R, то получим
27Г
47Г
/
H^{R)d(p = -Б^о,
или
27о
cR
Отсюда, пользуясь соотношением (2'), находим
dE,
dr
H^{R) = ^. (6)
r=R СД
''''lo. (7)
Таким образом, мы должны решить уравнение Бесселя
(5')

576 ПРИЛОЖЕНИЯ К ГЛАВЕ VII
при граничном условии
Ет = ^-^1о (Г)
и условии ограниченности при г = О
|S,(0)|<oo. (8)
Общее решение уравнения (5') имеет вид
AJo (агл/^Л + BNo (агл/^Л , (9)
где Jo VL No — функции Бесселя 1-го и 2-го рода (см. Дополнение II,
ч. I), Л и 5 — постоянные, подлежащие определению.
Функция А^о имеет логарифмическую особенность при г = 0.
Поэтому в силу условия (8) 5 = О и, следовательно,
E,{r)=AJo[ar^/^iy (10)
Коэффициент А определим из граничного условия (7):
А= ^Vffe^-^o (11)
acRJi [aR yj—г j
Отсюда для плотности тока
получаем
loOi
^ ^o^V г (ат^г) . (12)
'^ ^ 2t^RJi {aRy^i) V J ^ ^
В правой части этой формулы стоят функции Бесселя от комплексного
аргумента
Обычно пользуются для этих функций следующими обозначениями:
Jo ( X \[^% 1 = Ьего ж + г beio ж,
J\ ( X \f^i J = beri X -\- г beii x.
Нетрудно найти выражения для вещественных функций Ьегж и beix.

III. СКИН-ЭФФЕКТ
577
пользуясь разложением функций Бесселя в ряд. Например,
Jo (X \РА 1 = Jo (жг лЛ 1 =
(1!)2 "^ (2!)2 (3!)2 "^ (4!)2
= 1-ш.+ш.-.Л+^ш.-ж
(1!)2 (3!)2
+ ..
откуда получаем
ЬеГ(
° (2!)2 ^ (4!)2
beio ж =
(I)' (I)'
(1!)2 (3!)2 ' •••
Нетрудно убедиться подобным же образом, что
(13)
(14)
beri X
bail X =
( (^\^ (^\^ (^V
) а; , U/ V2/ V2/
х/2
2 "^ 1!2!
2!3!
3!4!
+ ...
л/2
Г /ж\3 /ж\5 /'а;\'^
I _ ^ + ilz_ + ilz_ _ ilz_
2 "^ 1!2!
2!3! 3!4!
(15)
(16)
В приложениях встречаются также производные
Ьегд ж, beig ж,
причем
Ji ( ж л/^ J = л/^ (beig ж — г Ьегд х).
(17)
Пользуясь введенными функциями, выражение (12) для тока
можно записать в виде
i(0
/о а Ьего аг -\- i beio ar
27rR beig «i^ — i Ьегд ai^
37 A. H. Тихонов, A. A. Самарский

578 ПРИЛОЖЕНИЯ К ГЛАВЕ VU
loot ((Ьего аг beig aR — beio ar Ьегд aR)
. (beio «r beig aR + bero ar Ьегд aR) 1
^' (bei[)ai^)2 + (ber[,ai^)2 J* ^ ^
Вычисляя абсолютную величину этого выражения, получим
I ./ ч| _ Ipa / (Ьегр агУ + (beip аг^
'•^ ^""^ ^~ 27tR\J {Ъет'о aRY + (bei[) ai^)^ ' ^ ^
Величиной, характеризующей распределение тока по сечению,
является OTHOHienne
Ь'(01 ^ / (Ьегр arY + (beip arf
\j{R)\ У (berp aRY + (beip ai^)^ ' ^ ^
Произведем расчет распределения тока по сечению для двух частот:
uji = 314 Гц (50 периодов в секунду), ио2 = 314 • 10^ Гц (5 • 10^ периодов
в секунду).
Все изложенные вып1е выкладки были произведены в гауссовой
симметричной системе. Поэтому при переходе к системе СГСЭ
следует учесть, что /^сгсэ = А^гаусс/с^- Все остальные величины, входящие
в формулы (12), (18) — (20), в обеих системах (гауссовой и СГСЭ)
совпадают. Поэтому в системе СГСЭ
а^ = 4:7T/jauj.
Для меди сг = 57 • 10^ СГСЭ, поэтому ai = 0,4444 (для uji), «2 = 44,44
(для UJ2)- Вычислим отношение модулей токов (20) для низкой частоты
LJi = 314 для двух значений г: г = О и г = 0,5 R. При этом R положим
равным единице.
Имея в виду-'^^ что
Ьегр О =1,
beip О =0,
Ьегр 0,222 = 1 - 0,000036 + ... = 0,999964,
beip 0,222 = 0,0123 - 0,000002 + ... = 0,012300,
berp 0,444 = 1 - 0,00061 + ... = 0,99939,
beip 0,444 = 0,493 - 0,0003 + ... = 0,4930,
найдем
i(0)
JiR)
= 0,9994, Щ1
= 0,9999,
=1
^ Cm. также: Янке E., Эмде Ф., Лёш Ф. Специальные функции,
формулы, графики, таблицы. М., 1977.

IV. РАСПРОСТРАНЕНИЕ РАДИОВОЛН НАД ПОВЕРХНОСТЬЮ 579
т. е. при небольшой частоте ток распределяется по сечению
приблизительно равномерно (скин-эффект отсутствует).
Рассмотрим теперь второй случай: uj2 = 314 • 10^. Так как значение
а велико, то для расчета удобнее исходить не из разложений функций
Ьег и bei в ряды, а из асимптотических формул
Ji
о (аг л/^ j
^ar/V2-i {аг/у/2-7т/8)
V2
ттаг
Jo (aR л/^ j =
^aR/V2-i {aR/V2-7T/8)
уДтшЕ
откуда получаем, задаваясь значениями г = 0,9 i^; R = 1,
JiO,9R)
т) 1л=1
= ^/_Le-440,i/V2^Q^Q47.
Этот результат свидетельствует о чрезвычайно быстром уменьп1ении
плотности тока по мере углубления внутрь проводника при высоких
частотах. Отметим в заключение, что скин-эффектом ninpoKO
пользуются на практике для закалки металлов.
IV. Распространение радиоволн над поверхностью земли
Проблемы, связанные с распространением радиоволн как в
свободном пространстве, так и при наличии поверхностей раздела,
имеют огромное теоретическое и практическое
значение. Этим вопросам посвящено
чрезвычайно большое количество работ советских и
иностранных авторов.
Мы рассмотрим задачу о влиянии земли
на распространение радиоволн, излучаемых
вертикальным диполем. При этом землю
будем считать плоской-'-^
Пусть над поверхностью земли на
расстоянии h в точке Ро находится диполь,
излучающий периодические колебания частоты
ио. Примем плоскость земли за плоскость 2; = О
и направим ось z по оси диполя (рис. 84). Положим, что в
атмосфере (2; > 0) го = А^о = 1, сгд = 0. Предположим далее, что земля {z < 0)
характеризуется диэлектрической постоянной г, проводимостью а, а
магнитная проницаемость fi может быть принята равной единице; е и
а будем считать постоянными.
^i
.]-
0
1
я,^
Уп'
^р
Рис. 84
' Эта задача была впервые решена Зоммерфельдом в 1909 г.
Первоначальное ренЕение содержало онЕибку, которая была исправлена В. А. Фоком.
37*

580
ПРИЛОЖЕНИЯ К ГЛАВЕ VU
Наша задача заключается в отыскании напряженности поля,
создаваемого диполем. Процесс распространения электромагнитных
волн описывается уравнением Максвелла.
Как было показано в Приложении П к гл. V, решение уравнений
Максвелла может быть сведено к решению волнового уравнения для
поляризационного потенциала П"*^^:
АП + А;^П = 0,
(1)
где
к'=(
'^0 - ^2 :
к =
Eijp' + i4:7ra(jj
z>0;
, z <0.
Потенциал П связан с напряженностями поля соотношениями
Е = Pn + graddivn,^
Н =
ко
rot П.
(2)
в нашем случае вектор П направлен параллельно излучающему
диполю:
П=(0,0,П,); Щ =n,(r,z).
(3)
Положив
п^ = е -\-i-
47Г сг
получим
к — ^ ^0-
Соотношения (2) и (3) дают
Ег = -^ -—^ , Н^ = -iko -^ , Е^= Нг = 0 при z > О, (4)
Ег = ^^, Щ = -'-^^, Е^=Нг = 0 при z<0. (5)
or oz ко or
^ Так как рассматривается установившийся процесс, то временной мно-
-icot
житель е можно опустить.

IV. РАСПРОСТРАНЕНИЕ РАДИОВОЛН НАД ПОВЕРХНОСТЬЮ 581
Чтобы получить граничные условия при 2; = О, воспользуемся
условием непрерывности тангенциальных составляющих напряженно-
стей полей. Эти условия, как показывают формулы (4) и (5), будут
выполнены, если положить
-—— = —— ; По = п Пз при 2; = 0. (6)
Будем искать решение уравнения (1) при граничных условиях (6) в
виде суперпозиции частных решений вида
Jo(Ar)e±^" {к" = \^ -11^).
Для неограниченной области вместо дискретного спектра
собственных значений Л получается непрерывный спектр. Поэтому решение П
можно искать в виде
сю
П= [ F{X)Jo{Xr)e^^'dX; (7)
о
знак у /J должен быть выбран таким образом, чтобы обеспечивалась
сходимость интеграла (7). Остающаяся пока не определенной функция
F{X) представляет собой амплитудный множитель отдельных
колебаний.
Воспользуемся интегральным представлением потенциала (см.
Дополнение П, ч. I, § 5)
AkR
СЮ
= /'jo(Ar)e-^l^-'>l— (8)
(^1л= Va2-A;2, i^ = у/г2 + (z - ну ) .
Рассмотрим две различные области.
а) Воздух (2; > 0). Поле в этой области имеет вид
-По ^ J-J-nepB ~г J-J-BTOP5
где
AkR
-l-1-перв = D v^/
— потенциал поля первичного возбуждения, создаваемого самим
диполем, а Пвтор — потенциал поля вторичного возбуждения, создаваемого
возникающими в земле токами.

582
ПРИЛОЖЕНИЯ К ГЛАВЕ VU
Используя представления (7), (8) и (9), мы можем записать
сю
XdX
J-J-nepB — 1^0
(Лг) е-
-/J, \z — h\
/^
сю
Пзтор = I F(X) Jo(Ar) е-^ ^'+'^'> dX,
(10)
где F{X) — пока что не определенная функция.
б) Земля (2; < 0). В этой области имеет место только вторичное
возбуждение, которое мы можем записать в виде
сю
П,= [р,{Х)МХг)е^^'-^ЫХ,
(11)
где /j^ = к^ — Х^. Так как 2; < О, то знак показателя экспоненты
обеспечит сходимость интеграла.
Для определения функций F{X) и ^з(Л) воспользуемся граничными
условиями (6), которые дают
сю
1 МХг) е-^^ [Л - fiF{X) - /^3^3(А)] ^Л = О,
о
сю
[ Jo(Xr) е-"'' [Л + цР(Х) - п^цР,{Х)] — = 0.
О
Условия (12) будут выполнены, если мы положим
1лР{Х) + n,F,{X) = X, Л
fiF{X)-n^liF,{X) = -X.f
Решая систему уравнений (13), найдем F{X) и ^з(Л) в виде
fJ. V Tl'^H + fJ,.,
(12)
(13)
^;(А)
2Л
n^fi + fJ,3
(14)

IV. РАСПРОСТРАНЕНИЕ РАДИОВОЛН НАД ПОВЕРХНОСТЬЮ 583
Подставляя выражения (14) в формулы (10) и (11), получим
следующие выражения для поляризационного потенциала поля
вертикального диполя:
сю сю
О о
сю
-2 j МХг)
о
сю
Пз = 2 /'jo(Ar)e^-^-^'' ^^^
fi {z+h)
-II {z-\-h)
1^3
XdX
XdX
n^/J + /ig /J
(15)
n^/J + /i3
Обозначая через расстояние от точки
наблюдения до диполя, через R' = у^г^ -\- [z -\- h)^ — расстояние от точки
наблюдения до зеркального отражения диполя в плоскости 2; = О и
пользуясь представлением (8), перепишем выражение для функции По
в виде
По
ЛкК ЛкК
R
+
-^-2у Jo(Ar),
-II {z-\-h)
1^3
XdX
n^/J + /is /i
(15')
Рассмотрим некоторые предельные случаи.
1. Идеально проводящая земля. В этом случае сг —>- оо, а
следовательно, \к>з\ и \п\ -^ оо. При этом формулы (15) и (15') дают
По =
+
R
R'
Пз = 0.
Этот же результат легко получить непосредственно, решая задачу
методом отражений.
2. Диполь в однородной среде. В этом случае ко = к^^; п =
= 1; fi = fi^. Формулы (15) и (15') дают
сю
JkR
R '
Т. е. имеет место одно первичное возбуждение, как и должно быть.
Полученные интегральные выражения (15) являются весьма
сложными для исследования и практического применения.
Подынтегральные выражения имеют точки ветвления и полюсы. Зоммерфельдом был
предложен метод приближенного вычисления этих интегралов путем

584
ПРИЛОЖЕНИЯ К ГЛАВЕ VU
деформации контура интегрирования"*^л При этом им была получена
следующая приближенная формула для поля вблизи поверхности
земли:
Пп
ikor
1 + i фГре-Р - 2фе-Р I е^^
da
\
(16)
/
где величина р — так называемое «численное расстояние» — связана
с полюсом р подынтегрального выражения (15) соотношением
p = i{ko -р) г.
Формула (16) совпадает с формулами, полученными совершенно иным
путем рядом других авторов (Вейль, Ван-дер-Поль, Фок).
^ Франк Ф., Мизес Р. Дифференциальные и интегральные уравнения
математической физики. М.; Л., 1937. Т. П.

ДОПОЛНЕНИЕ I
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ^)
§ 1. Основные понятия
Мы познакомились с аналитическими методами решения
уравнений с частными производными. Однако явное представление реп1ения
в виде ряда или интеграла не всегда возможно.
Рассмотрим, например, уравнение теплопроводности
=<-')!=i (*•')!). (1)
Метод разделения переменных применим только в случае с(ж, t) =
= Ci{x)c2{t), k{x^t) = ki{x)k2{t). Однако часто встречаются задачи,
когда коэффициенты теплоемкости и теплопроводности непредстави-
мы в таком виде или даже зависят от температуры
(квазилинейное уравнение теплопроводности). Представление решений
нелинейных уравнений в аналитической форме возможно в исключительных
случаях.
Универсальными методами приближенного решения
дифференциальных уравнений, применимыми для широкого класса уравнений
математической физики, являются численные методы, среди которых
выделим метод конечных разностей (или метод сеток).
Метод конечных разностей состоит в следующем. Область
непрерывного изменения аргументов (например, х vit) заменяется конечным
(дискретным) множеством точек (узлов), называемым сеткой; вместо
функций непрерывного аргумента рассматриваются функции
дискретного аргумента, определенные в узлах сетки и называемые сеточными
функциями. Производные, входящие в дифференциальное уравнение,
заменяются (аппроксимируются) при помощи соответствующих
разностных отношений; дифференциальное уравнение при этом
заменяется системой алгебраических уравнений (разностными уравнениями).
^^ См.: Самарский А. А. Теория разностных схем. М., 1989. Там же
дан список литературы.

586 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Начальные и краевые условия тоже заменяются разностными
начальными и краевыми условиями для сеточной функции.
Естественно требовать, чтобы полученная таким образом
разностная краевая задача была разрешима и ее решение при
увеличении числа N узлов сетки приближалось (сходилось) к решению
исходной задачи для дифференциального уравнения. Ниже понятия
аппроксимации, сходимости, точности и устойчивости иллюстрируются на
простейп1их примерах.
1. Сетки и сеточные функции. Рассмотрим простейшие
примеры сеток.
Пусть область изменения аргумента х есть отрезок О ^ х ^ I.
Разобьем этот отрезок точками Xi = ih (г = О, 1, 2, ..., А/"; h > 0) яа, N
равных частей длины h = l/N каждая. Множество точек Xi = ih, i =
= 0, 1, 2, ..., N, называется разностной сеткой на отрезке О ^ ж ^ / и
обозначается Со^ = {xi = г/г, г = О, 1, ..., N}, а число h — расстояние
между точками (узлами) сетки Сй^ — называется шагом сетки.
Отрезок [О, /] можно разбить на N частей, введя произвольные
точки О < Ж1 < Ж2 < ... < xn-i < I. Тогда получим сетку йо^ = {ж^, г =
= О, 1, ..., А/", жо = О, xn = /} с шагом hi = Xi — Xi-i, который зависит
от номера i узла Xi. Если hi ф /г^+1 хотя бы для одного номера г, то
сетка uj\i — о;^ называется неравномерной. Если hi — const — h — l/N для
всех г = 1, 2, ...,А/', то мы получаем построенную выше равномерную
сетку.
Функцию yi = y{xi) дискретного аргумента ж^,г = 0, 1, ...,А/',
называют сеточной функцией, определенной на сетке Coh-
Всякой непрерывной функции f{x) можно поставить в
соответствие сеточную функцию //^, полагая, например, //^ = f{xi). Впрочем,
в некоторых случаях удобнее устанавливать это соответствие другими
способами.
Пусть область изменения аргументов (ж, t) есть прямоугольник
Д=(0^ж^1,0^^^Т). Построим на отрезке О ^ ж ^ 1 сетку uoh =
= {xi = ih, г = О, 1, ..., N} с шагом h = l/N и на отрезке О ^ t ^Т
сетку LOr = {tj = jV, j = О, 1, ..., А^о} с шагом г = T/Nq. Множество
узлов {xi,tj) с координатами Xi = ih и tj = JT назовем сеткой в
прямоугольнике Д и обозначим Со^т = {(^г = '^h, tj = jr), г = О, 1, ..., А/",
j = О, 1, ..., А^о}- Эта сетка равномерна по каждому из переменных
ж и ^. Если хотя бы одна из сеток Си^ или (Jr неравномерна, то
сетка LOhr называется неравномерной. Сетка cohr, очевидно, состоит из
точек пересечения прямых ж = ж^, г = 0, 1, ...,А/^, и прямых t = tj,
j = 0, 1, ..., АГо.
Пусть у — сеточная функция, заданная на cohr- Будем обозначать
yj = y{xi,tj) значение сеточной функции у в узле {xi,tj) сетки со^т-
Непрерывной функции u{x,t), где (ж,^) — точка из Д, будем
ставить в соответствие сеточную функцию uj = и\ ^ ^ = u{xi,tj).
Возможны и другие способы такого соответствия, на которых мы
здесь не останавливаемся.

§ 1] ОСНОВНЫЕ ПОНЯТИЯ 587
2. Аппроксимация простейших дифференциальных
операторов. Оператор L^, преобразующий сеточную функцию у в сеточную
функцию Y = Lfii/, называют сеточным или разностным оператором.
Дифференциальный оператор L, заданный в классе функций
непрерывного аргумента, может быть приближенно заменен
(аппроксимирован) разностным оператором L/^, заданным на сеточных функциях.
Для этого каждая из производных заменяется разностным
отношением (отсюда и название «разностный оператор»), содержащим значения
сеточной функции в нескольких узлах сетки. Посмотрим, как это
делается для первых и вторых производных функции одного переменного.
Пусть LJh = {xi = ih} — сетка с шагом h на отрезке О ^ ж ^ 1.
Рассмотрим первую производную Lv = v' функции v{x). Заменить ее
разностным выражением можно бесчисленным множеством способов.
Простейшими являются замены
Vi-Vi-i
Lv ~ ; = L. Vi
h ^
— левая разностная производная, или левое разностное отношение,
h— " ^""^
— правая разностная производная,
— центральная разностная производная. Здесь Vi = v{xi), знак ~
означает соответствие или аппроксимацию. При замене Lv = v'
разностным выражением L^^Vi допускается погрешность L^^Vi — {Lv)i = ф^,
называемая погрешностью аппроксимации оператора L разностным
оператором L^. Естественно требовать, чтобы при стремлении h к
нулю эта погрешность стремилась к нулю. Для оценки ф^ надо
предположить, что v{x) — гладкая функция. Будем говорить, что v{x)
принадлежит классу (пространству) (7^^^[0,1] {v{x) G (7^^^[0,1]) функций,
заданных на отрезке О ^ ж ^ 1, если v{x) имеет т непрерывных на
отрезке О ^ ж ^ 1 производных. При ш = О получаем класс (7^^^[0,1]
непрерывных при О ^ ж ^ 1 функций.
Пусть |;(ж) е С(^)[0,1], где 771 ^ 2. Разложим v{x) в ряд Тейлора
в окрестности точки х = Xi'.
Vi±i =vi±hv[ + 0{h^)
и вычислим ф^ = L'^Vi — v[ = 0{h), ф^ = L^Vi — v[ = 0{h).
Будем говорить, что разностный оператор L^: 1)
аппроксимирует дифференциальный оператор L на сетке а;/^, если выражение
гаах!?/^^! = vimyi\LhVi — {Lv)i\ (где v{x) — достаточно гладкая функ-
^^ ^^
ция) стремится к нулю при /г —>- 0; 2) аппроксимирует L с порядком

588 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
п > О, если max l^/^f | = 0{h^) (или max l^/^f | ^ М/г^, где М — положи-
тельная постоянная, не зависящая от h).
Обращаясь к формулам для L^ , видим, что L'^Vi и L^Vi
аппроксимируют Lv = v' с 1-м порядком при V G , где 771 ^ 2. Увеличение
т не меняет порядка аппроксимации.
Выражение для L'^Vi содержит значения v в двух узлах х = Xi и
X = Xi-i сетки. Говорят, что оператор L^ является двухточечным, или
оператором 1-го порядка.
Множество узлов, значения сеточной функции в которых входят
в выражение L^Vi, называют шаблоном оператора L^ в точке Xi.
Очевидно, что шаблон оператора L^ состоит из двух узлов — ж^ и ж^_1, а
шаблон L^ — из узлов Xi и ж^+1.
Возьмем, например, трехточечный оператор, определенный на
шаблоне Xi-i, Xi, Xi-^i'.
L\ ^Vi = aLlvi + (1 - a) L^ Vi = -^ , (2)
где a — произвольное число. В частности, при а = 1/2 получаем цен-
тральную разностную производную Li^vi = — , которая, как
нетрудно показать, при v{x) G (7^^^[0,1] аппроксимирует v'[х) со 2-м
порядком.
В дальнейшем будем пользоваться обозначениями
_ Vj - Vj-i _ Vj^i - Vj
h h
(3)
'^^o = — = - (Vx i + Vx i).
x,i 2h 2 ^ ' '^
В тех случаях, когда номер i узла не имеет значения, будем его
опускать и писать Vx, Vx, Vo.
X
Рассмотрим теперь вторую производную Lv = v". На
двухточечном шаблоне, очевидно, ее аппроксимировать нельзя. Выберем
трехточечный шаблон, состоящий из узлов ж^_1, ж^, ж^+1, и рассмотрим
разностный оператор
LhVi = Vxx,i = -Г K,i - Vx,i) = 72 • (4)
Если^; G C(^)[0,1], 771 ^ 4, TO МОЖНО написать
щ±, =v,±hv[ + ^ v4 ± ^ vT + ^ «f ^) + o{h'). (5)
Отсюда следует (индекс г опускаем), что
^,,-^" = g«(IV)+o(/l2), (6)

§ 1] ОСНОВНЫЕ ПОНЯТИЯ 589
т. е. Vxx аппроксимирует v" со 2-м порядком.
Для аппроксимации четвертой производной Lv = v'^^^^ выберем
пятиточечный п1аблон, состоящий из узлов Xi -\- kh (/;; = О, =Ы, ±2), и
положим
J-'h'^i — '^xxxx,i — 74 • V'/
В ЭТОМ случае Vxxxx — '^'^^^^ = 0{h?) для v{x) G C^^^. Ha
пятиточечном п1аблоне {xi + kh)^ к = 0, =Ы, ±2, можно добиться аппроксимации
0{К^) для v"^ если г» G (7^^\ В самом деле, из (6) и (7) следует, что
оператор
LhV = Vxx - Y^ Vxxxx = v" + 0(/г^) (8)
имеет 4-й порядок аппроксимации.
На практике аппроксимация производных на многоточечных nia-
блонах используется редко, так как при увеличении п1аблона обычно
увеличивается объем вычислительной работы и ухудп1аются качества
получающихся разностных операторов (в смысле устойчивости).
Еще раз отметим, что порядок аппроксимации разностного
оператора Lh зависит от порядка т дифференцируемости функции v{x). Мы
везде фактически говорили о максимальном порядке аппроксимации,
который не меняется при увеличении номера т класса С^^\ считая,
что v{x) — любая функция из С^^\ Очевидно, что при специальном
выборе v{x) порядок аппроксимации может повыситься. Если,
например, v{x) = и{х) есть решение уравнения и" = ж, то и^^^^ = О и Uxx = и"^
т. е. Vxx аппроксимирует v" точно при v = и.
Рассмотрим более сложный оператор
ди д'^и
где и = u{x,t) — функция двух аргументов х и t, меняющихся в
области Д = (0^ж^1, О ^ t ^Т). Введем сетку
(^hr = {{xi = ih, tj = jr), г = 0, 1, ..., АГ, j = О, 1, ..., A^o}
с шагами h = 1/N и r = T/Nq.
Произведем замену
хх,г
В результате получим разностный оператор
^..пГ^ = ^^i^ - "--^"У+"-^^ , (10)

590 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
который можно записать в виде Ь^^-и = щ — и^ж, где и = щ, и = щ
Этот оператор определен на п1аблоне, состоящем из четырех точек:
(xi,^j+i), (xi^tj), (xi-i^tj), (xi-^i^tj) (рис. 85, б). Оператор Lh^
определен не во всех узлах cohr, ^ только при О < г < А/" и j > О, т. е. в
тех узлах, в которых п1аблон состоит только из узлов сетки Со^т-
Узлы {xi,tj), о < i < N, j > О, назовем внутренними и обозначим со^т =
= {{xi,tj), О < i < N, О < j ^ А^о} множество всех внутренних узлов.
Таким образом, оператор Ь^т определен на cohr, т. е. во внутренних
узлах. В остальных узлах, называемых граничными, должны быть за-
<7 = 1 <7 = о
T
a б в
Рис. 85
даны краевые и начальные условия. Оператор Ь^т имеет 1-й порядок
аппроксимации по г и 2-й по h:
m8ix\Lhrui - {Lu)i\ = 0(/г' +r), (11)
так как Uxx = и" + 0{h?)^ щ = й -\- 0{т) (й = (du/dty). Здесь штрихи
означают дифференцирование по ж, точка — дифференцирование по t.
Рассмотрим оператор
LhrW- = Г^ , или LhTU = Ut-Uxx,
(12)
определенный на четырехточечном шаблоне (xi_i,^j+i), (xi,^j+i),
(xi+i,^j+i), {xi,tj) (рис. 85, б). Он аппроксимирует Lu с тем же
порядком, что и оператор (10).
В § 2 будет рассмотрено однопараметрическое семейство
разностных операторов, аппроксимирующих оператор (9). Это семейство
содержит операторы (10) и (12).
До сих пор мы оценивали величину погрешности аппроксимации
ф = LhV — Lv для оператора L^ (или Ь^т) как шах \ф\, т. е. по норме^^
^ Каждой сеточной функции у ставится в соответствие некоторое
неотрицательное число II2/11, называемое нормой и представляющее собой аналог
расстояния от начала координат в обычной геометрии. Норма удовлетворяет
требованиям: 1) \\у\\ = О только при у{х) = 0; 2) \\су\\ = |с| • \\у\\, с = const; 3)
III/+ ^11 ^ lll/ll + Ikll (неравенство треугольника) (см.: Канторович Л. В.,
Акилов Г. Н. Функциональный анализ в нормированных пространствах.
М., 1984).

§ 1] ОСНОВНЫЕ ПОНЯТИЯ 591
(«в норме»)
||V^||o = max|V^(x)|. (13)
Для оценки величины сеточной функции ф можно использовать и
другие нормы, например
(7V-1 \ V2 дг_1
Т.^Щ ' ll^lli=E'*IV'*l и т. д. (14)
г=1 / г=1
Пусть II-011 — некоторая норма для функций -0, заданных на сетке
ujh' в дальнейп1ем будем говорить, что разностный оператор Ь^: 1)
аппроксимирует дифференциальный оператор L по норме || • ||, если
II-011 = \\LhV — Ьг'Ц —>- О при /г —>- 0; 2) аппроксимирует L с порядком
п > О (L/i имеет п-й порядок аппроксимации), если \\^\\ = 0{h^), или
II-011 ^ Mh'^, где М = const > О не зависит от /г.
Если V — достаточно гладкая функция, a,(Jh — равномерная сетка,
то все рассмотренные выше разностные операторы имеют один и тот
же порядок аппроксимации в любой из норм (13), (14).
Иначе обстоит дело в случае неравномерной сетки.
Пусть LJh = {xij г = О, 1, ..., А/", жо = О, xn = 1} — неравномерная
сетка с шагами hi = Xi — Xi-i, г = 1, 2, ..., А/", на отрезке О ^ ж ^ 1.
Рассмотрим оператор Lv = v". Ему поставим в соответствие
разностный оператор
LhVi
1
hi
'Vi^l -Vi
hi-\-i
Vi -Vi
hi
-1
(15)
где hi = {hi -\- hi-^i)/2, определенный на трехточечном шаблоне
(Xi_i, Xi, Xi+i).
Вычислим погрешность аппроксимации фi = L^Vi — Lvi.
Предполагая, что v{x) G C^^^[0,1] и пользуясь разложениями
Vi+i =Vi + hi+iv'i + ^ < + g h\+i<' + 0(/i^+i),
Vi_, =vi- hiv[ + i hlv'l - i f^v'l' + 0{ht).
находим
/ l^i-\-l ~ l^i III . ^/i2 I 7 2 \
V^i = ^ ^i +0(/г^ +/i^+i).
Отсюда видно, что HV^Hs = 0{ho), ho = шах/г^, где || • ||s при s =
= 0, 1, 2 — любая из норм (13), (14). Отсюда следует, что Lh имеет
1-й порядок аппроксимации в нормах || • ||о, || • ||i, || • ||2-

592
ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Покажем, что при надлежащем выборе нормы, а именно
7V-1
^ hi ^Пкфк
оператор (15) имеет в этой норме 2-й порядок аппроксимации:
\, = \\LhV-Lv\\s = 0{hl),
Так как < = ^^^ + 0(/ii+i), то (/г,+1 - hi)v'^' = ^^±^-^ v''' =
= -— {hlj^iv'l!^i — hjv'i") + 0{hj_^i) и поэтому фi представится в виде
Zfli
V)i = Vi + vr>
V* = 0(/if + /if+i),
° 1 1
V^i = ^ (^i+i - Vi), ^^ = б ^?^^'' = 0{hj).
о
Вычисляя J2l^^ fik^k = Y!k=i i'^k+i - Vk) = Vi+i - ^1 и учитывая,
о
ЧТО |?7| = 0(/io), получаем Ц^^Цз = 0{Н^) и, следовательно,
IIV'lls ^ ||^||з + IIV-lls ^ Mft2,
где М = const > О не зависит от сетки, т. е. (15) имеет 2-й порядок
аппроксимации в норме || • ||з на любой неравномерной сетке coh- Этот
результат сохраняет силу и для норм
V2
Зо
7V-1 /N-1
^hii^ Пкфк
г=1
. k=i
N-1
u = Y.^^
^^кФк
k=l
Отметим, что Ц^^Цз ^ IIV^IU, ^ = О, 1, 2.
В дальнейп1ем будем пользоваться обозначениями
Vj - Vj-l
hi
= hi,^''^
Vi+1 - Vi
hi-\-i
hi
Vx,i) =
hi
Vi^l -Vi Vi- Vi-i
hi-\-i
hi
(16)
Если сетка coh неравномерна, то при аппроксимации оператора (9)
используется оператор (15), так что вместо (10) и (12) будем иметь
разностные операторы L^rU = щ — йхх, L^rU = щ — Uxx- В этом случае
вместо (11) получим оценку
max \\LhrU - Ьи\\з = 0{hl + г), (17)
где максимум берется по j = 1, 2, ..., А^о-

у ОСНОВНЫЕ ПОНЯТИЯ 593
Сетка й!г также может быть неравномерной с тагом tj = tj —
ti
.bJ = l,2,...,Aro.npH3TOM(^-j ^___=(^_j +
+ 0(rj+i); тогда в (17) г = max tj.
3. Разностная задача. До сих пор мы занимались
аппроксимацией простейп1их дифференциальных операторов разностными
операторами. Обычно требуется реп1ить дифференциальное уравнение
Lu = — / с некоторыми дополнительными (начальными, краевыми)
условиями. Поэтому кроме построения разностного оператора
нужно аппроксимировать на сетке правую часть и дополнительные
условия, после чего можно поставить разностную задачу, т. е. написать
разностные (алгебраические) уравнения и дополнительные условия на
сетке. Получающуюся таким образом систему разностных уравнений
и дополнительных условий называют разностной схемой.
Рассмотрим несколько примеров постановки разностной задачи.
Пример 1. Задаче Коши для уравнения 1-го порядка
u'{x)=f{x), ж>0, u(0) = uo, (18)
на равномерной сетке соответствует разностная краевая задача
получаемая при замене оператора и' разностным оператором
LhU = Ux.
Пример 2. Краевой задаче для уравнения 2-го порядка
u" = -f{x), 0<ж<1, n(0)=/ii, n(l) = /i2, (19)
на равномерной сетке соответствует краевая задача
^i+l - 2у1 + ^i_i = -h^^Pi, У0= /J'l, yN = 1^2 {^i = /(Жг)),
получаемая при замене оператора и" разностным оператором Uxx •
Пример 3. Краевой задаче для уравнения теплопроводности
ди и и
^ = ^ + /(^,^), 0<х<1, 0<t<T, (20)
и{х,0) =uo{x), 0^ж^1, (21)
u{0,t) = fii{t), u{l,t) = fi2{t), O^t^T, (22)
на равномерной сетке cuhr = {xi = г/г, tj = jr (г = 0, 1, ..., A/", j =
= 0, 1, ..., A^o)} соответствует разностная краевая задача
(23)
(7=^, ^i^^ = f{xi,tj)j , y^ = uo{xi);
yo = f^i{tj)^ yN = f^2{tj), (24)
38 A. H. Тихонов, A. A. Самарский

594 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
получаемая при замене оператора теплопроводности разностным
оператором (10). Определим yj :
yi+' = (1 - 27) у{ + 7 (vU + vi+i) + ^^Г'- (25)
Если yj известно, то по этой формуле можно определить yj во
всех узлах г = 1, 2, ..., А/" — 1 (на слое j + 1). Так как при j = О задано
начальное условие у^ = u{xi), то формула (25) позволяет определить
от слоя к слою значения у- во всех узлах сетки cohr^ используя при
этом краевые условия (24). Схема (23) называется явной.
Пусть Lhr определяется формулой (12). Тогда уравнение
принимает вид
Уг ~ Уг Уг-1 "^Уг ^ Уг+1 , J + 1 /о^\
yt =Ухх-\-^ ИЛИ -^--- '- = — ^- + ipj^ . (26)
Для определения yj на новом слое j + 1 получаем систему
алгебраических уравнений
7y|+i' - (1 + 27) yt' + ly'iXl = -yi - Ы^'' о < г < ЛГ. (27)
Такая схема называется неявной или схемой с опережением.
4. Устойчивость. После того как разностная схема написана,
т. е. сформулированы разностное уравнение и все дополнительные
условия, возникает прежде всего вопрос о разрешимости полученной
алгебраической системы уравнений. Если эта система неразрешима,
то такую схему следует признать непригодной.
Пусть разностная задача разрешима. Тогда естественно
требовать, чтобы при неограниченном сгущении сетки решение разностной
задачи стремилось к решению исходной задачи для
дифференциального уравнения (схема сходилась). В этих рассуждениях мы
предполагаем, что разностная задача решается точно и решение может
быть найдено с любым числом знаков. Практически же все
вычисления ведутся с конечным числом знаков и на каждом этапе вычислений
допускаются ошибки округления. Если малые ошибки округления,
допускаемые на промежуточных этапах вычислительного процесса, при
сгущении сетки приводят к большим искажениям решения, то такую
схему называют неустойчивой. Она непригодна для практики.
Ошибки вычислений можно рассматривать как возмущение
начальных данных или правой части уравнения. Отсюда следует, что
от схемы надо требовать, чтобы решение разностной задачи мало
менялось при малом изменении входных данных задачи (правой части,
краевых и начальных условий), или, иными словами, чтобы решение
непрерывно зависело от входных данных при сгущении сетки. Если
это требование выполняется, то схема называется устойчивой, в
противном случае схема неустойчива. Ниже приводятся примеры
неустойчивых и устойчивых схем.

§ 1] ОСНОВНЫЕ ПОНЯТИЯ 595
Пример 4. Устойчивая схема. Рассмотрим задачу Коши для
уравнения
и' = —аи^ ж > О, и(0) = uo, а > О, (28)
имеющую решением и{х) = uoe"*^^, и заменим ее разностной схемой
=-ауг, г = 1, 2, ..., Уо = ио.
h
Из разностных уравнений получаем ^^ (1 + а/г) = yi-i или ^^ = s^i_i =
= s^yo, где S = < 1. Преобразуем выражение для s:
1 -\- ah
\ns = -\п{1 +ah) = -ah + 0{h^) = -h{a + 0{h)),
или ^ = g-M-+oW)^
Рассмотрим какую-либо точку х. Для простоты будем
предполагать, что эта точка является узлом последовательности сеток coh при
/г —>- 0. Номера г, соответствующие этой точке для сетки а;/^, равны
i = ж//г. Очевидно, что
Уг = s'yo = yoe-''(-+Om^/h ^ y^^-ax+0(h) ^ у^ [g-as ^ дщ^
откуда и следует сходимость разностной схемы.
Отсюда видно, что при малом изменении начального значения уо
решение у^ разностной задачи также меняется мало (непрерывно
зависит от ^о)-
Пример 5. Неустойчивая схема. Рассмотрим ту же задачу (28),
что и в примере 4.
Аппроксимируем уравнение и' = —аи разностной схемой
а h (1 - сг) \-ayi = 0, г = 1, 2, ..., (29)
где а — произвольный параметр, не равный единице.
Так как схема трехточечная, то начальные значения надо задавать
не только в точке ж = О, но и в точке xi = h: уо = щ, yi = щ. Из (29)
следует
{а - 1) yi^i - [{2а - 1) + ah] yi + ayi^i = 0. (30)
Будем искать частные решения этого уравнения в виде yi = s^. Для s
из (30) получим квадратное уравнение
{a-l)s^ -{2a-l + ah)s + a = О, (31)
дискриминант которого равен
А = (2а - 1 + ah)^ -4:a{a-l) = l + 2{2a-l)ah + a^h^,
38*

596 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
так что л/А = 1 + (2а - 1) а/г + 0{h^). Отсюда находим выражения для
корней si и S2 уравнения (31):
si = —^ (1 + а/г + 0{h^)), S2 = I - ah + 0{h^).
(7 — 1
Общее решение уравнения (30) имеет вид
yi = As{^Bsl (32)
где постоянные А и В определяются из начальных условий при г = О
и г = 1. Учитывая, что 1п(1 =Ь а/г + 0{h?)) = =Ь/г {а + 0(h)), находим
si = ^ е^ («^+о(/г)) ^ ^2 ^ g-/i (а+0(/г)) ^
сг — 1
Пусть ж — фиксированная точка, являющаяся узлом сетки а;/^, так
что X = г/г. Из (32) следует
у.=А (-^)" е* <"+''<''^^ + Se-*("+o(h))_
Отсюда видно, что поведение реп1ения зависит от значения
параметра а. Если сг > 1, то > 1 и первое слагаемое при любом
сг — 1
значении А ^ О неограниченно возрастает при /г —>- 0.
Коэффициент А зависит от уо, yi. Если при некотором выборе
начальных значений Л = О, то при сколь угодно малом возмущении
начальных данных, хотя бы за счет ошибки округления, мы получим
Л 7^ О и соответствующее решение будет неограниченно возрастать
при /г —>- 0.
Таким образом, при сг > 1 схема (29) неустойчива и непригодна
для вычислений■'■^
Приведенные выше примеры показывают, что если схема
устойчива, то малые изменения начальных данных или правой части
уравнения приводят к малым изменениям решения разностной задачи; если
же схема неустойчива, то малые изменения начальных данных и
правой части могут приводить на достаточно мелкой сетке к сколь угодно
большим изменениям решения. Поэтому неустойчивая схема
расходится.
Пусть ищется решение у^ некоторой разностной задачи с шагом
h на сетке coh, удовлетворяющее разностному уравнению с заданной
правой частью (р и дополнительными соотношениями (например,
начальным, краевым условиями), заданными в граничных узлах сетки.
Правую часть уравнения и известные функции, содержащиеся в
дополнительных условиях, называют входными данными. Решение
разностной задачи зависит от входных данных и от параметра h — шага
сетки. Меняя /г, мы получаем последовательность {у^} решений
разностной задачи.
При а = 0,5 схема (29) также неустойчива.

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 597
Говорят, что разностная задача поставлена корректно
(разностная схема корректна), если ее решение у^ при любом
достаточно малом h ^ ho
1) существует для произвольных входных данных;
2) непрерывно зависит от входных данных, причем эта
зависимость равномерна относительно niara h.
Свойство непрерывной зависимости реп1ения разностной задачи
от входных данных называется также устойчивостью разностной
задачи (схемы).
Penienne разностной задачи у^ рассматривается не при одном
фиксированном значении /г, а при любых /г ^ /го, т. е. на любых
последовательностях достаточно мелких сеток. Равномерная по h непрерывная
зависимость у^ от входных данных означает, что свойство
непрерывной зависимости сохраняется при /г —>- 0. Иными словами, если penie-
ние оценивать по норме || • ||п), а входные данные, например правую
часть (/?, по норме || • ||(2)5 то устойчивость (равномерная по h) схемы
по правой части означает существование такой постоянной М > О, не
зависящей от /г, что
\\У^\\(1) ^ М \\(f\\(2) при любых h ^ ho.
Данное вып1е определение корректности разностной схемы
аналогично определению корректности задачи для дифференциального
уравнения, с которым мы неоднократно встречались в курсе. Различие
между этими определениями состоит в требовании равномерной по h
устойчивости решения разностной задачи.
§ 2. Разностные схемы для уравнения теплопроводности
1. Схемы для уравнения с постоянными коэффициентами.
Рассмотрим первую краевую задачу для уравнения теплопроводности.
Найти непрерывную в прямоугольнике Д (0^ж^1, О ^ t ^ Т)
функцию и = u{x,t), удовлетворяющую условиям
ди д и Л
и{х,0) = uo{x), u{0,t) = Ui{t), u{l,t) = U2{t).)
Введем в Д описанную в § 1 сетку со^т = ^/г х ^г = {(^г = '^h, tj =
= jr), г = О, 1, ..., АГ, j = О, 1, ..., А^о} с шагами h = 1/N, т = Т/Щ.
Проведя замену
^^""^ _ Ui-i - 2ui ^ UiJ^i
\Цхх)г
/дЧ\
dtj

598 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
и введя произвольный вещественный параметр а (вес верхнего слоя
t = ^j+i), получим однопараметрическое семейство схем
J + 1 _ 3
^^ ^ = Л(а^/+^ + (1 - а)у{)^^\
г (2)
j=0, 1, ...,7Vo-l, г = 1, 2, ...,7V-1,
где h.yh = Ухх.г-
Схема (2) определена на шеститочечном шаблоне, состоящем из
узлов {xi^s^tj+k) (^ = —1, О, 1; /i; = О, 1), расположенных на двух слоях
t = tj VL t = ij-^i (см. рис. 85, a). Поэтому схему (2) часто называют
двухслойной шеститочечной схемой или схемой с весами.
Поскольку в (2) входит произвольный параметр а, то фактически
мы рассматриваем не одну схему, а однопараметрическое семейство
схем. В дальнейшем будет показано, что с помощью параметра а
можно управлять устойчивостью и точностью схемы (2). Так как схема
(2) пишется одинаково во всех внутренних (при l<i<N,j>0)
узлах (xi^tj) сетки (Jhr^ то индексы г, j можно опустить и пользоваться
безындексными обозначениями, полагая
J+1 - 3 У -у J+1
у = у1 , у = у1^ yt = , ^ = ^i •
г
в этих обозначениях схему (2) перепишем в виде
yt = A{ay + {l-a)y)+(f, {x,t)euJhT- (3)
Присоединяя сюда начальные и краевые условия
у{х,0) = uo{x), X е (Jh,
y{0,t) =Ui{t), y{l,t) =U2{t), teuJr,
(4)
получаем разностную задачу (3) — (4), соответствующую задаче
(1). Требуется найти сеточную функцию y{x,t), определенную для
{x,t) G LOhr и удовлетворяющую уравнению (3) во внутренних узлах
^hr — {{^i^tj)^ о < i < N, О < j ^ No} и условиям (4) в граничных
узлах jhr = {{xi^tj), г = о, о ^ j ^ TVo; г = TV, о ^ j ^ TVo; j = о, о ^ г ^ TV}
сетки ujhr-
Для определения у = у^'^'^ из (3) и (4) получаем задачу
criVi-i - (1 + 2сг7) yi + сг7^г+1 = -Fi, О <i < N,
Fi = {l- 27 (1 - a)) yi + {l-a)j {yi-i + ^i+i) + T(fi, '^ = ;^ '
Значения у = yj и, следовательно, Fi на нижнем слое (при t =
= tj) известны. Счет идет от слоя j к слою j + 1, начиная с j = О, при
котором задано у^ = uo{x).

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 599
При сг = О получаем явную схему (см. § 1, п. 2). Для нее i/i = Fi,
т.е. значения у определяются независимо в каждом узле сетки coh- При
сг 7^ О для определения у получаем систему алгебраических уравнений
порядка N — 1 (такие схемы называются неявными). Метод реп1ения
этой системы, учитывающий специальный вид (трехдиагональность
ее матрицы, у которой отличны от нуля только элементы, стоящие
вдоль главной диагонали и двух соседних с ней диагоналей), указан в
п. 10.
2. Погрешность аппроксимации. Пусть у = y{x,t) — решение
задачи (3) — (4), и = u{x,t) — решение исходной задачи (1).
Рассмотрим разность zj = yj — u{xi,tj-^i), или z = у — и, и подставим
у = Z -\- и в уравнение (3). Предполагая и = и{х, t) заданной функцией,
найдем
zt = K{az^{l -cr)i)+V^, {x,t) e uJhrA . .
z(x,0) = 0, z{0,t) = z{l,t) =0, J
где
Ф = A {au -\- {1 — a) u) -\- (f — Щ (6)
представляет собой погрешность, с которой решение и = u{x,t)
уравнения (1) удовлетворяет разностному уравнению (3). Сеточная
функция ф = ^{x^t^u] h,T,a), определяемая формулой (6), называется
погрешностью аппроксимации дифференциального
уравнения (1) разностным уравнением (3) в классе решений и = u{x,t)
уравнения (1) (или «погрешностью аппроксимации для схемы (3) на
решении уравнения (1)»).
Для оценки величины функции ф мы будем пользоваться
различными нормами (при фиксированном t G uJr), например
0= шах IV^il, (7)
l<t<N
/N-1
E^^i
(8)
a также нормами
maxllV^llo, max||'0||2 и т. д. (9)
Будем говорить, что схема (3) имеет по норме \\^)\\ т-й порядок
аппроксимации по /г и п-й — по г на решении и = u{x,t)
(аппроксимирует уравнение (1) с порядком {т,п)) или просто имеет аппроксимацию
0(/г^) + 0(г^), если
IIV^II ^М(/г^+г^) (ш>0, п>0), (10)
где М — положительная постоянная, не зависящая от/гиг, а||-|| —
некоторая норма (например, (7) или (8)).

600 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Для оценки порядка ф по h и т разложим и = u{x,t) в окрестности
точки {xi, i = ^7+V2 ~ ^J ~^ О?^'^) по степеням /гиг. Будем
предполагать, что u{x,t) имеет нужное по ходу изложения число производных.
Обозначивй = du/dt, и' = ди/дхи т. д., и = u(xi,^j+i), й = u{xi^t-j^ii)^
получим
(см. § 1, п. 2),
^2 _ _ _ ^2 _
U = й + 0,5гй+ --й + 0(г^), й = й - 0,5гй+ --й + 0(г^),
8 8
Пользуясь разложениями для и, й, Ли, находим
сги + (1 - сг) й = й + (сг - 0,5) гй + О(г^),
Л {аи + (1 - а) й) = о-и'' + (1 - 0-) и" + 0(/г^) =
= й" + (а - 0,5) ™ ' + 0(/г' + г').
Подставляя полученные выражения в (6), будем иметь
ф^й" -и^{а - 0,5) ти" + (/? + 0(/г^ + г^).
Так как и есть penienne уравнения (1), то й'' — й = — / и
ф = ^-/^(а- 0,5) гй'' + 0{h^ + г^) 1).
Выбирая (f так, чтобы (f = f -\- 0{h^ + r^), например (/? = /, если
/ G С^^\ получаем
ф = {а- 0,5) гй'' + 0(/г^ + г^). (11)
Обозначим через класс функций, имеющих ттг
производных по ж и п производных по t, непрерывных в Д. Из предыдущего
ясно, что
|о = 0(/г2+г) при (7 7^0,5 и и G С^^'^), (12)
|о = 0(/г2+г2) при (7 = 0,5 и и G С^^'^). (13)
Выбирая параметр а равным
и правую часть
'='■=1-^ м
"^^'^S- <'^'
^ Так как и" -\- f — й = О, то (6) можно было бы сразу записать в виде
V> = [Л (аи + (1 - а) й) - й"] + (¥'-/)- (и? - и).

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 601
получим схему повышенного порядка аппроксимации ф = 0(/г^ -\- т'^)^
еслииеС(^'^),/еС(2'^)^).
3. Энергетическое толсдество. Чтобы выяснить, при каких
значениях а схема (2) устойчива по начальным данным и по правой
части, найдем оценку реп1ения разностной задачи (3) — (4) с
однородными краевыми условиями {ui = ^2 = 0) через (/? и uq.
Для этого используем метод интегральных или энергетических
соотношений, который без существенных изменений переносится на
случай уравнений с переменными коэффициентами. Нам понадобится
небольшое число предварительных сведений. Пусть v{x) = Vi^ z{x) =
= Zi — произвольные функции, заданные на сетке ио^ = {xi = ih).
Имеют место следующие формулы.
1. Формула разностного дифференцирования произведения
{vz)x,i = ViZx,i + Vx,iZi^i. (16)
В самом деле, ViZ^^i + v^^iZi^i = [vi {zi^i - Zi) + {vij^i - Vi) Zi^i]/h =
= {vi-^iZi-^i — ViZi)/h = {vz)x,i' Формула (16) является разностным
аналогом формулы дифференцирования произведения {uv)' = u'v + uv'.
2. Формула суммирования по частям
{v,Zx) = -{z,Vx] + {vz)n -^0^1, (17)
где
7V-1 TV
(v^w) = 2Z ^i'^ih, {y,"^] = y^'^^i'^i^, (18)
i=l 1=1
являющаяся разностным аналогом формулы интегрирования по
частям.
Выразим из (16) ViZx^i = {vz)x^i — Vx,iZi-\-i и преобразуем сумму
(VjZx):
N-1 N-1 N-1
{v,Zx) = ^ ViZx,ih = ^[{vz)i^i - {vz)i] - ^ Vx,iZi^lh =
i=l i=l i=l
N
= {vz)n - VlZl - ^ Vx,iZih {Vx,i = Vx,i^l).
1=2
Затем, учитывая, что vi = v^ -\- {vi — v^) = г'о + hvx,i, получим
TV
{v, Zx) = {vz)n - {vo + hvx,i) ^1 - X^ ZiVx,ih = {vz)n - v^zx - {z, Vx].
^ к ПП. 1, 2 см.: Самарский A. A., Гулин A. В. Устойчивость
разностных схем. М., 1973; Саульев В. К. Интегрирование параболических
уравнений методом сеток. М., 1960.

602 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
3. Первая разностная формула Грина
{v,{ay^):,) = -{ay^.v^] + ay^v\N - voOiy^ |i. (19)
В самом деле, полагая в (17) z = аух, сразу получим (19). Из (19), в
частности, следует, что
{у, {аУх)х) = -{аух.Ух], если у = v = 0 при г = О, АГ; (20)
(^,(а^^)ж) =-(а, (^^)2], если уо = у^ = 0. (21)
Формула (19) является разностным аналогом формулы Грина
1 1
/ и {kw'Y dx = kuw' — I ku'w' dx.
0 0
4. Вторая разностная формула Грина
(^, {аУх)х) - {у, {cLVx)x) = CLN {уух - yVx)N " «i {vy^ - yVx)o (22)
получается из выражения (19), если в нем поменять местами у и v и
вычесть из (19) полученное равенство.
Нам понадобится также неравенство
\{y,zy\^^y{y,yy{z,zy, (23)
где
{у, zY = ^ ykZkh, г = 2, 3, ..., TV. (24)
к=1
Рассмотрим сумму
{у + Xz,y + XzY = {у, уУ + 2Л {у, zY + Х" {z, zf ^ О,
где л — любое вещественное число.
Если {z,zy ф О, то (^ + ^2;,^ + Л^;)* ^ О при любых
значениях Л только при условии, что дискриминант квадратного трехчлена
[(^,2;)*]^ — {у^уУ • {z^zy ^ 0. Отсюда и следует (23). В частности, при
i = N получаем неравенство Коши — Буняковского
\{y,z)\^\\y\\-\\z\\, (25)
где ( , ) — скалярное произведение в пространстве сеточных
функций — дается формулой (18), а ||^|| — норма сеточной функции у = yi —
равна
/N-1
V2
л/(^= Е^'^ • (26)

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 603
Докажем следующие неравенства:
1к11^:^11%Ь если zo = zn = 0, (27)
Ikllo ^ 2 II^^I' ^^™ zo = zn = 0, (28)
где ||2;||о = max \zi\, \\z\\ дается формулой (26), а
/ N \ V2
||%1 = (%,%]^/^ = (x^^l,i^J •
Замечая, что z^ = f J]l=i ^x,kh] = {T.k=i+i ^x,kh] , представим
z^ в виде
z^ = (l-Xi) i^z^^kh] +Xii^ z^^kh] .
\k=l I \fe=i+l /
Применив неравенство (23) для каждой из сумм, например
/ г \ 2 . . .
I Х^ %,fe/i I ^ Х^ (%,fe)^ /г • ^ 1^ /г = Xi ^ (%,fe)^ h,
\fe=i / fe=i fe=i fe=i
получим
^,2^x^(1-^0 (^(%,fe)'/г + ^ (%,fe)'/i] =Xi(l-xO||%F. (29)
Так как max x(\ — x) — 1/4, то отсюда следует, что ||2;||о ^ ||%]/2.
Умножив (29) на /г и просуммировав пог = 1, 2, ...,А/' — 1, будем
иметь \\z\\' ^ ||%р/4, или ||2;|| ^ ||%]/2, так как Yl,i^\ ih = {N — 1) h <
<1.
Пусть Av = {avx)xj а ^ ci > 0. Из (21) и (27) следует оценка
-(Л^;,^;) = -{{av^),,v) ^ 4ci \\vf. (30)
В самом деле, —{Av,v) = (а, (г^^)^] ^ ci Цг^^Р в силу (21). Пользуясь
затем неравенством (27), получаем (30).
Укажем еще одно неравенство:
2\аЬ\ ^соа^ + —&^ (31)
Со

604 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
где а и b — заданные числа, cq — произвольное положительное число.
В самом деле,
(«л/со) ! ,
Со
2 I b ^'
2\аЬ\ =
так как 2 \aibi\ ^ af + bf при любых ai и bi.
Перейдем теперь к изучению вопроса об устойчивости схемы (3)
по начальным данным и по правой части.
Папип1ем энергетическое тождество, соответствующее уравнению
с однородными граничными условиями
zt = Л^(") +ф, zo = ZN = о, z{x, 0) = zo{x), (32)
где
^И =crz + {l-a)z.
Умножим уравнение на 2тz^ ^h = 2 {zi — Zi) h vl просуммируем no
г = 1, 2, ..., АГ-1:
L, ^,
2rPf||' = 2r(Az('^),Zf) + 2r(^,Zf), Az = z-,,. (33)
Представляя 2;^^^ в виде
^И = 0,5 {z + z) + {a- 0,5) {z - z) = 0,5 {z + z) + {a - 0,5) rzt
и пользуясь первой формулой Грина (20) для а = 1, у = rz^ — z — z^
v = z-\-z'i/La = l,y = v = Zt, имеем"*-^
2т {Kz^''\zt) = -2 (сг - 0,5) r^ (%^-, z^^t] - (% + %, % - %] =
= _2 (а - 0,5) r^ ||z,,-f - ll^f + p,f.
Подставив это выражение в (33), получим энергетическое тождество
2т [\\ztf + {а- 0,5) г \\z,tf] + \\z^f = \\z,f + 2т {ф, zj). (34)
Отметим, что имеет место следующее неравенство:
Цг'жР ^ р-ll^'lP, если vo=vn = 0. (35)
В самом деле, суммируя неравенство
по г = 1, 2, ..., А/", приходим к (35).
^^ (A(^ + i),^-i) = -(^ж + ^ж,^ж - zx], {^zi.zi) = -{z^t^z^t].

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 605
4. Устойчивость. Как было указано в § 1, п. 4, устойчивость
схемы означает непрерывную зависимость решения разностной
задачи от входных данных (от начальных данных, от правой части и от
краевых условий в данном случае).
Выясним, при каких значениях параметра а схема (3)
устойчива по начальным данным и по правой части. Для этого рассмотрим
задачу (32) с однородными краевыми условиями. Уточним понятие
устойчивости.
Пусть penienne задачи (32) оценивается по норме ||2;||(i)
(например, ||2;||(1) = ||2;||о, ||2;||(1) = ||%1), а правая часть ф — по норме \\ф\\(2)
(например, ||V^||(2) = ||V^||o, ||V^||(2) = llV^lb).
Будем говорить, что схема (32) {или (3) — (4)) устойчива по
начальным данным и по правой части, если при достаточно малых h ^
^ ho и т ^ То имеет место неравенство
тах||^(ж,^)||(1) ^Mi||z(x,0)||(i)+M2max||V^(x,^)||(2), (36)
где Ml, М2 — полоэюителъные постоянные, не зависящие от h и т.
Для устойчивости схемы (32) достаточно, чтобы выполнялось
одно из условий:
1И1(1)^(1 + С1т)||г||(1)+С2г|И|(2) (37)
Z
|^l)^(l+Cir)||i||^l)+C2T||V||^2), (38)
где ci, С2 — положительные постоянные, не зависящие от /г и г.
В самом деле, пусть выполнено условие (37). Запишем его в виде
1кЛ1(1) ^ (1 + Cir) \\z^-%,) + С2Т ||V^||(2), (39)
i = 1, 2,...
Исключая из (39) последовательно ||^"^~"'"||(i), ||^"^~^||(i), ... и
учитывая, что (1 + cit)^ ^ e'^ib при к ^ j, получаем
\\z^\\(i)^e<^'b
||^(Ж, 0)11(1) +С2^ г IIV
А^- иг „(2)
к=1
(40)
Отсюда следует (36) при Mi = e^i^, М2 = С2М1Т. Предполагая, что
выполнено (38), аналогичными рассуждениями приходим к
неравенству вида (40), в котором следует заменить || • || выражениями || • |р. В
результате снова получим (36) с Mi = е2 ^1^, М2 = л/с2ТMi.
Пользуясь тождеством (34) для схемы (32), мы установим
неравенство вида (36), из которого и будет следовать в силу сказанного
выше устойчивость схемы (3).
Чтобы выяснить вопрос об устойчивости по начальным данным,
рассмотрим задачу (32) при -0 = О и положим ||2;||(i) = 11%].

606 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Тождество (34) при ф = О имеет вид
2г [\\ztf + {а- 0,5) г \\z,tf] + \\z,f = \\z,f. (41)
Пусть а ^ 0,5. Тогда выражение в квадратных скобках
неотрицательно и
\\z,f ^ \\z,f, или 1141 ^ 114-1 ^ 1141-
Отсюда в силу начального условия z^ = zo{x) следует, что
1кЛ1(1) ^ 1ко||(1), где ||2;||(1) = 11%]. (42)
Пусть а < 0,5, так что а — 0,5 < 0. Обозначая z^ = v и пользуясь (35),
находим
Wvf + {а- 0,5) г \\v,f ^ Wvf - (0,5 -^)г-^ М' =
l-{0,5-a)T~]\\vf^0
при
1-(0,5-а)г-^^0,
Т. е. при сг^сго = 1/2 — h? /{Ат). При этом условии выражение в
квадратных скобках в (34) неотрицательно и мы снова приходим к (42).
Таким образом, схема (32) (и схема (3)) устойчива по начальным
данным в норме ||^||(i) = ||%1, если выполнено условие
Рассмотрим частные случаи. Если а ^ 1/2, то условие (43) всегда
выполнено и схема (32) устойчива при любых h ж т.
Для явной схемы сг = О и условие (43) дает
г 1 1
т. е. явная схема условно устойчива (устойчива при условии (44),
связывающем г и /г). Можно показать, что при 7^1/2 +cir^,0^a<l,
явная схема неустойчива, т. е. условие 7 < 1/2 + cir*^ является
необходимым для устойчивости явной схемы (ci = const > О — произвольная
постоянная, не зависящая от /г и г).
Из (43) видно, что схема повышенного порядка точности {а = а^ =
= 1/2 — h'^ /{12т)) безусловно (при любых кит) устойчива, так как
сг* ^ ctq.
Перейдем к оценке устойчивости схемы (32) по правой части.
Будем исходить из тождества (34). Имеет место следующая теорема.

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 607
Разностная схема (32) устойчива по начальным данным и по
правой части при
1
так что для решения z задачи (32) верна оценка
114К1ко.1 + ^ fE^IIV-'in ■ (45)
Пользуясь неравенствами (26) и (31), имеем
2r(V^,z,)^cor||zdP + -|IV^lP. (46)
Со
Если а ^ 1/25 то мы получаем из (34) неравенство
2г IkdP + ll%F ^ P.F + сот ||^,|Р + - IIV^IP.
Со
Выбирая затем со = 2, будем иметь
Отсюда сразу следует
к=1
Так как а^ -\- Ь^ ^ {а -\- Ь)^ при а ^ О, b ^ О, то тем самым теорема
доказана.
Замечание. Несколько изменяя рассуждения, можно показать, что
1 1 - S 2
теорема верна при а ^ as = — h , где О < s ^ 1; в (45) следует вместо
2 4т
л/2 написать л/2в- Сравнение с (36) показывает, что ||^||(i) ^ ||^ж], ||'011(2) —
= \т, Ml = 1, М2 = vr/(2£).
Нетрудно получить оценку (36) с ||^||(i) = ||^||, ||'011(2) = IIV'II при сг ^ 1/2.
Ограничимся доказательством устойчивости по начальным данным.
Положим в уравнении (32) -0 = 0, умножим его на 2Tzf^^h и
просуммируем по z = l,2,...,iV — 1. Пользуясь формулой Грина (20) и
тождеством 2t{z^'^\z^) = {z-\-z,z-z) + 2г(сг-0,5) p^lP = \\z\\^ - \\z\\^ +
+ 2r (сг - 0,5) \\ztf, получим \\zf + 2т'^ {a - 0,5) p^-|p + 2r p^''^ = PiP-
Отсюда при a ^ 0,5 следует ||^|| ^ ||i|| и Ц^-^ || ^ ||^o||-
Эта оценка справедлива и при а ^ ао. Однако мы не имеем возможности
останавливаться на доказательстве этого факта.

608 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Мы доказали устойчивость схемы (32) в нормах ||%] и ||2;||,
являющихся разностными аналогами норм ( /^ (ди/дх)'^ dxj и (J^u^ dxj
Пользуясь разностным аналогом принципа максимума, можно
убедиться в том, что чисто неявная схема устойчива в равномерной
метрике, т. е.
Ikllo^lkollo при (7 = 1 (V' = 0). (47)
Оказывается, что для рассматриваемой одномерной параболической
задачи симметричная шеститочечная схема с сг = 0,5 также
равномерно устойчива при любых /гиг:
lkl|o^M||zo||o при (7 = 0,5. (48)
Рассмотрим явную схему (сг = 0). Запишем ее в виде
2/г = (1 - 27) Vi + l iVi-i + Vi+i) + r(fi.
Если 7 ^ 1/2, то \yi\ ^ (1 - 27) \yi\ + 7 {\yi_i \ + |^^+11) + r |(/р^| ^ ||^||o +
+ r \\(f\\oj так как 1 - 27 ^ 0. Отсюда следует ||^||o ^ ||^||o + r \\(f\\o при
7^ 1/2 и
y\\o^\\yo\\o+J2^\\^''\\^^ (49)
где, напомним, ||^||о = niax|^|. Таким образом, явная схема устойчива
^^
в равномерной норме по начальным данным и по правой части, если
выполнено условие 7 ^ 1/2.
5. Сходимость и точность. Будем говорить, что:
1) решение задачи (3) — (4) сходится к решению и = u{x,t) задачи
(1) (схема (3) — (4) сходится) при /г ^ О и г ^ О, если шах \\у^ —
— '^"^11(1) -^ О при /г ^ О и г ^ 0;
2) схема (3) — (4) сходится со скоростью 0(/г^ +г^),ш>0,п>0,
или имеет точность 0{К^ + г^) (порядка ттг по /г и порядка п по г),
если при достаточно малых h ^ ho и т ^ tq
шах |Ь^'-иЛ|п) ^М(/г^ + г^),
где М — const > О не зависит от /г и г.
Характеристикой точности схемы (3) — (4) является ||2;||(i) = ||^ —
— '^/||(1), где II • 11(1) — одна из введенных выше норм. Функция z —
— z{xi,tj-^i) является решением задачи (5). Так как z{x,0) = О, то из
(45) для Z следует оценка

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 609
Учитывая неравенство (28), получаем
ll^^'llo ^ ^^ maxllV^^II =M2max||V^^||. (51)
2 v2 ^^ ^^
Отсюда следует теорема.
Из устойчивости по правой части и аппроксимации схемы (3)
следует ее равномерная сходимость, причем порядок ее точности
совпадает с порядком аппроксимации^\
Иными словами, если схема (3) устойчива по правой части,
т. е. а ^ 1/2, и выполнены условия, при которых схема (3)
имеет максимальный порядок аппроксимации на peniennn и = u{x,t)
(см. (12), (13)), то она имеет точность 0{т^ + /г^), где ш = 2 при
а = 0,5, 771 = 1 при а ф 0,5:
||^^'-и^'||о^М(/г'+г^) при а фа,, (52)
где М — const > О не зависит от /г и г.
Из п. 2 следует, что оценка (52) имеет место, если и G (7^^'^\ Ч^ — f
при а ф 0,5, и е С(^'^), (f = f = Я+'/2 при а = 0,5.
Из неравенства (49) следует, что для явной схемы Ц^-^ — иЦ\о ^
^ М {h^ + г), если и G
Замечание. В силу замечания к теореме в п. 4 схема (3) при а =
= 1/2 - ну{12т) имеет для и G С^^'^), / G С^^'^) точность 0(/г4 + г^),
если (р определяется по формуле (15).
6. Разностные схемы для уравнений с переменными
коэффициентами. Перейдем теперь к изучению разностных схем для
численного решения уравнения теплопроводности (диффузии) с
переменными коэффициентами
где с = с(ж, t), к = к{х, t), q = q{x, t), f = /(ж, t) — заданные функции x
и t. Если, например, коэффициент теплопроводности к = k{x,t,u)
зависит от температуры и, то уравнение (53) называется квазилинейным.
Квазилинейные уравнения допускают аналитические решения
только в исключительных случаях. Развитие вычислительной техники и
применение метода конечных разностей сделали возможным решение
линейных и квазилинейных уравнений с переменными
коэффициентами. При этом выявилась необходимость развивать методы, пригодные
для решения по одним и тем же программам уравнений как с
непрерывными, так и с разрывными коэффициентами.
Задачи с разрывными коэффициентами встречаются очень часто
в физике и технике. Достаточно, например, указать задачи о диффузии
^ См.: Рябенький B.C., Филиппов А. Ф. Об устойчивости
разностных уравнений. М., 1956.
39 А. Н. Тихонов, А. А. Самарский

610 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
нейтронов и о термическом режиме в гетерогенном реакторе,
состоящем из большого числа зон с разными физическими свойствами, задачи
о движении границ фазовых переходов (см. Приложение IV к гл. П1,)
и т. д. Для решения задач с разрывными коэффициентами применяют
схемы «сквозного» счета, не использующие информации о положении
точек разрыва. При этом во всех узлах сетки и для любых
коэффициентов пишутся одни и те же формулы (без какого-либо изменения
формул в окрестности разрывов).
Требования сходимости и точности схем сквозного счета
накладывают ограничения на вид этих схем. Схемы, сходящиеся в случае
разрывных коэффициентов, можно получить при помощи метода
баланса, или интегроинтерполяционного метода.
7. Метод баланса. Консервативные схемы. Физические
процессы, с которыми мы познакомились в курсе, характеризуются
интегральными уравнениями сохранения (количества тепла, количества
движения, энергии и т. д.). Так, например, закон сохранения тепла
(уравнение баланса) на отрезке [xi, Ж2] за время А^ = ^2 — ti имеет вид
c[u{x,t2)-u{x,ti)]dx= [W{xi,t)-W{x2,t)]dt-\- f{x,t)dxdt,
Xl tl Xl ti
где u{x,t) — температура, с — теплоемкость единицы длины, f{x,t) —
uu
плотность источников тепла, W(x,t) = —k(x,t) -^— (x,t) — тепловой
ох
поток {k{x,t) — коэффициент теплопроводности). Если существуют
ди д Л ди\
непрерывные производные -^ и —— ( к -^ 1, то из уравнения баланса
(Jb (J X \ (J X J
следует дифференциальное уравнение теплопроводности
ди д (-, , . ди\
Естественно при написании разностных уравнений, приближенно
описывающих тот или иной процесс, исходить из уравнения баланса.
Пусть дана сетка [xi — ih, tj = jr). Для каждой элементарной
ячейки (прямоугольника) этой сетки пишется уравнение баланса, которое
содержит интегралы от функции и ее производных (потоки в случае
уравнения баланса тепла) вдоль границы ячейки. Для их вычисления
необходимы предположения о профиле функций. В зависимости от
выбора локальной интерполяции как по ж, так и по ^ мы получим
различные схемы. Вопрос о выборе интерполяций подчинен требованиям
устойчивости, точности и простоты реализации (в частности,
требованию минимума арифметических операций, которые надо произвести
для получения решения).
Проиллюстрируем метод баланса (интегроинтерполя-
ционный метод) примерами.

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 611
Сначала рассмотрим стационарное уравнение теплопроводности
-— (к{х)-^\ -q{x)u = -f{x), 0<ж<1, А;>0, ^^0;
(54)
здесь q{x) и — мощность стоков тепла (при ^ ^ О — источников),
пропорциональная температуре и{х).
Выберем на отрезке О ^ ж ^ 1 сетку й^ = {^г = ih, i = О, 1, ..., N}
с HiaroM h. HannnieM уравнение баланса тепла на отрезке x^_i/^ ^ х ^
^ ж^+1/2, ж^_1/2 = {xi-1 + Xi)/2 = Xi-i + /г/2:
^г-1/2-^г+1/2- / Q{x) u{x) dx + f f{x)dx = 0, (55)
г-72 г-72
где 1/Г(ж) = —к{х) du/dx — поток тепла. Чтобы получить схему,
заменим первый интеграл и W разностными выражениями. Возьмем
простейшую аппроксимацию {и = const = Ui при x^_ii^ ^ ж ^ ж^^х/^):
г+72 «+ /2
/ q{x) и{х) dx ^ hdiUi, di = — I q{x)dx. (56)
г-72 «- /2
Проинтегрируем равенство du/dx = — И^//;; на отрезке Xi-i ^ х ^ xf.
Xi
w
Щ-1 -щ= I
^ dx.
к
Xi-l
Так как W входит в (55) в полу целых точках x-^i/^ то, полагая W
= const = W^_i/^ при Xi-i ^ X ^ Xi, будем иметь
Xi-l
ИЛИ
Wi_i/ = -ai ———^— = -aiUx,i, (57)
и
-1
dx
к{х)
Xi-l
(57')
39*

612 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Отметим, что J * dx/k{x) есть тепловое сопротивление отрезка
[xi-i^Xi]. Заменяя интеграл, входящий в (57'), по одной из формул
1 J dx ^ 1 1 J dx ^1 г 1 1 \
получаем а^ = fc_i/o, сц = -, г~ и т. д. Эти коэффициенты отлича-
/2 ki-i + ki
ются друг от друга на величину 0{h?). Подставляя в (55) выражения
(56) и (57) и обозначая искомую функцию ^^, получаем разностную
схему, выражающую закон сохранения тепла на сетке (консервативную
схему):
tti+l {Уг+1 - У г) ai {уг - yi-i)
h h
diyi = -(fi, (58)
где
= - / q{x)dx, ^^ = /^ / /H^^' (^9)
г + 72 г+ /2
1
г-72 г-72
которую можно написать в виде
{0'Ух)х -dy = -(f. (58')
Метод баланса, таким образом, позволяет получать схемы,
коэффициенты которых во всех узлах сетки вычисляются по одним и тем же
формулам как средние значения коэффициентов дифференциального
уравнения в окрестности узла сетки.
Сами схемы (58) пишутся одинаково во всех узлах сетки и для
любых к{х), q{x), f{x). Такие схемы называются однородными. Для
практических целей целесообразно находить коэффициенты схемы а,
б?, ip по более простым формулам, используя значения к, q, f в
отдельных точках. При этом а, с?, (f определяются как средние значения к, q,
f в одной или нескольких точках, т. е.
а{х) = 2_] Cjk{x + Sjh), —1 ^ Sj ^ О, V^ Cj = 1, Cj ^ О,
j=ni j=ni
(60)
и аналогично для с?, ip. Совокупность точек {sjh} называется
коэффициентным шаблоном.
Обычно используют шаблоны из одной или из двух точек, полагая,
например,
ai = к^_у^, di = qi, (pi = /i, (61)

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 613
если к, q, / непрерывны. Если к, q, / разрывны, то в этих формулах
следует брать полусумму предельных значений слева и справа-*^^.
Схема (58) имеет 2-й порядок аппроксимации, если
^1±^ = k, + 0{h\ ^^±i-^ = к' + 0{h\
^ '^ (62)
di = qi + 0{h?), ipi = fi + 0{h?).
В самом деле, погреп1ность аппроксимации для схемы (58) на peniennn
и = и{х) уравнения (54) равна
'фi = {Аи - du-\-(p)i = — [tti+i (ui+i - щ) - ai {щ - Ui-i)] - diUi + (pi.
Подставляя сюда
щ±1 =Ui±hu[ + ^ u'l ± \ u'l' + 0(/г^)
л о
и учитывая, что {{ки')' — qu -\- f)i = О, получаем
Отсюда видно, что -0 = 0(/г^), если выполнены условия (62). Нетрудно
убедиться в том, что коэффициенты а, с?, (/?, написанные вып1е,
удовлетворяют этим условиям.
Таким образом, метод баланса приводит к однородным схемам
2-го порядка аппроксимации. Эти схемы сходятся в классе кусочно-
непрерывных коэффициентов и имеют по крайней мере 1-й порядок
точности (схема (58) с коэффициентами (57'), (59) — 2-й порядок).
Разностные схемы для уравнения (54) можно писать, исходя из
требования 2-го порядка аппроксимации. Однако иногда оказывается,
что схема порядка 0{h^) расходится в классе разрывных
коэффициентов. Примером может служить схема
Vi-i - 2yi + ^i+i ki^i - ki-i yi^i - Vi-i
Ay, = k, + q,y, = -/„ (63)
соответствующая уравнению {ки')' — qu = ки" + k'u' — qu = —/.
Имеется пример^^ (при q = О, / = О, и{0) = 1, и{1) = 0), показывающий,
что решение уравнения (63) при /г —>- О стремится к функции й{х),
не являющейся решением исходной задачи. Если вопрос о сходимо-
^ Тихонов А. П., Самарский А. А. Об однородных разностных
схемах // ЖВМ и МФ. 1961. Т. 1, № 1. С. 5-63.
^ См. там же.

614 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
сти схемы выяснять путем сгущения сеток (что часто делается на
практике), то можно прийти к onin-
■t = tj^i бочному выводу о ее сходимости (она
«сходится», но не к реп1ению
исходной задачи).
-t = tj 8. Двухслойные схемы для
^^Р
^ ^^'^ J ''^ ^^ ^ уравнения теплопроводности с
переменными коэффициентами.
Рис. 86 Обратимся теперь к
нестационарному уравнению теплопроводности (53). Для простоты положим с = 1,
q = 0. HannniCM уравнение баланса для прямоугольника {x^_i/^ ^ х ^
^ ж^+1/2, tj ^t ^ tj^i) (рис. 86):
' + 72
/ [и{х, tj-\-i) ~ '^(^5 tj)] dx
X . 1/
= I [И^(ж,_1/„ t) - WiXi^y^, t)] dt+ J J fix, t) dx dt, (64)
где W = —кди/дх. Возьмем простейшие формулы:
X . . I/
г+72
/ [u{x,tj-^i) — u{x,tj)]dx ^ h[u{xi,tj-^i) — u{xi,tj)], (65)
Ъ+1
I [W{x,^y^,t)-W{x,_y^,t)]dt:
та
г+ /2 *- /2,
+ т{1-а)
г+ /2 *- /2,
(66)
где a — произвольное число. Пользуясь для W^_i/^ формулой (57) и
подставляя (65), (66) в (64), получаем двухслойную консервативную
схему
^J + l _ yJ
)1+^Г
= a{Ay)i^' + {l-a){Ay)i+^i^\ Ку = {ay,),, (67)
^'
j+i
Ь + 1 "^^ + 1/2
hT
dxdt.
(68)
tj =5j_l/2

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 615
где а вычисляется (при фиксированном t) по формулам предыдущего
пункта, так что Аи = -^— к -^— -\-0{h ). Для ю можно пользоваться и
ох \ ох J
другими формулами, эквивалентными (68) с точностью до 0{h? + т^).
Если / — непрерывная функция, то полагаем ^^ = fl '^.
По аналогии с п. 3 убеждаемся в том, что схема (67) имеет
аппроксимацию 0(1? ^ [а — 1/2) г + г^). Если заменить а (Л^)^^ + (1 ~
— а) {Ау)1 выражением
Ai+V2 (^yi+i + (1 - а) yi) = (a^+V2 {ayi+' + (1 - a) yi)),,
TO получим схему того же порядка точности:
у ZJL = Ai+V2 ((^yi+i + (1 - а) у^) + ^р^+\
т
или
yt = A{ay + {l-a)y)+(f. (69)
Так как уравнение баланса может быть написано для любой
области G на плоскости (ж,^), ограниченной кривой Г:
/ {си dx-\-Wdt) = / / /(ж, t) dx dt,
г G
то его можно использовать для получения консервативных разностных
схем в случае тепловых задач с подвижными внутренними и внешними
границами на произвольных неравномерных сетках.
Аналогично можно получить консервативные схемы для
уравнений газодинамики, упругости и т. д. Во всех случаях необходимо у
полученных разностных схем проверять порядок аппроксимации,
устойчивость, сходимость и другие свойства, так как эти качества схемы
не следуют из ее консервативности.
Метод баланса, или интегроинтерполяционный метод (см. ссылку
на с. 613), широко применяется на практике-'^^ Получающиеся при этом
схемы сквозного счета сходятся в классе разрывных коэффициентов.
Рассмотрим теперь первую краевую задачу для уравнения
теплопроводности в области (0^ж^1,0^^^Т):
uu и I ди \
— =Lu + f{x,t), 0<Ж<1, ^>0, ^^= Q^i^Q^)
u{0,t) = fii{t), u{l,t) = fi2{t), u{x,0) = uo{x),
0 < ci ^ k{x^t) ^ C2,
(70)
^ См., например: Самарский A. A., Попов Ю. П. Разностные
методы репЕСния задач газовой динамики. М., 1992; Map чу к Г. И. Численные
методы расчета ядерных реакторов. М., 1958.

616 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
где ci, С2 — постоянные.
Для ее решения на сетке uhr (см. § 1, п. 1) воспользуемся
двухслойной схемой (69), полученной методом баланса:
y-t = k{ay^{l-a)y)^ip, О < ж = г/г < 1, t = jr > О,
y{0,t) =/Ji{t), y{l,t) =/J2{t), teOr,
y{x,0) = uo{x), X e (Jh,
(71)
где Л^ = {a{x,tj_^i/^)yx)x есть оператор 2-го порядка аппроксимации
по h.
Для определения у = yj из (71) получаем краевую задачу
^i+i2/i+i - Ciyi + Aiyi^i = -Fi, 0<i< nA
2/0 =/^1, VN = /J'2, J
где Ai = ar/h^ • ai, Ci = Ai -\- Л^+1 + 1, a F^ выражается через y^.
Оценим погрешность аппроксимации схемы (71). Пусть y{x,t) —
решение задачи (71), а и = u{x,t) — решение исходной задачи (70).
Подставляя в (71) у^ = z^ + и^, получим для разности z = у — и условия
Zt = A{az-\-{l-a)z)-\-ф, zq = zn = О, z{x,0) = 0, (73)
где ф = А {аи -\- {1 — а) й) -\- (р — щ — погрешность аппроксимации для
схемы (71) на решении и = и{х, t) уравнения (70). Учитывая, что Ки =
= Lu + 0(/г2), (^ = /i+V2^ щ = {du/dty+^l^ + 0{т'^), аи + (1 - а) й = (и +
+ (о- - 0,5) ru)^'+V2 + 0{т'^), получаем ф = {сг - 1/2) г (Lu)^'+V2 + 0{т'^ +
+ /г^), если u{x,t) и k{x,t) — достаточно гладкие функции {и G (7^^'^\
А; G С(^'О)).
Отсюда видно, что симметричная схема (а = 0,5) имеет 2-й
порядок аппроксимации по /г и г.
Перейдем к исследованию устойчивости схемы (71) по начальным
данным и по правой части. Так как az -\- {1 — а) z = 0,5 {z -\- z) -\- {а —
— 0,5) TZf, то (73) можно записать в виде
zt - {а - 0,5) rAzt - 0,5 A{z-\- z) =ф, zq = zn = 0. (74)
Будем предполагать, что
z{x,0) = zo{x), (75)
О < ci ^ а ^ С2, |а^| ^ сз, или |а — а| ^ гсз. (76)
Действуя так же, как в п. 3, напишем энергетическое тождество
для задачи (74) — (76), аналогичное тождеству (33):
2т \\ztf - 2г2 {а - 0,5) (Azj, z^) -{A{z + z), z-z)=2t (ф, zj). (77)

Fll(i
§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 617
В силу формулы Грина (19) имеем —{Av^v) = (а,г'|],
-{A{z-\- z),z - z) = {а (% + %), % - %] = (а, 2;|] - (а, i|]. Представляя
затем а в виде а = а -\- {а — а) = а + га^ и пользуясь условием |а^| ^ сз,
будем иметь а ^ (1 + тс^) а, С4 = сз/ci, (а, i|] ^ (1 + С4г) (a,i|].
Подставим эту оценку в (77):
2г [ll^ill' + (^ - V2) т (а, 4-]] + (а, zl] ^ (1 + С4г) (а, zl] + 2т (V, г?).
(78)
Исследуем сначала устойчивость схемы (74) по начальным
данным. Для этого положим в (78) -0 = 0. Покажем, что выражение в
квадратных скобках неотрицательно при сг ^ 0,5 — /г^/(4с2г). При а ^
^ 0,5 это очевидно. Пусть а < 0,5. По аналогии с п. 4 находим
||^||2 - (0,5 -а)т (а, ^?] ^ \\vf - (0,5 - а) с^т \\v-,f ^
^(l-(0,5-a)^)|H|2^0
при 1 — (0,5 — а^ 4с2г/г~^ ^ О (здесь v — zi). Поэтому из (78) следует
I , \ 11 112 1 ^ 4 iiiii2 iiii2 / 2i
1) ^ (1 + С4г)р||(1) ^ (^1 + —j р||(1), где ||z||(i) = (a,Zj],
(79)
РЛ1(1) ^ (1 + 0,5с4г) p^-i(i) ^ (l + Ц-) ||^0||(1) ^ е0-^<^4*, ii^^ii^^,.
(80)
Таким образом доказана следующая теорема.
Разностная схема (71) {или (74)) устойчива по начальным
данным в норме II2; 11(1) = л/{а, 2;|] при
Б этом случае для решения задачи (74) — (76) прг/ ф = О справедлива
оценка
||z^||(i) ^ Ml Poll(i), г<9е Mi=eO'5<^4T_ (§2)
Из (81) следует, что явная схема {а = 0) z^ = Az устойчива при
г ^ /г^/2с2, т. е. шаг по времени для устойчивости явной схемы
должен быть тем меньше, чем больше максимум коэффициента
теплопроводности. Поэтому явные схемы нецелесообразно использовать для
уравнений с переменными коэффициентами.
Докажем теорему.
Для решения разностной задачи (74) — (76) при а ^ 0,5
справедлива оценка
max||2;||(i) ^ Mi ||2;o||(i) + М2 max ||V^||, (83)

618
ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
где
11^11(1) = у(«'^й-
Обратимся к неравенству (78):
2r||z,-|p + (a,z|] ^ (l + C4r)(a,i|] + 2r(V^,z,-) при а^
Подставляя сюда оценку (46), получаем (при со = 2)
(a,z|]^(l + C4r)(a,i|] + ^ii^^'ii2
PeniHB это неравенство (по аналогии с п. 4):
(84)
(85)
koll^D + ^EllV'*
М[ = е"*'^,
приходим к оценке (83).
Если учесть, что (а, 2;|] ^ ci ||%|р ^ 4ci \\z\\^^ то из (83) для
решения задачи (73) получим
(86)
niax||2;||o ^ Mniax
где
М =
8с1 '
|2;||о = тах|2;|.
Тем самым доказана следующая теорема.
Если схема (71) устойчива {при а ^ 0,5) и аппроксимирует
уравнение (70); то она сходится, причем порядок ее точности совпадает
с порядком аппроксимации.
Пусть сетка cD/^ неравномерна, cD^ = {ж^, г = О, 1, ..., iV}, ее niar hi =
= Xi — Xi-i зависит от i. Тогда в (71) вместо А.у следует подставить
выражение (ср. с (15) из § 1, п. 2)
Аш = {аух)хл =
«г+1
f/i+l
yi-1
Ч+1
^i = 2 (^i + ^i+i).
(87)
HorpeniHOCTb аппроксимации для Л может быть представлена в виде
ipi = Ащ - Ьщ = — {rji^i - rji) -h 0{h1 -h /i?+i),
где Г] = 0{hi), т. е. HV'llo = 0{Но), \\'ф\\2 = 0{Но). Однако, как было показано
в п. 2, для IIV'lls верна оценка
V2
7V-1 / i
^ hi I ^П^Фк
i=i \к=1
Схема может быть получена методом баланса.
0(/го), где /го=п1ах/г^.

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 619
Если коэффициент k{xjt) имеет разрыв 1-го рода на линии х = const
(неподвижный разрыв) или х = ^(t) (движущийся разрыв), то схема (71) по-
прежнему сходится, однако порядок ее точности, вообще говоря, понижается.
В случае неподвижного разрыва (при х = const) целесообразно выбирать
сетку так, чтобы точка разрыва х = const была узлом сетки о;/^. Это приводит
к неравномерным сеткам. Однако порядок точности (2-й по h) схемы (71) на
такой сетке сохраняется и в случае разрывного к.
Оценка порядка точности в случае разрывных коэффициентов и
неравномерной сетки значительно усложняется. При этом справедлива оценка
вида (86), однако в правой части (86) вместо Ц-^Ц стоит норма специального
вида IIV'lls? указанная выпес.
До сих пор мы рассматривали краевые условия 1-го рода. Они
удовлетворяются на сетке (Jh точно, и поэтому точность разностной схемы
определяется порядком аппроксимации уравнения. Краевые условия
3-го рода аппроксимируются приближенно. Естественно требовать,
чтобы порядок их аппроксимации совпадал с порядком
аппроксимации дифференциального уравнения.
Приведем разностные краевые условия 3-го рода без вывода-*^^.
Рассмотрим сначала краевую задачу
{ки'У -qu = -f{x), 0<ж<1; к{х) > О, q{x) ^ 0;
к{0) и'{0) = /3iu(0) - /ii; -к{1) и'{1) = P2U{1) - /i2,
где /3i > О, /З2 > 0. Уравнение заменяется схемой (58), а условия при
ж = О, ж = 1 — разностными краевыми условиями 3-го рода
0'1Ух,о = А^/о - Дь -clnVx^n = hvN - Д2, (89)
где ai = а(/г), a^v = а{хм) = а(1), Pi= (ЗхЛ- 0,5 /гд'(О), /^2 = /?2 + 0,5 hq{l),
Д1 = A^i + 0,5/г/(0), Д2 = /^2 + 0,5/г/(1). Эти условия аппроксимируют
условия (88) на решении и = и{х) задачи (88) с порядком 0{h?).
Разрешая (89) относительно ^о и ^tv, получаем другую запись
краевых условий 3-го рода:
Уо = >^1У1 + г/1. Ум = >С2Ум-1 + г/2, (90)
где Ki = ai/(ai + h^i), у^2 = амЦам + h^2), 1^1 = hjj,i/{ai + hPi), г/2 =
= hjji2/{aN + hp2)-
Обратимся теперь к третьей краевой задаче для уравнения
теплопроводности (70). Пусть при ж = О, ж = 1 заданы условия
к—-=/3i{t)u —/Ji{t) при ж = О,
Ои
-к — = l32{t)u -/J2{t) при ж = 1.
(91)
^ См.: Самарский А. А. Однородные разностные схемы для
нелинейных уравнений параболического типа // ЖВМ и МФ. 1962. Т. 2, № 1. С. 25-
56. Условия (89) и (92) могут быть получены методом баланса.

620 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Разностные краевые условия 3-го рода в этом случае имеют вид
ai {сгУх,о -\-{1-(7)ух,о)=0,Ь hyt^Q + pi {ауо + (1 - сг) ^о) - Дь
Д1 =/ii+0,5/i/(0,^),
-CiN {cryx,N + (1 - сг) y^^N) = 0,5 hyt^N + P2 {сгум + (1 - сг) Ум) - Д2,
h =/^2 +0,5/г/(1,^),
(92)
где ai, адг, /3i, /З2, Д1, Д2 берутся в момент t = ^j+0,55 сг — параметр,
входящий в уравнение (71). Они имеют тот же порядок
аппроксимации 0(/г^ -\- {а — 0,5) г + г^) на решении и = u{x^t) (уравнения (70)
с условиями (91)), что и схема (71). Учитывая, что у = у-^ известны
для всех г = О, 1, ..., А/", нетрудно привести (92) к счетному виду (90).
Выражения для xi, Х2, i^i и г/2 не выписываем.
В результате для определения у = у^~^^ получим разностное
уравнение (72) с краевыми условиями (90).
9. Трехслойные схемы. Помимо двухслойных схем, рассмотренных
в п. 8, для численного ренхения уравнения теплопроводности (70)
используются трехслойные схемы, связывающие значения искомой функции у для
трех моментов времени t = ^j+i, ^j, ^j—i (^^ трех слоях) К
Часто применяются трехслойные симметричные схемы
y^^^^J^=A{ay^+' + {l-2a)y^+ay^-') + cp^ i'P^=f), (93)
где Ay = {a{xjtj) ух)х- Они имеют погрепЕность аппроксимации 0{h +т )
при любом а.
Для трехслойной схемы (93) помимо |/(ж,0) необходимо задавать
значение y{XjT) при t = т. Это можно сделать двумя способами: 1) используя
формулу и{х,т) = и{х,0) + т ^- (ж,0) + 0{т ) и уравнение (70), получить
у{х,т) = ио{х) + t[Lu + f]t=o = uo{x) + г [(А;(ж, 0)^0)' + /(ж,0)]; 2)
использовать для определения у(х,т) двухслойную схему 2-го порядка точности:
yt = 0,5 А {у -\- у) -\- ср при t = т. Итак, пусть заданы начальные условия
у{х,0) = ио{х), у{х,т) = йо{х), xeuJh- (94)
Нри ж = О, ж = 1 ставятся краевые условия, например, 1-го рода.
Покажем, что схема (93) устойчива по начальным условиям и по правой
части при
а ^ 1/4. (95)
Для этого рассмотрим однородные граничные условия |/о = О, у^ = 0. Введем
обозначения у = у-^ , у = у-^, у = у'^~ и перепиптем схему (93) в виде
Ау^""^ + (р, у^""^ =(ту+(1-2(т)у + а§. (96)
2т
^ См.: Рихтмайер Р. Д. Разностные методы рептения краевых задач.
М., 1972.

А
СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕНЛОНРОВОДНОСТИ
621
Умножим уравнение (96) т2ту\''\, просуммируем пог = 1, 2, ...,iV — 1и
учтем тождества
{у - у) У^""^ =
= [l{y' + y')+{^-l){y-^']-[l{y' + f)+{^-l){y-yf].
2 (2/^ + ^^) = 4 (2/ + yf + 4 (^ ~ ^)^-
В результате будем иметь
\\у\\1)+2т (а, [у^/^У] = 1|У||(1) +2г (^,2/('^)) ,
где
i) = \\\y + yf+{'^-\)\\y
(97)
(98)
2г (^,y('^)) ^ гсо ||2/(")||2 + ^ Mf, и (у*"^')
11г/11(1) > |11г/-у|| при <т^-.
Пользуясь затем неравенствами
со
и выбирая Со = 8ci, получаем
1Ы1(1) ^ 1Ы1(1) + 8^ 1ИГ-
Отсюда следует оценка
V2
^ 4с1 III/
И||2
1Ч|2
(99)
(^)^ll^^"^ll(^) + 7fcC^''''''''')
при сг ^ - . (100)
Эта оценка позволяет доказать сходимость схемы (93) — (94) со скоростью
0(/г^+г^) присг^ 1/4.
Укажем еще одну трехслойную схему:
^ (у^^' - у^) - ^ {у^ - у^-') = ^у^^' + ^^■+\ ^^^' = Я+\| (^Q^^
Л2/= (а(ж,^^+1)2/ж)^. J
Она безусловно устойчива и имеет точность 0{h + г ). Для определения
у^~^ из (101) получаем задачу (72) с
1 3
которая репЕается методом прогонки (см. п. 10).
^у1 - у1

622 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Для уравнения гиперболического типа
u{0,t)=ui{t), u{l,t)=U2{t),
Lu=-l[k{x,t)^),
ди
и{х,0) =ио{х), -—{х,0)--
(102)
= йо(х) (103)
разностные схемы должны содержать не менее трех слоев.
Симметричные схемы
У'^^-'^У'+У''^ = Л^' {ау^^^ + (1 - 2а) у^ + ау^'^) + /^' (104)
имеют аппроксимацию 0{h + г ) и устойчивы при
о- ^
1 h^
4 4:Т^С2 '
В частности, явная схема (а = 0) условно устойчива при
л/С2
Хотя все устойчивые схемы (104) имеют один и тот же порядок точности,
но на реальных сетках, как показывают численные эксперименты, точность
схемы увеличивается с уменьпЕением а. Поэтому можно рекомендовать
пользоваться безусловно устойчивыми схемами при а = 1/4.
10. Решение систем разностных уравнений. Метод
прогонки. Неявные схемы для уравнения теплопроводности приводят
к системе алгебраических уравнений для значения искомой функции
yj на новом слое t = ^j+i-
Эта система уравнений имеет вид
АгУг-1 - dyi + Biyi^i = -Fi, О < г < TV, (105)
где Fi — заданная функция.
Для уравнения с постоянными коэффициентами
т
Ai = СГ7, Bi = СГ7, Ci = 1 + 2сг7, ^ ^ h2 '
Для уравнения с переменными коэффициентами
Ai = ajai, Bi = ajai^i = Л^+1, d = Ai-\- Ai^i + 1.
В случае неравномерной сетки
crai ^ aai-\-i ^ . ^ _
^^ = ^^' ^^ = ^Т^^' Ci = Ai + Bi + l.
hihi fiihij^i
Краевые условия 1-го и 3-го рода, рассмотренные нами в § 1 и 2,
можно записать в виде
Уо = >^1У1 + г/1. Ум = >С2Ум-1 + г/2. (106)

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 623
При xi = О, Х2 = О отсюда следуют условия 1-го рода ^о = ^i, 2/7V = ^2-
Итак, рассмотрим уравнение (105) с краевыми условиями (106) и
предположим, что
Ai >0, Bi> О, Ci^Ai + Bi, или Ci = Ai^Bi^ А, А ^ 0,1
0^х^<1, а = 1, 2. J
При этих условиях, как будет показано ниже, задача (105) — (106)
разреп1има. Для нахождения ее реп1ения можно применять обычные
методы линейной алгебры. В методе прогонки, или методе фактори-
зации-'^^ учитывается специальный вид матрицы системы уравнений
(105): она трехдиагональна.
Будем искать решение задачи (105) — (106) в виде
Уг = «i+i2/i+i + А+ь г = О, 1, 2, ..., 7V - 1, (108)
где ai VL Pi — неизвестные пока функции. Подставляя yi-i = aiyi -\- Pi в
(105), исключим yi-i и получим {Aiai — Ci) yi + Biyi^i + {Ail3i + Fi) =
= 0, после чего при помощи (108) исключим yi'.
[{AiUi - Ci) «i+i + Bi] yi+^ + [{AiUi - Ci) A+i + {Aipi + Fi)] = 0.
Уравнение (105) будет удовлетворено, если выражения в квадратных
скобках равны нулю. Из этих двух равенств находим рекуррентные
формулы для определения а^+1 и /3i+i:
Bi AiPi -\- Fi • 1 о дг 1
<^i+i = 7^ л ' А+1 = п л ' г = 1, 2, ..., 7V - 1.
Ci — Aiai Ci — Aiai
(109)
Сравнивая формулу уо = aiyi -\- /3i с краевым условием (106) при г = О,
находим
«1 = XI, р1 =1У1. (110)
Решая (109) с начальными условиями (110), найдем а^, /3^, i =
= 1, 2, ..., N. Чтобы пользоваться формулой (108) начиная ci = N — 1,
надо знать у^.
Определим у^ через а^ и /3n из краевого условия (106) при i =
= N. Исключая y^-i из формул ум = >^22/7V-i + г/2, ум-1 = c^nVn + Pn,
находим
Vn = -^ (111)
1 — H2aN
при условии, что 1 — >C2aN ф 0.
' См.: Самарский А. А., Николаев Е. С. Методы решения сеточных
уравнений. М., 1978; Map чу к Г. И. Численные методы расчета ядерных
реакторов. М., 1958; Годунов С. К., Рябенький В. С. Разностные
схемы. Введение в теорию. М., 1977.

624 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Покажем, что из условий (107) следует О ^ а^ < 1 для всех i =
= 1, 2, ..., А^. Из формулы «i+i = Bi/[Bi + Ai{l - щ) + Di] видно,
что О < «i+i < 1, если О ^ «i < 1, и, следовательно, О ^ а^ < 1 для
г = 1, 2, ..., А/", так как ai = xi < 1. Таким образом, 1 — >C20ln > О при
О ^ Х2 < 1 и формула (111) имеет смысл.
Решение задачи (105) — (106) состоит из двух этапов: 1) по
начальным данным (110) и формулам (109) последовательно
определяются ai, затем /3i для г = 1, 2, ..., А/" (счет идет слева направо — от
г к г + 1); 2) из (111) находится у^ и затем по формуле (108)
последовательно (справа налево — от г + 1 к г) определяются ум-1, Ум-2, • • •
..., 2/ь Уо-
Счет по формулам (108) устойчив, так как О ^ а^ < 1.
Отметим также вариант формул прогонки:
А
^i^n W~c—' ^ = 1, 2, •••, ^-1, Ы = >^2] (112)
BiT^i+i + Fi
Ci — Bi^ij^i
1, 2, ..., АГ-1, т = 1^2] (113)
2/i+i=Ci+i2/i + ryi+i, г = 1, 2, ...,АГ-1, ^о = ^1±^. (114)
1 - xi4i
Порядок счета: 1) по формулам (112) и (113) последовательно от
г + 1 к г (справа налево) определяется сначала ^^, затем гц для i = N —
— 1, А/" — 2, ..., 1, 0; 2) по формулам (114) последовательно от г к г + 1
(слева направо) находятся yi, у2, ..., ум-
Нетрудно убедиться в том, что число арифметических действий,
производимых при peniennn задачи (105) — (Юб), пропорционально
числу уравнений.
11. Разностные методы решения квазилинейных
уравнений. При изучении высокотемпературных процессов необходимо
учитывать зависимость коэффициентов теплоемкости и теплопроводности
от температуры. Мощность тепловых источников также может
зависеть от температуры, если, например, тепло выделяется в результате
химической реакции. В результате мы получаем для описания
процесса распространения тепла квазилинейное уравнение теплопроводности
'^'''^ ж = ^ (^'''^ Э + ■^*''^' ^(")>0' Ни)>0. (115)
В общем случае с = с(ж, t,u), к = к{х, t,u), f = /(ж, t,и).
В неоднородной среде кис могут быть разрывными функциями
аргументов х и и (для разных веществ зависимость к, с от
температуры различна). Уравнение вида (115) встречается также при изучении
проникновения магнитного поля в среду, коэффициент магнитной
восприимчивости которой зависит от магнитного поля.

§ 2] СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 625
Уравнение (115) заменой искомой функции приводится к одному
из видов:
ди 9 / , , ди\ ,^^^,
т = Т. Г") di) ' ^'''^
В самом деле, введя, например, функцию v = J^ с{и) du, получим для
нее уравнение (116).
В настоящее время метод конечных разностей позволяет
эффективно найти penienne квазилинейных уравнений.
Рассмотрим простейп1ие двухслойные схемы для уравнения (115).
Они могут быть получены методом баланса по аналогии с п. 7, если
учесть, что W = —к{и) ди/дх.
Для квазилинейных уравнений использование явных схем
нецелесообразно, если к{и) является быстроменяющейся (например,
степенной) функцией, так как условие устойчивости
2 max/;; (и)
требует очень мелкого шага г по времени. Поэтому применяются
неявные схемы — линейные и нелинейные относительно у^^^. В случае
нелинейных схем применяются итерационные методы для нахождения
Рассмотрим некоторые неявные схемы.
а) Неявные схемы с погрешностью аппроксимации 0{h? + г):
J+1
-aiW){yi^'-yi^+f(yi), (118)
n _i
а,+1(2/^+^)(2/|+^-2/Г)
„i+i _ .,i
r ^ h?
где
При ж = О, ж = 1 ставятся краевые условия, например уо = uijVn = U2-
40 А. Н. Тихонов, А. А. Самарский
ady'^') {yt' - yi^l)\ + f{yi+'), (119)
аМ = к { У±±±У1 ) . (120)

626 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Первая схема линейна относительно yj — значения у на новом
слое t = tj-^i. Решение разностной краевой задачи для yj находится
методом прогонки (см. п. 10).
Вторая схема (119) нелинейна относительно yj . Для решения
получающейся системы нелинейных уравнений применяются итера-
ционные методы. Напишем уравнение для определения итераций ^^ в
случае простейп1его итерационного метода:
S S+1 S S+1 S S+1 S
Аг Уг-1- С г У г + Ai+lV i+1 = "Fi, (121)
где
li= ^ ai{y), Ci=Ai +li+i + 1, Fi= yj + rf{yi),
s = 0, 1, 2, ... — номер итерации.
В качестве нулевого приближения обычно берут значение yj с
о 7
предыдущего слоя, полагая ?/^= ^^; иногда применяют экстраполяцию
с использованием yj~ (если yj как функция j монотонна). Решение
уравнений (121) относительно У^ с краевыми условиями при г = О, г =
= N 1-го или 3-го рода находится методом прогонки (см. п. 10). Для
окончания итерации используется условие шах \У1 — У1\ < е или же
задается определенное число итераций. Обычно уже две-три итерации
заметно повышают точность. Итерационные схемы (119) позволяют
для обеспечения заданной точности использовать более крупный шаг
по времени по сравнению с безытерационными схемами (118), что
часто приводит к значительному уменьшению объема вычислительной
работы.
б) Симметричная шеститочечная схема 0(/г^ + т^):
yi^'-yi 1
AJ + 1
где
{ay,)Z + H.)1.J + / У' 2 ) ' ^^^^^
^ (Уг-1 ^УЛ гл " J + 1
ai = к \ 1. Зто нелинейная схема, и для определения ^^
нужны итерации.
В случае слабой квазилинейности, когда к не зависит от и, а
правая часть f{u) нелинейна, можно строить безытерационные схемы 2-го
порядка аппроксимации.
Напишем такую схему (при к = const = 1):
У—^ =Ку + fiy^), У'^' ~ У' = 0,5 Л (у^+1 + у^) + fiy),
0'5г г (123)
Лг/ = у XX,

А
СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕНЛОНРОВОДНОСТИ
627
где у — промежуточное значение. Сначала применяется с niaroM 0,5 г
и правой частью f{y^) чисто неявная схема, затем с niaroM г и
правой частью f{y) — симметричная п1еститочечная схема. В результате
получается схема 2-го порядка аппроксимации по /г и г.
Иногда для решения квазилинейных уравнений используются
симметричные трехслойные схемы (93); в этом случае к{и) и f{u) берутся
на шаге j. Однако предпочтения заслуживает нелинейная схема,
аналогичная схеме (101).
Пример. Приведем результаты численных расчетов по схеме
Ои
(119) для случая к{и) = xqu^, xq > О, сг > О, / = 0. Уравнение -^ =
д
ди
dt
_ . xqu 7^ имеет решения, производные которых в точках,
ох \ ох J
где U = О, разрывны, а поток kqu -^— непрерывен, т. е. существует
ох
фронт температуры, который распространяется с конечной скоростью
(рис. 87).
Примером такого решения является функция
1/а
u{x,t)
\[acKQ ^{ct — x)] , X ^ ct
о,
X ^ ct,
где с — скорость температурной волны. Эта функция является
решением задачи
ди
д_
дх
ж > О,
"^" д^
t>0,
и{х,0) = 0, u{0,t) =uo^^/^,
где 1,0
Uo
1/а
Рис. 87
1 — t = одо
2—t = 0Д2
3—t = 0Д6
4 — t = 0,20
Для этого примера по схеме
(119) были проведены
расчеты с параметрами сг = 2, xq =0,5, с = 5, /г = 0,2 (число точек N = 50)
и шагом г = 2 • 10~^. Точное решение и результаты расчета
нанесены на рис. 87. Всюду, кроме нескольких ближайших к фронту узлов,
отклонение сосчитанного решения от точного не превосходит 0,02. Чи-
40*

628 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
ело итераций г/ ^ 3 {s = 10~^). Сплошная линия на рие. 87 — точное
решение, кружки — расчетные точки-*^^.
Отметим, что схема (122) не удовлетворяет принципу
максимума (немонотонна) и поэтому при расчете температурной волны дает
худп1ие результаты по сравнению с монотонной схемой (119).
§ 3. Метод конечных разностей
для решения задачи Дирихле
1. Разностная аппроксимация оператора Лапласа. Пусть
на плоскости (ж1,Ж2) задана область G, ограниченная замкнутой
кривой Г. Рассмотрим задачу Дирихле (см. гл. IV)
"и д и
дх\ дх\
Аи= ^-^-\-—^ =-f{x) в G, и|г =/^(ж1,Ж2). (1)
Для решения задачи (1) методом конечных разностей надо в
области G + Г ввести сетку и аппроксимировать на этой сетке уравнение
и краевое условие.
Начнем с аппроксимации оператора Лапласа. Заменим вторые
производные д^и/дх^, д'^и/дх^ разностными выражениями:
д'^и u{xi + hi,X2) - 2u{xi,X2) -\-u{xi - /11,^2) _ _ .
dxl hi
д'^и u{xi, Ж2 + /^2) - 2и(ж1, Ж2) + u{xi, Ж2 -h2)
дх\ Щ
= Ux2X2 = ^2U,
где ha — шаг по Xq,, а = 1, 2.
Оператор Лапласа Аи заменим разностным оператором
который определен на пятиточечном шаблоне («крест»), состоящем из
точек (Ж1,Ж2), {Xi - /11,^2), {Xi + /11,^2), (Ж1,Ж2 - /i2), (Ж1,Ж2 +/^2). Он
изображен на рис. 88, а. Вычислим погрешность аппроксимации для
оператора Л. Так как (см. § 1, п. 2)
д'^и hi. д^и ^,,4ч . ^
«....= ^ + ^^ + 0(/.^J, « = 1,2,
ТО
Au-Au=^Llu+^Llu + 0{h\ + ht), Ьа = ^,
^ См.: Самарский А. А., Соболь И. М. Примеры численного расчета
температурных волн // ЖВМ и МФ. 1963. Т. 3, № 4. С. 702-719.

§ 3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ ЗАДАЧИ ДИРИХЛЕ 629
и, следовательно,
Kv - ^v = 0{\h\^),
где V — любая функция, имеющая не менее четырех производных по
5Х-
2
h2
-XI 5*
2
-¥-
h2
Щ1
2
¥
h2
5Х-
hi-
О hi
h2
-Kl
5)$_Ч Kl
X
4
Рис. 88
xi VL Х2 {v е C^^\ ш ^ 4). Таким образом, оператор Л аппроксимирует
оператор Лапласа со 2-м порядком.
Нетрудно убедиться в том, что оператор
A'^ = A^+M±MaiA2,;, (3)
определенный на девятиточечном nia6лоне («ящик») (рис. 88, б), имеет
на peniennn и = и{х) уравнения Аи = О 4-й порядок аппроксимации
{А'и - Аи = 0{\h\^) при и G С(^\ ш ^ 6) и б-й порядок {А'и - Аи =
= 0(|/г|^) при и е С^'^\ ш ^ 8) на квадратной сетке, т. е. при hi =
= h2 = h.
HannniCM подробнее выражение для Л в случае hi = h2 = h (на
квадратной сетке):
д _ _ У1+У2+УЗ+У4- 4^0
^^У — Ух1Х1 + Ух2Х2 ~ 7 2
Разреп1ая уравнение Л^ = О относительно уо, получим
Уо = ^ {У1 +У2+УЗ+ У4)

630
ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Значение у в центре шаблона есть среднее арифметическое
значений в остальных узлах шаблона.
Эта формула является
разностным аналогом формулы
среднего значения для гармонической
функции.
Уравнение Пуассона Аи =
= —f{xi,X2) заменяется схемой
i ^^-^т "^^ г
1 jyy 4 ж ^t
1—"f^ т т т 1^
^—т т т т т
т т т т т т
т^^ т т Т т 7"
■J —>it зк о ж м
Ау = -(р{х),
(f{x) = (f{xi,X2) = f{xi,X2)
(4)
Граничные узлы, а:: G 7/г
Нерегулярные узлы, х £ си'^
о
Регулярные узлы, х G (^н
Рис. 89
Перейдем теперь к
построению разностного аналога
задачи Дирихле (1) в области G +
+ Г. Проведем два семейства
параллельных прямых xi = iihi,
Х2 = ^2/^2, П, ^2 = о, =Ы, ...
(будем считать, что начало
координат (0,0) лежит внутри G).
Точки (u/ii,i2/i2) назовем узлами. Узлы х = (и/11,^2/12) и ж' = (г^/11,^2/12)
назовем соседними, если они лежат на прямой, параллельной либо оси
xi, либо оси Х2 И отстоят друг от друга на расстояние шага {hi или
/i2), так что \i[ — ill + 1^2 — ^2! = 1. Узел х = (и/11,^2/12) называется
регулярным, если его соседние узлы {{ii =Ь 1) /11,^2/^2), (u^i, (^2 =Ь 1) /^2),
образующие пятиточечный шаблон «крест», находятся либо внутри
области G, либо на ее границе. Если хотя
бы один из этих четырех соседних узлов
не принадлежит G + Г, то узел х = х* на-
о
зовем нерегулярным. Обозначим со^
множество всех регулярных узлов, о;^ —
множество всех нерегулярных узлов. Точки
пересечения прямых xi = iihi, Х2 = ^2^2
с границей Г назовем граничными
узлами. Множество всех граничных узлов
назовем границей сетки и обозначим 7/г-
Таким образом, области G + Г ставится в
соответствие сетка a;/i(G + r), т. е. множе-
- - ° *
ство точек X е (jJhj где а;/^ = а;/^ + о;^ + 7/г
(рис. 89).
Будем предполагать, что сетка
обладает свойством связности, т. е. любые два
внутренних узла можно соединить ломаной, целиком лежащей внутри
G и состоящей из звеньев, соединяющих узлы сетки и параллельных
либо Oxi, либо 0x2.
• Граничные узлы, а:: G 7/г
X Нерегулярные узлы, х £ си
о
о Регулярные узлы, х G (^н
Рис. 90

3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ ЗАДАЧИ ДИРИХЛЕ 631
В регулярных узлах пишем разностное уравнение (4), используя
пятиточечный п1аблон «крест» с П1агами hi и /12-
В граничных узлах ж G 7/г задаем значение искомой функции
ф),
X е 7/1-
(5)
В нерегулярных узлах могут быть написаны различные условия.
1. Интерполяция нулевого порядка. Значение у{х) L* полагается
h
равным /i(x) в ближайшем узле х границы "у^:
у{х) = ii{x) при X G о;^. (6)
2. Интерполяция 1-го порядка. Значение у{х) |^* определяется при
помощи линейной интерполяции. Например, для случая,
изображенного на рис. 90, значение у^ в узле О определяется по формуле
1 1 \ 1 1
hi hi- 1 hi hi-
(7)
которую можно записать в виде
^1У = О,
где Ai^ = Ух1Х1 — аппроксимация оператора Liu = d'^u/dxl на
неравномерной сетке (см. § 1, п. 2).
Муо ■■
^2У0 ■
У2 - УО УО - У4:
^^2 +
Ау = А1У + А2У, %! =0,5(/ii_ + /ii), %2 = 0,5 (/^2+ +/^2),
hi- =~03, /i2+ = '02
Рис. 91
3 Интерполяция 2-го порядка. В узле ж G о;^ пишется пятиточечная
схема на нерегулярном шаблоне (на неравномерной сетке)
Л*?/ = Ух1Х1 + Ух2Х2 = -^^
(8)
Нерегулярный шаблон изображен на рис. 91, а и 88, е. Узел 3 является
граничным, 1, 2, 4 — внутренними. Пусть hi- — расстояние между
узлами Зи 0. Тогда Aiy =
У1 -Уо Уо- Уз
hi \ hi
hi-
УХ1Х1 5 1^1
hi + hi-

Ai?/ =
Л22/ =
1
1
h~2
fyi -Уо
(У2 -Уо
2/0 -Уз
hi-
Уо -У4
h2
632 ДОПОЛНЕНИЕ 1. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
(см. § 1, п. 2), А2У = -^{у2- 2^0 + У4) = Ух2Х2, ^У = ^1^ + Лз^. Вто-
рой случай изображен на рис. 91, б и 88, г. Узлы ^ и .^ находятся на
границе, /^2+ — расстояние между узлами ^ и ^. В этом случае
Ух1Х1
• Ух2Х2^
где Ti2 = 0,5 (/i2 + ^2+)- Мы будем рассматривать 3-й способ задания
условий на о;^. Как будет показано ниже, он является наиболее точным.
Сформулируем теперь разностную краевую задачу,
соответствующую задаче (1):
Л^+ (/:? = О, хе^н, (9)
Л*^+ (/:? = О, xeujl, (10)
у = 11, xejh- (11)
Возникают два вопроса: 1) о разрешимости задачи, т. е. о
существовании решения системы алгебраических уравнений (9) — (И); 2) о
сходимости и точности схемы (9) — (И)- Ответы на эти вопросы мы
получим ниже при помощи принципа максимума.
Чтобы оценить погрешность, с которой мы определяем решение
задачи (1) из уравнений (9) — (И)? нужно оценить разность у{х) —
— и{х) = z{x)^ где у{х) — решение задачи (9) — (11), и{х) — решение
задачи (1), взятое в узлах сетки й^. Подставляя у = z -\-иъ (9) — (И),
получим
h.z = —-0, ф = Ли + (/?, ж G Ci;/^, I
A*z = -V^*, V^*=A*u + (/?, xeujlA (12)
^ = О, ж G 7/г. J
Из вышесказанного следует, что "ф = Ки-\- ^р = 0(|/гр), если (f = f[x),
ф* = 0(|/г|) для условия (8), ф* = 0(1) для условия (7). Чтобы
оценить решение задачи (9) — (11) через правую часть, нам понадобится
принцип максимума.
2. Принцип максимума. Рассмотрим задачу (9) — (И)-
Разрешим уравнение (9) относительно уо (см. рис. 88, а):
2 ( )^ + )^] ^0 = )^ (^1 + ^з) + ^ {У2 + У4) + V^O, X е UJh. (13)

§ 3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ ЗАДАЧИ ДИРИХЛЕ 633
Пусть О — нерегулярный узел (см. рис. 88, в). Тогда из уравнения
Л*^ + (/? = О следует
1 fyi-yo Уо-Уз\ , 1 (У2-уо Уо-уЛ
+ 7- ^ Z = -V^o,
hi \ hi hi- J h2 \ h2 h
где фо = ^0 -\- -r—r— l^{3)^ hi- — расстояние между узлом О и гранич-
nihi —
ным узлом 3^ hi = 0,5 {hi- -\-hi). Из (13) и (14) видно, что обе формулы
могут быть записаны в виде А{х)у{х) = Х^^^шЧж) ^{^Л)у{С) + F{x)
о .
ДЛЯ всех X ^ LUh = ^h -^ ^h, где суммирование проводится по всем
узлам шаблона с центром в узле ж, исключая сам узел х. Коэффициенты
А{х) и В{х^^) удовлетворяют условиям А{х) > О, В{х^^) > О,
У^ В{х,^)=А{х) при xeujh.
Если yljf^ =0, то по крайней мере один из коэффициентов В{х,^)
в пограничной зоне lj^ можно формально положить равным нулю,
так что Х^е5(ж,^) = А{х) — D{x), D{x) > 0. Если, например, узел 3
(см. рис. 91, а) находится на 7/г, то D{x) = D{0) = ——— ^ —^, так как
hihi— h-^
hi = 0,5 {hi- + hi) ^ hi. Если же два узла 2 vl 3 (см. рис. 91, б)
являются граничными, то D{x) = D{0) ^ l/hj + l/hj, Б(0, 2) = Б(0,3) = 0.
Таким образом, при ^ |^^ = О в о;^ всегда выполнено условие
D{x) ^ —, где /г = max(/z,i,/z,2). (15)
Итак, рассмотрим задачу: требуется найти функцию у{х),
определенную на a;/i = a;/i + 7/г и удовлетворяющую в со^ уравнению
А{х)у{х)= Y1 B{x,Oy{0+F{x), xeujh,
А{х)>0, В{х,О>0, Y1 В{х,О^А{х).
(16)
Справедлива следующая теорема (принцип максимума).
Если F{x) ^ О всюду в coh, шо решение задачи (16) {не равное
постоянной) не моэюет принимать наибольшего полоэюительного
значения во внутренних узлах сетки coh- Если эюе у{х) ^ const и F{x) ^ О

634 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
6 (jJhj fno у{х) не моэюет принимать внутри uoh наименьшего
отрицательного значения.
Доказательство. Пусть F{x) ^ О во всех внутренних узлах.
Допустим, что у{х) принимает положительное максимальное значение
в некотором внутреннем узле. Так как у{х) ^ const, то существует
такая точка х G cuhj в которой у{х) = тах^(ж) = Mq > О, а в соседнем
узле ^ G Ш'{х) имеем у{^) < Mq. Уравнение (16) в узле х перепип1ем в
виде
A{x)-Y,B{x,0
у{х) + Y,B{x,0 {У{х) - у{0) = F{x). (17)
Так как Е^ В{х, О {у{^) " У{0) ^ В{х, О {у{^) " У{0) > О, то из (17)
и (16) следует F{x) > О, что противоречит условию F{x) ^ 0. Первая
часть теоремы доказана.
Вторая часть доказывается аналогично.
Следствие 1. Если F{x) ^ О, ж G а;/^ и ^ |^^ ^0, то решение
задачи (16) неотрицательно: у{х) ^0 всюду в а;/^. В самом деле, пусть
хотя бы в одном узле х G coh функция у{х) отрицательна; тогда она
должна принимать отрицательное наименьшее значение во
внутреннем узле. Это невозможно в силу принципа максимума (если только
у{х) ^ const).
Следствие 2. Если F{x) ^ О, ж G а;/^ и ^ |^^ ^0, то у{х) ^0 для
всех X G LOh-
Следствие 3. Однородное уравнение
А{х)у{х)= Y1 В(^^Оу{0 (18)
при однородном граничном условии yljf^ =0 имеет только тривиальное
решение.
В самом деле, при F = О следствия 1 и 2 дают соответственно
у{х) ^ о, у{х) ^ О, т. е. у{х) = 0.
Таким образом, разностная задача (16) имеет единственное
решение.
Следствие 4. Для решения однородного уравнения (18) верна
оценка
\\у\\о ^ \\у\\о,^, (19)
где ll^llo = max |^(ж)|, ||^||о ^ = max \у{х)\ (решение уравнения (18) при-
нимает наибольшее и наименьшее значения на границе 7/г)-
Имеет место следующая теорема сравнения.

3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ ЗАДАЧИ ДИРИХЛЕ 635
Пусть у{х) — решение уравнения (16), а у{х) — решение того же
уравнения с правой частью F{x) ^ О и граничным значением у \^^ ^
^ 0. Если выполнены условия \F{x)\ ^ F{x) при х G coh, \у{х)\ ^ у{х)
при X е jhj fno \у{х)\ ^ у{х) для всех х G ион-
Следствие 1 сразу дает у{х) ^0 всюду в й^. Функции и = у -\-y,v =
= у — у удовлетворяют уравнению (16) с правыми частями Fu = F -\- F,
Fy = F — F и граничными значениями u = y-\-y\^,v = y — у\^. Так как
по условию Fu ^ о, u\j ^ о VL Fy ^ о, v\j ^ о, то в силу следствия 1
и ^ О или у ^ —у, V ^ О или у ^ у, т. е. \у\ ^ у при х G coh-
3. Оценка решения неоднородного уравнения. Рассмотрим
неоднородное уравнение
A{x)y{x)=Y,B{x,OyiO+F{^):
с однородным граничным условием
2/17 = 0-
Пусть выполнены условия
В{х,О>0^ Y,B{x^)=A{x)-D{x),
X G oJh,
(20)
D{x) ^ (5 > О (21)
для всех X ^ (Jh-
Тогда для решения задачи (20), (21) верна оценка
||л.<И=.
(22)
В силу теоремы сравнения \у\ ^ у, где у — решение задачи (20) с
правой частью F = |F|. Пусть у{х) принимает наибольшее значение в
узле X. Так как у{х) > О, то
А{х)у{х) = Y,B{x,Oy{0 + \F{x)\ ^ {А{х) - D{x))y{x) + \F{x)l
У{х) ^
\F{x)\
D{x)
<
niax \ф\).
Учитывая, что ||^||о ^ у{х) и D ^ S, получаем (22). Заметим, что
фактически нами получена оценка
Fix)
1Ы1о^
Dix)
Предположим, что
D{x) ^S>0 при X ecol, D{x) ^ О
F{x) =0 при ж G uoh, F{x) = F*
при
при
X е ujh,
X euot.
(23)
(24)

636 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Тогда для решения задачи (20), (23), (24) верна оценка
ll2/||o^i||F*||o. (25)
В самом деле, у{х) ^ О в силу принципа максимума и не может
иметь наибольп1его значения в узлах х G UJ^, в которых F{x) = 0.
Предполагая, что ж G о;^ есть точка, в которой достигается максимум,
получим оценку (25).
Наибольшие трудности при оценке решения задачи (21)
возникают в случае D{x) = 0 при х ^ coh- Тогда строится мажорантная
функция у{х) ^ \\у\\о, удовлетворяющая уравнению (20) с правой частью
F{x) ^ \F{x)\.
Итак, если выполнено условие D{x) ^ (5 > О, ж G а;/^, то для
решения задачи (20) — (21) верна оценка
IFI
о
11^11о^||?/||ол + ^, (26)
выражающая непрерывную зависимость решения от граничных
данных и от правой части.
4. Сходимость решения разностной задачи Дирихле.
Чтобы установить сходимость и порядок точности схемы (9) — (И), мы
должны оценить решение задачи (12).
Погрешность аппроксимации в регулярных узлах ф = {Аи -\- (р) —
— {Ьи + /) = 0(|/гр), если и G С^^^, и в нерегулярных узлах ф = ф* =
= 0{\h\).
Так как ||'0*||о = 0(|/г|), то для оценки z следует рассмотреть
отдельно вклад в Z погрешности аппроксимации в нерегулярных узлах.
о о
Представим z в виде суммы z = z -\- z*, где z и z* — решения задач
Az = -l хеип. ^1,, =0, V^=|^' ''^''1:^ (27)
[О, xeuj^]
\ф, X e о;*.
Так как z \^^ = О, то D{x) ^ 1/h^ = S > О при ж G о;^ и D{x) ^ О при
X G uJh-
Пользуясь (25), получаем
1к*||о^/г'||^*||о. (29)
О
Для оценки Z воспользуемся теоремой сравнения. Построим
мажорантную функцию
и{х) = K{R^ - г^), г^ = ж? + xj,

§ 3] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ ЗАДАЧИ ДИРИХЛЕ 637
где R — радиус круга с центром в точке (0,0) G G, содержащего
область G, К = const > 0. Вычислим разностные производные
-'^l' — V' Jxixi — X.'^lJxiXi — 7 2 — '
А2Г^ = 2 при X ^ (jJh- в нерегулярных узлах также имеем Air^ = 2.
Таким образом,
AU = -КЛг^ = -4:К при X eujh =^h+(^h-
о
Выберем К так, чтобы Ц^^Цо ^ 4Х. Для этого достаточно положить
К = ||V^||o/4. Учитывая, что [/ ^ О при х е jh, U ^ KR^ = i^^ ||^||о/4,
и пользуясь теоремой сравнения, находим
\\1\\^^\\иь^\к'Ш (30)
Объединяя неравенства (29) и (30) и учитывая, что ||^||о^||^||о + 1к*||о5
получаем
ll^llo^ft'llV'llo + J^'llV'llo. (31)
Тем самым доказана следующая теорема.
Для решения задачи (12) имеет место оценка (31).
Из (31) видно, что если и G С^^^((5), т. е. решение задачи имеет
непрерывные в замкнутой области G = G + Г вторые производные, так
о
что IIV'llo = p{\h\), ||V'*llo = p{\h\), где p{\h\) -^ 0 при \h\ ->• 0, то схема
(9) — (11) сходится:
\\А\о = \\у-и\\о = р{\Ц)- (32)
ТО справедливы оценки
o^T^I^^P, IIV^IIo ^ хМз/г, где М, = та_х
1-^ о a,G
д^и
дх'
(33)
(а = 1, 2, S = 3, 4). Применяя неравенство (31), видим, что для
решения задачи (12) верна оценка
Т. е. схема (9) — (11) равномерно сходится со скоростью 0(|/гр) (имеет
2-й порядок точности).
Заметим, что если у на о;^ задавать при помощи линейной
интерполяции (см. (7)), то -0* = 0(1) и оценка (31) дает
\\y-u\\, = 0{\h\'), (34)

638 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
т. е. и в этом случае схема (9) имеет 2-й порядок точности.
Для определения реп1ения разностной задачи Дирихле (9) — (11)
мы получаем систему линейных алгебраических уравнений больпюго
порядка, равного числу внутренних узлов сетки. При точном
решении этой системы известными методами линейной алгебры требуется
большое число арифметических действий и большой объем
оперативной памяти машины. Поэтому систему уравнений решают
итерационными методами, учитывающими специальный вид матрицы
системы. Ниже (в § 5) излагаются итерационные методы решения сеточных
уравнений.
§ 4. Разностные методы решения задач
с несколькими пространственными переменными
1. Многомерные схемы. В § 2 мы рассматривали разностные
схемы для решения задачи Дирихле в случае двух измерений (ж1,Ж2).
При написании разностных схем для уравнения теплопроводности
первым шагом является аппроксимация оператора Лапласа. Пусть
Л^ = Ai^ + К2У, АаУ = УхаХа ^ « = 1, 2, (2)
— пятиточечный оператор на coh с шагами hi и /12-
Как в § 2, п. 2, двухслойные схемы для (1) возьмем в виде
У- ^^ = л {ау^+' + {1-а) yi) + ^, (3)
Г
У^""^ = Vhk = yi'^ihi,i2h2,tj^i).
Пусть G — область на плоскости (xi, Ж2), ограниченная кривой Г.
Введем в (5 = G + Г сетку Со^, описанную в § 3. Будем рассматривать
задачу
— = Au + f{x,t), xeG, 0<t^T
и(ж,0) = ио(ж), и\г = fi{x,t).
Ей поставим в соответствие разностную схему (3) с краевыми
условиями
yUh =/^' У{х,0) =uo{x). (5)
По аналогии с § 2 устанавливается, что схема (3) устойчива при
1 h^ , , , ,ч
(^ ^ 7^ — -^ (если hi = П2 = h).
2 от

§ 4] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ 639
Отсюда следует, что явная схема {а = 0)
^ ^^ = Ау^ + ip^+'^, или у^+1 =у^ +т (Ау^ + ip>+'^), (6)
Г
условно устойчива при г ^ /г /4 (в одномерном случае при г ^ /^^/2,
см. § 2). Неявные схемы безусловно устойчивы при а ^ 1/2. В случае
трех измерений, когда х = (ж1,Ж2,жз), в (3) нужно подставить
Л^ = Ai^ + К2У + Лз^, Ку = Ухссхсс ^ а = 1, 2, 3.
Условие устойчивости имеет вид
1 /г^
^ ^ о ~ ТТГ (пР^ hi= h2 = Нз = h).
Z iZt
Явная схема {а = 0) устойчива при г ^ /г^/б. Порядок аппроксимации
ф = (Ли + (/? — и^) — {Lu + / — du/dty^ /2 зависит от сг: -0 = 0(|/гр +
+ г^) при а = 0,5, ф = 0{\h\^ + г) при а ф 0,5 (|/гр = ELi ^L Р = 2, 3)
для любого числа измерений.
Краевые условия на 7/г ставятся так же, как и в § 3 для задачи
Дирихле. В нерегулярных узлах о;^ оператор Л (Л ~ А) пишется на
неравномерной сетке. Для схемы с опережением (сг = 1) справедлив
принцип максимума. Она равномерно сходится со скоростью 0(|/гр +
+ г).
Не составляет труда написание (по аналогии с § 2 и 3) схем
повышенного порядка 0(|/г|^ + '^^) аппроксимации; например, при р = 2
{х — (ж1,Ж2)) схема 0(|/г|^ +'^^) имеет вид
У1 = Ai {аху + (1 - Ох) у) + Л2 {а2У + (1 - 02) у) (/ = 0),
1 h^
^OL — -^ — 77^ ' а = 1, 2 {G — прямоугольник).
2 12г
В случае уравнений с переменными коэффициентами для
получения схем можно воспользоваться методом баланса на сетке uj^. Пусть,
например, дано уравнение теплопроводности
ди '
Lu + f[x,i), ж = (ж1, ..., Жр), L = Li + L2 + ... + Lp,
dt
д (^ , . ди . ^ ^
LaU = -— I ка{х, t) -— ) , а = 1, 2, ..., р.
} (7)
Пустьр = 2. Возьмем объем ((ii — 1/2) hi ^ xi ^ {ii + 1/2) /ii, (^2 —
— 1/2) h2 ^ Х2 ^ (^2 + 1/2) h2, tj ^t^ tj+i) и напишем для него
уравнение баланса тепла
9

640 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Ь+1 Ь+1
/ hwi dx2 + W2 dxi) + f{x,t)dxidx2,
где д = ((п - 1/2) h ^ xi ^ (п + 1/2) /ii, (гз - 1/2) h2 ^ Х2 ^ (^2 +
+ 1/2) /12) — прямоугольник, с — его граница, Wa = —ка ди/дха —
тепловой поток по направлению оси Ох а • Заменяя интегралы и потоки
разностными выражениями, так же как в § 2, п. 8, приходим к схеме
вида
у ZA. = л (ii+V2) ((^yi+1 + (1 - а) yJ) + (^^+1, (8)
Г
или
^ ^ = а {АуУ+^ + {1-<т) {АуУ + ^^■+', (9)
Г
где
Л = Ai + А2, АаУ = {aaVxJ^^ , (10)
т. е. Aq, есть аналог разностного оператора А^ = {аух)х,
аппроксимирующего Lu = {ки')' (см. § 2, п. 7). Коэффициент аа определяется из
выражений вида (61) из § 2, например
^2 = {a2)ii,i2 = ^2 f П/^Ь f ^2 - 2 ) ^2,Л И Т. Д.
Для (/? = (/?-^ + -'- можно взять формулу (/?-^ + -'- = /(ii/ii, ^2/12,^7 + 1/2)•
Если коэффициенты /iJq, имеют разрывы при х^ = const, а = 1, 2, то
простейшее выражение для а^ запишется в виде
0^1 = т [^1 {hhi - О, i2h2 - О, ^) + ki {iihi - О, ^2/^2 + О, ^) +
+ A;i (n/ii + О, i2h2 + О, ^) + ki {hhi + О, ^2/^2 - О, t)]
и аналогично для а2.
Для полученных схем (8) справедливы результаты § 2, п. 8.
2. Экономичные схемы. При решении методом сеток
многомерных уравнений большое значение имеет объем вычислительной
работы, т. е. число арифметических действий для решения задачи
с требуемой точностью. Посмотрим с этой точки зрения на схемы,
полученные в предыдущем пункте.
Пусть G — квадрат (О ^ xi ^ 1, О ^ Ж2 ^ 1), ujh = {{iih,i2h), ii,
^2 = О, 1, ..., N} — сетка с шагом h. Она имеет {N — 1)^ = 0{l/h^)
внутренних узлов. Рассмотрим явную схему (6) и неявную схему (3)

§ 4] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ 641
при сг = 1. Обе схемы имеют один и тот же порядок точности. Число Q
действий для определения у^^^ во всех узлах uoh на новом слое t = ^j+i
по схеме (6) пропорционально числу {N — 1)^ узлов сетки а;/^, т. е.
В случае неявной схемы (3) при сг = 1 для определения у^^^ нужно
реп1ить систему {N — 1)^ уравнений. Для этого требуется значительно
больп1е вычислительной работы, чем для явной схемы.
С другой стороны, неявная схема (сг = 1) устойчива при любых г
и /г, а явная схема устойчива лишь при г ^ /г^/4.
Возникает вопрос: нельзя ли найти такие схемы, которые
сочетали бы лучшие качества явной (объем работы Q = 0{l/h?)) и неявной
(безусловная устойчивость) схем?
Такие схемы называют экономичными.
Было предложено много экономичных схем для различных задач
математической физики-'^л Экономичные схемы позволили найти
численное решение ряда сложнейших задач физики и техники, в
отношении которых еще несколько лет назад были сомнения в возможности их
приближенного решения даже с использованием самых совершенных
быстродействующих вычислительных машин.
В случае одного пространственного переменного неявные схемы
приводят, как мы видели в § 2, к системе уравнений (105), которые
решаются методом прогонки. При этом для нахождения у^^^ требуется
0{l/h) операций. Рассмотрим сетку й^ с шагом h = 1/N в квадрате
G (О ^ Ж1 ^ 1, О ^ Ж2 ^ 1). Сетку можно представить как
совокупность узлов, расположенных на «строках» ^2 = О, 1, 2, ..., А/", или как
совокупность узлов, расположенных на «столбцах» ii =0, 1, 2, ..., N.
Всего имеется {N + 1) строк и {N + 1) столбцов. Число узлов в каждой
строке (столбце) равно N -\-1.
Если на каждой строке (столбце) решать задачу вида (105) из § 2
методом прогонки при фиксированном 12 (и), то для нахождения
решения на всех строках (столбцах), т. е. во всех узлах сетки, потребуется
число действий 0(1//г^), пропорциональное числу узлов й^. Основная
идея экономичных методов и состоит в последовательном решении
одномерных задач вида (105) из § 2 вдоль строк и вдоль столбцов.
^ Peaceman D. W., Rachford Н. Н. The numerical solution of parabolic
and elliptic differential equations // SIAM J. 1955. Vol. 3, № 1. P. 28-41;
Douglas J. On numerical integration of Uxx + Uyy = щ implicit methods //
Ibid. P. 42-65; Яненко H. H. 06 одном разностном методе счета
многомерного уравнения теплопроводности // ДАН СССР. 1959. Т. 125, № 6. С. 1207-
1210; Дьяконов Е. Г. Разностные схемы с расщепляющимся оператором
для многомерных нестационарных задач // ЖВМ и МФ. 1962. Т. 2, № 4.
С. 549-568; Самарский А. А. Об одном экономичном разностном методе
репЕСния многомерного параболического уравнения в произвольной области
// Там же. № 5. С. 787-811.
41 А. Н. Тихонов, А. А. Самарский

642 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Наиболее четко выражает эту идею продольно-поперечная схема
(неявный метод переменных направлений):
y^-^-iyL = K^yi+'h + K^yi + P+'h^ (11)
0,5 Г
У—-^ = Л2у^+1 + Ai2/^+V2 + р+'/\ (12)
0,5 Г
Переход от слоя j к слою j + 1 соверп1ается в два этапа с П1агами 0,5 г:
сначала реп1ается уравнение (11), неявное по направлению xi и явное
по Ж2, затем уравнение (12), явное по xi и неявное по Х2. Значение
уЗ+ /2 является промежуточным.
Сформулируем краевые и начальные условия для схемы (11) —
(12) в случае, когда G = {О ^ Ж1,Ж2 ^ 1} — квадрат, й^ =
= {(и^1,^2^2)} — сетка с П1агами /ii, /12- Если краевые условия в (4) не
зависят от ^, т. е. /i = /i(x), то полагаем у^^ 1^ |^^ = у^^^ |^^ = \i[x) |^^.
Если же /J, = iJ,{x, t) зависит от ^, то для промежуточного значения у^~^ 1^
краевые условия при i\ =0, A^i задаются по формуле
yi+V2 = 1 (/,i+i + ^,i) _ 1 ^Лз (//^■+^ - /z^) = Д при ii = О, АГь (13)
а для у^^^ ставятся обычные условия
^j+i^^j+i при г2=0, 7V2. (14)
Присоединяя сюда начальное условие
у^^и^[х) при j = 0, (15)
получаем разностную задачу (11) — (15), соответствующую задаче
(4).
Продольно-поперечная схема (11) — (12) безусловно устойчива
(при любых г и /г) и имеет точность 0{т^ -\- h^).
Подставим в (11) — (12) вместо Ai^ и А2^ их выражения
Ai^ = {Aiy)i^i^ = j^ (^i^_i - 2yi^ + Vh+i),
А2У = (A22/)iii2 = J^ {Уг2-1 - ^Уг2 + 2/i2 + l)

4] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ 643
(пишем только тот индекс (ii или ^2), который меняется). Тогда для
у получим краевые задачи
yJ-\- /2 — у -^ У^^^
0,5 71у1+_'/^ - (1 + 71) уГ'/^ + 0,5 712/1-;^ = -Ff^''^
H = l,2,...,Ni
(О < гг < N2),
ydJ^ = Д Ui=o, y^ti' = ^ 1=^1=1' "^1 = "^/^1
'.«2
pi+V2 _
0,5 72 (2/4_i + 2/4+i) + (1 - 72) 2/4 + 0,5 r/i+V2 J
(16)
0,5 72у-2-1
^■+^ -(1 + ^2)у|+^+0,5 72у|+Л
(2 = 1,2, ...,N2-1 iO<H<Ni),
'+^ ^2=0, y-^"tiv2 = /"^"^^ 1^2=1' 72 = ^
F^+' = 0,5 71 bji^ + vt^) + (1 - 71) 4+'/^ + 0,5 r/i+V2. J
i+i
72 = -r//i|.
У (17)
Здесь /i определяется по формуле (13). Пусть у^ и, следовательно,
jpj-\- /2 известны. Фиксируем ^2 = 1 и на этой строке по формулам
прогонки решаем краевую задачу (16). Полагая затем ^2 = 2, ..., А^2 — 1,
последовательно находим у^~^ 1^ во всех узлах а;/^. После этого
вычисляем F^^ /2 и вдоль столбцов ii = l,2, ...,А^1 — 1 решаем краевые
задачи (17). В результате получаем значение у^^^ на новом слое. При
переходе от слоя j + 1 к слою j + 2 процедура счета повторяется.
Из сказанного выше ясно, что при переходе от слоя j к слою j +
+ 1 затрачивается 0{l/h?) арифметических действий. Чтобы найти у^^
при ^0 = Jo'T" по начальным данным, требуется, очевидно, 0(1//г^) jo =
= 0{1/{Ь?т)) операций, т. е. число операций пропорционально
числу использованных узлов пространственно-временной сетки ujhr —
= {(n/ii,i2/i2,jV)}.
В случае уравнения (7) с переменными коэффициентами в (11) —
(12) следует подставить, согласно (67) из § 2, выражения Kf^y =
= (ас(ж,^^+о,5)2/жа)жа5 « = 1, 2, L^u - K^u = 0{Н1). Операторы Ai
и А2 действуют только вдоль строк и столбцов соответственно.
Поэтому схемой (11) — (12) можно пользоваться и для произвольной
области, полагая, например, Д = 0,5 (/i-^ -\- fi^^^). Если G — область,
составленная из прямоугольников, то при
д = 0,5 (/i^' + /i^'+^) - 0,25 rL2 (/i^'+^ - 1л^)
продольно-поперечная схема имеет точность 0{т'^ + \Щ^)-
Схему (11) — (12) можно формально обобщить на случай трех
пространственных переменных xi, Ж2, жз, но так построенная схема
будет, вообще говоря, неустойчива.
41*

644 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Универсальным методом, пригодным для решения уравнения
теплопроводности с переменными и даже разрывными коэффициентами в
произвольной области G любого числа измерений, является локально-
одномерный метод. В основе его лежит понятие суммарной
аппроксимации схемы. Пусть дано уравнение (7). Будем искать его
приближенное решение v^^^ при t = ^j+i, последовательно (при а = 1, 2, ..., р)
решая одномерные уравнения теплопроводности
—^ = LaV^cx) + fa, tj ^t ^ tj^i, ^f^ = f^ a = 1, 2, ..., p,
a=l
(18)
С условиями v-J^ = yi^_i) 5 <^ = 2, ..., p, г'/^ч = v^ и естественными
краевыми условиями. Решением этой задачи, которую мы условно запишем
в виде Li —>- L2 —>-... —>■ Lp, является v^~^^ = v-! ^ . Зная v^ = uo{x),
находим V^'^'^ .
Каждое из уравнений номера а заменим двухслойной
шеститочечной схемой с весом а а (при этом dV(^(^^/dt « М^) ~ '^(а))/'^' ^а ^ -^а,
fa^(fa) вида
-1 .J
Учитывая, что v-J^ = WjLi), заменяя г» на ^ и опуская индекс j +
+ 1, получаем последовательность схем для одномерных уравнений
теплопроводности (одномерных схем), которую мы назовем локально-
одномерной схемой и условно запишем в виде Л-^^^^ —>- Лз ^ —>-...—>■
—>- Ар . Напишем локально-одномерную схему для случая а^ = 1
У(а) - У(а-1) д , / ^ч ^
= АаУ(а) + ^а, (ж, t) G UJhr,
(19)
а = 1, 2, ...,р, ^(0)=^^', У(р)=У^^^.
Здесь АаУ = (ао,(ж,Г)^жа)жа5 V^a = ^^а(ж,Г), где Г — любое значение
t на отрезке tj ^t ^ tj+i, например t* = ^j+i- Правые части (/?q,
выбираются так, что (fi-\-(f2 + --- + ^p = f{x,t*) + 0(|/гр + г), например
(fl= (f2 = ••• = (fp-1 =0, (fp = /.
Сформулируем краевые условия для У(^а)- Пусть G — р-мерная
область в пространстве х = (xi,..., Хр), Г — ее граница. Построим по
_ о
аналогии с§3, п. 2вС + Г сетку coh- Возьмем любую точку ж G ci;/^ и
проведем через нее прямую Са, параллельную оси Ох^- Рассмотрим
тот простейший случай, когда Са пересекает Г в двух точках: Р~ и
7 + 1 7

§ 4] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ 645
Р+. Множество всех точек Р~ и Р+ обозначим 7^, <^ = 1, 2, ..., р. Если
G = Go = {О ^ Ха ^ /а, а = 1, 2} — прямоугольник, то 7^ состоит из
узлов {iihi; ^2/^2), лежащих на сторонах Xq, = О {ia = 0) и х^ = la {^а =
= А^а), а = 1, 2. Краевые условия для ^(q,), очевидно, задаются только
на 7^:
^(с,) =/i(x,r) при же 7^, а = 1, 2, ...,р. (20)
В начальный момент ^ = О задано условие
у{х,0)=щ{х). (21)
Условия (19) — (21) однозначно определяют у^ при всех j =
= 1,2,... и X ^ (Jh- Для нахождения ^(^к) мы получаем уравнение
У (а) ~ ^^аУ(а) = ^ск = У(а-1) + '^V^a С красвыми УСЛОВИЯМИ (20). Эта
разностная задача реп1ается методом прогонки по переменным xi и
Х2.
Схема (19) аппроксимирует уравнение (7) в суммарном смысле:
погрешность аппроксимации ф для локально-одномерной схемы есть
сумма погрешностей аппроксимации ф^ на решении и = u{x,t) для
одномерных схем (19) номера а:
р
ф = "^ф^ = 0(|/г|2 + г), хотя все ф^ = 0(1). (22)
а=1
Схема (19) безусловно устойчива и равномерно сходится:
max|^^'-u^'| =0(|/г|2+г). (23)
В случае двух измерений (р = 2) схема (19) имеет вид
- {У(1) - У^) = Al^(i) +(/?!, - (^^ + ^ - ^(1)) = Л2^^ + ^ + (/?2,
так как ^(о) = у^, у(2) = У^^^ •
В схеме (19) не все направления равноправны. Симметризованная
локально-одномерная схема
0,5 Л^^^ ^0,5 Л^^^ ^ ... ^ 0,5 Л^,^) ^ 0,5 Л^,^) ^ ... ^ 0,5 Л^^^ ^0,5 Л^^^,
как показывают численные эксперименты, обладает большей
точностью по сравнению со схемой (19) с шагом 0,5 г.
Можно построить ряд симметричных схем, имеющих второй
порядок точности по г. Оказывается, что схема (11) — (12) также является
симметричной локально-одномерной схемой вида
0,5 Л^°^ ^ 0,5 Л^^^ ^ 0,5 Л^°^ ^ 0,5 Л^^^
с (fi = О, ^2 = 0,5 /, (рз = 0,5 /, (/?4 = 0. В этом можно убедиться,
если исключить ^(i) и ^(з) (сложив 1-е и 2-е, 3-е и 4-е уравнения) и
обозначить ^(2) = У'^'^ ^^-

646 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Напишем одну из симметричных локально-одномерных схем с ф =
= 0(|/гр + г^) для трех измерений (р = 3, ж = (ж1,Ж2,жз)):
0,5 Л(°) ^ 0,5 Л(°'^) ^ Л(°'^) ^ 0,5 Л(°'^) ^ 0,5 Л«. (24)
Эта схема, изученная И. В. Фрязиновым, является обобщением схемы
(11) — (12) на трехмерный случай.
Нетрудно написать локально-одномерную схему для
квазилинейного уравнения
Достаточно заменить каждую из одномерных схем (19) любой из схем,
рассмотренных в § 2, п. 12, для одномерных уравнений:
ди д
dt дхо
(ка{и) ^ j + /„И, J2 /«Н = /И- (26)
Так, например, для двумерного случая р = 2 достаточно в (19)
заменить Ai^(i) и К2у^^^ {у^^^ — У{2) при р = 2) выражениями
Ai?/(i) = (ai(^(i))^(i)^J^i, ^2^^+^ = («2(2/^+^) ?/f-^^
Х2 /Ж2'
= h , а2[у) = к2 '
(27)
и положить (pi = о, (/?2 = 1{У(1))-
На равномерной сетке А^у (а = 1, 2), очевидно, имеет вид
АаУ = -г^ [{aa{y))ia+i {yia+i -у)- аа{у) {у - yic^-i)] . (28)
Для определения ^(i) и у^'^'^ получаем нелинейные трехточечные
задачи, которые решаются по аналогии с § 2, п. 12 методом
итераций с использованием формул прогонки для каждой итерации. Если в
(27) положить ai = ai{y^) и а2 = a2(^(i)), то получим для определения
^(1) и у^^^ линейные краевые задачи, которые решаются сразу путем
прогонки по переменным xi и Х2 соответственно.
Приведем два примера.
Пример 1. Расчет двумерной температурной волны.
Рассмотрим двумерное уравнение теплопроводности
^=a^r(")a^j+a^r("'a^j' М«) =-««-, « = 1,2,
(29)

§ 4] РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ ЗАДАЧ 647
с параметрами ai = 4, xi = 4, сг2 = 2, Х2 = 0,25 и для расчета
используем точное penienne
u{xi,X2,t) = <
f 0,5 Y^-1 + v^l + 16 (^ - Ж1 - 2x^ при ^^Ж1+2ж2,
О
при ^ ^ Ж1 + 2Ж2.
(30)
Сетка грубая: hi = h2 = I; число узлов A^i • А^2 = 30 • 20 = 600. Из
точного решения взяты начальные значения, т. е. u{xi,X2, 0) = О, и краевые
условия на прямых xi = О, xi = 30, Ж2 = О и Ж2 = 20.
1 — Х2 = 3,0
Х2 = 7,0
Х2 = 11,0
1 — XI =1,0
XI = 21,0
XI = 11,0
15,0
Рис. 92
Расчеты проводились по локально-одномерной схеме (19) с
операторами Ai и А2, определяемыми формулами (27), с шагом по времени:
а) г = 0,2; б) г = 1,0; в) г = 2,0. Некоторые результаты при ^ = 30
нанесены на рис. 92, где крестиками обозначены результаты варианта
«в», точками — варианта «а», сплошные линии — это аналитическое
решение"'^^
Пример 2. Расчет задачи о фазовом переходе (задачи Стефана).
Предположим, что имеется две фазы 1,2 с коэффициентами
теплоемкости ci{u), С2{и) И теплопроводности ki{u), к2{и). В каждой из фаз
температура u{x,t) удовлетворяет уравнению теплопроводности
Cs{u)
ди
Е
д
дхо
ks(u)^] +fix,t),
1,2,
(31)
X — [Xi 1 - - - 1 Хр), р — 1, Z, о.
^^ См. ссылку на с. 628.

648 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
где f{x,t) — плотность тепловых источников. На границе раздела фаз
температура u{x,t) постоянна и равна температуре и* их фазового
перехода, тепловые потоки разрывны и их разность равна Xv, где Л —
теплота фазового перехода, v — скорость фронта границы фаз. В
одномерном случае условия на границе х = ^{t) раздела фаз имеют вид
(32)
если и < и* в фазе 1 и и > и* в фазе 2.
Вводя (5-функцию Дирака, запишем уравнение (31) в виде
{с{и) + XS{u — и
-))S = i:5|:(«»)|:)^/. (33.
^ ^ \с2, и> и*; ^ ^ \к2, и > и*.
Условия на границе фаз (в частности, условия (32) при р = 1) следуют
из уравнения (33).
Для решения задачи Стефана применяется метод сглаживания: S-
функция приближенно заменяется (5-образной функцией 5{и — и*. А),
отличной от нуля только на интервале (и* — А,и* + А) и
удовлетворяющей условию нормировки
/ 5{u-u*,A)du = l.
и*-А
Вводя эффективную теплоемкость
с{и) = с{и) + XS{u - п*. А)
и эффективный коэффициент к{и), совпадающий с ki (и) при и <и* — А
и с к2{и) при и > и* -\- А, мы получаем для определения и
квазилинейное уравнение теплопроводности
С соответствующими краевыми условиями на границе Г области G, в
которой ищется решение.
Отметим, что 5{и — и*. А) выбирается таким образом, чтобы с{и)
вблизи и = и'^ имело наиболее простой вид: «ступеньки», параболы и
т. д.

А
ИТЕРАЦИОННЫЕ МЕТОДЫ
649
Так как «размазывание» проводится по температуре, то оно
применимо для любого числа измерений и любого числа фаз. Для решения
уравнения (34) применяется локально-одномерная схема (19), (27).
А ^2
Рис. 93
Рис. 94
Были получены численные решения следующих задач, имеющих
точные аналитические решения-*^^:
1) задачи с косым плоским фронтом (рис. 93);
2) осесимметрической задачи, в которой граница фаз есть
окружность (рис. 94).
Решение этих задач проводилось в прямоугольной системе
координат. Результаты расчета показаны на рис. 93 и 94. Сплошные линии —
границы раздела фаз, крестики — расчетные точки, в которых и = и*.
§ 5. Итерационные методы решения сеточных уравнений
1. Модельная задача. Кратко обсудим возможности
нахождения приближенного решения сеточных эллиптических задач^^
итерационными методами. В качестве модельной рассматривается задача
^ Самарский А. А., Моисеенко Б. Д. Экономичная схема
сквозного счета для многомерной задачи Стефана // ЖВМ и МФ. 1965.
Т. 5, № 5. С. 816-827. См. также: Будак Б. М., Соловьева Е. Н.,
Успенский А. Б. Разностный метод со сглаживанием коэффициентов для
решения задач Стефана // Там же. С. 828-840.
^ Более полное и всестороннее обсуждение проблем рептения сеточных
уравнений проводится в книге: Самарский А. А., Николаев Е. С.
Методы репЕСния сеточных уравнений. М., 1978.

650
ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Дирихле для уравнения Пуассона в прямоугольнике G = {х \ х =
= (Ж1,Ж2), О ^Ха ^1а, « = 1, 2}:
О и О и
^^^ Ъ^^Ъ^^'"^^^^ ^^' ^Hlr = /^(ж). (1)
в области G введем равномерную прямоугольную сетку с шагами hi
и /i2, и пусть (см. § 2) a;/i — множество внутренних, а 7/г — множество
граничных узлов.
Дифференциальной задаче (1) ставится в соответствие разностная
задача
Ay = -(f{x), xeujhj
y{x) = fi{x), xejh,
(2)
(3)
где
A?/ = ^ АаУ, КУ = УхссХсс '
(4)
а=1
Исследование сходимости итерационных процессов проводится в
пространстве сеточных функций Н^ заданных на а;/^ = а;/^ + 7/г ^
равных нулю на 7/г- Для этого в разностной задаче (2) — (4) исключаются
с учетом (3) граничные узлы.
Для того чтобы записать разностную задачу (2) — (4) в виде
операторного уравнения 1-го рода
Ау = /, (5)
обозначим
Ау = -Л^, уеН. (6)
В приведенной записи уже у{х) =0, ж G 7/i5 т. е. в граничных узлах
эта сеточная функция не совпадает с разностным решением.
Неоднородность граничного условия учитывается дополнительной
неоднородностью правой части разностного уравнения (2). Правая часть
уравнения (5) отлична от правой части разностного уравнения (2) лишь в
приграничных узлах. Нетрудно убедиться, что f = ^ -\- ^ih^'^ + (/^2/^2^^,
где
(fi{x)
^2{х) = <
/^(
0,
/^(
к
0,
/^(
0,Ж2),
h,X2),
Ж1,0),
XI,h),
xi = hi,
2hi ^xi ^h
xi = h -hi;
X2 = /^2,
2/z,2 ^ Ж2 ^ /2 -
Ж2 = /2 - h2.
-2/ii,
-2/i2,

§ 5] ИТЕРАЦИОННЫЕ МЕТОДЫ 651
Аналогичная процедура применяется и для разностных задач с
другими типами неоднородных граничных условий.
На основе результатов § 2 устанавливается самосопряженность и
положительность оператора А {{Ay,v) = {y,Av), {Ay, у) > 0) в
сеточном гильбертовом пространстве Н, в котором
(У^^) = Y^ y{x)v{x)hih2, \\у\\ = Viy^y)'
На основании рассмотрения одномерных операторов (см. § 2, п. 3)
имеем оценки разностного оператора А снизу и сверху следующего вида:
KiE ^А^ К2Е, (7)
где (ср. с (27) и (35) в § 2)
4 4 4 4
"^ = /! + /|' ""'^ц^щ^ ^'^
д, Е — тождественный оператор.
2. Итерационные методы линейной алгебры. Будем
рассматривать вопросы итерационного решения системы линейных
уравнений (5), когда А — линейный оператор, действующий в конечномерном
гильбертовом пространстве Н, f — заданный элемент Н, а> у
необходимо найти.
Итерационный метод основан на том, что, начиная с некоторого
начального приближения уо G Н, последовательно определяются
приближенные решения уравнения (5) yi, у2, ..., у к, ••-, где к —
номер итерации. Значения Ук-\-1 определяются по ранее найденным ук,
Ук-1, ••• Если при вычислении Ук-\-1 используются только значения
на предыдущей итерации у к, то итерационный метод называется од-
ношаговым (двухслойным). Соответственно при использовании у к и
Ук-1 итерационный метод называется двухшаговым (трехслойным).
Любой одношаговый итерационный метод можно записать в виде
ВкУк+1 = СкУк + Tk+if, (9)
где Вк^ Ск — линейные операторы, а Тк+i — числовые параметры.
Решение уравнения (5) должно удовлетворять (9), т. е. ВкУ = СкУ +
+ Tj^+i/. С учетом уравнения (5) можно положить Вк — Ск = Tk-\-iA.
Выражая Ск через А и Вк, запишем (9) в виде
Вк ^'^' ~ ^' +Аук = 1, А; = О, 1, ... (10)
Это есть каноническая форма двухслойного итерационного метода.
При заданном уо все последующие приближения находят по (10).
Для характеристики точности приближенного решения
естественно ввести погрешность Zk = Ук ~ У- Итерационный метод сходится в
энергетическом пространстве Н^^ порожденном самосопряженным и

652 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
положительно определенным в Н оператором D (скалярное
произведение в Hd есть {у,у)о = {Dy,v)), если ||2;j^||d —>■ О при к ^ оо.В качестве
меры сходимости итераций принимают относительную погреп1ность г,
так что
\\Уп-у\\о^е\\уо-у\\о- (11)
В силу того что само точное penienne у неизвестно, оценка точности
приближенного решения проводится по невязке Vk = Ayk — / = Ayk —
— Ay, которая может быть вычислена непосредственно. Например,
итерационный процесс проводится до выполнения оценки
1кп||^е||го||. (12)
Использование критерия сходимости (12) соответствует выбору D =
= А* А в (11). Минимальное число итераций, которое гарантирует
точность е (выполнение (11) или (12)), обозначим по{е).
При построении итерационного метода мы должны стремиться
к минимизации вычислительной работы по нахождению
приближенного решения задачи (5) с заданной точностью. Пусть Qk — число
арифметических действий для нахождения приближения yk и пусть
делается п ^ по{е) итераций. Тогда общие затраты оцениваются
величиной Q{s) = J^^^i Qk- Применительно к двухслойному
итерационному методу (10) минимизация Q{e) может достигаться за счет выбора
операторов Bk и итерационных параметров tj^+i. Обычно операторы
Bk задаются из каких-либо соображений, а оптимизация
итерационного метода (10) осуществляется за счет выбора итерационных
параметров.
3. Выбор итерационных параметров. В теории
итерационных методов для выбора итерационных параметров получили
распространение два подхода. Первый из них связан с использованием
априорной информации об операторах итерационной схемы (В^ и Л в
(10)). При втором подходе (итерационные методы вариационного
типа) итерационные параметры определяются на каждой итерации из
минимума некоторых функционалов и явно не используется априорная
информация об операторах.
Будем рассматривать в качестве основной задачу (5), когда
оператор А самосопряжен и положительно определен (Л = Л* > 0) в
конечномерном гильбертовом пространстве Н. Рассматривается
итерационный процесс
вУ^±1^У1 + Ау, = /, к = 0,1,..., (13)
Тк + 1
Т. е. В отличие от общего случая (10) оператор Bk считается
постоянным (не изменяется в процессе итераций).
Метод простой итерации соответствует использованию в (13)
постоянного итерационного параметра tj^ = г, т. е. рассматривается
итерационный процесс
вУ^±1^У1+Ау, = /, к = 0,1,..., (14)

§ 5] ИТЕРАЦИОННЫЕ МЕТОДЫ 653
в предположении, что
Л = Л* > О, Б = Б* > 0. (15)
Итерационный метод (14) называется стационарным.
Пусть априорная информация об операторах В ж А задана в виде
двухстороннего операторного неравенства
^iB^A^ 72^, 71 > О, (16)
т. е. операторы В и А энергетически эквивалентны. Имеет место
следующее утверждение.
Итерационный метод (14) — (16) сходится в Hd, D = А, В
при О < г < 2/71- Оптимальным значением итерационного параметра
является г = го = 2/(71 + 72)5 ^ ^^^^ числа итераций п, необходимых
для достиэюения точности г, справедлива оценка
п^по{е) = -^^, (17)
\про
где
Ро = 7-Г7 ' е = ^
1 + С 72
Заметим, что в (17) по(е), вообще говоря, нецелое и п —
минимальное целое, при котором выполнено п ^ по{е). Сформулированное
утверждение указывает путь оптимизации сходимости
итерационного процесса (14) — (15) за счет выбора оператора В в соответствии
с (16), т. е. оператор В должен быть близок оператору А по
энергии. В этом смысле наиболее благоприятная ситуация соответствует,
конечно, выбору 5 = Лиго = 1,п = 1 (прямой метод).
Оптимальный набор итерационных параметров в (13) связан с
корнями полиномов Чебышёва, поэтому такой итерационный метод
называется чебышёвским итерационным методом (или методом
Ричардсона). Определим множество Adn следующим образом:
Мп = I-cos (——TTJ , г = 1, 2, ...,nL (18)
Для итерационных параметров Tk используется формула
Тк = ——-^ , fik ^ Мп, /i: = 1, 2, ..., п. (19)
1 + роР'к
Чебышёвский итерационный метод (13), (15), (16), (18), (19)
сходится в Hd, D = а, в, и для числа итераций п, необходимых для
достижения точности г, справедлива оценка
п^по{г)=Ы{2г-')/Ы{р^'), (20)
где

654 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Заметим, что в чебышёвском методе (см. (18), (19)) расчет
итерационных параметров осуществляется по заданному общему числу
итераций п. Естественно, что вырожденный случай п = 1 соответствует
рассмотренному вып1е методу простой итерации.
Практическая реализация чебып1ёвского итерационного метода
связана с проблемой вычислительной устойчивости, которая
порождена тем, что норма оператора перехода на отдельных итерациях больп1е
единицы и может происходить рост локальной погреп1ности до авоста.
Проблема вычислительной устойчивости реп1ается специальным
упорядочиванием итерационных параметров (выбором /Jk из множества
Л4п)- Для вычисления оптимальных последовательностей
итерационных параметров Tk по заданному числу итераций п предложены
различные алгоритмы.
4. Итерационные методы вариационного типа. Выше
рассматривались итерационные методы решения задачи (5) в условиях,
когда задана априорная информация об операторах В и А в виде
констант (см. (16)) энергетической эквивалентности 71 и 72- Через эти
постоянные определяются оптимальные значения итерационных
параметров. Получение этих постоянных может оказаться сложной
задачей, поэтому есть смысл пытаться строить итерационные методы, для
которых итерационные параметры вычисляются без такой априорной
информации. Этот класс методов известен как итерационные методы
вариационного типа. Начнем с рассмотрения двухслойного
итерационного метода (13) в предположениях (15).
Обозначая невязку Vk = Ayk — / и поправку Wk = B~^rk,
расчетную формулу для итерационных параметров можно представить в виде
{Dwk.Wk)
Итерационный процесс (13) запишется следующим образом:
Ук+1 =Ук - Tk+iWk, /1; = О, 1, ...
Конкретизация итерационного метода достигается за счет выбора
D = D* > 0. Этот выбор должен быть подчинен, в частности, условию
возможности вычисления итерационных параметров. В формулу (21)
входит невычисляемая величина Zk, и поэтому выбор D = В здесь не
проходит. Вторая отмеченная выше возможность — D = А —
приводит нас к методу скорейшего спуска, когда
Среди других возможностей выбора D отметим D = АВ~^А — метод
минимальных поправок.
Двухслойный итерационный метод вариационного типа сходится
не медленнее метода простой итерации. Сформулируем
соответствующий результат применительно к методу скорейшего спуска в виде
следующей теоремы.

§ 5] ИТЕРАЦИОННЫЕ МЕТОДЫ 655
Итерационный метод (13), (15), (16), (22) сходится в На, и для
числа итераций п, необходимых для достиэюения точности г,
справедлива оценка (17).
В вычислительной практике наибольшее распространение
получили трехслойные итерационные методы вариационного типа. По
скорости сходимости они не хуже итерационного метода с чебышёвским
набором итерационных параметров. В трехслойном (двухшаговом)
итерационном методе новое приближение находится по двум
предыдущим. Для реализации метода требуются два начальных
приближения уо, у1. Обычно уо задается произвольно, а yi находится по
двухслойному итерационному методу. Трехслойный метод записывается в
следующей канонической форме трехслойного итерационного метода:
Вук+1 = а^+1 {В - Tk^iA) Ук + {I- «fe+i) Вук-1 + «fe+iTjt+i/,
(23)
А; = 1, 2, ...,
Ву1 = {B-TiA)yo+Tif,
где ak-\-i и Tk-\-i — итерационные параметры.
Вычисления по (23) основаны на представлении
Ук+1 = OLk+iVk + (1 - OLk+i) Ук-1 - ak+iTk^iWk, (24)
где Wk = B~^rk. Реализация трехслойного итерационного метода часто
связана с использованием представления
Ук+1 =Ук + ^кРк, /i; = О, 1, ...,
(25)
Po = wo, Pk=Wk-\- l^kPk-i, к = 1,2,...
Сопоставляя (24) и (25), устанавливаем связь параметров Aj^ и /ij^ с
параметрами ak и tj^:
\ t -\\ ^к^к
Ak — -ak+l^k+l, fJ'k — [Oik^i — i)
O^k+l^k+1
С использованием введенных обозначений расчетные формулы
итерационного метода сопряженных направлений дают
{Dwk,Zk) J „ ^
П+1 = 77S V ' А; = О, 1, ...,
( Tk+i {Dwk,Zk) 1 ^"^ 7 1 о 1
«fe+1 = 1 77S \^] ' к = 1,2,..., «1 = 1.
(26)

656 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
В случае D = А, как следует из (26), итерационные параметры
рассчитываются по формулам
^к+1 = -Гл V ' А: = О, 1
{Awk,Wk) '
, J., ... 5
«fe+1 =1 7 V — ' А; = 1, 2, ..., ai = 1.
(27)
Расчет итерационных параметров трехслойного итерационного метода
(23) в соответствии с (27) определяет метод сопряженных градиентов,
который наиболее широко используется в вычислительной практике.
Метод сопряженных градиентов (23), (27) при выполнении (15), (16)
сходится в На, и для числа итераций п, необходимых для достижения
точности г, справедлива оценка (20).
5. Диагональный оператор В. Простейший класс
итерационных методов связан с выбором диагонального оператора В. В этом
случае
В = Ъ{х) Е (28)
и расчет нового итерационного приближения проводится по явным
формулам. К этому классу методов принадлежит и итерационный
метод Якоби, который соответствует выбору в качестве В диагональной
части оператора А и Tk = т = 1.
Задача оптимального выбора В в классе операторов (28) решена.
Отношение ^ = 71/72 в двухстороннем операторном неравенстве (16)
для Л = Л* > О будет максимальным, если в качестве В выбрать
диагональную часть оператора Л. И в этом смысле метод Якоби является
оптимальным.
При
с учетом (7), (8) имеем
Ь{х) = 2(/г-^ + /г-^) (29)
С=^ = 0(|/гП, \h\' = hl + hl
72
Для числа итераций метода простой итерации с оптимальным
значением г = Го = 2/(71+72) и метода скорейшего спуска при выборе В
согласно (28), (29) справедлива оценка
Тем самым, число итераций пропорционально общему числу узлов
(неизвестных) .

§ 5] ИТЕРАЦИОННЫЕ МЕТОДЫ 657
Для чебышёвского итерационного метода и метода сопряженных
градиентов вместо (30) имеем следующую оценку:
По сравнению с методом простой итерации метод с чебышёвским
набором итерационных параметров сходится значительно быстрее.
6. Попеременно-треугольный итерационный метод.
Рассмотрим задачу (5) в условиях, когда самосопряженный и
положительный оператор А представляется в виде
А = Аг+А2, Аг=А*. (32)
Пусть оператор V соответствует диагональной части А, С — нижней
треугольной матрице. Тогда в силу А = С -\- V -\- С* для операторов
Аа, а = 1, 2, из разложения (32) получим
Ai = ^V + C, A2 = ^V + C*. (33)
с учетом выбора
Vy = d{x) Е, d{x) = 2 (/г-^ + /г-^). (34)
Для операторов А^, а = 1, 2, разложения (32), (33) имеем следующие
представления на множестве сеточных функций, обращающихся в нуль
на 7/1:
^ly = -г-Ух1 + -г-Ух2, Му = --г-Ух1- -г-Ух2- (35)
All 1^2 1^1 1^2
Оператор В в попеременно-треугольном итерационном методе
является факторизованным и выбирается в виде произведения двух
треугольных и диагональной матриц:
B = {V + ljAi) V-^ {V + UJA2), (36)
где uj — числовой параметр.
Скорость сходимости итерационного метода (13), (15), (36)
определяется постоянными энергетической эквивалентности 7i ? 72 в
двухстороннем неравенстве (16). Найдем эти постоянные при априорной
информации в виде неравенств
5iV ^ Л, AiV-^A2 ^ ^ ^, (^1 > 0. (37)
Для оператора В имеем
B = {V + ljAi) V-^ {V + UJA2) = X) + о; (Л1 + Л2) + uj'^AiV-^A2. (38)
Принимая во внимание (37), получим
42 А. Н. Тихонов, А. А. Самарский

658 ДОПОЛНЕНИЕ I. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Тем самым для 71 имеет место выражение
Для получения постоянной 72 представим оператор В на
основании (38) в следующем виде:
В = V-uj{Ai+A2)+ uj^AiV-^A2 + 2uj {Ai + A2) =
= (X) - a;^i) V-^ {V - UJA2) + 2ujA.
Так как оператор X^ положителен, то отсюда получаем {By,у) ^
^ 2uj{Ay,y), т. е. Л ^ 72^, где
72 = ^. (40)
Сейчас мы можем выбрать параметр со в (36) исходя из условия
максимума ^ = ^{со) = 71/72- С учетом (39), (40) получим
Максимум ^{(jo)
и он равен
^(-) = ^
72
2ш1
>1
1+0)5 + u)'^5i5'2
достигается при
со = (
^ = а^о) --
^о = 2№Й2)-
277V2
-V2
5
г/ =
74
<5i
82
(41)
(42)
На основании полученных оценок можно сформулировать
соответствующий результат о сходимости попеременно-треугольного
итерационного метода при оптимальном выборе параметра ио.
Попеременно-треугольный итерационный метод (13), (32), (36),
(37), (41) с чебышёвским набором итерационных параметров
сходится в На и Нв, причем для числа итераций справедлива оценка п ^
^ по(г) = 1п(2г-1)/1п(р-^), где
1 - CV2
pi -
1 + CV2
(^ определяется согласно (42)).
Учитывая малость ?7, для числа итераций можно получить более
простое выражение:
по(е) = 1п(2е-1)/ {2у/2щ/*), tj = бг/62. (43)
Попеременно-треугольный метод может реализовываться и в
варианте метода сопряженных градиентов. И в этом случае число итераций
характеризуется оценкой (43).

§ 5] ИТЕРАЦИОННЫЕ МЕТОДЫ 659
Найдем теперь постоянные 5i и 52 в неравенствах (37). На
основе выбора (34) и оценки (7) — (8) имеем Si = 0(|/гр). Принимая во
внимание (34), (35), получаем
2 (hi + hi)
{AiV-^A2y,y) = ^,JJ,2. (^2У,А2У).
1 '..2 ,^ 2 ,„. „. X 1 Л.2
Для правой части имеем
{А2У,А2У) = -^ {у1^А) - J^ (Ухг^Ух^) + ^ (2/^2' !)•
Принимая во внимание, что
получаем
{А2у,А2у)^ (j^ + j^j {Ay,у).
Тем самым приходим к неравенству {AiV~^ А2у,у) ^ 0,5 {Ау,у).
Сопоставляя со вторым неравенством (37), имеем 52 = 2.
С учетом этого для чебып1ёвского итерационного метода верна
оценка числа итераций
Таким образом, число итераций пропорционально корню
квадратному из числа узлов по одному направлению (в нашей двумерной
задаче — корню четвертой степени из общего числа узлов). Оценка (44)
показывает, что рассмотренный метод значительно предпочтительнее
рассмотренных ранее других итерационных методов.
Параметр со в попеременно-треугольном методе (13), (36) можно
включить в оператор V и использовать (13) с В = {V -\- Ai) V~^ {V +
-\- А2). Оптимизация итерационного метода достигается только за счет
выбора оператора V. Это особенно важно при рассмотрении задач с
переменными коэффициентами. Заслуживает внимания попеременно-
треугольный итерационный метод в форме
B = {V + C) V-^ {V + £*). (45)
Если в качестве V взять OD, где в — постоянная, а, D — диагональная
часть Л, то выбор (45), как и в случае треугольных итерационных
методов, эквивалентен ранее рассмотренному выбору. Конечно, если
V ф OD, то эквивалентности между этими вариантами попеременно-
треугольного итерационного метода уже нет.
42*

ДОПОЛНЕНИЕ П
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
1. Введение. Метод разделения переменных для уравнений с
частными производными приводит к задаче Штурма — Л иу вил ля.
Для уравнений с постоянными коэффициентами и граничными
условиями 1-го рода, которые рассматриваются в гл. П, П1, V, мы получаем
задачу на собственные значения, или задачу Штурма — Л иу вил ля.
Найти значения Л, при которых однородное уравнение Av -\- Xv =
= О 6 области Т с однородным условием v\^ = О на границе Е имеет
нетривиальные решения v{P) ^ О (собственные функции).
Если Т — отрезок О ^ ж ^ /, прямоугольник (О ^ ж ^ /i, О ^ ^ ^ Ь)
или параллелепипед {О ^ х ^ li, О ^ у ^ I2, О ^ z ^ Is), то собственные
функции Vn{P) выражаются через тригонометрические функции.
Если Т — круг, цилиндр или шар, то для нахождения собственных
функций вводятся новые специальные функции — цилиндрические и
сферические.
Рассмотрим отдельные случаи.
1. Круг О^г^го.В полярных координатах (г, (f) задача
Штурма — Лиувилля имеет вид
A2V + Xv= -—[г--] + — --^ + Xv = 0, О < г < Го,
г or \ or J r^ Oip"^
(1)
V \r=ro =0, i; ^ 0.
Функцию V ищем в виде v{r^ ip) = К{г)Ф{(р). Подставим v = КФ в
уравнение и разделим переменные:
г{гЕ'У + Xr'^R Ф"
R Ф
Отсюда следует, что
/i, где /J = const.
ф'' + /^Ф = О,
J {rR'Y + (л - ^) i^ = О, R{ro) = 0.
В силу однозначности решения функция Ф{(р) должна быть
периодической, т. е. Ф{(р -\- 27г) = Ф((/?). Это условие дает /i = п^, где п —

ВВЕДЕНИЕ 661
целое число. Полагая х = л/Л ^, приходим к уравнению цилиндрических
функций, или уравнению Бесселя п-го порядка:
-y-f^?Vfl-^)2/ = 0, или y" + -y'+(l-'^\y = {),
X ах \ ах / \ х'^ J х \ х^)
(2)
причем R{r) =у{уДг). При п = 0 получаем уравнение Бесселя
нулевого порядка
1 d f dy\ ^ „1,
- :r h^:r + ^ = О' ™^ у" ^-y' ^y = {),
X ax \ ax J X
которое соответствует случаю решений задачи (1), обладающих
осевой симметрией.
Решения уравнения (2) называют цилиндрическими
функциями. К уравнению (2) приводят также задачи для уравнения
Лапласа и волнового уравнения в случае, когда область Т есть круговой
цилиндр.
2. Шар О^г^го. Рассмотрим задачу Штурма — Лиувилля
Av + Ai; = 0, 0<Г<Го, v\r=rQ=^- (3)
в сферических координатах
I д [ ^dv\ 1
j,z (jr \ or J r^
1 д f . ,dv\ 1 d'^v
smO aO \ do J ^m в d(f^
Положим V = R{r)w{e,(f) и проведем разделение переменных:
(4)
it W
откуда следует
^e,^w -\- ijw = 0, (5)
^ {r'R'Y + (a - ^) i^ = 0, i^(ro) = 0. (6)
Подстановка x = л/Л^, ?/ = R/^/x приводит (6) к уравнению
Бесселя
Для функции w{e,(p), определенной на сфере, мы получили
уравнение (5), которое имеет ограниченное решение (сферические
функции) только при /i = п(п + 1). Таким образом, при разделении

662 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ
переменных для оператора Лапласа в сферической системе координат
мы приходим к сферическим функциям. В частном случае, когда w =
= w{e) не зависит от (/?, уравнение (5) принимает вид
-— [(l-s^)-^ ] +/ii(; = 0, где s = cosi9, -1 ^ s ^ 1. (7)
Это уравнение Лежандра, имеющее только при /а = п{п -\- 1)
ограниченное решение (полиномы Лежандра). Сферические функции
выражаются через производные полиномов Лежандра и
тригонометрические функции.
В квантовой механике часто встречаются полиномы Чебышёва —
Эрмита и Чебышёва — Лагерра.
2. Общее уравнение теории специальных функций.
Уравнения для простейших специальных функций могут быть записаны в
виде
Ly + Хр{х)у = 0, а < X < Ь, р{х) > О,
Простейшая краевая задача у" + Л^ = О, ^(0) = у{1) = О,
соответствующая a = 0,b = l,q = 0,k = p = const, определяет
тригонометрические функции. Рассмотрим уравнения для других специальных
функций.
1. Уравнение Бесселя (2), или {ху'У + {Хх — 'п?/х) ^ = О,
соответствует к{х) = ж, р{х) = ж, q{x) = п^/ж, а = О, 6 = го-
2. При к{х) = 1 — ж^,р=1,д' = 0, а = —1,6=1 получаем уравнение
Лежандра
[{l-x^)y'] + \y = Q. (9)
3. Уравнение присоединенных функций Лежандра
2
ТП
[{1-х'')у']'- .2/ + Л2/ = 0 (10)
777/
соответствует к{х) = 1 — ж^, q{x) = -^ р = 1, а = —1, b = 1.
1 — ж^
4. Уравнение Чебышёва — Эрмита
{е-'^'у'У + Хе-'^'у = О, или у" - 2ху' + Ху = О, (11)
соответствует к{х) = е~^ , q{x) = О, р(ж) = е~^ , а = —оо, Ь = оо.
5. Уравнение Чебышёва — Лагерра
{хе-'^у'У + Ле-^^ = О, или у" + (1 - ж)^' + Л^ = О, (12)
соответствует к{х) = же~^, q = О, р = е~^, а = О, 6 = оо.

ВВЕДЕНИЕ 663
Характерной особенностью указанных уравнений является
обращение в нуль коэффициента к{х) по крайней мере на одном из концов
интервала (а, 6). Это свойство к{х), как будет показано ниже, играет
важную роль для постановки краевых задач для уравнения (8).
Рассмотрим поведение реп1ений уравнения (8) вблизи особой
точки, в которой к{х) обращается в нуль.
3. Поведение решений в окрестности ж = а, если к{а) = 0.
Рассмотрим случай, когда а конечно.
Если в уравнении (8) q{x) — \р{х) заменить функцией q{x)^ то все
результаты, полученные ниже для уравнения
Ly = {к{х)у'У - q{x)y = О, к{х) > О при а < х < Ь, {S')
будут справедливы и для уравнения (8).
Лемма 1. Пусть yi{x) и У2{х) — два линейно независимых
решения уравнения (8'), коэффициент которого к{х) имеет, вид
к{х) = {х — а) (f{x), (^(а) 7^ О, (13)
где (f{x) > О — непрерывная на {а^Ь) функция. Если yi{x) —
ограниченное решение^ представимое в виде
yi{x) = {x-a)''u{x), п^О, (14)
где и{х) — непрерывная на (а, Ь) функция и и{а) ф О, то второе
решение У2{х) при Ж —>- а является неограниченным.
Заметим, что У2{х) можно представить в виде квадратуры через
линейно независимое решение yi{x). В самом деле, из равенства О =
= y2Lyi - yiLy2 = [k{y2y'i - У1У2)]' следует, что вронскиан функций
yi{x) и у2{х) равен yiy!^ - у2у[ = С/к{х), где С ф О, так как yi{x) и
У2{х) линейно независимы. После деления на yf получим {У2/У1У =
= C/kyf. Интегрируя это уравнение от xq до ж, получим
У2{х) =yi{x)
J k{a)yl{a)
СI = const.
в силу линейной независимости yi{x) и У2{х) можно считать Ci =
= 0. Кроме того, можно положить (7 = 1, так как решение
однородного уравнения определено с точностью до постоянного множителя. В
результате будем иметь
X
У2{х) =yi{x)
da
k{a)yl{a)'
XQ
причем жо выберем так, чтобы yi{a) не обращалось в нуль на
интервале а < а < х^.

664
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Подставляя вместо к{х) и yi{x) их выражения и пользуясь
теоремой о среднем, находим (заменяя у2 на у2)
X
У2{х) = {х - а)''и{х) / / \ 2/ \ =
хо
X
{х — а)^и{х) f da
'0(ж*)
{х - а)^и{х)
J {а
\2n-\-l
хо
'0(ж*
2п{а - а)2^
при п > о,
хо
(15)
[ 1п{а - а)\1^ при п = О,
где ф{х) = (f{x)u^{x), X* е (ж,жо). Представим У2{х) в виде
У2{х) = fi{x) + /2(ж,жо),
где
/iH =
и{х)
-при п > о,
/2(ж,Жо)
'0(ж*)
и{х){х — а)^
'0(ж*)
2п(ж - а)^
[ 1п(ж — а) при п = 0;
1
[ — 1п(жо — а) при п = 0.
Отсюда видно, что функция /2(^,^0) при ж —>- а остается
ограниченной, а |/i(x)| ^ 00 при X ^ а либо как {х — а)~^, либо как 11п(ж — а)|.
Фактически доказана следующая лемма.
Лемма 2. Пусть выполнены условия леммы 1. Если yi{a) ф О,
т. е. п = О, то ^2(ж) имеет при х = а логарифмическую особенность:
У2{х) ^ \п{х — а) при yi{a) ф О (п = 0).
Если yi{x) имеет при х = а нуль п-го порядка: yi{x) = (ж — а)^и{х),
п > О, то У2{х) имеет при х = а полюс порядка п:
У2{х) ^ {х — а)~^, если yi{x) ^ {х — а)^, п > 0.
Лемма 3. Пусть выполнены условия леммы 1 и коэффициент
q{x) либо ограничен^ либо стремится к оо при ж —>- а, так что
q{x)
Qojx)
{х - аУ
сг ^ О, до{а)фО,

ВВЕДЕНИЕ 665
где qo{x) — непрерывная на [а, 6] функция. Тогда для ограниченного
решения уi{x) вида (14) выполняется условие
lim А;(ж)^(ж)=0, (16)
х^а йХ
еслщ кроме того, имеет место неравенство
п > а — 1.
В самом деле, фиксируем некоторое значение xi, а < xi < 6, и
проинтегрируем (8') от ж до Ж1, а < X < xi'.
X
Подставив сюда выражения для yi{x) и q{x), найдем
XI
^/ ч , / ч / / ч f QoM и(а) ,
Q X = fc XI у Ж1 - / Г \1 п da, п^О.
J [а — ау ^
Отсюда видно, что Q{x) — непрерывная на отрезке а ^ х ^ xi
функция, если сг — п < 1, или п > а — 1. Переходя к пределу при ж —>- а,
видим, что существует предел lim Q{x) = Q{a) и, следовательно,
ж—>-а
lim k{x)yi{x) = Q{a).
ж—>-а
Покажем, что Q{a) = 0. Для этого выразим yi{x) через Q{x)'.
XI XI
yi{x) = yi{xi) - / —-—da = yi{xi) - / —---da.
J k{a) J {a-a)(p{a)
X X
Отсюда видно, что yi{x) может быть ограничена в точке х = а лишь
при условии Q{a) = О, откуда и следует (16).
4. Постановка краевых задач. Перейдем к постановке краевых
задач для уравнения
Ьу + Хру = 0 и Ьу = 0 (17)
в промежутке (а, Ь), на одном или обоих концах которого к{х)
обращается в нуль. Если к{а) = О и выполнено условие (13), то при х = а мы
будем требовать ограниченности вида (14) решения уравнений (17).
При этом не требуется, чтобы решение у{х) при х = а принимало
заданное значение.
Общее решение уравнений (17) есть у{х) = Ayi{x) + Ву2{х), где
yi и у2 — любые линейно независимые решения уравнения (17), А
VL В — произвольные постоянные. Если yi{x) удовлетворяет условию

666 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ
ограниченности (14) при ж = а, то У2{х) при х ^ а обращается в
бесконечность (лемма 1). Поэтому из требования ограниченности (14),
которое мы будем записывать формально в виде
\у{а)\<оо (18)
И называть естественным условием ограниченности (поскольку оно
является следствием структуры оператора L), сразу следует В = 0.
В результате мы приходим к следующей краевой задаче.
Найти собственные значения и собственные функции у{х) ^ О
уравнения
{ку'У -qy + Хру = О, к{х) > О, а < х < Ь, (19)
где к{х) имеет вид (13), при условии ограниченности (14) или (18) и
обычном условии^ например 1-го рода:
у{Ь) = 0 при х = Ь. (20)
Если к{а) = О или к{Ь) = О (например, для уравнения Лежандра),
то на обоих концах интервала (а, Ь) ставится условие
ограниченности, так что yi{x) = {х — а)^^{Ь — х)^'^и{х)^ где ni ^ О, П2 ^ О, и{а) ф О,
и(\)) ф О, и{х) — непрерывная на (а, Ь) функция; это условие формально
записываем в виде
|2/(а)|<^, |у(Ь)|<оо. (20')
Если интервал (а, 6) бесконечен, как, например, а — —оо, b = оо
для уравнения Чебышёва — Эрмита или а = О, 6 = оо для уравнения
Чебышёва — Лагерра, то при а = — оо или при 6 = оо в этом случае
условие ограниченности (18) заменяется более слабым требованием:
решение на бесконечности не должно возрастать сильнее, чем конечная
степень х.
Сформулируем общие свойства собственных функций и
собственных значений поставленной краевой задачи (18) — (20).
1. Существует бесчисленное множество собственных значений
Ai < Л2 < Аз < ... < An < ..., которым соответствуют собственные
функции yi{x), У2{х), . . . , Уп{х), . . .
2. При q^ ^ все собственные значения неотрицательны:
Ап^О.
3. Собственные функции Уп{х) и ут{х), соответствующие разным
собственным значениям А^ и А^, ортогональны между собой с весом
р{х):
b
{Уп,Ут)= / Уп{х)Угп{х)р{х)(1х =0.
а
4. Имеет место теорема разложимости: функция f{x) разлагается
в абсолютно и равномерно сходящийся ряд по собственным функциям

ВВЕДЕНИЕ 667
Уп{х) данной задачи
fi^) = Y^fnyn{x), fn
^^1 {Уп^УпУ
если:
1) f{x) имеет при а < х < Ь непрерывную первую и кусочно-
непрерывную вторую производные]
2) f{x) удовлетворяет граничным условиям задачи; при этом,
если к{а) = О, то
|/(а)| < 00 при О ^ q{a) < оо,
/(а) =0 при q{x) > оо.
ж—>-а
Свойства 2 и 3 доказываются, как и в гл. II, § 3, с помощью формул
Грина. При этом используется ограниченность в точке х = а функции
Уп{х), а также следующее из леммы 3 равенство lim к{х)у' (х) = О, в
ж—^а
силу чего подстановки в формулах Грина при х = а обращаются в нуль.
Доказательство свойств 1 и 4 обычно проводится с помощью теории
интегральных уравнений. Для того чтобы 1 и 4 имели место, достаточно,
чтобы к{х) была непрерывной, а, q{x) — либо непрерывной, либо имела
вид qi{x)/{x — а), где qi{x) — непрерывная функция. Для изучаемых
ниже классов специальных функций эти условия выполнены.
Краевая задача (19) — (20) эквивалентна интегральному уравнению
ь
гдеК(ж,^) = G{x,^)^/~p(x)p(^, ip{x) = л^р{х) у{х), а G{x, ^) — функция Гри-
на для оператора L. В случае к{а) = О, к{Ь) / О, у{Ь) = О функция Грина
определяется следующим образом.
1. G{x,^) — непрерывная функция х при фиксированном ^, а ^ ^ ^ 6.
2. Первая производная dO/dx испытывает скачок при х = ^:
к{х)^{х,о
3. LxG{x,^) = О во всех точках а < х < Ь, кроме ж = ^.
4. С(ж,^) удовлетворяет граничным условиям
|G(a,OI<oo, G(b,O=0-
Из определения С(ж,^) следует, что С(ж,^) > О при ж,^ G (а, 6), С(ж,^) =
= С(^,ж) (симметрия).
Перейдем к изучению конкретных специальных функций:
цилиндрических и сферических функций, а также полиномов Чебышёва —
Эрмита и Чебышёва — Лагерра.

668 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
ЧАСТЬ I
ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
§ 1. Цилиндрические функции
При решении многих задач математической физики приходят к
обыкновенному дифференциальному уравнению
dx^ X dx
или (1)
X dx \ dx
называемому уравнением цилиндрических функций п-го
порядка. Это уравнение часто называют также уравнением
Бесселя п-го порядка.
Характерными задачами (см. гл. V, VI и УП), приводящими к
цилиндрическим функциям, являются краевые задачи для уравнения
Аи + А;^и = О (2)
вне или внутри круга (вне или внутри цилиндра в случае трех
независимых переменных). Введя полярные координаты, преобразуем
уравнение (2) к виду
I д f ди\ 1 д'^и ,2
г дг \ дг J г^ dip'^
Полагая и = R{r) Ф{(р) и разделяя в (3) переменные, получаем
1 d / dR\ /2 ^ ^ о _ п
г dr \ dr ) V г^ /
ф'' + ЛФ = 0.
Условие периодичности для Ф((/?) дает Л = п^, где п — целое число.
Полагая затем х = кг, приходим к уравнению цилиндрических
функций
X dx \ dx) V X
Г-(^з!) + (1-Г1)2/ = 0, R{r)=y{kr),
2/" + -2/'+fl-4)2/ = 0.
X \ х' '

§ 1] ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 669
В случае решений волнового уравнения (2), обладающих радиальной
(цилиндрической) симметрией, мы получим уравнение Бесселя
нулевого порядка
1 d [ dy\ ^ ,, 1 ,
--—ж-—+^ = 0, или у -\- -у -\-у = 0.
X ах \ ах J X
1. Степенные ряды. Уравнение Бесселя г/-го порядка
или
х^у" + ху' + {х^ -1У^)у = 0 (Г)
(г/ — произвольное действительное или комплексное число,
действительную часть которого мы можем считать неотрицательной) имеет
особую точку при X = 0. Поэтому решение у{х) следует искать в виде
степенного ряда-*^^
у{х) = х'^{ао + aix + а2Ж^ + ... + akX^ + •••), (4)
начинающегося с ж^, где а — характеристический показатель,
подлежащий определению. Подставляя ряд (4) в уравнение (1') и
приравнивая нулю коэффициенты при ж^, ж^+-^, ..., ж^+^, получаем уравнение
для определения а и систему уравнений для определения
коэффициентов ak'.
ао(а2 - г.2) = О,
ai[(a + l)2-j/2]=o,
а2[(ст + 2)2-г/2] + ао=0,
(5)
акЦо- + kf - г/2] + аи-2 = О
(fc = 2,3, ...).
Так как мы можем предположить, что ао т^ О, то из первого уравнения
(5) следует, что
а^ — v'^ = О, или а = =Ьг/. (6)
Перепишем к-е уравнение (5) {к > 1) ъ виде
{а ^кЛ- jy){(J -\- к - jy)ak + ak-2 = 0. (7)
^ См.: Степанов В. В. Курс дифференциальных уравнений. М., 1959;
Эльсгольц Л. Э. Дифференциальные уравнения и вариационное
исчисление. М., 1969.

670 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Оставим пока в стороне тот случай, когда а -\- и или сг — г/ (и
соответственно — 2г/ или 2г/) равно отрицательному целому числу.
Тогда из второго уравнения (5), в силу (6), будем иметь
ai = 0. (8)
Уравнение (7) дает рекуррентную формулу для определения ak
через ak-2'-
Cik-2 /Qx
Отсюда и из (8) заключаем, что все нечетные коэффициенты
равны нулю. Если 1У вещественно, то при а = —и решение обращается в
бесконечность в точке ж = 0.
Остановимся на случае сг = г/. Из (9) следует, что каждый четный
коэффициент может быть выражен через предыдущий:
0'2т = —0'2т-2-^ 7 \ Г- (Ю)
Последовательное применение этой формулы позволяет найти
выражение а2ш через а^:
а-гш = (-1)™ 22™т!(г/ + 1){„ + 2)... (г/ + т)" ^^^^
Воспользуемся свойством гамма-функции r(s)"'"^
r{s + 1) = sr{s) = ... = s{s-l)...{s- n)r{s - n).
Если s — целое число, то
r(s + l) = s\.
Коэффициент ao до сих пор оставался произвольным. Если v ф —п^
где п > О — целое число, то, полагая
И используя отмеченное выше свойство гамма-функций, получаем
аги = {-!)" 22ft+.r(fc + 1)Г(А; + j/ + 1)" ^^^'
Если же а = —1У, 1У ф п, где п > О — целое число, то, полагая
^ Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.

§ 1] ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 671
будем иметь
Ряд (3), соответствующий сг = г/ ^ О, с коэффициентами (12) и (13)
*W = |'-"'г№ + 1)щ + . + 1| (1)"*' <'^'
называется функцией Бесселя 1-го рода г/-го порядка. Ряд
соответствующий сг = — г/, представляет второе penienne уравнения (1),
линейно независимое от Jj^{x). Ряды (15) и (16), очевидно, сходятся на
всей плоскости х.
Рассмотрим теперь тот случай, когда f равно половине целого числа.
Пусть i/^ = (п + 1/2)^ , где п ^ О — целое число. Полагая в формулах
(5) сг = п + 1/2, получаем
2(n + l)ai = О,
к{к + 2п + l)ak + ak-2 =0 {к > 1),
так что
ai = О,
0'к = -
к{к-\-2п-\-1) '
Последовательно применяя эту формулу, находим
(-l)'ao
0'2к =
2 . 4 ... (2А;)(2п + 3)(2п + 5)... (2п + 2А; + 1)
Полагая здесь i/ = п + 1/2 , получаем формулу (11).
Положив далее
ао =
2^+V2r(n + 3/2) '
получим формулу (13).
Пусть
1
а = —п — -
2
тогда уравнения (5) для а^. принимают вид
ai • 1(-2п) = О,
к{к — 1 — 2n)aj. + aj._2 = 0.

672 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
По-прежнему все коэффициенты ai, аз, ..., CL2n-i равны нулю, но для
а2п+1 получаем уравнение О • a2n+i + ^2п-1 = О? которое удовлетворяется
при любом значении a2n+i- При к > п коэффициент a2k-\-i определяется
равенством
^2fe+l —
(-1)'-"а2п+1
(2п + 3)(2п + 5)... 2 . 4 ... (2А; - 2п)
Полагая a2n+i = О, ао = 1/[2~^~ /^Г(1/2 — п)], получаем формулу (14).
Таким образом, при v = d=(n + 1/2) не требуется никакого изменения в
определении функции Jv{x). Формулы (15) и (16) остаются в силе.
Отметим, что формула (16) определяет J-j^{x) лишь для
нецелых значений г/, поскольку определение ао по формуле (12) при целых
отрицательных г/ = — п лип1ено смысла. Продолжим по
непрерывности (16) на целые значения и = п. Поскольку Т{к — п + 1) = =Ьоо для
к ^ ко = п — 1, суммирование в (16) фактически начинается со
значений к = ко -\- 1 = п. Изменяя в (16) индекс суммирования к = п -\- к',
получаем
^ (-1)^' /Ж\2^'+п
^-..W = (-ТЕ г(^. + „ + 1№ + 1) (s) = '-""■'""•
так как суммирование начинается с к' = 0.
Выпип1ем в качестве примера ряды для функций Бесселя 1-го рода
нулевого (п = 0) и 1-го (п = 1) порядков:
Jo(x) = 1- (1)4 ^ (I)' - Щ^ (I)' + •••'
^ , , X 1 /ж\3 1 /х\^
'^^*^'=2-2!Ы +2!3!Ы -•••
Функции Jo (ж) и л (ж) наиболее часто встречаются в приложениях, и
для них имеются подробные таблицы-'^л На с. 767 приводятся графики
Jo (ж) и Ji{x).
функции Jn{x) и J-ri{x) (п — целое число), как мы видели,
линейно зависимы:
J.n{x) = {-1ГМх).
Для нецелых значений и функции Ju{x) и J-i^{x) линейно
независимы. В самом деле, Jjy{x) имеет нуль, а J-j^{x) — полюс г/-го порядка
^ Во всех таблицах специальных функций всегда имеются таблицы для
бесселевых функций 1-го рода (см., например, книгу Е. Янке, Ф. Эмде,
Ф. Jlenia «Специальные функции, формулы, графики, таблицы» (М., 1977),
где Jo (ж) и Ji{x) даны с пятью знаками для значений х в интервале от О до
14,9).

§ 1] ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 673
в точке X = 0. Таким образом, если и — нецелое число, то всякое
решение Уи{х) уравнения Бесселя (1) может быть представлено в виде
линейной комбинации функций Ju{x) и J-i^{x):
Угу{х) = CiJry{x) + C2J-u{x).
Если ищется ограниченное решение уравнения (1), то (72 = О и
Уи{х) = CiJjy{x) при Кег/>0.
2. Рекуррентные формулы. Установим следующие
соотношения, существующие между функциями Бесселя 1-го рода различных
порядков:
dx \ х"" ) ж^ ' ^ ^
^{x^J,{x))=x^J,_^{x). (18)
ах
Эти формулы проверяются непосредственным дифференцированием
рядов для бесселевых функций. Покажем, например, справедливость
соотношения (17):
1 /ж\2^-1 _
^ к=1
dx \ х"" ) 2^ ^' ' k\V{k^v ^\)
= У(-1)^ ^ рч-Я.-)
В последней сумме /;; меняется от 1 до оо. Введем новый индекс
суммирования I — к — \^ который будет меняться от О до оо. Тогда будем
иметь
^ d (Jv{x)
X '
dx V х^
- Z^^ ^^ г(/ + 1)г[/ + (г/ + 1) + 1] U; " ^-+1^^^'
что и доказывает формулу (17). Справедливость формулы (18)
доказывается аналогично.
Отметим два важных частных случая рекуррентных формул. При
г/ = О из (17) следует
J^(^) = -Ji(^). (19)
43 А. Н. Тихонов, А. А. Самарский

674 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Для случая и = 1 формула (18) дает
X
[xJi{x)]' = xJo{x), или xJi{x) = / ^MOd^ (20)
о
Установим рекуррентные формулы, связывающие Ju{x), J^y+i(x) и
Jy-i{x). Производя дифференцирование в (17) и (18), получаем
"'-^"^''^ -Jl{x) = J,+,{x), (17')
X
+ J^(x) = J,_i(x). (180
X
Складывая и вычитая (17') и (18'), находим рекуррентные
формулы
2г/
Л+1(ж) + Ju-l{x) = Л (ж),
X
Л+1(ж) - Ju-i{x) = -2Jl{x). J
(21)
С помощью формулы (21) можно вычислять J^y+i(x), если известны
Jy{x) и Л_1(ж):
Л+1(^) = -Л_1(^) + ?^^. (21')
3. Функции полуцелого порядка. Найдем выражения для
функций Ji/^{x) и J_y^{x):
^ f-ll^ /T\V2+2m
т=0
(-1)^ /X\-V2+2m
^-.« = Е;;,1^й^(Ю-'-^ (-)
ш!Г(1/2 + ш)
т=0 ^ ' ^
Пользуясь свойством гамма-функции, находим
(24)
где
г (|) = v^-

ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
675
Подставляя (24) в формулы (22) и (23), получаем
т=0 ^ '
^-v.(-) = \/-E
2 А (-ir^,^
'га; ^, (2т)!
(25)
(26)
Нетрудно видеть, что сумма в (25) представляет собой разложение
sin ж, а сумма в (26) — разложение cos ж по степеням х. Таким образом,
Jiu{x) И J_iu{x) выражаются через элементарные функции:
^1/9 (^)
1/2V^V - А/ — ^1^^'
J_i/Jx)
./\Jb) — \i COS Ж.
'"^ \l 7TX
(27)
(28)
Рассмотрим функции J^_^i/^{x), где n — целое число. Из (21')
следует
Js/Jx) = - JiJx) - J_i/Ax) =
7ГЖ
2
7ГЖ
■ COS X +
smx
JbiAx)
V 7ГЖ [
^4^-D + ^°K^-|)
= W — < sin(x — 7г) I 1 — ^7 I + cos(x — 7Г) • — > .
V 7ГЖ [ \ X^ J X }
sin Ж +
Применяя последовательно формулу (21'), найдем
^n+V2
(х)
= у^{^^Ч^-т)^"Ш+'^°К"-т)^"Ш}'
(29)
где Рп{1/х) — многочлен степени п относительно 1/ж, а Qn{^/x)
многочлен степени п — 1. Отметим, что Рп{0) = 1, а Qn(0) = О-
4. Асимптотический порядок цилиндрических функций.
Решения уравнения Бесселя обычно называют цилиндрическими
функциями. В п. 1 была определена одна из цилиндрических
функций — функция Бесселя.
43*

676 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Основным свойством цилиндрических функций является их
поведение при ж —>- О и ж —>- 00 (асимптотическое поведение). Ниже будет
показано, что любая цилиндрическая функция однозначно
определяется своей асимптотикой при ж —>- оо, точнее, главным членом
асимптотического разлоэюения.
Докажем, что любая вещественная цилиндрическая функция при
больп1их X представима в виде
уЛх) = Too —-д + О {-^\ , (30)
где 7оо 7^ О, ^оо — некоторые постоянные, 0{1/х Z^) означает члены
порядка не ниже 1/х 1^.
Полагая
вычисляя производные у' — —0,5ж~ l^v + х~ l^v', у" = х~ ^'^v" —
— х~ l^v' + 0,75ж~ l^v ж подставляя их в уравнение Бесселя,
получаем уравнение
являющееся частным случаем уравнения
i;'' + (l + p(x))i; = 0, (33)
где
р{х) = о (^) . (34)
Положим
г» = 7sin(x + (5), v' — ^ zo^{x-\-S), (35)
где 7(ж) и (5(ж) — некоторые функции ж, причем ^{х) не равна нулю
ни в одной точке, иначе v ж v^ одновременно обращались бы в нуль и
v{x) было бы тождественно равно нулю. Пользуясь (35) и (33), будем
иметь
г>' = 7 cos(x + (5) = 7' sin(x + (5) + ^[8' + 1) cos(x + (5),
^// _ у cos(x + (5) — 7(^' + 1) sin(x + (5) = — (1 + p)7sin(x + (5).
Отсюда находим
(5' = р8т'(ж + (5) = оГ^') , (36)
т' (5' / 1 \
— = - —-. гг = -psin(x + S) cos(x + (5) = о — . (37)
7 tg(x + ()) V^ У

§ 1] ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 677
Покажем, что существуют предельные значения j и 5 при ж —>- оо.
В самом деле,
S{x) =S{a)- / S\s)ds,
S{a) - I S'{
откуда в силу (36) следует, что существует предел lim S{a) = (5оо и
а—>-сю
S{x) =S^+o(-]. (38)
Аналогично находим из (37)
7(x)=7oo(l + O0j^, (39)
причем 7оо 7^ О-
Таким образом, всякое penienne уравнения (33) и, следовательно,
уравнения (32) при ж —>- оо имеет вид
v{x) = Too sin(x + (5оо) + О f - j . (40)
Тем самым установлена справедливость асимптотической формулы
(30) для любой цилиндрической функции Уи{х).
Покажем, что не может существовать двух различных
цилиндрических функций с одинаковой асимптотикой. В самом деле, пусть Уи{х)
и Уи{х) — две различные цилиндрические функции, для которых
Тсю ^ Тсю5 ^сю ^ ^сю- V^-'-J
Разность этих функций
Уи{х) =Уи{х) -Уи{х) ^ о
также является цилиндрической функцией, имеющей в силу (41)
следующую асимптотику:
У^{Х) = о ^ 3/2
Однако это противоречит формуле (30) для любой цилиндрической
функции Уи{х). Следовательно, Уи{х) = О и ^^^(ж) = Уи{х).
Реп1ением уравнения Бесселя может быть и комплексная
функция Zjy{x) = Zjy{x) + iZjy{x), где Zjy{x) и Zjy{x) — вещественные
цилиндрические функции. Из вышесказанного следует, что комплексная
цилиндрическая функция также однозначно определяется своей
асимптотикой при ж —>- 00.

678 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Значения постоянных 7оо и 5qq определяются с помощью
дополнительных исследований, которые дают
2
Too = А/ ~ для всех г/.
V 7Г
В § 1, П. 3 для г/ = п + 1/2 была получена формула (29), из которой
следует, что
В § 4 будет дан вывод асимптотической формулы для функции
Л (ж):
J.(.) = /Aeos(.-|.-J)+o(-L), (43)
где и — любое неотрицательное число (и ^ 0). Формула (43) имеет
место и при произвольном г/, так что
J-v{x)
\/^-(-r-j)-4i)- <^*'
§ 2. Краевые задачи для уравнения Бесселя
Простейп1ая краевая задача для уравнения Бесселя на отрезке
[О, Го] связана с задачей о собственных колебаниях круглой
мембраны
I д ( dv\ 1 d'^v
г дг \ дг) г^ д^'^
А2.; + Л.; = О, Д^^ =__( г —) + --- , (1)
^(^,V^)|r=ro =0, |i;(r,(/?)| < 00, i;(r,(/?)^0. (2)
Полагая v{r,(f) = К{г)Ф{(р) и разделяя переменные (см. Введение),
получаем
ф'' + z/Ф = О, (3)
Условие периодичности для Ф{(р) дает г/ = п^, где п — целое число.
Таким образом, функция R{r) должна определяться из уравнения
Бесселя
C[R] + XrR = 0 (m=l(rf)-yR) (5)

§ 2] КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ БЕССЕЛЯ 679
при граничном условии
ЯЫ = о (6)
И естественном граничном условии ограниченности в точке г = О
|Д(0)| < (Х). (7)
Полагая
X = л/Лг,
у{х) = Щг) =R[^^
(8)
приходим к уравнению
^1М)П'-^^|"=»- *'^''- <"
при дополнительных условиях
У
(\/Аго) = О, (10)
|у(0)| < (Х). (11)
Отсюда находим
у{х) = AJnix). (12)
В силу граничного условия у (гол/Л) = О имеем
MfJ.) = 0 (м = гол/л) . (13)
Это трансцендентное уравнение имеет бесчисленное множество
(п) (п) (п) 1) /-,4
вещественных корней /Ji , /^2 ? •••5 A^m , •••5 ? т. е. уравнение (1)
имеет бесчисленное множество собственных значений
AL")=('^^ (m = l,2,...), (14)
которым соответствуют собственные функции
R(r)=AjJ^r] (15)
краевой задачи (5) — (7).
^ На с. 766 дана таблица корней уравнения Jo(/^) = О, в частности первый
корень /i^°^ ^ 2,4048.

680 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Из способа построения собственных функций видно, что всякое
нетривиальное penienne рассматриваемой краевой задачи дается
формулой (15).
Из общей теории уравнений вида С[у] + Хру = О, рассмотренных
вып1е (см. Введение), следует ортогональность системы собственных
функций
Го
с весом г:
го
/
О
Jn ——^ r\jn\ ——^ г г б?Г = о при Ш1 ф Ш2. (16)
Вычислим норму собственных функций Ri{r) = Jn(<^i^), где ai =
= fJ'm /го. Попутно будет получено условие ортогональности (16). Для
этого рассмотрим функцию R2{r) = Jn(c^2^), где «2 — произвольный
параметр.
Функции Ri (г) и R2 (г) удовлетворяют уравнениям
d ( dRA f о п2\
d ( dRoX f r> n^
_2 \ I / ^,2
dr у dr
+ [air- —]R2 = 0,
причем Ri{ro) = 0, a R2{t) уже не удовлетворяет этому граничному
условию. Вычитая из первого уравнения второе, предварительно
умножив их соответственно на R2{t) и Ri{r), и интегрируя затем по г в
пределах от О до го, будем иметь
го
К - ^1) [ rRi{r)R2{r) dr + [г {R2R[ - RiR'2)]
о
откуда находим
го
го
/
„ D ^ roJn{oL2ro)aiJ'^{airo)-roJn{oLiro)a2Jn{oL2ro)
К1К2Т аг ^
Сх-| Схо
roJn{c^2ro)aiJn{c^iro)

§ 2] КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ БЕССЕЛЯ 681
Переходя к пределу при «2 —>■ «i и раскрывая неопределенность в
правой части, получаем выражение для квадрата нормы
\\R,f = \\Ua,r)\\' = J rRl{r)dr= ^ [j;(airo)f ,
или
7 / м X
Го
о ^ /
в частности, квадрат нормы функции Jq I —^ г 1 равен
V ^0 /
|лЧЛ')^
(п) (п)
Если положить «2 = —^^ ф 0L\— —^^ , то из формулы (17) сразу
Го Го
следует условие (16) ортогональности функций Бесселя.
Отметим, что имеются таблицы нулей /Jrn функции Jo(/i) и
соответствующих им значений Ji (/im ) (см. с. 766). Приведем несколько
первых значений fi^ • lA ^ 2,4048, /^2 ^ 5,5201, /ig ^ 8,6537, ii\ ^ «
?^ 11,7915.
Из асимптотической формулы (42) § 2 следует, что с возрастани-
(п) in) in)
ем номера т нуля /i^n разность /i^^i — lAn должна стремиться к тг.
П| " (0) /
Это можно проследить даже для нескольких первых значении jMn
(например, iif^ - /j'f^ ^ 3,1336, /jf^ - /j'f^ ^ 3,1378, /i^°^ - /j^Q^ ^ 3,1405 и
т. д.).
В силу общих свойств собственных функций краевых задач (см.
с. 666) имеет место теорема разложимости.
Всякая дваэюды дифференцируемая функция f{r), ограниченная
при г = О и обращающаяся в нуль при г = го, моэюет быть разло-
эюена в абсолютно и равномерно сходящийся ряд
ГХп) \
/(Г)= ^ArnJni^rV

682
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч.1
где
го
/
f{r)Jn
рттг
^0
Г \ Г dr
К
\Jn\?
и ||2 _ !i \v ("мЫ^
Вторая краевая задача для уравнения Бесселя
С[К) + \rR = О, R{r) ^ О,
i^'(ro) = 0, |i^(0)| <(Х)
решается аналогично. Собственные функции и собственные значения
также будут выражаться формулами (15) и (14), где под \Гш следует
понимать корень номера ттг уравнения
UiA = 0.
Собственные функции задачи ортогональны между собой с весом г
(см. (16)) и имеют квадрат нормы, равный
го
/
"I го
rdr
1-
{,Щ^
J:
п (/^т ) •
Аналогично решается и третья краевая задача. В этом случае для
(п)
определения /j^ получается уравнение вида
§ 3. Различные типы цилиндрических функций
1. Функции Ханкеля. Наряду с функциями Бесселя 1-го
рода Jjy{x) большое значение для приложений имеют другие
специальные виды решений уравнения Бесселя. К их числу относятся прежде
всего функции Ханкеля 1-го и 2-го рода: Н^ '(х) и Н^ (ж),
являющиеся комплексно-сопряженными решениями уравнения
Бесселя. С точки зрения физических приложений основной характеристикой
функций Ханкеля является асимптотическое поведение при больших
значениях аргумента. Поэтому мы определим функции Ханкеля как
цилиндрические функции, обладающие следующей асимптотикой:
V 7ГЖ
V 7ГЖ
,г (ж —7гг//2 —7г/4)
+
^(ж-7гг//2-7г/4)
+ ..
(1)
(2)

А.
РАЗЛИЧНЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ 683
где точками обозначены члены более высокого порядка малости
относительно 1/х. Условия (1), (2), в силу § 1, п. 4, определяют Н1 \х) и
Ни (х) однозначно. Разделяя действительную и мнимую части, пред-
(3)
ставим функции Ханкеля в виде
где функции
Мх)= \ [Я«(ж)+Я(2)(ж)]
N,{x)
2г
Hl'Hx) - Hl'Hx)
имеют асимптотический характер:
N^x)
(4)
(3')
(4')
(5)
(6)
ЧТО следует из формул (1) и (2).
Как будет показано ниже (см. § 4, п. 4), введенная здесь функция
Ju{x) является функцией Бесселя 1-го рода, рассмотренной в § 1.
Мнимая часть Njy (х) функции Ханкеля называется функцией Неймана
или цилиндрической функцией 2-го рода г/-го порядка.
Формулы (3) и (4) устанавливают связь между функциями
Ханкеля, Бесселя и Неймана, аналогичную связи между показательной
функцией мнимого аргумента, синусом и косинусом (формула
Эйлера). Асимптотические формулы (1), (2), (5) и (6) подчеркивают эту
аналогию.
Нри изучении решений уравнения колебаний
utt = a^{uxx +Uyy)
мы видели, что амплитуда v{x,y) установившихся колебаний
u{x,y,t) =v{x,y)e'''^
удовлетворяет волновому уравнению
к' =

684 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Если решение волнового уравнения обладает радиальной симметрией:
v{x, у) = v{r), то, как было отмечено в § 1, функция v{kr) удовлетворяет
уравнению Бесселя нулевого порядка.
Таким образом, функции
Я($'^ {кг)е'^' = J^ е' (^^+^") ^ + ... (у~г = е^"/^) , (7)
Н^^^ {кг)е'^' = W ^ е' (^^-^") лЛ + ... (8)
V тгкг
являются решениями уравнения колебаний, имеющими характер
цилиндрических волн. Функция Hq ' {кг)е^'^'^ соответствует
расходящимся цилиндрическим волнам, а функция Щ ' {кг)е^'^'^ — сходящимся
цилиндрическим волнам-'-^
Вторым важным свойством цилиндрических функций является их
(1 2)
поведение при ж —>- 0. В силу леммы 1 из Введения функции НЬ ' и
Ni, при ж —>- О обращаются в бесконечность (так как 7^/(0) конечно),
точнее, Н^^\х), Н^^\х), Щ{х) - 1п(1/ж), так как Jo(0) = 1 7^ 0; Н^^\х),
Hi {х)^ Njy{x) ~ 1/х^ при г/ > О, потому что Jjy{x) ~ х^ при х ^ 0.
Функции Ханкеля и Неймана нулевого порядка являются
фундаментальными решениями уравнения A2'L' -\- k^v = О, поскольку они
имеют нужную логарифмическую особенность при г = у ж^ + ^^ —>- О (см.
гл. Vn). Приведем (без доказательства) точные выражения для
главных членов разложения этих функций в окрестности точки ж = 0:
No{x) = - - In - + ..., H^^\x) = --ln- + ...,
7Т X 7Т X
Я^(х)=^1п1 + ...
7Г X
2. Функции Ханкеля и Неймана. Как было отмечено в п. 1,
всякое решение уравнения Бесселя нецелого порядка и выражается
через функции Jiy и J-iy. Установим связь между функциями Н1 , Н1 ,
А^^ и Л, J_^.
Так как всякое решение уравнения Бесселя при нецелом и можно
представить в виде линейной комбинации функций Ju{x) и J-i^{x), то
Hi^\x) = CiMx) + C2J-Ax), (9)
^ Если взять временной множитель е ^'^ , то расходящимся волнам
соответствует Hq \кг)е~^^^^ а сходящимся — Н^ \кг)е~^^^.

§ 3] РАЗЛИЧНЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ 685
где Ci и (72 — постоянные, подлежащие определению. Для главных
членов асимптотических разложений, очевидно, имеет место
аналогичное равенство:
^ ^г(ж-7гг//2-7г/4)
+C.^cos(x+|.-^). (10)
Преобразуем аргумент второго слагаемого к виду {х — 7гг//2 —
- 7Г/4):
/ 7Г 7Г\ Г/ '7Г 7Г\ 1
COS [х + — 1У — — = COS \[х — — 1У — — +7гг/ =
V 2 4/ LV 2 4/ J
/ 7Г 7Г\ . / '7Г 'ТГЧ .
! Ж — — г/ — — COS 7Г1У — sm [ X — — 1У — — sm тгг/.
V 2 4/ V 2 4/
cos
Сокращая обе части равенства (10) на ^J2pкx и пользуясь формулой
Эйлера для левой части, получаем
cos
— {С\ + (72 COS 7гг/) cos (^~":т^~т)~^2 sin тгг/ sin ( ж — — г/ — — J ,
откуда
или
С\ + (72 cosTTi/ = 1, —(72 sinvTi/ = г.
^2
smTTi/
_, cos7гг/- г sin7гг/ _, _-^
(И)
г smTTi/
Подставляя (11) в (9), находим
я^^\х) = - -^^ [Л(^)в-'"" - J-Л^)].
г smTTi/ "- -■
Аналогично
г smTTi/ ■- -■
Пользуясь формулой (4'), определяющей Njy{x), получаем из (12) и (13)
Jjy (х) cos 7Т1У — J-jy{x)
N,{x) =
smTTi/
(12)
(13)
:(13)
(14)

686
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч.1
Формулы (12), (13) и (14) получены нами для нецелых значений v.
Для целого значения г/ = п функции Ханкеля и Неймана могут быть
определены из (12), (13) и (14) с помощью предельного перехода при
г/ —>- п. Переходя в этих формулах к пределу при г/ —>- п и раскрывая
неопределенность по известному правилу, будем иметь
7Г
1^1 -(-!)'
1^1 -(-!)'
dv
dJ-г.
dv
1
7Г
ал
аг/
- (-1)"
dv
(12')
(13')
(14')
Пользуясь представлением функций J^^ и J_^y в виде степенных
рядов, можно получить аналогичные представления для Ni^{x), а также
Формулы (12) и (13) можно рассматривать как аналитическое
определение функций Ханкеля. Существуют, однако, и другие способы
введения функций Ханкеля. В § б будет дано представление функций
Ханкеля в виде контурных интегралов.
Если г/ = п + 1/2, то функции Ханкеля и Неймана выражаются в
конечном виде через элементарные функции. В частности, при г/ = 1/2
имеем
Ny^ix) = -J_v,(x) = -^Jf^ cosx = УА sin (х - I) ,
Hi^^i^) = Л/2(ж) + iNy^{x) = ^— [cos (x - I) + isin (x - |)] =
,J(a;-7r/2)
h[^^{x) = Jy^{x) - iNy^{x) = ^— [cos (x - I) - г Sin (x - |)] =
-г(ж-7г/2)
3. функции мнимого аргумента. Цилиндрические функции
можно рассматривать не только при действительных, но и при
комплексных значениях аргумента. В настоящем пункте мы рассмотрим
цилиндрические функции 1-го рода от чисто мнимого аргумента.

§ 3] РАЗЛИЧНЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ 687
Подставляя в ряд, определяющий Jjy{x), значение ix вместо ж,
получаем
^Л-) = г^ Е r(fe + l)rU.+ l) (2) = ^''^^f^'' (1^'
где
^^(-) = g r(fc + i)r(fc + . + i) [2) (^^'
— вещественная функция, связанная с Ju{ix) соотноп1ением
1^{х) = i-^J^{ix), или 1^{х) = е-^^^/2 Ju{ix).
В частности, при г/ = О
7.(x| = AM = l+(f)4pL (1)4^(1)'+..^ (171
Из ряда (16) видно, что 1и{х) являются монотонно возрастающими
функциями, имеющими при ж = О нуль г/-го порядка. Пользуясь
асимптотической формулой (5), получим, что для Ijy{x) должна иметь место
асимптотическая формула
ад.^^е^ (18)
при больп1их значениях аргумента х.
Аналогично вводится 1-^^{х). Функции 1^^ и /_^y при нецелом г/
линейно независимы, так как в точке ж = О при г/ > О функция 1у{х)
имеет нуль г/-го порядка, а I-jy{x) — полюс х~^. Если г/ = п — целое
число, то 1-п{х) = 1п{х).
Цилиндрические функции мнимого аргумента являются
решениями уравнения
И, В частности, функция /о (ж) удовлетворяет уравнению
у"+-у'-у = 0. (20)
Ж
Наряду с функцией Ijy{x) рассматривают функцию Макдональда
Kjy{x), определяемую с помощью функции Ханкеля чисто мнимого
аргумента
К^х) = ^TTie^"'/^ Hi'\ix). (21)

688 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Ki^{x) является вещественной функцией х. В самом деле, формулы (12)
и (13) дают
7Г
Kiy{x) = 7Г-- [1-1у{х) - Iiy{x)] при 1^ ^П,
д1-Л fdh
dv I,,__ V dv
(22)
Пользуясь асимптотическим выражением для Hi^ , находим
кл^) = ^ll^-^ + ■■■ (23)
Формулы (23) и (18) показывают, что К^^{х) экспоненциально
убывают, а Iv{x) экспоненциально возрастают при ж —>- оо. Отсюда следует
линейная независимость этих функций, а также возможность
представления любого реп1ения уравнения (19) в виде линейной комбинации
y = Ah{x)^BK^{x).
В частности, если у ограничено на бесконечности, то Л = О и ^ =
= BKjy{x); если же у ограничено при ж = 0, то5 = 0и^ = AIjy{x).
Из линейной независимости Ij^ и Kj^ следует, что Kj^{x) имеет в
точке ж = О полюс г/-го порядка {К^^{х) ~ х~^) при г/ т^ О и
логарифмическую особенность при г/ = 0. В п. 4 показано, что
Ко (ж) = In h ... при ж ^ 0.
X
На рис. 107 (с. 768) даны графики /о(ж) и К^{х). В отличие от
Jj^{x) и Njy{x) функции /г/(ж) И Kj^{x) являются монотонными (/г/(ж)
возрастает, а Kj,{x) убывает с ростом ж).
Наиболее важное значение имеет функция
К,{х)= уЯ«(г^).
4. Функция Kq[x). Покажем, что для функции Ко{х) справедливо
следующее интегральное представление:
сю
Ко(ж)= [ e-'^'^^^d^ {х>0). (24)
о
Нетрудно убедиться в том, что интеграл
сю
F{x)
о
сю
/'e-^<='^«dC (24')

§ 3] РАЗЛИЧНЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ 689
удовлетворяет уравнению
ЦУ) = у"+1у'-У = 0. (25)
В самом деле,
сю
о
сю сю
= f e-'^'^^sh^^d^- ^ f e-'''^^ch^d^ = Si-S2.
о о
Интегрируя второе слагаемое по частям, получаем
сю
X J X \о J
о о
откуда и следует
C{F) = 0.
Полагая ch^ = т/, преобразуем интеграл (24 ) для F{x) к виду
F{x) = / . dr].
1
Пользуясь этой формулой, можно выяснить характер поведения функции
F{x) при ж ^ оо. Производя еще раз замену переменной
x{n-\) = i,
получаем
сю
— ^ /. —С _г^
л/ж
При ж ^ оо
F{x) =
V^ J I
0 ^
e-«
'^(!-)
СЮ СЮ
0 0
Следовательно, при больпЕих значениях х
где е ^ О при ж ^ оо. Отсюда получаем асимптотическую формулу
F{x) = ^e-^ + ..., (26)
44 А. Н. Тихонов, А. А. Самарский

690 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
где точками отмечены члены более высокого порядка малости. Введенная с
помощью интеграла (24 ) функция F(x) является рептением уравнения (25),
ограниченным на бесконечности, поэтому
F{x) = ВКо{х).
Сравнение асимптотических формул для Kq(x) и F(x) показывает, что В = 1
и, следовательно,
сю
Ко{х)= [ e-'^'^^^d^ {х>0). (24)
о
Выясним характер функции Kq(x) при ж ^ 0. Представим интеграл
сю
J л/7/2 _1
Ko{x) = F{x)= / , ^ drj
1
в виде
сю
^°^^^ ^ / А 2 _ 2 "^^ ^^'^ ^ ^^-
X
Разбивая этот интеграл на три части:
А А
X X
где А — некоторая вспомогательная постоянная, видим, что первое
слагаемое равно
(в-^-
Л/Л2
-1) dX
— х^
сю
Ч
А
е-'
л/Л2
dX
— х^
A + VA^- х^ . ^
m = — m ж + ...,
X
а второе и третье слагаемые ограничены при ж ^ 0. Отсюда следует, что
Ко{х) = -1пж + ... = 1п^ +..., (27)
X
где точки означают слагаемые, остающиеся конечными при ж = 0. Таким
образом, функция Ко{х) является репЕСнием уравнения (25), имеющим
логарифмическую особенность в точке ж = О и экспоненциально убывающим при
ж -^ оо.
Следующая задача дает физическую интерпретацию функции Ко{х).
Пусть в начале координат действует стационарный источник
неустойчивого газа мощности Qq. Стационарный процесс диффузии сопровождается
распадом газа и описывается уравнением
Аи- >с и= -— [г^-)-\- -^ ^-^ - :и: и = 0 (28)
г or \ or J r^ о^р"^

§ 3] РАЗЛИЧНЫЕ ТИПЫ ЦИЛИНДРИЧЕСКИХ ФУНКЦИЙ 691
где (3 — коэффициент распада, D — коэффициент диффузии. Функция
источника этого уравнения обладает круговой симметрией и, следовательно,
удовлетворяет уравнению
I d ( du\
X ах \ ах J
кроме того, функция источника имеет логарифмическую особенность в
начале координат и ограничена на бесконечности. Отсюда следует, что функция
источника пропорциональна Ко{>сг):
С = АКо{:и:г). (29)
Для определения множителя А воспользуемся условием для источника
^lim / (-^^) ds = Qo, (30)
где интеграл слева выражает диффузионный поток через окружность Ке
радиуса е с центром в источнике. Подставляя в это условие вместо и функцию
G = АКо{>сг) и учитывая логарифмическую особенность функции Ко{х) при
ж = О, получаем
lim < - / D ^ ds\ = \im \в27геА-\ =27rAD = Qo.
е^О \ J or \ е^О I е )
Отсюда
Qo
2-kD
б=^КоЫ). (31)
Интегральную формулу (24) для Ко{х) можно получить, исходя из простых
физических соображений.
Рассмотрим нестационарную задачу диффузии газа с распадом. Пусть в
начале координат находится источник постоянной мощности Qg?
действующий начиная с момента ^ = 0. Будем предполагать, что в начальный момент
^ = О концентрация газа всюду равна нулю. Концентрация u{x,y,t) должна
удовлетворять уравнению
DAu-l3u = ut (32)
и соответствующим дополнительным условиям. Уравнение (32) при помощи
подстановки
и = ие ^
преобразуется в обычное уравнение диффузии
D Ай = щ,
44*

692 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
для которого функция влияния точечного источника имеет вид
^2
1
G= ^ в 4D(t-r) {D = a^).
Таким образом, функция влияния мгновенного точечного источника для
уравнения (32) равна
G .
Я е-шт^-/^(^-).
(2^^В{1-т)У
Функция влияния источника мощности Qo? непрерывно действующего от
^ = О до момента ^, дается формулой
t
.2
"^«"/i.i^^-"^-'"*-"-
О
Вводя новую переменную
получаем
t
^D J
G= -^ I е-шо-^^
4:7VD
о
Функция источника, соответствующая стационарной задаче, может быть
найдена предельным переходом при ^ ^ оо в предыдущей формуле:
^ Qo [
AttD J
r± 1
..... ^ , ^ 4D ^
t^oo AttD / 9
G= \im G= -^ I e~tDn -P^
Преобразуем этот интеграл при помощи подстановки в = Се^ (где С —
некоторая постоянная):
оо г 2
4:7ГВ J
— СЮ
Требуя, чтобы выполнялось равенство
находим
_ . . _ ^^ _ г I /3 _ >сг
2л/ДО iDC
вС- -^^ - — (х^-^\
^^" 2 V Д " 2 У" - d)-

§ 4] ПРЕДСТАВЛЕНИЕ В ВИДЕ КОНТУРНЫХ ИНТЕГРАЛОВ 693
Отсюда следует, что стационарная функция источника имеет вид
сю сю
-оо о
Таким образом, рассмотренная здесь задача приводит к интегральному
представлению (24) для функции Ко{х).
§ 4. Представление цилиндрических функций
в виде контурных интегралов
1. Контурные интегралы. Рассмотрим уравнение колебаний
Utt = o?{uxx + "^уу) = а^^2^ и будем искать его решение в виде
u{x^y^t) = г'(ж,^)е*^^; для v{x^y) получим уравнение А2г' + k'^v = О
{к = uj/a). Его частными решениями являются функции v = е^*^^ и
V = е^'^^У — амплитуды плоских волн и = е*(^^±^^) и и = е*(^^±^^) ^
распространяющихся соответственно вдоль оси х и вдоль оси у. Плоская
волна, распространяющаяся в направлении /, очевидно, имеет вид
—ik{\r) —ik{x cos (р-\-у sirup) —ikrcos{ip — a)
x = rcosa, ^ = rsina, 1 = (cos(/?, sin(/?).
Если a = 7г/2, TO на оси у амплитуда волны, падающей под углом ip к
оси ж, равна
^^^-ikrsin^^ (1)
Будем искать решение Zj^{x) уравнения Бесселя
L{y) = х^у" + ху' + {х^ - и^)у = О (2)
В виде суперпозиции плоских волн вида (1), считая при этом (р = (pi -\-
-\- i(f2 комплексными и обозначая кг = х. Положим
Z,{x) = j K{x,^)^,{^)d^ = I е-^-^-^ФЛ^)^^, (3)
с с
где С — некоторый контур на плоскости (р = (pi -\- г(/?2, К{х,(р) =
_ ^-гх8Ш(р^ ^и{^) — не определенный пока фазовый множитель.
Выберем С так, чтобы интеграл (3) сходился, а Фи{^) так, чтобы этот
интеграл удовлетворял уравнению Бесселя. Пайдем сначала Ф^^ ((/?),
предполагая, что интеграл (3) сходится и его можно дифференцировать под
знаком интеграла. Вычислим L{K). Замечая, что K^^ = —ix cos (рК,
К^^ = ix sin (рК — х^ cos^ (рК, Кх = —i sin (рК, К^х = —siv?(pK^
получим х'^Кхх + хКх + х'^К = К{х'^ cos^ (f — ix8in(p) = —К^^, L{K) =
= — (г/^Х + К^р^р) и, следовательно,
L{Z,) = - f {К^^ + и''К)Ф,{^) d^.
с

694
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч.1
Проинтегрируем по частям, считая, что подстановки обращаются в
*^2
Рис. 95
нуль (на бесконечности, если контур уходит в бесконечность):
{Ф'1 + рЧ,}К dip.
h
Для того чтобы L{Zi^) = О, достаточно, чтобы
Выберем Ф^ = е^^'^. Тогда Z^{x) = /^ e-i^smv^+i^^v. ^^^ ДJ^^ сходимости
этого интеграла достаточно, чтобы
Re{ix sin(р) = Re{ix sm{(pi -\-i(p2)) = —xcosipi sh(/?2 > 0 {^ = ^i -\-i^2)-
Это условие выполнено при ж > О, если
7Г 7Г
либо (/?2 < О, ~ "^ + ^^^ < V^l < ТТ + 2^^5
(4)
либо (/?2 > о, — + 2к7г < (fi < ——h 2к7г;
к = ±1, ±2, ...
На рис. 95 области, по которым должен проходить контур,
заштрихованы. В качестве контура С можно взять любой контур,
асимптотические ветви которого лежат в заштрихованных областях.

4] ПРЕДСТАВЛЕНИЕ В ВИДЕ КОНТУРНЫХ ИНТЕГРАЛОВ 695
2. Функции Ханкеля. Выберем два контура: Ci — контур,
состоящий из луча (—г(Х),0), отрезка (О, —тг) и луча (—тг, —тг + гоо), а
контур (72 = (гоо + 7г,7г) + (7г,0) + (О, —гоо) (рис. 96).
Соответствующие интегралы (3) определяют цилиндрические функции
-гх sin ip-\-ivip
dip,
к = 1,2.
(5)
В п. 4 будет показано, что определенные при помощи контурных
интегралов (5) функции Н1 (х) совпадают с функциями Ханкеля,
которые были введены в § 2. Для этого достаточно будет убедиться в
том, что функции (5) имеют асимптотику
Hi'^ (^) = \[^ е-" + ..., Я(2) {х) = J^ е--" + ...,
(6)
7Г 7Г
Пользуясь определением (5) функций Ханкеля Н^ ' (ж), можно
получить для них рекуррентные формулы
Выведем первую формулу. Замечая, что ^v+i + Ф
^IVip
, и интегрируя по частям.
находим
V-1
А^'
2С08(/?Ф^, Ф^
7Г + ioo
- I e-^^^^"'^+^^'^cos(/?^(/?:
Ck
2v r
X7T J
Ck
-ix sin (p-\-ii'(p
2v
d(f
Из (5) и формулы Jy{x) = {ш +
+ Hi ^)/2 можно получить
представление в виде контурного
интеграла для функции Бесселя J^, {х), полагая
Со
-ix sin (fi-\-iu(fi
df, (7)

696 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
где Со = Ci -\- С2 — контур, состоящий из луча (тг + г(Х),7г), отрезка
(тг, —7г) и луча (—7г, —7г + гоо). Направление обхода указано на рис. 96.
Чтобы убедиться в том, что интеграл (7) в самом деле дает
функцию, совпадающую с введенной в § 1 функцией Бесселя, надо показать,
что он разлагается в степенной ряд (15) из § 1. Для этого нам
понадобятся некоторые свойства гамма-функции.
3. Некоторые свойства гамма-функции. Гамма-функция
r(s), как известно, есть интеграл
сю
rW=/e-V-..., (81
о
где S, вообще говоря, комплексный аргумент, причем Res > 0. Помимо
элементарных свойств"*^^
Г(1) = 1, r(J\=V^, r(s + l) = sr(s) и т. д.,
нам понадобится свойство
r(s)r(l-s)= -,^. (9)
smTTS
В самом деле.
CXD CXD
rWr,I-,)=//e-"«V-H-...<.
о о
Будем рассматривать этот интеграл как двойной интеграл и
произведем замену переменных, полагая ^ = х -\-1, г] = x/t. Вычисляя ^хШ —
— ^tVx = — (1 + 'n)/tj получим dxdt = — d^ dr] и
сю сю сю
0 0 о
Интеграл, стоящий справа, вычисляется при помощи вычетов и равен
Для гамма-функции имеет место представление в виде контурного
интеграла (интеграла Римана — Ханкеля)
Г{з) = {е'^^' - 1) ' / е~^^"~^ d^^
(10)
^ Будак Б. М., Фомин СВ. Кратные интегралы и ряды. М., 1967.
^^ Лаврентьев М. А., Ша
плексного переменного. М., 1973.
' Лаврентьев М. А., Шабат Б. В. Методы теории функций ком-

4] ПРЕДСТАВЛЕНИЕ В ВИДЕ КОНТУРНЫХ ИНТЕГРАЛОВ 697
ук
= -Ф
Се
где 7 — любой контур (на плоскости комплексного переменного (f =
^1 + ^^2) указанного на рис. 97 вида; этот контур идет из +00, обходит
вокруг точки (/? = о и возвращается опять на +оо. Подынтегральная
функция f{(f) = e-'^(f'-^ = е-'^е^^-^)^"'^
комплексного переменного (р имеет точку
ветвления (f = 0. Проведем разрез вдоль
положительной части вещественной оси, полагая arg(/?
= О на верхнем берегу разреза и arg (/? = 27г на
нижнем берегу разреза. В силу теоремы Ко-
ши контур 7 можно без изменения величины
интеграла J f{(p) d(p произвольно деформировать, сохраняя обход
вокруг точки (/? = О и удерживая концы контура на +оо. Выберем в
качестве 7 контур, состоящий из луча (+00, г) на верхнем берегу
разреза, окружности Cs с центром (/? = О и радиусом е и луча (г, +оо)
вдоль нижнего берега. Тогда /((/?) = е~'^+(*~^)^"'^ на верхнем берегу
и /((/?) = е(*~-'-)^^*~'^+(*~-'-)^"'^ на нижнем берегу, где \п(р принимает
вещественные значения, так что
Рис. 97
/
f
-^ip
е сю
f е-^'х'-^ dx + е("-1) 2xi f ^-^j.s-1 dx+ f e-'^ip'-^ dip.
(11)
Покажем, что интеграл по С^ стремится к нулю при г —>- О, если
Res > 0. В самом деле, \е~'^\ на С^ ограничен:
1Г
= ^iso-l)\n\(f\-siarg(f _ ^

SCSI arg (р
S = So -\- isi,
I
Се
е-^^'
-^dif
< Л27гг"0е-"1^^§^^ ^0
при
г^О (so>0).
Поэтому предельный переход в (11) приводит к (10).
Формула (10) определяет справа от мнимой оси аналитическую
функцию T{s). В силу аналитического продолжения формула (10)
справедлива на всей плоскости и V{s) представляется в виде частного двух
целых функций. При s = —п (п ^ 0) функция V{s) имеет полюса.
Справедлива формула
Т{8
1 piTTS г
+ 1) 2тп J ^ ^
(12)

698 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Она следует из (9) и (10). В самом деле,
Т{8 + 1)
2ш (е-2^^^
7 7
4. Интегральное представление функции Бесселя.
Покажем теперь, что функция
Л(ж) = - - [ е-^^^^"'^+^^'^^(/? (13)
Со
разлагается в ряд (15) из § 1. Для этого преобразуем контур Со
(см. с. 696), полагая Р = -^ g-nv?-^) (^ > 0). Из таблицы
^
р
гоо + 7г
00
7Г
X
2
7Г
2
^ pi7r/2
2
0
2
— 7Г
^ ^г27г
2
—7г + гоо
00
видно, что Со преобразуется в контур 7? показанный на рис. 98 и
состоящий из луча (+оо,ж/2), окружности С* радиуса 0,5ж и луча
(0,5ж,+оо). Вычисляя
^ 2г ^ ^ 2 V2p ж у 4р ^'
преобразуем интеграл (13) к виду
7
Разложим ехр [х^ /Ар) в степенной ряд и подставим в (14):
■''W = -i ё wr «'-7'""''"'""''*•
Пользуясь затем формулой (12) для 1/V{k + г/ + 1), получим
^"^^^ " ^^"^^ Г(А; + 1)Г(г/ + А; + 1) UJ

§ 4] ПРЕДСТАВЛЕНИЕ В ВИДЕ КОНТУРНЫХ ИНТЕГРАЛОВ 699
Таким образом, функция (13) есть функция Бесселя Jjy{x), введенная
в § 1, п. 1. Преобразуем интеграл (13),
разбив его на три части: по оси (pi (от —тг до р^ ^
7г) и по бесконечным ветвям. Для вычисле- С*{^^^ ^ -
ПИЯ интеграла по ветвям (гЬтг + гоо) введем
новую переменную, полагая соответственно Pi^c. 98
(/? = г^ =Ь 7г. В результате получаем для функции Бесселя г/-го порядка
следующее интегральное представление:
7Г СЮ
27Г J 7Г J
-7Г О
Если и = п — целое число, то sinvri/ = О и
Jn{x)
7Г
— [ е-'''''''^^'''^dip. (16)
27Г J
Отсюда, в частности, следует, что для плоской волны е ^^^^^^
имеет место разложение в ряд Фурье
сю
п= — оо
так как (16) есть формула для коэффициента Фурье этого разложения.
Полагая (р = ф -\- 7т/2 и учитывая, что в силу периодичности
подынтегральной функции в (16) интегрирование можно производить по
любому промежутку длиной 27г, получаем вторую интегральную формулу
^п\Х ^
7Г
= — / e-^^^^^^+^^^^V^, (17)
которая соответствует следующему разложению плоской волны:
сю
n= —СЮ
в частности, при п = О имеем
7Г
Jo (ж) = ^ I e-^^^^^^^V^. (18)
27Г J
— 7Г
5. Интегральное представление К^{х). Покажем, что для
функции Макдональда Kjy{x), определяемой по формуле (см. § 3)
К,{х) = ^TTie-'"'/^ Hi'Hix), (19)

700
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[4.1
справедливо интегральное представление
1
к.
^Лх)= \ I е-^'^^^-^и^, х>0.
(20)
Отсюда видно, что К^^{х) — вещественная монотонно убывающая
положительная функция. При г/ = О формула (20) дает
сю
ch4
dC
(21)
Для доказательства (20) обратимся к (19) и представлению (5)
для функции Н1 \ Пусть Ci,^ — контур (рис. 99), у которого верти-
Рис. 99
кальные части пути Ci вместо — тг и О имеют абсциссы —тт — ф и ф
{ф < 0); в частности, Ci^o = Ci. В силу теоремы Konin замена Ci в
(5) контуром Ci^^ не влияет на значение интеграла, если при
больших |(/?2| выполнено условие сходимости интеграла Re{—ixsm(p) < О,
где X = xi -\- ix2j (f = (fi + i(f2- В силу (19) нас интересует функция
Ханкеля Н1 (ix) чисто мнимого аргумента. Условие сходимости при
Ж1 = О, ж = ix2, (р = ф имеет вид Х2 simpi ch(p2 < О или Х2 ^шф < 0.
Мы выберем контур Ci^_7r/2 при ф = —7г/2. Заменим Ж2 на ж и введем

§ 4] ПРЕДСТАВЛЕНИЕ В ВИДЕ КОНТУРНЫХ ИНТЕГРАЛОВ 701
новую переменную интегрирования ^, положив ^ = —7г/2 + г^; тогда
dip = i б?^, simp = cosi^ = ch^ и интеграл (5) по Ci,^ примет вид
сю
7гг J
ch^-z/^
сге
Отсюда и из (19) следует (20).
6. Асимптотические формулы для цилиндрических
функций. Пользуясь методом перевала-'^^ покажем, что для функций
Hiy ' (ж), определяемых при помощи контурных интегралов (5),
справедливы при больших значениях вещественного аргумента х > О
следующие асимптотические формулы:
Яа)(.)=уТ,.(™/2-./4)+0(-1.)
V 7ГЖ \Х /^
} х>0. (22)
Отсюда в силу § 1, п. 4 будет следовать, что функции (5)
тождественно совпадают с функциями Ханке ля, введенными в § 3 при помощи
формул (12), (13).
Из формул н1 '' = Jjy -\- iNy^ н1 ^ = Jjy — iNy и (22) следуют
асимптотические формулы для функций Бесселя Jj^ (ж) и функций Неймана
J.(.)=yAcos(.-|.-^)+o(-L), (23)
Ar.(.)=/Asin(.-|.-5)+0(-L). (24)
Напомним, что в п. 4 мы доказали тождественность функций
Ju{x), введенных при помощи контурных интегралов, с функциями
Ju{x), введенными в § 1 при помощи рядов.
При выводе асимптотических формул (22) мы будем пользоваться
контурными интегралами (5). Рассуждения достаточно провести для
Hiy ' (х). Подынтегральная функция
^-ix sin (p-\-iu(p X > О
В формуле (5) не имеет особенностей в конечной части плоскости
комплексного переменного (р.
^ Лаврентьев М. А., Шабат Б. В. Методы теории функций
комплексного переменного. М., 1973.

702
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч.1
Поэтому в силу теоремы Коши контур интегрирования в
конечной плоскости можно произвольно деформировать при условии, что
асимптоты ветвей контура, уходящих в бесконечность, лежат в тех же
зап1трихованных полосах плоскости (/?, что
и для контура Ci. Если выбранный контур
Ci целиком лежит в зап1трихованной
области (рис. 100), то во всех точках, где simp ф
Ф О, подынтегральная функция
экспоненциально стремится к нулю при ж —>- оо, так как
Imsin(/? < 0. Если отдельные части контура
проходят по незаштрихованной области, то
на этих частях в подынтегральном
выражении происходят сложные
интерференционные явления.
Для выяснения асимптотического
поведения функции Ну \х) при больших
значениях аргумента х целесообразно контур С\
выбрать так, чтобы он целиком лежал в
заштрихованной области. Такой контур,
очевидно, пройдет через точку —7г/2, в которой действительная часть
Re(—isin(/?) = cos (/?i sh (/?2 обращается в нуль. При ж —>- оо
подынтегральная функция в окрестности этой точки не ^тремится равномерно
к нулю, поэтому главной частью интеграла по С\ при ж —>- оо является
интеграл по малой дуге, содержащей точку ^ — — 7г/2. Поэтому С\
следует выбрать так, чтобы на нем множитель е-^^^шс/? убывал наиболее
быстро при удалении от точки ^ — —^к 12. Рассмотрим «топографию»
функции e-*^sin(/? g окрестности ^ — —7г/2. Положим ^ — —7г/2 + se^^.
Для малых значений s найдем
Рис. 100
г sin (/? = г cos(se'^) = г 1 - — е"^'^ +
jiie
2 /2
у sin 2i9 + г И - у cos 2i9 ) + ...
Для действительной части Re(—г sin(/?) = 1/2 • s^ sin 2^ точка s = О
является седловой точкой: в заштрихованных полосах эта функция
отрицательна, в незаштрихованных областях — положительна, а при s —
= О ((/? = —7г/2) обращается в нуль. Направление в = во = —7г/4,
очевидно, будет направлением наибыстрейшего спуска (убывания) для
функции s^/2 • sin2^. Отсюда следует, что и для модуля функции е"*^^^"'^
точка S = О является седловой, а ^о = —'7г/4 соответствует направлению
быстрейшего спуска.
Выберем контур Ci так, чтобы он содержал прямолинейный
отрезок Cis {—е < S < е), проходящий через точку s = О {(р = —'7г/2) под

§ 5] ИНТЕГРАЛ ФУРЬЕ — БЕССЕЛЯ 703
углом ^0 = ~'7г/4, а его ветви, уходящие в бесконечность, целиком
лежали в заштрихованных областях (рис. 100).
Подынтегральная функция в (5) экспоненциально убывает при
удалении от точки s = 0. Поэтому с точностью до экспоненциально
убывающего слагаемого можно написать
е
Я^1)(ж) = -- [ е-'''''''^^'''^dip^ - / e^(-^'/2+^)-^^^/2^se-^^/^
так как вдоль Cis (р = —7г/2 + se~*^/^, d(p = e~^^^^ds, —isiiKp «
« —s^/2 + г, e*^'^ « ^-гг/7г/2^ ^ ^ изменяется от г до —е. Введем
обозначения ^ = 8уж72, б?^ = ^/xJ2ds, а = л/х/2. Тогда
7Г V ж У
-С^
dt
Если ж —>- 00"*"^, т. е. а —>- 00, то J^*^ е ^ d^ ^ J^ е ^ d^ = л/тт.
Отсюда находим первый член асимптотической формулы (22). Следующие
члены разложения можно получить, если взять члены более
высокого порядка малости относительно s. Оценка 0{1/х Z^) для остаточных
членов в (22) следует из § 1, п. 4.
Отметим, что изложенный выше метод перевала, или метод сед-
ловой точки, применим для получения асимптотического разложения
ряда других функций, представимых в виде контурных интегралов, а
также для ii^) ^ [х) при г/ « ж ^ оо.
§ 5. Интеграл Фурье — Бесселя и некоторые интегралы,
содерлсащие функции Бесселя
1. Интеграл Фурье — Бесселя. Пайдем разложение заданной
функции /(г) в интеграл по функциям Бесселя. Интеграл Фурье для
функции f{x) и, соответственно, для функции двух переменных /(ж, у),
^ Ошибка, допускаемая при замене конечных пределов бесконечными,
имеет экспоненциальный характер убывания, так как
сю
/
е~^ d^^e~^ /2z.

704 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
как известно, имеет вид
сю сю
/(ж) = ^ I df, I /(бе*''*»^-?)^^, (1)
-СЮ —сю
сю сю сю сю
— СЮ —сю —сю —сю
Введя полярные координаты с помощью соотноп1ений
ж = г cos (/?, С = Р cos -0, /i = л cos в,
у = rsiiKf; V = Р sin ф; fi' = X sin О,
получим
/ix + fi'y = Лг cos(^ — ^)j А^С + /^'^ = ^Р cos('0 — 0).
Предполагая, что f{x,y) имеет вид
/(ж,2/) = /(r)e-^ (3)
где п — целое число, и преобразовывая с помощью написанных выше
соотношений интеграл Фурье (2), находим
сю сю 7Г
/(г)е*"*'= f I f{p)pdpXdX-^ /■ giArcos(e-v) +
in{e-v) ^Q . ginv X
0 0
n
X __ / g-iApcos(V^-6')+in(V^-6') ^^^ /^\
— 7Г
Воспользуемся формулами (см. (16), (17) из § 4, п. 4)
7Г
J„(^) = ^ I е*^<=°«^+*"^е-*'^"/2 сгб» Гб» = (^ - |V (5)
— 7Г
7Г
J„(^) = ^ / е-*^™'*^'+*"^'е*'^"/2 сгб»' (6* = 7Г + 6»'). (6)

§ 5] ИНТЕГРАЛ ФУРЬЕ — БЕССЕЛЯ 705
Так как подынтегральные выражения в (5) и (6) являются
периодическими функциями в VL в' VL интсгрировать поэтому можно по любому
промежутку длиной 27г, то можно написать
7Г
7Г
27Г J
— 7Г
где во и O'q — произвольные числа. Подставляя (7) и (8) в (4) и
сокращая обе части на е^'^^, получаем интеграл Фурье — Бесселя
сю сю
/(г) =11 f{p)Jn{\p)Jn{\r)\d\pdp, (9)
О о
или
сю сю
/(г) = / ip{\)Jn{\r)\d\ где (/^(А) = / f{p)Jn{Xp)pdp.
о о
Для того чтобы разложение в интеграл Фурье — Бесселя было
возможно, достаточно потребовать, чтобы для функции /(г),
определенной в промежутке (О, оо), выполнялись следующие условия:
1) /(г) непрерывна в промежутке (0,(Х));
2) /(г) имеет конечное число максимумов и минимумов во всяком
конечном промежутке;
3) существует интеграл
сю
I P\fip)\dp.
О
На доказательстве этого мы не останавливаемся.
2. Некоторые интегралы, содерлсащие функции Бесселя.
В различных приложениях часто встречаются определенные
интегралы, содержащие бесселевы функции.
К числу наиболее распространенных интегралов этого типа
принадлежит интеграл
сю
Bi= [ е-^^МрХ) dX = -т^= {Z > 0). (10)
J Jp^ + z^
о ^
45 А. Н. Тихонов, А. А. Самарский

706 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Для доказательства этой формулы заменим функцию Jo ее
интегральным выражением ((16) из § 4) и затем изменим порядок
интегрирования:
сю сю 7Г
Bi= I e-'^JoipX)dX = ^ I e-'^dX f е-'Р^'''^^ dip =
7Г СЮ
= ^ f d(f f е-(^+^^«^"'^)^^Л= ^ /
dip
z -\-гр sm if
-7Г 0 —7Г
7Г 7Г 7Г
1 Г zd^p i f psm(fd(f If
27Г У z^ -\- p^ sin^ Ш 27Г У z^ -\- p^ sin^ ю тг J z^ -\-
zd(f
27Г У z^ -\- p'^ sin^ (/? 27Г У z^ -\- p^ sin^ (/? "к j z^ -\- p^ sin^ (/? '
— 7Г —7Г 0
так как
7Г
/
sin ^d^
z'^ + p^ sin^ (f
в силу нечетности подынтегрального выражения.
Полагая сначала tg(/? = ^, а затем у — ^ = г], получаем
7г/2
^ . 2;б?(/? 2z f dip
Bi — —
1 Г 2;б?(/? 2z f
7г У z^ -\- р"^ sin^ (/? тг у
о о
2;^ + р^ sin^ (f 7г J z^ -\- р"^ sin^ (р
_ 2z Г d^ _ 2 Г dr] _ 1
о ^0 V г
тем самым формула (10) доказана. Пользуясь (10), сразу же находим
Полагая в формулах (10) и (11) z = га ж разделяя действительную и

А
ИНТЕГРАЛ ФУРЬЕ — БЕССЕЛЯ
707
мнимую части, получаем ряд следствии:
сю
1
О
сю
/л
COS аХ dX =
л/р^ - «2
(рЛ) sinaAc^A = О,
/ Л(рЛ)
о
сю
/ Ji(pA)si
cos аХ dX
sin аА dX =
р V^p2 _ д2
> при р > а; (12)
сю
о
сю
(рА) cosaAc^A = О,
(рА) sin аА dX
лА^^
сю
I МрХ)
COS аА б?А = - 1
Р \
л/а^ - Р^ ^
/ Ji(pA)si
sin аА б?А = О
> при а > р. (13)
Докажем вторую интегральную формулу
в, = /л(л.).-""л-'.л=1(|^)
1 /р\^ р2
(14)
Подставим в эту формулу вместо Jj^ степенной ряд и произведем
почленное интегрирование {t > О!):
52 = Е
(-1)'
fc=0
Г(А; + 1)Г(А;
СЮ
+ 1^-^А
е-*'' ^А.
45*

708 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. I
Вычисляя вспомогательный интеграл
сю сю
0
получаем
В2 =
0
. 1 (pYy- (-1)'
к=0
р^\^ _ 1 [ру -р^
и) ~ 2t \2t) ^ ^'
что и требовалось доказать.
Отметим, что вычисление Bi можно провести аналогично,
разлагая бесселеву функцию в ряд и производя затем почленное
интегрирование.
Рассмотрим интеграл
сю
С= J MXp)-^==^XdX. (15)
О
Нетрудно убедиться, что он является решением уравнения
/ Q2 Q2 02
\ аж^ оу"^ oz"^ J
Функция
oikr
также удовлетворяет волновому уравнению (г > 0)
^0
г
Ai;o + k^VQ = - тгт (^^о) + к^Щ =-к^ -— + k^vo = 0.
Разложим функцию vo{p) = е^^^/р в интеграл Фурье — Бесселя:
сю
[ F{X)Jo{pX)XdX, (16)
Р
где
сю
Р{Х)= 1 e"'PMXp)dp. (17)

полиномы ЛЕЖАНДРА
709
Для вычисления функции F{X) воспользуемся формулами (12):
сю
^W — / Jo{^p){(^o^kp-\-i^inkp) dp =
л/А2 - к^ '
I Vk^ - Л2 л/А2 - к^ '
если
если
Таким образом,
т. е. функция
сю
XdX
\/Л2 - А;2
Л > А;,
fc>A.
(18)
i;o =
совпадает с интегралом C{p^z) при 2; = 0. Итак, обе функции vo{p^z)
и С(р, 2;) являются реп1ениями волнового уравнения, совпадают при
2; = О и имеют в точке 2; = О, р = О одинаковую особенность.
Отсюда следует, что они тождественно равны друг другу, т. е.
I
Jo (Ар)
\/Л2 - fc2
AdA
(19)
Полученная формула широко применялась А. Зоммерфельдом в
физических исследованиях и часто называется формулой Зоммерфельда.
ЧАСТЬ II
СФЕРИЧЕСКИЕ ФУНКЦИИ
Сферические функции были введены в связи с изучением
решений уравнений Лапласа, и в частности с теорией потенциала. В § 1 мы
рассматриваем полиномы Лежандра, которые используются затем для
построения шаровых и сферических функций в § 2. Сферические
функции являются весьма мощным аппаратом для решения многих задач
математической физики.
§ 1. Полиномы Лелсандра
1. Производящая функция и полиномы Лелсандра.
Полиномы Лежандра тесно связаны с фундаментальным решением уравнения

710
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
Лапласа 1/i^, где R — расстояние точки М от фиксированной точки
Рис. 101
Мо. Пусть г и Го — радиусы-векторы точек М и Mq , а,в — угол между
ними (рис. 101). Очевидно, можно написать
R л/г1 -\-г^ — 2гго cos о
1
1
^0 л/1-\- р^ - 2рх
для г < Го,
(1)
ч/гт;
2рх
для
> ^0,
где X = cos^ (—1^ж^1) VL р = г/Го < 1 или р = Го/г < 1 (в обоих
случаях р меньше единицы).
Функция
Ф(р,ж)
л/1 + р^ - 2рх
(0<р<1, -1^ж^1)
(2)
называется производящей функцией полиномов Лежандра.
Разложим функцию Ф(р, ж) в ряд по степеням р:
np,x) = Y,Pn{x)p''.
(3)
п=0
Коэффициенты Р^ (ж) разложения (3) являются полиномами п-й
степени и называются полиномами Лежандра.
В силу теоремы Коши из формулы (3) следует, что
Рп{х)
1 а^Ф
п! др""
Р=0
2т J
2т J С"+^
с
(4)
где С — любой замкнутый контур в плоскости комплексного
переменного С = ^ + гту, содержащей точку ( = 0. Полагая ^/1 — 2х( + С^ =
= 1 - С^, находим ( = 2{z - x)/{z^ - 1), dC = 2(1 - (z) dz/{z^ - 1),
4f{C,x)dC = 2dz/{z'^-l).
Формула (4) примет вид
1 М^^ -1)"" ,
(5)

iL
полиномы ЛЕЖАНДРА
711
где Ci — любой контур, окружающий точку z = х.
Учитывая, что
27ri J
{z^ - ly
z — X
dz = [x^ - 1)^,
и пользуясь формулой для производной
d"" г (z'^ -IT , , f U^ - l)"" ,
-— / dz = nl / ——r dz,
dx'' J z-x J (^-ж)^+1
получаем из (5) формулу для Рп{х):
1 d^
Из формулы (6) непосредственно видно, что: 1) Рп{х) есть
полином степени п; 2) Рп{х) содержит только степени х той четности, что
и номер п, так что
Р„{-х) = {-1ГРп{х). (7)
Полагая х = 1, находим
Ф
^ сю
{р,1) = -,— = i+p+...+p" + ... = j2Pn{i)p'',
1 — р ^
п=0
Т. е. Рп{1) = 1, и в силу (7)
Формула (6) называется дифференциальной формулой для
полиномов Лежандра или формулой Родрига.
Заметим, что из (1) и (3) следует разложение потенциала
1
R
( 1_
Го
Е
п=0
PnicosO) при г < Го,
^ сю
- Х^ ( —) PnicosO) при Г>Го.
(8)
п=0
2. Рекуррентные формулы. Дифференцируя Ф(р, ж) по р и ж,
получаем два тождества:
(1 - 2рх + р2) ф^ _ (^ _ ^) ф = о.
(9)
(10)
Запишем левую часть формулы (9) в виде степенного ряда
относительно р, подставив в нее ряд (3) для Ф и ряд Фр = J^^o(^ + l)^n+i(^) р^.

712 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Коэффициент при р^ полученного ряда, в силу (9), равен нулю при
всех х:
(п + 1) Pn+i{x) - х{2п + 1) Рп{х) + nPn-i{x) = 0. (11)
Это тождество есть рекуррентная формула, связывающая три
последовательных полинома. Она позволяет найти последовательно все Рп (х)
(п > 1), если учесть, что (6) дает
Ро(ж) = 1, Pi{x)=x.
Так, например, полагая в (11) п = 1, находим Р2{х) = 1/2 • (Зж^ — 1)-
Выведем еще две рекуррентные формулы:
пР„(ж)-жр;(ж) + р;_1(ж) = о,
или
Р:,_,{х)=хР:,{х)-пРп{х), (12)
Р;(ж) - хР;^_,{х) - nPn-i{x) = 0. (13)
Исключив из (9) и (10) Ф, получим тождество рФр — (ж — р)Фж =
= О, из которого сразу следует (12), если в левую часть этого тождества
подставить ряд (3) и приравнять нулю коэффициент при р^.
Дифференцируя затем (11) по х и исключая P^_i = жР^ — пРп, получаем
Рп-\-1 ~ хР'п — {п -\- l)i^n = О ИЛИ (13) после замены п + 1 на п.
3. Уравнение Лелсандра. Найдем дифференциальное
уравнение, решением которого является Рп{х). Для этого исключим Pn-i и
Рп-1 из (12) и (13). Сначала подставим P^-i из (12) в (13):
Р; - жР;_1 - пРп-1 = (1 - ж')Р; + пхРп - пРп-1 = О,
затем продифференцируем полученное тождество по ж и еще раз
применим формулу (12) для P^-i'-
[(1 - Ж2)Р^]' + ПхР:, + пРп - ПР'„_^ =
= [(1 - х^)Р^]' + nxPl, + пРп - (пхР^ - п'^Рп) = 0.
В результате приходим к уравнению
[(1-ж2)р;]'+п(п + 1)Р„ = 0. (14)
Тем самым доказано, что полиномы Лежандра Рп{х) являются
собственными функциями, соответствующими собственным
значениям Л^ = п(п + 1), следующей задачи.
Найти такие значения Л, для которых на отрезке — 1 ^ ж ^ 1
существуют нетривиальные решения уравнения Леэюандра
d
dx
2 ч dy
^'-^'dx
+ Лу = 0, -1<ж<1, (15)

§ 1] полиномы ЛЕЖАНДРА 713
ограниченные при х = ±1 и удовлетворяющие условию нормировки
2/(1) = 1-
4. Ортогональность полиномов Лелсандра. Уравнение Ле-
жандра (15) является частным случаем (при q = О, р = 1, к{х) = 1 — ж^)
рассмотренного во Введении уравнения
(Мх)у'У-д(х)у + Хр(х)у = 0. (16)
Поэтому к нему применима общая теория для уравнения (16). Из этой
теории следует:
1) полиномы Лежандра разных порядков ортогональны между
собой:
1
/ Рп{х) Рт{х) dx = О при т ф щ
-1
2) второе линейно независимое решение уравнения Лежандра при
Л = п(п + 1) обращается в бесконечность при ж = =Ы как 1п(1 =р ж)-
Система ортогональных полиномов, как известно, является пол-
ной"*^^. Поэтому уравнение Лежандра не имеет нетривиальных
ограниченных решений ни при каком \ ф п{п -\- 1). В самом деле, если бы
^ Система ортогональных функций {^п} называется полной, если не
существует непрерывной функции, не равной тождественно нулю и
ортогональной ко всем функциям данной системы.
Система ортогональных функций {«^п} называется замкнутойв
промежутке (а, 6), если любую непрерывную функцию можно аппроксимировать в
среднем с любой степенью точности при помощи линейной комбинации
функций {(^п}- Иными словами, каково бы ни было s > О, всегда можно указать
такую линейную комбинацию функций
б'п = С1(^1 + . . . + Сп^п,
Ъ
а
[fix) - Sn{x)f dx < е.
Для замкнутой системы функций {(fn} имеет место соотноптение
b
о
/■
п=1
где /п — коэффициенты Фурье функции /(ж) (/п = (1/iVn) /^ /(С) ^п{0 ^0-
Полнота есть следствие замкнутости. Пусть дана некоторая
замкнутая система ортогональных функций {(^п(ж)}. Допустим, что существует

714 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
существовало решение у{х) для Л т^ п(п + 1), то оно было бы
ортогонально ко всем Рп{х). Отсюда, в силу полноты системы ортогональных
полиномов {Рп{х)}, следует, что у{х) = 0. Тем самым доказано, что мы
нашли все ограниченные нетривиальные решения уравнения Лежан-
дра.
5. Норма полиномов Лелсандра. Вычислим норму полиномов
Рп{х)
V2
Применим рекуррентную формулу (11) дважды: сначала выразим из
нее (предварительно заменив в (11) п + 1 на п) Рп через Pn-i и Рп-2,
а затем хРп через Pn+i и Pn-i- Учитывая ортогональность полиномов
Рп, Рп-1, Рп-2, получим
1
ll^nll' = - / Рп{х){{2п - 1) хРп-1 (х) - (п - 1)Рп-2} dx =
п J
(хРп) Рп-1 dx = -——-\\Pn-i\
п J 2n + 1
2
непрерывная функция /(ж) ^ О, ортогональная ко всем (рп{х). Тогда в силу
замкнутости системы функций {(fn} должно иметь место равенство
о
I
f(x)dx = Y,Nnfl=0,
так как /^ = О по предположению. Отсюда следует / = О, что противоречит
сделанному допущению, т. е. система {(^п(ж)} является полной.
Замкнутость и, тем самым, полнота системы ортогональных полиномов
{Рп{х)} является следствием теоремы ВейерпЕтрасса о возможности
равномерной аппроксимации непрерывной функции при помощи полиномов:
какова бы ни была непрерывная функция /(ж), заданная в промеэюутке
(а^Ь), и каково бы ни было s > О, существует такой полином Qn{x), что
\f(x)-Qn{x)\<e. (А)
В самом деле, представляя полином Qn{x) в виде линейной комбинации
ортогональных полиномов {Рп{х)} и пользуясь неравенством (Л), мы получим
условие замкнутости системы ортогональных полиномов.

полиномы ЛЕЖАНДРА
715
Последовательное применение этой формулы дает ||Рп|Р =
X ||Д)|Р- Подставив сюда ||Д)|Р = ||1|Р = 2, находим
2п + 1
2п + 1
Таким образом,
/
Рт{х) Рп{х) dx
О,
2п + 1
т ф п^
т
(17)
(18)
[(t^-i
2п + 1
6. Нули полиномов Лелсандра. С помощью формулы Родрига
(6) можно доказать следующую теорему.
Полином Леэюандра Рп{х) имеет п нулей, располоэюенных на
интервале — 1 < ж < 1, а его производная к-го порядка {к ^ п) имеет
п — к нулей внутри интервала (—1,1) и не обращается в нуль на его
концах.
Действительно, функция си = (ж^ — 1)^ обращается в нуль на
концах интервала (—1,1). Ее производная uj'{x) обращается в нуль при
X = 1 и X = —1 и по теореме о нуле производной имеет хотя бы
один нуль внутри интервала (—1,1).
Вторая производная uj"{x) имеет по
крайней мере два нуля внутри
интервала и обращается в нуль на его
концах (рис. 102). Продолжая
рассуждения, приходим к заключению,
что п-я производная а;^^^(ж) имеет
по крайней мере п нулей на
интервале (—1,1) или, точнее, ровно п
нулей, так как она есть полином п-й
степени. Первая часть утверждения
доказана. Производная Р^ (х) по той же теореме должна иметь по
крайней мере (п — 1) нулей внутри (—1,1), но она есть полином (п — 1)-й
степени и потому имеет ровно (п — 1) нулей внутри интервала. Далее
заключаем, что d^/dx^ Рп{х) имеет (п — к) нулей внутри интервала
(-1,1)-
7. Ограниченность полиномов Лелсандра. Покажем, что
полиномы Лежандра Рп{х) равномерно ограничены для всех значений
аргумента — 1 ^ ж ^ 1:
\Рп{х)\ ^ 1.
Для этого нам понадобится интегральное представление
27Г
Рис. 102
Рп{х) = -г- / [х-\-iyl — х'^ ^iiKf]'^ d(f.
27Г J
(19)

716 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Выведем формулу (19). Возьмем в (5) в качестве контура Ci
окружность радиуса R = л/1 — х^ {\х\ < 1) с центром в точке z =
= X. Тогда Z = X + Vl-x^e'"^, dz = Wl - х'^ е'"^ d^p, {z - ж)^+^ =
= (1 - ^2)^+1/2 ei(n+i).p^ ^2 _ ;l = ж^ - 1 + (1 - x'^)e^'^ + 2xVT^^e'^ =
= л/1 - ж2 e'"^ [2x + л/1 - ж2 {e'"^ - e"^'^)] = 2л/1 - x^ e'"^ [x + гл/1 - x^ x
X sin(/?]. Подставив эти выражения в (5), получим (19). Если —1 ^ ж ^
^ 1, то \х + гл/1 — х^ sin(/?| ^ 1 и из (19) сразу следует ограниченность
Рп{х).
§ 2. Присоединенные функции Лелсандра
1. Присоединенные функции. Рассмотрим следующую задачу.
Найти собственные значения и собственные функции уравнения
2^ dy
^'-^'^t
^-13^)2/ = О' -1<ж<1, (1)
d
dx
при условии ограниченности
\у{±1)\ < (Х). (2)
Уравнение (1) является частным случаем уравнения (8),
рассмотренного во Введении, при к{х) = 1 — ж^, q{x) = т?/{1 — ж^), р = 1,
а = — 1, 6 = 1. Так как коэффициент к{х) = 1 — х^' обращается в нуль
на обоих концах отрезка — 1 ^ ж ^ 1, то естественное условие
ограниченности ставится при ж = —1иж = 1. В силу леммы 2 из Введения
решение у{х) задачи (1) должно при ж = =Ы иметь нули порядка г/, где
V = т/2. Отсюда следует, что решение задачи (1) естественно искать
в виде
y{x) = {l-xT/^v{x), У{±1)ф0. (3)
Подставив (3) в уравнение (1), найдем
(1 - х'^У - 2(ш + 1)^;' + [Л - ш(ш + 1)]^; = 0. (4)
Это же уравнение получается для производной d^z/dx^ решения
уравнения Лежандра (15) из § 1, если его продифференцировать т раз.
Нетривиальное ограниченное решение z = Рп{х) уравнения Лежандра
существует лишь при Л = п(п + 1), где п — целое положительное
число. Отсюда следует, что
есть решение уравнения (1), а функция
лт р
pW(^) = (l-^2)™/2^Li^ (6)

А
ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
717
есть собственная функция задачи (1) — (2), соответствующая
собственному значению
Лп = п(п + 1), п = 1, 2, ... (7)
Функция Рп (х) называется присоединенной функцией Лежандра т-
го порядка. Очевидно, что Pfi
лишь при т ^
^ п.
2. Норма присоединенных функций. Согласно общей
теореме на с. 666 присоединенные функции Рп образуют ортогональную
систему. Вычислим норму ЦР^ ^|| присоединенных функций. Попутно
будет доказана их ортогональность. Умножим уравнение (4) на (1 —
— х^)^ и учтем (5). После замены ттг + 1 на ттг получим
d
dx
2\т
{1-х')
dTPn
dx""
= -[Л-ш(ш-1)](1-.2Г-^^.
(8)
Введем обозначение
1
LZ, = I PirHx)Pi'^\x)dx = l{
1-х
лт р лт р
dx"^ dx''
dx.
Интегрирование по частям дает
Lm
г, h —
d^-^Pu d^Pn
dx"^-^ dx"^
2\m
{1-х')
±
-/
(T-'^Pk d
dx"^ 1 dx
{1-х')
fimp
2\m ^ ^n
dx""
dx.
Подстановка обращается в нуль, а интеграл в силу (8) и (7)
преобразуется к виду
L™, = [п{п + 1) - т{т - l)]^-^^ = {п + т){п-т + l)L^j:\
Из этой рекуррентной формулы следует
L'^j^ = (п + ш) (п + ш - 1) ... (п + 1)п ... (п - ш + l)L^ri,k =
^ (п + ш)! п! о ^ (п + ш)! (0)
п! (п-ш)! ^'^~ (п-ш)! ^'^'
Выражение для L^ ^ дается формулой (18) из § 1, так как Рп =
= Рп- В результате получаем
О при к ф п^
I р!г\х.
)Pt\x)dx={
2 {n + mV. , (^)
при к = п,
[ 2п + 1 {п-ту.

718 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
т. е. присоединенные функции ортогональны между собой и квадрат
нормы присоединенной функции Рп равен
\\рМ\\^= ^ (п + ш)!
" ^ " 2п + 1 (п-ш)!' ^ ^
3. Полнота системы присоединенных функций. Докажем,
что система присоединенных функций {Р^ (ж)} полностью
исчерпывает все ограниченные решения уравнения (1).
В самом деле, при Л = п{п -\- 1) решение, линейно независимое с
Рп (х), обращается в бесконечность при х = ±1. Ограниченное же
решение при Л ^ п{п -\- 1) должно быть ортогонально ко всем Рп {х).
Для того чтобы убедиться, что не существует ограниченных
решений уравнения (1), отличных от Рп (х), достаточно установить, что
система присоединенных функций Рп (х) полна, т. е. что не
существует никакой непрерывной функции, не равной тождественно нулю,
которая была бы ортогональна ко всем функциям системы.
Лемма. Любая функция f{x)^ непрерывная на отрезке [—1,1] и
обращающаяся в нуль на его концах при х = 1 и х = —1, моэюет быть
равномерно аппроксимирована с любой степенью точности линейной
комбинацией из присоединенных функций любого порядка т.
Заметим прежде всего, что производные полиномов Лежандра
(F^/dx^ • Рп{х) являются полиномами степени п — т. Поскольку
любой полином по степеням х может быть представлен в виде линейной
комбинации этих полиномов, то в силу теоремы Вейерштрасса любая
функция /(ж), непрерывная на отрезке [—1,1], может быть равномерно
аппроксимирована с любой степенью точности при помощи линейной
комбинации d^/dx^ • Рп{х):
<г
fix)- Y, С„-—Рп{х)
п=т
< г, если По > N{e).
Умножая это неравенство на (1 — ж^)"^/^, получаем, что
по
fi{x)-j2 <^nPir\x)
< г, если По > N{e),
где
/l(x)=/»(l-x2r/2, (11)
Т. е. любая функция /(ж), представленная в виде (11), где f{x) —
функция, непрерывная на отрезке [—1,1], может быть равномерно
аппроксимирована с любой степенью точности линейной комбинацией
присоединенных функций.

§ 2] ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА 719
Будем говорить, что функция fi{x) принадлежит классу Hi, если
она непрерывна на отрезке [—1,1] и тождественно равна нулю в малых
окрестностях точек х = —1 и х = 1:
hix)=0 при |1-<5|^|ж|^1.
Так как для каждой функции Д (х) класса Hi функция
/н
(1_^2)т/2
является непрерывной на [—1,1], то тем самым лемма доказана для
функций класса Hi.
Рассмотрим некоторую функцию /(ж), непрерывную на отрезке
[—1,1], обращающуюся в нуль на концах. Очевидно, что эту функцию
можно равномерно аппроксимировать при помощи функции fi{x) из
класса Hi с точностью до г/2:
Аппроксимируя fi{x) линейной комбинацией из присоединенных
функций с точностью до г/2:
по
|/i(^) - El (^) I < I' El (^) = Е '^nPirH^),
п=т
получаем неравенство
|Лх)-^^(х)|<е,
которое и доказывает лемму.
С помощью этой леммы легко доказывается замкнутость системы
присоединенных функций, а тем самым и ее полнота.
Напомним, что система функций {(fn{x)} называется замкнутой
на некотором отрезке [а, 6], если любую функцию F{x), непрерывную
на [а, 6], можно аппроксимировать в среднем с любой степенью
точности при помощи линейной комбинации этих функций:
о
I
по
F{x) - ^ Cn(fn{^
п=1
2
dx < г, если по > N{e).
Очевидно, что всякую функцию, непрерывную на отрезке [—1,1],
можно аппроксимировать в среднем с любой степенью точности при
помощи функции /(ж), непрерывной на [—1,1] и обращающейся в нуль при
х = ±1:
I- -
[F{x) - f{x)f dx < е'.
1

720 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Беря линейную комбинацию присоединенных функций,
равномерно аппроксимирующих функцию f{x):
\fix)-'£^{x)\<e",
и пользуясь неравенством
(а + Ь)^ ^2{а^ + Ь^),
получаем
1
/
1
F{x) - Y,^ ^ dx^2 [[Fix) - fix)f dx + \
(если 2e' ^^[e"f ^ г),
что доказывает замкнутость, а тем самым и полноту системы
присоединенных функций.
§ 3. Гармонические полиномы и сферические функции
1. Гармонические полиномы. Гармоническим
полиномом называется однородный полином, удовлетворяющий уравнению
Лапласа
Аи = и^х + Uyy + Uzz = 0. (1)
Нетрудно убедиться, что первые два однородных гармонических
полинома имеют вид
их (ж, y,z) — Ах ^Ву ^Cz,
U2{x, у, z) = Ах'^ + Ву'^ - (^ + B)z'^ + Сху + Dxz + Eyz,
где А, В, С, D, Е — произвольные коэффициенты.
Определим число линейно независимых однородных
гармонических полиномов степени п:
Un= ^ ap^q^rX^y^z"^. (2)
p-\-q-\-r=n
Целая однородная функция степени п имеет (п + 1)(п + 2)/2
коэффициентов. Действительно, правую часть равенства (2) можно представить
в виде
0^0,0,71^"" + («1,0,п-1Ж + «0,l,n-l2/)^''~^ + . . . +
+ («п-1,о,1ж''-^ + ап-2,1,1х''-'^у + ... + ao,n-i,iy''~^)z+

3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 721
При z^ имеется один коэффициент, при z^~^ — два, ..., при z имеем
п коэффициентов, а при z^ число коэффициентов равняется п + 1, так
что общее число коэффициентов равно
1 + 2 + ... + п + (п + 1) =
(п + 1)(п + 2)
(3)
Уравнение (1) налагает на коэффициенты п{п — 1)/2 линейных
однородных соотноп1ений, так как Aun — однородная функция степени
п — 2. Таким образом, полином должен иметь не менее чем (п + 1)(п +
+ 2)/2 — (п — 1)п/2 = (2п + 1) независимых коэффициентов. Если бы
указанные (п — 1)п/2 соотноп1ений оказались линейно зависимыми, то
число независимых коэффициентов было бы больп1е 2п + 1.
Покажем, что только (2п + 1) коэффициентов линейно
независимы. Коэффициенты o^p^q^r однородного полинома можно представить в
виде
arj
д^Пгг
р\ q\ 1
число которых в точности равно
Л dxPdy^dz'^ '
Если Un — гармонический полином, то ap,q,r при г ^ 2 можно выразить
через коэффициенты «р,д,о и Q^p,g,i.
2п + 1.
Действительно,
-2
а.
^p,q,r
1
р\ q\ 'i
! dx^dy'^dz''
1
av
а^2
Qn-
p! q\ r\ dxP dy^ dz^
dx^' dy^'
/3ia
'p+2,gf,r-2
Поступая аналогично с коэффициентами «p+2,g,r-2 и «^,^+2,
конце концов выразим «p,g,r через коэффициенты типа о^р,д,о
gf+2,r-2-
2, МЫ В
{p^q
п) и Oip^q^i {р -\- q -\- 1 = п). Число коэффициентов вида ocp^q^o равно
п + 1, а OLp^q^i равно п. Таким образом, общее число линейно
независимых коэффициентов и, следовательно, независимых гармонических
полиномов п-й степени в точности равно 2п + 1.
Однородные гармонические полиномы называются шаровыми
функциями.
2. Сферические функции. Сферические функции проще всего
могут быть введены при решении уравнения Лапласа для шаровой
области методом разделения переменных.
Будем искать решение уравнения Лапласа в переменных (г, ^,(/?):
полагая
.2^
дг
-7Г- +
Г^ 8Ш (
д_
дв
8Ш1
дв '
г^ sin^
S = o,(i)
в dip'
46 А. Н. Тихонов, А
u(r,e,cp)=R(r)Y(e,cp).
А. Самарский

722 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Для определения R{r) получаем уравнение Эйлера
r'^R'' + 2rR' -XR = 0, (4)
а для определения ¥{в,(р) — уравнение
1 а / д¥\ 1 d^Y
Ae,^Y + ЛУ = -- - sin ^ — + —^ + ЛУ = О (5)
с дополнительным условием ограниченности функции У на всей сфере.
В частности, функция ¥{в,(р) удовлетворяет условиям
(5')
|У(0,^)|<<х), |y(7r,^)|<<x).J
Ограниченные решения уравнения (5), обладающие
непрерывными до 2-го порядка производными, называются сферическими
функциями.
Решение задачи для Y{e,(f) ищем также методом разделения
переменных, полагая
Функция Ф{(р) удовлетворяет уравнению
ф'' + /^Ф = О
и условию периодичности
Ф((/? + 27г) = Ф((/?).
Задача для Ф{(р) имеет решение лишь при целом /j = ттг^, и
линейно независимыми решениями являются функции С08икр и ^тпкр.
Функция 0(^) определяется из уравнения
s'mO dO \ dO J
8Ш
2,
И условий ограниченности при ^ = О и ^ = тг.
Вводя переменную
t = cos в
и обозначая X{t)\t=cosO = -^(cos^) = 0(^), получаем для X{t)
уравнение присоединенных функций
di
(>-'^'f
+ |Л-^—^|Л- = 0 (-КК1). (6)
Уравнение (6), как мы уже видели в § 2, допускает ограниченные
решения лишь при Л = п{п -\- 1):
X{t)\t=cosO = Pi"'Ht)\t=cosO = Pi'^HcOSe) = в{в),
где т ^ п.

3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 723
Выпишем полученную систему сферических функций п-го
порядка. Условимся приписывать отрицательный верхний индекс тем
функциям, которые содержат со^ k(f, и положительный — тем функциям,
которые содержат sin к(р. Тогда будем иметь
т = 0: yi'^(^,(/p)=Pn(cos^),
ш = 1: Yy^\0,(f) =P^^\co8 0)co8(f, Yj,^\o,(f) = Р^^\со8 0) siiKf,
т = к: ГУ^^ {в, (f) = Р^г"^ (cos в) cos k(f, Y^^^ {в, (f) = Р^^^ (cos в) sin k(f
(A; = 1,2, ...,n).
(m)
(7)
Число различных сферических функций n-го порядка Yn"^ равно 2п +
+ 1. Линейная комбинация этих (2п + 1) сферических функций (7)
п
Yn{0, (f) = У^ {Апт COS икр + Впт 81П m^)Pl™)(cos^), (7*)
m=0
ИЛИ
ул^,^)= Е Cmni;i^4^,^),
где
Сгг
Апт при Ш ^ О,
t Впт при Ш > О,
является также сферической функцией и называется сферической
гармоникой.
Функции Yn = Pn(cos^) не зависят
от (/? и называются зональными. Так
как Pn{t) в силу леммы из § 1, п. 6
имеет ровно п нулей внутри промежутка
(—1,1), то сфера разделяется на (п + 1)
широтных зон, внутри которых
зональная функция сохраняет знак.
Рассмотрим поведение функции
■Pn{t)\
У(=^*) = sin*^ в
dt>'
fsi
sin k(f,
C08k(f
Рис. 103
на сфере. Так как sin^ обращается в нуль
на полюсах, sin к(р или cos к(р обращаются
в нуль на 2к меридианах, а d^/dt^ • Pn{t) в силу той же леммы —
на (п — к) широтах, то вся сфера разбивается на клетки, в которых
46*

724 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Yn сохраняет постоянный знак (рис. 103). Функции Yn (при к >
> 0) называются тессеральными.
Вернемся теперь к отысканию функции R. Будем искать функцию
R{r) в виде
Подставив искомую форму реп1ения в уравнение (4), получим
характеристическое уравнение для определения а:
сг(сг + 1) -п(п + 1) = о,
откуда находим два значения а:
а = п и сг = —(п + 1).
Следовательно, частными реп1ениями уравнения Лапласа являются
функции
r"yi*=)(0,<^), (7')
^-^п+1)у(к)^0,^р), (7")
первая из которых, очевидно, соответствует реп1ению внутренних
задач, а вторая — внеп1них задач (см. § 4, п. 1).
Покажем, что найденные реп1ения уравнения Лапласа являются
однородными полиномами п-й степени. Общий член, например, в
формуле (7') можно записать так:
V ^г"" sin^ в cos к(р cos"""^"^^ в,
где q изменяется от О до (п — к)/2. Функцию v можно представить в
виде произведения трех полиномов:
где
ui = r^ sin^ в cos k(f = Re[rsin6>e^'^]^ = Re[{x -\-iy)^],
^ _ j,n — k — 2q ^Q^n — k — 2q Q _ ^n — k — 2q
Отсюда ясно, что функция r'^Yn {0,(f) есть однородный
гармонический полином степени к -\- п — к — 2q -\- 2q = п.
Очевидно, что сферические функции являются значениями
шаровых функций (7') и (7'') на сфере радиуса единица.
3. Ортогональность системы сферических функций.
Докажем, что сферические функции, соответствующие различным
значениям Л, ортогональны на поверхности сферы Е. Пусть Yi и Y2
удовлетворяют уравнениям
Ае.уП + AiFi = О, Ae,^Y2 + X2Y2 = О, (5)

|(""»-^«)+1^
§ 3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 725
где
Нетрудно видеть, что имеет место формула
//—--//{§§-^f-t}- <«'
Е Е
(б?0 = sin О dO dip),
легко получаемая интегрированием по частям.
На поверхности сферы
ди , 1 ди , ^, ^ 1
так что
Дб',(/?'^ = divgradu
и формулу (8) можно записать в виде
[ fY2AYidn = - [ [ grad Yi • grad У2 • dQ.
E E
Меняя местами в формуле (8) функции У1 и У2 и вычитая полученную
формулу из формулы (8), будем иметь
J = 11 {Y2 Ae,^Y, - Y, Ae,^Y2} dn = 0. (9)
E
Формулы (8) и (9) являются формулами Грина для оператора
сферических функций.
Из формулы (9) легко следует ортогональность функций Yi и У2 •
В самом деле, пользуясь уравнениями (5), получим из формулы (9)
J=(A2-Ai) //^1^2^0 = 0,
Е
откуда при Ai 7^ Л2
[ fYiY2dn = 0,
Е
ZTT 7Г
/ / Yi{e,^)Y2{e,^)8meded^ = 0.
о о

726
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
Тем самым доказана ортогональность сферических функций,
соответствующих разным Л.
Выше мы получили для Л = п{п -\- 1) систему (2п + 1)
сферических функций п-го порядка. Докажем, что и эти сферические функции
ортогональны меэюду собой на сфере.
(к^ ) (ко)
Пусть Yn и Уп — две сферические функции. Интегрируя их
произведение и пользуясь формулой (9) из § 2, получим
27Г 7Г
и yi*=i) У„(*2) dn = 1 1 У„(*1)(0, ^) ri*2) (^^ ^) sineded<p =
Е 0 0
27Г 7Г
= [ co8ki^co8k2^d^ / P^^i^ (cosi9)P^^2^ (cosi9) sin i9^i9 =
0 0
27Г +1
= <
0 при /iJi ^ k2,
27Г (n + A;)!
2n + l (n-A;)!
2.. ^
2n + l
при ki = k2 = к ^ 0,
при ki = k2 = 0,
(8')
T. e. сферические функции, определяемые формулой (7), образуют
ортогональную систему в области 0^^^7г,0^(/?^27ги имеют квадрат
нормы, равный
27Г 7Г
ll^i''lP = // [i^i''(^,^)]'sin^rf^#=;^7re,^^±|l:, (8")
О О
2п + 1 (п-А;)!
где го = 2, 6j^ = 1 при /;; > 0.
Предполагая возможность разложения произвольной функции
f{e,(f) в ряд по сферическим функциям (возможность такого
разложения для дважды непрерывно дифференцируемой функции будет
подробно обоснована ниже, в п. 5), допускающий почленное
интегрирование, получим
сю п
f{e, (f) = ^ ^ {Апт COS ПКр + Впт sin
п=0 т=0

3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 727
где Апгп и Впт — коэффициенты Фурье, определяемые формулами
27Г 7Г
f{0, (f) Р^^) (cos 0) cos m(f sin 0 dO d(f
A —
//
0 0
J-n
Zn 7Г
/ f f{e, if) P^^) (cos в) sin mip sin в dO d^p
■t^nm, —
0 0
I J-n
(^)||2
(9')
\\Yi
m)||2
2'K£m {n-\-m)\
2 при Ш = 0,
2n + l (n-m)! '
^m —
[ 1 при 771 > 0.
Общее решение внутренней краевой задачи для уравнения
Лапласа можно представить в виде
сю
п=0
Для внеп1ней краевой задачи общее penienne представимо в виде
Здесь
4-1
Yn{0,(f) = ^ {апт COSm(f + /З^т sinш(/?} Р^"^^ (cosl9)
— сферическая гармоника.
4. Замкнутость системы сферических функций. Докажем
замкнутость системы сферических функций, определяемых формулой
(7). Докажем сначала, что любая функция /{в, (/?), имеющая
непрерывные вторые производные, может быть равномерно аппроксимирована
некоторым полиномом из сферических функций. Рассмотрим
разложение такой функции в ряд Фурье
сю
f{0,(f) = У^ [Am (0) COS m(f + Вт (0) sin икр].
т=0
Используя ограниченность второй производной, легко оценить
коэффициенты Am И Вт ЭТОГО разложсния:
1Л I ^
Am < -^]
mZ
Вт < ^

728
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
где
М = тах|/^^|.
Отсюда следует, что для остаточного члена ряда Фурье имеет место
равномерная оценка
то
f — 2Z [^^ (^) ^^^ ^^ + ^^ (^) ^^^ ^^]
т=0
l^mol <
сю ^
2Л^ Е Л
<£'
m=mQ
(10)
где г' > О — любое наперед заданное число.
На основании § 2, п. 3 коэффициенты Фурье А^п{в) и B^aiO)^
являющиеся непрерывными функциями ^, обращающимися в нуль при ^,
равном О и 7г, могут быть равномерно аппроксимированы линейными
комбинациями присоединенных функций ттг-го порядка:
^™(^)-^afcP^™)(cos^)
к=0
B^{e)-Y,bkPt\cose)
к=0
<
<
2шо + 1 '
2шо + 1
(И)
Тогда из неравенств (10) и (11) будет следовать
то п
f{e,(f)— 2Z Х] [o^fe^j^ (cos^) С08Ш(/? + 6j^P^^^^(cos^) sinm(/?]
т=0 к=0 I
(12)
что и доказывает возможность равномерной аппроксимации любой
дважды дифференцируемой функции f{e,(p) полиномом из
сферических функций. Отсюда следует, что и любую непрерывную функцию
можно равномерно аппроксимировать полиномом сферических
функций, а это доказывает замкнутость системы функций, определяемых
формулой (7). Из замкнутости этой системы вытекает ее полнота.
Таким образом, доказано, что уравнение сферических функций не
имеет ограниченных решений при X ^ п{п -\- 1) и что всякая
сферическая функция п-го порядка (при Л = п(п + 1)) представима формулой
(Г).
5. Разлолсение по сферическим функциям. Сферические
функции являются собственными функциями уравнения
1 д
^шв дв \ дв
ди
+
1 д'^и
sin^ в d(f^
+ Ли = О, или Ао^^и + Ли = О, (13)
на поверхности сферы Е (О ^ (/? ^ 27г, О ^ ^ ^ тг) при дополнительных
условиях ограниченности.

§ 3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 729
Для обоснования разложимости произвольной дважды непрерывно
дифференцируемой функции f{e,(p) в ряд по сферическим функциям
перейдем к соответствующему интегральному уравнению. С этой
целью построим функцию источника уравнения
1 д f . ^ди\ 1 д'^и ^
«1п^^ +:г^^То =0, (14)
"'^ sin^ дв \ дв) s'm^O d(f^
удовлетворяющую условию ограниченности решения при ^ = О, тг.
Как было отмечено выше,
Ао^^и = (divgradu)6i,(p (15)
на поверхности сферы. Уравнение (14) можно рассматривать как
уравнение стационарного распределения температуры или стационарного
электрического тока на поверхности сферы.
С этой точки зрения понятно, что невозможно построить решение
однородного уравнения
Ао^^и = О (16)
с особенностью в одной только точке, так как для возможности
существования стационарной температуры необходимо, чтобы сумма
источников и стоков равнялась нулю.
Введем обобщенную функцию источника, которая в нашем случае
должна быть решением уравнения
Ae,^u = q (^ = 1/47г), (17)
регулярным всюду, кроме полюса ^ = О, где она должна иметь
логарифмическую особенность. Правая часть уравнения (17) означает
плотность отрицательных источников (стоков) тепла, равномерно
распределенных по поверхности сферы, так что
//
qda = l. (18)
Предполагая, что искомая функция источника и является функцией
только одного переменного в, получаем для нее обыкновенное
дифференциальное уравнение, решая которое, находим
и = —д' In sin ^ + с In tg - . (19)
Требуя, чтобы и имело особенность только при ^ = О, получаем
с= -q
и = —2q In sin - — q \п2.

730 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
Так как ui = const является решением однородного уравнения, то
функция источника G определена с точностью до произвольной
постоянной. Поэтому мы можем написать
G = -i-lnsin^. (20)
Если источник находится в некоторой точке Mq , то функция источника
имеет вид
G(M,Mo) = -^lnsin^, (21)
где 7мМо — угловое расстояние между точками Мо(^от'Ро} и М(в, срУ'.
Перейдем теперь к решению неоднородного уравнения
Д«,у«=ЗП7^ (sin^^) +—T^^^ = -F(^,^)- (22)
Это уравнение может иметь регулярное всюду на Е решение только
при выполнении условия
ffFda = 0, (23)
Е
означающего, что сумма источников и стоков должна быть равна
нулю. Его легко получить из формул Грина для оператора Аб',(/?,
установленных в п. 3.
Покажем, что всякое решение уравнения (22), удовлетворяющее
условию (23), представимо в виде
и{М) = / / G(M, Р) F{P) dap + Л,
Е
где А — некоторая постоянная, а G{M, Р) — функция источника,
определяемая формулой (21). Пусть М — некоторая фиксированная точка
сферы, в которую мы помещаем северный полюс (^ = 0), а Mi —
диаметрально противоположная ей точка. Точки М и Mi являются особыми
точками уравнения (22). Поэтому построим на Е в этих точках малые
кружки К^ и К^'^ и рассмотрим интеграл
//
(uAG-GAu)^a.
Ei=E-Ki^-Kfl
^ Угол 7 определяется из формулы
cos 7 = cos в cos ^0 + sin в sin ^о cos((^ — ipo)

3] ГАРМОНИЧЕСКИЕ ПОЛИНОМЫ И СФЕРИЧЕСКИЕ ФУНКЦИИ 731
Подставляя в правую часть выражения для Аи и AG, имеем
27Г 7Г — Е
//
О е
dOd(f +
+
7Г —е 27Г
J sin^ у
б?(/?.
о О
Учитывая, что в квадратных скобках стоят точные производные от
выражений
smf
|27Г _ I
до ^ди
до ^ди
причем v\q = О, получаем после интегрирования
27Г
ч
до ^ди^^^~'
dip.
Далее, замечая, что
до 1 д
дв- 2.с9/"'^"2
^''Ч
будем иметь
27Г
2^ у
sin - cos - ctg - • и
2 2^2
б?(/?-
1
smi
27Г
Insm-y -^^
о
= h+l2-
Отсюда видно, что
Следовательно,
lim /i = и(М) и lim /2 = 0.
i{M) = / / G(M, Р) F(P) dap + л,
Е
где
А
4^ У У
^б?сг
(24)

732 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
— постоянная. Решение нашей задачи определено с точностью до
аддитивной постоянной. То решение, для которого JJ^ uda = О,
определяется формулой
и{М)
11 G{M,P)F{P)dap.
Применяя (24) к уравнению сферических функций Aq^^u = —Хи,
приходим к следующему заключению.
Сферические функцищ определяемые формулой (7),
представляют совокупность всех линейно независимых собственных функций
интегрального уравнения
i{M) = А / / G(M, Р) и{Р) dap
с симметрическим ядром G{M,P), определяемым формулой (21).
К этому уравнению применима общая теория интегральных
уравнений с симметрическим ядром. Отсюда следует, что произвольная
дважды дифференцируемая функция /{в,(р) может быть разложена в
равномерно и абсолютно сходящийся ряд по сферическим функциям:
сю сю п
f{0,(f) = Y^Yn{0,(f) = Y^ ^ (лпш COSш(/? + Бпш sinш(/?)Р^^^ (cosi9),
п=0 п=0 т=0
(25)
где
п
Yn{0,ip) = ^ {Апш cosпыр + Впш sinпыр) Р^^^ (cos в), (26)
т=0
Апш И Впш — коэффициенты Фурье.
§ 4. Некоторые примеры
применения сферических функций
Рассмотрим несколько типичных задач математической физики,
требующих применения сферических функций.
Напомним, что общее решение уравнения Лапласа в сферической
системе координат (г, ^, (/?) имеет вид
и{г,в,^) = f; (л„г" + -^] Yn{9,'p),
где Уп(^5 Ф) — сферическая гармоника, т. е. линейная комбинация всех
(2п + 1) сферических функций. Если решение ищется в области г < а
(внутренняя задача), то Вп = 0; для задачи в области г > а (внешней

§ 4] ПРИМЕРЫ ПРИМЕНЕНИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ 733
задачи) следует положить An = 0; и, наконец, в случае области а <
< г < 6, не содержащей ниг = 0, ниг = (Х),в решение, вообще говоря,
входят слагаемые с г^ и l/r^^"'".
1. Задача Дирихле для сферы. Пусть дана сфера радиуса а.
Поместим в центр этой сферы начало сферической системы координат
(г, в, (f) и рассмотрим две задачи Дирихле:
Аи = О при г < а, u\r=a = f{0,^) (внутренняя задача), (1)
Аи = О при г > а, u\r=a = f{0,^) (внешняя задача), (1')
где / = f{e,(p) — заданная функция на поверхности сферы. Разложим
f{e,(p) в ряд по сферическим функциям:
сю
п=0
Yn{0,(p) = ^ {Аггт COS ПКр + Впт sin ПКр} Р^^ (cOS в),
где Апш и Впт ВЫЧИСЛЯЮТСЯ по формулам (9') из § 3.
Решение внутренней задачи ищем в виде
сю
и{г, 6>, (/?) = ^ (^-j Yn{0, (f) при г ^а.
Пользуясь граничным условием при г = а и учитывая разложение для
f{e,(p), находим
Аналогично находим решение внешней задачи (2):
сю I 1
и{г, e,(f) = 2_^ \^-j Yn{0, (f) при r^ а.
п=0
2. Проводящая сфера в поле точечного заряда. Найдем
электростатическое поле точечного заряда е в точке Р в присутствии
идеально проводящей сферы радиуса а. Будем предполагать, что сфера
заземлена, т. е. ее потенциал равен нулю. Поместим начало
сферической системы координат (г, в,(р) в центр О сферы, а полярную ось
{О = 0) проведем через точку Р; ОР = го > а.
Электростатическое поле Е = — gradu. Потенциал и = и{М) {М =
= М{г,в,(р)) удовлетворяет уравнению Лапласа всюду вне сферы,
кроме точки М = Р, в которой имеет особенность вида е/Кмр = '^о, где

734
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
uq — потенциал заряда е в неограниченном пространстве (в
отсутствие сферы). На поверхности сферы потенциал и\г=а = 0. Penienne
задачи естественно искать в виде
и{М) = ^ + v{M), R = Rmp = Y^r^+г2-2гго cosi9,
где V есть решение внешней задачи Дирихле
Av = О при г > а,
В данном случае / из (1) имеет вид /{в) = —e/R\
разложением 1/R в ряд при г < го (см. § 1, п. 1):
1 1 ^
- = -У
R Го
п=0
Го
Pn(cosl9),
г < Го.
(2)
Воспользуемся
(3)
Решение внешней задачи Дирихле (2) ищется в виде
(-) г^(в, ^).
Е
п=0
Из (2) и (3) находим Yn =
= -ea^r^^^'+^^Pn(cosl9). Таким
образом, потенциал и = и{г^в)
найден:
U = и{г,в) =
е
^2п+1
/7 ^
п=0 ^ ^0
3. Поляризация niapa в однородном поле. Пусть в
электростатическое поле в однородной изотропной среде с диэлектрической
постоянной El помещен шар радиуса а из диэлектрика с постоянной 62
(рис. 104). Будем искать потенциал создавшегося поля в виде суммы
{'^1 = '^0 + '^1 вне шара,
U2 = щ -\- V2 внутри шара,
где uo — потенциал невозмущенного (в отсутствие
диэлектрического шара) поля, а> v — возмущение, вызываемое помещенным в поле
шаром. Потенциал и удовлетворяет уравнению
Аи = 0

4] ПРИМЕРЫ ПРИМЕНЕНИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ 735
при дополнительных условиях
щ = U2 на 5,
dui du2 ^
El ^— = 82 ^— на 6,
on on
где S — граница шара, щ и U2 — значения функции и вне и внутри
шара. Отсюда следует, что потенциал v будет определяться условиями
Av = 0,
vi = V2 на 5,
dvi dv2 . .дщ
£i^ ^2^- = -{£i-£2)^- на S,
on on on
(4)
(4')
так как для функции щ имеем
Ащ = О,
{uo)i = (^0)2 на 5,
\дп ) ^ \дп
В правой части равенства (4') стоит известная функция в и (р,
которую мы разложим по сферическим функциям:
дп
S п=0
Полагая
VI
=E(;)""w^)^ -=f:©"f"
п=0 п=0
И пользуясь граничными условиями (4) и (4'), получаем
^^Е
-(п + 1) /а\^+1
п=0
С
■;
У„
п=0
= -{£1 -£2)Y^Yn,
п=0

736
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
откуда
^п — ^п
{ei -62) а
(Г)
е\ (п + 1) +62^ '
Рассмотрим теперь частный случай. Шар помещен в однородном
параллельном внеп1нем поле Е^о? направленном вдоль оси z. Потенциал
этого поля равен
По = —E^z = —EorcosO,
так что
дп
Формула (4'') дает
дщ
дг
Yn = 0
-Eoco8e = Yi{e).
при
n^l,
Yi = -Eocosi
{si -82) a
2ex + 62
Для потенциала возмущенного поля имеем
U\ — —EqZ
U2
-Eoz
1 +
3e
£1
261
1
-£2
+ £2
&
2^1 + 62
откуда следует, что
dui
~д7
E2 = -
вне шара {г > а),
внутри шара {г < а),
Ei =
£2 2а^
2е\ + 82 г^
£\
Ео,
du2
dz
Зб!
Ео,
2^1 + 82
Т. е. поле внутри шара параллельно и однородно.
Если 82 > -^i, то эквипотенциальные поверхности, оставаясь
плоскостями, перпендикулярными к направлению поля, будут
расположены реже, чем в невозмущенном поле. Силовые линии, являющиеся
ортогональными траекториями эквипотенциальных поверхностей, будут
втягиваться в шар с большей диэлектрической постоянной. В случае
8i > 82 картина будет обратной.
Этим же методом можно получить решение задачи о
поляризации шара в присутствии точечного источника, если воспользоваться
разложением 1/R по сферическим функциям (см. § 1).
Следует отметить, что аналогичные задачи встречаются при
изучении магнитных и термических полей, а также поля стационарного

§ 4] ПРИМЕРЫ ПРИМЕНЕНИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ 737
электрического тока при наличии сферического включения,
физические характеристики которого отличны от характеристик среды. Для
термической задачи в граничное условие (3) вместо ei и е2 будут
входить коэффициенты теплопроводности ki и к2, для магнитной
задачи — магнитные проницаемости /Ji и /i2, а для задачи, связанной с
полем электрического тока — проводимости Ai и Л2.
4. Собственные колебания сферы. Рассмотрим задачу о
собственных колебаниях сферы радиуса го с нулевыми граничными
условиями 1-го рода. Эта задача сводится к отысканию собственных
значений и собственных функций уравнения
А^ + Ai; = О (5)
с граничным условием на поверхности сферы
v = 0. (6)
Помещая начало сферической системы координат в центр сферы,
перепишем уравнение (5) в виде
(5')
г^ or \ or J r^
где
1 А (г^ ^Л
J.2 Qrp у Qrp J
1 9
smO од
1 + — A^,^i; + Ai; = 0,
f . ,dv\ 1 d'^v
Решение будем искать методом разделения переменных, полагая
v{r,в,^p)=R{r)Y{в,^p). (6')
После подстановки этого выражения в уравнение (5) получим
d ( 2 dR
''^/'^ +Xr^ + ^=0, (7)
откуда следует
Ae,^Y + nY = 0, (8)
Решая уравнение (8) при естественных условиях ограниченности в
полюсах сферы
\Y\e=o,n<^ (10)
И условии периодичности ио (р ¥{в,(р -\- 27г) = ¥{в,(р), получаем
собственные значения
^ = п(п + 1), (11)
47 А. Н. Тихонов, А. А. Самарский

738
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. П
каждому из которых соответствует (2п + 1) сферических функций:
Y^'\e,ip)=Pi^\co80) sinjV (i = 1, 2, ..., n).
(12)
Обратимся теперь к уравнению (9). Учитывая равенство (11),
граничные условия при г = Го и естественное условие ограниченности при
г = О, получаем для функции R{r) следующую задачу на собственные
значения:
1 d
J.2 ^j.
.2 ^^Л + Л - ''('' + ^^
dr J
R = 0,
С помощью подстановки
R{ro) = о,
|i^(0)| <(Х).
««=f
(9')
(13)
(14)
(15)
ЭТО уравнение приводится к уравнению Бесселя порядка (п + 1/2):
у" + -у' +
г
(п +1/2)2
У = 0,
(16)
общее решение которого имеет вид (см. Дополнение II, ч. I, § 1)
у{г) = AJ^^.i^ (лДг) + ВЛГ„+1/^ (лДг) . (17)
Из условия ограниченности (14) следует, что
В = 0.
Граничное условие (13) дает
^J„+i/2 (\/Аго) = 0.
Так как мы ищем нетривиальные решения уравнения, то Л ^ О и,
следовательно.
„+1/2 (л/Лго) = 0.
)рни тра
J,
Обозначив г/}^^, 1^2 , • • •, ^ш корни трансцендентного уравнения
(18)

§ 4] ПРИМЕРЫ ПРИМЕНЕНИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ 739
находим собственные значения
Л™.„ = i"^] . (19)
Каждому собственному значению Хт,п соответствует (2п + 1)
собственных функций. Введем обозначение
■Фп{х) = \1^ 4+1/2(^)-
(20)
Тогда собственные функции уравнения (5) при граничном условии (6)
можно представить в виде
(п)
Vr
^-'n,m,j \
V ^W (21)
(п = О, 1, ...; ш = 1, 2, ...; j = -п, ..., -1, О, 1, ..., п).
Рассмотрим теперь первую внутреннюю краевую задачу для
волнового уравнения
А^ + k^v = 0 (22)
при граничном условии
v = f{0,'p) (23)
на поверхности сферы радиуса го-
Из предшествующего изложения ясно, что решение этой задачи
представляется в виде
.(..»..) = £ E^lf^ei»..), (24)
п=0j=—n ^ ^
где fnj — коэффициенты разложения функции f{e,(p) по сферическим
функциям |yi"^^(l9,(/?)|:
сю п
/(^'^) = Е Е /nii^i'H^,^)- (25)
п=0j=—n
Если к^ совпадает с одним из собственных значений
/j,("o)\2
, 2 _ л _ / l^mp \
гь — ^топо — I I
\ Го
ТО краевая задача (22) — (23) имеет решение не для всякой функции
f{e,(p). Формула (24) показывает, что необходимым и достаточным
47*

740 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. П
условием разрешимости нашей краевой задачи в этом случае является
обраш:ение в нуль коэффициентов fnoj'-
jriQj — и,
или
7Г 27Г
1 I •'^"'-'^"0
О о
Если эти условия выполнены, то решение определяется формулой (24),
в которой слагаемые, соответствующие п = по, отсутствуют. Однако
при этом решение определено неоднозначно, так как к нему всегда
можно прибавить любую линейную комбинацию собственных
функций, соответствующих к'^ = A^q^o-
5. Внешняя краевая задача для сферы. Рассмотрим
внешнюю первую краевую задачу для сферы (см. гл. VH, § 3)
V = О I - ) при г —>- 00,
Иш г ( ——h ikv = О (условие излучения).
г^оо удг )
Как было показано в гл. VH, § 3, эта задача имеет единственное
решение. Разложим искомую функцию и функцию f{e,(p) в ряды по
сферическим функциям:
сю п
п=0j=—n
сю п
п=0 j= — n
Коэффициенты разложения Rn{r), очевидно, будут удовлетворять
уравнению
граничному условию
Rn{ro) = fn

§ 4] ПРИМЕРЫ ПРИМЕНЕНИЯ СФЕРИЧЕСКИХ ФУНКЦИЙ 741
и условиям излучения при г —>- оо
R^{r) = 0 (- ) , lim r{R'^ + ikRn) = 0.
Общее решение этого уравнения имеет вид (см. п. 4 и Дополнение П,
ч. I, § 3)
RAr)=A^CHkr)+B^C4kr),
где
С^п\р) = ^^н1^1у,{р) iP = kr).
Учитывая асимптотические формулы для функций Ханкеля
Нп (р) и Нп (р) (см. Дополнение П, ч. I, § 3):
V '^р
Н^^Нр) = /А e-*[''-W2-/4] + _ _ _
V ^р
(точками обозначены члены более высокого порядка малости
относительно 1/р), полу
ческие формулы:
енкг) = -—-—-+...,
тельно 1/р), получаем для функций Q и Q следующие асимптоти-
pi [кг —7гп/2 — 7г/4]
^ — г [fer —7гп/2 —7г/4]
е)(н = ^—-—+...
Отсюда видно, что условию излучения удовлетворяет лишь функция
Qi • Поэтому
Пользуясь граничным условием при г = го, находим
■t^ni —
Jnj
Таким образом, мы получаем функцию у{г,в,(р) в виде
п=0 j=-n Sn [l^l^o)

742
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. HI
где
7Г ZTT
I I f(e,cp)Yj,^He,cp) sineded^
О о
\^(i)||2
7Г 27Г
у(л
^//[^^
у(л
sin О dO d(f
27Tej (n + j)!
о о
квадрат нормы сферической функции Yn (O^ip).
2n + l (n-j)!
U)i
I ' ^j
2, J=0,
1, J>0,
ЧАСТЬ III
ПОЛИНОМЫ ЧЕБЫШЁВА — ЭРМИТА
И ЧЕБЫШЁВА — ЛАГЕРРА
§ 1. Полиномы Чебышёва — Эрмита
1. Дифференциальная формула. Полиномы Чебышёва—
Эрмита Нп{х) определим по аналогии с полиномами Лежандра при
помощи производящей функции Ф(р, ж), полагая
Ф(р,х)=е^-^-^'= Х^Я^х)
7,1 •
п=0
Отсюда в силу теоремы Коши следует
Нп{х) =
Р=0
п! [ Ф(С,ж)
(^-СГ
J е+1 ^ 2т J е+1
с с
(1)
■dC,
(2)
где С — замкнутый контур в плоскости комплексного переменного С,
охватывающий точку С = 0. Вводя новую переменную интегрирования
Z = X — (, преобразуем (2) к виду
Я„(х) = (-1)»е-' ^ / ^^
27гг J {z — X)
n+l
dz
Ci
(-l)^e^ <^
/
1 ^^
dz
(3)

§ 1] полиномы ЧЕБЫШЕВА — ЭРМИТА 743
где Ci — контур, охватывающий точку z = х. В силу теоремы Ко-
2
ши выражение в фигурных скобках равно d^{e~^ )/dx^. В результате
получаем из (3) дифференциальную формулу
Я„(х) = (-1)"е^^ £, (е-^) . (4)
Эта формула показывает, что Нп{х) есть полином степени п, причем
Нп{-х) = {-1ГНп{х), (5)
Из (4) находим Но{х) = 1^ Hi{x) = 2ж, Н2{х) = 4ж^ - 2 и т. д.
2. Рекуррентные формулы. Дифференцируя производящую
функцию по р и ж, находим
Ф, - 2рФ = О, Фр - 2 (ж - р) Ф = 0. (6)
В каждое из тождеств (6) подставим ряд (1) для Ф(р, ж). Собирая
члены при р^ и приравнивая их к нулю, получаем две рекуррентные
формулы:
Я;(ж) = 2пЯ,_1(ж), (7)
Hn+i{x) - 2хНп{х) + 2nHn-i{x) = 0. (8)
Формула (8) позволяет последовательно определять Нп для всех п,
зная, что Но{х) = 1, Hi{x) = 2х. Так, например, Н2{х) = 2xHi — 2Но =
= 4^2 - 2, Яз = 2жЯ2 - 4Я1 = Sx^ - \2х и т. д.
3. Уравнение Чебышёва — Эрмита. Найдем уравнение,
которому удовлетворяет Я^(ж). Для этого используем рекуррентные
формулы (7) и (8). Сначала с помощью (7) исключим из (8) 2пЯ^_1:
Я„+1 - 2жЯ„ + я; = 0;
это уравнение продифференцируем по х:
я;+1-2хя;-2я„ + я;' = о
и подставим сюда Я^_|_]^ = 2(п + 1)Я„ из (7). В результате получим
я;' - 2а;Я; + 2пЯ„ = О, или -^ ^6"=^" ^"j + 2пе-^'я„ = 0.
(9)
Отсюда видно, что полином Чебышёва — Эрмита является
собственной функцией, соответствующей собственному значению Л = 2п,
следующей задачи (задача Штурма — Лиувилля).
Найти те значения Л, при которых уравнение Чебышёва —
Эрмита
(е~^^^')'+ Ле~^^^ = О, -00 < ж < 00, (10)
имеет нетривиальное решение, возрастаюш^ее при х ^ оо не
быстрее, чем конечная степень х.

744 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
Решение этой задачи можно было бы искать в виде степенного
ряда у = ^^=QO"nX^- Подставив этот ряд в уравнение (10), получим
для коэффициентов рекуррентную формулу
2п-Л
"-+^= (п + 2)(п + 1)"- (11)
Из формулы (11) видно, что при л = 2п все коэффициенты ak = О
для к > п и ряд обрывается. Только при Л = 2п может быть
выполнено условие на бесконечности. Получающиеся полиномы определены
с точностью до постоянного множителя. Выбирая а^ = 2^, получаем
полиномы Нп{х).
4. Норма полиномов Нп{х). Докажем (не обращаясь к общей
теории), что полиномы Чебышёва — Эрмита образуют ортогональную
_ 2
С весом е ^ на бесконечной прямой — оо < ж < оо систему функций, и
2
ВЫЧИСЛИМ их норму (с весом р{х) = е~^ ):
||Я„|| = ^2»п! А. (12)
Рассмотрим выражение
сю сю
L,nn= I H^{x)Hn{x)e-^^dx = {-ir I HUx)£^ (е-"') dx.
— СЮ —СЮ
Положим для определенности, что т ^ п. Интегрируя по частям и
пользуясь формулой (7), а также тем, что на бесконечности обращает-
ся в нуль произведение полинома на е , получаем
сю
Я™_1 ^^^^ (е-^ ) dx =
СЮ
/г]п-т . .
(е-^ ) dx,
так как Н^ = 1. Отсюда видно, что
лп-т-1 . .
Если ш = п, то
при т < п.
сю
Lmn = 2^п! / е-^' dx = 2^п! ^ = ||Я^

§ 2] ПОЛИНОМЫ ЧЕБЫШЕВА — ЛАГЕРРА 745
Тем самым доказано, что
сю
/
Нт(х)Нгг(х)е "^ dx = < .'
Система полиномов Чебышёва — Эрмита является полной (на
доказательстве этого факта мы не останавливаемся), и, следовательно,
мы нап1ли все реп1ения задачи (10), т. е. Л т^ 2п не может быть
собственным значением.
5. Функции Чебып1ёва — Эрмита. В приложениях (см. с. 751)
часто пользуются функциями Чебып1ёва — Эрмита
ФЛх) = hn{x) е""^ /^ hn{x) = J" ,
\\Нп{х)\\
образующими ортогональную и нормированную с весом р{х) = 1
систему на бесконечном интервале — оо < ж < оо:
сю
I фп{х) фгп{х) dx = I ^^ ш = п!
Эти функции обращаются в нуль при ж —>- ±00 и удовлетворяют
уравнению
< + (A-x^)V^n = 0 при Л = 2п + 1.
§ 2. Полиномы Чебышёва — Лагерра
1. Дифференциальная формула. Полиномы Чебышёва —
Лагерра Ln{x) мы определим при помощи производящей функции
Ф(р,ж)= е-^. (1)
1- р
Разлагая ее в степенной ряд
^ 1 9^Ф
п=0 ' ^
(2)
р=0
и пользуясь теоремой Коши, находим
2т J С"^^
с
Ln{x)=— I ^^dC,
где С — контур, охватывающий точку С = 0. Введем новую
переменную интегрирования z, положив (" = 1 — x/z, d( = xdz/z^; тогда
1 f z^e~^

746 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
где Ci — контур, охватывающий точку z = х. Формула (3) дает
1 г1^
Отсюда заключаем, что Ln{x) есть многочлен степени п. В
частности, имеем Lo{x) = 1, Li{x) = 1 — х.
2. Рекуррентные формулы. Дифференцируя Ф(р, ж) по р и ж,
получаем два тождества:
(1-р)Чр-(1-р-х)^ = 0, (5)
(1-р)Ф,+/>Ф = 0. (6)
Подставим в (5) и (6) ряд (2) и приравняем коэффициенты при р^+-'^
нулю; это дает рекуррентные формулы
(п + l)Ln+i - (2п + 1 - x)Ln + nLn-i = О, (7)
L'^^^-L'^ + Ln = 0. (8)
Формула (7) устанавливает связь между полиномами L^+i, L^, L^_i
и позволяет последовательно определить все L^, например
Ых) = 2 [(3 - ^)^1 - ^о] = -х^ -2х + 1.
Выведем еще одну рекуррентную формулу
xL; + (п + 1 - x)Ln - (п + l)Ln+i = 0. (9)
Для этого заменим в (7) п на п + 1 и продифференцируем по х:
(п + 2)L'^^^ - (2п + 3 - x)L'^^^ + L^+i + (n + 1)L;, = 0;
дважды применив формулу (8), исключим отсюда L'^_^2 ^ ^n+i ^ ^
результате получим (9).
3. Уравнение Чебышёва — Лагерра. Найдем уравнение,
решением которого является Ln{x). Дифференцируя (9) по ж, получим
xL'^ + (п + 2 — x)L'^ — Ln — {п -\- l)L'^_^i = О, после чего исключим L'^_^i
при помощи (8). В результате приходим к уравнению для L^
xL'^ + (1 - x)L'^ + nLn = О, или -— [ же~^ —-^ ] + ne'^^Ln = О,
(10)
которое называется уравнением Чебышёва — Лагерра.
Тем самым доказано, что Ln{x) есть собственная функция,
соответствующая собственному значению Л = п следующей задачи.
Найти значения Л, при которых уравнение
{хе-'^у'У + Хе-''у = 0, О < ж < оо, (11)

§ 2] ПОЛИНОМЫ ЧЕБЫШЕВА — ЛАГЕРРА 747
имеет в области О < ж < оо нетривиальное решение^ ограниченное
при X = О и возрастающее при х ^ оо не быстрее, чем конечная
степень X.
Заметим, что уравнение (10) для L/ji (х) можно получить, если
продифференцировать (п + 2) раз функцию z = х^е~^ и воспользоваться
дифференциальной формулой (4).
4. Ортогональность и норма полиномов Чебышёва — Ла-
герра. Докажем ортогональность и нормированность с весом е~^
полиномов Ln{x), исходя из формулы (4). Рассмотрим интеграл
сю сю
/If (р
Lm{x) Ln{x) е-"" dx = — / Lm{x) — (ж^'е"'^) dx.
о о
Пусть т ^ п. Интегрируя т раз по частям и учитывая, что из-за
наличия множителя вида х^е~^ (к > 0) все подстановки обращаются в
нуль, получаем
сю
J^^ = (-1)- i- / ^-^ 4 (^"e--) dx. (12)
^ n! 7 dx^ dx^-^ ^ ^ ^ ^
0
Если m < n, TO, интегрируя еще раз, находим Jmn = О, так как
-——j- Lm = 0. В случае т = п имеем
dx^^^
лп т
dx"" ^ ^
И
сю
Jnn = Ц^ [ (-1) Ve-- dx = ^^^^^ = 1 = ||L„|p. (13)
n! J n!
0
Итак, полиномы Чебышёва — Лагерра образуют ортонормированную
с весом е~^ систему функций:
сю
I L^(x)L^)e-^dx=l^l ^^t^] (14)
О
5. Обобщенные полиномы Чебышёва — Лагерра. При
изучении движения электрона в поле кулоновых сил, а также в других
задачах современной физики наряду с полиномами Ln{x)
встречаются обобщенные полиномы Чебышёва — Лагерра Ь^(ж). Теорию этих
полиномов можно построить по аналогии с пп. 1 — 4, исходя из
производящей функции

748 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
и разлагая ее в ряд по степеням р:
4>\р,х)= Y,LUx)p"; К{х)= {р,х]
Повторяя рассуждения, проведенные для s = О в п. 1, находим
с Ci
Отсюда следует, что
1 d^
Ы{х)=-х-^е^—{х-+^е-^), (16)
Т. е. L^{x) действительно является многочленом п-й степени. В
частности, Lq{x) = 1, Lf (ж) = 1 + s — ж.
Вводя функцию Z = х^~^^е~^ и дифференцируя ее (п + 2) раз по ж,
находим для функции и = d'^z/dx'^ уравнение хи" + (ж + 1 — s)u' + (п +
+ 1)и = 0. Вычислим производные для L^{x) = 1/п! • х~^е^и и учтем
при этом уравнение для щ тогда получим уравнение
х{Щ"-(х-8-1){Щ'+пЬ^^ = 0, (17)
которому удовлетворяют обобщенные полиномы Ь^(ж). Тем самым
доказано, что обобщенные полиномы Чебышёва — Лагерра являются
собственными функциями, соответствующими собственным
значениям
Лп=П-\ -—
следующей задачи.
Найти значения Л, при которых уравнение
xy'' + {s + l-x)y'+ (х- ^^^ = 0,
S+1 —ж /\/ . « —^ /а -S + i
{х^+'е-^у'У + х^е-- (Л - -^ \ у = О, (18)
имеет в области О ^ ж < оо нетривиальное решение, ограниченное
при X = О и возрастающее при ж —>- оо ке быстрее конечной степени ж.
Исходя из дифференциальной формулы (16) и проводя
рассуждения по аналогии с п. 4, нетрудно доказать, что полиномы L^ образуют
ортогональную с весом е~^х^ систему функций:
ГО, т ф п {s > —1),
о
Г(п + 8 + 1)
; , т = п.

§ 3] ПРОСТЕЙШИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ШРЕДИНГЕРА 749
Полиномам Чебышёва — Лагерра Ь^(ж) соответствуют
ортогональные и нормированные с весом р{х) = 1 функции
где
11^:11 = 1,
которые являются решениями уравнения
(^^')' + (^ - I - £) V' = о (19)
при граничных условиях |'0(О)| < оо, lim 'ф[х) — О, соответствующими
ж—>-сю
собственным значениям
5 + 1
An = п + ^— .
Из формулы (18) видно, что Ь^(ж) = Ln{x) для X^ij равного п -\-
+ 1/2 (если в уравнении (18) Л заменить на Л + 1/2, то при s = О оно
совпадет с уравнением Чебышёва — Лагерра (10)).
В заключение отметим, что ортогональные системы полиномов
{Ln{x)} и {L^{x)} являются полными (на доказательстве этого факта
не останавливаемся). Тем самым мы нашли все собственные функции
задач (10) и (18).
§ 3. Простейшие задачи для уравнения Шрёдингера^^
1. Уравнение Шрёдингера. В квантовой механике поведение
частицы, находящейся в поле потенциальных сил, описывается
уравнением Шрёдингера
где h = 1,05 • 10~^^ эрг • с — постоянная Планка, i = л/—Т, /i —
масса частицы, и — ее потенциальная энергия в силовом поле, ф =
= ^){x^y^z^t) — волновая функция.
Если силы не зависят от времени, т. е. [/ = U{x,y,z), то
возможны стационарные состояния с заданным значением энергии, т. е.
существуют решения вида
V = V''(a;,y,z)e-f*, (2)
^ Рассматриваемые здесь задачи для уравнения Шрёдингера дают
примеры применения полиномов Чебынтёва — Эрмита и Чебынтёва — Лагерра.
Приведенное ниже изложение не претендует на полное освещение вопросов,
связанных с уравнением Шрёдингера. По университетской программе
квантовая механика изучается после курса математической физики.

Аф+ ^{Е-и)ф = 0. (4)
750 ДОПОЛНЕНИЕ П. СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
где Е — общая энергия частицы. Подставляя это выражение в
уравнение (1), приходим ко второму уравнению Шрёдингера
АГ+^{Е-и)ф''=0, (3)
В котором Е играет роль собственного значения, подлежащего
определению. В дальнейшем вместо ф^ мы будем писать ф:
В случае отсутствия силового поля {U = 0) уравнение (4)
принимает вид
AV+^V = 0. (5)
Нетрудно заметить сходство этого уравнения с волновым уравнением
классической физики
Аф + к^ф = О, (6)
где к = со/с = 27г/Л — волновое число, Л — длина волны. Однако это
сходство является чисто внешним и формальным в силу различия
физического смысла функций, входящих в уравнения (5) и (6).
В уравнении Шрёдингера непосредственный физический смысл
имеет не сама функция ф, а значение \ф\'^, которое истолковывается
в статистическом духе: выражение {ф]"^ dx dy dz означает вероятность
пребывания частицы внутри элементарного объема dx dy dz в точке
{x^y^z) пространства.
В связи с этим нормировка собственных функций к единице,
которой мы неоднократно пользовались ранее в целях математической
простоты, теперь приобретает фундаментальное значение. Условие
нормировки
^^dxdydz = l (7)
означает, что частица находится в каком-либо месте пространства и
поэтому вероятность найти частицу где-нибудь в пространстве равна
единице (достоверное событие).
Рассмотрим некоторые простейшие задачи для уравнения
Шрёдингера.
2. Гармонический осциллятор. Уравнение Шрёдингера для
гармонического осциллятора принимает вид
где и = ——^ ж^ {ujQ — собственная частота (циклическая)
осциллятора). Наша задача будет состоять в отыскании стационарных состоя-

§ 3] ПРОСТЕЙШИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ШРЕДИНГЕРА 751
НИИ, т.е. спектра собственных значений энергии Е и соответствующих
собственных функций ф из уравнения
^"+^(^-^х^)^ = 0 (8)
при дополнительном условии нормировки
сю
\ф^(1х = 1. (9)
— сю
Введя обозначения
сю
/
А=т—, хо = \ , ^=—, (10)
Пшо у fiuiQ хо
для функции ф = ф{^) после очевидных преобразований получим
уравнение
+ {\-е)Ф = ^ (11)
с дополнительным условием нормировки
сю
/
|V^P^C= -. (12)
Реп1ением этой задачи, в силу § 1, п. 5, будут функции
лАо V2^n!0r
соответствующие собственным значениям
Лп = 2п + 1.
Возвращаясь к исходным обозначениям, находим
2\xq) -- '
^п = 7га;о ("п + М (п = О, 1,2,...). (14)
В классической механике энергия осциллятора
2м 2 "^ '

752 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
где Рх — импульс частицы, может принимать непрерывный ряд
значений. С точки зрения квантовой механики энергия осциллятора, как
показывает формула (14), может принимать лишь дискретный ряд
значений Еп- В этом случае говорят, что энергия квантуется. Число п,
определяющее номер квантового уровня, называют главным
квантовым числом. В низшем квантовом состоянии при п = О энергия
осциллятора отлична от нуля и равна
Ео= - huj.
3. Ротатор. Найдем собственные значения энергии ротатора со
свободной осью, т. е. частицы, вращающейся на одном и том же
расстоянии вокруг неподвижного центра.
Потенциальная энергия U ротатора сохраняет одно и то же
значение во всех положениях частицы, и ее можно положить равной нулю:
и = о.
В сферической системе координат (г, в,(р) с началом координат в
неподвижном центре уравнение Шрёдингера для ротатора
можно записать в виде
д^ + ^ £;^ = О
sin^^ + -—^^ + -^£;V = 0. (15)
При этом используется условие
or
Вводя вместо массы /i момент инерции
получаем
sini9 дв \ дв) sin2|9 dip^
A^.vV + AV- = О, (16)
где
27"
Х= ^Е. (17)
Таким образом, мы приходим к краевой задаче на собственные
значения для уравнения
^в,^Ф + \Ф = о (16)

§ 3] ПРОСТЕЙШИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ШРЕДИНГЕРА 753
при естественном граничном условии ограниченности в точках ^ = О
и ^ = 7Г и условии нормировки
7Г 27Г
// '
\^\^^mededif = 1. (18)
о о
Решениями этой задачи, как мы знаем, являются нормированные
сферические функции
{21^1){1-т)\^гп).^ . ( /2 при ш = 0.
У/-^(^,^) = рГЧсов^) \^^"^^' (ш = О, 1,..., О,
I sm т^
(19)
соответствующие собственным значениям
Л = /(г + 1). (20)
Заменяя Л его значением согласно формуле (17), получаем формулу
для квантованных значений энергии ротатора
Ei,n = l{l + 1)^, / = 0,1,2,... (21)
4. Двилсение электрона в кулоновом поле. Одной из
простейших задач атомной механики является задача о движении электрона
в кулоновом поле ядра, имеющая большой практический интерес, так
как решение ее дает не только теорию спектра водорода, но и
приближенную теорию спектров атомов с одним валентным электроном
(водородоподобных атомов), например атома натрия.
В атоме водорода электрон находится в кулоновом
электростатическом поле ядра (протона), так что потенциальная энергия U{x,y,z)
равна
[/=--, (22)
Г
где г есть расстояние электрона от ядра, — е — заряд электрона, +е —
заряд ядра.
Уравнение Шрёдингера в этом случае имеет вид
2/i f^ ^ е^
AV^+^(^+-)V^ = 0. (23)
Наша задача состоит в отыскании таких значений Е^ для которых
уравнение (23) допускает решение, непрерывное во всем пространстве
48 А. Н. Тихонов, А. А. Самарский

754 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
и удовлетворяющее условию нормировки
сю
JJJ mx,y,z)\4xdydz = 1. (24)
— СЮ
Запишем уравнение (23) в сферической системе координат с
началом в ядре, которое предполагается неподвижным:
И будем искать penienne в виде
ф(г,в,^р)=х(г)¥^^"'\в,^р). (26)
Принимая во внимание дифференциальное уравнение для сферических
функций Yi' {в, (р)
Ай.^у/'") {9, ^) + /(/ + l)!-/"") [в, ^) = О,
получаем
dr^ г dr
2мf^^f!^ /(/+1)
X = 0. (27)
Введем в качестве единицы длины величину
а = Ь? / iie^ ^
в качестве единицы энергии — величину
^0 — —о- — — •
П^ а
Полагая
р = г/а, е = Е/Ео (е < 0),
перепишем уравнение (27) в виде
fA + l^ + (2s+ - - ^(^ + ^)У.=
dp"^ р dp \ р Р^ )
С помощью подстановки
1
= 0.
(28)
(29)
(30)
уравнение (29) приводится к виду
d^y ^ dy [^ 2 s^ .

§ 3] простейшие задачи для уравнения ШРЕДИНГЕРА 755
где
s = 2l + l.
Введя в качестве независимой переменной величину
х = рл/^8ё, (32)
получим вместо (31) уравнение
ху"+у'-(^^ + ^^у + уХ = 0, (33)
ИЛИ
где
i(4)-(i-S)"-»^=»-
совпадающее с рассмотренным нами в § 2 уравнением (19).
Найденные там собственные значения оказались равными
Л = Пг-\ — '
а собственные функции (определенные с точностью до постоянного
множителя) выражались через обобщенные полиномы Чебып1ёва —
Лагерра L^^:
УпАх)=х'^^е--^^Ь1(х), (35)
где L^^{x) определяются формулой (16) § 2.
Учитывая, что
s = 2/ + l,
получаем
Х = Пг + 1 + 1 = п (п = 1, 2,...). (36)
Целое число п называется главным квантовым числом, Пг —
радиальным квантовым числом, / — азимутальным квантовым числом.
Заменяя Л его выражением согласно формулам (34) и (28),
получаем квантованные значения энергии
(37)
Они
48*
зависят только от
Еп —
~2nV '
главного квантового числа п

756 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. HI
Положим Е равным энергии кванта, Е = —hcj = —/гг/, где и =
= uj/27T — частота. Тогда будем иметь
••- ^'" - ^ (38)
4 4
_, fie fie ^
где R = —7г- = о — так называемая постоянная Ридберга.
2h^h 47гП^
Найдем частоты спектральных линий. Наблюдаемая в
спектральной линии частота jynni соответствует переходу из состояния с
энергией Еп в состояние с энергией Е^-^.
Частота z/^ni кванта, излучаемого при таком квантовом переходе,
равна
.„„, = Д (^ - ^) . (39)
Полагая ni = 1 и п = 2, 3,..., мы получим ряд линий, составляющих
так называемую серию Лаймана:
Unni = R (1 — -^
Далее, значения rii = 2, п = 3, 4,... дают серию Бальмера
vnn, = ^ (^ - ;^ j '
значения ni = 3, п = 4, 5,... — серию Пашена
„ - р П _ J_
Перейдем теперь к определению собственных функций
водородного атома. Для этого в силу формулы (26) нам достаточно найти
радиальные функции х{р)-
Пользуясь формулами (35), (32), (30), (34), (36), можем написать
X„K^)=^n(^)'e-''/"eY-i(^), (40)
где An — нормировочный множитель, определяемый из условия
сю
I P^xli{p}dp=l. (41)
О

§ 3] ПРОСТЕЙШИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ШРЕДИНГЕРА 757
Вычисляя An, получаем следующее выражение для нормированных
радиальных функций:
В силу формул (26) и (19) нормированные собственные функции
имеют вид
/(2/ + l)(/-m)!^^(^)^^
у 2г^7г(/ + ш)!
где Xni{p) определяется формулой (42).
Число 771 (ттг = О, =Ы, ±2,..., =Ь/) называется магнитным
квантовым числом.
Так как Пг всегда неотрицательно (п^ = О, 1, 2, ...), то при
данном п в силу формулы
п = п^ + / + 1
квантовое число / не может быть больше п — 1 (/ = 0, l,2,...,n —
— 1). Поэтому при определенном значении главного квантового числа
п число / может принимать п значений: / = 0, 1,...,п — 1, а каждому
значению / соответствует (2/ + 1) значений т. Отсюда следует, что
заданному значению энергии Е^^ т. е. заданному значению п,
соответствует
п-1
^(2/ + 1) = 1 + 3 + 5 + ... + (2п - 1) = п^
различных собственных функций. Таким образом, каждый уровень
энергии имеет вырождение кратности in?.
Найденный нами дискретный спектр отрицательных собственных
значений энергии Е^ состоит из бесконечного множества чисел с
точкой сгущения в нуле.
Второй отличительной чертой рассматриваемой задачи для
уравнения Шрёдингера является наличие непрерывного спектра
положительных собственных значений (всякое положительное число Е
является собственным значением уравнения (23)). В этом случае электрон
уже не связан с ядром, но все еще находится в его поле
(ионизированный атом водорода). На доказательстве существования
сплошного спектра мы не останавливаемся, отсылая читателя к специальной
литературе"'^^
^ См., например: Фок В. А. Начала квантовой механики. М., 1976;
Курант Р., Гильберт Д. Методы математической физики. М.; Л., 1951.
Т. I, гл. V.

758
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. IV
ЧАСТЬ IV
ФОРМУЛЫ, ТАБЛИЦЫ И ГРАФИКИ
Ниже приводятся таблицы некоторых специальных функций, с
которыми мы встречались при peniennn краевых задач математической
физики. Таблицы сопровождаются перечнем простейп1их свойств
специальных функций.
I. Основные свойства специальных функций
1. Интеграл оп1ибок
1. Интеграл ошибок:
Ф{г
'=;!/-
da.
2. Разложение при малых z:
3. Асимптотическая формула при больших z:
2
Ф{г) ^1- ^^
1__ 3-4 _ 4-5-6
^Д Z \ (2^ ^ (2^ 'Щ^'^"
2. Цилиндрические функции
Ряды Асимптотические формулы
1. Функции Бесселя
W=(|)'
.2J Г(г/ + 1)
2. Функции Неймана
No{x)= ^Мх) (ln| +С) +
(С = 0,577215664901532 есть
постоянная Эйлера)
Jj,(x) = \ — cos (а
У 7ТХ \
7Г1У 7Г
Т ~ 4
)....
iv.w-y|;si„(x-j)+

I. ОСНОВНЫЕ СВОЙСТВА СПЕЦИАЛЬНЫХ ФУНКЦИЙ 759
Niix)
Ряды
2
+
^Л(.)(1п|+С)
+ ....
N^) = --(^) (п-1)! +
(П>1)
3. функции Ханке ля
Асимптотические формулы
Ni{x) ^
Nn{x) ^
I 2 / 7ГП 7Г\
Я(1)(х)
^ i(ж-7r^'/2-7r/4) ,
7ГЖ
Я(2)(а;) = Л(а;)-гАГДж)
4. Функции мнимого аргумента
/Да;) = i-ifMix) =
_ /ху 1
Я(2)(ж) ^ ./Ae-*(-W2-/4) +
V 7ТХ
Ко{х)= |гЯ«(гх)
(1п|+С7)/о(.)+(|)Ч....
/^1(х) = -|я«(гж)= 1+...,
ifn(a;)= |е-"/2я(1)(гх)
(п-1)! /2
Ш^^|^^e^ + .■
Ko{x) = sl^e- + .
^i(^) = a/^«"" + -'
if„(x)-,/-e- + .

760 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. IV
5. Рекуррентные формулы:
ах ах
Zy[x)
Zu^i{x)
2v
Z^_i{x) + Z^^iix) = — Z^{x)
X
где Zjy{x) — любая цилиндрическая функция вещественного
аргумента.
Частные случаи:
X
Jq{x) = -Ji{x), / Ji{x)dx = 1- Jo{x),
_d_
dx
X
[xJi{x)] = xJo(x), / ж Jo (ж) dx = xJi{x).
Для функций мнимого аргумента:
Iv-i{x) - Uj^i{x) = —Iv{x), K^-i{x) - K^^i{x) = K^{x),
X X
h-i{x) + h+i{x) = 2 — /^(ж), K^_i{x) + K^+i{x) = -2 ^ K^{x),
I'^{x)=h{x), Kl,{x) = -K,{x).
6. Определитель Вронского для цилиндрических функций:
2
Mx)Nl{x) - N,{x)Jl{x)
7ТХ
Я(1)(х)Я(2)'(х)-Я(2)(х)Я(1)'(х)
7ГЖ
h{x)Kl{x) - КЛх)1'Лх) = - - .
X

I. ОСНОВНЫЕ СВОЙСТВА СПЕЦИАЛЬНЫХ ФУНКЦИЙ 761
7. Интегральные формулы:
7Г
27Г J
( — Л'г^ г . . f —Л^
27Г
/■ g«cosv+mvp^^^ LJ!!! f е"<=°^'^ cos ГЫр dip,
Cl,2
где контуры интегрирования Ci и (72 изображены на рис. 96 (с. 695);
сю
— СЮ
8. функции полуцелого порядка:
Ji/Jx) = \ — sin ж,
/^ V 7ТХ
J-1/Лх) = \ COS ж,
/^ V 7ТХ
'^-^/^*^' = V;I(-^^-'^'^^)'
3. Полиномы Лежандра
1. Производящая функция:
^ сю
,, , , = Е Р"Рп{х), О < р < 1, -1 ^ X ^ 1.

762 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. IV
2. Рекуррентная формула:
(п + 1)Рп+1(ж) - х{2п + 1)Рп{х) + nPn-i{x) = 0.
3. Формула Родрига:
^ ^ 2^п! dx^ ^^ ^ ^
4. Уравнение полиномов Лежандра:
_d_
dx
(l-x^)
2^ dy
dx
-\-n{n-\- l)y = 0.
5. Интегральная формула:
27Г
Pn{x) = — / (ж + гу 1 — ж^ cos(/?j d(f,
о
-1 < ж < 1.
6. Квадрат нормы:
+1
/
P^{x)dx
2п + 1
7. Первые пять полиномов:
Ро(а;) = 1, Pi{x) = X, Р2{х) = - {Зх^ - 1),
Рз(а;) = 1 (5ж^ - Зх), Р4{х) = I (35а;* - ЗОж^ + 3).
2 8
4. Присоединенные функции
1. Уравнение присоединенных функций:
_d_
dx
(l-x^)
2^ dy
dx
m^
+ n(n + l)- h/ = 0.
l-x^
2. Дифференциальная формула:
РМ(Ж) = (1 - хТ'^^Рп{х) = (1 - ж2)™/2-Ц -^-^ [(^2 - 1)"1
б^Ж^
2^n! б^ж^

I. ОСНОВНЫЕ СВОЙСТВА СПЕЦИАЛЬНЫХ ФУНКЦИЙ 763
3. Квадрат нормы:
+1
\Pir^r= I [Pir4^)f dx= ^
2 (n + ш)!
(n — ш)!
5. Полиномы Чебышёва — Эрмита
1. Производящая функция:
2. Рекуррентные формулы:
Я;(ж) = 2nHn-i{x), Hn+i{x) - 2хНп{х) + 2nHn-i{x) = 0.
3. Дифференциальная формула:
2 ^^ 2
""^ ^ ^ ^ ^ж^
4. Квадрат нормы:
сю
||Я„||2 = f Я2(ж)е-^' dx = 2"п! лДР.
— СЮ
6. Полиномы Чебышёва — Лагерра
1. Производящая функция:
х±_ ею
е 1-*
Y:rr=T, ^»(^)*'
п=0
2. Дифференциальная формула:
3. Квадрат нормы:
\\Ln{x)r = 1.

764
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. IV
II. Таблицы
Таблица 1
« 2
Интеграл ошибок Ф(ж) = -^ J е~" da, О ^ ;г; ^ 2,8
Z
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
Ф(^)
0,0000
0,0113
0,0226
0,0338
0,0451
0,0564
0,0676
0,0789
0,0901
0,1013
0,1125
0,1236
0,1348
0,1459
0,1569
0,1680
0,1790
0,1900
0,2009
0,2118
0,2227
0,2335
0,2443
0,2550
0,2657
0,2763
0,2869
0,2974
0,3079
0,3183
0,3286
0,3389
0,3491
0,3593
0,3694
0,3794
0,3893
0,3992
0,4090
0,4187
Z
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
Ф(^)
0,4284
0,4380
0,4475
0,4569
0,4662
0,4755
0,4847
0,4937
0,5027
0,5117
0,5205
0,5292
0,5379
0,5465
0,5549
0,5633
0,5716
0,5798
0,5879
0,5959
0,6039
0,6117
0,6194
0,6270
0,6346
0,6420
0,6494
0,6566
0,6633
0,6708
0,6778
0,6847
0,6914
0,6981
0,7047
0,7112
0,7175
0,7238
0,7300
0,7361
Z
0,80
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
Ф(^)
0,7421
0,7480
0,7538
0,7595
0,7651
0,7707
0,7761
0,7814
0,7867
0,7918
0,7969
0,8019
0,8068
0,8116
0,8163
0,8209
0,8254
0,8299
0,8342
0,8385
0,8427
0,8468
0,8508
0,8548
0,8586
0,8624
0,8661
0,8698
0,8733
0,8768
0,8802
0,8835
0,8868
0,8900
0,8931
0,8961
0,8991
0,9020
0,9048
0,9076
Z
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
Ф(^)
0,9103
0,9130
0,9155
0,9181
0,9205
0,9229
0,9252
0,9275
0,9297
0,9319
0,9340
0,9361
0,9381
0,9400
0,9419
0,9438
0,9456
0,9473
0,9490
0,9507
0,9523
0,9539
0,9554
0,9569
0,9583
0,9597
0,9611
0,9624
0,9637
0,9649
0,9661
0,9661
0,9763
0,9838
0,9891
0,9928
0,9953
0,9970
0,9981
0,9989
0,9993
0,9996
0,9998
0,9999
0,9999

п. ТАБЛИЦЫ
765
Таблица 2
Значения функций Бесселя нулевого и 1-го порядка
от ж = О до ж = 12,00
X
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
Jo (ж)
+1,000
+0,997
+0,990
+0,977
+0,960
+0,938
+0,912
+0,881
+0,846
+0,808
+0,765
+0,720
+0,671
+0,620
+0,567
+0,512
+0,455
+0,398
+0,340
+0,282
+0,224
+0,167
+0,110
+0,056
+0,002
-0,048
-0,097
-0,142
-0,185
-0,224
-0,260
-0,292
-0,320
-0,344
-0,364
-0,380
-0,392
-0,399
-0,403
-0,402
Jl(x)
+0,000
+0,050
+0,099
+0,148
+0,196
+0,242
+0,288
+0,329
+0,369
+0,406
+0,440
+0,471
+0,498
+0,522
+0,542
+0,558
+0,570
+0,578
+0,582
+0,581
+0,577
+0,568
+0,556
+0,540
+0,520
+0,497
+0,471
+0,442
+0,410
+0,375
+0,339
+0,301
+0,261
+0,221
+0,179
+0,137
+0,095
+0,054
+0,013
-0,027
X
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70
6,80
6,90
7,00
7,10
7,20
7,30
7,40
7,50
7,60
7,70
7,80
7,90
Jo (ж)
-0,397
-0,389
-0,377
-0,361
-0,342
-0,321
-0,296
-0,269
-0,240
-0,210
-0,178
-0,144
-0,110
-0,076
-0,041
-0,007
+0,027
+0,060
+0,092
+0,122
+0,151
+0,177
+0,202
+0,224
+0,243
+0,260
+0,274
+0,285
+0,293
+0,298
+0,300
+0,299
+0,295
+0,288
+0,279
+0,266
+0,252
+0,235
+0,215
+0,194
Jl(x)
-0,066
-0,103
-0,139
-0,172
-0,203
-0,231
-0,257
-0,279
-0,298
-0,315
-0,328
-0,337
-0,343
-0,346
-0,345
-0,341
-0,334
-0,324
-0,311
-0,295
-0,277
-0,256
-0,233
-0,208
-0,182
-0,154
-0,125
-0,095
-0,065
-0,035
-0,005
+0,025
+0,054
+0,083
+0,110
+0,135
+0,159
+0,181
+0,201
+0,219
X
8,00
8,10
8,20
8,30
8,40
8,50
8,60
8,70
8,80
8,90
9,00
9,10
9,20
9,30
9,40
9,50
9,60
9,70
9,80
9,90
10,00
10,10
10,20
10,30
10,40
10,50
10,60
10,70
10,80
10,90
11,00
11,10
11,20
11,30
11,40
11,50
11,60
11,70
11,80
11,90
12,00
Jo (ж)
+0,172
+0,148
+0,122
+0,096
+0,069
+0,042
+0,015
-0,013
-0,039
-0,065
-0,090
-0,114
-0,137
-0,158
-0,177
-0,194
-0,209
-0,222
-0,232
-0,240
-0,246
-0,249
-0,250
-0,248
-0,243
-0,237
-0,228
-0,216
-0,203
-0,188
-0,171
-0,153
-0,133
-0,112
-0,090
-0,068
-0,045
-0,021
+0,002
+0,025
+0,048
Jl(x)
+0,235
+0,248
+0,258
+0,266
+0,271
+0,273
+0,273
+0,270
+0,264
+0,256
+0,245
+0,232
+0,217
+0,200
+0,182
+0,161
+0,140
+0,117
+0,093
+0,068
+0,043
+0,018
-0,007
-0,031
-0,055
-0,079
-0,101
-0,122
-0,142
-0,160
-0,177
-0,191
-0,204
-0,214
-0,222
-0,228
-0,232
-0,233
-0,232
-0,229
-0,223

766
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. IV
Таблица 3
Последовательные корни уравнения Jo(/in) = О и соответствующие
значения |Ji(/in)|
п
1
2
3
4
5
А*п
2,4048
5,5201
8,6537
11,7915
14,9309
1Л(/^п)|
0,5191
0,3403
0,2715
0,2325
0,2065
п
6
7
8
9
10
А*п
18,0711
21,2116
24,3525
27,4935
30,6346
\Jl{l^n)\
0,1877
0,1733
0,1617
0,1522
0,1442
Значения функций Kq(x) и К\{х)
Таблица 4
X
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1Д
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
К^{х)
2,4271
1,7527
1,3725
1,1145
0,9244
0,7775
0,6605
0,5653
0,4867
0,4210
0,3656
0,3185
0,2782
0,2437
0,2138
0,1880
0,1655
0,1459
0,1288
0,1139
0,1008
0,0893
0,0791
0,0702
0,0623
0,0554
0,0492
0,0438
0,0390
0,0347
К^х)
9,8538
4,7760
3,0560
2,1844
1,6564
1,3028
1,0503
0,8618
0,7165
0,6019
0,5098
0,4346
0,3725
0,3208
0,2774
0,2406
0,2094
0,1826
0,1597
0,1399
0,1227
0,1079
0,0950
0,0837
0,0739
0,0653
0,0577
0,0511
0,0453
0,0402
X
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
К^{х)
0,0310
0,0276
0,0246
0,0220
0,0196
0,0175
0,0156
0,0140
0,0125
0,0112
0,0098
0,0089
0,0080
0,0071
0,0064
0,0057
0,0051
0,0046
0,0041
0,0037
0,0033
0,0030
0,0027
0,0024
0,0021
0,0019
0,0017
0,0015
0,0014
0,0012
Ki{x)
0,0356
0,0316
0,0281
0,0250
0,0222
0,0198
0,0176
0,0157
0,0140
0,0125
0,0111
0,0099
0,0089
0,0079
0,0071
0,0063
0,0056
0,0051
0,0045
0,0040
0,0036
0,0032
0,0029
0,0026
0,0023
0,0021
0,0019
0,0017
0,0015
0,0013

III. ГРАФИКИ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
767
III. Графики специальных функций
1,0
-1,0
Рис. 105. Графики функций Бесселя 7о(ж), Ji{x) и J2{x)
-2,5
Рис. 106. Графики функций Неймана No{x) и Ni{x)

768
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. IV
5 X
Рис. 107. Графики цилиндрических функций мнимого аргумента
/о(ж), h{x), /2(ж), Kq{x), Ki{x)
Рис. 108. Графики полиномов Лежандра

IV. РАЗЛИЧНЫЕ ОРТОГОНАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ 769
IV. Различные ортогональные системы координат
Пусть X, у, Z — декартовы координаты некоторой точки, а xi, Ж2,
жз — криволинейные ортогональные координаты этой точки. Квадрат
элемента длины выражается формулой
ds^ = dx^ + dy^ + dz^ = h\dx\ + h\dx\ + h\dx\^
где
hi =
dx
dxj
dy_
dxj
+
dz
dxi
{i = 1, 2, 3)
— метрические коэффициенты, или коэффициенты Ламэ.
Ортогональная координатная система полностью характеризуется тремя
метрическими коэффициентами /ii, /12, Ы-
Приведем общее выражение для операторов grad, div, rot, А в
ортогональной криволинейной системе координат:
v-^ 1 du ,
gradn = ^-—1,,
3 = 1 ^ ^
div А =
hih2h3
f) f) f)
^— {h2h3Ai) + -— (/13/^1^2) + ^— {hih2A3)
OXi 0x2 0x3
rot A
hih2h3
hi'ii h2i2 h3\3
д д д
dxi дх2 дхз
hiAi /12^2 НзАз
Аи--
hih2h3
д f h2h3 ди\ д //гз^1 ди \ д f hih2 ди
dxi \ hi dxij дх2 V ^2 0x2; дхз \ Нз дхз
где ii, i2, 1з — единичные базисные векторы, А = (^1,^2,^3) —
произвольный вектор, и — скаляр.
1. Прямоугольные координаты:
Xi = ж.
Х2 =У,
хз
^ ди , ди , ди ^
gradu= ^-1+ ^-J+ ^-к,
ох Оу OZ
49 А. Н. Тихонов, А. А. Самарский
hi
div А =
/l2
дх
дАу
ду
/13 = 1,
дА,
dz

770
ДОПОЛНЕНИЕ Н. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[Ч. IV
rot А
д_ д_ д_
дх ду dz
^х ^у ^z
ЗА, дАу
ду
dz
i+...,
Дм
где i, j и к — направляющие единичные векторы осей ж, ^, z.
2. Цилиндрические координаты
Xi = г, Х2 = (f, Хз = Z
связаны с прямоугольными координатами уравнениями
X = г cos (/?, у = rsiiKf, Z = Z.
Координатные поверхности: г = const — цилиндры, (р = const —
плоскости, Z = const — плоскости.
Метрические коэффициенты равны
hi = 1, /z,2 = г. Из = 1,
так что
ди , 1 ди , ди ,
gradu = ^- 11 + - ^- 12 + ^- 1з,
or г 0(f OZ
div А = - — (rAi) + - —— + —— ,
г or г 0(f OZ
rot А
1 дАз дА2\ . fdAi дАз
г d(f dz
dz
дг
Id IdAi
- -^ M2) ^—
r or r 0(f
13,
r dr \ dr J r^ d(f'^ dz'^
3. Сферические координаты
Xi = r, X2 = 0, X3 = (f
связаны с прямоугольными координатами формулами
ж = г sin^cos(/?, ^ = г sin^sin(/?, 2; = rcos^.
Координатные поверхности: концентрические сферы г = const,
плоскости (р = const, конусы в = const.
Метрические коэффициенты равны
hi = l,
ho=^
hz = г sin t

IV. РАЗЛИЧНЫЕ ОРТОГОНАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ 771
так что
^ ди , 1 ди , 1 ди ,
gmdu = ^- 11 + - ^^ 12 + —^-^ ^- 13,
or г ов г 8т в 0(f
div А = — — r^i + —^-Б ^ smM2 +
J.Z ijj. г 8т в од
1 дА.
г sin ^ д^
rot А
•smt
11 +
+
1 a^i
д
sin ^ 9(/? 9г
Мз)
12 +
J.2 Qj. \ Qj.
1 д Г ди
^^^^^ дв г'"" М
1 э^п
г^ sin^ i9 9(/?2 '
4. Эллиптические координаты
xi = л, Ж2 = /i, жз = 2;
определяются с помощью формул преобразования
X = cA/i, ^ = с л/(А2 - 1)(1 - fi^),
где с — масп1табный множитель.
Метрические коэффициенты равны
hi
Л2-1 '
/12
/A2-/i2
/гя
1.
/i-
13,
Координатные поверхности: Л = const — цилиндры
эллиптического сечения с фокусами в точках х = ±с, ^ = 0; /i = const — семейство
конфокальных гиперболических цилиндров; z = const — плоскости.
5. Параболические координаты. Если г, в — полярные
координаты точки на плоскости, то параболические координаты могут
быть введены с помощью формул
xi = X = v2rsin - , Ж2 = /i = v2rcos - ,
хз
z.
Координатные поверхности Л = const и /i = const представляют
собой пересекающиеся параболические цилиндры с образующими,
параллельными оси Z. Связь с декартовыми координатами дают
формулы
х= 2(^'
Л^), У = Xfi, z = z.
Метрические коэффициенты равны hi = h2 = уЛ^+/?, hs = 1.
49*

772 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. IV
6. Эллипсоидальные координаты. Вводятся с помощью
уравнений {а > b > с):
Т ?У Z
+ — Н— = 1 {\> —(?) (уравнение эллипсоида),
а2 + Л 62 + Л с2 + Л
^2 2 ^2 (уравнение одно-
+ — \— = 1 {—(?> II > —Ъ^) полостного гипер-
о? -\-11 Ь^ -\-11 с^ -\-11
болоида),
^2 2 ^2 (уравнение двух-
+ — \— = 1 (—6^>г/>—а^) полостного гипер-
«2 +г. 62 + j, с2+г. болоида).
Каждой точке {x,y,z) соответствует только одна система
значений Л, /i, 1У. Параметры xi = Л, Ж2 = /i, жз = г^ и называются
эллипсоидальными координатами. Координаты х, у, z выражаются явно через
Л, /i, и:
/(A + a^)(/i + a^)(z/ + a^) _ {X + b^) {/i + b^) {и + b^)
""' V (&'- a2) (c2 - a2) ' ^~ V (c2 - 62) (a2 - 62)
^_^ /(A + c2)(/i + c2)(z/ + c2)
(a2 - c2) (62 _ c2)
Коэффициенты Ламэ равны
_ 1 (A-M)(A-t/) _ 1 {p,-v){p,-\)
_ 1 /(г.-Л)(г/-м)
'''- 2V Д>) '
где
^(s) = V(s + a2)(s + b2)(s + c2) (s = A, //, I/).
Оператор Лапласа можно представить в виде
4
Аи:
(Л - //) (Л - г/) (// - г/)
(м-.)вдА(вд|^) +
+ (.-л)ад|-(ад|)+(л-,)адА(ад|

U = A f -^ +B,
IV. РАЗЛИЧНЫЕ ОРТОГОНАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ 773
Частное решение уравнения Лапласа, зависящее только от Л, U =
= и{Х), дается формулой
ад
где А и В — произвольные постоянные.
7. Вырожденные эллипсоидальные координаты.
а) Вырожденные эллипсоидальные координаты {а,/3,(р) для
вытянутого эллипсоида вращения определяются при помощи формул
X = cshas'mP cos (/?, у = cshas'mP sin (/?, z = ccha cos /3,
где с — масштабный множитель, 0^а<оо,0^/3^7т, —тг < (р ^ тт.
Координатные поверхности: вытянутые эллипсоиды вращения
а = const, двухполостные гиперболоиды вращения Р = const и
плоскости (р = const.
Квадрат элемента длины дается выражением
ds^ = c^(sh^ а + sin^ р) {da^ + с?/?^) + с^ sh^ а sin^ /3 d^p^,
откуда для метрических коэффициентов получаются значения
hi = h2 = с л/sh а + sin^ /3, hs = h^p = csha sin/3.
Уравнение Лапласа имеет вид
Аи =
д ( , ди\ 1 д f . ^ди
sn а —- -\—;—- —- sm р
с^(sh^ а + sin^/3) [sha 9а \ да) sinf] д(3 \ д(3
1 1 \ д'^и
+ ■
,sh^a ' sin^/ЗУ 9(/?2_'
б) Система вырожденных эллипсоидальных координат {а,/3,(р)
для сплюснутого эллипсоида вращения определяется с помощью
равенств
X = ccha sin/3 cos(/?, у = ccha sin/3 sin(/?, z = csha cos/3,
0^a<(X), 0^/3^ 7Г, —7Г < (/? ^ 7Г.
Координатные поверхности: сплюснутые эллипсоиды вращения
а = const, однополостные гиперболоиды вращения /3 = const и
плоскости (/? = const, проходящие через ось z.
Квадрат линейного элемента и оператор Лапласа в
рассматриваемой системе координат имеют вид
ds^ = с^ (ch^ а - sin^ (3) {da^ + с?/?^) + с^ ch^ а sin^ [3 d(f'^,
1
Аи--
(? (ch а — sin /3)
1 а / au\ 1 а / ^au\
' cha^;— + ^-- —- sin/3—- +
c\iada\ да) sin/3 9/3 \ 9/3

774 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. IV
+
8. Тороидальные координаты. Система тороидальных
координат {а,/3,(р) определяется при помощи формул
с sh а cos (р с sh а sin (р с sin /3
^ = -^ о^ У =
cha — cos /3 ' cha — cos /3 ' ch a — cos /3 '
где с — масштабный множитель, О ^ а < оо, —тг < /3 ^ тг, —тг < (/? ^ тг.
Координатные поверхности суть торы а = const:
{p-ccthaf +z'^ = (^) (р= л/ж^Т^) ,
сферы Р = const:
2 I ^2
(z-cctg/3)'+p'
sin/3
плоскости (f = const.
Выражение для квадрата линейного элемента имеет вид
^2
ds'^ = — -—■ [da'^ + 6?/3^ + sh^ a d^\
(cha - cosp)"^
метрические коэффициенты равны
^ h csha
en a — cos p en a — cos p
и оператор Лапласа дается следующим выражением:
9а \chа — cospdaj др \ch.a — cosР дрJ
1 dhj^
(ch a — cos /3) sh a d(p^
Удобно вводить вместо и новую функцию v с помощью соотношения
и = v^2cha — 2cos/3 • г»,
при этом уравнение Аи = О приводится к уравнению
1 1
Vaa -\-Vf3f3-\-VaCtha-\- - V -\- —^- V^^ = 0.
4 sn а
9. Биполярные координаты.
а) Биполярные координаты на плоскости. Переменные
xi = а, Х2 = Р, хз = Z

IV. РАЗЛИЧНЫЕ ОРТОГОНАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ 775
называются биполярными координатами, если имеют место равенства
ash а asin/3
cha — cos /3 ' cha — cos P '
Метрические коэффициенты равны hi = h2 = — -, /гз = 1.
cha — cos p
6) Бисферические координаты xi = a, X2 = /3, xs = (p определяются
при помощи формул
с sin а cos (р с sin а simp csh/3
^ = -гъ ' У =
сЪ/З — cos а ' сЪ/З — cos а ' сЪ/З — cos а '
где с — постоянный множитель, О ^ а < /3, —оо</3<оо, —тг < (р ^тт.
Эти формулы можно представить в компактной форме:
Z + ip = cictg —-— (р = л/х^ +У^] .
Координатные поверхности суть веретенообразные поверхности
вращения а = const:
{p-cctgaf -\-z'^ = (- ) ,
сферы /3 = const:
ПЛОСКОСТИ (f = const.
Выражение для квадрата линейного элемента в бисферических
координатах имеет вид
ds^ = —-— — \da^ + df3^ + sin^ a d^\
(cnp - cosa)"^
откуда следует
с с sin a
III = П2 = -r-^ , пз = —— ,
СП p — cos a en p — cos a
и уравнение Лапласа принимает вид
д f sin а ди\
да \ ch /3 — cos а да J
д f sina ди\ 1 д'^и
др \сЪР — cosa дрJ sina(ch/3 — cosa) d(f'^
При решении уравнения Лапласа удобна подстановка
и
= л/2 ch/3 — 2 cos а • v.

776 ДОПОЛНЕНИЕ IL СПЕЦИАЛЬНЫЕ ФУНКЦИИ [Ч. IV
Тогда для функции v получается уравнение
1 1
4 sm а
10. Сфероидальные координаты.
а) Вытянутые сфероидальные координаты:
XI = Л, Х2 = 11, Хз = (fj
X = cXfi, у = слУ{Х^ — 1)(1 — /i^) cos(/?, z = с v^(A^ — 1)(1 — /i^) sin(/?,
6) Сплюснутые сфероидальные координаты:
Xi = Л, Ж2 = /i, Хз = v^,
ж = cXjj, sin (/?, ?/ = с v^(A^ — 1)(1 — /i^), 2; = cXjj, cos (/?.
Поверхности Л = const — сплюснутые сфероиды, /j, = const — однопо-
лостные гиперболоиды. Метрические коэффициенты равны
11. Параболоидные координаты. Переменные
Ж1 = Л, Ж2 = /i, хз = (/^,
определяемые соотношениями
X = XfiC08(f, у = XfisiiKf, z= -(Л^—/i^),
называются параболоидными координатами. Метрические
коэффициенты равны hi = h2 = уЛ^-Г/?, Из = Х/а.
Координатные поверхности Л = const, /i = const являются
параболоидами вращения вокруг оси симметрии Oz.

ДОПОЛНЕНИЕ Ш
ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
В предыдущих главах книги рассматривались в основном
классические решения краевых задач, т. е. решения, имеющие все
непрерывные производные нужного порядка и удовлетворяющие уравнению,
граничным и начальным условиям в каждой точке рассматриваемых
множеств. Рассмотрение таких решений накладывает существенные
ограничения на исходные данные задачи. Вместе с тем при выводе
основных дифференциальных уравнений (см., например, гл. П, § 2, п. 9)
было показано, что если исходить не из дифференциальных, а из
интегральных уравнений, то класс решений, а значит, и класс исходных
краевых задач можно существенно расширить. Такие решения
называют обобщенными. В зависимости от рассматриваемых интегральных
уравнений получают различные классы обобщенных решений.
Изучим вопрос об определении, существовании и единственности
в ограниченной области некоторого обобщенного решения задачи
Дирихле из класса функций Соболева для уравнения Нуассона Аи = /.
Для решения этого вопроса оказывается недостаточно понятия
интеграла в смысле Римана и требуется более общее определение
интеграла (в смысле Лебега). Кроме того, нам понадобится понятие
обобщенной частной производной от функции многих переменных. Поэтому
изложению теории обобщенных решений задачи Дирихле для уравнения
Нуассона будет предшествовать краткое изложение понятий интеграла
Лебега, обобщенных частных производных и некоторых
функциональных пространств"*^ л
§ 1. Некоторые понятия функционального анализа
1. Вспомогательные сведения об интеграле Лебега,
обобщенной частной производной и некоторых функциональных
пространствах. Пусть G — произвольная ограниченная область в
А/^-мерном евклидовом пространстве Е^ {N — некоторое натуральное
^ Более подробно изложение этих понятий см. в кн.: Соболев С. Л.
Уравнения математической физики. М., 1992. Лекция 6; Смирнов В. И.
Курс выспЕСЙ математики. Т. V. М., 1981.

778 ДОПОЛНЕНИЕ III. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
число), а f (х) = f {xi, Х2, ..., xn) —произвольная, заданная в этой
области неотрицательная функция. Обозначим через F произвольное
замкнутое подмножество точек области G, на котором функция / (х)
непрерывна. Тогда существует интеграл Римана
dx
N,
//...// (Ж1, Ж2, ..., xn) dxi dX2 ..
F
который мы кратко будем обозначать символом
f(x)dx. (1)
/■
Назовем внутренним интегралом от неотрицательной
функции / (ж) по области G точную верхнюю грань (если она
существует) интегралов Римана (1) по всем принадлежащим области
G замкнутым множествам F, на которых / (х) непрерывна, т. е.
величину
dx . (2)
Внутренний интеграл от неотрицательной функции / (ж) по
области G будем обозначать символом
вн. / / (х) dx. (3)
G
Итак, по определению
I. / / (х) dx = sup f (х) dx
G \F J
Ясно, что если f (x) = М = const > 0 в области G, то для такой
функции существует точная верхняя грань (2), а потому существует
внутренний интеграл (3), равный MmesG, где mesG — А/'-мерный
объем области G.
Далее, нетрудно видеть, что если для функции / (х) существует
внутренний интеграл по области G, а М > О — произвольная
постоянная, то и для функции / (х) + М существует внутренний интеграл
по области G.
Неотрицательная функция f (х) = / (xi, Ж2, ..., ждг) называется
интегрируемой по Лебегу в области G, если для этой
функции существует по области G внутренний интеграл (3) и для любой

§ 1] НЕКОТОРЫЕ ПОНЯТИЯ ФУНКЦИОНАЛЬНОГО АНАЛИЗА 779
постоянной М > о справедливо равенство
I- f[f{x)+M]dx = B^. [ f{x)dx + B^. I Mdx. (4)
вн.
G
При этом внутренний интеграл (3) называется интегралом
Лебега от функции / (ж) по области G и обозначается символом
j f{x)dx. (5)
G
Произвольная заданная в области G функция / (ж),
принимающая в этой области значения любых знаков, называется
интегрируемой по Лебегу в области G, если каждая из двух неотрица-
тельных функций ( /+ (ж) = '-^ ^ ^' -^ ^ ^ и /- (ж) = '-^ ^ ^' -^ ^ ^
интегрируема по Лебегу в области G. При этом разность интегралов
Лебега от указанных неотрицательных функций
I f+{x)dx- I f-{x)dx
называется интегралом Лебега от функции / (х) по области G
и обозначается символом (5).
Функцию f (х) называют измеримой в области G, если для
любого г > О у области G существует замкнутое подмножество F^,
на котором функция / (х) непрерывна и мера mesF^"'^^ которого
отличается от меры mesG области G меньше, чем на г^л
Оказывается, для того чтобы функция / (ж), обладающая в
ограниченной области G внутренним интегралом (3), была интегрируема
в этой области по Лебегу, необходимо и достаточно, чтобы она
являлась измеримой в этой области.
Достаточность этого условия доказывается совсем просто.
В качестве примера рассмотрим при А/" = 1 на интервале G =
= (О, 1) так называемую функцию Дирихле
I 1, если X иррационально,
I и, если X рационально.
^ Меру mesFs можно определить как интеграл J^ Idx.
^ Это определение измеримой функции принадлежит выдающемуся
математику, создателю московской математической пеколы Николаю
Николаевичу Лузину (1883 — 1950).

780 ДОПОЛНЕНИЕ III. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
Хорошо известно, что эта функция не интегрируема по Риману на
сегменте [О, 1]. Чтобы убедиться, что она интегрируема на G = (О, 1) по
Лебегу, фиксируем произвольное достаточно малое г > О и
пронумеруем все рациональные точки, лежащие на сегменте [е/4, 1 — е/4]. На
замкнутом множестве F^, получающемся вычитанием из [е/4, 1—г/4]
симметричной г/8-окрестности первой рациональной точки,
симметричной г/1б-окрестности второй рациональной точки и т. д., функция
/ (ж) непрерывна и равна единице. Поэтому J^ / (ж) dx существует и
его значение лежит в интервале (1 — г, 1 — s/2). Так как е произвольно,
отсюда следует, что внутренний интеграл (3), равный точной верхней
грани (2), существует и равен 1. Очевидно также выполнение
равенства (4).
К понятию интеграла Лебега можно прийти и из других
соображений. Рассмотрим множество всех непрерывных в ограниченной
области G функций / (ж) и введем для каждой из этих функций норму,
положив ее равной
/
\fix)\dx, (6)
т. е. превратим это множество в нормированное пространство.
Напомним, что последовательность { /п } элементов
произвольного нормированного пространства называется фундаментальной,
если при независимом стремлении двух номеров т и п к
бесконечности существует предел
lim 11/^ -/nil = 0.
Произвольное нормированное пространство называется
полным, если для любой фундаментальной последовательности {/п }
этого пространства существует элемент этого пространства /, к
которому сходится последовательность { /п } по норме, т. е. в смысле
соотношения
lim ||/„ - /II = 0. (7)
п—>-сю
Легко убедиться, что нормированное пространство всех
непрерывных в области G функций с нормой (6) не является полным (ибо
фундаментальная в смысле нормы (6) последовательность непрерывных в
G функций, вообще говоря, не сходится в смысле (7) к непрерывной в
области G функции /(ж)).
В силу теоремы Хаусдорфа любое нормированное пространство
может быть расширено до полного.
Естественно возникает идея — расширить указанное
пространство с нормой (6), пополнив его новыми элементами, так, чтобы
расширенное пространство стало полным. Интегрируемости по Риману для
такого расширения недостаточно: если расширить пространство всех

§ 1] НЕКОТОРЫЕ ПОНЯТИЯ ФУНКЦИОНАЛЬНОГО АНАЛИЗА 781
непрерывных в области G функций с нормой (6), пополнив его
всеми функциями, абсолютно интегрируемыми в области G по Риману,
расширенное пространство будет продолжать оставаться неполным.
Только дополнив указанное пространство всеми функциями,
интегрируемыми в области G по Лебегу, мы превратим его в полное
нормированное пространство с нормой (6). Такое пространство
принято обозначать символом Li (С).
Таким образом, интеграл Лебега совершенно естественно
возникает при расширении множества всех непрерывных в области G
функций с нормой (6) до полного нормированного пространства.
2. Функциональные пространства. В приложениях кроме
пространства Li (О) большую роль играет другое пространство,
элементами которого являются определенные в области G функции,
квадраты которых принадлежат Li (С). Это пространство является
полным в смысле нормы
V2
\f{x)\'dx^
и его принято обозначать символом L2 (G).
Для введения обобщенного решения задачи Дирихле нам
понадобится еще одно полное нормированное пространство, обозначаемое
символом W2 {G) и получаемое пополнением множества всех функций
/ (ж), имеющих в области G непрерывные частные производные 1-го
порядка и норму, определяемую равенством
1/(^)1^+ Е
. V2
дхь
dx ) . (8)
Оказывается, такое пополнение будет состоять из функций,
имеющих в области G принадлежащие L2 {G) частные производные 1-го
порядка в некотором обобщенном смысле-'^^
Для введения обобщенных частных производных обозначим через
С^^^ {G) множество всех функций, непрерывных в области G,
имеющих в этой области непрерывные частные производные 1-го порядка
и отличных от нуля только на некотором компакте открытой области
G (т. е. равных нулю в некоторой пограничной полосе области G).
Тогда, если функция / (ж) непрерывна в области G и имеет
непрерывную в этой области частную производную df/dxk, то в силу
^ Впервые понятие частных производных в обобщенном смысле было
введено С. Л. Соболевым.

782 ДОПОЛНЕНИЕ III. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
формулы Остроградского—Гаусса для любой функции ^ (х) из мно-
о . .
жества С^^ iG) справедливо тождество
dip {х) _ [ df {х)
/^«^—/
dxk
ip {х) dx.
Это тождество лежит в основе определения обобщенной частной
производной.
Если существует интегрируемая в области G по Лебегу
функция д{х)^ такая, что для данной интегрируемой по Лебегу функции
/ (ж) и для любой функции (/? (ж) из множества с'^^^ iG) справедливо
тождество
/ ^ ^^^ ~д dx = - д{х)(р (х) dx,
G G
ТО функция д (х) называется обобщенной частной
производной функции / (ж) по переменной Xk и обозначается символом
df/dxk.
Пространством W2 {G) называется полное в смысле нормы (8)
пространство, получаемое пополнением множества всех функций / (ж),
непрерывных в области G и имеющих в этой области непрерывные
частные производные 1-го порядка.
Пространство W2 {G) состоит из всех принадлежащих классу
L2 (G) функций / (ж), имеющих принадлежащие классу L2 (G)
обобщенные частные производные 1-го порядка.
Кроме W2 {G) нам понадобится его подпространство, обозначае-
о
мое символом W\ (G) и получаемое пополнением по той же норме (8)
множества всех функций из класса С''^'^ (G), равных нулю в
пограничных полосах области G.
§ 2. Обобщенное решение задачи Дирихле
для уравнения Пуассона
1. Определение обобщенного решения задачи Дирихле.
Пусть G — произвольная ограниченная область в А/'-мерном
евклидовом пространстве Е^, от границы Г которой не требуется никакой
гладкости.
В этой области мы рассмотрим задачу Дирихле (т. е. первую
краевую задачу) для уравнения Пуассона:
{Аи = — f (в области G),
^ (1)
и\т = (р.

§ 2] ОБОБЩЕННОЕ РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ 783
При этом f (х)—заданная функция из класса L2 (G), а (f (х) —
заданная во всей области G + Г функция, принадлежащая
пространству W2 {G) и имеющая на границе Г области G след,
совпадающий со значением реп1ения и {х) (такую функцию ip {х) называют
допустимой).
Дадим два определения обобщенного решения задачи Дирихле (1).
Для сокращения записи введем в рассмотрение следующие два
функционала, первый из которых определен на любой паре функций из класса
W2 (G), а второй — на любой паре функций из класса L2 (G):
G *^=1
Н{!,ф) = j f{x)xl,{x)dx. (3)
G
Определение 1. Назовем обобщенным решением
задачи Дирихле (1) функцию и (ж), удовлетворяющую следующим двум
требованиям:
1) u{x)-ip{x) ewl{G)]
о
2) для любой функции ф (ж) из класса W\ iG) функция и (ж)
удовлетворяет интегральному тождеству
G ^-^ G
С ПОМОЩЬЮ обозначений (2) и (3) тождество (4) можно записать в
виде
Е{и,ф)-Н{/,ф)=0. (5)
Определение 2. Назовем обобщенным решением
задачи Дирихле (1) функцию и (ж), которая доставляет минимум
функционалу ""^^
E(v,v)-2H(f,v) = IJ2(J^) dx-2 If{x)v(x)dx (6)
В классе всех функций v (ж), удовлетворяющих условию
v{x)-^p{x)€Wl{G). (7)
^ функционал (6) принято называть интегралом Дирихле или
основным энергетическим функционалом.

784 ДОПОЛНЕНИЕ HI. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
Замечание. Так как пространство W2 {^) является
подпространством W2 (G), то обобщенное penienne (и по определению 1, и
по определению 2) принадлежит пространству W2 {G).
Теорема (об эквивалентности двух определений
обобщенного реп1ения). Два определения обобщенного решения
задачи Дирихле (1) эквивалентны.
Доказательство. 1°. Сначала докажем, что если и{х) —
обобщенное penienne задачи (1) по определению 1, то эта же функция
является обобщенным реп1ением задачи (1) и по определению 2.
Заметим, что для любой функции и {х) из класса W2 {G) и любой
о
функции "ф {х) из класса W2 {G) справедливо тождество
E{u,u)-2H{f,u)
+ 2
Е{щф)-Н{!,ф)
+ Е{ф,ф), (8)
Так как для и (х) справедливо тождество (5) и Е {ф, ф) ^ О, то
из (8) получим неравенство
Е {и + ф, и + ф) - 2 Н {f, и + ф) ^ Е {и, и) - 2 Н {f, и). (9)
Любую функцию v{x), удовлетворяющую условию (7), в силу
о
ТОГО, что и{х) — (р (х) G Wl (G), можно представить в виде v (х) =
о
= и{х) + ф (ж), где ф (х) —некоторая функция из W2 {G).
Поэтому для любой функции V (ж), удовлетворяющей условию (7),
получим из (9)
Е{у, V) - 2Я(/, у) ^Е{и, и) - 2Я(/, и),
а это и означает, что функция и (х) доставляет минимум функционалу
(6) в классе всех функций v{x), удовлетворяющих условию (7), т. е.
и (х) является обобщенным решением задачи (1) по определению 2.
2°. Докажем теперь обратное утверждение, т. е. докажем, что если
и (х) является обобщенным решением задачи (1) по определению 2, то
эта же функция и (х) является обобщенным решением задачи (1) и по
определению 1.
Так как тождество (8) справедливо для и (х) G W2 {G) и для лю-
о
бой функции ф {х) из класса W2 (G), то в этом тождестве можно
заменить ф (х) на еф{х), где ф (х)—снова любая функция из класса
о
И^2 {G)j а е — любое вещественное число. При этом тождество (8)
принимает вид
Е{и-\-еф,и-\-еф) -2Н{/,и-\-еф)
Е{щи)-2Н{/,и)
= 2е
Е{щф)-Н{/,ф)
+ е'^Е{ф,ф). (10)

§ 2] ОБОБЩЕННОЕ РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ 785
Так как в силу определения 2 и (х) доставляет минимум
функционалу (6), то левая часть (10) неотрицательна. Поэтому для любого
о
вещественного числа е и любой функции ф (х) из класса Wl iP)
2е
Е{щф)-Н{/,ф)
+ е'Е{ф,ф)^0. (11)
Нам достаточно доказать, что и (х) удовлетворяет тождеству (5),
т. е. доказать, что выражение в квадратных скобках в (11) обращается
о
в нуль для любой функции ф (х) из класса W2 {^)- Предположим, что
о
для некоторой функции ф (х) из класса Wl {G) указанное выражение
в (11) отлично от нуля. Тогда, взяв для этой функции ф {х) число £
противоположным по знаку величине Е{и,ф) — Н{/,ф) и равным по
модулю
Е(ф,ф)
МЫ получим, что величина, стоящая в левой части (11), строго
отрицательна, а это противоречит неравенству (11). Полученное
противоречие доказывает, что выражение в квадратных скобках в (11) равно
о
нулю для любой функции ф (х) из класса Wl (G), т. е. справедливо
тождество (5), и и{х) является обобщенным решением задачи (1) по
определению 1. Теорема доказана.
2. Два основных неравенства.
1. Неравенство Пуанкаре. Пусть G—произвольная
ограниченная область в Е^. Тогда для всех функций ф (х) из класса
о
W\ (G) найдется постоянная 7, такая, что для величин,
определяемых соотношениями (2) и (3), справедливо неравенство
Н{ф,ф)^^Е{ф,ф), (12)
называемое неравенством Пуанкаре.
Доказательство. Достаточно доказать неравенство (12) для
любой функции ф (х) из класса С'^"'"'^ (G) (т. е. для любой функции,
имеющей в области G непрерывные частные производные 1-го
порядка и равной нулю всюду в некоторой пограничной полосе области G),
ибо пространство Wl iP) получается пополнением С^^ iG) по норме
(8) из § 1.
Рассмотрим любую функцию ф (ж) из класса (7^^^ (G) и
продолжим эту функцию нулем на некоторый «квадрат» со стороной 2а:
—a^Xk^OL^ к = 1, 2, ..., N, внутри которого содержится
рассматриваемая ограниченная область G. Тогда по формуле Ньютона —
50 А. Н. Тихонов, А. А. Самарский

786 ДОПОЛНЕНИЕ HI. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
Лейбница
Ук
-г
дф {У1, ^2, . . . , Ук-1, Xk, Ук+1, . . . , 2/7v)
дхь
dxk
и потому в силу неравенства Коши — Буняковского
Ф^ (у) ^ 2а
а
I
дф
dxk
dxk.
Тем более справедливо неравенство
V^' {у) ^ 2а
I
N
Е
дф
дхь
dxkj
интегрирование которого по координатам yi, У2, • • •, Vn в пределах
от —а до а по каждой из этих координат дает неравенство Пуанкаре
(12) с постоянной 7 = 4а^.
2. Оценка снизу основного функционала (6). Паша
цель — доказать, что в классе всех функций v{x), удовлетворяющих
условию (7), функционал (6) ограничен снизу постоянной, зависящей
лишь от области G и от заданных функций f (х) и (/? (ж).
Любую функцию v{x), удовлетворяющую условию (7), можно
представить в виде v (х) = (р (х) -\- ф (х), где ф (х) — некоторая функ-
о
ция из Wl iP). Таким образом.
= E{ip, ip)+2E{<p, ф)+Е{ф, ф) - 2Я(/, ip) - 2Я(/, ф).
Теперь заметим, что
(13)
E{ip, ip)+2E{ip, ф)+Е(ф, ф) = -Е{^, ср) + -Е{ф, ф) +
+
2Е{ср,^р)+2Е{ср,ф) + -Е{ф,ф)
-Е{ср,^р) + -Е(ф,ф) +
+ e(V2p+^,V2p+^^ ^-Е(р,р) + ^Е{ф,ф). (14)
Наконец, оценим сверху \2Н (f, ф)\, пользуясь неравенством
Пуанкаре (12) и неравенством 2 \А\ \В\ ^ А^ -\- В'^ при А = f -2 ^/7, В =

§ 2] ОБОБЩЕННОЕ РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ 787
Ф т.
= . в результате получим
2л/7
\2Н{!,ф)\^2 j\f{x)\\^{x)\dx ^
G
^ 4j I \f {х)\Чх+ ^ I \ф{х)\Чх ^4jH {f, Л + ^Е{ф, ф), (15)
G G
Сопоставляя равенство (13) и неравенства (14), (15), окончательно
получим
E{v, v)-2H{f, v) ^ -Е{^, ^) -47Я(/, f)-2H{f, ^) + \е{Ф, ф).
(16)
Так как Е {ф, ф) ^ О, ограниченность основного функционала (6)
снизу доказана.
3. Единственность и существование обобщенного
решения задачи Дирихле.
Теорема (о единственности обобщенного решения
задачи Дирихле). Моэюет существовать только одно
обобщенное решение задачи Дирихле (1).
Доказательство. Если бы существовало два обобщенных
решения задачи Дирихле (1) щ (х) и ^2 (ж), то их разность ф (х) =
о
= ui (х) — U2 (х) принадлежала бы классу Wl (G). Записав с
указанной функцией ф (х) тождество (5) сначала для щ (ж), а затем для
U2 (ж), мы получили бы равенства
E{ui,ui -U2) - H{f,ui -U2) = О, E{u2,ui -U2) - H{f,ui -U2) = О,
разность которых привела бы к соотношению
E{ui -U2, ui -U2) = 0. (17)
Из (17) в силу неравенства Пуанкаре (12) следовало бы, что и
Н {ui - U2, ui - U2) = 0. (18)
Соотношения (17) и (18) в силу определения (8) из § 1 нормы
пространства W2 {G) означали бы, что разность ui {х) — U2 {х) является
нулевым элементом пространства W2 (G), т. е. означали бы
совпадение элементов ui {х) и U2 {х). Теорема доказана.
Теореме существования обобщенного решения задачи Дирихле (1)
предпошлем определение минимизирующей
последовательности и доказательство вспомогательного утверждения.
Так как в силу неравенства (16) основной функционал (6)
ограничен снизу в классе всех функций, удовлетворяющих условию (7), то у
50*

788 ДОПОЛНЕНИЕ III. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
функционала (6) существует в указанном классе точная нижняя грань,
которую мы обозначим через d:
d= inf {E{v,v)-2H{f,v)}, (19)
v-(pewl (^)
По определению точной нижней грани, существуют последовательно-
о
сти {vn{x)} функций, удовлетворяющих условию Vn{x) — (f{x) ^WliG),
для которых числовые последовательности
dn = E{vn,Vn)-2H{f,Vn) (20)
СХОДЯТСЯ к точной нижней грани d.
Каждую такую последовательность { Vn (х) } назовем
минимизирующей.
Важное для нас свойство любой минимизирующей
последовательности выясняет следующая лемма.
Лемма. Если {vn{x)}—любая минимизирующая
последовательность, {фг1{х)}—последовательность функций из класса
о
Wl (G), для которых
Е{фггАп) ^M = COnst, (21)
то числовая последовательность
ап = Е{Уп,фп)-Н{/,фп) (22)
является бесконечно малой.
Доказательство. Положим an = dn — d, где {dn} — числовая
последовательность, определяемая соотношением (20), а d — точная
нижняя грань (19). Тогда в силу того, что последовательность
{ Vn (х) } является минимизирующей, можно утверждать, что
последовательность {(7п} является бесконечно малой при сг^ ^ О для всех
номеров п.
Для любого отличного от нуля е и любого номера п справедливо
неравенство
Е{Уп-\-ефп,Уп+£фп) -"^Н (/, Vn+e фп) ^ d,
которое может быть переписано в виде
E{vn, Vn) -2H{f, Vr,
d + 2e
E{vn, Фп) -H{f, фг,
+ е^Е{фп,фп) ^0.
Последнее неравенство с помощью обозначений (20) и (22), в свою
очередь, может быть переписано в виде
dn-d-\-2ean-\-€'^ Е {фп, фп) ^ О,
или
an + 2еап + е^ Е {фп, фп) ^ 0.

§ 2] ОБОБЩЕННОЕ РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ 789
В силу (21) тем более справедливо неравенство
сгп + 2гап + е^М ^ 0. (23)
Теперь, учитывая, что сг^ ^ О и что последовательность {сгп}
является бесконечно малой, для любого отличного от нуля е
фиксируем настолько большой номер N, что при п ^ N выполняется
неравенство
0^ап<е^ М.
Сопоставляя это неравенство с (23), мы получаем, что 2г а^ + 2 г^ М ^
^ 0. Теперь, если для каждого номера п взять знак е
противоположным знаку an, то мы получим, что произведение 2е an
неположительно и, следовательно, 2г^ М ^ 2\е\ \an\j откуда \ап\ ^ \е\ М (для всех
п^ N).
Лемма доказана.
Теорема (о существовании обобщенного решения
задачи Дирихле). Если G—произвольная ограниченная область
в пространстве Е^^ ^ (х)—произвольная допустимая функция,
f (х)—произвольная функция из класса L2 (G), то существует {и
притом единственное) обобщенное решение задачи Дирихле (1).
Доказательство. Прежде всего докажем, что любая
минимизирующая последовательность { Vn (х) } является фундаментальной в
смысле нормы (8) из § 1.
Заметим, что если {vn{x)} —минимизирующая
последовательность, то, положив Vn (х) = (f(x) -\- фп (х) и взяв в (16) такое Vn (х)
вместо v{x), мы получим, что левая часть (16) будет сходящейся,
а потому и ограниченной последовательностью. При этом из (16) мы
получим, что и последовательность { Е {ф^ Фп)} является
ограниченной. Таким образом, в силу тривиального неравенства
Е {vn, Vn) = Е {(f + Фп, (f + Фп) ^ '^ Е {(f, (f) + 2 Е {фп, Фп)
и последовательность Е {vn, Vn) является ограниченной. Отсюда, в
свою очередь, вытекает ограниченность последовательности Е (vn —
— Vm, Vn — Vm) при вссх п И вссх гп. Учитывая, что, кроме того, Vn —
о
— Vm ^ W\ (G) для любых номеров тип, мы получим, что разность
(vn — Vm) при фиксированном т можно взять в качестве фп (х) в
лемме, а при фиксированном п эту же разность можно взять в качестве
фт (х) В лемме. Мы получим при этом, что в силу леммы
Иш { Е {Vn, Vn -Vm) - Н (/, Vn -Vm)} = О,
n—>-CXD
lim { E {Vm, Vn -Vm) - H (/, Vn -Vm)} = 0.
Из последних двух соотношений вытекает, что
Иш Е {Vn -Vm.Vn- Vm) = О, (24)
ттг—>-cxD
n—>-CXD

790 ДОПОЛНЕНИЕ III. ОБОБЩЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
а из (24) и из неравенства Пуанкаре (12) — что и
lim Н {Vn -Vm,Vn- Vm) = 0. (25)
n—>-CXD
Из (24) и (25) следует, что минимизирующая последовательность
{ Vn (х) } является фундаментальной в смысле нормы (8) из § 1. По
тогда из полноты пространства W2 {G) вытекает, что существует такой
элемент v (ж) этого пространства, что
lim \\vn - v\\ = 0. (26)
n—>-CXD
Остается доказать, что v (х) и является обобщенным решением
задачи Дирихле (1).
Прежде всего заметим, что v (х) удовлетворяет условию (7), ибо
о
'^п (х) — (f{x) е W\ (G) для каждого номера п, а \\{vn — (f) — {v — (f)\\ =
= \\vn — г^Ц ^ 0 при n ^ 00.
о
Остается доказать, что для любой ф (х) из класса Wl iP)
функция V {х) удовлетворяет тождеству (5), т. е.
Е{у,ф)-Ни,ф)=0. (27)
О
в силу леммы для любой функции ф (ж) из класса W2 iP)
Е{Уп,ф)- Н{/,ф) ^0 при п^оо. (28)
Далее, из неравенства Коши — Буняковского
\E(v - Vn, [V -Vn, V -Vn
О
и ИЗ (26) следует, что для любой функции ф (х) из Wl (G)
Е {v — Vnj ф) ^ О при п ^ 00. (29)
Из (28) и (29) вытекает тождество (27).
Теорема доказана.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Арнольд В. И. Математические методы классической механики. М.:
Наука, 1989.
2. Бицадзе А. В. Уравнения математической физики. М.: Наука, 1982.
3. Владимиров В. С. Уравнения математической физики. М.: Наука,
1988.
4. Джефрис Г., Свирлс Б. Методы математической физики. М.: Мир,
1969.
5. Егоров Ю. В., Шубин М. А. Линейные дифференциальные
уравнения с частными производными // Современные проблемы математики.
Фундаментальные направления / ВИНИТИ. 1987. Т. 30. (Итоги науки и
техники).
6. Кондратьев А. Н., Рождественский Б. Л. Обыкновенные
дифференциальные уравнения и основы вариационного исчисления. М.:
Наука, 1986.
7. К о HI ел ев А. И. Регулярность репЕСний эллиптических уравнений и
систем. М.: Наука, 1986.
8. Кружков С. Н. Нелинейные уравнения с частными производными. М.:
Изд-во Моск. ун-та, 1970.
9. Крылов Н. В. Нелинейные эллиптические и параболические
уравнения второго порядка. М.: Наука, 1985.
10. Лаврентьев М. А., Шабат Б. В. Методы теории функций
комплексного переменного. М.: Наука, 1987.
11. Ладыженская О. А. Краевые задачи математической физики. М.:
Наука, 1973.
12. Ладыженская О. А., Солонников В. А., Уральцева Н. Н.
Линейные и квазилинейные уравнения параболического типа. М.: Наука,
1967.
13. Михайлов В. Т. Дифференциальные уравнения в частных
производных. М.: Наука, 1983.
14. М их ЛИН С. Г. Линейные уравнения в частных производных. М.: ВыспЕ.
шк., 1977.
15. Р о ж д ественский Б. Л., Яненко Н. Н. Системы квазилинейных
уравнений и их приложения к газовой динамике. М.: Наука, 1978.
16. СвепЕников А. Г., Боголюбов А. Н., Кравцов В. В. Лекции по
математической физике. М.: Изд-во Моск. ун-та, 1993.
17. Соболев С. Л. Некоторые применения функционального анализа в
математической физике. М.: Наука, 1988.
18. Фридман А. Уравнения с частными производными параболического
типа. М.: Мир, 1968.
19. Шипе марев И. А. Введение в теорию эллиптических уравнений. М.:
Изд-во Моск. ун-та, 1979.

предметный указатель
Автомодельное движение 173
Адиабата Гюгонио 167
— Пуассона 40
Адиабатический процесс 40, 164, 171
Аппроксимация дифференциального
оператора разностным 587
по норме 591
с порядком п 587, 591
— суммарная 644
Броуновское движение 282
Вектор Герца 473
— смещения 462
Векторный потенциал 464, 468
Волна бегущая 57
— гармоническая 78
— затухающая 79
— магнитная (типа ТМ) 558
— отраженная 72, 76
— плоская 434, 545
— разрежения 171
— распространяющаяся 57, 179, 181
— стоячая 93, 156, 450
— сферическая 429, 434
расходящаяся 429, 524
сходящаяся 429, 524
— температурная 256
— тепловая 273, 276
— ударная 165, 168
— цилиндрическая 434
— электрическая (типа ТЕ) 558
Волновая зона осциллятора 475
Волновое уравнение 443, 519
— число 78
Газовая динамика 163
Гамма-функция 696
Гармоника 94, 149, 155
— сферическая 723
Главное значение интеграла 365
Граничное условие 2-го рода 45
нелинейное 46, 200
1-го рода 45
3-го рода 45
Граничные условия 44, 45, 153, 196
Граничные условия однородные 45
(У-Функция 286, 288
Дисперсия волн 78
Дифракция 541
— на сфере 545
— плоской волны на сфере 547
Диффузия 189, 193, 283, 295, 511
— в движущейся среде 520
— при наличии распада и цепных
реакций 491, 520
Длина волны 78
Емкость уединенного проводника 398
Задача без начальных условий (на
установивп1ийся режим) 47, 111, 199,
250
— гравиметрии обратная 67
— Гурса 129
— Дирихле 296, 782
внеп1няя 322, 323
внутренняя 317
для сферы 733
разностная 632
— дифракции 542
— Коши 43, 47, 199, 228, 427
— краевая 45
внешняя 296, 322, 381
вторая 327
первая 323
внутренняя 296, 380
вторая 325
первая 317
вторая 46, 296, 325, 381
для уравнения Бесселя 678
первая 46, 49, 198, 199, 296, 381,
782
для круга 328, 383
для полупространства 385
разностная 586
с кусочно-непрерывными
начальными данными 216
с разрывными граничными
условиями 318, 336
коэффициентами 609

предметный указатель
793
Задача краевая с разрывными
начальными данными 215
смешанная 47
со стационарными неоднородно-
стями 109, 226
третья 46, 296
— Неймана 296
внешняя 327
внутренняя 325
— о движении твердого тела в
жидкости 416
электрона в кулоновом поле
ядра 753
колебании ограниченных объемов
444
тонкой пластинки 422
промерзании 279
размагничивании цилиндра с
обмоткой 514
распространении граничного
режима 76
начального возмущения 68
тепла в неограниченном
пространстве 477, 481
собственных значениях 89, 120,
154, 210, 423, 445, 660
фазовом переходе 277, 279
— об определении векторного поля по
заданным ротору и дивергенции 408
остывании равномерно нагретого
цилиндра 489
— обработки наблюдений 67
— поставленная корректно 65
— разностная, поставленная корректно
597
устойчивая 597
— с начальными условиями 47, 199,
228, 427
для уравнения Лапласа 66
— Стефана 279
— устойчивая 65
— Штурма — Лиувилля 89, 210, 445,
660
— электростатики основная 396
Закон Гука 462
— инерции 23
— Нернста 193
— Ньютона 192
— сохранения энергии 163
— Стефана — Больцмана 200
— Фурье 190, 194
второй 256
первый 257
третий 257
Законы Мерсена 96
Закрепление жесткое 45
— мягкое 45
— упругое 44
Изотерма Генри 175
— Ленгмюра 175, 183
Изотерма сорбции 175
Интеграл внутренний 778
— Дирихле 783
— Лебега 779
— несобственный 353
— ошибок 241, 246, 758, 764
— Пуассона 233, 334
для круга 347
для сферы 345
— Римана 778
— Римана — Ханкеля 696
— Фурье — Бесселя 705
Квантовое число азимутальное 755
главное 752, 755
магнитное 757
радиальное 755
Конденсация газа 40
Координаты биполярные 774
— бисферические 775
— криволинейные 298, 769
— параболические 771
— параболоидные 776
— прямоугольные 769
— сферические 301, 770
— сфероидальные 776
— тороидальные 774
— цилиндрические 301, 770
— эллипсоидальные 772
вырожденные 773
— эллиптические 771
Коэффициент диффузии 193
— жесткости закрепления 45
— кинетический 175
— пористости 194
— температуропроводности 192, 196,
258
почвы 257
— теплообмена 192
— теплопроводности 189
Коэффициенты Ламэ 769
— метрические 769
— Фурье 125
Краевые условия разностные 586
Кривая Ляпунова 371
Критические размеры 493
Локализация реп1ений уравнения
теплопроводности 276, 507
Метод баланса 610
— интегральных соотноп1ений 601
— интегроинтерполяционный 610
— итерационный 651
двухслойный 651
в канонической форме 651
двухп1аговый 651, 655
одноп1аговый 651

794
предметный указатель
Метод итерационный попеременно-
треугольный 657
стационарный 653
трехслойный 651, 655
в канонической форме 655
чебып1ёвский 653
— конечных разностей 282, 585
— конформного преобразования 412,
415, 419
— локально-одномерный 644
— минимальных поправок 654
— отражения 436
— перевала 701
— переменных направлений неявный
642
— подобия 185, 264, 281
— попеременно-треугольный 657
— последовательных приближений 129
— прогонки 623
— продолжения 68, 71
— простой итерации 652
— прямой 653
— разделения переменных 87, 119, 153,
209, 229, 328, 423, 445
— распространяющихся волн 54
— Ричардсона 653
— сглаживания для реп1ения задачи
Стефана 648
— седловой точки 703
— сеток 585
— скорейп1его спуска 654
— сопряженных градиентов 656
направлений 655
— спуска 433, 434
— усреднения 429
— факторизации 623
— Фурье 87
— электростатических изображений
343
— энергетических соотношений 601
— Якоби 656
Модуль сдвига 463
Момент диполя 367
— тока 471
Напряжения 462
— нормальные 462
— скалывающие 462
Начальные условия 43, 44, 197
разностные 586
Невязка 652
Неравенство Пуанкаре 785
Норма 780
— полиномов Лежандра 714
Чебышёва — Лагерра 747, 763
Чебышёва — Эрмита 747, 763
— присоединенных функций Лежандра
717, 763
— сеточной функции 591
— собственной функции 160, 161, 448,
680
Нули полиномов Лежандра 715
Обертон 95, 148
Обобщенное решение 68, 270, 271, 777,
783
Обтекание кругового цилиндра 418
— пластинки 419
Окрестность Ляпунова 371
Оператор Лапласа 41, 196
разностный 628
— разностный 587
двухточечный 588
1-го порядка 588
трехточечный 588
— самосопряженный 136
— сеточный 587
Операторы сопряженные 136
— энергетически эквивалентные 653
Ортогональность полиномов Лежандра
713
Чебышёва — Лагерра 747
Чебышёва — Эрмита 744
— присоединенных функций Лежандра
717
— с нагрузкой 158
— собственных функций 121, 124, 158,
161, 446, 666, 680
— сферических функций 724
Основной тон 95, 148, 155
— энергетический функционал 783
Переменная Лагранжа 31
— Эйлера 31, 38
Поверхность Ляпунова 371
HorpeniHOCTb аппроксимации
дифференциального оператора
разностным 587
уравнения разностным 599
схемы на peniennn уравнения 599
— итерационного метода 651
— относительная 652
Поле потенциальное 297
— электрическое полубесконечного
плоского конденсатора 413
— электромагнитное осциллятора 470
Полиномы гармонические 720
— Лежандра 662, 709, 761, 768
— Чебышёва — Лагерра 745, 763
обобщенные 747
— Чебышёва — Эрмита 742, 763
Пористость 187
Порядок аппроксимации
дифференциального оператора разностным 587,
591
разностной схемы 599
Последовательности эквивалентные 288
Последовательность минимизирующая
787
— нормированная локальная 288

предметный указатель
795
Последовательность фундаментальная
780
Постоянная Планка 749
— Ридберга 756
— Эйлера 758
Постоянные Ламэ 463
Потенциал 348
— векторный 464, 468
— двойного слоя 368, 371, 374, 529
— логарифмический 351
— объемный 348, 360, 363, 393, 528
— поверхностный 367, 371, 380
— поляризационный 473
— простого слоя 367, 371, 377, 530
— силового ПОЛЯ 349
— скалярный 464, 468
— скоростей 41, 296
Потенциалы тепловые 503
— электромагнитного поля 468
Потенциальное течение жидкости 296
Предельный элемент
последовательности 288
Преобразование Кельвина 306
— обратных радиусов-векторов 305
— переменных 16, 25
Принцип взаимности 342, 480, 527
— Гюйгенса 436
— Дюгамеля 249
— максимального значения 203, 315,
325, 522
— максимума 633
— предельного поглощения 532
— предельной амплитуды 534
— суперпозиции 48, 211, 235
обобщенный 97, 233
Проблема вычислительной
устойчивости чебып1ёвского итерационного
метода 654
Производная разностная левая 587
правая 587
центральная 587
— субстанциональная 39
— частная обобщенная 782
Пространство нормированное 780
полное 780
Li(G) 781
L2IG) 781
W^{G) 781, 782
Пучность стоячей волны 93, 450
Разностная схема 593
безытерационная 626
двухслойная шеститочечная 598
итерационная 626
консервативная 612
локально-одномерная 644
симметризованная 645
неустойчивая 594
неявная 594, 599, 622
однородная 612
Разностная схема повып1енного
порядка аппроксимации для уравнения
теплопроводности 601
продольно-поперечная 642
с весами 598
с опережением 594
симметричная п1еститочечная
для квазилинейного уравнения
теплопроводности 626
сквозного счета 610
трехслойная 620
симметричная 620
устойчивая 594, 596, 605
по начальным данным и по
правой части 605
экономичная 641
явная 594, 599
Разностное отноп1ение 587
— уравнение 585, 593
Разрыв сильный 170
— слабый 83, 170
Режим с обострением 274, 508
Резонанс 114, 119
Рекуррентные формулы для полиномов
Лежандра 711, 762
Чебышёва — Лагерра 746
Чебышёва — Эрмита 743,
763
Решение автомодельное 272, 274
— локализованное 276, 507
— обобщенное 68, 270, 271, 777, 783
— первой краевой задачи 200
— типа бегущей волны 268
— фундаментальное уравнения
Лапласа в пространстве 302
на плоскости 302
теплопроводности 230, 495
Ряд Фурье 92, 99
Серия Бальмера 756
— Лаймана 756
— Пашена 756
Сетка 585
— в прямоугольнике 586
— на отрезке 586
— неравномерная 586
— равномерная 586
— связная 630
Система ортогональных функций 713
замкнутая 713, 719
полная 713
Скалярный потенциал 464, 468
Скин-эффект 574
Скорость волны групповая 557
фазовая 78
— распространения звука 43
Собственная функция 89, 90, 120, 445,
563, 660, 666, 679
— частота 94, 157, 161
Собственное значение 89, 90, 120, 161,
445, 666, 679

796
предметный указатель
Собственные функции круглой
мембраны 565
прямоугольной мембраны 564
— электромагнитные колебания 565
Сопряженные точки 343
Сорбция 174
Суперпозиция 48
Сферическая гармоника 723
Сходимость последовательности
функций в среднем 287
равномерная 287
слабая 287
— разностной схемы 594, 608
Тембр 95, 148
Тензор деформаций симметрический
463
— напряжений симметрический 462
Теорема Вейерштрасса 714
— единственности 50, 205, 208, 217, 317,
318, 327, 532, 787
— о среднем значении 313
— разложимости 121, 446, 666, 681
— сравнения 634
— существования 50, 789
— Фредгольма вторая 389
первая 386
третья 390
— Цемплена 168
Теория упругости 461
Тепловые потенциалы 503
Теплосодержание 164
Тон 95, 148
— основной 95, 148, 155
Точность разностной схемы 608
Узел сетки 585, 630
внутренний 590
граничный 590, 630
нерегулярный 630
регулярный 630
— стоячей волны 93
Узловая линия (поверхность) стоячей
волны 450
Узлы сетки соседние 630
Уравнение акустики 42
— Бесселя 661, 662, 668
— бигармоническое 422
— волновое 443, 519
— газовой атаки 521
— Гельмгольца 443
— гиперболического типа 19, 22, 23, 25,
27
каноническая форма 20, 22, 24,
26
вторая 20
— Даламбера 427
— движения 163
Уравнение движения идеальной
жидкости в форме Эйлера 39
— дифференциальное с частными
производными 2-го порядка с двумя
независимыми переменными 15
со многими
независимыми переменными 22
— диффузии 194
— интегральное нагруженное 158
Фредгольма 2-го рода 382, 386
1-го рода 382
— квазилинейное 15
— кинетики сорбции 175
— колебаний 27, 31, 42, 427
интегральное 29, 32, 37, 79
мембраны 38
струны 27, 78, 128
— Ламэ 463
— Лапласа 65, 295, 301
— Лежандра 662, 712, 762
— линейное 16, 24
относительно старп1их
производных 15, 16
— непрерывности 40, 163
— нормального гиперболического типа
23
— однородное 16
— параболического типа 19, 20, 22, 23,
25, 189
вырождающееся 271
каноническая форма 21, 22, 24,
26
— поперечных колебаний стержня 152,
153
— присоединенных функций Лежандра
662, 762
— Пуассона 295
— разностное 585, 593
— с комплексным поглощением 1-го и
2-го типа 533
— состояния 40, 163, 171
— телеграфное 35, 79
— теплопроводности 189, 192, 196, 295,
477, 597
в интегральной форме 191
квазилинейное 193, 267, 624
неоднородное 222
— ультрагиперболического типа 23
каноническая форма 24
— Фредгольма 2-го рода 382, 386
1-го рода 382
— характеристическое 18, 25, 55
— цилиндрических функций 661, 668
— Чебышёва — Лагерра 662, 746
— Чебышёва — Эрмита 662, 743
— Шрёдингера 749
второе 750
для гармонического осциллятора
750
движения электрона в кулоно-
вом поле 753
ротатора 752

предметный указатель
797
Уравнение Эйлера 722
— Эйнштейна — Колмогорова 283
дифференциальное 285
— эллиптического типа 19, 21, 22, 23,
25, 295, 519
каноническая форма 22, 24, 26
Уравнения газовой динамики 163
— гидродинамики 40, 41
— интегральные сопряженные 382
— магнитостатики 467
— Максвелла 464
— поля материальные 465
— телеграфные 35, 185
— электромагнитного поля 464
— электростатики 467
Условие возбуждения 560
— исчезающего трения 115
— Леонтовича 572
— Лоренца 469
— нормировки 123, 140, 713, 750
— ограниченности 229, 455, 666
— отсутствия искажения 79
— периодичности 455
— прилипания 421
— свободного конца 44, 71
— упругого закрепления 44
Условия Гюгонио 165, 167
— динамической совместности 167
— Зоммерфельда 539
— излучения 539
— Коши — Римана 303
— сопряжения 30, 116, 156, 198
для уравнений Максвелла 466
Устойчивость разностной схемы 594,
596, 605
безусловная 606
по начальным данным и по
правой части 605
условная 606
— явной разностной схемы 606
Фазовая плоскость 57
Флажолет 96
Формула Грина 121
вторая 308
двумерная 136
основная интегральная 310
на плоскости 312
первая 308
разностная вторая 602
первая 602
— Даламбера 54, 56, 144
— дифференциальная для полиномов
Лежандра 711
— Зоммерфельда 709
— интегральная для волнового
уравнения 444
уравнения колебаний 437, 441
— Кирхгофа 441, 444
— Остроградского — Гаусса 307
— Пуассона 430
Формула разностного
дифференцирования произведения 601
— Родрига 711, 762
— суммирования по частям 601
Формулы прогонки 623, 624
Фронт распространяющейся волны
задний 58, 435, 436
передний 58, 435, 436
— тепловой волны 271
— ударной волны 165, 167
Функции Бесселя 671, 695, 699, 758, 765,
766, 767
от комплексного аргумента 576
полуцелого порядка 674, 761
— гармонические сопряженные 304
— зональные 723
— Лежандра присоединенные 717, 762
— Макдональда 687, 699, 759, 766, 768
— Пеймана 683, 684, 758, 767
— сферические 660, 661, 722
— тессеральные 724
— Ханкеля (1-го и 2-го рода) 682, 684,
695, 759
— цилиндрические 660, 661, 668, 675,
758
2-го рода 683
мнимого аргумента 686, 759, 768
— Чебышёва — Эрмита 745
— niapoBbie 721
Функция аналитическая 303
— бигармоническая 422
— влияния мгновенного импульса 107
сосредоточенного импульса 104,
140
точечного источника 497, 522
— гармоническая 295, 303, 305, 307
регулярная на бесконечности 321
— Грина 667
— Дирихле 779
— допустимая 783
— измеримая 779
— интегрируемая по Лебегу 778, 779
— источника 213, 225, 228, 291, 338, 477,
497, 500, 525
— мгновенного точечного источника
213
— обобщенная 286
— производящая обобщенных
полиномов Чебышёва — Лагерра 747
полиномов Лежандра 710, 761
Чебышёва — Лагерра 745, 763
Чебышёва — Эрмита 742, 763
— Римана 138, 139, 145
— сеточная 585
— собственная 89, 90, 120, 445, 563, 660,
666, 679
— температурного влияния 213, 225,
480, 497
— тепловая 164
— точечного источника первой краевой
задачи для уравнения Лапласа 339
— финитная 270

798
предметный указатель
Характеристика 18, 19, 25, 57, 83, 129,
176
Характеристический конус 438
— треугольник 58
— угол 62, 437
верхний 62
нижний 62
Шаблон девятиточечный «ящик» 629
— коэффициентный 612
— пятиточечный 589
«крест» 628
— разностного оператора 588
— трехточечный 588
— п1еститочечный 598
Шаг сетки 586
Цепные реакции 492
Энергетическое тождество 604
Частота 78, 155
— собственная 94, 157, 161
— собственная осциллятора 750
Шаблон двухточечный 588
Ядра повторные 386
— сопряженные 382
Ядро интегрального уравнения 382
— оператора 291
— Пуассона 334

Учебное издание
Тихонов Андрей Николаевич,
Самарский Александр Андреевич
УРАВНЕНИЯ математической физики
Зав. редакцией И. И. Щехура
Художественный редактор Ю. М. До брянская
Корректор Т. В. Властовская
Компьютерная верстка С. В. Полякову А. С. Болдарев
Изд. лиц. № 040414 от 18.04.97
Подписано в печать
Формат 60 X 90/16. Бумага офс. № 1.
Гарнитура Computer Modern. Офсетная печать.
Усл. печ. л. . Уч.-изд. л.
Тираж . Заказ № . Изд. №. 6811.
Ордена «Знак Почета» издательство Московского университета.
103009, Москва, ул. Б. Никитская, 5/7.
Отпечатано в