44зсГуъсьнные главъс
ВЫСШЕЙ МАТЕМАТИКИ
для инженеров и студентов, втузов
И.Г.ЛРАМАНОВИЧ и В.И.ЛЕВИН
УРАВНЕНИЯ
МАТЕМАТИЧЕСКОЙ
ФИЗИКИ

ИЗБРАННЫЕ ГЛАВЫ ВЫСШЕЙ МАТЕМАТИКИ
ДЛЯ ИНЖЕНЕРОВ И СТУДЕНТОВ ВТУЗОВ
И. Г. АРАМАНОВИЧ и В. И. ЛЕВИН
УРАВНЕНИЯ
МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Допущено Министерством
высшего и среднего образования РСФСР
в качестве учебного пособия
для высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
МОСКВА 1964

517.2
А 79
УДК 517.944(075.8)
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ

ОГЛАВЛЕНИЕ
Предисловие... 	 ...	7
Введение 	 9
1.	Дифференциальные уравнения с частными производными	9
2.	Однородные линейные дифференциальные уравнения
с частными производными и свойства их решений ...	14
3.	Оператор Лапласа в полярных, цилиндрических и сфе¬
рических координатах	,	 20
ГЛАВА I
УРАВНЕНИЯ КОЛЕБАНИЙ
§ 1. Уравнение колебаний струны	 24
4.	Вывод уравнения колебаний струны	 24
5.	Постановка начальных и краевых условий	 30
§ 2. Колебания бесконечной и полубесконечной струны.
Метод Даламбера	 33
6.	Бесконечная струна. Формула Даламбера	33
7.	Распространение волн отклонения	 37
8.	Распространение волн импульса	  .	46
9.	Полубесконечная струна 		 51
§ 3. Метод Фурье 	 54
10.	Метод Фурье	 54
11.	Стоячие волны	 62
12.	Примеры	 64
§ 4. Вынужденные колебания и колебания струны в среде
с сопротивлением	   71
13.	Вынужденные колебания струны	 71
14.	Колебания струны в среде с сопротивлением	 77
§ 5. Продольные колебания стержня	 80
15.	Постановка задачи и метод решения	 80
16.	Примеры	  .....	87

4
ОГЛАВЛЕНИЕ
§ 6» Крутильные колебания вала	 91
17.	Уравнение крутильных колебаний	  91
18.	Крутильные колебания вала с диском на одном конце 94
§ 7, Электрические колебания в длинных однородных
линиях	   .	99
19.	Телеграфное уравнение	  99
20.	Линия без потерь . . .	103
21.	Линия без искажения	•			105
22.	Линии конечной длины 	107
§ 8. Уравнение колебаний мембраны	114
23.	Вывод уравнения колебаний мембраны	  114
24.	Начальные и краевые условия 		 119
§ 9. Колебания прямоугольной мембраны	120
25.	Собственные функции	120
26.	Стоячие волны прямоугольной мембраны	  123
27.	Вторая часть метода Фурье. Двойные ряды Фурье . . 126
28.	Стоячие волны с одинаковой частотой	  128
§ 10. Уравнение и функции Бесселя	130
29.	Уравнение Бесселя	130
30.	Условие ортогональности функций Бесселя нулевого
порядка	  134
31.	Функции Бесселя первого порядка	  136
§ 11. Колебания круглой мембраны	  139
32.	Круглая мембрана . . . .	139
33.. Стоячие волны круглой мембраны	  143
ГЛАВА II
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ
§ 12. Уравнение линейной теплопроводности 	 145
34.	Вывод уравнения линейной теплопроводности . . . . . 145
35.	Начальное и краевые условия	  148
36.	Теплопроводность в стержне при наличии теплообмена
через боковую поверхность	151
§ 13. Теплопроводность в бесконечном стержне	153
37.	Метод Фурье для бесконечного стержня	  .	153
38» Преобразование решения уравнения теплопроводности 159

ОГЛАВЛЕНИЕ
5
39.	Фундаментальное решение уравнения теплопроводности
и его физический смысл	 162
40.	Примеры 	  168
§ 14. Теплопроводность в конечном стержне . ..... . 173
41.	Приведение к задаче с однородными краевыми усло¬
виями. Метод Фурье	173
42.	Распространение тепла в стержне в случаях постоянной
температуры на концах или теплоизоляции концов . . 177
43.	Общий случай краевых условий	•	. . 183
44.	Примеры	  186
г § 15. Теплопроводность в полубесконечном стержне . . . 196
45.	Распространение тепла при теплоизоляции или посто¬
янстве температуры конца стержня 		: . 196
46.	Примеры	200
§ 16. Некоторые пространственные задачи теплопровод¬
ности 	202
47.	Вывод уравнения теплопроводности в пространственном
случае 	202
48.	Начальное и краевые условия	207
49.	Распространение тепла в однородном цилиндре .... 210
50.	Распространение тепла в однородном шаре	214
§ 17. Задачи диффузии	216
51.	Уравнение диффузии	216
52.	Уравнения теплопроводности и диффузии с краевым
условием, зависящим от времени . •	219
53.	Примеры 	223
Г Л А В А III
УРАВНЕНИЕ ЛАПЛАСА
§ 18. Краевые задачи для уравнения Лапласа. Метод
функции Грина.  	  226
54.	Постановка краевых задач	226
65.	Метод функции Грина для задачи Дирихле (трехмерный
случай)	 230
56.	Метод функции Грина для задачи Дирихле (двумерный
случай)	 236
57.	Задача Неймана	  240
§ 19. Решение задачи Дирихле для шара и полупро¬
странства 		 .	. 		  242
58.	Сопряженные точки 		  .	242
-	59. Задача Дирихле для шара . . .... . . ,. . .. . .... 244

6
ОГЛАВЛЕНИЕ
60.	Задача	Дирихле	для внешности шара	252
61.	Задача	Дирихле	для полупространства	253
§ 20. Решение	задачи	Дирихле для круга и полуплоскости 258
62.	Задача	Дирихле	для круга	258
63.	Задача	Дирихле	для внешности круга	264
64.	Задача	Дирихле	для полуплоскости	264
§ 21. Метод Фурье для уравнения Лапласа	267
65.	Двумерное уравнение Лапласа и задача Дирихле для
круга	‘	267
66.	Разделение переменных в трехмернохм уравнении
Лапласа в сферических координатах. Многочлены
Лежандра	.	. 271
67.	Решение задачи Дирихле для шара в осесимметричном
случае разложением по многочленам Лежандра .... 278
Заключение	  282
68.	Классификация линейных дифференциальных уравнений
с частными производными второго порядка	282
69.	Корректность постановки задач математической физики 284
Литература	 287

ПРЕДИСЛОВИЕ
Несмотря на наличие богатой литературы по математи¬
ческой физике, студенты и аспиранты высших технических
учебных заведений, так же как и инженеры, работающие
в промышленности, которым необходимы первоначальные
сведения по уравнениям математической физики, испытывают
серьезные затруднения в подборе руководства по этой важ¬
ной отрасли прикладной математики. Это объясняется тем,
что почти все книги, существующие в этой области, либо
опираются на слишком большой объем математических зна¬
ний, либо написаны столь сжато и развивают математиче¬
ский аппарат столь далеко, что оказываются недоступными
для указанного выше круга возможных читателей настоящей
книги.
Авторы исходили из того, что читатель знаком только
с обычным курсом высшей математики, изучаемым в наших
втузах. Мы учитывали также, что читатель может интере¬
соваться не обязательно всеми задачами математической фи¬
зики, рассмотренными в книге, а только теми, которые имеют
непосредственное отношение к его специальности (одних,
например, могут интересовать только вопросы колебаний,
других — задачи теплопроводности). В соответствии с этим
книга построена так, что отдельные ее главы могут изучаться
сравнительно независимо друг ст друга. В частности, важней¬
ший метод решения многих задач математической физики —
метод Фурье — изложен с одинаковой степенью подробности
как в первой, так и во второй главе. *
Книге предпослано введение, в котором в помощь чита¬
телю собраны некоторые факты математического анализа
(в основном, обычно излагаемые в общем курсе втуза, но
также и некоторые дополнительные), которыми в дальней¬
шем приходится пользоваться.

8
ПРЕДИСЛОВИЕ
Большое внимание уделено физической стороне дела. Вы¬
воды основных уравнений изложены достаточно подробно,
а получаемые решения, как правило, исследуются с физи¬
ческой точки зрения. Всюду, где это возможно, указано на
связь с теми дисциплинами, в которых читатель найдет при¬
менение рассматриваемых в книге задач.
Вместе с тем чисто математическая сторона дела (тео¬
ремы существования, единственности, законность предельных
переходов и т. п.) почти не затрагивается. Читатель, инте¬
ресующийся вопросами такого рода, должен обратиться к
более полным руководствам (см. перечень литературы). Однако
даже при этом математический аппарат достаточно сложен
и от читателя потребуются известные усилия для его усвое¬
ния. Пункты и примеры, которые являются более трудными,
напечатаны мелким шрифтом; читатель, пропустивший эти
места, не будет испытывать затруднений при чтении основ¬
ного текста.
Чтобы, с одной стороны, избежать излишних повторений,
а с другой стороны, облегчить пользование книгой, изложе¬
ние сопровождается ссылками на книгу А. Ф. Берманта
«Краткий курс математического анализа для втузов» (Физ-
матгиз, М.), которая в дальнейшем именуется «Кр. к.».
Мы выражаем искреннюю благодарность Н. Я. Виленкину,
чьи советы повлияли на окончательную структуру книги,
а также Н. А. Угаровой и В. А. Угарову за их замечания
по тексту рукописи и Т. С. Плетневой, внимательно про¬
читавшей рукопись.
Авторы

ВВЕДЕНИЕ
1.	Дифференциальные уравнения с частными произ¬
водными. В дальнейшем будем предполагать, что читатель
уже знаком с основами теории обыкновенных дифферен¬
циальных уравнений, т. е, уравнений, связывающих неизвест¬
ную функцию одной независимой переменной, ее производные
и саму независимую переменную. Мы приведем лишь необ¬
ходимые сведения.
Дифференциальное уравнение первого порядка вида у' =
= У) имеет бесчисленное множество решений, опреде¬
ляемых формулой, содержащей одну произвольную посто¬
янную: у = ср(х, С). Аналогично общее решение дифферен¬
циального уравнения второго порядка у"==/(х, у, у') со¬
держит две произвольные постоянные: у = ср(х, СР С2). Выде¬
ление частного решения может быть произведено путем задания
начальных условий, которые для уравнения второго по¬
рядка обычно имеют вид у|х= =у0, у'|х=ЛГо = у'о. Подставляя
эти значения х, у и уг в общее решение и в его производную,
получим два уравнения для отыскания произвольных посто¬
янных Cj	л	_
f (х, у, у') — непрерывна в некоторой окрестности значений
^о» Уо и Уо и имеет там непрерывные частные производные
<V df
-g? и	то существует единственное частное решение,
удовлетворяющее данным начальным условиям (теорема су¬
ществования и единственности решения).
В дальнейшем особенно часто будут встречаться линей¬
ные дифференциальные уравнения второго порядка.
Для однородного уравнения
и С2. Если правая часть уравнения — функция
у" 4- а (х) у' + b (х) у = 0

10
ВВЕДЕНИЕ
общее решение есть линейная комбинация двух его частных
решений yj(x) и у2(х), если только эти решения линейно
независимы (т. е. у2 kyv где k — константа):
у = Ci У1 + С2 у2.
Общее решение неоднородного уравнения
у"+а(х)У + ^(х)у = /(х)
есть сумма какого-либо его частного решения и общего
решения соответствующего однородного уравнения.
В этой книге будут изучаться дифференциальные урав¬
нения с частными производными, т. е. уравнения, содер¬
жащие неизвестную функцию нескольких переменных
и ее частные производные. Обычно приходится иметь дело
с уравнениями для функций двух или трех независимых пе¬
ременных. Вот примеры таких уравнений (х, у, z— незави¬
симые переменные, и — неизвестная функция):
ди ] ди

дх'ду
д2и	д2и . ди

дх2	ду2 ' дх
д2и j д2и j д2и

дх2 ' ду2 * дг2
В первой строчке написаны уравнения, содержащие част¬
ные производные только первого порядка. Такие уравнения
называются уравнениями первого порядка. Соответственно
уравнения, написанные во второй строчке, являются приме¬
рами уравнений второго порядка.
Мы вовсе не ставим перед собой задачу изучать вообще
способы решений дифференциальных уравнений с частными
производными. Мы будем рассматривать только те конкрет¬
ные уравнения (да и то далеко не все), которые сущест¬
венны для физики, механики и техники. Именно эти урав¬
нения и называются дифференциальными уравнениями ма¬
тематической физики.
Предварительно без доказательств познакомимся с про¬
стейшими свойствами уравнений с частными производными;
будем считать, что неизвестная функция и зависит от двух
переменных х и у.
Возьмем уравнение
(1)

ВВЕДЕНИЕ
11
Ясно, что искомая функция и(х, у) не зависит от перемен¬
ной х, но может быть любой функцией от у:
й(х, у) = ?(у).	(2)
Действительно, дифференцируя функцию ср (у) по х, мы
получаем нуль, а это и значит, что равенство (1) соблю¬
дается. Следовательно, решение (2) уравнения (1) содержит
одну произвольную функцию ср (у). В этом и заключается
коренное отличие решения уравнения с частными произ¬
водными первого порядка от общего решения обыкновен¬
ного дифференциального уравнения первого порядка, кото¬
рое содержит лишь произвольную постоянную. По аналогии
решение (2), содержащее одну произвольную функцию, будем
называть общим решением уравнения (1).
Рассмотрим более сложное уравнение
Jy =/(>’).'	(3)
где f (у) — заданная функция. Все функции и(х, у), удо¬
влетворяющие уравнению (3), имеют вид
и(х, У)= f /(y)dy + <|>(x),	(4)
где ф (х)— произвольная функция от х. Это можно проверить,
дифференцируя обе части равенства (4) по у. Найденное
решение уравнения (3) зависит от одной произвольной функ¬
ции, т. е. является общим.
п	ди , ди
Легко проверить, что уравнение х-^ + у^у=0 имеет
общее решение и(х, у) = (р0^, где ср —произвольная диф¬
ференцируемая функция.
Напомним для этого правило дифференцирования слож¬
ной функции нескольких переменных (см. «Кр. к.», п. 97).
Если и = ср (v, . .., w), где v, ...» w — функции переменных
у, ...» t, то
ди   ди Эу .	, ди dw
дх	до дх' ’ * * ’ dw дх '
Аналогичные формулы имеют место и для производных
по у, ..., При этом число промежуточных аргументов
w, так же как и число независимых переменных
у, .... t, может быть любым.

12
ВВЕДЕНИЕ
В нашем примере м = 'р (-у)^ где v — ~. Поэтому
Подставляя эти выражения в уравнение, получим тождество
?'(■»)(--^) +У ?'(®) 7 = 0.
Точно так же можно проверить, что уравнение —
— -|у = 0 имеет общее решение и(х, у) = ср(х + у). а урав¬
нение — х ^- = 0 имеет общее решение и = ср(х2 + у2),
где ср— произвольная дифференцируемая функция.
Рассмотрим теперь уравнения второго порядка. Пусть
	— р
дх ду
Положим — v. Тогда уравнение (5) примет вид
~~	—— о. Общим решением уравнения = 0 бу¬
дет произвольная функция f (у). Возвращаясь к функции и,
получим опять уравнение первого порядка
(5)
Согласно (4) его общим решением будет функция
zz(x, у)= J/(y)rfy + <|>(x).
Так как f (у) — произвольная функция от у, то и инте¬
грал от нее также является произвольной функцией, которую
мы обозначим через ср (у). В результате мы получили реше¬
ние в виде
«(х. у) = ф(х)4-<р(у),	(6)
где ср (у) и ф (х)— произвольные дифференцируемые функции.
Легко проверить, что функция (6) действительно удовлет¬
воряет уравнению (5).

ВВЕДЕНИЕ	13
Решение (6) уравнения (5) с частными производными вто¬
рого порядка содержит уже две произвольные функции.
В этом случае оно называется общим решением.
Проверим, что функция и(х, у) = х<р(х + У)4-У1Нх + У)
является общим решением уравнения
а2м	о д2и	. д2и 0
дх2	2 дхду ду2 ~
Пользуясь приведенным выше правилом дифференцирования
сложной функции и обозначая х 4- у = v, последовательно
получим:
-g-= хт'^ + Ф^-Н’ф'^).
•др- = 2<р' (у) 4- х<?" (у) + Уф" (у),
W+2'К W+Я" О)-
gpgjT = (у)	х<?" (у) + ф' <у) 4- Уф" (У).
Подставляя выражения для производных в левую часть урав¬
нения, убеждаемся, что она обращается в нуль.
Предлагаем читателю проверить, что функция и (х, у) =
= ср (х + ay) -f- ф (х •— ау), где ср и ф — произвольные дважды
дифференцируемые функции, является общим решением урав-
непия — а14^=^' а Функция м(х- 0 = ?(У2*—0 +
4-ф (/2^ + 0 —• общим решением уравнения
о д2“	ди	&U
х дх2	дх	dt2 ~ и’
До сих пор мы еще не ставили вопроса об отыскании
частных решений. Позже будет выяснено, какие дополни¬
тельные условия нужно задать, чтобы с их помощью можно
было выделить частное решение, т. е. функцию, удовлетво¬
ряющую как дифференциальному уравнению, так и дополни¬
тельным условиям.
Оказывается, что дифференциальные уравнения математи¬
ческой физики, которыми мы будем в дальнейшем заниматься,
14
ВВЕДЕНИЕ
имеют между собой довольно много общих черт: все они —
второго порядка и линейны относительно неизвест¬
ной функции и ее частных производных. Чаще всего все ко¬
эффициенты перед функцией и ее производными — постоян¬
ные числа. Общий вид таких уравнений для функции и, за¬
висящей от двух переменных х и у, таков:
. д2и . D д2и . ^д2а . ~ ди . о да .	ч /7Ч
где А, В, С, D, Е и F— постоянные числа, а правая часть—•
заданная функция переменных х и у.
Отметим, что характер и поведение решений этого урав¬
нения существенно зависят от его коэффициентов. Об этом
мы скажем в заключении, после того как познакомим¬
ся с простейшими уравнениями типа (7) и способами их
решений !).
2.	Однородные линейные дифференциальные уравнения
с частными производными и свойства их решений. Если
в уравнении (7) правая часть равна нулю, то уравнение на¬
зывается однородным. Оно имеет вид
. д2и , D д2и . д2и \ г\ ди , да . с А /оч
Вообще в теории дифференциальных уравнений уравне¬
ние называется однородным, если функция, тождественно
равная нулю (я = 0), является его решением. Решения ли¬
нейных однородных уравнений вида (8) обладают следующим
свойством:
Если каждая из функций их (х, у), z/2 (х, у), ;.., uk (х, у)
является решением уравнения (8), то и их линейная
комбинация
Схих{х, у)-\-С2и2(х, у)+ ... -\-Ckuk(x, у),	(9)
*) Отчасти порядок изложения материала в книге будет напо¬
минать порядок изложения теории кривых второго порядка в курсе
аналитической геометрии. Там тоже вначале пишут общее уравне¬
ние кривых второго порядка Ах2 4- Вху 4- Су2 4" Ох 4- Еу + F = О,
а исследование его производят лишь после изучения свойств эл¬
липса, параболы и гиперболы, т. е. кривых, уравнения которых
представляют частные виды общего уравнения. Эта аналогия, как
мы увидим в заключении, не случайна, она служит основанием для
классификации уравнений типа (7).

ВВЕДЕНИЕ
15
где Ср С2, ...» Сл — произвольные постоянные, также
является решением этого уравнения»
Для доказательства достаточно заметить, что если и есть
линейная комбинация частных решений!
и = С1их-\-С2и2~^Г ... +
(для краткости аргументы функций не пишутся), то любая
производная функции и будет такой же линейной комбина¬
цией соответствующих производных функций //р и2, ..., uk\
ди 	£	dui	.	ди2 J	| q	duk
дх	1 дх	*	2 дх	'	‘	‘	k дх	’
ди _	ди{	.	ди2 .	| £	duk
ду	1 ду	'	2 ду	‘	'	k ду
Разумеется, так же будут выглядеть и производные вто¬
рого порядка. Если подставить выражения для производных
функций в левую часть уравнения (8) и перегруппировать
слагаемые, то получим
с'(л-??-+ ■■■ +f“0+
... +С,(л^-+ ... +F«t).
Поскольку по условию функции их, и2, . . ., uk являются ре¬
шениями уравнения (8), то каждая из скобок обратится
в нуль, а вместе с ними и вся левая часть уравнения; это
и означает, что функция и является его решением.
Точно такое же свойство, как известно, имеет место и для
обыкновенных линейных дифференциальных уравнений.
Однако надо иметь в виду, что обыкновенное линейное диф¬
ференциальное уравнение n-го порядка имеет в точности п
линейно независимых частных решений, линейная комбинация
которых и дает общее решение.
Уравнение же в частных производных может иметь, как
мы убедимся в дальнейшем, бесконечное множество ли¬
нейно независимых частных решений, т. е. такое мно¬
жество решений, любое конечное число которых являются
функциями линейно независимыми. (Система функций их(х, у),
н2(-я» У)» •• •»	(х« У) называется линейно независимой, если
ни одна из этих функций не является линейной комбинацией
остальных.) В соответствии с этим нам придется иметь дело
16
ВВЕДЕНИЕ
не только с линейными комбинациями конечного числа реше¬
ний, но и с рядами, членами которых служат произведения
произвольных постоянных на частные решения:
Схил{х, у)-^С2и2(х, у)+ . . . ~{~Спип(х, у)+
со
= ^Спип{х, у).	(10)
Л=1
Мы дадим здесь необходимые определения и укажем некото¬
рые свойства рядов, членами которых являются функции не¬
скольких переменных. Этими свойствами мы будем пользо¬
ваться в дальнейшем.
Будем считать, что члены ряда — функции двух перемен¬
ных; все определения легко переносятся на случай функций
трех переменных.
Рассмотрим функциональный ряд
«Л*.	у)+ ... +v„(x, у)4- ... =
оо
= 2 Vn (х, у).	(11)
п- 1
Этот ряд называется сходящимся в точке (х0, у0), если
со
числовой ряд 2 ^(xo’ Уо) сходится. Совокупность всех
zz= 1
точек, в которых ряд сходится, называется областью схо¬
димости ряда. Все члены ряда считаются непрерывными
и дифференцируемыми функциями переменных х и у во всей
области сходимости ряда.
Мы будем в дальнейшем рассматривать только такие ряды,
суммы которых есть непрерывные функции от х и у,
оо
•У(х, у) = 2 VAX’ У)-	' О2)
Л=1
Кроме того, будем предполагать, что все встречающиеся
ряды можно дважды почленно дифференцировать, т. е.
что
оо
до 	Vl dvn
дх	дх ’
л= 1
оо
до 	Vi dvn
ду ~	’
П=1
4-V4 <■’>
Лг1
и т. д.

ВВЕДЕНИЕ
17
Очень часто нам придется интегрировать ряд (12) либо
по некоторой области D, либо по одной из переменных. По¬
следнее означает, что мы полагаем, например, у = у0 и ин¬
тегрируем по х в некоторых пределах от х0 до Возмож¬
ность почленного интегрирования ряда заключается в том,
что
JCr	ОО
УоИ* = 2 f v„(x- Уо)ах- О4)
-Го	/2=1 -Л'о
(Разумеется, предполагается, что рассматриваемые значе¬
ния х и у0 принадлежат области сходимости ряда.)
Обозначим сумму ряда (10) через и(х, у) и будем считать,
что выполняются все введенные предположения. Тогда
ОО	ОО	ОО
ди 	дип ди 	дип д2и	X1 г» д2ип
дх	п дх ’ ду	п ду ’ дх2 Лк п дх2 ’ ’ ‘ ’
/2=1 11-1 /2=1
Отсюда ясно, что функция и(х, у) — сумма ряда (10),
так же как и члены ряда, является решением уравнения (8).
Можно указать сравнительно простые признаки, при соблюде¬
нии которых все высказанные предположения о рядах будут спра¬
ведливы. Введем для этого следующее определение.
Функциональный ряд
V\(x, y)+v2(x, у)+ ...	у)+ ...
называется правильно сходящимся в области D, принадлежа¬
щей области сходимости ряда, если все члены его по абсолют¬
ной величине не превосходят соответствующих членов некото¬
рого сходящегося знакоположительного числового ряда, т. е.
I vn (Л-, у) I < М„,
причем неравенство соблюдается во всех точках области D, а
Мп — член сходящегося числового ряда.
Для правильно сходящихся рядов имеют место следующие тео¬
ремы, которые мы приводим без доказательства.
1.	Сумма правильно сходящегося ряда из непрерывных функ¬
ций есть функция, непрерывная,
2.	Правильно сходящийся ряд можно почленно интегриро¬
вать.
3.	Если ряды, составленные из производных сходящегося
ряда, сходятся правильно, то ряд можно почленно дифферен¬
цировать.
Определение правильно сходящегося ряда без всяких измене¬
ний переносится как на функции одной переменной, так и на функ¬
ции трех и большего числа переменных.
2 И. Г. Араманович, В. И. Левин

18
ВВЕДЕНИЕ
Напомним, что все три сформулированные свойства имели ме-
оо
сто для степенных рядов 2 ап хП в интервале их сходимости (см.
п= о
«Кр. к.», п. 160). Нетрудно показать, что степенной ряд является
правильно сходящимся в любом интервале, целиком заключенном
в интервале сходимости ряда *).
В дальнейшем нам встретятся и такие случаи, когда функ¬
ция и(х, у, X) при всех значениях параметра К, заключен¬
ных в некотором интервале [Хо, XJ, является решением урав¬
нения (8). Тогда говорят, что частные решения зависят
от непрерывно изменяющегося параметра. Обычно ин¬
тервал изменения параметра К составляет или всю числовую
ось, или положительную полуось.
Мы будем в дальнейшем функцию и(х, у, X) записывать
в виде иу(х, у). Этой формой записи подчеркивается анало¬
гия между случаями, когда решения зависят от параметра,
принимающего только целые значения (uk(x, у)), и
когда решения зависят от параметра, принимающего любые
значения (ях(х, у)).
Покажем, что если мы умножим функцию ях(х, у) на
произвольную функцию С (X) и проинтегрируем в пределах
изменения параметра X:
X,
J С(Х)их(х, y)dX,	(15)
Хо
то вновь получим решение уравнения (8). Ясно, что инте¬
грал (15) есть некоторая функция переменных х и у.
Предварительно познакомимся с некоторыми свойствами
интегралов типа (15). Пусть дан интеграл
Xj
F(x, у)= J v(x, у, X)dX,	(16)
Хо
где Хо и Xj — конечные пределы. Имеет место следующая
теорема, которую мы приводим без доказательства.
9 Для читателей, знакомых с определением равномерной схо¬
димости ряда, отметим, что если ряд сходится правильно, то он
сходится и равномерно; однако не всякий равномерно сходящийся
ряд сходится правильно.

ВВЕДЕНИЕ
19
Если подынтегральная функция v(xt у, X), а также
ее частные производные по х и по у непрерывны при
всех рассматриваемых значениях аргументов х, у и X,
то и функция F(x, у) непрерывна вместе со своими
частными производными, причем
х.
д2Р
дх2
д2у
дх2
dX
(17)
f
и т. д.
В случае, когда хотя бы один из пределов интегриро¬
вания обращается в бесконечность, интеграл (16) ста¬
новится несобственным и указанные свойства функции F (х, у)
соблюдаются лишь при некоторых дополнительных условиях,
о которых мы скажем ниже.
Возвращаясь к интегралу (15), обозначим его через
U (х, у) и предположим, что для него справедливы фор¬
мулы (17). При этом пределы интегрирования Хо и Х} могут
быть как конечными, так и бесконечными. Тогда
X.	X,
dW _
дх
= /
dU
ду
= f
^0
Х0
м
д2 U	Г
дх2 — J
Хо
С(Х)
д2л^
дх2
и т. д.
Подставляя выражения для функции £7 (х, у) и ее про¬
изводных в уравнение (8) и заменяя сумму интегралов ин¬
тегралом от суммы функций, получим в левой части
...+™= f С(>.)[л^+
^0
Так как по предположению выражение в квадратных-
скобках при любом X равно нулю (ведь функция их(х, у)
при любом X является решением уравнения (8)), то и весь
интеграл равен нулю. Следовательно, функция U (х, у) дей¬
ствительно является решением уравнения.

20
ВВЕДЕНИЕ
Сформулируем простой признак, аналогичный соответствую¬
щему признаку для рядов, при соблюдении которого выполняются
все приведенные свойства для несобственных интегралов вида
J* yt X)dX, где один или оба предела интегрирования обра¬
зе	X
щаются в бесконечность.
Если можно указать такую положительную функцию ср (X),
что для всех рассматриваемых значений х, у и \ соблюдается
неравенство | v (х, у, X) | ср (А) и несобственный интеграл от
функции <р (X) сходится, то функция Е (х, у) непрерывна. Такую
сходимость несобственного интеграла от функции v (лг, у, X) будем
называть правильной.
Если аналогичное свойство имеет место и для интегралов от
частных производных функции v (л, у, X), то функция F (х, у)
дифференцируема и ее производные находятся по формулам (17).
Например, если I	I < Ф (ty и интеграл от ф (X) сходится,
xt
дЕ С dv ,,
то -дх=,1
3.	Оператор Лапласа в полярных, цилиндрических
и сферических координатах1). В этом пункте мы рассмо¬
трим вспомогательный вопрос о выражении оператора Лап¬
ласа в различных системах координат; эти выражения пона¬
добятся нам в дальнейшем. Напомним, что трехмерным
оператором Лапласа &и называется выражение
ч д2и , д2и ] д2и
*lt~ lx2 *” ~ду2 "дг2 ’
где и(х, у, z) — функция трех переменных. Если функция и
зависит только от двух переменных, то оператор Лапласа
л д2и . д2и
~	+ dp"
называется двумерным.
Начнем с двумерного оператора Лапласа и произведем
замену декартовых координат х и у полярными г и ср по
формулам
I
(18)
(19)
(20)
хг cos ср, у = г sin ср.
') Этот пункт следует прочесть или перед изучением задач,
в которых встретится необходимость преобразования оператора
Лапласа (п. 32, п. 49—50), или перед чтением гл. III.

ВВЕДЕНИЕ
21
Если в функцию //(х, у) подставить вместо х и у их
выражения, то получится функция и (г cos ср, г sin ср) перемен¬
ных г и ср. Выразив вторые производные от функции и по
х и по у через производные по г и ср и подставив затем
найденные выражения в формулу (19), мы и получим опера¬
тор Лапласа в полярных координатах.
По правилу дифференцирования сложной функции
ди   ди дг . ди ду
дх	дг дх' ду дх 1
ди 	 ди дг . ди ду
ду"~ Ir'dy’ ' lty"dy'
Для отыскания частных производных г и ср по х и у выра¬
зим из формул (20) г и ср. Находим, что
отсюда
дг х	дг у
17==T = C0St? и w = ^ = sinT.	(22)
Поскольку tg Ср =	, то
1 дер	 у	1 дер 	 1
cos2 ср дх	х2	cos2 ср ду х*
Заменяя х и у по формулам (20), получим
дер
дх
sin ср
г
д<р
ду
COS ср
(23)
и
Г
Подставив (22) и (23) в равенства (21),
ди
выражения частных производных
окончательно
ди
и	через
найдем
пере¬
менные г и ср и производные по этим переменным:
ди ди	ди sin ср
дх дг т дер г
ди
'ду
ди
~дг
sin ср-f
^-^F-(24)
Перейдем к отысканию вторых
« ди
к производной опять.правило
производных. Применим
дифференцирования слож-
ной функции
д2и 	 - \ дх ) дг .
дх2 ~ дг *дх '
о *_
д<р дх ’

22
ВВЕДЕНИЕ
Из равенств (24)
д<р Г2 *
dcp
д2и
<WC0Scp
д2и sin ср ди cos ср \
ду2 г ду г
дг
теперь первое равенство на = cos ср, а второе
— Sy и сложим. Приводя подобные члены, по-
ди ,
dTsincP
Умножим
ду
на =
дх
лучим
д2и 	 д2и	о д2и sin ср cos ср , о ди sin ср cos <р .
дх2 dr2 C0S	дг дер г * дер г2 ’
, ди sin2 ср . д2и sin2 ср 0-
+ dF~7	Ь-^г-тг--
Совершенно аналогично, воспользовавшись соотношением
г2
найдем, что
д2и
ду2
о
дг ду
ду>
д?
д2и	 д2и
'ду^ — 'дг2
Складывая
оператора
I о д*и sin ср cos ср о ди sin ср cos ср |
sin c?_t_2 dr dep r	d? r2 _r
1 dr r 1 d<p2 r2 v 7
(25) и (26), окончательно получим выражение
Лапласа в полярных координатах:
A „	 д2и .	д2и 	 д2и	,	1 du	]	1 д2и
U	дх2 '	ду2	дг2	*	г дг	‘	г2 д<р2
г2
(27)
Последнее выражение очень часто бывает удобно запи¬
сать в следующем виде:
А 1 д { ди \ .	1 д2и	zoq\
Дм = 7	+	(28)
Тождественность правых частей формул (28) и (27) легко
проверяется дифференцированием.
Перейдем к трехмерному случаю и начнем с цилин¬
дрических координат. Цилиндрические координаты г, ср
ВВЕДЕНИЕ
23
и z связаны с декартовыми соотношениями (см. «Кр. к.»,
п. 114)
х = г cos ср, у — г sin ср, z = z.
Функция н(х, у, z) преобразуется в функцию я (г cos ср,
г sin ср, z). Здесь третья переменная z остается неизменной,
и в выражении (27) двумерного оператора Лапласа в поляр¬
ных координатах добавляется только вторая производная
по z\
д2и , 1 ди ] 1 д2и t д2и	/ПЛч
— dr2 г dr “I” г2 д^2 + dz2 '
Для сферических координат г, 0 и ср имеем формулы:
x = rsin0coscp, у = г sin 0 sin ср, z = r cos0,
в которых г = ]/х2 4-у2 + z2 — расстояние точки (х, у, z)
от начала координат, 0 — угол между радиусом-вектором»
точки и осью Ozt а ср — угол между проекцией радиуса-
вектора на плоскость Оху и осью Ох. Здесь непосредствен¬
ное преобразование производных функции и (г sin 0 cos ср,
г sin 6 sin ср, г cos 0) очень громоздко, и мы его проводить
не будем1), ограничившись тем, что выпишем окончательное
выражение оператора Лапласа в сферических координатах:
л„	 д2и ]	2 ди , cos 0 ди (	1 д2и ,	1 д2и
г2 sin О +	г2 sin2 (W*
Эту формулу часто записывают в виде
+ Г2 sin2 0 1^2 *
Предоставляем читателю проверить тождественность обеих
формул.
’) Более подробные сведения о замене переменных в диффе¬
ренциальных выражениях читатель может почерпнуть в книге
А. Ф. Бер м ан та «Отображения. Криволинейные координаты.
Преобразования. Формулы Грина» (Физматгиз, 1958).

ГЛАВА I
УРАВНЕНИЯ КОЛЕБАНИЙ
§ 1. Уравнение колебаний струны
4. Вывод уравнения колебаний струны. Пусть конеч¬
ные точки струны закреплены, а сама струна туго натянута.
Если вывести струну из положения равновесия (например,
оттянуть ее или ударить по ней), то струна начнет коле¬
баться. Будем предполагать, что все точки струны движутся
перпендикулярно ее положению равновесия (поперечные коле¬
бания), причем в каждый момент времени струна лежит
в одной и той же плоскости.
в этой плоскости систему прямоугольных
Тогда, если в начальный момент времени струна
располагалась вдоль оси
Ох, то и будет означать
отклонение струны от
положения равновесия.
В процессе колебания ве¬
личина отклонения и бу¬
дет зависеть от абсциссы
точки струны х и от вре¬
мени t. Таким образом,
чтобы знать
любой точки
произвольный
найти зависимость и от х и t,
При каждом фиксированном
Возьмем
динат
коор-
положение
струны в
момент
т. е. найти
значении t
времени,
функцию
график функции и(х, f) представляет форму колеблющейся
струны в момент времени t (рис. 1), частная производная
'дх = и'Ах' О Дает ПРИ этом угловой коэффициент каса-
нам надо
и(х. t).

УРАВНЕНИЕ КОЛЕБАНИЙ СТРУНЫ
25
§ П
тельной в точке с абсциссой х. При изменении t форма
струны, очевидно, изменяется, и, чтобы представить себе
процесс колебаний, мы должны построить несколько гра¬
фиков функции и(х, t) при различных значениях /, т. е.
сделать несколько мгновенных снимков колеблющейся струны.
При постоянном значении х функция и(х, t) дает закон дви¬
жения точки с абсциссой х вдоль прямой, параллельной
оси Ои, производная -^ = и'(х, t) — скорость этого дви-
д2и
жения,. а вторая производная 	ускорение.
Наша задача состоит в том, чтобы составить уравнение,
которому должна удовлетворять функция и{х, t). Для этого
сделаем предварительно несколько упрощающих предположе¬
ний. Будем считать струну абсолютно гибкой, т. е. не
сопротивляющейся изгибу; это означает, что если удалить
часть струны, лежащую по одну сторону от какой-либо ее
точки, то сила натяжения Т, заменяющая действие удаленной
части, всегда будет направлена по касательной к струне
(рис. 1). Струна предполагается упругой и подчиняющейся
закону Гука; изменение величины силы натяжения при этом
пропорционально изменению длины струны. Примем, что
струна однородна} линейную плотность ее обозначим бук¬
вой р (р — масса единицы длины струны).
Предположим, далее, что на струну в плоскости колеба¬
ния действуют силы, параллельные оси Ои, которые могут
меняться вдоль струны и со временем. Силы эти будем счи¬
тать непрерывно распределенными вдоль струны; величину
силы, направленной вверх, условимся считать положительной,
а вниз — отрицательной. Плотность распределения этих сил
вдоль струны]) является функцией абсциссы х и времени t\
обозначим ее через g(x, f). Если, в частности, единствен¬
ной внешней силой является вес струны, то g(x, /) = — pg*,
где р — плотность струны, a g— ускорение силы тяжести.
Силами сопротивления среды, в которой колеблется
струна, мы пока пренебрегаем.
]) Плотность распределения параллельных сил, изменяющихся
вдоль линии, определяется как предел отношения величины равно¬
действующей этих сил, приложенных к малому участку, к длине
участка при условии, что участок стягивается в точку. Это опре¬
деление совершенно аналогично определению обычной плотности.

26
УРАВНЕНИЯ КОЛЕБАНИЙ
1ГЛ. I
Мы будем изучать только малые колебания струны. Если
обозначить через a(x, t) острый угол между осью абсцисс
и касательной к струне в точке с абсциссой х в момент
времени /, то условие малости колебаний заключается в том,
что величиной а2(х, t) можно пренебрегать:
а2^0.	(1.1)
Поскольку разложение функции sin а в ряд Маклорена имеет
вид
а3 .
sina = a —"3! ‘	• • ••
то в силу условия (1.1) можно считать, что
sina
(1.2)
а2
и,	следовательно,
cos а 1.	(1.3)
Наконец,	tg а — sin а =
= tga(l—cos а) О и
tga^sina. (1.4)
Так KaK-|^- = tga, то в си*
лу полученных условий заклю¬
чаем, что *)
Отсюда сразу следует, что в процессе колебания мы
можем пренебречь изменением длины любого участка струны.
Действительно, длина участка	в момент времени t
(рис. 2) равна
Хч.	-

Xi
*) Подобного рода предположения встречаются и в различных
других задачах. Так, при изучении движения кругового маятника
максимальный угол отклонения маятника считают настолько малым,
что его можно принять равным синусу; при рассмотрении изгиба
балки (в курсе сопротивления материалов) кривизну нейтральной
линии считают равной второй производной от неизвестной функции
(уравнения этой линии), пренебрегая квадратом первой производ¬
ной, и т. д.

I 1]
УРАВНЕНИЕ КОЛЕБАНИЙ СТРУНЫ
27
Согласно (1.5) заключаем, что
44^2	— хг	(1-7)
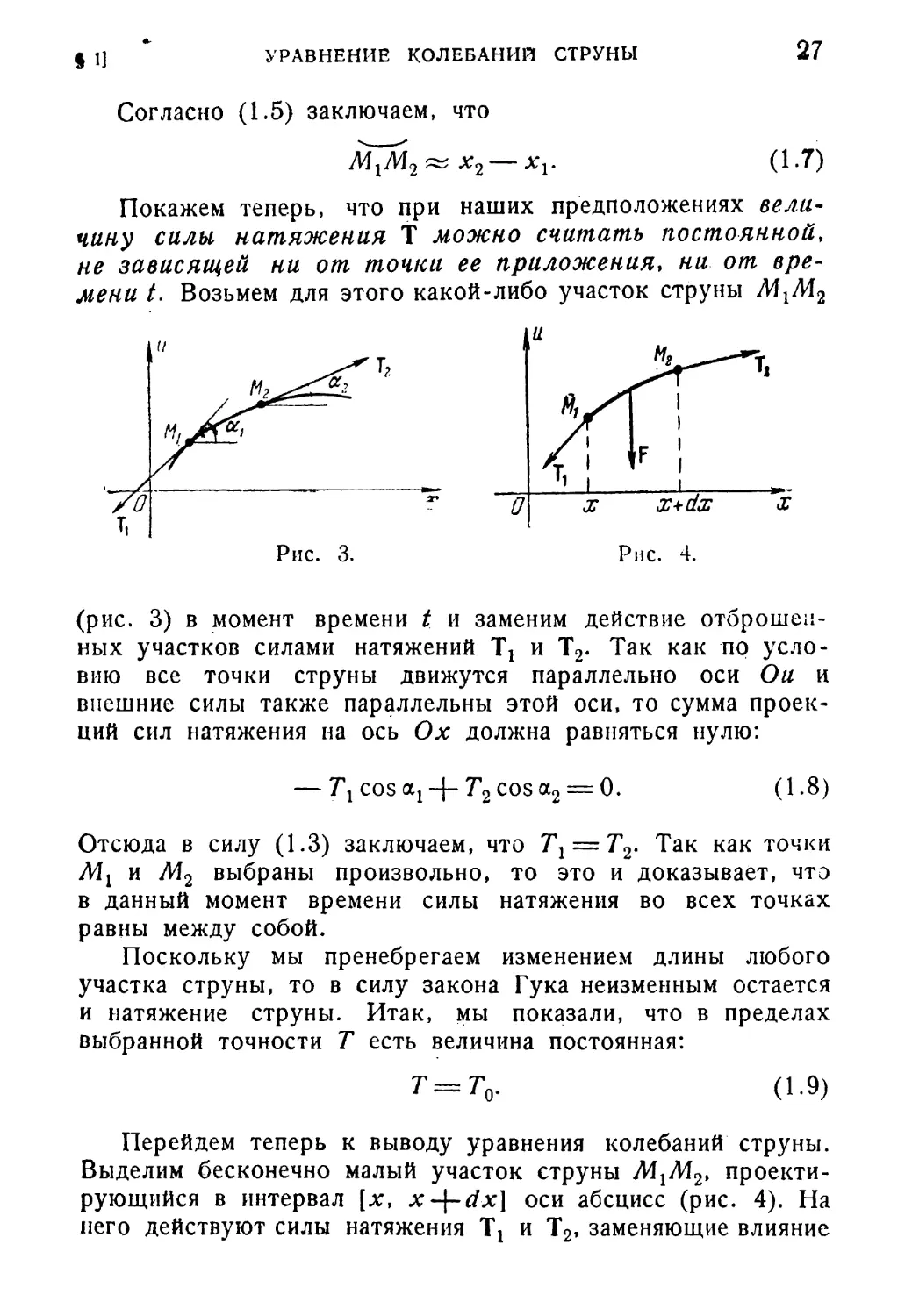
Покажем теперь, что при наших предположениях вели-
чину силы натяжения Т можно считать постоянной,
не зависящей ни от точки ее приложения, ни от вре¬
мени t. Возьмем для этого какой-либо участок струны
(рис. 3) в момент времени t и заменим действие отброшен¬
ных участков силами натяжений Tt и Т2. Так как по усло¬
вию все точки струны движутся параллельно оси Ои и
внешние силы также параллельны этой оси, то сумма проек¬
ций сил натяжения на ось Ох должна равняться нулю:
— 7\ cos 04 4~ Т2 cos а2 = 0.	(1.8)
Отсюда в силу (1.3) заключаем, что 7\ = Т2. Так как точки
Мг и М2 выбраны произвольно, то это и доказывает, что
в данный момент времени силы натяжения во всех точках
равны между собой.
Поскольку мы пренебрегаем изменением длины любого
участка струны, то в силу закона Гука неизменным остается
и натяжение струны. Итак, мы показали, что в пределах
выбранной точности Т есть величина постоянная:
Т=Т0.	(1.9)
Перейдем теперь к выводу уравнения колебаний струны.
Выделим бесконечно малый участок струны Л11Л12, проекти¬
рующийся в интервал [х, x-f-tfx] оси абсцисс (рис. 4). На
него действуют силы натяжения Tj и Т2, заменяющие влияние
28
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
отброшенных частей струны. Как уже отмечалось выше,
силы Tj и Т2 направлены по касательным к струне в точках
Л11 и М2; величина этих сил постоянно равна TQ. Согласно
равенству (1.8) сумма проекций сил Тт и Т2 на ось Ох
равна нулю. Вычислим сумму проекций этих же сил на
ось Ои:
— Tosin 0Ц	Tosina2 — T0(sina2 — sin 04).
В силу (1.4) можно записать, что
sina2 = tga2 = u'x(x-\-dx, t), sin qtj = tg 0^ = u'x (x, /).
Следовательно,
r0(sina2 — sin 04) —
Л2//
= r0[<,(x + dx, /)-<(x, t)] = TQ^dx. (1.10)
Здесь мы заменили частное приращение производной
при переходе от аргументов (х, Z) к аргументам (x-\-dx, t)
ее частным дифференциалом, т. е. dx.
Примечание. Если бы участок струны М^М2 располагался,
как на рис. 2, то сумма проекций сил Tj и Т2 равнялась бы
То (— sin a2 — sin aj; но теперь sin а2 = — их(х-}- dx, t), и в резуль¬
тате мы снова получили бы формулу (1.10).
Равнодействующую внешних сил, приложенных к участку
в момент времени t, обозначим через F. Согласно
определению функции g(x, t) и приближенному равенству
(1.7) можно считать, что
F^ g(x, t)M^2~ g(x, t)dx.	(1.11)
Направление равнодействующей F определится знаком
функции g(x, t) (направление F на рис. 4 соответствует
случаю g (х, t) < 0).
После того как найдены все силы, действующие на
участок Л41Л42, применим к нему второй закон Ньютона,
согласно которому произведение массы на ускорение равно
сумме всех действующих сил (в силу малости участка МгМ2
мы рассматриваем его просто как материальную точку).

§ 1]	УРАВНЕНИЕ КОЛЕБАНИЙ СТРУНЫ	29
Так как масса участка ТИРМ2 струны равна p441M2 = prfx,
то, используя формулы (1.10) и (1.11), получим
. д2и	д2и , ,	,	...
.4, - ?dx -^- = TQ-^dx-\-g{x, t)dx.
Сократив на dx и разделив все члены равенства на р, при¬
ведем, полученное уравнение к виду
д2и 9 д2и , 1	,
~dt2~ ~~ а	С1-12)
^а2=-^	положительная постоянная величина). В резуль¬
тате мы получили линейное дифференциальное уравнение с
частными производными второго порядка с постоянными коэф¬
фициентами. Уравнение (1.12) называется уравнением коле¬
баний струны, или одномерным волновым уравнением.
Это одно из простейших и в то же время важнейших диф¬
ференциальных уравнений математической физики. Как мы
позже увидим, к нему сводится не только рассматриваемая
задача, но и многие другие.
Если g(x, £)==0, то уравнение (1.12) называется одно¬
родным] оно описывает свободные колебания струны без
воздействия внешних усилий.
Если g(x, t) не тождественно равно нулю, то уравнение
называется неоднородным] в этом случае рассматриваются
вынужденные колебания струны. Когда на струну дей¬
ствуют только силы тяжести, а натяжение струны Го ве¬
лико, мы вправе пренебречь вторым слагаемым в правой
части уравнения струны по сравнению с первым и рассма¬
тривать, таким образом, колебания струны как свободные.
Читатель, конечно, обратил внимание на то, что вывод
уравнения колебаний струны (1.12) сопровождался целым ря¬
дом допущений как механического, так и геометрического
порядков. Такое же положение, разумеется, имеет место
и при выводе дифференциальных уравнений (как в частных
производных, так и обыкновенных) других задач математи¬
ческой физики. Вопрос о том, насколько точно уравнение
описывает физический процесс, может быть решен только
сравнением результатов, полученных при решении уравнения
и экспериментальным путем. В настоящей книге этим вопро¬
сом мы заниматься не будем, чтобы сосредоточить основное
внимание на методах решения уравнений.

30
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. 1
В связи со сказанным уместно сделать следующее заме¬
чание. Хорошо известна роль моделей при изучении раз¬
личных вопросов техники. Например, гидротехники при про¬
ектировании плотины часто строят в значительно уменьшен¬
ном размере ее модель, чтобы, производя опыты над ней
в лабораторных условиях, сделать некоторые заключения
о характере усилий, действующих на реальную плотину. Та¬
кую же роль играют модели проектируемых мостов, крыльев
и фюзеляжа самолетов и др. Разумеется, данные, полученные
при исследовании моделей, нельзя просто переносить на ре¬
альные объекты. Ведь в лаборатории нельзя создать все
условия, которые могут встретиться в действительности, да
и, кроме того, явления, происходящие при исследовании мо¬
дели, далеко не всегда в точности копируют соответствующие
явления в природе1). Однако наиболее существенные чер¬
ты процесса все-таки часто удается уловить, и дальнейшая
задача проектировщика в том и состоит, чтобы увязать на¬
блюденные на модели факты с теми, которые встретятся в
натуре.”
Подобную же роль в физике играет и изучение дифферен¬
циальных уравнений математической физики. Учитывая основ¬
ные закономерности физического процесса, мы создаем его ма¬
тематическую модель. Изучение этой модели и позво¬
ляет делать определенные суждения о характере процесса.
Образно говоря, в настоящей книге мы знакомим читателя
только а основными методами изучения математических
моделей, оставаясь, так сказать, в «лабораторных
условиях математики».
б. Постановка начальных и краевых условий. Как уже
отмечалось во введении, дифференциальные уравнения с част¬
ными производными второго порядка имеют бесчисленное мно¬
жество решений, зависящих от двух произвольных функций.
Чтобы определить эти произвольные функции, или, иначе го¬
воря, выделить необходимое нам частное решение, нужно
на искомую функцию и(х, t) наложить дополнительные усло¬
вия. С аналогичным явлением читатель встречался уже при
решении обыкновенных дифференциальных уравнений, когда
выделение частного решения из общего заключалось в про-
!) Вопросу о подобии явлений, протекающих в модели и в на¬
туре, посвящена обширная литература.

§ 1]	УРАВНЕНИЕ КОЛЕБАНИЙ СТРУНЫ	31
цессе отыскания произвольных постоянных по заданным на¬
чальным условиям.
При рассмотрении задачи о колебаниях струны дополни¬
тельные условия могут быть двух видов: начальные и кра¬
евые (или граничные).
Начальные условия показывают, в каком состоянии нахо¬
дилась струна в момент начала колебания. Удобнее всего
считать, что струна начала колебаться в момент времени
/ = 0. Начальное положение точек струны задается условием
=	о-13)
а начальная скорость
где /(х) и F (х)— заданные функции.
Запись й|/ж0 означает, что функция u(xt t) взята при
произвольном значении х и при / = 0, т. е. u\t^ — u{xt 0);
аналогично 4^-1	= ^(х, 0). Такая форма записи посто-
01 I/-0
янно применяется в дальнейшем; так, например, я|ж=ж0 = я (0, t)
и т. д.
Условия (1.13) и (1.14) аналогичны начальным условиям
в простейшей задаче динамики материальной точки. Там для
определения закона движения точки, помимо дифференциаль¬
ного уравнения, нужно знать начальное положение точки и ее
начальную скорость.
Иной характер имеют краевые условия. Они показывают,
что происходит на концах струны во все время колебаний.
В простейшем случае, когда концы струны закреплены (начало
сТруны — в начале координат, а конец — в точке (/, 0)),
функция я (х, 0 будет подчиняться условиям
wLo=o- ttL-z=°-	(1Л5>
С такими же точно условиями читатель встречался в курсе
сопротивления материалов при изучении изгиба балки, лежа¬
щей на двух опорах, под действием статической нагрузки.
Физический смысл того факта, что задание начальных
и краевых условий полностью определяет процесс, проще
всего проследить для случая свободных колебаний струны.

32
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Пусть, например, струну, закрепленную на концах, как-то
оттянули, т. е. задали функцию f (х) — уравнение начальной
формы струны, и отпустили без начальной скорости (это
значит, что F(x) = 0). Ясно, что этим самым дальнейший ха¬
рактер колебаний будет полностью определен и мы найдем
единственную функцию и(х, £), решая однородное уравнение
при соответствующих условиях. Можно заставить струну ко¬
лебаться и иначе, а именно придав точкам струны некоторую
начальную скорость. Физически ясно, что и в этом случае
дальнейший процесс колебаний будет вполне определен. При¬
дание точкам струны начальной скорости может быть осущест¬
влено при помощи удара по струне (как это имеет место при
игре на рояле); первый способ возбуждения струны применяется
при игре на щипковых инструментах (например, гитаре).
Сформулируем теперь окончательно математическую за¬
дачу, к которой приводит изучение свободных колебаний
струны, закрепленной на обоих концах.
Требуется решить однородное линейное дифферен¬
циальное уравнение с частными производными второго
порядка с постоянными коэффициентами
д2и 		 9 д2и
~dir~a'~dX^
(116)
при начальных условиях
и краевых условиях
ди
dt
|	=^(х)
1/=о
(М7)
(1.18)
Функции f(x) и F (х) определены на интервале [0, /] и, как
это следует из первого условия (1.17) и условий (1.18),
/(0) = /(0=0.
Можно доказать, не опираясь на физические представле¬
ния, что при некоторых ограничениях, наложенных на функ¬
ции f (х) и F (х), эта задача имеет единственное решение.
Примечание. Решение поставленной математической задачи
будет отражать реальный характер процесса колебаний лишь в том
случае, когда начальное смещение и начальные скорости точек
струны настолько малы, что соблюдаются все высказанные ранее
предположения. Имея в виду в дальнейшем главным образОхМ мате¬
матическую сторону вопроса, мы при решении конкретных приме¬
ров обращать на это внимания не будем*

МЕТОД ДА ЛАМБЕРА
33
§
§ 2. Колебания бесконечной и полубесконечной
струны. Метод Даламбера
6. Бесконечная струна. Формула Даламбера. Прежде чем
решать задачу о колебаниях закрепленной струны, мы рас¬
смотрим более простую задачу •—о колебаниях бесконечной
струны. Если представить себе очень длинную струну, то
ясно, что на колебания, возникшие в ее средней части,
концы струны не будут оказывать заметного влияния. Так,
если взять длинную натянутую веревку и слегка качнуть ее
в середине, то по веревке влево и вправо побегут волны.
Картина начнет искажаться только тогда, когда волны дойдут
до концов веревки и, отразившись, пойдут обратно. Следова¬
тельно, не учитывая влияния концов струны, мы тем самым
не будем учитывать влияния отраженных волн.
Рассматривая свободные колебания, мы должны, таким
образом, решить однородное уравнение
д2и 9 д2и
'дё=а~дх?-
(2.1)
при начальных условиях
«ко = /(*>’
ди I
|/=о
= F (х),
(2.2)
где функции /(х) и F (х) заданы на всей числовой оси. Ни¬
какие краевые условия на искомую функцию и(х, f) не на¬
кладываются. Такая задача называется задачей с начальными
условиями или задачей Коши. Метод решения ее, который
мы сейчас изложим, называется методом Даламбера или
методом бегущих волн.
Прежде всего покажем, что общее решение уравне¬
ния (2.1), т. е. решение, зависящее от двух произвольных
функций (см. введение), имеет вид
и(х, ^) = ср(х —+ at),	(2.3)
где функции «р и ф предполагаются дважды дифференцируе¬
мыми.
3 И. Г. Араманович, В. И. Левин

34
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ г
Действительно, последовательно дифференцируя, находим:
и'х = ф' (х — at) + </(* + «О»
и"хх = (х — ^0 4- ф" (х 4- at).
ut = —а<р' (х — at) 4- аф' (х 4- at).
и'{ = а2ср" (х — at) 4- а2ф" (х 4- at).
Отсюда ясно, что
д2а 	 2 д2и
~dF ~~ дх*’ ’
т. е. что равенство (2.1) соблюдается.
Наша задача состоит теперь в том, чтобы, пользуясь на¬
чальными условиями (2.2), определить неизвестные функции
<р и ф. Полагая в (2.3) f = 0 и подставляя выражение для
и (х, 0) в первое из условий (2.2), получим
?(х)4-ф(х) = /(х).	(2.4)
Полагая теперь t = 0 в выражении для и' и пользуясь вто¬
рым условием (2.2), придем к уравнению
— ау' (х) 4- аф' (х) = F (х).	(2.5)
Интегрируя это равенство в пределах от 0 до х, получим
соотношение
х
- а (с? (х) - ср (0)]	а [ф (х) - ф (0)] = f F (х) dx,
О
которое приведем к виду
г
— ср(х) + ф(х) = -1-jF(x)dx-(-C,	(2.6)
О
где С= —<р(0)4~ф(0) — некоторая постоянная величина.
Из системы уравнений (2.4) и (2.6) находим искомые функ¬
ции ср(х) и ф(х):
X
f(x)rfx-4.
о
х
=	F(x)rfx+£.
о
(2.7)

§ 2]
МЕТОД ДАЛАМБЕРА
35
Заменяя в формулах (2.7) аргумент х соответственно на
х	at и x-^at и подставляя полученные выражения в фор¬
мулу (2.3), найдем функцию и(х, t)\
х- at
и(х, 0 = 7 f(x — at)		 J F(x)dx-\-
'	' о
ха at
+ у f (х +	+ "2^" J F(x)dx.
о
Замечая, что
x-at	ха at
— f F(x)dx-j- f F(x)dx =
0	'0
0	xAat	XAat
= J" F (x)dx + J F(x)dx = J" F(x) dx,
x-at	0	x-at
придадим решению я(х, t) следующий вид:
Ц(х, t)= f(x-at)±f(x + at)	J F{x)dx, (2.8)
x-at
Формула (2.8) называется решением Даламбера задачи
Коши для уравнения колебаний струны.
Предоставляем читателю самостоятельно проверить, что
найденная функция я(х, /) действительно удовлетворяет как
уравнению (2.1), так и условиям (2.2)!).
*) При дифференцировании второго слагаемого формулы (2.8)
ха-at	XAat
учесть, что JL- /* F(x) dx = F(x-±at), а -4- I F(x)dx =
dx J	dt J
о	0
~aF(x-}-ai). Оба равенства немедленно следуют из правила диф¬
ференцирования интеграла по переменному верхнему пределу; нужно
только рассматривать интеграл как сложную функцию от хи/,
z
У* F (х) dx, где z = х-\-at.
о
Аналогичные формулы получаются при дифференцировании
x-at
интеграла F (х) dx.
6
3*

36
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
’ Для того чтобы выяснить физический смысл полученного
решения, рассмотрим прежде всего в отдельности функции,
входящие в общее выражение (2.3) для н(х, t). Начнем
с функции <р(х — at) и построим графики этой функции при
возрастающих значениях / = /0, t — tv t = t2 и т. д. (на
рис. 5 они расположены сверху вниз). Второй график будет
Рис. 5.
сдвинут относительно первого на величину atv третий — на
величину at2 и т. д. Если по очереди проектировать эти ри¬
сунки на неподвижный экран, то зритель увидит, что гра¬
фик, изображенный на верхнем рисунке, «побежит» вправо.
(Этот способ, изображения движения положен, между прочим^
в основу съемки мультипликационных фильмов.) При этом^
если мысленно перемещаться вправо вдоль струны с посто¬
янной скоростью а, то отклонение струны будет казаться все
время постоянным. Действительно, начав движение, скажем,

МЕТОД ДАЛАМБЕРА
37
§
в точке х0 и переместившись за время t в точку х> будем
иметь
х = xQ + at или х — at = х0.
Но тогда
«(х, /) = <Р (х — at) = (р (х0).
Процесс передвижения отклонения по струне называется
волной. При этом коэффициент а=^ в уравнении ко¬
лебаний струны является скоростью распространения
волны.
С частным случаем распространения волн, именно с сину-.
социальными волнами, читатель должен быть уже знаком из
курса физики. При этом, если скорость распространения
такой волны равна а и точка, совпадающая с началом коор¬
динат, колеблется по закону и = A sin (о/, то отклонение и (xt t)
равно
и (х, t) — A sin о)	.
Записав последнее выражение в виде A sin ~ (at—х), сразу
замечаем, что это функция аргумента at — х (или, что то
же самое, аргумента х — at).
Второе слагаемое формулы (2.3), функция ф(х + °0>
будет представлять такой же процесс, но только волна будет
распространяться со скоростью а влево (рис. 5 будет пока¬
зывать моментальные снимки такой волны, если на него
смотреть снизу вверх, т. е. считать t2 < tx < /0).
Теперь мы перейдем к исследованию решения, даваемого
формулой Даламбера (2.8), и рассмотрим два наиболее инте¬
ресных случая: когда отсутствуют начальные скорости
(F (х) = 0) и когда отсутствуют начальные отклонения
(/ (х) = 0). Общий случай будет являться результатом наложе¬
ния (суперпозиции) обоих случаев.
7. Распространение волн отклонения. Пусть начальные
скорости точек струны равны нулю и струна колеблется
в результате начального отклонения. В этом случае в фор¬
муле (2.8) надо положить F(x) = 0, и мы получим
f (х —— at) f (х at)
— 2
и(х, t)
(2.9)

38
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ Г
Так как функция / (х) известна, то мы можем вычислить
значение u(xt t) для любых х и t. Согласно сказанному
выше колебание w(x, t) слагается из двух волн: первая
волна у/(х— л О распространяется со скоростью а вправо
(прямая волна), а вторая волна -^f(x-^-at) распростра¬
няется с той же скоростью влево (обратная волна).
Рис. 6.
В начальный момент времени / = 0 профили обеих волн
совпадают.
Предположим, что в начальный момент функция f(x)
отлична от нуля только на некотором интервале (—/, /).
Для простоты изложения считаем функцию f (х) четной.
Тогда /(х) = 0 при х <—I и при х > I. Легко чисто
геометрически проследить за изменением формы струны
в любой момент времени. На рис. 6 в левом столбце изобра¬
жена в различные моменты времени волна у/(х-{-а/),
бегущая влево, а в правом столбце — в те же моменты вре¬
мени волна у/(х— бегущая вправо. В среднем столбце

МЕТОД ДАЛАМБЕРЛ
39
показана сумма этих волн, т. е. результирующее отклонение
точек струны. До тех пор, пока	есть участок, где
обе волны накладываются друг на друга; начиная с момента
Эти волны уже не накладываются и расходятся в раз-
а
ные стороны.
Йз сказанного можно сделать заключение о характере
колебания точки струны с фиксированной абсциссой х. Если
х > /, то в начальный момент точка струны лежит на оси
абсцисс, она не участвует в начальном отклонении. Волна,
бегущая вправо, дойдет до этой точки в момент времени
/1==	, и с этого момента точка струны начнет колебаться.
Как только волна пройдет через рассматриваемую точку,
т. е. начиная с момента /2 — —, эта точка снова будет
находиться в покое. В момент времени tx до точки х доходит
передний фронт волны, а в момент t2—«задний
фронт. Таким образом, рассматриваемая точка струны уча¬
ствует в колебательном процессе при -	*
Это неравенство удобнее записать так: — I < х — at < L
Если 0 < х < I, то через точку проходят уже как прямая,
так и обратная волны. Передний фронт обеих волн распо¬
лагается впереди точки; задний фронт обратной волны пройдет
I	х
через точку в момент tx =—-—, а задний фронт прямой
/ -4- х
волны — в момент t2 — —-—. При t > t2 точка струны будет
находиться в покое, т. е. лежать на оси Ох. Аналогично,
если х < — /, то точка участвует в колебательном процессе
при — I < х + at < /; если же 0 > х > — Z, то колебания за¬
кончатся, когда через точку пройдет задний фронт обратной
волны, т. е. при t =	.
Очень наглядное изображение описанного процесса можно
получить, введя фазовую плоскость xOt (рис. 7). Каждая
точка М(х, t) фазовой плоскости (при /^>0) соответствует
точке струны с абсциссой х в момент времени t. В част¬
ности, точки оси абсцисс (/==0) соответствуют точкам струны
в начальный момент времени. Точкам, лежащим на прямой
40
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ Г
/ = /0, соответствует положение точек струнькв фиксирован¬
ный момент времени tQ, а точкам, лежащим на прямой
х = х0,—положение фиксированной точки х0 в различные
моменты времени. Как мы уже видели, через точку х в момент
времени t проходит прямая волна, если —/ < х — at <1*
и обратная волна, если —I < x-\-at < I, Построим на фазо¬
вой плоскости прямые х — at= ±1 и % + at = ±/ (на рис. 7
изображены части этих прямых, лежащие в верхней полупло¬
скости). Эти прямые называются характеристиками.
При этом полуплоскость разбивается на шесть частей.
Колебание происходит только в тех точках и в те моменты
времени, которые соответствуют точкам зон /, II и III.
В зоне II действует только прямая волна, в зоне III—только
обратная, а в зоне I—и та и другая. Точкам построен¬
ных прямых соответствуют положения переднего и заднего
фронтов обеих волн. В точках, соответствующих зонам IV
и V, колебания еще нет, так как до них не дошел перед¬
ний фронт прямой (зона IV) и обратной (зона V) волн,
а в точках, соответствующих зоне VI, колебания уже нет,
так как через них задние фронты обеих волн уже прошли
(оба задних фронта проходят только через точки фазовой
плоскости, для которых —	через точки, для кото¬
рых х>/ или х < — /, проходит задний фронт только
одной из волн). Зафиксировав какую-либо точку х0 струны
и поднимаясь вверх по прямой х — х§, легко написать выра¬
жения для функции w(x0, t) в любой момент времени t.

§ 2]
МЕТОД ДАЛАМБЕРА
Пусть х0 > Z. Тогда при 0 < t <	— точка фазовой
х — Z
плоскости находится в зоне IV и и(х0, 1) = 0. Если—2	<
CL
< _X°~LL t то точка попадает в зону II — зону действия
прямой волны —и и(х0, t) =	— at). Второе слагае¬
мое у f(XQ-\~af) равно нулю, так как аргумент xQ-{-at > Z,
а у(х) = 0 при х > I. Наконец, при t > —точка по¬
падает в зону VI и снова w(x0, Z) = 0.
Читатель легко проверит, что в точке xv где 0< х1</,
функция и(х, t) будет принимать следующие значения:
tt(Xp t) —
/(X1_fl0 + /(X1 + fl0
при
2
^f(xx — at)
О
при
при
а	я
а
Ясно, что при переходе от одного интервала изменения t
к другому функция и(х, t) остается непрерывной.
Точно так же можно получить выражения для функции
w(x, t) при фиксированных значениях t. При t < ~ точка
фазовой плоскости при движении слева направо пересечет
последовательно зоны V, III, /, II и IV, а при t > ~ вместо
первой зоны она пройдет шестую. В первом случае
получим
и(х. /0) =
0
у / (■* + «У
при
при
—	оо < х < — at0—l,
—	1 — at0 < х < at0 — I,
_ 1
! /(х4-д/о) + /(х — ata)
2
при
ato — l<Zx<Zl — at0,
—а/0)
при
I — at0 < x < I
0
при
/-|-a/0<x < oo.

42
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
Рекомендуем читателю самостоятельно написать выражения
для и (х, /j) при > 4 *
Описанный процесс представляет распространение оди-
н очной волны отклонения; после прохождения такой волны
точка струны возвращаются в свое исходное положение
на оси абсцисс.
Как мы уже отмечали, такой процесс может наблюдаться
в очень длинной струне до тех пор, пока волны, бегущие
по струне, не дойдут до ее концов.
Перед тем как перейти к конкретному примеру, необхо¬
димо сделать одно важное замечание. Мы рассматриваем
уравнение
д2и 9 д2и
с начальными условиями
»U=/W.
Поэтому функция и(х, t), определяемая формулой (2.8):
»<А-	') + /(x+aQ+j_
x-at
только тогда будет решением уравнения, когда у. нее суще¬
ствуют вторые производные по х и по t. Для этого, как
легко проверить, пользуясь сноской на стр. 35, функция /(х)
должна иметь вторую производную, а функция F (х) — пер¬
вую. Между тем часто приходится рассматривать задачи,
в которых функции /(х) и F(x) не удовлетворяют указан¬
ным условиям. Уже в следующем примере начальная форма
струны будет иметь угловые точки (см. пример 1, рис. 8),
в которых функция /(х) не имеет производной (см. «Кр. к.»,
п. 49). В последующем нам встретятся примеры, в которых
функция F (х), определяющая начальные скорости, имеет
точки разрыва.
Во всех таких случаях функцию и(х, t), определяемую
формулой (2.8), мы все равно считаем решением задачи,
несмотря на то, что при некоторых значениях’ х и t она
может и не иметь соответствующих производных. Это
§ 2]
МЕТОД ДАЛАМБЕРА
43
объясняется тем,4 что всегда можно, чуть-чуть изменив началь¬
ные условия, добиться того, чтобы функции /(х) и F (х)
стали достаточно гладкими, т. е. имели нужные производные.
Заметим, что реальные начальные условия всегда имеют
именно такой сглаженный характер, так что придание им
формы, изображенной на рис. 8, является дополнительной
идеализацией процесса.
В то же время можно доказать, что малые изменения
начальных условий влекут за собой малые же изменения
решения. Поэтому решения,
полученные при помощи	и
сглаживания начальных ус¬
ловий, будут сколь угодно	уч
мало отличаться от тех, ко¬
торые мы получаем по фор- 		q	(
муле (2.8), когда функции
/(х) и F (х) имеют точ¬
ки разрыва или не везде	Рис-
дифференцируемы.
Вообще, если решение задачи единственно и непрерывно
зависит от начальных условий, т. е. малые изменения послед¬
них влекут за собой малое изменение решения, то говорят,
что решение задачи устойчиво или что задача поставлена
корректно.
Учитывая это замечание, мы в дальнейшем при рассмотре¬
нии примеров никогда не будем требовать, чтобы начальные
условия обязательно удовлетворяли условиям непрерывности
и дифференцируемости.
Пример 1. Начальные отклонения точек струны имеют
форму треугольника, изображенного на рис. 8, а начальные
скорости равны нулю. Составим выражения для функции
и(х, t) в разные моменты времени и при различных зна¬
чениях х.
Функция f (х) имеет вид
О
при
х < —Z,
/(х) =
при
—/<х<0.
при
О < х < I,
при
Х>1
Л(*-т)
О

44
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ Г
В точках х — — I, х = 0, х = 1 функция /(х) непрерывна,
но не имеет производной.
Как мы уже видели, выражения для отклонения и(х, t)~
f (х — at) + f (x 4- at)
~ Удобнее всего писать, рассматривая
движение точки (х, t) в фазовой плоскости. Здесь задача
осложняется только тем, что при переходе аргументов x-\-at
и х — at через нуль функции меняют свое выражение. Поэтому
на фазовой плоскости мы дополнительно проводим прямые
х±я£ = 0, в точках которых и происходит указанное изме¬
нение. Из рис. 9 видно, что точки струны, лежащие в интер¬
валах ^0, y) > (4’ 0’	°°^’ П0‘Разн0МУ пеРех°Дят из зоны
в зону (в силу четности функции /(х) мы рассматриваем
только положительные значения х). Проведя необходимые
выкладки (рекомендуем читателю проделать их самостоя¬
тельно), получим выражения для функции zz(x, t):
а) 0 < х < ~
X
а *
о,
0</<
а

МЕТОД ДАЛАМБЕРА
45
ч
А /
,	х—— at\' '
Z — х . ,	х
1 : )’
а <*<«■
4(
1 + V')'
а	а
0,
1+х-
1 > а *
• 0,
\ '■
h (
<	х — at\ ’
X — 1	X
2 (
1
	<.(< — ,
а	а
Если мы хотим получить форму волны в фиксированный
момент времени, то должны выписать значения функции и(х, t)
для трех интервалов времени: ^0,	ooj.
(Опять-таки, ограничиваемся значениями х 0.)
а) 0</<-^
ч
‘-4Ь
о х <
ч
at < х < / — at,
4(
t	х — at\ '
i J*
I — at х 1 —at,
0,
х	1 —j— at*,

46
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
«(Х, t) —
‘(■-4К
/г ] х — at\'
2\1+ I Г
h (1 х — at\
2 V Г“р
О,
О <^х < I — at,
I — at < х < at,
at < x < /+ а/,
x I —J— at}
В) t>-
7	а
и(х, t) =
И1
4(>
О,
I х — at\ '
_1	~ Г
х — at\
о,
О x <iat — I,
at 1 < x < at,
at < x < Z + at,
x > Z-f- at.
Во всех случаях функция u(x, t) непрерывна.
Советуем читателю построить формы струны в различные
моменты времени по найденным формулам и чисто геометри¬
чески и сравнить полученные графики.
8. Распространение волн импульса. Пусть теперь равны
нулю начальные отклонения точек струны и струна
колеблется в результате того, что в начальный момент ее
точки получили некоторые начальные скорости. В этом слу¬
чае говорят, что по струне распространяются волны импульса.
Полагая в формуле (2.8) функцию f (х) = 0,; получим
х vat
и(х, t) = -^ § F (x)dx = <b(x-V-at')—$(x—at'), (2.10)
x- at
где
X
F(x>dx- (2.11)
6
И здесь, как и в п. 7, решение и(х, t) слагается ~из двух
волн: прямой волны 1^ = -—Ф(х— at) и обратной волны

$ 2]
МЕТОД ДАЛАМБЕРА
47
^ = ф(х + at). Форма первой из них в начальный момент
/ = 0 имеет уравнение их = — Ф(х), а второй—уравне¬
ние =	В результате, как и следовало ожидать,
получим и(х> 0) = 0.
Чтобы наглядно представить себе картину процесса, будем
для простоты считать, что
функция F(x) равна нулю
всюду вне интервала (—/, /),
а в точках этого интервала
принимает постоянное зна¬
чение: F(x) — vQ. Иными
словами, точкам струны, ле¬
жащим в интервале (—/,./),
придана постоянная началь¬
ная скорость направлен¬
ная вверх. При этом функция F (х) в точках х=±/ имеет
разрывы.
Функция Ф(х) будет принимать следующие значения:
х
—	если ~
О
I
vodx=-^ — ^>	если х>/,
6
-Z
ф(х) = ^-./ v'>dx==~'W==~l>> если х< —/,
О
где h = Функция Ф(х) непрерывная и нечетная (рис. 10).
Перейдем теперь к геометрическому построению реше¬
ния и(х, t). В левом столбце рис. И построим графики
обратной волны и2 = Ф(х-}-аГ) в различные моменты вре¬
мени, а в правом столбце — графики прямой волны их =
— — Ф (х — at) в те же моменты времени (благодаря знаку
минус графики прямой волны окажутся по отношению к гра¬
фику функции Ф(х) перевернутыми). В среднем столбце
показано результирующее отклонение точек струны. Мы сразу
замечаем, что характер колебаний существенно отличается
от распространения волн отклонения. Начнем для определен-
48
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
кости.с точки струны, находящейся в момент / = 0в начале
координат. По мере увеличения t эта точка будет подни¬
маться вверх; это ясно видно и из формулы (2.10), так как
интервал интегрирования (—at, at) расширяется. При = ~
мы получим
й(°’ D = i ./ vodx = ^- = h.
-I
Если теперь брать t ~ > то все равно будет w(0, t) = h,
так как вне интервала (—Z, I) функция F (х) равна нулю.
Поэтому на рисунках, соответствующих значениям
отклонение zz(O, t) остается постоянным. Рассмотрим еще,
к примеру, поведение точки х1 = ^- Вначале, пока t < ~,
она будет подниматься вверх под действием обеих волн: пря¬
мой и обратной. При t > отклонение обратной волны
в этой точке примет постоянное значение ~ и точка будет
продолжать подниматься уже только под действием прямой
3Z
волны. Наконец, при t > отклонения обеих волн достигнут
величины — и смещение	tj станет равным h.
Если взять точку х2 > Z, то отклонение обратной волны
в этой точке постоянно равно ; отклонение прямой волны
/г
вначале равно — у > и точка начнет( подниматься вверх только
тогда, когда до нее дойдет наклонный участок прямой волны,
т. е. при t — ^-^—. Точка поднимется на максимальную вы¬
соту h, ко,гда через нер начнет снова проходить горизонталь¬
ный участок прямой волны, т. е. при t > Х~^~~ (рекомендуем
читателю^бычислить, аналитически по формуле (2.10) откло¬
нения zJ(^ » и и(?г2, О в рассмотренные моменты времени).
Таким образом, окончательно графики функции и(х> t)
при различных значениях t будут выглядеть так: при Z = 0

МЕТОД ДАЛАМБЕРА
49
Рис. 11.
4 И. Г. Араманович, В. И. Левин

60
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
прямая и = 0\ при 0</< —— профили в форме трапеций,
у которых верхнее основание поднимается и уменьшается
в размерах; при —“ — треугольный профиль и при t > ~
расширяющиеся профили, имеющие вид трапеций (рис. 11).
С течениехМ времени каждая точка струны под влиянием на¬
чальных скоростей, сообщенных участку струны (—/, /),
поднимется на высоту h и дальше будет все время оставаться
на этой высоте (остаточное смещение).
И в этом случае ход колебаний наглядно представляется
при помощи фазовой плоскости (рис. 12).
Пользуясь выражениями для функции Ф (х), легко по¬
лучим, что в зонах //, IV и VI отклонение обратной волны
Ф(х + а/) постоянно равно —, а в точках зон ///, V и VI
такое же отклонение имеет прямая волна — Ф(х— at). По¬
этому зона VI представляет зону остаточного смещения;
в точках, ей соответствующих, функция «(х, /)=Ф (x-\-at)—
— Ф(х— at) = h. В зоне IV прямая волна имеет отклоне¬
ние — такое же отклонение в зоне V имеет обратная
волна. Поэтому обе эти зоны являются зонами покоя точек
струны. Когда точка фазовой плоскости переходит из зоны IV
в зону VI. то по мере прохождения ею второй зоны откло¬
нение прямой волны изменяется от —4 до 4’ Г1°ЛЬЗУЯСЬ
§ 2]
МЕТОД ДАЛАМБЕРА
51
этими соображениями, напишем, например, выражения для
функции я(х0, /)> где *о>^:
о,	0 <7 < —~-Z-,
и(х0, 0 =
х0 — at \
'I )
h,
X0	I <2 t <1 X°
a	a
■
a
Рекомендуем читателю самостоятельно написать выраже¬
ния для w(xP /), где Xj < /, а также выражения для и(х, t),
рассмотрев случаи	и Z>~.
Разумеется, описанный процесс носит еще более идеали¬
зированный характер, чем в первом случае. Явление остаточ¬
ного смещения трудно себе представить еще и потому, что
если даже пренебречь влиянием концов струны, то неизбежно
будет сказываться влияние силы тяжести, т. е. колебания
нельзя будет рассматривать как свободные.
9. Полубесконечная струна. Метод решения задачи для
бесконечной струны, рассмотренный в п. 7, легко применить
и к случаю полубескопечной струны. Мы предположим
теперь, что струна в состоянии покоя располагается на по¬
ложительной полуоси Ох и ее конец, находящийся в на¬
чале координат, неподвижно закреплен. Тогда к уравне¬
нию колебаний струны
д2и 9 д2и
-5ё=а ы
и начальным условиям, заданным при х^О,
«1/=о = /(*)>	^.|^o = F(x)
необходимо добавить еще одно краевое условие:
а|х=о = О.
Из условий (2.13) и (2.14) следует, что /(0) = 0.
При исследовании этой задачи мы особое внимание уделим
колебаниям струны вблизи закрепленного конца и рассмотрим
важный вопрос об отражении волн.
Решение уравнения (2.12) при условиях (2.13) и (2.14)
может быть получено из формулы Даламбера (2.8) следующим
(2.12)
(2.13)
(2-14)
4’

52
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
образом. Допустим, что функции /(х) и F (х), определенные
сначала только при х^>0, доопределены нами произвольным
образом и при х < 0. Напишем выражение для zz (0, /):
«(0.	aV/(a°+A f F(x)dx. (2.15)
Чтобы и(0, t) было равно нулю при всех значениях t, нужно
значения функций /(х) и F (х) при х<0 выбрать так:
/(_ Х) = —/(х) и F( — х) = — F (х)>
т. е., как говорят, функции /(х) и F (х) продолжить
нечетным образом на всю числовую ось1). Первое сла¬
гаемое формулы (2.15) при этом, очевидно, равно нулю;
второе слагаемое также обращается в нуль, потому что мы
интегрируем нечетную функцию в интервале, симметричном
относительно начала координат. Продолжив таким образом
функции /(х) и F(x) на всю Числовую ось, напишем фор¬
мулу Даламбера:
x+at
и(х, t) = f(x-at) + f(x + at)	f p^dx (2.16)
a- at
Теперь это выражение определено для всех х и t и при
х>0 дает решение поставленной задачи. Действительно,
функция (2.16) удовлетворяет уравнению (2.12), условиям (2.13)
и, в силу доказанного, краевому условию (2.14).
Так же, как и раньше, укажем геометрический способ
построения решения и (х, /) в двух случаях: когда /7(х) = 0
{волна отклонения} й когда /(х) = 0 {волна импульса).
Рассмотрим сначала волну отклонения. Пусть функция /(х)
отлична от нуля на некотором интервале (а, р), где 0 < а < р.
Продолжая / (х) нечетным образом, определим ее на всей
числовой оси (рис. 13). Начало процесса будет полностью
’) С подобным продолжением читатель уже встречался; когда
функцию, заданную на половине периода, приходилось разлагать;
в . ряд Фурье или когда функцию, заданную в интервале (0, оо), при¬
ходилось представлять интегралом Фурье, (См. «Кр. к.», пп. 171
и 178).

$ 2]
МЕТОД ДАЛАМБЕРА
53
1
и
0 a	/
соответствовать случаю бесконечной струны (см. п. 7); за¬
данное отклонение следует разбить на две полуволны — одна
из них будет распространя¬
ться вправо, а другая влево.
Как только полуволна, бегу¬
щая влево, дойдет до на¬
чала координат, туда же по¬
дойдет и полуволна, бегущая
вправо по отрицательной
полуоси. В последующие мо¬
менты времени эти полувол¬
ны начнут накладываться
друг на друга, что и соответствует процессу отражения. Весь
процесс отражения показан на рис. 14. Сначала отражающаяся
Рис. 14.
м(х, t) при различных
димо учитывать, что в
волна укорачивается, потом исчезает
и наконец переворачивается. (Если
начальная форма волны не симмет¬
ричная, то полного исчезновения от¬
клонений может и не быть.)
Таким образом, после того как
волна полностью отразилась, откло¬
нения точек меняют свой знак: как
говорят, фаза волны изменила
знак. После этого по струне побегут
вправо с одинаковой скоростью
две волны, находящиеся в противо¬
положных фазах. (На рис. 14 изо¬
бражена только отраженная волна;
волна, с самого начала уходившая
вправо, не показана.)
Если мы захотим составить ана¬
литическое выражение для функции
rz(x, /), то опять-таки удобно вос¬
пользоваться фазовой плоскостью
(рис. 15). Рекомендуем читателю
составить выражения для функции
значениях х и t. При этом необхо-
заштрихованных треугольниках дей¬
ствуют одновременно две волны.
Перейдем к рассмотрению волны импульса и снова будем
считать, что только точки участка (а, р) струны получили

64
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ. I
Риз. 15.
U
Рис. 16.

МЕТОД ФУРЬЕ
55
§ з1
постоянные начальные скорости -у0. Начало процесса распро¬
странения волны полностью соответствует бесконечной струне,
по как только левый конец волны подойдет к началу коорди¬
нат, туда же подойдет и правый конец аналогичной волны,
распространяющейся от симметричного участка (—£, —а)
и находящейся в противоположной фазе. Процесс наложени1
этих волн и образования результирующей отраженной волны
изображен на рис. 16. После отражения по струне побежит
вправо с постоянной скоростью волна в форме трапеции.
(Процесс построения лишь чуть-чуть усложнится, если левый
конец распространяющейся волны достигнет начала координат
раньше, чем в середине интервала (а, р) отклонение достигнет
наибольшего значения.)
В случае конечной струны для получения решения можно
было бы применить метод Даламбера, воспользовавшись от¬
ражением от обоих концов струны (см. стр. 66). Однако для
конечной струны этот метод значительно менее нагляден. Мы
будем решать эту задачу методом Фурье, к изложению
которого сейчас и перейдем.
§ 3. Метод Фурье
10. Метод Фурье. Мы рассмотрим в этом параграфе за¬
дачу о свободных колебаниях*струны, закрепленной на обоих
концах. Как указано в § 1, задача сводится к решению одно-
родного уравнения струны
д2и
dt2
2 д2и
''а дхг
(3.1)
при начальных условиях
ди I
М=о
w|z=0 = /(*),
(3.2)
и краевых условиях
и L=o = 0»
и\х=Г-
= 0.
(3.3)
Метод Фурье (или, как его еще называют, метод раз¬
деления переменных) принадлежит к числу важнейших ме¬
тодов решения уравнений математической физики. Мы с ним
будем в дальнейшем неоднократно встречаться.
Первая часть метода Фурье состоит в том, что мы
отыскиваем частные решения уравнения (3.1), удовле-

56
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. Г
творяющие краевым условиям (3.3), вида
и(х, t) = X(x)T(t).
(3-4)
Каждое из искомых частных решений, таким образом,
представляется в виде произведения двух функций, одна
из которых зависит только от х, а другая—только от t.
Дифференцируя дважды выражение (3.4) по х и по /,
получим
d2Ur  YrfT	д^и

дх2 ~Л 1'	dt2	*
(Для сокращения записи мы не пишем аргументов функ¬
ций X (х) и Т(/).)
Подставляя выражения для производных в уравнение (3.1),
получим
XT" = а2Х"Т
или, деля обе части равенства на произведение а2ХТ,
1 Т" (/) _ X" (х)
a2 T(t) ~ Х(х) '
(3.5)
Чтобы функция и(х, f) = X(x)T(t) была решением уравне¬
ния (3.1), равенство (3.5) должно соблюдаться при всех зна¬
чениях х и t. Левая часть этого равенства зависит только
от переменной t и не может изменяться при изменении х.
Поэтому, если зафиксировать t и менять х, левая часть,
а следовательно и правая, будет сохранять постоянное зна¬
чение. Рассуждая аналогично, установим, что правая часть,
а следовательно и левая, не может изменяться и при изме¬
нении t. Это будет справедливо только в том случае, когда
обе части равенства (3.5) вообще не зависят ни от х,
1 Т"	Хп
ни от Л т. е. когда оба отношения —и являются
а2 Т	X
величинами постоянными:
1 Т" (0 _ X" (х) _
a2 t (t) ~ X (х) ~
с = const.
(3.6.)
Отсюда следует, что функции Т и X должны удовле¬
творять дифференциальным уравнениям
Х"(х) — сХ(х) = 0 и T"(t) — ca2T(t) = 0.	(3.7)

МЕТОД ФУРЬЕ
57
Поскольку мы ищем частные решения, удовлетворяющие
краевым условиям (3.3), то при любом значении t должны
соблюдаться равенства
«|х=о=* (0)т (0 = О’ «|Л=/=х (/) Т(О=0.
Если бы обращался в нуль второй множитель, то реше¬
ние и(х, t) равнялось бы нулю при всех значениях х и С
Поэтому, чтобы отыскать решения, не тождественно равные
нулю (а только такие нас и интересуют), мы должны счи¬
тать, что
Аг(0) = 0 и Х(/) = 0.
В результате для отыскания функции X (х) мы пришли
к следующей задаче1): найти решения линейного диф¬
ференциального уравнения второго порядна
Х"(л:) —сХ(х) = 0	(3.8)
при условиях
Х(0) = Х(/) = 0.	(3.9)
Разумеется, эта задача при любом с имеет решение, то¬
ждественно равное нулю: X(x)s0. Оказывается, однако, что
при некоторых значениях постоянной с эта задача имеет и
другие решения.
Заметим, что в этом состоит существенное отличие реше¬
ния рассматриваемой задачи от решения обыкновенных диф¬
ференциальных уравнений с начальными условиями, когда для
определения частного решения задаются значения функции и
ее производной в некоторой начальной точке. Как известно
(см. введение), последняя задача имеет единственное решение.
Полагая Х(х) = еГХ, составим для уравнения (3.8) харак¬
теристическое уравнение
г2 — с = 0
и рассмотрим различные случаи.
’) Эта задача является частным случаем общей задачи
Штурма — Лиувилля, заключающейся в отыскании решений линей¬
ного дифференциального уравнения второго порядка вида [р(л)у']'+
+ г (х) у — су = 0, удовлетворяющих некоторым краевым усло¬
виям, т. е. условиям, налагаемым на искомую функцию или ее про¬
изводную в точках х = а и х = b (концах интервала).

58
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
1)	Пусть с = Х2>0. Тогда корни характеристического
уравнения действительны, г=±Х, и общее решение урав¬
нения имеет вид
Чтобы соблюдались условия (3.9), мы должны положить
Ci ^2=
С1^ + С2в-х/ = 0.
Так как определитель этой однородной системы
1 1
ем е-м —е е
не равен нулю, то система имеет единственное решение
Cj = С2 = 0.
Таким образом, в этом случае решений, отличных от тожде¬
ственного нуля, не существует.
2)	Пусть с = 0. Тогда оба корня характеристического
уравнения равны нулю и
(х) =	б?2х.
Подставляя в условия (3.9), получим
= 0, Cj c2i== о»
т. е. опять-таки С1 — С2 = 0,
3)	Пусть, наконец, с ——X2 < 0. Корни характеристиче¬
ского уравнения мнимые, г = ± /X, и решение будет содер¬
жать тригонометрические функции
X (х) = С?! cos Хх 4- С2 sin Хх.
При х = 0 должно быть
Х(0) = С1 = 0,
а при х = 1
Ar(Z) = C2sinXZ = 0.
Последнее равенство возможно, когда С2 0, именно оно
будет удовлетворяться при
sinXZ = O,

§ з]
МЕТОД ФУРЬЕ
39
т. е. при
вуют решения уравнения (3.8), не равные тождественно
нулю.
Решение, отвечающее некоторому фиксированному k,
обозначим через Xk(x). Оно имеет вид
Хл(х) = Лй51п-^
(3.10)
где Ak — произвольная постоянная. Мы вправе в дальнейшем
придавать k только положительные значения: &=1, 2, . ..,
поскольку при отрицательных k будут получаться решения
того же вида (ведь Ak — произвольные постоянные, которые
могут иметь любые знаки).
Как мы видим, каждому значению ХЛ = -у- соответствует
бесчисленное множество решений (3.10), отличающихся друг
от друга постоянным множителем.
Величины Хй = -^- называют собственными числами.
а функции sin — собственными функциями дифферен¬
циального уравнения (3.8) с краевыми условиями (3.9).
Напомним читателю, что система функций (х), ср2(х),. •»
срл(х), ... называется ортогональной в интервале [а, Л],
если интеграл от произведения любых двух различных функ¬
ь
ций системы равен нулю: I срл(х)cpm(x)dx = 0, если п^т
а
(см. «Кр. к.», п. 175). Легко установить, что найденные
собственные функции ортогональны на интервале [0, /].
Действительно, при п =/= т
о
к (m — n) x	it (m n) x
sm	sin
m — n	m-\- n
“ 2k
m — n
о
I

60
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. Г
Теперь обратимся к отысканию функций Т (/). Каждому
собственному числу будет соответствовать своя функ¬
ция Tk(f), определяемая вторым из уравнений (3.7) (напоми¬
наем, что с — — X2):
Tht) + (~)2Tk(f) = Q.
Его общее решение имеет вид
T^O = Bftcos-^+0*sin-^,'’	(3.11)
где Bk и Dk — произвольные постоянные.
Подставляя выражения (3.10) и (3.11) в формулу (3.4),
найдем частные решения уравнения (3.1), удовлетворяющие
краевым условиям (3.3). При этом каждому значению ’Й = 1,
2, ... будет отвечать решение
ик{х, t) = \Bkcos-1- + Dks\n—r]Aks\n — .
Внося множитель Ak в скобку и вводя обозначения AkBk = ak
и AkDk = bk, запишем uk(x, t) в биде
z	{	knat . .	. kitat\ . knx
«*(*• 0 = ^ftcos-T-H-dftsin——Jsin —j—. (3.12)
Решения uk(x, f) называются собственными функциями
задачи; соответствующие им колебания струны называются
собственными колебаниями.
Физический смысл решений (3.12) мы рассмотрим не¬
сколько позже, а сейчас перейдем ко второй части метода
Фурье и при помощи собственных функций построим реше¬
ние, удовлетворяющее начальным условиям (3..2). В силу
линейности и однородности уравнения (3.1) сумма решений
(3.12) также будет являться его решением:
оо
/ м \? /	kitat , ,	. knat\ . knx
u(x, t) = 2jPacos“7	h^Sin—j— Isin-y- . (3.13)
Й = 1
Поскольку мы составили бесконечный ряд, то, разумеется,
нужно, чтобы он был сходящимся. Мы предположим также, что
его можно дважды почленно дифференцировать (см. введение).
Ясно, что функция и(х, ^ удовлетворяет краевым условиям
(3.3), так как им удовлетворяет каждая из функций ик(х, t).

§ 3]
МЕТОД ФУРЬЕ
61
Будем теперь подбирать цроизвольные постоянные ак
и bk так, чтобы функция (3.13) удовлетворяла начальным
условиям. Подставляя значение t — 0, получим
СТ'
«|/=0 =	=	(3.14)
/? = 1
Дифференцируя ряд (3.13) по /:
оо
ди	kita !	knat . . kizat\ . k~x
^=21—(-^sin—+^cos—)sin-r>
k=l
и подставляя t = 0, удовлетворим второму начальному усло¬
вию:
оо
Л = 1
Формулы (3.14) и (3.15) показывают, что величины ak
и J^Lbk являются коэффициентами разложения функ¬
ций f(x) и F (х) в ряд Фурье по синусам в интервале
(0, /) (см. «Кр. к.», п. 171). Вспоминая формулы для коэф¬
фициентов этого разложения, найдем ak*.
i
ak—~J f (x)sin-^- dx.	(3.16)
о
i
kna r	2	/* „ z к . knx ,
Так как —bk=-j- I F(x)sm—tZx, to
6
i
b*=^fF^n^rdx-	(3.17)
0
Подставляя выражения для коэффициентов ak и bk в ряд
(3.13), мы окончательно найдем решение поставленной за¬
дачи.
Мы не останавливаемся на условиях, которые надо нало¬
жить на функции /(х) и F(x), чтобы было оправдано сде¬
ланное допущение о возможности почленного дифференциро¬
62
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
вания ряда (3.13). Обычно в физических задачах эти условия
соблюдаются.
Формула (3.13) показывает, что в моменты времени
,	2/ Ы
t — —, t — — > ... струна возвращается в свое первона¬
чальное состояние; это означает, что колебания струны не¬
затухающие и периодически повторяющиеся, с периодом
2Z
Т = —. Так происходит потому, что мы пренебрегали си¬
лами трения. При учете их получились бы затухающие коле¬
бания, аналогично тому как это имеет место в случае обык¬
новенных гармонических колебаний точки. Решение задачи
в этом случае приведено в п. 14.
11. Стоячие волны. Прежде чем перейти к примерам,
выясним физический смысл собственных функций uk(x,
определенных формулой (3.12). Перепишем ее в виде
uk{x. =	(3.18)
где
Из формулы (3.18) видно, что все точки струны совер¬
шают гармонические колебания с одной и той же ча-
стотой = —— и фа¬
зой срй. Амплитуда ко¬
лебания зависит от абс¬
циссы х точки струны
Рис. 17?
новесия. Такие колебания
волнами.
гл	.
и равна Fk sin —j—.
При таком колебании
все точки струны одно¬
временно достигают сво¬
его максимального от¬
клонения в ту или иную
сторону и одновременно
проходят положение рав-
струны называются стоячими
На рис. 17 показана форма струны в различные моменты
времени для случая й=1; при этом неподвижными остаются

§ 3]
МЕТОД ФУРЬЕ
63
только концы струны, а наибольшего отклонения дости¬
гает только точка х —	, При k = 2 неподвижных точек
будет уже три: концы и середина струны	= sinrc=oj,
а точек, в которых от¬
клонения будут достигать
наибольшего значения, —
I	3/
две: х = т и х =
(рис. 18).
Вообще стоячая вол¬
на uk(x, t) будет иметь
столько неподвижных то¬
чек, сколько корней имеет
. knx А
уравнение sin -у- = и
в интервале [О, I]. Та¬
ких точек будет &4-1;
(£ — 1) Z ' ,
	g > i-
I ' 2Z
их абсциссы: 0, j, -у, ...
Неподвижные точки называются узлами стоячей волны.
Посередине между узлами располагаются точки, в которых
отклонения достигают максимума; такие точки называются
пучностями. Каждая струна может иметь собственные коле¬
бания лишь строго определенных частот =	Эти ча¬
стоты называются собственными частотами струны.
Наименьшей собственной частотой будет
(3.19)
где То — натяжение, а р— плотность струны.
Когда струна колеблется, она издает звук, высота кото¬
рого возрастает вместе с частотой колебаний. Если струна
совершает собственные колебания, то самый низкий тон будет,
когда частота равна а)Р Из формулы (3.19) видно, что при
этом звук тем выше, чем больше натяжение Го и чем короче

64
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
и легче струна1) (т. е. чем меньше I и р). Остальные тона,
соответствующие частотам называются обертонами или
гармониками. Если струна совершает свободные колебания,
определяемые начальными условиями, то функция и{х, t)
представляется, как это видно из формулы (3.13), в виде
суммы отдельных гармоник. При этом характер звучания
струны (тон, сила звука, тембр) будет зависеть от соотно¬
шения между амплитудами
£/	отдельных гармоник.
Основное назначение ре¬
шения (3.13) как раз и
заключается в том, что оно
позволяет произвести срав¬
нение этих амплитуд.
12. Примеры. Пример 1.
Найти колебания струны
Рис. Д9.	с закрепленными концами
х — 0 и х = I, если на-
0 с
чальные скорости точек
струны равны нулю, а начальное отклонение имеет форму
треугольника с вершиной в точке (с, й) (рис. 19). ^Натяжение
струны То, плотность р, величина а =	•)
Функция / (х) = и |/=0 задается формулами
/(*) =
hx
Т’
h(l — x)
1 — с
если
если с х /.
Функция F(x) —о» согласно условию, рав ла нулю.
Поэтому в общем выражении (3.13) для решения и (х, t) все
коэффициенты bk ==6.
О Читателю, ^имевшему дело со струнными инструментами, на¬
пример с балалайкой, хорошо известно, что, чем туже натянута
струна, тем более высокий звук она издает; точно так же можно
увеличить высоту звука, зажав струну в какой-либо ее точке, т. е.
укоротив ее.

§ 31
МЕТОД ФУРЬЕ
65
Коэффициенты ак находим по формуле (3.16):
i
2 Г , , ч . knx .
ak = TJ /(x)sin-y-dx =
6
с	I
h Г knx ,	. h /* z, ч . knx ,
— J x sin —dx + -j—- J (l — x)sin—rdx
0	c
Вычисляя интегралы по частям, получим:
с
I2
k2n*
Ic
kn
knx
Sin —j~
Io
cos
kne
I
и аналогично
i
(*z. 4 . knx . I (I — c) kne , Z2 kne
J (l-x)Sln-T-dx=	cos—+ ^-sm-r.
c
Следовательно,
_ 2AZ2	knC
аь~ Zf2TC2c(Z —c)sin I '
Подставляя выражение для ak в формулу (3.13), получаем
искомое решение
оо
z	2/zZ2 V1 1	. kne . knx knat
и(х’ 0= ^c(/_c) L^sin-rsin~z~cos~r- (3-20)
Л = 1
Если число k таково, что sin = 0, т. е. точка с
является узлом &-й гармоники, то ak = 0 ив найденное ре¬
шение соответствующая гармоника не входит (если kQ— наи¬
меньшее из таких чисел, то все остальные будут ему кратны).
Пусть, например, струна оттянута в середине, т. е. с = у.
Тогда	и при всех четных значениях k точка
является узлом; поэтому в решение будут входить только
нечетные гармоники. Читатель легко проверит, что в этом
случае = решение будет иметь вид
л = 0
5 И. Г. Араманович, В. И. Левин

66
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ. I
Выражение (3.20) для решения u(xt t} показывает, что
амплитуда &-й гармоники пропорциональна величине р-,
с* возрастанием номера k\
Это значит, что гармони¬
ки достаточно высоких
порядков на результиру¬
ющее колебание практик
чески никакого влияния
оказывать не будут.
Для построения фор¬
мы струны в любой мо¬
мент времени не обяза¬
тельно производить вы¬
числения по формуле
(3.20). Можно восполь¬
зоваться уже хорошо
изученным явлением от¬
ражения волны от закреп¬
ленного конца струны
(см. п. 9); теперь только
нужнр отразить волну от
обоих концов. Чтобы
произвести построение,
продолжим первоначаль¬
ный график струны на
интервале (0, Z) «нечет¬
ным» образом влево и
вправо и разобьем его
на прямую и обратную
волны. (На верхнем из
рисунков 20, соответст*
т. е. довольно быстро убывает
Рис. 20.
вующем моменту времени
/ = 0, графики обеих волн сливаются.) Затем обычным обра¬
зом строим графики прямой и обратной волн в разные мо¬
менты времени и складываем их в интервале (0, /). Весь
этот процесс в промежутке времени ^0, изображен на
рис. 20	= и рис. 21	= В следующий полупе¬
риод	j струна, пройдя в обратном порядке все отме*

§ 3j	МЕТОД ФУРЬЕ	67
ченные положения, вернется в первоначальное состояние (при
/ = 0), после чего процесс будет периодически повторяться
(21 \
с периодом Т-— I. Рис. 20 и 21 показывают существен¬
ное отличие характера
полученного колебания
от свойств стоячей вол¬
ны. Так, например, если
I
с =А ’ то точки струны
проходят положение рав¬
новесия в разные мо¬
менты времени; кроме
того, струна не будет за¬
нимать положения, сим¬
метричного с первона¬
чальным, относительно
оси Ох.
Предоставляем чита¬
телю доказать, что функ¬
ция и(х, t), определен¬
ная формулой (3.20),
удовлетворяет условию
“ (2~х’ 4 —2) =
•=—и(х, /), и объяс¬
нить его геометрический
смысл.
Пример 2. Пусть
в условиях предыдущего
примера начальная фор¬
ма струны задается функ¬
цией f(x) = A sinгде п — целое число, а начальные
скорости равны нулю.
В этом случае начальное положение струны совпадает
с графиком одной из собственных функций й решение осо¬
бенно просто. Помимо всех коэффициентов bk, обращаются
в нуль и все ак при k =£ я, так как собственные функции
ортогональны (см. стр. 59)>
5*

68
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. Г
Найдем коэффициент ап:
i
.2 Г . 9 mtx .	.
ап—A— I sin2——dx = At
о
и, следовательно,
и(х,
л . пкх .
/) = A sin -у- sin
nnat
~Т~
Таким образом, струна совершает стоячее колебание.
Пример 3. Пусть в условиях примера 1 начальная
форма струны — парабола, симметричная относительно сере¬
дины струны, и максимальное отклонение равно h (рис. 22).
Найдем колебания струны.
Составляя уравнение параболы, получим
/ (х) = ~р X (I — X).
По-прежнему все bk — 0, а
ak вычисляются по формулам
Дважды интегрируя по частям,
получим (необходимые выкладки читатель проведет само¬
стоятельно)
Отсюда следует, что если k четно, то aft = 0. Если же
k нечетно и равно 2п-4~Ь то
а2п+1 = _(2п+ 1)зкз (п = 0, 1, 2, . ..).
Окончательно получаем решение в виде
,	..	32h V 1
и(х, t)— тс3 2L (2п-{-l)3Sin
л = 0
(2n-f- 1)^АГ
I
cos
(3.22)
(2n+ 1)яд/
~1
Здесь амплитуды последовательных гармоник (нечетных) убы¬
вают еще быстрее, чем в первом примере. В подобных
§ 3)
МЕТОД ФУРЬЕ
69
случаях высшие гармоники оказывают влияние только на тембр
звука, издаваемого струной, в то время как тон определяется
основной наименьшей частотой а)х (см. формулу (3.19)).
Пример 4. Пусть в начальном положении струна на¬
ходится в покое и точкам ее на участке (а, р) придана
постоянная начальная скорость (этого можно добиться,
ударяя по струне на этом участке плоским жестким моло¬
точком). Найдем колебания струны.
Сохраняя предыдущие обозначения, будем иметь
/(х) = 0.
Р(х) =
0.
если
0 х < а
‘Wo-
если
а < х < 0
О.
если
0 < х
(мы уже отмечали тот факт, что функция F (х) может быть
разрывна). Коэффициенты ak общей формулы (3.13) равны
нулю, а коэффициенты bk находятся по формулам (3.17):
Р
,	2v0 Г . k-кх ,
™-rdx
	 2Z v0
kVa
COS
Лтф \
“Г
Следовательно,
ft = l
kna
COS
— COS 	T2-	,	,	,
I . knx . kitat
•p	Sin —— sin —* (3.23)
В частном случае, если начальные скорости v0 получают
все точки струны (а = 0, р = /), то
«(х, t)
	 4/v0 у 1
Li (2л+1)2
л = 0
(2л4-l)7tx .
sin -—-4-^	sin  	H-2

(для четных k разность 1—cos/гтс равна нулю, а для нечет¬
ных— двум). Нетрудно найти в этом случае наибольшее
отклонение струны от положения равновесия. Физически яс¬
но. что больше всего отклонится от положения равновесия
середина струны, т. е. точка х — Выбирая еще момент

70
УРАВНЕНИЯ КОЛЕБАНИИ ;
(ГЛ. I
времени
получим
JI		1	sin2 <2? + J)*.
\2* 2а) п*а	(2л4-1)* sin 2
Так как sin2	, то эт0 значение и и будет
наибольшим. Учитывая формулу1)
оо
1		 тс2
(2л+1)а ~ 8 ’
S
найдем, что wmax=4~~.
Пример 5. Пусть в условиях примера 4 струна возбу¬
ждается ударом очень острого молоточка, передающего струне
импульс I в точке с. Начальное отклонение точек струны
равно нулю.
В этой задаче мы имеем дело с так называемым сосре¬
доточенным импульсом. Будем понимать это следующим
образом: сначала положим, что импульс равномерно распре¬
делен по некоторому малому участку струны (с — 8, с+ 8),
окружающему точку с. Тогда, в силу закона сохранения
количества движения, будет соблюдаться равенство
2 8рт/0 — /,
где р—линейная плотность струны, a т/0— приобретаемая
ею на участке (с — 8, с + &) начальная скорость. Найдя
решение этой задачи и перейдя к пределу при 8—>0, мы
получим искомое решение.
!) Указанная формула следует из решения примера 1. Подставляя
в формулу (3.21) значения х = и £ = 0 и учитывая, что
.	(2п +1) тс	Z	,
sin	— = (—1)л, а начальное отклонение в точке равно А,
(1	и 8Л V 1	V 1	**
получим; 42-’°) = А = ^1(2^+1Р’ОТКУДа	У
л=0	л=0

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
71
fi
Положим в формуле (3.23) a = c—8, p = e4-8 и v0==~^:
„ kn (c — a) kit (e+a)
COS 	i-5	- — COS

	-	sin
I
k*
и (X, t) = -^2^ 2
Л = 1
По правилу Лопиталя
Лк (с —а)	Лк(с + а)
COS	~	- — COS 		-
lim 	-	.			=
8-»0 °
v kit г . Лк(с — a> . . лк(с + а) i
=Lmn“rLsin' ■ /—+sin-"-z7- -|
kitx , kitat
—Sln—•
2kit . kite
-j- sin —•'
Считая возможным почленный переход к пределу под знаком
суммы, получим решение задачи о колебаниях струны под
действием сосредоточенного импульса
kitat •
~~1
I
Пример 6. Пусть в условиях примера 4 начальное
распределение скоростей задается функцией
F(x) =
если	О С х < xQ — 8,
если х0— 8<х<х0 + 8,
если х04“ S < х /.
Показать, что колебания струны описываются функцией
cos
sin
кпх0
~Г'
itnx . itnat
Sin —т~ Sin —г— .!
I	I
§ 4. Вынужденные колебания и колебания струны
в среде с сопротивлением
13.	Вынужденные колебания струны. Методы, разви¬
тые в § 3, позволяют решать и задачу о вынужденных коле¬
баниях струны. Эта задача приводит к неоднородному

УРАВНЕНИЯ КОЛЕБАНИИ
(ГЛ. I
уравнению колебаний (см. § 1)
д2и 9 д2и .
G(x, t)
(4.1)
(йы обозначили через G(x, t) функцию yg(x, /), где
р — плотность струны, a g(x, t)— плотность распределения
внешних сил). Начальные и краевые условия примем такими же,
как и для случая свободных колебаний:
«L > = /(*)>	=
и
Так же как и при решении обыкновенных линейных
неоднородных дифференциальных уравнений (см. «Кр. к.»,
п. 145), будем искать решение уравнения (4.1) в виде суммы
двух функций:
и(х> t) = v{x, £) + w(x, /).	(4.2)
Функцию	t) выберем так, чтобы она удовлетворяла
d2v 9 d2v
однородному уравнению	—и условиям
Ч-о = /(*)•	=
Тогда функция w(x, /) должна удовлетворять неоднород¬
ному уравнению
G(x, t)
(4.3)
и нулевым начальным и краевым условиям
Легко проверить, что при таком выборе функций v и w
их сумма (4.2) будет являться искомым решением.
Функция v(х, t) описывает свободные колебания
струны, происходящие только вследствие придания точкам
струны начальных отклонений и скоростей. Функция w(x, t)
§ 4]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
73
описывает вынужденные колебания, которые совершаются
под действием внешних сил при отсутствии начальных
возмущений.
Поскольку функцию v(x, t) мы уже умеем отыскивать
(см. § 3), то займемся теперь только отысканием решения
неоднородного уравнения — функции w(x, /).
Будем искать функцию w(x, /) в виде ряда по соб¬
ственным функциям sin-^^- однородной задачи*.
оо
да (х, 0 = X} (t) sin ~,	(4.4)
Л = 1
где 7^(0 — не определенные пока функции от t. Прежде
всего заметим, что функция w(x, /) действительно удовле¬
творяет краевым условиям w |	0 = w | z = 0, так как все
собственные функции обращаются в нуль при х = 0 и х = /.
Чтобы функция ,w(x, /) удовлетворяла и нулевым начальным
условиям, достаточно считать, что 7л(0) = 0 и ^(0) = 0.
Запишем уравнение (4.3) в виде
d2w
~д?
d2w
~дх2
G(x, t)
и заменим функцию w(x, t) рядом (4.4). Тогда получим
оо
S [т*(А> + Л2/гд2	w] sin = °(х< *)■	(4-5)
Л = 1
Разложим теперь функцию G(x, t) в интервале (0, /)
в ряд по синусам по аргументу х (это производится точно
так же, как и разложение в ряд Фурье функции одной пере¬
менной, но только коэффициенты разложения будут являться
функциями переменной t):
оо
G (х, t) = J] gk (t) sin ,	(4.6)
k=l
где
i
gk (0 = 7 f 0 (x’ 0sin	dx-
0
(При интегрировании t считается постоянным.)
(4.7)

74
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Если, в частности, плотность распределения внешних сил
не зависит от времени, то функция G(x, t) не зависит от Z,
т. е. G(x, t) = G(x) и формула (4.6) представляет собой
обычное разложение в ряд Фурье по синусам. В этом случае
функции gk(t) постоянны.
Если же функция G(x, /) не зависит от х, а зависит
только от времени Л т. е. G(x, t) — G(t), то функции gk(t)
будут равны
„ ...	2G(t) f . knx ,
= J sm — dx =
0
4
-r-G(f), если k нечетное,
(4,8)
О, если k четное.
Приравнивая в разложениях (4.5) и (4.6) коэффициенты
при собственных функциях, составим дифференциальные урав¬
нения для отыскания неизвестных функций (^):
(0 = ^(0-	(4.9)
К полученному неоднородному уравнению второго порядка
следует присоединить установленные выше начальные условия
т*(°) = °>	ъ(°)=°-
(4.Ю)
Общее решение однородного уравнения, соответствующего
уравнению (4.9), имеет вид
Ak cos
knat
~Г'
BAsin
kizat
Решение неоднородного уравнения (4.9) в случае, когда
функция gk (t) имеет специальный вид (в частности, постоянна),
может быть найдено методом неопределенных коэффи¬
циентов (см. «Кр. к.», п. 147). При произвольной правой
части решение следует искать методом вариации произ¬
вольных постоянных (см. «Кр. к.», п. 148).
Пользуясь этим методом, можно показать, что при любой пра¬
вой части gk (t) решение уравнения (4.9) с начальными усло¬
виями (4.10) дается формулой
t
=	<т>Sln —1—-dx-
о
(4.11)

§ 4]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
75
Выводить эту формулу мы не будем, и рекомендуем читателю сде¬
лать это самостоятельно.
После того как все функции yk(t) найдены, остается
подставить их в формулу (4.4), и мы получим искомую функ*
цию w(x, t).
Пример 1. Найти вынужденные колебания струны,
находящейся под действием силы тяжести.
В этом случае функция G(x, t) = — g и задача сильно
упрощается, поскольку все коэффициенты	разложе¬
ния (4.6) постоянны.
По формуле (4.8)
= — sin-^-dx= — -^(1— cosAk),
6
откуда
g2„ = 0 и g2n+i=s— (2n+l)it •
Функции T2/i(O тождественно равны нулю, так как они
удовлетворяют однородному уравнению
с ну левыми начальными условиями у2п = 0 и |^_q=0.
Для функций с нечетными индексами 72я+1 (0 уравне¬
ние (4.9) принимает вид
(2 л +1)2 к2а2
Т2
Т2я+1
4g
(2л-|-1)п *
(4.12)
Частное решение неоднородного уравнения находится сразу;
это есть постоянная величина, равная—(2л+1)3гс34? * ^ле"
довательно, общим решением уравнения (4.12) будет функция
Л2я+1 cos
(2n+l)iwf I
I
В2п+^\п
(2л -f- 1) Tzat
7
4gl2
(2л +1)3 тс3л2 *
Подставляя начальные условия, находим произвольные постоян-
ные Л2я+1 и В2я+1:
А		 ^g12	g		 Q
л2л+1	(2л4-1)3тс3л2 ’	2л + 1 —

76
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
Итак, функции 72«+iW найдены:
1Л^Л, <4 ,3>
Подставляя полученные выражения в формулу (4.4), полу¬
чим решение w(x, /), описывающее вынужденные колебания
струны, совершающиеся под действием силы тяжести:
п = 0
(Знак минус указывает на то, что в начале колебания точки
струны отклоняются вниз.) Каждая точка струны совершает
сложное периодическое колебание с периодом —. В моменты
2/
времени t = — k (& = 0, 1, 2, ...) все точки струны про¬
ходят положение равновесия. Легко заметить, что наибольшие
отклонения от положения равновесия будут наблюдаться
для середины струны = в моменты времени t = ^
— и т. д. I Это можно установить и аналитически; при х =
J I .	2п/	dw dw
и t = — ~\—— обе частные производные и обра¬
щаются в нуль.) Поскольку
sin (2п+1)тс.| = (_1)л, а
cos (2я+1>”д.-£ = _1,
/	а
ТО
Н lmax = H (4 ’ 1)1
Известно, что !)
у (~1)л
яЗд2	(2и+1)3	•
Л = 0
и t = 0, получим: и
V (— 1)" _ я3
(2/i-J- l)3 ~ 32 ’ .
л-0
*) Указанная формула следует из решения примера 3 п. 12.
Полагая в (3.22) х — ~
32 А V (— О"
(2п+1)3 ,0ТКУДа
л=0
(у. °Н-

§ 41
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
77
следовательно,
|w|
max
gJL
4а2 ’
Пример 2. Найдем вынужденные колебания струны без на¬
чальных смещений и скоростей, если на струну действует равно¬
мерно распределенная сила с плотностью g (х, t) = Лр sin со/, зави¬
сящей от времени (р— линейная плотность струны).
В этом случае функция G (х, t) = О = A sin»/ не зависит
от х и по формуле (4.8) мы получим:
4А
g2n (0 = 0,	£2я+ , (0 =	- sin
Как и в предыдущем примере, замечаем, что Т2я(0 = 0* Функ¬
ции же Тгл+1 (О находим по общей формуле (4.11):
Т2Л+1 (0 =
41А	/ ,
о / Sin (ОТ Sin
(2л +1)2 J
о
(2п+1)тсд(/~т)
Вводя обозначение
(2п4-1)ка
ш2л+1 —	/

и производя все необхо-
димые вычисления, получим, что
72/1+1(0 =
41А
(2 л 4- 1)2А
(02я+1 Sin (oZ — со sin (О2Л+ \t
“2,1 + 1— “2
Найденное выражение имеет смысл для любого п только в случае,
если частота <о вынуждающей силы не совпадает ни с одной из не¬
четных собственных частот струны (отсутствует резонанс).
Подставляя выражения для 72л+1 (0 в общую формулу (4.4),
завершаем решение задачи:
w (X, t) =
4/Л у	1
п2а (2п+ I)2
n = 0v	‘
Рекомендуем читателю самостоятельно установить, что если
для какого-нибудь k имеет место равенство со2й+1 = со, то соответ¬
ствующее слагаемое в выражении w (х, t) надо заменить на
2/Л	(О2^_|_ COS 4-]^ — Sin (O2£ -f-
rc2a(2#-f-l)2	<02ft+i
2/2Л
= К3Л2 (2Л | l)3	— W2fe + ^ COS «2ft + l0-
14.	Колебания струны в среде с сопротивлением. До сих
пор мы все время рассматривали колебания струны, не учитывая
78
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
сопротивления окружающей среды. Естественно, что при этом
получались незатухающие колебания. Рассмотрим теперь слу¬
чай, когда колебания струны происходят при наличии сопро¬
тивления среды. Силу сопротивления, возникающую при этом,
примем пропорциональной скорости движения (такой же закон для
силы сопротивления принимается и при изучении гармонических ко¬
лебаний точки). Тогда на бесконечно малый участок струны МХМ2
(см. § 1, рис. 4) действует сила
/='сопР = а-^-^.	(4.14)
где а — коэффициент пропорциональности. Рассуждая так же, как
при выводе уравнения (1.12), и учитывая, что сила сопротивления
всегда направлена против движения, придем к уравнению
д2и __ 2 д2и
~dfl~a дх*~
(4.15)
| g<x, t).
где введено обозначение ~ = 2m (все остальные обозначения та¬
кие же, как в § 1). Ограничиваясь случаем свободных колебаний,
запишем уравнение (4.15) в виде
д2и
dt
д2и
дх2
(416)
Начальные и краевые условия имеют прежний вид, т. е.
«I/=O = /W.	4г|,_о = /7(х)’	“1х=о = и1х=г = О. (4.17)
Решение уравнения (4.16) с условиями (4.17) опять будем произ¬
водить методом Фурье.
Полагая и (х, t) = X (х) Т (t) и поступая, как в § 3, получим
1 ( Т" + 2тТ' \ X"
Т J ” X ’
(4.18)
Поскольку краевые условия для функций X (х) остались та¬
кими же, как и для случая колебаний без сопротивления, то равен¬
ство (4.18) будет возможно, если обе его части равны—.где
kit
= —- собственные числа (k = 1, 2,...); при этом собствен¬
ные функции Хь(х) определяются по формуле (3.10) (мы опускаем
числовые коэффициенты):
д» . х , kitx
XA,(x) = sin—у-.
Для определения функций Гл(/) получим дифференциальное
уравнение
^ + 2т7’;4-(-~-)27’А = 0.	(4.19)

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
79
§ Ч
Его характеристическое уравнение
r2 + 2mr+(^y=0
имеет корни		___
rli2 = —m ± |/”т2 —
Мы будем предполагать, что коэффициент трения т настолько
мал, что подкоренное выражение отрицательно для любых значе¬
ний к. Ясно, что это будет тогда, когда т <	. Вводя обозначе-
/ kita \2	2	2
ние I —у—• I — т = qk, получим
гЬ2 = —m ± iqk.
Следовательно, общее решение уравнения (4.19) таково !):
Тк Ю = e~mt (ak cos Чц* + ьк sin 4kty
По функциям Xk (x) и Tk(t) составим выражения для частньГх
решений uk (х, Z):
= e~mt (ак cos чк(+ьк sin qkt) sm .
Каждая из полученных стоячих волн благодаря множителю е~т
является затухающей.
Переходя ко второй части метода Фурье, составим ряд
и (х, /) = e-mt	(at cos qj + b* sin qkf) sin
fc=i
и подберем его коэффициенты так, чтобы удовлетворялись началь¬
ные условия. При / = 0
«к=в= a*sln =
Й=1
и величины ak определяются уже известной формулой (3.16):
i
Uk=j J'/(x)sln-^-rfx.
о
!) Если выражение т2—	при небольших значениях к
положительно, то общее решение уравнения (4.19) для этих к
иметь другой вид, содержащий показательные функции.
Дальнейшее решение в этом случае несколько усложняется.

80
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Находя производную и полагая t = 0, получим
оо
(— mak + bkqk) sin	= F (х),
Л=1
откуда
— mak + bkqk = j- l' F(x)s\n^-dx
о
н
/
Ь*= ТУ"./ F (х) sin ~rdx+ — all.
k Q	R
Пример. Пусть в примере 1 п. 12 дополнительно предполо¬
жено, что струна колеблется в среде с сопротивлением, причем
т = — < —— . По условию начальные скорости г (х) = 0, и по¬
этому
, т
Предоставляем читателю установить, что решение будет иметь вид
и(х, z) =
. 2Л/2
п2С (/ — С)
е' Ъ 1? sin —sin “ cos qk* + 7"sin qk ]9
*=i	'	k	'
где
§ 5. Продольные колебания стержня
15.	Постановка задачи и метод решения. В этом пара¬
графе нами будет рассмотрена задача о продольных колеба¬
ниях однородного стержня. Стержень — это тело цилиндри¬
ческой (в частности, призматической) формы, для растяжения
или сжатия которого надо приложить известное усилие. Мы
будем считать, что все силы действуют вдоль оси стержня
и каждое из поперечных сечений стержня pqrs (рис. 23)
перемещается поступательно только вдоль оси стержня.
§ 5]	ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ	81
Обычно это предположение оправдывается, если поперечные
размеры стержня малы по сравнению с его длиной, а силы,
действующие вдоль оси стержня, сравнительно невелики !).
На практике продольные колебания возникают чаще всего
тогда, когда стержень предварительно немного растягивается
или, наоборот, сжимается, а затем предоставляется самому
себе. В этом случае в нем возникают свободные продольные
колебания. Выведем уравнения этих колебаний.
Направим ось абсцисс по оси стержня (рис. 23); в со¬
стоянии покоя концы стержня имеют соответственно абс¬
циссы х = 0 и х — 1. Рассмотрим сечение pqrs\ х — его
ч
x*dx
7^~
\ 1
1
1
1
1
1
1
абсцисса в состоянии покоя. Смещение этого сечения в любой
момент времени t будет характеризоваться функцией я(х, Z),
для отыскания которой мы и должны составить дифферен¬
циальное уравнение. Найдем прежде всего относительное
удлинение участка стержня, ограниченного сечениями pqrs
и pxqxrxsr Если абсцисса сечения P\qp\sx в состоянии покоя
x-\-dx, то СхМещение этого сечения в момент времени t
с точностью до бесконечно малых высшего порядка равно
u(x-j-dx, t) — u(x, 0 + dx.
Поэтому относительное удлинение стержня в сечении с абс¬
циссой х в момент времени t равно
u(x + dx, f) — u(x, t) _ ди	,	-
	dJc	—~д^ ~их	1 >
!) Если эти силы велики, то стержень может начать изгибаться.
В курсе сопротивления материалов устанавливается, что наимень¬
шая нагрузка Р, при которой стержень может принять устойчивое
изогнутое положение (критическая нагрузка), определяется по фор-
7^2 pf
муле Эйлера Р — ——> где — модуль Юнга, J—момент инер¬
ции поперечного сечения относительно его центра тяжести,
1 — длина стержня.
6 И, Г. Араманович, В, И. Левин
82
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
Считая, что силы, вызывающие это удлинение, подчиняются
закону Гука, найдем величину силы натяжения Т, действую¬
щей на сечение pqrs*
Т = ESu'x(x, t).	(5.2)
где S — площадь поперечного сечения стержня, а Е— модуль
упругости (модуль Юнга) материала стержня. Формула (5.2)
должна быть хорошо известна читателю из курса сопроти¬
вления материалов.
Соответственно сила Tv действующая на сечение
равна
Тг = ESu'x(x dx, t).
Поскольку силы Г и 7\ заменяют действие отброшенных
частей стержня, то их результирующая равна разности
Tl — T = ES [их (х + dx, t) — и'х(х, ^)] = ES dx. ,
Считая выделенный участок стержня материальной точкой
с массой pSdx, где р— объемная плотность стержня, и при¬
меняя к нему второй закон Ньютона, составим уравнение
?Sdx^- = ES^dx.	(5.3)
Е
Сокращая на Sdx и вводя обозначение —= а2, получим диф¬
ференциальное уравнение свободных продольных коле¬
баний стержня
д2и _ 2 д2и
dt2 ~а дх2'
(5.4)
Если дополнительно предположить, что к стержню приложена
внешняя сила g (х, /), рассчитанная на единицу объема и действую¬
щая вдоль оси стержня, то к правой части соотношения (5.3)
добавится слагаемое g (х, t) S dx и уравнение (54) примет вид
д2и 2 д2и 1	z--.
■ж-=**^+уг(*.э.	(55)
что в точности совпадает е уравнением вынужденных колебаний
струны.
Перейдем теперь к установлению начальных и краевых
условий задачи и рассмотрим практически наиболее интерес¬
$ 51
ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
83
ный случай, когда один конец стержня закреплен, а дру¬
гой— свободен.
внешние силы отсутствуют.
Если считать неподвижным конец стержня, совпадающий
с началом координат, то й| ^=о = О.
На свободном конце краевое условие будет иметь иной
вид. Так как на этом конце
то должна быть равна нулю и сила Т, действующая в сече¬
нии х — 1» т. е.
откуда
л-1	= °»
дх |*=г
4^1	=о.
дх \x=i
Колебания происходят оттого, что в начальный момент
стержень был деформирован (растянут или сжат) и точкам
стержня были приданы некоторые начальные скорости. Сле¬
довательно, мы должны знать смещение поперечных сечений
стержня в момент / = 0
«|#=0 = /(*)’
а также начальные скорости точек стержня
ди
It
Итак, задача о свободных
продольных
колебаниях
стержня, закрепленного на
одном
конце, возникающих бла-
годаря начальному сжатию
к уравнению
или
растяжению,
привела нас
д2и	9 д2и
dt* ~а дх^
где
(5.6)
с начальными условиями
и |/=0 == / (•*).
ди
(5-7)
и краевыми условиями
«1х=0 = °-
ди
дх
I =0.
1л = »
(5.8)
Именно последнее условие и отличает с математической
точки зрения рассматриваемую задачу от задачи о колебаниях
струны, закрепленной на обоих концах.
6*

84
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
Будем решать поставленную задачу методом Фурье, т. е.
отыскивать частные решения уравнения, удовлетворяющие
краевым условиям (5.8), в виде
«(х, /) = Аг(х)Т(О.	(5.9)
причем X (0) — 0 и X' (/) = 0.
Так как дальнейший ход решения аналогичен уже изло¬
женному в § 3, ограничимся только краткими указаниями.
Дифференцируя функцию и(х, t), подставляя полученные
выражения в (5.6) и разделяя переменные, получим
1 Т" _ X” _	)2
а2 Т ~ X ~	’
(Предоставляем читателю самостоятельно установить, что
в силу краевых условий постоянная в правой части не может
быть числом положительным или нулем.) Общее решение
уравнения X" 4~X2X = 0 имеет вид
X (х) = Cj cos Хх + С2 sin Хх.
В силу условий, наложенных на функцию X (х), будем
иметь
X (0) = С} = 0, X' (/) = С2Х cos X/ = 0.
Решения, не тождественно равные нулю, будут получаться
только при соблюдении условия cosX/ = 0, т. е. при Х/ =
= ^--\-kTzt где k может принимать значения 0, 1, 2, ...
Итак, собственными числами задачи служат числа
(^+1)я (й = 0. 1, 2, ...).	(5.10)
Каждому Xfe соответствует собственная функция
=	(5.11)
Как мы уже знаем, умножая любую из собственных функ¬
ций на произвольную постоянную, будем получать решение
уравнения X" -4-Х2Х = 0 с поставленными краевыми усло¬
виями. Легко проверить, что, придавая числу k отрицатель¬
ные значения, мы не получим новых собственных функций
(например, при k = —3 будет получаться функция, отли¬
чающаяся от собственной функции Х2(х) только знаком).

§ 5]	ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ	85
Докажем прежде всего, что собственные функции (5.11)
ортогональны в интервале (0, Z). Действительно, при
[ sin (Jm.+ lUx sin (2n+^ .x dx =
0
, (tn — п)кх	. (/n-l-n4-l) лх 1 1
sin -	z-2-—	sin i/—-—
Z
2л
m — n	m-j-n-t-l Jo’
Если же m = n, то
У Sin2 <2П±11^^ = |У[1_СОЗ	=
О	о
Доказать ортогональность собственных функций (х) можно
и иначе, не опираясь на их явные выражения, а пользуясь только
дифференциальным уравнением и краевыми условиями. Пусть \т
и \п — два различных собственных числа, Хт и Хп — соответ¬
ствующие им собственные функции. По определению эти функции
удовлетворяют уравнениям
<я+х2Л = о, <+хХ = о
и краевым условиям. Умножим первое из уравнений на Хп, второе
на Хт и вычтем одно из другого:
- Х''ПХт + tfn - ХЛ = О-
Интегрируя это равенство в пределах от 0 до Z и замечая, что
(^Х-<Х) = Х^-^Х)'. получим, что
/
(*JX - х'пхт)	- X2) f ХтХп dx = 0.
о
Первое слагаемое обращается в нуль при любой из следующих
комбинаций начальных условий: 1) X (0) = 0, X (Z) = 0 (задача
о колебаниях струны), 2) X (0) = 0, X' (Z) = 0 (колебания стержня
со свободным концом), 3) X' (0) = 0, Xr (Z) = 0 (колебания стержня,
у которого оба конца свободны). Следовательно, во всех случаях
i
j XmXndx = 0,
о
так как по условию \т =# \п. Приведенное здесь рассуждение будет
неоднократно встречаться в дальнейшем.

86
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
При Х = Хл общее решение уравнения т"	— О
имеет вид
Тк (О = ак cos <2А+ЦT'at + sin (2* + р■♦ (5.12)
Поэтому частным решением uk(x, t), соответствующим соб¬
ственному числу Хл, будет функция
/) =
=[«, cos У"+-»’•“ + Ь, sin <"+toq sin	-1
(5.13)
Для окончательного решения задачи составляем ряд
и(х, t) =
= Х [«» t’’" - + -У "'] 5|" (И V“
k = Q
(5-14)
В силу начальных условий (5.8)
«1«=о = § ak sin	= f (х),
л=о
ди I _ У (2Л+1)ДД b . (2fe+l)KX _ р , .
dt |/=0 ~ Zl 21	&к S П 21
л=о
Чтобы найти коэффициенты ak и bk, заметим, что написан¬
ные равенства представляют разложения функций f (х)
и F(x) в ряды по ортогональной системе функций
sin	(см. «Кр. к.», п. 175). Предполагая такое раз¬
ложение возможным, легко находим коэффициенты ап и Ьп,
*	. (2л4-1)тех
умножая обе части разложения на sin-1		и интегри¬
руя в пределах от 0 до I. Так как интеграл от квадрата

§ 5]
ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
87
любой собственной функции равен , то
о
(5.15)
Подставляя в ряд (5.14) найденные значения ап и Ьп> получим
искомое решение.
16.	Примеры. Пример 1. Пусть однородный стержень
плотности р и длины Z, закрепленный в точке х = 0, рас¬
тянут силой Р, приложенной к другому его концу. В мо¬
мент времени £ = 0 действие силы мгновенно прекращается,
после чего стержень предоставлен самому себе. Найти воз¬
никающие продольные колебания стержня.
Будем считать, что сила Р, действующая на стержень
в начальный момент, такова, что применим закон Гука, и най¬
дем начальное смещение точек стержня и |/=0 — /(•*)• Так как
в каждом сечении сила натяжения Т постоянна и равна Р,
то по формуле (5.2)
где Е— модуль упругости, 5 — площадь поперечного сече¬
ния. Интегрируя и учитывая, что /(0) = 0 (стержень при
х = 0 закреплен), получим
т. е. смещение любого сечения в начальный момент про¬
порционально его абсциссе. (Заметим, что если бы стер¬
жень сжимался силой Р, то в выражении для f (х) изме¬
нился бы только знак.) Так как начальные скорости равны
нулю, то р(х) = 0 и все bk обращаются в нуль. Найдем
теперь по формуле (5.15) коэффициенты ak:
п — 2Р
ttk ~ IES

88
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Подставляя выражения для ak в формулу (5.14), получим функ¬
цию и(х, /)к описывающую продольные колебания стержня:
,	..	8Р1 v
U ^Х’	~ r?£S
й=0
(-D* гп, (2*+l)x<rt s. (2*+l)*.t
(2А—1-1)2 C0S 21	21
где
sin
то на свободном конце стержня все гармоники имеют пуч¬
ность (см. стр. 63). Ясно, что в закрепленном конце всегда
будет узел. Первая гармоника имеет частоту	|/ у;
это есть основная частота колебаний стержня. Частоты осталь¬
ных гармоник будут получаться при умножении основной
частоты на последовательные нечетные числа.
Пример 2. Пусть стержень примера 1 выводится из со¬
стояния равновесия ударом по его свободному концу в про¬
дольном направлении. Найти возникающие колебания стержня,
если импульс, сообщенный стержню при ударе, равен
В этом примере наибольшую трудность представляет фор¬
мулировка начальных условий. Сообщение стержню ударного
импульса приводит к тому, что точки его свободного конца
получают начальные скорости. Удар предполагается мгновен¬
ным, поэтому начальные скорости, строго говоря, должны по¬
лучать только те точки стержня, которые лежат в сечении
х = 1. Однако физически это нереально. Ведь по второму
закону Ньютона сообщенный импульс должен быть равен изме¬
нению количества движения, т. е. произведению массы на ско¬
рость, а масса сечения стержня х = /, очевидно, равна нулю.
Поэтому мы выделяем малый участок стержня I — е <С
<х<1 и считаем, что все его точки получили в резуль¬
тате удара одну и ту же скорость vQ. Масса выделенного
участка равна р£г, где р — плотность стержня и S — площадь
готеречного сечения. Приравнивая изменение количества дви¬
жения импульсу силы, получим
р5ег»0 =

§ 5)
ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
89
откуда
Функции /(х) и F(x), определяющие начальное состояние
стержня, будут равны:
/(х) = 0.
при
при
О < х < Z—е,
I— е х
О
(знак минус берется потому, что скорость *и0 направленя
в отрицательную сторону оси Ох). Коэффициенты, входящие
в общую формулу (5.14), находим по формулам (5.15):
4е)=°-
I
	 Г sin (2#-J-1) тех ,
(2£-H)™pSe J	21 ил~
l—s
4сЯ
Так как
21
8^Z	(2^ + 1)k(Z-«)
(2^ + 1)2к2ар5е
cos
(2^+ 1)к (/-£)
2Z
= сю
(2k + l)^-[
21 J —
,	.	(2k + 1) nt
= (— lfSin-	L

2Z
то
2Z
-(~l)fe8^/	(2fe+D^
(2Л + 1)2тс2дрЗе Ь1П
В полученных выражениях для b(k легко перейти к пределу
при е->0. Поскольку
(26 + фи
..	21	(2*4-1) я
||т	1	= - Т/ •
е->0	£
то, обозначая lim	получим
в->0
h —	(-О*-4^
к ~	(2k + 1) uapS ’

90
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Подставляя выражения для b
тельно получим
4<Р
icapS
л=о
(-1)*
(2Л4-1)
k в формулу (5.14), оконча-
(2Л4-1)яа/	(2*4-1) их !
sin	г» *	sin	•
н(х, t) =
Если нас интересуют колебания конца стержня, то мы должны
положить х = 1\ тогда
со Cin(2*+D^
4^> V	2Z
«(/,/)_ явр5 2*4-1
А = 0
Период колебания Т= —. Смещение u(l, t) равно нулю
2/	41
при £ = 0,	... Наибольшее смещение конца стер¬
жня от положения равновесия будет при t—~\
|И|	=_4^_у .(-П6 .
|max TtapS Ju 2* + 1
л=о
Сумма написанного ряда, как известно, равна (этот
числовой ряд получается, если в разложении arctgx в ряд
Маклорена принять х = 1; см. «Кр. к.», п. 164). Поэтому
«I _ & _	&
|и|тах_ aps~ S/£T’	‘
где Е — модуль упругости.
Пример 3. Пусть стержень длины Z, конец которого
х — 0 закреплен, находится в состоянии покоя. В момент t = 0
к его свободному концу приложена сила Q, действующая вдоль
стержня. Показать, что задача сводится к решению урав¬
нения свободных колебаний стержня (5.6) с условиями и |/=о=О,
=0, н! о = О, —I =пЯг и что колебания
ся |/=о	dt \x=i ES
стержня описываются функцией
«(х, t)=-Q$ X
(—I)"	(2n+l)«xz.nr(2n+l)«aZ
n2ESZj (2n -J-1)’sln 2Z C ~2l	’
л=0

6 6]
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
91
§ в. Крутильные колебания вала
17.	Уравнение крутильных колебаний. Для того чтобы
вывести дифференциальное уравнение крутильных колебаний
вала (круглого цилиндрического стержня), напомним основ¬
ные положения, лежащие в основе теории кручения круглых
стержней,,изучаемой в курсах сопротивления материалов. Со¬
гласно этой теории поперечные круговые сечения стержня
при кручении остаются плоскими и сохраняют между собой
первоначальные расстояния; радиусы, проведенные в этих
сечениях, не искривляются1). Таким образом, кручение круг¬
лого вала можно представить как результат сдвигов, вызван¬
ных поворотом поперечных сечений друг относительно друга,
причем все повороты совершаются вокруг оси вала. Вслед¬
ствие этого в поперечных сечениях возникают только каса¬
тельные напряжения, действующие в плоскости сече¬
ния, а нормальные напряжения равны нулю. Так как
касательные напряжения симметричны относительно центра
поперечного сечения, то они приводятся к паре сил, момент
которой называется крутящим моментом.
Поскольку нас интересуют только относительные повороты
сечений, то любое из них можно принять за неподвижное.
Будем считать, что неподвижен левый конец вала (как говорят,
левый конец заделан). Поместим начало координат в центр
неподвижного сечения и направим ось абсцисс по оси стержня
!) Если стержень не круглый, то эти положения не могут со-
‘ блюдаться. Решение задач кручения некруглых стержней значи¬
тельно сложнее; оно рассматривается в курсах теории упругости.

92
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
(рис. 24). В результате закручивания вала поперечное сече¬
ние АВ, взятое на расстоянии х от заделки, повернется от¬
носительно неподвижного сечения на некоторый угол 9, зави¬
сящий от х; сечение А'В', отстоящее от сечения АВ на
расстояние dx, повернется при этом на угол 9 -f-dfl. Таким
Рис. 25.
образом, поворот сечения
А'В' относительно сечения
АВ будет равен dO.
Вычислим сначала кру¬
тящий момент Л4Г, прило¬
женный к сечению АВ. Вы¬
делим для этого отдельно
участок вала, ограниченный
сечениями АВ и А'В'
(рис. 25), сдвинутыми друг
относительно друга на угол
K'O'L' — d9. Возьмем про¬
извольный элемент площа¬
ди da, расположенный на расстоянии г от центра сечения,
и определим величину напряжения т, вызванного сдвигом эле¬
ментарного волокна КК' в положение KL'. Считая, что мы
находимся в пределах применимости закона Гука, получим
т — G7,
где 7—угол сдвига волокна, a G — постоянная для данного
материала величина, называемая модулем сдвига. В силу
малости угла 7 дугу K'L' можно принять за хорду, и тогда
7 ~‘£7
K'L’
dx
С другой стороны, дуга K'L' равна
K'L' = rdQ
и, следовательно,
dO	/Д 14
7 = (6-1)
Таким образом, напряжение т прямо пропорционально рас¬
стоянию г рассматриваемого волокна КК' от центра сечения.
Усилие, приходящееся на площадку da, выразится произве¬
дением
т da = Gr da
dx

§ в]
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
93
и будет направлено перпендикулярно радиусу. Обозначая
через dMx элементарный закручивающий момент, приложен¬
ный к элементу Ja, получим
dMx = rxda = Or2 da.	(6.2)
Величину искомого момента Мх найдем, интегрируя выраже¬
ние (6.2) по площади сечения АВ:
гр	dft
Так как для всех точек поперечного сечения величина Q
одна и та же, то ее можно вынести за знак интеграла; тогда
MX = GJO^,	(6.3)
где Jo = ff г2 da — полярный момент инерции поперечного
сечения АВ относительно его центра.
Перейдем к выводу дифференциального уравнения кру¬
тильных колебаний вала, рассматривая по-прежнему эле¬
ментарную часть его, заключенную между сечениями АВ
и А'В'. По второму закону Ньютона, примененному к вра¬
щательному движению тела вокруг оси, произведение момента
инерции тела относительно оси на угловое ускорение равно
моменту внешних сил относительно оси вращения.
Угол 6 поворота сечения зависит теперь уже как от
абсциссы х, так и от времени Л т. е. б = 0(х, Z). Угловое
ускорение элементарного участка вала будет равно
Если через К обозначить величину момента инерции вала
относительно оси вращения, приходящуюся на единицу его
длины, то момент инерции рассматриваемого участка будет
равен К dx. Момент внешних сил найдем как разность кру¬
тящих моментов, приложенных к сечениям АГВГ и АВ.
Согласно формуле (6.3), в которой заменено на 6^-,
Мх+с1х — Мх = Щ К (•* + dx> Г) — 0х {х, О] = О/0 dx.

94
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. F
Таким образом, мы выразили все величины, входящие в закон
Ньютона. Применяя его, получим
К	dt2	дх2 ^Х’
или
=	(6.4)
где
Таким образом, дифференциальное уравнение крутильных
колебаний вала, так же как и продольных колебаний стержня,
полностью совпадает с уравнением колебаний струны.
Однако обычно встречающиеся конкретные задачи приводят
к иным краевым условиям, нежели те, которые были рас¬
смотрены в §§ 3 и 5.
Так как вал однородный, то, обозначая его плотность
через р и учитывая, что К — момент инерции единицы длины
вала, найдем
1
к = р J dx J* J r2da = p/0.
Отсюда
0
в =	(6.5)
Примечание. В то время как уравнение продольных коле¬
баний выведено для любых призматических стержней, уравнение
крутильных колебаний применимо только для круглых стержней
(валов). Для некруглых стержней, как мы уже отмечали, задача
становится значительно более сложной.
18.	Крутильные колебания вала с диском на одном конце.
Пусть один конец вала длины I закреплен, а на другой его конец
насажен массивный диск, момент инерции которого относительно
оси вала равен Jx. В начальный момент диск закручивается
на малый угол а и отпускается без начальной скорости. Изучим
характер возникающих при этом крутильных колебаний вала.
Сохраняя введенные выше обозначения, составим прежде всего
начальные и краевые условия, которым должна удовлетворять
функция, являющаяся решением задачи.

§ в]
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
95
Чтобы найти 01/=0» рассмотрим рис. 26. Так как угол а мал,
то, рассуждая так же, как при выводе формулы (6.1), получим
соотношения (R — радиус вала)
h = R« а *Т=ЯЧ=о’
откуда
Далее, согласно условию
дО
dt
Поскольку конец вала х = 0 неподвижен, то
О
(6.6)
(6.7)
(6-8)
Если бы диска на правом конце вала не было, то крутящий
момент Mt = GJq -ч—
д* \х=1
был бы просто равен нулю,
так как внешние силы от¬
сутствуют. Это привело бы
dO I л
к условию	=0,
и решение в точности сов¬
пало бы с решением при¬
мера 1 п. 16 (см. стр. 87).
В нашем же случае на¬
до приравнять нулю сумму
крутящего момента М[ и
произведения момента инерции диска на его угловое ускорение
d20 I
-таЧ (момент силы инерции диска):
01 1ж =Z
гт dO I ,, d20 I л
Gj 0 “3— I	+ J 1 "ЗТо"	= 6.
дх |х=^ dt2 |х=1
Полученное условие удобнее записать в виде
где
<r I	2 <?е I
dt2 |x=z с дх |ж=1’
(6.9)
Итак, будем искать решение уравнения (6.4), удовлетворяющее
условиям (6.6) — (6.9).
Запишем искомую функцию в виде 0 (х, t) = T (t) X (л), под¬
ставим в уравнение (6.4) и разделим переменные:
1 Т" _ X"
а2 Т ~ X

96
У РАВ Н ЕН ия КОЛ Е БЛII11П
1Г-Л. I
(Предоставляем читателю доказать, что и здесь в силу условий,
которые налагаются на функцию Х(х), постоянная в правой части
равенства обязательно отрицательна.)
Функции Т (t) и X (х) являются решениями обыкновенных диф¬
ференциальных уравнений:
Г' + а2Х2Т = 0,	(6.10)
Х"-|-Х2Х = 0,	(6.11)
причем из (6.8) следует, что функция Х(х) должна удовлетворять
условию X (0) = 0. Далее, из краевого условия (6.9) получим
Т"Х(1) = — c2TXr (Z)
и, заменяя, согласно уравнению (6.10), Г" на —а2Х2Г, придем
ко второму условию, налагаемому на функцию Х{х)\
с2Х' (Z) — аЖХ (Z) = 0.	(6.12)
Заметим, что в рассматриваемой задаче постоянная X входит
не только в дифференциальные уравнения, определяющие функции
Т (Z) и X (х), как это было во всех предыдущих случаях, но и
в краевое условие, которому должна удовлетворять функция X (х).
Это приведет, как мы увидим в дальнейшем, к некоторому услож¬
нению решения.
Решение уравнения (6.11) имеет вид
X (х) — cos Хх + С2 sin Хх.
Из условия X (0) = 0 следует, что С!=0. Второе условие для
функции X (х) приводит к уравнению
X (с2 cos — а2Х sin XZ) С2 = 0.
Так как С2 =# 0 и X 0 (иначе мы получаем тривиальное решение
X (х) = 0), то для определения собственных чисел мы приходим
к трансцендентному уравнению
с2 cos XZ — а2Х sin XZ = 0
или
ctgM = -£*.	(6.13)
Из формул, определяющих а и с, следует, что = на¬
помним, что Ji — момент инерции диска, а К—момент инерции
единицы длины вала. Полагая XZ = р. и обозначая -тЛ- = ш, пере-
Zv
пишем уравнение (6.13) в виде
cig р- = /пр..
(6.14)

§ 6]
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
97
Как мы сейчас покажем, это уравнение имеет бесчисленное
множество корней; будем обозначать их Каждому корню
соответствуют собственное число = и собственная функция
Xk (х) = sin \kx = sin	(6.15)
Так как обе части уравнения (6.14) — нечетные функции отно¬
сительно р., то каждому положительному корню соответствует
равный ему по абсолютной величине отрицательный. Поскольку
изменение знака приводит к изменению знака Хд, что не влечет
за собой образования новых собственных функций (они только из¬
менят знак, что несущественно), будем отыскивать только положи¬
тельные корни уравнения (6.14). Для этого построим графики функ¬
ций u = ctgu. и и = т& (рис. 27). Ясно видно, что эти графики
имеют бесчисленное множество точек пересечения, т. е. что урав¬
нение имее?бесчисленное множество корней (k = 1, 2, ...). Поль¬
зуясь каким-нибудь способом приближенного решения уравнений
(см., например, «Кр. к.», п. 62), можно вычислить значения корней
(при заданном т) с любой степенью точности. Из рис. 27 видно
также, что при больших значениях k корни приблизительно равны
Рй ~ (k — 1) к.
После того как собственные числа найдены, ищем соответ¬
ствующие им решения уравнения (6.10):
Tk (t) = ak cos a\kt 4- bk sin a\kt.	(6.16)
Перемножая функции Xk (x) и Tk(t), найдем решения уравнения
колебаний (6.4), удовлетворяющие краевым условиям:
О* (л, t) = (ak cos a\kt 4- sin аХл/) sin Xftx.
7 И. Г. Араманович, В, И. Левин

98
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
Как обычно, решение, удовлетворяющее начальным условиям (6.6)
и (6.7), ищем в виде суммы:
оо
0 (х, 0=2 (ak cos abJ + bk abJ) sin Ьгх> (6-17)
fc = i
Для определения неизвестных коэффициентов ak и bk получаем
два условия:
оо
61,=о = 2 sin “ т ’
<6Л8>
|	= ® ^к&к Sin = 0.
k = 1
Из второго условия заключаем, что все = 0.
Заметим, что собственные функции sin \kx не ортого¬
нальны в интервале [0, ZJ. Поэтому мы не можем отыскивать ak,
пользуясь формулами Фурье для коэффициентов разложения в ряд
по ортогональным функциям. В этом и заключается та сложность;
задачи, о которой говорилось выше. Оказывается, что это затруд¬
нение легко обойти, поскольку производные от собственных
функций (т. е. функции cos Xkx) уже образуют ортогональную си¬
стему. Действительно, при п k имеем
L
J* cos \kx cos \пх dx =
о
_ JL Г sin(Xfe4-X„)x sin (Kk — ln) x 11* __
2 L bi +	bt — b J Io
 sin X^Z cos XrtZ — \n sin Хп1 cos X^Z

sin XijZ sin X«Z z. » r »	»
= ?2 ?2 С
Воспользовавшись уравнением (6.13), корнями которого являются
числа Х* и Хл, найдем, что
а2
b ctg — bi ctg bit = (Х^ХЯ ХЯХ£) = 0.
Сл едовательно, при k п
i
J* cos bix cos bix dx == 0.
о
(6.19)

8 7]
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
99
Если же k = nt то
(6.20)
Дифференцируя первое из условий (6.18), получим
со
а
Т
Умножим
интервалу
зовавшись
обе части равенства на cos \пх и проинтегрируем по
[0, /]. Так как у J cos \пх dx = sin AnZ, то, восполь-
о	”
равенствами (6.19) и (6.20), найдем, что
)=
откуда
sin 2ХЛ/
Заменим через и придадим выражению для ап более удоб-
ный вид:
4а sin
ап	V-n (2цп + Sin	•
Подставляя найденные коэффициенты в ряд (6.17), окончательно
получим решение задачи:
со
6 (х, 0 = 4а
Л=1
sin
Р-к (%4t + sin
COS
Wk*
I
sin
-цу sin Хл/’
Для того, чтобы произвести числовые расчеты, нужно знать
корни уравнения (6.14). Отметим, что значения этих корней при
различных значениях ш можно найти в специальных таблицах.
§ 7. Электрические колебания в длинных
однородных линиях
19. Телеграфное уравнение. Знакомясь с теорией обык¬
новенных линейных дифференциальных уравнений с постоян¬
ными коэффициентами, читатель, наверное, сталкивался с
применениями этой теории к расчету электрических цепей
7*

100
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ I
переменного тока, содержащих сосредоточенные пара¬
метры.
Важнейшим примером такой цепи является колебательный
контур, состоящий из последовательно соединенных сопро¬
тивления, емкости и катушки самоиндукции. При этом счи¬
тается, что все сопротивление контура сосредоточено только
в реостате, т. е. что ни катушка самоиндукции, ни соединяю¬
щие провода при прохождении электрического тока не вы¬
деляют тепла. Точно так же переменный магнитный поток
индуцирует электродвижущую силу только в катушке, а токи
электрического смещения возникают только между обкладками
конденсатора. В курсах электротехники подробно изучаются
вопросы возможности таких предположений; в частности,
при периодических процессах они считаются допустимыми,
если линейные размеры всех элементов цепи малы по срав¬
нению с длиной электромагнитной волны в окружающем цепь
диэлектрике.
Если протяженность цепи велика (например, телеграф¬
ные линии или линии передачи энергии), то такую цепь уже
нельзя характеризовать сосредоточенными параметрами. В про¬
стейшем случае, когда цепь имеет большую протяженность,
можно говорить о линиях с распределенными пара¬
метрами !).
При изучении таких линий учитывают сопротивление про¬
водов, индуктивность линии, утечку тока в атмосферу вслед¬
ствие отсутствия изоляции провода или ее несовершенства,
а также взаимную емкость между проводами (или между про¬
водом и землей). Мы будем рассматривать однородную
линию, т. е. линию, сопротивление, индуктивность, утечка
и емкость которой распределены вдоль провода непрерывно
и равномерно; для большей наглядности будем считать линию
двухпроводной (рис. 28). Пусть напряжение между про¬
водами и ток на расстоянии х от начала линии в момент
времени t равны соответственно н(х, /) и Z(x, t)\ эти функ¬
ции и являются искомыми.
’) Если длина электромагнитной волны настолько мала, что она
сравнима с поперечными размерами проводника, то выводимые
в дальнейшем уравнения становятся неприменимыми. В этом случае
необходимо прибегать к решению уравнений электромагнитного
поля, излагаемому в более подробных курсах.

§ 7]	ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ	10!
Пусть R— сопротивление, L — коэффициент самоиндук¬
ции, С — емкость и G — коэффициент утечки, рассчитан¬
ные на единицу длины провода. Напомним, что коэффи¬
циент самоиндукции L есть коэффициент пропорциональности,
связывающий электро¬
движущую силу само¬
индукции со скоростью
изменения тока, т. е.
г dl	S'*
= A -st ; емкость С
с	ot
есть коэффициент про¬
порциональности между
током смещения и ско-
ди
ростью изменения напряжения, т. е. iCM = G это равен¬
ство получается дифференцированием соотношения q = Cut
где q — количество электричества, остающегося на участке
провода, рассматриваемого как обкладка конденсатора, а и —
напряжение. Наконец, коэффициент утечки G есть коэффи¬
циент пропорциональности между током утечки и напряже¬
нием: iy — Gu.
Для составления дифференциальных уравнений, которым
должны удовлетворять функции z/(x, t) и Z(x, /), выделим
участок провода от точки с абсциссой х до точки с абсцис¬
сой x-^-dx. Если обозначить для краткости через и и i на¬
пряжение и ток в точке х в момент времени Z, то в точке
x-^dx в тот же момент времени значения этих величин
(с точностью до бесконечно малых величин высших порядков,
чем dx) будут равны	и	Падение на¬
пряжения на рассматриваемом участке будет вызываться поте¬
рей напряжения в проводе, т. е. величиной Rdxi, и возник¬
новением противодействующей электродвижущей силы само¬
индукции uz — Ldx-^. (Величины R и L рассчитаны на
единицу длины.) Поэтому
и — (и Н- tfjcj = R dx i-j- L dx ~,
t. e.
OU I n- I 7 dl C\
(7.1)

102
УРАВНЕНИЯ КОЛЕБАНИЙ
(ГЛ. Г
Далее, изменение тока на этом же участке обусловлено
током утечки и током смещения. Следовательно,
I — (/ + ~ dx) = Gdx и + С dx	,
откуда
^+О« + С^ = 0.	(7.2)
Полученные уравнения (7.1) и (7.2) представляют систему
двух уравнений с частными производными первого по¬
рядка. Из них легко исключить любую из неизвестных функ¬
ций, например ток. Дифференцируем для этого уравнение (7.1)
по х, а уравнение (7.2) по Z:
д2и | р di . , дЧ
dx»	дх dtdx
д21	, п ди , с д2и

дх dt	dt	dt2 ~
(7.3)
--	оt	OU	~ U U ■■
Из второго равенства находим:	= — О 	С .
Выражая еще из уравнения (7.2): ^- = — Ои — С ,
и подставляя все в первое из равенств (7.3), получим
д2и
дх2
-«(o“+cS-)-'-(ot+cS-)=0'
или окончательно
д2и , RC + LG ди f RG tt 1 д2и _
dt2	LC dt ' LC U LC dx2 ~
Полученное уравнение называется телеграфным уравне¬
нием. Рекомендуем читателю проверить самостоятельно, что,
исключая функцию и, мы придем к точно такому же урав¬
нению и для функции Г.
дЧ , RC+LG dl , RG ,	1 дЧ
~дГ2^	LC—-dF + -LCl-LC-dJ? = Q- <7-5>
Полное исследование уравнения (7.4) (или (7.5)) требует
применения специальных методов и выходит за рамки книги.
Мы ограничимся рассмотрением частных случаев, впрочем
играющих значительную роль в курсах электротехники. При
этом сначала отвлечемся от краевых условий, т. е. будем
§ 7]
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
103
считать линию бесконечно простирающейся в обе стороны.
Предполагается, что в начальный момент, т. е. при / = 0,
вдоль линии задано распределение напряжения и тока:
(7.6)
Пользуясь уравнениями (7.2) и (7.1), легко найти	и
| о . Из (7.2) следует
Поскольку	= ср' (х), то
ох |/ = о
(7.7)
Аналогично
(7.8)
20. Линия без потерь. Если сопротивление провода
очень мало и он хорошо изолирован, то приближенно можно
положить
A? —G —0.
Уравнение (7.4) обращается при этом в обычное уравне¬
ние колебаний струны:
Как мы уже знаем из § 2, общее решение этого уравне¬
ния имеет вид
и (х, /) = ф (х —	(х “I- at}
и представляет результат наложения двух волн, распро¬
страняющихся вправо и влево со скоростью а =		.
Произведенные измерения величин А и С для воздушных
линий показали, что скорость распространения волн в этих
линиях практически совпадает со скоростью света в воздухе.
Это явилось в свое время убедительным доказательством
электромагнитной природы света.

104
УРАВНЕНИЯ КОЛЕБАНИЯ
[ГЛ Г
Начальные условия для функции и(х, f), согласно (7.6)
и (7.7), таковы (напомним, что 0 = 0):
"Ь=о = /(*)•	-Й-|/=о = —
Воспользовавшись общей формулой Даламбера (см. стр. 35),
сразу получим выражение для напряжения:
x+at
()=/<* + »0 + №—0	f
x-at
Вычисляя интеграл и учитывая, что аС =
запишем
С
Vlc
и(х, =	+
ср (х — at) — ср (х at)
2
(7.10)
Для функции Z(x, /), как мы уже отмечали, уравнение (7.9)
сохраняет свой вид; начальными условиями будут
Опять-таки по формуле Даламбера получим
9(* + аО + ?(* — лО | i/ZT/(-у — ДО —/U + дО.
2	у L	2
(7.Н)
Формулы (7.10) и (7.11) и дают решение поставленной задачи.
Как легко заметить, в любой точке линии отношение напря¬
жения к току для прямой волны равно	, а для обрат¬
ной—	• Величина	называется волновым со¬
противлением линии.
Возникновение волн в линии очень часто бывает связано
с атмосферными разрядами. Если в линии на некотором ее
протяжении внезапно возникает индуцированный заряд, то
вдоль линии начинают распространяться волны напряжения
и тока с одинаковой скоростью. Так как начальный ток
равен нулю, то <р(х) = 0. Функция / (х) будет отлична от
§ п
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
105
нуля на некотором участке, именно на том, где возник инду¬
цированный заряд. Процесс графического построения таких
волн был подробно рассмотрен в § 2.
21. Линия без искажения. Линией без искажения назы¬
вается линия, параметры которой связаны соотношением
RC = LO.	(7.12)
Покажем, что в такой линии волны напряжения и тока рас¬
пространяются таким же образом, как и в линии без потерь,
но с той разницей, что амплитуда волны при ее продвижении
по линии все время уменьшается, т. е. происходит зату¬
хание волн.
Рассмотрим снова уравнение (7.4)-и введем вспомогатель¬
ную неизвестную функцию v(x, t), связанную с и(х, t) соот¬
ношением
и(х> t) — e L v(x, /).	(7.13)
Дифференцируя ее дважды по х и /, получим:
д2и
дх2
--?■ t d2v ди
е	~д1 =
2R ди , д2о \
д2и
dt2
Подставим выражения для производных в (7.4), сократим
на е L и сгруппируем члены:
d2v . dv ( 2R . RC + LGX ,
dt I- L • LC ) +
j JR2 R RC+LG , RG\ 1	n
*V\L2 L LC	LC) LC dx2~^
В последнем уравнении коэффициенты при v и равны
нулю (первый — тождественно, а второй — в силу усло¬
вия (7.12)); поэтому для функции ^(х, t) мы получили
опять-таки уравнение колебаний струны
d2v 9 д2о
dt2 ~а 'дх2 9
1
где по-прежнему а =	.

106
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Считая, как и раньше, заданными начальное напряжение
и ток, составим начальные условия для функции v(x, t).
Из (7.13) и (7.6) следует, что
Ч-о = 4-0 = /(*)•
•п	dv R t ,	~т~ t ди	.
Далее, — е ■ u-\-eL	учитывая условия (7.7)
и (7.12), получим
L=i f (х) “ % f(х) “ i ч'(х)=“ i ч' <*>•
Сразу замечаем, что уравнение и начальные условия
для функции v(x, t) точно такие, какими они были
в п. 20 при отыскании напряжения в линии без потерь.
Следовательно, функция v (х, I) определится по формуле (7.10)
и функция и(х, t) будет равна
и(х, t) =
|7(* + e0 + /(* —<>0 _|_	<p(x—д/)—<p(x4-a/)j .:
Проделав аналогичные преобразования для уравнения (7.5)
(настоятельно рекомендуем читателю выполнить их самостоя¬
тельно), установим, что
l(x, t) =
'jjC*+ «0+ ?(*--| р/С~7(* —<*0—+ i •
Таким образом, в линии без искажений, так же как
и в линии без потерь, между напряжением и током в прямой
и обратной волнах сохраняется постоянное отноше¬
ние j/^(волновое сопротивление). Волны напряжения
и тока распространяются опять-таки, как в линии без потерь,
но с той существенной разницей, что благодаря множи-
_ R .
телю е
закону затухают. Ясно, что причиной затухания
является рассеяние энергии, вызванное выделением
в проводах, а также утечкой тока.
Если соотношение RC = LG не выполняется, то
между напряжением и током становится значительно
— t
L обе волны со временем по показательному
волн
тепла
связь
более

ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
107
§ Л
сложной. В этом случае волновое сопротивление уже не
является величиной постоянной, а существенно зависит
от характера возбуждения линии.
В курсах электротехники и связи подробно рассматри¬
вается вопрос б распространении по длинной линии перемен¬
ного синусоидального тока с частотой <о. Нарушение соот¬
ношения RC — LG приводит здесь к тому, что и скорость
распространения тока, и его затухание зависят от частоты ш.
Если по линии распространяется сложный импульс, являющийся
наложением простых синусоидальных токов, то каждый такой
ток будет иметь свою скорость распространения и свой коэффи¬
циент затухания. Это и приводит к искажению сигналов
при передаче по такой линии.
22. Линии конечной длины. Рассмотрим наиболее часто
встречающиеся краевые условия в линиях конечной длины /.
Если в начале линии (х = 0) включен источник питания
с постоянной электродвижущей силой f, то
И1х=0 = £-
Если к началу линии подключено синусоидальное напряже¬
ние, то
и |д.=0 = Е sin о)£.
Если на конце (х = /) линия коротко замкнута (при одно¬
проводной линии ее конец в этом случае заземлен), то
MLz=°;
если же конец линии изолирован, то
Из уравнения (7.1) отсюда следует, что -з—	=0.
0Х \х = 1
Если считать линию полубесконечной, то поставленные
краевые условия при х = 0 приводят к явлению отражения
волн напряжения и тока. С математической точки зрения эти
задачи аналогичны тем, какие были рассмотрены в § 2
при изучении полубесконечных струн.
Часто встречается случай, когда двухпроводная линия
на конце имеет приемник тока с сопротивлением и само¬
108
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
индукцией Lt (рис. 29). Тогда, рассуждая так же, как
при выводе уравнения (7.1), получим
“Ia-=z==/?izIx=z + li
Рекомендуем читателю написать краевое условие, если прием¬
ник тока содержит еще и конденсатор.
ul&=o
L
Рис. 29.
Разумеется, можно рассматривать любую комбинацию
условий при х = 0 и х = /.
Перейдем к рассмотрению конкретных примеров.
Пример 1. Пусть линия длины /, свободная от искаже¬
ний (/?C = £G), заряжена до потенциала Е (по отношению
к земле). Один конец линии (х — 1) изолирован, а другой
(х = 0) в начальный момент заземляется. Найдем распределе¬
ние потенциала вдоль линии.
Если потенциал обозначить через и(х> f), то в результате
введения новой функции (см. (7.13)) v(x, f) = eL и(х, t)
уравнение (7.4), согласно результатам п. 21, обращается
а «	d2v 9 d2v	1
в уравнение колебаний струны 	— а2	, где а =	,
dt2	дх2	^LC
что
ди I
1/ = 0
Так как zz|?=0
a i |/=0 = 0, то согласно (7.7) найдем,
Перейдем к составлению начальных условий для функции
v(x, /). Первое остается без изменения: г/|/=0 —Так как
R т
dt L е
* u-\-eL
ди
~dt
то
dv !	R р G
Ot\^o~ L С

§ Л
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
109
Краевые условия таковы:	==0,	=0. Для функ-
ции v эти условия имеют тот же вид:
L
v
= 0,
ду
дх
Окончательно
уравнения
задача формулируется так. Найти решение
д2у	9 д2у
St? = a д?
dv I
L-o
с начальными условиями
4.0 = *’
и краевыми условиями
dv I
= 0.
= 0
Заметим, что на первый взгляд условия w|/=0 = /7 и ц|^=о==О
противоречат друг другу, так как из первого следует, что и (0,0) = £,
а из второго и (0, 0) = 0. Дело в том, что при заземлении потен¬
циал на конце х = 0 исчезает не мгновенно, а за некоторый малый
промежуток времени, в течение которого и происходит непрерыв¬
ное убывание потенциала. Пренебрегая этим, мы и приходим
к нашим условиям.
Уравнение, к которому свелась задача, мы уже решали
в § 5, рассматривая продольные колебания стержня. (Реко¬
мендуем читателю самостоятельно восстановить это решение.)
Согласно (5.14) решение ищется в виде ряда по собственным
функциям
v(x> t) =
= v С05 g-+o.“' +4,sl„
Коэффициенты ak и bk отыскиваются по
где /(x) = v|/-0 = £,1 F(x)==^-| ° = 0.
i
2Е f .	(2k + 1) itx .
ak— i J sin 21 dx~ л(2*+1)’
0
формулам (5.15),
Имеем
4Е
»,=0.

по
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Переходя к функции и (х, /), окончательно получим
лЕ	cos
u{x,f) = — e L 2 —
л=о
(2Л -|- 1) nat (2£ + 1)
21 21
2k+ \
Пример 2. Пусть у линии длины /, для которой соблю¬
дается условие RC = LG, оба конца изолированы. Найдем
распределение потенциала вдоль линии, если в начальный
момент потенциал распределен по линейному закону, т. е.
«|/_0 = Лх.
началь-
условия
обычно,
О, X1 (Z) = 0. В отличие от предыдущих
Рассуждая так же, как и в примере 1, получим для функ-
,	.. y-i	..	d2v 9d2v
ции v(xt t) — eL и(х, t) уравнение	,
ные условия с/|/е=0 = Дх, |	=0 и краевые
dv I	А dv I	А „
= 0 и -V—	=0. Если положить, как
|Xss0	дх |Жя/
г/(х, t) = X (х)Т (/), то для отыскания собственных функт
ций X (х) придем к уравнению Xй -|-^2Х — 0 с краевыми
условиями Хг (0)	‘	' *
случаев Хо = О является собственным числом. Действи¬
тельно, при этом общее решение X = Сгх-\-С2 удовлетво¬
ряет обоим краевым условиям при Cj = O. Мы положим
JCO=1; функция Го(/) найдется из уравнения 7о=О, т. е.
То = а0+#(/- Если Х=£0, то X = C1coskx + ^2SinXx.
Краевые условия приводят к уравнениям
ХС2 = О и —\СХ sin U — 0.
Собственные числа суть корни уравнения sinXZ = 0, откуда
. Собственные функции Xk (х) = cos - (здесь к
может равняться нулю). Ортогональность собственных функ¬
ций доказана на стр. 85; впрочем, ее легко установить
и непосредственным интегрированием. Функцию v(x, f) за¬
пишем в виде ряда
оо
v (х, t) = а0 +	(ak cos a\kt + bk sin a\kt) cos ,
* = i
где член	отвечает собственному числу Х0 = 0.

§ Л
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
111
Рекомендуем читателю дальнейшие выкладки проделать
самостоятельно и получить следующий ответ:
и(х, t) =
_R_
= Ale L
2
I
I
Любопытно отметить, что если бы в этом примере началь¬
ное распределение потенциала было постоянным: u\tssQ = E,
t
то мы получили бы, что т>(х, t) = E и н(х, t) = Ee L .
Физически картина в этом случае ясна: в любой момент вре¬
мени все точки линии имеют одинаковый потенциал, который
уменьшается вследствие тока утечки.
Пример 3. Задача о включении линии. Пусть
линия длины / без потерь (R = G — 0) подключается одним
концом (х = 0) к источнику переменного тока, электро¬
движущая сила которого равна Zssino)/. Найдем напряжение
zz(x, t) линии при условии, что на другом конце (х = 1) она
накоротко замкнута и в момент включения напряжение и ток
в линии равны нулю.
Функция н(х, О должна удовлетворять уравнению
д2и	 2
дР"
при начальных условиях
и краевых условиях
a|Xe0 = Esino>O
Краевые условия последнего типа нам раньше не встречались;
они называются неоднородными условиями.
Метод Фурье здесь непосредственно неприменим, поскольку
сумма частных решений, каждое из которых удовлетворяет
краевым условиям, уже не удовлетворяет краевому условию
при х = 0. Поэтому будем отыскивать решение нашей задачи
в виде суммы двух функций
д(х, t) = v(x> 0 + w(x*

112	УРАВНЕНИЯ КОЛЕБАНИЙ	ГГЛ Г
каждая из которых является решением уравнения колебаний.
Первую функцию v(x, t) выберем так, чтобы она удовле¬
творяла только краевым условиям
|д,=0 — Е sin v L=z — °-
Для этого положим
v (х,-1) = X (х) sin «)Л
где X (х)— неизвестная пока функция. Дифференцируя функ¬
цию v(xt t) и подставляя в уравнение колебаний, придем
(после, сокращения на sin ш/) к обыкновенному дифферен¬
циальному уравнению для функции X (х):
Г(х) + ^-/(х) = 0
при условиях Х(0) = Е, Х(1) = 0.
Произвольные постоянные в общем решении
X (х) = Cj cos — + С2 sin —
определятся из системы
С! — Е, С, cos —	£9sin ~ = О»
откуда Сг — Е, C2= — Ectg-^-' Отметим, что при этом
— Ф &7г, т. е. -—у—. Последнее условие означает, как мы
CL	I
сейчас увидим, что частота внешнего напряжения не совпа¬
дает ни с одной из частот собственных колебаний (т. е. нет
резонанса).
Следовательно, функция *у(х, /) найдена:
7	74 I Г? ШХ „ ,	(О/	.	(0Х\ .	,
v(x, t) = \E cos	Еctg — sin -— sin &t.
CL	CL	CL J
Последнее выражение легко преобразовать к более простому
виду:
£sin
tj(x, t) —		sino)/.
sin —
а

§ 7]
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
ИЗ
^Если бы линия была подключена к источнику с постоянным
напряжением н|х=0 = £’, то, как легко проверить, v(x, t)=s
_ Е^х) .)
Перейдем теперь к отысканию функции w(x, t). Она
также удовлетворяет уравнению колебаний, но уже с одно¬
родными (нулевыми) краевыми условиями
(Ясно, что при этом u = v-\-w удовлетворяет требуемым
краевым условиям.)
Начальные же условия для функции w(x, t) уже будут
иные. Так как
и
dv I , dw I

|/=з0 dt |/=0
то, находя xf|/=0
dv
"~di
l/=o
из выражения для функции v(x, f),
получим:
w|,=0 = °.
dw I
£co sin
(O (Z x)
a
Как мы видим, для отыскания функции w(x, t) мы пришли
к задаче, подробно разобранной в § 3. По формуле (3.13)
оо
,	/	knat . ,	. knat\ . knx
w(x, Z) = 2^ l^cos~7	r^sin-y-l sin—j—.
k = i
Так как w |/=0 = 0, то все ak — Q. Коэффициенты bk находим
по формуле (3.17):
kitx
T
Заменяя
sin
ш (Z — x)
a
sin
8 И. Г. Араманович, В. И. Левин

114
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
и интегрируя, получим
А 	 2£<оя
Как уже отмечалось выше, знаменатель ни при каком
значении k не обращается в нуль. Числа как раз пред¬
ставляют частоты собственных колебаний.
Беря сумму функций v(x, t) и w(x, t), окончательно
получаем
/•sin
и(х, t) =	—	sin ut
sin —
а
Отметим, что задача о включении линии без искажения
решается точно так же, но приводит к значительно более
громоздким выкладкам, даже в случае подключения постоян¬
ной электродвижущей силы.
§ 8. Уравнение колебаний мембраны
23. Вывод уравнения колебаний мембраны. В преды¬
дущих параграфах рассматривались задачи, приводящие
к одномерному волновому уравнению
д2и 	л2 д2и
~<№—а ’
Сейчас мы перейдем к изучению двумерного волнового
уравнения, т. е. уравнения вида
Покажем, что к этому уравнению сводится задача о сво¬
бодных колебаниях однородной мембраны. Говоря
о мембране, мы подразумеваем упругую свободно изгибаю¬
щуюся натянутую пленку. Пусть в состоянии покоя мембрана
занимает некоторую область D в плоскости хОу, а затем,
будучи каким-то образом выведена из этого состояния, начи¬
нает колебаться так, что все ее точки движутся перпенди¬
кулярно плоскости хОу (поперечные колебания мембраны).
§ 81
УРАВНЕНИЕ КОЛЕБАНИЙ МЕМБРАНЫ
115
Отклонения точек мембраны от плоскости хОу будем обо¬
значать через и. Величина и зависит от координат точки
(х, у) мембраны и от времени t. Функция и(х, у, t) и
является искомой. При фиксированных х и у эта функция
дает закон колебания точки (х, у) мембраны; при этом
ди д2и
частные производные и определяют соответственно
скорость и ускорение движущейся точки. Если зафикси¬
ровать t9 то поверхность и — и(х, у, /) представляет форму
колеблющейся мембраны в момент времени t\ с изменением t
эта форма, очевидно, будет изменяться. Как известно
(см. «Кр. к.», п. 100), нормаль N к рассматриваемой поверх-
( ди	ди л }
пости имеет проекции |	1|; знаки проек¬
ций выбраны так, чтобы нормаль образовывала острый угол
с осью Oz. Направляющие косинусы нормали находятся
по формулам:
4
“У
, cos р =
cos а =
1
+“у+1
cos 7 = - ,

И и*+иу+1
Ких+иу+1
Мы будем изучать малые колебания мембраны, т. е. счи-
тать угол 7
малым, что
отклонения нормали от оси Oz настолько
cos 7^1.
Из формулы для cos 7 следует, что при этом мы пренебре¬
гаем квадратами частных производных и'х и я':
(8.2)
можно также принять, что и
Условия (8.2) совершенно аналогичны условию (1.5),
введенному при изучении малых колебаний струны. Приняв
условия (8.2), получим:
cos а
ди
~~^х 9
COS р =
ди
cos 7 = 1.	(8.3)
8*

116
УРАВНЕНИЯ КОЛЕБАНИИ
|ГЛ Г
Следовательно, вектор N является единичным вектором:
| N | = У"и* + иу ~Ь 1 = И"cos2 а + cos2 Р + cos2 Т = 1 •
Вычислим еще площадь поверхности мембраны в произ¬
вольный момент времени t. Она выражается интегралом
(см. «Кр. к.», п. 128)	1 + и* 4- «'2 dx dy.
D
В силу условий (8.2) заключаем, что изменением площади
поверхности мембраны в процессе колебания можно прене-
бречь. Это, разумеется, от¬
носится как ко всей мембране,
так и к любой ее части.
Перейдем теперь от гео¬
метрических предположений
к механическим. Если выре*
зать какой-нибудь участок мем¬
браны, то действие отброшен¬
Рис. 30.
ной ее части следует заменить,
силами, распределенными вдоль контура L выделенного
участка. Поскольку мембрана свободно изгибается, то эти
силы будут действовать в касательных плоскостях к мембране
по направлению нормалей к контуру L (рис. 30). Будем
считать, что мембрана находится под действием рав¬
номерного натяжения.
Это значит, что величина си¬
лы, приложенной к любому
элементу ds линии разреза,
равна Т dst т. е. пропор¬
циональна длине элемента
ds. Площадь вырезанной
части мембраны во все вре¬
мя колебаний считается не¬
изменной, и поэтому вели¬
чину Т также можно считать
постоянной.
Прежде всего найдем
равнодействующую сил на¬
тяжения. приложенных к контуру L. Выберем направление
обхода этого контура, как на рис. 31. и обозначим через ds
вектор, направленный по касательной к контуру и по модулю

§
УРАВНЕНИЕ КОЛЕБАНИЙ МЕМБРАНЫ
117
равный дифференциалу длины дуги ds. (Направление каса¬
тельной считается совпадающим с выбранным направлением
на контуре.) Если х, у. и — координаты точек контура,
то (см. «Кр. к.», п. 131)
ds — dxi 4- dyj 4* duk.
Поскольку точки контура лежат на поверхности мембраны,
аппликата и определяется из уравнения и — и(х, у, t)
.	. ди ,	• ди ,
dy.
TO
при фиксированном t. Поэтому du = dx 4- -gy
Вектор n, вдоль которого направлена сила натяжения,
перпендикулярен вектору ds и нормали N (N — нормаль
к поверхности мембраны). Следовательно, он имеет напра¬
вление векторного произведения векторов ds X N; из рис. 31
видно, что вектор п направлен как раз в сторону отбро¬
шенной части мембраны. Вычисляя
получим
векторное произведение,
i
dx
ди
дх
j
du
~~dy
k
du
1
Так как | N | — 1, то | n | — ds • 1 • sin 90° = ds. Это зна¬
чит, что сила натяжения, действующая на элемент ds,
равна Tn; направление ее совпадает с направлением вектора п,
а величина равна Т [ п | = Т ds. Проекция этой силы на
ось Ои равна
7’(прОвп) = т(-^-^ + -^4.
Чтобы найти проекцию равнодействующей всех сил натя¬
жения, надо полученное выражение проинтегрировать по кон-
туру L, т. е.
вычислить интеграл
L
Подынтегральное выражение зависит только от х и у,
поэтому криволинейный интеграл по контуру L можно за¬
менить интегралом по контуру L' (//—^проекция L на
118
УРАВНЕНИЯ КОЛЕБАНИИ
(ГЛ. Г
плоскость хОу). Преобразуя последний интеграл по формуле
Грина (см. «Кр. к.», п. 118), получим
L'	Д
(направление обхода* контура L' положительно, как это и
требуется в формуле Грина).
Воспользовавшись условиями малости частных производных
их и иу1 легко проверить, что проекции равнодействующей сил
натяжения на оси Ох и Оу равны нулю. Действительно,
7’(ПРохП)=7’(^+1Г</“)-
Но
ди , ди ди ,	, ( ди\2 ,	_
^au=w<^dx+Mdyx0’
a J* Т dy, очевидно, равен нулю, как интеграл по замкнутому кон-
L
туру от полного дифференциала. Аналогично доказывается и вторая
часть утверждения.
Чтобы вывести дифференциальное уравнение колебаний
мембраны, выделим бесконечно малый участок do области D,
окружающий точку (х, у). В любой момент времени масса
части мембраны, проектирующейся в этот участок, равна pda,
где р — поверхностная плотность, считающаяся постоянной
(мембрана предполагается однородной). Ускорение точек
выбранного элементарного участка равно	При свобод¬
ных колебаниях мембраны единственной действующей силой
будет проекция на ось Ои сил натяжения, определяемая
по формуле (8.4). Применяя к двойному интегралу, взятому
по области da, теорему о среднем, запишем выражение для
этой проекции в виде	Рассматривая выде¬
ленный участок как материальную точку и применяя закон
Ньютона, составим уравнение

§ 8]	УРАВНЕНИЕ КОЛЕБАНИЙ МЕМБРАНЫ	119
т
Сокращая на da и вводя обозначение — = л2, окончательно
получим
— „гр2" I д2“\
dt2	\ дх2 ' ду2 J ’
Поскольку выражение в скобках есть двумерный оператор
Лапласа Ди, запишем полученное уравнение в виде
(8.5)
Отметим, что имеется много задач, приводящих к трехмер¬
ному волновому уравнению
где Ди — трехмерный оператор Лапласа.
К этому уравнению сводятся задачи колебания газа, находя¬
щегося в некотором объеме, ‘ задачи теории распространения зву¬
ковых волн (акустические волны) и ряд других. Решение трехмер¬
ных задач еще более сложно, чем двумерных, и мы их касаться
не будем, отсылая читателя к более подробным курсам.
24. Начальные и краевые условия. Сформулируем
начальные и краевые условия задачи о колебаниях мембраны.
Если в состоянии покоя мембрана занимала в плоскости хОу
область D, ограниченную контуром Г, то, чтобы мембрана
начала колебаться, нужно ее точкам придать либо начальные
отклонения, либо начальные скорости, либо и то и другое.
Это значит, что заданы функции
U |/=0 = f(x< У)’
-S- /=o = F(X’ У)>
(8.6)
определенные в области D.
Будем считать, что край
мембраны закреплен.
Тогда.
и
|г = 0,
(8.7)
где символ и|г дает значения функции и(х, у, t) в точках
контура Г в любой момент времени /.
Трудность решения двумерного уравнения колебаний суще¬
ственно зависит от геометрической формы мембраны. Как мы
увидим дальше, даже для сравнительно простых случаев

120
УРАВНЕНИЯ КОЛЕБАНИЙ
[Г.П Г
прямоугольной и круглой мембран способы решения будут
различны. В случае же мембран другого вида уже требуются
специальные приемы, которые мы в настоящем курсе изу¬
чать не будем.
§ 9. Колебания прямоугольной мембраны
25. Собственные функции. Пусть мембрана в состоянии
пэкоя имеет форму прямоугольника, ограниченного прямыми
х = 0, х = 1, у = 0 и у = т
1У
т
0
1	Е
(рис. 32). Согласно резуль¬
татам § 8 задача о колеба¬
ниях мембраны сводится к
решению уравнения
с начальными условиями
5 «1/=о=/(•«>
Рис. 32.
ди I
М=о
-=F(x, у)
(9.2)
и краевыми условиями, заданными на границе прямоугольника,
“1х=0 = °> “L=i = °- а|у=о = О. «|у=т = 0.	(9.3)
Поставленную задачу будем [ешать методом Фурье.
Ищем решения уравнения (9.1), удовлетворяющие краевым
условиям (9.3), в виде произведения трех функций, каждая
из которых зависит только от одного аргумента:
и(х, у, t) = X (x)Y(y)T(t).
(9-4)
Из первого условия (9.3) следует, что X (0) К (у) T(t) = 0.
Так как нас интересуют решения, не тождественно равные
нулю, то X (0) = 0. Аналогично составим и остальные усло¬
вия, налагаемые на функции X (х) и Y (у). Выписав их все
вместе, получим:
Аг(0) = 0,	Аг(/) = 0,	Г(0) = 0,	Г(/?г) = О. (9.5)
Дифференцируем дважды функцию (9.4) по каждому из аргу¬
ментов:
д2и
дх2
= X"YTt
д2и
dt2
= XYT"

§
КОЛЕБАНИЯ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ
121
(как и раньше, аргументы у функций для сокращения записи
опущены).
Подставляя выражения для производных в уравнение (9.1)
и разделяя переменные, придадим ему вид
Т" __ X" Y”
а2Т ~ X ' Y *
Левая часть равенства не зависит от переменных х и у,
а правая часть — от переменной t. Поэтому оно может соблю¬
даться только при условии, что ни левая, ни правая части
не зависят ни от одной из переменных, т. е.
Т" X” Y"
—г- = -V- + -17- — const.
„	X"
Далее, так как отношение	зависит только от х,
Y"	X" . Y”	л
а -у	только от у, то сумма	может быть
постоянной лишь при условии, что каждое из этих слагаемых
есть в свою очередь величина постоянная, т. е.
X"
X
X2,
Обе последние постоянные выбраны отрицательными, так
как в противном случае функции X (х) и Y (у) не могли бы
удовлетворять краевым условиям (9.5). Доказательство этого
было приведено в § 3 (стр. 58).
В результате для отыскания функций X (х), F(y) и T(t)
получены уравнения:
X” (х) + \2Х (х) = О,	X (0) = X (/) = 0,	(9.6)
У" (У) + и2Г (у) = 0,	У (0) = У (т) = 0,	(9.7)
Т" (О + а2 (X2 + pi2) Т (t) = 0.	(9.8)
Решения уравнений (9.6) и (9.7) имеют вид
X (х) = Сг cos Хх + С2 sin Хх,
У (у) = Dx cos рх 4- sin р.х.
Краевые условия Х(0) = X (/) = 0 приводят к соотношениям
Cj = O и Х/ = А?к, где k — целое число. Только при соблю¬
дении последнего требования уравнение (9.6) имеет ненулевое
решение. Аналогично из условий У (0) = У (гп) = 0 следует»
122
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. Г
что D} = 0 и |х/п = птс (п— целое число). Собственные
числа \k и определяются формулами
4 = -^’	=	(9-9)
где k и п — любые целые положительные числа. Каждой
паре собственных чисел соответствуют собственные функции
Xft(x) = sin-^,.	^B(y) = sin-^-.	(9.10)
Из (9.10) ясно, что если брать числа k и п отрицательными,
то новых собственных функций не получится. (Напомним,
что, умножая любую из собственных функций на произволь¬
ную постоянную, мы будем снова получать решение урав¬
нения (9.6) или (9.7) с нулевыми краевыми условиями.)
Перейдем к уравнению (9.8). Для каждой пары собствен-
kn пп
них чисел -у- и оно примет вид
Т" (/) +	(V- + -g) т (0 = 0.
Решение этого уравнения обозначим функцией Tk п (t)
с двумя индексами; произвольные постоянные, входящие в его
общее решение, придется также обозначить буквами с двумя
индексами: ak,n и bkifl. Имеем
тк, п (0 = Oft, „ cos <0ft( nt + bk> n sin nt, (9.11)
/"^2
где =	+	— собственные частоты ко¬
лебаний мембраны.
Составив произведение функций (9.10) и (9.11), образуем
функции uk,n(x, у, t), удовлетворяющие уравнению (9.1)
и краевым условиям (9.3). Каждой паре положительных
чисел k и п Соответствует функция
«*,»(*• У- =
— (ak, П cos + bk, П sin	«О sin Хйх sin |*„y. (9.12)
Прежде чем переходить ко второй части метода Фурье —
отысканию решения, удовлетворяющего начальным усло¬
виям,— выясним свойства функций (9.12).

§ 9]
КОЛЕБАНИЯ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ
123
26.	Стоячие волны прямоугольной мембраны. Функции
ял>л(х, у, t) описывают собственные колебания мем¬
браны. Каждая из них представляет стоячую волну для
прямоугольной мембраны. Запишем формулу (9.12) в виде
«»,„(*•	^ = /7fc,nsin(U)*,^ + c?ft.n)sinXHsinM'
где
^,. = У«Ь+Ч,.- 4?.,.= »—■
п
Ясно видно, что каждая точка (х, у) мембраны совершает
простое гармоническое колебание с частотой п и ампли-
тудой Ffti„sinXftxsin|*„y.
Все точки проходят положение равновесия в одни и те же
моменты времени, определяемые равенствами	п = гк*
где г принимает значения 0, 1, 2, 3, ... Точно так же одно¬
временно точки достигают максимального отклонения (в ту
или другую сторону). Для большей наглядности рассмотрим
сначала самое простое колебание, соответствующее случаю
k = п — 1:
«1,1 у, t) = Flt! sin (U)b it + <plr 1) sin ~ sin .
Его
частота T = na
является наименьшей
паУ2 _ тгу 2 ,/■ Т
I ~ I V р
собственной частотой и характеризует основной тон
мембраны. Особенно просто выражение для частоты основ¬
ного тона в случае квадратной пластинки (т — /). Здесь <оь т =
, где Т—натяжение, а р—плотность.
При колебании мембраны контур ее остается неподвижным.
Так как внутри прямоугольника 0 < х < / и 0 < у < /п,
,	. кх . яу
то функции sin —у— и sin -положительны и все точки
мембраны одновременно находятся то по одну сторону
плоскости хОу, то по другую (в зависимости от знака
sin((Dlt xt + i)).
Наибольшую амплитуду колебаний будет иметь точка,
для которой sin-y- = 1 и sin-— — 1, т. е. точка с коор¬
124
УРАВНЕНИЯ КОЛЕБАНИЙ
ГГЛ. Т
динатами » -yj—центр мембраны. Так же как и для струны,
такие точки называются пучностями. Линии, точки кото¬
рых не колеблются, называются узловыми линиями
(для рассматриваемого простейшего случая узловые линии
совпадают с контуром
мембраны). На рис. 33
изображена мембрана в
тот момент, когда все
ее точки достигают наи¬
большего отклонения
вверх. Затем все от¬
клонения уменьшаются,
становятся равными ну¬
лю, после чего мембра¬
на начинает прогибаться
вниз. Так же просто про¬
анализировать колебания мембраны, описываемые функцией
'gjt X	7* V
«2,1 (х, у, t) = F2> i sin (ш2> / + ?2( j) sin -у- sin .
Узловые линии определятся из уравнений sin
= 0
и
/
sin -у- = 0. Помимо точек контура, это будет отрезок прямой
= При 0 < х < у функция sin-^^- положительна,
а при -ту < х < I — отрицательна; функция же .sin везде
положительна. Поэтому левая и правая половины мембраны
будуъпрогибаться в разные стороны (рис. 34). Соответственно

§ 9]
КОЛЕБАНИЯ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ
125
будет две пучности — точки пересечения прямой у = —-
I	31 /п
с прямыми х =-^ и х = -£-. (При этих значениях х и
Рекомендуем читателю так же подробно рассмотреть коле¬
бания, соответствующие функциям и1>2 и и2 2 (рис. 35 и 36).
«г
Рис. 36.
Другие стоячие волны имеют более сложный вид. При
колебаниях
иь,п(х- У- 0 = /7ft,nsin(a>fti„/+ n)sin-^sin-^,
помимо линий контура, будет k—1 узловая линия, парал-
I	21	(k —1)1
лельная оси Оу: х = -£, x —	х = -—, и
.	т	2т
п—1 линия, параллельная оси Ох: у = — 9 у = —, .. .
126
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ Г
...» у = ——(при этих значениях х и у собственные
функции обращаются в нуль). Эти линии разобьют мембрану
на nk прямоугольников, причем в двух соседних (т. е. имеющих
общую сторону) отклонения будут направлены в разные сто¬
роны. Центр каждого такого прямоугольника будет являться
пучностью.
27.	Вторая часть метода Фурье. Двойные ряды Фурье.
Вернемся теперь к задаче отыскания решения, удовлетворяю¬
щего начальным условиям (9.2). Как обычно, будем искать
его в виде ряда, составленного из частных решений (9.12).
Каждое частное решение зависит от двух индексов: k и
поэтому нам придется образовать двойную сумму
и(х, у, /) =
со оо
= X X (а*>» cos п sin sin sin •(9-13)
А=1л=1
Заставляя индексы суммирования k и п пробегать все
положительные числа независимо друг от друга, мы тем самым
учтем все частные решения вида (9.12). Подставляя значение
2 = 0 в функцию м(х, у, t) и в производную получим:
оо оо
Ч=о = Х Xc*-'>sin ^rsin =	У)’ (9-14)
Л=1 л=1
. knX .
Sin—j- sin
пку
m
F(x, у).	(9.15)
Формулы (9.14) и (9.15) представляют разложения функ¬
ций двух переменных в двойные ряды Фурье. С подобным
разложением мы сталкиваемся впервые и поэтому рассмотрим
его подробнее. Возьмем систему функций sin sin
и покажем, что в области D	0<^у<^/п) она
ортогональна. Это значит, что двойной интеграл, взятый
по области D от произведения двух различных функций

127
§ 91
системы, равен нулю. Действительно,
I т
Г I* •	k'KX	..	fliTty .	k2nx .	п2пу j ,
I	/ sin	—4—	sin	——sin sin dx dy =
J J	I	tn	I	m
о 0
КОЛЕБАНИЯ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ
Поскольку система функций sin —j— ортогональна в интер¬
вале [О,/], а система sin ~~ — в интервале [0, т] (см.
стр. 59), то написанное выражение равно нулю, если соблю¬
дается хотя бы одно из неравенств kr^=k2 и пг^п2. Если же
k2 — kr = k и п2 — пг = п, то
I tn
Я. 9 knX . 9 MW
sin2 —j— sin2	dx dy =
о о
I	т
/* . 9 knx , Г . 9 пку . 1т
= I s\v?—j—dx I sin2 dy = -j-.
о	о
Исходя из установленных соотношений, легко цайти все
коэффициенты разложений (9.14) и (9.15). Формулы для их
отыскания совершенно аналогичны обычным формулам Фурье:
I т
an,n = T^fJ f (х, y)sin-^ sin-^dxdy, (9.16)
o b
I m
bk’n	f F^X' y)^^-sin^-dxdy. (9.17)
0 0
Мы не останавливаемся на тех условиях, которые надо
наложить на функции /(х, у) и F(x, у), чтобы они могли
быть разложены в двойные ряды Фурье. В практически
встречающихся задачах они всегда выполняются.
Подставив выражения для коэффициентов akt п и bkttl
в формулу (9.13), завершим решение задачи.
Пример. Найти колебания квадратной мембраны
(/ = /п=1), всем точкам которой приданы одинаковые

128
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. Т
начальные скорости v0. (Разумеется, это не касается непод¬
вижно закрепленных точек контура мембраны !).)
Начальные условия (9.2) имеют вид
/(X, у) = 0, F(x, y) — v0.
Следовательно, в решении (9.13) все коэффициенты aktn = 0.
Коэффициенты Ьк п найдем по формуле (9.17), полагая в ней
F(x, у) = <и0,	/==;п=1, (oktn = тш
1 1
Ьь п =	— / / sin &тсх sinnTry dxdy.
k,n KaVk2 + n2J J	?	?
r 1 о 0
Двойной интеграл разбивается на произведение двух обыкно¬
венных интегралов, и мы получим
Ъ ,
	4у0

ъ3акп Yk2 + п2
cos kitx |J cos птсу J* =
r3akti k2-\- n2
(1 	C0S&tc)(1 —coshtc).
Если хотя бы одно из чисел k или п четно, то bktn — 0,
так как тогда по крайней мере одна из скобок равна нулю.
Поэтому нужно считать, что £ = 2г+1 и /z = 2s—J— 1—<■ не¬
четные числа. При этом
h	=	16vp

2Г+1,25+1 кза (2r	(2s 4- 1) /(2г + 1)2 4- (2s 4- I)2
и решение примет вид
ОО ОО .
и(Х, у, 0 = 2 2*2г+1,25+1Х
г = 0 6 = 0
х sin тс a yr(2r+ I)2—|—(2 s —|— I)2/ sin (2r—J— 1) tcjc sin (2s —J— 1) тсу.
Так как знаменатели у коэффициентов #2r+i, 2s+i быстро
возрастают, то ряд хорошо сходится и для вычисления зна¬
чений функции и(х, у, I) придется брать очень небольшое
число его членов.
28.	Стоячие волны с одинаковой частотой. В заключение
кратко остановимся на одной важной особенности колебаний мем¬
браны. При колебаниях струны каждой собственной частоте соот¬
*) При этом функция F (х, у) оказывается разрывной. Объясне¬
ние этого факта аналогично приведенному на стр. 42.

§ 91
КОЛЕБАНИЯ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ
129
ветствовала одна стоячая волна, вполне определяющая форму
струны. При колебаниях мембраны одной и той же собственной
частоте может соответствовать несколько различных стоя¬
чих волн. Проще всего это проследить па квадратной мем¬
бране. Примем для простоты, что стороны квадрата равны те
(т = I = те) и что начальные скорости точек мембраны равны
нулю: F (х, у) = 0. Тогда из (9.17) следует, что все bk, п = 0, и общее
выражение для решения и(х, у, t) примет вид (см. формулу (9.13))
, оо оо
и(х, у, 0=2 2 аь>п cos sin sln пУ* (9.18)
fe=l n=l
В разложении (9.18) содержится только одна стоячая волна,
соответствующая наименьшей частоте соь , = аУ~2. Это будет волна
1 cos аУ 2/ sin х sin у. Следующие частоты, w2>, = аУ 22 + I2
и (оЬ2==лК12 + 22, обе равны аУ5. Поэтому частоте аУ~5 соот¬
ветствуют в рассматриваемом колебании две волны:
а2,1 cos аУ51 sin 2х sin у и 2 cos а У51 sin х sin 2у.
Общее колебание квадратной пластинки с частотой аУЪ пред¬
ставляется суммой стоячих волн
2	cos а У51 sin х sin у (а2, i cos х + а}> 2 cos у).
Узловые линии такого колебания, отличные от сторон мембраны,
будут иметь уравнение
а2,1 cos х + aXt 2 cos у = 0.
Если а2>! = 0, то узловой линией служит отрезок прямой у
те
(рис. 37), а если а1>2 = 0, то отрезок прямой х = ~2 (Рис- 38).
В случае, когда а2) j =—aXt 2, из уравнения следует, что cos у = cos х,
т. е. что у = х; узловой линией будет диагональ квадрата (рис. 39).
Если же a2t 1 = а1>2, то cosy = — cos х= cos (те — х) и узловой
линией будет другая диагональ: у = те — х (проведена пунктиром
на рис. 39). При произвольных a2tX и аь2 узловая линия может
9 И. Г. Араманович, В. И. Левин

130
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
иметь очень сложную форму; отметим только, что она всегда про-
/	л	те
ходит через центр квадрата 1при х =2"» У левая часть УРав-
нения обращается в нуль^.
При рассмотрении более высоких частот могут встретиться
самые разные случаи. Так, частоте w2j2 == У"8 соответствует только
одна стоячая волна; частоте арТб—две волны: и3>j и иьз, а частоте
а|<5б — три: ub7, u5,5 и u7>1. Ясно, что, чем больше различных
волн соответствует данной частоте, тем сложнее картина распре¬
деления узловых линий.
Существует любопытный прием, при помощи которого можно
практически получать узловые линии. Пластинку посыпают тонким
слоем песка и заставляют колебаться, проводя по краю смычком.
Тогда мембрана совершает колебания с одной из собственных
частот и песок, скатываясь с пучностей, будет скапливаться вдоль
узловых линий. Образующиеся при этом фигуры называются фигу¬
рами Хладни !).
§ 10. Уравнение и функции Бесселя
29. Уравнение Бесселя. Для того чтобы перейти к реше-;
нию задачи о колебаниях круглой мембраны, мы предвари¬
тельно должны познакомиться с функциями Бесселя. Функ¬
ции Бесселя являются решениями линейного дифференциального
уравнения второго порядка с переменными коэффициентами
у"+-7/+(1-$)у = °-	(10Л)
Это уравнение называется уравнением Бесселя. И само
уравнение, и его решения встречаются не только в задаче
о колебаниях круглой мембраны, но и в очень большом
числе других задач.
Параметр k, входящий в уравнение (10.1), может, вообще
говоря, принимать любые положительные значения. Решения
уравнения при заданном k называются бесселевыми функ¬
циями порядка k (иногда их называют цилиндрическими
функциями). Мы рассмотрим детально лишь наиболее про¬
стые случаи, когда Л = 0 и Л=1, так как в дальнейшем
изложении нам встретятся только бесселевы функции нуле¬
вого и первого порядков. Для общего изучения бесселе-
По имени немецкого физика Э. Хладни (1756—1827).
§ W]	УРАВНЕНИЕ И ФУНКЦИИ БЕССЕЛЯ	131
вых функций мы отсылаем читателя к специальным руко¬
водствам.
Уравнение Бесселя нулевого порядка имеет вид
= (10.2)
При х = 0 коэффициент при первой производной терпит
разрыв; как говорят, точка х = 0 для уравнения. (10.2)
является особой. В этом случае мы не можем заранее сказать,
существуют ли решения уравнения, принимающие определен¬
ные значения при х = 0; теорема существования и единствен¬
ности решения (см. введение) здесь неприменима.
Уравнение (10.2) не принадлежит ни к одному из типов
уравнений второго порядка, допускающих решение простыми
приемами; поэтому будем его решать при помощи степенных
рядов. ' Предположим, что решение можно представить
в виде ряда
№^о+^1х + с2х24“гзх34“ •••	(Ю.З)
Продифференцируем этот ряд дважды:
у' =^1_|_2с2^+Зб?3х24- ... 4-пслх/1~1+ ...,
у" —2е2+3 • 2c3x-f-4 • 3qx2 + ... +^(п—1)спхп~2-\-
и подставим в дифференциальное уравнение (10.2):
(2с2 + 3 • 2с3х + 4 • Зс4х2+ ... -\-п(п— 1)^дхя"2+ ...)-}-
+2с2х +Зе3х24-	+ пелхл“1 + •..) +
+ ••• ..-.) = 0.
Приравнивая нулю коэффициенты при всех степенях х, мы
и получим систему уравнений для отыскания неопределенных
коэффициентов с0,	...
Начнем с члена, содержащего коэффициент при нем
^ = 0.	(10.4)
Условие (10.4) показывает, что решение в виде ряда (10.3)
может существовать только тогда, когда с1 = у'];г=о = О.
Это и означает, что произвольно задавать значение первой
производной у' при х = 0 нельзя.
9*

132
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
Выпишем теперь коэффициенты при нечетных степенях х:
х, х3 и т. д.:
3	• 2сд—Зс34- Су =2 О,
5 ’ 4^5	5с5	£3 = 0,
Поскольку q = 0, то и все последующие коэффициенты
с нечетными индексами равны нулю:
С3 = е5 — ••• =С2Л + 1= ••• =0.	(10.5)
Перейдем к отысканию коэффициентов с четными
индексами. Последовательно выбирая слагаемые, содержащие
свободный член, х2, х4 и т. д., составим систему уравнений
2с24- 2г2+ г0 = 0,
4	• 5с4 4~ 4с4 4~ г2 = 0,
Можно написать и общую рекуррентную формулу, связы¬
вающую любые два коэффициента, индексы которых отли¬
чаются друг от друга на две единицы. Собирая члены,
содержащие хп, получим
(п4“ 2) (п4- 1) сл4.24- (п 4- 2) сп+24“ = 0,
или
(п + 2)2сп+2+сп = 0.	(10.6)
Легко проверить, что все написанные выше уравнения
представляют частные случаи равенства (10.6).
Оставляя коэффициент г0 произвольным, последовательно
выразим через него все остальные четные коэффициенты:
г 		 Со	е 		 		Со
L2	22 ’	^4	42	2242 ’	—	62 —	224262
и вообще
С2п = (-1)" 2Ф-. (2п)2 = (-1)" -22^ •	(10-7)

5 101
УРАВНЕНИЕ И ФУНКЦИИ БЕССЕЛЯ
133
Таким образом, найдено решение уравнения Бесселя при А=0:
у=с0(1
X2
22
х4
24(2!)2
хб
26(3!)2
сю
=со2(-1)я
/1=0
х2л
22л(п!)2
х2п
22я (я!)2
...) =
(10.8)
(0! считается равным 1).
Покажем, что ряд (10.8) сходится при всех значениях х.
Применяя признак Даламбера, составим отношение абсолют¬
ных величин двух последовательных членов ряда:
х2(л+1)
х2л
X2
22(л+1’[(л+1)!]2 '
' 22л(п!)2
22(п+1)2
Это отношение при любом значении х стремится к нулю,
что и доказывает абсолютную сходимость ряда.
Постоянная с0 = у |	0 может быть выбрана произвольно.
Если ее положить равной единице, то получающаяся функция
сю
^oW = X(-1)'l2^!7	(10-9)
п=0
и называется функцией Бесселя первого рода порядка 0.
Она является решением уравнения (10.2) при начальных
условиях
У|х=о=1>	/1ж=о = °-
Как известно, общее решение линейного дифференциаль¬
ного уравнения второго порядка представляет линейную ком¬
бинацию двух его частных решений и у2 при условии,
что их отношение — не является постоянной величиной.
У2
Одним из таких решений является функция Бесселя J0(x).
Второе частное решение уже не будет функцией, непрерыв¬
ной при х = 0; аналитическое выражение этого решения
значительно более сложное, и мы его не приводим. Отметим
только, что это второе решение называют функцией Бесселя
второго рода (или еще функцией Неймана} и обычно
обозначают через N0(x)- Отличительная его черта состоит
в том, что \Nq (х) | -> оо при х_>0.

134
УРАВНЕНИЯ КОЛЕБАНИИ
ГГЛ. Г
Для функции Бесселя JQ(x) составлены подробные
таблицы1). График функции J0(x) приведен на рис. 40;
он похож на график затухающих колебаний. Эта функция
четная, и поэтому на рисунке изображена только половина
графика, соответствующая положительным значениям х. Функ¬
ция Jq(x) имеет бесчисленное множество корней pz, кото¬
рые в дальнейшем исследо¬
вании будут играть важную
роль. Приведем значения
первых из них с двумя
знаками после запятой:
[i1 = 2,40; рь2 = 5,52;
|л3 = 8,65; р4= 11,79 ит. д.
Отметим, что для больших номеров п разность \ьп— рл-1 тс.
30. Условие ортогональности функций Бесселя нуле¬
вого порядка. Рассмотрим теперь уравнение несколько более
общего вида
У" + |/-Н2У = 0	(10.10)
и покажем, что оно сводится к уравнению Бесселя нулевого
порядка. Введем для этого вместо х новую независимую пере¬
менную £ = Ах. Тогда
, dy dy dt . dy
У ~ dx~ dt dx~^ dt ’
После подстановки производных
множитель К2 сократится, и мы
с новой независимой переменной
ч d2y . 1 dy
~d^^ 6 ~d£'
</(/) dt _ I2 d?v
У	dt dx	dt2 ’
у' и у" в уравнение (10.10)
придем к уравнению (10.2)
+-у = о.
Его частным решением является функция Бесселя Ja(S); сле¬
довательно, решением уравнения (10.10) будет функция J0(Xx).
Пусть теперь X последовательно принимает значения
ji2, ... положительных корней функции Бесселя J0(x).
Последовательность функций	*А)(Р2Х)» • • •» ^о(Рлх)» • • •
9 См., например, Люстерник Л. А., АкушскийИ. Я.,
Диткин В. А., Таблицы бесселевых функций, Гостехиздат, 1949
или Янке Е., Эм де Ф., Таблицы функций с формулами и кри¬
выми, Физматгиз, 1959.

§ Ю]
УРАВНЕНИЕ И ФУНКЦИИ БЕССЕЛЯ
135
будет удовлетворять на интервале [0, 1] следующим усло¬
виям ортогональности*.
1
J= если
0	,	(Ю.И)
f xJ20 (у.кх) dx = ± J*
6
Эти условия ортогональности отличаются от обычных только
тем, что под интегралом содержится еще множитель х
(в таких случаях часто говорят об «ортогональности
с весом»).
Докажем условия (10.11). Функции Jo(px) и J0(qx) удовлетво¬
ряют уравнению (10.10) при X, соответственно равных р и q\
»+2^fcl + ?voM = o.
Умножим первое из равенств на х/0 (£•*)> второе на х/0 (Рх) и
вычтем одно из другого:
* ['. м	+
+ (Рг — ?2) xJ0 (рх) Ja (qx) = Л
Полученному равенству можно придать вид
+ (Р2 — 92) xJ9 (рх) Jo (qx) = 0
(рекомендуем читателю проверить это самостоятельно).
Интегрируя последнее равенство по х в пределах от 0 до 1»
получим
1
+ (Рг — 92) У xJo (рх) Jo (qx) dx = 0. (10.12)
б

136
УРАВНЕНИЯ КОЛЕБАНИИ
[ГЛ. I
До сих пор мы не делали никаких предположений относительно
чисел р и q. Пусть теперь р = pft, a q = рл, где и рп — два
различных положительных корня уравнения Jo(х) = 0. Тогда
в результате подстановки пределов выражение в фигурных скобках
обратится в нуль, так как JQ(р^) = JQ (рл) = 0; поскольку
окончательно заключаем, что
1
f xJ^kx)Ja(^nx)dx = Q.
о
Чтобы доказать второе из соотношений (10.11), положим в равен¬
стве (10.12) Р = Р'£ и перепишем его в виде
1 ,
f , , sr /	Jo(<?VoOfe)
J xJo(V-kx)Ja^dx =	23~	•	(1013)
n	0
I..	dJQ(px) dJn(px) rt,	.	\ „
^Мы учли, что —■■ =	P = (Px) P-) Будем считать q
переменной величиной и заставим ее стремиться к р^. Числитель
и знаменатель в правой части равенства (10.13) стремятся при этом
к нулю (JQ (р^) = 0), поэтому для отыскания предела мы восполь¬
зуемся правилом Лопиталя
J0 (V) К Oft) v-k J'o Oft) J’o (^k) V-k 1 ,'a , 4
lim 		x	=			= — J Q (pfe),
q2-V2k	2fx6	2	1 k>
Левая часть равенства (10.13) при q — p. обращается в интересую-
1 л
щий нас интеграл J xJ$ (pftx) dxt так что и второе соотноше-
о
ние (10.11) доказано.
31. Функции Бесселя первого порядка. Найдем еще
выражение для функции Бесселя первого порядка, т. е. Jx (х).
Подставляя ряд (10.3) и его производные в уравнение
У" + ^У' + (1-2г)у = 0.
(10.14)

§ 10]
УРАВНЕНИЕ И ФУНКЦИИ БЕССЕЛЯ
137
получим
оо	оо
2 П{п—	ficnx«-l-{-
п=2	п=1
оо	оо
+ S спхЯ— 4? 2 спх"=0.
п=0	л=0
Объединяя первую, вторую и четвертую суммы вместе и за¬
мечая, что слагаемые, содержащие (во второй и четвертой
суммах), уничтожаются, перепишем последнее равенство в виде
(п2—1) спхп~2—	спхп — 0.
п=2	л=0
Отсюда ясно, что со = О.
Рекуррентная формула, при помощи которой коэффи¬
циент сп выражается через сл_2, выглядит так:
(и2—1)с„Ч-ся_2 = 0	(д>2).
Поскольку со = О, то отсюда последовательно получаем, что
все коэффициенты с четными индексами равны нулю:
Коэффициенты с нечетными индексами можно выразить
через ср
Cj
сз = — (32 — 1) ’ С5 = (32 _ 1) (52 _!) • • • •
• • • • с2л+1 = (— О" (З2 —1)(52 —1)[(2п4-1)2 —1] •
Знаменателю выражения для с2л+1 удобнее придать несколько
иной вид:
(32— 1)(52— 1)... [(2я-{~1)2 — 11 =
= (2 • 4) (4 • 6) ... 2л(2л + 2) =
= (2-4 ... 2я)(4-6 ... 2(л4~ 1)) = 22ял1(я-|-1)1.

138
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Подставляя коэффициенты сп в разложение (10.3) и полагая
сх = у, получим функцию Бесселя порядка 1 (первого рода)
00.15)
л=0	'
График функции Jx(x) показан, на рис. 41; эта функция
нечетная. Функция ^(х), так же как и функция J0(x),
имеет бесчисленное множество корней vz. Приведем значения
первых из них с двумя знаками после запятой:
v1 = 3,83, v2 = 7,02,	v3= 10,17,	v4= 13,32.
Как и на стр. 134, отметим, что ул —	Для больших п.
Относительно таблиц значений функции JT(x) смотри сноску
на стр. 134. Отметим часто встречающуюся формулу
j'(x) = -Ji(x),	(10.16)
которая получается почленным дифференцированием ряда (10.9)
для J0(x). Эта формула позволяет при помощи таблиц для (х)
вычислять значения /о(|хл),
входящие в формулу (10.11).
Согласно формуле (10.16)
функция J0(x) имеет экстре¬
мумы именно в тех точках,
в которых функция /Х(х) об¬
ращается в нуль, т. е. в
точках Из рис. 42 вид¬
но, что корни функций Бес¬
селя нулевого и первого порядков перемежаются, т. е. меж¬
ду двумя любыми последовательными корнями функции J0(x)
лежит обязательно один корень функции Jx(x), и наоборот.

§ II]
КОЛЕБАНИЯ КРУГЛОЙ МЕМБРАНЫ
139
Рассуждая аналогично, можно найти выражения для функций
Бесселя любого целого порядка k:
«,2/1+Z?
A (•*) = У (-1)"	,, ,	• (Ю-ID
2zn+ltnl (« + *)!
Из общей формулы (10.17) при k = 0 и k = 1 получаются функ-
ции Бесселя Jo (■*) и Jx (х). Во всех случаях мы каждый раз на¬
ходим одно частное решение уравнения; формула для второго част¬
ного решения имеет более сложный вид. Соответствующая функция
I Nk (х) | также стремится к оо при х->0. Выражения для бессе¬
левых функций не целого порядка мы не приводим.
§ И. Колебания круглой мембраны
32. Круглая мембрана. В § 9 методом Фурье была ре¬
шена задача о колебаниях прямоугольной мембраны.
Сейчас мы покажем, как, пользуясь результатами предыду¬
щего параграфа, можно тем же методом решить задачу о ко-
лебаниях круглой мембраны.
Пусть мембрана в состоянии покоя занимает круг радиуса R
с центром в начале координат. Введем полярные коорди¬
наты г и ср. Уравнение границы круга будет при этом r = R.
Отклонение точек мембраны и является теперь функцией
полярных координат г и ср и времени t:
и = и(г, ср, t).
Воспользуемся результатами п. 3 введения, где было по?
казано, что выражение для оператора Лапласа Ди в полярных
координатах имеет вид
А д2и .	1 ди .	1 д2и
дг2 ' г дг ' г2 д<р2
д2и
Тогда уравнение колебаний мембраны = а2 &и пере¬
пишется следующим образом:
д2и	 2 / д2и .	1 ди f 1 д2и \
~д^~~а \дг* ' 7~дг~г*	}’
(И.1)
Краевое условие в полярных координатах записывается осо¬
бенно просто:
«|г=л = 0.
(11-2)

140
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
Начальные условия имеют вид
«|/=о==/(г. ф),	^|<=o = F(r. ?).
(И.З)
Мы будем рассматривать только осесимметричные ко¬
лебания мембраны, т. е. предполагать, что начальные функ¬
ции f(r, ср) и F(r, ср) не зависят от угла ср. Это значит,
что величины начальных отклонений и скоростей зависят только
от расстояния точки мембраны до ее центра. Иначе говоря,
все точки окружности, концентрической с границей круга,
в начальный момент имеют одни и те же скорости и отклоне¬
ния. Тогда ясно, что и в любой момент времени величина
отклонения не будет зависеть от полярного угла ср и будет
являться функцией только г и £, т. с. u = u(r, t). Это зна¬
чит, что при любом фиксированном t форма колеблющейся
мембраны будет поверхностью вращения.
При этом упрощающем предположении задача сводится
к уравнению
(11.4)
I 1
dt2	\ дг2 г дг)
с начальными условиями
H.« = F(r)
и краевым условием
и 1г=/? = 0-
(И.5)
(11.6)
Как обычно в методе Фурье, полагаем
W(r, /)==6Л(Г)Т(О
(11.7)
и отыскиваем частные решения, удовлетворяющие краевому
условию (11.6). Подставляя (11.7) в краевое условие, найдем,
что U(R) = 0.
Дифференцируя функцию (11.7), подставляя в уравне¬
ние (11.4) и разделяя переменные, получим
Т" (t)
a*T(t)
U40 + --U' (г)
W)
(И.8)
= — R
Постоянная выбрана в виде —X2 из тех же соображений,
что и раньше. Доказательство того, что функция U (г) при
ином выборе постоянной не может удовлетворять условию

§ 111
КОЛЕБАНИЯ КРУГЛОЙ МЕМБРАНЫ
141
= мы опускаем. Впрочем, физически ясно, что про¬
цесс носит колебательный характер, а уравнение для T(t)
только тогда имеет решения в виде тригонометрических функ¬
ций, когда в правой части (11.8) стоит отрицательная вели¬
чина. Равенства (11.8) приводятся к двум уравнениям:
Г'(^) + Х2а2Т(О = 0,	(11.9)
t/"(r)+y t/'(r)4_^2^(r) = o.	(11.10)
Уравнение (11.10) совпадает с уравнением (10.10), изученным
в § 10. Одним из его частных решений является функ¬
ция J0(Xr). Второе частное решение — функцию 7V0— мы
брать не будем потому, что в центре мембраны (при г = 0)
оно обращается в бесконечность. В то же время ясно, что
прогиб мембраны всегда есть величина конечная.
Поскольку произвольные постоянные войдут в общее ре¬
шение уравнения (11.9), то решение уравнения (11.10) просто
берем в виде
t7(r) = J0(Xr).
Подстановка краевого условия (11.6) приводит к уравнению,
определяющему собственные числа задачи:
Jo(X/?) = O.
Таким образом, собственными числами задачи являются ве¬
личины
(И.11)
где — корни функции Бесселя JQ(x). После того как
собственные числа найдены, решаем уравнение (11.9). Получим
Tk (t) = ak cos \kat + bk sin\kat.
Собственные функции uk(r, t) таковы:
uk (r, t) = (ak cos \kat + bk sin XAa/) Jo (Xftr). (11.12)
Как видим, в выражение для собственных функций, в от¬
личие от всех предыдущих задач, входят не только тригоно¬
метрические функции, но и функции Бесселя.

142	УРАВНЕНИЯ КОЛЕБАНИИ	[ГЛ. I
Составляем теперь сумму собственных функций
оо
u(r,	(afecosXftaf+ ^sinXftaO4)(4r) (И-13)
А=1
и подбираем коэффициенты так, чтобы выполнялись началь¬
ные условия
« 1<=о = 2 а*7° (^А ■£) =
Л = 1
Л= 1
(Мы заменили собственные числа Хй их значениями.) Введем
новую переменную, положив — х (это равносильно тому,
что мы выбрали масштаб, при котором радиус круга R равен
единице; х, конечно, не является декартовой координатой
точек мембраны). Тогда написанные ряды примут вид
fiakJ0M = f(Rx),	(11.14)
k = 1
оо
^^kJ0M = F(Rx).	(11.15)
Л = 1
Последние же равенства означают, что мы раскладываем
функции f(Rx) и F (Rx) в ряды по функциям /0(рлх), кото¬
рые, как мы показали в § 10, удовлетворяют в интер¬
вале [0, 1] почти обычным условиям ортогональности. Пред¬
полагая, что разложения (11.14) и (11.15) имеют место и
допускают почленное интегрирование, находим все неопреде¬
ленные коэффициенты, воспользовавшись условиями ортого¬
нальности (10.11). Для этого умножим обе части каждого
разложения на xJQ(pnx) и интегрируем в пределах от 0 до 1;
тогда слева останется только по одному слагаемому:
1
1 '2 (*
Jq ([\z) = I xJq (pnx)f (Rx) dx,
6
1
bn 4 Jo2 (b,) = f XJO (Ипх) F (Rx) dx.
0

§ и]
КОЛЕБАНИЯ КРУГЛОЙ МЕМБРАНЫ
143
^2	о
Воспользовавшись равенством JQ (pQ = Л (pQ (см. формулу
(10.16)), окончательно получим (индекс п мы заменили на А):
1
йл = -лТ-Г / xJ0(^kx)f(Rx)dx,
Ji(M ё
1
bk =		 Г xJQ (^х) F (Ях) dx.
Подставляя коэффициенты ak и bk в ряд (11.13), мы и
завершаем решение задачи.
33.	Стоячие волны круглой мембраны. Как и во всех
предыдущих случаях, функции uk(r, t), определенные фор*
мулой (11.12), представляют стоячие волны. Пучности и
узлы располагаются здесь по концентрическим окружностям.
Узловые окружности получаются при тех значениях г, для
которых
•/о(М=л(^) = о.
Кроме очевидного значения г = R (края мембраны), это будут
значения, определяемые из соотношений
?кг	^kr	^kr
-Д- = Р-2	-^-=^-1’
т. е.
r _	» г - R	г -
гх — — к, г2 — — К, ..rk_x -
__	^kr
Ясно, что нет смысла приравнивать
Бесселя J0(x) с индексами большими, чем k,
получилось бы больше R. Если, скажем,
корням функции
так как тогда г
^kr
ТО
г = -Ш- R> R.
Следовательно, стоячая волна uk(r, t) имеет k узловых
окружностей (считая и край мембраны). Между ними распо¬
лагаются окружности пучностей. Они соответствуют тем зна¬
чениям г, при которых функция	достигает максимума

144
УРАВНЕНИЯ КОЛЕБАНИЙ
[ГЛ. I
или минимума. Это будут корни уравнения	= или,
если воспользоваться связью между Jo(x) и Л(х), корни
уравнения	= 0. В частности, пучность будет всегда
при г = 0.
Решение . конкретных примеров на колебания круглых
мембран вызывает обычно значительные затруднения, так как
в формулы для коэффициентов ak и bk входят функции Бес¬
селя под знаком интеграла. Эти интегралы крайне редко вы¬
ражаются через известные функции, и приходится прибегать
к численному интегрированию; последнее, впрочем, весьма
облегчено наличием подробных таблиц бесселевых функций.

ГЛАВА II
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ
§ 12. Уравнение линейной теплопроводности
34.	Вывод уравнения линейной теплопроводности. Рас¬
смотрим металлический стержень, боковая поверхность кото¬
рого теплоизолирована. Теплоизолированность боковой
поверхности стержня означает, что через поверхность не про¬
исходит теплообмена с окружающей средой х). Если этот
стержень в начальном состоянии неравномерно нагрет, то бла¬
годаря теплопроводности в нем будет происходить передача
тепла от более нагретых частей к менее нагретым. В про¬
стейшем случае, когда притока тепла извне нет и концы
стержня тоже теплоизолированы, температура точек стержня
с течением времени будет, изменяясь, выравниваться и в ко¬
нечном итоге станет постоянной во всем стержне. Если возмо¬
жен теплообмен с окружающей средой через концы стержня
(торцевые сечения) или в некоторых участках стержня выде-
R-'-	-е—
О	х
Рис. 43.
ляется тепло, то распределение температуры будет соответ¬
ственно усложняться.
В задаче линейной теплопроводности стержень предполага¬
ется настолько тонким, что в каждый момент времени темпера¬
тура всех точек данного поперечного сечения стержня (рис. 43)
1) Задача о теплопроводности стержня при условии теплооб¬
мена с внешней средой через боковую поверхность будет рассмот¬
рена в п. 36.
10 И. Г. Араманович, В. И. Левин

146 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
будет одной и той же. Если принять ось стержня за ось
абсцисс, то температура и будет являться функцией
координаты х и времени t. При постоянном t функ¬
ция u(x, t) представляет зависимость температуры точек
стержня в данный момент времени от их расстояния до на-
du
чала координат; частная производная выражает при этом
скорость изменения температуры в направлении оси Ох.
Если зафиксировать абсциссу х, то u(x, t) выражает закон
изменения температуры в данном сечении стержня с течением
времени.
Вывод дифференциального уравнения теплопроводности
основан на следующих физических предпосылках:
1.	Количество тепла, которое необходимо сообщить одно¬
родному телу, чтобы повысить его температуру на Ди, равно
срУДи,	(12.1)
где V — объем тела, р — его плотность, с — удельная тепло¬
емкость.
2.	Количество тепла, протекающее через поперечное се¬
чение стержня за момент времени Д£ (тепловой поток),
пропорционально площади сечения, скорости изменения тем¬
пературы в направлении, перпендикулярном к сечению, и
промежутку времени ДЛ т. е. равно
— kS~M,	(12.2)
где S — площадь поперечного сечения, k — коэффициент
теплопроводности.
Знак минус в формуле (12.2) объясняется тем, что вели¬
чину теплового потока мы будем, считать положительной»
когда тепло проходит в сторону возрастания х. Если
> 0, то это значит, что с возрастанием х температура
повышается, а так как тепло переходит от более нагретых
участков к менее нагретым, то тепловой поток будет напра¬
влен в сторону уменьшения х, т. е. его величина будет
отрицательной. Мы будем считать коэффициент теплопро¬
водности постоянным; это предположение оправдывается,
если стержень однородный и температура меняется
в небольших пределах. Заметим еще, что способы экспери¬
УРАВНЕНИЕ ЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ
147
ментального определения коэффициентов теплопроводности
различных материалов весьма сложны и во многом опираются
на развиваемую дальше математическую теорию теплопро¬
водности.
Выделим участок стержня, ограниченный поперечными
сечениями с абсциссами х и х + Дх, и составим для него
уравнение теплового баланса. По формуле (12.2) количе¬
ство тепла, входящее через поперечное сечение с абсцис¬
сой х за промежуток времени Д/, равно —Если
отбросить бесконечно малые величины высших порядков,
то значение частной производной по х в точке х-\-кх бу¬
ди .	, (ди \ ди | д2и А z	тг
дет равно —=	(см. «Кр. к.»,
п. 91). Поэтому величина, теплового потока, выходящего
через сечение x-j-Дх, равна — kS	Взяв
разность величин входящего и выходящего тепловых пото¬
ков, мы получим количество тепла &Q, сообщенное выбран¬
ному участку стержня за время Д/:
А« = -kS £ и+kS (■£•+"=ss
С другой стороны, за этот же промежуток времени темпе¬
ратура изменилась на величину Д£ (опять-таки с точ¬
ностью до бесконечно малых высшего порядка). Поэтому
по формуле (12.1) сообщенное количество тепла равно
(объем V равен SДх).	'/	/
Приравнивая полученные выражения для Дф и сокращая
на общий множитель ЗДхД/, составим уравнение
dzz , д2 и	/1 о
<12-3)
Введя обозначение — = а2, окончательно получим основное
ср
уравнение теплопроводности для однородного стержня
без тепловых источников'.
ди 9 д2 и
~ а'
(12.4)
10*

148 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
Постоянную а=]/Г-~ называют коэффициентом темпе¬
ратуропроводности. Уравнение (12.4) является однород¬
ным и линейным.
Предположим теперь дополнительно, что в некоторых
участках стержня может возникать или поглощаться тепло.
Как говорят, внутри стержня имеются тепловые источники.
Выделение (или поглощение) тепла очень удобно характери¬
зовать с помощью плотности тепловых источников. Под
плотностью тепловых источников понимают функцию F (х, О
такую, что на малом участке стержня (х, х-|-Дх) за малый
промежуток времени (/, t-{-kt) выделяется количество тепла,
равное (с точностью до бесконечно малых высшего порядка)
F (х, t) kx kt.
(12.5)
(Если F (х, t) < 0, то тепло не выделяется, а поглощается.)
Например, при пропускании через стержень постоянного
электрического тока в нем будет выделяться тепло, причем
в этом случае F(x, t) = const = I2 R, где / — ток, a R —
сопротивление единицы длины стержня.
При составлении уравнения теплового баланса (12.3) надо
учесть тепло, возникающее в рассматриваемом участке стержня.
Для этого прибавим к правой части уравнения (12.3) вели¬
чину, определяемую формулой (12.5) и разделенную на S kxkt.
Получим:
Разделив обе части равенства на ср и введя обозначение
(12.6)
Уравнение (12.6), полученное в предположении, что внутри
стержня имеются тепловые источники, в отличие от уравне¬
ния (12.4) является неоднородным.
Разумеется, полученные уравнения теплопроводности вы¬
ведены при условии некоторой идеализации процесса.
35.	Начальное и краевые условия. Перейдем теперь к
начальному и краевым условиям. Начальное условие
для уравнения теплопроводности состоит в задании темпе¬
§ 12] УРАВНЕНИЕ ЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ	149
ратуры во всех точках стержня в некоторый момент, от ко¬
торого ведется отсчет времени; обычно полагают, что в на¬
чальный момент t =0; тогда начальное условие имеет вид
и(х, 0) = «|<=0 = /(х),	(12.7)
где /(х)— данная функция.
Краевые условия должны выполняться там, где стержень
может'иметь теплообмен с окружающей средой, т. е. на
торцевых сечениях стержня (напомним, что боковая поверх¬
ность тела по условию теплоизолирована). Пусть начало
стержня совпадает с началом координат (х = 0), а его ко¬
нец имеет абсциссу х = 1. Самый простой случай краевых
условий тот, когда концы стержня поддерживаются при
постоянной температуре. Это значит, что
И(О, f) = «lx,o	О2-8)
где uQ и ut—заданные числа.
Возможны, однако, и более общие краевые условия,
когда на торцевых сечениях стержня происходит теплообмен
с окружающей средой по закону Ньютона. Этот закон со¬
стоит в том, что поток тепла через единицу поверх¬
ности в единицу времени пропорционален разности
температур тела и окружающей среды, т. е. равен
h(u — и),	(12.9)
где и — температура конца стержня, и — температура окру¬
жающей среды и h — коэффициент пропорциональности, за¬
висящий от физических свойств стержня и среды. Коэффи¬
циент h называется коэффициентом теплообмена (или еще
коэффициентом внешней теплопроводности); мы будем считать
его для данного торцевого сечения стержня постоян¬
ным х). Условимся также, что h > 0, т. е. что поток тепла
считается положительным, когда тепло уходит из стержня
!) Как показывают точные эксперименты, коэффициент h зави¬
сит также от температуры. Мы эту зависимость учитывать не
будем. Отметим лишь, что в связи с этим обстоятельство:)! в
экспериментах по теплопроводности стараются по возможности
уменьшить теплообмен.

150 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
в окружающую среду {и > а), и отрицательным в противо¬
положном случае. Количество тепла, передаваемое со всего
торцевого сечения за момент ДЛ будет равно h(u— u)S&t.
По закону сохранения энергии количество уходящего
тепла должно быть в точности равно потоку тепла, прохо¬
дящего через рассматриваемое торцевое сечение в силу теп¬
лопроводности стержня.
Согласно формуле (12.2) тепловой поток, проходящий
через поперечное сечение стержня в направлении оси Ох,
равен —	На правом конце стержня направление
потока, идущего во внешнюю среду, совпадает с направле¬
нием оси Ох и поток равен — kS № I . На л е в о м
ох \х=1
конце эти направления противоположны и поэтому поток
равен kS	1	. Мы также будем считать, что внешние
Ох L=0
среды могут быть на концах стержня разными, так что могут
быть различными h и и; пусть на левом конце h = hQ и
u=uQ, а на правом h — ht, и = и1. Тогда краевые усло¬
вия на торцевых сечениях запишутся в виде
, ди I
дх 1х=1
= M“lx=z —“ib
(12.10)
где а0 и ut— заданные температуры внешней среды, которые
мы будем считать известными функциями времени, а в наи¬
более простОхМ случае — постоянными величинами.
Если какой-либо конец стержня теплоизолирован, то со¬
ответствующий коэффициент теплообмена равен нулю и крае¬
вое условие на этом конце примет вид
ди
~дх
= 0.
(12.11)
Условия (12.8) также можно рассматривать как частный слу¬
чай общих условий (12.10) при очень больших значениях

УРАВНЕНИЕ ЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ
151
§ 12]
коэффициентов теплообмена. Записав, например, первое усло¬
вие (12.10) в виде
k ди I 	 *	~
|л=0	и '*=о	йо
и перейдя к пределу при й0—>оо, получим первое из усло¬
вий (12.8). Разумеется, можно рассматривать любую комби¬
нацию краевых условий на разных концах стержня.
Подводя итоги сказанному в двух последних пунктах,
мы можем следующим образом сформулировать математи¬
ческую задачу теплопроводности для однородного стержня
с теплоизолированной боковой поверхностью без тепловых
источников.
Отыскивается температура и = и(х, f), удовлетворяющая
уравнению (12.4)
ди 	 2 д2 и
~dt~~a ~дх^'
начальному условию (12.7)
и краевым условиям (12.10)
*^L=o=M«L=o-«ob
(или их частным случаям (12.8) и (12.11)).
В теории дифференциальных уравнений с частными про¬
изводными доказывается, что эта задача всегда имеет един¬
ственное решение (при некоторых достаточно общих пред¬
положениях относительно заданных функций /(х), uQ(t) и
МО)-
36.	Теплопроводность в стержне при наличии теплообмена
через боковую поверхность. Сформулируем задачу теплопровод¬
ности в стержне при условии теплообмена с внешней средой через
боковую поверхность. Правда, здесь предположение постоянства
температуры по любому сечению в каждый момент времени яв¬
ляется физически менее оправданным, поскольку в этом случае
вблизи контура сечения температура должна меняться довольно

152
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
резко. В этой задаче дифференциальное уравнение имеет уже вид,
отличный от (12.4). Для вывода этого уравнения обозначим через
S площадь поперечного сечения стержня, через р — периметр по¬
перечного сечения и рассмотрим произвольный отрезок стержня
от сечения с абсциссой х до сечения с абсциссой x-J- Дх. Как было
установлено в п. 34, количество тепла, сообщенное выбранному
участку стержня за промежуток времени (/, t Д/) в результате про¬
хождения вдоль стержня теплового потока, равно	-2- Дх Д/. По
закону Ньютона количество тепла, поступающего в отрезок стержня
через боковую поверхность за этот же промежуток времени, равно
h [и(х, t) — и (х, t) ] р Дх Д/,
где р Дх — площадь боковой поверхности, h — коэффициент тепло¬
обмена и и (х, t) — температура внешней среды. Составляя уравне¬
ние теплового баланса, получим
Дх Д/ + h[u — и]р Дх At = c?S Ах	At,
где правая часть представляет тепло, благодаря которому темпера¬
тура точек стержня изменилась на . Разделив обе части ра¬
венства на cpS Дх At, приведем уравнение к виду
<=*2S+*2	<12Л2>
где а= 1/ — — коэффициент температуропроводности, а
V с?
д2 = 7^ * ^СЛИ h ~ О’ Т‘е’ б°ковая поверхность стержня теплоизоли¬
рована, то 62 = 0 и мы вновь получаем уравнение (12.4). Началь¬
ное и краевые условия для уравнения (12.12) формулируются так же,
как и для уравнения (12.4) (см. п. 35). Важно отметить, что в слу¬
чае постоянной температуры внешней среды, т. е. в практи¬
чески наиболее интересном случае, уравнение (12.12) с помощью
замены неизвестной функции может быть сведено к уравнению (12.4).
Действительно, пусть и — const. Можно считать, что и = 0, так
как иначе нам достаточно было бы начать отсчет температуры
от значения и, что равносильно введению новой функции
их = и — н. Легко проверить, что при такой замене уравнение (12.12)
приобретает вид
ди 9 д2и
~dt ~а "дх2" —
b2u.
(12.13)

8 13]
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
153
Полагая u = v(x, t), где v— новая искомая функция, най¬
дем, что
v+tT™ — .
dt ° е	di ’
d2u _	д2<и
дх2 ~ е	дх2
Подставляя в уравнение (12.13), получим
_ 62 е-ъч v + е-»ч dv=ai е-ьч
1	dt	дх2
b2e~bu v
или, после сокращения,
dv 9 d2v
~дГ “ а
(12.14)
Начальное условие для функции v (х, t) сохраняется, так как
v|/=o = “k=o-
Краевые условия изменятся и, например, для случая постоянства
температуры на концах стержня (см. (12.8)) примут вид
v 1х=о = «О > v\x=i =	•	(12.15)
Здесь правые части являются уже не постоянными величинами,
а известными функциями времени /. Метод решения таких задач
будет указан в п. 52.
§ 13. Теплопроводность в бесконечном стержне
37.	Метод Фурье для бесконечного стержня, рассмот¬
рим тонкий длинный теплопроводящий стержень, боковая
поверхность которого теплоизолирована. Согласно результа¬
там § 12 температура zz(x, /) точек этого стержня при отсут¬
ствии тепловых источников удовлетворяет уравнению
du 9 d2u
(13.1)
Если стержень очень длинный, то на процессы, протекающие
в его средней части, главное влияние оказывает начальное
распределение температуры; влияние температурных условий
на концах стержня в течение довольно длительного времени
почти не будет сказываться. В задачах такого типа стержень
считают бесконечным. Краевые условия при этом отпа¬
154 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
дают, и на искомую функцию u(xt t) накладывается только
начальное условие
в|,=0 = /(х),	(13.2)
где функция /(х) определена на всей числовой оси
(—оо < х < оо). Задача решения уравнения (13.1) при усло¬
вии (13.2) называется задачей с начальным условием или
задачей Коши.
Прежде чем решать уравнение (13.1) при начальном усло¬
вии (13.2), мы несколько упростим задачу, введя вместо вре¬
мени t новую переменную
т = а2/.	(13.3)
Тогда
ди	ди dt	 2 ди
dt dt dt а дх 9
и уравнение (13.1) примет вид
ди	 д2и
'dt~'dx29
(13.4)
не зависящий от физических свойств стержня. Так как при
/ = 0 и т = 0, то в качестве начального условия мы будем
иметь
Ч=о = /(х).	(13.5)
Чтобы решить эту задачу, применим метод разделения
переменных и суперпозиции частных решений Фурье.
Этот, метод состоит из двух частей. Сначала мы находим
частные решения уравнения (13.4), имеющие вид X(x)T(t)
произведения двух функций, каждая только от одной из не¬
зависимых переменных. Подставляя это произведение вместо и
в уравнение (13.4), получим:
или
Х(х) Г(т) = Х"(х)Т(т),
Г(т) _ X" (х)
T(t) — X (х) *
(13.6)
Обе части этого уравнения должны быть постоянными, по¬
скольку его левая часть не зависит от х, а правая — от т,
т. е. ни левая, ни правая части не могут зависеть ни от х,
ни от т. В этом рассуждении — ключ к методу разделения
переменных Фурье. Обозначим теперь постоянную, которой
5 13]
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
155
должны быть равны и левая и правая части равенства (13.6),
через с. Тогда уравнение (13.6) распадается на два уравнения:
Г(т)_	*"(•*)_
Т(г) ~С‘	Х(х) —
(13.7)
Первое из них имеет общее решение
л	Т(у) = Сес\
Поскольку ни в одном сечении стержня (т. е. ни при каком
фиксированном х) температура и — Х(х)Т(х) не может не¬
ограниченно возрастать по абсолютной величине при т—>оо
(т. е. при t—>оо), с должно быть отрицательно. Поло¬
жим с = — X2; тогда
Т(т) = Се~^.
Второе из уравнений (13.7) принимает вид
JV" (х)Х27С (х) = 0
и имеет общее решение
X (х) = A cos Хх + В sin Хх.
Таким образом, мы получили частное решение нашего урав¬
нения (13.4):
и = (AC cos Хх + ВС sin Хх)
или
и = (a cos Хх + р sin Хх) е~к\	(13.8)
где а = ДС и р = ВС. Здесь С, Д, В, а следовательно а
и р, — произвольные постоянные; X также обозначает произ¬
вольное число.
Функция (13.8) является при любом фиксированном X
решением уравнения (13.4), и мы можем, конечно, для каждого
значения X выбирать разные постоянные аир. Это означает,
что аир могут быть произвольными функциями от X:
а==а(Х), р = р(X), так что окончательно мы имеем семейство
частных решений уравнения (13.4):
ик(х, т; = [а(X)cosХхsinХх]	(13.9)

156 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
зависящее от параметра X, который может принимать все
значения от —оо до 4~оо. Тем самым первая часть метода
Фурье завершена.
Вторая часть метода Фурье — суперпозиция полученных
решений их(х, *0— состоит в следующем. Уравнение *(13.4)
линейное и однородное; оно имеет, как мы только
что установили, бесчисленное множество частных решений,
зависящих от непрерывно изменяющегося параметра X. Со¬
гласно п. 2 введения функция
и(х, т) = J их(х, x)d\ = J [a(X)cosXx4~P(X)sinXx]
— со	—оо
(13.10)
также является решением уравнения (13.4).
Нам остается теперь только подобрать неизвестные функ¬
ции а(Х) и Р(Х) так, чтобы решение (13.10) удовлетворяло
начальному условию (13.5), т. е. чтобы
н|т=0 = у [a(X)cosXx4~P(X)sinXx]rfX = /(x).	(13.11)
— оо
Последнее равенство означает, что функцию f (х) надо раз¬
ложить в интеграл Фурье (см. «Кр. к.», гл. XII, § 3).
Напомним, что разложение функции /(х) в интеграл
Фурье возможно, если функцию /(х) можно разложить
в ряд Фурье в любом конечном интервале и если инте-
оо
грал J* lf(x)fdx сходится, т. е., как говорят, функ-
— оо
ция /(х) абсолютно интегрируема на всей оси Ох.
Оба условия выполняются во всякой физической задаче
(функция /(х) — начальное распределение температуры).
оо
Второе условие, т. е. сходимость интеграла £ |/(х)|^х,
— оо
означает конечность тепловой энергии стержня (так как
тепловая энергия пропорциональна абсолютной температуре).

$ 13]
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
157
Разложение функции /(х) в интеграл Фурье имеет вид1)
ОО	оо
f(x) = -~ f dX f /(?)cosXG — X)dl.
—oo	—oo
Так как cos X (£ — x) = cos X$ cos Xx + sin X? sin Xx, то инте¬
грал Фурье можно переписать в виде
оо
оо
оо
□о
dX.
Сравнивая это разложение и формулу (13.11), заключаем, что
неизвестные пока функции а(Х) и Р(Х) должны определяться
по формулам:
оо
a(k)=^ f /($)cos^,
— ОО
оо
f /(OsinM^.
— оо
(13.12)
Отметим, что из второго условия, наложенного выше на функ¬
цию f (х), вытекает, что а (X) и р (X) ограничены:
оо	оо
— oo	—oo
!) Так как cosX(£— x)— четная функция относительно X, то
разложение можно написать и так:
оо	оо
/(х) = 1 У* л У*/G)cosX(? — x)di
О	—оо
(именно в таком виде оно записано в «Кр. к.»).

158 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ* II
Найдя таким образом функции а(Х) и 0(Х) по формулам
(13.12) и подставив их в решение (13.10), мы получим функцию
оо	оо
И(х, х) = ъft® {cos Хх cosX£4~
— оо	—оо
4-Sin Хх Sin Х£}	=
оо	оо
= i / dX f /©cosX(x —	(13.13)
—оо	— оо
которая одновременно удовлетворяет и уравнению (13.4) и
начальному условию (13.5). Эта функция (13.13) решает,
следовательно, поставленную в этом параграфе задачу
о теплопроводности в бесконечном стержне.
Докажем, что интеграл (13.10) действительно является реше¬
нием уравнения (13.4) для всех х и т > т0 > 0. Как было отмечено
выше, функции а (X) и 0 (X) ограничены: [а (А) | < К и | 0 (X) | < К
со
для всех X, где К =
этих предположениях
в
— оо
I и). (х, т) | = | а (X) cos Хх + ? (X) sin Хх | е Х2т < 2Ке
Далее,
-4^.	— [а (л) cos \х з (X) sin Хх] X2# Х2т
л при соблюдении тех же условий
I 1
|1хН
Совершенно аналогично получим, что
<2/<X2^-Z2t\
В правых частях неравенств, полученных для функции (х, т)
и ее производных, стоят функции, зависящие только от пара¬
метра X, причем интегралы от этих функций сходятся. Для
доказательства этого напомним предварительно, что
оо
J e~v =
— 00

£ 135
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
159
— со
У Л
2т0У Т, ’
2т0 .
—со
(этот интетрал— интеграл Пуассона — вычислен в «Кр. к.», п. 111).
.00
Интеграл ^_Х2т° dk вычисляется с помощью замены перемен-
— оо
ной. Полагая = Н находим, что
оо	оо

— ОО
Далее, интегрируя по частям, полагая к = и и ke~^dkt=dv, по¬
лучим
-OQ
так как первое слагаемое стремится к нулю при X -> ± оо.
оо
Таким образом, мы доказали, что как сам интеграл J* (х, т) dk,
— оо
так и интегралы от частных производных подынтегральной функции
сходятся правильно. Согласно п. 2 введения (см. мелкий шрифт
на стр. 20) в этом случае функция (13.10) действительно является
решением уравнения (13.4). Это справедливо для всех значений х
и для всех положительных значений т.
38.	Преобразование решения уравнения теплопровод¬
ности. Для того чтобы решение (13.13) можно было физи¬
чески истолковать, необходимо его преобразовать. Прежде
всего заметим, что если в правой части формулы (13.13)
изменить порядок интегрирования, то получится следующая
формула для и(х, т):
оо
и(х, t) = ^_ I/(У f «-XJtcosX(x —OdX (13.14)
со
—со
— оо
где внутренний интеграл по X в правой части уже не со¬
держит заданной функции f (£). Если мы произведем замену
0		 с
переменной Х = —— и введем обозначение ——- = ш, то
К т	/ т
будем иметь
ОО	ОО
/ ^-x**cosX(x— tydk = -l— I е-’2 cos aw da = —L-/ (ш).
«/	у t J	у t
— ОО	—оо

160 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. п
Интеграл
оо
/(а))= J* е~°2 cos go) da
— оо
может быть вычислен следующим специальным приемом.
Во-первых, мы замечаем, что /(0) есть интеграл Пуассона
(см. «Кр. к.», п. 111):
оо
7(0)= Je-‘2d0 = -|/T.
— ОО
Образуем далее (см. формулу (17) введения) производную
оо
/' (ф) = — J* oe“ff2stn coo da. Преобразуем /' (to), интегрируя.по
—оо
частям:
со
= ~ e“ff2 sin со |	—-у y\“ff2cosoo)do = — -^-/((о)
(так как внеинтегральный член обращается в нуль при
о—>4"Оо и о —> — оо). Решая получившееся дифференциаль¬
ное уравнение для функции / (о), получаем
со2
/(ш) = С^ 4 .
Пользуясь тем, что /(0) = ]/^, находим произвольную по¬
стоянную: С = У к.
Итак,
/ (со) = у к е 4 ,
х— 6
а так как о = —, то
К *
/? 1 (х~^2
J 0-Z2xcosX(x — $)dX =	/(о) = |/ -_е 4х .
—оо

§ 13]
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
161
Подставляя найденное
окончательно найдем, что
1
выражение в формулу
(13.14),
и(х, х)_—
2 у тет
J f&e~ * db
— oo
(13.15)
После того как решение (13.13) преобразовано к виду
(13.15), можно непосредственно проверить, что функция
и(х, т) удовлетворяет уравнению (13.4) и начальному усло¬
вию (13.5). Второе легче всего сделать, если вместо В ввести
новую переменную интегрирования:
х —5
о) =
£ = х — 2ю ]/" т, = — 2 У т du),
и записать интеграл (13.15) в таком виде, чтобы т уже не
стояло
знаменателе, т. е.
Тогда
ОО
u(x,-t) = -L- J* f(x — ZvVt'je-
"	— oo
0,2 da.
ОО
f	=	f е~ш2 d<i> = f (х),
—	— ОО
ОО
— ОО
г. e. условие (13.5) выполняется.
Чтобы проверить, удовлетворяет ли функция (13.15) урав¬
нению (13.4), заметим, что функция
2 j/tct
(13.16)
в
=	t)
является решением уравнения
тельно,
(13.4) при любом Действи-
И


дъ [	4т Y ят
И И. Г. Араманович, В. И. Левин

162 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. и
д^ d2fy
Следовательно, = -^~-, т. е. уравнение (13.4) удо¬
влетворяется. Поэтому функция и(х, т), полученная интегри¬
рованием функции ср^(х, т) по параметру £, также является
решением уравнения (13.4) (см. п. 2 введения).
Чтобы от функции и(х, т), являющейся решением урав¬
нения (13.4) с начальным условием (13.5), перейти к реше-
z	ди 9 д2и
нию и(х, t) исходного уравнения = а-^рг с начальным
условием и |/=0 = /(х), мы должны вспомнить, что т = а2/,
и тогда по формуле (13.15) получим
И(Х’ (13Л7)
39.	Фундаментальное решение уравнения теплопро¬
водности и его физический смысл. Перейдем теперь
к выяснению физического смысла полученного решения (13.17).
Как мы уже видели, функция ср^(х, т), определенная фор¬
мулой (13.16), является решением уравнения (13.4). Подста¬
вляя x — a2t, мы получим функцию
’ (13Л8)
являющуюся решением исходного уравнения (13.1). Функция
<р£(х, t) зависит от х и Р) и, кроме того, от произволь¬
ного параметра £. Она называется фундаментальным ре¬
шением уравнения теплопроводности и имеет важный
физический смысл, связанный с понятием теплового импульса.
Физическим тепловым импульсом мы будем называть
следующее начальное распределение температуры:
у/')—./"0’ если 1х~хо1<е’
Jsk J I g, если |х — х0|>е
(см. рис. 44), где w0—постоянная и е > 0. Такое начальное
распределение температуры возникает, если в стержень, тем-
!) При t = 0 функция (х, t) не определена. Исследование ее
поведения при £->0 будет проведено несколько позже.

Рис. 44,
§ 13} ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ	163
пература которого в каждой точке первоначально равна
нулю, в момент t = 0 на отрезке от xQ — е до х04-£ вне¬
запно введено некоторое количество тепла (например, если
к этому отрезку на мгновение поднесено высокотемпера¬
турное пламя, так что температура -этого отрезка в мо¬
мент ^ = 0 подскакивает до значения zz0). Это количе¬
ство тепла 60 пропорционально заштрихованной на
рис. 44 площади 2еи0, а
именно, если S — пло¬
щадь сечения стержня,
т. е. 2eS— объем отрез¬
ка стержня, 2eSp — его
масса, то 60=2eSpcw0,
где с — удельная тепло¬
емкость.
Практически темпера¬
тура, конечно, не может
представляться разрывной функцией /е(х), но график
температуры будет очень близок к графику /в(х) (он будет
иметь примерно вид пунктирной линии на рис. 44) и будет
тем меньше отличаться от графика /е(х), чем резче и кратко¬
временное будет подогрев. Тот факт, что на графике функ¬
ции /£(х) температура в точках х0— е и х04~е не опреде¬
лена, не имеет для нас никакого значения (если разрывную
функцию /е(х) представить интегралом Фурье, то его зна¬
чение в этих точках будет равно -у-, поэтому можно счи¬
тать, что и температура равна
При таком физическом тепловом импульсе в качестве на¬
чального распределения температуры решение (13.17) задачи
теплопроводности будет иметь вид
“<*•«= 2^=? ./ е_ “ А <13Л9)
г х0-е
По теореме о среднем интегрального исчисления
•Vе	(X-Ir
I e ш d^=2ee 4°2' ,
*o-»
11*

164 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. и
где £ — некоторая точка, лежащая внутри интервала интегри-
рования: х0 — е < ? < х0-|-е. Таким образом, решение (13.19)
может быть записано и так:
о ,	а '1	{Х~Ъ2
и (х, t) = — е 4д2/ = —	-==■ е 4a2t
2а У Tit	Spc 2а УтЛ
(так как 2еи0 = -^-). Предположим конкретно, что подве¬
денное количество тепла 60 = Sgc (чтобы исключить физи¬
ческие параметры стержня). Тогда мы получим решение
в случае физического теплового импульса в виде
1	Сг-О2
u(x,t) =—_^е 4a2t .	(13.20)
2аУ тЛ	4
От физического теплового импульса перейдем теперь
к точечному (идеальному) тепловому импульсу, устрем¬
ляя е к нулю. Так как в наших предположениях 2ея0=1,
то при е—>0 имеем н0 —>4"со- Кроме того, очевидно, что
так что решение (13.20) превратится теперь (для то¬
чечного теплового импульса) в функцию
1 (х~х<^ *
U(X’t)==2^ie' 4О2‘ =^(хЛ)’	(13'21>
т. е. в фундаментальное решение (13.18) при значении
параметра (• = х0.
Точечный тепловой импульс является, конечно, еще в боль¬
шей мере абстракцией, чем физический импульс на отрезке.
Но он также может быть приближенно реализован, если
пламя, о котором шла речь выше, будет очень узким.
Математически начальное распределение температуры при то¬
чечном импульсе представляется так называемой импульсной функ¬
цией Дирака S (х — х0), представляющей как бы предел физиче¬
ского импульса Д (х) при е —> 0. Ей приписываются следующие
свойства:
0, если х ■=£ х0,
4-оо, если х = л'о
(1)	В(х-х0) =

§ 131
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
165
(последнее объясняется тем, что и0->-|-со при е —> 0; это значит,
что температура в точке х0 становится равной со).
оо
(2) J*3(x — x0)dx=l,
— ОО .
так как в наших предположениях 2eu0 = 1 при любом е (в послед¬
нем интеграле нижний предел может быть заменен любым числом,
меньшим xQ, а верхний — любым числом, большим х0).
Итак, фундаментальное решение уХо (а, /) является решением
задачи теплопроводности в бесконечном стержне (с теплоизолиро¬
ванной боковой поверхностью) при начальном распределении тем¬
пературы f (х) = & (х —- А'о).
Рассмотрим теперь, как распространяется тепло в стержне
после точечного импульса. Для этого надо исследовать гра¬
фики фундаментального решения фХо(*, О	формулу
(13.21)] для разных зна¬
чений t > 0. Эти кривые	м
называются кривыми
Г а у с с а (сама функция
<р и ее график играют
важную роль в теории
вероятностей).
Мы установим следу¬
ющие свойства функции
(*» t) и ее графика.
1. График функции
ФЛо(х, t) при любом зна¬
чении t симметричен от¬
носительно прямой х = х0
(см. рис. 45). Максимум
достигается при х = х0,
1
и он равен 	=? (из
физических соображений
также ясно, что в каждый
момент максимальная температура будет в той точке стержня,
где был приложен импульс). Если мы рассмотрим фиксирован¬
ный момент t > 0, то эта максимальная температура будет обрат¬
но пропорциональна коэффициенту температуропроводности
166 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
fl = |/"(качественно это очевидно из физических сообра¬
жений: в каждый момент времени максимальная температура
по стержню будет тем меньше, чем больше коэффициент
внутренней теплопроводности k и чем меньше удельная теп¬
лоемкость с и плотность р материала стержня).
2. Площадь под каждой кривой равна 1 (см., например,
заштрихованную площадь на рис. 45). Чтобы это доказать,
вычислим интеграл
ОО	оо
t}ix = ^va J "" ix-
— ОО
— оо
В результате замены переменной: ^-р^==ш, dx — Za ]A(Za),
он принимает вид
Физически это означает, что количество тепловой энер¬
гии, сообщенной стержню в начальный момент t = 0 в резуль-
им
каждой фикси-
точке х 4-- х9
?Хо(х, t), как
времени Z, сна-
тате импульса, остается
неизменным с течением
времени.
3. В
рованной
функция
функция
чала возрастает от 0 (при
/ = 0) до некоторого
максимального зна¬
чения Z7 (х) и затем
монотонно убывает, стре¬
мясь к нулю при t —>OQ
(см. рис. 46). При £ = 0 функция <f>Vo(-v, t) не определена,
и мы имеем в виду ее предел при >0:
1	(Х-Хр)2. ж
lim ср (х, t) = lim	■= е АаЧ
/->0 2aVTt
1

§ 13] ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ	167
Записав последний предел
к нему правило Лопиталя,
в виде lim
/->о
получим
1
(Х-*о)2.
е 4fl2'
и применив
1
limo (х, t) = lim
f->o
	 а
~ (х —х0)2
Ит
(Х“*с)2
, 4аЧ
= 0.
Разумеется, этого заключения нельзя сделать при х = х0.
Также ясно, что limcp (х, £) = 0.
t+oo 0
Чтобы найти максимальное значение U (х)> найдем произ¬
водную функции срХо(х, О по t\
Приравняв выражение в квадратной скобке нулю, найдем то
значение / = £тах, при котором <р = £7:
/	_ (х— х0)2
‘шах—	2а2
(Читатель легко проверит, что при этом значении t функция
действительно имеет максимум.)
Следовательно,
(*) =	(*> W = 77=-^		 •	(13.22)
0	у [ х — х01
Таким образом, температура в любой точке х =£ х0 сна¬
чала повышается до значения U (х), а затем убывает и стре¬
мится к нулю. Максимально достигаемая температура в точке
х =/= стержня обратно пропорциональна при этом расстоя¬
нию этой точки от точки приложения импульса, а время,

168 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. н
необходимое для достижения этой максимальной температуры,
прямо пропорционально квадрату указанного расстояния.
Нам остается только применить разъясненный выше фи¬
зический смысл фундаментального решения (13.18) к физи¬
ческому толкованию решения (13.17). Решение (13.17) задачи
теплопроводности в бесконечном стержне при начальном
условии (13.2) может рассматриваться как результат су¬
перпозиции (наложения) температур, возникающих
в точке х в момент времени t вследствие непрерывно
распределенных по стержню тепловых импульсов «ин¬
тенсивности» f (£) в точке 5, приложенных в момент
/ = 01). Такие импульсы можно приближенно реализовать
в виде большого числа языков пламени разной температуры,
поднесенных в момент t — 0 на очень краткий промежуток
времени к стержню так, что в каждой точке 5 стержня
мгновенно возникает температура f (£) (конечно, это очень
приближенная картина, однако она наглядно описывает
характер происходящего процесса).
Рис. 47.
40. Примеры. Пример 1. Пусть начальное распреде¬
ление температуры
( «О’
/(х) = { 0,
если Xj < х < х2,
если либо х < хр либо х > х2
(см. рис. 47). Тогда в качестве решения по формуле (13.17)
!) Начальное распределение температуры f (х) можно предста¬
вить себе «разложенным» на импульсы:
оо
/(*) = f /(5)8(«-x)d«
— ОО
(это соотношение является следствием свойства (2) импульсной
Функции Дирака).

§ 13]
ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ
169
мы получим
и0
(13.23)
Эта функция выражается через одну важную специальную
функцию, называемую интегралом вероятностей*.
Z
г о
(13.24)
х —• 8
Действительно, полагая в нашем решении -	= Iх» =
= — 2а У* tdpt найдем, что
X—Xj
2aV7
f =
=

У к
X-Xi
2a VI
X—Xg
2a V7
=Л /
= т[ф(^)-ф(^)]- <’3'25>
u(xt t)
и0
X-Xj
2aV7
f* e"1^ =
0
Остановимся на свойствах функции Ф(г). Эта функция
нечетная: Ф(— z) = — Ф(z). Действительно,
~z
®(—<г) = -Д^ /* e~*‘dp.=
—yd1'”'*-
-z	r 0
Последнее равенство следует из того, что подынтегральная

170 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. и
функция четная. Далее, если z _•> 4- оо, то Ф (z) стремится
оо
к интегралу
1. Следовательно,
Ф (оо) =1 и Ф (— оо) — — 1.
График функции Ф(г) изображен на рис. 48; для этой
функции имеются специальные таблицы!).
Исходя из свойств функции Ф(г), нетрудно проверить,
что функция (13.25) действительно удовлетворяет начальному
условию. Если х < Xj или х > х2, то оба аргумента
и
2aV t
при t ->0 одновременно
стремятся или к —оо
стоящих в квадратных скобках формулы (13.25), стремятся
к одному и тому же пределу (—1 или 1), а их разность —
к нулю.
Если же Xj < х < х2, то первый аргумент стремится
к + оо, а второй к —со; выражение в скобках при этом
стремится к 2, т. е. я(х, О) = яо.
Наконец, если х = хх или х = х2 (точки разрыва началь¬
ного распределения температур), то при t —>0 температура
2 .
’) Дальнейшие сведения об интеграле вероятностей см. в книге
Н. Н. Лебедева «Специальные функции и их приложения»
(Физматгиз, 1963), гл. II.

§ 131 ТЕПЛОПРОВОДНОСТЬ В БЕСКОНЕЧНОМ СТЕРЖНЕ	17$
Пример 2. Пусть начальное распределение температуры
для
/(*) =
ДЛЯ
О для х> /и
(см. рйс. 49). Тогда формула (13.17)
о	(х-Е)2
/(1+4/ - «+
и (X, t) =

2а/itf
для
дает
'	(х-Е)2
х	$
Полагая вновь 	— = pi, преобразуем решение к виду
2а У t
х+1	X
2а V7	2а V7
(1 + 4) f ,-■ <+ + (!-+) f
X	x-l
w0
и (х, 0 =
у тс
х-1
2а УТ	2а V7
Х + 1	X
2а V7	2а	V7
— 2у/7	/*	R?-1*2 Ф +	/	pe~^dp	=
X	х-1
2а У 7	2а V7
=т{0+>Ш-*Ш]+
	 ( {Х+1)2	X2	X2	(х-1)21
t 1 „ 4аЧ „ wt „ 4а2« I 4а2‘ f
- [е	— е	— е +е J =
= 7 {(■+т)Ф Ш -2 7 Ф Ш-(‘- 7)	Ь
r (х+1}2	х2	(Х-1)2
+ во^|/Ар- _2е'^+е- ™ J.

172 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
Полученное решение имеет довольно громоздкий вид, но оно
позволяет судить о поведении температуры в стержне. Легко про¬
верить, что оно является четной функцией от х, что начальное
условие выполняется и что а->0 при Z->co в любой точке х.
Установим, как понижается температура в точке х = 0:
где z = ■. Покажем, что полученное выражение для «|х_0
может быть преобразовано следующим образом. Заметим, что
производная выражения, стоящего в прямых скобках, равна
1 —e~z*
2z2e-zl — 1 + е~г2
z2
1 1—
V л z2 ’
кроме того, само это выражение стремится к 0 при г->0, так как
Ф (0) = 0 и Пт —	— = 0. Поэтому
2->0 zy К
I
2а V t
1—Z2
Поскольку —1 —2Г + • • •> то для больших /, т. е. малых
значений верхнего предела	,
2а/7

§ 14)
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
178
Примерз. Показать, что если / (х) = иае , и0 > 0, а > 0, то
и (х, t) =
Ug
/ 1 -J-4a2a2Z
а2Х2
H-4aW ,
е
показать, что в тех точках стержня, в которых кривая начального
распределения температуры выпукла / |х| <—т^)» температура
монотонно убывает к нулю с возрастанием /, а в тех точках, где
эта кривая вогнута [ |х| >—— температура сначала повы-
\ а у 2 /
шается до —, а затем уже монотонно убывает к нулю,
о К 2е | х |	J
•Пример 4. Показать, что если f (х) =	то
“ '> = т [> + - (& Н /7)]+
показать, что
« L=o= tttfa44 h—ф (да2 К"*)) =
оо
__ 2и0 Г -2a<J2 V ty-v2 j ~
/к J	~
для больших t.
§ 14. Теплопроводность в конечном стержне
41.	Приведение к задаче с однородными краевыми
условиями. Метод Фурье. Задача линейной теплопровод¬
ности в конечном стержне отличается от задачи для
бесконечного стержня, рассмотренной в предыдущем
параграфе, тем, что необходимо учитывать краевые условия
на торцевых сечениях (концах) стержня. Как мы увидим,
наличие краевых условий вносит весьма существенные изме¬
нения в метод Фурье по сравнению с задачей без краевых
условий.
Предположим, что длина стержня равна I. Начало коор¬
динат на оси х выберем в левом конце стержня; тогда его
торцевые сечения будут х=0 и х=/. Температура н=«(х, t)
174
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. П
должна удовлетворять (при условии теплоизоляции боковой
поверхности) для 0 < х < I уравнению (13.1):
ди 9 д2и
Начальное условие имеет прежний вид (13.2):
Ц=о = /(х)’
но только теперь функция f (х) (начальное распределение
температуры) должна быть задана лишь на интервале 0<х</.
Общие краевые условия на торцах стержня были установлены
в п. 35 (формулы (12.10)). Если температурные условия
на концах стержня различны, то
*lH-o = M4=o-«o).
, <fc|" HI ~1	(14Л)
Напомним, что k — коэффициент теплопроводности стержня,-
Ло и ht — коэффициенты теплообмена на торцах стержня,
w0 и иг — заданные температуры концов стержня.
Метод Фурье, с помощью которого мы предполагаем
решить задачу, в случае краевых условий (14.1) непосред¬
ственно неприменим, так как они неоднородны, если
ио=#О или ut + 0: решение я = 0 им не удовлетворяет. Это
значит, что сумма двух решений их(х, t) и zz2(x, /), каждое
из которых в отдельности удовлетворяет условиям (14.1),
этим условиям уже не удовлетворяет; точно так же не удо¬
влетворяет этим условиям произведение любого решения на
постоянную величину (читатель легко убедится в этом само¬
стоятельно). Поэтому, прежде чем применять метод Фурье,
мы должны свести задачу к такой, в которой краевые усло¬
вия однородны. Мы это сделаем в предположении, что
температуры, внешних сред uQ и ut постоянны,.
Для этого введем новую искомую функцию w = te/(x, f),
связанную с и формулой
и(х, f) — w(x, O+t + Ti*»	(14.2)
где 7 и 7j — некоторые постоянные коэффициенты, которые
мы будем пытаться подобрать так, чтобы для функции w полу¬
§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
175
чились однородные краевые условия. Так как =
то условия (14.1) перепишутся в виде
ь	u+м——Мо.
ил 'х=0
— А-4^-1	=М1х=/+М + (/й1 + &)1Г1 —Мр
л ljr=z
Требование однородности этих условий состоит в выполне¬
нии равенств
АоТ —ftTi = Mo>
^zl Н" (^z + ^) Ti = *zaz*
(14.3)
Система уравнений (14.3) относительно у и имеет един¬
ственное решение, поскольку определитель этой системы
не равен нулю:
/г0
ht
—k
k
= Hq (Ihi “4~ k) "4“ kh^ 0,
так как Ло, hv k и I — положительные числа. Найдя из урав¬
нений (14.3) 7 и Тр получим для w(x, t) краевые условия
в виде
k ■эг 1=0 = №	- k L=U’ <14Л>
которые уже являются однородными.
С другой стороны, в качестве начального условия для
функции w мы получаем
<Ц=о = Ч=о — 7 —71X = /(X) — т —Т1* = /1(*).	(14.3)
где ^(х), как и /(х),— функция, заданная на интервале
0 < х < /. Наконец, уравнение, которому должна удовле¬
творять функция не отличается от исходного уравне¬
ния (13.1), так как
ди __ dw	w	д2и d2w
~dt~~ST	И	"дх* ~~ дх2 *

176 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. п
Таким образом, мы приходим теперь к следующей задаче:
найти функцию •w = tw(xt t), удовлетворяющую для
О < х < Z и всех t > 0 уравнению
dw
d2w
"дх2*
(М.6)
начальному условию (14.5) и краевым условиям (14.4).
Эта задача уже решается методом Фурье, так как краевые
условия однородны (им удовлетворяет решение w = 0).
Первая часть метода Фурье — разделение переменных —
применяется без каких бы то ни было изменений, и мы найдем,
как в предыдущем параграфе, частные решения вида (13.8):
w(x, Z) = (acosXx4-?sinXx)^~w/	(14.7)
(где вместо т подставлено аЧ). Но если в случае бесконечного
стержня X оставалось совершенно произвольным,
то наличие краевых условий, как мы сейчас увидим, накла¬
дывает на X определенные требования. Действительно, под¬
ставляя функцию w(x, t) из (14.7) в условия (14.4) и сокра¬
щая на е-12аЧ, мы найдем, что для первого множителя
в правой части (14.7):
a cos Хх -|- р sin Хх = X (х),
должны выполняться равенства
kX' (0) = hQX (0),	— kX' (Z) = htX (Z).	(14.8)
Заменяя значения функций X и Xf их выражениями, получим
ЛрХ = Лоа, ЛаХ sin X/ — ЛрХ cos X/ = /zza cos XZ 4~ M sin X/,
откуда, с одной стороны,
а с другой стороны,
р	sin XZ 4-	cos XZ) = a (AX sin XZ — ht cos XZ),
t. e.
a   ht sin AZ + H cos XZ   hi tgXZ 4- h\
P kXsinXl— hi cos \l	kXtgXl— hi
Таким образом, X должно удовлетворять уравнению
ht tg XZ + kl
Ao Л kXtgXl— h[ ’

§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
177
или
t	k (hb + hiYK
Прежде чем рассматривать решение в общем случае, займемся
наиболее важными частными задачами.
42.	Распространение тепла в стержне в случаях
постоянной температуры на концах или теплоизоляции
концов. В п. 35 мы уже видели, что краевые условия зна¬
чительно упрощаются, если концы стержня либо теплоизоли¬
рованы, либо поддерживаются при постоянной температуре.
В случае теплоизоляции какого-либо конца надо соответ¬
ствующий коэффициент теплообмена положить равным нулю,
а в случае постоянства температуры устремить этот коэф¬
фициент к бесконечности.
При этом мы условимся говорить об одинаковом режиме
на концах стержня, если они оба либо теплоизолированы,
либо поддерживаются при постоянной температуре, и о раз¬
ном режиме, если один из них (для определенности левый:
х = 0) теплоизолирован, а другой (правый: х = Г) поддер¬
живается при постоянной температуре.
Пусть сначала концы стержня находятся при одинако¬
вом режиме. Если они теплоизолированы, то hQ — hl = 0
и уравнение (14.9) примет вид tgXZ = O.
Чтобы рассмотреть случай постоянства температуры на
концах, разделим числитель и знаменатель правой части
формулы (14.9) на произведение /z0/zz:
Переходя к пределу при Л0->оо, >оо, замечаем, что
снова получаем условие tgXZ = O.
Итак, в случае одинакового режима на концах
стержня X должно являться корнем уравнения
lgXZ = O.	(14.10)
Пусть режим на концах разный. Если, скажем, Ло = О,
то tgXZ = ~j- или ctgU — — , При /zz->oo получается
12 И. Г. Арамановнч, В. И. Левин

178 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
уравнение ctg XZ = 0. Поменяв ролями hQ и hv мы снова при¬
дем к этому же уравнению1).
Таким образом, в случае разного режима на концах
стержня X должно удовлетворять уравнению
ctgXZ = O.	(14.11)
Начнем со случая одинакового режима; X должно
быть корнем уравнения (14.10), т. е. должно быть
XZ = п-гс,
где п — любое целое число. Таким образом, X может прини¬
мать только значения из бесконечной последовательности
Х = Х„ = -^-,	« = 0,1,2,...	(14.12)
Эти значения называются собственными числами задачи.
Отметим, что мы не учитываем отрицательных значений п
потому, что в решении (14,7), куда мы должны подставить
Х==ХЛ, знак Х/2 не играет никакой роли (в показатель е~>2аЧ
число X входит в квадрате, cosXx — четная функция от X,
а знак синуса может быть включен в произвольную постоян¬
ную Р).
В случае разных режимов X должно удовлетворять
уравнению (14.11), т. е. собственными числами в этой
задаче являются
Х = Х„ =	« = 0,1,2,...	(14.13)
(отрицательные значения X мы не учитываем по указанным
выше соображениям).
Каждому из собственных чисел \п будут соответствовать
свои коэффициенты ап и в формуле (14.7).
Таким образом, решения уравнения (14.6), удовлетворяю¬
щие поставленным краевым условиям, должны иметь вид
-Х2а2^
^ ==wn(x, t) = (ап cosX^x + pn sinХлх) e~ n ,	(14.14)
!) Если в формуле (14.9) сначала устремить /г0 к оо, то полу¬
чим tg U = X или ctg М — Положив hi = 0, мы опять при¬
ходим к уравнению ctg XZ = 0.

§ 14]	ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ	179
где % и связаны соотношением (14.87). В частности, О,
если /го = О, и ад = 0, если Ло —оо (в этом мы еще непо¬
средственно убедимся ниже).
Ввиду того, что в дальнейшем выражение ал cos \пх4-
4-Pnsin/</zx из формулы (14.14) будет фигурировать в каче¬
стве общего члена ряда Фурье, условимся, что при п = 0
это выражение мы будем заменять на
Рассмотрим подробнее все три решаемые нами задачи.
Задача А. Оба конца теплоизолированы.
Задача Б. На обоих концах поддерживается по¬
стоянная температура.
Задача В. Левый конец теплоизолирован, а на пра¬
вом конце поддерживается постоянная температура*
В задачах А и Б собственные числа \п = и
,	пЧ?аЧ
t) = (a„cos — 4-^sin-y-je 1	,
Но в задаче А должно быть
dwn I _п	I _п
дх |х=0	’ дх \х = 1
(/zo = /zz = O в краевых условиях (14.4)), откуда вытекает,
что pn = 0, n = 0, 1, 2, ... Таким образом, уравнению и
краевым условиям задачи А удовлетворяют функции
п2к2аЧ
Wn(x, t) = а„ cos ^-е~ 12 .	(14.15А)
В задаче Б должно быть
®Л=О = 0’	= °
(hQ = hl = oo в краевых условиях (14.4)), откуда следует,
что art = 0, n = 0, 1, 2, ... Таким образом, уравнению и
краевым условиям задачи Б удовлетворяют функции
п2п2аЧ
wn(x, O = P«sin^-e 12 .	(14.15Б)
Наконец, в задаче В собственные числа Х/3 =	и
(*■<) = («/acos  	F sin А——] е	41	♦
12*

180 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
Здесь мы должны иметь
д™п I
дх |х=0
откуда вытекает, что — 0, я = 0, 1, 2, ... Таким образом,
уравнению и краевым условиям задачи В удовлетворяют
функции
/9	(2д+1)2 1?аЧ
wn(x, 0 — ап cos' -1-	е	• (14.15В)
Решения (14.15А)— (14.15В) однородного уравнения (14.6)
удовлетворяют соответствующим, и тоже однородным, крае¬
вым условиям задач А — В. Следовательно, сумма ряда, со¬
ставленного из этих решений,
t)	(14.16)
л = 0
также удовлетворяет и уравнению и соответствующим крае¬
вым условиям.
Заметим, что выделение с помощью краевых условий послё-
довательности собственных чисел каждой задачи существенно
отличает эти зад1чи от задачи Коши без краевых условий,
которую мы решили в предыдущем параграфе для бесконеч¬
ного стержня. Там X оставалось произвольным и, чтобы
использовать все полученные частные решения, нам надо было
интегрировать их по К. Здесь К может пробегать только
последовательность собственных чисел и мы должны сум¬
мировать частные решения по всем собственным числам.
Там произвольные коэффициенты а(Х) и Р(Х) определялись
из разложения начального распределения температуры в инте¬
грал Фурье. Здесь произвольные коэффициенты ап и
определятся, как мы сейчас увидим, из разложения началь¬
ного распределения температуры в ряд Фурье. В этом и
заключается существенное отличие второй части метода Фурье
(суперпозиция частных решений) в применении к задачам без
краевых условий — бесконечный стержень — и к задачам,
с краевыми условиями — конечный стержень, о котором мы
упоминали в самом начале этого параграфа.
Перейдем к определению произвольных коэффициентов ап
или из начального условия (14.5). Это мы должны по
отдельности сделать для каждой из задач А, Б и В.

§,14]	ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ	181
Задача А. Решение имеет вид (см. (14.15А))
°°	пЧРаЧ
tej(x, Z) = ane /2 cos^, (14.17А)
п = 0
и начальное условие (14.5) записывается так:
оо
®lf=o=:^®»cos-^r = /iW'	0 < х </.
л = 0
Мы должны, следовательно, разложить функцию /j(x),
заданную на интервале 0 < х < Z, в неполный ряд
Фурье — ряд косинусов. Как известно из теории рядов Фурье
(см. «Кр. к.», п. 171), коэффициенты разложения находятся
по формулам
a„ = -| [ fx(x)co5~-dx.	(14.18А)
О
Подставляя это выражение для а/г в формулу (14.17А), полу¬
чим искомое решение задачи.
Задача Б. Здесь решение имеет вид (см. (14.15Б))
°°	пЮаЧ
=	12 sin-^ (14.17Б)
п = 1
и начальное условие записывается так:
оо
wi/=o=S^sin'^F'=^i(x)’ °<x<z-
Л = 1
Здесь мы должны разложить функцию /2(х), заданную на
интервале 0 < х < Z, в ряд по синусам. Коэффициенты
вычисляются по формулам
i
= /i(x)sin^dx,	(14.18Б)
О
и, подставив это выражение в формулу (14.17Б), получим
искомое решение задачи.

182 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
Задача В. Решение имеет вид (см. (14.15В))
®(х, 0 =	4/2 cos -(2" +1)л1*,	(14.17В)
2Z
и начальное условие записывается так:
оо
1/=о = ал cos ^2p1tX- = fi (*)’	0 < х </.
Легко проверить, что система функций cos-——•
(n = 0, 1, 2, ...) ортогональна на интервале (0, Z)
(см. аналогичное доказательство на стр. 85). Поскольку
6
то коэффициенты ал разложения функции J\(x) по ортого¬
нальной системе функций находятся по формулам (см. «Кр. к.»,
п. 175)
i
о
(14.18В)
Подставляя выражение (14.18В) в формулу (14.17В), полу¬
чаем искомое решение задачи.
Заметим, что формулу (14.18В) можно получить иначе, опираясь
только на знание обычных рядов Фурье. Сумма тригонометриче¬
ского ряда
оо
Л=0
является четной функцией с периодом 4Z, обладающей еще спе¬
циальным свойством: /j (х-\-21)=—(х), где 2Z—половина периода.
Действительно, достаточно убедиться в том, что каждое слагаемое
меняет знак на обратный при замене х на х-\-21, а это очевидно:
(2п	1) к (x-{-2Z)

( (2п + 1)лх ,	)	(2тг-|“1)гсх
cos ( '	21	Ь (2« +1) л J = - cos —

§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
183
Графически это свойство иллюстрируется так: чтобы получить гра¬
фик функции на левой половине периода (—2/, 0), можно график на
правой половине (0, 2/) зеркально отобразить относительно оси х
и затем сдвинуть на 2Z влево («зеркально-сдвинутые» полуволны).
Процесс построения графика в интервале (—2Z, 2Z) показан на
рис. 50. Сначала кривая (/) из основного интервала (0, Z) четно
продолжается в интервал (— Z, 0), в результате чего получается
кривая (2). Затем кривую (2) сдвигаем на 2Z вправо и берем ее
зеркальное отображение относительно оси Ох; получаем кривую (3).
Наконец, кривая (4) строится так: берем зеркальное отображение
кривой (/) относительно оси Ох и сдвигаем его на 2Z влево; то же
получится, если кривую (3) зеркально отобразить относительно
оси Оу.
Коэффициенты ап вычисляются по обычным формулам Фурье
для четных функций, и мы вновь получим формулу (14.18В):
an — ^[f fl (•*) cos ^2n ~2/)	f fl W cos X dx'
6 6
так как подынтегральная функция имеет равные интегралы по чет¬
вертям периода: (0, Z) и (Z, 2Z).
43.	Общий случай краевых условий. Аналогично обстоит дело
и в случае общих краевых условий (14.4), когда X должно удовле¬
творять трансцендентному уравнению (14.9):
	 £ (Ло + hi) Л
— kW — hshi ’
простейшие частные случаи которого мы рассматривали выше.
Уравнение (14.9) также имеет бесконечное множество корней, обра¬
зующих последовательность А/г>-0 (см. рис. 51, где жирными ли¬
ниями изображены графики левой и правой частей уравнения (14.9):
сплошной линией — график левой части (тангенсоида) и пункта-

184 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ (ГЛ. II
ром — график правой части). Нетрудно видеть, что в этом общем
случае лл для больших п очень близки к последовательности (14.12)
собственных значений для задач А и Б. В соответствующих реше¬
ниях для общего случая
(х, t) = (ая cos Хях + sin \пх) ё п
коэффициенты а„ и ря должны быть связаны соотношением (14.8'):
№л(х, 0 = ?n^Xncos Xnx-f-sinX„xp "	.	(14.19)
Ряд
(X, 0 =	хл cos ^Пх + sin Хях) ё п (14.20)
л=0	л=0
будет решением уравнения (14.6), удовлетворяющим условиям (14.4).
Чтобы удовлетворить начальному условию (14.5), мы должны по¬
ложить
^P„(-^XncosXnx-f-slnXnxj = ft(x), 0<х<1,	(14.21)
л=0

§ 14]	ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ	185
Докажем прежде всего, что система функций
k
Хп (х) = — \п cos Хях + sin Хлх, п = О, 1, 2, .
«о
ортогональна на интервале (0, /), т. е. что для т =£ п
i
f Xm(x)Xn(x)dx = 0.	(14.22)
О
Из определения функций Хт (х) и Хп (х) следует, что они удо¬
влетворяют уравнениям
+	= о « <+^Х = о.
Умножим левую часть первого уравнения на Хп, а второго — на Хт
и вычтем одно из другого:
(й - хпхт = хтх"п - хах"т = М - хах'ту.
Интегрируя в пределах от 0 до Z, получим
I
(4 - $ f	(0 *'п (0 -	(0 Х'т (/) -
О
-Xm(0)4(0)-hX„(0)X;(0).
Но Хт и Хп должны удовлетворять условиям (14.8), так что
<(0)=4^(0)’	4(0)=4*«<0)’
=	X'n(l) = —!±Xn(l).
Учитывая это, мы сразу находим, что
i
f Vndx=^0,
О
а так как Х^ =£ Х^, то равенство (14.22) доказано. Записывая раз¬
ложение (14.21) в виде
2	(-*•)= /г
п= о
186 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. й
находим коэффициенты разложения функции j\ (х) по ортого¬
нальной системе функций Хл(х):
где
/
?л = 4- /* f^Xn(,x)dx,
ln.J
I
X?n(x)dx.
0
(14.23)
Последний интеграл может быть выражен через Хл. Общую фор¬
мулу ввиду ее громоздкости мы не выписываем; частные случаи
приведены в примерах 9 и 10 п. 44. Подставляя выражение (14.23)
в формулу (14.20), получим искомое решение задачи в общем
случае.
44.	Примеры. Пример 1. В конечном стержне (с тепло¬
изолированной боковой поверхностью) оба торцевых сечения
теплоизолированы, а начальная температура постоянна по
стержню: / (х) = uQ (0 < х < /). Тогда мы имеем hQ = ht = 0
и w из (14.2) совпадает с и, a /j(x) из (14.5) — с f (х),
так как в силу уравнений (14.3) 7 = у1 = 0. Это — задача А,
а по формуле (14.18А)
2rz0 7* ппх
=	cos —
о
2«0>
0.
если
если
п = 0,
п>0.
Следовательно, по формуле (14.17А)
«о
W==tf = -^- = tf0
(см. замечание к формуле (14.14». Таким образом, мы по¬
лучили физически очевидный результат: при полной тепло¬
изоляции стержня постоянная начальная температура
сохраняется в нем для всех t > 0.
Пример 2. При тех же условиях, что и в примере 1»
предположим, что начальное распределение температуры
f(x)~
если 0 < х <	,
0, если < х < I.

§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
187
Тогда по формуле (14.18А) а0 = я0, а для л > О
2
2
2а0 Г
an = -f-J cos
6
£
mzx .	2a0	. пкх 12
—— dx == —- sin —
l	n* I l0
О при n = 2tn,
< / i \m
'	(2m + 1) те
т— 1, 2, 3, ...
n — 2tn-\- 1,
т — 0, 1, 2, ...
формуле (14.14)),
при
Следовательно (учитывая замечание к
решением задачи будет (см. (14.17А))
n	COS	Р(2т + 1)2т^аЧ
да = и==^.+ 2^^(_]Г		е~ Р
т = 0
I
2m 4-1
косинусы меняют знак на обратный, так что при любом t > 0
график и симметричен относительно точки	-~-j
(см. рис. 52). Поэтому для любого t > 0
i
j* udx = ^ UqI
о

188 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
(эта площадь, пропорциональная количеству тепла в стержне,
заштрихована на рис. 52). Теплоизоляция концов стержня
находит свое выражение в том, что кривые распределения
температуры при t = const имеют горизонтальные касатель¬
ные при х = 0 и х = 1. При >оо главным членом ряда
является первый, так что
е 12 cos~7“ (для больших t).
Пример 3. При тех же условиях, что в примере 1,
предположим, что начальное распределение температуры
таково:
-у2- х,	если 0 < х /•
~ (I — х), если i I < х < I
/(•*) =

§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
189
(см. рис. 53). Тогда а0=и0, а для п>0
£
2	i
4w0 Г	ппх . . 4м0 Г	пкх ,
ап = -~- / х cos —dx +	/ (Z— x)cos —— dx.
6 2
2
Сделаем во втором интеграле подстановку y = Z — х и
новую переменную интегрирования снова обозначим через х;
тогда
£
2
ал = -7Г П + (— О”} f xcos-^~dx =
6
О,	если п — 2т — 1,
~	-^2 {(— 1)” — !}• если П = 2т.
т—1, 2, 3, ... Таким образом, отличными от нуля ал,
кроме а0, будут те, для которых zz = 2/n, а т = 2s-1,
s = 0, 1, 2, ...» т. е. /г = 4$ + 2, причем
«45 + 2	(2$+1)2тс2’
Следовательно, как в предыдущем примере, получим
4и0 V
5 = 0
(4s 4- 2) т.х
COS 3

(2s+D2
I2
е
При x — lft и х = 3//4 все косинусы равны нулю, так
что в этих точках и = uQ для любого t > 0. Ясно также,
что при каждом фиксированном t график и симметричен от¬
носительно прямой x = Z/2 и что каждая его половина сим¬
метрична относительно, соответственно, точек (Z/4, и0/2) и
(3Z/4, я0/2). Поэтому для любого t > 0

190 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ? IT
(см. заштрихованную на рис. 53 площадь). Для больших t
л	Wt	п
4w0 Г2—	2пх
—-е	1 cos—у—
ТС2
Пример 4. В конечном стержне (с теплоизолированной
боковой поверхностью) концы поддерживаются при постоян¬
ных температурах: u\x=iQ—u^ u\x=tl = ul (задача Б), а на¬
чальная температура постоянна по стержню: /(x) = w0
(0 < х < Г). Тогда 7z0 = /zz = oo и уравнения (14.3), которые
можно записать в виде
т + (/+^')'Г1=“г’
превращаются в 7 = uQt 7 + 1ул — itt, т. е, 7 = uQt
71 = y(wz — w0), и по формуле (14.5)
/1 (*) = uq — uq—y^i — uq).
Поэтому по формуле (14.17Б)
60	пЫаЧ
■йу(х,/) = ^ ₽„е	11 sin-^,
/2=1
где (см. формулу (14.18Б))
i
?п = Т f /i(x)sin-^dx =
о
I
= т/ {“о — «о— т(а1~ «o)}sin-^rf* =
О
I
= -^ («о — «о) {1 — (—Ь"} —— «о) / к sin dx =
=	(«о- «о) {1 - (-!)"}	(-1)" («, - «о) =
= ЛК 	 «о+(—	«о)}’

§ 14!
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
191
Таким образом»
о	~ „ sin —у— пЫаЧ
w(x, О = 4(ио~“о)2 	п—е	1> +
/1=1
О	00	sin —у—' пЧРаЧ
л= 1
а
и(х, /) = w(x, 0+т +71* = «'(*> t) + “о + Ц< f Ц°-*•
Чтобы по существу разобраться в полученном решении,
—>оо и, следовательно, я—>н0-|-
и
заметим, что >0 при t
~ Uq- х, т. е. к. линей¬
ному распределению темпе¬
ратуры между температура¬
ми на концах (см. рис. 54,
где принято uQ > uQ > ut).
Для сравнительно малых
£>0 график и должен резко
спускаться из точки (0, w0),
примыкать к прямой и — uQ
и затем опускаться в точ¬
Рис. 54.
ку (/, ut) (кривая (/)). Для
больших t
кх
2 ~
w «7(«о— ио)е
n2a?t
12 sin
тРаЧ
ч п2аЧ
)	7Г~	•
— иЛе 12 sin-p,
±( Цр + Ц/
и 2
т. е. ордината графика и ниже ординаты соответствующей
точки прямой, соединяющей точки (0, uQ) и (/, я*), на вели¬
чину, пропорциональную sin-^ : получается кривая (2).
Вид графиков и может резко меняться в зависимости от
соотношения величин uQ, uQ и ut. Так, если w0 = ~(zz0-|-tfi)

192 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
(начальная температура равна среднему арифметическому темпе¬
ратур концов), то uQ — uQ =—~(я0— ui) = ui — я0 и в вы-
ражении для w(x, t) останутся
ними индексами п = 2пг.
только
слагаемые с ч е т-
оо
, 2тпх
sin ——
4r?z2ir2a2/
/А	и1
2
т- 1
1
-е	12
w ( X , L )

7	те
т
И 'а'|лг=//2==0. В этом случае графики и симметричны отно¬
сительно точки	zzoj; они
изображены на рис. 55. Здесь
для больших t
ЫаЧ п
Uq—Ui л	— 2тех
Ж	“	— е I	sin —7-г-.
те	I
Рис. 55.
ксами п = 2/п4-1 и, полагая
будем иметь
Представляет интерес ча¬
стный случай я0=яр Тогда
в сумме останутся только сла¬
гаемые с нечетными инде-
для определенности uQ > uQ,
со
w(x. О = 7(«о — «о) S
гп = 0
. (2т	1) тех
Sln ТГ —
2т+1
(2т + 1)2 т?аЧ
и н(х, f) = w(x, /) + ^0. Графики и симметричны относи¬
тельно прямой х = —; они изображены на рис. 56 для воз¬
растающих t: (/), (2), (3).
Заметим, что в этом примере количество тепла, содержа¬
щееся в стержне, изменяется с течением времени, хотя боковая
поверхность стержня теплоизолирована: теплообмен с внеш-

§ Н] ТЕПЛОПРОВОДНОСТЬ в конечном СТЕРЖНЕ	193
ней средой происходит через торцевые сечения. Например,
в последнем рассмотренном случае тепло уходит из стержня
через торцевые сечения в более холодную внешнюю среду.
Пример 5. В конечном стержне (с теплоизолированной
боковой поверхностью) концы поддерживаются при постоян¬
ной температуре Uq — u^ а начальная
«!/=о=/(*) —
2и0
~ х,	если
2uq	х
-р- (/ — х), если
температура
13 И. Г. Араманович, В. И. Левин

194 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ, II
(см. рис. 57, где принято 0 < uQ < zz0). Показать, что
Провести исследование полученного решения для малых t > О
(кривая (7)) и больших t (кривая (3)). Найти приближенное
выражение и для больших значений t и установить, что для
них и > uQ, если f/0 > | ^0’ и и < если ио < z/o- ^на"
логично исследовать случай 0 < uQ < uQ,
Пример 6. В конечном стержне (с теплоизолирован¬
ной боковой поверхностью) левый конец теплоизолирован:
= 0, правый поддерживается при постоянной темпе¬
ратуре: и\х=1 = и1, а начальная температура постоянна по
стержню: u\t=Q = uQ, Это — задача В. Предварительно опре¬
делим 7 и 7j из уравнений (14.3). Так как здесь /го = О,
hl = coi то эти уравнения принимают вид y1 = 0, 7 = ut и
мы имеем « =	/1(x) = zz0— иг (по формулам (14.2)
и (14.5)). Далее, по формуле (14.17В)
л = 0
где по формуле (14.18В)
Таким образом, решением будет

§ 14]
ТЕПЛОПРОВОДНОСТЬ В КОНЕЧНОМ СТЕРЖНЕ
195
(см. рис. 58, где принято я0> uj). Для больших t
~ т?аЧ
cos^
(кривая (3)).
7. Пусть в условиях примера 6 я|/=0=-у-#
П р и мер
(О < х < /). Показать, что тогда
~	0°	COS <2п+1)**
(-,)“■■ 2J‘,
n = Q
(2 л 4-1)2 тёаЧ
4Р
со
8и0 у
я2 Л4
п = 0
(2л 4-1)2 т?аЧ
41?
е
Построить приближенно графики и для случаев zz0 > ut и
«о < ui-
Пример 8. Пусть в условиях примера 6
л|,=0 = -^-(/-х)	(0 < х </).
Показать, что тогда
~ ОО	cos (2”+1)^
2„+а.
п=0
(2л + 1) tzx
c°s
(2л+1)2 е
(2л-!-1)2 ч&аЧ
оо
8w0 V
л2
л=0
(2л +1)2 т&аЧ
+
13*

196 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. П
Построить приближенно графики и для случаев «0 > ut и
«о < «р
Пример 9. Пусть в общем краевом условии (14.8)
Ло = О и ht = h. Тогда в выражении (14.14) рл = 0 и
Ч - Л	Ч	. Ч .	/l
wn —a.ncosHnxe п , где Ал — корень уравнения tgи —
(частный случай уравнения (14.9)). Непосредственным вы¬
числением проверить, что функции Хп (х) = cos ортого-
i
нальны в интервале (О, I) и J* X„(x)dx = -|-	•
Пример 10. Пусть в общем краевом условии (14.8)
hQ — ^ — h. Показать, что в этом случае
Г ч	1 / л \	Л
§ 15. Теплопроводность в полубесконечном стержне
45.	Распространение тепла при теплоизоляции или
постоянстве температуры конца стержня. Стержень, огра¬
ниченный только с одной стороны, а в другую сторону про¬
стирающийся в бесконечность, называется по луб ес конечным.
Будем по-прежнему считать, что боковая поверхность стержня
теплоизолирована и что его единственный — левый — конец
расположен при х = 0. Тогда мы имеем только одно крае¬
вое условие, относящееся к х = 0, и в общем виде оно за¬
писывается так:
k¥x\ =Ао{“1х=о-«о)	(15.1)
(первое равенство (14.1)). Начальное условие имеет преж¬
ний вид:
u\t^f(x) (х>0).	(15.2)
где начальное распределение температуры /(х) должно быть
задано лишь на полуоси х > 0.
Задача теплопроводности в полубесконечном стержне легко
решается при помощи формул § 13 в случаях Ло = О (тепло-

I 15] ТЕПЛОПРОВОДНОСТЬ ПОЛУБЕСКОНЕЧНОГО СТЕРЖНЯ 197
изоляция на конце) и hQ — oo (постоянная температура на
конце). Действительно, если мы сначала рассмотрим случай
теплоизолированного конца:
ди I
м=о
= 0,
(15.1')
и продолжим f(x) на отрицательную полуось х = 0 чет¬
ным образом: /(—х) = /(х), то функция (13.17):
u(xt t)
— оо
(x-W
4аЧ
я.
(15.3)
будет являться решением нашей задачи. Как мы знаем, она
является решением линейного уравнения теплопровод¬
ности (13.1) и удовлетворяет начальному условию (15.2).
Чтобы проверить, что она удовлетворяет и краевому усло¬
вию (15.1'). образуем
,	.	?	U-E)2
— =	/ /($)(? — х)е	dZ
дх 4a3tVnt J J
— ОО
И
ди I
дх L=o
1
Последний интеграл равен нулю, так как /($) по построе¬
нию— четная функция, £/(£), следовательно, нечетна и вся
подынтегральная функция нечетна. Таким образом, усло¬
вие (15.1') выполняется.
Решение задачи (15.3) может быть в этом случае не¬
сколько преобразовано. Используя четность / (х), получим
1	/»	(-У-Е)2
и(х’ Jf®e' 4а2'*+
ЛаЧ d'=
198 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ, II
где в первом интеграле В заменено —таким образом, при
краевом условии (15.1х) решением будет
1 г (	(х~^2	(х+®2 1
U(Xt t)=	/С0Г 4fl2Z+^4fl2/J^.	(15.3х)
Перейдем к случаю, когда конец х = 0 поддерживается
при постоянной температуре zz0:
"L=o="o-	(15.1хх)
(Решение для случая, когда и0 есть функция времени t, при¬
ведено в п. 52.) Сначала сведем краевое условие к одно¬
родному, полагая
w =	и0, Л (х) = / (х) — «о (х>0),
и продолжим (х) на отрицательную полуось х < 0 не¬
четным образом: Д(—х) = —	Тогда функция
— оо
dw о d2w
удовлетворяет уравнению = а2~дхг' начальному условию
w|/=0 = /1(x) (х > 0) и краевому условию ^|х=о = О. По¬
следнее вытекает из того, что
00 &
поскольку J\(%) — нечетная функция. Следовательно,
1 г (х~®2
“(X1 ,)=i'+W J/,(E)e'di =
— oo
0 /
_ ~ , 1
“° ‘ 2a Yrf
— оо
H-

I 15] ТВПЛОПРОВОДНОСТЬ ПОЛУБЕСКОНЕЧНОГО СТЕРЖНЯ 199
1 г (	(х~&	(х+^)2 )
-2тй//1(Че_ 4ач ~е'4а2‘ г
(АЧ-Н)2
(
f /©
А '
оо
(x-Е)2
— e
Преобразуем эту
стей Ф (z)
	 	 x — i
11 ~ 2a pT ’
формулу,
пример
(см.
заметим, что
привлекая
1	§	13).
интеграл вероятно-
Для этого, полагая
1
(х-ф
оо
—f е~^~dt —
2aVrd J
1
а полагая и = —,
— что
'п
—^=- / e ™ di
2аУтЛ J
ОО
X
2а V7
1
вследствие чего
Поэтому окончательно мы получим решение задачи в случае
краевого условия (15.1") в виде

200
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ, ,11
Решение задачи теплопроводности в полубесконечном
стержне при общем краевом условии (15.1) представляет
значительно большие трудности и требует иных средств.
46.	Примеры. Пример 1. Левый конец х = 0 полу-
бесконечного стержня (как и его боковая поверхность) тепло¬
изолирован. Начальное распределение температуры:
0,
если
0 < х < хг
«Ь=о = /(х) =
«0-
если
Xj X х2
. 0,
если
Х2 < X.
Найти я== zz(x, /). По формуле (15.3х) имеем
и —
(х-ф
4аЧ
(х+Е)г )
+ е" 4аЧ к';
полагая для первого слагаемого
х -4“ 6
и = —, найдем» что
r 2aVt
а для второго
и =
Но
X-Xi
Х+Хг
2aVT
2а VT
f е'
e-^dp
x~x2_
X + Xt
2а V t
*	2a V 7
(15.4)
В частности, полагая Xj = 0, х2 = /, получим
(15.5)
Вид графиков и при фиксированных значениях /> 0 виден
на рис. 59; Так как теплообмена с окружающей средой нет.

§15] ТЕПЛОПРОВОДНОСТЬ ПОЛУБЕСКОНЕЧНОГО СТЕРЖНЯ 201
то площадь под каждым графиком равна uQl (заштрихована
на рис. 59).
Представляет интерес предельный случай решения (15.4) при
«о==	!	 и х2->х{. Если положим х2 — *i + *	(е->0),
ф (Sr)"* (Sr)
_ J. чг(Х1+ О-^(лч)
и 2	е	’
так что
Нт и = — ~ «'' (.<!).
в->0
Дифференцируя 4г(х0 по хп найдем, что
Так как
Z
Ф(г) = ~— У е~^
2 ,2
то Ф' (г) = -77— е и, следовательно,
U-.rtP
4a2i .	*	4а2?
+ <?
(15.6)

202
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. и
Но очевидно, что осуществленный в начальном условии предель¬
ный переход означает, что
—*i).	(15.7)
где & (х — хх) — функция Дирака (см. стр. 164). Таким образом,
решением задачи для полубесконечного стержня при краевом усло¬
вии (15.Г) и начальном условии (15.7) является сумма фундамен¬
тальных решений
{х-ху- _ (х+х,)2
е 4аЧ _|_е ЬаЧ 1 = ^ ^ О + ?_Х1(Х, О
(см. формулу (13.18)). Это можно усмотреть и непосредственно.
Пример 2. Левый конец х — 0 полубесконечного стержня
(с теплоизолированной боковой поверхностью) поддерживается
при постоянной температуре «0: и |х=0 = zz0. Начальное рас¬
пределение температуры то же, что в примере 1. Показать,
что в этом случае (по формуле (15.3"))
рассмотреть частный случай решения при х} = 0, х2 — 1 и
приближенно нарисовать графики и при фиксированных зна¬
чениях t >*0.
Пример 3. Показать, что при условиях примера 2, но при
начальном условии zz|/=()=o(x— xt) решение имеет вид
и (.Г, О = иа | 1 — Ф	j +	(*> 0 — ‘t’-x, (А’> О-
§ 16. Некоторые пространственные задачи
теплопроводности
47.	Вывод уравнения теплопроводности в простран¬
ственном случае !). Рассмотрим неравномерно нагретое тело.
Пусть температура в каждой точке (х, у, z) тела в момент
!) Перед чтением этого пункта читателю необходимо вспомнить
теорию поля (векторный анализ). Все необходимые сведения
содержатся в «Кр. к.», гл. VII, п. 106 и 107 и гл. IX, пп. 130—132.

§ 16] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 203
времени t определяется функцией я(х, у, z, t). Физические
предпосылки были подробно рассмотрены в п. 34 при выводе
уравнения линейной теплопроводности. Поэтому мы ограни¬
чимся краткими замечаниями, обратив основное внимание
на те усложнения математической стороны дела, которые
возникают в пространственном случае.
В любой момент времени t функция и определяет ска¬
лярное поле — поле температуры. В общем курсе анализа
обычно ограничиваются изучением стационарных полей,
когда температура и не зависит от времени1). Нам же
сейчас придется рассматривать нестационарное поле, по¬
скольку мы предполагаем, что температура точек тела изме¬
няется со временем. Если зафиксировать момент времени t,
то совокупность точек, в которых температура и(х, у, z, t)
принимает одно и то же значение, образует изотермическую
поверхность (поверхность уровня). В отличие от стацио¬
нарного случая, форма и расположение изотермических
поверхностей с течением времени будут изменяться.
Как известно, направление наибольшей скорости изме¬
нения температуры и совпадает с направлением градиента
функции и(х, у, z, t) при данном значении t. При этом
В точках изотермической поверхности градиент направлен
по нормали к этой
чений и и модуль
направлению:
поверхности в сторону увеличения зна-
градиента равен производной по этому
lsradw!- дп •
Обобщая формулу (12.2), считают, что величина теплового
потока через малый участок Да изотермической поверх¬
ности за время равна
Дф = — йДе Д/,	(16.1)
*) Задачи о стационарных температурных полях приводят
к уравнению Лапласа, которое мы рассматриваем в гл. III.

204
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ (ГЛ. II
где k — коэффициент теплопроводности, который мы считаем
постоянным (см. стр. 146)!).
Обратим особое внимание на роль знака «минус» в фор¬
муле (16.1). Условимся считать величину теплового потока
положительной, если направление потока тепла совпа¬
дает с выбранным направлением нормали, и отрицатель¬
ной, если оно ему противоположно. Для нормали, совпа¬
дающей с направлением градиента, > 0; тепло же пере¬
ходит от более нагретых участков к менее нагретым, т. е.
как раз в противоположную сторону, и, следовательно,
по определению, AQ < 0, что и объясняет знак «минус»
в формуле (16.1). Изменив направление нормали на противо¬
положное, мы получили бы, что < 0; но тогда AQ > О
и опять-таки знак «минус» сохраняется.
В линейном случае изотермическими поверхностями
являются сечения стержня, перпендикулярные оси Ох\ нор¬
маль к ним совпадает с осью Ох, и	(если напра¬
вление нормали совпадает с положительным направлением
оси Ох).
В теории теплопроводности доказывается, что фор¬
мула (16.1) для величины теплового потока справедлива
для любых поверхностей (не только для изотермических).
Производная по направлению нормали к выбранной по¬
верхности равна проекции градиента на эту нормаль, т. е.
скалярному произведению grad и на единичный вектор нор¬
мали п:
ди	.
-^ = gradM'n-
!) Вообще коэффициент k может зависеть от температуры и
координат точки х, у и z (для неоднородного тела). Возможен и
более сложный случай, когда тело обладает свойством тепловой
анизотропии, т. е. когда коэффициент теплопроводности зависит
от направления, в котором происходит передача тепла (например,
для тел с волокнистым строением). Любое из этих предполо¬
жений приводит к значительному усложнению уравнения тепло¬
проводности.

$ 16] ’ ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 205
Поэтому поток тепла через участок Да- любой поверх¬
ности за время будет равен
&Q =— & grad и * пДаД/.	(16.2)
Для краткости назовем вектор — k grad и вектором тепло¬
вого потока и обозначим через А:
А — — k grad и.
Тогда Дф есть поток вектора А через элементарную пло¬
щадку Да за время Д/:
ДQ — Ап Да At
Если теперь выделить в теле
ченную замкнутой поверхностью S,
через эту замкнутую поверх¬
ность за время А? будет равен
произведению потока вектора А
на At
Q = Xf A„da, (16.3)
где Ап — проекция А на внеш¬
нюю нормаль (рис. 60).
Поток Q будет положитель¬
ным, если выбранная часть тела
теряет тепло, и отрицательным,
некоторую часть, ограни-
то поток тепла изнутри
если приобретает.
Применяя к интегралу в формуле (16.3) теорему Гаусса —
Остроградского, запишем, что
5
/ J/divAdti.
где V — часть тела, ограниченная поверхностью S, и
div А = — k div grad и = —	+ ■§■) = — k
. д2и , d2u . d2u
где Ди = -gp- + -^+оператор Лапласа.
Таким образом, количество тепла Qv приобретенное
выделенной частью тела за счет прохождения теплового

206
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
потока, будет
равно (оно противоположно по знаку вели-
чине Q)
<?! = J J* § k budv.	-	(16.4)
V
Предположим, далее, что в теле имеются тепловые
источники, плотность которых характеризуется функцией
F(x, у, zt t) (см. стр. 148). Тогда за промежуток времени
(Z, £-}-Д/) в выбранной части тела выделится тепло Q2»
равное (с точностью до бесконечно малых высшего порядка)
Q2 = М Iff F(x, у, z, t)dv.	(16.5)
v
Общее количество тепла, сообщенного выделенному
объему V, будет равно сумме Qj + Q2- Подсчитаем теперь
это тепло иначе, учитывая изменение температуры в точках
тела, лежащих внутри поверхности S. В точке (х, у, z)
за промежуток времени &t температура изменится на величину
и(х, у, z, / +	— «(*» У» -?>	=
Поэтому элементарному объему Дг/ для такого изменения
температуры потребуется количество тепла, равное ср М,
где с — удельная теплоемкость, р — плотность, а всему
объему — количество
Q3 = btff f c^dv,	(16.6)
V
которое должно быть равно сумме	Следовательно,
f [ f	f I f k&udv-{- f J*У* F(x, y, z, t)dv.
V	V	V
Перенося все слагаемые в левую часть, приходим к равенству
dt
(16.7)

§ 16] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 207
Равенство (16.7) должно соблюдаться для любой части
тела V. Это возможно только тогда, когда в каждой точке
внутри тела
сР^~ kAu — F = 0.	(16.8)
Это заключение справедливо, когда все слагаемые в левой
части равенства (16.8) — непрерывные функции. Действительно,
если предположить, что в точке М (х, yt z) равенство (16.8) нару¬
шается, т. е., например,	— /г Ди—	>0, то в силу непре¬
рывности это же неравенство будет соблюдаться и в некоторой
области Q, окружающей точку М. Но тогда интеграл по этой
области, вопреки условию (16.7), был бы величиной положительной.
Подобное же рассуждение неоднократно встречалось в курсе ана¬
лиза (см., например, «Кр. к.», стр. 437).
Переписав -равенство (16.8) в виде
т=“!4“+4-л	(16-9)
получим основное уравнение теплопроводности (а =
	коэффициент температуропроводности). Если
тепловые источники внутри тела отсутствуют, то F = 0
и уравнение становится однородным:
du 9А	9/d2u	. д2и . д2и\
— = = + (16.10)
Еще раз отметим, что уравнения (16.9) и (16.10) выве¬
дены в предположении, что все физические величины, характе¬
ризующие свойства тела (плотность, удельная теплоемкость,
коэффициент теплопроводности), постоянны.
Ясно, что уравнение (12.4) линейной теплопроводности
является частным случаем уравнения (16.10).
48.	Начальное и краевые условия. Перейдем теперь
к начальному и краевым условиям. Начальное
условие для уравнения теплопроводности состоит в задании
температуры во всех точках тела в некоторый данный момент,
от которого ведется отсчет времени. В этот начальный момент
поэтому полагают £ = 0, так что начальное условие прини¬
мает вид
и(_х, у, Z, 0) = «[<=0 = /(х, у, Z),
(16.11)

208 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. п
где /(х, у, z) — данная функция» определенная и непрерыв¬
ная во всех точках тела.
Краевое условие должно выполняться на поверхности Г,
ограничивающей тело. Вдоль Г тело граничит с окружающей
средой, имеющей в каждой точке	С границы Г свою
температуру и = и ($, tj, С. /). Разность и (5, tj, С, /)■—«($, tq, Ц t)
между температурой тела в точке границы и температурой
окружающей среды в этой точке называется перепадом
температур в точке tq, С границы. Существует физиче¬
ский закон, устанавливающий, что поток тепла изнутри,
тела через любую часть поверхности Г пропорциона¬
лен перепаду температур на этой части границы.
Если выделить некоторую часть границы, то поток тепла
через нее за время ДГ будет равен
Д/ If h(u — и) da,
г»
где Гт — рассматриваемая часть границы Г, a h — коэффи¬
циент теплообмена, зависящий от физических свойств тела
и окружающей среды. Вообще говоря, h может изменяться
от точки к точке границы, т. е. /г = /г(£, tq, С), но в случае
однородности тела и среды h = const. Поскольку поток
тепла, уходящий в окружающее пространство, должен рав¬
няться потоку тепла, подходящему изнутри, то, применяя
формулу (16.3) к участку Гр получим
J* Anda —§ j*/г(и — и) da,
г,	г.
Так как Г* — любая часть границы, то, повторяя рассужде¬
ния, обосновывающие равенство (16.8), придем к условию
на границе Г:
Ап = й(и — и).
Вспоминая, что Ап=—k grad и • п=—где -^-—произ¬
водная и в точке границы по направлению внешней нормали
к ней, запишем последнее равенство так:
- AS-|r=4“ir-«]•
(16.12)

§ 16] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 209
Здесь черта подстановки |г означает, что имеется в виду
значение соответствующей величины в точке границы Г.
Общее краевое условие (16.12) может в частных случаях
иметь более простой вид.
Первый частный случай h = 0. Это означает, что переход
тепла через границу тела исключен, т. е. что, как говорят,
граница тела теплоизолирована. В этом случае крае¬
вое условие принимает вид
£|г = 0.	(16.13)
Второй случай соответствует очень большому коэффи¬
циенту внешней теплопроводности /г. Тогда условие (16.12),
записанное в виде
в пределе при h —>оо приводит к равенству
я|г=£,	(16.14)
выражающему тот факт, что на границе тело имеет темпера¬
туру внешней среды.
Следует отметить, что разные части границы тела могут
находиться в задачах теплопроводности в разных условиях,
выраженных разными значениями h. Так, например, одна
часть границы может быть теплоизолирована, а на другой
температура тела может совпадать с температурой окру¬
жающей среды.
Подводя итоги, мы можем следующим образом сформули¬
ровать математическую задачу теплопроводности (для одно¬
родного тела без тепловых источников): ищется температура
и — и(х, у, z, t) внутри тела, удовлетворяющая там уравне¬
нию (16.10), начальному условию (16.11) и краевому усло¬
вию (16.12) (или условиям (16.13) или (16.14)). В теории
дифференциальных уравнений в частных производных показы¬
вается, что эта задача имеет одно и только одно решение
[при некоторых достаточно общих требованиях к заданным
функциям f и и, следующих из условий (16.11) и (16.12)].
Перейдем теперь к решению этой задачи для простейших
случаев.
14 И. Г. Араманович, В. И. Левин

210 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
49.	Распространение тепла в однородном цилиндре1).
Пусть боковая поверхность бесконечного круглого цилиндра
радиуса /? поддерживается при постоянной температуре. Если
в начальный момент времени температура в каждой точке
зависит только от ее расстояния г до оси цилиндра, то ясно,
что и в последующем температура а будет зависеть лишь от г
и времени t. Тепловой поток при этом всегда направлен
по радиусам цилиндра. Таким образом, и —и (г, £).
Преобразуем общее уравнение теплопроводности (16.10)
ди	9 А
-vy- = а2&и
dt
(а — коэффициент температуропроводности) к цилин¬
дрическим координатам, учитывая, что функция и не зависит
от ср и z. Придем к уравнению радиального распростра¬
нения тепла в цилиндре*.
ди 9/ д2и .	1 ди \	/1 с 1
Начальное условие имеет вид
f/|/=o = cp(r),	(16.16)
где ср (г) — заданная функция в интервале
Краевым условием будет условие постоянства температуры
боковой поверхности цилиндра
ы !,=/?= “о-	(16.17)
Будем считать, что но = О, т. е. что краевое усло¬
вие (16.3) однородное. В противном случае нужно ввести
новую функцию u(r, t) = u(r, t) — и^. Уравнение (16.15)
не изменится, а начальное и краевое условия примут вид
«|<=о = '?(г) — «о и	«1г=я = 0-
Применим к решению задачи метод Фурье. Полагая
и (rt t) = U (г) Т (t), разделим переменные:
т-т __
a2?(t)~ U (г)
!) Перед чтением этого пункта рекомендуем вспомнить содер¬
жание § 10, касающегося уравнения и функций Бесселя.

$ 16) ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 211
(Соображения, в силу которых постоянная в правой части
не может быть положительной, приведены при решении
задачи о конечном стержне.) Отсюда
T(t) = Ce-)^t.
Для функции U (г) получаем уже знакомое нам уравнение
(см. п. 30):
U" (г) +1 U' (г) 4- KU (г) = 0,	(1.6.18)
одно частное решение которого выражается через функцию
Бесселя нулевого порядка:
U(r) = J0(lr).
Второе линейно независимое решение уравнения (16.18) —
функцию Неймана NQ — мы не принимаем в расчет, так как
она обращается в бесконечность при г = 0.
Чтобы решение удовлетворяло однородному краевому
условию, нужно положить
уо(Х/?) = О.	(16.19)
Таким образом, собственными числами задачи являются
величины = где |хй — корни функции Бесселя нуле¬
вого порядка. Каждому собственному числу соответ¬
ствует собственная функция
uk(r, t) = e~'ka ‘j0^.kr).
Образуем теперь функцию
«(Г,	(16.20)
Л=1
и подберем коэффициенты Ck так, чтобы
оо	оо
« |/=о = 2 М = 2 CkJ0 (^) = ф (г).
й=1	Л=1
Полагая r — Rx, придадим последнему равенству вид
со
2 CkJQ <РН) = <Р ('’*)»
к= 1
14*

212 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
после чего, основываясь на условиях ортогональности функ¬
ций /0(Хлг), выраженных формулами (10.11), найдем коэф¬
фициенты Ck*.
1
Сй = ~7Г— f xJ0(y.kx)<?(x)dx.	(16.21)
4) (^/г) 6
Напомним еще, что J'2 (у.^) — J\ (р^) (см. формулу (10.16)
п. 31).
Вычисляя коэффициенты Ck по формулам (16.21) и под¬
ставляя в ряд (16.20), мы и завершим решение задачи1).
Почти так же решается задача в случае теплоизоля¬
ции боковой поверхности цилиндра»
Краевое условие запишется теперь в виде
S-|^s = 0	(16.22)
(нормаль к боковой поверхности цилиндра направлена по
радиусу).
Для определения собственных чисел взамен уравне¬
ния (16.19) мы получим уравнение Jo — 0 или, согласно
формуле (10.16),
J1(X/?) = O.	(16.23)
Таким образом, собственными числами являются величины
\k =	, где — нули функции Бесселя первого порядка
(см. п. 31).
Собственные функции uk(x, f) — е
отличаются от собственных функций предыдущей задачи
(постоянство температуры на поверхности цилиндра) только
тем, что в аргумент функции Бесселя входят множителями
корни не самой функции J0(x), а корни функции Jx(x).
Ряд (16.20) запишется теперь в виде
00 2 2
«(х. O =	(16.24)
Л=1
!) Решение почти полностью повторяет решение задачи о коле¬
баниях круглой мембраны, разобранное в п, 32.

§ 16] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 213
и, чтобы удовлетворялось начальное условие (16.16), должно
соблюдаться равенство
оо
2CftJ0(vftx) = ?(/?x),	(16.25)
где х = -~.
Оказывается, что функции JQ(ykx) в интервале [О, 1]
удовлетворяют такому же условию ортогональности, что
и функции J0(|a^x). Это следует из формулы (10.12) п. 30.
Напомним» что, согласно этой формуле и примечанию к фор¬
муле (10.13), для любых чисел р и q
p2 — q2
1
f . z ч , z ч	PWW
J xJQ(px) JQ(qx) dx =
6
Отсюда сразу следует, что при p — vk и q = vn, где
правая часть обращается в нуль, так как Jq (yk) = Ji (^) = 0
и */о(^л) = О. Если же k = ti, то, полагая p = vk и переходя
по правилу Лопиталя к пределу при q->vk, получим
/‘ хЛ М dx = lim	= _	,
о	Ч-Я
Из уравнения Бесселя Jq (х) +	«/о (аг) + Jq (х) = 0 и условия
Л(Ук) = ® следует, что Jo (v*) = — Jo(^). Поэтому
i
f хЛ O'ax) dx = -i- л (Ун)-
о
Воспользовавшись этим соотношением, сразу получим, что
коэффициенты Ck в формуле (16.25) равны
1
= ,2.2	/ xjo(vftx)<p(/?x)rfx.
•'оО'а) о
Подставляя найденные значения Ck в ряд (16.24), завер¬
шим решение задачи.

214 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ, II
Общий случай краевых условий 1	+ Л«1г=^ = 0 может
быть рассмотрен точно так же, однако уравнение для отыскания
собственных чисел приобретает более сложный вид: Мо (XT?) -j-
4- hJQ (KR) = 0. Решение этого уравнения и доказательство орто¬
гональности' получающихся собственных функций требуют более
детального знакомства с теорией бесселевых функций; мы этим
заниматься не будем.
50.	Распространение тепла в однородном шаре. В ка¬
честве второй пространственной задачи рассмотрим радиаль¬
ное распространение тепла в однородном шаре ра¬
диуса R. Мы предполагаем, что как в начальный, так и
в произвольный момент времени температура одна и та же
во всех точках, находящихся на одинаковом расстоянии г
от центра шара. Если ввести сферические координаты, то это
означает, что температура зависит только от г и t. Переходя
в общем уравнении (16.10) к сферическим координатам,
получим (см. п. 3 введения)
<1626>
Начальное и краевое условия примем такими же, как
в задаче о цилиндре:
«Uo = <?(r)>	= °	(16.27)
(как уже отмечалось, неоднородность краевого условия
u\r=R—uQ легко устраняется введением вспомогательной
функции).
При решении нам даже не понадобится заново применять
метод Фурье. Введем новую неизвестную функцию
v(r, f) = ru(r, f).	(16.28)
Тогда
dv 	 ди dv 	 ди	f	d2v 	 d2u	(	0 du
dt	Г dt	' dr	Г dr	*	dr2	Г dr2	' dr
Уравнение (16.26) преобразуется при этом к виду
dv 9 d2v
Начальное условие примет вид
Ч=о = '■'?('•).
(16.29)

§ 16] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ 215
а краевое останется без изменения:
1г = /? = 0-
Кроме того, появится новое условие
П=о = 0.
В результате мы пришли к задаче о теплопроводности
в конечном стержне длины /?, на концах которого поддер¬
живается температура, равная нулю, а начальное распределе¬
ние температур задается функцией v |/=0 = гу(г). Эта задача
уже решена в п. 42 (задача Б).
Согласно формуле (14.17Б) ее решение имеет вид
00	п2к2а2(
v(r, — рле R2 sin ,	(16.30)
Л=1
где коэффициенты определяются по формулам (14.18Б),
в которых функцию j\(x) надо заменить на хср(х):
/г
О
Чтобы вернуться к функции я (г, /), надо найденную функ¬
цию v (г, t) разделить на г:
. ~пг
п2^аЧ sin
* —г—	(16.31)
п = 1
Из формулы (16.31) получается, что температура в центре
шара (г = 0) будет для любого t > 0 равна
00	пЫаЧ
и(0, j‘) = liin«(r, О = У РУ я*
г^° «=1 *
Если на поверхности шара задано общее краевое условие
(однородное)
ди I
‘зг|г=я
+ ,2“ 1г = /? = 0,

216
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
то для вспомогательной функции v оно преобразуется в следующее:
71 dv
\r dr
или
dv I
1г=Я
= 0.
При этом вновь добавляется условие ^|г=о = О’
Решение задачи с такими краевыми условиями приведено
в п. 43, и мы его повторять не будем. Отметим только, что урав¬
нение (14.9) для определения собственных чисел принимает более
простой вид:
tgX/?= \ —hR
(это соответствует случаю hQ = oo, k = 1, hi~h— -i-
§ 17. Задачи диффузии
51. Уравнение диффузии. В процессе диффузии иско¬
мой функцией является концентрация диффундирующего
вещества, которую обычно обозначают через с=с(х, у, z, /).
Этот процесс во многом схож с распространением тепла,
и в предположениях, аналогичных тем, которые мы делали
в § 16 при выводе уравнения теплопроводности, функция
с(х, у, z, t) удовлетворяет уравнению
(17.1)
тождественному с уравнением теплопроводности (16.10). По¬
ложительный коэффициент D называется коэффициентом
диффузии. Он играет роль коэффициента а2 в теории те¬
плопроводности. Начальное условие
=	(17.2)
задает начальную концентрацию. В качестве краевых усло¬
вий рассматриваются главным образом условия
£|г=°
и
с|г = 0,
(17.3")

§17]
ЗАДАЧИ ДИФФУЗИИ
217
где Г — граница области, в которой происходит диффузия.
Условие (17.3') означает, что Г является непроницаемой
для диффундирующего вещества стенкой, а условие
(17.3") задает концентрацию на границе Г.
Линейные задачи диффузии в тонкой трубке с непро¬
ницаемой стенкой:
дс	п д2с
~dt~U дх2 *
с|,=0 = /(х)
и на конце или на концах ду = 0 или с —с, решаются при
помощи методов, изложенных в §§ 13, 14 и 15. В соответ¬
ствующих формулах следует только и заменить на с и а
на УЪ.
В большинстве практически интересных задач коэффи¬
циент D является переменным. Это приводит к дальней¬
шему усложнению задачи. Мы рассмотрим три наиболее
часто встречающихся случая переменного коэффициента диф¬
фузии для линейных задач.
I. В первую очередь D зависит от температуры. По¬
скольку температура в условия задачи явно не входит, но
закон зависимости температуры от времени, как правило,
известен, то коэффициент диффузии может рассматриваться
как функция времени: D — D(t). Уравнение диффузии ста¬
новится уже уравнением с переменным коэффициентом:
дс
~dt
— D(t)
д2^
дх2 *
(17.4)
Однако это уравнение легко привести к более простому
виду, введя вместо независимой переменной t новую пере¬
менную:
t
& = f D(x)dn.
О
Так как D > 0, то & = &(0 монотонно возрастает с t (а при
/ = 0 также и & = 0). Поэтому существует однозначная
обратная функция t = /(&), так что концентрацию с можно
считать функцией х и Но
дс		 дс
dt~ dfr dt ~ dti

218
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. II
(так как -^- = £)(f)j.
простой вид:
Поэтому уравнение (17.4) принимает
дс	 д2с
~д§ ~~ Sx2 '
т. е. вид уравнения теплопроводности с а2=1. Начальное
условье не меняется: с|$=0 = /(х), краевое условие также
остается прежним.
II.	Если отвлечься от изменения коэффициента диффузии
со временем (например, если процесс диффузии происходит
при постоянной температуре), то D не обязан все же быть
постоянным. Процесс диффузии может происходить в неод¬
нородной среде, и тогда D будет зависеть от х: D = D(x).
Уравнение
значительно сложнее уравнения (17.4), так как в него вхо¬
дит вторая производная искомой функции по переменной х,
от которой зависит коэффициент D. Уравнение (17.5) уже
не может быть сведено к уравнению с постоянным коэффи¬
циентом, его приходится решать приближенно. Одним из
простых методов приближенного решения является замена
D (х) к у с о ч н о-п остоянной функцией. Для этого интер¬
вал изменения х (всю ось, конечный интервал или полуось)
разбивают на частичные интервалы (xk_v xk) и в каждом
частичном интервале считают D постоянным: D = Dk (в ка¬
честве Dk можно взять значение D(x) в любой точке
частичного интервала: Dk = D (£ft)). В каждом частичном
интервале задача решается методами §§ 13—15 с краевыми
условиями «склеивания» решения: если xk — точка деления
(граница двух соседних частичных интервалов), то в ней
концентрация с должна быть непрерывной.
Практически важным является и несколько более простой
случай, когда диффузия проходит через конечное число
сред с разными коэффициентами диффузии (т. е. через
кусочно-однородную среду); задачи подобного рода при¬
ведены в п. 53.
III.	При достаточно больших концентрациях коэффициент
диффузии зависит от самой концентрации: D—-D (с). Соот-

17]
ЗАДАЧИ ДИФФУЗИИ
219
ветствующее уравнение
дс
~dt
будет уже нелинейным и может быть решено только при¬
ближенно специальными методами.
52. Уравнения теплопроводности и диффузии с краевым
условием, зависящим от времени. До сих пор, рассматривая за¬
дачи теплопроводности с краевыми условиями для полубесконеч-
ного или конечного стержня, мы ограничивались случаями, когда
температура внешней среды и была постоянной (см. стр. 174
и 197). Однако во многих важных задачах диффузии для кусочно¬
однородных сред приходится иметь дело и с такими краевыми
условиями, когда концентрация вещества на границе (в терминах
теплопроводности — температура конца стержня) является некото¬
рой заданной функцией времени. Сейчас мы рассмотрим такую за¬
дачу, ограничиваясь случаем полубесконечной трубки (стержня).
Имея в виду последующие примеры, будем считать, что трубка
занимает интервал Z < х < оо, где />0. Соответствующая задача
формулируется так:
Найти решение уравнения диффузии (теплопроводности)
дс п д2с
~дГ	~дх2'
(17.6)
удовлетворяющее начальному условию
Н/=о = °	С*>0
(17.7)
и краевому условию
С|Х=/ = ?(О	(/>0),
(17.8)
где ?(/)-> 0 при t -> 0.
Это — более сложная задача, чем те, которые решались нами
в §§ 14 и 15, так как краевое условие неоднородно и непо¬
стоянно.
Для того чтобы ее решить, необходимо в первую очередь за¬
менить краевое условие (17.8) однородным путем введения
новой искомой функций
g (х, t) = C (X, t) — <Р (/).
(17.9)
Тогда для g (х, t) уравнение (17.6) примет вид
dg _ п d2g	dt?
dt	дх2	dt ’
(17.10)
начальное условие (17.7) сведется к
1/=о
(Х>0
(17.11)

220 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ, и
(поскольку ? (/) = 0 при t = 0), а краевое условие (17.8) — к
*lx=Z = °-	(17.12)
Таким образом, мы заменили однородное уравнение (17.6) с неод¬
нородным краевым условием (17.8) неоднородным уравнением
(17.10) с однородным краевым условием (17.12).
Рассмотрим теперь выражение
t
Ох (О dx,
о
называемое сверткой функций ф и у. Чтобы найти производную
свертки по /, воспользуемся правилом Лейбница (для диф¬
ференцирования интеграла от функции, зависящей от параметра,
при условии, что пределы интегрирования также являются функ¬
циями этого параметра):
*(0	b(t)
4- J f	оdz = / (*> оъ' ю	о а' <0 + f dx-
a\t)	a\t)
Частным случаем этого правила, когда а и b не зависят от /. яв¬
ляется теорема, упомянутая в п. 2 введения. Производная свертки
будет равна
t	t
± f ф(<-г)Х(О Л = ф(0)Х(О + / Ф'	dx.
6 , 6
Воспользуемся этой формулой, взяв в качестве ф любое реше¬
ние Ci (х, t) однородного уравнения (17.6) и положив
Тогда
t
J Cj (х, t — т) Х (т) dx = gt (х, t).
О
(17ЛЗ)
так что
дсх (х, t — т)
д2сх (х, t — т)
дх2
I X СО dx.
D

ЗАДАЧИ ДИФФУЗИИ
221
Поскольку функций Cj (х, t) выбрана так, что она является реше¬
нием уравнения (17.6), то подынтегральное выражение равно нулю
при любом значении t > т и, следовательно,
dgi
dt
__
дх2
Ci (х, О)х(0.
(17.14)
Пусть теперь функция (х, t) удовлетворяет начальному условию
(х, 0) = — 1 (х > Z)	(17.15)
и краевому условию
Cj(Z, 0 = 0	(/>0).	(17.16)
Функция С[ (х, 0, как решение уравнения (17.6) при условиях
il7«15) и (17.16), может быть найдена из решения примера 2 п. 46.
[ля этого надо в формуле (15.8) положить
а2 = D, wo = O, uQ =—1,	Xi=0, х2 = оэ
Г
и заменить х на х — I. Мы получим (рекомендуем читателю всё
выкладки провести самостоятельно)
=	(х>/Л>0),
где Ф (х) — интеграл вероятностей. Легко проверить, что при х > I
и Z->0 функция q(x, 0->—1, а при Z>0 и x = Z функция
Cj(Z, 0 = 0. Именно так следует понимать начальное и краевое
условия. Тогда функция gx (х, 0, определенная формулой (17.13),
примет вид
t
Согласно равенству (17.14) и условию (17.15) она является реше¬
нием уравнения
дх*
~Х(0.
а согласно (17.13) и (17.16) удовлетворяет условиям
^|/=0=0, ^|х=/ = 0.
Остается только положить

222
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ [ГЛ. п
и задача решена. Окончательно функция g (х, t), удовлетворяющая
неоднородному уравнению (17.10) и условиям (.17.11) и (17.12), будет
иметь вид
t
о
или, после интегрирования по частям,
t
10
Так как <р (0) = 0, Ф (оо) = 1 (получается при х > I и z = t) и
Х-1
2VD (/-?)
X — I
(Х-1У
0
е 4D ,
то
2/тсО (/ — т)г/2
(x-Z)2
Согласно формуле (17.9) окончательное решение поставленной за¬
дачи будет
(17.17)
Тот факт, что функция с (х, t) удовлетворяет начальному и крае¬
вому условиям, следует понимать так: при х>1 и Z_>0 функция
с(х, 0->О, а при />0 и х->1 функция с (х, t) -> с (Z, /) = ? (О-
Проверка последнего условия наиболее важна, так как на первый
взгляд из формулы (17.17) следует, что при х — 1 функция с(/, t)
равна нулю благодаря множителю перед интегралом. На самом же
деле при х = I интеграл становится расходящимся; это осо¬
бенно ясно видно, если <рСО = с^=0. Действительно,

!§ 17]
ЗАДАЧИ ДИФФУЗИИ
223
2 I*
. ■ г	 • и при т = t правая часть обращается в оо. Таким
Vt — ' to
образом, просто подставлять значение х = 1 в формулу (17.17)
нельзя. Чтобы все-таки проверить требуемое условие, преобразуем
эту формулу, произведя замену переменной (как это уже неодно¬
кратно делалось раньше):
. _Л~1 ■ =,	= T = z-.(x~/)2t
— t) ’	4^D (t —’	4Dz2
Тогда
oo
r x—l
2VDt
Теперь видно, что при х = I и t > О
оо
V 71 о
(здесь мы воспользовались значением интеграла Пуассона).
53. Примеры. Пример 1. В тонкой бесконечной непроницае¬
мой трубке находятся две среды: 1) х < Z (Z > 0) с коэффициентом
диффузии D{ и 2) х > I с коэффициентом диффузии D2. В момент
t = 0 в трубку при х = 0, вводится («вспрыскивается») «погонная
единица» диффундирующего вещества (т. е. такое количество, кото¬
рое при равномерном распределении по единице длины трубки дает
концентрацию, равную единице !)). Тогда в среде 1, т. е. для х < Z,
решением будет фундаментальное решение
X2
?0 (Х, t) =	Л е 4Dlt = ct (х, t).
Чтобы найти решение в среде 2, мы должны для отрезка трубки
х > I поставить следующую задачу: найти решение уравнения диф¬
фузии
_ п д2с2
dt 2 дх2 ’
удовлетворяющее начальному условию
!) Можно сказать, что начальным условием является с |/=0 = & (*),
где & (х) — импульсная функция Дирака (см. стр. 164).

224 УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ И ДИФФУЗИИ 1ГЛ. п
и краевому условию (условию «склеивания»)
= c,(Z, t).
Это в точности та задача, которая была нами решена в п. 52. По
формуле (17.17)
c2(x,t)=-x~L f е~4О>('~х) dx,
J (f-x)3'2
где
c, (/, 0 =
	i2
1 „
2 J/tcDjT
При фактическом отыскании функции с2 (•*, 0 возникают серьезные
затруднения, связанные с необходимостью численно вычислять не¬
собственные интегралы.
Пример 2. В полубесконечной (непроницаемой) тонкой трубке
х > 0 конец х = 0 закрыт непроницаемой перегородкой. В отрезке
О < х < I имеется постоянная концентрация с0 в среде с коэффи¬
циентом диффузии В отрезке трубки х > I диффундирующего
вещества нет (концентрация равна нулю); этот отрезок заполнен
средой с коэффициентом диффузии D2. При х = I находится непро¬
ницаемая перегородка, которая в момент / = 0 удаляется. С этого
момента начинается процесс диффузии, в течение которого надо
определить концентрацию с (х, t) (х > 0).
Для участка трубки 0 < х < Z решение совпадает (с соответ¬
ствующими изменениями) с решением примера 1 п. 46. Заменяя
в формуле (15.5) на с0 и а на УDlf получим
При х = I концентрация будет равна
и это значение служит (в силу условия «склеивания») краевым
условием для концентрации с2 (х, t) на отрезке х > Z. Таким обра¬
зом, мы должны решить для с2 следующую задачу:
<Эс2	д2с2
~~dF Ui~dx2'
«»|<=о = 0 (х>1).

§ 17]
ЗАДАЧИ ДИФФУЗИИ
225
Эта задача совпадает с задачей п. 52 при
Решение дается, как мы видели, формулой (17.17), т. е.
с2 (х, /)
‘ ф ( 1— 'j
= Со(х —Z) /	£>,/ ] с	dx
(*>/).

ГЛАВА III
УРАВНЕНИЕ ЛАПЛАСА
§ 18. Краевые задачи для уравнения Лапласа.
Метод функции Грина
54. Постановка краевых задач. У равнением Лапласа
называется уравнение
Aw = 0,	(18.1)
где Azz— лапласиан, имеющий в декартовых, цилиндрических
и сферических координатах соответственно следующий вид
(см. введение, п. 3):
(18.2х)
.	1 д2и
' г2 sin2 0 ду2
(18.2")
(18.2)
Уравнение Лапласа играет важную роль в приложениях.
Например, ему должно удовлетворять всякое стационар¬
ное распределение температуры в теле (см. § 12). Действи¬
тельно, если температура и = и(х, у, z, t) не зависит от Л
то -^ = 0 и уравнение теплопроводности (12.10) сводится
к уравнению Лапласа (18.1)1). Применение уравнения Лапласа
выходит далеко за рамки вопроса стационарного распреде¬
ления температуры. Однако при изучении этого уравнения
9 Уравнению Лапласа удовлетворяет также потенциал стацио¬
нарного электрического поля во всякой области, где отсутствуют
заряды.

§ 18]
КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
227
представление функции и как температуры очень удобно и
наглядно.
Функции, удовлетворяющие уравнению Лапласа, назы¬
ваются гармоническими, В каждой задаче» связанной с урав¬
нением Лапласа, искомое решение выделяется из множества
всех гармонических функций определенным дополнительным
условием, которое чаще всего является краевым. Если
обратиться к «тепловой» иллюстрации, то общим, краевым
условием является условие (16.12) п. 48. Таким образом,
возникает следующая краевая задача: в области про¬
странства, ограниченной замкнутой поверхностью Г,
ищется гармоническая функция и(х, у, z), удовле¬
творяющая на границе Г краевому условию (п — напра¬
вление внешней нормали к Г)
где Н и и — функции, заданные на границе Г. В задаче ста-
ционарного распределения температуры п— — и—тем¬
пература внешней среды на границе тела.
Наиболее важным является частный случай /7 = 0 этой
краевой задачи, соответствующий случаю /г = оо, т. е. зада¬
нию температуры границы тела: и |г = и. Эта краевая задача
называется задачей Дирихле.
Задача Дирихле в пространстве формули¬
руется так:
Найти функцию и(х, у, z), удовлетворяющую внутри
замкнутой поверхности Г уравнению Лапласа Azz = O
и принимающую на границе Г заданные значения'.
и]Т = и.	(18.3)
То, что задача Дирихле всегда имеет решение (при не¬
которых весьма общих предположениях относительно Г и zz),
можно считать очевидным по физическим соображениям. Дей¬
ствительно, если каждая точка границы тела постоянно под¬
держивается при определенной температуре (которая может
быть разной в разных точках границы), то в каждой точке
тела установится в конце концов своя температура, кото¬
рая и дает решение задачи Дирихле при данных граничных
15*

228
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
значениях. Кроме того, очевидно, что по тем же соображе¬
ниям это решение будет единственным.
Задача Дирихле может, конечно, интерпретироваться также и
в терминах диффузии: ее решением будет стационарная концен¬
трация (см. § 17) при условии, что концентрация на границе известна.
Задача Дирихле может быть поставлена и в д в у х изме¬
рениях. Если и зависит только от двух пространственных
координат, например х и у (или только от г и ср в поляр¬
ной системе координат), то уравнение Лапласа (18.2) или
(18.2') принимает более простой вид:
д2и . д2и а	/юоч
= 0	<18-2а>
или
Задача Дирихле на плоскости формулируется так:
Найти функцию и(х, у), удовлетворяющую внутри
замкнутой кривой Г уравнению Лапласа &и = 0 и при¬
нимающую на границе Г заданные значения'.
и\Т = и.	(18.3а)
Эта задача тоже имеет единственное решение. Она может
возникнуть в физических задачах двух типов, которые мы
разъясним опять на примере тела, распределение темпера¬
туры в котором стационарно. Первый тип задачи относится
к стационарному распределению температуры в тонкой одно¬
родной пластинке, параллельной плоскости хОу с теплоизо¬
лированными нижней и верхней поверхностями. Край пла¬
стинки Г поддерживается при определенной температуре и.
Пластинка должна быть настолько тонкой, чтобы можно было
пренебречь изменениями температуры по ее толщине. Тогда
температура и будет функцией только х и у.
Второй тип задачи возникает при рассмотрении стацио¬
нарного распределения температуры в бесконечном однород¬
ном цилиндре, у которого образующие параллельны оси г,
направляющая Г лежит в плоскости хОу, а боковая поверх¬
ность поддерживается при определенной температуре и (см.
п. 49). Здесь и тоже остается постоянной на любой прямой, па¬
раллельной оси г, проходящей в цилиндре, так что и=и (х, у).

§ 18] КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	229
Заметим, что задача Дирихле решается очень просто
в одномерном случае, т. е. когда в соответствующей
системе координат неизвестная функция и зависит только от
одной из координат.
В случае декартовых координат одномерное уравнение
„	d2u А
Лапласа принимает вид — О и его решениями являются
линейные функции и = Ах-]- В (стационарное распределение
температуры в тонком стержне с теплоизолированной боко¬
вой поверхностью всегда линейно). Задача Дирихле имеет
в этом случае решение и — —х 4~ где г/о — w L=o»
ai = и lx=z-
В случае задач с осевой симметрией запишем урав¬
нение Лапласа в цилиндрических координатах (18.2'), считая,
что и не зависит от ср и z\
Отсюда г= А и и = А\пг-\-В, где А и В — произволь¬
ные постоянные. Задача Дирихле и \г=а = иа, и \г=ь — иь имеет,
как это легко проверить, решение
" = [(и“ ~ Иг>) 1п г 1п а ~ “в 1П
,пт
= «а + («й —«а)—Х--
In—
а
Эта формула дает решение задачи о стационарном распреде¬
лении тепла в пространстве между двумя цилиндрами с общей
осью при условии, что на поверхностях цилиндров поддер¬
живается постоянная температура1). (Ясно, что если иа — иъ,
то и^иа.) Заметим, что полученное решение теряет смысл
при г — 0.
Наконец, если гармоническая функция и зависит только
от расстояния точки до начала координат, то, воспользовав-
*) Можно также сказать, что и — потенциал электростатиче¬
ского поля в цилиндрическом конденсаторе, на обкладках которого
потенциалы соответственно равны иа и

230	УРАВНЕНИЕ ЛАПЛАСА	[ГЛ. ПГ
шись сферическими координатами (см. (18.2")), получим
уравнение
9 du л du А	А . о гт
откуда г* 2—=	= — и « =	—+ ^. Поставив за¬
дачу Дирихле u\r=a—ua, и\г=ь~иь, найдем стационарное
распределение температуры в сферическом слоеJ) а г Ь'.
_L _ JL
u = tta + {ub — Ua} п	г
b а
(и здесь решение не имеет смысла при г — 0).
Трехмерные и двумерные задачи Дирихле могут быть
точно решены только для сравнительно простых областей
(приближенные методы решения мы не рассматриваем). Мы
сейчас изложим основы общего метода решения задачи Ди¬
рихле, называемого методом функции Грина2).
55. Метод функции Грина для задачи Дирихле (трех¬
мерный случай). Метод функции Грина базируется на фор¬
муле Грина, являющейся следствием формулы Остроград¬
ского— Гаусса (см. «Кр. к.», п. 130):
Anda = fff divAdv,	(18.4)
5	v
где S — граница области Vt n = cos aicos [Уcos 7k—
единичный вектор внешней нормали к S, Лл = Ап — проек¬
ция вектора А на направление п.
Пусть и=и(х, у, z) и <о = <о(Х' у, z) — две любые
дважды дифференцируемые функции и
А = и grad v — v grad и.
Тогда
= (я grad — ^grad7z)n= и grad v • n — v grad и • n.
*) и является также потенциалом электростатического поля
в шаровом конденсаторе.
2) Если читатель интересуется только применением метода
Фурье, то он может прямо перейти к чтению § 21.

§ 18]
КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
231
Поскольку скалярное произведение градиента функции на
единичный вектор равно производной функции по направле¬
нию этого вектора, то
.	dv	,	ди
grade-11 = -^, grada-n = ^-.
Поэтому выражение для Ап примет вид
Ап = и
dv
~дп
Перейдем теперь к вычислению di*vA:
div А = div (и grad v—v grad u) = div (u grad -u) — div (vgrad tt).
Преобразуем каждое из выражений в правой части:
div(Mgradu) = div[a-^-i + K-^-j4-w-^- k) =
d2v .	d2v	. d2v \ .	du dv	.	du dv	,	du
dx2 ‘	dy2	* dz2 / *	dx dx	'	dy dy	'	dz
dv
~dz
= и М/ grad u * grad v
и аналогично
div (v grad u) = v Azz + grad v • grad u.
Поэтому
div A = u&v — v hu.
Подставляя выражения для An и div А через и и v в фор¬
мулу (18.4), получим формулу Грина
§(u^—v^)dc = ff J\uto-v&u)dv. (18.5)
5	V
Нам понадобится, однако, обобщение этой формулы на
тот случай, когда область ограничена не одной, а двумя
поверхностями. Пусть область W ограничена снаружи
замкнутой поверхностью S и изнутри замкнутой поверх¬
ностью лежащей целиком внутри S (так что W— это
часть внутренности S, внешняя относительно Sj). Тогда фор¬
мула Остроградского — Гаусса (18.4) запишется в виде
АПг de 4~ Ап de == ш div Atfv,
5	vz

232
• УРАВНЕНИЕ ЛАПЛАСА
(ГЛ. иг
где tij — единичный вектор внешней нормали к SP т. е. век¬
тор, направленный внутрь (внутренность Sj не принад¬
лежит W и поэтому является областью, внешней относи¬
тельно W). Соответственно формула Грина (18.5) примет вид
(и Дг/ — v&u) dv. (18.6)
w
Эта формула и служит основой метода функции Грина реше¬
ния задачи Дирихле в пространстве.
Введем теперь определение самой функции Грина для
трехмерного случая. В качестве поверхности S возьмем гра-
Рис. 61.
точку области 2, отличную
между точками А и Р\
ницу Г области 2, для которой
мы решаем задачу Дирихле,
и выберем внутри Г произволь¬
ную, но фиксированную точку
Д(х0; у0; ^0), которую окру¬
жим сферой радиуса е >0
с центром в А. При этом
мы предположим, что сфера
целиком лежит внутри Г (рис.
61). Тогда между «Sj и Г мы
имеем область UZ. Обозначим,
далее, через Р(х, у, z) любую
от Л, и через гАР — расстояние
г АР = V (X — х0)2 + (У — Уо)2 Н- (2 — *о)2-
Легко проверить, что функция
1
W =

ГАР
является гармонической, т. е. удовлетворяет уравнению
Лапласа Aw = 0, во всех точках, кроме самой точки Д,
в которой она обращается в бесконечность.
Действительно,
дГАР _X~V dW =	1 дГАР	. Х~Х0
дх ■ Г АР '	. дх	г2ар дх	■ г*АР

$ lei
КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
233
и
d2tv	1
‘"'др _	1	. „ (х — х0)2 _
д„	г3 ~1_	г5	’
. Ох	г АР	ГАР
_ 2 (х — х0)2 — (у — у0)2 — (г — z0)2 ,
—	s	•	»
аналогично
д2а> _ 2 (у — у0)2 — (х — хр)2 — (г — г0)2
<>?	г\р
d2w __ 2 (z — Zp)2 — (х — Хр)2 — (у — уо)2
г5лр
и
d2w ( d2w | d2w 	n
"5yr	~
Еще проще в этом можно убедиться, если рассмотреть ла¬
пласиан в сферической системе координат с началом в точке А
(см. (18.2")); тогда гАР=г, ■а>= у и Д® =	~ (г2 -^=0,
9 dw	i	л
так как г2-^ ——1 и w не зависит от 0 и ср.
Обозначим, далее, через Wj решение задачи Дирихле для
области 2 с краевым условием
Wllr = Wlr-	(18.7)
Согласно определению функция юг — гармоническая уже
во всей области 2, в то время как w — гармоническая только
в области W, получающейся удалением из области 2 сферы
содержащей точку А (таким образом, область W не содер¬
жит точки А). Поясним это простым примером. Пусть
2 — шар радиуса 1 с центром в начале координат, Г — его
граница и точка А совпадает с началом координат. Тогда
-^и w |г = w |г=1 — 1. В то же время функция, прини¬
мающая на Г значения, равные 1, и гармоническая во всем
шаре, будет, очевидно, тождественно равна единице: Wj-^1
(это особенно ясно из физических соображений: если темпе¬
ратура в точках тела не меняется с течением времени, а на
границе тела постоянна, то она вообще будет величиной
234
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
постоянной). Этим примером подчеркивается, что функции w
и Wi совпадают, вообще говоря, только на границе Г.
Разность функций wx— w называется функцией
Грина для области 2 и обозначается обычно через
G = G(x, у, z\ х0, у0,	—	=	—	(18.8)
АР
Обратим внимание на то, что функция Грина зависит как от
координат х, у, z текущей точки Р, так и от координат х0,
у0, Zq произвольно выбранной, но фиксированной точки А
(последние входят в явном виде в w, но они войдут также
через краевые значения и в W0.
Особо отметим, что, в силу условия (18.7), функция
Грина на границе Г обращается в нуль'.
G|r = 0.	(18.9)
Пусть теперь и — искомая гармоническая функция в об¬
ласти 2, принимающая на границе Г значения и\ положим
v = Q и применим к области W формулу Грина (18.6). Тогда,
ввиду того что в этой области Ди = 0 и До = 0, правая
часть формулы Грина обращается в нуль, и мы получим сле¬
дующее равенство:
+ а^)л = °-
5,	Г
Второй из этих интегралов в силу равенства (18.9) и усло¬
вия и |г = и сведется к
г
Для вычисления первого интеграла введем систему сфе¬
рических координат г, 0, ср с началом в точке А. Тогда на Sj
ГАР = г = е>	=	^=s2sin9d9d?.
Следовательно, равенство (18.10) перепишется в виде
е2 fd<? f {и	-G	L.s 1 n 6 d9=§ “ d9'
о о	г

§181 КРАЕВЫЕ З’АДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	235
Правая часть этого равенства, очевидно, не зависит от е.
Поэтому она должна быть равна также и пределу левой
части при е->0:
2те	тс
J Л “ т -	} L.
: Л‘ «'>■ (is.il)
г
Чтобы вычислить этот предел, заметим, что по фор¬
муле (18.8) G = wl — у (так как мы теперь гАР обозначаем
через г). Тогда
Функции и и Wj—гармонические во всей области 2, вклю¬
чая точку А. Поэтому они вместе со своими производными
ограничены (точное доказательство этого факта мы
не проводим; отметим лишь, что с физической стороны он
совершенно ясен: функции и и Wj можно толковать как не¬
которые стационарные распределения температур в однород¬
ном теле). Это значит, что
Se2/dtP/{“^L_W1lF}LeSin9d9=O-
вторым интегралом дело
==__1_ и II ==±
•=•	е2 И г |г=а е
обстоит сложнее, так как
неограниченно возрастают

236
УРАВНЕНИЕ ЛАПЛАСА
(ГЛ пт
при е->0. Найдем предел каждого слагаемого в отдельности:
2тс	тс
lime2
«->о
sin 9 d6 =
Так как функция и непрерывна, то lim и |г=6 — и |г=0. Вынося
£->0
эту постоянную за знак интеграла, получим
2тс тс
ulr=of Ж? f sin 9	= 4itu |r=0.
о о
Далее,
в силу ограниченности
ди
дг
Таким образом, предел в левой части равенства (18.11) есть
просто 4тш|г=0 = 4тш(х0, у0, г0), так как при г = 0 в каче¬
стве аргументов функции и мы получаем координаты точки А,
Теперь формула (18.11) принимает окончательный вид:
и(х0. уо. =	<18Л2)
Г
Эта формула дает решение задачи Дирихле в про¬
странстве, если известна функция Грина О; действи-
тель ю, мы получили значение искомой функции и в любой
точке А области 2.
56. Метод функции Грина для задачи Дирихле (дву¬
мерный случай). Здесь метод функции Грина также осно¬
вывается на формуле Грина, аналогичной формуле (18.5),

§ 181
КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
237
а именно:
(18.13)
где С — замкнутая кривая на плоскости, ограничивающая
область О, а ~ и — производные по направлению внеш¬
ней нормали к С. При ^этом интегрирование по С ведется
в направлении, оставляющем область D слева, или, как
говорят, в направлении, согласованном с направлением внешней
нормали.
Эта формула может быть получена из формулы (18.5), приме
ценной к цилиндру высоты 1, построенному на С как на напра
вляющей с образующими, параллельными оси z. Тогда, поскольку и
и v не зависят от z,
Iff (и Av — v Au) d\r = 1 • ff (и Av — v Au) da,
2	D
а
ди \
v-d^}ds
^плюс
нулю,
д
=°).
интегралы по основаниям цилиндра, которые, однако, равны
д д
так как на верхнего основании	, на нижнем
_	д	ди   dv
дп ~~	dz '	dz ~~ dz	,
Отметим, что формула (18.13) может быть выведена из фор?
мулы Грина на плоскости.
Нам нужна обобщенная формула Грина, ана¬
логичная формуле (18.6), а именно:
du \
ds —
— v ко) de,
(18.14)
где — замкнутая кривая, лежащая внутри С, а Е — область,
заключенная между Cj и С. При этом интегрирование по Д
ведется по направлению, также согласованному с направле-

238
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ИГ
нием внешней нормали гц к Сг (рис. 62), т. е. по направле¬
нию, оставляющему область Е слева.
Функция Грина на плоскости вводится теперь следующим
образом. В качестве кривой С возьмем границу Г области D,
для которой мы решаем задачу
Дирихле, и выберем внутри Г
произвольную, но фиксирован¬
ную точку Д(х0, у0); за кон¬
тур (?! примем окружность ра¬
диуса е > 0 с центром в точ¬
ке Д. При этом мы предполо¬
жим, что окружность Cj цели¬
ком лежит внутри Г. Тогда
между Cj и Г мы имеем область
Е (заштрихованную на-рис. 62).
Обозначим вновь через Р(х, у)
любую точку области D, отличную от Д, и через гАР—рас¬
стояние между точками А и Р:
ГАР = У(Х —Х0)2Ч-(у —у0)2.
Проверим, что функция
* 1
= In 	=
ГАР
является гармонической, т. е.
Aw = 0.
Действительно,
дГАР
дх
Х XQ
г АР
dw
~дх
\пгАр
удовлетворяет уравнению
1 дГАР
гАР дх
х-х0
г2
'АР
I
и
d2w
Аналогично
d2w 	 (У — Уо)2 —(х —х0)2
^у2
ГАР
.2
И

§ 18] КРАЕВЫЕ З’АДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	23'9
В этом можно также убедиться, если рассмотреть лапла¬
сиан в полярной системе координат с началом в точке 4
(см. (18.2')); тогда rAP=r, w——In г и	~^г	)=0,
dw	.
так как г — — 1 и w не зависит от ср.
Отметим, что функция w— гармоническая в области Е
(так как эта область не содержит точки А).
Обозначим, далее, через <о)х решение задачи Дирихле
для области D с краевым условием
^|r = w|r.	(18.15)
Функция Wj—гармоническая уже во всей области D, (Разли¬
чие между функциями w и Wj было выяснено на стр. 233.)
Тогда функция Грина для области D будет иметь вид
G = G(x, у; х0, Уо) = ‘^1 — w = w1— In—?—. (18.16)
ГАР
Как и в трехмерном случае, функция Грина и здесь зависит
от координат точек Р и Д, и-по определению (18.16) и
условию (18.15)
G |г = 0.	(18.17)
Для искомой гармонической функции и, удовлетворяющей
условию и\Т = и, и функции v = G запишем формулу (18.14),
правая часть которой обратится в нуль (так как Дя=Д<1>=0):
<1818>
с,	г
причем в силу равенства (18.17)
ф О ds = 0.
Если мы введем полярные координаты г, ср с началом
д
dtii
в точке Д, то гАР = г,
~. На окружности Сх

240
УРАВНЕНИЕ ЛАПЛАСА
(ГЛ. Ш
г = е и ds = zdy. Учитывая все это, мы можем переписать
формулу (18.18) в виде
о	г
так как zz|r = zz (перед интегралом слева стоит знак минус,
так как контур Ст обходится по часовой стрелке).
Поскольку правая часть равенства (18.19) не зависит
от е, то в левой части можно перейти к пределу при е—>0
аналогично тому, как это было сделано в предыдущем пункте
(см. (18.11)). Подставим G из формулы (18.16); разбивая
интеграл в левой части формулы (18.19) на два слагаемых
и учитывая, что функции и, и их производные ограни¬
чены ]) в области Z), получим, что искомый предел равен
2тс
п2Гое S у—1п г 4т) |r=e d<?=2кн (х°’Уо)’
так как sine—>0 при е—>0, а и |г=е —> и |г=0 = и (х0, у0).
Поэтому
И Оо- уо) = 4? $ “ 4т ds‘	<18-2°)
Г
Эта формула дает решение задачи Дирихле на пло¬
скости, если известна функция Грина G.
57. Задача Неймана. В приложениях встречается еще одна
краевая задача для уравнения Лапласа, так называемая задача
Неймана, Задача Неймана состоит в следующем:
Найти функцию и, удовлетворяющую внутри замкнутой
поверхности (или кривой) Г уравнению Лапласа &и = 0 и на гра¬
нице Г условию
ди I ~
-у—I —
ОН |р
(18.21)
где 1Гг —производная по направлению внешней нормали к Г,
a Ui — функция, заданная на Г.
’) Точное доказательство этого факта мы опускаем (см. соот¬
ветствующее замечание на стр. 235).

§ 18}
КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
241
Прежде всего отметим, что функция и} на поверхности (или
кривой) Г не может быть задана произвольно. Если в формуле (18.5),
верной для любых функций и и v, положить v = 1, то = О
и Av = О и формула примет вид
f
s	V
Поэтому для любой функции и, гармонической в области
соблюдаться равенство
Следовательно, граничное значение производной на
ция их — должно удовлетворять условию
их dv = 0.
5
V9 должно
Г — функ¬
(18.22)
(Аналогично в двумерном случае из формулы (18.13) будет следо¬
вать, что	где Г — граница области £>.) При соблюде¬
те
нии условия (18.22) задача Неймана всегда имеет решение. При этом
очевидно, что вместе с любым решением и решением будет также
const. Можно доказать, что других решений задача Неймана
не имеет, т. е. что разность двух любых решений задачи Неймана
постоянна. Это означает, что решение задачи Неймана единственно
с точностью до аддитивной постоянной.
Задача Неймана не имеет наглядной «тепловой) иллюстрации
(за исключением простейшего случая Wj==O, т. е. теплоизоляции
границы, когда решением является и = const). Однако эта задача
играет важную роль в теории волновых процессов, в частности
в теории электромагнетизма.
Метод функции Грина может быть применен и к решению
задачи Неймана на основе формул (18.6) (для пространства)
и (18.14) (для плоскости). Но функция Грина для задачи Неймана
должна быть определена несколько иначе. Мы по-прежнему пола¬
гаем G = wx— w, где w =	 для пространства и w = in

ГАР	ГАР
для плоскости; однако на гармоническую функцию wt накладываем
теперь краевое условие
dtv, I   dw I
дп |р	дп |р
16 И. Г. Арамановнч, В. И. Левин

242
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. III
(вместо (18.7) или (18.15)). Тогда
и формулы (18.6) и (18.14) приводят нас к решению задачи Неймана
я (*о, Уо. ^о) =	«1^ da	(18.23)
г
(в пространстве) и
« (*0, У о) =	ds	(18.24)
г
(на плоскости).
Задачу Дирихле часто называют первой краевой задачей для
уравнения Лапласа, а задачу Неймана — второй краевой задачей.
Рассматривается еще третья краевая задача', найти функцию а,
удовлетворяющую внутри замкнутой поверхности (или кривой)
Г уравнению Лапласа Aw = О и на границе Г условию
+ Мг = Ъ
г
где а, f— функции, заданные на Г. Очевидно, что задачи Дирихле
и Неймана являются частными случаями этой задачи. Однако третьей
краевой задачи мы касаться не будем.
§ 19. Решение задачи Дирихле для шара
и полупространства
58. Сопряженные точки. Основной трудностью при ре¬
шении задачи Дирихле является нахождение функции Грина,
которая в явном виде известна только для небольшого числа
простых областей. В частности, функция Грина известна
для шара, круга, полупространства и полуплоскости.
Поэтому мы и займемся решением задачи Дирихле для этих
областей. Решения, которые мы получим, играют важную
роль в приложениях.
При построении функций Грина нам понадобится понятие
сопряженных точек.
Две точки А и А* называются сопряженными относи¬
тельно плоскости (в пространстве) или прямой (на плоско¬
сти), если они симметричны относительно этой плоско¬
сти или прямой. Так, точки A(xQ, у0, zQ) и Л*(х0, у0, — г0)
сопряжены относительно плоскости z = 0, а точки Д(х0, у0)
и А* (х0, — у0) — относительно прямой у — 0.

§ 19)
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
243
Несколько сложнее понятие сопряженности относительно
сферы (в пространстве) или окружности (на плоскости).
Точки А и Д* назидаются сопряженными относительно
сферы или окружности, если они лежат на одном луче,
исходящем из центра О сферы или окружности, и про¬
изведение их расстояний от центра равно квадрату
радиуса:О А • О А* = R2, где R — радиус сферы или окруж¬
ности.
Если центр сферы совпадает с началом координат, то
в пространстве точка Д(х0, у0, £0) сопряжена с точкой
хо- Уо>	V где г0 = О А = ]/y2 + z2.
Чтобы в этом убедиться, обозначим координаты сопряженной
точки Д* через х*, у*, z*Q, тогда г* = ОД* = \ х*2 +у*2 +г*2.
В силу определения гг* = /?2. Поскольку точки Д и Д*
лежат на одном луче, выходящем из начала координат, то
т. е.
*
*
-Z1 —
R2
*
Уо

R2
*
^0 __
л2
А'о
г0
г2 '
г0
>’о
^0
г0
*
о
R2
(19.1)
х
Совершенно аналогично получим, что точки Д(х0, у0) и
Д* ( х0’ Уо V где го = 0Л ~ Vхо+	сопряжены
\ го го /
относительно окружности радиуса R с центром в начале
координат.
Очевидно, что если точка А лежит внутри сферы или
окружности, то точка Д* находится вне сферы, соответ¬
ственно окружности; если А лежит на сфере (окружности),
то Д* совпадает с Д. Центру сферы или окружности не со¬
пряжена никакая точка. Для сферы и окружности геометри¬
ческое построение сопряженных точек состоит в следующем.
Пусть А лежит внутри окружности и не совпадает с ев
центром (рис. 63); проведем через А хорду ТТ1г перпенди¬
16*

244
УРАВНЕНИЕ ЛАПЛАСА
(ГЛ. (If
кулярную лучу О А, и через концы Т и 7\ — касательные
к окружности; эти касательные пересекаются в точке Д*
на луче О А, так как из подобия треугольников О АТ и ОТА"
ОА ОТ
вытекает, что ‘qt* ='дГдг»
откуда ОА • ОА* = ОТ2 — R2.
Если мы будем вращать
• фигуру на рис. 63 вокруг
оси ОАА\ то возникает
соответствующее постро¬
ение для сферы. Очевид¬
но, что указанным обра¬
зом можно по точке А
построить точку А (т. е.
сопряженную с точкой,
лежащей вне сферы или
окружности).
59. Задача Дирихле
для шара. Рассмотрим
шар радиуса R с цент-
Пусть А(хп, у0, z0) — фикси-
*	*\	л •.. v
г*
ром в начале координат.
рованная точка шара, Д*(х*, у*, z^— точка, ей сопряженная,
и Р(х, у, г) — произвольная переменная точка. Тогда
ГАР = У(х — хо)2 + (У — Уо)2 + (z — го)2
ГА»Р = /(* — Хо)2 + (У - < + (* -
Если ввести обозначения ОР==г, ОА~г{Г О.А* — г* и
£~АОР = $ (рис. 64), то по теореме косинусов
r4P = jA2 + ro-2"ocos'l' н гА’>Р^\Гг' + г^~2гг*^^-
Так как г0г* = /?2, то
Согласно доказанному в п. 55, функция w =	 удовле-
г АР
творяет уравнению Лапласа во всех точках, кроме точки Д»
Поэтому функция

§ 191
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
245
будет гармонической всюду внутри шара, так как точ¬
ка Л* лежит вне шара (точка Л* — сопряженная с точкой,
лежащей внутри шара).
Далее, если точка Р расположена на границе шара —
сфере Г, то г = R и
Гдр1г=/«2 + ^-2^0СО8'Ь
1г = 1//?2+^-2^со5ф =
V	, го го
=	V^2+r0 —2/?Г0СОЗФ = £ ГАР If
(19.2)
R_
R	f
Поэтому функция	— w2 =—— является гармонической
Г0	ГА*Р
во всем шаре, и ее значения на сфере Г совпадают со зна¬
чениями функции iw = —1—, так как
АР
я
>0
ГА*Р
1г
Г

246
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. Т1Г
Согласно определению (см. п. 55) функция
шара имеет вид
R
G = wr — w = —	—.
rA*P rAP
Грина для
(19.3)
После того как функция Грина найдена, можно по общей
формуле (18.12) написать решение задачи Дирихле для шара.
Для этого нужно предварительно вычислить значения произ¬
водной от функции Грина по внешней нормали, т. е.
при r = R. Согласно формулам, определяющим G, гАР
и	имеем
dG	1 дгАР	R 1 дгА*р
дг	г2ар дг	г0 г2а*р дг
Р2	г
.	~ Г	COS ф
	 г — r0 cos ф R	г0	т
г3	г	г3
Г АР	*0	ГА*Р
Учитывая формулы (19.2), получим
,	г»	f г» R	COS Ф
dG 	 R — rQ cos ф	R	rQ т
\r = R	f^Ap |г
'о
я3 3
~3ГАР
•
г0
Г
R2 — r2	R2 — Гд
	1 =	2	. (19.4)
#гар |r R (R2 + ro *“ 2^ro cos Ф)3/г
Введем теперь сферические координаты с началом в О:
х = г sin 6 cos ср, у = r sin 0 sin ср, z = г cos 6.
Обозначим координаты точки Р через г, 9, ср, а координаты
точки А — через г0, 90, ср0. Тогда в формуле (18.12)
da = R2 sin 9 d9 rfcp,
и будет функцией 9 и ср, и нам остается только выразить
через введенные сферические координаты величину соэф
$ 19]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
247
из выражения (19.4). Это можно сделать при помощи еди¬
ничных векторов е0 и е направлений ОА и ОР. Так как
04 = х014- У oJ + £ок —
— r0 sin 0О cos <р01.+ Го sin 0о sin	+ ro cos 90k,
OP = г sin 9 cos cpi —г sin 9 sin <pj + r cos 0k,
TO
e0 = — 0Д = sin90coscp0i4“Sin90sincp0j-[-cos 90k,
г 0
e = у OP = sin 9 cos cpi + sin 9 sin cpj 4- cos 9k.
Следовательно,
cos ф = eoe = sin 90 sin 9 cos (cp — <p0) + cos 90 cos 9.	(19.5)
Таким образом, мы получаем окончательное решение за¬
дачи Дирихле для шара в следующем виде:
1	R2 — 4
«(г0. 0О> ?о) = 7-<й>а(0- &—Т-7,	2	Th da=s
4тс у	R (R2 + Го — 2/?г0 cos ф)
2те	it
= — f dv Г и(9, ср)	1		j-sin0d9, (19.S)
‘■s' s' ’ (К! + ^-2Яг, cos (.)■'■
где вместо cos<^ нужно подставить его выражение (19.5).
Интеграл (19.6) называется интегралом Пуассона для
шара.
Следует обратить внимание на то, что при выводе фор¬
мулы (19.6) мы должны были предполагать, что точка А
не совпадает с началом координат, т. е. что г0=А О (так как
центр сферы не имеет сопряженной точки). Но по непре¬
рывности решения формула (19.6) останется в силе и при
го = 0; она тогда примет вид
«Uo=4^-§«(0-<p)^	а9-7)
г
означающий, что в центре сферы гармоническая функция
имеет значение, равное среднему ее значений на сфере
{теорема о среднем для гармонических функций).

248
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ИГ
Формула решения (19.6) довольно сложна, однако ею
можно воспользоваться в некоторых частных случаях.
Если мы предположим, что граничная температура и = 1
на всей сфере, то в силу единственности решения задачи
Дирихле всюду внутри шара и=1. Это означает» по фор¬
муле (19.6), что
2тс	к
— Fd<f f ——sinO <i6 === 1 (19.8)
4яо о (R2 + r20-2Rr0 cos ф)А
для всех	0<е()<тс, 0	<р0 2тс (соэф опре¬
деляется по формуле (19.5)). Указанный факт можно про¬
верить и непосредственно, правда, при этом приходится иметь
дело с весьма сложными интегралами.
Пример 1. Дан однородный шар радиуса R, верхняя
половина границы которого поддерживается при темпера-
туре 1, а нижняя — при темпе¬
ратуре 0. Найти стационарное
распределение
вдоль диаметра
(рис. 65).
Для точек верхней
сферы 0 G < у , для
нижней полусферы < G <1 тс;
следовательно.
температуры
шара
SN
полу-
точек
если 0	0 < —,
Сложность формулы Пуас¬
сона (19.6) видна из того, что
случае распределения внешней тем-
даже в этом простейшем
пературы получить выражение для температуры во всех точках
шара очень затруднительно. Поэтому мы и ограничиваемся
лишь частным случаем.
Будем искать температуру в точках вертикального диа¬
метра SA7. Если точка А лежит на радиусе ON (т. е.
в верхней части шара), то 0о = О и cos<|> = cosG (см. фор*

§ 191
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
249
мулу (19.5)). Если же точка А лежит на радиусе OS, то
60 —тс и cos<p =— cos 6.
По формуле (19.6) для точки А. лежащей на радиусе ON
на расстоянии г0 от О, получим
/9	21Г	ТС/2
Я(Я2 — Го) ?	Г	sinOrfO
4с о о (Я2 + г2 — 2/?r0cos б) /г
тс/2
/?(/?2 — Tq) f*	sin O dO
2 о (Я2-Но — 2#r0cos °)’/!
	/?2-г2	1	_
2fo	У /?2 -Но — 2/?г0 cos О
2г0
1
Я —г0
1
Уяйн«
2	2г0
Для точки А, лежащей на радиусе OS на расстоянии г0 от О,
п	л 2тс	тс/2
fa, Г		=
4*	» о	'
Я2-г2 1
1 1
1
2г0
я-Ио	/7?+г2
1 1
R —
Я2 —г2
2	2г0
Уя2+г2
вертикальном диаметре SN
Таким образом, температура на
1 равна
ы=1±_1
2	2г0
/?2-г2
Я —^==
+ го
где верхний знак берется для верхней половины диаметра,
а нижний — для нижней. Любопытно отметить, что полу-
сумма температур в точках, одинаково удаленных от центра
250
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
шара, равна у. Это же значение получится, если найти пре¬
дел а при г0—>0. Можно показать, что полусумма темпера¬
тур двух точек, лежащих на любом диаметре и равно-
1
удаленных от центра, равна у.
Значительно более сложным оказывается вычисление темпера¬
туры в точках экваториальной плоскости. Здесь 0о=-^- и cos ф =
= sin 6 cos (ср — <ро). Согласно формуле (19.6)
/ к \	1 /• (•	tf — rl
u ( го. — > ?о ) = — /	/	—тг da,
\	2	/ kt. J J	+	—2/?r0COS<p)'2
где интеграл распространен по верхней полусфере. Вычисление
( те \	1
этого интеграла показывает, что и I г0,, ср01
Пример 2. Дан однородный шар радиуса R и на его
границе — сфере Г — точка М со сферическими координа¬
тами 6' и ср' (рис. 66). Проведем на Г с центром в точке М
маленький кружок, видный из центра сферы под углом 2s
(е > 0). Площадь полученного сферического сегмента Е (за¬
штрихован на рис. 66) равна 2те/?2(1 —cos г) — 4тс/?2 sin2!).
Пусть граничная температура и на всей сфере Г, кроме сег¬
мента Е, равна 0, а на S равна 			, т. е. величине,
sin2-^-
обратной площади сегмента S. Найти стационарное распре¬
деление температуры внутри шара при малых значениях
угла е.
9 Если совместить ось сегмента с осью Ozt то площадь его
выразится с помощью интеграла

РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
251
Применяя формулу (19.6), найдем, что в данном случае
«(г0. 90.	=
Е
1	R2-rl
4nR2 sin2 R (R? 4“ '‘о — ^Rrо cos ф)
da,
где da = /?2sin6d6dcp — дифференциал площади сферы Г.
По теореме о среднем интегрального исчисления это может
быть записано в виде
z л	.	1
«('о» °0’
1
?о) —	о	*
4kR (/?2 -j~ Гд — 2£r0 cos <0
причем через ф обозначено среднее значение ф, соответствую¬
щее некоторой точке М со сферическими координатами 0 и ср,
лежащей в сегменте Е. При е—>0 граничная температура
сведется к нулю на всей сфере Г, кроме точки М, где тем¬
пература будет бесконечна (двумерная импульсная функ¬
ция Дирака\ см. стр. 164). Так как при е->0	и
ср-хр', то стационарное распределение температуры будет
стремиться к
J

4nR \R2 + Tq — 2/?r0 cos ф')’/а

252
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. III
где согласно формуле (19.5)
cos <[/ = sin 90 sin О' cos (<р0—?') + cos 90 cos S'.
Опуская теперь штрихи, мы можем сказать, что выра¬
жение
J	^2-Гр2
4nR (Л2 + г2 — 2Rr0 cos ’
(19.9)
где соэф определен формулой (19.5), является стационар-
ным распределением температуры в точке (г0, 90, <р0),
если на границе шара поддерживается всюду темпера¬
тура 0, кроме одной точки Л1 с координатами 6 и ср,
в которой температура бесконечна (в смысле указан¬
ного выше предельного перехода при г—>0).
Выражение (19.9) называется ядром Пуассона для шара.
По формуле (19.8) интеграл от ядра Пуассона для шара по
граничной сфере Г равен 1 для любых г0, 90 и ср0: 1
1 ГС
(Я24-Го — 2«r0cos'|/)*'2
sin6<Z9 = l.
60. Задача Дирихле для внешности шара. Можно пред¬
ставить себе теплопроводящее пространство, из которого
изъят шар. Границей оставшейся бесконечной области
будет сфера, являющаяся и границей шара (только темпера¬
туру, поддерживаемую на этой границе, мы должны себе
теперь представить «приложенной» изнутри). Очевидно, что
решение задачи о распределении температуры в такой бес¬
конечной области, внешней к шару, может быть получено
так же, как и формула (19.6); единственное изменение, ко¬
торое мы должны произвести в выводе, заключается в том,
что нужно точки А и А* поменять местами, т. е. г0 в фор-
р>
муле (19.6) заменить на у-. Тогда мы получи^ искомую
§191
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
253
температуру
«(го- °о- ?о) =
2л:	ТС
— f d(?f и(-°1
6 о
r0(r20 — R2)
(/?2 + ^ —2/?r0cos<p)’/2
sin 0 db.
2тс тс
И /“(»■?>
о о
(19.10)
где уже, конечно, г0 > R.
Пример. В условиях граничной температуры примера 1
п. 59 стационарное распределение температуры во внешности
шара на продолжениях вертикального Диаметра мы получим,
поменяв местами г0 и R в соответствующих формулах для
температуры внутри шара (именно такая замена переводит
интеграл (19.6) в интеграл (19.10)).
Таким образом,
1
1
~2R
с верхним знаком для верхнего продолжения диаметра SN
и с нижним — для нижнего. Отметим, что в обе стороны
1
при г0~>оо.
61. Задача Дирихле для полупространства. Для полу¬
пространства z > 0 функция Грина имеет вид
О(х. у. z\ х0, у0, z0) = ~—
ГА*Р
1
г ар ’
где А(х0, у0, z0)— произвольная точка полупространства
z > 0 и Д*(хо« Уо’ —*о)— точка, ей сопряженная. В этом
случае
ГАР = У(* — *о)2 + (У ~ Уо)2 + {Z. — д0)2.
ГА*Р = Г(х — хо)2 + (У ~ У о)2 + (2 + Zo)2
и границею Г служит плоскость z = 0.

254
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
1
Действительно, при этом
1
ция --—
ГА*Р
rAP z=q ГА*Р
гармоническая при z^Q. Далее,
dG I _	dG I
дп |г—	dz [z=0
z=0
и функ-
(так как внешняя нормаль к Г направлена вниз, в сторону
отрицательных z), а
дО __	,	1 дгАР _ _ z + zo , z — zo
dz	г2 dz r\p dz	r3A*p	r3AP
Следовательно,
dG I 	 2z0
|r r3AP
так как при z = 0 r„p = rAP = /(x -x0)2+(y—y0)2+z2.'
Граничные значения и здесь заданы на плоскости z = Q, т. е.
и-и(х.у) (—оо<х<оо, —се < у < оо), и по фор¬
муле (18.12)
Интеграл (19.11) называется интегралом Пуассона для
полупространства. Если ввести в пространстве цилиндри¬
ческие координаты, положив х — г cos ср, у — г sin ср, z = z,
то формула (19.11) может быть записана в виде
Следует иметь в виду, что интегралы (19.11) и (19.12)
несобственные и для их сходимости (тем более пра¬
вильной) граничные значения и должны достаточно хорошо
вести себя на бесконечности, например быть ограниченными.

§ 191
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
255
Ядро Пуассона для полупространства
га	1		 	1

2Я [(* — хо)2 + (У ~ Уо/ + 4]’/s 2к [r2+ro—2rr0 cos (T—cPo)+*ol’/’
физически может быть (по аналогии со случаем шара) интер¬
претировано как стацио¬
нарное распределение
температуры в одно¬
родном полупростран¬
стве £>0, на границе
которого — плоскости
z=Q— поддерживается
температура 0 всю¬
ду, кроме точки (х, у)
этой плоскости, где
она бесконечна. Дей¬
ствительно, если и — §
вне квадрата xf — е<
СхСх' + е, у' — е<
< У < у' + е И равно
то по формуле (19.11)
Х'+Е	У'4-S
“=-₽ f dx f 7—
x'-s у’-г Lv
Рис. 67.
внутри этого квадрата (рис. 67),
	dy	=
хо)2 + (У “ Уо)2 + ги) /2
	1

2те [(•*—хо)2+(у — Уо)2+j''
где хг— е<х<х, + £> у' — £<У<У + £- В пределе
при е->0 мы получаем
и
	1

& К-—.)“+(/-»«)’+<■■
т. е., опуская штрихи, ядро Пуассона для полупространства.
Как следует из единственности решения задачи Дирихле,
оо	оо
	1

[(•* — хо)2 + (У — Уо)2 + *о|/а
dy= 1.

256
УРАВНЕНИЕ ЛАПЛАСА
1ГЛ. Ill
т. е. интеграл от ядра Пуассона для полупространства по всей
граничной плоскости равен 1. Это может быть проверено
непосредственно интегрированием.
Перейдем к примерам.
Пример 1. На границе z = 0 однородного полупро¬
странства z > 0 температура равна 0 для х < 0 и равна 1
для х > 0. Найти стационарное распределение температуры
в пола пространстве.
По формуле (19.11)
со	оо
f
0	— оо
	1

[(* - -*о)2 + (у - Уо)2 + *of’
dy.
Очевидно, что это выражение не зависит от у0, так как
замена у — у0 = приведет к выражению
оо	оо
Вычислим внутренний интеграл, обозначив для краткости
(х— х0^24-2'2 = X2 и совершая подстановку 7] = ktgf:
ОО
Г d-Ч
— оо
1
\2
Тогда
ОО
И==Л1 Г	**

" I (х-х^ + 4
Таким образом,
и (х0, г0) = 1 +1 arctg .
1	, X	Ха
-2 = -arctg	5
’>	*	го
°° —А
о“2
4- — arctg —
Л	20
В этом случае температурное поле в каждой плоскости
у0 = const одно и то же. В разрезе плоскостью уо=О
мы получим картину, изображенную на рис. 68. Изотермами
§ 19]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ШАРА
257
являются лучи, исходящие из начала координат; луч, накло¬
ненный к положительному направлению оси xQ под углом ак,
< а < 1, является изотер¬
мой и — 1—а. Изометриче¬
скими поверхностями слу¬
жат плоскости, проходя¬
щие через ось у0.
Пример 2. На грани¬
це г = 0 однородного по¬
лупространства z > 0 под¬
держивается температура О
всюду вне круга радиуса У?
с центром в начале коор¬
динат, а внутри этого круга поддерживается температура 1.
Найти стационарное распределение температуры на положи¬
тельной полуоси z0.
Здесь удобнее применить формулу (19.12). Ввиду осевой
симметрии задачи искомая температура и не будет зависеть
от ср0, и мы получим
2к R
и(г0’ ^о) = >У d^ j
О о
г dr
[г2 н- Г2 — 2rr0 cos <Р 4-
На оси имеем го = О, поэтому подынтегральное выраже¬
ние значительно упрощается. Интегрируя, получим
и(0,	= Г а<? f rdr f ■■■r-df—==
4 J e2+4/2	/ e2+<
1 — 1 = 1	. ..
Температура «(0, zQ), таким образом, монотонно убывает
от 1 до 0 при возрастании zQ от 0 до оо.
Для точек, не лежащих на оси z0, т. е. при г0 > 0,
внутренний интеграл по г может быть вычислен точно,
однако интегрирование по ? приводит к интегралам, не беру¬
щимся в элементарных функциях, именно к эллиптиче-
с к и м интегралам !).
]) См. книгу Н. Н. Лебедева, указанную в сноске на стр. 170.
. 17 И. Г. Араманович, В. И. Левин

258	УРАВНЕНИЕ ЛАПЛАСА	[ГЛ. III
§ 20. Решение задачи Дирихле для круга
и полуплоскости
62. Задача Дирихле для круга. Эта задача решается
аналогично соответствующей задаче для шара, только фор¬
мулы, естественно, получаются
JC более простыми. Покажем, что
функция Грина для круга ра¬
диуса R с центром в начале
координат имеет вид
Рис. 69.
О(х, у; х0, у0) =
_R_
=inA-'
1п7^ (20-1)
(ср. с формулой (19.3)), где
х, у — координаты точки Р,
х0, Уо— координаты точки А. Точки А и Д* сопряжены, и
г АР =У(Х — хо)2 + (У — У о)2 >
Я2 ?2	7
Х~^ Х0
Г0 у
а г0 = Ух2 + у2 (рис. 69). Нетрудно проверить, что функ-
г	1
ция w1 = ln—— = 1п	(-const удовлетворяет уравнению
ГА*Р	ГА*Р
_	dwi , d2w< ~
Лапласа	— 0 всюду внутри круга, так
точка А* лежит вне его. Это доказывается так же,
на стр. 238 для функции w = ln —. Из рис. 69 видно,
ГАР
ГА*Р
Я2 \2 -
как
как
что
Я4 о R2 ,	.
— —		COS (ср — ср0) ,
''о	''о
где г = ОР = ]/х2 + у2.

i 20]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ КРУГА
259
Если точка Р попадает на границу круга (т. е. г == /?), то
Следовательно, значения функций *а/=1п — и Wi = ln —
Г АР	ГАЧ
совпадают на границе круга, и согласно определению (см.
п. 56) правая часть формулы (20.1) действительно предста¬
вляет собой функцию Грина для круга.
Чтобы воспользоваться общей формулой (18.20), нам
осталось вычислить
Поскольку
dG I _ dG I
дп |г dr \r=R*
г	cos (т — сро) -
дг
ГА*Р
то из формулы (20.1\ которую удобно записать в виде
дг гАР дг гА*Р дг
г	— cos (т — <Ро)
Отсюда
r-~r0 cos (у —?0)
где г^р — /?2 + Гд — 2/?r0 cos — т0). Таким образом, окон¬
чательно
dG
1г
r=R R (Я2 + / о — 2/?Г0 cos (? — ?о) ) ’
17*

260
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
и решение задачи Дирихле для круга по формуле (18.20)
примет вид
1 2тс	У?2	2
и (Га, ср0) = — / и (ср)—			tZcp (20.2)
W^ + r2_2^oCOS(?_?o) т k /
(дифференциал длины дуги ds окружности Г заменен на R dy).
Интеграл (20.2) называется
интегралом Пуассона для
круга, а выражение
1	Я2-г2
2~R У?2 4-Гц — 2/?r0 cos (<? —<р0)
(20.3)
— ядром Пуассона для кру¬
га. Физической иллюстрацией
его является стационарное рас¬
пределение температуры вну¬
три круга радиуса R, граница
которого — окружность Г —
поддерживается при температуре 0 всюду, кроме одной точки
М с полярной координатой ср, в которой температура бесконеч¬
на. Для доказательства положим в формуле (20.2) и=0,
если (ср — ср'|>е, и и= , если [ср—ср' | < е (рис. 70). По
формуле (20.2)
Я2-/2
1
и (го* То) 2яУ? /?2 4- г% — 2RrQ cos (£ — <р0) ’
где ср — некоторое среднее значение ср, [ср — ср'[<£ (здесь мы,
как и в пространственном случае, применили теорему о сред¬
нем интегрального исчисления). При е—>0 ср->ср\ и в пре¬
деле мы получаем стационарное распределение температуры
1 -
2nR У?2 4. г2 — 2У?г0 cos (<р' — <о0) ’
которое и является ядром Пуассона для круга, если мы
опустим штрих при ср. Нетрудно видеть также, что инте¬
грал от ядра Пуассона для круга по граничной окружности Г

§ 20]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ КРУГА
261
Это вновь следует из единственности решения задачи Дирихле и
может быть также Проверено непосредственно интегрированием.
Пример., Дана тонкая однородная круглая пластинка
радиуса /?, верхняя половина границы которой поддержи¬
вается при температуре 1, а нижняя — при температуре 0
(рис. 71). Найти стационарное распределение температуры
на пластинке и определить форму изотерм.
В формуле общего решения (20.2) мы должны положить
н(ср) = О для тс < ср < 2тс и и (ср) — 1 для 0 < ср < тс; сле¬
довательно, искомое распределение температуры будет дано
формулой
«(Г0.
1 Г	.а.
2л о ^2 + r(> — 2Rr<) Cos (V — ?.))
Этот интеграл надо вычислять с осторожностью. Предположим

262
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. Ilf
сначала, что 0 < <р0 < тс (т. е. что точка
в верхнем полукруге); тогда разность
в пределах от — ср0 до тс — ср0, а этот
не содержит	’	“
ta То,
* 2
получаем
t,
точек ± тс. Поэтому
cos(? —?0) = 4^J.
г0, ?0 расположена
ср — ср0 изменяется
интервал длины тс
законна подстановка
, 2dt
= T+F’ и Mbl
«('о-То) = 4 f
(Я-Го)2 + (Я + го)2'2 dt~
= larclg(4±i<',^ =
it	&\R — ra
= | { arctg	etg -^) + arctg (-J±^tg	.
Чтобы представить найденное выражение в более удобном
виде, вычислим
tg(WTC)		/рд_г \2

Я2-/-2
— 4Rr<>
Так как правая часть отрицательна, то это означает, что и
для 0 < ср0 < тс удовлетворяет неравенствам у < и < 1. Таким
образом,
Я2-г2
tg(^ ^)-2y?roSin?o.
или
g = 1-7arctg^Mn;. (О <%<*)•	(20.5)
Если тс < <р0 < 2тс (точка (г0, ср0) расположена в нижнем по¬
лукруге), то интервал (—ср0, тс—<р0) изменения ср—ср0 содержит
точку — тс, но не содержит точку 0 и мы можем сделать под-
. <р — Фо 4.	(	\	— 1 w	^dt
становку etg -т- 2Т° — t, cos (<р — %) =	, dy=— .

I 20]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ КРУГА
263
Таким образом, для этих значений %
*г>
ч	1	/	№-г2
м(го-?о) —— я J ^ + ro)2 + ^_roytdt-
- ctg
- Т { arct£ (^77 f) + arcts (tTR? ctg	} •
Преобразовывая, как и раньше, найдем
tg'O)
R — rQ
R + rQ
2RrQ sin cf>o
R — r0
R + r0
?о
2
— прежний результат, с тем лишь различием, что теперь
правая часть положительна, так как sin ср0 < 0. Следовательно,
a==_larctg_±Z21_ (К<то<2к)	(20.6)
и О < и < ~.
Изотермы в верхнем полукруге по формуле (20.5) будут
иметь уравнение [а постоянно, < и < 1 j
tg К1 ~ “И = 2RrQ sin
или, если перейти к декартовым координатам x0 = r0coscp0,
у0 = r0sin ср0, уравнение
tg((l-zz)rc)
т» е,
2/?у0
R2
Это — уравнение окружности с центром в точке
р
(0, — R tg [(1 — и) к]) радиуса	’ пР0Х°ДяЩей через
точки (± /?; 0); однако нашей изотермой является лишь дуга
этой окружности, лежащая в верхней полуплоскости у0>0
264
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
(так как sin<p0 > 0), Аналогично показывается, что в-нижнем
полукруге у0 < 0 изотермами также являются дуги окруж¬
ностей, проходящих через точки (± /?; 0) (рис. 71). Уравнения
этих окружностей: х20 + (у0 — tg к«)2 = —^г.и ‘
63.	Задача Дирихле для внешности круга. Так же, как мы
поставили и решили выше задачу Дирихле для внешности шара
(см. п. 60), можно поступить и с внешностью круга. Решением
будет формула (20.2), в которой нужно поменять местами и R',
2тс
«(Го. <Po)=i / “(?)
о
'о-/?2
л2 + Гц — 2RrQ cos (<? — 90)
('"о > R)-
Если мы теперь поставим задачу об изотермах во внешности
круга радиуса Rt верхняя половина границы которого поддержи-
Рис. 72.
вается («изнутри») при темпе¬
ратуре 1, а нижняя — при тем¬
пературе 0, то эти изотермы
будут продолжением изотерм
для внутренности круга, т. е.
дополнительными дугами соот¬
ветствующих окружностей. При
этом, если дуга такой окруж¬
ности является внутри круга
радиуса R изотермой и, то ее
г дополнительная дуга вне этого
круга является изотермой
1 — и (рис. 72). Это легко
доказать таким же образом,
как мы это делали выше для
внутренности круга.
64.	Задача Дирихле
для полуплоскости. Функ¬
ция Грина для полуплоско¬
сти у0 > 0 имеет вид
G(x, у; х0, у0) =
— In —1	In — ,(20.7)
Га*р гар
где А(х0, у0)— произвольная точка полуплоскости у0 > 0,
а Д*(х0, —у0) — точка, ей сопряженная. В этом случае
ГАР = У <4 ~ *о)2 4~ (У ~ Уо)2 ♦
га*р==V(x — хо)2 4- (у 4- Уо)2

§20]
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ КРУГА
265
и границей Г служит прямая у = 0. (Рекомендуем читателю
получить формулу (20.7) самостоятельно.) Далее (см. задачу
Дирихле для полупространства, п. 61),
dG | _	I _
д* |г— ду |у=0“
= 1 дГА*Р	1 дГАР	Ч	'
ГА*Р дУ	ГАР дУ	(•"^V + O'-V ’
и решение запишется в виде (по формуле (18.20))
(20.8)
— ОО
Выражение (20.8) называется интегралом
полуплоскости, а
Уо	1
л (* —*о)2 + Уо
Пуассона для
(20.9)
— ядром Пуассона для полуплоскости.
Физический смысл ядра Пуассона для полуплоскости со¬
стоит в том, что функция
Уо t 1
и ' (х'—х0у + у2и
представляет стационарное распределение температуры в полу¬
плоскости у0>0, если граница — ось х — поддерживается
при температуре « = 8(х— х') (см. стр. 164), т. е. при
температуре 0 для всех х^хг и температуре оо в точке х'
(в смысле предельного перехода, который ведет к импульс¬
ной функции Дирака 8 (х — хг)). Интеграл от ядра Пуас¬
сона для полуплоскости по границе полуплоскости равен I:
оо
Уо Г	dx		 J
л _•£ (*-*о)2 + у«
Все эти утверждения предоставляем доказать читателю.
Рассмотрим в заключение еще один пример.
Пример. Дана однородная полуплоскость у0>0, гра¬
ница которой — ось х — поддерживается при температуре О
для |х|>/ и при температуре 1 для |х|</. Найти

266
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. III
стационарное распределение температуры в полуплоскости
и соответствующие изотермы. В интеграле формулы (20.8)
сделаем замену переменной х — х0 = $;
i
и(х0, у0) = — /
тогда
“и"’	ньр
=Iaici" i IX.=-И,ret® +аие -4?} •
Начнем с изотермы и = у . На ней
a,ctg±^+a,ctg'±it=^,
I — Xq	Уо
т. е. —— =	откуда
-^=1. =
Уо
Эта изотерма является верхней полуокружностью радиуса /
с центром в начале координат (рис. 73). Для и < ~
I — Xq	Z + *0
Уо
2Zyo
1

f 2t]
МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
267
т. е,
	Z

sin (ик)
эта прохо-
>1.
Изотермой является дуга окружности радиуса
лежащая в верхней полуплоскости. Окружность
дит через точки (±Z, 0) и имеет свой центр на положитель¬
ной полуоси у0 в точке (0, Zctg(//7c)). Для ~ < и < 1 мы
приходим к аналогичному результату, только центр окруж¬
ности будет располагаться на отрицательной полуоси у0
(рис. 73).
§ 21. Метод Фурье для уравнения Лапласа
65.	Двумерное уравнение Лапласа и задача Дирихле
для круга. Метод Фурье разделения переменных, кото¬
рый играет большую роль в задачах колебаний и тепло¬
проводности (см. гл. I и II), применим также к решению
уравнения Лапласа и задачи Дирихле для таких простых
областей, как круг, прямоугольник и т. п. В этом пункте
мы решим методом Фурье задачу Дирихле для круга. Радиус
круга обозначим через R, центр поместим в начало коорди¬
нат. Очевидно, что целесообразно решать задачу в полярных
координатах. Тогда задача формулируется так: ищется ре¬
шение и = и(г, ср) уравнения Лапласа
1 д / ди\ .	1 д2и л	/О1
для г < R, принимающее на границе круга, т. е. при r = R,
заданные значения rz (ср):
и1г=я = «(т)-	(21.1а)
Метод Фурье заключается в том, что мы сначала, ищем
решения уравнения (21.1) в виде и = U (г) Ф (ср), где неиз¬
вестные функции U (г) и Ф (ср) зависят каждая только от
одной переменной, соответственно г и ср. Тогда для этих
неизвестных функций из уравнения (21.1) находим:
1 d ( dU\
г dr \ dr J
г2 d'f2 и’

268
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. III
или
Г d ( dU\
и dr V dr J
1 d2$
~ Ф dy2 '
(21.2)
Так как левая часть уравнения (21.2) не зависит от ср, а пра¬
вая—от г, то ни левая, ни правая части этого равенства
не могут зависеть ни от ср, ни от г, т. е. являются по¬
стоянными:
г d
U dr
1 Л2Ф
Ф_ dy2
(21.3)
где X — постоянная разделения. Постоянная X, как мы сейчас
увидим, должна быть неотрицательной.
Второе из уравнений (21.3),	ХФ == О, имеет общее
решение
Ф (ср) = A cos /X ср + В siп /X ср,	(21.4)
где А и В — произвольные постоянные. Покажем теперь,
что X не может принимать любые значения. Это выте-.
кает из того, что увеличение ср на 2тс возвращает точку (г, ср)
в исходное положение; значит, все функции от ср, которые
мы рассматриваем, должны быть периодическими по ср с пе¬
риодом 2тс. Таким образом, и Ф (ср4_2т:) = Ф (ср), а это по
формуле (21.4) означает, что fA должен равняться целому
числу n(n = 0, 1, 2, ...). Отрицательные п мы можем
отбросить, так как знак п влияет только на знак произвольной
постоянной В. Итак, \ — п2 {собственные числа) и
ф (ср) = Л cos/гср-|-Bsin/гср.	(21.4а)
Вернемся теперь к первому уравнению (21.3), в котором
заменим X на п2:
г d
U~ ~d r
откуда
2 d4J , dU	■>,,	n
г2 —.-у- + г 	п2и	= 0.
dr2 1	dr
Это уравнение для функции U (г) может быть решено под¬
становкой U = га, причем для показателя а легко получаем
уравнение
а (а — 1)	-j- ага —г п2га = 0

«211
МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
269
или
а (а—1)4-а— п2 = 0, а2 = п2, а = ± п.
Следовательно,
U(r) = rn либо U(r) — r~n.
Второе из этих решений мы должны отбросить, так как при
п > 0 оно обращается в бесконечность в центре круга г — 0.
Окончательно
«я(г. 'p) = /’"(AC0S«cp + s«sinra?)-
Здесь мы полученное частное решение уравнения Лапласа
(21.1), которое мы искали в виде и — U (г) Ф (ср), обозначили
через ип, так как оно зависит от п так же, как и произ¬
вольные постоянные Ап и Вп.
В силу линейности и однородности уравнения Лапласа
сумма частных решений
«(■'■• ?)=£«„ (г. ?у=^гп (Ап cos «<? + В„ sin «<?) (21.5)
л = 0	л = 0
будет также решением уравнения Лапласа; но это решение
уже содержит две бесконечные последовательности неопре¬
деленных коэффициентов (произвольных постоянных) Ап и Вп.
Чтобы придать решению (21.5) вид, напоминающий ряд
Фурье, положим
Л =	Ап = ап. Вп — Ьп («=1.2....)..
Тогда «(г, ср) может быть записано в виде
«(г, <р) = -у +	cos ivf + b„ sin «?)/•'’.	(21.5а)
л= 1
Оставшиеся неопределенными коэффициенты а0, ап и Ьп мы
определим из граничного условия (21.1а), в котором задан¬
ная функция и (ср) также должна быть периодической с пе¬
риодом 2тс. Полагая в решении (21.5а) r = получим гра¬
ничное условие в виде соотношения
оо
« (?) = -у- 4- 2 ^"ал C0S «? + Si n «?)>
270
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПТ
которое представляет собой разложение я (ср) в ряд Фурье.
По известным формулам для коэффициентов Фурье мы можем
теперь установить, что
2те
Rnan = I* и (ф) cos пф t/ф
о
и
2«
Rnbn = ^ J* и (ф) sin пф (/ф,
о
т. е. что
2те	2л
f /7(ф)созпф^ф, bn = ^f 2(ср) sin/гф
6	о
(21.6)
Чтобы получить решение задачи Дирихле для круга, остается
только подставить формулы для коэффициентов (21.6) в вы¬
ражение (21.5а).
Покажем, что полученное решение совпадает с интегралом
Пуассона для круга (см. формулу (20.2)). Действительно, подста¬
новка формул (21.6) в выражение (21.5а) дает
оо	1
и. {г, ?) = ф f 4 + 2 cos П р (Ф) <+
0 [	Л=1	J
Сумма в фигурных скобках может быть вычислена. С этой целью
заметим, что согласно формуле Эйлера (см. «Кр. к.», п. 168)
cos п (<р — ф) = Re е1п
где Reозначает вещественную часть г. Поэтому
cos л с?—Ф)=Re
Л=1
п = 1
Для г < R отношение 4 < 1 и ряд
2Ш”	=2’"=+
П=1	Л=1

$ 21]	МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	271
является бесконечной геометрической прогрессией с знаменателем
q =	модуль которого \q\ =-^ < 1. Следовательно, ряд
сходится и его сумма равна
оо	r pl (<р-ф)
1Ц. у ((?-ф) _± , R	_ 1 я+г<<?-*>
2+2Дя/	”2	1 r	“2 R-re^-»'
n=1	i~'Re
Чтобы отделить вещественную часть этого выражения, умножим
числитель и знаменатель дроби на сопряженный знаменатель:
р Г1 R+re'1^-® 1	Г_1_ (Тг + п/в-Ф)) (У? —ге-Н?-Ф)) 1
Ке[2 fl —г? <’-'»]	L2 (Я —ге/(¥_ф,)(Я —J
_ Rp Г1 Я2 — г2 + 2/Яг sin (у — ф) q _
1.2 Я2 —2Яг cos& — <{>) +г2_| —
1	Я2 — г2
“2 Я2 — 2Яг cos (<р — <р) + г2 ’
так что
1 Vi ( г \п	1	R2	г2
"2 + 2Д Я") cos и (? — ф) = 2- Я2 —2Яг cos (? —4.)4-г2"
п=1
и
2тс
1 f ~	R2 — г2
. и(г’ ?) = 2^ ./ и.Я2—2Яг cos (? —<р)4-г2
О
Это и есть интеграл Пуассона для круга (отличие от формулы
(20.2) состоит только в том, что вместо rOl ср0 мы теперь пишем г,
у, а вместо ср применяем переменную интегрирования ф).
66.	Разделение переменных в трехмерном уравнении
Лапласа в сферических координатах. Многочлены Ле¬
жандра. Применим теперь метод Фурье к трехмерному урав¬
нению Лапласа в сферических координатах-
1 д / 2	[	1	д / . л ди\	j 1	д2и	п
Т2 дг К	дг / *	г2 sin 0	<20 \Sin dO ) г2 sin2 в	ду2
Мы рассмотрим здесь наиболее простой и важный случай,
когда и не зависит от ср: u — u(rt 9). Это—:так называемый
осесимметричный случай, в котором и постоянно на каждом
круге широты: г — const, 9 = const, О^ср^тс. Тогда

272
УРАВНЕНИЕ ЛАПЛАСА
!гл. пт
уравнение Лапласа принимает вид после сокращения на
общий множитель
(21.7)
Посмотрим, каковы могут быть решения этого уравнения
вида и = U (г)Ф (6), ограниченные в шаре радиуса R с цен¬
тром в начале координат. Подставляя и = U (г) Ф (0) в урав¬
нение (21.7), находим
или
1 d ( 9 dU \	1 d I . « d$ \
U dr \	’ Ф sin 0 d0 ^Sin dft /
(21.8)
По стандартному для метода Фурье рассуждению, поскольку
левая часть уравнения (21.8) не зависит от 6, а правая — от г,
обе они должны быть постоянными:
таг ж (si"e	<2L9>
где X — постоянная разделения, которую опять-таки считаем
неотрицательной. Для дальнейших вычислений нам удобнее
вместо X ввести другую произвольную постоянную v, связан¬
ную с X соотношением
Х = v(v+ 1).
Тогда первое уравнение (21.9) примет вид
г2
d2U
dr2
+ 2r
dU
dr
_v(v+l)^ = 0.
Полагая U — r\ мы найдем для показателя а уравнение
а (а—1)-(-2а— v(v-|-l) = O или
а(а+1)=л,+ 1).'
Очевидно, что это квадратное уравнение относительно а
имеет следующие два корня: a = v и а = — —1. Считая
мы можем второй из этих корней отбросить, поскольку
соответствующая функция U (г) = г~'>~х обращается в бес¬
конечность при г = О (напомним, что наша цель — найти
s 21J ‘	МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	273
ограниченные решения). Таким образом, остается решение
U(r) = r (v>0).
Вернемся теперь ко второму уравнению (21.9):
Ф1	(21.10)
Так как сферическая координата 6 изменяется от 0 до тс:
О<0<тс, то мы должны искать решения уравнения (21.10),
ограниченные для всех таких 0. Преобразуем уравнение (21.10),
введя вместо 0 новую независимую переменную
x = cosO.	(21.11)
При 0, изменяющемся от 0 до тс, х изменяется от 1 до —1:
— 1<^х<3. Кроме того, при дифференцировании по 0 мы
должны учесть, что по правилу дифференцирования сложной
функции в силу подстановки (21.11)
z/Ф dx	. п г/Ф
=		УК =	Sin 0 -у— ,
dO dx J0	dx
и уравнение (21.10) должно быть записано в форме
■iH’-S-h-"(-+1)ф
или
[(1 ~ х2)	+v (?н- о ф=
Если мы, кроме того, обозначим зависимую переменную Ф
как функцию от x = cos0 через у:
ф (0) = Ф (arccos х) = у (х),
то получим для определения искомой функции у уравнение
•fe[<1-jc2)®+v<v+1)y=o,	<21Л2>
называемое уравнением Лежандра. Решения этого уравне¬
ния играют важную роль во многих прикладных вопросах.
Точки х=± 1 являются особыми для дифференциального
уравнения (21.12), и поэтому не все решения уравнения Ле¬
жандра будут ограничены на отрезке — 1 х 1 (анало¬
гичную картину мы наблюдали для других дифференциальных
18 И. Г. Арамановнч, В. И. Левин
274
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ИГ
уравнений этой главы, а также для уравнения Бесселя
(см. п. 29)). Можно показать, что уравнение Лежандра
имеет ограниченные решения только в том случае,
когда v = n — целому числу (п 0). Для таких v ограни¬
ченными решениями уравнения Лежандра (21.12) являются
некоторые многочлены, называемые многочленами Ле¬
жандра. Эти многочлены имеют довольно простое замкну¬
тое выражение:
у = Р„(х)=24Г-^г[(х2-1)"].	(21.13)
Покажем, что многочлены (21.13) действительно удовлетворяют
уравнению (21.12) при \ = п. Положим (х2— 1)п = 2 и y = zW.
Тогда z' = 2nx(x2— l)"”1 и (х2— 1)г'=2пхг. Дифференцируя
последнее равенство п раз по х>, будем иметь
[(х* - 1) г'} =	(**)•	(21.14)
Но по правилу Лейбница дифференцирования произведения (см.
«Кр. к.», п. 51)
(uv) = uv^ nuv^"+
4~ 11 ^2! •— *Л/Л“2)	• • • + nu^v' u^v,
и при и = х2 — 1, и = zr получим
. [(х2— l)zz] = (х2— 1)г(л+1) + 2/гхг(л) 4“ 2
ахп	z\
так как все производные функции и = х2 — 1 порядка выше вто¬
рого равны нулю. Точно так же по правилу Лейбница при и = х,
v = z найдем, что
-^■(хг) = хг(л) + пг(и-1).
Следовательно, равенство (21.14) может быть также записано в виде
(х2 — 1)	л+1) 4“ 2пхг(л) 4- п (п — 1) z{n~1} = 2nxz^n>> 4- 2п2г(л_1)
или
(х2 — 1) г(л+1) — п (л+ 1) /л_1) = 0.
Дифференцируя это последнее равенство еще раз по х, придадим
ему вид
-А [(1 _ х2) г(л+1>] + „ („ + 1) 2(л) = о

f 21]
МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
275
или, поскольку z^ = у,
Это показывает, что у == г(л) =-^^-[(х2— 1)л] является решением
уравнения (21.12) при № п, а следовательно, при любой постоян¬
ной Си Су = С [(х2 — 1)л] является решением этого же. урав¬
нения.
Выбор постоянной C = '2«^j’ в многочлене Лежандра (21.13)
зависит от условия нормировки: потребуем, чтобы при л = 1 много¬
член Лежандра Рп (х) принимал значение 1: Рп (.1) = 1, п = 0,1,2,.. ♦
Тогда нужно выбрать С так, чтобы выполнялось условие
=	(21.15)
По правилу Лейбница, уже использованному выше,
-<x+l)"-^rt<x-l)"j +
+„JL(U+I>«i^t<x-1)")+...-
= (1 + 1)" л! + Л [(X + 1)")	К*— 1)”) + ..
но все члены последнего выражения, начиная со второго, содержат
разность х — 1 в качестве множителя и поэтому обращаются в нуль
при х = 1. В силу этого
■^>((хг-1)п]
Из условия нормировки (21.15) теперь действительно следует, что
С=2Щ-'
Таким образом, мы установили, что в качестве Ф(0) сле¬
дует взять Рп (х) = Рп (cos 6) и что, следовательно, ограни¬
ченными решениями вида £/(г)Ф(0) уравнения Лапласа (21.7)
будут функции
«Я(Г, 6) = 1/п(г)Фя(6) = г’Ря(СО8е). (21.16)
18*

276
УРАВНЕНИЕ ЛАПЛАСА
(ГЛ. IIГ
Рассмотрим некоторые свойства многочленов Лежандра.
1.	Многочлен Рп(х) содержит только степени х одина¬
ковой с п четности, а именно: хп, хп~2, хл“4, ..низшей
степенью х в Рп(х) будет первая, если п нечетно, и нуле¬
вая, если п четно.
В качестве примера приведем первые пять многочленов
Лежандра, вычисленных по формуле (21.13)!):
Р0(х)=1. Р1(х) = х, Р2(х) = 1 (3x2-1).
Р3 (х) = у (5х3 — Зх). Pi (х) = -i- (35 х4 — ЗОх2 + 3).
Графики этих многочленов изображены на рис. 74.
2.	При х = 1 значение Р/г(1)= 1 и при х =—1 значе¬
ние Рп(—1) = (—l)rt для всех n = 0, 1, 2, ...
Выше (см. формулу (21.15) и связанный с ней текст) уже
показано, что Рл(1)=1. Ввиду того, что при п четном
Рп(—х) = Рп(х)> а при п, нечетном Рп{—х) = — Рп(х).
очевидно и соотношение Рп{—1) = (—1)л. Графики Рп(х)
при четном п симметричны относительно оси у, а при нечет¬
ном п обладают центральной симметрией относительно начала
координат.
3.	На отрезке — 1 х 1 многочлены Лежандра сами
по абсолютной величине не превосходят единицы:
1Л1(*)1<1 для
Для первых пяти многочленов Лежандра это видно из рис. 74,
в общем случае мы доказательства не приводим.
4.	Многочлен Рп(х) для п > 1 имеет п действительных
простых корней, расположенных в интервале —1<х<1.
Например, на рис. 74 отмечены 4 корня Р4(х), Доказатель¬
ство в общем случае мы также опускаем.
5.	Многочлены Лежандра ортогональны на интервале
(—1, 1), т. е. для
1
f Рп(х) Рт(х) dx = 0.	(21.17)
-1
*) Таблицы многочленов Лежандра имеются в книге Янке Е.»
Эм де Ф. (см. список литературы),

§21]
МЕТОД ФУРЬЕ &ЛЯ УРАВНЕНИЯ ЛАПЛАСА
277
Докажем это важное свойство методом, неоднократно приме¬
нявшимся ранее. Пусть п=рт, и запишем, что Рп(х) и Рт(х)
удовлетворяют уравнению Лежандра (21.12) соответственно для
и \ = т\
г[<'— ’i^q+^ + DP.-o.
Умножим первое из этих равенств на Рт (х), а второе на Рл(л),
и вычтем из первого полученного равенства второе:
Нетрудно видеть, что

278
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. IIF
интегрируя это последнее равенство по л в пределах от х = —1
до х = 1, найдем, что
1
{m(m4-l) —п(п-Н)}	/ Р„ (х) Рт (х) dx =
так как последнее выражение из-за множителя 1 — х2 обращается
в нуль при х = ± 1. У читывая, что т (т +1) — п (п + 1) =/= 0, мы
приходим к равенству (21.17).
6.	В приложениях многочленов Лежандра важную роль
играет еще формула
1
fpl(x)dx = li~ (и = 0,1.2,...),	(21.18)
-1
которую мы не будем выводить (но полезно ее проверить
для малых n = 0, 1, 2, 3, 4: так, например,
1 1
f р1 (х) dx = f | (5х3 — Зх)2 dx =
Доказательства всех приведенных свойств многочленов
Лежандра имеются в более полных курсах,
67.	Решение задачи Дирихле для шара в осесиммет¬
ричном случае разложением по многочленам Лежандра.
Осесимметричная задача Дирихле для шара радиуса R с цен¬
тром в начале координат состоит в определении функции и {г, 0),
удовлетворяющей уравнению Лапласа (21.7)для г < R и гра¬
ничному условию
(21.19)
Выше мы установили, что дляп = 0, 1, 2, ... решениями
уравнения (21.7) являются функции (21.16):	(cos 0).
Ввиду линейности и однородности уравнения Лапласа его
$ 211
МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
279
решением будет также функция
оо
и(г, 6)= 2СЛГПРЛ(СО8 6),	(21.20)
л = 0
где Сп — произвольные постоянные коэффициенты, которые
мы определим так, чтобы функция (21.20) удовлетворяла гра¬
ничному условию (21.19). Для этого надо потребовать,
чтобы по 9, 0<^9<^гс, тождественно имело место соотношение
оо
^(0)= 2C„7?"P„(cos9).	(21.21)
п = о
В предположении, что тождество (21.21) имеет место, мы
можем эти коэффициенты найти, воспользовавшись свойством
ортогональности многочленов Лежандра (свойство 5 в пре¬
дыдущем п. 66). Действительно, умножим тождество (21.21)
на Рт (cos 6), где т 0 — некоторое фиксированное целое
число, и проинтегрируем его по граничной сфере радиуса /?:
§ И (9) Рт (cos 9) da = V CnRn $ Рп (cos 9) Рт (cos 9) da.
S	n = 0	5
(21.22)
Элемент площади поверхности сферы da = /?2sin 6 dft dy, и
интегрирование по сфере означает интегрирование по 9
в пределах от 0 до z и по ср в пределах от 0 до 2тс.
Следовательно,
$ Рп (cos 9) Рт (cos 9) da —
s
2-	u
—	d<? Рл (cos 9) (cos 9)/?2 sin 9 <f9=s
6 о
It
= 2itR2 I*Prt(cos G)Pm(cos 9)sin9d9 =
6
1
= 2k/?2 fPn(x)Pm(x)dX=:
-1
0
если n=km
2
I 2m-hi'’ еСЛИ n~m

280
УРАВНЕНИЕ ЛАПЛАСА
[ГЛ. ПГ
Здесь интегрирование по ср дало множитель 2 г, а последую¬
щая замена переменной cos 0 = х, —sin9rfO = Jx приводит
к последнему интегралу, который по свойствам 5 и 6 много-
9
членов Лежандра (п. 66) равен 0 при	и	г
при п = т.
Таким образом, в правой части равенства (21.22) все
члены суммы, кроме одного, равны нулю; действительно,
когда п, пробегая все значения от 0 до оо, принимает зна¬
чения, отличные от фиксированного номера т, соответствую¬
щий интеграл равен 0; только в единственном члене суммы,
соответствующем значению п = т> интеграл оказывается
отличным от нуля. Следовательно, правая часть, равен¬
ства (21.22) равна
откуда следует, что
Ст =	(2т + 1)	§ и (0) Рт (cos 9) da. (21.23)
Так как т— произвольный фиксированный номер, т = 0,
1, 2	 то мы можем заменить его на п, и подставить
выражение (21.23) в решение (21.20). Тогда мы получим
окончательное решение задачи Дирихле для шара радиуса /?.
Мы уже имели выше (см. п. 59) решение задачи Дирихле
для шара в виде интеграла Пуассона в более общем (не осе¬
симметричном) случае зависимости граничной функции и и
решения от ср. Можно показать, что решение (21.20) совпа¬
дает с решением (19.6) из гТ. 59 в том частном случае,
когда и не зависит от ср.
Формула (21.20), представляющая решение задачи Дирихле
(в осесимметричном случае) в виде ряда по многочленам
Лежандра, имеет некоторые преимущества перед решением
в виде интеграла Пуассона. Мы ограничимся только одним
простейшим следствием из этой формулы. Очевидно, что
если граничные значения zz(9) сами являются одним из много¬
членов Лежандра или их конечной линейной комбинацией,
то в правой части формулы (21.20) останется только одно
или несколько слагаемых, отличных от нуля. Например,
если zz(0) = cos9 = P1(cos9), то в формуле (21.23) интеграл

§ 21]	МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА	281
будет отличен от нуля только для т—\ и при этом
тс
Ci = ^4^^cos0-P1(cos9)da = ^ У*cos29-sin9
5	6
Таким образом, по формуле (21.20) решением задачи Дирихле
для шара радиуса R при граничных значениях и (0) == cos 6
будет «(г, 9) = -^-cos 9. Рассмотрим еще один такой при¬
мер: пусть и (0) = cos 26; представим cos 29 в виде линейной
комбинации многочленов Лежандра:
cos 29 — 2 cos2 9 — 1 = 2х2 — 1 =
' — у Р<1 (*) — j ро (X) = Р2 (cos 9) — 1 Ро (cos 9),
где x = cos9. Следовательно, в решении (21.20) от суммы
останутся только два отличных от нуля члена, соответствую¬
щих // —О и п = 2, причем
Со = 4^г § «(0) Ро (cos 9)	1,
5
С2=^Г4^Г§ Р2(cos0)=
s
так что решением задачи Дирихле при этом граничном усло¬
вии будет
“(Г- 0>=4(^)2p2<COS0)—I-
Изложенный выше метод Фурье решения задачи Дирихле
для шара применим не только в осесимметричном случае.
Однако в общем случае при разделении переменных в урав¬
нении Лапласа в сферических координатах мы получаем
вместо уравнения Лежандра (21.12) более сложное уравне¬
ние, решения которого — так называемые присоединенные
функции Лежандра—тесно связаны с многочленами Лежандра.
Соответственно и формула решения в виде ряда примет более
сложный вид. Подробнее эти вопросы рассматриваются в спе¬
циальных руководствах.

ЗАКЛЮЧЕНИЕ
68.	Классификация линейных дифференциальных урав¬
нений с частными производными второго порядка. Как
уже отмечалось во введении, общий вид линейного диффе¬
ренциального уравнения второго порядка при условии, что
неизвестная функция и зависит от двух переменных х и у,
таков:
. д2и . D д2и . д2и , гу ди , „ ди . „	. . ч /1Ч,
Как и раньше, мы предполагаем, что все коэффициенты
уравнения постоянны !).
Большинство дифференциальных уравнений математиче¬
ской физики, которые изучались в настоящем курсе, пред¬
ставляют частные случаи общего уравнения (1).
Так, если для единообразия обозначений вместо пере¬
менной t (времени) писать переменную у, то уравнение сво¬
бодных колебаний струны (§ 1) примет вид
д2и
дх2
а
2
(2)
а уравнение линейной задачи теплопроводности (§ 12)
ди
~ду
= 0.
(3)
Наконец, уравнение Лапласа (§ 18) ъ двумерном случае
имеет вид
д2и ( д2и
9 Приводимая ниже классификация линейных уравнений пере¬
носится и на уравнения с переменными коэффициентами, которые
в нашей книге не рассматриваются.
(4)

ЗАКЛЮЧЕНИЕ
283
В уравнении (4) обе вторые частные производные входят
в левую часть с одинаковыми знаками, в уравнении (2) —
с противоположными знаками, а в уравнении (3) — вторая
производная по одной из переменных вовсе не входит.
Л. Эйлер доказал, что любое дифференциальное урав¬
нение вида (1) с помощью замены независимых переменных
х и у может быть приведено к одному из следующих трех
видов.
В2
1.	Если АС	4~>0> то после введения новых незави¬
симых переменных £ и т?1) уравнение (1) примет вид
д2и . д2и , ~ ди .	„ ди . „	£ ч
д'? drf 01 дЬ + дц	~ f1
В этом случае уравнение называется эллиптическим. Наи¬
более простым эллиптическим уравнением является уравнение
Лапласа (4).
В2
2.	Если АС	< 0, то уравнению (1) можно при¬
дать вид
д2и д2и . ди .	„ ди .	„	. „	.	z_4
E2~d^ + F2U = f^’	<6>
Такое уравнение называется гиперболическим} простей¬
шим примером его является одномерное уравнение свободных
колебаний (2).
В2
3.	Если АС-	4- = 0, то уравнение (1) приводится
к следующему:
^ + °з^+£3-^-+ лза==/з(;> <	(7)
и называется параболическим. Примером его служит урав¬
нение линейной теплопроводности (3).
Наименования уравнений объясняются тем, что при
исследовании общего уравнения кривых второго порядка
Ах2 + Еху + Су2 + Dx + Еу -J- F = 0 оказывается, что
!) Мы ограничиваемся только принципиальной стороной вопроса
и не указываем формул, по которым фактически производится
замена переменной. Читатель, интересующийся этим вопросом,
должен обратиться к более полным курсам.

284
ЗАКЛЮЧЕНИЕ
в случае АС	> 0 кривая представляет эллипс, в случае
В2	В2
АС	j- <0 — гиперболу и в случае АС	= О —
параболу1).
Уравнения (5), (6) и (7) можно еще более упростить
введением новой неизвестной функции. Именно, вводя функ¬
цию v($, т]) по формуле
tf(t =	(8)
мы можем всегда подобрать числа аир так, что в эллипти¬
ческом и гиперболическом уравнениях исчезнут члены с про¬
изводными первого порядка, а в параболическом — член
с первой производной по одной из независимых переменных
(в уравнении (7) по 5) и член с самой функцией.
Введение вспомогательной функции по формуле (8) уже
встречалось нам в п. 21 при изучении телеграфного
уравнения для линии без искажений (см. формулу (7.13)).
Окончательно любое уравнение вида (1) может быть,
с учетом сделанных замечаний, приведено к одному из сле¬
дующих канонических типов'.
д2и
, д2и
1 д'Г?
си
=g
д2и
д2и
1 Г11
дф
дт?
| С LL
д2и
ди
д?
дт]
= g
(эллиптический тип),
(гиперболический тип)
(параболический тип)
(с — постоянное число, g— функция переменных х и у).
69.	Корректность постановки задач математической
физики. Уравнения гиперболического и параболического
типов возникают чаще всего при изучении процессов, про¬
текающих во времени (в нашем курсе это были уравнения
колебаний, распространения электрических волн, распростра¬
нения тепла, диффузии). В одномерном случае всегда уча¬
ствовала одна координата х и время t.
’) Поскольку бывают еще случаи вырождения кривых
второго порядка, то чаще говорят, что в первом случае кривая
эллиптического типа, во втором — гиперболического и в тре¬
тьем — параболического (см., например, книгу Н. В. Ефимова
«Квадратичные формы и матрицы», Физматгиз, М.» 1962).

ЗАКЛЮЧЕНИЕ
285
Поэтому канонические уравнения этих типов обычно за¬
писываются так:
д2и
lx2
д2и
dt2
■+-CU=g(X, t)
д2и
дх2
ди
dt
= g(x, t)
(гиперболический тип).
(параболический тип).
Для задач, приводящих к таким уравнениям, дополни¬
тельные условия разделяются на начальные и краевые.
Начальные условия, как мы видели, состоят
в задании при t = 0 значений искомой функции и и ее про¬
изводной (в гиперболическом случае) или только значений
самой функции (в параболическом случае).
Краевые условия для этих задач заключаются в том,
что указываются значения неизвестной функции и(х, t)
на концах интервала изменения координаты (в задаче о коле¬
баниях струны это концы струны !), в задаче о распростра¬
нении электрических колебаний это концы линии, в задаче
о линейной теплопроводности это концы стержня и т. д.).
Если процесс протекает в бесконечном интервале
изменения координаты х (бесконечная струна, бесконечный
стержень и т. д.), то. краевые условия отпадают и полу¬
чается задача только с начальными условиями, или, как ее
часто называют, задача Коши.
Если ставится задача для конечного интервала, то
должны быть заданы и начальные и краевые условия. Тогда
говорят о смешанной задаче.
Уравнения эллиптического типа возникают обычно
при исследовании стационарных процессов. Время t в эти
уравнения не входит, и обе независимые переменные являются
координатами точки. Такими оказываются уравнения стацио¬
нарного температурного поля, электростатического поля и
уравнения многих других физических задач, которые мы
в курсе не рассматривали.
Для задач такого типа ставятся только краевые усло¬
вия, т. е. указывается поведение неизвестной функции
на контуре области. Это может быть задача Дирихле,
когда заданы значения самой функции; задача Неймана,
когда заданы значения нормальной производной искомой
!) В задаче о колебаниях мембраны задаются значения неиз¬
вестной функции на контуре мембраны.

286
ЗАКЛЮЧЕНИЕ
функции, и, наконец, задача, когда на контуре задана
линейная комбинация функции и ее нормальной производной.
В основных задачах математической физики, рассматри¬
вавшихся в настоящей книге, именно физические соображения
подсказывали, какие дополнительные условия следует поста¬
вить в той или иной задаче, чтобы получить единственное
ее решение, отвечающее характеру изучаемого про¬
цесса.
Кроме того, следует иметь в виду, что все выведенные
уравнения носят идеализированный характер, т. е. отражают
лишь наиболее существенные черты процесса. Функции, вхо¬
дящие в начальные и краевые условия, в физических задачах
определяются из экспериментальных данных и могут счи¬
таться известными лишь приближенно. Поэтому мы должны
быть уверены в том, что решения задачи при прибли¬
женных исходных данных будут близки к тем решениям,
которые получились бы при точных исходных данных.
Таким образом, важно, чтобы малые изменения данных
задачи вызывали лишь малые изменения в ее решении
во всей области, в которой эти решения рассматри¬
ваются. В этом случае говорят об устойчивости задачи
относительно начальных и краевых условий.
Все задачи, рассмотренные в книге, принадлежат к типу
задач, имеющих единственное решение, устойчивое относи¬
тельно исходных данных. Как говорят, эти задачи поста¬
влены корректно.
Исследование корректности более сложных задач матема¬
тической физики представляет очень важную и трудную
задачу теории этих уравнений.

ЛИТЕРАТУРА
1.	Кошляков Н. С., Глинер Э. Б., Смирнов М. М.,
Основные дифференциальные уравнения математической физики,
Физматгиз, 1962.
2.	Левин • В. И., Г р о с с б е р г Ю. И., Дифференциальные
уравнения математической физики, Гостехиздат, 1951.
3.	Смирнов В. И., Курс высшей математики, т. III и т. IV,
Физматгиз, 1958.
4.	Тихонов А. Н., Самарский А. А., Уравнения матема¬
тической физики, Гостехиздат, 1953.
5.	Лебедев Н. Н., Специальные функции и их приложения,
Физматгиз, 1963.
6.	Будак Б. М., Самарский А. А., Тихонов А. Н.,
Сборник задач по математической физике, Гостехиздат, 1956.
7.	Лебедев Н. Н., Скальская И. П., Уфлянд Я. С.,
Сборник задач по математической физике, Гостехиздат, 1955.
8.	С м и р н о в М. М., Задачи по уравнениям математической
физики, Физматгиз, 1961.
9.	Янке Е., Эм де Ф., Таблицы функций с формулами и кри¬
выми, Физматгиз, 1959.

Исаак Генрихович Араманович
и Виктор Иосифович Левин.
Уравнения математической физики.
М., 1964 г.,	288 стр. с илл.
(Серия: «Избранные главы высшей математики
для инженеров и студентов втузов»).
Редактор Н. А. Угарова.
Техн, редактор И. Ш. Аксельрод.
Корректор Т. С. Плетнева.
Сдано в набор 10/1 1964 г. Подписано к печати
14/V 1964 г. Бумага 84х1081/з2« Физ. печ. л. 9.
Условн. печ. л. 14,76. Уч.-изд. л. 13,3. Тираж 34 500 экз.
Т-04587. Цена книги 50. коп.	Заказ № 42. '
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71,Ленинский проспект, 15.
Ленинградская типография № 2
имени Евгении Соколовой «Главполиграфпрома»
Государственного комитета Совета
Министров СССР по печати.
Измайловский проспект, 29.

50 к.
«нм