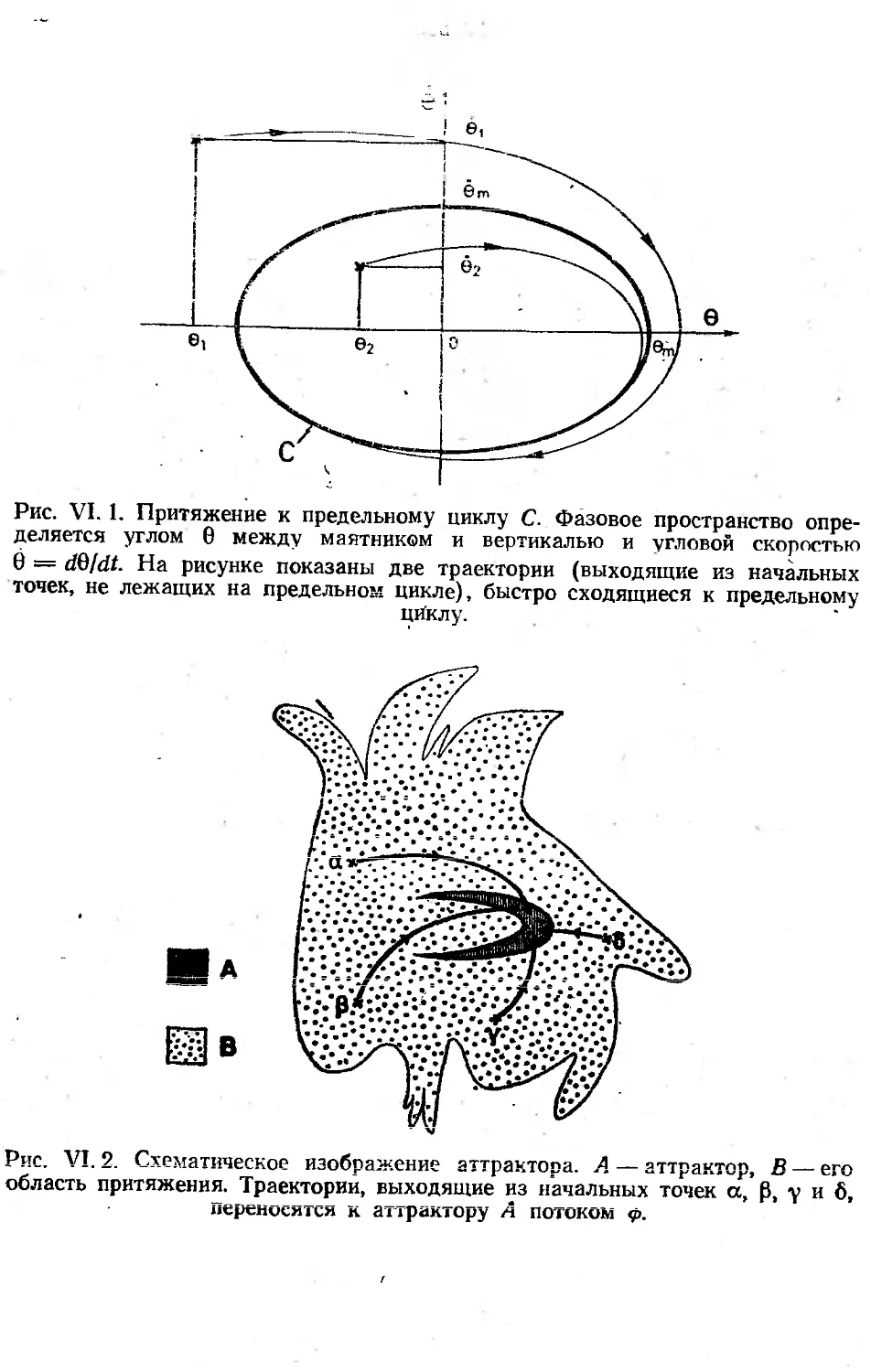
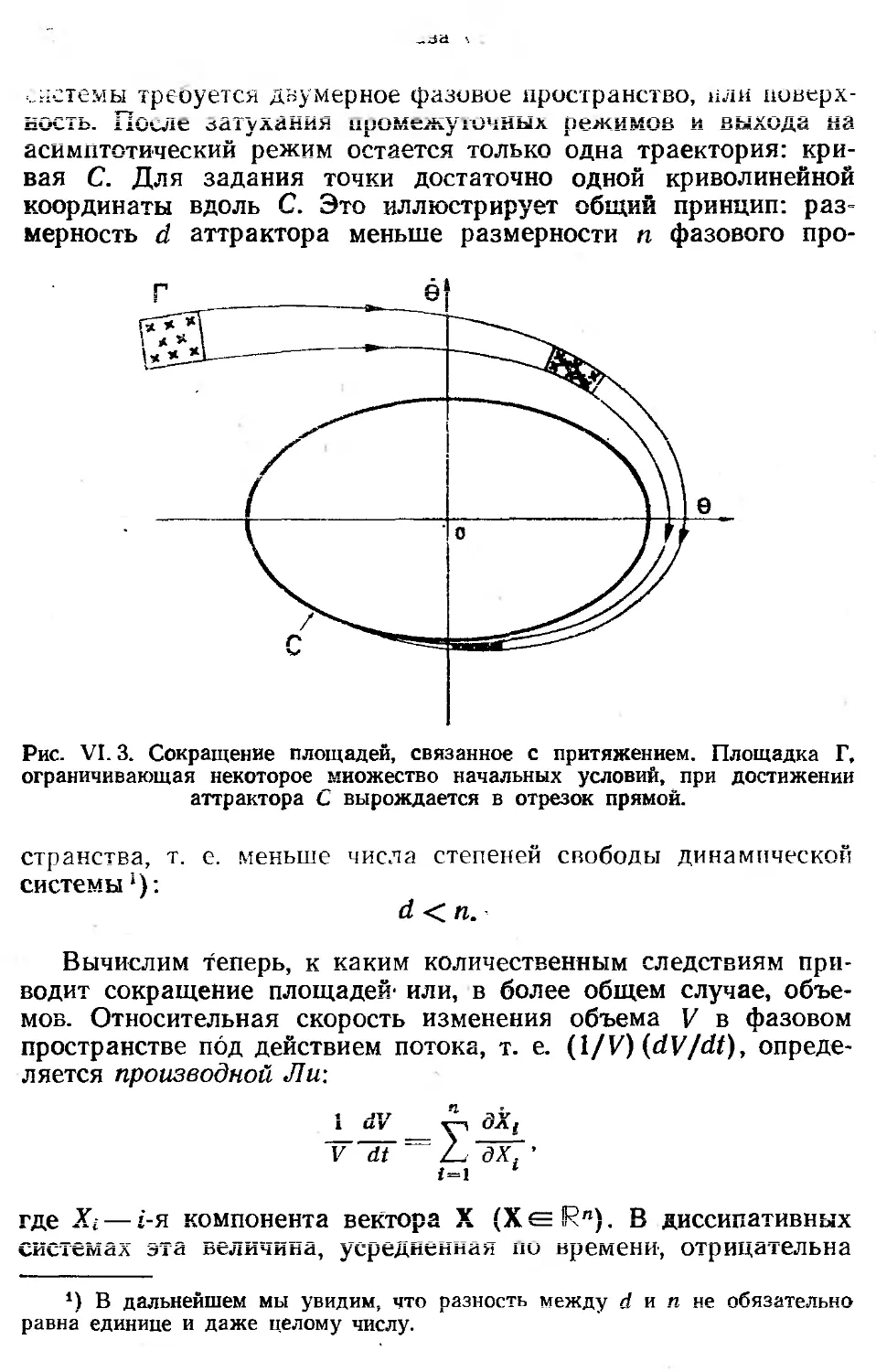
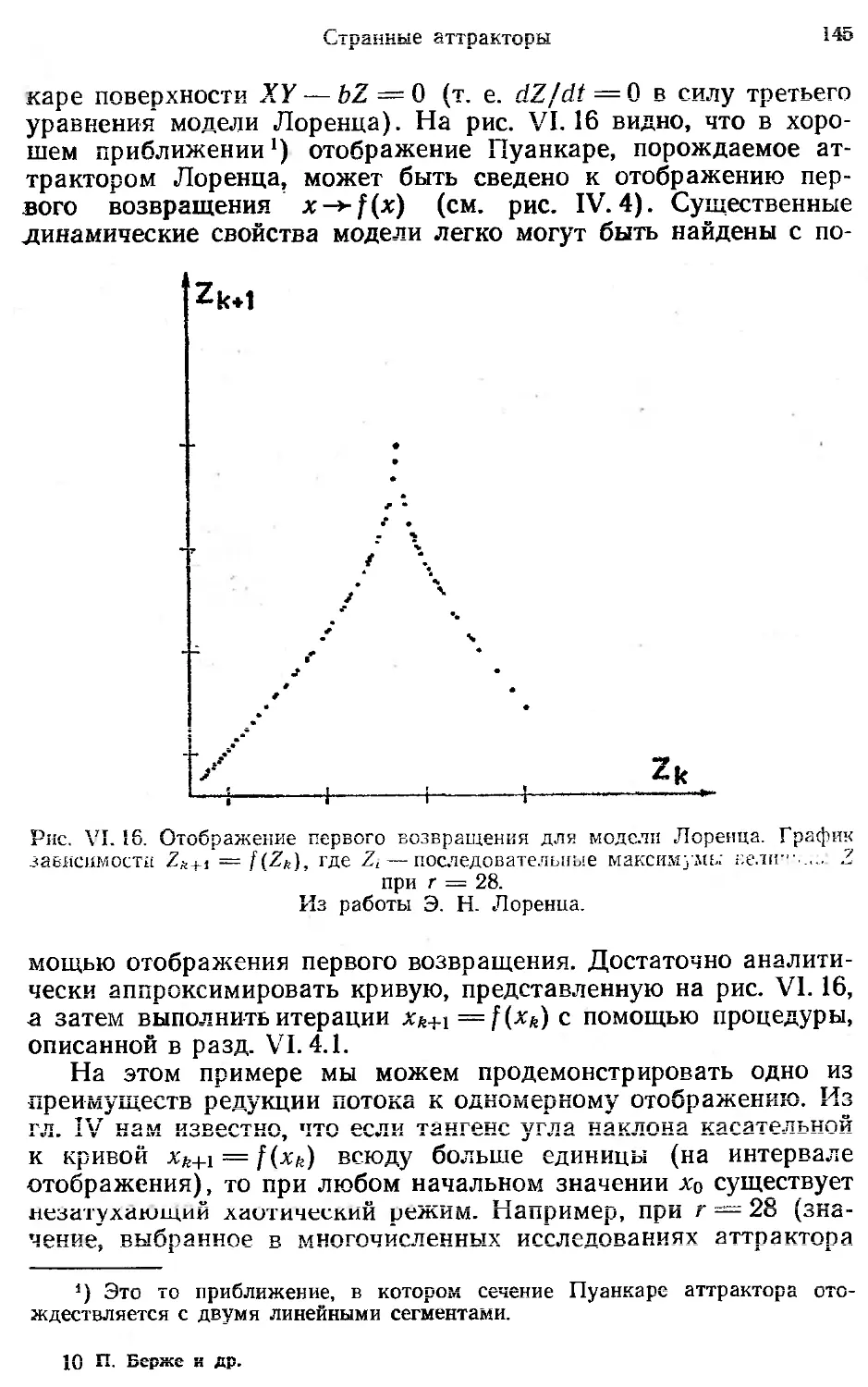
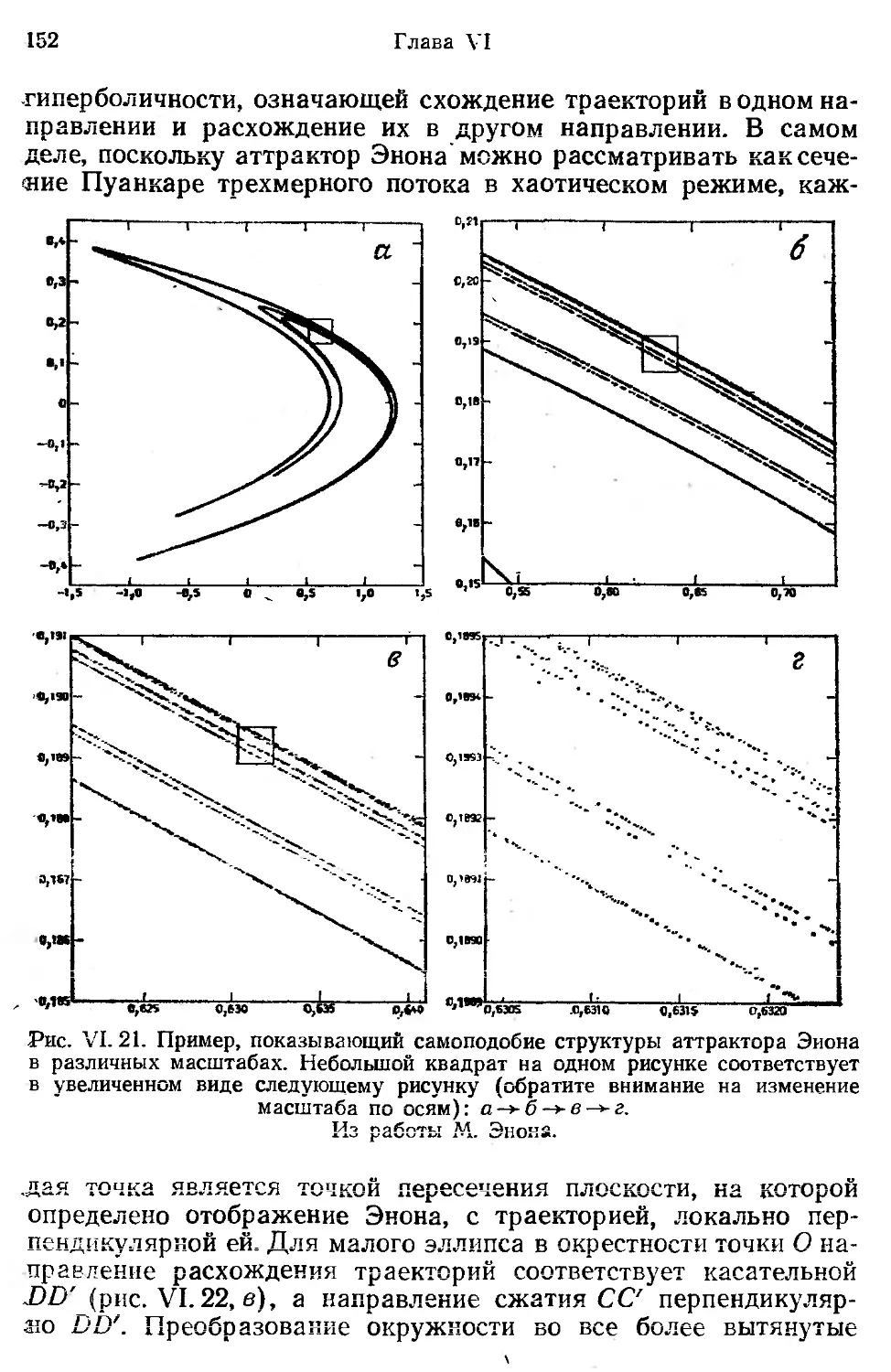
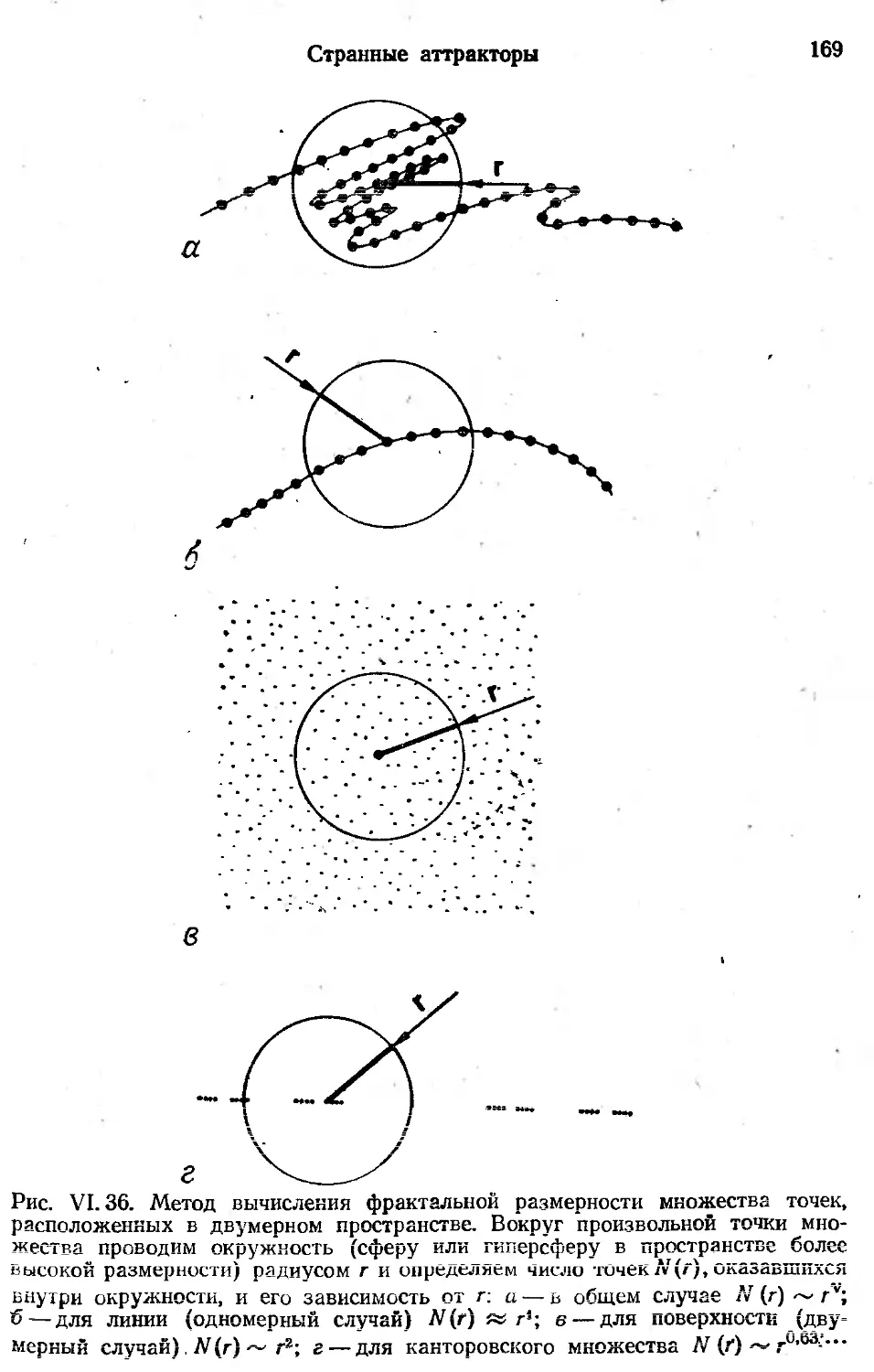
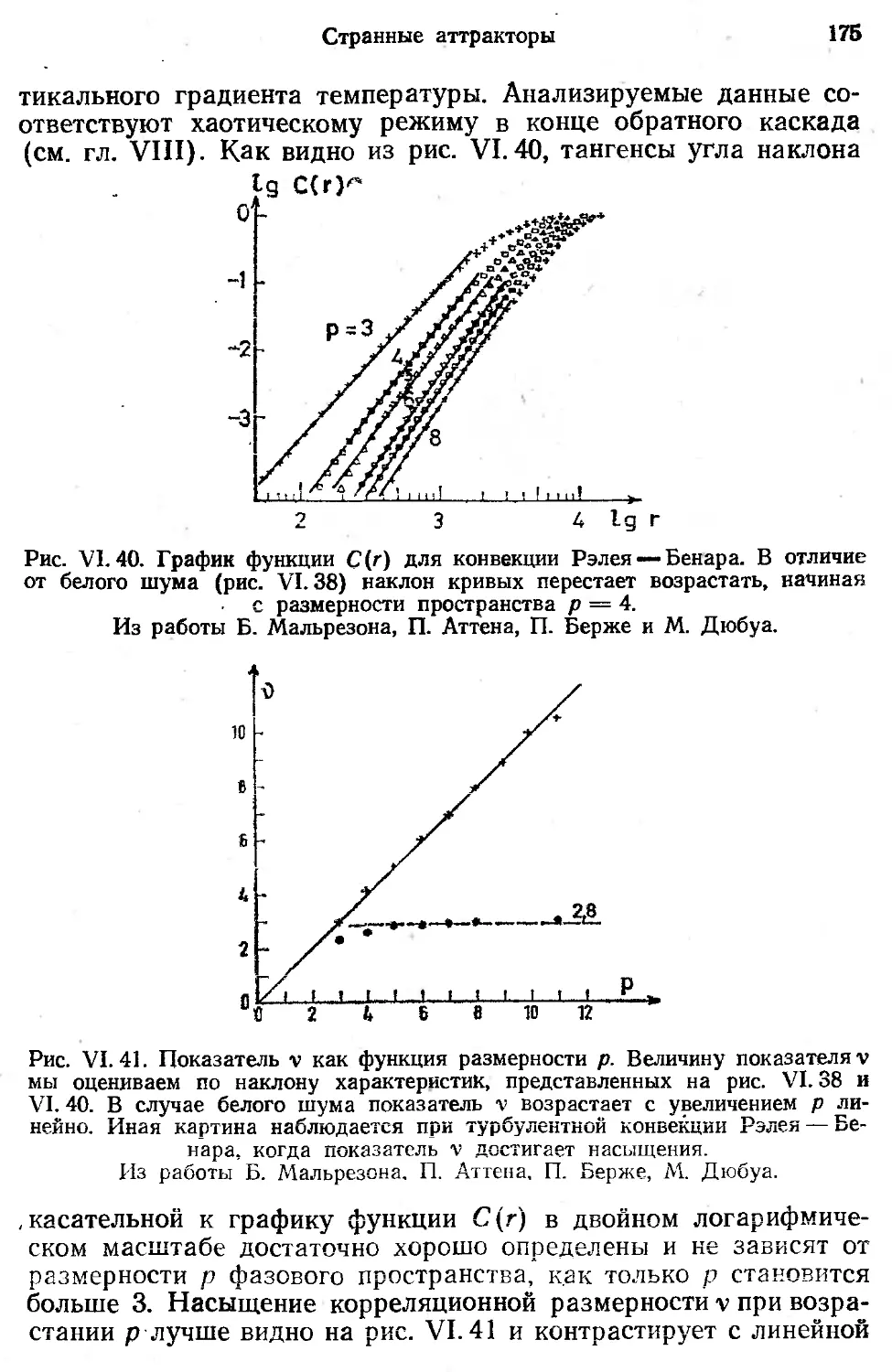
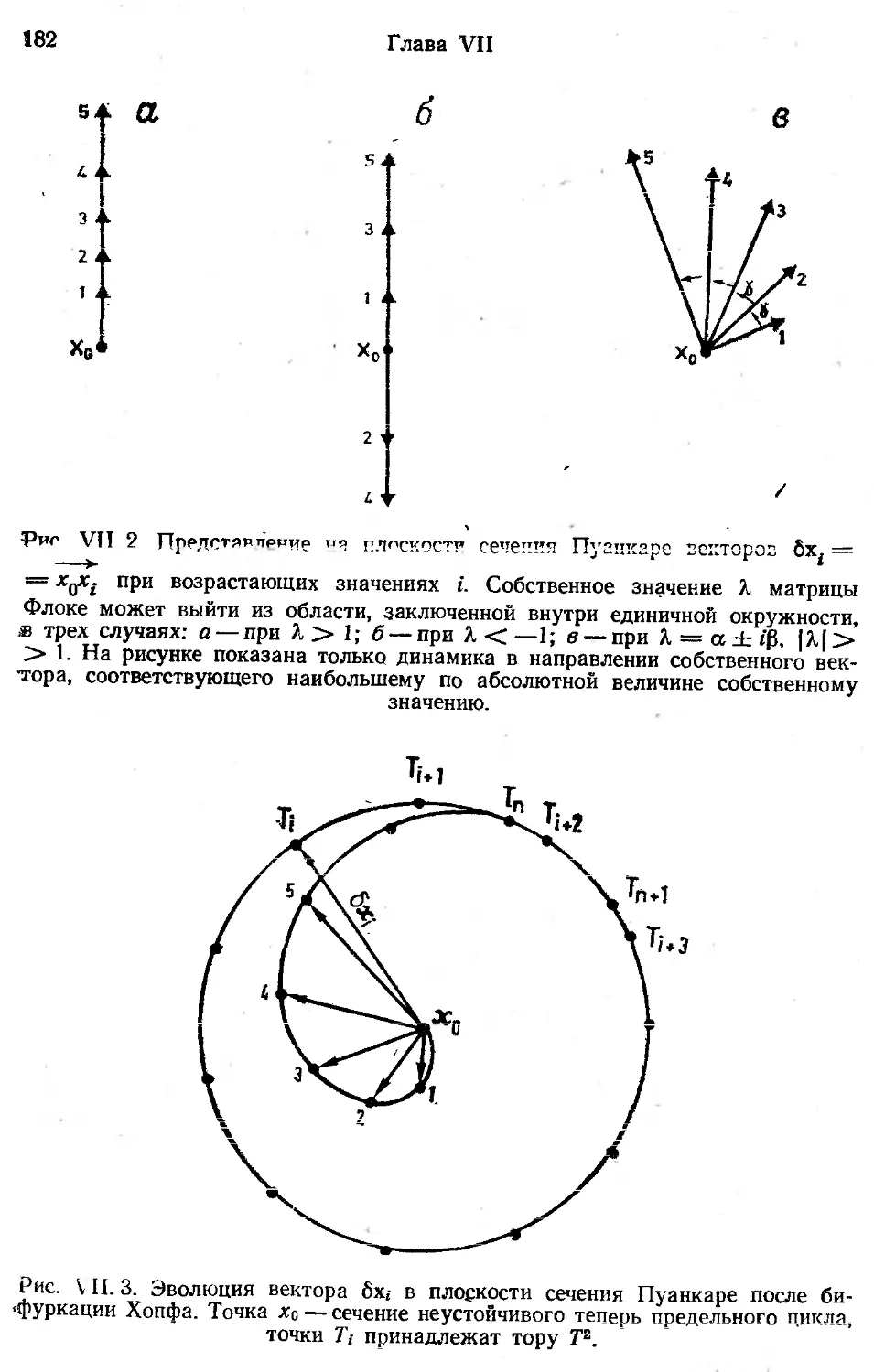
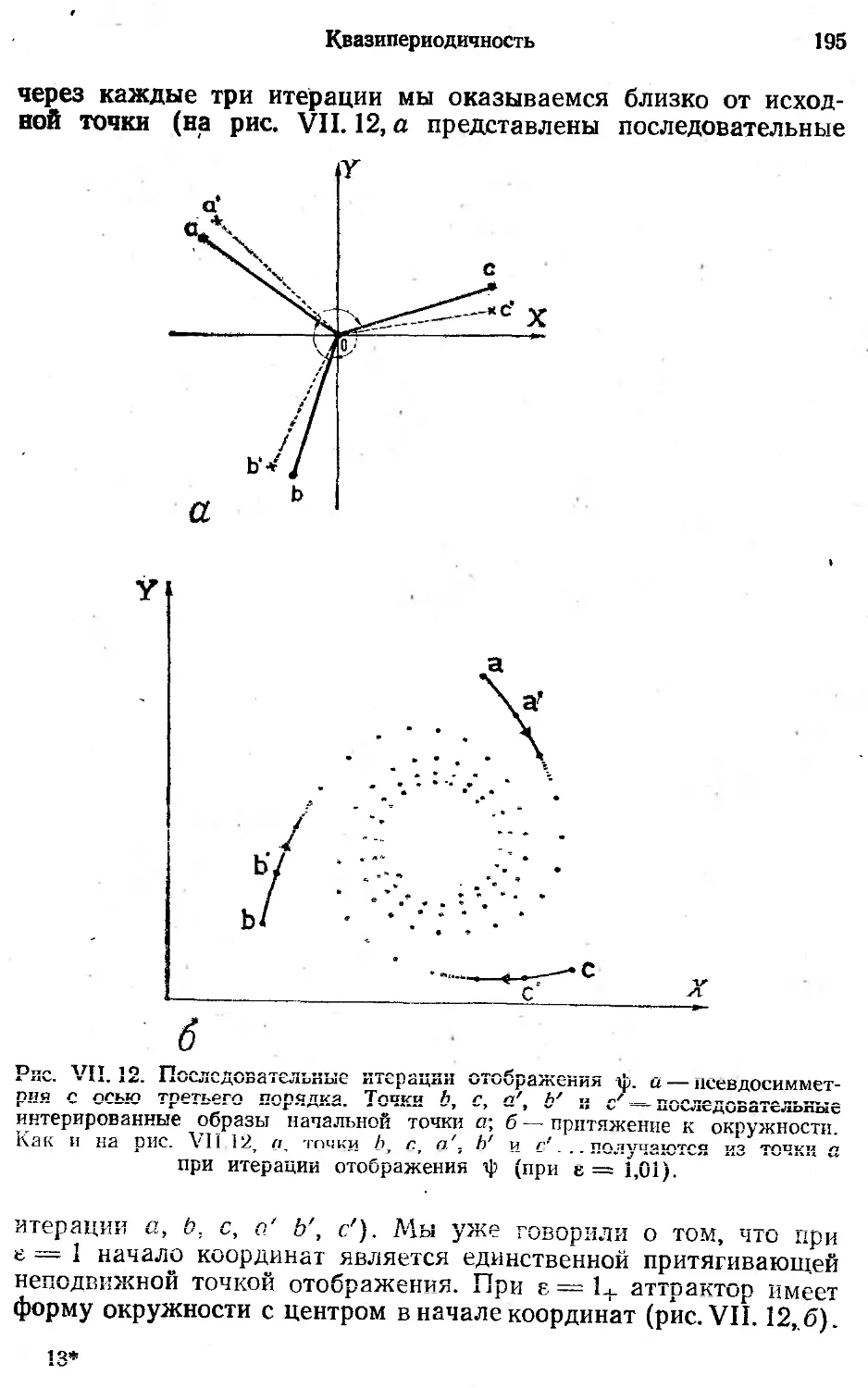
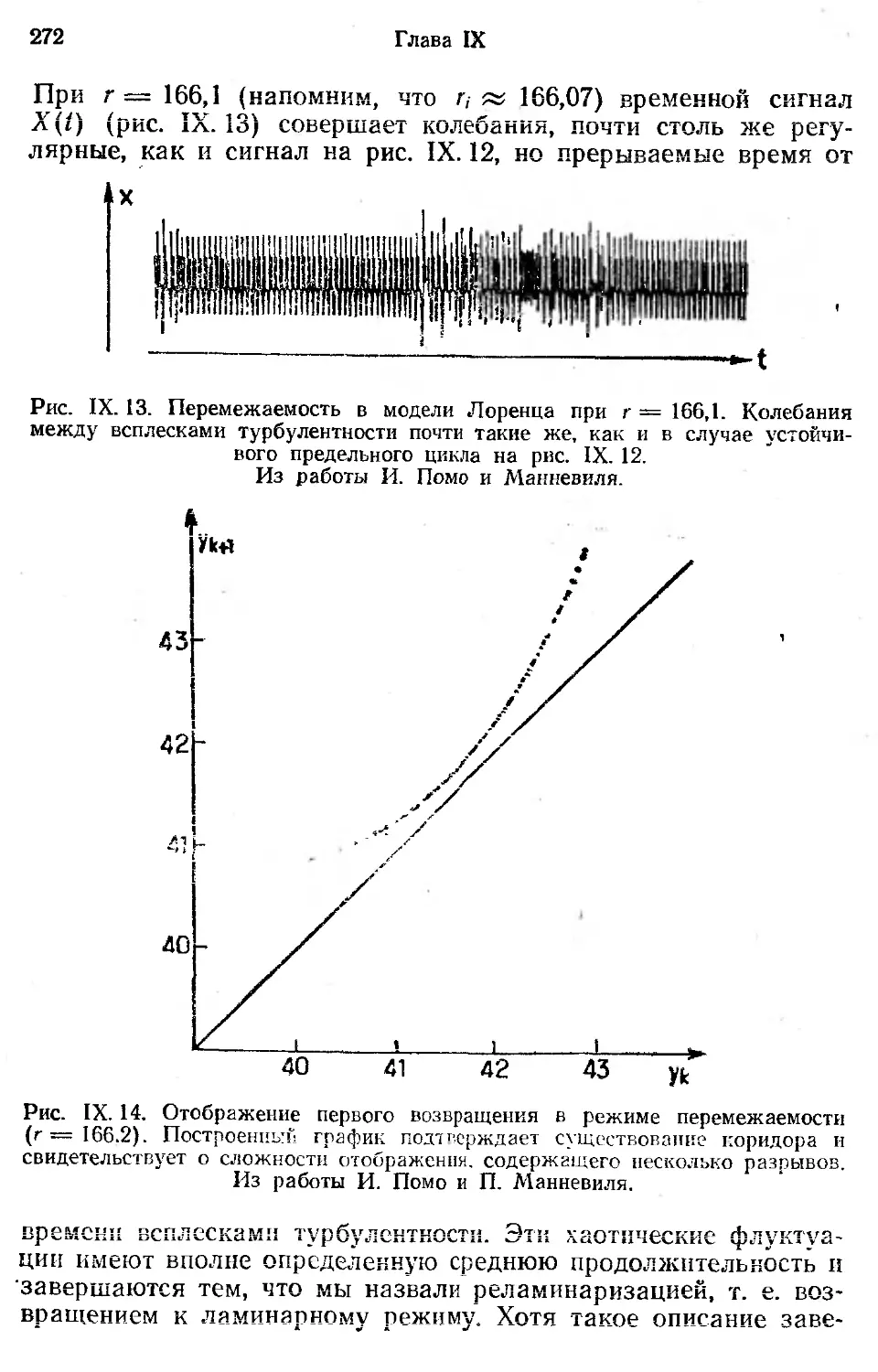
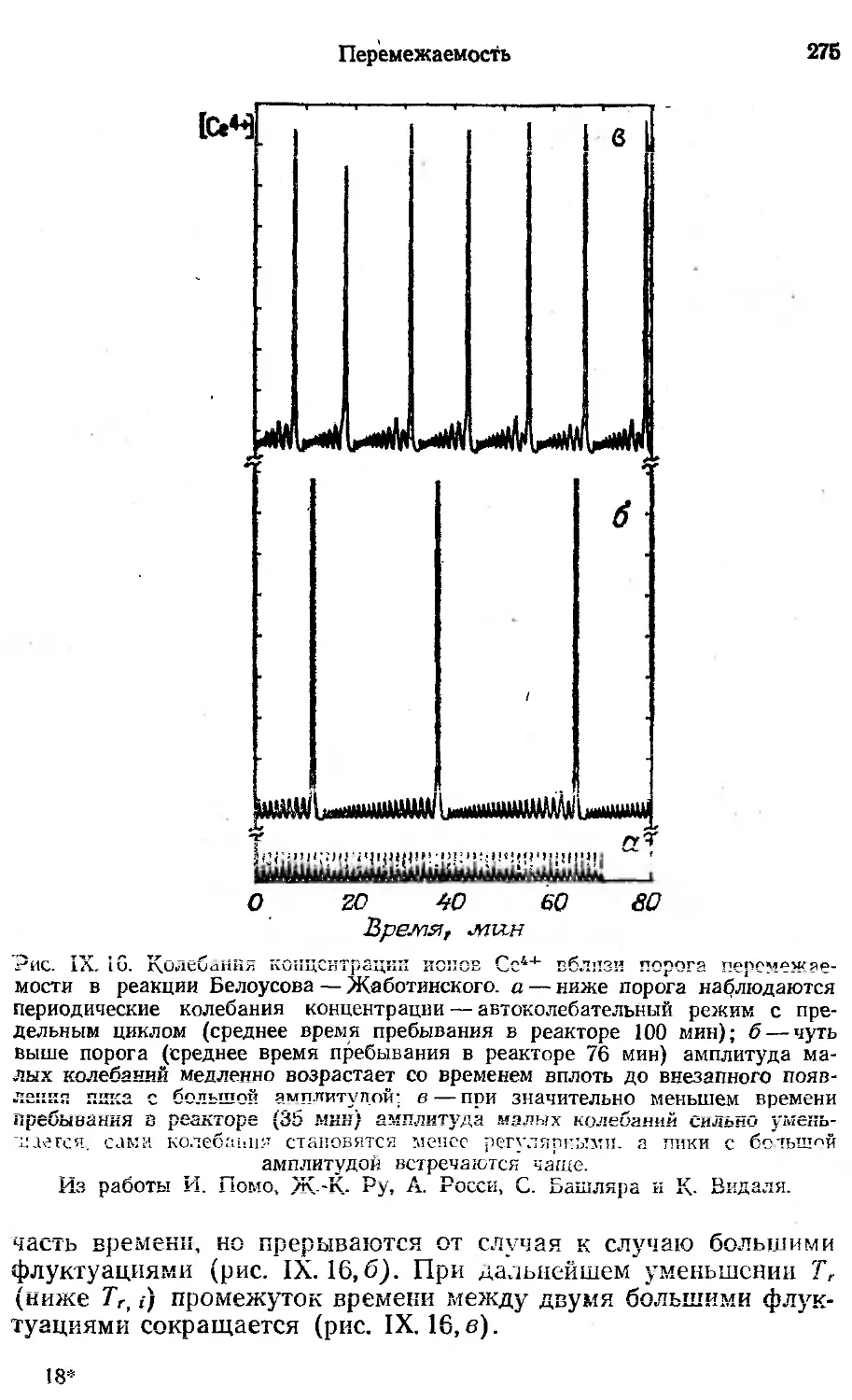
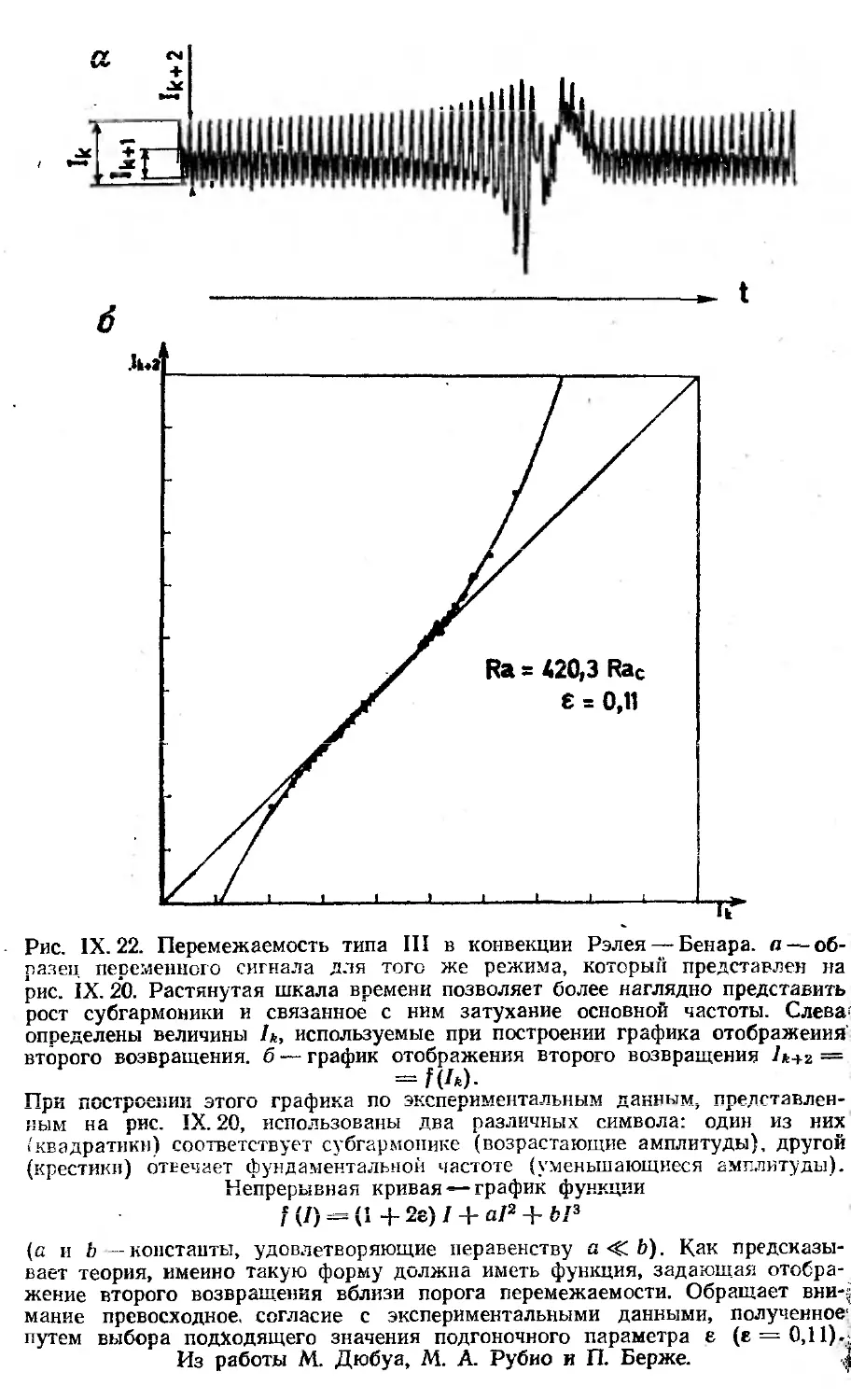
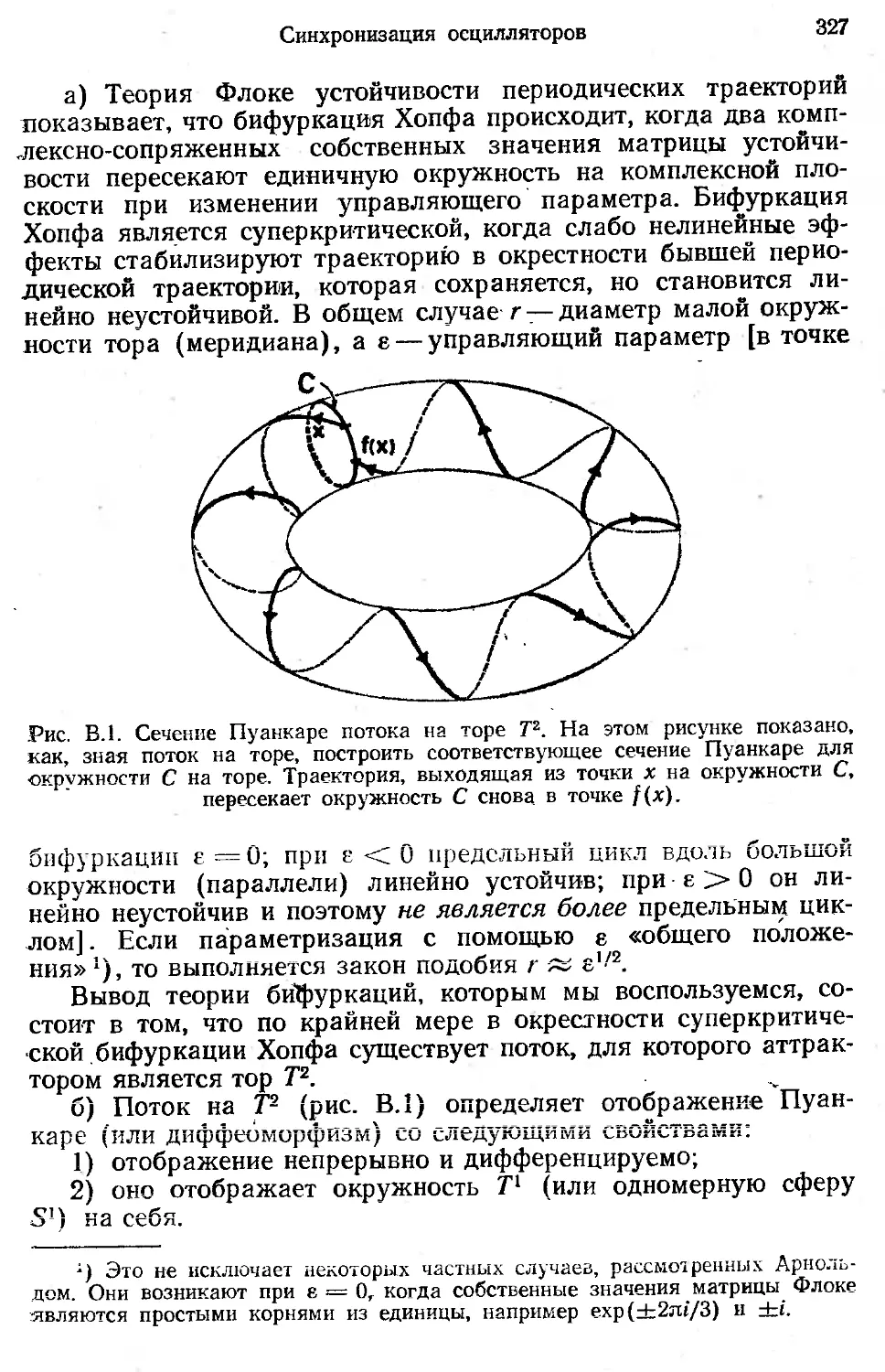
Порядок в хаосе. О детерминистском подходе к турбулентности - Берже П., Помо И., Видаль К.

Автор: Берже П. Помо И. Видаль К.

Теги: аппаратура для изучения и демонстрации явлений физика турбулентность

ISBN: 5-03-001804-2

Год: 1991

Похожие

Нелинейные колебания, динамические системы и бифуркации векторных полей

Введение в теорию динамических систем с обзором последних достижений

Хаос и интегрируемость в нелинейной динамике

Механизмы возникновения, структура и свойства динамичного хаоса в в радиофизических системах

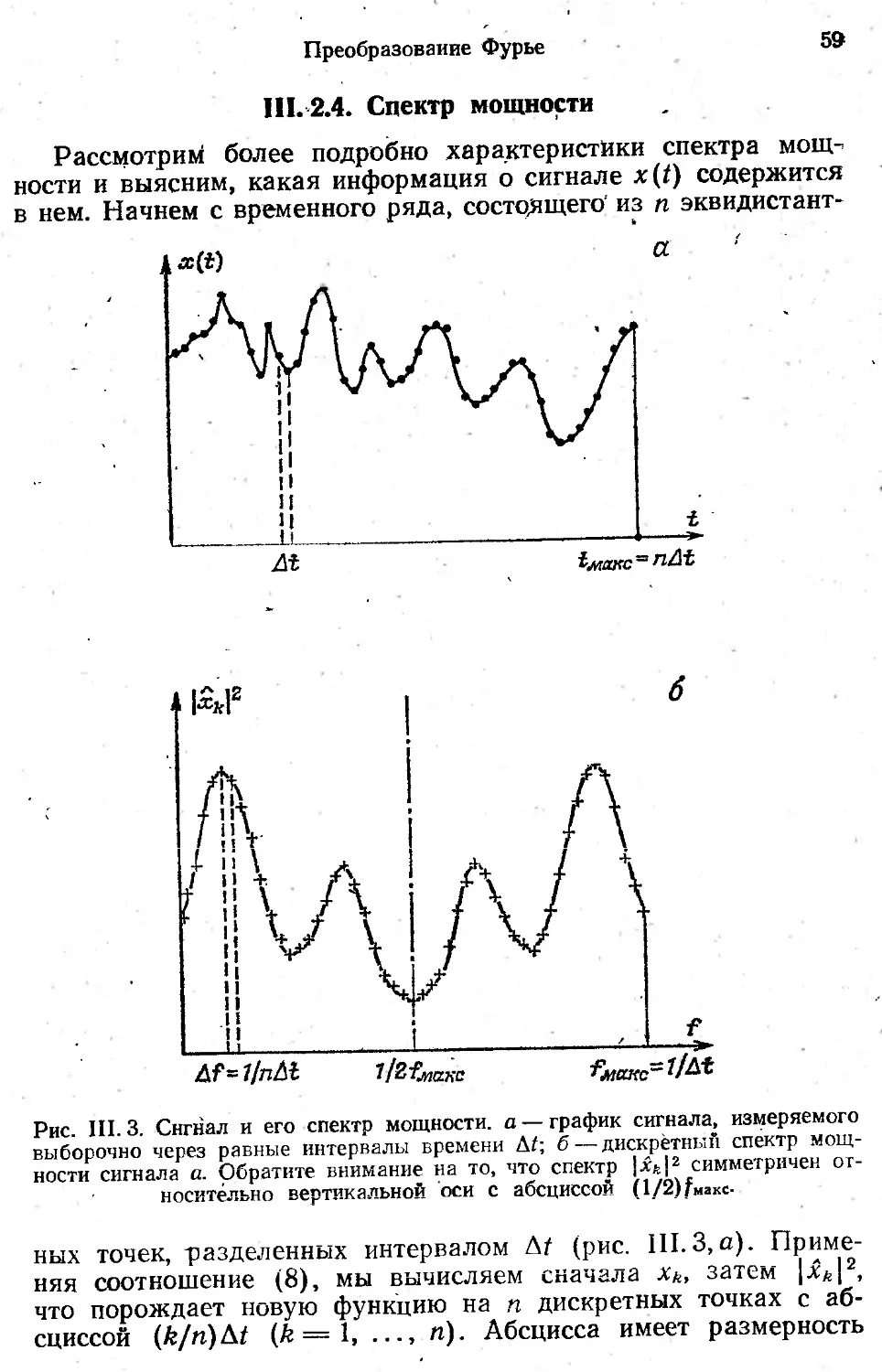
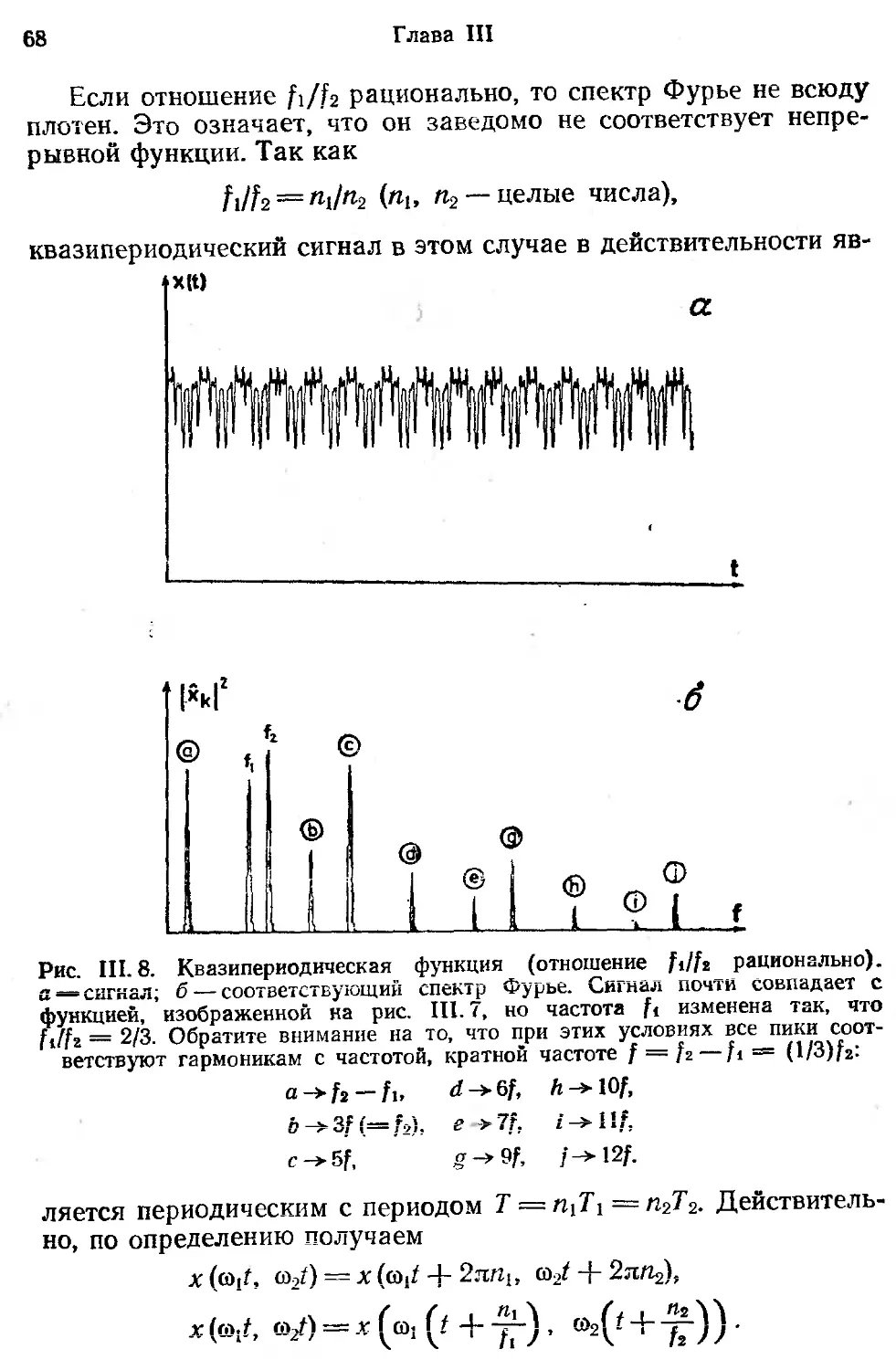
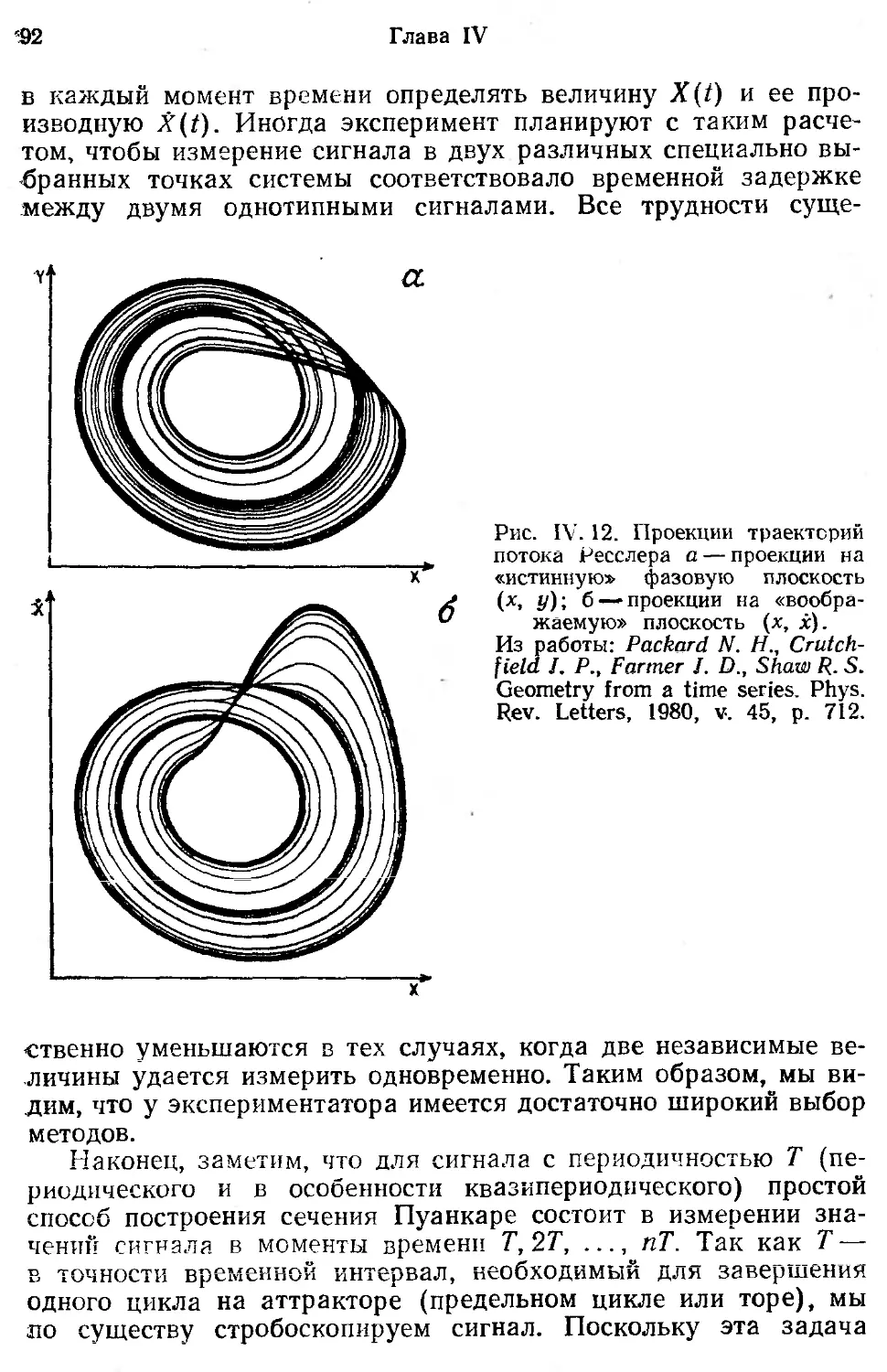
Текст

ПОРЯДОК В ХАОСЕ

PIERRE BERGE
С. E. A. SACLAY, Service de physique du solide
et de resonance magnetique
YVES POiViEAU
С E. A. SACLAY, Service de physique theorique
CHRISTIAN VIDAL
C. N. R. S., Centre de recherches Paul Pascal
L'ORDRE DANS LE CHAOS
Vers une approche deterministe
de la turbulence
Preface de David Ruelle
Institut des Hautes Etudes Scientifiques
Hermann, Editeurs des sciences et des arts

П.Берже, И.Помо, К.Видалъ
Порядок
вхаосе
О детерминистском подходе
к турбулентности
Перевод с французского
Ю. А. Данилова
Москва «Мир» 1991

I ЙДУЧЙОЙ JIHTEFAi.f-и ,
ББК 22.317
Б48
УДК 53.072.1!
Берже П., Помо И., Видаль К.
Б48 Порядок в хаосе. О детерминистском подходе к турбу-
турбулентности: Пер. с франц.— М.: Мир, 1991.— 368 с, ил.
ISBN 5-03-001804-2
Книга французских авторов представляет собой введение в область
исследований, называемую синергетикой. Авторам, удалось в живой,
непринужденной, вполне доступной форме дать ясное представление
о современных познаниях в области физики турбулентности и коопе-
кооперативных процессов, которыми интенсивно занимаются специалисты по
проблемам аэро- и газодинамики, физики плазмы, оптики, химической
кинетики, биологии и т. д. Может служить пособием для студентов ву-
вузов и читателей с высшим образованием, желающих иметь доступное
введение в проблемы синергетики.
1604030000-113 ВПК 22 417
Б 041@1)—91 31~91 ББК 22.317
Редакция литературы по физике и астрономии
1001ЬФ
Трудов
/Irn ,tSf fSfta'\ ® 1988> Hermann- *« r«e Lecourbe. 75015 Pa-
ISBN 2-7056-5980-3 (франц.) ris, Nouvelle edition corrigee
© перевод на русский язык, Данилов Ю. А.
1991 '

ПРЕДИСЛОВИЕ АВТОРОВ
Эта книга задумана как введение в теорию диссипативных
, динамических систем. Она написана на сравнительно элемен-
к тарном (насколько это возможно) уровне и предназначена
в первую очередь, для студентов и во вторую — для аудитории,
' имеющей научную подготовку, но не специализирующейся в дан-
данной области.
Под динамической системой мы понимаем любую систему,
• какой бы ни была ее природа (физическую, химическую, элек-
электромагнитную, биологическую, экономическую и т. д.), которая
может принимать различные математические формы: обыкно-
¦ венных дифференциальных уравнений (автономных и неавто-
неавтономных), дифференциальных уравнений в частных производных,
- отображений [обратимых или необратимых) прямой или пло-
плоскости. Таким образом, область исследования здесь необычайно
'' обширна, поскольку охватывает анализ всех зависящих от вре-
' мени явлений. Рассматривая большинство типов режимов или
эволюции безотносительно к конкретным особенностям систем,
1 в которых они проявляются, теория диссипативных динамиче-
динамических систем обладает высокой степенью общности и универсаль-
универсальности и в этом отношении напоминает такую мощную и вы-
\. строенную по определенному плану физическую теорию, как,
; например, термодинамика. Несомненно, что именно отсюда про-
проистекает в основном интерес к этой теории.
^ четкое различие ме-
г Жду системами с трениеми системами без трения, поскольку
; системы этих двух типов не приводят к одному и тому же
> классу задач. Наличие внутреннего трения (в самом широком
смысле) влечет за собой существование аттрактора, т. е. асимп-
асимптотического предела (при t-+<x>) решений, предела, на который
у не оказывает прямЪтО"'влияния"начальное условие — исходная
точка. В механике, где трение приводит к постоянному убыва-
. нию энергий, соответствующие системы"до этой причине лри-
нятчо называть диссипативными. Этим прилагательным мы будем
1 пользоваться впредь применительно и к немеханическим си-
' Стемам.

6 Предисловие авторов
Системы без трения, называемые консервативными или га-
мильтоновыми, представляют интерес и находят приложения
в механике. В частности, к теории подобных систем относятся
такие вопросы, имеющие неоспоримое практическое значение,
как, например, эволюция солнечной системы и поведение плазмы
в ускорителе. Исследование систем без трения требует своих спе-
специфических методов главным образом потому, что в отсутствие
аттрактора начальное условие обретает решающее значение.
«Среди больших нерешенных проблем классической физики
турбулентность, несомненно, является старейшей. Как ни уди-
удивительно, но еще двадцать лет назад о турбулентности было
известно немногим больше, чем в начале XIX века, когда Навье
вывел уравнения, описывающие течение жидкости. Такое поло-
положение нельзя не признать совершенно необычным, если принять
во внимание гигантский прогресс, достигнутый с тех пор в по-
понимании структуры материи и Вселенной, тем более что гидро-
гидродинамика была и остается областью науки, легко доступной для
эксперимента: установки в гидродинамических лабораториях по
своей сложности или стоимости не идут ни в какое сравнение
с ускорителями, используемыми для исследования субатомных
частиц! Несмотря на свою банальность, это замечание подни-
поднимает вопрос, который рано или поздно привлечет внимание ис-
историков науки, а именно вопрос о глубинных причинах (вызван-
(вызванных стечением обстоятельств или эпистемологического харак-
характера) относительного застоя в научной дисциплине, никогда не
страдавшей от недостатка практической и экономической моти-
мотивации.
Как бы то ни было, но в 60-х годах нашего столетия ситуа-
ситуация начала существенно изменяться. Мы еще далеки, даже
очень далеки от решения проблемы турбулентности, т. е. от
того, чтобы дать точное объяснение турбулентности и механиз-
механизмов ее возникновения. Тем не менее были развиты новые ме-
методы, позволившие осуществить анализ явлений, упорно не под-
поддававшихся прежде научному описанию из-за кажущегося пол-
полного отсутствия в них какой-либо закономерности. Первым и
наиболее важным было открытие странных аттракторов. Стран-
Странный аттрактор был обнаружен численно в 1963 г. Э. Лоренцом,
но математически понятие было сформулировано в 1971 г.
Д. Рюэлем и Ф. Такенсом как ключевой элемент в понимании
иррегулярного поведения, описываемого детерминистскими урав-
уравнениями главным образом в понимании турбулентности. Тем
самым было положено начало исследованиям того, что теперь
нередко называют детерминированным хаосом, первому этапу
в анализе явлений, обладающих еще более сложной зависи-
зависимостью от пространства и времени. «Достигнутый прогресс ока-

Предисловие авторов 7
зал благотворное влияние на многие области науки помимо гид-
гидромеханики.
Теперь, по прошествии примерно одного десятилетия после
того, что можно было бы назвать существенным обновлением,
настал подходящий момент для осмысления и выделения тех
идей и методов, которые отныне должны стать неотделимой
целью нашей научно-образовательной программы. Именно эту
цель мы ставили перед собой, работая над этой книгой, отра-
отражающей, разумеется, наши педагогические вкусы и пристрастия.
В силу этого наш выбор в ряде случаев произволен и поэтому
уязвим для критики. Во-первых, спорен избранный нами метод
изложения: мы неизменно стремились быть конкретными, иллю-
иллюстрируя свои соображения при каждом удобном случае приме-
примерами, заимствованными из эксперимента. Кроме того, мы часто
заменяли строгие математические доказательства, необходи-
необходимость, а иногда и красота которых неоспорима, упрощенными
вычислениями «на пальцах». Учитывая это, отсутствие формули-
формулировок теорем и лемм не следует относить за счет отсутствия
строгости теории. Во-вторых, спорен наш выбор вопросов, под-
подлежащих обсуждению: не претендуя на исчерпывающее изложе-
изложение, мы ограничились рассмотрением диссипативных систем,
наиболее широко распространенных в природе. Кроме того, мы
не пытались систематически исследовать все вопросы, представ-
представляющие интерес, предпочитая нарисовать для читателя широкую
панораму, которая была бы самосогласованной и доступной по-
пониманию, несмотря на неполноту. Наконец, на уровне органи-
организации наша книга состоит из двух частей. Изложение основных
понятий (гл. I—IV), аналитические методы (гл. III и IV), три
экспериментальные ситуации (магнит, помещенный в магнитное
поле, тепловая конвекция в слое жидкости, химическая реакция
в открытой среде), приведенные в качестве иллюстраций
(гл. V), включены в первую часть. Она называется «От по-
порядка...» и посвящена в основном рассмотрению регулярных,
в частности периодических, режимов. Описав средства исследо-
исследования, мы используем их затем во второй част», само название
которой «..j^ хаосу» говорит о ее содержании. Понятие стран-
'ного аттрактора"вводится самым прагматическим образом
в гл. VI. Затем обсуждаются различные способы перехода от
периодического режима к хаотическому: квазипериодичность
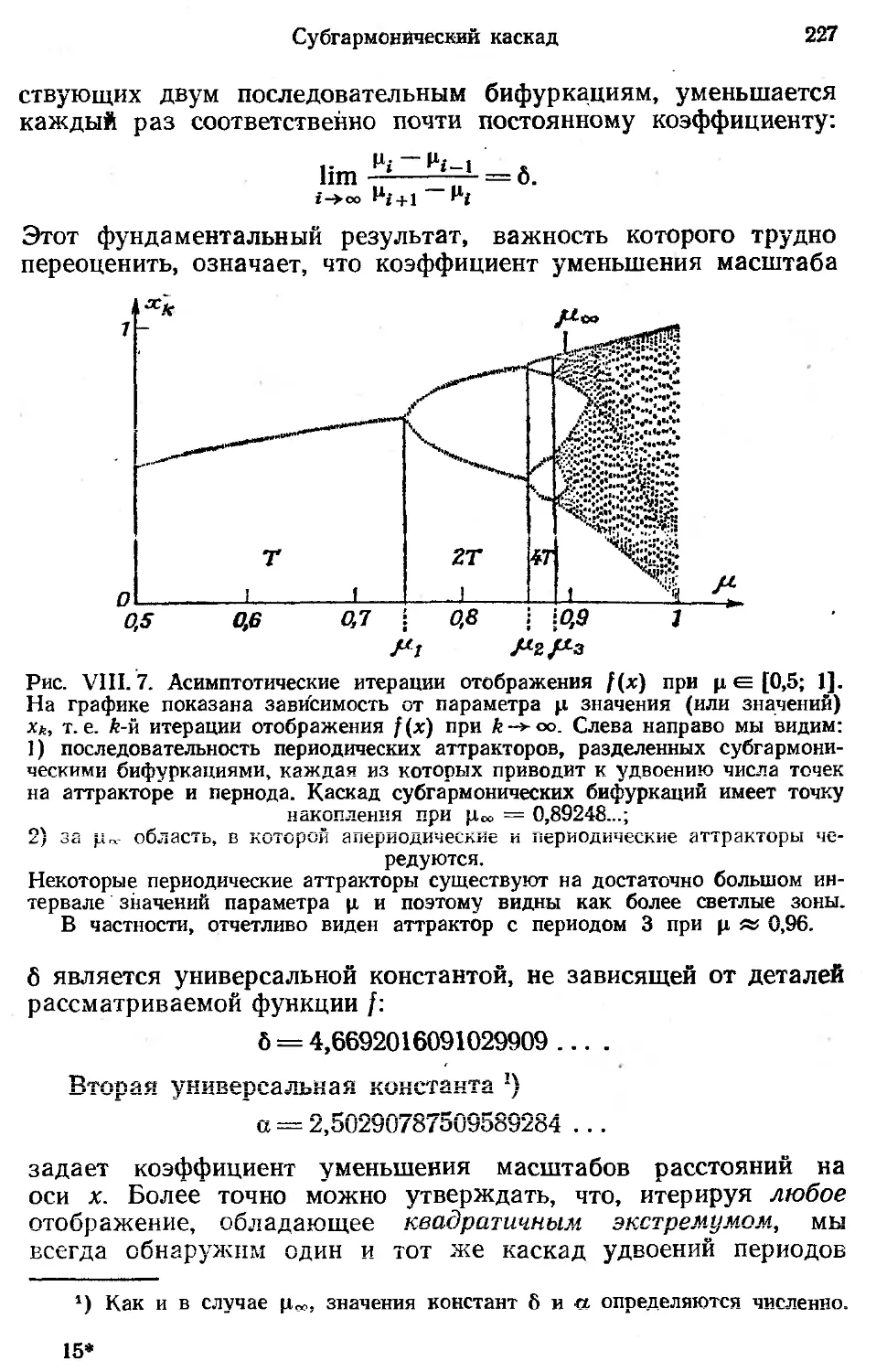
(гл. VII), субгармонический каскад (гл. VIII), перемежаемость
(гл. IX). Новые вопросы более специального или технического
характера отнесены в приложения, чтобы избежать длинных
экскурсов, прерывающих последовательный ход рассуждений.
Краткий предметный указатель и избранная библиография за-
завершают нашу книгу.

8 Предисловие авторов
Любая книга, написанная с образовательными целями
(а наша книга принадлежит к числу именно таких книг), не
претендует на полный обзор литературы. В любом случае со-
составление такого обзора было бы нелегкой задачей, поскольку
излагаемый нами предмет уже насчитывает сотни статей и этот
поток, далекий от исчерпания, с каждым днем становится все
обильнее. Учитывая это, мы просто приводим несколько наибо-
наиболее важных ссылок в дополнение к тем статьям, из которых
нами были заимствованы результаты численных или натурных
экспериментов. Аналогично мы, как правило, не упоминали
в тексте имена авторов, предпочитая сосредоточить основное
внимание на научном содержании их работ. Мы даже не пыта-
пытались проследить первоисточники различных основополагающих
результатов. Мы лишь констатируем, что в целом 1) исследо-
исследование динамических систем проводится совместными усилиями
огромного числа выдающихся ученых, особенно математиков и
физиков, усилий, предпринимаемых во всем мире; 2) француз-
французские ученые своими теоретическими и экспериментальными ра-
работами вносят достойный вклад в развитие этой области науки.
Если не считать нескольких изданий, рассчитанных на спе-
специалистов, не существует пока книги, посвященной элементар-
элементарному изложению теории динамических систем, которая была бы
доступна студентам. Наша книга, сколь бы далека она ни была
от совершенства (впрочем, чего еще можно ожидать от книги,
посвященной столь новой и бурно развивающейся области
науки?), все же обладает, по нашему мнению, одним достоин-
достоинством, поскольку представляет собой первую попытку воспол-
восполнить указанный выше пробел в научной литературе. Наша цель
будет достигнута, если, несмотря на все недостатки, предлагае-
предлагаемая вниманию читателя книга будет способствовать распростра-
распространению идей и методов, развитых за последние годы для иссле-
исследования детерминированного хаоса.
Мы выражаем глубокую благодарность Шанталь Помо, взяв-
взявшей на себя труд по перепечатке рукописи, Жаку Муано, Бер-
нару Озенде, Жослин Дюсотуар и Мадлен Порнеф, оказавшим
различную помощь при подготовке рукописи.
Мы от души благодарим Анну-Мари Берже, Моник Дюбуа
и Поля Манневиля, которые своими замечаниями, критикой и
предложениями позволили в ряде пунктов улучшить первона-
первоначальный текст; их вклад был весьма ценным для нас.
Давид Рюэль согласился написать предисловие, чтобы чи-
читатель мог рассматривать нашу книгу в должной перспективе.
Мы признательны Д. Рюэлю за этот знак дружбы и уважения.
Бордо — Париж, Пьер Берже, Ив Помо, Кристиан Видаль
февраль 1984 г.

ПРЕДИСЛОВИЕ ДАВИДА РЮЭЛЯ
В последние годы возникла новая область физики, которую
называют по-разному: нелинейной физикой, теорией турбулент-
турбулентности или хаоса. Предмет ее необычайно широк и разнообразен
и включает в себя гидродинам^ическую кинетику и исследование
электронных цепей.]"Возникает вопрос: можёт~лй существовать"
общий подход¦'к~столь, казалось бы, разнородным и сложным
проблемам? Как показал тщательный анализ, временная эво-
эволюция таких систем имеет много общего, что и делает возмож-
возможным единый подход к их исследованию. Мы имеем в виду не
статистический или стохастический подход и не внешнее сход-
сходство явлений на описательном уровне. Внутренняя аналогия ме-
между сложными режимами в гидродинамике, химической кине-
кинетике, механике и электронике проявляется в экспериментально
установленных деталях, которые стали известными лишь не-
недавно. В основе замеченного сходства лежит глубокая матема-
математическая теория: современная теория нелинейных систем или,
точнее, качественная теория дифференцируемых динамических
систем.
Новая, нелинейная физика занимается изучением интересней-
интереснейших явлений: турбулентности и колебаний в физико-химиче-
физико-химических и биологических системах. Хаотические и причудливые,
почти непредсказуемые внешние эффекты ныне уступают место
неожиданной концептуальной, унификации на основе таких по-
понятий, как бифуркации, странные аттракторы, показатели Ля-
Ляпунова и т. д. До сих пор удалось приподнять лишь краешек
завесы и многие явления все еще остаются непонятными^ййе-
объяснймьТми, хотя мы, по-видимому, уже вступили на путь,
предсказанный в «Фейнманоэских лекциях по физике»:
«Следующая эра пробуждения человеческого интеллекта
вполне может породить метод понимания качественного содер-
содержания уравнений. Сегодня мы не в состоянии увидеть, что урав-
уравнения гидродинамики содержат такие вещи, как вихревая струк-
структура турбулентности, наблюдаемая между вращающимися
цилиндрами. Сегодня мы не знаем, содержит ли уравнение
Шрёдингера лягушек, сочинителей музыки и мораль или не

10 Предисловие Давида Рюэля
содержит. Мы не можем сказать, есть ли необходимость в чем-
нибудь, помимо уравнения Шрёдингера, вроде Бога или такой
необходимости нет. Пока каждый из нас может придерживаться
как одной, так и другой точки зрения».
О нелинейных динамических системах можно было бы напи-
написать книгу с математическим уклоном. В книге, предлагаемой
вниманию читателя — первой в своем роде — основное внимание
уделяется физике и химии. Она написана теоретиком И. Помо
и двумя экспериментаторами П. Берже и К- Видалем, прини-
принимающими активное участие в разработке новых идей. Они кон-
конкретно описывают важные динамические явления и то, как те
или иные эффекты появляются в экспериментальной реальности,
не вдаваясь в излишние математические детали. По прочтении
этой книги физик, химик и физиолог смогут самостоятельно
применять приобретенные знания при интерпретации явлений,
встречающихся в изучаемой ими области. Они смогут также
продолжить свое математическое образование, опираясь на за-
заложенную прочную основу.
Давид Рюэль

ЧАСТЬ 1
ОТ ПОРЯДКА ...
ВВЕДЕНИЕ. НЕМОНОТОННАЯ ЭВОЛЮЦИЯ
I. ОСЦИЛЛЯЦИИ, КОЛЕБАНИЯ, НЕМОНОТОННАЯ ЭВОЛЮЦИЯ
Понятия осцилляции, или колебаний, играют важную роль
при изучений "динамики нёШШ?о1йно"й"эволюции, характеризуе-
характеризуемой движением' туда и обратно, регулярным или'нерегулярным.
Дл^зтого та
явлениянеобыч^
ском мире, так "ив живых* организмах, чтб"самоГпо сёбе~при-
дает значимость жсл^ованшо~'^^шШ'^^ШТ^в11Шу1иГ"Кройе
1 ^1,0, временную '"эволюцию люё'ои" вёличкнъГ'сГ"помощью преоб-
разования"Фу^ь"е"мо"жнр,Т1р^Ж!^6^ь"''в"вйд"е'"сум[мы периодиче-
периодических чденрв.„,Э!эсЕ.. Два обстоятельства, взятые вместе, делают
периодическое движение краеугольным камнем любой теории,
созданной для описания эволюции во времени. Отсюда непосред-
непосредственно ясна^J^Ba^a^jgOJib^jcoTopyio играет осциллятор_„к#к
архетип зависящего от времени режимаГНе вдаваясь в детали,
мы хотим л^шь подчеркнуть во введении распространенность пе-
риодических явлений в окружающем нас мире. Несколько при-
примеров, заимствованных из различных областей, послужат иллю-
иллюстрациями, подкрепляющими правильность этого утверждения.
II. ПРИМЕРЫ—ОТ НЕОРГАНИЧЕСКОГО МИРА...
Напомним, что пдмимо простого маятника (к которому мы
еще вернемся в гл. 1) в различных "областях физики существует
несколько реализации 7осДВДл.?тВДа- Приведём несколько изве-
известных примеров: груз, подвешенный на упругой пружине, тра-
традиционный колебательный контур и акустический резонатор
Гельмгольца принадлежат к числу классических моделей, эво-
эволюция которых описывается дифферейциальными уравнениями
с периодическими решениями. Было бы неверно рассматривать
эти элементарные осцилляторы как'про'стые физические'задачи.
не имеющие реальной пользы или значения. Наоборот, осцилля-
осцилляторы находят многочисленные приложения в механике, электро-
электротехнике, электронике и акустике — перечень, как нетрудно
видеть, достаточно внушительный. В промышленную эпоху ос-
осциллятор стал одной из основных компонент многих созданных
человеком машин.

12
Введение
Упомянем также о колебательных, ил» осцилляторных, яв-
явлениях, которые возникают спонтанно. Анализ их проводится
теми же методами, а важную роль, которую они играют в по-
повседневной жизни, вряд ли можно преувеличить. Так, любое
вращающееся устройство, будь то колесо, двигатель, вант/тур-
вант/турбина и т. д., порождает колебания, которые 'могут нарушить его
работу и даже привести к разрушению устройства; поэтому не-
необходима тщательная "балансировка двигателя или колес авто-
автомашины, .КолебанйСвалхш и балок, обычно используемых в кон-
конструкциях (крыльев самолетов, мостов и т. д.), могут приводить
а О
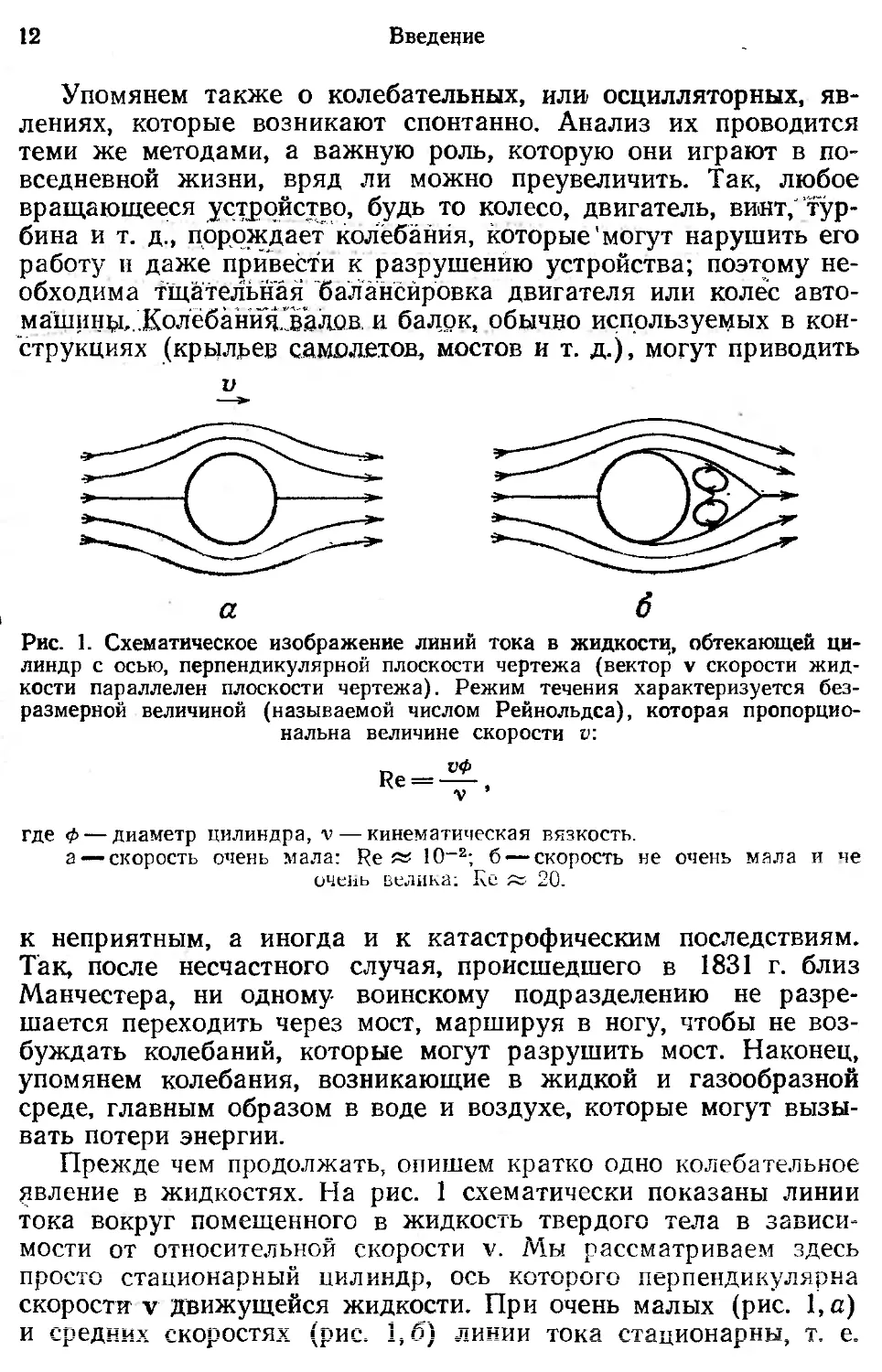
Рис. 1. Схематическое изображение линий тока в жидкости, обтекающей ци-
цилиндр с осью, перпендикулярной плоскости чертежа (вектор v скорости жид-
жидкости параллелен плоскости чертежа). Режим течения характеризуется без-
безразмерной величиной (называемой числом Рейнольдса), которая пропорцио-
пропорциональна величине скорости v:
где Ф — диаметр цилиндра, v — кинематическая вязкость.
а —скорость очень мала: Re « 10~2; б —скорость не очень мала и не
очень велика: Re « 20.
к неприятным, а иногда и к катастрофическим последствиям.
Так, после несчастного случая, происшедшего в 1831 г. близ
Манчестера, ни одному воинскому подразделению не разре-
разрешается переходить через мост, маршируя в ногу, чтобы не воз-
возбуждать колебаний, которые могут разрушить мост. Наконец,
упомянем колебания, возникающие в жидкой и газообразной
среде, главным образом в воде и воздухе, которые могут вызы-
вызывать потери энергии.
Прежде чем продолжать, опишем кратко одно колебательное
явление в жидкостях. На рис. 1 схематически показаны линии
тока вокруг помещенного в жидкость твердого тела в зависи-
зависимости от относительной скорости v. Мы рассматриваем здесь
просто стационарный цилиндр, ось которого перпендикулярна
скорости' v движущейся жидкости. При очень малых (рис. 1,с)
и средних скоростях (рис. 1,6) линии тока стационарны, т. е.

Немонотонная эволюция
13
остаются неизменными с течением времени. Но после того, как
скорость превысит некоторый порог, рециркуляционные вихри
в следе за цилиндром (рис. 1,6) становятся неустойчивыми.
Стационарный режим исчезает, уступая место цепочке вихрей,
вращающихся попеременно то в одну, то в другую сторону и
Снимок 1. След Бенара — Кармана. Цилиндр помещен в воздушный поток.
Дым поступает в поток из двух щелей, параллельных образующим цилиндра.
Визуализация движения частиц дыма в плоскости осуществляется плоским
лазерным лучом, направленным вдоль оси потока (перпендикулярно оси ци-
цилиндра), а — Re — Rec = 2,4; б —Re —Rec = 13,6. Здесь Re — число Рей-
нольдса, отвечающее диаметру цилиндра A см), Rec — критическое число
Рейнольдса, при котором возникает неустойчивый след (экспериментальное
значение Rec « 70).
Взято из работы: Mathis С. Proprietes des composantes de vitesse trans-
verses dans l'ecoulement de Benard— von Karman aux faibles nombres de
Reynolds.
увлекаемых движущейся жидкостью. На снимке 1 показана
мгновенная фотография такой конфигурации в следе за цилинд-
цилиндром, известной под названием вихревой дорожки Бенара — Кар-
Кармана. Подчеркнем универсальный характер описываемых перио-
периодических явлений: о чем бы ни шла речь, будь то вихри за
фермами моста, структура облаков, создаваемая ветром над ост-
островом Мадера, или вихри за Большим красным пятном на Юпи-
Юпитере, мы всегда обнаруживаем описанную выше дорожку Бе-
Бенара— Кармана. Одно из следствий такого явления — звучание

14
Введение
так называемой «эоловой арфы», воспринимаемое непосред-
непосредственно на слух. Когда из-за ветра вихри, образующиеся по-
позади твердого тела, начинают периодически отрываться, на тело
действует переменная сила, заставляющая его колебаться с ча-
частотой отрыва вихрей. При этом тело издает характерный звук,
частота которого возрастает с увеличением скорости ветра. На
рис. 2 показана запись такого ветрового шума. В зависимости
Скорость
Время
Рис. 2. «Шум» воздушного потока: изменение скорости течения воздуха во
времени. Описание эксперимента см. в подписи к снимку 1, число Рейнольдса
Re = 72,9 (Фцил = 0,7 см, Rec = 59,4).
от осс;о;пельств звучание головой арфы» может сыть прият-
приятным (музыкальным) или, наоборот, резким и раздражающим
(шумI)-
Помимо колебательных физических процессов менее изве-
известные осцилляторы встречаются в химии. Восстановительные
реакции в кислой среде и горение в газовой фазе способны
осциллировать во времени. То, что принято называть химиче-
химическими осцилляторами, было впервые открыто случайно, однако
это отнюдь не умаляет их концептуального значения2). Их важ-
М Поиск альтернативных источников энергии привел к проекту создания
мощных ветряных двигателей — своего рода современных ветряных мельниц.
Но, поскольку по самой своей природе ветровые установки — устройства
весьма шумные и при работе слышны издалека, возможность их сооружения
дое !-:¦'• ограниченна.
-) Поведение колебательных химических систем удовлетворительно опи-
сызег""".- дифференциальными уравнениями, выводимыми в термодинамика и
друп. областях физики. Колебательные химические системы можно исследо-

Немонотонная эволюция ' 15
ность подтверждается еще и тем, что, как будет показано в сле-
следующем разделе, существуют также биохимические и биологиче-
биологические осцилляторы, действие которых может быть лучше понято,
если воспользоваться в качестве экспериментальных моделей
химическими осцилляторами. Все это объясняет, почему с конца
60-х годов нашего столетия колебательные реакции в жидкой
среде стали предметом весьма активного исследования. Их при-
принято классифицировать по окислителю: иодату, бромату или
хлориту. Восстановитель (чаще всего органическое соединение)
и возможный катализатор могут варьировать в широких преде-
пределах, что открывает возможность для многочисленных комби-
комбинаций ').
III. ...ДО ЖИВОТНОГО МИРА
Химия приводит нас к биологическим системам, в периоди-
периодическом поведении которых так много общего с периодическим
поведением нелуиьой материи, В биологических системах на-
наблюдение и анализ периодических явлений находятся в центре
внимания многих исследований. К числу таких явлений отно-
относятся биологические ритмы. Некоторые из них известны со вре-
времен античности: дыхание, сокращение сердечной мышцы, чере-
чередование бодрствования и сна, циклическое размножение у рас-
растений и т. д. Некоторые из биоритмов, получивших название
экзогенных, возникают под воздействием циклических вариаций
среды, в которой живет организм: времен года, лунных фаз,
'смены дня и ночи. Мы говорим о циркадных (с периодом около
24 часов) и цирканнуальных (с периодом около 365 дней) рит-
ритмах. Источник других ритмов находится на клеточном или ме-
метаболическом уровне. Такие ритмы получили название эндоген-
эндогенных. Их периоды заключены в диапазоне от нескольких долей
секунды до 20—30 минут. Например, у млекопитающих наблю-
наблюдаются колебания 1) некоторых гладких (желудок, кишечник,
матка и т. д.) или полосатых (жестких) мышц, а также мышеч-
мышечных клеток в культуре; 2) центральной нервной системы (ЭЭГ),
а также потенциала действия нейронов, ответственного за рас-
распространение нервных импульсов.
вать математически, в частности с точки зрения теории динамических систем,
как это намереваемся сделать мы. Кроме того, такие системы легко наследо-
наследовать экспериментально в лабораторных условиях. Термодинамика необрати-
необратимых процессов показывает, что второе начало не запрещает существования та-
таких немонотонных режимов, как колебания, если рассматриваемая система
достаточно далека от равновесия.
*) Выбрав химический осциллятор для иллюстрации некоторые аспектов,
затрагиваемых в нашей книге, мы отсылаем читателя к разд. V. 4, где изло-
изложены дополнительные подробности на эту тему, все еще весьма мало из-
известные вне узкого круга специалистов.

16
Введение
У животных и растений, а также у бактерий синтез белков
и метаболическая активность, например гликолиз и фотосинтез,
ЧЗпуоресцещия
' NADH
Захват Н+
Захват К+
На чало и
Рис. 3. Колебания в реакциях гликолиза, а — одновременная запись флуорес-
флуоресценции NADH (одной из компонент гликолитической цепи), захвата ионов
Н+ и К+ и увеличения объема популяции митохондрий, обнаруживающая вы-
вызванные гликолизом колебания.
Из работы: Boiteux A., Hess В. Oscillations in glycolysis, cellular respi-
respiration and communication. Faraday Symposium of the Chemical Society, 1975,
v. 9, p. 202.
б — запись флуоресценции I^IADH in vivo от интактной клетки Saccharo-
rnyces carlbergensis через 2 мин после введения глюкозы.
Из работы: Chance В., Willianson G., Lee Mela I. Y., De Vault D., Ghosh A.,
Pye E, K. Synchronization phenomena in oscillations of yeast cells and Isolated
mitochondria. — In: Biological and Biochemical Oscillators. — Eds. B. Chance,
E. K. Pye, A. Ghosh, B. Hess. — 'N. Y.: Academic Press, 1973, p. 285. Колеба-
Колебания б реакциях гликолиза наблюдаются in vitro (а) и in vivo (б) с перио-
периодом порядка 1 мин.
могут происходить в периодическом режиме. Пока из всех этих
колебательных биохимических и биологических реакций наибо-
наиболее твестен и изучен гликолиз. Интерес к гликолизу понятен,

Немонотонная эволюция 17
если учесть ту роль, которую эта последовательность фермен-
ферментативных реакций играет в клеточном метаболизме '). Открытые
в 1957 г. гликолитические колебания с тех пор неоднократно
наблюдались in vitro и in vivo, что подтверждается, например,
рис. 3. На этом рисунке показаны записи вариаций во времени
некоторых свойств, главным образом флуоресценции одной из
компонент гликолитической последовательности NADH:
в популяции митохондрий — клеточных органелл, образую-
образующих АТФ (рис. 3, а),
в изолированной интактной клетке Saccharomyces carlsber-
gensis (рис. 3,6).
Заметим, что период гликолитических колебаний в обоих
случаях составляет величину порядка минуты.
Периодическими являются также развитие и рост многочис-
многочисленных клеток и одноклеточных организмов. На другом уровне
организации мы наблюдаем периодическое поведение некоторых
Г1Г»ГГ\7"ГТСГТТ
1) движение слизевиков, или миксомицетов (таких, как
Dyctyostelium discoideum), собирающихся в спорангий, когда
в среде, в которой они обитают, истощается запас питательных
веществ и они не могут выжить порознь;
2) испускание света группами светляков;
3) развитие в противофазе многих пар хищник — жертва.
Из этого краткого обзора видно, что периодические режимы
действительно распространены необычайно широко как на ин-
индивидуальном уровне — от клетки до целого организма, так и
на уровне популяций.
\! IV. КЛЮЧ К АНАЛИЗУ: ОСЦИЛЛЯТОР
Поскольку колебательные явления встречаются столь часто,
внутринаучныи интерес к осциллятору вполне естествен. Но
в действительности интерес к осциллятору простирается гораздо
дальше, если в приведенный выше обзор мы включим всю не-
немонотонную эволюцию, в которой колебания играют роль и при-
примера, и неотъемлемой составной части. Мы уже упоминали
о том, что преобразование Фурье2) приводит к описанию произ-
произвольной эволюции (временной зависимости) как к алгебраиче-
алгебраической сумме периодических членов. Именно поэтому прежде, чем
!) Напомним, что гликолиз является важным путем распада глюкозы,
на котором происходит восстановление молекул АТФ (можно сказать, «горю-
«горючего» клеточного «мотора») из молекул АДФ. Таким образом, гликолиз со-
составляет существенную часть процесса превращения энергии в клетке.
2) См. "гл. III.

18 Введение
мы сумеем построить любую теорию зависящих от времени яв-
явлений, нам необходимо понять, как происходят колебания. Это
объясняет, почему наиболее ценные аналитические идеи есте-
естественно приводят к рассмотрению такого элементарного осцил-
осциллятора, как маятник, изучению которого посвящена первая гла-
глава нашей книги. Мы видим, что выбор такой исходной точки не
является произвольным и не продиктован чисто педагогическими
соображениями.. Его настоятельно требует природа рассматри-
рассматриваемой проблемы — немонотонное поведение во времени, или
немонотонная эволюция.

ГЛАВА I
СВОБОДНЫЙ ОСЦИЛЛЯТОР, ОСЦИЛЛЯТОР
С ВЫНУЖДАЮЩЕЙ СИЛОЙ
1.1. СВОБОДНЫЙ ОСЦИЛЛЯТОР
1.1.1. Уравнение простого маятника без трения
Простой маятник, пожалуй, самый известный пример свобод-
свободного осциллятора. Это маССат в гравитационном поле ускоре-
ускорения g, подвешенная в точке О на жесткой проволоке длиной '/
(рис. 1.1). Эта масса колеблется в вертикальной плоскости. Две
точки на вертикальной прямой, проходящей через точку под-
подвеса О, являются точками равновесия, из них R устойчивая, _§
неустойчивая. Если 8@ —угол в момент времени t между про-
проволокой и вертикалью^)/?, то основной закон механики приводит
к уравнению
F = ml —щ- = — mg sin 8,
т. е. '"^
-g/+J.sine==0. A)
Следует иметь в виду, что уравнение A) предполагает идеали-
идеализацию описанного выше устройства. В частности, неявно пред-
предполагается, что масса имеет точечные размеры, отсутствует тре-
трение, а различные характеристики маятника постоянны1).
При малых углах 0, при которых sin 8».,8 (линейная ап-
аппроксимация), уравнение A) легко интегрируется при заданных
начальных условиях, и мы получаем классический результат:
G == 9о cos (at + ?),
где о:> — угловая частота, Г—период, Ф — фаза.
Такое движение точно периодическое:'это изохронные малые
колебания, используемые в часовых механизмах.
') Существует естественная связь между геометрией и механикой: первая
отражает абстрактные, а вторая — конкретные аспекты многочисленных об-
общих понятий, таких, как движение, кривая, траектория и т. д. Мы предпо-
предполагаем, что читателю известно это глубокое эпистемологическое различение,
восходящее к Декарту.
2*

20
Глава I
Рассмотрим проблему с более общей точки зрения, а именно
попытаемся определить, какая информация необходима для пол-
полного описания мгновенного состояния маятника. Ясно, что для
этого необходимо и достаточно знание двух величин: положения
Рис. I. 1. Простой маятник. Масса т подвешена в гравитационном поле g на
одном конце жесткой проволоки, другой конец которой закреплен в точке О.
Движение происходит по окружности, на которой имеются две точки равно-
равновесия R H»j? Одна из точек равновесия (R') расположена над точкой О,
другая (R) — под точкой О. В отличие от состояния покоя R точка R' соот-
соответствует неустойчивому состоянию равновесия. Обычно состояние маятника
описывают с помощью таких переменных, как угол 0 и мгновенное значение
его производной 9 = dQ/dt.
Q(t) и скорости dQ/di = Q. Следовательно, вместо интегрирова-
интегрирования уравнения A) можно просто представить решение на пло-
плоскости с прямоугольной системой координат (8,8). В рассмат-
рассматриваемом нами идеальном случае решением является замкнутая
кривая, т. е. орбита, на плоскости. На практике такого рода
представление играет существенную роль во всех исследованиях
динамики по следующей простой причине: такое представление
служит альтернативой в тех случаях, когда аналитическое ин-

Свободный осциллятор, осциллятор с вынуждающей силой 28
тегрирование дифференциальных уравнений оказывается невоз-
невозможным. Именно поэтому мы будем часто использовать такое
представление.
В общем случае мы можем определить фазовое простран-
пространство — пространство, в котором осями координат служат поло-
положение и скорость1), и фазовую траекторию — кривую в фазовом
пространстве, описывающую эволюцию системы. Совокупность,
фазовых траекторий образует фазовый портрет. Другим важ-
важным понятием является степень свободы, по-разному определяе-
определяемая. Под степенью свободы по определениям понимается либо<
каждая пара координат положение —скорость, связанная с пе-
перемещением, либо только один из двух элементов — положение
или скорость.
Таким образом, система N тел, способных свободно двигать-
двигаться по трем пространственным направлениям, обладает либо 3JV,
либо GN степенями свободы в зависимости от принятого опреде-
определения. Число степеней свободы соответствует числу начальных
условий, которые могут быть выбраны независимо, и поэтому
действительно близко к этимологии выражение «степень сво-
свободы». В рассматриваемом нами примере осциллятора началь-
начальное положение и скорость являются двумя величинами, которые
могут быть заданы произвольно, поэтому мы говорим, что маят-
маятник— это система с двумя степенями свободы, фазовое про-
пространство которой двумерно.
1.1.2. Описание движения в фазовом пространстве
Применим приведенные выше определения и понятия к ис-
исследованию нелинейного уравнения A). В каждой точке на фа-
фазовой плоскости @, 6) это уравнение определяет ориентацию-
касательной к траектории. Следовательно, фазовую траекторию,
по крайней мере в принципе, можно построить методом после-
последовательных приближений2). В рассматриваемом нами примере
важное упрощение проистекает от того, что величина ?(8, 6)t.
определяемая соотношением
есть интеграл движения. Действительно,
') Точнее, импульс (см. разд. 1.2.1).
2) Мы будем использовать метод последовательных приближений в боль-
большинстве случаев, в частности всякий раз, когда не будем знать, как интегри-
интегрировать уравнение движения.

22
Глава I
Заметим, что с точностью до множителя размерности ml эта
величина есть не что иное, как энергия маятника, которую при-
принято считать равной нулю в состоянии покоя (в точке R на
рис. 1.1):
?@,0) = 0.
Следовательно, траектории, удовлетворяющие уравнению A),
являются кривыми постоянной энергии, или контурами энергии
Е, на фазовой плоскости. Так как энергия Е — периодическая
Сепаратрисы
Рис. 1.2. Фазовый портрет простого маятника. Кривые на плоскости
F, 6)—линии постоянной энергии маятника. Картина периодична по оси 9
(perjod 2л). В области применимости линейного приближения A) линии по-
постоянной энергии принимают форму окружностей с центрами в точках 9 = 0,
0 = ±2л.т, где п — целое число. Такие кривые соответствуют колебаниям,
период которых не зависит от амплитуды (изохронизм малых колебаний).
При ббльших значениях энергии окружности переходят в овалы и период
начинает зависеть от амплитуды. Когда энергия становится больше 2g/l,
колебания сменяются непрерывным вращением вокруг тотки О. Каждая из
двух кривых, отделяющих область колебаний от области вращений, назы-
называется сепаратрисой. Стрелки указывают направление движения по времени.
функция угла в (с периодом 2я), траектории достаточно по-
построить в области
ве[-я,+п], ёе(-оо, +оо).
Чтобы подчеркнуть это свойство, на рис. I. 2 траектории по-
показаны в более широкой области значений б. Здесь уместно
¦сделать несколько замечаний относительно рис. 1.2. Окружность
с центром в точке 0=0 (или при более общем подходе в точке
0 ± 2лп, где п — целое число) соответствует изохронным коле-
колебаниям, период которых, как было показано в предыдущем раз-
разделе (в линейном приближении), не зависит от амплитуды и

Свободный осциллятор, осциллятор с вынуждающей силой 2$
массы. Такие колебания отвечают наименьшим значениям энер-
энергии. В отличие от этого в нелинейной области период колеба-
колебаний возрастает с увеличением амплитуды (и соответственно
энергии). Соотношение между периодом Т и энергией Е имеет
вид
Функция F{lE/g) есть эллиптический интеграл, который расхо-
расходится, когда мы приближаемся к сепаратрисе, т. е. контуру энер-
энергии, проходящему через неустойчивые точки равновесия маят-
маятника с координатами 6 = 0, в = ±Bn-f-1)я (верхнее положе-
положение маятника — точка R' на рис. 1.1). На этой сепаратрисе
энергия равна 2g/l, а период бесконечен. Априори это второе
свойство может показаться несколько курьезным и даже пара-
парадоксальным, хотя в действительности лишь отражает тот факт»
что маятнику требуется бесконечно много времени для достиже-
достижения неустойчивого состояния равновесия, когда имеющаяся
энергия в точности равна энергии, необходимой для достижения
точки R'.
При любом значении Е, превышающем 2g/l, существуют две
возможные траектории, симметричные относительно оси 8. Они
соответствуют вращению маятника вокруг точки О либо в од-
одном, либр в другом направлении.
/
1.1.3. Каноническая форма уравнений движения
Уравнение A) нетрудно преобразовать в два дифференци-
дифференциальных уравнения первого порядка
dt аре'1" m
dt ~~Pe~Z.^_ dQ >
где ре — угловой момент:
Ре = /в,
а Я — гамильтониан, или функция Гамильтона, маятника. Не-
Нетрудно видеть, что
2
Е (9, 9) = Н (ре, 6) = i -?¦ + 4- A - cos 6).
Переменные В и ре канонически сопряжены в смысле Гамильто-
Гамильтона— Якоби. Так как
tf<fte) fS/>e+«2e 0

24 Глава I
энергия остается постоянной при движении. (К такому заклю-
заключению мы пришли в предыдущем разделе.) Это свойство позво-
позволяет отнести маятник к классу консервативных (или гамильто-
мовых) систем, для которых характерна инвариантность энергии.
1.2. КОНСЕРВАТИВНЫЕ СИСТЕМЫ
I. 2.1. Закон сохранения энергии
Вывод, к которому мы пришли относительно простого маят-
иика, имеет гораздо более широкое применение. Классическая
механика показывает, что теоретически возможно описать по-
поведение любой системы без диссипации с помощью функции
Гамильтона Н, которая зависит от обобщенных пространствен-
яых координат (обозначаемых через qi), обобщенных канони-
канонически сопряженных импульсных координат (обозначаемых че-
через р) и, возможно, времени1):
Н{Яъ Чъ •••> Яп, Ръ Р2, • ••> Рп> О-
С помощью принципа наименьшего действия мы устанавли-
устанавливаем, что эта функция удовлетворяет системе 2п дифферен-
дифференциальных уравнений
d?L — n дН
dt Pi dqi '
i=l, .... n;
частным случаем является система уравнений B). Нетрудно
убедиться, что, когда Н не зависит явно от времени,
дН __ dH _n
dt.~-~dT—u>
•откуда Н (q, р) = Е = const.
Таким образом, все системы, описываемые не зависящим от
времени гамильтонианом, например простой маятник [уравне-
яие A)], консервативны.
1,2.2. Сохранение площадей в фазовом пространстве
Из сохранения энергии следует одно очень важное свойство:
сохранение площадей в фазовом пространстве. Исходя из урав-
уравнений C), можно доказать, что площадь элемента поверхности
') Ниже мы приводим без доказательств краткий обзор наиболее суще-
существенных понятий и результатов механики, которые читатель найдет в любом
учебнике.

Свободный осциллятор, осциллятор с вынуждающей силой 25»
фазовой плоскости сохраняется при движении, если Я не
зависит явно от времен»1). Что следует из такого результата?
Рассмотрим сначала случай, когда имеется только одна пара
канонических сопряженных переменных {q, p). Предположим,,
что имеется множество точек, заполняющих поверхность о@)
в окрестности начальной точки. В любой последующий момент
времени эти точки заполняют поверхность o(t), такую, что-
а(^)== а@) (в соответствии с упомянутым выше свойством)-
Рис. 1.3. Сохранение площади в фазовом пространстве (р, q). Элемент пло-
площади о@), который мояшо рассматривать как множество начальных условий,
вследствие движения преобразуется в другой элемент, площадь которого"
равна a (t). Если система консервативна, то элемент a(t) при любых значе-
значениях t имеет такую же площадь (но не обязательно такую же форму), как
и исходный элемент 0@).
Для того чтобы это равенство выполнялось, расстояние между
соседними траекториями должно оставаться почти постоянным
(рис. 1.3). Но это не требуется при более высоких размерностях.
Коль скоро существуют по крайней мере две пары канонически
сопряженных переменных (<7ьРь 92, Рг), движение происходит
по энергетической поверхности2)
H(qu q2, Pi, p2) = ? = const.
1) За доказательством этого свойства, достаточно простым, но сравни-
сравнительно длинным, мы отсылаем читателя к курсам механики. Понятие «пло-
«площадь» подлежит обычному обобщению и замене понятием меры двумерной
поверхности. Две канонически сопряженные переменные qi и pi изменяются
на плоскости, а элемент площади bpi bqi сохраняется в силу уравнений C).
Множество начальных условий, занимающее поверхность меры а на плоско-
плоскости (qi, pi), будет занимать поверхность такой же меры в процессе эволюции.
Это свойство гамильтоновых систем гораздо более ограничительно, чем про-
просто сохранение энергии или обратимость уравнений движения. Оно влечет
за собой сохранение объема в фазовом пространстве, так как элемент объема
равен произведению элементов площади каждой пары сопряженных перемен-
переменных. Фазовое пространство имеет в этом случае четную размерность.
2) Эта поверхность эквивалентна линиям уровня простого маятника. Сле-
Следовательно, она (по крайней мере локально) может быть отображена н»
обычное пространство R3. ,,

26 Глава I
Так как площадь множества данных начальных условий
qp сохраняется во времени, расстояние между начальными
точками не может убывать, поскольку в противном случае пло-
площадь убывала бы со временем. Но сохранение площади может
быть гарантировано одним из двух способов:
1) либо, как прежде, элемент поверхности переносится вдоль
траектории по существу без деформации, 2) либо он экспонен-
экспоненциально удлиняется со временем, т. е. как еи, % > 0, в одном
направлении и экспоненциально сжимается, как е~и, в перпен-
перпендикулярном направлении. Так как ё>-*е~м нз 1, площадь во вто-
втором случае также сохраняется.
Если при первой гипотезе две траектории, близкие первона-
первоначально, остаются близкими при любом t, то при второй гипо-
гипотезе они стремятся разойтись экспоненциально. Подчеркнем, что
с динамической точки зрения различие существенно: в первом
случае траектории устойчивы, в то время как во втором случае
они неустойчивы, так как малое начальное расхождение очень
быстро усиливается со временем.
I. 2.3. Инвариантность уравнений относительно
обращения времени
Еще одно важное свойство уравнения A) и более общих
уравнений C) состоит в том, что на них никак не сказывается
изменение знака времени (замена -j-t на —/). В нашем конк-
конкретном примере это означает, что кинофильм о движении маят-
маятника можно прокручивать как в одну, так и в другую сторону
без сколько-нибудь заметного различия. Именно поэтому гово-
говорят, что динамика консервативных систем обратима.
Чтобы понять особую природу обращения времени, следует
иметь в виду одно обстоятельство: оно не является свойством
большей части наблюдаемой нами эволюции во времени. Если
мы пускаем в правильную или в обратную сторрну кино- или
телефильм, то зритель через несколько секунд замечает разли-
различие: волны движутся от берега, дым втягивается в сигареты
и т. д. Следовательно, инвариантность относительно обращения
времени отнюдь не является общим свойством. Она характерна
для консервативных систем и отражает тот факт, что фунда-
фундаментальные физические законы, заключенные в уравнениях
C) — инерция, гравитация, — одного и того же рода. Как мы
увидим в дальнейшем, необратимость возникает, если энергия
рассеивается вместо того, чтобы сохраняться.
С точки зрения фазового пространства ясно, что сохранение
площадей остается в силе при обращении времени. Аналогично
устойчивые траектории остаются устойчивыми: независимо от

Свободный осциллятор, осциллятор с вынуждающей силой 27
того, в каком направлении течет время, они не расходятся. В от-
отличие от этого если площадь сохраняется за счет удлинения
в одном направлении и сокращения в перпендикулярном на-
направлении, то обращение времени приводит к тому, что эти два
направления обмениваются характером устойчивости: первона-
первоначально устойчивое направление (сжатия) становится неустой-
неустойчивым (направлением растяжения), и наоборот.
1.3. ОСЦИЛЛЯТОР С ЗАТУХАНИЕМ
.3.1. Диссипация энергии при трении
Как мы видели в разд. 1.1, описание свободного осциллятора
было получено путем идеализации простого маятника. В ча-
частности, мы пренебрегли всеми видами трения — трением про-
проволоки и массы о воздух, а также трением в точке подвеса О.
На практике движение реального маятника всегда1) прекра-
прекращается из-за трения: амплитуда колебаний со временем неумо-
неумолимо убывает. Это весьма общее явление рассеяния, или дисси-
диссипации, энергии необходимо учесть в математическом описании.
Если говорить более конкретно, то уравнение A) необходимо
модифицировать. Простое замечание поможет понять, в каком
направлении следует действовать. Мы подчеркивали, что урав-
уравнение A) инвариантно относительно обращения времени. Но
механизм затухания нарушает это свойство, так как приводит
в конце концов к прекращению колебаний. Следовательно, не-
необходимо нарушить инвариантность относительно обращения
времени.
I. 3.2. Уравнение для осциллятора с затуханием
Проще всего это сделать, добавив к уравнению A) член,
пропорциональный производной какого-нибудь нечетного по-
порядка, например первую производную, от угла Э. Тогда в ли-
линейном приближении получаем У~
где у — коэффициент затухания, ш2 = g/Z —квадрат угловой
частоты.
В результате мы приходим к линеаризованному уравнению
маятника с затуханием. Как показывает опыт, это уравнение
') Говоря так, мы исключаем случайное движение маятника под дей-
действием тепловых флуктуации. В наших масштабах это вполне оправданно в
силу того, что постоянная Больцмана очень мала.

28 Глава I
дает удовлетворительное описание в случае трения типа «тре-
«трение в жидкости»1). Рассмотрим более подробно эволюцию
энергии в этом случае:
е, в) = | № +
как (по предположению, необходимому для линеаризации)
1 —cose »(92/2).
Используя уравнение D), мы видим,
Таким образом, энергия сохраняется, если 7 = 0 (трение от-
отсутствует), и убывает, если у >¦ 0. Так как по определению
Е ^ 0, энергия стремится к нулю. Следовательно, состояние
с нулевой энергией (состояние покоя) устойчиво, поскольку
маятник с необходимостью эволюционирует к этому состоянию.
Забудем теперь, как мы вывели уравнение D|, и сосредото-
сосредоточим внимание на его внутренних свойствах. Заметим, что если
7 < 0, то энергия Е априори неограниченно возрастает, разу-
разумеется, за исключением того случая, когда исходным является
состояние покоя (в этом случае из 0 = 0 = 0 следует, что
dE/dt = 0). Но состояние покоя неустойчиво, так как малейшее
смещение маятника из состояния покоя со временем только уси-
усиливается.
I. 3.3. Фазовый портрет
Решениями уравнений D) являются траектории, касающиеся
в каждой точке вектора локальной скорости, две компоненты
которого (х — 0, у = 0) по определению удовлетворяют урав-
уравнениям ' ¦'¦
dx а
-& = 0 = - 76 _ ©20 = - у у - ©2JC.
Пользуясь математической терминологией, можно сказать, что
траектории являются силовыми линиями такого векторного
*) Сила такого трения пропорциональна скорости. Примеры:
1) маятник с плотностью груза, во много раз превышающей плотность
жидкости, в которую он погружен (таков, в частности, обычный маятник
в воздухе);
2) электрический колебательный контур, демпфируемый сопротивлением
цепи.
Существует также другая разновидность трения — «трение твердых тел>.
Включить его в уравнения гораздо труднее, в основном из-за эффектов ги-
гистерезиса.

Свободный осциллятор, осциллятор с вынуждающей силой 29
поля. Существенно, что через каждую точку, кроме особых то-
точек, в которых векторное поле не определено, проходит только
одна силовая линия. Начало координат (8=6=0)—един-
(8=6=0)—единственная особая точка на плоскости (только в ней обе компо-
компоненты скорости равны нулю).
Мы уже видели (рис. 1.2), что при у = 0 траектории обра-
образуют непрерывное семейство замкнутых кривых, охватывающих
точку равновесия 0 = 8=0. Если уфО, то такое семейство
кривых трансформируется в множество траекторий, которые
либо сходятся к началу координат, либо расходятся из него
в зависимости от знака: у > 0 или у < 0. Покажем, что при сла-
слабом затухании, т. е. когда |y| ¦< ©, эти траектории имеют форму
спиралей. Действительно, при малом коэффициенте затухания у
временная эволюция угла, 8 не может сильно отличаться от
эволюции при у = 0. Следовательно, в качестве первого прибли-
приближения мы можем положить
о cos (©/ + ?),
где p(t)— функция времени, медленно изменяющаяся по срав-
сравнению с периодом Т = 2я/со. Используя это приближенное вы-
выражение, вычислим среднее изменение энергии за один период
двумя способами. Во-первых, проинтегрируем мгновенное изме-
изменение энергии:
и+т
dE 1 Г / dE \ .. Ъ,
—=— \ \-w)dt=-^-
и
Пренебрегая малым изменением функции р за один период, по-
получаем
Во-вторых, воспользуемся тем, что в том же приближении энер-
энергия имеет значение
Е = i- [pV sin2 (<ot + ф) + р2©2 cos2 (Ш + ф)] = i p V,
а ее среднее изменение за период определяется выражением
dE d
~dT =

30
Глава I
Комбинируя эти два результата, мы видим, что за период
dp5 _ 2
~dT ~ ~ Yp *
Если коэффициент затухания y очень мал по сравнению с со, то,
интегрируя это соотношение по времени, получаем
Таким образом мы вывели параметрическое уравнение траекто-
траекторий на плоскости (9,9):
9 ~ р @) ехр (- ¦#-) cos (со/ + <j>),
9 « — р @) соехр (— -^) sin (со* + ф).
Это уравнение описывает спирали, закручивающиеся (у > 0)
или раскручивающиеся (y*<0), и окружности (y = 0). Напом-
Напомним, что мы используем здесь линейное приближение [уравне-
[уравнение D)]. ,
Рис. 1.4. Фазовый портрет уравнения D) вблизи начала координат. При
Y = 0 ситуация такая же, как в случае простого маятника в линейном при-
приближении, поэтому мы получаем семейство окружностей с центром в начале
координат. Если же у Ф 0, то траектории имеют форму спиралей, раскручи-
раскручивающихся из начала координат (у < 0, усиление) или сходящихся к началу
(у > 0. затухание). Чтобы не загромождать чертеж, для каждого из этих
двух случаев изображена только одна спираль.
На рис. 1.4 схематически показаны фазовые портреты кото-
которые получаются в каждом из этих трех случаев.
Заметим, что при любом значении y начало координат яв-
является особой точкой, соответствующей стационарному решению
уравнения движения. Это стационарное решение устойчиво при
Y > 0 и неустойчиво при y < 0. так как в первом случае все
траектории сходятся к нему, а во втором расходятся от него.
При y = 0 говорят, что начало координат обладает нейтральной

Свободный осциллятор, осциллятор с вынуждающей силой 31
устойчивостью, поскольку смещения не усиливаются и не зату-
затухают со временем.
При v > 0 все траектории на фазовой плоскости заканчи-
заканчиваются в начале координат, которое поэтому называется при-
притягивающей точкой или аттрактором. Это фундаментальное по-
- нятие, допускающее немедленное обобщение на случай много-
многообразий более высоких размерностей (кривых, поверхностей
и т. д.). Мы неоднократно будем использовать понятие аттрак-
аттрактора.
К/ 1.4. ДИССИПАТИВНЫЕ СИСТЕМЫ
\J 1.4.1. Существенные свойства
Осциллятор с затуханием служит типичным примером дис-
сипативной системы. Динамические свойства диссипативных си-
систем во многих отношениях противоположны свойствам консер-
консервативных систем. Мы можем вернуться к соображениям, рас-
рассмотренным в разд. I. 2. Для диссипативных систем, вообще
говоря, не существуют гамильтонианы, не зависящие от вре-
времени *); следовательно, энергия не сохраняется. С другой сто-
стороны, в определенных случаях существует функция динамиче-
динамических переменных, называемая .функцией Ляпунова, которая по-
положительна и монотонно убывает со временем (обусловливая
тем самым необратимость). Такая функция Ляпунова суще-'
ствует не всегда. Диссипативные системы могут обладать го-
гораздо более сложным эволюционным режимом, чем просто за-
затухание, в особенности если динамика включает в себя и эф-
эффекты затухания, и механизмы, поддерживающие движение. Во
всяком случае если существует диссипация, то уравнения дви-
движения изменяются при обращении времени; эволюция диссипа-
диссипативных систем не является обратимой. Наконец, нельзя не упо-
упомянуть еще об одном важном обстоятельстве: площади в фазо-
фазовом пространстве диссипативных систем не сохраняются.
1.4.2. Сжатие площадей в фазовом пространстве
В свете того, что нам уже известно, это свойство является
почти очевидным. Обратимся, например, снова к рис. 1.4 и рас-
рассмотрим «настоящее» трение (v>0). Ясно, что при таком дви-
движении не может сохраняться элемент поверхности 68 -66, так
как все траектории, которые проходят через него, заканчи-
заканчиваются в начале координат. Мы встречаемся здесь со свойством,
') Увеличивая число степеней свободы, диссипативную систему всегда
можно погрузить в «объемлющую» гамильтонову систему. Но этот искус-
искусственный прием не приносит сколько-нибудь существенной пользы при иссле-
исследовании диссипативных систем.

32
Глава I
характерным для диссипативных систем: площадь любого мно-
множества начальных условий в среднем уменьшается во времени.
Это свойство часто выражают, утверждая, что поток в фазо-
фазовом пространстве сжимает площади.
Приводимые далее в нашей книге несколько примеров пока-
показывают, что такое сжатие происходит по-разному. Однако было
бы неверно думать (и этой ошибки следует избегать), будто
сокращение площадей непременно означает сокращение длин.
?
Рис. I. 5. Два разных случая сжатия площадей. В первом ряду (по горизон-
горизонтали) длина и ширина уменьшаются одновременно и одинаково. Во втором
ряду ширина возрастает, но высота убывает быстрее. И в первом, и во вто-
втором случае площадь убывает в одном и том же темпе. Таким образом,
уменьшение площади в фазовом пространстве отнюдь не обязательно озна-
означает, что все размеры области уменьшаются.
В действительности все обстоит совсем не так.. Результат здесь
полностью аналогичен результату, упомянутому в разд. 1.2.2:
площади могут сохраняться и в том случае, если расхождение
траекторий в одном направлении компенсируется их сближе-
сближением в другом направлении. Аналогично в рассматриваемом
случае сокращение площадей может быть достигнуто не только
за счет сокращения всех длин, но и за счет уменьшения одних
длин, сопровождаемого менее быстрым увеличением других
длин.
Простая схема на рис. 1.5 иллюстрирует обе указанные воз-
возможности (причем в качестве начального элемента поверхности
выбран квадрат).
Это замечание очень важно для понимания того, что расхож-
расхождение траекторий по некоторым направлениям остается возмож-
возможным даже в случае диссипативной системы. Разумеется, знание
того, как именно происходит сжатие площадей, и его скорости
существенно для завершения динамического описания. В этом
одна из причин важности и полезности якобиана '),
•) См. приложение Д.

ГЛАВА II
ОСЦИЛЛЯТОР С ВЫНУЖДАЮЩЕЙ СИЛОЙ,
ПАРАМЕТРИЧЕСКИЙ ОСЦИЛЛЯТОР
II. 1. ОСЦИЛЛЯТОР ПОД ДЕЙСТВИЕМ ВЫНУЖДАЮЩЕЙ СИЛЫ
II. 1.1. Уравнение Ван дер Поля
Каким должно быть подходящее описание поведения осцил-
осциллятора с вынуждающей силой? Во введении мы упоминали
о том, что в природе существуют многочисленные примеры ос-
осцилляторов с вынуждающей силой. Ясно, что уравнение D) не
подходит для этой цели и не только из-за затухания. У этого
уравнения имеются два других недостатка. Один из них со-
состоит в том, что в случае у <С О энергия маятника неогпянчченнб
возрастает, а это не имеет физического смысла. Другим недо-
недостатком уравнения D) является то, что веди 9(/)—решение,
то любое произведение сев @ также есть решение при любом •
вещественном а, поскольку уравнение D) линейно по 0. Ясно,
что такая инвариантность относительно растяжения несовме-
несовместима с существованием колебаний, обладающих заданной
амплитудой. Следовательно, для случая осциллятора с вынуж-
вынуждающей силой уравнение D) надлежит изменить так, чтобы:
1) нарушить инвариантность относительно растяжения,
2) ограничить рост энергии при у < О,
3) ввести непрерывный источник энергии1), компенсирую-
компенсирующий потери на вязкое затухание при у > 0.
Приняв это за отправной пункт, Ван дер Поль заметил, что
математически простое изменение состоит во, введении коэффи-
коэффициента трения у, зависящего от амплитуды 8 колебаний.
') Практическая реализация стационарного движения маятника имела
большое историческое значение, так как была необходима* для усовершен-
усовершенствования механических часов и, следовательно, для точного измерения' вре-
времени. Физику Гюйгенсу мы обязаны изобретением храпового колеса -!• устрой-
устройства, регулирующего ход маятника. Восемнадцатый век стал свидетелем раз-
развития крутильного маятника — спирали, регулирующей ход механических
наручных часов, в которых колебания поддерживаются пружинным механиз-
механизмом, в наше время появление электроники привело к созданию автоколеоа-
тельных цепей с частотой, стабилйзируембй колебаниями пьезоэлектрического
кварца. Такие же цепи настраиваются на колебания с частотами, связанными
с разностями между энергетическими уровнями атоме в соотношением П.'анкл
(A? = frv). Это позволяет создавать атомные часы с необычно высокой точ-
точностью хода («10~!3 с). В качестве конкретной иллюстрации приведем такой
пример: чтобы показания двух атомных часов разошлись всего лишь на се-
секунду, нам потребовалось бы ждать около 300 000 лет.
3 П. Берже и др.

34 Глава II ;
ч
Сделав так,, чтобы параметр,у был отрицательным при малых
амплитудах и положительным при больших, мы достигнем же-
желаемой цели. Так как существенна только абсолютная величина,
а не знак амплитуды, естественно выбрать зависимость у (9) от
'82. Простейшее возможное выражение, удовлетворяющее всем
условиям, имеет вид
где yo > 0, 0о,—исходная амплитуда. Тогда
. у < 0 при 92 < во,
у> 0 при 92>8<>.
Подставляя наше выражение в уравнение D), получаем так на-
называемое уравнение Ван дер Поля ')
Оно описывает поведение осциллятора с вынуждающей силой,
в котором колебания с малой амплитудой усиливаются, а коле-
колебания с большой амплитудой затухают. Полезно привести это
уравнение к безразмерному виду, выбирая ©dVWYo ?a единицу
амплитуды и 1/ш — за единицу времени. Исходное уравнение
Ван дер Поля переходит в уравнение
-2-^- —(е — в2) — + 9^=0, E)
содержащее только безразмерный параметр е = Yo/<»-
II. 1.2. Фазовый портрет
Если параметр г положителен, то траектории в окрестности
начала координат расходятся, как спирали. Действительно,
в этой окрестности угол 0 всегда мал и членом 02 можно пре-
пренебречь. Таким образом, мы находимся Точно в той ситуации,
которая представлена на рис. 1.4 с у < 0. Наоборот, вдали от
начала координат траектории стремятся к началу координат,
так как коэффициент затухания yF) на достаточно большом
расстоянии от начала координат положителен. Исходя из ин-
интуитивных соображений можно предположить, что между этими
') Ван дер Поль предложил это уравнение в 1922 г. для объяснения
работы триодного генератора.

Осциллятор с вынуждающей силой, параметрический осциллятор 35
двумя крайностями должна существовать замкнутая траекто-
траектория. Более тщательное исследование уравнения Ван дер Поля
позволяет установить существование, единственность и устойчи-
устойчивость такой замкнутой траектории; которую Пуанкаре назвал
предельным циклом. Все фазовые траектории, расположенные
как 'внутри, так и вне предельного цикла, асимптотически стре-
стремятся к нему. Таким образом, перед нами новый пример аттрак-
аттрактора (рис. II. 1).
м0» -
9
-"
Предельный,
цикл
\
Рис. II. 1. Фазовый портрет уравнения Ван дер Поля. Одно из решений
этого уравнения представлено на фазовой плоскости F, 6) замкнутой кри-
кривой — предельным циклом, к которому сходятся все траектории. Мы выбрали
две начальные точки: одну (Мо) вне, а' другую' (м'о) внутри предельного
цикла при е = 0,4.
Форма предельного цикла и колебаний, как видно из
оис. П, 2, сильно зависит от значения положительного пара-
параметра е. Здесь мы изобразили решения уравнения E), исходя-
исходящие из заданной начальной точки (начального условия) в си-
системах координат (9,0) и @, t). Рассмотрены два значения г:
одно очень малое (рис. 11.2,а), другое гораздо больше
(рис. II. 2,р). В первом случае предельный цикл имеет форму
окружности и колебания квазйсинусоидальны. Во втором случае
эволюция происходит в двух, различных масштабах; вслед за

36
Глава II
медленным дрейфом происходит ¦ резкая вариация амплитуды.
Такая характерная временная зависимость получила название
релаксационных колебаний^
Режим предельного цикла описывается периодической функ-
функцией 9(*), которая может быть разложена в ряд Фурье. Это
а
\
ю
1 \
\
t
го
7 \
V
А
V
да
1
\
г.
7
Ъ
1
Рис. II. 2. Влияние параметра г. а — при малых значениях этого параметра
(в = 0,01) временные колебания квазисинусоидальны .и предельный цикл по
форме мало отличается от окружности; б —при гораздо больших значениях
параметра е (е = 4,0) предельный цикл имеет почти прямоугольную форму,
что приводит к появлению двух разных масштабов времени. Пилообразные
изменения амплитуды U называются релаксационными колебаниями.
очень рбщее свойство всех „динамических систем с режимами
такого типа. Следовательно, как только мы оказываемся в ре-
режиме предельного цикла, временная зависимость любой наблю-
наблюдаемой X(t) имеет вид

Осциллятор с вынуждающей силой, параметрический осциллятор 37
II. 1.3. Амплитуда колебаний при 6 = 0
В выбранных единицах энергия определяется выражением
Закон ее изменения во времени может быть выведен из уравне-
уравнения E)
AT! 1 .
¦— —g- B96 + 288) = (е - в2) 92.
Средняя энергия определяется выражением
dE
dt
= lim X \ 4гЛ,
Из приведенного выше' выражения dE/dt получаем
Таким образом, выделяемая энергия ев2 в среднем точно ком-
компенсируется диссипацией 9282 из-за нелинейности. Вычислим
теперь приближенно амплитуду предельного цикла при е=0+.
В этом случае мы можем предположить, что .
8@ я* psinr
{см. рис. II.2,а). Отсюда заключаем, что
Приведенный выше баланс средней энергии показывает, что
в этой области
Таким Образом, размер р предельного цикла (почти окружности)
изменяетсй как квадратный корень ий параметра е. Мы устано-
установили этот результат в частном случае — для уравнения Ван дер
Поля, — но „область его применимости гораздо шире. Действи-
Действительно, член с в2 можно рассматривать как представляющий
любую нелинейность при малых 9. Это — стандартная форма

38 i Глава II
первого нелинейного члена разложения в ряд Тейлора произ-
произвольной функции').
_3аметим, что зависимость размеров предельного цикла от
У? и от амплитуды соответствующих колебаний формально
может быть исключена. Принимая за единицу амплитуды во
(вместо 90/Уе). мы получаем вмесдю уравнения E) новое урав-
уравнение
Разумеется, по форме оно в точности эквивалентно уравнению
E) при заданном значении е. Однако повторяя приведенные
выше вычисления, мы приходим к выводу о том, что размер
предельного цикла на плоскости @,0) теперь не зависит от е.
Определенная выше зависимость от д/е полностью маскируется
выбором единицы измерения угла 0,
II. 2. ПАРАМЕТРИЧЕСКИЙ ОСЦИЛЛЯТОР
II. 2.1. Уравнение движения
Вернемся к примеру простого маятника без трения в грави-
гравитационном поле и представим себе, что точка подвеса О
(рис. I. 1) колеблется в вертикальном направлении. Это другой
способ поддержания движения. Тем самым мы определяем па-
параметрический маятник, т. е. маятник, один из параметров ко-
которого изменяется со временем2). Можно было бы поступить
иначе и (что эквивалентно) поместить простой маятник в гра-
гравитационное поле, зависящее от времени:
') Если рассмотреть разложение в ряд Тейлора коэффициента затухания
Y). to можно было бы считать, что оно начинается с линейного члена
(в то время как мы начали с квадратичного члена):
Этот линейный член не оказывает (по крайней мере вблизи е = 0) прямого
влияния на эволюцию энергии. Действительно, его вклад в среднее dE/dt
имеет вид <х992 и обращается в нуль при 9 = р sin t. Это объясняет, по-
почему мы не удерживали линейный член «9 в выражении для y(Q), а также,
почему соотношение р»-уе имеет совершенно общий характер.
2) Возможны также многочисленные другие реализации, например ем-
емкостный колебательный контур с сопротивлением, зависящим от времени. Эта
ситуация на первый взгляд могла бы показаться весьма необычной, хотя в
действительности она соответствует общей проблеме — поведению любого
осциллятора- с зависящим от времени параметром.

Осциллятор с вынуждающей силой, параметрический осциллятор 39
В описанном выше случае р(/) характеризует вертикальное
ускорение точки О. В линейном приближении уравнение дви-
движения, выведенное из уравнения A), имеет вид
^ + Шв=о. F)
Несмотря на формальное сходство с уравнением A), уравнение
F) существенно отличается от него: при произвольной функ-
функции g(t) уравнение F) неинтегрируемо. Это означает, что мы
не знаем, как решать это обыкновенное дифференциальное урав-
уравнение в квадратурах, т. е. выразить решение 6(/) этого уравне-
уравнения как явную функцию времени через интегралы (или квад-
квадратуры) qj обычных элементарных или трансцендентных функ-
функций, таких, как рациональные дроби, экспоненты, эллиптические
функции'и т. д. Что же касается уравнения A), то оно, наобо-
наоборот, интегрируемо, так как член с (g/l) sin 8 не зависит явно
от времени').
Несмотря на это различие, состояние покоя 8=0=0 по-
прежнему остается тривиальным решением приведенного выше
уравнения. Однако в том случае, когда g зависит от времени,
устойчивость тривиального решения отнюдь не гарантируется
и подлежит определению с помощью детального анализа. Хотя
априори любая форма функции g(t) заслуживает изучения, мы
рассмотрим только g(t), периодическую по времени: уравнение
движения называется в этом случае уравнением Хилла. Упро-
Упрощая задачу еще больше и предполагая, что $(t) — тригономет-
тригонометрическая функция, мы приходим к частному случаю уравнения
Хилла, известному под названием уравнения Матье. Выбирая
ё ('•) = go + gi cos BШ),
получаем 2)
45- + ©2 [1 + h cos Burf)] 8 = 0, G)
') Понятие интегрируемости и неинтегрируемости может быть сразу же
обобщено на любую систему обыкновенных дифференциальных уравнений- За-
Заметим/что решение уравнения или системы уравнений в квадратурах принад-
принадлежит к числу математических проблем, рассматриваемых теорией Галуа
алгебраических (и дифференциальных) уравнений.
2) Такой выбор функции g(t) помимо удобства вычислений обусловлен
более глубокой причиной, ибо позволяет нам упомянуть об общей проблеме
связанных осцилляторов. Введем переменную а = h cosBa>/) и рассмотрим
вместо уравнения F) систему двух уравнений
dt2 °

40 Глава II
где
Возбуждение, представленное членом hcosBo)t), имеет период
Т = я/со. He умаляя общности, мы можем предположить, что
h ^ 0. Заметим, что соо—угловая частота маятника в отсут-
отсутствие внешнего возбуждения (h = 0). Так как уравнение G)
линейно и второго порядка по 6, начальное условие 0@), 0@)
через каждый период (я/ю, 2(я/со), 3(я/со), .-...) претерпевает
линейное преобразование, эквивалентное умножению координат
на плоскости @, 6) на матрицу М (см. приложение Д). На ос-
основе этого замечания в теории Флоке линейных уравнений с пе-
периодическими коэффициентами показано, что решения уравне-
уравнения Матье имеют вид
Здесь ц — собственное значение матрицы М, называемое иногда
характеристическим показателем, a P(t) —функция с периодом
Т — я/со, т. е. такая, что
Поиск решений уравнения G) мы разделили на две части. Пер-
Первая часть сводится к нахождению функции P(t), которая, как
уже упоминалось, не может быть выражена через обычные
функции: необходимо ввести новый класс трансцендентных
функций, называемых функциями Матье (мы не будем останав-
останавливаться здесь на их описании). Вторая часть состоит в вычис-
вычислении характеристического показателя ц,. Знак вещественной
части ц определяет, возрастает ли решение 0@ или убывает.
Если вещественная часть р, положительна, то 9@ неограни-
неограниченно возрастает со временем. В этом случае состояние покоя,
а в действительности любое решение уравнения G), неустой-
неустойчиво, так как любое малое возмущение формы 0@ неограни-
ченро возрастает. Именно вопросом устойчивости мы займемся
описывающих поведение двух осцилляторов с амплитудами 0 и а. Уравнения
связаны перекрестным членом со^ав. Такая модель почти очевидна, так как
периодические изменения функции git) означают, что ею управляет внешний
осциллятор с амплитудой, пропорциональной а. Этот внешний осциллятор
должен быть нечувствительным к движению параметрического маятника, чем
и объясняется отсутствие члена, зависящего от 6, во втором уравнении. Та-
Такова специфическая форма связи, при которой второй осциллятор действует
на первый как вынуждающая сила.

Осциллятор с вынуждающей силой, параметрический осциллятор 41
II. 2.2. Устойчивость решений
При малых значениях возбуждения (при ft, близких к нулю)
показатель ц может быть вычислен по теории возмущений1).
Известно, что при Л=0 общее решение уравнения G) имеет
вид
По непрерывности при ft, близких, но не равных нулю, решение
е»*Р {t) должно мало отличаться от приведенного выше. Мы за-
заключаем поэтому, что выражение
дает удовлетворительно приближение при малых ц и частоте а»,
близкой к а>о- Подставляя это приближение в уравнение Матье»
получаем
[? + h со* Bш/))] eat cos (со/ \ f) -
= | («о — а2 + ц2) cos (Ы + Ф) — 2<йц sin (<в/ + ф) +
+ 4 <о2 cos (arf - ф) + | a§ cos
Отбрасывая член с cosCW + ^), который, как показывают бо-
более подробные вычисления, пренебрежимо мал, попытаемся
найти условия, при которых правая часть равна нулю при
всех/. Чтобы это произошло, коэффициенты при e^cos((oO' и
e^fsin(cof) должны быть равны нулю:
2 jCQS ^ 2(i sin ^> = О,
2сйц cos ф + (ю2, — со2 + И2 — 4 ио) sin Ф = °-
Эта система двух линейных неоднородных уравнений относи-
относительно cos^ и sin# имеет решение только в том ^случае, если
детерминант системы равен нулю, т. е.
'(cog - со2 + и.2J - -у-со* -f 4a>V = О,
или
со2) ^ + (е^ - со2J - ^- со* = 0.
4) В частном случае уравнения Матье известно, как проводить вычисле-
вычисления и в пределе при /г-»-оо, но используемые при этом математические ме-
методы характерны именно для уравнения Матье. Именно поэтому мы излагаем
здесь метод вычислений, пригодный при h, близких к нулю, но применимый
зато в самом общем случае.

42
Глава II
Перед нами квадратное уравнение относительно ц2, сумма кор-
корней которого всегда отрицательна, а дискриминант всегда поло-
положителен. Существуют два вещественных корня, по крайней мере
один из которых отрицателен. Так как отрицательному значе-
значению (х2 соответствует чисто мнимый характеристический показа-
показатель ц, оно не может быть источником неустойчивости. Наобо-
Наоборот, решение неустойчиво, если существует вещественное поло-
Недстаичцвоапь
/х.г>0
х' СО/С00
Рис. II. 3. Диаграмма устойчивости уравнения Матье на плоскости
Внутри заштрихованной зоны существует положительное значение VM^ и
уравнение не имеет устойчивого периодического решения. В окрестности точ-
точного резонанса (о = соо) это утверждение верно даже при самой малой ам-
амплитуде возбуждения к вплоть до предельного значения 0. Существуют и
другие области субгармонической неустойчивости, не изображенные на это»
рисунке. Их вершины имеют координаты
h = 0; со/Шо = 1/я, п — положительное целое число.
жительное значение ц2 и, следовательно, ц. Для этого необхо-
необходимо, чтобы произведение корней было отрицательно, т. е.
А>2
1 —
На плоскости параметров возбуждения (А, <о) с прямоугольной
системой координат это условие задает сектор с вершиной
в точке Л = 0, ю/шо = 1 (рис. П. 3).
Внутри сектора (заштрихованная зона) ,u2 имеет положи-
положительный корень и у уравнения G) нет устойчивого решения.
Под этим мы подразумеваем следующее: существуют началь-
начальные условия, очень близкие к состоянию покоя и такие, что
выходящие из начальных точек траектории расходятся экспонен-
экспоненциально. Состояние покоя неустойчиво относительно возбужде-
возбуждения с амплитудой, стремящейся к нулю (А -*¦ 0), если выпол-
выполняется условие со = соо (в этом случае мы говорим, что имеет

Осциллятор с вынуждающей силой, параметрический осциллятор 43
место точный резонанс). Такого рода неустойчивость часто на-
называют субгармонической, так как она приводит к колебаниям
маятника с частотой й/2л, равной' половине частоты 2со/2я
внешнего возбуждения.
Вне области неустойчивости оба возможных значения ц2 от-
отрицательны. При частоте ю, близкой к ©о, и малых А, как не-
нетрудно проверить, одно из мнимых значений ц, близко к нулю,
а другое приближенно равно 2icoq- Эффект, производимый при
этом на колебания, состоит в следующем:
1) основная частота слегка изменяется из-аа наличия ха-
характеристического показателя, близкого к 2?со0;
2) малое отрицательное значение ц,2 приводит к низкочастот-
низкочастотной модуляции колебаний. Следовательно, режим, вообще го-
говоря, оказывается квазипериодическим (точное определение см.
в разд. III. 3.2);
3) амплитуда этой модуляции произвольна, так как уравне-
уравнение G) линейно по 9. ¦ •
Когда иарамехры возбуждения на плоскости (А,о>) прибли-
приближаются к области неустойчивости, низкочастотная модуляция
уменьшается. Она стремится к нулю, как соответствующее зна-
значение (д2 на границе области. На самой границе множитель е»1
теории Флоке заменяется членом, полиномиальным по вре-
времени. Затем внутри сектора неустойчивости показатель стано-
становится вещественным. Резюмируя, можно сказать, что при дви-
движении в пространстве параметров мы видим, как одна частота
уменьшается и затем обращается в нуль, причем одновременно
возникает неустойчивость. Режим, который появляется в об-
области неустойчивости, определяется нелинейными эффектами,
которые не охватываются приведенным выше анализом.
Прежде чем завершить этот раздел, упомянем о том, что
на плоскости (А, ю) существуют и другие области неустойчи-
неустойчивости. Они соответствуют секторам шириной А", не показанным
на рис. II. 3, вершины которых расположены в точках А = 0 и
/ = 1/п (гс—*положительное целое числоI).
>) Проницательный читатель, возможно, заметил, что с точностью до
различий в обозначениях (t вместо х, постоянная h включена в определе-
определение \) уравнение Матье — Хилла совпадает со стационарным уравнением
Шрёдингера для одного пространственного измерения. Между развитой нами
теорией параметрического резонанса и теорией электронов (без взаимодей-
взаимодействия) в периодическом потенциале одномерного кристалла существует пол-
полная параллель. По историческим причинам аналог теории Флоке называют
в последнем случае теорией Блоха — Ваннье, несмотря на то что работа
Флоке включает в себя значительную часть теории электронов в металле.
В случае электронов существуют области, аналогичные зонам параметриче-
параметрической неустойчивости, которые называются запрещенными энергетическими
зонами.

44
Глава II
II. 2.3. Эффект затухания
Так как во всех физических системах имеется трение, есте-
естественно спросить, как изменятся приведенные выше результаты
при наличии затухания. При слабом трении типа трения в жид»
С затуханием
л
Без ва,туха.ния
О 1
Рис. II. 4. Влияние затухания. Нсли имеется затухание, то область субгармо-
субгармонической неустойчивости сужается и оказывается внутри зоны неустойчивости
в отсутствие затухания. Обращаем особое внимание читателя на то, что даже
при точном. резонансе для дестабилизации параметрического осциллятора не-
необходимо превысить некоторый, отличный от нуля, порог возбуждения.
кости, т. е. при 0 < у «С wo, мы можем-повторить все предыду-
предыдущие вычисления, начиная с уравнения
Если величина h мала, то из существования решения в форме,
постулируемой теорией Флоке, следует, что
- -? < + B«>fH- «>YJ = 0.
Нейтральная устойчивость, соответствующая ц = 0, достигается
при
Таким образом, при точном резонансе (со = соо) состояние покоя
является параметрически неустойчивым, если
Для дестабилизации этого состояния необходим некоторый ми-
минимальный уровень возбуждения. Это не удивительно и легко
объясняется необходимостью компенсировать затухание осцил-

Осциллятор с вынуждающей силой, параметрический осциллятор 45
лятора. На этот раз главная область субгармонической неустой-
неустойчивости на. плоскости (ft, со) ограничена непрерывной кривой,
которая лежит внутри сектора, вычисленного в отсутствие зату-
затухания (рис. П. 4).
II. 2.4. Механизм параметрического усиления
Попытаемся установить физическую причину субгармониче-
субгармонической неустойчивости. Вместо синусоидального возбуждения рас-
рассмотрим функцию g(t) с периодом Т = л/а>, состоящую из ко-
коротких импульсов длиной х, где х<Г (рис. П.5).
X
Рис. 11.5. Схематическое представление функции g(t). Предполагается, что
длительность т каждого импульса пренебрежимо мала по сравнению с пе-
периодом Т.
Проинтегрируем уравнение F) по интервалу х (продолжи-
(продолжительности импульса) в предположении, что амплитуда импульса,
хотя и велика, не может вызывать существенных изменений
угла 0 за это время. При таких условиях для любой функции
f(8) справедливо соотношение
\ / (8) dt = х ¦ (среднее значение /F)).
(т)
Но потребуем также, чтобы в нашем приближении выполнялось
равенство
где [dQ/dt] — среднее изменение скорости, вызванное импуль-
импульсом. Тогда из уравнения F) получаем
где
G = j\ g(t)dt,
Q(t)—среднее положение маятника за импульс.

46 Глава II
В момент, когда маятник достигает своего максимального от-
отклонения, его скорость и кинетическая энергий равны нулю,
а его потенциальная энергия пропорциональна A/2Nмакс Пред-
Предположим, что именно в этот момент мы прикладываем к маят-
маятнику импульс. Потенциальная энергия при этом не изменяется,
так как положение маятника остается прежним. Но скорость
получает приращение [dQ/dt\——Обмане, и поэтому кинетиче-
кинетическая энергия после импульса равна A/2) <526макс- В результате
импульс увеличивает энергию осциллятора в A + G2) раз, при-
причем этот множитель больше единицы. Если следующий импульс
поступает в тот самый момент, когда отклонение снова макси-
максимально, то маятник дестабилизируется. Для наступления потери
устойчивости необходимо, чтобы последовательные импульсы
были разделены интервалом времени, равным целому кратному
полупериодов невозмущенного движения маятника/ Априори
кратное может быть любым, не обязательно целым, но ясно, что
такой процесс параметрического усиления особенно эффекти-
эффективен, когда импульс поступает каждый полупериод, как это было
выше. Сказанное объясняет, почему на диаграмме устойчивости
уравнения Матье мы имеем на плоскости (Л, со) последователь-
последовательность областей неустойчивости, исходящих из точек с абсцис-
абсциссами \/п. В соответствии с нашей интерпретацией это соответ-
соответствует импульсному воздействию через полупериод, период, пол-
полтора периода и т. д.
II. 3. ВВЕДЕНИЕ В ТЕОРИЮ БИФУРКАЦИЯ
II. 3.1. Понятие бифуркации1)
Описание осцилляторов с вынужденной силой и параметри-
параметрических осцилляторов позволяет нам рассмотреть другое поня-
понятие, имеющее фундаментальное значение для исследования ди-
динамических систем — понятие бифуркации. Мы уже отмечали
выше на примере, что при движении в плоскости (Л, со) пара-
параметрического маятника наблюдается полное изменение характе-
характера колебаний при пересечении границ, разделяющих устойчивые
решения от неустойчивых., Когда решение любого уравнения или
системы уравнений претерпевает качественное изменение при
фиксированном значении параметра, называемом критическим
значением, это называется бифуркацией. Точка в параметриче-
параметрическом пространстве, в котором происходит такое изменение, на-
называется точкой бифуркации. Из точки бифуркации исходят
') Более подробное изложение локальных бифуркаций коразмерности 1
см. в приложении А,

Осциллятор с вынуждающей силой, параметрический осциллятор 47
Максимальное
растяжение _
Уапвинквт
предельный.
. ' цикл
УЬтойчивал
неподвижная
точна
неустойчивая
неподвижная
точка
Рис. II. 6. Бифуркационная диаграмма для уравнения E). а — при е?-— О
устойчивое решение претерпевает качественные изменения: вместо притяги-
притягивающей неподвижной точки появляется предельный цикл, начальная ампли-
амплитуда которого равна нулю; б — справа схематически изображены некоторые
фазовые траектории в трех случаях: е < ес, е — ес и е > ес- Для удобства
ось е выбрана вертикальной.

48 Глава II
несколько (две или более) ветвей решения, устойчивых или не-
неустойчивых. Представление любого характеристического свой-
свойства решений как функции бифуркационного параметра образует
бифуркационную диаграмму.
Чтобы пояснить эти понятия, продемонстрируем их на при-
примере осциллятора с вынуждающей силой или, точнее, уравне-
уравнения E), которое мы будем рассматривать независимо от физи-
физического смысла параметра е. При всех значениях (положитель-
(положительных и отрицательных) бифуркационного параметра е начало
координат 8 — 6 — 0 всегда является особой точкой. При е < О
начало координат устойчивЪ (и, следовательно, является аттрак-
аттрактором), но становится неустойчивым при е > 0 и переходит
в другой аттрактор—. предельный цикл. Таким образом, при
критическом значении параметра гс =0 происходит изменение
характера устойчивого решения. Построив график какого-ни-
какого-нибудь типичного свойства решения, например максимального, от-
отклонения, как¦ функцию паргмстра е, пслуч;:;»! диаграмму, изо-
изображенную на рис. II. 6, о. Чтобы подчеркнуть значение этой
бифуркационной диаграммы, мы показали также на фазовой
плоскости форму траекторий (рис. 11.6,6).
Напомним, что при е==ес=0 осциллятор находится в со-
состоянии нейтральной устойчивости: в фазовой плоскости больше
нет аттрактора и всякое начальное условие порождает свою соб-
собственную траекторию.
II. 3.2. Бифуркация Хопфа
Когда (как в предыдущем примере) при достижении крити-
критического значения параметра из точки рождается предельный
цикл, мы имеем дело с вполне определенным явлением, изве-
известным под названием бифуркации Хопфа. Это понятие имеет
гораздо более широкую область применения, чем приводимый
ниже ограниченный перечень примеров. Бифуркации Хопфа
встречаются в векторных полях и диффеоморфизмах. Их меха-
механизм не зависит ни от числа степеней свободы, ни от конкрет-
конкретной формы уравнений, ни от приложений. Для наших целей до-
достаточно упомянуть два главных свойства предельного цикла
в окрестности точки бифуркации Хопфа. Одно из этих свойств
было доказано в разд. II. 1.3, исходя из уравнения E): ампли-
амплитуда предельного цикла пропорциональна |е — ес||/2, т. е. ампли-
амплитуда растет как квадратный корень из расстояния от этой точки
бифуркации'). С другой стороны, можно показать, что период
') В частном случае уравнения E) гс = 0, что объясняет зависимость
от к'/2, которая была выведена нами.

Осциллятор с вынуждающей силой, параметрический осциллятор 49
колебаний не зависит от е — е;С по крайней мере в первом при-
приближении (в действительности до второго приближения вклю-
включительно). Эти две типичные особенности представляют боль-
большой практический интерес, так как их можно использовать для
идентификации бифуркации Хопфа.
I
II. 3.3. Субкритическая и суперкритическая бифуркация
Бифуркация, порождаемая уравнением E) пр.и е = ес = 0,
называется суперкритической (надкритической) или нормаль-
нормальной. Предельный цикл рождается с нулевой амплитудой, и
в точке бифуркации система находится в состоянии нейтральной
устойчивости. Обусловлена она наличием диссипативного члена
020, противодействующего неустойчивости. Соответственно этому
решение не претерпевает резкого преобразования в точке би-
бифуркации, но изменяется постепенно. В общем случае так про-
происходит всякий раз, когда нелинейные члены низшего порядка
в точности компенсируют неустойчивость (см. приложение А).
Нетрудно представить себе диаметрально противоположную
ситуацию, когда нелинейные члены стремятся усилить неустой-
неустойчивость (достаточно, например, изменить знак члена 029 в урав-
уравнении E) и добавить какие-нибудь члены старшего порядка,
скажем 040, чтобы погасить колебания большой амплитуды).
То же происходит и с другими уравнениями и приводит к суд-,
критической бифуркации, изображенной схематически на
рис. II. 7. В этом случае из-за усиления неустойчивости нели-
нелинейностью устойчивое решение всегда находится ks конечном
расстоянии от решения, которое становится неустойчивым в
точке бифуркации. Проходя ось е справа налево, мы видим, что
ес — неустойчивая неподвижная точка — порождает устойчивую
неподвижную точку и неустойчивый предельный цикл. Эта би-
бифуркация обратна нормальной бифуркации на рис. П. 6, и она
действительно называется обратной или субкритической бифур-
бифуркацией. В интервале \е'с, еЛ сосуществуют два устойчивых ре-
решения: одно стационарное (притягивающая неподвижная точ-
точка), другое колебательное (предельный цикл).
С практической точки зрения необходимо подчеркнуть сле-
следующее:
1) эти два решения не наблюдаются одновременно в одной
и той же системе, и только начальное решение определяет,
какое из них реализуется;
2) устойчивый предельный цикл с самого начала возни-
возникает как цикл конечной амплитуды и исчезает, также имея
конечную амплитуду.
4 П. Берже и др.

so
Глава II
Свойство
Неустойчивый
4v^ / предельный
"-<. цикл
Устойчивая*
неподвижная
точка
Y7
Неустойчивая
неподвижная
точка
Устойчивый.
предельный
цикл
а
Рис. II. 7. Пример обратной, или субкритической, бифуркации, а — график
такого же типа, как на рис. II. 6. Б интервале j г'с, ecj устойчивы два реше-
решения; одно из них стационарное, другое — периодическое; б — чтобы не загро-
загромождать чертеж, на фазовой плоскости при разных значениях параметра е
изображены только аттракторы {неподвижная точка и предельный цикл).

Осциллятор с вынуждающей силой, параметрический осциллятор 51
Представим себе, что параметр б сначала изменяется в одну,
а затем в другую сторону. В этом случае мы увидим явление
гистерезиса, схематически изображенное на рис. II. 8. При уве-
увеличении бифуркационного параметра переход от неподвижной
точки к предельному циклу происходит, при е = гс- Обратный
Свойство
Устойчивое
решение 2
Устойчивое решение I
Рис. II. 8. Явление гистерезиса, связанное с субкрнтической бифуркацией. Так
как два устойчивых решения сосуществуют на ненулевом интервале значений
бифуркационного параметра, переход от одного решения к другому (при пе-
пересечении параметром границ интервала) происходит при различных значениях
параметра в зависимости от направления, в котором текущее значение пара-
параметра пересекает границу: при е = гс, когда параметр пересекает границу,
возрастая, и при 8 = ес, когда параметр пересекает границу, убывая (на-
(направления, в которых изменяется параметр е, указаны стрелками).
переход при уменьшении е происходит при г = г'с. Таким обра-
образом, мы видим, что в отсутствие нейтральной устойчивости ко-
колебания с ненулевой амплитудой в точке перехода и гистерезис
являются свойствами субкритической бифуркации, качественно
отличными от свойств нормальной (суперкритической) бифур-
бифуркации Хопфа.
4*

ГЛАВА III
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
III. 1. ИДЕНТИФИКАЦИЯ И УСТАНОВЛЕНИЕ ХАРАКТЕРИСТИК
ДИНАМИЧЕСКОГО РЕЖИМА
Когда в результате эксперимента или численного моделиро-
моделирования мы получаем зависящий от времени сигнал, x(t) (назы-
(называемый временным радом), одна из наиболее важных задач со-
состоит в определении того, какого рода временной эволюцией
порожден этот сигнал. Ответить на этот вопрос,мы сумеем, если
нам удастся сжать информацию так, чтобы подчеркнуть наибо-
наиболее значительные динамические характеристики. Имеем ли мы
дело с колебаниями более или менее сложной формы, но обла-
обладающими совершенно определенным периодом? |}меем ли мы
дело с более или менее линейной суперпозицией нескольких
различных колебаний? Может быть, перед нами нечто совсем
иное?
Ответ на эти вопросы отнюдь не тривиален, за исключением
весьма простых случаев типа тех, которые были рассмотрены
в предыдущей главе. В этих случаях нам удалось удостове-
удостовериться в существовании периодических решений уравнения дви-
движения осциллятора с вынуждающей силой. Описание таких ре--
шений включает в себя период (или, что эквивалентно, частоту)
и амплитуду: по существу амплитуду предельного цикла ') и
время, за которое фазовая точ'ка его описывает. Эти две харак-
характеристики получаются почти автоматически, если уравнения
движения известны. Важно подчеркнуть, что эти характери-
характеристики остаются в силе и продолжают играть столь же суще-
существенную роль для любого периодического явления, механизм
возникновения и поддержания которого неизвестен, или перио-
периодического явления, описываемого аналитически неразрешимыми
уравнениями, как это чаще всего бывает на практике.
Некоторые динамические режимы представляют собой супер-
суперпозиции колебаний с различными амплитудами, периодами, от-
J) Существование предельного цикла (или аттрактора любого рода) с
необходимостью влечет за собой вывод о диссипативности системы. Именно
это мы и будем предполагать впредь. Консервативная система не может
иметь аттрактор, так как ее эволюция не сопровождается сокращением пло-
площадей в фазовом пространстве.

Преобразование Фурье 53
ношениями гармоник и т. д. С одним из примеров таких режи-
режимов мы познакомились при рассмотрении уравнения Матье,
с другими примерами встретимся дальше. Аттрактором, соответ-
соответствующим суперпозициям колебаний, является не предельный
цикл, а тор. Такого рода режимы называются квазипериодиче-
квазипериодическими. '
Труднее понять природу других режимов. Внешне они ка-
кажутся совершенно беспорядочными и поэтому получили назва-
название «хаотических»1). Если динамика носит детерминированный
характер (т. е. представима конечным числом связанных между
собой нелинейных дифференциальных уравнений или каким-ни-
каким-нибудь эквивалентным способом), то траектории в фазовом про-
пространстве сходятся к странному аттрактору, топологические свой-
свойства которого резко отличаются от топологических свойств тора.
Чтобы ответить на вопросы, заданные в начале этой главы,
мы должны использовать какие-то «объективные» методы ана-
анализа, а не просто полагаться на суждение наблюдателя о регу-
регулярности временного ряда. Существует несколько способов,
позволяющих идентифицировать динамический режим и уста-
устанавливать его характеристики. Мы изложим два часто исполь-
используемых метода: в этой главе — метод Фурье2) и сечение Пуан-
Пуанкаре— в гл. IV. В гл. VI мы познакомимся с, развитым
недавно методом, позволяющим исследовать непосредственно
аттрактор. -
III. 2. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
III. 2.1. Дискретизация сигнала
Быстрое развитие вычислительных методов привело к тому,
что сигнал x(t)—-непрерывную функцию времени — очень часто
измеряют, производя выборку и дискретизацию. При таком под-
подходе эксперимент обычно дает некоторую дискретную последот
') Такие режимы называются также турбулентными, апериодическими
или непериодическими. Все эти прилагательные являются более или менее
синонимическими, так как терминология до сих пор не установилась. Отличи-
Отличительная особенность хаотических режимов состоит в том, что в соответствую-
соответствующем временном ряде x(t) невозможно обнаружить никакой долговременной
регулярности.
2) Преобразование Фурье было разработано в XIX в. математиком Жаном-
Батистом Фурье в ходе его исследований уравнения теплопроводности. Ана-
Аналогичными свойствами обладают и другие преобразования, в частности пре-
преобразования Радемахера и Адамара. Мы не приводим здесь описания этих
преобразований и многочисленных математических результатов относительно
преобразования Фурье, а ограничиваемся изложением только тех практиче-
практических результатов, которые наиболее существенны для наших целей.

S4
Глава III
вательность') вещественных чисел л/0'eZ), расположенных
через регулярные интервалы времени At (рис. III. 1).
На практике такая последовательность чисел с необходи-
необходимостью конечна и содержит п значений при общей продолжи-
продолжительности эксперимента tMaKC = nAt. Выбор двух величин п и
Ы определяется практическими соображениями', такими; как
приемлемая продолжительность эксперимента, емкость памяти,
ос - ¦ -
Hi j
Рис. III. 1. Дискретизация непрерывной функции. Кривая непрерывной функ-
функции (например, экспериментальная кривая) представлена сплошной жирной
линией. Дискретные значения х, выбираются в равноотстоящие моменты вре-
времени ..., /—1,'¦/, /+1, ••• (с интервалом At между двумя последователь-
последовательными моментами), после чего непрерывная функция заменяется последова-
последовательностью точек Pj.
в которой хранятся результаты эксперимента, и пр'опускная спо-
способность устройств, обрабатывающих измерения. Преобразова-
Преобразование Фурье применимо как к непрерывным функциям (с интегра-
интегралами вместо суммирования), так и к дискретным последователь-
последовательностям. Однако мы ограничимся рассмотрением дискретных по-
последовательностей, подразумевая, что сигнал x(t) математически
является интегрируемой и квадратично интегрируемой функ-
функцией.
III. 2.2. Определение дискретного преобразования Фурье
Определим преобразование Фурье дискретного временного
ряда X,- как операцию, порождающую соответствующий ему ди-
') Говоря о недостатках дискретизации, не следует упускать из виду ее
значительное преимущество, состоящее в том, что она позволяет обрабаты-
обрабатывать сигнал численно от начала и до конца. Современная электронная тех-
техника позволяет производить выборку значений с интервалом времени А/,
меньшим 10~6 с, и преобразовывать сигнал в цифровую форму в реальном
времени.

Преобразование Фурье 55-
скретный ряд хк, такой, что
k=.l, ..., я,
/ = V"—1 — мнимая единица.
Выберем для удобства At за единицу времени так, что уве-
увеличение / на единицу соответствует эволюции на интервале вре-
времени А/. Преобразование (8) можно рассматривать как своего
рода вращение, отображающее .вектор (xi,x2, ...,*/, ..., х„)
в вектор (xi;x2, ..., Хк, ..., Хп). Это не вращение в обычном
смысле, так как евклидова длина X/х) не сохраняется. Вели-
Величина, остающаяся инвариантной относительно преобразования-
(8), называется эрмитовой длиной1). Сохранение эрмитовой»
длины выражается равенством Парсеваля — Планшереля:
tiftk?
/-1 6=1
Заметим, что х — функция переменной, сопряженной с време-
временем, т. е. частоты /. Частота также изменяется дискретными*
приращениями А/:
Если ряд Xj вещественнозначный (как мы предполагаем), то
знание комплексных компонент xk означает, что известны 2п
вещественных величин (вещественной и мнимой частей каждой
&к)- Ясно, что имеется избыточность этих данных, выражаема»
соотношением
лп~к>
которое легко выводится.
С помощью обратного преобразования мы можем вернуться
от вектора х к начальному вектору
'•) Зрмитовой длиной называется величина ^ хх* = ^ j х \2, где х* —
величина, комплексно-сопряженная с числом х.

66 ' Глава III
Заметим, что это соотношение может быть использовано для
определения компонент х,- не только при /е [1, п], но и при всех
целых значениях /. Эта функция х периодична по п (в действи-
действительности по nht), так как
Это объясняет, почему любой сигнал x(t) может быть представ-
представлен в виде суммы'периодических функций,, как в формуле (8').
x(i)
A
i
j.
i
i
i
i
г
. гл/i
'V i
/ "'•••'
1
A
... i ••• •
О
Рис. III.2. Выборка значений, принимаемых функцией x(t) на конечном вре-
временном интервале. Измеренный интервал [0, ^макс] эквивалентен одному пе-
периоду функции, определенной при всех значениях / е (—<», +°°) и имеющей
перИОД /макс
Конечный интервал [0, ?макс] можно рассматривать просто1 как
один период функции, которая, если ее определить при всех /,
периодична по ^макс, как показано на рис. III. 2.
III. 2.3. Теорема Винера — Хинчина
Определим автокорреляционную функцию сигнала Xj как
п
Единица времени по-прежнему равна Д?, поэтому
Физически эта функция есть среднее произведения значений
сигнала в данный момент времени и в более поздний момент
времени mAt. Следовательно, зная tym> мы можем установить
наличие или отсутствие зависимости текущего значения сигнала
от его предыдущих значений, отсюда и название функции. Иначе

Преобразование Фурье 57
говоря, корреляционная функции служит мерой степени сход-
сходства сигнала с,самим собой в прошлом ').
Так как ряд х/ периодичен по п, автокорреляционная функ-
функция также обладает периодичностью:
Применяя обратное преобразование Фурье, получаем
/ = 1 ft,
п.
2
Используя свойство %*k' — x*n-k' и суммируя по индексам / и
мы устанавливаем, что
Это означает, что с точностью до коэффициента пропорциональ-
пропорциональности автокорреляционная функция просто совпадает ^преоб-
^преобразованием Фурье величины | х |2.
Выведем теперь обратное соотношение между \хц\2 и if>m~
Пусть Sh — функция, определяемая формулой
m=l
Подставляя в это определение вычисленное выражение для
получаем
п п
о г., « I Р ( 2nmk \ / 2ят1 \
Используя равенство
1 Г ^ • 2ятр \ . / . 2яотр \1
4) Если автокорреляционная функция заметно отлична от нуля, то это
означает, что сигнал остается относительно предсказуемым: знание сигнала
на достаточно большом интервале Бремени позволяет с достаточной уверен-
уверенностью вычислять его значение в более поздний момент времени путем экстра-
экстраполяции. С другой стороны, если iji,™ стремится к нулю, то временное само-
самоподобие сигнала исчезает и предсказание его эволюции становится невоз-
невозможным.

58 Глава III
преобразуем сумму по т в отрезок геометрической прогрессии
длиной в п членов. Суммируя прогрессию, приходим к формуле
п
„„„ Bnmk \ „пг. ( 2nml
cos \~~^~) C0S
где величина б/ге) равна 1, если / = 0* и 0 в противном случае.
Комбинируя этот результат с соотношением симметрии |in-;|2 =
= |х/|2, получаем,
Это и есть обратное соотношение, которое требовалось найти.
Полученное соотношение есть одна из форм теоремы Винера —
Хинчиня1), утверждающей, что функция |-?*]2 пропорциональна1
преобразованию-Фурье автокорреляционной функции ipm сиг-
сигнала. График величины [хк[2 как функции частоты / (f = kAf)
.называется спектром мощности.
Спектр мощности вещественной функции обладает свойством
которое следует из равенства xk = x"n_k. Оно выражает тот оче-
очевидный факт, что информация о фазе компонента ^теряется2),
когда мы рассматриваем \xk\2.
*) Эта теорема была доказана Н. Винером после работы Дж. Тейлора,
который аналогичным образом измерял величину; аналогичную |i*|2, по тур-
турбулентному сигналу (изменению сопротивления анемометра .с нагреваемой
проволокой).
2) Заметим попутно, что потеря информации о фазе наблюдается в физи-
физике довольно часто, например при дифракции электронов и при столкновении
элементарных частиц высокой энергии. Информация, содержавшаяся в фазе,
связана со средней обратимостью сигнала. В таких функциях, как \хц\г я
¦фт, не изменяющихся при обращении порядка индексов переменной х, (они
имеют одни и те же значения, когда временной ряд рассматривается в по-
порядке 1, 2, ..., геи когда он рассматривается в обратном порядке п, ...
..., 2, 1), эта информация не может сохраняться, С другой стороны, это
неверно для корреляционной функции *„-, определяемой соотношением
„2 >
Xj + r;ixi)
и изменяющей знак при рассмотрении временного ряда в обратном порядке.

Преобразование Фурье ' 59
III. 2.4. Спектр мощности
Рассмотрим более подробно характеристики спектра мощ-<
ности и выясним, какая информация о сигнале x(t) содержится
в нем. Начнем с временного ряда, состоящего; из п эквидистант-
1л ip
Af-1/nui
'макс
-I/At
Рис. III. 3. Сигнал и его спектр мощности, а —график сигнала, измеряемого
выборочно через равные интервалы времени Д?; б — дискретный спектр мощ-
мощности сигнала а. Обратите внимание на то, что спектр \хк\2 симметричен от-
относительно вертикальной оси с абсциссой A/2)fикс-.
ных точек, разделенных интервалом At (рис. III.3,а). Приме-
Применяя соотношение (8), мы вычисляем сначала xk, затем \хк\2,
что порождает новую функцию на п дискретных точках с аб-
абсциссой (k/n)At (k = 1, ..., п). Абсцисса имеет размерность

вО Глава III
обратного времени, т. е. частоты, отчего и происходит название
«спектр», закрепившееся за графиком \хк\2. Интерпретация оси
, ординат зависит от природы измеряемого сигнала.
Традиционное название «спектр мощности» установилось по
аналогии с случаем, когда ордината означает мощность, т. е.
количество энергии в единицу времени. Рассмотрим сигнал
x(t), возникающий при приеме волн (электромагнитных, звуко-
звуковых и т. д.) антенной. Если детектор линеен и не вносит иска-
искажений в. рассматриваемой полосе частот, то измеряемая им
величина пропорциональна изменениям электрического поля или
давления вблизи антенны. Из теории волн известно, что мощ-
мощность, переносимая волной, пропорциональна квадрату ампли-
амплитуд волны (так же, как энергия гармонического осциллятора
пропорциональна квадрату амплитуды его колебаний), усред-
усредненной по времени. Формула Парсеваля — Планшереля позво-
позволяет» заменить среднее по времени средним по частоте. Это оп-
оправдывает название «спектр мощности», которое мы для удоб-
удобства сохраняем во всех случаях1).
Спектр мощности на рис. III. 3, б соответствует сигналу на
рис. III. 3, а. Величина шага f=l/(nAt) по оси абсцисс соот-
соответствует спектральному разрешению. Чтобы повысить разре-
разрешение, следует увеличить произведение nAt. Наибольшая ча-
частота спектра равна /Иакс = I/At. Чтобы расширить исследуе-
исследуемый диапазон частот, следует уменьшить At. В силу соотно-
соотношения
спектр всегда симметричен 2) относительно вертикальной пря-
прямой f = ('/2^макс. Таким образом, эффективно полезный диа-
диапазон частот (содержащий неизбыточную информацию) про-
простирается только от 0 до l/BAt).
Для полной строгости заметим, что спектр состоит из после-
последовательности «шагов» шириной Af (рис. III. 4).* На практике
часто просто проводят отрезки вертикальных линий высотой
|i*|2 через точки с абсциссами f — kAf. Но обычно соседние
точки (kAf, \xk\ 2) соединяют отрезками прямых (рис. III. 3,6).
Нередко амплитуда \?k\2 изменяется на несколько порядков, и
в таких случаях удобно откладывать ординаты в логарифми-
') В действительности соотношение между мощностью (в смысле энер-
энергии, принимаемой в единицу времени) и амплитудой спектра выходного сиг-
сигнала усилителей или вообще приемно-регистрирующей системы может быть
очень сложным. Это замечание еще более верно, если детекторы производят
нелинейное преобразование сигнала.
-} Напомним, что это свойство является следствием предположения о ве-
щественнозначности ряда X;.

Рис. III. 4. Периодические функ-
функции и их спектры Фурье, а —чи-
—чисто синусоидальная функция; б~
периодическая функция, содержа-
содержащая различные гармоники. Пока-
Показаны только первые четыре гармо-
гармоники. (Здесь и далее спектры мощ-
мощности и спектры Фурье, если нет
специальных указаний, приводятся
в логарифмическом масштабе.)
ыг
vf гл iix

62 Глава II! ,
ческом масштабе. За единицу измерения вдоль оси ординат вы-
выбирают децибел, равный десятикратному десятичному лога-
логарифму. Разность в а децибел соответствует отношению ампли-
амплитуд 10°-1а.
III.3. РАЗЛИЧНЫЕ ТИПЫ СПЕКТРОВ ФУРЬЕ
III. 3.1. Периодический сигнал
Вид спектра мощности, как нетрудно понять, зависит от
того, как именно сигнал x[t) изменяется со временем. Спектр
Фурье интересен тем, что позволяет выявить такие свойства
эволюции во времени, которые в противном случае остались бы
скрытыми.
Рассмотрим сначала простой случай, когда л; (^ — периоди-
периодический сигнал с периодом Т, т. е.
Такой сигнал порождает генератор Ван дер Поля в режиме
предельного цикла.
В предельном случае период в точности равен продолжи-
продолжительности измерения
I — чиакс
Тогда, как следует из формулы (8), компоненты Фурье сосре-
сосредоточены на частотах
_2_ _3_ п_
Т ' Т ' Т
В простейшем случае, когда x(t)—круговая тригонометриче-
тригонометрическая функция (синус или косинус), спектр состоит только из
одной ненулевой компоненты с абсциссой 1/7 (или k = \,
рис. III,4,а). Для сигнала другой формы,, например в случае
релаксационных колебаний, амплитуда гармоник с частотой
2/7", 3/Г, ... уже не равна нулю. Именно поэтому'наличие гар-
гармоник в спектре указывает на несинусоидальный характер сиг-
сигнала (рис. 111.4,6).
Изложенные выше соображения легко могут быть обобщены
на случай, когда продолжительность измерений tM3KC есть целое
кратное периода сигнала Т:
/макс = рТ, р — положительное целое число > 1.
В этом случае ненулевые компоненты спектра по-прежнему со-
сосредоточены на частотах \/Т, 2/Т, ... , но разрешение по ча-

Преобразование Фурье 63
стоте в р раз лучше. Следовательно, все компоненты |яй|2 с ин-
индексом k, отличным от целого кратного р\ равны нулю.
В дейстрительности описанная нами ситуация носит весьма
абстрактный характер, так как на практике период сигнала
либо неизвестен, либо известен неточно. Это означает, что отно-
отношение кикс/Т, вообще говоря, не является целым числом,. Как
это сказывается на форме спектра? Чтобы ответить на этот
вопрос, вычислим преобразование Фурье в простом случае кру-
круговой тригонометрической функции
/. 2nj\t \
/==exp^-y— J,
/=1
Полагая фк = At/T — k/n, получаем
1 „..„^^(''Н)-1
exp ('2Я0А) - 1
Принимая дополнительную гипотезу больших п (и, следователь-
следовательно, малых пфк), получаем асимптотически
(ш^)
sin
Следовательно, |#&|2 ведет себя, как функция sin2 z/z2, график
которой вы видите на рис. III. 5. Эта функция имеет максималь-
максимальную амплитуду, равную единице при 2 = 0, и серию вторичных
максимумов в точках ±(/+1/2)я (/ — положительное целое
число), амплитуды которых ^убывают как 1 /г2. Таким образом,
\xk\2 достигает максимума при &, равном ko — ближайшему
к n&t/T целому числу; дискретная переменная фк в этой точке
близка нулю. Кроме того, так как целые значения k, близкие ko,
соответствуют боковым дугам функции sin2 z/z2, амплитуда
\xk\2 при k — ko±l не равна нулю, хотя и быстро убывает
с увеличением /. Окончательный результат состоит в том, что
помимо одного пика, возникающего в том случае, когда между
периодом сигнала и продолжительностью. измерений имеется
резонанс, существуют также вторичные пики, называемые

64
Глава III
побочными, которые расположены симметрично относительно ча-
частоты 1/7. Ширина линии — порядка нескольких единиц часто-
частоты Af и максимальна, когда отношение пМ/Т полуцелое. На
рис. III. 6 показано, как эта ситуация отличается от резонанса.
s;nz\2
'k\zl
-Z7C ~Л О П.
Рис. III. 5. График функции sin2 г/г2.
hist2
х—х—* f
О о- О *¦
Рис. III. 6. Форма одной спектральной компоненты при двух различных усло-
условиях получения выборочных значений: сплошная линия (кружки) удовлетво-
удовлетворяет условию резонанса: nAt/T — целое число; штриховая линия (крестики)
¦ удовлетворяет другому условию: пЫ/Т —.полуцелое число.
Резюмируя, можно сказать, что спектр периодического сиг-
сигнала с периодом Т состоит из пика на частоте 1/7, побочных
пиков и, возможно, несколько других пиков (и их побочных пи-
пиков)— гармоник основной частоты.

Преобразование Фурье 65
III. 3.2. Квазипериодический сигнал
Функция у, зависящая от г независимых переменных
ti, U tr, называется периодической с периодом 2л по каж-
каждому из своих аргументов, если значение ее не изменяется при
увеличении любой из своих переменных на 2я:
y(tlt t2 tj, ..., tr) — y(tu h t] + 2n, ..., tr), j — 1 r.
Такая функция называется квазипериодической по времени,
если все ее г переменных пропорциональны времени /:
tl = ajt, / = 1, ..., г.
i
Квазипериодическая функция имеет г основных частот
/S i=l г'
и, следовательно, г периодов 7/ = 1/// = 2я/ю/.
Прежде чем мы перейдем к форме спектра Фурье такой
функции, напомним, что приведенное выше ее формальное опре-
определение относится к любому явлению кратной периодичности.
Приведем один пример этого явления из многих: астрономиче-
астрономическое положение точки на поверхности Земли описывается квази-
квазипериодическим законом, так как обусловлено вращением Земли
вокруг своей оси Gi = 24 ч), вращением Земли вокруг Солнца
(Т2 « 365,242 дней) и, наконец, прецессией земной оси G3 «¦
« 25 800 лет; период Г3 иногда называют платоническим го-
годом) '). Мы уже упоминали о том, что фазовая траектория, со-
соответствующая квазипериодической функции, определена на
торе2) размерности г, который принято обозначать символом Тг.
Как нетрудно догадаться, спектр Фурье функции, квазипе-
квазипериодической по времени, в общем случае имеет сравнительно
сложный вид. Однако существует одно исключение — когда ква-
квазипериодический сигнал лг(со1^, ..., сйг^) есть сумма периодиче-
периодических функций:
г
, ..., a>rt) = Yu xt (a>tt).
?1
!) Очень малыми возмущениями этих основных движений мы пренебре-
пренебрегаем. Если учесть различие в порядке величин временных масштабов движе-
движений. то_взаимодействие между ними пренебрежимо мало.
2) В простейшем случае г = 2 можно показать при совершенно общих
условиях, что траектория, описываемая параметрически тремя функциями
времени x(ait, a2t), (d/dt)x(e>it, wrf) и (d2ldt2)x(a>it, <a20, действительно
лежит на торе в R3, т.е. на торе в обычном смысле.
5 П. Берже и др.

66 Глава III
В этом случае, используя линейность соотношения (8), можно
показать, что спектр мощности есть сумма г спектров каждой
из функций Xi((dit). Следовательно, он состоит из множества пи-
пиков на частотах /ь /2, ..., fr и их гармониках:
mJu m2f2 mrfr
(mi, m2, ..., mr — положительные целые числа). Но, вообще
говоря, ниоткуда не следует, что квазипериодический сигнал
должен быть суммой г периодических слагаемых. Если квазипе-
квазипериодическая функция содержит член типа произведения круго-
круговых тригонометрических функций, например sin (ant) sin (©//), то
ее спектр Фурье содержит основные частоты \f{ — f,-\ и \fi-\-fj\,
а также их гармоники, поскольку
sin (ш,0 sin (И/0 = 1 cos (| ft - ft 12я/) - 4 cos (| /, + f, \ 2nt).
Обобщая этот результат, мы можем утверждать, что спектр
Фурье квазипериодической функции x(t), нелинейно зависящей
от периодических функций переменных ant, содержит компо-
компоненты со всеми частотами вида
I /я,/, + m2f2 + • ¦ • + mrfr |,
где mi — произвольные целые числа.
В дальнейшем мы ограничимся пока двумя периодами (г=2)
и оставим в стороне то обстоятельство, что разрешение Af
спектра мощности конечно. Каждая ненулевая компонента
спектра сигнала x(ti>it,a2t) есть пик с абсциссой |mifi + «2/21>
который мы обозначим для краткости через (т\,т2). Отноше-
Отношение fi//2 может быть либо рациональным, либо иррациональным
числом. В последнем случае из теории чисел известно, что сум-
суммы вида \m\f\-\- т2\2\ образуют на положительной веществен-
вещественной полуоси всюду плотное множество. Иначе говоря, любое ве-
вещественное положительное число сколь угодно близко к одной
из таких сумм. Следовательно, спектр сигнала с двумя перио-
периодами: также всюду плотен. Но это не означает, что его можно
представить с помощью непрерывной функции. Действительно,
два пика, близких друг к другу на оси частот, априори отнюдь
не обязательно должны иметь близкие амплитуды. Следова-
Следовательно, в большинстве случаев мы будем наблюдать весьма огра-
ограниченное число частот, соответствующих линиям с большой
амплитудой, поскольку линии более высоких порядков (т. е. соот-
соответствующие значениям гп\ и т2, превышающим несколько еди-
единиц) имеют слишком малые амплитуды, чтобы их можно было

Преобразование Фурье
67
обнаружить1). На практике квазипериодический спектр иденти-
идентифицируют, пытаясь найти две основные частоты /i и /2, которые
позволили бы представить частоты линий с большой амплитудой
x|t)
, ?
@
®
©
,1
о
©
Рис. III. 7. Квазипериодическая функция с двумя частотами /i и /2 (отноше-
(отношение fi/fi иррационально), а — сигнал; б — его спектр Фурье, содержащий по-
помимо основных частот /4 и }г главные пики с комбинационными частотами
/р = niifi + Ш2/2:
а —> /г — f\, в -> 5/1 — ^г, j -> 5/i + /2,
Ъ -> 3f ] — /2» & ~* 3/1 -|- /2»
с -* /i + /2. А -> 5fь
d->3f,, i-^lfx-h.
в виде простых комбинаций \mifi + -""г/г! с небольшими mi и /тгг:
О, ±1,±2, ... (рис. III. 7).
амплитуды пиков высокого порядка убывают как ехр(—ai|mi| —
ai и аз — положительные числа. При больших \mi] и |И2| эти амплитуды
становятся пренебрежимо малыми. Обнаружить их практически невозможно,
если индексы nit и тг по абсолютной величине существенно превышают а^1
и а
-1
5*

68
Глава III
Если отношение U/h рационально, то спектр Фурье не всюду
плотен. Это означает, что он заведомо не соответствует непре-
непрерывной функции. Так как
fi/f2 = nl/n2 {щ, п2 — целые числа),
квазипериодический сигнал в этом случае в действительности яв-
x(t)
а.
ыг
©
©
©
®
ф
2Л.
f
Рис. III. 8. Квазипериодическая функция (отношение filfz рационально),
а — сигнал; б — соответствующий спектр Фурье. Сигнал почти совпадает с
функцией, изображенной на рис. III. 7, но частота ft изменена так, что
filfz = 2/3. Обратите внимание на то, что при этих условиях все пики соот-
соответствуют гармоникам с частотой, кратной частоте / = /2—/i = A/3)?г:
a-i.ft-fu d->6f, A-MOf,
c->5f, g^9f,
ляется периодическим с периодом Т =
но, по определению получаем
a2i) = х (со,/ + 2кпь a
х (co.f, co2f) = х
= п2Т2. Действитель-
Действитель2лп2),
+ f) ) .

Преобразование Фурье 69
Говорят, что происходит синхронизация частот /? и /2 (или затя-
затягивание частоты). Все линии спектра Фурье являются гармони-
гармониками низшей частоты
f — -L =_ 1l = JL
/0 Г re, /i2 "
Эта ситуация изображена на рис. III. 8. Соседние линии спектра
всегда разделены одинаковым расстоянием \/Т.
III. 3.3. Апериодический сигнал
Если сигнал x(t) не является ни периодическим, ни квазипе-
квазипериодическим, то его называют апериодическим (или иногда не-
непериодическим) . Позднее в этой книге нам встретятся несколько
примеров такой ситуации, и мы увидим, что спектр Фурье апе-
апериодического сигнала непрерывен1). Реальная трудность со-
состоит в том, что спектр Фурье, кажущийся непрерывным, не мо-
может быть автоматически приписан апериодическому сигналу,
так как такой спектр может соответствовать квазипериодиче-
квазипериодическому сигналу с очень большим (в пределе — бесконечным) чис-
числом частот.
Если предположить, что сигнал действительно апериодиче-
апериодический, то все равно нам придется решать (по чисто методическим
соображениям), мало ли число степеней свободы (например,
меньше, чем 10) или, наоборот, очень велико. В первом случае
перед нами открывается возможность дать полностью детерми-
детерминированное описание системы. В отличие от этого во втором
случае при современном состоянии знаний мы можем развить
только вероятностный подход. Он состоит в том, что вводят по-
понятие случайности, не ставя под сомнение (скрытую) детерми-
детерминированность явлений. Хотя второй случай выходит за рамки
книги, все же уместно остановиться несколько подробнее на том,
что мы имеем в виду, когда проводим различие между «детер-
«детерминированным» и «случайным».
Предельный случай случайного сигнала известен под назва-
названием белого шума. Этот термин вызывает ассоциации с шумом.
*) Спектр апериодического сигнала стремится к непрерывной функции
только в среднем. Действительно, если вычислить дискретный спектр сигнала
продолжительностью /маКс с помощью описанного выше метода выборочных
значений, то окажется, что амплитуды соседних \хк\г очень сильно изме-
изменяются независимо от того, сколь большим мы выбрали iM»Kc- Разность ме-
между ]хк\г и |x*±i|2 обычно сравнима с самими этими величинами. Следова-
Следовательно, чтобы получить непрерывный спектр (или по крайней мере разумное
приближение к нему) исходя из последовательности \xk\%, необходимо либо
произвести усреднение по многим спектрам, взяв каждый из них во времен-
временном окне шириной {макс/А/ (Л —большое число), либо, что эквивалентно, ус-
усреднить \хь\г локально по некоторому числу последовательных значений k.

Глава III
(звуком, лишенным какой бы то ни было гармоничности) и со
светом без окраски. Таким образом, белый шум можно видеть
как белый свет или слышать, например, как шум водопада. Бе-
Белый шум порождает множество независимых источников: атомы
раскаленной нити в лампе, испускающей белый свет, или брызги
водопада, низвергающегося на скалистое основание.
Порождаемый белым шумом сигнал x(t) в каждый момент
времени можно считать «новым»') по крайней мере в первом
приближении. Покажем, что соответствующий спектр мощности
«плоский», т. е. амплитуда не зависит от частоты, так что его
наиболее существенная характеристика в том, что он лишен ка-
какой бы то ни было гармоничности.
Пусть x(t)—сигнал с нулевым средним и дисперсией х2. От-
Отсутствие корреляции между значениями сигнала в различные
моменты времени выражается условием 2)
где 8т — дельта-функция Кронекера (80=l, 6m = 0 при тфО).
Из теоремы Винера — Хинчина получаем
Это показывает, что средняя амплитуда спектра мощности сиг-
сигнала не зависит от k. Иначе говоря, средняя амплитуда белого
шума не зависит от частоты.
Описанная выше ситуация весьма широко встречается на
практике: высокочастотная компонента многих природных шу-
шумов есть такой белый шум. Действительно, шум, обусловленный
молекулярным возбуждением, включает в себя действие почти
бесконечно многих независимых агентов: молекул, электронов
') Чтобы быть вполне строгими, заметим следующее. Шум является бе-
белым, если отдельные источники не только независимы, но и порождают сиг-
сигналы, представляющие собой импульсы бесконечно малой продолжительности.
Если же спектр каждого такого элементарного сигнала наделен какой-нибудь
структурой, то свет или звук становится окрашенным.
2) В приводимом выражении под средними понимаются средние по ан-
ансамблю. Мы неявно рассматриваем автокорреляционые функции ¦$„ и фурье-
образы |?*|2, получаемые из ряда, содержащего п значений х — индивидуаль-
индивидуальной реализации этих величин. Затем мы берем их среднее арифметическое
{ ) . Заметим, что в данной реализации среднеквадратичное расстояние ме-
между величиной \?k\2 и ее средним значением есть величина такого же поряд-
порядка, как и среднее. Как мы уже упоминали, это объясняет, почему спектры
турбулентных сигналов, чтобы получить непрерывные функции частот, сле-
следует либо сглажвать, либо усреднять по ансамблю реализаций.

Преобразование Фурье 7t
проводимости, упругих колебаний атомов кристаллической ре-
решетки и т. д.
Теория термодинамического шума принадлежит к числу наи-
наиболее выдающихся достижений физики первой половины XX в.
В качестве конкретного примера рассмотрим классический при-
пример шума Найквиста, названного так в честь физика, предло-
предложившего объяснение этого явления. Пусть RC-цепъ (R — сопро-
сопротивление, С — емкость) находится в тепловом равновесии (в от-
отсутствие приложенного извне напряжения}. Чувствительный
вольтметр измеряет флуктуации напряжения V(t) на конденса-
конденсаторе или резисторе. Энергия, запасенная в конденсаторе ем-
емкостью С, выраженная через напряжение на его обкладках, ра-
равна CV2/2. Эта энергия обусловлена тепловыми флуктуациями,
и по теореме Эренфеста о равнораспределении энергии ее сред-
среднее значение равно kT/2, где k — постоянная Больцмана (k =
= Rj/N, Rj — джоулевская постоянная, N — число Авогадро),
Т — абсолютная температура системы. Таким образом, имеем
_ кТ
где среднее берется либо по времени, либо по термодинамиче-
термодинамическому ансамблю. Но эта величина есть среднее мгновенных зна-
значений, а мы хотели бы знать частотную структуру такого шума.
Определить ее можно следующим образом. Если V(t) — напря-
напряжение на конденсаторе в момент времени t, то напряжение в по-
последующий момент времени t + т обусловлено двумя факторами.
С одной стороны, конденсатор разряжается через резистор R,
создавая напряжение V(t)e~T-/RC, где {RC) — постоянная времени
цепи. С другой стороны, на обкладках конденсатора тепловые
флуктуации создают новый электрический заряд. Эти флуктуа-
флуктуации не коррелированы с начальным зарядом конденсатора и
тем самым с V(t). Так как RC-цепь линейна, мы получаем
(V (t) V(t + т)> = (V № ехр (-1 т \/RC),
где в случае отрицательного значения т следует взять его абсо-
абсолютную величину |т]. Спектр шума определяется теоремой Ви-
Винера — Хинчина для непрерывных переменных
оо
S (со) = ± \ dx (V (t) V (t + т)> cos (сот),
«irlw ™!?
~ v-/ я A + a'R'C2) '

72
Глава III
В этом формализме соотношение Парсеваля — Планшереля
имеет вид
Эта формула дает спектральное распределение флуктуации на-
напряжения на емкости в #С-цепи. В пределе нулевой емкости
а
о
Рис. III. 9. Апериодическая функция, а — сигнал; б — его спектр Фурье.
Спектр непрерывный в отличие от линенчатых спектров рис. Ш.7 и Ш, 8,
достаточно положить С = 0 в выражении для 5(о>), и мы полу-
получаем классическое выражение для шума Наиквиста:
Следовательно, тепловой шум на резисторе есть белый шум, так
как 5 (а) не зависит от со. Амплитуда такого шума пропорцио-
пропорциональна абсолютной температуре и сопротивлению. Заметим, что

Преобразование Фурье 73
в рассматриваемом пределе (С = 0) среднее величины V2 рас-
расходится, так как (V2) = kT/C. На практике V2 не обращается
в бесконечность, так как при очень высоких частотах в цепи
всегда имеется паразитная емкость, и поэтому С никогда не бы-
бывает в точности равной нулю.
Шум, производимый простым резистором, есть белый шум,
спектр мощности которого не зависит от частоты. Наоборот,
тепловые флуктуации напряжения ^С-цепи образуют окрашен-
окрашенный шум: спектр его также является непрерывной функцией
частоты, но отличен от константы.
Завершив это отступление о случайных сигналах, возвра-
возвратимся к нашей главной цели, т. е. к исследованию сигналов, воз-
возникающих в детерминистской динамике. Как мы уже отмечали,
апериодический сигнал имеет спектр мощности, который ка-
кажется непрерывным, как в примере на рис. III. 9. Следователь-
Следовательно, выбранный нами метод анализа не позволяет провести раз-
различие между апериодическим и случайным сигналами. Это огра-
ограничивает применимость преобразования Фурье и вынуждает нас
обратиться к другим методам, главным образом к методу сече-
сечений Пуанкаре.
III. 4. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (БПФ)
Мы видели, что существует тесная взаимосвязь между перио-
периодическим, квазипериодическим или апериодическим характером
сигнала x{t) и формой его спектра мощности. Чтобы определить
характер динамического режима, остается явно вычислить |**|2.
Теоретически это нетрудно сделать, используя формулу (8). Но
на практике объем вычислений становится устрашающим, как
только я принимает достаточно большие значения. Тем не менее
удобно выбирать п большим, а А/ малым, чтобы воспроизвести
сигнал x(t) как можно точнее. При п=103 (т. е. еще при сравни-
сравнительно малом значении п) нам пришлось бы вычислить
1000 сумм, каждая из которых содержит 1000 членов! Вообще
вычисление п компонент спектра требует выполнения числа опе-
операций (сложения и умножения) порядка п2. Столь быстрое воз-
возрастание числа операций долгое время было ограничивающим
фактором, сдерживавшим применение преобразования Фурье,
Даже появление первых компьютеров не слишком исправило
ситуацию.
Но в тех случаях, когда п есть степень двойки, алгоритм, из-
известный под названием БПФ1), позволяет вычислять спектр за
') БПФ означает быстрое преобразование Фурье. Этот алгоритм был
предложен в 1965 г. Кули и >Тьюки. Впоследствии авторы обнаружили, что
тот же алгоритм был разработан еще в 1942 г. другими исследователями,
работа которых в то время не привлекла к себе должного внимания.

74 Глава III
существенно меньшее число операций порядка п log2 п. При я =
= 210 = 1024 спектр вычисляется в 100 раз быстрее, а при п_=
=r= i0iS — в 7000 раз быстрее, чем традиционным методом. Это
приводит к ощутимой разнице в стоимости вычислений. Именно
благодаря столь фантастической экономии времени анализ
Фурье стал стандартной процедурой в научно-исследовательских
лабораториях и помимо исследования динамических систем по-
позволил достичь большого прогресса во многих других обла-
областях1).
Упомянем среди прочих областей различные виды спектро-
спектроскопии: инфракрасную, комбинационного рассеяния, рентгенов-
рентгеновскую, на основе магнитного резонанса, фотонных биений и т. д.
На рынке появились цифровые анализаторы Фурье, которые,
комбинируя БПФ с другими трюками, позволяют получать
спектр мощности сигнала, содержащего тысячи точек, всего
лишь за несколько секунд.
') Методы обработки сигналов (главным образом фильтрования и по-
повышения отношения сигнал/шум) претерпели существенные технические усо-
усовершенствования, в которых немалую роль сыграло БПФ.

ГЛАВА IV
СЕЧЕНИЯ ПУАНКАРЕ
IV. 1. ОПРЕДЕЛЕНИЕ ПОТОКА
Примем теперь весьма общую точку зрения и начнем с того,
что, как было показано в трех предыдущих главах, эволюция
многочисленных систем может быть описана системой п обык-
обыкновенных дифференциальных уравнений
-§r\{t) = F(\, t), (9)
где X — вектор из Rn (фазового пространства), a F — векторное
поле над этим пространством. Как мы уже знаем, именно та-
такой вид1) имеют законы, управляющие поведением различных
осцилляторов.
Система дифференциальных уравнений типа системы (9) на-
называется потоком в R". Если F не зависит явно от времени, а
зависит только от X:
F = F(X(t)),
то поток называется автономным. Уравнение E) может служить
типичным примером автономного потока. С другой стороны, если
F зависит явно от времени, то поток называется неавтономным.
Примером такого потока может служить уравнение Матье G).
Найти аналитическое выражение для решений уравнений (9)
удается лишь в отдельных частных случаях, когда поток инте-
интегрируем. В большинстве случаев поток неинтегрируем, и нам
приходится исследовать каждое решение, рассматривая соот-
соответствующую ему траекторию в фазовом пространстве. По-
Поскольку часто и это бывает очень трудно, мы упростим задачи,
используя для этого один метод, развитый Анри Пуанкаре.
*) Это согласуется с тем, что с помощью подходящей замены переменных
мы всегда можем преобразовать одно дифференциальное уравнение /i-го по-
порядка в систему п дифференциальных уравнений первого порядка. Этим
свойством мы уже воспользовались при построении фазового портрета для
генератора Ван дер Поля.

76 Глава IV
IV.2. СЕЧЕНИЯ ПУАНКАРЕ
IV. 2.1. Построение и свойства
Теоретически не существует никаких ограничений на размер-
размерность п фазового пространства. Однако в этой главе по сообра-
соображениям дизактического и практического порядка мы рассмотрим
только трехмерный случай'). Кроме того, нас будет инте-
интересовать только асимптотическое поведение при t-+oo. Иссле-
Исследование переходных состояний, обладающих значительно мень-
меньшей общностью, мы оставим в стороне.
Рис. IV. 1. Схематическое изображение сечения Пуанкаре. Фазовая траекто-
траектория Г последовательно пересекает плоскость S (с д'-3 < 0) в точках Л„ Яь
Рг Эти точки принадлежат сечению Пуанкаре траектории Г плоскостью S.
Вместо прямого изучения решения системы уравнений (9)
в R3 может оказаться полезным рассмотреть точки пересечения
траектории с плоскостью. Схематически эта процедура изобра-
изображена на рис. IV. 1. Для иллюстративных целей мы выбрали пло-
плоскость 5, заданную уравнением х% = const, и отметили точки
пересечения, соответствующие заданному направлению эволюции
(i3<0). Высота плоскости выбрана с jaKHM расчетом, что
траектория Г пересекает S в точках Ро, Р\, Р2 Динамика
в этих точках такова, что х3 непрерывно переходит с одкой сто-
стороны плоскости S на другую. В действительности 5 может быть
любой плоскостью, но подходящий выбор ее приводит к сече-
сечениям, более легко поддающимся анализу. Итак, исходя из на-
') В этой главе либо п. = 3, либо мы рассматриваем проекцию фазовых
траекторий на трехмерное подпространство.

Сечения Пуанкаре 77
чальной точки, мы получаем множество точек, образующих се-
сечение Пуанкаре, т. е. некоторый граф в двух измерениях.
Преобразование, переводящее точку в следующую, является
непрерывным отображением плоскости S на себя, называемым
отображением Пуанкаре:
Pk+i = T(Pk) = Т (Т (Р4_,)) = Г2(Р*_.) =*.... A0)
Так как решение системы (9) единственно, точка Ро однозначно
определяет точку Pi, которая в свою очередь определяет Р2
и т. д. Если, наоборот, Pi однозначно определяет точку Ро при
изменении знака t в уравнениях (9), то Т — обратимое отобра-
отображение плоскости S на себя.
Заметим, что сечение Пуанкаре заменяет эволюцию с непре-
непрерывным временем, описываемую уравнениями (9), отображе-
отображением A0) с дискретным временем. Если не считать особых (но
тем не менее интересных) случаев, то интервал времени между
псслс^оезт^лын/мн точками непостоянен
Наконец, подчеркнем, что по построению сечение Пуанкаре
и отображение Пуанкаре обладают топологическими свойствами
того же рода, что и породивший их поток. Например, если по-
поток (9) диссипативен и объемы в фазовом пространстве сжи-
сжимаются, то отображение Т сокращает площади на плоскости S.
Наоборот, отображение Т сохраняет площади, если поток (9)
консервативен, или гамильтонов. Аналогично если у потока име-
имеется аттрактор, то его структурные характеристики могут быть
найдены в сечении Пуанкаре.
!V. 2.2. Практический интерес
Метод сечений Пуанкаре упрощает исследование непрерыв-
непрерывных потоков по трем причинам. Во-первых, мы переходим от по-
потока в R3 к отображению на плоскости, понижая тем самым
число координат на единицу1). Во-вторых, время дискретизуется
и дифференциальные уравнения заменяются разностными урав-
уравнениями, определяющими отображение Пуанкаре Р-*-Т(Р).
Эти алгебраические уравнения значительно легче поддаются ре-
решению. Наконец, в-третьих, резко сокращается число данных,
подлежащих обработке, так как почти всеми точками на траек-
траектории можно пренебречь. Покажем теперь, какие преимущества
проистекают из этих упрощений.
Первое преимущество — на уровне математического модели-
моделирования. Итерация отображения
Xi(k-\-l) = T(xt(k)), / = 1,2,
') В более общем случае непрерыннътм поток r> R" сгодится к дискрет-
дискретному отображению R"-' на себя.

78
Глава IV
осуществляется несравненно легче, чем интегрирование такого
потока, как (9), если говорить о времени вычислений и необхо-
необходимой производительности ЭВМ1). Следовательно, итерирован-
итерированные отображения позволяют апробировать адекватность модели
ценой меньших затрат. В гл. VI мы познакомимся с примером
того, как метод сечений Пуанкаре позволяет открыть фундамен-
фундаментальные свойства. Хотя априори область сечения Пуанкаре трех-
трехмерного потока есть поверхность, задача может быть нередко
сведена далее к (необратимому) отображению прямой IR1 на
себя. ,
Рис. IV. 2. Сечение Пуанкаре для квазипериодического режима. Показаны
часть траектории в трехмерном пространстве, спроектированной на плоскость
(*ь х2), и (штриховой линией) соответствующее сечение Пуанкаре.
Метод Пуанкаре имеет и другие преимущества помимо упро-
упрощения математического моделирования. В трехмерном про-
пространстве мы можем изображать траектории только либо в пер-
перспективе, либо в проекции. И в том и в другом случае трудно
получить представление об их расположении в пространстве.
Сечение Пуанкаре траекторий быстро дает хорошую картину.
Подтверждением этому может служить рис. IV. 2. На нем изо-
изображена проекция трехмерной траектории на плоскость. Много-
оборотная кривая с самопересечениями не много говорит о ди-
динамике системы (за исключением того, что динамика сложная).
Но стоит лишь провести сечение Пуанкаре, как тотчас же ста-
становится ясно, что эта траектория, по-видимому, лежит на
торе Г2, который, как мы знаем, является аттрактором режима
') В случае отображения плоскости на себя вычисления могут быть прак-
практически выполнены с помощью карманного калькулятора. Именно так Энон
открыл аттрактор, носящий ныне его имя, определяемый итерацией отобра-
отображения {х, {/)->- (рг/, 1— ах2 + у). где а = 1,4; р = 0,3 (см. гл. VI).

Сечения Пуанкаре
79
с двумя периодами. Сечение Пуанкаре может характеризовать
трехмерный поток и по-другому (хотя и в том же духе). Точки
сечения Пуанкаре могут быть расположены более или менее
сложным образом на кривой или распределены по поверхности,
как на рис. IV. 3. Во втором случае мы заключаем с полной уве-
уверенностью, что поток апериодический. Если же сечение Пуан-
а
Рис. IV. 3, Примеры сечений Пуанкаре, а — квазипериодический режим; б —
хаотический режим.
каре выглядит как кривая, то мы имеем дело с динамическим
режимом, который либо квазипериодический, либо апериодиче-
апериодический с сильным сжатием. Действительно, если сокращение пло-
площадей в фазовом пространстве происходит очень быстро, то про-
протяженность в «боковом» направлении (т. е. в направлении сжа-
сжатия) сечения Пуанкаре становится пренебрежимо малой1). Для
того чтобы определить истинный характер потока, необходим
более подробный анализ.
IV. 3. РАЗЛИЧНЫЕ ТИПЫ СЕЧЕНИЙ ПУАНКАРЕ
IV. 3.1. Периодическое решение
Следуя процедуре, изложенной в разд. III. 3, исследуем со-
соответствие между видом сечения Пуанкаре аттрактора и дина-
динамическими свойствами решения. Если решение периодическое,
то, как мы уже упоминали, фазовая траектория представляет
') В качестве примера см. поток Лоренца в приложении Г.

80
Глава IV
собой замкнутую орбиту — предельный цикл. Соответствующее
сечение Пуанкаре устроено очень просто: это либо одна точ-
точка Ро (рис. IV. 4), либо несколько точек, если предельный цикл
очень извилист. Точка /V является неподвижной точкой отобра-
отображения 7, так как
Это свойство позволяет сделать еще один шаг и исследовать
устойчивости периодического решения. Поскольку этот вопрос
Рис. IV. 4. Сечение Пуанкаре предельно-
предельного цикла. В этом очень простом случае
сечение Пуанкаре представляет собой
одну точку Ро.
важен для последующего, рассмотрим проблему устойчивости
несколько подробнее.
Итак, нас интересует устойчивость замкнутой траектории от-
относительно бесконечно малых возмущений. В этом случае до-
достаточен линейный анализ устойчивости, ограниченный членами
первого порядка по возмущению. Отображение Пуанкаре (в
первом порядке теории возмущений) описывается матрицей М,
определенной в окрестности точки Ро как
м =
. * = 1. 2.
Эта матрица, называемая матрицей Флоке, обладает тем свой-
свойством, что после одной петли (одного периода) образ точки
Ро+б, выбранной очень близко к точке Ро, находится на рас-
расстоянии ')
Устойчивость траектории определяется собственными значения-
значениями матрицы М. В самом деле, через m периодов мы имеем
1) Для простоты мы не приводим вычислений координат точек пересече-
пересечения с плоскостью сочемчя Пуанкаре. Хотя приводимая далее процедура по
существу описывает то, что происходит вдоль собственного вектора матрицы
Флоке. ока равным образом применима н к смещениям в общем направлении.

Сечения Пуанкаре 81
т. е. начальное отклонение увеличивается в Мт раз. В резуль-
результате смещение экспоненциально убывает со временем, если все
собственные значения матрицы М по абсолютной величине мень-
меньше единицы, т. е. если все собственные значения лежат внутри
единичной окружности на комплексной плоскости. В этом слу-
случае периодическая траектория линейно устойчива, так как лю-
любое смещение из неподвижной точки стремится к уменьшению.
В противоположном случае, когда по крайней мере одно соб-
собственное значение матрицы М по абсолютной величине больше
единицы, смещение растет со временем по экспоненте, т. е. пре-
предельный цикл неустойчив. Разумеется, экспоненциальный рост
продолжается не бесконечно, но ограничивается нелинейными
эффектами, которые не принимаются во внимание в линейном
анализе. Таким образом, потеря устойчивости предельным цик-
циклом соответствует пересечению одним или несколькими соб-
собственными значениями матрицы Флоке. Во второй части этой
1шиги мы erne вернемся к вопросу о потере устойчивости.
IV. 3.2. Квазипериодическое решение
В случае двоякопериодического решения с двумя основными
частотами /i и f2 известно, что аттрактором является тор Г2,
который может быть проведен в R3. Любую траекторию на по-
поверхности тора можно рассматривать как суперпозицию двух
движений1): вращения по большей окружности (параллелям)
и вращения вокруг «цилиндра», образующего тор (рис. IV. 5).
Каждая из основных частот fi и f2 соответствует этим враща-
вращательным движениям. Точки пересечения траектории с плоскостью
сечения S возникают через регулярные интервалы времени, рав-
равные периоду первого движения (в нашем примере 7\ = l/fi).
Точки пересечения расположены на замкнутой кривой С, форма
которого может быть:
1) либо простой, т. е. без точек самопересечения (окруж-
(окружность, эллипс и т. д.);
2) либо более сложной (восьмерка, циклоида и т. д.) при
наличии гармоник с частотами f\ и f2.
') Если (х, у, г) —координаты в фазовом пространстве R3, то одно из
возможных параметрических представлений траектории имеет вид
х — a, sin Bnftt + а.) + а2 sin !2nf2t + а»),
у = ft, sin Bnftt + Р,) + 62 sin Bnf2t + р2),
z = с, sin Bnfit + Vi) + C2 sin
где а,:, bi, d, а,, р,- и yi — вещественные константы, ft и /г — две частоты
движения. В этом частном случае движение представляет собой просто сумму
двух периодических движений. В общем случае суперпозиция двух частот
имеет более сложный вид.
6 П Берже и др.

82
Глава IV
Точная форма сечения Пуанкаре зависит от отношения fi//2-
Если оно иррационально, то траектория не замыкается и всюду
плотно покрывает поверхность тора. В этом случае говорят, что
частоты /i и /2 несоизмеримы. Замкнутая кривая С непрерывна.
• Рис. IV. 5. Тор Тг и его сечение Пу-
Пуанкаре плоскостью S. Через /4 и /г
обозначены две частоты, определяю-
определяющие перемещение по поверхности то-
тора. Если отношение fjfz иррацио-
иррационально, то сечение Пуанкаре есть за-
замкнутая кривая С.
Так как каждая из ее точек есть образ ,некоторой другой точки
кривой С под действием преобразования Т, кривая С инвариант-
инвариантна относительно отображения Т:
Т(С) = С.
Хотя кривая' С непрерывна, последовательные точки пересече-
пересечения траектории с плоскостью S не покрывают ее сплошь. На-
а 6
Рис. IV. 6, Сечение Пуанкаре для квазипериодического режима с двумя ча-
частотами fi и h. а — отношение /<//, иррационально; б — отношение /<//2 ра-
рационально (в нашем примере /i/г = 3/5). Индекс указывает, в каком порядке
траектория проходит точки Рс„ Р\, Я2, Рг, Р{.
оборот, отображение Т соответствует сдвигу вдоль С на конеч-
конечный интервал.
Если отношение fi/f2 рационально, то сечение Пуанкаре со-
состоит из конечного множества точек, распределенных по С. Од-
Однако на этот раз С — уже не непрерывная кривая, так как тра-

Сечения Пуанкаре 83
ектория уже не образует всюду плотного покрытия на торе.
Между /i и /2 возникает затягивание частоты: отношение U/U
равно отношению двух целых чисел п\ и п2. Завершив П\ обо-
оборотов по «параллелям» и п% оборотов по «меридианам», траек-
траектория замыкается. Следовательно, мы имеем в действительно-
действительности дело с периодическим решением [с периодом Т = (fti//i) =
= («2/f2)]. Сечение Пуанкаре содержит только п\ точек, таких,
что
Обе указанные возможности представлены на рис. IV. 6.
IV. 3.3. Апериодическое решение
Чтобы понять, как выглядит сечение Пуанкаре апериодиче-
апериодического решения трехмерного потока, очень важно разобраться
в слоистой структуре сгранных аиракшров. Мы огложим рас-
рассмотрение этого вопроса до гл. VI, которая посвящена описа-
описанию этих сложных аттракторов. Напомним, что, когда поток
сильно диссипативен и приводит к быстрому сокращению площа-
площадей, его сечение Пуанкаре практически можно рассматривать
как множество точек, распределенных вдоль некоторой кривой
(отрезка прямой, дуги кривой и т. д.). В этом случае мы можем
определить координату х для каждой точки на кривой и иссле-
исследовать, как изменяется х со временем. Отображение Пуанкаре
на таком одномерном графике называется отображением пер-
первого возвращения. Следовательно, естественным обобщением
исследования сечения Пуанкаре является анализ отображения
первого возвращения, т. е. итерации
выражающей зависимость между координатами текущей и пред-
предшествующей точек.
IV. 4. ОТОБРАЖЕНИЕ ПЕРВОГО ВОЗВРАЩЕНИЯ
Во второй части книги нам часто придется исследовать од-
одномерные нелинейные отображения вида
В частности, мы покажем, что такое отображение может порож-
порождать хаотическое поведение. В гл. IX мы убедимся в том, что
отображения первого возвращения имеют самое непосредствен-
непосредственное отношение к явлениям перемежаемости. Но прежде, чем мы
б*

84
Глава IV
займемся выяснением этого вопроса, уместно обсудить, как ис-
используются отображения первого возвращения в более простых
ситуациях.
IV. 4.1. Итерация одномерного отображения
Классическими средствами исследования одномерного ото-
отображения являются графики на плоскости (xk,xk+\) функции /:
Хь+1 = f(xk) и тождественного отображения хк+\ = хк. Чтобы
О х0 X] х"хг 1
Рис. IV. 7. Отображение /(*) при \и = 0,7. Неподвижными точками отображе-
отображения являются точки пересечения графика функции f(x) с диагональю, т.е. с
графиком функции х, задающей тождественное отображение (геометрический
метод построения последовательных итераций отображения / ел. в тексте).
Существует устойчивая неподвижная точка х*, к которой сходятся итерации
всех начальных условий в интервале @, 1). Начало координат — неустойчи-
неустойчивая неподвижная точка. В этом представлении устойчивость неподвижной
точки можно определить по угловому коэффициенту касательной к кривой,
задающей отображение, в неподвижной точке: если абсолютная величина
углового коэффициента меньше единицы, то неподвижная точка устойчива
(как точка х*). В противном случае неподвижная точка неустойчива (как
точка 0).
продемонстрировать этот метод, выберем в качестве примера не-
нелинейное отображение1)
хк+1 = 4№ A - xk\ xk е= [0, ! ].
График функции /(.г) = 4цлA—х) при заданном значении ц,
заключенном между 0,25 и 0,75 (на рис. IV. 7 jj = 0,7), имеет
два нуля (при х = 0 и x=i) и максимум, равный ,«, в точке
!) Как будет показано в гл. VIII, это отображение (квадратичная итера-
итерация на единичном интервале) обладает необычайно богатыми и разнообраз-
разнообразными динамическими режимами.

Сечения Пуанкаре 85-
х = 0,5. Пользуясь этим графиком, исследуем заданную выше
итерацию с начального условия jco- Первая итерация xi = f(xo)
есть точка пересечений вертикали с абсциссой х0 и графика
функции f (см. рис. IV. 7). Аналогично вторая итерация х2 =
= f(x\) расположена на пересечении вертикали с абсциссой х\
и графика функции f и т. д. Простой и эффективный метод по-
построения последовательных итераций состоит в использовании
тождественного отображения, или диагонали, xk+\ = xk. Дей-
Действительно, горизонталь хн+\ = х\ пересекает диагональ Xk+\=Xk
в точке xk = x\. Следовательно, достаточно провести вертикаль
через эту точку, не обращаясь к оси абсцисс.
Таким образом, повторяя последовательность операций
1) проведение вертикали от диагонали до пересечения с гра-
графиком функции f{x);
2) проведение горизонтали из полученной точки до пересе-
пересечения с диагональю,
мы получаем последопзтельпые итерации отображения. Из
рис. IV. 7 видно, что итерации сходятся к точке с абсциссой х*—
пересечению диагонали с графиком функции f. Читатель может
легко убедиться в том, что при любом начальном условии Хо,
кроме концевых точек интервала 0 и 1, итерации функции f
сходятся к х*. Ясно, что любая точка пересечения графика функ-
функции f(x) с диагональю (графиком тождественного отображе-
отображения) является итерацией самой себя; это неподвижная точка
отображения /. Именно с такой ситуацией мы встречаемся при
рассмотрении начала координат: выбирая х0— 0, получаем
v, = о, х2 = 0 и т. д. Но при значении хв, сколь угодно близком,
не равном нулю, итерации сходятся к х*. Это означает, что лю-
любое смещение из начала координат, каким бы малым оно ни
было, увеличивается при итерациях. Точка, находящаяся на ма-
малом расстоянии от начала координат, движется от этой непо-
неподвижной точки, которая поэтому называется неустойчивой, В от-
отличие от нее неподвижная особая точка х*, к которой сходятся
итерации при любом начальном условии из @, 1), является
устойчивой неподвижной точкой.
Существует критерий, позволяющий определять устойчивость
или неустойчивость неподвижной точки без громоздких вычис-
вычислений. Графическое построение показывает, что если тангенс
угла наклона касательной к кривой f(x) по абсолютной вели-
величине больше единицы, то неподвижная точка неустойчива:
именно так обстоит дело с началом координат на рис. IV. 7.
С другой стороны, если тангенс угла наклона касательной к кри-
кривой / по абсолютной величине меньше единицы, то итерации
сходятся к неподвижной точке: так обстоит дело с неподвижной
точкой х*.

86
Глава IV
Результаты относительно существования и устойчивости не-
неподвижной точки одномерного отображения справедливы не
только для квадратичной функции, выбранной в качестве иллю-
иллюстрации, но и для более общих отображений.
IV. 4.2. Предельный цикл генератора Ван дер Поля
Теперь мы уже в состоянии легко установить результат, сфор-
сформулированный в разд. II. 1.2, без доказательства, а именно су-
существование устойчивого периодического решения уравнения E)
при е > 0. Это уравнение определяет поток на плоскости с пря-
прямоугольными координатами (9, 9). Мы уже упоминали о том,
что фазовые траектории имеют форму спиралей, раскручиваю-
раскручивающихся из начала координат и сходящихся вдали от него.
Рис. IV. 8. Две траектории для урав-
уравнения Ван дер Поля. Образом точки
Ра служит точка Pi, образом точки
—точка Р
Рассмотрим на фазовой плоскости луч, исходящий из начала
координат, и его пересечения с траекториями, начинающимися
в точках Ро и Р'о (рис. IV. 8). Поступая таким образом, мы
в действительности строим сечение Пуанкаре в R2; в данном
случае «плоскость» сечения вырождается в полупрямую, или
луч.
Каждой точке на луче мы можем поставить в соответствие
координату х, измеряющую расстояние от этой точки до начала
координат (т. е. радиус окружности, проходящей через эту
точку на плоскости F,8)). Зададим функцию x^-f(x), сопо-
сопоставляющую каждой точке на луче другую точку, именно точку
первого пересечения луча с траекторией выходящей из точки х.
Такая функция f обладает некоторыми легко проверяемыми,
но важными свойствами:
1) f однозначно определена, т. е. f отображает каждую точку
луча в другую (одну и только одну) точку луча;

Сечения Пуанкаре
8?
2) f непрерывна;
3) в окрестности начала координат тангенс угла наклона ка-
касательной к кривой f больше единицы (в противном случае мы,
имели бы в этой области неравенство f(x)<.x, поэтому после-
последовательность итераций
Х1 ~
X2~
<ХХ< Хо,
сходилась бы к началу координат, а это противоречит утверж-
утверждению о том, что траектории расходятся);
4) при больших х тангенс угла наклона касательной к кри-
кривой / меньше единицы (сходящиеся спирали);
Рис. IV. 9. График отображения
x-+f{x), имеющего устойчивую
неподвижную точку х0.
5) f — обратимая функция, а тангенс угла наклона касатель-
касательной к ее графику всюду имеет один и тот же знак (положите-
(положителен). Действительно, мы можем единственным образом вер-
вернуться «вспять» вдоль траектории [уравнение E1)]. Следова-
Следовательно, каждому значению f(x) соответствует одно и толька
одно значение х.
Если учесть все эти свойства, то простейшая форма графика
функции f такая, как на рис. IV. 9. Так как / — непрерывна»
функция, существует по крайней мере одно1) положительное
значение х0) при котором график функции f пересекается с гра-
графиком тождественного отображения:
/(*о) = По-
Последовательно, отображение первого возвращения в сечени»
Пуанкаре имеет неподвижную точку. Это означает, что поток,
') Как показывают вычисления, для уравнения Ван дер Поля существует
только одна неподвижная точка.

«8 Глава IV
из которого возникает сечение Пуанкаре, должен иметь пре-
предельный цикл. В силу условия | df/dx ^ < 1 неподвижная точ-
точка х0 является аттрактором. Следовательно, периодическое ре-
решение устойчиво.
IV. 4.3. Редукция трехмерного потока
Некоторые (но отнюдь не все) трехмерные потоки могут
быть сведены к отображениям меньшей размерности. В качестве
иллюстративного примера рассмотрим следующий поток, пред-
предложенный Рёсслером:
х = — у — г,
у = х + ау, A1)
2 = 6 + XZ — CZ,
г Ас л, у и г — переменные, а, О и с — параметры, значения ко-
которых требуется выбрать. При некоторых значениях парамет-
параметров (например, при а=й=0,2; с=5,7) решения уравнений A1)
обнаруживают апериодическое или хаотическое поведение. На
рис. IV. 11 эволюция переменных x{t), y(t) и z(t) кажется со-
совершенно некогерентной, хотя сами уравнения очень просты.
На рис. IV. 12, а мы видим проекцию фазовой траектории на
плоскость (х, у). Среди многих возможных сечений Пуанкаре
существует одно, которое особенно просто реализуемо на прак-
практике, а именно сечение, соответствующее плоскости, определяе-
определяемой уравнением
Первое из уравнений A1) показывает, что переменная достигает
в этом сечении максимума, так как х = 0. Численно интегрируя
уравнения A1), мы можем получать значение х каждый раз,
когда эта переменная достигает экстремума определенного
типа, например максимума. Пусть Xk — последовательность та-
таких значений. Априори не существует причины, по которой
между двумя последовательными значениями не могло бы су-
существовать какое-нибудь соотношение. Но если мы построим
график зависимости xfe+. от предыдущего значения x-R, то полу-
получим поразительный результат, изображенный на рис. IV. 10: вме-
вместо того чтобы рассеяться по всей плоскости, точки уклады-
укладываются на кривую с «горбом». В этой связи можно сделать два
замечания. Во-первых, не вызывает сомнений тесная связь
между потоком A1) и кривой на рис, IV. 10. Следовательно, ис-
исследуя только отображение первого возвращения и не анали-
анализируя полностью поток, мы можем прийти к некоторым выводам

Сечения Пуанкаре
ck*f
+
+
%
iii iii i i i
Рис. IV. 10. Зависимость последовательных максимумов апериодического ре-
решения х потока A1) от значения предыдущего максимума. Обратите внима-
внимание на регулярный характер полученной кривой и на существование у нее-
одного максимума.
Z0
10
Рис. IV. П. Апериодическое решение потока A1), полученное с помощью чис-
численного интегрирования. Несмотря на простоту дифференциальных уравнений,
описываемая ими эволюция далеко не регулярна, как видно на примере функ-
функций x(t) и г@- Такой вывод подтверждается сечением Пуанкаре, а также
анализом Фурье.

¦90 Глава IV
о потоке. Сведение трехмерного потока к отображению на ин-
интервале позволяет достичь существенного упрощения. Во-вто-
Во-вторых, что еще более важно, мы можем повторить замечание,
высказанное в предыдущем разделе: сравнительно простое де-
детерминистское описание [уравнение A1)] может порождать
поведение, не обладающее никакой видимой регулярностью. Из-
Изменение во времени переменных x(t), y(t), r(t) представляется
совершенно некоррелированным (рис. IV. 11), тогда как закон,
определяющий это изменение [поток A1)] совершенно регуля-
регулярен (рис. IV. 11)). Здесь мы затрагиваем существенный вопрос,
которому посвящена вторая часть нашей книги — вопрос о су-
существовании детерминистского хаоса.
IV.5. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ
Изложенные выше соображения относительно метода Пуан-
кяпр ттрр.ттолагают знание базового гтпостпзнства исследуемой
динамической системы. Однако на практике мы никогда, по
крайней мере в экспериментальных исследованиях реальных си-
систем, не располагаем подобной информацией. Чаще всего нам
приходится ограничиваться измерением изменений лишь одного
свойства, связанного более или менее сложной зависимостью
с одной из независимых переменных соответствующей задачи
(а иногда и с несколькими переменными). Может создаться впе-
впечатление, что любая попытка практически реализовать изложен-,
ный выше анализ обречена на провал.
Должны ли мы сделать вывод о том, что метод Пуанкаре
применим только для численного моделирования потоков типа
A1) и не может быть использован для исследования поведения
реальных систем? Безусловно, не следует, по крайней мере если
число степеней свободы остается малым, как в случае тех си-
систем, которые рассматриваются в нашей книге. Мы надеемся,
что каждая из переменных достаточно хорошо отражает общее
поведение, и это обстоятельство позволяет нам проводить полный
анализ. Отсюда напрашивается гипотеза: по-видимому, возмож-
возможно восстановить топологию аттрактора, исходя из наблюдений
только сигнала X(t) и выбирая в качестве фазового простран-
пространства либо X(t),X(t+x),X(t+2x), ..., m6oX(t),X(t),X(t), ... .
Иначе говоря, мы можем считать, что сигнал X(t) не зависит
от значений, принимаемых им же в более поздний момент вре-
времени X(t-rt), где т — произвольная постоянная, называемая
запаздыванием. Можно поступить по-другому и рассматривать
сигнал X(t) и его производную по времени А'(г) как независи-
независимые сигналы. Сказанное отнюдь не означает, будто аттрактор,
получаемый в новом пространстве, тождествен аттрактору в ис-

Сечения Пуанкаре 91
ходном фазовом пространстве. Мы утверждаем лишь, что новое
представление аттрактора сохраняет основные топологические
свойства первого и этого может оказаться достаточно для иссле-
исследования существенных характеристик исходного аттрактора.
В случае простого аттрактора (неподвижной точки или пре-
предельного цикла) топологическая эквивалентность почти очевид-
очевидна, однако она отнюдь не очевидна для более сложного аттрак-
аттрактора— тора или странного аттрактора, а именно такие аттрак-
аттракторы мы намереваемся исследовать. Поскольку точных границ
области топологической эквивалентности двух представлений не
существует, полезно обратиться к примеру. Для потока A1) чис-
численное интегрирование позволяет получить все переменные
x(t), у if), г {t), x(t), y(t\ z(t), x(t), ij{t), 2@.
С этого момента и впредь мы можем сравнивать характеристики
аттрактора в фазовом пространстве (х. и. z) с его характеристи-
характеристиками в любом другом представлении. На рис. IV. 12 сравни-
сравнивается проекция фазовых траекторий на плоскость (х, у) с про-
проекцией на плоскость (х, х) траекторий в пространстве (х,х,х) ')..
Сходство топологий этих двух кривых очевидно. Кроме того»
наибольшие показатели Ляпунова2) также дают великолепное
количественное согласие: значения, вычисленные в двух пред-
представлениях, различаются менее чем на 1 %!
Остается практически осуществить процедуру. Один из мето-
методов состоит в численной обработке сигнала X(t) для определе-
определения X(t-\-x) или X(t): Если сигнал хранится в памяти компью-
компьютера, то такая обработка проводится без труда. Возможны и
другие методы, более физические, чем вычислительные. Напри-
Например, с помощью аналогового электронного устройства можно
') Для уравнений Рёсслера соотношения, позволяющие совершить пере-
переход от координат (х, х, х) к координатам (х, у, г) исходного фазового про-
пространства, таковы:
y Л- In In х\ y А- х. -4- h
с — а —. х
¦ — ах + х А- Ь
с — а — х
Формально замена переменных {х, у, г) -> (х, х, х) есть криволинейное пре-
преобразование координат в фазовом пространстве. При естественных предполо-
предположениях о непрерывности подобного рода преобразование сохраняет тополо-
топологию таких объектов, как аттракторы потоков.
2) Показатель Ляпунова служит мерой средней скорости расхождения
двух траекторий (см. приложение Б).

'92
Глава IV
в каждый момент времени определять величину X(i) и ее про-
производную X(t). Иногда эксперимент планируют с таким расче-
расчетом, чтобы измерение сигнала в двух различных специально вы-
выбранных точках системы соответствовало временной задержке
между двумя однотипными сигналами. Все трудности суще-
Рис. IV. 12. Проекции траекторий
потока Ресслера а — проекции на
«истинную» фазовую плоскость
(х, у); б — проекции на «вообра-
«воображаемую» плоскость (х, х).
Из работы: Packard N. #., Crutch-
field I. P., Farmer I. D., Shaw R. S.
Geometry from a time series. Phys.
Rev. Letters, 1980, v. 45, p. 712.
егвенно уменьшаются в тех случаях, когда две независимые ве-
величины удается измерить одновременно. Таким образом, мы ви-
видим, что у экспериментатора имеется достаточно широкий выбор
методов.
Наконец, заметим, что для сигнала с периодичностью Т (пе-
(периодического и в особенности квазипериоднческого) простой
способ построения сечения Пуанкаре состоит в измерении зна-
значений сигнала в моменты времени Г, 2 Г, ..., пТ. Так как Т —
в точности временной интервал, необходимый для завершения
одного цикла на аттракторе (предельном цикле или торе), мы
ло существу стробоскопируем сигнал. Поскольку эта задача

Сечения Пуанкаре 93
легко выполнима, стробоскопические') методы часто исполь-
используются для идентификации и исследования квазипериодических
решений.
Завершив обзор различных методов измерения характери-
характеристик, зависящих от времени режимов динамических систем, мы
проиллюстрируем теперь эти методы на конкретных случаях. Мы
избрали несколько архетипов, которые проливают свет и на ме-
методы анализа, и на ¦ получаемые с их помощью результаты.
В следующей главе подробно описаны три экспериментальные
ситуации.
4) Метод стробоскопирования равным образом применим и к анализу
систем с периодической вынуждающей силой. В этом случае частота выну-
вынуждающего воздействия задает естественный интервал для стробоскопической
выборки значений сигнала.

ГЛАВА V
ТРИ ПРИМЕРА ДИНАМИЧЕСКИХ СИСТЕМ
V.I. ВВЕДЕНИЕ
Чтобы проиллюстрировать на конкретных примерах теорети-
теоретические идеи, которые будут развиты в оставшейся части книги,,
мы решили сосредоточить внимание на трех различных экспери-
экспериментальных ситуациях. В своем выборе мы исходили из богат-
богатства их динамического поведения и обилия известных резуль-
результатов.
Наш первый пример — электромеханическое устройство с тре-
тремя степенями свободы, а именно магнит, помещенный в магнит-
магнитное поле. Мы будем называть это устройство вращающимся маг-
магнитом. Наш второй пример заимствован из гидродинамики —
это движение горизонтального слоя жидкости, подогреваемого*
снизу. Ключевое явление в этом случае называется неустойчи-
неустойчивостью Рэлея — Бенара. Именно она вызывает спонтанное дви-
движение жидкости. Говоря об этом явлении, мы будем использо-
использовать сокращенное обозначение РБ (Рэлей — Бенар). Наконец,
свой третий пример мы взяли из химии. Это наиболее известная
и хорошо изученная ¦ из колебательных химических реакций —
реакция Белоусова — Жаботинского (сокращенно БЖ).
В этой главе мы намереваемся изложить то, что известно
о дифференциальных уравнениях, описывающих каждый из трех
осцилляторов, и в общих чертах охарактеризовать методы и экс-
экспериментальное оборудование, используемые для исследования
выбранных нами систем.
V.2. ВРАЩАЮЩИЙСЯ МАГНИТ
V. 2.1. Описание
Вращающийся магнит, о котором идет речь, — не более чем
искусная реализация параметрического маятника, позволяющая
удобно производить точные наблюдения поведения системы
с тремя степенями свободы. Как и другие аналогичные устрой-
устройства, установка была создана отчасти с демонстрационными це-
целями. Один из наиболее привлекательных аспектов этого уст-
устройства состоит в том, что оно позволяет в широких пределах

Три примера динамических систем
Щ Ось
95
Генератор
(л)
Катушка.
АЦП
АЦП
Макропро-
Макропроцессор
*(*)
Рис. V. 1. Схема установки для исследования динамического поведения вра-
вращающегося магнита. На магнит, который может вращаться на оси, действуют
стационарное и вращающееся магнитные поля (см. также рис. V. 2). Дисси-
Диссипация контролируется изменением вязкости масла в подшипнике, температура
которого регулируется с высокой точностью. Положение магнита определяется
по ЭДС, наводимой при его движении в катушках-датчиках. Эта ЭДС x(t)
пропорциональна мгновенной угловой скорости вращения магнита. Аналого-
Аналоговая схема дает производную i(t) этой ЭДС по времени. Частота вращающе-
вращающегося магнитного поля служит тактовой частотой для включения двух ана-
аналого-цифровых преобразователей, благодаря чему за каждый оборот поля
в ЗУ компьютера вводится пара значений x(t) и x(t). Таким образом за до-
достаточно большое время эксперимента регистрируется сечение Пуанкаре
траекторий.

96 Глава V
изменять уровень трения. В свою очередь это открывает воз-
возможность наблюдения и анализа влияния диссипации энергии
при переходе от консервативной или квазиконсервативной си-
ситуации (с нулевым или пренебрежимо слабым трением) к си-
ситуации все более и более диссипативнои.
Блок-схема установки изображена на рис. V. 1. Магнит, ко-
который может вращаться вокруг вертикальной оси, помещен
между двумя парами катушек Гельмгольца с горизонтальными
осями, расположенными под прямым углом друг к другу. К каж-
каждой паре катушек подается переменный (синусоидальный) ток
с угловой частотой <о и переменной интенсивностью. Так как
токи сдвинуты по фазе на я/2, эти пары катушек создают ста-
стационарное магнитное поле и магнитное поле, вращающееся во-
вокруг оси магнита с угловой частотой со тока. Вращающееся маг-
магнитное поле стремится привести магнит в движение. Приемные
катушки, перпендикулярные катушкам Гельмгольца, располо-
расположены вблизи магнита и детектируют его движение по индуци-
индуцируемой электродвижущей силе. Наведенный в катушках сигнал
X(t) зависит от мгновенной угловой скорости магнита. После
усиления и фильтрации сигнал поступает на анализатор Фурье,
который вычисляет спектр мощности.
Построение сечения Пуанкаре фазовых траекторий прово-
проводится прямо, поскольку магнит представляет собой осциллятор
с вынуждающей силой. Действительно, период вращения нало-
наложенного магнитного поля служит естественным интервалом вре-
времени для стробоскопии. Достаточно измерять сигнал х каждый
раз, как вращающееся поле совершает поворот на 2я. Иначе го-
говоря, период переменного тока, текущего по обмотке катушек
Гельмгольца, используется как интервал, через который произ-
производится выборка значений сигнала. Что касается двумерного
представления, то две величины записываются в цифровой фор-
форме одновременно: сам сигнал X и получаемая аналогично его
производная X.
Подшипники оси магнита изготовлены из рубина, чтобы све-
свести до минимума трение между твердыми телами. Погружая
нижнюю опору оси в масла с различной вязкостью, можно варь-
варьировать уровень трения в жидкости и связанной с вязкостью
диссипацией энергии. Одно и то же устройство может быть и
диссипативным, и почти консервативным.
V. 2.2. Уравнение эволюции
Рассмотрим случай, когда трение пренебрежимо мало. Дви-
Движение магнита определяется приложенными к нему силами.
Магнит с моментом инерции / и магнитным моментом Jt поме-

Три примера динамических систем
97
щен в суперпозицию двух магнитных полей: одного стационар-
стационарного с индукцией В\ и другого с индукцией Во, вращающегося
с угловой скоростью со (рис. V. 2). Изменения угла 0 между маг-
магнитом и выбранным фиксированным направлением в горизон-
12 = li ¦ lo cos аи
13 = lo sin wt
Рис. V. 2. Схема расположения магнита М относительно катушек, создающих
поле. Вращающееся магнитное поле Во создается двумя парами катушек
Гельмгольца с взаимно перпендикулярными осями. К обмоткам катушек под-
подведен ток /о sin Ш и /о cos Ш. Стационарное магнитное поле Bi создаете*
постоянным электрическим током /ь пропускаемым через одну из пар ка-
катушек.
Из работы В. Крокетта.
тальной плоскости определяются дифференциальным уравне-
уравнением - ¦ '
/-^5- = — --5i s'«е — -"о sin (9- <з>).
Приведем это уравнение к безразмерному виду, полагая
и выбирая I/O) за единицу времени. Получаем
?*. = ё = — М sin 9 — Р sin (9 — О-
7 П. Берже н др.

98 Глава V
I
Чтобы прийти к выражению, стоящему в правой части, необхо-
необходимо принять допущение (вполне,обоснованное для данной экс-
экспериментальной установки) о том, что магнитные поля не зави-
зависят от положения магнита. .
Трение в жидкости, как известно( приводит к замедлению
движения силой, пропорциональной скоростью. Следовательно,
когда трение перестает быть пренебрежимо малым, мы должны
ввести в предыдущее уравнение член, пропорциональный 8:
ё + аё = — Afsin6 — P sin (в-0- A2)
Это неавтономное обыкновенное дифференциальное уравнение
второго порядка, эквивалентное потоку в R3, который мы запи-
запишем с помощью трех переменных у, 6, ф: '.. ¦'
у = — щ/ — М sin9 — Р sin (9 — ^>),
Итак, мы имеем нелинейную систему с тремя степенями сво-
свободы1). Физически переменная ф (связанная с со/) представляет
собой угол между вращающимся магнитным полем и фиксиро-
фиксированным направлением плоскости. Именно поэтому решение по-
потока всегда перибдично (с периодом 2я в единицах I/to) по
компоненте ф. Заметим, что в отсутствие вращающегося поля,
т. е. при Р = 0, уравнение A2) переходит в уравнение для про-
простого маятника с затуханием 2), линейная аппроксимация кото-
которого была рассмотрена в разд. I. 3.2.
После того как магнит выбран и тем самым выбраны значе-
значения / и Ж и фиксирована угловая частота о> синусоидального
тока, управляющими параметрами остаются индукции В\ и Во
стационарного и вращающегося магнитных полей. Их можно
регулировать, изменяя интенсивность электрического тока, про-
пропускаемого через обмотку катушек Гельмгольца. Таким обра-
•) В более общем случае неавтономный поток можно представить в виде
автономного потока в фазовом пространстве более высокой размерности с по-
помощью подходящей замены переменных.
2) Заметим, что к аналогичному результату мы приходим, когда стацио-
стационарное поле обращается в нуль (Л1 = 0), если за движением наблюдать в
системе отсчета, вращающейся с угловой скоростью со. Действие двух полей
симметрично: вращающееся поле становится стационарным в системе отсчета,
вращающейся с угловой скоростью поля, и наоборот. Кроме того, в отсутствие
трения и при наличии только одного магнитного поля намагниченный стер-
стержень совершает регулярные колебания относительного поля. При малых ам-
амплитудах колебания имеют угловую частоту Л/М в случае стационарного
поля и V "• если поле вращается.

Три примера динамических систем 99
зом, экспериментатор может по своему желанию варьировать
параметры М и Р, чтобы наблюдать различные возможные ди-
динамические режимы, а также переходы и бифуркации между
ними.
V.3. КОНВЕКЦИЯ РЭЛЕЯ —БЕНАРА
V. 3.1. Неустойчивость Рэлея — Бенара
В жидкости с достаточно большим коэффициентом тепло-
теплового расширения любая разность температур порождает раз-
разность плотностей. Если такую жидкость поместить в гравита-
гравитационное поле, то поле в свою очередь создает силы, которые
приводят к движению жидкости, называемому тепловой конвек-
конвекцией. Для количественного исследования этого, явления необхо-
необходимо контролировать разность температур, приложенную к жид-
жидкости, так как именно разность температур приводит жидкость
То
Ж
gL d Жидкость
Г0+8Т
Температура.
Рис. V. 3. Схема опыта Рэлея —Бенара. В жидкости, заключенной между
двумя теплопроводящими пластинами, существует (в отсутствие конвекции)
постоянный градиент температуры (как показано на графике справа). Темпе-
Температура изменяется от 7 о + 67 на нижней границе слоя жидкости до Го на.
его верхней границе.
в движение. На рис. V. 3 изображена принципиальная, схема ти-
типичного устройства, используемого для этого. Слой жидкости;
толщиной d ограничен двумя твердыми горизонтальными пла-
пластинами с высокой теплопроводностью. Верхняя пластина под-
поддерживается при фиксированной температуре То, а нижняя —
при температуре Г0 + б7" F7 >0). Слой ограничен также вер-
вертикальными стенками (не показанными на рис. V. 3), теплопро-
теплопроводность которых, как правило, близка к теплопроводности
жидкости. С экспериментальной точки зрения существенно,,
чтобы теплообмен между жидкостью и пластинами был очень-
хорошим; тогда линейный вертикальный градиент температуры
устанавливается в слое без разрыва на границах. По сравнению»
с другими более или менее естественными типами конвекции
¦ 7* ¦

100
Глава V
такая геометрия характеризуется отсутствием горизонтального
градиента температуры до наступления конвекции.
Любая жидкость с достаточно большим коэффициентом теп-
теплового расширения, помещенная между двумя пластинами, под-
подвержена двум противоборствующим тенденциям. Холодная
жидкость, более плотная и расположенная в верхней части слоя,
стремится опуститься, в то время как нижняя часть слоя, более;
теплая и менее плотная, стремится подняться. Но коль скоро
разность температур ЬТ остается малой, конвективное движение
"
Рис. V. 4. Возникновение движения в жидкости. Два элемента жидкости Я
и В перемещаются в новые положения Н' и В'. В зависимости от величины
6Г возникающее движение затухает или не затухает.-
не возникает из-за стабилизирующих эффектов трения1). Воз-
Возникновение неустойчивости можно объяснить, следующим обра-
образом. Если элементы жидкости перемещаются по траекториям
HW и ВВ' на рис. V. 4, то крутящий момент усиливает возни-
возникающее перемещение. После того как два элемента жидкости
переместятся соответственно на НН' и ВВ', разность температур
между ними уменьшится из-за теплопроводности (с коэффи-
') Иначе обстоит дело, если градиент температуры не вертикален, а го-
горизонтален. В этом случае жидкость стремится подниматься вдоль более теп-
теплой границы и опускаться вдоль более холодной. Силы не уравновешивают
друг друга, а создают крутящий момент. Независимо от того, насколько мала
А
разность температур (даже если она бесконечно мала), этот момент приводит
жидкость в движение. Следовательно, если мы хотим наблюдать четко выра-
выраженный порог конвекции, то в эксперименте РБ горизонтальных градиентов
температуры следует избегать.

Три примера динамических систем 101
циентом теплопроводности Dt), причем характерное время со-
составляет величину порядка
Характерное время перемещения НН'— ВВ' зависит от сил, дей-
действующих на жидкость, т. е. от архимедовой силы (плавучести),
обусловленной разностью температур, и силы вязкости трения.
Это характерное время %т определяется соотношением:
PogaddT '
где т] — динамическая вязкость, а — коэффициент теплового рас-
расширения, ро — средняя плотность жидкости, g — ускорение силы
тяжести. Условие наступления незатухающего движения со-
состоит в том, что время ттепл (время жизни причины) должно
быть, больше, чем'тш (времени внешнего проявления эффекта).
Следовательно, условие для затухающей конвекции имеет вид
неравенства
Щ^бТ^ const.
r\DT ^
Величина, стоящая в левой части, называется числом Рэлея Ra
и является безразмерной мерой разности температур ЬТ. Нера-
Неравенство означает, что существует критическое число Рэлея Rac
(или, что эквивалентно, критическая разность температур 6ГС),
выше которого состояние покоя теряет устойчивость и начи-
начинается конвекция. Конвективные неустойчивости впервые от-
отчетливо наблюдались в экспериментах Бенара A900) и полу-
получили теоретическое объяснение в работе Рэлея A916). Именно
поэтому с этим явлением связаны эти два имени. '
За порогом конвекции движение жидкости отнюдь не ста-
становится беспорядочным. Наоборот, в жидкости образуется ре-
регулярная структура валов с параллельными горизонтальными
осями1) (рис. V. 5). В срединной плоскости мы наблюдаем по-
последовательность чередующихся восходящих и нисходящих по-
потоков. Потоки расположены эквидистантно, расстояние между
*) В оригинальном варианте эксперимента Бенара использовался тонкий
слой китового спермацетового масла со свободной верхней границей. В этих
условиях из-за эффектов поверхностного натяжения на границе раздела мас-
масло — воздух возникали не валы, а шестиугольные ячейки с вертикальными
осями. Такого рода неустойчивость, называемая теперь эффектом Марангони,
обусловлена температурной зависимостью поверхностного натяжения.

102
Глава V
соседними потоками составляет величину порядка d. Два сосед-
соседних вала вращаются в противоположные стороны. Но если взять
всю систему валов, то нетрудно заметить, что направление вра-
вращения каждого вала можно изменить на противоположное, не,
ОООООО-
SSS^^N^^^W^^ Тл+бТ
Рис. V. 5. Схема организации движения жидкости в конвективных валах
(изображено поперечное сечение валов). Соседние валы вращаются навстречу
друг другу, как шестерни в зацеплении. Обратите внимание на то, что рас-
расстояние между двумя соседними вертикальными токами (которое можно при-
принять за диаметр конвективного вала) по порядку величины сравнимо с d —
расстоянием между двумя жесткими горизонтальными пластинами, ограничи-
гающгаи слой' жидкости снизу к сверху.
внося при этом глобальных изменений в геометрические и дина-
динамические свойства движущейся жидкости. Именно поэтому в
идеальном эксперименте Рэлея —Бенара оба направления вра-
вращения валов строго равновероятны. То же утверждение можно
Рис. V. 6. Бифуркационная диаграмма вблизи порога Rac неустойчивости теп-
тепловой конвекции. В идеальном эксперименте конвективные валы, возникающие
при Rac, с равной вероятностью вращаются как в одну, так и в другую
сторону. Это отражается в существовании двух ветвей, обозначенных симво-
символами V+ И V—
сформулировать и в другой эквивалентной форме: в любой точке
жидкости скорость может быть направлена как в одну, так и
в противоположную сторону. Это свойство отражено на бифур-
бифуркационной диаграмме (рис. V. 6). На ней построен график зави-
зависимости скорости v в некоторой точке слоя как функция числа
Рэлея Ra. При Ra < Rac единственное возможное состояние
есть состояние покоя (и = 0). На пороге неустойчивости Rac
происходит бифуркация; выше порога при любом заданном зна-

Три примера динамических систем 103
чении Ra экспериментально реализуемы') два конвективных со-
состояния с равными, но противоположно направленными скоро-
скоростями. При Ra > Rac конвективные валы имеют стационарную
конфигурацию: скорость и температура описываются функция-
функциями, не зависящими от времени. С точки зрения теории динами-
динамических систем переход при Ra = Rac является бифуркацией
между двумя стационарными состояниями: состоянием покоя
и конвективным состоянием. Разумеется, , пространственная
структура этих состояний весьма различна.
Нельзя не упомянуть здесь о главном преимуществе конвек-
конвекции. РБ перед другими гидродинамическими ситуациями: отсут-
отсутствие какого бы то ни было механического движения, поддержи-
поддерживаемого извне. Это замечательное свойство делает конвекцию
РБ особенно удобной системой для изучения возникновения тур-
турбулентности. . ¦ ¦ ..
i ' ¦
V. 3.2. Конвективные структуры
Если слой достаточно широк, то конвективные валы могут
образовывать многочисленные конфигурации, или «конвектив-
«конвективные структуры», в горизонтальной плоскости. ^Процесс отбора
структур представляет собой сложную проблему, которая сей-
сейчас находится в стадии изучения. В случае прямоугольных кю-
кювет 2) структура может состоять главным образом из прямоли-
прямолинейных эквидистантных валов, оси которых параллельны более
коротким сторонам прямоугольника. Мы видим в такой струк-
структуре аналогию с одномерным кристаллом (снимок V. 1).
Flpii дальнейшем увеличении разности температур &Т струк-
структура "сначала становится более сложной, но сохраняет опреде-
определенную регулярность. Однако при еще большем увеличении 8Т
структура полностью разрушается, как бы «расплавляется». На
смену упорядоченной стационарной структуре приходит непре-
непрестанно изменяющаяся неупорядоченная конфигурация: движе-
движение жидкости становится турбулентным. Ясно, что это сложное
непредсказуемое поведение обусловлено множеством возможных
пространственных структур, каждая из которых эволюционирует
по-своему. Их взаимодействие порождает турбулентный режим.
•) При более высоких значениях Ra возникают и другие неустойчивости,
которые р. значительной мере зависят от условий эксперимената. Разнообра-
Разнообразие их столь велико, что для описания всех неустойчивостей вряд ли хватило
6w ::i!nnt. Несколько примеров таких неустойчивостей мы приводим во второй
части книги в качестве иллюстраций к теории динамических систем.
2) В действительности для того чтобы возникла конвективная структура,
.изображенная на снимке V. !, ее необходимо предварительно индуцировать.

104
Глава V
который называют хаотическим, с большим- числом степеней
свободы1).
Как можно сохранить первую конвективную структуру и пре-
предотвратить возникновение хаоса указанного типа? Достаточно
резко снизить число возможных конфигураций, совместимых
Фотография V. 1. Конвективная структура из упорядоченных валов. Конвек-
Конвекция создается в слое силиконового масла толщиной 2,5 мм с горизонталь-
горизонтальными размерами 98 X 60 мм. Если верхняя пластина прозрачна, а в качестве
нижней ьз.чга полированная медь с оптически гладкой поверхностью, то кон-
конвективные валы можно визуализовать, используя преломление света,"прохо-
света,"проходящего сквозь слой жидкости. Вокруг более холодных нисходящих ^ токов
жидкости горизонтальные градиенты температуры создают градиенты пока-
показателя преломления, фокусирующие свет в определенных направлениях. В ре-
результате этого широкий пучок света, проходящий вертикально сквозь слон
силиконового масла, претерпевает периодическую фокусировку и наблюдатель
видит нисходящие токи как светлые лолосы на темном фоне. Небольшие
градиенты температуры вдоль двух меньших боковых границ созданы для
стабилизации фазы боковых валов и обеспечения правильной периодической
структуры.
с наложенными связями. Естественно поместить жидкость
в ячейку с горизонтальными размерами Lx, Ly того же масшта-
масштаба, что и высота. Аспектное отношение, определяемое как Г =
= L/d, такой ячейки мало и число конвективных валов ограни-
') Используемое здесь определение степени свободы отличается от дан-
данного в гл. I.

Три примера динамических систем
105
чено. Например, в ячейке формата Г = 2 умещаются только два
вала (рис. V. 7). Как показывает эксперимент, в ячейках такого
типа пространственный порядок действительно сохраняется в
очень широком диапазоне чисел Рэлея Ra. Это не означает, что
динамическое поведение не зависит от Ra. Действительно, при
увеличении Ra возникает то, что называется вторичными не-
устойчивостями, которые влияют да временное поведение кон-
конвективных структур. Например; одна бифуркация приводит
L = Zd
Рис. У. 7. Схема ячейки с небольшим удлинением (T — Lld — 2). Наличие
боковых границ из плексигласа, расстояние между которыми лишь вдвое пре-
превышает толщину слоя, стабилизирует конвективную структуру и уменьшает
число валов (по крайней мере при средних значениях Ra) до двух. Следует
подчеркнуть, что в направлении, перпендикулярном плоскости рисунка, рас-
расстояние U между границами из плексигласа еще меньше: для описанных в
тексте экспериментов с силиконовым маслом L' = l,2d.
к строго периодическим колебаниям скорости в точке. О такой
системе говорят, что она обладает малым числом степеней сво-
свободы (сравнимым с числом пространственных мод, вовлеченных
в конвективную структуру) в отличие от ситуации, с которой
мы сталкиваемся в ячейках с большим аспектным отношением.
V. 3.3. Уравнения эволюции
L Уравнения, описывающие конвективные явления, связывают
скорость v элемента жидкости с возмущением температуры 6 ').
Установленные в XIX в. эти уравнения были выведены путем
рассмотрения локального баланса импульса (уравненияНавье —
Стокса), массы (уравнения непрерывности) и тепла. Немного-
Немногочисленные приближения, вполне приемлемые для описания
') Возмущение 0 есть разность между температурой в конвективном ре-
режиме и температурой, которую имела бы жидкость в отсутствие конвекции.
Следовательно, в состоянии покоя разность температур 6 всюду тождествен-
тождественно равна нулю.

106 Глава V •
тепловой конвекции в обычных экспериментальных условиях,
приводят к следующим безразмерным уравнениям1):
1) уравнение Навье — Стокса - . .
Pr~' (If + v ' Vv) = - Vp'+ 8Я, + V2v; A3a)
2) несжимаемость жидкости (если все скорости малы по
сравнению со скоростью звука)
' , V-v = 0; A36)
3) распространение тепла
^ - " A3в)
где р — гидростатическое давление, X—единичный вектор, на-
направленный вдоль' вертикальной оси (направления силы тя-
тяжести), а Рг — отношение кинематической вязкости v жидкости
к ее температуропроводности:
Эта безразмерная величина, называемая числом Прандтля, за-
зависит от природы жидкости и (в меньшей степени) от темпе-
температуры жидкости.
В уравнениях эволюции существуют два нелинейных члена:
v-Vv (в уравнении A3а)] и v-V0 [в уравнении A3в)]. Их от-
относительная значимость зависит от значения Рг, Если число
Прандтля Рг мало (как, например, для жидкого гелия, где
Рг <; 1), то доминирует член v-Vv. Таким образом, следует
ожидать, что вторичные неустойчивости, которые развиваются
в жидкости, находящейся в режиме стационарной конвекции,
по существу имеют гидродинамическое происхождение. Qhh
обусловлены неоднородностью поля скоростей и возникают
вследствие естественной тенденции поля гидродинамических
скоростей к однородности. С другой стороны, в жидкостях
с большими числами Прандтля, таких, как некоторые силико-
силиконовые масла (Рг > 100), член vV8 становится доминирующим
нелинейным членом и вторичные неустойчивости имеют глав-
главным образом тепловое происхождение. Между этими двумя
') V означает оператор дифференцирования по пространственным коорди-
координатам в поймоугольной системе координат:
а точкой обозначено екалярное, или внутреннее, произведение.

¦ Три примера динамических систем 107
крайностями существуют такие жидкости, как вода (Рг = 5—10
в зависимости от температуры), в которых гидродинамические
и тепловые эффекты, конкурируя, порождают боле сложные ре-
режимы ').
V, 3.4. Эксперимент
Для данной жидкости при выбранном аспектном отношении
единственным унравляющим параметром остается число Рэлея
Ra. Поскольку оно пропорционально 6Г, изменяя разность тем-
температур, экспериментатор может либо вызывать переход от од-
одного динамического режима к другому, либо изменять относи-
относительную значимость нелинейных эффектов в рамках данного
режима. Выбор экспериментальной установки диктуется жид-
жидкостью, которая также определяет временной масцггаб конвек-
конвективных явлений. Существует огромная разница между исследо-
исследованием поведения жидкого гелия при температурах порядка не-.
скольких градусов Кельвина и исследованием воды, ртути или
силиконовых масел при комнатной температуре, т. е. при 300 К-
Мы не будем вдаваться в подробности относительно устройства
ячеек и способов контроля температуры. В табл. V. 1 сведены
Жидкость
Ртуть
Ртуть
Гелий ,
Гелийi
Силико-
Силиконовое
масло
Силико-
Силиконовое
масло
Г
2
4
3
2—3
2
2
, Условия
Магнитное
поле
Р = 0,3 МПа
Р= •
= 0,1— 0,5 МПа
V =
= 3-10~6m2/c
V =
Таблица 1
Рг
0,031
0,031
0,5
d,
см
0,8
0,7
0,125
0,4-0,8*0,125
38
130
1,25
2
7.1
К
273
273
3,5
[2,5;
4]
~300
~300
вгс, к (R
0,91
~ 1,3
2,5 • 10~3
~КГ3
~3- 10~г
~2-10~2
i
6
4
' 43
80 .
450
600
\
— 6
— 5,5
~0,1
~0,2
~13
^ 12
условия экспериментов, при которых получены результаты, при-
приводимые во второй части нашей книги.
*) Из педагогических соображений наблюдения, упоминаемые в нашей
книге, были выбраны из выполненных на ячейках с малыми аспектными
отношениями при очень малых или очень больших числах Прандтля.

108 Глава V
Переменные, подлежащие измерению — скорость v и 6 или
по крайней мере тесно связанные с ними свойства1). В опти-
оптически прозрачной среде лучшим методом определения локаль-
локальной скорости v в точке жидкости является лазерная доплёров-
ская анемометрия. Так как этот метод позволяет непосред-
непосредственно, измерить одну из динамических переменных, его
используют всюду, где только возможно. Однако к измерениям
такого типа примешивается экспериментальный шум, уровень
которого для некоторых целей'может оказаться чрезмерно вы-
высоким. Часто применяется и другой оптический метод с большим
отношением сигнал/шум. В основе его лежит тот факт, что гра-
градиент температуры в жидкости создает градиент показателя
преломления. Измерению подлежит угол отклонения луча света
из-за неоднородности показателя преломления. Такое измере-
измерение технически легко осуществимо и позволяет получать сиг-
сигнал, соответствующий среднему градиенту температуры, прой-
пройденному лучом света на всем пути в жидкости. Таким образом,
результат, измерения имеет лишь полулегальный лара^ср и
связан с переменной 0 довольно сложным образом, но тем не
менее в некоторых случаях оказывается весьма полезным. Ис-
Использование измерений отклонения света ограничено прозрач-
прозрачными средами с достаточно большой вязкостью, поскольку
только в таких жидкостях могут существовать значительные
градиенты температуры и, следовательно, показателя прелом-
преломления. '
В непрозрачных жидкостях (ртути, жидком калии и т. д.)
оба предыдущих метода становятся неприменимыми. От идеи
оптического измерения локальной скорости v приходится отка-
отказаться. С другой стороны, невозможно ввести датчик темпера-
температуры (термометр, термистор, термопару и т. д.), не возмущая
движения жидкости. Невозмущающий датчик температуры
можно поместить только на границу слоя жидкости —на пла-
пластины. Но теоретически возмущение температуры 0 на границе
всегда равно нулю. Экспериментаторы решили эту Дилемму, по-
поместив болометры на поверхности пластин2). Такого рода де-
детектор измеряет тепловой поток, а не возмущение темпера-
температуры 0. Тем не менее получаемая информация представляет
большую ценность и может служить основой анализа динами-
динамического поведения жидкости в зависимости от числа Рэлея.
') Производимые измерения должны быть невозмущающими, т.е. не долж-
должны оказывать воздействие на наблюдаемые явления. Этому очевидному тре-
требованию трудно удовлетворить, особенно вблизи порога неустойчивости.
2) Болометр — это измерительное устройство, электрическое сопротивле-
сопротивление которого сильно зависит от температуры. Включая болометр в мостик
Уитстона, можно с высокой точностью измерять изменения температуры.

Три примера динамических систем
109
Ячейка. РБ
Рис. V. 8а. Экспериментальное определение сечений Пуанкаре при конвекции
Рэлея — Бенара; схема установки. Конвективный режим считается дважды
периодическим; осцилляторы тепловой конвекции обозначены цифрами 1 и 2.
Сквозь жидкость проходят два пучка света — по одному пучку вблизи каж-
каждого осциллятора. На осях пучков находятся два фотодиода Pt и Рг- Не-
Нестационарный градиент температуры, создаваемый осцилляторами тепловой
конвекции, приводит к отклонению пучков света, модулируя фототок в фото-
фотодиодах Рх и р2. Пусть ДГ и ДГ'— сигналы, измеряемые фотодиодами Pi и
Рг, a ft и f2 — характерные частоты осцилляторов 1 и 2. Тогда модуляции
величины ДГ с частотой ft сильнее, чем с частотой f2, а модуляции величины
hi' с частотой /2 сильнее, чем с частотой /j.
Из работы М. Дюбуа.
Графопостроитель
к
AT л
/1 1 ft
1
. г
' 1 '
j !
¦ 1 1
/Г\
\IV
i
i
l
I
l/l
J
i
1
l
«r
Рис. V. 86. Экспериментальное определение сечений Пуанкаре при конвекции
Рэлея — Бенара. Суть метода. В трехмерном фазовом пространстве можно
ввести координаты ДГ, Д*Г и ДГ', где Д'Г производная величины ДГ по
времени, получаемая при помощи аналоговой схемы. Проекции траекторий на
это пространство мы получаем, подавая сигналы ДГ и Д'Г на вход двух-
координатного самописца.
При построении сечений Пуанкаре сигнал ДГ' служит опорным: когда он
достигает заданного значения К, опускается перо самописца и регистрируется
точка с координатами (ДГ, Д'Г). В тех особенно благоприятных случаях,
когда оказывается возможным зарегистрировать сигнал ДГ', определяющийся
-л основном вторым осциллятором, используется тот же стробоскопический
метод, что и в эксперименте с вращающимся магнитом: за каждый период
изменения ДГ' регистрируется одна точка с координатами (ДГ, Д'Г).
Из работы М. Дюбуа. .

110 , Глава V
Независимо от метода измерения сигнал затем анализирует-
анализируется методами, описанными в гл. III и IV: с помощью преобразо-
преобразования Фурье, исследования тополо.гии аттрактора. Обработка
сигналов осуществляется с помощью либо цифровых, либо ана-
аналоговых вычислительных средств (см. рис. V. 8а и 86).
V.4. РЕАКЦИЯ БЕЛОУСОВА —ЖАБОТИНСКОГО
V. 4.1. Краткая история химических осцилляторов
При изучении Окисления лимонной кислоты броматом ка--
лия, катализируемого окислительно-восстановительной парой
Се^/Се4*, русский биохимик. Б. П. Белоусов случайно') заме-
заметил концентрационные колебания, проявлявшиеся в регулярном
изменении окраски реакционной смеси от бледно-желтого до бес-
бесцветного. Однако, когда Белоусов опубликовал свою работу
в 1958 г. (через восемь лет после открытия), реакции такого
рода отнюдь не были неизвестными. В 1921 г. Брей сообщил
о том, что разложение перекиси водорода в присутствии ионов
Юз происходит в колебательном режиме. И в этом случае на-
наблюдение носило случайный характер и было датировано 1917 г.
Несмотря на необычность обеих реакций (большинство химиче-
химических реакций протекают' монотонно2), оба открытия колебатель-
колебательных гомогенных реакций в жидкостях не привлекли к себе долж-
должного внимания. В начале 60-х годов молодой советский химик
А. М. Жаботинский посвятил свою диссертацию исследованию
механизма и свойств реакции, открытой Белоусовым. Но лишь
после достижений в термодинамике необратимых процессов и
открытия колебаний на клеточном и метаболическом уровнях
в биологии важность открытия Белоусова была оценена по до-
достоинству. G тех пор исследования этой реакции ведутся во все
возрастающих масштабах как в химии, так и в биохимии.
Реакционная среда БЖ бесспорно является наиболее изу-
изученной из колебательных химических реакций. Поведение реак-
реакций БЖ весьма необычно и во времени, и в пространстве. В од-
однородной смеси реагентов БЖ пространственная структура воз-
возникает за несколько минут либо в виде цилиндрических, колец
1) Более подробные сведения об открытии Б. П. Белоусова и его статью
читатель сможет найти в сборнике «Колебания и бегущие волны, в химиче-
химических системах». — М.: Мир,-1988. — Прим. перев.
2) Линейная термодинамика необратимых процессов показывает, что ко-
колебания не могут происходить относительно равновесного .состояния. Но з
нелинейной области из второго начала термодинамики не обязательно следует
монотонная эволюция. Поэтому вдали от равновесия ничто не запрещает ре-
реакций быть колебательной из-за диссипации имеющейся химической энергии.

Три примера динамических систем 111
в пробирке, либо в виде концентрических круговых волн в тон-
тонком слое. Из дальнейшего нам станет ясно, почему эта необыч-
необычная реакция вызвала столь большой интерес в научном мире.
V. 4.2. Схема экспериментальной установки
Реагенты БЖ— серная кислота H2SO4, малоновая кислота
СН2(СООНJ или другие органические восстановители, бромат
натрия ЫаВЮз, сульфат церия Сe2(S04K или другие катализа-
катализаторы окислительно-восстановительных реакций — легко До-
Доступны коммерчески. Достаточно приготовить'их водный рас-
раствор и смешать в надлежащих концентрациях, чтобы возникли
знаменитые колебания. Добавление окрашенного индикатора
окислительно-восстановительных процессов позволяет визуаль-
визуально наблюдать регулярные изменения окраски. Например, если
в качестве катализатора выбран ферроин, то окраска раствора
изменяется от красной до синей. Приводим состав смеси [в мо-
молях на литр (Л!)]; позволяющей наблюдать колебания при ком-
комнатной температуре:
-H2S04l,5Af,' СН2(СООНJ0,002М,
' ЫаВгОз 0.08М, Се2EО4K 0,002 М,
' Ферроин 3-10~4М.
Количественные измерения налагают дополнительные требо-
требования. Прежде всего чтобы получить характеристики динамиче-
динамического режима, его требуется поддерживать в течение достаточно
долгого времени. С точки зрения практической реализации это
означает, что необходимо использовать открытый реактор с не-
непрерывным подводом реагентов и отводом продуктов реакции.
Для того чтобы концентрации реагентов были постоянны и рав-
равномерно распределены по реакционному общему, смесь необхо-
. димо быстро и интенсивно перемешивать. Наконец, так как ско:
рость химических реакций чувствительна к температуре, необ-
необходима терморегуляция реактора. За протеканием реакции
экспериментаторы следят, измеряя какое-нибудь свойство среды.
На рис. V. 9 показана принципиальная схема установки для
эксперимента БЖ. Реагенты БЖ поступают из резервуаров в ре-
реактор по трем трубам. Мгновенное состояние среды измеряется
с помощью потенциометрии или спектрофотометрии. Сигнал от
детекторов (электродов или спектрофотометра) усиливается и
после дискретизации через регулярные интервалы времени пре-
преобразуется в цифровую форму. Компьютер осуществляет управ-
управление экспериментом и хранит в памяти результаты последова-
последовательных измерений. Файл данных может вмещать сотни тысяч

112
Глава V
значений X{i) для последующего анализа данных с помощью
различных методов: преобразования Фурье, фазового портрета,
сечения Пуанкаре и т. д.
Динамическими переменными в этой системе являются мгно-
мгновенные концентрации некоторых веществ, измеряемые с по-
Реактор
Расходомеры
Перистальтичес-
Перистальтические нсссосы
¦ Термостат
Цетектор
Слив
излишков
смеси.
{Усилитель
АЦП
Компьютер
Емкости с реагентами
Рис. Y. 9. Схема 'экспериментально!"! установки ллг. с.сслсдовзг.ия динамиче-
динамического поведения химической реакции. Динамический режим (стационарный,
периодический или апериодической) поддерживается в течение нужного вре-
времени в открытом реакторе с помощью системы питания, создающей на входе
в реактор постоянный поток с надлежащим соотношением реагентов. На-
Наблюдение за протеканием реакции ведется спектрофотометрическим или по-
тенциометрическим методом. Контроль за параметрами эксперимента осу-
осуществляется с помощью компьютера, который помимо этого производит
выборку сигнала в реальном времени и записывает ее в память для после-
последующей численной обработки (например, для вычисления преобразований
¦Фурье, сечений Пуанкаре и т. д.). Реагенты указаны для реакции Белоусо-
ва —— /Каботпнекого.
Из работы К.. Видзля, С. Башляра к А. Росси.
мощью потенциометрии или спектрофотометрии, В области при-
применимости уравнения Нернста разность потенциалов между эта-
эталонным и измерительным электродами пропорциональна лога-
логарифму концентрации, а по закону Бэра — Ламберта оптическая
плотность пропорциональна самой концентрации. Во "избежание
«смешанной» информации, отражающей вариацию концентра-

Три примера динамических систем 113
ций нескольких реагентов, часто используют электроды, обла-
обладающие специфической чувствительностью к определенному ве-
веществу и измеряющие только его концентрацию (например, кон-
концентрацию иона Вг~). Аналогично производят измерение опти-
оптической "плотности на 340 нм — длине волны, на которой в реак-
реакционной среде БЖ заметное поглощение наблюдается только
У Се4+. .
V. 4.3. Уравнения эволюции
Химическую реакцию можно рассматривать как последоваг
тельность элементарных стадий, которые символически можно
представить в виде .
где i, /=1, ..., L — индекс L реаге'нтов; r = l, ...,*/? —
индекс R элементарных стадий; Xt — реагенты, X't — продукты;
vir — стехиометрический коэффициент i-ro вещества в г-н
стадии; kr — константа скорости r-й стадии.
Это точное описание содержания табл. V. 2, в которой со-
собраны сведения о механизме реакции БЖ,
Таблица V. 2. Механизм Филда — Кёрёша — Нойеса реакции
Белоусова — Жаботинского
НОВг + Br~ + Н+~ ч=>:
НВгО2 + Вг~ + Н4" ¦—>
ВгО3" + ВГ + 2Н+ ¦—v
2НВгО2 —у
ВгО- + НВгО2 + Н+ ч=±:
ВгО" + Се" 4-Н+ ^=t
Вг2 4- ОН2(СООНJ —>
6Се<+ 4- СН2(СООН}2 4- 2Н2О —*-
4Се4+ 4- ВгСН(СООНJ 4- 2Н2О »-
Нг„ 4- НГПГГн *.
Вг2 4- Н2О,
2НОВг
НВгО2
ВгО; 4
2ВгО2"
НВгО2
4- НОВг,
- НОВг + Н\
4- Н2О,
+ Се4\
ВгСН(СООНJ 4- Вг" 4- Н+,
6Се3+ -
4Се3+ -
2ВГ 4-
f НСООН + 2СО2 4- 6Н+,
h НСООН 4- 2СО2 + 5Н+ 4- Вг"
СО2 4- 2Н+.
и гомогенной среде при постоянном объеме вариации моляр-
молярных концентраций [Xi] реагентов, возникающие вследствие

114 Гляня V
реакции, удовлетворяют уравнениям
dt
r=l <
Если реакция происходит в открытом реакторе объемом V, пи-
питаемом потоком с объемным расходом /, то каждый реагент
попадает в реактор с концентрацией [Х]о и покидает реакцион-
реакционную зону через отводную трубу с мгновенной концентрацией
[X]. Поэтому в предыдущее уравнение мы должны ввести ад-
аддитивный член," учитывающий проточность реактора:
1=1 L.
, A4)
Эта система дифференциальных уравнений обладает некоторым
сходством с уравнением неустойчивости РБ. Уравнения A4) не-
нелинейные, первого порядка по времени. Нелинейность обуслов-
обусловлена взаимодействием реагентов (Дг №]v'r). Управляющих па-
параметров можно использовать, несколько, один из них, а именно
температура, от которой зависят константы скоростей kr", явно
не входит в уравнения A4). Остальные легко изменяемые па-
параметры— это концентрации любого из реагентов на входе
№]0. Наконец, что наиболее важно, отношение \i = (J/V) также
можно варьировать, изменяя объемный расход ) с помощью ре-
регулируемых насосов. Физический смысл параметра |л ясен: это
величина, обратная времени наполнения реакционной "'омы ре-
реактора, или среднего времени пребывания реагента в реакторе.
Математически-ц входит в каждое из L уравнений как коэффи-
коэффициент при линейном члене, описывающем проточность реактора.
Изменяя ц, мы можем по своему произволу изменять относи-
относительную значимость линейных (транспортных) и нелинейных
(химических) эффектов. Именно поэтому \i частр выбирают в ка-
качестве управл'яющего параметра при поиске бифуркаций между
различными динамическими режимами. Если параметр |л доста-
достаточно велик и член, описывающий взаимодействие реагентов,
доминирует над членом, описывающим проточность реактора, то
поток A4) становится практически линейным и допускает три-
тривиальное стационарное решение
[Xi\ ~ l/Ti/Jo, i. = 1, .. ., L,
практическое значение которого очевидно: при больших расхо-
расходах реагенты остаются в реакторе слишком мало и не успевают

ическкх систем
прореагировать с другими реагентами. Нестационарные режимы
могут наблюдаться и при умеренных значениях J'.
Мы могли бы пойти дальше и выписать в-явном виде урав-
уравнения A4) для реакции БЖ. Но это вряд ли полезно, поскольку
с динамической то^ки зрения, знания структуры уравнений
вполне достаточно. Кроме того, механизм любой реакций яв-
является следствием предположений, значительное число которых
не допускает прямой проверки. Механизм реакции БЖ, предло-
предложенный в 1972 г. Филдом, Кёрёшом. Нойесом, и включающий
в себя тринадцать реакций, в которых участвуют четырнадцать
реагентов, не является исключением (см. табл. V. 2). Для изу-
изучения различных динамических режимов, периодических и хао-
хаотических, с помощью численного моделирования на основе со-.
ответствующих дифференциальных уравнений можно восполь-
воспользоваться упрощенным вариантом модели ФКН, состоящим из
пяти стадий и включающим в себя только четыре реагента.
ЛИТЕРАТУРА
Berge P., Experiments on hydrodynamics instabilities and the transition to tur-
turbulence. — In: Lectures Notes in Phvsics, 104, p. 189 A979).
Berge P., Dubois M., Study of Rayleigh — Benard convection properties through
optical measurements. — In: Scattering Techniques Applied to Supramole-
cular and Nonequilihrium Systems, eds. S. H. Chen, B. Chu, R. Nossal,
Plenum Publishing Corporation, p. 493 A981).
Croquette V., Determinism et chaos, Pour la science, 62, p. 62 A982).
Croquette V., Poitou C, Cascades de dedoublements de periode et stdchasticite
a grande echelle des mouvements d'une boussole, Compt. Rend, /de ГАса-
demie des Science de Paris, C292, p. 1353 A981).
Dubois M., Hxperimental study of transition to turbulence in convective sys-
systems, cours de l'lnstitut von Karman de dynamique des lluides, se.ne
1982—07 (Bruxelles). ¦ "
Dubois Al, Berge P., Experimenatl evidence for the oscillators in a convective
biperiodic regime, Physics Letters, 76A, p. 53 A980),.
Vidal C, Roux I.-C, Comment nait la turbulence, Pour la Science, 39. p. 50
A981).
Vidal C, Bachelart S., Rossi A., Bifurcations en cascade conduisant a la tur-
bubence dans la reaction de Belousoy — Zhabotisky, Journal de Physique,
43, p. 7 A982). ,

ЧАСТЬ 2
... К ХАОСУ
ВВЕДЕНИЕ. ВРЕМЕННЫЙ ХАОС
I В ДИССИПАТИВНЫХ СИСТЕМАХ
I. АСИМПТОТИЧЕСКОЕ ПОВЕДЕНИЕ ДИССИПАТИВНОИ СИСТЕМЫ
Большинство понятий и идей, необходимых для описания и
понимания нестационарного поведения динамических систем,
бцло введено нами в первых пяти главах. Сформулируем наи-
наиболее существенные моменты. Мы намереваемся анализировать
эволюцию произвольных диссипативных систем. Эти системы по
предположению детерминированные, так как их описание до-
достигается с помощью либо непрерывного автономного потока
либо .отображения с дискретным временем
где X — вектор кзгЕ^_1т ^0). Функция F содержит один или
несколько управляющих параметров^^выражающих связи, на-
налагаемые внешним миром на исследуемую систему. Связью
может быть, например, интенсивность магнитного поля, число
Рэлея или среднее время пребывания в реакторе. Варьируя уп-
управляющий параметр, мы получаем возможность изменять пове-
поведение системы. В ходе измерения управляющий параметр под-
поддерживается (или предполагается) постоянным.
Нас главным образом интересует долговременное поведение
диссипативных систем. Мы предполагаем, что выполнены неко-
некоторые «технические» условия (в действительности удовлетво-
удовлетворить им весьма трудно даже в такой простой модели, как урав-
уравнение Ван дер Поля), при: которых траектории остаются в огра-
ограниченном объеме фазового пространства.
Если поток диссипативный, то в этом конечном объеме тра-
траектории сходятся к аттрактору — компактному множеству в фа-
фазовом пространстве, инвариантному относительно потока или
отображения. Сам аттрактор имеет нулевой объем, но.его об-
область притяжения имеет конечный (или даже бесконечный)
объем. Область притяжения мы определяем как множество на-
начальных условий, таких, что выходящие из него траектории схо-
сходятся к аттрактору. Поток может иметь несколько различных

временный хаос в ч.чссиративных системах ¦ ¦ •
аттракторов, у каждого из которых имеется своя область при-
притяжения. Были даже построены отображения, имеющие беско-
бесконечное (счетное) множество аттракторов. Мы ограничимся рас-
v^Mvy I px^hKt-ivi \^tii у чал kj^ukji. u ai ipuiviujju.
Исследование аттрактора означает существенное упроще-
упрощение, так как мы можем пренебречь переходными эффектами и
сосредоточить внимание на асимптотическом режиме. Разу-
Разумеется, такая процедура неприменима к анализу гамильтоновых
систем, лишенных по определению трения: понятие аттрактора
чуждо им1). Таким образом, соображения, развитые во второй
части нашей книги, относятся исключительно к диссипативным
системам. Об этом не следует забывать.
Наш анализ будет состоять из двух частей:
1) определения простейших типов аттракторов;
2)-. каталогизации способов перехода между аттракторами.
Цель, которую мы ставим перед собой, состоит в том, чтобы
понять, как возникают и какими свойствами характеризуются
все типы временной эволюции, какие только встречаются, в том
числе и режимы, кажущиеся на первый взгляд совершенно бес-
беспорядочными. *w~^_™-^_™.,.-
Л\.
ПРОСТЕЙШИЕ АТТРАКТОРЫ
Напомним кратко три типа аттракторов, уже описанных
в первой части, и основные свойства соответствующих динами-
динамических режимов.
Аттрактор-точка представляет собой решение, не зависящее
от времени, т. е. стационарное состояние. В этой ситуации нет
никаких неясностей, так как система не эволюционирует.
Решение, периодическое по времени, соответствует предель-
предельному циклу, характеризуемому своей амплитудой и периодом.
Спектр Фурье такого решения содержит одну основную частоту
'и, возможно,- некоторое число гармоник (в зависимости от фор-
формы колебаний). Решение для потока всегда представимо в виде
ряда Фурье: если состояние системы в данный момент времени
известно, то ее состояние в любой последующий момент времени
предсказуемо.
'¦) Вряд ли нужно говорить о том, что сказанное отнюдь не означает,
будто гамильтонсвъ! системы пс представля'ют интереса. Мы утгермсг-ясм
лишь, что гкмильтоновы системы не имеют аттракторов. Аналогичное заме-
замечание можно было бы сделать и относительно притяжения: в отсутствие за-
затухания малая флуктуация никогда ие обращается в нуль. Это верно, на-
например, для устойчивости нелттееппатипнь'х (нег-ччкпх) течений жчл'-гстп:
линейная устойчивость таких течений не позволяет сделать скол1::о":'будь
далеко идущие выводы относительно их устойчивости на больших iih;cur.daax
времени относительно флуктуации конечной амплитуды, даже малых. Этот
важный Факт чясто \тпускятот ич punv

третьим типом аттрактора, также относительно простым, яв-
является Topv Гг X''^> 2), соответствующий квазипериодическому
режиму с. г'независимыми основными частотами1), В этом слу-
случае спектр Фурье также состоит из Множества линий, частоты
которых являются линейными комбинациями основных частот.
Хотя решение для потока, вообще говоря, не представимо в виде
обычного ряда Фурье, мы можем тем не менее, исходя из на-
начального состояния, вычислить состояние системы в любой по-
последующий момент времени.
УIII. ПСЕВДООПРЕДЕЛЕНИЕ ХАОСА
Поскольку строго научного определения терминов «хаос» и
«хаотический» не существует, мы будем считать их синонимами
некоторых типичных свойств2). Условимся называть динамиче-
динамический режим хаотическим, если его спектр мощности содержит
непрерывную часть (широкую полосу) независимо от возмож-
возможного наличия пиков. Мы можем также воспользоваться крите-
критерием: автокорреляционная функция временного сигнала должна
иметь конечный носитель, т. е. обращаться в нуль вне конеч-
конечного интервала, времени. И в том и в другом случае в основе
лежит одно и то же понятие: потеря сигналом памяти о самом
себе. Это означает, что знание состояния системы в течение
сколь угодно продолжительного интервала времени не позво-
позволяет предсказывать дальнейшую эволюцию системы. Тем самым
мы признаем непредсказуемость3) тем качеством, которое опре-
определяет хаос. Такое определение хаоса чисто прагматическое;
ему недостает строгости, и оно неизбежно таит в себе неодно-
неоднозначность. Между предсказуемостью и непредсказуемостью не
') Торы Т с г > 3 теоретически несомненно могут существовать, однако
относительно их структурной устойчивости, без которой их невозможно на-
наблюдать экспериментально, имеются сомнения. Мы называем свойство струк-
структурно устойчивым, если оно способно «устоять» против малых вариаций па-
параметров потока (обычная устойчивость означает способность «сопротив-
«сопротивляться» малым вариациям начальных условий). Тем не менее взаимосвязь
между наблюдаемостью и структурной устойчивостью свойства не является
абсолютной. Свойство «структурной неустойчивости» (как и свойство отсут-
отсутствия затягивания частот в режиме с двумя периодами) может быть наблю-
наблюдаемым, если сущес?вует отличная от нуля вероятность возникновения этого
свойства при произвольном выборе параметров (см. приложение В).
2) То же самое в полкой мере относится и к терминам «турбулент-
«турбулентность» и «турбулентный». Мы отдаем предпочтение термину «хаос», поскольку
пространство не входит в интересующие нас здесь проблемы, а термин «тур-
«турбулентность» неизбежно рождает ассоциации с пространственно-временным
поведением нерегулярных гидродинамических течений.
3) ьолее точно термин «непредсказуемость» употребляется в том смысле,
что точное знание эволюции системы в прошлом в течение сколько угодно
продолжительного интервала времени не помогает предсказывать ее после-
последующую эволюцию за пределами некоторого ограниченного интервала вре-
времени.

существует разделяющей их четкой границы, поэтому остаются
открытыми такие вопросы:
1) В каком масштабе времени должен быть предсказуемым
поток?
2) Насколько точным должно быть предсказание?
3) Допустимо ли статическое предсказание?
Различие между теоретической и практической невозмож-
невозможностью предсказания также проблематично. Но при нынешнем
состоянии знаний было бы преждевременным пытаться вносить
какие-либо уточнения. ч
IV. СТРАННЫЕ АТТРАКТОРЫ
какого рода аттрактор связан с режимом, спектр Фурье ко-
которого содержит-широкую полосу? Советский физик Л. Д. Лан-
Ландау впервые попытался ответить на этот вопрос в 1944 г. Стре-
Стремясь объяснить, каким образом в жидкости происходит пере-
переход- от ламинарного течения к турбулентному при увеличении
числа Рейнольдса Re (управляющего параметра ц), Ландау
выдвинул следующие идеи, ныне известные как теория турбу-
турбулентности Ландау. Выше первого порога неустойчивости ско-
скорость жидкости, бывшая ниже порога постоянной по времени
(ламинарное течение),, становится периодической: скорость мо-
модулируется с определенной частотой /ь При дальнейшем уве-
увеличении числа Рейнольдса Re периодический режим в свою
очередь теряет устойчивость. Появляется вторая частота /;,, не-
несоизмеримая с /i и устанавливается квазипериодический режим.
Продолжая этот ход рассуждений, мы ожидаем последова-
последовательного появления других частот f^,, f4, • • • , fr путем деста-
дестабилизации все большего числа колебательных мод. В резуль-
результате при достаточно больших г получается турбулентный по-
поток1). А поскольку различие между спектром Фурье, состоящим.
'•) Рассматривая произвольную фазу, входящую в описание жидкости
вместе с каждой хаарктеристической частотой, как одну степень своб:ды и
используя колмогоровскую теорию турбулентности при подсчете чисЛа степе-
степеней свободы турбулентного течения. Ландау показал, что в пределе при
г->оо непрерывный спектр соответствует пределу бесконечно большого числа.
Рейнольдса Re (т.е. нулевой диссипации). Хотя теперь теория турбулентно-
турбулентности Ландау не считается точной, определение числа степеней свободы турбу-
турбулентного течения (при больших Re) остается нерешенной проблемой. При
таком подходе «число степеней свободы» имеет следующий конкретный смысл.
Пусть Х\ ;=г Я2 + Я3 ^ . .. будет убывающая (не но абсолютной величине, а
по алгебраическим значениям) последовательность показателей Ляпунова (ем.
приложение Б) рассматриваемой динамической системы. Тогда ее числом
степеней свободы называется максимальное число п показателей, таких, что
1-1

¦ведение
iij многих близких инков, и непрерывным спектром носит чисто
теоретический характер, аттрактор турбулентного потока дол-
должен быть тором Тг достаточно большой размерности г.
Следствием из этого соблазнительно простого предположе-
предположения является то, что хаотическое поведение может наблюдаться
только у систем с большим числом степеней свободы, поскольку
размерность фазового пространства должна быть больше раз-
размерности аттрактора. Но, как мы знаем сегодня (главным об-
образом из численного моделирования трехмерных течений), та-
такой вывод неверен:. трех степеней свободы (в указанном выше
смысле) достаточно для возникновения хаотического режима.
Прогрессом в этом круге проблем мы обязаны Рюэлю и
Такенсу, которые в 1971 г. ввели аттракторы, топологически от-
отличные от тора и названные странными аттракторами1), и щ-
казали, что такие аттракторы играют важную роль в физиче-
физических проблемах, в том числе и в гидродинамической турбулент-
xiocTii. Термин «странный аттрактор» указывает на необычные
свойства таких аттракторов, из которых наиболее важным яв-
является чувствительная зависимость от начальных условий
(ЧЗНУ). Вследствие ЧЗНУ любые две первоначально близкие
траектории на аттракторе в конце концов расходятся. Более
того, расхождение траекторий (усредненное по коротким интер-
интервалам времени) возрастает со временем экспоненциально.
На рис. 1 схематически иллюстрируется свойство ЧЗНУ. Мы
видим, что две траектории, первоначально почти неразличимые,
со временем не имеют ничего общего между собой. Обращение/
в нуль автокорреляционной функции, широкополосный спектр
Фурье и внутренняя непредсказуемость системы — все это след-
следствия ЧЗНУ. В частности, ясно, что малейшая ошибка или не-
неточность в задании начального условия не позволяет нам ре-
решить, по какой траектории пойдет эволюция системы, и вы-
1) В действительности работы, описывающие по крайней мере два таких
аттрактора, были опубликованы Рикитаке A958) и Лоренцом A963) еще до
появления статьи Рюэля и Такенса, но не привлекли к себе должного внима-
внимания. Приложение Г посвящено подробному описанию модели Лоренца. Рики-
Рикитаке и Аллен предложили модель для объяснения геофизического динамо —
опрокидывания земного магнитного дииильною Момента за геологические
масштабы времени. Их простая модель показала, что высшие случайное
опрокидывание магнитного диполя может быть результатом детерминирован-
детерминированного процесса. Она поставила под сомнение другие объяснения, связывавшие
опрокидывание магнитного диполя с такими внешними по отношению к ди-
динамике геомагнитного поля, явлениями, как катаклизмы, аномальная солнеч-
солнечная актиг;юсть. хаотические конвективные потоки в недрах Земли и т. д.
Ныне причина, обусловливающая опрокидывание магнитного диполя, по-преж-
по-прежнему остается загадкой, хотя общепризнаны удивительные регулярности в
траектории магнитных полюсов.

нуждает шраннчитьси статистическим предсказанием долгор;ч'-
менного будущего системы. Таким образом, мы приходим к ре-
результату, в высшей степени, нетривиальному: выводу о непред-
Рис. 1. Чувствительность к начальным условиям. На странном аттракторе две-
соседние "траектории всегда расходятся независимо от того, как близки они
были первоначально. Поэтому траектория, по которой реально происходит
эволюция системы, очень сильно зависит от начальной точки.
сказуемости поведения некоторых детерминированных потоков '
всего лишь с тремя степенями свободы!
\/ V. ПУТИ ВОЗНИКНОВЕНИЯ ХАОСА
Введение странных аттракторов оживило и революционизи-
революционизировало исследование хаоса и турбулентности. Убедительное
тому свидетельство — появившиеся после 1971 г. бесчисленные
статьи, книги и конференции по странным аттракторам. Но
само по себе понятие странного аттрактора не решает проблемы,
поскольку немедленно возникает другой вопрос: как возникает
странный аттрактор или, если угодно, как устанавливается хао-
хаотический режим? Какими маршрутами переходит динамическая
система от регулярного режима к хаотическому? Чтобы отве-
ответить на этот вопрос, нам необходимо перечислить различные-
возможные переходы между аттракторами — задача столь же
необходимая, как и идентификация аттракторов.
Б первой части мы подчеркивали тенденцию многих динами-
динамических систем к переходу в периодический режим независимо
от других характеристик этих систем. Сама по себе такая тен-
тенденция отнюдь не очевидна1). Хотя периодичность далеко не'
') Для объяснения такой относительной «универсальности» периодиче-
периодического режима привлекается двойной аргумент устойчивости. Во-первых, тео-
теория Флоке (см. ниже) показывает, что устойчивость периодической траекто-
траектории относительно малых изменений начальных условий определяется-

"еденне
псчерпывает всех возможностей, первый шаг к ответу на по-
поставленный выше вопрос состоит в выяснении условий, при ко-
которых периодический режим теряет устойчивость. Мы рассмот-
рассмотрим два метода: вб-первых, теорию Флоке линейной устойчи-
устойчивости периодических решений и, во-вторых, анализ нелинейных
эффектов, которые могут ограничить рост неустойчивости.
VI. ТЕОРИЯ ФЛОКЕ
В этом разделе иы напомним суть теории Флоке, кратко
изложенной в разд. IV. 3.1. Рассмотрим нелинейный автоном-
автономный поток в и-мерном фазовом пространстве, допускающий пе-
периодическое решение с периодом Т:
Чтобы определить, устойчиво или неустойчиво решение, до-
достаточно выяснить, как будет развиваться со временем малое
начальное возмущение 6Х ^эешёняя. Линеаризуя поток относи-
относительно периодической- тръекЩуШ, мы обнаруживаем,^ что на-
начальное условие Хо + 6Х FХ — бесконечное малое возмуще-
возмущение) отображается-в конце периода Т в вектор ХО+Л46Х, где
М — матрица m X tn, называемая матрицей Флоке.
Тем самым проблема линейной устойчивости периодического
решения сводится к исследованию собственных значений мат-
матрицы М. Прежде всего заметим, что эта матрица всегда имеет
одно собственное значение, равное единице, оно соответствует
смещению 6Х вдоль траектории. Это просто означает, что, оста-
оставаясь на предельном цикле, в конце периода мы в точности
возвращаемся в исходную точку — тривиальное заключение о
периодическом решении, из которого мы ничего не узнаем об
устойчивости этого решения. Ь1то действительно требуется, так
это выяснить, как ведут себя возмущения в направлениях, пер-
перпендикулярных траектории, как на рис. 2. Интуитивно ясно, что
если-собственные значения матрицы М зависят от вида пре-
некоторьиуШ неравенствами и не требует какой-либо исключительной ситуации.
Во-вторых, эта устойчивость в - обычном смысле подразумевает к тому же и
структурную устойчивость: если некий поток имеет линейно устойчивую пе-
периодическую траекторию (предельный цикл), то всякий близкий к нему поток
(получаемый практически изменением управляющих параметров) тоже имеет
устойчивый предельный цикл. Поэтому велика вероятность того, что заданная
диссипативная динамическая система обнаружит такое периодическое поведе-
поведение. Конечно, остается открытым вопрос о том, что происходит, когда перио-
периодическая траектория теряет свою устойчивость (в обычном смысле слова).
Далее мы увидим, что ответ на этот вопрос отнюдь не однозначен. Он
частично зависит от нелинейных эффектов в амплитуде флуктуации, стремя-
стремящихся удалить траекторию от ставшего неустойчивым предельного цикла,
когда последний еще существует.

¦ .;<v,Hiia i НШ1Ы\ ...
дельного цикла, то они не зависят от выбранной на предель-
предельном цикле начальной точки Хо. Так как через период вектор
Хо + 6Х отображается в Хп + Л46Х, решение линейно устойчиво,
если все собственные значения матрицы М расположены внутри
единичной окружности D на комплексной плоскости. В этом
случае все компоненты вектора 6Х, перпендикулярного предель-
предельному циклу, с каждом периодом уменьшаются. С другой сто-
стороны,-если (по крайней мере) одно из собственных значений
матрицы М лежит вне D, то 6Х непрерывно растет по крайней;
Предельный
цикл
Рис. 2. Основы теории Флокё. Чтобы определить устойчивость периодического-
решения (предельного цикла), необходимо проследить, как изменяется за
один период малое начальное смещение траектории 6Х. Б зависимости от
того, убывает ли начальное смещение по всем направлениям или возрастает
хотя бы в одном направлении, предельный цикл устойчив или, как показано на
рисунке, неустойчив. В данном примере начальное смешение 5Х выбрано
вдоль одного из собственных направлений в плоскости сечения S.
мере в одном направлении: траектория все дальше и дальше
отклоняется от предельного цикла, который поэтому неустойчив.
При непрерывном изменении параметра ц периодическое ре-
щение постепенно изменяется; то же справедливо и относительно
матрицы М и ее собственных значений. Каждому из собственных
значений на комплексной плоскости соответствует кривая, пара*
метризованная величиной ц. Потеря устойчивости периодическим
решением, сопровождаемая бифуркацией, происходит тогда, ког-
когда одна из этих кривых при изменении параметра \i выхо-
выходит из единичной Окружности. Существуют три') генерических
') В случае потока в Rz собственное значение может выйти из единич-
единичной окружности через точку +1, так как Траектория не может самопересе-
самопересекаться.1 Два других варианта пересечения единичной окружности возможны
только при т ^ 3 (см. гл. VI).

iinia-j пересечения единичной окружности (рис. 3): в точке — i.
н точке —1 и в двух комплексно-сопряженных собственных зна-
значениях а ± ,g. Домимо потери устойчивости каждый из трех ти-
лов пересечения по-своему сказывается на последующем поведе-
i
I
.lm
"^
0
^^
\f cc+ifi
p Re
Рис. 3. Три возможных случая пересечения
единичной окружности D собственными зна-
значениями матрицы Флоке.
нии системы в зависимости от нелинейности и в тесной связи с
типом соответствующих бифуркаций.
VII. ПЕРЕХОДЫ ПРИ ПОТЕРЕ ЛИНЕЙНОЙ УСТОЙЧИВОСТИ
При пересечении единичной окружности в точке +1 возни-
возникает бифуркация седло — узел (см. приложение А). Периодичен
ское решение не только становится неустойчивым, но полностью
исчезает. В области параметра чуть выше порога бифуркации
система переходит в режим, который называется перемежае-
перемежаемостью I типа. Он характеризуется фазами регулярного, по.чти
периодического поведения (ламинарные фазы), время от вре-
времени прерываемого фазами беспорядочного, «анархического»
поведения (турбулентные всплески).
Если собственное значение выходит из. единичной окруж-
окружности в точке —1, то бифуркация называется субгармонической
и может быть либо суперкритической; либо обратной. В случае
супер критической субгармонической бифуркации (см. гл. VIII)
новое устойчивое периодическое решение с удвоенным периодом
заменяет старое решение, которое становится неустойчивым.
Удвоение периода повторяется всякий раз, когда возникает но-
новое периодическое решение, что приводит к бесконечной после-
последовательности бифуркаций, называемой субгармоническим ка-
каскадом, заканчивающейся хаосом. С другой стороны, субкрити-
') «Генерический тип» здесь означает, что при малом изменении решения
(например, при изменении второго управляющего параметра у.') характер
пересечения не изменяется.

ческан иифуркация приводит к перемежаемости Ш iiina, i.uiu-
рая качественно напоминает перемежаемость I типа: длинные
фазы почти периодического поведения, время от времени пре-
прерываемые хаотическими всплесками. Однако тип III характе-
характеризуется монотонным увеличением амплитуды субгармоники на
протяжении почти периодической фазы из-за того, что нелиней-
нелинейные эффекты усиливают субгармоническую неустойчивость пре-
предельного цикла. Амплитуда возрастает с каждым колебанием.
Когда она превышает некоторое критическое значение, лами-
ламинарная фаза прерывается.
Наконец, неустойчивость третьего типа возникает, когда два
комплексно-сопряженных собственных значения а ± ф одно-
одновременно пересекают единичную окружность: это называется
бифуркацией Хопфа1). Если бифуркация Хопфа суперкритиче-
суперкритическая, то она приводит к устойчивому аттрактору вблизи пре-
предельного дикла, который становится неустойчивым (но все еще
существует). Этот аттрактор — тор Т~, на поверхности которого
л«жит новое решение, соответствующее квазипериодическому
режиму. Вторая суперкритическая бифуркация Хопфа может
порождать переход Т2-*-Т3, а в результате третьей (иногда
после второй) бифуркации возникает странный аттрактор. Если
бифуркация Хопфа субкритическая, то может встретиться дру-
другое явление, называемое перемежаемостью II типа. Глобальные
качественные особенности у перемежаемости II типа такие же,
как у I и III типов, за исключением того, что неустойчивости,
Точка'
пересечения
с единичной
окружностью
+1
а ± /р
Бифуркация
Седло — узел
Субгармоническая:
Нормальная
Обратная
Хопфа:
Нормальная
Обратная
Явление
Перемежаемость
1 типа
Субгармонический
каскад
Перемежаемость
III типа
Квазипериодичность
Перемежаемость
11 типа
Глава
IX
УШ
IX
УП
IX
1) Арнольд называет ее бифуркацией Пуанкаре — Андронова. Мы будем
придерживаться термина «бифуркация Хопфа», более распространенного в
западной литературе.

газвивающиеся в ламинарных фазах, имеют частоту, не связан-
связанную с основной частотой исходного цикла. Новая частота свя-
связана с отношением а/р для (а ± tp)—собственных значений,
пересекающих единичную окружность при бифуркации. Дина-
Динамический процесс, дающий начало новой ламинарной фазе
после турбулентного всплеска, слишком сложен, чтобы описы-
описывать его здесь, поскольку речь идет о потоке в шестимерном
фазовом пространстве, а это соответствует, сечению Пуанкаре
В следующей таблице сведены различные ситуации, описан-
описанные йыше, и указаны главы, в которых проводится их анализ.
VIII. СОВРЕМЕННЫЕ ПРЕДЕЛЫ ТЕОРИИ
Исследование переходов с потерей периодическим решением
линейной устойчивости является удобным способом классифи-
классификации ряда процессов, приводящих к установлению хаотического
режима. Однако следует соблюдать осторожность, и в этой связи
мы сделаем два замечания.
Во-первых, как мы уже указывал», периодическая эволюция
является не необходимым условием возникновения хаоса,
а всего лишь благоприятным обстоятельством. Необязатель-
Необязательность периодического режима убедительно подтверждается на
примере модели Лоренца.
Во-вторых, необходимо ясно сознавать ограниченность дан-
. ной теории в ее современном состоянии. Мы перечислили и
проанализировали три явления, ведущие к хаосу: квазиперио-
дичность, субгармонический каскад и перемежаемость. Но не
были указаны никакие необходимые или достаточные условия,
при которых возникают эти явления, на основе характерных
особенностей потока. В этом отношении симфония динамиче-
динамических систем остается незавершенной.

¦ ¦-¦ b A • ¦
СТРАННЫЕ АТТРАКТОРЫ
VI. 1. ДИССИПАЦИЯ И АТТРАКТОРЫ
VI. 1.1. Явление притяжения
Диссипативные динамические системы (а мы рассматриваем
только такие системы) характеризуются притяжением всех тра-
траекторий, проходящих через некоторую область фазового про-
пространства, к геометрическому объекту, называемому аттракто-
аттрактором,. Проиллюстрируем это на простом примере: маятник под
действием вынуждающей силы. Энергия, подводимая к маят-
,1шку извне, компенсирует затраты энергии и, таким образом,
диссипируется системой. Когда колебания маятника достигают
амплитуды/при которой энергия, подводимая за один цикл,
в точности равна энергии, диссипируемой за один цикл, уста-
устанавливается стационарное состояние. Режим периодический:
амплитуда колебаний постоянна, а траектория в фазовом про-
пространстве есть предельный цикл С (рис. VI. 1). В притягиваю-
притягивающем характере цикла мы убедимся, слегка сместив систему
с предельного цикла. Например, возмутим маятник толчком,
придав ему амплитуду 0i и скорость 0ь значительно превышаю-
превышающие максимальные значения Вт и 0т для предельного цикла.
По прошествии некоторого времени диссипация вынудит траек-
траекторию быстро приблизиться к предельному циклу С, на кото-
котором диссипация коменсируется подводимой энергией. Анало-
Аналогично временное торможение маятника, находящегося под дей-
действием вынуждающей силы, уменьшит амплитуду его колебаний
и скорость до В2 и 8г (рис. VI. 1), но затем траектория снова
приближается к С,1).
Сказанное о предельном цикле можно обобщить следующим
образом. В фазовом пространстве решения системы п обыкно-
обыкновенных дифференциальных уравнений
^ XgR",
') Последнее утверждение нуждается в уточнений: «наматывается» на С
любая траектория, исходящая из окрестности предельного цикла С, образую-
образующей его область притяжения (см. ниже).

Рис. VI. 1. Притяжение к предельному циклу С. Фазовое пространство опре-
определяется углом 9 между маятником и вертикалью и угловой скоростью
9 = dQ/dt. На рисунке показаны две траектории (выходящие из начальных
точек, не лежащих на предельном цикле), быстро сходящиеся к предельному
циклу.
Рис. VI. 2. Схематическое изображение аттрактора. А — аттрактор, В — его
область притяжения. Траектории, выходящие из начальных точек а, р, у и 6,
переносятся к аттрактору А потоком <р.

аттрактор. По определению ~-трактором ] называется лом-
пактное множеству в фазовом пространстве, обладающее сле-
следующими свойствами:
1) А инвариантен относительно действия потока, т. е.
фА = Л;
2) А имеет нулевой объем в «-мерном фазовом пространстве
(см. следующий разд.);
3) Л содержится в области В ненулевого объема, которая
является областью притяжения аттрактора. По определению
областью притяжения называется множество точек, таких, что
выходящие из них траектории при t—>-oo стремятся к А
(рис. VI. 2).
Мы видим, что аттрактор А есть асимптотический предел ре-
решений, начальные точки которых принадлежат его области при-
притяжения В. Заметим, что даже если А — простой геометриче-
геометрический объект, то В может иметь очень сложную форму.
VI. 1.2. Два следствия из сокращения площадей
Обратимся снова к примеру с предельным циклом, чтобы
исследовать две очень важные характеристики притяжения: по-
потерю памяти о начальных условиях и то, что из этого происте-
проистекает для размерности аттракторов.
Рассмотрим множество начальных условий на фазовой пло-
плоскости @,9), занимающее область размером Г (рис. VI. 3).
Вследствие диссипации поток приводит к сокращению площа-
площадей. Следовательно, поверхность Г под действием потока вы-
рождаетчл до линейного отрезка па аттракторе С. Стало быть,
происходит потеря информации относительно взаимного распо-
расположения точек, первоначально принадлежавших поверхности Г;
по достижении аттрактора информация утрачивается необра-
необратимо. Этот вывод опирается исключительно на сокращение
площадей и на одновременное существование аттрактора. Следо-
Следовательно, вывод остается в силе независимо от типа аттрак-
аттрактора. Именно поэтому информация о начальных условиях те-
теряется и в двоякопериодическом режиме, траектории которого
эволюционируют в фазовом пространстве размерности не
меньше трех и стремятся к тору Т2. Аналогичный вывод спра-
справедлив и для апериодических режимов, и для связанных с ними
аттракторов.
Потеря памяти о точных начальных условиях мы продемон-
продемонстрируем на примере с маятником. Сначала (т. е. вдали от пре-
предельного цикла) для задания состояния динамической системы
необходимы дре координаты 9,- и 0, а поэтому для описания
9 П. Берже и др.

системы требуется двумерное фазовое пространство, или поверх-
поверхность. После затухания промежуточных режимов и выхода на
асимптотический режим остается только одна траектория: кри-
кривая С. Для задания точки достаточно одной криволинейной
координаты вдоль С. Это иллюстрирует общий принцип: раз-
размерность d аттрактора меньше размерности п фазового про-
Рис. VI. 3. Сокращение площадей, связанное с притяжением. Площадка Г,
ограничивающая некоторое множество начальных условий, при достижении
аттрактора С вырождается в отрезок прямой.
странства, т. е. меньше числа степеней свободы динамической
системы'):
d <n.
Вычислим теперь, к каким количественным следствиям при-
приводит сокращение площадей'или, в более общем случае, объе-
объемов. Относительная скорость изменения объема V в фазовом
пространстве под действием потока, т. е. A/V) (dV/dt), опреде-
определяется производной Ли:
1 dV
дХ,
~дТ,
где Xi — i-я компонента вектора X (XgR"). В диссипативных
системах эта величина, усредненная по времени, отрицательна
') В дальнейшем мы увидим, что разность между d и я не обязательно
равна единице и даже целому числу.

.л служит мерой скорости сокращения'), из отрицательности'
производной Ли следует, что при t-*-oo, после того как траек-
траектории достигают аттрактора, любое множество начальных усло-
условий объемом V отображается в множество нулевого объема:
объем самого аттрактора равен нулю.
В трехмерном пространстве термин «объем» имеет свое
обычное значение (элемент пространства R3). Следовательно,
чтобы удовлетворять сформулированному выше условию а < п,
любой аттрактор должен иметь размерность меньше трех.
VI. 1.3. Непересечение фазовых траекторий
Траектории динамической системы в фазовом пространстве
не могут пересекаться2) (нигде, кроме особых точек, в которых
они «сливаются»). Это — неизбежное следствие детерминист-
детерминистского характера описания. В противном случае одно начальное
условие (ючка пересечения) порождало бы различные траек-
траектории или система по прохождении точки'пересечения могла бы
вести себя различным образом, т. е. поведение ее было бы не-
неопределенным. Такая неопределенность противоречила бы гипо-
гипотезе детерминистского описания системы конечной совокуп-
совокупностью обыкновенных дифференциальных уравнений.
На первый взгляд такое замечание может показаться до-
довольно бессодержательным, но в действительности оно приво-
приводит к весьма глубоким следствиям, в чем мы еще неоднократно
будем иметь случай убедиться, а пока выясним, что следует
из него для двоякопериодического режима. В этом случае ат-
грактор имеет вид тора Г2, который мы для удобства «развер-
«развернем» на плоскость. Такая операция топологически осуществима,
поскольку поверхность тора двумерна.
Разворачивание тора состоит из трех этапов, которые изо-
изображены на рис. VI. 4. На первом этапе мы разрезаем тор по
малой окружности {SC), разделяющей области С и С, и, разги-
разгибая, превращаем его в цилиндр. Проводя второй разрез вдоль
образующей АА' цилиндра и разворачивая еще раз цилиндри-
цилиндрическую поверхйость, получаем прямоугольник АА'В'В. Сторона
А.В (или А'В') соответствует малой окружности («меридиану»)
!) Как мы уже упоминали, для консервативных, или гамильтоновых, си-
систем объем сохраняется:
2) Для случая векторных полей об этом уже упоминалось в разд. 1.3.3.
9*

PC на тире, а сторона АА' (или БВ') — большой окружности
(«параллели») GC, Пусть ©: и ©2 — угловые частоты вращений
траекторий соответственно по большим и малым окружностям.
Полному обороту по большой окружности на прямоугольной раз-
развертке соответствует отрезок, параллельный большей стороне
АА' прямоугольника (при переходе из В в В' фаза изменяется
от 0 до 2я). Аналогично отрезок, параллельный меньшей сто-
с
в'
'А'
Рис. VI. 4. Развертка поверхности
тора Тг. Развертывание поверхности
тора производится в два этапа. Сна-
Сначала мы разрезаем тор по малой ок-
окружности (меридиану) С и распрям-
распрямляем его. В результате получаем
трубку, ограниченную окружностями
С и С' (первоначально на торе эти
две окружности совпадали). Затем
разрезаем трубку по линии АА'(ВВ')
и, развернув, получаем прямоуголь-
прямоугольник АА'В В (первоначально на торе
точки А, А', В' и В совпадали с од-
одной точкой /). О том, как изобра-
изображается фазовая траектория Т на та-
таком прямоугольнике, рассказано в
тексте.
2п В1
роне ВА прямоугольника, соответствует вращению по малой
окружности тора. Вообще любая фазовая траектория на торе
представляет собой некоторую комбинацию двух движений, и
на прямоугольнике ей соответствует некоторый прямолинейный
отрезок, например отрезок ТТ. Так как линии АВ и А'В' на
торе совпадают, продолжая таекторию!) за точку Т, мы
должны «перепрыгнуть» в точку Т\ и из нее провести прямую,
параллельную ТТ. Аналогично, дойдя до точки Т'2, мы должны
перепрыгнуть в точку Т'г и т. д. Вся траектория в таком пред-
представлении состоит из множества параллельных прямолинейных
') Естественно, что при монотонно возрастающем t движение по траек-
траектории происходит только в одну сторону.

этрезков. На рис. VI. 5 показан пример -фаектории, возникаю-
возникающей в случае, когда отношение частот oji/o>2 равно четырем.
Детерминированность запрещает разбегание траекторий: если
две траектории расходятся, то они непременно должны пере-
пересечься, как на рис. VI. 6, и число точек пересечения со временем
, cuzt
Рис. VI. 5. Представление траектории на развертке тора Г2. В этом примере
(ui/(»2 = 4. Из-за периодичности стороны прямоугольника нормированы к от-
отрезку [0, 2я].
возрастает. Следовательно, фазовый портрет такого типа, как на
рис. VI. 6, исключается.
Резюмируя, мы можем утверждать, что на притягивающем
тор« Т2 существуют тольке две возможности. Если отношение
Рис. VI. 6. Невозможность расхождения траекторий на Г2. Две расходящиеся
траектории должны были бы пересекаться, что невозможно.
toi/a>2 иррационально, то прямолинейные отрезки всюду плотно
покрывают прямоугольник (т. е. развертку тора): это двояко-
перкодический, или квазипериодический, режим. Если же
отношение o)i/©2 рационально, то траектория состоит из ко-
конечного числа параллельных прямолинейных отрезков, по-
последовательно проходимых с течением Бремени, как на
рис. VI. 5: режим периодический. Единственный тип структурной

неустойчивости, которой подвержен двоякопериодический ре-
режим,— затягивание частоты, или синхронизация'), означаю-
означающее, что отношение частот из иррационального становится ра-
рациональным. Следовательно, тор Р не может быть аттрактором
апериодического режима.
VI. 2. АПЕРИОДИЧЕСКИЕ АТТРАКТОРЫ
VI. 2.1. Характеристики хаотического режима
Резюмируем то, что было сказано в гл. III о хаотических ре-
режимах, с тем, чтобы вывести свойства аттракторов, связанных
с такими режимами..
В хаотическом режиме спектр мощности одной из перемен-
переменных X динамической системы содержит непрерывную часть, что
соответствует неупорядоченной и хаотической эволюции этой
переменной (рис. VI.7,а). Чтобы оценить интенсивность хаоса,
S(f)
С (г)
Рис. VI. 7. Апериодический режим, а — спектр мощности S(f); б—автокорре-
б—автокорреляционная функция С(т).
полезно ввести функцию, служащую мерой сходства значения
сигнала X в момент времени t с значением того же сигнала в бо-
более поздний момент времени t-\-x. Величина С(х), о которой
идет речь, получается путем усреднения большого числа произ-
произведений X (t) X (t + т):
и
^^ x)dt,
или, в более сжатых обозначениях,
Изменяя интервал т, мы строим величину С(х), которая назы-
называется временной автокорреляционной функцией, В гл. III было
') Подробнее об этом явлении см. в приложении В.

-рппные аттпакторы •->
показано, что по теореме Винера — Хинчина С (г) есть преоб-
преобразование Фурье спектра мощности. Если X(t)—константа, пе-
периодический или квазипериодический режим, то спектр мощ-
мощности состоит из отдельных пиков. Следовательно, С (т.) остает-
остается отличной от нуля при т->- оо.
Периодический (или квазипериодический) сигнал обладает
сходством с самим собой в более поздние моменты времени. Это
означает, что поведение системы предсказуемо, так как, зная
его поведение на достаточно большом интервале времени, мы
можем с помощью простого сравнения построить точный про-
прогноз на все последующие времена. С другой стороны, в хаоти-
хаотическом режиме, в котором спектр мощности обязательно содер-
содержит непрерывную часть, автокорреляционная функция С (т.)
Рис. VI. 8. Пример расхождения первоначально близких фазовых траекторий.
стремится к нулю при возрастающем х (см. рис. VI. 7, б). Авто-
Автокорреляционная функция имеет конечную протяженность: сход-
сходство сигнала с самим собой со временем ослабевает, а по исте-
истечении достаточно продолжительного большого времени исчезает
совсем. Следовательно, наблюдение сигнала X(t) на любом ко-
конечном интервале времени недостаточно для предсказания по-
поведения сигнала в будущем. Хаотический режим принципиально
непредсказуем в силу все возрастающей потери самоподобия.
В разд. VI. 1,1 мы уже встречались с потерей памяти о началь-
начальных условиях. В действительности это отражает только нечув-
нечувствительность к начальным условиям и обеднение, информации,
так как многие начальные состояния вне аттрактора, эволюцио-
эволюционируя, «оседают» на аттракторе. Но когда речь идет о забыва-
забывании начальных условий в хаотическом режиме, мы понимаем
под этим нечто другое: множество незначительно различающих-
различающихся начальных состояний на аттракторе порождает непредска-
непредсказуемым образом многие конечные состояния. Таким образом,

¦ ¦» i лава \ i
информация в этом случае не теряется, а в определенном смысле
приобретается1). Это приводит к решающим последствиям для
динамики: две траектории, первоначально близкие, расходятся,.
что приводит к полной потере всякого сходства за конечное
время (рис. VI. 8). Наоборот, если режим представлен аттрак-
аттрактором, на котором соседние тракетории расходятся, то такой
режим хаотический. Это очень важное свойство — усиление (в
действительности экспоненциальное усиление) ошибок или неоп-
неопределенности в начальных данных — хаотического режима на-
называется чувствительностью к заданию начальных условий
(ЧЗНУ).
VI. 2.2. Свойства апериодических аттракторов
Идея Ландау состояла в том, чтобы объяснить существова-
существование непрерывного спектра Фурье наличием бесконечно боль-
большого числа независимых частот2). Но для описания хаоса вовсе
не требуется тор Тг очень большой размерности г: из сказан-
сказанного выше ясно, что любой аттрактор даже малой размерности,
обладающий ЧЗНУ, соответствует хаотическому режиму.
Представление об аттракторе с ЧЗНУ содержит двойной па-
парадокс и весьма противоречит нашей интуиции. Этим, по-види-
по-видимому, объясняется позднее открытие хаоса с малым числом сте-
степеней свободы — детерминированного хаоса. Первый парадокс
кроется в кажущемся противоречии между притяжением, кото-
которое обусловливает схождение траекторий, и ЧЗНУ, которая
приводит к расхождению траекторий. В действительности же
расходимость траектории только устанавливает нижнюю гра-
границу размерности аттрактора. Как было показано в разд. VI. 1.3,
по топологическим причинам ЧЗНУ для двумерного аттрактора
невозможна: фазовые траектории должны эволюционировать
в пространстве, размерность которого не меньше трех. Для про-
простоты мы будем рассматривать только трехмерное фазовое про-
пространство. На рис. VI. 9 схематически изображена одна из
новых ситуаций 3), коренным образом отличающихся от тех, ко-
которые могут встретиться на торе Т2, и открывающих путь к ат-
аттрактору нового типа. Траектории расходятся на плоскости как
раскручивающиеся спирали, затем выходят из плоскости и воз-
') В отличие от временной потери информации из-за притяжения к ат-
аттрактору на самом аттракторе происходит непрестанный процесс производства
информации.
2) Во введении к второй части мы определили такую ситуацию, как хаос
с бесконечно большим числом степеней свободы.
а) Это не единственная возможная ситуация; мы выбрали ее лишь в ка-
качестве примера.

вращаются, попадая в центр спирали. Такой процесс повто-
повторяется до бесконечности. Для этого необходимы две операции:
растяжение вследствие ЧЗНУ и складывание, без которого
траектории не могли бы оставаться в ограниченной части про-
пространства.
Чтобы понять, как возникает такой поток, представим себе
трехмерный поток, расходящийся в направлении хх' и сходя-
Рис. VI. 9. Схематическое изображение расхождения двух траекторий в трех-
трехмерном фазовом пространстве. Соседние траектории 1 и 2 выходят из гори-
горизонтальной плоскости, «перекрещиваются», не пересекаясь, и возвращаются
к спирали. Траектории проведены на упрощенном изображении аттрактора
Рёсслера.
И^ работы Абрахама и Шоу.
щийся в перпендикулярном направлении у у' (рис. VI. 10, а).
Некоторое множество начальных условий порождает квазидву-
квазидвумерный лист АВЕС, на котором траектории расходятся, как это
требуется для ЧНЗУ (рис. VI. 10,б). После первой операции —
растяжения — необходимо убедиться в том, что поток остается
в ограниченной части трехмерного пространства, т. е. в том, что
происходит складывание1). После того как ширина листа уд-
удвоится (СЕ = 2АВ), сторона СЕ складывается вдвое вдоль Cut
(рис. VI. 10, г). В результате мы получаем трехмерный поток,
обладающий ЧНЗУ в конечной части пространства2).
!) Позднее мы увидм, что именно повторное складывание потока по-
порождает характерную слоистую структуру странных аттракторов.
2) Построенный нами с помощью операций растяжения и складывания
объект обладает по существу такой же топологией, как аттрактор Рёсслера,
изображенный на рис. VI. 9.

Мы видим, что в трехмерном фазовом пространстве проти-
противоречивые требования притяжения и ЧЗНУ удается ппкмипить
с помощью понятия гиперболичности: притяжение происходит
в одном направлении, а расхождение траекторий в другом. На
Рис. VI. 10. Этапы построения странного аттрактора, о — сокращение (притя-
(притяжение) по направлению уу' и растяжение (расхождение) по направлению хх'-г
б — лист, на котором динамика обладает^ высо_кой чувствительностью к на-
начальным условиям , (в данном случае СЕ = 2АВ); в — первое складывание
листа (длина стороны СЕ, сложенной вдоль CDE, становится сравнимой с
длиной стороны АВ); г — второе складывание, в результате которого «выход»
(CDE) совмещается с «входом» (АВ).
В результате всех проделанных операций мы получаем объект такого же
типа, как на рис. VI. 9.
Из работы Р. Шоу.
рис. VI. 11 изображена плоскость, перпендикулярная среднему
направлению потока. По аналогии с аналитической геометрией
точка О называется гиперболической. Вдоль листа, т. е. в на-
направлении хх', траектории расходятся от точки О, а в перпенди-
перпендикулярном направлении уу' траектории сходятся к точке О. Вне
этих двух осей точки движутся по кривым, проекции которых

эзкторы
на плоскость рис. VI. 11 напоминают гиперболы'). Таким обра-
образом, притяжение, уничтожающее информацию, уравновешивает-
уравновешивается расхождением траекторий, рождающим информацию.
Здесь кроется второй парадокс: придя к заключению о том,
что ЧЗНУ требует размерности аттрактора d, удовлетворяющей
у'
Рис. VI. 11. К понятию гиперболичности. Жирными линиями на рисунке слева
вверху изображены расходящиеся траектории, а тонкими линиями сходя-
сходящиеся траектории. Стрелка 00' указывает направление среднего потока,
хх' — направление, в котором происходит растяжение, уу' — направление, в
котором происходит сжатие. На рисунке справа внизу показана проекция
потока на плоскость, перпендикулярную направлению 00'. Поверхность, на
которой лежат сходящиеся траектории (в нашем случае плоскость YY'OO'),
называется устойчивым многообразием. Поверхность, на которой лежат не-
неустойчивые траектории (в нашем случае плоскость ХХ'ОО'), называется не-
неустойчивым многообразием.
неравенству d > 2, мы можем спросить, может ли трехмер-
трехмерный поток обладать ЧЗНУ. Этот вопрос возникает потому, что
в случае диссипативной системы (т. е. системы, обладающей
') Описанное выше построение позволяет определить две различные ли-
1 нии, «параллельные» одной и той же «прямой» (точнее, геодезической). Один
из способов построения прямой, параллельной данной прямой D и проходя-
проходящей через точку Р, не лежащую на D, основан на использовании точки М,
движущейся по D. Прямая, параллельная прямой D и проходящая через
точку Р, есть предельное положение прямой МР, когда точка М уходит по D
в бесконечность. Пятый постулат Евклида эквивалентен утверждению о том,
что предельная прямая не зависит от того, в какую сторону движется по D
точка М- Но на гиперболической плоскости (для которой пятый постулат не
выполняется) что не так: в зависимости от того, в какую сторону движется
по D точка М, существуют две различные параллельные. Это замечание ле-
лежит в основе неевклидовой геометрии Гаусса — Ббльяя — Лобачевского, не-
некоторые идеи, используемые при изучении хаотических систем в конечном
фазовом пространстве, берут начало в гиперболических геометриях. Напри-
Например, числа Ляпунова, о которых пойдет речь в дальнейшем (см. приложе-
приложение Б), связаны с понятием внутренней кривизны гиперболической плоскости.

140 Глава VI
аттрактором) объемы в фазовом пространстве со временем со-
сокращаются (см. гл. I). Следовательно, объем аттрактора должен
быть равен нулю, что в трехмерном фазовом пространстве при-
приводит к неравенству d < 3. Аттрактор '), который может пред-
представлять хаотический режим (и тем самым обладать ЧЗНУ),
должен быть таким, чтобы выполнялось неравенство 2 < d < 3.
Казалось бы, такое условие должно исключать существование
аттракторов, поскольку евклидова размерность должна быть
цельш числом. Однако аттракторы, удовлетворяющие неравен-
неравенству 2 •< d < 3, все же существуют. Помимо многих других
необычных свойств они обладают нецелой размерностью, кото-
которая называется фрактальной размерностью2) (см. разд. VI. 4.2).
Из-за своих необычных свойств такие аттракторы получили на-
название странных аттракторов.
Резюмируя, можно утверждать, что диссипативная динами-
динамическая система может стать хаотической, если размерность фа-
фазового пространства больше или равна трем. Такой хаос (с ма-
малым числом степеней свободы) обусловлен ЧЗНУ траекторий
на странном аттракторе. Наиболее важные свойства странного
аттрактора состоят в следующем:
1) фазовые траектории (по крайней мере те, которые исхо-
исходят из точек, расположенных достаточно близко к аттрактору)
стремятся к аттрактору;
2) близкие траектории расходятся на аттракторе (ЧЗНУ);
3) аттрактор имеет фрактальную размерность d.
VI. 3. ПРИМЕРЫ АТТРАКТОРОВ
VI. 3.1. Аттрактор Лоренца
Изложение этой модели турбулентности и ее основных
свойств читатель найдет в приложении Г. Если принять неко-
некоторые сильно упрощающие предположения, то динамическое по-
поведение жидкости в условиях конвекции может быть описано
') Напоминаем, что мы рассматриваем трехмерное фазовое пространство.
2) В отличие от евклидовой размерности фрактальная размерность опре-
определяется несколькими формально неэквивалентными способами, которые в
конкретных примерах приводят к различным численным значениям. Сильно
упрощая, можно сказать, что одни определения фрактальной размерности
более чувствительны к внутренней связности объекта, другие — к способу
погружения объекта в объемлющее пространство. Эти свойства, ныне тща-
тщательно изучаемые, входят в описание таких явлений, как перколядия (проте-
(протекание), турбулентность и физика полимеров. Позднее мы рассмотрим размер-
размерность Хаусдофра, называемую также размерностью Хаусдорфа — Безиковича
(которая будет определена и разд. VI. 4), — одну из возможных фракталь-
фрактальных размерностей.

транные аттракторы
тремя обыкновенными дифференциальными уравнениями1), оп-
определяющими поток в трехмерном фазовом пространстве с пе-
переменными X, У и Z:
!L
Значения Рг и Ь обычно фиксированы (часто выбирают значе-
значения Рг = 10 и Ъ = 8/3; этих же значений придерживаемся
и мы), а параметр г остается управляющим. Эта система свя-
связанных между собой нелинейных уравнений кажется простой,
но, вообще говоря, она (аналитически) неинтегрируема. Тем не
менее, задавая начальные значения (Х@), У@), 2@)) и ис-
используя калькулятор, мы можем шаг за шагом численно ре-
решить систему Лоренца и найти поток X(t), Y(t) Z(t).
При малых значениях г устойчивые решения стационарны 2)
(см. приложение Г). Когда параметр г превышает 24, 74 (на-
(например, при г =28), проекции траекторий на плоскость {Y,Z)
становятся нерегулярными орбитами вокруг точек С и С
(рис. VI. 12)—неустойчивых неподвижных точек потока. На
рис. VI. 13 мы видим, что временная эволюция, наприглер X(t),
обладает всеми внешними признаками хаотического поведения.
Если начальные значения (л@), Y{0), Z@)) выбраны слу-
случайным образом, то соответствующие траектории быстро устрем-
устремляются к области А, состоящей из множества траекторий, опи-
описывающих петли вокруг точек С и С (рис. VI. 14). Аттрактор А
(которому соответствует хаотический режим) является стран-
странным аттрактором. Более того, это первый странный аттрактор 3),
который был открыт и исследован. Мы можем вычислить сокра-
сокращение объемов под действием потока, если воспользуемся про-
производной Ли:
дХ dY.dZ__ /Pr,A,n_ 41
!) Обыкновенным дифференциальным уравнениям б отличие от диффе-
ренциальных уравнений с частными производными удовлетворяют функции
только одной переменной, в данном случае времени.
2) Напомним, что в этом разделе Рг = 10 и Ь = 8/3.
3) Когда Лоренц занимался исследованием своей модели, термин «стран-
«странный аттрактор» еще не существовал и не были известны необычные евойстъа
странных аттракторов. В более ранней работе Рикитаке и Аллена были по-
получены результаты, которые ныне принято связывать со свойствами странных
аттракторов.

Глада VI
-20
-10
О
1П
20
30
Рис. VI. 12. Аттрактор Лоренца. Проекция части траектории на плоскость
(К, Z) фазового пространства при г = 28; Си С — неустойчивые неподвиж-
неподвижные точки.
-2QL
Рис. VI. 13. График зависимости X(t) при г = 28. Обратите внимание на
неупорядоченную эволюцию, происходящую то в окрестности среднего значе-
значения .Y, то в окрестности другого значения X' (X и X' —координаты неустой-
неустойчивых неподвижных точек С и С).

Странные аттракторы
143
За единицу времени (которая в данном случае примерно равна
периоду одного оборота вокруг С или С) объем уменьшается
в "е-41/3 ж Ю-6 раз. Это означает, что модель Лоренца сильно
диссипативна.
Сечение Пуанкаре траекторий плоскостью1) Z — r—1, со-
содержащей точки С и С', показано на рис. VI. 15. На первый
взгляд кажется, что это сечение состоит из двух сегментов,
Рис. VI. 14. Аттрактор Лоренца при г = 28. Кажущаяся асимметрия аттрак-
аттрактора обусловлена только перспективой изображения. Двумя штриховыми от-
отрезками показаны пересечения траекторий с плоскостью сечения S (задавае-
(задаваемой уравнением Z = т — 1 = 27) при условии Z > 0, т. е. сечение Пуанкаре
аттрактора этой поверхностью.
Из работы О. Ланфорда.
каждый из которых соответствует вращению вокруг одной из
неустойчивых неподвижных точек С и С в данном направлении.
Отсюда следует, что траектории почти ложатся на поверхность
и что аттрактор имеет размерность, равную двум. Действи-
Действительно, «проткнув» кажущийся двумерным лист, мы обнаружим
сложную структуру, состоящую из большого числа плотно упа-
упакованных листов. Таким образом, аттрактор Лоренца является
не поверхностью, но вместе с тем не имеет объема: листы не
имеют «толщины» (протяженности в поперечном направлении)
и С.
') Плоскость Z = r—1 содержит неустойчивые неподвижные точки С

Глаза VI
и разделены пустым пространством. Действительно, вычисляя
размерность Хаусдорфа — Безиковича (которая будет опреде-
определена в разд. VI. 4.2) аттрактора Лоренца, мы получаем число,
очень близкое к двум, но все же большее двух:
d = 2,06
Этот результат подверждает, что аттрактор Лоренца — не про-
простая поверхность. То, что его фрактальная размерность очень
30
20-
Ю
-30 -20 -10 0 10 20
-10 ¦
-20-J
-30
Рис. VI. 15. Сечение Пуанкаре аттрактора Лоренца. Плоскость сечения совпа-
совпадает с плоскостью S на рис. VI. 14. В плоскости сечения лежат неустойчивые
неподвижные точки С и С. Сечение Пуанкаре состоит из двух почти прямо-
прямолинейных отрезков.
близка к двум, обусловлено сильным сжатием объемов, о кото-
котором мы упоминали выше. Сильным сжатием объемов объяс-
объясняется и то, что отображение Пуанкаре может быть описано
одномерным отображением первого возвращения xk+i = f(xb)
(см. разд. IV. 4). Сам Лоренц получил это отображение! по-
построив график зависимости последовательных максимальных
значений Z, т. е. Zk+X, от предыдущих максимумов Zk. Эти зна-
значения 2Макс являются координатами Z точек'в сечении Пуан-

Странные аттракторы
145
каре поверхности XY — bZ = О (т. е. dZ/dt = 0 в силу третьего
уравнения модели Лоренца). На рис. VI. 16 видно, что в хоро-
хорошем приближении') отображение Пуанкаре, порождаемое ат-
аттрактором Лоренца, может быть сведено к отображению пер-
первого возвращения x^*-f(x) (см. рис. IV. 4). Существенные
динамические свойства модели легко могут быть найдены с по-
Рис. VI. 16. Отображение первого возвращения для модели Лоренца. График
зависимости Zk + l = f(Zk). где Z; — последовательные максимумы a.e,w:'i..:.: 2
при г = 28.
Из работы Э. Н. Лоренца.
мощью отображения первого возвращения. Достаточно аналити-
аналитически аппроксимировать кривую, представленную на рис. VI. 16,
а затем выполнить итерации Xk+i =f(xk) с помощью процедуры,
описанной в разд. VI. 4.1.
На этом примере мы можем продемонстрировать одно из
преимуществ редукции потока к одномерному отображению. Из
гл. IV нам известно, что если тангенс угла наклона касательной
к кривой xk+i = f(Xk) всюду больше единицы (на интервале
отображения), то при любом начальном значении х0 существует
незатухающий хаотический режим. Например, при г — 28 (зна-
(значение, выбранное в многочисленных исследованиях аттрактора
!) Это то приближение, в котором сечение Пуанкаре аттрактора ото-
отождествляется с двумя линейными сегментами.
Ю П. Берже и др.

146
Глава VI
35
27
а
25 Zo 31
Рис. VI. S7. Отображение первого возвращения для модели Лоренца, а — при
г = 24,06; б — при г < 24,06.
На рисунке а показан предельный случай, когда угловой коэффициент каса-
касательной к кривой по абсолютной величине всюду больше единицы.
Из работы Дж. А. и Э. Д. Иорк.

Странные аттракторы 147
Лоренца) тангенс угла наклона к кривой Zk+i — f(Zb), действи-
действительно, в рассматриваемом интервале всюду больше единицы.
Следовательно, независимо от начального значения Zo режим
будет хаотическим. При уменьшении параметра г ситуация из-
изменяется. В частности, очень интересный случай возникает, если
1
10
«f6
Ю"8
б
12 5
л.
. . . '¦>¦ t
Рис. VI. 18. Временная эволюция расстояния б между траекториями, задавае-
задаваемыми уравнениями Лоренца. Траектории исходят из двух точек, выбранных
вблизи аттрактора на расстоянии всего лишь 80 = 10~8 друг от друга.
В среднем расстояние б между двумя траекториями возрастает со временем t
как б = 60 exp(Xi/), где Я4 — наибольший показатель Ляпунова. В логариф-
логарифмическом масштабе оценка показателя Ляпунова Xi определяется средним
наклоном кривой б = бо exp{kit). В рассматриваемом случае Ai « 0,9, что
дает разумное согласие с результатами более подробных численных расчетов.
Разумеется, максимальное расстояние б ограничено размерами аттрактора,
чем и объясняется насыщение, наблюдаемое при больших Г.
мы выберем значение г чуть меньше 24,06, чтобы неподвижные
точки С а С были устойчивы. При таких значениях г отображе-
отображение первого возвращения выглядит, как на рис. VI. 1/, б: тан-
тангенс угла касательной к одной части кривой меньше единицы
(Z < Zo), из чего следует вывод о существовании неустойчивой
неподвижной точки Zo (пересечения графиков отображения пер-
первого возвращения и тождественного отображения). Траектории,
Ю*

148 Глава VI
выходящие из начальных точек с Z< Zo, устремляются прямо
к устойчивой неподвижной точке ниже Zo. С другой стороны,
траектории, выходящие из точки с Z > Zo, ведут себя хаоти-
хаотически, затем попадают в область с Z < Zo, где быстро сходятся
к устойчивой неподвижкой точке. Такого рода хаос, называе-
называемый метастабильным, обладает интересными свойствами, кото-
которые могут быть выведены из формы отображения первого воз-
возвращения.
В заключение продемонстрируем ЧЗНУ аттрактора Лоренца
при значении г = 28. Для этого вычислим поток, выходящий
из двух очень близких начальных точек, и посмотрим, как бы-
быстро расстояние, разделяющее эти две точки, эволюционирует
во времени. Из рис. VI. 18 видно, что в среднем расстояние 6
между траекториями возрастает экспоненциально, как и пред-
предсказывает общая теория.
VI. 3.2. Аттрактор Энона
Разумеется, весьма заманчиво продвинуться дальше и выйти
за рамки предпринятого Лоренцом моделирования тепловой
конвекции. Дополнительное упрощение, которое можно внести
в модель, состоит в преобразовании уравнений с непрерывным
временем в итерации с дискретным временем. Это позволяет
заменить систему трех дифференциальных'уравнений, аналогич-
аналогичных уравнениям модели Лоренца, двумерным отображением1).
В этом случае последовательные точки, получаемые в R2, сле-
следует рассматривать как принадлежащие сечению Пуанкаре по-
потока, порождаемого тремя дифференциальными уравнениями.
Исходя из этой идеи, Энон предложил следующее отобра-
отображение плоскости на себя:
— Yk + 1 — o,Xk,
где коэффициент а управляет нелинейностью итерации, а коэф-
коэффициент р учитывает диссипацию. Обычно используются сле-
следующие значения а и р:а= 1,4 и р = 0,3. Именно эти значе-
значения приняты в этом разделе. Исходя из точки плоскости с ко-
координатами (Хо, Уо) можно вычислить координаты (Хи Y\)
следующей точки и т. д. Следует заметить, что преобразование,
о котором идеть речь, обратимо: зная любую точку Рь, мы мо-
можем найти предшествующие точки Pk-u Pk-2 и т. д. Иначе го-
говоря, итерации можно производить как по возрастающим k
*) Это позволяет понизить на один порядок мощность компьютера, не-
необходимого для/построения аттрактора.

странные аттракторы
149»
(аналогу времени), так и по убывающим k (вспять во вре-
времениI).
Если начальные точки лежат внутри области притяжения
(имеющей очень сложную структуру), то последовательные ите-
итерации чрезвычайно быстро сходятся к аттрактору, изображен-
изображенному на рис. VI. 19. Мы видим, что последовательные точки
0,1
о
¦—••-.'.'.¦' ——
-
-
0
^ ^ \ 1 f 1 t*7""l f I r f t 1 1 f t I 1 I 1 1 Г I
У
¦•*** •
1 i i | t f i 1 ?
/
Уу
.--¦-"
•
\ 4,:
e" i ',
Рис. VI. 19. Аттрактор Энона (а = 1,4; р = 0,3). Обратите внимание на раз-
различие в масштабах по осям абсцисс и ординат.
располагаются иррегулярно, непредсказуемо и случайно. В этом
отношении динамика на аттракторе Энона обладает ярко выра-
выраженным хаотическим характером.
Исследование расстояния между траекториями (первона-
(первоначально очень малого) как функции последовательных итераций,
подтверждает прогноз о хаотическом характере отображения,
поскольку становится очевидной ЧЗНУ. На рис. VI. 20 пока-
показано, что расстояние между соседними траекториями возрастает
в среднем экспоненциально. В основу рисунка положены резуль-
результаты численных расчетов, поэтому можно заключить, что ат-
аттрактор Энона (при а = 1,4 и 3 = 0,3) является странным
аттрактором2).
отличается от квадратичных отображений
а на себя (см. гл. VIII).
2) Ввиду чрезвычайной простоты исходных уравнений приводить строгое
доказательство этого утверждения было бы излишне.
') Этим отображение Энона
отрезка на себя (см. гл. VIII).
2) Вду чрезыйй

150
Глава VI
ибратимся теперь к отображению Знона и продемонстри-
продемонстрируем на нем некоторые из упомянутых выше свойств или поня-
понятий. Прежде всего нас будет интересовать вопрос о сокращении
площадей (аналогичный проблеме сокращения объемов под дей-
действием трехмерных диссипативных потоков). В случае двумер-
Рис. VI. 20. Временная эволюция расстояния б между траекториями, зада-
задаваемыми отображением Энона. Траектории исходят из двух точек, выбранных
вблизи аттрактора на расстоянии всего лишь б0 = 10~8 друг от друга.
В среднем расстояние между двумя траекториями возрастает с числом ите-
итераций k на б = 6oexp(A,ik), где X.i — наибольший показатель Ляпунова. В ло-
логарифмическом масштабе оценка показателя Xi может быть получена как
средний наклон кривой 8 = бо ехр(/ч&). В рассматриваемом случае ).< « 0.50.
что находится в разумном согласии с результатами более подробных числен-
численных расчетов. Насыщение угла наклона кривой обусловлено теми же причи-
причинами, что и в случае, представленном на рис VI. 18. (См. также рис. VIII. Э.)
ного отображения якобиан играет роль производной Ли (см.
приложение Д). Для отображения Энона он равен
дХ
Таким образом, при каждой итерации площади умножаются ка
коэффициент |3|- Следовательно, если |Р|<1, то мы имеем
сжатие. При Р = 0,3 (мы рассматриваем здесь только этот слу-
случай) площадь, бывшая единичной после k-и итерации, станет
равной 0,3 после (к + 1)-й итерации.

Странные аттракторы 151
Это сжатие, относительно умеренное, отличается от сжатия
в модели Лоренца, в которой за время, разделяющее две после-
последовательные точки в сечении Пуанкаре, объем сжимается
в 10~6 раз (в модели Энона этому промежутку времени соот-
соответствует интервал времени между двумя последовательными
итерациями). Столь быстрое сжатие мешает различить фрак-
фрактальную структуру сечения Пуанкаре аттрактора Лоренца.
Иначе обстоит дело в случае аттрактора Энона, на котором,
вследствие умеренного сжатия (|Р| = 0,3) легко различить
фрактальную структуру. Некоторые из приведенных графиков
(с все возрастающим увеличением) позволяют уточнить послед-
последнее замечание. Так, на рис. VI. 21, с в рамке мы видим три па-
параллельные линии, которые почти сливаются одна с другой.
После первого увеличения выясняется, что верхняя линия в дей-
действительности представляет собой три параллельные линии.
Аналогично после второго увеличения становится видно, что
верхняя из трех линий, обнаруженных после первого увеличе-
увеличения, также оказывается тройной и т. д. Иначе говоря, струк-
структура аттрактора повторяется в последовательных масштабах1)
наблюдения. Такую структуру, характерную для фрактального
объекта2), можно рассматривать как сечение множества, со-
состоящего из большего числа листов, т. е. как странный аттрак-
аттрактор. Аттрактор Энона (объект, занимающий промежуточное по-
положение между линией и поверхностью) имеет размерность
Хаусдорфа d = 1,26.
Аттрактор Энона можно использовать для иллюстрации со-
сосуществования сокращения площадей и ЧЗНУ. Напомним, что<
это сокращение происходит с постоянной скоростью: в |Р|~' =
= @, 3)~' раза за одну итерацию. Сокращение не изотропно:
в первом приближении окружность (радиусом г, малым по
сравнению с размером аттрактора) становится эллипсом, все
более удлиняющимся в одном направлении и сжимающимся в
другом (рис. VI. 22). Длины главных осей после итераций соот-
соответственно равны г Ал и гА.2, где Ai и Аг — две константы, зна-
значения ¦ которых могут быть определены только численно3).
При Ai > 1 и Л2 < 1 (и AiA2 = |P|< 1, так как имеет ме-
место глобальное сокращение) длины растягиваются в одном
направлении и сжимаются в перпендикулярном направлении
(рис. VI. 22, б). Мы снова встречаемся здесь с понятием.
') В некоторых случаях это масшабная инвариантность.
2) Простейшим и наиболее известным примером объекта такого типа
является канторовское множество, описанное в разд. VI. 4.2.
3) Мы не знаем, как вычислять Л4 и Л2 аналитически, хотя умеем вы-
вычислять AiA2 = | РI.

152
Глава VI
гиперболичности, означающей схождение траекторий в одном на-
направлении и расхождение их в другом направлении. В самом
деле, поскольку аттрактор Энона можно рассматривать как сече-
сечение Пуанкаре трехмерного потока в хаотическом режиме, каж-
о,м
0,!В92
P.53OS
¦-...
.0,6310
0,6315
г
' ""•- .'-'¦.¦"•¦¦=
•
0,6320
Рис. VI. 21. Пример, показывающий самоподобие структуры аттрактора Энона
в различных масштабах. Небольшой квадрат на одном рисунке соответствует
в увеличенном виде следующему рисунку (обратите внимание на изменение
масштаба по осям): а-+б-*¦ в->-г.
Из работы М. Энона.
.дая точка является точкой пересечения плоскости, на которой
определено отображение Энона, с траекторией, локально пер-
перпендикулярной ей. Для малого эллипса в окрестности точки О на-
направление расхождения траекторий соответствует касательной
JDD' (рис. VI. 22, в), а направление сжатия СС' перпендикуляр-
зга DD'. Преобразование окружности во все более вытянутые

Странные аттракторы
!53
а
\
В
В'
' t* * •••• * : '. '- ••
«Г.*.*. .-;••"'** • *' *
Рис. VI. 22. Деформация окружности при итерации отображения Энона.
\Л Л1Ш LS LAW W1TX Li X \J XX XJ VL^^^YX XVX XX^^ifXVW^ X XJ ^»/ -* \/ ~4 WXb J i • L/ U. ^X4 V/^lVilWUllULA XX ti VXb \J T H»liu ^ i ix*
центр которой лежит на аттракторе. После первой итерации мы получаем
множество В. Обратите внимание па растяжение в направлении каеатслъ:::;";
к аттрактору и на сжатие в направлении, которое приближенно можно счи-
считать перпендикулярным касательной. Вторая итерация преобразует множе-
множество В в множестве С; б — это преобразование переводит окружность в
эллипсы. Увеличение и переобозначение множеств А, В и С в А'. В' л С
позволяет сделать сокращение площадей более заметным; в — гнперболич-
ность и роль коэффициентов Ляпунова как пример преобразования окруж-
окружности в эллипсы.

Глава VI
¦эллипсы служит конкретной иллюстрацией коэффициентов Ляпу-
Ляпунова (см. приложение Б): в пределе малых г и больших k числа
Ai и А2 являются двумя коэффициентами Ляпунова для отобра-
отображения Энона. В другом предельном случае — при г порядка
В
~,, /
•- ¦> ;::>
Рис. VI. 23. Образование складки при отображении Энона. Процедура остает-
остается такой же, как на рис. VI. 22, но окружность А на этот раз сравнима по
размерам с аттрактором. На множествах В и С, получающихся из окружно-
окружности А в результате первой и второй итераций, видно комбинированное дей-
действие растяжения и складывания.
размеров аттрактора — рис. VI. 23 показывает также, что эволю-
эволюция на аттракторе включает две операции: растяжение и скла-
складывание.
VI. 3.3. Экспериментальные примеры странных аттракторов
Приводимые далее примеры заимствованы из экспериментов,
-выполненных на трех динамических системах, описанных в гл. V.
Начнем с вращающегося магнита, обладающего таким пре-
преимуществом, как регулируемость диссипации. При умеренных
величинах трения в жидкости мы можем экспериментально на-
илюдзть четко выраженную слоистую структуру странного ат-
аттрактора. Наш магнит (см. гл. V) испытывает совместное дей-
действие стационарного магнитного поля с индукцией В\ и другого
магнитного поля с индукцией Во, вращающегося с угловой ча-
частотой се. Вязкое трение создается маслом в одном из подшип-
подшипников магнита. Нетрудно построить сечение Пуанкаре фазо-

Странные аттракторы 155
вых траекторий, поскольку перед нами осциллятор с вынуждаю-
вынуждающей силой, для которого период 2л/© вращающегося поля яв-
является естественным, интервалом времени, через который про-
производится выборка значений сигнала. Таким образом, доста-
достак
-л-- •¦
\ V
-*- л:
Рис. VI. 24. Сечение Пуанкаре аттрактора в хаотическом режиме вращающе-
вращающегося магнита. Угловая скорость магнита пропорциональна х.
Из работы В. Крокетта.
точно фиксировать переменную x(t), пропорциональную ско-
скорости магнита, и ее производную x(t) каждый раз, когда Во по-
поворачивается на 2я. Результат проведения такой операции над
хаотическим режимом представлен на рис. VI. 24. Мы видим
характерную структуру странного аттрактора с большим чис-
числом складок — сложную структуру, напоминающую аттрактор
Энона.

t56
Глава VI
другое, еще более поразительное сходство между аттракто-
аттрактором Энона и экспериментом можно обнаружить в неустойчи-
неустойчивости РБ. Экспериментальная процедура несколько отличается
от той, которая применялась в случае магнита: так как конвек-
AT
//¦:
AT
Рис. VI. 25. Сечение Пуанкаре аттрактора в хаотическом режиме конвекции
Рэлея —Бенара. Величина Д71 приблизительно пропорциональна вертикаль-
вертикальному градиенту температуры в данной точке слоя жидкости. Сечение Пуан-
Пуанкаре было получено стробоскопированием сигналов с частотой одного из
двух осцилляторов тепловой конвекции.
Из работы М. Дюбуа.
ция РБ не испытывает периодического внешнего воздействия,
вычисление сечений Пуанкаре оказывается более сложным. На-
Напомним то, что было сказано в гл. V: две переменные1) (АГ)
s) Обычно (ДГ) и (Д7') измеряют, пропуская сквозь жидкость в гори-
горизонтальном направлении узкие пучки света. Эти пучки отклоняются пропор-
пропорционально градиенту температуры.

Странные аттракторы
157
я (AT)' измеряются в двух различных точках жидкости, в ко-
которой происходит тепловая конвекция (см. рис. V. 8). Трехмер-
Трехмерное фазовое пространство определяется координатами (AT),
(AT) и (AT)'. Если удается детектировать сигнал (AT)', пред-
представляющий в основном один из осцилляторов тепловой конвек-
конвекции, то его период можно использовать в качестве интервала
времени для стробоскопирования траекторий, проектируемых на
плоскость (AT, AT). Но получить сигнал (AT)', обладающий
достаточной спектральной чистотой, обычно очень трудно даже
Рис. VI. 26. Предельный цикл при периодическом режиме в реакции Белоу-
«ова — Жаботинского. Измеренный сигнал (потенциал специального электро-
электрода) пропорционален логарифму концентрации ионов Bi". Используемое здесь
представление основано на методе «задержек»: строится график зависимости
сигнала, измеренного в момент времени t + т, от сигнала, измеренного в мо-
момент времени t (в данном случае время задержки равно 8,8 с).
Из работы Ж.-К. Ру, Р. Симон и X. Суинни.
после фильтрования. Поэтому сечекие Пуанкаре строят как пе-
пересечение траекторий в фазовом пространстве (AT), (AT), (AT)'
с плоскостью (AT)' = К. Для этого наносят на график коорди-
координаты (AT), (AT) всякий раз, когда координата (AT)' достигает
заданного значения К (при определенном условии для знака
d(AT)'/dt, например при d(AT)'/dt > 0).
Именно так было получено сечение Пуанкаре на рис. VI. 25
в конвективном режиме, спектр Фурье которого содержит не
только дискретные линии, но и существенный широкополосный
шум. Мы видим (рис. VI. 25), что точки в сечении Пуанкаре
образуют сложную, но вполне определенную структуру1).
') В случае недетерминированного хаотического режима мы увидели бы
облако точек, не обладающее тонкой структурой.

158
Глава VI
X(tj+t)
X (til
Рис. VI. 27. Апериодический режим в реакции Белоусова—Жаботинского.
Диаграмма такого же типа, как и на рис. VI. 26, но для хаотического режима.
Петли являются проекциями траекторий на плоскости (А'(^), X(t-, + x)).
Из работы Ж.-К. Ру, X. Суинни.
Рис. VI. 28. Сечение Пуанкаре. Это сечение пересекает те самые траектории
в пространстве X(ti), X(ti-\-r), А'(^ + 2т), проекция которых изображена на
рис. Vi. 27. Плоскость сечения перпендикулярна плпгкости рисунка VI у7. ня
которой след пересечения двух плоскостей отмечен штриховой линией. Заме-
Заметим, что квазилинейный вид сечения — чистая случайность.
Из работы Ж.-К. Ру, X. Суинни.

Странные аттракторы
!59
Рис. VI. 29. Отображение первого возвращения, ьеличина Хь — ордината точ-
точки сечения на рис. VI. 28. Для получения отображения первого возвращения
мы строим график зависимости ординаты Xj+1 от ординаты Хк ближайшей
предшествующей точки, а — множество точек, полученных при хаотическом
режиме аттрактора. Непрерывная кривая проведена только для удобства
прослеживания общей зависимости; б— сплошная кривая, изображенная на
рисунке а, начерчена повторно. При записи серии точек с номерами от 1 до 13
возникло ппим
в тот момент, ког
л ~
Последующие точки быстро вернулись к асимптотической кривой, что свиде-
свидетельствует об эффекте притяжения.
Из работы Ж.-К. Ру, X. Суинни,

X(ti +r) I
1
V* v--.
/// ill
f/i
X(tj)

Странные аттракторы !6!
Обратимся теперь к химической реакции БЖ, чтобы изучить
один аспект, непосредственно связанный с динамикой. Подле-
Подлежащей измерению величиной является концентрация ионов
брома в реакторе. Записи временных рядов X(ti), содержащие
несколько десятков тысяч точек, производились при фиксиро-
фиксированном значении потока реагентов (управляющий параметр ц).
Фазовые диаграммы построены методом временных задержек
(см. разд. IV. 5), позволяющим получить представление аттрак-
аттрактора в трехмерном фазовом пространстве с координатами X(t;),
X )X( 2)
Простейший пример, иллюстрирующий эту процедуру, вы ви-
видите на рис. VI. 26. При некоторых значениях потока реагент.а
реакция БЖ становится периодической, и ее фазовая диаграмма
(предельный цикл) представима в двумерном пространстве. Си-
Ситуация радикально изменяется при других значениях потока1:
как свидетельствует проекция фазовой диаграммы, представ-
представленная на рйс. VI. 27, среди режимов могут быть обнаружены
хаотические. Выбранными координатами являются величины
X = X(tt),
Y = X(tt + x),
где т = 8,8 с1).
Кроме чисто эстетического интереса эта проекция мало го-
говорит о динамическом состоянии системы. Было бы рискованно
делать какие-либо заключения о существовании странного
аттрактора только на основании рис. VI. 27. Та же неопреде-
неопределенность сохранилась бы, даже если бы мы попытались пред-
представить аттрактор в трехмерном фазовом пространстве. Однако
решающий шаг будет сделан, если мы проведем сечение Пуан-
Пуанкаре через трехмерное представление аттрактора, третьей коор-
координатой которого служит X(ti -)- 2т). Плоскость сечения перпен-
перпендикулярна плоскости рис. VI. 27, на которой след сечения
проведен штриховой линией. Построенное сечение Пуанкаре по-
показано на рис. VI. 28. Подчеркнем, что квазилинейный вид
сечения Пуанкаре обманчив: при другом выборе т и другой
4) Это время следует сравнить с временем обхода аттрактора представ-
представляющей точкой, которое имеет порядок сотен секунд.
Рис. VI. 30. Чувствительная зависимость от начальных условий. Штриховые
линий соответствуют некоторым траекториям, изображенным на рис. V1/27.
положение точек при f = 0 отмечено буквой О. а — положение точек при
t = 60Дг; б— положение точек при i— 105ДГ; в — положение точек при
I = 210At. (At = 0,88 с. Среднее время, за которое точка успевает описать
петлю, составляет — 120А/.)
Из nofm-ru Ж -К Pv и Y ГЧ/иииы
, , ,.ч. -х. - j .. „. K^j
11 П. Берже и др.

162 Глава VI
плоскости сечения мы получили бы другую кривую (как мы уви-
увидим дальше). Однако узость этого квазилинейного объекта на-
напоминает аттрактор Лоренца. Причина та же: система БЖ (при
рассмотренных выше условиях) сильно диссипативна, отсюда и
очень малая ширина аттрактора. В дальнейшем мы узнаем и
другие подтверждения столь сильного сжатия.
Детерминированный характер хаотического поведения, соот-
соответствующего аттрактору, убедительно подтверждается отобра-
отображением первого возвращения, которое можно построить по ото-
отображению Пуанкаре при столь сильной диссипации, как в \дан-
ном случае. Построив график зависимости ординаты Xk+i точки
на рис. VI. 28 от ординаты Хк предыдущей точки, мы увидим на
рис. VI. 29, а, что все точки ложатся на четкую кривую. Таким
образом, знание одной точки определяет положение следующей
точки. Это свидетельствует о порядке, управляющем траекто-
траекториями на аттракторе.
Чтобы продемонстрировать два решающих свойства стран-
странного аттрактора, рассмотрим, как появляются в данном случае
сжатие и ЧЗНУ. Первое из этих явлений можно проиллюстри-
проиллюстрировать, введя возмущение: например, пузырек воздуха, увлекае-
увлекаемый потоком одного из реагентов, на какое-то время нарушает
нормальный ход реакции. На рис. VI. 29, б вы видите построен-
построенное отображение первого возвращения, а также непрерывную
кривую, которая воспроизведена с рис. VI. 29, а. После точки 4
пузырек нарушает на время состояние реактора. Действие этого
возмущения отчетливо видно на точке 5, которая явно не лежит
на кривой. Последующие точки 6, 7 и 8 снова приближаются
к кривой (и тем самым к аттрактору), а после точки 9 изме-
измерения недостаточно точны для того, чтобы мы могли обнару-
обнаружить любое отклонение от кривой. Так сила притяжения воз-
возвращает «заблудшую» точку на аттрактор в Четыре орбиты.
Что же касается ЧЗНУ (т. е. экспоненциального уси пения
отклонений), то обратимся снова к проекции фазовой диа-
диаграммы. Фигура, которую вы видите на рис. VI. 27, получена
путем нанесения на график большого числа точек с координа-
координатами (X(ti), Х(^ + т)), где моменты времени U разделены ин-
интервалом Ai (в данном случае 0,88 с), составляющем около од-
одной сотой продолжительности одного обхода аттрактора. Вме-
Вместо систематического нанесения на график всех точек поступим
следующим образом: каждый раз, когда точка пройдет вблизи О
(рис. VI.30), будем следить за ее эволюцией, нанося на гра-
график ее последующие положения. На рис. VI. 30, а показано мно-
множество точек в момент времени t = 80At, где 4=0 соответ-
соответствует моменту прохождения точки вблизи О. Множество точек
на рис. VI. 30, б соответствует значению t = 105Д?, а на

Странные аттракторы
163
рис. VI. 30, в — значению f = 210Af. Повторим такую операцию
несколько десятков раз. Мы видим, что при t = 0 существует
множество точек, расположенных так близко друг от друга, что все
они практически неотличимы от О. При t = 8(Ш мы замечаем,
Рис. VI. 31. Проекция аттрактора при другом времени запаздывания т'. Вы-
Выбранные траектории соответствуют тому же хаотическому режиму, который
представлен на рис. VI. 27, но т'= 53 с (вместо т/ = 8,8 с). Штриховыми
линиями показаны различные' секущие плоскости (перпендикулярные плоско-
плоскости чертежа), которые использовались для построения сечений Пуанкаре^
представленных на рис. VI. 32.
Из работы Ж.-К. Ру, Р. Симой и X. Суинни.
что эти точки начинают разделяться (рис. VI.30,а, зона А).
Расстояние между точками быстро возрастает со временем:
к моменту времени ^ = 210Л/ (времени, которое (приблизи-
(приблизительно) необходимо, чтобы совершить дважды обход аттракг
тора) точки рассеиваются , почти по всему аттрактору
(рис. VI. 30, в, зона С). Это означает, что начальное условие
11*

164
Глава VI
(все точки практически неотличимы от О) забывается из-за рас-
расхождения начальных отклонений от точки О. Перед нами ЧЗНУ.
Рис VI. 32. Сечения Пуанкаре. Каждое сечение Пуанкаре имеет свой номер
(N) и соответствует отличной от других плоскости сечения, проекция которой
имеет на рис. VI. 31 такой же номер. Масштабы меняются от сечения к се-
сечению. Для каждого сечения N коэффициенты изменения масштабов по оси
абсцисс ЕХ и оси ординат ? У указаны ниже как (N) EXXEY-
A) 0,3X0,2; B) 1,1X0.9; C) 1.0XL0; D) 0.5X0,9; E) 0,5X0,9;
F) 0,5X0,8; G) 0,4X0,5; (8) 0,4X0,2; (9) 0,4X0,08.
Из работы Ж--К. Ру. Р. Симон, X, Суинни.
Мы можем даже показать, каким образом d реакции Б.Ж
осуществляются две операции (растяжения и складывания),
общие для всех странных аттракторов. При изменении времени
задержки % (по сравнению с т, принятым на рис. VI. 27) фазо-

Странные аттракторы 165,
вая диаграмма претерпевает существенную деформацию, как
видно из рис. VI. 31, на котором -показаны траектории, спроек-
спроектированные на плоскость (X(ti), Х(^+т')) с т' = 53 с1).
Чтобы проследить за эволюцией соответствующего потока, рас-
рассмотрим сечения Пуанкаре плоскостями, перпендикулярными
плоскости рис. VI.31 и обозначенными цифрами 1, 2, 3, ..., 9.
На рис. VI. 32 показано, что сечение Пуанкаре постепенно
на протяжении среднего периода обхода аттрактора, изобра-
изображенного на рис. VI. 31. Мы видим, что образование складки
происходит между 2 и 8. Растяжение (менее заметное, так как
масштабы сильно изменяются от одной фигуры к другой) про-
происходит главным образом между 9 и Г. Именно поэтому ши-
ширина сечения гораздо меньше на плоскости 1, чем на пло-
плоскости 9.
VI. 4. ИЗМЕРЕНИЕ РАЗМЕРНОСТИ СТРАННЫХ АТТРАКТОРОВ
VI. 4.1. Проблемы получения количественных характеристик
динамических режимов
Динамический режим можно охарактеризовать с помощью
анализа Фурье. Но анализ Фурье не позволяет провести разли-
различие между хаосом с небольшим числом степеней свободы (де-
(детерминированным хаосом) и белым шумом2). В этом отноше-
отношении исследование фазовых траекторий с помощью сечений Пу-
Пуанкаре обладает важным преимуществом. Но получить' при
этом удается только качественную информацию. Кроме того,
мерными фазовыми пространствами.
Охарактеризовать хаотический режим количественно можно,
определяя наибольший показатель Ляпунова (см. приложе-
приложение Б). Мы не будем обсуждать здесь алгоритмы определения
наибольшего показателя Ляпунова по экспериментальным дак-
ным, поскольку все они еще не очень, эффективны. Другой ин-
интересной характеристикой хаотического режима является фрак-
фрактальная размерность аттрактора, которой посвящен этот раз-
раздел. Поскольку размерность странного аттрактора, как правило,
нецелая, остановимся на этом понятии несколько подробнее.
') На рис. VI. 31 и VI. 32 использованы те же экспериментальные дан-
данные, что к на рис. VI. 27 и VI. 28. Это еще раз подтверждает, что сечение
Пуанкаре на рис, VI. 28 имеет лишь видимость квазилинейного.
2) Под «белым шумом» мы понимаем (в отличие от детерминированного
хаоса) хаотический режим, в основе которого лежит очень большое число
независимых мод или степеней свободы (см. разд. VII. 3.3).

166
Глава VI
VI. 4.2. Фрактальные размерности
Рассмотрим множество точек в р-мерном пространстве. Мы
хотим покрыть это множество (гипер)кубами с ребром е. Пусть
Af(e) — наименьшее число кубов, необходимых для покрытия
множества (рис. VI. 33). Размерность Хаусдорфа (называемая
также размерностью Хаусдорфа — Безиковича) точки D опре-
определяется как предел, если он существует, отношения
Рис. VI. 33. Покрытие объекта (множества точек) кубами с длиной ребра е.
In Л^(е)/1пA/е) при ребре е гиперкуба, стремящемся к нулю, т. е.
г. 1- 1пЛГ(е)
lnd/e)
То же самое можно сформулировать иначе: минимальное
число N (г) кубов, необходимое для покрытия множества точек,
зависит от е как e~D. Если множество состоит из одной точки, то
N (е) = const = 1.
Следовательно, размерность Хаусдорфа точки D равна нулю
(евклидова размерность точки также равна нулю). Если мно-
множество представляет собой отрезок линии длиной L, то
поэтому ?> = 1, в то время как для поверхности с площадью S
откуда и = 2.
До сих пор определение размерности Хаусдорфа ничего не
добавило к определению евклидовой размерности. Обратимся
теперь к канторовскому множеству, получаемому с помощью
итерационного процесса. Сначала из единичного отрезка уда-

Странные аттракторы 167
ляется средняя треть. Затем каждый из двух оставшихся отрез-
отрезков также подвергается удалению средней трети. Эта операция
повторяется до бесконечности, как показано на рис. VI. 34. В ре-
результате мы получаем бесконечное множество несвязных то-
точек1), размерность которого заключена между нулем и едини-
единицей. Размерность Хаусдорфа канторовского множества нетрудно
получить по его построению. При е= 1/3 число элементов (в
to 1/3 2/з И
I,
1/3 2/9
Рис. VI. 34. Первые стадии построения канторовского множества.
данном случае гиперкубы вырождаются просто в отрезки), не-
необходимых для того, чтобы покрыть множество, равно
ЛгA/3) = 2. Аналогично при 8=1/9 мы получаем N(e) = 4 и
в общем случае при е = A/3)т имеем N(e) = 2m. По определе-
определению размерность Хаусдорфа есть величина
D = lim J[fJ-« 0,63.
m->oo 1п6
На этом примере мы видим, что размерность Хаусдорфа есть
обобщение обычной геометрической размерности, позволяющее
характеризовать «фрактальные» объекты.
Рассмотрим теперь второй классический фрактальный объ-
объект, называемый снежинкой. Снежинка обладает одним необыч-
4) Заметим, что построенная структура инвариантна относительно изме-
изменения масштаба. «Издали» канторовское множество выглядит как отрезок,
из которого выкинута средняя треть. Вблизи мы увидим такую же картину
при любом' увеличении, т. е. на любых масштабах. След такой масштабной
инвариантности сохраняется в структуре странных аттракторов — их разбие-
разбиении на листы.

168
Глава VI
ным свойством (разделяемым сечениями Пуанкаре многих
странных аттракторов): она имеет бесконечный периметр, хотя
ограничивает конечную область плоскости. Возьмем равносто-
равносторонний треугольник, разделим каждую из его сторон на три рав-
равные части и на каждой из трех центральных третей построим во
внешнюю сторону по равностороннему треугольнику меньших
размеров (рис. VI. 35). Итерируя это построение бесконечно
Рис. VI. 35. Фрактальный объект в форме снежинки (первые стадии по-
построения) .
много раз, мы получаем фрактальный объект1), называемый
иногда кривой Коха. Рассуждая так же, как прежде, находим,
что ее размерность Хаусдорфа равна ;
D=— ~126
и 1пЗ 1'zo>
К сожалению, во многих других случаях, представляющих прак-
тичсскнй интерес, вычисления размерности Хаусдорфа непо-
непосредственно из ее определения как предела сходятся слишком
') Подобно канторовскому множеству, этот объект обладает масштабной
инвариантностью.

Странные аттракторы
169
в
Рис. VI. 36. Метод вычисления фрактальной размерности множества точек,
расположенных в двумерном пространстве. Вокруг произвольной точки мно-
множества проводим окружность (сферу или гиперсферу в пространстве более
высокой размерности) радиусом г и определяем число точек Л'(г), оказавшихся
внутри окружности, и его зависимость от г: а — в общем случае N (г) ~ г";
б — для линии (одномерный случай) N{r) « г1; в — для поверхности (дву-
(двумерный случай), Л7(г) ~ тг\ г — для канторовского множества iV (/*) — г".ол;...

170 Глава VI
медленно, если размерность р фазового пространства больше
двух. Поэтому приходится использовать другую фрактальную
размерность v, которая может быть вычислена быстрее. Хотя v,
называемая корреляционной размерностью, вообще говоря, не
равна в точности размерности Хаусдорфа D, она ограничивает
D снизу:
Проиллюстрируем наш второй подход на примерах из пла-
планиметрии. Рассмотрим множество точек на плоскости, представ-
представляющее, например, сечение. Пуанкаре какого-то потока в R3,
и пусть N(r) — число точек этого множества, расположенных
внутри окружности радиусом г. В случае дискретного множе-
множества точек, равномерно распределенных по кривой (размер-
(размерность 1), получаем при достаточно малых г:
N(r)~r,
т. е. N(r) ~ rv с v=l (рис. VI. 36, б). С другой стороны, если
точки равномерно распределены по поверхности (размерность 2;
см. рис. VI.36,в), то
N{r)~r2, v = 2.
Теперь мы уже можем рассмотреть общие объекты произволь-
произвольной размерности, такие, как описанное выше канторовское мно-
множество (рис. VI.36,г). Число точек N(r), расположенных внутри
окружности, растет в среднем медленнее, чем радиус г. Полагая
N(r) ~ rv, можно вычислить, что v ж 0,63. Это равно вычислен-
вычисленной выше размерности Хаусдорфа. Аналогично для аттрактора
Энона (см. разд. VI. 3.2) мы получаем среднюю зависимость
N(r)~rv, где v « 1,26.
Метод допускает обобщение на р-мерные пространства, если
под N (г) понимать число точек, содержащихся в р-мерной ги-
гиперсфере радиусом г1).
') Корреляционная размерность v зависит от плотности точек на аттрак-
аттракторе, так как связана с подсчетом точек. В отличие от нее размерность' Хаус-
Хаусдорфа и множества зависит только от геометрии множества. По определе-
определению D есть «максимальная» размерность объекта. Основной вклад в D дает
та компонента объекта, для покрытия которой требуется наибольшее число
сфер. Это наиболее «складчатая» часть, если объект является странным ат-
аттрактором, получающимся в результате растяжения и складывания. Если
распределение точек на аттракторе имеет низкую плотность именно в склад-
складчатой части, то эта часть не даст существенного вклада в v. Таково каче-
качественное обоснование того, что корреляционная размерность v ограничена
сверху размерностью Хаусдорфа D. Для таких конструкций, как канторовское
множество или снежинка Коха, эти две размерности равны, если плотность
точек, используемых при вычислении v, однородна по объекту.

Странные аттракторы
171
VI. 4.3. Геометрическая характеристика аттрактора
В последнее время был предложен эффективный метод оцен-
оценки геометрических характеристик аттрактора на основе описан-
описанного выше подхода в сочетании с возможностью восстановления
траекторий в фазовом пространстве по задержкам времени.
Напомним, что, исходя из одной зависящей от времени пе-
переменной X(t), мы можем восстановить траекторию в р-мерном
фазовом пространстве (см. разд. IV. 5), выбирая в качестве ко-
Рис. VI. 37. Схематическое изображение траектории, восстанавливаемой по-
поточечно по значениям простой переменной X(t) методом запаздывающего ар-
аргумента. В этом примере использовано трехмерное пространство с координа-
координатами X(t), X(t + x), X(t + 2x).
ординат величины X(t), X(t -\- х), X(t -\- 2т), ..., X(t-\-(p—- 1)т),
где х — надлежащим образом выбранная временная задержка ').
На практике время t дискретизуется, в результате чего мы по-
получаем серию р-мерных векторов, представляющих фазовую
диаграмму динамической системы (рис. VI. 37).
В хаотическом режиме (соответствующем странному аттрак-
аттрактору) положения двух точек на одной и той же траектории, но
разделенных во времени, некоррелированы2) вследствие ЧЗНУ.
Так как все точки лежат на аттракторе, существует простран-
пространственная корреляция, которую можно попытаться охарактеризо-
охарактеризовать с помощью какой-то функции. Мы можем написать
С (г)— lim (l//n2) X [число пар i, j, для которых |хг — \}\<г],
!) Оптимальный выбор т сильно зависит от конкретной
X(t) и определяется отчасти эмпирически.
2) И в этом случае «виновницей» является ЧЗНУ.
ормы сигнала

172 Глава VI
где i и / — индексы, упорядочивающие точки вдоль траектории,
на которой расположено всего т точек (рис. VI. 37). Функцию
С (г) можно определить более строго:
т
С (г) = Цт^ -ij- ? Я (г -1 х, - х, |),
где Н — функция Хевисайда, равная по определению единице
при положительных х и нулю при остальные значениях х. Число
пар точек I, /, расстояние между которыми меньше г, есть вме-
вместе с тем сумма всех N(r) (см. выше) — величин, «пересчиты-
«пересчитывающих» точки в гиперсферах с центрами в каждой') точке ат-
аттрактора. Следовательно, С (г) пропорциональна N(r):
C(r)~r\
Заметим, что применимость этого степенного закона ограни-
црря ЯНЯЧРНЧ^МИ г ^ОСТЯТОЧЧ^ МАЛЫМИ Т7О СПЗВНСНИЮ п noo^f6n-
ностями аттрактора. При увеличении г величина N(r) достигает
насыщения, когда г принимает значения, сравнимые с размером
аттрактора, поскольку тогда учитываются т точек и, следова-
следовательно, С(г)-»-1. С другой стороны, при очень малых значе-
значениях г число пзр точек i, j, расстояние между которыми мень-
меньше г, становится малым, поскольку число точек на аттракторе
конечно и статистика становится бедной. Кроме того, приобре-
приобретает решающее значение относительный вклад инструменталь-
инструментальной ошибки. Следовательно, на практике степенной закон
С(г)~гу выполняется только в ограниченном диапазоне зна-
значений г и может быть использован для определений v — корре-
корреляционной размерности аттрактора.
VI. 4.4. Реализация процедуры
Исходя из дискретных значений X(tt), полученных экспери-
экспериментально, мы восстанавливаем траекторию в р-мерном про-
пространстве, как описано выше, при возрастающих целых значе-
значениях р:
р = % 3, 4, 5,
При каждом значении р мы вычисляем С (г) и определяем
тангенс угла наклона касательной к графику функции /, опре-
4) Суммирование по всем парам i, j приводит к дополнительному благо-
благоприятному эффекту — погашению статистической точности функции С (г).
С другой стороны, эта процедура сопряжена с большой затратой машинного
времени. Как показывает опыт, весьма разумное усреднение достигается уже
при сотне или около того операций, тогда как число точек т « 10*. что
приводит к значительной экономии машинного-времени.

Странные аттракторы
173
деляемой равенством С (г) = f (log г), достигаемым при некото-
некотором показателе v. Для периодического режима, на фазовой диа-
диаграмме которого мы имеем предельный цикл, зависимость. С (г)
от г строго линейна (с точностью до эффектов, связанных с раз-
размером объекта). С совершенно иной ситуацией мы встречаемся
в случае белого шума1). Сигнал можно рассматривать как су-
суперпозицию бесконечного числа независимых колебательных
мод. Следовательно, такой режим может быть описан с помощью
Хд С (г)
2 3 U
Рис. VI. 38. График функции С (г) для белого шума в двойном логарифми-
логарифмическом масштабе. Обратите внимание на то, что наклон кривых (позволяю-
(позволяющий судить о величине показателя v) возрастает с увеличением размерности р
пространства представления.
Из работы Б. Мальрезона, П. Аттена, П. Берже и М. Дюбуа.
аттрактора Тп с очень большим п. Траектории плотно покры-
покрывают любое фазовое пространство размерности
Действительно, как показывает рис. VI. 38, у характерных функ-
функций С (г), получаемых из белого шума, тангенсы углов наклона
касательных к их графикам в двойном логарифмическом мас-
масштабе продолжают возрастать с увеличением р: v ~ р. Этот ре-
результат допускает обобщение: если вычисленное значение v
равно р (или продолжает возрастать вместе с о), то это озна-
означает, что размерность пространства, используемого для вычис-
вычислений, меньше размерности соответствующего аттрактора (или
сравнима с ней). С другой стороны, если размерность v, вычис-
вычисленная для хаотического режима, становится не зависящей от р,
то хаос детерминированный и соответствующий аттрактор
странный.
Определение белого шума см. в разд. III. 3.3.

174
Глава VI
В качестве иллюстрации этого метода вычисления корреля-
корреляционной размерности v для странных аттракторов рассмотрим
аттрактор Энона, определенный в разд. VI. 3.2. На рис. VI. 39
показан график функции С (г) в двойном логарифмическом мас-
масштабе. Значение v, которое можно получить из этого графика,
составляет
v= 1,25 ±0,05,
что согласуется с значением размерности Хаусдорфа, вычис-
вычисленной исходя из ее определения:
?>=1,26.
Наконец рассмотрим пример из области неустойчивости РБ
в ограниченной геометрии (см. разд. V. 3). В качестве жидкости
log С (г)
log r
Рис. VI. 39. График функции С (г) для аттрактора Энона в двойном логариф-
логарифмическом масштабе. В этом частном случае вычисления проведены только
для двумерной задачи (в плоскости X, Y аттрактора), поэтому на графике-
представлена только одна кривая:
выберем силиконовое масло с числом Прандтля 40 в ячейке
с аспектным отношением (ширина/высота), равным 2. Конвек-
Конвективная структура состоит из двух валов. Увеличивая число Рей-
нольдса, мы переходим от периодического режима к хаосу через
субгармонический каскад (см. гл. VIII). Отслеживаемой пере-
переменной и на этот раз является отклонение узкого пучка света,
пропускаемого сквозь ячейку. Это отклонение служит мерой вер-

Странные аттракторы
175
тикального градиента температуры. Анализируемые данные со-
соответствуют хаотическому режиму в конце обратного каскада
(см. гл. VIII). Как видно из рис. VI. 40, тангенсы угла наклона
tg CCr)"
0'-
-1
~2
-3
2 3 4 tgr
Рис. VI. 40. График функции С (г) для конвекции Рэлея—-Бенара. В отличие
от белого шума (рис. VI. 38) наклон кривых перестает возрастать, начиная
с размерности пространства р = 4.
Из работы Б. Мальрезона, П. Аттена, П. Берже и М. Дюбуа.
10 -
10 12
Рис. VI. 41. Показатель v как функция размерности р. Величину показателя v
мы оцениваем по наклону характеристик, представленных на рис. VI. 38 и
VI. 40. В случае белого шума показатель v возрастает с увеличением р ли-
линейно. Иная картина наблюдается при турбулентной конвекции Рэлея — Бе-
Бенара, когда показатель v достигает насыщения.
Из работы Б. Мальрезона, П. Аттена, П. Берже, М. Дюбуа.
, касательной к графику функции С (г) в двойном логарифмиче-
логарифмическом масштабе достаточно хорошо определены и не зависят от
размерности р фазового пространства, как только р становится
больше 3. Насыщение корреляционной размерности v при возра-
возрастании р лучше видно на рис. VI. 41 и контрастирует с линейной

176 Глава VI
зависимостью v от р для белого шума (или случайного сиг-
сигнала). Анализ данных такого типа свидетельствует о детерми-
детерминированном характере хаотического поведения в этом режиме
и, кроме того, определяет нижнюю границу числа возбужденных
степеней свободы.
VI. 5. АТТРАКТОР ТИПА ПОДКОВЫ
На протяжении этой главы мы занимались описанием раз-
различных свойств странных аттракторов, Смейл, обобщив более
раннюю работу Левинсона, предложил отображение плоскости
на себя, ставшее теоретической моделью, позволяющей иллю-
иллюстрировать эти свойства.
Основной операцией, необходимой для создания странного
аттрактора, является растяжение в сочетании со складыванием,
порождающие аттрактор, который занимает ограниченную часть
•^ji-io^Ii'jj.^ iij^Ct-j.^cii.i^i.jJU.. ,и,Бо 71 1С и. 71 ОПСр dii,iiyi- \J u<-1 Aii.v\b,i.n:i/i.-^I\.»Jici(u,1JA~
вания и была выбрана за исходный пункт при построении мо-
модели. Возьмем прямоугольник ABCD (рис. VI. 42) и, растянув
его (например) в 2 раза по оси х и одновременно сжав в 2т] раз
по оси у, получим прямоугольник AiBiCiDi. При ц > 1 такая
операция приводит к сокращению площади, что необходимо для
диссипативной системы. Сложим прямоугольник A\B\C\D\ в виде
подковы и наложим на исходный прямоугольник ABCD. Именно
форма изогнутого прямоугольника A\BiC\D\ и дала название
модели. Повторяя операцию (снова растяжение по оси х и скла-
складывание по оси у), мы получаем образ подковы, напоминающий
по форме двойную заколку для волос1) (рис. VI. 43). Итерируя
операцию бесконечно много раз, мы получаем сложную много-
многослойную структуру s&, обладающую, как будет показано, всеми
свойствами странного аттрактора2).
') Модель Смейла и преобразование пекаря, с которым мы встретимся
в гл. IX, тесно связаны между собой. Вместе с тем следует обратить внима-
внимание на два существенных различия между ними; преобразование пекаря
разрывно и, кроме того, сохраняет площади.
2) Строго говоря, jif есть пересечение всех итераций исходного прямо-
прямоугольника R. Если / — отображение Смейла, то
п
В ;;.:ль;1с;шс;,г ни будс:.: предполагать, что до:.;шшрующий эффект преобра-
преобразовании состоит в растяжении горизонтальных участков, и не будем учиты-
учитывать действия преобразования на изогнутую часть подковы. Иначе говоря,
мы ь:ожем предположить, что длина прямоугольника ABCD по оси х во
много <аз превосходит его ширину.

Странные аттракторы
177
Рис. VI. 42. Первая итерация преоб-
преобразования типа подковы. Исходный
прямоугольник ABCD мы растягиваем
вдвое в направлении оси х и сжи-
сжимаем более чем вдвое в направлении
оси у. Сжатый и растянутый таким
образом прямоугольник складываем
вдвое, и получаем образ исходного
прямоугольника при данном преобра-
преобразовании, напоминающий по форме
подкову.
А
Г)
А|—
_, 1
А
D
1
г
1
1
У
1
В
—л
с
в
i
Рис. VI. 43. Вторая итерация прсоб-
pajobaniii: чипа подковы. Операция,
изображенная на рис. VI. 42, повто-
повторяется на подкове. На первом этапе
получаем сильно вытянутую подкову.
(Мы предполагаем, что ширина обра-
образа подковы постоянна. Строго говоря,
такое предположение неверно, по-
поскольку изогнутая часть подковы так-
также подлежит растяжению.) После
складывания мы получаем нечто вро-
вроде двойной заколки для - волос'
12 П. Берже и др.

178
Глава VI
То, что структура s& есть аттрактор, гарантируется значением
г\ > 1, которое приводит к сокращению площадей: образ каж-
каждой точки исходного прямоугольника ABCD лежит внутри *s?.
Кроме того, аттрактор s4- странный, так как обладает ЧЗНУ:
каждая итерация удваивает компоненту х расстояния между
двумя точками, тем самым порождая экспоненциальное увели-
увеличение расстояния между точками.
Преобразование Смейла служит особенно простым приме-
примером гиперболичности. Растяжение происходит по оси х (можно
k=0 k=i k=2
А
| 1
I
D
0
0
Рис. VI. 44. Поперечные сечения, проведенные через несколько первых обра-
образов исходного прямоугольника при преобразовании типа подковы. Попереч-
Поперечные сечения вдоль оси 00' проведены через исходный прямоугольник (k=0),
его первую итерацию (подкову, k = 1) и вторую итерацию (двойная заколка
для волос, k = 2). Сравнивая с рис. VI. 34, мы обнаруживаем тот же прин-
принцип, что и используемый при построении канторовского множества.
сказать также, что ось х соответствует неустойчивому многооб-
многообразию) , а сжатие — по оси у (ось у соответствует устойчивому
многообразию). С этими двумя направлениями х и у (перпен-
(перпендикулярными аттрактору типа подковы) связаны два коэффи-
коэффициента Ляпунова отображения. Больший коэффициент (вдоль
оси х) равен Ai = 2, а другой коэффициент Ляпунова равен
Аг = 1/21]. Произведение этих коэффициентов AiA2—1/т] слу-
служит мерой степени сжатия площадей (см. также рис. VI. 22),
а показатели Ляпунова соответственно равны A,i = In А- и Я2 =
= In A2.
Наконец убедимся, что аттрактор ._s# является фрактальным
объектом. На рис. VI. 44 показана эволюция сечения 00', про-
проведенного через прямоугольник, при повторяющихся итерациях.
В начале (« = 0) мы имеем прямоугольник ABCD, и его сече-
сечение 00' имеет вид прямолинейного отрезка. После одной итера-
итерации (k—\) мы получаем подкову, а сечение состоит из двух

Странные аттракторы 179
отрезков. После второй итерации сечение, проведенное через
«двойную заколку для волос», состоит из четырех отрезков
и т. д. Мы легко узнаем принцип построения канторовского мно-
множества в том виде, как оно описано в предыдущем разделе.
Можно вычислить, как это было сделано для канторовского
множества, размерность Хаусдорфа сечения 00' аттрактора:
U In 2T1 •
В результате получаем фрактальную размерность аттрактора^:
" ~ х ^ In 2т) '
которая характеризует объект, занимающий промежуточное по-
положение между линией и поверхностью1).
Заметим, что в пределе при i\-*-l (пренебрежимо слабая
диссипация, почти полное отсутствие сокращения площадей) D'
стремится к двум, а поэтому итерации точек прямоугольника
ABCD практически заполняют всю его поверхность. В противо-
противоположном предельном случае сильной диссипации ti >• 1 раз-
размерность D' стремится к единице и аттрактор «5$ почти вырож-
вырождается в линию (как сечение Пуанкаре аттрактора Лоренца).
Аттрактор ?ф является сравнительно простой иллюстрацией
свойств странных аттракторов. Помимо педагогического инте-
интереса существенно и то, что основные свойства аттрактора типа
подковы обнаруживаются у. многих сечений Пуанкаре хаотиче-
хаотических потоков. Например, численные эксперименты показывают,
что при некоторых значениях параметра сечение Пуанкаре ат-
аттрактора Лоренца возникает при повторных итерациях отобра-
отображения типа подковы. В основу самого отображения Энона было
положено следующее замечание: оно сводится к отображению,
которое при каждой итерации растягивает, сокращает и склады-
складывает данную фигуру. На рис. VI. 23 показано, к чему приводит
отображение Энона. Результаты очень похожи на то, к чему
приводит отображение Смейла.
ЛИТЕРАТУРА
Brandstiiter A., et al., Physical Review Letters, 51, p. 1442 A983).
Croquette V., Poitou C," Compte-rendus de l'Academie des Sciences de Paris.
C292, p. 1353 A981).
Croquette V., Pour la Science, 62, p. 62 A982).
!) Подобно аттрактору Энона, аттрактор типа подковы может рассматри-
рассматриваться как сечение Пуанкаре хаотического трехмерного потока.
12*

180 Глава VI
Dubois M., Lecture Notes in Physics, 164, p. 117 A982).
Grassberger P., Procaccia I., Physical Review Letters, 50, p. 346 A983).
Grassberger P., Procaccia I., Physica, 9D, p. 189 A983).
Guckenhelmer /., Buzina G., Physical Review Letters, 51, p. 1438 A983).
Нёпоп M., Pomeau Y., Lecture Notes in Mathematics, 565, p. 29 A976).
Нёпоп М., Communications in Mathematical Physics, 50, p. 69 A976).
Lorenz E. N., Journal of Atmospheric Sciences, 20, p. 130 A963).
Malraison В., et al., Comptes rendus de l'Academie des Sciences de Paris, C297,
p. 209 A983).
Roux J.-C, et al., Physica, 8D, p. 257 A983).
Roux J.-C, Swinney H. L: In: Non linear phenomena in chemical dynamics,
ed. С Vidal, A. Pacalilt, Springer-Verlag, p. 38 A981).
Simo C, Journal of Statistical Physics, 21, p. 465 A979).
Tresser C, et al., Le Journal de Physique Letters, 13, p. L123 A980).
Yorke /., Yorke E., Journal of Statistical Physics, 21, p. *263 A979).

ГЛАВА VII
КВАЗИПЕРИОДИЧНОСТЬ
VII. 1. БИФУРКАЦИЯ ХОПФА ИЗ ПРЕДЕЛЬНОГО ЦИКЛА
В, гл. VI было показано, что странные аттракторы харак-
характерны для хаотического поведения в диссипативной динамиче-
динамической системе с небольшим числом степеней свободы. Вопрос, на
который мы пытаемся ответить в этой главе и в последующих
главах, можно было бы сформулировать так: с помощью каких.
Рис. VII. 1. Сечение Пуанкаре фазовых траекторий вблизи предельного цик-
цикла С.
механизмов осуществляется перелод между периидическим а
странным аттрактором? Отвечая на него, исследователи устано-
установили «маршруты», или «сценарии», переходов к хаосу, характе-
характеризуемые ограниченным числом бифуркаций. Их удалось разде-
разделить на три главных типа маршрутов в зависимости от того,
каким образом периодический режим утрачивает свою устойчи-
устойчивость. Анализ сечения Пуанкаре показывает, что предель-
предельный цикл линейно неустойчив: последовательные пересечения
Л'1,Л'2, ... траектории, первоначально близкой к предельному
циклу, с плоскостью S (рис. VII. 1), удаляются от точки л'О:

182
Глава VII
5|
в
1 ..
X
2 ' ¦
L i '
Vwr VTI 2 Предстячлриие на плоскости сечения Пуанкаре зсптороп бх, =
= xQx{ при возрастающих значениях i. Собственное значение к матрицы
Флоке может выйти из области, заключенной внутри единичной окружности,
,« трех случаях: а — при Я> 1; б — при Я<—1; в-^-при X = а ± (J3, |Я|>
> 1. На рисунке показана только динамика в направлении собственного век-
вектора, соответствующего наибольшему по абсолютной величине собственному
значению.
•Ti
Рис. \ II. 3. Эволюция вектора бх,- в плоскости сечения Пуанкаре после би-
•фуркации Хопфа. Точка Хо — сечение неустойчивого теперь предельного цикла,
точки Ti принадлежат тору Г2.

Квазипериодичность 18$
Полагая 6х1 = х0хи bx2 = xQx2, мы видим, что бх2 = М6хи где
М — матрица Флоке. Условие неустойчивости предельного цикла
состоит в том, что модуль по крайней мере одного собственного
значения А матрицы М должен быть больше единицы. Если Я,=
= 1 + е, то каждый вектор бх* увеличивается в одном и том же
направлении с каждым оборотом. Если А = —A + в), то после-
последовательные векторы бх,- увеличиваются по модулю, но попере-
попеременно направлены то в одну, то в противоположную сторону.
Наконец в случае двух комплексно-сопряженных собственных
значений векторы бх,- с каждым циклом поворачиваются на
угол у, а их длина увеличивается (рис. VII. 2). Если бифурка-
бифуркация, сопровождающая неустойчивость последнего типа, супер-
суперкритическая, то нелинейные эффекты (не учитываемые в приве-
приведенных выше рассуждениях) ограничивают удлинение модуля
|бхг| до некоторой конечной величины. Предельный цикл, кото-
которому в сечении Пуанкаре соответствует точка х0, преобразуется
бифуркацией Хопфа в тор Т2, сечение Пуанкаре которого со-
состоит из множества точек Г,-, Г,+ь •¦• (рис. VII. 3). ¦*
В этой главе мы рассмотрим события, которые ведут от
тора Т2 (квазипериодического режима) к странному аттрактору,
соответствующему хаотическому режиму.
VII. 2. ТЕОРИЯ РЮЭЛЯ - ТАКЕНСА (РТ)
VII. 2.1. Описание
Эта теория, выдвинутая в 1971 г. и развитая в 1978 г. Рюэ-
лем, Такенсом и Ньюхаусом (РТН), имеет большое историче-
историческое значение, поскольку она впервые достаточно обоснованно
поставила под сомнение механизм турбулентности, предложен-
предложенный Ландау, согласно которому для возникновения турбулент-
турбулентности требуется бесконечное число бифуркаций Хопфа. Выдвинув
эту революционную идею, Рюэль и Такенс (РТ) пошли на эпи-
эпистемологический разрыв с традицией: оказалось, что для генера-
генерации хаотического режима достаточно очень небольшого числа
бифуркаций. Если не воспроизводить здесь доказанную ими
весьма абстрактную математическую теорему, то подход РТН
схематически сводит к следующему. Рассмотрим динамическую
систему в стационарном состоянии, например ламинарное тече-
течение вязкой жидкости. Предположим, что, когда управляющий
параметр (число Рейнольдса) возрастает, режим утрачивает
свою устойчивость и переходит в колебания с частотой /ь Пред-
Предположим, что такой же процесс повторяется еще 2 раза, т. е. что
всего происходят три последовательные бифуркации Хопфа, по-
порождающие три независимые частоты /ь /2 и /з- 'огда, согласно-

184
Глава VII
теории РТН, соответствующий тор Тг при весьма общих усло-
условиях может стать неустойчивым и перейти в странный аттрак-
аттрактор. Нестационарное поведение перестает быть квазипериодиче-
квазипериодическим с тремя частотами (на торе Г3), а становится явно хаоти-
хаотическим (рис. VII. 4).
Рюэль, Такенс и Ньюхаус показали, что некоторые возмуще-
возмущения могут разрушить тор Г3 и преобразовать его в странный
Неподвижная Предельный
тючка цикл
_ _, „ Управляющий
Тор Тг Тор Т?-** СЛ .параметр
Р
QP,
QP.3"*- Лаос
Рис. VII. 4. Схематическое изображение последовательных бифуркаций Bit B%
и'Вз, приводящих, согласно теории Рюэля — Такенса, к хаосу. 5 — стационар-
стационарное состояние; Р — периодическое состояние; QP2 — квазипериодический ре-
режим с двумя частотами; QPs — квазипериодический режим с тремя частота-
/ ми; СА —странный аттрактор.
аттрактор. Но в отличие от тора странный аттрактор обладает
устойчивостью по отношению к действующим на систему возму-
возмущениям. Можно ожидать, что при этих условиях спектр мощно-
мощности динамической системы будет эволюционировать как функ-
функция управляющего параметра следующим образом. Спектр мощ-
б
4 S(f)
а
S(f)
Рис. VII. 5. Схема эволюции спектра мощности согласно теории Рюэля —
Такенса. а — периодический режим; б — квазипериодический режим с двумя
частотами; в — хаотический режим. S(f)—спектр мощности, определенный
в гл. III (и обозначенный там через \хь\ 2).
ности будет содержать сначала одну частоту (ft), затем две час-
частоты (/2 и /3) и иногда три частоты (fu f2 и /3). Как только
в спектре появляется третья частота, возникает характерная для
хаоса широкополосная шумовая компонента (рис. VII. 5). Третья
частота может обнаруживаться (а может и не обнаруживаться)
в спектре перед тем, как мы идентифицируем хаос. Нельзя не
подчеркнуть еще раз принципиальное различие между механиз-
механизмом РТН и механизмом Ландау: вместо бесконечно большого
числа частот достаточно трех частот. Это говорит о том, что си-
система с небольшим числом степеней свободы может порождать

Квазипериодичность 186-
хаотический режим. Попытаемся теперь обосновать необходи-
необходимость возникновения квазипериодического режима с тремя час-
частотами перед появлением на этом маршруте странного аттрак-
аттрактора.
VII. 2.2. Топологическая интерпретация
В предыдущей главе было показано, что для существования
странного аттрактора необходимо фазовое пространство с раз-
размерностью не ниже трех1). Вернемся к последовательности из
трех бифуркаций Хопфа, идущих одна за другой. Первая би-
бифуркация ведет к переходу от начального стационарного состоя-
состояния (неподвижная точка, размерность 1) к периодическому со-
состоянию (предельный цикл, размерность 1). Вторая бифуркация
Хопфа преобразует периодический режим (с частотой /i) в ква-
квазипериодический режим (с частотами /i, f2 и иррациональным
,»_>,_,.,, ... С /С \ (Г^ г> -г v. ,-..,.,-,,.,,.,.,J* ^^,^-^^,,-~.^ _„ „ „ Т""? _
Vj i iiOii-i^lIiiClVJ i L/ i 2/ ' uCuTBi-jCi l>y XOXl^iiMi U A IL/UJii Op 1 Op Л. С ptiG"
мерностью 2. На торе T2 траектории могут подвергаться тополо-
топологической деформации только при синхронизации, т. е. когда
отношение fi/fi становится рациональным (см. разд. VI. 1.3 и
примечания к нему). Третья бифуркация Хопфа, если она супер-
суперкритическая, порождает переход (в линейном приближении) от
квазипериодического режима с двумя частотами к квазипериоди-
квазипериодическому режиму на торе Т3 с тремя частотами (/ь /2 и f3). По-
Подобно тому как Т2;— двумерный аттрактор, тор Т3 — трехмер-
трехмерный аттрактор. Мы можем построить развертку аттрактора Тг
в Ч'3 так же, как можно построить развертку тора Т2 в Р.2. В слу-
случае тора Т2 траектории должны ложиться на отрезки прямых
в прямоугольнике (прямоугольник представляет собой раз-
развертку тора Т2; см. разд. VI. 2.2). Но траектории на Т3 «живут»
в кубе2) (рис. VII. 6), поэтому они могут не быть параллель-
параллельными и тем не менее не пересекаться (см. разд. VI. 2.2). Таким
образом, дополнительная степень свободы3), возникающая с по-
') Подчеркнем еще раз, что размерность аттрактора не следует смеши-
смешивать "с размерностью фазового пространства, в котором находится аттрактор.
2) Подобно тому как траектории на торе Г2 удобно изображать на
прямоугольнике (см. разд. VI. !.3), траектории на торе Т9 можно представить
линиями, проходящими внутри прямоугольного параллелепипеда с отождеств-
отождествленными противоположными гранями. (Соответствующее фазовое простран-
пространство должно быть не менее чем четырехмерным; см. рис. VII. 6 и подпись
к нему.)
3) Заметим, что появление у режима новой частоты требует учета допол-
дополнительной размерности фазового пространства, причем каждая новая ча-
частота соответствует пог.п*' степени свободы. Согласно интерпретации Л":'д:г.',
каждой частоте соответствует фаза, значение которой зависит от деталей,
процесса возникновения турбулентности. Эта «свободная» фаза и есть сте-
степень свободы.

186
Глава VII
¦явлением третьей частоты, привносит в картину совершенно но-
новый элемент. Она позволяет развиваться неустойчивостям
(рис. VII. 7), отличным от синхронизации — единственной воз-
а
Рис. VII. 6. Развертки торов Т2 и Т3, а —развертка тора Тг в прямоугольник.
Дсст!:г;;у^ степки, траектория скачком дерелидш на ^(лдиьиао^ожную с/ен-
ку, после чего продолжается' в ту же сторону, что и раньше; б '¦— каждая из
граней тора Г3 отождествлена с противоположной гранью. Угловые частоты
квазипериодического движения равны a>f, ш2 и со3.
, Неподвижное*
Ч^ точка.
Предельный цикл
Netjcmoiz 41zsocvt^^^"\
Странный
Рис. VII. 7. Последовательные фазовые диаграммы в теории Рюэля — Такенса.
После каждой бифуркации Хопфа размерность фазового пространства повы-
повышается на единицу.
можности, существующей для Т2, как было показано в
разд. VI. 1.3. Исходя из этих элементарных топологических со-
соображений, мы можем попытаться интерпретировать кеобходи-

Квазипериодичность 187
мость наличия по крайней мере трех степеней свободы') для
получения хаоса, описываемого странным аттрактором. Но до-
достаточно ли это условие? Ответить на этот вопрос мы попы-
попытаемся в следующем разделе.
, VII. 2.3. Практическое значение: численное моделирование
В рамках обсуждаемого здесь подхода, для того чтобы по-
поток в фазовом пространстве имел странный аттрактор, необхо-
необходимы три независимые частоты. Наша цель состоит в том, чтобы
определить, могут ли малые' возмущения дестабилизировать
тор Т3 и превратить его в странный аттрактор. Существование
устойчивых экспериментально наблюдаемых режимов, квазипе-
квазипериодических с тремя частотами и свободных от хаоса, доказы-
доказывает, что по крайней мере не все возмущения дестабилизируют
тор Т3.
Эти соображения, а также абстрактный математический ха-
характер теоремы РТН наводят на мысль проиллюстрировать их
теорему численными экспериментами. Рассмотрим квазиперио-
квазипериодическую функцию X(t) с тремя частотами fu f2, fc
= F(fJ, f2t, fzt).
Введем в уравнение потока контролируемое возмущение, чтобы
проанализировать устойчивость потока относительно таких воз-
возмущений. Устойчивость функции X(t) исследуется с помощью
сечения Пуанкаре потока. В частности, мы выбираем поверх-
поверхность сечения так, чтобы значения X(t) можно было получать
через времена, кратные периоду Т\ = \/f\, т. е. в дискретные
моменты времени 2) Ik = k/f\.
Сечение Пуанкаре аттрактора Т3, соответствующее функ-
функции X(t), есть тор Т2, который может быть описан двумя уг-
углами 0 и ф. Последовательные пересечения с поверхностью се-
сечения удовлетворяют уравнениям 3)
e*+i = [e* + «>i] (modi),
(modi). (VH-1)
Мы определяем устойчивость режима X(t), возмущая отображе-
отображение Пуанкаре, заданное системой (VII. 1). Пусть еР(8, Ф)— воз-
') Отсюда необходимость трех последовательных бифуркаций Хопфа.
2) Мы снова прибегаем здесь к стробоскопическому методу, описанному
в предыдущей главе в связи с вычислениями сечений Пуанкаре в эксперимен-
экспериментах с тепловой конвекцией.
3-) Мы снова используем преимущество метода Пуанкаре, сводя квази-
квазипериодический потоя с тремя частотами к итерационному двумерному ото-
отображению.

188 Глава VII
«лущение !)^ приложенное для выяснения устойчивости решения.
Амплитуда возмущения управляется параметром е, где е = 1
соответствует полному возмущению.
Возмущенное отображение Пуанкаре тора Та принимает вид
(modi), _„
^+i = [^+«2 + eP2(9b фк)] (modi). (V11'2)
Над системой (VII. 2) с случайно выбранными Pj и Р2 возра-
возрастающим параметром е выполнено много численных экспери-
экспериментов. Заключения относительно возмущенной системы (VII. 2)
мы извлекаем, вычисляя показатели Ляпунова этого отображе-
отображения (см. приложение Б). Возникающие режимы можно класси-
классифицировать, разделяя их на четыре типа в зависимости от зна-
знаков показателей Ляпунова:
1) квазипериодические режимы с тремя частотами @,0,
О, —);
2) квазипериодические режимы с двумя частотами @, 0,
> ) >
3) периодические режимы с одной частотой @, —,:—, —);
4) хаотические режимы (+, 0,—,.—).
Статистические результаты многих численных экспериментов,
соответствующие возмущениям Р(в,,ф) различного рода и раз-
различным отношениям частот, показаны на- круговых диаграм-
диаграммах 2) (рис. VII. 8) при трех различных значениях s (т. е. при
трех амплитудах возмущений). Эти результаты явно подтверж-
подтверждают конкретные следствия из теоремы РТН: тор Т3 неустойчив
относительно некоторых (достаточно больших) возмущений, под
действием которых он переходит в странный аттрактор, устой-
устойчивый, как показывают дальнейшие численные эксперименты.
Ясно, однако, что в пределе при е-»-0 вероятность получения
хаотического режима обращается в нуль. Можно провести ана-
аналогию между структурной неустойчивостью траекторий на Т2 и
, Г3. Единственная неустойчивость траекторий на Т2 приводит к
явлению синхронизации, подробно исследованному в приложе-
приложении В. Нетрудно видеть, что по мере приближения к порогу би-
бифуркации Хопфа, при которой впервые проявляется аттрактор
Т2, синхронизация встречается редко. Аналогично не следует
!) Здесь РF, Ф) — функция, периодическая по 9 и ф, амплитуда и фаза
которой выбрана случайным образом. Средняя амплитуда возмущения управ-
управляется параметром е,
-) Например, 7 % хаотического режима означает, что ¦ из N численных
экспериментов, проведенных над системой (VII. 2), 7- (Л^/100) привели к хао-
хаотическому режиму.

Квазипериодичнвсть
189
удивляться тому, что неустойчивость на Г3, приводящая к хаосу,
также становится редкой (для сла0ых возмущений) при произ-
произвольном выборе параметров бифуркации. Это обстоятельство,
е*0.25
е=0,50
= 0,76
Рис. VII. 8. Процентное соотношение различных динамических режимов, на-
наблюдаемых в численных экспериментах при трех различных амплитудах е
(тор Г3). Р — периодический режим; QPz— квазипериодический режим с дву-
двумя-частотами; QPs—квазипериодический режим с тремя частотами. Точками
выделен сектор, соответствующий хаотическому режиму.
отмеченное Арнольдом, согласуется с результатами численных
экспериментов на основе приведенных выше моделей.
VII. 2.4. Экспериментальный пример
Проиллюстрируем теорию РТ на примере неустойчивости РБ.
Жидкостью, в которой происходит конвекция, является вода со
средней температурой, соответствующей числу Прандтл;:, раг.-
ному 5. Аспектное отношение ячейки Г* = 3,5, а поэтому обра-
образуются три конвективных вала. Управляющим параметром слу-
служит отношение Ra/Rac1)- При возрастании отношения Ra/Rac
стационарная конвекция теряет устойчивость и переходит в пе-
периодический режим, начиная с Ra/Rac = 30 (перзой бифурка-
бифуркации Хопфа). При Ra/Rac = 39,5 периодический режим в свою
очередь теряет устойчивость и сменяется квазипериодическим
режимом с двумя частотами (вторая бифуркация Хопфа). На-
Наконец при Ra/Rac = 41,5 происходит третья бифуркация Хопфа,
соответствующая появлению квазипериодического режима с тре-
тремя частотами, спектр которого показан на ркс. VII. 9.
Заметим, что идентификация такого спектра, содержащего
большое число трех несоизмеримых частот, — задача весьма не-
*) Ra/Rac есть отношение числа Рэлея в эксперименте к критическому
числу Рэлея Rac, соответствующему возникновению конвекции в бесконеч-
бесконечной геометрии.

190
Глава VII
тривиальная. Необходимо показать, что частота каждой из ли-
линий может быть индексирована комбинацией трех частот / =
=¦ mifi + tn^i + rtisfs, где rti\, Шг, т3 — целые числа (не превы-
превышающие некоторого максимального числа, например 20), и (что
особенно важно) не может быть индексирована комбинацией
двух частот f = m[f[ + rn'2f2. Для установления этого факта тре-
требуются многочисленные подгоночные расчеты на компьютере.
Для проверки несоизмеримости необходимо удостовериться в
том, что отношения U/h> h/h и h/h непрерывно изменяются
10 -
S(f)
Рис. VII. 9. Спектр мощности квазипериодического режима с тремя несоизме-
несоизмеримыми частотами, наблюдаемого при неустойчивости Рэлея — Бенара. В ка-
качестве жидкости выбрана вода с Ra/Rac = 42,3. Спектральная плотность как
функция частоты в герцах представлена в логарифмическом масштабе.
Из работы Дж. Голлуба и С. Бенсона.
при изменении отношения Ra/Rac. Если бы возникала синхро-
синхронизация (например, при рациональном отношении /1//2), то это
проявлялось бы в существовании интервала захвата частоты,
т. е. конечного интервала значений Ra/Rac, в котором отноше-
отношение частот fi//2 остается постоянным (о синхронизации см. при-
приложение В).
После четкой идентификации квазипериодического режима
с тремя частотами, как показывают эксперименты, в небольшой
области значений отношения Ra/Rac соответствующие спектры
(с точностью до погрешности измерений) свободны от шума.
Это подтверждает один из выводов, сделанных на основе чис-
численной модели в предыдущем разделе: пои тех же условиях
трехчастотный режим устойчив. Но выше некоторого значения
Rt = Ra/Rac « 43 становится заметным широкополосный шум,

4 Квазипериодичность 191
одновременно происходит уширение пиков: режим становится
хаотическим. На рис. VII. 10 показана последовательность раз-
различных режимов, приводящая к хаосу, в данном конкретном
эксперименте.
Очень трудно установить, существует ли порог Rt возникно-
возникновения хаоса, отличный от порога квазипериодичности с тремя
частотами, или эти два порога в действительности совпадают.
РисУП.9
S . Р " QPZ QP3 Хаос
30 39,5 41,5 RT
Рис. VII. 10. Стадии маршрута, ведущего к хаосу через квазипериодический
i режим с тремя частотами.
Наблюдения были проведены на примере неустойчивости Белоусова — Жабо-
тинского (в воде).
Следует иметь в виду, что может существовать достаточно вы-
высокий уровень шума инструментального происхождения: если
порог Rt превзойден, то можно утверждать, что уровень внут-
внутреннего шума системы выше уровня инструментального шума.
Анализируя только экспериментальные данные, мы не можем
исключать возможность того, что при пренебрежимо низком
уровне инструментального шума порог Rt возникновения хаоса
и порог появления третьей частоты совпадают.
VII. 3. ПЕРЕХОД К ХАОСУ ОТ ТОРА
VII. 3.1. Модель Керри—Йорке
Мы описали маршрут, ведущий к хаосу, — маршрут, на ко-
котором тор Т3 трансформируется в странный аттрактор. Рас-
смотрим теперь другой маршрут _также через__квази.пеЕиодич-
щ;^~Ш~Шй лохощш л^ос'возшкаёт непосредственно из квази-
периодического режима' с двумя_ чайотами ,.(x™ew6e3- «вдаьавн»я
третьей частоты). Иначе говоря™ этот маршрут соответствует
дестабилизации или, точнее,^разрушению, т6р~а~Т2." Жёжду~дёСта-
билизацией тора Г2 и изложенными выше соображениями отно-
относительно того, что Т3 имеет наименьшую размерность, необходи-
необходимую для возникновения странного аттрактора, нет противоре-
чия. Действительно, в случае, о котором сейчас пойдет речь,
хаос, хотя он и возникает'из тора Т2, обусловлен тем не менее
появлением дополнительной '.степени свободы, но не в форме
третьей частоты, а посредством постепенного отклонения траек-

192 Глава VII
a Р, приводящего вконце.,концов к...его разру-
разрушению. __
Доказательство существования такого маршрута следует не
из строгой, обоснованной" теории, а из. результатов численных
экспериментов с итерациями некоторого двумерного отображе-
отображения, * соответствующего сечению Пуанкаре трехмерного потока.
Такое отображение удовлетворяет нескольким критериям:
1) оно должно "быть нелинейным;
2) оно должно быть сжимающим (т. е. соответствовать дис-
сипатйвнои системёр, ' '
3) оно_ должно .обладать бшртркядией. Хопфа.
При увеличении управляющего параметра неподвижная точ-
точка отображения должна терять устойчивость и через бифурка-
бифуркацию Хопфа переходить в предельный цикл. Для трехмерного
потока, отображение Пуанкаре которого требуется рассмотреть,
эта бифуркация Хопфа соответствует бифуркации предельный
Тттгтгтт ^_v T*2
Керри и Йорке построили модель, удовлетворяющую всем
этим условиям. Рассмотрим композицию двух гомеоморфизмов
(см: приложение Д) на R2:
гр = -ф! о 1|з2,
где символом !°j обозначена композиция отображений1).
Отображение ifi определяет (в полярных координатах
(р, 8)) {k -j- 1)-ю итерацию как функцию .%-й по формулам
где е — управляющий параметр (е ^ 1) и угол Эо > 0 фиксиро-
фиксирован для данной серии экспериментов.
Отображение $2 определяется следующим соотношением
между прямоугольными координатами (X,Y) (&-f 1)-й и k-й
итераций:
X X
1) Композицию i|? = \|L о ф2 можно было бы также представить в форме,
аналогичной модели Энона:
Но при этом окончательная формулировка становится весьма громоздкой и
малопригодной для интуитивного понимания.

Квазипериодичность
193
Нетрудно убедиться/что отображения ipl; if-1, -ф2 и ф непре-
непрерывны, а поэтому "ф действительно является гомеоморфизмом.
Начнем с рассмотрения того, как действует отображение чрь
Результат преобразования p^+i = elog(l + Р*) представлен на
в
Рис. VII. 11. Модель Карри —Иорка. а —график отображения p*+i =
= elog(l+p*) при е<1; б — график того же отображения, при е>1;
в — итерация отображения 4>i только при е > 1. Любая начальная точка Pi
после нескольких итераций отображается на притягивающую окружность С;
г — представление композиции отображений i|) = \|)i\jj2 на плоскости с прямо-
прямоугольной системой координат. Отображение 1|>4 переводит Ро в Ри а отображе-
отображение iji2 переводит Р< в Я,.
графиках рис. VII. 11. Тангенс угла наклона касательной к кри-
кривой в начале координат равен е. Следовательно, если е < 1, то
начало координат является устойчивой неподвижной точкой:
при итерациях все начальные значения р стремятся к нулю
(рис. VII. И, а). При е> 1 существует еще одна неподвижная
точка помимо начала координат: при итерациях все начальные
13 П. Берже и др.

194 , Глава VII
значения Р стремятся к пределу pL — положительному отлич-
отличному от нуля решению уравнения (рис. VII. 11,6).
Вторая часть .отображения фь а именно отображение 0^+1 =
= б* -»- Эо, есть простой поворот на угол 0О. На рис. VII. 11, по-
показана комбинация двух типов итерированных графиков ото-
отображения t|)i; При е s=; 1 начало координат О является един-
единственной притягивающей точкой, в то время как при е > 1
отображение ij^i имеет притягивающую окружность') С радиу-
радиусом pi, возрастающим с увеличением 8. Нетрудно видеть, что
сформулированные в начале раздела условия (диссипация и су-
существования бифуркации Хопфа) выполнены. Отображение if>i
в действительности описывает диссипативную систему. В соот-
соответствующем трехмерном потоке (сечение Пуанкаре которого
представлено графиком отображения if>i) существует бифурка-
бифуркация от предельного цикла к инвариантному тору Т2 при е= 1.
Композиция отображений г|э нелинейна, так как, во-первых,
ih; сопрржит логарифмический член, а ф? — квадратичный член:
= Yk -\r Xk.
Действие2) отображения г|э2 состоит в установлении существую-
существующей в t|)i связи между 0 («углом») и р («действием»). Пока угол
и действие не связаны, аттракторами преобразования могут
быть ТОЛЬКО ОКРУЖНОСТИ. КрОМе ТОГО, В КОМПОЗИЦИИ 1J) — if>i ° 1р2
нелинейные эффекты усиливаются с увеличением е.
На рис. VII. 11, г показано, как действует преобразование if»
на плоскости (X, Y). Выбрав точку Ро с координатами (Хо, Yo)
за начальную, мы вычисляем ее образ Р\ под действием преоб-
преобразования t.. затем образ точки Р' пол. действием преобразова-
преобразования -ф2 и получаем точку Р2. Потом.повторяем процедуру, дей-
действуя преобразованием i|) на точку Ро- Итерации могут продол-
продолжаться до бесконечности. После того как затухают переходные
эффекты (на практике, чтобы исключить их, достаточно отбро-
отбросить первые 100 итераций), точки оказываются на аттракторе.
VII. 3.2. Поведение модели в зависимости от е
Пусть 0о = 2 (в' радианах). Так как это значение близко
к 2л/3, при каждой итерации вк+г = вй -4- Go мы совершаем при-
примерно треть полного оборота (рис. VII. 12, а). Следовательно,
J) /Можно провести параллель между итерированным отображением \|>i
при е > 1 и фазовой диаграммой генератора Ван дер Поля. В обоих случаях
растяжение, дейетт'гпще;3 пб.ипт; начала коор iv.h&t. вдали от н?чала сме-
сменяется сжатием, а поэтому аттрактор существует на конечном расстоянии от
начала _координат (си. ра^д. II. 1.1).
2) Заметим, что в отличие от ipi отображение фг сохраняет площади
(его якобиан равен единице).

Квазипериодичность
195
через каждые три итерации мы оказываемся близко от исход-
исходной точки (на рис. VII. 12, а представлены последовательные
Рис. VII. 12. Последовательные итерации отображения ф. а — псевдосиммет-
псевдосимметрия с осью третьего порядка. Точки Ь, с, а', Ь' и с' — последовательные
интерированные образы начальной точки а; б — притяжение к окружности.
Как и на рис. VII,12, о, точки Ь, с, а', Ь' и с'... получаются из точки а
при итерации отображения цз (при s = 1,01).
итерации а, Ь, с, о/ Ь', с'). Мы уже говорили о том, что при
е = 1 начало координат является единственной притягивающей
неподвижной точкой отображения. При е = 1+ аттрактор имеет
форму окружности с центром в начале координат (рис. VII. 12,6).
13*

196
Глава VII
С увеличением е радиус окружности быстро возрастает. Нели-
Нелинейные эффекты деформируют окружность и приводят к возник-
возникновению симметрии с осью 3-го порядка замкнутой петли, ко-
которая является аттрактором (петля остается топологически эк-
эквивалентной ') окружности). Обращает на себя внимание нали-
наличие трех зон (рис. VII. 13), плотность которых намного выше
X
Рис. VII. 13. Асимптотическое поведение отображения ¦$ при е = 1,27.
Оставаясь гомеоморфной окружностью, кривая приобретает форму, обла-
обладающую псевдосимметрией третьего порядка, и вариация плотности обна-
обнаруживает первые признаки синхронизации с /i//z = 3.
плотности остальной части аттрактора. Это предвестник затяги-
затягивания частоты третьего порядка, но пока режим носит отчет-
отчетливо выраженный квазипериодический характер с двумя несо-
несоизмеримыми частотами. Аттрактором служит тор Г2, сечением
Пуанкаре которого является замкнутая кривая, представленная
на рис. VII. 13. Продолжая увеличивать е, т. е. делая нелиней-
нелинейные эффекты все более важными, мы видим, как то, что было
тенденцией к затягиванию частоты, становится подлинным затя-
затягиванием частоты 3-го порядка. Иначе говоря, график состоит
только из трех точек и орбита имеет период, равный трем. С фи-
физической точки зрения это означает, что две частоты м и U ис-
исследуемого квазипериодического режима становятся соизмери-
соизмеримыми: fi/f-i = 3.
•) Математически более точным было бы выражение: петля «гомеоморф-
на окружности».

Квазипериодичность
,197
Затягивание частоты существует в диапазоне 1,28 < е <
< 1,3953. Сразу же над порогом ес = 1,3953 вновь появляется
замкнутая петля. Она сильно напоминает ту петлю, которая
возникает при значениях е, несколько меньших 1,28. Но новая
петля не гОмеоморфна окружности. Подобное исследование (на
рис. VII. 14 мы имеем е = 1,48) открывает качественно новое яв-
явление: на петле появляются «зазубрины»') (таких выступов
даже бесконечно много), отчего она обретает определенную
Рис. VII. 14. Асимптотическое поведение отображения г|з при 8 = 1,48. Так
как режим хаотический, кривая более не гомеоморфна окружности: ее
можно рассматривать как сечение Пуанкаре странного аттрактора. Обра-
Обратите внимание на выступы, свидетельствующие о том, что образуются
складки.
«толщину»2). Размерность петли более не равна единице (т. е.
размерности прямой или окружности), а становится фракталь-
фрактальной (близкой к единице, но несколько большей ее). Следова-
Следовательно, график представляет собой сечение странного аттрак-
аттрактора и упорядочение точек на петле теперь несколько хаотично.
Иначе говоря, тор Т2 разрушен; выше е = ес аттрактор обретает
4) Такая структура, едва различимая непосредственно над порогом f.c,
при увеличении е становится все более заметной.
2) Второе сечение, перпендикулярное петле, обнаружило бы, что петля
состоит из бесконечно большого числа листов со структурой капторовского
множества.

198
Глава VII
некоторую толщину в форме мелких складок («морщин»), по-
покрывающих поверхность тора.
Вернемся к преобразованию if>, чтобы проиллюстрировать
происхождение хаотического режима. Рассмотрим две точки Pt
и Р2, первоначально близкие в сечении Пуанкаре (рис. VII. 15),
р
'1
' 1
¦РР
Рис. VII. 15. Чувствительная зависимость отображения ф от начальных
условий. Pt и Рг — две первоначально очень близкие точки на аттракторе.
Хотя точки Pi и Рг почти неотличимы друга от друга, после сорока ите-
итераций их образы Pj и Р2 разделены уже вполне отчетливо.
т. е. две соседние траектории трехмерного потока. При выпол-
выполнении итераций (т. е. со временем) образы Р[ — §ь(РЛ я Р'2 =
¦== -ф* (Р2) все более удаляются друг от друга до тех пор, пока
не окажутся на противоположных сторонах петли. Расхождение
итераций свидетельствует о расхождении соседних траекторий
(ЧЗНУ), характерном для странных аттракторов. После рас-
расхождения на максимальное расстояние образы Р'. и Pi начи-
начинают сближаться вследствие образования складок. Сойдясь на
минимальное расстояние, они снова расходятся и т. д. С такой
комбинацией растяжения и складывания — необходимым и

Квазипериодичность 199
достаточным условием существования хаоса1)—мы уже встре-
встречались неоднократно.
На рис. VII. 16 показаны различные маршруты, ведущие
к.хаосу в модели Керри — Йорке. Заметим, что в области Е>ес,
соответствующей хаотическому режиму, встречаются «окна» пе-
периодических режимов. При соответствующих значениях е ат-
аттрактор перестает быть странным и становится периодическим.
Puc.VIl.13 Рис. VII. 74
Синхронизация
3-го порядка
^^ Лаос -
1,28 ¦ ес=7,3953
Рис. VII. 16. Последовательность этапов перехода к хаосу в модели Кер-
Керри—Йорка.
(_. аналогичной ситуацией мы встретимся также при рассмотре-
рассмотрении маршрута, ведущего к хаосу через удвоение периода (см.
гл. VIII).
VII. 3.3. Некоторые экспериментальные примеры
Некоторые экспериментальные наблюдения возникновения
хаоса из квазипериодического режима могут быть ошибочно
приняты за результаты численных экспериментов, выполненных
на основе модели Керри — Йорке, — настолько сильно сходство.
Приводимые ниже иллюстративные примеры заимствованы
хЛ'лЬаЫм образом из кеустоГ•;;;гост:-; РБ п ограниченной геомет-
геометрии, приводящей в этой области к необычайно разнообразным
режимам2). Управляющий параметр Ra/Rac уже был опреде-
определен. Но знание Ra/Rac бесполезно, если мы, кроме того, не за-
зададим, конвективную структуру 3) в ячейке. Поэтому мы, не вда-
вдаваясь в подробности относительно самой структуры, обозначим
1) Как будет показано в дальнейшей, это двоякое явление вводит «пере-
«перемешивание»—одну из существенных характерных особенностей хаоса.
2) Поддержание одной и той же конвективной структуры на протяжении
всего маршрута, ведущего к хаосу, — ограничение, выполнить которое экспе-
экспериментально необычайно трудно. Малейшее во.чмушение кош.ективной струк-
структуры изменяет динамическое поведение. Нередко неполнота наблюдений объ-
объясняется отнюдь не тем, что экспериментатор не пожелал выйти за пределы
исследуемого диапазона параметров, а обусловлена тем, что конвективная
1'ч'оvktv-" теряет устойчивость.
3i Описание конвективной структуры должно включать в себя число кон-
конвективных валов, их симметрию, направление вращения, дефекты структуры
и т. д.

200 . Глава VII
каждую структуру символически буквой А, В или С. Мы можем
воспользоваться этим случаем, чтобы продемонстрировать раз-
разнообразие проявлений неустойчивости РБ в жидкостях при боль-
больших числах Прандтля. Если в качестве жидкости выбрано сили-
силиконовое масло, то его прозрачность в сочетании со значитель-
значительными тепловыми вариациями показателя преломления наводит
на мысль об использовании локальных или полулокальных оп-
оптических измерений. Это позволяет постоянно следить за типом
и качеством конвективной структуры. В частности, оптические
методы позволяют локализовать (и тем самым исследовать в от-
отдельности) осцилляторы тепловой конвекции, ответственные за
наблюдаемые режимы.
На рис. VII. 17, а вы видите спектр, снятый на структуре А
при Ra/Rac = 569 и свидетельствующий о квазипериодичности
с двумя частотами, для которых' /i/,f2 = 2,91. Два осциллятора
тепловой конвекции I и II были идентифицированы и локализо-
локализованы. Иначе говоря, если мы нацеливаем оптическое устройство
на малую окрестность осциллятора 1, то при этом детектируется
в основном ') частота /i (аналогичное утверждение справедливо
относительно осциллятора II и частоты /2). Ясно, что эта инфор-
информация представляет необычайную ценность для понимания про-
процессов, происходящих в жидкости, и однозначной идентифика-
идентификации главных частот спектра.
Возможность разделения вкладов двух осцилляторов также
облегчает построение сечений Пуанкаре. На одном детекторе,
мы собираем вклад главным образом осциллятора I, который
обозначим через AT. Одновременно мы с помощью аналогового
устройства (RC-цеии) дифференцируем AT и получаем Л Т. Сиг-
Сигналы AT и А" Г поступают на входы двух каналов графопострои-
графопостроителя (см. рис. V. 8 и разд. VI. 3.3). Можно построить фазовые
траектории на плоскости (А7, ДТ). На рис. VII. 17, б показано,
насколько сложными могут быть эти траектории. Если теперь
мы с помощью второго детектора регистрируем второй сигнал,
поступающий главным образом от осциллятора II, то эту ин-
информацию можно использовать для стробоскопирования 2) тра-
траектории при фиксированной фазе колебаний осциллятора II. Ре-
Результат этой процедуры показан на рис. VII. 17, в. Сравнивая
рис. VII. 17, б и в, мы можем оценить упрощения, проистекающие
4) Разумеется, осцилляторы I и II связаны между собой гидродинамикой.
В колебаниях осциллятора I мы обнаруживаем примесь частоты /г, характер-
характерной для осциллятора II, и наоборот (см. подпись к рис, V, 8).
") На практике, вместо того чтобы постоянно держать перо графопо-
графопостроителя в нижнем положении (именно так был построен график на
рис. VII. 17,6), мы опускаем перо только в те моменты, когда осциллятор II
находится в определенной фазе.

M-
5 If)
+.ДТ
ДТ
в
3
AT
Рис. VII. 17. Конвекция Рэлея—Бенара. Структура A, Ra/Rac = 569.
а — комбинационный спектр мощности градиента температуры. Две харак-
характеристические частоты обозначены через fi и f2, остальные пики соответ-
соответствуют их линейным комбинациям[jntfi + тг\г_ с filfz = 2,91; б — фазовые
траектории на плоскости [ДГ, Д*Г], где ДГ — градиент температуры и
Д*Г — производная от него по времени; в — сечение Пуанкаре траекторий
на рис. о, полученное с помощью строооскопирования сигналов на частоте
одного из двух осцилляторов тепловой конвекции. Зоны наибольшей плот-
плотности, обозначенные буквами а, 0 -и у, — предвестники сиихоонизации
с fJh = 3. "
Из работы М. Дюбуа, П. Берже, В. Крокетта.

202
Глава VII
от метода сечений Пуанкаре. Расшифровать запутанные траек-
траектории на рис. VII. 17,6 невозможно, тогда как на рис. VII. 17, в
мы легко узнаем сечение Пуанкаре тора. Теперь мы уже в со-
состоянии различить некую более тонкую деталь: большую плот-
ДТ
AT
ДТ
v...
ТОООс
Время
Рис. VII. 18. Конвекция Рэлея —Бенара. Структура A, Ra/Rac = 590.
а —сечение Пуанкаре: отношение частот fil{% равно 2,99. Обратите вни-
внимание на сильнейшее различие в плотности точек между тремя наиболее
темными областями и остальной частью кривой; б —величина Д'Г как
функция времени: после продолжительного периода (обратите внимание на,
масштаб времени) медленной эволюции происходит резкий поворот на 2л/3.
Из работы М. Дюбуа, П. Берже и В. Крокетта.
ность точек на участках а, р й у. Это связано с тем, что, по-
поскольку отношение /i//2 равно 2,91, рассматриваемый режим
близок к простому затягиванию частоты 3-го порядка. Осцилля-
Осцилляторы I и II интенсивно взаимодействуют, и поэтому тенденция
к синхронизации с отношением частот, близким к 3, сохраняется
в течение какого-то времени.

Квазипериодичность
203
При больших значениях управляющего параметра Ra/Rac
эта замечательная тенденция к временной1) синхронизации еще
больше усиливается. При Ra/Rae = 590 отношение f\/fi стано-
становится равным 2,99, что очень близко к 3. На рис. VII. 18, а мы
Puc.Vff.17 РисЖ.18
\4i' чиа
Рис. VII. 19. Последовательность смены динамических режимов структуры А
в зависимости от значений параметра Ra/Rac.
видим, что три зоны содержат почти все точки сечения Пуан-
Пуанкаре. Еще отчетливее это видно на рис. VII, 18,6, где величина
(AT)- представлена как функция времени. Заметим, что относи-
относительная фаза изменяется сначала очень медленно2), а затем
ДТ
,_¦•
ДТ
Рис. VII. 20. Конвекция Рэлея — Бенара. Структура В, Ra/Rac « 520. Сече-
Сечение Пуанкаре проведено для квазипериодического режима с двумя частотами.
Самопересечение кривой обусловлено наличием в сигнале гармоники второго
порядка с большой амплитудой.
скачком на 2л/3. Чередование периодов медленного и быстрого
изменения соответствует чередованию синхронизации и десин-
хронизации. Это чередование строго периодично с периодом
l/(/i — 3f2), где /i — 3/2 — отклонение от синхронизации. При
дальнейшем увеличении параметра Ra/Rac мы достигаем значе-
') Обратите внимание на поразительное сходство с затягиванием частоты
в численной модели из разд. VII. 3.2.
2) В отсутствие связи между осцилляторами относительная фаза изменя-
изменялась бы линейно со временем.

204
Глава VII
ния Ra/Rae = 593, соответствующего точной и постоянной син-
синхронизации с /1//2 = 3, при которой сечение Пуанкаре состоит
только из трех точек. Различные описанные выше стадии пред-
представлены на рис. VII. 19.
Что произойдет, если мы увеличим параметр Ra/Rac выше
значений, соответствующих синхронизации при fi/f2 = 3? Как
показывают эксперименты, исчезнет структура А. Динамический
режим, который придет ей на смену, не имеет никакого отноше-
дт
AT
Рис. VII. 21. Конвекция Рэлея — Бенара. Структура В, Ra/Rac«563. На се-
сечении Пуанкаре видны складки, характерные для странного аттрактора.
ния к маршруту, который мы рассматривали до сих пор.. Необ-
Необходимо рассмотреть другую структуру, которая, хотя и соответ-
соответствует более слабой связи между осцилляторами, выходит на
хаотический режим. Пусть В — эта новая структура. При
Ra/Rac = 520 структура В находится в квазипериодическом ре-
режиме, о чем свидетельствует сечение Пуанкаре1) на рис. VII. 20.
При дальнейшем увеличении управляющего параметра Ra/Rac
сечение Пуанкаре приобретает характерную структуру, изобра-
изображенную на рис. VII. 21, где Ra/Rac —563. Появление морщин
и складок на поверхности аттрактора типично для двойной опе-
операции, приводящей к возникновению странного аттрактора2):
растяжения и складывания.
') Заметим, что кривая на рис. VII. 20 не замкнутая, а с самопересече-
самопересечением. Это обусловлено только наличием второй гармоники в сигнале, исполь-
использованном для построения сечения Пуанкаре.
2) Так как Ra/Rac = 563 соответствует появлению мелких складок на
поверхности тора, хаос выражен еще недостаточно отчетливо. В спектре мощ-
мощности видны только пики квазипериодического режима, а уровень шума
остается низким.

Квазипериодичность 205
Сходство между таким аттрактором и аттрактором в модели
Керри — Иорке заметно на рис. VII. 22, где представлены сече-
\'
\
а
Рис. VII. 22. Сравнение двух сечений
Пуанкаре, а — сечение Пуанкаре для
модели Керри — Иорка при е =1,465;
N^ \ б — сечение Пуанкаре для термокон-
\ -V*1 \ Л векции в условиях эксперимента,
^ -¦ Ч ¦' "^ Бросается в глаза разительное сход-
1^\ %t ство сечений Пуанкаре а и б.
ния Пуанкаре этих двух аттракторов. В обоих случаях мелкие
складки на поверхности аттрактора появляются в окрестности
Puc.41l.Z0 Puc.VlL21 ^
% Синхронизация
1
Хаотический ^
режим 570 '*' г 590
Рис. VII. 23. Последовательность смены динамических режимов структуры В ¦
в зависимости oi значений параметра Ra/Rac. Возможность пояьлсипя «окоп»
периодичности в хаотической области не исключается, хотя имеющиеся в на-
настоящее время экспериментальные методы не позволяют обнаружить их.
синхронизации 3-го порядка. Но на структуре В появление мел-
мелких складок непосредственно предшествует синхронизации, ко-
которая наступает при 570 < (Ra/Rac) < 590 (рис VII. 23), в

206
Глава VII
&
- 218
¦•• t •¦.,.. „,„
I*
дт
Ra/Rac= 219/
ДТ
Ra/Rac= 220
дт
Рис. VII. 24. Конвекция Рзлся — Бенара. Структура С. Сечения Пуанкаре при
трех очень1 близких значениях параметра Ra/Rac. а — квазипериодический ре-
режим; б и а — хаотические режимы. Усиливающийся разброс точек может
отражать существование странного аттрактора с размерностью большей 3
(или очень близкой к 3).
Кз раооты М. ДюОуа и ii. Берже.

Квазипериодичность 207
/
отличие от модели Керри — Йорке, в которой мелкая «рябь» на
поверхности аттрактора появляется после синхронизации.
Наконец упомянем о переходе к хаосу через периодичность,
для которого в отличие от рассмотренных нами переходов се-
сечение Пуанкаре не дает информации. Измерения, производимые
на структуре третьего типа, обозначенной нами через С, полу-
получены в экспериментах с силиконовым маслом при малом, а не
большом, как в предыдущих примерах, числе Прандтля (Рг—38
вместо Рг = 130). На рис. VII. 24, а видно, что при Ra/Rac=2l8
структура С находится в квазипериодическом режиме. При чрез-
чрезвычайно малом увеличении управляющего параметра Ra/Rac
(менее чем на 1 %) мы наблюдаем не появление мелких скла-
складок в сечении, а разброс точек (рис. VII.24,б). Когда Ra/Rac
достигает значения 220 (рис. VII. 24, е), в сечении существует
только облако точек. В этом случае нет оснований для заключе-
заключения о том, что наблюдаемый хаотический режим соответствует
странному аттрактору с размерностью большей 3Чили несколько
меньшей 3), а не тору с высокой размерностью (недетермини-
(недетерминированный хаос). Вопрос о размерности аттрактора может быть
решен только с помощью' метода, описанного в разд. VI. 4.4.
VH. 4. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПЕРЕХОДА
К ХАОСУ ОТ ТОРА Г2
Как было показано, простая математическая модель позво-
позволяет воспроизводить переход от тора Р непосредственно к
странному аттрактору без изменения числа степеней свободы1).
Ниже мы попытаемся рассмотреть это явление в более широких
рамках.
Отображение первого возвращения для потока на 72 может
быть описано с помощью непрерывного обратимого отображе-
отображения окружности Т1 на себя. Отображение fF) (график которого
представлен на рис. VII. 25) задается монотонно возрастающей
(или убывающей) функцией с двумя фиктивными разрывами,
обусловленными только тем, что идентифицированы точки 0 и 1
на окружности. Такое отображение окружности на себя харак-
характеризуется числом вращений2). Если число вращений рацио-
рационально, то говорят, что имеет место затягивание частоты, или
синхронизация. Затягивание частоты в общем случае происхо-
происходит в некотором открытом интервале значений управляющих
параметров. Иррациональное число вращений соответствует ква-
квазипериодическому режиму. Чтобы проанализировать эту фено-
') Число степеней свободы зд«хь г.оиима^юд ь icm сл;ь;с.~:, г* :;?л:ом сно
определено в примечании 3 на с. 185.
2) См. приложение В.

208
Глава VII
менологию, желательно ввести двухпараметрическое отображе-
отображение /@). Например, Арнольд предлагает отображение
Двумя управляющими параметрами являются а и 8о. Каждой
паре значений этих параметров, представленной точкой на пло"-
скости с прямоугольными системами координат, соответствует
некоторое точное значение числа вращений. Плоскость плотно
покрыта множеством непересекающихся полос конечной ши-
ширины (в основном очень узких), таких, что внутри каждой по-
Рис. VII. 25. Представление отображения окружности на себя в прямоуголь-
прямоугольной системе координат. Разрывы на графике функции /(б) фиктивные и ис-
исчезают при отождествлении 0 и 1 по осям абсцисс и ординат.
лосы число вращений постоянно и рационально. Эти полосы,
называемые полосами синхронизации, плотны на плоскости (по-
(подобно тому, как рациональные числа всюду плотны на интер-
интервале). Затягивание частоты с отношением р3/<7з. заключенным
между Р\1ц\ и Рг/Цг (например, отношение 3/5 заключено ме-
между 1/2 и 2/3), происходит в полосе (рз/#з), расположенной
между полосами (pi/qi) и (ргА/г), где pi, a, — положительные
целые числа. Структура множества полос синхронизации (по
крайней мере локально) напоминает структуру канторовского
множества: между любой парой полос синхронизации мы на-
находим другие полосы, между которыми в свою очередь распо-
располагаются другие полосы синхронизации и т. д.
Нетрудно представить, как деформировать /9 а F), чтобы
касательная к кривой 80(а) на плоскости управляющих пара-

Квазипериодичность
209
метров стала горизонтальной (рис. VII. 26 и VII. 27). Образо-
Образование -складки на кривой Эо(а) означает потерю устойчивости
отображения /, которой можно объяснить переход Г2-»-стран-
ЦЬ СС 2UCrlfl Д
отображения G —>feo> a (9) с двумя параметрами 8о и а. Внутри каждой по-
полосы число вращений постоянно и рационально. Полосы плотны на плоскости
параметра и не пересекаются. Кривая 0о(а) отделяет в пространстве пара-
параметров область, в которой функция f обратима, от области, в которой функ-
функция f необратима (см. рис. VII. 27).
ный аттрактор, о котором идет речь в этой главе. В связи с опи-
описанной выше конструкцией возникают два вопроса.
О 0 10 Т
ео>ео(а) 90=е0(а) во<ео{<х}
Рис. VII. 27. Деформация графика функции /еоа(в). Когда параметр 80
пересекает на плоскости параметров кривую 60(«), касательная к графику
функции Д6) принимает горизонтальное положение (см. рис. б). На рис. а
отображение обратимо, на рис. в оно необратимо.
1) Что происходит при итерации 8-*-/е а (9) вблизи значения
параметра 00(а)?
2) Как может произойти потеря устойчивости отображения
первого возвращения плоскости на себя?
14 П. Еерже к др.

210 Глава VII
Попытаемся ответить на эти вопросы по очереди.
1) Если ограничиться областью 0с > Во (а) (где сохраняется
обратимость отображения), то в ней доминирует явление син-
синхронизации в окрестности значения 0о(а). Действительно, мы
знаем, что в указанной окрестности существует затягивание ча-
частоты и при итерации отображения Э-»-/(9) две первоначально
близкие точки сближаются. Можно представить себе, что кри-
кривая f@) содержит почти горизонтальное плато, т. е. значение 9»
несколько больше Э0(а). • .
Простые вычисления показывают, что расстояние между
двумя близкими точками при каждой итерации умножается на
\df/dQ\. Следовательно, если существуют значения 0, при ко-
которых производная очень мала, то отображение сильно сбли-
сблизит итерации соседних точек, что, как уже говорилось, харак-
характерно для синхронизации. Кроме того, Херман показал, что ве-
вероятность иррационального числа вращений (т. е. отсутствия
синхронизации) при случайном выборе точки па кривей 0и(а)
равна нулю. Можно представить себе (хотя доказать это труд-
трудно), что при приближении к 90(а) синхронизация становится
доминирующим явлением, хотя при некоторых значениях
@о, а) синхронизация отсутствует, так как при непрерывном
переходе от одного рационального значения к другому число
вращений должно принимать иррациональное значение1).
В той области пространства параметров, где отображение f
необратимо, мы наблюдаем очень сложную картину, которая
понята еще не до конца. Тем не менее можно утверждать, что
по крайней мере в части области сохраняется синхронизация.
Это объясняется тем, что синхронизация с рациональным чис-
числом вращений p/q зависит только от существования решения
уравнения р>@)=9. Мы почти всегда можем по непрерыв-
непрерывности продолжить это решение за 0о(а), хотя для разреши-
разрешимости уравнения не требуется обратимости ни f, ни f<<7). Но
в отличие от случая, когда отображение f обратимо, полосы
синхронизации имеют сложную внутреннюю структуру.
Как возникает синхронизация (например, с периодом 3)'при
отображении 9->/@) окружности на себя? Синхронизация об-
обусловлена наличием трех неподвижных точек отображения fC>
(третьей итерации отображения f). График отображения f<3> ко-
колеблется относительно диагонали, с которой он пересекается
6 раз: три точки пересечения образуют устойчивый цикл
') Одновременное исчезновение квазипериодических орбит было предме-
предметом весьма подробного исследования, отчасти в связи с разрушением магнит-
магнитных поверхностей, удерживающих горячую плазму в тороидальных конфигу-
конфигурациях.

Квазипериодичность
211
с периодом 3, а три остальные точки пересечения образуют неус-
неустойчивый цикл с периодом 3 (рис. VII. 28). Деформация графика
отображения fC), соответствующего затягиванию частоты, вы-
выглядит как простой сдвиг по вертикали, возникающий в резуль-
результате прибавления постоянного угла 6* к fC)@). Пусть 0Ь 02 и
63 — точки устойчивого цикла, Q[, Qr2, % — точки неустойчивого
цикла. Когда цикл возникает, график отображения /C>(9) (штри-
Рис. VII. 28. Деформация графика функции /C)(9) в окне синхронизации с
периодом 3. Двумя штриховыми линиями обозначены кривые (каждая из ко-
которых касается диагонали), указывающие верхний и нижний пределы окна
синхронизации с периодом 3. Стандартной ситуации внутри окна соответ-
соответствует сплошная линия, на которой расположены три устойчивые неподвиж-
неподвижные точки Fi, 02, 9з) и три неустойчивые неподвижные точки @j, 92, 83)
ховая кривая ка рис. VII. 28) касается диагонали. Следова-
Следовательно, два цикла совпадают и 6, = 8р 62 = Q'2, в3 = д'3. Когда
цикл исчезает, т. е. когда значение G* достаточно велико (верх-
(верхняя кривая на рис. VII. 28), происходит такое же слияние устой-
устойчивого и неустойчивого циклов, но на этот раз при Э,=9з,
02 = вС и 63 = 91 (за циклами и точками при трансляции гра-
графика отображения f!3) мы следим по непрерывности). Таким
образом мы получаем геометрическое объяснение процесса воз-
возникновения и исчезновения цикла по обе стороны интервала
синхронизации.
14*

212
Глава VII
Посмотрим теперь, что происходит, когда отображение /@)
имеет экстремум') и, следовательно, перестает быть обрати-
обратимым. Используя формулы дифференцирования композиции
функций, находим, что если производная от / обращается в нуль
при одном значении 0, то производная от f<«> обращается в Нуль
по крайней мере при q различных значениях 0, если только она
Рис. VII. 29. Пример неустойчивого отображения /@) с двумя неустойчивыми
3-циклами. В отличие от обратимого случая, которому на рис. VII. 28 соот-
соответствует сплошная линия, цикл (9f, 82, 9з) не обязательно устойчив, так
как производная от /<3)@) по 0 в любой из трех точек может быть мень-
меньше — 1.
не обращается тождественно в нуль на всем периоде. В нашем
примере 3-цикла /C> имеет нулевую производную (в точке ло-
локального максимума или минимума) между каждой парой не-
неподвижных точек (рис. VII. 29). Как показывает исследование
кривой на рис. VII. 29, в отличие от случая, когда отображе-
отображение / (и, следовательно, fC)) обратимо, мы не можем более оп-
определить априори устойчивость точки 0], например, как непод-
неподвижной точки отображения fC>. Но по-прежнему выполняется
') Если (как мы будем предполагать) / отображает ни себя интервал
[О, 1], т.е. значения f@) пробегают один раз единичный интервал, когда 0
пробегает один раз единичный интервал, то / имеет четное число экстремумов
(в рассматриваемом случае два экстремума).

Квазипериодичность - .
21$
неравенство (dfC)/d9) le'> 1, а поэтому точка 0{ неустойчива и
по-прежнему (d[i3>/dQ) |9i < 1. Но, кроме того, справедливо нера-
неравенство (dfW/dQ) |9; < Ои точка 9i неустойчива, если (d/<3yd6) |Qi <
<—1, а в этом случае неустойчивы оба 3-цикла отображе-
отображения /. Таким образом, внутри полосы синхронизации 3-цикла на
плоскости параметров (9о, а) мы обнаруживаем две области
в зависимости от того, больше или меньше единицы величина
| dfi3)/dQ |9, т. е. в зависимости от того, существуют ли один или
два неустойчивых 3-цикла. Область неустойчивости обоих цик-
<х
Один устойчивый
3-цикл
nU OoHOZO
устойчивого
3-цикли
граница.
обратимости.
Полоса, синхронизации
З-циклами
Рис. VII. 30. Полоса синхронизации с периодом 3 на плоскости параметров
(So, а). В области, где отображение f необратимо, а именно выше и левее
кривой 6о(сс), внутри полосы синхронизации существует подобласть, в кото-
которой оба 3-цикла неустойчивы. В остальной части полосы синхронизации один
из 3-циклов устойчив. В заштрихованной области могут наблюдаться хаоти-
хаотические режимы.
лов образует своего рода полосу с полосой синхронизации
внутри (рис. VII. 30). Аналогичным образом подразделяется на
две части каждая полоса синхронизации с числом вращений
p/q. Чем больше знаменатель q, тем ближе граница между
двумя частями к кривой бо(а).
Внутри области неустойчивости обоих циклов мы встречаем
большое разнообразие режимов. Как видно на рис. VII. 29,
у отображения fC>F) имеются локально параболические об-
области, аналогичные тем, которые рассматриваются в гл. VIII.
Они могут порождать хаос с помощью механизма каскада
удвоений периода, который анализируется в гл. VIII. Суще-
Существуют и другие более сложные возможности, поскольку /C) не
отображает интервал ('8', 6,4j на себя. В частности, если образ

214 Глава VII
максимума функции /<3), расположенного между Q[ и 8,, попа-
попадает в интервал [9^, 92] и если образ минимума, расположен-
расположенного между .6, и 02, попадает в интервал [0, 8{], то итерация
отображения f<3> сопровождается явлением, которое не встре-
встречается ни в каскаде удвоений периода, ни в обратимых отобра-
отображениях окружности на себя: суперпозицией случайной диффу-
диффузии на окружности и хаотического режима.
Рис. VII. 31. Обратимое отображение плоскости. При сжатии кольца отобра-
отображение порождает аттрактор, имеющий форму окружности. Заштриховано то-
точечное множество — образ внешнего кольца.
2) Как мы уже знаем, некоторые отображения плоскости
имеют «круговой» аттрактор, т. е. аттрактор в форме простой
замкнутой кривой, которую можно рассматривать как сечение
Пуанкаре притягивающего тора трехмерного потока. На ок-
окружности отображение есть непрерывное и обратимое преобра-
преобразование, характеризуемое некоторым числом вращений. По-
Поэтому интерес к переходам, связанным с потерей обратимости
отображений окружности на себя,' может показаться парадок-
парадоксальным. Однако мы покажем, что потеря обратимости на ок-
окружности все же совместима с обратимостью исходного отобра-
отображения на плоскости. Следовательно, такая ситуация может воз-
возникнуть и для данной динамической системы с варьируемыми
параметрами.
Обоснование этого утверждения состоит в следующем. Из
работ Пуанкаре нам известно, что круговой аттрактор для ото-
отображения на плоскости возникает из диеснпативного преобразо-
преобразования кольца в себя (рис.УИ. 31). Это преобразование само

Квазипериодичность
215
можно рассматривать как результат радиального сжатия с по-
последующим поворотом относительно центра кольца. В этом про-
простом случае аттрактор представляет собой окружность нулевой
толщины, возникающей от кумулятивного влияния радиального
сжатия на конечную толщину кольца. Представим теперь, что
кольцо одновременно подвергается складыванию (рис. VII. 32).
Рис. VII. 32. Необратимое отображение плоскости. Как и на рис. VII. 31, за-
заштриховано точечное множество — образ внешнего кольца. Один и тот же
угол 6 для образа может быть получен из трех различных значений угла
в кольце. Это означает, что по углам отображение становится необратимым.
Если свести такое преобразование к его действию на угол, то
мы увидим, что складывание разрушает необратимость, по-
поскольку порождает максимум и минимум у функции f(8), опре-
определяющей действие преобразования на углы. Разумеется, само
отображение кольца на себя остается обратимым: точки, об-
образы которых, находятся под одним и тем же углом, разли-
различаются своим радиальным положением (рис. VII. 32).
Другой способ убедиться в этом состоит в следующем.
В «стандартном» случае, т. е. до потери обратимости, образ
кольца при итерированном отображении есть замкнутая кривая
конечной длины, которая может быть параметризована с по-
помощью угла. Увеличение длины этой замкнутой кривой при
складывании1) обладает тем свойством, что в момент потери
обратимости (т. е. в каждой точке рассмотренной выше крИЕ
') Напомним, что
разд. 1.4.2).
сатие площадей не означает сжатия всех длин (см.

216 Глава VII
во (а) в пространстве параметров) длина кривой становится
бесконечной и это исключает параметризацию с помощью угла.
Мы видели, что на кривой 0о(а) вероятность обнаружить
квазипериодический режим априори очень мала. Тем не менее
мы обсуждаем этот случай, когда итерация описывает кривую
бесконечной длины. Если окружность имеет конечную длину и
число вращений иррационально, то различные возможные зна-
значения угла посещаются с равной вероятностью. Но в момент
потери необратимости (и в отсутствие синхронизации) посещае-
посещаемые точки образуют по значениям угла канторовское множество.
Практическая ценность такого результата ограничена тем,
что при приближении к кривой 0о(а) доминирующим стано-
становится периодический режим. По-видимому, этим объясняется,
что в экспериментах хаос часто появляется через синхрониза-
синхронизацию. Такая ситуация встречается далеко за порогом потери
обратимости, который мы только что обсуждали.
ЛИТЕРАТУРА
Berge P., Dubois M., Physics Letters, 93A, p. 365 A983).
Berge P., Physica Scripta, Tl, p; 71 A982).
Curry I. M., Communications in Mathematical Physics, 60, p. 193 A978).
Curry I., Yorke J, A., — In: The structure of attractors in dynamical systems,
Springer Notes in Mathematics, 668, p. 48, Springer-Verlag, A977).
Dubois M., — In: Symmetries and Broken Symmetries in,Condensed Matter
Physics, ed. N. Воссагя, I, D. S. E. Т. Paris A98!).
Dubois M., Berge P., Croquette V., Compt. Rend, de l'Academie des Sciences
de Paris, C293, p. 409 A981).
Dubois M., Berge P., Le Journal de Physique. 42. p. 167 A981).
Collub J. P., Benson S. V., Journal of" Fluid Mechanics, 100, p. 449 A980).
Gollub I. P., Benson S. V., — In: Pattern Formation, ed. H. Haken, Springer-
Verlag, p. 74 A979).
Gollub I. P., Brunner T. O., Danly B. G., Science, 200, p. 48 A978).
¦Grebogi С, ОН E., Yorke I. A., Physical Review Letters, 51, p. 339 A983).
Herman M., Publications mathematiques-de I'l. H. E. S., 49, p. 5 A979).
Ландау Л. Д., Лифшиц Е. М. Гидродинамика. Изд. 3-е, перераб. — М.: Наука,
1986.
Newhouse S., Ruelle D., Takens F., Communications in Mathematical Physics,
64, p. 35 A978).
Ostlund S., Rand D.,_Sethna J., Siggia E., Physica, 8D, p. 303 A983).
Ruelle D., Tokens /•"., Communications in Mathematical Physics, 20, p. 167
A971). [Имеется перевод: Рюэль Д., Такенс Ф. О природе турбулент-
турбулентности.— В сб.: Странные аттракторы. — М.: Мир, 1981, с. 117.]

ГЛАВА VIII
СУБГАРМОНИЧЕСКИЙ КАСКАД
VIII. 1. ВВЕДЕНИЕ
VIII. 1.1. Субгармоническая неустойчивость
В гл. II мы уже обсуждали субгармоническую неустойчи-
неустойчивость в связи с параметрическим осциллятором. Мы увидели
механизм, посредством которого возбуждение, даже если ампли-
амплитуда его мала, приводит к срыву устойчивости движения маят-
маятника при условии, что внешняя сила воздействует на маятник
в моменты времени, разделенные целым числом полупериодов
(см. разд. II. 2.4). Возбуждение наиболее эффективно, когда оно
происходит каждые полпериода: частота колебаний равна по-
половине частоты (период равен удвоенному периоду) возбужде-
возбуждения, о чем и говорит прилагательное «субгармоническая» в на-
названии неустойчивости. Этот результат следует расширить и
обобщить.
Поскольку процесс субгармонической неустойчивости инте-
интересен для нас сам по себе, мы рассмотрим субгармоническую
неустойчивость общего периодического решения безотноситель-
безотносительно к параметрическому осциллятору. Заметим, что по аналогич-
аналогичным причинам решение с частотой f/2 (или периодом 2 Т)
может в свою очередь претерпевать субгармоническую неустой-
неустойчивость, что приводит к половинной частоте //¦! (периоду 4 Т)
и т. д. Иначе говоря, соответствующая вариация управляющего
параметра должна позволить нам наблюдать целую серию суб-
субгармонических неустойчивостей, что порождает решения с пе-
периодами 2 Т, 4 Т, 8 Т и т. д. Мы называем это явление каскадом
субгармонических бифуркаций или субгармоническим каскадом,
каждый этап которого сопровождается уменьшением частоты
вдвое, т. е. удвоением периода.
VIII. 1.2. Механизм удвоения периода
Теория Флоке объясняет процесс, при котором происходит
удвоение периода. На рис. VIII. 1 показаны основные ингре-
ингредиенты, необходимые для исследования линейной устойчивости
периодического решения: сечение Пуанкаре траектории
(рис. VIII. 1, а) и пересечение единичной окружности на комп-
комплексной плоскости собственным значением матрицы Флоке

2!8
Глава VIII
(рис. VIII. 1,6). Посмотрим, что происходит, когда собственное
значение приближается к критическому значению —1 и, нако-
наконец, достигает его. Пусть х — собственный вектор, соответствую-
соответствующий этому собственному значению, и 5 — плоскость сечения, со-
(неустойчивый}-
Рис. VIII. 1. Устойчивость предельного цикла в линейном приближении, а—ис-
а—используя сечение Пуанкаре предельного цикла, мы можем определить эволю-
эволюцию начального возмущения дх под действием потока. В зависимости от того,
становится ли Мох больше (как на рисунке) или меньше, чем бх, предельный
цикл неустойчив или устойчив; б —нейтральная устойчивость возникает в том
случае, когда собственное значение матрицы М (которая называется матрицей
Флоке) пересекает на комплексной плоскости единичную окружность D.
В случае субгармонической неустойчивости собственное значение пересекает
окружность D в точке —1.
держащая х. Не "уменьшая общности, мы можем рассматривать
только эволюцию последовательных точек пересечения фазовой
траектории с плоскостью S (рис.'УШ. 2). До бифуркации любое
смещение начальной амплитуды д'о убывает с каждым периодом,
так как значение х умножается на отрицательный коэффициент,
абсолютная величина которого меньше единицы (рис. VIII. 2, а).
Следовательно, предельный цикл с периодом Т линейно устой-

Субгармонический каскад 21Ф
чив. Его сечение Пуанкаре вырождается в точку, выбранную
на рис. VIII. 2 за начало координат. Но, когда собственное зна-
значение становится равным —1, ситуация изменяется. Расстояние
от начала координат не убывает fco временем: при каждом пере-
пересечении отклонение от начала изменяет свой знак, но модуль
его остается неизменным. Через каждые два пересечения (обо-
I
Рис. VIII. 2. Последовательность итераций потока. Показано, что происходит
вдоль собственного вектора х, соответствующего тому собственному значению
матрицы Флоке, которое ' пересекает единичную окружность в точке —1-
а —до бифуркации предельный цикл устойчив. Итерации начальной точки хъ
сходятся к нулю — сечению Пуанкаре предельного цикла. Так как собствен-
собственное значение отрицательно, итерации попеременно оказываются то по одну,
то по другую сторону от нуля; б —в точке бифуркации итерации перестают
сходиться. Модуль любого начального смещения х0 сохраняется, тогда как
знак смещения изменяется при каждой итерации.
значенные на рис. VIII. 2, б через Х2, х4 и т. д.) мы возвращаем-
возвращаемся в исходную точку Хо- Мы видим, что возникает новая перио-
периодическая орбита с периодом, вдвое большим периода исходной
орбиты. Новая орбита зависит от выбора начального смещения
л'о. Кроме того, оставаясь в рамках линейной теории Флоке. мы
ничего не можем сказать об устойчивости новой орбиты. Прав-
Правдоподобно, однако, чги непосредственно за точкой бифуркации
возникает устойчивый предельный цикл с периодом 2 Т (если.
бифуркация суперкритическая).

220 Глава VIII
VIII. 1.3. Отображение первого возвращения
В предыдущем разделе снова показана центральная роль
критического собственного значения матрицы Флоке и связан-
связанного с ней собственного вектора. Учитывая это, мы сосредото-
сосредоточим внимание на сечении Пуанкаре и на этом собственном век-
векторе и оставим в стороне остальную часть траектории, имею-
имеющую второстепенное значение. Это приводит нас к исследованию
эволюции начального условия через дискретные интервалы вре-
времени Т, 2Т, 4 7,..., т. е. к анализу свойств итерированного
преобразования точки на оси. Поведение потока можно выяс-
выяснить с помощью одномерного отображения вида
связывающего координату Xk+i точки в момент времени (k + 1O"
г. координатой хк предыдущей точки в момент времени kT и яв-
являющегося отображением первого возвращения исходного по-
потока. Мы снова видим эвристическое преимущество сведения
анализа нелинейного потока к математически гораздо более
простой задаче1).
Еще в 1918 г. исследования того, что мы называем итера-
итерациями отображений интервала на себя, были предприняты' Жю-
Жюлиа и Фату. Но в то время эта проблема казалась весьма экзо-
экзотической и ее практическое значение не было оценено по до-
достоинству. Важность работ Жюлиа и Фату была осознана лишь
в свете современных достижений теории динамических систем.
С 1975 г. число работ по этому кругу вопросов необычайно воз-
возросло, и дать их исчерпывающий обзор не представляется воз-
возможным. Именно поэтому мы ограничимся изложением наибо-
наиболее существенных результатов, имеющих непосредственное от-
отношение к возникновению хаоса. Напомним, что одномерный
подход, как было показано в гл. IV, обоснован, когда мы имеем
дело с сильно диссипативной системой. Действительно, в силу
крайне быстрого сокращения площадей, обусловленного силь-
сильной диссипацией, существенную роль играет лишь одна степень
свободы. Таким образом, вся полезная информация сосредото-
сосредоточена в одном выделенном направлении в фазовом простран-
пространстве, и мы можем спокойно пренебречь остальными. В этой
главе мы излагаем анализ субгармонического каскада и свой-
свойства квадратичных отображений интервала на себя.
') Отображение первого возвращения широко применяется и не ограничи-
ограничивается отображением интервала на себя, которое мы рассматриваем в этой
главе. Другие примеры применения отображения первого возвращения приве-
приведены в гл. IX в связи с анализом перемежаемости.

Субгармонический каскад 221
VIII. 2. СУБГАРМОНИЧЕСКИЙ КАСКАД
VIII. 2.1. Квадратичное отображение интервала
Рассмотрим непрерывную функцию
jc), хе[0, 1].
При 0 < \х =sj 1 эта функция описывает отображение первого
возвращения
4U) f() (VIII. 1)
которое каждой точке xk из единичного интервала ставит в со-
соответствие другую точку Xk+\ единичного интервала, называе-
называемую итерацией точки хн- Условие ц ^ 1 необходимо (для того
чтобы гарантировать принадлежность f(xk), как и хк, единич-
единичному интервалу [0, 1]). В действительности ни точная форма1)
функции, ни ограничение значений х единичным ишерБалом не
ограничивают общность излагаемых ниже соображений. Но, для
того чтобы прийти к определенным выводам, мы должны вы-
выбрать вполне определенную функцию; приведенная выше форма
функции и нормировка интервала на единичный интервал [0, 1]
выбраны нами из соображений удобства.
Прежде всего построим график функции f при каком-нибудь
заданном значении ц, например при [л = 0,7 (рис. VIII. 3). Не-
Нетрудно видеть, что f обращается в нуль при х — 0 и х— 1 и что
эта парабола достигает максимума при х = 0,5. Методом, опи-
описанным в гл. IV, исходя из произвольного начального условия
А'о, исследуем с помощью этого графика, как ведут себя итера-
итерации отображения. Как видно из рис. VIII. 3, итерации сходятся
к точке с абсциссой х* (точке пересечения графика функции /
с диагональю) независимо от абсциссы х0 начальной точки, за
исключением двух случаев: концов интервала 0 и 1. Выбирая
х0 = 0 или х0 = 1, мы получаем х\ ¦.= 0, х2 = 0, ... . Но при лю-
любом положительном значении х0, сколь угодно близком к нулю,
но отличном от нуля, итерации сходятся к х*. Можно сказать,
что любое смещение из начала координат, сколь бы малым оно
') Функция f должна удовлетворять на интервале |0, 11 только следую-
следующим условиям: а) быть непрерывной и дифференцируемой; б) иметь один
экстремум; в) иметь отрицательную производную Шварца. Второе условие
требует, чтобы f была нелинейной функцией. Ни одно из описываемых в этой
глапе явлений не может порождаться линейной функцией и вообще функ-
функцией, монотонной на интервале. Третье условие, которое мы не используем
з явном виде, можно рассматривать как требование вогнутости графика
функции f. Оно обеспечивает суперкритичность всех бифуркаций отображения
x^-j(x). Квадратичное отображение удовлетворяет этому последнему ус-
условию.

222
Глава VIII
ни было, усиливается итерациями и образы начальной точки
удаляются от начала координат. Следовательно, начало коор-
координат— неустойчивая неподвижная точка. Наоборот, неподвиж-
неподвижная точка с абсциссой х*, к которой сходятся итерации, если
начальная точка принадлежит открытому интервалу (О, 1), ус-
устойчива, т. е. является аттрактором. Чтобы обозначить как-то си-
ситуацию, когда на каждом этапе итерации мы находимся в одной
Рис. VIII. 3. График отображения f(x) при ц = 0,7. Начало координат —
неустойчивая неподвижная точка. Точка х* пересечения графика отображе-
отображения / с диагональю —устойчивая неподвижная точка, к которой сходятся
итерации всех начальных условий в открытом интервале @, 1).
и той же неподвижной точке, условимся говорить, что перед нами
аттрактор с периодом 1 (за единицу времени неявно принят
один шаг итерации). Можно было бы также сказать, что за
единицу времени мы выбрали период предельного цикла, сече-
сечением Пуанкаре которого является данная неподвижная точка.
VIII. 2.2. Каскад удвоений периода
Ситуация, изображенная на рис. VIII. 3, не единственно воз-
возможная. Действительно, кривая f(x) зависит от значения пара-
параметра и, который, как мы видели, задает максимальное значе-
значение функции /. Варьируя \_i. мы изменяем кривую, что может
иметь решающие последствия для всей серии итераций. Чтобы
убедиться в этом, обратимся к рис. VIII. 4, для которого ц =0,8,
Неподвижная точка х* неустойчива, так как тангенс угла на-

Субгармонический каскад
223
клона касательной к кривой в этой точке по абсолютной вели-
величине больше единицы. Как показывает графическое построение,
у отображения имеются две такие особые точки с абсциссами
к' и х' что
и x; =
Иначе говоря, итерации попеременно совпадают то с одной из
них, то с другой. Начав с любой из этих точек, мы через две
Рис. "viil. 4. График отображения {(х) при A = 0,8. При згом значении на-,
-л мет г а и о'1 непоч^'Ж'Гло точки отображения f не\'сто;;ч1:г,!;Т. Нотрулнп
видеть, что асимптотическим пределом итераций при любом начальном усло-
условии из открытого интервала @, 1) служит пара точек х1 и х2> с которыми
попеременно совпадают образы начальной точки.
итерации вернемся в нее. Такие две точки образуют аттрактор
с периодом 2, который называется также 2-циклом. Так как
то эти две точки (не являющиеся неподвижными точками ото-
отображения /) являются неподвижными точками функции
з чем мы легко убеждаемся, взглянув на рис. VIII. 5. Более
подробное исследование показывает, что существует непре-
непрерывный переход от первой ситуации (рис. VIII. 3) ко второй

224
Глава VIII
(рис. VIII. 4) при увеличении значения параметра ц. Сам
переход происходит при единственном значении jxi = 0,75.
В этот момент устойчивая неподвижная точка отображения f
становится неустойчивой и соответственно появляются две ус-
устойчивые неподвижные точки отображения f2. Аттрактор с пе-
периодом 2 возникает вместо аттрактора с периодом 1: происходит
удвоение периода, как предсказывает теория Флоке при пере-
пересечении единичной окружности в точке —1.
О
1
Рис. VIII. 5. График отображения g(x) = /(/(*)) = f2(x) при ц = 0,8. Это
отображение имеет четыре неподвижные точки, дне ил которых (.", и х0) ус-
* * * *
тойчивы. Отображение f(x) переводит точку х{ в х2, а х2 — в Ху
Два квадрата, построенные вокруг неподвижных точек, призваны подчеркнуть
структурное сходство этого графика с графиком отображения f(x) на
рис. VIII. 3.
Что происходит при дальнейшем увеличении параметра ц?
Кривые / и f2 постепенно деформируются так, что неподвижные
точки отображения /2 также в конце концов теряют устойчи-
устойчивость. Следующее простое графическое построение позволяет
предсказать и понять последовательность событий. Рассмо-
Рассмотрим квадрат вокруг неподвижной точки с абсциссой х'2 на
рис. VIII. 5'). Внутри квадрата мы видим локально параболи-
параболическую кривую с устойчивой неподвижной точкой, т. е. обнару-
обнаруживаем ситуацию, полностью аналогичную той, которая изобра-
*) Те же рассуждения применимы и к неподвижной точке
также является экстремумом, но минимумом.
которая

Субгармонический каскад
225
жена на рис. VIII. 3. Следовательно, когда при деформации кри-
кривой эта неподвижная точка становится неустойчивой, мы можем
ожидать такого же явления, как прежде: замены неподвижной
точки отображения g двумя точками, которые являются непод-
неподвижными точками функции
Такой же вывод применим к двум неподвижным точкам отобра-
отображения g с абсциссами
устойчивость при
х\ и х'2, которые одновременно теряют
== 0,86237....
Выше этого значения отображение g не имеет устойчивых не-
неподвижных точек. Но, как видно из рис. VIII. 6, отображение А
О Г
Рис. VIII. 6. График отображения h(x) — g(g(x)) — fl(x) при ц = 0,875.
Это отображение имеет восемь неподвижных точек, четыре из них устойчивы.
Квадрат, построенный вокруг одной из них, показывает, что мы снова вос-
воспроизводим ситуацию, изображенную на рис. VIII. 3. Это позволяет сказать,
что в действительности речь идет о бесконечном повторении одного и того же
процесса.
имеет при \i = 0,875 четыре неподвижные точки. Они образуют
аттрактор, состоящий из четырех последовательно посещаемых
точек отобпзжснйЯ- ттпрлгтяр.ленного нз г>но VITT 1. О. кзкой бы
из этих четырех точек мы ни начали, для возвращения в нее
нам потребуются четыре последовательные итерации: период
аттрактора равен 4 D-цикл). Таким образом, снова произошло
удвоение периода при субгармонической бифуркации.
15 П. Берже и др.

226
Глава VIII
При дальнейшем увеличении параметра р, в отображении
(VIII. 1) то же явление повторяется до бесконечности: мы полу-
получаем каскад бифуркаций, каждая из которых сопровождается
удвоением периода, связанным с субгармонической неустойчи-
неустойчивостью. Квадрат, очерченный вокруг одной из неподвижных то-
точек функции h(x) на рис. VIII.6, подчеркивает сохранение
структуры, представленной на рис. VIII. 3. Мы замечаем анало-
аналогию между структурами во всех масштабах, о которой уже упо-
упоминали в связи с канторовским множеством. При уменьшении
параметра ц мы наблюдаем последовательность аттракторов
с периодами 21, или 2(-циклов, где / — целое число от 0 (при
ц ^ 0,75) до бесконечности. Значения ц, при которых происхо-
происходит этот каскад бифуркаций, обладают замечательным свой-
свойством: они образуют возрастающую последовательность, быстро
сходящуюся к точке накопления ц^,. Значение ц,» может быть
найдено численно:
,^ = 0,892486418 ....
В табл. VIII. 1 приведены значения (х, соответствующие несколь-
нескольким первым бифуркациям субгармонического каскада.
Таблица VIII. 1
Период аттрактора
1 • 2° = 1
1-2!=2
1 • 22 = 4
1-23 = 8
1 • 2*= 16
1 • 25 = 32
1 • 2°° = оо
Значение ц^ в точке бифуркации
ц,=0,75
ц2 — 0,86237...
Из = 0,886 02...
ц« = 0,892 18...
fi5 = 0,892472 8...
ц6 = 0,892483 5...
^ = 0,892 486 418...
VIII. 2.3. Законы подобия
Внимательное изучение чисел, представленных в табл. VIII. 1,
показывает, что их сходимость к точке накопления подчиняется
простому и строгому закону: разность значений \х, соответ-

Субгармонический каскад
227
ствующих двум последовательным бифуркациям, уменьшается
каждый раз соответственно почти постоянному коэффициенту:
Этот фундаментальный результат, важность которого трудно
переоценить, означает, что коэффициент уменьшения масштаба
0,5
0,6
0,1
0,8
[49
Mi Мг/*з
Рис. VIII. 7. Асимптотические итерации отображения f(x) при ц е [0,5; 1].
На графике показана зависимость от параметра ц значения (или значений)
Xk, т.е. k-й итерации отображения f(x) при &->оо. Слева направо мы видим:
1) последовательность периодических аттракторов, разделенных субгармони-
субгармоническими бифуркациями, каждая из которых приводит к удвоению числа точек
на аттракторе и периода. Каскад субгармонических бифуркаций имеет точку
накопления при ц» = 0,89248...;
2) за ц^ область, в которой апериодические и периодические аттракторы че-
чередуются.
Некоторые периодические аттракторы существуют на достаточно большом ин-
интервале значений параметра |х и поэтому видны как более светлые зоны.
В частности, отчетливо виден аттрактор с периодом 3 при ц ж 0,96.
6 является универсальной константой, не зависящей от деталей
рассматриваемой функции /:
6 = 4,6692016091029909 ....
Вторая универсальная константа !)
а = 2,50290787509589284 ...
задает коэффициент уменьшения масштабов расстояний на
оси х. Более точно можно утверждать, что, итерируя любое
отображение, обладающее квадратичным экстремумом, мы
всегда обнаружим один и тот же каскад удвоений периодов
Как и в случае и», значения констант S и а определяются численно.
15*

228 Глава VIII
с одними и теми же законами подобия, которые приведены
выше. Мы располагаем весьма общей теорией, которая апосте-
апостериори обосновывает наш выбор конкретной функции f. Замеча-
Замечательно, что эта теория позволяет делать количественные пред-
предсказания, если выполнено простое качественное условие1).
График, на котором значения х в точках на каждом аттрак-
аттракторе представлены в зависимости от ц,, позволяет наглядно
представить описанный выше субгармонический каскад
(рис. VIII. 7). Первые бифуркации с удвоением числа точек
аттрактора видны особенно ясно. Но бифуркации быстро сни-
снижаются и становятся неразличимыми, если значения ц, откла-
откладывать в линейном масштабе. На рис. VIII. 7 аттрактор с пе-
периодом 8 — последний, который различим без труда. Эти ре-
результаты следуют из приведенного выше закона сходимости —
геометрической прогрессии: значения, приведенные в табл. VIII. I,
показывают, почему аттракторы с периодами 16, 32 и т. д. в мас-
масштабе, выбранном на рис. VIII. 7, практически неразличимы.
VIII. 3. ХАРАКТЕРИСТИКИ ХАОСА
VIII. 3.1. За субгармоническим каскадом
При возрастании параметра jj, и его стремлении к (Лею появ-
появляются аттракторы со все большим периодом 2'. Следовательно,
для того чтобы установить соответствующую периодичность, за
явлением требуется наблюдать в течение все более продолжи-
продолжительного (бесконечно большого в точке Цоо) времени. Но что
происходит за точкой накопления?
Численное моделирование показывает, что за критическим
значением [i = 0,892486418 ... начинается очень сложная об-
область. На графике, представленном на рис. VIII. 7, появляются
различные зоны, одни более светлые, другие более темные. Под-
Подробный анализ обнаруживает, что в закритической области пе-
периодические аттракторы чередуются с режимом, который теперь
принято называть хаосом.
В последнем случае итерации функции f порождают после-
последовательность таких значений х, которые а) не повторяются,
б) зависят от начального условия хо- В частности, две перво-
первоначально близкие точки порождают две последовательности ите-
итераций (или траекторий), которые расходятся друг от друга.
Для столь простого преобразования такое поведение весьма не-
') Хорошо известна аналогия между упомянутой теорией и теорией фя-
зовых переходов, в частности процедурой и терминологией теории ренорм-
группы. Константы б и а можно рассматривать как «критические показатели»
в точке накопления.

Субгармонический каскад
229
•ожиданно! Мы попытаемся понять, чем оно вызвано,.и рассмот-
рассмотри два существенных свойства этого отображения, ключевых
для понимания хаотического поведения.
VIII. 3.2. Два фундаментальных свойства отображения
Чтобы понять эти два свойства — необходимость преобразо-
преобразования и его ЧЗНУ, —достаточно рассмотреть график функции
а
Рис. VIII. 8. Фундаментальные свой-
свойства отображения f(x). а —растяже-
—растяжение и складывание. Функция f ото-
Оражает первую половину шлераалч
[О, 1/2] на весь интервал [0, 1].
Вторая половина также отображает-
отображается на весь интервал, но в обратном
направлении (см. стрелки). Можно
сказать, что отображение f сначала
растягивает интервал вдвое, а затем
складывает его так, как это требует-
требуется для того, чтобы образ интервала
совпадал с интервалом [0, 1]. б —
необратимость.
Из формы кривой f видно, что любая
итерация Xk+i имеет два прообраза:
хк и xk. Это означает, что отобра-
отображение / необратимо, так как из-за
неопределенности в выборе прообра-
прообраза оно может быть выполнено только
в одном направлении. Необрати-
Необратимость — важное свойство, которое
необходимо для того, чтобы отобра-
отображение прямой R в R могло поро-
порождать хаос.
1 ос
(.V)
при значениях ц, близких к единице. Построим график
,.„т, t (mm Л7ТТТ Й л\ о ппл nr-Kin v nnraioneu ГООИЗОНТ8ЛЬ-
кую линию, на которой будем откладывать образы f(x). выяс-
выясним, что происходит, когда х принимает значения из интервала

230 Глава VIII
10, 1]. Образ точки х = 0 есть 0, образ точки х=\/2 есть L
Следовательно, первая половина интервала [0, 1/2] «растяги-
«растягивается» при отображении на весь интервал 10, 1J. Нетрудно ви-
видеть также, что образ точки х = 1 есть 0 и что преобразование
растягивает вторую половину интервала [1/2, 1] на весь интер-
интервал и при этом изменяет направление его на обратное. Иначе
говоря, когда х однократно пробегает единичный интервал, об-
образ точки х проходит единичный интервал туда и обратно. Та-
Такое поведение образа можно рассматривать как результат двоя-
двоякой операции: растяжение [в нашем примере в среднем в.
2 раза1)] в сочетании со складыванием (необходимым, чтобы
образ интервала покрыл интервал [0, 1]). Каждая из этих двух
операций приводит к важному следствию.
1. Растяжение приводит к тому,, что образ малого началь-
начального смещения 8хо (в среднем) умножается при каждой опера-
операции на коэффициент растяжения. Если коэффициент растяже-
растяжения больше единицы, то этот геометрический процесс приводит
к экспоненциальному росту смещения. Эти события происходят
за критическим значением jioo, когда не существует периодиче-
периодический аттрактор: именно они и обусловливают ЧЗНУ, о которой
говорилось в гл. VI. Средняя скорость увеличения данного сме-
смещения измеряется параметром Я экспоненциального закона:
bxk = бдг0 ехр (Щ,
где Я — показатель Ляпунова (см. приложение Б) одномерного
отображения. Этот экспоненциальный рост отчетливо заметен
на рис. VIII. 9.
2. Складывание, необходимое для того, чтобы растяжение
было совместимо с ограниченностью области (в данном случае
интервала), приводит к «перемешиванию» образов различных
точек. Оно также является важной характеристикой хаоса.
Именно образование складок не позволяет однозначно указать
для точки предшествующую ей точку: у каждой точки хк+\
имеются два прообраза xk в предыдущей итерации
(рис. VIII. 8, б), четыре прообраза еще на одну итерацию раньше
и т. д. Следовательно, преобразование, легко выполнимое при
возрастающих значениях k, не может быть выполнено в обрат-
обратную сторону. Такое преобразование называется необратимым 2).
Следовательно, наше преобразование запрещает знание прош-
*) При заданной параболической форме f(x) может быть определено
только растяжение р. среднем. Области вблизи концов х = 0, х = 1 единич-
единичного отрезка растянуты сильнее всего, тогда как область вблизи максимума
х = 1/2 сжата.
2) Справедливо более общее утверждение: любое непрерывное отображе-
отображение R в R должно быть необратимым, чтобы оно приводило к хаосу.

Субгармонический каскад
231
лых значений х, а также (вследствие ЧЗНУ) предсказание бу-
будущих значений х через какой-то период времени. Долговремен-'
яг*
Ю'в
ю~8
S
ю
-
-
го
30
40
60
70 ZO 30 40 SO 60 к
1СГг
ю-"
Ю'6
Рис. VIII. 9. Эволюция расстояния б между двумя итерациями отображения
jyx) = 4цхA — х) при различных начальных значениях. Чтобы исключить
переходные эффекты, связанные с погрешностью в начальных условиях х0,
отображение подвергалось ШО-кратной итерации. Для вычисления двух се-
серий итераций в качестве начальных условий выбирались точки х0 и х<> + бо-
Абсолютная величина расстояния между двумя k-ын итерациями изменяется
по закону
6 = 60ехр (Щ,
где X — показатель Ляпунова. Таким образом, показатель Ляпунова характе-
характеризует средний угловой коэффициент графика зависимости б от k в полуло-
полулогарифмическом масштабе, как на рис. а и б.
а — при [д, = 0,7 показатель Ляпунова X да —0,02. Соответствующий режим
периодический, и расстояние б убывает: показатель Ляпунова отрицателен;
б — при ц = 0,95 показатель Ляпунова X « +0,4. Соответствующий режим
хаотический, и расстояние б возрастает: показатель Ляпунова положителен.
Когда б достигает величины, сравнимой с длиной интервала [0, 1], насту-
наступает насыщение.
ное предсказание значений х потребовало бы, чтобы начальное
условие было известно с бесконечной точностью, так как малей-
малейшая (даже бесконечно малая) неопределенность в х0 не позво-
позволяет нам различать траектории, которые непременно разойдутся

232
Глава VIII
по истечении достаточно большого промежутка времени. Разу-
Разумеется, бесконечная точность недостижима на практике. По-
Поэтому, несмотря на то что она описывается детерминированным
уравнением (VIII. 1), эволюция остается принципиально не-
непредсказуемой и представляется нам неупорядоченной и хаотич-
хаотичной. Вопреки широко распространенному мнению детерминиро-
детерминированность и хаос не являются взаимно исключающими противо-
противоположностями.
VIII. 3.3. Обратный каскад
Сказанное выше позволяет полагать, что хаотический режим
при |х > ц™ не полностью лишен определенного порядка, хотя;
этот порядок на первый взгляд, возможно, и не виден. Другим
0,25
Рис. VIII. 10. Прямой и обратный каскады. Этот схематический рисунок при-
приведен для того, чтобы привлечь внимание читателя к одной детали, которая
не видна на рис. VIII. 7: обратный каскад — своего рода нечеткое отражение
прямого каскада относительно вертикали, соответствующей значению пара-
параметра |Хоо. По оси абсцисс взята неравномерная шкала у th Dц — ^„J; вы-
выбор ее обусловлен исключительно удобством построения графика и не дол-
должен мешать пониманию того, что «естественным» представлением решений
следует считать то, которое можно видеть на рис. VIII. 7.
Из работы С. Гроссманна и С. Томе.
элементом порядка, свидетельствующим о том же, являются
«окна периодичности» (разд. VIII. 3.4) — периодические аттрак-
аттракторы в интервале (|Лм>, 1). Некоторые из них можно наблюдать
в виде более светлых зон!) на рис. VIII. 7. Периодические и
апериодические аттракторы тесно взаимосвязаны. Действитель-
Действительно, как показывает тщательный анализ апериодических аттрак-
аттракторов, они являются своего рода «шумовыми предельными цик-

Субгармонический каскад 233
лами» с периодом 21, где / — целое число, неограниченно воз-
возрастающее, когда ц стремится к [х» сверху. Более точно, образ
точки последовательно посещает множество, состоящее из 21 не-
непересекающихся отрезков из интервала @, 1). После 2' итера-
итераций мы возвращаемся на исходный отрезок: это позволяет гово-
говорить о цикле. Вместе с тем поведение внутри каждого отрезка
полностью хаотическое: отсюда прилагательное «шумовой». Ко-
Короче говоря, все итерации порядка 2' содержатся внутри малого
отрезка, но там они полностью неупорядочены. Аналогичное
утверждение справедливо относительно каждого из 2' отрезков.
При возрастании ц мы видим, что при некоторых значениях
этого параметра отрезки расщепляются на два. Вместо шумо-
шумового цикла с периодом 21 возникает другой шумовой цикл с вдвое
меньшим периодом, т. е. с периодом 2'-1. При дальнейшем воз-
возрастании (л процесс повторяется до тех пор, пока не будет до-
достигнут «период» 2° = 1. На рис. VIII. 10 схематично показана
серия изменений периода. Мы видим, что наряду с субгармони-
субгармоническим каскадом существует4 другой каскад с близкой структу-
структурой, но ведущий в противоположном направлении по оси ji.
Обычно первый каскад принято называть прямым, а второй об-
обратным. Результат, который по самым скромным оценкам может
быть назван замечательным, состоит в том, что значения пара-
параметра ц, при которых происходят бифуркации обратного ка-
каскада, также сходятся к \lx с тем же масштабным множителем
б = 4,669 ..., что и прямой каскад. В этом еще одно подтверж-
подтверждение того, что в хаосе существует некоторый порядок (если
это утверждение нуждается в подтверждении)!
VIII. 3.4. Окна периодичности
Как мы уже упоминали, интервал [цоо, 1] содержит не толь-
только хаос. В нем встречаются также узкие диапазоны значений
ц, в которых траектории строго периодические. Сначала рож-
рождается цикл с основным периодом р (р>1), затем процесс,
аналогичный описанному выше,- приводит к появлению после-
последовательности аттракторов с периодом р-21 A = 1, 2, ..., оо).
Это, несомненно, субгармонический каскад, удовлетворяющий
приведенным выше законам подобия. Точкой накопления
(/—>-оо) отмечен конец окна периодичности с периодом р. Каж-
Каждое окно занимает отрезок оси \i, длина которого варьируется
в широких пределах, но в большинстве случаев отрезки очень
малы. Именно поэтому их невозможно разглядеть на рис. VIII. 7,
где почти весь интервал [(!«>, 1] кажется хаотическим. Наиболь-
Наибольшее окно @.9571 ... <!;!¦< 0,9624 ...) содержит циклы с ос-
основным периодом, равным 3. Его мы и используем в качестве

234
Глава VIII
примера (поскольку его численная реализация наиболее удоб-
удобна), на котором можно показать, как рождается цикл.
Когда мы говорим о цикле с периодом р, это означает, что
после р итераций мы возвращаемся в исходную точку. Чтобы
идентифицировать такой цикл, удобно построить график ото-
отображения р-ro возвращения, т. е. функции xk+p = ff (xk). На
О
Рис. VIII. 11. Рождение цикла с периодом 3. Наибольшее окно периодично-
периодичности @,9571 ...< цО,9624...) содержит циклы с периодом 3-2' A = 0, ...
..., оо). Чтобы объяснить, как рождается цикл с периодом 3, построим гра-
график отображения третьего возвращения:
а — немного ниже порогового значения (при ц = 0,9) отображение не имеет
устойчивой неподвижной точки; б — при достижении порога (при jx =
= 0,9751 ...) график отображения /3 касается диагонали в трех точках. Эти
три точки, первоначально нейтрально устойчивые, становятся устойчивыми,
как только параметр ц превысит пороговое значение. Бифуркация касания
порождает цикл с периодом 3.
рис. VIII. 11 вы видите такое отображение при р==3 и двух
значениях щ одно несколько выше, а другое несколько ниже
порога появления цикла. Ниже порога неподвижные тбчки
(точки пересечения диагонали с кривой) неустойчивы (тангенс
угла наклона касательной к кривой по абсолютной величине
больше единицы). При вариации параметра ц, кривая, деформи-
деформируясь, касается диагонали в трех точках— рождаются три не-
неподвижные точки, нейтпально устойчивые на пороге и асимпто-
асимптотически устойчивые пад порогом. Позтому бифуркация такого
типа называется касательной или тангенциальной бифуркацией.
Если параметр ц продолжает возрастать, то следует ожидать,
что субгармоническая неустойчивость дестабилизирует этот

Субгармонический каскад 235
режим, как прежде. И действительно, цикл с периодом 3 пости-
постигает судьба, аналогичная той, которая постигла цикл с перио-
периодом 1, что приводит к хаосу') через субгармонический каскад,
все еще удовлетворяющий тем же законам подобия.
VIII. 3.5. Универсальная последовательность
Другое весьма необычное свойство относится к иерархии от-
относительного расположения окон периодичности вдоль оси ц,.
Действительно, если абсолютное расположение и длина окон
зависят от рассматриваемого нами конкретного отображения f,
то порядок, в котором эти окна включаются при увеличении
а.
6
Рис. VIII. 12. Два аттрактора с циклами периода 4. Для каждого периоди-
периодического аттрактора характерен свой порядок обхода образующих его точек
при итерациях. Возможны два различных цикла с периодом 4: а—1—2—3—4;
б—1—3—2—4. Других циклов с периодом 4 при заданной форме отобра-
отображения не существует.
параметра ц, остается неизменным. Иначе говоря, при любой
функции f (лишь бы она имела один экстремум, квадратичный
или неквадратичный) периодические аттракторы образуют по-
последовательность всегда в одном и том же порядке, которая по-
поэтому называется универсальной последовательностью.
Характеризуя периодический аттрактор, следует иметь ввиду,
что два аттрактора с одним и тем же периодом могут разли-
различаться порядком обхода принадлежащих им точек. Используя
простейший пример аттракторов с периодом 4, изобразим схе-
схематически четыре точки на оси х (рис. VIII. 12). Мы видим, что
i) Когда последовательность образов полученных численно, кажется
хаотической, естественно нозникяет вопрос: является ли данная последова-
последовательность действительно хаотической или периодической с очень большим
периодом и сопровождается долгоживущими переходными режимами? Окон-
Окончательный ответ на этот вопрос пока не получен, хотя некоторые факты
подтверждают гипотезу истинного хаоса.

236
Глава VIII
существуют два 4-цикла1), соответствующие замкнутым марш-
маршрутам 1-2-3-4 и 1-3-2-4.
Полезно поэтому идентифицировать периодический аттрак-
аттрактор по расположению его компонент на оси х. Различные ат-
аттракторы с одним и тем же периодом могут быть охарактери-
охарактеризованы двумя способами. Один способ состоит в том, чтобы
сначала пронумеровать точки аттрактора в порядке их обхода
при итерации отображения, а затем записать, в каком порядке
они располагаются на оси х. Следуя второму методу, мы при-
приписываем каждой точке букву П или Л в зависимости от того,
находится ли она справа или слева от максимума функции /v
Перечисляя буквы в порядке обхода точек, мы получаем харак-
характеристическую последовательность букв П и Л. Можно пока-
показать, что в любом окне периодичности существует такое значе-
значение ц, при котором сам максимум является частью аттрактора.
Следовательно, итерации достаточно начать с максимума, кото-
который мы обозначим символом 0 (не смешивать с левым концом
интервала — точкой х — 0). Так как нуль расположен не слева
и не справа от максимума, в последовательности букв Пи Л
знаков на один меньше, чем точек в периодическом аттракторе.
Данные о различных аттракторах универсальной последова-
последовательности с периодом от 1 до 6 представлены в табл. VIII. 2.
Таблица VIII. 2
Период
Р
6
5
3
6
5
6
4
6
5
6
Последовательность точек
2—0-4-3-5-1
2—0-4-3-1
2—0—1
2—5—3—0—4—1
2—3—0—4—1
2-3-0-4-5-1
2-3-0—1
2—3—4—0-5—1
2—3—4—0—1
2—3—4—5—0—1
Последовательность
символов П и Л
ПЛППП
плпп
пл
пллпл
пллп
пллпп
плл
ПЛЛЛ11
пллл
плллп
Из-за формы кривой f(x) образ максимума (точки 0) всегда
является крайней правой точкой (точкой 1), образ которой
в свою очередь совпадает с крайней левой точкой. Именно по-
') Если форма рассматриваемой функции f задана, то существуют только
два различных аттрактора. Из формы" этой функции (рис." VIII. 3)_ следует,
что образ крайней левой точки совпадает с крайней правой точкой. Уто озна-
означает, что любой цикл должен начинаться с точки ! и заканчиваться в точке 4.

Субгармонический каскад 237
этому последовательность точек всегда начинается с 2, а закан-
заканчивается 1, в то время как последовательность символов П и Л
для любого периодического аттрактора начинается с комбина-
комбинации ПЛ.
VIII. 4. ЭКСПЕРИМЕНТАЛЬНЫЕ ПРИМЕРЫ
VIII. 4.1. Природа наблюдений
Экспериментальная идентификация некоторых явлений, опи-
описанных при рассмотрении квадратичного отображения, не долж-
должна быть особенно трудной. Если периодический режим с часто-
частотой f в результате субгармонической неустойчивости переходит
в другой периодический режим с удвоенным периодом, то такой
переход должен сопровождаться
1) удвоением числа точек сечения Пуанкаре;
2) появлением в спектре Фурье частоты f/2 и ее нечетных
гармоник C//2, 5//2 и т. д.).
В субгармоническом каскаде такой процесс повторяется не-
неоднократно и поэтому легко наблюдаем, если мы можем доста-
достаточно точно регулировать управляющий параметр.
Аналогично в случае обратного каскада мы ожидаем, что
должны наблюдаться:
1) удлинение отрезков, образующих сечение Пуанкаре, когда
они попарно сливаются (рис. VIII. 10);
2) связанный с хаотическим режимом шум, который после-
последовательно уничтожает субгармоники ..., f/16, f/8, f/4, f/2 в по-
порядке, обратном последовательности их появления в прямом
каскаде, прежде чем они заполнят весь спектр.
Исследование универсальной последовательности предпола-
предполагает точную идентификацию типа периодического аттрактора.
Эта задача, недоступная спектральному анализу, требует ис-
использования сечения Пуанкаре.
Многие эксперименты, значительная часть которых была вы-
выполнена на трех системах, описанных в гл. V, подтвердили адек-
адекватность теоретических выводов, к которым мы пришли
в гл. VIII. Наблюдения не оставляют сомнений в том, что
1) субгармонический каскад действительно является одним
из способов перехода к хаосу;
2) если управляющий параметр возрастает за точкой накоп-
накопления \ix субгармонического каскада, то мы действительно на-
наблюдаем обратный каскад. Он сопровождается постепенным
уширением линий спектра Фурье и, следовательно, ростом хаоса;
3) за прямым каскадом мы встречаем периодические аттрак-
аттракторы, принадлежащие универсальной последовательности.

238 Глава VIII
Если измерения достаточно точны, то мы можем даже про-
проверить законы подобия: согласие между теорией и эксперимен-
экспериментом носит не только качественный, но и количественный ха-
характер.
VIII. 4.2. Субгармонический каскад: конвекция РБ
Начнем с описания эксперимента, выполненного на жидкой
ртути при очень, малом числе Прандтля (Рг да 0,03). Чтобы ста-
стабилизировать конвективную структуру, воспользуемся ячейками
с малым аспектным отношением (Г = 4 или Г = 6), которые,
кроме того, поместим в магнитное поле. Два обстоятельства спо-
способствуют успеху экспериментов. Во-первых, вследствие высо-
высокой электропроводности ртути конвективные валы имеют силь-
сильную тенденцию выстраиваться в направлении, параллельном
магнитному полю. Это фиксирует пространственный порядок и
препятствует расплыванию структуры при увеличении пара-
параметра Ra (см. разд. V. 3.2). Во-вторых, магнитное поле способ-
способствует затуханию некоторых мод, вызывающих колебания ва-
валов, делает более интенсивной диссипацию, что, как мы видели,
благоприятно для использования отображения первого возвра-
возвращения.
Ртуть мы помещаем между двумя толстыми медными пла-
пластинами. Конвективные движения измеряются болометрами, так
как оптические моды неприменимы в непрозрачной среде. На
первом этапе эксперимента мы фиксируем интенсивность маг-
магнитного поля на нуле и увеличиваем разность температур до
возникновения конвекции при критическом значении числа Рэ-
лея Rac. Продолжая увеличивать Ra, мы замечаем, что вблизи
2Ra наступает новая неустойчивость. Сигнал, зарегистрирован-
зарегистрированный болометром, начинает осциллировать во времени с часто-
частотой fi. Эта осцилляторная неустойчивость может быть обуслов-
обусловлена волной, распространяющейся вдоль осей валов. При даль-
дальнейшем увеличении параметра Ra периодический режим в свою
очередь становится неустойчивым и в спектре мощности сигнала
появляется вторая частота1) f2, близкая, но все же отличная от
fi/2. Физические колебания, связанные с этой второй частотой,
до сих пор достоверно не идентифицированы. При несколько
большем значении Ra происходит синхронизация двух осцилля-
осцилляторов, если выполняется условие субгармонического резонанса
/2=/l/2.
Тенденция к синхронизации знаменует начало второго этапа
эксперимента. Ячейку мы помещаем в постоянное и однородное
!) Происходит переход от предельного цикла к тору Р через бифурка-
бифуркацию, описанную в гл. VII.

Субгармонический каскад
239
магнитное поле, интенсивность которого сравнима с амплиту-
амплитудами двух осцилляторов. Постепенно увеличивая число Рэлея,
мы встречаем последовательность четко определенных значений
Рис. VIII. 13а. Субгармонический каскад в эксперименте с тепловой конвек-
конвекцией. Изменение формы сигнала (температуры жидкости в одной точке как
функции времени) отчетливо указывает на то, что при увеличении параметра
Ra/Rac происходит процесс удвоения периода. Отрезки соответствуют длине
периода, определяемой основным мотивом, который повторяется неограни-
неограниченно.
Из работы А. Либхабера, С. Фова и К. Лароща.
Ra, при которых один периодический режим после бифуркации
переходит в другой, с удвоенным периодом. На рис. VIII. 13, а
представлены экспериментальные сигналы нескольких последо-
последовательных периодических режимов. Появление в спектре Фурье
субгармоник 'fi/4, ft/8, ft/16, ft/32 (и их нечетных гармоник)
свидетельствует об удвоениях периода (рис. VIII. 13,6). По этим

240
Глава VIII
результатам можно попытаться оценить скорость сходимости
последовательных бифуркаций. Полученное значение 4,4 очень
близко к значению 4,669 ..., предсказываемому теорией уни-
универсального асимптотического режима.
Этот эксперимент с конвекцией РБ убедительно подтверж-
подтверждает существование субгармонического каскада в физической си-
&Б
-70
в
= 3,-64
Рис. VIII. 136. Субгармонический каскад в эксперименте с тепловой конвек-
конвекцией. Анализ Фурье со всей определенностью подтверждает вывод, к кото-
которому приводит рассмотрение рис. VIII. 13. а: при возрастании параметра
Ra/Rac появляются субгармоники — сначала с частотой fi/2 (а), затем с ча-
частотами /i/4 (б), Д/8 (е) и /i/16 (г), а также их нечетные субгармоники.
Из работы А. Либхабера, С. Фова и К. Лароша.
стеме. Особенно важно, что измерение таких величин, как отно-
отношение амплитуд последовательных субгармоник, подтверждает
теоретические предсказания. Упомянем также о том, что тепло-
тепловая конвекция в других жидкостях (жидком гелии, воде и т. д.)
также приводит к возникновению каскада удвоений периода.
VIII. 4.3. Обратный каскад: вращающийся магнит
Субгармонический каскад легко наблюдается и з экспери-
эксперименте с магнитом, что еще раз подтверждает универсальность
теории. Ось магнита (см. гл. V) погружена в масло с большой

Субгармонический каскад 241
вязкостью, чтобы обеспечить сильную диссипацию энергии. За-
Зафиксировав амплитуду и частоту вращающегося магнитного
поля, мы постепенно изменяем амплитуду В\ стационарного маг-
магнитного поля, в свою очередь изменяющую управляющий пара-
параметр М в уравнении A2) гл. V. В эксперименте используются
следующие значения параметров:
а = 0,174; Р = 0,335; Me [0, 1600; 0, 2321].
Варьируя Л!, мы порождаем последовательность периодиче-
периодических режимов, характеризуемых на каждом этапе удвоением
периода. В качестве примера на рис. VIII. 14 показаны резуль-
результаты, полученные после четвертой бифуркации. В спектре Фурье
мы различаем субгармоники fi/2, fi/4, fi/8 и /i/16 начальной
частоты fi, а также их нечетные гармоники. Аналогично в сече-
сечении Пуанкаре мы видим 16 точек, подразделенных на две груп-
группы. В свою очередь каждая группа подразделяется па четыре
пары точек, что составляет всего восемь пар. Такого рода рас-
распределение мы получили бы, проведя вертикальную прямую на
рис. VIII. 7 в области существования аттрактора с периодом
16Г. Продолжая увеличивать М выше значения, близкого
к 0,2285 (численной оценки точки накопления), мы увидим за-
заметное изменение в эволюции спектра Фурье и сечения Пуан-
Пуанкаре. Дополнительные субгармонические пики высших порядков
в спектре не появляются. Вместо этого шум начинает уширять
основания некоторых пиков, прежде чем поглотить их. Этот про-
процесс происходит на нечетных гармониках сначала частоты fi/16
(рис. VIII. 15,а), затем частоты fi/8 (рис. VIII. 16,а) и т. д. Ана-
Аналогично в сечении Пуанкаре прекращается образование пар но-
новых точек за счет «удвоения» существующих точек. Вместо
этого дополнительные точки мало-помалу распространяются по
коротким сегментам, удлиняющимся при увеличении М, прежде
чем слиться попарно. Мы видим это на рис. VIII. 15,6, где все
еще можно различить восемь групп, и на рис. VIII. 16, б, где
различимы только четыре группы. Такое поведение вполне пред-
предвидимо, если на рис. VIII. 10 передвинуть вертикальную прямую
вправо за (л-с*,. Как предсказывает теория, вслед за прямым ка-
каскадом идет обратный каскад.
Заметим, что с точностью до ошибок измерений точки сече-
сечения Пуанкаре (рис. VIII. 16, б) не покрывают поверхность,
а располагаются вдоль двух дуг кривых. Так происходит по-
потому, что диссипация энергии достаточно велика и маскирует
структуру апериодического аттрактора. Именно это служит
обоснованием анализа режимов с помощью отображения интер-
интервала на себя,
16 П. Берже и др.

242
Глава VIII
S(fHlog)
ее
Рис. VIII. 14. Режим вращающегося магнита с частотой fi/!6. Описанный в
гл. V вращающийся магнит претерпевает субгармонический каскад. Спектр
Фурье (а) и сечение Пуанкаре (б) плоскостью (х, х) получены для предель-
предельного цикла после четырех субгармонических бифуркаций. Форма спектра и
разбиение сечения Пуанкаре на шестнадцать групп точек соответствуют пред-
предсказаниям теории.
Из работы В. Крокетта и К. Пуату.

Субгармонический каскад
243
а.
Рис. VIII. 15. Исчезновение частоты fi/16 в обратном каскаде, а — пики, со-
соответствующие нечетным гармоникам частоты fi/16, поглощены шумом и не
видны в спектре Фурье, но субгармоники частоты /4/8 еще отчетливо видны;
а —точки сечения Пуанкаре "разделены на восемь групп. В каждой из групп
точки уже не разбиты на пары.
Из работы В. Крокетта и К. Пуату.
16*

244
Глава VIII
Рис. VIII. 16. Исчезновение частоты, fi/8 в обратном каскаде, а — спектр, на-
напоминающий спектр на рис. VIII. 15, но без пиков с частотами, кратными /\/8;
б —сечение Пуанкаре состоит лишь из четырех дуг кривых, длина которых
заметно увеличилась.
Из работы В. Крокетта и К. Пуату.

Субгармонический каскад 245>
VIII. 4.4. Универсальная последовательность: реакция Б Ж
Реакция БЖ в открытом реакторе обладает последователь-
последовательностью периодических режимов с удвоением периода на каждой
ступени каскада бифуркаций — так же, как в конвекции РБ и
в случае вращающегося магнита. Реально наблюдаются не-
несколько первых бифуркаций каскада — режимы с периодом Т,,
2Т, 47, 8Т и т. д. Причина обрезания каскада чисто экспери-
экспериментальная: управляющим параметром в этом примере являет-
является величина, обратная среднему времени пребывания реагентов»
в реакторе, которое можно изменять, варьируя скорость потока
на входе с помощью питательных насосов. Но стабилизировать,
скорость потока-(по крайней мере на протяжении длительного
интервала времени) удается на уровне не выше 0,5—1 %. Зада-
Задавая значение универсальной постоянной б геометрической про-
прогрессии, мы можем определить, как далеко нам удастся продви-
продвигаться в наблюдении режимов с периодами больше 87\
Помимо субгармонического каскада, более наглядно иллю-
иллюстрируемого другими экспериментами, реакция БЖ позволяет-
продемонстрировать весьма интересный аспект теории. Весь на-
набор наблюдаемых режимов представлен в табл. VIII. 3 в ис-
использованных ранее обозначениях. Сравнивая табл. VIII. 2 и
VIII. 3, мы идентифицируем несколько первых элементов уни-
универсальной последовательности. Наблюдаются даже режимы
с периодом больше 6. Хотя весьма вероятно, что другие перио-
периодические режимы также присутствуют, но не детектируемы; так
как их области существования на оси управляющего параметра
Таблица VIII. 3
Период Последовательность точек
см
а
Л
Е-
а S
— 7ц
3 й
51
3 ч
? 5
о
1
2
4
8
10
6
5
3
6
9
5
4
8
0
0—1
2—0—3—1
2—6—0—4—3—7—5— 1
2—8—6—0—4—3—9—5—7— 1
2—0-4-3-5-1
2—0—4—3—1
2—0—1
2—5—3—0—4—1
2—8-5-3—0—6—4-7-1
2-3-0—4—1
2—3-0—1
2-6—3—7—4—0—5— 1
—
П
плп
плппплп
плппплплп
ПЛПП11
плпп
пл
пллпл
пллплппл
пллп
плл
плллплл

246
Глава VIII
¦слишком узки, можно сказать, что эти режимы неустойчивы от-
относительно экспериментальных возмущений. Аналогичным обра-
образом можно интерпретировать отсутствие в табл. VIII. 2 и VIII. 3
некоторых элементов, и это не должно нас интересовать.
Рассмотрим табл. VIII. 3 более подробно. На протяжении
каждого эксперимента мы записываем временную вариацию по-
потенциала электрода, обладающего специфической чувствитель-
Рис. VIII. 17. Периодические режимы в реакции Белоусова — Жаботинского.
.Для идентификации нескольких периодических режимов, соответствующих
различным значениям потока реакционной смеси, использовался сигнал элек-
электрода, обладающего селективной чувствительностью к ионам Вг~. Эти сиг-
сигналы (выборка из сигналов, полученных после субгармонического каскада)
описывают движение на аттракторах, принадлежащих универсальному кас-
каскаду, представленному на рис. VIII. 3. Точки над сигналами указывают на-
начало и конец периодов.
Из работы Р. Симой, А. Вольфа и Г. Суинни.
костью к иону Вг~. Это позволяет нам проследить за ходом ре-
реакции, измеряемым логарифмом концентрации иона. Варьируя
среднее время пребывания одного из реагентов в активной зоне
реактора и роддерживая все остальные параметры (например,
концентрации реагентов в резервуарах, откуда они поступают
в реактор, температуру реактора) на постоянном уровне, мы
б
различные "бжкмы, кногдз
иодическ
иногда непериодические. На рис. VIII. 17 видно, что сигналы
записаны от нескольких периодических режимов1). Как можно
воспользоваться этой информацией для идентификации типа ат-
аттрактора, который мы наблюдаем?
') Обращаем внимание на сходство между этими сигналами и сигналами,
представленными на рис. VIII. 13 и соответствующими конвекции РБ.

Субгармонический каскад
24Г
Для ответа на этот вопрос читателю следует иметь в виду>
что экспериментатор проходит тот же путь, какой выпадает тео-
теоретику, но в противоположном направлении! Теоретик начинает
с функции, определяющей последовательные итерации. Экспе-
Экспериментатор сначала идентифицирует итерации по измерениям «
надеется затем реконструировать функцию, задающую итера-
итерации (или по крайней мере ее график), которая является «не-
«неизвестной» в задаче.
X(t+53s)
X(ti)
Рис. VIII. 18. Апериодический аттрактор. Форма аттракторов в пространстве
X(t), Х(< + т), X(t + 2x) с т = 53 с восстановлена по сигналу X(t). Изобра-
Изображена проекция аттрактора на плоскость X(t), X(t-\-x). Сечение Пуанкаре
восстановленного аттрактора плоскостью, перпендикулярной плоскости рисун-
рисунка, проведено вдоль штриховой прямой.
Из работы Р. Симой, А. Вольфа и Г. Суинни.
Если измерена толькр одна из динамических переменных, то
восстановить аттрактор в исходном фазовом пространстве не
представляется возможным. Но метод, описанный в конце
гл. IV, позволяет построить проекцию аттрактора в трехмерном
фазовом пространстве, если в качестве координат выбрать зна-
значение сигнала в момент времени t и в два более поздних
момента времени t -\- х и ' -j- 2т. Зятем мы находим точки пере-
пересечения траектории с плоскостью, например с плоскостью, пер-
перпендикулярной плоскости рис. VIII. 18 (след пересечения пока-
показан штриховой линией). Мы видим, что точки пересечния рас-
распределены отнюдь не случайно, а расположены на одной кривой
(почти на прямой). Это признак сильной диссипации. При та-
таких условиях мы можем построить график зависимости абсцис-
абсциссы точки на кривой от абсциссы предшествующей точки и

¦248
Глава VIII
получить отображение первого возвращения: график Xk+i как
функции Xk. Если наши предположения верны, то следует ожи-
ожидать, что множество точек распределится вдоль некоторой кри-
кривой. Эта кривая должна быть графиком той функции, которая
задает итерации. Именно так и происходит, в чем нас убеждает
рис. VIII. 19, а: мы получаем кривую, а это свидетельствует
Ряс. V11I. 19. Отображение первого возвращении, а — после того как построе-
построено сечение Пуанкаре аттрактора, динамика может быть исследована путем
построения графика зависимости координаты точки Xp.+i от координаты пред-
предшествующей точки Xk. Для экспериментатора важно восстановить по этим
данным график отображения первого возвращения. Как видно из рисунка а,
мы получаем кривую, а не набор отдельных точек и построеипап кривая
имеет экстремум; б — плавно деформируя кривую, построенную на рис. а, мы
наблюдаем переход от апериодического аттрактора к соседнему периодиче-
периодическому аттрактору с периодом 6.
Из работы Р. Симой, А. Вольфа и Г. Суинни.
о том, что дисперсия на плоскости (xk, xk+\) очень мала. В ча-
частности, заметим, что эта кривая не монотонна: она имеет мак-
максимум («горб»), как используемая в рассматриваемой теории
квадратичная функция. На этой стадии сравнение с теорией са-
самоочевидно. Медленно варьируя управляющий параметр, мы
можем постепенно изменять форму кривой и, следовательно, по-
последовательность режимов, одни из которых хаотические, дру-
ГНР ПРШТПГТииРГЧГ ITP t-Гя ПНР \7TTT 1 Q ft Пт/а-зопп т/птг птпплнтттг
- — _ ?. г-1— - --— I4" ч л л л. л \st \j axwllu^uiiv, UUU Г1Х V-^/ иЦ11и1>
ная кривая, представленная на рис. VIII. 19, о, порождает пер-
первый аттрактор с периодом 6 универсальной последователькости,
идентифицируемый как аттрактор 2-0-4-3-5-!, или ПЛППП.

Субгармонический каскад 249*
ЛИТЕРАТУРА
Collet P., Eckmann J. P., Iterated Maps on the Interval as Dynamical Systems.
Birkhauser, Boston A980).
Croquette V., Determinisme et chaos, Pour la Science, 62, 62 A982).
Feigenbaum M. J., Quantitative universality for a class of non-linear transfor-
transformations, Journal of Statistical Physics, 19, 25 A978).
Grossmann $., Thomae S., Invariant distributions and stationary correlation
functions of one-dimensional discrete processes, Zeitschrift fur Naturfors-
chung, A32, 1353 A977).
Libchaber A., Fauve S., Laroche C, Two-parameter study of the routes to»
chaos, Physica, 7D, 73 A983).
May R. M., Simple mathematical models with very complicated dynamics, Na-
Nature, 261, 459 A976).
Metropolis M., Stein M. L, Stein P. R., On finite limit sets for transformations,
of the unt interval, Journal of Combinatorial Theory, A15, 25 A973).
Simoyi R. H., Wolf A., Swinney H. L., One-dimensional dynamics in a multi-
component chemical reaction, Physical Review Letters, 49, 245 A982).
Tresser C, Coullet P., Iterations d'endomorphisme et groupe de renormalisation,.
Compt. Rend, de FAcademie des Sciences de Paris, A287, 577 A978).
Derrida В., Gervois A., Pomeau Y., Iteration of endomorphisms on the real axis
and representation of numbers, Annales de l'lnstitut Henri Poincare, 29,,
305 A978).
Derrida В., Gervois A., Pomeau Y., Universal metric properties of bifurcations,
of endomorphisms, Journal of Physics, A12, 269 A979).

ГЛАВА IX
ПЕРЕМЕЖАЕМОСТЬ
IX. 1. ВВЕДЕНИЕ
Во введении ко второй части этой книги мы уже охарактери-
охарактеризовали перемежаемость как один из типичных маршрутов пере-
перехода от периодического состояния к хаосу. В этой главе мы под-
подкрепим наше утверждение как теоретическими аргументами, так
и анализом типичных и тщательно выбранных экспериментов.
В данном введении мы впервые попытаемся объяснить, что
кроется за термином «перемежаемость». Затем мы кратко рас-
рассмотрим содержание последующих разделов.
Строго говоря, перемежаемость не имеет канонического оп-
определения. Мы называем сигнал перемежающимся, если он под-
подвержен резким вариациям большой амплитуды. Под такое
•несколько расплывчатое определение можно подвести много слу-
случайных явлений природы, не столь легко поддающихся тради-
традиционному статистическому описанию в терминах распределений
вероятности, средних значений (математических ожиданий),
дисперсий и т. д. Приведем теоретический пример такой ситуа-
ситуации. Предположим, что нам необходимо выбрать вещественную
случайную величину х с распределением вероятности Р(х) =
= A + х2)~1/2. В элементарной теории вероятностей такое рас-
распределение недопустимо, поскольку оно ненормируемо: интеграл
P(x)dx, который выражает вероятность того, что х прини-
— оо
мает какое-нибудь значение и поэтому должен быть равен еди-
единице, в действительности логарифмически расходится при боль-
больших \х\. Это означает, что гистограмма значений х, взятых из
конечной выборки (хи хг, ..., xN) объемом N, сильно растянута
и, если ее нормировать, стремится к нулю при любом значении
х. В отличие от этого гистограмма нормируемого распределения
вероятности Р0(х) (такого, что интеграл \ P0(x)dx сходится)
*» —оо '
стремится к Ро(х) при каждом значении х, если число N выбо-
выборок стремится к бесконечнЬсти. При нормируемом распределе-
распределении ненормированная гистограмма возрастает в среднем как N
при больших N [в интервале (х — (Дх/2). х + (Ах/2)) оказы-

Перемежаемость 25В
вается примерно Р0(х)Ах N выбранных значений х]. В случае
же «распределения» A + х2)~1/2 ненормированная гистограмма
растет только как N/\n N. Причина различия состоит в том, что
при возрастании N мы выбираем все большие значения х с та-
таким весом, который достаточен для непрерывного уменьшения:
относительного веса любого конечного значения х. На этом ос-
основано одно из возможных определений перемежаемости: слу-
случайная величина х называется перемежающейся, если относи-
относительный вес больших флуктуации непрерывно возрастает для
статистических выборок возрастающего объема. На практике
мы не будем пользоваться этим формальным математическим:
определением.
Многочисленные примеры перемежающихся процессов мы
находим в природе и физике. В частности, в гидродинамике
перемежаемость возникает в нескольких классах эксперимен-
экспериментальных явлений. Если мы возмутим быстрое течение (с боль-
большим числом Рсйпольдса), поместив в пего пластину, парал-
параллельную среднему направлению течения, то в окрестности;
пластины образуется пограничный слой. Такой турбулентный по-
пограничный слой, если его усреднить по времени, имеет четкую-
пространственную границу. Но по не понятным до конца причи-
причинам эта граница в отдельные редкие интервалы времени испы-
испытывает очень большие мгновенные смещения. Соответствующие
флуктуации в поле скоростей становятся все более перемежаю-
перемежающимися, если мы производим измерения на все больших расстоя-
расстояниях от пограничного слоя. Мы можем также упомянуть мелко-
мелкомасштабную перемежаемость в полностью развитой турбулент-
турбулентности—явлении, объяснение которого все еще остается спорным.
Переходные течения в трубах (т. е. течения с числами Рей-
нольдса, точно соответствующими экспериментальной точке пе-
перехода между ламинарным и турбулентным режимами) также
имеют перемежающуюся структуру: турбулентность имеет тен-
тенденцию сосредоточиваться в зонах пространства с четко выра-
выраженной границей, как показал Рейнольде более ста лет назад.
Вполне возможно (хотя и не абсолютно достоверно), что
в основе всех упомянутых нами явлений перемежаемости в гид-
гидродинамике лежит пространственная структура явлений: «боль-
«большие флуктуации», о которых идет речь, локализованы в про-
пространстве и во времени. Но цель нашей книги состоит в описа-
описании главным образом динамических явлений, в которых про-
пространственная структура не играет важной роли: описание
пространственной структуры мы свели к описанию амплитуд не-
небольшого числа четко выраженных мод. Было показано (и тео-
теоретически, и экспериментально), что в динамических системах
с небольшим числом степеней свободы при переходе от

252 Глава IX
периодического') к хаотическому (или квазипериодическому)
режиму может существовать временная перемежаемость. Даже
при столь ограничительных условиях существует несколько, а
именно три перехода через перемежаемость, каждый со своими
отличительными особенностями.
Опишем кратко феноменологию, общую для всех трех типов.
Когда значение г управляющего параметра меньше некоторого
критического значения г,-, рассматриваемая динамическая си-
система (будь то экспериментальная система типа систем РБ или
БЖ или теоретическая типа модели Лоренца, отображения ок-
окружности и пространства более высокой размерности на себя)
имеет предельный цикл (или в случае отображений — устойчи-
устойчивый дискретный цикл). Система совершает регулярные колеба-
колебания и устойчива относительно малых возмущений. При г, лишь
незначительно большем п (порога перемежаемости), мы имеем
перемежающийся динамический режим. Временной сигнал со-
состоит из колебаний, которые кажутся регулярными и напоми-
напоминают устойчивый колебательный режим при г < г,-. Но на этот
раз колебания время от времени прерываются «аномальными»
флуктуациями, амплитуда и направление остаются примерно
одними и теми же от флуктуации к флуктуации » слабо завися-
зависящими от г. Мы называем этот переход перемежающимся, по-
поскольку, когда г приближается к^в перемежающейся области
(г,!^, г,), флуктуации становятся все более редкими и полностью
исчезают при r.^ri. Подчеркнем, что в точке перехода к нулю
стремится не амплитуда и не частота исключительных флук-
флуктуации, а только их средняя частота.
Теория перемежающихся переходов состоит из двух частей.
Первая часть (теория Флоке) занимается изучением линейной
неустойчивости предельного цикла, объясняющей «спонтанный»
рост флуктуации относительно режима, близкого к периодиче-
периодическому режиму. Вторая часть описывает процесс «реинъекции»,
или «реламинаризации», в ходе которого перемежающиеся
флуктуации затухают, уступая место новой фазе регулярных
колебаний. В основе классификации перемежаемости на типы I,
II и III лежат три типа линейных неустойчивостей периодиче-
периодических траекторий: пересечения единичной окружности мультипли-
') Можно представить себе переход через перемежаемость непосредствен-
непосредственно от стационарного состояния к турбулентному режиму. Например, такого
рода переход может происходить, если устойчивое и неустойчивое многообра-
многообразия неподвижной точки потока в фазовом пространстве двумерны. В модели
Лоренца такого произойти не может, поскольку размерность фазового про-
пространства равна только трем. Зтот тип перемежаемости не был исчерпываю-
исчерпывающим образом изучен ни экспериментально, ни теоретически, и мы не будем
рассматривать его здесь.

Перемежаемость 253
катерами Флоке в точке +1 (I тип), —1 (III тип) или в двух
комплексно-сопряженных собственных значениях (II тип). В сле-
следующих трех разделах мы дадим более полное теоретическое
описание каждого из этих трех типов и дополним его экспери-
экспериментальными примерами, подтверждающими существование пе-
перемежаемости I и III типов.
Пути мультипликаторов Флоке на комплексной плоскости за-
зависят только от линеаризации динамических уравнений относи-
относительно предельного цикла. Это приближение, линейное по ам-
амплитуде флуктуации, приводит к неконтролируемому росту
флуктуации. Однако в нашем чисто качественном обзоре явле-
явления перемежаемости мы описываем флуктуации как достигаю-
достигающие со временем конечного уровня. Следовательно, теория
требует анализа эффектов, которые по крайней мере слабо не-
нелинейны по амплитуде флуктуации. В случае II и III типов пере-
перемежаемость возможна лишь в том случае, если бифуркация
субкритическая, т. е. если нелинейные эффекты имеют тенден-
тенденцию к усилению неустойчивости. Но в случае перемежаемости
I типа мы можем не спрашивать, будет ли бифуркация супер-
суперкритической или субкритической, так как существует только
один тип бифуркации, которая (в определенном смысле) всегда
субкритическая (см. приложение А).
IX. 2. ПЕРЕМЕЖАЕМОСТЬ I ТИПА
IX. 2.1. Общие теоретические соображения
В этом случае периодическая траектория, устойчивая при
г ^ rt, теряет устойчивость (и фактически исчезает) при г = г,,
так как собственное значение матрицы Флоке выходит из еди-
единичной окружности через точку +1. Наш анализ подразде-
подразделяется на две части, о которых упоминалось выше. Сначала мы
рассмотрим явления в окрестности периодической траектории,
теряющей устойчивость. Для этого мы воспользуемся локаль-
локальным анализом в духе теории Ландау с учетом нелинейных эф-
эффектов в членах низшего порядка ряда Тейлора по амплитуде
флуктуации. Несмотря на сравнительно элементарный характер
такого подхода, он все же позволяет высказать ряд количествен-
количественных предсказаний, которые впоследствии подлежат сравнению
с результатами численного моделирования системы Лоренца и
с данными экспериментов с реакцией БЖ.
На второй стадии нашего анализа мы обсудим определен-
определенный выше процесс реинъекции, или реламинаризации. Этот
процесс зависит от глобальной структуры потока в фазовом
пространстве в следующем смысле; если траектория покидает

254 Глава IX 1
окрестность потерявшего устойчивость предельного цикла, она
должна «обследовать» части фазового пространства, находя-
находящиеся на конечном расстоянии от предельного цикла, и тем са-
самым обрести чувствительность к глобальной структуре потока.
В частности, мы покажем, что реламинаризация допускает очень-
простое объяснение для потоков на торе Г2. Как известно, на Т2
возможны только периодические или квазипериодические ре-
режимы. Отсюда следует, что для некоторых переходов между
двумя регулярными (нехаотическими) режимами, например для
переходов от периодического режима к квазипериодическому,,
может наблюдаться перемежаемость I типа. Как показывает
проводимое ниже обсуждение модели Лоренца, перемежаемость
I типа может возникать при переходе от периодического режима
к хаотическому. Все эти соображения мы рассмотрим более под-
подробно в разделе, посвященном реламинаризации.
IX. 2.2. Локальный анализ
Собственному значению матрицы Флоке, пересекающему
единичную окружность, вообще говоря, соответствует единич-
единичный собственный вектор. Именно так, как мы увидим-
в разд. IX. 2.5, обстоит дело в случае модели Лоренца. Опреде-
Определим на плоскости сечения Пуанкаре координату и, откладывае-
откладываемую по направлению собственного вектора. Следовательно, ум-
умножение на матрицу Флоке сводится к простому умножению
координаты и на собственное значение Я,(г):
и' = 1(г)и. (IX. 1>
Пересечение единичной окружности в точке +1 при г = rt озна-
означает, что А (г,) = 1 и (dX/dr) \n Ф 0. Чтобы получить представле-
представление о том, как трансформируется отображение Пуанкаре, когда
параметр г изменяется в окрестности п, воспользуемся упро-
упрощающим предположением (которое будет обосновано в дальней-
дальнейшем) о том, что выражение (IX. 1) при г = rt есть начальный,
отрезок ряда Тейлора функции и!(и,г) в окрестности и=0 и
г == п. Тогда для объяснения перемежаемости I типа достаточно
учесть члены старших порядков.
Предельный цикл для динамической системы мы обнаружи-
обнаруживаем как неподвижную точку отображения Пуанкаре. Вблизи
неподвижных точек при г < г,- график функции и'(и) почти ка-
касается диагонали (графика тождественного отображения), так
как (du!jdu) \r. = к (rt) -= 1. Таким образом, мы находимся в си-
ситуации, схематически изображенной на рис. IX. \,а. В точке би-
бифуркации (г — п) кривая и'(и) касается диагонали, так как

Перемежаемость
255
{du'/du)—\ в неподвижной точке (рис. IX. 1.6I). Переход от
рис. IX. 1, а к рис. IX. 1,6 осуществляется сдвигом кривой «'(и)
вверх. При дальнейшем увеличении параметра г кривая про-
продолжает подниматься, и между кривой и диагональю образуется
узкий канал (рис. IX. 1,в).
и±
и
Рис. IX. 1. График отображения и-*-и'(и) вблизи его неподвижной точки.
Когда угловой коэффициент кривой и'(и) на рис. б становится равным еди-
единице, график отображения касается диагонали. При изменении управляющего
параметра г происходит непрерывный переход от а к в. На рис. а отображе-
отображение и-* и'(и) имеет две неподвижные точки и±, которые исчезают на рис. в.
Однопараметрическое семейство кривых вблизи контакта
представимо в следующей общей для и' форме:
и' = ы + е + «2. (IX. 2)
Коэффициент при и2 (втором члене разложения величины и'
в ряд Тейлора относительно и = О и r = rt) при подходящем
выборе масштаба переменной и можно выбрать равным еди-
единице. Параметр е, пропорциональный г — rl, является управ-
управляющим параметром, варьируя который, мы осуществляем пере-
переход от рис. IX. 1,с к рис. IX. 1,6.
d) Эта бифуркация возникает при слиянии двух неподвижных точек
(одной устойчивой и другой неустойчивой) и называется бифуркацией седло-
узел. Является ли она' суперкритической или субкритической, безразлично,
поскольку такая бифуркация сопровождается исчезновением всех решений
как устойчивых, так и неустойчивых (см. приложение А)-

256
Глава IX
Ситуация при е=0 изображена на рис. IX. 1,6: уравнение
г/(и)=ы имеет двойной корень при ы=0 с тангенсом угла
наклона касательной (du'/du) |u=o^= +1. При гФО неподвиж-
неподвижные точки уравнения (IX. 2) являются решениями уравнения
и'(и)=и, т. е. м± = ±(—гI12, и существуют только при усло-
условии, если е < 0. Их собственные значения Флоке равны
(du'/du) | и± = 1 ± 2 (—еI/2; поэтому решение ы_ устойчиво,
а решение и+ неустойчиво. В этом нетрудно убедиться, если вос-
воспользоваться графическим построением для итераций преобразо-
преобразования и-*-и'(и) (рис. IX.2).
и
Рис. IX. 2. Итерации отображения и-*-и'(и) для случая, когда существуют
две неподвижные точки и±. Точка и_ локально устойчива: итерации, начи-
начинающиеся вблизи точки и_, сходятся к ней. Точка и+ неустойчива: итерации,
начинающиеся вблизи точки и+, удаляются от нее.
Устойчивая неподвижная точка и~ служит аттрактором для
начальных условий и < и+, а неподвижная точка и+ неустой-
неустойчива. Итерации, начинающиеся си>«+, быстро расходятся как
(м<0)J" при большом п и ы°, близком к начальному условию.
Графическое представление перехода от режима с е<0 к ре-
режиму с е>0 также показывает, что обрыв ряда Тейлора для
и'(и, г) на члене первого порядка по (г—г,) и второго порядка
по и дает правильное описание окрестности перехода: кривизна
кривой и'(и), тангенс угла наклона касательной, близкий к +1
в области касания, и подъем кривой представлены верно.
Мы видели, что при малом положительном б между диаго-
диагональю и кривой и'(и) образуется узкий канал: Это приводит
к двум важным следствиям.

Перемежаемость
257
1) При е>0 (r^rj) в рассматриваемой области не суще-
существует более неподвижной точки отображения первого возвра-
возвращения. Это ясно из того, что неподвижные точки представимы
в виде«± = ±(—еI/2.
2) Итерации, начинающиеся с отрицательного значения "и,
систематически дрейфуют в область и >0 (рис. IX. 3): так как
е и е2 положительны, справедливо неравенство и' = и + е -f-
+ и2 > и.
г»'
О
и
Рис. IX. 3. Итерации отображения и-> и'= и-\-ъ-\-иг при е > 0. В отличие
от отображения на рис. IX. 2 (е<0) это отображение не имеет ни одной
неподвижной точки. При малых положительных е итерации, начинающиеся
при отрицательных значениях и, проводят много времени в узком коридоре,
отделяющем график отображения и' от графика тождественного отображения.
Но если параметр е очень мал, то последовательные итера-
итерации накапливаются в самой узкой части канала. Это возвра-
возвращает нас к вопросу о перемежаемости. Область канала (точнее,
значений и, которые действительно наблюдаемы) очень близка
к неподвижным точкам, существующим при е < 0. Следова-
Следовательно, если мы обратимся снова к непрерывному временному
сигналу потока, соответствующего прохождению через канал для
отображения Пуанкаре, то обнаружим временную зависимость,
во многом аналогичную временной зависимости устойчивых ко-
колебаний, происходящих при е < 0. Но колебания более не ус-
устойчивы, так как отображение первого возвращения и~+и'(и, г)
не имеет неподвижной точки вблизи нуля и поэтому не суще-
существует периодического решения, устойчивого или неустойчивого,
уравнений движения вблизи предельного цикла.
17 П. Берже и др.

258 Глава IX
Это первое теоретическое описание перемежающегося пере-
перехода оставляет открытыми несколько вопросов.
1) Существует ли простая динамическая модель, позволяю-
позволяющая воспроизвести перемежающийся переход только что опи-
описанного типа? В разд. IX. 2.5 будет показано, что в модели Ло-
Лоренца такой переход существует.
2) Позволяет ли теория высказывать количественные пред-
предсказания, сравнимые с экспериментом?
3) Если итерации прошли сквозь канал и траектория вышла
из почти регулярного колебательного режима, то как она мо-
может войти снова в канал слева, чтобы начать новую фазу коле-
колебаний?
Рассмотрим два последних вопроса. v
IX, 2.3. Количественные предсказания модели
В нашей теоретической модели исключение физических пара-
параметров прнводш к универсальной форме преобразования «-*¦
-+и'(и):
и = и -J- е -+- и ,
справедливой в окрестности и = 0. Количественные предсказа-
предсказания, вытекающие из этого описания, принимают форму законов
подобия, например, управляющих средней продолжительностью
ламинарных фаз вблизи 8 = 0. Чтобы найти эти законы, заме-
заметим следующее: если величина и' близка к и, то разность и' — и
можно заменить производной du/dk. При этом индекс итерации
k надлежит рассматривать как непрерывную переменную, что
законно, если разность и' — и мала. Таким образом, разностное
уравнение мы заменяем дифференциальным уравнением
Это уравнение имеет общее решение
u(k) = BWtgWi*{k-ka)), (IX. 4)
где ko (приближенно) фиксирует шаг, на котором итерация про-
проходит наиболее узкую часть канала. Для удобства записи поло-
положим «о—О. Функция u(k) расходится при k = ±(п/2)е~1/2.
Смысл этой расходимости состоит в том, что, когда k достигает
значений порядка е-'/2, разность и' — и перестает быть малой
величиной, а поэтому разностное уравнение (IX. 2) не может
быть заменено дифференциальным уравнением (IX. 3). Это сви-
свидетельствует помимо прочего о том, что число итераций, необ-
необходимое для прохождения через канал, составляет величину по-

Перемежаемость
259
рядка е-'/2, так как именно такая величина соответствует ин-
интервалу значений между двумя последовательными особыми
точками решения (IX. 4). Данная оценка является первым зако-
законом подобия: средняя продолжительность ламинарных фаз рас-
расходится как е~1/2 ~ \г— г;}-1'2 по мере приближения к порогу.
Когда мы имеем переход через перемежаемость между пе-
периодическим и турбулентным режимом, число Ляпунова у (г),
характеризующее уровень неустойчивости турбулентных траек-
траекторий, становится величиной такого же порядка, как величина,
обратная времени корреляции сигнала с собой. Предполагая,
(~ ? ' "*) X
Рис. XI. 4. Распределение длин ламинарных фаз в режиме перемежаемости
типа I. На рисунке представлен лишь качественный характер распределения,
так как вид кривой зависит от деталей процесса реламинаризации. Верхняя
граница порядка г~1/2 вблизи 8 = 0+ характерна для перемежаемости типа I
и соответствует максимальному времени прохождения коридора на рис. IX. 3.
что корреляция почти полностью исчезает во время турбулент-
турбулентных всплесков, мы заключаем, что время корреляции составляет
величину порядка е~1/2, как среднее время прохождения канала,
и что обратная ему величина (число Ляпунова) удовлетворяет
закону Y(e)s->-(H-'~ e1/2. Этот закон действительно подтверждает-
подтверждается моделью Лоренца (разд. IX. 2.5).
Другой интересной величиной является статистическое рас-
распределение продолжительности х ламинарных фаз, т. е. Р(х,е).
В выборке из N ламинарных фаз (N — целое число) существует
С х
N \ йт'и (т', е) фаз продолжительностью менее т. Мы уже знаем,
*j О
что средняя продолжительность ламинарной фазы равна
п. ОО
\ dxP(x, е)т ~ е~1/2. При фиксированном s продолжительность
Jo
ламинарных фаз ограничена сверху величиной порядка г~^2, и
чем ближе мы подходим к порогу, тем меньше флуктуирует
17*

260 Глава IX
продолжительность ламинарных фаз. Эти соображения позво-
позволяют нам прийти к качественным заключениям относительно
формы функции Р(х, е) в перемежающемся режиме (рис. IX. 4).
Точная форма функции Р(т, е) зависит от деталей рассмат-
рассматриваемой задачи, так как флуктуации параметра т отражают
флуктуации процесса реинжекции в* канал. Распределение
Р{х, е) априори более легко измеримо, чем упомянутые выше
законы подобия, требующие точной локализации порога е = 0
и, следовательно, серии экспериментов с очень близкими значе-
значениями управляющего параметра. Заметим также, что в случае
перемежаемости других типов (II и III) распределение продол-
. жительности ламинарных фаз подчиняется закону, весьма от-
отличному от того, которому подчиняется распределение в случае
перемежаемости I типа. Этот другой закон распределения имеет
максимум при малых временах и убывает алгебраически при
больших временах.
IX. 2.4. Реламинаризация
До сих пор мы не рассматривали, как ведут себя переме-
перемежающиеся решения вне области канала. Этот вопрос связан
с реламинаризацией — процессом, позволяющим траектории вер-
вернуться в канал. Мы ограничимся качественными соображениями,
так как процесс реинжекции приводит к исследованию областей
фазового пространства, имеющих конечные размеры. Следова-
Следовательно, только топологический подход позволяет нам прийти
к заключениям, обладающим некоторой общностью.
Ниже мы опишем три возможных варианта реинжекции:
1) поток на торе; 2) преобразование пекаря (с незначительными
модификациями, позволяющими применять его к модели Ло-
Лоренца); 3) аттрактор Смейла.
Реламинаризация на юре
Напомним, что, когда мы рассматриваем поток на, торс Р,
преобразованием Пуанкаре является просто обратимое отобра-
отображение окружности в себя. Это отображение можно представить
в виде графика отображения полуоткрытого интервала [0, 1)
в [0, 1) при условии, что определяемая им непрерывная функ-
функция (¦¦-*-f(f3) строго монотонна (например, монотонно возрас-
возрастает) и точки 0 и 1 отождествлены. В прямоугольной системе
координат ня графике (рис, IX, 5) возникают кажущиеся раз-
разрывы, которые исчезают, если отождествить 0 и !. Рис. IX. 5
позволяет наглядно представить, как происходит переход с пе-
перемежаемостью I типа в случае диффеоморфизма окружности.

Перемежаемость
26!
Как показано на рис. IX. 6, график функции f касается диаго-
диагонали, а затем отрывается от нее. В этом случае процесс реин-
жекции протекает очень просто: итерации, выйдя из канала,
описывают круг и входят в канал с другой стороны. Это не
переход к турбулентности. Действительно, как мы уже знаем,
поток на Г2 может быть периодическим или квазипериодиче-
квазипериодическим, но не хаотическим, т. е. турбулентным. В перемежаемости
такого типа «турбулентные» всплески наступают приближенно
периодически и их период либо соизмерим, либо несоизмерим
1 9
Рис. IX. 5. Общий вид отображения первого возвращения для потока на Т*.
Сечение Пуанкаре имеет вид окружности, параметризованной интервалом
[A ! 1 ¦: (•"¦".-клест1; TOii'iv:.:;; ,.р:-ц;г-:и. Р.прыпм графика отображения в точку:
О, Оо и I —кажущиеся. Они обусловлены выбором представления для отобра-
отображения.
с периодом быстрого движения ка топе б зависимости от того,
является ли перемежающийся режим периодическим или квази-
лериодическим.
Когда канал закрыт, как на рис. IX. 6, а, существуют две не-
неподвижные точки отображения f; это соответствует затягиванию
частоты, или синхронизации (см. гл. VII и приложение В).
В этом случае после n-кратного обхода тора по большой окруж-
окружности (параллели) траектория возвращается в исходную точку
на малой окружности. Знание отображения Пуанкаре не задает
однозначно значение п: число вращений определено лишь по
модулю S. В случае перемежаемости (рис. IX.6,в), предше-
ствующей синхронизации, на временном сигнале наблюдается
«проскальзывание фазы» между двумя «квазирегулярными» пе-
периодами колебаний. Это явление можно объяснить следующим

262
Глаза IX
образом. При прохождении через канал вращения по большой
и малой окружностям четко согласованы по фазе. Во времен-
временном сигнале это создает видимость регулярных колебаний толь-
только с одним периодом. Между двумя прохождениями канала
траектория совершает один дополнительный оборот по малой
1 в
О
1 в
Рис. IX. Ь. Переход с перемежаемостью для диффеоморфизма окружности.
На рис. а устойчивый 1-цикл сосуществует с неустойчивым 1-циклом. В пе-
переходной ситуации б остается лишь один 1-цикл, который исчезает на рис. в.
В возникающем режиме перемежаемости реламинаризация происходит тогда,
когда точка, выходящая из коридора справа, возвращается в коридор слева
после однократного обхода окружности.
окружности. Это означает, что один из осцилляторов сдвигается
по фазе на один период относительно другого, отсюда и про-
проскальзывание фазы на временном сигнале. Проскальзывание
фазы является признаком аномальной «флуктуации» переме-
перемежающегося режима. Может случиться далее так. что для ка-
какой-нибудь динамической переменной проскальзывание фазы
служит единственным, проявлением аномальной флуктуации, не
сопровождающейся сколько-нибудь заметным изменением ампли-
амплитуды колебаний. Так происходит, например, в случае релакса-
релаксационного осциллятора.

Перемежаемость 263
Переход через перемежаемость и преобразование пекаря
В этом разделе мы объясним процесс реламинаризации, воз-
возникающий при преобразовании пекаря. Как чбудет показано
ниже, сказанное с незначительными видоизменениями приме-
применимо к переходу через перемежаемость в модели Лоренца. Сна-
Сначала мы приведем несколько результатов относительно отобра-
отображения сдвига Бернулли и, тесно связанного с ним преобразо-
преобразования пекаря. Затем покажем, что, несмотря на кажущиеся
разрывы, преобразование пекаря может быть отображением пер-
первого возвращения непрерывного потока. И в заключение объяс-
объясним, как может произойти переход через перемежаемость от
периодического режима к хаотическому и, в частности, как про-
происходит реламинаризация.
Преобразованием полуоткрытого интервала [0, 1) в себя
с характерной ЧЗНУ является сдвиг Бернулли х-*-{2х}, где
{2х} есть по определению дробная часть числа 2 (например,
{2- C/5)}= 1/5). При каждой итерации преобразования все
расстояния умножаются на 2. Таким образом, даже первоначаль-
первоначально бесконечно малое расстояние возрастает в ходе итераций в
геометрической прогрессии. Сдвиг Бернулли не может быть ото-
отображением первого возвращения по двум причинам: оно не яв-
является однозначно обратимым (например, 2- A/4)} = {2- C/4)} =
= 1/2) и непрерывным ({2х}— *- О, а {2л;} >- IV
' ' V V V ' х-УП/2+0) ' 1 ' х-»A/2-0) )
На первый взгляд кажется, что разрывность отображения
несовместима с непрерывностью уравнений движения (таких,
как уравнения Лоренца). В действительности это не так. Не
вдаваясь в детали, можно утверждать, что, поскольку в мо-
модели Лоренца всегда существует неустойчивая неподвижная
точка (например, конвективное состояние (X, Y, Z) = @,0, 0)),
существует и множество начальных условий, приводящих при
больших временах к неустойчивой неподвижной точке.
Такое множество, называемое устойчивым многообразием не-
неподвижной точки, образует поверхность') нулевой меры (нуле-
(нулевая мера означает, что вероятность случайного выбора началь-
начальных условий, при которых траектория достигает неподвижной
точки, чрезвычайно мала и попасть в точку можно, только спе-
специальным образом выбрав начальные условия). Если неустой-
неустойчивая неподвижная точка не принадлежит плоскости сечения
1) Эта поверхность называется устойчивым многообразием неподвижной
точки. У неустойчивой неподвижной точки, кроме того, имеется неустойчивое
многообразие (состоящее из всех начальных условий, из которых траектории
достигают неподвижную точку за отрицательное бесконечно большое время).
В отличие от неустойчивой точки устойчивая точка имеет только устойчивые
многообразия.

-'-I Глава IX
Пуанкаре, то пересечение (если оно существует) устойчивого
многообразия с плоскостью Пуанкаре содержит точки, ке имею-
имеющие образа при отображении первого возвращения. Именно
вдоль кривой пересечения отображение Пуанкаре может быть
разрывным. Примером такого поведения может служить пло-
плоское сечение Z = г— 1 в модели Лоренца.
Итак, мы хотим построить обратимое, но разрывное отобра-
отображение, исходя из сдвига Бернулли. При сдвиге Бернулли у
каждой точки имеются ровно два прообраза, т. е. два числа х0
и д-1, такие, что
О ^ хо ^ ~2 • xi = хо + Y •
{2х0} = {2*,}.
Чтобы сделать это преобразование обратимым, необходимо
ввести еще одну координату у, позволяющую различать два
прообраза точки. Определим преобразование квадрата [О, 1]Х
Х[0, 1] в себя, называемое преобразованием пекаря, как
(*, у)-*Ц2х], у'(у, х)),
где
Г у/2, если 0 < х < ^ <
У (У, х) = )
((у+1)/2, если 1/2<*<1.
tit,'
дх
9
0
1
~2
Это обратимое преобразование сохраняет площади, так как яко-
якобиан его равен единице:
дх
дх'
ду
Заметим, что по оси х мы сохранили сдвиг Бернулли х'={2х}.
Для большей наглядности мы нарисовали голову кошки («кош-
(«кошка Арнольда») на единичном квадрате плоскости (х, у) и на
его образе после разрезания пополам и растяжения под дей-
действием преобразования пекаря (рис. IX. 7). Растяжение вдоль
оси абсцисс отражает ЧЗНУ преобразования Бернулли.
Весьма простое обобщение предыдущей конструкции позво-
позволяет нам построить обратимое и разрывное (двумерное) ото-
отображение, исходя из любого двукратного разрывного отобра-
отображения x-+f(x) интервала [0, 1] в себя, которое монотонно воз-
возрастает. Другое обобщение приводит к отображению, которое
сокращает площади, что отражает диссипативный характер рас-
рассматриваемой динамической системы. Вследствие этого отобра-

Перемежаемость
жение имеет аттрактор, наделенный слоистой структурой, в то
время как изображенное на рис. IX. 7 преобразование пекаря
не имеет такого аттрактора, поскольку оно сохраняет площади.
Например, вместо отображения у, определяемого по правилу
у-*-у/2 и у-*(у-\- 1)/2, мы могли бы воспользоваться отобра-
отображением у-*Р({//2) и у-+${у + 1)/2, где 0< р < 1. С каждой
итерацщей площадь сокращается в 1/р (Р < 1) раз. Любое ото-
отображение f, удовлетворяющее выдвинутым выше условиям
Рис. IX. 7. Отображение пекаря. Действие преобразования пекаря можно на-
наглядно представить себе, прослеживая преобразования какой-нибудь фигурки,
нарисованной на единичном квадрате (в данном случае головы кошки —при-
—пример, предложенный В. И. Арнольдом). Смысл названия отображения пекаря
ясен из следующего описания. Квадрат из теста а сжимают вдоль оси у и
растягивает вдоль оси х. Затем его разрезают пополам по вертикали и одну
':Оло-л':г\' тпдружоЮ" roBcnv другой, образуя мчдрат б. Объем тестя при
этой операции остается неизменным. Разрывное отображение пекаря сохра-
сохраняет площади: сжатие в 2 раза вдоль оси у в точности компенсируется
растяжением в 2 раза вдоль оси х.
(функции f монотонно возрастает, и у каждой точки имеются
два прообраза), может порождать переход с перемежаемостью,
аналогичный рассмотренному нами в случае отображения ок-
окружности, и аналогичное утверждение справедливо относительно
отображения (x,y)-^(f(x), y'(y,x)). На рис. IX.8 показано,
как изменяется f при переходе через порог перемежаемости.
Итерируя отображение, представленное на рис. IX. 8, е, мы
нндн.м, что процесс репнжекции (или реламинаризацпн) про-
происходит при пересечении разрыва отображения х-^}(х). По вы-
выходе из канала итерации возрастают до тех пор, пока они не
оказываются по другую сторону разрыва (обозначенного на
рис. IX. 8, с через л>;). За исключением особых случаев, итера-
итерации не попадают точно в точку при х = х0, а поэтому следую-
следующая итерация (в общем случае) смещает точку в область

лалых положительных оначенни х. хак как начало лоординат
является неустойчивой неподвижной точкой, итерации начинают
снова расти, в конце концов снова входят в канал и т. д. Заме-
Заметим, что в отличие от рассмотренной ранее ламинаризации на
Т2 в интересующем нас сейчас случае всегда остается (неустой-
(неустойчивая) неподвижная точка отображения, которая на рис. IX. 8
выбрана за начало координат. Наконец, упомянем о том, что
Рис. IX. 8. Переход с перемежаемостью типа I в преобразовании пекаря.
Тесто растягивается вдоль оси х. Разрыв (подлинный, а не кажущийся) в
точке Ха вводится при разрезании куска теста на две части.
между двумя «ламинарными фазами» траектория попадает в
неустойчивые области фазового пространства. В таких областях,
например в области х0 < х < 1 на рис. IX. 8, производная функ-
функции f больше единицы. Следовательно, флуктуации соответ-
соответствующего Бременноги сигнала существенно непредсказуемы,
хотя их средние характеристики не изменяются от одного тур-
турбулентного всплеска к другому, так как траектория блуждает
в одной и той же части пространства. Таким образом, "вполне
допустимо говорить о подлинно «турбулентном всплеске». На-
Например, это проявляется в рассматриваемой ниже модели Ло-
Лоренца.

¦ ¦-'ламинириллция в аучие ujтрактора
- этом разделе мы пштытаемсм ибьисшпь, как
лать обратимыми сдвиг Бернулли и аналогичное отображение,
добавляя по двум другим вещественным координатам отобра-
отображение, сокращающее площади. Это отображение (известное
топологам еще в 20—30-е годы XX столетия) позволило Смейлу
показать, что непрерывная динамическая система может обла-
обладать «устойчивой» ЧЗНУ (это означает, что ЧЗНУ характерна
не только для самой системы, но и для близких к ней систем).
В модели Смейла отображение первого возвращения по одной
из координат такое же, какое было выведено нами для отобра-
отображения, близкого к сдвигу Бернулли. Следовательно, если от-
отвлечься от второстепенных деталей, то это отображение по
существу сводится к сдвигу Бернулли, а поскольку сдвиг Бер-
Бернулли порождает перемежаемость, в модели Смейла, основан-
основанной на преобразовании пекаря, нет ничего принципиально но-
нового. Но интерпретация процесса реламинаризации отличается
от предыдущего случая, поскольку в случае отображения Смей-
Смейла нет разрыва в отображении первого отображения. Мы обсу-
обсудим кратко последний вопрос после того, как рассмотрим ат-
аттрактор Смейла.
Рассмотрим еще раз двукратное отображение x->f(x) ин-
интервала [0, 1] на себя, порождающее переход через перемежае-
перемежаемость, которая связана с исчезновением пары неподвижных то-
точек (схематически это исчезновение изображено на рис, IX, 9),
Но в отличие от предыдущего случая мы исключаем разрыв, вы-
выбирая в качестве х угловую переменную так, чтобы отожде-
сгвшь 0 и 1 (рис. IX. 9,«). Разрыв при таком выборе устра-
устраняется:
/(хо-О) = +1 и
Чтобы сделать отображение обратимым и непрерывным, мы до-
добавляем к фазовому пространству еще две переменные у и z
вместо одной переменной, как в предыдущем случае. Для коор-
координат у и 2 область определения отображения есть внутрен-
внутренность окружности С. Рассмотрим образ окружности при двух
значениях х — ха и хь, таких, что f(xa) = f(Xb). Образ отображе-
отображения, который требуется гшстриить, имеет вид двух небильшид
непересекающихся окружностей, расположенных диаметрально
противоположно внутри С (рис. IX.9,б). Одна из малых окруж-
окружностей Са есть образ окружности С при х = ха, другая окруж-
окружность Сь есть образ окружности С при х = Хь. Когда ха изме-
изменяется от 0 до :;а, а хь от х0 до 1, каждая из окружностей Са
и Сь поворачивается на угол я вдоль кривой Г, изображенной
на рис. IX. 9, б. Следовательно, когда х принимает значения от

д'.алые окружности :;;кже совершают лолньш
вая непрерывность отображения по у и г.
а
Рис. IX. 9. Действие преобразования Смейла на координаты, а — отображение
первого возвращения по угловой переменной х. Отображение необратимо:
когда х совершает однократный обход окружности (представленной здесь в
виде интервала [0, 1] с отождественными концами), образ j(x) точки х
дважды обходит окружность; б — преобразование координат у и z.
Круг С отображается либо па Са, либо на Сь в зависимости от того, чему
равен х: ха или хь (см. рис. а). Таким образом, глобальнее отображение
обратимо. Когда точка х '.бхолит окружность, кр;.гп С,, и Сь. остс,1.,усь диа-
диаметрально противоположными, совершают пол:;:=';"| обход окружности Г.
Мы можем также разложить это отображение, отправляясь
от «бублика», или «полного» тора Т2 (а не только его поверх-
поверхности). Полный тор есть фазовое пространство: он образуется
при обнесении диска, ограниченного окружностью С на пло-

[л, у), ли икрулнос! и при iiJMCHtniiii величины л. Умень-
Уменьшим объем тора, одновременно удвоив длину его большой ок-
окружности (параллели). Сложим затем тор в форме восьмерки
и вложим в исходный тор (рис. IX. 10). Эта конструкция иллю-
иллюстрирует возможное отображение Пуанкаре для четырехмер-
четырехмерного потока, сечение Пуанкаре которого порождает трехмерные
Р'с. SX. Hi. Схема отобрйжс-'мк <--:];"!ны-> ~- .?.".:>joo ге^я "Х'-л raicofp::"-4 г ; ¦ m>
Смейла. Шина растягивается по большому кругу и складывается в восьмерку.
Одна петля восьмерки укладывается поверх другой, после чего шину вкла-
вкладывают в первоначальную шину. Такое вложение возможно, так как сечение
и объем шины уменьшаются вследствие диссипации.
объекты. Она показывает также, что отображение «полного»
тора на себя может определить отображение первого возвра-
возвращения, поскольку оно возникает от последовательности непре-
непрерывных деформаций. Вопрос о том, является ли данное отобра-
отображение фазового пространства более или менее высокой пазмвр-
т-ссти на себя отображением первого возвращения, может быть
несьма нетривиальным. Следует заметить также, что такое ото-
отображение никогда не наблюдалось в физической системе, не-
несомненно, из-за его сложности.
Качественное описание перехода через перемежаемость в фа-
фазовом пространстве и процесса реламинаризации в рассматри-
рассматриваемом непрерывном случае отлично от приведенною выше опи-
описания для (разрывного) преобразования пекаря. Следовательно,

О О I П.Ш Т.гГ\Т'Г\Г\Г\еГ± i^ Т. Y IIQ ЛПППО ПЛ/iL UO П1ОП LI DUAPTL иОРРМПТПЫ М О li* -
рестность неподвижной точки, исчезающей при переходе через
перемежаемость. Эта неподвижная точка слабо устойчива в на-
направлении оси х и обладает конечной устойчивостью в направ-
направлениях осей у и г [такая устойчивость соответствует сокраще-
сокращению площадей в плоскости (у, z) — см. рис. IX. 9]. Когда непод-
неподвижная точка исчезает и открывается канал (в отображении по
координате х), конечное притяжение в направлении осей у и z
Рис. IX. 11. Окрестность неподвижной точки преобразования Смейла. Итера-
Итерации быстро сходятся к оси х вдоль осей у и г, но медленно движутся вдоль
самой оси х. При переходе от а к б подвижная точка исчезает.
CO-Ypdii/iC I L'n. 1>с1иПЧ11Ь0С r.iiiOI OOUpa JtiC Б панраБЛСШШ OCii X libl-
рождается в линию С, которая притягивает близко расположен-
расположенные точки из своей окрестности и вдоль которой отображением
первого возвращения является отображение x-+f{x) с каналом
(рис. IX. 11). Если в своем хаотическом движений (т. е. в фазе
турбулентного всплеска) траектория попадает в окрестность
«признака» неподвижной точки, то предварительно ее притяги-
притягивает линия С. Процесс притяжения к линии С протекает с ко-
конечной скоростью, в то время как в направлении, параллельном
линии С, траектория очень медленно приближается к порогу
перемежаемости. Оказавшись почти па линии С, точка начинает
ощущать (медленную) динамику одномерного отображения
вдоль оси х и медленно дрейфует в канале. Именно поэтому
продолжительность ламинарных фаз велика и намного превы-
превышает продолжительность «хаотических» блужданий в фазовом
пространстве между двумя посещениями «призрака» неподвиж-
неподвижной точки. Следовательно, на долю ламинарных фаз приходит-
приходится подавляющая часть временного поведения системы.

wr.i.jici введена о '-i. v н at
предметом подробного анализа в приложении Г, мы лишь на-
напомним здесь, что она состоит из трех обыкновенных диффе-
дифференциальных уравнений и предназначается для моделирования
конвекции Рэлея — Бенара. Уравнения имеют следующий вид:
(IX. 5.1)
(IX. 5.2)
(IX. 5.3)
Y = —XZ + rX — Y,
Z=XY-bZ.
Модель Лоренца стала предметом интенсивных исследований
как функция параметра г и иногда начальных условий при обыч-
обычных значениях параметров Рг =10, Ь = 8/3. Эти исследования
Рис. IX. 12. Периодические колебания в модели Лоренца при г = 166.
Из работы И. Помо и П. Манневиля.
позволили получить множество различных результатов. В ча-
частности, были открыты два сценария перехода к турбулентности:
переход через субгармонический каскад (гл. VIII) и переход
через перемежаемость. В этом разделе мы опишем в общих чер-
чертах, как переход через перемежаемость осуществляется в модели
Лоренца.
Один из возможных типов динамических режимов в модели
Лоренца связан с существованием предельного цикла. При
;- = го = 166 выбранные случайным образом начальные условия
после затухания переходных процессов выходят на совершенно
регулярные колебания, в чем нетрудно убедиться, взглянув на
графики X(t), Y(J) Zit) или любой функции этих величин
(РИС. 1Л. iZ).
Когда г чуть больше го, мы наблюдаем устойчивые колебания,
аналогичные изображенным на рис. IX. i2, на всем интер-
интервале [то, л], где пi = 166, 07. «Прочность» режима, соответствую-
соответствующего предельному циклу, выражает глубокое свойство струк-
структурной устойчивости (устойчивых) колебаний. Но когда г ста-
становится чуть больше п, типичные решения модели Лоренца
становятся «турбулентными», но весьма характерного вида.

272
Глава IX
При г= 166,1 (напомним, что г, ж 166,07) временной сигнал
X(i) (рис. IX. 13) совершает колебания, почти столь же регу-
регулярные, как и сигнал на рис. IX. 12, но прерываемые время от
Рис. IX. 13. Перемежаемость в модели Лоренца при г = 166,1. Колебания
между всплесками турбулентности почти такие же, как и в случае устойчи-
устойчивого предельного цикла на рис. IX. 12.
Из работы И. Помо и Манневиля.
43
42
41 Ь
лоь
40
41
42
43
Рис. IX. 14. Отображение первого возвращения в режиме перемежаемости
(г =166,2). Построенный график подтверждает существование коридора и
свидетельствует о сложности отображении, содержащего несколько разрывов.
Из работы И. Помо и П. Манневиля.
времени всплесками турбулентности. Эти хаотические флуктуа-
флуктуации имеют вполне определенную среднюю продолжительность и
завершаются тем, что мы назвали реламинаризацией, т. е. воз-
возвращением к ламинарному режиму. Хотя такое описание заве-

Перемежаемость
273
домо включает в себя переход через перемежаемость, мы не
можем немедленно решить, каким типом перемежаемости A, II
или III) обусловлено описанное выше явление.
Перемежаемость II типа в случае модели Лоренца (с поло-
положительными значениями параметров) исключается, так как при
такой перемежаемости наблюдалось бы локальное расширение
объемов в фазовом пространстве, в то время как система"Ло-
0,65-
0,60
0,55
0,50
X Угрозой
коэффициент
-3
-2
-1
tee
Рис. IX. 15. Вариация числа Ляпунова вблизи порога перемежаемости. На-
Наблюдаемый: рост в соответствии с теорией пропорционален квадратному корню
т'"- рзесто;'^ г от порогя. р, чем мы легко убежтярмся благодаря логариф-
у...\:-чаг.-У'У ¦.¦;"ir;i:T;;f:y по ос;: :^"С1::.;:с¦_-
Из работы И.¦ Помо и П. Манневиля.
ренца глобально1), т. е. всюду, сокращает площади. Не столь
определенно мы можем исключить также перемежаемость
III типа, анализируя рис. IX. 13. В этом сигнале не наблюдается
характерная особенность перемежаемости III типа (см.
разд. IX. 3)—рост субгармонических колебаний в ламинарной
фазе. Доказательство того, что в модели Лоренца имеет место
перемежаемость I типа, опирается главным образом ка числен-
численное построение отображения первого возвращения, в котором
обнаруживается характерное для перемежаемости I типа явле-
явление «открывания канала». Рис. IX. 14 позволяет со всей опре-
определенностью заключить, что в модели Лоренца вблизи г х- г,
М Впрочем, по iion самой причине лорепцеза систем- >:е может иметь
инвариантного тора Г2: в> противном случае внутренний'объем тора глобаль-
глобально сохранялся бы данной динамикой. Экспоненциальным сжатием же всех
сохранялся
объемов это исключается.
18 П Серже и ар

274 Глава IX
наблюдается перемежаемость I типа. Поскольку в численной,
модели величинам могут быть приданы любые значения, другие
теоретические предсказания также допускают проверку. Напри-
Например, рис. IX. 15 показывает, что вблизи порога перемежаемости
число Ляпунова у (г) возрастает, как е1/2. Это подтверждает
также хаотический характер турбулентных всплесков в том
смысле, что они разрушают временную корреляцию сигнала
с собой. Переход действительно происходит от периодического-
режима к хаотическому режиму с положительным числом Ля-
Ляпунова. Наконец, упомянем о том, что процесс реламинариза-
ции в принципе аналогичен преобразованию пекаря. Отображе-
Отображение первого возвращения имеет разрывы, связанные с пересе-
пересечением устойчивого многообразия неподвижной точки @, 0, 0)
с плоскостью сечения Пуанкаре. К таким следствиям приводит
сложность (странного) аттрактора траекторий в режиме пере-
перемежаемости.
IX. 2.6. Перемежаемость в реакции БЖ
Введенная в гл. V химическая реакция БЖ обладает не-
необычайным разнообразием пространственно-временного поведе-
поведения. Сосредоточим внимание на переходах через перемежае-
перемежаемость I типа, наблюдавшихся экспериментально в гомогенной
фазе в открытом реакторе. Управляющим параметром служит
среднее время пребывания Тг реагентов. Физико-химические ус-
условия поддерживаются как можно более точно при следующих
значениях параметров:
Реакционный объем 28 мл,
Температура 39,6 °С.
Концентрации реагентов в молях на литр: •
NaBrO3
CH2(COOHJ
Ce2(SO4K
ti9'6Ui
1,8-
5,6-
5,8-
1,5
ю-3
io-3
io-4
Концентрация ионов Се4~, определяемая по оптической плот-
плотности реакционной среды на длине волны 340 нм, изменяется
и позволяет следить за ходом реакции.
При среднем времени пребывания Тг около 100 мин реакция
совершает абсолютно правильные колебания (рис. IX. 16, а)
с периодом порядка минуты. Когда Тг становится меньше крити-
критического значения Тт, ,¦ да 76 мин, колебания длятся большую

Перемежаемость
275
idWuHw 1иш№\и''М1 b**wr
О 20 40 60 SO
Время, мин
Ряс. IX. 1G. Колебания концентрации ионов Сс4+ вблизи порога перемежге-
мости в реакции Белоусова — Жаботинского. а — ниже порога наблюдаются
периодические колебания концентрации — автоколебательный режим с пре-
предельным циклом (среднее время пребывания в реакторе 100 мин); б— чуть
выше порога (среднее время пребывания в реакторе 76 мин) амплитуда ма-
малых колебаний медленно возрастает со временем вплоть до внезапного появ-
лгнкг. п:п-са с большой амплитудой: в — при значительно меньшем времени
пребывания а реакторе C5 мни) амплитуда .малых колебаний сильно умекь-
•илегсл., саки колебали;' становятся менее ретуляршлти. а пики с большой
амплитудой встречаются чаще.
Из работы И. Помо, Ж--К- Ру. А. Росси, С. Башляра и К- Видаля.
часть времени, ко прерываются от случая к случаю большими
флуктуациями (рис. IX. 16,б). При дальнейшем уменьшении Тг
(ниже Тг, i) промежуток времени между двумя большими флук-
флуктуациями сокращается (рис. IX. 16,б).
18*

276
Глава IX
Такое поведение естественно наводит на мысль о переходе
через перемежаемость. Гипотеза о перемежаемости подтверж-
подтверждается существованием канала в отображении первого возвра-
возвращения, который может быть найден экспериментально»
го«
Рис. IX. 17. Отображение первого возвращения..**-. = f{xk). В качестве ко-
координаты х при построении этого графика выбрана амплитуда малых коле-
колебаний сигнала на рис. IX. 16, б. Экспериментальные точки пронумерованы к-
хронологическом порядке, что позволяет проследить за медленным движением
вдоль диагонали при прохождении коридора.
Из работы И. Помо, Ж-К. Ру, А. Росси, С. Башляра и К. Видаля.
(рис. IX. 17) путем построения графика зависимости амплитуды
fi м НГ>ГГ| п'О.ЛР^ЯН'им ПТ Я пИП 7Т1Т~1*Л ПЛ О 77 ХЛ 7V »ГТ!Т?1Г^~» ^Л ПОмОим И T-T-jTriti
утверждение о том, что этот переход, по-видимому, приводит
к хаотическому режиму, опирается в основном на расплывание
распределения вероятности интервалов между большими флук-
туациями (рис. IX. 18). Заметим, что это распределение имеет
форму, предсказываемую теорией (см. рис. IX. 4).
Другие результаты, также согласующиеся с теоретическими
предсказаниями, были получены в экспериментах с тепловой
конвекцией. На рис. IX. 19 показаны два сигнала (один выше,.

Перемежаемость
277
Р(п)
0,3-
0,2
0,1
гП
гт
ю
п
Рис. IX. 18. Гистограмма для фаз периодических колебаний вблизи порога
перемежаемости. По оси ординат отложена вероятность Р{п) наблюдения п
периодических колебаний между двумя пиками с большими амплитудами.
Данные заимствованы из экспериментального сигнала, часть которого пред-
представлена на рис. IX. 16, б. Построенная гистограмма явно подтверждает тео-
теоретические предсказания (см. рис. IX. 4).
Из работы И. Помо, Ж.-К. Ру, А. Росси, С. Башляра и К. Видаля.
а
^ 270 Rd с
^^ ЛЧЛ-71 J
rail. \ \. |У; поведение cKupucin ЕиЛйЗИ iiGpGia и?р?ГисЖ
"екнни Рэлея — Бенара. Конвективная структура в этом эксперименте состоит
;:j двух валов вдоль каждого из двух гори шиталишлх нанрииленш; :::;е;';;:п.
Используется один осциллятор тепловой конвекции типа ^теплой каллк».
" — периодический режим при Ra <. Rai, где Ra; = 295Rac — порог наступле-
наступления перемежаемости: б — режим с перемежаемостью при Ra > Ra.. Обра-
!':яют па себя внимание длинные (неравной длины) последовательности
:лаио B03MytL;eii:i^:x лолиСаи;:й (прохождение :срс.:; корпдер), нгг:р:.:гт-:т!>.?е
внезапными всплесками. Поразительно сходство между этими эксперимен-
экспериментальными сигналами и поведением модели Лоренца (см. ряс. IX. \2 и IX. 13).
Из работы П. Берже, М. Дюбуа, П. Манневиля и И. Помо.

278 Глава IX
другой ниже порога перемежаемости). Бросается в глаза их
сходство с результатами численного моделирования системы Ло-
Лоренца (см. рис. IX. 12 и IX. 13).
IX. 3. ПЕРЕМЕЖАЕМОСТЬ HI ТИПА
В этом случае собственное значение матрицы Флоке пересе-
пересекает единичную окружность на комплексной плоскости в точке
—1 и соответствующая бифуркация субкритическая, а поэтому
нелинейные эффекты низшего порядка не стабилизируют траек-
траектории (или поток) или последовательные итерации (для отобра-
отображения) в окрестности прежнего аттрактора1). В этом разделе
мы разовьем теорию перемежаемости III типа и проиллюстри-
проиллюстрируем экспериментально существование такой перемежаемости
в неустойчивости РБ.
IX. 3.1. Теория перемежаемости Ш типа
Как и в случае перемежаемости I типа, теория перемежае-
перемежаемости III типа состоит из нескольких частей.
1) Описание локальных явлений в слабо неустойчивой об-
области (соответствующей ламинарным фазам в динамике).
2) Количественные следствия для статистики ламинарных
фаз вблизи порога.
3) Описание процесса реламинаризации: как может начаться
ламинарная фаза после турбулентного всплеска?
Как и в случае перемежаемости I типа, мы можем, исходя
из простой модели, сделать количественные предсказания отно-
относительно ламинарных фаз динамики, так как эти фазы по су-
существу соответствуют пребыванию траектории в окрестности
бывшего аттрактора. Во введении к этой главе и ко второй ча-
части книги мы уже упоминали о том, что феноменология пере-
перемежаемости относительно независима от типа. Если значения
управляющего параметра меньше критического, то мы имеем
устойчивый предельный цикл. Если управляющий параметр не-
незначительно превосходит критическое значение, то на протяже-
протяжении большей части времени мы по-прежнему наблюдаем перио-
периодический режим, но он от случая к случаю прерывается турбу-
турбулентными всплесками. Когда мы приближаемся к критическому
!) Наоборот, б случае удвоения периода (или, возможно, каскада удвое-
удвоений периода) нелинейные эффекты стабилизируют линейно неустойчивые суб-
субгармонические флуктуации (см. гл. VIII).

Перемежаемость
279
значению управляющего параметра, при котором мультиплика-
мультипликатор Флоке пересекает единичную окружность в точке —1,
всплески становятся более редкими. Как видно по эксперимен-
экспериментально полученным сигналам (наблюдавшимся в случае не-
неустойчивости РБ, рис. IX. 20), ламинарная фаза наблюдается
как интервал, на протяжении которого амплитуда субгармо-
субгармоники нарастает до тех пор, пока не происходит своего рода
Рис. IX. 20. Временная зависимость горизонтального градиента температуры
вблизи порога перемежаемости типа III при конвективном режиме Рэлея —
Зенара. Этот эксперимент приведен для конвекции Рэлея—Бенара с отно-
отношением Ra/Rac « 420, несколько превышающим порог nepe.Me>KatMOci)i
(Ra/Rac « 416,5). Отмечается непрерывный рост с последующим резким уве-
увеличением амплитуды субгармоники, сопровождающийся уменьшением ампли-
амплитуды основной частоты.
Из работы М. Дюбуа, М. А. Рубио и П. Берже.
катастрофа, знаменующая начало турбулентного всплеска. Сле-
Следуя подходу, близкому к тому, которым мы воспользовались при
анализе перемежаемости I типа, исследуем динамику ламинар-
ламинарных фаз с помощью одномерного отображения. Это отображе-
отображение должно соответствовать слабо неустойчивому многообразию
замкнутой траектории.
В линейном приближении это отображение принимает вид
х^х' = -(\+г)х. (IX.6)
Неподвижная точка .v — 0 при е=0 становится нейтрально
устойчивой. При малых положительных (отрицательных) значе-
значениях эта неподвижная точка неустойчива (устойчива). Муль-

280 Глава IX
типликатор Флоке (дх'/дх)\х=0 равен —A + е) при пересече-
пересечении единичной окружности в точке —1 и е = 0-. Неподвижная
точка имеет координату х =0 вдоль слабо устойчивого (при
е < 0) или слабо неустойчивого (при г > 0) многообразия. Как
и в случае перемежаемости I типа, дополним линейный анализ,
введя в уравнение (IX. 6) члены, нелинейные по х. Как будет
показано в дальнейшем, для самосогласованности необходимо
ввести члены второго и третьего порядков по х. Новое отобра-
отображение имеет вид
х-*х' = — A-\-е)х + ах2 + $'х3. (IX. 7)
Для дифференциальных уравнений коэффициенты аир' мо-
могут быть определены явными формулами. Заметим, что значения
этих коэффициентов определяют выбор масштаба по х, так как
они входят в кубический полином, неоднородный по х.
Чтобы проанализировать отображение, задаваемое уравнение
(IX. 7) но причинам, которые станут ясными из дальнейшего,
желательно проитерировать дважды. Если ограничиться чле-
членами, кубическими по х и линейными по е (так как нас интере-
интересуют только значения х и е в окрестности нуля), то отображе-
отображение второго возвращения принимает вид
х -+ х" = х' [х! (х)] « A + 2е)-х + рг3, (IX. 8)
где
В выражение для В мы включили только члены, не зависящие1)
от р. так как нас интересует, что произойдет в пределе при
Отметим две отличительные особенности уравнения (IX. 8).
1) Коэффициент при линейном члене имеет значение, близ-
близкое к +1 [а не —1. как в уравнении (IX. 7)]. Это связано про-
просто с тем, что мультипликатор Флоке при каждой вдерации
умножается на себя. В результате после второй итерации пер-
первоначальный коэффициент (—1) переходит в (—IJ —+1-
2) Уравнение (IX. 8) не содержит (по крайней мере в низ-
низшем члене по е) члена, квадратичного по х. Это резко контра-
контрастирует с моделью перемежаемости I тща, развитой выше, и
обусловлено отбрасыванием после двух итерации всех старших
членов [а фактически всех членов четного порядка в разложе-
разложении х'(х}} и сохранением только членов низшего порядка по е.
J) Мы предполагаем также, что C имеет вполне определенный знак
вблизи 8 = 0. Действительно, f> — коэффициент при кубическом члеце в раз-
разложении функции х'(х) в ряд Тейлора — зависит от е. Мы не рассматриваем
случай E (е = 0) = 0, который соответствует коразмерности 2.

Перемежаемость 281
Уравнение (IX. 8) можно представить в виде
Нелинейный член $х2 в зависимости от знака коэффициента б
порождает два противоположных эффекта. Если C < 0, то мы
имеем суперкритическую бифуркацию с удвоением периода.
В слабонелинейной области («^.0) отображение, задаваемое
уравнением (IX. 8), имеет устойчивую неподвижную точку (точ-
(точка х = 0 неустойчива). Следовательно, отображение х' имеет
устойчивый 2-цикл: существуют значения х\ и х2, такие, что
где
*1>2 - ±(ф)
с-»0+
И
I (dx'/dx) \Xi • (dx'/dx) \X21 < 1 (условие устойчивости).
Наоборот, если Р > 0, то нелинейный член |3х2 оказывает
такой же эффект, как и е > 0: с каждой итерацией он увеличи-
увеличивает мультипликативный коэффициент при х. Таким образом, не-
нелинейность усиливает неустойчивость и мы имеем субкритиче-
субкритическую бифуркацию. Именно этот последний случай приводит
к перемежаемости III типа, которая нас сейчас интересует.
Как и в случае перемежаемости I типа, мы проанализируем
субкрнтическую бифуркацию (р>-0), заменив вблизи непод-
:м':-кной точки разность х" — х производной dx/dk п разностное
уравнение (IX. 8) дифференциальным уравнением
-g- = .vBe + ^2). (IX. 9)
Вводя в х нормирующий множитель Bе/РI/2, а вА нормирую-
нормирующий множитель е~', приведем это уравнение к универсальной
форме
-% = х(\+х% (IX. 10)
Это масштабное преобразование само по себе полезно для тео-
теоретических предсказаний. Индекс k, задающий число колебаний
на основной частоте, является мерой времени. Естественным
масштабом для k служит величина е~;. Мы заключаем, что
средняя продолжительность ламинарных периодов вблизи по-
порога перемежаемости расходится, как е-1. Вблизи того же по-
порога среднее время корреляции сигнала также сравнимо по-

282 Глава IX
порядку величины с средней продолжительностью ламинарной
фазы. Это время есть величина, обратная показателю Ляпу-
Ляпунова, характеризующему среднюю скорость расходимости траек-
траекторий в фазовом пространстве. Мы заключаем, что показатель
Ляпунова, характеризующий турбулентность, возрастает в фазе
перемежаемости, как е. Аналогичным образом мы можем ут-
утверждать, что, так как масштабом х служит величина Bе/р) Х12,
средняя амплитуда субгармонических флуктуации в ламинарных
фазах вблизи порога есть величина порядка г1/2.
Вместо интегрирования уравнения (IX. 10) попытаемся объ-
объяснить, как вывести из него статистическое распределение длин
ламинарных периодов.
Статистика ламинарных периодов
Уравнение (IX. 9) показывает, что при данном малом значе-
значении параметра в существуют два режима. Если л; достаточно
лревосходит величину Bе/рI/2, то доминирует член $х2. При
этих условиях уравнение (IX. 9) сводится к уравнению
которое имеет решение
х0
с начальным условием x(k — д) = х0. Когда знаменатель обра-
обращается в нуль, т. е. при
это решение расходится. Продолжительность интервала вре-
времени, к концу которого решение уравнения (IX. 11) расходится,
можно отождествить с концом ламинарной фазы, измеряемой
в периодах основного колебания.
Это соображение позволяет нам получить первую оценку
статистического распределения ламинарных фаз. Предположим,
что начальное значение Хо выбрано случайным образом, т. е.,
иначе говоря, ;:з однородного распределения б окрестности не-
неустойчивой неподвижной точки (гипотеза, которая должна быть
подтверждена впоследствии при исследовании процесса релами-
наризации). Соотношение между х0 и k (длиной ламинарной
фазы), задаваемое формулой (IX. 12), приводит к следующему
соотношению дифференциалов:

11еремежаемость
которое может быть представлено в виде
?
-3/2
Это соотношение позволяет нам связать распределение длин
k с распределением начальных условий хо. Если величина хо
произвольна, то в достаточно большой статистической выборке
доля значений Хо, заключенных между х0 и х0 + dx0, пропор-
пропорциональна dx0. Предыдущее соотношение между дифференциа-
дифференциалами показывает, что относительное число ламинарных фаз, за-
заключенных между k и k-\-dk, есть величина порядка P(k)dk ~
$V2k3'2dk
Разумеется, при малых k этот закон распределения не вы-
выполняется. По определению малые k означают, что длина лами-
ламинарной фазы есть величина порядка нескольких основных пе-
периодов. При столь коротких фазах последовательные итерации
расходятся слишком быстро для того, чтобы мы могли считать
разность х" — х малой и заменить отображение (IX. 8) уравне-
уравнением (IX.9I). Следовательно, распределение P(k)~ к~Ъ12 спра-
справедливо только при достаточно больших значениях k. Но эти
значения не должны быть и слишком большими. Если k стано-
становится большим, то, как показывает уравнение (IX. 12), началь-
начальная точка итерации приближается к нулю, а это противоречит
гипотезе о том, что х >> (е/В)х/2, которая была использована при
выводе уравнения (IX. 11) из уравнения (IX. 9).
Если эта гипотеза не выполняется (т. е. если исходная точка
недостаточно близка к неустойчивой неподвижной точке), то ла-
¦':п:йрная фаза разделяется на две т;асш. В пернсп из них глав-
главным в уравнении (IX. 9) является член, линейный по х, а по-
поэтому x(k) ~ ХоехрB&е). Эта часть заканчивается приблизи-
приблизительно тогда, когда х « (е/В) V2, так что k ~ A/4е) In (е/(Щ). Как
показывают рассуждения, аналогичные приведенным выше, да-
далее при k 3> е-' (что реализуется при х0 <С (е/РI/2) распреде-
распределение вероятности Р (k) убывает по закону ехр(—2zk).
J) Строго говоря, разностное уравнение (IX. 8) предсказывает, что ите-
итерации расходятся как
X (к) » Р% (Хо)8*.
Однако это весьма быстрая расходимость не приводит к особенности за ко-
конечное время в отличие от того, что происходит в дифференциальном урав-
лсшш (IX. 10). Ко, как бы то ни было, используемое нами приближение
сшачает, что значения х малы, и это позволяет нам оборвать разложение
х' (х) в ряд Тейлора после нескольких первых членов. Быстрая расходимость
итерации, или особенности в дифференциальном уравнении, вынуждает х
покинуть область применимости уравнений.

284 Глава IX
Резюмируя, можно утверждать, что P{k) имеет два асимпто-
асимптотических предела: при 1 < А С s-' мы получаем P{k) ~ k~3/2,
а при к 3> е мы имеем P(k) ~ ехр(—2ея).
Реламинаризация
Как и в случае перемежаемости I типа, анализ реламинари-
зации не может быть в той же мере количественным, что и ана-
анализ ламинарной фазы: реламинаризация зависит от глобальной
структуры потока, и поэтому ее анализ должен носить тополо-
топологический, т. е. качественный, характер.
Прежде всего заметим, что мультипликатор Флоке не может
пересечь единичную окружность в точке —1 в случае, когда по-
поток определен на Т2 или на плоскости. Действительно, построив
соответствующие графики, нетрудно понять, что слабо неустой-
неустойчивая траектория, отщепляющаяся от замкнутой траектории,
должна быть проведена на листе Мёбиуса, срединной линией
которого служит замкнутая траектория. Лист Мёбиуса неориен-
неориентируем ') и поэтому не может быть частью плоскости или Г2,
которые являются ориентируемыми поверхностями. Это озна-
означает, что в случае перемежаемости III типа процесс реламина-
ризации (в отличие от перемежаемости I типа) не может проис-
происходить на торе. Что же касается реламинаризации посредством
преобразования пекаря или на аттракторе Смейла, то она мо-
может происходить при перемежаемости как III, так и I типа.
Чтобы в конструкции, представленной на рис. IX. 9, перейти
от I типа к III типу, достаточно после завершения процесса
(или перед его началом, так как система итерационная) произ-
произвести дополнительно поворот тора на 180е. Эта операция изме-
изменяет знак мультипликатора Флоке, перемещая его из окрестно-
окрестности точки -f-1 (перемежаемость I типа) в окрестность точки —Г
(перемежаемость III типа). В результате отображение на
рис. IX. 9 переходит от x-*-f(x) в ?->/ (х)~ {A—х)
(рис. IX. 21). Такого рода топологические построения устанав-
') Поверхность называется ориентируемой, если на замкнутых кривых,
проведенных на ней, можно однозначно задать направление вращения. Пло-
Плоскость, .поверхность сферы и тор Г2 ориентируемы. Проведя на одной из этих
поверхностей небольшую окружность и непрерывно перемещая ее по уэвер.х-
постп, мы однозначно определим направление вращения (например, по часо-
часовой стрелке) в каждой точке поверхности. В отличие от этого лист Мёбиуса
«ли, например, бутылка Клейна неориентируемы. Перемещая по листу Мёбиуса
нсболыуу:о (ориентированную) окружность, мы можем оказаться на оборот-
оборотной стороне листа. Окружности, проведенные па слпцевон» и на оборотной
Мёби'/са — односторонняя поверхность (у которой лицевая сторона и «из-
«а-п-.я» отождествлены). Это доказывает, что лист Мёбиуса неориентируем.

Перемежаемость
285
ливают связь между перемежаемостью типа I и типа III лишь
в довольно общем виде, не детализируя ее. В частности, такие
глобальные построения в общем случае не сохраняют непод-
неподвижные точки.
Все эти соображения применимы к проблеме реламинариза-
ции. В случае перемежаемости I типа реламинаризация возни-
возникает в результате прохождения итераций через канал, образую-
образующийся между графиком функции f(x) и диагональю. В случае
Рис. IX. 2!. Отображение окружности при перемежаемости типа III. Если
угловой коэффициент в точке Р становится меньше —I it сопровождается
субарктической бифуркацией, то возникает перемежаемость типа III. Суще-
Существует (^устойчивая) неподвижная точка Р, имеющая д;:а прообраза: себл
". длиту^ точку Р'. Когдл итерация попадает и окрестность точки Р', от -
'¦¦ .г;;:^ иереводш ее is окр;_'С'П!ость точки Р: ~то к есть процесс рсламм;:а-
ризации.
перемежаемости III типа ничего такого не наблюдается, так как
пересечение единичной окружности мультипликатором Флоке не
сопровождается исчезновением неподвижной точки отображе-
отображения. В случае отображения, схематически изображенного на
рис. IX. 21, перемежаемость III типа может возникнуть, когда
тангенс угла наклона касательной к кривой f(x) в неподвижной
точке Р станет меньше —1 и будет выполнено условие р > О
¦--а нерпые члены разложения функции / п ряд Тейлора в окре-
окрестности точки Р, обеспечивающее субкритичность сопровождаю-
сопровождающей бифуркации. Как известно, эти условия не гарантируют ис-
исчезновения неподвижной точки Р. Реламинаризация гю:шикж--т,
когда у неподвижной точки имеются два прообраза: она сама
и точка, обозначенная на рис. IX. 21 буквой Р. Тогда если траек-
траектория, блуждая во время турбулентного всплеска, окажется в

286 Глава IX
окрестности точки Р', то следующие итерации вернут ее в ок-
окрестность точки Р — слабо неустойчивой неподвижной точки.
Это будет означать наступление новой ламинарной фазы. Мо-
Может показаться, что такой процесс исключается для реальных
систем, описываемых детерминистическими уравнениями, кото-
которые позволяют нам единственным способом возвращаться вспять
по времени1). Такое соображение априори исключало бы необ-
необратимое отображение Пуанкаре. Но мы уже увидели, что, когда
отображение Пуанкаре является достаточно сильно сжимающим
вдоль некоторых направлений пространства, порождаемое им
отображение первого возвращения свободно от ограничения об-
обратимости. В случае перемежаемости достаточно даже слабого-
сжатия вдоль устойчивого многообразия. Если начальная точка
оказывается в достаточно близкой окрестности устойчивого мно-
многообразия траектории, то выходящая из нее траектория экспо-
экспоненциально быстро устремляется к периодической траектории
(или к неподвижной точке сечения Пуанкаре) вдоль этого мно-
многообразия и медленно удаляется от нее вдоль неустойчивого
многообразия, так как вблизи порога перемежаемости неустой-
неустойчивость всего лишь нейтральна. Используя отображение на>
рис. IX. 21 в качестве модели, мы можем свести приближение
к неустойчивой неподвижной точке вдоль ее устойчивого много-
многообразия к единственной итерации— той, которая переводит
Р' в Р.
При этих условиях мы можем обосновать случайный выбор
начальной точки итерации в ламинарной фазе в окрестности-
точки Р. Действительно, по крайней мере на рис. IX. 21, отобра-
отображение x^-f(x) является сильно растягивающим вне достаточно
') Возможность вернуться вспять во времени понятна, когда мы рассма-
рассматриваем обыкновенные дифференциальные уравнения вида (dxjdt) = F(х)~
С другой стороны, для дифференциальных уравнений.с диссипацией, напри-
например уравнений гидродинамики, вообще говоря, невозможно вернуться назад
во времени, даже если речь идет о бесконечно малых интервалах. Если мы
попытаемся вернуться вспять во времени в уравнении теплопроводности, или-
уравнении Фурье, Tt = кТхх (х>0), т.е. найти T(t, x) no T(t + x, x') приг
т > О, то получим некорректную задачу (в смысле Адамара). Поэтому н&
вполне ясно, является ли условие единственности траекторий при обращении»
времени столь ограничительным, каким оно кажется. Необратимость происте-
проистекает из существования флуктуации, затухающих си времена»;, со сколь угодно
v.vibiiin постоянными г.ременп. При обращении времени эти флуктуации уси-
усиливаются сколь угодно быстро и становятся неконтролируемыми. В случае'
гидродинамики можно принять точку зрения, согласно которой в сокращен-
сокращенном описании (например, в описании, приводящем к обыкновенным дифферен-
дифференциальным уравнениям, как в случае модели Лоренца) такие флуктуации
пренебрежимо малы независимо от направления времени. Такая гипотеза
(формально) делает возможной обратимость сокращенного описания. Более
подробное обоснование обратимости увело бы нас слишком далеко в сторону
от темы нашей книги.

Перемежаемость 287
малой окрестности точки Р. Это растяжение, или ЧЗНУ, как мы
знаем, означает; что начальные условия забываются, т. е. что
точки реинжекции по существу выбираются случайным образом.
В следующем разделе мы приведем описание эксперимента РБ,
з котором наблюдался такой переход через перемежаемость
III типа.
IX. 3.2. Перемежаемость III типа в конвекции РБ
Эксперимент проводился при следующих условиях: конвек-
конвекция наблюдалась в силиконовом масле с числом Прандтля
Рг « 38, высотой ячейки d x 1,5 см, длиной Lx = 2d и шириной
Ly — \,2d. Число Рэлея Ra примерно в 380—400 раз больше
критического значения Rac. Измеряется отклонение узкого пуч-
пучка света, вызванное градиентом температуры в конвектирую-
щей жидкости/. Непосредственные наблюдения сводятся к сле-
следующему. При Ra/Rac между 333 и 377 вызванные тепловой
конвекцией течения совершают почти регулярные колебания')
с частотой порядка 1,7-10~2 Гц (т. е. с периодом около 1 мин).
При Ra/Rac « 416,7 в сигнале возникает субгармоническая ча-
частота, сопровождаемая перемежаемостью. Типичный сигнал
представлен на рис. IX. 20. Между двумя турбулентными вспле-
всплесками отчетливо видны увеличение амплитуды субгармоники
и заметное уменьшение основной частоты. Когда амплитуда суб-
субгармоники достигает того же порядка величины, что » ампли-
амплитуда основного колебания, возникает флуктуация, или турбу-
турбулентный всплеск, нарушающая регулярность сигнала. Сразу же
после этого устанавливается регулярный режим с малой случай-
случайно:: амплитудой субгармоники. Начальная амплитуда опреде-
определяет продолжительность ламинарной фазы до следующего
турбулентного всплеска. Чем меньше начальная амплитуда суб-
субгармоники, тем больше продолжительность ламинарной фазы.
Режим перемежаемости обратим, и это подтверждает соображе-
') Физическая природа этих колебаний весьма сложна и связана с гео-
геометрией конвективных течений в ячейке. В описываемом эксперименте коле-
колебания связаны с пульсацией холодного «шлейфа». Шлейф — это локальная
флуктуация температуры жидкости, в данном случае понижение по сравне-
сравнению с окружающей жидкостью. Шлейф отделяется через более или менее
; :-";'л:тр[:Ь!е интервалы времени от границ, создающих градиент температуры
в жидкости. Шлейфы существуют главным образом r жидкостях при больших
числах Прандтля по следующим причинам. Большое число Прандтля озна-
означает, что кинематическая вязкость жидкости во много раз больше ее темпера-
гуропповодности. Поэтому последняя малоэффективна, что позволяет боль-
:'шм градиентам температуры и плотности долго существовать в жидкости,
прежде чем они релаксируют. В свою очередь это вызывает большие флук-
флуктуации архимедовой силы, которая служит причиной движения шлейфа.

а
Рис. IX. 22. Перемежаемость типа III в конвекции Рэлея—-Бенара. а — об-
образец переменного сигнала для того же режима, который представлен на
рис. IX. 20. Растянутая шкала времени позволяет более наглядно представить
рост субгармоники и связанное с ним затухание основной частоты. Слева;
определены величины /*, используемые при построении графика отображения
второго возвращения, б — график отображения второго возвращения ln-ц =
= f(/*)-
При построении этого графика по экспериментальным данным, представлен-
представленным на рис. IX. 20, использованы два различных символа: один из них1
• квадратики) соответствует субгармонике (возрастающие амплитуды), другой
(крестики) отвечает фундаментальной частоте (уменьшающиеся амплитуды).
Непрерывная кривая —график функции
{а и Ь — константы, удовлетворяющие неравенству а<.Ь). Как предсказы-
предсказывает теория, именно такую форму должна иметь функция, задающая отобра-
отображение второго возвращения вблизи порога перемежаемости. Обращает вни-j
мание превосходное, согласие с экспериментальными данными, полученное;
путем выбора подходящего значения подгоночного параметра е (е = 0,11).;
Из работы М. Дюбуа, М. А. Рубио и П. Берже. |

Перемежаемость
289
ние о том, что переход к хаотическому состоянию через пере-
перемежаемость обратим.
Используя экспериментальные данные, можно показать, что
в ламинарных фазах отображение второго возвращения имеет'
форму, предсказанную уравнением (IX. 8). Пусть 1к — значение
k-то максимума физического сигнала, например сигнала, пред-
представленного на рис. IX. 20. Отображение второго возвращения
определяется графиком зависимости,/*+2 = /(/*) для последо-
60 80
Тч JUU.H
140
Рис. IX. 23. Гистограмма для ламинарных фаз. Наблюдаемые длины варьи-
"•г.ются от 18 мин до 2 ч и более. Наиболее существенной особенностью и
распределения является длинный хвост при больших 7', характерный для пе-
перемежаемости типа III. Форма распределения заметно отличается от рас-
распределения, характерного для перемежаемости типа 1( см. рис. IX. 4 и IX. 18).
Из работы М: Дюбуа и М. А. Рубио.
вательности значений k. Напомним, что теория предсказывает
следующую форму функции:
/ft+1==(l + 2e)/ft -f Ы\. (IX. 13)
Как видно из рис. IX. 22, б, эта форма хорошо согласуется с экс-
экспериментальными данными. В частности, обращает на себя
внимание существование точки перегиба в окрестности непод-
неподвижной точки отображения /(/*)• Это соответствует отсутствию
квадратичного члена в разложении функции f(h) в ряд Тей-
Тейлора.
Другим характерным признаком перемежаемости является
статистическое распределение длин т ламинарных фаз
19 П. Берже и др.

290 Глава IX
[{рис. IX. 23)I Как показывают вычисления, аналогичные прове-
проведенным в разд. IX. 3.1, если P(x)dx — доля ламинарных фаз
в интервале времени от т до т + dx (dx — малая величина), то
р (%).-_- ^Р <~257>
[1-«ср(-4втI3'2
При т > е~' имеем Р(х) ~ ехр(—2ет), в то время как при 1 >С
<т<8-' справедливо соотношение -р(т) ~ Dет)~3/2 (оба со-
соотношения подтверждают теоретические предсказания). Время
J4O
Рис. IX. 24. Число ламинарных фаз, продолжительность которых превышает То.
Экспериментальные точки получены путем суммирования гистограммы на
рис. IX. 23. Непрерывная линия — теоретическая кривая, подогнанная к экс-
. пе^иментальным точкам путем изменения свободного параметра е. Пора-
Поразительно, что выбранное значение (е = 0,1) оказалось очень близким к зна-
значению, определенному независимо от отображения второго возвращения
(рис. IX. 21). '. : , _
Из -работы М. Дюбуа, М. А. Рубио и ГЬ Берже.
т= 1, ограничивающее область применимости последней оцен-
оценки, можно интерпретировать как период колебаний с основной
частотой. Действительно, представление о ламинарной фазе
имеет смысл только в том случае, если на протяжении интервала
времени, в течение которого длится такая фаза, мы можем на-
наблюдать большое число колебаний с основной частотой. Сравне-
Сравнение теории и эксперимента в рассматриваемом случае произвО'

Перемежаемость 291
дится путем подсчета числа ламинарных фаз Лг(т > т0),. для-
длящихся больше т0. При то ~> 1 получаем
Эта функция параметра т0 полностью определяется значением
параметра е. На рис. IX. 24 показаны результаты сравнения
уравнения (IX. 14) и экспериментальных данных. Согласие пре-
превосходное, так как наилучшая аппроксимация уравнением ¦
(IX. 14) экспериментальных данных осуществляется при е да 0,1,
в то время как сами экспериментальные данные (рис. IX. 22, б
и IX. 23) приводят к б х- 0,11. Это позволяет идентифицировать
наблюдаемое явление как перемежаемость III типа. Заметим
также, что одна; из гипотез, сформулированных в разд. IX. 3.1,
согласно которой ламинарные фазы начинаются случайно в ок-
окрестности неподвижной точки, хорошо подтверждается статисти-
статистическими исследованиями, приводящими к рис. IX. 24.
1Х.4. ТЕОРИЯ ПЕРЕМЕЖАЕМОСТИ И ТИПА
Мы ограничим'свой анализ слабо нелинейными, или локаль-
локальными, явлениями, т. е. процессами, происходящим» в окрестно-
окрестности слабо неустойчивой замкнутой траектории. Мы можем по-
построить модель отображения, первого возвращения—непрерыв-
возвращения—непрерывную, обратимую и порождающую переход через перемежаемость
II типа. Помимо прочего такая модель указывает возможный
путь для реламинаризации. В основе модели лежит весьма
сложное геометрическое построение в пятимерном пространстве,
причем главная идея по существу совпадает с той, которая по-
положена в основу аттрактора Смейла. .
Когда два комплексно-сопряженных мультипликатора Флоке
выходят из единичной окружности на комплексной плоскости,
периодическая траектория утрачивает свою устойчивость. Не-
Неустойчивое возмущение экспоненциально возрастает по модулю
(в линейном приближении), одновременно поворачиваясь на ко-
конечный угол в своей плоскости при каждой итерации. Для опи-
описания линейных и слабо нелинейных явлений при таких бифур-
бифуркациях естественно (и это уже традиция) воспользоваться комп-
комплексными числами. Пусть (х, у) — прямоугольные ксюрдинаты на
плоскости малых отклонений (возмущений) от неподвижной
точки в направлении собственных векторов, соответствующих
двум комплексно-сопряженным собственным значениям, поки-
покидающим единичную окружность. Мы определяем комплексное
число z — х + iy так, что в линеаризованном приближении для
¦ 19*

292 Глава IX
амплитуд малых возмущений действие отображения первого воз-
возвращения сводится к умножению z на Хе1*, где Я—положитель-
Я—положительное вещественное число, а ^ — просто вещественное число. На
пороге неустойчивости параметр % равен единице, ф— угол по-
поворота образа точки при каждой итерации (см. приложение В).
В этих обозначениях два комплексно-сопряженных собственных
значения матрицы Флоке имеют вид Хе±1ф и определение линей-
линейной устойчивости сводится к исследованию необычайно простой
итерации - .
г-+г' = №Фг. (IX. 15)
Как и в случае перемежаемости двух рассмотренных выше
типов, введем малый управляющий, параметр е, обращение ко-
которого в нуль совпадает с нейтральной устойчивостью; т. е.
с i = 1. Таким образом, мы получаем К= 1 + е. Угол ф, вхо-
входящий в уравнение (IX. 15), априори также зависит от е. Но
мы предполагаем, что ф(е — 0) не совпадает с одним из спе-
специальных углов: 0, я/2, я, 2я/3, ... .Как будет показано ниже,
исключение таких ситуаций позволяет пренебречь зависимостью
ф от е в окрестности е = 0.
Как и в случае перемежаемости I и III типов, анализ слабых
нелинейностей мы начинаем с интерпретации правой части урав-'
нения (IX. 35) как начало разложения в ряд Тейлора функции
z'(z). Но в рассматриваемом случае не существует причины, по
которой разложение должно идти только по степеням z. Это
означает, что мы должны рассматривать на равных основания
степени z и z* (величины, комплексно-сопряженной с г) и клас-
классифицировать члены ряда только по степени модуля величины z.
Как и в случае перемежаемости III типа, мы должны удержи-
удерживать члены до третьего порядка, чтобы получить теорию пер-
первого порядка по нелинейностям. Мы получаем отображение
z -+ z' = Яе'*г + щг2 + а2 (z'
+ btf + MV + h {*У z + h (z'f +...', (IX. 16)
где a-t и bi — комплексные коэффициенты, которые в аналитиче-
аналитическом примере могут быть вычислены на основе общих принципов
разложения типа Ландау. Так же как линейные члены, нели-
нелинейные члены порождают два эффекта: они поворачивают z во-
вокруг начала координат и изменяют модуль числа z. Как разде-
разделить эти два эффекта, вообще говоря, неясно, так как они тесно
связаны нелинейностью уравнения (IX. 16). Но в рассматривае-
рассматриваемом нами примере можно воспользоваться упрощениями, воз-
возникающими вблизи 2 = 0ил=!, т, а в окрестности, где спра-
справедливо разложение (IX. 16). Эффект нелинейностей весьма раз-

Перемежаемость 293
личен в зависимости от того, рассматриваем ли мы модуль z
или угол числа г. Неустойчивость сказывается главным образом
на поведении модуля, который нейтрально устойчив при е = 0.
Это означает, что при %, близком к 1 (или е близком к 0), мо-
дуль числа z эволюционирует, как мы и предполагаем, очень
медленно. Но угол, на который z поворачивается с каждой ите-
итерацией, ост'ается конечным, при е — 0. Следовательно, предпо-
предполагая, что угол z изменяется значительно, в то время как мо-
модуль z остается почти неизменным, мы по существу принимаем
адиабатическое приближение1). В качестве примера рассмот-
рассмотрим случай, когда нелинейности ,в уравнении (IX. 16). сводятся
к одному члену a\z2:
(IX. 17.1)
Уравнение для комплексно-сопряженного числа г* имеет вид
z'-^z'^le-^z' + a^izy. (IX. 17.2)
Умножая почленйо эти два выражения, получаем
. (IX. 18)
Теперь нас интересует средняя эволюция величины \z'\2 р
числе итераций, достаточно большом для того, чтобы угол z
мог принимать многие значения, но в то же время достаточно
малом для того, чтобы модуль z мог изменяться лишь незначи-
незначительно. В первом приближении отображение, действующее на
углы, есть поворот на постоянный угол ф с начальным значе-
значением гр0- Известно2), что если ф— произвольный иррациональ-
иррациональный угол, то углы (if)о + кф) (mod 2л) равнораспределены на ин-
интервале [0, 2я], где k принимает многие различные целые зна-
значения. Следовательно, среднее, которое мы хотим найти, есть
*) Адиабатическим приближением называется такое приближение, в ко-
котором параметр изменяется медленно, в то время как система испытывает
быстрые изменения (обычно быстрые колебания). Такая терминология берет
.начало в термодинамике: процесс там называется адиабатическим, если про-
протекает настолько медленно, что позволяет пренебречь необратимыми явления-
явлениями, обусловленными вязким трением, пропорциональным скорости процесса.
Несмотря на кажущуюся простоту, адиабатические теории отличаются тон-
тонкостью и глубиной: они связаны с такими проблемами, как долговременная
устойчивость Солнечной системы, микроскопические основания второго начпла
термодинамики и классический предел квантовой механики.
2) Именно здесь входит условие, согласно которому угол Ф(е = 0) не
принимает специальные значения я/2, 2я/3 и т. д. В противном случае мы
не могли бы принять гипотезу о том, что значения D'о + кФ) равномерно
распределены по окружности. Так как Ф зависит от \z\- мы рассматриваем
гораздо более сложный случай: необходимо в явном виде учитывать связь
•между Ф и модулем Ы_ Соответствующая теория напоминает знаменитую
-теорию КАМ (Колмогорова — Арнольда — Мозера).

294 Глава IX
простое среднее по углу числа г. с однородным распределением
на [0,2л]. Усредняя уравнение (IX. 18), мы оставляем неизмен-
неизменными члены Я.2|;г|2 и |ai|2|z4|, не зависящие от угла. Наоборот,
рассмотрим последний член в уравнении AХ.Л8): если i|> — угол
комплексного числа z, то последний член зависит от if> как
cos (ф — ifi) и при усреднении по г|) дает нуль. Обобщая эти рас-
рассуждения, мы заключаем, что средняя эволюция модуля \z\ (ко-
(который мы обозначим через р) в адиабатическом приближении
определяется соотношением
р_>р' = (ку + Ар* + ...I/2. / (IX. 19)
Сумма в скобках представляет собой ряд по р2, коэффициенты
которого могут быть почленно вычислены') путем разложения
соотношения (IX. 16) и усреднения по г|з. Коэффициент А в фор-
формуле (IX. 19) зависит явно от коэффициентов'с,- и 6, соотноше-
соотношения. {\Х. 16).
В рассматриваемом приближении модуль р близок к 0 и член
Ар'4 можно считать малым по сравнению с %2р2. Это позволяет
разложить в ряд квадратный корень в соотношении (IX. 19) и
получить
(ig ) (IX.20)
(Напомним, что параметр К положителен и близок к единице.)
Здесь также члены в скобке являются началом ряда по р2.
В дальнейшем мы ограничимся только членами, явно выписан-
выписанными в соотношении (IX. 20), т. е. отображение модуля имеет
вид
^^) (IX.21)
Различие между субкритической и суперкритической бифур-
бифуркацией зависит от знака коэффициента А. Чтобы убедиться
в этом, мы можем рассматривать в первом приближении дей-
действие нелинейных членов в р'(р) только как замену множителя
X величиной %[\ +(.Д/2&2)р2]. Если К >Л (т. е. в условиях -ли-,
нейной неустойчивости), неустойчивость может компенсировать-
компенсироваться нелинейностями низшего порядка при А < 0 и усиливаться
при А > 0. Чтобы придать нашему анализу более количествен-
')¦ Заметим, что в эти выражения угол Ф явно не входит. Это отражает
глубокое свойство адиабатического приближения: «быстрая» переменная {в
нашем, случае ф) не связана с «медленной» переменной (в нашем случае р)
во всех алгебраических порядках разложения. Связь возникает только в транс-
трансцендентных порядках по р, например в ехр(— 1/р).

Перемежаемость 295
ный характер, рассмотрим окрестность точки к= 1; т, е. значе-
значения % = 1 + е, где |е|< 1. Отображение, задаваемое соотноше-
соотношением (IX. 21), имеет одну или несколько неподвижных точек,
которые являются решениями уравнений: р=(—2е/ЛI/2 при
А < 0 и р = 0. (Мы видим здесь квадратично-корневую зави-
зависимость, характерную для теории бифуркаций Ландау.) Если
А < О, то существует супер критическая бифуркация и непод-
неподвижная точка р== (—2е/ЛI/2 линейно устойчива при е > О,
а р = 0 неустойчива. Если же Л > 0 (мы здесь рассматриваем
именно этот улучай), то бифуркация субкритическая: Это озна-
означает, что при е < 0 линейно устойчивая точка сосуществует с не-
неустойчивой неподвижной точкой р =(-^-2е/ЛI/2. При 8 = 0 не-
неустойчивая неподвижная точка [в действительности инвариант-
инвариантная окружность на плоскости (х,у) неустойчивых направлений
матрицы Флоке] сливается с точкой р=0'—проекцией пре-
предельного цикла на плоскость (х,у). Следовательно, при е > 0
не существует устойчивого аттрактора в области фазового про-
пространства вблизи интересующей нас замкнутой траектории.
Именно в этом случае становится возможной перемежаемость
II типа, которую мы исследуем, используя задаваемое соотно-
соотношением (IX. 21) отображение. Приведя р к безразмерной форме
делением на B№/АI/2, запишем соотношение (IX. 21) в «стан-
«стандартном» виде -
р-^р' = A+е)р + р3. (IX.22)
Формально перед нами то же итерационное соотношение,
с которым мы истречались при анализе перемежаемости
III типа. Следовательно, соотношение между длиной ламинар-
ламинарных периодов (обозначенной через N), значение р в начале ла-
ламинарного периода (обозначенное через, р0) и параметр е ос-
остаются по существу такими же, как в случае перемежаемости
III типа. Если^ е1/2 ^ ро «С 1, то в итерациях, задаваемых соот-
соотношением (IX. 22),главным является кубический члени ЛГ~р^2.
С другой стороны, если ро <S е1/2, то увеличение амплитуды ко-
колебаний в ламинарной фазе управляется членом ер в уравнении
(IX. 22) и поэтому N ~ —e-1 In p0. Таким образом, как и в слу-
случае перемежаемости III типа, гистограмма длин Лг ламинарных
фаз состоит из двух частей, отвечающих неравенствам N ~> е-1
и 1 -с N <С е~!. Однако эта элементарная теория распределения
отличается от аналогичной теории, развитой для перемежае-
перемежаемости III типа. Б последнем случае неустойчивым многообра-
многообразием является линия, и ламинарная фаза начинается на этой
линии в случайной точке вблизи неустойчивой неподвижной точ-
точки. Иначе говоря, если so — расстояние между начальной точкой

296 Глава IX
и неустойчивой неподвижной точкой, то вероятность того, что So
принадлежит интервалу [so,so + ds0], равна просто дифферен-
дифференциалу ds0, умноженному на нормирующий множитель, но в слу-
случае перемежаемости II типа неустойчивое многообразие дву-
двумерно. Продолжительность ламинарной фазы, как и прежде, оп-
определяется расстоянием р0 между начальной точкой и неустой-
неустойчивой неподвижной точкой, измеренным на поверхности обычным
способом. Если начальная точка выбрана случайным образом
на поверхности, то вероятность того, что р0 лежит в интер-
интервале [ро, ро + ф0], равна величине 2ярофо,. умноженной на
константу, так как 2яр»фо — площадь кольца, ограниченного
окружностями радиусов р0 и (р0 + фо) с центром в неподвиж-
неподвижной точке. Так как ро ~ N~lJ2, мы получаем следующее соот-
соотношение между дифференциалами:
dpo~N~3l2dN.
Предположим теперь, что начальная точка выбрана на не-
неустойчивом многообразии случайным образом, т. е: с мерой ф,
пропорциональной площади многообразия. Тогда ф ~ рофо,
' или ф ~ QoN-^^dN ~ N~2dN. Если мы находимся точно на по-
пороге неустойчивости (е=0), то это означает, что средняя про-
продолжительность ламинарной фазы расходится, так как она оп-
определяется интегралом, который при больших ./V ведет себя как
х N (dN/N2). Но при, конечном (малом) е среднее значение <Л/>
величины N не расходится.' Действительно, распределение ве-
вероятности P(N) ведет себя как 1/.V2 при в <.V< 1 (что со-
соответствует е1/2 <С ро <С 1) и как ехр(—2eAf) при N >¦ е-1 (или,
что эквивалентно, р0 <С е1/2). Таким образом, если параметр е
конечен, то интеграл, определяющий среднее <ЛГ>, сходится
при больших N, так как в этой области F(N) убывает экс-
экспоненциально. Характерный временной масштаб, ограничи-
ограничивающий продолжительность ламинарной фазы,. изменяется
вблизи е = 0 как е-1. Поскольку интеграл, определяющий сред-
среднее <ЛО, при г = 0 логарифмически расходится в области боль-
больших N, мы заключаем, что в окрестности s = 0 среднее <Av
ведет себя как е-1. Предположим теперь, что число Ляпунова
у{г)—величина того же порядка, что и (N}-1, и сигнал утра-
утрачивает память после каждого турбулентного всплеска. Тогда
у(е)~ 1/1пA/е). В заключение укажем, что тщательные чис-
численные исследования обнаруживают тонкие статистические эф-
эффекты, которые вносят изменения в приведенное выше элемен-
элементарное описание статистики.

Перемежаемость 297
ЛИТЕРАТУРА
Berge P., Dubois P., Manneville P., Pomeau Y., Intermittency in Rayleigh —
Benard convection, Le Journal de. Physique — Letters, 41, L341 A980).
Dubois M., Approach of the turbulence' in hydrodynamic instabilities. — In:
Symmetries and Broken Symrnetries in Condensed Matter physics,
I.D.S.E.T. Paris A981). '
Dubois M., Rubio M: A., Berge P., Experimental Evidence of Intermittencies
Associated with a Subharmonic Bifurcation, Physical Review Letters, 51,
1446 A983).,
Manneville P., Pomeau Y., Intermittency and the Lorenz Model. — In: Sym-
Symmetries and Broken Syrrimetries in Condensed Matter Physics, I. D. S. E. T.
Paris A981). ,
Manneville P., Pomeau Y., Different ways to turbulence in dissipative dyna-
dynamical systems, Physica, ID, 219 A980).
Manneville P., Intermittency, Self Similarity and I If Spectrum, Le Journal de
Physique, 41, 1235 A980).
Pomeau Y., Approche de la turbulence, Actes de la conference de la Societe
franeaise de Physique, Clermont-Ferraind, Les editions de physique, Orsay
A981).
Pomeau Y., Manneville P., Intermittent Transition to Turbulence in Dissipative
Dynamical Systems, Communications in Mathematical Physics, 74, 189
A980).

ЗАКЛЮЧИТЕЛЬНАЯ ДИСКУССИЯ
К. Видаль: «Прежде всего мне хотелось бы затронуть один
принципиально важный аспект, не получивший должного разви-
развития в книге: область, в пределах которой теория динамических
систем верна и применима, до сих пор остается неопределенной.
Мы располагаем описаниями отдельных событий й последова-
последовательностей событий, приводящих к хаотическим ситуациям: иа
таких описаний состоит вторая часть книги. Это означает, что
при определенных условиях мы в состоянии предсказать, каким
образом возникнет апериодический режим, т. е/ произойдет пе-
переход. Но теория ничего не говорит ч о том, сочетание каких
условий гарантирует, что данная последовательность событий
завершится установлением' хаотического режима. Теория не оп-
определяет (по крайней мере в существующем ныне виде) пред-
предпосылки хаотического режима, и это, несомненно, следует от-
отнести к числу ее недостатков».
И. Помо: «Я полностью согласен с этой точкой зрения. Мож-
Можно сказать, однако, что проделанный анализ переходов к хаосу
и хаотических явлений, несмотря на все недостатки, обладает
или должен обладать большой прогностической силой, посколь-
поскольку экспериментаторы наблюдали и переходы к хаосу, и хаоти-
хаотические явления. Это позволяет нам * надеяться на то, что, ана-
анализируя более подробно эксперименты, пытаясь разобраться в-
деталях наблюдавшихся явлений, мы поймем, наконец, почему
в данном эксперименте удалось наблюдать именно тот, а не
другой сценарий перехода к хаосу,- почему наблюдался тот или
иной тип турбулентности, почему было большим или малым
число степеней свободы. Неясно пока другое: потребуется ли
для того, чтобы узнать все это, чудовищный объем, вычислений,
ставящий под сомнение эффективность предсказаний, поскольку
эти расчеты сопряжены с неприемлемо большими затратами ма-
машинного времени и в конце концов не слишком проясняют су-
существо дела, или мы можем разработать промежуточную тео-
теорию, менее общую, чем теория динамических систем в том виде,
как она существует теперь, но достаточно подробную, чтобы
предсказывать происходящее в данной ситуации, не вда-

Заключительная дискуссия 239
ваясь в детали конкретных уравнений, описывающих си-
систему».
П. Берже: «В связи с высказанными замечаниями по поводу
предсказаний я хотел бы подчеркнуть определенную практиче-
практическую ценность понятий, изложенных в этой книге. Например, мы
можем надеяться, что когда-нибудь нам удастся уточнить про-
прогнозы погоды, если бы только мы сумели обобщить метод ото-
отображений первого возвращения. *Мы видел», что такие отобра-
отображения действительно позволяют определить будущее, хотя и не
позволяют предсказывать долговременное поведение хаотиче-
хаотической системы, т. е. найти «порядок в хаосе». Можем ли мы, опи-
опираясь на такого рода методы, усовершенствовать прогноз по-'
годы? Можем ли мы лучше понять исследования зависящий от
двух параметров популяций живых организмов и эволюцию по-
популяций различных видов с разнотипными циклами и, следова-
следовательно, лучше управлять этими популяциями? Мы считаем, что
это возможно. Следует отметить также, важность того, что в по-
последнее время теорий детерминированных динамических систем
нашли применение в гидродинамике, по крайней мере для ана-
анализа некоторых типов турбулентности. В настоящее время нет
сомнения в том, что во многих экспериментах, в которых эффект-
эффектное число степеней свободы мало, нам удалось понять несколько
вполне определенных маршрутов, ведущих к хаосу. Возникает
серьезный вопрос: можем ли мы продвинуться, гораздо дальше
на пути к развитой турбулентности, в которой число степеней
свободы очень .велико? В этой связи следует упомянуть не-
несколько самых последних работ по моделям, занимающим в не-
некотором смысле промежуточное положение между моделями
с небольшим числом степеней свободы, рассмотренными в этой
книге, и моделями с очень большим, практически бесконечным
числом степеней свободы. Мы начинаем понимать механизмы,
возникающие в модельных системах с 50 или около того етегТе-
нями свободы. Небезынтересно отметить, что прогресс, достиг-
достигнутый в понимании промежуточных случаев, подготавливает нас
к преодолению пропасти, отделяющей в настоящее время детер-
детерминированную турбулентность от обширнойЛ области развитой
турбулентности, в которой пока остается много неясного».
И. Помо: «Интересно, что были предложены модели для опи-
описания таких достаточно конкретных явлений, как химическая
турбулентность и -неустойчивости в пламенах. Эти модели зани-
занимают промежуточное положение между системами с небольшим
числом степеней свободы и полностью развитой турбулентностью
со всеми примыкающими проблемами. В частности, эти модели
обладают тем преимуществом, что позволяют понять взаимо-
взаимодействие между описанными в книге эффектами сложной дина-

300 Заключительная дискуссия
мики и не менее сложными эффектами пространственной струк-
структуры— двумя элементами, которые, несомненно, должны помочь
нам объяснить развитую турбулентность. Важно понимать, что
исследования, проводимые на основе этих моделей, сопряжены
с большим объемом вычислений, но наша цель состоит отнюдь
не в проведении этих громоздких вычислений, а в анализе ре-
результатов вычислений для достижения лучшего понимания. Про-
Проводимым до сих пор исследованиям развитой турбулентности не-
недоставало не средств для выполнения большого объема вычис-
вычислений, а скорее способа анализа их результатов, опиравшегося
на слишком рудиментарные понятия и потому не вносившего
сколько-нибудь существенного вклада в понимание статистиче-
статистической механики, лежащей в основе теории турбулентности. Ныне
мы постепенно выходим из этой ситуации слишком грубого ана-
анализа проблем нелинейной эволюции, но пока лишь начинаем
использовать сравнительно тонкие методы, анализа, применяв-
применявшиеся к системам с небольшим числом степеней свободы».
К. Видаль: «Если мы попытаемся (как вы только что сде-
сделали) заглянуть в будущее/ то разумно ожидать, что нас под-
подхватит течение и наш путь будет пролегать от систем с неболЬг
шим числом степеней свободы к системам с большим числом
степеней свободы, прежде чем будет достигнуто более общее
описание с элементами понимания полностью развитой турбу-
турбулентности. Кроме того, мы должны предпринять попытку под-
подняться против течения, т. е- найти что-нибудь, напоминающее
первое и- даже второе начало теории динамических систем по
аналогии с термодинамикой. Я должен признать, что задача эта
весьма амбициозна. Знание общих начал позволило бы вывести
минимальные условия, необходимые для наблюдения того или
иного режима, а это десятикратно усилит мощь теории.
Построение теории, как мы только что видели, уже идет по
одному пути: это направление является естественным продол-
продолжением достижений последних десяти лет или около того. Дру-
Другой путь уводит к самым глубоким корням анализа: если на
этом пути когда-нибудь и удастся достичь прогресса, то весьма
вероятно, что продвижение будет очень медленно. Из множе-
множества многообещающих идей и фактов, изложенных нами так,
как мы понимаем их сейчас, следует особо выделить один эле-
элемент, имеющий первостепенное значение: я имею в виду ту
концептуальную методологическую и педагогическую роль, ко-
которую теория динамических систем играет в точных науках».
к. немо: <м"»1ы уже неоднократно отмечали в книге практи-
практическое значение такого понятия, как чувствительная зависимость
от начальных условий, и я хотел бы кратко вернуться к нему
еще раз. Необходимо отчетливо сознавать, что введение чувстви-

Заключительная дискуссия 301:
тельной зависимости от начальных условий знаменует подлин-
подлинный прогресс в точных науках. Анализ многих явлений, о кото-
которых мы бегло упоминали (в метеорологии, биологии, турбулент-
турбулентности, экономике), был пересмотрен на основе понятия ЧЗНУ.
Выяснилось, что даже, казалось бы, строгий математический
формализм может приводить к понятию статистической вариа-
вариации без необходимости введения флуктуации внешнего проис-
происхождения, и, как мы знаем, несмотря на этот статистический
аспект, можно что-то сделать, например проанализировать рас-
распределения вероятности. флуктуации или кратковременную эво-
эволюцию, установление хаоса через показатели Ляпунова или воз-
возникновение непредсказуемости. В определенном смысле именно
этот аспект явлений, исследованный нами, отсутствует в той ма-
математике, "которую мы изучали до сих пор, и становится все
более важным для понимания затронутого нами круга явлений.
В этой связи уместно подчеркнуть новизну методов, исполь-
используемых и внедренных в практику. Новизна практически состоит
только в одном: хотя фундаментальные идеи, о которых идет
речь, начали широко применяться лет 10—20 назад, они были
высказаны такими учеными, как Пуанкаре и Адамар, еще в на-
начале столетия. Случилось так, что их практическое проникно-
проникновение в физику произошло лишь совсем недавно. Они оказались
весьма эффективными, в чем мы уже успели убедиться, и таят
в себе необычайно богатые возможности с точки зрения обра-
образовательного "аспекта, что > делает желательным включение их
в программу высшей школы. Еще один важный аспект новых
идей и понятий — универсальность».
П. Берже: «Я хотел бы дополнить сказанное и подчеркнуть
«достоинства» новой области в надежде на то, что по крайней
мере некоторые из них не прошли незамеченными для читателя
нашей книги. Первое достоинство — искусство упрощения, при-
приводящее к моделям, имеющим некий смысл, несмотря на все
огрубляющие предположения. Приведу конкретный пример: .
конвекцию Рэлея — Бенара даже в малой ячейке, где уме-
умещаются только два конвективных вала, описывают уравнения
гидродинамики — уравнения Навье— Стокса, которые, как пра-
правило, не поддаются решению. Без упрощений и аппроксимаций
самые мощные компьютеры не позволяют получить численные
решения. Один из возможных подходов состоит в том, чтобы
построить модель, сильно урезав исходные уравнения. Как из-
известно, именно так была построена модель Лоренца. Такой под-
подход нельзя не признать многообещающим, но мы можем пойти
дальше и перейти от дифференциальных уравнений к разно-
разностным с тем, чтобы закончить дву- и даже одномерными ото-
отображениями. Проделав этот переход, мы приходим к предельно

302 , Заключительная дискуссия
простой формулировке, для реализации которой требуются са-
самые скромные вычислительные средства. На'этом пути нам уда-
удалось помимо прочего найти маршрут, ведущий к турбулентности
через каскады удвоений периодов, убедительно подтвержден-
подтвержденный экспериментально.
Второе, что мне хотелось бы отметить особо — силу идеи
универсальности. Мы упростили исходные уравнения до пре-
предела, и теперь наша модель универсальна. Какой смысл мы
вкладываем в это понятие? Универсальность означает, что не
только уравнение, f(x) = 4\ix(l — x), описывающее каскад
удвоений периода, но и почти любая нелинейная функция пе-
переменной х порождает тот же каскад: сценарий нечувствителен
к деталям модели. Другой аспект, связанный с универсаль-
универсальностью, состоит в том, что удвоение периода, приводящее к
хаосу, обнаружено экспериментально: в колебаниях параметри-
параметрического маятника, в некоторых системах электронных генера-
генераторов, в особом режиме работы синхронного двигателя, в неко-
некоторых немонотонных химических реакциях, в движении жид-
жидкости в тепловой конвекции и т,. д. Мы видим здесь подлинную
универсальность поведения, что убеждает нас в правильности
наблюдений и показывает, сколь широка сфера применимости
проведенного анализа. Наконец, среди общих особенностей, ко-
которые я с удовольствием отмечаю в исследованиях динамиче-
динамических систем, существует взаимно обогащающее сотрудничество
между теоретиками и экспериментаторами и, что еще более за-
замечательно, между математиками и физиками. Кроме того, тео-
теории динамических систем представляют собой область, в разви-
развитие ь'птпппй мпжнп внргти гиггтялг пягппттягяа птнпгнтрльнп
скромными материальными средствами, но обладая богатым
воображением: она как бы воплощает в себе триумф «легкой
физики».
К. Видаль: «Весьма близкая идея, которая не может не вол-
волновать физика, состоит в тесной взаимосвязи методологии (даже
в ходе рассуждений), существующей между теорией" динамиче-
динамических систем и методами, на протяжении ряда лет применявши-
применявшимися для исследования фазовых переходов. Разумеется, я имею
в виду метод ренормгруппы, которым мы можем воспользовать-
воспользоваться для определения знаменитого параметра 6=4,6692 ... суб-
субгармонического каскада. Ясно, что в свое время непременно
будет достигнут глобальный, синтез, поскольку между двумя
теориями имеется слишком много формальных аналогий, чтобы
их нельзя было объединить в рамках единого более широкого
подхода.
В более широком плане следует, несомненно, подчеркнуть
элемент, приводящий к многочисленным и разнообразным эпи-

Заключительная дискуссия 303
стемолошческим следствиям, которые мы лишь бегло затро-
затронули в нашей дискуссии: я имею в виду проблему пересмотра
традиционных представлений о детерминированности и случай-
случайности. Ясно, что серьезный пересмотр научных определений
этих понятий настоятельно необходим и нто теперь мы должны
выйти за рамки идей, сформулированных впервые Лапласом
около двух столетий назад. Замечательно также, что понятие
странного аттрактора, необычайно расширившего признанную
область детерминированности, одновременно подводит гораздо
более прочную,-чем прежде, основу под необходимость обраще-
обращения к статистическим методам. Необходимость использования
статистических методов теперь обосновывается не соображе-
соображениями прагматического характера, а как бы внутренней логи-
логикой самой математики».
И. Помо: «Хотя в книге об этом ничего не говорится, мы
можем также упомянуть о гамильтоновых системах, играющих
важную роль, с одной стороны, в небесной механике, а с дру-
другой— имеющих самое непосредственное отношение к проблемам
термоядерной плазмы, т. е. к решению самых важных техни-
технических и научных проблем нашей эры. Как показали различ-
различные исследователи, в гамильтоновых системах, например в дви-
движении частиц в неоднородных магнитных полях, также суще-
существуют законы универсальности, принципы которых были
открыты методами ренормгруппы, разработанными в связи с ис-
исследованием критических явлений. Здесь таЮке произошла сво-
своего рода перегруппировка понятий: например, в случае гамиль-
гамильтоновых систем была доказана взаимосвязь между одномерными
кристаллами, проблемами квантовой механики с квазипрриоди-
ческими потенциалами и проблемой движения заряженных ча-
частиц в сравнительно сложных магнитных полях термоядерных
реакторов. И в этом случае можно утверждать, что у нелиней-
нелинейной физики, о которой мы попытались рассказать в этой книге,
хватило сил, чтобы обнаружить универсальные явления. Можно
сказать, что блоки, на которые делились принципиальные про-
проблемы, связанные с нелинейностью, начали мало-помалу рассы-
рассыпаться, И теперь м,ы являемся свидетелями возникновения но-
нового единого подхода к нелинейным явлениям, что следует счи-
считать неожиданным поворотом событий».
К- Видаль: «С философской точки зрения здесь можно усмот-
усмотреть необычайно мощную идею, которой несомненно потребует-
потребуется время для того, чтобы проникнуть в умы ученых. Она выте-
вытекает из центрального понятия чувствительной зависимости от
начальных условий, которое иногда принято называть слабо
устойчивой динамикой. Эта фундаментальная идея состоит
в том, что через понятие ЧЗНУ наука снова приходит к осозна-

304 Заключительная дискуссия
нию, идентификации своих пределов. Здесь уместно провести
параллель с принципом неопределенности Гейзенберга. Соглас-
Согласно этому принципу, самое совершенное лабораторное оборудо-
оборудование не позволяет измерить одновременно сколь угодно точно
координату и импульс частицы. Аналогичным образом чувстви-
чувствительная зависимость от начальных условий запрещает нам пред-
предсказывать будущее динамической системы,' поток которой на-
находится на странном аттракторе, независимо от того, каким
образом мы будем это делать. Разумеется, эту параллель не сле-
следует проводить слишком далеко, поскольку между принципом
неопределенности Гейзенберга и ЧЗНУ существуют многочис-
многочисленные различия. Наиболее очевидное различие состоит в том,
что теория динамических систем есть феноменология на макро-
макроскопическом уровне, в то время как малость постоянной ft
(кванта действия) ограничивает действие принципа неопреде-
неопределенности Гейзенберга микроскопическим уровнем. Тем не менее
и в том и в другом случае речь идет об идентификации вну-
внутренних пределов науки и тем самым ее силы. Существование
этой .силы неоспоримо, но она ограничена в самом математи-
математическом смысле слова. Теория динамических систем по мере сво-
своего развития обнаруживает способность находить пределы
сферы своей собственной эффективности, что отнюдь не три-
тривиально и отнюдь не лишено интереса».

ПРИЛОЖЕНИЕ А
ЛОКАЛЬНЫЕ БИФУРКАЦИИ КОРАЗМЕРНОСТИ 1
I. ЛОКАЛЬНЫЕ БИФУРКАЦИИ
В гл. II понятие бифуркации вводится на отдельных приме-
примерах—в контексте параметрических осцилляторов и осциллято-
осцилляторов с вынуждающей силой. Но это понятие более фундамен-
фундаментально: оно имеет "основополагающее значение для целой обла-
области математики, известной под названием теории бифуркаций1).
В данном приложении мы сформулируем основные положения
этой теории.
Рассмотрим автономный поток на R":
XeR".
Этот поток зависит от некоторого множества параметров, пред-
представляемого символически буквой ц, выбранной в качестве ин-
индекса правой части F (если существует k параметров, то ц<= R*).
Ими могли бы быть Ra и Рг в эксперименте по тепловой кон-
конвекции; Рг, Ь и г в модели Лоренца; концентрация реагента
[Х]ь объемный расход У и температура Т в химических реак-
реакциях и т. д. Решения системы алгебраических уравнений
являются неподвижными точками потока, т. е. особыми точ-
точками сопряженного векторного поля, или стационарными со-
состояниями физической системы. Разумеется, поток имеет и дру-
другие решения иной природы, например периодические решения.
В пространстве параметров существование данного решения
может быть прослежено с помощью графика, описывающего
зависимость решения от р.: решение как функция параметра ц
называется ветвью решения. Точка в пространстве параметров,
от которой расходятся несколько ветвей, называется точкой би-
бифуркации.
Часто по причинам, связанным с существующими методами
анализа, мы вынуждены ограничиться рассмотрением непосред-
') Теория бифуркаций берет начало в работах Анри Пуанкаре по систе-
системам дифференциальных уравнений в начале этого столетия. Термин «бифур-
«бифуркация» был предложен Пуанкаре для обозначения ситуации, когда из данного
решения рождается несколько решений.
20 П. Берже и др.

306 Приложение А
ственной окрестности бифуркации. Основная идея состоит в том,
чтобы вывести наиболее существенные свойства, сохраняя в1
разложении в ряд Тейлора только члены низшего порядка. Та-
Такая процедура не является слишком серьезным ограничением,
ее наиболее заметным следствием является в принципе некото-
некоторое сужение области применимости наших выводов. Такое ло-
локальное математическое описание называется локальными би-
бифуркациями в отличие от глобальных бифуркаций. Это озна-
означает, что мы рассматриваем малую окрестность данного реше-
решения, а не то, что происходит на конечном расстоянии от него.
Н. КОРАЗМЕРНОСТЬ
Хотя размерность k пространства параметров ' зависит от
рассматриваемой задачи, мы хотим развить общий подход, сво-
свободный от ограничений, возникающих в связи с конкретными
условиями. Имея это в виду, мы определяем коразмерность би-
бифуркации как наименьшую размерность пространства парамет-
параметров, в котором может происходить такая бифуркация. Пояс-
Поясним это понятие на примере трехмерного пространства пара-
параметров (& —3). Геометрическое место точек в пространстве
параметров, удовлетворяющих некоторому условию, например
потери устойчивости решения, в общем случае имеет вид по-
поверхности Q (рис. АЛ,а). Почти любая прямая D пересекает
эту поверхность: двигаясь 119 прямой D (размерность 1), мы
в конце концов пересекаем поверхность Q и наблюдаем соот-
соответствующую бифуркацию. В этом случае мы говорим, что на-
наблюдается бифуркация коразмерности 1. Если мы наложим не
одно, а два условия, то они выполняются только вдоль линии
пересечения L двух поверхностей Qi и Q2, соответствующих вы-
выбранным нами двум условиям. Априори произвольная линия не
имеет шанса пересечься-с L: чтобы пересечь линию бифурка-
бифуркации коразмерности 2 (рис.; АЛ,б), мы должны двигаться вдоль
поверхности (размерность 2). ' '
Сказанное выше для случая k = 3 легко обобщается на лю-
любое другое значение k путем простой замены слов- «простран-
«пространство»; «поверхность» и т. д. словами «гиперпространство», «ги-
«гиперповерхность» и т. д. Таким образом, существенным элемен-
элементом является не само значение размерности k, а коразмерность,
т. е, минимальное число параметров, которые необходимо варьи-
варьировать для того, чтобы наблюдать бифуркацию определенного
типа. Исследование бифуркаций при этом упрощается, так как
используются только геометрические свойства соответствующего
пространства и не учитывается конкретная размерность про-
пространства параметров. Кроме того, поскольку характеристики

Локальные бифуркации коразмерности !
307
каждого типа бифуркации (диаграмма, свойства) устанавли-
устанавливаются без явной ссылки на какие-либо специфические условия,
результаты приобретают совершенно общую приложимость.
Рис. АЛ. Коразмерности бифуркаций в трехмерном пространстве параметров.
а — одно простое условие обычно соответствует заданию некоторой поверх-
поверхности Q. Произвольная линия D пересекает эту поверхность (кроме исключи-
исключительных случаев). Следовательно, для того чтобы обнаружить бифуркацию,
достаточно. двигаться вдоль линии D. Именно поэтому о такой .бифуркации
принято говорить как о бифуркации коразмерности один; б — два условия,
соответствующие поверхностям fii и ?3г, одновременно удовлетворяются
только ндоль их линии пересечения L. Ненулевую вероятность пересечения
с линией L имеет только поверхность (не изображенная на нашем рисунке).
И поэтому о бифуркациях, возникающих на линии, говорят как о би-
бифуркациях коразмерности два.
Нади простоты мы рассмотрим только локальные бифурка-
бифуркации коразмерности 1, отсылая читателя, который заинтересуется
бифуркациями коразмерности 2 и 3, к более специальным кни-
книгам и статьям. ,
20*

308 Приложение А
III. СУПЕРКРИТИЧЕСКИЕ БИФУРКАЦИИ КОРАЗМЕРНОСТИ
1 НЕПОДВИЖНЫХ ТОЧЕК
Математики доказали, что при весьма общих условиях ло-
локальное исследование, бифуркаций коразмерности 1 неподвиж-
неподвижной точки может быть сведено к нескольким архетипам. Точнее
говоря, было доказано; что существуют разложения в ряды и
замены переменной, такие, что вблизи "неподвижной точки по-
поведение системы описывается небольшим числом дифференци-
дифференциальных уравнений, зависящих от одного параметра, который мы
обозначим через \i. Интуитивно это заключение кажется доста-
достаточно разумным для бифуркаций коразмерности 1. Более уди-
удивительно то, что в фазовом пространстве также достаточно,
только одной переменной. Под действием преобразований, пере-
переводящих неподвижную точку в начало координат,, уравнения
принимают одну из классических нормальных форм. Ограни-
Ограничиваясь третьим порядком, мы перечислим кратко четыре наи-
наиболее часто встречающиеся формы, представленные в табл. I.
Поскольку типичные случаи собраны, описаны и проанализиро-
проанализированы, нам достаточно решить, какой из них соответствует рас-
рассматриваемой проблеме, и обратиться к имеющейся полной (ло-
(локальной) теории.
Таблица I. Бифуркации коразмерности 1 неподвижных точек
Нормальная фпр*а Название бифуркации
(суперкритическая) . .
х = \* — х2 Седло — узел (или точка возврата)
х = \ix — х2 Транскритическая (или со сменой
устойчивости)
х = \ix — х3 Типа вилки
2 = (ji + iy)z — z \z\2 Хопфа
X—вещественная переменная;
z—комплексная переменная;
ц —расстояние от точки бифуркации;
i—мнимая единица;
у—произвольная постоянная.
III. 1. Бифуркации седло — узел л; = ju — х"
Стационарное решение имеет вид х = ± Уц . Оно опреде-
определено только при A > 0 и впервые возникает при ц = 0. При
|л •< 0 решение не существует (ни устойчивое, ни неустойчивое).
В результате мы получаем бифуркационную диаграмму, изо-
изображенную на рис. А.2.

Локальные бифуркации коразмерности 1
309
III. 2. Транскритическая бифуркация: х = \*х — х2
Два стационарных решения х =^= 0 и х = \i сосуществуют.
Нетрудно видеть, что решение х = 0 устойчиво при ц < 0 и не-
неустойчиво при (л > 0, а для решения х — ц, все наоборот; в точке
Рис. А.2. Схема бифуркации седло — узел. Неподвижная точка расположена
в начале координат (х = 0, (х = 0). Из точки бифуркации выходят две ветви
стационарных состояний: одна устойчивая (сплошная жирная линия), другая
неустойчивая (штриховая линия). Вертикальные линии соответствуют сило-
силовым линиям векторного поля. Стрелками указано направление.
бифуркации
(рис. А.З).
Рис. А.З. Схема транскритической бифуркации.
эти два решения обмениваются устойчивостью
III. 3. Бифуркация типа вилки: х — цх— дс3
Стационарные решения в этом случае имеют вид х — 0 и
+ у'ц (последкие два решения определены только при
>0). Заметим, что эта нормальная форма инвариантна отно-

310
Приложение А
сительно преобразования *-*-(—х). Каждый раз, когда задача
нечувствительна к симметрии относительно отражения (напри-
(например, образование конвективных валов РБ при первой конвек-
_ 1
X
1
Рис. А.4. Схема бифуркации типа вилки.
Рис. А.5. Схема бифуркации Хопфа. На этой диаграмме имеется дополни-
дополнительное измерение у. Стрелки-указывают направление силовых линий вектор-
векторного поля.
гивной неустойчивости), следует ожидать нормальную форму
этого типа. Ее бифуркационная диаграмма представлена на
рис. А,4,
III. 4. Бифуркация Хопфа: г= (fi -f i\)z — z\z\2
На этот раз z—комплексная переменная, а у — произволь-
произвольная константа, которая не играет роли бифуркационного пара-

Локальные бифуркации коразмерности 1 31В
метра. Заметим, что эта нормальная форма является комплекс-
комплексным эквивалентом нормальной формы бифуркации типа вилки.
Чтобы найти решения, удобно перейти к вещественным перемен-
переменным, используя прямоугольные или полярные координаты.' По-
Полагая z — x + iy, приводим нормальную форму к следующему
виду: ,-
[B2)]
Помимо решения г = 0 (т. е. х = у = 0) существует другое ре-
решение, для которого |z|2 не зависит от времени:
Это условие определяет на плоскости (х,, у) окружность радиу-
радиусом д/ц (рис. А.5).
IV. СУБКРИТИЧЕСКИЕ БИФУРКАЦИИ
Все нормальные формы, рассматриваемые в предыдущем
разделе, являются суперкритическими (называемыми также
нормальными). Под этим мы понимаем, что нелинейные члены
х2 и х3 оказывают действие, противоположное неустойчивости,,
обусловленной членом низшего порядка. Возьмем форму х =
= цх — .V3. При малых х мы можем сохранять только линей-
линейный член. Получаемое тогда решение х — exp {\xt) расходится
на бесконечности при ц, > 0. Но решение полного уравнения не
расходится экспоненциально, так как линейный член компенси-
компенсируется членом —х3, который возрастает слишком быстро для
того, чтобы им можно было пренебречь. Записывая уравнение
к виду . ' ¦
мы видим, что нелинейный член вызывает «насыщение» эффекта
линейной неустойчивости при х2 — ii-
Однако ничто не мешает нелинейному члену низшего по-
порядка оказывать на решение дестабилизирующее действие..
В этом случае бифуркация называется субкритической, а иногда
обратной. Все перечисленные выше нормальные формы могут
быть сделаны субкритическими: для этого достаточно лишь.

312
Приложение А
Рис. А.6. Схемы субкритических (или обратных) бифуркаций,
а) ? = ц + х2; б) х = цх + х2; в) х = ц* + л;3; г) г = (jx + iy) г + г |-г |
изменить знак нелинейного члена. В результате мы получаем
бифуркационную диаграмму на рис. А.6.
V. БИФУРКАЦИИ КОРАЗМЕРНОСТИ 1 ПЕРИОДИЧЕСКИХ ОРБИТ
Естественно спросить, какого рода бифуркации могут проис-
происходить локально не из неподвижной точки, а из периодической
орбиты. Трудно удержаться от искушения еще больше обоб-
обобщить предыдущие результаты, особенно если учесть, что сече-
сечением Пуанкаре периодической орбиты является неподвижная
точка. Возникает вопрос: как далеко можно провести аналогию
между неподвижной точкой потока и неподвижной точкой се-
сечения Пуанкаре. Можно предсказать, что соответствующая ма-.
тематическая задача могла бы оказаться трудно разрешимой.
Действительно, чтобы определить, где теория возвращается
в плоскость сечения, нам потребовалось бы проинтегрировать
уравнения вдоль орбиты. Но теория Флоке (см. разд. IV. 3.1)

Локальные бифуркации коразмерности 1 ' 313-
позволяет обойти эту трудность й заняться исследованием ли- .
нейнои устойчивости периодической орбиты без необходимости
прослеживать эволюцию потока шаг за шагом. Мы можем за-
заключить, что собственное значение может пересечь единичную^
окружность на комплексной плоскости тремя возможными спо-.
собами.
Если пересечение происходит в точке -f-1, то теория не слиш-
слишком отличается от той, которая была развита? выше для непод-
неподвижных точек потока. Нормальная форма, топологически экви-
эквивалентная нормальной форме бифуркации седло-узел, предста-
вима в виде
X = X + (X — X2,
где член х введен собственным значением +1- Аналогично су-
существуют нормальные формы, приводящие к бифуркациям типа
вилки н транскритическим бифуркациям.
Когда собственное значение, равное —i, приводит к потере
линейной устойчивости, эта ситуация не имеет аналогов среди
бифуркаций неподвижной точки потока. Для этого случая необ-
необходимо развить свой особый подход, как мы сделали в гл. VIII.
На этот раз бифуркация приводит к возникновению орбиты
с удвоенным периодом через субгармоническую неустойчивость.
Бифуркационная диаграмма совпадает с диаграммой бифурка-
бифуркации типа вилки (см.рис. А.4),но поведение решения радикально'
отличается. После субгармонической бифуркации периодическое
решение попеременно посещает обе ветви. С другой стороны*
после выбора одной из ветвей, или геометрического места то-
точек, в случае бифуркации типа вилки устанавливается одно и
только одно решение.
Наконец, если потеря устойчивости обусловлена пересече-
пересечением единичной окружности двумя комплексно-сопряженными
собственными значениями, то возникает явление, которое напо-
напоминает бифуркацию Хопфа и часто так называется, несмотря-
на некоторые различия между этими двумя бифуркациями.
В сечении Пуанкаре неподвижная точка заменяется множеством
точек на кривой, напоминающей предельный цикл. Однако наш
анализ нуждается в уточнении, так как эта кривая сама не яв-
является траекторией и траектории пересекают ее весьма необыч-
необычным образом. Именно здесь становится существенным число
вращений и его рациональность или иррациональность. Эти во-
вопросы рассмотрены в приложении В, посвященном квазиперио-
квазипериодичности и синхронизации (затягиванию частоты).

ПРИЛОЖЕНИЕ Б
ПОКАЗАТЕЛИ ЛЯПУНОВА
I. ОПИСАНИЕ -
Чем быстрее расходятся траектории на аттракторе, тем труд-
труднее следить за эволюцией хаотического потока. Именно- по-
поэтому мы пытаемся оценить или измерить скорость разбёгания
траектории. Величина, используемая как мера расходимости
траекторий, называется показателем Ляпунова или числом Ля-
Ляпунова1).
Чтобы продемонстрировать важность этой величины, рас-
рассмотрим поведение траектории вблизи решения ф(г) потока:
Без ограничения общности мы будем рассматривать трехмер-
«ый потокф(г) = (ХУ), Y(t), Z(t)) и воспользуемся в качестве
примера моделью Лоренца (приложение Д). Линеаризуя поток
относительноф(г), получаем уравнение, описывающее эволюцию
разности, которую мы обозначим через 6^ (t):
4^-
(Б.П
где dF/дф — матрица, которая зависит как от потока, так и от
рассматриваемого частного решения. Для решения X(t), Y(t),
Z(t) модели Лоренца получаем
5F
-Рг
О
Рг
Y(t) X(t) -b
Проинтегрировать уравнение (Б.1) аналитически, за исключе-
нем особых частных случаев, невозможно. Однако его всегда
можно проинтегрировать численно и найти матрицу L{t), та-
такую, что
') Иногда оба термина используют как синонимы, ь более точной версии
под показателем Ляпунова понимают натуральный логарифм числа Ляпуно-
Ляпунова. — Прим. перев.

Показатели Ляпунова 315
где ЬфУ)—решение уравнения (Б. 1), соответствующее началь-
начальному смещению 60@). В силу предыдущего соотношения L@) =
= 1. Для /n-мерного потока матрица L имеет размеры т X тп
и m собственных значений.
Это очень напоминает теорию Флоке линейной устойчивости
периодической траектории.. Процедура имеет те же корни: ли-
линейный анализ поведения в окрестности траектории. Но если
в теории Флоке нас интересует только то, что происходит через
один период Т при движении по замкнутой орбите, то в данном
случае это ограничение снимается. Если собственные значения
матрицы Флйке дают информацию о линейной устойчивости пре-
предельного цикла, то собственные значения матрицы L дают ин-
информацию об эволюции в окрестности траектории, которая от-
отнюдь не обязательно должна-замыкаться на себй.
Вместе с тем уравнения (Б.1) легко интегрируются анали-
аналитическими, если производная dF/дф не зависит от времени1) и
ее собственные значения — числа (возможно, комплексные) к\,
Я2, %$. Мы приходим к матрице L{t), которая диагональна в си-
системе координат, образованной ее собственными векторами:
л, < о
0
О ем О
О 0 ем
Пусть L+—матрица, эрмитово-сопряженная с матрицей L. След
произведения L+L равен:
Tr (L+ @ L @) = е^+Х") * + е^)' + е^^ \
При возрастании t показатель с наибольшей вещественной
частью % в конце концов подавляет два остальных члена; по-
поэтому
Я= Ига-g-In [Tr(L+@L (/))].
Это выражение позволяет найти наибольшую вещественную
часть X, не прибегая к обычным методам определения собствен-
собственных значений, что весьма важно с практической точки зрения,
поскольку X определяет долговременное поведение системы. По-
Попытаемся обобщить полученное выражение на не столь частные
ситуации.
') В нелинейном потоке так будет только в том случае, если- само реше-
решение ф.уьj стационарно, тз чем можке убедиться, исходя непосредственно из
Уравнений модели Лоренца. Хотя это не соответствует интересующей нас
проблеме эволюции вблизи траектории, кз'учепке такой гипотезы тем не менее
полезно для дальнейшего.

316 \ Приложение Б ' ¦ 1
В большинстве случаев матрица dF/дф зависит от времени»
и матрица L(t) не представима в таком простом виде, как|
выше. Для этого существуют две причины: во-первых, собствен'-!
ные значения матрицы dF/дф не постоянны и, во-вторых, мат-|
рица L не диагонализуема в фиксированной системе отсчета.|
„Однако мы можем по-прежнему определить величину |
км= lira'4-In [Tr {L+(t)L(t))]t. . vj
поскольку так называемые мультипликативные эргодические|
теоремы гарантируют существование этого предела для широ-ij
кого круга ситуаций. Этот предел называется показателем Ля-|
пунова (или числом Ляпунова), соответствующим решению?
фЦ). Он выражает тот факт, что при больших временах раз-!
ность 6$ возрастает или убывает в' среднем экспоненциально!
в зависимости от того, положительна или отрицательна вели-J
чина К[ф].
II. АНАЛИЗ ПРОСТЫХ СЛУЧАЕВ
Из многих возможных вариантов сосредоточим внимание н
трех случаях, которые легче понять, так как матрица dF/дф
(и, следовательно, L) диагонализуема в фиксированной си
стеме координат. '
Если dF/дф имеет постоянные собственные значения, то соб
ственные значения матрицы L(t) имеют вид е1'*, где X,- не за
р
висят от t при любых i; поэтому Х\ф\ действительно является!
наибольшей вещественной частью1) собственных значений Xi.4
В качестве второго случая рассмотрим . матрицу dF/дф, со-
соответствующую умножению на скаляр а, который стохастически
флуктуирует во времени (эффект «мультипликативного шума»);
Так как в этой ситуации '
матрица L(t) вырождается в скаляр:
\nL{t)=\dt'a{t').
i
') Матрица L имеет на самом деле т собственных значении, или показа-1»
телей, каждое из которых соответствует поведению в одном -из собственны^
направлений. Но данный метод вычислений позволяет выделить только однсЦ
собственное значение — с наибольшей вещественной частью. Я

Показатели Ляпунова 317
Рассмотрим среднее значение этой величины
t
Если статистический ансамбль, по которому мы вычисляем сред-
среднее, стационарен (не зависит от времени), то эргодическая тео-
теорема1) позволяет заменить а (Г) средним а по (не зависящему
от времени) ансамблю:
1
и поэтому2)
Обобщая, можно утверждать, что, когда dF/дф и L диаго-
нализуемы в фиксированной системе отсчета, матричное урав-
уравнение (Б.1) принимает вид
= C[j>(f)]6Z,
где А, В и С — собственные значения (по предположению ве-
вещественные) матрицы dF/дф в фиксированной системе отсчета.
Решения известны:
6Х@ = бX @) ехр \\dfA [ф {t')] I,
1) Эргодическая теорема по существу утверждает, что если x{t) —зави-
—зависящая от времени случайная величина с распределением вероятности Р(х),
то среднее функции f(x) по времени для реализации x(t) не зависит от вре-
времени и равно:
2) Более подробные вычисления показывают, что если а(^) не имеет «па-
«памяти», то при больших временах
(lr.-L (ОJ = а'/2 + ct,
где коэффициент с зависит от двойной корреляции a(t) при малых временах,
т.е. от величины a (<i) — б) — (a (ti) — а). В свою очередь корреляция за-
иисит только от разности \ti — <г|, если, как сказано выше, а — стационар-
[,;,:¦' случайный процесс. При большой разности \ti — i2\ корреляция стре-
стремится к нулю, так как а(?4) и CL(h) при этом становятся независимыми
случайными величинами и (a (t) — а) =0. Таким образом, при больших вре-
времена:; среднее а (/) функции L(t) статистически определено с точностью до
флуктуации порядка t~l/2.

318 - Приложение Б %
где величина X выбрана нами в направлении собственного век-
вектора с наибольшим в среднем собственным значением. По-
Поскольку нас интересует поведение 8Х при больших временах,
а не мгновенные значения этой случайной величины, наше вни-
внимание привлекает величина
t
Эргодическая теорема, о которой мы уже упоминали, утверж-
дает, что если <Л> — среднее величины А [ф] по множеству зна-
значений ф, то <Л> есть и среднее по времени. Следовательно,
\im ±
и поэтому
Нас интересует среднее значение логарифма отношения
\bX{t)/bX(Q)\, а не среднее значение самого отношения потому,
что логарифм флуктуирует гораздо слабее и поэтому его сред-
среднее значение имеет больший физический смысл. Чтобы проде-
продемонстрировать это, разделим интервал, по которому проводится
интегрирование, на множество интервалов длиной т, где г —
характерная длина корреляции для А\ф(?)}. Пусть Af — число
таких интервалов. Тогда
где Л,—среднее значение А по одному из малых интервалов.^
Заметим, что Л, с различными индексами статистически неза-
независимы, так как длина интервалов меньше длины корреляции. I
Этому разложению показателя в сумму соответствует, разложе-!
ние экспоненты в произведение:
t N . '
ь (Б.З)
где р,(= ехр(тЛ,)) образуют последовательность из N незави-
независимых множителей.
Предположим теперь, что R. с равной вероятностью прини-я
мают значения 1/2 и I. Вычислим среднее и среднеквадратич-:
л

Показатели Ляпунова 319
яое значения E(t):
~?-(|+ if-®1.
Отношение среднего квадрата к квадрату среднего значения
равно ' • л. ¦
(?»(<)) _ f ЮУ*
(Е (t)f 4 9/ '
При очень больших N это отношение также становится очень
большим. Следовательно, нескольких очень больших значений ?
достаточно для того, чтобы средний квадрат <?2> был гораздо
больше!), чем квадрат среднего значения <?>2. Это означает,
что распределение вероятности случайной величины Е с увели-
увеличением ^испытывает сильный разброс: мы показали, что за-
задаваемая выражением (Б.?) величина Е сильно флуктуирует при
больших N. Как показывает приведенный в примечании пример,
мы можем ожидать, что выбор среднего значения логарифма
величины Е будет гораздо более «разумным». Именно так и
происходит: экспонента от среднего логарифма случайной вели-
величины E(t) дает наиболее вероятное значение E(t). Тем не ме-
менее не следует упускать из виду, что со временем отношение
\8X(t)/8X@) | сильно флуктуирует относительно наиболее ве-
вероятного значения. В частности, его всегда можно умножить
') Чтобы показать правдоподобность такого заключения, приведем про-
простой числовой пример. Рассмотрим случайную величину X, принимающую зна-
значение 1 с вероятностью 99,9,% и значение 1000 с вероятностью 0,1 %. Сред-
Среднее значение такой величины X равно 0,999-1+0,001-1000 «2, а ее
средний квадрат равен 0,999-1+0,00.1-10" « 103. Это показывает, что
средний квадрат величины X гораздо чувствительнее к присутствию редких
больших флуктуации, чем ее среднее значение. Наш пример показывает так-
также, что для сильно флуктуирующей случайной величины среднее значение
утрачивает свой смысл. Действительно, утверждение 6 том, что среднее вели-
величины X равно 2, мало что говорит о распределении этой величины. Гораздо
более содержательным было бы утверждение о том, что наиболее вероятное
значение X равно 1. Нетрудно показать, что это наиболее вероятное значение
может быть найдено из среднего значения логарифма:
(lg X) = 0,999 • 0 + 0,001 • 3 да 0,003.
Следовательно," s
что и требовалось показать. Качественно полученный результат объясняется
тем, что логарифм является очень медленно возрастающей функцией своего
аргумента. Таким обпазом, большие флуктуации случайной величины X иска-
искажают статистику In \Х\ гораздо меньше, чем статистику \Х\ и тем более Хг,

320 Приложение Б
на коэффициент (},-, который будет уменьшать (или увеличивать)
отношение в 10 раз по истечении интервала времени т. Следо-
Следовательно, если
fc <ln?@> ~ а, .
то мы не можем заключить, что
<?(/)> ~ е«
так как отношение (E(t))/elt испытывает по крайней мере ко-
конечные флуктуации и, следовательно, не стремится к постоян-
постоянному пределу, как того требует последнее равенство,
'' III. МЕТОДЫ ОПРЕДЕЛЕНИЯ
^Определяющее соотношение (Б.2) имеет большое практиче-
практическое значение, так как лежит в основе некоторых алгоритмов
определения Х[ф\ по данным экспериментального измерения
8X(t). Принцип состоит в следующем: предположим, что мы
"свели непрерывную экспериментальную динамику к отображе-
отображению первого возвращения x-+f(x), также экспериментальному,
в некотором конечномерном фазовом пространстве (на практике
1R2 или R3). От этого экспериментального отображения мы мо-
можем с помощью какой-нибудь численной процедуры1) перейти
к аналитическому представлению отображения f. После того
как это сделано, нам остается только найти число Ляпунова
аттрактора, порождаемого приближенным аналитическим ото-
отображением /. Для дтого мы воспользуемся непосредственно
определением. Выберем последовательность из Л' итераций
(хи х2, ..., xh) и вычислим произведение ма/гриц Якоби
Так как при каждой итерации вектор флуктуации умножается
(в линейном приближении) на матрицу Якоби df/dx\Xl, после N
4) Как видно из рис. VI. 24 и VI. 25, сечения Пуанкаре некоторь;;; ат-
аттракторов напоминают аттрактор Энона. Поскольку аттрактор Энона возни-
возникает в преобразовании, явно зависящем от двух вещественных чисел а и J3,
мы пытаемся определить значения параметров с, и 6 в экспериментальной
ситуации. Для этого можно воспользоваться, например, методом ;;ашу:ен;Л1п;х
квадратов, т.е. минимизировать су^му^ \%i.ri — ?а g(-*j)|2 п0 а и "¦ где
?а а— преобразование Энона. a Xi — упорядоченная последовательность
экспериментальных точек.

Показатели Ляпунова ' 321
итераций получаем
6х
•лг
— Л.
дх
дх
Среднее по времени (соответствующее непрерывному времени)'
заменено средним по числу N итераций, и показатель Ляпунова,
который требуется найти, равен
где Jn заменяет матрицу L(t). Ясно, что такой метод лучше
всего работает, когда f может быть сведено к отображению
прямой на себя. Заметим также, что показатель Я безразмерен,
в то время как рассмотренная ранее величина <Л> имеет раз-
размерность частоты (обратного времени). Для перехода от <Л>
к А. достаточно умножить <Л> на среднее время между двумя
пересечениями траектории с поверхностью сечения: показатель
X есть скорость расхождения траекторий за «средний период»
(и, следовательно, безразмерен), тогда как <Л> есть скорость
расхождения траекторий в единицу времени.
При численном моделировании нелинейных потоков опреде-
определение наибольшего показателя Ляпунова осуществляется непо-
непосредственно, если имеется доступ к адекватным вычислитель-
вычислительным средствам. Исходя из вычисленного выше решения <j>{t),
мы можем с помощью численного интегрирования уравнения
(Б.1) найти матрицу L(t) и, пользуясь определением, оценить
Я[ф]. Подчеркнем, что, согласно эргодической теореме, для этого
'iv требуется предположения о дпагоиалиоацнн матрицы dF/дф.
Это было сделано для модели Лоренца с Рг = 10, b == 8/3 и
параметром г, близким к порогу перемежаемости ri (см. гл. IX).
Мы видим, что в этом случае (см. рис. IX. 15) наибольший по-
показатель Ляпунова возрастает как квадратный корень из г — г{
(это подтверждает одно из предсказаний теории перехода че-
через перемежаемости). Другим примером служит модель Рёс-
слера, введенная в гл. IV [уравнение A1)}. При фиксированных
значениях параметров а и Ь (а = 6 = 0,2) мы варьируем тре-
третий ПЯГ5Я ДЯРТГ! Г IT II7J."-77?iETUri ТТГЛ-^Г-Г-.ГЛтггОйя ТТГ*.<г#-.т^ АЛ ит плп^ттоа,,-
несколько режимов, одни из которых периодические, другие
хаотические. На рис. Б.1 (графике наибольшего отличного от
нуля показателя как функции параметра с) видно, что % при-
принимает положительные значения, а они соответствуют расхож-
расхождению траекторий на аттракторе.
С другой стороны, когда мы сталкиваемся с решением <j>(t),
полученным экспериментально, вычисление показателя Ляпу-
21 П. Берже и др.

322
Приложение Б
нова становится гораздо более деликатной задачей из-за по-
погрешностей в измерениях и неизбежного экспериментального
шума. Если предположить, что фЦ) флуктуирует в некотором;
статистическом ансамбле, то теоретически -возможно найти ин-
интервал времени [^,^1». на котором реализация (т. е. определен-
определенЛериодинеский. ХКаотииескгш.
' резким
Рис. Б.1. Наибольший отличный от нуля показатель % модели Рёсслера как:
функция параметра с [уравнение_A1) из первой части нашей книги]. Поло-
Положительные значения показателя Я свидетельствуют о расхождении первона-
первоначально близких траекторий на аттракторе (чувствительной зависимости от
начальных данных). Непрерывная кривая проходит через 300 отдельно вы-
вычисленных точек (а = Ь = 0,2; параметр с принимает значения из интервала
[2,5; 6]).
Из работы Дж. Кратчфилда, Д. Фармера, Н. Паккарда, Р. Шоу, Г. Джонса
и Р. Дж. Доннелла.
ная последовательность значений) величины <p{i), сколь угодно
близка к опорной реализации, заданной на интервале времени
[гь щ такой же длины. Для этого необходимо удовлетворить
условию близости траекторий в начальный момент времени.
Сравнивая поведение системы между t2 и t'2. мы можем прийти
к заключению о различии в эволюции между соседним» траек-
траекториями. Конкретная трудность такого подхода проистекает от
того, что показатель Ляпунова отражает средний эффект: еле-

Показатели Ляпунова ,
323
довательно, для получения его статистически значимого сред-
среднего значения необходимо произвести многочисленные сравне-
сравнения1)-
IV. ХАРАКТЕРИСТИКИ АТТРАКТОРА
Для хаотического решения *j>(t), связанного со странным
аттрактором, ЧЗНУ означает существование положительного
Рис. Б.2. Знаки показателей Ляпунова для аттракторов различных типов в
трехмерном фазовом пространстве. Нетрудно узнать аттракторы, описанные
в нашей книге: предельный цикл Ван дер Поля (s = 0,4) и аттрактор Ло-
Лоренца (г = 28).
показателя Ляпунова К[ф). Это — прямое следствие среднего
расхождения соседних траекторий. Следовательно, получение
положительного показателя Ляпунова есть верный признак
') Для определения наибольшего показателя Ляпунова по эксперимен-
экспериментальным временным рядам предложено несколько алгоритмов. Судя по от-
отсутствию значительного прогресса, удовлетворительного результата пока до-
достичь ке удалось. Именно поэтому мы не излагаем здесь эти попытки.
21*

324 Приложение Б
хаотического режима. Вычисляя по определению показатель Ли-
пунова периодического или квазипериодического решения, мы по-
получаем Х[ф] = 0. Если решение устойчиво, то любое смещение,
«перпендикулярное» траектории, со временем убывает, и, следо-
следовательно, соответствующие собственные значения матрицы L
всегда меньше единицы. С другой стороны, смещение вдоль са-
самой траектории не затухает и не усиливается; оно эквивалентно
просто сдвигу начальной точки х0. Инвариантность такого сме-
смещения во времени выражается существованием постоянного соб-
собственного значения Л, равного единице, которое в этом случае
больше всех остальных собственных значений. Следовательно,
наибольший показатель Ляпунова Я,,- равен нулю.
Обобщая эти простые рассуждения, естественно идентифи-
идентифицировать аттракторы по знакам показателей Ляпунова А,;. Для
трехмерного потока это приводит к результатам, представлен-
представленным в таблице. Все перечисленные в ней аттракторы изобра-
изображены на рис. Б.2.
Тип аттрактора Знаки показателей Ляпунова
Неподвижная точка (—,—.—)
Предельный цикл @,—,—)
Тор Г2 @,0,-)
Странный аттрактор (+.0,-*-)

ПРИЛОЖЕНИЕ В
СИНХРОНИЗАЦИЯ ОСЦИЛЛЯТОРОВ
I. ОБЩИЕ СВЕДЕНИЯ
Проблема синхронизации связанных нелинейных осциллято-
осцилляторов требует для своего решения сложных и глубоких математи-
математических теорий и привлекает внимание великих умов, начиная
с Пуанкаре. В настоящее время ее можно считать решенной,
но крайней мере с точки зрения физика. Мы не собираемся про-
проводить здесь исчерпывающий анализ огромного объема накоп-
накопленных значений, для которого нам потребовалось бы вводить
сложные понятия из анализа, топологии и теории чисел, и огра-
ограничимся изложением наиболее важных практических результа-
результатов теории.
Если говорить не слишком строго, то можно утверждать, что
в синхронизации осцилляторов существуют две компоненты.
а) Во-первых, необходимо иметь два или более независимых
осцилляторов, описываемых, например, двумя уравнениями
Ван дер Поля с различными значениями параметра е, и иметь
возможность связать их (позднее мы поясним на примерах, что
имеется в виду под Связью).
б) Во-вторых, необходима диссипация. В противном случае
мы имели бы гамильтонову систему, для которой связанные
осцилляторы (по крайней мере частично) описываются так на-
называемой теорией К.АМ1).
Наиболее известным примером синхронизации является дви-
движение Земли и Луны. Вращение Луны вокруг своей оси синхро-
синхронизуется с ее обращением вокруг Земли, поэтому мы всегда
видим обращенную к нам одну и ту же сторону Луны. С точки
зрения математики это затягивание частоты простейшего типа
1:1, так как оба осциллятора имеют одинаковую частоту. Фи-
Физическая интерпретация двух осцилляторов в случае движения
Луны очень проста: одно твердое тело вращается с постоянной
частотой вокруг оси инерции, а другое обращается по кеплеров-
ской орбите. Механизм связи между этими двумя осцилляторами
') Теория названа в честь се создателей Колмогорова, Арнольда и Мо-
зера. Было бы неверно утверждать, что в теории связанных осцилляторов
все до конца понятно.

326 Приложение В
гораздо менее очевиден и имеет двоякое происхождение. Во-пер-
Во-первых, распределение масс на Луне обладает определенной
асимметрией (Луна сферически несимметрична). Во-вторых,эта
асимметрия связана силой ньютоновской гравитации с анало-
аналогичной асимметрией, вызываемой на Земле распространением
приливов. Несмотря на малую интенсивность, эта связь приво-
приводит к весьма важным последствиям, поскольку вызываемые эф-
эффекты накапливаются на протяжении длительного периода вре-
времени (ситуация, часто встречающаяся в астрономии). Затуха-
Затухание обусловлено трением приливной волны о Землю (о конти-
континенты и о морское дно). Величину силы трения можно оценить
по запаздыванию между приливом и вызывающим его притя-
притяжением Луны. Следует заметить, однако, что создание количе-
количественной теории приливов все еще остается делом будущего.
Можно привести много других примеров синхронизации. Ин-
Интуитивно ясно, что для синхронизации осцилляторов с близкими
частотами достаточно слабого взаимодействия. Например, из-
известно, что если просто положить рядом на стол два экземпляра
механических наручных часов одной модели, то механическая
передача толчков от одной пары часов к другой обеспечивает их
синхронизацию. Нельзя не вспомнить и биологические примеры:
циркадные ритмы, синхронизованные со сменой дня и ночи, и
более курьезные явления, такие, как синхронизация менстру-
менструальных циклов у женщин, живущих повседневно общающейся
группой.
Многочисленные примеры синхронизации мы находим в ок-
окружающих нас различных механических и электрических коле-
колебательных устройствах. Так, субгармоническая неустойчивость
параметрического осциллятора означает, что между частотами
собственных колебаний и вынуждающей силы имеет место
арифметическое соотношение (см. гл. II). Процесс синхрониза-
синхронизации того или иного рода часто лежит в основе точных методов
измерения и регистрации: гетеродин в радиотехнике, нониус
в механике, муар в оптике. Само слово «синхронизация» стало
достоянием широких кругов общества и в повседневной речи
употребляется в смысле одновременности событий, происходя-
происходящих далеко друг от друга, а не совпадения частот.
II. АНАЛИЗ ПРОБЛЕМЫ
Теоретический подход к явлению синхронизации, которого
мы будем здесь придерживаться, основывается главным обра-
образом ка исследовании отображения Пуанкаре на окружности. На-
Напомним кратко взаимосвязь между синхронизацией и диффео-
диффеоморфизмами на окружности.

Синхронизация осцилляторов 327
а) Теория Флоке устойчивости периодических траекторий
показывает, что бифуркация Хопфа происходит, когда два комп-
комплексно-сопряженных собственных значения матрицы устойчи-
устойчивости пересекают единичную окружность на комплексной пло-
плоскости при изменении управляющего параметра. Бифуркация
Хопфа является суперкритической, когда слабо нелинейные эф-
эффекты стабилизируют траекторию в окрестности бывшей перио-
периодической траектории, которая сохраняется, но становится ли-
линейно неустойчивой. В общем случае г — диаметр малой окруж-
окружности тора (меридиана), а е — управляющий параметр [в точке
С-
Рис. В.1. Сечение Пуанкаре потока на торе Г2. На этом рисунке показано,
как, зная поток на торе, построить соответствующее сечение Пуанкаре для
•окружности С на торе. Траектория, выходящая из точки х на окружности С,
пересекает окружность С снова в точке f(x).
бифуркации е—0; при е<0 предельный цикл вдоль большой
окружности (параллели) линейно устойчив; при е > 0 он ли-
линейно неустойчив и поэтому не является более предельным цик-
циклом] . Если параметризация с помощью е «общего положе-
положения» !), то выполняется закон подобия г « е1/2.
Вывод теории бифуркаций, которым мы воспользуемся, со-
состоит в том, что по крайней мере в окрестности суперкритиче-
ской бифуркации Хопфа существует поток, для которого аттрак-
аттрактором является тор Т2.
б) Поток на Т2 (рис. В.1) определяет отображение Пуан-
Пуанкаре (или диффеоморфизм) со следующими свойствами:
1) отображение непрерывно и дифференцируемо;
2) оно отображает окружность Г1 (или одномерную сферу
S1) на себя.
;) Это не исключает некоторых частных случаев, рассмотренных Арноль-
Арнольдом. Они возникают при 8 = 0, когда собственные значения матрицы Флоке
являются простыми корнями из единицы, например ехр(±2ш'/3) и ±i.

328
Приложение. В
Окружность удобно параметризовать с помощью криволи-
криволинейной координаты, «развертывая» окружность в . единичный
¦Хп 1
сг е R
Рис. В.2. Представление двух непрерывных обратимых отображений в прямо-
прямоугольной системе координат, а — отображение f окружности на себя описы-
описывает поток на торе как сечение Пуанкаре этого потока (см. рис. В.1). Ка-
Кажущиеся разрывы в точках 0, 1 и х0 устраняются, если вспомнить, что как
на оси абсцисс, так и на оси ординат 0 и 1 соответствуют одной и той_же
точке на разрезе развернутой окружности; б — второе отображение f(x\
х е R построено по отображению f и может быть использовано для опреде
ления числа вращений р^| на торе.
интервал [0, 1]. При этом точки 0 и 1 соответствуют одной и
той же окружности. После этого диффеоморфизм можно пред-
представить отображением x—>~f(x) интервала [0,1] на себя, та-
таким, что /(*)е[0, 1], f@)=i(l) и прообраз f-''ix) каждой

Синхронизация осциллятбров 32S*
точки единствен. Последнее свойство связано с тем, что рас-
рассматриваемые потоки однозначно обратимы. График отобра-
жения f(x) в прямоугольной системе координат имеет кажу-
кажущийся разрыв (рис. В.2), возникающий из-за невозможности
представить циклическую координату на плоском графике. Ус-
Условие непрерывности диффеоморфизма на окружности состоит
в том, что если /(хо + О)=1, то /(х0 —0) = 0 и /@) = f(l) =
= xi, как показано на рис. В.2, а. Отображение f обратимо,
если условие (df/dx) > 0 выполняется всюду [возможно также
неравенство (df/dx) < 0, но рассматривая вместо f двукратную
итерацию / °/, мы снова возвращаемся к случаю (df/dx) > 0].
Приняв все сказанное за отправной пункт, исследуем свой-
свойства диффеоморфизмов на окружности, аналогичных диффео-
диффеоморфизму на рис. В.2, где изображено отображение первого
возвращения потока на торе (см. рис. В. 1). Существенным эле-
элементом анализа является число вращений отображения /, обо-
обозначенное через р[л, — еще одно понятие, введенное Пуанкаре..
III. ЧИСЛО ВРАЩЕНИИ
Чтобы понять, какой смысл имеет число вращений, рассмот-
рассмотрим сначала простейшую из возможных функций /, удовлетво-
удовлетворяющих условиям, которые наложены на отображение первого
возвращения — поворот окружности на постоянный угол а:
где {у}—дробная часть числа у. Здесь а — произвольное поло-
положительное вещественное число, которое меньше или равно еди-
единице. Исходя из этого отображения, мы можем затем опреде-
определить другое отображение, которое непрерывно и переводит R
в себя, с помощью простого сдвига:
х -> у + а, х е R:
Мы видим, что при 0 < х < 1 второе отображение порождает
либо {х + а}-\-1, либо {х-\-<х}. Итерируя это отображение п
раз, получаем
jc<") = х + па,
откуда находим значение а:
а= lim —.
С помощью аналогичного построения мы можем определить
угол поворота любого диффеоморфизма на S1, представленного

.330 Приложение В
Отображением x-*-f{x). Первый этап состоит в построении по
отображению / диффеоморфизма f на R, который относится к /,
как х + а, к {х-\-а}. Пусть х0 — точка из 10,1], такая, что
,/(*о)= 1. Определим ]{х), просто полагая (рис. В.2,б), что
а) f(x) — f (х) при 0 < х < х0;
б) f(x) = f(x)+ 1 при' хо<х<1;
в) при всех остальных значениях х е R диффеоморфизм
f(x) полностью определяется условием периодичности f(jc +
-f- n) = f (х) + п, где п — целое число.'
Нетрудно проверить, что если f(x) = {x + а}, то ](х) = х-\-
+а, и что в общем случае f(x) наследует от f(x) свойства не-
непрерывности и обратимости. Число вращений по определению
-есть величина
fflLf (B.i)
где /(л) (х) есть n-я итерация отображения f.
Число вращений не зависит от выбора начальной точки х.
В этом можно убедиться, есл» учесть, что, поскольку f моно-
монотонно возрастает, f(x) и, следовательно, ](п)(х) изменяются са-
самое большее на единицу, когда х принимает значения, заклю-
заключенные между 0 и 1. Следовательно, «остаток», обусловленный
выбором точки х в определении p(fJ, составляет лишь l/п в пра-
правой части соотношения (В.1) и обращается в нуль в пределе
больших п.
Важность числа вращений обусловлена главным образом
тем, что величина p[f, инвариантна относительно сопряжения.
В некотором смысле число вращений полностью описывает диф-
диффеоморфизм / (за исключением того случая, когда p[f] обла-
обладает «исключительными» арифметическими свойствами). Под
сопряжением мы понимаем изменение параметризации (или за-
замену переменной) окружности. Пусть х-^С(х)—преобразова-
х-^С(х)—преобразование координат, где С — обратимое отображение интервала [0, 1]
на себя. В результате преобразования координат С диффеомор-
диффеоморфизм / переходит в отображение
где о означает композицию функций. Мы можем построить по
С преобразование координат С на R, такое, что
где операция _~ расширяет диффеоморфизм на S1 до диффео-
диффеоморфизма на R, определенного выше.

Синхронизация осцилляторов 331
Ясно, что
а поскольку композиция функции и обратной функции есть тож-
тождественное отображение:
СьС~1 = 1,
мы получаем
1С = С» ° / °С
ив общем случае
Используя определение числа вращений, можно показать, что
а это доказывает инвариантность р относительно сопряжения,
т. е. р не изменяется при произвольном преобразовании коор-
координат х-*- С (х).
Важность числа вращений проистекает из обращения сле-
следующего свойства: если два диффеоморфизма на S1 имеют одно
и то же иррациональное число вращений, то существует преоб-
преобразование координат С(х), связывающее их сопряжением. До-
Доказательство этого утверждения сложно и основано на нетри-
нетривиальном использовании алгебраических свойств p,f,, а поэтому
мы не будем останавливаться на нем.
Таким образом, мы видим различие между двумя типами си-
ситуаций: в одних случаях р.,. рационально (сопряжения, вообще
говоря, не существует), в других иррационально (сопряжение
существует). Такое заключение часто считают «нефизическим»,
так как оно придает решающее значение природе потока на
торе и алгебраическим свойствам числа вращений. Мы подробно
рассмотрим, к каким физическим следствиям приводит такое
различие после того, как выясним, какие математические след-
следствия из него проистекают.
IV. РАЦИОНАЛЬНОЕ ЧИСЛО ВРАЩЕНИИ, СИНХРОНИЗАЦИЯ
Заглядывая вперед, мы можем утверждать, что случай,
когда число вращений р„, рационально, важен, поскольку со-
соответствует синхронизации двух частот вращения по большой
и малой окружности тора (см. рис. B.I). Пусть PIfj={p/o}
(р, ц — целые числа). Прежде всего мы можем ограничиться
случаем р[п = 0. Действительно, используя определение числа

332 Приложение В
вращений, можно показать, что
а поэтому
Покажем теперь, что если число вращений равно нулю, то*
уравнение f(x) = x имеет в интервале [0, 1] по крайней мере
один корень. Если бы это было не так, то (поскольку интервал
[О, 1] компактен) для \f(x) — х\ должна была бы существовать
нижняя граница >| и верхняя граница |', такие, что 0 <.? <
<\f(x)—х\<Ц' <1. Следовательно, расстояние между гра-
графиком функции f(x) и- диагональю (или, графиком любой из
функций х-\-п) всегда было бы больше, чем min(g, 1 — ?'). От-
Отсюда мы заключаем, что
0<inf(g, l-6')<p[fi<l-inf(|, I — ГX 1,
а это противоречит гипотезе, согласно которой р.,. = 0. Следо-
Следовательно, уравнение f(x) = x имеет на S1 по крайней мере один
корень. Мы можем доказать более сильное утверждение: при
общем выборе отображения /, такого, что pIf] = 0, отображение
x-^-f(x) имеет по крайней мере две неподвижные точки, из ко-
которых одна устойчивая, а другая неустойчивая. Это свойство
лучше всего доказывать графически. Рассмотрим случай, когда
f(x)—х имеет корень между 0 и точкой ^..удовлетворяющей
уравнению f(xQ — 0)=1, и f @) —jci > 0 (как на рис. В.З).
Тогда функция f(x)— x положительна между 0 и ха (наимень-
(наименьшим корнем уравнения f(x) = х) и обращается в нуль в точке
ха. Если (dfJdx)\X!=x Ф 1, то график функции f(x) не касается
диагонали в точке ха и при значениях х, чуть ббльших ха, функ-
функция (f(x) — х) отрицательна. Так как при х=.х0 функция (f(x) —
— х) снова положительна, между х'а и х0 заведомо существует
второй корень хь функции (f(x)—х). Это общая ситуация в том
смысле, что мы приняли только одно предположение:
(df/dx)\x^x Ф\. Обобщение этого рассуждения показывает
что корни функции (f(x) — х) встречаются парами, если каж-
каждую точку касания графика функции f(x) и диагонали считать
за два корня.
Выясним, что происходит при итерации отображения х-*-
-»-/(Y). Корни функции (f(x) — а-) являются неподвижными точ-
точками итерации. Рассмотрим простейший случай, когда (f(x) —
— х) имеет в интервале [0, 1] только два корня ха и хь, таких,
что 0 < ха < хь < х0 (см. рис. В.З). Каким будет результат

Синхронизация осцилляторов
333
итерации х-*- f (х)? Так как 0 < (dfjdx) \х^х < 1, ха — устойчивая
неподвижная тбчка, а так как (df/dx)\XTnX =±xb->l, хь— не-
неустойчивая неподвижная точка. Применяя изложенные в гл. IV
графические методы, мы видим, что при. всех начальных точках
итерации отображения / сходятся к ха, за исключением того
•случая, когда в качестве начальной точки мы выбираем неустой-
неустойчивую неподвижную точку Хь.
Рис. В.З. Итерации отображения на окружности x-*-f(x). Существуют две
неподвижные точки: ха (з'стойчивая) и хь (неустойчивая). Итерации всех
начальных условий на [0, 1], кроме х = Хь, сходятся к точке ха.
Если ха и хь в действительности совпадают с одной и той же
точкой касания графика функции f(x) и диагонали, то итера-
итерации отображения / всегда сходятся к той же точке касания.
В этом случае заключительная фаза сходимости к неподвижной
точке происходит медленнее, чем в том случае, когда
и1
Напомним, что по предположению число вращений равно
нулю .¦•'.¦
а) либо потому, что отношение p/q — целое число и тогда по
определению
Plf ] = {plq) = 0.
б) либо потому, что мы рассматриваем q-ю (а не первую)
итерацию отображения (f(<7)), используя сравнение по модулю
единица, входящее в определение числа вращений1).
J) Этот случай соответствует затягиванию частот с отношением 1 : 1 (как
вращение Луны вокруг своей оси и ее обращение вокруг Земли). Период
вращения по малой окружности тора кратен периоду вращения по большой

334 Приложение В
Если р и q — взаимно простые (т. е. не имеющие общего
делителя) целые числа, то, как известно, отображение *->-¦
—*-f№(x) имеет по крайней мере одну пару неподвижных точек,,
поскольку p[f] = 0. Но что можно сказать о самом отображе-
отображении /? Пусть х — одна из неподвижных точек отображения f(<?).
Показатель q— наименьшее число, такое, что /<'?>(#) = х. Дей-
Действительно, предположим, что существует целое число q* < q,
для которого f<4*} (х) — х. Тогда число вращений отображения
f4*'1 было бы равно нулю, а число вращений отображения f
было бы вида p*/q*. Это противоречит предположению о том,,
что в отношении p/q числа р и q взаимно простые. Кроме того,
q последовательных итераций точки X, т. е. <f(X), ..., f(l?)(X),,'
образуют последовательность точек (Х\, Х2, ..., Xq) на S1, на-
называемую ^-циклом и такую, что
*/ = /(*/_,); Х,ФХН, Kj<k^q,
где индекс j берется по модулю q, так что Xi=f(Xg). По-
Поскольку f(<?) имеет две неподвижные точки, существуют по край-
крайней мере две такие последовательности (с периодом q), одна
из которых неустойчива. В нейтральном случае, когда график
отображения /w касается диагонали в точке Хх \а также в точ-
точках Хч, Хз, ..., Xq, поскольку производная (df/dx)fw прини-
принимает в каждой точке последовательности одно и то же значе-
значение], обе последовательности совпадают. В остальных случаях
между любыми двумя точками устойчивой последовательности
всегда найдется одна точка неустойчивой последовательности^
и наоборот. Таким образом, устойчивая последовательность при-
притягивает' все начальные точки, за исключением точек неустой-
неустойчивой последовательности. Обобщая эти рассуждения, можно
показать, что если существуют другие последовательности, устой-
устойчивые или неустойчивые, то они также имеют период q.
Если отображение Пуанкаре x-*-f(x\ имеет устойчивый
q-йпкл, то соответствующий непрерывный поток имеет предель-
предельный цикл. Устойчивая траектория системы пересекает себя'
после q оборотов и, следовательно, является простой замкнутой
кривой. Спектр Фурье состоит из линий на частотах, кратных
некоторой основной частоте. Мы говорим, что это синхрониза-
синхронизация, поскольку две основные частоты, соответствующие движе-
движениям по большой и малой окружности тора, связаны между
окружности. Сводя поток на торе к диффеоморфизму на окружности, мы
не можем различить, сколько оборотов (один, два или больше) по большой
окружности совершила траектория между двумя последовательными пере-
пересечениями с малой окружностью. Следовательно, с точки зрения диффеомор-
диффеоморфизма на S1 отношения двух периодов движения определены только с точ-
точностью до целого числа.

Синхронизация осцилляторов 335
собой рациональным отношением. Однако при очень больших q
основной период становится очень длинным, а так как расстоя-
расстояние между соседними линиями спектра Фурье порядка \/q, ана-
анализ спектра может стать затруднительным и даже невозмож-
невозможным, поскольку неизбежный экспериментальный шум увеличи-
увеличивает ширину линий (см. гл. III).
V. ИРРАЦИОНАЛЬНОЕ ЧИСЛО ВРАЩЕНИЙ,
КВАЗИПЕРИОДИЧЕСКИЙ РЕЖИМ
Изложение в этом разделе неизбежно должно быть более
сухим из-за математических трудностей, связанных с анализом
в случае иррациональных чисел вращений. Мы уже говорили
о том, что два диффеоморфизма / и /' на S1 называются сопря-
сопряженными, т. е. связанными заменой переменной, если их числа
вращений равны и иррациональны. Это позволяет нам рассмот-
рассмотреть то'лько простое вращение *->¦{* + P[f]}- В теории чисел
существует множество результатов, имеющих отношение к вра-
вращениям на иррациональные углы. Один из важных 'результатов
состоит в том, что если число а иррационально, то последова-
последовательные образы х, {х+а}, {х-\-2а}, ..., {х-\-па} постепенно
покрывают окружность непрерывно и равномерно. Соответствую-
Соответствующая траектория всюду плотно наматывается на тор без само-
самопересечений.
В анализе Фурье такой непрерывной временной последова-
последовательности мы обнаружим две различные угловые частоты ©i и
о>2, соответствующие периодам вращения по большой и малой
окружности тора. Так как отношение этих двух угловых частот
иррационально, квазипериодический сигнал обнаруживает (ап-
(априори, так как осцилляторы не гармонические) всюду плотное
бесконечное множество пиков на всех частотах | nicoj ± Пг<»21,
где rii, п% — целые числа (см. гл. III). Строго говоря, несколько
более сложная ситуация возникает, если иррациональное отно-
отношение fc>i/co2 «слишком близко» к рациональному. Такая ситуа-
ситуация, хотя и вызывает восторг у математиков, по-видимому, не
играет особо важной роли в физике (см. ниже).
VI. СТРУКТУРНАЯ УСТОЙЧИВОСТЬ И СИНХРОНИЗАЦИЯ,
«ЧЕРТОВА ЛЕСТНИЦА»
До сих пор мы ограничивались анализом явлений, исходя из
арифметической природы числа вращений. Было показано, что
если число вращений иррационально, то происходит синхрониза-
синхронизация, а если оно иррационально, то возникает квазипериодич-
квазипериодичность. Чтобы продвинуться дальше, нам необходимо оценить
относительную важность этих двух ситуаций. Следует ли

336 Приложение В
считать синхронизацию, соответствующую рациональному числу
вращений, чем-то исключительным, как рациональные числа
в множестве вещественных чисел? Из работы М. Хермана мы
знаем, как отвечать на такого рода вопрос, требующий нетри-
нетривиального анализа, поскольку мы находимся в рамках весьма
общего подхода и не используем индивидуальные особенности
выбранной модели. С этой точки зрения следует отметить два
•особенно замечательных свойства.
1) Синхронизация — явление структурно устойчивое, чем
(в принципе) и объясняется его относительная универсальность.
2) Вариация числа вращений как функция управляющего
параметра в общем, случае имеет своим графиком «.чертову ле-
лестницу».
Эти два утверждения заслуживают обоснования и более под-
подробного объяснения. ^
VI. 1. Структурная устойчивость синхронизации
Предположим, что число вращений рационально (например,
равно нулю). Тогда в стандартном случае график,отображения
jc-+f(x) пересекает диагональ в двух точках. Если мы, изменяя
управляющий параметр, слегка деформируем отображение /, то
две точки пересечения останутся (по крайней мере в том слу-
случае, когда возмущение не слишком велико). Именно это мы и
имеем в виду, когда говорим о структурной устойчивости, кото-
которую не следует смешивать с динамической устойчивостью в ее
обычном смысле (т. е. с устойчивостью относительно изменения
начальных данных). Пока число точек пересечения остается
равным двум, число вращений сохраняет свое нулевое значение.
К аналогичному результату мы придем всякий раз, когда число
вращений будет рациональным. Следовательно, p[fj, когда оно
рационально, есть константа на открытых интервалах значений
управляющего параметра.
Концы этих интервалов соответствуют нейтральным ситуа-
ситуациям, когда график функции \f(x) касается диагонали. Здесь
также число вращений равно нулю, но бесконечно малое изме-
изменение управляющего параметра может привести к отрыву гра-
графика f(x) от диагонали и, следовательно, к изменению числа
вращений (см. гл. IX).
VI. 2. «Чертова лестница»
Число вращенийг'р(/Г, есть непрерывная функция отображе-
отображения f и, следовательно, любого непрерывного параметра ?., ха-
характеризующего /. Следовательно, изменение величины pIf, как
функции параметра % имеет весьма необычный вид: каждый

Синхронизация осцилляторов
337
раз, когда р проходит через рациональное значение, в графике
р(Я) появляется горизонтальная ступень, так как эта функция
постоянна на открытом интервале значений параметра Я. Но
это еще и непрерывная функция параметра Я.
Пусть 1 и 2 — два интервала значений параметра Я, на ко-
которых р принимает рациональные значения pi/qi и Рг/щг
(рис. В.4). Тогда заведомо существует другой интервал 3 зна-
значений Я, расположенный между 1 и 2, на котором р = рз/Яз, где
/ — любое рациональное число, заключенное между pi/qi в
г
Рис. В.4. Построение. «чертовой лестницы». Показана зависимость числа вра-
вращений р(Х) от управляющего параметра X. На открытых интервалах 1 и 2
число вращений рационально и равно соответственно Pi/qi и Pzlqz- В интер-
интервале 3 между интервалами 1 и 2 число вращений равно pi/qt — рациональ-
рациональному числу, заключенному между числами pi/qi и рг/Яг- Следовательно,
функция р(Я) постоянна на некотором открытом интервале значений пара-
параметра Л всякий раз, когда она принимает рациональное значение. Оконча-
Окончательно мы получаем функцию, состоящую из бесконечного числа ступеней,
которая изчестна под названием «чертовой лестницы».
р2/<72, например (pi + p?)/(<7i + b)- Та же процедура повто-
повторяется для нового рационального числа, заключенного между
p\/qi и р3/<7з (или p2/q2 ичрзУ<7з)> и т- Дг Для всех интервалов
значений Я, остающихся' между интервалами синхронизации.
Ось Я в конце концов оказывается всюду плотно покрытой ин-
интервалами синхронизации. Но это не исчерпывает всех возмож-
возможностей: так как функция р(Я) непрерывна, она должна также
принимать все иррациональные значения, заключенные между
любыми рациональными. Иррациональные значения р должны
вклиниваться между интервалами синхронизации. График р(Я)
образует то, что получило название чертовой лестницы, так как
между любыми двумя ступенями заключено бесконечно много
ступеней. Но, естественно, большинство ступеней имеет беско-
бесконечно малую ширину, так как в любом ограниченном интер-
интервале содержится (счетное) бесконечное множество ступеней.
22 П. Берже в др.

338 Приложение В
На практике ступени со сколько-нибудь заметной шириной соот-
соответствуют синхронизации с «простым» рациональным числом
p/q, т. е. с отношением небольших целых чисел, например 1/1,
1/2, 2/3 и т. д.
Возникает вопрос: каково практическое значение иррацио-
иррациональных значений р? Действительно, для физики имеют значе-
значение только такие явления, которые имеют ненулевую меру. Дело
в том, что для реальной физической системы значение К никогда
точно не известно, и поэтому мы не знаем, располагаем ли точ-
точным значением X, соответствующим иррациональному числу вра-
вращений, или близким к нему значением из очень узкого интер-
интервала синхронизации. Очень разумная точка зрения, позволяю-
позволяющая учитывать экспериментальные «впечатления», состоит в
принятии вероятностного подхода. Иррациональные числа вра-
вращений обретают «физический» смысл (как квазипериодические
режимы, противопоставляемые режиму синхронизации), если
значение %, выбранное случайным образом в интервале (напри-
(например, между 1 и 2 на рис. В.4), имеет шанс оказаться соответ-
соответствующим иррациональному p[f]. Ответ, данный математиками
на этот вопрос, можно сформулировать в виде двух утверж-
утверждений., ,
1) Вблизи нормальной (суперкритической) бифуркации
Хопфа, т. е. в момент, когда в спектре Фурье сигнала возникает
вторая частота с очень малой амплитудой, два осциллятора
«игнорируют» друг друга. Это означает, что мы почти заведомо
находимся вне интервала синхронизации (несмотря на то что
интервалы синхронизации расположены всюду плотно!).
2) По мере возрастания амплитуды колебаний второго осцил-
осциллятора, т. е. когда мы покидаем точку, бифуркации Хопфа, ве-
вероятность оказаться вне интервала синхронизации убывает и
обращается в нуль при значениях управляющего параметра,
превышающих некоторое критическое конечное значение. Как
было показано в гл. IVII, это значение такое, что график ото-
отображения x-*-f(x) имеет точку перегиба с горизонтальной ка-
касательной.

ПРИЛОЖЕНИЕ Г
МОДЕЛЬ ЛОРЕНЦА
I. КОНВЕКЦИЯ РЭЛЕЯ — БЕН АРА
Рассмотрим слой жидкости бесконечной протяженности по
горизонтали, подогреваемый снизу. В приближении Буссинеска
безразмерные уравнения, описывающие связанный перенос им-
импульса жидкости [через ее скорость v (г, /) J и тепла [через от-
отклонение температуры Э(г,/)], имеют вид1)
(Г.Щ
il + vve = Rabv + ve
с числом Прандтля Рг = v/DT и числом Рэлея
Наличие оператора дифференцирования V по пространствен-
пространственным переменным означает, что перед нами дифференциальные
уравнения с частными производными, не слишком удобные в об-
обращении. Следовательно, желательно преобразовать их в какую-
нибудь конечную систему дифференциальных уравнений, т. е.
в поток (разумеется, в математическом смысле, а не в поток
жидкости). Для этого мы воспользуемся методом Галеркина,
который можно рассматривать как своего рода экстраполяцию»
разложений типа Ландау. Основная задача состоит в том, чтобы
определить неустойчивые моды, которые надлежит сохранить
в обрезанном разложении, поскольку подход в духе Ландау не
может удовлетворительно учитывать все нелинейности, когда
входят флуктуации конечной амплитуды. Несколько правил по-
помогают правильно отбирать моды.
з) Не следует вводить неустранимые особенности. Б нели-
нелинейной динамике это не всегда легкая задача. Например, про-
простейшее нелинейное дифференциальное уравнение
dt ~х
*) Здесь мы снова используем обозначения из гл. V, где читатель может
найти все необходимые определения.
22*

340 Приложение Г
имеет решение
которое обращается в бесконечность при t= 1/jc@), т. е. за ко-
конечное время, если *@)>0. Разумеется, для исключения всех
расходимостей из исходных уравнений необходимо использовать
физику задачи. Но для того чтобы произвести вычисления, почти
всегда необходимо обращаться к тем или иным приближениям
и очень трудно проследить за тем, чтобы введение приближе-
приближений не сопровождалось появлением новых особенностей.
б) Количественные свойства уравнений должны оставаться
неизменными, в частности законы сохранения таких экстенсив-
экстенсивных переменных, как масса, импульс и т. д.
в) Усеченные уравнения следует выбирать как можно ближе
к исходным. Если мы пытаемся моделировать дифференциаль-
дифференциальные уравнения с частными производными, как в случае задачи
РБ, то желательно взять столько узлов в разностной схеме (или
столько мод Фурье), сколько требуется для эффективности вы-
вычислений.
Вывод модели Лоренца из уравнений (Г.1) требует в основ-
основном правил «а» и «б». Что же касается правила «в», то в нем
выражается требование максимального упрощения представле-
представления динамики. Апостериори, по крайней мере если судить по
обильному урожаю полученных результатов1-), такая процедура
представляется вполне разумной.
II. ВЫВОД МОДЕЛИ ЛОРЕНЦА
Самое первое упрощение состоит в том, чтобы считать кон*
вективные валы, возникающие за порогом неустойчивости РБ,
параллельными (рис. Г.1). Тогда вектор скорости любого эле-
элемента жидкости перпендикулярен оси валов. Вдоль оси валов
существует трансляционная инвариантность, поэтому перемен-
переменные в уравнениях (Г.1) зависят только от двух пространствен-
пространственных координат: высоты z и горизонтальной координаты х. пер-
перпендикулярной оси валов (рис. Г.Г).
Пусть u(x,z,t) и w(x,z,t)—компоненты поля скоростей по
осям х и z. Тогда уравнение несжимаемости (Г. 16) запишется
') Напомним, что первоначально A963) Лоренц намеревался создать
хотя бы грубую модель земной атмосферы, которая позволила бы произво-
производить расчеты на бывшем тогда в его распоряжении сравнительно небольшом
компьютере LPG30.

Модель Лоренца
341
в виде')
ди , dw
дх ' дг
Вводя функцию тока Лагранжа гр(лг, z, t), замечаем, что уравне-
уравнению несжимаемости удовлетворяют
дг ' дх ' ™х'
Поле скоростей должно удовлетворять условиям, наложенным
на верхнюю и нижнюю поверхности жидкости, задаваемые в
Рис. Г.). Схематическое изображение конвекционных валов при тепловой
конвекции- Рэлея — Беиара. Все валы прямые, с параллельными осями. Вся
структура периодична по оси х. Высота валов d по оси г принята за единицу
длины, поэтому верхняя и нижняя поверхности жидкости определяются урав-
уравнениями
z=-1/2 и z = +1/2.
Направление градиента температуры противоположно направлению гравита-
гравитационного поля g.
единицах длины d уравнениями z = -fl/2 и z = —1/2. Первое
требование состоит в том, что, не должно быть потока жидкости
через поверхности:
'•) Мы используем обычные обозначения:

342 Приложение Г
Кроме того, если обе поверхности считаются «свободными» (это
означает, что мы пренебрегаем силами поверхностного натяже-
натяжения), то сдвиговая компонента тензора напряжения должна
быть равной нулю:
i Г
= 0.
откуда
ди
дг z-±i/2
Нетрудно видеть, что эти условия выполняются, если ¦ф удовлет-
удовлетворяет условиям
Этим двум условиям удовлетворяет член типа cos(яг). Так как
линии уровня функции \|р являются линиями тока поля скоро-
скоростей, они должны адекватно воспроизводить систему валов в на-
направлении оси х. Этого можно достичь с помощью члена типа
sin(^) с периодом 2n/q в направлении оси х.
Используя метод Галеркина, мы произвольно ограничиваем
описание функции ф одним членом:
Ц> (х, z, t) = if>! (/) cos (яг) sin (qx),
что приводит к следующим выражениям для компонент поля
скоростей:
и = яф, (/) sin (яг) sin (qx), (Г.2а)
w = qyfr! (t) cos (nz) cos (qx). (Г-26)
Запишем теперь уравнение (Г.1а) для компонент х иг1):
' = -Рж + А«, (Г.За)
= — pz + bw + Q. (Г.Зб)
Действуя на уравнение (Г. 1а) оператором rot [вычисляя (д/дг)
(Г.За) — (д/дх) (Г.36)], получаем
^- (иих + тиг) - -A. (UWx + WWz)\ = - Л2ф - 9„
(Г.Зв)
') а означает оператор Лапласа в прямоугольных координатах (х, z):

Модель Лоренца 343
где мы воспользовались соотношением \
*¦--(?—-¦&•)•
Придерживаясь метода Галеркина, мы должны далее вы-
выбрать произвольную, но подходящую форму для 9. Если дано,
что отклонение температуры 8 связано с полем скоростей урав-
уравнениями (Г. 1а) и (Г.Зв), то естественно наложить на в ту же
периодичность по х, какой обладает поле скоростей. Именно
поэтому мы принимаем для 0 такую же зависимость от х, как
для w (компоненты скорости по оси г). Кроме того, мы считаем,
что температура жестко задана на двух поверхностях. Это озна-
означает, что отклонение температуры G обращается на поверхно-
поверхностях в нуль:-
0U±1/2 = O.
Таким образом, мы приходим к следующей форме для 6:
rQ,{t)sinBnz), (Г.4)
согласующейся с граничными условиями. Второй член, не за-
зависящий от х, оказывается необходимым, как мы увидим в
дальнейшем, для включения хотя бы части нелинейностей си-
системы (Г.1).
Подставляя в уравнение (Г.Зв) приведенные выше уравнения
для и, ш, ф и 9, получаем
Pr'^^^-i^ + ^t. (Г.5)
— линейное дифференциальное уравнение первого порядка1)
для ij)i.
Из уравнения теплопроводности (Г.1в) следует, что
в, + ФА - №* = Ra 4>х + Ав. (Г.6 )
Величина ф*9г — ф29* в этом уравнении —наследие нелинейного
члена v-V0 в уравнении (Г.1в); она равна
г fl п
[ — -j- sin (nz) + 9, cos (ax) (cos (яг) + cosCnz))J.
Подставляя в уравнение (Г.6) выражения для поля скоростей
(Г.2) и температуры (Г.4), приходим к уравнению, допускаю-
допускающему только неконвективные решения (it>i=0). Следовательно,
4) В результате обрезания исходных уравнений за счет выбора соответ-
соответствующих функциональных форм для 1|з и 0 нелинейный член v«vv уравне-
уравнения (Г. 1а) исчез.

344 Приложение Г
вместо того чтобы требовать точного равенства, как мы обычно
делали, потребуем равенства членов cos(qx)cos(nz) и sinBnz)
и пренебрежем членом cos(^x)cosCkz). В результате получим
два уравнения
в, = - nqb&2 + q Ra ф, - (я2 + q2) в,, (Г.7а)
92 = 1 я^в, — 4я2в2 (Г.76)
относительно членов, входящих в cos (qx)cos (яг) и sinBnz).
Уравнения (Г.5), (Г.7а) и (Г.76) образуют систему трех обык-
обыкновенных нелинейных дифференциальных уравнений для ампли-
амплитуд ifi, 6i и 02- Удобно произвести замену переменных
У = я<?2 8 • Z =
V2(* + *) "
и ввести два параметра
г= (л2Ч-<72K **а; Ь
В результате мы приходим к так называемой модели Лоренца
X=Pr(Y-X), (Г.8а)
Y = -XZ + rX-Y, (Г.86)
Z = A"r-6Z. (Г.8в)
III. НЕПРОТИВОРЕЧИВОСТЬ МОДЕЛИ
Прежде всего убедимся в том, что обрезание не ввело не-
неявно в модель какую-нибудь нежелательную особенность. До-
Достаточно показать, что ни одно решение уравнений (Г.8) не
обращается в бесконечность; иначе говоря, что векторное поле
в R3 на поверхности, окружающей начало координат и прохо-
проходящей на большом расстоянии от него, всюду направлено к на-
началу. Пусть f(X,Y,Z) = 0 будет уравнение такой поверхности.
Необходимое и достаточное условие существования векторного
поля состоит в том, чтобы скалярное произведение вектора ско-
скорости и нормали, направленной наружу от поверхности, было
всюду отрицательным:
Bf = Xfx + Yfy + ZL<0.
Подставляя X, ?, 1 из уравнений (Г.8), получаем
Df = Рг (X - X) fx + {-XZ + rX - Y) f9 + (AT - bZ) fz.

Модель Лоренца 345
Из большого запаса возможных поверхностей f выберем эллип-
эллипсоид, уравнение которого имеет вид
f(X, Y, z) = ^L + -Y- + j|L-(r+l)Z-n = O
с произвольно большим ц^О. Подставляя уравнение эллип-
эллипсоида, получаем
Df = - X2 - Y2 — bZ2 + (r + 1) bZ.
Из определения поверхности ясно, что при достаточно большом
р. доминируют квадратичные члены, а членом, линейным по Z,
можно пренебречь. Следовательно, величина Df всегда отрица-
отрицательна: ни одна траектория, выходящая из начала координат,
не может на конечном расстоянии от Него уйти в бесконеч-
бесконечность1).
Нельзя не отметить еще одно обстоятельство: объемы в фа-
фазовом пространстве сокращаются. Это означает, что поток, оп-
определяемый уравнениями (Г.8), диссипативен, как и исходные
уравнения. Сокращение объема следует из того, что поле ско-
скоростей имеет постоянную отрицательную дивергенцию: /
Ж +# + # —(Pr+1+ft).
Если в некоторый момент ^ = 0 мы рассмотрим множество на-
начальных данных, занимающих объем ?2@), то концы траекто-
траекторий, выходящих из точек множества, в момент времени t запол-
заполнят объем Щ/J, равный
Q @ = Q @) ехр [- (Рг + 1 + b) t].
Таким образом, объем монотонно убывает со временем. Попутно
заметим, что, поскольку модель Лоренца задает поток в R3, экс-
экспоненциальное сокращение объема запрещает существование
аттрактора на торе Т2, так как в противном случае объем внутри
тора сохранялся потоком. Следовательно, в силу своей внутрен-
внутренней структуры модель Лоренца не может иметь квазипериоди-
квазипериодического решения2).
Нам остается определить волновое число q валов вдоль
оси х. Так как одна из наших целей состоит в моделировании
порога конвекции, представляется естественным выбрать (как
') Приведенное выше доказательство использует метод, характерный для
модели Лоренца. Установить регулярность решений нелинейного потока при
всех t не всегда так просто.
2) Это свойство является общим для всех потоков в R3 с всюду отри-
отрицательной дивергенцией.

346 Приложение Г
делал сам Лоренц) волновое число флуктуации, дестабилизи-
дестабилизирующих состояние, в котором конвекция отсутствует и передача
тепла осуществляется только за счет теплопроводности. По оп-
определению такое состояние характеризуется тем, что
Его линейная устойчивость зависит от эволюции бесконечно ма-
малой флуктуации 6Х, 8Y и 6Z, удовлетворяющей уравнениям
ЬХ = Pr FY - 6Х),
получающимся при линеаризации потока (Г.8) относительно
доконвективного состояния. Компонента 8Z всегда затухает, так
как коэффициент Ь положителен. Что же касается компонент
8Х и б У, то они имеют вид
где а — корень характеристического уравнения:
(а + Рг)(а+ 1) —гРг = 0,
или
а2 + (Рг+ 1)а + РгA —г) = 0.
Так как Рг > 0, мы видим, что один из вещественных корней
этого квадратного уравнения становится положительным, как
только параметр г превосходит единицу. Следовательно, докон-
вективное состояние линейно неустойчиво при г ^ 1, т. е. при
Соответствующими флуктуациями на пороге неустойчивости яв-
являются такие, которые приводят к минимуму Ra, т. е. такие, при
которых правая часть достигает минимума:
о 1 о
Следовательно, Ra = 27я4/4.
k^Tn X<j^OIII<-> riooGCTKbie ЗНаЧсНИл опсриЫс иыли isbiL;BU'ichbi
Рэлеем. Параметр Ъ в этом случае равен 8/3. Это значение
часто используется при численном моделировании системы Ло-
Лоренца.

Модель Лоренца 347
IV. БИФУРКАЦИОННАЯ ДИАГРАММА (Рг = 10; Ъ = 8/3)
После того как система Лоренца выведена, поток (Г.8) сам
по себе может быть предметом исследования безотносительно
к его гидродинамическому происхождению. Поскольку в общем
случае модель Лоренца не интегрируема, ее решения могут быть
найдены численно с помощью компьютера, если фиксировать
три параметра Рг, Ъ и г. Много исследований было проведено
с значениями параметров, первоначально выбранными самим
Лоренцом1):
Рг=10, 6 = 8/3, г>0.
Параметр "г, непосредственно связанный с параметром Ra в про-
проблеме РБ, т. е. с приложенной разностью температур, служит
бифуркационным, или управляющим, параметром. Совершим
краткий обзор бифуркационной диаграммы.
Стационарные решения по определению таковы, что
Y = X; Z = ±X2; X = ±[b(r- I)]1'2.
При 0 ^ гг^ 1 существует только одно решение такого типа —
чисто теплопроводящее состояние:
j = r = z = o.
Когда параметр г становится больше единицы, это решение те-
теряет устойчивость. Возникают два стационарных решения:
Мы имеем здесь бифуркацию типа вилки, при которой устойчи-
устойчивая неподвижная точка рождает две другие неустойчивые не-
неподвижные точки. Эти результаты следуют из инвариантности
потока (Г.8) относительно симметрии
(X, Y, Z)-*(-*, -Y, -Z).
Очень простые вычисления подтверждают, что два решения
при г !>> 1 линейно независимы. -Физически они соответствуют
наступлению конвекции, и каждое из них связано с одним из
двух возможных направлений вращения валов. Они теряют ли-
линейную устойчивость при г = 24,74, где каждое решение пре-
претерпевает субкритическую бифуркацию Хопфа; выше точки
бифуркации существует только апериодическое решение. Хотя
- 1 \J\Jl \J\-
1) Были исследованы и некоторые другие комбинации параметров, в ос-
основном Рг =16, 6 = 4. Для наших целей достаточно результатов, получен-
полученных Лоренцом. (

348
Приложение Г
видимому, мы имеем здесь дело со странным аттрактором. При
бифуркации Хопфа наблюдается гистерезис, и при значениях
параметра г от 24,06 до 24,74 сосуществуют три аттрактора:
два стационарных решения и странный аттрактор, который
Странный
аттр/хктпор
Субкрштсческая
бифуркация
тфа
\ i ! ! ? -1ГГ*хуА
Бифуркация
вилки.
1 стационарное
состояние
Z стационарное
состояние
Хаотическое
состояние
Рис. Г.2. Бифуркационная диаграмма для модели Лоренца (Рг =10, b =
= 8/3). Первая бифуркация (г — I)—суперкритическая бифуркация типа
вилки, обусловенная симметрией (X, У, Z)-*- (—X, —У, Z) данной модели.
Втирая бифуркация \г = 24,74) — субкритическая бифуркация Хопфа. Вели-
Величины, отложенные по оси ординат, изменяются как X или У. Как обычно,
штриховые линии соответствуют неустойчивым, а сплошные — устойчивым
состояниям.
Из диссертации К. Трессера «Простые модели перехода к турбулентности»
на звание доктора философии, защищенной в Университете Ниццы в 1981 г.
иногда называется «нестандартным». Упомянем также о том,
что метастабильный хаос, о котором шла речь в гл. VI, полу-
получается при меньших значениях г (до г =13,926). На рис. Г.2
схематически изображена бифуркационная диаграмма. Заме-
Заметим, что хаос на ней появляется не через потерю устойчивости
периодической траектории. Эта мода перехода «не впр.сывает-
ся* в один из трех маршрутов, описанных во второй части книги.
При re [24,74; 30,1] странный аттрактор составляет только
устойчивое решение потока (Г,8), Нетрудно понять, почему так
мйого математических исследований было выполнено при г = 28,
т. е. в самом центре зтой области. Выше г = 30,3 и до г « 214
диаграмма решений становится необычайно сложной, с чередо-

Модель Лоренца
349
ванием хаотических и периодических режимов, внешне напо-
напоминающих соответствующие режимы, которые возникают при
О/хно
ераодютости
Обратный
катод
чести * Перемежав*
мост
Рис. Г.З. Типичное окно периодичности и процессы, предшествующие его по-
появлению и исчезновению. Численные эксперименты, с необходимостью ограни-
ограниченные лишь самыми широкими (по г) окнами, показывают, что появлению
окон периодичности всегда предшествует обратный каскад. Прямой субгар-
субгармонический каскад завершается основным предельным циклом, который впо-
впоследствии разрушается перемежаемостью типа I.
квадратичном отображении интервала на себя при ц. е [0,892,...
...; 1] (см. рис. VIII. 7). Имеются веские основания считать,
что «окон периодичности» бесконечно много. Мы упомянем лишь
три самых больших окна !):
99,524 ... <г< 100,795 ...,
145, ... <г< 166
214,364 ... < г.
Эти области, как объяснялось в разд. VIII. 3.5, являются обла-
областями различных периодических аттракторов. Интересно, что их
появление и исчезновение подчиняются той последовательности
событий, которую мы сейчас описываем (см. рис. Г.З). Незадолго
до того, как действительно начинается окно периодичности,
наблюдается обратный каскад бифуркаций того типа, кото-
который описан в разд. VIII. 3.3. В спектре Фурье шум и, следо-
следовательно, хаос монотонно убывают. Обратный каскад сменяется
прямым субгармоническим каскадом, который заканчивается
основным предельным циклом, а вся совокупность режимов
*) Границы окон указаны в соответствии с имеющимися данными. Утим
(и только этим) объясняется различное число десятичных знаков.

350
Приложение Г
в целом составляет окно периодичности1). Так же, как окну
периодичности всегда предшествует обратный каскад (по край-
крайней мере во всех достаточно хорошо изученных случаях), пере-
Мегппстабильньтй
исаос
ТНГ
ZKT
2НТ,
Странный,
шттптрсскшрр
ZHT+CA СА
ГА/ПА
1
СА/ПА ,
13,928
ПА ,
ZfifiB
СА/ЛА ,
24,7*
Перемежаемость
типа I
ПА ,,
. СА/ЛА
Щ1
99,524 100,155
16В
214,354
Рис. Г.4. Последовательность аттракторов в модели Лоренца (Рг = 10,
b = 8/3). НТ — неподвижная точка; СА —странный аттрактор; ПА — перио-
периодический аттрактор (окно периодичности); «+» — сосуществование, а «/»—
чередование различных аттракторов.
межаемость I типа каждый раз указывает на его конец 2). Когда
основной предельный цикл утрачивает устойчивость, это проис-
происходит из-за перехода через точку +1 одного из собственных
значений матрицы Флоке. Переход к хаосу при этом осуществ-
осуществляется от периодического решения и вписывается в один из сце-
сценариев теории.
Аналитическое исследование модели (Г.8) в пределе боль-
больших значений г показывает, что последний аттрактор непре-
непременно является предельным циклом, и этот вывод убедительно
подкрепляется данными численного моделирования. Последнее
окно периодичности начинается при г = 214,364, а заканчивается
обратным каскадом, который начинается при г = 197,4. Прямой
каскад заканчивается при г = 313. Выше этого значения пара-
параметра г остается только соответствующий основной предель-
предельный цикл в качестве устойчивого аттрактора. На рис. Г.4 пока-
показаны последовательность аттрактора вдоль оси х и явления, под-
подробно описанные в других частях этой книги.
') Подробно эта ситуация была объяснена в гл. VIII, где мы рассматри-
рассматривали субгармонический каскад, встречающийся при квадратичном отображе-
отображении интервала на себя. Для восстановления той же последовательности
(прямого каскада, за которым следует обратный каскад) достаточно выбрать
в качестве бифуркационного параметра а какую-нибудь убывающую функ-
функцию от г, например 1/г.
2) Перемежаемость I типа была открыта и исследована при численном
моделировании с г > 166.

ПРИЛОЖЕНИЕ Д
МАТЕМАТИЧЕСКИЕ ДОПОЛНЕНИЯ
I. МАТРИЦЫ
Мы опишем здесь некоторые свойства квадратных матриц,
иллюстрирующих основы теории матриц Флоке в том числе,
в каком они встречаются в различных частях нашей книги.
1.1. Общие сведения
Пусть So —начало координат в сечении Пуанкаре устойчи-
устойчивого предельного цикла и пусть Si. S%, ..., Sn — последова-
последовательность точек пересечения траектории, первоначально близкой
к предельному циклу.
Рис. Д.1. Две системы координат Sox' и Soj/' —два собственных направления
матрицы (если она имеет действительные собственные значения).
Выясним, как Si, ¦ ¦ ¦, Sn можно получить из .Si в зависи-
зависимости от типа используемого отображения. Пусть (Sox, Soy) —
прямоугольная система и пусть х\ и у\ — координаты точки Si
(рис. Д.1). Рассмотрим линейное преобразование, определяю-
определяющее координаты образа 52 точки Si:
Уг = сху + dyx

352 Приложение Д
и в общем случае /г-я итерация Sn:
s ( xn = axn_i + byn_u
Матрица М этого линейного преобразования имеет вид
Га ЪЛ
и мы можем написать
или ад.-**"-1 ад-
Обычно вычисление матрицы М"~1 сопряжено с громоздкими и
трудными выкладками. Однако мы можем в общем случае
найти другую систему координат (х', у') и два числа hi и h2
(которые могут быть комплексными), таких, что координаты
образа Si связаны с координатами точки Si более просто:
Аналогично
, Xn Al Xl,
Матрица NV в новой системе координат диагональна:
ГА,! О
М = I I, и в этом случае
L U Л2 J
[кГ1 о ]
вычислить
нетрудно.
Величины hi и Я2 называются собственными значениями
матрицы М. Они являются корнями уравнения
а-Х Ь I
I Г)
С ^ — Л | '
т. е.
Я2 - (а + d) Я + (ad — be) = 0.

Математические дополнения 353
Нетрудно понять, при каких условиях собственные значения
могут быть комплексными. Тогда (в случае матрицы М) они
непременно комплексно-сопряженные:
Собственными векторами V матрицы М называются такие век-
векторы, для которых М-У/ = к\. Один из них параллелен оси
Sox', другой — оси Stfy' новой системы координат; поэтому эти
оси называются собственными направлениями матрицы М.
Оси Soxr и SQyf определяются (в системе координат х, у) со-
соотношениями
ах + by = кх,
+ d X ' г
Так как
1 Уп = &2 У\,
асимптотическое поведение преобразования 5П определяется
наибольшим по модулю значением К. Пусть |А.| + —модуль этого
значения. Тогда
1) если |А,|+<С 1, то А,"-»-0 и Sn сходятся к началу коорди-
координат So;
2) если | А,|+ > 1, то А,"-»- оо и Sr. стремятся к бесконечности.
I. 2. Матрица вращения
Матрицей вращения Мг называется матрица
Нетрудно убедиться, что ее собственные значения А, (два
комплексно-сопряженных К) по модулю равны единице и что
действие ее на вектор сводится к повороту его на угол v» такой,
что cos~ = Oj sin у = Ь. Матрицу вращения можно представить
в виде
cosy —sm У 1
sin y cos y J
~L
Мы рассмотрим несколько конкретных примеров, чтобы проил-
проиллюстрировать эволюцию последовательных образов начальной
точки ка плоскости (х, у) (по предположению — плоскости се-
сечения Пуанкаре).
n верже и др.

354
Приложение Д
I. 3. Матрица, у которой наибольшее по модулю собственное
значение вещественно и больше единицы
С таким случаем мы встречаемся, когда потеря устойчивости
вызвана пересечением единичной окружности в точке +1. Пред-
Предположим, что | Xi | <; 1 < А,2.
При каждой итерации абсцисса х' умножается на число A,i,
абсолютная величина которого меньше единицы, в то время как
ордината у' умножается на число \2, которое больше единицы.
Итерации любой начальной точки S\ при этом быстро (экспо-
(экспоненциально) сходятся к оси у', а вдоль нее расходятся, удаляясь
г
f
V
у
У
Рис. Д.2. Первые несколько итераций для матрицы М = -'к „' I с соб-
|_ и,о и,У J
ственнымн значениями Xi = 0,16 и Яг = 1,23. На этом и последующих ри-
рисунках (до рис. Д4б) начальной точке присвоен номер 1, а итерации прону-
пронумерованы последовательными натуральными числами в порядке возрастания.
в бесконечность. Следует отметить сильное сходство между та-
таким поведением и описанием (см. разд. VI. 3.2) гиперболичности
отображений Пуанкаре. В случае гиперболичности также суще-
существуют сжимающее направление х' и растягивающее направле-
направление и два (локальных!) коэффициента Ляпунова К\, Яг. Заме-
Заметим, что сжимающее направление не обязательно перпендику-
перпендикулярно растягивающему направлению.
На рис. Д.2 показаны положения нескольких первых итера-
итераций линейного преобразования, матрица которого
м =
0,5 0,5
0,5 0
¦51
,9j

Математические дополнения 355
имеет собственные значения
А,, = 0,16;
Я2=1,23.
1.4. Матрица, у которой наибольшее по модулю собственное
значение вещественно и меньше единицы
Я2<—1, ~1<Я,1<1.
Этот случай встречается, когда потеря устойчивости вызвана
пересечением единичной окружности в точке —1. При каждой
^" ' I
/*¦
/
Рис. ДЗа. Первые итерации для матрицы М =| ' . с собственными
значениями Xi = 0,36 и к2 = —1,36.
итерации абсцисса х' умножается на число Я;, абиолютная ве-
величина которого меньше единицы, в то время как ордината у'
умножается на отрицательное число Я2, абсолютная величина
которого больше единицы. Как и в предыдущем случае, суще-
существует экспоненциальная сходимость к оси уг, вдоль которой
образы экспоненциально расходятся, но на этот раз оказывают-
оказываются попеременно то на положительной, то на отрицательной по-
полуоси из-за умножения на отрицательное число л2, изменяю-
изменяющего при каждой итерации знак ординаты уг.
23*

356
Приложение Д
На рис. Д.За показано действие линейного преобразования,
матрица которого
Г—1,3 1 1
М~[ 0,1 0,3 J
имеет собственные значения
Я, = 0,36;
1.5. Матрица, у которой наибольшее по абсолютной величине
собственное значение вещественно и равно —1
Может показаться, что этот случай не представляет особого
практического интереса. В действительности же его можно рас-
рассматривать как асимптотическую ситуацию, возникающую, когда
А
Рис. ДЗб. Сходимость последовательных итераций к двум пределам S^ и S^,
(четные итерации сходятся к S^, нечетные — к S^). Линейное преобразова-
преобразование имеет матрицу Af =1 ' с собственными значениями Xt = 0,5 и
линейное нарастание неустойчивости насыщается действием не-
нелинейных членов.
На рис. Д.36 показана эволюция последовательных итераций
при умножении на матрицу

Математические дополнения 357
с собственными значениями
*i = 0,5;
По достижении прямой Soy' (действие собственного значения
Ki) точки попеременно оказываются то на STO, то на 5^. На
этом графике мы видим сечение Пуанкаре после субгармониче-
субгармонической бифуркации, а на рис. Д.За изображена фаза экспонен-
экспоненциального роста (линейная теория).
1.6. Матрицы с комплексно-сопряженными собственными
значениями, модуль которых больше единицы
Этот случай встречается, когда предельный ци.кл теряет ус-
устойчивость из-за пересечения единичной окружности е комп-
комплексно-сопряженных точка* а ± ifi. Собственных направлений
х' и у' при этом не существует, и вместо них нам необходимо
вычислить матрицу вращений и угол у (исходя из заданной
матрицы). Например, рассмотрим преобразование, матрица ко-
которого
Г1 -11
М = , имеет собственные значения А.^ 2 = 1 ± i,
модуль которых равен д/2.
Записав исходную матрицу в виде
,_Г 1/V2 -1/V2 1
L1/V2 1/V2 J
мы узнаем матрицу вращения
cos y —
ч
' sin y cos •
Умножение на М сводится к растяжению в л/ 2 раз и после-
последующему повороту на угол л/4 (рис. Д.4а).
Нейтральный случай, когда модуль собственных значений
равен единице, соответствует асимптотическому состоянию сече-
сечения Пуанкаре режима после того, как нелинейные эффекты по-
погасили экспоненциальный рост, вызванный линейной неустойчи-
неустойчивостью (см., например, рис. Д.4а). На рис. Д.46 показано дей-

358
Приложение Д
в
6<
7
*
Рис. Д4а. Первые итерации для матрицы М = I . . I с собственными
значениями kit Яг = 1 ± «.
Гл/З/2 —1/2 1
Рис. Д4б. Итерации для матрицы т ~\ ._ ,_,_ .j с комплексными
L" I/a 'V'3/2 J
собственными значениями, равными по модулю 1.

Математические дополнения
359
етвие преобразования с матрицей
М =
1_
2
2
Модуль ее собственных значений равен единице, и М есть про-
просто матрица вращений (у = л/6). На рис. Д.46 показано, что
итерации 5,- обходят поочередно 12 эквидистантных точек на
единичной окружности. Их можно рассматривать как сечение
Пуанкаре потока, который после бифуркации Хопфа Претерпе-
Претерпевает синхронизацию 12-го порядка.
II. ЯКОБИАН
II. 1. Линейное преобразование
Рассмотрим две системы координат (Ох,Оу) и {Oz,Ot) и
линейное преобразование, которое отображает точку М с коор-
координатами х, у в первой системе в точку Р с координатами z, t
/
-7
/
/
о щ ^ о
Рис. Д.5. Схематическое представление линейного преобразования.
"во второй системе (рис. Д.5) и определяется уравнениями
.. z = ах + $у,
t = yx + by,
где а, В. v. 6 — вещественные числа. Пусть Afi и М2 — две точки
с^координатами A,0) и @, 1), a Pi и Р2 —их образы с коорди-
координатами (а, у) и (р1, б).
Единичный квадрат 0М,АШ2 преобразуется в параллело-
параллелограмм ОР\РР2, площадь которого (величина векторного произ-
произведения) равна абсолютной величине определителя
р*
= аб—BV
Ь ¦ . .

360
Приложение Д
(знак определителя указывает ориентацию преобразования:
плюс соответствует сохранению направления отсчета углов).
Если |аб — Py|> 1, то происходит растяжение площадей, а при
| аб — Pv I < 1 их сокращение.
Заметим, что особый случай аб — $у — 0 соответствует пре-
преобразованию единичного квадрата в отрезок прямой. Такое пре-
0 х0 ccgt-Ax х 0 Az
Рис. Д.6. Векторы, иллюстрирующие локальную линеаризацию преобразования.
образование не биективно, т. е. х и у не могут быть однозначно
определены по z и t; преобразование перестает быть обрати-
обратимым1).
II. 2. Локальное исследование произвольного преобразования
Пусть z=f(x,y) и t=g{x,y)—нелинейное преобразование.
В окрестности точки Мо(хо, г/о), т. е. при малых приращениях
Ах. Дг/, членами второго порядка можно пренебречь (рис. Д.6).
Если
то
') Мы говорим, что отображение, действующее из множества А в мно-
множество В, обратимо, или биективно, если у каждого элемента множества В
существует единственный прообраз в множестве А. Например, отображение
окружности на себя, переводящее точку М, расположенную под углом 0,
в точку М'. расположенную под углом 2G, не является обратимым (точка М'
повернута на вдвое больший угол, чем точка М), в то время как отображе-
отображение вращения
в
обратимо. Заметим, что если отображение есть числовая функция одной пере-
переменной, то обратимое отображение должно быть монотонным (иначе у ка-
каких-то образов окажется по крайней мере два прообраза; см. гл. VIII). По
непрерывность для обратимости не обязательна (см. разд. VII. 4 и приложе-
приложение В).

Математические дополнения
361
и аналогично для АГи g(x, у). Если SP —образ вектора 6М
в окрестности точки Мо, то
6Р
Гх(хо> Уо) f'y{xo> Уо)'
.ё'х(хо'Уо) 8у{хО'Уо).
6М.
Эта матрица называется матрицей Якоби и определяет линей-
линейное отображение1), возвращающее нас к рассмотренному в на-
начале этого раздела случаю преобразований. Если определитель
г __
называемый определителем Якоби или якобианом, в точке
{хо,уо), отличен от нуля, то отображение локально обратимо.
Если |/|>;1, то в окрестности точки Мо площади растягивают-
растягиваются; если |/|< 1, то площади сокращаются.
Пример: отображение Энона
fe+i — "* ¦ — *^й»
В приведенных выше обозначениях
g (х, У) =
якобиан равен
—2си
О
a
В случае отображения Энона якобиан есть константа. При ите-
итерации отображения площадь каждый раз умножается на р и
после k итераций становится равной
При р = 0,3 площади сокращаются.
Предельный случай I = 0, т. е. р = 0, должен соответство-
соответствовать потере обратимости: действительно, координата yk+i =
= 0-л:й=0 и отображение становится нелинейным одномерным
отображением, о котором уже известно (см. гл. VIII), что оно
необратимо.
•) Это отображение называется линейным касательным отображением..

362 Приложение Д
III. ГОМЕОМОРФИЗМЫ, ДИФФЕОМОРФИЗМЫ
Пусть f(x,y,z, ...) — функция п вещественнозначиых пере-
переменных, задающая отображение, которое действует из некото-
некоторой части п-мерного пространства R" в множество веществен-
вещественных чисел 'R:
f: R"-».R
(если бы было р функций и переменных, то отображение дей-
действовало бы из IR" в R)
III. 1. Гомеоморфизмы
Отображение типа отображения f из подмножества А про-
пространства Rn в подмножество В пространства Rp называется
гомеоморфизмом А на В, если оно обратимо и непрерывно в обе
стороны (т. е. непрерывно само отображение f и обратное ото-
отображение f-1: /?->-Л). Непрерывность определяется в естествен-
естественной топологии n-мерного пространства (индуцированной евкли-
евклидовой метрикой) и предполагает, что каждое из подмножеств
А и В содержит вместе с любой своей точкой некоторую ее ок-
окрестность.
Например, рассмотрим окружность внутри равностороннего
треугольника, центр масс G которого совпадает с центром масс
окружности. Любая прямая, исходящая из G. пересекает окруж-
окружность в точке М, а треугольник — в точке М'. Отображение
/: М~уМ'
ставит в соответствие каждой точке окружности некоторую
точку треугольника, и наоборот. Кроме того, две соседние точки
каждой из фигур отображаются в две соседние точки другой
фигуры. Отображение f является гомеоморфизмом. Можно
также сказать, что окружность и треугольник гомеоморфны.
III. 2. Диффеоморфизмы
Диффеоморфизм должен удовлетворять более ограничитель-
ограничительному условию, чем гомеоморфизм: отображение f называется
диффеоморфизмом из Л в В, если оно обратимо и имеет на А
непрерывные частные производные первого порядка. (Можно
показать, что обратное отображение имеет непрерывные ча-
частные производные первого порядка на В.) Любой диффео-
диффеоморфизм есть гомеоморфизм. Обратное утверждение неверно.

Математические дополнения 363
Вещественнозначная функция / вещественной переменной, опре-
определенная на интервале /, на котором i она имеет непрерывную
производную постоянного знака, есть диффеоморфизм /на об-
образ интервала f(I).
Отображение окружность ->- треугольник из предыдущего
раздела не является диффеоморфизмом из-за разрывов произ-
производной в вершинах треугольника. Аналогичное отображение из
окружности в эллияс является диффеоморфизмом. Другой при-
пример диффеоморфизма, приведенный в разд. VII. 4 и в приложе-
приложении В — биективное отображение окружности в интервал [0,1)«
НЕКОТОРЫЕ ОБЩИЕ РАБОТЫ
I Книги
Abraham R. H., Shaw С. D., Dynamics: the Geometry of Behavior, Aerial Press,.
Santa Cruz, 1983,
Арнольд В. И. Обыкновенные дифференциальные уравнения. — М.: Наука,.
1971.
Арнольд В. И. Дополнительные главы теории обыкновенных дифференциаль-
дифференциальных уравнений, —М.: Наука, 1978.
Арнольд В. И. Математические методы небесной механики. — М.: Наука,
1974.
Arnol'd V., Avez A., Ergodic Problems of Classical Mechanics, Benjamin, New
York, 1968.
Collet P., Eckmann I.-P., Iterated Maps on the Interval as Dynamical Systems,.
Birkhauser, Boston, 1980.
Ekeland I., Le calcul, l'imprevu, Le Seuil, Paris, 1983.
Guckenheimer /,, Holmes P., Non-Linear Oscillations, Dynamical Systems and
Bifurcations of Vector Fields, Springer-Verlag, New York, 1983.
Haken H., Advanced Synergetics, Springer-Verlag, Heidelberg, 1983. [Имеется
перевод: Хакен Г. Синергетика. Иерархия неустойчивостей в самооргани-
самоорганизующихся системах и устройствах. — М.: Мир, 1985.]
Hirsch M. W., Smale S., Differential Equations, Dynamical Systems and Linear
A'gebra. Academic Press, New York, 1974.

364 Некоторые общие работы
Joseph D., Stability of Fluid Motion, Springer-Verlag, 1976»
Ландау Л. Д., Лифшиц E. M. Гидродинамика. — M.: Наука, 1986.
Lin С. С, The Theory of Hydrodynamic Stability, Cambridge University Press,
Cambridge, 1955. [Имеется перевод: Линь Цзя-цзяо. Теория гидродинами-
гидродинамической устойчивости. — М.: ИЛ, 1958.]
Mandelbrot В. В., Les objets fractals: forme, hasard et dimension, Flammarion,
Paris, 1975.
Marsden I. ?., McCracken M., The Hopf Bifurcation and its Applications,
Springer-Verlag, New York, 1976. [Имеется перевод: Марсден Д., Мак-
Кракен М. Бифуркация рождения цикла и ее приложения. — М.: Мир,
1980.]
Minor sky N.. Nonlinear Oscillations, Van Nostrand, New York, 1962.
Nayfeh A. M., Mook D. Т., Nonlinear Oscillations, Wiley, New York, 1979.
Prigogine /., Physique, temps et devenir, Masson, Paris, 1980.
Rocard Y., Dynamique generate des vibrations, Masson, Paris, 1949.
Smale S., The Mathematics of Time: Essays on Dynamical Systems, Economic
Processes and Related Topics, Springer-Verlag, New York, 1980.
Sparrow C, The Lorenz Equations, Springer-Verlag, New York, 1982.
Thorn R., Stabilite structurelle et morphogenese, Benjamin, New York, 1972.
II Обзоры
Abraham N. В., Gollub I. P., Swinney H. L., Testing Nonlinear Dynamics,
Physica, 11D, 252 A984).
Berge P., Pomeau Y., La turbulence, La Recherche, ПО, 422 A980).
Croquette V., Determinisme et chaos, Pour la Science, 62, 62 A982).
Dubois M., Attracteurs etranges et dimension fractale, Images de la Physique,
92 A984).
Eckmann I.-P., Roads to Turbulence in Dissipative Dynamical Systems, Review
of Modern Physics, 53, 643 A981).
Ott F. Strano^ Attractors and Chaotic Motions of Dynamical Systems, Reviev/
of Modern Physics, 53, 655 A981).
Рабинович М. И. Стохастические автоколебания и турбулентность. УФН.
1978, т. 125, вып. 1, с. 123.
Ruelle D., Deterrninisrne et predictibiiite. Pour la Science, 82, 58 A984).
Ruelle ?>., Les attracteurs etranges, La Recherche, 108, 132 A980).
Shaw R. S., Strange Attractors, Chaotic Behavior and Information Flow, Zeits-
chrift fur Naturforschung, A36, 80 A981).
Swinney H. L, Gollub I. P., The Transition to Turbulence, Physics Today, 31,
41 A978).
Vidal C, Roux I.-C, Comment nait la turbulence, Pour la Science, 39, 50
A981).

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автокорреляционная функция 56—57
Аспектное отношение 104
Аттрактор 6
— Сжила 176
— странный 6
Бифуркации точка 46, 305
Биоуркаций теория 305
Бифуркационная диаграмма 48
Бифуркационный параметр 48
Бифуркация 46
— глобальная 306
— касательная 234
— локальная 306
— нормальная 49
— обратная 49, 311
— субкритическая 49, 311
— суиеркритичеСкая 49, 311
— Хопфа 48
Отображение Энона 148—154
Показатель Ляпунова 314
Поток 75
— автономный 75
— Лоренца 141
— неавтономный 75
— Рёсслера 88—91
Производная Ли 130
Размерность евклидова 166
— корреляционная 170
— фрактальная 140
— Хаусдорфа 166
— Хаусдорфа — Безиковича 166—167
Растяжение 176
Ритм циркадный 15
•— цирканнуальный 15
Ветвь решения 305
Геофизическое динамо 120
Гиперболичность 138—140, 178
Детерминированность 69
Детерминированный хаос 7 -
Колебания изохронные 19
— релаксационные 36
Коэффициент Ляпинова 178
Кривая Коха 168
Критическое значение 46
Сепаратриса 23
Сигнал апериодический 69
— квазипериодический 65—69
— непериодический 69
Система гамильтонова 6, 24
— динамическая 6
— диссипативная, 6
— консервативная 6, 24
— обратимая 26
Складывание 176
Случайность 69
Спектр мощности 58—60
Степень свободы 21
Субгармоническая неустойчивость 43
Субгармонический каскад 217
Сценарий 180
Матрица Флоке 80, 122
Модель Рикитаке — Аллена 120
Трение в жидкости 28^
Трение твердых тел 28

366 Предметный указатель
Теория Блоха — Ваннье 43 Функция Ляпунова 31
— Галуа 39 •— Матье 40
— Флоке 40, 43
Характеристический показатель 40
Уравнение интегрируемое 39
~4^
30—31 -"•"""¦ У™» J2°
p
— структурная 271
Шум белый 69—70, 72
— окрашенный 70, 73
Фазовая траектория 21
Фазовое пространство 21
Фазовый портрет 21 Эолова арфа 14

/
ОГЛАВЛЕНИЕ
Предисловие авторов 5
Предисловие Давида Рюэля 9
ЧАСТЬ I.jQt порядка 11
Введение. Немонотонная1 эволюция 11
Глава I. Свободный осциллятор, осциллятор с вынуждающей силой . . 19
Глава П. Осциллятор с вынуждающей силой, параметрический осциллятор 33
Глава III. Преобразование Фурье 52
Глава IV. Сечения Пуанкаре 75
Глава V. Три примера динамических систем . 94
ЧАСТЬ 2. ... К хаосу .116
Введение. Временный хаос в диссипативных системах 116
Глава VI. Странные аттракторы 127
Глава VII. Квазипериодичность 181
Глава VIII. Субгармонический каскад 217
Глава IX. Перемежаемость 250
Заключительная дискуссия 298
Приложение А. Локальные бифуркации коразмерности 1 305
Приложение Б. Показатели Ляпунова 314
Приложение В. Синхронизация осцилляторов ........... 325
Приложение Г. Модель Лоренца 339
Приложение Д. Математические дополнения 351
Некоторые общие работы 363
Предметшй указатель 335

Учебное издание
Пьер Берже, Ив Поыо, Кристиан Вндаль
ПОРЯДОК В ХАОСЕ
О детерминистском подходе к турбулентности
Заведующий редакцией проф. А. Н. Матвеев. Зам. зав. редакцией
С. М. Жебровский. Научн. редактор Е. С. Куранский. Мл. ред. Р. X. Заце-
Зацепина, Г. Г. Сорокина, В. Н. Цлаф. Художник К. В. Радченко. Художест-
Художественные редакторы И. Калеэин, О. Адаскина. Технический редактор
Т. А. Мирошина. Корректор Н. А. Мистрюкова
ИБ Jft 7391
Сдано в набор 29.06.90. Подписано к печати 15.01.91. Формат 60Х90'/н. Бу-
Бумага типографская № 1. Печать высокая. Гарнитура литературная. Объем
11,50 бум. л. Усл. печ. л. 23,00. Усл. кр.-отт. 23,00. Уч. изд. л. 19,05. Изд.
№ 2/7805. Тираж 6000 экз. Зак. 592. Цена 4 р. 90 к.
Издательство «Мир*
В/О «Совэкспорткнига» Государственного комитета СССР по печати
129820, ГСП, Москва, 1-й Рижский пер. 2.
Набрано в Ленинградской типографии J* 2, головного предприятия ордена
Трудового Красного Знамени Ленинградского объединения «Техническая
книга* им. Евгении Соколовой Государственного комитета СССР по печати.
198052, Ленинград, Л-52, Измайловский проспект, 29.
Отпечатано в Ленинградской типографии Jw S ордена Трудового Красного
Знамени Ленинградского объединения «Техническая книга» им. ьвгении
Соколовой Государственного комитета СССР по печати.
190000, Ленинград, Прачечный пер., 6.