Вероятностное программирование на практике - Ави Пфеффер

ЧАСТЬ I Введение в вероятностное программирование и систему Figaro

Глава 1. О вероятностном программировании в двух словах

1.1.2. Системы вероятностных рассуждений помогают принимать решения

1.1.3. Система вероятностных рассуждений может рассуждать тремя способами

1.1.4. Система вероятностного программирования: система вероятностных рассуждений, выраженная на языке программирования

1.2. Зачем нужно вероятностное программирование?

1.2.2. Улучшенные языки имитационного моделирования

1.3. Введение в Figaro, язык вероятностного программирования

Глава 2. Краткое руководство по языку Figaro

2.2. Создание модели и выполнение алгоритма вывода на примере Hello World

2.2.2. Выполнение алгоритма вывода и получение ответа на запрос

2.2.3. Построение моделей и задание наблюдений

2.2.5. Повторяющиеся элементы: когда они совпадают, а когда различаются?

2.3. Базовые строительные блоки: атомарные элементы

2.4. Комбинирование атомарных элементов с помощью составных

2.4.3. Составные версии атомарных элементов

2.5. Построение более сложных моделей с помощью Apply и Chain

2.6. Задание фактов с помощью условий и ограничений

Глава 3. Создание приложения вероятностного программирования

3.3. Архитектура приложения фильтра спама

3.4. Проектирование модели почтового сообщения

3.4.4. Использование числовых параметров

3.4.5. Работа с дополнительными знаниями

3.5. Разработка аналитического компонента

ЧАСТЬ II Написание вероятностных программ

Глава 4. Вероятностные модели и вероятностные программы

4.1.2. Подробно о распределении вероятности

4.2. Использование вероятностной модели для ответа на запросы

4.3. Составные части вероятностных моделей

4.5.2. Представление непрерывных переменных

Глава 5. Моделирование зависимостей с помощью байесовских и марковских сетей

5.2.2. Как байесовская сеть определяет распределение вероятности
5.2.3. Рассуждения с применением байесовской сети

5.3.2. Рассуждения с помощью модели диагностики компьютерной системы

5.4. Применение вероятностного программирования для обобщения байесовских сетей: предсказание успешности продукта

5.4.2. Рассуждения с помощью модели для предсказания успешности продукта

5.5.2. Представление марковских сетей и рассуждения с их помощью

Глава 6. Использование коллекций Scala и Figaro для построения моделей

6.1.3. Моделирование одновременной зависимости от двух переменных....

6.2.2. Иерархическая модель и коллекции Figaro

6.2.3. Совместное использование коллекций Scala и Figaro

6.3. Моделирование ситуаций с неизвестным числом объектов

6.3.3. Операции над массивами переменной длины

6.3.4. Пример: прогнозирование продаж неизвестного числа новых продуктов

6.4.2. Пример: моделирование состояния здоровья во времени

Глава 7. Объектно-ориентированное вероятностное моделирование

7.1.3. Рассуждения о нескольких принтерах

7.2. Добавление связей в объектно-ориентированные модели

7.2.3. Представление модели социальной сети на Figaro

7.3. Моделирование реляционной неопределенности и неопределенности типа

7.3.2. Модель социальной сети с реляционной неопределенностью

7.3.3. Модель принтера с неопределенностью типа

8.2.4. Модели с нестационарной структурой

8.3. Моделирование систем, работающих неопределенно долго

8.3.2. Использование универсумов для моделирования постоянно работающих систем

Глава 9. Три правила вероятностного вывода

9.2. Правило полной вероятности: получение ответов на простые запросы из совместного распределения

9.3. Правило Байеса: вывод причин из следствий

9.4.2. Предсказание результата следующего подбрасывания

10.1.2. Факторизация распределения вероятности с помощью цепного правила

10.1.3. Задание запросов с факторами с помощью правила полной вероятности

10.2.2. Исключение переменных как алгебраическая операция

10.3.2. Проектирование модели, эффективно поддерживающей ИП

10.5.2. Проектирование модели, эффективно поддерживающей РД

11.2.3. Полезность выборки по значимости

11.2.4. Приложения алгоритма выборки по значимости

11.3. Алгоритм Монте-Карло по схеме марковской цепи

11.3.2. Алгоритм МСМС в Figaro: алгоритм Метрополиса-Гастингса

12.2. Вычисление наиболее вероятного объяснения

12.2.2. Использование алгоритмов для ответа на запросы НВО

12.3.2. Выполнение алгоритмов вычисления вероятности фактов

Глава 13. Динамические рассуждения и обучение параметров

13.2.2. Обучение методом максимального правдоподобия и МАВ

Приложение А. Получение и установка Scala и Figaro

Приложение В. Краткий обзор систем вероятностного программирования

Автор: Ави Пфеффер

Теги: программирование на эвм компьютерные программы программирование

ISBN: 978-5-97060-410-6

Год: 2017

Похожие

Искусственный интеллект. Современный подход.

Структуры данных в С++

Паттерны проектирования для C# и платформы .NET Core

Грокаем алгоритмы. Иллюстрированное пособие для программистов и любопытствующих

Текст

Ави Пфеффер
Вероятн
остное
мирование
практике
MANNING
програм
на

Ави Пфеффер
Вероятностное
программирование
на практике

Practical
Probabilistic
Programming
AVIPFEFFER
MANNING
Shelter Island

Вероятностное
программирование
на практике
АВИ ПФЕФФЕР
ЛfrMkit lit*ll
Москва, 2017

УДК 004.42
ББК 32.973
П91
Ави Пфеффер
Вероятностное программирование на практике. / Пер. с англ. Слин-
кин А. А. - М.: ДМК Пресс, 2017. - 462 с: ил.
ISBN 978-5-97060-410-6
Книга представляет собой введение в вероятностное программирование
для программистов-практиков. Описан вероятностный вывод, где
алгоритмы помогают прогнозировать использование социальных сетей. Приведены
примеры построения фильтра спама, диагностики ошибок в вычислительной
системе, восстановления цифровых изображений. Представлен
функциональный стиль программирования для анализа текстов,
объектно-ориентированных моделей и моделей с открытой вселенной.
Издание рассчитано на широкий круг читателей: специалистов по анализу
данных и машинному обучению, программистов, студентов вузов и др.
УДК 004.42
ББК 32.973
Original English language edition published by Manning Publications Co., Rights and
Contracts Special Sales Department, 20 Baldwin Road, PO Box 261, Shelter Island, NY
11964. © 2016 by Manning Publications Co. All rights reserved. Russian-language edition
copyright © 2016 by DMK Press. All rights reserved.
Все права защищены. Любая часть этой книги не может быть воспроизведена
в какой бы то ни было форме и какими бы то ни было средствами без письменного
разрешения владельцев авторских прав.
Материал, изложенный в данной книге, многократно проверен. Но, поскольку
вероятность технических ошибок все равно существует, издательство не может
гарантировать абсолютную точность и правильность приводимых сведений. В связи
с этим издательство не несет ответственности за возможные ошибки, связанные с
использованием книги.
ISBN 978-1-61729-233-0 (англ.)
ISBN 978-5-97060-410-6 (рус.)
© 2016 by Manning Publications Co.
© Оформление, перевод на русский язык,
издание, ДМК Пресс, 2017

Памяти любимой матушки,
Клэр Пфеффер.
Да будет память её благословенна.

ОГЛАВЛЕНИЕ
Предисловие 13
Вступление 15
Благодарности 17
Об этой книге 19
Структура книги 20
О коде и упражнениях 21
Об авторе 21
Автор в сети 22
Об иллюстрации на обложке 22
ЧАСТЬ I
Введение в вероятностное программирование и систему Figaro 23
Глава 1. О вероятностном программировании в двух словах 24
1.1. Что такое вероятностное программирование? 24
1.1.1. Как мы высказываем субъективное суждение? 25
1.1.2. Системы вероятностных рассуждений помогают принимать решения 26
1.1.3. Система вероятностных рассуждений может рассуждать тремя
способами 28
1.1.4. Система вероятностного программирования: система вероятностных
рассуждений, выраженная на языке программирования 32
1.2. Зачем нужно вероятностное программирование? 37
1.2.1. Улучшенные вероятностные рассуждения 37
1.2.2. Улучшенные языки имитационного моделирования 38
1.3. Введение в Figaro, язык вероятностного программирования 40
1.3.1. Figaro и Java: построение простой системы вероятностного
программирования 43
1.4. Резюме 48
1.5. Упражнения 48
Глава 2. Краткое руководство по языку Figaro 50
2.1. Введение в Figaro 50
2.2. Создание модели и выполнение алгоритма вывода на примере Hello World 52
2.2.1. Построение первой модели 53
2.2.2. Выполнение алгоритма вывода и получение ответа на запрос 54

2.2.3. Построение моделей и задание наблюдений 55
2.2.4. Анатомия построения модели 56
2.2.5. Повторяющиеся элементы: когда они совпадают,
а когда различаются? 58
2.3. Базовые строительные блоки: атомарные элементы 59
2.3.1. Дискретные атомарные элементы 60
2.3.2. Непрерывные атомарные элементы 61
2.4. Комбинирование атомарных элементов с помощью составных 64
2.4.1. Элемент If 64
2.4.2. Элемент Dist 65
2.4.3. Составные версии атомарных элементов 66
2.5. Построение более сложных моделей с помощью Apply и Chain 67
2.5.1. Элемент Apply 67
2.5.2. Элемент Chain 70
2.6. Задание фактов с помощью условий и ограничений 73
2.6.1. Наблюдения 73
2.6.2. Условия 74
2.6.3. Ограничения 75
2.7. Резюме 78
2.8. Упражнения 78
Глава 3. Создание приложения вероятностного
программирования 80
3.1. Общая картина 80
3.2. Выполнение кода 83
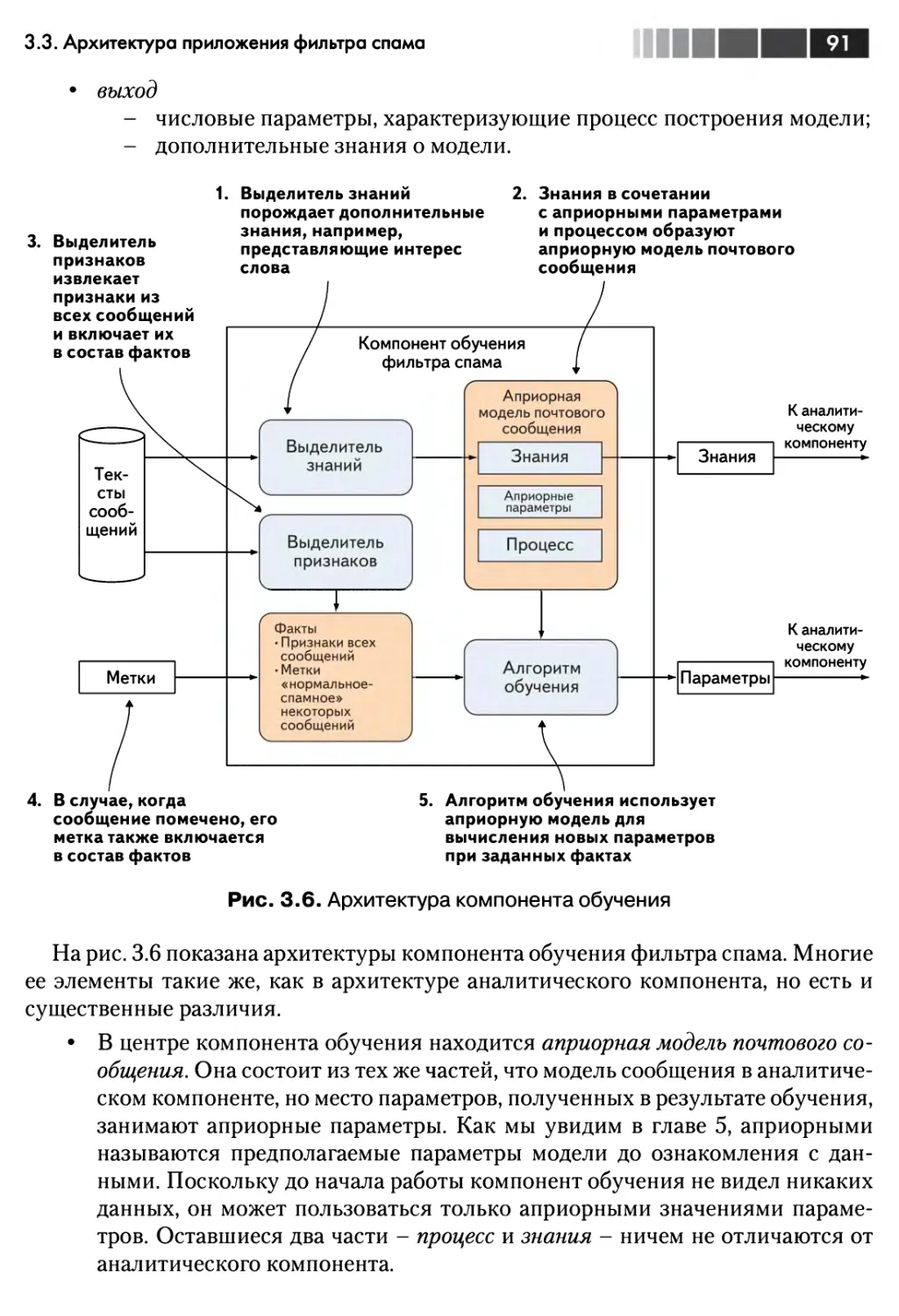
3.3. Архитектура приложения фильтра спама 86
3.3.1. Архитектура аналитического компонента 86
3.3.2. Архитектура компонента обучения 90
3.4. Проектирование модели почтового сообщения 92
3.4.1. Выбор элементов 93
3.4.2. Определение зависимостей 95
3.4.3. Определение функциональных форм 97
3.4.4. Использование числовых параметров 100
3.4.5. Работа с дополнительными знаниями 102
3.5. Разработка аналитического компонента 104
3.6. Разработка компонента обучения 108
3.7. Резюме 112
3.8. Упражнения 113
ЧАСТЬ II
Написание вероятностных программ 115
Глава 4. Вероятностные модели и вероятностные программы 116
4.1. Определение вероятностной модели 117
Оглавление
7

4.1.1. Выражение общих знаний в виде распределения вероятности
возможных миров 117
4.1.2. Подробно о распределении вероятности 120
4.2. Использование вероятностной модели для ответа на запросы 121
4.2.1. Применение условий для получения апостериорного
распределения вероятности 122
4.2.2. Получение ответов на запросы 124
4.2.3. Применение вероятностного вывода 126
4.3. Составные части вероятностных моделей 127
4.3.1. Переменные 127
4.3.2. Зависимости 129
4.3.3. Функциональные формы 134
4.3.4. Числовые параметры 138
4.4. Порождающие процессы 140
4.5. Модели с непрерывными переменными 144
4.5.1. Бета-биномиальная модель 145
4.5.2. Представление непрерывных переменных 146
4.6. Резюме 150
4.7. Упражнения 150
Глава 5. Моделирование зависимостей с помощью байесовских
и марковских сетей 152
5.1. Моделирование зависимостей 153
5.1.1. Направленные зависимости 153
5.1.2. Ненаправленные зависимости 159
5.1.3. Прямые и косвенные зависимости 162
5.2. Байесовские сети 163
5.2.1. Определение байесовской сети 163
5.2.2. Как байесовская сеть определяет распределение вероятности 166
5.2.3. Рассуждения с применением байесовской сети 166
5.3. Изучение примера байесовской сети 169
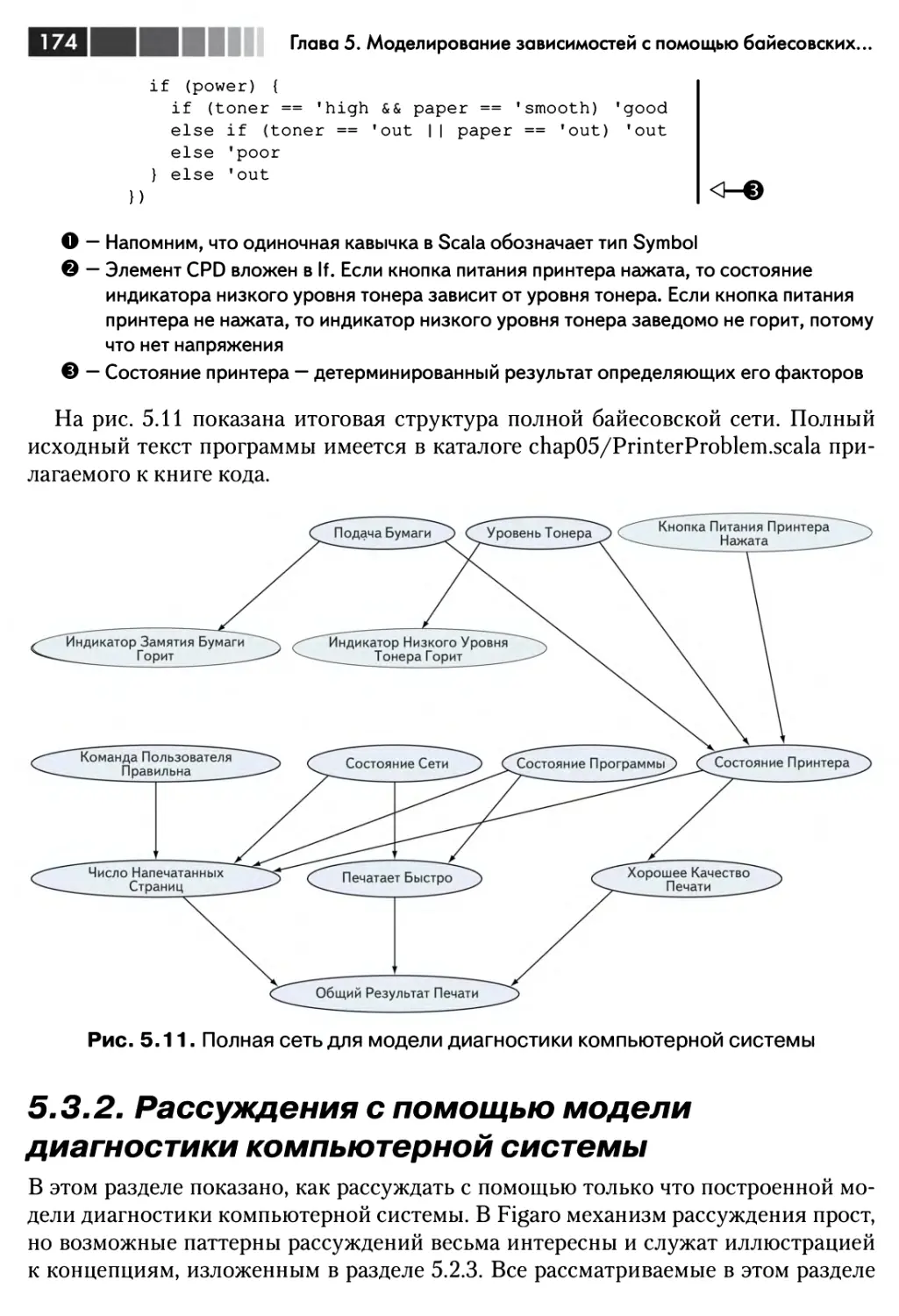
5.3.1. Проектирование модели диагностики компьютерной системы 169
5.3.2. Рассуждения с помощью модели диагностики компьютерной
системы 174
5.4. Применение вероятностного программирования для обобщения
байесовских сетей: предсказание успешности продукта 179
5.4.1. Проектирование модели для предсказания успешности продукта.... 180
5.4.2. Рассуждения с помощью модели для предсказания успешности
продукта 185
5.5. Марковские сети 187
5.5.1. Определение марковской сети 187
5.5.2. Представление марковских сетей и рассуждения с их помощью 191
5.6. Резюме 195
5.7. Упражнения 195
8
Оглавление

Глава 6. Использование коллекций Scala и Figaro для построения
моделей 198
6.1. Работа с коллекциями Scala 199
6.1.1. Моделирование зависимости многих переменных от одной 200
6.1.2. Создание иерархических моделей 203
6.1.3. Моделирование одновременной зависимости от двух переменных.... 205
6.2. Работа с коллекциями Figaro 208
6.2.1. Почему коллекции Figaro полезны? 208
6.2.2. Иерархическая модель и коллекции Figaro 210
6.2.3. Совместное использование коллекций Scala и Figaro 212
6.3. Моделирование ситуаций с неизвестным числом объектов 215
6.3.1. Открытая вселенная с неизвестным числом объектов 215
6.3.2. Массивы переменной длины 216
6.3.3. Операции над массивами переменной длины 217
6.3.4. Пример: прогнозирование продаж неизвестного числа новых
продуктов 218
6.4. Работа с бесконечными процессами 220
6.4.1. Характеристика Process 220
6.4.2. Пример: моделирование состояния здоровья во времени 222
6.4.3. Использование процесса 224
6.5. Резюме 225
6.6. Упражнения 226
Глава 7. Объектно-ориентированное вероятностное
моделирование 228
7.1. Объектно-ориентированные вероятностные модели 229
7.1.1. Элементы объектно-ориентированного моделирования 230
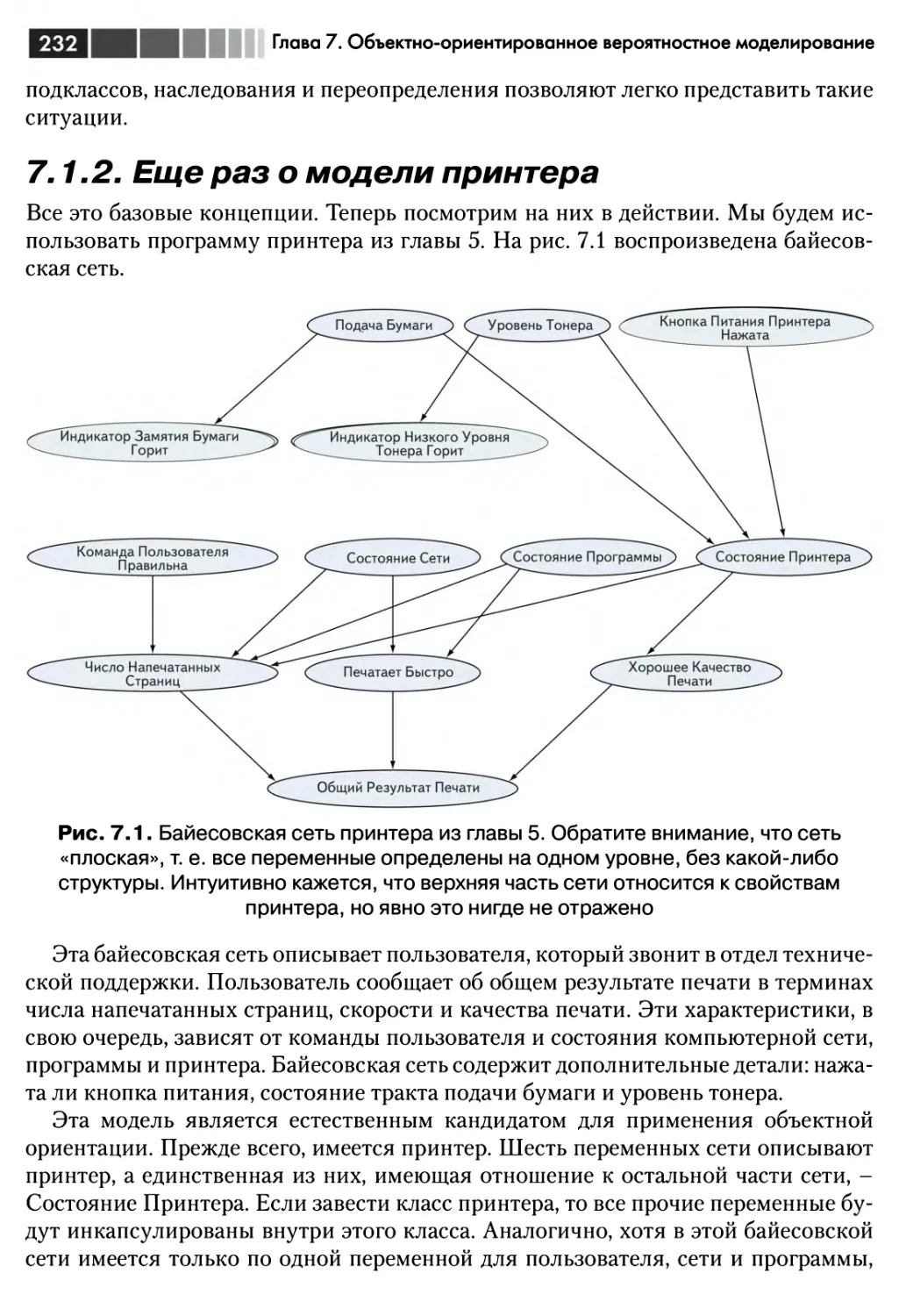
7.1.2. Еще раз о модели принтера 232
7.1.3. Рассуждения о нескольких принтерах 236
7.2. Добавление связей в объектно-ориентированные модели 240
7.2.1. Описание общей модели на уровне классов 240
7.2.2. Описание ситуации 243
7.2.3. Представление модели социальной сети на Figaro 246
7.3. Моделирование реляционной неопределенности и неопределенности
типа 249
7.3.1. Коллекции элементов и ссылки 249
7.3.2. Модель социальной сети с реляционной неопределенностью 252
7.3.3. Модель принтера с неопределенностью типа 254
7.4. Резюме 257
7.5. Упражнения 257
ГЛАВА 8. Моделирование динамических систем 259
8.1. Динамические вероятностные модели 260
8.2. Типы динамических моделей 261
Оглавление
9

8.2.1. Марковские цепи 261
8.2.2. Скрытые марковские модели 265
8.2.3. Динамические байесовские сети 268
8.2.4. Модели с нестационарной структурой 272
8.3. Моделирование систем, работающих неопределенно долго 277
8.3.1. Универсумы в Figaro 277
8.3.2. Использование универсумов для моделирования постоянно
работающих систем 279
8.3.3. Следящее приложение 281
8.4. Резюме 284
8.5. Упражнения 284
ЧАСТЬ III
Вывод 287
Глава 9. Три правила вероятностного вывода 288
9.1. Цепное правило: построение совместных распределений по условным
распределениям вероятности 290
9.2. Правило полной вероятности: получение ответов на простые запросы
из совместного распределения 294
9.3. Правило Байеса: вывод причин из следствий 297
9.3.1. Понимание, причина, следствие и вывод 297
9.3.2. Правило Байеса на практике 299
9.4. Байесовское моделирование 301
9.4.1. Оценивание асимметрии монеты 303
9.4.2. Предсказание результата следующего подбрасывания 307
9.5. Резюме 312
9.6. Упражнения 312
Глава 10. Факторные алгоритмы вывода 314
10.1. Факторы 315
10.1.1. Что такое фактор? 315
10.1.2. Факторизация распределения вероятности с помощью цепного
правила 318
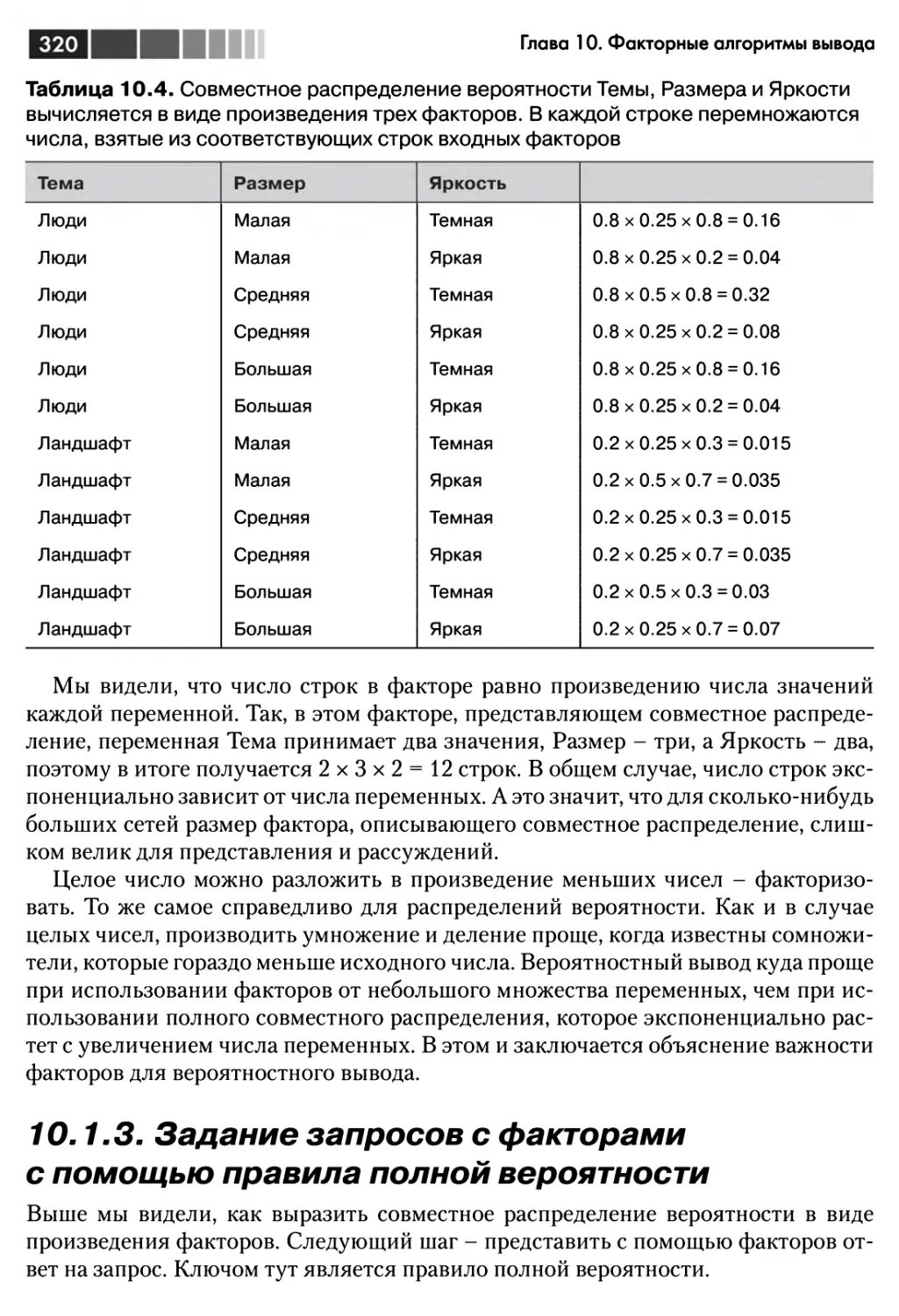
10.1.3. Задание запросов с факторами с помощью правила полной
вероятности 320
10.2. Алгоритм исключения переменных 324
10.2.1. Графическая интерпретация ИП 325
10.2.2. Исключение переменных как алгебраическая операция 329
10.3. Использование алгоритма ИП 332
10.3.1. Особенности ИП в Figaro 332
10.3.2. Проектирование модели, эффективно поддерживающей ИП 334
10.3.3. Приложения алгоритма ИП 338
10.4. Распространение доверия 342
10
Оглавление

10.4.1. Основные принципы РД 342
10.4.2. Свойства циклического РД 343
10.5. Использование алгоритма РД 345
10.5.1. Особенности РД в Figaro 346
10.5.2. Проектирование модели, эффективно поддерживающей РД 347
10.5.3. Приложения алгоритма РД 349
10.6. Резюме 350
10.7. Упражнения 350
Глава 11. Выборочные алгоритмы 353
11.1. Принцип работы выборочных алгоритмов 354
11.1.1. Прямая выборка 355
11.1.2. Выборка с отклонением 360
11.2. Выборка по значимости 363
11.2.1. Как работает выборка по значимости 364
11.2.2. Выборка по значимости в Figaro 367
11.2.3. Полезность выборки по значимости 368
11.2.4. Приложения алгоритма выборки по значимости 370
11.3. Алгоритм Монте-Карло по схеме марковской цепи 373
11.3.1. Как работает МСМС 374
11.3.2. Алгоритм МСМС в Figaro: алгоритм Метрополиса-Гастингса 378
11.4. Настройка алгоритмами 382
11.4.1. Специальные схемы предложения 384
11.4.2. Избежание жестких условий 388
11.4.3. Приложения алгоритма МГ 389
11.5. Резюме 391
11.6. Упражнения 392
Глава 12. Решение других задач вывода 394
12.1. Вычисление совместных распределений 395
12.2. Вычисление наиболее вероятного объяснения 397
12.2.1. Вычисление и запрос НВО в Figaro 400
12.2.2. Использование алгоритмов для ответа на запросы НВО 402
12.2.3. Приложения алгоритмов НВО 409
12.3. Вычисление вероятности фактов 410
12.3.1. Наблюдение фактов для вычисления вероятности фактов 411
12.3.2. Выполнение алгоритмов вычисления вероятности фактов 414
12.4. Резюме 415
12.5. Упражнения 415
Глава 13. Динамические рассуждения и обучение параметров 417
13.1. Мониторинг состояния динамической системы 418
13.1.1. Механизм мониторинга 419
13.1.2. Алгоритм фильтрации частиц 421
Оглавление
и

13.1.3. Применения фильтрации 424
13.2. Обучение параметров модели 425
13.2.1. Байесовское обучение 426
13.2.2. Обучение методом максимального правдоподобия и МАВ 430
13.3. Дальше вместе с Figaro 439
13.4. Резюме 440
13.5. Упражнения 440
Приложение А. Получение и установка Scala и Figaro 443
А.1. Использование sbt 443
А.2. Установка и запуск Figaro без sbt 444
А.З. Сборка из исходного кода 445
Приложение В. Краткий обзор систем вероятностного
программирования 447
Предметный указатель 450
12
Оглавление

ПРЕДИСЛОВИЕ
В 1814 году Пьер-Симон Лаплас писал: «по большей части важнейшие
жизненные вопросы являются на самом деле лишь задачами теории вероятностей».
Спустя сто лет после этих слов на такие вопросы можно было ответить только одним
способом (сохраняя верность мнению Лапласа): проанализировать каждую задачу
на бумаге, выразить результат в виде формулы и вычислить значение формулы,
вручную подставив в нее числа. Наступление эры компьютеров мало что
изменило. Просто стало возможно вычислять более сложные формулы, а анализ с
помощью «пера и бумаги» теперь может занимать сотни страниц.
Для анализа вероятностной задачи необходимо построить вероятностную
модель, в которой описывается пространство возможных исходов и каждому из них
каким-то образом сопоставляется числовая вероятность. Раньше вероятностные
модели формулировались на смеси естественного языка и полуформальной
математической нотации. На основе модели с помощью некоторых математических
манипуляций выводилась формула или алгоритм для вычисления ответов. Обе
стадии были трудоемкими, чреватыми ошибками и зависели от конкретной
задачи, поэтому применение теории вероятностей на практике сталкивалось с
серьезными ограничениями. Вопреки Лапласу, важнейшие жизненные вопросы
оставались неразрешенными.
Первым крупным продвижением стала разработка формальных языков, в
частности байесовских и марковских сетей, для выражения вероятностных моделей. У
формального языка имеется точный синтаксис, определяющий, какие выражения
допустимы, и точная семантика, определяющая, что означает каждое допустимое
выражение (т. е. какая именно вероятностная модель представлена данным
выражением). Поэтому появилась возможность описывать вероятностные модели
в машиночитаемом виде и разработать единый алгоритм вычисления следствий
любой выразимой вероятностной модели.
Но в этой бочке меда есть одна ложка дегтя: отсутствие выразимых вероятностных
моделей. Байесовские и марковские сети как формальные языки обладают очень
ограниченными выразительными возможностями. В каком-то смысле их можно
назвать вероятностными аналогами булевых схем. Чтобы понять, в чем состоит
ограничение, рассмотрим написание программы расчета платежной ведомости
для крупной компании. На языке высокого уровня, например Java, она может
состоять из десятков тысяч строк кода. А теперь представьте себе реализацию той
же функциональности посредством соединения логических вентилей. Эта задача,

Предисловие
по всей видимости, абсолютно неразрешима. Схема оказалась бы невообразимо
огромной, сложной и непонятной, поскольку логическим схемам недостает
выразительной силы, соответствующей структуре задачи.
В 1997 году Ави Пфеффер, автор этой книги, тогда еще студент, в соавторстве
со своим научным руководителем Дафной Коллер и коллегой Дэвидом Макал-
лестером, опубликовал пионерскую работу по языкам вероятностного
программирования (ЯВП) (probabilistic programming language - PPL), в которой
высказана важнейшая идея, связывающая теорию вероятностей с выразительными
возможностями языков программирования высокого уровня. Идея заключалась в
том, что программу можно рассматривать как вероятностную модель, если ввести
некоторые стохастические элементы и определить смысл программы как
вероятность каждого возможного пути выполнения. Эта идея вводит полезную связь
между двумя важнейшими областями математики, и мы еще только приступаем к
исследованию открывающихся на этом пути возможностей.
Книга представляет собой неформальное введение в круг этих идей на
примере языка Figaro для иллюстрации основных концепций и их применения. Автор
избегает ненужной математики и акцентирует внимание на реальных тщательно
подобранных примерах, которые подробно объясняет. Книга доступна любому
человеку со стандартной подготовкой в области программирования. Заодно
трудолюбивый читатель с меньшими, чем обычно, усилиями освоит принципы и
технику байесовского вывода и статистического обучения. Но, пожалуй, еще важнее
тот факт, что читатель приобретет навыки моделирования - одно из важнейших
умений любого ученого или инженера. Figaro и другие ЯВП позволяют выражать
такие модели непосредственно, быстро и точно.
Эта книга - важный шаг на пути вывода вероятностного программирования из
научно-исследовательских лабораторий, где оно зародилось, в реальный мир. Без
сомнения, такое столкновение с реальностью выявит ограничения имеющихся
систем ВП, и у лабораторий появятся новые задачи. С другой стороны,
читатели этой книги обязательно откроют неожиданные способы применения Figaro и
подобных ему языков к широкому кругу новых задач, о которых авторы даже не
подозревали.
Стюарт Рассел
профессор информатики
Калифорнийский университет в Беркли
14

ВСТУПЛЕНИЕ
Вероятностное программирование - новая захватывающая область исследований,
которая привлекает все больший интерес. Постепенно она прокладывает себе
дорогу из академических кругов в мир программистов. По сути дела, вероятностное
программирование - это новый способ создания вероятностных моделей,
позволяющих предсказывать или выводить новые факты, которых нет в результатах
наблюдений. Вероятностные рассуждения давно считаются одним из основных
подходов к машинному обучению, где модель описывает то, что известно из опыта.
Но раньше такие системы были ограничены простыми фиксированными
структурами типа байесовских сетей. Вероятностное программирование освобождает
системы вероятностных рассуждений от этих оков, предоставляя всю мощь языков
программирования для представления моделей. Можно считать, что это аналог
перехода от логических схем к языкам высокого уровня.
Я начал заниматься вероятностным программированием с подростковых лет,
когда писал футбольный симулятор на BASIC, хотя в то время еще не осознавал
этого. В программе встречались предложения вида «GOTO 1730 + RANDOM * 5»,
призванные выразить случайную последовательность событий. После тщательной
настройки эмулятор оказался настолько реалистичным, что я мог развлекаться с
ним часами. Разумеется, с тех пор вероятностное программирование далеко ушло
от предложений GOTO со случайным адресом.
В 1997 я в соавторстве с Дафной Коллер и Дэвидом Макаллестером написал
одну из первых работ по вероятностному программированию. В ней описывался
Lisp-подобный язык, но главным новшеством был алгоритм выведения вероятных
аспектов программы на основе наблюдаемых результатов ее работы. Это и вывело
вероятностное программирование из разряда типичных языков вероятностного
моделирования, предоставив средства, позволявшие программе не только
продвигаться вперед по одному из возможных путей выполнения, но и строить обратные
рассуждения и делать выводы о том, почему получен наблюдаемый результат.
В начале 2000-х годов я разработал IBAL (произносится «айболл») - первую
систему вероятностного программирования общего назначения, основанную на
функциональном программировании. IBAL обладала высокой выразительной
способностью и содержала инновационные алгоритмы вывода, но с годами меня
все сильнее раздражали ее ограничения и главное из них - трудность
взаимодействия с данными и интеграции с приложениями. Поэтому в 2009 году я начал
разрабатывать новую систему вероятностного программирования, которую назвал

Вступление
Figaro. При проектировании Figaro на первый план выдвигалась практичность, но
не жертвуя мощью вероятностного программирования. Это навело меня на мысль
реализовать Figaro в виде библиотеки на языке Scala, что упрощает интеграцию
вероятностных моделей с приложениями для виртуальной машины Java. В то же
время Figaro предлагала, пожалуй, самый широкий спектр средств представления
и алгоритмов выводов из всех известных мне систем вероятностного
программирования. В настоящее время Figaro - проект с открытым исходным кодом на
GitHub, его текущая версия имеет номер 3.3.
Овладеть вероятностным программированием не так-то просто, потому что
необходимы разнообразные навыки и, прежде всего, умение строить вероятностные
модели и писать программы. Для многих программистов написание программ -
естественный процесс, но вероятностные модели окутаны тайной. Эта книга
призвана сорвать покров таинственности, показать, как можно эффективно
программировать в процессе создания моделей и помочь в освоении систем
вероятностного программирования. Не предполагается, что читатель имеет подготовку
в области машинного обучения или вероятностных рассуждений. Знакомство с
функциональным программированием и языком Scala будет полезно, но для
чтения книги не нужно быть опытным специалистом по Scala. Зато вполне может
статься, что после прочтения вы станете программировать на Scala увереннее.
Прочитав книгу, вы сможете проектировать вероятностные модели для
различных приложений, извлекающих осмысленную информацию из данных, и степень
доктора по машинному обучению для этого не потребуется. Если вы
специализируетесь в какой-то предметной области, то книга поможет выразить модели,
которые имеются у вас в голове или на бумаге, и сделать их операционными, т. е.
допускающими вычисление и анализ вариантов. Если вы - специалист по анализу
данных, то, прочитав книгу, сможете разрабатывать более развитые, детальные и
потенциально более точные модели, чем позволяют другие средства.
Программисту или архитектору, стремящемуся включить в свою систему умение рассуждать
в условиях неопределенности, книга поможет не только построить вероятностную
модель, но и интегрировать ее с приложением. По какой бы причине вы ни
выбрали эту книгу, я надеюсь, что она доставит вам удовольствие и окажется полезной.
16

БЛАГОДАРНОСТИ
Эта книга потребовала многих лет работы: от первых идей, касающихся
вероятностного программирования, через создание систем IBAL и Figaro до замысла,
написания и шлифовки книги в сотрудничестве с издательством Manning. He счесть
людей, усилия которых помогали созданию книги.
Своим существованием эта книга в значительной степени обязана трудам моих
коллег из компании Charles River Analytics: Джо Гормана (Joe Gorman),
Скотта Харрисона (Scott Harrison), Майкла Ховарда (Michael Howard), Ли Келлога
(Lee Kellogg), Элисон О'Коннор (Alison O'Connor), Майка Репоза (Mike Reposa),
Брайна Раттенберга (Brian Ruttenberg) и Гленна Таката (Glenn Takata). Также
спасибо Скотту Нилу Рейли (Scott Neal Reilly), который поддерживал Figaro с самого
начала.
Большую часть того, что я знаю об искусственном интеллекте и машинном
обучении, я почерпнул от Дафны Коллер, моего научного руководителя и коллеги.
Стюарт Рассел предоставил мне первую возможность изучать искусственный
интеллект и воодушевлял на протяжении всей моей карьеры. А недавно мы начали
работать в одном проекте, и он написал предисловие к этой книге. Майкл Стоун-
брейкер предоставил мне шанс заняться исследованиями в своем проекте СУБД
Postgres, и я много узнал о построении систем, работая в его группе. Алон Халеви
(Alon Halevy) пригласил меня провести лето вместе с ним с в AT&T Labs, где я
имел первые беседы о вероятностном программировании с Дэвидом Макаллесте-
ром; в результате родилась на свет статья о вероятностном диалекте Lisp,
написанная в соавторстве с Дафной. С Лайзой Гетур (Lise Getoor), делившей со мной
кабинет и общую работу, я мог обсуждать идеи, которые вынашивал.
Я глубоко признателен Алексу Ихлеру (Alex Ihler), который любезно проверил
книгу на предмет отсутствия технических ошибок. Алекс также оказался
великолепным слушателем, на котором последние пару лет я опробовал все идеи,
относящиеся к логическому выводу.
Многие люди делились своими замечаниями на различных этапах разработки,
в том числе Равишанкар Раджагопалан (Ravishankar Rajagopalan) и Шабеш Ба-
лан (Shabeesh Balan), Крис Хенеган (Chris Heneghan), Клеменс Баадер (Clemens
Baader), Кроистофер Вебер (Cristofer Weber), Эрл Бингэм (Earl Bingham), Джу-
зеппе де Марко (Giuseppe de Marco), Джауме Валлс (Jaume Vails), Хавьер Гуэр-
ра Гиральдес (Javier Guerra Giraldez), Костас Пассадис (Kostas Passadis), Лука
Кампобассо (Luca Campobasso), Лукас Наллиндо (Lucas Gallindo), Марк Элстон

Благодарности
(Mark Elston), Марк Миллер (Mark Miller), Нитин Годе (Nitin Gode), Одиссеас
Пентаколос (Odisseyas Pentakolos), Петр Рабинович (Peter Rabinovitch), Филлип
Брэдфорд (Phillip Bradford), Стивен Уэйкли (Stephen Wakely), Тапош Дутта Рой
(Taposh Dutta Roy), Унникришнан Кумар (Unnikrishnan Kumar).
Я благодарен многим замечательным сотрудникам издательства Manning,
которые способствовали выходу книги из печати. Отдельное спасибо редактору Дэну
Махарри (Dan Maharry), который сделал книгу куда лучше, чем мог бы я сам, и
Фрэнку Полманну (Frank Pohlmann), который посоветовал мне написать книгу и
помогал на подготовительных этапах.
Спасибо Исследовательской лаборатории ВВС и Управлению перспективных
научно-исследовательских проектов Министерства обороны США (DARPA)
за финансирование части описанной в этой книге работы в рамках программы
PPAML (вероятностное программирование для развития методов машинного
обучения). Отдельная благодарность нескольким руководителям программ в
DARPA: Бобу Кохоуту (Bob Kohout), Тони Фальконе (Tony Falcone), Кэтлин
Фишер (Kathleen Fisher) и Сурешу Джаганнатану (Suresh Jagannathan), которые
поверили в вероятностное программирование и прилагали все силы, чтобы оно стало
реальностью. Этот материал основан на работе, которая финансировалась ВВС
США по контракту № FA8750-14-C-0011. Мнения, открытия и заключения или
рекомендации автора, встречающиеся в этом материале, не обязательно отражают
точку зрения ВВС США.
И наконец, эта книга не состоялась бы без любви и поддержки со стороны моей
семьи. Спасибо моей супруге Дебби Гелбер и моим детям Дине, Номи и Рути за
то, что они такие чудесные. И вечная благодарность моей маме Клэр Пфеффер,
воспитавшей меня с любовью. Эту книгу я посвящаю твоей памяти.
18

ОБ ЭТОЙ КНИГЕ
Многие решения, будь то в бизнесе, науке, военном деле или повседневной
жизни, принимаются в условиях неопределенности. Если разные факторы толкают
в разных направлениях, то как узнать, на что обращать больше внимания?
Вероятностные модели дают средство выразить всю информацию, относящуюся к
конкретной ситуации. Вероятностные рассуждения позволяют использовать эти
модели, чтобы найти вероятности величин, наиболее существенных для принятия
решения. С помощью вероятностных рассуждений можно предсказать наиболее
вероятное развитие событий: хорошо ли будет продаваться ваш продукт по
назначенной цене, будет ли пациент отвечать на предложенное лечение, сможет ли
кандидат победить на выборах, если займет определенную позицию? Вероятностные
рассуждения можно использовать и для вывода вероятных причин уже
случившихся событий: если продажи провалились, то не потому ли, что была назначена
слишком высокая цена?
Вероятностное рассуждение также является одним из основных подходов к
машинному обучению. Мы представляем исходные допущения о предметной
области в виде вероятностной модели, например общей модели поведения
пользователей в ответ на появление продуктов на рынке. Затем, получив обучающие данные,
скажем о реакции пользователей на конкретные продукты, мы модифицируем
первоначальные представления и получаем новую модель. Эту модель можно уже
использовать для предсказания будущих событий, например успеха
перспективного продукта, или для объяснения причин наблюдавшихся событий, скажем
провала нового продукта.
Раньше для выражения вероятностных рассуждения применялись
специализированные языки представления вероятностных моделей. В последние годы мы
поняли, что можно использовать обычные языки программирования, и это
положило начало вероятностному программированию. У такого подхода три
основных достоинства. Во-первых, при построении моделей в нашем распоряжении
все средства языка программирования: развитые структуры данных, поток
управления и т. д. Во-вторых, вероятностную модель легко интегрировать с другими
приложениями. И, в-третьих, для рассуждений о моделях можно использовать
универсальные алгоритмы логического вывода.
Задача этой книги - вооружить вас знаниями, необходимыми для
использования вероятностного программирования в повседневной деятельности. В
частности, объясняется:

• как строить вероятностные модели и выражать их в виде вероятностных
программ;
• как устроены вероятностные рассуждения и как они реализованы в
различных алгоритмах вывода;
• как с помощью системы вероятностного программирования Figaro
создавать практичные вероятностные программы.
Система Figaro реализована в виде библиотеки на языке Scala. Как и в Scala,
в ней сочетаются функциональный и объектно-ориентированный стили
программирования. Некоторое знакомство с функциональным программированием было
бы полезно. Но в этой книге не используются сложные концепции
функционального программирования, так что для понимания хватит и скромных познаний.
Знание Scala также не помешало бы. Хотя встречающиеся конструкции Scala
часто объясняются, эта книга не является введением в Scala. Но экзотические
особенности Scala почти не используются, так что поверхностного знакомства будет
достаточно.
Структура книги
Часть 1 представляет собой введение в вероятностное программирование и
систему Figaro. В начале главы 1 объясняется, что такое вероятностное
программирование и почему оно полезно, а затем приводится краткое введение в Figaro.
Глава 2 - учебное пособие по работе с Figaro, она позволит вам быстро приступить к
написанию вероятностных программ. В главе 3 вы найдете полное приложение
вероятностного программирования - фильтр спама - включающее компонент,
который рассуждает о том, является данное почтовое сообщение хорошим или
спамным, и компонент, который обучает вероятностную модель на данных. Цель
главы 3 - дать общую картину взаимосвязей разных частей, перед тем как
приступать к детальному изучению приемов моделирования.
Часть 2 целиком посвящена построению вероятностных программ. В главе 4
представлены основные сведения о вероятностных моделях и вероятностных
программах, которые необходимы для понимания того, что в действительности
стоит за созданием таких программ. В главе 5 описаны две системы моделирования,
лежащие в основе вероятностного программирования: байесовские и марковские
сети. Главы 6-8 содержат набор полезных приемов программирования,
применяемых при создании более сложных программ. В главе 6 речь идет о коллекциях в
Scala и Figaro, позволяющих скомпоновать много переменных одного типа.
Глава 7 посвящена объектно-ориентированному программированию, которое в
функциональных программах не менее полезно, чем в обычных. В главе 8 рассказано о
моделировании динамических систем. Динамической называется система,
состояние которой изменяется со временем, и в этой главе подробно рассматривается
это весьма распространенное и важное применение вероятностных рассуждений.
Из части 3 вы узнаете о вероятностных алгоритмах вывода. Понимать, что такое
вывод, необходимо для эффективного применения вероятностного
программирования; это позволит выбрать подходящий для решения задачи алгоритм, правиль-
20
Об этой книге

Об авторе
но настроить его и выразить модель так, чтобы она эффективно поддерживала
рассуждения. Я старался соблюсти баланс между изложением теории, стоящей за
алгоритмами, и практическими примерами их использования. В
основополагающей главе 9 сформулированы три правила, в которых заключены основные идеи
вероятностного вывода. В главах 10 и 11 описаны два основных семейства
алгоритмов вывода. В главе 10 рассматриваются факторные алгоритмы, в том числе
введение в факторы и принципы их работы, а также алгоритмы исключения
переменных и распространения доверия. В главе 11 обсуждаются выборочные
алгоритмы с акцентом на выборку по значимости и методы Монте-Карло по схеме
марковской цепи. Если в главах 10 и 11 упор сделан на базовом запросе -
вычислении вероятностей величин, представляющих интерес, то в главе 12 показано, как
факторные и выборочные алгоритмы можно использовать для вычисления других
запросов, например, совместной вероятности нескольких переменных, наиболее
вероятных значений переменных и вероятности эмпирических данных. Наконец,
в главе 13 обсуждаются две более сложных, но важных задачи вывода: мониторинг
динамической системы, изменяющейся во времени, и нахождение числовых
параметров вероятностной модели на основе обучающих данных.
Каждая глава сопровождается упражнениями. Это могут быть как простые
вычисления, так и задачи на размышление, не предполагающие однозначного ответа.
В книге есть еще два приложения. Приложение А содержит инструкцию по
установке Figaro, а приложение В - краткий обзор других систем вероятностного
программирования.
О коде и упражнениях
Код набран моноширинным шрифтом, чтобы не путать его с обычным текстом. Многие
листинги сопровождаются аннотациями, в которых объяснены важные
концепции. В некоторых случаях за листингом следует несколько комментариев,
оформленных как отдельные пункты.
Многие примеры кода имеются в сети, найти их можно на сайте книги по адресу
www.manning.com/books/practical-probabilistic-programming. Там же есть ответы
на избранные упражнения.
Об авторе
Ави Пфеффер - пионер вероятностного программирования, работающий в этой
области с момента ее зарождения. Ави - ведущий проектировщик и разработчик
Figaro. В компании Charles River Analytics Ави занимается применением Figaro
к различным задачам, в том числе к анализу вредоносного ПО, мониторингу
исправности транспортных средств, моделированию климата и оценке инженерных
систем.
В свободное время Ави поет, сочиняет музыку и продюсирует музыкальные
произведения. Ави живет в Кембридже, штат Массачусетс, с женой и тремя
детьми.
21

Об этой книге
Автор в сети
Приобретение книги «Практическое вероятностное программирование»
открывает бесплатный доступ к закрытому форуму, организованному издательством
Manning Publications, где вы можете оставить свои комментарии к книге, задать
технические вопросы и получить помощь от автора и других пользователей.
Получить доступ к форуму и подписаться на список рассылки можно на странице
www.manning.com/books/practical-probabilistic-programming. Там же написано,
как зайти на форум после регистрации, на какую помощь можно рассчитывать, и
изложены правила поведения в форуме.
Издательство Manning обязуется предоставлять читателям площадку для
общения с другими читателями и автором. Однако это не означает, что автор
обязан как-то участвовать в обсуждениях; его присутствие на форуме остается чисто
добровольным (и не оплачивается). Мы советуем задавать автору какие-нибудь
хитроумные вопросы, чтобы его интерес к форуму не угасал!
Форум автора в сети и архивы будут доступны на сайте издательства до тех пор,
пока книга не перестанет печататься.
Об иллюстрации на обложке
Рисунок на обложке книги называется «The Venetian», или «Житель Венеции».
Он взят из книги Жака Грассе де Сен-Совера «Энциклопедия путешествий»,
опубликованной в 1796 году. Путешествие ради удовольствия в те времена было в
новинку, а путеводители, подобные этому, были весьма популярны - они
знакомили настоящих туристов и путешественников, не покидающих своего кресла, с
жителями других регионов Франции и всего мира.
Разнообразие иллюстраций в «Энциклопедии путешествий» красноречиво
свидетельствует об уникальности и индивидуальности городков и провинций,
которое можно было наблюдать каких-то 200 лет назад. То было время, когда по
манере одеваться, отличающейся в местах, разделенных всего несколькими
десятками миль, можно было сказать, откуда человек родом. Этот путеводитель
возвращает к жизни ощущение изолированности и удаленности, свойственное тому
периоду, да и всем остальным историческим периодам, кроме нашего
гиперактивного настоящего.
С тех пор манера одеваться сильно изменилась, и различия между областями,
когда-то столь разительные, сгладились. Теперь трудно отличить друг от друга
даже выходцев с разных континентов, что уж говорить о странах или областях. Но
можно взглянуть на это и с оптимизмом - мы обменяли культурное и визуальное
разнообразие на иное устройство личной жизни - основанное на многостороннем
и стремительном технологическом и интеллектуальном развитии.
Издательство Manning откликается на новации и инициативы в компьютерной
отрасли обложками своих книг, на которых представлено широкое разнообразие
местных укладов быта в позапрошлом веке. Мы возвращаем его в том виде, в каком оно
запечатлено на рисунках из разных собраний, в том числе из этого путеводителя.
22

Часть I
ВВЕДЕНИЕ
В ВЕРОЯТНОСТНОЕ
ПРОГРАММИРОВАНИЕ
И СИСТЕМУ FIGARO
-Lto такое вероятностное программирование? Почему оно полезно? Как им
пользоваться? Ответы на эти вопросы составляют основное содержание первой
части. В главе 1 излагаются основные идеи вероятностного программирования.
Прежде всего, мы познакомимся с концепцией системы вероятностных
рассуждений и покажем, как вероятностное программирование соединяет традиционные
системы вероятностных рассуждений с технологией языков программирования.
В этой книге мы будем использовать систему вероятностного
программирования Figaro. В главе 1 дается краткое введение в Figaro, а глава 2 представляет
собой пособие по основным понятиям Figaro, позволяющее быстро приступить к
написанию вероятностных программ. Глава 3 содержит законченное
вероятностное приложение, из которого вы поймете, как реальная программа собирается из
различных частей. Эта глава находится в начале книги, чтобы можно было
составить общую картину, но имеет смысл возвращаться к ней и позже, после более
глубокого знакомства с различными концепциями.

ГЛАВА 1 .
О вероятностном
программировании в двух словах
В этой главе.
■ Что такое вероятностное программирование?
■ Какое мне до него дело? А моему начальнику?
■ Как оно работает?
■ Figaro - система вероятностного
программирования.
■ Сравнение вероятностных приложений, написан
ных с применением и без применения
вероятностного программирования.
Из этой главы вы узнаете, как принимать решения с помощью вероятностной
модели и алгоритма вывода - двух главных составных частей системы
вероятностных рассуждений. Вы также узнаете, как современные языки вероятностного
программирования упрощают создание подобных систем по сравнению с
такими универсальными языками, как Java или Python. Здесь же вы познакомитесь с
Figaro, основанным на Scala языком вероятностного программирования, которым
мы будем пользоваться в этой книге.
1.1. Что такое вероятностное
программирование?
Вероятностное программирование - это способ создания систем, помогающих
принимать решения в условиях неопределенности. Многие решения,
принимаемые нами каждодневно, подразумевают учет релевантных факторов, которые мы
не наблюдаем непосредственно. Исторически одним из способов принять
решение в таких условиях неопределенности стали системы вероятностного рассужде-

1.1. Что такое вероятностное программирование
щи
ш
ния. Вероятностное рассуждение позволяет объединить наши знания о ситуации
с вероятностными законами и таким образом учесть ненаблюдаемые факторы,
важные для принятия решения. До недавнего времени область применения
систем вероятностного рассуждения была ограничена, и ко многим возникающим
на практике задачам их удавалось применить с большим трудом. Вероятностное
программирование - это новый подход, позволивший упростить построение
систем вероятностного рассуждения и расширить их применимость.
Чтобы понять, в чем смысл вероятностного программирования, начнем с
рассмотрения того, как принимается решение в условиях неопределенности и какую
роль в этом играют субъективные суждения. Затем посмотрим, как может помочь
система вероятностного рассуждения. Мы познакомимся с тремя видами
рассуждений, присущих таким системам. После этого станет понятно, что такое
вероятностное программирование и как оно позволяет использовать всю мощь языков
программирования для построения систем вероятностного рассуждения.
7.7.7. Как мы высказываем субъективное
суждение?
В реальном мире интересующие нас вопросы редко допускают недвусмысленный
ответ: да или нет. Например, при выводе на рынок нового продукта хотелось бы
знать, хорошо ли он будет продаваться. Вы полагаете, что его ждет успех, потому
что продукт хорошо спроектирован и изучение рынка показало, что в нем есть
потребность, но полной уверенности нет. Быть может, ваш конкурент представит
лучший продукт, а, быть может, в вашем продукте обнаружится фатальный изъян,
из-за которого рынок от него отвернется. Или экономическая ситуация
повернется к худшему. Если вы хотите стопроцентной уверенности, то никогда не сможете
принять решение о начале продаж (см. рис. 1.1).
Для принятия решений такого рода помогает язык вероятностей. Запуская
продукт, мы можем воспользоваться прошлым опытом продажи похожих продуктов
для оценки вероятности того, что этот окажется успешным. А зная эту вероятность,
мы сможем решить, выводить продукт на рынок или нет. Возможно, нас
интересует не только сам факт успешности продукта, но и размер ожидаемого дохода или,
напротив, размер убытков, которые мы понесем в случае неудачи. Знание
вероятностей различных исходов помогает принимать более обоснованные решения.
Ну хорошо, вероятностное мышление может помочь в принятии трудных
решений с элементами субъективности. Но как это выглядит на практике? Общий
принцип выражен в виде следующего факта.
Факт. Субъективное суждение основано на знании + логике.
Вы располагаете некоторыми знаниями об интересующей вас проблеме.
Например, вы много знаете о своем продукте и, возможно, провели исследование
рынка, чтобы понять, кто будет его покупать. Возможно, вы также кое-что знаете о
конкурентах и знакомы с прогнозом развития экономики. Логика же позволяет
получать ответы на вопросы с использованием имеющихся знаний.

Рис. 1 -1 ■ В прошлом году мой продукт всем нравился, но как будет в следующем?
Нам необходим способ описания своих знаний и логика получения ответов на
вопросы с использованием этих знаний. Вероятностное программирование дает
то и другое. Но прежде чем переходить к описанию системы вероятностного
программирования, я опишу более общую концепцию системы вероятностных
рассуждений, которая предоставляет базовые средства для спецификации знаний и
реализации логики.
1.1.2. Системы вероятностных рассуждений
помогают принимать решения
Вероятностные рассуждения - это подход, в котором модель предметной
области используется для принятия решений в условиях неопределенности. Возьмем
пример из области футбола. Предположим, что по статистике 9 % угловых
завершаются голом. Требуется предсказать исход конкретного углового удара. Рост
центрального нападающего атакующей команды равен 193 см, и известно, что он
отлично играет головой. Основного вратаря защищающейся команды только что
унесли на носилках, и на замену ему вышел вратарь, который проводит свой пер-
26
Глава 1. О вероятностном программировании в двух словах
Показатели
прошлого
года
Показатели
будущего
года

1.1. Что такое вероятностное программирование
вый матч. Кроме того, дует сильный ветер, который затрудняет контроль над
полетом мяча. И как при таких условиях вычислить вероятность?
1. Вы кодируете свои знания
об угловых ударах и
релевантных факторах
5. Система возвращает
ответ в виде набора
вероятностей
Система
вероятностных
рассуждений
С Модель углового Л
I удара )
Алгоритм вывода
NJ
Ответ
• Да: 20%; Нет: 80%
2. Вы предоставляете
знания о предусловиях
конкретного углового
удара
Факт
• Высокий центральный
нападающий
• Неопытный вратарь
• Сильный ветер
Запрос
• Будет ли забит гол?
4. Система применяет алгоритм
вывода для предсказания исхода
3. Вы говорите
системе, что
хотите узнать
Рис. 1 .2. Как система вероятностных рассуждений предсказывает
исход углового удара
На рис. 1.2 показано, как получать ответ с помощью системы вероятностных
рассуждений. Все свои знания об угловых ударах и релевантных факторах мы
кодируем в виде модели углового. Затем мы предоставляем факты о конкретном
угловом ударе: что центральный нападающий высокий, что вратарь неопытный и
что дует сильный ветер. Мы говорим системе, что хотели бы узнать, будет ли забит
гол. Алгоритм вывода возвращает ответ: гол будет забит с вероятностью 20 %.
Основные определения
Общие знания - что известно о предметной области в общем, без деталей,
описывающих конкретную ситуацию.
Вероятностная модель - представление общих знаний о предметной области в
количественном виде, в терминах вероятностей.
Факты - имеющаяся информация о конкретной ситуации.
Запрос - свойство ситуации, о котором мы хотели бы узнать.
Вывод - процесс использования вероятностной модели для получения ответа на
запрос при известных фактах.
В системе вероятностных рассуждений мы создаем модель, в которой отражены
все релевантные общие знания о предметной области в виде вероятностей. В
нашем примере это может быть описание ситуации углового удара и всех релевант-
27

Глава 1. О вероятностном программировании в двух словах
ных характеристик игроков и окружающих условии, которые могут повлиять на
исход. Затем модель применяется к конкретной ситуации, для которой мы хотим
получить заключение. Для этого мы передаем модели имеющуюся информацию,
которая называется фактами. В данном случае есть три факта: центральный
нападающий высокий, вратарь неопытный и дует сильный ветер. Полученное от
модели заключение поможет принять решение - например, что на следующую игру
нужно поставить другого вратаря. Сами заключения предстают в виде
вероятностей, например, вероятностей других игровых навыков вратаря.
Соотношение между моделью, предоставляемой вами информацией и
ответами на запросы математически строго определено законами теории вероятностей.
Процесс использования модели для получения ответов на запросы при известных
фактах называется вероятностным выводом, или просто выводом. По счастью,
разработаны алгоритмы, которые выполняют необходимые вычисления, скрывая от
вас всю математику. Они называются алгоритмами вывода.
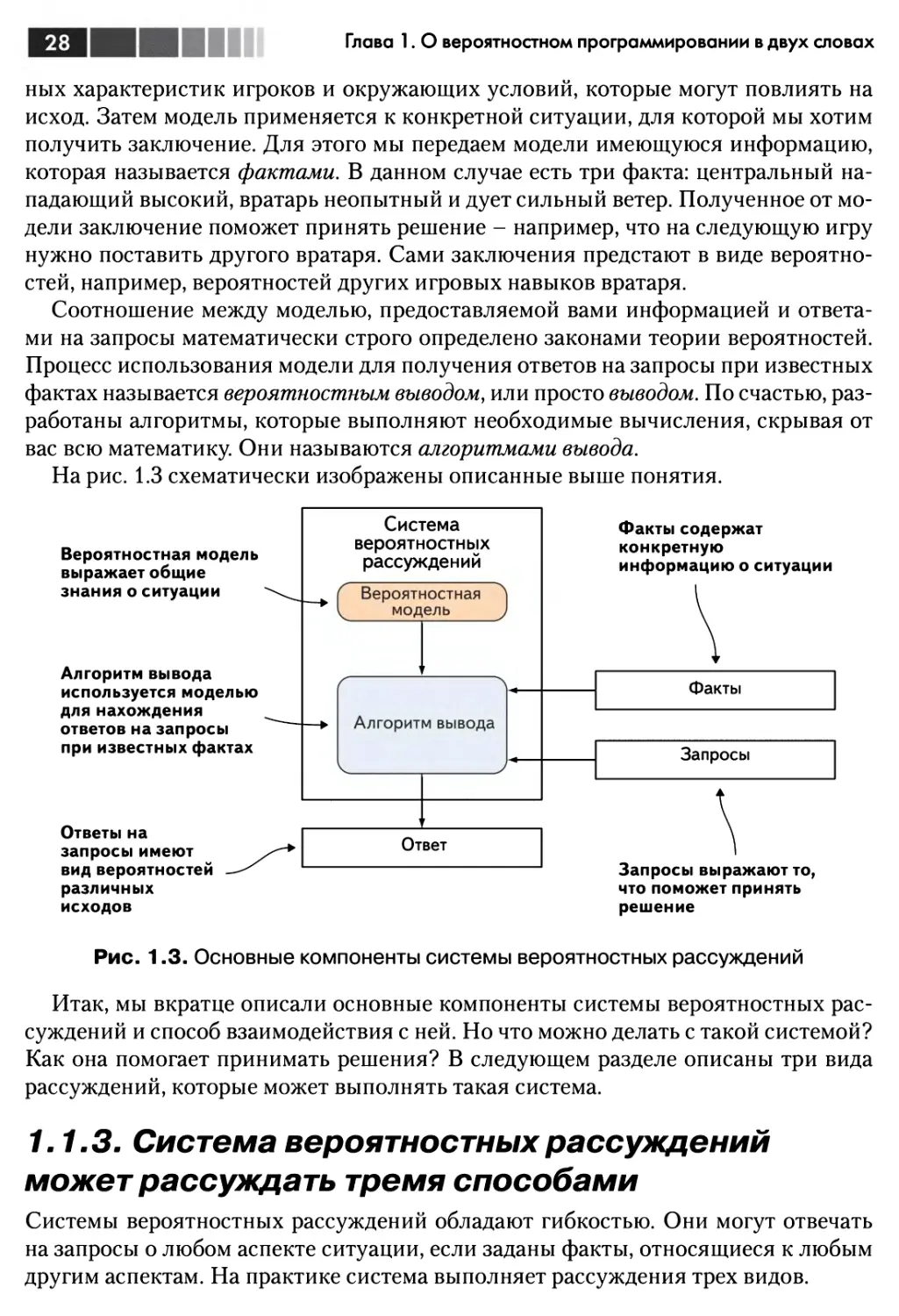
На рис. 1.3 схематически изображены описанные выше понятия.
Вероятностная модель
выражает общие
знания о ситуации
Алгоритм вывода
используется моделью
для нахождения
ответов на запросы
при известных фактах
Ответы на
запросы имеют
вид вероятностей
различных
исходов
Система
вероятностных
рассуждений
с
Вероятностная
модель
j
Алгоритм вывода
Факты содержат
конкретную
информацию о ситуации
Факты
Запросы
Ответ
Запросы выражают то,
что поможет принять
решение
Рис. 1.3. Основные компоненты системы вероятностных рассуждений
Итак, мы вкратце описали основные компоненты системы вероятностных
рассуждений и способ взаимодействия с ней. Но что можно делать с такой системой?
Как она помогает принимать решения? В следующем разделе описаны три вида
рассуждений, которые может выполнять такая система.
7.7.3. Система вероятностных рассуждений
может рассуждать тремя способами
Системы вероятностных рассуждений обладают гибкостью. Они могут отвечать
на запросы о любом аспекте ситуации, если заданы факты, относящиеся к любым
другим аспектам. На практике система выполняет рассуждения трех видов.
28

Что такое вероятностное программирование
Предсказание будущих событий. Мы уже видели это на рис. 1.2, где
система предсказывает, будет ли в данной ситуации забит гол. Факты обычно
включают информацию о текущей ситуации, например рост центрального
нападающего, опытность вратаря и силу ветра.
Вывод причины событий. Прокрутим пленку вперед на 10 секунд. Высокий
центральный нападающий только что забил гол головой, протолкнув мяч
под корпусом вратаря. Что можно сказать об этом вратаре-новобранце при
таких фактах? Можно ли заключить, что ему не хватает умения? На рис. 1.4
показано, как использовать систему вероятностных рассуждений для
ответа на этот вопрос. Берется та же модель углового удара, что и для прогноза
гола. (Это полезное свойство вероятностных рассуждений: одну и ту же
модель можно использовать как для предсказания будущего результата, так
и для объяснения причин, приведших к известному результату.) Факты те
же, что и прежде, плюс тот факт, что гол забит. Запрос касается
квалификации вратаря, а ответ дает вероятности различных уровней квалификации.
Факты включают
знание предусловий
и исходов
Алгоритм вывода
рассуждает о
запросе, зная
все известные
предусловия и
исходы
Система
вероятностных
рассуждений
Модель углового
удара
Г
Алгоритм вывода
Ответ
• Плохая: 50 %; Средняя:
30%; Хорошая: 20%
Факты
• Предусловия
> Высокий
центральный нападающий
> Неопытный вратарь
> Сильный ветер
• Исход
> Забит гол
Запрос
* Какова квалификация
вратаря?
Задается запрос о
возможной причине
данного исхода
Рис. 1.4. Если изменить запрос и факты, то система сможет
сделать вывод о том, почему был забит гол
Немного поразмыслив, вы поймете, что первый способ - рассуждения с
прямым ходом времени, т. е. предсказание будущих событий на основе того,
что известно о текущей ситуации, а второй - рассуждения с обратным ходом
времени, когда требуется вывести прошлые условия из известных
результатов. Типичная вероятностная модель следует естественному ходу времени.
29

Глава 1. О вероятностном программировании в двух словах
Игрок подает угловой, затем ветер воздействует на летящий мяч, затем
центральный нападающий прыгает, пытаясь достать мяч головой, и, наконец,
вратарь пытается спасти ворота. Но процесс рассуждения может
происходить как в прямом, так и в обратном порядке. Это ключевая особенность
вероятностного рассуждения, которую я не раз буду подчеркивать:
направление рассуждения необязательно совпадает с направлением модели.
Обучение па прошлых событиях, чтобы лучше предсказывать будущие.
Прокрутим пленку еще на 10 минут вперед. Та же команда заработала еще
один угловой. Все так же, как и раньше - высокий центральный
нападающий, неопытный вратарь - только ветер теперь стих. Вероятностное
рассуждение позволяет использовать информацию о том, что случилось при
подаче предыдущего углового, чтобы лучше предсказать исход
следующего. На рис. 1.5 показано, как это делается. В состав фактов входит все то, что
и в прошлый раз (с пометкой, что это было в прошлый раз), а также новая
информация о текущей ситуации. Отвечая на вопрос, будет ли забит гол
на этот раз, алгоритм вывода сначала определяет свойства ситуации,
которые привели к голу в первый раз, например, квалификацию нападающего
и вратаря. А затем эти свойства используются для предсказания исхода в
новой ситуации.
Факты включают знание
предусловий и исходов прошлых
ситуаций, а также предусловия
текущей ситуации
Факты
Алгоритм вывода
рассуждает о
предыдущих
ситуациях, пытаясь
определить
факторы (например,
квалификацию
вратаря),
существенные и в
новой ситуации
Алгоритм использует
эти факторы,
чтобы улучшить
предсказание
исхода в новой
ситуации
Система
вероятностных
рассуждений
С Модель углового ^
удар* J
Алгоритм вывода
Ответ
• Да: 25%; Нет: 75%
Предыдущий угловой удар
> Высокий центральный
нападающий
> Неопытный вратарь
> Сильный ветер
> Был забит гол
Текущий угловой удар
> Высокий центральный
нападающий
> Неопытный вратарь
> Слабый ветер
Запрос
• Будет ли забит гол в
этот раз?
Задается запрос об исходе
в новой ситуации
Рис. 1.5. Принимая во внимание факты, относящиеся к результату прошлого
углового, система вероятностного рассуждения может лучше
предсказать результат следующего
30

1.1. Что такое вероятностное программирование
III!
ЕЛ
Запросы перечисленных видов могут помочь в принятии различных решений.
• Зная вероятность гола при наличии или отсутствии дополнительного
защитника, можно решить, не стоит ли заменить атакующего защитником.
• На основе оценке квалификации вратаря можно решить, какую зарплату
предложить ему в следующем контракте.
• Получив информацию о вратаре, можно решить, стоит ли ставить его на
следующую игру.
Обучение улучшенной модели
Выше были описаны способы рассуждения о конкретных ситуациях при
известных фактах. Но система вероятностных рассуждений позволяет сделать еще
одну вещь: обучаясь на прошлом опыте, улучшить общие знания. Третий способ
рассуждений - это использование прошлых результатов для лучшего
предсказания исхода в конкретной новой ситуации. А сейчас мы говорим об улучшении
самой модели. Если имеется обширный прошлый опыт, т. е. информация о многих
угловых ударах, то почему бы не обучить новую модель, представляющую общие
знания о том, что обычно происходит при подаче углового? На рис. 1.6
показано, что это достигается с помощью алгоритма обучения. В отличие от алгоритма
вывода, его задача состоит не в том, чтобы отвечать на вопросы, а в том, чтобы
породить новую модель. На вход алгоритма обучения подается исходная модель,
а он обновляет ее на основе опыта. Затем новую модель можно использовать для
ответа на будущие запросы. Предположительно ответы новой модели будут более
обоснованы, чем ответы исходной.
Системы вероятностных рассуждений и точные предсказания
Как и в любой системе машинного обучения, чем больше данных у системы
вероятностных рассуждений, тем точнее ее ответы. Качество предсказания зависит от двух
факторов: верности отражения реального мира в исходной модели и объема
предоставленных данных. Вообще говоря, чем больше данных, тем менее существенно
качество исходной модели. Причина в том, что новая модель - комбинация исходной и
информации, содержащейся в данных. Если данных очень мало, то доминирует
исходная модель, поэтому чем она точнее, тем лучше. Если же данных много, то
доминируют именно они, так что в новой модели остается очень мало от исходной, поэтому ее
точность не слишком важна. Например, если мы обучаем модель по данным за весь
футбольный сезон, то факторы, от которых зависит результативность углового, будут
учтены весьма точно. Если же имеются данные только об одном матче, то придется
изначально задать хорошие значения факторов, иначе на точность предсказаний
можно не рассчитывать. Системы вероятностного программирования умеют
пользоваться моделью и имеющимися данными так, что предсказания получаются максимально
точными.

Глава 1. О вероятностном программировании в двух словах
Обучающий алгоритм
использует исходную
модель и данные для
порождения новой
модели
Алгоритм вывода
использует новую
модель для ответа
на запросы о новой
ситуации
Система
вероятностных
рассуждений
Исходная модель
углового,адара
Алгоритм
обучения
До
После
Новая модель
углового удара
Алгоритм вывода
Ответ
• Да: 15%; Нет: 85%
Данными являются факты о
предыдущих ситуациях
Прошлый опыт 1
• Высокий центральный
нападающий
• Неопытный вратарь
• Сильный ветер
Прошлый опыт 2
Прошлый опыт 3
И т. д.
Факты о новой ситуации
Новые факты
• Высокий центральный
нападающий
• Неопытный вратарь
• Слабый ветер
Запрос
• Будет ли забит гол в
этот раз?
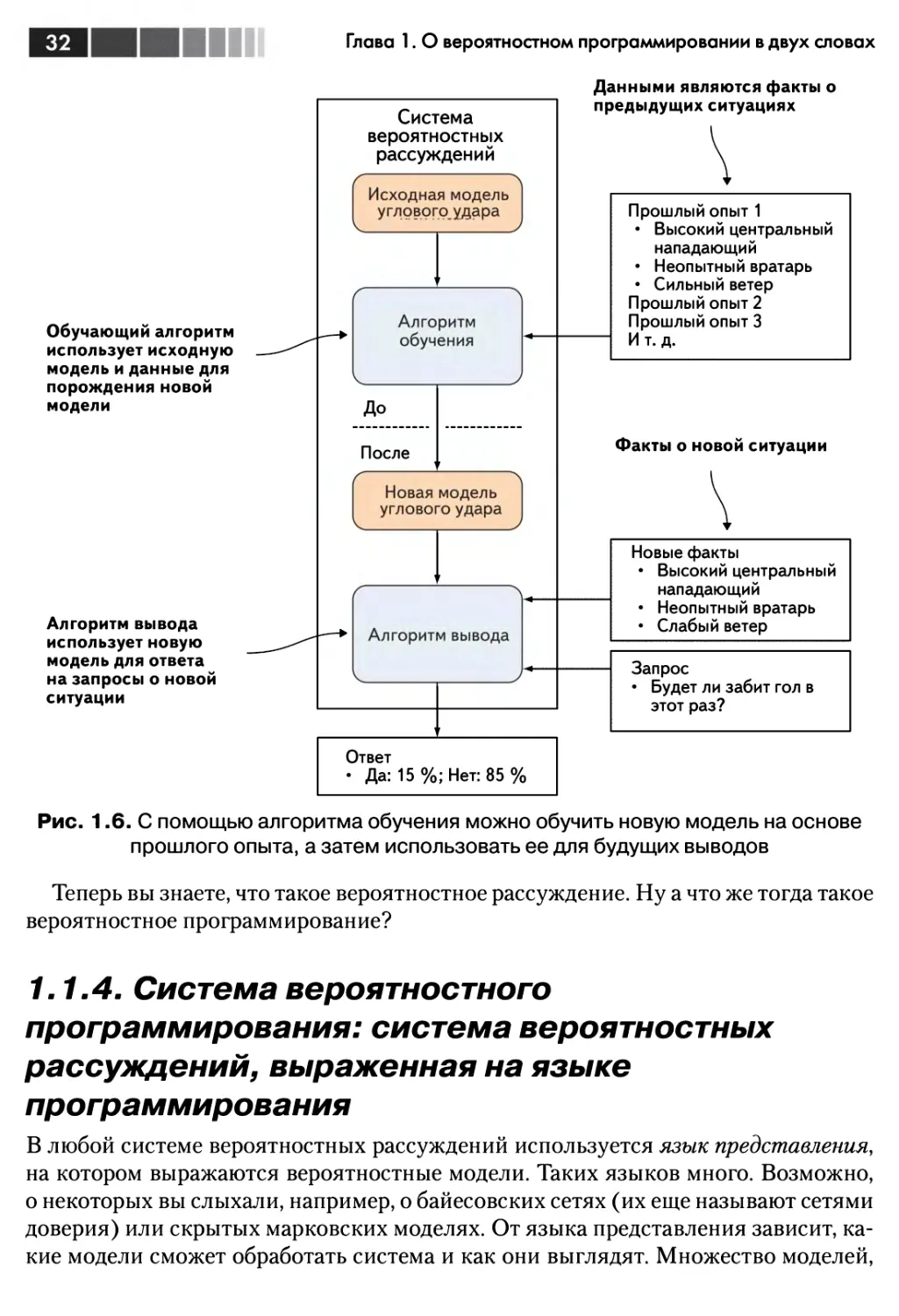
Рис. 1.6. С помощью алгоритма обучения можно обучить новую модель на основе
прошлого опыта, а затем использовать ее для будущих выводов
Теперь вы знаете, что такое вероятностное рассуждение. Ну а что же тогда такое
вероятностное программирование?
7.7.4. Система вероятностного
программирования: система вероятностных
рассуждений, выраженная на языке
программирования
В любой системе вероятностных рассуждений используется язык представления,
на котором выражаются вероятностные модели. Таких языков много. Возможно,
о некоторых вы слыхали, например, о байесовских сетях (их еще называют сетями
доверия) или скрытых марковских моделях. От языка представления зависит,
какие модели сможет обработать система и как они выглядят. Множество моделей,
32

1.1. Что такое вероятностное программирование
представимых языком, называется выразительной силой языка. Для разработки
приложений требуется, чтобы выразительная сила была как можно больше.
Система вероятностного программирования - это просто система
вероятностных рассуждений, для которой языком представления является язык
программирования. Говоря «язык программирования», я имею в виду, что он обладает всеми
возможностями, которые принято ожидать от типичного языка
программирования: переменными, развитой системой типов данных, средствами управления
потоком выполнения, функциями и т. д. Как вы вскоре увидите, языки
вероятностного программирования способны выразить широкий спектр вероятностных
моделей, далеко выходящий за рамки большинства традиционных систем
вероятностных рассуждений. Выразительная сила языков вероятностного
программирования очень высока.
На рис. 1.7 иллюстрируется соотношение между системами вероятностного
программирования и вероятностных рассуждений в общем случае. Сравните этот
рисунок с рис. 1.3, чтобы стали яснее различия между двумя системами.
Основное изменение состоит в том, что модели выражаются в виде программ на
некотором языке программирования, а не в виде математических конструкций типа
байесовской сети. Поэтому факты, запросы и ответы становятся переменными
программы. Факты можно представить конкретными значениями переменных,
запрос - это получение значения переменной, а ответ - вероятности того, что
переменные принимают те или иные значения. Кроме того, система вероятностного
программирования обычно включает набор алгоритмов вывода. Эти алгоритмы
применяются к моделям, написанным на языке системы.
Модель выражена
в виде программы
на некотором языке
программирования,
а не в виде
математической
конструкции
Система вероятностного
программирования
предоставляет набор
алгоритмов вывода,
которые применяются к
моделям,написанным
на языке системы
Ответы представляются
в виде вероятностей
значений переменных,
указанных в запросе
Figaro
с
Вероятностная
модель
пая |
Алгоритм вывода
Факты — это значения
переменных программы
Факты
Запросы
Ответ
Запросы — это значения
других переменных
программы
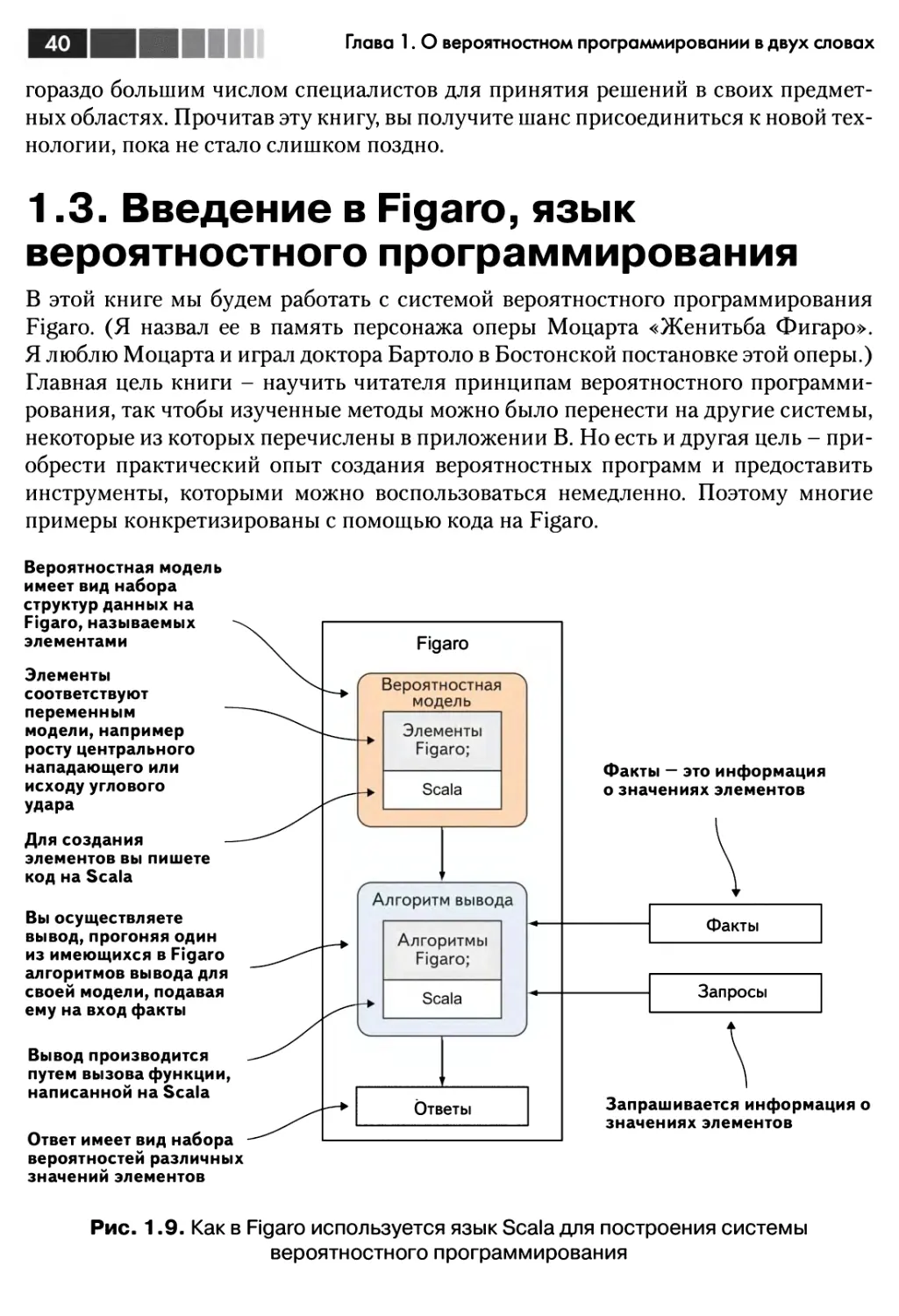
Рис. 1.7. Система вероятностного программирования - это система
вероятностных рассуждений, в которой для представления вероятностных
моделей применяется язык программирования
33

Глава 1. О вероятностном программировании в двух словах
Существует много систем вероятностного программирования (см. обзор в
приложении В), но в этой книге рассматриваются только функциональные, полные
по Тьюрингу системы. Функциональные означает, что они основаны на
функциональном языке программирования, но пусть это вас не пугает - чтобы пользоваться
функциональной системой вероятностного программирования, не нужно знать, что
такое лямбда-функция. Просто функциональное программирование составляет
теоретическое основание, благодаря которому язык имеет возможность представлять
вероятностные модели. А полным по Тьюрингу называется язык, на котором можно
закодировать любое вычисление, которое способен выполнить цифровой
компьютер. Если нечто вообще можно сделать с помощью компьютера, то это можно сделать
на любом полном по Тьюрингу языке. Большинство языков программирования, с
которыми вы знакомы, например С, Java и Python, являются полными по Тьюрингу.
Поскольку системы вероятностного программирования основаны на языках
программирования, полных по Тьюрингу, то они обладают выдающейся гибкостью в
части типов моделей, которые можно построить с их помощью.
Основные определения
Язык представления - язык для кодирования знаний о предметной области в модели.
Выразительная сила - способность языка представления кодировать различные виды
знаний.
Полный по Тьюрингу - язык, позволяющий выразить любое вычисление, которое
можно выполнить на цифровом компьютере.
Язык вероятностного программирования - язык представления системы
вероятностных рассуждений, в котором для представления знаний используется полный по
Тьюрингу язык программирования.
В приложении В приведен обзор некоторых систем вероятностного
программирования, помимо используемой в этой книге системы Figaro. В большинстве
из них используются полные по Тьюрингу языки. В некоторых, например BUGS
и Dimple, это не так, но они все равно полезны для тех приложений, на которые
рассчитаны. В этой книге мы будем заниматься исключительно возможностями
полных по Тьюрингу языков вероятностного программирования.
Представление вероятностных моделей
в виде программ
Но каким образом язык программирования становится языком вероятностного
моделирования? Как представить вероятностную модель в виде программы?
Сейчас я дам очень краткий ответ на этот вопрос, а более глубокое обсуждение
отложу на потом, когда мы станем лучше понимать, как выглядит вероятностная
программа.
Главная идея любого языка программирования - выполнение. Мы выполняем
программу, порождающую некоторый выход. Вероятностная программа в этом
смысле аналогична, только она может иметь не один, а несколько путей выполнения,
каждый из которых порождает свой выход. По какому пути следовать, определяется
случайным выбором, совершаемым внутри программы. Каждый случайный выбор
34

1.1. Что такое вероятностное программирование
имеет несколько возможных исходов, и в программе закодирована вероятность
каждого исхода. Поэтому можно считать, что вероятностная программа - это
программа, при выполнении которой случайным образом генерируются выходные
данные.
Эта идея иллюстрируется на рис. 1.8. Здесь система вероятностного
программирования содержит программу углового удара, которая описывает случайный
процесс генерации исхода углового. Программа принимает ряд входных данных;
в нашем примере это рост центрального нападающего, опытность вратаря и сила
ветра. На основе этих данных программа случайным образом выполняется и
генерирует выходные данные. Каждое случайное выполнение дает на выходе
конкретный результат. Поскольку каждый случайный выбор может иметь несколько
исходов, то существует много возможных путей выполнения, дающих различные
результаты. Любой заданный результат, например взятие ворот, может быть
сгенерирован на различных путях выполнения.
1. Вероятностная
программа описывает
процесс случайной
генерации выходных
данных по известным
входным
Высокий центральный
нападающий
Неопытный вратарь
Сильный ветер
Вероятностная
система
программирования
с
Программа
углового удара
Случайное
выполнение
Нет гола
Гол!!!
Нет гола
Чуть не
забили
При заданных входных
данных программа может
случайно выполняться
многократно и каждый
раз порождать новые
результаты
Вероятность некоторого
результата — это вероятность
выбора пути выполнения,
порождающего такой
результат. В данном случае
вероятность гола равна %
Рис. 1.8. Вероятностная программа определяет процесс случайной
генерации выходных данных по известным входным
Рассмотрим, как эта программа определяет вероятностную модель. Любое
конкретное выполнение программы является результатом последовательности
случайных выборов. Каждый случайный выбор происходит с некоторой
вероятностью. Если перемножить все эти вероятности, то получится вероятность пути
выполнения. Таким образом, программа определяет вероятность каждого пути
выполнения. Если представить себе, что программа прогоняется многократно, то
доля прогонов, на которых генерируется заданный путь выполнения, равна его
вероятности. Вероятность некоторого результата равна доле прогонов, на которых
35

Глава 1. О вероятностном программировании в двух словах
был получен этот результат. На рис. 1.8 гол получается в 1/4 всех прогонов,
поэтому вероятность гола равна 1/4.
Примечание. Возможно, вы недоумеваете, почему один из блоков на рис. 1.8
назван «Случайное выполнение», а не «Алгоритм вывода», как на других рисунках. На
рис. 1.8 показан смысл вероятностной программы - определение процесса
случайного выполнения, а не как использовать систему вероятностного программирования -
выполнить алгоритм вывода для получения ответа на запрос при заданных фактах.
Поэтому хотя структурно рисунки похожи, они иллюстрируют разные концепции. На
самом деле, случайное выполнение лежит в основе и некоторых алгоритмов вывода, но
есть много алгоритмов, которые не основаны на простом случайном выполнении.
Принятие решений с помощью вероятностного
программирования
Легко видеть, как можно использовать вероятностную программу для
предсказания будущего. Нужно просто выполнить ее случайное число раз, подавая на
вход известные данные о настоящем, и посмотреть, сколько раз порождается
каждый результат. В примере с угловым ударом на рис. 1.8 мы выполняли
программу много раз, подавая на вход такие данные: высокий центральный нападающий,
неопытный вратарь и сильный ветер. Поскольку в 1/4 прогонов получился гол,
можно сказать, что при этих входных данных вероятность гола равна 25 %.
Однако прелесть вероятностного программирования заключается в том, что его
можно с тем же успехом использовать для любых видов вероятностных
рассуждений, описанных в разделе 1.3.1. Оно позволяет не только предсказывать
будущее, но и выводить факты, приведшие к наблюдаемым результатам; можно
«открутить» программу назад и посмотреть, какие причины породили данный исход.
Можно также применить программу в одной ситуации, обучиться на полученном
результате и использовать новую программу для получения более точных
предсказаний в будущем. Вероятностное программирование помогает принимать
любые решения в рамках вероятностных рассуждений.
Как все это работает? Вероятностное программирование стало применяться на
практике, когда было осознано, что алгоритмы вывода, работающие для более
простых языков представления, например байесовских сетей, можно обобщить и на
программы. В части 3 описаны разнообразные алгоритмы вывода, благодаря
которым это возможно. К счастью, в состав вероятностных систем программирования
входит ряд встроенных алгоритмов вывода, которые применяются к программам
автоматически. Вам нужно лишь предоставить знания о предметной области в
виде вероятностной программы и описать факты, а система сама позаботится о
выводе и обучении.
В этой книге мы будем изучать вероятностные рассуждения через призму
вероятностного программирования. Прежде всего, мы узнаем, что такое вероятностная
модель и как ее использовать для вывода заключений. Мы также научимся
производить некоторые простые манипуляции для вывода таких заключений из
модели, составленной из простых компонентов. Мы рассмотрим различные приемы
36

1.2. Зачем нужно вероятностное программирование
ни
Шум
моделирования и покажем, как реализовать их с помощью вероятностного
программирования. Мы разберемся в том, как работают вероятностные алгоритмы
вывода, и это позволит эффективно проектировать и использовать модели. К
концу книги вы сможете уверенно пользоваться вероятностным программированием
для вывода полезных заключений и принятия обоснованных решений в условиях
неопределенности.
1.2. Зачем нужно вероятностное
программирование?
Вероятностные рассуждения - одна из фундаментальных технологий машинного
обучения. Такие системы используются компаниями Google, Amazon и Microsoft
для извлечения смысла из имеющихся данных. Вероятностные рассуждения
применялись в таких разных приложениях, как прогнозирование цены акций, ре-
комендование фильмов, диагностика компьютеров и обнаружение вторжений в
вычислительные системы. Во многих из этих приложений используются методы,
описанные в этой книге.
В предыдущем разделе следует выделить два важнейших положения:
• вероятностные рассуждения можно использовать для предсказания
будущего, объяснения прошлого и обучения на прошлом опыте для лучшего
предсказания будущего;
• вероятностное программирование - это вероятностное рассуждение, в
котором для представления используется полный по Тьюрингу язык
программирования.
В сочетании эти два положения позволяют отчеканить следующую формулу.
Факт. Вероятностное рассуждение + полнота по Тьюрингу = вероятностное
программирование.
Обоснованием вероятностного программирования является тот факт, что из
двух концепций, которые сами по себе являются достаточно мощными,
составляется новая. В результате получается более простой и гибкий способ применения
компьютеров для принятия решений в условиях неопределенности.
7.2.7. Улучшенные вероятностные рассуждения
У большинства современных вероятностных языков представления имеются
ограничения на сложность представляемых систем. В таких относительно
простых языках, как байесовские сети, предполагается фиксированный набор
переменных, поэтому они не обладают достаточной гибкостью для моделирования
предметных областей, в которых состав переменных может изменяться. В
последние годы были разработаны более гибкие языки. В некоторых (например, BUGS)
даже имеются возможности, характерные для языков программирования, напри-

Глава 1. О вероятностном программировании в двух словах
мер итерация и массивы, хотя полными по Тьюрингу они все же не являются.
Успех языков, подобных BUGS, ясно говорит о необходимости более развитых и
структурированных представлений. Но движение в сторону полноценных полных
по Тьюрингу языков открывает целый мир новых возможностей для
вероятностных рассуждений. Теперь стало возможно моделировать длительные процессы с
большим числом событий и взаимодействующих сущностей.
Снова рассмотрим пример на футбольную тематику, но теперь представьте, что
вы занимаетесь спортивной аналитикой и хотите порекомендовать решения по
подбору игроков в команду. Можно было бы воспользоваться для этой цели
накопленной статистикой, но статистика не улавливает контекст, в котором была
собрана. Можно провести более тонкий контекстный анализ, построив детальную
модель футбольного сезона. Для этого придется моделировать много
взаимосвязанных событий и взаимодействие игроков и команд. Трудно представить себе,
как построить такую модель без структур данных и управляющих конструкций,
имеющихся в полноценном языке программирования.
Вернемся к вопросу о выводе продукта на рынок и взглянем на процесс
принятия решений по развитию бизнеса во всей его полноте. Запуск продукта - не
изолированное событие, ему предшествуют этапы анализа рынка, исследований и
разработок, и исход каждого этапа не предрешен. Результаты запуска продукта
зависят от всех предшествующих этапов, а также от анализа того, что еще имеется на
рынке. Полный анализ должен также учитывать, как отреагируют на наш продукт
конкуренты и какие новые продукты они смогут предложить. Это трудная
задача, т. к. приходится выдвигать гипотезы о конкурирующих продуктах. Возможно
даже, что существуют конкуренты, о которых вы еще не знаете. В этом примере
продукты оказываются структурами данных, порождаемыми сложными
процессами. Поэтому наличие полноценного языка программирования было бы крайне
полезно для создания модели.
У вероятностного программирования есть одна приятная особенность: если вы
хотите использовать более простой каркас вероятностных рассуждений -
пожалуйста. Системы вероятностного программирования позволяют представить
широкий спектр существующих каркасов, а также такие системы, которые ни один
из существующих каркасов представить не в состоянии. В этой книге вы узнаете о
многих каркасах, в которых используется вероятностное программирование.
Поэтому, изучая вероятностное программирование, вы заодно освоите многие
современные каркасы вероятностных рассуждений.
1.2.2. Улучшенные языки имитационного
моделирования
Полные по Тьюрингу языки вероятностного моделирования уже существуют.
Обычно они называются языками имитационного моделирования (simulation
languages). Мы знаем, что можно построить имитационную модель такого
сложного процесса, как футбольный сезон, пользуясь языками программирования.
В этом контексте я буду использовать термин язык имитационного моделирова-
38

1.2. Зачем нужно вероятностное программирование
III!
Еа
ния для описания языка, который позволяет представить выполнение
сложного процесса с элементами случайности. Как и вероятностные программы, такие
имитационные модели выполняются случайным образом и порождают различные
результаты. Имитационное моделирование широко используется как
вероятностное рассуждение и применяется в самых разных областях, например: военном
планировании, проектировании компонентов, здравоохранении и прогнозировании
спортивных результатов. На самом деле, широкое распространение изощренных
имитационных моделей говорит о потребности в развитых языках вероятностного
моделирования.
Но вероятностная программа - нечто гораздо большее, чем имитационная
модель. Имитационное моделирование позволяет реализовать лишь один аспект
вероятностного программирования: предсказание будущего. Его нельзя
использовать для объяснения причин наблюдаемых результатов. И хотя модель можно
улучшить, дополнив ее новой актуальной информацией, трудно включить
неизвестную информацию, которую нужно вывести. Поэтому способность к обучению
на прошлом опыте с целью улучшения будущих прогнозов и анализа оказывается
ограниченной. Использовать имитационные модели в машинном обучении
невозможно.
Вероятностную программу можно уподобить имитационной модели, которая
допускает не только выполнение, но и анализ. При разработке вероятностного
программирования пришло осознание того, что многие алгоритмы вывода,
используемые в более простых системах моделирования, можно использовать и для
имитационного моделирования. Поэтому открывается возможность создать
вероятностную модель, написав имитационную модель и применив к ней алгоритмы
вывода.
И последнее. Системы вероятностных рассуждений уже существуют, например
программы Hugin, Netica и BayesiaLab предлагают реализацию байесовских сетей.
Но более выразительные языки представления, применяемые в вероятностном
программировании, настолько новые, что мы лишь начинаем открывать для себя
таящуюся в них мощь. Положа руку на сердце, не могу сказать, что вероятностное
программирование уже используется во многих прикладных системах. Но
некоторые нетривиальные приложения все же существуют. Microsoft с помощью
вероятностного программирования научилась определять истинный уровень умения
игроков в онлайновые игры. Стюарт Рассел из Калифорнийского университета
в Беркли написал программу, которая следит за соблюдением Договора о
всеобъемлющем запрещении ядерных испытаний, определяя сейсмическую активность,
которая могла бы указывать на ядерный взрыв. Джош Тененбаум из Массачусет-
ского технологического института и Ноа Гудман из Стэнфордского университета
создали вероятностные программы для моделирования когнитивных
способностей человека, они обладают очень неплохими объяснительными возможностями.
В компании Charles River Analytics мы использовали вероятностное
программирование для вывода заключений о компонентах вредоносного ПО и определения
их эволюции. Но я полагаю, что все это - только вершина айсберга. Системы
вероятностного программирования достигли такого уровня, что могут использоваться

Глава 1. О вероятностном программировании в двух словах
гораздо большим числом специалистов для принятия решений в своих
предметных областях. Прочитав эту книгу, вы получите шанс присоединиться к новой
технологии, пока не стало слишком поздно.
1.3. Введение в Figaro, язык
вероятностного программирования
В этой книге мы будем работать с системой вероятностного программирования
Figaro. (Я назвал ее в память персонажа оперы Моцарта «Женитьба Фигаро».
Я люблю Моцарта и играл доктора Бартоло в Бостонской постановке этой оперы.)
Главная цель книги - научить читателя принципам вероятностного
программирования, так чтобы изученные методы можно было перенести на другие системы,
некоторые из которых перечислены в приложении В. Но есть и другая цель -
приобрести практический опыт создания вероятностных программ и предоставить
инструменты, которыми можно воспользоваться немедленно. Поэтому многие
примеры конкретизированы с помощью кода на Figaro.
Вероятностная модель
имеет вид набора
структур данных на
Figaro, называемых
элементами
Элементы
соответствуют
переменным
модели, например
росту центрального
нападающего или
исходу углового
удара
Для создания
элементов вы пишете
код на Scala
Вы осуществляете
вывод, прогоняя один
из имеющихся в Figaro
алгоритмов вывода для
своей модели, подавая
ему на вход факты
Вывод производится
путем вызова функции,
написанной на Scala
Ответ имеет вид набора
вероятностей различных
значений элементов
Figaro
' Вероятностная
модель
Элементы
Figaro;
Scala
V
Г
Алгоритм вывода
Алгоритмы
Figaro;
Scala
Ответы
Факты — это информация
о значениях элементов
Факты
Запросы
Запрашивается информация о
значениях элементов
Рис. 1 -9. Как в Figaro используется язык Scala для построения системы
вероятностного программирования
40

1.3. Введение в Figaro, язык вероятностного программирования
Исходный код Figaro открыт, поддержка осуществляется с помощью GitHub,
а сама система разрабатывается с 2009 года. Она реализована в виде библиотеки,
написанной на Scala. На рис. 1.9 показано, как в Figaro используется Scala для
реализации системы вероятностного программирования. Это уточнение рис. 1.7, где
описаны основные компоненты такой системы. Начнем с вероятностной модели.
В Figaro модель состоит из структур данных, называемых элементами. Каждый
элемент представляет переменную, которая может принимать произвольное
число значений. Структуры данных реализованы на Scala, и для создания модели, в
которой они используются, вы пишете программу на Scala. Программе можно
подать на вход факты, содержащие информацию о значениях элементов, а в запросе
указать, какие выходные элементы вас интересуют. Вы выбираете один из
встроенных в Figaro алгоритмов выбора и применяете его к своей модели, чтобы
получить ответ на запрос при заданных фактах. Алгоритмы вывода реализованы на
Scala, а применение алгоритм сводится к вызову функции Scala. Результатом
вывода являются вероятности различных значений элементов, указанных в запросе.
Тот факт, что Figaro написана на Scala, дает ряд преимуществ. Некоторые из них
связаны с использованием языка общего назначения вместо
специализированного, другие - со спецификой именно Scala. Сначала остановимся на преимуществах
вложения в язык общего назначения.
• Факты можно представлять, используя программу на объемлющем языке.
Например, программа может прочитать данные из файла, каким-то образом
обработать их и представить в виде фактов для модели Figaro. На
специализированном независимом языке сделать это было бы гораздо труднее.
• Аналогично ответы, возвращенные Figaro, можно использовать в
программе. Например, если менеджер футбольной команды работает с некоторой
программой, то эта программа может запросить вероятность гола с тем,
чтобы порекомендовать менеджеру варианты действий.
• Код на языке общего назначения можно включить в вероятностную
программу. Рассмотрим, к примеру, физическую модель траектории мяча после
удара головой. Эту модель можно было бы сделать частью элемента Figaro.
• Для построения модели Figaro можно использовать стандартные приемы
программирования. Например, можно завести словарь, который содержит
элементы Figaro, соответствующие всем игрокам команды, и выбирать из
него элементы, исходя из ситуации, складывающейся на поле.
Теперь перечислим причины, по которым Scala особенно хорошо подходит на
роль объемлющего языка для системы вероятностного программирования.
Поскольку Scala - функциональный язык программирования, Figaro также
получает все преимущества функционального программирования, что позволяет
естественно записывать многие модели. Я продемонстрирую это во второй части
книги.
Scala - объектно-ориентированный язык, и то, что он сочетает в себе
функциональные и объектно-ориентированные черты, является дополнительным
преимуществом. Figaro также является объектно-ориентированным. Во второй части
41

Глава 1. О вероятностном программировании в двух словах
я покажу, что это полезно для выражения некоторых паттернов проектирования в
вероятностном программировании.
Наконец, ряд преимуществ Figaro не связан с вложением в Scala.
• На Figaro можно представить чрезвычайно широкий спектр
вероятностных моделей. Элементы Figaro могут принимать значения любого типа,
в том числе: булевы, целые, с двойной точностью, массивы, деревья, графы
и т. д. Связи между элементами можно определить с помощью
произвольной функции.
• Figaro предоставляет развитые средства задания фактов с помощью
условий и ограничений.
• В Figaro имеется обширный набор алгоритмов вывода.
• Figaro позволяет представлять динамические модели ситуаций,
изменяющихся во времени, и рассуждать о них.
• Figaro дает возможность включать в модель явные решения и
поддерживает вывод оптимальных решений.
Использование Scala
Поскольку система Figaro реализована в виде библиотеки на Scala, для работы с ней
необходимы практические навыки работы со Scala. Эта книга посвящена
вероятностному программированию, поэтому я не ставил себе задачу научить Scala. Для этой
цели есть немало замечательных ресурсов, например Школа Scala в Твиттере (http://
twitter.github.io/scala_school). Но на случай, если вы пока не уверены в своих
познаниях, я буду объяснять используемые средства Scala по ходу дела. Вы сможете читать
книгу, даже если совсем не знаете Scala.
Чтобы пользоваться всеми преимуществами вероятностного программирования и
Figaro, не нужно знать Scala в совершенстве. В этой книге я избегал продвинутых и
малопонятных возможностей Scala. С другой стороны, чем лучше вы знаете Scala, тем
больших успехов достигнете в работе с Figaro. Возможно даже, что после прочтения
этой книги вы станете лучше владеть Scala.
Есть несколько причин, по которым Figaro - удобный язык для изучения
вероятностного программирования.
• Будучи реализован в виде библиотеки на Scala, Figaro может быть
использован в программах, написанных на Java и Scala, что упрощает его
интеграцию с приложениями.
• По той же причине Figaro позволяет использовать для построения моделей
все богатство объемлющего языка. Scala - современный передовой язык
программирования, обладающий множеством полезных средств для
организации программ, и все это вы автоматически получаете в свое
распоряжение, работая с Figaro.
• Figaro располагает полным набором алгоритмов.
В этой книге упор сделан на практические приемы и примеры. Всюду, где
возможно, я объясняю общие принципы моделирования и описываю, как они реали-
42

1.3. Введение в Figaro, язык вероятностного программирования
зованы в Figaro. Это сослужит вам добрую службу, если вы решите обратиться к
другой системе вероятностного программирования. Не во всех системах
описанные здесь приемы реализуются с одинаковой легкостью. Так, в настоящее время
еще мало объектно-ориентированных систем вероятностного программирования.
Но обладая фундаментальными знаниями, вы найдете способ выразить свои
потребности на выбранном языке.
7.3.7. Figaro и Java: построение простой системы
вероятностного программирования
Для иллюстрации достоинств вероятностного программирования и языка Figaro
я покажу два способа написания простого приложения: сначала на языке Java, с
которым вы, возможно, знакомы, а потом на Figaro. Хотя у Scala есть некоторые
преимущества по сравнению с Java, не в этом состоит различие, которое я хочу
подчеркнуть. Основная идея в том, что Figaro содержит такие средства для
представления вероятностных моделей и выполнения вывода из них, которые
недоступны без вероятностного программирования.
Наше скромное приложение будет играть роль примера «Hello World» для Figaro.
Представьте, что человек просыпается утром, смотрит, ясно ли на улице, и
произносит приветствие, зависящее от погоды. Так происходит два дня подряд. Кроме того,
погода во второй день зависит от первого: если в первый день было ясно, то
вероятность, что и на завтра будет солнечно, повышается. Эти предложения на
естественном языке можно записать количественно, как показано в табл. 1.1.
Таблица 1.1. Количественные вероятности в примере «Hello World»
Ясно
Пасмурно
Погода сегодня
0.2
0.8
Приветствие сегодня
Если сегодня на улице ясно
Если сегодня на улице пасмурно
Если сегодня на улице ясно
Если сегодня на улице пасмурно
«Здравствуй, мир!»
«Здравствуй, вселенная!»
«Здравствуй, мир!»
«О нет, только не это»
Погода завтра
Ясно
Пасмурно
Ясно
Пасмурно
0.6
0.4
0.2
0.8
0.8
0.2
0.05
0.95
43

Глава 1. О вероятностном программировании в двух словах
Если завтра на улице ясно
Если завтра на улице пасмурно
Приветствие завтра
«Здравствуй, мир!»
«Здравствуй, вселенная!»
«Здравствуй, мир!»
«О нет, только не это»
0.6
0.4
0.2
0.8
В следующих главах будет точно объяснено, как интерпретировать эти числа.
А пока достаточно интуитивного понимания того, что означает фраза «сегодня
будет ясно с вероятностью 0.2». Аналогично, если завтра на улице будет ясно,
то с вероятностью 0.6 будет произнесено приветствие «Здравствуй, мир!» и с
вероятностью 0.4 - «Здравствуй, вселенная!».
Наметим три задачи, которые должна решать эта модель. В разделе 1.1.3 мы
видели три типа рассуждений, доступных вероятностной модели: предсказание
будущего, вывод прошлых событий, приведших к наблюдаемому результату, и обучение
на прошлом опыте для лучшего предсказания будущего. Все это мы сделаем с
помощью нашей простой модели. Точнее, задачи формулируются следующим образом.
1. Предсказать сегодняшнее приветствие.
2. Зная, что сегодня было произнесено приветствие «Здравствуй, мир!»,
сделать вывод о том, ясно ли на улице.
3. Зная, что сегодня было произнесено приветствие «Здравствуй, мир!»,
научиться предсказывать завтрашнее приветствие.
Посмотрим, как решить эти задачи на Java.
Листинг 1,1, Программа Hello World на Java
class HelloWorldJava {
static String greetingl
static String greeting2
static String greeting3
"Здравствуй, мир!";
"Здравствуй, вселенная!";
"О нет, только не это";
<ь-о
static Double pSunnyToday = 0.2;
static Double pNotSunnyToday = 0.8;
static Double pSunnyTomorrowIfSunnyToday = 0.8;
static Double pNotSunnyTomorrowIfSunnyToday = 0.2;
static Double pSunnyTomorrowIfNotSunnyToday = 0.05;
static Double pNotSunnyTomorrowIfNotSunnyToday = 0.95;
static Double pGreetinglTodaylfSunnyToday = 0.6;
static Double pGreeting2TodayIfSunnyToday = 0.4;
static Double pGreetinglTodaylfNotSunnyToday = 0.2;
static Double pGreeting3IfNotSunnyToday = 0.8;
static Double pGreetinglTomorrowIfSunnyTomorrow = 0.5;
static Double pGreeting2TomorrowIfSunnyTomorrow = 0.5;
static Double pGreetinglTomorrowIfNotSunnyTomorrow = 0.1;
static Double pGreeting3TomorrowIfNotSunnyTomorrow = 0.95;
<-e
44

1.3. Введение в Figaro, язык вероятностного программирования
static void predict() {
Double pGreetinglToday =
pSunnyToday * pGreetinglTodaylfSunnyToday +
pNotSunnyToday * pGreetinglTodayIfNotSunnyToday;
System.out.printIn("Сегодня будет приветствие " +
greetingl + " с вероятностью " + pGreetinglToday + ".");
}
static void infer() {
Double pSunnyTodayAndGreetinglToday =
pSunnyToday * pGreetinglTodaylfSunnyToday;
Double pNotSunnyTodayAndGreetinglToday =
pNotSunnyToday * pGrееtinglTodayIfNotSunnyToday;
Double pSunnyTodayGivenGreetinglToday =
pSunnyTodayAndGreetinglToday /
(pSunnyTodayAndGreetinglToday +
pNotSunnyTodayAndGreetinglToday);
System.out.printIn("Если сегодня произнесено приветствие " +
greetingl + ", то сегодня ясно с вероятностью " +
pSunnyTodayGivenGreetinglToday + ".");
}
static void learnAndPredict() {
Double pSunnyTodayAndGreetinglToday =
pSunnyToday * pGreetinglTodaylfSunnyToday;
Double pNotSunnyTodayAndGreetinglToday =
pNotSunnyToday * pGreetinglTodayIfNotSunnyToday;
Double pSunnyTodayGivenGreetinglToday =
pSunnyTodayAndGreetinglToday /
(pSunnyTodayAndGreetinglToday +
pNotSunnyTodayAndGreetinglToday);
Double pNotSunnyTodayGivenGreetinglToday =
1 - pSunnyTodayGivenGreetinglToday;
Double pSunnyTomorrowGivenGreetinglToday =
pSunnyTodayGivenGreetinglToday *
pSunnyTomorrowIfSunnyToday +
pNotSunnyTodayGivenGreetinglToday *
pSunnyTomorrowlfNotSunnyToday;
Double pNotSunnyTomorrowGivenGreetinglToday =
1 - pSunnyTomorrowGivenGreetinglToday;
Double pGreetinglTomorrowGivenGreetinglToday =
pSunnyTomorrowGivenGreetinglToday *
pGreetinglTomorrowIfSunnyTomorrow +
pNotSunnyTomorrowGivenGreetinglToday *
pGreetinglTomorrowIfNotSunnyTomorrow;
System.out.printIn("Если сегодня произнесено приветствие " +
greetingl + ", то завтра будет сказано " + greetingl +
" с вероятностью " +
pGreetinglTomorrowGivenGreetinglToday);
}
public static void main(String[] args) {
predict();
infer () ;
learnAndPredict();
45

Глава 1. О вероятностном программировании в двух словах
О — Определяем приветствия
© — Задаем числовые параметры модели
© — Предсказываем сегодняшнее приветствие, применяя правила вероятностного вывода
© — Из того, что было произнесено приветствие «Здравствуй, мир!», выводим
сегодняшнюю погоду, применяя правила вероятностного вывода
© — Из того, что было произнесено приветствие «Здравствуй, мир!», обучаемся
предсказывать завтрашнее приветствие, применяя правила вероятностного вывода
© — Метод main, который выполняет все задачи
Не буду здесь описывать, как выполняются вычисления с применением правил
вероятностного вывода. В коде используются три правила вывода: цепное правило,
правило полной вероятности и правило Байеса. Все они будут объяснены в главе 9.
А пока выделим две серьезные проблемы в этой программе.
• Не существует способа определить структуру модели.
Определение модели содержится в списке имен переменных,
принимающих значения типа double. Когда в начале этого раздела я описывал модель
и приводил числа в табл. 1.1, структура модели была очевидна и
более-менее понятна, пусть и на интуитивном уровне. У списка же переменных нет
вообще никакой структуры. Назначение переменных закодировано только
в их именах, что нельзя назвать хорошей идеей. Следовательно, написать
модель таким образом трудно, и этот путь чреват ошибками. К тому же,
написанный код трудно читать и сопровождать. Если потребуется
модифицировать модель (например, сделать так, чтобы приветствие зависело
еще и от того, хорошо ли вы спали), то, скорее всего, придется переписать
большие куски кода.
• Самостоятельно кодировать правила вывода трудно и чревато ошибками.
Вторая серьезная проблема связана с кодом, в котором для ответа на
запросы используются правила вероятностного вывода. Чтобы написать такой
код, необходимо хорошо знать правила вывода. Даже если такие знания
имеются, написать код правильно все равно тяжело. И проверить,
получен ли правильный ответ, тоже трудно. А ведь это очень простой пример.
В сложном приложении написать код рассуждений подобным способом
вообще нереально.
А теперь познакомимся с кодом, написанным на Scala/Figaro.
Листинг 1 -2, Программа Hello World на Figaro
import com.era.figaro.language.{Flip, Select}
import com.era.figaro. library. compound. If
import com.era.figaro.algorithm.factored.VariableElimination
<M>
object HelloWorld {
val sunnyToday = Flip(0.2) © ^
val greetingToday = If(sunnyToday,
Select (0.6 -> "Здравствуй, мир!", 0.4 -> "Здравствуй, вселенная!"),
46

1.3. Введение в Figaro, язык вероятностного программирования
Select (0.2 -> "Здравствуй, мир!", 0.8 -> "О нет, только не это"))
val sunnyTomorrow = If(sunnyToday, Flip(0.8), Flip(0.05))
val greetingTomorrow = If(sunnyTomorrow,
Select (0.6 -> "Hello, world!", 0.4 -> "Howdy, universe!"),
Select (0.2 -> "Hello, world!", 0.8 -> "Oh no, not again"))
def predict() {
val result = VariableElimination.probability(greetingToday,
"Здравствуй, мир!")
printIn("Сегодня будет приветствие \"Здравствуй, мир!\" " +
'с вероятностью
+ result +
')
©->
<ь-®
def infer () { Q [>
greetingToday.observe("Здравствуй, мир!")
val result = VariableElimination.probability(sunnyToday, true)
println("Если сегодня произнесено приветствие \"3дравствуй, мир\", " +
"то будет солнечно с вероятностью " + result + ".")
}
def learnAndPredict() {
greetingToday.observe("Здравствуй, мир!")
val result = VariableElimination.probability(greetingTomorrow,
"Hello, world!")
println("Если сегодня произнесено приветствие \"3дравствуй, мир!\",
"то завтра будет сказано \"Здравствуй, мир!\" " +
0->
'с вероятностью
+ result +
')
def main(args: Array[String])
predict()
infer ()
learnAndPredict()
}
<!-©
О — Импортируем конструкции Figaro
© — Определяем модель
© — Предсказываем сегодняшнее приветствие, применяя алгоритм вывода
© — Применяем алгоритм вывода, чтобы вывести сегодняшнюю погоду из того, что
сегодня было произнесено приветствие «Здравствуй, мир!»
© — Применяя алгоритм вывода, обучаемся предсказывать завтрашнее приветствие,
зная, что сегодня было произнесено «Здравствуй, мир!»
© — Метод main, который выполняет все задачи
Я подробно объясню этот код в следующей главе. А пока хочу отметить, что он
решает обе проблемы, встретившиеся в программе на Java. Во-первых,
определение модели точно описывает ее структуру - в полном соответствии с табл. 1.1. Мы
определяем четыре переменные: sunnyToday, greetingToday, sunnyTomorrow И
greetingTomorrow, Как ОПИСанО В табл. 1.1. Вот, например, определение greetingToday!
val greetingToday = If(sunnyToday,
Select (0.6 -> "Здравствуй, мир!", 0.4 -> "Здравствуй, вселенная!"),
Select(0.2 -> "Здравствуй, мир!", 0.8 -> "О нет, только не это"))
47

Глава 1. О вероятностном программировании в двух словах
Здесь говорится, что если сегодня ясно, то с вероятностью 0.6 будет
произнесено приветствие «Здравствуй, мир!» и с вероятностью 0.4 - «Здравствуй,
вселенная!». Если же сегодня пасмурно, то с вероятностью 0.2 будет сказано
«Здравствуй, мир!» и с вероятностью 0.8 - «О нет, только не это». Это в точности то
же самое, что говорит табл. 1.1 о сегодняшнем приветствии. Поскольку код явно
описывает модель, то писать, читать и сопровождать его гораздо проще. А если
потребуется изменить модель (например, добавить переменную sieepQuaiity), то
это можно будет сделать модульно.
Теперь рассмотрим код задач рассуждения. В нем нет никаких вычислений, а
просто создается экземпляр объекта-алгоритма (в данном случае алгоритма
исключения переменных, одного из встроенных в Figaro), и у него запрашивается
искомая вероятность. В части 3 будет показано, что этот алгоритм основан на тех
же правилах вывода, что и алгоритм из программы на Java. Всю сложную работу
по организации и применению правил вывода берет на себя алгоритм. Даже если
модель велика и сложна, можно прогнать алгоритм, и он отлично справится с
выводом.
1.4. Резюме
• Для субъективных суждений нужны знания + логика.
• В системах вероятностных рассуждений вероятностная модель выражает
знания, а алгоритм вывода инкапсулирует логику.
• Вероятностные рассуждения можно использовать для предсказания
будущих событий, для вывода причин произошедших событий и обучения на
прошлом опыте с целью улучшения предсказаний.
• Вероятностное программирование - это вероятностное рассуждение, в
котором вероятностная модель выражена на языке программирования.
• В системе вероятностного программирования используется полный по
Тьюрингу язык программирования для представления моделей и включены
алгоритмы вывода для работы с этими моделями.
• Figaro - это система вероятностного программирования, реализованная на
языке Scala, предлагающем функциональный и
объектно-ориентированный стили программирования.
1.5. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Пусть требуется использовать систему вероятностных рассуждений для
рассуждения об исходе сдачи карт в покере.
a. Какие общие знания вы закодировали бы в этой модели?
b. Опишите, как можно воспользоваться системой для предсказания
будущего. Что в этом случае является фактами? А что - запросом?
48

1.5. Упражнения
c. Опишите, как бы вы использовали систему для вывода причин
наблюдаемого результата. Что является фактами и что - запросом?
d. Опишите, как выведенные причины произошедшего события могут
улучшить будущие предсказания.
2. В примере «Hello World» измените вероятность ясной погоды сегодня, как
показано в таблице ниже. Как изменится результат работы программы?
Почему вы так думаете?
Погода сегодня
Ясно
Пасмурно
0.9
0.1
Добавьте в пример «Hello World» еще одно приветствие «Здравствуй,
галактика!». Назначьте ему некоторую вероятность при ясной погоде, не
забыв уменьшить вероятности других приветствий, так чтобы сумма
вероятностей осталась равной 1. Кроме того, модифицируйте программу, так
чтобы там, где раньше ответом на запрос было приветствие «Здравствуй,
мир!», теперь печаталось «Здравствуй, галактика!». Попробуйте сделать
это для обеих версий программы: на Java и на Figaro. Сравните
трудоемкость.
49

ГЛАВА 2.
Краткое руководство
по языку Figaro
В этой главе.
■ Создание моделей, задание фактов, прогон
алгоритма вывода и получение ответов на запросы.
■ Основные строительные блоки моделей.
■ Построение сложных моделей из строительных
блоков.
Итак, мы узнали, что такое вероятностное программирование и теперь готовы
ближе познакомиться с системой Figaro, начать писать простые программы и
получать от них ответы на свои запросы. В этой главе я хочу как можно быстрее
ввести вас в курс основных идей Figaro. А в последующих главах подробно объясню,
что означает модель и как ее следует интерпретировать. Приступим.
2.1. Введение в Figaro
Для начала взглянем на Figaro с высоты птичьего полета. Как было сказано в
главе 1, Figaro - это система вероятностных рассуждений. Но прежде чем
рассматривать ее компоненты, вспомним о компонентах общей системы вероятностных
рассуждений, чтобы была основа для сопоставления с Figaro. На рис. 2.1 повторена
самая суть системы вероятностных рассуждений. Напомню, что в вероятностной
модели закодированы общие знания о ситуации, а факты сообщают информацию
о конкретной ситуации. Алгоритм вывода пользуется моделью и фактами для
получения ответов на запросы о ситуации.

2.1. Введение в Figaro
Факты содержат
информацию
о конкретной
ситуации
В запросе
описывается, что
мы хотим узнать
Ответы на запросы
представлены в
виде вероятностей
различных исходов
Факты
Запросы-
Ответы
Система
вероятностных
рассуждений
' N
Вероятностная
модель
v >
Алгоритм
вывода
Вероятностная модель
выражает общие знания
о ситуации
Алгоритм вывода
пользуется моделью
для получения ответов
на запросы при
заданных фактах
Рис. 2.1. Обзор основных частей системы вероятностных рассуждений
Теперь обратимся к Figaro. На рис. 2.2 показаны его основные концепции. Как
видим, компоненты те же самые, что на рис. 2.1. Общие знания выражаются в виде
модели Figaro. Знания о конкретной ситуации представлены в виде фактов. Запрос
говорит системе, что мы хотим узнать. Алгоритм вывода Figaro принимает запрос
и использует модель для получения ответов на запросы.
Факты включают
наблюдения, условия
и ограничения на
значения элементов
Г
Факты
Замечания
Условия
Ограничения
Г
Запросы
Целевые элементы
В запросах
указываются целевые
элементы
Модель Figaro состоит из
набора структур данных,
называемых элементами
Г
Модель Figaro
Атомарные элементы
Составные элементы
Apply
Chain
Алгоритмы вывода Figaro
Instantiate
Run
Clean up
r
Ответы
Вероятности значений
Наиболее вероятные значения
Атомарные элементы
являются базовыми
строительными блоками
Составные элементы
связывают более простые
элементы
Apply и Chain — важные
примеры составных
элементов
Алгоритмы Figaro
вычисляют информацию о
запрошенных элементах
Обычно экземпляр
алгоритма создается,
исполняется и в конце
уничтожается
В Figaro имеются методы
для выполнения всех
перечисленных шагов
В ответах содержится
информация о
целевых элементах
Рис. 2.2. Взаимосвязь основных концепций Figaro
51

Глава 2. Краткое руководство по языку Figaro
Рассмотрим каждую часть поочередно. Большую часть интерфейса Figaro
занимают различные способы спецификации моделей. Модель Figaro состоит из
набора структур данных, которые называются элементами. Каждый элемент
представляет одну из переменных ситуации и может принимать одно из множества
значений. В элементе закодирована информация, определяющая вероятности
различных событий. В примере 2.2.1 мы увидим базовое определение элементов в
контексте примера «Hello World».
Элементы бывают двух видов: атомарные и составные. Можно считать, что
Figaro - это конструктор для сборки моделей. Атомарные элементы - это
основные строительные блоки, они представляют базовые вероятностные переменные,
которые не зависят от других элементов. Атомарные элементы обсуждаются в
разделе 2.3, где приведены различные примеры. Составные элементы - это
соединители. Из одного или нескольких элементов они конструируют более сложные
элементы. Подробнее о составных элементах вы узнаете в разделе 2.4. В Figaro
много составных элементов, но два - Apply и Chain - особенно важны, речь о них
пойдет в разделе 2.5.
Переходим к фактам. В Figaro имеется развитый механизм для задания фактов.
Чаще всего вы будете использовать простейшую форму фактов - наблюдение.
Наблюдение говорит, что значение элемента известно и равно заданному. Как
специфицируются наблюдения, рассказано в разделе 2.2.3. Иногда необходим более
общий способ задания фактов. Для этой цели в Figaro имеются условия и
ограничения. То и другое рассматривается в разделе 2.6.
В запросах указывается, какие целевые элементы представляют интерес и что
мы хотим о них знать. Для получения информации о целевых элементах
используется алгоритм вывода, которому передаются факты. Как правило, необходимо
создать экземпляр алгоритма, выполнить его и в конце уничтожить. Я
предоставил простые методы, которые выполняют все эти шаги с подразумеваемыми по
умолчанию параметрами. После прогона алгоритма можно получить ответы на
запросы. Чаще всего ответы имеют вид вероятностей значений целевых элементов.
Иногда вместо вероятностей сообщаются наиболее вероятные значения каждого
целевого элемента, т. е. значения с наибольшей вероятностью. В разделе 2.2.2
показано, как задавать запросы, выполнять алгоритмы и получать ответы.
2.2. Создание модели и выполнение
алгоритма вывода на примере
Hello World
Познакомившись с основными понятиями Figaro, посмотрим, как они
взаимосвязаны. Вернемся к примеру «Hello World» из главы 1 и покажем, как в нем
материализуются концепции, показанные на рис. 2.2. Мы увидим, как построить модель из
атомарных и составных элементов, задать наблюдаемые факты, сформулировать
запрос, прогнать алгоритм вывода и получить ответ.
52

2.2. Создание модели и выполнение алгоритма вывода ...
Выполнить код из этой главы можно двумя способами. Первый -
воспользоваться консолью Scala и вводить в ней предложения последовательно,
сразу же получая результаты. Для этого зайдите в корневой каталог проекта
PracticalProbProg/examples и наберите sbt console. Вы увидите приглашение
Scala. После этого можете вводить строки приведенного кода и наблюдать за
реакцией системы.
Второй способ традиционный: написать программу, содержащую метод main.
В этой главе я не буду описывать стереотипный способ превращения кода в
исполняемую программу Здесь приведен лишь код, имеющий отношение к Figaro.
Но я обязательно отмечу, что необходимо импортировать и откуда это берется.
2.2.7. Построение первой модели
Начнем с построения простейшей модели Figaro, в которой будет всего один
атомарный элемент. Но прежде необходимо импортировать необходимые
конструкции Figaro:
import com.cra.figaro. language._
В результате ИМПОрТИруЮТСЯ ВСе КЛаССЫ ИЗ пакета com.cra.figaro. language, KO-
торый содержит базовые конструкции Figaro. Один из этих классов называется
Flip. С его помощью можно построить простую модель:
val sunnyToday = Flip(0.2)
Эта строка объясняется на рис. 2.3. Важно четко понимать, что относятся к Scala,
а что - к Figaro. В этой строке мы создали переменную Scala sunnyToday и
присвоили ей значение Flip(0.2). Значение Flip(0.2) - это элемент Figaro,
представляющий случайный процесс, который порождает значение true с вероятностью 0.2
и false - с вероятностью 0.8. Элемент - это структура данных, представляющая
процесс, который случайным образом порождает некоторое значение. Число
исходов случайного процесса может быть произвольным. Каждый возможный исход
называется значением процесса. Таким образом, Flip (0.2) - элемент с двумя
возможными булевыми значениями: true и false. Итак, мы имеем переменную Scala,
принимающую значение в смысле Scala. Это значение является элементом Figaro
и представляет различные возможные исходы процесса.
Scala: Figaro:
sunnyToday
Переменная
\ Элемент
- _^ - Flip(0.2)
Значение -"^
* ^--Возможные значения
true false «-^
Рис. 2.3. Связь между переменными и значениями Scala
и элементами Figaro и их возможными значениями
53

Глава 2. Краткое руководство по языку Figaro
В Scala тип может быть параметризован другим типом, описывающим его
содержимое. Возможна, эта идея знакома вам по универсальным типам Java, где можно,
например, определить список целых чисел или список строк. Все элементы Figaro
являются экземплярами класса Element, который параметризуется типом
значения элемента. Поскольку элемент Flip (0.2) может принимать булевы значения,
то типом его значения является Boolean. Формально говоря, Flip (0.2) является
Экземпляром Класса Element [Boolean].
Основные определения
Элемент- структура данных Figaro, представляющая случайный процесс.
Значение - возможный исход случайного процесса.
Тип значения - тип Scala, представляющий возможные значения элемента.
Как много слов для такой простой модели! Но, к счастью, все, что вы сейчас
узнали, относится ко всем моделям Figaro. В Figaro модели создаются из простых
элементов - строительных блоков, которые комбинируются в более сложные
элементы и наборы взаимосвязанных элементов.
Прежде чем переходить к более сложным моделям, посмотрим, как модель
позволяет проводить рассуждения.
2.2.2. Выполнение алгоритма вывода и получение
ответа на запрос
Итак, мы построили простую модель. Теперь прогоним алгоритм вывода и
запросим вероятность того, что переменная sunnyToday равна true. Сначала нужно
импортировать используемый алгоритм вывода:
import com.era.figaro.algorithm.factored.VariableElimination
Здесь импортируется алгоритм исключения переменных, относящийся к классу
точных алгоритмов, т. е. он точно вычисляет вероятности, исходя из модели и
фактов. Вероятностный вывод - сложная задача, поэтому иногда точные алгоритмы
работают очень долго или им не хватает памяти. Figaro предлагает также
приближенные алгоритмы, которые обычно вычисляют ответы, близкие к точным.
Поскольку все модели в этой главе простые, то алгоритм исключения переменных
будет работать без проблем.
В Figaro имеется команда, позволяющая за одно действие задать запрос,
выполнить алгоритм и получить ответ:
println(VariableElimination.probability(sunnyToday, true))
Эта команда напечатает 0.2. Наша модель состоит только из элемента Flip (0.2),
который принимает значение true с вероятностью 0.2. Алгоритм исключения
переменных правильно вычисляет вероятность, что sunnyToday равно true, - она
равна 0.2.
54

2.2. Создание модели и выполнение алгоритма вывода ...
щи
1*1
Еще раз поясним, что показанная выше команда выполняет несколько
операций. Сначала она создает экземпляр алгоритма исключения переменных. Затем
сообщает этому экземпляру, что целевым элементом является sunnyToday. Далее
она выполняет алгоритм и возвращает вероятность того, что значение sunnyToday
равно true. Команда также подчищает за собой, т. е. освобождает ресурсы,
захваченные алгоритмом.
2.2.3. Построение моделей и задание
наблюдений
Теперь приступим к построению более интересной модели. Нам понадобится
конструкция Figaro if, поэтому импортируем ее. Еще будет нужна конструкция
select, НО Она уже импортирована В СОСТаве пакета com. era . figaro . language!
import com.era.figaro.library.compound.If
Воспользуемся элементами if и select для построения более сложного
элемента:
val greetingToday = If(sunnyToday,
Select (0.6 -> "Здравствуй, мир!", 0.4 -> "Здравствуй, вселенная!"),
Select (0.2 -> "Здравствуй, мир!", 0.8 -> "О нет, только не это"))
Мы интерпретируем элемент как случайный процесс. В таком случае элемент
greetingToday представляет процесс, КОТОрыЙ Сначала проверяет Значение
sunnyToday. Если это значение равно true, то он выбирает приветствие «Здравствуй,
мир!» с вероятностью 0.6, а приветствие «Здравствуй, вселенная!» с вероятностью
0.4. Если же значение sunnyToday равно false, то «Здравствуй, мир!» выбирается с
вероятностью 0.2, а «О нет, только не это» с вероятностью 0.8. Элемент greeting-
today составной, потому что он построен из трех элементов. Так как возможные
значения greetingToday - строки, то этот элемент является экземпляром класса
Element[String].
Теперь допустим, что сегодня мы наблюдали приветствие «Здравствуй, мир!».
Этот факт можно задать в виде наблюдения следующим образом:
greetingToday.observe("Здравствуй, мир!")
Мы можем найти вероятность того, что сегодня ясно, зная, какое было
приветствие:
println(VariableElimination.probability(sunnyToday, true))
Печатается 0.4285714285714285. Отметим, что этот ответ значительно больше
предыдущего (0.2). Причина в том, что приветствие «Здравствуй, мир!» гораздо
вероятнее, если сегодня ясно, поэтому факт говорит в пользу того, что сегодня
действительно ясно. Этот вывод - простой пример применения правила Байеса, о
котором мы узнаем в главе 9.

Глава 2. Краткое руководство по языку Figaro
Далее мы разовьем эту модель и выполним дополнительные запросы с другими
фактами, НО Предварительно удаЛИМ Наблюдение ДЛЯ Переменной greetingToday.
Это делает такая команда:
greetingToday.unobserve()
Если теперь выполнить запрос
println(VariableElimination.probability(sunnyToday, true))
то получится тот же ответ 0.2, что и раньше, до того как был сообщен этот факт.
Прежде чем закончить этот раздел, усложним модель:
val sunnyTomorrow = If (sunnyToday, Flip(0.8), Flip(0.05))
val greetingTomorrow = If(sunnyTomorrow,
Select (0.6 -> "Здравствуй, мир!", 0.4 -> "Здравствуй, вселенная!"),
Select (0.2 -> "Здравствуй, мир!", 0.8 -> "О нет, только не это"))
Вычислим вероятность того, что завтра будет произнесено приветствие
«Здравствуй, мир!», если известно, какое приветствие было сегодня, и если неизвестно:
println(VariableElimination.probability(greetingTomorrow, "Здравствуй, мир!"))
// печатается 0.27999999999999997
greetingToday.observe("Здравствуй, мир!!")
println(VariableElimination.probability(greetingTomorrow, "Здравствуй, мир!"))
// печатается 0.3485714285714286
Как видим, если известно, что сегодня произнесено приветствие «Здравствуй,
мир!», то вероятность того, что оно будет произнесено и завтра, возрастает.
Почему так? Потому что если сегодня было сказано «Здравствуй, мир!», то высока
вероятность, что на улице ясно, а это значит, что с высокой вероятностью и завтра
будет ясно, а это, в свою очередь, значит, что и завтра будет сказано «Здравствуй,
мир!». В главе 1 мы назвали это выводом прошлого для лучшего предсказания
будущего, и Figaro производит все необходимые вычисления самостоятельно.
2.2Л. Анатомия построения модели
Итак, мы рассмотрели все шаги создания модели, задания фактов и запросов,
выполнения алгоритма и получения ответа. Теперь внимательнее приглядимся
к модели «Hello World», чтобы понять, как она конструируется из строительных
блоков (атомарных элементов) и соединителей (составных элементов).
На рис. 2.4 приведено графическое изображение этой модели. Сначала
повторено ее определение, причем каждая переменная Scala показана в отдельном блоке.
А в блоках ниже представлены соответствующие элементы модели. Некоторые
элементы являются значениями самих переменных Scala. Например, значение
переменной sunnyToday представлено элементом Flip (0.2). Если элементом
является значение переменной Scala, то в графе показано имя и переменной и элемента.
В модели присутствуют также элементы, не являющиеся значениями переменных
Scala. Например, ПОСКОЛЬКУ переменная sunnyTomorrow определена Как If (sunnyTo-
56

2.2. Создание модели и выполнение алгоритма вывода
day, Flip (0.8), Flip (0 . 05) ), ТО ЭЛвМеНТЫ Flip (0 . 8) И Flip (0.05) ТОЖе ЯВЛЯЮТСЯ
частью модели, поэтому они показаны в вершинах графа.
val sunnyToday = Flip(0-2)
val greetingToday = If(sunnyToday,
Select (0.6->"Hello, world!",0^4->MHowdy, universe!"),
Select (C^2->"Hello, world! ", 0 . 8->"Oh no, not again") )
val sunnyTomorrow=If(sunnyToday,Flip(0,8), Flip(0.05))
i 1
| val greetingTomorrow = If (sunnyTomorrow,
Select (£L_£->"Hello, world!",0.4->"Howdyr universe!"),
Select (Q^2->"Hello, world!",QJJ->"0h no, not again"))
sunnyToday: Flip(0.2)
Select(0,6->"Hello, world!",
0.4->"Howdy, universe!")
Select(0.2->"Hello, world!",
0.8->"Oh no, not again")
sunnyTomorrow: If( , , )
Select(0.6->"Hello, world!",
ч 0.4->"Howdy, universe!")
Рис. 2.4. Структура модели «Hello World» в виде графа. Каждая вершина соответствует
элементу. Ребра графа показывают, что один элемент используется другим
57
greetingToday: If( , , )
Select{0.2->"Hello, world!",
0,8->"Oh no, not again")
greetingTomorrow: If{ , , )
Flip(0.8)
Flip(O-OS)

Глава 2. Краткое руководство по языку Figaro
Элементы в вершинах графа соединены ребрами. Например, существует ребро,
идущее из Flip(0.8) в элемент if, являющийся значением переменной sunnyTo-
morrow. Элемент Flip(0.8) используется элементом if. В общем случае ребро из
одного элемента в другой существует, если в определении второго элемента
используется первый. Поскольку только составные элементы конструируются из
других элементов, конечная вершина любого ребра обязательно является
составным элементом.
2.2.5. Повторяющиеся элементы: когда они
совпадают, а когда различаются?
Обратите внимание, ЧТО элемент Select (0.6 -> "Здравствуй, мир!", 0.4 ->
"Здравствуй, вселенная!") встречается В Графе ДВаЖДЫ, Как И Элемент Select (0.2 ->
"Здравствуй, мир!", 0.8 -> "О нет, только не это"). Причина В ТОМ, ЧТО Само
определение дважды встречается в коде, один раз для greetingToday, другой - для
greetingTomorrow. Это два разных элемента, хотя их определения одинаковы. Они
могут принимать различные значения в ходе одного и того же выполнения
случайного процесса, определяемого моделью Figaro. Например, первый экземпляр
элемента мог бы принять значение «Здравствуй, мир!», а второй - «Здравствуй,
вселенная!». Это имеет смысл, потому что один используется в определении
переменной greetingToday, а Другой - В определении greetingTomorrow. Вполне
ВОЗМОЖНО, что сегодняшнее и завтрашнее приветствия будут различаться.
Тут уместна аналогия с обычным программированием. Пусть имеется такой
Класс Greeting!
class Greeting {
var string = "Здравствуй, мир!"
}
val greetingToday = new Greeting
val greetingTomorrow = new Greeting
greetingTomorrow.string = "Здравствуй, вселенная!"
ХОТЯ определения переменных greetingToday И greetingTomorrow В ТОЧНОСТИ
Совпадают, ЭТО два разных экземпляра Класса Greeting. Поэтому значение
greetingTomorrow. string МОЖет ОТЛИЧатьСЯ ОТ Значения greetingToday. string, KOTO-
рое по-прежнему равно «Здравствуй, мир!». Точно так же конструкторы Figaro, в
частности select, создают новые экземпляры соответствующего класса элемента.
Так, greetingToday И greetingTomorrow - два раЗНЫХ экземпляра Элемента Select И
потому могут принимать различные значения при одном и том же прогоне.
С другой стороны, заметим, что переменная Scala sunnyToday также дважды
встречается в коде: один раз в определении greetingToday, другой - в
определении sunnyTomorrow. Но Элемент, ЯВЛЯЮЩИЙСЯ Значением sunnyToday, встречается В
графе только один раз. Почему? Потому что sunnyToday - переменная Scala, а не
определение элемента Figaro. Переменная Scala, несколько раз встречающаяся в
коде, - это одна и та же переменная, поэтому ее значение всюду одинаково. В на-
58

2.3. Базовые строительные блоки: атомарные элементы
Ш
шей МОДеЛИ ЭТО имеет СМЫСЛ: В определениях greetingToday И sunnyTomorrow речь
идет о погоде в один и то же день, поэтому при любом случайном выполнении
модели значения в обоих случаях должны быть одинаковы.
То же самое происходит в обычной программе. Если написать
val greetingToday = new Greeting
val anotherGreetingToday = greetingToday
anotherGreetingToday.string = "Здравствуй, вселенная!"
TO anotherGreetingToday - В ТОЧНОСТИ та Же переменная Scala, ЧТО И
greetingToday, поэтому после выполнения этого кода greetingToday будет иметь значение
«Здравствуй, вселенная!». Аналогично, если одна и та же переменная Scala,
представляющая некоторый элемент, встречается в программе несколько раз, то она
всюду будет иметь одно и то же значение.
Этот момент важно понимать, чтобы правильно конструировать модели Figaro,
поэтому я рекомендую перечитать этот подраздел, пока вы не будете уверены, что
все усвоили. Теперь у вас должно сложиться общее представление об основных
концепциях Figaro и их взаимосвязях. В следующих разделах мы изучим
некоторые концепции более детально. И начнем с атомарных элементов.
2.3. Базовые строительные блоки:
атомарные элементы
Настало время поближе познакомиться с элементами Figaro. Начнем с базовых
строительных блоков - атомарных элементов. Слово «атомарный» означает, что
элемент не зависит ни от каких других элементов. Не буду здесь приводить
полный список атомарных элементов, а ограничусь наиболее употребительными.
Атомарные элементы подразделяются на дискретные и непрерывные, в
зависимости от типа значения. Значения дискретных элементов имеют такие типы,
Как Boolean ИЛИ Integer, а непрерывных - ТИП Double. Технически ДИСКретНОСТЬ
означает, что значения достаточно далеко отстоят друг от друга. Например,
между целыми числами 1 и 2 нет других целых чисел, поэтому можно сказать, что
они отделены друг от друга. С другой стороны, значения непрерывных элементов
образуют неразрывный континуум, как, например, вещественные числа. Между
любыми двумя вещественными числами найдется еще одно вещественное число.
Различие между дискретными и непрерывными элементами существенно для
вычисления вероятностей, мы увидим это в главе 4.
Предупреждение. Некоторые думают, что дискретный означает конечный. Это не так.
Целых чисел бесконечно много, но между любыми двумя соседними имеется
промежуток, в котором нет ни одного целого числа, так что они образуют дискретное множество.
Основные определения
Атомарный элемент - элемент, не зависящий ни от каких других элементов.
Составной элемент - элемент, построенный из других элементов.

Глава 2. Краткое руководство по языку Figaro
Дискретный элемент - элемент, значения которого отстоят «далеко» друг от друга.
Непрерывный элемент- элемент, между значениями которого нет промежутков.
2.3.1. Дискретные атомарные элементы
Рассмотрим Примеры ДИСКреТНЫХ аТОМарНЫХ Элементов: Flip, Select И Binomial.
Элемент Flip
Мы уже встречались с дискретным атомарным элементом Flip. Его код
находится в пакете com.era.figaro.language вместе со многими другими широкоупо-
требительными элементами. Я рекомендую импортировать этот пакет целиком в
начале программы. Элемент Flip принимает один аргумент/? - вероятность того,
что значение элемента равно true; р должно быть числом от 0 до 1 включительно.
Вероятность того, что элемент принимает значение false, равна 1 - р. Например:
import com.era.figaro. language._
val sunnyToday = Flip(0.2)
println(VariableElimination.probability(sunnyToday, true))
// печатается 0.2
println(VariableElimination.probability(sunnyToday, false))
// печатается 0.8
Элемент Flip (0.2) Имеет Официальный ТИП AtomicFlip - ПОДКЛаСС Класса
Element [Boolean]. Этим он отличается от элемента compoundFiip, который будет
рассмотрен ниже.
Элемент Select
С элементом select мы тоже встречались в программе «Hello World». Вот
пример: Select(0.6 -> "Здравствуй, мир!", 0.3 -> "Здравствуй, вселенная!", 0.1 ->
"о нет, только не это"). На рис. 2.5 показано, как строится этот элемент. Внутри
скобок находится несколько частей. Каждая часть состоит из вероятности,
стрелки и возможного исхода. Количество частей произвольно. На рисунке мы видим
три части. Поскольку все исходы имеют тип string, то элемент принадлежит
классу Element [String]. Официально его ТИПОМ является AtomicSelect [String] - ПОД-
КЛаСС Element [String].
Естественно, элемент select соответствует процессу, возможные исходы
которого выбираются с указанными вероятностями. Вот как это будет работать для
примера на рисунке:
val greeting = Select (0.6 -> "Здравствуй, мир!",
0.3 -> "Здравствуй, вселенная!", 0.1 -> "О нет, только не это")
println(VariableElimination.probability(greeting,
"Здравствуй, вселенная!"))
// печатается 0.30000000000000004
60

2.3. Базовые строительные блоки: атомарные элементы
III!
HI
Select (0.6 -> "Hello, world!", 0.3 "Howdy, iverse!", 0Л -> "Oh no, not again1')
Возможные исходы
Рис. 2.5. Структура элемента select
Отметим, что сумма вероятностей в select не обязательно равна 1. Если она
отлична от 1, то вероятности нормируются, т. е. умножаются на некоторый (один
и тот же) коэффициент, так чтобы получилась сумма 1. В следующем примере
вероятности вдвое больше, чем в предыдущем, поэтому их сумма равна 2.
Нормировка приводит к таким же вероятностям, как и выше, поэтому результаты будут
совпадать.
val greeting = Select(1.2 -> "Здравствуй, мир!",
0.6 -> "Здравствуй, вселенная!", 0.2 -> "О нет, только не это")
println(VariableElimination.probability(greeting,
"Здравствуй, вселенная!"))
// печатается 0.30000000000000004
Элемент Binomial
Binomial- еще один полезный дискретный элемент. С каждым из семи дней
недели может быть связан элемент Flip(0.2), определяющий будет ли в этот день
ясно. А нам нужен элемент, значением которого является число ясных дней на
неделе. Для этого можно взять элемент Binomial (7, 0.2). Его значением является
количество испытаний, результат которых равен true, при том, что всего
проводится семь испытаний, и каждое дает true с вероятностью 0.2. Используется этот
элемент так:
import com.era.figaro.library.atomic.discrete.Binomial
val numSunnyDaysInWeek = Binomial(7, 0.2)
println(VariableElimination.probability(numSunnyDaysInWeek, 3))
//печатается 0.114688
Элемент Binomial принимает два аргумента: количество испытаний и
вероятность того, что испытание даст результат true. В определении Binomial
предполагается, что испытания независимы; от того, что первое дало true, вероятность
получения true во втором не меняется.
2.3.2. Непрерывные атомарные элементы
В этом разделе описаны два распространенных непрерывных элемента: Normal и
uniform. В главе 4 непрерывные элементы рассматриваются подробно.
Непрерывное распределение вероятности отличается от дискретного тем, что задается не
Вероятности
Стрелки связывают
вероятности
с исходами

Глава 2. Краткое руководство по языку Figaro
вероятность каждого значения, а плотность вероятности, описывающая
вероятность интервала вокруг значения. Тем не менее, можно считать, что плотность
вероятности похожа на обычную вероятность, т. е. показывает, насколько данное
значение вероятно по сравнению с другими. Поскольку эта глава - учебное
пособие по Figaro, то я отложу более подробное обсуждение до главы 4, где
рассматриваются вероятностные модели. Но не беспокойтесь, в свое время все станет ясно
и понятно.
Элемент Normal
Вы, наверное, знакомы с нормальным распределением вероятности. У него есть
и другие названия, например: колоколообразная кривая или гауссово распределение.
На рис. 2.6 показана функция плотности вероятности для нормального
распределения. (Строго говоря, это одномерное нормальное распределение\ потому что
определено для одной вещественной переменной, а бывают и многомерные нормальные
распределения нескольких переменных, но не будем придираться.) У этой функции
есть среднее значение - центральная точка (1 на рисунке) - и стандартное
отклонение, т. е. степень разброса функции вокруг центральной точки (0.5 на рисунке).
Примерно в 68 % процентах случаев значение с нормальным распределением будет
отстоять от среднего не далее, чем на одно стандартное отклонение. В
статистике и в вероятностных рассуждениях нормальное распределение обычно задается
средним и дисперсией, равной квадрату стандартного отклонения. Поскольку на
рисунке ниже стандартное отклонение равно 0.5, то дисперсия равна 0.25.
Следовательно, это нормальное распределение задается как Normal а, 0.25).
Normal (1,0.25)
0.9 п
Среднее
Рис- 2.6. Функция плотности вероятности нормального распределения
62

2.3. Базовые строительные блоки: атомарные элементы
El
Figaro точно следует этому соглашению. Он предоставляет элемент Normal,
принимающий в качестве аргументов среднее и дисперсию, например:
import com.era.figaro.1ibrary.atomic.continuous.Normal
val temperature = Normal(40, 100)
Здесь среднее равно 40, а дисперсия 100, т. е. стандартное отклонение равно 10.
Предположим теперь, что мы хотим выполнить вывод с помощью этого элемента.
Увы, алгоритм исключения переменных в Figaro работает только для элементов,
принимающих конечное число значений, а, значит, к непрерывным элементам он
неприменим. Поэтому придется взять другой алгоритм. Мы воспользуемся
приближенным алгоритмом выборки по значимости, который хорошо работает с
непрерывными элементами. Выполнить этот алгоритм можно так:
import com.era.figaro.algorithm.sampling.Importance
def greaterThan50(d: Double) = d > 50
println(Importance.probability(temperature, greaterThan50 _))
Выборка по значимости - это рандомизированный алгоритм, который каждый
раз дает новый ответ, близкий к истинному значению - в данном случае 0.1567.
Отметим, что запрос немного отличается от того, что мы видели раньше.
Вероятность, что значение непрерывного элемента будет в точности равно заданному,
например 50, очень близка к 0, поскольку значений бесконечно много, и
промежутков между ними нет. Шансы на то, что процесс вернет значение, равное точно
50, а не, скажем, 50.000000000000001, бесконечно малы. Поэтому мы обычно не
запрашиваем у непрерывного элемента вероятность точного значения.
Вместо этого указывается диапазон вероятностей. В данном случае в запросе
задан предикат greaterThanSO, который принимает в качестве аргумента значение
типа Double и возвращает true, если аргумент больше 50. Предикатом
называется булева функция от значения элемента. Спрашивая, удовлетворяет ли элемент
предикату, мы на самом деле интересуемся, с какой вероятностью применение
предиката к значению элемента вернет true. В этом примере запрос вычисляет
вероятность того, что температура больше 50.
Замечание о Scala. Знак подчеркивания после greaterThanSO говорит Scala, что
greaterThanSO следует рассматривать как функциональное значение, передаваемое
методу importance .probability. Без подчеркивания интерпретатор Scala мог бы
подумать, что мы пытаемся вызвать функцию без аргументов, а это ошибка. Иногда Scala
может разобраться в такой ситуации автоматически, даже если подчерка нет, а иногда
сдается и просит добавить подчерк.
Элемент Uniform
Рассмотрим еще элемент uniform (равномерное распределение), который
возвращает значения в указанном диапазоне с равной вероятностью:

Глава 2. Краткое руководство по языку Figaro
import com.era.figaro.library.atomic.continuous.Uniform
val temperature = Uniform(10, 70)
Importance.probability(temperature, greaterThan50 _)
// печатается число, близкое к 0.3334
Элемент uniform принимает два аргумента: начало и конец диапазона.
Плотность вероятности всех значений в этом диапазоне одинакова. В примере выше
минимальное значение равно 10, а максимальное 70, так что длина диапазона
равна 60. Предикат в запросе проверяет, находится ли значение между 50 и 70;
длина этого промежутка равна 20. Следовательно, для этого предиката вероятность
равна 20/60, или 1/3, и легко видеть, что алгоритм выборки по значимости дает
близкий результат.
И напоследок одно замечание: официально этот элемент называется
непрерывный uniform. Существует также дискретный uniform, находящийся в
пакете com. era. figaro. library, atomic, discrete. Как легко догадаться, ДИСКретныЙ
uniform возвращает каждое значение из переданного списка с одинаковой
вероятностью.
Итак, мы познакомились со строительными блоками, теперь посмотрим, как из
них собираются более крупные модели.
2.4. Комбинирование атомарных
элементов с помощью составных
В этом разделе мы рассмотрим несколько составных элементов. Напомним, что
составной элемент строит из нескольких элементов новый, более сложный.
Составных элементов много, но для начала мы рассмотрим только два: if и Dist,
а затем посмотрим, как использовать составные версии большинства атомарных
элементов.
2.4.7. Элементе
Мы уже встречались с одним примером составного элемента - if. Он состоит из
трех элементов: условия, предложения then и предложения else. Случайный
процесс, представленный элементом if, сначала проверяет условие. Если результат
вычисления условия равен true, то процесс порождает значение предложения
then, иначе значение предложения else. На рис. 2.7 показан пример элемента if.
Как видим, if принимает три аргумента. Первый аргумент - представляющий
условие - имеет тип Element [Boolean] и в данном случае является элементом
sunnyToday. Второй аргумент - предложение then; если значение
элемента-условия равно true, то выбирается этот элемент. Если же значение элемента-условия
равно false, то выбирается третий аргумент - предложение else. Типы значений
предложений then и else должны совпадать, и этот общий тип является типом
значения if.
64

Предложение
then
Предложение
else
Select (0.2 -> "Hello, world!", 0.8 -> "Oh no, not again"))
Рис. 2.7. Структура элемента if
Ниже показан элемент if в действии:
val sunnyToday = Flip(0.2)
val greetingToday = If(sunnyToday,
Select (0.6 -> "Здравствуй, мир!", 0.4 -> "Здравствуй, вселенная!"),
Select (0.2 -> "Здравствуй, мир!", 0.8 -> "О нет, только не это"))
println(VariableElimination.probability(greetingToday, "Здравствуй, мир!"))
// печатается 0.27999999999999997
Поясним, почему печатается 0.28 (с некоторой погрешностью). Предложение
then выбирается с вероятностью 0.2 (когда sunnyToday равен true), и в этом
случае строка «Здравствуй, мир!» выбирается с вероятностью 0.6. С другой стороны,
предложение else выбирается с вероятностью 0.8, и в этом случае строка
«Здравствуй, мир!» выбирается с вероятностью 0.2. Следовательно, полная вероятность
выбора строки «Здравствуй, мир!» равна (0.2 х 0.6) + (0.8 х 0.2) = 0.28. В этом
можно убедиться, явно вычислив два случая:
sunnyToday.observe(true)
println(VariableElimination.probability(greetingToday, "Здравствуй, мир!"))
// печатается 0.6, потому что всегда выбирается предложение then
sunnyToday.observe(false)
println(VariableElimination.probability(greetingToday, "Здравствуй, мир!"))
// печатается 0.2, потому что всегда выбирается предложение else
2.4.2. Элемент Dist
Dist - еще один полезный составной элемент. Он похож на select, но выбор
производится не из множества значений, а из множества элементов. Поскольку каждый
вариант выбора сам является элементом, Dist оказывается составным элементом.
Элемент Dist полезен, когда нужно выбрать один из случайных процессов.
Например, угловой удар в футболе может быть коротким пасом или сразу навесом на
ворота. Это можно представить элементом Dist, выбирающим один из двух
процессов: короткий пас и навес на ворота.
Элемент Dist находится в пакете com.era.figaro.language. Ниже приведен
пример его использования:
val goodMood = Dist(0.2 -> Flip(0.6), 0.8 -> Flip(0.2))
По структуре (см. рис. 2.8) он похож на элемент select (рис. 2.5). Разница в том,
что исходами являются не значения, а элементы. Можно представлять себе это
2.4. Комбинирование атомарных элементов с помощью составных
65
Условие
If(sunnyToday, «
Select(0.6 -> "Hello, world!", 0.4 -> "Howdy, universe!"),

Глава 2. Краткое руководство по языку Figaro
так: select выбирает одно из множества значений непосредственно, без
промежуточного процесса, а Dist опосредованно - сначала выбирается процесс, а тот уже
генерирует значение в ходе выполнения. В данном случае с вероятностью 0.2
будет выбран процесс, представленный элементом Flip (0. б), и с вероятностью 0.8 -
процесс, представленный элементом Flip (0.2).
Стрелки связывают
вероятности с
Вероятности исходами
Dist (0.2 -> Flip(0.6), 0.8 Flip(0.2))
Возможные элементы-исходы
Рис- 2.8. Структура элемента Dist
Вот что получается в случае запроса к этому элементу:
println (VariableElimination.probability(goodMood, true))
// печатается 0.28 = 0.2 * 0.6 + 0.8 * 0.2
2.4.3. Составные версии атомарных элементов
Мы видели примеры атомарных элементов, принимающих числовые аргументы.
Например, Flip принимает вероятность, a Normal - среднее и дисперсию. А если
мы не знаем точно значения числовых аргументов? В Figaro ответ прост: сделайте
их элементами.
Когда числовые аргументы являются элементами, мы получаем составные
версии исходных атомарных элементов. Например, ниже определен составной Flip, к
которому предъявляется запрос:
val sunnyTodayProbability = Uniform(0, 0.5)
val sunnyToday = Flip(sunnyTodayProbability)
println(Importance.probability(sunnyToday, true))
// печатается число, близкое к 0.2548
Здесь элемент sunnyTodayProbability представляет неизвестную верОЯТНОСТЬ
ясной погоды сегодня; мы полагаем, что равновероятно любое значение от 0 до 0.5.
Тогда sunnyToday paBHO true С ВерОЯТНОСТЬЮ, раВНОЙ Значению Элемента
sunnyTodayProbability. В общем случае составной Flip принимает один аргумент типа
Element [Double], ПреДСТаВЛЯЮЩИЙ ВерОЯТНОСТЬ ТОГО, ЧТО Flip Вернет true.
Элемент Normal предоставляет больше возможностей. В вероятностных
рассуждениях часто предполагают, что дисперсия нормального распределения известна,
а вот насчет среднего полной уверенности нет. Так, можно предположить, что
дисперсия температуры равна 100, а среднее примерно равно 40, но точное его
значение неизвестно. Эту ситуацию можно смоделировать следующим образом:
66

2.5. Построение более сложных моделей с помощью Apply и Chain
val tempMean = Normal(40, 9)
val temperature = Normal(tempMean, 100)
println(Importance.probability(temperature, (d: Double) => d > 50))
// печатается число, близкое к 0.164
С другой стороны, может быть неизвестна дисперсия. Допустим, у нас есть
основания полагать, что она равна 80 или 105. Тогда можно написать такой код:
val tempMean = Normal(40, 9)
val tempVariance = Select (0.5 -> 80.0, 0.5 -> 105.0)
val temperature = Normal(tempMean, tempVariance)
println(Importance.probability(temperature, (d: Double) => d > 50)
// печатается число, близкое к 0.154 9
Дополнительные сведения. В этой главе описана лишь небольшая часть атомарных
и составных элементов, имеющихся в Figaro. Другие примеры можно найти в
документации Scaladoc no Figaro. Scaladoc (www.cra.com/Figaro) - это автоматически
генерируемая HTML-документация по библиотеке Figaro в формате, похожем на Javadoc. Она
также имеется в двоичном дистрибутиве Figaro, выложенном на веб-странице Figaro.
Дистрибутив находится в файле с именем вида figaro_2.11-2.2.2.0-javadoc.jar.
Распаковать архив можно с помощью программы 7-Zip, WinZip или их аналогов.
2.5. Построение более сложных
моделей с помощью Apply и Chain
В Figaro имеются два весьма полезных для построения моделей элементов:
Apply и chain. Apply позволяет выполнять из Figaro произвольный код на Scala,
предоставляя тем самым всю мощь Scala в распоряжение разработчика, chain дает
возможность создавать бесконечно разнообразные зависимости между
элементами. Составные элементы if и Flip, которые мы рассматривали до сих пор, умеют
создавать только зависимости предопределенного вида. A chain позволяет создать
любую нужную вам зависимость.
2.5.1. Элемент Apply
Элемент Apply находится в пакете com. era .figaro. language. Он принимает на входе
произвольный элемент и функцию Scala. Представляемый им процесс применяет
функцию к значению элемента с целью получения нового значения. Например:
val sunnyDaysInMonth = Binomial(30, 0.2)
def getQuality(i: Int): String =
if (i > 10) "хорошее"; else if (i > 5) "среднее"; else "плохое"
val monthQuality = Apply(sunnyDaysInMonth, getQuality)
println(VariableElimination.probability(monthQuality, "хорошее"))
// печатается 0.025616255335326698
Во второй и третьей строке определена функция getQuality. Она принимает
аргумент типа integer, который внутри функции именуется i, и возвращает строку.
67

Глава 2. Краткое руководство по языку Figaro
В четвертой строке определен элемент Apply с именем monthQuaiity. Структура
элемента Apply показана на рис. 2.9. Apply принимает два аргумента. Первый
является Элементом, В ДаННОМ Случае ЭТО Элемент sunnyDaysInMonth ТИПа Element [Int].
Второй - функцией, аргумент которой должен иметь тот же тип, что и тип
значения элемента. В нашем примере функция getQuaiity принимает аргумент типа
integer, так что это условие соблюдается. Функция может возвращать значение
любого типа, в нашем случае она возвращает string.
Элемент, к которому
применяется функция
Apply(sunnyDaysInMonth, getQuaiity)
Функция, применяемая
к значениям элемента
Рис. 2.9. Структура элемента Apply
Элемент Apply определяет случайный процесс следующим образом. Сначала
генерируется значение элемента, переданного в первом аргументе. В нашем примере
это число ясных дней в месяце. Допустим, что получено значение 7. Затем процесс
применяет к этому значению функцию, переданную во втором аргументе. В
нашем случае вызывается функция getQuaiity с аргументом 7, которая возвращает
строку среднее. Эта строка и становится значением элемента Apply. Таким
образом, значения, возвращаемые Apply, имеют тот же тип, что возвращаемое значение
фуНКЦИИ. В Нашем Случае ЭЛемеНТ Apply Принадлежит ТИПу Element [String].
Тех, кто раньше не работал со Scala, я хочу познакомить с анонимными
функциями. Определять отдельную функцию для каждого элемента Apply скучно и
утомительно, особенно если мы собираемся использовать ее только в одном месте, а
сама функция совсем коротенькая. В языке Scala имеется механизм анонимных
функций, которые определяются прямо в месте использования. На рис. 2.10
показана структура анонимной функции, эквивалентной функции getQuaiity. Все
выглядит так же, как для именованной функции. У функции есть аргумент с
именем i. Он имеет тип integer. Символ => означает, что мы определяем анонимную
фуНКЦИЮ. И За НИМ Следует ТеЛО фуНКЦИИ - Такое Же, Как у getQuaiity.
Аргумент Символ определения
функции функции
(i: Int) => if (i > 10) "good"; else if (i > 5) "average"; else "poor"
Тип аргумента Тело функции
Рис. 2.10. Структура анонимной функции
68

2.5. Построение более сложных моделей с помощью Apply и Chain
Ниже показан элемент Apply, эквивалентный предыдущему, но определенный с
помощью анонимной функции:
val monthQuality = Apply(sunnyDaysInMonth,
(i: Int) => if (i > 10) "хорошее"; else if (i > 5) "среднее"; else "плохое")
Теперь можно опросить элемент monthQuality. Обе версии дают одинаковый
ответ:
println(VariableElimination.probability(monthQuality, "хорошее"))
// печатается 0.025616255335326698
Это, конечно, искусственный пример, но есть много практических причин для
применения Apply. Назовем лишь некоторые из них.
• Имеется элемент типа Double, значение которого нужно округлить до
ближайшего целого.
• Имеется элемент, значение которого имеет тип структуры данных, и
требуется как-то агрегировать некоторое свойство этой структуры. Например,
элемент определен над списками, и мы хотим узнать вероятность того, что
количество элементов в списке больше 10.
• Связь между двумя элементами лучше всего представить в виде
физической модели. В таком случае мы можем воспользоваться функцией Scala
для представления физической связи и включить эту модель в Figaro
посредством Apply.
Apply с несколькими аргументами
Элемент Apply принимает также функции Scala с несколькими аргументами, но
не более пяти. Такое применение Apply полезно, когда для воздействия на
некоторый элемент нужно более одного элемента. Приведем пример.
val teamWinsInMonth = Binomial(5, 0.4)
val monthQuality = Apply(sunnyDaysInMonth, teamWinsInMonth,
(days: Int, wins: Int) => {
val x = days * wins
if (x > 20) "хорошее"; else if (x > 10) "среднее"; else "плохое"
})
Здесь Apply передаются в качестве аргументов два элемента: sunnyDaysInMonth и
teamwinsinMonth, оба они имеют тип Element [int ]. Переданная в третьем аргументе
функция принимает два аргумента типа integer, названные days и wins, и создает
локальную переменную х со значением days * wins. Отметим, что поскольку days
и wins - обычные переменные Scala типа integer, то х также обычная переменная,
а не элемент Figaro. На самом деле, все внутри переданной Apply функции -
обычный код на Scala. Элемент Apply принимает эту обычную функцию Scala,
работающую с обычными значениями Scala, и «возводит» ее в ранг функции, работающей
с элементами Figaro.
Теперь ПреДЪЯВИМ Запрос ЭТОЙ ВерСИИ monthQuality!
69

Глава 2. Краткое руководство по языку Figaro
println(VariableElimination.probability(monthQuality, "хорошее"))
// печатается 0.15100056576418375
Вероятность немного подросла. Похоже, софтбольная команда, за которую я
болею, имеет шанс порадовать меня. Важнее, впрочем, тот факт, что несмотря на
простоту примера, без помощи Figaro вычислить эту вероятность было бы
затруднительно.
2.5.2. Элемент Chain
Как явствует из названия, элемент chain служит для сцепления элементов в
модель, где один элемент зависит от другого, который, в свою очередь зависит от
других, и так далее. Он имеет отношение к цепному правилу из теории вероятностей,
с которым мы познакомимся в главе 5. Но чтобы понимать работу chain, знать
цепное правило необязательно.
Элемент chain также находится в пакете com.era.figaro.language. Проще всего
объяснить принцип его работы с помощью картинки. На рис. 2.11 изображены два
элемента; goodMood зависит от monthQuality. Соответствующий случайный процесс
сначала генерирует значение monthQuality, а затем на его основе генерирует
значение goodMood. Это простой пример байесовской сети, о которой речь пойдет в главе
4. Заимствуя терминологию байесовских сетей, элемент monthQuality на рисунке
называется родителем, а элемент goodMood - потомком.
Родитель
Потомок
Рис. 2.11. Модель с двумя переменными,
одна из которых зависит от другой
ПОСКОЛЬКУ goodMood зависит ОТ monthQuality, TO goodMood определен С ПОМОЩЬЮ
chain. Элемент monthQuality уже был определен в предыдущем разделе. А вот как
ВЫГЛЯДИТ Определение goodMood!
val goodMood = Chain(monthQuality, (s: String) =>
if (s == "good") Flip(0.9)
else if (s == "average") Flip(0.6)
else Flip(O.l))
На рис. 2.12 показана структура этого элемента. Как и Apply, элемент chain
принимает два аргумента: элемент и функцию. В данном случае элементом является
родитель, а в роли функции выступает так называемая цепная функция. Разница
между chain и Apply состоит в том, что передаваемая функция в случае Apply
возвращает обычные значения Scala, а в случае chain - элемент. В нашем примере
функция возвращает элемент Flip, а какой именно, зависит от значения month-
70

2.5. Построение более сложных моделей с помощью Apply и Chain
Quality. Таким образом, эта функция принимает аргумент типа string и
возвращает экземпляр Класса Element [Boolean].
Родитель
\
Chain(monthQuality,
(s: String) => if (s == "good") Flip(0.9); else if (s == "average") Flip(0.6); else Flip(O.l))
1 1 '
Цепная функция
Рис. 2.12. Структура элемента chain
Случайный процесс, определенный этим элементом chain, показан на рис. 2.13.
Он состоит из трех шагов. Во-первых, генерируется значение родителя. У нас это
значение среднее элемента monthQuality. Во-вторых, к этому значению
применяется цепная функция, которая возвращает результирующий элемент. В данном
случае из определения цепной функции видно, что это элемент Шр(О.б).
В-третьих, результирующий элемент генерирует значение - в нашем случае % Это
значение и становится значением потомка.
Значение родителя
Результирующий
элемент
Значение цепочки
true
Рис. 2.13. Случайный процесс, определяемый элементом chain.
Сначала генерируется значение родителя. Затем с помощью цепной функции
выбирается результирующий элемент. И наконец, генерируется значение
результирующего элемента
Подведем итог, перечислив типы всех компонентов, участвующих в работе
chain. Элемент chain параметризован двумя типами: типом значения родителя
(обозначим его т) и типом значения потомка (обозначим его и):
• Родитель Имеет ТИП Element [T].
• Значение родителя имеет тип т.
• Цепная функция имеет тип т => Element [и]. Это означает, что функция
получает аргумент типа т и возвращает значение типа Element [и].
• РезуЛЬТИруЮЩИЙ Элемент Имеет ТИП Element [U].
• Значение цепочки имеет тип и.
• ПОТОМОК Имеет ТИП Element [U]. Это И еСТЬ ТИП СаМОГО Элемента Chain.
В нашем примере goodMood имеет тип Element [Boolean], поэтому можно
запросить вероятность того, что он равен true:
println(VariableElimination.probability(goodMood, true))
// печатается 0.3939286578054374
71

Глава 2. Краткое руководство по языку Figaro
Элемент Chain с несколькими аргументами
Рассмотрим чуть более сложную модель, в которой goodMood зависит как от
monthQuality, так И ОТ sunnyToday (СМ. рис. 2.14).
Рис. 2.14. Модель с тремя переменными,
в которой goodMood зависит от двух других переменных
Для этого нам понадобится элемент chain с двумя аргументами. В данном
случае цепная функция принимает два аргумента: quality типа string и sunny типа
Boolean, а ВОЗВращает Элемент ТИПа Element [Boolean]. goodMood, Как И раньше, ИМе-
ет ТИП Element [Boolean]. Вот Как ВЫГЛЯДИТ КОД!
val sunnyToday = Flip(0.2)
val goodMood = Chain(monthQuality, sunnyToday,
(quality: String, sunny: Boolean) =>
if (sunny) {
if (quality == "хорошее") Flip(0.9)
else if (quality == "среднее") Flip(0.7)
else Flip(0.4)
} else {
if (quality == "хорошее") Flip(0.6)
else if (quality == "среднее") Flip(0.3)
else Flip(0.05)
})
println(VariableElimination.probability(goodMood, true))
// печатается 0.2896316752495942
Примечание. В отличие от Apply, у элемента Chain может быть только один или два
аргумента. Если необходимо больше, то можно скомбинировать chain с Apply. Сначала
Apply используется для объединения переданных в аргументах элементов в один
элемент, значением которого является кортеж, содержащий значения аргументов. Затем
этот один элемент передается chain. После этого цепочка получает доступ ко всей
необходимой информации через значение этого элемента.
Реализация тар и flatMap с применением Apply и Chain
Эта врезка для тех, кто знаком со Scala. Элементы Figaro в каком-то смысле
напоминают коллекции Scala, например List. Если List содержит список значений,
то элемент - случайное значение. И точно так же, как функцию можно применить к
каждому значению в списке для получения нового списка, так можно применить ее и
к случайному значению в элементе для получения нового элемента. Но именно это и
monthQuality
sunnyToday
goodMood
72

2.6. Задание фактов с помощью условий и ограничений
III!
ш
делает Apply! Для списков применение функции к каждому значению осуществляет
метод шар. То есть с помощью Apply мы просто определили тар для элементов.
Поэтому вместо Apply (Flip {0 ,2) , (b: Boolean) => lb) можно написать
Flip{0.2),map{!_).
Аналогично мы можем применить к каждому значению в списке функцию, которая
возвращает список, а затем объединить все получившиеся списки в один с помощью
метода flatMap. Точно так же Chain применяет функцию к случайному значению,
содержащемуся в элементе, для получения другого элемента, а затем получает
от этого элемента значение. Поэтому с помощью Chain определяется flatMap для
элементов. Таким образом, можно написать Uniform(0, 0.5) -flatMap(Flip (_) )
вместо Chain (Uniform (0, 0-5), (d: Double) => Flip (d) ). (Попутно заметьте,
что мы определяли составной Flip посредством Chain. Многие составные элементы
в Figaro можно определить с помощью Chain.)
У Scala есть одна замечательная особенность: любой тип, обладающий методами
тар и flatMap можно использовать в операторе генерации списков for. А значит, этот
оператор применим и к элементам. Можно написать такое предложение:
for { winProb <- Uniform{0, 0.5); win <- Flip(winProb) } yield !win
На этом заканчивается краткое пособие по конструированию сложных
моделей из простых элементов. Но прежде чем завершить эту главу, я хочу описать
несколько способов задания фактов и наложения ограничений на модели.
2.6. Задание фактов с помощью
условий и ограничений
Мы уже достаточно подробно познакомились с процедурой построения моделей.
Именно этим вы в основном и будете заниматься при работе с Figaro. Но не стоит
забывать и о задании фактов. Figaro предлагает три механизма для этой цели:
наблюдения, условия и ограничения.
2.6.1. Наблюдения
Мы уже видели один способ задания фактов - с помощью наблюдений. В примере
программы «Hello World» это делалось так:
greetingToday.observe("Здравствуй, мир!")
Вообще, метод элемента observe принимает в качестве аргумента возможное
значение элемента и говорит, что элемент должен действовать на основе этого
значения. Запрещаются случайные вычисления, в которых предполагается другое
значение. Это наблюдение оказывает влияние на вероятности связанных
элементов. Например, в программе «Hello World» мы видели, что после задания такого
наблюдения переменная sunnyToday с большей вероятностью будет равна true,
потому что, согласно модели, в ясный день приветствие «Здравствуй, мир!»
более вероятно, чем в пасмурный. Мы видели также другой метод, относящийся к
наблюдениям:

Глава 2. Краткое руководство по языку Figaro
greetingToday.unobserve()
Он удаляет наблюдение, заданное для элемента greetingToday (если таковое
было), ПОЭТОМУ ДОПуСКаЮТСЯ Любые Случайные ВЫЧИСЛеНИЯ. В результате
greetingToday не оказывает влияние на вероятности других элементов.
2.6.2. Условия
Метод observe задает конкретное значение элемента. А что, если нам известно что-
то о значении элемента, но чему оно точно равно мы не знаем? Figaro позволяет
задавать в качестве факта произвольный предикат, который называется условием.
Значение допустимо, только если условие принимает значение true. Например:
val sunnyDaysInMonth = 31110111131(30, 0.2)
println(VariableElimination.probability(sunnyDaysInMonth, 5) <3—О
sunnyDaysInMonth.setCondition((i: Int) => i > 8) <3—©
println(VariableElimination.probability(sunnyDaysInMonth, 5) <]—©
О - Печатается 0.172279182850003
© — Факт означает, что ясных дней больше 8
© — Печатается 0, потому что, согласно условию, 5 ясных дней быть не может
Использование наблюдаемых фактов для вывода вероятностей других
переменных - самое главное в вероятностных рассуждениях. Например, из наблюдения за
количеством ясных дней в месяце мы можем заключить, насколько вероятно, что
у человека будет хорошее настроение. Воспользуемся примером из раздела 2.5:
val sunnyDaysInMonth = Binomial(30, 0.2)
val monthQuality = Apply(sunnyDaysInMonth,
(i: Int) => if (i > 10) "хорошее"; else if (i > 5) "среднее";
else "плохое")
val goodMood = Chain(monthQuality, (s: String) =>
if (s == "good") Flip(0.9)
else if (s == "average") Flip(0.6)
else Flip(O.l))
println(VariableElimination.probability(goodMood, true))
// печатается 0.3939286578054374 with no evidence
Теперь Зададим уСЛОВИе, КОТОрое ГОВОРИТ, ЧТО Значение sunnyDaysInMonth
ДОЛЖНО быть больше 8, И ПОСМОТрИМ, Как ЭТО ВЛИЯеТ На goodMood!
sunnyDaysInMonth.setCondition((i: Int) => i > 8)
println(VariableElimination.probability(goodMood, true))
// печатается 0.6597344078195809
Вероятность хорошего настроения резко возросла, потому что мы запретили
рассматривать случаи, когда в месяце только 8 или меньше ясных дней.
Figaro позволяет задать несколько условий, которым должен удовлетворять
элемент. Для этого предназначен метод addcondition, который добавляет условие
к уже существующим. В результате значение элемента должно удовлетворять как
прежним условиям, так и новому.
sunnyDaysInMonth.addCondition((i: Int) => i % 3 == 2)
74

2.6. Задание фактов с помощью условий и ограничений
III!
ша
ЗдеСЬ МЫ ГОВОРИМ, ЧТО Значение sunnyDaysInMonth ДОЛЖНО быть Не ТОЛЬКО боЛЬ-
ше 8, но и давать при делении на 3 остаток 2. Тем самым значения 9 и 10
исключаются, и наименьшее возможное значение равно 11. Понятно, что вероятность
хорошего настроения при таких условиях будет еще больше:
println(VariableElimination.probability(goodMood, true))
// печатается 0.9
Метод removeconditions удаляет все условия, заданные для элемента:
sunnyDaysInMonth.removeConditions()
println(VariableElimination.probability(goodMood, true))
// снова печатается 0.3939286578054374 again
Кстати, наблюдение - это частный случай условия, в котором требуется, чтобы
элемент принимал в точности заданное значение. Резюмируем.
• Метод элемента setcondition принимает в качестве аргумента предикат,
т. е. функцию, которая принимает аргумент того же типа, что значение
элемента, и возвращает значение типа Boolean. После выполнения этого
метода в элементе остается только заданное им условие, все ранее
существовавшие условия и наблюдения удаляются.
• Метод addcondition тоже принимает предикат такого же типа, как описано
выше, и добавляет его к существующим условиям и наблюдениям.
• Метод removeconditions удаляет все условия и наблюдения, ранее
заданные для элемента.
2.6.3. Ограничения
Ограничения - это более общий способ что-то сказать об элементе. Ограничения
служат двум целям: (1) для задания «неточного» факта; (2) для организации
дополнительных связей между элементами модели.
Ограничения как неточные факты
Предположим, что вам известен какой-то факт об элементе, но вы в нем не
вполне уверены. Например, вам кажется, что я сегодня угрюм, но определенно судить о
моем настроении во внешнему виду вы не решаетесь. Поэтому вы не задаете точный
факт - goodMood равно false, а сообщаете, что goodMood скорее равно false, чем true.
Для этого можно применить ограничение - функцию, которая принимает
значение элемента и возвращает Double. Хотя Figaro этого не требует, ограничения
работают лучше всего, когда значение функции - число от 0 до 1 (включительно).
Например, чтобы выразить тот факт, что мое настроение ближе к угрюмому, но
вы в этом не вполне уверены, можно было бы добавить к goodMood ограничение,
КОТОрое Порождает Значение 0.5, еСЛИ goodMood раВНО true, И 1.0 - еСЛИ goodMood
равно false!
goodMood.addConstraint((b: Boolean) => if (b) 0.5; else 1.0)
Это ограничение интерпретируется следующим образом: при прочих равных
условиях вероятность, что переменная goodMood равно true, вдвое меньше, чем веро-

Глава 2. Краткое руководство по языку Figaro
ятность, что она равна false, потому что 0.5 вдвое больше 1.0. Точная математика,
стоящая за этим утверждением, обсуждается в главе 4, а пока просто отметим, что
вероятность значения элемента умножается на результат вычисления ограничения
для этого значения. Поэтому в данном примере вероятность значения true
умножается на 0.5, а вероятность значения false - на 1.0. После такой операции сумма
вероятностей может оказаться отличной от 1, поэтому они нормируются, так чтобы
в сумме получилась 1. Предположим, что без этого факта я полагаю, что значения
true и false переменной goodMood равновероятны, т. е. обе вероятности равны 0.5.
Увидев факт, я должен буду сначала умножить обе вероятности на результат
вычисления ограничения, т. е. получу, что true имеет вероятность 0.25, a false - 0.5. Сумма
этих чисел не равна 1, поэтому я нормирую их и получаю окончательный ответ:
вероятность, ЧТО goodMood paBHO true Составляет 1/3, а ЧТО goodMood paBHO false - 2/3.
Разница между условием и ограничением состоит в том, что в случае
условия некоторые состояния объявляются невозможными (т. е. имеющими
вероятность 0), а ограничения лишь изменяют вероятности различных состояний,
но не запрещают их, если только результат вычисления ограничения не равен 0.
Иногда условия называют жесткими условиями, потому что они устанавливают
непреложное правило касательно возможных состояний, а ограничения -
мягкими ограничениями.
Вернемся к нашей программе. Если после добавления этого ограничения
опросить goodMood, то мы увидим, что вероятность уменьшилась, но не стала равна 0,
как было бы в случае сообщения о моей угрюмости, как о точном факте:
println(VariableElimination.probability(goodMood, true))
// печатается 0.24527469450215497
С ограничениями связан дополнительный набор методов - как для условий.
• Метод элемента setconstraint принимает в качестве аргумента предикат,
принимающий значение элемента и возвращающий Double. Метод
setconstraint делает этот предикат единственным ограничением для элемента.
• Метод addconstraint тоже принимает аналогичный предикат и добавляет
его к существующим ограничениям.
• Метод removeconstraints удаляет все ограничения, ранее заданные для элемента.
Условия и ограничения отделены друг от друга, т. е. установка условия или
удаление всех условий никак не затрагивает существующие ограничения. И наоборот.
Ограничения для связывания элементов
Это еще одно полезное применение ограничений. Допустим, у нас есть
основания полагать, что значения двух элементов взаимосвязаны, но эта связь не
улавливается определениями элементов. Например, предположим, что ваша любимая
софтбольная команда выигрывает в 40 % матчей, поэтому каждый матч определен
элементом Flip (0.4). Предположим также, что вы полагаете, что в игре команды
случаются полосы везения и неудач, т. е. последовательные матчи с высокой
вероятностью закончатся одинаково. Эту гипотезу можно выразить, добавив
ограничение на пары последовательных матчей, которое говорит, что вероятность одинако-
76

2.6. Задание фактов с помощью условий и ограничений
шгш
вых результатов в них выше, чем различных. Ниже показан соответствующий код.
Я написал его для трех матчей, но он легко обобщается на любое число с помощью
массивов и оператора генерации for.
Сначала определим результаты трех матчей:
val resultl = Flip(0.4)
val result2 = Flip(0.4)
val result3 = Flip(0.4)
Теперь, чтобы показать, что происходит, создадим элемент aiiwins,
принимающий значение true, когда все результаты равны true:
val allWins = Apply(resultl, result2, result3,
(wl: Boolean, w2: Boolean, w3: Boolean) => wl && w2 && w3)
Спросим, какова вероятность выигрыша всех матчей до того, как добавлены
ограничения:
printIn(VariableElimination.probability(allWins, true))
// печатается 0.064000000000000002
Теперь добавим ограничения. Определим функцию makestreaky, которая
принимает два результата и добавляет для них ограничение «полосатости жизни»:
def makeStreaky(rl: Element[Boolean], r2: Element[Boolean]) {
val pair = Apply(rl, r2, (bl: Boolean, b2: Boolean) => (bl, b2))
pair.setConstraint((bb: (Boolean, Boolean)) =>
if (bb._l == bb._2) 1.0; else 0.5
)}
Эта функция принимает в качестве аргументов два булевых элемента,
представляющих результаты двух матчей. Поскольку ограничение можно применить только
к одному элементу, а мы хотим создать связь между двумя элементами, то сначала
упакуем ДВа Элемента В ОДИН. ЭТО Делает КОНСТРУКЦИЯ Apply (rl, r2, (Ы: Boolean,
Ь2: Boolean) => (bi, Ь2)). Теперь у нас есть один элемент, значением которого
является пара результатов двух матчей. Наложим на эту пару ограничение в виде
функции, которая принимает пару ьь значений типа Boolean и возвращает 1.0, если
ьь._1 == ьь._2 (первый и второй элементы пары равны), и 0.5 в противном случае.
Это ограничение означает, что при прочих равных условиях вероятность
совпадения двух результатов вдвое больше, чем вероятность их различия.
Теперь можно наложить это ограничение на каждую пару соседних результатов
и спросить, с какой вероятностью все матчи будут выиграны:
makeStreaky(resultl, result2)
makeStreaky(result2, result3)
printIn(VariableElimination.probability(allWins, true))
// печатается 0.11034482758620691
Как видим, при наличии ограничения вероятность резко возросла.
Примечание. Читатели, знакомые с графическими вероятностными моделями,
заметят, что продемонстрированное в этом разделе использование ограничений позволяет
Figaro представить неориентированные модели, например марковские сети.

Глава 2. Краткое руководство по языку Figaro
Наша краткая экскурсия по Figaro подошла к концу. В следующей главе мы
рассмотрим законченный пример использования Figaro в приложении.
2.7. Резюме
• В Figaro используется такая же общая структура, как в других системах
вероятностных рассуждений: модели, факты, запросы и алгоритмы вывода,
дающие ответы.
Модель в Figaro состоит из множества элементов.
Элементы Figaro - это структуры данных Scala, представляющие
случайные процессы, которые генерируют экземпляры типа значения.
Для построения модели Figaro мы начинаем с атомарных элементов и
объединяем их, используя составные элементы.
Элемент Apply позволяет включить в модель Figaro произвольную
функцию, написанную на Scala.
Элемент chain позволяет создавать интересные и сложные зависимости
между элементами.
Условия и ограничения предоставляют средства для задания фактов и
дополнительных связей между элементами.
2.8. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Обобщите программу «Hello World», добавив переменную,
показывающую, с какой ноги вы встали (правой или левой). Встав не с той ноги, вы
всегда произносите приветствие «О нет, только не это», в противном случае
логика остается прежней.
2. В исходной версии программы «Hello World» задайте наблюдение, что
сегодня было произнесено приветствие «О нет, только не это», и спросите,
какая сегодня погода. Теперь добавьте то же наблюдение в
модифицированную программу из упражнения 1. Как изменился ответ? Можете ли вы
объяснить результат на интуитивном уровне?
3. В Figaro код выражение х ===== z означает то же самое, что
Apply(x, z, (bl: Boolean, Ь2: Boolean) => bl === Ь2
Другими словами, оно порождает элемент, принимающий значение true,
если значения обоих его аргументов равны. Не прибегая к Figaro,
попробуйте угадать, что порождают следующие две программы:
a. val х = Flip(0.4)
val у = Flip(0.4)
val z = x
78

2.8. Упражнения
val w = х === z
println(VariableElimination.probability(w, true))
b.val x = Flip(0.4)
val у = Flip(0.4)
val z = у
val w = x === z
println(VariableElimination.probability(w, true))
Проверьте свой ответ, выполнив программы.
4. Следующие упражнения убедят вас в полезности элемента FromRange,
который принимает два целых числа т и п и порождает случайное целое число
от т до п - 1. Например, FromRange (о, 3) порождает числа 0, 1, 2 с равной
вероятностью. Напишите программу Figaro, которая вычисляет
вероятность выпадения 11 при бросании двух правильных шестигранных костей.
5. Напишите программу Figaro, которая вычисляет вероятность того, что на
первой кости выпало 6, если бросаются две правильные шестигранные
кости и общее число выпавших очков больше 8.
6. В игре «Монополия» дублем называется выпадение одинаковых чисел на
двух шестигранных костях. Три раза подряд выкинув дубль, игрок
отправляется в тюрьму. Напишите программу Figaro, которая вычисляет
вероятность такого исхода.
7. Представьте игру, в которой имеется волчок и пять костей с разным
числом граней. Волчок может с равной вероятностью остановиться в одном из
пяти положений: 4, 6, 8, 12, 20. Сначала игрок вращает волчок, а затем
бросает правильную кость с выпавшим числом граней. Напишите программу
Figaro, представляющую эту игру.
a. Вычислите вероятность бросания 12-гранной кости.
b. Вычислите вероятность выпадения 7 на кости.
c. Вычислите вероятность, что вы бросали 12-гранную кость при
условии, что выпало 7.
d. Вычислите вероятность, что выпадет 7 при условии, что вы бросали
12-гранную кость.
8. Теперь модифицируем игру из упражнения 6, считая, что волчок склонен
залипать и показывать одно и то же число при двух последовательных
вращениях. Применяя такую же логику, как в функции makestreaky, напишите
ограничение, согласно которому результаты двух последовательных
вращений с большей вероятностью окажутся одинаковыми, чем различными.
Допустим, что вы играете два раза подряд.
a. Вычислите вероятность, что во второй раз выпадет 7.
b. Вычислите вероятность, что во второй раз выпадет 7 при условии, что
в первый раз выпало 7.
79

ГЛАВА 3.
Создание приложения
вероятностного
программирования
В этой главе.
■ Общая архитектура приложений вероятностного
программирования.
■ Проектирование реалистичных моделей с
помощью одних лишь простых средств языка.
■ Обучение моделей на данных и использование
результатов для рассуждения о будущих примерах.
На данный момент вы имеете какое-никакое представление о многих возможностях
Figaro. Что с этим можно сделать? Как написать на этой основе полезную
программу? В этой главе вы увидите, как с помощью Figaro построить реальное
приложение.
Мы спроектируем фильтр спама, основанный на вероятностном
программировании: модель, компонент, который оценивает входящие сообщения и
классифицирует их как нормальные или спамные, и компонент, который обучает модель
фильтрации спама на наборе почтовых сообщений. По ходу дела мы обсудим
архитектуру, которая часто применяется в приложениях вероятностного
программирования.
3.1. Общая картина
Мы собираемся создать фильтр спама. Как он встраивается в объемлющее
приложение электронной почты? На рис. 3.1 показано, как все работает. Допустим, что у
нас имеется почтовый сервер. Одна из его задач - получать входящую почту и рас-

3.1. Общая картина
сылать ее пользователям. Когда поступает сообщение, сервер передает его
оценивающему компоненту фильтра спама. Этот компонент с помощью вероятностных
рассуждений вычисляет вероятность того, что сообщение спамное, и передает ее
фильтру, который на основе полученной вероятности и заданной политики
решает, пропустить ли сообщение.
Сообщение
поступает
на сервер
Входящее
сообщение
Сервер передает
сообщение
аналитическому
компоненту
фильтра спама,
перед тем как
отправить его
пользователю
Почтовый сервер
с
Политика
•с
Фильтр
Аналитический
компонент фильтра
спама
Модель почтового
сообщения
С
Алгоритм вывода
J
■d
*4 Вероятность спама
3. Аналитический компонент использует
вероятностное рассуждение, применяя
алгоритм вывода к модели почтового
сообщения и к входящему сообщению
Фильтр оценивает
вероятность спама с
помощью политики.
Если вероятность
не слишком высока,
то сообщение
переправляется
пользователю
^

Отфильтрованное
сообщение
Аналитический
компонент
возвращает
выведенную
вероятность того,
что сообщение
является спамом
Рис. 3.1. Как фильтр спама встраивается в почтовый сервер. Эта процедура
выполняется всякий раз, как поступает новое почтовое сообщение
Напомним (см. главу 1), что система вероятностных рассуждений применяет
алгоритм вывода к модели, чтобы получить ответ на запрос при заданных фактах.
В данном случае система применяет модель почтового сообщения, описывающую,
что такое нормальные и спамные сообщения. В запросе спрашивается, является ли
сообщение спамом, а ответ содержит вероятность спама. Аналитическому
компоненту для работы нужно откуда-то получить модель сообщения. Откуда она
берется? Строится на основе обучающих данных компонентом обучения.
В системах вероятностных рассуждений обучением называется процесс
построения модели по обучающим данным. В главе 1 мы вкратце описали обучение, как
нечто такое, что умеет делать система вероятностных рассуждений. Например,
система, рассуждающая о футболе, могла бы использовать данные обо всех
угловых в сезоне, чтобы обучить модель углового удара, которую затем можно будет
применять для предсказания результата следующего углового. В реальных прило-
81

Глава 3. Создание приложения вероятностного программирования
жениях обучение действительно используется для построения модели. Другой
метод - ручное создание модели с использованием знаний о моделируемой системе.
Набор данных
включает много
примеров почтовых
сообщений
Компонент обучения пользуется
априорной моделью сообщений
и набором данных для
построения модели, с которой
работает аналитический
компонент
1 'X
■N.
Набор
данных
/
Компонент обучения
фильтра спама
( Априорная модель |
1 сообщений \
Алгоритм обучения
1^
Модель

сообщений
Априорная модель
сообщений описывает
все, что известно о
почтовых сообщениях,
до обучения на данных
Рис. 3.2. Как компонент обучения порождает модель почтового сообщения.
Обучение может занимать много времени и производится в пакетном режиме
На рис. 3.2 показан процесс построения модели почтового сообщения
компонентом обучения. Он запускается в пакетном режиме, а не для каждого
поступающего сообщения, так что может работать настолько долго, насколько необходимо
для построения наилучшей возможной модели. Компонент обучения должен
закончить работу, чтобы аналитический компонент мог воспользоваться
построенной им моделью. После этого компонент обучения не нужен до тех пор, пока не
понадобится обновить модель.
Компонент обучения использует обучающие данные, представляющие собой
набор почтовых сообщений. В него входят как нормальные, так и спамные
сообщения, но не требуется, чтобы все они обязательно несли метку типа. Нельзя сказать,
что в начале работы компонент обучения не располагает вообще никакими
знаниями: в его распоряжении имеется алгоритм обучения, который принимает
априорную модель почтовых сообщений и преобразует ее в модель, с которой работает
аналитический компонент. Возможно, вам показалось, что имеет место порочный
круг: если задача компонента обучения - создать модель почтового сообщения, то
откуда же берется априорная модель сообщения?
В данном случае априорная модель содержит минимальные структурные
предположения, необходимые для построения фильтра спама. В частности, модель
говорит, что спамность сообщения зависит от наличия или отсутствия некоторых
слов, но ничего не говорит ни о том, какие это слова, ни о вероятности того, что
сообщение окажется спамом. Эта информация появляется в результате обучения
82

3.2. Выполнение кода
на данных. Априорная модель также утверждает, что количество необычных слов
в сообщении имеет некоторое отношение к его спамности, но не говорит, что это
за отношение. Его характер также определяется из данных.
Ниже я расскажу подробнее о том, что именно выясняет компонент обучения,
но вкратце речь идет о следующем:
• Какие слова полезны для классификации сообщения как нормального или
спамного. Такие слова называются признаками.
• Множество параметров, представляющих следующие вероятности: что
данное почтовое сообщение окажется спамом еще до его рассмотрения; что в
сообщении встречается конкретное слово при условии, что оно нормальное
или спамное: что сообщение содержит много необычных слов, опять-таки
при условии, что оно нормальное или спамное.
Множеств слов извлекается непосредственно из набора данных при его первом
чтении. Смысл же компонента обучения - вычисление параметров на основе
обучающих данных. Это те самые параметры, которые затем используются
аналитическим компонентом.
Построению эффективных фильтров спама посвящено много исследований.
В этой главе описано сравнительно простое решение, достаточное для
демонстрации основных принципов, но для сборки практически полезного приложения
можно сделать гораздо больше.
3.2. Выполнение кода
В этой главе будет приведен весь код той части приложения, которая имеет
отношение к вероятностному программированию. Но в приложении также много
кода, связанного с файловым вводом-выводом, в частности с чтением почтовых
сообщений из файла, записью обученной модели в файл и последующим
считыванием ее. Этот код я не привожу, потому что иначе глава получилась бы слишком
длинной. Чтобы выполнить программу, вы можете скачать файл http://manning.
com/pfeffer/PPP_SourceCode.zip. содержащий полный код.
Компоненту обучения нужны данные. Данные нужны также для тестирования
и оценки системы на этапе разработки. Существует несколько реальных наборов
данных, относящихся к спаму, но приводить их адреса в Интернете
бессмысленно, т. к. они могут измениться. Поэтому, чтобы у вас гарантированно был набор, с
которым можно работать, я подготовил свой собственный. Он состоит не из
реальных почтовых сообщений, каждое «сообщение» представлено в виде списка слов,
не образующих предложений; заголовки также исключены. Однако
распределение слов между нормальными и спамными сообщениями такое же, как в
действительности, так что с этой точки зрения набор можно считать реалистичным. Для
объяснения встречающихся в этой главе концепций такого набора достаточно.
В реальном приложении лучше бы работать с настоящими сообщениями.
В каталоге Chapter3Data этот набор занимает два подкаталога: Training,
содержащий 100 примеров сообщений (60 нормальных и 40 спамных), используемых
83

Глава 3. Создание приложения вероятностного программирования
для обучения, и Test, содержащий 100 сообщений для тестирования результатов
обучения. Кроме того, имеется файл Labels.txt, содержащий метки всех
сообщений (1 - спам, 0 - нормальное). В самой модели метки не используются - это
было бы жульничеством. Но при ее оценке метки нужны, чтобы проверить
правильность ответа, формируемого аналитическим компонентом. В принципе,
необязательно помечать все обучающие данные. Алгоритм обучения может работать
даже тогда, когда помечена только часть сообщений, и приведенный в этой главе
код в действительности работает только с подмножеством меток. Но для простоты
включены метки для всех примеров из набора данных.
При разработке приложения, обучающего модель, необходим какой-то способ
оценки качества модели. В репозитории кода имеется программа для решения
этой задачи. Но поскольку она не входит в состав развернутого приложения, то и
описывать ее в книге я не стану. Программа прямолинейная, вы легко разберетесь
в ее коде в файле Evaluator.scala, руководствуясь пояснениями в тексте.
Для исполнения приведенного в этой главе кода проще всего воспользоваться
средством сборки Scala-программ sbt. Сначала нужно прогнать компонент
обучения на каких-то обучающих данных. Этот компонент принимает три аргумента:
путь к каталогу, содержащему обучающие примеры, путь к файлу меток и путь к
файлу, в котором сохраняются результаты обучения. Например:
sbt "runMain chap03.LearningComponent Chapter3Data/Training Chapter3Data/
Labels.txt Chapter3Data/LearnedModel.txt"
В результате выводятся следующие сообщения (показаны только самые
интересные строки, а не полная - довольно длинная - распечатка):
Number of elements: 31005
Training time: 4876.629
Здесь мы видим, что было создано 31 005 элементов Figaro, а обучение заняло
4876 секунд.
Самый важный результат работы компоненты обучения состоит в том, что
теперь у нас в каталоге проекта есть файл LearnedModel.txt. Это текстовый файл,
содержащий информацию, необходимую аналитическому компоненту, и, в
частности, список всех релевантных слов, используемых для классификации, и
значения параметров модели. Формат файла ориентирован специально на приложение
для фильтрации спама, и аналитический компонент умеет его читать.
Примечание. Компонент обучения потребляет очень много памяти. Возможно,
придется явно увеличить размер кучи для виртуальной машины. Обычно для этого задается
флаг вида -Xmx8096m при запуске Java-программы. При работе с Eclipse этот флаг
указывается в файле eclipse.ini в установочном каталоге Eclipse. В данном случае мы просим
Java выделить для кучи 8096 МБ (8 ГБ).
Имея модель, мы можем использовать аналитический компонент для
классификации почтового сообщения. Аналитический компонент принимает в качестве
84

3.2. Выполнение кода
аргументов путь к классифицируемому сообщению и путь к обученной модели.
Например:
sbt "runMain chap03.ReasoningComponent Chapter3Data/Test/TestEmail_3.txt
Chapter3Data/LearnedModel.txt"
Эта команда выводит вероятность того, что третье сообщение - спам.
Наконец, можно проверить результаты обучения на тестовом наборе данных.
Для этого вызывается программа оценки, которая принимает четыре аргумента.
Первые три - путь к каталогу, содержащему тестовые сообщения, путь к файлу
меток и путь к файлу обученной модели. Последний аргумент соответствует
политике, показанной на рис. 3.1, и равен пороговой вероятности классификации
сообщения как спама. Если аналитический компонент сочтет, что сообщение является
спамом с вероятностью выше пороговой, то классифицирует его как спам, иначе
как нормальное сообщение. Пороговая вероятность определяет чувствительность
фильтра. Если задать ее равной 99 %, то фильтр будет задерживать только
сообщения, которые почти наверняка являются спамом, однако при этом может
просочиться много спамных сообщений. Если же установить порог 50 %, то может быть
заблокировано много нормальных сообщений. Например, команда
sbt "runMain chap03.Evaluator Chapter3Data/Test Chapter3Data/Labels.txt
Chapter3Data/LearnedModel.txt 0.5"
выводит такую информацию:
True positives: 44
False negatives: 2
False positives: 0
True negatives: 54
Threshold: 0.5
Accuracy: 0.98
Precision: 1.0
Recall: 0.9565217391304348
Эти строки описывают общее качество фильтра спама. Строка «true positives»
{истинно положительных) показывает, сколько раз спам был классифицирован как
спам, а строка «false positives» (ложноположительных) - сколько раз нормальные
сообщения были ошибочно классифицированы как спам. Строка «false negatives»
(ложноотрицателъных) прямо противоположна: сколько раз спамные
сообщения были классифицированы как нормальные. Наконец, строка «true negatives»
(истинно отрицательных) показывает, сколько раз нормальные сообщения были
правильно классифицированы как нормальные. В следующей строке показана
использованная пороговая вероятность. Последние три строки содержат различные
показатели качества. Вопрос об измерении качества классификаторов интересен,
но к вероятностному программированию как таковому имеет косвенное
отношение, поэтому детали вынесены на врезку «Измерение качества классификаторов».
Код из этой главы работает достаточно быстро на обучающих наборах,
содержащих до 200 сообщений. Figaro позволяет обучать модели и на гораздо более
объемных наборах с помощью более изощренных методов, обсуждаемых в главе 12.
85

Глава 3. Создание приложения вероятностного программирования
Измерение качества классификаторов
Количественная оценка качества классификаторов - непростая задача. Самый
очевидный показатель - верность (accuracy), т. е. доля правильных классификаций. Но
он может вводить в заблуждение, если в большинстве случаев классификация
отрицательна, а нас интересуют только положительные результаты. Допустим, к примеру,
что в 99 % случаев классификатор дает отрицательный результат. Тогда для получения
верности 99 % достаточно было бы классифицировать все вообще примеры как
отрицательные, но такой классификатор никуда не годится, потому что не находит
интересующие нас случаи. Поэтому часто используют показатели точности (precision) и
полноты (recall). Точность измеряет, насколько хорошо классификатор избегает лож-
ноположительных результатов, а полнота - насколько хорошо он распознает
положительные примеры (т. е. избегает лож неотрицательных результатов).
Обозначим ТР - количество истинно положительных результатов, FP - количество
ложноположительных, FN - количество ложноотрицательных, a TN - количество
истинно отрицательных. Тогда
Верность
Точность =
Полнота =
TP + TN
TP + FP + FN + TN
ТР
ГР + FP
ТР
TP + FN
Разобравшись, как обучить и выполнить фильтр спама, посмотрим, как он
работает. Начнем с общей архитектуры приложения, а затем перейдем к деталям
модели и кода.
3.3. Архитектура приложения фильтра
спама
Напомним (см. раздел 3.1), что фильтр спама состоит из двух компонентов.
Оперативный аналитический компонент выполняет вероятностное рассуждение -
классификацию почтового сообщения - и решает, пропустить его или нет. Пакетный
компонент обучает модель почтового сообщения на обучающем наборе данных. В
следующих разделах описана архитектура аналитического компонента, а затем и
компонента обучения. Как мы увидим, между ними много общего.
3.3.1. Архитектура аналитического компонента
Обдумывая архитектуру компонента, нужно, прежде всего, определить входные и
выходные данные и связи между ними. Задача нашего приложения - получить на
входе почтовое сообщение и определить, является оно нормальным или спамным.
86

3.3. Архитектура приложения фильтра спама
Поскольку речь идет о вероятностном программировании, приложение выдает не
просто булев признак: спам-неспам, а вероятность, с которой сообщение, на его
взгляд, является спамом. Кроме того, для простоты я буду предполагать, что
входное сообщение поступает в виде текстового файла.
Итак, для аналитического компонента нашего фильтра спама определены:
• вход - текстовый файл, представляющий почтовое сообщение;
• выход - число типа Double, равное вероятности того, что сообщение
является спамом.
Теперь можно шаг за шагом разрабатывать архитектуру фильтра.
Шаг 1: определение верхнеуровневой архитектуры как системы
вероятностных рассуждений
Для начала можно вернуться к базовой архитектуре системы вероятностных
рассуждений, которые была описана в главе 1, и на ее основе нарисовать первый
вариант архитектуры приложения фильтра спама (рис. 3.3). Аналитический
компонент фильтра спама должен определить, является сообщение спамным или
нормальным. Факт - это текст сообщения, запрос - является ли сообщение
спамом, а ответ - вероятность того, что сообщение является спамом.
Факт
• Текст сообщения
Запрос
• Является ли
сообщение спамом?
Аналитический
компонент фильтра
спама
г Модель почтового ^
^ сообщения j
j
Г Л
Алгоритм
вывода
V. )
у
*-
г
Ответ
• Вероятность
спама
^— Модель нормальных и
у/ спамных сообщений
Алгоритм вывода
вероятности того,что
сообщение является
спамом, по фактам,
касамщптии сииищсппи
Рис. 3.3. Первый вариант архитектуры аналитического компонента.
В фильтре спама используется алгоритм вывода, который получает
на входе модель почтового сообщения и вычисляет вероятность того,
что сообщение является спамом при заданном тексте сообщения
Для получения ответа в аналитическом компоненте используется
вероятностная модель почтового сообщения и алгоритм вывода. В модели инкапсулированы
общие знания о почтовых сообщениях, в том числе свойства самого сообщения и
сведения о том, как анализировать его на предмет спамности. Алгоритм вывода
пользуется этой моделью, чтобы ответить на вопрос, является ли сообщение
спамом при условии имеющихся фактов.
Шаг 2: уточнение архитектуры приложения фильтра спама
Вы хотим представить свою вероятностную модель с помощью вероятностной
программы. В Figaro вероятностная программа состоит из элементов. Напомним,
87

Глава 3. Создание приложения вероятностного программирования
что в Figaro факты применяются к отдельным элементам в виде условий или
ограничений. Поэтому необходимо как-то превратить текст сообщения в факт,
который можно применить к элементам модели. В машинном обучении компонент,
который преобразует исходные данные в факты об элементах модели, обычно
называют выделителем признаков. А те аспекты данных, которые применяются в
модели в качестве фактов, называются признаками. Как показано на рис. 3.4,
выделитель признаков получает на входе текст сообщения и преобразует его в набор
признаков сообщения, который становится фактом для алгоритма вывода.
^
Текст

сообщения
Аналитический компонент фильтра
Г >
Выделитель
признаков
L J
'
спама
Модель почтового
сообщения
г
Факт
- Признаки сообщения
V J
1
'
Г
Алгоритм
вывода
1 )
<
'
Ответ
• Вероятность
спама
Рис. 3.4. Второй вариант архитектуры аналитического компонента
фильтра спама. Добавлен выделитель признаков и удален запрос,
потому что он всегда один и тот же
Кроме того, это конкретное приложение всегда отвечает на один и тот же запрос:
является ли сообщение спамом? Делать запрос входными данными приложения
нет необходимости, поэтому мы исключили его из архитектуры.
Шаг 3: детальная спецификация архитектуры
Пора присмотреться к модели поближе. На рис. 3.5 показана уточненная
модель, в которой выделено три части: процесс, содержащий структурные знания,
запрограммированные автором модели; параметры, полученные в результате
обучения на данных, и дополнительные знания, которые напрямую не связаны с
элементами, но используются в рассуждениях.
Для создания модели нужен навык, и в этой книге мы встретим много примеров,
но, вообще говоря, любая вероятностная модель содержит одни и те же составные
части. В разделе 3.4 мы подробно рассмотрим, как они выглядят в фильтре спама,
но уже сейчас я хотел бы кратко описать их. Модель состоит из пяти частей.
• Шаблоны, определяющие, какие элементы встречаются в модели.
Например, один элемент представляет спамность сообщения, а другие -
присутствие в нем определенных слов. Конкретные слова не указываются; эту
88

3.3. Архитектура приложения фильтра спама
часть знаний я поместил в конец списка. Выбор элементов фильтра спама
обсуждается в разделе 3.4.1.
С\
Текст
сообще
ния
Аналитический компонент фильтра спама
Выделитель
признаков
Модель почтового
сообщения
{ Факт ~~Л
'Признаки ►
I сообщения J
Алгоритм
вывода
Шаблоны элементов,
представляющих спайность
сообщения и присутствие
слов; зависимости между
этими элементами;
'функциональные формы
этих зависимостей и т. д.
Числовые параметры
функциональных
форм
\Параметры
Знания
Результаты обучения
Дополнительные
знания, например,
слова, представляющие
особый интерес
Ответ
• Вероятность
спама
Рис- 3.5. Третий вариант архитектуры аналитического компонента
фильтра спама. В модели выделен процесс, параметры и знания.
Параметры и знания получены в результате обучения
Зависимости между элементами. Например, элемент, обозначающий
присутствие конкретного слова, зависит от элемента, представляющего спам-
ность сообщения. Напомним, что в вероятностной модели направление
зависимости необязательно совпадает с направлением рассуждения. Мы
используем слова, чтобы определить, является ли сообщение спамом, но в
модели можно считать, что отправитель первым делом решает, какое
сообщение послать («А пошлю-ка я спам»), а уже потом подбирает слова.
Обычно зависимости моделируются в направлении от причины к следствию.
Поскольку вид сообщения определяет выбор слов, зависимости
направлены от элемента, представляющего спамность сообщения, к каждому слову.
Определение зависимостей в модели фильтра спама подробно обсуждается
в разделе 3.4.2.
Функциональные формы этих зависимостей. Функциональная форма
элемента определяет его тип, например: if, атомарный Binomial или составной
Normal. В функциональной форме не задаются параметры элемента.
Например, вышеупомянутая зависимость имеет форму if с двумя Flip: если
сообщение спамное, то слово rich (богатый) присутствует с вероятностью 1,
89

Глава 3. Создание приложения вероятностного программирования
иначе с какой-то другой вероятностью. Функциональные формы модели
фильтра спама определены в разделе 3.4.3.
Первые три части, составляющие процесс на рис. 3.5, - это то, что известно
приложению до обучения. Они определяются проектировщиком
приложения и образуют структуру модели почтового сообщения.
• Числовые параметры модели, находящиеся в блоке «Параметры» на
рис. 3.5. Например, одним из параметров является вероятность спамности
сообщения. Другой - вероятность присутствия слова rich, если сообщение
спамное, третий - вероятность присутствия слова rich, если сообщение
нормальное. Параметры отделены от процесса, потому что они определяются
в ходе обучения. Параметры модели обсуждаются в разделе 3.4.4.
• Знания. На рис. 3.5 показаны дополнительные знания, необходимые для
построения модели и применения к ней фактов в конкретной ситуации.
Термин «знания» я употребляю для всего, что было получено в результате
обучения и не связано с элементами, их зависимостями, функциональными
формами и числовыми параметрами. В нашем приложении знания
включают перечень слов, встречающихся в обучающих примерах сообщений, и
счетчики эти слов. Эти знания нужны, к примеру, для того чтобы решить,
представляет ли интерес слово rich. Таким образом, знания помогут
определить параметры модели: вероятность вхождения слова rich в сообщение
является параметром, только если это слово нас интересует.
Дополнительные знания обсуждаются в разделе 3.4.5.
Итак, с архитектурой аналитического компонента мы определились. Пора
рассмотреть компонент обучения.
3.3.2. Архитектура компонента обучения
Возвращаясь к разделу 3.1, напомним, что задача компонента обучения - по
обучающему набору примеров построить модель почтового сообщения, которая будет
использоваться аналитическим компонентом. Как и раньше, первым делом нужно
определить вход и выход компонента обучения. Из рис. 3.5 понятно, что на
выходе должны быть параметры и знания о модели. Но что подается на вход? Можно
предположить, что частью входа является заданный обучающий набор
сообщений. Однако обучение заметно упростится, если хотя бы некоторые сообщения
будут кем-то помечены как нормальные или спамные. Поэтому будем считать, что
задан обучающий набор сообщений и метки для некоторых из них. Необязательно
помечать все сообщения, достаточно, если будет помечена небольшая часть.
Итак, для компонента обучения нашего фильтра спама определены:
• вход
- набор текстовых файлов, представляющих почтовые сообщения;
- файл, содержащий метки (нормальное или спамное) подмножества
сообщений.
90

3.3. Архитектура приложения фильтра спама
выход
- числовые параметры, характеризующие процесс построения модели;
- дополнительные знания о модели.
Выделитель
признаков
извлекает
признаки из
всех сообщений
и включает их
в состав фактов
Метки
1. Выделитель знаний
порождает дополнительные
знания, например,
представляющие интерес
слова
Знания в сочетании
с априорными параметрами
и процессом образуют
априорную модель почтового
сообщения
Компонент обучения
фильтра спама
Выделитель
знаний
Выделитель
признаков
Факты
■ Признаки всех
сообщений
* Метки
«нормальное-
сламное»
некоторых
сообщений
Априорная
модель почтового
сообщения
Знания
Априорные
параметры
Процесс
Г
Алгоритм
обучения
Знания
К
аналитическому
компоненту
Параметры
К
аналитическому
компоненту
4. В случае, когда
сообщение помечено, его
метка также включается
в состав фактов
Алгоритм обучения использует
априорную модель для
вычисления новых параметров
при заданных фактах
Рис. 3.6. Архитектура компонента обучения
На рис. 3.6 показана архитектуры компонента обучения фильтра спама. Многие
ее элементы такие же, как в архитектуре аналитического компонента, но есть и
существенные различия.
• В центре компонента обучения находится априорная модель почтового
сообщения. Она состоит из тех же частей, что модель сообщения в
аналитическом компоненте, но место параметров, полученных в результате обучения,
занимают априорные параметры. Как мы увидим в главе 5, априорными
называются предполагаемые параметры модели до ознакомления с
данными. Поскольку до начала работы компонент обучения не видел никаких
данных, он может пользоваться только априорными значениями
параметров. Оставшиеся два части - процесс и знания - ничем не отличаются от
аналитического компонента.
91

Глава 3. Создание приложения вероятностного программирования
• Знания извлекаются непосредственно из обучающих сообщений
выделителем знаний. Например, знания могут состоять из слов, которые чаще
всего встречаются в сообщениях. Эти знания являются частью выхода
компонента обучения и передаются аналитическому компоненту.
• Как и в аналитическом компоненте, выделитель признаков извлекает
признаки из всех сообщений и преобразует их в факты. Если сообщение
помечено, то метка тоже включается в состав фактов.
• Место алгоритма вывода занимает алгоритм обучения. Он получает на
входе факты для всех сообщений и с помощью модели вычисляет значения
параметров. Figaro предоставляет не только алгоритмы выводы, но и
алгоритмы обучения, речь о них пойдет ниже.
Удобная особенность описанной архитектуры с разделением на два компонента
состоит в том, что компонент обучения можно выполнить один раз, а результат
многократно использовать в аналитическом компоненте. Обучение на примерах
данных - длительный процесс, и повторять его при поступлении каждого
сообщения нежелательно. Наш дизайн позволяет обучить модель один раз, сохранить
вычисленные параметры и добытые знания и использовать их для быстрого
анализа поступающих сообщений.
Познакомившись с архитектурой, посмотрим, как все это работает на практике.
В следующем разделе представлен дизайн модели и приведен код, который строит
модель для каждого сообщения. Затем будет показана реализация аналитического
компонента и, наконец, компонента обучения.
3.4. Проектирование модели
почтового сообщения
В этом разделе показан дизайн вероятностной модели нормальных и спамных
сообщений. Поскольку в аналитическом компоненте и в компоненте обучения
используется один и тот же процесс и знания, а отличаются только параметры, то
этот дизайн применим в обоих случаях.
При построении вероятностной модели в Figaro необходимо смешать четыре
основных ингредиента:
• элементы модели;
• способ соединения элементов между собой (зависимости);
• функциональные формы элементов. Это конструкторы классов элементов,
используемые для реализации зависимостей. Например, атомарный Flip -
конструктор класса булевых элементов, не зависящих ни от каких других
элементов, тогда как составной Flip - конструктор элементов типа Double,
зависящий от другого элемента, определяющего его среднее;
• числовые параметры функциональных форм.
Ниже мы рассмотрим эти ингредиенты, а в конце я опишу дополнительные
знания, являющиеся частью модели.
92

3.4. Проектирование модели почтового сообщения
3.4.1. Выбор элементов
При проектировании фильтра спама необходимо решить, какие характеристики
сообщения помогут выяснить, нормальное оно или спамное. Перечислим
некоторые из них.
• Конкретные слова в заголовке или теле сообщения. Например, слово rich
скорее встретится в спамном сообщении, чем в нормальном.
• Слова с орфографическими ошибками и другие необычные слова. Спам-
ные сообщения часто содержат неправильно написанные слова и слова, не
встречающиеся в нормальных сообщениях.
• Появление определенных слов рядом с другими словами.
• Особенности естественного языка, например, части речи.
• Поля заголовка, например адреса отправителя и получателя,
задействованные при доставке серверы и т. д.
Чтобы не слишком усложнять приложение, примем следующие проектные
решения.
• Использовать только первые две из перечисленных выше характеристик:
набор слов в сообщении и присутствие необычных слов.
• Хотя анализировать заголовок и тело сообщения раздельно имеет смысл,
мы не будем их различать.
• При создании элемента, описывающего слова сообщения, есть две
возможности: использовать целое число, равное количеству вхождений слова в
сообщение, или использовать булев элемент, показывающий, встречается
слово или нет, не обращая внимания на количество вхождений. Мы
выберем второй вариант.
• Что касается необычных слов, то можно искать каждое слово в словаре -
это покажет, является ли слово «узаконенным» или необычным. Чтобы
не зависеть от внешних приложений, мы выберем другой подход - будем
считать необычными слова, которые встречаются в одном и только одном
сообщении.
Сформулировав предположения, займемся выбором элементов модели. У нас
будет три набора элементов. Первый набор показывает, является ли сообщение
спамом. Для этого достаточно одного элемента типа Boolean. Второй набор
отражает наличие или отсутствие конкретных слов в сообщении, а третий -
количество необычных слов в сообщении.
Представления наличия и отсутствия слов
При создании элементов, представляющих наличие или отсутствие слов,
нужно подумать, какие слова включать в модель. Можно было бы завести по одному
элементу для каждого слова, встречающегося хотя бы в одном обучающем
сообщении. Но тогда количество элементов будет огромно. Например, в типичном
обучающем наборе из 1000 сообщений число различных слов превышает 40 000.
93

Глава 3. Создание приложения вероятностного программирования
Слишком много элементов плохо по двум причинам. Во-первых, это ведет к
переобучению, когда обученная модель точно соответствует обучающим данным, но
плохо обобщается на новые. Если количество элементов слишком велико, то
велики шансы, что некоторые из них по чистой случайности объясняют обучающие
данные, хотя и не способны предсказать, является ли сообщение спамом. Чтобы
убедиться в этом, представим, что некоторое слово случайным образом включили
в пять сообщений. Предположим, что 1/3 обучающих примеров - спам.
Вероятность, что все пять сообщений, в которых встречается это слово, - спам,
составляет примерно 1/250. Это означает, что если имеется 40 000 слов, встречающихся
по пять раз, то приблизительно 160 из них будут встречаться только в спамных
сообщениях. Эти 160 слов могли бы объяснить все спамные сообщения. Но, по
условиям эксперимента, они были включены в обучающие сообщения случайным
образом, поэтому никакой предсказательной силы не имеют.
Еще одна причина не создавать слишком много элементов состоит в том, что это
замедляет как анализ, так и обучение. Мы хотим, чтобы аналитический компонент
работал максимально быстро, поскольку он применяется к каждому приходящему
на сервер сообщению. Что касается обучения вероятностной модели, то это и так
медленный процесс, особенно когда обучающих примеров тысячи и более. Если
при этом еще и элементов чересчур много, то он может стать недопустимо
медленным.
С учетом этих соображений создадим элементы для 100 слов. Тогда возникает
следующий вопрос: какие 100 слов выбрать? Решить, какие элементы, или
признаки, включать в модель, поможет заимствованная из машинного обучения техника
отбора признаков. В случае фильтра спама цель отбора признаков - найти слова,
являющиеся наиболее убедительными индикаторами спамности или
нормальности сообщения. Методы отбора признаков бывают весьма изощренными. При
построении фильтра промышленного качества одним из таких методов и следовало
бы воспользоваться. Но в этой главе мы ограничимся техникой попроще.
Эта техника основана на двух наблюдениях. Во-первых, использование слов,
которые встречаются редко, ведет к переобучению, поскольку их
предсказательная сила невелика. Во-вторых, такие часто встречающиеся слова, как the и and,
тоже вряд ли могут что-то предсказать, потому что встречаются чуть ли не всех
нормальных и спамных сообщениях. Они называются стоп-словами. Поэтому при
создании списка слов для модели, мы удалим слова, встречающиеся слишком
часто, а из оставшихся выберем первые 100 по частоте встречаемости.
Представление числа необычных слов
Желание включить в модель необычные слова продиктовано тем, что спам
обычно содержит больше необычных слов, чем нормальное сообщение. На самом
деле, в обучающем наборе из 1000 сообщений 28 % слов были необычными, тогда
как в нормальных сообщениях таковых было всего 18 %. Но при более
внимательном изучении обнаруживаются нюансы. В некоторых спамных сообщениях число
необычных слов очень велико, тогда как другие в этом отношении не отличаются
94

3.4. Проектирование модели почтового сообщения
от нормальных сообщений. Чтобы уловить эту деталь, мы включим в модель
элемент hasManyUnusuaiwords, который показывает, что в сообщении много
необычных слов. Это скрытый элемент. Непосредственно в данных он не присутствует,
но включение его в модель повышает ее качество.
Итак, в модель почтового сообщения включаются следующие элементы:
• isspam - элемент типа Boolean, принимающий значение true, если
сообщение спамное;
• hasWordl, ..., hasWordlOO - Элемент ТИПа Boolean ДЛЯ КаЖДОГО ИЗ 100 СЛОВ,
принимающий значение true, если слово присутствует в сообщении;
• hasManyUnusuaiwords - элемент типа Boolean, принимающий значение true,
если в сообщении много необычных слов;
• numUnusualWords - Элемент ТИПа Integer, Значение КОТОрОГО paBHO ЧИСЛу
слов, встречающихся только в данном сообщении.
Все описанные выше элементы сведены в показанный ниже класс Model. Это
абстрактный класс, поскольку в нем имеются лишь объявления элементов, но
отсутствуют определения. Мы завели его, имея в виду расширить классами Rea-
soningModel И LearningModel. Ниже МЫ уВИДИМ, ЧТО Существуют ТОНКИе ОТЛИЧИЯ,
из-за которых необходимы два разных класса для модели анализа и обучения.
Абстрактный базовый класс позволяет писать методы, например применение
фактов, общие для обеих моделей. В главе 12 мы познакомимся с общим способом
создания аналитического и обучающего компонентов с единым классом модели,
так что не придется создавать два разных класса. Но этот способ опирается на
такие средства Figaro, о которых мы еще не говорили.
Листинг 3.1. Абстрактный класс Model
abstract class Model(val dictionary: Dictionary) { <]—О
val isSpam: Element[Boolean] I
val hasManyUnusuaiwords: Element[Boolean] <3—©
val numUnusualWords: Element[Int] I
val hasWordElements: List[(String, Element[Boolean])] <)—©
}
О — Класс модели принимает словарь в качестве аргумента. В разделе 3.4.5 мы увидим,
что словарь содержит дополнительные знания о словах в обучающем наборе
© — Объявления описанных выше элементов модели
© — hasWordElements— это список пар (слово, элемент), каждый элемент которого
описывает, встречается ли слово в сообщении
3.4.2. Определение зависимостей
Для начала определим зависимости между элементом isspam и всеми элементами
word. При определении зависимостей в вероятностной модели действует общее
эвристическое правило: класс объекта определяет свойства объекта, т. е. свойства
зависят от класса в модели зависимости. В нашем примере от того, является ли
сообщение спамом, зависит наличие или отсутствие всех слов. Я уже отмечал этот
95

Глава 3. Создание приложения вероятностного программирования
момент выше, но он заслуживает повторения, потому что многие в этом месте
путаются. Мы используем слова, чтобы определить, является ли сообщение спамом.
Так почему же я говорю, что класс сообщения определяет слова, а не наоборот?
Очень важно запомнить, что в вероятностных рассуждениях направление
вывода необязательно совпадает с направлением зависимостей в модели. С тем же
успехом, оно может быть и противоположно, коль скоро мы пытаемся определить
факторы, обусловившие наблюдаемый результат. В данном случае мы
моделируем сущностную характеристику почтового сообщения (является оно нормальным
или спамным) как ненаблюдаемый фактор, обуславливающий наблюдаемые
слова. Поэтому зависимость направлена от класса сообщения к словам.
Разобравшись с этим вопросом, мы должны еще решить, будем ли
моделировать зависимости между словами. В английском и многих других языках выбор
первого слова предложения тесно связан со вторым словом. В действительности
слова не являются независимыми. Но чтобы не усложнять эту главу сверх меры,
я буду предполагать, что слова независимы при условии, что известен класс
сообщения (нормальное или спамное).
Мы можем нарисовать так называемую байесовскую сеть, на которой
показаны зависимости в модели. Подробно байесовские сети рассматриваются в главе 5.
Пока же отметим лишь, что между двумя узлами сети существует ребро, если
второй узел зависит от первого. Байесовская сеть для нашего фильтра спама на
данный момент выглядит, как показано на рис. 3.7. Сеть такого вида называется
наивной байесовской моделью, причем слово «наивный» употребляется из-за
предположения о независимости слов.
Рис- 3-7. Наивная байесовская модель зависимостей
Элементов isSpam И hasWord
Теперь рассмотрим элементы, относящиеся к необычным словам. Напомним,
ЧТО у Нас ДВа ТаКИХ Элемента: hasManyUnusualWords И numUnusualWords. Элемент has-
ManyUnusualWords ПОКаЗЫВаеТ, МНОГО ЛИ В Сообщении НеобыЧНЫХ СЛОВ, a
numUnusualWords содержит точное их количество. Понятно, что numunusuaiwords зависит от
hasManyUnusualWords, поскольку если необычных слов много, то их число заведомо
больше НуЛЯ. В СВОЮ ОЧереДЬ, Элемент hasManyUnusualWords, ЯВЛЯЮЩИЙСЯ
СВОЙСТВОМ сообщения, зависит от is spam, представляющего класс сообщения.
Наконец, в соответствии с наивным байесовским допущением мы считаем, что наличие
необычных слов не зависит от наличия любого конкретного слова при условии,
что класс известен. Получается байесовская сеть, изображенная на рис. 3.8. Это
окончательная модель зависимостей в нашем фильтре спама.
96

3.4. Проектирование модели почтового сообщения
Рис. 3.8. Полная модель зависимостей, включающая необычные слова
3.4.3. Определение функциональных форм
Необходимо определить функциональные формы наших элементов. Напомним,
что функциональная форма - это конструктор класса элемента, используемый
при построении модели. Они содержат все необходимое для выражения модели
за исключением числовых параметров. Пойдем по порядку. Сначала определим
функциональные формы для аналитического компонента, предполагая, что
значения параметров вычисляет компонент обучения. Ниже приведен код модели
аналитического компонента. Подробные объяснения приведены после кода.
Листинг 3.2. Модель аналитического компонента
i
class ReasoningModel(
dictionary: Dictionary,
parameters: LearnedParameters
) extends Model(dictionary) {
val isSpam = Flip(parameters.spamProbability)
val hasWordElements = {
for { word <- dictionary.featureWords } yield {
val givenSpamProbability =
parameters.wordGivenSpamProbabilities(word)
val givenNormalProbability =
parameters.wordGivenNormalProbabilities(word)
val hasWordlfSpam = Flip(givenSpamProbability)
val hasWordlfNormal = Flip(givenNormalProbability)
val hasWord = If(isSpam, hasWordlfSpam, hasWordlfNormal)
(word, hasWord)
В
val hasManyUnusuallfSpam =
Flip(parameters.hasManyUnusualWordsGivenSpamProbability)
val hasManyUnusuallfNormal =
Flip(parameters.hasManyUnusualWordsGivenNormalProbability)
val hasManyUnusualWords =
If(isSpam, hasManyUnusuallfSpam, hasManyUnusuallfNormal)
В
val numUnusuallfHasMany =
Binomial(Model.binomialNumTrials,
В
isSpam
hasManyUnusualWords
numUnusualWords
hasWordlOO
hasWordl
97

Глава 3. Создание приложения вероятностного программирования
parameters.unusualWordGivenManyProbability),
val numUnusuallfHasFew =
Binomial(Model.binomialNumTrials,
parameters.unusualWordGivenFewProbability),
val numUnusualWords =
If(hasManyUnusualWords, numUnusuallfHasMany, numUnusuallfHasFew)
}
Й
О — Аргументы модели аналитического компонента — это словарь и параметры,
найденные в процессе обучения
© — ReasoningModel реализует абстрактный класс Model
© — Элемент, показывающий, что сообщение спамное
© — Элементы, показывающие, присутствует ли слово в сообщении. Этот код создает
список пар (слово, элемент), по одной для каждого слова-признака
© — Элемент, показывающий, много ли необычных слов в сообщении
© — Элемент, представляющий количество необычных слов
Теперь рассмотрим каждый элемент подробно.
• isSpam - вероятность, что этот элемент типа Boolean равен true,
совпадает с вероятностью того, что сообщение спамное. Поэтому определяем его
с помощью элемента Flip. В Figaro это записывается в виде val isSpam
= Flip (parameter. spamProbability). Это Отражает нашу априорную - ДО
предъявления каких-либо слов - веру в то, что сообщение является спам-
ным. Поскольку слова зависят от спамности сообщения, и мы наблюдаем
именно слова, то на основе слов делается вывод о том, спамное сообщение
или нет. Как видим, в этом случае направление зависимости отличается от
направления вывода. В вероятностных рассуждениях иногда идут от
следствия к причине.
• wordi,..., wordioo - каждое слово присутствует с некоторой вероятностью.
Эта вероятность зависит от того, является сообщение нормальным или
спамным. Поэтому элемент if подходит идеально. Базовая форма имеет
вид:
val hasWordlfSpam = Flip(givenSpamProbability)
val hasWordlfNormal = Flip(givenNormalProbability)
val hasWord = If(isSpam, hasWordlfSpam, hasWordlfNormal)
Предупреждение. Возможно, вам показалось, что определение hasWord можно
упростить, исключив hasWordlf Spam и hasWordlfNormal:
val hasWord = If(isSpam, Flip(givenSpamProbability),
Flip(givenNormalProbability) )
К сожалению, в Figaro есть ограничение: элемент, который зависит от параметра,
вычисляемого в процессе обучения (например, Flip (givenSpamProbability),
зависящий от параметра givenSpamProbability), нельзя определять внутри Chain.
A if - частный случай Chain, поэтому приведенная выше конструкция недопустима. Мы
надеемся снять это ограничение в будущей версии Figaro.
98

<-©
3.4. Проектирование модели почтового сообщения
• givenSpamProbability И givenNormalProbability - ЭТИ параметры ПСфОЖДа-
ются в результате обучения, они свои для каждого слова. Указанные выше
формы if создаются для каждого слова, выделенного в качестве признака.
В Scala мы создаем список пар, состоящих из слова и соответствующего ему
элемента hasword. Ниже приведен соответствующий код:
val hasWordElements = {
for { word <- dictionary.featureWords } yield { <|—Q
val givenSpamProbability =
parameters.wordGivenSpamProbabilities(word)
val givenNormalProbability =
parameters.wordGivenNormalProbabilities(word)
val hasWordlfSpam = Flip(givenSpamProbability) .
val hasWordlfNormal = Flip(givenNormalProbability) <1_£|
val hasWord = If(isSpam, hasWordlfSpam, hasWordlfNormal) |
(word, hasWord) <}—ф
}
}
О - dictionary.featureWords порождает список 100 слов-признаков. В этом цикле
производится обход этого списка
© - Вероятность вхождения слова в зависимости от того, является сообщение
нормальным или спамным
© - Создаем элемент Figaro, показывающий, присутствует ли слово
© - Пара, состоящая из слова и соответствующего ему элемента. Все такие пары
помещаются в список
• :: i :; : i . i i - этот элемент принимает значение true с
вероятностью, зависящей от спамности сообщения. И в этом случае подходящей
формой является if:
val hasManyUnusuallfSpam =
Flip(parameters.hasManyUnusualWordsGivenSpamProbability)
val hasManyUnusuallfNormal =
Flip(parameters.hasManyUnusualWordsGivenNormalProbability)
val hasManyUnusualWords =
If(isSpam, hasManyUnusuallfSpam, hasManyUnusuallfNormal)
• numunusuaiwords - этот элемент типа integer представляет количество нео-
бычных слов в сообщении. Чем больше в сообщении слов, тем больше
среди них может быть необычных. В модели каждому слову сопоставляется
вероятность того, что оно необычное. Это естественно представить
биномиальным распределением, в котором общее число испытаний равно
количеству слов в сообщении. Однако слов может быть больше 1000, а при
таком большом числе испытаний вероятность многих значений numunusu-
aiwords будет очень малой. Поэтому и вероятность сообщения может
оказаться очень малой. При большом числе сообщений это может привести к
ошибкам из-за потери значимости: вероятности округляются до 0, потому
что столь малые числа непредставимы в компьютере.
99

Глава 3. Создание приложения вероятностного программирования
Чтобы обойти эту проблему, мы устанавливаем фиксированное число
испытаний, например 20. Это число представлено в коде константой Model.
binomiaiNumTriais. Тогда число необычных слов в сообщении
масштабируется и представляет долю 20. Мы вспомним об этом позже, когда будем
применять факты. При описанном подходе определение numunusuaiwords
выглядит так:
val numUnusuallfHasMany =
Binomial(Model.binomiaiNumTriais,
parameters.unusualWordGivenManyProbability),
val numUnusuallfHasFew =
Binomial(Model.binomiaiNumTriais,
parameters.unusualWordGivenFewProbability),
val numUnusualWords =
If(hasManyUnusualWords, numUnusuallfHasMany, numUnusuallfHasFew)
С моделью аналитического компонента всё. Модель компонента обучения
отличается только тем, что вместо вероятности, вычисленной в процессе обучения,
используется элемент, представляющий априорную вероятность. Например:
val isSpam = Flip(parameters.spamProbability)
Сравните с тем, как это выглядит в модели аналитического компонента:
val isSpam = Flip(parameters.spamProbability)
На первый взгляд, совершенно одинаково. Однако имеется существенное
различие. В модели аналитического компонента parameters.spamProbability -
фиксированное число. А в модели компонента обучения :■ » i .-.,•« , ; i > r ::; • -
случайный элемент, который может принимать много разных значений. В процессе
обучения мы не знаем, с какой вероятностью конкретное сообщение является спа-
мом, поэтому представляем эту вероятность случайным элементом. В результате
обучения вычисляется значение этой вероятности, которое затем используется в
аналитическом компоненте. Вот как выглядит код модели компонента обучения:
class LearningModel(
dictionary: Dictionary,
parameters: PriorParameters <3—О
) extends Model(dictionary) { <}—ф
// тело точно такое же, как в модели аналитического компонента
}
О — Элементы, представляющие априорные параметры
© — LearningModel также расширяет абстрактный класс Model
3.4.4. Использование числовых параметров
Вот мы и подошли к обсуждению числовых параметров. В аналитическом
компоненте эти параметры берутся из результатов обучения. Класс LearnedParam-
eters определяет все параметры модели:
100

3.4. Проектирование модели почтового сообщения
Листинг 3-3- Класс LearnedParameters
class LearnedParameters(
val spamProbability: Double,
val hasManyUnusualWordsGivenSpamProbability: Double,
val hasManyUnusualWordsGivenNormalProbability: Double,
val unusualWordGivenManyProbability: Double,
val unusualWordGivenFewProbability: Double,
val wordGivenSpamProbabilities: Map[String, Double],
val wordGivenNormalProbabilities: Map[String, Double]
)
Для компонента обучения необходимы априорные значения параметров. В
нашей модели используются составные элементы Flip и Binomial. Напомним (см.
главу 2), что оба принимают в качестве аргумента объект Element [Double], т. е.
Element [Double] является параметром составных Flip и Binomial. Обычно мы
хотим, чтобы в качестве этого параметра выступал непрерывный атомарный
элемент. И существует непрерывный атомарный элемент Beta, прекрасно
подходящий на роль параметра составных Flip и Binomial, так что им мы и воспользуемся.
Подробнее об элементе Beta будет сказано в главах 4 и 5.
Атомарный элемент Beta принимает в качестве аргументов два значения типа
Double. В показанном ниже коде эти значения тщательно подобраны, но чтобы
понять, почему они именно такие, придется немного подождать - объяснения будут
Даны В ПОСЛедуЮЩИХ Главах. ВОТ КОД Класса PriorParameters.
Листинг 3.4. КлассPriorParameters
class PriorParameters(dictionary: Dictionary) {
val spamProbability = Beta (2,3) <]—©
val wordGivenSpamProbabilities =
dictionary.featureWords.map(word => (word, Beta(2,2)))
val wordGivenNormalProbabilities =
dictionary.featureWords.map(word => (word, Beta(2,2)))
val hasManyUnusualWordsGivenSpamProbability = Beta (2,2)
val hasManyUnusualWordsGivenNormalProbability = Beta(2,
val unusualWordGivenManyProbability = Beta (2,2)
val unusualWordGivenFewProbability = Beta(2,7)
<-Q
21)
<-©
<-o
val fullParameterList =
spamProbability ::
hasManyUnusualWordsGivenSpamProbability ::
hasManyUnusualWordsGivenNormalProbability ::
unusualWordGivenManyProbability ::
unusualWordGivenFewProbability ::
wordGivenSpamProbabilities.map(pair => pair._2) :
wordGivenNormalProbabilities.map(pair => pair._2)
<^-0
101

Глава 3. Создание приложения вероятностного программирования
О — Априорная вероятность спама
© — Вероятность, что слово встречается в спамном или нормальном сообщении
© — Априорные вероятности необычности слова при условии, что сообщение имеет
много и мало необычных слов
© — Априорные вероятности наличия многих необычных сообщений в спамном и
нормальном сообщении
© — Говорит алгоритму обучения, какие параметры нужно определить. См. врезку
Рассмотрим более внимательно следующие строки:
val wordGivenSpamProbabilities =
dictionary.featureWords.map(word => (word, Beta(2,2)))
val wordGivenNormalProbabilities =
dictionary.featureWords.map(word => (word, Beta(2,2)))
Для каждого слова существуют вероятности его появления в спамном и в
нормальном сообщении. Априорная вероятность в обоих случаях равна Beta(2,2).
В этом коде создается список пар (слово, элемент), по одной паре для каждого
слова-признака. В роли априорного элемента во всех парах выступает Beta (2,2). Одна
важная деталь: элементы Beta для каждого случая различны. У каждого слова свои
собственные вероятности встретиться в нормальном и спамном сообщении.
Нотация Scala
Рассмотрим более пристально код определения full Parameters. В нем создается
список всех параметров модели. Следует обратить внимание на две вещи. Во-первых,
взгляните на Строку wordGivenNormalProbabilities.map (pair => pair ._2) . Здесь
мы перебираем все пары (слово, элемент) в списке wordGivenNormalProbabilities.
К каждой паре применяется функция, которая получает на входе пару и возвращает
ее второй компонент, т. е. элемент. Поэтому результатом этого предложения является
набор всех элементов, представляющих вероятности появления слов-признаков в
нормальных сообщениях. Предложение wordGivenSpamProbabilities .map (pair =>
pair .2) делает то же самое в отношении спамных сообщений.
Второе, что нужно отметить, - как элементы объединяются в список. Взглянув на
определение, вы увидите, что в каждой из первых пяти строк находится по одному
элементу, а последние две строки содержат списки элементов. В Scala оператор ; :
принимает элемент х и список xs и помещает х в начало xs, А оператор : : :
конкатенирует два списка. Таким образом, этот код создает один список, содержащий все
параметры модели.
3.4.5. Работа с дополнительными знаниями
Чтобы построить модель конкретного сообщения, нужно знать, какие слова
являются признаками. Кроме того, нужно как-то определять, является ли слово
необычным. Для этого мы используем структуру данных Dictionary. Ниже приведен
код класса Dictionary. Все пояснения приведены в аннотациях.
102

3.4. Проектирование модели почтового сообщения
Листинг 3-5. Класс Dictionary
class Dictionary(initNumEmails: Int) { О—О
val counts: Map [String, Int] = Map () 0—©
var numEmails = initNumEmails <3—©
def addWord(word: String) {
counts += word -> (getCount(word) + 1)
}
E
def addEmail(email: Email) {
numEmails += 1
for { word <- email.allWords
addWord(word)
<-0
object OrderByCount extends Ordering[String] {
def compare(a: String, b: String) = getCount(b) - getCount(a)
}
def words = counts.keySet.toList.sorted(OrderByCount)
В
в
def nonStopWords =
words.dropWhile(counts(_) >=
numEmails * Dictionary.stopWordFraction)
def featureWords = nonStopWords.take(Dictionary.numFeatures)
def getCount(word: String) =
counts.getOrElse(word, 0)
E
def isUnusual(word: String, learning: Boolean) =
if (learning) getCount(word) <= 1
else getCount(word) <= 0
W
О — В классе Dictionary запоминается количество сообщений, по которым он был
построен. initNumEmails — начальное значение
© — Отображает слово на счетчик сообщений, в которых оно встречается
© — Число сообщений, по которым построен этот словарь Dictionary
© — Добавляем слово в словарь, увеличивая его счетчик на 1
© — Добавляем сообщение в словарь, увеличивая numEmails и добавляя каждое слово,
встречающееся в сообщении
© — Слова, хранящиеся в словаре, отсортированные в порядке убывания счетчика
© — Получить слова, встречающиеся не слишком часто
© — Отобрать numFeatures самых часто встречающихся из оставшихся слов
© — Получить количество сообщений, в которых встречается данное слово
© — Определить, является ли слово необычным
Несколько комментариев по поводу этого кода.
• Аргумент initNumEmails класса Dictionary - это начальное число
сообщений в словаре. В аналитическом компоненте общее число сообщений уже
103

Глава 3. Создание приложения вероятностного программирования
известно от компонента обучения, поэтому initNumEmaiis устанавливается
равным этому числу В компоненте обучения сообщения добавляются по
ОДНОМу, ПОЭТОМУ initNumEmaiis paBHO 0.
• numEmails - ЧИСЛО Сообщений В СЛОВаре. В Начале ОНО раВНО initNumEmaiis
и увеличивается на единицу при добавлении каждого сообщения.
Сообщения добавляются в словарь только компонентом обучения.
• words - список всех слов словаре, отсортированный в порядке убывания
счетчика - от наиболее частых к наименее частым. Метод sorted
принимает аргумент ordering - объект, предоставляющий метод compare для
сравнения двух элементов списка. Порядок сортировки реализован объектом
OrderByCount.
• Множество слов-признаков формируется из всего множества слов в два
этапа. На первом этапе мы обходим отсортированный список слов и удаляем
слова, которые встречаются слишком часто (стоп-слова). Слово считается
стоп-словом, если доля сообщений, в которых оно встречается, не меньше
Dictionary. stopWordFraction. Например, еСЛИ Dictionary. stopWordFraction
равно 0.2 и всего существует 50 сообщений, то стоп-словом будет считаться
слово, встречающееся как минимум в 10 сообщениях. На втором этапе мы
Отбираем первые Dictionary. numFeatures ИЗ СПИСКа nonStopWords.
• В методе get count используется метод getorEise из библиотеки Scala. Он
ищет слово в отображении counts и, если не найдет, возвращает 0.
• В методе isunusuai реализована логика определения необычных слов.
Слово считается необычным, если не встречается ни в каких других
сообщениях. В процессе обучения слово заведомо встречается в рассматриваемом
в данный момент сообщении, поэтому его счетчик <= 1. В аналитическом
компоненте словарь состоит только из сообщений, встречавшихся в
процессе обучения, поэтому если слово необычно, то оно вообще не может
оказаться в словаре.
3.5. Разработка аналитического
компонента
Еще раз рассмотрим архитектуру аналитического компонента, повторенную на
рис. 3.9. Мы уже видели части, относящиеся к модели сообщения, порождающему
процессу, параметрам, найденным на этапе обучения, и знаниям - в виде словаря,
построенного в ходе обучения. Осталось разобраться с выделителем признаков,
применением фактов и выполнением алгоритма вывода.
Для выделения признаков и формирования наблюдаемых фактов используется
класс Email. Ниже приведен аннотированный код этого класса. После уже
проделанной работы выделение признаков и формирование фактов не представляет
сложностей.
104

3.5. Разработка аналитического компонента
^
Текст

сообщения
Аналитический ко
( >
Выделитель
признаков
L J
1
мпоне!
t
f Факт Л
■ Признаки
^ сообщения j
нт фильтра
спама
Модель
почтового
V
сообщения
Процесс
Параметры
Знания \
)
*
Алгоритм
вывода
V )
1
>
Ответ
• Вероятность
спама
Параметры
Знания
Результаты
обучения
Рис. 3.9. Архитектура аналитического компонента (повтор)
Листинг 3.6. Класс Email
class Email (file: File) {
def getAHWords () = ...
val allWords: Set [String] = getAHWords ()
def observeEvidence(
model: Model, <3—©
label: Option[Boolean], <]—Q
learning: Boolean <]—Q
) {
label match {
case Some(b) => model.isSpam.observe(b)
case None => ()
}
for {
(word, element) <- model.hasWordElements
} {
element.observe(allWords.contains(word))
П
В
В
val obsNumUnusualWords =
allWords.filter ( (word: String) =>
model.dictionary.isUnusual(word, learning)).size
Ш
105

Глава 3. Создание приложения вероятностного программирования
val unusualWordFraction =
obsNumUnusualWords * Model.binomialNumTrials / allWords.size
model.numUnusualWords.observe(unusualWordFraction)
}
}
О — Получить все слова сообщения с помощью операций ввода-вывода (не показано)
© — Метод для передачи фактов модели, основанной на признаках сообщения
© — Модель, которой передаются наблюдаемые факты
© — Метка, которая может и отсутствовать
© — Флаг режима: обучение или анализ
© — Если метка имеется, применить ее к элементу модели isSpam
© — Для каждого слова и соответствующего ему элемента модели наблюдаемым фактом
является вхождение слова в множество allWords
© — Подсчитать число необычных слов в сообщении
© — Применить наблюдаемый факт к элементу модели numUnusualWords
И снова несколько комментариев.
• При создании объект Email читает указанный в аргументе файл для
получения всех слов, встречающихся в сообщении. Они сохраняются в поле aii-
words. Отметим, что aiiwords - множество, что согласуется с моделью, в
которой нас интересует только, присутствует ли слово в сообщении или
нет, а сколько раз оно встречается, неважно.
• Аргумент label метода observeEvidence имеет ТИП Option [Boolean], ЭТО
означает, что он может и отсутствовать. В Scala структура данных option
может принимать значение some (с) или None. В данном случае, если класс
сообщения известен, то label будет содержать этот класс, а в противном
случае равно None. Если метка имеется (значение label равно some (b)), то
она будет применена в качестве факта к model.isSpam.
• Для подсчета необычных слов в сообщении используется стандартный
метод Scala niter. Здесь filter получает множество строк aiiwords и удаляет
из него все строки, не удовлетворяющие заданному в аргументе условию.
Аргументом filter является функция, которая возвращает true, если
слово необычное. Таким образом, niter удаляет все строки, кроме необычных.
Размер оставшегося множества и является количеством необычных слов.
Отметим, что метод isunusuai принимает флаг режима обучения во втором
аргументе.
• В последних трех строках задается наблюдаемое количество необычных
слов. Напомним, что элемент numUnusualWords определен с помощью
биномиального распределения, в котором число испытаний задано константой
Model.binomialNumTrials. Поэтому МЫ ПРОИЗВОДИМ НОрМИрОВКу, Чтобы ВЫ-
раЗИТЬ ЧИСЛО obsNumUnusualWords Как ДОЛЮ ОТ Model.binomialNumTrials.
Зная, как выделять признаки и применять факты, и имея модель вместе с
найденными в результате обучения параметрами, мы теперь можем
классифицировать сообщения как нормальные или спамные. Для этого служит алгоритм вывода.
106

3.5. Разработка аналитического компонента
Мы воспользуемся точным алгоритмом исключения переменных (ИП). Для
одного сообщения этот алгоритм работает достаточно быстро, а, в силу своей точности,
дает наилучший из возможных ответов. Ниже приведен его код.
Листинг 3.7. Метод classify
def classify( I
dictionary: Dictionary, I <^—U
parameters: LearnedParameters,
fil eName: String
) = {
val file = new File (fileName)
val email = new Email (file)
«-©
val model = new ReasoningModel(dictionary, parameters) O—©
email.observeEvidence(model, None, false) <]—©
val algorithm = VariableElimination(model.isSpam)
algorithm.start()
<^-0
val isSpamProbability = algorithm.probability(model.isSpam, true) <J—©
println("Вероятность спама: " + isSpamProbability) |
algorithm, kill () <—©
isSpamProbability O—©
}
© — Метод classify принимает результаты обучения в виде словаря и параметров, а также
имя файла, содержащего классифицируемое сообщение, и возвращает вероятность
того, что это сообщение спамное
© — Создать объект Email на основе файла с именем filename
© — Создать аналитическую модель с применением результатов обучения;
© — Передать модели наблюдения относительно этого сообщения. Поскольку мы
сейчас не занимаемся обучением, необязательная метка равна None, а флаг режима
обучения равен false
© — Создать и выполнить алгоритм исключения переменных, передав в качестве запроса
элемент модели isSpam
© — Получить вероятность спамности сообщения и напечать сообщение
© — Почистить за собой, уничтожив алгоритм. Алгоритм нельзя уничтожать, пока не
будет получен ответ на запрос
© — Вернуть вероятность того, что сообщение спамное
Наконец, в аналитическом компоненте имеется метод main. Он вызывается,
когда приложение запускается из командной строки.
Листинг 3-8- Метод main аналитического компонента
def main(args: Array[String]) = {
val emailFileName = args(O) <3—©
107

Глава 3. Создание приложения вероятностного программирования
val learningFileName = args(l) <3—©
val (dictionary, parameters) = loadResults(learningFileName) <}—©
classify(dictionary, parameters, emailFileName) <3"-0
}
О — Получить имя файла сообщения из первого аргумента командной строки
© — Получить имя файла с результатами обучения из второго аргумента командной
строки
© — Загрузить результаты обучения из файла с помощью метода loadResults (не
показан)
© — Использовать результаты обучения для классификации сообщения, прочитанного из
файла
Я не привожу код метода loadResults, поскольку он длинный и не содержит
ничего, кроме обычных операций ввода-вывода. Опишу лишь вкратце, что он делает.
1. Прочитать общие параметры модели, например вероятность спама и
вероятность, что в сообщении много необычных слов.
2. Прочитать все слова вместе со счетчиками вхождения.
3. Прочитать слова-признаки вместе с вероятностями присутствия при
условии, что сообщение нормальное или спамное.
Формат файла разработан специально для этого приложения. В Figaro нет
общего формата файла с результатами обучения.
3.6. Разработка компонента обучения
Определив модель и разработав аналитический компонент, мы имеем почти все
необходимое для создания компонента обучения. Еще раз посмотрим на
архитектуру этого компонента, повторенную на рис. 3.10. Модель почтового сообщения
мы уже видели. Как отмечалось выше, различие между моделью сообщения в
компоненте обучения и в аналитическом компоненте заключается в том, что первом
случае используются априорные параметры, состоящие из элементов Beta.
При разработке аналитического компонента мы уже видели, как работает
выделитель признаков и как применяются факты при наличии сообщения и
факультативной метки «нормальное-спам». В аналитическом компоненте мы
анализировали одно сообщение. Напротив, в компоненте обучения имеется весь обучающий
набор сообщений. Выделитель признаков извлекает из всех сообщений признаки
и преобразует их в факты. Он также читает файл Labels, содержащий метки
некоторых обучающих сообщений, и если метка имеется, то применяет
соответствующий факт.
В архитектуре на рис. 3.10 присутствует также выделитель знаний, задача
которого - извлечь дополнительные знания из текстов сообщений. Мы уже знаем,
что эти знания представлены в виде словаря - класса Dictionary, имеющего метод
addEmaii, поэтому выделитель знаний в нашем фильтре спама несложен. Мы
определим объект Scala с именем Dictionary. В Scala объект можно считать классом,
108

3.6. Разработка компонента обучения
имеющим единственный экземпляр. Его можно использовать для определения
аналога статических методов в Java. Мы определяем метод fromEmaiis, который
конструирует объект Dictionary по экземпляру класса Traversable,
параметризованного КЛаССОМ Email (Traversable - ЭТО баЗОВЫЙ КЛаСС Scala, Которому НаСЛеду-
ют многие коллекции, в том числе списки и множества). Для вызова этого метода
НуЖНО Написать Dictionary. fromEmaiis (emails). ОТМСТИМ, ЧТО у нас уже еСТЬ КЛаСС
Dictionary, т. е. разрешается использовать одинаковые имена для класса и объекта.
Тексты

сообщений
Метки
Компонент обучения фильтра спама
Выделитель
знаний
Выделитель
признаков
Факты
* Признаки всех
сообщений
* Метки
«нормалычое-
спамное»
некоторых^
сообщений
Модель почтового
сообщения в
компоненте обучения
Знания
Априорные
параметры
Процесс
Алгоритм
обучения
Знания
Найденные
параметры
Рис. 3.10. Архитектура компонента обучения (повтор)
Листинг 3-9- Объект Dictionary
object Dictionary {
def fromEmaiis(emails: Traversable[Email]) = {
val result = new Dictionary(0)
for { email <- emails } { result.addEmail(email)
result
}
}
<M>
О — Создать экземпляр класса Dictionary, для которого начальное число сообщений
равно 0. Добавить в словарь все сообщения и вернуть его
Вот мы и добрались до самого главного кода в компоненте обучения -
применения алгоритма обучения с целью определить параметры модели. Мы
воспользуемся ЕМ-алгоритмом (expectation-maximization). Это «мета-алгоритм», поскольку в
его внутреннем цикле используется регулярный алгоритм вывода. Подробнее о
109

Глава 3. Создание приложения вероятностного программирования
ЕМ-алгоритме будет сказано в главе 12. Опуская детали, можно сказать, что ЕМ
сначала выдвигает гипотезу о значениях параметров, вычисляет вероятности
элементов модели в предположении этой гипотезы, а затем с помощью вычисленных
вероятностей улучшает гипотезу Этот процесс повторяется столько раз, сколько
необходимо. Для вычисления вероятностей элементов используется алгоритм
вывода.
Figaro предоставляет реализации ЕМ-алгоритма с различными алгоритмами
вывода. В данном приложении мы воспользуемся алгоритмом распространения
доверия (belief propagation - РД). Алгоритм РД похож на ИП, но для больших
моделей работает быстрее. Принцип его работы основан на распространении
сообщений между элементами, повторяемом на протяжении нескольких итераций.
При выполнении ЕМ-алгоритма с РД в качестве алгоритма вывода необходимо
задать число итераций для того и другого. В данном случае мы оставим для обоих
значение по умолчанию (10), которое дает хорошие результаты.
Ниже показан метод learnMAP, в котором применяется алгоритм обучения. Он
принимает априорные параметры и возвращает параметры, найденные в
результате обучения. Акроним MAP означает «maximum a posteriori» {максимум
апостериорной вероятности - МАВ) - используемый нами метод обучения: мы
возвращаем значения параметров, доставляющие максимум апостериорной вероятности
параметров при известных данных. ЕМ-алгоритм порождает именно МАВ-значе-
ния.
Листинг 3.10. Метод learnMAP
LearnedParameters = {
def learnMAP(params: PriorParameters):
val algorithm =
EMWithBP(params.fullParameterList:_*]
algorithm.start()
val spamProbability = params.spamProbability.MAPValue
val hasUnusualWordsGivenSpamProbability =
params.hasManyUnusualWordsGivenSpamProbability.MAPValue
val hasUnusualWordsGivenNormalProbability =
params.hasManyUnusualWordsGivenNormalProbability.MAPValue
val unusualWordGivenHasUnusualProbability =
params.unusualWordGivenManyProbability.MAPValue
val unusualWordGivenNotHasUnusualProbability =
params.unusualWordGivenFewProbability.MAPValue
Я
val wordGivenSpamProbabilities =
for { (word, param) <- params.wordGivenSpamProbabilities }
yield (word, param.MAPValue)
val wordGivenNormalProbabilities =
for { (word, param) <- params.wordGivenNormalProbabilities }
yield (word, param.MAPValue)
В
algorithm.kill()
В
new LearnedParameters(
spamProbability,
Й
no
i

3.6. Разработка компонента обучения
hasUnusualWordsGivenSpamProbability,
hasUnusualWordsGivenNormalProbability,
unusualWordGivenHasUnusualProbability,
unusualWordGivenNotHasUnusualProbability,
wordGivenSpamProbabilities.toMap,
wordGivenNormalProbabilities.toMap
)
g
О — Создать и выполнить экземпляр ЕМ-алгоритма, в котором для вычисления
вероятностей используется алгоритм РД. Число итераций в алгоритмах ЕМ и РД оставлено
подразумеваемым по умолчанию
© — Вычислить самое вероятное значение типа Double для каждого параметра-элемента
© — Для каждого слова-признака вычислить наиболее вероятное значение параметра,
т. е. вероятность присутствия слова в спамном сообщении, и аналогично для
нормальных сообщений. Поместить найденные значения в список пар (слово, значение)
© — Почистить за собой, уничтожив экземпляр алгоритма. Алгоритм нельзя уничтожать,
пока не будут получены МАВ-значения, поскольку после уничтожения они будут
неверны.
© — Вернуть экземпляр класса Learned Parameters, содержащий найденные в процессе
обучения параметры
Наконец, в компоненте обучения имеется метод main, который вызывается при
запуске из командной строки. Он принимает три аргумента: путь к каталогу,
содержащему все сообщения из обучающего набора, путь к файлу меток некоторых
обучающих сообщений и путь к файлу, в котором будут сохранены результаты
обучения. Сначала метод читает входные файлы и строит словарь. Затем создаются
модели всех сообщений. И наконец, метод выполняет алгоритм обучения и
сохраняет результаты. Впоследствии эти результаты могут быть многократно
использованы аналитическим компонентом.
Важно отметить, что параметры всех сообщений одинаковы. Однако элементы
в моделях различных сообщений различны. Например, у каждого сообщения свой
элемент is spam. Если бы это было не так, то этот элемент принимал бы одно и то
же значение для всех сообщений, т. е. все сообщения были бы либо спамными,
либо нормальными. С другой стороны, по структуре и параметрам модели всех
сообщений идентичны.
Ниже приведен код метода main.
Листинг 3.11. Метод main компонента обучения
def main(args: Array[String]) {
val trainingDirectoryName = args(O)
val labelFileName = args(l)
val learningFileName = args(2)
val emails = readEmails(trainingDirectoryName) ^3—©
val labels = readLabels(labelFileName)
in
s

Глава 3. Создание приложения вероятностного программирования
val dictionary = Dictionary.fromEmails(emails.values) O—©
val params = new PriorParameters (dictionary) i <|_Л
val models =
for { (fileName, email) <- emails }
yield {
val model = new LearningModel(dictionary, params)
email.observeEvidence(model, labels.get(fileName), true)
model
}
val learnedParameters = learnMAP(params) <]—©
saveResults(learningFileName, dictionary, learnedParameters) 0—©
}
О — Прочитать все сообщения из каталога, содержащего обучающий набор. Метод
readEmails (не показан) возвращает отображение имен файлов на экземпляры Email
© — Прочитать метки из файла меток. Метод readLabels (не показан) возвращает
отображение имен файлов на метки. Файлы, для которых нет меток, в этом
отображении не представлены
© — Построить словарь по значениям отображения emails (всем сообщениям)
© — Построить модели и сформировать наблюдаемые факты. Отметим, что у всех
моделей одинаковые априорные параметры, но разные экземпляры LearningModel. Еще
отметим, что для получения необязательного аргумента метода observeEvidence
используется метод labels.get(filename). Он возвращает None, если метки нет, и
Some(class), если метка есть и обозначает определенный класс
© — Выполнить алгоритм обучения
© — Сохранить результаты обучения в файле для аналитического компонента (метод не
показан)
Ну, вот и все. Мы рассмотрели всю процедуру создания полного приложения:
разработку архитектуры, проектирование модели, реализацию аналитического
компонента, а затем и компонента обучения. Сейчас вы знаете об основных
возможностях Figaro и располагаете более-менее приличными средствами для
написания приложений.
В следующей части книги мы рассмотрим моделирование более детально.
Сначала мы отступим на шаг назад и углубим понимание вероятностных моделей и
вывода, а затем разберем различные способы использования Figaro для создания
развитых практически полезных вероятностных моделей.
3.7. Резюме
• Вероятностные программы части применяются в приложениях, где
требуется обучить модель на данных, а затем многократно применять ее к новым
примерам.
• У многих вероятностных программ схожая архитектура, в которой
выделяются два компонента: аналитический и обучения.
112

3.8. Упражнения
В обоих компонентах используется модель, включающая спецификацию
порождающего процесса, параметры этого процесса и дополнительные
знания.
Компоненту обучения передаются априорные параметры, а он на основе
данных определяет их истинные значения, которые затем используются в
аналитическом компоненте.
3.8. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
Упражнения к этой главе требуют от читателя размышлений общего характера.
Вам предлагается подумать о том, как бы вы спроектировали приложение с
вероятностными рассуждениями и компонентом обучения для решения реальной
задачи - по образцу примера из этой главы. Прорабатывая упражнения, обращайте
внимание на общую архитектуру и дизайн, не отвлекаясь на детали модели.
1. Вы разрабатываете поисковую систему, которая ищет изображения,
содержащие указанные объекты, даже если эти объекты явно не аннотированы
в изображении. Система содержит блок распознавания объектов, который
снабжает изображение меткой - аннотацией, содержащей сведения об
изображенных объектах. Вы решили разработать распознаватель как
приложение с вероятностными рассуждениями и компонентом обучения.
a. Набросайте архитектуру поисковой системы и опишите роль
распознавателя объектов.
b. Набросайте архитектуру аналитического компонента. Каковы вход и
выход распознавателя? Возможно, вы захотите работать не с
пикселями, а сначала извлечь высокоуровневые признаки, например
гистограмму распределения цветов и выделенные границы. Как это
укладывается в архитектуру?
c. Набросайте архитектуру компонента обучения. Каковы входы и
выходы? Как результаты обучения передаются аналитическому
компоненту?
2. Вы проектируете компонент охранного приложения, задача которого -
распознавать аномальную активность в сети универсама. Вы решили, что
аномальной считается активность, имеющая низкую вероятность. Вы
хотите обучить вероятностную модель сетевой активности. Всякий раз,
замечая некоторую активность в сети, система вычисляет ее вероятность. Если
вероятность оказывается низкой, то система сигнализирует об аномалии.
a. Каковы входы и выходы детектора аномалий и как он вписывается в
структуру охранного приложения?
b. При таком дизайне не существует переменной, представляющей
класс активности. Вместо этого вы создаете вероятностную модель,
основанную на переменных, описывающих активность. Что это могут
из

быть за переменные? Какие между ними существуют связи и
зависимости?
с. Что должно входить в состав обучающих данных для детектора
аномалий? Какого рода знания можно получить в результате обучения на
этих данных?
Вы проектируете программу для игры в покер. Перед ней стоят две задачи:
хорошо играть с противником в первый раз и улучшать игру со временем.
a. В покере есть два основных источника случайности: сдача карт и
действия игроков. Опишите некоторые переменные, связанные с вашей
программой, и каждую пометьте источником случайности. Как вы
думаете, почему с точки зрения обучения следует различать,
обусловлена переменная сдачей карт или действиями игроков?
b. Для программы игры в покер нужны два вида обучения. Во-первых,
она должна знать, как вообще играют люди. Это поможет ей при
первой встрече с соперником. Во-вторых, в ходе нескольких игр против
одного и того же соперника программа должна обучаться
особенностям его манеры игры. Опишите архитектуру системы обучения,
которая решала бы обе эти задачи. Какая информация передается
между различными компонентами?
114
Глава 3. Создание приложения вероятностного программирования

Часть II
НАПИСАНИЕ
ВЕРОЯТНОСТНЫХ
ПРОГРАММ
Ч
.асть 2 целиком посвящена тому, как писать вероятностные программы,
описывающие любую интересующую вас ситуацию. Моя задача - не только
вооружить вас инструментами для разработки программ, но и добиться, чтобы вы
хорошо понимали, что эти программы означают и когда следует выбирать ту или иную
технику программирования. Глава 4 содержит введение в вероятностное
моделирование и основные идеи вероятностного программирования; хотя собственно
программирования в этой главе почти нет, она позволит заложить
принципиальный фундамент. В главе 5 представлены две основных парадигмы моделирования,
находящиеся в центре вероятностного программирования: байесовские и
марковские сети. Главы с 6 по 8 базируются на материале глав 4 и 5 и содержат
продвинутые методы моделирования, в т. ч. коллекции, объектно-ориентированное
программирование и моделирование динамических систем.

ГЛАВА 4.
Вероятностные модели
и вероятностные программы
В этой главе.
■ Определение вероятностной модели.
■ Как вероятностные модели используются для
ответа на запросы,
■ Ингредиенты вероятностной модели: переменные,
зависимости, функциональные формы и числа.
■ Как в вероятностной программе представлены
ингредиенты вероятностной модели.
Первая часть книги представляла собой введение в вероятностное
программирование. Мы узнали, что в системах вероятностных рассуждений вероятностная
модель используется для получения ответов на запросы при заданных фактах и что
вероятностное программирование - это создание программ для представления
вероятностных моделей. В этой части мы глубже изучим представление
вероятностных моделей и познакомимся с различными приемами написания вероятностных
программ.
Но сначала необходимо в общих чертах понимать, что такое вероятностная
модель, как она конструируется и как используется для ответов на запросы. Этим
вопросам и посвящена данная глава. Интуитивное понятие о предмете вы получили
в главе 1, теперь самое время заняться фундаментальными принципами.
В этой главе мы разовьем темы, затронутые в главе 1, поэтому полезно было
бы сначала ее прочитать. Здесь же будет описано, как в вероятностной
программе и, в частности, в программе на Figaro определяется вероятностная модель,
поэтому не помешает знакомство с базовыми сведениями о Figaro, изложенными
в главе 2.

4.1. Определение вероятностной модели
4.1. Определение вероятностной
модели
Вероятностная модель - это способ кодирования общих знаний о
неопределенной ситуации. Допустим, к примеру, что вы - искусствовед, пытающийся
определить, является ли некая картина подлинным Рембрандтом или подделкой. Вы
располагаете следующей информацией:
1. Рембрандт любил темные цвета.
2. Он часто рисовал людей.
3. Новые подлинники великих мастеров открывают редко, но подделок на
рынке пруд пруди.
4. На этой картине имеется большое пятно ярко-желтого цвета.
5. На картине изображен моряк.
6. Картина была продана на аукционе в 2003 году.
Пункты 1-3 - это общие знания, а пункты 4-6 - конкретные знания. Отметим,
что общие знания формулируются в виде тенденций: «любил», «часто», «редко»,
«пруд пруди», а конкретные предельно специфичны: «на этой картине», «на
картине изображен», «картина была продана». В вероятностном моделировании
общие знания представляются в виде вероятностной модели, которая применяется
к конкретным знаниям с целью рассуждения о конкретной имеющейся ситуации.
Конкретные знания также называют фактами, а то, что вы пытаетесь выяснить -
является ли картина подлинным Рембрандтом, - запросом. Таким образом, вы
применяете общие знания о живописи и Рембрандте, содержащиеся в
утверждениях 1-3, к фактам, сообщаемым в утверждениях 4-6, чтобы получить ответ на
запрос, является ли данная картина подлинником.
4.1.1. Выражение общих знаний в виде
распределения вероятности возможных миров
На рис. 4.1 приведены примеры общих знаний о предметной области. Общие
знания сообщают нам две вещи: (1) что является возможным и (2) что является
вероятным. Сначала поговорим о том, что возможно: при создании вероятностной
модели мы рисуем в воображении много возможных состояний дел - и каждое
называется возможным миром. Так, один из возможных миров - тот, в котором
картина является подделкой, другой - тот, в котором это подлинный ландшафт,
написанный Рембрандтом. Каждый возможный мир описывает одну из ситуаций,
которые вы считаете возможными до знакомства с фактами.
Например, ландшафт Рембрандта - один из возможных миров, пока вам не
предъявили факты. Позже, узнав, что на картине изображены люди, вы отвергнете
этот мир. Это хорошо сочетается с описанными нами различиями между общими
и конкретными знаниями. Возможный мир - то, что может произойти в принципе:
определение картины как ландшафта Рембрандта возможно. Факты
характеризуют то, что вам известно здесь и сейчас: это портретная живопись.
117

Глава 4. Вероятностные модели и вероятностные программы
Варианты,которые мы
считаем возможными
Знания об общих характеристиках
предметной области
г
Общие знания о предметной области
Возможности:
• Рембрандт или
подделка?
- Яркие или темные
цвета?
• Люди или ландшафт?
• В каком году продана?
Тенденции:
• Подделки встречаются часто,
подлинники Рембрандта редко
- Рембрандт любил темные цвета
• Рембрандт часто рисовал людей
Рис. 4.1. Общие знания о предметной области включают
знания о том, что возможно, и о том, что вероятно
Так, в нашей ситуации можно вообразить следующие возможные миры:
w1 - картина поддельная;
w2 - картина действительно написана Рембрандтом, это изображение людей в
темных тонах;
w3 - картина действительно написана Рембрандтом, это изображение людей в
ярких тонах;
w4 - картина действительно написана Рембрандтом, это изображение
ландшафта.
Отметим, что возможные миры - это то, что мы считаем возможным до
ознакомления с фактами. Важно понимать, что факты - не часть вероятностной
модели. Модель описывает общие знания. В вероятностных рассуждениях модель
используется для кодирования общих знаний и применяется к фактам о
конкретной ситуации с целью получить ответы на запросы об этой ситуации. Поскольку
факты не являются частью модели, а модель составлена из возможных миров, то
факты нельзя использовать для определения того, какими должны быть
возможные миры. Поэтому мы имеем, например, миры w2 и w4, хотя они и противоречат
фактам в утверждениях 4 и 5.
Теперь поговорим о второй составляющей общих знаний: что является
возможным? Для кодирования этой информации каждому возможному миру
сопоставляется число - его вероятность. В табл. 4.1 показано, как назначены вероятности
всем четырем возможным мирам. Сумма вероятностей всех миров должна быть
равна 1. Назначение вероятностей возможным мирам называется распределением
вероятности. Этим термином обозначается любое назначение вероятностей
мирам, вне зависимости от того, на каких знаниях оно базируется.
Таблица 4.1. Распределение вероятности возможных миров
Возможный мир
wl
Описание
Подделка
Вероятность
0.9
118

4.1. Определение вероятностной модели
Возможный мир
w2
wz
w4
Описание
Рембрандт, люди, темные
Рембрандт, люди, яркие
Рембрандт, ландшафт
Вероятность
0.09
0.009
0.001
Процесс представления общих знаний, включающих все мыслимые
возможности и применимые к ним тенденции, в виде распределения вероятности
возможных миров описан на рис. 4.2. Возможности диктуют определение возможных
миров, а тенденции - вероятности этих миров.
Варианты,которые мы
считаем возможными
Знания об общих характеристиках
предметной области
Общие знания о предметной области
Возможности:
■ Рембрандт или
подделка?
- Яркие или темные
цвета?
• Люди или ландшафт?
• В каком году продана?
Тенденции:
• Подделки встречаются часто,
подлинники Рембрандта редко
- Рембрандт любил темные цвета
■ Рембрандт часто рисовал людей
Возможные миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
Распределение
вероятности
00 © ©
0.9 0.09 0.009 0.001
Возможные миры описывают
все ситуации, считающиеся
возможными до ознакомления
с фактами
С каждым миром связана
вероятность. Сумма вероятностей
равна 1
Рис. 4.2. Знания о предметной области представлены в виде распределения
вероятности возможных миров. На этом рисунке величина вероятности
представлена размером соответствующего мира
Разобравшись с возможными мирами и распределением вероятности, можно
перейти к определению вероятностной модели. Вероятностная модель - это
формальное представление распределения вероятности возможных миров.
И это все. В определении не говорится, что вероятностная модель является
распределением вероятности. На самом деле, это лишь представление такого рас-
119

пределения. Само распределение - это математическая концепция явного
сопоставления числа каждому возможному миру Возможных миров может быть очень
много, а распределение сопоставляет вероятность каждому из них. Представление
же - это нечто, что можно записать, и с чем можно работать. Простейшая
вероятностная модель - это таблица, в которой явно перечислены вероятности
возможных миров, но, как мы увидим далее, модель может быть весьма компактной, пусть
даже количество миров огромно. В определении говорится, что представление
должно быть формальным. Это значит, что имеются точные правила определения
вероятности каждого мира, хотя явной формулы ее вычисления может и не быть.
Я определил вероятностную модель, но не описал, как ее создать - как описать
все возможные миры и их вероятности. Искусство и наука вероятностного
моделирования в том и состоят, чтобы представить распределение вероятности точно
и компактно. Как это делать, вы узнаете, читая книгу.
Узнав о важной роли распределений вероятности в вероятностном
моделировании, познакомимся с это концепцией поближе.
4.7.2. Подробно о распределении вероятности
Распределение вероятности несет информацию не только о вероятностях
возможных миров, но и о вероятностях различных фактов. Любой факт в одних мирах
имеет место, а в других - нет. Чтобы узнать вероятность этого факта, нужно
сложить вероятности тех миров, в которых он имеет место.
Например, рассмотрим факт - картина действительно написана
Рембрандтом. Этот факт имеет место в мирах wv w3 и wv но не в мире w{. Его вероятность
равна сумме вероятностей миров, в которых он имеет место, т. е. 0.09 + 0.009 +
0.001 =0.1. Поэтому мы говорим, что Рембрандт написал эту картину с
вероятностью 0.1, или - в разговорной речи - 10 %. Стандартно это записывается в виде
Р(Рембрандт) = 0.1. Изложенная концепция изображена на рис. 4.3.
Распределение вероятности до ознакомления с фактами принято называть
априорным распределением вероятности. Противоположностью ему служит
апостериорное распределение вероятности - после ознакомления с фактами.
Соответственно, величина Р(Рембрандт), вычисленная выше, называется априорной
вероятностью факта в противовес апостериорной вероятности, вычисляемой
после ознакомления с фактами. В следующем разделе мы увидим, как принимать в
расчет факты для нахождения апостериорной вероятности.
Возможные миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
-~""***""^ Распределение ^^^
вероятности
Q0 © ©
0.9 0.09 0.009 0.001
Вероятность, что картина
написана Рембрандтом
£
0.09
V
)©
©
*- 0,009 + 0,001 =0.1
J
Рис. 4.3. Вероятность факта равна сумме вероятностей возможных миров,
в которых этот факт имеет место
Глава 4. Вероятностные модели и вероятностные программы
120

4.2. Использование вероятностной модели для ответа на запросы
Существует много способов перебрать возможные миры и назначить им
вероятности. Распределение вероятностей, показанное в табл. 4.1 и повторенное в
табл. 4.2, соответствует общим знаниям, описанным в пунктах 1, 2 и 3 в начале
раздела. В пункте 3 говорится, что подделки встречаются чаще, чем
подлинники Рембрандта, и в нашем распределении подделка имеет место в мире wv
вероятность которого равна 0.9, а подлинники в остальных трех мирах с суммарной
вероятностью 0.1. В пункте 1 говорится, что Рембрандт любил темные цвета. И в
таблице мы видим, что мир w2 (Рембрандт, люди, темные) в 10 раз вероятнее мира
w3 (Рембрандт, люди, яркие). И хотя в оставшемся мире тл ничего не говорится о
цветах, в нашем распределении его вероятность крайне мала - всего 0.001.
Наконец, в пункте 2 говорится, что Рембрандт часто рисовал людей. Миры w2 и w3
согласуются с этим фактом, поэтому согласно нашей модели вероятность, что
картина написана Рембрандтом и на ней изображены люди, равна сумме вероятностей
w2 и wy т. е. 0.099. А вероятность, что ландшафт написан Рембрандтом, равна всего
0.001 - в 99 раз меньше, чем для картины с людьми.
Таблица 4.2. Все та же вероятностная модель. Подделка гораздо вероятнее
подлинника, поэтому вероятность w} больше, чем трех других миров вместе
взятых. Аналогично, если картина написана Рембрандтом, то на ней скорее будут
изображены люди, чем ландшафт, а темные тона гораздо вероятнее ярких
Возможный мир
иг,
w2
wz
w4
Описание
Подделка
Рембрандт, люди, темные
Рембрандт, люди, яркие
Рембрандт, ландшафт
Вероятность
0.9
0.09
0.009
0.001
В данном примере построить правдоподобную модель можно, не применяя
никаких методов, но в более сложных ситуациях эта затея наталкивается на
серьезные трудности. В разделе 4.3 мы начнем изучать структурированные методы
представления распределений вероятности.
Но прежде чем вдаваться в детали представления моделей, нужно в общих
чертах понять, как модели используются для рассуждений о конкретной ситуации.
4.2. Использование вероятностной
модели для ответа на запросы
Мы закодировали общие знания в виде распределения вероятности миров. Как
применить эту модель к фактам (конкретным знаниям) и получить ответ на
запрос? Например, мы знаем, что на картине есть большое ярко-желтое пятно, что
это портрет моряка и что она была продана на аукционе в 2003 году. Это факты.
Мы хотим узнать, написана ли картина Рембрандтом. Это запрос. Как с помощью
121

Глава 4. Вероятностные модели и вероятностные программы
модели вывести ответ на запрос при заданных фактах? Состояние наших знаний
сведено в табл. 4.3.
Таблица 4.3. Модель и факты - все наши знания о ситуации. Каждый факт
аннотирован его релевантностью модели
Модель
Подделка
Рембрандт, люди, темные
Рембрандт, люди, яркие
Рембрандт, ландшафт
0.9
0.09
0.009
0.001
Факты
Большое ярко-желтое пятно ==> Яркие
Портрет моряка ==> Люди
Продана в 2003 году (не релевантен)
4.2.7. Применение условий для получения
апостериорного распределения вероятности
Процедура использования распределения вероятности с целью учесть факты
называется применением условий, или обусловливанием. Результатом применения
условий является апостериорное распределение вероятности.
Процедура проста и состоит из двух шагов.
1. Исключить все возможные миры, не согласующиеся с фактами.
В данном случае таких миров два: wv в котором используются только
темные тона, и w4, в котором на картине изображен ландшафт. Вычеркиваем
эти меры, сопоставляя им вероятность 0. Тот факт, что картина была
продана на аукционе в 2003 году, не является поводом для вычеркивания - этот
факт не релевантен модели.
2. Увеличить вероятности оставшихся миров, так чтобы их сумма осталась
равной 1.
Это называется нормировкой вероятности. Смысл нормировки в том, что
вероятности вычеркнутых миров распределяются между оставшимися.
Вероятность каждого мира увеличивается пропорционально его
априорной вероятности. Например, раз априорная вероятность wx была в 100 раз
больше априорной вероятности wv то из суммы вероятностей вычеркнутых
миров на долю wx придется в 100 раз больше, чем на долю wy В результате
после распределения вероятность w{ по-прежнему будет в 100 раз больше
вероятности w3.
Существует математически простой метод корректной нормировки
вероятностей. Сначала вычислим сумму вероятностей миров, которые
совместимы с фактами и не вычеркнуты. Эта сумма называется нормировочным
коэффициентом. В нашем случае он равен 0.9 + 0.009 = 0.909. Затем
поделим вероятность каждого совместимого мира на нормировочный
коэффициент. Этим гарантируется, что сумма вероятностей по-прежнему равна 1,
а пропорции сохранены. В результате получится распределение
вероятности, показанное в табл. 4.4.
122

4.2. Использование вероятностной модели для ответа на запросы
Таблица 4.4. Апостериорное распределение вероятности после применения
условий. Сначала вероятности несовместимых миров обнуляются. Затем
оставшиеся вероятности нормируются путем деления на сумму вероятностей
совместимых миров. Тем самым гарантируется, что сумма вероятностей равна 1
Возможный мир
IV,
w2
W3
wA
Описание
Подделка
Рембрандт, люди, темные
Рембрандт, люди, яркие
Рембрандт, ландшафт
Вероятность
0.9/0.909 = 0.9901
0
0.009 / 0.909 = 0.0099
0
Применение условий, основанных на фактах, сводится к вычеркиванию
возможных миров, не совместимых с фактами, и нормировки вероятностей
оставшихся миров. Полученное распределение вероятности называется апостериорным,
поскольку оно вычислено после ознакомления с фактами. Весь процесс -
априорное распределение, применение условий и получение апостериорного
распределения - показан на рис. 4.4.
Факты
представляют
конкретные
знания о
ситуации
Распределение вероятности
до ознакомления с фактами
Возможные миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
Факты:
• Ярко-желтое пятно
• «Пьяный моряк»
• Продана на аукционе
в 2003 году
Совместимые миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
Вычеркиваем миры,
не совместимые
с заданными фактами
Распределение
вероятности после
применения условий,
основанных на фактах
Нормируем вероятности
оставшихся миров, чтобы
их сумма была равна 1
Рис- 4.4. Применение условий, основанных на фактах.
Мы вычеркиваем миры, не совместимые с фактами, и нормируем
вероятности оставшихся миров, чтобы их сумма была равна 1
123
Распределение
вероятности
0.9 0.09 0.009 0.001
Апостериорное
распределение вероятности
0.9/(0.9 + 0.009) 0.009/(0.9 + 0.009)

Глава 4. Вероятностные модели и вероятностные программы
4.2.2. Получение ответов на запросы
Как, зная апостериорное распределение, получить ответы на запросы? Нас
интересует, является ли Рембрандт автором картины. В предыдущем разделе было
сказано, что распределение вероятности задает не только вероятности отдельных
возможных миров, но и фактов, которые в одних мирах имеют место, а в других -
нет. Например, w3 - единственный возможный мир, совместимый с авторством
Рембрандта, для которого апостериорная вероятность больше 0. Поэтому
апостериорная вероятность того, что картина написана Рембрандтом, равна 0.0099.
Для записи ответа на запрос при условии известных фактов имеется
специальная нотация: Р(Рембрандт | ярко-желтый, портрет моряка, продана в 2003
году) = 0.0099. Здесь вертикальная черта (|) отделяет запрос от фактов. Слева от
черты находится событие, вероятность которого мы хотим знать, а справа -
известные факты. Такая нотация называется условной вероятностью, поскольку
представляет вероятность запрошенного события при условии некоторых фактов.
На рис. 4.5 показано, как устроена нотация условной вероятности.
Запрос Факты
Р(Rembrandt I bright yellow, picture of sailor, sold in 2003) = 0.0099
/
Символ условия Вероятность
Рис. 4.5- Строение нотации условной вероятности
Предупреждение. Если рассматривать только саму нотацию, то кажется, что можно
применить условия, основанные на фактах, которые мы считаем невозможными
(факты с нулевой вероятностью). Например, что произойдет, если попытаться указать в
качестве факта, что на картине изображен натюрморт, написанный Рембрандтом?
Предположим, что мы хотим запросить яркость картины. С применением нотации условной
вероятности надо было бы написать Р(яркая | натюрморт, Рембрандт). Но вероятность,
что натюрморт написан Рембрандтом, равна нулю, поскольку это не совместимо ни с
одним из возможных миров. Применяя условие, основанное на таком факте, мы
вычеркнем вообще все возможные миры. Следовательно, мы не сможем вычислить
апостериорное распределение вероятности и сказать, с какой вероятностью картина яркая.
В попытках придать смысл условной вероятности при невозможных условиях было
израсходовано немало чернил, но итог таков: этого следует избегать. Применение
условий, основанных на невозможных фактах, приводит к непредсказуемым результатам,
зависящим от конкретной системы вероятностного программирования.
На рис. 4.6 все идеи из двух предшествующих разделов сведены в общую
картину вероятностного моделирования. Общие знания о предметной области
представлены в виде распределения вероятности возможных миров. Конкретные
знания принимают вид фактов, которые используются для вычисления
апостериорного распределения вероятности. Наконец, апостериорное распределение
124

4.2. Использование вероятностной модели для ответа на запросы
используется для получения ответов на запросы об интересующих нас сведениях
в свете имеющихся фактов.
1. Варианты, которые мы
считаем возможными
2. Знания об общих характеристиках
предметной области
Общие знания о предметной области
Возможности:
" Рембрандт или
подделка?
• Яркие или темные
цвета?
" Люди или ландшафт?
• В каком году продана?
Тенденции:
" Подделки встречаются часто,
подлинники Рембрандта редко
• Рембрандт любил темные цвета
* Рембрандт часто рисовал людей
Возможные миры:
1. Подделка
2. Рембрандт, люди, темные|
3. Рембрандт, люди, яркие
4. Рембрандт, ландшафт
Факты:
• Ярко-желтое пятно
• «Пьяный моряк»
• Продана на аукцио-]
не в 2003 году
Распределение
вероятности
0.9 0.09 0.009 0001
Совместимые миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ланд-
шафт
Факты
представляют
конкретные
знания об этой
ситуации
Апостериорное
распределение вероятности
0,9/(0.9 + 0,009) 0.009/(0.9 + 0.009)
3. Распределение
вероятности до
ознакомления
с фактами
Вероятность, что
автор картины —
Рембрандт, при
заданных фактах
0.009/(0,9 + 0.009)
= 0.0099
Распределение вероятности
после применения условий,
основанных на фактах
6. Вероятность события при условии
имеющихся фактов равна сумме
вероятностей миров, совместимых
с этим событием
Рис. 4.6. Общая картина использования вероятностной модели
Основные определения
Возможные миры - все состояния, которые мы считаем возможными.
Распределение вероятности - сопоставление вероятности от 0 до 1 каждому
возможному миру, так что сумма всех вероятностей равна 1.
Вероятностная модель - формальное представление распределения вероятности
возможных миров.
Факты - имеющиеся знания о конкретной ситуации.
Априорное распределение вероятности - распределение вероятности до
ознакомления с фактами.
125
1
2
3
4
1
3
3

Глава 4. Вероятностные модели и вероятностные программы
Применение условий, основанных на фактах - процедура применения фактов к
распределению вероятности.
Апостериорное распределение вероятности - распределение вероятности после
ознакомления с фактами; результат применения условий.
Нормировка - процедура пропорционального изменения чисел из некоторого
множества, так чтобы их сумма стала равна 1.
Теперь вы знаете, что такое вероятностная модель и на каких принципах
основано получение ответов на вопросы. Но как все это выглядит на практике?
Возможных миров может быть очень много, поэтому проверка их совместимости с
фактами не всегда осуществима. Задача вероятностного алгоритма вывода -
эффективное получение ответов.
4.2.3. Применение вероятностного вывода
Основная задача вероятностного вывода - вычислить апостериорное
распределение вероятности представляющих интерес переменных при заданных фактах.
В нашем примере было легко вычеркнуть миры, не совместимые с фактами, и
нормировать вероятности оставшихся миров. В реальных же задачах число
возможных миров обычно очень велико, количество переменных модели может
расти экспоненциально. Поэтому миры нельзя даже выписать, что уж говорить о
вычислении их вероятностей. Нам необходим алгоритм вероятностного вывода,
умеющий эффективно вычислять апостериорные вероятности. Системы
вероятностного программирования и, в частности, Figaro включают такие алгоритмы.
Подобные алгоритмы основаны на трех правилах вероятностного вывода:
цепное правило, правило полной вероятности и правило Байеса. Подробно о них вы
узнаете в третьей части книги. А пока достаточно знать, что алгоритмы
вероятностного вывода сводятся к механическому применению этих правил и вытекающих
из них. Алгоритмы ориентированы на работу с конструкциями языка
вероятностного программирования, для которого определены, поэтому могут использоваться
даже в сложных программах на этом языке. Это одно из преимуществ
вероятностного программирования: если вы можете написать программу на некотором языке,
то можете применить в ней алгоритм вывода.
На практике алгоритм вероятностного вывода может столкнуться с
трудностями, даже если он в принципе работает. Легко написать обычную программу,
которая имеет экспоненциальную сложность и, стало быть, очень долго работает на
интересующих нас задачах. И с вероятностными программами точно так же - для
получения точного ответа алгоритму вывода иногда требуется много времени. Во
многих типичных применениях вероятностный вывод в вашей программе будет
работать так, как нужно. Однако в больших и сложных задачах даже самые
эффективные алгоритмы могут работать долго.
Алгоритмы вероятностного вывода могут быть точными или приближенными.
Точный здесь означает, что апостериорные вероятности вычислены в точном
соответствии с тремя правилами вывода. Поскольку точный вывод иногда обходится
126

4.3. Составные части вероятностных моделей
дорого, возникает нужда в приближенных алгоритмах, которые обычно - но не
всегда - дают ответ, близкий к точному.
В системах вероятностного вывода часто предлагается широкий ассортимент
алгоритмов для решения данной задачи - как точных, так и приближенных.
Некоторые из них еще и допускают настройку. На сложность вывода также
оказывает сильное влияние выбранный способ выражения модели. Поэтому, если вы
собираетесь использовать язык вероятностного программирования при создании
больших и сложных моделей, то стоит потратить некоторое время на то, чтобы
понять, как работает вероятностный вывод, и приобрести навыки выбора наиболее
эффективного алгоритма. Этим вопросам посвящена третья часть книги.
4.3. Составные части вероятностных
моделей
Вероятностная модель - это формальное представление распределения
вероятности, и таких представлений может быть много. Одно из них - таблица с явно
выписанными вероятностями, но оно пригодно разве что для самых простых задач.
В этом разделе мы познакомимся с общим, практически применимым подходом к
построению вероятностных моделей, включающих четыре составные части. Это
не единственный, но широко распространенный способ создания моделей. Он
также лежит в основе вероятностного программирования.
В главе 3 мы уже познакомились с четырьмя ингредиентами модели фильтра
спама, а здесь рассмотрим их более подробно.
• Переменные, например, является картина подлинным Рембрандтом или
подделкой.
• Зависимости между переменными, например, яркость красок зависит от
того, писал ли картину Рембрандт.
• Функциональные формы, которые принимают зависимости, например,
можно ли смоделировать подлинность картины как результат
подбрасывания асимметричной монеты.
• Числовые параметры этих форм, например, степень асимметрии монеты
при определении подлинности картины.
В следующих разделах мы увидим, как задается каждый ингредиент.
4.3.1. Переменные
Первым делом следует решить, какие переменные включать в модель. Как и в
языке программирования, переменная - это нечто, способное принимать различные
значения. Возможный мир определяет конкретные значения каждой переменной.
В любом возможном мире переменная имеет вполне определенное значение, но в
разных мирах ее значения могут различаться. Хотя выбор переменных - всего лишь
первый шаг построения вероятностной модели, здесь, как и в программировании,
127

Глава 4. Вероятностные модели и вероятностные программы
полная свобода творчества. Принимаемые на этом этапе решения оказывают
сильное влияние на эффективность модели.
В примере из раздела4.1 в описаниях возможных миров неявно подразумевались
следующие переменные:
• Рембрандт: является ли картина подлинным Рембрандтом или подделкой?
• Яркость: написана она в ярких или темных тонах?
• Тема: изображены люди или ландшафт?
Отметим, что мы не включили переменную, касающуюся продажи на аукционе.
Хотя она и входила в состав конкретных знаний, мы посчитали ее нерелевантной.
У каждой переменной есть тип, определяющий, какого рода значения она
может принимать. Непрерывные переменные принимают в качестве значений
вещественные числа (как переменные типа Double); например, высоту можно измерить
в сантиметрах. Существуют также перечисления, целые числа или структурные
переменные типа списков. Противоположностью непрерывным являются
дискретные переменные. Все переменные, с которыми мы до сих пор встречались,
были дискретными, более того - перечислениями. Переменные типа
перечисления часто называют категориальными. У переменной есть также область
значений, т. е. множество значений, считающихся допустимыми. Например, в модели
может присутствовать целая переменная, принимающая только значения от 1 до
10, в этом случае областью ее значений является множество целых чисел от 1 до 10.
В табл. 4.5 приведены примеры переменных, которые можно было бы
использовать в модели картины, вместе с типами и некоторыми возможными значениями.
Таблица 4.5. Примеры переменных, их типы и возможные значения
Переменная
Рембрандт
Размер
Высота (в см)
Год последней продажи
Годы всех продаж
Тип
Boolean
Enumeration
Real
Integer
List[Integer]
Примеры значений
true,false
малая, средняя, большая
25.3, 14.9,68.24
1937,2003
List(1937), List( 1969, 2003)
Между переменными вероятностной модели и вероятностной программы
существует очевидная связь. В Figaro элементы программы соответствуют
переменным модели, а типы их значений будут вычислительными представлениями
соответствующих типов модели. Например:
val rembrandt: Element[Boolean] = // здесь будет определение
val size: Element[Symbol] = // здесь будет определение
val height: Element[Double] = // здесь будет определение
val lastYearSold: Element[Int] = // здесь будет определение
val allYearsSold: Element[List[Integer]] = // здесь будет определение
Если известен набор переменных, то построить возможные миры проще всего,
создав таблицу, в которой будет по одному столбцу для каждой переменной и по
128

4.3. Составные части вероятностных моделей
одной строке для каждой возможной комбинации значений переменных.
Например, в табл. 4.6 перечислено восемь возможных миров с переменными Рембрандт,
Яркость и Тема.
Таблица 4.6. Возможные миры для переменных Рембрандт, Яркость и Тема.
Всего существует восемь комбинаций их значений и, следовательно, восемь миров
W,
w2
W3
W4
W5
we
w7
WB
Рембрандт
False
False
False
False
True
True
True
True
Яркость
Темная
Темная
Яркая
Яркая
Темная
Темная
Яркая
Яркая
Тема
Люди
Ландшафт
Люди
Ландшафт
Люди
Ландшафт
Люди
Ландшафт
4.3.2. Зависимости
Я говорил, что зависимости можно использовать для структурирования
распределения вероятности. Зависимости характеризуют, как переменные связаны между
собой. Интуитивно представляется, что распределение вероятности огромного
числа возможных миров можно разбить на локальные компоненты модели,
характеризующие эти связи.
В нашем примере есть три переменные: Рембрандт, Яркость и Тема. Как они
связаны? В вероятностном моделировании связи между переменными
характеризуются зависимостями, которые описывают, как значение одной переменной
зависит от значений других. Не менее чем зависимости, важны отношения
независимости, описывающие ситуации, когда значение некоторой переменной вообще
не зависит от значения какой-то другой переменной.
Отношение независимости
Две переменные независимы, если знание одной ничего не говорит о другой.
Например, допустим, что есть еще переменная Размер (с допустимыми
значениями Малая, Средняя и Большая), описывающая размер картины. Что означает
фраза «Размер не зависит от Яркости»? У нее есть совершенно точный смысл.
Рассмотрим какое-нибудь значение Яркости, например, Темная. Пусть
известна априорная вероятность Р(Яркость = Темная). Теперь рассмотрим
произвольное значение Размера, например, Большая. Спрашивается, дает ли знание того,
что Размер = Большая, какую-то дополнительную информацию об истинности
утверждения Яркость = Темная. В данном случае фактом является утверждение
Размер = Большая, а запросом - утверждение Яркость = Темная, поскольку нас
129

Глава 4. Вероятностные модели и вероятностные программы
интересует именно его истинность. Если применить к модели условие Размер =
Большая, то получится апостериорная вероятность Р(Яркость = Темная | Размер =
Большая). Так вот, если переменные Яркость и Размер независимы, то
апостериорная вероятность будет совпадать с априорной. Знание того, что картина
большая, ни на йоту не изменяет нашей веры в том, что она написана в темных тонах.
Чтобы Яркость и Размер были независимы, это утверждение должно выполняться
при любых значениях этих переменных. Должны быть справедливы следующие
равенства (как их читать, объяснено на рис. 4.7).
Р(Яркость = Темная | Размер = Большая) = Р(Яркость = Темная)
Р(Яркость = Темная | Размер = Средняя) = Р(Яркость = Темная)
Р(Яркость = Темная | Размер = Малая) = Р(Яркость = Темная)
Р(Яркость = Яркая | Размер = Большая) = Р(Яркость = Яркая)
Р(Яркость = Яркая | Размер = Средняя) = Р(Яркость = Яркая)
Р(Яркость = Яркая | Размер = Малая) = Р(Яркость = Яркая)
Вероятность, что Яркость = Темная Вероятность, что Яркость =
при условии, что Размер = Большая Темная безо всяких условий
Р(Яркость = Темная I Размер = Большая) = Р(Яркость = Темная)
Запрос Символ Факт
условия
Рис. 4.7. Объяснение равенства, описывающего отношение независимости
Независимость - симметричное свойство. Если известно, что знание размера
картины не сообщает никакой новой информации о ее яркости, то верно и
обратное: знание яркости ничего не говорит о размере. В математических обозначениях
из того, что
Р(Яркость = Темная | Размер = Большая) = Р(Яркость = Темная)
следует, что
Р(Размер = Большая | Яркость = Темная) = Р(Размер = Большая)
Уравнение независимости иллюстрируется на рис. 4.8. Мы начинаем с
априорного распределения вероятности Размера и Яркости. Вероятность, что Яркость =
Темная, равна сумме вероятностей всех возможных миров, в которых Яркость =
Темная, т. е. 0.8. Затем мы наблюдаем факт Размер = Малая и вычеркиваем
несовместимые с ним миры. Нормируя вероятности оставшихся миров, мы вычисляем
апостериорную вероятность, что Яркость = Темная. Она оказывается равной 0.8,
т. е. такой же, как до наблюдения факта. Легко видеть, что для любого значения
Размера отношение вероятности мира, в котором Яркость = Темная, к вероятности
130

4.3. Составные части вероятностных моделей
мира, в котором Яркость = Яркая, равно 4:1. Поскольку отношение вероятностей
одинаково, то наблюдение конкретного значения Размера не изменяет отношение
Темной к Яркой по сравнению с априорным распределением.
Факт
• Размер=
Малая
Размер Яркость Вероятность
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Средняя-
Средняя -
Большая-
Большая -
Темная
Яркая.
Темная
Яркая
Темная
Яркая
0.2
0.05
0.2
0.05
0.4
0.1
Размер Яркость Вероятность
Темная
Яркая
I емная
0.2
0.05
-&т2—
Яркая-
-Темная-
-&S5-
-&4-
-Вркая-
-9+
Р(Яркость = Темная):
0.2 + 0.2 + 0.4 = 0.8
Р(Яркость = Темная | Размер = Малая):
0.2 / (0.2 + 0.05) = 0.8
Рис. 4.8- Независимость: вероятность, что Яркость = Темная,
не изменяется после ознакомления с фактом Размер = Малая
Условная независимость
Следующий шаг - рассмотреть случай, когда связь между двумя
переменными зависит от того, что мы уже знаем. Бывает, что две переменные не являются
независимыми, если никакой дополнительной информации нет, но становятся
таковыми после добавления информации. Например, мы можем сказать, что
ландшафты чаще бывают большими и яркими. Тогда переменные Размер и Яркость не
являются независимыми, поскольку знание того, что картина большая, повышает
нашу веру в том, что это ландшафт, а это, в свою очередь, увеличивает шансы, что
картина яркая. С другой стороны, если мы уже знаем, что на картине изображен
ландшафт, то известие о том, что она большая, не дает новой информации о типе
картины и потому не изменяет нашу веру в том, что она яркая. В таком случае мы
говорим, что Яркость и Размер условно независимы при условии Тема = Ландшафт.
Можно выписать такие равенства:
Р(Яркость = Темная | Размер = Малая, Тема = Ландшафт) =
Р(Яркость = Темная | Тема = Ландшафт)
Подобные равенства можно написать для всех возможных значений Яркости,
Размера и Темы.
131

Глава 4. Вероятностные модели и вероятностные программы
Факт
• Размер=
Малая
Р(Яркость=Темная | Тема=
Ландшафт, Размер = Малая) =
0.015/(0.15 + 0.35) =
0.3
Тема
Размер Яркость Вероятность
Люди
Люди
Люди
Люди
Люди
Люди
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Средняя
Средняя
Большая
Большая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
0.16
0.04
0 16
0+04
032
0.08
0.015
0.035
0.03
0.07
0.015
0.035
Р(Яркость = Темная) =
0.16 + 0.16 + 0.32 +
0.015 + 0.03 + 0.015 = 0.7
Тема
Размер Яркость Вероятность
-Люди
-Люди
—Малая -
-Темная-
-вгНЗ-
-Мэлэя-
-Люди
-Люди
-Средняя Темная-
-е^-
-е-46-
Люди
Люди
-Средняя Яркая-
Большая Темная-
-Ъ&г-
-Gt32-
Ландшафт
Ландшафт
Малая
Малая
Яркая —
Темная
Яркая
-Тетч
-9:08-
0.015
0.035
-Ландшафт—Средняя Темная 9т9в—
-Ландшафт—Средняя Яркая &9?—
-Ландшафт—Большая Темная 0015
Ландшафт—Большая Яркая 0035
Факт
• Тема =
Ландшафт
Р(Яркость = Темная |
Тема = Ландшафт) =
0.015 + 0.03 + 0.015/
(0.015 + 0.03 + 0.015 +
0.07 + 0.015 + 0.035) =
0.3
Тема
Размер Яркость Вероятность
-Люди
-Люди
-Малая-
-Темная-
-6т4€-
"Малая-
-л ркв
-Ы±-
Люди
Люди
-Средняя Темная-
-fr46-
Люди
-Люди
Средняя Яркая —
"Ьольшая I емная-
-0:0^
-&32-
"Ьоль
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Малая
Малая
Средняя
Средняя
Большая
Большая
-Яркая-
Темная
Яркая
Темная
Яркая
Темная
Яркая
-От£в-
0.015
0.035
0.03
007
0015
0.035
Рис. 4.9. Условная независимость: факт Тема = Ландшафт изменяет
нашу веру в то, что Яркость = Темная, но следующий факт Размер = Малая
не дает новой информации
Чтобы понять это равенство, представим себе двухшаговую процедуру,
показанную на рис. 4.9. В начале мы ничего не знаем о картине и имеем априорное
распределение вероятности Темы, Размера и Яркости. Согласно этому распределению,
Р(Яркость = Темная) = 0.7. Затем мы наблюдаем факт Тема = Ландшафт и
вычисляем апостериорное распределение вероятности Р(Яркость = Темная | Тема =
Ландшафт) = 0.3. Согласно априорному распределению, ландшафты бывают
темными реже, чем портреты, поэтому знание факта Тема = Ландшафт уменьшило
нашу веру в то, что Яркость = Темная. А теперь хитрость: это апостериорное
распределение становится априорным распределением для следующего
наблюдаемого факта: Размер = Малая. Мы вычисляем новое апостериорное распределение,
132

4.3. Составные части вероятностных моделей
согласно которому Р(Яркость = Темная | Размер = Малая, Тема = Ландшафт)= 0.3,
т. е. дополнительный факт Размер = Малая не дал никакой информации о Яркости
в дополнение к той, что мы уже имели после ознакомления с фактом Тема =
Ландшафт. Внимательно взглянув на априорное распределение, мы заметим, что в
нижней части таблицы, где Тема = Ландшафт, отношение Темной Яркости к Яркой
везде равно 3:7, тогда как в верхней половине, где Тема = Люди, оно равно 4:1. Эти
отношения различны, но после фиксации Темы отношение тоже становится
фиксированным, так что Размер и Яркость условно независимы при условии Темы.
Кодирование зависимостей в вероятностной программе
Зависимостям посвящена глава 5. Там в качестве представления в основном
используются байесовские сети. Сейчас я хочу дать их предварительное описание.
Одна из сквозных тем этой книги заключается в том, что зависимости между
переменными можно закодировать в виде сети, в которой от родительской
переменной к дочерней направлена стрелка, если значение родителя влияет
на значение потомка. В нашем примере можно представить себе, что художник
сначала выбирает Тему картины, а это влияет на Размер и Яркость, но друг на друга
Размер и Яркость не влияют. Эти связи улавливаются сетью на рис. 4.10. Ребра в
байесовской сети всегда направлены от родителя к потомку, и обычно наличие
ребра означает, что родитель как-то влияет на потомка. В главе 5 рассматриваются
детали эти причинно-следственных связей и правила изображения байесовской
сети.
Размер зависит
от Темы
Яркость зависит от
Темы, но не зависит от
Размера
Рис. 4.10. Простая байесовская сеть, отражающая условную
независимость Размера и Яркость при условии заданной Темы
Сеть, в которой таким образом показаны зависимости между переменными,
называется байесовской сетью. Узлы сети соответствуют переменным модели,
и два узла соединены ребром, если первый влияет на второй. Как станет ясно в
главе 5, в байесовской сети хранится очень много информации о зависимостях,
существующих в модели.
Структура байесовской сети естественно транслируется в структуру
вероятностной программы. Если одна переменная является родителем другой в сети, то
133

Глава 4. Вероятностные модели и вероятностные программы
первая влияет на вторую. В обычной программе мы считаем, что одна переменная
влияет на другую, если первая встречается в определении второй. Точно так же
обстоит дело и в вероятностном программировании: если в байесовской сети
существует ребро, ведущее из одной переменной в другую, то первая будет входить в
определение второй. Это одна из фундаментальных связей между вероятностным
моделированием и программированием, благодаря которой вероятностное
программирование вообще возможно.
Уяснив этот момент, уже просто понять, как представляются зависимости в
вероятностных программах. В Figaro программа имеет следующую структуру:
val subject = // определение
val size = // в определении используется subject
val brightness = // в определении используется subject
Важно, что в определении brightness не используется size. В главе 5 мы узнаем,
что таким образом отражается факт условной независимости brightness от size
При УСЛОВИИ subject.
Сейчас у нас есть четыре переменных, и мы знаем их зависимости, выраженные
в виде сети. Но мы еще не знаем, как выглядят эти зависимости и какую форму
они принимают. Для описания этих аспектов нужны еще два ингредиента:
функциональные формы и числовые параметры.
4.3.3. Функциональные формы
Итак, мы выбрали переменные и описали их зависимости в виде сети. Я уже
говорил, что зависимости - ключ к описанию распределения вероятности
нескольких переменных с помощью простых компонентов. Эти компоненты
должны характеризовать переменные только в терминах тех переменных, с которыми
они связаны. Следующий шаг - определить точные формы компонентов,
характеризующих такие связи. Для примера на рис. 4.10 нам надо было бы описать,
как выбирается значение Темы и как оно используется для выбора значений
Размера и Яркости.
Базовые функциональные формы
Начнем с первого вопроса: как выбирается значение Темы. Поскольку Тема ни
от каких переменных не зависит, то нужно всего лишь задать распределение
вероятности ее значений. В нашем примере тип Темы - перечисление, она может
принимать два значения: Люди и Ландшафт, вот их вероятности и нужно задать.
Явное задание вероятностей - самый простой способ описать распределение
вероятности. Но если значений много или непосредственно выразить вероятности
затруднительно, то такой подход неосуществим.
Вместо этого распределение вероятности часто задается в виде одной из
стандартных функциональных форм. Вообще говоря, выбор формы зависит от типа
переменной. У каждой формы имеются специфические свойства, и каждая рас-
134

4.3. Составные части вероятностных моделей
считана на определенное применение. Чтобы выбрать форму, подходящую для
приложения, нужно понимать, как различные формы используются.
Например, для непрерывных переменных нередко применяется нормальное
или экспоненциальное распределение. А для целочисленных переменных -
биномиальное и геометрическое распределение. В этой книге мы, как правило, не
будем вдаваться в детали конкретных функциональных форм. На эту тему есть
масса материалов, в том числе и в википедии.
В Figaro имеются представления многих функциональных форм, мы видели это в
главе 2. Для представления формы одной переменной обычно используется
атомарный элемент. Например, элемент select представляет явное назначение
вероятностей с заданным средним и дисперсией, а элемент Binomial - биномиальное
распределение с заданными числом испытаний и вероятностью успеха в одном испытании.
Условные распределения вероятности
Ну а что сказать о двух других переменных - Размер и Яркость, - зависящих
от Темы? Для них недостаточно просто задать базовую функциональную форму,
нужно еще определить, как изменяется распределение вероятности для разных
значений Темы. С этой целью мы определяем условное распределение
вероятности, т. е. для каждого значения Темы задается распределение вероятности
Размера. Например, задается вероятность, что Размер = Большая при условии Тема =
Ландшафт, или в нашей нотации Р(Размер = Большая | Тема = Ландшафт). Проще
всего это сделать, задав для каждого возможного значения Темы
соответствующую функциональную форму Размера.
В нашем примере Размер является перечислением, поэтому функциональная
форма естественно принимает вид явного задания вероятностей. Представить
условное распределение Размера при условии Темы можно в табличном виде, как
показано в табл. 4.7. Я пользуюсь стандартным представлением, в котором
показана зависимая переменная и переменные, от которых она зависит. Последние
находятся слева. В данном случае независимая переменная всего одна, Тема, и она
занимает левый столбец. Но можно представить себе модель, в которой одна
переменная зависит от нескольких, тогда все они располагались бы слева. Справа мы
видим переменную, для которой определяется условное определение, под каждое
возможное значение отведен отдельный столбец. Здесь зависимая переменная
Размер принимает три значения: Малая, Средняя и Большая. Для каждого
возможного значения зависимой переменной имеется отдельная строка. У нас таких
значений два: Люди и Ландшафт. Если бы независимых переменных было
больше, то в таблице было бы по одной строке для каждой комбинации их возможных
значений. Наконец, в ячейке на пересечении строки г и столбца^ находится
вероятность того, что зависимая переменная принимает значение в столбце^ при
условии, что независимые имеют значения, указанные в строке L Например, в ячейке
(Люди, Малая) находится вероятность Р(Размер = Малая | Тема = Люди). Я
сопоставил вероятностям метки от pi до рб, которые используются во фрагменте кода
ниже и позволяют сравнить код с таблицей.
135

Глава 4. Вероятностные модели и вероятностные программы
Таблица 4.7. Форма условного распределения вероятности Размера
при условии Темы
Тема
Люди
Ландшафт
Размер
Малая
р1 = Р( Размер = Малая |
Тема = Люди)
р4 = Р( Размер = Малая |
Тема = Ландшафт)
Средняя
р2 = Р( Размер = Средняя |
Тема = Люди)
р5 = Р( Размер = Средняя |
Тема = Ландшафт)
Большая
рЗ = Р(Размер = Большая |
Тема = Люди)
рб = Р(Размер = Большая |
Тема = Ландшафт)
В Figaro условное распределение вероятности можно реализовать с помощью
составного элемента, который точно описывает, как одна переменная зависит от
других. В главе 2 мы видели, что в общем виде определить произвольную
функциональную зависимость между независимой переменной и элементом над
зависимой переменной позволяет составной элемент chain. Но существует также много
конкретных функциональных форм.
Одна полезная форма, естественно, называется cpd (conditional probability
distribution - условное распределение вероятности). В Figaro ее можно
использовать следующим образом:
val size = CPD(subject,
fpeople -> Select (pi -> 'small, p2 -> fmedium, p3 -> flarge),
'landscape -> Select(p4 -> 'small, p5 -> 'medium, рб -> 'large)
)
Переменные Scala pi,..., рб представляют числовые вероятности, о которых мы
будем говорить в следующем разделе.
Примечание. Одиночная кавычка ' означает, что дальше идет символ. Символом в
Scala называется уникальное имя чего-то. Например, символ 'small имеет одно и то
же значение всюду, где встречается, и отличается от значения любого другого символа.
Символы можно только сравнивать между собой на равенство. Они полезны, когда
требуется создать конечный набор значений переменной.
Форму cpd можно использовать и когда переменных больше двух. Например,
допустим, что переменная Цена зависит от того, написана ли картина
Рембрандтом, и от ее темы. В этом случае можно написать такую форму:
val price = CPD(rembrandt, subject,
(false, 'people) -> Flip(pi),
(false, 'landscape) -> Flip(p2),
(true, 'people) -> Flip(p3),
(true, 'landscape) -> Flip(p4)
Конструктор cpd принимает два набора аргументов:
1. Родители определяемой переменной. Их может быть не больше пяти.
136

4.3. Составные части вероятностных моделей
2. Несколько ветвей, число которых зависит от возможных значений
родителей. Каждая ветвь (clause) включает условие - комбинацию значений
родителей - и результирующий элемент. Например, в первой ветви cpd
для size условием является 'people, а результатом - элемент select (pi ->
'small, p2 -> 'medium, рЗ -> ' large). Это Означает, ЧТО еСЛИ subject paBHO
'people, ТО Значение size Выбирается В СООТВетСТВИИ С Элементом Select.
Если родитель всего один, то условие состоит просто из значения
родителя. Если же родителей несколько, то условием будет кортеж значений
каждого родителя. Например, в первой ветви cpd для price условие имеет
вид (false, 'people), т. е. ветвь применяется, когда переменная rembrandt
равна false, а переменная subject равна 'people.
Другие способы задания зависимостей в Figaro
В Figaro имеется также конструктор RichCPD, позволяющий представить
условные распределения вероятности гораздо более компактно - не выписывая
целиком всю таблицу. RichCPD похож на cpd, но условие в каждой ветви описывает
множество возможных значений, а не одно значение. Множество можно задать
одним из трех способов: (1) oneof (values) означает, что ветвь применяется, если
родитель принимает любое из перечисленных значений; (2) Noneof (values)
означает, что родитель не должен принимать ни одно из перечисленных значений;
(3) * означает, что ветвь применяется, если родитель принимает любое значение
в предположении, что у остальных родителей подходящие значения. Для
конкретного множества значений родителей выбирается первая подходящая
ветвь, которая и определяет распределение для элемента.
RichCPD полезен, когда имеются условные распределения вероятности с
несколькими родителями. Обычно число строк в условном распределении равно
произведению количества возможных значений каждого родителя. Если один
родитель может принимать два значения, второй - три, а третий - четыре, то число
строк в условном распределении равно 2 х 3 х 4 = 24. Как видим, явно описывать
распределение, когда родителей несколько или они принимают достаточно много
значений, утомительно. Как раз для таких ситуаций и предназначена форма
RichCPD. Приведем пример:
val xl = Select (0.1 -> 1, 0.2 -> 2, 0.3 -> 3, 0.4 -> 4)
val x2 = Flip(0.6)
val у = RichCPD (xl, x2, <—©
(OneOf(l, 2), *) -> Flip(O.l), <3—©
(NoneOf(4), OneOf(false)) -> Flip(0.7), <3—©
(*, *) -> Flip(0.9)) <J—О
О — RichCPD с двумя родителями
© — Соответствует случаю, когда х1 равно 1 или 2, а х2 любое
© — Соответствует случаю, когда х1 — любое значение, кроме 4, а х2 равно false
© — Ветвь выбирается по умолчанию во всех остальных случаях
137

Глава 4. Вероятностные модели и вероятностные программы
Предупреждение. Важно, чтобы условия в конструкторах cpd и RichCPD покрывали
все значения родителей, имеющие ненулевую вероятность. В противном случае Figaro
не будет знать, что делать, когда встретится значение, не соответствующее ни одному
условию. Для cpd это означает, что таблица должна быть задана полностью, а для
RichCPD можно последней указать ветвь «по умолчанию», в которой для значения каждого
родителя задана *, - как в приведенном выше примере.
cpd и RichCPD - два явных способа записи зависимостей, полезные для
дискретных переменных. Но не думайте, что ничего другого в Figaro нет - это лишь самые
простые и явные методы. А в более общих случаях зависимости можно описать с
помощью элементов Apply и chain. Напомним (см. главу 2), что:
• Apply принимает в качестве аргументов элементы и функцию. Результатом
Apply является элемент, значение которого получено применением
функции к значениям аргументов. Таким образом, Apply определяет зависимость
между аргументами и результатом.
• chain принимает в качестве аргументов один элемент и функцию, которая
принимает значение этого элемента и возвращает новый элемент. То есть
результатом chain является элемент, значение которого порождается следующим
образом: взять значение аргумента, применить к нему функцию для
получения нового элемента и сгенерировать значение этого элемента. Таким образом,
chain также определяет зависимость между аргументом и результатом.
• Многие элементы, например if и составной Normal, определены с
использованием chain. Поэтому они тоже определяют зависимости.
До сих пор мы говорили о том, что такое функциональные формы, и убедились,
что Figaro предоставляет их в изобилии. Но без чисел, подставляемых вместо
параметров, это не более чем пустая оболочка. Поэтому к ним и перейдем.
4.3.4. Числовые параметры
Последний ингредиент вероятностной модели - числовые параметры.
Концептуально это самая простая часть. У любой функциональной формы имеются
некоторые параметры, вместо которых нужно подставить числа. Однако необходимо,
чтобы подставляемые значения были допустимы. Например, если явно задаются
вероятности, то их сумма должна быть равна 1. В табл. 4.8 показано конкретное
условное распределение вероятности Размера при условии Темы. Заметьте, что
суммы значений в каждой строке равны 1. Это обязательно, поскольку в строке
находится распределение вероятности Размера.
Таблица 4.8. Конкретное условное распределение вероятности
Размера при условии Темы
Тема
Люди
Ландшафт
Размер
Малая
0.5
0.1
Средняя
0.4
0.6
Большая
0.1
0.3
138

4.3. Составные части вероятностных моделей
Несмотря на концептуальную простоту, подстановка числовых значений на
практике может оказаться самым трудным шагом. Оценка вероятностей на основе
опыта - непростое дело. Напомним, что в начале этой главы приводились общие
экспертные суждения о картинах: Рембрандт «любил» темные тона, он «часто»
рисовал людей, открытие новых подлинников случается «редко», а подделок «пруд
пруди». Эксперт в предметной области с легкостью высказывает такие общие
суждения, но приписать им числовые значения - совсем другое дело. Рембрандт
«любил» темные тона - значит ли это, что Р(Яркость = Темная | Рембрандт =
True) = 0.73? Трудно сказать.
Но есть и две хорошие новости. Во-первых, как выясняется, во многих
случаях точные значения и не нужны. Ответы на запросы обычно оказываются
примерно одинаковыми, даже если числовые значения вероятностей немного
различаются. Например, если модель говорит, что Р(Яркость = Темная | Рембрандт =
True) = 0.77, то заключение о поддельности картины будет почти таким же, как в
случае, когда эта вероятность равна 0.73. Это, однако, уже не так, если вероятности
близки к 0. Переход от вероятности 0.001 к вероятности 0.0001 может радикально
изменить заключение. На границах диапазона важны порядки величины. С другой
стороны, эксперту проще дать оценку с точностью до порядка.
Во-вторых, эти числа обычно можно вывести из данных методами машинного
обучения. Пример мы видели в главе 3. Проблема в том, что для вывода
параметров из данных нужно задать какие то априорные значения. Но для них достаточно
минимальных предположений, и при наличии достаточно большого объема
данных априорные значения слабо влияют на окончательные. Вообще возможность
задавать априорные параметры - благо, т. к. это позволяет эксперту в предметной
области оказывать влияние на обучение. Если же экспертных знаний нет, то
можно задать нейтральные априорные значения, которые не будут смещать
результаты обучения ни в каком направлении.
В главах 9 и 12 мы узнаем об основных принципах выведения параметров из
данных. В главе 9 описываются два общих подхода к машинному обучению. В
первом - байесовском обучении - в модель включается распределение вероятности
самих значений параметров, и тогда для обучения параметров достаточно
обычного вероятностного вывода, в результате которого получается апостериорное
распределение их значений. Во втором подходе апостериорное распределение не
вычисляется, а генерируется детерминированная оценка значений параметров по
результатам обучения на данных. В главе 12 показано, как эти подходы
реализованы в Figaro.
Итак, мы рассмотрели все ингредиенты практического подхода к
представлению вероятностных моделей. Но один важный вопрос остался без ответа.
Предположим, что мы строим модель из этих ингредиентов. Как представить в ней
распределение вероятности возможных миров? В следующем разделе описываются
порождающие процессы, эта концепция очень важна для понимания
вероятностного программирования и представления вероятностных моделей.
139

Глава 4. Вероятностные модели и вероятностные программы
4.4. Порождающие процессы
Мы начали эту главу с определения вероятностной модели как формального
представления распределения вероятности возможных миров. В разделе 4.3 было
показано, как строить вероятностные модели из переменных, зависимостей,
функциональных форм и числовых параметров, и высказана мысль, что такой подход
к представлению - неотъемлемая часть вероятностного программирования. Для
ясного понимания смысла вероятностных программ остается замкнуть круг и
показать, как в определенных таким образом моделях задается распределение
вероятности возможных миров. Здесь нам не обойтись без концепции
порождающего процесса.
Вероятностное программирование опирается на аналогию между
вероятностными моделями и программами на языке программирования. Суть этой аналогии
в следующем.
• Вероятностные модели, например байесовские сети, можно рассматривать
как процесс порождения значений переменных. Этот процесс определяет
распределение вероятности возможных миров.
• Но и обычная, не вероятностная программа определяет процесс
порождения значений переменных.
• Объединяя то и другое, получаем, что вероятностная программа
пользуется языком программирования, чтобы описать процесс порождения
переменных, основанный на случайном выборе. Этот порождающий процесс и
определяет распределение вероятности возможных миров.
Последнее утверждение нуждается в обосновании. Я объясню, как байесовские
сети определяет распределение вероятности с помощью порождающего процесса.
А затем проведу аналогию с вероятностными программами.
Посмотрим, как байесовская сеть определяет процесс порождения значений
переменных. На рис. 4.11 воспроизведена сеть с рисунка 4.10 вместе с условным
распределением вероятности каждой переменной при условии переменной, от
которой она зависит.
Представим себе процесс порождения значений всех переменных в этой сети.
Нельзя породить значение переменной, пока не станут известны значения всех
переменных, от которых она зависит. Этот процесс иллюстрируется на рис. 4.12. Мы
начинаем с Темы, потому что она не зависит ни от каких переменных. Согласно
условному распределению вероятности Темы, значение Люди имеет вероятность
0.8, а значение Ландшафт - вероятность 0.2. Случайно выберем одно из этих
значений, соблюдая распределение вероятности. Допустим, что выбран Ландшафт.
Затем переходим к выбору Размера. Это можно сделать, потому что значение
переменной Тема, от которой зависит Размер, уже известно. Ищем в таблице
условного распределения вероятности Размера строку, соответствующую Ландшафту.
В ней значение Малая имеет вероятность 0.25, Средняя - 0.5, а Большая - 0.25.
Случайно выберем одно из трех значений, не забывая о вероятностях. Допустим,
выбрано значение Средняя.
140

4.4. Порождающие процессы
Значения вероятности Темы
Тема
Люди
0.8
Ландшафт
0.2
Значения вероятности Размера
при условии Темы
Значения вероятности Яркости
при условии Темы
Тема
Люди
Ландшафт
Малая
0.25
0.25
Размер
Средняя
0.25
0.5
Большая
0.5
0.25
Тема
Люди
Ландшафт
Яркость
Темная | Яркая:
0.8 0.2
0.3 0,7
Рис. 4-11. Байесовская сеть с тремя узлами и условные распределения
вероятности
1. Выбираем
значение Темы
из этой строки
РЕЗУЛЬТАТ:
Ландшафт
Значения вероятности Темы
Тема
Люди
0.8
Ландшафт
0.2
Значения вероятности Размера
при условии Темы
Значения вероятности Яркости
при условии Темы
Тема
Люди
Ландшафт
Размер
Малая Средняя Большая
0.25 0.25 0.5
0.25 0.5 0.25
;
Тема
Люди
Ландшафт
Яркость
Темная Яркая
0.8 0.2
0.3 0.7
Выбираем значение
Размера из этой строки
РЕЗУЛЬТАТ: Средняя
Строка условного
распределения вероятности,
соответствующая значению
Тема = Ландшафт
Выоираем значение
Яркости из этой строки
РЕЗУЛЬТАТ: Яркая
Рис. 4.12. Процесс порождения значений всех переменных в сети с тремя узлами.
Значение переменной порождается путем выбора значения с соблюдением
условного распределения вероятностей в строке, зависящей от значений родителей
141
Тема
Яркость ;
Размер
Тема
Яркость
Размер

Глава 4. Вероятностные модели и вероятностные программы
Наконец, мы выбираем значение Яркости. Делается это аналогично выбору
значения Размера, потому что Яркость зависит только от Темы. Допустим, выбрано
значение Яркая. В итоге сгенерированы значения всех трех переменных: Тема =
Ландшафт, Размер = Средняя, Яркость = Яркая.
В процессе порождения значений для каждой переменной есть несколько
возможностей. Можно нарисовать дерево, на котором все они будут изображены.
Такое дерево для нашего примера показано на рис. 4.13. В корне находится первая
переменная, Тема. Из нее исходят ветви для обоих возможных значений: Люди
и Ландшафт. Каждая ветвь аннотирована вероятностью ее выбора. Так, согласно
распределению вероятности Темы, ветвь Ландшафт помечена вероятностью 0.2.
Затем мы переходим к следующей переменной, Размер, которая находится в двух
узлах дерева, соответствующих различным выборам значения Темы. Из
каждого узла Размер исходят три ветви, соответствующие трем возможным значениям.
Отметим, что для разных узлов этим ветвям сопоставлены разные вероятности,
поскольку их значения берутся из разных строк таблицы условного
распределения Размера. На конце каждой ветви, исходящей из обоих узлов Размер,
находится узел Яркость с двумя исходящими ветвями, соответствующими значениям
Яркая и Темная. Вероятности, проставленные на этих ветвях, как и раньше, берутся
из соответствующих строк таблицы условного распределения Яркости. Отметим,
что для всех трех узлов в левой части вероятности ветвей одинаковы, и то же самое
верно для трех узлов в правой части. Объясняется это тем, что Яркость зависит
только от Темы и не зависит от Размера. А для трех узлов в левой части значение
Темы одно и то же.
Тема
Люди 0.8 J
Ландшафт 0.2
Размер
Размер
Малая 0,25
Большая 0,5
Малая 0,25
Средняя 0.25
I
Яркость Яркость Яркость Яркость
Темная 0,8
Темная 0,8;
Темная 0,8
Темная 0,3
Темная 0,3
Яркая 0,2 / Яркая 0,2 / Яркая 0.2 / Яркая 0.7 / Яркая 0.7
I / ' \ I ' \ I \ I ' \
0.16 0.04 0.16 0.04 0.32 0.08 0.015 0.035 0.03 0.07 0.015
Большая 0,25
Средняя 0.5
I
Яркость Яркость
Темная 0,3
Яркая 0,7
0.035
Вероятности возможных миров вычисляются путем перемножения
вероятностей на пути к миру. В сумме эти вероятности дают 1
Рис. 4.13. Дерево порождения для байесовской сети с тремя узлами
142

4.4. Порождающие процессы
Спускаясь по дереву на рис. 4.13, мы делаем выбор в каждом узле. Получается
последовательность выборов, изображенная на рис. 4.14. Путь в дереве
определяет один из возможных миров. Какова его вероятность? Ответ следует из цепного
правила - одного из правил вывода, о которых мы узнаем в третьей части.
Согласно этому правилу, вероятность мира равна произведению вероятностей ветвей,
выбиравшихся при порождении этого мира. В нашем примере вероятность мира
Тема = Ландшафт, Размер = Средняя, Яркость = Яркая равна 0.2 х 0.5 х 0.7 = 0.07.
Нетрудно доказать, что сумма вероятностей всех возможных миров равна 1.
Поэтому байесовская сеть определяет распределение вероятности возможных миров.
Теперь стало понятно, как байесовская сеть описывает процесс порождения
значений переменных. Но и программа на обычном языке программирования тоже
описывает процесс порождения значений переменных, только в ней нет места
случайному выбору. Стало быть, вероятностная программа похожа на обычную с тем
отличием, что процесс порождения значений включает случайный выбор.
Вероятностная программа напоминает байесовскую сеть, только для описания
порождающего процесса в ней используются конструкции языка программирования.
А раз в нашем распоряжении имеется язык программирования, то возможностей
гораздо больше, чем в байесовской сети. У нас есть средства управления потоком
выполнения, например циклы и функции, и сложные структуры данных такие, как
множества и деревья. Но принцип тот же самый: программа описывает процесс
порождения значений всех переменных.
Малая 0.25
Темная 0.8
Яркость
/
Тема
Люди 0.8
Ландшафт 0.2
Размер
Большая 0.5
Средняя 0.25
I
Яркость Яркость I Яркость
Темная 0.8 / \ Темная 0.8 / \ Темная 0.3 / \ Темная
Большая 0.25
Яркая 0.2
I
0.16
0.04
Яркая 0.2
\
0.16 0.04
Яркая 0.2
\
0.32 0.08
Яркая 0.7
\
0.015 0.035
Яркая 0.7
\
0.03 0.07
Яркая 0.7
\
0.015 0.035
Вероятность выбранного мира
равна 0.2 х 0.5 х 0.7 = 0.07
Рис. 4.14. Последовательность выборов и ее вероятность
Выполняя вероятностную программу, мы порождаем значения каждой
переменной, пользуясь определением, в котором указано, от каких переменных она
Малая 0.25
Размер
Средняя 0.5
Яркость
Яркость
Темная 0.3
143

■Illl
Глава 4. Вероятностные модели и вероятностные программы
зависит. По завершении программы переменные из некоторого набора получают
значения. Этот набор переменных вместе с порожденными значениями
определяет возможный мир. Как и в байесовской сети, вероятность этого мира равна
произведению вероятностей каждого случайного выбора.
Но существует и важное различие между вероятностными программами и
байесовскими сетями: набор переменных, которым программа присваивает значения,
может изменяться от прогона к прогону. Рассмотрим такую программу на Figaro:
Chain(Flip(0.5), (b: Boolean) => if (b) Constant(0.3) else Uniform(0, 1))
Элемент constant (0.3) создается, только если Flip принимает значение true,
а элемент uniform(0, 1) - если Flip равен false. Ни в каком прогоне программы
не могут быть созданы оба элемента. Тем не менее, каждый прогон дает
возможный мир с корректно определенной вероятностью. И хотя доказать это несколько
труднее, сумма вероятностей всех возможных миров по-прежнему равна 1.
Поэтому вероятностная программа описывает распределение вероятности возможных
миров.
Предостережение. На языке программирования можно написать программу, которая
никогда не завершается, и то же верно в отношении вероятностных программ. Если
существует ненулевая вероятность, что случайный процесс, определяемый вероятностной
программой, не завершится, то эта программа не определяет корректное
распределение вероятности возможных миров. Представьте вероятностную программу, в которой
определена рекурсивная функция, продолжающая вызывать себя до бесконечности;
процесс, описываемый такой программой, не завершается.
Теперь вы, надо думать, понимаете, что такое вероятностная модель и как ей
пользоваться. А равно и то, как вероятностная программа представляет все
составные части вероятностной модели. Прежде чем закончить эту главу, осталось
рассмотреть один технический вопрос: как использовать в вероятностной модели
непрерывные переменные?
4.5. Модели с непрерывными
переменными
В примерах вероятностных моделей, которым нам встречались до сих пор,
использовались дискретные переменные, значения которых далеко отстоят друг от друга,
как у перечислений и целых чисел. В то же время значения непрерывных
элементов не разделены промежутками - как в случае вещественных чисел. В главе 2 мы
мельком отмечали, что непрерывные переменные требуют другого обращения,
нежели дискретные, и обещали дать подробные объяснения позже. Теперь для этого
настало время.
Проблема заключается в том, что трудно определить распределение
вероятности всех значений непрерывного элемента. Рассмотрим произвольный интервал
вещественных чисел. Если приписать всем числам из этого интервал положитель-

4.5. Модели с непрерывными переменными
ные вероятности, то сумма вероятностей будет бесконечна. И это верно даже для
самого маленького интервала. Ну и как же тогда определять вероятности
непрерывных переменных? Ответ дается в этом разделе.
В качестве конкретного примера возьмем бета-биномиальную модель, которая
применяется во многих приложениях. В главе 3 мы использовали ее для описания
количества необычных слов в почтовом сообщении. А сейчас детализируем эту
модель, чтобы проиллюстрировать изученные выше идеи. Модель содержит
непрерывную переменную, и я объясню, как эту переменную представить, а попутно
мы поговорим о непрерывных переменных вообще.
4.5.1. Бета-биномиальная модель
Модель называется бета-биномиальной, потому что в ней одновременно
используется два распределения: бета и биномиальное. Рассмотрим простой пример.
Пусть имеется несимметричная монета, т. е. вероятность выпадения орла и решки
различна. Наша цель - предсказать вероятность выпадения орла при условии, что
известны результаты прошлых подбрасываний монеты. Допустим, что мы
наблюдали 100 подбрасываний и хотим узнать, с какой вероятностью в 101-ый раз
выпадет орел.
Сначала определим переменные. В этом примере их будет три:
• Степень асимметрии монеты, так и назовем ее Асимметрия.
• Сколько раз в предыдущих 100 подбрасываниях выпадал орел. Назовем эту
переменную ЧислоОрлов. Это целочисленная переменная, принимающая
значения от 0 до 100.
• Результат 101-го подбрасывания - Бросок101.
Модель зависимостей представлена байесовской сетью на рис. 4.15. Напомним,
что хотя мы выводим степень асимметрии из числа выпавших орлов,
зависимости в модели направлены в противоположную сторону. В причинно-следственном
смысле именно асимметрия монеты определяет результат подбрасывания, что, в
свою очередь, определяет число выпавших орлов, поэтому ребро и направлено от
Асимметрии к ЧислуОрлов.
Рис. 4.15. Байесовская сеть в примере с подбрасыванием монеты.
Результаты первых 100 подбрасываний представлены
в виде одной переменной, равной количеству выпавших орлов
Вы, наверное, задаетесь вопросом, почему нет ребра из ЧислаОрлов в Бросок101.
Ведь число орлов, выпавших в первых 100 подбрасываниях, дает информацию,
145
Ассиметрия
ЧислоОрлов
Бросок
10;

Глава 4. Вероятностные модели и вероятностные программы
имеющую прямое отношение к 101-му броску. Причина в том, что вся эта
информация поглощается асимметрией монеты. Первые 100 подбрасываний говорят нам
о степени асимметрии, а эта информация затем используется для предсказания
значения Броска10Г Если мы уже знаем степень асимметрии, то первые 100
подбрасываний к этому ничего не добавят. Другими словами, переменная Бросок101
условно независима от ЧислаОрлов при условии Асимметрии.
Теперь можно выбирать функциональные формы. Для каждой переменной у
нас будет своя форма. Начнем с Броскашг Это подбрасывание монеты, в
результате которого выпадает орел или решка. Тут подойдет одна из простейших форм.
Требуется только задать вероятность выпадения орла или решки. В нашем случае
вероятность орла определяется значением переменной Асимметрия. Орел
выпадает с вероятностью Асимметрия, а решка - с вероятностью 1 - Асимметрия.
В Figaro мы можем воспользоваться составным элементом Flip.
Далее нужна функциональная форма, характеризующая вероятность того, что
при 100 подбрасываниях выпадает заданное число орлов при условии, что
вероятность одного выпадения орла равна значению Асимметрии. В главе 2 мы видели,
что для этой цели подходит биномиальное распределение, которое описывает
результат повторения эксперимента, имеющего два возможных исхода. Оно
показывает, с какой вероятностью будет иметь место заданное число исходов одного
вида. В нашем примере это вероятность выпадения заданного числа орлов после
100 подбрасываний.
В общем случае биномиальное распределение зависит от двух параметров:
количества испытаний (в нашем примере - 100) и вероятности желаемого исхода
испытания (в нашем примере - выпадения орла). Зная эту вероятность, легко
вычислить вероятность выпадения заданного количества орлов, скажем 63. Но
в нашем примере эта вероятность определена значением переменной Асимметрия.
Нам нужна функциональная форма для Асимметрии. Вы, конечно,
догадались - по названию модели - что асимметрия будет подчиняться
бета-распределению. Вообще, бета-биномиальной называется вероятностная модель, которая
содержит биномиальную переменную, представляющую количество успешных
исходов испытаний таких, что вероятность успеха в одном испытании
определяется переменной, подчиняющейся бета-распределению.
Итак, мы знаем, что асимметрия имеет бета-распределение. Но в чем точный
смысл этого утверждения? Как все-таки определить распределение вероятности
непрерывной переменной?
4.5.2. Представление непрерывных переменных
Значением Асимметрии является вещественное число от 0 до 1, и это непрерывная
переменная. Для непрерывных переменных необходимо по-другому определять
распределение вероятности. Пусть, например, мы предполагаем, что высота
картины находится в пределах от 50 до 150 см и что нет оснований полагать, что одна
высота более вероятна, чем любая другая. Тогда область значений - диапазон от
50 до 150, и предполагается, что вероятность принадлежности этому диапазону
146

4.5. Модели с непрерывными переменными
распределена равномерно. Пусть мы хотим узнать, с какой вероятностью высота
картина в точности равна 113.296 см. Проблема в том, что возможных значений
высоты бесконечно много. Если бы у любой возможной высоты была
положительная вероятность, скажем 0.2, и мы считаем, что все значения высоты
равновероятны, то оказалось бы бесконечно много значений с вероятностью 0.2, так что сумма
всех вероятностей попадания в диапазон от 50 до 150 см была бы бесконечна. А мы
знаем, что полная вероятность должна быть равна 1.
Решение заключается в том, чтобы рассматривать не вероятности отдельных
значений высоты, а вероятности интервалов высот. Например, на вопрос, какова
вероятность, что высота находится между ИЗ и 114 см, можно было бы ответить
«1 из 100», потому что длина этого интервала равна 1, т. е. это один из 100
равновероятных интервалов такой длины. На самом деле, можно поинтересоваться
вероятностью любого, сколь угодно малого интервала вокруг значения 113.296.
Например, вероятность интервала от 113.2 до 113.3 равна 1 из 1000, интервала от
113.29 до 113.30 - 1 из 10 000 и т. д.
Итак, для непрерывных переменных вероятность отдельного значения обычно
равна 0. Рассмотрим степень асимметрии монеты. Вероятность, что она равна в
точности 0.49326486..., нулевая, поскольку значений бесконечно много. Но у
интервалов, содержащих значение, вероятность положительна. Например,
асимметрия может находиться в интервале от 0.49326 до 0.49327.
Существует математически корректный способ определить вероятность любого
интервала. Он изображен на рис. 4.16 и называется функцией плотности
распределения вероятности (ФПР). ФПР позволяет задать вероятность любого интервала.
Плотность задается в каждой точке. Если интервал мал, то плотность часто
оказывается приблизительно одинаковой в каждой его точке, поэтому вероятность
интервала равна значению этой константы, умноженному на длину интервала. На
рис. 4.16 показана равномерная ФПР, т. е. плотность всюду равна 0.01, поэтому
вероятность интервала единичной длины (ИЗ, 114) равна 0.01. Если функция
плотности распределения постоянна, то умножение этой константы на длину
интервала равно площади под кривой плотности на этом интервале. В общем случае
плотность в разных точках может быть различна. Но и тогда вероятность
интервала равна площади под кривой на этом интервале. Если вы еще не забыли
математический анализ, то знаете, что эта площадь равна интегралу от функции
плотности распределения на интервале. Я не стану в этой книге ни экзаменовать вас по
матанализу, ни вычислять площади под кривыми - Figaro об этом позаботится, но
я хочу, чтобы вы понимали различие между непрерывными и дискретными
распределениями и знали, что такое функция плотности.
Вернемся к нашему примеру. Мы ищем функциональную форму для
Асимметрии, для этого нужно задать ФПР. Мы знаем, что значение асимметрия -
число от 0 до 1, поскольку это вероятность, поэтому плотность должна быть равна
0 вне интервала (0, 1). Оказывается, что есть функциональная форма, прекрасно
подходящая как раз к этому случаю, - бета-распределение. Оно применяется для
моделирования вероятности определенного исхода в одном испытании, если
исходов всего два. На рис. 4.17 показан пример бета-распределения. Как видим, оно
147

Глава 4. Вероятностные модели и вероятностные программы
положительно в интервале от 0 до 1 и имеет один пик. Чуть ниже мы покажем, как
охарактеризовать местоположение и остроту этого пика.
Плотность
распределения
0.0 Н
Функция плотности распределения (ФПР)
Вероятность интервала
(113,114) = площадь
под кривой ФПР = 0.01
50 113114 150
Высота (см)
Рис. 4.16. Функция плотности распределения вероятности (ФПР):
вероятность интервала равна площади под кривой ФПР на этом интервале
Мы выбрали именно бета-распределение для характеристики асимметрии
монеты, потому что оно отлично уживается с биномиальным распределением.
Точнее, если имеется факт - ЧислоОрлов - и известно, что Асимметрия имеет
априорное бета-распределение, то ее апостериорное распределение после ознакомления с
числом выпавших орлов тоже будет бета-распределением. В третьей части книги
мы увидим, что это позволяет без труда предсказать исход 101-го подбрасывания.
Подведем итоги. У нас имеются следующие переменные и функциональные
формы:
• Асимметрия, характеризуемая бета-распределением;
• ЧислоОрлов, характеризуемое биномиальным распределением с общим
числом испытаний 100 и вероятностью выпадения орла в одном
испытании, равной значению Асимметрии;
• Бросок101, характеризуемый элементом шр, в котором вероятность
выпадения орла равна значению Асимметрии.
Программу на Figaro для этой модели можно начать так:
val bias = Beta(?,?)
val numberOfHeads = Binomial(100, bias)
val tosslOl = Flip(bias)
Теперь время выполнить четвертый шаг: выбрать числовые параметры. Из
заготовки программы видно, что параметры для переменных numberofHeads и tossioi
определяются значением bias, которой уже является элементом программы.
Остается задать только параметры bias. Для этого нужно понимать, как выбираются
параметры бета-распределения.
148

4.5. Модели с непрерывными переменными
У бета-распределения много вариантов, на рис. 4.7 изображен только один из
них. Каждый вариант характеризуется двумя числовыми параметрами: а и (3. на
рисунке показано распределение beta (2, 5), для которого а = 2, а (3 = 5.
Как выясняется, у а и (3 имеется естественная интерпретация. Это число
наблюдений каждого из двух исходов плюс 1. В нашем примере а - число выпавших
орлов плюс 1, а р - число выпавших решек плюс 1. Следовательно, априорные
значения а и (3 - до подбрасывания монеты - это наша гипотеза о поведении
монеты, выраженная в терминах воображаемых предыдущих подбрасываний. Если на
основе экспериментов с подобными монетами вы полагаете, что эта монета будет
чаще выпадать орлом, чем решкой, то можете задать а > р. И чем больше вы
доверяете своему опыту, тем больше будут значения аир.
Плотность
распределения
2.5
1.5 Ч
И
0.5
0
О СМ "^ Ю 00 .
О О О О q
о о о о
^с\1^сососчс\1^союсосч^<ода^сч^юдаюсч^ю»сосч^юдаг^сч^юда
Qr•т•^т-Q(^Jc^lc^^(^J^nAcocoQ^^тr^QlOюююQ<DЮ(o<DQN^^^QOOooooooQO><»o>0)
оооо оооо оооо оооо оооо оооо оооо оооо оооо
Асимметрия
Рис. 4,17. Функция плотности распределения beta (2, 5)
Так, на рис. 4.17, а = 2, (3 = 5. Из того, что (3 больше а, следует, что априорно мы
склонны считать, что асимметрия в пользу решки (вероятность выпадения орла
мала). И действительно, мы видим, что плотность вероятности малых значений
асимметрии (< 0.5) выше плотности вероятности больших значений (> 0.5).
Кроме того, такой выбор значений свидетельствует о том, что в воображаемом
эксперименте выпал один орел и четыре решки, и мы заложили в модель эти априорные
знания об асимметрии - потому-то ФПР не является постоянной функцией.
Ну, вот, наконец, и всё. Мы рассмотрели все четыре составные части
вероятностной модели и видели, как они представляются в вероятностной программе.
Теперь можно с головой погрузиться в методы моделирования и паттерны
проектирования. В следующей главе мы начнем детально обсуждать зависимости и две
системы их представления: байесовские и марковские сети.
149
2

Глава 4. Вероятностные модели и вероятностные программы
4.6. Резюме
• Вероятностные модели представляют общие знания о предметной области
в виде распределения вероятности возможных миров.
• Факты используются для исключения несовместимых с ними миров и
нормировки вероятностей оставшихся. В системах вероятностного
программирования для этого применяются алгоритмы вывода.
• Для построения вероятностной модели необходимо определить
переменные и их типы, задать зависимости между переменными в виде сети, а
также выбрать функциональную форму и числовые параметры для каждой
переменной.
• Функциональная форма непрерывной переменной задается в виде
функции плотности распределения вероятности.
• Составные части вероятностной модели определяют процесс порождения
значений всех переменных.
• В вероятностных программах порождающие процессы описываются на
языке программирования.
4.7. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Рассмотрим игру в покер с колодой из пяти карт: туз пик, король пик,
король червей, дама червей и дама пик. Каждый игрок получает по одной
карте. Каковы возможные миры? В предположении, что колода хорошо
перетасована, какова вероятность каждого возможного мира?
2. В той же игре мы наблюдаем факт: у одного игрока на руках картинка (дама
или король). Какова вероятность, что у другого игрока на руках пика?
3. Усложним правила этой игры, добавив торговлю. Правила торговли
таковы:
• Игрок 1 может сделать ставку или спасовать.
• Если игрок 1 делает ставку, то:
- игрок 2 может сделать свою ставку или сбросить карты.
• Если игрок 1 пасует, то:
- игрок 2 может сделать ставку или спасовать.
• Если игрок 2 делает ставку, то:
- игрок 1 может сделать свою ставку или сбросить карты.
Возможные исходы раунда торговли таковы: (1) оба игрока сделали
ставки; (2) оба игрока спасовали; (3) один игрок сделал ставку, а другой
спасовал. Если оба спасовали, то никто ничего не выиграл и не проиграл. Если
один сделал ставку, а другой сбросил карты, то сделавший ставку
выигрывает 1 доллар. Если оба сделали ставку, то игрок, имеющий на руках карту
150

1.7. Упражнения
более высокого достоинства, выигрывает 2 доллара. Если у обоих на руках
карты одного достоинства, то пики бьют червы.
Требуется построить вероятностную модель этой игры в покер. Цель
модели - помочь выбрать действие в любой момент игры, основываясь на
прогнозе развития событий при каждом действии.
a. Какие переменные будут в модели?
b. Каковы зависимости между переменными?
c. Каковы функциональные формы этих зависимостей?
d. Какие числовые параметры точно известны? А какие придется
оценивать или получать методами машинного обучения?
4. Напишите на Figaro программу, представляющую вероятностную модель
этой игры. Сделайте какие-нибудь предположения о значениях
параметров, подлежащих оцениванию. С помощью своей программы примите
следующие решения:
a. Вы игрок 1 и получили короля пик. Пасовать или поставить?
b. Вы игрок 2 и получили короля червей, противник поставил.
Поставить или сбросить карты?
c. Посмотрите, можно ли изменить значения оцениваемых параметров,
так чтобы программа подсказывала другие решения.
5. Опишите три разных последовательности выборов при выполнении
порождающего процесса в программе из упражнения 4. В предположении,
что выбраны параметры для первой версии программы, какова вероятность
каждой последовательности в отсутствие наблюдаемых фактов?
6. Вы подозреваете, что противник сдает нечестно. Точнее, вы полагаете, что с
некоторой неизвестной вероятностью р он сдает вам даму червей, а с
вероятностью 1 - р сдает карты случайно, с равномерным распределением. Вы
полагаете, чтор подчиняется бета-распределению Beta(l, 20). В 100 сдачах
вы 40 раз получили даму червей. С помощью Figaro вычислите, с какой
вероятностью следующая сданная карта окажется дамой червей.
151

ГЛАВА 5.
Моделирование зависимостей
с помощью байесовских
и марковских сетей
В этой главе.
в Типы связей между переменными в
вероятностной модели и как эти связи трансформируются в
зависимости,
в Как выразить различные типы зависимостей в
Figaro.
в Байесовские сети: модели, представляющие
направленные зависимости между переменными.
в Марковские сети: модели, представляющие
ненаправленные зависимости между переменными.
в Практические примеры байесовских и
марковских сетей,
В главе 4 мы узнали о связях между вероятностными моделями и вероятностными
программами, а также рассмотрели составные части вероятностной модели:
переменные, зависимости, функциональные формы и числовые параметры. В этой
главе мы займемся двумя системами моделирования: байесовскими и
марковскими сетями. Эти системы основаны на различных способах представления
зависимостей.
Зависимости отражают связи между переменными. Ясное понимание типов
связей и их трансформаций в зависимости вероятностной модели - одно из
важнейших умений проектировщика моделей. Вообще говоря, существуют два вида
зависимостей между переменными: направленные (асимметричные) и
ненаправленные (симметричные). Байесовские сети представляют направленные зависи-

5.1. Моделирование зависимостей
мости, а марковские сети - ненаправленные. Мы также узнаем, как язык
программирования позволяет обогатить байесовские сети и тем самым воспользоваться
всей мощью вероятностного программирования.
Усвоив материал этой главы, вы получите твердые знания об основах
вероятностного программирования. Все вероятностные модели сводятся к набору
направленных и ненаправленных зависимостей. Вы узнаете, когда следует заводить
зависимость между переменными, делать ли ее направленной или
ненаправленной и, если направленной, то в какую сторону. В главе 6 мы на основе этих знаний
будем создавать более сложные модели с использованием структур данных, а в
главе 7 включим в свой арсенал еще и объектно-ориентированное моделирование.
В этой главе предполагаются знания об основах Figaro в объеме главы 2.
В частности, необходимо понимать элемент chain, лежащий в основе
направленных зависимостей, а также условия и ограничения, составляющие основу
ненаправленных зависимостей. Еще мы будем использовать элементы cpd и RichCPD,
описанные в главе 4. Если вы что-то забыли, ничего страшного - я напомню,
когда понадобится.
5.1. Моделирование зависимостей
В основе вероятностных рассуждений лежат зависимости между переменными.
Две переменные называются зависимыми, если знания об одной дают
информацию и о другой. Наоборот, если никакие знания об одной переменной не
позволяют сказать что-то о другой, то переменные независимы.
Рассмотрим приложение для диагностики компьютерной системы, в котором
мы пытаемся рассуждать о сбоях в процессе печати. Пусть есть две переменные:
Кнопка Питания Принтера Нажата и Состояние Принтера. Если мы замечаем, что
кнопка не нажата, то можем заключить, что принтер не работает. Наоборот, если
мы знаем, что принтер не работает, то можем заключить, что, возможно, кнопка
питания не нажата. Две переменные, очевидно, зависимы.
Зависимости используются для моделирования переменных, которые как-то
связаны между собой. Между переменными может быть много разных связей, но
только два вида зависимостей.
• Направленная зависимость идет от одной переменной к другой. Обычно
так моделируются причинно-следственные связи между переменными.
• Ненаправленная зависимость моделирует связи, в которых нет очевидного
влияния одной переменной на другую.
В следующих двух разделах эти виды зависимостей объясняются подробнее и
приводятся примеры.
5.7.7. Направленные зависимости
Направленная зависимость ведет от одной переменной к другой, обычно они
используются для представления причинно-следственных связей. Например, если
кнопка питания принтера не нажата, то принтер не работает, поэтому существует
153

Глава 5. Моделирование зависимостей с помощью байесовских.
направленная зависимость между переменными
Кнопка Питания Принтера Нажата и Состояние
Принтера. Эта зависимость показана на рис. 5.1,
где между узлами, представляющими переменные,
проведено ориентированное ребро {ребро -
стандартный термин для обозначения стрелки между
двумя вершинами, или узлами графа). Первая Рис, 5.1. Направленная
переменная (в данном случае Кнопка Питания зависимость, выражающая
Принтера Нажата) называется родителем, вторая причинно-следственную связь
(Состояние Принтера) - потомком.
Почему стрелка направлена от причины к следствию? Объяснение, лежащее на
поверхности, - потому что причина случается раньше следствия. Более глубокий
ответ связан с концепцией порождающей модели, о которой шла речь в главе 4.
Напомним, что порождающая модель описывает процесс порождения значений
всех переменных модели. Типичный порождающий процесс имитирует то, что
происходит в реальном мире. Если некая причина вызывает некое следствие, то
сначала мы хотели бы породить значение причины, а затем использовать его для
порождения следствия. В примере с моделью принтера сначала нужно породить
значение переменной Кнопка Питания Принтера Нажата, а затем на его основе -
значение Состояния Принтера.
Еще раз повторю, что направление зависимости необязательно совпадает с
направлением рассуждения. Можно рассудить, что если кнопка питания не нажата,
то принтер не работает, но можно и в обратном направлении: если принтер
включен, то кнопка питания наверняка нажата. Многие совершают типичную ошибку:
строят модель в том же направлении, в каком рассуждают. В приложении для
диагностики мы наблюдаем, что принтер не работает, и пытаемся определить
причины, поэтому рассуждение идет в направлении от Состояния Принтера к Кнопка
Питания Принтера Нажата. Возможно, вы испытываете соблазн провести стрелку
в том же направлении, но это было бы ошибкой. Стрелка описывает порождающий
процесс, который развивается в направлении причинно-следственной связи.
Я сказал, что направленные зависимости, как правило, моделируют причинно-
следственные связи. На самом деле, связь причины со следствием - лишь один
пример общего класса асимметричных связей между переменными. Рассмотрим
различные виды асимметричных связей более пристально, начав с причинно-
следственных.
Разновидности причинно-следственных связей
Существует несколько видов причинно-следственных связей.
• Произошедшее раньше с произошедшим позже - самый очевидный тип
причинно-следственной связи: сначала происходит одна вещь, затем другая.
Например, сначала кто-то выключает питание, затем принтер перестает
работать. Такая временная последовательность - настолько обычная
характеристика причинно-следственной связи, что кажется, будто время - его
неотъемлемое свойство. Однако я с этим не согласен.
154
Состояние Принтера
Кнопка Питания Принтера Нажата

5.1. Моделирование зависимостей
• Связь состояний - иногда две переменные описывают различные аспекты
состояния объекта в заданный момент времени. Например, одна
переменная может представлять состояние кнопки питания, а другая -
работоспособность принтера. Оба состояния имеют место одновременно. В данном
случае, ненажатая кнопка влечет за собой неработающий принтер.
• Связь истинного значения с измерением - если одна переменная является
результатом измерения значения другой переменной, то мы говорим, что
истинное значение - причина измерения. Предположим, к примеру, что
имеется переменная Индикатор Питания Горит, показывающая
состояние лампочки питания принтера. Существует асимметричная связь между
переменными Кнопка Питания Принтера Нажата и Индикатор Питания
Горит. Обычно измерения производятся датчиками, и для одного и того
же значения может быть несколько измерений. Кроме того, наблюдаются
обычно именно результаты измерений, и мы хотим на основе измерений
делать выводы об истинных значениях. Таким образом, налицо еще один
пример, когда направление зависимости противоположно направлению
рассуждения.
• Связь между параметром и переменной, в которой он используется -
рассмотрим, к примеру, степень асимметрии монеты, представляющую
вероятность выпадения орла, и подбрасывание этой монеты. Для определения
исхода подбрасывания используется асимметрия. Ясно, что сначала
порождается асимметрия, а лишь потом подбрасывание монеты. Если
подбрасываний несколько, то все они порождаются после асимметрии.
Дополнительные асимметричные связи
Рассмотренные выше случаи - самые важные и не вызывающие недоразумений.
Если вы их поняли, то в 95 % случаев не затруднитесь с определением правильного
направления зависимости. Но давайте копнем глубже и рассмотрим другие
связи, которые, несмотря на очевидную асимметричность, вызывают сложности при
определении направления зависимости. Я перечислю эти связи, а затем опишу
эвристическое правило, помогающее разрешить неоднозначность.
• Связь части с целым - нередко свойства части объекта определяют свойства
всего объекта. Например, рассмотрим принтер с тонером и устройством
подачи бумаги. Неполадки того и другого могут привести к неполадкам
принтера в целом. А иногда, наоборот, свойства целого определяют свойства его
части. Например, если принтер плохо изготовлен, то, вероятно, плохо
изготовлены также устройство подачи бумаги и тонер.
• Связь частного и общего - и эта связь может быть направлена в обе стороны.
Пользователь может сталкиваться с самыми разными ошибками принтера,
например, с замятием бумаги или с плохим качеством печати.
Столкнувшись с любой частной проблемой, пользователь сталкивается и с более
общей проблемой плохой работы принтера. В этом случае частное является
причиной общего. С другой стороны, представьте себе процесс порождения
155

Глава 5. Моделирование зависимостей с помощью байесовских.
объекта. Обычно, сначала порождаются общие свойства, а затем
уточняются частности. Так, в случае принтера сначала нужно решить, является
он лазерным или струйным, а затем уже порождать отдельные свойства.
Действительно, не имеет смысла порождать частные свойства, не зная тип
принтера - ведь свойство может быть применимо только к принтеру
определенного типа.
Связь конкретного/детального с абстрактным/суммарным - примером
связи между конкретным и абстрактным может служить связь между
экзаменационными баллами и общей оценкой. Различные комбинации баллов
приводят к одной и той же оценке. Понятно, что преподаватель выставляет
оценку, исходя из результатов экзаменов, поэтому баллы являются
причиной оценки. С другой стороны, рассмотрим процесс порождения студента
и результатов экзамена. Сначала порождается абстрактный тип студента
(например, студент А или студент В), а только потом - конкретная оценка
на экзамене.
Устранение неоднозначности причинно-следственных связей
Как видно из предыдущих примеров, даже в случае, когда асимметричность
зависимости не вызывает сомнений, определить ее направление может быть нелегко. Иногда
в таких случаях помогает следующее соображение. Представьте, что один человек
произносит предложение, а другой слушает. Говорящий знает, что именно он хочет сказать и
соответственно подбирает слова. Это связь между целым и частью. Слушающий уясняет
смысл предложения по отдельным словам - это связь между частью и целым.
Целое
Целое
Произнесение и восприятие предложения: говорящий
вкладывает смысл в целое предложение, произнося слова (части).
Из этих слов слушающий восстанавливает смысл всего
предложения
Внимательно проанализировав этот пример, мы увидим, что в процессе произнесения
предложения сначала определяется его общий смысл, а потом подбираются слова. А в
процессе восприятия сначала собираются слова, а затем на их основе устанавливается
156

Вкладываемый смысл

Воспринимаемый смысл

5.1. Моделирование зависимостей
общий смысл. Это правило не высечено в камне, но часто в жизни мы сначала делаем
нечто общее/абстрактное/целое, а потом уточняем это с целью получить нечто частное/
конкретное/детальное, состоящее из нескольких частей. В случае принтера мы сначала
порождаем общий класс принтера в целом. Затем порождаем конкретный тип принтера
и детальную информацию о его компонентах. Точно так же в случае студента мы сначала
порождаем абстрактный класс студента, а затем наполняем его конкретными
результатами ответов на экзаменационные вопросы. С другой стороны, в процессе
восприятия мы сначала воспринимаем частную/конкретную/детальную информацию, а затем
путем обобщения выводим из нее общие/абстрактные представления о целом.
Например, пользователь, столкнувшийся с конкретной неполадкой принтера, пытается
обобщить ее, а преподаватель, оценивающий студента, сначала видит его экзаменационные
баллы, а потом выводит общую оценку. Можно сформулировать такое эвристическое
правило:
При моделировании процесса создания или определения свойств
зависимость направлена от общего, абстрактного или целого к частному, конкретному
или части. При моделировании восприятия и перечислении свойств
зависимость направлена от частного, конкретного или части к общему, абстрактному
или целому.
Как я уже сказал, понимая основные причинно-следственные связи, вы почти
никогда не будете испытывать затруднений с выбором направления зависимости.
Но в исключительных случаях даже опытные разработчики иногда расходятся во
мнениях о направлении. Надеюсь, что приведенное эвристическое правило
поможет вам при создании моделей.
Направленные зависимости в Figaro
Вы еще не забыли о четырех ингредиентах вероятностной модели? Повторим:
переменные, зависимости, функциональные формы и числовые параметры. До
сих пор мы предполагали, что переменные уже даны и акцентировали внимание на
зависимостях. Желая выразить зависимость в Figaro, мы должны выбрать
функциональную форму и задать числовые параметры.
В Figaro направленные зависимости можно выразить разными способами.
Общий принцип - использовать тот или иной элемент chain в качестве
функциональной формы. Напомним, что chain принимает два аргумента:
• родительский элемент;
• цепную функцию, которая получает значение родительского элемента и
возвращает результирующий элемент.
ВЫЗОВ Chain (parentElement, chainFunction) определяет следующий
порождающий Процесс: ПОЛуЧИТЬ Значение рОДИТеЛЯ ОТ parentElement, Применить
chainFunction ДЛЯ Получения resultElement И, наконец, ПОЛуЧИТЬ Значение ОТ resultElement.
Когда элемент chain применяется для выражения направленной зависимости,
parentElement, естественно, является родителем. Цепная функция описывает
распределение вероятности потомка для каждого значения родителя. В Figaro име-
157

Глава 5. Моделирование зависимостей с помощью байесовских...
ется немало конструкций с использованием chain, так что во многих случаях вы
будете работать с chain, даже не осознавая этого.
Ниже приведено несколько эквивалентных примеров, в каждом из которых
выражается одно и то же: если кнопка питания принтера не нажата, то принтер
определенно не работает, но если кнопка питания нажата, то принтер может как
работать, так и не работать.
val printerPowerButtonOn = Flip(0.95)
val printerState = <-0
Chain(printerPowerButtonOn, <]—©
(on: Boolean) => <3—©
H
if (on) Select(0.2 -> 'down, 0.8 -> fup)
else Constant('down)
val printerState = 0—©
If(printerPowerButtonOn, <J—©
Select (0.2 -> fdown, 0.8 -> fup), <—©
Constant(fdown)) <—©
val printerState = O—©
CPD (printerPowerButtonOn, O—©
false -> Constant('down), <3—©
true -> Select(0.2 -> 'down, 0.8 -> 'up)) <|—©
v.; pi.:глог.чч". <МЕ)
RichCPD(printerPowerButtonOn, <\—©
OneOf(false) -> Constant (' down) , <—©
-> Select (0.2 -> 'down, 0.8 -> 'up)) <—©
•
© — Использование Chain
© — Родительский элемент
© — Аргумент цепной функции
© — Тело цепной функции
© — Использование If
© — Родительский элемент
© — Использование CPD
© — Исход, если родитель равен true
© — Исход, если родитель равен false
© — Родительский элемент
ф — Ветвь, описывающая исход, когда родитель равен false
© — Ветвь, описывающая исход, когда родитель равен true
© — Использование RichCPD
ф — Родительский элемент
© — Ветвь, описывающая исход, когда значение родителя принадлежит множеству {false}
© — Ветвь, описывающая исход, когда родитель принимает любое другое значение
Как уже отмечалось, одним из видов асимметричной связи является связь
между параметром и переменной, зависящей от этого параметра, например, между
158

5.1. Моделирование зависимостей
асимметрией монеты и подбрасыванием этой монеты. Такую связь тоже можно
выразить с помощью chain или составного варианта атомарного элемента. Вот два
эквивалентных примера:
val toss = Chain(bias, (d: Double) => Flip(d))
val toss = Flip(bias)
5.7.2. Ненаправленные зависимости
Мы видели, что направленные зависимости представляют различные виды
асимметричных связей. Что касается ненаправленных зависимостей, то они
моделируют связи между переменными, не имеющие очевидного направления. Такие связи
называются симметричными. Если имеются коррелированные переменные, но не
видно, какой порождающий процесс должен был бы породить одну раньше
другой, то подойдет ненаправленная зависимость. Симметричные связи возникают
двумя способами.
• Два следствия одной причины в случае, когда причина явно не
присутствует в модели. Например, два измерения одной величины, когда для этой
величины не заведена переменная, или два последствия одного события,
которому не соответствует никакая переменная. Понятно, что если мы не
знаем истинного значения величины или события, то два измерения или
последствия связаны. Допустим, что в примере с принтером имеются две
переменные, представляющие качество и скорость печати. Если бы не было
переменной, представляющей состояние принтера, то эти две переменные
были бы связаны, поскольку это два аспекта печати, у которых может быть
общая причина.
Может возникнуть вопрос, что мешает включить в модель переменную,
представляющую эту причину. Один из возможных ответов состоит в том,
что причина может быть гораздо сложнее следствий, так что ее точное
моделирование проблематично. В этой главе мы будем рассматривать пример
реконструкции изображения, являющегося двумерным следствием
сложной трехмерной сцены. Создать корректную вероятностную модель
трехмерной сцены труднее, чем смоделировать связи между пикселями
изображения.
• Две причины известного следствия. Это интересная ситуация. Обычно
между причинами одного следствия нет никакой связи. Например, и состояние
устройства подачи бумаги, и уровень тонера влияют на состояние принтера
в целом, но эти два фактора независимы. Однако если мы знаем, что
принтер работает плохо, то внезапно они оказываются зависимыми. Если мы
знаем, что тонера осталось мало, то можем предположить, что качество
печати плохое именно по этой причине, а не из-за препятствий на тракте
движения бумаги. В этом примере состояние принтера в целом - следствие, а
уровень тонера и состояние устройства подачи бумаги - возможные причи-
159

Глава 5. Моделирование зависимостей с помощью байесовских...
ны, которые становятся зависимыми, если известно следствие. Это пример
наведенной зависимости, о которой подробнее будет сказано в разделе 5.2.3.
Если переменной для следствия в модели нет, то появляется симметричная
связь между двумя причинами. Но вывод за пределы модели общего
следствия двух причин - явление не слишком частое.
Выражение ненаправленных зависимостей в Figaro
Симметричные зависимости можно выразить в Figaro двумя способами: с
помощью ограничений и условий. У каждого есть свои плюсы и минусы. Достоинством
ограничений является концептуальная простота. Но числовые значения,
входящие в состав ограничений, зашиты в код, и Figaro не может найти их методами
машинного обучения, потому что они недоступны алгоритму обучения. С другой
стороны у условий есть то достоинство, что их числовые параметры можно
вывести с помощью обучения.
Общий принцип обоих подходов один и тот же. В разделе 5.5 о кодировании
ненаправленных зависимостей рассказано детально, здесь же дадим конспективное
описание. Если между двумя переменными существует ненаправленная
зависимость, то некоторые пары их значений являются более предпочтительными. Это
можно обеспечить, назначив веса различным парам значений. В случае
ограничения веса задаются с помощью функции, которая сопоставляет паре значений
вещественное число. А в случае условия та же по существу информация кодируется
более сложным способом.
Давайте, например, закодируем связь между двумя соседними пикселями
изображения. Это связь типа «при прочих равных условиях». Так, мы, возможно,
имеем основания считать, что при прочих равных условиях два соседних пикселя в
три раза вероятнее будут одноцветными, чем разноцветными. На самом деле, на
цвета пикселей могут влиять различные факторы, поэтому их шансы оказаться
одноцветными не равны в точности 3:1.
Как с помощью ограничений выразить эту связь в Figaro? Обозначим цвета
пикселей coiori и coior2. Чтобы не усложнять пример, будем считать цвета
булевыми величинами. Напомним, что ограничение - это функция, отображающая
значение элемента в Double. Мы должны создать элемент, который представляет
пару color 1, color2 в виде, допускающем задание ограничения. Можно поступить
так:
import com.cra.figaro. library. compound. Л/ч
val pair = ЛЛ(со1ог1, color2) <\—Q
О — л/ч в Figaro обозначает конструктор пары
Теперь нужно определить функцию, реализующую ограничение:
def sameColorConstraint(pair: (Boolean, Boolean)) =
if (pair._l == pair._2) 0.3; else 0.1 <—О
О — Здесь проверяется, что первый компонент пары равен второму
160

5.1. Моделирование зависимостей
Наконец, применяем ограничение к паре цветов:
pair.setConstraint(sameColorConstraint _) <J—О
О — Знак подчеркивания говорит, что мы хотим получить саму функцию, а не вызвать ее
Figaro интерпретирует ограничение именно так, как мы и ожидаем. При прочих
равных условиях состояние, в котором оба компонента пары равны (т. е. цвета
одинаковы), в три раза вероятнее, чем противоположное. Эти ограничения корректно
учитываются при определении распределения вероятности, как будет показано в
разделе 5.5. Но, к сожалению, числа 0.3 и 0.1 зашиты в код функции ограничения,
так что получить их из обучающих данных не получится.
Подход с применением условий я сначала продемонстрирую на примере кода, а
затем объясню, почему он работает правильно. Первым делом определим
вспомогательный булев элемент samecoiorconstraintvaiue, так чтобы он принимал
значение true с вероятностью, заданной в постановке задачи. Затем добавим условие,
которое говорит, что этот элемент должен быть равен true. Это можно сделать с
помощью наблюдения:
val sameColorConstraintValue =
Chain(colorl, color2,
(Ы: Boolean, Ь2: Boolean) =>
if (bl == Ь2) Flip(0.3); else Flip(O.l))
sameColorConstraintValue.observe(true)
Этот код эквивалентен коду с ограничением. Действительно, условие
означает, что любое нарушающее его значение имеет вероятность 0, а удовлетворяющее
ему - вероятность 1. Полная вероятность любого состояния вычисляется путем
комбинирования вероятностей, следующих из определения элементов и условий
или ограничений. Например, допустим, что два цвета совпадают. Из определения
Chain Следует, ЧТО sameColorConstraintValue будет Иметь Значение true С ВерОЯТ-
НОСТЬЮ 0.3, a false - С верОЯТНОСТЬЮ 0.7. ЕСЛИ sameColorConstraintValue ОКажет-
ся равным true, то условие будет иметь вероятность 1, а если false - то
вероятность 0. Следовательно, комбинированная вероятность условия равна (0.3 х 1) +
(0.7 х 0) = 0.3. Аналогично, если цвета различаются, то комбинированная
вероятность равна (0.1 х 1) + (0.9 х 0) = 0.1. Мы видим, что при прочих равных условиях
вероятность одинаковых цветов в три раза больше, чем различных. Это именно тот
результат, который мы получили с применением ограничений.
Конструкция на основе условий достаточно общая, она применима к любым
асимметричным связям. Достоинство этого подхода в том, что числа 0.3 и 0.1
встречаются внутри элементов Flip, поэтому их можно было бы сделать
зависимыми от других аспектов модели. Допустим, к примеру, что мы хотим с помощью
обучающих данных узнать, насколько одинаковый цвет соседних пикселей
вероятнее различного. Можно создать элемент, скажем имеющий бета-распределение,
который будет представлять вес, а затем использовать этот элемент внутри Flip
вместо 0.3. Тогда, воспользовавшись обучающими данными, мы сможем узнать
распределение вероятности веса.
161

Глава 5. Моделирование зависимостей с помощью байесовских...
5.7.3. Прямые и косвенные зависимости
Прежде чем переходить к байесовским и марковским сетям, я хочу подчеркнуть
один важный момент. В типичной вероятностной модели много пар переменных
таких, что знание одной изменяет наши предположения о другой. По
определению, все это примеры зависимостей между переменными. Но большинство этих
зависимостей косвенные: они связывают две переменные не напрямую, а
опосредованно, через промежуточные переменные. Точнее, наши знания о первой
переменной изменяют предположения о второй, потому что они изменяют предположения
о некоей промежуточной переменной, а это, в свою очередь, изменяет
предположения о второй переменной.
Например, на рис. 5.2 показаны три переменные: Кнопка Питания Принтера
Нажата, Состояние Принтера и Число Напечатанных Страниц. Очевидно, что
между переменными Кнопка Питания Принтера Нажата и Число Напечатанных
Страниц существует зависимость. Если мы знаем, что кнопка питания не нажата,
то полагаем, что число напечатанных страниц равно нулю. Но на рисунке
зависимость между этими переменными проходит через промежуточную переменную
Состояние Принтера. Это означает, что причина, по которой знание о переменной
Кнопка Питания Принтера Нажата изменяет предположения о Числе
Напечатанных Страниц, заключается в том, что сначала изменяются предположения о
Состоянии Принтера, а уже эти измененные предположения меняют наши
предположения о числе напечатанных страниц. Зная, что кнопка питания не нажата, мы
понимаем, что принтер не работает, а, значит, не напечатано ни одной страницы.
Кнопка Питания Принтера Нажата
Состояние Принтера
Число Напечатанных Страниц
Рис. 5.2. Переменная Кнопка Питания Принтера Нажата косвенно связана
с Числом Напечатанных Страниц, эта связь опосредована промежуточной
переменной Состояние Принтера
Рассмотрим еще один пример косвенной зависимости. В примере с соседними
пикселями изображения зависимость была прямой. А если пиксели не соседние?
Взгляните на рис. 5.3. Если мы знаем, что пиксель 11 красный, то есть
основания полагать, что пиксель 12 тоже красный, а отсюда следует, что и пиксель 13 с
большой вероятностью красный. Это очевидный пример косвенной зависимости,
поскольку знания о пикселе 11 влияют на предположения о пикселе 13 через
промежуточный пиксель 12.
162

5.2. Байесовские сети
Важно понимать, какие зависимости в предметной области прямые, а какие
косвенные. И в байесовских, и в марковских сетях мы строим граф, в котором ребра
представляют зависимости между переменными. В байесовской сети ребра
направленные, в марковской ненаправленные. Ребра проводятся только для прямых
зависимостей. Если две переменные связаны лишь косвенной зависимостью, то
ребра между ними не будет.
Рис- 5-3. Между пикселями 11 и 13 имеется косвенная связь,
опосредованная промежуточным пикселем 12
Далее мы рассмотрим байесовские сети, моделирующие направленные
зависимости, а затем марковские сети, моделирующие ненаправленные зависимости.
Однако хочу подчеркнуть - из того, что для моделирования зависимостей разных
видов используются разные системы, не следует, что нужно выбирать для
модели только ту или другую. Существуют способы, позволяющие комбинировать
направленные и ненаправленные зависимости в одной модели. В вероятностной
программе это сделать легко: для представления направленных зависимостей
используем порождающие определения элементов, а для ненаправленных -
добавляем ограничения.
5.2. Байесовские сети
Мы видели, что представление связей между переменными - одна из основ
вероятностного моделирования. В этом разделе мы изучим байесовские сети -
стандартную систему представления асимметричных связей с применением
направленных зависимостей. Мы уже встречались с байесовскими сетями в главе 4, когда
рассматривали пример экспертизы картины Рембрандта. А сейчас дадим полное
определение и объясним, какие существуют способы рассуждений.
5.2.7. Определение байесовской сети
Байесовской сетью называется представление вероятностной модели, состоящее
из трех компонентов:
• множество переменных, каждая со своей областью значений;
• ориентированный ациклический граф, вершинами которого являются эти
переменные;
• условное распределение вероятности каждой переменной при условии ее
родителей.
Множество переменных со своими областями значений
На рис. 5.4 показаны три переменные: Тема, Размер и Яркость. Область
значений переменной описывает, какие значения она может принимать. Областью
значений переменной Тема является множество {Люди, Ландшафт}, переменной Раз-
Пиксель 11
Пиксель 12
Пиксель 13
163

Глава 5. Моделирование зависимостей с помощью байесовских.
мер - множество {Малая, Средняя, Большая}, а переменной Яркость - множество
{Темная, Яркая}.
Значения вероятности Темы
Тема
Люди
0,8
Ландшафт
0,2
Значения вероятности Размера
при условии Темы
Значения вероятности Яркости
при условии Темы
Тема
Размер
Малая Средняя Большая
Люди 0.25 0.25 0,5
Ландшафт 0.25 0.5 0.25
Тема
Люди
Ландшафт
Яркость
Темная | Яркая |
0.8 0.2
0.3 0.7
Рис. 5.4. Байесовская сеть с тремя узлами
Ориентированный ациклический граф
Слово ориентированный означает, что у каждого ребра графа имеется
ориентация, или направление; ребро направлено от одной переменной к другой.
Начальная переменная называется родителем, конечная - потомком. На рис. 5.4 Тема
является родителем Размера и Яркости. Слово ациклический означает, что в графе
нет ориентированных циклов, т. е. нельзя, отправившись из одной вершины и
следуя в направлении стрелок, вернуться в ту же самую вершину. Однако
неориентированные циклы, в которых направление стрелки игнорируется, допускаются. Эта
концепция изображена на рис. 5.5. В графе слева имеется ориентированный цикл
A-B-D-C-A. А в графе справа в цикле A-B-D-C-A встречаются ребра с разными
ориентациями, т. е. этот цикл неориентированный.
Ориентированный цикл Ориентированного цикла нет
Рис. 5.5. Обход ориентированного цикла производится
по стрелкам и заканчивается в исходной вершине
164
Тема
Размер
Яркость
к
А
С
D
В
С
D
В

5.2. Байесовские сети
Условное распределение вероятности переменной
Речь идет об условном распределении переменной-потомка при условии
известных значений ее родителей. Учитываются все возможные комбинации
допустимых значений родителей. Для каждой комбинации определяется
распределение вероятности потомка. На рис. 5.6 у каждой переменной имеется условное
распределение вероятности. Переменная Тема - корневая вершина сети, у нее нет
родителей. Если у переменной нет родителей, то условное распределение
описывает единственное распределение вероятности этой переменной. В нашем
примере переменная Тема принимает значение Люди с вероятностью 0.8 и значение
Ландшафт с вероятностью 0.2. У переменной Размер есть родитель - Тема,
поэтому в ее условном распределении имеется по одной строке для каждого значения
Темы. Мы видим, что если Тема принимает значение Люди, то в распределении
Размера значение Малая имеет вероятность 0.25, Средняя - 0.25 и Большая - 0.5.
Если же Тема принимает значение Ландшафт, то у Размера другое распределение.
Наконец, родителем Яркости тоже является Тема, и в ее условном распределении
тоже имеется по одной строке для каждого значения Темы.
Р(Тема + Люди)
Тема
Люди
0.8
Ландшафт
0.2
Малая
Люди
Яркая
Р(Размер = Малая |
Тема = Люди)
Тема
Люди
Ландшафт
Малая
0,25
0.25
Размер
Средняя Большая
0.25 0.5
0.5 0.25
Р(Яркость = Яркая
Тема = Люди)
Тема
Яркость
Темная 1 Яркая 1
Люди 0.8 0.2
Ландшафт Q.3 0.7
Р((Тема = Люди, Размер = Малая, Яркость = Яркая) = 0.8 х 0.25 х 0.2 = 0.04
Рис. 5.6. Вычисление вероятности возможного мира путем перемножения
элементов условных распределений вероятности
165

Глава 5. Моделирование зависимостей с помощью байесовских...
5.2.2. Как байесовская сеть определяет
распределение вероятности
Байесовскую сеть мы определили. Теперь посмотрим, как она определяет
распределение вероятности. Прежде всего, необходимо определить возможные миры.
Для байесовской сети возможный мир - это комбинация значений всех
переменных, причем значение каждой должно принадлежать ее области значений.
Например, <Тема = Люди, Размер = Малая, Яркость = Яркая> - возможный мир. Затем
мы определяем вероятность возможного мира. Это просто. Нужно лишь найти в
условном распределении вероятности каждой переменной запись,
соответствующую значениям родителей и потомка в данном возможном мире. Этот процесс
иллюстрируется на рис. 5.6. Так, для мира <Тема = Люди, Размер = Малая,
Яркость = Яркая> в записи, соответствующей Теме, находится 0.8, это значение
взято из столбца Люди. Для Размера мы ищем строку, соответствующую значению
Тема = Люди, и в столбце, соответствующем значению Размер = Малая, находим
число 0.25. Наконец, для Яркости мы снова ищем строку, соответствующую
значению Тема = Люди, и берем число 0.2 из столбца Яркая. Вероятность мира
получается путем перемножения найденных чисел: 0.8 х 0.25 х 0.2 = 0.04.
Если повторить эту процедуру для каждого возможного мира, то сумма
вероятностей окажется равна 1, как и должно быть. Это справедливо для любой
байесовской сети. Итак, мы рассмотрели, как байесовская сеть определяет допустимое
распределение вероятности. Поняв, как строится байесовская сеть и что она
означает, посмотрим, как ее можно использовать для высказывания предположений об
одних переменных, если что-то известно о других.
5.2.3. Рассуждения с применением байесовской
сети
В байесовской сети закодирован большой объем информации о независимости
переменных. Напомним, что две переменные называются независимыми, если, зная
что-то об одной из них, мы ничего не можем сказать о другой. Из предыдущего
примера понятно, что переменные Число Напечатанных Страниц и Кнопка
Питания Принтера Нажата независимыми не являются. Знание о том, что не
напечатано ни одной страницы, уменьшает вероятность того, что кнопка питания нажата.
С условной независимостью дело обстоит похоже. Две переменные называются
условно независимыми, если после получения информации о некоей третьей
переменной знание чего-то об одной из них не позволяет сказать ничего нового о другой. Так
называемый критерий d-разделенности позволяет определить, когда две переменные
в байесовской сети являются условно независимыми относительно набора
переменных. Критерий звучит довольно сложно, поэтому я не буду приводить его точную
формулировку, а опишу основные принципы и приведу несколько примеров.
Основная идея заключается в том, что рассуждение протекает вдоль пути от
одной переменной к другой. В примере на рис. 5.4 рассуждение может протекать от
Размера к Яркости вдоль пути Размер-Тема-Яркость. Отблеск этой идеи мы виде-
166

5.2. Байесовские сети
ли в разделе 5.1.3, когда говорили о прямых и косвенных зависимостях. В случае
косвенной зависимости рассуждения протекает от одной переменной к другой,
проходя через промежуточные переменные. В данном случае Тема - промежуточная
переменная на пути от Размера к Яркости. В байесовской сети рассуждение может
протекать вдоль пути при условии, что он не блокирован в некоторой переменной.
В большинстве случаев путь блокирован в переменной, если эта переменная
наблюдается. Таким образом, если Тема наблюдается, то путь Размер-Тема-Яркость
блокирован. Это означает, что, наблюдая Размер, мы не узнаем ничего нового о
Яркости, если Тема тоже наблюдается. По-другому можно сказать, что Размер
условно независим от Яркости при условии Темы. В нашей модели выбор темы
художником определяет размер и яркость, но после выбора темы размер и яркость
порождаются независимо.
Сходящиеся стрелки и наведенные зависимости
Есть еще один случай, который поначалу может показаться противоречащим
интуиции: путь блокирован в переменной, если переменная не наблюдается, но
разблокируется, когда переменную наблюдают. Я проиллюстрирую эту ситуацию,
дополнив пример, как показано на рис. 5.7. Здесь появилась новая переменная
Материал: масло, акварель или еще что-то. Естественно, Материал обусловливает
Яркость (допустим, масляные картины ярче акварелей), поэтому в сети имеется
ориентированное ребро от Материала к Яркости. В данном случае у одного
потомка два родителя. Эта ситуация называется сходящимися стрелками, потому что
ребра, исходящие из Темы и Материала, сходятся в Яркости.
Рис. 5.7. Дополненный пример с живописью, включающий
сходящиеся стрелки от двух родителей к общему потомку
Теперь обратимся к вопросу о рассуждении, касающемся Темы и Материала.
Согласно модели, Тема и Материал порождаются независимо. Поэтому
справедливо следующее утверждение:
(1) Тема и Материал независимы, когда ничего не наблюдается.
Ну а если мы наблюдаем, что картина яркая? Согласно нашей модели,
ландшафты обычно ярче, чем изображения людей. Зная, что картина яркая, мы
заключаем, что на ней с большей вероятностью изображен ландшафт, а не люди.
Предположим, что затем мы узнали, что картина написана маслом, а это также тяготеет
к большей яркости. Это наблюдение дает другое объяснение тому, почему картина
яркая. Следовательно, вероятность ландшафта несколько уменьшается по срав-
167
Размер
Тема
Сходящиеся
стрелки
Материал
Яркость

Глава 5. Моделирование зависимостей с помощью байесовских.
нению с тем, что было после наблюдения яркости, но до наблюдения масляной
краски. Как видим, рассуждение протекает от материала к Теме вдоль пути
Материал-Яркость-Тема. Поэтому можно высказать такое утверждение:
(2) Тема и Материал не являются условно независимыми при условии Яркости.
Встретившийся здесь паттерн противоположен обычному. Мы имеем путь,
который блокирован, когда промежуточная переменная не наблюдается, и
разблокируется, когда эта переменная наблюдается. Такая ситуация называется наведенной
зависимостью - зависимость между двумя переменными появляется в результате
наблюдения третьей. Любые сходящиеся стрелки в байесовской сети могут приводить
к наведенной зависимости. Путь между двумя переменными может включать как
обычные ситуации, так и сходящиеся стрелки. Рассуждение может протекать вдоль
пути, только если оно не блокируется ни в какой вершине, лежащей на этом пути. На
рис. 5.8 показаны четыре примера для пути Размер-Тема-Яркость-Материал. В левом
верхнем примере ни Тема, ни Яркость не наблюдаются, а путь блокирован в Яркости,
потому что в нем имеются сходящиеся стрелки. В следующем примере (справа) Тема
наблюдается, поэтому путь блокирован и в Теме, и в Яркости. В следующем примере
(слева) Тема не наблюдается, но наблюдается Яркость, это в точности то условие,
которое необходимо, чтобы путь не блокировался ни в Теме, ни в Яркости. Наконец, в
последнем примере наблюдаются Тема и Яркость, поэтому путь блокирован.
Размер
Блокирован
в Теме и
Яркости
Яркость
Рис. 5.8. Примеры блокированных и неблокированных путей, в которых
обычный паттерн сочетается со сходящимися стрелками. На всех рисунках
показан путь от Размера к Материалу, когда переменные Тема и Яркость
наблюдаются и не наблюдаются
168
Размер
Тема
Материал
Тема
Блокирован
в Яркости
Материал
Яркость
Тема
Не
блокирован
Размер
Яркость
Тема
Размер
Блокирован
в Теме
Материал
Яркость

5.3. Изучение примера байесовской сети
5.3. Изучение примера байесовской
сети
Рассмотрев основные концепции байесовских сетей, исследуем пример
диагностики неисправности принтера. Сначала я покажу, как проектируется сеть, а затем
продемонстрирую все способы рассуждения в этой сети. Вопрос обучения
параметров сети отложим до главы 12, где будет приведен полезный паттерн
проектирования, относящийся к этой теме.
5.3.7. Проектирование модели диагностики
компьютерной системы
Представьте, что вы проектируете приложение для отдела технической поддержки.
Ваша задача - помочь сотруднику как можно быстрее идентифицировать
причины неисправности. В этом приложении можно использовать систему
вероятностных рассуждений: зная факты - сообщение пользователя и результаты
диагностических тестов, - определить внутреннее состояние системы. Для представления
вероятностной модели было бы естественно воспользоваться байесовской сетью.
В проектировании байесовской сети обычно выделяются три этапа: выбор
переменных и их областей значений, задание структуры сети и представление
условных распределений вероятности. Мы увидим, как это делается в Figaro.
На практике эти этапы обычно не выполняются линейно: сначала выбрать
все переменные, потом построить структуру всей сети и напоследок выписать
условные распределения. Как правило, сеть строится по частям, и сделанное ранее
уточняется впоследствии. Так мы и поступим. Сначала построим сеть для модели
общей неисправности принтера, а затем будем уточнять детали.
Модель общей неисправности принтера: переменные
Мы хотим смоделировать возможные сообщения пользователя, потенциальные
неисправности и факторы внутри системы, которые могли бы стать причиной
неисправностей. Для всего этого нам понадобятся переменные.
Начнем с Общего Результата Печати. Эта переменная представляет общее
впечатление пользователя от результатов печати на верхнем уровне абстракции.
Когда пользователь впервые обращается в отдел поддержки, он сообщает лишь такую
общую информацию. Возможны три варианта: (1) к печати нет претензий (вы
ставите метку «отлично»); (2) печатается, но не так, как надо (неудовлетворительно);
(3) вообще ничего не печатается (ничего).
Затем рассматриваются конкретные аспекты результата печати, а именно:
Число Напечатанных Страниц - ни одной, несколько страниц, все страницы; Печатает
Быстро - булева переменная, показывающая, завершилась ли печать за разумное
время; Хорошее Качество Печати - еще одна булева переменная. Эти аспекты
моделируются по отдельности, потому что помогут дифференцировать различные
неисправности. Например, если не напечатано ни одной страницы, то, возможно,
169

Глава 5. Моделирование зависимостей с помощью байесовских...
не работает сеть. Если же несколько страниц (но не все) все же напечатано, то
проблема, скорее всего, не в сети, а в ошибке пользователя.
Рассматриваем все элементы системы, которые могут повлиять на результат
печати, а именно: Состояние Принтера - хорошее, плохое, не работает; Состояние
Программы - корректное, глючит, крах; Состояние Сети - работает, нестабильна,
не работает; Команда Пользователя Правильна - булева переменная.
Модель общей неисправности принтера:
структура сети
Отобранные нами переменные можно скомпоновать в три группы: абстрактный
Общий Результат Печати, различные конкретные аспекты результата печати и
состояния системы, влияющие на результат печати. Соответственно имеет смысл
заложить в проект сети три уровня. Но каким должен быть порядок уровней?
Между переменными состояния системы и переменными, описывающими
конкретный результат печати, существуют причинно-следственные связи. Например,
Состояние Сети «не работает» - причина того, что переменная Печатает Быстро
равна false. Кроме того, между индивидуальными переменными, описывающими
результат печати, и Общим Результатом Печати существует связь типа
конкретное-абстрактное. В разделе 5.1.1 я говорил, что такие связи могут быть направлены
в любую сторону. В нашем приложении моделируется восприятие системы
пользователем и его сообщение о результатах печати, поэтому, согласно введенному
там же эвристическому правилу, правильным будет направление от конкретных
результатов печати к абстрактному общему результату. Поэтому порядок уровней
в нашей сети таков: (1) переменные состояния системы, (2) переменные,
описывающие конкретный результат печати, (3) Общий Результат Печати.
Структура сети показана на рис. 5.9. Мы видим три уровня, но не всегда
существует ребро от переменной на одном уровне ко всем переменным на следующем
уровня. Дело в том, что некоторые переменные, описывающие результат печати,
зависят от состояния лишь некоторых компонентов системы. Например, качество
печати зависит от состояния принтера, но не зависит от сети. Аналогично
скорость печати, согласно нашей модели, зависит только от сети и программного
обеспечения. О том, справедливы эти утверждения или нет, можно спорить; я хотел
показать, что в любом приложении можно привести аргументы в пользу удаления
некоторых ребер. А чем меньше ребер, тем короче описание условного
распределения вероятности.
Модель общей неисправности принтера:
условные распределения вероятности
Я продемонстрирую проектирование условного распределения вероятности в
виде кода на Figaro, объясняя наиболее интересные моменты. В разделе 5.1.1 были
показаны различные способы определения условных распределений на Figaro.
Здесь мы встретим многие из них.
170

5.3. Изучение примера байесовской сети
Ком ан да П о л ьзо вате л я
Правильна
Число Напечатанных
Страниц
Рис. 5.9- Структура сети той части модели диагностики компьютерной системы,
которая относится к общим неисправностям принтера
Листинг 5-1. Реализация модели общей неисправности принтера
val printerState = ... О—О
val softwareState =
Select(0.8 -> 'correct, 0.15 -> 'glitchy, 0.05 -> 'crashed)
val networkState =
Select (0.7 -> 'up, 0.2 -> 'intermittent, 0.1 -> 'down)
val userCommandCorrect =
Flip(0.65)
val numPrintedPages =
RichCPD(userCommandCorrect, networkState,
softwareState, printerState,
(*, *, *, OneOf('out)) -> Constant('zero),
(*, *, OneOf('crashed), *)
(*, OneOf('down), *
(OneOf(false), *, *
Select(0.3 -> 'zero, 0.6
(OneOf(true), *, *, *) ->
Select(0.01 -> 'zero, 0.01 -> 'some,
1
-> Constant('zero),
*) -> Constant('zero),
*) ->
-> 'some, 0.1 ->
'all),
0.98 -> 'all))
1
val printsQuickly =
Chain(networkState, softwareState,
(network: Symbol, software: Symbol) =>
if (network == 'down || software == 'crashed)
Constant(false)
else if (network == 'intermittent I I software == 'glitchy)
Flip(0.5)
else Flip(0.9))
И
val goodPrintQuality =
CPD(printerState,
'good -> Flip(0.95) ,
'poor -> Flip(0.3),
'out -> Constant(false))
I
171
Состояние Сети
Печатает Быстро
Состояние Программы
Состояние Принтера
Хорошее Качество
Печати
Общий Результат Печати

Глава 5. Моделирование зависимостей с помощью байесовских.
val printResultSummary = I <^1Л
Apply(numPrintedPages, printsQuickly, goodPrintQuality,
(pages: Symbol, quickly: Boolean, quality: Boolean) =>
if (pages == 'zero) 'none
else if (pages == 'some || Iquickly || Iquality) 'poor
else 'excellent)
О — Берется из детальной модели принтера, которая будет показана ниже
© — Для корневых переменных имеем атомарные условные распределения вероятности,
например Select или Flip
© — для переменной numPrintedPages используется элемент RichCPD, представляющий
зависимость от команды пользователя и от состояний сети, программы и принтера
© — для printsQuickly используется элемент Chain, представляющий зависимость от
состояний сети и программы
© — для goodPrintQuality используется элемент simpleCPD, представляющий
зависимость от состояния принтера
© — используется элемент Apply, т. к. переменная printResultSummary однозначно
определена своими родителями
Здесь используется несколько приемов представления вероятностной
зависимости потомка от родителей.
• Для переменной numPrintedPages используется элемент RichCPD, реализую-
щий следующую логику: если принтер не работает или сеть не работает или
программа завершилась аварийно, то не будет напечатано ни одной
страницы вне зависимости от состояния других родителей. В противном случае,
если пользователь дал неправильную команду, то вряд ли будут
напечатаны все страницы, а если команда правильна, то с высокой вероятностью
будут напечатаны все страницы.
• Для переменной printsQuickly используется элемент chain, реализующий
следующую логику: есть сеть не работает или программа завершилась
аварийно, то принтер безусловно не будет печатать быстро. В противном случае,
если сеть работает нестабильно или программа «глючит», то будет принтер
печатать быстро или нет - вопрос везения. Если сеть и программа работают
нормально, то обычно принтер печатает быстро (хотя гарантии нет).
• ДЛЯ Переменной goodPrintQuality ИСПОЛЬЗуеТСЯ ПрОСТОЙ Элемент CPD.
Если принтер не работает, то ожидать хорошего качества печати точно не
приходится. Но даже если принтер в хорошем состоянии, высокое качество
печати не гарантируется (ну так уж они устроены, эти принтеры).
• Переменная printsummary детерминированная, т. е. однозначно определена
своими родителями, без какой-либо неопределенности. Для
детерминированной переменной можно применить элемент Apply вместо chain.
Детальная модель принтера
В этом разделе мы бегло рассмотрим детальную модель принтера, потому что
многие принципы те же самые. Структура сети показана на рис. 5.10. На состояние
172

5.3. Изучение примера байесовской сети
принтера влияют три фактора: Подача Бумаги, Уровень Тонера и Кнопка Питания
Принтера Нажата. В модели имеется также переменная еще не встречавшегося
нам вида: индикатор, или измерение. Переменная Индикатор Замятия Бумаги
Горит - это результат измерения Подачи Бумаги, а переменная Индикатор
Низкого Уровня Тонера Горит - результат измерения уровня тонера. В разделе 5.1.1
отмечалось, что между истинным значением и результатом его измерения имеется
причинно-следственная связь, поэтому от Подачи Бумаги к Индикатор Замятия
Бумаги Горит и от Уровня Тонера к Индикатор Низкого Уровня Тонера Горит
проведены ребра.
Индикатор Замятия Бумаги
Горит
Рис. 5.10. Структура сети для детальной модели принтера
Ниже приведен код определения условных распределений вероятности, по
большей части прямолинейный.
Листинг 5.2. Детальная модель принтера на Figaro
val printerPowerButtonOn = Flip(0.95)
val tonerLevel = Select (0.7 -> 'high,
val tonerLowIndicatorOn =
If(printerPowerButtonOn,
CPD(paperFlow,
'high -> Flip(0.2) ,
'low -> Flip(0.6) ,
'out -> Flip(0.99)) ,
Constant(false) )
val paperFlow = Select(0.6 -> 'smooth,
0.2 -> 'low, 0.1 -> 'out)
0.2 -> 'uneven, 0.2 -> 'jammed)
val paperJamlndicatorOn =
If(printerPowerButtonOn,
CPD(tonerLevel,
'high -> Flip(O.l),
'low -> Flip(0.3),
'out -> Flip(0.99)),
Constant(false))
val printerState =
Apply(printerPowerButtonOn, tonerLevel, paperFlow,
(power: Boolean, toner: Symbol, paper: Symbol) =>
В
Ё
173
Подача Бумаги
Уровень Тонера
Кнопка Питания Принтера
Нажата
Состояние Принтера
1

Глава 5. Моделирование зависимостей с помощью байесовских.
if (power) {
if (toner == 'high && paper == 'smooth) 'good
else if (toner == 'out || paper == 'out) 'out
else 'poor
} else 'out
>:
§
О — Напомним, что одиночная кавычка в Scala обозначает тип Symbol
© — Элемент CPD вложен в If. Если кнопка питания принтера нажата, то состояние
индикатора низкого уровня тонера зависит от уровня тонера. Если кнопка питания
принтера не нажата, то индикатор низкого уровня тонера заведомо не горит, потому
что нет напряжения
© — Состояние принтера — детерминированный результат определяющих его факторов
На рис. 5.11 показана итоговая структура полной байесовской сети. Полный
исходный текст программы имеется в каталоге chap05/PrinterProblem.scala
прилагаемого к книге кода.
Рис. 5.11. Полная сеть для модели диагностики компьютерной системы
5.3.2. Рассуждения с помощью модели
диагностики компьютерной системы
В этом разделе показано, как рассуждать с помощью только что построенной
модели диагностики компьютерной системы. В Figaro механизм рассуждения прост,
но возможные паттерны рассуждений весьма интересны и служат иллюстрацией
к концепциям, изложенным в разделе 5.2.3. Все рассматриваемые в этом разделе
174
Подача Бумаги
Уровень Тонера
Кнопка Питания Принтера
Индикатор Замятия Бумаги
Горит
Индикатор Низкого Уровня
Тонера Горит
Команда Пользователя
Правильна
Состояние Сети
Состояние Принтера
Состояние Программы
Число Напечатанных
Страниц
Печатает Быстро
Хорошее Качество
Печати
Общий Результат Печати

5.3. Изучение примера байесовской сети
паттерны рассуждений разбиты на отдельные шаги в прилагаемом к главе коде.
Можете закомментировать шаги, которые не хотите выполнять.
Запрос априорной вероятности
Прежде всего, запросим вероятность того, что кнопка питания принтера нажата,
в отсутствие каких-либо фактов, т. е. априорную вероятность. Для запроса можно
выполнить такой код:
val answerWithNoEvidence = Л_{>
VariableElimination.probability(printerPowerButtonOn, true)
printIn("Априорная вероятность, что кнопка питания принтера нажата = " +
answerWithNoEvidence)
О — Вычислить Р(Кнопка Питания Принтера Нажата = true)
В результате печатается:
Априорная вероятность, что кнопка питания принтера нажата = 0.95
Вернувшись к модели, мы увидим, что переменная printerPowerButtonOn
определена в такой строке:
val printerPowerButtonOn = Flip(0.95)
Таким образом, ответ на наш запрос в точности такой, как если бы мы
проигнорировали всю модель, кроме этого определения. Это проявление общего правила:
все, что находится в сети после определения переменной, имеет значение, лишь
если имеются факты. Для априорных вероятностей никаких фактов не нужно,
поэтому то, что расположено в сети ниже, нас не интересует.
Запрос с фактами
А что произойдет, если добавить факты? Спросим у модели, какова
вероятность, что кнопка питания нажата при условии, что результат печати
неудовлетворительный, т. е. какой-то результат имеется, но не тот, что хотел бы видеть
пользователь. Напишем такой код:
printResultSummary.observe ('poor) О—D>
val answerlfPrintResultPoor =
VariableElimination.probability(printerPowerButtonOn, true)
println("Вероятность, что кнопка питания принтера нажата, при условии, "
+ "что результат неудовлетворительный = " + answerlfPrintResultPoor)
О — Вычислить Р(Кнопка Питания Принтера Нажата = true | Результат Печати =
неудовлетворительный)
В результате печатается:
Вероятность, что кнопка питания принтера нажатия, при условии,
что результат неудовлетворительный = 1.0
175

Глава 5. Моделирование зависимостей с помощью байесовских...
Однако же это странно! Вероятность выше той, что была в отсутствии фактов,
касающихся результата печати. Но если обратиться к модели, то становится
понятно, почему Результат печати может оказаться неудовлетворительным, только
если хотя бы одна страница напечатана, а это невозможно, если нет питания.
Поэтому питание включено с вероятностью 1.
Теперь спросим то же самое, указав в качестве факта, что ничего не напечатано.
printResultSummary.observe ('none) Л_Г>
val answerlfPrintResultNone =
VariableElimination.probability(printerPowerButtonOn, true)
println("Вероятность, что кнопка питания принтера нажата, при условии, "
+ "ничего не напечатано = " + answerlfPrintResultNone)
О — Вычислить Р(Кнопка Питания Принтера Нажата = true | Результат Печати = ничего)
В результате печатается:
Вероятность, что кнопка питания принтера нажатия, при условии,
ничего не напечатано =0.8573402523786461
Что и следовало ожидать. Не нажатая кнопка питания объясняет отсутствие
напечатанных страниц, поэтому задание такого факта повышает вероятность.
Независимость и блокировка
В разделе 5.2.3 было введено понятие блокированного пути и описана его
связь с условной независимостью. Эту концепцию иллюстрируют три
переменные: Общий Результат Печати, Кнопка Питания Принтера Нажата и Состояние
Принтера. На рис. 5.11 видно, что путь от переменной Кнопка Питания Принтера
Нажата к Общему Результату Печати проходит через Состояние Принтера. Здесь
нет сходящихся стрелок, поэтому путь блокирован, если Состояние Принтера
наблюдается. И так оно и есть, как мы сейчас увидим:
printResultSummary.unobserve() A
printerState.observe(f out) " ^
val answerlfPrinterStateOut =
VariableElimination.probability(printerPowerButtonOn, true)
println("Вероятность, что кнопка питания принтера нажата, при условии, "
+ "что принтер не работает = " + answerlfPrinterStateOut)
printResultSummary.observe('none)
val answerlfPrinterStateOutAndResultNone = d~4>
VariableElimination.probability(printerPowerButtonOn, true)
println("Вероятность, что кнопка питания принтера нажата, при условии, "
+ "что принтер не работает и ничего не напечатано = "
+ answerIfPrinterStateOutAndResultNone)
О — Вычислить Р(Кнопка Питания Принтера Нажата = true | Состояние Принтера =
не работает)
© — Вычислить Р(Кнопка Питания Принтера Нажата = true | Состояние Принтера =
не работает, Общий Результат Печати = ничего)
176

5.3. Изучение примера байесовской сети
В результате печатается:
Вероятность, что кнопка питания принтера нажата, при условии,
что принтер не работает = 0.6551724137931032
Вероятность, что кнопка питания принтера нажата, при условии,
что принтер не работает и ничего не напечатано = 0.6551724137931033
Как видим, знание того, что ничего не напечатано, не изменяет вероятность того,
что кнопка питания принтера нажата, если мы уже знаем, что принтер не работает.
Объясняется это тем, что Общий Результат Печати условно независим от
переменной Кнопка Питания Принтера Нажата при заданном Состоянии Принтера.
Рассуждения относительно различных следствий
одной причины
До сих пор все пути рассуждения вели вверх по сети. Но можно
комбинировать в одном рассуждении разные направления. Это происходит, например, когда
мы рассматриваем, что говорит результат измерения об измеряемой величине, и
какие выводы из этого можно сделать. В нашем примере переменная Индикатор
Низкого Уровня Тонера Горит является потомком переменной Уровень Тонера, а
Уровень Тонера - родитель Состояния Принтера. Если уровень тонера низкий,
то вероятность хорошего качества печати будет ниже. В то же время горящий
индикатор низкого уровня тонера свидетельствует о том, что уровень тонера
низкий. Поэтому вполне логично, что наблюдение горящего индикатора низкого
уровня тонера понижает вероятность хорошего качества печати. Убедиться в этом
поможет следующий код:
<з-о
<^©
printResultSummary.unobserve()
printerState.unobserve()
val printerStateGoodPrior =
VariableElimination.probability(printerState, 'good)
printIn("Априорная вероятность, что состояние принтера хорошее = "
+ printerStateGoodPrior)
tonerLowIndicatorOn.observe(true)
val printerStateGoodGivenTonerLowIndicatorOn =
VariableElimination.probability(printerState, 'good)
println("Вероятность, что состояние принтера хорошее, при условии
+ "горящего индикатора низкого уровня тонера = "
+ printerStateGoodGivenTonerLowIndicatorOn)
О — Вычислить Р(Состояние Принтера = хорошее)
© — Вычислить Р(Состояние Принтера = хорошее | Индикатор Низкого Уровня Тонера
Горит = true)
В результате печатается:
Априорная вероятность, что состояние принтера хорошее = 0.39899999999999997
Вероятность, что состояние принтера хорошее, при условии
горящего индикатора низкого уровня тонера = 0.23398328690807796
177

Глава 5. Моделирование зависимостей с помощью байесовских...
Как видим, вероятность хорошего состояния принтера уменьшается, если
наблюдается горящий индикатор низкого уровня тонера. Этого следовало ожидать.
Рассуждения относительно различных причин
одного следствия: наведенные зависимости
В разделе 5.2.3 мы видели, что рассуждения в ситуации, когда имеются
различные причины одного следствия, отличаются от других видов рассуждений из-за
феномена сходящихся стрелок, который приводит к наведенной зависимости.
Рассмотрим, например, переменные Состояние Программы и Состояние Сети,
обе они являются родителями переменной Печатает Быстро. Сначала получим
априорную вероятность корректного состояния программы:
tonerLowIndicatorOn . unobserve () Л_Г>
val softwareStateCorrectPrior =
VariableElimination.probability(softwareState, f correct)
println("Априорная вероятность корректного состояния программы = " +
softwareStateCorrectPrior)
О — Вычислить Р(Состояние Программы = корректное)
В результате печатается:
Априорная вероятность корректного состояния программы = 0.8
Далее мы наблюдаем, что сеть работает, и снова запрашиваем состояние
программы:
networkState.observe(f up)
val softwareStateCorrectGivenNetworkUp =
VariableElimination.probability(softwareState, f correct)
println("Вероятность корректного состояния программы при условии, что "
+ "сеть работает = " + softwareStateCorrectGivenNetworkUp)
О — Вычислить Р(Состояние Программы = корректное | Состояние Сети = работает)
В результате печатается:
Вероятность корректного состояния программы при условии, что
сеть работает = 0.8
Вероятность не изменилась, несмотря на то, что имеется чистый путь из
Состояния Сети в Состояние Программы через узел Печатает Быстро! Таким
образом, мы видим, что в общем случае две причины одного следствия независимы.
Это согласуется с интуицией: тот факт, что сеть работает, никак не сказывается на
корректности состояния программы.
Но если мы знаем, что принтер печатает не быстро, то все меняется. Наша
модель предлагает два объяснения медленной печати: проблема с сетью и проблема
с программой. Если мы наблюдаем, что сеть работает, значит, дело должно быть в
программе. В этом позволяет убедиться следующий код:
networkState.unobserve() ft—Г>
printsQuickly.observe(false)
val softwareStateCorrectGivenPrintsSlowly =
178

5.4. Применение вероятностного программирования для обобщения ...
VariableElimination.probability(softwareState, f correct)
println("Вероятность корректного состояния программы при условии, что "
+ "печатается медленно = " + softwareStateCorrectGivenPrintsSlowly)
networkState . observe (f up) Л_гч
val softwareStateCorrectGivenPrintsSlowlyAndNetworkUp = "
VariableElimination.probability(softwareState, f correct)
println("Вероятность корректного состояния программы при условии, что "
+ "печатается медленно и сеть работает = "
+ softwareStateCorrectGivenPrintsSlowlyAndNetworkUp)
О — Вычислить Р(Состояние Программы = корректное | Печатает Быстро = false)
© — Вычислить Р(Состояние Программы = корректное | Печатает Быстро = false,
Состояние Сети = работает)
В результате печатается:
Вероятность корректного состояния программы при условии, что
печатается медленно = 0.6197991391678623
Вероятность корректного состояния программы при условии, что
печатается медленно и сеть работает = 0.39024390243902435
Знание о том, что сеть работает, заметно уменьшает вероятность
корректности программы. Поэтому переменные Состояние Программы и Состояние Сети
независимы, но не являются условно независимыми при условии Печатает
Быстро. Это пример наведенной зависимости.
Подведем итоги.
• Когда мы выполняем рассуждение от следствия X к его непрямой причине
Y, переменная X не является независимой от Y, но становится условно
независимой при условии Z, если Z блокирует путь от X к Y.
• То же самое справедливо, когда выполняется рассуждение от причины к
непрямому следствию или в отношении двух следствий одной причины.
• Для двух причин X и Y одного следствия Z верно обратное. X и Y
независимы, но не являются условно независимыми при условии Z; это результат
наведенной зависимости.
На этом можно закончить пример диагностики компьютерной системы. Мы
видели не вполне тривиальную сеть с интересными паттернами рассуждений. В
следующем разделе мы выйдем за рамки традиционных байесовских сетей.
5.4. Применение вероятностного
программирования для обобщения
байесовских сетей: предсказание
успешности продукта
В этом разделе мы покажем, как обобщить модель байесовской сети для
предсказания успешности маркетинговой кампании и размещения скрытой рекла-
179

Глава 5. Моделирование зависимостей с помощью байесовских...
мы. Цель примера двоякая: во-первых, продемонстрировать возможности
языков программирования в плане обобщения байесовских сетей, а, во-вторых,
показать, что байесовские сети можно использовать не только для вывода причин
наблюдаемых событий, но и для предсказания будущих событий. Как и в примере
диагностики компьютерной системы, я сначала покажу, как спроектировать
модель и выразить ее на Figaro, а затем как с ее помощью рассуждать.
5.4.1. Проектирование модели для предсказания
успешности продукта
Представим, что имеется новый продукт, и мы хотим обеспечить ему успех. Этого
можно достичь разными способами. Можно вложить деньги в упаковку и другие
приманки для покупателей. Можно поставить такую цену, при которой продукт
купят с большей вероятностью. Или продвигать продукт, раздавая бесплатные
версии, в надежде, что пользователи расскажут о них своим друзьям. Прежде чем
выбирать стратегию, нужно знать относительную важность каждого фактора.
В этом разделе описывается каркас модели, который можно использовать в
приложении. Я говорю «каркас», потому что это не более чем скелет реальной
модели, но для понимания идеи его достаточно. Ниже будет представлена простая
байесовская сеть всего с четырьмя узлами, но интересны типы узлов и условные
распределения вероятности.
В модели имеются четыре переменные, показанные на рис. 5.12.
• Типом переменной Социальная Сеть Целевого Покупателя является
социальная сеть. Это один из способов с помощью языка программирования
выйти за рамки обыкновенной байесовской сети, где переменные могут быть
только булевыми, перечислениями, целыми или вещественными. Условное
распределение вероятности этой переменной случайным образом
генерирует сеть на основе популярности целевого покупателя. Что касается самой
популярности, то, поскольку это управляющий параметр, мы моделируем
ее как известную константу, а не переменную. Но при желаниии можно
было бы внести неопределенность и сделать популярность еще одной
переменной.
• Целевому Покупателю Нравится - булева переменная, показывающая,
нравится ли продукт целевому покупателю, это функция качества продукта.
Качество продукта тоже считается известной константой, но можно было
бы сделать ее переменной, зависящей от капиталовложений в продукт.
• Скольким Друзьям Нравится - целая переменная, но при вычислении ее
условного распределения вероятности производится обход Социальной
Сети Целевого Покупателя, чтобы узнать количество друзей, которым
продукт был показан и понравился. Это условное распределение гораздо
богаче, чем возможно в традиционных байесовских сетях.
• Число Купивших - целая переменная. При ее моделировании считается,
что любой человек, которому понравился продукт, купит его с вероятное-
180

5.4. Применение вероятностного программирования для обобщения ...
тыо, зависящей от ценовой доступности, каковая является еще одним
управляющим параметром с известным постоянным значением.
Следовательно, число купивших продукт подчиняется биномиальному
распределению.
Ниже приведен код этой модели на Figaro. Сначала я опишу, как он
работает на верхнем уровне, а потом перейду к деталям.
Тип: Network
Социальная сеть
целевого покупателя
Тип: Boolean Нравится
ли продукт целевому
покупателю
Социальная Сеть Целевого
Покупателя
Тип: Integer Сколько
друзей целевого
покупателя купят продукт
после его предложения
покупателю
Целевому Покупателю
Нравится
Скольким Друзьям Нравится
Тип: Integer Скольким
друзьям целевого
покупателя понравится
продукт после его
предложения покупателю
Рис. 5.12. Сеть для предсказания успешности продукта
Листинг 5-3- Модель для предсказания успешности продукта на Figaro
class Network(popularity: Double) { I <]—A
val numNodes = Poisson(popularity)
}
class Model(targetPopularity: Double, productQuality: Double,
affordability: Double) {
def generateLikes(numFriends: Int,
productQuality: Double): Element[Int] = {
def helper(friendsVisited: Int, totalLikes: Int,
unprocessedLikes: Int): Elementflnt] = {
if (unprocessedLikes == 0) Constant(totalLikes)
else {
val unvisitedFraction =
1.0 - (friendsVisited.toDouble - 1) / (numFriends - 1)
val newlyVisited = Binomial(2, unvisitedFraction)
val newlyLikes =
Binomial(newlyVisited, Constant(productQuality))
Chain(newlyVisited, newlyLikes,
(visited: Int, likes: Int) =>
<ъ-в
<h-©
181

Глава 5. Моделирование зависимостей с помощью байесовских.
helper(friendsVisited + unvisited,
totalLikes + likes,
unprocessedLikes + likes - 1)
}
helper(1, 1, 1)
val targetSocialNetwork = new Network(targetPopularity) <]—©
val targetLikes = Flip(productQuality) <]—0
' <-0
■ ;:i.t.
( i : :«•
•:'<Г.,
■) )
val numberBuy =
Binomial(numberFriendsLike, Constant(affordability))
}
<ь-о
О — Определяем класс Network с единственным атрибутом, определенным с помощью
элемента Poisson (см. в тексте)
© — Создаем класс Model, принимающий известные управляющие параметры в качестве
аргументов
© — Определяем рекурсивный процесс для порождения числа людей, которым нравится
продукт (см. в тексте)
© — Социальная сеть целевого покупателя определяется как случайная сеть, основанная
на популярности этого покупателя
© — Нравится ли продукт целевому покупателю — булев элемент, зависящий от качества
продукта
© — Если целевому покупателю продукт нравится, вычисляем число людей, вызывая
метод generateLikes. Если не нравится, то он не расскажет о нем своим друзьям,
значит, это число будет равно нулю
© — Число купивших продукт, подчиняется биномиальному распределению (см. в тексте)
Три места в коде нуждаются в дополнительных пояснениях: элемента Poisson в
Классе Network, процесс generateLikes И определение переменной numberBuy.
Сначала поговорим об элементе Poisson и логике, стоящей за numberBuy, а затем
перейдем к процессу generateLikes - самой интересной части модели.
• Элемент Poisson - это целочисленный элемент, в котором используется
распределение Пуассона. Как правило, оно применяется для
моделирования числа возникновений события в течение некоторого промежутка
времени, например, числа отказов сети за месяц или числа угловых ударов в
футбольном матче. Проявив творческий подход, распределение Пуассона
можно использовать для моделирования любой ситуации, в которой нужно
знать количество некоторых объектов в области. В данном случае мы с его
182

5.4. Применение вероятностного программирования для обобщения ...
помощью моделируем число людей в социальной сети целевого
покупателя; это отличается от типичного применения, но является вполне
разумным выбором.
Элемент Poisson принимает в качестве аргумента среднее число событий,
ожидаемых в течение заданного промежутка времени, но допускает, что
фактическое число будет больше или меньше среднего. В нашей модели
аргументом является популярность целевого покупателя; по определению,
это оценка среднего числа людей в его социальной сети.
• Здесь сосредоточена логика вычисления числа купивших продукт. Каждый
человек, которому продукт понравился, купит его с вероятностью, равной
значению параметра ценовой доступности. Поэтому общее число купивших
подчиняется биномиальному распределению, в котором число испытаний
равно числу друзей, которым понравился продукт, а вероятность покупки
зависит от доступности продукта. Поскольку число людей, которым
понравился продукт, само является элементом, то необходимо использовать
составной элемент Binomial, принимающий элементы в качестве аргументов.
Составной элемент Binomial требует, чтобы вероятность успеха испытания
также задавалась элементом, потому-то мы и обернули параметр
доступности af f ordability Элементом Constant. Элемент Constant принимает обыч-
ное значение Scala и порождает элемент Figaro, который всегда принимает
это значение.
ЦеЛЬ фуНКЦИИ generateLikes - Определить, СКОЛЬКИМ ЛЮДЯМ ПОНраВИТСЯ
продукт после того, как он будет предложен целевому покупателю,
социальная сеть которого содержит заданное количество людей. В этой
функции предполагается, что самому целевому покупателю продукт нравится,
иначе она не была бы вызвана вовсе. Функция моделирует случайный
процесс рекламирования понравившегося продукта друзьям. Она принимает
два аргумента: (1) количество людей в социальной сети целевого
покупателя, это переменная типа integer и (2) качество продукта - переменная типа
Double, принимающая значения от 0 до 1.
• Точная логика функции generateLikes не так важна, главное для нас -
показать, что можно использовать нетривиальную рекурсивную функцию
в качестве условного распределения вероятности. Но я все же объясню
ЛОГИКу, Чтобы Пример был ПОНЯТеН. ОСНОВНУЮ ЧаСТЬ работы
generateLikes поручает вспомогательной функции, которая вычисляет три
переменные.
- friendsvisited равна числу людей в социальной сети целевого
покупателя, уже проинформированных о продукте. В начальный
момент она равна 1, т. к. проинформирован только один человек.
- totaiLikes равна числу людей из числа уже посещенных, которым
понравился продукт. В начальный момент она равна 1, поскольку мы
предполагаем, что generateLikes вызывается, только если целевому
покупателю продукт понравился.
183

Глава 5. Моделирование зависимостей с помощью байесовских...
- unprocessedLikes - ЧИСЛО ЛЮДвЙ, КОТОрЫМ Продукт ПОНраВИЛСЯ, НО ДЛЯ
которых мы еще не успели смоделировать рекламирование продукта
друзьям.
Логика вспомогательной функции подробно объяснена ниже.
Листинг 5.4. Вспомогательная функция для обхода социальной сети
def helper(friendsVisited: Int, totalLikes: Int,
unprocessedLikes: Int): Element[Int] =
<-0
if (unprocessedLikes == 0) Constant(totalLikes) <3—©
else {
val unvisitedFraction =
1.0 - (friendsVisited.toDouble - 1) / (numFriends - 1)
val newlyVisited = Binomial(2, unvisitedFraction) <3—©
<^©
val newlyLikes =
Binomial(newlyVisited, Constant(productQuality))
<-0
Chain(newlyVisited, newlyLikes,
(visited: Int, likes: Int) =>
helper(friendsVisited + visited, <}—©
}
totalLikes + likes, <]_ф
unprocessedLikes + likes - 1)) <]—©
О — Вспомогательная функция принимает в качестве аргументов обычные значения
Scala, а возвращает элемент. Ее можно использовать внутри chain
© — Критерий остановки: если больше некого обрабатывать, то число людей, которым
понравился продукт, равно числу найденных к этому моменту
© — Вычисляем вероятность, что случайный член социальной сети (за исключением
обрабатываемого в данный момент лица) еще не посещался
© — Обрабатываемый человек рекламирует продукт двум друзьям. Вероятность, что
каждый из этих друзей еще не посещался, задается параметром unvisitedFraction
© — Вероятность, что данному человеку понравится продукт, определяется параметром
productQuality, который обернут элементом Constant, поскольку этого требует
интерфейс составного элемента Binomial
184

5.4. Применение вероятностного программирования для обобщения ...
© — Рекурсивный процесс часто программируется с помощью chain
© — Каждый новый человек, которому понравился продукт, — еще не обработанное
лицо, а единица вычитается, чтобы учесть того, кто только что обработан
© — Новое значение числа посещенных людей равно старому значению плюс число тех,
кто был посещен в этом вызове
© — Новое значение числа людей, которым продукт понравился, равно старому
значению плюс число тех, кому он понравился в этом вызове
В этом примере необходимо больше навыков работы со Scala, но
принципиально техника моделирования та же, что для байесовских сетей. Основная задача -
представить процесс порождения возможных миров. В данном случае мы имеем
сравнительно простой процесс распространения продукта по социальной сети, но
можно закодировать и более сложные процессы.
5.4.2. Рассуждения с помощью модели
для предсказания успешности продукта
Поскольку мы спроектировали модель для предсказания успеха, то ее типичное
применение сводится к заданию управляющих параметров и предсказанию числа
людей, купивших продукт. Так как число людей - переменная типа integer с
широкой областью значений, то предсказание вероятности конкретного значения не
интересно. А интересно узнать среднее ожидаемое значение, или математическое
ожидание.
В теории вероятностей математическое ожидание - общее понятие. Берется
какая-нибудь функция, определенная для переменной, и возвращается среднее
значение этой функции. Пример приведен на рис. 5.13. Начинаем с распределения
вероятности значений произвольного типа, в данном случае типа integer. Затем
применяем к каждому значению функцию, возвращающую значение типа Double.
В данном случае функция преобразует число типа integer в его представление
типа Double. Далее вычисляется взвешенное среднее этих значений типа Double с
весами, равными вероятностям значений. То есть мы умножаем каждое значение
типа Double на его вероятность и суммируем результаты.
В нашем примере требуется вычислить математическое ожидание числа людей,
купивших продукт, т. е. переменную типа integer. Для этого напишем такую
строку на Figaro:
algorithm.expectation(model.numberBuy, (i: Int) => i.toDouble)
Здесь algorithm - ссылка на используемый алгоритм вывода. В данном случае
используется алгоритм выборки по значимости, который особенно хорошо
подходит для предсказания исхода сложного порождающего процесса. Поскольку нам
нужна ссылка на алгоритм, для выполнения вывода придется написать чуть более
сложный код, чем раньше. Он показан в следующем фрагменте. Весь процесс
получения управляющих констант и вычисления ожидаемого числа купивших
продукт Заключен В фуНКЦИЮ predict!
185

Глава 5. Моделирование зависимостей с помощью байесовских.
0.1 -► 0 0.2 -^ 1 0.4 —» 2
(i: Int) => i.toDouble
0.1 -► 0.0 0.2 -► 1.0 0.4 -► 2.0
Expectation
Начинаем с
О.з -► з «--"^распределения значений
произвольного типа
.Преобразуем каждое
значение к типу Double,
применяя некоторую
функцию
0.3 -*- 3.0
Вычисляем произведения
"каждого значения типа
Double на его вероятность
0.1 х 0.0 = 0.0
0.2 х 1.0 = 0.2
0.4 х 2.0 = 0.
0.3 х 3.0 = 0.9
-Складываем результаты
0.0 + 0.2 + 0.8 + 1.0 = 1.9
Рис. 5.13. Вычисление математического ожидания распределения целых
значений элемента. Сначала значения элемента преобразуются к типу Double.
Затем каждое полученное значение умножается на его вероятность,
и результаты суммируются - получается среднее
def predict(targetPopularity: Double, productQuality: Double,
affordability: Double): Double = {
val model =
new Model(targetPopularity, productQuality, affordability)
val algorithm = Importance(1000, model.numberBuy) <]—©
algorithm, start () O—©
val result =
algorithm.expectation(model.numberBuy, (i: Int) => i.toDouble)
algorithm.kill() <3—©
result
D
И
О — Создаем экземпляр модели предсказания с заданными управляющими константами
© — Создаем экземпляр алгоритма выборки по значимости. 1000 — размер выборки,
a model. numberBuy — то, что мы хотим предсказать
© — Прогоняем алгоритм
© — Вычисляем ожидаемое число людей, купивших продукт
© — Очистка и освобождение ресурсов, захваченных алгоритмом
Чтобы понять, как различные параметры влияют на число людей, купивших
продукт, нужно выполнить функцию predict много раз с различными входными
параметрами. Ниже приведен потенциальный результат.
186

100
100
100
100
10
10
10
10
0.5
0.5
0.9
0.9
0.5
0.5
0.9
0.9
5.5. Марковские сети
Популярность Качество продукта Доступность Предсказанное число купивших
0.5 2.0169999999999986
0.9 3.7759999999999962
0.5 29.21499999999997
0.9 53.13799999999996
0.5 0.7869999999999979
0.9 1.4769999999999976
0.5 3.3419999999999885
0.9 6.066999999999985
Из этой таблицы можно вывести несколько заключений. Число покупателей
примерно пропорционально доступности продукта. Но зависимость от качества
продукта нелинейна: для каждой комбинации популярности и доступности число
покупателей при качестве 0.9 в несколько раз выше, чем при качестве 0.5. Если
популярность равна 100, то аж в 15 раз выше. Похоже, существует связь между
популярностью и качеством продукта, причем популярность определяет предел
числа охваченных рекламой людей при высоком качестве. Если качество низкое,
то популярность не играет особой роли.
В этом примере мы видели, как Figaro используется в качестве языка
имитационного моделирования. Прогнозирование того, что случится в будущем, -
типичная задача имитационного моделирования, и именно этим мы здесь и занимались.
Ничуть не сложнее использовать эту модель для рассуждений в обратном
направлении. Например, после того как продукт предложен нескольким целевым
покупателям и стало известно, сколько друзей они убедили купить продукт, можно
оценить качество продукта. Это тоже ценное применение модели.
5.5. Марковские сети
В предыдущих разделах нас интересовали байесовские сети, представляющие
направленные зависимости. Теперь настало время обратиться к ненаправленным
зависимостям. Их моделируют марковские сети. Принцип работы марковской сети
я объясню на примере типичного приложения для восстановления изображений.
А затем покажу, как представить ее в Figaro и как с ее помощью проводить
рассуждения.
5.5.1. Определение марковской сети
Марковская сеть - это представление вероятностной модели, состоящее из трех
частей:
• Множество переменных - у каждой переменной имеется область
допустимых значений.
• Неориентированный граф, вершинами которого являются переменные -
ребра, соединяющие вершины, не ориентированы, т. е. лишены стрелок.
Допускаются циклы в графе.
• Множество потенциалов - потенциалы определяют числовые параметры
модели. Подробнее о них чуть ниже.
187

Глава 5. Моделирование зависимостей с помощью байесовских.
На рис. 5.14 изображена марковская сеть для восстановления изображений.
Каждому пикселю изображения соответствует переменная. В данном случае мы
имеем массив пикселей 4x4, но сеть легко обобщить на изображение любого размера.
В принципе, пиксель может быть любого цвета, но для простоты предположим,
что его значением является булева величина, описывающая, является пиксель
ярким или темным. Между любой парой пикселей, соседних по горизонтали или по
вертикали, проведено ребро. Ребра представляют тот факт, что при прочих равных
условиях два соседних пикселя с большей вероятностью будут одинаковыми, а не
различными.
Пиксель 31
Рис. 5.14. Марковская сеть для пиксельного изображения
Оговорка «при прочих равных условиях» важна для понимания семантики
модели. Если на время забыть о ребрах между пикселями и рассмотреть
индивидуальные распределения вероятности значений каждого пикселя, то может
оказаться, что они с большой вероятностью различны. Например, принимая во внимание
все известные дополнительные факты, мы можем предполагать, что пиксель 11
яркий с вероятностью 90 %, а пиксель 12 - с вероятностью 10 %. В таком случае
пиксели 11 и 12 с большой вероятностью различны. Но наличие ребра между
пикселями 11 и 12 означает, что они одинаковы с большей вероятностью, чем были бы в
отсутствие ребра. Ребро добавляет знание о том, что пиксели, вероятно,
одинаковы. Этому знанию противостоит знание о том, что они, вероятно, различаются, но
полностью изменить общий вывод оно неспособно. Конкретное знание,
выраженное в ребре между пикселями И и 12, представлено потенциалом на этом ребре.
А теперь дадим определение потенциалов.
Потенциалы
Как определяются числовые параметры марковской сети? В байесовской сети
у каждой переменной имеется условное распределение вероятности. В
марковской же сети все не так просто. У переменных нет своих числовых параметров.
Их заменяют функции, называемые потенциалами, которые определены на
множествах переменных. Если существует симметричная зависимость, то некоторые
совместные состояния переменных, зависящих друг от друга, более вероятны,
188
Пиксель 41
Пиксель 42
Пиксель 43
Пиксель 44
Пиксель 32
Пиксель 33
Пиксель 34
Пиксель 21
Пиксель 22
Пиксель 23
Пиксель 24
Пиксель 11
Пиксель 12
Пиксель 13
Пиксель 14

5.5. Марковские сети
чем другие, - при прочих равных условиях. Потенциал определяет вес каждого
совместного состояния. Совместные состояния с большими весами вероятнее
совместных состояний с малыми весами, при прочих равных условиях.
Относительная вероятность двух совместных состояний равна отношению их весов, опять же
при прочих равных условиях.
Математически потенциал - это просто функция, отображающая значения
переменных в неотрицательные вещественные числа. В табл. 5.1 приведен пример
унарного потенциала одиночного пикселя в приложении восстановления
изображения, а в табл. 5.2 - бинарный потенциал, определенный для пар пикселей.
Таблица 5.1. Унарный потенциал одиночного пикселя, кодирующий тот факт,
что при прочих равных условиях пиксель освещен с вероятностью 0.4
Пиксель 31
F
Т
Значение потенциала
0.6
0.4
Таблица 5.2. Бинарный потенциал пар пикселей, кодирующий тот факт,
что при прочих равных условиях вероятность, что два пикселя одинаковы,
в девять раз больше, чем вероятность, что они различны
Пиксель 31
F
F
Т
Т
Пиксель 32
F
Т
F
Т
Значение потенциала
0.9
0.1
0.1
0.9
Как потенциальные функции взаимодействуют со структурой графа? Есть два
правила:
• в потенциальной функции могут упоминаться только переменные
соединенные ребром в графе;
• если две переменные соединены ребром, то они должны упоминаться
совместно в какой-то потенциальной функции.
В нашем примере с каждой переменной связана копия унарного потенциала из
табл. 5.1, а с каждой парой соседних по горизонтали или по вертикали пикселей -
копия бинарного потенциала из табл. 5.2. При таком назначении потенциалов оба
правила соблюдены.
Как марковская сеть определяет распределение
вероятности
Мы только что дали определение марковской сети. Но как она определяет
распределение вероятности? Каким образом назначить вероятность каждому воз-
189

Глава 5. Моделирование зависимостей с помощью байесовских...
можному миру, так чтобы сумма вероятностей была равна 1? Ответ не такой
простой, как для байесовской сети, но и не слишком сложный.
Как и в байесовской сети, возможный мир в марковской сети - это сопоставление
каждой переменной значения из ее области значений. Какова вероятность такого
возможного мира? Будем действовать последовательно.
Для простоты рассмотрим массив пикселей 2x2 со следующими значениями:
пиксель 11= true, пиксель 12 = true, пиксель 21 = true, пиксель 22 = false. Для
этого мира рассмотрим значения всех потенциалов в модели. Унарные потенциалы
определены в табл. 5.3. Для пикселей, равных true, значение потенциала равно 0.4,
а для пикселей, равных false, оно равно 0.6. В табл. 5.4 показаны бинарные
потенциалы четырех пар пикселей. Если оба пикселя совпадают, то потенциал пары
равен 0.9, в остальных случаях - 0.1. Других потенциалов в модели нет.
Таблица 5.3. Значения унарных потенциалов для примера возможного мира
Переменная
Пиксель 11
Пиксель 12
Пиксель 21
Пиксель 22
Значение потенциала
0.4
0.4
0.4
0.6
Таблица 5.2. Бинарные потенциалы для примера возможного мира
Переменная 1
Пиксель 11
Пиксель 21
Пиксель 11
Пиксель 12
Переменная 2
Пиксель 12
Пиксель 22
Пиксель 21
Пиксель 22
Значение потенциала
0.9
0.1
0.9
0.1
Теперь перемножим значения всех потенциалов: 0.4 х 0.4 х 0.4 х 0.6 х 0.9 х 0.1 х
0.9 х 0.1 = 0.00031104. Зачем нужно перемножать? Вспомните об оговорке «при
прочих равных условиях». Если в двух мирах вероятность одинакова всюду,
кроме одного потенциала, то вероятности миров пропорциональны значениям этого
потенциала. Это именно то, что мы получаем, помножив вероятности на значение
потенциала. Продолжая рассуждать в том же духе, мы придем к произведению
значений всех потенциалов как «вероятности» возможного мира.
Я заключил слово «вероятность» в кавычки, потому что на самом деле это не
вероятность. Вычисляя произведение потенциалов таким образом, мы обнаружим,
что сумма «вероятностей» не равна 1. Но это легко исправить. Нужно лишь
нормировать «вероятности», полученные перемножением потенциалов. Исходные
произведения называются ненормированными вероятностями, а их сумма -
нормировочным коэффициентом, который принято обозначать буквой Z. Таким
образом, для получения вероятностей миров мы делим ненормированные вероятности
на Z. Не пугайтесь - Figaro принимает на себя все хлопоты.
190

5.5. Марковские сети
По ходу обсуждения обнаружился удивительный факт. В байесовской сети
вероятность возможного мира можно было вычислить, перемножив релевантные
условные распределения вероятности. В марковской сети вероятность одного мира
невозможно определить без учета всех вообще миров. Чтобы вычислить
нормировочный коэффициент, необходимо знать ненормированные вероятности всех
возможных миров. По этой причине многие считают, что представление с
помощью марковской сети труднее, чем с помощью байесовской, т. к. числа сложнее
интерпретировать как вероятности. Но я считаю, что если вы будете помнить о
принципе «при прочих равных условиях», то сможете уверенно определить
параметры марковской сети. А вычисление нормировочного коэффициента оставьте
Figaro. Разумеется, параметры байесовских и марковских сетей можно получить с
помощью машинного обучения. Используйте структуру, которая лучше отвечает
связям в приложении.
5.5.2. Представление марковских сетей
и рассуждения с их помощью
В одном отношении марковские сети определенно проще байесовских: когда речь
заходит о паттернах рассуждений. В марковской сети нет понятия наведенной
зависимости. Рассуждения могут проходить по любому пути между переменными,
не блокированному наблюдавшейся переменной. Две переменные зависимы, если
между ними существует путь, но становятся условно независимыми при условии
некоторого множества переменных, если эти переменные блокируют все пути
между ними. Вот и всё.
Кроме того, поскольку все ребра марковской сети неориентированны, то нельзя
говорить о причине и следствии или о прошлом и будущем. Обычно не ставится
задача предсказания будущих исходов или вывода причин сделанных
наблюдений. Требуется просто вывести значения одних переменных, если известны
значения других.
Представление модели восстановления
изображения на Figaro
В приложении для восстановления изображения предполагается, что одни
пиксели наблюдаемы, а другие - нет. Требуется восстановить ненаблюдаемые
пиксели. Для этого используется описанная в предыдущем разделе модель, в которой
потенциалы соседних пикселей одинаковы. Ниже показан код представления этой
модели на Figaro. Напомним, что в разделе 5.1.2 были упомянуты два способа
задания симметричных связей: ограничения и условия. Сейчас мы воспользуемся
ограничениями.
val pixels = Array .fill (10, 10) (Flip (0 . 4) )
def setConstraint (il: Int, jl: Int, i2: Int, j2: Int) {
val pixell = pixels(il)(jl)
<^-©
191

Глава 5. Моделирование зависимостей с помощью байесовских.
val pixel2 = pixels(i2)(j2)
val pair = /4/4(pixell/ pixel2)
pair.addConstraint(bb => if (bb._l == bb._2) 0.9; else 0.1)
}
<-o
<ь-®
for {
i <- 0 until 10
j <- 0 until 10
} {
if (i <= 8) setConstraint(i, j, i + 1, j)
if (j <= 8) setConstraint(i, j, i, j+1)
О — Задать для каждой переменной унарное ограничение
© — Задать для пар переменных бинарные ограничения, зависящие от координат
© — Применить бинарные ограничения ко всем парам соседних переменных
Уместно будет сделать несколько замечаний.
• Выражение Array, пи (Ю, Ю) (Fiip(0.4)) в определении переменной pixels
создает массив 10x10 и заполняет его элементы различными экземплярами
элемента Flip (0.4). Каждому пикселю соответствует свой элемент Flip, и
это важно, поскольку значения пикселей должны быть различны.
• Возможно, вы недоумеваете, зачем вообще для унарных потенциалов
использовать элемент Flip, а не ограничение. Но в этом случае безразлично,
к чему прибегнуть: к обычному для Figaro способу или к ограничению -
результат один и тот же. Flip возвращает true с вероятностью 0.4 и false -
с вероятностью 0.6. Произведение этих вероятностей дает
ненормированную вероятность возможного мира - точно так же, как при задании с
помощью ограничения.
На самом деле, каждый элемент Figaro следует определять обычным
способом, с помощью того или иного конструктора, даже при использовании
языка для представления марковской сети. Если для элемента нет унарного
ограничения, то обычный конструктор Figaro должен быть нейтральным,
т. е. не дающим одному возможному миру предпочтение перед другими.
ДЛЯ ЭТОГО МОЖНО ВОСПОЛЬЗОВаТЬСЯ ЭЛемеНТОМ Flip (0 . 5) ИЛИ Uniform.
• КОНСТРУКЦИЯ АА В Определении setConstraint - ЭТО КОНСТруКТОр Пары В
Figaro. Следовательно, АА (pixeli, pixei2) создает элемент, значением
которого является пара значений элементов pixeii и pixei2.
• В операторе спискового включения for конструкция о until ю означает
диапазон целых чисел от 0 до 10, не включая правый конец, т. е. множество
целых чисел 0, 1,..., 9. Если нужно включить правый конец, то следует
написать о to ю.
• Тот же оператор for дает пример вложенного цикла. В других языках
нужно было бы написать два цикла for, один внутри другого. В Scala
разрешается поместить оба цикла в один заголовок for.
192

5.5. Марковские сети
Рассуждения с помощью модели восстановления
изображения
Мы хотим использовать модель восстановления изображения для вывода
значений ненаблюдаемых пикселей по известным наблюдаемым. Для этого нужно
три вещи: способ задания и обработки фактов, способ вычисления наиболее
вероятных состояний пикселей и способ получения результатов. Рассмотрим их
поочередно.
Обработка фактов: массив пикселей 10x10 можно было бы построить по
массиву символов 10x10, в котором символ равен 0, если пиксель не освещен, 1 - если
освещен, и ? - если состояние неизвестно. Для обработки этих данных можно
применить Следующую Простую фуНКЦИЮ setEvidence:
def setEvidence(data: String) = {
for { n <- 0 until data.length } {
val i = n / 10
val j = n % 10
data(n) match {
case '0' => pixels (i) (j) .observe(false)
case '1' => pixels(i)(j).observe(true)
case => ()
<M>
О — Используется механизм сопоставления с образцом в Scala, который в данном
случае напоминает предложение switch в других языках. Знак _ обозначает
вариант по умолчанию. Следовательно, если символ равен ' ? ', то пиксель
ненаблюдаемый
Вычисление наиболее вероятных состояний пикселей: в этом примере
встретился новый вид запроса. Раньше нас интересовала оценка апостериорных
вероятностей элементов, а на этот раз - наиболее вероятные значения элементов. Однако
нас интересуют не наиболее вероятные значения по отдельности, безотносительно
к другим элементам, а наиболее вероятное совместное распределение значений
всех переменных. Мы хотим знать, какой из возможных миров наиболее вероятен.
Запрос такого вида в Figaro называется наиболее вероятным объяснением
(НВО), потому что нам нужен мир, дающий наиболее вероятное объяснение
данных. Алгоритмы обработки НВО-запросов отличаются от встречавшихся
ранее алгоритмов вычисления вероятности, хотя они и взаимосвязаны. В этом
примере мы воспользовались вариантом алгоритма распространения доверия
MPEBelief Propagation, Предназначенным ДЛЯ ВЫЧИСЛеНИЯ НВО. Это ИТераТИВНЫЙ
алгоритм, и количество итераций можно задать с помощью параметра. В данном
случае мы проведем 10 итераций. Чтобы создать и выполнить экземпляр
алгоритма MPEBelief Propagation, нуЖНО написать:
val algorithm = MPEBeliefPropagation(10)
algorithm.start()
193

Глава 5. Моделирование зависимостей с помощью байесовских.
Просмотр результатов: нам нужно просто перебрать все пиксели и напечатать
их наиболее вероятные значения. Для получения наиболее вероятного значения
Элемента Предназначен МеТОД mostLikelyValue Класса MPEBeliefPropagation. Код
приведен ниже.
for {
i <- 0 until 10
} {
for { j <- 0 until 10 } {
val mlv = algorithm.mostLikelyValue(pixels(i)(j))
if (mlv) print(flf) else print('O')
}
println ()
}
Для прогона модели нужно подать на вход какие-то данные. Обычно они
читаются из файла или формируются программно другим модулем. Но для простоты
мы определим входные данные прямо в этой программе:
D
val data =
f,,,,,00?000?000
0?010?0010
1107010011
11??000111
1101100071
1707100710
0000170700
0010770100
0170100170
077000110?""".filterNot(_.isWhitespace)
setEvidence(data)
О — В Scala конструктор " " " позволяет создавать длинные строки, занимающие
несколько строчек на экране. Для создания строки длиной 100 мы
отфильтровываем все пробельные символы
При прогоне с этими данными программы выводит такой результат:
0000000000
0001000010
1100010011
1100000111
1101100011
1000100010
0000100000
0010000100
0100100100
0000001100
Это все, что я хотел сказать о марковских сетях. Глава получилась длинной, зато
и узнали вы много. Теперь вы знакомы со всеми основными принципами вероят-
194

5.7. Упражнения
ностных моделей и можете писать вероятностные программы для различных
приложений. В следующих главах мы закрепим и расширим материал, чтобы можно
было писать еще более интересные программы. И начнем с рассмотрения того, как
контейнеры Scala и Figaro позволят создавать более крупные и
структурированные модели.
5.6. Резюме
• Предметом вероятностного моделирования являются связи между
переменными. Симметричные связи порождают ненаправленные зависимости,
асимметричные - направленные.
• Направленная зависимость ведет от причины к следствию. Существуют
разные виды причинно-следственных связей.
• В байесовских сетях направленные зависимости представляются с
помощью ориентированного ациклического графа.
• Направление стрелок в байесовской сети необязательно совпадает с
направлением рассуждения. Байесовская сеть позволяет проводить
рассуждение в любом направлении.
• Марковские сети служат для представления ненаправленных
зависимостей с помощью неориентированного графа.
• Идентификация типов связей между переменными в модели и написание
программы на этой основе - шаг в правильном направлении.
5.7. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Для каждой из перечисленных ниже пар переменных решите, является ли
зависимость между ними направленной или ненаправленной, и, если
направленной, то в какую сторону.
a. Карты игрока в покер и его торговля.
b. Карты первого и второго игрока в покер.
c. Мое настроение и сегодняшняя погода.
d. Мое настроение и позавтракал я или нет.
e. Температура в моей гостиной и настройки домашнего термостата.
f. Температура в моей гостиной и показания находящегося в ней
термометра.
g. Температура в моей гостиной и на кухне,
h. Тема и содержание статьи.
i. Краткое и полное содержание статьи.
2. Для каждого из перечисленных ниже наборов переменных нарисуйте
байесовскую сеть.
195

a. Карты первого игрока в покер, карты второго игрока, торговля
первого игрока, последующая торговля второго игрока.
b. Мое настроение сразу после просыпания, мое настроение в 10 утра,
сегодняшняя погода и позавтракал я или нет.
c. Температура в моей гостиной, температура на кухне, настройки
домашнего термостата, показания термометра в гостиной, показания
термометра на кухне.
d. Тема статьи, краткое содержание статьи, полное содержание статьи,
комментарии к статье.
Вы должны спроектировать байесовскую сеть, моделирующую процесс
приготовления супа. Ее задача - помочь в принятии решения о том, какие
ингредиенты использовать и в каком количестве, а также в определении
таких переменных, как время и температура готовки, всё это с целью
оптимизировать различные качества пищи, например остроту и консистенцию.
a. Какие переменные будут в вашей модели?
b. Нарисуйте байесовскую сеть с этими переменными.
c. Выберите функциональную форму Figaro для каждой переменной..
d. Определите числовые параметры функциональных форм.
e. Воспользуйтесь моделью Figaro для ответа на различные вопросы,
например, сколько времени следует готовить суп из заданных
ингредиентов для достижения оптимальной консистенции.
Теннисный матч состоит из нескольких сетов, а каждый сет - из
нескольких геймов. Игрок, первым выигравший два сета, выигрывает матч. Игрок,
первым выигравший шесть геймов, выигрывает сет. (Пока не будем
обращать внимание на тай-брейки, но, выполнив упражнение 5, вы сумеете
смоделировать и их тоже.) Подача чередуется при смене геймов. Напишите на
Figaro программу, которая принимает два аргумента: вероятности, что
каждый игрок выигрывает гейм, в котором подает. С ее помощью предскажите
победителя матча.
Усложним модель тенниса, включив очки. В рамках одного гейма игроки
набирают очки. Игрок, первым набравший четыре очка, выигрывает гейм,
если только перед этим оба игрока не набрали по три очка. Напишите на
Figaro программу, которая также принимает два аргумента, но теперь это
вероятности, что каждый игрок наберет очко на своей подаче. Снова
воспользуйтесь ей для предсказания победителя.
Еще усложним модель, включив моделирование очков в виде результата
обмена ударами. Игрок характеризуется таким переменными, как
результативность подачи, скорость и частота ошибок. Можете включить в модель
столько деталей, сколько сочтете нужным, в том числе положения игроков
и мяча при каждом ударе.
В моем доме имеется центральное кондиционирование, управляемое
термостатом на первом этаже. На втором этаже обычно теплее, чем на первом.
Глава 5. Моделирование зависимостей с помощью байесовских...
196

5.7. Упражнения
Создайте марковскую сеть для представления температуры в доме (пока не
принимая во внимание термостат). Напишите на Figaro модель для
представления этой сети. С помощью своей модели вычислите вероятность, что
температура на втором этаже не ниже 27 градусов, если на первом этаже она
равна 22 градуса.
8. Теперь добавим в модель термостат, а также температуру на улице и
информацию о том, открыты ли окна. В этой модели сочетаются направленные и
ненаправленные зависимости, поэтому она не является чистой марковской
сетью, однако в Figaro такие комбинации вполне возможны. Напишите на
Figaro программу и воспользуйтесь ей, чтобы решить, стоит ли мне
открывать окно на втором этаже.
9. Рассмотрим фильтр спама из главы 3. В этом приложении все почтовые
сообщения считались независимыми. Теперь предположим, что имеется
несколько сообщений от одного отправителя. Их спамность заведомо
сильно коррелирована.
a. Создайте марковскую сеть, улавливающую такие корреляции.
b. Байесовская сеть для спамных сообщений показана на рис. 3.8.
Воспроизведите эту сеть в марковской сети из упражнения 9а. В этом
случае мы также имеем комбинацию направленной и
ненаправленной сети.
Примечание. Хотя я говорил, что между классом объекта и его свойствами имеется
причинно-следственная связь, и именно такой подход принят в фильтре спама, иногда
имеет смысл двигаться в обратном направлении. Так обстоит дело, когда все признаки
всегда наблюдаемы, как в фильтре спама. В таком случае расточительно явно
моделировать распределение вероятности наблюдаемых признаков. Вместо этого можно создать
модель, в которой признаки почтового сообщения определяют его класс. Классы
сообщений затем связываются с помощью марковской сети из упражнения 9а. Модель такого
вида называется условным случайным полем, они широко используются для понимания
естественных языков и в компьютерном зрении.
Я не собираюсь здесь вдаваться в детали условных случайных полей, но для тех, кто с
ними знаком, отмечу, что их легко представить в Figaro. Особенность состоит в том,
чтобы сделать наблюдаемые признаки сообщений не элементами Figaro, а переменными
Scala, которые помогают определить распределение вероятности элемента,
представляющего спамность сообщения. Все обучаемые параметры модели, конечно, будут
элементами Figaro, и они смогут взаимодействовать с переменными Scala, которые
представляют признаки, определяющие вероятность спама.
197

ГЛАВА 6.
Использование коллекций Seal а
и Figaro для построения моделей
В этой главе,
■ Как коллекции используются для организации
вероятностных моделей.
■ Различия между коллекциями Scala и Figaro,
роли тех и других и совместное применение.
■ Типичные паттерны моделирования, выражаемые
с помощью коллекций, в том числе иерархическое
байесовское моделирование, моделирование
сетей с неизвестным числом объектом и модели над
непрерывной областью.
В предыдущих двух главах был заложен солидный фундамент вероятностного
моделирования. В этой главе мы сконцентрируемся на программировании и
покажем, чем различные возможности языка программирования могут быть полезны
для построения вероятностных моделей. В частности, мы обратим внимание на
коллекции
Коллекции - один из наиболее полезных механизмов высокоуровневого языка,
позволяющий рассматривать несколько объектов одного типа как единое целое.
Например, если нужно обработать много целых чисел, то можно поместить их в
массив, а затем написать цикл, в котором все элементы массива умножаются на
два и суммируются. Или, если говорить в терминах функционального
программирования, то можно написать функцию тар, которая умножает каждый элемент
массива на 2, и функцию fold, выполняющую сложение. То же самое справедливо
и для вероятностного программирования; если имеется много переменных одного
типа, то мы можем поместить их в коллекцию и применять к ней функции типа
тар И fold.

6.1. Работа с коллекциями Seal а
В Figaro это можно сделать двумя способами. Первый - воспользоваться
обычными коллекциями Scala. Если вы опытный программист, то, без сомнения,
знакомы с такими коллекциями, как массивы, списки, множества, отображения и т. д. В
составе Scala имеется обширная библиотека коллекций, которой вы можете
пользоваться для организации элементов и создания вероятностных программ.
Figaro также предоставляет библиотеку коллекций, которая добавляет
возможности для работы со многими элементами. Коллекции Figaro позволяют делать
такие вещи, которые с помощью обычных коллекций Scala выполнить нелегко.
С другой стороны, и коллекции Scala могут предложить такое, чего нет в
коллекциях Figaro, так что для работы с вероятностными моделями полезны и те, и
другие.
Начнем с обычных коллекций Scala, а затем перейдем к коллекциям Figaro и
посмотрим, что они позволяют. После этого обсудим, когда лучше
воспользоваться коллекциями Scala, а когда применить коллекции Figaro. В последних двух
разделах этой главы мы рассмотрим два весьма полезных применения коллекций
Figaro: использование массивов переменной длины для моделирования ситуаций
с неизвестным числом объектов и определение вероятностной модели над
непрерывной областью пространства или времени.
Примечание. Поскольку эта глава посвящена программированию, в ней вы найдете
много кода. Приведено семь полных программ, код которых имеется на сайте книги.
Знакомство с коллекциями Scala было бы полезно, хотя в коде и не используются
особенно заумные конструкции. Кроме того, вы должны уверенно владеть концепциями
байесовских сетей в объеме главы 5.
6.1. Работа с коллекциями Scala
До сих пор в рассмотренных примерах было всего по одному. В примере с
установлением подлинности Рембрандта была одна картина, у которой была одна тема,
один размер и одна яркость. А если требуется работать с несколькими объектами,
например, построить модель, где много картин, у каждой из которых может быть
больше одной темы?
В программировании для хранения нескольких объектов одного типа,
обрабатываемых как единое целое, применяются коллекции. Например, можно завести
массив чисел и использовать его для применения некоторой операции к каждому
числу или для сложения всех чисел. Возможность в цикле обойти все числа в
массиве намного сокращает программы и повышает их гибкость, потому что размер
массива достаточно изменить только в одном месте. Не будь массивов, цикл
пришлось бы полностью развернуть, и было бы гораздо труднее написать общий код
для массивов разной длины в одной программе.
Коллекции Scala привносят те же удобства в вероятностное программирование.
Я приведу примеры нескольких типичных ситуаций, в которых полезны
коллекции Scala, начав со случая, когда есть много переменных одного типа, зависящих
от одной переменной.
199

Глава 6. Использование коллекций Scala и Figaro для построения...
6.1.1. Моделирование зависимости многих
переменных от одной
Рассмотрим классический пример, с которым впервые столкнулись в главе 4.
Имеется монета сомнительного происхождения. Монета может оказаться
асимметричной, и мы не знаем, с какой вероятностью при подбрасывании выпадет орел.
Мы хотим оценить степень асимметрии монеты (вероятность выпадения орла).
И, кроме того, хотелось бы предсказать результаты последующих подбрасываний.
На рис. 6.1 показана байесовская сеть для этой задачи. В корневом узле
находится переменная Асимметрия. Эта вещественная переменная представляет
вероятность выпадения орла при одном подбрасывании. На рисунке показаны узлы
для 101 подбрасывания, но вообще число подбрасываний может быть любым. При
каждом подбрасывании вероятность выпадения орла равная значению
Асимметрии. Можно представить себе, что мы наблюдали результаты первых 100
подбрасываний и хотим предсказать результат 101-го.
Результат каждого подбрасывания
зависит от степени асимметрии
Асимметрия —
корневой узел
Рис. 6.1. Байесовская сеть для подбрасывания асимметричной монеты
Представление модели подбрасывания монеты
на Figaro
Этот пример легко представить на Figaro, воспользовавшись массивом Scala для
хранения результатов предыдущих подбрасываний монеты. Наша программа
будет читать заданную в командной строке последовательность символов Н (орел)
и Т (решка), описывающих результаты предыдущих подбрасываний. Для
установления размера массива достаточно этого аргумента. Ниже приведен код модели:
val outcomes = args(O)
val numTosses = outcomes.length
val bias = Beta(2,5)
val tosses = Array.fill (numTosses) (Flip (bias) )
val nextToss = Flip(bias)
«-o
О — Создаем массив размера numTosses, состоящий из отдельных экземпляров
элемента Flip(bias). Элементы массива представляют подбрасывания монеты
200

6.1. Работа с коллекциями Seal а
Для моделирования асимметрии мы используем элемент Beta. В главе 3 при
проектировании фильтра спама мы уже пользовались элементом Beta для
моделирования вхождений слов в сообщение. Я говорил, что этот элемент отлично
работает совместно с Flip и Binomial, так что использование Beta для
подбрасывания монеты оправдано. На врезке ниже сказано еще несколько слов о связи между
Элементами Beta И Flip.
Далее мы строим массив для представления всех ранее наблюдавшихся
подбрасываний. Для этого используется метод Array.пи, который создает массив
заданной длины и предоставляет определение элемента. Это определение вычисляется
заново для каждого элемента массива, т. е. в данном случае каждый элемент
массива - отдельный экземпляр элемента Figaro Flip (bias), определяющего выпадение
орла с вероятностью bias. И в самом конце мы создаем еще один элемент Flip,
описывающий следующее подбрасывание, исход которого требуется предсказать.
Сопряженное априорное распределение и почему элементы
Beta и Flip работают совместно
В теории вероятностей элементу Flip соответствует стандартное название -
распределение Бернулли. А бета-распределение называется сопряженным априорным к
распределению Бернулли. Это означает, что если имеются переменные,
подчиняющиеся распределениям бета и Бернулли, и бета-переменная представляет вероятность
того, что переменная Бернулли принимает значение true, то распределение
бета-переменной при условии исхода переменной Бернулли также является
бета-распределением.
Присмотримся внимательнее к двум аргументам элемента Beta. Первый
аргумент, а, представляет воображаемое число уже наблюдавшихся орлов плюс 1.
Второй аргумент, р, -тоже самое, но для решек. В нашем примере используется элемент
Beta (2, 5), т. е. предполагается, что еще до обучения мы видели, что выпал один орел
и четыре решки. (Кстати, прибавление единицы к числу орлов и решек -
математическое удобство; как мы увидим ниже, оно упрощает предсказание исхода
следующего подбрасывания.) Это позволяет закодировать тот факт, что мы имеем априорные
предположения об асимметрии еще до ознакомления с данными. Если никаких
априорных предположений нет, можете взять Beta (1,1).
Предположим теперь, что в результате подбрасывания выпал орел. Тогда для
получения апостериорного распределения прибавляем к а единицу. А если выпала решка,
то прибавляем 1 к р. Вообще, если наблюдается h орлов и t решек, то а увеличивается
на h, a р - на t. Так, если априорное распределение описывалось элементом Beta (2r
5) и выпало три орла и две решки, то апостериорное распределение будет
описываться элементом Beta {5, 7). Потому-то бета-распределение и является сопряженным
априорным к распределению Бернулли.
Также легко предсказать, выпадет ли при следующем подбрасывании орел, если
асимметрия подчиняется бета-распределению. Это произойдет с вероятностью
а/(а + р), т. е. 5/12 для случая Beta (5,7).
Все вычисления в этом примере просты, для них не нужен никакой язык
программирования. Но так бывает далеко не всегда, обычно вычислить апостериорное
распределение и сделать прогноз с помощью такой простой формулы не удается. И, кроме
того, в Figaro не обязательно использовать сопряженные априорные распределения.
Но лучше все же использовать, если это возможно, поскольку это разумный способ
представления априорных знаний о параметрах.
201

Глава 6. Использование коллекций Scala и Figaro для построения...
Массивы Scala также упрощают задание фактов. Напомним, что переменная
outcomes читается из командной строки и является последовательностью
символов Н и Т, по одному для каждого подбрасывания. Чтобы указать исходы ранее
наблюдавшихся подбрасываний, можно написать такой код:
for {
toss <- 0 until numTosses
} {
val outcome = outcomes(toss) == fHf
tosses(toss).observe(outcome)
}
Вывод с помощью алгоритма с отсечением по времени
Итак, мы создали модель и задали факты, пора приступать к выводу. В этой
главе описан новый способ вывода, при котором вы полностью контролируете время
работы: использование алгоритмов с отсечением по времени. Так называется
алгоритм, который выдает наилучшее решение на тот момент, когда его прервали. Вы
можете точно указать, сколько времени алгоритм должен работать, и он
постарается сделать все возможное.
В Figaro алгоритмы с отсечением по времени используются, как обычные
алгоритмы. Мы создаем экземпляр алгоритма и запускаем его. Алгоритм с отсечением
по времени работает в отдельном потоке, поэтому параллельно программа может
делать что-то еще. Обычно она спит в течение времени, отведенного алгоритму для
работы. Затем мы запрашиваем у алгоритма интересующую нас информацию. И в
конце уничтожаем экземпляр алгоритма. Это важно, потому что вместе с
экземпляром уничтожается и поток, иначе алгоритм будет и дальше потреблять ресурсы.
Ниже приведен код выполнения вывода для нашей модели подбрасывания
монеты с использованием алгоритм выборки по значимости. У этого алгоритма
есть как версия без отсечения по времени, которая после запуска отрабатывает до
естественного завершения, так и версия с отсечением. Две версии есть и у многих
других алгоритмов в Figaro. В случае версии без отсечения мы сообщаем
алгоритму объем выборки. А в версии с отсечением объем выборки заранее не задается,
поскольку алгоритм сам выбирает столько примеров, сколько может обработать за
имеющееся в его распоряжении время.
val algorithm = Importance(nextToss, bias) О—О
algorithm.start()
Thread.sleep(1000) <3—©
algorithm.stop()
println("Средняя асимметрия = " + algorithm.mean(bias))
println("Вероятность орла при следующем подбрасывании = " +
algorithm.probability(nextToss, true))
algorithm.kill() <3—®
О — Создаем экземпляр алгоритма выборки по значимости, намереваясь опросить
nextToss и bias. Figaro знает, что это версия с отсечением по времени, поскольку
объем выборки не задан
202

6.1. Работа с коллекциями Seal а
© — Ждать 1000 миллисекунд
© — Освободить все ресурсы
При запуске с аргументом нтнннннтнтнннтнннннн эта программа работает 1
секунду и печатает такой результат:
Средняя асимметрия = 0.6641810675997326
Вероятность орла при следующем подбрасывании = 0.6414832927224574
6.1.2. Создание иерархических моделей
В этом разделе показано, как создать последовательность последовательностей и
тем самым обобщить предыдущий пример, добавив иерархию. Предположим, что
мы подбрасываем монету, выбрав ее из многих монет в мешке, который выбирается
из многих мешков в ящике... Ну и так далее. Для простоты будем моделировать
подбрасывание монет из одного и того же мешка, так что у нас будет всего два уровня
последовательностей. Но подход легко обобщается на произвольное число уровней.
В предыдущем разделе мы видели, что свойство подбрасывания (выпадение
орла) зависит от свойства монеты (асимметрии). В этом разделе асимметрия
монеты зависит от свойства мешка. Точнее, некоторые монеты в мешке
правильные, т. е. орел выпадает точно в 50 % случаев, тогда как другие - неправильные.
У мешка имеется свойство: вероятность, что выбранная наугад монета окажется
правильной.
На рис. 6.2 изображена байесовская сеть для этого примера. В ней три
уровня, соответствующих уровням иерархии. На первом уровне представлен мешок и
ассоциированная с ним переменная ВероятностьПравильной. На втором уровне
представлены монет и их асимметрия. Здесь монет три, но их число может быть
произвольным. На третьем уровне находятся подбрасывания монет. С каждым
подбрасыванием связаны два нижних индекса: номер монеты и номер
подбрасывания. Результат подбрасывания зависит от асимметрии монеты. Количество
подбрасываний для разных монет может различаться; в данной сети третья монета
подбрасывается три раза, а первые две - по два раза.
Эту ситуацию можно описать с помощью двух уровней последовательностей.
На первом уровне мы имеем две последовательности, содержащие элементы
Figaro, относящиеся к отдельным монетам: является ли монета правильной и какова
степень ее асимметрии. Для каждой монеты на втором уровне находится
последовательность элементов Figaro, представляющих подбрасывания монеты. В Scala
последовательность легко создать с помощью оператора генерации списков for.
Ниже приведен код модели. Программа ожидает, что в командной строке будет
по одному аргументу для каждой наблюдавшейся монеты. Один аргумент
содержит последовательность символов Н и Т, описывающих отдельные
подбрасывания, - так же, как в предыдущем примере.
val numCoins = args.length
val fairProbability = Uniform(0.0, 1.0)
203

val isFair =
for { coin <- 0 until numCoins
yield Flip(fairProbability)
Глава 6. Использование коллекций Scala и Figaro для построения.
val biases =
for { coin <- 0 until numCoins }
yield If (isFair (coin), Constant (0.5), Beta(2,5))
val tosses =
for { coin <- 0 until numCoins }
yield { |
for { toss <- 0 until args(coin).length }
yield Flip(biases(coin) )
} |«-®
<^-в
<i-o
О — Создаем последовательность длины numCoins элементов Flip(fairProbability)
© — Если монета правильная, то ее асимметрия заведомо равна 0.5, иначе описывается
элементом Beta(2, 5)
© — Порождается последовательность последовательностей подбрасываний, по одной
для каждой монеты
© — Для данной монеты порождается последовательность элементов Flip(biases(coin)),
длина которой равна числу подбрасываний монеты, полученному из аргумента в
командной строке
Первый уровень
представляет
мешок
Второй уровень
представляет
монеты в мешке
Третий уровень представляет
подбрасывания одной монеты
Рис. 6.2. Байесовская сеть для иерархической модели
Теперь можно написать двумерный оператор for для задания фактов:
for {
coin <- 0 until numCoins
toss <- 0 until args(coin).length
} {
204
Вероятность-
Правильной
Асимметрия З
Асимметрия 1
Асимметрия 2
Подоpa
сывание
■ i
Подбра
сывание
а
Подбра
сывание
21
Подбра
сывание
jj
Подбра
сывание
ti
Подбра
сывание
ц
Подбра
сывание
3J

6.1. Работа с коллекциями Seal а
val outcome = args(coin) (toss) == fHf
tosses (coin) (toss).observe(outcome)
}
И наконец, выполнить вывод:
val algorithm = Importance(fairProbability, biases(0))
algorithm.start()
Thread.sleep(lOOO)
algorithm.stop()
val averageFairProbability = algorithm.mean(fairProbability)
val firstCoinAverageBias = algorithm.mean(biases(0))
println("Средняя вероятность правильности: " + averageFairProbability)
println("Средняя асимметрия первой монеты: " + firstCoinAverageBias)
algorithm.kill()
Если этой программе передать аргументы нтннт н тннн ннт, то она напечатает
такой результат:
Средняя вероятность правильности: 0.7079517451620699
Средняя асимметрия первой монеты: 0.4852371044437457
6.1.3. Моделирование одновременной
зависимости от двух переменных
В предыдущем разделе мы видели, как исход подбрасывания монеты зависит от
степени ее асимметрии, которая, в свою очередь, зависит от вероятности выборки
правильной монеты из мешка. Это иерархически организованная модель.
Альтернативой является зависимость переменной сразу от двух других переменных, не
связанных никакой иерархией. В последнем примере использования коллекций
Scala мы рассмотрим моделирование таких ситуаций с помощью двумерных
массивов, когда одна переменная зависит от двух других, каждая из которых является
коллекцией. Например, объем продаж продукта в регионе может зависеть от
качества продукта и от известности в этом регионе торговой марки. В таком случае мы
имеем массив продуктов, массив регионов и двумерный массив продаж, в котором
каждый элемент зависит от соответствующего продукта и региона.
Примечание. В этом разделе речь идет только о двумерных массивах. Но, вообще
говоря, число измерений может быть любым. Это массивы Scala, поэтому работа с ними
устроена так же, как в обычных программах.
На рис. 6.3 показана байесовская сеть для этого примера. Разобраться в ней не
сложно. Имеются две переменные, относящиеся к качеству продуктов, две
переменные, относящиеся к известности марки, и шесть переменных, относящихся к
продажам, - по одной для каждой комбинации качества продукта и известности в регионе.
Несмотря на простоту сети, она допускает содержательные рассуждения,
особенно если известны результаты наблюдения продаж, а требуется вывести каче-
205

Глава 6. Использование коллекций Scala и Figaro для построения..
ство продукта и известность марки. Например, объем продаж продукта 1 может
предоставить информацию о качестве продукта 2. Чтобы понять, как это
возможно, предположим, что в регионе 1 высоки продажи продукта 1. Отсюда можно
сделать вывод, что марка хорошо известна в регионе 1. А если продажи продукта 2
в регионе 1 низкие, то можно предположить, что качество продукта 2 оставляет
желать лучшего. С другой стороны, если продажи продукта 1 в регионе 1 также
низкие, то мы уже не будем так уверены, что продукт 2 низкокачественный,
потому что есть основания полагать, что в регионе 1 плохо известна сама марка.
С каждым Продуктом I
связано Качество Продукта I
Продажи., связана
с Качество Продукта I и
Известностью В Регионе J
С каждым Регионом J связана
Известность В Регионе J
Рис- 6.3. Байесовская сеть для двумерной модели продаж
Если вы еще не забыли обсуждение паттернов рассуждений в байесовских сетях
(глава 5), то сразу заметите, что путь Продажии - Известность В Регионе 1 -
Продажи^ - Качество Продукта 2 активен. Действительно, единственная
наблюдаемая на этом пути промежуточная переменная - Продажи2Г Но в ней сходятся
стрелки, а, значит, путь не блокируется наблюдением этой переменной. Вместе с
тем, переменная Известность В Регионе 1 не наблюдается, и стрелки в ней не
сходятся, так что путь не блокирован и здесь. Следовательно, путь активен.
Как видим, при наблюдении продаж в этой модели все переменные связаны
друг с другом. Значит, при выполнении вывода будут вычислены сразу все
переменные, относящиеся к качеству продуктов и известности марки в регионе. Такой
вывод называется коллективным, и подобные рассуждения встречаются в
вероятностном программировании достаточно часто.
Двумерная модель продаж на Figaro
Эту ситуацию легко представить на Figaro с помощью двумерных массивов.
Я приведу весь код целиком, потому что его составные части мы уже видели.
206
Качество Продукта 1
Качество Продукта 2
Качество Продукта 3
Продажи
м
Продажи
\7
Продажи
г
Продажи
22
Продажи
Г
Продажи
V?
Известность В
Регионе 1
Известность В
Регионе 2

6.1. Работа с коллекциями Seal а
Листинг 6.1. Двумерная модель продаж
import com.era.figaro.library.atomic.continuous.Beta
import com. era.figaro. language . Flip
import com.era.figaro.algorithm.sampling.Importance
object Sales {
def main(args: Array[String]) {
val numProducts = args.length I <l—ft
val numRegions = args(0).length
val productQuality = Array.fill(numProducts)(Beta(2,2))
val regionPenetration = Array.fill(numRegions)(Beta(2,2))
def makeSales(i: Int, j: Int) =
Flip(productQuality(i) * regionPenetration(j))
val highSales =
Array.tabulate(numProducts, numRegions)(makeSales
m
for {
i <- 0 until numProducts
j <- 0 until numRegions
} {
val observation = args(i)(j) == fTf
highSales(i)(j).observe(observation)
}
s
val targets = productQuality ++ regionPenetration
val algorithm = Importance(targets:_*)
algorithm.start()
Thread.sleep(lOOO)
algorithm.stop()
for { i <- 0 until numProducts } {
println("Качество продукта " + i + ": " +
algorithm.mean(productQuality(i)))
}
for { j <- 0 until numRegions } {
println("Известность в регионе " + j + ": " +
algorithm.mean(regionPenetration(j) ) )
}
algorithm.kill()
E
§
}
О — В командной строке задается несколько аргументов — по одному для каждого
продукта. Каждый аргумент — строка, содержащая по одному символу для каждого
региона, все строки должны быть одинаковой длины
© — Конструкция Array.tabulate(numProducts, numRegions) создает двумерный массив,
элементы которого соответствуют комбинациям продукта и региона. Каждый
элемент массива — это элемент Flip, в котором вероятность равна произведению
качества продукта на известность в регионе
207

лава 6. Использование коллекций Scala и Figaro для построения..
© — Результаты наблюдения продаж берутся из командной строки; Т означает
высокие продажи для комбинации продукта и региона. Для каждого элемента массива
highSales задается соответствующий ему факт
О — Создаем экземпляр алгоритма выборки по значимости с отсечением по времени,
указывая, что нас интересует качество каждого продукта и известность марки в каждом
регионе
© — Печатаем среднее качество каждого продукта и среднюю известность в каждом
регионе
Итак, мы рассмотрели три практически полезные модели, которые можно
представить с помощью коллекций Scala. Пора расширить арсенал, включив него
коллекции Figaro.
6.2. Работа с коллекциями Figaro
В предыдущем разделе мы узнали, как коллекции Scala помогают создавать
интересные модели со многими переменными определенного вида. В этом разделе
мы познакомимся с коллекциями Figaro. Коллекция Figaro - это структура данных
для хранения нескольких элементов Figaro одного вида. Вы наверняка подумали,
что это ничем не отличается от коллекции Scala - так зачем же еще какие-то
коллекции?
6.2.7. Почему коллекции Figaro полезны?
Особенность коллекций Figaro состоит в том, что они содержат элементы,
определяющие распределение вероятности значений, - и знают об этом! Они позволяют
заглядывать внутрь элементов и производить операции над значениями. Как это
работает, показано на рис. 6.4.
Коллекция
Figaro
Элементы
Значения
Новые
коллекции
Новые
элементы
Новые
значения
Рис. 6.4. Коллекция Figaro содержит
элементы, определяющие распределение
вероятности значений. Она позволяет
применять к этим значениям операции и тем
самым порождать новые элементы и новые
коллекции
Это открывает возможность делать разные полезные вещи, некоторые из них
перечислены ниже.
• ЕСЛИ с - КОЛЛеКЦИЯ Figaro Элементов ТИПа Integer, ТО ВЫЗОВ стар ( (i: Int)
=> i * 2) порождает новую коллекцию Figaro. Каждому элементу е
исходной коллекции соответствует элемент, эквивалентный результату Apply (e,
d: int) => i * 2), в новой коллекции. Поэтому новая коллекция состоит
208

6.2. Работа с коллекциями Figaro
из элементов типа integer. Каждый ее элемент соответствует процессу,
который начинается с элемента исходной коллекции, порождает его
значение и умножает это значение на 2. Например, если с - коллекция Figaro,
содержащая два элемента uniform (2, 3) и constant (5), то коллекция Figaro
c.map((i: Int) => i * 2) СОДерЖИТ Элементы Apply (Uniform (2, 3) , (i:
Int) => i * 2) И Apply (Constant (5) , (i: Int) => i * 2). На Практике ЭТО
означает, что коллекция содержит два элемента, один из которых
определяет равномерное распределение значений 4 (2 * 2) и б (з * 2), а другой
является константой ю (5 * 2).
• ЕСЛИ с - КОЛЛеКЦИЯ Figaro Элементов ТИПа Double, TO ВЫЗОВ с. chain ((d:
Double) => Fiip(d)) порождает новую коллекцию Figaro, в которой
каждому Элементу е ИСХОДНОЙ КОЛЛеКЦИИ СООТВеТСТВуеТ Элемент Chain (e, (d:
Double) => Fiip(d)). Первая коллекция содержит параметры, а вторая -
элементы Flip, так что каждый Flip зависит от соответственного
параметра. Например, еСЛИ с СОДерЖИТ ЭЛемеНТЫ Beta (2, 1) И Beta(l, 2), ТО В
НОВОЙ КОЛЛеКЦИИ ИМ будут СООТВеТСТВОВаТЬ ЭЛемеНТЫ Flip (Beta (2, 1) ) И
Flip (Beta (l, 2)) (напомним, что составной Flip - это сокращенная запись
Chain).
• Если с - коллекция Figaro, содержащая элементы типа integer, то вызов
c.exists((i: int) => i < 0) возвращает булев элемент, показывающий,
если ли в исходной коллекции элементы с отрицательными значениями.
Аналогично вызов с.count ((i: int) => i < 0) возвращает количество
таких элементов.
• К контейнеру можно применить любую операцию сворачивания или
агрегирования. Опытные программисты на Scala наверняка знакомы с
операциями типа foidLeft. Например, если с - коллекция Figaro, содержащая
элементы типа integer, то вызов с. foidieft (_ + _) создает элемент,
представляющий сумму значений всех элементов коллекции. Рассмотрим, к
примеру, коллекцию Figaro, содержащую элементы uniform (2, з) и constant (5).
Сумма может принимать два значения: 2 + 5 = 7иЗ + 5 = 8. Поскольку
вероятность значений 2 и 3 в первом элементе равна 1/2, то и вероятность
каждой из этих сумм равна 1/2. Следовательно, элемент с. f oidief t (_ + _)
определяет равномерное распределение значений 7 и 8.
• Существует целый ряд других операций над контейнерами Figaro,
подробности смотрите в Scaladoc.
Это основная причина полезности коллекций Figaro. Но есть и другие.
• Коллекции Figaro переменной длины позволяют представить ситуацию,
когда количество объектов заранее неизвестно.
• Они также позволяют представить ситуации, когда множество переменных
бесконечное и даже не счетное.
Обо всем этом будет рассказано ниже.
209

Глава 6. Использование коллекций Scala и Figaro для построения...
6.2.2. Иерархическая модель и коллекции Figaro
В качестве первого примера вернемся к иерархической модели подбрасывания
монет, выбираемых из мешка, и посмотрим, как ее можно представить с
помощью коллекций Figaro. Для этого мы воспользуемся простейшей коллекцией:
FixedsizeArray. Она содержит фиксированное число элементов, каждый из
которых генерируется тем или иным способом. На рис. 6.5 показано, что
конструктор FixedsizeArray принимает два аргумента: количество элементов и генератор
элементов. Генератор - это функция, которая принимает аргумент типа integer,
равный индексу элемента в массиве, и возвращает элемент, зависящий от этого
индекса. Код на рис. 6.5 создает коллекцию Figaro из 10 элементов, в которой i-ый
элемент (нумерация начинается с 0) равен Flip(l.o / ц + щ.
Количество
элементов Генератор элементов
л
new FixedsizeArray (10, i => Flipd.O / (i + 1)))
Индекс в Определение
массиве элемента
Рис. 6.5. Конструирование массива фиксированной длины
Поскольку иерархическую модель мы уже видели, я приведу код, выделив
изменения полужирным шрифтом. Для иллюстрации использования контейнеров
Figaro я немного усложнил пример, разрешив включать в аргумент командной
строки также символы ?, означающие, что исход подбрасывания монеты не
наблюдался. Тогда можно будет запросить у модели, выпадал ли орел при каком-либо
подбрасывании конкретной монеты.
Листинг 6.2. Иерархическая модель с применением контейнеров Figaro
import com.era.figaro.language.{Flip, Constant}
import com.era.figaro.library.atomic.continuous.{Uniform, Beta}
import com.era.figaro.library.compound.If
import com.era.figaro.algorithm.sampling.Importance
import com. era.figaro. library. process . FixedsizeArray <3—©
object HierarchicalContainers {
def main(args: Array[String]) {
val numCoins = args.length
val fairProbability = Uniform(0.0, 1.0)
val isFair =
new FixedsizeArray (numCoins + 1, i => Flip (fairProbability)) <]—©
210

6.2. Работа с коллекциями Figaro
val biases = isFair.chain(if (_) Constant(0.5) else Beta(2,5))
val tosses =
for { coin <- 0 until numCoins } yield
new FixedSizeArray(args(coin).length, i => Flip(biases(coin)))
val hasHeads =
for { coin <- 0 until numCoins
tosses(coin).exists(b => b)
yield
a
for {
coin <- 0 until numCoins
toss <- 0 until args(coin).length
} {
args (coin) (toss) match {
case fHf => tosses(coin)(toss).observe(true)
case 'T' => tosses(coin)(toss).observe(false)
case => ()
}
}
В
val algorithm = Importance(fairProbability, hasHeads(2))
algorithm.start()
Thread.sleep(lOOO)
algorithm.stop()
printIn("Вероятность, что хотя бы в одном подбрасывании третьей
"монеты выпал орел = " +
algorithm.probability(hasHeads(2), true))
algorithm.kill()
}
}
О — com.cra.figaro.library.process — пакет, содержащий библиотеку коллекций Figaro
© — В этом массиве фиксированной длины каждый элемент — Flip(fairProbability), вне
зависимости от индекса
© — Для каждой монеты создаем новый элемент, равный либо Constant(0.5), либо
Beta(2, 5) в зависимости от значения isFair(coin)
© — Переменная tosses ссылается на последовательность Scala (одну для каждой монеты),
в которой каждый элемент — это коллекция Figaro, содержащая элементы Flip, для
которых вероятность выпадения орла равна асимметрии соответствующей монеты
© — hasHeads(coin) — элемент, описывающий, выпал ли орел хотя бы при одном
подбрасывании монеты. Пояснения к конструкции tosses(coin).exists(b => b) приведены в тексте
© — Задание фактов производится почти так же, как и раньше, tosses(coin) — коллекция
FixedSizeArray, для получения элемента из нее можно использовать выражение
tosses(coin)(toss) — так же, как для массива Scala
В пояснениях больше всего нуждается строка tosses (coin) .exists (b => b).
Выделим в ней отдельные части. Начнем с того, что переменная tosses определена
как следующий код:
for { coin <- 0 until numCoins } yield
new FixedSizeArray(args(coin).length, i => Flip(biases(coin)))
211

Глава 6. Использование коллекций Scala и Figaro для построения...
Конструкция for...yieid создает последовательность Scala, в которой каждой
монете соответствует массив фиксированной длины. Длина этого массива равна
числу подбрасываний монеты, а эта величина определяется соответствующим
аргументом в командной строке. В каждом элементе массива находится
элемент Figaro Flip, аргумент которого равен асимметрии монеты. Таким образом,
tosses (coin) - массив фиксированной длины.
exists - это метод коллекций Figaro, который создает новый элемент,
описывающий, есть ли среди элементов коллекции такие, которые удовлетворяют
заданному предикату. В данном случае задан предикат ь => ь, т. е. функция, которая
принимает значение ь и возвращает его же. Поскольку исход подбрасывания
монеты - булева величина, то ь имеет тип Boolean, и этот предикат возвращает true
тогда и только тогда, когда элемент принимает значение true (т. е. при
подбрасывании выпал орел). Следовательно, tosses (coin) .exists (b => ь) возвращает
элемент, принимающий значение true, если хотя бы при одном подбрасывании
монеты выпал орел.
Итак, мы познакомились с первым примером коллекций Figaro, теперь пойдем
дальше и изучим связь между коллекциями Scala и Figaro.
6.2.3. Совместное использование коллекций
Scala и Figaro
Увидев, как коллекции Figaro позволяют применять операции к значениям
элементов, вы, наверное, задаетесь вопросом, а нужны ли вообще в Figaro
коллекции Scala. Нужны - потому что различных коллекций Scala больше, и многие
методы коллекций Scala для коллекций Figaro не определены. Если вам не
нужны операции над значениями элементов коллекции, то лучше работать с
коллекцией Scala.
Преобразование коллекции Scala в коллекцию Figaro
и наоборот
Иногда нужно то и другое: гибкость коллекций Scala в сочетании с
возможностью применять операции к значениям. По счастью, совсем нетрудно
преобразовать коллекцию Scala в коллекцию Figaro и наоборот. Опишем несколько
способов такого преобразования.
• Конструктор класса container. В Figaro container - это общий класс
коллекций, содержащих конечное число элементов. Его конструктор
принимает переменное число аргументов, все они должны быть элементами,
принимающими значения одного и того же типа. Конструктор возвращает
коллекцию Figaro, содержащую эти элементы. Для создания коллекции
Figaro, состоящей из трех подбрасываний можно написать container (toss i,
toss2, toss3).
Если коллекция Scala - последовательность (т. е. реализует
характеристику seq, как массив или список), то ее можно преобразовать в переменное чис-
212

6.2. Работа с коллекциями Figaro
ЛО аргументов С ПОМОЩЬЮ КОНСТРУКЦИИ :_*. Так, еСЛИ tosses = List(tossl,
toss2, toss3), TO KOHCTpyKTOp Container (tosses :_*) порождает ту Же КОЛ-
лекцию Figaro, что и выше. Если же коллекция больше походит на
множество, не являющееся последовательностью, то для преобразования можно
сначала воспользоваться методом toList, а затем применить конструкцию
:_*, например! Container (Set (tossl, toss2, toss3) . toList :_*). Любую
коллекцию Scala, реализующую характеристику Traversable, - а это
большинство коллекций - можно преобразовать в список указанным способом,
а затем преобразовать список в коллекцию Figaro.
• Перечисление элементов контейнера. Если имеется экземпляр класса
Figaro container (конечная коллекция), то его можно преобразовать в
Последовательность Scala Seq С ПОМОЩЬЮ Метода elements. Так,
Container (tossi, toss2, toss3) .elements возвращает последовательность Scala,
содержащую элементы tossi, toss2 и toss3. Затем эту последовательность
seq можно преобразовать в любую коллекцию Scala, например, список
или множество.
• Порождение отображения индексов на элементы. Фундаментальное
определение коллекции Figaro - это отображение значений множества
индексов на элементы. Мы более внимательно изучим эту концепцию в разделе
6.4, когда будем рассматривать бесконечные процессы, в которых
множество индексов состоит из вещественных чисел. Для коллекции Fixedsize-
Array множество индексов состоит из целых чисел от 0 до числа элементов
минус 1. Для класса container множество индексов конечно. Поэтому легко
преобразовать container в явное отображение Scala (мар) индексов на
значения. Для этого предназначен метод toMap класса container.
Пример: предсказание продаж
Для иллюстрации совместной работы Scala и Figaro усложним пример с
продажами из раздела 6.1.3. Как и раньше, имеется некоторый набор продуктов, каждый
со своим качеством, и некоторый набор регионов, каждый со своей степенью
известности торговой марки. Мы наблюдаем продажи каждого продукта в каждом
регионе за последний год и хотим предсказать продажи в будущем году. Кроме
того, мы хотим узнать, сколько людей могла бы нанять компания для поддержки
каждой линейки продуктов и в региональные отделы продаж.
Как и раньше, начнем с одномерных массивов Scala, содержащих продукты и
регионы, и с двумерного массива продаж:
val productQuality = Array.fill(numProducts)(Beta(2,2))
val regionPenetration = Array.fill(numRegions)(Beta(2,2))
def makeSales(i: Int, j: Int) =
Flip(productQuality(i) * regionPenetration(j))
val highSalesLastYear =
Array.tabulate(numProducts, numRegions)(makeSales _)
val highSalesNextYear =
Array.tabulate(numProducts, numRegions)(makeSales )
213

Глава 6. Использование коллекций Scala и Figaro для построения...
Это полная модель всех продуктов, регионов и продаж в прошлом и будущем
году. Ее можно использовать, чтобы спрогнозировать продажи в будущем году на
основе данных о продажах в прошлом году. Для этой цели достаточно коллекций
Scala, так что если вам не нужны дополнительные возможности коллекций Figaro,
то и не используйте их. Но мы хотим также предсказать количество новых
сотрудников в разрезе продуктов и регионов, а вот для этого понадобятся
коллекции Figaro. Приведенный ниже код создает массив Scala, содержащий по одному
элементу на каждый продукт, причем этим элементом является объект Figaro
container, в котором хранятся элементы, представляющие прогноз продаж
соответствующего продукта во всех регионах:
def getSalesByProduct(i: Int) =
for { j <- 0 until numRegions } yield highSalesNextYear(i)(j)
val salesPredictionByProduct =
Array.tabulate(numProducts)(i => Container(getSalesByProduct(i):_*))
А вот теперь воспользуемся коллекциями Figaro для прогнозирования
количества вновь нанятых сотрудников. Сначала для каждого продукта создаем элемент,
представляющий количество регионов с высоким объемом продаж в будущем
году:
val numHighSales =
for { predictions <- salesPredictionByProduct }
yield predictions.count(b => b)
numHighSales - массив Scala, содержащий по одному объекту - элементу Figaro
ТИПа Integer - ДЛЯ КаЖДОГО продукта. Мы СДелаЛИ salesPredictionByProduct мас-
сивом коллекций Figaro, чтобы для каждого объекта-коллекции можно было
вызвать метод predictions.count(b => b) и получить элемент, представляющий
количество продуктов, для которых прогнозируется высокий объем продаж. Это
было бы трудно сделать по-другому, но совсем легко с помощью коллекции Figaro.
Затем для каждого продукта создаем элемент, представляющий число вновь
нанятых под него сотрудников, оно зависит от соответствующего продукта элемента
numHighSales. Как обычно в Figaro, такого рода зависимости создаются с помощью
chain. Я покажу два эквивалентных способа добиться нужного результата: с
помощью коллекций Scala и коллекций Figaro. Сначала вариант с коллекциями Scala:
val numHiresByProduct =
for { i <- 0 until numProducts }
yield Chain(numHighSales(i), (n: Int) => Poisson(n + 1))
Здесь создается массив Scala элементов chain. Теперь - с помощью коллекций
Figaro:
val numHiresByProduct =
Container(numHighSales:_*).chain((n: Int) => Poisson(n + 1))
Здесь создается контейнер Figaro, содержащий элементы chain.
214

6.3. Моделирование ситуаций с неизвестным числом объектов
ни
НЕ
С моделью мы закончили. Код задания фактов и выполнения вывода по
существу не отличается от рассмотренного выше. Но одна тонкость достойна
упоминания. Мы Запрашиваем Сведения об Элементах В КОЛЛеКЦИИ numHiresByProduct,
поэтому для варианта, когда numHiresBy Product является контейнером Figaro,
необходим какой-то способ получить эти элементы и передать их алгоритму
выборки по значимости. Делается это так:
val targets = numHiresByProduct.elements
val algorithm = Importance(targets:_*)
Осмыслим, что же мы сделали. У коллекций Scala и Figaro есть свои - важные -
роли. С одной стороны, в Scala имеются удобные и простые многомерные
массивы. Создать объекта Figaro container с двумерным множеством индексов тоже
можно, но это куда более утомительно. С другой стороны, подсчет, т. е. операция
агрегирования, легко реализуется с помощью контейнеров, но гораздо сложнее в
Scala. Собственно говоря, для агрегирования пришлось бы повторить логику, уже
реализованную в Figaro, а это не тривиально.
Теперь, освоив принципы работы с коллекциями в Figaro, рассмотрим более
экзотические, но от того не менее полезные виды коллекции.
6.3. Моделирование ситуаций
с неизвестным числом объектов
Встречавшиеся нам до сих пор коллекции Figaro содержали фиксированное
число объектов. Но во многих ситуациях число объектов неизвестно и может быть
переменным. Для таких случаев в Figaro имеются массивы переменной длины.
Сначала я расскажу, когда такие массивы полезны, затем представлю структуру
данных variabiesizeArray и, наконец, приведу пример массивов переменной
длины в действии.
6.3.7. Открытая вселенная с неизвестным числом
объектов
Пусть мы реализуем систему наблюдения за дорожным движением на
автомагистрали. Наша цель - следить за потоком машин и предсказывать возникновение
пробок. В стратегически важных точках установлены видеокамеры. Для решения
задачи нужны две вещи. Во-первых, требуется вывести число проезжающих в
каждой точке машин с учетом отождествления одной и той же машины, проехавшей
мимо двух разных камер. Во-вторых, нужно уметь прогнозировать появление
новых машин на автомагистрали и возникающие в результате пробки.
В обоих случаях требуется рассуждать о системе с неизвестным числом
объектов. Когда мы анализируем поток машин, находящихся на магистрали в данный
момент, мы не знаем, сколько их, и не можем получить точную информацию на
этот счет от видеокамер. Иногда на изображении несколько машин сливаются в

Глава 6. Использование коллекций Scala и Figaro для построения...
одну, а какие-то машины и вовсе остаются незамеченными. А уж при
прогнозировании пробок мы совсем не знаем, сколько будет машин.
Ситуация, когда число объектов неизвестно, называется открытой вселенной
(объяснение названия см. на врезке ниже) и характеризуется двумя свойствами.
• Точное число объектов, например транспортных средств, неизвестно. Это
называется неопределенностью количества.
• Нет уверенности в том, что два объекта совпадают. Например, мы не знаем,
запечатлена ли на двух изображениях одна и та же машина. Это называется
неопределенностью тождества.
В этом разделе мы сосредоточимся на неопределенности количества, для
разрешения этой проблемы предназначены массивы переменной длины. Figaro
позволяет справиться и с неопределенностью тождества, но тут вам придется потерпеть
до следующей главы.
Моделирование открытой вселенной
Термин открытая вселенная (open universe) ввел в вероятностное программирование
Стюарт Рассел {Stuart Russell) со своей группой при работе над языком BLOG, который
предназначен в первую очередь для представления ситуаций с открытой вселенной
и рассуждения о них. Истоки термина следует искать в математической логике, где
замкнутый мир или замкнутая вселенная означает, что существуют лишь объекты, явно
упомянутые в модели или выводимые из нее.
Читатели, знакомые с языком программирования Prolog, знают, что в нем
применяется принцип отрицания как неудачи: если невозможно доказать, что некоторое
утверждение является истинным, то оно предполагается ложным. Например, если вы
пытаетесь доказать, что на изображении имеется зеленая машина, но не можете это
сделать, опираясь на имеющуюся информацию о машинах, то предполагаете, что
такой машины не существует. Не требуется доказывать, что не существует никакой
другой машины, о которой вы просто не знаете. Отрицание как неудача - вид рассуждений
в замкнутой вселенной.
Напротив, логика первого порядка является открытой вселенной. Чтобы доказать,
что на изображении нет зеленой машины, необходимо доказать, что ее не может быть,
даже если вы о ней не знаете. Моделирование открытой вселенной - вещь, которую
можно сделать с помощью вероятностных языков программирования, но трудно в
других системах вероятностных рассуждений.
6,3.2. Массивы переменной длины
В Figaro для моделирования открытой вселенной применяются массивы
переменной длины. Конструктор такого массива принимает два аргумента: элемент,
значение которого равно размеру массива, и генератор элементов, аналогичный
генератору элементов для массива фиксированной длины. На рис. 6.6 показан пример
конструирования массива переменной длины. Первым аргументом конструктора
VariableSizeArray ЯВЛЯеТСЯ Элемент ТИПа Integer, ПреДСТаВЛЯЮЩИЙ КОЛИЧеСТВО
элементов в массиве. Второй аргумент - генератор элементов, т. е. функция, полу-
216

6.3. Моделирование ситуаций с неизвестным числом объектов
ни
НЕ
чающая индекс массива и возвращающая определение элемента. На рис. 6.6
массив СОСТОИТ ЦеЛИКОМ ИЗ ЭЛемеНТОВ Beta, Значения КОТОРЫХ ИМеЮТ ТИП Double.
Что происходит при конструировании массива переменной длины? Технически
массив переменной длины и не массив вовсе, а случайная переменная, значением
которой может быть один из многих массивов различной длины, номер которого
ЗавИСИТ ОТ Значения аргумента number. При ВЫЗОВе КОНСТруКТОра VariableSizeAr-
гау создается элемент MakeArray, представляющий эту случайную переменную.
Все операции над массивом переменной длины применяются к этому элементу.
Под капотом Figaro реализует MakeArray максимально эффективно, так чтобы
массивы различного размера разделяли как можно больше данных. В частности,
короткие массивы являются префиксами более длинных и включают одни и те же
элементы. От программиста все это скрыто, а говорю я об этом только для того,
чтобы вы знали об элементе MakeArray, потому что можете встретить упоминание
этого типа.
Элемент, представляющий
количество элементов в
массиве Генератор элементов
VariableSizeArray(Binomial(20, 0.3), i => Beta(l, i + 1))
; \
Индекс в Определение
массиве элемента
Рис. 6.6. Устройство конструктора массива переменной длины
6.3.3. Операции над массивами переменной
длины
Что можно делать с массивами переменной длины? В общем, то же самое, что и с
массивами фиксированной длины, но есть несколько важных различий. В
примерах ниже vsa обозначает массив переменной длины, состоящий из элементов типа
string. Вот некоторые операции над массивами переменной длины.
• Получение элемента в позиции с указанным индексом. В принципе, vsa (5)
возвращает элемент с индексом 5 (шестой элемент массива). Но тут есть
опасность. В массиве должно быть не менее шести элементов, иначе вызов
ЭТОГО Метода ЗаКОНЧИТСЯ Исключением IndexOutOfRangeException.
• Безопасное получение элемента в позиции с указанным индексом. Во
избежание описанной выше проблемы Figaro предоставляет безопасный
способ получить элемент с указанным индексом. Вызов vsa. get (5) возвращает
Element [Option [String] ]. Это ТИП Scala, Совпадающий С Some [String], еСЛИ
строка имеется, и None, если строки нет. Выполнение vsa.get (5)
представляет следующий случайный процесс:

Глава 6. Использование коллекций Scala и Figaro для построения...
- выбрать элементы в количестве, определяемом аргументом number;
- получить массив фиксированной длины соответствующего размера;
- если в массиве есть хотя бы шесть элементов, положить s равным
значению элемента с индексом 5 и вернуть some (s);
- Иначе Вернуть None.
Как видим, в обоих случаях случайный процесс возвращает элемент типа
Option [String], а ЗНаЧИТ, Представляет ТИП Element [Option [String] ]. ЭТОТ
элемент можно использовать по-разному, например, передать его элементу
Apply, который делает что-то интересное, если аргумент имеет тип some (s),
и порождает значение по умолчанию, если аргумент равен None.
• Отображение массива переменной длины на значения с помощью какой-то
функции. То же самое, что для массива фиксированной длины, только
теперь Figaro сначала заглядывает внутрь массива переменной длины,
находит массив фиксированной длины, на который тот указывает, а затем
заглядывает внутрь этого массива и получает значения элементов. Например,
вызов vsa .map (.length) порождает новый массив переменной длины, в
котором вместо каждой строки находится ее длина.
• Подать массив переменной длины на вход цепной функции, которая
отображает значения на элементы. И эта операция аналогична операции над
массивом фиксированной длины, но Figaro сначала заглядывает внутрь
массива переменной длины, находит массив фиксированной длины и
подает каждый из его элементов на вход цепной функции. Так, vsa.map(
(s: String) => discrete .Uniform (s :_*)) СОЗДает маССИВ переменной ДЛИНЫ,
в котором каждый элемент содержит случайный символ, взятый из
соответствующий строки. В этом примере s:_* преобразует строку в
последовательность СИМВОЛОВ, a discrete. Uniform (s :_* ) Выбирает Случайный Член
этой последовательности.
• Свертки и агрегаты. Все свертки и агрегаты, имеющиеся для массивов
фиксированной длины, доступны и для массивов переменной длины.
Например, vsa.count (_. length > 2) ВОЗВращаеТ Элемент Element [Int], Пред-
ставляющий число строк длины больше 2 в массиве. Интерпретировать
этот вызов можно как случайный выбор массива фиксированной длины в
соответствии с аргументом number и последующий подсчет числа строк в
это массиве, длина которых больше 2. В документации Scaladoc описаны
все имеющиеся свертки и агрегаты.
6.3.4. Пример: прогнозирование продаж
неизвестного числа новых продуктов
В этом примере предполагается, что мы планируем финансирование отдела
исследований и разработок на будущий год. Чем больше финансирование, тем больше
будет разработано новых продуктов, что повысит продажи. Однако, принимая
решение об уровне финансирования, мы еще не знаем точно, сколько новых
продуктов будет разработано при таком уровне.
218

6.3. Моделирование ситуаций с неизвестным числом объектов
Поэтому для представления новых продуктов используется массив переменной
длины. Модель определяется следующим образом:
1. Она принимает аргумент rNDLevei типа Double, представляющий уровень
финансирования исследований и разработок.
2. Элемент numNewProducts, представляющий число новых
разработанных продуктов, - это элемент типа integer, определяемый элементом
Geometric (rNDLevei). Элемент Geometric характеризует процесс, СОСТОЯЩИЙ
из нескольких шагов. После каждого шага процесс может завершиться или
перейти к следующему шагу. Вероятность перехода к следующему шагу
определяется параметром элемента (а данном случае rNDLevei).
Значением процесса является число шагов, выполненных до завершения.
Вероятность числа шагов убывает в геометрической прогрессии со знаменателем
rNDLevei. Чем больше rNDLevei, тем дольше будет продолжаться процесс и
тем больше будет разработано новых продуктов.
3. Мы создаем массив переменной длины productQuaiity, представляющий
качество вновь созданных продуктов. Аргумент number конструктора этого
массива равен numNewProducts, а генератор элементов - функция,
сопоставляющая индексу i элемент Beta a, i + 1). В разделе 6.1.1 мы говорили,
что математическое ожидание Beta(1, i + d равно i / ц + 2), так что
чем больше новых продуктов разрабатывается, тем ниже их качество, т. е.
эффективность инвестиций падает.
4. Затем мы преобразуем качество продуктов в прогноз объема продаж
каждого продукта. Это делается в два шага. Сначала генерируется объем
продаж в виде элемента Normal со средним, равным качеству продукта. Но
элемент Normal может принимать отрицательные значения, а отрицательные
продажи - вещь невозможная, поэтому на втором шаге мы отсекаем все
отрицательные значения, устанавливая нулевую нижнюю границу. Это
делается Комбинированием МеТОДОВ chain И тар Класса VariableSizeArray.
5. Наконец, мы вычисляем общий объем продаж, применяя функцию sum к
маССИВу Переменной ДЛИНЫ productSales.
Ниже приведен полный код модели:
val numNewProducts = Geometric(rNDLevei)
val productQuaiity =
VariableSizeArray(numNewProducts, i => Beta(l, i + 1))
val productSalesRaw = productQuaiity.chain(Normal(_, 0.5))
val productSales = productSalesRaw.map(_.max(0))
val totalSales = productSales.foldLeft(0.0)(_ + _)
В этом примере вероятностное программирование позволило реализовать весь
содержательный процесс с помощью всего нескольких строк кода. Далее мы
рассмотрим фундаментальные концепции, лежащие в основе коллекций Figaro, и
увидим, как они применяются к бесконечным коллекциям.
219

Глава 6. Использование коллекций Scala и Figaro для построения...
6.4. Работа с бесконечными
процессами
В этом разделе показано, как работать с коллекциями Figaro, определенными над
бесконечным пространством. Сразу возникает вопрос: как можно определить
коллекцию с бесконечным числом элементов в памяти конечного объема? И как
произвести обработку такой коллекции за конечное время?
Ответ - элементы коллекции определяются неявно. Мы никогда не обращаемся
к бесконечно большому числу элементов. Но любой элемент доступен, коль скоро
в нем возникает необходимость.
Предупреждение. Материал в этом разделе довольно сложный. Можете пропустить
его при первом чтении, нигде в книге он не понадобится. Но возвращайтесь, когда
захотите глубже понять коллекции Figaro и оценить всю их мощь.
Характеристика (trait) Process является в Figaro общим представлением
любой коллекции, конечной или бесконечной. Далее объясняется, как процесс
позволяет неявно представить элементы и как работать с процессом. После этого мы
рассмотрим пример процесса, определенного для моментов времени.
6.4.1. Характеристика Process
В Figaro процесс - это неявное представление коллекции элементов, определенных
над множеством индексов. Говоря «неявно», я имею в виду, что по любому индексу
можно получить соответствующий элемент. Для массивов это определение
естественно: зная индекс из некоторого диапазона, мы можем получить элемент в
позиции с этим индексом. Но в процессах Figaro тип индекса может быть любым. Таким
образом, характеристика Process параметризуется двумя типами: типом индекса и
типом значения, который представляет типы значений элементов процесса.
ОСНОВНОЙ МеТОД, КОТОрЫЙ Необходимо реализовать ДЛЯ Process [Index, Value], -
ЭТО generate. В простейшей форме generate принимает ИНДеКС ТИПа Index И ВОЗВра-
щает Element [value]. Будучи вызван, этот метод должен создать и вернуть
элемент, соответствующий индексу.
При работе с процессом не следует вызывать метод generate напрямую. Выше мы
видели, что если р - массив фиксированного размера, то р (5) получает элемент р в
позиции с индексом 5. Вызывать generate нет необходимости. На самом деле,
нотация р(5) даже безопаснее, чем явный вызов generate. Конструкция р(5) приводит
к вызову generate для порождения элемента, который затем кэшируется, и таким
образом мы будем получать тот же самый элемент при повторном вызове. Если же
вызывать generate напрямую, то при каждом вызове с одним и те же индексом будет
возвращаться новый элемент, хотя может статься, что это нежелательно.
Примечание. В Scala р (5) - сокращенная запись для р. apply (5). У характеристики
Process имеется метод apply, который вызывает generate и кэширует результат, что
позволяет использовать нотацию р (5) для получения нужного элемента.
220

6.4. Работа с бесконечными процессами
И снова о контейнерах
В разделе 6.2 было сказано, что Container - это обобщенный суперкласс,
представляющий конечные коллекции в Figaro. Теперь, когда мы знаем о еще более
общей характеристике Process, самое время вернуться к классу Container, Класс
Container - это процесс, предоставляющий конкретную конечную
последовательность индексов. Индексы, принадлежащие этой последовательности, и только они
считаются допустимыми. В классе Containe r, как в любом процессе, имеются методы
generate для получения одного или нескольких элементов.
Поскольку число элементов в контейнере конечно, мы можем определить свертки и
агрегаты. Операция свертки требует перебора всех элементов коллекции, а это можно
сделать только для конечных коллекций. Поэтому характеристика Process не
поддерживает ни сверток, ни агрегатов. Однако же она поддерживает операции тар и chain -
как и Container.
FixedSizeArray является подклассом Container, специализированным в двух
отношениях. Во-первых, допустимыми индексами являются целые числа отО до размера
массива минус 1. Во-вторых, предполагается, что элементы FixedSizeArray
независимы. Неважно генерируем мы один элемент или сразу несколько, каждый из них
создается генератором элементов, и никакие дополнительные элементы для
кодирования зависимостей не генерируются.
Другая форма generate позволяет получать элементы, указав сразу несколько
индексов. Эта специальная возможность иллюстрирует одно из различий между
коллекциями Figaro и обычными коллекциями. В процессе Figaro могут
существовать зависимости между элементами с разными индексами. Предположим, к
примеру, что процесс представляет количество осадков, выпавших в разных
точках региона. Очевидно, что элементы, представляющие осадки в близких точках,
должны быть зависимы. Если брать элементы по отдельности, то мы не сможем
уловить эти зависимости, но если выбрать сразу все элементы для интересующих
нас точек, то зависимости удастся построить.
Вторая форма generate принимает список индексов и возвращает отображение
Map [Index, Element [Value] ] ИНДеКСОВ На элементы. В ЭТОМ отображении ДОЛЖеН
присутствовать элемент для каждого переданного индекса. За кулисами generate
порождает также элементы, представляющие зависимости между элементами,
соответствующими индексам, но в отображение они не включаются. Например, если
имеется Процесс, Содержащий КОЛИЧеСТВО ОСаДКОВ В раЗНЫХ ТОЧКаХ, ТО ВЫЗОВ generate CO
списком этих точек породит элементы, представляющие количество осадков, а также
элементы, описывающие зависимости между количеством осадков в разных точках.
Как это работает, мы скоро увидим.
У характеристики Process имеется еще один метод, который необходимо
реализовать. Не каждое значение типа index является допустимым индексом процесса, т. е. не
с каждым значением ассоциирован элемент. Например, в случае массива допустимы
только целые индексы от 0 до размера массива минус 1. Метод Process под названием
rangecheck принимает в качестве аргумента индекс и возвращает булево значение,
которое равно true, если индекс допустим. Когда мы вызываем для получения элемента
221

Глава 6. Использование коллекций Scala и Figaro для построения...
метод процесса apply, сначала проверяется, принадлежит ли индекс допустимому
диапазону; еСЛИ нет, возбуждается ИСКЛЮЧение IndexOutOfRangeException.
6.4.2. Пример: моделирование состояния
здоровья во времени
И напоследок мы рассмотрим темпоральный процесс, который представляет
значение, изменяющееся с течением времени. Это моделирование состояния
здоровья пациента. К моделированию темпоральных процессов есть два подхода.
Первый - задать дискретные моменты через одинаковые интервалы (например,
каждую минуту) и определить случайную переменную, представляющую
состояние здоровья в каждый из этих моментов. Второй - считать время непрерывным,
а переменную состояния здоровья - определенной в каждый момент времени. Это
позволяет получать значение переменной в любой интересующий нас момент. Для
иллюстрации беконечных процессов в Figaro я выберу второй подход.
Определим класс HeaithProcess, расширяющий Process, для которого индекса-
ми являются числа двойной точности, представляющие моменты времени, а
элементы имеют тип Boolean и говорят, здоров ли пациент в данный момент. Вот как
ВЫГЛЯДИТ объявление HeaithProcess!
object HeaithProcess extends Process[Double, Boolean]
Мы должны реализовать три метода: (1) вариант generate, порождающий
элемент для одного момента времени; (2) вариант generate, порождающий элементы
ДЛЯ НеСКОЛЬКИХ МОМеНТОВ, а Также ЗаВИСИМОСТИ Между НИМИ; (3) rangeCheck.
Начнем с самого простого - метода rangeCheck. Предположим, что у процесса
существует начальный момент 0, и допустимым считается любой момент,
больший или равный 0. Тогда rangeCheck определяется следующим образом:
def rangeCheck(time: Double) = time >= 0
Теперь реализуем метод generate, который порождает состояние здоровья
пациента в один момент времени. Если рассматривать один момент изолированно
от всех остальных, то состояние здоровья определяется простым элементом Flip.
Предположим, однако, что мы не знаем ассоциированную с Flip вероятность и
хотим вывести ее из обучающих данных. Можно ввести параметр heaithyPrior для
представления этой вероятности. Переменная heaithyPrior и одиночный вариант
метода generate определены ниже:
val heaithyPrior = Uniform((0.05 to 0.95 by 0.1):_*)
def generate(time: Double): Element[Boolean] = Flip(heaithyPrior)
В качестве функциональной формы heaithyPrior мы взяли дискретный эле-
мент uniform, выбирающий одно из значений 0.05, 0.15,..., 0.95.
Переходим к самому интересному. Мы хотим реализовать функцию generate,
которая умеет порождать элементы для нескольких моментов времени, а также
222

6.4. Работа с бесконечными процессами
зависимости между этими элементами. Как моделировать зависимости между
моментами времени? Естественно считать, что в близких точках высока
вероятность одинаковых значений. Истинность этого утверждения зависит от близости
точек. Будем предполагать, что влияние одной точки на временной оси на другую
экспоненциально убывает с ростом расстояния между точками. Заведем параметр
heaithChangeRate для описания скорости изменения состояния здоровья со
временем и выведем его значение из обучающих данных.
Таким образом, нам предстоит создать два набора элементов. Первый - это
элементы, соответствующие моментам времени, они создаются одиночным методом
generate. Второй - зависимости между парами соседних моментов. Мы
перебираем моменты времени по порядку и для каждой пары создаем элемент,
кодирующий тот факт, что в соседних точках вероятность одинакового состояния здоровья
больше, чем различного. Сила этого ограничения зависит от расстояния между
ТОЧКамИ И регулируется параметром heaithChangeRate!
def generate(times: List[Double]): Map[Double, Element[Boolean]] = {
val sortedTimes = times.sorted <)—О
val healthy = sortedTimes.map(time => (time, generate(time))).toMap <]—©
def makePairs(remaining: List[Double]) {
if (remaining.length >= 2) {
val timel :: time2 :: rest = remaining
<ь-©
«-O
val probChange =
Apply(heaithChangeRate,
(d: Double) => 1 - math.exp(- (time2 - timel) / d))
val equalHealth = healthy(timel) === healthy(time2)
val healthStatusChecker =
If(equalHealth, Constant(true), Flip(probChange))
healthStatusChecker.observe(true)
makePairs (time2 : : rest) O—©
} '
}
makePairs(sortedTimes)
healthy
}
О — Сортируем моменты времени, чтобы можно было без опаски предполагать, что они
упорядочены
© — Порождаем отображение временных индексов на элементы, описывающие
состояние здоровья
© — Перебираем моменты времени по порядку, обрабатывая каждую пару соседних
© — Создаем элемент, кодирующий зависимость между состоянием здоровья в соседние
моменты времени
Опишем, как создается элемент, кодирующий зависимость между состоянием
здоровья в соседние моменты времени. Будем моделировать эту зависимость как
223

Глава 6. Использование коллекций Scala и Figaro для построения...
косвенную. Напомним (см. главу 5), что в Figaro есть два способа представления
косвенных зависимостей. Самый простой метод - ограничение. Но он не позволяет
обучить параметры, характеризующие зависимость, а нам хотелось бы таким
образом узнать значение параметра heaithchangeRate. Поэтому воспользуемся
вторым методом - создадим булев элемент, который принимает значение true с
вероятностью, зависящей от двух состояний здоровья, и зададим в качестве наблюдаемого
факта, что этот элемент равен true. Вот как выглядят входные данные:
• healthy (timei) - состояние здоровья в первый момент времени;
• healthy (time2) - состояние здоровья во второй момент времени;
• heaithchangeRate - СКОрОСТЬ Изменения СОСТОЯНИЯ ЗДОрОВЬЯ.
В показанном выше коде создается элемент heaithstatuschecker, для
которого наблюдается значение true. Если healthy (timei) и healthy (time2) равны, то
heaithstatuschecker определенно равен true. Это то же самое, что сказать:
когда healthy (timei) И healthy (time2) равны, Значение Ограничения равно 1. ЕСЛИ
healthy (timei) И healthy (time2) не равны, ТО верОЯТНОСТЬ, ЧТО heaithstatuschecker
принимает значение true, зависит от расстояния между time2 и timei.
Интуитивно кажется, что чем больше расстояние между time2 и timei, тем вероятнее, что
состояние здоровья изменилось. Согласно определению probchange, вероятность,
что состояние здоровья не изменилось, экспоненциально затухает с увеличением
раЗНОСТИ time2 - timei, ПОДеленНОЙ на heaithchangeRate. Следовательно, верОЯТ-
ность, что состояние здоровья изменилось тем ближе к 1, чем больше разность во
времени.
6.4.3. Использование процесса
Итак, процесс мы определили. Теперь надо его использовать. Для этого
предположим, что имеются данные, описывающие состояние здоровья в некоторые
моменты времени. Мы хотим запросить состояние здоровья в какие-то другие
моменты времени. Кроме того, мы хотим узнать значения параметров heaithyPrior и
heaithchangeRate, полученные на ОСНОВе Данных.
Самый важный шаг - одновременная генерация элементов для всех
интересующих нас моментов времени - как заданных изначально, так и указываемых в
запросе. Попутно будут созданы все необходимые зависимости. Если бы мы
генерировали элементы для данных и запроса порознь, то не смогли бы получить
зависимости между ними, а, стало быть, не сумели бы использовать имеющиеся
данные для предсказания состояния здоровья в другие моменты.
В этом примере для вывода применяется алгоритм исключения переменных.
Это точный алгоритм, который хорошо работает для данной модели, поэтому наш
выбор оптимален. Однако метод исключения переменных в Figaro работает
только тогда, когда переменные могут принимать конечное число значений. Именно
ПОЭТОМУ При Моделировании Параметров heaithyPrior И heaithchangeRate МЫ
ВЗЯЛИ дискретное конечное множество значений. Ниже приведен код, который
генерирует необходимые элементы, задает факты, выполняет вывод и получает ответы
на запросы.
224

6.5. Резюме
val data = Map(0.1 -> true, 0.25 -> true, 0.3 -> false,
0.31 -> false, 0.34 -> false, 0.36 -> false,
0.4 -> true, 0.5 -> true, 0.55 -> true)
D
val queries = List(0.35, 0.37, 0.45, 0.6)
val targets = queries ::: data.keys.toList
val healthy = generate(targets)
H
for { (time, value) <- data }
healthy(time).observe(value)
В
val queryElements = queries.map(healthy(_))
val queryTargets = healthyPrior :: healthChangeRate
val algorithm = VariableElimination(queryTargets:_*)
algorithm.start()
queryElements
H
for { query <- queries } {
printIn("Вероятность, что пациент здоров в момент " + query + " = " +
algorithm.probability(healthy(query), true))
}
println("Ожидаемая априорная вероятность здоровья = " +
algorithm.mean(healthyPrior))
println("Ожидаемая скорость изменения состояния здоровья = " +
algorithm.mean(healthChangeRate))
algorithm.kill()
О — data — отображение моментов времени на состояние здоровья
© — Порождаем элементы для всех изначально заданных и интересующих моментов
времени
© — Задаем факты. Переменная healthy, возвращенная методом generate, содержит
отображение моментов времени на элементы
© — Выполняем вывод для целевых элементов. И снова для получения релевантных
элементов используется отображение healthy
Это пример несколько сложнее разобранных ранее в этой главе. Класс Fixed-
si zeArray берет на себя заботу об определении метода rangecheck и обоих
вариантов generate. Но теперь вы знаете, что делать, если нужен процесс или контейнер,
отсутствующий в библиотеке.
Вот мы и подошли к концу главы. Мы начали с относительно простых, но
полезных паттернов проектирования и постепенно перешли к более развитым и
многообещающим концепциям. В следующей главе мы узнаем, как с помощью Figaro
создавать объектно-ориентированные вероятностные модели, которые расширят
возможности применения моделей на практике.
6.5. Резюме
• Как и в обычном программировании, коллекции позволяют организовать
множество объектов и применить к ним единообразный код.
225

Глава 6. Использование коллекций Scala и Figaro для построения...
• Коллекции Scala предоставляют полезные и эффективные структуры для
организации элементов Figaro, позволяя создавать модели с
иерархическими или многомерными зависимостями.
• Коллекции Figaro предоставляют дополнительные средства организации
элементов, наделенные возможностью заглядывать внутрь элементов и
манипулировать их значениями. Тем самым мы можем реализовать такие
операции, как свертывание и кванторы.
• Кроме того, коллекции Figaro позволяют моделировать открытую
вселенную с неизвестным числом объектов.
• Процессы Figaro дают возможность моделировать коллекции с
бесконечным множеством индексов, например, временные или пространственные.
6.6. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. В вашем городе три школы. В каждой школе имеются классы от первого
до шестого. В каждом классе 30 учеников. Каждый ученик сдает экзамен
по математике. Оценка на экзамене зависит от способностей ученика и
мастерства учителя. Напишите вероятностную программу для
представления этой ситуации и выведите мастерство учителя из результатов экзамена.
При написании программы используйте коллекции Scala.
2. Вы повели свое семейство в парк развлечений. В парке семь аттракционов,
одни - захватывающие дух, другие - спокойные. Каждый аттракцион
характеризуется качеством: высоким, средним или низким. Является ли аттракцион
захватывающим дух или спокойным - наблюдаемый факт, чего нельзя сказать
о качестве. У вас трое детей 16, И и 7 лет. Нравится аттракцион ребенку или
нет, зависит от его возраста, качества аттракциона и его рискованности; дети
постарше предпочитают захватывающие дух аттракционы, и все без
исключения любят аттракционы высокого качества. Ваш 16-летний отпрыск уже
бывал в парке развлечений прежде и сказал, какие аттракционы ему нравятся.
Воспользовавшись коллекциями Scala, напишите программу, которая будет
предсказывать, какие аттракционы понравятся детям 11 и 7 лет.
3. В гольфе у каждой лунки имеется пар, т. е. количество ударов, за которое
игрок должен закатить мячик в лунку по регламенту. Обычно пар равен 3,
4 или 5. Определим квалификацию гольфиста s как математическое
ожидание числа ударов, необходимых ему для прохождения лунки.
Квалификация - это вещественное число, равномерно распределенное в диапазоне
от 0 до 8/13. Точнее, вероятность, что понадобится заданное число ударов,
определяется следующей таблицей.
Пар-2
s/8
Пар- 1
s/2
Пар
s
Пар+1
4/5x(1-13s/8)
Пар+ 2
1/5 х(1 -13S/8)
226

Упражнения
Создайте структуру данных, описывающую поле для гольфа с 18 лунками
разных паров. Напишите на Figaro программу, представляющую игрока в
гольф.
a. С помощью этой программы предскажите, с какой вероятностью
игрок наберет больше 80 очков, если известна его квалификация.
b. Ответьте на тот же запрос при условии, что квалификация не
меньше 0.3.
c. С помощью своей программы найдите вероятность, что
квалификация игрока не меньше 0.3, если известно, что он набрал 80 очков.
4. В игре «Сапер» вы должны определить, в каких ячейках сетки находятся
мины. Каждая ячейка может находиться в одном из четырех состояний:
(1) в ней точно мина, (2) точно безопасна, (3) есть мина, но это еще
неизвестно (4) безопасна, но это еще неизвестно. В каждой заведомо безопасной
ячейке находится число, показывающее, сколько мин (известных и
известных) находится в восьми соседних ячейках (по горизонтали, по вертикали
и по диагонали). Напишите вероятностную программу, которая получает
на входе сетку «Сапера» и для каждой ячейки с неизвестным состоянием
предсказывает вероятность нахождения в ней мины.
5. Вы владелец кондитерского магазина и хотите спрогнозировать,
сколько конфет продадите в один день. Предположим, что число детей,
заглянувших в магазин в определенный день, подчиняется распределению
Binomial(100, 0.1). Каждый ребенок покупает конфеты с вероятностью 0.5
и, если вообще покупает, то количество купленных конфет равномерно
распределено в диапазоне от 1 до 10. Воспользовавшись массивом переменной
длины, предскажите, сколько конфет вы продадите в день.
6. Вы снова владелец кондитерского магазина, но теперь дети заходят в
магазин группами, и решение одного купить конфеты влияет на решения
других. Точнее, если один ребенок покупает, то вероятность, что другой
тоже купит, возрастает. Количество конфет, купленных одним ребенком
(если он решил купить), неизменно. Предположим, что количество групп
детей, заходящих каждый день в магазин, подчиняется распределению
Binomial(40, 0.1) и что число детей в группе равномерно распределено в
диапазоне от 1 до 5. Создайте процесс Figaro, описывающий логику этой
ситуации, и с его помощью предскажите, сколько конфет будет продано за
день.
227

ГЛАВА 7.
Объектно-ориентированное
вероятностное моделирование
В этой главе.
я Применение методов
объектно-ориентированного (ОО) программирования для организации
сложных вероятностных моделей.
в Комбинирование ОО с идеями реляционных баз
данных для создания гибких моделей,
содержащих объекты и связи между ними.
в Конструкции Figaro, поддерживающие ОО-мо-
делирование, в том числе коллекции элементов и
ссылки.
в Использование конструкций Figaro для
представления неопределенности знаний о типах объектов
и связях.
В предыдущей главе мы узнали о применении коллекций для структурирования
вероятностных программ. В этой главе мы продолжим тему использования
типичных языковых конструкций для создания вероятностных программ. В фокусе
этой главы находится применение методов объектно-ориентированного
программирования для представления вероятностных моделей. Объектная ориентация -
это весьма эффективная общая техника программирования, которая, как мы
убедимся, прекрасно сочетается с вероятностным моделированием, т. к. позволяет
естественно описать ситуацию в терминах объектов и связей между ними. Язык
Scala особенно хорошо подходит для вероятностного программирования,
поскольку является одновременно функциональным и объектно-ориентированным.
Это одна из основных причин, по которой именно Scala был выбран в качестве
объемлющего языка для Figaro.

7.1. Объектно-ориентированные вероятностные модели
III!
УШ
Мы начнем эту главы с изложения основных объектно-ориентированных
концепций в применении к вероятностному программированию. Мы увидим, как с
помощью классов, экземпляров, подклассов и наследования собирать программы
из объектов, рассматриваемых как строительные блоки. В разделе 7.2
представлены реляционные вероятностные модели, в которых центральное место занимают
связи между объектами. Начав работать со связями, мы будем естественно
сталкиваться с ситуациями, когда неизвестно, какие связи существуют. Эта реляционная
неопределенность является основной темой раздела 7.3.
Вы узнаете о средствах Figaro, позволяющих представлять реляционную
неопределенность и рассуждать о ней. Эти же средства можно использовать для
моделирования неопределенности типа, когда неточно известен тип объекта.
Предполагается, что вы освоили концепции, изложенные в предыдущих главах,
в частности основы Figaro (глава 2) и моделирование зависимостей с помощью
байесовских и марковских сетей (глава 5). Кроме того, вам должны быть знакомы
средства объектно-ориентированного языка в таких языках, как Java или Scala.
Как правило, я не буду использовать такие специфичные для Scala возможности,
как характеристики, хотя объекты Scala все же используются. В общем, если вы
владеете Java, то сможете понять встречающиеся в этой главе
объектно-ориентированные конструкции.
7.1. Объектно-ориентированные
вероятностные модели
Скорее всего, вы знакомы с объектно-ориентированным программированием и
его достоинствами, но я хочу конкретно указать, какие именно его черты я считаю
особенно важными. А по ходу главы буду отмечать, как эти черты применяются к
вероятностному программированию.
Чтобы лучше понять, зачем методы ОО нужны в вероятностном
программировании, вернемся к примеру с угловыми ударами из главы 1. Напомню, что
моделируется угловой в футболе с учетом различной информации: мастерство
атакующей и обороняющейся команды, условия окружающей среды, в
частности сила ветра, и т. д. К моделированию такой ситуации естественно
применяется объектно-ориентированный подход. Игроки рассматриваются как объекты.
Игроки принадлежат командам, также являющимся объектами. Игроки
выполняют определенные действия: перемещаются или бьют по мячу. Различные амплуа
игроков, например центральный нападающий и вратарь, можно моделировать с
помощью подклассов класса Player. Игроки взаимодействуют друг с другом и с
мячом, который, кстати, - тоже объект. Окружающие условия, также
моделируемые в виде объекта, взаимодействуют с игроками и мячом.
У объектно-ориентированного программирования два основных достоинства.
• Внесение структуры в сложную программу. Объекты - это внутренне
связные единицы, инкапсулирующие данные и поведение. Любой объект
предоставляет единый интерфейс к данным и поведению, а его внутреннее

Глава 7. Объектно-ориентированное вероятностное моделирование
устройство недоступно из других частей программы. Это позволяет
программисту модифицировать внутреннее устройство объекта модульным
образом, не затрагивая остальной программы. Например, полная модель
вратаря при ближайшем рассмотрении может включать множество
переменных и зависимостей, но лишь небольшая их часть, например умение в
броске парировать удар, может оказать влияние на прочие части модели.
• Возможность повторного использования кода. Во-первых, один и тот же
код класса, со всей его внутренней структурой, можно повторно
использовать во всех экземплярах класса. Одна и та же модель игрока применима
ко многим игрокам одной команды. Во-вторых, наследование позволяет
повторно использовать общие части разных классов. Так, у центрального
нападающего и вратаря может быть много общих переменных и
зависимостей.
Указанные черты, конечно, применимы и к вероятностному
программированию. Но этим полезность объектной ориентации для вероятностных моделей не
исчерпывается. В вероятностном программировании мы строим модели
реального мира, а реальный мир естественным образом описывается в терминах объектов.
В этом разделе мы сначала обсудим такие базовые концепции, как классы,
экземпляры, атрибуты, подклассы, и их применение в вероятностном
моделировании. Затем будет представлено два примера, относящихся к принтеру (см.
главу 5). В первом примере показано, как превратить плоскую байесовскую сеть в
объектно-ориентированную модель, а во втором - как повторно использовать код
для моделирования различных видов принтеров в одной сети.
7.7.7. Элементы объектно-ориентированного
моделирования
В объектно-ориентированной программе имеются классы, описывающие данные
и поведение в общем виде, и экземпляры этих классов, которые содержат
конкретные данные и конкретизации поведения. Например, может существовать общий
класс принтера и конкретный принтер, являющийся экземпляром этого класса.
Класс принтера описывает поведение, общее для всех принтеров, а в экземпляре
принтера хранятся данные, специфичные именно для этого принтера, и
поведение, являющееся специализацией поведения класса.
Примечание. Термином «объект» иногда называют класс, а иногда - экземпляр. В
языке Scala имеется еще и ключевое слово object, которое определяет экземпляр клас-
са-синглтона (класса, у которого существует единственный экземпляр). Из-за этой
путаницы я далее не буду употреблять слово объект, а ограничусь классом и экземпляром,
которые не приводят к двусмысленности.
Что все это означает с точки зрения вероятностной программы? А вот что.
• Вероятностная модель класса определяет общий процесс порождения
значений случайных переменных. Например, модель класса принтера описы-
230

7.1. Объектно-ориентированные вероятностные модели
вает общий процесс порождения таких переменных, как «питание
включено», «бумага замялась», «общее состояние принтера» и т. д.
• Экземпляром будет конкретизация модели общего класса, которая
описывает процесс порождения значений случайных переменных, относящихся
к конкретному экземпляру. Например, экземпляр принтера пользуется
моделью класса, чтобы описать процесс порождения переменных,
показывающих, включено ли питание этого принтера, замялась ли бумага в этом
принтере и каково общее состояние этого принтера.
Для представления вероятностных классов и экземпляров в Figaro можно
пользоваться обычными конструкциями Scala. Атрибутами класса Scala будут
элементы. Так, для представления принтера в классе Scala могут понадобиться
атрибуты powerButtonOn, paperFiow и state, каждый из которых определяется как
элемент. В Scala атрибут класса является частью общего определения. А у
каждого экземпляра класса имеется конкретный атрибут, определенный именно в
этом элементе. Например, экземпляр класса принтера myPrinter имеет атрибуты
myPrinter.powerButtonOn, myPrinter.paperFiow И myPrinter.state. Это обычные
атрибуты Scala, которые просто являются элементами Figaro. Таким образом, мы
определили порождающий процесс для значений атрибутов myPrinter. В
следующем фрагменте кода приведено определение класса Printer с тремя атрибутами и
определение конкретного экземпляра myPrinter этого класса, у которого имеются
КОНКреТНЫе атрибуты: myPrinter.powerButtonOn - Элемент Flip (0.95), myPrinter.
paperFiow - элемент Select И Т. Д.
class Printer {
val powerButtonOn = Flip(0.95)
val paperFiow = Select (0.6 -> 'smooth, 0.2 -> "uneven, 0.2 -> 'jammed)
val state = // etc.
}
val myPrinter = new Printer
Другой способ выразить ту же мысль - сказать, что определение
вероятностного класса - это определение случайного процесса, который можно повторно
использовать для разных экземпляров. Это полная аналогия с ОО-программиро-
ванием, в котором класс можно повторно использовать для определения
различных экземпляров. Так, классы принтера, сети и программы можно использовать
для определения различных экземпляров принтера, сети и программы, создавая
из них произвольные конфигурации. Например, в системе могут быть разные
принтеры, управляемые разными программами. Можно даже завести несколько
экземпляров одного и того же класса, скажем, несколько принтеров в одной сети.
Поскольку Scala поддерживает подклассы и наследование, те же механизмы
доступны и в моделях Figaro. Это позволяет повторно использовать части
определения класса в различных классах. Так, могут существовать различные виды
принтеров, например, лазерные и струйные. У разных принтеров может быть как
общее поведение, скажем, склонность к замятию бумаги, так и различное -
отсутствие тонера характерно только для лазерных принтеров. Знакомые концепции
231

Глава 7. Объектно-ориентированное вероятностное моделирование
подклассов, наследования и переопределения позволяют легко представить такие
ситуации.
7.7.2. Еще раз о модели принтера
Все это базовые концепции. Теперь посмотрим на них в действии. Мы будем
использовать программу принтера из главы 5. На рис. 7.1 воспроизведена
байесовская сеть.
Индикатор Замятия Бумаги
Горит
Кнопка Питания Принтера
Нажата
Индикатор Низкого Уровня
Тонера Горит
Ком ан да П о л ьзо вате л я
Правильна
Число Напечатанных
Страниц
Рис- 7.1. Байесовская сеть принтера из главы 5. Обратите внимание, что сеть
«плоская», т. е. все переменные определены на одном уровне, без какой-либо
структуры. Интуитивно кажется, что верхняя часть сети относится к свойствам
принтера, но явно это нигде не отражено
Эта байесовская сеть описывает пользователя, который звонит в отдел
технической поддержки. Пользователь сообщает об общем результате печати в терминах
числа напечатанных страниц, скорости и качества печати. Эти характеристики, в
свою очередь, зависят от команды пользователя и состояния компьютерной сети,
программы и принтера. Байесовская сеть содержит дополнительные детали:
нажата ли кнопка питания, состояние тракта подачи бумаги и уровень тонера.
Эта модель является естественным кандидатом для применения объектной
ориентации. Прежде всего, имеется принтер. Шесть переменных сети описывают
принтер, а единственная из них, имеющая отношение к остальной части сети, -
Состояние Принтера. Если завести класс принтера, то все прочие переменные
будут инкапсулированы внутри этого класса. Аналогично, хотя в этой байесовской
сети имеется только по одной переменной для пользователя, сети и программы,
232
Подача Бумаги
Уровень Тонера
Состояние Сети
Состояние Программы
Состояние Принтера
Печатает Быстро
Хорошее Качество
Печати
Общий Результат Печати

7.1. Объектно-ориентированные вероятностные модели
III!
¥Ш
эти сущности могли бы оказаться сложнее и содержать какое-то
инкапсулированное внутреннее состояние. Наконец, имеется объект, представляющий общий
результат печати.
Чтобы преобразовать эту модель принтера в объектно-ориентированную
байесовскую сеть, мы можем сгруппировать взаимосвязанные переменные, как
показано на рис. 7.2. Здесь шесть переменных, относящихся к принтеру, помещены в
класс Принтер. Точно так же, четыре переменные, связанные с результатом
печати, помещены в класс Результат Печати. Ну а для пользователя, сети и программы
я решил завести отдельные классы. Хотя сейчас в них всего по одной переменной,
наличие класса позволит в будущем детализировать его структуру, не затрагивая
модель в целом. Это общая причина использовать объектно-ориентированный
стиль.
Рис. 7.2. Объектно-ориентированное представление байесовской сети принтера.
В серых блоках сгруппированы взаимосвязанные переменные. Метка слева
вверху от блока содержит название класса. Обратите внимание, что в этой модели
имеется структура, которой не было видно в сети на рис. 7.1
Ниже приведена программа для решения задачи о принтере
объектно-ориентированным способом. Код простой, а стиль покажется знакомым любому, кто
писал объектно-ориентированные программы. Из относящегося к
вероятностному программированию здесь почти ничего нового. Код представляет собой
трехшаговый процесс:
1. Определить классы модели.
2. Создать экземпляры этих классов.
Подача Бумаги
Уровень Тонера
Кнопка Питания Принтера
Нажата
Индикатор Замятия Бумаги
Горит
Индикатор Низкого Уровня
Тонера Горит
Состояние
Команда Правильна
Принтер
Пользователь
Сеть
Программа
Состояние
Состояние
Результат печати
Число Напечатанных
Страниц
Печатает Быстро
Хорошее Качество
Печати
Общий Результат Печати

I Глава 7. Объектно-ориентированное вероятностное моделирование
3. Выполнить рассуждение с помощью созданных экземпляров.
В этом примере экземпляры используются, чтобы вывести вероятность
нажатия кнопки питания при условии, что известен общий результат печати, но можно
было бы поддержать и любой другой паттерн рассуждений, допускаемый
байесовской сетью. Листинг разбит на три части. В первой находятся классы модели
принтера, программы, сети и пользователя. Эти классы такие же, как и раньше,
только переменные теперь помещены внутрь определения класса.
Листинг 7.1. Объектно-ориентированное решение задачи о принтере: классы модели
package chap07
import com.cra.figaro. language.__
import com. era.figaro. 1 ibrary. compound.___
import com.era.figaro.algorithm.factored.VariableElimination
object PrinterProblemOO {
class Printer {
val powerButtonOn = Flip(0.95)
val tonerLevel = Select (0.7 -> 'high, 0.2 -> 'low, 0.1 -> 'out)
val tonerLowIndicatorOn =
If(powerButtonOn,
CPD(tonerLevel,
•high -> Flip(0.2),
'low -> Flip(0.6),
'out -> Flip(0.99)),
Constant (false))
val paperFlow = Select (0.6 -> 'smooth, 0.2 -> 'uneven, 0.2 -> 'jammed)
val paperJamlndicatorOn =
If(powerButtonOn,
CPD(paperFlow,
'smooth -> Flip(0.1),
'uneven -> Flip(0.3),
'jammed -> Flip(0.99)),
Constant(false) )
val state =
Apply(powerButtonOn, tonerLevel, paperFlow,
(power: Boolean, toner: Symbol, paper: Symbol) => {
if (power) {
if (toner == 'high && paper == 'smooth) 'good
else if (toner == 'out I| paper == 'out) 'out
else 'poor
} else 'out
})
}
class Software {
val state = Select(0.8 -> 'correct, 0.15 -> 'glitchy, 0.05 -> 'crashed)
}
class Network {
val state = Select(0.7 -> 'up, 0.2 -> 'intermittent, 0.1 -> 'down)
234

7.1. Объектно-ориентированные вероятностные модели
ЕЕ
}
class User {
val commandCorrect = Flip(0.65)
}
Далее следует определение класса PrintExperience. Его аргументами служат
предыдущие четыре класса, и в определении имеются ссылки на переменные,
объявленные внутри этих классов.
Листинг 7.2. Задача о принтере: класс PrintExperience
class PrintExperience(printer: Printer, software: Software, network:
Network, user: User) { <J—©
val numPrintedPages =
RichCPD(user.commandCorrect, network.state, software.state,
printer.state.
(*, *, *, OneOf(fout)) -> Constant('zero),
(*, *, OneOf('crashed), *) -> Constant('zero) ,
(*, OneOf(fdown), *, *) -> Constant(fzero),
(OneOf(false), *, *, *) -> Select (0.3 -> 'zero, 0.6 -> 'some, 0.1
-> 'all),
(OneOf(true), *, *, *) -> Select(0.01 -> 'zero, 0.01 -> 'some, 0.98
-> 'all))
val printsQuickly =
Chain(network.state, software.state, <]—©
(network: Symbol, software: Symbol) =>
if (network == 'down || software == 'crashed) Constant(false)
else if (network == 'intermittent || software == 'glitchy)
Flip(0.5)
else Flip(0.9))
val goodPrintQuality = <]—®
CPD(printer.state,
'good -> Flip(0.95),
'poor -> Flip(0.3),
'out -> Constant(false))
val summary =
Apply(numPrintedPages, printsQuickly, goodPrintQuality, <]—©
(pages: Symbol, quickly: Boolean, quality: Boolean) =>
if (pages == 'zero) 'none
else if (pages == 'some I I Iquickly || Iquality) 'poor
else 'excellent)
}
О — Результат печати зависит от конкретного принтера, программы, сети и
пользователя, поэтому конструктор класса PrintExperience принимает экземпляры этих
классов в качестве аргументов
© — Результат печати зависит от определенных атрибутов принтера, программы, сети
и пользователя. Чтобы сослаться на них, мы записываем сначала имя экземпляра,
затем точку и затем имя атрибута. Например, «printer.state» — ссылка на атрибут
«state» экземпляра с именем «printer»

Глава 7. Объектно-ориентированное вероятностное моделирование
Определив все классы, мы можем приступить к созданию и связыванию их
экземпляров. Тем самым определяется процесс порождения атрибутов экземпляров,
иначе говоря, конкретная вероятностная модель. После этого можно задать факты
и поинтересоваться значениями атрибутов.
Листинг 7.3, Задача о принтере: создание экземпляров и опрос модели
val myPrinter = new Printer I <]_Л
val mySoftware = new Software
val myNetwork = new Network
val me = new User
val myExperience = new PrintExperience(myPrinter, mySoftware,
myNetwork, me)
<ъ-в
def stepl() {
val answerWithNoEvidence =
VariableElimination.probability(myPrinter.powerButtonOn, true)
println("Априорная вероятность, что кнопка питания нажата = " +
answerWithNoEvidence)
}
def step2() {
myExperience.summary.observe (fpoor) <]_Л
val answerlfPrintResultPoor =
VariableElimination.probability(myPrinter.powerButtonOn, true) |
println("Вероятность, что кнопка питания нажата, при условии плохого " +
"результата = " + answerlfPrintResultPoor)
}
def main(args: Array[String]) {
stepl()
step2()
}
}
О — Создаем экземпляры классов. Связь myExperience с myPrinter, mySoftware,
myNetwork и me задается в конструкторе PrintExperience
© — В фактах и запросах фигурируют конкретные атрибуты экземпляров
С простой моделью мы разобрались. Далее усложним ее, включив несколько
принтеров.
7.1.3. Рассуждения о нескольких принтерах
До сих пор мы рассматривали, как объектную ориентацию можно использовать
для структурирования моделей и получения выгоды от инкапсуляции. Но одно из
главных преимуществ объектно-ориентированного программирования -
повторное использование кода. Есть два механизма повторного использования:
несколько экземпляров одного класса в одной модели и несколько подклассов одного
класса с различающимися определениями.
236

7.1. Объектно-ориентированные вероятностные модели
В этом разделе будет показано, как реализовать оба механизма в Scala. Сначала
взглянем на определение нескольких подклассов одного класса. Допустим, что
существует два вида принтеров: лазерные и струйные. У того и другого есть кнопка
включения питания и механизм подачи бумаги, но имеются и уникальные
характеристики. Для создания подклассов можно использовать стандартные
механизмы наследования.
В ЛИСТИНГе 7.4 Приведен КОД Класса Printer И Двух его ПОДКЛаССОВ: LaserPrinter
и inkjetPrinter. Printer - абстрактный класс, в котором отсутствует
определение атрибута state; оно предоставляется подклассами. В этом классе определены
три атрибута, общие для всех принтеров. У такого дизайна есть два достоинства.
Во-перВЫХ, ОН обеспечивает ПОВТОрНОе ИСПОЛЬЗОВание чаСТИ КОДа Классами Laser-
Printer и ink jet Printer. Во-вторых, определяется общий интерфейс принтеров, на
который может полагаться остальная часть модели. Если myPrinter - экземпляр
любого подкласса Printer, то можно быть уверенным в наличии атрибута state.
Листинг 7-4- Иерархия класса Printer
abstract class Printer { <]_Q
val powerButtonOn = Flip(0.95)
val paperFlow =
Select (0.6 -> 'smooth, 0.2 -> 'uneven, 0.2 -> 'jammed)
val paperJamlndicatorOn =
If (powerButtonOn,
CPD(paperFlow,
'smooth -> Flip(0.1),
'uneven -> Flip(0.3),
'jammed -> Flip(0.99)),
Constant(false))
g
val state: Element[Symbol]
}
<-o
class LaserPrinter extends Printer {
val tonerLevel = Select (0.7 -> 'high,
val tonerLowIndicatorOn =
If (powerButtonOn,
CPD(tonerLevel,
'high -> Flip(0.2),
'low -> Flip(0.6),
'out -> Flip(0.99)),
Constant(false))
0.2 -> 'low, 0.1 -> 'out)
E
val state =
Apply(powerButtonOn, tonerLevel, paperFlow,
(power: Boolean, toner: Symbol, paper: Symbol) =>
if (power) { //
if (toner == 'high && paper == 'smooth) 'good
else if (toner == 'out I I paper == 'out) 'out
else 'poor
} else 'out
s
237

Глава 7. Объектно-ориентированное вероятностное моделирование
class InkjetPrinter extends Printer {
val inkCartridgeEmpty = Flip(0.1)
val inkCartridgeEmptylndicator =
If(inkCartridgeEmpty, Flip(0.99), Flip(0.3)
val cloggedNozzle = Flip(0.001)
val state =
Apply(powerButtonOn, inkCartridgeEmpty,
cloggedNozzle, paperFlow,
(power: Boolean, ink: Boolean,
nozzle: Boolean, paper: Symbol) => {
if (power && link && Inozzle) {
if (paper == 'smooth) 'good
else if (paper == 'uneven) 'poor
else 'out
} else 'out
}
Й
g
О — Это абстрактный класс, т. к. он содержит атрибут state, не имеющий определения
© — Код, общий для всех принтеров
© — Общий интерфейс, в котором объявлен атрибут, имеющийся у всех принтеров.
Определить этот атрибут обязаны конкретные подклассы
© — Атрибуты, специфичные для подкласса LaserPrinter
© — Разные реализации общего интерфейса
© — Атрибуты, специфичные для подкласса InkjetPrinter
Вот так создаются модели с несколькими классами с частично совпадающим
кодом и общим интерфейсом. Поскольку LaserPrinter и InkjetPrinter -
подклассы одного и того же класса Printer, то их экземпляры можно передавать в качестве
аргументов КОНСТруКТОру PrintExperience, КОТОрыЙ ОЖИДаеТ ПОЛуЧИТЬ ЭКЗеМПЛЯр
Printer. МОЖНО Даже ИМеТЬ В ОДНОЙ МОДеЛИ ДВа Экземпляра PrintExperience, ОДНО-
Му ИЗ КОТОРЫХ Передан LaserPrinter, а Другому Ink j etPrinter. A CeTb, ПОЛЬЗОВатеЛЬ
и программа у этих экземпляров могли бы быть общими. Вот как это выглядит:
val myLaserPrinter = new LaserPrinter
val mylnkjetPrinter = new InkjetPrinter
val mySoftware = new Software
val myNetwork = new Network
val me = new User
val myExperiencel =
new PrintExperience(myLaserPrinter, mySoftware, myNetwork, me)
val myExperience2 =
new PrintExperience(mylnkjetPrinter, mySoftware, myNetwork, me)
Теперь можно порассуждать об элементах, общих для этих двух результатов
печати: программе, сети и пользователе:
238

7.1. Объектно-ориентированные вероятностные модели
F5M
def stepl() {
myExperiencel.summary.observe(fnone)
val alg =
VariableElimination(myLaserPrinter.powerButtonOn, myNetwork.state)
alg.start ()
println("После наблюдения, что печать на лазерном принтере " +
"не дала никакого результата:")
println("Вероятность, что кнопка питания лазерного принтера нажата = " +
alg.probability(myLaserPrinter.powerButtonOn, true))
println("Вероятность, что сеть не работает = " +
alg.probability(myNetwork.state, 'down))
alg.kilK)
}
def step2() {
myExperience2.summary.observe('none)
val alg =
VariableElimination(myLaserPrinter.powerButtonOn, myNetwork.state)
alg.start ()
println("ХпПосле наблюдения, что печать на струйном принтере " +
"тоже не дала никакого результата:")
println("Вероятность, что кнопка питания лазерного принтера нажата = " +
alg.probability(myLaserPrinter.powerButtonOn, true))
println("Вероятность, что сеть не работает = " +
alg.probability(myNetwork.state, 'down))
alg.kilK)
}
Эта программа печатает следующее:
После наблюдения, что печать на лазерном принтере не дала никакого
результата:
Вероятность, что кнопка питания лазерного принтера нажата =
0.8573402523786461
Вероятность, что сеть не работает = 0.2853194952427076
После наблюдения, что печать на струйном принтере тоже не дала никакого
результата:
Вероятность, что кнопка питания лазерного принтера нажата =
0.8978039844824163
Вероятность, что сеть не работает = 0.42501359502427405
Логика понятна: после того как стало известно, что струйный принтер тоже не
печатает, вероятность, что первая проблема была связана с лазерным принтером
уменьшается (поскольку это означало бы, что струйный принтер тоже
неисправен), зато повышается вероятность, что проблема в чем-то другом, например, в
сети. Поэтому вероятность, что кнопка питания лазерного принтера нажата,
возрастает, а вероятность сбоя сети убывает.
Прежде чем перейти к следующему разделу, представим, что мы не знаем, какой
у нас принтер. Точнее известно, что либо лазерный, либо струйный, но вот, какой
именно... Это называется неопределенностью типа, и для обработки этой
ситуации требуются дополнительные ухищрения, о которых мы узнаем в разделе 7.3.
Однако предварительно нам нужно сделать еще один шаг обобщения: от объек-

Глава 7. Объектно-ориентированное вероятностное моделирование
тно-ориентированных моделей к моделям со связями общего вида. Такие
реляционные вероятностные модели - тема следующего раздела.
7.2. Добавление связей
в объектно-ориентированные модели
Представим, что мы пытаемся смоделировать посетителей сайта какой-нибудь
социальной сети, например Facebook, и хотим вывести интересы и связи, наблюдая
за постами и комментариями. Социальная сеть, по определению, реляционная,
т. к. целиком посвящена отношениям между людьми. Между людьми, их
постами и комментариями существуют естественные связи. В этой предметной
области имеется также естественная объектно-ориентированная структура, в которой
классами представлены люди, посты и комментарии. Но для ее моделирования
необходима реляционная вероятностная модель.
Реляционная вероятностная модель - это не что иное, как
объектно-ориентированная модель, в которой связи сделаны явной и центральной частью
представления. За последние несколько лет был разработан ряд языков описания
реляционных вероятностных моделей, например: Probabilistic Relational Models и Markov
Logic. В этом разделе мы будем говорить не о каком-то определенном языке, а об
общем стиле программирования, в котором объединены черты многих языков.
Изложение вопроса о проектировании и реализации реляционной
вероятностной модели я разобью на три части. Сначала покажу, как описать общую модель с
помощью классов вероятностной модели, затем продемонстрирую, как применить
эту общую модель к описанию конкретной ситуации, и, наконец, расскажу, как все
это реализовать на Figaro.
7.2.7. Описание общей модели на уровне классов
В реляционной вероятностной модели классы служат двум целям:
• описать структуру модели, в том числе ее классы, их атрибуты и связи
между классами;
• определить вероятностные зависимости, функциональные формы и
числовые параметры вероятностной модели.
Понять, как выглядит реляционная вероятностная модель, проще всего,
взглянув на ее структуру. На рис. 7.3 показана структура модели для приложения
социальной сети.
• В модели имеется четыре класса: Персона, Отношение, Пост,
Комментарий.
• У класса имеются атрибуты. Есть два вида атрибутов.
- Простые атрибуты, изображенные в виде овалов, представляют
случайные переменные со значениями некоторого типа. Например, в
классе Персона есть атрибут Интересы - случайная строковая
переменная. В классе Пост есть атрибут Тема - тоже строковая перемен-
240

7.2. Добавление связей в объектно-ориентированные модели
ная. В классе Связь есть атрибут Тип, это может быть семья, близкий
друг или знакомый. В классе Комментарий есть атрибут
Соответствует - булева переменная, которая равна true, если имеется
соответствие между интересами комментатора и темой поста.
Комплексные атрибуты, изображенные в виде прямоугольников,
определяют связи с другими объектами. Например, в классе Пост
есть атрибут Отправитель, представляющий человека, отправившего
пост. Для любого экземпляра класса Пост значением атрибута
Отправитель будет экземпляр класса Персона. Поэтому атрибут
Отправитель определяет связь между экземплярами Поста и Персоны.
В классе есть простые и комплексные атрибуты
Простые атрибуты
(овалы)
представляют случайные
переменные
Стрелки показывают
конец связи, например,
концом связи Пост.
Отправитель является
Персона
Комплексные атрибуты
(прямоугольники)
представляют связи с
другими объектами
Рис. 7-3. Структура реляционной вероятностной модели
Описав реляционную структуру, можно переходить к следующему шагу -
определению вероятностных аспектов представления. Главное, что нужно сделать, -
определить зависимости. Сначала прикинем, что это значит на уровне
экземпляров. Основной принцип заключается в том, что атрибут экземпляра может
зависеть от других атрибутов этого экземпляра или атрибутов связанных с ним
экземпляров. Например, если имеется экземпляр Пост 1 класса Пост и экземпляр
Эми класса Отправитель такие, что Пост 1.Отправитель - это Эми, то Пост 1.Тема
может зависеть от Эми.Интересы.
Такого рода зависимости мы хотели бы видеть на уровне экземпляра. Но как
представить их на уровне класса? Да просто! Нужно лишь нарисовать стрелку от
241
Персона
Интересы
Отношение
Персона 1
Персона 2
Тип
Пост
Отправитель
Тема
Комментарий
Комментатор
Пост
Соответствует

Глава 7. Объектно-ориентированное вероятностное моделирование
атрибута Интересы класса Персона к атрибуту Тема класса Пост. На рис. 7.4
показаны вероятностные зависимости в нашей модели социальной сети. Они
изображены жирными стрелками поверх реляционной структуры (рис. 7.3), чтобы сразу
бросались в глаза. В этом примере имеются как направленные зависимости,
показанные жирными сплошными линиями со стрелками, так и одна ненаправленная
зависимость, показанная жирной пунктирной линией.
Пунктирной линией показана симметричная
зависимость, например, между атрибутами
Комментарий.Соответствует и Отношение
(Комментарий. Пост.Отправитель,
Комментарий.Комментатор).Тип
Класс Персона продублирован,
потому что Комментатор может
отличаться от Отправителя,
поэтому атрибут Интересы,
влияющий на Тему, отличается
от атрибута Интересы,
влияющего на Соответствует
Жирными стрелками показаны
вероятностные зависимости,
например, Пост.Тема зависит
от Пост.Отправитель.Интересы
Комментатор
^
Рис. 7.4. Вероятностные зависимости в реляционной модели социальной сети
Задав зависимости, можно переходить к определению функциональных форм
и числовых параметров. Ничего необычного здесь нет, можно применять те же
методы, что и раньше. Напомним (см. главу 5), что направленные зависимости в
байесовской сети задаются с помощью условных распределений вероятности, а
ненаправленные зависимости в марковской сети - с помощью потенциалов.
Напомним также, что потенциал - это функция, определенная на множестве
переменных, которая сопоставляет неотрицательное вещественное значение каждой
комбинации значений переменных.
В нашем примере:
• атрибут Персона.Интересы не имеет родителей, поэтому имеем
распределение вероятности возможных интересов;
242
Персона
Интересы
Отношение
Персона 1
Тип
Персона 2
Персона
Интересы
Тема
Отправитель
Пост

Комментарий
Пост
Соответствует

7.2. Добавление связей в объектно-ориентированные модели
• атрибут Отношение.Тип тоже не имеет родителей, поэтому имеем
распределение вероятности возможных типов отношений;
• для атрибута Пост.Тема имеем условное распределение вероятности при
условии Пост.Отправитель.Интересы, которое говорит, что тема поста
обычно соответствует интересам отправителя;
• для атрибута Комментарий.Соответствует имеем условное распределение
вероятности при условии Комментарий.Пост.Тема и Комментарий.Ком-
ментатор.Интересы. Детерминированное условное распределение
вероятности говорит, что соответствие существует, если тема поста совпадает с
интересами комментатора;
• имеется также потенциал для зависимости между соответствием
комментария посту и типу отношений между отправителем и комментатором. Тип
отношения можно определить как атрибут Тип того класса Отношение, в
котором Персона 1 - Комментарий.Пост.Отправитель, а Персона 2 -
Комментарий. Комментатор. Назовем этот атрибут Отношение (Комментарий.
Пост.Отправитель, Комментарий.Комментатор).Тип. Для любого
экземпляра с класса Комментарий находим два экземпляра класса Персона:
с.Пост.Отправитель и с.Комментатор. Затем находим экземпляр класса
Отношение, соединяющий эти две персоны и берем его атрибут Тип. Таким
образом, потенциал определен для этого атрибута и с.Соответствует.
Потенциал говорит, что Комментарий с высокой вероятностью соответствует
посту, если тип отношения - знакомство, с меньшей вероятностью, если тип
отношения - близкий друг, и с еще меньшей, если тип отношения - семья.
На этом завершается определение реляционной вероятностной модели на
уровне класса. Следующий шаг - создать экземпляры и определить связи между ними.
Я покажу, как при этом определяется распределение вероятности атрибутов
экземпляров.
7.2.2. Описание ситуации
Для описания ситуации необходимо точно определить, какие экземпляры
каждого класса в ней участвуют и как они соединены. Так, в нашей модели социальной
сети ситуацию можно описать, как показано в табл. 7.1.
Таблица 7.1. Задание экземпляров в модели социальной сети и связей между ними.
В первой таблице описаны три экземпляра класса Персона, во второй - три
экземпляра класса Пост и для каждого - значение комплексного атрибута Отправитель.
В третьей таблице описаны четыре экземпляра класса Комментарий и для каждого -
значения атрибутов Пост и Комментатор
Персона
Эми
Брайан
Черил
Пост
Пост1
Пост 2
ПостЗ
Отправитель
Эми
Брайан
Эми
Комментарий
Комментарий 1
Комментарий 2
Комментарий 3
Комментарий 4
Пост
Пост1
Пост1
Пост 2
ПостЗ
Комментатор
Брайан
Черил
Эми
Черил
243

Глава 7. Объектно-ориентированное вероятностное моделирование
Необязательно описывать экземпляры Отношения, потому что они выводятся
автоматически. Для каждого экземпляра с класса Комментарий мы автоматически
выводим Отношение(с.Пост.Отправитель, с.Комментатор). Для Комментария 1
Пост.Отправитель - Эми, а Комментатор - Брайан, поэтому выводим Отноше-
ние(Эми, Брайан). Аналогично для Комментариев 2 и 3 выводим Отношение(Эми,
Черил) и Отношение(Брайан, Эми).
Для Комментария 4 выводим также Отношение(Эми, Черил). Это тот же
экземпляр Отношения, что и выведенный для Комментария 2. Это важный момент.
Мы хотим делать выводы из обоих комментариев Черил к постам Эми. Если бы
для каждого комментария использовались разные экземпляры Отношения, то мы
не смогли бы сделать заключение о типе отношения по комбинации
комментариев. А используя один и тот же экземпляр Отношения, мы задействуем все
комментарии Черил к постам Эми для вывода типа отношения. (С другой стороны, в
нашей модели Отношение(Эми, Брайан) отличается от Отношение(Брайан, Эми).
Это осознанное проектное решение - мы считаем, что отношения асимметричны.
Можно было бы поступить по-другому и моделировать симметричные
отношения, тогда существовал бы единственный экземпляр Отношения для
Комментария 1 и Комментария 3.)
Вывод вероятностной модели для ситуации
Одно из главных преимуществ вероятностных моделей с классами
заключается в том, что модель для ситуации выводится автоматически, синтезировать ее
вручную не нужно. Но важно понимать, как это работает. Мы действуем обычным
образом. Сначала решаем, какие переменные будут описывать ситуацию. Затем
определяем зависимости. И наконец, выбираем функциональные формы и задаем
числовые параметры, описывающие зависимости.
Что касается переменных, то определенные экземпляры и связи автоматически
определяют множество простых атрибутов для всех участвующих в ситуации
экземпляров, и каждый из них становится переменной модели. В данном примере
получаются такие переменные:
• Эми.Интересы, Брайан.Интересы, Черил.Интересы;
• Пост 1.Тема, Пост 2.Тема, Пост З.Тема;
• Комментарий 1.Соответствует, Комментарий 2.Соответствует,
Комментарий 3.Соответствует, Комментарий З.Соответствует;
• Отношение(Эми, Брайан).Тип, Отношение(Эми, Черил).Тип, Отноше-
ние(Брайан, Эми).Тип.
Для каждого из этих атрибутов мы можем, пользуясь общей моделью на
уровне классов, найти, от каких атрибутов он зависит. Это позволяет построить граф
зависимостей в рассматриваемой ситуации (рис. 7.5). Так, согласно модели класса
Персона, у атрибута Персона.Интересы нет родителей, а значит, это
справедливо для атрибутов Эми.Интересы, Брайан.Интересы и Черил.Интересы. Согласно
модели класса Пост, родителем Пост.Тема является Пост.Отправитель.Интересы.
Это означает, что на уровне экземпляра родителем Пост 1.Тема является Эми.
244

7.2. Добавление связей в объектно-ориентированные модели
III!
fH*j
Интересы, родителем Пост 2.Тема - Брайан.Интересы, а родителем Пост З.Тема -
снова Эми.Интересы.
Теперь рассмотрим атрибут Комментарий 1.Соответствует. Согласно моделям
классов, у атрибута Комментарий.Соответствует два родителя: Комментарий.
Пост.Тема и Комментарий.Комментатор.Интересы. Кроме того, имеется
неориентированное ребро, соединяющее с узлом Отношение(Комментарий.Пост.Отпра-
витель, Комментарий.Комментатор).Тип. Для экземпляра Комментарий 1 класса
Комментарий имеет место следующее: Комментарий 1.Пост - это Пост 1,
Комментарий 1.Комментатор - Брайан, Комментарий 1.Пост.Отправитель - Эми.
Следовательно, родителями атрибута Комментарий 1.Соответствует являются Пост
1.Тема и Брайан.Интересы. Имеется также неориентированное ребро с узлом От-
ношение(Эми, Брайан).Тип. Именно эти ребра мы видим в байесовской сети.
Аналогичная история и с другими экземплярами Комментария.
Строго говоря, граф зависимостей не является ни байесовской, ни марковской
сетью, потому что содержит как ориентированные, так неориентированные ребра.
Тем не менее, разобраться в определяемой им вероятностной модели сравнительно
легко. Ту часть, которая содержит ориентированные ребра, можно рассматривать
как обычную байесовскую сеть. А неориентированные ребра налагают
дополнительные ограничения на эту сеть - по аналогии с ограничениями Figaro. Именно
так мы и реализуем эту модель в следующем разделе.
Рис. 7.5. Граф зависимостей для социальной сети. Он строится автоматически
по изображенной на рис. 7.3 модели уровня классов и по спецификации ситуации
в табл. 7.1. Каждому простому атрибуту уровня класса в сети соответствует
множество переменных, по одной для каждого экземпляра класса. Понятно, что если
число экземпляров сколько-нибудь велико, граф становится весьма запутанным
Эми.Интересы
Брайан,Интересы
Черил.Интересы
Пост 1.Тема
Пост 2. Тем а
Пост З.Тема
Комментарий 1,
Соответствует
Комментарий 2.
Соответствует
Комментарий 3.
Соответствует
Комментарий 4,
Соответствует
Отношение(Эми, Брайан),Тип
Отношение(Эми, Черил).Тип
Отношение(Брайан, Эми).Тип

Глава 7. Объектно-ориентированное вероятностное моделирование
После того как граф зависимостей построен, числовые параметры для ситуации
естественным образом выводятся из модели уровня класса. Например, условное
распределение вероятности Пост 1.Тема при условии Эми.Интересы выводится
из условного распределения вероятности атрибута класса Пост.Тема при условии
Пост.Отправитель.Интересы. Аналогично ограничение на Комментарий
1.Соответствует и Отношение(Эми, Брайан).Тип выводится из потенциала для
Комментарий.Сооответствует и Отношение(Комментарий.Пост.Отправитель, Коммента-
рий.Комментатор).Тип на уровне класса.
Теперь у нас есть все необходимое для определения совместного распределения
вероятности значений всех простых атрибутов всех экземпляров в предложенной
ситуации. Еще раз напомним, что реляционная вероятностная модель - это
способ описания вероятностной модели над атрибутами экземпляров в некоторой
ситуации. По сравнению с непосредственным построением модели в виде графа
на рис. 7.4 она имеет два серьезных преимущества, которые в точности отражают
преимущества объектной ориентации, отмеченные в начале главы.
• Описывая предметную область с помощью объектов и связей, мы вносим
структуру в потенциально сложные ситуации. Граф на рис. 7.4 не так уж
плох, но ведь в нем только три пользователя, три поста и четыре
комментария. А представьте, что пользователей, хостов и комментариев тысячи.
Попытка построить и сопровождать такую сеть стала бы сущим кошмаром.
Тогда как наша модель уровня классов на рис. 7.3 не меняется, сколько
бы экземпляров ни было. Да, придется описать экземпляры и связи, как в
табл. 7.1, но эта задача не в пример проще. Полно инструментов для работы
с реляционными базами данных, которые помогут организовать
экземпляры и связи между ними.
• Модели с классами можно применять ко многим экземплярам с разными
связями. Это мощный механизм повторного использования, поскольку
единственное определение вероятностной модели уровня классов годится
для многих ситуаций.
Ну что ж, мы поняли, что такое реляционная вероятностная модель и как она
определяет распределение вероятности, теперь самое время посмотреть, как
реализовать ее на языке вероятностного программирования.
7.2.3. Представление модели социальной
сети на Figaro
Представить реляционную вероятностную модель на Figaro совсем не сложно.
Мы уже убедились, что идеи, встретившиеся в объектно-ориентированной модели
принтера из раздела 7.1.2 и в модели социальной сети, похожи.
Для начала создадим классы модели с атрибутами, как и раньше. В нашем
примере комплексные атрибуты можно сделать аргументами классов. Получается вот что:
class Person() {
val interest = Uniform("sports", "politics")
246

7.2. Добавление связей в объектно-ориентированные модели
Ша
}
class Post(val poster: Person) {
val topic = If(Flip(0.9), poster.interest, Uniform("sports", "politics"))
}
Замечание об одной проблеме и ее решении. В рассматриваемом примере можно
было бы сделать poster аргументом Post, потому что пост зависит от отправителя, но
отправитель не зависит от поста. Поэтому можно сначала сгенерировать отправителя, а
затем пост. Если бы отправитель зависел от поста, то сделать poster аргументом Post
было бы невозможно, потому что отправителя нельзя сгенерировать раньше поста. Эту
проблему можно разрешить двумя способами. Первый - воспользоваться механизмом
отложенных (ленивых) вычислений в Scala, тогда пост мог бы зависеть от отправителя,
но атрибуты отправителя не вычислялись бы до момента, когда понадобятся. Второй -
включить в класс Post внутренний атрибут poster, первоначально равный null, и
присвоить ему значение позже, перед вызовом алгоритмов вывода. При условии, что все
ссылки на poster встречаются только в элементах chain (в нашем случае внутри if,
который является синтаксической оберткой chain), элементы poster не понадобятся
вплоть до вывода, а к тому времени значение атрибута poster уже будет правильно
установлено.
Остальные два класса можно определить аналогично. Но с классом connection
надо поступить осторожно. Отношения бывают между двумя людьми. Чтобы
создать ОТНОШеНИе, МЫ ДОЛЖНЫ ИМеТЬ ВОЗМОЖНОСТЬ НаПИСаТЬ Connection (personl,
person2). И ДОЛЖНа быть Гарантия, ЧТО еСЛИ ВЫЗВаТЬ КОНСТруКТОр Connection
(personl, person2) несколько раз, то мы всегда будем получать один и тот же
экземпляр. Figaro предлагает простой способ добиться этого с помощью функции memo
из пакета com.era .figaro.utn, которая гарантирует, что функция возвращает одно
и то же значение при каждом вызове с одними и теми же аргументами. Работает
это так:
import com.era.figaro.util .memo
class Connection(personl: Person, person2: Person) {
val connectionType = Uniform("acquaintance", "close friend", "family")
}
def generateConnection(pair: (Person, Person)) =
new Connection(pair._1, pair._2)
val connection = memo(generateConnection _)
В случае класса comment мы используем комбинацию направленных и
ненаправленных зависимостей. Такие вещи мы уже делали прежде. Код приведен ниже.
Тремя знаками === обозначается равенство в Figaro. Это булев элемент, который
принимает значение true, если значения обоих аргументов равны.
class Comment(val post: Post, val commenter: Person) {
val topicMatch = post.topic === commenter.interest
val pair =

Глава 7. Объектно-ориентированное вероятностное моделирование
ЛЛ(topicMatch, connection(post.poster, commenter).connectionType)
def constraint(pair: (Boolean, String)) = {
val (topicMatch, connectionType) = pair
if (topicMatch) 1.0
else if (connectionType == "family") 0.8
else if (connectionType == "close friend") 0.5
else 0.1
}
pair.addConstraint(constraint _)
Далее задаем факты:
postl.topiс.observe("politics")
post2.topic.observe("sports")
post3.topic.observe("politics")
И наконец, получаем ответы на запросы:
println("Вероятность, что Эми интересуется политикой = " +
VariableElimination.probability(amy.interest, "politics"))
println("Вероятность, что Брайан интересуется политикой = " +
VariableElimination.probability(brian.interest, "politics"))
println("Вероятность, что Черил интересуется политикой = " +
VariableElimination.probability(cheryl.interest, "politics"))
println("Вероятность, что Брайан является членом семьи Эми = " +
VariableElimination.probability(connection(amy, brian).connectionType,
"family"))
println("Вероятность, что Черил является членом семьи Эми = " +
VariableElimination.probability(connection(amy, cheryl).connectionType,
"family"))
println("Вероятность, что Черил является членом семьи Брайана = " +
VariableElimination.probability(connection(brian, cheryl).connectionType,
"family"))
Вот что напечатала эта программа:
Вероятность, что Эми интересуется политикой = 0.9940991345397325
Вероятность, что Брайан интересуется политикой = 0.10135135135135132
Вероятность, что Черилинтересуется политикой = 0.7692307692307692
Вероятность, что Брайан является членом семьи Эми = 0.5472972972972974
Вероятность, что Черил является членом семьи Эми = 0.4205128205128205
Вероятность, что Черил является членом семьи Брайана = 0.3333333333333333
Отметим, что Эми почти наверняка интересуется политикой, потому что она
дважды отправляла посты на эту тему. Черил также с большой вероятностью
интересуется политикой: сама она ни разу не постила на эту тему, но зато
прокомментировала два поста Эми. С другой стороны, Брайан откликнулся на один
пост Эми о политике, поэтому он, вероятно, член семьи Эми, т. к. политикой
не интересуется. Наконец, Черил ни разу не комментировала посты Брайана,
поэтому вероятность, что она является членом его семьи не изменилась по
сравнению с априорной, 1/3.
248

7.3. Моделирование реляционной неопределенности...
as
7.3. Моделирование
реляционной неопределенности
и неопределенности типа
Усложним наш пример, касающийся социальной сети. Предположим, что в любой
момент есть какие-то горячие темы, которым посвящено больше сообщений. Для
моделирования этой ситуации сделаем темы не строками, а объектами, т. е.
создадим класс Topic с атрибутом hot. Атрибут topic класса Post теперь становится
комплексным атрибутом, указываются на класс Topic. Пока все нормально.
Предположим теперь, что тема поста р неизвестна. Быть может, для
определения темы мы пользуемся средствами обработки естественного языка, и наши
алгоритмы несовершенны. Стало быть, имеет место неопределенность значения
комплексного атрибута р. topic. Иными словами, мы не уверены в связи между
постом и его темой, которая могла бы быть одним из многих потенциальных
экземпляров класса Topic. Такая ситуация называется реляционной неопределенностью.
Иногда употребляют также термина ссылочная неопределенность, потому что мы
не знаем, на какой объект ссылается p. topic.
В примере с принтером возможна похожая ситуация - тип принтера не всегда
известен. Скажем, вы работаете в службе техподдержки, и звонит пользователь,
который не знает, какой у него принтер. Технически это означает, что неизвестен
класс аргумента printer объекта PrintExperience. Такая ситуация называется
неопределенностью типа. Это частный случай реляционной неопределенности,
потому что мы можем создать гипотетические принтеры всех возможных классов, и
тогда останется неопределенной связь с конкретным принтером.
Концептуально реляционная неопределенность и неопределенность типа
понятны, но для их обработки в Figaro нужны дополнительные средства. В этой
главе мы рассмотрим главную цель - обработку реляционной неопределенности.
А в следующей поговорим о еще одной важной задаче - работе с динамическими
моделями. Сначала мы изложим основы коллекций элементов и ссылок, а затем
покажем, как поступать в случае неизвестной темы в примере социальной сети.
И напоследок разберем пример с неопределенностью типа принтера.
7.3.7. Коллекции элементов и ссылки
Вы, наверное, еще не знаете, что у каждого элемента Figaro есть имя, и он
принадлежит некоторой коллекции элементов. Коллекция элементов - это коллекция Figaro,
в которой элемент индексируется строкой - своим именем. А не знали вы этого,
потому что по умолчанию задавать имя и коллекцию элемента необязательно. Если
не указано противное, то именем элемент является пустая строка ,,п. И существует
коллекция элементов по умолчанию, в которую попадает элемент, если не указано
ничего другого. До этого места у нас не было причин присваивать элементам особые
имена или помещать их в специальную коллекцию, поэтому я и не рассказывал об
этом. Но вот при рассмотрении реляционной неопределенности они понадобятся.

Глава 7. Объектно-ориентированное вероятностное моделирование
Коллекции элементов полезны, потому что дают отличный от переменных Scala
способ идентификации элементов. Если ее - коллекция элементов, то получить
элемент с именем п можно, написав ec.get(n). Иногда это единственный способ
добраться до элемента. Во время составления программы не всегда заранее
известно, какой элемент будет иметь имя п. Тут можно провести аналогию с проверкой
типов на этапе компиляции и выполнения. Иногда во время компиляции тип
переменной неизвестен, поэтому приходится выполнять проверку во время
выполнения. Точно так же, на этапе компиляции не всегда известно, как добраться до
конкретного элемента, а коллекции элементов дают способ получить переменную
динамически во время выполнения.
Немного поразмыслив, вы поймете, что это позволяет разрешить реляционную
неопределенность. Мы не уверены в значении атрибута topic класса Post. У темы
есть атрибут hot, который является элементом. Нам необходимо как-то сослаться
на topic.hot изнутри класса Post. Но Scala не позволяет это сделать, потому что
topic не является известным экземпляром класса Topic! Ну что ж, сделаем Post и
Topic коллекциями элементов и вызовем get ("topic.hot"), чтобы получить
нужный нам элемент.
Но тогда возникает вопрос, как это работает, ведь topic. hot - не имя. На самом
деле, это конкатенация двух имен. Первая часть, topic, - имя элемента в
коллекции Post. В данном случае оно ссылается на элемент Element [Topic], значение
которого представляет конкретную тему поста. Вторая часть, hot, - имя элемента в
коллекции Topic. Такая конкатенация имен называется ссылкой. На рис. 7.6
показано, как разбирается эта ссылка. Основная идея заключается в том, что каждое
последующее имя в ссылке определяется относительно коллекции элементов,
являющейся возможным значением предыдущего элемента.
Коллекция
элементов
Имя
Элементе
указанным
именем
Post
"topic1
Topic
'hot1
-Коллекция элементов,
являющаяся типом
значения предыдущего
элемента
Element[Topic;
Element[String]
РИС. 7.6. Разбор ССЫЛКИ topic.hot
Как следует интерпретировать ссылки? Будем рассматривать их как способ
определения случайных процессов. Предположим, что возможны две темы: sports
и politics. Каждая из них - экземпляр класса Topic. При этом Topic - коллекция
элементов и имеет атрибут hot с именем "hot". (Вообще говоря, не требуется,
чтобы имя атрибута в смысле Figaro совпадало с именем переменной Scala, но часто
это имеет смысл.) Пост posti является экземпляром класса Post, который также
является коллекцией элементов и имеет атрибуты poster и topic. Атрибут topic
250

7.3. Моделирование реляционной неопределенности...
имеет имя "topic". Вызов posti. get ("topic, hot") определяет случайный процесс,
шаги которого изображены на рис. 7.7.
1. Имя "topic" в posti 4. Имя "hot" в sports
выбирает атрибут выбирает атрибут
postl.topic sports.hot
3. Предположим,
что выбран
sports
posti
5. Значение sports,
hot случайно
выбирается из true
и false
sports
0.1
true
6. Предположим,
что выбрано
false
0.9
false
Значение postl.topic
случайно выбирается из
объектов sports и politics
7. Выражение posti.get ("topic.hot") породило
значение false
Рис. 7.7. Ссылка как случайный процесс, порождающий значения. На этой диаграмме
процесс порождает значение ссылки topic. hot в коллекции элементов posti
Вы помните, что элемент в Figaro представляет случайный процесс? Для
представления случайного процесса, определенного выражением posti.get ("topic,
hot"), тоже можно использовать элемент. Получение ссылки на элемент в
коллекции элементов реализовано именно так, потому что при этом возвращается
элемент, представляющий случайный процесс. Этот элемент можно использовать
в моделях, как любой другой. Дополнительная «приятность» заключается в том,
что Figaro берет на себя все хлопоты по отслеживанию ссылки и всех возможных
способов ее разрешения, так что вам об этом задумываться не надо.
Следует упомянуть одну тонкость. Что, если в классе Topic имеется также
атрибут important и существует зависимость между ним и атрибутом hot? Допустим,
что мы создали элемент, представляющий posti.get ("topic.hot") и другой
элемент, ПреДСТаВЛЯЮЩИЙ posti. get ("topic, important"). В Любом ВОЗМОЖНОМ МИре
topic - это либо sports, либо politics, но не то и другое одновременно. В любом
возможном мире неопределенность атрибута topic в posti должна быть
разрешена одинаково, вне зависимости от того, какой элемент мы собираемся получить:
important ИЛИ hot. Тем Самым образуется ЗавИСИМОСТЬ Между posti.get ("topic,
hot") И posti. get ("topic, important"). Это ТО, ЧТО МЫ ИНТУИТИВНО ОЖИДаем, И ал-
горитмы Figaro корректно обрабатывают этот случай.
251
true
0.1
false
0.9
hot
politics
hot
0.5
0.5
poster
topic

Глава 7. Объектно-ориентированное вероятностное моделирование
7.3.2. Модель социальной сети с реляционной
неопределенностью
Получив в свое распоряжение описанный механизм, мы можем вернуться к
модели социальной сети, на этот раз допустив неопределенность в теме поста. Сначала
СОЗДаДИМ КЛаСС Topic!
class Topic() extends ElementCollection {
val hot = Flip(O.l)("hot", this)
}
В первой строке говорится, что всякий экземпляр Topic одновременно является
и экземпляром Eiementcoilection, а, значит, элементам можно давать имена и
помещать их в коллекцию элементов. Во второй строке создается элемент Flip (О. i),
ему присваивается имя hot, и он помещается в коллекцию элементов this. В
контексте класса Topic ключевое слово this ссылается на данный экземпляр класса
Topic. Таким образом, данный экземпляр Topic является коллекцией элементов, в
которой имеется элемент с именем hot, и это элемент Flip (0. i).
Здесь мы впервые встретились с двумя дополнительными аргументами
конструктора Flip. Они необязательны и обычно опускаются. А задаются только
тогда, когда мы хотим присвоить элементу имя или поместить его в определенную
коллекцию. Но если нужно только присвоить элементу имя или только поместить
его в коллекцию, все равно придется задать второй необязательный аргумент. Flip
- не единственный конструктор, принимающий эти необязательные аргументы.
Конструкторы всех встроенных в Figaro элементов позволяют задавать имя и
коллекцию элементов.
Теперь мы можем определить два экземпляра класса Topic:
val sports = new Topic()
val politics = new Topic()
В классе Person имеется атрибут interest, ссылающийся на неизвестный
экземпляр Topic. Ниже ЭТОТ атрибут Определяется Как Element [Topic] I
class Person() {
val interest = Uniform(sports, politics)
}
КлаСС Post Также расширяет ElementCollection. В нем Имеется атрибут topic.
ЭТО Элемент ТИПа Element [Topic], ЗавИСЯЩИЙ ОТ poster, interest:
class Post(val poster: Person) extends ElementCollection {
val topic =
If(Flip(0.9), poster.interest,
Uniform(sports, politics)) ("topic", this)
}
Ссылка topic.hot используется в классе comment. Идея в том, что люди
оставляют комментарии на горячие темы, даже если обычно ими не интересуются. По-
252

7.3. Моделирование реляционной неопределенности...
in
ш\
этому комментарий возможен, если тема отвечает интересам комментатора или
является горячей. Вот соответствующий код из класса comment:
class Comment(val post: Post, val commenter: Person) {
val isHot = post.get[Boolean]("topic.hot")
val appropriateComment =
Apply(post.topic, commenter.interest, isHot,
(tl: Topic, t2: Topic, b: Boolean) => (tl == t2) || b)
// как и раньше, добавить ненаправленное ограничение на appropriateComment
//и тип отношения
}
Взглянув на определение is Hot выше, нетрудно заметить, что мы должны
задавать тип значения элемента (в данном случае Boolean). На самом деле, тип
значения нужно задавать всегда. Компилятор Scala не может по одному лишь имени
элемента определить тип его значения. Но чтобы использовать isHot, тип
значения необходимо знать. Задание типа значения в виде аргумента-типа get (в
квадратных скобках) сообщает компилятору интересующую его информацию.
На этом определение модели закончено. Мы можем создавать экземпляры и
связи в точности, как и раньше, - не стану снова приводить этот код, а лучше
покажу, как задавать факты, касающиеся комплексного атрибута. Делается это так же,
Как ДЛЯ ПРОСТЫХ атрибутов. Мы МОЖеМ НаПИСаТЬ postl. topic, observe (politics),
если хотим сообщить, что результатом наблюдения атрибута topic является
экземпляр politics Класса Topic.
Мы можем также запросить значение комплексного атрибута. Эта модель
поддерживает некоторые интересные запросы и способы вывода. Начнем с примеров,
которые показывают, как формулировать запросы об интересах людей и темах
постов - экземплярах класса Topic:
println("Вероятность, что Эми интересуется политикой = " +
VariableElimination.probability(amy.interest, politics))
println("Вероятность, что темой поста 2 является спорт = " +
VariableElimination.probability(post2.topic, sports))
println("Вероятность, что темой поста 3 является спорт = " +
VariableElimination.probability(post3.topic, sports))
println("Вероятность, что Эми является членом семьи Брайана = " +
VariableElimination.probability(connection(brian, amy).connectionType,
"family"))
Эта программа печатает:
Вероятность, что Эми интересуется политикой = 0.9656697011762803
Вероятность, что темой поста 2 является спорт = 0.24190044937009825
Вероятность, что темой поста 3 является спорт = 0.06958146174469142
Вероятность, что Эми является членом семьи Брайана = 0.3791735849751334
Теперь предположим, что известно, что спортивная тема горячая (sports.hot.
observe (true)), и выполним те же запросы. Будет напечатано:

Глава 7. Объектно-ориентированное вероятностное моделирование
Вероятность, что Эми интересуется политикой = 0.9609178093049061
Вероятность, что темой поста 2 является спорт = 0.3729396845525878
Вероятность, что темой поста 3 является спорт = 0.0900555124038995
Вероятность, что Эми является членом семьи Брайана = 0.33670840928905443
Отметим возросшую вероятность того, что посты 2 и 3 посвящены спорту. Это
может показаться странным, потому что в модели класса Post «температура» не
учитывается при выборе темы. Но рассуждение производится следующим
образом. Ранее мы наблюдали, что тема поста 1 - политика. Эми отправила пост 1,
поэтому высока вероятность, что она интересуется политикой. Мы также знаем,
что Брайан отправил пост 2, а Эми оставила комментарий к нему. Поскольку люди
чаще комментируют посты на интересующие их темы, если только речь не идет
о горячей теме, есть основания полагать, что темой поста 2 является политика.
Но теперь мы еще знаем, что спорт - горячая тема. В результате вполне может
оказаться, что темой поста 2 является спорт, а свой комментарий Эми оставила,
потому что это горячая тема, а не потому что интересуется спортом. Поэтому
увеличивается вероятность, что тема поста 2 - спорт. Аналогичное рассуждение
можно отнести и к посту 3.
Теперь подумаем, почему уменьшилась вероятность принадлежности Эми к
семье Брайана. Мы знаем, что Эми с большой вероятностью интересуется
политикой. Для поста 2 есть две возможности: либо он посвящен политике, и в этом
случае не нужно объяснять, почему Эми его прокомментировала, либо спорту - и
тогда это нуждается в объяснении. Объяснения может быть два: либо Эми - член
семьи Брайана, либо спорт - горячая тема. До того как стало известно, что тема
спорта горячая, вероятность, что Эми - член семьи Брайана, составляла 38 %.
Знание о том, что спорт - горячая тема, дает альтернативное объяснение, а потому
снижается ценность первоначального объяснения, т. е. вероятность, что Эми и
Брайан - члены одной семьи, уменьшается. Это пример наведенной зависимости,
о которой шла речь в главе 5, посвященной байесовским сетям. Априори два
события - Эми является членом семьи Брайана и спорт - горячая тема - независимы.
Нет никаких причин, по которым они должны быть как-то связаны. Но после того
как стало известно, что Эми с большой вероятностью интересуется политикой и
что она прокомментировала пост Брайана, эти события становятся связанными.
Это классический пример паттерна рассуждения, который называется
оправданием (explaining away), когда есть два альтернативных объяснения одного и того
же наблюдения и эмпирическое наблюдение одного объяснения снижает ценность
другого.
7.3.3. Модель принтера с неопределенностью
типа
Итак, мы теперь знаем, как реализовать модель с реляционной
неопределенностью, и можем заняться проблемой неопределенного типа в модели принтера, где
тип принтера неизвестен. Принцип похож: используются коллекции элементов
и ссылки. Мы создаем несколько экземпляров принтера, по одному для каждого
254

7.3. Моделирование реляционной неопределенности...
щи
*Ш
возможного типа, и элемент, значением которого является один из созданных
экземпляров. Этот элемент будет представлять неизвестный принтер.
Но есть две трудности, которых не было в предыдущем разделе. Во-первых,
требуется предъявлять факты и формулировать запросы, относящиеся к
неизвестным элементам. Поэтому мы будем использовать get как в наблюдениях, так и в
запросах. Это просто.
Вторая трудность заключается в том, что мы не хотели бы кардинально
изменять первоначальное определение класса PrintExperience, который принимает
Printer в качестве аргумента. Но у нас нет конкретного принтера, а имеется
элемент Element [Printer], представляющий неизвестный принтер, и при этом нужно
СОЗДатЬ ЭКЗемПЛЯр PrintExperience И ПОЛуЧИТЬ ДОСТуП К его атрибутам. Для ЭТОГО
мы воспользуемся элементом Figaro Apply. Если имеется неизвестный принтер,
представленный в виде Element [ Printer], то применим Apply для создания
элемента ТИПа Element [PrintExperience], где PrintExperience ОСНОВан на ТОМ принтере,
что имеется.
Как мы увидим, потребуется внести минимальные изменения в модель, всего
пять строчек. Правда, способ создания экземпляра модели и его опроса изменится
сильнее, но это как раз то место, где изменения ожидаемы и желательны. Вот все
пять изменений, внесенных в модель.
1. object PrinterProblemTypeUncertainty extends ElementCollection {
Мы помещаем всю модель в коллекцию элементов.
2. abstract class Printer extends ElementCollection {
Принтер является коллекцией элементов.
3. val powerButtonOn = Flip(0.95)("power button on", this)
Запрашиваемый атрибут powerButtonOn получает имя и помещается в
коллекцию элементов принтера, к которому он относится.
4. class PrintExperience(printer: Printer, software: Software, network:
Network, user: User) extends ElementCollection {
Результат печати - также коллекция элементов.
5. val summary = Apply (...) ("summary", this)
Мы наблюдаем общий результат печати, поэтому присваиваем ему имя и
помещаем в коллекцию элементов результата печати.
Вот и всё. Теперь нужно описать конкретную ситуацию. Именно здесь вступает
в игру неопределенность типа. Действуем следующим образом. Сначала случайно
Выбираем myPrinter ИЗ Принтеров раЗНЫХ ТИПОВ, Присваиваем myPrinter ИМЯ И
помещаем его в коллекцию элементов модели в целом:
val myPrinter =
Select(0.3 -> new LaserPrinter,
0.7 -> new InkjetPrinter) ("my printer", this)
Затем, Как И раньше, СОЗДаеМ ЭКЗеМПЛЯрЫ КЛаССОВ Software, Network И User!

Глава 7. Объектно-ориентированное вероятностное моделирование
val mySoftware = new Software
val myNetwork = new Network
val me = new User
Наконец, ДЛЯ СОЗДаНИЯ myExperience ИСПОЛЬЗуеМ Apply И Существующий КЛаСС
PrintExperience, который принимает в качестве аргументов конкретные принтер,
программу, сеть и пользователя. Присваиваем myExperience имя и помещаем его в
коллекцию элементов верхнего уровня:
val myExperience =
Apply(myPrinter,(p: Printer) =>
new PrintExperience (p, mySoftware, myNetwork, me)) ("print experience",
this)
Теперь всё готово к заданию фактов и опросу. Наблюдается общий результат
печати. Но ведь myExperience - Элемент ТИПа Element [PrintExperience], Как Же ПО-
лучить для него общий результат? Да с помощью ссылки, конечно! Мы можем это
сделать, потому что присвоили элементу, описывающему общий результат, имя и
ПОМеСТИЛИ его В КОЛЛеКЦИЮ PrintExperience, а Элемент myExperience ТОЖе ИМеНО-
ванный и находится в коллекции верхнего уровня. И вот как это выглядит в коде:
val summary = get[Symbol]("print experience.summary")
summary.observe(f none)
Зная, что ничего не было напечатано, мы зададим два вопроса. Первый: нажата
ли кнопка питания? И снова, поскольку myPrinter - элемент, опросить его
непосредственно невозможно, но можно воспользоваться ссылкой:
val powerButtonOn = get[Boolean] ("my printer.power button on")
Второй запрос интереснее. Представьте, что вы сотрудник службы техподдерж-
ки и хотите узнать, какой принтер у пользователя. Послушав рассказ
пользователя о том, что он наблюдает, мы можем выдвинуть гипотезу о типе принтера, а
затем запросить у модели тип принтера, исходя из наблюдаемых фактов. Для этого
воспользуемся имеющимся в Scala методом проверки типа во время выполнения
isinstanceof. Точнее, мы можем определить элемент, значение которого равно
true, если myPrinter является лазерным принтером:
val isLaser =
Apply(myPrinter, (p: Printer) => p.isInstanceOf[LaserPrinter])
Теперь можно выполнить вывод и получить ответ на запрос в таком виде:
После наблюдения отсутствия печати:
Вероятность, что кнопка питания принтера нажата = 0.8868215502107177
Вероятность, что принтер является лазерным = 0.23800361000850662
Априорная вероятность, что принтер является лазерным, была равна 0.3. После
того как стало известно, что принтер печатает плохо, вероятность уменьшилась.
Согласно нашей модели, лазерные принтеры надежнее струйных, поэтому плохой
результат более вероятен для струйного принтера.
256

7.5. Упражнения
Надеюсь, вы теперь понимаете, что моделирование объектов и связей с учетом
неопределенности - реляционной и типа - позволяет описывать интересные и
нетривиальные ситуации, а также производить разного рода рассуждения.
Наряду с коллекциями, описанными в предыдущей главе, объектно-ориентированная
и реляционная парадигмы моделирования дают возможность использовать
знакомые по обычному программированию приемы для создания вероятностных
моделей. В следующей главе мы опишем моделирование и рассуждения в одном
важном частном случае - динамической модели ситуации, которая изменяется с
течением времени.
7.4. Резюме
• Объектно-ориентированная и реляционная парадигмы программирования
позволяют структурировать сложные модели и повторно использовать
компоненты моделей.
• Эти парадигмы подразумевают определение классов моделей с атрибутами
и вероятностными зависимостями, функциональными формами и
числовыми параметрами.
• На уровне экземпляра мы таким образом определяем распределение
вероятности атрибутов всех экземпляров; мы можем задать факты и запросить
у модели значения атрибутов.
• Коллекции элементов и ссылки - это механизм, применяемый в Figaro для
доступа к элементам, которые на этапе компиляции еще неизвестны.
• Чтобы представить реляционную неопределенность или неопределенность
типа, мы создаем элемент, значением которого является коллекция
неизвестных элементов, и пользуемся ссылками для доступа к атрибутам этой
коллекции.
7.5. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. В вашей компании пять отделов: исследований и разработок,
производственный, продаж, кадров и финансовый. Постройте
объектно-ориентированную модель, которая описывает взаимозависимости этих отделов. С
помощью этой модели ответьте на запросы о благополучии компании, исходя
из информации о состоянии ее отделов.
2. Вы занимаетесь моделированием популярности фильмов. В каждом
фильме занято несколько актеров, и каждый актер играет в нескольких
фильмах. С каждым актером связана переменная, показывающая, насколько он
нравится публике. Популярность фильма зависит от симпатий публики к
актерам. Имея набор данных о фильмах, их популярности и занятых в них
257

Глава 7. Объектно-ориентированное вероятностное моделирование
актерах, предскажите популярность нового фильма с заданным актерским
составом.
3. В вашем колледже студенты могут посещать курсы по разным предметам.
Один преподаватель может вести несколько курсов, и один курс может
читаться разными преподавателями. Оценка студента по курсу зависит от
трех факторов: способности студента, сложность предмета и квалификация
преподавателя. Разработайте вероятностную модель для представления
этой ситуации. Имея набор данных о студентах, посещаемых ими курсах,
преподавателях и полученных оценках, выведите способности заданного
студента, трудность заданного курса и квалификацию заданного
преподавателя.
4. Продолжая упражнение 3, представьте, что вы студент, планирующий, на
какие курсы записаться в следующем семестре. К сожалению, неизвестно,
кто их будет читать, но можно предположить, что преподавать данный курс
будет кто-то из ранее преподававших его. Воспользовавшись реляционной
неопределенностью, представьте эту ситуацию и предскажите свою оценку
по выбранному курсу.
5. Рассмотрим приложение для слежения за транспортными средствами. Есть
несколько видов транспортных средств, например: грузовики, легковые
машины и мотоциклы. У каждого транспортного средства имеются свойства,
например, размер и цвет. Распределение вероятности этих переменных
различно для разных транспортных средств. Имеется камера, которая снимает
транспортные средства, заезжающие на вашу территорию, и алгоритм
анализа изображений, который умеет оценивать размер и цвет транспортного
средства. Оценки размера и цвета зависят от истинных размера и цвета, но
необязательно совпадают с ними. Разработайте реляционную модель с
неопределенностью типа для представления этой ситуации. С помощью своей
модели выведите тип заданного транспортного средства, зная оценки его
размера и цвета.
258

ГЛАВА 8.
Моделирование
динамических систем
В этой главе.
■ Создание вероятностной модели динамической
системы.
■ Использование различных видов динамических
моделей, в том числе марковских цепей, скрытых
марковских моделей и динамических
байесовских сетей,
■ Использование вероятностных моделей для
создания новых видов динамических моделей,
например, моделей с нестационарной структурой.
■ Непрерывный мониторинг динамической
системы.
В предыдущих главах мы многое узнали об использовании вероятностного
программирования для построения вероятностных моделей. Сейчас у вас уже
довольно богатый арсенал методов, в том числе моделирование зависимостей, функции,
коллекции и объектно-ориентированное моделирование. В этой главе мы
воспользуемся всем этим для моделирования особенно важного вида систем:
динамических систем, изменяющихся с течением времени.
В разделе 8.1 мы познакомимся с общей концепцией динамических
вероятностных моделей, а в разделе 8.2 подкрепим этот материал рядом примеров, начиная
с простейших временных рядов и заканчивая системами, в которых изменяется
сама структура. В начале главы мы будем предполагать, что динамическая система
функционирует в течение фиксированного промежутка времени, но в разделе 8.3
ослабим это предположение, допустив системы, работающие сколь угодно долго.
Для этого нам понадобится новое понятие Figaro - универсум. Мы увидим, как
универсумы Figaro позволяют моделировать постоянно работающие системы и
рассуждать о них.

Глава 8. Моделирование динамических систем
8.1. Динамические вероятностные
модели
В главе 1 мы говорили о том, как рассуждать об угловых ударах в футболе.
Вероятностная система рассуждения позволяет отвечать на запросы трех видов:
• предсказание исхода углового с учетом таких факторов, как ветер, рост
центрального нападающего и т. д.;
• вывод свойств, которые могли стать причиной наблюдаемого исхода,
например, квалификации вратаря;
• использование сведений об исходе одного углового для вывода свойств,
которые могут оказать влияние на исход другого углового, и предсказание
исхода второго углового на основе этой информации.
В этой главе мы перейдем от моделирования отдельных угловых ударов,
рассматриваемых как изолированные события, к моделированию всего футбольного
матча как последовательности взаимосвязанных событий. Футбольный матч -
пример динамической системы. Это означает две вещи:
• У футбольного матча имеется состояние в каждый момент времени.
Состояние может включать, к примеру, счет, владение мячом, уверенность обеих
команд в своих силах.
• Состояние в данный момент времени зависит от предшествующих
состояний. Например, в футбольном матче счет зависит от предыдущего счета и
от того, засчитан ли гол; владение мячом зависит от того, кто владел мячом
ранее, поскольку команда, владеющая мячом, имеет все шансы владеть им
и далее; уверенность команды также зависит от уверенности в
предшествующий период времени, потому что уверенность обычно не пропадает и не
появляется внезапно.
Приняв во внимание обе эти характеристики, мы приходим к следующему
определению: динамическая система - это система, обладающая в каждый момент времени
состоянием, причем состояния в различные моменты времени взаимозависимы.
Можно привести много примеров динамических систем. Очевидно, что такой
системой является погода, потому что сегодняшняя погода зависит от погоды в
предшествующие дни. Эффективность бизнеса - тоже динамическая система;
ее состояние включает различные показатели, например выручку и прибыль, а
значения этих показателей в разные моменты времени взаимозависимы. Третий
пример - движение транспорта на автомагистрали; состоянием может быть
количество машин на каждой полосе и понятно, что эта величина в данный момент
зависит от того, какой она была раньше.
Мы будем рассматривать создание вероятностных моделей динамических
систем. Такие модели называются динамическими вероятностными моделями.
Состояние динамической вероятностной модели представляется случайными
переменными. Например, в случае эффективности бизнеса переменные могут
описывать величину выручки и прибыли в каждый момент времени. Эти пере-
260

8.2. Типы динамических моделей
менные называются переменными состояния. Вероятностная модель определяет
вероятностные зависимости между значениями переменных состояния в разные
моменты времени.
Способы использования динамической вероятностной модели аналогичны
тому, как мы используем обычную статическую вероятностную модель.
• Предсказание состояния системы в будущий момент времени с учетом
текущего состояния и временных зависимостей между состояниями.
Например, можно предсказать окончательный счет футбольного матча, зная
текущий счет и степень уверенности команд.
• Вывод прошлых причин текущего состояния. Например, если ваша команда
проиграла матч, то можно попытаться выяснить, какие принятые во время
игры решения привели к поражению.
• Мониторинг состояния системы, основанный на наблюдениях в различные
моменты времени. Например, мы можем непрерывно оценивать
уверенность и качество игры двух команд, основываясь на наблюдениях за
происходящим на поле. А затем воспользоваться этими оценками, чтобы
предсказать, что произойдет на следующем отрезке игры.
Все три возможности были бы весьма полезны главному тренеру команды. На
самом деле, динамические системы настолько важны и вездесущи, что для их
вероятностного моделирования разработано множества методов. Системы
вероятностного программирования могут предложить многие из давно сложившихся
методов построения динамических вероятностных моделей, в т. ч. скрытые
марковские модели и динамические байесовские сети, рассматриваемые в следующем
разделе, а также многое сверх того - за счет включение таких средств, как
развитые структуры данных и управление потоком выполнения. Но хватит
предисловий, давайте рассмотрим некоторые подходы и покажем, как они выражаются на
языке вероятностного программирования.
8.2. Типы динамических моделей
В этом разделе представлены различные виды динамических моделей. Мы
начнем с самой простой - марковских цепей, а затем рассмотрим ее широко
распространенное обобщение - скрытые марковские модели. После этого мы перейдем
к динамическим байесовским сетям, которые, как следует из названия,
являются обобщением байесовских сетей на динамические модели. Все это стандартные
системы, существовавшие до появления вероятностного программирования. Во
всех них предполагается, что структура модели со временем не изменяется. Но
вероятностное программирование позволяет пойти дальше и описать модели с
нестационарной структурой; мы увидим, как это делается, в разделе 8.2.4.
8.2.1. Марковские цепи
Для динамической системы характерно изменение состояния во времени, но
так, что состояния в различные моменты времени взаимозависимы. Марковская
261

Глава 8. Моделирование динамических систем
цепь - простейший вид динамической системы, характеризуемый двумя
свойствами. Во-первых, состояние исчерпывается единственной переменной. Во-вторых,
переменная состояния в каждый момент времени вероятностно зависит от
переменной в предшествующий момент времени, но не от более ранних переменных
состояния.
На рис. 8.1 приведен пример марковской цепи для футбольного матча. В этой
модели состоянием является единственная переменная, показывающая, какая
команда владеет мячом в конкретный момент времени. Для удобства можно считать,
что моменты времени совпадают с минутами, но вообще разбивать время матча на
промежутки можно произвольным образом.
Владение(О)
Рис. 8.1. Марковская цепь. Состояние в момент времени описывается
единственной переменной, которая зависит от той же переменной в предыдущий
момент. Владение(1) непосредственно зависит от Владения(О), Владение(2) -
от Владения(1) и вообще Владение(п) непосредственно зависит от Владения(п - 1)
На рис. 8.1 видно, что стрелки последовательно ведут из предыдущего состояния
в следующее, а это означает, что:
• Владение( 1) непосредственно зависит от Владения(О);
• Владение(2) непосредственно зависит только от Владения( 1), но не от
Владения^);
• Любое влияние Владения(О) на Владение(2) опосредовано Владением(1).
Ту же мысль можно выразить по-другому, сказав, что Владение(2) условно
независимо от Владения(О) при условии Владения(1). Это верно и для всех остальных
моментов времени: владение мячом в любой момент времени условно независимо от
владения во все предшествующие моменты времени при условии владения в
предыдущий момент. Это утверждение - пример свойства, которое называется
марковским предположением.
Марковское предположение. Динамическая вероятностная модель удовлетворяет
марковскому предположению, если состояние в любой момент времени зависит
только от состояния в предыдущий времени; состояние в любой момент времени условно
независимо от всех предшествующих состояний при условии предыдущего состояния.
Задание марковской цепи
Для создания марковской цепи необходимо несколько действий.
1. Определить множество значений переменной состояния. Это те значения,
которые вы считаете релевантными в какой-нибудь момент времени. В
общем случае не следует выбирать больше значений, чем необходимо. Как
мы вскоре увидим, размер представления марковской цепи квадратично
зависит от количества значений переменной состояния, и мы не хотели
бы, чтобы он оказался слишком велик. Например, можно было бы создать
262
Владение{1)
Владение(2)

8.2. Типы динамических моделей
для футбольного матча марковскую цепь, в которой переменная состояния
представляет разность количества забитых и пропущенных голов.
Теоретически эта разность могла бы быть велика - если каждую минуту
забивать по голу, то окончательный счет будет 90:0! Но на практике большая
разность в счете - редкость, а, кроме того, разница между опережением на
5 и 15 голов уже несущественна, потому что в матче профессиональных
команд отыграть пять мячей практически невозможно. Поэтому можно
ограничить разность количества забитых и пропущенных голов значениями от
-5 до +5.
2. Сделать одно из двух:
• Задать начальное значение марковской цепи, т. е. значение первой
переменной состояния. Например, разность количества забитых и
пропущенных голов в начале футбольного матча равна 0.
• Определить распределение начального значения. Это необходимо, если
точное значение неизвестно. Например, кто будет владеть мячом в
начале матча, определяется подбрасыванием монеты, так что для каждой
команды вероятность владения равна 0.5.
3. Задать модель переходов, которая определяет, как следующее состояние
зависит от предыдущего. На рис. 8.1 модель переходов определяет
вероятность Владения(1) при условии Владения(О), вероятность Владения(2)
при условии Владения(1) и т. д. В символьных обозначениях модель
переходов определяет Р(Владение(£) | Владение(£-1)) для любого t > 1.
На шаге 3 я предположил, что вероятности перехода в разные моменты времени
в точности одинаковы. Вообще говоря, для марковских цепей такое
предположение необязательно, но практически удобно и применяется во многих
приложениях. При таком предположении для определения марковской цепи достаточно
простого цикла.
Работа с динамическими моделями требует значительных накладных расходов.
Сложность представления динамической модели и рассуждений определяется в
первую очередь числом состояний. В марковской цепи количество параметров в
модели переходов квадратично зависит от числа значений переменной состояния.
В нашем примере модель переходов определяет величины Р(Владение(£) |
Владение^-!). Это условное распределение вероятности можно описать таблицей,
содержащей вероятности для всех возможных значений Владения(£-1) и
Владения^). Число ячеек в этой таблице равно квадрату числа возможных значений
переменной Владение.
Марковские цепи в Figaro
Если нам заранее известно общее число временных шагов, то задать
марковскую цепь на Figaro легко. Если это число неизвестно и система может работать
сколь угодно долго, то требуются более хитрые методы, описанные в разделе 8.3.
А для цепи с известным числом шагов можно написать простой цикл. Ниже
приведен код для марковской цепи, изображенной на рис. 8.1.
263

Глава 8. Моделирование динамических систем
Листинг 8,1, Кодирование марковской цепи
val length = 90 <—О
val ourPossession: Array[Element[Boolean]] =
Array .fill (length) (Constant (false) )
В
ourPossession(0) = Flip(0.5) <\—©
for { minute <- 1 until length } {
ourPossession(minute) =
If(ourPossession(minute - 1), Flip(0.6), Flip(0.3))
О — Длина цепи
© — Массив переменных состояния, по одной для каждого момента времени
© — Задаем распределение вероятности начального состояния последовательности
© — Модель переходов, определяющая распределение переменной состояния в каждый
момент времени при условии ее значения в предыдущий момент
Сначала мы задаем длину последовательности - 90 минут. Затем создаем
массив, содержащий по одному элементу для каждой минуты от 0 до 89, который
представляет булеву переменную состояния, показывающую, владеет ли мячом
наша команда на этой минуте. Метод Scala Array.пи создает массив, длина
которого задается первым аргументом length, а все элементы инициализированы
значением constant (false). Начальное значение несущественно, потому что мы его
перезапишем в следующем же предложении.
Далее мы определяем распределение вероятности того, что наша команда будет
владеть мячом в момент 0. Выбрав элемент Flip (0.5), мы указали, что в начальный
момент времени мяч окажется у нашей команды с вероятностью 0.5.
Затем идет цикл, в котором мы перебираем все моменты времени от 1 до 89.
В каждый момент определяется, владеем ли мы мячом, на основе информации
о том, кто владел им в предыдущий момент. Точнее, если мячом владели мы, то
он у нас и останется с вероятностью 0.6, а если не владели, то завладеем с
вероятностью 0.3.
Мы можем запросить у этой марковской модели распределение вероятности
переменной состояния в любой момент времени, если имеются наблюдения в
какие-то другие моменты. Пусть, например, нас интересует, с какой вероятностью наша
команда будет владеть мячом в момент 5. Сначала можно спросить, чему равна эта
вероятность, если нет никаких наблюдаемых фактов:
VariableElimination.probability(ourPossession(5), true)
Модель говорит, что априорная вероятность владения мячом в момент 5 равна
0.428745.
Затем мы сообщаем, что владели мячом на шаге 4:
ourPossession(4).observe(true)
264
в

8.2. Типы динамических моделей
Теперь тот же самый запрос возвращает 0.6. Как видим, вероятность возрастает,
если известно, что мы владели мячом на предыдущем шаге. Она в точности равна
вероятности сохранить владение мячом в следующий момент.
А что произойдет, если мы знаем, что владели мячом и на шаге 3 тоже? В ответ
на запрос модель возвращает то же значение 0.6. Новое наблюдение не изменило
вероятность. Объясняется это марковским предположением: владение мячом в
момент 5 не зависит от того, владели ли мы им в момент 3, при условии, что мяч
был у нас в момент 4.
Можно также сообщить модели о том, что мы владели мячом в момент 6. Это
показывает, что можно рассуждать не только в прямом направлении марковской
цепи для предсказания будущего, но и в обратном для вывода прошлых состояний
из результата будущих наблюдений. Если добавить этот факт, то вероятность
владения мячом в момент 5 возрастет до 0.75.
Наконец, сообщим, что владели мячом и в момент 7. В ответ по-прежнему
получим 0.75 (с точностью до ошибки округления). Это еще одно проявление
марковского предположения. Тот факт, что мы владели мячом в момент 7, не добавляет
новой информации для момента 5 при условии, что известно, кто владел мячом в
момент 6.
Марковские цепи - простейший случай динамических вероятностных моделей,
но они лежат в основе более сложных. В следующих разделах мы рассмотрим эти
более развитые модели.
8.2.2. Скрытые марковские модели
Скрытая марковская модель (СММ) - этот обобщение марковской цепи на
случай, когда в каждый момент времени существуют две переменные: одна
представляет «скрытое» состояние, а другая - наблюдение. На рис. 8.2 приведен пример
СММ. Скрытое состояние - это информация об уверенности команды в каждый
момент времени. Мы никогда не знаем точно, уверена команда в своих силах или
нет, а вынуждены строить умозаключения, исходя из того, что происходит на поле.
Потому-то это состояние и называется скрытым. А непосредственно можно
наблюдать, кто владеет мячом.
Уверена(О)
Владение(О)
Рис. 8.2. Скрытая марковская модель. Уверена - переменная скрытого
состояния, а Владение описывает непосредственное наблюдение. Переменные
скрытого состояния образуют марковскую цепь, а наблюдение зависит
только от скрытого состояния в данный момент времени
265
Уверена{1)
Уверена(2)
Владение(1)
Владение(2)

Глава 8. Моделирование динамических систем
Из рис. 8.2 видно, что СММ удовлетворяет двум предположениям:
• скрытые состояния образуют марковскую цепь, удовлетворяющую
марковскому предположению;
• наблюдение в любой момент времени зависит только от скрытого
состояния в этот момент. Наблюдение не зависит от всех предыдущих скрытых
состояний и наблюдений, если известно скрытое состояние в данный
момент.
Отсюда также следует, что скрытое состояние в конкретный момент времени не
зависит от всех предыдущих состояний, если известно предыдущее скрытое
состояние. Но тут следует сделать важную оговорку. Предыдущее состояние, по
определению, скрыто, т. е. обычно неизвестно достоверно. Текущее скрытое состояние
не является независимым от предыдущих наблюдений, если предыдущее скрытое
состояние неизвестно. Так, на рис. 8.2 Владение(О) не является независимым от
Уверена(2), если мы не наблюдали Уверена(О) или Уверена(1).
Это существенно для понимания того, почему СММ - полезное представление,
обладающее широкими возможностями. Два вышеупомянутых предположения
позволяют также сделать представление СММ компактным, а вывод -
эффективным. В то же время они не препятствуют использованию всей последовательности
наблюдений для вывода скрытых состояний.
Задание СММ на Figaro
Мы знаем, как описать марковскую цепь, а описание СММ не намного сложнее.
Необходимо сделать следующее.
1. Определить множество значений переменной скрытого состояния. В
нашем примере переменную Уверена можно сделать булевой. Поскольку
переменные скрытого состояния образуют марковскую цепь, размер
представления будет квадратично зависеть от числа значений переменной.
2. Определить множество значений наблюдаемой переменной. В нашем
примере Владение можно сделать булевой переменной, показывающей,
владеет ли наша команда мячом в данный момент времени. Поскольку
наблюдаемая переменная зависит от скрытого состояния, но не от предыдущих
наблюдений, размер представления будет пропорционален произведению
числа значений скрытой переменной на число значений наблюдаемой
переменной.
3. Определить распределение вероятности начального скрытого состояния.
Оно называется начальной моделью. В нашем примере это Р(Уверена(0)).
4. Определить модель переходов для переменных скрытого состояния,
которая представляет условное распределение переменной состояния в каждый
момент времени при условии известного значения в предыдущий момент.
В нашем примере это Р(Уверена(£) | Уверена(£-1)).
5. Определить модель наблюдения, которая описывает условное
распределение вероятности наблюдаемой переменной в каждый момент времени при
266

8.2. Типы динамических моделей
условии известной переменной скрытого состояния в этот момент. В
нашем примере это Р(Владение(£) | Уверена(£)).
Ниже показано, как эти шаги реализуются в коде.
Листинг 8-2- Описание СММ
val length = 90
val confident: Array [Element [Boolean] ] =
Array.fill (length) (Constant (false) )
val ourPossession: Array[Element[Boolean]] =
Array.fill (length) (Constant (false) )
confident (0) = Flip (0.4) <]—ф
for { minute <- 1 until length } {
confident (minute) = If (confident (minute - 1) , Flip (0.6), Flip (0.3))
} //
for { minute <- 0 until length } {
ourPossession(minute) = If(confident(minute), Flip(0.7), Flip(0.3))
} //
H
и
О — Массив переменных скрытого состояния, по одной для каждого момента времени
© — Массив наблюдаемых переменных, по одной для каждой переменной скрытого
состояния
© — Задаем распределение начального скрытого состояния
© — Модель переходов, определяющая распределение вероятности каждой переменной
скрытого состояния на основе предшествующей ей
© — Модель наблюдений, определяющая распределение вероятности каждой
наблюдаемой переменной на основе соответствующей переменной скрытого состояния
При выводе скрытого состояния в некоторый момент времени из наблюдений
мы можем рассматривать наблюдения трех видов: текущее, прошлые и будущие.
Словосочетание «будущие наблюдения» звучит парадоксально: как можно что-то
наблюдать в будущем? Я просто хочу сказать, что можно вывести скрытое
состояние в предшествующий момент времени, основываясь на наблюдениях, сделанных
в промежутке от этого момента до настоящего времени. По отношению к
прошлому моменту эти наблюдения являются будущими.
Как уже было отмечено, для вывода скрытого состояния необходимо
принимать во внимание все наблюдения, а не только текущее и соседние с ним. Это
можно продемонстрировать на примере следующих запросов к нашей модели.
Листинг 8.3. Запросы к СММ
println ("Вероятность, что команда уверена в момент 2")
println("Априорная вероятность: " +
VariableElimination.probability(confident(2), true))
D
В
267

Глава 8. Моделирование динамических систем
ourPossession(2).observe(true)
println ("После наблюдения за текущим владением мячом в момент 2: " +
VariableElimination.probability(confident(2), true))
ourPossession(1).observe(true)
println ("После наблюдения за предыдущим владением мячом в момент 1: " +
VariableElimination.probability(confident(2), true))
ourPossession(0).observe(true)
println ("После наблюдения за предыдущим владением мячом в момент 0: " +
VariableElimination.probability(confident(2), true))
ourPossession(3).observe(true)
println ("После наблюдения за будущим владением мячом в момент 3: " +
VariableElimination.probability(confident(2), true))
ourPossession(4).observe(true)
println ("После наблюдения за будущим владением мячом в момент 4: " +
VariableElimination.probability(confident(2) , true))
Вот результаты:
Вероятность, что команда уверена в момент 2
Априорная вероятность: 0.42600000000000005
После наблюдения за текущим владением мячом в момент 2: 0.6339285714285714
После наблюдения за предыдущим владением мячом в момент 1: 0.6902173913043478
После наблюдения за предыдущим владением мячом в момент 0: 0.7046460176991151
После наблюдения за будущим владением мячом в момент 3: 0.7541436464088398
После наблюдения за будущим владением мячом в момент 4: 0.7663786503335885
Как видим, каждое новое наблюдение повышает нашу веру в уверенность
команды в момент 2.
8.2.3. Динамические байесовские сети
Хотя СММ умеют выводить скрытое состояние из последовательности
наблюдений, это все-таки простое представление, в котором в каждый момент времени
имеются только две переменные. В общем случае нас может интересовать
много переменных, которые зависят друг от друга самыми разными способами. Для
этого предназначены динамические байесовские сети (ДБС), обобщающие СММ.
В основе их работы лежит тот же принцип моделирования временной
последовательности переменных, что и в СММ, но переменных может быть много, а
зависимости между ними разнообразны. Как следует из названия, ДБС похожа на
байесовскую сеть и включает аналогичные данные.
ДБС состоит из следующих компонентов.
1. Множество переменных состояния в каждый момент времени. На рис. 8.3
имеются следующие переменные:
Выигрывает - показывает, какая команда ведет в счете в данный момент;
Уверена - показывает, уверена ли наша команда в своих силах;
Владение - показывает, какая команда владеет мячом;
Гол - показывает, был ли забит гол на данной минуте;
Разность - показывает разность забитых и пропущенных мячей.
268

Рис. 8.3. Динамическая байесовская сеть. В каждый момент времени существует
несколько переменных. Переменная может зависеть от других переменных в тот же
или предшествующие моменты времени
2. Множество возможных значений каждой переменной. В нашем примере:
• Выигрывает может принимать значения «мы», «они», «никто»;
• Уверена - булева переменная;
• Владение - булева переменная;
• Гол - булева переменная;
• Разность - целое число от -5 до 5.
3. Модель переходов, содержащая:
• Множество родителей для каждой переменной. Это могут быть другие
переменные в тот же момент времени или какие-то переменные в
предшествующие моменты. На родителей налагается только два
ограничения: (1) никакое ребро не может пересекать более одного промежутка
времени и (2) ребра не могут образовывать ориентированные циклы -
как и в обычной байесовской сети. В нашем примере имеются
следующие зависимости:
- Выигрывает в некоторый момент времени зависит от Разности в
предыдущий момент;
- Уверена в некоторый момент времени зависит от того, кто сейчас
Выигрывает и была ли команда Уверена в предыдущий момент;
- Владение зависит от уверенности в текущий момент;
- Гол (для любой команды) зависит от владения мячом и уверенности.
- Новая Разность определяется предыдущей Разностью и тем, был ли
забит Гол и кто его забил, что, в свою очередь, зависит от того, кто
владел мячом.
269
8.2. Типы динамических моделей
Выигрывает{1)
Выигрывает(2)
Уверена(О)
Уверена(1)
Уверена(2)
Владение(1)
Владение(2)
Гол{1)
Гол (2)
Разность(О)
Разность(1)
Разность(2)

Глава 8. Моделирование динамических систем
• Для каждой переменной условное распределение вероятности для
каждой комбинации значений родителей. В нашем примере условные
распределения вероятности таковы.
- Выигрывает: определяется по предыдущей Разности очевидным
способом.
- Уверена: вероятность уверенности больше, если команда Выигрывает
и была Уверена в предыдущий момент;
- Владение: вероятность Владения больше, если команда Уверена;
- Гол более вероятен, если команда, владеющая мячом, уверена в своих
силах. Это означает, что если команда владеет мячом и уверена в себе или
не владеет мячом и не уверена в себе, то вероятность гола повышается;
- новая Разность - детерминированная функция предыдущей
Разности, Гола и того, кто владел мячом (от этого зависит, какая команда
забила гол).
4. Начальная модель, которая описывает распределение вероятности
переменных в начальный момент времени. Как правило, это обычная байесовская сеть
с начальными переменными. Но для запуска ДБС необходимо распределение
только для тех переменных, которые влияют на состояние в следующий
момент времени. В нашей ДБС это переменные Уверена(О) и Разность(О).
Как видно из этого перечня, основным в спецификации ДБС является модель
переходов. Обычно вместо того чтобы показывать временную последовательность
переменных, как на рис. 8.3 (где показаны переменные в моменты 0, 1, 2 и т. д.)
показывают только связь между текущим и предыдущим моментами. Эту связь
называют двухэтапной байесовской сетью, или сокращенно 2ЭБС. На рис. 8.4
изображена 2ЭБС для нашего примера.
Рис. 8.4. Двухэтапная байесовская сеть (2ЭБС) для нашего примера. В 2ЭБС
показаны переменные в момент t и их зависимости от переменных в момент t - 1
270
Выигрывает(/)
Уверена(^1)
Уверена(0
Владение(/)
Гол (О
Разность(/— 1)
Разность(0

8.2. Типы динамических моделей
Как видно из рисунка, 2ЭБС аналогична обычной байесовской сети, в которой
переменными являются переменные состояния ДБС в моменты t и t - 1.
Единственное различие заключается в том, что переменные в момент t - 1 не имеют
ни родителей, ни условного распределения вероятности; определены только
зависимости и распределения для переменных в момент L 2ЭБС - это представление
модели переходов определенной ранее ДБС, и именно в таком виде обычно
изображается ДБС.
Задание ДБС на Figaro
Мы уже знаем, как задавать на Figaro обычные байесовские сети и СММ.
Поскольку ДБС - комбинация того и другого, у нас есть всё необходимое для их
задания.
Листинг 8-4. Реализация на Figaro ДБС, изображенной на риа 8.3
val length = 91
val winning: Array[Element[String]] = Array.fill(length) (Constant (""))
val confident: Array [Element [Boolean] ] =
Array .fill (length) (Constant (false) )
val ourPossession: Array[Element[Boolean]] =
Array.fill (length) (Constant (false) )
val goal: Array[Element[Boolean]] =
Array.fill (length) (Constant (false) )
val scoreDifferential: Array[Element[Int]] =
Array.fill (length) (Constant (0) )
D
confident (0) = Flip (0.4)
scoreDifferential(0) = Constant(0)
В
for { minute <- 1 until length } {
winning(minute) =
Apply(scoreDifferential(minute - 1), (i: Int) =>
if (i > 0) "us" else if (i < 0) "them" else "none")
confident (minute) =
CPD (confident (minute - 1), winning (minute) ,
(true, "us") -> Flip(0.9),
(true, "none") -> Flip(0.7),
(true, "them") -> Flip(0.5),
(false, "us") -> Flip(0.5),
(false, "none") -> Flip(0.3),
(false, "them") -> Flip(O.l))
ourPossession(minute) = If(confident(minute), Flip(0.7), Flip(0.3))
goal(minute) =
CPD (ourPossession (minute) , confident (minute) ,
(true, true) -> Flip(0.04),
(true, false) -> Flip(O.Ol),
(false, true) -> Flip(0.045),
(false, false) -> Flip(0.02))
scoreDifferential(minute) =
If(goal(minute),
Apply(ourPossession(minute), scoreDifferential(minute - 1),
i
271

Глава 8. Моделирование динамических систем
(poss: Boolean, diff: Int) =>
if (poss) (diff + l).min(5) else (diff - l).max(-5)),
scoreDifferential(minute - 1))
В
О — Создаем массив, содержащий пять переменных состояния, по одной на каждый
момент времени
© — Создаем элементы Figaro для представления начальных значений переменных
confident и scoreDifferential
© — В цикле определяем переходы в каждый момент времени. Модель переходов
описывает, как все пять переменных состояния зависят от предыдущего состояния и
переменных confident и scoreDifferential. Каждая переменная может также зависеть
от переменных, определенных выше в цикле. В этом примере confident зависит от
winning в тот же момент времени
Этой модели ДБС можно предъявлять различные запросы. Например,
попросить предсказать развитие матча на основе текущего состояния или вывести
предыдущее состояние, ставшее причиной наблюдаемого результата. Тренеру (или
человеку, поставившему деньги на исход матча) может быть интересно, кто
выиграет. ЗапрОСИВ у Программы Окончательное Значение Переменной
scoreDifferential, мы узнаем, что вероятность выиграть матч равна примерно 0.4. Но если
известно, что наша команда забила гол на четвертой минуте, то вероятность
повышается до 0.73.
8.2.4. Модели с нестационарной структурой
Три рассмотренных до сих пор вида моделей - марковские цепи, скрытые
марковские модели и динамические байесовские сети - это стандартные конструкции.
В каждой из них имеется фиксированное множество переменных с фиксированной
структурой. Но вероятностное программирование открывает возможность работать
с более сложными моделями, структура которых может изменяться во времени.
Представьте, например, владельца ресторана, который хочет знать, сколько
гостей будет вечером указанного дня. Это поможет решить, сколько готовить еды,
следует ли поторапливать постоянных гостей или дать им посидеть подольше и
т. д. Ресторан - это динамическая система, в которой гости приходят, ужинают и
уходят. Состояние системы можно описать текущим числом гостей в ресторане
и проведенным ими временем, а также числом гостей, ожидающих, пока
освободится место. Поскольку число гостей изменяется со временем, структура система
нестационарна. Более того, мы не знаем заранее, какой будет структура в будущем;
в любой момент времени следует рассматривать много возможных структур.
Применение вероятностного программирования
для моделирования систем с переменной структурой
Самый простой способ моделирования подобных систем средствами
вероятностного программирования - создать множество переменных состояния,
типами которых являются изменяемые структуры данных. В примере, показанном на
рис. 8.5, можно завести две переменные состояния:
272

8.2. Типы динамических моделей
Усаженные - представляет гостей, которые уже сидят за столиками, и
время, проведенное ими в ресторане. Тип данных этой переменной - список
целых чисел. Длина списка - число усаженных гостей, а каждое целое
число - время, проведенное одним гостем.
Ожидающие - представляет число гостей, ожидающих освобождения
места. Это целое число.
Рис. 8.5. Динамическая модель, содержащая переменные с изменяющейся структурой.
Показаны три возможных значения каждой переменной состояния. Возможными
значениями переменной Усаженные являются массивы переменной длины
При таких переменных состояния модель становится похожа на ДБС, и
кодировать ее можно аналогично. Но для работы с переменными, типы которых
характеризуются изменчивостью, необходимы кое-какие дополнительные приемы. Будем
строить модель постепенно.
Для начала зададим вместимость ресторана и число шагов выполнения модели.
Для простоты предположим, что в ресторане имеется десять столиков
одинакового размера и что каждая группа гостей занимает один столик, так что вместимость
равна 10. Кроме того, предположим, что один шаг модели длится 5 минут, а всего
модель охватывает один час, поэтому количество шагов равно 12.
val numSteps = 12
val capacity = 10
Значения каждой из двух описанных выше переменных состояния в разные
моменты времени будут представлены массивами соответствующего типа. Так,
ТИП КаЖДОЙ переменной seated - Element [List [Int] ], а переменной waiting -
Element [int]:
val seated: Array[Element[List[Int]]] =
Array .fill (numSteps) (Constant (List () ) )
val waiting: Array[Element[Int]] = Array.fill(numSteps)(Constant(0))
В этом примере предполагается, что модель ресторана начинает работу в
известном состоянии, поэтому мы присваиваем переменным состояния начальные
значения с помощью конструкции Figaro constant. В начальный момент ресторан
уже заполнен, и три гостя стоят в очереди:
273
Усаженные(^1)
Усаженные{/)
Ожидающие^ 1)
Ожидающие(5)

Глава 8. Моделирование динамических систем
seated(O) = Constant(List(0, 5, 15, 15, 25, 30, 40, 60, 65, 75))
waiting(O) = Constant(3)
Представление модели переходов
Мы подошли к интересной части: модели переходов. Напишем ее в два этапа:
сначала скелет, а потом детали. Скелет приведен ниже.
Листинг 8-5- Динамическая модель с переменной структурой - скелет кода
def transition(seated: List[Int], waiting: Int):
(Element[(List[Int], Int)]) = {
// здесь будут детали
AA (allSeated, newWaiting)
}
for { step <- 1 until numSteps } {
val newState =
Chain(seated(step - 1), waiting(step - 1),
(1: List[Int], i: Int) => transition (1, i))
в
seated(step) = newState._1
waiting(step) = newState._2
}
I
О — Определяем функцию перехода, которая принимает предыдущие переменные
состояния и возвращает совместное распределение вероятности новых переменных
© — Порождаем совместное распределение вероятности новых переменных состояния
на основе распределений предыдыщих переменных
© — Извлекаем новые переменные состояния из этого совместного распределения
Этот код демонстрирует общий паттерн, поэтому присмотримся к нему
внимательнее. Возможно, у вас возник вопрос, есть ли какая-то связь между словом
«цепь» в марковских цепях и цепочками в Figaro. Есть - и очень тесная.
Раньше мы не акцентировали на этом внимание, но сцепление переменных состояний
на двух соседних шагах можно реализовать с помощью элемента Figaro chain.
Напомним, что chain принимает распределение вероятности родителя и
условное распределение потомка при условии родителя, а порождает распределение
вероятности потомка. В марковской цепи родителем является переменная вида
possession (t - 1), потомком - переменная вида possession (t), а условное
распределение вероятности - это модель переходов, которая описывает распределение
верОЯТНОСТИ possession (t) При УСЛОВИИ possession (t - 1). ПоЭТОМу, Чтобы ПОЛу-
чить распределение possession (t), можно написать:
Chain (possession(t - 1), transitionModel)
В приведенном выше коде логика похожая. Мы имеем состояние в момент
step - 1, Складывающееся ИЗ seated (step - 1) И waiting (step - 1).ФунКЦИЯ
перехода принимает значения seated и waiting и порождает элемент в следующем
274
1

8.2. Типы динамических моделей
СОСТОЯНИИ, Т. е. Пару ИЗ List [Int] (ДЛЯ seated) И Int (ДЛЯ waiting). Мы ИСПОЛЬЗуеМ
chain, чтобы получить элемент в следующем состоянии по текущему состоянию.
Следующее состояние - это элемент, построенный по паре значений seated и
waiting. Он Определяет СОВМеСТНОе распределение Переменных seated И waiting В
следующий момент времени. В функции перехода этот элемент конструируется
с помощью конструктора Figaro AA, который создает элемент из двух (или
большего числа) отдельных элементов. В нашей функции это элементы ail seated и
newwaiting. Как они порождаются, мы увидим чуть ниже.
Наконец, результатом цепочки является элемент, содержащий пару. Мы хотим
извлечь из этой пары отдельные элементы seated и waiting. Это делается с
помощью операции извлечения i и 2. Нотация i означает, что мы создаем элемент
из первого компонента пары, нотация 2 - то же самое для второго компонента.
Ниже приведен полный код функции перехода.
Листинг 8-6- Динамическая модель с переменной структурой - полный код функции
перехода
def transition(seated: List [Int], waiting: Int):
(Element[(List[Int], Int)]) = {
val newTimes: List[Element[Int]] =
for { time <- seated }
yield Apply(Flip(time / 80.0),
(b: Boolean) => if (b) -1 else time + 5)
E
val newTimesListElem: Element[List[Int]] = Inject(newTimes:_*)
val staying = Apply(newTimesListElem,
(1: List[Int]) => 1.filter (_ >= 0))
val arriving = Poisson(2)
val totalWaiting = Apply(arriving, (i: Int) => i + waiting)
val placesOccupied =
Apply(staying, (1: List[Int]) => 1.length.min(capacity))
val placesAvailable =
Apply(placesOccupied, (i: Int) => capacity - i)
val numNewlySeated =
Apply(totalWaiting, placesAvailable,
(tw: Int, pa: Int) => tw.min(pa))
val newlySeated =
Apply (numNewlySeated, (i: Int) => List .fill (i) (0) )
val allSeated =
Apply(newlySeated, staying,
(11: List[Int], 12: List[Int]) => 11 ::: 12)
val newWaiting = Apply(totalWaiting, numNewlySeated,
(tw: Int, ns: Int) => tw - ns)
№
В
(allSeated, newWaiting)
275
В
Й
и
5
Ш

Пересчитываем для каждого гостя время его пребывания за столиком. —1 означает,
что гость уходит, что случается с вероятностью time/80
newTimes — список Element[lnt]. Нам нужно преобразовать его в Element[List[lnt]],
что можно сделать с помощью Inject
Определяем, сколько людей уходит, удаляя тех, для кого время пребывания за
столиком стало меньше О
Определяем, сколько людей пришло в ресторан и сколько из них будут ждать в очереди
Определяем, сколько ожидающих можно усадить за столик
Строим новый список усаженных гостей
Определяем новое число ожидающих гостей
Возвращаем элемент, содержащий пару (новый список усаженных гостей, новое
число ожидающих гостей)
Поскольку в этом коде используются в основном уже знакомые средства Figaro,
я не стану объяснять его в деталях. Но одну вещь стоит отметить: элемент Figaro
inject, который преобразует список элементов в элемент, состоящий из списков.
Что это означает? Предположим, что имеется список из трех Element [int]. Один
из возможных наборов значений этих элементов: 5, 10, 15. Мы можем
преобразовать их в список, содержащий значения 5, 10, 15. В данном случае значением
Inject (1) будет List (5, 10, 15).
Почему это полезно? Некоторые операции в нашей модели, а именно
определение нового времени пребывания гостя за столиком и факта его ухода из ресторана,
применяются к отдельным элементам. Другие же операции, например, построение
списка остающихся гостей, применяются к списку гостей как к единому целому.
Нам нужен элемент, содержащий список, и inject его как раз и дает.
Рассуждения с помощью модели
Мало что нового можно сказать о выполнении вывода в этой модели, всё
делается так же, как в других динамических вероятностных моделях, которые мы уже
видели. Как и раньше, модель можно использовать для предсказания будущего
или для вывода причин наблюдаемых событий. В разделе 8.3 показано, как эту же
модель использовать для мониторинга состояния ресторана во времени.
В общем случае не имеет смысла применять факторные алгоритмы, например
исключения переменных или распространения доверия, к моделям с переменной
структурой. Число возможных значений переменных состояния огромно. В
примере с рестораном время пребывания за столиком для каждого гостя может быть
любым целым числом от 0 до 75, которое делится на 5 (по истечении 75 минут
гость безусловно покидает ресторан на следующем шаге). Таких чисел 16.
Следовательно, число возможных списков из 10 усаженных гостей равно 1610. Да еще
нужно рассмотреть случаи, когда гостей меньше 10. Столько возможностей не
перебрать.
Поэтому лучше применить выборочный алгоритм. В данном примере
используется выборка по значимости для предсказания длины в очереди в конце
следующего часа. Вот как это делается:
276
Глава 8. Моделирование динамических систем
1
2
3
4
5
6
7
8

8.3. Моделирование систем, работающих неопределенно долго
val alg = Importance(10000, waiting(numSteps - 1))
alg.start()
println(alg.probability(waiting(numSteps - 1), (i: Int) => i > 4))
В результате выполнения этого кода получается примерно 0.4693, т. е. с
вероятностью около 47 % в конце часа в очереди у входа будет больше четырех человек.
Итак, мы рассмотрели различные динамические вероятностные модели - от
простых до более сложных. Но у всех них есть общее ограничение - количество
шагов моделирования нужно задавать заранее. В следующем разделе будет
показано, как снять это ограничение.
8.3. Моделирование систем,
работающих неопределенно долго
В этом разделе наша цель - определить динамические вероятностные модели,
способные работать сколь угодно долго. С их помощью можно вести непрерывный
мониторинг состояния системы на основе фактов, собираемых на протяжении
длительного времени. Механизм достижения этой цели несложен, но нам
понадобится новое понятие - универсум.
8.3.1. Универсумы в Figaro
В главе 7 мы узнали о коллекциях элементов. Коллекция элементов - это структура
данных, позволяющая обращаться к элементу по имени. Универсум (universe) - это
специальный вид коллекции элементов, который предоставляет дополнительные
средства, полезные алгоритмам вывода, например управление памятью и анализ
зависимостей. Поэтому алгоритмы вывода обычно работают с универсумами.
До сих пор концепция универсума нам была не видна, и, как правило, думать о
ней не приходится. Однако каждый элемент принадлежит какому-то универсуму.
Всегда существует универсум по умолчанию, и, если не указано противное,
элемент помещается в него.
Понятия коллекции элементов и универсума тесно связаны. Вот что нужно
запомнить:
• каждый универсум - коллекция элементов, но не каждая коллекция
элементов - универсум;
• с любой коллекцией элементов ассоциирован некоторый универсум. Если
коллекция элементов сама является универсумом, то ассоциированный
универсум - это она сама;
• когда элемент помещается в коллекцию, его универсумом становится
универсум, ассоциированный с этой коллекцией.
Напомним, что для помещения элемента в коллекцию элементов необходимо
задать необязательные аргументы: имя и коллекцию элемента. Например, если
написать:
Flip(0.5) ("coin", collection)
277

Глава 8. Моделирование динамических систем
то элемент Flip (0.5) получит имя coin и будет помещен в коллекцию элементов
collection. Поскольку универсум - это коллекция элементов, мы можем
поместить элемент сразу в универсум, указав его в качестве второго аргумента:
Flip(0.5) ("coin", universe)
Всегда существует текущий универсум по умолчанию. Если при создании
элемента не задавать явно необязательные имя и коллекцию, то коллекцией
и универсумом элемента становится этот универсум по умолчанию. Ссылка на
универсум по умолчанию хранится в переменной Scala universe.universe из
пакета com. era .figaro. language.
Алгоритмы также работают с универсумом. Если не указано противное, то
таковым является текущий универсум по умолчанию. Но можно указать и другой
универсум, задав его в качестве необязательного аргумента в собственном списке
аргументов. Например, выражение variabieEiimination(target) создает
алгоритм исключения переменных с аргументом target в универсуме по умолчанию.
А выражение VariabieEiimination (target) (u2) СОЗДает таКОЙ Же алгоритм С тем
же аргументом, но в универсуме и2. При использовании однострочной
сокращенной НОТаЦИИ, Например VariabieEiimination.probability, Всегда Подразумевается
универсум по умолчанию.
Получить новый универсум можно одним из двух способов. Первый - вызвать
конструктор
new Universe
который создает новый универсум без элементов. Второй способ - написать
Universe.createNew()
Тогда новый универсум не только создается, но и становится универсумом по
умолчанию. Это удобный способ начать работу с новым универсумом: помещать
в него новые элементы и запускать в нем алгоритмы. Например, можно было бы
написать:
Universe.createNew()
val x = Betad, 2)
val у = Flip(x)
printIn (VariabieEiimination.probability(y, true))
Элементы х и у будут помещены в новый универсум, и в нем же будет работать
алгоритм исключения переменных.
Всё сказанное об универсумах применимо и в ситуации, когда Figaro
выполняется в интерактивном интерпретаторе Scala. Все создаваемые элементы
помещаются в какой-то универсум - по умолчанию, если не указано противное. Если вы
хотите забыть все, что делали до определенного момента, и начать с чистого листа,
введите команду universe. createNew (). Все вновь создаваемые элементы будут
помещаться в новый универсум, а старые станут недоступны.
278

8.3. Моделирование систем, работающих неопределенно долго
8.3.2. Использование универсумов для
моделирования постоянно работающих систем
Чтобы представить в Figaro динамическую вероятностную модель без
ограничений по времени, мы создаем на каждом временном шаге универсум, содержащий
все переменные для этого шага. Модель обычно задается в виде двух частей:
• начальный универсум;
• функция, отображающий предыдущий универсум в следующий.
Эти две части следующим образом определяют динамическую вероятностную
модель, показанную на рис. 8.6.
1. Начать с распределения вероятности начального состояния в момент О,
определяемого всеми элементами в начальном универсуме.
2. Применить функцию к начальному универсуму и получить универсум в
момент 1. Элементы нового универсума определяют распределение
вероятности состояния в момент 1.
3. Применить функцию к универсуму в момент 1 и получить универсум в
момент 2. Элементы нового универсума определяют распределение
вероятности состояния в момент 2.
4. Продолжать, пока не надоест.
universe(0) - initial
universe(1) -
nextUniverse(universe(O))
universe(2) -
nextUniverse(universe(1))
Рис. 8.6. Развитие динамической модели как череды универсумов. Каждый
универсум содержит переменные состояния в данный момент времени. Первый
универсум определяется начальной моделью, а каждый последующий создается
путем применения функции nextuniverse к предыдущему
Любой элемент на некотором временном шаге, непосредственно влияющий на
элемент на следующем шаге, должен иметь имя. Это имя позволяет программе
сослаться на элемент в предыдущем универсуме. В примере с рестораном
количество ожидающих гостей в конце временного шага влияет на состояние
на следующем шаге. Элементу, представляющему это количество, необходимо
ПРИСВОИТЬ ИМЯ, МЫ Назвали еГО waiting.
Функция перехода принимает предыдущий универсум в качестве аргумента.
Допустим, что этот универсум хранится в переменной Scala previous. Тогда для
получения элемента с именем waiting в предыдущем универсуме можно написать:
279
Seated(0)
Seatedtl}
Seated(2)
Waiting(O)
Waiting(l)
Waiting (2)

previous.get[Int]("waiting")
Отметим, что нам пришлось сообщить Scala о типе значения этого элемента
(int), потому что иначе метод get не знал бы, какого вида элемент возвращать.
Любому элементу, который мы хотим запросить или пронаблюдать, также
необходимо присвоить имя. Это позволит единообразно ссылаться на элемент на
каждом временном шаге. После этого краткого введения мы можем представить
скелет постоянно работающей модели ресторана.
Листинг 8.7. Реализация функции nextUniverse
def transition(seated: Listflnt], waiting: Int):
(Element[(List[Int], Int, Int)]) = {
// детали такие же, как и выше
АА (allSeated, newWaiting, arriving)
}
def nextUniverse(previous: Universe): Universe = {
val next = Universe.createNew() <]—
val previousSeated = previous.get[List[Int]]("seated")
val previousWaiting = previous.get[Int]("waiting") .
val state = Chain(previousSeated, previousWaiting, transition _)
О — Единственное изменение в функции перехода — включение числа прибывающих
гостей в возвращаемый элемент, поскольку мы наблюдаем это число
© — Определяем функцию перехода от предыдущего универсума к следующему
© — Создаем новый универсум, делаем его универсумом по умолчанию, присваиваем
переменной Scala
© — Получаем переменные предыдущего состояния из предыдущего универсума
© — Используем Chain для получения элемента, представляющего новое состояние
© — Получаем от него элементы, представляющие отдельные переменные состояния, и
присваиваем каждому имя в следующем универсуме
© — Возвращаем следующее состояние
Как видим, в коде мало что изменилось по сравнению с предыдущей версией
модели, где время работы было ограничено. В частности, почти не изменилась
функция перехода, в которой и сосредоточена основная логика. Наиболее
существенное новшество - использование имен для идентификации элементов,
представляющих переменные состояния в каждом универсуме. Мы получаем
элементы по именам от предыдущего универсума и присваиваем им соответственные
имена при помещении в новый универсум.
С представлением модели мы разобрались. Теперь рассмотрим приложение для
непрерывного мониторинга состояния системы.
280
Глава 8. Моделирование динамических систем
1
Apply(state, (s: (List[Int], Int, Int)) => s._1)("seated", next)
Apply(state, (s: (List[Int], Int, Int)) => s._2)("waiting", next)
Apply(state, (s: (List[Int], Int, Int)) => s. 3)("arriving", next)
В
next
и
5
4
3
2

8.3. Моделирование систем, работающих неопределенно долго
8.3.3. Следящее приложение
Наша цель - начав с исходной гипотезы о состоянии системы, обновлять ее на
основе фактов, наблюдаемых на каждом временном шаге. Точнее, мы хотим
выполнить процесс, изображенный на рис. 8.7.
1. Начать с распределения вероятности состояния системы в момент 0.
2. Учесть наблюдения в момент 1 для порождения распределения состояния
в момент 1.
2. Учесть наблюдения в момент 2 для порождения распределения состояния
в момент 2.
4. Повторять, пока не надоест.
Распределение
State(0)
Распространить динамику
и наблюдаемые условия
Observations(1)
Распределение
State(l)
Т
Распространить динамику
и наб л ю д ае м ы е уел ов и я
Observations(2)
Распределение'
State{2)
Рас п р остра н ить динами ку
и наблюдаемые условия
Observations(3)
Распределение-
State(3)
Рис. 8.7. Процесс фильтрации. Figaro пересчитывает распределение вероятности
состояния системы в каждый момент времени. При переходе от предыдущего
момента к следующему Figaro принимает во внимание динамику модели и
наблюдаемые условия в следующий момент и порождает распределение
вероятности нового состояния
Этот процесс называют по-разному: мониторинг, оценка состояния,
фильтрация. Все эти названия означают одно и то же. Алгоритмы выполнения этого
процесса часто называют алгоритмами фильтрации, именно это название
используется в Figaro. Пожалуй, самым популярным из таких алгоритмов является фильтр
частиц. Это выборочный алгоритм, в котором распределение состояния системы
в каждый момент времени представлено множеством «частиц». Более подробное
описание алгоритма фильтрации частиц приведено в главе 12.
В Figaro конструктору алгоритма фильтрации частиц передаются три аргумента:
• начальный универсум;
• функция перехода от предыдущего универсума к следующему;
• количество частиц на каждом временном шаге.
В примере с рестораном алгоритм создается так:
val alg = ParticleFilter(initial, nextUniverse, 10000)
281

Глава 8. Моделирование динамических систем
Следующий шаг такой же, как для всех алгоритмов в Figaro: запустить алгоритм
методом aig. start (). В случае фильтра частиц это порождает распределение
вероятности начального состояния.
Основная работа производится в методе advanceTime, который переводит
систему в новое состояние с учетом новых фактов. В данном случае мы вызываем:
alg.advanceTime(evidence)
Факты задаются не так, как раньше. Мы уже привыкли к тому, что факты
задаются путем добавления ограничений или условий к элементам. Здесь это
невозможно, потому что отсутствуют прямые ссылки на элементы, представляющие
состояние системы в произвольный момент времени; они скрыты внутри
функции nextuniverse. Поэтому мы ссылаемся на эти элементы по именам. То есть мы
должны сообщить фильтру частиц имена элементов, для которых у нас имеются
факты, а также характер этих фактов.
Например, можно задать факт следующим образом:
NamedEvidence("arriving", Observation(3))
ЭТО ЭКЗеМПЛЯр КЛаССа NamedEvidence, КОТОрыЙ СВЯЗЫВаеТ ИМЯ (arriving) С На-
блюдаемым фактом (в данном случае - элемент с именем arriving имеет
значение з). Фактом может быть и более общее условие или ограничение. Аргументом
Метода advanceTime фиЛЬТра чаСТИЦ ЯВЛЯетСЯ СПИСОК объеКТОВ NamedEvidence, ОПИ-
сывающих все вновь полученные факты.
В примере с рестораном предположим, что владелец фиксирует число людей,
заходящих в ресторан в начале очередного временного шага, но делает это
нерегулярно, т. е. для некоторых шагов новые факты есть, а для некоторых - нет. В Scala
ЭТО МОЖНО ВЫраЗИТЬ С ПОМОЩЬЮ ТИПа Option [ Int ], КОТОРЫЙ МОЖеТ быТЬ равен None
или конкретному наблюдаемому числу людей. Это факультативное наблюдение
МОЖНО СЛедуЮЩИМ обраЗОМ Преобразовать В аргумент advanceTime:
val evidence = {
arrivingObservation(time) match {
case None => List()
case Some(n) => List(NamedEvidence("arriving", Observation(n)))
}
}
alg.advanceTime(evidence)
После вызова advanceTime мы можем запросить состояние системы в текущий
момент времени. Для этого фильтр частиц предоставляет несколько методов:
currentProbability, currentExpectation И currentDistribution. И СНОВа, ПОСКОЛЬКУ
ссылки на конкретные элементы нам недоступны, будем задавать опрашиваемые
элементы по именам. Например, чтобы узнать, с какой вероятностью места
ожидают более четырех человек, можно написать:
alg.currentProbability("waiting", (i: Int) => i > 4)
282

8.3. Моделирование систем, работающих неопределенно долго
А для получения ожидаемого (среднего) числа усаженных гостей, пишем:
alg.currentExpectation("seated", (1: List[Int]) => 1.length)
Итак, чтобы прогнать алгоритм фильтрации частиц, зная начальный универсум
и функцию перехода от предыдущего универсума к следующему, нужно
выполнить следующие шаги:
1. Создать фильтр частиц.
2. Запустить фильтр частиц для получения начального распределения.
3. Выполнить следующие действия на каждом временном шаге:
• собрать факты для этого временного шага;
• вызвать метод advanceTime, передав ему эти факты, чтобы получить
распределение вероятности нового состояния;
• запросить новое распределение.
В коде, прилагаемом к этой главе, имеется программа, иллюстрирующая эти
шаги. Она печатает следующие строки:
Time 1: expected customers = 9.6498, expected waiting = 1.2325
Time 2: expected customers = 9.2651, expected waiting = 0.7388
Time 3: expected customers = 9.3622, expected waiting = 1.2295
Time 4: expected customers = 9.4169, expected waiting = 1.7192
Time 5: expected customers = 9.6011, expected waiting = 2.0629
Time 6: expected customers = 9.5866, expected waiting = 2.4307
Time 7: expected customers = 8.9794, expected waiting = 1.3958
Time 8: expected customers = 9.489, expected waiting = 2.2148
Time 9: expected customers = 9.5205, expected waiting = 2.5118
Time 10: expected customers = 9.5373, expected waiting = 2.8227
Time 11: expected customers = 9.5656, expected waiting = 3.1624
Time 12: expected customers = 9.4327, expected waiting = 2.6614
Как видим, это программа отслеживает количество усаженных и ожидающих
гостей с течением времени. Наша цель достигнута. Мы построили модель сложной
динамической системы и умеем вести мониторинг ее состояния во времени.
На этом заканчивается часть книги, посвященная методам моделирования. Мы
рассмотрели важнейшие идеи и самые распространенные сценарии. Имеющихся
у вас знаний Figaro уже достаточно для разработки большинства приложения и
понимания документации в формате Scaladoc.
Примечание. Я не пытался осветить абсолютно все возможности Figaro. Полное
описание имеется в официальной документации. Если что-то останется неясным, пишите на
адрес fiaaro@cra.com: мы всегда готовы улучшать документацию.
В следующей части книги рассказано о том, как работает вероятностный вывод,
позволяющий извлечь из моделей все, что те могут предложить.
283

Глава 8. Моделирование динамических систем
8.4. Резюме
• Состояние динамической системы изменяется со временем, состояния в
разные моменты времени взаимозависимы.
• Во многих динамических вероятностных моделях реализовано марковское
предположение о том, что текущее состояние условно независимо от всех
предыдущих состояний, если известно непосредственно предшествующее
состояние.
• Хотявскрытоймарковскоймоделиреализованомарковскоепредположение,
при выводе текущего состояния необходимо рассматривать все предыдущие
факты, потому что предыдущее состояние ненаблюдаемо.
• Динамическая байесовская сеть - это обобщение скрытой марковской
модели на несколько переменных состояния; сделав типы эти переменных
развитыми структурами данных, мы можем моделировать системы с
нестационарной структурой.
• Мониторинг, или фильтрация - это процесс отслеживания состояния
системы во времени с учетом наблюдаемых фактов; одним из применяемых
для этого алгоритмов является фильтрация частиц.
• В Figaro для фильтрации необходимо создать начальный универсум и
функцию перехода от предыдущего универсума к следующему.
• В процессе фильтрации в Figaro доступ к элементам, влияющим на
следующий временной шаг, а также к элементам, описывающим факты, и к
опрашиваемым элементам производится по именам.
8.5. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. В настольном теннисе выигрывает тот, кто первым набрал 21 очко. Алиса и
Боб играют в настольный теннис, причем Алиса играет чуть лучше,
поэтому вероятность выигрыша очка для нее составляет 52 %. Постройте модель
игры в настольный теннис с помощью марковской цепи и оцените
вероятность выигрыша партии Бобом.
2. Теперь рассмотрим вариант упражнения 1. Относительные уровни
мастерства Алисы и Боба неизвестны, и в начале игры предполагается, что Алиса
выигрывает очко с вероятностью Beta(2, 2). Такую ситуацию тоже можно
смоделировать марковской цепью, только вероятности переходов будут
зависеть от неизвестного параметра. С помощью этой модели вычислите, с
какой вероятностью выиграет Боб, если текущий счет 11:8 в пользу Алисы.
3. Смоделируем освоение студентом материала, изложенного в 10 главах все
возрастающей трудности. В конце каждой главы имеется тест. Результат
теста зависит от того, насколько хорошо студент усвоил материал. Кроме
того, последующая глава основывается на предыдущих, поэтому усвоение
284

материала одной главы зависит от усвоения предыдущих. Смоделируйте
эту ситуацию с помощью скрытой марковской модели и предскажите, с
какой вероятностью студент пройдет последний тест при условии, что
успешно прошел первые три.
4. Воспользуйтесь ДБС для создания простой экономической модели
деятельности компании. В ДБС три переменные: инвестиции, прибыль и
основной капитал. В любой момент времени значение капитала равно
предыдущему значению плюс новая прибыль минус новые инвестиции. Величина
прибыли в каждый момент времени неопределенная, но обычно тем выше,
чем больше объем инвестиций. Рассмотрите различные стратегии, при
которых объем инвестиций в данный момент времени равен фиксированной
доле от размера капитала в предыдущий момент. Для заданного
начального размера капитала спрогнозируйте его размер после 10 временных шагов
при различных стратегиях инвестирования.
5. Создадим простую модель эволюции графа со временем. В каждый момент
времени может произойти одно из двух. С вероятностью 0.1 в граф
добавляется новая вершина, которая случайным образом соединяется с какой-то
из существующих. С вероятностью 0.9 состояние ребра между двумя
существующими вершинами изменяется на противоположное: если ребра не
было, оно добавляется, иначе удаляется.
Для заданного начального графа напишите на Figaro модель его эволюции
на протяжении 100 временных шагов. Предскажите количество ребер в
графе после 100 шагов.
6. Создадим модель успешности новой песни в хит-парадах поп-музыки.
После выхода песни с ней знакомятся все новые и новые люди, так что ее
популярность растет. Рано или поздно наступает момент, когда большинство
тех, кого песня могла бы заинтересовать, уже знают про нее, поэтому ее
покупают меньше, и она начинает опускаться в хит-парадах.
Мы создадим модель с пятью переменными. Переменная Качество
описывает качество песни; переменная Вновь Услышавших - количество людей,
впервые услышавших песню на данной неделе; Всего Слышавших - общее
количество людей, слышавших песню; Вновь Купивших - количество
людей, купивших песню на этой неделе; Всего Купивших - общее количество
людей, купивших песню. Качество со временем не изменяется, а Всего
Купивших равно предыдущему значению Всего Купивших плюс значение
Вновь Купивших, и то же самое справедливо для Всего Слышавших.
Переменная Вновь Купивших зависит от переменных Качество и Вновь
Услышавших; чем больше людей впервые услышали песню, тем больше ее купят,
однако это зависит и от качества песни. Наконец, переменная Вновь
Услышавших зависит от Всего Слышавших и от Вновь Купивших; чем больше
людей уже слышало песню, тем меньше услышат ее впервые, а, с другой
стороны, чем больше людей купило песню в течение данной недели, тем
чаще она звучит в эфире, так что ее слышит больше народу.
8.5. Упражнения
285

Поскольку длительность нахождения песни в хит-параде не ограничена,
придется воспользоваться универсумами Figaro для создания постоянно
работающей модели. Переменная Вновь Купивших наблюдаемая, а узнать
мы хотим значение переменной Всего Слышавших. Напишите на Figaro
программу, реализующую эту модель.
a. Сгенерируйте данные, исходя из модели. Воспользуйтесь фильтром
частиц без фактов для создания последовательности значений
переменной Вновь Купивших. Остановитесь, когда число вновь купивших
окажется меньше некоторого порога (при котором песня исчезает из
хит-парада).
b. Затем, используя сгенерированные данные, задайте наблюдаемые
значения переменной Вновь Купивших и оцените изменение Всего
Слышавших со временем.
Глава 8. Моделирование динамических систем
286

Часть III
вывод
и
так, вы написали вероятностную программу. Но как ей воспользоваться?
Необходимо применить алгоритм вывода. Чтобы получить максимум от
вероятностного программирования, нужно понимать, что такое алгоритмы вывода и как их
использовать. Часть 3 целиком посвящена выводу. В главе 9 описываются
основные понятия вероятностного вывода, а в главах с 10 по 13 - различные алгоритмы
вывода. Я пытался соблюсти баланс между теоретическими описаниями
алгоритмов и практическими соображениями, касающимися их применения, а также
привести примеры использования алгоритмов в реальных задачах.
Мы узнаем о двух основных семействах алгоритмов вывода: факторных и
выборочных алгоритмах. Понимание принципов, на которых они основаны,
поможет разобраться в большинстве алгоритмов, встречающихся в вероятностном
программировании. Факторным алгоритмам посвящена глава 10, а выборочным -
глава И. В главе 12 показано, как адаптировать изученные в главах 10 и И
алгоритмы для ответа на различные запросы. Наконец, в главе 13 рассмотрены два
более сложных, но очень важных типа вывода: рассуждения о динамических
системах и получение числовых параметров модели методами машинного обучения.

ГЛАВА 9.
Три правила
вероятностного вывода
В этой главе.
■ Три важных правила работы с вероятностными
моделями:
- цепное правило, позволяющее строить
сложные модели из простых компонентов;
- правило полной вероятности, позволяющее
упростить сложную модель для ответа на
простые запросы;
- правило Байеса, позволяющее строить
заключения о причинах на основе наблюдаемых
следствий.
■ Основы байесовского моделирования, в т. ч.
оценки параметров модели по данным и
использования их для предсказания.
Во второй части книги мы узнали о написании вероятностных программ для
различных приложений. Мы знаем, что в системах вероятностного
программирования для ответов на запросы применяются алгоритмы вывода, которым
сообщаются факты. Но как они работают? Этому вопросу и посвящена третья часть книги.
Знать об этом необходимо, чтобы проектировать модели и выбирать те алгоритмы
вывода, которые будут быстро давать точные результаты.
Мы начнем эту главу с основ: трех правил вероятностного вывода. Сведения о
входных и выходных данных для каждого из трех правил приведены на рис. 9.1.
• Первым будет рассмотрено цепное правило, которое позволяет перейти
от простого (локальные условные распределения вероятности отдельных
переменных) к сложному (полное совместное распределение вероятности
всех переменных).

Глава 9. Три правила вероятностного вывода
Цепное правило
Р(Тема)
Р(Размер | Тема)
Р(Яркость | Тема)
Р(Тема, Размер, Яркость)
Правило полной вероятности
Р(Тема, Размер, Яркость)' | ► Р(Тема)
Правило Байеса
Р(Тема)
Р(Размер | Тема)
Р(Размер | Тема)
Рис. 9.1. Входные и выходные данные для каждого из трех правил вероятностного
вывода. Цепное правило преобразует набор условных распределений вероятности
в совместное распределение. Правило полной вероятности принимает на входе
совместное распределение множества переменных и порождает распределение
одной переменной. Правило Байеса позволяет «инвертировать» условное
распределение вероятности следствия при условии причины в условное
распределение причины при условии следствия
• Правило полной вероятности, описанное в разделе 9.2, позволяет перейти
от сложного (полное совместное распределение) обратно к простому
(распределение одной переменной).
• Наконец, описанное в разделе 9.3 правило Байеса является, пожалуй, самым
известным правилом вывода. Оно позволяет изменить направление
зависимости, т. е. преобразовать условное распределение вероятности следствия
при условии причины в распределение причины при условии следствия.
Правило Байеса необходимо для того, чтобы из фактов, каковые обычно
являются результатом наблюдения следствия, делать выводы о причинах.
Эти три правила вывода используются для ответов на запросы.
Прежде чем с головой погружаться в новый материал, вспомним некоторые
определения из главы 4, они нам скоро понадобятся.
• Возможные миры - все состояния, которые мы считаем возможными.
• Распределение вероятности - сопоставление вероятности от 0 до 1
каждому возможному миру, так что сумма всех вероятностей равна 1.
• Априорное распределение вероятности - распределение вероятности до
ознакомления с фактами.
• Применение условий, основанных на фактах - процедура применения
фактов к распределению вероятности.
• Апостериорное распределение вероятности - распределение вероятности
после ознакомления с фактами; результат применения условий.
289

Глава 9. Три правила вероятностного вывода
• Условное распределение вероятности - правило, определяющее
распределение вероятности одной переменной для каждой комбинации значений
других переменных.
• Нормировка - процедура пропорционального изменения чисел из
некоторого множества, так чтобы их сумма стала равна 1.
Примечание. Для всех этих правил на врезке приведены математические
определения. Они полезны для более глубокого понимания. Если вы уверенно владеете
математической нотацией, то обсуждение на более абстрактном уровне поможет лучше усвоить
принципы. Если же нет, можете спокойно пропустить врезки. Главное - понимать, как и
почему используется каждое правило.
9.1. Цепное правило: построение
совместных распределений
по условным распределениям
вероятности
Вы, наверное, еще не забыли (см. главу 4), как вероятностная модель определяет
распределение вероятности возможных миров, а также ингредиенты
вероятностной модели: переменные, зависимости, функциональные формы и числовые
параметры. Я говорил, что цепное правило - важнейший механизм преобразования
этих ингредиентов в распределение вероятности возможных миров, и обещал
подробно обсудить это правило в главе 3. Теперь время настало.
Как цепное правило определяет распределение вероятности возможных
миров? Иными словами, как оно сопоставляет каждому возможному миру число от О
до 1? Вернемся к примеру с картиной Рембрандта из главы 4. Начнем с
переменных Тема, Размер и Яркость и предположим, что дана модель, в которой Размер и
Яркость зависят от Темы, но не зависят друг от друга. Кроме того, задано
распределение вероятности Темы, условное распределение Размера при условии Темы и
условное распределение Яркости при условии Темы. Эти ингредиенты
представлены на рис. 9.2. (Для Темы, которая ни от чего не зависит, я использую ту же
нотацию условного распределения вероятности, что и для других переменных, только
переменные условия отсутствуют и в таблице всего одна строка.)
В любом возможном мире все три переменные Тема, Размер и Яркость имеют
некоторые значения. Как определить вероятность возможного мира? Например,
чему равна вероятность Р(Тема = Люди, Размер = Большая, Яркость = Темная)?
Цепное правило дает простой ответ: нужно найти подходящие записи в таблицах
условного распределения вероятности и перемножить их. В данном случае
Р(Тема = Люди, Размер = Большая, Яркость = Темная) =
Р(Тема = Люди) х Р(Размер = Большая | Тема = Люди) х Р(Яркость = Темная |
Тема = Люди) =
0.8 х 0.5 х 0.8 =
0.32
290

9.1. Цепное правило: построение совместных распределений...
Значения вероятности Темы
Тема
Люди Ландшафт
0.8 0.2
Значения вероятности Размера
при условии Темы
Значения вероятности Яркости
при условии Темы
Тема
Люди
Ландшафт
Малая
0.25
0,25
Размер
Средняя! Большая
0.25 0.5
0,5 0,25
Тема
Люди
Ландшафт
Яркость .
Темная 1 Яркая 1
0.8 0.2
0.3 0.7
Рис. 9-2. Структура байесовской сети и условное распределение
вероятности для примера цепного правила
Одну и ту же формулу можно использовать для всех возможных значений
Темы, Размера и Яркости. В результате получатся значения, сведенные в табл. 9.1.
Эта таблица называется совместным распределением вероятности Темы, Размера
и Яркости, потому что в ней заданы вероятности каждой комбинации этих трех
переменных.
Таблица 9.1 - Совместное распределение вероятности, получающееся
применением цепного правила к условным распределениям вероятности,
показанным на рис. 9.1. Мы умножаем Р(Тема) на Р(Размер | Тема)
и Р(Яркость | Тема). Сумма вероятностей равна 1
Тема
Люди
Люди
Люди
Люди
Люди
Люди
Ландшафт
Ландшафт
Размер
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Яркость
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Вероятность
0.8x0.25x0.8 = 0.16
0.8x0.25x0.2 = 0.04
0.8x0.25x0.8 = 0.16
0.8x0.25x0.2 = 0.04
0.8x0.5x0.8 = 0.32
0.8x0.5x0.2 = 0.08
0.2x0.25x0.3 = 0.015
0.2x0.25x0.7 = 0.035
291
Тема
Размер
Яркость

Глава 9. Три правила вероятностного вывода
Тема
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Размер
Средняя
Средняя
Большая
Большая
Яркость
Темная
Яркая
Темная
Яркая
Вероятность
0.2x0.5x0.3 = 0.03
0.2x0.5x0.7 = 0.07
0.2x0.25x0.3 = 0.015
0.2x0.25x0.7 = 0.035
По правде говоря, я немного смухлевал. Стандартное цепное правило для трех
переменных гласит, что вероятность третьей переменной нужно брать при
условии первых двух. То есть вместо
Р(Тема = Люди, Размер = Большая, Яркость = Темная) =
Р(Тема = Люди) х Р(Размер = Большая | Тема = Люди) х Р(Яркость = Темная |
Тема = Люди)
следовало бы вычислять
Р(Тема = Люди, Размер = Большая, Яркость = Темная) =
Р(Тема = Люди) х Р(Размер = Большая | Тема = Люди) х Р(Яркость = Темная |
Тема = Люди, Размер = Большая)
Так выглядит официальная формулировка цепного правила. Но я
воспользовался знаниями о зависимостях в данном конкретном случае, а именно тем, что
Яркость зависит только от Темы, но не от Размера, т. е. Яркость условно
независима от Размера при условии Темы:
Р(Яркость = Темная | Тема = Люди, Размер = Большая) =
Р(Яркость = Темная | Тема = Люди)
Поэтому я вправе упростить цепное правило, что я и сделал. Всегда, когда
имеется байесовская сеть, и мы хотим воспользоваться цепным правилом для
вычисления полного распределения вероятности всех переменных, мы вправе упрощать
правило таким образом, что каждая переменная зависит только от своих
родителей в сети. С другой стороны, если бы Яркость не была условно независима от
Размера при условии Темы, пришлось бы использовать более длинную форму.
Байесовские сети идут рука об руку с цепным правилом. Байесовская сеть точно
определяет вид цепного правила, применяемого для построения совместного
распределения.
Это все, что я хотел сказать о цепном правиле - простом, но чрезвычайно
важном для вероятностного моделирования. Цепное правило необходимо для
понимания не только байесовских сетей, но и порождающих моделей вообще.
Поскольку вероятностные программы - это способ представления порождающих моделей,
то, поняв смысл цепного правила, вы тем самым поняли фундаментальную
природу вероятностной модели, определяемой вероятностной программой.
292

Цепное правило: построение совместных распределений.
Общая формулировка цепного правила
Цепное правило - это общий принцип, применимый к любой модели зависимостей и
к любому множеству условных распределений вероятности переменных, какова бы ни
была их функциональная форма. Коль скоро у каждой переменной имеется условное
распределение, которое определяет распределение вероятности ее значений для
любых возможных значений переменных, от которых она зависит, мы можем вычислить
совместное распределение вероятности всех переменных, перемножив подходящие
элементы условных распределений.
В математической нотации мы начинаем с двух переменных X и У, из которых У
зависит отХ. Дано Р(Х) - распределение вероятности значений X и P(Y\ X) -условное
распределение Упри условии X, Согласно цепному правилу, из этих двух распределений
получается совместное распределениеXи Y- P(X,Y). Для любых возможных значений
х переменной X и у переменной Y цепное правило определяется формулой:
Р(Х = хтУ=у) = Р(Х=х)Р(У = у \х = х)
О нотации. Принято использовать заглавные буквы, например X и У, для
обозначения переменных, а строчные - х и у - для значений.
Существует удобный способ показать, что эта формула верна для любых х и у:
Р(Ху) = Р(Х)Р(У|Х)
Эта простая формула - пример сокращенной записи многих формул, относящихся к
произвольным значениям х и у.
А что, если значений больше двух? Цепное правило обобщается на любое число
переменных. Пусть имеются переменные^, Хг, ...»Хп. В стандартной формулировке
цепного правила не делается никаких предположений о независимости, т. е. считается,
что каждая переменная зависит от всех предшествующих ей. В сокращенной нотации
полное цепное правило выглядит так:
Р(Х11Х2 XJ = P{X1)P(X2|X1)P(^|X1^)--P(XJX^-.^J
Разберемся, что означает эта формула. Она говорит, что для получения совместного
распределения вероятности Xv X2, ,,,, Хп нужно начать с вероятности Х(, затем взять
условное распределение вероятности Х2 при условии Хг Далее мы берем условное
распределение переменной Х3, которая зависит от Х1 иХ2. И продолжаем рекурсивно,
пока не получим условное распределение переменной Хт, которая зависит от всех
предыдущих переменных. Кстати говоря, именно по этой причине правило и называется
цепным. Совместное распределение вероятности вычисляется по цепочке условных
распределений.
В нашей формулировке цепного правила для нескольких переменных не делалось
никаких предположений об их зависимостях, а, уж тем более, о независимости.
Добавление информации о независимости может заметно упростить формулу- Вместо того
чтобы указывать все предыдущие переменные справа от знака «|», нужно включать
лишь те, от которых переменная слева от «|» непосредственно зависит. Рассмотрим,
к примеру, три переменные Тема, Размер и Яркость. Следуя приведенной выше
формуле, мы получили бы
Р(Тема, Размер, Яркость) = Р(Тема) Р(Размер | Тема) Р(Яркость | Тема, Размер)
Но согласно нашей байесовской сети, Яркость не зависит от Размера, а зависит
только от Темы. Поэтому формулу можно упростить до:
Р(ТемаР Размер, Яркость) = Р(Тема) Р{Размер | Тема) Р{Яркость | Тема)
Именно в таком виде формула использовалась для заполнения табл. 9.1.
293

Глава 9. Три правила вероятностного вывода
9.2. Правило полной вероятности:
получение ответов на простые
запросы из совместного
распределения
Цепное правило позволяет построить совместное распределение из простых
условных распределений, например, совместное распределение Темы, Размера и
Яркости. Но обычно мы задаем вопрос о конкретной переменной или небольшом
числе переменных. Например, нас может интересовать вывод личности
художника из наблюдений о картине. Допустим, что имеется совместное распределение
всех переменных. Как получить распределение вероятности одной переменной?
Принцип простой: вероятность любого значения некоторой переменной равна
сумме вероятностей тех совместных распределений всех переменных, которые
совместимы с этим значением.
Мы уже видели проявление этого принципа в главе 4: вероятность любого
факта равна сумме вероятностей возможных миров, совместимых с этим фактом.
Так, чтобы вычислить вероятность того, что Тема = Ландшафт, мы складываем
вероятности всех возможных миров, совместимых с условием Тема = Ландшафт.
Поскольку каждый мир получается путем присваивания значений всем
переменным, включая Тему, мы ищем те миры, в которых Тема имеет значение Ландшафт.
Этот простой принцип части называют законом полной вероятности, но я
предпочитаю не столь категоричное название - правило полной вероятности.
Применение правила полной вероятности показано на рис. 9.3. Начинаем с
априорного распределения вероятности, показанного в верхней части. Затем
применяем к фактам условие Размер = Малая и получаем апостериорное
распределение, показанное в средней части. Мы выполняем обычные два шага: сначала
вычеркиваем все присваивания переменным значений, несовместимых с фактом
Размер = Малая, а затем нормируем оставшиеся вероятности, так чтобы их сумма
была равна 1. В нижней части рисунка правило полной вероятности применяется
для вычисления вероятности того, что на картине изображен ландшафт при
условии имеющегося факта. Для этого мы складываем вероятности во всех строках, в
которых переменная Тема принимает значение Ландшафт.
Обратите внимание, что апостериорная вероятность строки, в которой значение
Размера отлично от Малая, равна 0. Так бывает всегда, потому что миры,
несовместимые с фактами, вычеркиваются, а их вероятность приравнивается нулю. То
есть равенство
Р(Тема = Ландшафт, Яркость = Темная | Размер = Малая)
на самом деле эквивалентно такому:
Р(Тема = Ландшафт, Яркость = Темная, Размер = Малая | Размер = Малая)
294

9.2. Правило полной вероятности: получение ответов на запросы.
Р(Тема, Размер, Яркость)
1. Начинаем
со всех
возможных
миров и их
вероятностей
Факт
• Размер=
Малая
Используем факты
для вычеркивания
несовместимых
миров путем
приравнивания их
вероятностей нулю
Тема
Размер Яркость Вероятность
Люди
Люди
Люди
Малая
Малая
Средняя
Люди
Люди
Люди
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Средняя
Большая
Большая
Малдя
Малая
Средняя
Средняя
Большая
Большая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
0.16
0.04
0.16
0.04
0.32
0.08
0.015
0.035
0.03
0.07
0,015
0.035
Р(Тема, Размер, Яркость | Размер = Малая)
Тема
Размер Яркость Вероятность
Люди
Люди
-Люди
Малая
Малая
-Люди
-Люди
-л^редняя-
-Средняя-
Темная
Яркая
-Темная-
-Темная-
Люди
-Большая -
Ландшафт
Ландшафт
Малая
Малая
-Средняя-
Яркая-
Темная
Яркая
-Яркая -
-Ландшафт Большая Темнад-
-Ландшафт Большая Яркая—
0.64
0.16
0
0
0
0
0.06
0.14
0
0
0
О
Р(Тема = Ландшафт |
|_ Размер = Малая) =
0.06+0.14+0+0+0+0=0.2
Затем нормируем
для получения
апостериорного
распределения
вероятности
4. Складываем
вероятности миров,
совместимых
с запросом Тема =
Ландшафт
Рис. 9-3- Использование правила полной вероятности для получения ответа
на запрос. Полная вероятность некоторого значения переменной равна сумме
вероятностей всех совместных распределений, совместимых с этим значением
Легко видеть, что вероятность Р(Тема = Ландшафт | Размер = Малая), равную
сумме двух строк в средней таблице на рис. 9.3, можно выразить следующим
образом:
295

Глава 9. Три правила вероятностного вывода
Р(Тема = Ландшафт | Размер = Малая) =
Р(Тема = Ландшафт, Яркость = Темная | Размер = Малая) + Р(Тема = Ландшафт,
Яркость = Яркая | Размер = Малая)
В математике для записи суммы принято использовать греческую букву 2:
Р(Тема = Ландшафт | Размер = Малая) =
Х/; Р(Тема = Ландшафт, Яркость = Ъ | Размер = Малая) (1)
В правой части этого равенства Ъ обозначает любое допустимое значение
Яркости, а Ъь - сумму последующих членов для всех допустимых значений Яркости.
Мы говорим, что «производится суммирование по» Яркости. Таким образом,
формула (1) имеет место для всех возможных значений Темы и Размера, мы можем
воспользоваться сокращенной нотацией, введенной в предыдущем разделе:
Р(Тема | Размер) = Z/; Р(Тема, Яркость = Ъ | Размер)
Общая формулировка правила полной вероятности
Познакомившись с применением правила полной вероятности к конкретному
примеру, мы готовы рассмотреть общую математическую формулировку. Принцип столь же
прост, но нотация несколько более запутанна. Мы имеем совместное распределение
вероятности множества переменных и хотим выполнить суммирование по некоторым
из них для получения распределения других переменных. Например, пусть имеется
совместное распределение Цвета, Яркости, Ширины и Высоты, а требуется получить
распределение Цвета и Яркости, просуммировав по Ширине и Высоте. При этом
совместное распределение всех переменных может быть обусловлено множеством
каких-то других переменных, например Рембрандт и Тема. Чтобы не удлинять формулы,
мы будем использовать первую букву имени каждой переменной. Предположим еще,
что допустимыми значениями Ширины и Высоты являются «малая» и «большая». По
правилу полной вероятности
Р(Ц = желтый, Я = яркая | Р = true, T = ландшафт) =
Р{Ц = желтый, Я = яркая, Ш = малая, В = малая | Р = true, T = ландшафт) +
Р{Ц = желтый, Я = яркая1, Ш = малая, В = большая | Р = true, T = ландшафт) +
Р{Ц = желтый, Я = яркая, Ш = большая, В = малая | Р = true, T = ландшафт) +
Р(Ц = желтый, Я = яркая, Ш = большая, В = большая | Р = true, T = ландшафт)
Для записи этого тождества можно использовать математическую нотацию.
Обозначим Хх Хп переменные, чье совместное распределение нас интересует, а
V^ Ym - переменные, по которым производится суммирование. Обозначим Z1 Z,
- переменные, фигурирующие в условии. Правило полной вероятности утверждает,
что для любых значений х1 х переменных X, X и значений z1 z{ переменных
zv...,z-
P(*i=* Xn=xn\Z,=z Z=z,) =
^iV"*V3P(Xi=*, \ = Xn^ = yv-<ym = ym\Z,=zv...,Z,=z1)
Это означает, что для вычисления условной вероятности того, что переменные
X ,..., Хп принимают значения x1f.,., хп, нужно просуммировать те элементы полного
условного распределения всех переменных, для которых эти переменные принимают
указанные значения.
296

9.3. Правило Байеса: вывод причин из следствий
III!
LpT*VJ
Поскольку это равенство справедливо для всех значений х^..., xnv\zv...,zr мы можем
воспользоваться сокращенной нотацией, введенной в разделе 2.1, и написать:
Р(Х15...,Х |Z1M..iZJ = X^lL-..XrtP(X; ХУ=у, У =у |Z1f...,Zt)
Есть еще одно соглашение об обозначениях, благодаря которому формулу проще
запомнить. Если имеется множество переменных X,,..., Хл, то их совокупность обозначают
полужирным написанием X. ТоестьХ- сокращенное обозначение дляХ^-.-.Х.
Аналогично полужирная строчная буквах- сокращенное обозначение множества значенийхг..,хп.
О нотации. Принято использовать обычные курсивные буквы, например X их, для
обозначения отдельных переменных или значений, а полужирные начертания -Хи
х-для обозначения множеств переменных или значений.
Таким образом, для конкретных значений х и z имеем
Р(Х = х | Z = z) = ЕуР(Х = х,У=у | Z = z)
Обобщая на все значения х и z, получаем окончательную лаконичную формулу
P(X\Z) = ZyP(X,Y=y\Z)
Это и есть правило полной вероятности.
Существует термин, который может вам встретиться при чтении технической
литературы. Если начать с совместного распределения множества переменных и
просуммировать по некоторым переменным для получения распределения
вероятности остальных, то результирующее распределение называется маргинальным
распределением оставшихся переменных, а процесс исключения переменных
путем суммирования по ним называется маргинализацией. Чаще всего суммируют по
всем переменным, кроме одной, и таким образом получают маргинальное
распределение одной переменной.
Итак, мы разобрали два из трех правил вероятностного вывода. Обратимся
теперь к последнему - самому интересному.
9.3. Правило Байеса: вывод причин
из следствий
Последний кусочек пазла, касающегося рассуждений о вероятностных моделях, -
это правило Байеса, названное в честь Томаса Байеса, математика XVIII века,
который впервые открыл, как делать выводы о причинах по наблюдаемым
следствиям. Правило Байеса позволяет вычислить вероятность причины при условии
ее следствия, зная априорную вероятность причины (до получения какой-либо
информации о следствии) и вероятность следствия при условии причины.
9.3.1. Понимание, причина, следствие и вывод
Правило Байеса связано с понятиями причины и следствия, которые, в свою
очередь, связаны с зависимостями в модели. В обычной программе, если в определе-

Глава 9. Три правила вероятностного вывода
ние переменной X входит переменная У, то изменение У может привести к
изменению X. Таким образом, У в некотором смысле является причиной X. Точно так же
при построении вероятностной модели, в которой X зависит от У, У часто является
причиной X. Рассмотрим, к примеру, Тему и Яркость. Строя модель, мы считали,
что Яркость зависит от Темы, ведь, как правило, художник решает, что изобразить,
а только потом - насколько яркой должна быть картина. Поэтому в некотором
смысле Тема является причиной Яркости.
Я употребляю слово «причина» неформально. Точнее было бы сказать, что мы
моделируем процесс, порождающий данные. При этом мы считаем, что художник
сначала выбирает тему, а затем - на ее основе - яркость. То есть художник сначала
порождает значение переменной Тема, которое затем передается процедуре,
порождающей значение переменной Яркость. Если модель следует порождающему
процессу, то мы неформально употребляем слова «причина» и «следствие», желая
сказать, что значение одной переменной используется при порождении другой.
На рис. 9.4 показан чуть более сложный пример порождающего процесса,
описываемого байесовской сетью. В этом примере первой порождается переменная,
описывающая, является ли автором картины Рембрандт, поскольку личность
художника влияет на все его картины. Затем художник выбирает Тему, что, в свою
очередь, помогает определить Размер и Яркость. Размер зависит от переменных
Рембрандт и Тема, потому что ландшафты, написанные разными художниками,
обычно различаются по размеру, и то же самое справедливо для Яркости.
Порождающий процесс
Следует в
направлении
стрелок
Рембрандт
Вывод
А
Производится
в любом
направлении
Рис, 9-4. Стрелки в сети часто повторяют ход порождающего процесса,
но вывод можно производить в любом направлении
В правой части рис. 9.4 отмечен важный момент. Хотя порождающий процесс
следует стрелкам в модели, вывод может производиться в любом направлении.
На самом деле, в этом примере мы хотим выяснить, является ли автором картины
Рембрандт, поэтому направления вывода и порождающего процесса
противоположны. Я уже неоднократно подчеркивал эту мысль: направление стрелок в сети
необязательно совпадает с направлением вывода. Не поддавайтесь искушению
структурировать сеть точно так, как вы обычно рассуждаете о предметной области
(например, «глядя на яркость картины, я пытаюсь определить ее автора»). Вме-
298
Тема
Размер
Яркость

9.3. Правило Байеса: вывод причин из следствий
сто этого держите в голове порождающий процесс. В большинстве случаев
следование порождающему процессу приводит к самой простой и понятной модели.
А рассуждать о ней можно в любом направлении.
Как я сказал, вывод можно производить в направлении, противоположном
стрелкам в сети. Но как это делается? Секрет кроется в применении правила
Байеса! Взгляните на пример с двумя переменными на рис. 9.5. Здесь сеть следует
естественному порождающему процессу, в котором Тема определяет Размер. Нам
известны Р(Тема) и Р(Размер | Тема). Сначала, подумаем, как производится вывод
в прямом направлении - совпадающем с направлением порождающего процесса.
Допустим, что мы видим, что Тема = Ландшафт, и хотим запросить апостериорную
вероятность Размера. Ее можно получить непосредственно из условного
распределения Р(Размер | Тема). Если мы хотим вывести следствие из фактов о причине,
то все уже под рукой.
Значения вероятности Размера
Значения вероятности Темы при условии Темы
Люди
0.8
Тема
Ландшафт
0.2
СГ Тема
^)—*-(^~ Размер "^)
Тема
Люди
Ландшафт
Малая
0.25
0.25
Размер
Средняя Большая
0.25 0.5
0.5 0.25
Рис. 9.5- Модель с двумя переменными, иллюстрирующая правило Байеса
Но часто мы наблюдаем факты, касающиеся следствия, а узнать хотим что-то
о причине, вызвавшей такое следствие. То есть требуется инвертировать модель,
т. к. нам нужно получить Р(Тема | Размер) - вероятность причины при условии
следствия. Это и позволяет сделать правило Байеса.
9.3.2. Правило Байеса на практике
Принцип применения правила Байеса прост. Сначала я покажу, как оно работает,
а затем объясню каждый шаг. Процесс целиком изображен на рис. 9.6. Начинаем
мы с модели на рис. 9.5. Затем наблюдаем факт - Размер = Большая. И
требуется вычислить апостериорное распределение вероятности Темы при условии этого
факта, т. е. Р(Тема | Размер = Большая). Вот как это делается:
1. Вычислить Р(Тема = Люди) Р(Размер = Большая | Тема = Люди) =
0.8 х 0.5 = 0.4 и Р(Тема = Ландшафт) Р( Размер = Большая | Тема =
Ландшафт) = 0.2 х 0.25 = 0.05. Эти числа показаны в средней таблице на рис. 9.6.
2. Нормировать эту таблицу для получения искомого ответа.
Нормировочный коэффициент равен 0.4 + 0.05 = 0.45. Таким образом, Р(Тема = Люди |
Размер = Большая) = 0.4 / 0.45 = 0.8889, а Р(Тема = Ландшафт | Размер =
Большая) = 0.05 / 0.45 = 0.1111. Ответ показан в нижней таблице на рис. 9.6.
А почему это работает? Составные части этого процесса дают цепное правило и
правило полной вероятности. Мы построим совместное распределение
вероятности по условным распределениям, применяя цепное правило, как описано в разде-
299

Глава 9. Три правила вероятностного вывода
ле 9.1. Затем снова применим цепное правило, но на этот раз в противоположном
направлении. И наконец, завершим вычисление, применив правило полной
вероятности. Вот эти шаги:
1. Берем Р(Тема) и Р(Размер | Тема) и, применив цепное правило, получаем
Р(Тема, Размер) = Р(Тема) Р(Размер | Тема).
2. Применяем цепное правило, но в обратном направлении:
Р(Размер, Тема) = Р(Размер) Р(Тема | Размер).
3. Поскольку величины Р(Размер, Тема) и Р(Тема, Размер) равны, то можно
объединить 1 и 2, получив при этом
Р(Размер) Р(Тема | Размер) = Р(Тема) Р(Размер | Тема).
4. Делим обе части этого равенства на Р(Размер) и получаем
Р(Тема | Размер) =
Р(Тема)Р(Размер | Тема)
Р(Размер)
Тема
Люди
0.8
Ландшафт
0.2
<^~ Тема ^>—^С^ Размер ^)
Факт
• Размер=
Большая
Тема
Люди
0.8x0.5 = 0.4
Ландшафт
0.2x0.25 = 0.05
Тема
Люди
0.4/(0.4 +
0.05) = 0.8889
Ландшафт
0.05/(0.4 + 0.05):
0.1111
Тема
Люди
Ландшафт
Размер
Малая Средняя Большая
0.25 0.25 0.5
0.25 0.5 0.25
Вычисляем Р(Тема = Люди) Р(Размер = Большая | Тема =
Люди). Вычисляем Р(Тема = Ландшафт) Р(Размер =
Большая | Тема = Ландшафт). В результате получаем таблицу,
которая сопоставляет число 0.4 переменной Люди и число
0.05 переменной Ландшафт
2. Нормируем эту таблицу, так чтобы сумма чисел в ней
равнялась 1. Для этого нужно разделить каждое число
на 0.4 + 0.05
Это дает числовые значения Р(Тема = Люди | Размер =
Большая) и Р(Тема = Ландшафт | Размер = Большая).
Получаем таблицу, представляющую Р(Тема | Размер:
Большая)
Рис. 9.6. Правило Байеса в действии
Теперь ответ на интересующий нас вопрос, Р(Тема | Размер), находится в левой
части. Эту формулу принято называть правилом Байеса, но в таком виде она
неудобна для применения, потому что включает неизвестную величину Р(Раз-
мер). Необходим еще один шаг.
300

9.4. Байесовское моделирование
1. Применяя правило полной вероятности и цепное правило, выразим
Р(Размер) через известные нам величины. Сначала, пользуясь правилом полной
вероятности, напишем Р( Размер) = Хд. Р(Тема = 5, Размер). Затем, пользуясь
цепным правилом, записываем Р(Тема = s, Размер) = Р(Тема = $)Р(Размер |
Тема = s). Наконец, объединяя то и другое, получаем Р(Размер) = Z, Р(Те-
ма = 5)Р(Размер | Тема = s).
2. И вот он, окончательный ответ:
Р(Тема)Р(Размер = Большая | Тема)
Р(Тема | Размер = Большая) =
Zs. Р(Тема = s)Р(Размер = Большая | Тема = s)
Легко видеть, как этот ответ соотносится с двумя шагами, показанными на
рис. 9.6. На первом шаге вычисляется числитель Р(Тема)Р(Размер = Большая |
Тема) для каждого из двух возможных значений Темы. Далее рассмотрим
знаменатель. Мы складываем величины Р(Тема = $)Р(Размер | Тема = s) для
каждого возможного значения s Темы. Но это в точности величина, вычисленная на
первом шаге для каждого значения Темы. Знаменатель - это просто сумма всех
величин, вычисленных на первом шаге. Поэтому нам нужно разделить каждую
величину на их сумму, иначе говоря, нормировать их. В этом и состоит
содержание шага 2.
Правило Байеса выглядит просто, но мы еще не все сказали о нем. Это правило
лежит в основе системы байесовского моделирования - темы следующего
раздела. В нем мы более глубоко рассмотрим, как работает правило Байеса, и на врезке
дадим общую формулировку.
9.4. Байесовское моделирование
Правило Байеса лежит в основе общего подхода к моделированию, в котором мы
выводим причины из наблюдений над следствиями, а затем применяем эти знания
к другим потенциальным следствиям.
В этом разделе мы продемонстрируем байесовское моделирование на примере
подбрасывания монеты из главы 2. Основываясь на результатах 100
подбрасываний (следствия модели), мы сделаем вот что:
• применим правило Байеса для вывода асимметрии монеты (причина
следствий);
• покажем несколько методов предсказания исхода 101-го подбрасывания:
- метод максимума апостериорной вероятности (МАВ);
- метод максимального правдоподобия (ММП);
- полный байесовский метод.
На рис. 9.7 воспроизведена байесовская сеть для примера, где мы пытаемся
предсказать исход 101-го подбрасывания монеты, зная исходы первых 100
подбрасываний. Имеются три переменные: Асиммметрия монеты, ЧислоОрлов, вы-
301

Глава 9. Три правила вероятностного вывода
павших в первых 100 подбрасываниях, и исход Броска10Г Сначала порождается
Асимметрия, от которой зависят исходы всех подбрасываний. Если Асимметрии
известна, то подбрасывания монеты независимы. Напомню, что слова «сначала
порождается Асимметрия» описывают порождающий процесс, а не тот факт, что
Асимметрия заранее известна. Это еще один пример, доказывающий, что порядок
порождения переменных не обязательно совпадает с порядком вывода. В нашем
примере Асимметрия порождается первой, но вывод производится в направлении
от ЧислаОрлов к Асимметрии.
Рис. 9.7. Байесовская сеть для примера
с подбрасыванием монеты
Мы используем бета-биномиальную модель, поэтому Асимметрия
характеризуется бета-распределением, а ЧислоОрлов - биномиальным распределением,
зависящим от Асимметрии. Напомним некоторые факты.
• Биномиальная переменная характеризует, сколько случайных попыток
завершается исходом определенного вида. В нашем примере речь идет о
выпадении орла при подбрасывании монеты. Параметром биномиального
распределения является вероятность «правильного» исхода.
• Эта вероятность и измеряет степень асимметрии монеты. В данном
случае асимметрия нам неизвестна, и мы хотели бы оценить ее по результатам
подбрасываний монеты. Поэтому мы моделируем асимметрию случайной
переменной. Конкретно для моделирования используется непрерывное
бета-распределение. Непрерывное распределение описывается функцией
плотности распределение вероятности (ФПВ), а не вероятностями
каждого значения. Бета-распределение характеризуется двумя параметрами,
а и (3. Параметр а интуитивно можно представлять себе как число ранее
наблюдавшихся орлов плюс 1, а параметр (3 - как число ранее
наблюдавшихся решек плюс 1. Как отмечалось в главе 4, бета-распределение хорошо
работает совместно с биномиальным. Почему это так, мы увидим в
следующем разделе.
Исход любого будущего подбрасывания описывается элементом Flip, в
котором вероятность выпадения орла равна Асимметрии. Как следует из байесовской
сети, исход будущего подбрасывания напрямую зависит только от асимметрии.
Если асимметрия известна, то новое подбрасывание не дает дополнительной
информации. Если же она неизвестна, то первые 100 подбрасываний дают
информацию об асимметрии, которую можно использовать для предсказания исхода 101-
го подбрасывания.
302
Ассиметрия
ЧислоОрлов
Бросок
101

9.4. Байесовское моделирование
9.4.1. Оценивание асимметрии монеты
Как воспользоваться этой моделью для предсказания исхода будущего
подбрасывания на основе результатов первых 100 подбрасываний? Тут-то и выходит на
сцену байесовское моделирование, суть которого состоит в использовании
правила Байеса для вывода апостериорного распределения вероятности асимметрии по
наблюдаемому числу выпавших орлов. Затем это апостериорное распределение
можно применить для предсказания исхода следующего подбрасывания.
Этот процесс изображен на рис. 9.8. Если в 40 % из тысячи подбрасываний
выпадал орел, то можно сделать вывод, что асимметрия близка к 0.4. Чем
меньше подбрасываний, тем ниже уверенность в правильности вывода. Такой вывод
является прямым результатом применения правила Байеса. Вернемся к нашему
примеру: если в 100 подбрасываниях мы наблюдали 63 орла, то можем вычислить
апостериорное распределение Асимметрии при условии, что ЧислоОрлов = 63, и
использовать его для предсказания Броска10Г
2. Выводим апостериорное распределение
Асимметрии, пользуясь правилом Байеса
1. Наблюдаем
число орлов
3. Используем
апостериорное
распределение
Асимметрии для
предсказания
исхода следующего
подбрасывания
Рис. 9.8. Порядок вывода в примере с асимметричной монетой
Для этого начнем с априорного распределения Асимметрии.
Бета-распределение характеризуется двумя параметрами, аир. Обозначим параметры априорного
бета-распределения а0 и (30. Напомним (см. главу 2), что а0 и (30 представляют
число воображаемых орлов и решек, выпавших до наблюдения результатов реальных
подбрасываний, плюс 1. Для получения апостериорного распределения мы
прибавляем фактическое число выпавших орлов и решек к этим умозрительным
величинам. Предположим, что мы начали с распределения beta(2, 5). Это означает,
что умозрительно мы предполагаем, что выпадет 1 орел и 4 решки (т. к. а0 -
воображаемое число выпавших орлов плюс 1, а (30 аналогично вычисляется для решек).
Затем мы наблюдаем 63 орла и 37 решек. Апостериорное распределение
асимметрии имеет вид beta(65,42). Обозначив параметры апостериорного
бета-распределения а{ и (Зг будем иметь простую формулу:
at = а0 + число наблюдаемых орлов
(3j = (30 + число наблюдаемых решек
303
Ассиметрия
ЧислоОрлов
Бросок
101

Глава 9. Три правила вероятностного вывода
Примечание. На практике производить эти вычисления самостоятельно вам не
придется. Обо всем позаботятся алгоритмы, входящие в состав системы вероятностного
программирования. Вы говорите, что хотите использовать бета-биномиальную модель,
а алгоритм производит все необходимые вычисления. Но важно понимать принципы,
лежащие в основе системы, потому-то мы и тратим сейчас время.
На рис. 9.9 показано распределение beta(65, 42), наложенное на исходное
распределение beta(2,5). Бросаются в глаза два момента. Во-первых, пик
распределения сместился вправо, потому что доля реально выпавших орлов (63 из 100)
больше предполагавшейся априори (1 из 5). Во-вторых, пик стал острее, поскольку,
имея 100 дополнительных наблюдений, мы гораздо увереннее смотрим на оценку
асимметрии.
9
8
7
6
5
4
3
2
1
0
beta(65, 42)
Рис. 9.9. Вывод асимметрии монеты из ряда наблюдений.
Выпало 63 орла и 37 решек, эти числа мы прибавили к параметрам альфа и бета.
Апостериорная функция плотности вероятности beta(65, 42) наложена
на априорную beta(2, 5)
Эта простая формула сложения исходов для создания новой
бета-биномиальной модели апостериорного распределения является результатом применения
правила Байеса. В примере с подбрасыванием монеты мы имеем дело с тремя
величинами:
• р(Асимметрия = Ь): априорная плотность вероятности значения
Асимметрии Ъ (здесь и ниже используется строчная буква р, чтобы подчеркнуть, что
это плотность вероятности, а не вероятность).
• Р(ЧислоОрлов = 631 Асимметрия = Ь): вероятность, что выпадет ЧислоОр-
лов = 63 при условии Асимметрии Ь. Эта вероятность называется
правдоподобием Ъ при условии данных.
• р( Асимметрия = Ъ | ЧислоОрлов = 63): апостериорная плотность
вероятности значения Асимметрии Ь.
304
beta(2, 5)

9.4. Байесовское моделирование
Поскольку в этом примере переменная (асимметрия) непрерывна, он
оказывается несколько сложнее, чем пример с картиной из раздела 9.3.2. Я повторю здесь,
чем закончилось рассмотрение того примера, чтобы вы убедились, что все
работает и для асимметричной монеты. В разделе 9.3.2 мы получили следующее
выражение для распределения вероятности темы картины при известном размере:
Р(Тема)Р(Размер = Большая | Тема)
Р(Тема | Размер = Большая)
Zs. Р(Тема = s)Р(Размер = Большая | Тема = s)
Обратите внимание на знаменатель. Это сумма значений числителя для всех
возможных значений Темы. Таким образом, это нормировочный коэффициент,
который гарантирует, что (а) левая часть всегда пропорциональна числителю в
правой части и (Ь) сумма значений в левой части равна 1. Суть формулы можно
описать с помощью следующей нотации:
Р(Тема | Размер = Большая) ос Р(Тема)Р(Размер = Большая | Тема)
Знак ос означает, что левая часть пропорциональна правой, причем
коэффициент пропорциональности равен 1/Е.Р(Тема = s) Р(Размер = Большая | Тема = 5).
В левой части находится апостериорное распределение вероятности Темы.
Первый член в правой части - априорное распределение, а второй член, вероятность
наблюдения конкретного Размера при заданном значении Темы, - правдоподобие.
Следовательно, смысл приведенной выше формулы можно выразить так:
Апостериорное ос Априорное х Правдоподобие
Составные части этой формулы показаны на рис. 9.10. Если вы в силах
запомнить только одну формулу, относящуюся к байесовскому моделированию, то
запомните эту. И хотя мы вывели ее применительно к примеру с картиной, она
отражает общий принцип, справедливый для любых применений правила Байеса.
Чтобы найти апостериорное распределение некоторой величины Ь, нужно
вычислить правую часть этого равенства для каждого возможного значения b и, сложив
все результаты, получить суммарное значение В - нормировочный коэффициент.
Затем произведение Априорного на Правдоподобие делится на В для получения
Апостериорного.
В случае непрерывной переменной процесс нормировки может оказаться
сложным, поскольку требует интегрирования по всем возможным значениям Ь. Вот что
говорит правило Байеса для примера с подбрасыванием монеты:
р(Асимметрия = Ъ | ЧислоОрлов = 63) =
Р(Асимметрия = &)Р(ЧислоОрлов = 63 | Асимметрия = Ь)
Jj°P(Асимметрия = х)Р(ЧислоОрлов = 63 | Асимметрия = x)dx
Применив нотацию пропорциональности, эту формулу можно переписать в виде:
р(Асимметрия = Ъ | ЧислоОрлов = 63) ос Р(Асимметрия = &)Р(ЧислоОрлов =
63 | Асимметрия = Ъ)
305

Глава 9. Три правила вероятностного вывода
Символ
пропорциональности
Априорная
вероятность
значения
Вероятность
факта при условии
этого значения
Апостериорное <* Априорное х Правдоподобие
V У
Нормировать
для получения
апостериорного
распределения
этой переменной
т
1. Вычислить правую часть для
каждого значения переменной,
для которой производится вывод
Рис. 9.10. Структура формулы байесовского моделирования
И в этом случае апостериорное распределение пропорционально
априорному, умноженному на правдоподобие. И хотя последнее равенство выглядит
просто, в нем скрыт интеграл, который не всегда легко оценить. По счастью, в
случае бета-биномиальной модели у этого уравнения существует простое решение,
которое мы уже видели в начале раздела. Нужно прибавить число наблюдаемых
успешных и неудачных исходов к параметрам бета-распределения. Именно
поэтому бета-распределение так хорошо работает с биномиальным. Попытавшись же
скомбинировать произвольное непрерывное распределение с биномиальным, мы
получим задачу интегрирования, у которой нет простого решения.
При работе с системами вероятностного программирования вам никогда не
придется вычислять интегралы вручную. Система часто способна применить
приближенные алгоритмы для решения трудных задач интегрирования, поэтому мы
не обязаны использовать только такие функциональные формы, которые хорошо
работают вместе. Тем не менее, если такая форма имеется, то было бы оптимально
воспользоваться ей.
Примечание. В главе 6 нам впервые встретился термин сопряженное априорное
для описания априорного распределения, которое хорошо работает с
распределением, зависящим от параметра. Технически это означает, что апостериорное
распределение имеет такой же вид, как априорное. В частности, бета-распределение является
сопряженным априорным к биномиальному, потому апостериорное распределение
параметра также является бета-распределением. Если имеется сопряженное априорное
распределение, то интегрирование в байесовском правиле производится просто.
Потому-то сопряженные распределения так часто используются в байесовской
статистике. Но при использовании вероятностного программирования мы не ограничены только
сопряженными распределениями.
Общая формулировка правила Байеса
Теперь, когда мы больше знаем о правиле Байеса и особенно о свойстве
пропорциональности, настало время сформулировать его в общем виде. Как и правило полной
вероятности, правило Байеса обобщается на любое число переменных и может вклю-
306

9.4. Байесовское моделирование
чать условия. В обозначениях раздела 9.2 мы имеем три набора переменных: X1f,,,,Xn
(«причины»), Yv,..t Ym («следствия») и Z^.,,, Z; (условные переменные}. Известна
величина Р(Х ,..., Хп | Z^..., Z;) - априорная вероятность причин при заданных условных
переменных и величина P{YV..., Ym | X1t..., ХЛ, Z1f..., Z;) - условная вероятность следствий
при условии причин и условных переменных. Требуется найти вероятность причин при
условии следствий и условных переменных, т. е. Р(Х1,...,Хя | Yv...,Ym,Zv...}Zf). Правило
Байеса говорит, что
P(X,,...,XJY, Ym,Z,t...,Z,) =
РУ< xjz1,...,z,)P(y ут\хл,...,х„,г z)
£,...Е Р(Х=х, X =х |Z, Z)P(V„..., У |X1=xi,...X=xe,Z1 Z)
х1 хп * 1 1' 'п п1 1* ' /' * 11 ' m ' I 11 'л п'1' ' /'
Я обещал упростить нотацию в этой формуле. Поскольку знаменатель - это
нормировочный коэффициент, мы можем воспользоваться символом пропорциональности и
сделать запись гораздо понятнее:
P{Xv...,Xn\Yv...,Ym,Zv...,Z)~P{Xv...,Xn\Z Z)P(Yv...,Ym\Xv„.,Xn,Zv...,Z}
Это то же самое, что равенство Апостериорное «= Априорное Правдоподобие,
только вместо апостериорного используется совместное распределение нескольких
переменных причины, в выражении правдоподобия также рассматривается несколько
переменных следствия и имеется ряд nepeMei-mbixZ, влияющих на причины и следствия.
Наконец, вспомним об использовании полужирного шрифта для обозначения
множеств переменных. Тогда правило Байеса можно записать совсем кратко:
Р(Х | Y, Z) - р(х | Z)P{Y | X,Z)
где X обозначает все причины, У - все следствия, aZ- все условные переменные. Эта
лаконичная формула - лучший способ запомнить общее правило Байеса.
Итак, мы научились оценивать Асимметрию. Следующий шаг - предсказать Бро-
сок|0|.
9.4.2. Предсказание результата следующего
подбрасывания
Пусть мы получили апостериорное распределение Асимметрии в виде
бета-распределения. Как предсказать результат следующего подбрасывания монеты?
Существует три распространенных способа, и все они для бета-биномиальной
модели оказываются простыми:
• метод максимума апостериорной вероятности (МАВ);
• метод максимального правдоподобия (ММП);
• полный байесовский метод.
Рассмотрим их поочередно.
Метод максимума апостериорной вероятности
В этом методе мы вычисляем значение Асимметрии с наибольшей
апостериорной плотностью вероятности. Это значение, которое максимизирует произведе-
307

Глава 9. Три правила вероятностного вывода
ние априорной вероятности на правдоподобие, называется наиболее
правдоподобным значением Асимметрии. Затем оно используется для предсказания результата
следующего подбрасывания.
Метод МАВ иллюстрируется на рис. 9.11. Первый шаг - вычислить
апостериорное распределение Асимметрии, как описано в предыдущем разделе. Мы
начинаем с априорного распределения beta(2,5), наблюдаем 63 орла и 37 решек и
получаем апостериорное распределение beta(65,42). На следующем шаге вычисляется,
при каком значении Асимметрии кривая beta(65,42) (см. рис. 9.9) достигает пика.
Иными словами, нас интересует мода beta(65, 42). Для нахождения моды
существует простая формула:
л — 1
mode(beta(a,p)) = ————
a + p - 2
В нашем примере мода равна (65 - 1)/(65 + 42 - 2), т. е. приблизительно 0.6095.
Предположим далее, что Асимметрия равна 0.6095, и вычислим вероятность, что в
результате Броска101 выпадет орел при условии, что наблюдалось 63 орла и 37
решек. Функциональная форма Броска101 говорит, что вероятность выпадения орла
равна значению Асимметрии, которое, по предположению, равно 0.6095. Поэтому
мы получаем ответ 0.6095.
Априорное Апостериорное
beta(2, 5) *" beta(2 + 63, 5 + 37) = beta(65, 42)
ч
Наиболее правдоподобное значение
(65-1)/(65 + 42-2) = 0.6095
Р(Бросок101 = Орел | данные) = 0.6095
Рис. 9.11. Предсказание результата следующего подбрасывания монеты
методом МАВ
Метод максимального правдоподобия
Распространенный частный случай МАВ называется методом максимального
правдоподобия (ММП). В этом случае мы подбираем значения параметров,
которые наилучшим способом «аппроксимируют данные», не обращая внимания на
априорное распределение. Метод ММП иногда считается небайесовским, но он
хорошо укладывается в схему байесовского моделирования, если предположить,
что априорная вероятность любого значения Асимметрии одинакова. Тогда
формула
Апостериорное ос Априорное х Правдоподобие
сводится к
Апостериорное <* Правдоподобие
308
63 орла, 37 решек
Ассиметрия
ЧислоОрлов
Бросок
■01

9.4. Байесовское моделирование
Поэтому наиболее правдоподобным значением апостериорной вероятности
является то, которое максимизирует правдоподобие. Отсюда и название метод
максимального правдоподобия.
Метод максимального правдоподобия иллюстрируется на рис. 9.12. Он
похож на метод МАВ (рис. 9.11), только начинаем мы с априорного распределения
beta(l, 1), которое назначает одну и ту же плотность вероятности всем значениям
между 0 и 1. Вспомнив, что параметрами априорного распределения являются
воображаемые числа выпавших орлов и решек плюс 1, мы поймем, что такое
распределение представляет случай, когда мы вообще не ожидаем увидеть ни орлов, ни
решек. Затем выполняются те же вычисления, что и раньше, которые дают
прогноз 0.63. И это не совпадение. В 100 подбрасываниях мы наблюдали 63 орла.
Значение Асимметрии, максимально совместимое с такими наблюдениями, - то, при
котором любое подбрасывание монеты с вероятностью 0.63 завершается
выпадением орла. Следовательно, метод максимального правдоподобия действительно
выбирает значение параметра, наилучшим образом аппроксимирующее данные,
тогда как метод МАВ уравновешивает наблюдаемые данные и априорное
распределение.
Априорное Апостериорное
beta(1, 1) *" beta(1 + 63, 1 + 37) = beta(64, 38)
Р(Бросок101 = Орел | данные) = 0.63
Рис. 9-12. Предсказание результата следующего подбрасывания
монеты методом максимального правдоподобия
Полный байесовский метод
Третий способ предсказания результата следующего подбрасывания иногда
называют полным байесовским методом, потому что вместо оценки одного значения
Асимметрии, в нем используется полное апостериорное распределение. Процесс
иллюстрируется на рис. 9.13. Все начинается так же, как в методе МАВ, с
вычисления апостериорного распределения Асимметрии. Чтобы использовать это
распределение для предсказания Броска101, мы пользуемся формулой Р(Бросок101 =
Орел | данные), которая приведена на рисунке. Эта формула получается в
результате применения правила полной вероятности и цепного правила. Важно
отметить, что она подразумевает интегрирование, потому что Асимметрия -
непрерывная переменная. Как и в случае оценивания апостериорного значения параметра,
интегрирование может оказаться трудной задачей. Но в бета-биномиальной
модели все просто: если апостериорное распределение имеет вид beta(ar (3j), то
вероятность, что в следующий раз выпадет орел, равна
309
63 орла, 37 решек
Ассиметрия
Бросок
ш
ЧислоОрлов
Наиболее правдоподобное значение
(64-1)/(64 + 38-2) = 0.63

Глава 9. Три правила вероятностного вывода
а.
a, + ft-2
Таким образом, в нашем примере вероятность выпадения орла равна 65 / (65 +
42) = 0.6075. И, чтобы уж все стало на свои места, эта простая формула для
вероятности выпадения орла и есть причина, по которой мы прибавляем 1 к
счетчикам орлов и решек в параметрах бета-распределения; иначе формула оказалась бы
сложнее.
Априорное Апостериорное
beta(2, 5) *" beta(2 + 63, 5 + 37) = beta(65, 42)
Р(Бросок101 = Орел | данные)
^р(Асимметрия = b\ данные) Р(Бросок101 = Орел |
0 Асимметрия = b)dp
ч
Р(Бросок101 = Орел | данные) =
65/(65 + 42) = 0.6075
Рис. 9-13. Предсказание результата следующего подбрасывания
монеты полным байесовским методом
Сравнение методов
Теперь давайте сравним рассмотренные методы.
• Метод ММП дает наилучшую аппроксимацию данных, но чреват
переобучением. Так в машинном обучении называется ситуация, когда алгоритм
чересчур хорошо подгоняет модель к случайным особенностям данных,
в результате чего она не поддается обобщению. Такая проблема особенно
опасна, когда число подбрасываний мало. Например, если в 10
подбрасываниях выпало 7 орлов, станете ли вы утверждать, что асимметрия монеты
составляет 0.7? Даже правильная монета может выпасть орлом 7 раз из 10,
так что наблюдение не дает достаточных свидетельств в пользу
асимметричности.
Два преимущества метода ММП делают его популярным. Во-первых, он
сравнительно эффективен, поскольку не требует интегрирования по
значениям параметра для предсказания исхода следующего испытания.
Во-вторых, ему не нужно априорное распределение, которое нелегко получить,
не имея каких-либо оснований. Тем не менее, уязвимость к переобучению
может оказаться серьезной проблемой.
• Метод МЛВ может стать неплохим компромиссом. Включение априорного
распределения служит двум целям. Первая - представление имеющихся
априорных знаний. Вторая - противодействие переобучению. Например,
если начать с априорного распределения beta(l 1, 11), то мы не сместим
результаты ни в одну сторону, но особенности данных будут сглажены за счет
310
63 орла, 37 решек
Ассиметрия
ЧислоОрлов
Бросок
'01

9.4. Байесовское моделирование
прибавления 10 воображаемых орлов и решек к наблюдаемым величинам.
Чтобы убедиться в этом, предположим, что в 10 подбрасываниях выпало 7
орлов. Вспомним - априорное распределение beta(l 1,11) означает, что мы
наблюдали 10 воображаемых орлов и 10 воображаемых решек. Прибавив
еще 7 орлов и 3 решки, получим в итоге 17 орлов и 13 решек. Поэтому
оценка асимметрии методом МАВ будет равна 17 / (17 + 13) = 17/30 ~ 0.5667.
То же самое показывает приведенная выше формула моды
бета-распределения
При семи орлах и трех решках апостериорное распределение имеет вид
beta(18, 14), его мода равен 17/30. И хотя в 70 % случаев выпадал орел,
апостериорное доверие к орлам лишь немногим больше 0.5, а вовсе не 0.7,
как в методе ММП. Помимо противодействия переобучению, метод МАВ
сравнительно эффективен, потому что не нуждается в интегрировании по
значениям параметра. Однако ему необходимо априорное распределение,
которое не всегда легко получить.
• Полный байесовский метод в тех случаях, когда его применение возможно,
может оказаться лучше других подходов, потому что в нем используется
полное распределение. В частности, когда мода распределения не может
считаться репрезентативной характеристикой полного распределения,
другие методы могут давать недостоверные результаты. Для
бета-распределения это не слишком серьезная проблема - предсказания МАВ и полного
байесовского метода в нашем примере очень близки. Точнее, имея
априорное распределение beta(l 1, 11), а также результаты наблюдений - семь
орлов и три решки, - мы получаем апостериорное распределение beta(18,14).
Байесовская оценка вероятности следующего подбрасывания равная 18 /
(18 + 14) = 18/32 = 0.5625, немногим меньше оценки МАВ. Но для других
распределений, особенно с несколькими пиками, полный байесовский
метод дает гораздо лучшие оценки, чем МАВ. Хотя в методе МАВ и
используется априорное распределение, он удовольствуется одним каким-нибудь
пиком, полностью игнорируя важные участки распределения. Однако с
вычислительной точки зрения байесовский подход труднее.
Системы вероятностного программирования отличаются в плане
поддерживаемых подходов. Как правило, они поддерживают полный байесовский метод.
Но поскольку в нем часто требуется интегрирование, используются
приближенные алгоритмы. Некоторые системы поддерживают также методы максимального
правдоподобия и оценки максимальной апостериорной вероятности для моделей
специального вида, что позволяет повысить эффективность вычислений. В
частности, Figaro поддерживает полный байесовский метод и МАВ. В главе 12
показано, как они используются на практике.
311
а + р-2
а-1

Глава 9. Три правила вероятностного вывода
Итак, теперь мы знаем об основных правилах вывода и понимаем, как в
байесовском моделировании используется правило Байеса, чтобы обучаться на данных и
применять полученные знания для предсказания будущего. Далее мы рассмотрим
конкретные алгоритмы вывода. В вероятностном программировании есть два
основных семейства таких алгоритмов: факторные и выборочные. Им посвящены
следующие две главы.
9.5. Резюме
• Цепное правило позволяет построить совместное распределение
вероятности нескольких переменных, если известны условные распределения
каждой из них.
• Правило полной вероятности позволяет из совместного распределения
вероятности нескольких переменных получить распределение каждой из них.
• Стрелки в графе вероятностной модели обычно направлены так же, как в
процессе порождения данных, однако вывод на основе этой модели может
производиться в любом направлении. Это возможно благодаря правилу
Байеса.
• В байесовском моделировании правило Байеса используется для вывода
причин из наблюдений над их следствиями, а результаты вывода
применяются для предсказания будущих исходов.
• В байесовском выводе апостериорная вероятность значения переменной
пропорциональна произведению априорной вероятности этого значения на
его правдоподобие, т. е. вероятность факта при условии данного значения.
• В методе оценки максимальной априорной вероятности (МАВ) для
предсказания будущих исходов используется наиболее правдоподобное
апостериорное значение параметра.
• В методе максимального правдоподобия априорное распределение
игнорируется, я для предсказания используется значение параметра, при котором
достигается максимум правдоподобия. Это самый простой метод, но он
подвержен переобучению.
• В полном байесовском методе для предсказания будущих исходов
используется полное апостериорное распределение вероятности значений
параметра. Это самый точный, но и самый вычислительно сложный метод.
9.6. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Рассмотрим детальную модель принтера из примера с диагностикой
принтера. Ее байесовская сеть показана на рис. 5.11. Возьмем следующий
случай:
• Кнопка Питания Принтера Нажата = true
312

9.6. Упражнения
• Уровень Тонера = низкий
• Индикатор Низкого Уровня Тонера Горит = false
• Подача Бумаги = беспрепятственная
• Индикатор Замятия Бумаги Горит = false
• Состояние Принтера = плохое
a. Выпишите выражение для вероятности такого случая, применив
полное цепное правило, в котором каждая переменная обусловлена
всеми предыдущими переменными.
b. Упростите это выражение, приняв во внимание отношения
независимости, существующие в сети.
c. Выпишите выражение для совместного распределения вероятности,
которое было бы применимо в общем случае, без задания конкретных
значений переменных.
Для сети из упражнения 1:
a. Выпишите выражение для вероятности того, что Кнопка Питания
Принтера Нажата = true.
b. Выпишите выражение для вероятности того, что Кнопка Питания
Принтера Нажата = true и Состояние Принтера = плохое.
Предположим, что 1 из 40 миллионов американцев становится
Президентом США.
a. Предположим, что 50 % президентов - левши, тогда как всего среди
населения левшей 10 %. Какова вероятность стать президентом, если
человек - левша?
b. Предположим теперь, что 15 % президентов США учились в
Гарварде, тогда как для всего населения это соотношение составляет 1:2000.
Какова вероятность стать президентом у выпускника Гарварда?
c. В предположении, что леворукость и учеба в Гарварде условно
независимы при условии, что человек стал президентом, какова
вероятность стать президентом США у левши, учившегося в Гарварде?
313

ГЛАВА 10.
Факторные алгоритмы вывода
В этой главе.
■ Основы факторного вывода, определение
факторов и операции над факторами.
■ Алгоритм исключения переменных.
■ Алгоритм распространения доверия.
Познакомившись с основными правилами вероятностного вывода, мы в
следующих двух главах будем рассматривать некоторые алгоритмы вывода,
применяемые в вероятностном программировании. Это позволит лучше понять, какой
алгоритм оптимален для данной задачи и как спроектировать модель, адаптированную
к данному алгоритму
Существует два основных типа алгоритмов вывода:
• факторные алгоритмы, работающие со структурами данных, которые
называются факторами и улавливают особенности вероятностной модели;
• выборочные алгоритмы, которые создают примеры возможных миров,
исходя из распределения вероятности, и используют их для ответов на
запросы.
Выборочные алгоритмы мы отложим до следующей главы. А эту посвятим
факторным алгоритмам и рассмотрим следующие вопросы.
• Факторная структура данных и как она представляет вероятностную
модель и запрос. Мы увидим, что эта структура тесно связана с цепным
правилом и правилом полной вероятности, о которых шла речь в предыдущей
главе.
• Алгоритм исключения переменных (Я/7). Это точный алгоритм, то есть, зная
факты, он точно вычисляет запрошенную вероятность в соответствии с
моделью. Следовательно, это отличный выбор, если модель поддерживает его,
но работать он может долго.

10.1. Факторы
• Алгоритм распространения доверия (РД). Это приближенный алгоритм.
Он может работать быстро и обычно - но не всегда - возвращает результат,
близкий к истинному.
• Компромиссы между точностью и скоростью работы, на которые
приходится идти, выбирая между точным и приближенным алгоритмом, и
методы проектирования вероятностной модели, отвечающей типу выбранного
алгоритма.
Для объяснения концепций, встречающихся в этой главе, я опирался на
материал по байесовским и марковским сетям из главы 5. Методы моделирования на
языке Figaro, применявшиеся в главе 5, являются базовыми, поэтому рекомендую
освежить их в памяти, прежде чем читать главы с 6 по 8. Кроме того, вы должны
свободно владеть правилами вывода из главы 9, особенно цепным правилом и
правилом полной вероятности.
10.1. Факторы
Идея факторизации распределения вероятности аналогична идее факторизации
(разложения на множители) целого числа. Число 15 можно разложить в
произведение 3x5, поэтому 3 и 5 - множители 15. Точно так же можно разложить
распределение вероятности на «множители» - факторы. В этом разделе мы узнаем,
что такое факторы, а затем увидим, как разложить распределение вероятности на
факторы с помощью цепного правила. Наконец, мы расскажем, как,
воспользовавшись правилом полной вероятности, выразить ответ на запрос с помощью
факторов.
10.1.1. Что такое фактор?
Сначала я дам общее определение фактора, а затем объясню, как оно согласуется
с вероятностной моделью. Фактор - это представление функции, отображающей
множество значений переменных в вещественное число. Существуют разные
представления факторов, но в этой книге мы будем использовать только табличное.
В табл. 10.1 показан фактор от двух переменных: Тема и Размер. В этой таблице
имеется по одному столбцу для каждой переменной и еще один столбец (справа),
содержащий вещественные числа. Каждая строка фактора соответствует
некоторой комбинации значений переменных. Так, в первой строке Тема = Люди,
Размер = Малая. Фактор сопоставляет этой комбинации вещественное число 0.25.
Таблица 10.1. Фактор от двух переменных Тема и Размер.
Каждая строка соответствует комбинации значений переменных
и сопоставляет ей вещественное число
Тема
Люди
Люди
Размер
Малая
Средняя
0.25
0.25
315

Глава 10. Факторные алгоритмы вывода
Тема
Люди
Ландшафт
Ландшафт
Ландшафт
Размер
Большая
Малая
Средняя
Большая
0.5
0.25
0.5
0.25
Почему факторы полезны для вероятностных рассуждений? Вернемся к
основополагающим принципам.
• Распределение вероятности - это сопоставление числа от 0 до 1 каждому
возможному миру.
• В вероятностной модели, определенной множеством переменных,
возможный мир - это комбинация значений всех переменных.
Распределение вероятности - это функция, которая сопоставляет значениям
переменных модели числа от 0 до 1. Поэтому распределение можно представить
фактором и рассматривать распределение вероятности как таблицу, в которой
строки соответствуют всем возможным комбинациям переменных. В качестве
примера мы будем использовать уже привычный пример с определением
подлинности картины, в котором есть три переменные: Тема, Размер и Яркость. На
рис. 10.1 воспроизведена байесовская сеть для этого примера вместе с условными
распределениями вероятности.
Значения вероятности Темы
Тема
Люди
0Я
Ландшафт
0.2
Значения вероятности Размера
при условии Темы
Значения вероятности Яркости
при условии Темы
Тема
Люди
Ландшафт
Малая
0.25
0.25
Размер
Средняя Большая
0.25 0.5
0.5 0,25
Тема
Яркость
Темная Яркая
Люди 0.8 0.2
Ландшафт 0.3 0.7
Рис. 10.1. Повтор байесовской сети Тема-Размер-Яркость из главы 5
Каждое условное распределение вероятности в этой сети можно представить
фактором, как в табл. 10.1. На самом деле, в табл. 10.1 как раз и представлено
316
Тема
Яркость
Размер

10.1. Факторы
Р(Размер | Тема) - распределение Размера при условии Темы, изображенное на
рис. 10.1. Так, согласно этому условному распределению, вероятность Р(Размер =
Малая | Тема = Люди) равна 0.25. Соответственно в табл. 10.1 в строке Тема =
Люди, Размер = Малая мы видим число 0.25. А в табл. 10.2 показан фактор,
соответствующий распределению Р(Тема). Поскольку у переменной Тема нет
родителей, то в этой таблице есть только столбец для самой Темы. Наконец, в табл. 10.3
приведен фактор, соответствующий Р(Яркость | Тема).
Таблица 10.2. Фактор, соответствующий Р(Тема)
Тема
Люди
Ландшафт
0.8
0.2
Таблица 10.3. Фактор, соответствующий Р(Яркость | Тема)
Тема
Люди
Люди
Ландшафт
Ландшафт
Яркость
Темная
Яркая
Темная
Яркая
0.8
0.2
0.3
0.7
Размышляя о стоимости представления и использования фактора, важно
принимать во внимание число строк в факторе. Для подсчета числа строк можно
воспользоваться простой формулой: перемножить количество различных значений
каждой переменной, от которой зависит фактор. Например, в табл. 10.2 есть одна
строка для каждого значения Темы, т. е. всего две строки. А в табл. 10.1 имеются
строке для каждой комбинации значений Темы и Размера. Поскольку число таких
комбинаций равно 2 х 3, то всего мы имеем шесть строк.
Примечание. Все факторы, которые мы видели до сих пор, представляли собой
условные распределения вероятности, но бывают и более общие факторы. Например, при
выполнении алгоритма исключения переменных создаются различные факторы,
которым не соответствует никакое условное распределение. Они могут представлять
произвольную функцию, отображающую значения переменных на вещественное число. Кроме
того, хотя значение фактора - всегда вещественное число, оно не обязано быть
вероятностью, т. е. находиться в диапазоне от 0 до 1. Например, в марковской сети факторы
выводятся из потенциалов и могут быть больше 1.
Теперь мы понимаем, что такое факторы. Но какое отношение они имеют к
факторизации распределения вероятности?
317

Глава 10. Факторные алгоритмы вывода
10.1.2. Факторизация распределения
вероятности с помощью цепного правила
Цепное правило (см. главу 9) - ключ к пониманию факторов и факторных
алгоритмов. Напомним, что это правило позволяет вычислять совместную
вероятность значений нескольких переменных в виде произведения условных
вероятностей. Цепное правило тесно связано с байесовскими сетями и принципиально
важно для понимания того, как байесовская сеть определяет распределение
вероятности.
Рассмотрим, к примеру, всего две переменные: Тема и Яркость. Цепное правило
говорит, что вероятность того, что картина яркая и изображает людей,
вычисляется по формуле
Р(Тема = Люди, Яркость = Яркая) =
Р(Тема = Люди) Р(Яркость = Яркая | Тема = Люди) =
0.8x0.2 = 0.16
Откуда взялись числа 0.8 и 0.2? А из факторов. Точнее, 0.8 происходит из
фактора для Р(Тема), показанного в табл. 10.2, в строке, где Тема принимает значение
Люди. Аналогично 0.2 берется из фактора для Р(Яркость | Тема), показанного в
табл. 10.3, из строки, где Тема принимает значение Люди, а Яркость - значение
Яркая.
Строки выделены
цветом фона
Строки выделены
шрифтом
Получить значения из строк
нужного цвета и с нужным шрифтом
Тема
Люди
Ландшафт
0.8
0.2
Тема
Люди
ЛЮДИ
Ландшафт
Ландшафт
Яркость
Темная
ЯРКАЯ
Темная
Яркая
0.8
0.2
0,3
0.7
Тема
Люди
ЛЮДИ
Ландшафт
Ландшафт
Яркость
Темная
ЯРКАЯ
Темная
Яркая
0.8x0.8 = 0.64
0.8x0.2 = 0.16
0.2x0.3 = 0.06
0.2x0.7 = 0.14
Рис. 10.2. Факторное произведение. Строки показаны так,
чтобы было видно, откуда берутся числа в результирующем факторе.
Например, строка результирующего фактора для комбинации (Люди, Яркая)
получена из строки Люди (темный фон) первого фактора
и строки (Люди, Яркая) (заглавными буквами) второго фактора
Подобные вычисления можно выполнить для всех значений Темы и Яркости,
беря числа из соответствующих строк факторов. На рис. 10.2 показан результат
перемножения двух факторов, который часто называют факторным произведением.
Идея факторного произведения в том, чтобы перемножить числа,
ассоциированные со строками, в которых переменные принимают одинаковые значения. Но
некоторые переменные встречаются только в одном факторе. В строке результирую-
318

10.1. Факторы
щего фактора упоминаются (а) все переменные, встречающиеся в обоих факторах,
(Ь) все переменные, встречающиеся только в первом факторе, (с) все переменные,
встречающиеся только во втором факторе. Чтобы получить число,
ассоциированное со строкой результирующего фактора, нужно найти строку в первом факторе
с одинаковыми значениями переменных (а) и (Ь) и строку во втором факторе с
одинаковыми значениями переменных (а) и (с), а затем перемножить числа,
ассоциированные с этими строками. Рассмотрим эту процедуру на примере факторов
для Р(Тема) и Р(Яркость | Тема). Для перемножения этих факторов мы поступаем
следующим образом.
1. Создадим новый фактор от всех переменных, встречающихся в любом из
двух входных сомножителей. Его строки соответствуют всем возможным
комбинациям значений этих переменных. В нашем примере переменными
являются Тема и Яркость, а строками - (Люди, Темная), (Люди, Светлая),
(Ландшафт, Темная) и (Ландшафт, Светлая).
Для каждой строки результирующего фактора, например (Люди,
Светлая), найдем совместимую с ней строку первого сомножителя и возьмем
число из этой строки. В нашем примере переменная Тема в
результирующей строке принимает значение Люди, поэтому в исходном факторе ищем
строку, в которой Тема = Люди. На рисунке применяется цветовое и
шрифтовое кодирование. Строка Тема = Люди имеет темный фон, поэтому фон
строки (Люди, Светлая) в результирующем факторе тоже темный. В
исходной строке находится число 0.8.
2. Так же поступаем со вторым фактором: находим строку, совместимую со
строкой результирующего фактора, и берем из нее число. В данном случае
строке (Люди, Светлая) во втором факторе соответствует строка,
набранная заглавными буквами. В ней число равно 0.2.
Зная, как перемножить два фактора, мы можем перемножить сколько угодно
факторов. В главе 9 мы видели, что распределение вероятности, определяемое
байесовской сетью, можно выразить с помощью цепного правила. Чтобы сделать
формулы компактными, я буду использовать следующие сокращения:
• Т - Тема;
• Р - Размер;
• Я - Яркость.
В нашем примере можно написать:
Р(Т, Р, Я) = Р(Т) Р(Р | Т) Р(Я | Т)
В этой формуле не заданы конкретные значения Темы, Размера и Яркости. Она
применима к любым значениям этих переменных. Поскольку Р(Тема), Р(Размер |
Тема) и Р(Яркость | Тема) - факторы, эта формула означает, что совместное
распределение Темы, Размера и Яркости можно выразить в виде произведения трех
факторов, что показано в табл. 10.4.
319

Глава 10. Факторные алгоритмы вывода
Таблица 10.4. Совместное распределение вероятности Темы, Размера и Яркости
вычисляется в виде произведения трех факторов. В каждой строке перемножаются
числа, взятые из соответствующих строк входных факторов
Тема
Люди
Люди
Люди
Люди
Люди
Люди
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Размер
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Средняя
Средняя
Большая
Большая
Яркость
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
0.8x0.25x0.8 = 0.16
0.8x0.25x0.2 = 0.04
0.8x0.5x0.8 = 0.32
0.8x0.25x0.2 = 0.08
0.8x0.25x0.8 = 0.16
0.8x0.25x0.2 = 0.04
0.2x0.25x0.3 = 0.015
0.2x0.5x0.7 = 0.035
0.2x0.25x0.3 = 0.015
0.2x0.25x0.7 = 0.035
0.2x0.5x0.3 = 0.03
0.2x0.25x0.7 = 0.07
Мы видели, что число строк в факторе равно произведению числа значений
каждой переменной. Так, в этом факторе, представляющем совместное
распределение, переменная Тема принимает два значения, Размер - три, а Яркость - два,
поэтому в итоге получается 2x3x2 = 12 строк. В общем случае, число строк
экспоненциально зависит от числа переменных. А это значит, что для сколько-нибудь
больших сетей размер фактора, описывающего совместное распределение,
слишком велик для представления и рассуждений.
Целое число можно разложить в произведение меньших чисел - факторизо-
вать. То же самое справедливо для распределений вероятности. Как и в случае
целых чисел, производить умножение и деление проще, когда известны
сомножители, которые гораздо меньше исходного числа. Вероятностный вывод куда проще
при использовании факторов от небольшого множества переменных, чем при
использовании полного совместного распределения, которое экспоненциально
растет с увеличением числа переменных. В этом и заключается объяснение важности
факторов для вероятностного вывода.
10.1.3. Задание запросов с факторами
с помощью правила полной вероятности
Выше мы видели, как выразить совместное распределение вероятности в виде
произведения факторов. Следующий шаг - представить с помощью факторов
ответ на запрос. Ключом тут является правило полной вероятности.
320

10.1. Факторы
Запросы без фактов
Для начала предположим, что никаких фактов нет. Нас интересует
распределение вероятности одной переменной, скажем Яркости. Начинаем с совместного
распределения вероятности; в нашем примере оно приведено в табл. 10.4. Правило
полной вероятности гласит, что для того чтобы узнать вероятность конкретного
значения Яркости, скажем Яркая, нужно сложить вероятности всех
встречающихся в совместном распределении случаев, для которых Яркость принимает это
значение. Это показано в табл. 10.5, где приведено то же самое совместное
распределение, но строки, в которых Яркость = Яркая, выделены полужирным шрифтом.
Вероятность, что Яркость = Яркая, равна сумме чисел в этих строках, т. е.
Р(Яркость = Яркая) = 0.04 + 0.08 + 0.04 + 0.035 + 0.035 + 0.07 = 0.3
Таблица 10.5. Совместное распределение вероятности Темы, Размера и Яркости.
Строки, для которых Яркость = Яркая, выделены полужирным шрифтом.
Р(Яркость = Яркая) равна сумме чисел в этих строках
Тема
Люди
Люди
Люди
Люди
Люди
Люди
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Размер
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Средняя
Средняя
Большая
Большая
Яркость
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
0.16
0.04
0.32
0.08
0.16
0.04
0.015
0.035
0.015
0.035
0.03
0.07
Точно так же следует поступить для вычисления вероятности того, что
Яркость = Темная: просуммировать числа в строках, где Яркость принимает значение
Темная (они набраны светлым шрифтом). Из этих двух чисел получается фактор,
показанный в табл. 10.6.
Таблица 10-6. Фактор, представляющий распределение вероятности Яркости. Каждая
строка является суммой значений в соответствующих строках совместного распределения.
Строка, в которой Яркость = Яркая, выделена полужирным шрифтом, чтобы подчеркнуть,
что она получена суммированием чисел в полужирных строках табл. 10.5
Яркость
Темная
Яркая
0.16 + 0.32 + 0.16 + 0.015 + 0.015 + 0.03 = 0.7
0.04 + 0.08 + 0.04 + 0.035 + 0.035 + 0.07 = 0.3
321

Глава 10. Факторные алгоритмы вывода
У только что проделанной нами операции есть два общеупотребительных
названия. Первое - факторная сумма. Только следует понимать, что сумма здесь
означает не сложение двух факторов, а сложение чисел в строках одного фактора
для получения нового - более простого - фактора. Выполняя такое
суммирование, мы исключаем некоторые переменные из результирующего фактора - в
нашем случае переменные Тема и Размер. Говорят, что производится суммирование
по этим переменным. Второе название - маргинализация. Получающееся в
результате распределение Яркости называется маргинальным, в отличие от исходного
совместного распределения. Я не буду употреблять термин «маргинализация», но
само понятие факторной суммы не раз будет встречаться при обсуждении
вероятностного вывода.
Мы можем записать эту идею в виде математической формулы. Факторная
сумма обозначается греческой буквой £. Тот факт, что Р(Тема, Размер, Яркость)
суммируется по Теме и Размеру, записывается так:
Р(Я) = 1трР(Т,Р,Я)
В предыдущем разделе мы видели, что
Р(Т, Р, Я) = Р(Т) Р(Р | Т) Р(Я | Т)
Объединяя оба равенства, получаем
Р(Я) = 2тр Р(Т) Р(Р | Т) Р(Я | Т)
Мы выразили ответ на запрос в виде выражения, содержащего произведения и
суммы факторов. Оно называется выражением в виде суммы произведений.
Числами в результирующем факторе будут суммы произведений чисел в исходных
факторах. Факторные алгоритмы вывода для получения ответа на запрос
манипулируют такими суммами произведений.
Запросы с фактами
А что, если добавить факты? Допустим, мы знаем, что Яркость = Яркая, и хотим
запросить апостериорную вероятность Темы, т. е. вычислить Р(Тема | Яркость =
Яркая). Для этой цели проще всего ввести новые факторы, представляющие
известные факты.
Как было сказано в главе 4, для применения условий в виде фактов нужно
вычеркнуть все возможные миры, несовместимые с фактами, т. е. присвоить им
вероятности 0. Для этого можно создать фактор, который сопоставляет 0 состояниям,
несовместимым с фактами. В нашем примере фактор для представления факта
Яркость = Яркая показан в табл. 10.7
Таблица 10.7. Фактор для представления факта Яркость = Яркая
Яркость
Темная I 0
Яркая 1
322

10.1. Факторы
Каков эффект этого фактора? Если умножить один фактор на другой, то во всех
строках, где Яркость принимала значение Темная, окажется число 0, а остальные
строки не изменятся. По существу, мы вычеркиваем из совместного
распределения строки, в которых Яркость равна Темная, оставляя прочие без изменения.
Если назвать этот фактор Ея, то получится такая сумма произведений:
Р(Т, Я = Яркая) = Етя Р(Т) Р(Я | Т) Р(Р | Т) ЕЯ(Я)
В табл. 10.8 показано совместное распределение, являющееся произведением
Р(Тема), Р(Яркость | Тема), Р(Размер | Тема), умноженным на фактор Е(Яркость =
Яркая). Обратите внимание, что во всех строках, несовместимых с фактом,
стоит 0; эти строки «вычеркнуты».
Таблица 10.8. Совместное распределение вероятности Темы, Размера и Яркости
умноженное на фактор, представляющий факт Яркость = Яркая
Тема
Люди
Люди
Люди
Люди
Люди
Люди
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Ландшафт
Размер
Малая
Малая
Средняя
Средняя
Большая
Большая
Малая
Малая
Средняя
Средняя
Большая
Большая
Яркость
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
Темная
Яркая
0.16x0 = 0
0.04 х 1 = 0.04
0.32x0 = 0
0.08x1 =0.08
0.16x0 = 0
0.04 х 1 = 0.04
0.015x0 = 0
0.035x1 =0.035
0.015x0 = 0
0.035x1 =0.035
0.03x0 = 0
0.07 х 1 = 0.07
Следующий шаг - суммирование по переменным, не встречающимся в запросе:
Размер и Яркость. Для каждого значения Темы мы складываем все строки фактора
из табл. 10.8, в которых число отлично от 0. В табл. 10.9 показан результирующий
фактор, представляющий распределение вероятности Р(Тема, Яркость = Яркая).
Таблица 10.9. Результат суммирования по Размеру и Яркости фактора из табл. 10.8
Тема
Люди
Ландшафт
0.04 + 0.8 + 0.04 = 0.16
0.035 + 0.035 + 0.07 = 0.14
Внимательно взглянув на этот фактор, мы увидим, что он не точно отвечает на
запрос. Мы хотели получить условную вероятность Р(Тема | Яркость = Яркая);
323

Глава 10. Факторные алгоритмы вывода
например, вероятность, что на картине изображены люди при условии, что она
яркая. Однако фактор дает совместное распределение Р(Тема, Яркость = Яркая),
из которого можно узнать, какова вероятность, что на картине изображены люди
и она яркая.
Но это легко исправить. Распределение вероятности Р(Тема, Яркость =
Яркая) - это ненормированный ответ на наш запрос. Легко видеть, что сумма чисел
в табл. 10.9 не равна 1, но их отношение равно 16:14. Чтобы получить ответ на
запрос, мы нормируем фактор, так чтобы сумма была равна 1, а отношение
сохранилось. Окончательный результат показан в табл. 10.10.
Таблица 10.10. Распределение Р(Тема | Яркость = Яркая),
полученное нормировкой фактора в табл. 10.9
Тема
Люди
Ландшафт
0.16/(0.16 + 0.14) = 0.5333
0.14/(0.16 + 0.14) = 0.4667
Итак, мы разобрались в том, что такое факторы, узнали об операциях
умножения и суммирования факторов и видели, как можно выразить ответ на запрос в
виде суммы произведений. Сейчас может показаться, что для получения ответов
на запросы нужно перемножить все факторы и создать совместное распределение.
Но размер полного совместного распределения экспоненциально зависит от
количества переменных в модели. Поэтому основная цель факторных алгоритмов
вывода - избежать создания полного распределения и работать с более компактными
представлениями. Как это делается, мы начнем изучать в следующем разделе.
10.2. Алгоритм исключения
переменных
В предыдущем разделе мы видели, что ответ на запрос можно выразить в виде
суммы произведений факторов. Алгоритм исключения переменных (ИП)
манипулирует такими выражениями. Базовая операция такова: по одной исключать из
выражения не входящие в запрос переменные, применяя простые алгебраические
преобразования. Отсюда и название алгоритма. Алгоритм ИП является точным,
поскольку для преобразования выражений в нем применяются только правила
алгебры.
Хотя исключение переменных, по сути своей, алгебраический алгоритм, его
можно интерпретировать и графически. Графическое представление дает
интуитивно понятное объяснение процедуры исключения и позволяет оценить
сложность алгоритма. А алгебраическое представление важно для понимания деталей
работы алгоритма. Поэтому сначала я расскажу о графическом представлении,
чтобы вы поняли общее устройство алгоритма, а затем перейду к
алгебраическому.
324

10.2. Алгоритм исключения переменных
1. Исходная байесовская сеть
2. В начальном графе ИП ребрами соединены
все пары вершин, упоминаемых в одном и
том же факторе
3. Граф ИП после исключения
Материала
Граф ИП после исключения Темы;
добавлено ребро между Размером и
Яркостью, потому что обе переменные
встречаются в факторе, образовавшемся
после исключения Темы
5. Граф ИП после исключения
Яркости
Размер
6. Полный индуцированный
граф
Материал
Рис. 10.3. Построение графа ИП путем исключения переменных
70.2.7. Графическая интерпретация ИП
Графическая интерпретация ИП интуитивно понятно, для ее объяснения
достаточно нескольких предложений и картинки. В состав запроса входит одна или
несколько переменных. Мы исключаем все переменные, кроме этих, в определенном
порядке. Исключая переменную, мы находим все факторы, в которых она
упоминается, и порождаем новый фактор. Цель создаваемых графов - следить, какие
переменные встречаются в одном и том же факторе на каком-то шаге вычисления.
На рис. 10.3 изображена байесовская сеть, содержащая переменные Тема,
Размер, Яркость и Материал. В запрос входит переменная Размер, а исключаются
переменные Материал, Тема и Яркость - в указанном порядке. Этот порядок выбран
произвольно. Можно использовать любой порядок исключения, но, как мы скоро
увидим, он небезразличен. На рис. 10.3 показаны следующие шаги.
1. На шаге 1 просто копируется исходная байесовская сеть.
2. Имея исходную сеть, мы строим начальный граф ИП. В нем имеется
вершина для каждой вершины сети, а две вершины, упоминаемые в одном
и том же факторе, соединены неориентированным ребром. Сюда входят
ребра между каждым родителем и потомком в байесовской сети, а также
325
Тема
Материал
Размер
Яркость
Тема
Тема
Размер
Яркость
Размер
Яркость
Тема
Размер
Яркость
Размер
Яркость

Глава 10. Факторные алгоритмы вывода
ребра между родителями одного и того же потомка. Например, Тема и
Материал являются родителями Яркости и оба упоминаются в факторе,
который представляет условное распределение вероятности Яркости, поэтому
между ними проведено ребро.
3. Исключаем переменные по одной. Если некоторая переменная
исключается, то добавляем ребро между любыми двумя переменными, которые были
соединены с исключенной переменной, если между ними еще нет ребра.
Обе эти переменные войдут в фактор, созданный в процессе исключения.
А раз так, то они должны быть соединены ребром.
В нашем примере первой исключается переменная Материал. Поскольку
вершины Тема и Яркость уже соединены, новые ребра не добавляются.
4. Затем исключается переменная Тема. Поскольку Размер и Яркость
соединены Темой, то они соединяются между собой в результирующем графе.
5. Последней исключается переменная Яркость, новые ребра при этом не
добавляются, и остается только переменная Размер.
6. Наконец, помещаем в один граф все ребра, входящие хотя бы в один из
промежуточных графов. Этот граф называется графом, индуцированным
исключением переменных Материал, Тема и Яркость, или просто
индуцированным графом.
Терминология. Начальный граф ИП называется моральным графом. Такое название
объясняется тем, что для его получения мы «женим» родителей одного и то же ребенка,
соединяя соответствующие вершины.
Оценка сложности алгоритма
Графическая интерпретация полезна тем, что позволяет оценить сложность
алгоритма. Алгоритм ИП включает много операций сложения и умножения. Их
количество тесно связано с размерами создаваемых факторов. Индуцированный
граф дает неплохое представление о размерах факторов, потому что говорит, какие
переменные входят в один и тот же фактор.
Анализ основан на графическом понятии клики. Кликой называется множество
вершин такое, что каждые две соединены ребром. Если некое множество вершин
образует клику в индуцированном графе, то в какой-то момент все эти вершины
должны встретиться в одном факторе. На самом деле, нетрудно доказать, что
максимальное число переменных, встречающихся в одном факторе, в точности равно
размеру наибольшей клики в индуцированном графе.
Например, в индуцированном графе в нижней части рис. 10.3 переменные Тема,
Размер и Яркость соединены друг с другом и, следовательно, образуют клику.
Все они встречаются в промежуточном факторе, порожденном при исключении
Темы, - после перемножения факторов, в которых упоминается Тема, но до
суммирования по Теме с целью исключения ее из результата. Аналогично соединены
друг с другом Тема, Материал и Яркость, и все они встречаются в условном
распределении Яркости. Однако Размер и Материал не соединены, так что Размер,
326

10.2. Алгоритм исключения переменных
Тема, Яркость и Материал не образуют клику. И действительно, ни на каком шаге
алгоритма не появляется фактор, в котором одновременно упоминались бы
Размер и Материал.
Итак, мы знаем, что максимальное число переменных, встречающихся в одном
факторе, равно размеру наибольшей клики. И насколько же велик этот фактор?
Вспомним формулу: чтобы узнать количество строк в факторе, нужно
перемножить число значений всех входящих в него переменных. Результат
экспоненциально зависит от количества переменных. Таки образом, получаем следующий
ключевой результат: сложность алгоритма ИП при заданном порядке исключения
экспоненциально зависит от размера наибольшей клики в графе, индуцированном
этим порядком.
Альтернативные порядки исключения
Приведенный выше анализ был основан на конкретном порядке исключения.
Играет ли роль этот порядок? Да, и очень большую. В индуцированном графе на
рис. 10.3 есть две клики размера 3, т. е. размер наибольшей клики равен 3.
На рис. 10.4 показаны графы, индуцированные двумя другими порядками
исключения. В левом наибольшая клика имеет размер 4, поскольку все переменные
соединены. Это означает, что при таком порядке сложность ИП оказалась бы
выше. В случае порядка, показанного справа, не пришлось добавлять никаких
новых ребер. И хотя размер наибольшей клики, как и раньше, равен 3, существует
лишь одна клика такого размера, поэтому исключение переменных в таком
порядке обойдется дешевле.
Если первой исключается
Тема, то Размер и Материал
будут соединены ребром, что
приводит к клике размера 4
Если первым исключается Материал,
затем Яркость, а затем Тема, то новые
ребра не добавляются, что приводит к
клике размера 3
Рис. 10.4. Графы, индуцированные двумя другими порядками исключения.
Слева: Тема-Материал-Яркость. Справа: Материал-Яркость-Тема
Последний порядок исключения интересен тем, что не добавляется ни одно
ребро. Добавляя ребро, мы включаем соединенные им переменные в один фактор.
В результате факторы увеличиваются, и вывод становится более накладным. Если
существует порядок исключения, при котором ребра не добавляются, то ничего
лучшего добиться нельзя, т. к. факторы, порождаемые в процессе вывода, не привносят
никаких пар переменных, которые бы не входили в какой-то фактор с самого начала.
327
Тема
Тема
Материал
Материал
Размер
Яркость
Размер
Яркость

Глава 10. Факторные алгоритмы вывода
Возникает естественный вопрос: всегда ли существует порядок исключения, не
добавляющий новых ребер. Ответ связан с понятием триангуляции. Граф
называется триангулированным, если все циклы в нем являются «треугольниками»; на
врезке ниже объясняется точный смысл этой фразы. Если начальный граф ИП
триангулирован, то существует по меньшей мере один порядок исключения, не
требующий добавления ребер. Наоборот, если начальный граф ИП не
триангулирован, то при любом порядке исключения придется добавить хотя бы одно
ребро. Один из способов (не единственный) добиться того, чтобы начальный граф
ИП не был триангулирован, - начать с сети, в которой вообще нет циклов. Таким
образом, если в начальном графе ИП нет циклов, то всегда можно организовать
исключение, начав с концевых вершин и двигаясь внутрь графа, так что не будет
добавлено ни одного ребра.
Триангулированные графы
Граф называется триангулированным, если все циклы в нем составлены из
треугольников. Строго говоря, это означает, что в графе не существует цикла длины 4
или более, в котором имеются две несмежные вершины, не соединенные поперечным
ребром. Проще показать это на картинке.
Рис. Триангулированные графы. Левый граф содержит
цикл A-B-D-C, в котором нет поперечного ребра, поэтому он
не является триангулированным. В правом графе этот цикл
содержит поперечное ребро В-С, поэтому граф триангулирован.
И действительно, он состоит из двух треугольников А-В-С и B-C-D
Почему от триангуляции зависит, можно ли исключить переменные, не добавляя
ребер? Из левого графа видно, что если сначала исключить А или D, то придется
добавить ребро В-С, а если сначала исключить В или С, то будет добавлено ребро A-D.
Как ни поступить, ребро добавляется. В правом графе можно сначала исключить А,
не добавив новое ребро. В этот момент останется треугольник B-C-D, в котором все
вершины соединены между собой, поэтому при любом порядке их исключения новых
ребер не возникнет.
Это общий принцип. В нетриангулированном графе существует цикл длины 4 или
более без поперечного ребра. При первом же исключении вершины из этого цикла
придется добавить поперечное ребро. С другом стороны, в триангулированном графе
всегда найдется вершина, начав с которой мы не добавим ребро. После исключения
328
А
В
С
D
D
В
С
А

10.2. Алгоритм исключения переменных
этой вершины граф останется триангулированным, поэтому можно будет продолжить
исключение, не добавляя ребер. Мы приходим к выводу, что порядок исключения
без добавления ребер существует тогда и только тогда, когда начальный граф ИП
триангулирован.
Что отсюда следует? Если граф триангулирован, то факторы, порождаемые в
процессе вывода, будут не больше факторов, существовавших в самом начале.
Поэтому если вам удалось изначально представить модель должны образом, то вывод
будет эффективным. С другой стороны, если граф не триангулирован, то в процессе
вывода могут создаваться факторы гораздо большего размера.
Раз порядок исключения столь важен, то как найти наилучший? К сожалению,
это вычислительно трудная задача, сложность которой в общем случае
экспоненциально зависит от размера наибольшей клики при оптимальном порядке. Но для
нахождения хорошего порядка можно воспользоваться эвристическими
соображениями. Одна популярная эвристика основана на интуитивно понятном
стремлении по возможности избежать добавления ребер. Поэтому на каждом шаге мы
выбираем ту переменную, исключение которой создаст минимальное число новых
ребер. В Figaro применяется вариант этой эвристики, в котором учитывается еще
количество значений переменных.
70.2.2. Исключение переменных как
алгебраическая операция
В этом разделе подробно объясняется алгоритм ИП. Если детали вам не
интересны, можете, ничего не потеряв, перейти сразу к итоговой части в конце раздела.
Давайте рассмотрим простой пример. Требуется вычислить вероятность Р(Те-
ма, Яркость = Яркая), определенную как следующая сумма произведений:
Р(Т, Я = Яркая) = 2РЯР(Я) Р(Я | Т) Р(Р | Т) ЕЯ(Я)
Распишем фактор Р(Т, Я = Яркая), явно выписав вычисления каждого
слагаемого. В символьном виде вычисления показаны в табл. 10.11, а в числовом -
в табл. 10.12.
Таблица 10.11. Фактор для запроса Р(Яркость) с явно выписанными вычислениями
каждого слагаемого. Поскольку известен факт Яркость = Яркая, во всех строках, где
Яркость = Темная, число будет сброшено в 0, поэтому из фактора, описывающего
этот факт, такие строки можно попросту удалить
Тема
Люди
Р(Т = Люди) Р(Я = Яркая | Т = Люди) Р(Р = Малая | Т = Люди) ЕЯ(Я = Яркая) +
Р(Т = Люди) Р(Я = Яркая | Т = Люди) Р(Р = Средняя | Т = Люди) ЕЯ(Я = Яркая) +
Р(Т = Люди) Р(Я = Яркая | Т = Люди) Р(Р = Большая | Т = Люди) ЕЯ(Я = Яркая) +
Р(Т = Люди) Р(Я = Темная | Т = Люди) Р(Р = Малая | Т = Люди) ЕЯ(Я = Темная) +
Р(Т = Люди) Р(Я = Темная | Т = Люди) Р(Р = Средняя | Т = Люди) ЕЯ(Я = Темная) +
Р(Т = Люди) Р(Я = Темная | Т = Люди) Р(Р = Большая | Т = Люди) ЕЯ(Я = Темная)
329

Глава 10. Факторные алгоритмы вывода
Тема
Ландшафт
Р(1 =
Р(Т =
Р(Т =
Р(Т =
Р(Т =
Р(Т =
= Ланд.)Р(Я =
= Ланд.)Р(Я =
= Ланд.)Р(Я =
= Ланд.)Р(Я =
= Ланд.)Р(Я =
= Ланд.)Р(Я =
= Яркая | Т = Ланд.) Р(Р = Малая | Т = Ланд.) ЕЯ(Я = Яркая) +
= Яркая | Т = Ланд.) Р(Р = Средняя | Т = Ланд.) ЕЯ(Я = Яркая) +
= Яркая | Т = Ланд.) Р(Р = Большая | Т = Ланд.) ЕЯ(Я = Яркая) +
= Темная | Т = Ланд.) Р(Р = Малая | Т = Ланд.) ЕЯ(Я = Темная) +
= Темная | Т = Ланд.) Р(Р = Средняя | Т = Ланд.) ЕЯ(Я = Темная) +
= Темная | Т = Ланд.) Р(Р = Большая | Т = Ланд.) ЕЯ(Я = Темная)
Таблица 10.12. Фактор для Р(Яркость), в котором каждый член заменен числом,
взятым из условных распределений вероятности. Числа набраны разными
шрифтами, чтобы показать из какого фактора они происходят. Набранные
уменьшенным шрифтом числа происходят из Р(Тема), полужирным шрифтом -
из Р(Яркость | Тема), обычным шрифтом - из Р(Размер | Тема), а курсивом - из
Ея(Яркость). Это поможет не запутаться, когда будете следить за вычислениями
Тема
Люди
Ландшафт
0.8 х 0.8 х 0.25 х 1 + 0.8 х 0.8 х 0.25 х 1 + 0.8 х 0.8 х 0.5 х 7 +
0.8 х 0.2 х 0.25 х 0 + 0.8 х 0.2 х 0.5 х 0 + 0.8 х 0.2 х 0.25 х 0
0.2 х 0.3 х 0.25 х 1 + 0.2 х 0.3 х 0.25 х 1 + 0.2 х 0.3 х 0.5 х 1 +
0.2 х 0.7 х 0.25 х 0 + 0.2 х 0.7 х 0.5 х 0 + 0.2 х 0.7 х 0.25 х 0
Алгоритм ИП производит эти вычисления, чтобы исключить одну за другой
переменные, не участвующие в запросе. В нашем примере требуется исключить
переменные Яркость и Размер. Начнем с исключения Яркости. Мы должны
перемножить числа из всех факторов, в которых упоминается Яркость, избегая
умножения на другие числа.
Для этого мы первым делом переставим сомножители в произведениях, так
чтобы числа, происходящие из факторов, в которых упоминается Яркость,
оказались справа, а числа из других факторов - слева. В нашем случае полужирные и
курсивные числа происходят соответственно из Р(Яркость | Тема) и Ея(Яркость),
поэтому смещаются вправо, а остальные числа влево. Это допустимая операция,
потому что умножение коммутативно, т. е. не зависит от порядка сомножителей.
Результат показан в табл. 10.13. Обратите внимание, что полужирные и курсивные
числа в каждом произведении находятся справа.
Таблица 10.13. Суммы произведений для Р(Яркость), в которых сомножители,
происходящие из факторов, где упоминается Яркость, перемещены вправо
Тема
Люди
Ландшафт
0.8 х 0.25 х 0.8 х 1 + 0.8 х 0.25 х 0.8 х 1 + 0.8 х 0.5 х 0.8 х 1 +
0.8 х 0.25 х 0.2 х 0 + 0.8 х 0.5 х 0.2 х 0 + 0.8 х 0.25 х 0.2 х 0
0.2 х 0.25 х 0.3 х 1 + 0.2 х 0.25 х 0.3 х 1 + 0.2 х 0.5 х 0.3 х 1 +
0.2 х 0.25 х 0.7 х 0 + 0.2 х 0.5 х 0.7 х 0 + 0.2 х 0.25 х 0.7 х 0
Важно отметить, что хотя я показал перемещение самих чисел, в табл. 10.13
представлены суммы произведений, выписанные для факторов; если быть точ-
330

10.2. Алгоритм исключения переменных
ным, то, как показывает следующее равенство, мы переместили Р(Я | Т) и ЕЯ(Я)
вправо от факторов, в которых Яркость не упоминается.
Р(Т, Я = Яркая) = 1ряР(Я) Р(Р | Т) Р(Я | Т) ЕЯ(Я)
Следующий шаг - воспользоваться законом дистрибутивности:
axb + axc = ax(b + c)
В нашем случае это означает:
0.8 х 0.25 х 0.8 х 1 + 0.8 х 0.25 х 0.3 х 0 = 0.8 х 0.25 х (0.8 х 1 + 0.3 х 0)
Пользуясь этим законом, мы можем переписать фактор из таблицы 10.13, как
показано в табл. 10.14.
Таблица 10.14. Результат переписывания фактора из табл. 10.13
с выделением внутренних сумм, в которых участвуют только числа
из факторов, где упоминается Размер
Тема
Люди
Ландшафт
0.8 х 0.25 х (0.8 х 1 + 0.2 х0) +
0.8 х 0.25 х (0.8 х 1 + 0.2 х0) +
0.8 х 0.5 х (0.8 х 1 + 0.2 х 0)
0.2 х 0.25 х (0.3 х 1 + 0.7 х 0) +
0.2 х 0.5 х (0.3 х 1 + 0.7 х 0) +
0.2 х 0.25 х (0.3 х 7+0.7x0)
Мы снова выполнили операцию над факторами: выделили внутреннюю сумму,
в которой участвуют только числа из факторов, где упоминается Размер. Это те
числа, которые мы переместили вправо на предыдущем шаге. В терминах
факторов мы создали следующую сумму произведений:
Р(Т, Я = Яркая) = Хр Р(Т) Р(Р | Т) \ Р(Я | Т) ЕЯ(Я)
И последний шаг исключения Яркости состоит в том, чтобы вычислить
внутреннюю сумму произведений, т. е. Хя Р(Я | Т) ЕЯ(Я). Результатом этого
вычисления является фактор. Поскольку вычисление началось с факторов, в которых
встречается Яркость и Тема, и мы просуммировали по Яркости, то в
результирующем факторе осталась только Тема. Этот фактор показан в табл. 10.15.
Таблица 10.15. Фактор, получившийся в результате вычисления
£я Р(Я | Т) ЕЯ(Я). Числа из этого фактора набраны фантазийным шрифтом
Тема
Люди
Ландшафт
0.8 х 1 +0.2x0 = 0.8
0.3 х 7 + 0.7x0 = 0.8
Назовем этот фактор Ря, т. е. фактор, полученный путем исключения Яркости.
Подставив этот фактор в равенство (3), получим:
331

Глава 10. Факторные алгоритмы вывода
P(T)-ZpP(T)P(P|T)F„(T)
И вот наконец-то - перед нами сумма произведений, в которой не упоминается
Яркость. Мы успешно исключили Яркость, и для этого не пришлось перемножать
все факторы.
Краткое изложение алгоритма
Выше я описал процесс во всех скучных деталях, но по существу-то он очень
простой. Вот краткое изложение алгоритма исключения переменной V из суммы
произведений S:
Eliminate(V, S) {
Переместить сомножители из факторов в S, в которых упоминается V, вправо
Произвести суммирование по V, т. е. выделить суммы, включающие только
эти сомножители.
Вычислить внутреннюю сумму произведений, включающую сомножители из
факторов, в которых упоминается V.
Заменить эту сумму произведений в S результирующим фактором
}
Это и есть основная часть алгоритма ИП. Теперь сформулируем алгоритм целиком:
VariableElimination(S) {
Выбрать порядок исключения О, содержащий все переменные, кроме
участвующих в запросе
Для каждой переменной V из О {
Eliminate(V, S)
10.3. Использование алгоритма ИП
Итак, теперь мы знаем, как работает алгоритм ИП, и настало время поговорить о
его практическом использовании. Сначала я скажу несколько слов о механизме
использования ИП в Figaro, отметив различные варианты. Затем обсудим общие
принципы проектирования модели, ориентированной на ИП. И напоследок я
опишу некоторые реальные приложения.
70.3.1. Особенности ИП в Figaro
До сих пор мы рассматривали простые примеры на основе байесовских сетей. Но
вероятностные программы могут быть гораздо сложнее байесовских сетей, они
могут включать дополнительные переменные, структуры данных, команды
управления потоком выполнения и даже рекурсию. К счастью, Figaro берет все
сложности на себя.
ПрОСТеЙШИЙ Вариант ИП В Figaro - алгоритм VariableElimination, С КОТОрЫМ
мы уже не раз встречались. Напомню, что конструктору VariableElimination
передается список целевых переменных, а затем мы опрашиваем созданный экземпляр
алгоритма. Например:
332

10.3. Использование алгоритма ИП
val algorithm = VariableElimination(elementl, element2)
algorithm.start()
println(algorithm.probability(elementl, 0)) <3_©
println(algorithm.probability(elementl, (i: Int) => i > 0)) <]—©
println(algorithm.distribution(elementl) .toList) O—©
println(algorithm.mean(element2)) <3—©
println(algorithm.expectation(element2, (d: Double) => d * d) O—©
© — Печатаем вероятность того, что значение elementl = 0
© — Печатаем вероятность того, что значение elementl больше 0
© — Получаем распределение вероятности elementl в виде потока, а затем преобразуем
его в список для печати
© — Печатаем среднее значение элемента element2 типа Element[Double]
© — Печатаем математическое ожидание квадрата element2
Мы также встречали однострочную нотацию:
VariableElimination.probability(element, 0)
VariableElimination.probability(element, (i: Int) -> i > 0)
Простейший алгоритм ИП, реализованный в Figaro, преобразует
вероятностную программу в гигантскую байесовскую сеть. Для этого должно выполняться
следующее условие: число переменных, потенциально существующих в модели,
конечно. Тем самым исключаются некоторые модели с открытой вселенной, в
которых нет ограничения сверху на число объектов. Исключаются также
рекурсивные модели с неограниченной глубиной рекурсии.
Кроме того, ИП - принципиально дискретный алгоритм, поэтому применение к
непрерывному распределению сопряжено с некоторыми сложностями. Figaro
решает эту проблему, делая выборку из множества значений каждого непрерывного
атомарного элемента. Но коль скоро используется лишь небольшое подмножеств всего
множества значений, ИП перестает быть точным алгоритмом. Однако этого может
оказаться достаточно, особенно если в модели не так много непрерывных элементов.
Если вы хотите придерживаться стандартного алгоритма, можете сразу перейти
к следующему разделу. Но команда Figaro неустанно стремится
усовершенствовать алгоритмы вывода в вероятностном программировании, и алгоритм ИП - не
исключение. Если вы готовы копнуть немного глубже, то сможете
воспользоваться плодами этих трудов.
Один из вариантов ИП, реализованный в Figaro, - так называемый алгоритм
ленивого ИП - ослабляет запрет на неограниченную рекурсию. Полное объяснение
этого алгоритма выходит за рамки книги, но я хочу, чтобы вы знали о его
существовании. На интуитивном уровне главная идея ленивого ИП заключается в том,
чтобы частично расширить модель и вычислить нижнюю и верхнюю границу ответа
на запрос, выполнив ИП для такой расширенной модели. Представьте, к
примеру, программу, которая порождает граф некоторого размера и оценивает какое-то
свойство этого графа. Размер графа может быть не ограничен сверху, поэтому
применить к нему обычный алгоритм ИП невозможно. Однако ленивый алгоритм ИП
мог бы частично расширить модель, породить графы, размер которых не превыша-
333

Глава 10. Факторные алгоритмы вывода
ет заданную верхнюю границу, а затем оценить распределение вероятности
интересующего свойства на таком частичном расширении.
Команда разработчиков Figaro работает также над новой общей системой
факторного вывода - так называемым структурным факторным выводом. В нее
входит и структурный алгоритм ИП. Сейчас он находится в экспериментальном
пакете, но вскоре будет перенесен в основной (возможно, в момент, когда вы читаете
эти строки, это уже произошло). Идея структурного ИП состоит в том, чтобы
воспользоваться структурой вероятностной программы для управления процессом
поиска решения. При каждом расширении цепочки создается подзадача, которая
представляет все элементы, созданные цепной функцией. Все переменные внутри
подзадачи можно исключить в отдельном процессе ИП, работающим только над
этой подзадачей. Одно из основных достоинств такого подхода - тот факт, что
если одна и та же подзадача встречается в задаче несколько раз, то решением,
полученным в первый раз, можно снова воспользоваться в дальнейшем.
70.3.2. Проектирование модели, эффективно
поддерживающей ИП
Как же воспользоваться знаниями об ИП и сложности этого алгоритма при
проектировании моделей? В этом разделе будет предложено несколько советов.
Избегайте слишком большого числа циклов
Первый и самый очевидный совет - по возможности избегать циклов, в
которых нет поперечных ребер. При наличии такого цикла придется рано или поздно
добавить ребро, что увеличит время вывода. Мы видели, что в триангулированной
сети, где каждый цикл длины 4 и более имеет полный набор поперечных ребер,
можно произвести ИП без добавления новых ребер.
Если невозможно обойтись совсем без циклов, то лучше, чтобы циклы были
изолированы, а не расположены близко друг к другу. Сеть, изображенная на
рис. 10.5, плохо приспособлена для И П. Это марковская сеть для восстановления
изображения из главы 5. Здесь показана сеть 4 х 4, но вообще количество пикселей
по каждому измерению могло бы составлять сотни или тысячи.
Пиксель 21
Пиксель 43
Рис. 10.5. Сеть для восстановления изображения из главы 5. Сложность алгоритма
ИП в такой сети экспоненциально зависит от числа пикселей вдоль стороны
334
Пиксель 11
Пиксель 12
Пиксель 13
Пиксель 14
Пиксель 22
Пиксель 23
Пиксель 24
Пиксель 31
Пиксель 32
Пиксель 33
Пиксель 34
Пиксель 41
Пиксель 42
Пиксель 44

10.3. Использование алгоритма ИП
К сожалению, вне зависимости от выбранного порядка исключения
невозможно избежать добавления ребер, создающих клику, размер которой равен числу
пикселей вдоль короткой стороны изображения. Сложность ИП
экспоненциально зависит от размера сетки. Поэтому, хотя в принципе ИП для подобных сетей
работает, на практике он занимает недопустимо много времени.
Разлагайте условные распределения вероятности
с большим числом родителей
Еще одна причина увеличения стоимости ИП - размер начальных факторов.
Даже если новые вершины не создаются, алгоритм может работать долго, если
имеются большие факторы. Если начальные факторы происходят из условного
распределения вероятности, то число переменных, упоминаемых в одном
условном распределении, равно числу родителей плюс один (для потомка). Это
означает, что размер фактора экспоненциально зависит от числа родителей. Поэтому
число родителей следует минимизировать.
Практический пример такой ситуации дают элементы Apply. Figaro позволяет
передавать конструктору Apply до пяти аргументов. Функции с пятью
аргументами соответствует фактор от шести переменных. Если каждый аргумент может
принимать 10 значений, то существует 100 000 комбинаций значений. Как видим,
факторы растут очень быстро.
Справиться с элементом Apply, можно, разложив его на несколько функций.
Пусть, например, требуется сложить четыре биномиальных элемента. Можно
было бы написать:
val х =
Apply(Binomial(10, 0.1), Binomial(10, 0.2),
Binomial(10, 0.3), Binomial(10, 0.4),
(xl: Int, x2: Int, x3: Int, x4: Int) => xl + x2 + x3 + x4)
Каждый элемент Binomial может принимать И значений (от 0 до 10), поэтому
существует 14 641 комбинаций значений аргументов, что приводит к большому
фактору. Лучше было бы разложить этот код на три сложения по два аргумента в каждом:
val xl2 = Apply(Binomial(10, 0.1), Binomial(10, 0.2),
(xl: Int, x2: Int) => xl + x2)
val x34 = Apply(Binomial(10, 0.3), Binomial(10, 0.4),
(x3: Int, x4: Int) => x3 + x4)
val x = Apply(xl2, x34,(xl2: Int, x34: Int) => xl2 + x34)
Здесь имеется три функции с двумя аргументами. Для первых двух функций
число комбинаций аргументов равно 121. xi2 и х34 могут принимать значения
от 0 до 20 (10 + 10), т. е. число комбинаций аргументов третьей функции равно
21x21= 441. Таким образом, суммарное число строк во всех факторах равно 683 -
намного лучше, чем прежние 14 641.
На самом деле, для операций типа сложения, применимых к любому числу
аргументов, существует естественное разложение в последовательность операций
335

Глава 10. Факторные алгоритмы вывода
Apply с двумя аргументами. По счастью, реализовывать это разложение
самостоятельно вам не придется. Figaro уже предлагает решение в виде конструктора
FoidLef t. Он похож на метод Scala f oidLef t, который итеративно применяет
операцию к последовательности элементов. Например, в Scala можно написать:
val х = List (l, 2, 3, 4)
val у = x.foldLeft(0) ((xl: Int, x2: Int) => xl + x2)
и тогда у будет равно сумме всех х. А в Figaro можно использовать аналогичную
КОНСТРУКЦИЮ, ИМПОрТИрОВав Пакет com. era. figaro. library, compound!
FoldLeft(0, (xl: Int, x2: Int) => xl + x2)(
Binomial(10, 0.1), Binomial(10, 0.2),
Binomial(10, 0.3), Binomial(10, 0.4)
)
При этом происходит автоматическое разложение на функции с двумя
аргументами. A Figaro имеются также конструкторы FoidRight и Reduce, аналогичные
методам Scala foldRight И reduce.
Подумайте об инкапсуляции
Если вам доводилось писать на объектно-ориентированном языке, то вы
знакомы с идеей инкапсуляции, которая помогает бороться со сложностью кода за счет
сокрытия внутренних деталей объектов, не важных для остальной части
программы. Оказывается, что инкапсуляция полезна и для ИП. Если объект
предоставляет интерфейс, который скрывает все детали от остальной части модели, то все
внутренние элементы, представляющие детали, можно исключать внутри объекта,
не привлекая к этому модель в целом. Результатом исключения внутренних
элементов является фактор от интерфейса. Он улавливает все, что модели
необходимо знать об объекте.
Ключ к эффективному использованию инкапсуляции - уменьшение размера
интерфейса. Это стандартная рекомендация по объектно-ориентированному
проектированию, так что хороший ОО-проект и эффективный вывод идут рука об
руку. Примером может служить модель диагностики компьютера из главы 7. В ней
мы создали отдельные объекты для Принтера, Сети, Программы и Пользователя.
Каждый объект взаимодействует с моделью путем использования всего одной
переменной. Например, Принтер взаимодействует с моделью через переменную
Состояние. Это означает, что все внутренние детали Принтера, какими бы сложными
они ни были, можно свести к фактору от одной переменной.
Чтобы извлечь максимум из этой идеи, можно воспользоваться иерархической
декомпозицией модели. Например, объект Принтер может содержать вложенные
объекты Подача Бумаги и Тонер, каждый из которых общается с Принтером через
компактный интерфейс, а Принтер, в свою очередь, раскрывает компактный
интерфейс остальной части модели. Ниже показано, как это можно было бы сделать.
Но следует помнить, что если требуется опрашивать элемент или задавать
относящиеся к нему факты, то такой элемент не может быть закрытым. В примере ниже
336

10.3. Использование алгоритма ИП
мы хотим иметь возможность сообщить о состоянии индикатора низкого уровня
тонера, поэтому элемент tonerLowindicatorOn вынесен из вложенного закрытого
Класса Toner И Сделан ОТКРЫТЫМ В Классе Printer!
class Printer {
val powerButtonOn = Flip(0.95) <\—О
private val heavyUsage = Flip(0.5) <J—®
class Toner {
private val adequateColorToner =
If (heavyUsage, Flip(0.8), Flip(0.95)) <\—©
private val adequateBlackToner =
If(heavyUsage, Flip(0.7), Flip(0.9)) <}—©
val adequateToner = adequateColorToner | | adequateBlackToner <]—©
}
private val toner = new Toner <}_ф
val tonerLowindicatorOn = <}—©
If (powerButtonOn,
CPD(toner.adequateToner,
true -> Flip(O.l),
false -> Flip(0.99)),
Constant (false))
val state = <]—©
Apply(powerButtonOn, toner.adequateToner,
(power: Boolean, toner: Boolean) => {
if ( Ipower) out
else if (toner) 'good
else 'poor
})
}
О — Часть интерфейса Printer
© — Инкапсулировано внутри Printer
© — Инкапсулировано внутри Toner
© — Часть интерфейса Toner
© — Вложенный объект, инкапсулированный внутри Printer
© — Вынесено наружу из Toner, чтобы было видно в остальной части модели
© — Часть интерфейса Printer
Получить выгоду от инкапсуляции можно и не прибегая явно к объектно-
ориентированному проектированию. Конструкция цепочки также предоставляет
возможность инкапсуляции. Цепочка подразумевает наличие родителя и потомка,
и применение цепной функции к каждому значению родителя приводит к
созданию набора элементов. При условии, что эти элементы не ссылаются на элементы
вне цепочки, они инкапсулированы внутри цепочки и видны только ее родителю и
потомку. Если же используются какие-то элементы вне цепочки, то они
становятся частью интерфейса. Если таких элементов немного, мы получаем в свое распо-
337

Глава 10. Факторные алгоритмы вывода
ряжение все преимущества инкапсуляции. И алгоритм структурного ИП, кратко
упомянутый в предыдущем разделе, явно применяет такую инкапсуляцию.
Упростите сеть
Если ваша сеть слишком сложна для ИП, а вы хотите использовать ИП,
поскольку это точный алгоритм, то сеть придется упростить. Сделать это можно
путем удаления ребер или вершин. Какие ребра и вершины наименее ценны для
сети и при этом способны дать наибольший эффект в случае удаления, решать
вам. Альтернативой упрощению модели является применение приближенного
алгоритма вывода, но упрощение и использование ИП имеют то преимущество, что
вы получаете заведомо правильный ответ и сами контролируете, что включить в
модель.
70.3.3. Приложения алгоритма ИП
Поскольку ИП - точный алгоритм вычисления вероятностей, то может сложиться
впечатление, что к реальным приложениям со сложными моделями он
неприменим. Однако это не так. ИП широко используется; проблема не в размере модели,
а в правильности ее структуры, и, прежде всего, нас интересует, можно ли
исключать переменные без добавления слишком большого числа ребер в граф ИП, так
чтобы размер наибольшей клики в графе оставался небольшим, а сложность
низкой. В этом разделе описаны две предметные области, в которые ИП применяется
особенно часто.
Распознавание речи
Для применения ИП особенно хорошо подходят скрытые марковские модели
(СММ), с которыми мы познакомились в главе 8. На рис. 10.6 повторен пример
СММ из этой главы. СММ - динамическая вероятностная модель, в которой
переменная состояния изменяется со временем, а наблюдение зависит от
переменной состояния в каждый момент времени.
Скрытые марковские модели используются во многих приложениях, в
частности, для распознавания речи. В этом случае наблюдением является
изменяющийся во времени аудиосигнал, а вывести требуется произнесенное слово.
Уверена(О)
Рис. 10.6. Воспроизведение скрытой марковской модели из главы 8
Каждое слово моделируется в виде СММ, которая проходит через
последовательность состояний, соответствующих типам звуков, издаваемых в ходе
произнесения слова. Например, произнесение слова «саг» может начинаться со звука
338
Уверена(1)
Уверена(2)
Владение(О)
Владение(1)
Владение(2)

10.3. Использование алгоритма ИП
к, за которым следует долгое а и в конце, возможно, р. Сколько времени занимает
произнесение каждого звука, точно не известно. Само наличие некоторых звуков
не гарантируется; так, некоторые люди не произносят р в конце слова саг.
Неопределенный процесс произнесения представлен моделью переходов СММ. А в
модели наблюдения закодирована вероятностная зависимость признаков
аудиосигнала от звуков, произносимых говорящим. Таким образом, произнесение слово
хорошо моделируется с помощью СММ.
Рассуждая о СММ, мы обычно располагаем конкретной последовательностью
наблюдений (например, аудиосигналом определенной длины). Мы можем
«развернуть» СММ в четыре временных интервала и получить байесовскую сеть,
показанную на рис. 10.7.
Рис- 10-7. Байесовская сеть для СММ, развернутой
в четыре временных интервалах
Следует отметить, что в этой сети у каждой вершины не более одного родителя.
Отсюда вытекает, что при построении для нее морального графа нам не придется
соединять вершины. В результате получается граф, показанный на рис. 10.8.
В(0)
ВО)
В(2)
В(3)
Рис. 10.8. Моральный граф для СММ на рис. 10.7
Отметим также, что в графе на рис. 10.8 нет циклов. Как мы уже знаем, отсюда
следует, что существует порядок исключения, не требующий добавления ребер.
Пусть, например, нас интересует апостериорная вероятность У(2). Мы можем
исключать переменные в следующем порядке: В(0), У(0), В(1), У(1), В(2), В(3),
У(3). При таком порядке каждая исключаемая переменная принадлежит ребру
графа и соединена только с одной переменной, поэтому ребра не добавляются.
Следовательно, граф на рис. 10.8 является также индуцированным графом ИП
при таком порядке исключения.
Взглянув на рис. 10.8 внимательнее, мы увидим, что пары соседних скрытых
состояний соединены, и то же можно сказать о каждом скрытом состоянии и
соответствующем ему наблюдении. Эти соединения образуют клики размера 2. Нет
ни одной группы из трех переменных, которые были бы соединены между собой,
поэтому размер наибольшей клики равен 2. И это утверждение не зависит от дли-
339
У(0)
У(1)
У(2)
У(3)
У(0)
У(1)
У(2)
У(3)
В(0)
В(1)
В(2)
В(3)

Глава 10. Факторные алгоритмы вывода
ны последовательности наблюдений и количества развернутых временных шагов.
Следовательно, стоимость ИП в СММ линейно зависит от длины
последовательности наблюдений. Потому-то ИП и является таким эффективным алгоритмом
для СММ.
Для распознавания речи применяется вариант вывода в СММ. Прежде всего,
нас обычно не интересует конкретное скрытое состояние, а хотим мы знать
вероятность последовательности наблюдений для заданной СММ. Предположим,
например, что мы не уверены, произнес ли говорящий слово «саг» или «jar», и хотим
узнать, что вероятнее. Для этого можно было бы воспользоваться байесовским
рассуждением. Напомним (см. главу 9), что в байесовском рассуждении
апостериорная вероятность событий пропорциональна произведению его апостериорной
вероятности на правдоподобие.
• Априорная вероятность могла бы выражать тот факт, что слово саг
встречается чаще, чем jar, поэтому в отсутствие фактов мы склонны считать, что саг
вероятнее. Априорную вероятность часто получают методами машинного
обучения (сравнительная частота употребления слов cam jar). Но в любом
случае к моменту классификации слова априорная вероятность известна.
• Правдоподобие слова саг - это вероятность наблюдаемого аудиосигнала
при условии, что произнесено саг(и аналогично для^яг). Эта вероятность
определяется с помощью СММ для саг и jar соответственно. Иными
словами, чтобы вычислить правдоподобие, мы должны вычислить вероятность
последовательности наблюдений в СММ.
Простой способ решить эту задачу - исключить все переменные и посмотреть
на конечный нормировочный коэффициент. Он равен вероятности наблюдаемого
факта. К сожалению, сейчас в Figaro нет удобного интерфейса для доступа к
нормировочному коэффициенту. Однако имеются другие алгоритмы для вычисления
вероятности факта, которые подробно рассматриваются в главе 12. В частности,
алгоритм вероятности факта, основанный на распространении доверия, ведет себя
практически так же, как ИП для СММ.
Чтобы воспользоваться СММ в таких приложениях, как распознавание речи,
необходимо обучить параметр модели на данных. Данные обычно представляют
собой примеры аудиосигналов вместе с метками произнесенных слов. Обучение
параметров СММ производится с помощью ИП в сочетании с ЕМ-алгоритмом
(expectation-maximization). О применении ЕМ-алгоритма к обучению параметров
модели мы узнаем в главе 12.
Понимание естественного языка
СММ - не единственная структура, приспособленная к алгоритму ИП. При
обработке естественного языка часто используются деревья грамматического
разбора, показывающие, как предложение составлено из частей.
На рис. 10.9 показано дерево разбора для предложения «The cat drank milk»
(Кошка пила молоко). На верхнем уровне разбора находится символ
Предложение, соответствующий предложению в целом. Дерево показывает, как этот символ
340

10.3. Использование алгоритма ИП
разбивается на именные и глагольные группы. Именная группа состоит из слов
«The cat», а глагольная - из слов «drank milk». Таким образом, результатом
грамматического разбора является иерархическая структура предложения.
Предложение
Именная группа
Глагольная группа
Определитель Имя существительное Глагол
The
cat
drank
Именная группа
Имя существительное
milk.
Рис. 10.9. Грамматический разбор предложения «The cat drank milk».
Предложение состоит из именной и глагольной группы. В свою очередь,
глагольная группа состоит из глагола («drank») и именной группы и т. д.
Для понимания естественного языка одной из типичных задач является
нахождение правильного разбора предложения. Грамматикой называется свод правил
построения предложений. Зачастую для применения этих правил требуется
делать выбор. Например, глагольная группа может содержать только глагол (как в
предложении «Кошка села») или глагол с последующей именной группой
(«Кошка пила молоко»). Как оказалось, вероятностные грамматики, которые
описывают такой выбор в терминах вероятностей, эффективно генерируют правильный
разбор. Например, вероятность, что именная группа содержит только глагол,
могла бы быть равна 40 %, тогда как вероятность, что она состоит из глагола и
именной группы, - 60 %.
Один из видов вероятностных грамматик, завоевавший популярность
благодаря простоте и легкости вывода, называется вероятностной контекстно-свободной
грамматикой (ВКСГ). Не буду вдаваться в детали определения ВКСГ, скажу лишь,
что ее основной характеристикой является независимость принятия решений в
различных точках разбора. Это свойство и позволяет эффективно применять
алгоритм ИП к ВКСГ.
Идея заключается в том, чтобы завести для каждой непустой подстроки
предложения переменную, которая будет представлять ассоциированный с этой
подстрокой символ. В нашем примере подстроками будут The, cat, drank, milk, The cat,
cat drank, drank milk, The cat drank, cat drank milk и The cat drank milk. Согласно
правилам ВКСГ, поскольку предложение «The cat drank milk» может быть составлено
из The cat и drank milk, символ, ассоциированный с «The cat drank milk», может
повлиять на символы, ассоциированные с The cat и drank milk. Этот общий процесс
определяет байесовскую сеть, состоящую из всех таких переменных.
341

Глава 10. Факторные алгоритмы вывода
В этой сети мы можем определить разбор предложения, исключая переменные
снизу вверх. Например, можно начать с переменных, соответствующих отдельным
словам. Исключив их, мы затем можем исключить переменные, соответствующие
подстрокам длины 2. По предположению независимости ВКСГ, все они могут
быть исключены по отдельности. Продолжаем действовать таким же образом,
двигаясь вверх по дереву; на каждом этапе после исключения переменных для
всех подстрок длины меньше п можно переходить к независимому исключению
переменных, ассоциированных с подстроками длины п.
Можно доказать, что сложность ИП для ВКСГ кубически зависит от длины
предложения. Для типичных предложений, встречающихся в большинстве
приложений, это вполне приемлемо, поэтому алгоритм широко применяется. Но часто
нас не интересует распределение вероятности символов, а нужно вывести
наиболее вероятный разбор. Эта задача относится к категории запросов наиболее
вероятного объяснения. Мы будем говорить о таких запросах в главе 12 и, в частности,
о применении алгоритма ИП для вычисления наиболее вероятного объяснения,
именно с этой целью он и используется в ВКСГ.
10.4. Распространение доверия
ИП порождает точный результат, если дорабатывает до конца. К сожалению,
иногда нет возможности упростить модель настолько, чтобы можно было выполнить
ИП. Мы видели, что сложность ИП экспоненциально зависит от размера
наибольшей клики в графе, индуцированном порядком исключения. Что, если
добавленных ребер так много, что индуцированный граф становится чрезмерно плотным?
По счастью, приближенный алгоритм распространения доверия (РД) справляется
и с такими случаями. Я не стану объяснять алгоритм РД во всех деталях, но
расскажу об основных принципах, так чтобы вы понимали, как он работает и когда
работает хорошо.
10.4.1. Основные принципы РД
Алгоритм РД опирается на моральный граф (начальный граф ИП), но работает
без добавления ребер. Если наибольшая клика в моральном графе не слишком
велика, то РД будет работать эффективно. Поскольку новые ребра не добавляются,
алгоритму удается избежать создания больших клик, что теоретически позволяет
получать результат значительно быстрее И П. Но у всего есть своя цена.
Добавление ребер необходимо для правильности вывода, а отказ от добавления может
приводить к ошибкам. Тем не менее, можно добиться приблизительно
правильного результата вывода даже без добавления ребер.
В разделе 10.2.1 мы говорили, что если моральный граф триангулирован, то
существует такой порядок исключения, при котором для порождения
индуцированного графа не нужно добавлять ребер. Как выясняется, алгоритм РД в
триангулированном графе дает точный ответ. На самом деле, сложность РД и ИП для
342

10.4. Распространение доверия
триангулированных графов одинакова. Но в случае нетриангулированного графа
РД является приближенным алгоритмом и потенциально значительно
эффективнее И П. Если граф не триангулирован, то алгоритм РД иногда называют
циклическим РД.
РД - это алгоритм передачи сообщений. Понять его проще всего, рассмотрев
работу для триангулированных графов, где алгоритм точен. В таком случае он
преобразует сумму произведений, как и И П. Но делает это не с помощью
алгебраических манипуляций, а путем передачи сообщений между вершинами сети.
Сообщения основаны на факторных операциях. Не стану объяснять детали
вычисления сообщений, но скажу, что они имитируют те же произведения и суммы
факторов, что в алгоритме ИП.
Однако между ИП и РД есть важное различие. РД выполняет эти вычисления
для запросов ко всем переменным сети одновременно. По завершении РД мы
можем получить апостериорную вероятность любой переменной при условии
фактов. В триангулированной сети РД может достичь этого результата за два
прохода по сети, если правильно организовать передачу сообщений. (К сожалению,
как мы увидим, Figaro не способен организовать передачу сообщений нужным
образом, поэтому требуется больше двух проходов, но в принципе алгоритм РД
обладает этим свойством.) Если нас интересует несколько переменных, то РД
дает существенное преимущество по сравнению с ИП - даже в
триангулированных графах.
В триангулированной сети циклическое РД работает точно так же, как ИП, но
не завершается после двух проходов (если передача сообщений организована
правильно), а продолжает работать столько, сколько вы пожелаете. Сообщения
передаются по сети, и, если моральный граф содержит циклы, то сообщения
также передаются по циклу. Число итераций в алгоритме РД произвольно,
мы можем прервать его в любой момент и получить наилучший вычисленный
к этому моменту ответ. В идеале чем больше итераций, тем ближе ответ к
истинному.
10.4.2. Свойства циклического РД
Удивительно, что циклическое РД вообще работает. Как выясняется, причина
связана со статистической физикой. Коротко говоря, алгоритм циклического РД
вычисляет так называемую свободную энергию Бете сети. Не буду объяснять, что
это за зверь, но ее можно использовать для аппроксимации апостериорного
распределения переменных в сети, хотя это не одно и то же.
При достаточно большом числе итераций алгоритм циклического РД во многих
случаях должен сходиться к свободной энергии Бете. К несчастью, невозможно
гарантировать точность аппроксимации апостериорного распределения свободной
энергией Бете. На врезке «О точности циклического РД» приведены два примера
программ. Они почти не отличаются друг от друга, но в одной циклическое РД
дает точный ответ, а в другой - весьма далекий от действительности.
343

Глава 10. Факторные алгоритмы вывода
О точности циклического РД
Рассмотрим две программы.
Пример хорошего циклического РД
val el = Flip(0,5)
val e21: Element[Boolean] = Apply(el, (b: Boolean) => b)
val e31: Element[Boolean] = Apply(e21, (b: Boolean) => b)
val e22: Element[Boolean] = Apply(el, (b: Boolean) => b)
val e32: Element[Boolean] = Apply(e31, (b: Boolean) => b)
val e4: Element[Boolean] - Dist(0.5 -> e31, 0.5 -> e32)
println(BeliefPropagation-probability(e4, true))
printIn(VariableElimination-probability(e4, true))
О — Здесь производится случайный выбор между е31 и е32
Пример плохого циклического РД
II
val el = Flip{0.5)
val e21: Element[Boolean] - Apply(el, (b: Boolean) => b)
val e31: Element[Boolean] = Apply(e21, (b: Boolean) => b)
val e22: Element[Boolean] = Apply(el, (b: Boolean) -> b)
val e32: Element[Boolean] = Apply(e31, (b: Boolean) => b>
val e4: Element[Boolean] = e31 === e32
println(BeliefPropagation,probability(e4, true))
println(VariableElimination.probability(e4, true))
О — e4 равно true тогда и только тогда, когда е31 и е32 равны
Обе программы сначала печатают вычисленную РД оценку вероятности того, что е4
равно true, а затем точный ответ, вычисленный ИП. Чем лучше аппроксимация, тем
ближе должны быть ответы. В случае первой программы оба алгоритма дают ответ
0.5, т. е, аппроксимация идеальна. Во второй программе РД дает 0.5, а ИП -1.0, т. е.
аппроксимация никуда не годится.
Что же происходит? Структурно обе программы одинаковы. Их моральный граф
показан на рисунке ниже. Единственное различие заключается в определении е4.
Рис. Моральный граф в примере
циклического РД. Переменные е31 и е32 соединены
ребром, потому что обе являются родителями е4.
Сеть содержит цикл е1-е21-е31-е32-е22 без
поперечного ребра, т. е. не является
триангулированным графом
344
1
е1
е21
е22
е31
е32
е4

10.5. Использование алгоритма РД
Присмотревшись к этим определениям внимательно, мы увидим, что секрет в
степени взаимодействия между е31 и е32 при определении е4. В первой программе е4
случайно выбирается из е31 и е32. Переменные е31 и е32 никак не взаимодействуют
в ходе выбора е4; если е31 оказывает влияние на е4, потому что выбрана, то е32 не
оказывает никакого влияния, и наоборот. Во второй программе е4 равно true тогда и
только тогда, когда значения е31 и е32 равны. Это крайняя степень взаимодействия
между е31 и е32; достаточно взглянуть на определение е4, чтобы понять, что знание
е31 ничего не говорит о значении е4без знания также и е32. Но на самом деле мы
знаем, чтое31 и е32 обязаны быть равны, потому что обе равны (косвенно) е1. Поэтому е4
обязательно будет равно true, вследствие чего ИП порождает ответ 1.0.
Это подводит нас к главному пункту. Получение правильного ответа в программе 2
требует нелокальных рассуждений: обратной трассировки общей зависимости е31 и
е32 от е1. Алгоритм РД не рассчитан на нелокальные рассуждения. РД хорошо
работает, если эффект дальнодействия мал. Так обстоит дело во многих задачах; влияние
переменных ослабевает с увеличением расстояния. Поэтому РД зачастую хорошо
работает для типичных моделей. На самом-то деле, программа 2 - искусственный
пример. Чтобы добиться нужного эффекта, мне пришлось сделать е21 точно такой, каке1,
ае31 -точно такой, каке21. Реальная модель не была бы определена таким способом.
И еще одно замечание по поводу производительности циклического РД: к
сожалению, сходимость этого алгоритма не гарантируется. Иногда в процессе передачи
сообщений по циклам они продолжают осциллировать. Но такие ситуации -
редкость. Куда неприятнее, что аппроксимация, к которой сходится циклическое РД,
иногда далеко отстоит от истинного апостериорного распределения.
Подведем итог: на практике алгоритм циклического РД работает быстро и во
многих случаях порождает достаточно точные аппроксимации. Но в общем
случае не дается никаких гарантий: ни в части сходимости вообще, ни в части
точности аппроксимации, к которой алгоритм сходится. Поэтому рекомендуется такая
стратегия.
1. Попробовать алгоритм ИП. Если он завершается за разумное время, то мы
получаем точный результат, и это замечательно.
2. Если ИП не завершается достаточно быстро, то попробовать РД.
Проверить, дает ли он разумный ответ. Хочется надеяться, что у вас есть
интуитивные соображения о том, каким должен быть ответ, или хотя бы
контрольные данные, на которых ответ можно проверить.
3. Если РД тоже работает слишком медленно или вы не удовлетворены
полученным результатом, то попробуйте один из выборочных алгоритмов,
обсуждаемых в следующей главе.
10.5. Использование алгоритма РД
Как и в случае ИП, я сначала обсужу варианты использования РД в Figaro, потом
изложу общие принципы эффективного применения РД и закончу перечислением
некоторых практических приложений.
345

Глава 10. Факторные алгоритмы вывода
10.5.1. Особенности РД в Figaro
Основной вопрос при работе с РД - число итераций. Существует три варианта.
• Задать число итераций явно, передав его конструктору алгоритма:
val algorithm = BeliefPropagation(100, element)
algorithm.start()
println(algorithm.probability(element, true))
• Воспользоваться алгоритмом с отсечением по времени. В этом случае мы
не задаем число итераций, а разрешаем алгоритму работать определенное
время. Напомню, как это делается:
val algorithm = BeliefPropagation(element)
algorithm.start()
Thread.sleep(1000) <3—О
println(algorithm.probability(element, 0))
Thread.sleep(1000) <J—О
println(algorithm.probability(element, 0))
algorithm.kill () <]_Q
О — Подождать 1 секунду
© — Исходная оценка ответа
© — Вторая, предположительно улучшенная, оценка ответа
© — По завершении важно уничтожить экземпляр алгоритма с отсечением по
времени, чтобы освободить занятый им поток
• ИспоЛЬЗОВатЬ ОДНОСТРОЧНУЮ НОТаЦИЮ, например Belief
Propagation.probability (element, 0). В этом случае подразумевается число итераций по
умолчанию; чтобы задать другое, нужна длинная форма.
Сколько нужно итераций? В Figaro используется асинхронная форма РД, в
которой порядок передачи сообщений по сети невозможно контролировать. В
общем случае, чтобы информация из одной вершины гарантированно дошла до
другой, число итераций должно быть не меньше расстояния между вершинами.
В разделе 10.4.1 я говорил, что в сети без циклов алгоритм РД может получить
правильный ответ за два прохода по сети. В Figaro это означает, что число
итераций должно быть как минимум равно удвоенному диаметру сети плюс один
(диаметром графа называется максимальное расстояние между парой его вершин).
Отсюда следует, что в Figaro алгоритм РД эффективнее работает в сетях с малым
диаметром.
В случае циклического РД ситуация аналогична. Задание числа итераций
равным диаметру сети эквивалентно одному циклу обхода сети. Поэтому, выбирая
число итераций самостоятельно, умножайте диаметр на желаемое число циклов.
Точность здесь не обязательна, просто задавайте столько итераций, чтобы
сообщения гарантированно обошли сеть несколько раз. Обычное эвристическое
правило - 10 циклов обхода. Если вам не хочется «заморачиваться», пользуйтесь
вариантом алгоритма с отсечением по времени.
346

10.5. Использование алгоритма РД
10.5.2. Проектирование модели, эффективно
поддерживающей РД
Сложность РД зависит от размера наибольшей клики в моральном графе, а не в
индуцированном графе, как в случае ИП. Кроме того, как мы знаем, алгоритм РД
точен, если моральный граф триангулирован. Многие соображения, высказанные
для ИП, сохраняют силу и для РД, но есть и специфика.
Избегайте слишком большого числа циклов
Хотя циклы не оказывают на сложность РД такого влияния, как в случае ИП,
они вносят погрешность, которую, как мы видели, трудно оценить. Чем больше
циклов, тем больше потенциальная погрешность. Поэтому стремление ограничить
число циклов по-прежнему оправдано, хотя и не так важно, как для ИП.
Объединяйте элементы
Один из способов избежать цикла - вручную устранить его, объединив
вершины. Снова рассмотрим худшую из двух программ, приведенных на врезке:
val el = Flip(0.5)
val e21: Element[Boolean] = Apply(el, (b: Boolean) => b)
val e31: Element[Boolean] = Apply(e21, (b: Boolean) => b)
val e22: Element[Boolean] = Apply(el, (b: Boolean) => b)
val e32: Element[Boolean] = Apply(e31, (b: Boolean) => b)
val e4: Element[Boolean] = e31 === e32
Чтобы устранить цикл, мы можем объединить элементы е21 и е22 в один элемент
е2, а элементы е31 и е32 - в элемент еЗ, как показано на рис. 10.10. Поскольку
элементы е21 И е22 булевы, ТО е2 будет Элементом ТИПа Element [ (Boolean, Boolean) ],
значением которого является пара, составленная из значений е21 и е22.
Следовательно, число возможных значений е2 равно 2 х 2 = 4, и то же самое относится к еЗ.
Исходный моральный граф
е1
е22
е32
е21
е2
е22
е31
еЗ
е32
Вершины е21 (2 значения)
~и е22 (2 значения) объединяются в
«супервершину» е2, принимающую
2x2 = 4 значения
-Аналогично для еЗ
В результате из графа
-устраняется цикл ценой
появления переменных с
большим числом значений
Рис. 10.10. Объединение вершин для устранения циклов.
Слева показан исходный моральный граф, который давал неточные
результаты, а справа - граф с объединенными вершинами без циклов
347
е21
е31
е4
е1
е4

Глава 10. Факторные алгоритмы вывода
Мы можем написать такую программу
val el = Flip(0.5)
val e2: Element[(Boolean, Boolean)] = Apply(el, (b: Boolean) => (b, b)) О—О
val e3: Element[(Boolean, Boolean)] =
Apply(e2, (bb: (Boolean, Boolean)) => (bb._l, bb._2)) <—©
val e4: Element[Boolean] =
Apply(e2, (bb: (Boolean, Boolean)) => bb._l == bb._2)
О — Создаем элемент из пар, в котором каждый компонент равен значению е1 — так же,
как элементы е21 и е22 в исходной программе
© — Создаем элемент из пар, в котором первый компонент равен значению первого
компонента е2, и аналогично для второго компонента
Очевидно, что эту программу читать не так легко, как исходную. Но у нее есть
важное преимущество - РД теперь дает правильный ответ.
Разлагайте условные распределения вероятности
с большим числом родителей
Поскольку алгоритм РД работает с моральным графом, а в моральном графе
имеется клика для каждого условного распределения вероятности, то наличие
условных распределений с большим числом родителей составляет для РД такую же
проблему, как для ИП. В частности, сложность РД экспоненциально зависит от
максимального числа родителей вершины. Поэтому стоит попытаться разложить
такие условные распределения, применяя технику из раздела 10.3.2.
Применяйте ослабляющие условные распределения
вероятности
Алгоритм циклического РД работает хуже при наличии эффекта
дальнодействия, когда значение в одной вершине сильно влияет на значение в другой,
далеко отстоящей от нее, вершине посредством цикла. Эффект дальнодействия
особенно заметен, если связи между переменными вдоль пути детерминированы.
Пример приведен на врезке в разделе 10.4.2, где промежуточные переменные в
точности равны первой переменной. Такие эффекты можно ослабить, устранив
детерминированность за счет условных распределений, содержащих некоторую
долю случайности.
Ослабляющие условные распределения вероятности не только улучшают
работу РД, но и могут дать более точную модель. Рассмотрим, к примеру, модель
принтера из главы 5. Там мы говорили, что если кнопка питания нажата, уровень
тонера достаточен и бумага подается беспрепятственно, то принтер находится в
исправном состоянии. Это детерминированная связь. Но всегда ли это верно? На
самом деле, нет - принтер может не работать из-за каких-то других электрических
или механических повреждений. Мы часто пользуемся детерминированными
связями, чтобы упростить модель, однако добавление шума может дать более точный
результат. А поскольку это также улучшает работу РД, то к этой идее стоит при-
348

10.5. Использование алгоритма РД
смотреться. В следующей главе мы увидим, что включение слабого шума может
также повысить точность выборочных алгоритмов.
Упростите сеть
Если другие подходы ничего не дали, то имеет смысл упростить сеть, как и
в случае ИП. Упрощение сети должно преследовать две цели. Первая и самая
важная - уменьшить число родителей в условном распределении вероятности и
тем ускорить вывод. Вторая - по возможности устранить эффекты дальнодействия,
например, путем удаления циклов без поперечных ребер.
70.5.3. Приложения алгоритма РД
Для применения алгоритма ИП модель должна иметь определенную структуру.
Мы видели два примера такой структуры на примере СММ и ВКСГ. У алгоритма
РД таких ограничений нет, поэтому он распространен более широко. РД можно
рассматривать как хорошего кандидата для любой модели с дискретными
переменными. И даже если переменные непрерывны, РД все равно можно
использовать, если вы готовы ограничить множество значений некоторой выборкой.
Ниже перечислены некоторые типичные приложения РД.
• Анализ изображений. В главе 5 мы видели, что двумерный массив пикселей
можно смоделировать в виде марковской сети. На рис. 10.5 показан пример
марковской сети для изображения 4x4. Тогда я говорил, что такие сети
плохо приспособлены для алгоритма ИП, потому что сложность вывода
экспоненциально растет с увеличением размера изображения. Напротив, РД
прекрасно применим к такого рода моделям. Сложность вывода зависит от
размера всего лишь линейно.
• Медицинская диагностика. В типичной задаче медицинской диагностики
пациент перечисляет симптомы, а врач должен установить их причину. На
рис. 10.11 показана байесовская сеть для такой задачи. Существует ряд
заболеваний, которыми может страдать пациент, и ряд симптомов, о которых
он сообщает. Каждый симптом может быть вызван несколькими
болезнями. Обычно такие байесовские сети содержат много циклов. В общем
случае по мере увеличения количества болезней и симптомов клики
становятся большими, так что ИП неприменим. Но РД вполне успешно справляется
с такими сетями.
Заболевание
Симптом
Рис. 10.11. Байесовская сеть для медицинской диагностики
349
Заболевание
2
Заболевание
з
Заболевание
■i
Симптом
2
Симптом
3

Глава 10. Факторные алгоритмы вывода
• Мониторинг состояния зданий, транспортных средств и оборудования.
Мониторинг состояния сложной системы - важное приложение
вероятностных рассуждений. Допустим, что требуется следить за температурой
и энергопотреблением в центре обработки данных. Можно завести
переменные, представляющие температуру и энергопотребление каждого
компонента. Температура расположенных рядом компонентов
взаимозависима вследствие теплопереноса. Величины энергопотребления соединенных
между собой компонентов также взаимозависимы. Кроме того,
энергопотребление оказывает влияние на температуру. В результате получается
большая вероятностная модель с циклами. В данном случае температура и
энергопотребление - непрерывные переменные, которые необходимо дис-
кретизировать. Тем не менее, алгоритм РД эффективно применяется для
решения таких задач.
10.6. Резюме
Факторы - это структуры данных, с помощью которых организуются
вычисления, выполняемые в процессе вероятностного вывода.
Фактор определяется множеством переменных, набором строк для всех
возможных комбинаций значений переменных и числом,
ассоциированным с каждой строкой.
Факторы можно складывать и умножать, производя операции над
соответствующими строками.
Ответ на запрос, предъявляемый вероятностной модели, можно
определить в виде суммы произведений факторов.
Исключение переменных - точный алгоритм, который преобразует сумму
произведений, не порождая полного совместного распределения.
Сложность алгоритма исключения переменных зависит от порядка
исключения; при заданном порядке исключения сложность экспоненциально
зависит от размера наибольшей клики в индуцированном графе.
В алгоритме распространения доверия передаются сообщения, над
которыми производятся факторные операции. В триангулированной сети этот
алгоритм является точным. В сети с циклами алгоритм дает
приближенные результаты. И хотя результат не гарантирован, на практике алгоритм
успешно применяется.
Алгоритм циклического распространение доверия работает тем точнее, чем
меньше эффектов дальнодействия, вызываемых наличием циклов в сети.
10.7. Упражнения
Первые пять упражнений к этой главе основаны на байесовской сети на рис. 10.12,
которая описывает жизненный цикл младенца. На рисунке приведены
также условные распределения вероятности всех четырех переменных. Решения
350

10.7. Упражнения
избранных упражнений имеются на сайте www.manning.com/books/practical-
probabilistic-programming.
Голоден
False
False
True
True
Устал
False
True
False
True
Плачет
False True
5/6 1/6
1/6 5/6
1/6 5/6
0 1 |
Голоден
False
3/4
True
1/4
Голоден
Ест
Устал
Голоден
False
True
Ест
Ничего
Мало
Много
Ест
Ничего Мало
2/3 1/3
1/6 1/3
Устал
False I True
3/4 1/4
1/2 1/2
1/4 3/4
Много
0
1/2
Рис. 10.12. Сеть, описывающая жизненный цикл младенца
1. Запишите каждое условное распределение вероятности в виде фактора.
2. Выпишите выражение для совместного распределения вероятности всех
переменных, пользуясь цепным правилом. Вычислите это совместное
распределение, перемножив все факторы.
3. Выпишите выражение для Р(Плачет), пользуясь правилом полной
вероятности. Вычислите фактор для Р(Плачет), просуммировав совместное
распределение по переменным Голоден, Ест и Устал.
4. Выпишите выражение для Р(Ест | Плачет = True). Начав с совместного
распределения, вычислите ответ на этот запрос следующим образом:
a. Обнулить строки, в которых Плачет не равно True.
b. Просуммировать по переменным Голоден и Устал.
c. Нормировать результат.
5. Рассмотрим процесс вычисления Р(Плачет) методом исключения
переменных.
a. Нарисуйте моральный граф байесовской сети.
b. Нарисуйте граф, индуцированный порядком исключения
переменных Ест, Голоден, Устал. Каков размер наибольшей клики?
c. Нарисуйте граф, индуцированный порядком исключения
переменных Голоден, Устал, Ест. Каков размер наибольшей клики?
6. Для сети, соответствующей изображению 4x4 (рис. 10.5), попробуйте
различные порядки исключения переменных. Убедитесь, что при любом
порядке появляется клика размером не меньше 4.
351
Плачет

Глава 10. Факторные алгоритмы вывода
7. Представьте на Figaro CMM, подобную изображенной на рис. 10.6.
Напишите функцию, которая принимает последовательность наблюдений,
разворачивает СММ на длину этой последовательности и с помощью
исключения переменных вычисляет распределение вероятности конечного
скрытого состояния. Измерьте время работы при различной длине
последовательности наблюдений. Как выглядит зависимость времени работы от
длины последовательности?
8. Создайте на Figaro общее представление сети пикселей, изображенной на
рис. 10.5, с переменным числом пикселей по каждой стороне. При разном
числе пикселей проделайте следующие эксперименты.
a. Выполните случайное наблюдение 1/3 пикселей, исключая левый
верхний угол.
b. Измерьте, сколько времени занимает исключение переменных,
необходимое для вычисления вероятности, что пиксель в левом верхнем
углу включен. Вы обнаружите, что если число пикселей относительно
велико, то исключение переменных занимает много времени, поэтому
остановите процесс. Как выглядит график времени исключения
переменных?
c. Измерьте, сколько времени занимает вычисление вероятности того,
что пиксель в левом верхнем углу включен, методом
распространения доверия. Как выглядит график времени работы этого алгоритма?
d. В случае, когда алгоритмы исключения переменных и
распространения доверия естественно завершаются, вычислите разность между
полученными ответами. Поскольку алгоритм исключения
переменных дает точный ответ, эта величина является погрешностью
алгоритма распространения доверия.
9. Рассмотрим сеть для медицинской диагностики, изображенную на
рис. 10.11, где заболевания расположены в одной строке, а симптомы - в
другой.
a. Напишите функцию, которая генерирует случайные сети такого вида.
Эта функция должна принимать три параметра: число заболеваний,
число симптомов и вероятность существования ребра между
заболеванием и симптомом.
b. Как в упражнении 8, проведите эксперимент по изучению поведения
алгоритмов исключения переменных и распространения доверия
при различных значениях параметров. Как изменяется время
исключения переменных? А время распространения доверия? Какова
погрешность алгоритма распространения доверия в случае, когда оба
алгоритма естественно завершаются?
352

ГЛАВА 11.
Выборочные алгорижмы
В этой главе.
■ Основы выборочных алгоритмов.
■ Важность выборочных алгоритмов,
■ Алгоритм Монте-Карло по схеме марковской
цепи (МСМС).
■ Вариант МСМС Метрополиса-Гастингса.
Мы продолжим тему предыдущей главы - представление основных алгоритмов
вывода, применяемых в вероятностных программах. Если в главе 10 нас
интересовали факторные алгоритмы, в частности исключение переменных и
распространение доверия, то сейчас мы займемся выборочными алгоритмами, которые для
ответа на запрос генерируют выборку возможных состояний переменных в
соответствии с заданным программой распределением вероятности. Конкретно будут
рассмотрены два полезных алгоритма: выборка по значимости и алгоритм
Монте-Карло по схеме марковской цепи (Markov chain Monte Carlo - МСМС).
Прочитав эту главу, вы будете хорошо понимать алгоритмы вывода,
используемые в системах вероятностного программирования и, в частности, в Figaro. Это
поможет при проектировании моделей и управлении выводом с целью
повышения его эффективности. МСМС в особенности требует дополнительных усилий
по настройке, и в этой главе будут показаны два метода достижения нужного
результата. В главе 12, которая опирается на изложенный материал, будет показано,
как использовать похожие алгоритмы для получения ответов на другие запросы.
Эта глава практически не зависит от предыдущей. Хотя я иногда сравниваю
выборочные алгоритмы с факторными, понимать, как работают факторные
алгоритмы, не обязательно. Кроме того, в выборочных алгоритмах в меньшей степени
используются правила вывода, представленные в главе 9. Но, конечно, вы должны
понимать, как писать программы на Figaro. Наконец, алгоритм МСМС опирается
на понятие марковской цепи, введенное в начале главы 8, поэтому имеет смысл
предварительно перечитать эту часть.

Глава 11. Выборочные алгоритмы
11.1. Принцип работы выборочных
алгоритмов
Выборочные алгоритмы - альтернатива факторным алгоритмам вероятностного
вывода. Их основной принцип прост: вместо того чтобы представлять
распределение вероятности всех возможных миров, мы берем только некоторые примеры
возможных миров, и называем это множество выборкой.
Идея выборки иллюстрируется на рис. 11.1. В этом примере имеется
единственная переменная, принимающая значения малая, средняя и большая. Возможный
мир определяется значением этой переменной. Существует истинное
распределение вероятности возможных миров, показанное в верхней строке. Оно могло
бы стать ответом на запрос, но в общем случае неизвестно. Вместо того чтобы
вычислять распределение напрямую, мы порождаем множество примеров.
Каждый пример является возможным миром, а вероятность порождения конкретного
мира должна быть равна его вероятности. На рисунке показан результат такого
порождения миров:
• два примера, в которых переменная имеет значение «малая»;
• пять примеров, в которых она имеет значение «средняя»;
• три примера, в которых она имеет значение «большая».
Оценить вероятность возможного мира можно, посчитав долю примеров,
совпадающих с этим миром. Подведем итог:
• существует истинное распределение, которое требуется вычислить;
• генерируется выборка из истинного распределения;
• на основе выборки дается оценка истинного распределения.
0.23
0.2
малая
0.46
0.5
средняя
0.31
0.3
большая
Истинные вероятности
Примеры
Оценки вероятностей
Значения
Рис. 11.1. Принцип работы выборочных алгоритмов. Существует истинное
распределение, которое требуется вычислить. Для его оценки генерируется
множество примеров - выборка. Вероятность генерирования конкретного
значения должна быть равна вероятности этого значения. Имея выборку,
мы можем оценить вероятность каждого значения, посмотрев,
сколько примеров принимают это значение
В предыдущем примере была одна дискретная переменная, принимающая всего
три значения. Но принцип выборки применим также к переменным с
бесконечным числом значений, в том числе непрерывным. На самом деле, именно для
таких переменных выборка особенно полезна. Напомним, что распределение веро-
354

11.1. Принцип работы выборочных алгоритмов
ятности непрерывной переменной описывается функцией плотности. На рис. 11.2
показаны две непрерывные переменные со значениями от 0 до 1; возможный мир
определяется комбинацией их значений. Пространство возможных миров разбито
на области с разной плотностью вероятности. Чем темнее область, тем выше
плотность. Эта область покрыта множеством примеров. Плотность примеров в области
приблизительно соответствует плотности вероятности в ней. Количество
примеров в области может служить оценкой вероятности этой области.
Возможные
миры
Области
с наибольшей
плотностью
Рис. 11.2. Покрытие пространства возможных миров выборкой.
Чем темнее закрашенная область, тем выше плотность вероятности.
Количество примеров больше в областях с высокой плотностью
и меньше - в областях с низкой плотностью
Есть два вида выборочных алгоритмов. В первом, более простом, случае мы
напрямую генерируем выборку из желаемого распределения, выполняя
вероятностную программу. Это так называемая прямая выборка, которую я опишу ниже.
Практический пример прямого выборочного алгоритма, реализованный во
многих системах вероятностного программирования и в том числе в Figaro, -
алгоритм выборки по значимости, описанный в разделе 11.2.
Второй вид выборочных алгоритмов называется методом Монте-Карло по
схеме марковской цепи (Markov chain Monte Carlo - MCMC). Его основная идея - не
формировать выборку из распределения непосредственно, а определить процесс
выборки, который сходится к истинному распределению. Это подробно
объяснено в разделе 11.3.
7 7.7.7. Прямая выборка
В случае прямой выборки мы генерируем значения переменных вероятностной
программы по одному. Когда значения всех переменных будут сгенерированы, мы
получим возможный мир, т. е. один пример из выборки. Для генерации значения каждой
переменной используется ее определение: зависимость от родителей, описываемая
функциональной формой и числовыми параметрами. Следовательно, определение
переменной задает распределение ее вероятности, а ее значение выбирается в
соответствии с этим распределением. Прямая выборка производится в порядке тополо-
355

Глава 11. Выборочные алгоритмы
гическои сортировки: значения родителей генерируются раньше значения потомка,
поэтому мы всегда точно знаем, какое распределение использовать.
Ниже приведен псевдокод прямой выборки. В нем генерируется один пример,
состоящий из значений всех переменных.
1. Обозначим О - топологический порядок на множестве переменных.
2. Для каждой переменной V в порядке О:
a. Обозначим Par родителей V.
b. Обозначим хРаг уже сгенерированные значения Par.
c. Выбрать xv из P(V | Par = х)аг).
3. Вернуть х (вектор, содержащий значения xv для каждой переменной V).
Процесс прямой выборки показан на рис. 11.3. Вероятностная программа, в
которой определены переменные, находится слева. В середине расположено дерево,
содержащее все возможные пути генерирования значений переменных в этой
программе. Жирными стрелками показан один проход выборки. Сначала
генерируется значение переменной rembrandti, описывающей вероятность того, что первая
из двух картин принадлежит кисти Рембрандта. Поскольку она определена как
Flip (0.4), то значение true генерируется с вероятностью 0.4, a false - с
вероятностью 0.6. На показанном пути выборки сгенерировано значение true. Затем
генерируется значение rembrandt2. Эта переменная не зависит ни от какой другой и
также определена элементом Flip, поэтому процесс аналогичен. На показанном пути
сгенерировано значение false. Наконец, генерируется переменная samePainter,
показывающая, написаны ли обе картины одним художником. (Рассматривается
только два возможных художника, поэтому если ни одна картина не написана
Рембрандтом, то обе написаны вторым художником.) Переменная samePainter зависит
от rembrandti и rembrandt2, а они к этому моменту уже сгенерированы. Поскольку
rembrandti равна true, a rembrandt2 равна false, TO samePainter равна false.
Программа
rembrandti = Flip(0.4)
rembrandt2 = Flip(0.2)
samePainter = x === у
Flip(0.4)
Сгенерированный мир
true
false
rembrandti
rembrandt2
samePainter
true
false
false
Flip(0.2)
Flip(0.2)
true
false
true
false
rl===r2
rl===r2
rl===r2
rl===r2
true
true false false
Рис. 11.3. Процесс прямой выборки. Дерево показывает все возможные пути
генерирования значений в данной программе, а также конкретный обход.
Справа приведен возможный мир, получившийся в результате этого обхода
(rl И г2 - Сокращения rembrandti И rembrandt2)
356

11.1. Принцип работы выборочных алгоритмов
При прямой выборке мы прогоняем этот процесс многократно, каждый раз
генерируя новый возможный мир - пример. В табл. 11.1 показаны четыре примера,
сгенерированные этой программой. Отметим, что один и тот же пример может
быть сгенерирован несколько раз; в данном случае совпадают второй и четвертый
примеры. Вероятность возможного мира оценивается как доля примеров,
совпадающих с этим миром. Например, вероятность мира, в котором rembrandti равно
false, rembrandt2 paBHO false, a samePainter paBHO true, Оценивается Как 1/2,
ПОСКОЛЬКУ два из четырех примеров совпадают с этим миром.
Таблица 11.1. Четыре примера, сгенерированные для программы на рис. 11.3
Элемент
rembrandti
rembrandt2
samePainter
Пример 1
true
false
false
Пример 2
false
false
true
Примерз
true
true
true
Пример 4
false
false
true
Оценку распределения вероятности можно использовать также для ответа на
запросы. Например, пусть мы хотим знать вероятность того, что обе картины
написаны одним художником. Мы видим, что в трех из четырех примеров
переменная samePainter принимает значение true. Поэтому ответ - 3/4.
Зачем использовать выборку?
Важно подчеркнуть, что конкретное множество примеров - лишь одно из
возможных представлений распределения вероятности возможных миров. Прямая
выборка - случайный процесс, поэтому каждый раз может генерироваться новый
результат. Оценка распределения, получаемая при разных прогонах, обычно
различается. Кроме того, как правило, мы получаем не точно то распределение,
которое определено вероятностной программой. Действительно, в нашем примере
элемент Flip (0.4) равен false с вероятностью 0.6, в Flip (0.2) равен false с
вероятностью 0.8. Вероятность, что оба элемента равны false, составляет 0.6 х 0.8 = 0.48.
А в нашем случае Flip (0.4) === Flip (о. 2) всегда равно true. Поэтому правильная
вероятность возможного мира, совпадающего со вторым и третьим примером,
равна 0.48, а не 0.5. В данном случае значения близки, но, вообще говоря, нет никакой
гарантии близости ответа к истинному, особенно если генерируется мало
примеров.
Почему же тогда выборка считается хорошей идеей? В этом примере всего
три переменных, и все необходимые вычисления можно проделать напрямую с
помощью сложений и умножений. Но во многих программах переменных
гораздо больше, а их типы более сложны и допускают много, иногда даже бесконечно
много, значений. В таких программах не всегда возможно даже создать все
необходимые факторы для прогона факторного алгоритма вывода, что уж говорить о
выполнении умножений и сложений. А выборка позволяет ограничиться рассмо-
357

Глава 11. Выборочные алгоритмы
трением сравнительно небольшого числа возможностей и получить оценку
искомого распределения вероятности.
Вот пример программы, иллюстрирующий эту мысль:
val х = Apply(Normal(0.4, 0.3), (d: Double) => d.max(0).min(1))
val у = Flip(x)
Здесь x представляет нормально распределенную переменную в диапазоне от 0
до 1. Переменная у определена как составной Flip, что эквивалентно chain (x,
(d: Double) => Fiip(d)). На рис. 11.3 было показано все дерево возможных
проходов выборки. На практике, однако, никогда не создается полное дерево, а лишь
поддерево, соответствующее генерируемым значениям. В данном примере полное
дерево бесконечно, поэтому вычислить точное распределение вероятности было
бы невозможно. В процессе выборки вычисляется только конечное подмножество
дерева, которое затем используется для оценки распределения.
На рис. 11.4 показано дерево, сгенерированное выборкой по этой программе. На
каждом проходе генерируется вещественное значение Apply. Это значение
передается в качестве аргумента элементу chain, так что каждый раз порождается новый
элемент Flip. Если сгенерировать только четыре примера, то будет сгенерировано
четыре конкретных элемента Flip; остальные элементы, каковых бесконечно
много, никогда не появятся на свет.
Apply(Normal(0.4, 0.3), (d: Double) => d.max(0).min(1))
Результирующий элемент: Flip (0 .1129) Flip (0. 8482) Flip (0 . 6437) Flip (0)
Сгенерированный пример: false true false true
Рис. 11.4. Частичное дерево, сгенерированное в результате выборки
Если выборочное распределение - лишь оценка истинного, то что можно
сказать о результате выборки? Тут следует отметить два важных момента, которые
согласуются с интуицией.
В среднем выборочное распределение совпадет с истинным. Любое конкретное
выборочное распределение отличается от истинного, но если усреднить все
найденные распределения, то получится истинное. Это интуитивно понятно, потому
что каждый пример выбирается из истинного распределения. Для этого свойства
имеется специальный термин - говорят, что процесс выборки несмещенный.
Чем больше выборка, тем ближе выборочное распределение будет к истинному.
Иначе эту мысль можно выразить, сказав, что ожидаемая погрешность
уменьшается с ростом числа примеров. Но это только ожидаемая погрешность; гарантий
никто не дает. Если не повезет, то погрешность может возрастать с увеличением
358
Сгенерированный пример: 0.1129 0.8482 0.6437 0

11.1. Принцип работы выборочных алгоритмов
числа примеров, но в среднем она будет убывать. Говорят, что дисперсия процесса
выборки убывает сростом выборки.
На рис. 11.5 иллюстрируется типичное поведение выборочного алгоритма. На
графике показана зависимость вероятности, оцененная по выборке, от числа
примеров в выборке. Видно, что в начале оценка быстро приближается к истинной
вероятности и в конечном итоге сходится к ней, но временами отклонение оценки
увеличивается, а сходимость медленная.
Истинная
вероятность
Вероятность, оцененная
по выборке
Вероятность
Размер выборки
Рис. 11.5. Типичное поведение выборочного алгоритма во времени.
Вероятность, оцененная по выборке, сходится к истинной вероятности,
но иногда отклоняется от нее
Эти два свойства - ключ к пониманию того, почему приближенный
выборочный алгоритм полезен в вероятностных рассуждениях. Согласно этим свойствам,
в результате выборочного алгоритма мы получаем приближенное распределение,
в среднем близкое к истинному, и ожидается, что расхождение тем меньше, чем
больше размер выборки. При достаточно большом размере выборке можно
получить оценку, сколь угодно близкую к истинному распределению.
Предупреждение. Решений, пригодных для всех случаев, не бывает. Вывод - это
трудная задача, а выборка - не всегда идеальный подход. Иногда для получения
достаточно близкой аппроксимации приходится брать выборку очень большого размера.
Сгенерированную выборку легко использовать для ответа на запросы.
Например, чтобы оценить, с какой вероятностью переменная принимает определенное
значение, нужно вычислить долю примеров, в которых эта переменная равна
указанному значению. Повторим, в чем состоит привлекательность выборочных
алгоритмов: при достаточном размере выборки можно получить сколь угодно
близкую аппроксимацию истинного распределения и использовать выборку для ответа
на запросы.
359

Глава 11. Выборочные алгоритмы
11.1.2. Выборка с отклонением
До сих пор мы видели процесс прямой выборки, который генерирует значения
элементов модели, основываясь на определениях этих элементов. Мы пока не
рассматривали фактов в форме условий или ограничений. Без фактов программа
определяет априорное распределение возможных миров. Следовательно,
процедура прямой выборки генерирует выборку из априорного распределения
вероятности.
Для понимания процесса это, возможно, и полезно, но обычно нас интересуют
ответы на запросы об апостериорном распределении, которое получается после
задания фактов. Нужен какой-то способ получать выборку из апостериорного
распределения.
Для этого применяется процедура выборки с отклонением. Принцип прост:
использовать прямую выборку, как и раньше, но отклонять примеры,
противоречащие фактам. Сохраняются только примеры, совместимые с фактами.
Примечание. Представленный ниже алгоритм - частный случай общей
математической теории. Изложенный алгоритм выборки с отклонением применим только к
вероятностным программам, в которых есть условия, но не мягкие ограничения.
Выборка с отклонением проистекает из фундаментального принципа
применения условий в виде фактов, описанного в главе 4. Рис. 11.6 напоминает, как он
работает. Мы начинаем с априорного распределения вероятности возможных миров.
Наблюдая эмпирические факты, мы «вычеркиваем» несовместимые с ними миры,
сопоставляя им нулевую вероятность. Затем получившиеся вероятности
нормируются для получения апостериорного распределения.
В процессе выборки с отклонением используется тот же принцип
вычеркивания миров, несовместимых с фактами. Для этого мы удаляем из выборки
несовместимые примеры. Те же, что останутся, представляют апостериорное
распределение после применения условий. Получившуюся выборку можно использовать для
ответа на запросы.
Рассмотрим программу, использованную для получения данных в табл. 11.1, но
добавим факты. Вот как выглядит модифицированная программа:
val rembrandtl = Flip(0.4)
val rembrandt2 = Flip(0.2)
val samePainter = rembrandtl === rembrandt2
rembrandt2.observe(false)
Табл. 11.2 получена так же, как табл. 11.1, но примеры, несовместимые с
наблюдениями, удаляются. Оставшиеся примеры представляют апостериорное
распределение вероятности.
360

11.1. Принцип работы выборочных алгоритмов
Факты
представляют
конкретные
знания о
ситуации
Возможные миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
Факты:
• Ярко-желтое пятно
• «Пьяный моряк»
• Продана на аукционе в
2003 году
Совместимые миры:
1. Подделка
2. Рембрандт, люди,
темные
3. Рембрандт, люди,
яркие
4. Рембрандт, ландшафт
1. Распределение вероятности
до ознакомления с фактами
3. Вычеркиваем миры,
не совместимые с
заданными фактами
Распределение
вероятности после
применения условий,
основанных на фактах
Нормируем вероятности
оставшихся миров, чтобы
их сумма была равна 1
Рис. 11.6. Повтор рис. 4.4: процесс применения условий в виде фактов
В табл. 11.2 продемонстрирован базовый процесс выборки с отклонением, но в
реальном алгоритме есть две оптимизации. Во-первых, бессмысленно расходовать
память на хранение примеров, которые в конечном итоге будет отклонены. Если
таких примеров большинство, то память вообще может закончиться до того, как
будет получена достаточно большая выборка из апостериорного распределения.
Поэтому примеры, несовместимые с фактами, отбрасываются сразу после
создания и не хранятся.
Таблица 11.2. Выборка с отклонением при условии, что элемент Flip (о, 2)
принимает значение true. Примеры, несовместимые с этим фактом, отклоняются
Элемент
rembrandtl
rembrandt2
samePainter
Пример 1
true
false
false
Пример 2
false
false
true
Пример 3
true
true
true
Пример 4
false
false
true
361
Распределение
вероятности
0.9 0.09 0.009 0.001
Апостериорное
распределение вероятности
0.9/(0.9 + 0.009) 0.009/(0.9 + 0.009)
1
2
3
4
1
3

Глава 11. Выборочные алгоритмы
Во-вторых, необязательно генерировать пример целиком, чтобы проверить его
совместимость с фактами. Пример можно отбросить, как только выяснится, что
значение некоторого элемента несовместимо с фактом для этого элемента. Третий
пример в табл. 11.2 можно отклонить после того, как для rembrandt2
сгенерировано значение true, и не генерировать samePainter. Это может дать существенную
экономию времени.
Ниже показан псевдокод алгоритма выборки с отклонением. Программа
продолжает попытки, пока не сгенерирует один пример, совместимый с фактами.
1. Обозначим О топологический порядок на множестве переменных.
2. Для каждой переменной V в порядке О:
a. Обозначим Par множество родителей V.
b. Обозначим хРаг ранее сгенерированные значения Par.
c. Вывести ху из P(V | Par = х ).
d. Если xv несовместимо с фактом, относящимся к V, перейти к шагу 2
(пример немедленно отклоняется).
3. Вернуть х.
Отметим главное, что нужно знать о выборке с отклонением.
• Достоинством выборки с отклонением является то, что оставленные
примеры выбраны из апостериорного распределения, обусловленного фактами.
Чем больше примеров, тем ближе выборочное распределение к истинному.
Здесь все обстоит так же, как для прямой выборки, только дополнительно
учитываются имеющиеся факты.
• Недостаток заключается в том, что может быть отклонено большинство
примеров. В таком случае большая часть работы напрасна, и приходится
долго ждать, пока не наберется достаточно много примеров. В общем
случае вероятность принятия примера равна вероятности факта.
Следовательно, если факт маловероятен, то большинство примеров отклоняются.
Можно ли оценить вероятность факта? Допустим, мы 10 раз подбрасываем
правильную монету. Число возможных исходов равно 210. Поэтому вероятность
каждого конкретного исхода 10 подбрасываний равна 1/(210). Если подбрасываний 20,
то вероятность конкретного исхода равна 1/(220). Значит, если в этом случае
использовать выборку с отклонением, то оставлен будет лишь один из каждых 220
примеров - очень мало. В общем случае вероятность факта экспоненциально
убывает с ростом числа переменных, к которым относится факт. Отсюда следует, что
объем работы, которую нужно проделать для генерации хорошей выборки с
отклонением экспоненциально возрастает с ростом числа переменных. Если вы думаете,
что способность быстро отклонять несовместимые примеры спасает, то вынужден
вас огорчить - сэкономленное время зависит от числа переменных линейно, что
никак не компенсирует экспоненциальный рост.
Из-за этой проблемы выборка с отклонением, хотя и полезна для иллюстрации
общих принципов, на практике обычно не применяется. К тому же, этот алгоритм
может работать только с условиями Figaro, но не с более общими ограничениями.
362

11.2. Выборка по значимости
В следующих двух разделах мы рассмотрим два практически применимых
алгоритма: выборку по значимости и метод Монте-Карло по схеме марковской цепи.
Выборка по значимости похожа на выборку с отклонением, но для учета фактов
используется более рациональный подход. Напротив, в метод Монте-Карло по
схеме марковской цепи применяется совершенно иной подход к формированию
выборки.
11.2. Выборка по значимости
Выборка по значимости похожа на выборку с отклонением - обнаружив
невыполненное условие, алгоритм точно так же отклоняет пример. Но есть два отличия.
Во-первых, напомним, что Figaro поддерживает не только условия, но и
ограничения, которые не просто принимают значение true или false, а сопоставляют
каждому состоянию вещественное число. Алгоритм выборки с отклонением не способен
обработать такие ограничения, потому что пример не то что совсем несовместим с
фактом, а просто имеет меньшую вероятность. Алгоритм же выборки по
значимости может обрабатывать ограничения, не отклоняя примеры. Во-вторых, при
определенных обстоятельствах выборка по значимости позволяет избежать отклонения
по условиям за счет преобразования условий в ограничения на другие переменные.
Примечание. Выборка по значимости - более общая схема, чем описано в этом
разделе. Я рассказываю о том ее варианте, который используется в Figaro.
Прежде чем описывать алгоритм выборки по значимости, я хотел бы уточнить
смысл условий и ограничений в Figaro.
• Жестким условием называется функция, сопоставляющая значению
элемента булеву величину. Оно определяет свойство, которым значение
обязано обладать, чтобы его вероятность была положительна. Точнее,
вероятность любого мира, в котором значение данного элемента не удовлетворяет
условию, будет равна 0. Поэтому условие можно рассматривать как
умножение вероятности возможного мира на 0, если значение элемента ему не
удовлетворяет, и на 1 - в противном случае.
• Мягким ограничением называется функция, сопоставляющая значению
элемента вещественное число. Я говорил, что ограничение можно
интерпретировать как фразу «при прочих равных условиях». Рассмотрим, к
примеру, элемент с ограничением, которое возвращает 1.0, если значение
элемента равно true, и 0.5, если оно равно false. Если имеются два возможных
мира, отличающиеся только значениями этого элемента, чьи вероятности в
противном случае были бы равны, то вероятность мира, а котором элемент
равен true, в два раза больше, чем того, в котором он равен false.
Приведу более точное определение. Рассмотрим элемент Е с ограничением С.
Без этого ограничения все возможные миры имели бы некоторую вероятность р0.
Обозначим значение элемента в некотором возможном мире е. Тогда ненормиро-
363

Глава 11. Выборочные алгоритмы
ванная вероятность элемента с учетом ограничения равна ро х С(е). Я говорю
ненормированная, потому что при такой интерпретации ограничений сумма чисел в
общем случае будет отличаться от 1, так что для превращения их в вероятности
необходима нормировка.
После этого введения мы готовы рассмотреть работу алгоритма выборки по
значимости.
7 7.2. Т. Как работает выборка по значимости
Основной принцип выборки по значимости, отличающий его от предыдущих
алгоритмов, - использование взвешенных примеров: мы учитываем не весь пример, а
лишь его часть, определяемую весом. Распределение вероятности возможных
миров тогда определяется весами примеров. Ниже я объясню, как это работает, а затем
покажу, как выборка по значимости позволяет избежать отклонения примеров.
Взвешенные примеры
В алгоритме выборки по значимости каждому примеру назначается вес,
зависящий от значений условий и ограничений для данного образца. Встретив
ограничения, мы должны умножить вероятность возможного мира на значение этого
ограничения. Для этого мы умножаем вес примера на значение ограничения.
Итоговый вес будет равен произведению значений всех ограничений.
Чтобы понять, как это работает, модифицируем программу, с помощью которой
строилась табл. 11.2:
val rembrandtl = Flip(0.4)
val rembrandt2 = Flip(0.2)
val samePainter = rembrandtl === rembrandt2
rembrandt2.addConstraint((b: Boolean) => if (b) 0.1 else 1.0)
Мы заменили жесткое условие мягким ограничением. Если переменная
rembrandt2 равна false, то ограничение принимает значение 1.0, иначе - 0.1. При
генерации тех же примеров, что в табл. 11.1 и 11.2, мы ассоциируем с каждым
примером вес, равный значению ограничения. Получившийся набор взвешенных
примеров приведен в табл. 11.3.
Таблица 11.3. Взвешенные примеры. Каждому примеру назначен вес, равный
значению ограничения на элементе fi ip (о, 2)
Элемент
rembrandtl
rembrandt2
samePainter
Weight
Пример 1
true
false
false
1.0
Пример 2
false
false
true
1.0
Пример 3
true
true
true
0.1
Пример 4
false
false
true
1.0
Множество взвешенных примеров определяет распределение вероятности
возможных миров. Представим процесс случайного выбора примера, в котором веро-
364

11.2. Выборка по значимости
ятность выбора пропорциональна весу примера. Чтобы определить, с какой
вероятностью будет выбран некоторый пример, мы просто делим его вес на сумму всех
весов, которая в случае четырех примеров из табл. 11.4 равна 3.1. Так, вероятность
выбора первого примера равна 1.0/3.1, а второго - 0.1/3.1. Тогда вероятность
возможного мира равна сумме вероятностей выбора примеров, совместимых с этим
миром. Для мира, соответствующего второму и четвертому примерам, вероятность
будет равна 2.0/3.1. Таким образом, взвешенные примеры из табл. 11.3 определяют
апостериорное распределение вероятности, показанное в табл. 11.4.
Таблица 11.4. Апостериорное распределение вероятности, определяемое
множеством взвешенных примеров, порожденных алгоритмом выборки
по значимости. Вероятность возможного мира пропорциональна сумме весов
примеров, совместимых с этим миром
Flip(0.4)
true
false
true
Flip (0,2)
false
false
true
Flip{0,4) == Flip(0.2)
false
true
true
Вероятность
1.0/3.1=0.3226
2.0/3.1 =0.6452
0.1/3.1=0.0322
Поскольку взвешенные примеры определяют распределение вероятности, их
можно использовать для ответа на запросы. Делается это просто. Пусть,
например, нас интересует вероятность, что элемент х (шр (0.4)) равен true. Такое
значение этот элемент принимает в первом и третьем примерах. Их суммарный вес
равен 1.1. Делим эту величину на общий вес всех примеров (3.1) и получаем
оценку Р(х = true) = 1.1 /3.1 = 0.3548.
В алгоритме выборки по значимости, когда имеются факты для нескольких
элементов, мы перемножаем значения ограничения для каждого из таких элементов.
Допустим, мы добавили в программу второе ограничение:
val rembrandtl = Flip(0.4)
val rembrandt2 = Flip(0.2)
val samePainter = rembrandtl === rembrandt2
rembrandt2.addConst raint((bi Boolean) —> if (b) 0.1 else 0.9)
rembrandtl.addConst raint((bi Boolean) —> if (b) 0.8 else 0.3)
Вероятность мира, в котором обе переменные rembranti и rembrandt2
принимают значение true, равна 0.8 х 0.1 = 0.08.
Как и в случае прямой выборки, это не точная апостериорная вероятность, а
лишь оценка, основанная на сгенерированной выборке. Справедливы те же самые
утверждения:
• в среднем выборочное распределение совпадает с истинным;
• чем больше размер выборки, тем ближе выборочное распределение к
истинному.
Таким образом, выборка по значимости потенциально является хорошим
приближенным методом вывода в вероятностном программировании.
365

Глава 11. Выборочные алгоритмы
Предотвращение отклонений
В предыдущем примере факты задавались в виде мягкого ограничения. Это
хорошо, потому что одна из целей выборки по значимости - обработка ограничений.
Но что делать, если у нас имеется не ограничение, а условие?
Условие эквивалентно ограничению, в котором фигурируют только значения О
и 1. Так, факт
у.observe(false)
можно записать в виде
y.addConstraint((b: Boolean) => if (b) 0.0 else 1.0)
Поскольку мы умеем обрабатывать ограничения в алгоритме выборке по
значимости, то можем обработать и условия. Но есть один нюанс. Если пример
несовместим с жестким условием, то его вес будет равен 0, поэтому он не дает никакого
вклада в апостериорное распределение. Это эквивалентно отклонению примера.
Поскольку мы знаем, что в конечном итоге вес примера окажется равным 0, то
можем отклонить его сразу, чтобы не делать лишнюю работу.
Сейчас мы в состоянии написать псевдокод базового алгоритма выборки по
значимости. Он возвращает пример и его вес.
1. Обозначим О топологический порядок на множестве переменных.
2. w ч- 1 (вес инициализируется значением 1; если ограничений нет, то таким
же будет и окончательный вес).
3. Для каждой переменной V в порядке О:
a. Обозначим Par множество родителей V.
b. Обозначим хРаг ранее сгенерированные значения Par.
c. Вывести xv из P(V | Par = хадг).
d. Если xv несовместимо с условиями, относящимися к V, перейти к
шагу 2.
e. w <- w * (произведение ограничений на V, примененных к xv).
3. Вернуть (х, w).
Этот алгоритм ничем не лучше выборки с отклонением при жестких
ограничениях, который, как я говорил, практически непригоден, потому что требует
слишком много времени для генерирования даже одного примера. Отклонение
примеров, несовместимых с условиями, - вещь, которой хотелось бы по возможности
избежать. Решение проблемы заключается в том, чтобы попытаться «протолкнуть
факт назад», так чтобы жесткие условия на последующие элементы превратились
в мягкие ограничения на предыдущие. Общая процедура довольно сложна, но я
могу проиллюстрировать ее на примере:
val х = Betad, l)
val у = Flip(x)
у.observe(false)
366

11.2. Выборка по значимости
Проанализируем этот пример. Сначала генерируется значение х, допустим 0.9.
Затем элемент шр(0.9) генерирует значение у. Оно будет равно true с
вероятностью 0.9 и false с вероятностью 0.1. Таким образом, у согласуется с наблюдением
с вероятностью 0.1. Чтобы узнать это, выбирать у вообще не нужно, т. к.
утверждение непосредственно следует из определения Flip. Сгенерировав значение 0.9
для х, мы сразу можем назначить примеру вес 0.1 и не выбирать у. Аналогично,
если для х сгенерировано значение 0.3, то вероятность совместимости с
наблюдением равна 0.3, поэтому примеру можно сразу назначить вес 0.7.
В общем случае, если при выборке х сгенерировано значение р, то вероятность
наблюдения равна 1 - р. Назначение примеру веса 1 - р можно имитировать,
наложив на х ограничение, равное 1 минус значение х. Затем можно принудительно
положить у равным false; мы знаем, что эта переменная должна быть равна false
вследствие наблюдения, и мы уже учли эффект этого наблюдения в ограничении
на х. В итоге исходная программа оказывается эквивалентна такой:
val х = Beta(l, 1)
x.addConstraint((d: Double) => 1 - d)
val у = Constant(false)
Как видите, мы преобразовали жесткое условие в мягкое ограничение. В
результате примеры не будут отклоняться, а получат веса, основанные на значении х.
Примечание. В Figaro нет общей процедуры, которая производила бы такие
преобразования для всех условий. Но есть набор простых эвристик для обработки типичных
ситуаций. Преобразование программы для переноса условий и ограничений на более
ранние стадии - область активных исследований, и мы надеемся в будущем улучшить
Figaro в этом отношении.
7 7.2.2. Выборка по значимости в Figaro
Применение алгоритма выборки по значимости в Figaro не вызывает затруднений.
Существует как стандартный вариант, когда размер выборки задается заранее, так
и вариант с отсечением по времени, который работает столько времени, сколько
указано, и позволяет получить ответ в любой момент. Оба варианта находятся в
пакете com. era. figaro. algorithm, sampling. Importance. Ниже ПОКазанО, Как Запу-
стить стандартный вариант с размером выборки 10 000 и целевыми переменными
rembrandti и rembrandt2, а затем запросить результаты:
val algorithm = Importance(10000, rembrandti, rembrandt2)
algorithm.start()
println(algorithm.probability(rembrandti, true))
printIn(algorithm.distribution(rembrandt2).toList)
algorithm.kill()
Алгоритм с отсечением по времени продолжает выбирать примеры, пока
работает, что дает возможность получать все более точные ответы на запросы. Чтобы
367

Глава 11. Выборочные алгоритмы
запустить версию с отсечением, нужно просто не задавать размер выборки,
ограничившись целевыми переменными. Обычно, пока алгоритм работает, программа
делает что-то другое, но можно просто подождать указанное время (выраженное в
МИЛЛИСекуНДах), ВЫЗВаВ МеТОД Thread, sleep.
В следующем фрагменте алгоритм выборки по значимости работает 1
секунду, затем печатает ответ на запрос, потом работает еще секунду и снова печатает
ответ:
val algorithm = Importance(x, у)
algorithm.start()
Thread.sleep(lOOO)
println(algorithm.probability(x, true))
printIn (algorithm.distribution(y) .toList)
Thread.sleep(lOOO)
println(algorithm.probability(x, true))
println(algorithm.distribution(y).toList)
algorithm.kill()
Алгоритм с отсечением по времени работает в отдельном потоке. Важно по
завершении вызывать его метод kin, чтобы освободить поток, иначе алгоритм будет
и дальше потреблять системные ресурсы.
Если вы хотите на время приостановить алгоритм и возобновить его позже, то
можете воспользоваться методами algorithm, stop о и algorithm, resume о,
например:
val algorithm = Importance(x, у)
algorithm.start()
Thread.sleep(lOOO)
algorithm.stop()
// Выполнить интерактивную визуализацию и подождать, пока пользователь
// работает
algorithm.resume()
Thread.sleep(lOOO)
algorithm.stop()
// Снова показать результаты визуализации и т. д.
7 7.2.3. Полезность выборки по значимости
Когда следует использовать алгоритм выборки по значимости? Основных
причины две.
В модели имеются непрерывные переменные. В главе 10 мы видели, что хотя
факторные алгоритмы и могут работать с непрерывными переменными, обычно
им приходится строить выборку из небольшого числа значений переменных,
поэтому они не столь эффективны, как для дискретных переменных с относительно
узким диапазоном значений. Если мы хотим рассматривать всю область значений
непрерывных переменных, то следует использовать какой-нибудь выборочный
алгоритм, например по значимости.
368

11.2. Выборка по значимости
• Примером модели с непрерывными переменными может служить модель
для прогнозирования продаж различных продуктовых линеек. Объем
продаж, измеряемый в долларах, естественно моделируется с помощью
непрерывной переменной. При использовании факторного алгоритма нам
пришлось бы ограничиться относительно небольшим числом значений, что
помешало бы получить нужную точность.
• Модель имеет переменную структуру. Если некоторые части модели
существуют лишь для определенных значений переменных, то алгоритм
выборки по значимости будет генерировать только релевантные переменные
для каждого примера. Примером такой динамической модели с
переменной структурой может служить модель ресторана из главы 8. Количество
усаженных гостей на каждом временном шаге переменно. В разделе 8.2.4
было показано, как использовать выборку по значимости для рассуждений
об этой модели.
Подчеркну, что выборка по значимости - не панацея даже для тех типов
моделей, на которые ориентирована. Проблема в том, что собрать заданное число
взвешенных примеров - совсем не то же самое, что столько же обычных
примеров. Ценность миллиона взвешенных примеров, собранных с помощью выборки
по значимости, может оказаться не лучше, чем 100 примеров, собранных методов
выборки с отклонением. Есть специальный показатель - эффективный размер
выборки, который характеризует количество обычных примеров, эквивалентное
данному множеству взвешенных.
Эффективный размер выборки трудно формализовать строго, но на
интуитивном уровне чем меньше суммарный вес примеров, тем меньше эффективный
размер выборки. Вообще говоря, средний вес примера равен вероятности факта,
выраженного в виде условий и ограничений. Поэтому чем меньше вероятность
факта, тем меньше ожидаемый эффективный размер выборки. Проблема похожа
на возникающую в случае выборки с отклонением, где чем меньше вероятность
факта, чем меньше ожидаемое число пригодных примеров.
Принимая во внимание всё сказанное, для применения выборки по
значимости с пользой рекомендуется избегать крайне маловероятных фактов. Например,
вместо жесткого условия, которое вряд ли когда-нибудь будет выполнено, а,
значит, станет причиной большого числа отклонений, воспользуйтесь ограничением
с малым, но ненулевым значением в ситуации, когда условие не удовлетворяется.
Если таких условий много, и все они заменены ограничениями, то окажется, что
примеры, совместимые с большинством условий, имеют больший вес, чем
примеры, совместимые с немногими условиями. Во многих случаях это позволит
получить вполне приемлемые ответы на запросы. К сожалению, несмотря на простоту
этих интуитивных соображений, на практике трудно понять, когда они
действительно дадут эффект. Ключевое условие - чтобы примеры, совместимые с
большим числом условий, были ближе к истине, чем те, что совместимы с меньшим
числом. Описание конкретной ситуации приведено на врезке ниже.
369

Глава 11. Выборочные алгоритмы
Пример: расшифровка криптограммы методом выборки
по значимости
Представьте, что вы пытаетесь с помощью вероятностных рассуждений
расшифровать криптограмму. Криптограммой называется текст, в котором каждая буква
заменена некоторой другой буквой алфавита. Допустим, имеется вероятностная модель,
которая случайным образом выбирает подстановку букв. И есть два условия: разные
буквы нельзя заменять одной и той же и каждое слово исходного текста должно быть
допустимым словом английского языка.
В случае выборки с отклонением мы выбрали бы случайный набор подстановок, а
затем проверили, удовлетворяют ли они условиям. Вероятность, что выбранный набор
будет удовлетворять всем условиям, крайне мала, поэтому даже на генерирование
одного примера уйдет масса времени. Но если заменить условия мягкими
ограничениями, то можно будет сгенерировать подстановки, удовлетворяющие большинству,
хотя и не всем условиям. Но даже эти примеры могут дать полезную оценку
апостериорного распределения. Хотя маловероятно, что будет сгенерирован абсолютно
правильный ответ, может оказаться, что в большинстве примеров с высоким весом буква
Е заменена буквой N. Это позволит высказать гипотезу, которая даст возможность
продвинуться и в конечном итоге решить головоломку. Примерно так люди и
расшифровывают криптограммы.
Подведем итог всему сказанному о выборке по значимости.
• Это общий алгоритм, применимый практически к любой модели.
• Он работает плохо, если факты маловероятны, поскольку эффективный
размер выборки оказывается слишком малым. Но это можно несколько
поправить, ослабив условия, входящие в состав фактов.
7 7.2.4. Приложения алгоритма выборки
по значимости
Мы видели, что алгоритм выборки по значимости работает лучше, если нет крайне
маловероятных фактов. Поэтому на практике он чаще всего применяется в
ситуациях, где фактов мало или нет вовсе.
Прогнозирование с помощью имитационной модели
Если фактов нет вообще (в программе нет ни условий, ни ограничений), то
выборка по значимости - то же самое, что простейший алгоритм прямой выборки,
описанный в разделе 11.1.1. В этом случае предсказание будущего
осуществляется путем генерирования большого числа возможных будущих путей выполнения.
При таком использовании Figaro по существу работает как система
имитационного моделирования, и его можно применять во многих приложениях такого
характера: выборы, планирование военных операций, экономические системы,
спортивные прогнозы.
Допустим, к примеру, что мы хотим смоделировать футбольный сезон и
предсказать положение любимой команды в турнирной таблице. Мы можем создать
370

11.2. Выборка по значимости
модель отдельного матча, зависящую от силы двух соперников, и включить ее в
модель всего сезона, состоящую из всех матчей. Модель может учитывать
различные факторы, например, травмы игроков. Применяя прямую выборку, мы
моделируем исходы всех игр на протяжении сезона и получаем окончательную
турнирную таблицу. Используя результаты имитационного моделирования, мы можем
подсчитать шансы нашей команды стать чемпионом. Если брать весь сезон, то
модель окажется весьма сложной, и выборка представляется естественным способом
рассуждений о ней.
При таком использовании выборки по значимости обычно имеются начальные
условия, например, начальная сила всех команд лиги. Смоделировать их можно
тремя способами.
• Как фиксированные значения Scala. Это позволяет эффективно рассуждать
о них, но не дает возможности смоделировать случайные изменение силы
команд на протяжении сезона. Если вы не собираетесь изменять модель, то
это, наверное, самый лучший подход.
• Как константные элементы Constant Например, начальную силу
команды 0.96 можно было бы представить элементом constant(0.96). Тогда в
разные моменты на протяжении сезона представлять силу команды можно
было бы разными элементами. Преимущество такого подхода в том, что он
позволяет изменять силу команды со временем, не вводя никаких фактов,
относящихся к ее силе в начале сезона. Элемент constant может принимать
только одно значение, поэтому начальная сила команды всегда будет
равна 0.96. Это позволяет эффективно использовать прямую выборку.
• Как элементы Figaro с непостоянным распределением. Так имеет смысл
поступать, если начальные условия характеризуются неопределенностью.
Например, возможно, есть основания полагать, что сила каждой
команды изменяется в определенном диапазоне, для вашей команды это мог бы
быть диапазон от 0.94 до 0.98, и тогда можно было бы использовать элемент
uniform(0.94, 0.98). Преимущество такого подхода состоит в том, что не
нужно фиксировать какое-то определенное значение. Если же
определенное значение таки существует (скажем, 0.96), то лучше взять элемент
constant, чем элемент uniform вместе с фактом, говорящим, что его значение
равно 0.96.
Прогнозирование при наличии фактов о начальном
состоянии
Если начальное состояние точно не известно, то, возможно, есть какие-то
относящиеся к нему факты. Например, вы считаете, что сила команды связана с ее
положением в прошлогодней турнирной таблице, дополненными сведениями о
выбытии и приобретении игроков в межсезонье. Чтобы включить эти факты,
можно было бы сделать выборку из предыдущего сезона, взяв окончательную
турнирную таблицу в качестве факта, и вывести вероятную силу всех команд в прошлом
сезоне. Затем полученные величины силы корректируются с учетом выбытия и
371

Глава 11. Выборочные алгоритмы
приобретения игроков. И наконец, моделируется новый сезон с вычисленными
оценками силы в качестве начальных условий. Ниже приведен набросок
соответствующей программы на Figaro:
val lastYearsStrengths = Array.fill(Uniform(0, 1))
val lastYearsTable = playSoccerSeason(lastYearsStrengths)
lastYearsTable.observe(actualTable)
val thisYearsStrengths =
lastYearsStrengths.map((strength: Element[Double]) => adjust(strength))
val thisYearsTable = playSoccerSeason(thisYearsStrengths)
println(Importance.probability(thisYearsTable, (t: Table) => myTeamTop(t)))
Если вероятность фактов, относящихся к начальному состоянию, не слишком
мала, то выборка по значимости - прекрасный кандидат для решения этой задачи.
Если в качестве наблюдений брать результаты матчей во всем сезоне, то фактов
оказалось бы слишком много для алгоритма выборки по значимости, поэтому
лучше было бы использовать МСМС.
Можно представить себе обобщение этого рассуждения на несколько сезонов.
Быть может, для определения начальных условий стоит взять данные о трех
прошлых сезонах. В каждом из них мы задаем начальную силу команд, прогоняем
модель сезона, наблюдаем турнирную таблицу и вносим корректировки, связанные с
выбытием и приобретением игроков, - в результате получаем силу команд в
начале следующего сезона. Все это можно сделать с помощью выборки по значимости.
Все здесь описанное составляет основу алгоритма фильтрации частиц,
применяемого для рассуждений о динамических моделях. Работа этого алгоритма
начинается с множества примеров, представляющих состояние системы в некоторый
момент времени. Затем выборка по значимости используется, чтобы учесть
факты в этот момент. Алгоритм фильтрации частиц добавляет шаг перевыборки. Весь
процесс можно повторять сколько угодно раз. Подробнее об алгоритме
фильтрации частиц мы будем говорить в главе 12, а сейчас я хочу подчеркнуть, что это одно
из основных применений выборки по значимости.
Выводы о сложном процессе при наличии немногих
фактов
Выборка по значимости используется не только для предсказания будущего.
Она эффективно применяется также для задач вывода, когда целью является
вывод значения запрашиваемой переменной на основе знания о его следствиях.
Обычно алгоритм выборки по значимости используется таким образом, когда
процесс порождения следствия сложен, а фактов немного. Приведем пример.
При анализе социальных сетей применяются различные модели порождения
сетей, например, модель Эрдеша-Реньи или модель предпочтительного
присоединения Барабаши-Альберта. Исследователя может интересовать, какая модель
лучше подходит для описания наблюдаемой сети. Разные модели
характеризуются различными статистиками, например, максимальным числом соседних
вершин или средним расстоянием между вершинами. Зная эти статистики, можно
372

11.3. Алгоритм Монте-Карло по схеме марковской цепи
III!
SHE]
вывести, каким процессом, скорее всего, была порождена сеть. В Figaro различные
модели порождения сетей возвращали бы элемент Element [Network]. Статистики
применялись бы к этому элементу и возвращали Element [Double]. Вот набросок
программы такого типа:
class Network { ... }
def erdosRenyi: Element [Network] = ...
def barabasiAlbert: Element [Network] = ...
def maxNeighbors (n: Network) = ...
def averageDistance (n: Network) = ...
val er = erdosRenyi()
val ba = barabasiAlbert()
val myNetwork = discrete.Uniform(er, ba)
val mn = myNetwork.map (maxNeighbors) <3—©
val ad = myNetwork.map(averageDistance)
mn.observe(7)
ad.addCondition( (d: Double) => d > 0.31 && d < 0.35) <3—©
println(Importance.probability(myNetwork, er))
О — Сокращенная запись Apply(myNetwork, (n: Network) => maxNeighbors(n))
© — Используем для условия диапазон, чтобы оно не оказалось слишком
маловероятным
Выборка по значимости здесь работает, потому что имеется единственный
факт - сводная статистика сети. Хотя генерирование какой-то конкретной сети
маловероятно, статистика у многих сетей похожа, поэтому вероятность сводной
статистики не так уж мала. С другой стороны, если бы мы наблюдали
порождение определенной сети, то было бы крайне маловероятно найти метод, который
порождает именно такую сеть, поэтому применение выборки по значимости
оказалось бы неэффективным.
Из этого обсуждения видно, что алгоритм выборки по значимости практически
полезен только тогда, когда переменных, содержащих факты, немного, а
вероятность самих фактов не слишком мала. Многие реальные ситуации не
удовлетворяют этим условиям, поэтому возникает необходимость в другом алгоритме. Как
правило, в качестве такого алгоритма выступает МСМС, который мы и обсудим в
следующем разделе.
11.3. Алгоритм Монте-Карло по схеме
марковской цепи
Метод Монте-Карло по схеме марковской цепи (МСМС)снимаетфундаментальное
ограничение алгоритма выборки по значимости, в котором генерирование одного
«хорошего» примера с большим весом может занимать длительное время. А
сгенерировав один пример, нужно начинать все заново и генерировать следующий.
Главный принцип МСМС заключается в том, чтобы не начинать работу заново
при генерировании следующего примера, а на следующем шаге продолжать с того
места, где закончился предыдущий. Это дает два преимущества:

Глава 11. Выборочные алгоритмы
• МСМС быстрее доходит для примеров с высокой вероятностью;
• найдя пример с высокой вероятностью, МСМС имеет тенденцию
оставаться в области таких примеров;
• МСМС - гибкий и мощный алгоритм. Прежде чем переходить к
практическим вопросам, обсудим, как он работает.
11.3.1. Как работает МСМС
Для иллюстрации работы МСМС рассмотрим следующую программу:
val х = Normal(0.75, 0.2)
val у = Normal(0.4, 0.2)
x.setCondition((d: Double) => d > 0 && d < 1)
y.setCondition((d: Double) => d > 0 && d < 1)
val pair = AA(x, y)
println(MetropolisHastings.probability(pair,
(xy: (Double, Double)) => xy._l > 0.5 && xy._2 > 0.5))
В ней определены два случайных числа с нормальным распределением и
заданы условия, согласно которым их значения должны быть заключены между 0
и 1. Затем программа создает пару, состоящую из значений обоих чисел. Наконец,
с помощью алгоритма Метрополиса-Гастингса (так МСМС называется в Figaro)
вычисляется вероятность того, что оба числа больше 0.5.
На рис. 11.7 показано, как работает МСМС. Мы видим множество возможных
миров (квадрат, в котором х и у принимают значения от 0 до 1). Существует
некоторое распределение возможных миров; круг - это область миров с высокой
вероятностью. Алгоритм МСМС проходит через последовательность состояний.
На каждом шаге он случайным образом переходит в новое состояние. Но хотя
шаг случайный, наблюдается тенденция движения в сторону более вероятных
состояний. В конечном итоге алгоритм обычно достигает области состояний с
высокой вероятностью.
Возможные
миры
Области
высокой
вероятности
Рис. 11.7. Работа МСМС: алгоритм случайным образом переходит из одного
состояния в другое, постепенно приближаясь к состояниям с высокой вероятностью
374
1
г
О
х
О
1

11.3. Алгоритм Монте-Карло по схеме марковской цепи
Почему МСМС работает
Попробуем разобраться, почему алгоритм МСМС работает. Нужно понять три
ключевых момента; уяснив их, вы будете знать самую суть алгоритма.
Как следует из названия, алгоритм МСМС опирается на теорию марковских
цепей, с которой мы познакомились в главе 8. Напомню, что марковская цепь -
это вероятностная модель динамической системы, которая переходит из одного
состояния в другое. Переход на каждом шаге определяется некоторым условным
распределением вероятности. Легко видеть, почему МСМС определяет
марковскую цепь: он описывает последовательность состояний, причем переход из
одного состояния в другое производится согласно заранее определенному процессу.
На рис. 11.8 показана диаграмма (по аналогии с главой 8), иллюстрирующая эту
марковскую цепь.
Состояние(О)
Рис. 11.8. Марковская цепь, показывающая состояния,
через которые проходит алгоритм МСМС
Теперь сделаем мысленное усилие и перейдем от последовательности
состояний к последовательности распределений. Логика такая. При каждом выполнении
марковской цепи система проходит по некоторой последовательности состояний.
В каждый момент времени система может находиться в любом из нескольких
состояний. Всегда существует распределение вероятности текущего состояния
системы; в каждый момент имеется распределение вероятности для этого момента.
Иными словами, марковская цепь определяет последовательность распределений,
по одному для каждого момента времени.
Определим эту последовательность распределений. Если имеется текущее
распределение в некоторый момент времени, то модель переходов марковской цепи
определяет следующее распределение. В Figaro для этой цели можно
использовать элемент chain:
val nextDistribution = Chain(currentDistribution, (s: State) =>
transition(s))
Следующее распределение определяется таким порождающим процессом:
начать с состояния, выбранного из текущего распределения, и применить функцию
перехода для получения следующего состояния. В результате получаем
следующие свойства.
• Пункт 1 - начав с заданного распределения, марковская цепь определяет
последовательность распределений вероятности состояний системы.
А теперь тонкое и красивое утверждение относительно алгоритма МСМС,
которое и объясняет, почему он работает.
• Пункт 2 - для любой марковской цепи, удовлетворяющей некоторым
математическим условиям, все последовательности распределений сходятся
к одному и тому же распределению.
375
Состояние(1)
Состояние{2)

Глава 11. Выборочные алгоритмы
Это конечное распределение называется стационарным распределением
марковской цепи. Весь процесс иллюстрируется на рис. 11.9. Главное, что нужно в нем
понять, - тот факт, что закрашенная область показывает не возможные состояния
х и у, а пространство распределений вероятности х и у. Каждая точка этого
пространства - целое распределение, а не одиночные значения х и у.
Стационарное распределение,
к которому сходится цепь
Заданное
начальное
распределение
Все возможные
распределения
вероятности
Рис. 11.9. Сходимость распределений состояний, определяемых марковской
цепью. Закрашенная область показывает все возможные распределения
состояний. Каждый путь описывает последовательность распределений, причем
все последовательности начинаются из разных распределений. Каким бы ни
было начальное состояние, процесс сходится к одному и тому же стационарному
распределению
Марковская цепь начинается с некоторого начального распределения. В
алгоритме МСМС это начальное распределение определяется процессом, который
выбирает начальное состояние системы. В нашем примере это процесс, выбирающий
начальные значения х и у. Так, процесс может установить х и у равными 0.5; тем
самым будет определено распределение вероятности, при котором это состояние
будет иметь вероятность 1.
Стрелками на рисунке показан процесс перехода от предыдущего
распределения к следующему; еще раз подчеркну, что это переход не между состояниями,
а между распределениями вероятности состояний. Как видно из рисунка, при
любом начальном распределении последовательность распределений сходится
к некоторому пределу - стационарному распределению. Возможно, она никогда
не достигнет стационарного распределения, но приблизится к нему сколь угодно
близко, если сделать достаточно большое количество шагов. Кроме того, если
последовательность достаточно близко подошла к стационарному распределению,
то она и останется близко к нему.
376

11.3. Алгоритм Монте-Карло по схеме марковской цепи
III!
aa
И последний момент.
• Пункт 3 - если марковская цепь спроектирована так, что стационарное
распределение является апостериорным распределением, из которого мы
хотим производить выборку, то выборка из стационарного распределения
будет близка к выборке из апостериорного распределения.
Определение алгоритма МСМС
Существо алгоритма заключается в том, что, начав с некоторого состояния, мы
используем марковскую цепь для последовательных переходов в новое
состояние. Известно, что спустя длительное время распределение текущего состояния
окажется близко к апостериорному распределению, из которого производится
выборка. В этот момент мы производим выборку. Число шагов марковской цепи
до выборки называется периодом приработки. Чем дольше период приработки,
тем ближе получившееся в его конце распределение к апостериорному. С другой
стороны, чем этот период дольше, чем больше времени потребуется МСМС для
взятия выборки.
В начале раздела 11.3 я отмечал, что одно из основных достоинств МСМС
состоит в том, что, раз достигнув состояния с высокой вероятностью, он там и
останется, а не будет начинать все сначала. Алгоритм МСМС никогда не возвращается
в начальное состояние, в продолжает использовать марковскую цепь для перехода
между состояниями. В принципе, после выборки первого примера мы знаем, что
уже близки к апостериорному распределению, поэтому дальше могли бы выбирать
пример на каждом шаге.
Но есть одна тонкость: состояния на соседних шагах МСМС не являются
независимыми. Рассмотрим наш пример программы. Допустим, что значение х в
некоторый момент времени равно 0.9. Если марковская цепь изменяет х небольшими
приращениями, то в следующий момент значение х будет близко к 0.9. Оно
сильно зависит от предыдущего значения. В результате ответы на запросы могут быть
смещены. Поэтому имеет смысл задать интервал между отбираемыми примерами,
чтобы уменьшить их взаимозависимость. На практике, однако, выясняется, что
задание интервала не всегда повышает качество работы МСМС, поскольку число
примеров резко уменьшается.
На рис. 11.10 показан ход отбора примеров МСМС при использовании периода
приработки и интервала. Как видим, период приработки призван обеспечить
отбор первого примера в области высоких вероятностей. Однако никаких гарантий
тут нет. Вам остается догадываться, сколько шагов сделать, и надеяться, что их
окажется достаточно. Кроме того, из рисунка видно, что интервал 2 обеспечивает
довольно большое расстояние между соседними примерами, так чтобы сделать их
достаточно независимыми.
Ниже приведено формальное описание алгоритма МСМС. Алгоритм
принимает три параметра: количество примеров, период приработки и величину
временного интервала.

Глава 11. Выборочные алгоритмы
Приработка
Возможные
миры
Области
высокой
вероятности
Интервал = 2
Рис. 11.10- Ход отбора примеров МСМС при использовании
периода приработки и интервала. Примеры, попадающие
в период приработки, пропускаются, после этого берется
каждый второй пример, поскольку интервал равен 2
1. Выбрать начальное состояние из начального распределения марковской
цепи.
2. Фаза приработки - повторять на протяжении периода приработки:
а. Перейти в новое состояние, применяя модель перехода.
3. Взять текущее состояние в качестве первого примера.
4. Фаза выборки - повторять, пока не набрано заданное число примеров.
a. Повторять в течение заданного временного интервала:
i. Перейти в новое состояние, применяя модель перехода.
b. Взять текущее состояние в качестве примера.
7 7.3.2. Алгоритм МСМС в Figaro:
алгоритм Метрополиса-Гастингса
Согласно пункту 3, если марковская цепь спроектирована так, что стационарным
распределением является апостериорное распределение, из которого будет
производиться выборка, то мы имеем основу для алгоритма выборки из
апостериорного распределения. Существует много способов спроектировать марковскую цепь
с желаемым свойством. В Figaro применяется алгоритм Метрополиса-Гастингса
(МГ). Этот алгоритм широко известен благодаря своей общности, а возможность
выразить различные виды моделей делает его пригодным для вероятностного
программирования.
Основная идея алгоритма Метрополиса-Гастингса состоит в том, чтобы
использовать марковскую цепь, в которой модель перехода состоит из двух шагов.
1. Зная текущее состояние (множество значений переменных модели),
предложить новое. Это новое состояние выбирается в соответствии со
вспомогательным распределением - распределением вероятности следующего
378
1
у
о
х
О
1

11.3. Алгоритм Монте-Карло по схеме марковской цепи
III!
НЕ
состояния при условии текущего. Это вспомогательное распределение
зависит от текущего состояния; например, оно может отдавать предпочтение
небольшим шагам из текущего состояния. Искусство применения
алгоритма МГ во многом определяется именно выбором вспомогательного
распределения.
2. С вероятностью перехода принять новое состояние или оставить текущее.
Вероятность перехода зависит как от свойств вспомогательного
распределения, так и от отношения вероятностей нового и текущего состояния.
В Figaro вспомогательное распределение определяется с помощью схемы
предложения. Существует схема предложения по умолчанию, а также API для задания
собственной схемы. Схема по умолчанию работает следующим образом.
1. Случайным образом выбрать один недетерминированный элемент.
Недетерминированность означает, что элемент порождает случайное значение,
даже если его аргументы известны. Например, элементы Flip и Normal
недетерминированные, a constant и if - нет.
2. Предложить новое значение выбранного элемента.
3. Обновить значения элементов, зависящих от выбранного.
В схеме по умолчанию вы никак не контролируете, какой элемент выбирается
на шаге 1; он равновероятно выбирается из всех недетерминированных элементов.
В специальной схеме предложения вы можете предлагать несколько элементов
и сами управляете тем, какие элементы предлагаются. В некоторых случаях
схема по умолчанию дает хорошие результаты, так что всегда имеет смысл начать с
нее. Но иногда приходится придумывать собственную схему. Специальные схемы
предложения обсуждаются в разделе 11.4.1.
Создание алгоритма Метрополиса-Гастингса в Figaro
Figaro предлагает несколько способов создать экземпляр алгоритма МГ с
различными конфигурациями аргументов. В самом распространенном случае
задается требуемое количество примеров, схема предложения и опрашиваемые
переменные. Например, вызов
MetropolisHastings(100000, ProposalScheme.default, x, у)
означает, что мы хотим отобрать 100 000 примеров, используя схему предложения
по умолчанию для получения приближенных апостериорных распределений х и у.
Это стандартный вариант алгоритма, который работает, пока не наберется нужное
число примеров. Есть также вариант с отсечением по времени; в этом случае число
примеров не задается, а алгоритм работает, пока не будет остановлен, например:
MetropolisHastings(ProposalScheme.default, x, у)
В этих вариантах нет периода приработки, поэтому МГ сразу же начинает
отбирать примеры. Интервал равен 1, т. е. каждое состояние отбирается в качестве
примера. При желании можно также задать период приработки и интервал. На-

Глава 11. Выборочные алгоритмы
пример, чтобы набрать 100 000 примеров с периодом приработки 1000, нужно
было бы написать:
MetropolisHastings(100000, ProposalScheme.default, 1000, х, у)
Здесь интервал по умолчанию равен 1. Период приработки обычно задается,
чтобы не отбирать примеры из распределений, образующихся в начале
марковской цепи, т. к. они могут сильно отличаться от истинного. А интервал нас в
большинстве случаев не волнует, и его можно оставить равным 1. Если же вы все-таки
хотите задать интервал, то должны будете задать и период приработки тоже.
Период приработки задается первым, а интервал - за ним. Так, чтобы задать
приработку 1000 и интервал 10, мы пишем:
MetropolisHastings(100000, ProposalScheme.default, 1000, 10, х, у)
В любом случае можно использовать также вариант с отсечением по времени.
На рис. 11.11 показана структура конструктора МГ со всеми необязательными
аргументами:
MetropolisHastings(100000, ProposalScheme.default, 1000, 10, х, у)
Количество экземпляров Схема Период Целевые переменные
(для варианта с отсечением предложения приработки (в произвольном
по времени опускается) , (необязательный) количестве)
\
MetropolisHastings(100000, ProposalScheme.default, 1000, 10, х, у)
Интервал
(необязательный)
Рис. 11.11. Структура конструктора МГ в Figaro
Свойства МГ
Алгоритм МГ широко распространен благодаря своей общности. Его основное
достоинство заключается в том, что вместо случайной выборки нового состояния
на каждой итерации имеется процесс, который направляет алгоритм в область
высоких вероятностей. А дойдя до этой области, алгоритм имеет тенденцию
оставаться в ней. Поэтому выборочный алгоритм может оказаться практически
полезным даже в тех случаях, когда выборка по значимости работает плохо из-за
слишком низкой вероятности фактов.
Чтобы понять, почему МГ может находить состояния с высокой вероятностью,
а выборка по значимости - нет, рассмотрим простой пример с двумя переменными
х и у. Предположим, что имеются ограничения на х и у, которым трудно удов-
380

11.3. Алгоритм Монте-Карло по схеме марковской цепи
inn
летворить. Для определенности пусть ограничение принимает большое значение
из узкого диапазона, что случается 1 раз из 10 при выборке х и у из априорного
распределения. В остальных 9 случаях ограничение принимает малое значение.
Применяя выборку по значимости, мы каждый раз генерировали бы новые
значения х и у из их априорного распределения, поэтому вероятность того, что оба
ограничения примут большое значение, равна 1 из 100. То есть для получения
одного пригодного примера потребовалось бы 100 итераций.
С другой стороны, представим алгоритм МГ, который позволяет раздельно
предлагать х или у. В среднем после 10 предложений х или у в одном
ограничение примет большое значение. Допустим, это оказалась переменная х. Когда
впоследствии МГ снова предложит х, переход, при котором ограничение принимает
низкое значение, почти наверняка будет отклонен. Поэтому х почти всегда будет
оставаться в области высокой вероятности. А тем временем еще после нескольких
предложений ограничение на у также примет большое значение.
Пусть теперь переменных не две, а 100. В случае выборки по значимости
вероятность генерирования примера, для которого все ограничения принимают
большое значение, равна 1 / 10100. На практике это означает невозможность. Но
МГ может продвигать каждую переменную к области ее высокой вероятности по
отдельности и в конце концов найдет состояние, в котором ограничения для всех
переменных принимают большие значения.
Это преимущество делает алгоритм МГ привлекательным решением для
многих приложений, но у него есть и недостатки. Главный недостаток в том, что
алгоритм может работать медленно. Если не задавать интервал между примерами,
то в общем случае мы должны отобрать гораздо больше примеров, чем в алгоритме
выборки по значимости, потому что примеры не являются независимыми.
Бывают задачи, где примеров должно быть на несколько порядков больше. Если же мы
решим задать интервал, то его нужно делать достаточно большим, чтобы
примеры оказались практически независимыми, но тогда для генерирования хотя бы
одного примера понадобится много времени. Кроме того, много времени может
занять период приработки, необходимый, чтобы приблизиться к области высокой
вероятности. Поэтому в ситуациях, когда вероятность фактов не слишком низкая,
лучше отдать предпочтение выборке по значимости.
Второй недостаток МГ состоит в том, что его поведение трудно понять,
предсказать и контролировать. Эффективность МГ зависит от того, насколько хорошо
определено вспомогательное распределение. Интуитивно нам хотелось бы иметь
алгоритм, который достаточно быстро перемещается по пространству состояний,
чтобы нахождение области высокой вероятности не занимало слишком много
времени, но не настолько быстро, чтобы покинуть эту область после ее обнаружения.
Эти свойства чувствительны к выбору вспомогательного распределения;
спроектировать хорошее вспомогательное распределение, обладающее такими
свойствами, - непростая задача, а предсказать, как поведет себя конкретное распределение,
зачастую нелегко. К тому же, велики шансы по неосторожности определить такое
вспомогательное распределение, в котором пространство состояний исследуется
не полностью. Я еще вернусь к этому вопросу в следующем разделе.

Глава 11. Выборочные алгоритмы
Сложность прогнозирования поведения МГ имеет побочный эффект:
непонятно, чему должен быть равен период приработки и сколько всего отбирать
примеров. Если мы не знаем, сколько времени потребуется для достижения области
высокой вероятности, то как узнать, когда прекращать приработку? А если
неизвестно, сколько времени нужно для перехода из текущего состояния в состояние,
которое почти не зависит от него, но при этом все еще находится в области
высокой вероятности, то как решить, сколько нужно примеров? Поэтому в общем
случае рекомендуется дать МГ поработать длительное время и посмотреть,
разумно ли выглядят ответы. Один из вариантов - прогнать алгоритм несколько раз и
сравнить ответы; если окажется, что они не похожи, то, наверное, отобрано
недостаточно примеров.
В силу всего сказанного, несмотря на мощь и общность алгоритма МГ, я обычно
рассматриваю его как последнюю надежду. Обращайтесь к нему, если все
остальные алгоритмы не работают, но помните, что для его настройки, возможно,
придется немало потрудиться. В следующем разделе мы рассмотрим приемы такой
настройки.
11.4. Настройка алгоритма МГ
В этом разделе представлено несколько способов настройки алгоритма МГ. Я буду
рассматривать задачу, которую трудно решить без настройки.
Допустим, требуется предсказать, кто получит приз Оскар за лучшую
актерскую игру. Имеется множество кандидатов. Каждый кандидат представляет собой
роль конкретного актера в конкретном фильме. Согласно модели, станет ли роль
победителем, зависит от известности актера и качества фильма.
Первая попытка смоделировать эту ситуацию на Figaro выглядит следующим
образом:
class Actor {
val famous = Flip(0.1)
class Movie {
val quality = Select (0.3 -> flow, 0.5 -> 'medium, 0.2 -> fhigh)
class Appearance(val actor: Actor, val movie: Movie) {
val award: Element[Boolean] =
CPD(movie.quality, actor.famous,
('low, false) -> Flip(0.001),
(•low, true) -> Flip(O.Ol),
('medium, false) -> Flip(O.Ol),
('medium, true) -> Flip(0.05),
('high, false) -> Flip(0.05),
('high, true) -> Flip(0.2))
382

11.4. Настройка алгоритма МГ
Здесь используются объектно-ориентированные паттерны из главы 7, никаких
дополнительных пояснений код не требует. Ничто не мешает атрибуту award
принимать значение true для нескольких ролей. Поэтому возможны миры, в которых
несколько ролей получают приз. Как мы знаем, в реальности такого быть не
может, поэтому необходимо добавить условие, гарантирующее, что награды будет
удостоена только одна роль. Делается это так:
def uniqueAwardCondition(awards: List[Boolean]) = {
awards.count(b => b)== 1
}
val allAwards: Element[List[Boolean]] =
Inject(appearances.map(_.award): _*)
allAwards.setCondition(uniqueAwardCondition) O—©
О — Проверяем, что число присужденных наград равно 1
© — Создаем элемент, значением которого является список Boolean, извлеченных из
массива ролей
© — Задаем для этого элемента условие, гарантирующее единственность награды
Чтобы завершить описание ситуации, мы должны создать несколько
экземпляров актеров и фильмов и составить из них роли. На практике актеры, фильмы и
роли могут выбираться из базы данных. В коде, прилагаемом к книге, я создаю
роли случайным образом:
val numActors = 200
val numMovies = 100
val numAppearances = 300
val actors = Array.fill (numActors) (new Actor)
val movies = Array.fill (numMovies) (new Movie)
val appearances =
Array .fill (numAppearances) (new Appearance (
actors(random.nextlnt(numActors)),
movies(random.nextlnt(numMovies))))
К сожалению, если просто применить МГ к этой задаче, то ничего работать не
будет. Проблема в том, что в любом возможном мире награды может быть
удостоена только одна роль. Мы хотим, чтобы МГ исследовал пространство возможных
миров с высокой вероятностью. Если начать с какого-то мира, в котором
награждена одна роль, то следующим должно быть состояние, в котором эта роль не
награждена, но награждена какая-то другая роль, причем только одна. На рис. 11.12
показано, почему этого не будет. Изображена байесовская сеть для двух актеров,
фильмов и ролей, но проблема существует при любом количестве. В соответствии
со схемой предложения по умолчанию, может быть изменена известность одного
актера, качество одного фильма или присвоение награды одной роли. Изменение
известности актера или качества фильма не приводит ни к каким сложностям. Но
если текущее состояние удовлетворяет условие уникальности награды, то
после изменения статуса награжденности это условие обязательно будет нарушено.
383
п
в

Глава 11. Выборочные алгоритмы
Если отобрать награду у роли, которая ее имеет, то мы перейдем в состояние, где
нет ни одной награжденной роли, а если дать награду роли, которая ее не имеет,
то в новом состоянии окажутся две награжденных роли. В любом случае условие
уникальности нарушено, и новое состояние отклоняется. За один шаг МГ
невозможно передать награду от одной роли другой.
true
false low
medium
high
false ► true medium
low
high
true
allAwards
Нарушает условие
Нарушает условие
Рис. 11.12. Возможные одношаговые предложения для наивного применения
МГ к задаче об актерах и фильмах. Переменные заключены в закругленные
прямоугольники. Для каждой переменной слева от стрелки показано текущее
значение, а справа - возможные альтернативы. Схема предложения по умолчанию
позволяет за один шаг заменить текущее значение одной переменной другим.
Изменить сразу два значения невозможно. Поэтому любое предложение,
изменяющее значение переменной award, обязательно нарушит условие
уникальности награды и потому не будет принято.
Как все же применить МГ к этой задаче? Есть две основных идеи. Первая -
использовать специальную схему предложения. Например, она могла бы предлагать
изменение сразу двух элементов. Вторая идея - вообще избегать жестких условий,
которые не разрешается нарушать. Одна из проблем в нашей задаче заключается
в том, что условие уникальности награды должно удовлетворяться, иначе
предложение будет отклонено. Если бы можно было ослабить это условие и иногда
принимать предложения, в которых награды удостоены две роли или ни одной, то
алгоритм МГ смог бы передавать награду. В следующих разделах эти идеи получат
развитие.
7 7.4.7. Специальные схемы предложения
Первая проблема связана с использованием схемы предложения по умолчанию.
В Figaro включен язык описания специальных схем. Напомню, что схема
предложения по умолчанию случайным образом выбирает один недетерминированный
Actorl♦famous
Moviel.quality
Actor2♦famous
Movie2♦quality
Appearancel.award
Appearance2.award
false

11.4. Настройка алгоритма МГ
элемент, а специальная схема позволяет предлагать несколько элементов и
управлять их выбором. В частности, специальная схема предложения позволяет делать
следующее:
• последовательно предлагать несколько элементов;
• выбирать из нескольких альтернатив;
• начать с одного элемента, а затем на основе его значения решить, как
продолжить.
На врезке ниже подробно описано, как реализуется каждый вариант. Я же
покажу, как создать специальную схему предложения для задачи об актерах и
фильмах. В данном случае мы хотим одновременно предлагать две роли. Figaro
позволяет последовательно предлагать несколько элементов с помощью такой
конструкции:
ProposalScheme (elementl, element2, ...)
ТаКИМ обраЗОМ, еСЛИ appearances - маССИВ экземпляров Класса Appearance
ДЛИНОЙ numAppearances, то можно создать схему предложения, которая предлагает
элементы award двух случайно выбранных ролей:
ProposalScheme(
appearances(random.nextInt(numAppearances)).award,
appearances(random.nextInt(numAppearances)).award)
Кроме того, мы хотели бы иногда предлагать известность актера или
качество фильма. Для достижения желаемого эффекта воспользуемся функцией
Disjointscheme, которая позволяет алгоритму выбирать одну из нескольких схем
предложения с заданными вероятностями. Для нашей задачи создадим
переменную Scala scheme И С ПОМОЩЬЮ DisjointScheme ПРИСВОИМ ей Нужную Нам Схему
предложения:
val scheme: ProposalScheme = {
DisjointScheme(
(0.5, () =>
ProposalScheme(appearances(random.nextlnt(numAppearances)).award,
appearances(random.nextlnt(numAppearances)).award)),
(0.25, () =>
ProposalScheme(actors(random.nextlnt(numActors)).famous)),
(0.25, () =>
ProposalScheme(movies(random.nextlnt(numMovies)).quality)))
}
Теперь у нас имеется нужная схема предложения. Мы можем предложить либо
две случайно выбранные роли, что, возможно, приведет к взаимному изменению
их статуса награжденности, либо известность случайного актера, либо качество
случайного фильма.
385

Глава 11. Выборочные алгоритмы
Общий взгляд на схемы предложения
Figaro предоставляет простой язык для определения схем предложения. Ниже
перечислены возможные действия.
* Выбор из нескольких альтернатив. Допустим, мы хотим случайно выбрать
одну из нескольких схем предложения, для каждой из которых задана
вероятность. Это позволяет сделать функция DisjointScheme (probability1 ->
schemeFunction , „., probability -> schemeFunctionJ . Каждая схемная
функция schemeFunction возвращает схему предложения, не принимая
никаких аргументов. В задаче об актерах и фильмах примером такой функции служит
() => ProposalScheme(actors(random.nextlnt(numActors)).famous) .
Функция DisjointScheme выбирает одну из схемных функций, руководствуясь
их вероятностями, а затем применяет ее для получения схемы предложения.
* Последовательное предложение нескольких элементов. Функция
ProposalScheme (element,, ..., elementj поочередно предлагает элементы
element^ ..., element^ Поскольку обычно мы не хотим предлагать в точности
одинаковые элементы на каждой итерации МП эта схема предложения, как
правило, является результатом схемной функции, например выбираемой с помощью
DisjointScheme. Именно так мы поступили в нашей задаче.
* Начать с одного элемента, а затем на основе его значения решить, как
продолжить. Иногда мы хотели бы предложить один элемент, а затем в зависимости
от его значения решить, что делать дальше. Пример - предложение
известности актера и качества фильма, если роль удостоена награды. В таких
ситуациях используется функция TypedScheme, принимающая два аргумента. Первый
аргумент - функция, возвращающая первый элемент. Она имеет тип () =>
Element [т], где т - тип значения первого элемента. Второй аргумент имеет
тип т => Option [ProposalScheme]. To есть это функция, которая принимает
сгенерированное значение первого элемента (типа т) и в зависимости от него
возвращает либо None - больше не предлагать, либо Some [proposalScheme] -
предлагать дальше, используя схему proposalScheme. Рассмотрим, например,
такой код:
val appearance = appearances(random»nextlnt(numAppearances)>
TypedScheme(
() => appearance.award,
(b: Boolean) =>
if (b) Some (ProposalScheme(appearance.actor.fame,
appearance.movie,quality))
else None)
Эта схема предложения случайным образом выбирает роль и сначала предлагает
статус награжденное™ для этой роли. Если новое значение appearance, award равно
true, TO дальше последовательно предлагаются appearance < actor . fame И
appearance.movie, quality. В противном случае больше ничего не предлагается.
Существует также функция UntypedScheme, которая позволяет принимать решение
о продолжении вне зависимости от выбранного значения первого элемента.
К сожалению, в задаче об актерах и фильмах остается одна техническая
загвоздка, связанная с тем, как алгоритм МГ работает в Figaro. Еще раз взглянем на
определение атрибута award:
386

11.4. Настройка алгоритма МГ
class Appearance(val actor: Actor, val movie: Movie) {
val award: Element[Boolean] =
CPD(movie.quality, actor.famous,
('low, false) -> Flip(O.OOl),
('low, true) -> Flip(O.Ol),
('medium, false) -> Flip(O.Ol),
(fmedium, true) -> Flip(0.05),
(•high, false) -> Flip(0.05),
(•high, true) -> Flip(0.2))
}
Проблема в том, что атрибут award класса Appearance определен как cpd. Но
cpd - детерминированный элемент; хотя внутри него встречаются элементы Flip,
но если их значения фиксированы, то значение cpd полностью детерминировано.
Элементы Flip внутри элемента cpd - это его аргументы. Когда предлагается
некоторый элемент, его аргументы фиксируются, и генерируется значение элемента.
Поскольку cpd - детерминированный элемент, при заданных значениях элементов
Flip всякий раз будет генерироваться одно и то же значение. В результате мы
никогда не получим предложение изменить значение award.
Хотя приведенное выше объяснение носит технический характер, из него следует
практический вывод: всегда стремитесь предлагать недетерминированные
элементы. Все атомарные элементы, кроме constant, недетерминированны. Составные же
элементы, как правило, детерминированы, но есть несколько исключений:
составной Flip, составной select и составной Dist. Прочие составные элементы, например
составной Normal, определены с помощью chain и потому детерминированы.
Как же сделать award недетерминированным элементом? Хитрость в том, чтобы
преобразовать программу в эквивалентную, но такую, что award станет
недетерминированным. Это можно сделать так:
class Appearance(val actor: Actor, val movie: Movie) {
def getProb(quality: Symbol, famous: Boolean): Double =
(quality, famous) match {
case
case
case
case
case
case
!low, false) => 0.001
flow, true) => 0.01
'medium, false) => 0.01
'medium, true) => 0.05
'high, false) => 0.05
'high, true) => 0.2
}
0
val probability: Element[Double] =
Apply(movie.quality, actor.famous,
(q: Symbol, f: Boolean) => getProb(q, f))
val award: Element[Boolean] =
Flip(probability)
}
s
H
О — Функция, возвращающая вероятность в зависимости от качества фильма и
известности актера
© — Элемент, представляющий эту вероятность
© — Выбираем значение award, подбрасывая монету с заданной вероятностью
387

Глава 11. Выборочные алгоритмы
Легко видеть, почему это определение эквивалентно исходному определению
award. В исходном определении каждая ветвь cpd возвращала Flip с некоторой
вероятностью. В новом определении тоже используется Flip, а вероятность в
каждом случае такая же, как раньше. Но это составной Flip, который, как было
сказано выше, не детерминирован. Поэтому предложение такого элемента Flip может
привести к смене значений, а, значит, МГ сможет работать правильно.
/7.4.2. Избежание жестких условий
Даже после реализации специальной схемы предложения и преобразования
программы, показанного в предыдущем разделе, наш пример все-таки может работать
некорректно. Проблема вот в чем. Допустим, в начальном состоянии награды были
удостоены четыре фильма. На каждом шаге наша специальная схема предложения
позволяет изменить не более двух наград. В конце шага награждены окажутся по
меньшей мере два фильма, поэтому предложение не удовлетворяет условию
уникальности награды и автоматически отклоняется. Поэтому мы никогда не сможем
перейти в состояние, удовлетворяющее условию.
Корень проблемы в том, что имеется жесткое условие, которое обязано
удовлетворяться, иначе предложение отклоняется. В разделе 11.2.3 мы видели, что
жесткие условия могут представлять проблему в алгоритме выборки по значимости.
Это верно и для алгоритма МСМС. При наличии жестких условий бывает трудно
найти хотя бы одно удовлетворяющее им состояние. А если алгоритму удастся
найти такое, то из него будет сложно перейти в другое.
Решение заключается в замене жесткого условия мягким ограничением. В
идеале ограничение должно направлять алгоритм к состояниям с большей
вероятностью. В нашем примере можно задать такое ограничение:
def uniqueAwardConstraint(awards: List[Boolean]) = {
val n = awards.count(b => b)
if (n == 0) 0.0 else 1.0 / (n * n)
}
Это ограничение подсчитывает число атрибутов award, равных true, и
записывает это число в переменную п. Затем оно возвращает оценку, зависящую от п.
Если п отлично от нуля, то оценка равна 1/п2. Это означает, что при /2=1 оценка
равна 1 и быстро убывает с ростом п. Если же п = 0, то возвращается оценка 0, т. е.
состояние оказывается невозможным при данном ограничении.
Что дает такое ограничение? Рассмотрим начальное состояние.
• Если в начальном состоянии число наград было равно нулю, то любое
новое состояние, в котором есть хотя бы одна награда, принимается.
• Если в начальном состоянии была одна награда, то алгоритм обычно
принимает только новые состояния с одной наградой, но иногда (в одном
случае из четырех) примет состояние с двумя наградами и еще реже (в одном
случае из девяти) - состояние с тремя наградами.
• Если в начальном состоянии было несколько наград, то алгоритм всегда
принимает состояние с меньшим числом наград, поскольку ограничение
388

11.4. Настройка алгоритма МГ
в этом случае принимает большее значение. Иногда он принимает также
состояния с большим числом наград, но общая тенденция - двигаться в
сторону хорошего состояния с одной наградой.
Можно рассматривать это ограничение как «смазку», которая облегчает
переход марковской цепи от одного состояния к другому, способствуя движению
к состояниям с одной наградой. Без смазки цепь заедает и не может двигаться
правильно. Техника использования ограничений в качестве смазки широко
применяется. Она помогает не только добраться до состояний с высокой
вероятностью, но и беспрепятственно перемещаться в области таких состояний, после
того как она найдена.
Полный код этого примера имеется в сопутствующем коде. Он показывает, что
иногда приходится прилагать значительные усилия - специальные схемы
предложения, преобразование программы, настройка ограничений - чтобы заставить
алгоритм МСМС работать, как надо. Если вам повезет, то достаточно будет схемы
предложения по умолчанию. Если же нет, то настройка этого алгоритма окажется
гораздо труднее, чем всех остальных. По этой причине я и считаю МСМС
алгоритмом последней надежды. Вместе с тем, если вы готовы усердно поработать, то труд
может окупиться сторицей, поскольку иногда удается решить задачу, для которой
никакие другие алгоритмы не работают.
7 7.4.3. Приложения алгоритма МГ
МГ применялся к самым разным задачам, но, как было сказано выше, для его
применения необходимо приложить усилия. Каждое приложение уникально, и,
к сожалению, мне неизвестны волшебные заклинания, способные заставить
конкретное приложение хорошо работать. Могу сказать, что лучше всего МГ
работает в тех случаях, когда наблюдения являются результатом большого числа малых
взаимодействий между переменными и не зависят от комбинации многих
переменных. В предыдущем разделе мы видели, что условие уникальности награды
зависит от комбинации переменных award, поэтому пришлось немало потрудиться,
чтобы всегда использовались только допустимые комбинации. Если ничего такого
не требуется, то заставить МГ работать гораздо проще.
Вернемся к модели предсказания результатов футбольных матчей из
раздела 11.2.4. Там я говорил, что алгоритм выборки по значимости может хорошо
работать, когда единственное наблюдение - турнирная таблица, а если наблюдаются
результаты всех матчей, то ничего хорошего ждать не приходится и лучше
обратиться к МГ. На самом деле, именно для этого приложения МГ отлично работает
безо всякой настройки. Каковы случайные переменные в этой модели? Сила
игроков и другие характеристики команды, а также результаты всех матчей. Никакая
одна переменная не определяет все остальные, а исход матча кумулятивно зависит
от различных переменных. Например, если в команде хороший центральный
нападающий, то одно это позволит ей выиграть больше матчей вне зависимости от
значений прочих переменных. Для такой задачи схема предложения по
умолчанию, скорее всего, будет работать приемлемо.
389

Глава 11. Выборочные алгоритмы
На практике МГ часто применяется для анализа изображений и видео. Если мы
стремимся распознать в изображении какой-то один объект, то лучше
воспользоваться невероятностным подходом, например глубокой нейронной сетью. Но
если требуется более полная интерпретация изображения или видео (например,
распознавание связей между объектами или действиями), то у вероятностной
модели есть преимущества. Вероятностная модель может предложить свод знаний, в
рамках которого интерпретируется изображение. Рассмотрим, к примеру,
последовательность действий футболиста, бьющего по воротам, и вратаря,
пытающегося отразить удар. В динамической вероятностной модели можно представить
вероятности таких последовательностей событий. Каждое конкретное событие в
последовательности порождает в качестве факта определенные свойства
изображения или видео. Для вывода вероятных последовательностей действий при
условии этих фактов можно применить алгоритм вероятностного вывода.
Обычно для решения этой задачи используются алгоритмы МСМС, и тому есть
несколько причин. Во-первых, структура последовательности действий гибкая и
изменчивая, поэтому уловить ее с помощью небольшого числа случайных
переменных сложно, а, значит, она с трудом поддается факторному выводу. Во-вторых,
в изображениях и видео велико число значений переменных, например цветов и
уровней яркости, что также затрудняет применение факторных алгоритмов.
Наконец, выборка по значимости неприменима, потому что конкретное изображение
или видео - крайне маловероятный факт.
Для практического применения МГ к этой задаче можно рассматривать
переменные, представляющие последовательность действий, как единое целое с точки
зрения предложений. Допустим, к примеру, что текущая последовательность
действий такова: центральный нападающий бьет в левый угол, а вратарь бросается
вправо от себя (влево от нападающего). Если затем предложить, что
центральный нападающий бьет в правый угол, то вратарю не имеет смысла по-прежнему
бросаться вправо. Поэтому нужна схема предложения, которая одновременно
отправит вратаря влево. Путем тщательной настройки схем предложения можно
добиться эффективной работы МГ.
Научные приложения МГ. Алгоритм МГ особенно популярен в биологии и физике.
Так, в биологии вероятностную модель можно использовать для изучения связи между
генотипом организма, представляющим его генетический материал, и фенотипом,
показывающим, как гены проявляются в организме, формируя его свойства и признаки.
В частности, интересен вопрос о том, какой ген несет ответственность за данный
признак. Осложняет дело тот факт, что мы не всегда знаем конкретный вариант гена в
данном организме, однако версии близких генов в одной и той же хромосоме коррелируют.
Различные гены, а также признаки можно представить случайными переменными, а для
генотипа и фенотипа построить совместную вероятностную модель. К этой модели
можно применить алгоритм МГ, чтобы, во-первых, методами машинного обучения выявить
связи между генами и признаками, а, во-вторых, вывести, какие версии генов имеются
у данного индивидуума.
Из двух предыдущих глав мы многое узнали об алгоритмах, применяемых
для вывода в вероятностном программировании. Я рассматривал, прежде всего,
390

11.5. Резюме
задачу вычисления апостериорного распределения вероятности запрашиваемой
переменной при условии фактов, но есть и другие полезные запросы, например,
нахождение наиболее вероятных значений переменных или вычисление
вероятности факта. Для этих задач существуют специальные алгоритмы, являющиеся
варинтами алгоритмов, изученных в этих двух главах. Важно также уметь обучать
параметры вероятностных программ на данных. В следующей главе
рассматриваются все эти вопросы.
11.5. Резюме
• Выборочные алгоритмы генерируют состояния, выбираемые из
распределения вероятности возможных миров, и позволяют отвечать на запросы,
исходя из частоты значений в выборке.
• В среднем выборочное распределение совпадает с истинным, но любое
конкретное выборочное распределение отличается от истинного.
• Чем больше размер выборки, тем ближе выборочное распределение к
истинному и тем точнее ответы на запросы. К сожалению, чтобы подойти к
истинному распределению сколь угодно близко, размер выборки должен
быть велик.
• Выборка с отклонением - простой выборочный алгоритм, который
генерирует примеры из априорного распределения вероятности, определенного
в программе, и отклоняет примеры, не удовлетворяющие условиям. Этот
алгоритм не поддерживает ограничения и плохо работает, если условий
много.
• В алгоритме выборки по значимости используются взвешенные
примеры, что позволяет включить в рассмотрение ограничения и по
возможности избежать отклонений. Это повышает производительность по
сравнению с выборкой с отклонением. Но из-за низкого эффективного
размера выборки этому алгоритм может потребоваться много примеров,
если условиям трудно удовлетворить или имеются ограничения с
малыми значениями.
• Метод Монте-Карло по схеме марковской цепи (МСМС) - алгоритм,
позволяющий повторно использовать результаты работы по мере
продвижения вперед. Он случайным образом ищет область высокой вероятности в
пространстве состояний, а найдя ее, имеет тенденцию в ней и оставаться.
В результате производительность может оказаться выше, чем у выборки
по значимости, в случаях, когда имеются трудновыполнимые условия или
ограничения с малыми значениями.
• Иногда алгоритму МСМС нужно много примеров, а понять и
контролировать его поведение проблематично. Для успешного применения МСМС к
реальным задачам зачастую требуется приложить дополнительные усилия,
например, разработать специальные схемы предложения и настроить
ограничения.
391

Глава 11. Выборочные алгоритмы
11.6. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Для следующей программы:
val х = Flip(0.8)
val у = Flip(0.6)
val z = If(x === y, Flip(0.9), Flip(O.l))
z.observe(false)
a. Методом исключения переменных вычислите точную
апостериорную вероятность того, что у равно true при условии наблюдения
относительно Z.
b. Выполните выборку по значимости на 1000, 2000 и т. д. вплоть до
10 000 примеров. Для каждого числа примеров прогоните программу
100 раз. Вычислите среднеквадратичную ошибку выборки по
значимости при данном числе примеров. Эта величина определяется
следующим образом.
i. Для каждого прогона измерить разность между вероятностью,
вычисленной методом выборки по значимости, и точной
вероятностью, полученной в результате исключения переменных. Это
ошибка.
и. Вычислить квадрат ошибки для каждого прогона.
iii. Вычислить среднее всех квадратов ошибки.
iv. Извлечь квадратный корень из среднего. Это и есть
среднеквадратичная ошибка - стандартный способ измерения
погрешности алгоритма вывода.
c. Нарисуйте график среднеквадратичной ошибки. Заметили ли вы
какие-нибудь тенденции?
2. Повторите упражнение 1 для алгоритма Метрополиса-Гастингса со схемой
предложения по умолчанию. На этот раз берите 10 000,20 000 и т. д. вплоть
до 100 000 примеров.
3. Теперь немного изменим программу, взяв более экстремальные значения
числовых параметров:
val х = Flip(0.999)
val у = Flip(0.99)
val z = If(x === y, Flip(0.9999), Flip(0.0001))
z.observe(false)
a. Методом исключения переменных вычислите точную
апостериорную вероятность у.
b. Выполните алгоритм выборки по значимости с 1 000 000 примеров.
c. В этой программе вероятность факта мала. Но вы увидите, что
выборка по значимости дает точный результат. Как вы это объясните?
392

11.6. Упражнения
4. Выполните алгоритм Метрополиса-Гастингса для той же программы со
схемой предложения по умолчанию и 10 000 000 примеров. Результат
получится плохой. (Возможно, не каждый раз, но при нескольких прогонах
будет видна тенденция к плохому результату.) Как вы думаете, почему эта
задача так трудна для алгоритм Метрополиса-Гастингса?
5. Попробуйте написать специальную схему предложения для алгоритма МГ.
a. Поскольку мы предлагаем элементы Flip внутри определения z, то
должны сделать их отдельными переменными, на которые будем
ссылаться. Заведите для Flip (0.9999) переменную zi, для Flip (O.oooi) -
переменную z2 и воспользуйтесь новыми переменными в
определении Z.
b. Создайте специальную схему предложения со следующим
поведением.
i. С вероятностью 0.1 предлагать zi.
ii. С вероятностью 0.1 предлагать z2.
iii. С вероятностью 0.8 предлагать х и у.
c. Выполните алгоритм Метрополиса-Гастингса с такой схемой
предложения. Результаты должны быть лучше. Объясните, почему.
6. В упражнении к главе 6 было предложено написать вероятностную
программу для игры «Сапер». Воспользуйтесь этой программой для
вычисления вероятности мины в квадратике. Поэкспериментируйте с разными
алгоритмами.
393

ГЛАВА 12.
Решение других задач вывода
В этой главе.
■ Как опрашивать совместное распределение
нескольких переменных.
■ Как вычислить наиболее вероятные значения
всех переменных модели.
■ Как вычислить вероятность наблюдаемого факта.
До сих пор мы рассматривали различные способы ответа на запросы вида: «Какова
вероятность, что кнопка питания принтера не нажата, если принтер не печатает
правильно?» или «Какова вероятность, что я получу Оскара при условии моего
таланта и качества фильма?». Во всех таких запросах речь идет о вычислении
апостериорного распределения вероятности одной переменной при условии
известных фактов. Но вероятностное программирование позволяет решать и другие
задачи вывода. К ним относятся:
• вычисление совместного распределения вероятности нескольких
переменных;
• вычисление наиболее вероятных значений переменных при условии фактов;
• вычисление вероятности факта (вероятности того, что возможный мир,
сгенерированный моделью, будет согласован с фактом);
• мониторинг состояния динамической системы во времени;
• обучение параметров модели, чтобы впоследствии их можно было
использовать в рассуждениях.
В этой главе рассказано, как решать первые три задачи, а две оставшиеся будут
рассмотрены в следующей. Для каждой задачи я опишу, в чем ее суть и зачем это
нужно, потом представлю примеры, а в конце объясню, как работают алгоритмы и
как выполнить их в Figaro. По счастью, алгоритмические принципы, изложенные
в предыдущих главах, переносятся и на эти задачи, так что материал, в основном,
будет знакомый, хотя появятся и новые интересные идеи.

12.1. Вычисление совместных распределений
Для чтения главы необходимо понимание основ моделирования в Figaro, более
сложные приемы не используются. Поскольку описанные в этой главе алгоритмы
основаны на алгоритмах из главы 10 и И, то вы должны владеть изложенным в
них материалом.
12.1. Вычисление совместных
распределений
До сих пор мы видели различные алгоритмы, вычисляющие распределение
вероятности одной переменной, которое называется маргинальным распределением.
Вызывая алгоритм, например исключения переменных или выборки по
значимости, мы передаем ему список опрашиваемых переменных. Пусть, например,
имеется вероятностная программа, которая прогнозирует объем продаж различных
продуктовых линеек. Тогда элементы, соответствующие каждой линейке, станут
целями запроса. Можно будет запросить вероятность того, что объем продаж
данной продуктовой линейки превысит определенный уровень или выйдет на
ожидаемый уровень.
Но что, если требуется запросить совместное распределение нескольких
переменных? Зачем это может понадобиться? Да потому что совместное
распределение содержит информацию, отсутствующую в индивидуальных маргинальных
распределениях. Например, нас может интересовать вероятность того, что
продажи двух продуктовых линеек одновременно окажутся низкими, поскольку это
очень плохо для бизнеса. Вот несколько ситуаций, когда знание совместного
распределения было бы полезно.
• Продажи двух продуктовых линеек независимы; хорошо или плохо
продается один продукт, на продажи другого это не влияет.
• Между продажами двух продуктовых линеек существует положительная
корреляция: если один продукт продается плохо, то и другой, скорее всего,
будет продаваться плохо. Такая ситуация чревата рисками.
• Между продажами двух продуктовых линеек существует отрицательная
корреляция: если один продукт продается плохо, то другой, скорее всего,
продается хорошо. Это менее рискованная ситуация, потому что
маловероятно, что объемы продаж одновременно окажутся низкими.
Зная только индивидуальные маргинальные распределения, мы не сможем
сказать, какая из этих ситуаций имеет место на самом деле. Но как вычислить
совместное распределение?
В Figaro нет особого алгоритма для вычисления совместных распределений.
Вместо этого нужно создать специальный элемент, улавливающий совместное
поведение элементов, чье совместное распределение мы хотим опросить. А затем
можно применить любой алгоритм вывода из числа описанных ранее. Для
создания специального элемента в Figaro используется конструктор кортежа -
оператор АА.
395

Глава 12. Решение других задач вывода
Пусть, например, имеется массив элементов, описывающих продажи. В
следующем предложении создается пара, содержащая первые два элемента:
val salesPair = AA (sales (0), sales (1))
А так создается кортеж из четырех элементов:
val sales4Tuple = AA (sales (0) , sales (1), sales (2), sales (3))
Примечание. Конструктор кортежа АА принимает до пяти аргументов. Если нужно
больше, используйте вложенные кортежи, например: АА (АА (sales (0), sales (l),
sales(2)), AA(sales(3), sales(4), sales(5))).
Затем можно указать кортеж в запросе, как будто это один элемент, например:
VariableElimination.probability(salesPair,
(pair: (Double, Double)) => pair._l < 100 && pair._2 < 100)
Создание кортежей и рассуждения о них в факторных алгоритмах обходятся не
бесплатно. Создание кортежа эквивалентно созданию фактора от всех
компонентов кортежа. Так, в случае saies4Tupie мы имеем фактор от элементов sales (0),
sales (1), sales (2) и sales (3). Если такой фактор уже встречается в программе, то
никаких проблем не возникает. В противном случае его создание заметно
увеличивает время работы алгоритма.
В случае выборочных алгоритмов такой проблемы нет. Мы лишь выбираем
значения каждого компонента кортежа, и каждая комбинация компонентов
становится одним значением кортежа. Поэтому, обнаружив, что факторный алгоритм
вычисления совместной вероятности работает слишком долго, попробуйте
выборочный.
В общем случае при увеличении числа совместно опрашиваемых элементов
количество возможных значений кортежа растет экспоненциально. Совместное
распределение многих переменных трудно не только вычислить, но и
интерпретировать. Если вам кажется, что необходимо знать совместное распределение многих
переменных, попробуйте вместо этого сводную статистику. Например, почему бы
вместо совместного распределения объема продаж многих продуктовых линеек не
вычислить распределение суммарного объема продаж? Это легко сделать с
помощью коллекций Figaro:
val allSales = Container(sales:_*) <J—Л
val totalSales =
allSales.foldLeft((x: Int, y: Int) => x + y) <—©
printIn(Importance.probability(totalSales,
(i: Int) => i > 1000))
О — Нотация :_* преобразует массив sales в список переменной длины, передаваемый
конструктору
© — Метод foldLeft применяет функцию сложения ко всем элементам массива sales для
вычисления их суммы
396

12.2. Вычисление наиболее вероятного объяснения
III!
шш
Примечание. Полный код программы, иллюстрирующий идеи этого раздела, имеется
в прилагаемом к книге коде. Это относится ко всем разделам данной главы.
12.2. Вычисление наиболее
вероятного объяснения
Иногда нас интересует не распределение вероятности исходов, а то, какие исходы
наиболее вероятны. Возьмем задачу диагностики принтера. Мы наблюдаем
симптомы, например: принтер печатает медленно. Задача вероятностного вывода -
определить наиболее вероятное состояние системы (принтера, программы, сети
и пользователя), приведшее к наблюдаемому поведению. Зная наиболее
вероятное состояние, мы сможем назвать вероятные причины неисправности, а затем и
устранить их.
Запрос о наиболее вероятном состоянии переменных модели называется
наиболее вероятным объяснением (НВО). В процессе диагностики мы хотим получить
наилучшую гипотезу, объясняющую, как устранить неисправность. Типичный
процесс показан на рис. 12.1.
1. Наблюдаем исходные симптомы - факты модели. Например, пользователь
сообщает, что ничего не печатается, т. е. в байесовской сети, описывающей
принтер, переменная Общий Результат Печати равна «ничего».
2. Вычисляем НВО, чтобы определить наиболее вероятное состояние
системы. На рисунке показано, что в наиболее вероятном объяснении кнопка
питания принтера не нажата, а все остальные возможные причины плохой
печати не представлены. Поэтому наиболее вероятное объяснение
отсутствия результата печати - ненажатая кнопка питания.
3. Проверяем, действительно ли имеет место одна или несколько
неисправностей, найденных на шаге 2. Если да, пытаемся устранить их. В нашем случае
пользователь нажимает кнопку питания.
4. Проверяем, решена ли проблема. Если да, то все сделано. В нашем примере
дело было не в кнопке питания, т. е. проблема еще не решена.
5. Если проблема не решена, добавляем новый факт и возвращаемся к шагу 2.
В нижней части рисунка показан дополнительный факт - переменная
Кнопка Питания Принтера Нажата равна true - и получившееся в
результате НВО. В этом НВО наиболее вероятной причиной отказа названа
неработающая сеть. Пользователь может проверить, так ли это, и попытаться
исправить ошибку. В нашем случае пользователь замечает, что сетевой
кабель вытащен из розетки, и решает проблемы, вставив его.

Глава 12. Решение других задач вывода
Факт; Ничего
Нет
Факт: True
Факт: Ничего
Нет
Рис. 12.1. Применение НВО для диагностики. На верхнем рисунке показан первый вывод
для сети принтера из главы 5. Пользователь сообщает, что принтер ничего не печатает,
поэтому мы имеем факт - переменная Общий Результат Печати равна «ничего». Показаны
наиболее вероятные значения всех переменных после выполнения запроса НВО. Как видим,
наиболее вероятная причина неисправности - ненажатая кнопка питания. Проверяется,
нажата кнопка или нет, и оказывается, что нажата. Поэтому добавляется новый факт -
переменная Кнопка Питания Принтера Нажата равна true. В нижней части показано НВО
после добавления этого факта. Наиболее вероятные значения, изменившиеся по сравнению
с первым запросом, выделены полужирным шрифтом. Теперь наиболее вероятной причиной
неисправности является отсутствие сети
398
Подача
Бумаги
Беспрепятствен ная
Высокий
False
Уровень
Тонера
Кнопка Питания
Принтера Нажата
Индикатор Замятия
Бумаги Горит
Индикатор Низкого
Уровня Тонера Горит
False
False
Команда Пользователя
Правильна
True
Работает
Корректное
Состояние
Сети
Состояние
Программы
Состояние
Принтера
Неисправен
Число Напечатанных
Страниц
Печатает
Быстро
Качество
Печати Хорошее
Общий Результат
Печати
Подача
Бумаги
Уровень
Тонера
Кнопка Питания
Принтера Нажата
Высокий
Беспрепятственная
Индикатор Замятия
Бумаги Горит
Индикатор Низкого
Уровня Тонера Горит
False
False
True
True
Команда Пользователя
Правильна
Не работает
Корректное
Состояние
Сети
Состояние
Программы
Состояние
Принтера
Исправен
Число Напечатанных
Страниц .
Печатает
Быстро
Качество
Печати Хорошее
True
Нуль
False
Общий Результат
Печати

12.2. Вычисление наиболее вероятного объяснения
Возьмем другой пример. Допустим, имеется поврежденное изображение, и нам
нужно его восстановить. Можно воспользоваться вероятностным выводом для
восстановления истинного изображения при известных пикселях. Вариантов
действий несколько.
Вычислить маргинальное распределение вероятности каждого пикселя по
отдельности. С вычислительной точки зрения, это осуществимо, но для
восстановления полного изображения не идеально, т. к. мы получаем лишь индивидуальные
распределения пикселей и ничего не можем сказать о том, какие значения
пикселей с большой вероятностью встречаются вместе. Вполне возможно, что выбор,
сделанный для одних пикселей, должен оказать влияние на другие, но
маргинальные распределения таких нюансов не улавливают.
Вычислить совместное распределение вероятности всех пикселей
изображения. Увы, это неосуществимо из-за объема вычислений. Количество возможных
комбинаций экспоненциально зависит от числа пикселей, а оно может быть
весьма велико.
Вычислить НВО - наиболее вероятное совместное значение всех пикселей
изображения, а не механический конгломерат наиболее вероятных значений
отдельных пикселей. С точки зрения объема вычислений, это возможно, поскольку
мы вычисляем всего одно значение. К тому же, НВО улавливает взаимодействия
между пикселями, в отличие от индивидуальных маргинальных распределений.
НВО показано в табл. 12.1. Мы имеем два пикселя, которые могут находиться
в состояниях Вкл и Выкл. В таблице приведены четыре возможных мира для этих
двух пикселей вместе со своими вероятностями. Если рассматривать только
первый пиксель, то сумма вероятностей миров, в которых он равен Выкл, равна 0.65,
а тех, в которых он равен Вкл, - 0.35. Поэтому наиболее вероятно значение Выкл.
Аналогично для второго пикселя наиболее вероятно значение Выкл. Но мир, в
котором пиксель 1 равен Выкл, а пиксель 2 - Вкл, имеет вероятность 0.45. Из всех
возможных миров это самая большая вероятность, значит, это и есть НВО.
Очевидно, что НВО не получается механическим объединением наиболее вероятных
значений отдельных переменных.
Таблица 12.1. Наиболее вероятное объяснение необязательно является
комбинацией наиболее вероятных значений отдельных переменных.
Здесь наиболее вероятное значение каждого пикселя равно Выкл,
но в наиболее вероятном объяснении Пиксель 1 = Выкл, а Пиксель 2 = Вкл
Пиксель 1
Выкл
Выкл
Вкл
Вкл
Пиксель 2
Выкл
Вкл
Выкл
Вкл
Вероятность
0.2
0.45
0.35
0
Таким образом, НВО - полезный запрос во многих приложениях. Посмотрим,
как вычислить НВО в Figaro.
399

Глава 12. Решение других задач вывода
12.2.7. Вычисление и запрос НВО в Figaro
Интерфейс для вычисления и запроса НВО в Figaro прост. В Figaro имеется три
алгоритма ВЫЧИСЛенИЯ НВО: Два фаКТОрНЫХ (MPEVariableElimination И МРЕВе-
lief Propagation) И ОДИН выборочный (MetropolisHastingsAnnealer). Я объясню ИХ
в следующем разделе, но сначала посмотрим, как они используются.
Все три алгоритма являются экземплярами класса MPEAigorithm. У этого класса,
как и у прочих, есть два варианта: без отсечения и с отсечением по времени. Для
алгоритмов MPEBeliefPropagation И MetropolisHastingsAnnealer определены оба
варианта, а для MPEVariableElimination - только вариант без отсечения. В
примере ниже демонстрируется использование алгоритмов без отсечения по времени.
Варианты с отсечением применяются, как обычно.
Вспомним задачу о восстановлении изображения из главы 5. Мы пытались
предсказать цвет пикселя. Изображение описывалось марковской сетью. На
каждый пиксель налагалось унарное ограничение, согласно которому пиксель равен
Вкл с вероятностью 0.4. На каждую пару соседних пикселей налагается бинарное
ограничение, которое говорит, что при прочих равных условиях вероятность их
совпадения в два раза больше вероятности различия. Марковская сеть для этого
примера показана на рис. 12.2, где массивы начинаются с пикселя 11, как и в
примере восстановления изображения из главы 5.
Пиксель 14
Пиксель 32
Пиксель 43
Рис. 12.2. Марковская сеть для восстановления изображения
(повтор рисунка из главы 5)
В следующем листинге приведен код, показывающий, как использовать
вышеупомянутые алгоритмы для вычисления НВО в задаче о восстановлении
изображения. Индексы пикселей начинаются с 00.
Листинг 12.1. Восстановление изображения с помощью НВО
val pixels = Array.fill (4, 4 ) (Flip (0 . 4 ) ) <\—Q
def makeConstraint(pixell: Element[Boolean],
pixel2: Element[Boolean]) {
val pairElem = AA(pixell, pixel2)
В
400
Пиксель 11
Пиксель 12
Пиксель 13
Пиксель 21
Пиксель 22
Пиксель 23
Пиксель 24
Пиксель 31
Пиксель 33
Пиксель 34
Пиксель 41
Пиксель 42
Пиксель 44

12.2. Вычисление наиболее вероятного объяснения
pairElem.setConstraint (pair
=> if (pair._l == pair._2) 1.0 else 0.5)
}
В
for {
i <- 0 until 4
j <- 0 until 4
} {
if (i > 0) makeConstraint(pixels(i-1)(j), pixels(i)(j))
if (j > 0) makeConstraint(pixels(i) (j-1) , pixels(i) (j))
g
И
pixels(0)(0).observe(true)
pixels(O)(2).observe(false)
pixels(1)(1).observe(true)
pixels(2)(0).observe(true)
pixels(2)(3).observe(false)
pixels(3)(1).observe(true)
def run (algorithm: OneTimeMPE) { O—0
algorithm.start() <3—©
for { i <- 0 until 4 } {
for { j <- 0 until 4 } {
print(algorithm.mostLikelyValue(pixels(i)(j)))
print("\t")
}
В
println()
}
println()
algorithm.kill()
def main(args: Array[String] ) {
println("HBO методом исключения переменных") I
run(MPEVariableElimination() ) |
println("HBO методом распространения доверия")
run(MPEBeliefPropagation(10))
println("Имитация отжига")
run(MetropolisHastingsAnnealer(100000, ProposalScheme.default,
Schedule.default(1.0)))
W
О — Создаем элементы, представляющие пиксели, и унарные ограничения для них
© — Добавляем бинарные ограничения для пар пикселей
© — Применяем бинарные ограничения к соседним пикселям
О-В роли фактов выступают наблюдаемые значения некоторых пикселей
© — Этот метод применяет заданный алгоритм к модели, определенной выше.
Пиксели — это элементы модели, к которым применяется алгоритм
© — Создаем и выполняем алгоритм без отсечения по времени для вычисления НВО.
По завершении этого вызова будут вычислены наиболее вероятные значения всех
пикселей
© — Запрашиваем наиболее вероятное значение данного пикселя и печатаем результат
401
8
9

Глава 12. Решение других задач вывода
© — Конструктор MPEVariableElimination не имеет аргументов
© — Конструктор MPEBelief Propagation принимает в качестве аргумента число итераций
распространения доверия
© — Три аргумента конструктора MetropolisHastingsAnnealer описаны в следующем
разделе
Как видно из листинга 12.1, порядок вычисления и запроса НВО такой же, как
в обычных запросах вероятностей.
1. Создать все элементы.
2. Добавить условия и ограничения, являющиеся частью определения
модели.
3. Задать наблюдаемые факты.
4. Создать экземпляр алгоритма.
5. Запустить алгоритм.
6. Запросить наиболее вероятные значения индивидуальных элементов. Хотя
элементы запрашиваются по одному, их значения образуют наиболее
вероятное совместное состояние.
Эта программа печатает такие результаты:
НВО методом исключения переменных
true true false false
true true false false
true true false false
true true false false
HBO методом распространения доверия
true true false false
true true false false
true true false false
true true false false
Имитация отжига
true true false false
true true false false
true true false false
true true false false
Этот пример очень прост, и все алгоритмы быстро находят правильный ответ.
Но в более сложных случаях у каждого алгоритма есть свои плюсы и минусы.
Рассмотрим алгоритмы более пристально и поймем, когда они работают хорошо и
почему.
72.2.2. Использование алгоритмов для ответа
на запросы НВО
Алгоритмы для ответа на запросы НВО обычно являются вариантами алгоритмов
для ответа на обычные запросы вероятностей. Точно так же мы можем
использовать факторные или выборочные алгоритмы. Сначала я опишу два факторных
402

12.2. Вычисление наиболее вероятного объяснения
алгоритма, а затем - один выборочный. Поскольку вы уже знакомы с основными
принципами, не буду вдаваться в детали, а лишь выделю основные идеи.
Факторные алгоритмы НВО
Цель НВО - вычислить возможный мир с наибольшей вероятностью. Пусть,
например, возможный мир состоит из значения р00 Пикселя 00, значения р01
Пикселя 01 и т. д. вплоть до значения р33. Вероятность этого мира равна Р(Пиксель 00
= р00, Пиксель 01 = р01,..., Пиксель 33 = р33), и мы хотим ее максимизировать, т. е.
узнать, чему равна величина
max 00max 01 ...max 33 Р(Пиксель 00 = р00, Пиксель 01 = р01,..., Пиксель 33 = р33)
Напомним (см. главу 10), что вероятность возможного мира равна
произведению факторов. В данном случае это произведение унарных факторов от
индивидуальных пикселей и бинарных факторов от соседних пикселей. Максимальная
вероятность возможного мира равна максимуму произведений факторов. Если
унарные факторы обозначить U, а бинарные - В, то можно записать такое
выражение максимума произведений:
ЩПиксель 00 = р00)и(Пиксель 01 = р01) ...ЩПиксель 33 = р33) х
max)00max)01 ...тах)33В(Пиксель 00 = р00, Пиксель 01 = р01) ...В(Пиксель 32 = р32,
Пиксель 33 = р33) х
В(Пиксель 00 = роо, Пиксель 10 = pio) ...В(Пиксель 23 = р2з, Pixel 33 = рзз)
Первая строка этого выражения содержит унарные факторы, вторая -
бинарные факторы от пар пикселей, соседних по горизонтали, третья - бинарные
факторы от пар пикселей, соседних по вертикали. Берется максимум произведения
факторов по всем переменным.
Если в обычном алгоритме исключения переменных (ИП) производятся
операции с суммой произведений, то в алгоритме НВО ИП - с максимумом
произведений. Исключается по одной переменной за раз. Процедура исключения показана
на рис. 12.3. Начинается она так же, как в обычном алгоритме - мы перемножаем
все факторы, в которых эта переменная встречается. Но вместо суммирования по
исключаемой переменной производится взятие максимума по ней. В результате
порождается фактор от всех переменных, которые упоминались в факторе,
содержащем исключаемую переменную. В данном примере создается фактор от
пикселя 21 и пикселя 12.
Операция взятия максимума по переменной аналогична суммированию по
переменной. В обоих случаях заданная переменная исключается из фактора. В
случае суммирования для каждой комбинации значений остальных переменных
фактор содержит сумму чисел, ассоциированных с этими значениями. А в случае
максимизации фактор будет содержать максимум из чисел, ассоциированных со
значениями оставшихся переменных.
403

Глава 12. Решение других задач вывода
Таблица
возвратов
Фактор от
Пикселей 21 и 22
Пиксель 24
Рис. 12.3. Результат исключения Пикселя 11 с помощью алгоритма НВО ИП.
Создается новый фактор от Пикселей 21 и 12. Кроме того, создается таблица
возвратов, которая позволяет восстановить наиболее вероятное значение
Пикселя 11 после того, как станут известны значения Пикселей 21 и 22
Этот процесс иллюстрируется на примере в табл. 12.2, где показаны две
переменные, Пиксель 1 и Пиксель 2, связанные фактором. В табл. 12.3 мы видим
фактор, получающийся исключением Пикселя 2. Переменные, от которых зависит
этот фактор, - это все переменные, встречающиеся в факторе, где упоминается
исключаемая переменная, кроме нее самой. В данном случае, в этом факторе есть
еще только одна переменная - Пиксель 1. Для любого значения Пикселя 1
(например, Выкл) элементом результирующего фактора будет максимум по всем строкам
исходного фактора, совместимым с этим значением. В двух строках, совместимых
со значением Выкл Пикселя 1, находятся числа 0.2 и 0.45, поэтому максимум
равен 0.45.
Таблица 12.2. Исходный фактор, из которого исключается Пиксель 2
Пиксель 1
Выкл
Выкл
Вкл
Вкл
Пиксель 2
Выкл
Вкл
Выкл
Вкл
Вероятность
0.2
0.45
0.35
0
404
Пиксель 11
Пиксель 12
Пиксель 21
Пиксель 13
Пиксель 14
Пиксель 22
Пиксель 23
Пиксель 31
Пиксель 32
Пиксель 33
Пиксель 34
Пиксель 41
Пиксель 42
Пиксель 43
Пиксель 44

12.2. Вычисление наиболее вероятного объяснения
Таблица 12.3. Фактор, получившийся после взятия
максимума по Пикселю 2 в факторе, показанном в табл. 12.2
Пиксель 1
Выкл
Вкл
Вероятность
0.45
0.35
Помимо фактора, являющегося результатом взятия максимума, при
исключении переменной создается еще таблица возвратов, которая позволяет
восстановить наиболее вероятное значение исключаемой переменной после того, как
определены наиболее вероятные значения остальных переменных. Ведь при решении
задачи о НВО нас интересует не только нахождение возможного мира с
наибольшей вероятностью, а еще значения переменных в этом мире. Именно для этого
предназначена таблица возвратов. В ней для каждого возможного значения
оставленных переменных указано значение исключенной переменной, при котором в
исходном факторе достигался максимум.
Таблица возвратов для нашего примера приведена в табл. 12.4. Оставлена
переменная Пиксель 1, а исключена переменная Пиксель 2. В таблице для
каждого значения Пикселя 1 показано то значение Пикселя 2, при котором достигался
максимум фактора, показанного в табл. 12.2. Рассмотрим значение Выкл
Пикселя 1. Исходный фактор был равен 0.2, когда Пиксель 2 принимал значение Выкл,
и 0.45 - когда он принимал значение Вкл. Поэтому максимум для значения
Пикселя 1, равного Выкл, достигался, когда Пиксель 2 был равен Вкл. Это и записано
в таблице возвратов.
Таблица 12.4. Таблица возвратов, созданная в процессе
исключения Пикселя 2 из фактора в табл. 12.2
Пиксель 1
Выкл
Вкл
Пиксель 2
Вкл
Выкл
В конце процесса будут исключены все переменные. Теперь можно пройти назад
по всем таблицам возвратов и найти НВО. Начнем с последней исключенной
переменной, пусть это будет Пиксель 1. Раз после нее уже ничего не исключалось, то у
нас будет таблица с единственным значением Пикселя 1; допустим, что оно равно
Выкл. Это и есть наиболее вероятное значение Пикселя 1. Затем возвращаемся на
шаг назад; предположим, что предпоследней исключалась переменная Пиксель 2.
Переходим к таблице возвратов, созданной в процессе исключения Пикселя 2, она
показана в табл. 12.4. Ищем строку, в которой Пиксель 1 = Выкл, и читаем из нее
наиболее вероятное значение Пикселя 2 - Вкл. Эта процедура продолжается в
порядке, обратном исключению переменных, и в конце мы имеем полное НВО.
Алгоритм вычисления НВО методом распространения доверия (РД) очень
похож на обычный алгоритм РД. В нем тоже передаются сообщения между вершина-
405

Глава 12. Решение других задач вывода
ми и над этими сообщениями производятся факторные операции. Единственное
различие состоит в том, что в каждой вершине вместо выполнения суммирования
производится максимизация - точно такая же, как в табл. 12.3. алгоритм НВО РД
часто называют алгоритмом максимизации произведений.
Главное, что нужно запомнить об алгоритмах НВО ИП и НВО РД, - тот факт,
что по своим свойствам они аналогичным обычным алгоритмам ИП и РД.
Алгоритм НВО ИП точный, поэтому если он применим, то это оптимальный выбор.
Его сложность такая же, как у обычного ИП: экспоненциально зависит от размера
наибольшей клики в графе, индуцированном порядком исключения. Поэтому он
хорошо работает для точно такого же класса задач, что и обычный ИП. В задаче
восстановления изображения размер наибольшей клики равен числу пикселей
вдоль стороны изображения. В нашем примере, когда пикселей было всего четыре,
алгоритм НВО ИП практически реализуем, но по мере увеличения числа
пикселей его сложность экспоненциально возрастает.
НВО РД - приближенный алгоритм, его свойства аналогичны РД. Зачастую он
работает хорошо и быстро, но без гарантии нахождения оптимального результата.
Все соображения, относящиеся к обычному РД, справедливы и для НВО: избегать
слишком большого числа циклов, объединять элементы, разлагать условные
распределения вероятности с большим количеством родителей и использовать
ослабляющие условные распределения. Упрощение сети положительно сказывается
на работе как НВО ИП, так и НВО РД.
Область высокой
вероятности
Наиболее вероятное
состояние
Возможные миры
Алгоритм
Метрополиса-Гастингса Имитация отжига
Рис. 12.4. Сравнение алгоритма Метрополиса-Гастингса и имитации отжига
Имитация отжига
Самый распространенный выборочный алгоритм НВО называется
имитацией отжига (ИО). Он тесно связан с алгоритмом Метрополиса-Гастингса. В МГ
формирователь выборки случайно блуждает в пространстве состояний и в
конце концов достигает некоторого состояния с вероятностью, равной вероятности
406
1
У
О
о
1
х
1
У
О
0
х
1

12.2. Вычисление наиболее вероятного объяснения
этого состояния. Он может и не найти наиболее вероятное состояние, но имеет
тенденцию перебирать состояния, имеющие высокую вероятность. Напротив, ИО
ищет самое вероятное состояние. Он перемещается по пространству состояний и,
вообще говоря, движется в сторону максимальной вероятности, хотя временами
может «отступать» к состояниям с меньшей вероятностью. На рис. 12.4 показано
различие между траекториями алгоритмов МГ и имитации отжига.
Эпизодический возврат к состояниям с меньшей вероятностью в алгоритме ИО
нужен для более полного исследования пространства состояний. Если бы
алгоритм двигался только в сторону более вероятных состояний, то мог бы застрять
в локальном максимуме, т. е. в состоянии, вероятность которого больше, чем у
ближайших соседей, хотя подальше имеются состояния с гораздо большей
вероятностью. Исследование пространства состояний дает ИО возможность избегать
застревания в локальном максимуме и находить лучшие области пространства
состояний. ИО стремится поддержать баланс между исследованием пространства
состояний и движением в сторону более вероятных состояний. В начале работы
он отдает предпочтение случайному блужданию, а в конце сосредотачивается на
поиске близлежащих состояний с высокой вероятностью.
Для достижения баланса в ИО используется понятие температуры. На
интуитивном уровне температура управляет исследованием пространства состояний.
Если температура высока, то алгоритм случайным образом исследует
пространство, а если низка, то агрессивно движется в сторону более вероятных состояний.
Стратегия ИО состоит в том, чтобы начать работу при высокой температуре и
охлаждаться со временем, т. е. сначала больше исследовать, а в конце полностью
сосредоточиться на поиске вероятных состояний.
В различных реализациях И О температура используется по-разному. В Figaro
принят следующий подход. Допустим, работа начинается в состоянии с
вероятностью/^, а новое предложенное состояние имеет вероятность pv Если температура
равна t, то новое состояние принимается с вероятностью
/ V7'
Р\
Ро)
Какой эффект дает температура? Посмотрим, как изменяется вероятность
принятия нового состояния в зависимости от температуры. Если рх больше р0, то
это число больше 1, и новое состояние принимается безоговорочно. В противном
случае вероятность зависит от температуры. Если температура t бесконечна, то
вероятность принятия равна 1, т. е. новое состояние точно принимается. Это
соответствует чистому исследованию. Если t равна 0, то новое состояние может быть
принято, только если его вероятность не меньше вероятности текущего, так что
имеет место движение в сторону более вероятных состояний. Промежуточные
значения t дают различные соотношения между исследованием и максимизацией
вероятности. В общем случае, чем меньше t, тем меньше алгоритм склонен к
исследованию.
407

Глава 12. Решение других задач вывода
Примечание. В строгом описании алгоритма вероятность принятия зависит еще и
от свойств вспомогательного распределения, которое используется для предложения
нового состояния. В Figaro члены, зависящие от свойств вспомогательного
распределения, обычно взаимно уничтожаются, поэтому можно считать, что вероятность зависит
только от отношения вероятностей состояний.
Скорость изменения температуры со временем управляется режимом
охлаждения, который определяет, когда и как быстро понижается температура. Иными
словами, от режима охлаждения зависит, как долго алгоритм будет исследовать
пространство состояний, прежде чем приступит к максимизации вероятности. По
умолчанию Figaro предлагает стандартный режим охлаждения, которого должно
быть достаточно в большинстве случаев.
У стандартного режима охлаждения имеется один параметр, контролирующий
скорость охлаждения. Чем он больше, тем медленнее происходит охлаждение.
Вообще говоря, чем больше этот параметр, тем дольше алгоритм отжига будет искать
наиболее вероятное значение, но тем меньше вероятность застрять в локальном
максимуме. Можно, например, начать со скорости 1.0 и увеличивать ее, если есть
подозрение, что обнаружен локальный максимум.
Контекст. В физике отжигом называется метод нахождения
низкоэнергетических состояний вещества путем его постепенного охлаждения. Низкоэнергетическое
состояние соответствует состоянию с высокой вероятностью. При высоких
температурах вещество переходит из одного энергетического состояния в другое, а при более
низких стремится снизить энергию непосредственно. Режим охлаждения управляет тем,
сколько энергетических состояний будет исследовано и насколько быстро будет
найдено состояние, соответствующее минимуму энергии.
Для создания экземпляра алгоритма ИО нужно написать:
MetropolisHastingsAnnealer(100000, ProposalScheme.default,
Schedule.default(1.0))
Стандартный КОНСТруКТОр MetropolisHastingsAnnealer ПрИНИМаеТТрИ
аргумента: число отбираемых примеров, схема предложения (мы здесь используем схему
по умолчанию) и режим охлаждения (мы используем стандартный режим с
параметром 1.0).
Свойства ИО во многом напоминают свойства МГ. Это общий алгоритм,
применимый к различным типам моделей. Но он может работать медленно, и для его
настройки нужно приложить усилия. Требуется не только подобрать схему
предложения, но и задать режим охлаждения. И даже если имеется хорошая схема
предложения, существуют тонкие взаимодействия между режимом охлаждения
и числом итераций. Наилучший способ настроить их - действовать методом проб
и ошибок.
Один из возможных подходов - сравнить результаты, полученные на разных
итерациях. Если мы устойчиво получаем один и тот же результат, то, наверное, он
правильный. Если получаются разные результаты, то, вероятно, мы натыкаемся
на локальные максимумы и должны замедлить охлаждение, увеличив параметр.
408

12.2. Вычисление наиболее вероятного объяснения
Если получаются похожие, но не совсем одинаковые результаты, то, скорее всего,
ИО еще не сошелся к максимуму. Тогда нужно либо ускорить охлаждение, либо
увеличить число итераций.
72.2.3. Приложения алгоритмов НВО
На практике вычисление НВО встречается почти так же часто, как вычисление
вероятности отдельных переменных при известных фактах. Вот некоторые примеры.
• Распознавание вероятных последовательностей действий. Если дана
последовательность изображений или видео, то иногда хочется узнать, какие
сняты действия. Например, если имеется видеозапись футбольного матча,
то хорошо бы уметь распознавать происходящие на поле действия
(подается угловой, центральный нападающий головой направляет мяч в ворота,
вратарь прыгает и отражает удар). Возможные последовательности
действий и результирующие изображения в футбольном матче можно
представить в виде скрытой марковской модели (СММ).
В случае СММ задача НВО заключается в том, чтобы вычислить
наиболее вероятную последовательность скрытых состояний при условии
имеющихся наблюдений. В главе 10 мы видели, что исключение переменных -
хороший алгоритм для СММ в силу их линейной структуры. Точно так же
НВО ИП удобен для решения задачи НВО в СММ. В этой ситуации НВО
ИП называется алгоритмом Витерби.
• Порождение наиболее вероятного разбора предложения на естественном
языке. В главе 10 мы видели, что вероятностные контекстно-свободные
грамматики (ВКСГ) - простая и популярная система представления
вероятностных моделей предложений. Имея ВКСГ, мы можем запросить у
нее наиболее вероятный разбор. И в этом случае НВО ИМ дает хорошие
результаты.
• Анализ изображений. Выше в тексте был приведен пример восстановления
изображения, это типичное применение рассуждений на основе НВО. Дано
частичное изображение, и мы хотим найти его вероятные продолжения.
Например, построить полное изображение человека по фрагменту лица
(на фотографии видна только часть лица человека). Это может быть
полезно для идентификации. Здесь пригодятся как НВО РД, так и имитация
отжига.
• Диагностика. Модель диагностики принтера, рассмотренная в начале этого
раздела, - пример общего класса задач. Другой пример - медицинская
диагностика, цель которой - определить заболевание пациента по известным
симптомам и результатам анализов. В случае диагностики часто
желательно знать наиболее вероятные состояния всех переменных, например,
наиболее вероятное совместное состояние принтера, сети, программы и
пользователя. Это показывает, какие тесты (анализы) выполнить сначала и на
какие потенциальные неисправности обратить внимание.
409

Глава 12. Решение других задач вывода
Для диагностики годится любой алгоритм НВО, но выбирать его надо с
учетом структуры модели. Так, в главе 10 была приведена двухуровневая
сеть для медицинской диагностики, в которой на первом уровне
расположены заболевания, а на втором - симптомы. Для этой структуры хорошо
подходит алгоритм НВО РД.
Научные приложения. В главе 11 обсуждалось применение алгоритма МГ в
биологии, когда ставится задача определить, имеет ли данный индивидуум
некоторые гены, если известен его фенотип, т. е. проявление генов в виде
признаков. Этот запрос можно преобразовать в запрос НВО, цель
которого - найти наиболее вероятный генотип индивидуума. Как МГ оказался
хорошим алгоритмом для вычисления маргинального распределения в
главе 11, так ИО - хороший алгоритм для вычисления максимальной
апостериорной вероятности (МАВ) в данном случае.
Маргинальная МАВ
Еще один вид запросов - комбинация вычисления маргинальных вероятностей
запрашиваемых переменных при условии фактов и МАВ. Такой запрос называется
маргинальной МАВ. В этом случае мы хотим вычислить наиболее вероятные значения
некоторых переменных, суммируя или беря максимум по остальным переменным.
Например, в задаче о диагностике принтера нас может интересовать наиболее
вероятное состояние принтера после агрегирования по сети, программе и пользователю.
Вообще говоря, маргинальная МАВ - полезный вид запроса, но иногда вычислить
ее гораздо труднее, чем обычные маргинальные вероятности или просто МАВ. При
вычислении маргинальной МАВ приходится иметь дело с максимумами сумм
произведений. В факторных алгоритмах, например ИП и РД, важную роль играет произвольное
перемещение переменных в выражениях. Но при вычислении маргинальной МАВ
проблема заключается в том, что нельзя переместить взятие максимума под знак суммы,
а это существенно ограничивает набор допустимых операций. Исследование
алгоритмов вычисления маргинальной МАВ - передний край науки о вероятностных
рассуждениях. В Figaro таких алгоритмов пока нет, но мы планируем добавить их в будущем.
12.3. Вычисление вероятности фактов
Помимо распределения вероятности запрашиваемых переменных или наиболее
вероятного объяснения, иногда требуется вычислять вероятность наблюдаемых
фактов. Предположим, к примеру, что наша задача - мониторинг сети и
обнаружение попыток проникновения в нее. Мы хотели бы применить вероятностный
подход для принятия решения о том, является ли наблюдаемая активность
нормальной или признаком атаки, но, к сожалению, в нашем распоряжении
недостаточно примеров атак с проникновением в сеть, чтобы обучить на них модель.
Кроме того, нас беспокоят новые виды атак, отличные от всего, что наблюдалось
раньше.
410

12.3. Вычисление вероятности фактов
В такой ситуации можно попытаться создать совместное распределение
вероятности с такими переменными: (а) является активность нормальной или опасной,
(Ь) активность, зависящая от вида активности. Но такая модель работать не будет,
потому что мы не знаем условную вероятность атаки при условии, что активность
свидетельствует о попытке проникновения. Альтернативный подход - создать
вероятностную модель нормальной активности и отмечать флагом все, что
оказывается относительно нее необычным. Такой подход называется обнаружением
аномалий. Видя определенную активность, мы сообщаем ее характеристики
модели в виде факта и просим вычислить вероятность этого факта. Если вероятность
достаточно мала, активность помечается как аномальная. Это необязательно
означает попытку проникновения, но является основанием для расследования.
Вычисление вероятности фактов применяется также для классификации.
Вернемся к задаче о распознавании речи, которая в главе 10 обсуждалась в
контексте СММ. При распознавании речи каждое слово моделируется в виде СММ, где
скрытые состояния соответствуют стадиям произнесения слова, а наблюдения -
порождаемым звуковым сигналам. Чтобы определить вероятность слова с
помощью байесовского вывода, мы должны рассмотреть (а) априорную вероятность
слова и (Ь) правдоподобие слова, равное вероятности наблюдаемой
последовательности при условии этого слова. Следовательно, для вычисления
апостериорного распределения вероятности слов придется вычислить вероятность факта в
СММ для каждого слова.
Поскольку вычисление вероятности фактов довольно сильно отличается от
ранее рассмотренных способов вероятностных рассуждений, я проиллюстрирую его
на рис. 12.5, похожем на диаграммы из главы 1.
Первые два шага - точно такие же, как при обычном вероятностном
рассуждении: представить общие знания в виде вероятностной модели, а конкретные
знания о ситуации - в виде фактов. В данном случае общие знания касаются
нормальной активности в сети. Запрос же состоит в вычислении вероятности фактов, и
система применяет алгоритм вывода, чтобы ответить на запрос и вернуть искомую
вероятность. При таком использовании вероятностного рассуждения имеется
заключительный шаг: решающий модуль, который определяет, что делать с ответом.
В этом модуле закодирована некая политика. Например, простая политика могла
бы заключаться в отправке уведомления всякий раз, как вероятность факта
оказывается ниже предопределенного порога.
72.3.7. Наблюдение фактов для вычисления
вероятности фактов
В этом разделе мы продолжим обсуждение примера восстановления изображения
из предыдущего раздела, только теперь нас будет интересовать вероятность
наблюдаемых пикселей. Модель та же, что и раньше. Ниже я покажу, как описать
наблюдаемые пиксели.
Возможно, вы считаете, что о наблюдении фактов мы уже все знаем: нужно
использовать условия или ограничения. Однако условия и ограничения - часть мо-
411

Глава 12. Решение других задач вывода
дели, а не фактов. Так, в модели изображения ограничение, говорящее о том, что
соседние пиксели с большой вероятностью одинаковы, - это часть модели, а вовсе
не факт. При вычислении вероятности фактов нас не интересует вероятность этих
ограничений; мы хотим знать вероятность фактов в рамках модели, включающей
такие ограничения.
1. Представить
знания о
нормальной
активности в сети
и релевантных
факторах в виде
модели
5. Система
возвращает
ответ
Система
вероятностных
рассуждений
/*" Модель
[ нормальной
V активности
Алгоритм вывода
Ответ: 0.0001392
Решающий
модуль
2. Предоставить знания о
конкретной активности
в виде фактов
Факты:
• Сетевой трафик
• Данные пакетов
Запрос:
• Какова
вероятность факта?
4. Система применяет
вероятностный
вывод для
получения ответа
на запрос
3. Сообщить
системе, что
мы хотим
знать
6. Решающий модуль решает,
что делать с ответом.
Например, он может
отправить уведомление, если
вероятность оказалась ниже
пороговой
Рис. 12.5. Шаги применения вероятностных рассуждений для вычисления
вероятности фактов в приложении, распознающем попытку проникновения в сеть
Примечание. Причина этой проблемы состоит в том, что условия и ограничения в
Figaro служат двум целям: модифицировать модель и сообщить о фактах. До сих пор
это нас не беспокоило, потому что обе цели отражаются на запросах одинаково. Но при
вычислении вероятности фактов нужно явно указать, в чем факты заключаются.
По этой причине Figaro предлагает дополнительный механизм явного задания
фактов. Чтобы воспользоваться им, нужно выполнить следующие шаги.
1. Ассоциировать с элементом, для которого задаются факты, имя и
коллекцию элементов. В примере с изображением факты задаются для отдельных
пикселей, поэтому пишем:
412

12.3. Вычисление вероятности фактов
val pixels =
Array.tabulate(4, 4)((i: Int, j: Int) =>
Flip(0.4) ("pixel (" + i + "," + j + ")", Universe.universe))
В результате создается массив пикселей 4 4. Каждый пиксель представлен
элементом Flip(0.4), с которым ассоциировано имя, зависящее от
индекса пикселя. Например, пикселю в позиции (0, 0) будет сопоставлено имя
pixel (0,0). С КаЖДЫМ ПИКСелеМ ассоциирована КОЛЛеКЦИЯ Элементов
Universe, universe - универсум по умолчанию (напомним, что универсум -
это коллекция элементов).
2. Преобразовать каждый факт в экземпляр класса Evidence. Вот несколько
примеров Класса Evidence!
- observation (true) i утверждается, что элемент типа Boolean
принимает значение true;
- Condition ( (i: Int) => i > 0)! утверждается, ЧТО Элемент ТИПа
Integer принимает положительное значение;
- constraint ((d: Double) => l / (d + l) * (d + i)): применяется
ограничение К Элементу ТИПа Double.
3. Ассоциировать с каждым фактом конкретный элемент, воспользовавшись
экземпляром класса NamedEvidence. Его конструктор принимает два
аргумента: ссылка на элемент, для которого задается факт, и экземпляр класса
Evidence, представляющий факт. Так, в следующей строчке задается факт,
говорящий о том, что пиксель в позиции (0,0) принимает значение true:
NamedEvidence("pixel(0,0)", Observation(true))
4. Поместить все экземпляры NamedEvidence, задаваемые в виде фактов, в
список. Приведенный ниже код создает все факты для программы
обработки изображения:
def makeNamedEvidence(i: Int, j: Int, obs: Boolean) =
NamedEvidence("pixel(" + i + "," + j + ")", Observation(obs))
val evidence =
List(makeNamedEvidence(0, 0, true) ,
makeNamedEvidence(0, 2, false),
makeNamedEvidence(1, 1, true),
makeNamedEvidence(2, 0, true),
makeNamedEvidence(2, 3, false),
makeNamedEvidence(3, 1, true))
Описанный способ использования именованных фактов работает так же, как
задание фактов с помощью условий и ограничений. Все элементы (в данном
случае пиксели) генерируются, как обычно, в соответствии с порождающей моделью.
Затем к каждому элементу, для которого имеется именованный факт,
применяется условие или ограничение. Результат добавления именованного факта такой
же, как для добавления условия или ограничения. Именованный факт позволяет
получить доступ к элементам, к которым нужно применить условие или
ограничение.
413

Глава 12. Решение других задач вывода
Теперь, разобравшись в том, как выразить знания о конкретной ситуации в
форме именованных фактов, посмотрим, как задать вопрос о вероятности фактов и
получить на него ответ.
72.3.2. Выполнение алгоритмов вычисления
вероятности фактов
Теперь все готово к вычислению вероятности фактов. Базовый интерфейс прост.
Figaro Предлагает ДВа алгоритма ДЛЯ ЭТОЙ Цели: Выборочный - ProbEvidenceSam-
pler - ПОХОЖИЙ На Выборку ПО ЗНаЧИМОСТИ, И фаКТОрНЫЙ - ProbEvidenceBelief-
Propagation. Так, Чтобы ВЫПОЛНИТЬ алгоритм ProbEvidenceSampler ДЛЯ 10 000 при-
меров при заданных фактах и напечатать вероятность, нужно написать:
println(ProbEvidenceSampler.computeProbEvidence(10000, evidence))
А ЧТОбы Дать алгоритму ProbEvidenceSampler ВОЗМОЖНОСТЬ поработать фиКСИ-
рованное время (скажем, 1 секунду), пишем:
println(ProbEvidenceSampler.computeProbEvidence(1000L, evidence))
He забудьте включить суффикс l в число ioool. Он говорит Scala, что это
длинное целое число, а, значит, речь идет о времени в миллисекундах, а не о количестве
примеров. Количество примеров задается обычным целым числом, а, чтобы задать
время работы, нужно использовать длинное целое.
АлГОрИТМ ProbEvidenceBeliefPropagation аналогичен. НуЖНО ПрОСТО Задать
число итераций и факты, например:
println(ProbEvidenceBeliefPropagation.computeProbEvidence(20, evidence))
Алгоритм вычисления вероятности фактов методом распространения доверия
характеризуется теми же достоинствами и недостатками, что и обычный алгоритм
РД. Он может работать быстро, но поскольку алгоритм приближенный, то ответ, к
которому он сходится, может сильно отличаться от правильного, особенно в сети
с циклами. Именно так обстоит дело в случае сети, описывающей изображение;
выполнив алгоритм, включенный в прилагаемый к книге код, вы увидите, что РД
дает ответ, отличающийся от результата выборочного алгоритма, даже если
производить выборку много раз, включая много примеров. Так что для этой задачи
РД не подходит.
Насколько хорош выборочный алгоритм вычисления вероятности фактов? Это
зависит от того, что понимать под словом «хороший». Определим абсолютную и
относительную погрешность.
• Абсолютной погрешностью называется разность между оценкой значения
и истинным значением. Например, если истинная вероятность факта равна
0.0001, а в результате вычисления получилось 0.001, то абсолютная
погрешность равна 0.0009, что вроде бы и неплохо.
414

12.5. Упражнения
• Относительная погрешность равна абсолютной погрешности, поделенной
на истинное значение. В данном случае вычисленный ответ (0.001) в 10 раз
больше истинной вероятности (0.0001), поэтому относительная
погрешность равна 0.0009/0.0001 = 9. Это не очень хорошо.
Выборочные алгоритмы вычисления вероятности фактов обычно дают хорошую
абсолютную погрешность, но с относительной дело обстоит хуже. Иными словами,
алгоритм может сообщить, что вероятность близка к нулю, но вот сколько нулей
предшествует первой значащей десятичной цифре, определить затрудняется.
Хорошо это или плохо, зависит от приложения. В случае обнаружения аномалий
все зависит от того, близка ли к нулю вероятность фактов в нормальной ситуации.
Если она достаточно далека от нуля, то выборочный алгоритм будет работать
хорошо, т. к. быстро определит, что имеющаяся ситуация не входит в эту категорию.
Если же вероятность в нормальной ситуации уже близка к нулю, а в аномальной
еще ближе, то у выборочного алгоритма возникнут проблемы. Это общее свойство
выборочных алгоритмов, но для вычисления вероятности фактов, которая часто
бывает мала, о нем нужно помнить особенно.
Помогают те же методы, что при выборочном вычислении обычной
вероятности. Самое главное - избегайте жестких условий. Если в модели много жестких
условий, например, имеется мало состояний, удовлетворяющих всем условиям, то
будет трудно найти хотя бы один пример. Оценка вероятности обычно будет равна
нулю, а не малому положительному числу. С точки зрения абсолютной
погрешности это правильно, но с точки зрения относительной - катастрофа.
12.4. Резюме
• Чтобы вычислить совместное распределение вероятности нескольких
переменных, мы можем создать кортеж переменных и применить обычный
вывод. Но если переменных много, что лучше завести переменную,
каким-то образом агрегирующую их в сводную статистику.
• Для вычисления наиболее вероятного совместного значения всех
переменных можно запросить HBO. Figaro предлагает факторные и выборочные
алгоритмы для этой цели. Во многих приложениях запросы НВО можно
использовать как альтернативу запросам маргинальной вероятности.
• Вычисление вероятности фактов полезно в таких приложениях, как
обнаружение аномалий и классификация. Figaro предоставляет факторные и
выборочные алгоритмы и для этой цели тоже.
12.5. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Пользуясь программой диагностики принтера из главы 5, вычислите
совместную вероятность состояния принтера и состояния сети при условии,
415

Глава 12. Решение других задач вывода
что результат печати неудовлетворительный. Являются эти переменные
положительно коррелированными, отрицательно коррелированными или
независимыми?
2. С помощью той же программы выполните шаги диагностики, описанные в
начале раздела 12.2.
3. С помощью той же программы вычислите вероятность факта
неудовлетворительной печати.
4. Продолжая упражнение 10.7 к главе 10, создайте представление СММ
на Figaro. При условии, что задана некоторая последовательность
наблюдений, вычислите наиболее вероятную последовательность скрытых
состояний, порождающих такие наблюдения.
5. В этом упражнении используется сеть для восстановления изображения из
главы 5. При решении следующих двух задач поэкспериментируйте с
различными алгоритмами вычисления вероятности фактов.
a. Вычислить вероятность того факта, что левый верхний пиксель
включен.
b. Вычислить вероятность факта, представленного в поле данных в
коде.
416

ГЛАВА 13.
Динамические рассуждения
и обучение параметров
В этой главе,
■ Как вести мониторинг состояния динамической
системы.
■ Как обучить параметры вероятностной
программы.
В предыдущей главе были описаны различные виды запросов, которые можно
предъявлять вероятностной модели. В этой главе мы продолжим тему и
познакомимся еще с двумя задачами - важными и широко применяемыми. В разделе 13.1
рассматривается задача мониторинга изменяющегося со временем состояния
динамической системы с помощью информации, получаемой от датчиков. А в
разделе 13.2 речь пойдет о задаче обучения параметров вероятностной модели на
данных. И хотя методы рассуждения в этих задачах различны, они попадают в
категорию продвинутых методов, необходимость в которых возникает во многих
приложениях. Поэтому имеет смысл потратить время, чтобы понять, как устроены
и используются эти методы. Главу завершает короткий раздел, в котором
подводятся итоги тому, что мы изучили, и упоминается о не рассмотренных
возможностях Figaro.
Раздел 13.1 опирается на материал главы 8, в которой рассматривались
динамические вероятностные модели. Алгоритм фильтрации частиц, описанный в этом
разделе, основан на выборке по значимости, обсуждавшейся в главе 11. В
разделе 13.2 используется материал из главы 9. В частности, вы должны понимать
различные подходы к обучению, а именно: максимальная апостериорная вероятность
(МАВ) и байесовский подход.

Глава 13. Динамические рассуждения и обучение параметров
13.1. Мониторинг состояния
динамической системы
В главе 8 мы обсуждали, как представить динамическую вероятностную модель.
Существует два способа рассуждения о динамической модели, изображенной на
рис. 13.1:
Поток рассуждения
Владение(О)
Владение(90)
Развертывание модели
Поток рассуждения
Владение(О)
Владение{1)
Владение{1)
Владение(2)
Владение(2)
Владение(З)
Мониторинг
Рис. 13.1. Два способа рассуждения о динамических моделях. В верхней части
рисунка показана модель, развернутая на все временные шаги, для создания
байесовской сети. Серыми стрелками показан поток рассуждений, который
в данном случае может быть направлен как вперед, так и назад во времени.
В нижней части показан мониторинг, здесь рассуждение производится рекурсивно
только в прямом направлении - от предыдущего шага к следующему
• Как показано в верхней части рисунка, мы можем развернуть
динамическую модель на фиксированное число временных шагов. Например, начав с
состояния, описывающего начало футбольного матча, мы могли бы
развернуть его вперед на 90 шагов, по одной минуте каждый. В результате
получается обычная вероятностная модель, к которой применимы все способы
рассуждения, описанные в предыдущих главах. Основное достоинство
такого подхода в том, что он позволяет вести рассуждения как в прямом, так
и в обратном направлении. Например, можно было бы на основе условий в
418
Владение(89)
Владение{90)

13.1. Мониторинг состояния динамической системы
начале игры предсказать ее результат или, зная результат, вывести
начальные условия.
• В нижней части рисунка видно, что мы можем рекурсивно отслеживать
состояние системы во времени. При таком подходе модель не
разворачивается, но в каждый момент времени хранится текущее и предыдущее
состояние. Двигаясь вперед во времени, мы генерируем новое состояние,
которое становится текущим. Состояние, которое было текущим, становится
предыдущим, а то, что было предыдущим, отбрасывается. Главные плюсы
такого подхода в том, что в каждый момент времени хранятся только два
состояния, и это позволяет продолжать мониторинг сколь угодно долго.
Минус же в том, что рассуждение возможно только в прямом направлении.
В этом разделе рассматривается второй подход. У него есть несколько названий:
мониторинг состояния системы, оценка состояния и более техническое -
фильтрация.
13,1.1. Механизм мониторинга
В главе 8 показано, как такое рассуждение производится механически, и я
напомню основные положения. В Figaro мониторинг основан на понятии универсума.
На каждом временном шаге создается новый универсум. Предпоследний
универсум отбрасывается и уничтожается сборщиком мусора. В самом начале мы создаем
начальный универсум, представляющий начальное состояние, и функцию
перехода, которая принимает предыдущий универсум и возвращает следующий.
Элементам, переходящим из одного универсума в другой, должны быть присвоены имена.
Также должны быть поименованы наблюдаемые и опрашиваемые элементы.
Ниже эти шаги описаны более подробно, и приведены также фрагменты
программы мониторинга заполненности ресторана из главы 8. Напомним, что в этой
модели имеется две именованные переменные состояния:
• seated - список целых чисел, показывающих, сколько времени провела за
столиком каждая усаженная группа гостей;
• waiting - целое число, показывающее, сколько людей ждет освобождения
столика.
Вот эти шаги.
1. Создать универсум, представляющий начальное состояние системы.
Присвоить всем релевантным элементам имена и поместить их в начальный
универсум.
val initial = Universe.createNew()
Constant(List (0, 5, 15, 15, 25, 30, 40, 60, 65, 75))
("seated", initial)
Constant(1)("waiting", initial)
О — Создаем универсум, представляющий начальное состояние;
© — Создаем два элемента с именами «seated» и «waiting» и помещаем их в
начальный универсум
419
1
В

Глава 13. Динамические рассуждения и обучение параметров
2. Создать функцию перехода. Ко всем элементам из предыдущего универсума,
которые влияют на текущий, можно обратиться по имени.
Соответствующие им элементы с такими же именами должны быть созданы в следующем
универсуме.
def nextUniverse (previous: Universe): Universe = { <3_ф
val next = Universe.createNew() <d—©
val previousSeated = previous.get[List[Int]]("seated")
val previousWaiting = previous.get[Int]("waiting")
<ь©
Q—О val newState = Chain(previousSeated, previousWaiting, transition _)
0—О Apply (newState, (s: (List[Int], Int, Int)) => s. 1) ("seated", next)
next
}
<b-©
О — Функция перехода принимает предыдущий универсум в качестве аргумента и
возвращает следующий универсум
© — Создаем следующий универсум
© — Получаем элементы «seated» и «waiting» из предыдущего универсума
О — Логика порождения нового состояния из предыдущего инкапсулирована в
функции перехода. Знак подчеркивания сообщает Scala, что transition здесь
используется как функция
© — Создаем в следующем универсуме элемент с именем «seated», чтобы его
можно было использовать и дальше
© — Функция перехода принимает предыдущий универсум в качестве аргумента и
возвращает следующий универсум
3. Создать экземпляр алгоритма мониторинга. Figaro предоставляет два
таких алгоритма: фильтрация частиц и факторный рубеж (factored frontier).
Фильтрация частиц - это выборочный алгоритм, а факторный рубеж -
факторный (как явствует из названия). Чаще всего используется алгоритм
фильтрации частиц, его я и опишу ниже.
val alg = ParticleFilter(initial, nextUniverse, 10000)
4. Запустить алгоритм. В результате порождается распределение вероятности
в начальный момент времени.
alg.start()
5. В цикле переходить к следующему моменту времени, вызывая метод advan-
ceTime. Этот метод позволяет задавать факты на каждом шаге. Для задания
фактов используется интерфейс NamedEvidence. Именно поэтому элементы,
наблюдаемые в качестве фактов, должны быть поименованы.
alg.advanceTime(List(NamedEvidence("waiting", Observation(1))))
6. В каждый момент времени можно запросить текущее распределение
вероятности элементов. Опрашиваемые элементы должны быть поименованы.
420

13.1. Мониторинг состояния динамической системы
III!
ЕСТ1
Например, чтобы получить ожидаемую длину списка усаженных за столик,
можно написать:
alg.currentExpectation("seated", (1: Listflnt]) => 1.length)
Теперь, уяснив себе порядок применения алгоритмов фильтрации, рассмотрим
один из наиболее распространенных алгоритмов такого рода - фильтрацию частиц.
73.7.2. Алгоритм фильтрации частиц
Фильтрация частиц - алгоритм, основанный на выборке по значимости. Слово
частица здесь - синоним примера, а фильтрация означает мониторинг, т. е. это
алгоритм мониторинга с использованием примеров.
Схема работы алгоритма
Схема работы алгоритма фильтрации частиц показана на рис. 13.2. Основная
идея заключается в том, что распределение состояний в любой момент времени
представлено множеством примеров. В левой части рисунка находится множество
частиц, представляющее предыдущее распределение, а в правой - множество
частиц, представляющее текущее распределение. Между ними показаны две
промежуточных стадии.
На первом шаге алгоритма мы берем все примеры из предыдущего состояния
и распространяем их в соответствии с функцией перехода. В результате создается
новое распределение текущего состояния системы, но в нем не учтены имеющиеся
факты о текущем состоянии. Поэтому на следующем шаге мы применяем
условия в виде фактов. Делается это так же, как в случае выборки по значимости, но
каждому примеру назначается вес в соответствии с вероятностью факта для этого
примера. (Точнее, вес равен 0, если пример нарушает какие-либо условия, а в
противном случае вес равен произведению значений ограничений, определенных для
элементов.)
В этот момент у нас имеется множество взвешенных примеров, обозначенное
цифрой 3 на рис. 13.2. Диаметр черного кружка на рисунке пропорционален весу
примера. Однако для завершения алгоритма нам нужно вернуться к множеству
невзвешенных примеров и представить распределение на текущем временном
шаге.
Для этого применяется процесс перевыборки. Смысл его в том, чтобы создать
новое множество невзвешенных примеров, которое аппроксимирует то же
распределение вероятности, что и взвешенные примеры. Алгоритм выбирает новые
невзвешенные примеры из множества взвешенных примеров. Вероятность
выбора данного взвешенного примера пропорциональна его весу. Допустим, что один
взвешенный пример имеет вес 1/3, а другой - 2/3. Пример с весом 2/3 будет
встречаться в новом множестве невзвешенных примеров приблизительно в два раза
чаще, чем имеющий вес 1/3. Поэтому вероятность этого состояния в множестве
невзвешенных частиц будет приблизительно в два раза больше - как и в
множестве взвешенных.

Глава 13. Динамические рассуждения и обучение параметров
Пространство
состояний
Взвешенные
примеры; диаметр
пропорционален
весу
Невзвешенные
примеры
1. Начинаем с
примеров из
предыдущего
шага
Формируем
выборку состояний
на следующем
временном шаге,
применяя модель
перехода
Взвешиваем
каждый пример,
учитывая факты
на новом шаге
4. Строим новое
множество невзвешен-
ных примеров,
производя выборку из
взвешенных, тем
самым получаем
примеры на новом шаге
Рис. 13.2. Алгоритм фильтрации частиц: показан процесс перехода от оценки
распределения состояний в предыдущий момент времени к оценке в текущий
момент
Свойства алгоритма фильтрации частиц
Перевыборка - важнейшая часть алгоритма фильтрации частиц. Возникает
вопрос: а зачем она вообще нужна? Почему бы просто не пользоваться все время
взвешенными частицами? Нельзя ли распространять взвешенные частицы,
следуя динамике системы, а затем применить основанные на фактах условия путем
вычисления новых весов? Но при таком подходе мы рано или поздно получим
множество примеров с очень маленькими весами. На каждом шаге алгоритм будет
умножать текущий вес примера на значения ограничений, что лишь уменьшит его
вес. Если делать это достаточно долго, то вряд ли хоть один пример будет
представлять траекторию с высокой вероятностью. Поэтому множество примеров не
будет репрезентативно для истинного распределения состояний.
Перевыборка решает эту проблему, избавляясь от частиц с наименьшей
вероятностью на каждой итерации и сохраняя лишь те, которые лучше представляют
истинное состояние. Это не гарантирует получение примеров с высокой
вероятностью; есть небольшой шанс, что будут выбраны примеры с низким весом. Но
в среднем процесс перевыборки стремится оставлять примеры с высоким весом.
Поэтому сохраняемые примеры, вообще говоря, представляют более вероятные
траектории.
Хотя в этом смысле перевыборка помогает, у нее есть и неблагоприятный эффект:
снижение разнообразия примеров на каждой итерации. Если у одного взвешенного
422
Невзвешенные
примеры

13.1. Мониторинг состояния динамической системы
примера вес гораздо больше, чем у всех остальных, то с большой вероятностью
почти все невзвешенные примеры на следующем шаге будут соответствовать
именно этому примеру И все бы хорошо, если этот пример представляет истинное
состояние системы, а если нет? Алгоритму фильтрации части трудно исправить
«ошибки», допущенные ранее.
Этот феномен называется истощением частиц. Приведем пример. Допустим, что
фильтрация частиц применяется для мониторинга состояния футбольного матча
между командами А и В. Пусть имеется переменная, описывающая относительную
силу команд. Если команда А забьет гол первой, то может оказаться, что все
примеры будут свидетельствовать о том, что эта команда сильнее. И алгоритм не
сможет исправить эту ошибку, даже если команда В потом забьет 10 голов! Просто не
осталось примеров, в которых команда В сильнее, чем А. На рис. 13.3 показано, что
истощение частиц может случиться даже в течение одного временного шага.
1. В начале
множество
примеров
достаточно
разнообразно
После выборки из
модели перехода
разнообразие
сохраняется
3. Но после учета
фактов одна из
взвешенных частиц
получает гораздо
больший вес, чем все
остальные
4. Все
перевыбранные примеры
соответствуют этому
взвешенному
примеру; разнообразие
утрачено
Рис. 13.3. Истощение частиц происходит, когда из-за перевыборки утрачивается
разнообразие примеров. Это может случиться даже в течение одного шага
Как видно из этого примера, проблема истощения частиц стоит особенно остро,
если переменные не изменяются со временем. Сила команды в описанной выше
модели фиксирована, поэтому после того как фильтр частиц принял решение о
силе команды, он уже не сможет изменить его. Но это же подсказывает и способ
смягчить проблему: ввести небольшую вероятность изменения переменных со
временем. Например, если с вероятностью 1 % относительная сила команд
каждую минуту меняется на противоположную, то даже если алгоритм решит, что
все примеры подтверждают большую силу команды А после забитого ей гола,
некоторые из них смогут изменить свое мнение на следующем шаге. И тогда
после гола, забитого командой В, у этих частиц окажется больший вес, и они будут
перевыбираться чаще. В конечном итоге, если команда В забьет несколько голов
подряд, доминировать будут примеры, в которых команда В сильнее.
423

Глава 13. Динамические рассуждения и обучение параметров
Помимо проблемы истощения, для алгоритма фильтрации частиц характерны
и общие проблемы выборки по значимости. Если факт на одном временном шаге
маловероятен, то множество примеров не станет хорошим представлением
апостериорного распределения. Сгладить проблему помогают стандартные меры.
• Избегать жестких условий и по возможности использовать мягкие
ограничения. Например, условие, состоящее в том, что освобождения столика
ожидают ровно пять человек, трудно удовлетворить, и, значит, оно может
приводить к большому числу бесполезных примеров с весом 0. Лучше
добавить ограничение, значение которого максимально, если в очереди ровно
пять человек, и уменьшается, когда длина очереди отличается от пяти.
• Ослаблять мягкие ограничения, избегая чрезмерно малых значений.
За обеими мерами стоит один и тот же принцип. Мы заменяем вероятностную
модель более «гладкой» аппроксимацией. И хотя новая модель не вполне точна,
рассуждать о ней с помощью выборочного алгоритма проще, и результаты
получаются лучше. Разумеется, если зайти по этому пути слишком далеко, то модель
чересчур сильно разойдется с истинной, поэтому выдаваемые ей результаты будут
бесполезны. Для отыскания правильного баланса лучше всего воспользоваться
методом проб и ошибок.
73.7.3. Применения фильтрации
Динамические модели встречаются в вероятностных рассуждениях повсеместно,
а фильтрация - пожалуй, самый распространенный способ рассуждения о
динамических вероятностных моделях. Поэтому у фильтрации много применений.
Приведем лишь несколько примеров.
• Мониторинг состояния здоровья человека или исправности системы.
Например, пациент лежит в травматологическом отделении, и к нему
подсоединены различные датчики, скажем, температуры и сердечного ритма.
Требуется следить за его состоянием, чтобы быстро прийти на помощь в случае
каких-либо проблем. Состояние пациента характеризуется скрытыми
переменными, например кровопотерей. Задача - вывести эти переменные из
показаний датчиков.
• Локализация робота. Роботу, перемещающемуся в окружающей среде,
необходимо определять свое местоположение, исходя из показаний датчиков,
например, радиолокатора. В этом приложении скрытыми переменными
являются местоположение и скорость движения робота. Задача - определять
эти переменные в различные моменты времени, зная показания датчиков.
У этого приложения есть вариант - одновременная локализация и
построение карты (SLAM). В этом случае робот оказывается в неизвестной среде
и должен строить ее карты, одновременно пытаясь определить, где он
находится.
• Наблюдение и слежение. В охранном приложении имеется несколько
датчиков, которые покрывают какую-то область и получают сигналы при появ-
424

13.2. Обучение параметров модели
лении в этой области объекта. В роли датчиков могут выступать, например,
видеокамеры, а сигналами могут быть последовательности изображений
людей или транспортных средств. Скрытыми переменными являются
объекты, находящиеся в области. Основываясь на сигналах от датчиков, мы
должны вычислить, какие объекты присутствуют в охраняемой области.
Задача тесно связанного следящего приложения - вести наблюдение за
отдельными объектами и строить траектории их перемещения в области.
• Моделирование сложных непрерывных процессов. Фильтрация полезна для
моделирования длительных сложных процессов. Один такой пример -
выборы. Скрытыми переменными в модели выборов являются
характеристики кандидатов, например, популярность кандидата в различных слоях
населениях. Состояние скрытой переменной изменяется во времени. Для
моделирования такой системы можно воспользоваться динамической
моделью, в которой временной шаг соответствуют одному дню. В роли
датчиков выступают опросы. В период избирательной кампании часто
проводятся опросы, проливающие свет на скрытое состояние. Желая предсказать
результаты выборов на основании опросов, мы можем запоминать
состояние скрытых переменных за каждый день. Допустим, до даты выборов
осталось 30 дней. Применяя фильтрацию, мы можем получить
распределение вероятности состояния кандидатов в данный момент времени. Затем
можно развернуть динамическую модель на 30 шагов, начиная с текущей
оценки начального состояния, и предсказать окончательный итог выборов.
13.2. Обучение параметров модели
Третья часть этой книги посвящена выводу: вычислению ответов на запросы при
заданных фактах. Другая важная задача систем вероятностного
программирования - обучение: улучшение модели с учетом имеющихся данных. В обучающих
приложениях неизвестны точные числовые параметры модели, поэтому для их
оценки мы используем прошлые данные. В байесовской парадигме обучения мы
используем прошлые данные для создания апостериорного распределения
вероятности значений параметров, тогда как в парадигмах максимального
правдоподобия (МП) и максимальной апостериорной вероятности (МАВ) используется
алгоритм обучения для оценки одного набора значений параметров, который затем
можно подставить в модель.
Я сосредоточился на выводе, а не на обучении по двум причинам.
• В байесовской парадигме обучение выполняется с помощью алгоритма
вывода.
• В парадигмах МП и МАВ алгоритмы вывода применяются во внутреннем
цикле обучения, а сам алгоритм обучения оказывается сравнительно
простой оберткой.
Теперь мы обсудим эти два момента и покажем, как выполнить обучение в
байесовской парадигме и в парадигме МАВ. Я опишу оба алгоритма и продемонстри-
425

Глава 13. Динамические рассуждения и обучение параметров
рую их применение в Figaro. Мы будем рассматривать только задачу обучения
параметров модели, а на врезке скажем несколько слов об обучении структуры.
73.2.7. Байесовское обучение
При байесовском подходе к обучению, который был описан в главе 9,
вероятностная программа состоит из двух основных частей.
Априорное распределение параметров модели. Обозначим его Р0(Параметры).
Индекс 0 означает, что это значения параметров до ознакомления с данными.
Условное распределение вероятности значений переменных для каждого
примера данных. Обозначим его Р(Данные | Параметры). Отметим, что поскольку
это вероятностная программа, данные в разных примерах могут иметь различную
структуру. Например, примером может служить предложение на английском
языке, и в разных примерах длина предложения будет различаться.
Имея эти две части, мы можем определить совместное распределение
параметров и данных с помощью цепного правила:
Р(Параметры, Данные) = Р0(Параметры) Р(Данные | Параметры)
Затем с помощью правила полной вероятности можно получить распределение
вероятности данных, просуммировав по параметрам. Получается формула,
показанная на рис. 13.4.
Априорное Вероятность данных
распределение р при условии р
P(Data = d) = J_p P0(Parameters = p) P(Data = of | Parameters = p)
Суммирование
по значениям
параметров р
Рис. 13.4. Вычисление вероятности данных по априорному
распределению вероятности параметров
Примечание. Поскольку обычно параметры являются непрерывными переменными,
принимающими бесконечное множество значений, то используется не суммирование, а
интегрирование - аналог суммирования для непрерывных функций.
Данные состоят из набора примеров, а каждый пример содержит множество
значений переменных. Правдоподобием заданного набора значений параметров
при условии данных называется вероятность данных при условии таких значений
параметров. Оно равно произведению - по всем примерам данных - вероятности
данных в каждом примере при условии значений параметров.
426

13.2. Обучение параметров модели
Ключевая концепция байесовского обучения - правило Байеса, которое
гласит, что апостериорная вероятность значений параметров р при условии данных
пропорциональна произведению априорного распределения р на правдоподобие
р. Обозначим Pj(Параметры) апостериорное распределение, a d - наблюдаемые
данные. Тогда апостериорное распределение можно вычислить по формуле,
показанной на рис. 13.5.
Апостериорное Априорное Правдоподобие
распределение распределение i
Р1 (Parameters = р) <* P0(Parameters = р) P(Data = d | Parameters = р)
/
Пропорционально
Рис. 13.5. Правило Байеса для обучения параметров
Применение байесовского обучения для предсказания
будущих наблюдений
При байесовском подходе мы вычисляем апостериорное распределение и
используем его для предсказания будущих примеров данных, которые ранее
предъявлялись. По-другому эту мысль можно выразить, сказав, что для будущих
примеров данных апостериорное распределение становится априорным.
Обозначим апостериорное распределение Р^Параметры), а будущий пример данных -
Данныег Рассуждая так же, как на рис. 13.4, получаем формулу, показанную на
рис. 13.6.
Вероятность Апостериорное Вероятность данных
новых данных распределение р при условии р
P(Data1 = d<i) = J_p Р^(Parameters = р) P(Data1 = с/1 | Parameters = р)
Суммирование по
значениям параметровр
Рис. 13.6. Для вычисления вероятности новых данных используем
апостериорное распределение значений параметров
Подставляя эту формулу в выражения для Pt на рис. 13.5, получаем
окончательную формулу для предсказания новых данных (Данные^ после обучения на
исходных данных (Данные0). Она показана на рис. 13.7.
427

Глава 13. Динамические рассуждения и обучение параметров
Пропорционально
Л
PfData! = с/-! | Data0 = d0 ) «=
Zp Po(Parameters = p) P(Data0 = d0 | Parameters = p) P(Data1 = d^ | Parameters = p)
ft ♦
Априорное Правдоподобие Вероятность новых
распределение данных при условии р
Рис. 13.7. Окончательная формула вероятности новых данных
после наблюдения обучающих данных
Величина Р(Данные1= dx | Данные = d0) называется апостериорным
предиктором, поскольку представляет собой предсказание новых данных на основе
апостериорного распределения значений параметров. Отметим важный момент:
формула апостериорного предиктора имеет вид суммы произведений. Для ее вычисления
можно использовать любой алгоритм вывода. Байесовское обучение выполняется с
помощью вывода и не нуждается в специальном алгоритме.
Применение байесовского обучения в Figaro
Коль скоро для байесовского обучения не нужен специальный алгоритм,
значит, у нас уже есть все необходимые инструменты. Для иллюстрации я
воспользуюсь упрощенной моделью фильтра спама из главы 3. Необходимо выполнить
следующие действия.
1. Определить параметры и их априорные распределения.
val spamProbability = Beta (2,3) <1—©
val wordGivenSpamProbabilities =
featureWords.map(word => (word, Beta (2,2))) .toMap
val wordGivenNormalProbabilities =
featureWords.map(word => (word, Beta(2,2))).toMap
В
О — Параметр, описывающий вероятность того, что данное сообщение является
спамом
© — Параметры, представляющие вероятности появления отдельных слов в
почтовом сообщении при условии, что это не спам. featureWords — слова,
выделенные из обучающих сообщений и используемые в качестве признаков
2. Создать класс, описывающий отдельные примеры данных (т. е. почтовые
сообщения) и распределение вероятностей примеров при условии
параметров.
class EmailModel { <]—О
val isSpam = Flip (spamProbability) <]—©
val hasWordElements = { <]—®
428

13.2. Обучение параметров модели
for { word <- featureWords } yield {
val givenSpamProbability =
wordGivenSpamProbabilities(word)
val givenNormalProbability =
wordGivenNormalProbabilities(word)
val hasWord =
If(isSpam,
Flip(givenSpamProbability) ,
Flip(givenNormalProbability))
(word, hasWord)
}
}
val hasWord = hasWordElements.toMap
В
}
О — Класс, представляющий почтовое сообщение
© — Элемент, представляющий, является ли сообщение спамом. В нем
используется параметр, задающий вероятность спама
© — Элементы, представляющие наличие отдельных слов в зависимости от того,
является ли сообщение спамом. В них используются соответствующие
параметры, задающие вероятности слов при условии, что сообщение спамное или
нормальное
© — Создаем отображение слов на ассоциированные с ними элементы
Создать экземпляры класса, по одному для каждого примера данных
(сообщения в обучающем наборе). Для каждого сообщения передать модели
сообщения относящиеся к нему наблюдаемые факты. Отметим, что все
сообщения в обучающем наборе описываются одной и той же моделью с
одними и теми же параметрами.
for { email <- trainingEmails } { <3—©
val model = new EmailModel <3—©
for { word <- featureWords } {
model.hasWord(word).observe(email.text.contains(word))
}
model.isSpam.observe(email.label == "spam")
1
О — Обходим все сообщения в обучающем наборе
© — Создаем новую модель для каждого сообщения
© — Передаем модели факты, относящиеся к файлу сообщения
Создать экземпляр класса для каждого будущего примера данных
(будущего сообщения), для которого мы собираемся делать предсказания. В данном
случае делается предсказание для одного будущего сообщения, но их число
может быть произвольным. Снова отметим, что модель будущего
сообщения совпадает с использованной для обучающих сообщений, и параметры
те же самые.
val futureModel = new EmailModel(dictionary)
429
в

Глава 13. Динамические рассуждения и обучение параметров
5. Теперь можно отвечать на запросы о будущих примерах, как мы это обычно
делаем. Так, можно задать все слова будущего сообщения и спросить,
является ли оно спамом.
for { word <- featureWords } { О-^
futureModel.hasWord(word).observe(futureEmail.text.contains(word))
}
©—1> println (MetropolisHastings .probability (futureModel. isSpam, true) )
О — Сообщаем слова будущего сообщения, но не его метку, поскольку она
неизвестна
© — Вывести, является ли будущее сообщение спамом, зная список входящих в
него слов и значения обученных параметров
Какой алгоритм следует использовать? В этом примере я воспользовался
алгоритмом Метрополиса-Гастингса, обычно это первый кандидат для байесовского
обучения. И хотя факторные алгоритмы тоже годятся, они выбирают значения
параметров из априорного распределения и считают их единственно возможными.
В результате есть риск пропустить хорошие значения параметров с высокой
апостериорной вероятностью. А вот о выборке по значимости лучше забыть, потому
что при большом числе примеров данных вероятность фактов очень мала. Таким
образом, алгоритм Метрополиса-Гастингса оказывается лучшим кандидатом.
В предыдущей главе было сказано, что для эффективной работы алгоритма
Метрополиса-Гастингса его обычно нужно настраивать. Набор данных, прилагаемый
к этой главе, простой - в отличие от главы 3. Для него настройки МГ по
умолчанию работают неплохо. Но в реальном наборе данных должно быть гораздо
больше примеров, либо надо дать алгоритму поработать достаточно долго. К
сожалению, заранее трудно сказать, насколько долго, поэтому лучше посмотреть, сколько
примеров необходимо для получения стабильных результатов. Возможно, также
понадобится специальная схема предложения.
73.2.2. Обучение методом максимального
правдоподобия и МАВ
В этом разделе показано, как организовать обучение методом МАВ, раньше этот
вопрос рассматривался в главе 9. Сначала я опишу механизм, имеющийся для
этой цели в Figaro, а потом объясню применяемые алгоритмы. Напомним, что при
обучении методом МАВ мы выбираем такие значения параметров, которые
максимизируют произведение априорной вероятности на правдоподобие. Затем эти
параметры используются для предсказания будущих примеров.
Примечание. Обучение методом максимального правдоподобия (МП) - это то же
обучение методом МАВ, только с равномерным априорным распределением, когда
вероятности всех значений одинаковы. Так что сказанное ниже применимо и к обучению
методом МП.
430

13.2. Обучение параметров модели
Механизм обучения методом МАВ в Figaro
Figaro предлагает общую схему обучения методом МАВ. Основная проблема
при кодировании этого метода показана в верхней части рис. 13.8 и заключается
в том, что мы хотели бы использовать одну и ту же модель как для обучения
параметров, так и для последующего вывода на тестовых примерах, но параметры
этих моделей по необходимости различаются. Во время обучения это те
параметры, которые мы обучаем. Например, для представления вероятности спама
можно было бы использовать бета-распределение. Но в процессе последующего
вывода значения параметров уже фиксированы. Так, на этапе обучения мы могли
прийти к выводу, что вероятность спама равна 0.4, и дальше использовать только
это значение. Поскольку параметры - это разные элементы, нам пришлось бы
создать две разные модели и заняться копированием общего кода, что чревато
ошибками.
Без схемы обучения
Параметры для обучения Параметры для рассуждения
Модель для обучения ► Модель для рассуждения
Копирование и вставка
Со схемой обучения
Параметры модели
Априорные ^/^ ^^ Апостериорные
Модель для обучения Модель для рассуждения
/
Общая модель
Рис. 13.8. Создание моделей для обучения и рассуждения.
В верхней части показано, что мы должны были бы сделать, не будь схемы
обучения. Поскольку для обучения и рассуждения используются разные
элементы-параметры, то пришлось бы создать две модели и скопировать
код из одной в другую. Благодаря схеме обучения (нижняя часть) параметры
инкапсулированы в классе ModeiParameters и используется общая модель,
которая специализируется под обучение или рассуждение в зависимости от того,
какие параметры выбраны - априорные или апостериорные
431

Глава 13. Динамические рассуждения и обучение параметров
Схема обучения Figaro, показанная в нижней части рис. 13.8, позволяет
использовать одну и ту же модель для обучения и вывода. В ней используется структура
данных Parametercoiiection - коллекция элементов, специально предназначенная
для хранения параметров модели. Чтобы воспользоваться схемой обучения, мы
создаем экземпляр класса ModeiParameters. От него можно получить либо апри-
орные параметры priorParameters для обучения, либо апостериорные параметры
posteriorParameters для последующего вывода; то и другое - экземпляры класса
ParameterCollection. Все параметры В КОЛЛеКЦИИ ParameterCollection ИМеЮТ ИМе-
на, по которым мы обращаемся к ним из модели.
Ниже описан порядок действий. Полная программа имеется в файле MapLearn-
ing.scaia в приложенном к книге коде.
1. Создать Экземпляр ModeiParameters.
val params = ModeiParameters()
2. ПрИСВОИТЬ КаЖДОМу Параметру ИМЯ И ассоциировать ИХ С ЭКЗеМПЛЯрОМ
ModeiParameters.
val spamProbability = Beta (2,3) ("spam probability", params)
val wordGivenSpamProbabilities = .
featureWords.map(word =>
(word, Beta (2,2) (word + " given spam", params))).toMap
val wordGivenNormalProbabilities =
featureWords.map(word =>
(word, Beta (2,2) (word + " given normal", params))).toMap
О — Для каждого слова-признака создаем два элемента с подходящими именами
для нормального и спамного сообщения. Помещаем эти элементы в два разных
отображения
3. Наша модель должна принимать ParameterCollection в качестве аргумента.
class EmailModel(paramCollection: ParameterCollection) {
4. Внутри модели обращаемся к параметрам по имени.
val isSpam = Flip(paramCollection.get("spam probability"))
5. ДЛЯ обучаЮЩИХ Примеров Передаем Создаваемой МОДеЛИ ПОЛе
priorParameters Экземпляра ModeiParameters.
for { email <- trainingEmails } {
val model = new EmailModel(params.priorParameters)
6. Для обучения значения параметров методом МАВ используем алгоритм
ожидания-максимизации (expectation maximization - ЕМ). Ниже я
поясню, что ЕМ - это «мета-алгоритм», обертывающий любой алгоритм
вывода. В Figaro имеются варианты ЕМ для алгоритмов ИП, РД, выборки по
значимости и МГ.
ЕМ - итеративный алгоритм, который выполняет несколько итераций
цикла. Первый аргумент любого варианта ЕМ - число итераций, а
остальные передаются обернутому алгоритму. Например, в случае ЕМ поверх
432

13.2. Обучение параметров модели
РД мы должны будем передать число итераций РД, тогда как в случае ЕМ
поверх выборки по значимости - число примеров. Последним аргументом
любого варианта ЕМ является экземпляр ModeiParameters, содержащий
подлежащие обучению параметры. В данном случае я воспользовался ЕМ
поверх И П. Вот как создается и запускается алгоритм:
val learningAlg = EMWithVE(10, params)
learningAlg.start()
7. После этого значения параметров обучены методом МАВ. Теперь
апостериорные параметры можно использовать в модели для предсказания
будущих примеров данных.
val futureModel = new EmailModel(params.posteriorParameters)
8. Теперь можно рассуждать о будущих примерах, как мы обычно и делаем:
задать факты и выполнить стандартный алгоритм вывода.
val result = VariableElimination.probability(futureModel.isSpam,true)
println("Новое сообщение является спамом с вероятностью = " + result)
ЕМ-алгоритм
Цель ЕМ-алгоритма - обучить конкретный набор значений параметров на
данных. Алгоритм опирается на понятие достаточной статистики. Чтобы объяснить,
что это такое, я вернусь к бета-биномиальной модели, с которой мы сталкивались
в главах 4 и 9. На рис. 13.9 повторена модель из главы 4.
Рис. 13.9. Бета-биномиальная модель
Вспомним структуру этой модели.
• Существует переменная, представляющая непрерывный параметр,
моделируемый с помощью бета-распределения. Эта переменная соответствует,
например, асимметрии монеты. У бета-распределения два параметра: аир.
Поскольку это параметры параметра, их иногда называют
гиперпараметрами.
• Существует переменная, представляющая число успехов в заданном
количестве испытаний посредством параметра, моделируемого с помощью
биномиального распределения. Она соответствует, к примеру, числу
выпадений орла при подбрасывании монеты, причем асимметрия монеты
представлена описанным выше параметром.
433
Ассиметрия
ЧислоОрлов
Бросок
101

Глава 13. Динамические рассуждения и обучение параметров
Напомним, что в априорном распределении бета-распределенный параметр а
интерпретируется как воображаемое число успехов до наблюдения данных плюс 1,
ар- как воображаемое число неудач плюс 1. Если мы затем наблюдали Nsуспехов
и NF неудач, то апостериорное распределение параметра будет равно Beta(a + N9
(5 + Nj). А мода этого распределения, которая представляет МАВ-значение
параметров, равна
a + JV5-l
a + Ns+$ + NF
Помнить точную формулу необязательно. Важно лишь понимать, что, зная
число успехов Ns и число неудач Np мы имеем всю необходимую информацию для
вычисления апостериорного распределения параметров и МАВ-значений
параметров. Неважно, в каком порядке имели место успехи и неудачи. Ns и NF
называются достаточными статистиками для бета-распределения, т. к. их достаточно для
вычисления апостериорного распределения. А поскольку Ns и NF обычно
наблюдаются для биномиального распределения, знание числа различных исходов дает
достаточные статистики для бета-распределенного параметра.
Существует много примеров распределений параметров и достаточных
статистик для них. В Figaro включена лишь малая их часть, но в этом смысле он легко
расширяется. Приведем наиболее употребительные примеры:
• ТОЛЬКО ЧТО рассмотренные Beta И Binomial.
• Beta и Flip; каждый элемент Flip предоставляет один исход - успех или
неудачу - бета-распределенного параметра, и, если имеется много элементов
Flip, зависящих от такого параметра, то мы складываем вместе все успехи
и неудачи, точно как в случае биномиального распределения.
• Если Flip позволяет выбрать между двумя исходами (true и false), то select
выбирает один из нескольких исходов, например: select (0.2 -> i, о.з ->
2, 0.5 -> 3). Как Flip можно параметризовать бета-распределенным
параметром, так параметр select может иметь распределение Дирихле. Параметр
с распределением Дирихле аналогичен бета-распределенному параметру
с тем отличием, что допускает несколько исходов и имеет гиперпараметр
для каждого возможного исхода. Как и бета-распределенный параметр,
параметр с распределением Дирихле представляет число наблюдений
конкретного варианта плюс 1. Например, Dirichiet(2, 4, 3) могло бы быть
априорным распределением для выбора одного из трех вариантов. Оно
соответствует воображаемой ситуации, когда первый исход наблюдался один
раз, второй - три раза, а третий - два раза. Имея параметр d с
распределением Дирихле, мы можем написать select (d, Listd, 2, 3)) для создания
элемента select с параметром d, для которого возможны исходы 1, 2, 3.
• Нормальное распределение, представляющее среднее других
нормальных распределений. Предположим, к примеру, что имеется переменная m с
распределением Normal (2, 1), представляющая среднее других
нормальных распределений, каждое из которых определено как Normal (m, о.5).
Допустим, что имеются наблюдения этих распределений. Тогда среднего
434

13.2. Обучение параметров модели
значения этих наблюдений достаточно для определения МАВ-значения т,
равного этому среднему. Поэтому в данном случае среднее значение
наблюдений - достаточная статистика для т.
Основной принцип прост. Если известна достаточная статистика, то можно
вычислить МАВ-значения параметров. Но, к сожалению, в большинстве случаев
примеры данных недоступны для прямого наблюдения, поэтому достаточные
статистики неизвестны.
С другой стороны, если имеется корректно определенная вероятностная
модель, то можно применить вероятностный вывод для вычисления ожидаемых
значений переменных, которые вообще-то хотелось бы наблюдать непосредственно.
В случае бета-биномиального распределения можно было бы вычислить
ожидаемое число успехов и неудач. А в случае нормально-нормального распределения -
ожидаемое значение среднего нормальных распределений. Эти ожидаемые
значения называются ожидаемыми достаточными статистиками. А зная ожидаемые
достаточные статистики, мы могли бы вычислить МАВ-значения параметров.
Увы, это тоже не идеал, потому что, не зная значений параметров, вычислить
ожидаемые достаточные статистики трудно.
Подведем итоги:
• Зная только ожидаемые достаточные статистики, мы можем вычислить
МАВ-значения параметров по формуле.
• Зная только МАВ-значения параметров, мы можем вычислить ожидаемые
достаточные статистики, применив вероятностный вывод.
Похоже, мы оказались в затруднительном положении, но эти два факта
предлагают решение, воплощенное в ЕМ-алгоритме. Блок-схема алгоритма показана на
рис. 13.10. Мы начинаем со случайной гипотезы о значениях параметров. Затем
попеременно выполняются два шага, давшие название алгоритму: Е-шаг, или
ожидание, на котором текущие значения параметров используются для вычисления
достаточных ожидаемых статистик с помощью вероятностного вывода, и М-шаг,
или максимизация, на котором вычисленные достаточные ожидаемые статистики
применяются для вычисления МАВ-значений параметров. Эти два шага
повторяются на протяжении заданного максимального числа итераций или пока
параметры не сойдутся. Сходимость означает, что значения параметров на двух
последовательных итерациях почти не отличаются; если такое происходит, то алгоритм
заведомо не даст дальнейшего улучшения, поэтому можно останавливаться.
Гипотеза о
начальных
значениях
параметров
Е-шаг: вычислить
ожидаемые
достаточные
статистики с
помощью вывода
М-шаг: присвоить
параметрам
МАВ-значения,
вычисленные по
формуле
Вернуть

окончательные значения
параметров
Рис. 13.10. Блок-схема ЕМ-алгоритма
435
Параметры
сошлись или
уже выполнено
максимальное
число
итераций?
Нет
Да

Глава 13. Динамические рассуждения и обучение параметров
Замечания об использовании ЕМ-алгоритма
Нетрудно доказать, что, дав ЕМ-алгоритму возможность доработать до
сходимости, мы получим максимум в пространстве значений параметров. Но это может
быть локальный максимум, т. е. для возвращенных значений параметров
апостериорная вероятность выше, чем у близлежащих, но в отдалении могут быть значения
параметров с более высокой вероятностью. Разные прогоны ЕМ-алгоритма могут
давать различные результаты в зависимости от начальной гипотезы. На практике
это означает, что имеет смысл прогнать ЕМ-алгоритм несколько раз с разными
случайно выбранными начальными гипотезами и посмотреть, какая дает
наилучшие результаты. Эта методика называется случайным перезапуском.
Я называю ЕМ мета-алгоритмом, потому что он вызывает другой алгоритм
для вывода на Е-шаге. Поэтому ЕМ-алгоритм может обертывать произвольный
алгоритм вывода, и в Figaro предлагается несколько вариантов. Большую часть
времени ЕМ-алгоритм проводит на Е-шаге, поэтому важно правильно выбрать
алгоритм вывода. Соображения здесь те же, что при обычном выводе для каждого
отдельного примера данных. Алгоритм, который хорошо ведет себя в конкретной
модели при обычном выводе, годится и для обучения с применением ЕМ. В
модели почтового сообщения для каждого примера данных можно использовать
точный алгоритм исключения переменных, поэтому подойдет поверх ИП.
Но ЕМ-алгоритм, вообще говоря, гораздо медленнее, чем вывод для одного
примера данных. Прежде всего, на каждой итерации ЕМ необходимо выполнить
вывод для всех примеров, а их может быть много. И это еще нужно повторить столько
раз, сколько производится итераций. Наконец, возможно, вы захотите произвести
несколько случайных перезапусков ЕМ-алгоритма.
Сколько должно быть итераций? Это существенно зависит от задачи, и дать
общий ответ невозможно. Но мой опыт показывает, что иногда после 10 итераций
достигается насыщение, после которого лучше перезапустить алгоритм с новой
начальной гипотезой.
При выполнении ЕМ-алгоритма с большим набором данных может возникнуть
проблема нехватки памяти. Для одновременного прогона ЕМ на всех примерах
данных требуется все их хранить в памяти, а вдобавок еще и структуры данных,
используемые при выводе. Особенно остро эта проблема стоит для факторных
алгоритмов, потому что факторы могут занимать много памяти, но и для
выборочных алгоритмов она тоже возникает. Так что при обработке больших наборов
данных памяти вполне может не хватить.
Онлайновый ЕМ-алгоритм
Чтобы избежать проблемы нехватки памяти, Figaro предлагает альтернативный
онлайновый ЕМ-алгоритм. Вместо того чтобы обрабатывать все примеры данных
одновременно и для всех выполнять Е-шаг на каждой итерации, этот алгоритм
перебирает примеры по одному. Он выполняет Е-шаг для одного примера, а затем на
М-шаге добавляет полученные в результате ожидаемые достаточные статистики к
накопленным в ходе обработки предыдущих примеров.
436

13.2. Обучение параметров модели
Как правило, мы перебираем все имеющиеся примеры данных и применяем
ЕМ к каждому. Но иногда возникает ситуация, когда имеется постоянный поток
данных, и мы хотим непрерывно обучаться на данных по мере их поступления.
В любой момент времени мы можем использовать уже обученные параметры для
анализа новых примеров, а затем продолжить обучение. Приведенный ниже код
демонстрирует использование онлайнового ЕМ-алгоритма в Figaro.
Листинг 13.1. Онлайновый ЕМ-алгоритм
val parameters = ModelParameters()
val d = Dirichlet(2.0,2.0,2.0)("d",parameters)
D
class Model(parameters: ParameterCollection, modelUniverse: Universe) { //
val s = Select(parameters.get("d"), 1, 2, 3) ("s", modelUniverse) //
} ©-0
def f = () => {
val modelUniverse = new Universe
new Model(parameters.priorParameters, modelUniverse)
modelUniverse
}
s
val em = EMWithVE.online(f, parameters)
em.start()
И
for (i <- 1 to 100) {
val evidence = List(NamedEvidence("s", Observation(1))) // <3—®
em.update(evidence)
}
val futureUniversel = Universe.createNew() //
©-t>
val futureModell = new Model(parameters.posteriorParameters, futureUniversel) //
printIn(VariableElimination.probability(futureModell.s, 1))
for (i <- 101 to 200) {
val evidence: List(NamedEvidence("s", Observation (2))) // <]—©
em.update(evidence) <3—©
}
val futureUniverse2 = Universe.createNew() //
val futureModel2 = new Model(parameters.posteriorParameters, futureUniverse2) //
printIn(VariableElimination.probability(futureModel2.s, 1))
О — Используем схему обучения, основанную на ModelParameters, чтобы было проще
использовать априорные и апостериорные параметры в одной модели
© — Ради максимальной гибкости класс Model принимает в качестве аргументов
коллекцию параметров и универсум
© — Каждый пример данных живет в собственном универсуме. Функция f без
параметров возвращает этот универсум
© — Первый аргумент онлайнового ЕМ-алгоритма — функция, порождающая универсум.
Второй аргумент — ModelParameters
437

Глава 13. Динамические рассуждения и обучение параметров
© — Для каждого примера данных создаем список экземпляров Named Evidence,
содержащих факты, относящиеся к этому экземпляру (быть может, читая их из файла)
© — Вызываем метод update онлайнового ЕМ-алгоритма с этими фактами
© — По завершении обучения можно создать модель с апостериорными параметрами и
рассуждать о ней обычным образом
© — Вызываем метод update онлайнового ЕМ-алгоритма с этими фактами
© — После завершения рассуждения могут поступить дополнительные обучающие
данные. Мы можем переходить из режима обучения в режим рассуждения сколь угодно
часто
Эта программа печатает строки вида:
0.9805825242718447
0.4975369458128079
При первом рассуждении обучающие данные содержали 100 единиц, поэтому
после обучения вероятность генерирования 1 была очень близка к 1. Затем мы
добавили 100 двоек, и в результате вероятность генерирования 1 стала близка к 1/2.
Обучение структуры модели
В этом разделе мы говорили о задаче обучения параметров модели на данных. Я
предполагал, что структура модели (переменные, функциональные формы и
зависимости) известна, а неопределенными остаются только числовые параметры. Но что,
если структура неизвестна?
В идеале хотелось бы узнать из данных как структуру, так и параметры модели, К
сожалению, обучить структуру трудно, поскольку пространство возможных структур
программы огромно. Допустим, нам даны примеры входных и выходных данных
программы, а хотим мы получить программу, которая преобразует одно в другое. Эта задача
называется индукцией программы (program induction) и, несмотря на многолетние
исследования, до сих пор не найдены надежные универсальные методы ее решения.
Так что же делать, если структура модели неизвестна? Наилучший подход - явно
включить неопределенность структуры в модель. Например, если мы точно не знаем,
должна ли присутствовать в модели некоторая переменная, создадим два варианта
модели - с переменной и без нее. Если непонятно, как должна быть направлена
зависимость, включим в модель обе возможности. Если неизвестно, имеет ли
переменная нормальное или равномерное распределение, закодируем оба варианта. В любом
случае добавим переменную, показывающую, какая модель правильна. Она
называется структурной переменной (structural variable).
Если пытаться включить каждую комбинацию в отдельную модель, то получится
прорва моделей. По счастью, многие структурные решения независимы. Например,
решение о том, содержит ли модель некую переменную, может не зависеть от того, какое
распределение - нормальное или равномерное - имеет другая переменная. Штука в
том, как обеспечить максимальную гибкость структуры в минимальной по размеру
модели.
После того как в модели представлено несколько альтернативных структур, выбор
между ними производится с помощью вероятностного вывода, который позволяет
определить апостериорные вероятности структурных переменных. Вместо этого
можно было бы воспользоваться выводом НВО и найти наиболее вероятные значения,
получив тем самым единственную модель, пригодную для анализа будущих примеров.
438

13.3. Дальше вместе с Figaro
13.3. Дальше вместе с Figaro
Примите поздравления! Вдумчиво прочитав книгу, вы очень много узнали о
вероятностном моделировании и программировании, в том числе: основы
моделирования и вывода, различные парадигмы моделирования, несколько алгоритмов
вывода и порядок их использования. Мы дошли до конца книги, но тем, кто хочет
углубить знания о вероятностном программировании и применении Figaro, хочу
дать несколько советов:
• Создайте свою библиотеку классов атомарных элементов. Возможно, вы
хотели бы использовать какое-нибудь распределение вероятности,
отсутствующее в текущей версии Figaro. Добавить свой элемент нетрудно.
Можно взять за образец определения классов элементов - непрерывных и
дискретных - В пакете com. era. figaro. library, atomic.
• Создайте собственные составные элементы. Это даже проще создания
атомарных элементов. Если вы видите, что приходится часто писать и
использовать функцию, которая принимает некоторые элементы и возвращает
другой элемент, попробуйте преобразовать ее в класс составного элемента.
Такой элемент проще использовать в любой модели. Как это делается,
можно ПОСМОТреТЬ В Определениях КЛаССОВ ИЗ Пакета com. era. figaro. library,
compound.
• Поинтересуйтесь отладочными версиями алгоритмов. У большинства
алгоритмов в Figaro имеется флаг debug, который по умолчанию равен false.
Если присвоить ему значению true, то будут выдаваться подробные
сообщения, которые помогут понять, почему алгоритм работает не так, как вы
ожидали. Разумеется, для понимания отладочных сообщений необходимо
представлять себе, что алгоритм делает, но базовой информации,
почерпнутой из этой книги, должно быть достаточно. Например, в отладочных
сообщениях для алгоритма исключения переменных перечисляются все
факторы, созданные в процессе решения. При отладке моделей очень полезно
давать всем элементам уникальные имена.
• При работе с алгоритмом Метрополиса-Гастингса может быть полезен
метод MetropolisHastings.test. Он ПОЗВОЛЯеТ установить KOHKpeTHOe СОСТОЯ-
ние системы, задав значения интересующих вас переменных методом
Element.set. Затем можно протестировать возможности, возникающие, если
выполнить один шаг алгоритма МГ из этого состояния. Нужно задать
число предикатов, которым могло бы удовлетворять результирующее
состояние, и посмотреть, сколько раз удовлетворялся каждый предикат.
• Используйте концепцию универсума при решении трудных задач вывода.
Например, в одном универсуме можно выполнить имитацию отжига и
найти наиболее вероятные значения некоторых переменных, а в другом
универсуме вычислить вероятность фактов, получающуюся при таких
значениях переменных. На самом деле, в алгоритм исключения переменных уже
встроена концепция использования другого алгоритма для вычисления
439

Глава 13. Динамические рассуждения и обучение параметров
вероятности фактов в зависимом универсуме, но сама идея использования
нескольких универсумов носит общий характер. Команда Figaro работает
над модернизацией каркаса универсумов, стремясь предоставить единый
интерфейс, который позволил бы одному и тому же алгоритму работать в
разных универсумах и прозрачно комбинировать алгоритмы через
границы универсумов. Так что потенциал использования этой техники в
будущих версиях будет раскрыт полнее.
Если у вас есть идеи насчет того, как сделать Figaro лучше и полезнее,
поделитесь ими на нашем сайте в GitHub (https://github.com/p2t2/figaroy Мы
приветствуем все предложения и всегда рады ответить на ваши вопросы. Спасибо, что
прочли книгу, и желаем вам успехов в вероятностном программировании.
13.4. Резюме
• Чтобы рассуждать о динамической вероятностной модели, можно либо
развернуть ее на фиксированное число временных шагов, либо
воспользоваться алгоритмом фильтрации для мониторинга состояния модели во
времени. Разворачивание позволяет рассуждать в прямом и обратном
направлении, зато фильтрация дает возможность гонять модель сколь угодно
далеко вперед, экономя при этом память.
• Для выполнения байесовского обучения можно использовать любой
стандартный алгоритм вывода. При этом цель обучения - найти апостериорное
распределение вероятности значений параметров и использовать его для
анализа новых примеров.
• Конструкция Figaro ModeiParameters упрощает обучение методом МАВ,
которое производится с помощью ЕМ-алгоритма, обертывающего
произвольный стандартный алгоритм вывода.
• Онлайновый ЕМ-алгоритм полезен, когда имеется много примеров
данных, а памяти недостаточно, а также в случае, когда обучение ведется на
постоянном потоке данных.
13.5. Упражнения
Решения избранных упражнений имеются на сайте www.manning.com/books/
practical-probabilistic-programming.
1. Одна из тысячи машин, собираемых на заводе, где была изготовлена ваша
машина, имеет дефект. В любой заданный день топливная экономичность
двигателя либо высокая, либо низкая и определяется следующим
правилом. Если в предыдущий день топливная экономичность была низкой, то
на следующий день она будет низкой с вероятностью 90 %. Если в
предыдущий день топливная экономичность была высокой, то на следующий она
будет низкой с вероятностью 90 % для дефектных машин и с вероятностью
5 % для исправных. Ваша машина оборудована датчиком экономии топли-
440

13.5. Упражнения
ва, который показывает, была ли топливная экономичность в данный день
высокой или низкой. Датчик показывает значение правильно с
вероятностью 0.95 и неправильно - с вероятностью 0.05.
a. Нарисуйте динамическую байесовскую сеть для представления этой
системы.
b. Напишите на Figaro программу, представляющую эту систему.
c. Пользуясь этой программой, создайте две последовательности
наблюдений длины 100 - для исправной и для дефектной машины.
d. Примените метод фильтрации частиц для мониторинга состояния
системы. Выполните фильтр частиц для обеих последовательностей
наблюдений. Используйте 100 примеров. Скорее всего, вы обнаружите,
что в большинстве случаев не удается распознать дефектную машину.
Как вы думаете, почему?
e. Теперь повторите часть (d) на 10 000 примеров. Как правило,
результат будет другим. Можете ли вы объяснить это? (Обязательно
выполните эксперимент несколько раз - метод фильтрации частиц не
всегда дает одинаковые ответы.)
2. Теперь немного изменим модель из предыдущего упражнения, чтобы
алгоритм фильтрации частиц работал более гладко. Дефектная машина не
всегда остается дефектной, с некоторой вероятностью неисправность сама
собой пропадает на каждом временном шаге. Аналогично исправная
машина может сломаться. Точнее, состояние наличия или отсутствия дефекта
сохраняется на следующем временном шаге с вероятностью 0.99 и меняется
на противоположное с вероятностью 0.01.
Выполните фильтрацию частиц для этой модели на 100 примерах. Есть ли
разница с предыдущими результатами? Повторите эксперимент на 10 000
примеров. Оцените компромисс.
3. В этом упражнении обсуждается подвох в ЕМ-
алгоритме. Рассмотрим простую байесовскую сеть,
показанную на рис. 13.11. Требуется обучить
параметры этой сети.
a. Напишите на Figaro программу для
представления этой сети с применением схемы обучения
параметров модели. Считайте, что априорное
распределение всех параметров - Beta(l, 1).
b. Создайте обучающий набор, содержащий
порядка 10 примеров, в которых наблюдаются Рис. 13.11.
только переменные X и Z. В каждом обучаю- Байесовская сеть
щем примере X и Z должны быть одинаковы: Д™ упражнения 3
иногда обе равны true, а иногда обе - false.
c. Воспользуйтесь ЕМ-алгоритмом для обучения параметров модели.
Поэкспериментируйте с различными вариантами ЕМ.
441
X
Y
Z

Глава 13. Динамические рассуждения и обучение параметров
d. Теперь создайте тестовый сценарий с использованием апостериорных
параметров. Вычислите вероятность, что Z равно true, при условии,
что X равно true. Скорее всего, окажется, что эта вероятность далека
от 1, несмотря на то, что X равно true и X и Z в обучающем наборе
всегда принимали одинаковые значения. Попробуйте объяснить, чем
это вызвано.
e. Исправим эту проблему. Измените априорное распределение Y при
условии, что X равно true, на Beta(2, 1), а априорное распределение
X при условии, что Y равно true, на Beta(l, 2). Снова воспользуйтесь
ЕМ-алгоритмом, чтобы обучить параметры, и выполните тест. На
этот раз вероятность, что Z равно true, должна быть близка к 1. Как вы
думаете, почему в этом случае обучение дало правильный результат?
Какую мораль следует извлечь из этого упражнения при
использовании ЕМ в собственных программах?
4. Повторите упражнение 3, используя байесовское обучение вместо ЕМ-
алгоритма.
a. Попробуйте применить к этой задаче разные алгоритмы вывода.
Какой алгоритм работает лучше? Почему?
b. Сравните результат байесовского обучения с результатами ЕМ-
алгоритма. Есть ли значительное различие в результатах
байесовского обучения, когда для всех переменных задано априорное
распределение Beta(l, 1) и когда заданы распределения Beta(2,1) и Beta(l, 2)?
Сильно ли отличаются результаты при распределениях Beta(2, 1) и
Beta(l, 2) от тех, что дает ЕМ-алгоритм? Если да, то как вы думаете,
почему?
5. Узнав, как работает обучение параметров, самое время вернуться к фильтру
спама из главы 3.
a. Перепишите эту программу, применив схему обучения параметров
модели.
b. Замените метод обучения: вместо использованного в главе 3 базового
ЕМ-алгоритма, который обучает параметры сразу на всех
сообщениях, попробуйте онлайновый алгоритм.
442

ПРИЛОЖЕНИЕ А.
Получение и установка
Seal а и Figaro
В этом приложении приведены инструкции по установке и запуску Figaro.
Проще всего воспользоваться системой сборки Scala Build Tool (sbt). Инструкции по
сборке проекта с помощью sbt приведены в разделе А.1. Если по какой-то причине
вы не можете или не хотите использовать sbt, то ознакомьтесь с инструкциями по
ручной сборке в разделе А.2.
Код в этой книге тестировался для версии Figaro 3.3. Более ранние версии Figaro
поддерживают не все описанные в книге возможности. Мы стараемся сохранять
в новых версиях обратную совместимость там, где это возможно, поэтому можете
попробовать и более поздние версии.
Figaro 3.3 использует версию Scala 2.11.x. К сожалению, разработчики Scala не
заботятся об обратной совместимости версий, а для переноса Figaro на более
свежую версию Scala требуется время, поэтому работа Figaro с последними версиями
Scala не гарантируется, sbt автоматически следит за зависимостями и позаботится
о том, чтобы использовалась подходящая версия Scala.
А.1. Использование sbt
Простейший способ выполнить приведенный в книге код - воспользоваться
системой sbt. Сопровождающий книгу код организован в виде пакета для проекта
sbt. Вам нужно только скачать и установить sbt с сайта www.scala-sbt.org. Позже,
когда вы начнете использовать sbt в проекте, она автоматически загрузит нужные
версии Scala и Figaro, так что вам больше ничего устанавливать не придется, sbt
также правильно настроит путь к классам, избавив вас от лишней мороки.
В этой книге вам понадобятся только две команды sbt:
sbt console «-О
sbt "runMain object arguments"
О — Запускает интерактивную оболочку Scala
© — Выполняет метод main указанного объекта, передав ему заданные в командной
строке параметры. Имя объекта должно быть задано полностью, вместе с пакетом,
например: «chap01 .HelloWorldFigaro».

Приложение А. Получение и установка Scala и Figaro
Для выполнения этих команд нужно находиться в каталоге проекта верхнего
уровня PracticalProbProg/examples.
Примечание. Если вы уже находитесь в консоли sbt, то вводить sbt еще раз не надо,
достаточно набрать runMain object arguments.
У sbt много возможностей, ее можно использовать также для сборки и запуска
собственного кода. В качестве отправной точки можете использовать в нашем
проекте Build.scala. Eclipse также поддерживает sbt.
А. 2. Установка и запуск Figaro без sbt
Хотя sbt - полезное средство, вы, возможно, предпочитаете управлять своим
рабочим пространством по-другому. Далее описано, как установить и запустить
Figaro, не прибегая к sbt.
Для запуска Figaro, прежде всего, понадобится Scala. Компилятор Scala можно
запустить как из командной строки, так и из интегрированной среды разработки
(IDE). Разработку на Scala поддерживают как Eclipse, так и IntelliJ IDEA. Для
NetBeans тоже есть подключаемый модуль Scala, но он, похоже, не
поддерживает последние версии. Ниже я расскажу, как получить Scala и Figaro и запустить
Scala-программы, использующие Figaro, из командной строки. Инструкции для
конкретных IDE не приводятся. О том, как подключить к ним библиотеку Figaro,
читайте в документации по IDE и подключаемым модулям Scala.
1. Чтобы начать работу со Scala, скачайте версию, соответствующую
имеющейся у вас версии Figaro, с сайта http://scala-lang.org/download/.
Следуйте инструкциям по установке Scala на странице http://scala-lang.org/
download/install.html и убедитесь, что можете откомпилировать и
выполнить программу «Hello World», приведенную в документации.
2. Следующий шаг - получить Figaro. Двоичный дистрибутив Figaro
размещен на сайте компании Charles River Analytics Inc. Перейдите по адресу
www.cra.com/figaro. Проверьте, что версия Figaro соответствует версии
Scala. Все ссылки ведут на сжатый архив, содержащий JAR-файл Figaro
(JAR - формат для хранения откомпилированного байт-кода на Java и
Scala), примеры, документацию, Scaladoc-файлы и исходный код. Суффикс
«fat» в названии JAR-файла Figaro означает, что файл содержит все
необходимые для работы Figaro библиотеки. Перейдите по нужной вам ссылке и
распакуйте скачанный архив.
3. [Необязательный шаг] Добавьте полный путь к JAR-файлу Figaro в путь к
классам. Для этого можно добавить путь к переменную окружения class path
в операционной системе. Как это сделать, зависит от операционной
системы. Подробные сведения о переменных окружения path и classpath
можно прочитать на странице http://docs.oracle.com/javase/tutorial/essential/
environment/paths.html.
444

А.З. Сборка из исходного кода
a. Если переменной classpath не существует, создайте ее. Я
предпочитаю, чтобы classpath включала текущий каталог, поэтому сначала
сделайте ее равной «.».
b. Теперь добавьте в classpath путь к JAR-файлу Figaro classpath. Так, в
Windows 7, если файл figaro_2.11-3.3.0.0-fat.jar находится в каталоге
C:\Users\apfeffer folder, и classpath равна «.», то сделайте ее равной
С : \Users\apf ef f er\figaro_2 .11-3.3.0. 0-f at; .. Вместо 2.11 ПОДСТавьте
номер подходящей версии Scala, а вместо 3.3.0.0 - номер подходящей
версии Figaro.
4. Теперь программы на Figaro можно компилировать и выполнять, как любые
Scala-программы. Запишите текст приведенной ниже тестовой программы
в файл Test.scala. Сначала будем предполагать, что вы задали переменную
classpath, как описано на шаге 3.
a. Если команда scaia Test.scala выполняется из каталога, где
находится файл Test.scala, то программа сначала будет
откомпилирована, а затем выполнена. Она должна напечатать 1.0.
b. Если выполняется команда scaiac Test.scala (обратите внимание
на букву с в конце scaiac), то запустится компилятор Scala и
сгенерирует файлы с расширением .class. Затем программу можно будет
выполнить, введя команду scala Test в том же каталоге.
c. Если вы проигнорировали шаг 3, то задать путь к классам можно
прямо в командной строке с помощью флага -ср. Так, чтобы
откомпилировать и выполнить программу Test.scala в предположении, что
файл figaro_2.11-3.3.0.0-fat.jar находится в каталоге C:\Users\apfeffer,
можно ввести команду
scala -ср C:\Users\apfeffer\ figaro_2.11-3.3.0.0-fat Test.scala.
Вот текст тестовой программы:
import com. cra.figaro. language ._
import com. era .figaro. algorithm, sampling ._
object Test {
def main(args: Array[String] ) {
val test = Constant("Test")
val algorithm = Importance(1000, test)
algorithm.start()
println(algorithm.probability(test, "Test"))
}
}
Эта программа должна напечатать 1.0.
А.З. Сборка из исходного кода
Figaro распространяется в исходных кодах и сопровождается на сайте GitHub.
Проект GitHub называется «Probabilistic Programming Tools and Techniques»
445

Приложение А. Получение и установка Scala и Figaro
(Р2Т2) и размещен по адресу https://github.com/p2t2. В настоящее время Р2Т2
содержит только исходный код Figaro, но мы планируем включить в него
дополнительные инструменты. Если вы хотите заглянуть в исходный код и собрать
Figaro самостоятельно, добро пожаловать на наш сайт GitHub.
Для управления сборкой Figaro используется sbt. Чтобы собрать Figaro из
исходного кода на GitHub, создайте копию репозитория в своей учетной записи на
GitHub, а затем воспользуйтесь функцией клонирования, чтобы скопировать
исходный код из учетной записи на GitHub на свою машину:
git clone https://github.com/[your-github-username]/figaro.git
Существует несколько веток; выгружайте ветку «master», содержащую
последнюю стабильную версию или последнюю ветку «DEV», если хотите иметь самые
свежие возможности (поскольку над ними ведется работа, возможны ошибки).
Скачайте и установите sbt, запустите программу и в ответ на приглашение
введите такие команды:
> clean
> compile
> package
> assembly
> exit
В результате будет создана версия Figaro, соответствующая версии Scala;
сгенерированные файлы вы найдете в каталоге «target».
446

ПРИЛОЖЕНИЕ В.
Краткий обзор систем
вероятностного
программирования
Сейчас разрабатывается много систем вероятностного программирования (СВП),
и их число постоянно растет. В этом обзоре я кратко опишу некоторые наиболее
распространенные системы и отмечу их основные особенности. Там, где возможно,
я указываю URL-адрес страницы, с которой можно скачать систему. Я не пытаюсь
охватить все системы на свете, приношу извинения разработчикам тех систем, о
которых не упомянул. Также заранее прошу прощения за неточности и упущения
в описании систем.
СВП можно охарактеризовать со следующих позиций.
• Выразительность языка. Например, поддерживает ли язык
пользовательские функции, ненаправленные модели, дискретные и непрерывные
переменные, модели с открытой вселенной и переменные произвольных типов?
• Стратегия развертывания системы. Предлагается ли автономный язык,
библиотека на существующем языке или новая реализация существующего
языка с вероятностными расширениями? Если это автономный язык,
существует ли интерфейс к нему из какого-нибудь существующего языка?
• Какой стиль программирования используется: функциональный,
логический, императивный, объектно-ориентированный и т. п.?
• Какие поддерживаются алгоритмы вывода: факторные, выборочные и т. п.?
Поддерживаются ли динамические рассуждения?
• Какого рода запросы поддерживает система?
Ниже описано несколько примеров СВП.
BUGS (www.mrc-bsu.cam.ac.uk/software/bugs/)
BUGS означает Bayesian Inference Using Gibbs Sampling (байесовский вывод с
использованием выборки по Гиббсу). Как следует из названия, система построена
на базе алгоритма Монте-Карло по схеме марковской цепи (МСМС), который
называется выборкой по Гиббсу. BUGS была одной из первых СВП и получила
широкое распространение в социальных науках. Если говорить о представлении,

Приложение В. Краткий обзор систем вероятностного программирования
то BUGS не поддерживает пользовательские функции и ориентирована, главным
образом, на непрерывные переменные. Зато она предлагает широкий спектр
распределений переменных. BUGS реализована в виде автономного языка.
STAN (http://mc-stan.org/)
Stan - популярная система вероятностного программирования, особенно в
области статистики. Она поддерживает многочисленные виды статистического
вывода. Основной алгоритм вывода в Stan - эффективный вариант МСМС. Как и
BUGS, Stan ориентирована на непрерывные переменные и предлагает широкий
спектр распределений. Stan, как и BUGS, представляет собой автономный язык,
но имеет интерфейсы к таким популярным языкам, как R, Python и MATLAB.
FACTORIE (http://factorie.cs.umass.edu/)
Система вероятностного программирования FACTORIE добилась большого
успеха в обработке естественного языка. В отличие от большинства других СВП,
в FACTORIE применяется императивный стиль для явного построения
факторных графов, на которых она может выполнять такие алгоритмы, как МСМС. Как
и Figaro, FACTORIE представляет собой библиотеку, написанную на Scala.
PROBLOG (https://dtai.cs.kuleuven.be/problog/)
ProbLog отличается от других СВП, упомянутых в этом обзоре, тем, что
основана на логическом программировании. Если вам нравятся такие языки логического
программирования, как Prolog, то ProbLog - система для вас. Можно считать, что
ProbLog - расширение Prolog с поддержкой вероятностей. Основная идея
вероятностного логического программирования состоит в том, что имеется множество
неопределенных базовых фактов и множество логических правил, позволяющих
выводить другие - производные - факты. Вероятность любого производного
факта равна вероятности того, существует множество базовых фактов, из которых
следует производный. ProbLog может работать только с дискретными
переменными. Для вывода в ProbLog используется применяемая в логическом
программировании техника формального доказательства.
BLOG (https://sites.google.com/site/bloginference/)
BLOG (Bayesian Logic) - некий гибрид логической и функциональной СВП.
Предложения в BLOG похожи на высказывания в логике, но существует
порождающий поток в сторону BLOG-моделей, который представляет способы
генерирования возможных миров - как в функциональных СВП типа Figaro. В BLOG
используется моделирование с открытой вселенной, когда неизвестны ни
количество, ни виды объектов. Если у вас именно такая модель, то BLOG вам
подойдет. Для вывода в BLOG применяется алгоритм МСМС. Это автономный язык, но
специальные схемы предложения можно писать на Java.
CHURCH (https://probmods.org/play-space.html)
Church - функциональная СВП, основанная на языке Scheme, похожем на LISP.
С точки зрения представления, она похожа на Figaro тем, что поддерживает
сложный поток управления и рекурсию, а также развитые структуры данных, хотя и не
448

Приложение В. Краткий обзор систем вероятностного программирования
является объектно-ориентированной. У Church есть несколько реализаций.
Приведенный выше URL-адрес относится к WebChurch - веб-приложению с удобным
интерактивным пособием по вероятностному программированию.
ANGLICAN (www.robots.ox.ac.uk/-fwood/anglican/)
Anglican - сравнительно новый язык, похожий на Church в плане
представления. Основная особенность Anglican - эффективные и точные выборочные
алгоритмы.
VENTURE (http://probcomp.csail.mit.edu/venture/)
Venture - новый язык, созданный несколькими разработчиками Church.
Основное новшество в Venture - программируемый вывод (inference programming),
который предоставляет пользователю выразительный, детальный, интерактивный
контроль над выводом, преимущественно с помощью выборочных алгоритмов.
DIMPLE (http://dimple.probprog.org/)
СВП Dimple разработана компанией Gamalon. Она способна представлять
дискретные и непрерывные переменные, направленные и ненаправленные модели, но
ограничена только конечными моделями с фиксированной структурой. Для таких
моделей Dimple предлагает высокоэффективные факторные алгоритмы вывода.
449

предметный указатель
Символы
лл, конструктор в Figaro 275
::, оператор Scala 102
:::, оператор Scala 102
?, символ 210
А
addCondition, метод 74
addConstraint, метод 76
advanceTime, метод 420
и фильтрация частиц 282
algorithm.resumeO, метод, выборка по
значимости 368
Anglican, система вероятностного
программирования 449
apply(), метод 220
Apply, элемент Figaro 52, 67, 255, 335
в сочетании с Chain 72
задание зависимостей 138
практические причины для применения 69
с несколькими аргументами 69
структура 68, 71
Array.fill, метод Scala 264
В
Beta, элемент 101, 201
Binomial, элемент 101, 201
дискретный атомарный 61
составной 183
BLOG
система вероятностного
программирования 448
язык вероятностного программирования 216
Boolean, тип значения и дискретный
атомарный элемент 59
BUGS, система вероятностного
программирования 34, 447
С
Chain, элемент Figaro 52, 70, 98, 136
flatMap 72
map 72
задание зависимостей 138
направленные зависимости 157
отличие от элемента Apply 70
представление условных распределений
вероятности 136
проектирование структуры сети 172
Charles River Analytics Inc. 39, 444
Church, система вероятностного
программирования 448
classify, метод 107
CLASSPATH, переменная окружения 444
com.cra.figaro.language, пакет 53, 60, 65
com.cra.figaro.library.atomic, пакет 439
com.cra.figaro.library.compound, пакет 439
com.cra.figaro.util, пакет 247
Constant, элемент 183
Container, конструктор 212
CPD, конструктор, два набора аргументов 136
currentExpectation, метод 282
currentProbability, метод 282
D
Dictionary, класс 102
DIMPLE, система вероятностного
программирования 449

Предметный указатель
DisjointScheme, функция 385
Dist, составной элемент 65
Double, тип значения и непрерывный
атомарный элемент 59
d-разделенности критерий 166
Е
Element, класс 54
ЕМ-алгоритм 109, 340, 432
блок-схема 435
замечания об использовании 436
как итеративный алгоритм 432
как мета-алгоритм 436
цель 433
Evidence, класс 413
exists, метод коллекций Figaro 212
F
FACTORIE, система вероятностного
программирования 448
Figaro 24
алгоритмы вычисления НВО 400
версии 443
встроенные алгоритмы вывода 41
вычисление совместных распределений
395
динамические модели без ограничений по
времени 279
и концепция универсума 419
и процесс фильтрации 281
как объектно-ориентированный язык 41
как язык имитационного моделирования 187
конструкторы встроенных элементов 252
основные концепции 51
особенности алгоритма распространения
доверия 346
преимущества погружения в Scala 41
применение байесовского обучения 428
пример программы Hello World 44
filter, метод 106
FixedSizeArray 210, 221
Flip, класс 53
Fold Left, конструктор 336
foldLeft, операция Scala 209
fold, функция 198
FromRange, элемент 79
G
generate, метод 220
Geometric, элемент 219
getOrElse, метод Scala 104
getQuality, функция 68
GitHub 41, 446
I
If
составной элемент 64
Inject, элемент 276
Integer, элемент 59, 99, 216
J
Javadoc 67
L
leamMAP, метод 110
M
map, функция 198
memo, функция 247
MetropolisHastingsAnnealer, конструктор 408
Model Parameters, класс 432
moslikelyValue, метод 194
MPEAIgorithm, с отсечением и без отсечения
повремени 400
MPEBeliefPropagation, алгоритм 193, 400
MPEVariableElimination, алгоритм 400
N
NamedEvidence, класс 413
nextUniverse, функция 280
Normal, непрерывный атомарный элемент
62, 219
О
OrderByCount, объект 104
451

р
ParameterCollection, класс 432
Poisson, элемент 182
predict, функция 185
PriorParameters, класс 101
ProbEvidenceBeliefPropagation, факторный
алгоритм 414
ProbEvidenceSampler, выборочный
алгоритм 414
ProbLog, система вероятностного
программирования 448
Process, характеристика 220
R
rangeCheck, метод 221
removeConditions, метод 75
removeConstraints, метод 76
RichCPD, конструктор 137, 172
S
Scala 99
достоинства в качестве объемлющего
языка 41
консоль 53
механизмы повторного использования 237
скачивание подходящей версии 444
учебные ресурсы 42
Scala Build Tool (sbt) 443
Select, дискретный атомарный элемент 60
Seq, характеристика 212
setCondition, метод 75
setConstraint, метод 76
setEvidence, функция 193
Stan, система вероятностного
программирования 448
Т
toList, метод коллекции 213
toMap, метод 213
Traversable, характеристика 109, 213
TypedScheme, функция 386
Предметный указатель
U
Uniform, непрерывный атомарный элемент
63, 222
UntypedScheme, функция 386
V
VariableSizeArray, структура данных 215
Venture, система вероятностного
программирования 449
А
абсолютная погрешность 414
алгоритм вывода 28, 81, 224, 353
встроенный 36
и системы вероятностного
программирования 288
типы 314
алгоритм Монте-Карло по схеме марковской
цепи (МСМС) 353
выборка с отклонением 362
описание 374
определение 377
основные преимущества 373
параметры 377
алгоритм фильтрации частиц 421
создание 281
алгоритмы
Витерби 409
выборочные 314, 353
вывода 28
имитации отжига 406
исключения переменных 107
максимизации произведений 406
Метрополиса-Гастингса 378
Монте-Карло по схеме марковской цепи 353
наиболее вероятное объяснение (НВО) 193
обучающие 32
ожидания-максимизации (ЕМ) 432
ответ на запросы НВО 402
оценка сложности 326
приближенные 127, 315
452

Предметный указатель
распространения доверия 342
создание экземпляра 52
с отсечением по времени 202, 346
выборка по значимости 367
точные 126, 314
факторные 403
фильтрации 281
фильтрации частиц 421
анализ изображений, как типичное
применение НВО 409
анализ изображений, приложение РД 349
апостериорное распределение
вероятности 122, 289
и байесовское обучение 427
и применение условий 122
определение 126
получение выборки из 360
апостериорный предиктор 428
априорное распределении вероятности 289
байесовское обучение 426
определение 125
прямая выборка 360
априорные параметры 91
архитектура
компоненты и принятие решений 86
сходство во многих вероятностных
приложениях 112
асимметричные отношения 244
асимметричные связи 155, 158
достоинства условий 161
конкретное/детальное с абстрактным/
суммарным 156
ограничения и условия 160
разновидности 154
части с целым 155
частного и общего 155
Асиммметрия
бета-распределение 302
наиболее правдоподобное значение 308
с наибольшей апостериорной плотностью
вероятности 307
атомарный элемент 52, 59
базовые строительные блоки 59
и схема предложения 387
подразделение 59
составные версии 66
атрибут
комплексный 241, 253
простой 240
Б
Байеса правило 46, 289
включение фактов 289
и направление зависимости 289
и сопряженное распределение 306
как основа байесовского моделирования 301
ключевая концепция байесовского
обучения 427
математическая нотация 307
модель с двумя переменными 299
на практике 299
общая формулировка 306
определение 297
пример применение 304
причина, следствие и вывод 297
байесовская сеть 133, 143, 152, 232
бета-биномиальная модель 145
иерархические модели 203
и распределение вероятности 166
направление стрелок 195
объектно-ориентированное
представление 233
определение 163
ориентированные ребра 164
основные этапы проектирования 169
переменные 169
представление направленных
зависимостей 153
проектирование 169
процесс порождения значений
переменных 140
рассуждения 166
блокированный путь 167, 168
относительно различных причин одного
следствия 178
относительно различных следствий
одной причины 177
скрытая марковская модель 339
453

течение вдоль пути 166
байесовское моделирование 301
иерархическое 198
сравнение методов 310
структура формулы 306
байесовское обучение 426
выбор алгоритма 430
Байес Томас 297
Барабаши-Альберта модель
предпочтительного присоединения 372
Бернулли распределение 201
бесконечный процесс 220
бета-биномиальная модель 145, 302
вычисление ожидаемого числа успехов и
неудач 435
и ЕМ-алгоритм 433
бета-распределение 147, 431
байесовское моделирование 303
пары 433
сопряженное распределение 306
функция плотности вероятности 149
бинарный потенциал 189
биномиальное распределение 99, 106, 146
наблюдение исходов 434
В
верность классификации 86
вероятностная контекстно-свободная
грамматика (ВКСГ) 341
и приложение НВО 409
вероятностная модель 116
динамическая 260
как программа 34
общая картина использования 125
объектно-ориентированная 228
определение порождающего процесса 140
получение ответов на запросы 121
связи между переменными 129
составные части 88
вероятностное программирование
использование для обобщения байесовской
сети 179
иязык8са1а 229
определение 24
Предметный указатель
принятие решений 36
фильтр спама 83
вероятностное рассуждение
направление вывода и направление
зависимостей 96
определение 25
вероятность
возможного мира 143
неизвестная 66
ненормированная 190
нормировка 122
оценка на основе опыта 139
состояния, полная 161
факта
выборочные алгоритмы 415
вычисление 394, 410
вероятность перехода 379
ветвь 137
взвешенное среднее 185
Витерби алгоритм 409
возможные миры 117, 125, 289
и байесовская сеть 166
и переменные 128
оценка вероятности 354
перечисление 121
выборка
взвешенные примеры 364
дисперсия 359
интервал между примерами 377
истинное распределение 391
несмещенная 358
ответы на запросы 359
период приработки 377
примеры, несовместимые с условиями 366
выборка по значимости 202
и алгоритм фильтрации частиц 421
описание 363
приложения 370
псевдокод 366
выборка с отклонением 360
достоинства 362
и выборка по значимости 363
и условия Figaro 362
невозможность работы с ограничениями 362
454

Предметный указатель
псевдокод 362
Выборка с отклонением 360
выборочное распределение 358
выборочный алгоритм 353
и динамическая модель 276
метод Монте-Карло по схеме марковской
цепи 355
описание 354
пример типичного поведения 359
вывод 27, 372
и обучение параметров модели 425
направление 299
выделитель признаков 88, 92, 108
выразительная сила
определение 34
языка вероятностного программирования 33
Г
генератор элементов 210
и массивы переменной длины 216
генетика, приложения алгоритма МГ 390
геометрическое распределение 135
гиперпараметр 433
грамматика, понимание естественного
языка 341
грамматический разбор 340
наиболее вероятный 342
граф, нетриангулированный 343
Д
детерминированные связи 348
динамическая байесовская сеть
задание на Figaro 271
как обобщение скрытой марковской
модели 284
описание 268
динамическая модель
иллюстрация потока рассуждения 418
определение 260
постоянно работающая 277
разворачивание на фиксированное число
шагов 418
различные виды 261
рассуждения с помощью 276
с переменной структурой
полный код функции перехода 275
скелет кода 274
динамическая система
вывод причин текущего состояния 261
мониторинг состояния 418
общее число временных шагов 263
пример 260
Дирихле распределение 434
дискретная переменная 128
дискретные атомарные элементы 60
дополнительные знания 88, 90, 102
достаточная статистика 434
ожидаемая 435
дочерняя переменная 133, 154
Ж
жесткое условие 76
преобразование в мягкое ограничение 366
3
зависимости 127, 129
выбор правильного направления 157
кодирование в вероятностной программе 133
косвенные 162
между атрибутами экземпляров 241
наведенные 179
направленные 153
ненаправленные 153
определение 95
функциональные формы 134
замкнутый мир (замкнутая вселенная) 216
запрос 117
без фактов 321
и правила вывода 289
определение 27
получение ответа 124
с фактами 322
И
иерархическая модель, создание 203
имитация отжига 406
455

индукция программы 438
индуцированный граф 326
инкапсуляция 229
и конструкция цепочки 337
исключение внутренних элементов 336
интервал, функция плотности вероятности 147
исключения переменных (ИП) алгоритм
314, 324, 403
внутреннее суммирование 332
графическая интерпретация 325
как алгебраическая операция 329
ленивый 333
особенности в Figaro 332
приложения 338
испытания независимые и элемент
Binomial 61
истинное распределение 358
истинно отрицательные результаты 85
истинно положительные результаты 85
истощение частиц 423
К
класс
cbyuknjy 230
атрибуты 240
объектно-ориентированное
моделирование 230
классификатор, измерение качества 86
классификация 411
коллективный вывод 206
коллекции Scala
использование совместно с коллекциями
Figaro 212
удобства с точки зрения вероятностного
программирования 199
коллекция
бесконечная 220
и языки высокого уровня 198
переменной длины 209
преобразование между Scala Figaro 212
коллекция элементов 249
и неопределенность типа 254
и универсум 277
неизвестных 257
Предметный указатель
конкретные знания 117
и переменные 127
контейнер 221
перечисление элементов 213
кортежей конструктор 395
криптограмма
определение 370
Л
ложноотрицательные результаты 85
ложноположительные результаты 85
локализация робота, применение
фильтрации 424
локальный максимум в ЕМ-алгоритме 436
М
МАВ, обучение 430
механизм 431
максимальное правдоподобие (МП) 425
обучение 430
максимум апостериорной вероятности (МАВ),
метод 110, 307, 425
байесовское моделирование 301
сравнение с другими методоами 310
маргинализация 297
маргинальная МАВ 410
маргинальное распределение 297, 395
марковская сеть 152, 187
и кодирование ненаправленных
зависимостей 153
определение 187
сравнение с байесовской сетью 191
факторы 317
марковская цепь 259
в Figaro 263
задание модели переходов 263
запросы 264
и алгоритм МСМС 375
мягкие ограничения как смазка 389
начальное значение 263
определение 261
пример простого цикла 263
рассуждения в прямом и обратном
направлении 265
456

Предметный указатель
сходимость 375
марковское предположение 262
массив 199
двумерный 206
переменной длины 215
MakeArray, элемент 217
построение 216
фиксированного размера 210
число измерений 205
массив переменной длины
операции 217
свертки и агрегаты 218
математическое ожидание 185
машинное обучение 88
медицинская диагностика, приложение РД 349
метод максимального правдоподобия
(ММП) 308
сравнение с другими методами 310
Метрополиса-Гастингса алгоритм 378
байесовскове обучение 430
настройка 382
научные приложения 390
недостатки 381
свойства 380
специальные схемы предложения 384
модель
двумерная 206
и алгоритм обучения 31
иерархическая декомпозиция 336
обучение параметров 425
обучение структуры 438
объектно-ориентированная байесовская
сеть 232
описание 27
создание экземпляров и опрос 236
модель переходов 269, 274
и скрытая марковская модель 266
описание 263
мониторинга состояния системы 280
мониторинг состояния оборудования,
приложение РД 350
моральный граф 326, 342
мягкое ограничение 76
замена жестких условий 388
Н
наблюдение 55
будущее 267
как механизм задания фактов 52
распознавание речи 338
наблюдение и слежение, применение
фильтрации 424
наведенная зависимость 160, 167, 178
наиболее вероятное объяснение (НВО)
вычисление 397, 400
и индивидуальные маргинальные
распределения 399
приложения алгоритмов 409
сравнение алгоритмов ИП и РД 406
наивная байесовская модель 96
наследование 230
независимость
блокировка 176
как симметричное свойство 129
уравнение 130
ненаправленные зависимости 153, 159
неопределенность количества 216
неопределенность тождества 216
неориентированный граф марковской сети 187
неориентированный цикл 164
нормально распределение 62, 135
нормировка 126, 290, 305
нормировочный коэффициент 122, 190, 340
О
обнаружение аномалий 411, 415
обучающие данные 92
общие знания 27
и вероятностная модель 117
объектная ориентация
и структурирование модели 230
описание 228
объектно-ориентированное моделирование
230, 240
объемлющий язык, универсальный 41
ограничение
и наблюдение фактов 412
мягкое 76
457

настройка 391
определение 75
унарное 400
ограничение бинарное, вычисление и запрос
НВО в Figaro 400
одновременная зависимость от двух
переменных, моделирование 205
одновременная локализация и построение
карты (SLAM) 424
одномерное нормальное распределение 62
онлайновый ЕМ-алгоритм 436
ориентированный ациклический граф,
байесовская сеть 163
ориентированный цикл 164
отбор признаков, техника машинного
обучения 94
открытая вселенная 215
относительная погрешность 415
охлаждения режим 408
оценивание, полный байесовский метод 311
П
параметр 92, 188
перевыборка 421
переменная 127
детерминированная 172
дискретная 138
зависимая 153
исключенная, и таблица возвратов 405
и условная независимость 166
непрерывная
и выборка 355
и выборка по значимости 368
случайная 230
совместное состояние 188
типы 128
переобучение 94
и метод максимума апостериорной
вероятности 310
плотность вероятности 62
полнота классификатора 86
полный байесовский метод 301, 309
пороговая вероятность 85
Предметный указатель
порождающий процесс 140, 154
и правило Байеса 298
порядок исключения 327, 335
поиск наилучшего 329
потенциал 188, 242
потенциальная функция, взаимодействие со
структурой графа 189
почтового сообщения модель
в фильтре спама 87
компонент обучения 81
правило полной вероятности 294
и вероятностный вывод 126
общая формулировка 296
переход от сложного к простому 289
предикат, определение 63
признаки, определение 88
приработки фаза, марковские цепи 378
причинно-следственные связи 154, 170
и направленные зависимости 153
устранение неоднозначности 156
программируемый вывод 449
процесс
в Figaro 220
использование 224
прямая выборка 355
Пуассона распределение 182
путь выполнения 35
Р
развертывания стратегия (системы
вероятностного программирования) 447
распознавание речи
вариант на тему СММ 340
и приложение алгоритмов НВО 411
применение алгоритма ИП 338
распределение вероятности 61, 118, 242, 288
и вероятности различных фактов 120
ограничения 161
одной переменной 294
определение 125
факторизация 315
распространения доверия алгоритм 110, 276,
315, 340, 342
458

Предметный указатель
асинхронная форма в Figaro 346
приложения 349
сложность 347
циклический 343
рассуждение нелокальное 345
ребро 154
реляционная вероятностная модель 240
реляционная неопределенность 229, 249
родительская переменная 133, 154
С
связь
между двумя причинами одного
следствия 159
между частью и целым 155
символ 136
симметричная зависимость, и потенциалы 188
симметричная связь 159
система вероятностного программирования
выбор алгоритма 127
обзор различных систем 447
определение 33
скрытая марковская модель (СММ) 259
задание на Figaro 266
описание 265
распознавание речи 338
скрытая марковская приложения НВО 409
слова-признаки 83
случайный перезапуск 436
случайный процесс 231
и ссылки 251
определяемый элементом Chain 71
совместное распределение
вычисление 395
и информация, отсутствующая в
индивидуальных маргинальных
распределениях 395
и создание кортежей 396
соединитель (как составной элемент) 56
сопряженное априорное распределение 306
бета-распределение 201
составной элемент 52, 59
и реализация условного распределения
вероятности в Figaro 136
состояние 260
низкоэнергетическое 408
новое, вероятность принятия 407
с высокой вероятностью 380
скрытое 266
условно независимое 262
ссылка 250
ссылочная неопределенность 249
стандартное отклонение 62
статистическая физика, и циклический
алгоритм РД 343
стационарное распределением 376
структурная переменная 438
структурный факторный вывод 334
сумма произведений 322, 428
схема обучения, в Figaro 432
схема предложения
жесткие условия 388
по умолчанию 379
специальная 384
сходящиеся стрелки, байесовская сеть 167
Т
таблица возвратов 405
температура, в алгоритме имитации
отжига 407
темпоральный процесс, моделирование 222
тип значения 54
точность классификатора 86
триангуляция графа 328
У
унарное ограничение 192
унарный потенциал 189
универсум 259, 277
моделирование постоянно работающих
систем 279
получение нового 278
по умолчанию 277
трудные задачи вывода 439
условие
задание фактов с помощью 73
и наблюдение фактов 412
определение 74
459

отличие от ограничения 76
условная независимость 131
условное распределение вероятности
135, 165, 242, 290
байесовское обучение 426
и рекурсивные функции 183
пример проектирования байесовской
сети 170
условное случайное поле 197
Ф
фактор
и потенциалы 317
и условное распределение вероятности 316
определение 315
от двух переменных 315
правило полной вероятности и запросы 320
умножение 319
число строк 317
факторная сумма 322
факторное произведение 318
факторный алгоритм 314
непрерывные и дискретные переменные 368
факторный алгоритм НВО, максимизация
вероятности 403
факторный вывод 390
факторный рубеж, алгоритм 420
факты 28
вычисление вероятности 411
добавление при вычислении НВО 397
дополнительный механизм явного задания
в Figaro 412
задание 73
и запросы 175, 321
избегать крайне маловероятных 369
именованные 413
маловероятные и выборка
с отклонением 362
наблюдаемые 74
невозможные в качестве условий 124
несовместимые меры 122
о начальном состоянии, выборка по
значимости 371
определение 125
Предметный указатель
оценка вероятности 362
применение к модели 90
фильтрация
алгоритм 281
применения 424
функциональная форма 127
базовая 134
определение 97
функциональное программирование и
полные по Тьюрингу системы 34
функция плотности распределения (ФПР) 147
функцияплотностираспределения(ФПР) 355
Ц
цепная функция 70
цепное правило 46, 143
и вероятностный вывод 126, 288
и пример умножения факторов 318
общая формулировка 293
определение распределения вероятности
возможных миров 290
факторизация распределения
вероятности 318
циклы
и графы ИП 328
избежание с помощью объединения
элементов 347
Ч
числовые параметры 100, 127, 138
и бета-распределение 149
Э
экспоненциальное распределение 135
элемент 53
два основных вида 52
и распределение вероятности значений 208
конструктор класса 92
недетерминированный 379, 387
повторяющийся 58
последовательное предложение
нескольких 386
скрытый 95
460

Предметный указатель
соединительные ребра 58
создание для вычисления совместного
распределения 395
универсум 419
Эрдеша-Реньи модель 372
эффективный размер выборки 369
Я
язык представления 32, 34
461

Книги издательства «ДМК Пресс» можно заказать в торгово-издательском
холдинге «Планета Альянс» наложенным платежом, выслав открытку или письмо по
почтовому адресу: 115487, г. Москва, 2-й Нагатинский пр-д, д. 6А.
При оформлении заказа следует указать адрес (полностью), по которому
должны быть высланы книги; фамилию, имя и отчество получателя. Желательно также
указать свой телефон и электронный адрес.
Эти книги вы можете заказать и в интернет-магазине: www.alians-kniga.ru.
Оптовые закупки: тел. (499) 782-38-89
Электронный адрес: books@alians-kniga.ru.
Ави Пфеффер
Вероятностное программирование на практике
Главный редактор Мовчан Д. А.
dmkpress@gmail.com
Перевод с английского Слинкин А. А.
Корректор Синяева Г. И.
Верстка Паранская Я. В.
Дизайн обложки Мовчан А. Г.
Формат 70x100*/^ Гарнитура «Петербург».
Печать офсетная. Усл. печ. л. 37,54.
Тираж 200 экз.
Веб-сайт издательства: www.flMK.pc|)

Вероятностное программи
— ЭТО НОВЫЙ
способ создания вероятностных моделей,
позволяющих предсказывать или выводить новые
факты, которых нет в результатах наблюдений.
Это позволяет, к примеру, прогнозировать такие
будущие события, как тенденции продаж, отказы
вычислительных систем, исходы экспериментов и
многое другое.
Книга представляет собой введение в
вероятностное программирование для программистов-
практиков. Автор почти сразу переходит к
практическим примерам: построению фильтра спама,
диагностике ошибок в вычислительной системе,
восстановлению цифровых изображений. Вы
познакомитесь с вероятностным выводом, где
алгоритмы помогают прогнозировать,
например, использование социальных сетей. Попутно
узнаете о применении функционального стиля
программирования для анализа текстов,
объектно-ориентированных моделей —для
прогнозирования распространения твитов, и моделей с
открытой вселенной —для измерения явлений,
имеющих место в социальной сети. В книге есть
также главы о том, как вероятностные модели
помогают в принятии решений и моделировании
динамических систем.
Собираемые вами данные о клиентах, продуктах
и пользователях сайта могут оказать помощь не
только в интерпретации прошлого, но и в
предсказании будущего!
Краткое содержание:
• введение в вероятностное моделирование;
• написание вероятностных программ на Figaro;
• построение байесовских сетей;
• прогнозирование жизненного цикла продукта;
• алгоритмы принятия решений.
— главный разработчик
языка вероятностного программирования Figaro.
Предварительные знания по вероятностному
программированию для чтения книги не нужны. Знание языка
Scala было бы полезно.
на
«Важный шаг на пути вывода
вероятностного
программирования из
научно-исследовательских лабораторий в
реальный мир.»
— Стюарт Рассел,
Калифорнийский университет
«Ясные примеры и доступные
объяснения трудной темы.»
— Марк Элстон,
Advantest America
«Последовательно,
практично и доступно.
Великолепный справочник по
вероятностному
программированию на языке Scala.»
— Кос mac Пассадис, IPTO
«Вероятностное
программирование — трудная тема!
Но Ави ухитрился сделать ее
простой и понятной.»
— Эрл Бингэм, Eye lock
Интернет-магазин: www.dmkpress.com
Книга почтой: orders@aIians-kniga.Ri
Оптовая продажа: "Альянс-книга"
Тел.(499)782-3889, books@alians-kniga.ai
- t i i УЕМ V** ГА
www. дм к. рф
рование
практике